Casio GRAPH 100+_Users Guide 1_Fr GRAPH100_MAN1 GRAPH100 MAN1 FR
User Manual: Casio GRAPH100_MAN1 GRAPH 100+ | Calculatrices | Manuels | CASIO
Open the PDF directly: View PDF ![]() .
.
Page Count: 442 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- AVANT D’UTILISER LA CALCULATRICE POUR LA PREMIÈRE FOIS...
- Démarrage rapide
- Précautions de manipulation
- Table des matières
- Familiarisation — A lire en premier!
- Chapitre 1 Opérations de base
- Chapitre 2 Calculs manuels
- Chapitre 3 Listes
- Chapitre 4 Calcul d’équations
- Chapitre 5 Représentation
graphique de fonctions
- 5-1 Exemples de graphes
- 5-2 Contrôle des paramètres apparaissant sur un écran graphique
- 5-3 Tracé d’un graphe
- 5-4 Stockage d’un graphe dans la mémoire d’images
- 5-5 Tracé de deux graphes sur le même écran
- 5-6 Représentation graphique manuelle
- 5-7 Utilisation de tables
- 5-8 Représentation graphique dynamique
- 5-9 Représentation graphique d’une formule de récurrence
- 5-10 Changement de l’aspect d’un graphe
- 5-11 Analyse de fonctions
- Chapitre 6 Graphes et calculs statistiques
- Chapitre 7 Système d’algèbre informatique
- Chapitre 8 Programmation
- 8-1 Etapes de la programmation de base
- 8-2 Touches de fonction du mode de programmation
- 8-3 Edition du contenu d’un programme
- 8-4 Gestion de fichiers
- 8-5 Guide des commandes
- 8-6 Utilisation des fonctions de la calculatrice dans un programme
- 8-7 Liste des commandes de programmation
- 8-8 Bibliothèque de programmes
- Chapitre 9 Menu de réglages du système
- Chapitre 10 Communication de données
- Appendice

Conservez la documentation à portée de main pour
toute référence future.

Manufacturer:
CASIO COMPUTER CO., LTD.
6-2, Hon-machi 1-chome
Shibuya-ku, Tokyo 151-8543, Japan
Responsible within the European Union:
CASIO EUROPE GmbH
Casio-Platz 1
22848 Norderstedt, Germany

AVANT D’UTILISER LA CALCULATRICE
POUR LA PREMIÈRE FOIS...
La calculatrice ne contient pas de piles principales lors de l’achat. N’oubliez pas
d’effectuer les opérations suivantes pour mettre les piles en place, reinitialiser la
calculatrice et régler le contraste avant d’essayer d’utiliser la calculatrice.
1. A veillant à ne pas appuyer accidentellement sur la touche o, faites glisser l’étui sur
la calculatrice et retournez la calculatrice. Enlevez le couvercle arrière de la calculatrice
en tirant avec le doigt au point indiqué par 1.
2. Insérez les quatre piles fournies avec la calculatrice.
•Assurez-vous que les extrémités positives (+) et négatives (–) des piles sont
dirigées dans le bon sens.
3. Enlevez la pellicule isolante à l’endroit marqué “BACK UP” en tirant dans le sens de
la flèche.
4. Remettez-le couvercle arrière en faisant bien entrer les griffes dans les orifices
indiqués par 2 et retournez la calculatrice, face vers le haut. La calculatrice doit
s’allumer automatiquement et réinitialiser la mémoire.
P
1
BACK UP
BACK UP
2
19990401

5. Appuyez sur m.
•Si le menu principal indiqué à droite n’apparaît pas,
appuyez sur le bouton P au dos de la calculatrice pour
réinitialiser la mémoire.
6. Utilisez les touches de curseur (f, c, d ou e) pour sélectionner l’icône
SYSTEM et appuyez sur w, puis sur 2 ( ) pour afficher l’écran de réglage du
contraste.
7. Ajustez le contraste.
• La touche de curseur e rend le contraste plus sombre.
• La touche de curseur d rend le contraste moins sombre.
• 1 (INIT) rétablit le contraste initial.
8. Pour quitter l’écran de réglage du contraste, appuyez sur m.
Bouton P
20001202

19990401
1
Démarrage rapide
Démarrage rapide
Bienvenue dans le monde des calculatrices graphiques.
Ce sommaire n’est pas un guide complet, mais il vous initie aux fonctions les plus
communes, de la mise sous tension aux équations graphiques complexes. Quand
vous l’aurez lu, vous maîtriserez les opérations de base de cette calculatrice et serez
prêt à aborder la suite de ce mode d’emploi pour faire connaissance avec toutes les
fonctions disponibles.
Toutes les phases des exemples du sommaire sont illustrées graphiquement pour
vous aider à comprendre rapidement et facilement l’opération. Si vous devez entrer
le nombre 57 par exemple, nous l’indiquons comme suit:
Appuyez sur fh
Chaque fois que c’était nécessaire, nous avons inséré des exemples d’écran. Si
votre écran ne correspond pas à l’exemple, vous pouvez recommencer depuis le
début en appuyant sur le bouton o “All Clear” (vidage complet).
MISE SOUS/HORS TENSION
Pour mettre sous tension, appuyez sur o.
Pour mettre hors tension, appuyez sur !o.
La calculatrice s’éteint automatiquement si vous n’effectuez aucune opération pendant
le délai de mise hors tension automatique spécifié. Ce délai peut être réglé sur six ou
60 minutes.
UTILISATION DES MODES
Cette calculatrice facilite la réalisation d’un grande nombre de calculs par simple
sélection du mode approprié. Avant d’aborder les calculs et les opérations par des
exemples réels, voyons comment passer d’un mode à l’autre.
Pour sélectionner le mode RUN·MAT
1. Appuyez sur m pour afficher le menu principal.
OFF
20001202
19990401
2. Utilisez defc pour mettre
RUN • MAT en surbrillance et appuyez surw.
C’est l’écran initial du mode RUN • MAT, dans
lequel vous pouvez effectuer les calculs manuels,
les calculs matriciels et exécuter des pro-
grammes.
CALCULS DE BASE
Avec les calculs manuels, vous entrez vos formules de gauche à droite, simplement
comme elles s’écrivent sur une feuille de papier. Avec les formules qui comprennent
des opérateurs arithmétiques et des parenthèses, la calculatrice applique
automatiquement la logique algébrique vraie pour calculer le résultat.
Exemple:
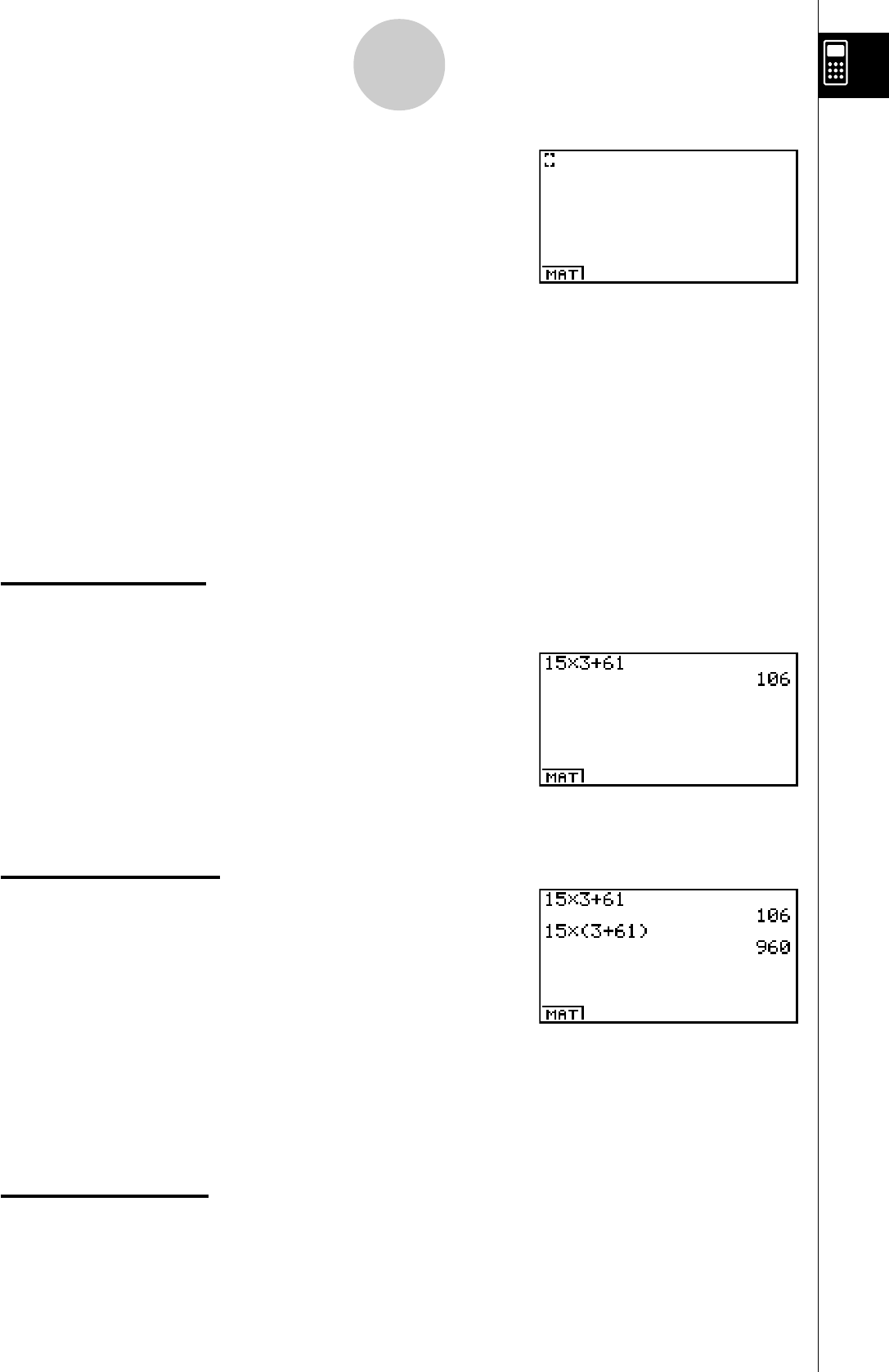
15 × 3 + 61
1. Appuyez sur o pour vider la calculatrice.
2. Appuyez sur bf*d+gb
w.
Calculs avec parenthèses
Exemple:
15 × (3 + 61)
1. Appuyez sur bf*(d
+gb)w.
Fonctions incorporées
Cette calculatrice comprend un certain nombre de fonctions scientifiques, dont les
fonctions trigonométriques et logarithmiques.
Exemple:
25 × sin 45˚
Important!
Spécifiez bien Deg (degré) comme unité d’angle avant de tenter de réaliser cet
exemple.
2
Démarrage rapide

19990401
3
Démarrage rapide
1. Appuyez sur u3 pour afficher l’écran de
configuration.
2. Appuyez sur cccc1 (Deg)
pour spécifier les degrés comme unité de
mesure angulaire.
3. Appuyez sur i pour quitter le menu.
4. Appuyez sur o pour vider la calculatrice.
5. Appuyez surcf*sefw.
FONCTION DE RÉPÉTITION
Avec la fonction de répétition, appuyez simplement sur d ou e pour rappeler le
dernier calcul effectué et faire les changements souhaités ou pour l’exécuter une nouvelle
fois.
Exemple:
Changer le calcul de l’exemple précédent (25 × sin 45˚) en (25 × sin 55˚)
1. Appuyez sur d pour afficher le dernier calcul.
2. Appuyez deux fois sur d pour amener le
curseur (t) sur 4.
3. Appuyez sur D pour effacer 4.
4. Appuyez sur f.
5. Appuyez sur w pour exécuter le calcul à nouveau.
REPLAY
SET UP

19990401
4
Démarrage rapide
CALCULS DE FRACTIONS
Vous pouvez utiliser la touche N pour introduire des fractions dans un calcul. Le
symbole “ { ” est utilisé pour séparer les diverses parties d’une fraction.
Exemple:
1+
1. Appuyez sur o.
2. Appuyez sur bNbfN
bg+dhN
jw.
Conversion d’une fraction mixte en un nombre
fractionnaire
Quand une fraction mixte est affichée à l’écran, appuyez sur !N pour le
convertir en un nombre fractionnaire.
Appuyez à nouveau sur !N pour le reconvertir en une fraction mixte.
Conversion d’une fraction en son équivalent décimal
Lorsqu’une fraction est affichée à l’écran, appuyez sur N pour la convertir en
son équivalent décimal.
Appuyez à nouveau sur N pour revenir à la fraction.
d/c
d/c
+
15
16
37
9
Indique
6
+7
144

19990401
5
Démarrage rapide
EXPOSANTS
Exemple:
1250 × 2,065
1. Appuyez sur o.
2. Appuyez sur bcfa*c.ag.
3. Appuyez sur M. L’indicateur ^ apparaît à l’écran.
4. Appuyez sur f. Le ^5 à l’écran indique que 5 est l’exposant.
5. Appuyez sur w.

19990401
6
Démarrage rapide
FONCTIONS GRAPHIQUES
Les capacités graphiques de la calculatrice permettent de tracer des graphes com-
plexes à partir de coordonnées rectangulaires (axe horizontal: x ; axe vertical: y) ou de
coordonnées polaires (angle:
θ
; distance de l’origine: r).
Tous les exemples de graphes suivants s’effectuent depuis le réglage valide immédiatement
après la réinitialisation.
Exemple
1: Représenter graphiquement = X(X + 1)(X – 2)
1. Appuyez sur m.
2. Utilisez defc pour mettre
GRPH • TBL en surbrillance, puis appuyez sur
w.
3. Entrez la formule.
v(v+b)
(v-c)w
4. Appuyez sur 5 (DRAW) ou w pour tracer
le graphe.
Exemple
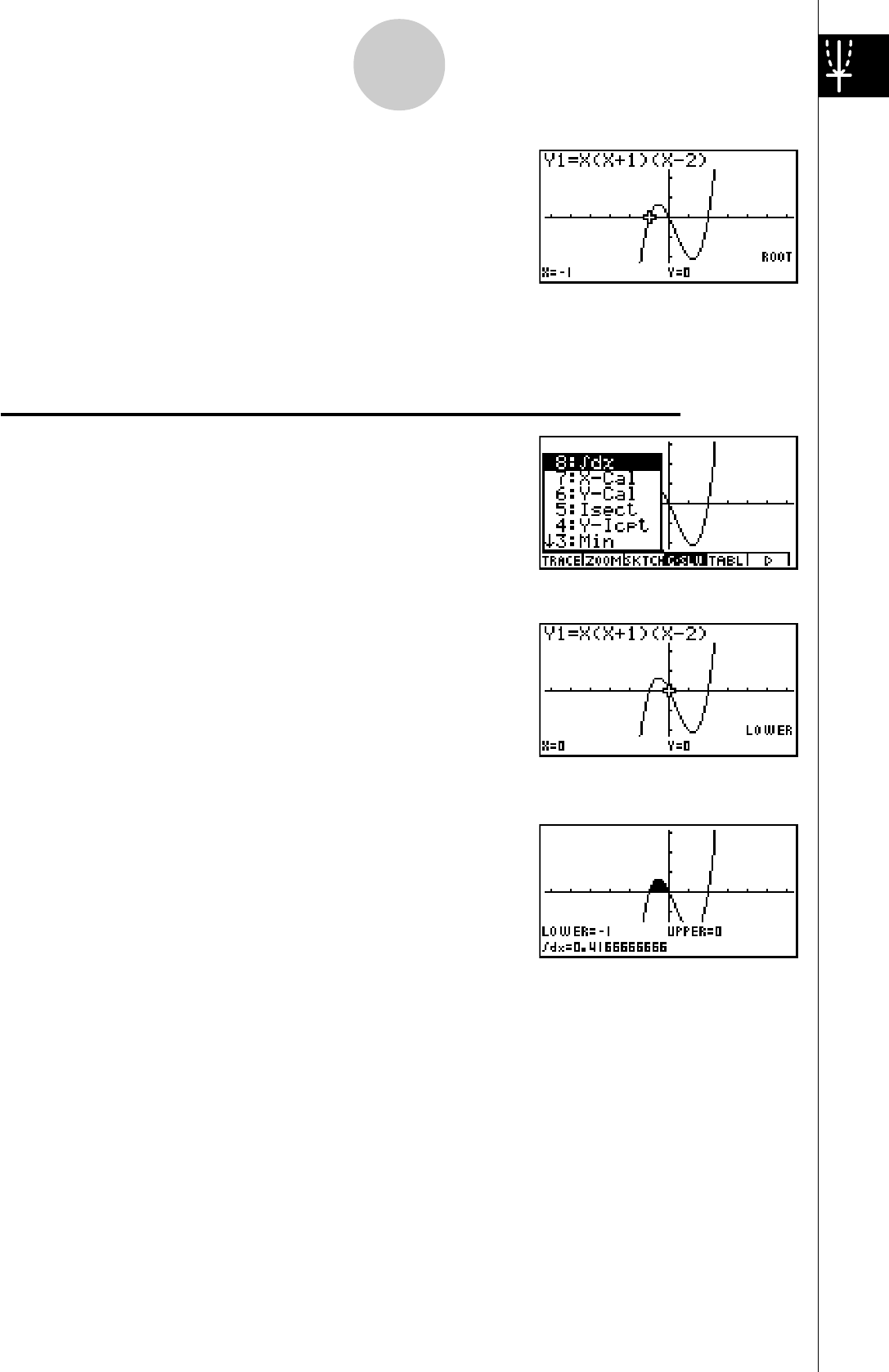
2: Déterminer les racines de Y = X(X + 1)(X – 2)
1. Appuyez sur 4(G-SLV) pour afficher le menu
déroulant.
19990401
7
Démarrage rapide
2. Appuyez sur b(Root).
Appuyez sur e pour d’autres racines.
Exemple
3: Déterminer la zone délimitée par l’origine et la racine X = –1
obtenue pour
Y = X(X + 1)(X – 2)
1. Appuyez sur i4(G-SLV)c.
2. Appuyez sur i(∫dx).
3. Utilisez d pour amener le pointeur à l’endroit où
X = –1 puis appuyez sur w. Utilisez e pour
amener le pointeur à l’endroit où X = 0, puis
appuyez sur w pour indiquer la plage
d’intégration, qui apparaît en sombre à l’écran.

19990401
8
Démarrage rapide
GRAPHE DOUBLE
Cette fonction vous permet de diviser l’écran en deux zones et d’afficher deux graphes
sur le même écran.
Exemple:
Tracer les deux graphes suivants et déterminer les points d’intersection
Y1 = X(X + 1)(X – 2)
Y2 = X + 1,2
1. Appuyez suru3ccc2(G+G)
pour spécifier “G+G” comme réglage de double
écran.
2. Appuyez sur i, puis entrez les deux fonctions.
v(v+b)
(v-c)w
v+b.cw
3. Appuyez sur 5(DRAW) ou wpour tracer
les graphes.
ZOOM SUR CADRE
Utilisez la fonction zoom sur cadre pour délimiter la zone d’un graphe que vous voulez
agrandir.
1. Appuyez sur 2(ZOOM) b(Box).
2. Utilisez defc pour amener le
pointeur sur un angle de la zone que vous voulez
spécifier, puis appuyez sur w.
SET UP
19990401
9
Démarrage rapide
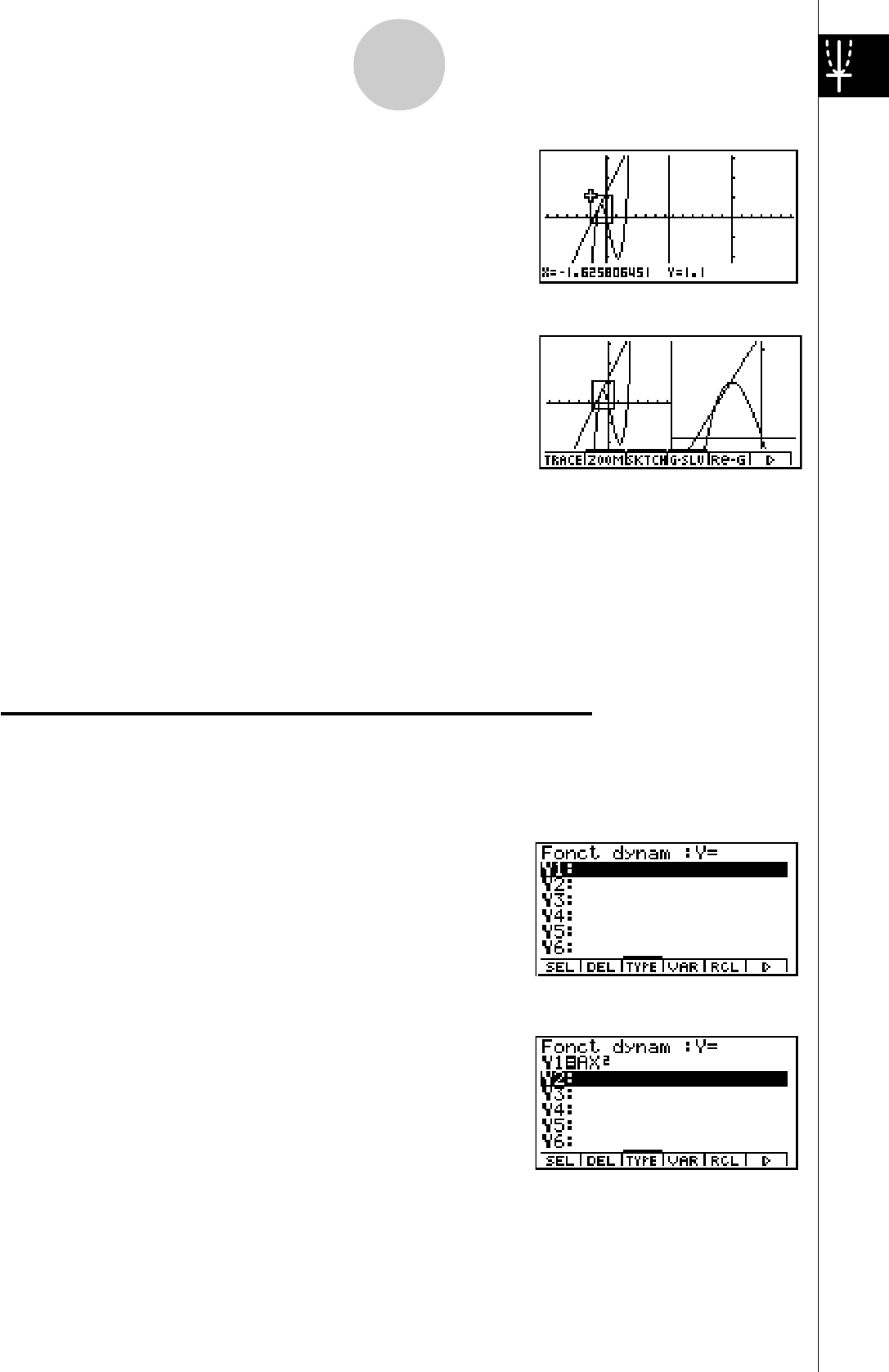
3. Utilisez defc pour déplacer une
nouvelle fois le pointeur. Un cadre apparaît sur
l’écran. Déplacez le pointeur de façon à encadrer
la zone que vous voulez agrandir.
4. Appuyez sur w. La zone agrandie apparaît sur
l’écran inactif (côté droit).
GRAPHE DYNAMIQUE
Le graphe dynamique vous permet de voir de quelle façon la forme d’un graphe est
affectée par le changement de valeur d’un des coefficients de la fonction.
Exemple:
Tracer les graphes lorsque la valeur du coefficient A
change de 1 à 3 dans la fonction suivante
Y = AX2
1. Appuyez sur m.
2. Utilisez defc pour mettre DYNA
en surbrillance, puis appuyez sur w.
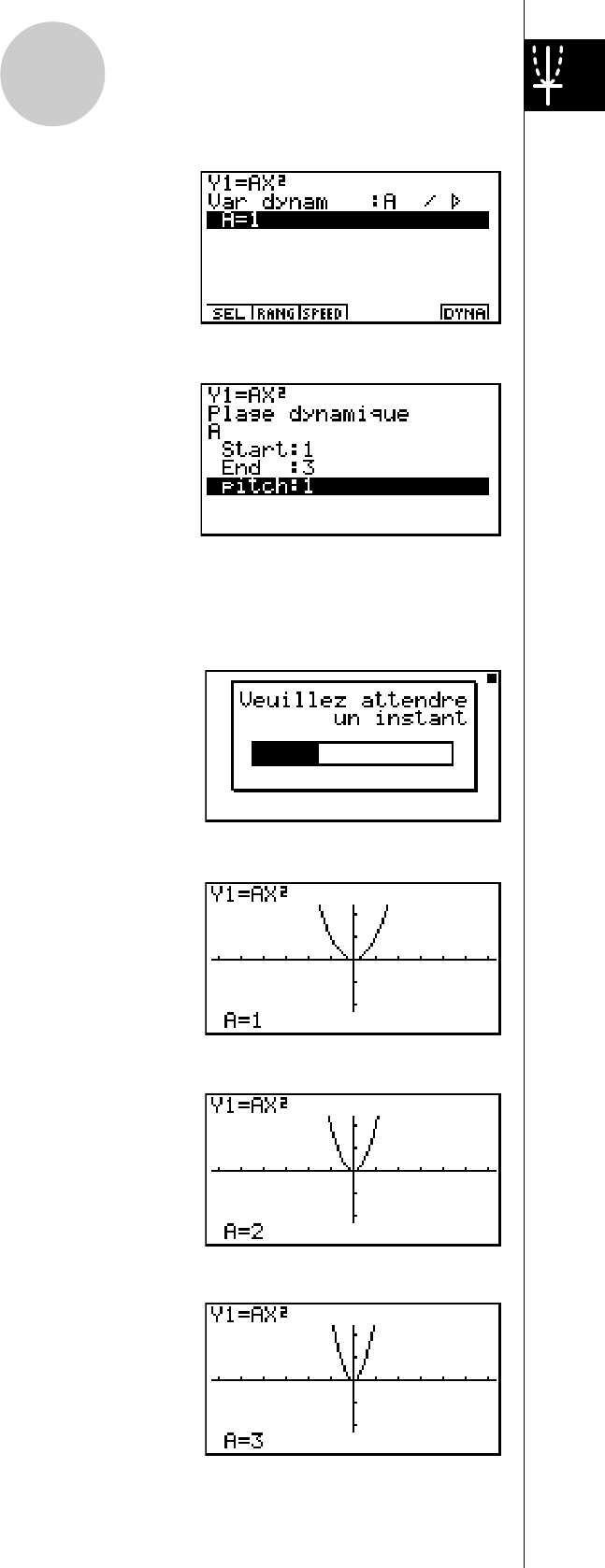
3. Entrez la formule.
avvxw
A
19990401
10
Démarrage rapide
4. Appuyez sur 4(VAR) bw pour affecter la
valeur initiale 1 au coefficient A.
5. Appuyez sur 2(RANG) bwdw
bw pour spécifier la plage et l’incrément pour
le changement de valeur du coefficient A.
6. Appuyez sur i.
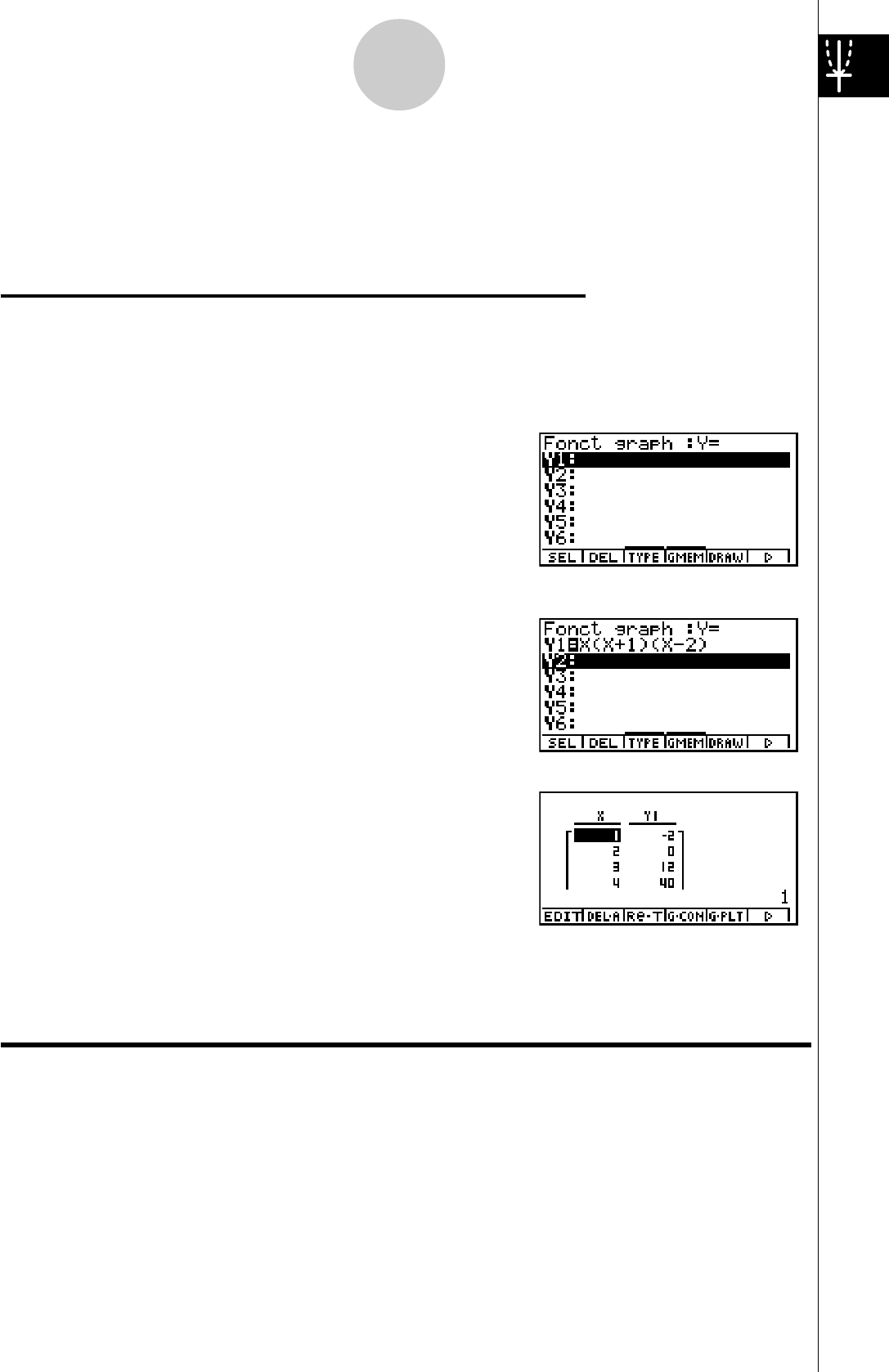
7. Appuyez sur 6(DYNA) pour commencer le tracé
de graphe dynamique. Les graphes sont tracés 10
fois.
↓↑
↓↑
↓
19990401
11
Démarrage rapide
FONCTION DE TABLE
Cette fonction permet de produire une table de solutions quand différentes valeurs
sont affectées aux variables d’une fonction.
Exemple:
Créer une table numérique pour la fonction suivante
Y = X (X + 1) (X – 2)
1. Appuyez sur m.
2. Utilisez defc pour mettre
GRPH • TBL en surbrillance, puis appuyez sur
w.
3. Entrez la formule.
v(v+b)
(v-c)w
4. Appuyez sur 6(g)5(TABL) pour créer une
table numérique.
Pour tout connaître sur les nombreuses caractéristiques de cette calculatrice, lisez et
explorez!

19990401
Précautions de manipulation
• Votre calculatrice est constituée de composants de précision et ne doit jamais être démontée.
• Eviter de la laisser tomber et de lui faire subir des chocs violents.
• Ne pas ranger ou laisser la calculatrice dans des endroits exposés à une température et
humidité élevées ou à de grandes quantités de poussière. Lorsqu’elle est exposée à de faibles
températures, la calculatrice peut nécessiter plus de temps pour afficher les réponses et même
ne pas fonctionner du tout. L’affichage redevient normal lorsque la température atteint un
niveau normal.
• L’affichage est vide et les touches ne fonctionnent pas pendant les calculs. Lorsque vous
utilisez le clavier, contrôlez l’affichage pour vérifier que toutes vos opérations de touches sont
correctement effectuées.
• Remplacer les piles principales au moins une fois tous les 2 ans, même si la machine n’est pas
utilisée pendant cette période. Ne jamais laisser de piles mortes dans le logement des piles.
Elles pourraient fuir et endommager la machine.
• Rangez les piles hors de portée des enfants en bas âge. En cas d’ingestion, consultez
immédiatement un médecin.
• Eviter d’utiliser des liquides volatils tels que diluant ou benzine pour nettoyer la machine.
L’essuyer avec un chiffon doux et sec ou un chiffon légèrement mouillé d’une solution d’eau et de
détergent neutre, puis essoré.
• Enlevez la poussière de l’écran avec précaution pour ne pas le rayer.
• En aucun cas le fabricant et ses fournisseurs ne seront tenus pour responsables de dégât,
dépense, perte de profits, perte d’économies ou autre dommage résultant d’une perte de
données et/ou de formules survenue à la suite d’un fonctionnement défectueux, de réparations
ou du remplacement des piles. Vous devez préparer des copies des données pour vous
protéger contre de telles pertes de données.
• Ne jamais incinérer les piles, le panneau à cristaux liquides ou d’autres composants.
• Lorsque le message ‘‘Piles principales faibles!’’ ou “Pile sauvegarde faible!” apparaît sur l’écran,
remplacer aussitôt que possible les piles d’alimentation principale ou la pile de sauvegarde.
• Vérifier que la machine est hors tension lors du remplacement des piles.
• Si la calculatrice est exposée à de fortes charges d’électricité statique, le contenu de sa
mémoire peut être endommagé ou les touches cesser de fonctionner. Dans ce cas, effectuer
une réinitialisation (Reset) pour effacer la mémoire et rétablir le fonctionnement normal des
touches.
• Si la calculatrice cesse de fonctionner correctement pour une raison quelconque, appuyez sur
le bouton P au dos de la calculatrice avec un objet fin et pointu. Notez qu’à ce moment toutes
les données mémorisées sont effacées.
• Notez que de fortes vibrations ou de violents chocs pendant l’exécution des programmes
peuvent provoquer l’arrêt de l’exécution ou endommager le contenu de la mémoire de la
calculatrice.
• L’utilisation de la calculatrice à proximité d’un téléviseur ou d’une radio peut provoquer des
interférences sur la réception de la télévision ou de la radio.
• Avant de supposer un mauvais fonctionnement de la calculatrice, veuillez relire avec soin ce
manuel et vous assurer que la panne n’est pas due à une alimentation insuffisante, des erreurs
opérationnelles ou de programmation.

19990401
Toujours garder des copies de toutes données importantes!
Une faible puissance des piles ou le remplacement incorrect des piles alimentant l’appareil peut
entraîner une modification des données sauvegardées en mémoire ou même leur disparition
complète. Les données sauvegardées peuvent également être affectées par une forte charge
électrostatique ou un coup violent. Vous devez toujours garder des copies de toutes vos données
importantes pour vous protéger contre de telles pertes.
En aucun cas CASIO Computer Co., Ltd. ne sera tenu pour responsable de dommages
spéciaux, collatéraux, indirects ou consécutifs liés à ou résultant de l’achat ou de l’utilisation de
ce matériel. De plus, CASIO Computer Co., Ltd. ne sera pas tenu pour responsable de
réclamation quelle qu’elle soit, faite contre l’utilisation de ce matériel par un tiers.
• Le contenu de ce manuel est susceptible d’être modifié sans préavis.
• Aucune partie de ce manuel ne peut être reproduite sous quelque forme que ce soit sans
la permission écrite du fabricant.
• Les options décrites dans le chapitre 10 de ce manuel ne sont pas disponibles dans
certaines zones géographiques. Demandez à votre distributeur ou au revendeur CASIO le
plus proche quelles sont les options qui sont disponibles dans votre pays.

19990401
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
GRAPH 100
+
20001202

19990401
Table des matières
Familiarisation — A lire en premier!
Chapitre 1 Opérations de base
1-1 Touches ............................................................................................ 1-1-1
1-2 Affichage .......................................................................................... 1-2-1
1-3 Saisie et édition de calculs ............................................................... 1-3-1
1-4 Menu d’options (OPTN) ................................................................... 1-4-1
1-5 Menu de données de variables (VARS) ........................................... 1-5-1
1-6 Menu de programmation (PRGM) ................................................... 1-6-1
1-7 Utilisation de l’écran de configuration.............................................. 1-7-1
1-8 En cas de problème... ...................................................................... 1-8-1
Chapitre 2 Calculs manuels
2-1 Calculs de base ............................................................................... 2-1-1
2-2 Fonctions spéciales ......................................................................... 2-2-1
2-3 Désignation de l’unité d’angle et du format d’affichage .................... 2-3-1
2-4 Calculs de fonctions ......................................................................... 2-4-1
2-5 Calculs numériques ......................................................................... 2-5-1
2-6 Calculs avec nombres complexes ................................................... 2-6-1
2-7 Calculs binaire, octal, décimal et hexadécimal ............................... 2-7-1
2-8 Calculs matriciels ............................................................................. 2-8-1
Chapitre 3 Listes
3-1 Saisie et édition d’une liste (Menu STAT) ......................................... 3-1-1
3-2 Traitement des données d’une liste (Menu RUN
•
MAT) .................... 3-2-1
3-3 Calculs arithmétiques à partir de listes (Menu RUN
•
MAT)............... 3-3-1
3-4 Changement de fichiers de listes ..................................................... 3-4-1
Chapitre 4 Calcul d’équations
4-1 Equations linéaires simultanées ....................................................... 4-1-1
4-2 Equations de degré élevé ................................................................. 4-2-1
4-3 Calculs avec résolution..................................................................... 4-3-1
4-4 Que faire quand une erreur se produit ? .......................................... 4-4-1
1
Table des matières

19990401
Chapitre 5 Représentation graphique de fonctions
5-1 Exemples de graphes....................................................................... 5-1-1
5-2 Contrôle des paramètres apparaissant sur un écran graphique ...... 5-2-1
5-3 Tracé d’un graphe ............................................................................ 5-3-1
5-4 Stockage d’un graphe dans la mémoire d’images ........................... 5-4-1
5-5 Tracé de deux graphes sur le même écran ...................................... 5-5-1
5-6 Représentation graphique manuelle ................................................ 5-6-1
5-7 Utilisation de tables .......................................................................... 5-7-1
5-8 Représentation graphique dynamique ............................................. 5-8-1
5-9Représentation graphique d’une formule de récurrence .................. 5-9-1
5-10 Changement de l’aspect d’un graphe............................................. 5-10-1
5-11 Analyse de fonctions ...................................................................... 5-11-1
Chapitre 6 Graphes et calculs statistiques
6-1 Avant d’effectuer des calculs statistiques ......................................... 6-1-1
6-2 Calcul et représentation graphique de données statistiques à
variable unique ................................................................................. 6-2-1
6-3 Calcul et représentation graphique de données statistiques à
variable double ................................................................................. 6-3-1
6-4 Exécution de calculs statistiques...................................................... 6-4-1
Chapitre 7 Système d’algèbre informatique
7-1 Utilisation du mode CAS (Système d’algèbre informatique) ............ 7-1-1
7-2 Précautions concernant le mode CAS ............................................. 7-2-1
Chapitre 8 Programmation
8-1 Etapes de la programmation de base .............................................. 8-1-1
8-2 Touches de fonction du mode de programmation ............................ 8-2-1
8-3 Edition du contenu d’un programme ................................................ 8-3-1
8-4 Gestion de fichiers............................................................................ 8-4-1
8-5 Guide des commandes .................................................................... 8-5-1
8-6 Utilisation des fonctions de la calculatrice dans un programme....... 8-6-1
8-7 Liste des commandes de programmation ........................................ 8-7-1
8-8 Bibliothèque de programmes ........................................................... 8-8-1
Chapitre 9 Menu de réglages du système
9-1 Utilisation du menu de réglages du système.................................... 9-1-1
9-2 Opérations concernant la mémoire .................................................. 9-2-1
9-3 Réglages du système ....................................................................... 9-3-1
9-4 Initialisation....................................................................................... 9-4-1
2
Table des matières
20091001

19990401
Chapitre 10 Communication de données
10-1 Connexion de deux calculatrices ................................................. 10-1-1
10-2 Connexion de la calculatrice à une imprimante d’étiquettes
CASIO .......................................................................................... 10-2-1
10-3 Connexion de la calculatrice à un ordinateur ............................... 10-3-1
10-4 Communication des données....................................................... 10-4-1
10-5 Précautions lors la communication de données ........................... 10-5-1
10-6 Envoi d’une copie d’écran ............................................................ 10-6-1
10-7 Ajouts ........................................................................................... 10-7-1
10-8 Mode MEMORY ........................................................................... 10-8-1
Appendice
1 Tableau des messages d’erreur ..........................................................
α
-1-1
2 Plages d’introduction ..........................................................................
α
-2-1
3 Spécifications.......................................................................................
α
-3-1
4 Index ....................................................................................................
α
-4-1
5 Index des touches ................................................................................
α
-5-1
6 Bouton P (en cas de blocage) ............................................................
α
-6-1
7 Alimentation .........................................................................................
α
-7-1
3
Table des matières

19990401
Familiarisation
— A lire en premier!
A propos du manuel de l’utilisateur
u!
x( )
Cette suite de touches indique que vous devez appuyer sur ! puis sur x pour écrire le
symbole . Toutes les opérations qui nécessitent l’utilisation de plusieurs touches sont
indiquées de cette façon. Les indications sur les touches proprement dites sont suivies du
caractère ou de la commande à saisir entre parenthèses.
uTouches de fonction et menus
• Un certain nombre d’opérations effectuées par la calculatrice peuvent être exécutées en
utilisant les touches de fonction 1 à 6. L’opération affectée à chaque touche de
fonction dépend du mode dans lequel se trouve la calculatrice, et les opérations
disponibles sont indiquées sur les menus de fonctions qui apparaissent au bas de
l’écran.
• Dans ce manuel, l’opération actuellement affectée à une touche de fonction est indiquée
entre parenthèses après le nom de la touche. 1 (Comp), par exemple, indique que par
une pression sur 1 vous sélectionnez {Comp}, qui apparaît aussi sur le menu de
fonctions.
• Quand (g) est indiqué sur le menu de fonctions pour la touche 6, ce symbole signifie
qu’en appuyant sur 6 vous afficherez la page suivante ou précédente des options de
ce menu.
uu
uu
uTitres des menus
• Les titres des menus dans le manuel de l’utilisateur indiquent l’opération de touches
nécessaire pour afficher le menu expliqué. Par exemple, [OPTN]-[MAT] indique qu’il
faut appuyer sur K puis sur {MAT} pour afficher le menu.
• L’utilisation de la touche 6 (g) pour le changement de page d’un menu n’est pas
indiquée dans les titres des menus.
0
19990401
0-1-1
Familiarisation
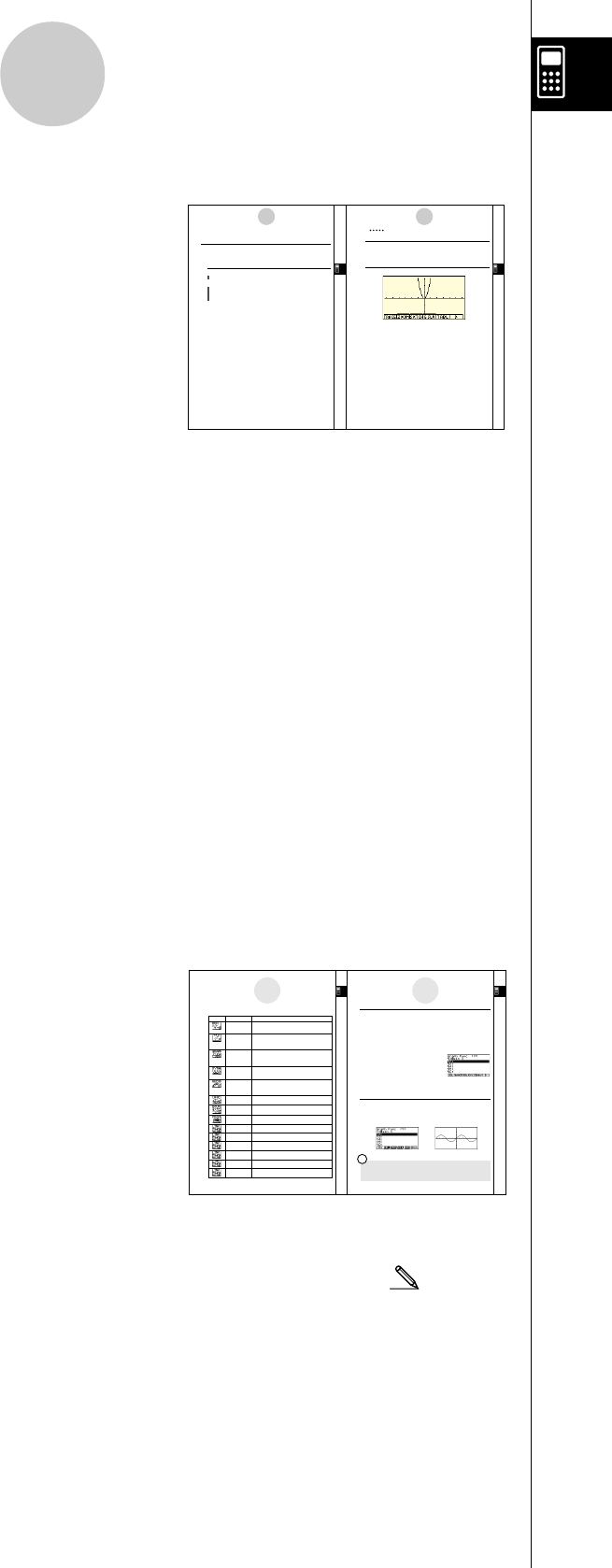
uGraphes
En règle générale, les opérations concernant les
graphes sont indiquées sur deux pages en vis à vis,
avec des exemples de graphes sur la plage droite. Vous
pouvez produire le même graphe sur votre calculatrice
en effectuant les étapes de la procédure au-dessus du
graphe. Recherchez le type de graphe souhaité sur la
page de droite, puis allez à la page indiquée pour ce
graphe.
Les étapes de la “ Procédure ” utilisent toujours les
réglages initiaux.
Les numéros d’étapes dans les sections “Réglage” et “Exécution” sur la page de gauche
correspondent aux numéros d’étapes de “Procédure” sur la page de droite.
Exemple:
Page de gauche Page de droite
3. Tracez le graphe. 35(DRAW)(ou w)
uu
uu
uListe de commandes
La liste des commandes de programmation (page 8-7) fournit un organigramme des
différents menus correspondant aux touches de fonction. EIle vous indique comment
accéder au menu de commandes souhaité.
Exemple: L’opération suivante affiche Xfct: [VARS]-[FACT]-[Xfct]
uu
uu
uContenu de la page
Un numéro de page divisé en trois se trouve au haut
de chaque page. Le numéro de page “ 1-2-3 ”, par
exemple, indique les chapitre 1, partie 2 et page 3.
uu
uu
uInformations complémentaires
Des informations complémentaires apparaissent au bas de chaque page sous “ ”
(Remarques).
* renvoie à une note sur un terme qui apparaît dans la même page.
# Indique une remarque qui fournit des informations d’ordre général sur un sujet traité dans
la même section que la remarque.
1-2-2
Affichage
1-2-3
Affichage
19981001 19981001
La signification de chaque symbole est la suivante.
Description
Icon Mode Name
RUN
STATistics
(statistiques)
GRaPH-TaBLe
(graphe)
DYNAmic graph
(graphe
dynamique)
RECURsion
(récurrence)
CONICS
(coniques)
EQUAtion
(équation)
PRoGraM
(programme)
Computer Algebra
System
ALGEBRA
TUTORial
LINK
MEMORY
SYSTEM
k A propos du menu de fonction
Utilisez les touches de fonction (1 à 6) pour accéder aux menus et commandes dans la barre
de menu au bas de l’écran. Les menus et les commandes se différencient par leur aspect.
• Commande (Exemple : DRAW )
Une commande s’exécute par une pression sur la touche de fonction correspondant à la
commande dans la barre de menu.
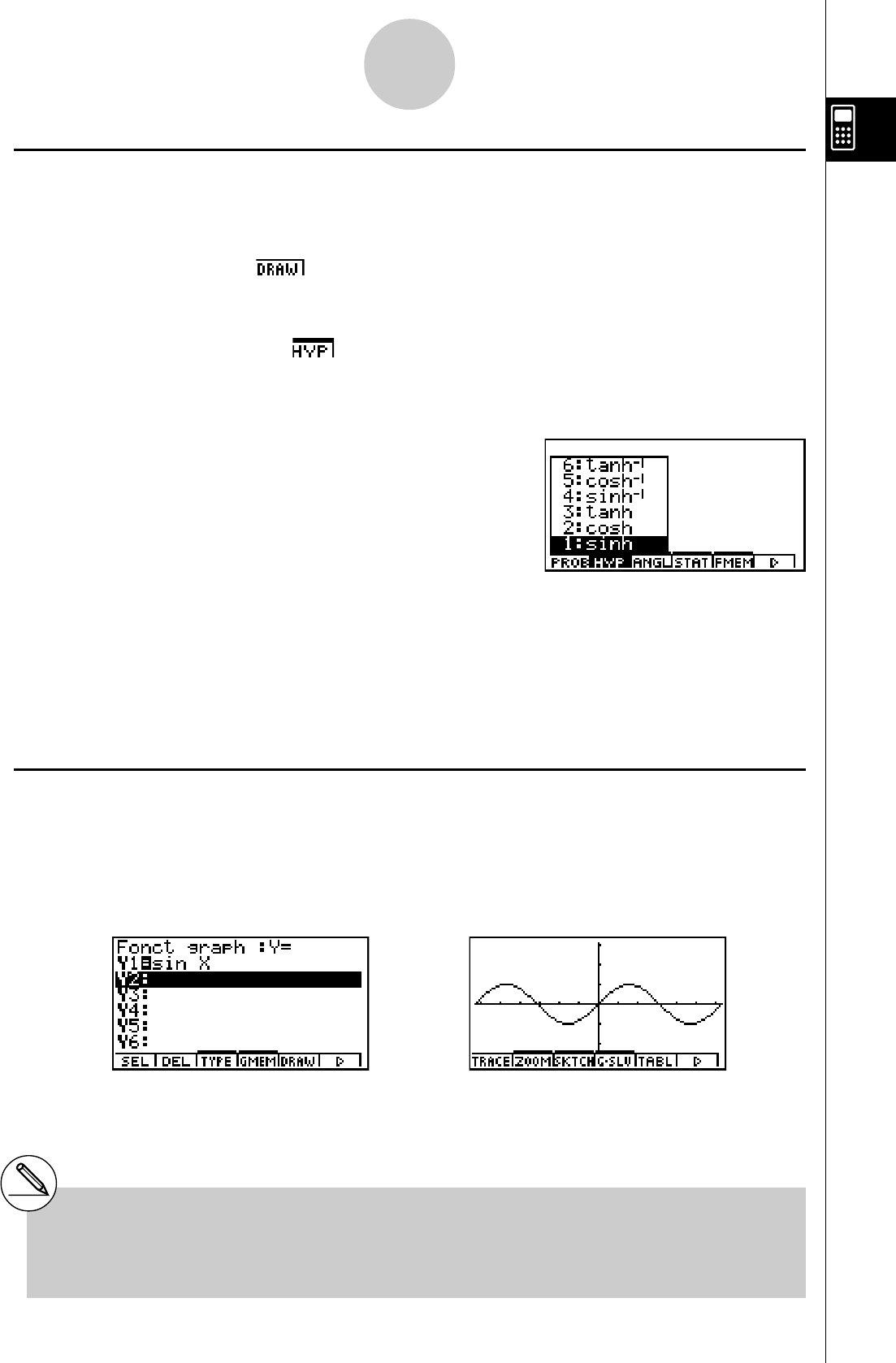
• Menu déroulant (Exemple: HYP )
Un menu s’ouvre par une pression sur la touche de fonction correspond à ce menu.
Vous pouvez choisir une des deux méthodes suivantes pour sélectionner une commande
sur un menu déroulant.
k About Display Screens
This calculator uses two types of display screens: a text screen and a graphic screen. The
text screen can show 21 columns and eight lines of characters, with the bottom line used for
the function key menu. The graph screen uses an area that measures 127 (W) × 63 (H) dots.
•Tapez le code à la gauche de la commande sur le menu déroulant.
•Utilisez les touches de curseur f et c pour amener la surbrillance sur la commande souhaitée
puis appuyez sur w.
Le symbole ' à droite de la commande indique que l’exécution de la commande affichera un sous-
menu.
Pour annuler le menu déroulant sans exécuter la commande, appuyez sur i.
Text Screen Graph Screen
Le contenu de chaque écran est stocké dans des zones de mémoire indépendantes.
Appuyez sur u5(G´T) pour passer de l’écran graphique à l’écran de texte.
Utilisez ce mode pour les calculs arithmétiques et les calculs
de fonction, ainsi que pour les calculs impliquant des valeur
binaires, octales, décimales et hexadécimales et des matrices.
Utilisez ce mode pour effectuer des calculs statistiques
statistiques à variable unique (écart-type) ou à variable double
(régression), pour effectuer des tests, analyser des donn ées et
pour tracer des graphes statistiques.
Utilisez ce mode pour stocker des fonctions, créer une table
numérique présentant différentes solutions quand les valeurs
affectées aux variables d’une fonction changent et pour en
tracer les graphes.
Utilisez ce mode pour stocker des fonctions graphiques et pour
tracer plusieurs versions d’un graphe en changeant les valeurs
affectées aux variables d’une fonction.
Utilisez ce mode pour stocker les formules de récurrence, créer
une table numérique présentant les différentes solutions quand
les valeurs affectées aux variables d’une fonction changent et
pour en tracer les graphes.
Utilisez ce mode pour tracer des graphes de fonctions implicites.
Utilisez ce mode pour résoudre des équations deux à six
inconnues, des équations quadratiques et des équations cubiques.
Utilisez ce mode pour stocker des programmes dans la
zone de programme et lancer des grammes.
Utilisez ce mode pour effectuer des calculs algébriques.
Utilisez ce mode pour la résolution détaillée d’expressions.
Utilisez ce mode pour déterminer le type d’expression et le mode de
résolution, et pour les solutions d’équations interactives.
Utilisez ce mode pour transférer le contenu de la mémoire ou
des données de sauvegarde sur une autre machine.
Utilisez ce mode pour travailler sur des données stockées
dans la mémoire.
Utilisez ce mode pour initialiser la mémoire, ajuster le contraste et
effectuer d’autres réglages du système.
Le contenu de chaque écran est
stocké dans des zones de mémoire
indépendantes.
Le contenu de chaque écran est
stocké dans des zones de mémoire
indépendantes.
5-1-1
Exemples de graphes
5-1-2
Exemples de graphes
Réglage
1. Depuis le menu principal, accédez au mode GRPH• TBL.
Exécution
2. Input the function you want to graph.
Vous pouvez ici utiliser la fenêtre d’affichage pour définir la plage et d’autres
paramètres du graphe. Voir 5-2-1.
3. Tracez le graphe.
k Comment tracer un graphe simple (1)
Description
Pour tracer un graphe, saisissez simplement la fonction appropriée.
Procédure
1 m GRPH-TBL
2 dvxw
35(DRAW) (ou w)
Exemple Représenter graphiquement la fonction
y
= 3
x
2
Rcran de résultat
19990401 19990401
5-1 Exemples de graphes

19990401
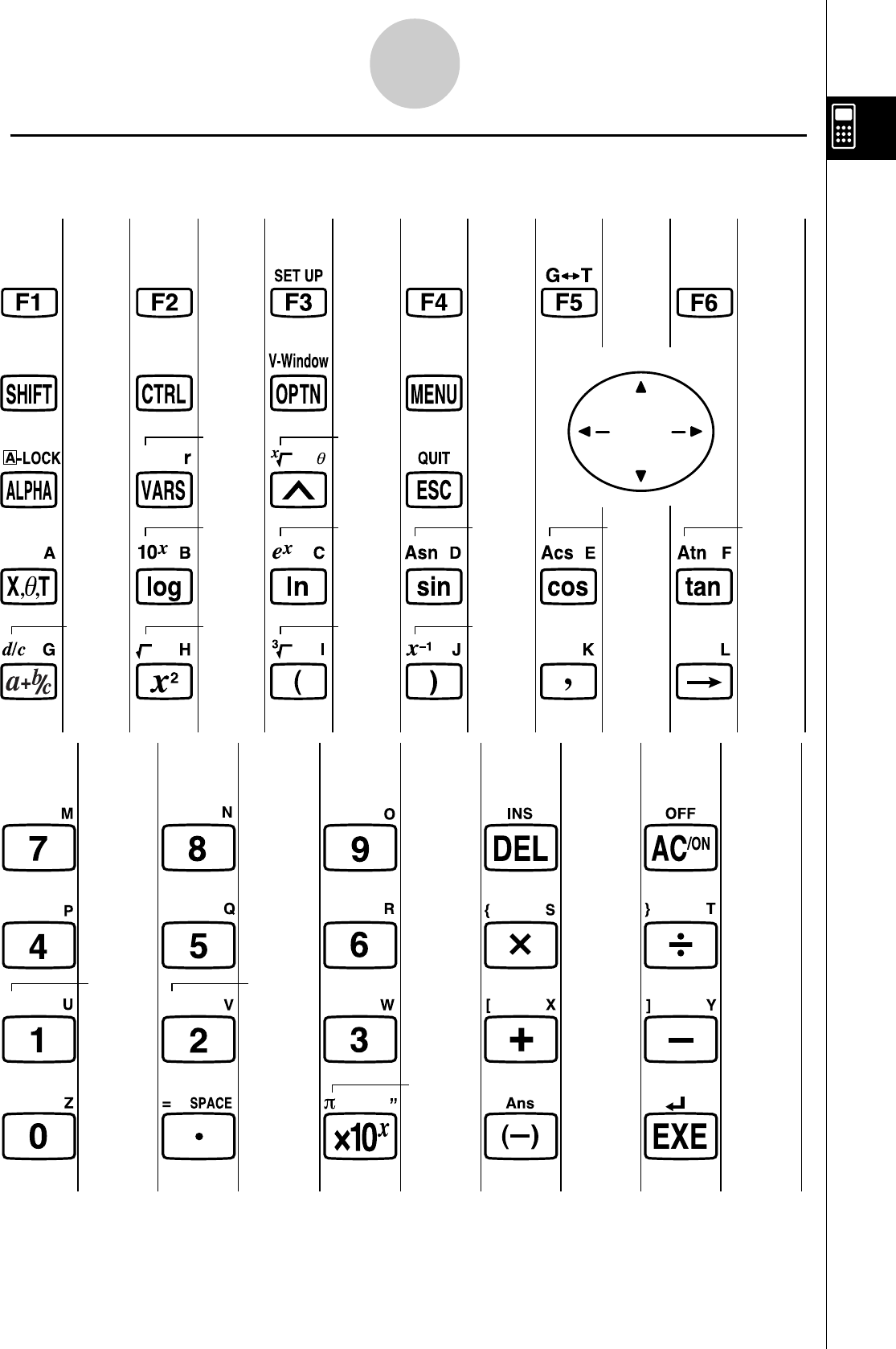
1-1 Touches
1-1-1
Touches
REPLAY
COPY PASTE CAT/CAL
H-COPY
PRGM
List Mat
i
1999040120001202
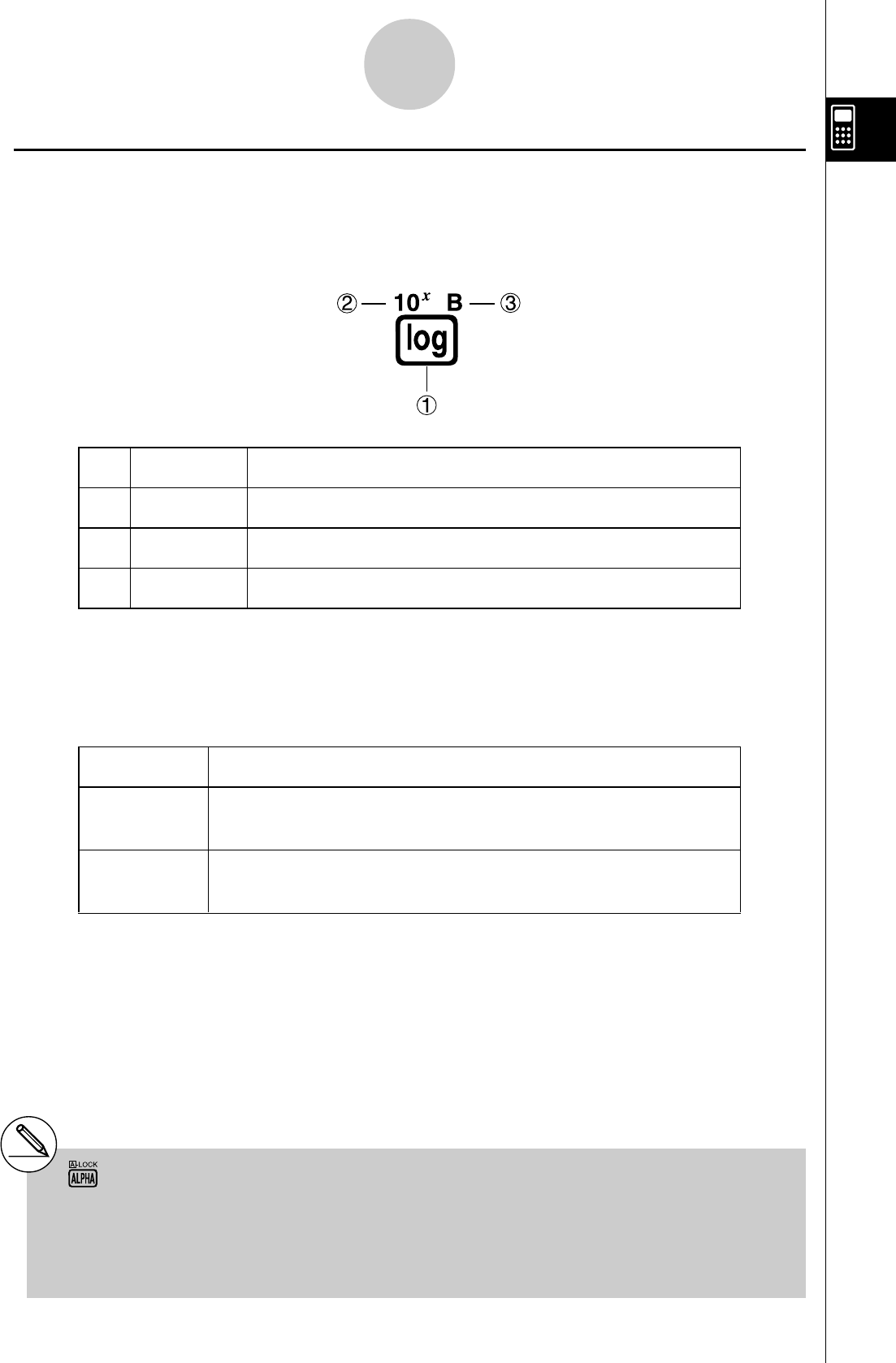
1-1-2
Touches
kk
kk
kTableau des touches
Page Page Page Page Page Page
1-3-5
Page Page Page Page Page
1-3-5 1-7-1
1-6-1 2-4-4
1-1-3 1-5-1 2-4-4
1-3-5 5-3-6 10-6-1
5-2-1
1-1-3 1-3-4 1-4-1 1-2-1
2-4-4 2-4-4
2-4-4 2-4-4
2-4-3 2-4-3
2-4-3 2-4-3
1-3-3
1-3-1
2-1-1
2-1-1
2-1-1
2-1-1
2-2-5
2-1-12-1-1
2-4-6
2-1-1
2-4-10
2-4-10
3-1-2 2-8-11
2-4-3
2-4-6 2-4-6
2-1-1
2-4-3
2-4-3
2-2-1
2-4-6
COPY PASTE
CAT/CAL
H-COPY
PRGM
List Mat
i
REPLAY
19990401
1-1-3
Touches
kk
kk
kInscriptions sur le clavier
De nombreuses touches de la calculatrice servent à exécuter plus d’une fonction. Les
fonctions indiquées sur le clavier sont codées par couleur pour vous aider à trouver
rapidement et aisément celle dont vous avez besoin.
Fonction Opération de touche
1log l
210x!l
3Bal
Le codage couleur utilisé pour les inscriptions du clavier est le suivant.
Couleur Opération de touche
Orange Appuyez sur ! puis sur la touche pour exécuter la fonction
indiquée.
Rouge Appuyez sur a puis sur la touche pour exécuter la fonction
indiquée.
# Verrouillage alpha
Normalement, après avoir appuyé sur a
puis sur une touche pour saisir un caractère
alphabétique, le clavier revient immédiatement
à ses fonctions primaires. Si vous appuyez sur
! puis sur a, le clavier se verrouillera sur
l’entrée alphabétique jusqu’à ce que vous
appuyiez de nouveau sur a.

19990401
1-2-1
Affichage
1-2 Affichage
kSélection d’une icône
Ce paragraphe décrit comment sélectionner une icône sur le menu principal pour entrer
dans le mode souhaité.
uu
uu
uPour sélectionner une icône
1. Appuyez sur m pour afficher le menu principal.
2. Utilisez les touches de curseur (d, e, f, c) pour mettre l’icône souhaitée en
surbrillance.
3. Appuyez sur w pour afficher l’écran initial du mode correspondant à l’icône
sélectionnée.
Ici nous choisissons le mode STAT.
• Vous pouvez aussi accéder au mode sans mettre l’icône en surbrillance dans le menu
principal en entrant le nombre ou la lettre indiqué dans le coin inférieur droit de l’icône.
Icône actuellement
sélectionnée
20001202
19990401
La signification de chaque icône est la suivante.
Icône Nom de mode Description
RUN • MATrix
Utilisez ce mode pour les calculs arithmétiques et les calculs
(RUN
•
matrices)
de fonction, ainsi que pour les calculs impliquant des valeurs
binaires, octales, décimales et hexadécimales et des matrices.
STATistics
Utilisez ce mode pour effectuer des calculs statistiques à
(statistiques)
variable unique (écart-type) ou à variable double
(régression), pour analyser des données et pour tracer des
graphes statistiques.
GRaPH-TaBLe
Utilisez ce mode pour stocker des fonctions, créer une table
(graphe-Table)
numérique présentant différentes solutions quand les valeurs
affectées aux variables d’une fonction changent et pour en
tracer les graphes.
DYNAmic graph
Utilisez ce mode pour stocker des fonctions graphiques et pour
(graphe
tracer plusieurs versions d’un graphe en changeant les valeurs
dynamique)
affectées aux variables d’une fonction.
RECURsion
Utilisez ce mode pour stocker les formules de récurrence, créer
(récurrence)
une table numérique présentant les différentes solutions quand
les valeurs affectées aux variables d’une fonction changent et
pour en tracer les graphes.
CONICS
Utilisez ce mode pour tracer des graphes de fonctions implicites.
(coniques)
EQUAtion
Utilisez ce mode pour résoudre des équations linéaires de 2 à
(équation)
30 inconnues et des équations du 2
e
au 30
e
degré.
PRoGraM
Utilisez ce mode pour stocker des programmes dans la zone de
(programme)
programmes et lancer des programmes.
Computer Algebra
Utilisez ce mode pour effectuer des calculs algébriques.
System
TVM (finance)
Utilisez ce mode sert pour effectuer des calculs financiers.
DIFFerential
Utilisez ce mode sert pour résoudre les équations différentielles.
EQuation
(équation différentielle)
E-CON
Utilisez ce mode sert pour piloter un CASIO EA-100 depuis
la calculatrice.
LINK
Utilisez ce mode pour transférer le contenu de la mémoire ou
(liaison)
des données de sauvegarde sur une autre machine.
MEMORY
Utilisez ce mode pour travailler sur des données stockées dans
(mémoire)
la mémoire.
SYSTEM
Utilisez ce mode pour initialiser la mémoire, ajuster le contraste
(système)
et effectuer d’autres réglages du système.
1-2-2
Affichage
20001202
19990401
kk
kk
kA propos du menu de fonction
Utilisez les touches de fonction (
1
à
6
) pour accéder aux menus et commandes dans la
barre de menu au bas de l’écran. Les menus et les commandes se différencient par leur aspect.
• Commande (Exemple: )
Une commande s’exécute par une pression sur la touche de fonction correspondant à la
commande dans la barre de menu.
• Menu déroulant (Exemple: )
Un menu s’ouvre par une pression sur la touche de fonction correspond à ce menu.
Vous pouvez choisir une des deux méthodes suivantes pour sélectionner une commande
sur un menu déroulant.
• Tapez le code à la gauche de la commande sur le menu déroulant.
• Utilisez les touches de curseur f et c pour amener la surbrillance sur la commande
souhaitée puis appuyez sur w.
Le symbole ' à droite de la commande indique que l’exécution de la commande affichera un
sous-menu.
Pour annuler le menu déroulant sans exécuter la commande, appuyez sur i.
kk
kk
kA propos des écrans
La calculatrice emploie deux types d’écrans: un écran de texte et un écran graphique.
L’écran de texte peut contenir 21 caractères sur une ligne et 8 lignes, y compris la ligne
inférieure utilisée pour le menu de touches de fonction. L’écran graphique utilise une zone
de 127 points (l) × 63 points (h).
Ecran de texte Ecran graphique
Le contenu de chaque écran est stocké dans des zones de mémoire indépendantes.
Appuyez sur u5(G↔T) pour passer de l’écran graphique à l’écran de texte et
inversement.
1-2-3
Affichage
# Le symbole ↑ dans le coin supérieur droit d’un
menu déroulant indique qu’il n’y a plus de
commandes au haut de l’écran.
Utilisez les touches de curseur pour faire défiler le
contenu du menu et voir les commandes qui
n’apparaissent pas au haut de l’écran.

19990401
kk
kk
kAffichage normal
La calculatrice est capable normalement d’afficher des valeurs contenant 10 chiffres. Les
valeurs qui dépassent cette limite sont automatiquement converties et affichées sous forme
exponentielle.
uComment interpréter le format exponentiel
1.2E+12 indique que le résultat est égal à 1,2 × 1012. Cela signifie que vous devez déplacer
la virgule des décimales dans 1,2 de douze rangs vers la droite, puisque l’exposant est
positif. Le résultat est 1 200 000 000 000.
1.2E–03 indique que le résultat est équivalent à 1,2 × 10–3, ce qui signifie que vous devez
déplacer la virgule des décimales dans 1,2 de trois rangs vers la gauche puisque l’exposant
est négatif. Le résultat est 0,0012.
Vous pouvez choisir une des deux plages pour l’affichage automatique normal.
Norm 1 .................. 10–2 (0,01) > |x|, |x| > 1010
Norm 2 .................. 10–9 (0,000000001) > |x|, |x| > 1010
Tous les exemples de calculs dans ce manuel affichent des résultats avec Norm 1.
Voir page 2-3-2 pour les détails sur la commutation entre Norm 1 et Norm 2.
1-2-4
Affichage
19990401
kk
kk
kFormats d’affichage spéciaux
Cette calculatrice emploie des formats d’affichage spéciaux pour indiquer les fractions, les
valeurs hexadécimales et les valeurs exprimées en degrés/minutes/secondes.
uFractions
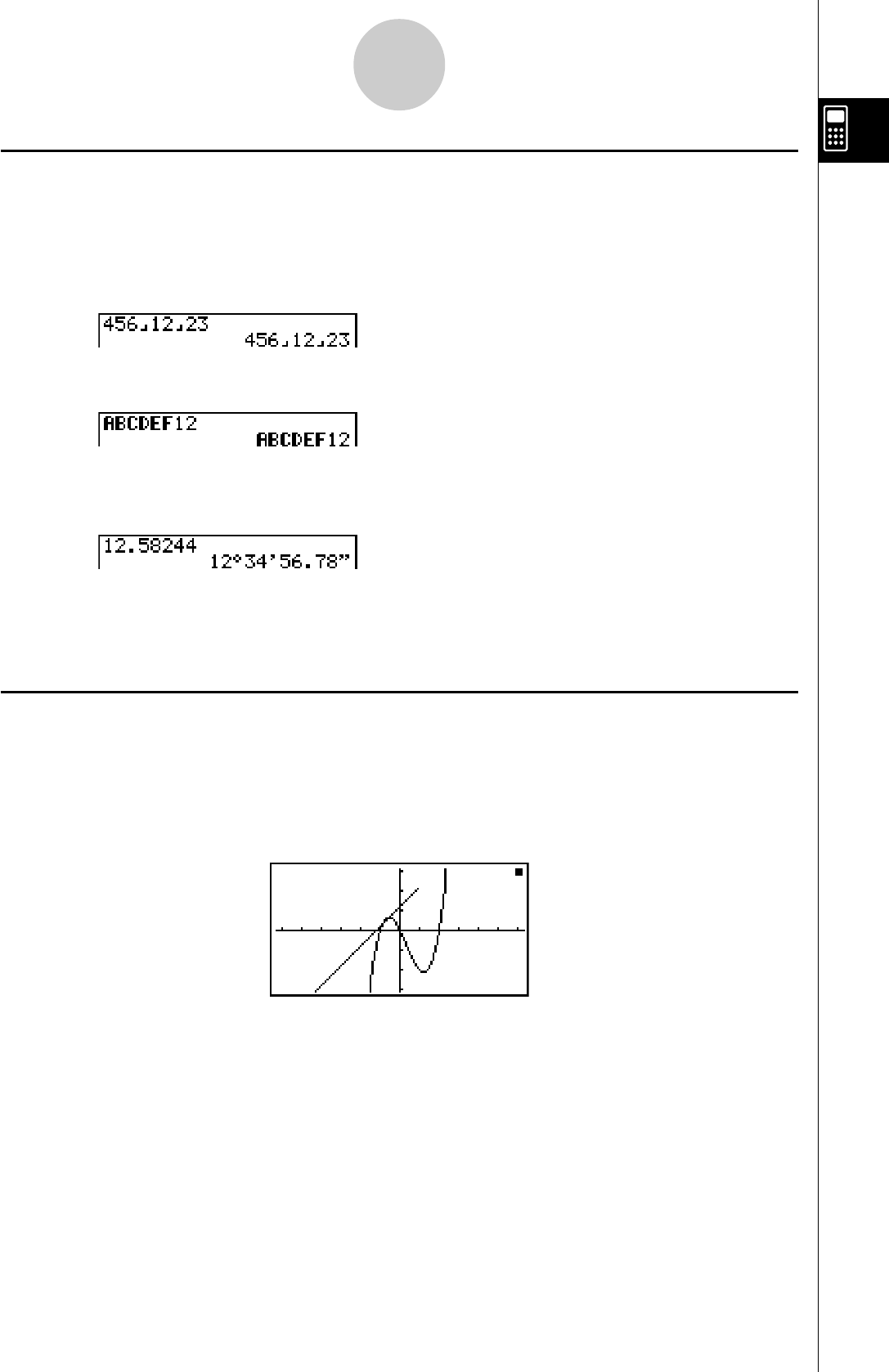
................. Indique: 456+
uValeurs hexadécimales
................. Indique: ABCDEF12(16), qui est égal à
–1412567278(10)
uValeurs en degrés/minutes/secondes
................. Indique: 12° 34’ 56,78”
• Outre ces formats spéciaux, la calculatrice utilise aussi d’autres indicateurs et
symboles qui sont décrits dans chaque paragraphe concerné de ce mode d’emploi.
kk
kk
kIndicateur d’exécution de calcul
Quand la calculatrice est en train de dessiner un graphe ou d’exécuter un calcul ou un
programme long et complexe, un carré noir “k” clignote dans le coin supérieur droit de
l’écran. Ce carré vous signale que la calculatrice effectue une opération interne.
1-2-5
Affichage
12
––––
23

19990401
1-3 Saisie et édition de calculs
kk
kk
kSaisie de calculs
Lorsque vous êtes prêt à saisir un calcul, appuyez d’abord sur la touche A pour effacer
l’affichage. Introduisez ensuite vos formules de calcul, exactement comme elles sont
écrites, de gauche à droite et appuyez sur w pour obtenir le résultat.
Exemple 1 2 + 3 – 4 + 10 =
Ac+d-e+baw
Exemple 2 2(5 + 4) ÷ (23 × 5) =
Ac(f+e)/
(cd*f)w
kÉdition de calculs
Utilisez les touches d et e pour amener le curseur sur la position à changer, puis
effectuez une des opérations décrites ci-dessous. Après avoir édité le calcul, vous pouvez
l’exécuter en appuyant sur w. Vous pouvez aussi utiliser e pour aller à la fin du calcul
et continuer à saisir des données.
uPour changer un pas
Exemple Changer cos60 en sin60
Acga
ddd
D
s
1-3-1
Saisie et édition de calculs

19990401
uPour effacer un pas
Exemple Remplacer 369 × × 2 par 369 × 2
Adgj**c
ddD
uPour insérer un pas
Exemple Remplacer 2,362 par sin2,362
Ac.dgx
ddddd
s
uPour changer le dernier pas saisi
Exemple Remplacer 396 × 3 par 396 × 2
Adgj*d
D
c
1-3-2
Saisie et édition de calculs

19990401
kk
kk
kUtilisation de la mémoire de répétition
Le dernier calcul est toujours stocké dans la mémoire de répétition. Le contenu de la
mémoire de répétition peut être rappelé par une pression sur d ou e.
Lorsque vous appuyez sur e, le calcul apparaît avec le curseur au début. Une pression
sur d permet de faire apparaître le curseur à la fin du calcul. Vous pouvez effectuer des
changements dans le calcul, puis le réexécuter.
Exemple 1 Effectuer les deux calculs suivants
4,12 × 6,4 = 26,368
4,12 × 7,1 = 29,252
Ae.bc*g.ew
dddd
!D(INS)
h.b
w
Une fois que vous avez appuyé sur A, vous pouvez appuyer sur f ou sur c pour
rappeler des calculs précédents, dans l’ordre, en commençant par le plus récent pour finir
par le plus ancien (Fonction de multi-répétitions). Vous pouvez utiliser e et d pour
déplacer le curseur dans un calcul et faire des changements pour créer un nouveau calcul.
Exemple 2
Abcd+efgw
cde-fghw
A
f (Un calcul précédent)
f (Deux calculs précédents)
1-3-3
Saisie et édition de calculs
# Une pression sur !D(INS) change la
forme du curseur en “ _ ”. La valeur ou fonction
suivante que vous introduirez sera inscrite à la
position de “ _ ”. Pour désactiver cette fonction,
appuyez une nouvelle fois sur !D(INS).
# Un calcul reste sauvegardé dans la mémoire
de répétition jusqu’à ce que vous en réalisiez
un nouveau ou changiez de mode.
# Le contenu de la mémoire de répétition n’est pas
effacé lorsque vous appuyez sur la touche A,
vous pouvez donc rappeler un calcul et
l’exécuter même après avoir un effacement
général.
19990401
1-3-4
Saisie et édition de calculs
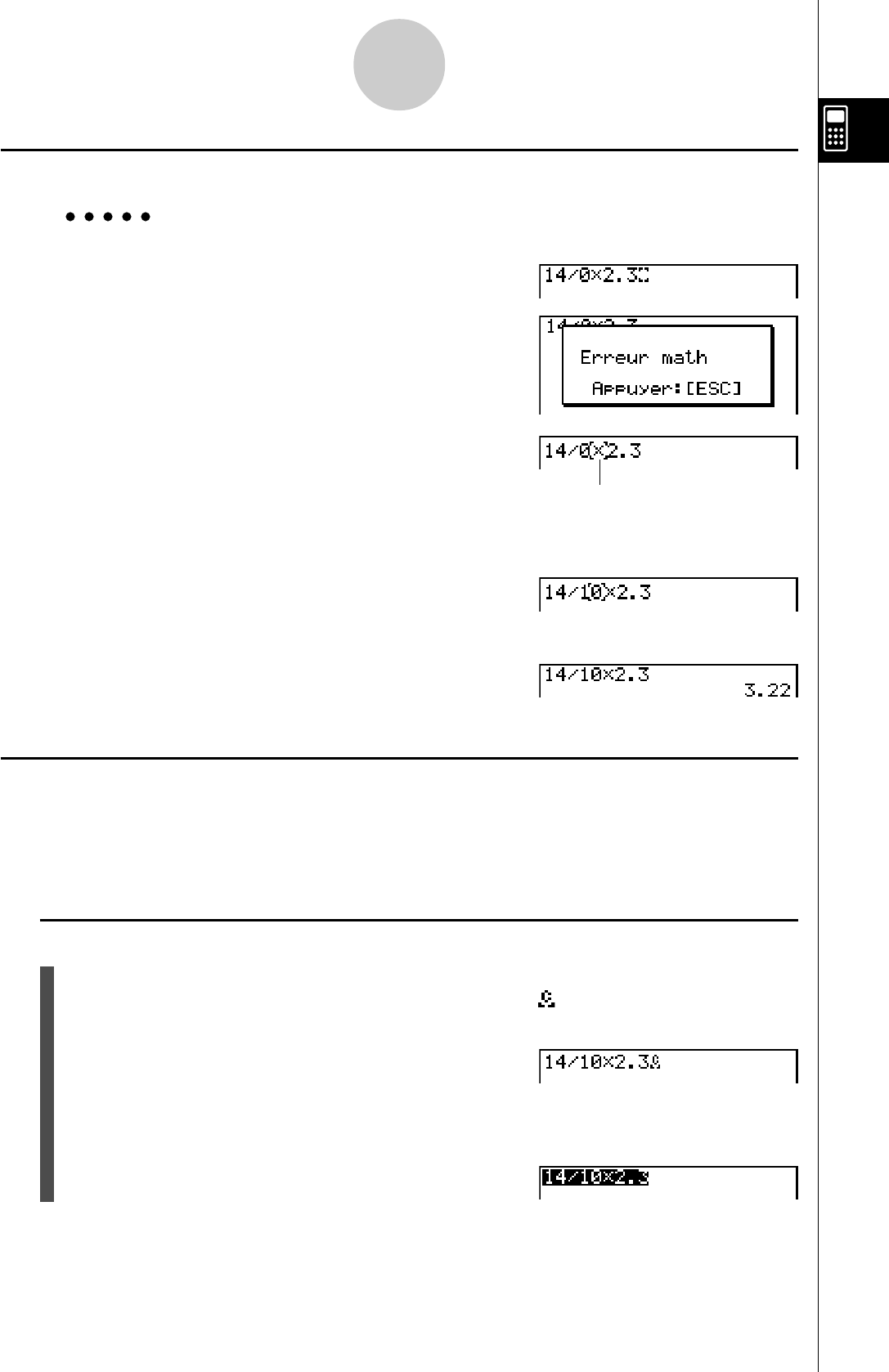
kPour faire des corrections dans le calcul d’origine
Exemple 14 ÷ 0 × 2,3 tapé par erreur à la place de 14 ÷ 10 × 2,3
Abe/a*c.d
w
Appuyez sur i.
Faites les changements nécessaires.
db
Réexécutez le calcul.
w
kk
kk
kCopie et collage
Les données de commandes, de programmes et de texte peuvent être copiées
provisoirement dans une zone de la mémoire appelée “presse-papiers” pour être ensuite
collées à un autre endroit de l’écran.
uPour définir le texte à copier
1. Amenez le curseur (t) au début ou à la fin du texte que vous voulez copier, puis
appuyez sur la touche u. Le curseur prend la forme “ ” .
2. Utilisez les touches de curseur pour amener le curseur sur le texte et mettre en
surbrillance le texte que vous voulez copier.
Le curseur se met automatiquement à
l’emplacement de la cause de l’erreur.

19990401
3. Appuyez sur u1 (COPY) pour copier le texte en surbrillance dans le presse-
papiers, puis sortez du mode de sélection de texte.
Pour annuler la surbrillance sans copier le texte, appuyez sur la touche i.
uCollage du texte
Amenez le curseur à l’endroit où vous voulez coller le texte et appuyez sur u2(PASTE).
Le contenu du presse-papiers est collé à la position du curseur.
A
u2(PASTE)
kk
kk
kFonction de catalogue
Le catalogue est une liste alphabétique de toutes les commandes présentes dans la
calculatrice. Vous pouvez saisir une commande en affichant le catalogue et en sélectionnant
cette commande.
uUtilisation du catalogue pour la saisie d’une commande
1. Appuyez sur u4(CAT/CAL) pour afficher le
catalogue au bas de l’écran.
2. Appuyez sur la touche de fonction correspondant à la première lettre de la commande
que vous voulez saisir.
3. Sélectionnez la commande sur le menu déroulant.
Exemple 1 Utiliser le catalogue pour saisir la commande ClrGraph
Au4(CAT/CAL)3(C~)h(CLR)
b(Graph)
1-3-5
Saisie et édition de calculs

19990401
Exemple 2 Utiliser le catalogue pour saisir la commande Prog
Au4(CAT/CAL)6(g)6(g)
5(P)I(Prog)
Le catalogue se ferme par une pression sur i ou !i(QUIT).
1-3-6
Saisie et édition de calculs

19990401
1-4 Menu d’options (OPTN)
Le menu d’options vous permet d’accéder aux fonctions scientifiques et caractéristiques
qui ne sont pas indiquées sur le clavier de la calculatrice. Le contenu du menu d’options
varie en fonction du mode dans lequel est la calculatrice quand vous appuyez sur la
touche K.
Voir “8-7 Liste des commandes de programmation” pour les détails sur le menu d’options
(OPTN).
uMenu d’options dans le mode RUN
•
MAT ou PRGM
•{LIST} ... {menu de fonctions de listage}
•{MAT} ... {menu d’opérations matricielles}
•{CPLX} ... {menu de calculs avec nombres complexes}
•{CALC} ... {menu d’analyse de fonctions}
•{NUM} ... {menu de calculs numériques}
•{PROB} ... {menu de calculs de probabilité/distribution}
•{HYP} ... {menu de calculs hyperboliques}
•{ANGL} ... {menu pour la conversion d’angles/coordonnées, entrée/conversion DMS}
•{STAT} ... {menu de valeurs statistiques estimées à variable double}
•{FMEM} ... {menu de mémoires de fonctions}
•{ZOOM} ... {menu de fonctions de zoom}
•{SKTCH} ... {menu de fonctions de dessin}
•{PICT} ... {menu de mémoires d’images}
•{SYBL} ... {menu de symboles}
•{° ’ ”} … {DMS}
•{ ° ’ ”} … {conversion DMS}
•{ENG}/{ ENG} … {conversion ENG}
1-4-1
Menu d’options (OPTN)
# Le menu d’options (OPTN) n’apparaît pas
pendant les calculs binaires, octaux, décimaux
et hexadécimaux.

19990401
Les menus de fonctions suivants apparaissent dans d’autres circonstances.
uMenu d’option lorsqu’une valeur de la table numérique est affichée dans
le mode GRPH
•
TBL ou RECUR
•{LMEM} … {menu de mémoires de listes}
•{ ° ’ ”}/{ENG}/{ ENG}
uMenu d’options dans le mode CAS
•{∞} … {infini}
•{Abs} … {valeur absolue}
•{x!} … {factorielle}
•{sign} … {fonction signum}
•{HYP}/{FMEM}
Vous trouverez la signification des paramètres de chaque menu d’options dans les parties
décrivant chaque mode.
1-4-2
Menu d’options (OPTN)

19990401
1-5 Menu de données de variables (VARS)
Pour rappeler des données de variables, appuyez sur J pour afficher le menu de données
de variables.
{V-WIN}/{FACT}/{STAT}/{GRPH}/{DYNA}/
{TABL}/{RECR}/{EQUA*1}
Voir “8-7 Liste des commandes du mode de programmation” pour les détails sur le menu de
données de variables (VARS).
u V-WIN — Rappel des valeurs de la fenêtre d’affichage
•{Xmin}/{Xmax}/{Xscale}/{Xdot}
…{valeur minimale}/{valeur maximale}/{échelle}/{valeur de points*2} de l’axe X
•{Ymin}/{Ymax}/{Yscale}
…{valeur minimale}/{valeur maximale}/{échelle} de l’axe Y
•{T
θ
min}/{T
θ
max}/{T
θ
ptch}
…{valeur minimale}/{valeur maximale}/{pas} de T,
θ
•{R-Xmin}/{R-Xmax}/{R-Xscl}/{R-Xdot}
…{valeur minimale}/{valeur maximale}/{échelle}/{valeur de points*2} de l’axe X du
graphe droit d’un double graphe
•{R-Ymin}/{R-Ymax}/{R-Yscl}
…{valeur minimale}/{valeur maximale}/{échelle} de l’axe Y du graphe droit d’un
double graphe
•{R-Tmin}/{R-Tmax}/{R-Tpch}
… {valeur minimale}/{valeur maximale}/{pas} de T,
θ
du graphe droit d’un double
graphe
u FACT — Rappel des facteurs de zoom
•{Xfact}/{Yfact}
... {facteur de l’axe x}/{facteur de l’axe y}
1-5-1
Menu de données de variables (VARS)
*1Le paramètre EQUA n’apparaît que lorsque
vous accédez au menu de données de
variables depuis le mode RUN
•
MAT ou
PRGM.
# Le menu de données de variables n’apparaît
pas si vous appuyez sur J lorsque le
système binaire, octal, décimal ou
hexadécimal est défini par défaut.
*2La valeur de points indique la plage d’affichage
(valeur Xmax – valeur Xmin) divisée par le pas
des points (126).
Cette valeur est normalement calculée
automatiquement à partir des valeurs maximales
et minimales. Le changement de la valeur des
points se répercute automatiquement sur le
maximum.

19990401
u STAT — Rappel de données statistiques
• {n} … {nombre de données}
• {X} … {données x à variable unique, variable double}
•{
oo
oo
o}/{Σx}/{Σx2}/{x
σ
n}/{x
σ
n–1}/{minX}/{maxX}
…{moyenne}/{somme}/{somme des carrés}/{écart-type sur une population}/
{écart-type sur un échantillon}/{valeur minimale}/{valeur maximale}
• {Y} ... {données y à variable double}
•{
pp
pp
p
}/{Σ
y}/{Σ
y2}/{Σ
xy}/{
y
σ
n}/{
y
σ
n–1}/{minY}/{maxY}
…{moyenne}/{somme}/{somme des carrés}/{somme des produits de données x et
de données y}/{écart-type sur une population}/{écart-type sur un échantillon}/
{valeur minimale}/{valeur maximale}
•{GRAPH} ... {menu de données de graphes}
•{a}/{b}/{c}/{d}/{e}
... {coefficient de régression et coefficients multinominaux}
•{r}/{r2}
... {coefficient de corrélation}/{coefficient de détermination}
•{Q1}/{Q3}
... {premier quartile}/{troisième quartile}
•{Med}/{Mod}
... {médiane}/{mode} des données saisies
•{H-Strt}/{H-ptch}
... {division initiale}/{pas} de l’histogramme
•{PTS} ... {menu de données de points récapitulatifs}
•{
x1}/{y1}/{x2}/{y2}/{x3}/{y3} ... {coordonnées de points récapitulatifs}
1-5-2
Menu de données de variables (VARS)
20091001

19990401
u GRPH — Rappel des fonctions graphiques
•{Yn}/{rn}
... {fonction de coordonnées rectangulaires ou d’inégalités}/
{fonction de coordonnées polaires}
•{Xtn}/{Ytn}
... fonction de graphe paramétrique {Xt}/{Yt}
•{Xn} ... {fonction de graphe avec constante=X}
(Appuyez sur ces touches avant de désigner la zone de stockage.)
u DYNA — Rappel des données de configuration de graphes dynamiques
•{Start}/{End}/{Pitch}
... {valeur initiale de la plage de coefficient}/{valeur finale de la plage de
coefficient}/{incrément du coefficient}
uTABL — Rappel des données de configuration et du contenu de Table
et Graphe
•{Start}/{End}/{Pitch}
... {valeur initiale de la plage de la table}/{valeur finale de la plage de la table}/
{incrément des valeurs de la table}
•{Result*1}
... {matrice du contenu de la table}
1-5-3
Menu de données de variables (VARS)
*1 Le paramètre Result n’apparaît que si le menu
TABL est affiché dans le mode RUN
•
MAT ou
PRGM.

19990401
u RECR — Rappel des données de formules de récurrence*1, de plages
de tables et du contenu de tables
• {FORM}... {menu de données de formules de récurrence}
• {an}/{an+1}/{an+2}/{bn}/{bn+1}/{bn+2}/{cn}/{cn+1}/{cn+2}
... expressions {an}/{an+1}/{an+2}/{bn}/{bn+1}/{bn+2}/{cn}/{cn+1}/{cn+2}
• {RANGE} ... {menu de données de plages de tables}
• {R-Strt}/{R-End}
... {valeur initiale}/{valeur finale} de la plage d’une table
• {a0}/{a1}/{a2}/{b0}/{b1}/{b2}/{c0}/{c1}/{c2}
... valeur {a0}/{a1}/{a2} {b0}/{b1}/{b2}/{c0}/{c1}/{c2}
• {anStrt}/{bnStrt}/{cnStrt}
... origine du graphe de convergence divergence d’une formule de récurrence
{an
}/{bn}/{cn} (graphe WEB)
• {Result*2} ... {matrice du contenu d’une table*3}
u EQUA — Rappel des coefficients et des solutions d’équations*4 *5
•{S-Rslt}/{S-Coef}
... matrice de {solutions}/{coefficients} pour les équations linéaires*6
•{P-Rslt}/{P-Coef}
... matrice de {solutions}/{coefficients} pour les équations de degré élevé
1-5-4
Menu de données de variables (VARS)
*1Une erreur se produit s’il n’y a pas de fonction
ni de table numérique de formules de
récurrence dans la mémoire.
*2 “Result” n’est disponible que dans les modes
RUN
•
MAT et PRGM.
*3Le contenu d’une table est automatiquement
stocké dans la mémoire de réponse matricielle
(MatAns).
*4Les coefficients et les solutions sont
automatiquement stockés dans la mémoire de
réponse matricielle (MatAns).
*5 Dans les cas suivants, une erreur se produit:
— Aucun coefficient n’a été saisi pour
l’équation.
— Aucune solution n’a été obtenue pour
l’équation.
*6 Le coefficient et la solution mémorisés d’une
équation linéaire ne peuvent pas être rappelés
en même temps.

19990401
1-6 Menu de programmation (PRGM)
Pour afficher le menu de programmation (PRGM), accédez d’abord au mode RUN • MAT ou
PRGM à partir du menu principal, puis appuyez sur !J(PRGM). Les sélections
disponibles dans le menu de programmation (PRGM) sont les suivantes.
• {Prog} ........ {rappel de programme}
• {JUMP} ...... {menu de commande de saut}
• {?} .............. {commande d’entrée}
• {^} ............. {commande de sortie}
• {I/O}............ {menu de commande de contrôle/transfert d’entrée/sortie}
• {IF} ............. {menu de commande de saut conditionnel}
• {FOR} ......... {menu de commande de boucle}
• {WHLE} ...... {menu de commande de contrôle de boucle conditionnelle}
• {CTRL}....... {menu de commande de contrôle de programmation}
• {LOGIC} ..... {menu de commande d’opérations logiques}
• {CLR} ......... {menu de commande de suppression}
• {DISP} ........ {menu de commande d’affichage}
• {:} ............... {séparateur d’instructions multiples}
Le menu de touches de fonction suivant apparaît si vous appuyez sur !J(PRGM)
dans le mode RUN • MAT ou PRGM, quand le système numérique par défaut est binaire,
octal, décimal ou hexadécimal.
• {Prog}/{JUMP}/{?}/{^}/{:}
• {= GG
GG
G <} ....... {menu d’opérateurs relationnels}
Les fonctions attribuées aux touches de fonction sont identiques à celles du mode Comp.
Pour les détails sur les commandes disponibles dans les différents menus auxquels vous
avez accès à partir du menu de programmation, voir “8. Programmation”.
1-6-1
Menu de programmation (PRGM)

19990401
1-7 Utilisation de l’écran de configuration
L’écran de configuration de mode indique l’état actuel des réglages de mode et permet
d’effectuer les changements souhaités. Vous pouvez changer les réglages d’un mode de
la façon suivante.
uPour changer la configuration d’un mode
1. Sélectionnez l’icône souhaitée et appuyez sur w pour acceder au mode et
en afficher l’écran initial. Ici nous choisissons le mode RUN • MAT.
2. Appuyez sur u3(SET UP) pour afficher l’écran
de configuration de ce mode.
• Cet écran de configuration est utilisé à titre
d’exemple. Le contenu de l’écran peut être
différent en fonction du mode dans lequel
vous êtes et des réglages actuels de ce mode.
3. Utilisez les touches de curseur f et c pour mettre le paramètre dont vous voulez
changer le réglage en surbrillance.
4. Appuyez sur la touche de fonction 1 à 6 qui indique le réglage que vous voulez
faire.
5. Quand vous avez fait les changements nécessaires, appuyez sur i pour revenir à
l’écran initial de ce mode.
kMenus de touches de fonction sur l’écran de configuration
Cette partie détaille les réglages que vous pouvez effectuer à l’aide des touches de fonction
de l’écran de configuration.
indique le réglage par défaut.
uMode (calcul/mode binaire, octal, décimal, hexadécimal)
•{Comp} ... {mode de calcul arithmétique}
•{Dec}/{Hex}/{Bin}/{Oct}
... {décimal}/{hexadécimal}/{binaire}/{octal}
1-7-1
Utilisation de l’écran de configuration
...

19990401
uFunc Type (type de fonction graphique)
Une pression sur une des touches de fonction suivantes commute aussi la fonction de la
touche v.
•{Y=}/{r=}/{Parm}/{X=c}
... graphe à {coordonnées rectangulaires}/{coordonnées polaires}/{coordonnées
paramétriques}/{X = constante}
•{Y>}/{Y<}/{Yt}/{Ys}
... graphe d’inéquation {y>f(x)}/{y<f(x)}/{y≥f(x)}/{y≤f(x)}
uDraw Type (méthode de tracé du graphe)
•{Con}/{Plot}
... {par points connectés}/{par points séparés}
uDerivative (affichage de la valeur de la dérivée)
•{On}/{Off}
... {affichage activé}/{affichage désactivé} pendant l’utilisation de Graph-to-Table,
Table & Graph et de Trace.
uAngle (unité par défaut de l’unité d’angle)
•{Deg}/{Rad}/{Gra}
... {degrés}/{radians}/{grades}
uComplex Mode
•{Real} ... {calcul dans la plage des nombres réels seulement}
•{a + bi}/{r
·
e^
θ
i}
... affichage d’un calcul complexe à {format rectangulaire}/{format polaire}
uCoord (affichage des coordonnées du pointeur graphique)
•{On}/{Off}
... {affichage activé}/{affichage désactivé}
uGrid (affichage de la trame du graphe)
•{On}/{Off}
... {affichage activé}/{affichage désactivé}
uAxes (affichage de l’axe du graphe)
•{On}/{Off}
... {affichage activé}/{affichage désactivé}
uLabel (affichage du nom de l’axe graphique)
•{On}/{Off}
... {affichage activé}/{affichage désactivé}
1-7-2
Utilisation de l’écran de configuration

19990401
uDisplay (format d’affichage)
•{Fix}/{Sci}/{Norm}/{Eng}
... {nombre de décimales défini}/{nombre de chiffres significatifs}/{réglage
d’affichage normal}/{mode Ingénieur}
uStat Wind (méthode de réglage de la fenêtre d’affichage de graphes
statistiques)
•{Auto}/{Man}
... {automatique}/{manuel}
uReside List (calcul résiduel)
•{None}/{LIST}
... {pas de calcul}/{spécification de la liste pour les données résiduel les calculées}
uList File (réglages d’affichage de fichier de listes)
•{FILE} ... {réglages du fichier de liste affiché}
uVariable (réglages pour la génération de tables et le tracé de graphes)
•{Rang}/{LIST}
... {utilisation de la plage d’une table}/{utilisation des données d’une liste}
uGraph Func (affichage de la fonction pendant le tracé d’un graphe et
l’affichage des coordonnées d’un point)
•{On}/{Off}
... {affichage activé}/{affichage désactivé}
uDual Screen (état du mode écran double)
•{T+G}/{G+G}/{GtoT}/{Off}
... {graphe d’un côté et table numérique de l’autre côté de l’écran double}/{tracé
graphique sur les deux côtés de l’écran double}/{graphe sur un côté et table
numérique de l’autre côté de l’écran double}/{écran double désactivé}
uSimul Graph (mode de graphe simultané)
•{On}/{Off}
... {tracé de graphes simultanés activé (tous les graphes sont tracés
simultanément)}/{tracé de graphes simultanés désactivé (tous les graphes sont
tracés les uns après les autres)}
uBackground (arrière-plan d’affichage de graphe)
•{None}/{PICT}
... {pas d’arrière-plan}/{désignation de l’image en arrière-plan du graphe}
1-7-3
Utilisation de l’écran de configuration

19990401
uDynamic Type (réglage du lieu du graphe dynamique)
•{Cnt}/{Stop}
... {sans arrêt (continu)}/{arrêt automatique après 10 tracés}
uΣ Display {affichage de la valeur Σ dans une table de récurrence}
•{On}/{Off}
... {affichage activé}/{affichage désactivé}
uSlope (affichage de la dérivée à la position actuelle du pointeur dans un
graphe de fonction implicite)
•{On}/{Off}
... {affichage activé}/{affichage désactivé}
uAnswer Type (définition de la plage de résultats)
•{Real}/{Cplx}
... résultat avec {nombre réel}/{nombre complexe}
uH-Copy (réglages de copie d’image)
•{Dirct}/{Mem}
... {envoi direct}/{stockage en mémoire}
1-7-4
Utilisation de l’écran de configuration

19990401
1-8En cas de problème...
Si vous rencontrez un problème pendant que vous effectuez une opération, effectuez les
opérations suivantes avant de supposer que la calculatrice ne fonctionne pas.
kk
kk
kRétablissement des réglages de modes initiaux de la calculatrice
1. Depuis le menu principal, accédez au mode SYSTEM.
2. Appuyez sur 5(Reset).
3. Appuyez sur 1(S/U) et sur w(Oui).
4. Appuyez sur m pour revenir au menu principal.
Accédez maintenant au mode correct et effectuez à nouveau votre calcul en vérifiant les
résultats sur l’écran.
kk
kk
kEn cas de blocage
• Si la calculatrice se bloque et ne répond plus à la saisie au clavier, appuyez sur le
bouton P au dos de la calculatrice pour réinitialiser la calculatrice à ses réglages par
défaut (voir page α-6-1). Notez qu’à ce moment toutes les données mémorisées
dans la calculatrice risquent d’être effacées.
1-8-1
En cas de problème...
19990401
kk
kk
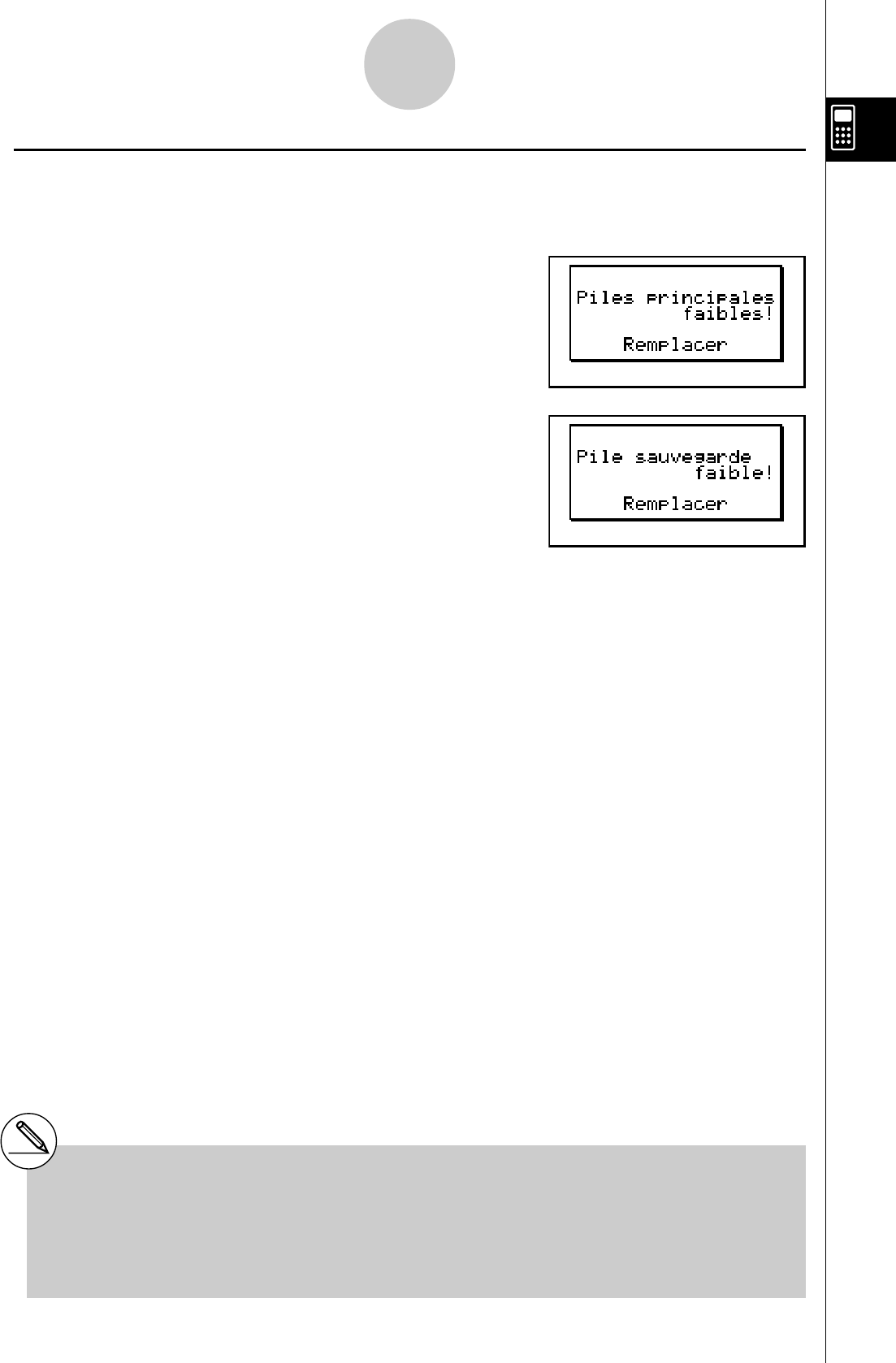
kMessage de faible tension des piles
Si un des messages suivants apparaît à l’écran, éteignez immédiatement la calculatrice et
remplacez les piles principales ou la pile de sauvegarde de la mémoire de la façon indiquée.
# Vous ne pouvez effectuer aucun transfert de
données après l’apparition du message de
faible tension des piles.
1-8-2
En cas de problème...
Si vous continuez d’utiliser la calculatrice sans remplacer les piles principales, l’alimentation
sera automatiquement coupée afin de protéger le contenu de la mémoire. Le cas échéant, il
sera impossible de remettre la calculatrice sous tension et le contenu de la mémoire risque
d’être vérolé ou entièrement perdu.
# Si les piles principales et la pile de sauvegarde
deviennent faibles en même temps (ce qui est
indiqué par l’apparition des deux messages ci-
dessus), remplacez d’abord la pile de sauvegarde
puis les piles principales.

19990401
Chapitre 2
Calculs manuels
2-1 Calculs de base
2-2 Fonctions spéciales
2-3 Désignation de l’unité d’angle et du format
d’affichage
2-4 Calculs de fonctions
2-5 Calculs numériques
2-6 Calculs avec nombres complexes
2-7 Calculs binaire, octal, décimal et hexadécimal
2-8Calculs matriciels
Choisir le menu RUN
•
MAT
Régler l’écran de configuration u3(SET UP)

19990401
2-1-1
Calculs de base
2-1 Calculs de base
kk
kk
kCalculs arithmétiques
• Introduisez les calculs arithmétiques comme ils sont écrits, de gauche à droite.
• Utilisez la touche - pour saisir le signe moins devant une valeur négative.
• Les calculs sont effectués internement avec une mantisse de 15 chiffres. Le résultat
est arrondi à une mantisse de 10 chiffres avant d’être affiché.
• Pour les calculs arithmétiques mixtes, la multiplication et la division ont priorité sur
l’addition et la soustraction.
Exemple Opération
23 + 4,5 – 53 = –25,5 23+4.5-53w
56 × (–12) ÷ (–2,5) = 268,8 56*-12/-2.5w
(2 + 3) × 102 = 500 (2+3)*1Z2w*1
1 + 2 – 3 × 4 ÷ 5 + 6 = 6,6 1+2-3*4/5+6w
100 – (2 + 3) × 4 = 80 100-(2+3)*4w
2 + 3 × (4 + 5) = 29 2+3*(4+5w*2
(7 – 2) × (8 + 5) = 65 (7-2)(8+5)w*3
6= 0,3 6 /(4*5)w*4
4×5
(1 + 2i) + (2 + 3i) = 3 + 5i(b+c!a(i))+(c+
d!a(i))w
(2 + i) × (2 – i) = 5 (c+!a(i))*(c-!a(i)
)w
*1(2+3)Z2 ne donne pas le bon
résultat. Toujours introduire ce calcul de la
manière indiquée.
*2Les fermetures de parenthèses
(immédiatement avant une opération de la
touche w) peuvent être omises, quel qu’en
soit le nombre.
*3Un signe de multiplication se trouvant
immédiatement devant une ouverture de
parenthèses peut être omis.
*4Identique à 6 / 4 / 5 w.

19990401
2-1-2
Calculs de base
*1Les valeurs affichées sont arrondies à la
décimale spécifiée.
kk
kk
kNombre de décimales, nombre de chiffres significatifs, plage
d’affichage normal [SET UP]- [Display] -[Fix] / [Sci] / [Norm]
• Même après que le nombre de décimales ou le nombre de chiffres significatifs a été
défini, les calculs internes sont effectués avec une mantisse de 15 chiffres et les
valeurs affichées sont enregistrées avec une mantisse de 10 chiffres. Utilisez Rnd du
menu de calculs numériques (NUM) (page 2-4-1) pour arrondir la valeur affichée au
nombre de décimales et au nombre de chiffres significatifs spécifié.
• Le réglage du nombre de décimales (Fix) et de chiffres significatifs (Sci) reste valide
tant que vous ne les changez pas ou tant que vous ne changez pas le réglage
d’affichage normal (Norm).
Exemple 100 ÷ 6 = 16,66666666...
Condition Opération Affichage
100/6w16.66666667
4 décimales u3(SET UP)
cccccccccc
*1
1(Fix)ewiw16.6667
5 chiffres significatifs u3(SET UP)
cccccccccc
*1
2(Sci)fwiw1.6667E+01
Annule la spécification u3(SET UP)
cccccccccc
3(Norm)iw16.66666667

19990401
2-1-3
Calculs de base
Exemple 200 ÷ 7 × 14 = 400
Condition Opération Affichage
200/7*14w400
3 décimales u3(SET UP)
cccccccccc
1(Fix)dwiw400.000
Le calcul continue en 200/7w28.571
utilisant l’affichage *Ans ×
de 10 chiffres. 14w400.000
• Si le même calcul est effectué avec le nombre de chiffres spécifié:
200/7w28.571
La valeur interne K5(NUM)e(Rnd)w28.571
sauvegardée est *Ans ×
arrondie au nombre 14w399.994
de décimales spécifié.
kk
kk
kSéquence de priorité de calcul
Cette calculatrice emploie la vraie logique algébrique pour calculer les parties d’une
formule dans l’ordre suivant:
1Transformation de coordonnées Pol (x, y), Rec (r,
θ
)
Calculs de différentielles, différentielles quadratiques, intégrations, Σ
d/dx, d2/dx2, ∫dx, Σ, Mat, Solve, FMin, FMax, List→Mat, Seq, Min, Max, Median, Mean,
Augment, Mat→List, P(, Q(, R(, t(, List
Fonctions composites*1 fn, Yn, rn, Xtn, Ytn, Xn
2Fonctions de type A
Avec ces fonctions, la valeur est introduite, puis la touche de fonction enfoncée.
x2, x–1, x !, ° ’ ”, symboles ENG, unité d’angle o, r, g
20001202
*1Vous pouvez combiner le contenu de plusieurs
endroits de la mémoire de fonctions (fn) ou de
la mémoire de graphes (Yn, rn, Xtn, Ytn, Xn) en
fonctions composites. Par exemple, lorsque
vous spécifiez fn1 (fn2), vous obtiendrez la fonction
composite fn1°fn2 (voir page 5-3-3).
Une fonction composite peut comprendre jusqu’à cinq
fonctions.

19990401
20001202
2-1-4
Calculs de base
3Puissance/Racine ^(xy), x
4Fractions a+b/c
5Format de multiplication abrégé devant π, nom de mémoire ou nom de variable.
2π, 5A, Xmin, F Start, etc.
6Fonctions de type B
Avec ces fonctions, la touche de fonction est enfoncée, puis la valeur introduite.
, 3, log, In, ex, 10x, sin, cos, tan, Asn, Acs, Atn, sinh, cosh, tanh, sinh–1, cosh–1, tanh–1,
(–), d, h, b, o, Neg, Not, Det, Trn, Dim, Identity, Sum, Prod, Cuml, Percent, AList, Abs, Int,
Frac, Intg, Arg, Conjg, ReP, ImP
7Format de multiplication abrégé devant les fonction de type B
2, A log2, etc.3
8Permutation, combinaison nPr, nCr
9× , ÷
0+, –
!Opérateurs relationnels >, <, ≥, ≤
@Opérateurs relationnels =, G
#and (opération de bits)
$xnor, xor (opérations de bits)
%or (opération de bits)
^And (opération logique)
Or (opération logique)
Exemple 2 + 3 × (log sin2π2 + 6,8) = 22,07101691 (unité d’angle = Rad)
1
2
3
4
5
6
# Lorsque des fonctions ayant la même priorité
sont utilisées en série, l’exécution est effectuée
de droite à gauche.
exIn → ex{In( )}
120 120
Sinon, l’exécution se fait de gauche à droite.
# Les fonctions composées sont exécutées de
droite à gauche.
# Tout ce qui se trouve entre parenthèses a la
plus grande priorité.

19990401
20001202
2-1-5
Calculs de base
kOpérations de multiplication sans signe de multiplication
Vous pouvez omettre le signe de multiplication (×) dans toutes les opérations suivantes.
• Avant la transformation de coordonnées et les fonctions de Type B (1 (page 2-1-3) et 6
(page 2-1-4)), sauf pour les signes négatifs.
Exemple 2sin30, 10log1,2, 2 , 2Pol(5, 12), etc.
• Devant les constantes et les noms de variables et de mémoires
Exemple 2π, 2AB, 3Ans, 3Y1, etc.
• Devant une ouverture de parenthèses
Exemple 3(5 + 6), (A + 1)(B – 1), etc.
kDépassement de capacité et erreurs
Le dépassement d’une plage de calcul ou de définition spécifiée, ou une tentative d’entrée
invalide entraîne l’apparition d’un message d’erreur sur l’affichage. Toute autre opération
est impossible quand un message d’erreur est affiché. Les opérations suivantes entraînent
l’apparition d’un message d’erreur sur l’affichage.
• Lorsqu’un résultat, intermédiaire ou final, ou une valeur en mémoire, dépasse
±9,999999999 × 1099 (Erreur math).
• Lorsque vous essayez d’effectuer un calcul de fonction qui dépasse la plage de définition
(Erreur math).
• Lorsque vous faites une opération invalide pendant des calculs statistiques (Erreur
math). Par exemple, tentative d’obtenir 1VAR sans introduction de données.
• Lorsqu’un type de données inadapté est désigné comme argument dans le calcul d’une
fonction (Erreur math).
• Lorsque la capacité de la pile de valeurs numériques ou de la pile de commandes est
dépassée (Erreur pile). Par exemple, introduction de 25 ( successives, suivie de 2 +
3 * 4 w.
• Lorsque vous essayez d’effectuer un calcul en utilisant une formule invalide (Erreur
syntaxe). Par exemple, 5 ** 3 w.
# D’autres erreurs peuvent se produire
pendant l’exécution d’un programme.
Lorsqu’un message d’erreur est affiché, la
plupart des touches de la calculatrice sont
inopérantes.
Appuyez sur i pour annuler l’erreur et
afficher sa position (voir page 1-3-4).
# Voir le “ Tableau des messages d’erreur ” à la
page α-1-1 pour de plus amples informations au
sujet des erreurs.

19990401
• Lorsque vous essayez d’effectuer un calcul qui provoque un dépassement de la mémoire
(Erreur mémoire).
• Lorsque vous utilisez une commande qui exige un argument mais qu’aucun argument
valide n’est spécifié (Erreur argument).
• Lorsque vous essayez d’utiliser une dimension invalide pendant des calculs matriciels
(Erreur dimension).
• Lorsque vous essayez de faire un calcul contenant un chiffre réel comme argument et
obtenez une solution avec nombre complexe, alors que “ Real ” est sélectionné comme
réglage du mode Complex sur l’écran de configuration (Erreur non réel).
kCapacité de la mémoire
Chaque fois que vous appuyez sur une touche, un octet ou deux octets de mémoire sont
utilisés. Les fonctions qui n’utilisent qu’un octet sont les suivantes: b, c, d, sin, cos,
tan, log, In, et π. Les fonctions qui utilisent deux octets sont les suivantes: d/dx(, Mat,
Xmin, If, For, Return, DrawGraph, SortA(, PxIOn, Sum et an+1.
2-1-6
Calculs de base
# Lorsque vous entrez des valeurs
numériques ou des commandes, elles
apparaissent sur l’affichage à partir de la
gauche. Cependant, les résultats des
calculs sont affichés à partir de la droite.
# La plage admissible pour les valeurs d’entrée
et de sortie est de 15 chiffres pour la mantisse
et de 2 chiffres pour l’exposant. Les calculs
internes sont aussi effectués avec 15 chiffres
pour la mantisse et 2 chiffres pour l’exposant.

19990401
2-2 Fonctions spéciales
kk
kk
kCalculs avec variables
Exemple Opération Affichage
193.2aav(A)w193.2
193,2 ÷ 23 = 8,4 av(A)/23w8.4
193,2 ÷ 28 = 6,9 av(A)/28w6.9
kk
kk
kMémoire
uVariables
Cette calculatrice est dotée de 28 variables en standard. Vous pouvez utiliser les variables
pour sauvegarder les valeurs à utiliser à l’intérieur des calculs. Les variables sont
identifiées par des noms d’une lettre, correspondant aux 26 lettres de l’alphabet plus r et
θ
. La taille maximale des valeurs que vous pouvez affecter aux variables est de 15 chiffres
pour la mantisse et 2 chiffres pour l’exposant.
uPour affecter une valeur à une variable
[valeur] a [nom de la variable] w
Exemple Affecter 123 à la variable A
Abcdaav(A)w
Exemple Ajouter 456 à la variable A et sauvegarder le résultat dans la variable B
Aav(A)+efgaa
l(B)w
2-2-1
Fonctions spéciales
# Le contenu des variables est retenu même
lorsque la calculatrice est mise hors tension.

19990401
uPour afficher le contenu d’une variable
Exemple Afficher le contenu de la variable A
Aav(A)w
uPour effacer une variable
Exemple Effacer la variable A
Aaaav(A)w
uPour affecter la même valeur à plus d’une variable
[valeur]a [nom de la première variable*1]K6(g)6(g)4(SYBL)d(~)
[nom de la dernière variable*1]w
Exemple Affecter la valeur 10 aux variables A à F
Abaaav(A)
K6(g)6(g)4(SYBL)d(~)
at(F)w
uMémoire de fonctions [OPTN]-[FMEM]
La mémoire de fonctions est pratique pour le stockage provisoire d’expressions souvent
utilisées. Pour le stockage d’expressions à long terme, il est conseillé d’utiliser le mode
GRPH • TBL pour les expressions et le mode PRGM pour les programmes.
•{Store}/{Recall}/{fn}/{SEE} ... {sauvegarde de la fonction}/{rappel de la fonction}/
{désignation de la zone de la fonction comme nom de variable dans une
expression}/{liste des fonctions}
2-2-2
Fonctions spéciales
*1 Vous ne pouvez pas utiliser “r” ou “
θ
” comme
nom de variable.

19990401
uPour sauvegarder une fonction
Exemple Sauvegarder la fonction (A+B) (A–B) dans la mémoire de fonctions 1
(av(A)+al(B))
(av(A)-al(B))
K6(g)5(FMEM)
b(Store)bw
uPour rappeler une fonction
Exemple Rappeler le contenu de la mémoire de fonctions 1
K6(g)5(FMEM)
c(Recall)bw
uPour afficher une liste des fonctions disponibles
K6(g)5(FMEM)
e(SEE)
2-2-3
Fonctions spéciales
# Si le numéro de mémoire de fonctions où
vous sauvegardez une fonction contient déjà
une fonction, celle-ci sera remplacée par la
nouvelle.
# La fonction rappelée apparaît à l’emplacement
actuel du curseur sur l’écran.
19990401
2-2-4
Fonctions spéciales
uPour effacer une fonction
Exemple Effacer le contenu de la mémoire de fonctions 1
AK6(g)5(FMEM)
b(Store)bw
• L’exécution d’une sauvegarde quand l’affichage est vierge supprime la fonction de la
mémoire de fonctions spécifiée.
uPour utiliser les fonctions mémorisées
Exemple Stocker x3 + 1, x2 + x dans le mémoire de fonctions, puis représenter
graphiquement y = x3 + x2 + x + 1
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = – 4, Xmax = 4, Xscale = 1
Ymin = –10, Ymax = 10, Yscale = 1
u3(SET UP)c1(Y=)i
AvMd+bK6(g)5(FMEM)b(Store)bw(stocke (x3 + 1))
iAvx+v5(FMEM)b(Store)cw(stocke (x2 + x))
iAK6(g)6(g)2(SKTCH)b(Cls)w
2(SKTCH)e(GRAPH)b(Y=)
K6(g)5(FMEM)d(fn)b+
5(FMEM)d(fn)cw
• Pour tous les détails au sujet de la représentation graphique, voir “5. Représentation
graphique de fonctions”.

19990401
kk
kk
kFonction de réponse
La fonction de réponse sauvegarde le dernier résultat obtenu après une pression sur w(à
moins la pression de la touche w n’entraîne une erreur). Le résultat est sauvegardé dans
la mémoire de dernier résultat.
uPour utiliser le contenu de la mémoire de dernier résultat dans un calcul
Exemple 123 + 456 = 579
789 – 579 = 210
Abcd+efgw
hij-!-(Ans)w
kk
kk
kExécution de calculs continus
La mémoire de réponse permet d’utiliser le résultat d’un calcul comme argument dans le
calcul suivant.
Exemple 1 1 ÷ 3 =
1 ÷ 3 × 3 =
Ab/dw
(En continuant)*dw
Les calculs continus peuvent également être utilisés avec les fonctions de type A (x2, x-1,
x!, page 2-1-3), +, –, ^(xy), x, ° ’ ”, etc.
2-2-5
Fonctions spéciales
# La valeur la plus élevée que peut contenir
la mémoire de dernier résultat est 15
chiffres pour la mantisse et 2 chiffres pour
l’exposant.
# Seuls les valeurs numériques et les résultats
de calculs peuvent être stockés dans la
mémoire de dernier résultat.
# Le contenu de la mémoire de dernier résultat
n’est pas effacé lorsque la touche A est
enfoncée ou l’appareil mis hors tension.
# Le contenu de la mémoire de dernier résultat
n’est pas changé par une opération qui affecte
des valeurs à la mémoire de valeurs (tel que:
faav(A)w).
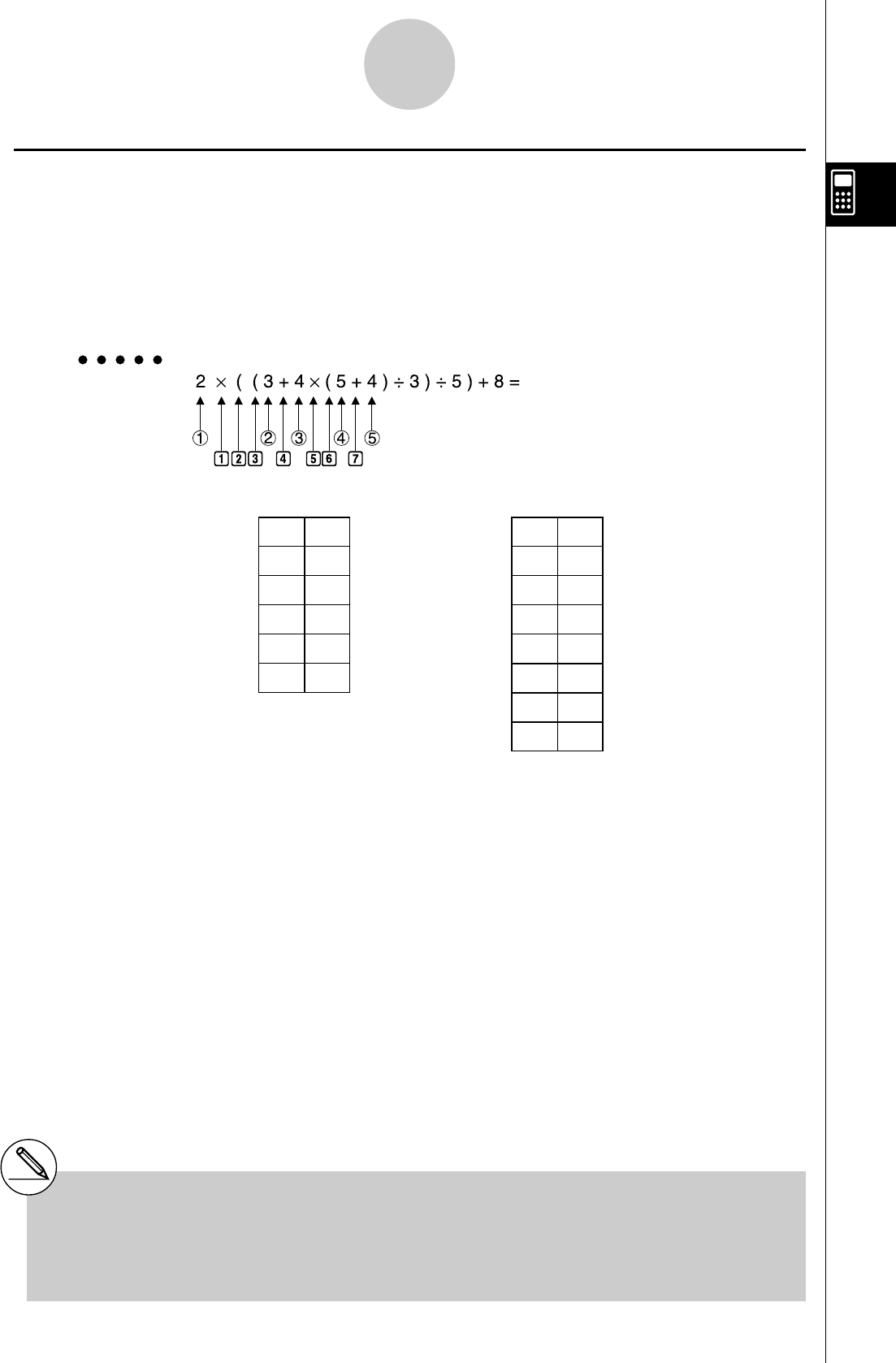
19990401
kPiles
L’appareil utilise des blocs de mémoire appelés “
piles
” pour la sauvegarde des valeurs et
des commandes de faible priorité. La
pile de valeurs numériques
a 10 niveaux, la
pile de
commandes
26 niveaux et la
pile de sous-programmes
10 niveaux. Une erreur se produit
si vous effectuez un calcul trop complexe pour la capacité restante de la pile de valeurs
numériques ou de la pile de commandes, ou si l’exécution d'un sous-programme dépasse
la capacité de la pile de sous-programmes.
Exemple
2-2-6
Fonctions spéciales
# Les calculs sont effectués dans l’ordre de
priorité. Une fois un calcul exécuté, il est
effacé de la pile.
# La sauvegarde d’un nombre complexe occupe
deux niveaux de la pile de valeurs numériques.
# La sauvegarde d’une fonction à 2 octets occupe
deux niveaux de la pile de commandes.
2
1
2
3
4
5
b
c
d
e
f
g
h
3
4
5
4
×
(
(
+
×
(
+
...
...
Pile de valeurs numériques Pile de commandes
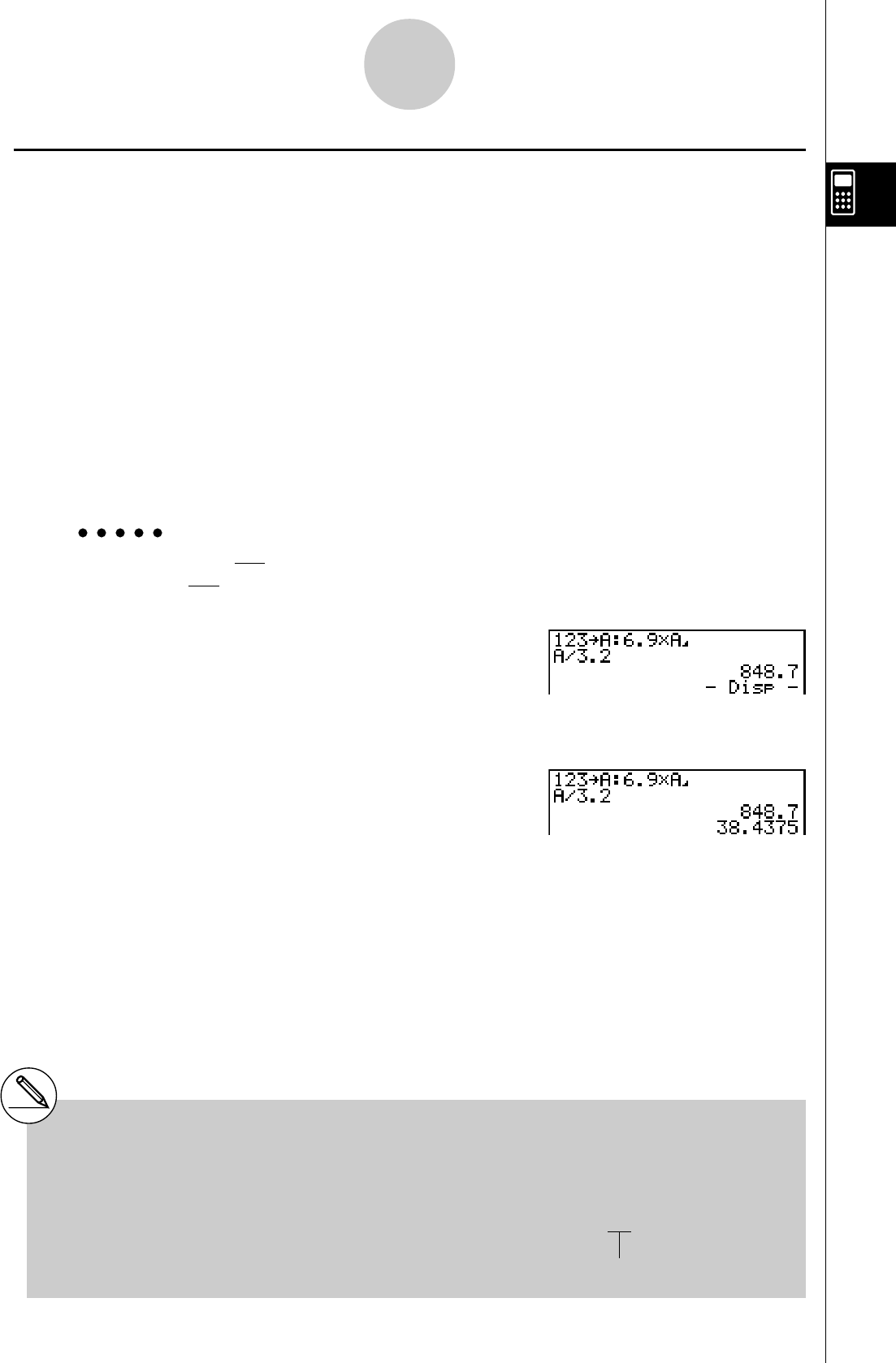
19990401
kUtilisation d’instructions multiples
Les instructions multiples consistent en un certain nombre d’instructions individuelles
reliées entre elles pour une exécution séquentielle. Vous pouvez utiliser les instructions
multiples dans les calculs manuels et dans les calculs programmés. Il y a deux manières
de relier des instructions en instructions multiples.
• Deux-points (:)
Les instructions qui sont reliées par deux-points sont exécutées de gauche à droite, sans
arrêt.
• Commande d’affichage de résultat (^^
^^
^)
Lorsque l’exécution atteint la fin d’une instruction suivie d’une commande d’affichage de
résultat, l’exécution s’arrête et le résultat jusqu’à ce point apparaît à l’écran. Vous pouvez
continuer en appuyant sur la touche w.
Exemple 6,9 × 123 = 848,7
123 ÷ 3,2 = 38,4375
Abcdaav(A)
!J(PRGM)6(g)6(g)3(:)g.j
*av(A)!J(PRGM)4(^)
av(A)/d.cw
w
2-2-7
Fonctions spéciales
# Le résultat final d’une instruction multiple
est toujours affiché, qu’il se termine ou non
par une commande d’affichage de résultat.
Exemple : 123 × 456: × 5
Invalide
# Vous ne pouvez pas construire une instruction
multiple dans laquelle une instruction utilise
directement le résultat de l’instruction
précédente.

19990401
2-3 Désignation de l’unité d’angle et du format
d’affichage
Avant d’effectuer un calcul pour la première fois, vous devez définir l’unité d’angle et le
format d’affichage sur l’écran de configuration.
Effectuez les opérations de touche suivantes pour afficher l’écran de configuration: mRUN
•
MAT wu3(SET UP).
kk
kk
kPour définir l’unité d’angle [SET UP]- [Angle]
1. Sur l’écran de configuration, mettez “ Angle ” en surbrillance.
2. Appuyez sur la touche de fonction correspondant à l’unité d’angle que vous voulez
spécifier, puis appuyez sur i.
•{Deg}/{Rad}/{Gra} ... {degré}/{radian}/{grade}
• La relation entre les degrés, les grades et les radians est la suivante.
360° = 2π radians = 400 grades
90° = π/2 radians = 100 grades
kk
kk
kPour définir le format d’affichage [SET UP]- [Display]
1. Sur l’écran de configuration, mettez “Display” en surbrillance.
2. Appuyez sur la touche de fonction correspondant au paramètre que vous voulez
spécifier, puis appuyez sur i.
•{Fix}/{Sci}/{Norm}/{Eng} ... {désignation du nombre de décimales}/{désignation
du nombre de chiffres significatifs}/{normal affichage}/{mode Ingénieur}
uPour définir le nombre de chiffres après la virgule (Fix)
Exemple Définir deux chiffres après la virgule
1(Fix) cw
Appuyez sur la touche de fonction qui corres-
pond au nombre de chiffres après la virgule
que vous souhaitez (
n
= 0 à 9).
2-3-1
Désignation de l’unité d’angle et du format d’affichage
# Les valeurs affichées sont arrondies au
nombre de chiffres après la virgule que
vous avez spécifié.

19990401
uPour définir le nombre de chiffres significatifs (Sci)
Exemple Définir trois chiffres significatifs
2(Sci) dw
Appuyez sur la touche de fonction qui
correspond au nombre de chiffres
significatifs que vous souhaitez
(
n
= 0 à 9).
uPour définir l’affichage normal (Norm 1/Norm 2)
Appuyez sur 3(Norm) pour alterner entre les deux plages, Norm 1 et Norm 2.
Norm 1: 10–2 (0,01)>|x|, |x| >1010
Norm 2: 10–9 (0,000000001)>|x|, |x| >1010
Ab/caaw(Norm 1)
(Norm 2)
uPour définir l’affichage en notation ingénieur (Mode Eng)
Appuyez sur 4(Eng) pour alterner entre la notation ingénieur et la notation normale.
L’indicateur “/E” apparaît sur l’écran quand la notation ingénieur est validée.
Vous pouvez utiliser les symboles suivants pour convertir les valeurs en notation
ingénieur, comme 2.000 (= 2 × 103) → 2k.
E (Exa) × 1018 m (milli) × 10–3
P (Péta) × 1015 μ (micro) × 10–6
T (Téra) × 1012 n (nano) × 10–9
G (Giga) × 109p (pico) × 10–12
M (Méga) × 106f (femto) × 10–15
k (kilo) × 103
2-3-2
Désignation de l’unité d’angle et du format d’affichage
# Les valeurs affichées sont arrondies au nombre
de chiffres significatifs que vous avez spécifié.
# Si vous spécifiez 0, le nombre de chiffres
significatifs sera 10.
# La calculatrice sélectionne automatiquement le
symbole ingénieur qui fait rentrer la valeur de
la mantisse dans la plage de 1 à 1000 quand
la notation ingénieur est validée.

19990401
2-4 Calculs de fonctions
kMenus de fonctions
La calculatrice comprend cinq menus de fonctions pour l’accès aux fonctions scientifiques
qui ne sont pas indiquées sur le clavier.
• Le contenu de chaque menu de fonctions varie selon le mode que vous avez choisi sur le
menu principal avant d’avoir appuyé sur la touche K. Les exemples suivants indiquent
les menus de fonctions qui apparaissent dans le mode RUN • MAT.
uu
uu
uCalculs numériques (NUM) [OPTN]-[NUM]
•{Abs} ... {sélectionnez ce paramètre et entrez une valeur pour obtenir la valeur absolue
de cette valeur.}
•{Int}/{Frac} ... Sélectionnez le paramètre et saisissez une valeur pour extraire la partie
{entière}/{fractionnaire}.
•{Rnd} ... {arrondit la valeur utilisée pour les calculs internes à 10 chiffres significatifs
(en fonction de la valeur enregistrée dans la mémoire de dernier résultat), ou au
nombre de décimales (Fix) et au nombre de chiffres significatifs (Sci) que vous
avez définis.}
•{Intg} ... {sélectionnez ce paramètre et saisissez une valeur pour obtenir le plus grand
entier qui n’est pas supérieur à cette valeur.}
•{E-SYM} ... {symbole ingénieur}
•{m}/{μ}/{n}/{p}/{f} ... {milli (10–3)}/{micro (10–6)}/{nano (10–9)}/{pico (10–12)}/ {femto
(10–15)}
•{k}/{M}/{G}/{T}/{P}/{E} ... {kilo (103)}/{méga (106)}/{giga (109)}/{téra (1012)}/
{péta (1015)}/{exa (1018)}
uu
uu
uCalculs de probabilité/répartition (PROB) [OPTN]-[PROB]
•{x!} ... {appuyez après avoir saisie une valeur pour obtenir la factorielle de cette valeur}
•{nPr}/{nCr} ... {permutation}/{combinaison}
•{Ran#}... {génération de nombres pseudo-aléatoires (0 à 1)}
•{P(}/{Q(}/{R(} ... probabilité {P(t)}/{Q(t)}/{R(t)}
•{t(} ... {valeur de la variante normalisée t(x)}
2-4-1
Calculs de fonctions

19990401
uu
uu
uCalculs hyperboliques (HYP) [OPTN]-[HYP]
•{sinh}/{cosh}/{tanh} ... hyperbolique {sinus}/{cosinus}/{tangente}
•{sinh–1}/{cosh–1}/{tanh–1} ... hyperbolique inverse {sinus}/{cosinus}/{tangente}
uu
uu
uUnités d’angle, conversion de coordonnées, opérations en notation
sexagésimale (ANGL) [OPTN]-[ANGL]
•{°}/{r}/{g} ... {degré}/{radian}/{grade} pour une valeur saisie particulière
•{° ’ ”} ... {définit les degrés (heures), minutes, secondes lors de la saisie de valeurs
exprimées en degrés, minutes ou secondes}
•{'DMS} ... {convertit une valeur décimale en valeur sexagésimale}
•{Pol(}/{Rec(} ... conversion de coordonnées {rectangulaires en polaires}/{polaires en
rectangulaires}
uu
uu
uFonctions instantanées
•{ ° ’ ”} ... {convertit la valeur décimale en degrés/minutes/secondes}
•{ENG}/{ENG} ... déplace la virgule des décimales de la valeur affichée de trois
chiffres vers la {gauche}/{droite} et {réduit}/{augmente} l’exposant de trois.
Quand vous utilisez la notation Ingénieur, le symbole Ingénieur change en
conséquence.
• Les opérations de menus { ° ’ ” }, {ENG} et { ENG} ne sont disponibles que si un
résultat de calcul est affiché.
kk
kk
kUnités d’angle
Pour changer l’unité d’angle d’une valeur, appuyez d’abord sur K3(ANGL), puis sur le
menu déroulant qui apparaît, sélectionnez “°”, “r”, ou “g”.
• Veillez à désigner Comp pour Mode sur l’écran de configuration.
Exemple Opération
Convertir 4,25 radians en degrés:
u3(SET UP)cccc1(Deg)i
243,5070629 4.25K6(g)3(ANGL)c(r)w
47,3° + 82,5rad = 4774,20181°
47.3+82.5K6(g)3(ANGL)c(r)w
2-4-2
Calculs de fonctions
# Après avoir spécifié une unité d’angle, celle-ci
reste valide jusqu’à ce qu’une autre unité soit
spécifiée. La spécification est retenue même si
l’appareil est mis hors tension.

19990401
kk
kk
kFonctions trigonométriques et trigonométriques inverses
• Toujours régler l’unité d’angle avant d’effectuer des calculs de fonction trigonométrique
et de fonction trigonométrique inverse.
• Veillez à désigner Comp pour Mode sur l’écran de configuration.
Exemple Opération
sin 63° = 0,8910065242 u3(SET UP)cccc1(Deg)i
s63w
π
cos (–– rad) = 0,5 u3(SET UP)cccc2(Rad)i
3c(!Z(π)/d)w
tan (– 35gra) = – 0,6128007881
u3(SET UP)cccc3(Gra)i
t-35w
2 • sin 45° × cos 65° = 0,5976724775
u3(SET UP)cccc1(Deg)i
2*s45*c65w*1
cosec 30° = 1
= 2 1/s30w
sin30°
Asn 0,5 = 30°!s(Asn)0.5*2w
(x quand sinx = 0,5)
2-4-3
Calculs de fonctions
*1* peut être omis. *2La saisie du zéro initial n’est pas nécessaire.
π
(90° = ––– radians = 100 grades)
2

19990401
kFonctions logarithmiques et exponentielles
• Veillez à désigner Comp pour Mode sur l’écran de configuration.
Exemple Opération
log 1,23 (log101,23) = 8,990511144 × 10–2 l1.23w
In 90 (loge90) = 4,49980967 I90w
101,23 = 16,98243652
(Pour obtenir l’antilogarithme du logarithme !l(10x)1.23w
décimal 1,23)
e4,5 = 90,0171313
(Pour obtenir l’antilogarithme du logarithme !I(ex)4.5w
népérien 4,5)
(–3)4 = (–3) × (–3) × (–3) × (–3) = 81 (-3)M4w
–34 = –(3 × 3 × 3 × 3) = –81 -3M4w
1
7 (= 1237) = 1,988647795 7!M(x )123w
2 + 3 × 3 – 4 = 10 2+3*3!M(x )64-4w*1
2-4-4
Calculs de fonctions
123
64
*1^ (xy) et x ont priorité sur la multiplication
et la division.

19990401
kFonctions hyperboliques et hyperboliques inverses
• Veillez à désigner Comp pour Mode sur l’écran de configuration.
Exemple Opération
sinh 3,6 = 18,28545536 K6(g)2(HYP)b(sinh)3.6w
cosh 1,5 – sinh 1,5 K6(g)2(HYP)c(cosh)1.5-
= 0,2231301601 2(HYP)b(sinh)1.5w
= e–1,5 (Affichage: –1.5) I!-(Ans)w
(
Preuve de
cosh x ± sinh x = e±x)
cosh–1 20 = 0,7953654612 K6(g)2(HYP)f(cosh–1)(20/15)w
15
Déterminer la valeur de x
lorsque tanh 4 x = 0,88
x = tanh–1 0,88 K6(g)2(HYP)g(tanh–1)0.88/4w
4
= 0,3439419141
2-4-5
Calculs de fonctions

19990401
kAutres fonctions
• Veillez à désigner Comp pour Mode sur l’écran de configuration.
Exemple Opération
+ = 3,65028154 !x( )2+!x( )5w
25
= 1,755317302 !x( )(d+!a(i))w
(3 + i)
+0,2848487846i
(–3)2 = (–3) × (–3) = 9 (-3)xw
–32 = –(3 × 3) = –9 -3xw
(3!)(x–1)-4!)(x–1))!)(x–1)w
8! (= 1 × 2 × 3 × .... × 8) 8K6(g)1(PROB)b(x!)w
= 40320
3 = 42
!(
(3 )
(36*42*49
)w36 × 42 × 49
Quelle est la valeur absolue du
logarithme décimal de
|
log
|
= 0,1249387366 K5(NUM)b(Abs)l(3/4)w
Quelle est la partie entière de K5(NUM)c(Int)-3.5w
– 3,5? – 3
Quelle est la partie décimale de K5(NUM)d(Frac)-3.5w
– 3,5? – 0,5
Quel est le chiffre entier le plus K5(NUM)f(Intg)-3.5w
proche, ne dépassant pas
– 3,5? – 4
2-4-6
Calculs de fonctions
3
4?
3
4
1
–––––– = 12
11
–– – ––
34

19990401
kGénération de nombres aléatoires (Ran#)
Cette fonction génère un nombre réellement aléatoire ou séquentiellement aléatoire de 10
chiffres, supérieur à zéro et inférieur à 1.
• Un nombre réellement aléatoire est généré si vous ne désignez rien comme argument.
Exemple Opération
Ran # (Génère un nombre aléatoire) K6(g)1(PROB)e(Ran#)w
(A chaque pression sur w, un nouveau w
nombre aléatoire est généré.) w
• La spécification d’un argument compris entre 1 et 9 génère des nombres aléatoires
basés sur cette séquence.
• La spécification de 0 comme argument initialise la séquence.*1
Exemple Opération
Ran# 1 (
Génère le premier nombre aléatoire de la séquence 1.
)1(PROB)e(Ran#)bw
(Génère le second nombre aléatoire de la séquence 1.) w
Ran# 0 (Initialise la séquence.) 1(PROB)e(Ran#)aw
Ran# 1 (
Génère le premier nombre aléatoire de la séquence 1.
)1(PROB)e(Ran#)bw
2-4-7
Calculs de fonctions
*1Le changement de séquence ou la
génération d’un nombre totalement aléatoire
(sans argument) initialise la séquence.
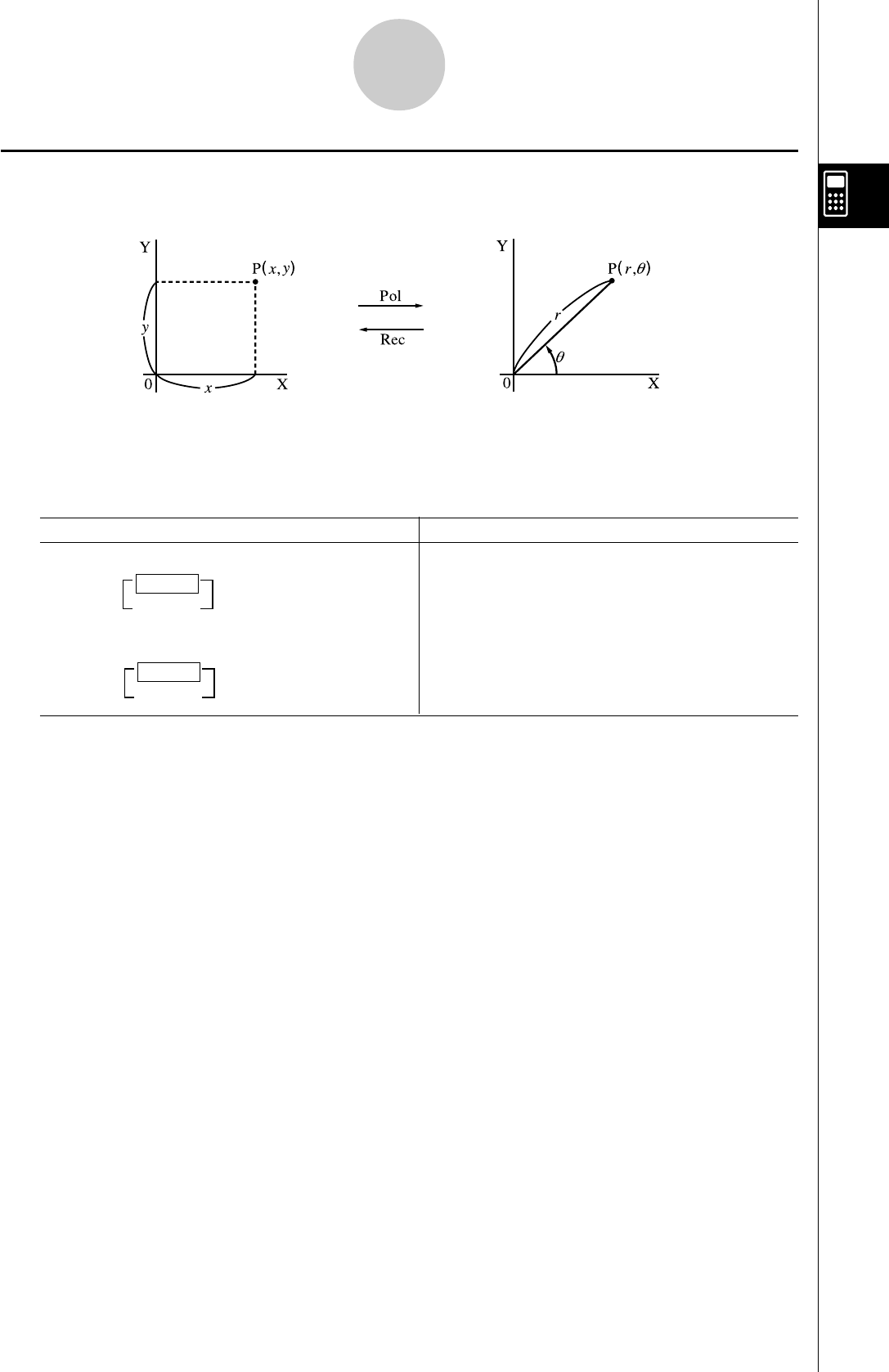
19990401
2-4-8
Calculs de fonctions
kConversion de coordonnées
uu
uu
u Coordonnées rectangulaires uu
uu
u Coordonnées polaires
• Avec les coordonnées polaires,
θ
peut être calculé et affiché dans une plage de
–180°<
θ
< 180° (les radians et les grades ont la même plage).
• Veillez à désigner Comp pour Mode sur l’écran de configuration.
Exemple Opération
Calculer r et
θ
° lorsque x = 14 et y = 20,7 u3(SET UP)cccc1(Deg)i
K6(g)3(ANGL)g(Pol()
14,20.7)w
Calculer x et y lorsque r = 25 et
θ
= 56°u3(SET UP)cccc1(Deg)i
K6(g)3(ANGL)h(Rec()
25,56)w
• Pour rappeler les valeurs et les utiliser dans des calculs.
r : ListAns [ 1 ]w
θ
: ListAns [ 2 ]w
x : ListAns [ 1 ]wy: ListAns [ 2 ]w
List est obtenu par K1b (ou !b).
1 24.989 →24.98979792 (r)
2 55.928 →55.92839019 (
θ
)
1 13.979 →13.97982259 (x)
2 20.725 →20.72593931 (y)

19990401
2-4-9
Calculs de fonctions
n!n!
nPr = ––––– nCr = –––––––
(n – r)! r! (n – r)!
kPermutation et combinaison
uu
uu
u Permutation uu
uu
u Combinaison
• Veillez à désigner Comp pour Mode sur l’écran de configuration.
Exemple Calculer le nombre possible d’arrangements différents quand 4
éléments sont sélectionnés parmi 10 éléments
Formule Opération
10P4 = 5040 10K6(g)1(PROB)c(nPr)4w
Exemple Calculer le nombre possible de combinaisons différentes de 4
éléments pouvant être sélectionnés parmi 10 éléments.
Formule Opération
10C4 = 210 10K6(g)1(PROB)d(nCr)4w
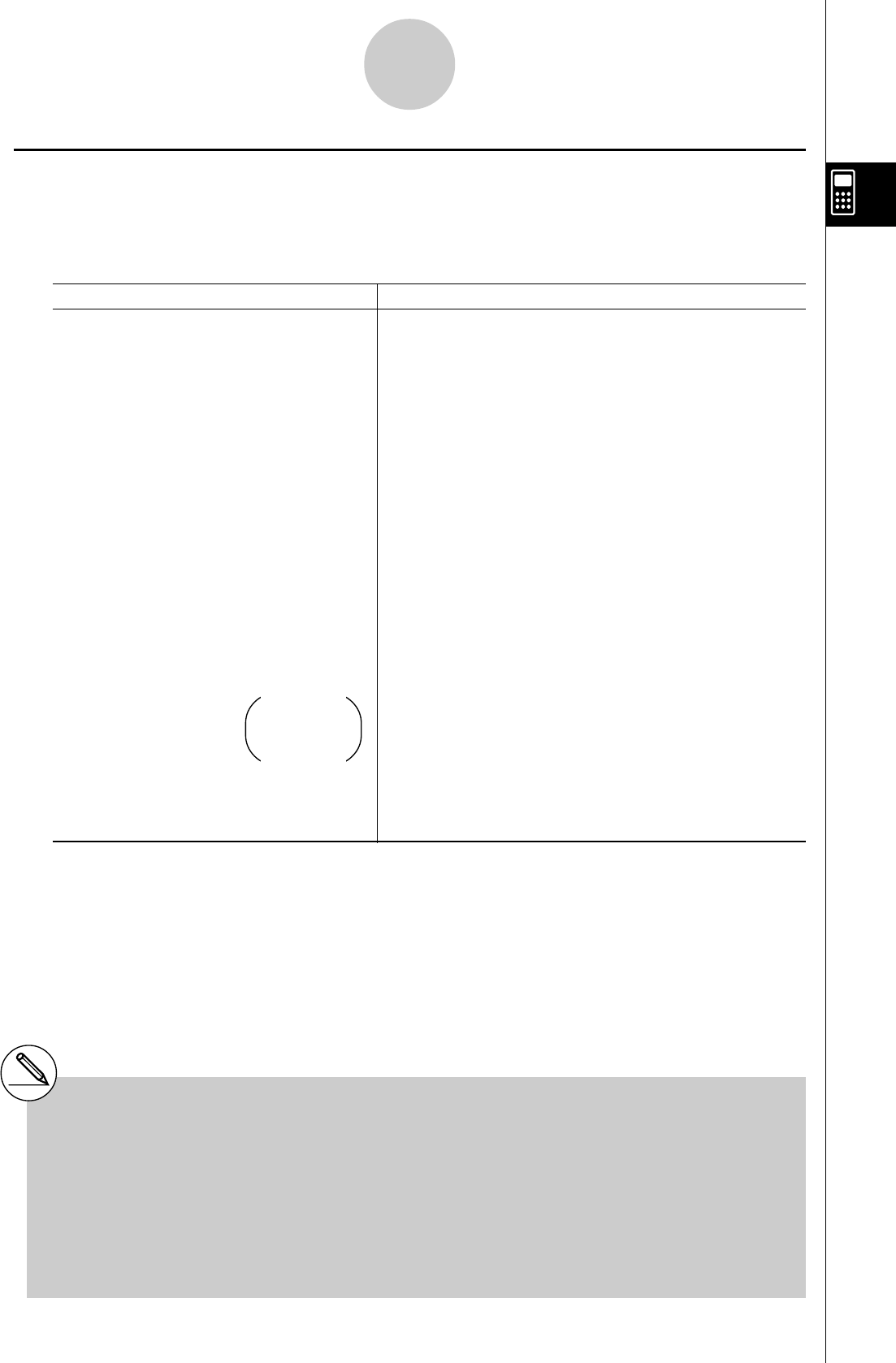
19990401
kk
kk
kFractions
• Les valeurs fractionnaires sont affichées avec le nombre entier en premier, puis le
numérateur et enfin le dénominateur.
• Veillez à désigner Comp pour Mode sur l’écran de configuration.
Exemple Opération
2N5+3N1N4w
= 3,65 N(Conversion en décimale)
N(Conversion en fraction)
1N2578+1N4572w
1N2*.5w
N
1.5+2.3!a(i)w
NN*3
1N(1N3+1N4)w*4
2-4-10
Calculs de fonctions
11
––––– + –––––
2578 4572 = 6,066202547 × 10–4
1
–– × 0,5 = 0,25*2
2
(Affichage: 6.066202547E–04*1)
(Format d’affichage Norm 1)
1
= ––
4
*1Lorsque le nombre total de caractères, y
compris le nombre entier, le numérateur, le
dénominateur et le séparateur, dépasse 10,
la fraction introduite est automatiquement
affichée sous forme décimale.
*2Les calculs contenant à la fois des fractions
et des décimales sont effectués sous forme
décimale.
*3Une pression unique sur N, lorsque la partie
décimale d’un nombre complexe est converti
d’abord en fraction, affiche la partie réelle et la
partie imaginaire sur des lignes séparées.
*4Vous pouvez inclure des fractions dans le
numérateur ou le dénominateur d’une fraction
en mettant le numérateur ou le dénominateur
entre parenthèses.
13
1,5 + 2,3i = 1+–– +
2+––i
210
21 13
–– + 3 –– = 3+
–––
54 20
(Affichage: 3{13{20)
Affichage:
1{1{2
+2{3{10i
(Affichage: 1{5{7)
15
–––––– = 1+––
11 7
–– + ––
34

19990401
2-4-11
Calculs de fonctions
kCalculs en notation Ingénieur
Introduisez les symboles Ingénieur sur le menu de notation Ingénieur.
• Veillez à désigner Comp pour Mode sur l’écran de configuration.
Exemple Opération
u3(SET UP)cccccccccc
4(Eng)i
999k (kilo) + 25k (kilo) 999K5(NUM)g(E-SYM)g(k)+255(NUM)
= 1,024M (méga) g(E-SYM)g(k)w
9 ÷ 10 = 0,9 = 900m (milli) 9/10w
= 0,9 K6(g)6(g)6(g)3(ENG)*1
= 0,0009k (kilo) 3(ENG)*1
= 0,9 2(ENG)*2
= 900m 2(ENG)*2
*1Convertit la valeur affichée à l’unité ingénieur
supérieure suivante, en déplaçant la virgule
décimale de trois unités vers la droite.
*2Convertit la valeur affichée à l’unité ingénieur
inférieure suivante, en déplaçant la virgule
décimale de trois unités vers la gauche.

19990401
2-5 Calculs numériques
Ce paragraphe décrit les paramètres qui sont disponibles sur les menus que vous utilisez
pour effectuer des calculs avec différentielles/différentielles quadratiques, intégration, Σ,
valeur maximale/minimale et résolution.
Quand le menu d’options est affiché, appuyez sur 4(CALC) pour faire apparaître le menu
d’analyse de fonction. Les paramètres de ce menu servent à effectuer des calculs de type
particulier.
•{d/dx}/{d2/dx2}/{∫dx}/{Σ}/{FMin}/{FMax}/{Solve} ... Calculs de {différentielle}/{différentielle
quadratique}/{intégration}/{Σ (sigma)}/{valeur minimale}/{valeur maximale}/{résolution}
Calcul de résolution
La syntaxe requise pour l’utilisation de la fonction de résolution dans un programme est la
suivante.
Solve( f(x), n, a, b) (a: limite inférieure,
b: limite supérieure,
n: valeur initiale estimée)
• Deux méthodes différentes peuvent être utilisées pour le calcul de résolution:
l’affectation directe et l’introduction d’une table de variables.
Avec l’affectation directe (méthode décrite ici), vous attribuez directement des valeurs
aux variables. Cette méthode est identique à celle qui est utilisée avec la commande
de résolution dans le mode de programmation.
L’introduction d’une table de variables est utilisée avec la fonction de résolution du
mode d’équation. Cette méthode est recommandée pour la saisie de la plupart des
fonctions de résolution ordinaires.
Une erreur (Erreur d’itération) se produit lorsqu’il n’y a pas de convergence dans la
solution.
2-5-1
Calculs numériques

19990401
kCalculs de différentielles [OPTN]-[CALC]-[d
/dx]
Pour effectuer des calculs de différentielles, affichez d’abord le menu d’analyse de
fonctions, puis saisissez les valeurs indiquées dans la formule suivante.
K4(CALC)b(d/dx) f(x),a,tol)
La différentiation pour ce type de calcul est définie par:
Dans cette définition,
infinitésimal
est remplacé par
suffisamment petit
Ax, avec la valeur
aux environs de f ' (a) calculée par:
Afin offrir la meilleure précision possible, la machine emploie la différence moyenne pour
réaliser les calculs différentiels.
Utilisation d’un calcul différentiel dans une fonction graphique
• L’omission de la valeur de tolérance (tol) lorsque la commande différentielle est utilisée
à l’intérieur d’une fonction graphique simplifie le calcul pour le tracé du graphe. Dans ce
cas, la précision est sacrifiée pour obtenir un tracé plus rapide. La valeur de tolérance
est définie et le graphe est tracé avec la précision que vous obtenez lors de l’exécution
d’un calcul différentiel.
• Vous pouvez aussi omettre le point de dérivée en utilisant la formule de graphe
différentiel suivante: Y2=d/dx(Y1). Dans ce cas, la valeur de la variable X est utilisée
comme point de dérivée.
2-5-2
Calculs numériques
d
d/dx ( f (x), a) ⇒ ––– f (a)
dx
f (a + Ax) – f (a)
f '(a) = lim –––––––––––––
Ax
Ax→0
f (a + Ax) – f (a)
f '(a) –––––––––––––
Ax
(a: point pour lequel la dérivée doit être
déterminée, tol: tolérance)

19990401
Exemple Déterminer la dérivée au point x = 3 pour la fonction
y = x3 + 4x2 + x – 6, avec pour tolérance “tol” = 1E – 5
Introduisez la fonction f(x).
AK4(CALC)b(d/dx)vMd+evx+v-g,
Indiquez le point x = a pour lequel vous voulez déterminer la dérivée.
d,
Indiquez la valeur de tolérance.
bZ-f)
w
# Dans la fonction f(x), seule X peut être
utilisée comme variable dans les expressions.
Les autres variables (A à Z, r,
θ
) sont traitées
comme constantes, et la valeur affectée à
cette variable est utilisée au cours du calcul.
# La valeur de tolérance (tol) et la fermeture de
parenthèses peuvent être omises. Si vous
omettez la valeur de tolérance (tol) la
calculatrice utilisera automatiquement tol =
1E-10 comme valeur.
# Indiquez comme tolérance la valeur (tol) = 1E-14
ou une valeur inférieure. Une erreur d’itération se
produira si aucune solution satisfaisant la valeur
de tolérance ne peut être obtenue.
# Les points ou sections discontinus soumis à un
changement important peuvent affecter la
précision du calcul ou même provoquer une
erreur.
2-5-3
Calculs numériques

19990401
uApplications des calculs différentiels
• Les différentielles peuvent être additionnées, soustraites, multipliées et divisées par
chacune d’elles.
Par conséquent:
• Les résultats de différentielles peuvent être utilisés dans les additions, soustractions,
multiplications et divisions et dans les fonctions.
2 × f '(a), log ( f '(a)), etc.
• Des fonctions peuvent être utilisées pour tous les termes ( f (x), a, tol) d’une
différentielle.
2-5-4
Calculs numériques
# Vous ne pouvez pas utiliser d’expression avec,
différentielle, différentielle quadratique,
intégration, Σ, valeur maximale/minimale ou de
calcul de résolution à l’intérieur d’un terme du
calcul différentiel.
# Le fait d’appuyer sur A pendant le calcul d’une
différentielle (lorsque le curseur n’est pas affiché
à l’écran) interrompt le calcul.
# Utilisez toujours le radian (mode Rad) comme
unité d’angle pour effectuer des différentielles
trigonométriques.
dd
––– f (a) = f '(a), ––– g (a) = g'(a)
dx dx
f '(a) + g'(a), f '(a) × g'(a), etc.
d
––– (sinx + cosx, sin0,5, 1E -8), etc.
dx

19990401
kk
kk
kCalculs de différentielles quadratiques [OPTN]-[CALC]-[d2/dx2]
Après avoir affiché le menu d’analyse de fonctions, vous pouvez saisir des différentielles
quadratiques en utilisant un des deux formats suivants.
K4(CALC)c(d2/dx2) f(x),a,tol)
Les calculs de différentielles quadratiques produisent une valeur différentielle approximative
avec la formule de différentielle de second ordre suivante qui se base sur l’interprétation
polynomiale de Newton.
2 f (a + 3h) – 27 f(a + 2h) + 270 f (a + h) – 490 f (a)+270 f(a – h) – 27 f (a – 2h) +2 f (a – 3h)
f''(a) = –––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
180h2
Dans cette expression, les valeurs pour les “ incréments suffisamment petits de h” sont utilisées
pour obtenir une valeur proche de f ”(a).
Exemple Déterminer le coefficient différentiel quadratique au point où
x = 3 pour la fonction y = x3 + 4x2 + x – 6
Ici nous utiliserons tol = 1E – 5 comme tolérance
Introduisez la fonction f(x).
AK4(CALC)c(d2/dx2) vMd+
evx+v-g,
Saisissez 3 comme point a qui est un point de coefficient différentiel.
d,
Indiquez la valeur de tolérance.
bZ-f)
w
2-5-5
Calculs numériques
# Dans la fonction f(x), seule X peut être utilisée
comme variable dans les expressions. Toutes
les autres variables (A à Z, r,
θ
) sont traitées
comme constantes et la valeur actuellement
attribuée à cette variable est utilisée pendant
le calcul.
# La valeur de tolérance (tol) et la fermeture de
parenthèses peuvent être omises.
# Des points ou des sections discontinus avec
d’importantes fluctuations peuvent affecter la
précision, voire causer une erreur.
(a: point de coefficient différentiel, tol: tolérance)
d
2
d
2
––– (f (x), a) ⇒ ––– f (a)
dx
2
dx
2

19990401
uApplications des calculs de différentielles quadratiques
• Les opérations arithmétiques peuvent être effectuées en utilisant deux différentielles
quadratiques.
Par conséquent:
f ''(a) + g''(a), f ''(a) × g''(a), etc.
• Le résultat d’un calcul de différentielle quadratique peut être utilisé dans un calcul
ultérieur arithmétique ou de fonction.
2 × f ''(a), log ( f ''(a) ), etc.
• Les fonctions peuvent être utilisées à l’intérieur des termes ( f(x), a, tol ) d’une
expression différentielle quadratique.
2-5-6
Calculs numériques
d2d2
––– f (a) = f ''(a), ––– g (a) = g''(a)
dx2dx2
d2
––– (sin x + cos x, sin 0,5, 1E -8), etc.
dx2
# Vous ne pouvez pas utiliser d’expression avec
de différentielle, différentielle quadratique,
intégration, Σ, valeur maximale/minimale ou
calcul de résolution à l’intérieur d’un terme du
calcul de différentielle quadratique.
# Indiquez la valeur tol = 1E-14 comme
tolérance ou une valeur inférieure.
Une erreur d’itération se produira si aucune
solution satisfaisant la valeur de tolérance ne
peut être obtenue.
# Vous pouvez interrompre un calcul de
différentielle quadratique en cours en appuyant
sur la touche A.
# Utilisez toujours les radians (mode Rad) comme
unité d’angle quand vous effectuez des
différentielles quadratiques trigonométriques.
# Pour l’tilisation d’un calcul de différentielle
quadratique dans une fonction graphique, voir
page 2-5-2.
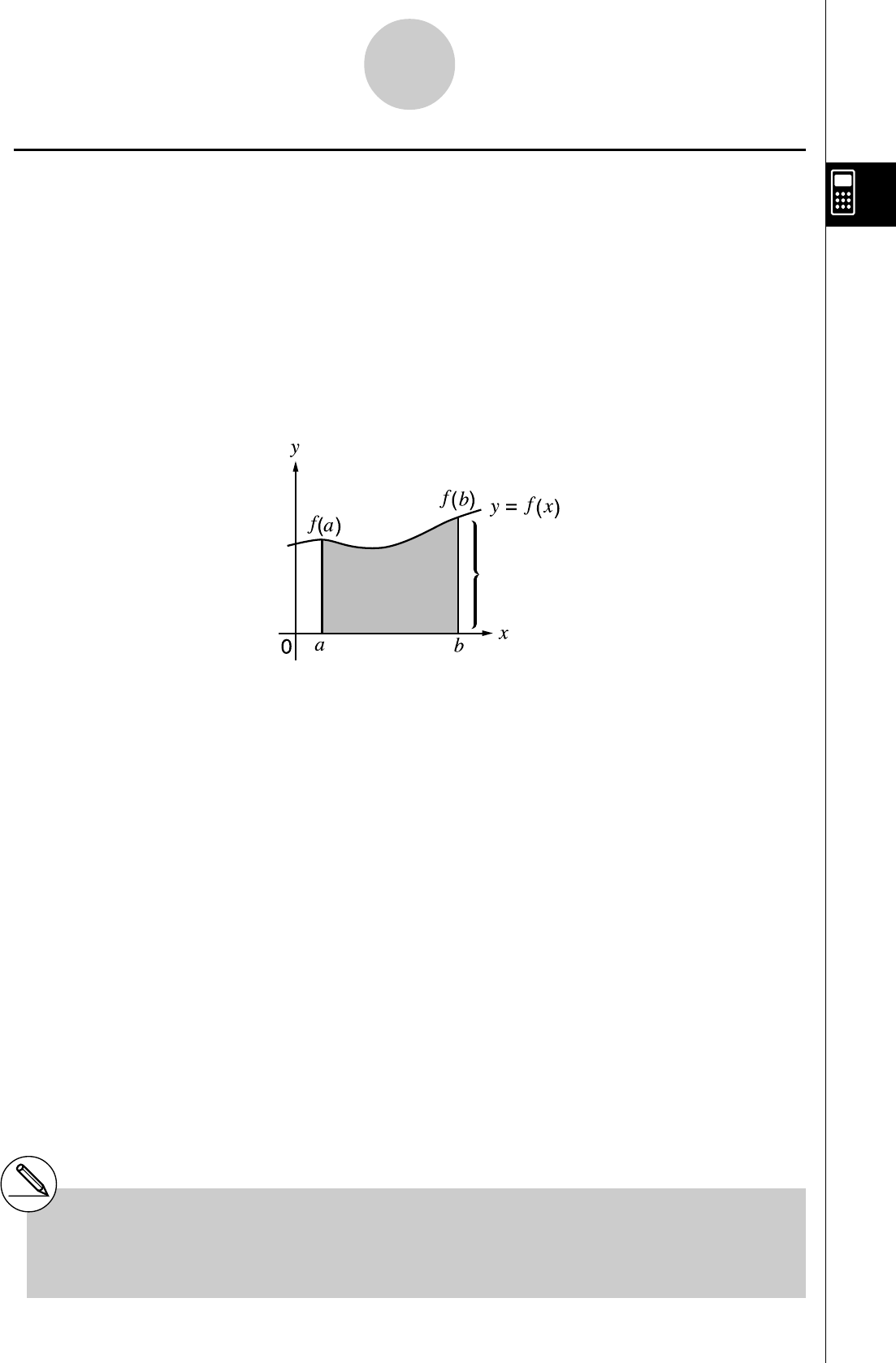
19990401
kk
kk
kCalculs d’intégrations [OPTN]-[CALC]-[
∫
dx]
Pour effectuer des calculs d’intégration, affichez d’abord le menu d’analyse de fonctions,
puis entrez les valeurs indiquées dans la formule suivante.
K4(CALC)d (
∫
dx) f(x) , a , b , tol )
∫
( f(x), a, b, tol) ⇒
∫
a
b f(x)dx
Comme indiqué sur l’illustration ci-dessus, les calculs d’intégration sont exécutés en
calculant les valeurs intégrales de a à b pour la fonction y = f (x) quand a < x < b et f (x) > 0.
L’aire de la zone ombrée sur l’illustration est ainsi calculée.
2-5-7
Calculs numériques
(a: point initial, b: point final, tol: tolérance)
#Si f (x) < 0 quand a < x < b, le calcul de l’aire
produit des valeurs négatives (aire × – 1).
Zone calculée par
∫
a
b f(x)dx

19990401
Exemple Effectuer un calcul d’intégration pour la fonction indiquée ci-dessous
avec une tolérance de “tol” = 1E - 4
∫
1
5 (2x2 + 3x + 4) dx
Introduisez la fonction f (x).
AK4(CALC)d(∫dx)cvx+dv+e,
Indiquez le point initial et le point final.
b,f,
Indiquez la valeur de tolérance.
bZ-e)
w
uu
uu
uApplication des calculs d’intégration
• Les intégrales peuvent être utilisées dans les additions, soustractions, multiplications et
divisions.
∫
a
b f(x) dx +
∫
c
d g(x) dx, etc.
• Les résultats d’intégration peuvent être utilisés dans les additions, soustractions,
multiplications, divisions et dans les fonctions.
2 ×
∫
a
b f(x) dx, etc. log (
∫
a
b f(x) dx), etc.
• Les fonctions peuvent être utilisées dans chacun des termes (f(x), a, b, tol) d’une
intégrale.
∫
cos 0,5
(sin x + cos x) dx =
∫
(sin x + cos x, sin 0,5, cos 0,5, 1E -4)
sin 0,5
2-5-8
Calculs numériques
# Dans la fonction f(x), seule X peut être utilisée
comme variable dans les expressions. Les
autres variables (A à Z, r,
θ
) sont traitées comme
constantes, et la valeur affectée à cette variable
est utilisée au cours du calcul.
# Il est inutile d’indiquer la valeur “tol” et de
fermer la parenthèse. Si vous n’indiquez pas
la valeur “tol” , la calculatrice utilisera
automatiquement 1E-5 comme valeur par
défaut.
# Les calculs d’intégration peuvent prendre un
certain temps.
# Vous ne pouvez pas utiliser d’expression avec
différentielle, différentielle quadratique,
intégration, Σ, valeur maximale/minimale ou
calcul de résolution à l’intérieur d’un terme du
calcul d’intégration.
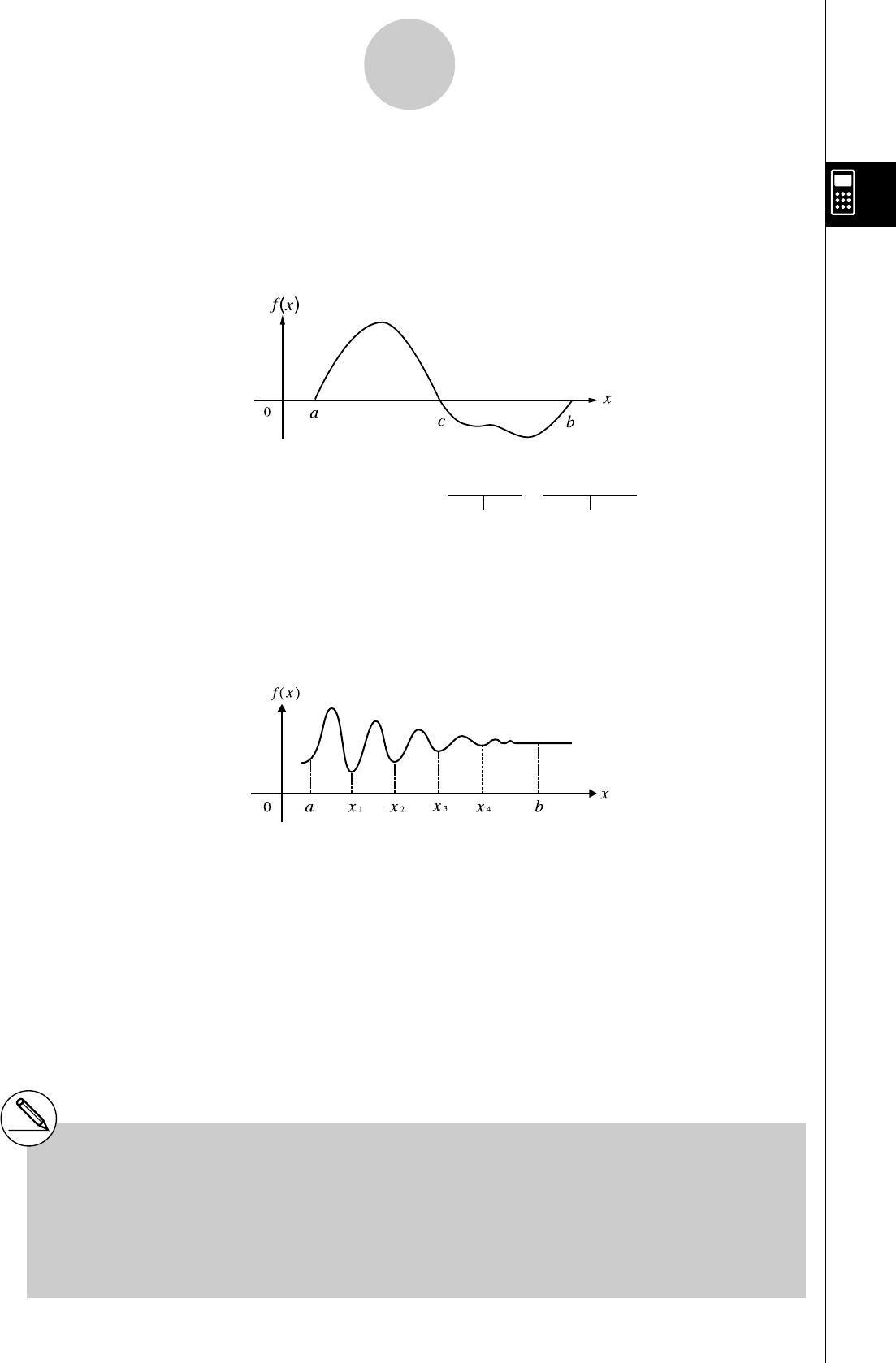
19990401
Notez les points suivants pour obtenir de bonnes valeurs d’intégration.
(1) Lorsque les fonctions cycliques pour les valeurs d’intégration deviennent positives ou
négatives pour différentes divisions, effectuez le calcul pour des cycles uniques ou
divisez entre négatif et positif, puis ajoutez les résultats.
∫
a
b f(x)dx =
∫
a
c f(x)dx + (–
∫
c
b f(x)dx)
Partie positive (
S
) Partie négative (
S
)
(2) Lorsque des changements minimes dans les divisions d’intégration donnent des
changements importants dans les valeurs d’intégration, calculez séparément les
divisions d’intégration (divisez les grandes zones de changement en zones plus
petites), puis ajoutez les résultats.
∫
a
b f(x)dx =
∫
a
x1 f(x)dx +
∫
x1
x2 f(x)dx +.....+
∫
x4
b
f(x)dx
2-5-9
Calculs numériques
Partie négative (S)
Partie
positive (S)
# Le fait d’appuyer sur A pendant le calcul
d’une intégrale (lorsque le curseur n’est pas
affiché à l’écran) interrompt le calcul.
# Utilisez toujours le radian (mode Rad)
comme unité d’angle pour effectuer des
intégrations trigonométriques.
# Une erreur d’itération se produira si aucune
solution satisfaisant la valeur de tolérance ne
peut être obtenue.

19990401
kk
kk
kCalculs de Σ[OPTN]-[CALC]-[Σ ]
Pour effectuer des calculs de Σ , affichez d’abord le menu d’analyse de fonctions, puis
entrez les valeurs indiquées dans la formule suivante.
K4(CALC)e(Σ) ak , k ,
α
,
β
, n )
Exemple Effectuer le calcul suivant:
Utilisez n = 1 comme distance entre les partitions.
AK4(CALC)e(Σ)a,(K)x
-da,(K)+f,
a,(K),c,g,b)w
2-5-10
Calculs numériques
6
Σ (k2 – 3k + 5)
k = 2
β
Σ (ak, k,
α
,
β
, n) = Σ ak = a
α
+ a
α
+1 +........+ a
β
k = α(n: distance entre les partitions)
# Vous pouvez utiliser seulement une variable
dans cette fonction comme séquence ak.
# Saisissez des nombres entiers seulement
pour le terme initial (
α
) de la séquence ak et
pour le terme final (
β
) de la séquence ak.
# La saisie de n et la fermeture de parenthèses
peuvent être omises. Si vous omettez n, la
calculatrice utilisera automatiquement n = 1.

19990401
uApplications des calculs de Σ
• Opérations arithmétiques utilisant des expressions avec calculs de Σ
Expressions:
Opérations possibles: Sn + Tn, Sn – Tn, etc.
• Opérations arithmétiques et de fonctions utilisant les résultats de calculs de Σ
2 × Sn, log (Sn), etc.
• Opérations de fonctions utilisant des termes de calculs de Σ (ak, k)
Σ (sink, k, 1, 5), etc.
2-5-11
Calculs numériques
nn
Sn = Σ ak, Tn = Σ bk
k = 1k = 1
# Vous ne pouvez pas utiliser d’expression avec
différentielle, différentielle quadratique,
intégration, Σ, valeur maximale/minimale ou
calcul de résolution à l’intérieur d’un terme de
calcul de Σ.
# La valeur utilisée comme terme final
β
doit être
supérieure à la valeur utilisée comme terme
initial
α
, sinon une erreur se produira.
# Pour interrompre un calcul de Σ en cours
(indiqué par l’absence de curseur sur l’écran),
appuyez sur la touche A.
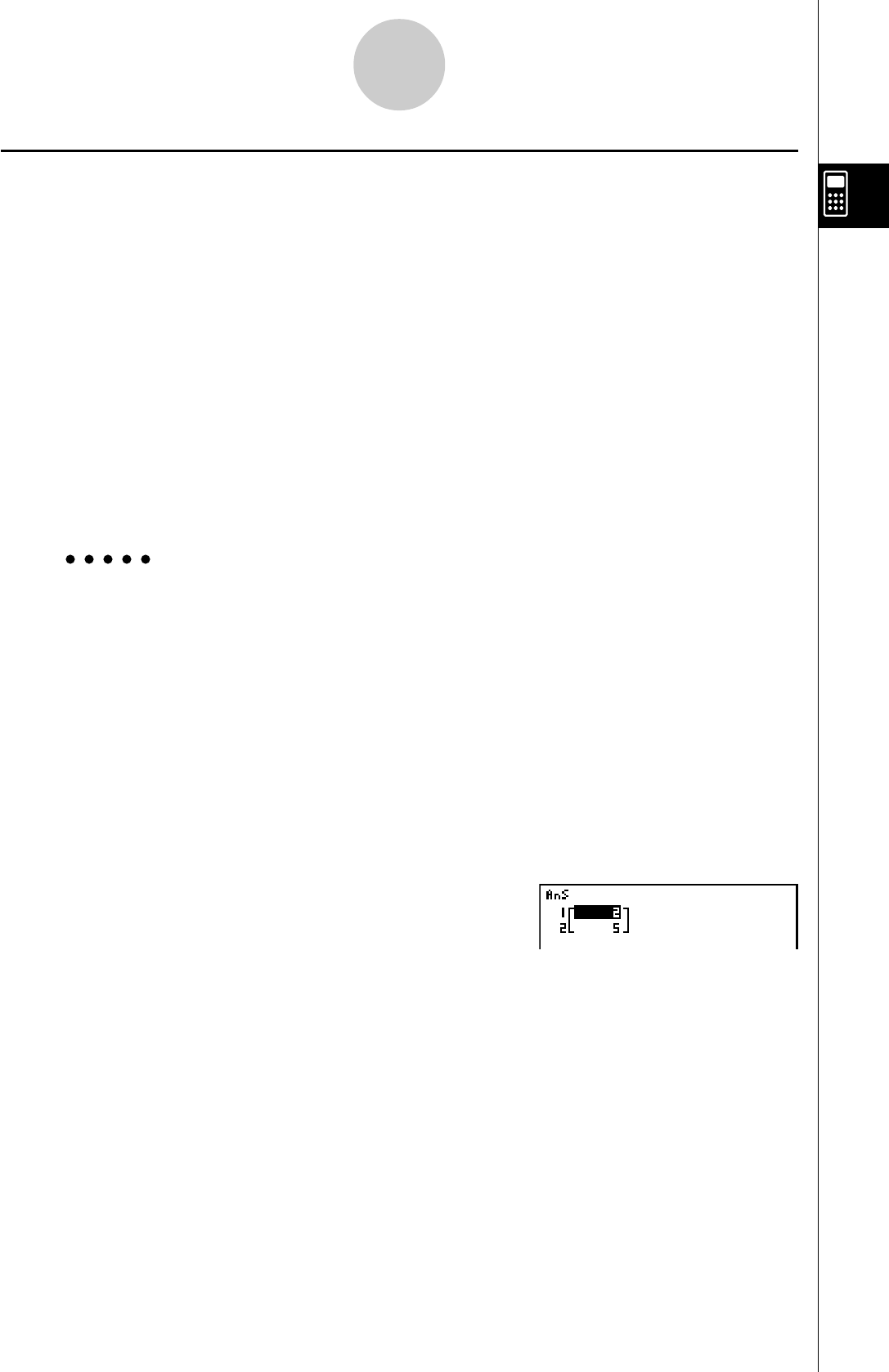
19990401
2-5-12
Calculs numériques
kk
kk
kCalculs de valeurs maximale/minimale [OPTN]-[CALC]-[FMin]/[FMax]
Après avoir affiché le menu d’analyse de fonctions, vous pouvez effectuer des calculs de
valeurs maximale/minimale en utilisant les formats suivants et trouver le maximum et le
minimum d’une fonction dans un intervalle tel que a < x < b. (a: point initial de l’intervalle,
b: point final de l’intervalle, n: précision (n = 1 à 9))
uu
uu
uValeur minimale
K4(CALC)f(FMin) f(x) , a , b , n )
uu
uu
uValeur maximale
K4(CALC)g(FMax) f(x), a , b , n )
Exemple 1 Déterminer la valeur minimale de l’intervalle défini par le point
initial a = 0 et le point final b = 3, avec une précision de n = 6 pour la
fonction y = x2 – 4x + 9
Saisissez f(x).
AK4(CALC)f(FMin) vx-ev+j,
Saisissez l’intervalle a = 0, b = 3.
a,d,
Saisissez la précision n = 6.
g)
w
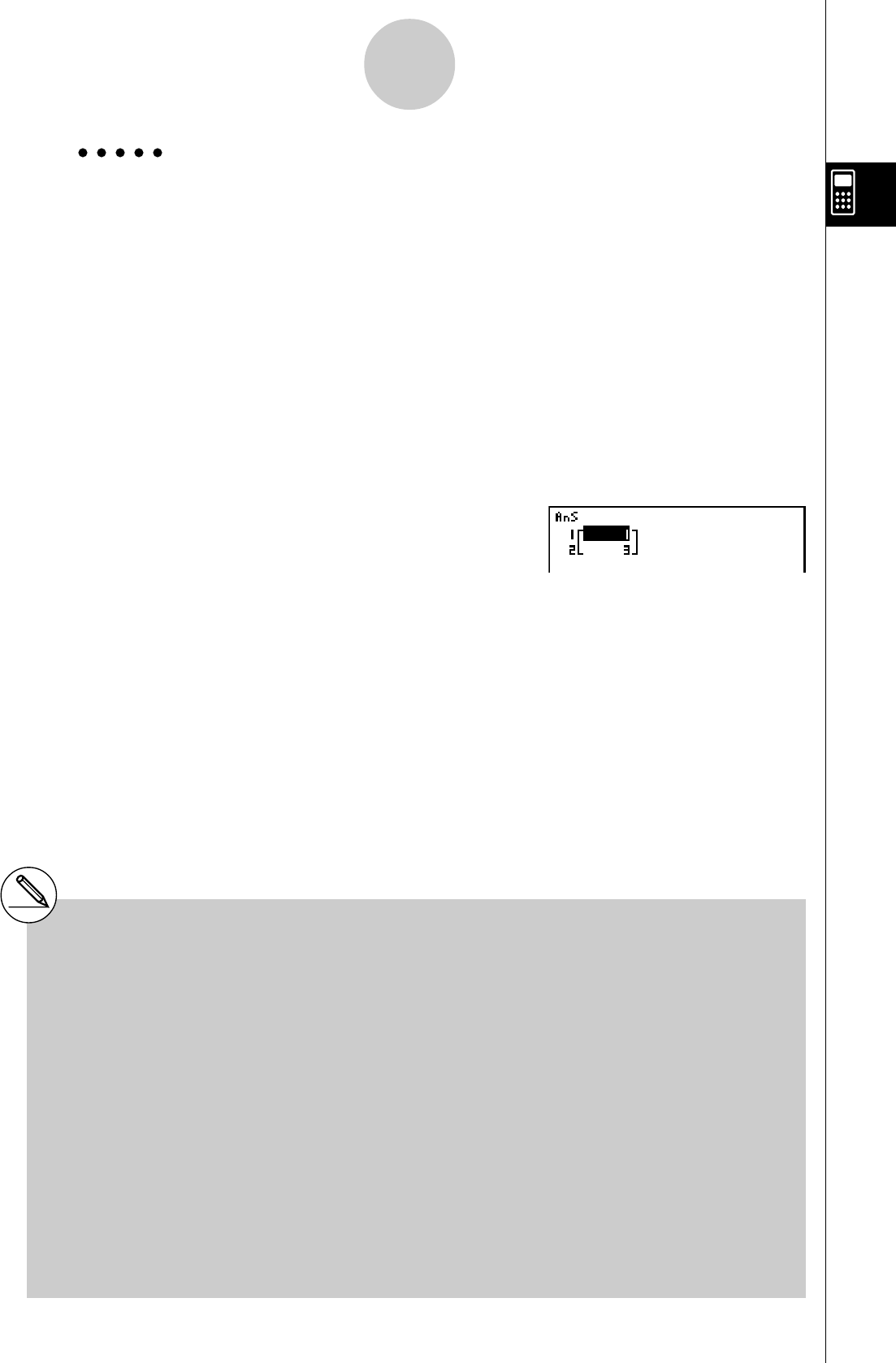
19990401
2-5-13
Calculs numériques
# Dans la fonction f(x), seule X peut être
utilisée comme variable dans les expressions.
Les autres variables (A à Z, r,
θ
) sont traitées
comme constantes, et la valeur affectée à
cette variable est appliquée au cours du
calcul.
# La saisie de n et la fermeture de parenthèses
peuvent être omises.
# Les points ou sections discontinus soumis à
un changement important peuvent affecter la
précision du calcul ou même provoquer une
erreur.
# Vous ne pouvez pas utiliser d’expression avec
différentielle, différentielle quadratique,
intégration, Σ, valeur maximale/minimale ou
calcul de résolution à l’intérieur d’un terme du
calcul des valeurs maximale et minimale.
# La saisie d’une valeur plus grande pour n
augmente la précision du calcul, mais aussi le
temps de calcul requis.
# Le point final de l’intervalle (b) doit avoir une
valeur supérieure à celle du point initial (a),
sinon une erreur se produira.
# Vous pouvez interrompre un calcul de valeurs
maximale/minimale en cours en appuyant sur la
touche A.
# Vous pouvez utiliser un entier de 1 à 9 comme
valeur de n. L’utilisation d’une valeur hors de
cette plage cause une erreur.
Exemple 2 Déterminer la valeur maximale de l’intervalle défini par le point
initial a = 0 et le point final b = 3, avec une précision de n = 6 pour la
fonction y = –x2 + 2x + 2
Saisissez f(x).
AK4(CALC)g(FMax) -vx+cv+c,
Saisissez l’intervalle a = 0, b = 3.
a,d,
Saisissez la précision n = 6.
g)
w

19990401
2-6 Calculs avec nombres complexes
Vous pouvez effectuer des calculs avec addition, soustraction, multiplication, division, des
calculs de fonctions, parenthèses et des calculs à partir de la mémoire avec les nombres
complexes comme vous le faites avec les calculs manuels décrits aux pages 2-1-1 et 2-4-6.
Vous pouvez sélectionner le mode de calcul de nombre complexe en sélectionnant un des
réglages suivants comme paramètre “Complex Mode” sur l’écran de configuration.
• {Real} ... Calcul dans la plage des nombres réels seulement*1
• {a+bi} ... Exécution d’un calcul de nombre complexe et affichage des résultats par des
coordonnées rectangulaires
• {re^
θ
i} ...Exécution d’un calcul de nombre complexe et affichage des résultats par des
coordonnées polaires*2
Appuyez sur K3(CPLX) pour afficher le menu de calcul de nombre complexe, qui
contient les paramètres suivants.
• {Abs}/{Arg} ... obtention de {la valeur absolue}/{l’argument}
• {Conjg} ... {calcul du conjugué}
• {ReP}/{ImP} ... extraction de la partie {réelle d’un nombre}/{imaginaire d’un nombre}
• {'re^
θ
i}/{'a+bi} ... convertit le résultat sous forme (polaire)/(linéaire)
2-6-1
Calculs avec nombres complexes
*1 Lorsque l’argument contient un nombre
imaginaire, cependant, le calcul du nombre
complexe est effectué et le résultat est affiché
avec des coordonnées rectangulaires.
Exemple:
ln 2i= 0,6931471806 + 1,570796327i
ln 2i + ln(-2) = (Erreur non réel)
*2 La plage d’affichage de
θ
dépend de l’unité
d’angle désigné sur l’écran de configuration.
• Deg ... –180 <
θ
< 180
• Rad ... – π <
θ
< π
• Gra ... –200 <
θ
< 200
# Les solutions obtenues par les modes Real et
a+bi / re^
θ
i sont différentes pour les calculs de
puissance (xy) lorsque x < 0 et y = m/n quand n
est un nombre impair.
Exemple:
3x (- 8) = – 2 (Réel)
= 1 + 1,732050808i(a+bi / re ^θi)
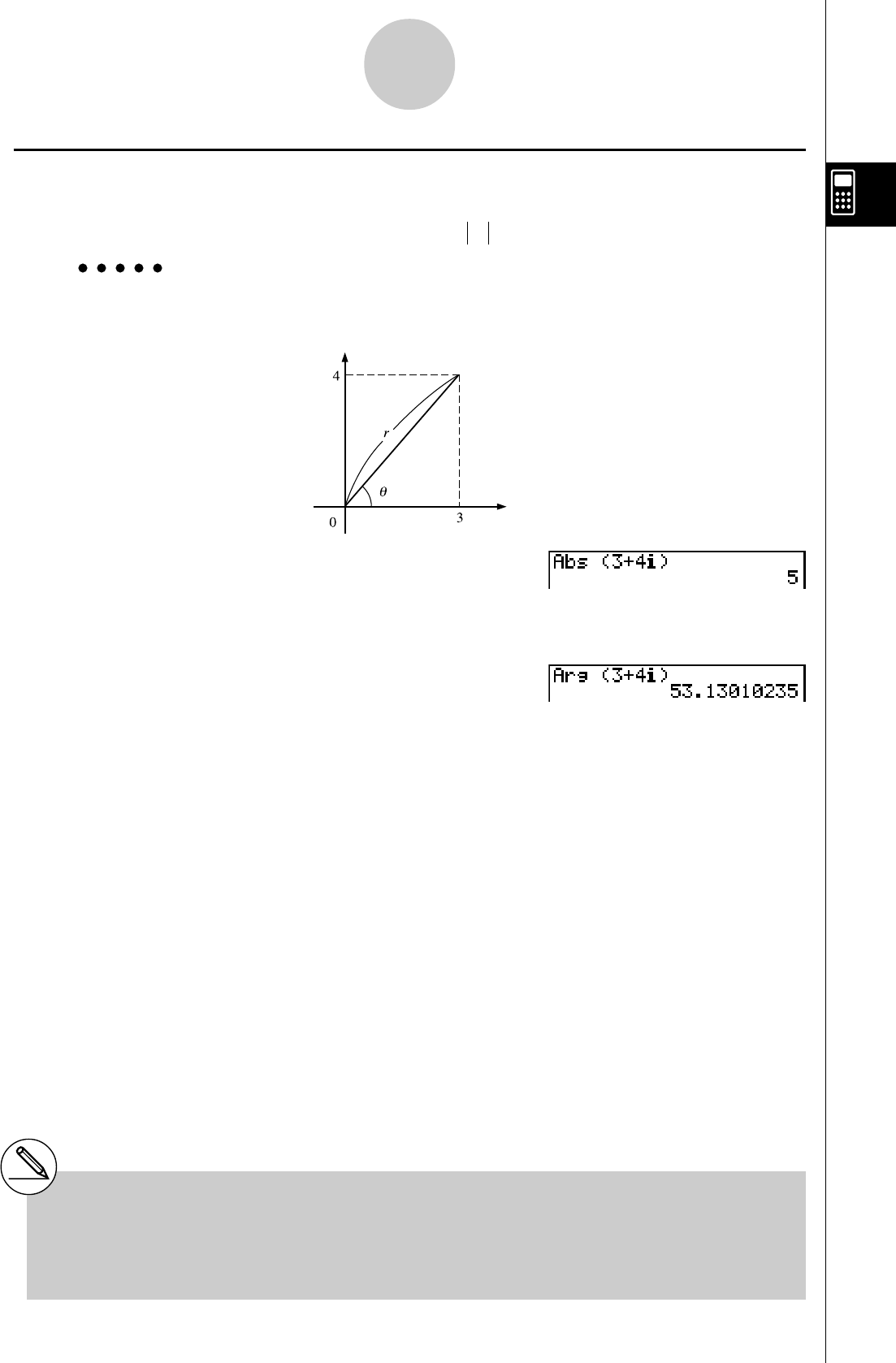
19990401
2-6-2
Calculs avec nombres complexes
kk
kk
kValeur absolue et argument [OPTN]-[CPLX]-[Abs]/[Arg]
La machine considère un nombre complexe dans la formule Z = a + bi comme coordonnée
sur un plan de Gauss et calcule la valeur absolue Z et l’argument (arg).
Exemple Calculer la valeur absolue (r) et l’argument (
θ
) du nombre complexe 3
+ 4i, avec le degré comme unité d’angle
AK3(CPLX)b(Abs)
(d+e!a(i))w
(Calcul de la valeur absolue)
AK3(CPLX)c(Arg)
(d+e!a(i))w
(Calcul de l’argument)
# Le résultat du calcul de l’argument change
selon l’unité d’angle (degré, radian, grade)
sélectionnée.
Axe de nombres imaginaires
Axe de nombres réels
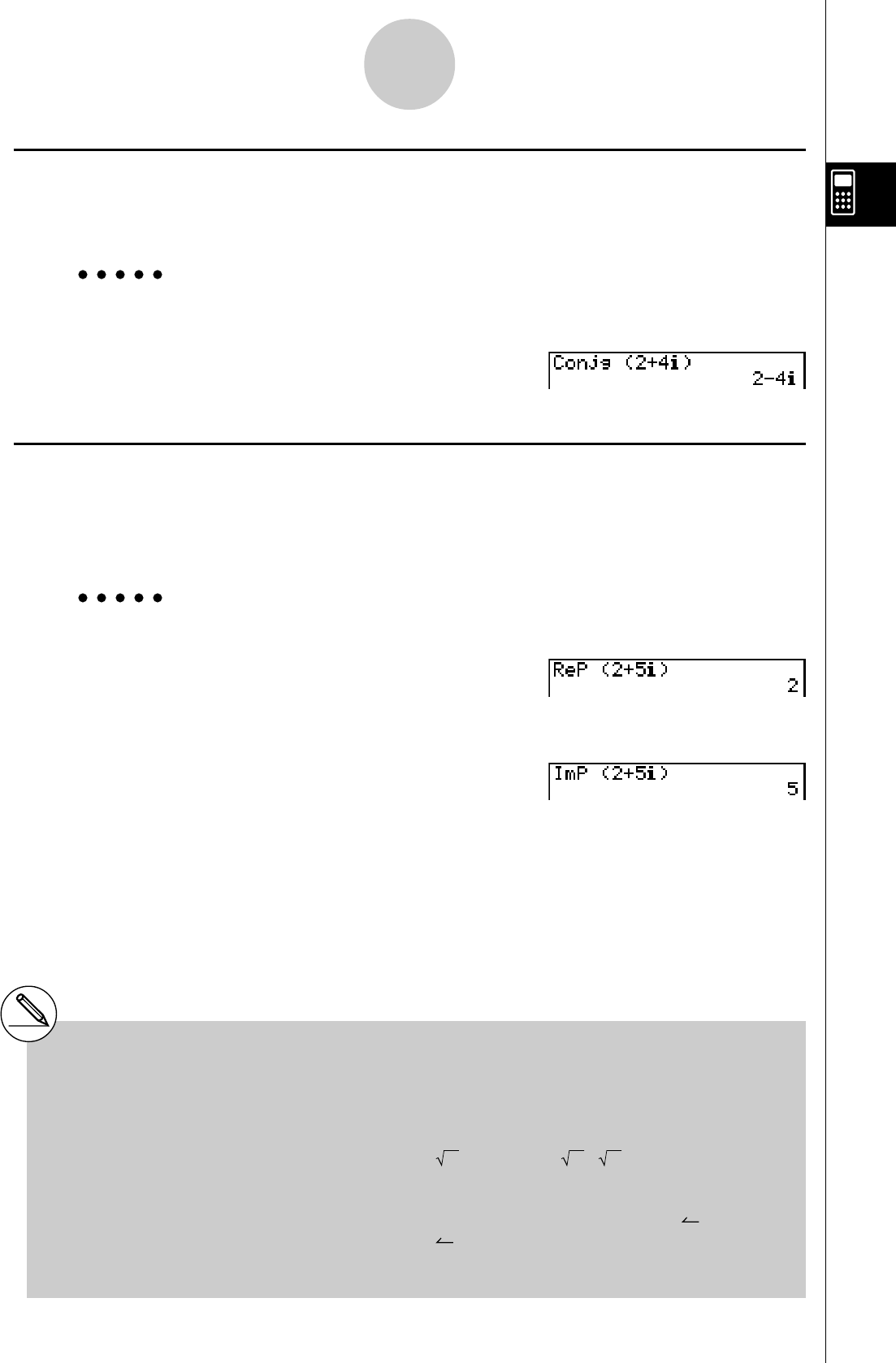
19990401
kk
kk
kNombres complexes conjugués [OPTN]-[CPLX]-[Conjg]
Un nombre complexe de format a + bi devient un nombre complexe conjugué de format a
– bi.
Exemple Calculer le nombre complexe conjugué pour le nombre complexe 2
+ 4i
AK3(CPLX)d(Conjg)
(c+e!a(i))w
kk
kk
kExtraction des parties réelle et imaginaire d’un nombre
[OPTN]-[CPLX]-[ReP]/[lmP]
Utilisez la méthode suivante pour extraire la partie réelle a et la partie imaginaire b d’un
nombre complexe dont le format est a + bi.
Exemple Extraire les parties réelle et imaginaire d’un nombre complexe 2 + 5i
AK3(CPLX)e(ReP)
(c+f!a(i))w
(Extraction de la partie réelle)
AK3(CPLX)f(ImP)
(c+f!a(i))w
(Extraction de la partie imaginaire)
2-6-3
Calculs avec nombres complexes
# La plage d’entrée/sortie des nombres
complexes est normalement de 10 chiffres
pour la mantisse et de deux chiffres pour
l’exposant.
# Lorsqu’un nombre complexe a plus de 21
chiffres, la partie réelle et la partie imaginaire
du nombre sont affichées sur deux lignes
séparées.
# Lorsque la partie réelle ou la partie imaginaire
d’un nombre complexe est égale à zéro, elle
n’est pas affichée sous forme rectangulaire.
# Vous utilisez 18 octets de mémoire chaque fois
que vous affectez un nombre complexe à une
variable
.
# Les fonctions suivantes peuvent être utilisées
avec les nombres complexes.
, x2, x–1, ^(xy), 3, x, In, log, 10x, ex, sin,
cos, tan, Asn, Acs, Atn, sinh, cosh, tanh, sinh–1,
cosh–1, tanh–1,
Int, Frac, Rnd, Intg, Fix, Sci, ENG, ENG, ° ’ ”,
° ’ ”, a+b/c, d/c

19990401
kk
kk
kForme polaire et transformation sous forme rectangulaire
[OPTN]-[CPLX]-[''
''
're^
θ
i]
Procédez de la façon suivante pour transformer un nombre complexe affiché sous forme
rectangulaire en forme polaire, et inversement.
Exemple Transformer la forme rectangulaire du nombre complexe 1 + 3
i sous
sa forme polaire
Ab+(!x( )d)!a(i)
K3(CPLX)g('re^
θ
i)w
2-6-4
Calculs avec nombres complexes

19990401
2-7 Calculs binaire, octal, décimal et hexadécimal
Vous pouvez utiliser le mode RUN • MAT et les réglages de système binaire, octal, décimal
et hexadécimal pour effectuer des calculs qui contiennent des valeurs binaires, octales,
décimales et hexadécimales. Vous pouvez aussi convertir les systèmes numériques entre
eux et effectuer des opérations logiques.
• Vous ne pouvez pas utiliser de fonctions scientifiques dans les calculs binaires, octaux,
décimaux et hexadécimaux.
• Vous ne pouvez utiliser que des entiers dans les calculs binaires, octaux, décimaux et
hexadécimaux, ce qui signifie que les valeurs fractionnaires ne sont pas admises. Si
vous introduisez une valeur qui comprend une partie décimale, la machine élimenera
automatiquement la partie décimale.
• Si vous essayez d’introduire une valeur invalide pour le système de notation (binaire,
octale, décimale, hexadécimale) utilisé, la calculatrice affichera un message d’erreur.
Voici les chiffres qui peuvent être utilisés dans chaque système de notation.
Binaire: 0, 1
Octale: 0, 1, 2, 3, 4, 5, 6, 7
Décimale: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Hexadécimale: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
• Les valeurs binaires, octales et hexadécimales négatives sont produites en utilisant le
complément de deux de la valeur d’origine.
• La capacité d’affichage de chacun des systèmes de notation est la suivante.
Système numérique Capacité d’affichage
Binaire 16 chiffres
Octal 11 chiffres
Décimal 10 chiffres
Hexadécimal 8 chiffres
2-7-1
Calculs binaire, octal, décimal et hexadécimal
# Les caractères alphabétiques utilisés dans
la notation hexadécimale apparaissent
différemment sur l’écran pour les distinguer
des caractères de texte.
Texte normal: A, B, C, D, E, F
Valeurs hexadécimales: u, v, w, x, y, z

19990401
• Les plages de calcul pour chacun des systèmes de notation sont les suivantes.
Valeurs binaires
Positive: 0 < x < 111111111111111
Négative: 1000000000000000 < x < 1111111111111111
Valeurs octales
Positive: 0 < x < 17777777777
Négative: 20000000000 < x < 37777777777
Valeurs décimales
Positive: 0 < x < 2147483647
Négative: –2147483648 < x < –1
Valeurs hexadécimales
Positive: 0 < x < 7FFFFFFF
Négative: 80000000 < x < FFFFFFFF
uu
uu
u Pour effectuer un calcul binaire, octal, décimal ou hexadécimal
[SET UP]- [Mode] -[Dec]/[Hex]/[Bin]/[Oct]
1. Sur le menu principal, sélectionnez RUN • MAT.
2. Appuyez sur u3(SET UP), puis définissez le système numérique par défaut en
appuyant sur 2(Dec), 3(Hex), 4(Bin) ou 5(Oct).
3. Appuyez sur i pour changer d'écran pour la saisie du calcul. Un menu de fonctions
apparaît avec les paramètres suivants.
•{d~o}/{LOGIC}/{DISP}/{SYBL} ... menu de {désignation du système numérique}/
{opérations logiques}/{conversion décimale/hexadécimale/binaire/octale}/
{symboles}
2-7-2
Calculs binaire, octal, décimal et hexadécimal

19990401
kk
kk
kSélection du système numérique
Vous pouvez désigner le système décimal, hexadécimal, binaire ou octal sur l’écran de
configuration. Une fois que vous avez appuyé sur la touche de fonction qui correspond au
système que vous voulez utiliser, appuyez sur w.
• Les résultats seront convertis dans le système choisi sur l’écran de configuration.
uu
uu
u Pour définir un système numérique pour la saisie d’une valeur seulement
Vous pouvez définir un système numérique pour chaque valeur que vous entrez. Appuyez
sur 1(d~o) pour afficher un menu de symboles représentant les systèmes numériques.
Appuyez sur la touche de fonction correspondant au symbole que vous voulez sélectionner
et indiquez la valeur souhaitée.
•{d}/{h}/{b}/{o} ... {décimal}/{hexadécimal}/{binaire}/{octal}
uu
uu
u Pour saisir des valeurs dans différents systèmes numériques
Exemple Saisir 12310 ou 10102 quand le système numérique par défaut est le
système hexadécimal
u3(SET UP)3(Hex)i
A1(d~o)b(d)bcdw
1(d~o)d(b)babaw
kk
kk
kOpérations arithmétiques
Exemple 1 Calculer 101112 + 110102
u3(SET UP)4(Bin)i
Ababbb+
bbabaw
2-7-3
Calculs binaire, octal, décimal et hexadécimal

19990401
Exemple 2 Saisir et exécuter 1238 × ABC16, quand le système numérique de par
défaut est décimal ou hexadécimal
u3(SET UP)2(Dec)i
A1(d~o)e(o)bcd*
1(d~o)c(h)ABCw
3(DISP)c(Hex)w
kk
kk
kValeurs négatives et opérations logiques
Appuyez sur 2(LOGIC) pour afficher un menu de négations ou d’opérateurs logiques.
•{Neg} ... {négation}
•{Not}/{and}/{or}/{xor}/{xnor} ... {NOT}/{AND}/{OR}/{XOR}/{XNOR}
uValeurs négatives
Exemple Déterminer la valeur négative de 1100102
u3(SET UP)4(Bin)i
A2(LOGIC)b(Neg)
bbaabaw
uOpérations logiques
Exemple 1 Saisir et exécuter “12016 and AD16”
u3(SET UP)3(Hex)i
Abca2(LOGIC)
d(and)ADw
2-7-4
Calculs binaire, octal, décimal et hexadécimal

19990401
Exemple 2 Afficher le résultat de “368 or 11102” par une valeur octale
u3(SET UP)5(Oct)i
Adg2(LOGIC)
e(or)1(d~o)d(b)
bbbaw
Exemple 3 Mettre en négation 2FFFED16
u3(SET UP)3(Hex)i
A2(LOGIC)c(Not)
cFFFEDw
uTransformation du système numérique
Appuyez sur 3(DISP) pour afficher un menu des fonctions de transformation du système
numérique.
• {''
''
'Dec}/{''
''
'Hex}/{''
''
'Bin}/{''
''
'Oct} ... transformation de la valeur affichée en son équivalent
{décimal/hexadécimal/binaire/octal}
u Pour convertir une valeur affichée d’un système numérique dans un autre
Exemple Convertir 2210 (système numérique par défaut) dans sa valeur binaire
ou octale correspondante
Au3(SET UP)2(Dec)i
1(d~o)b(d)ccw
3(DISP)d(''
''
'Bin)w
3(DISP)e(''
''
'Oct)w
2-7-5
Calculs binaire, octal, décimal et hexadécimal

19990401
2-8-1
Calculs matriciels
2-8Calculs matriciels
Depuis le menu principal, accédez au mode RUN • MAT et appuyez 1(MAT) pour effectuer
des calculs matriciels.
Vous pouvez effectuer les opérations suivantes grâce aux 26 mémoires matricielles (Mat A
à Mat Z) et à la mémoire matricielle de dernier résultat (MatAns).
• Addition, soustraction, multiplication
• Calculs de produits scalaires
• Calculs de déterminant
• Transposition d’une matrice
• Inversion d’une matrice
• Élévation d’une matrice au carré
• Élévation d’une matrice à une puissance
• Calculs de valeur absolue, extraction de la partie entière, extraction de la partie
fractionnaire d’un nombre, nombre entier maximal
• Modification de matrices à l’aide des commandes de matrice
• Valeur absolue, argument, calcul complexe conjugué pour une matrice à nombres
complexes
• Extraction de la partie réelle et de la partié complexe d’un nombre d’une matrice
comprenant des nombres complexes.
Le nombre maximal de lignes pouvant être spécifiées pour une matrice est 255 et le nombre
maximal de colonnes est également 255.
# Au sujet de la mémoire matricielle de
dernier résultat (MatAns)
La calculatrice stocke automatiquement
les résultats de calculs matriciels dans la
mémoire matricielle. Il faut noter les points
suivants concernant la mémoire matricielle
de dernier résultat:
• Quand vous effectuez un calcul avec matrice, le
contenu de la mémoire matricielle est remplacé
par le nouveau résultat. Le contenu précédent
est effacé et ne peut pas être récupéré.
• L’introduction de valeurs dans une matrice
n’affecte pas le contenu de la mémoire
matricielle de dernier résultat.

19990401
k Saisie et édition de matrices
Appuyez sur 1(MAT) pur afficher l’écran d’édition de matrice. Utilisez cet écran pour saisir
et éditer des matrices.
• {DIM} ... {définit les dimensions de la matrice (nombre d’éléments)}
• {DEL}/{DEL·A} ... suppression {d’une matrice particulière}/{de toutes les matrices}
u Création d’une matrice
Pour créer une matrice, vous devez définir ses dimensions (sa taille) dans la liste de
matrices. Vous pouvez ensuite introduire des valeurs dans la matrice.
u Pour définir les dimensions (taille) d’une matrice
Exemple Créer une matrice de 2 lignes × 3 colonnes dans la zone nommée
Mat B
Mettez Mat B en surbrillance.
c
1(DIM)
Spécifiez le nombre de lignes.
cw
Spécifiez le nombre de colonnes.
dw
w
• Tous les éléments de la nouvelle matrice contiennent la valeur 0.
2-8-2
Calculs matriciels
# Si “Erreur mémoire” reste à côté du nom de la
zone de matrice après l’introduction des
dimensions, c’est que la mémoire n’est pas
suffisante pour créer la matrice souhaitée.
m × n … Matrice de m (lignes) × n (colonnes)
None… Aucune matrice définie

19990401
u Pour introduire des valeurs dans la matrice
Exemple Introduire les données suivantes dans la matrice B:
123
456
c (Sélectionne Mat B.)
w
bwcwdw
ewfwgw
(La donnée est introduite dans l’élément
en surbrillance. A chaque pression sur
w, l’élément suivant de droite est mis en
surbrillance.)
# Vous pouvez introduire des nombres
complexes dans un élément.
# Les valeurs affichées des éléments
indiquent des nombres entiers positifs de six
chiffres au maximum et des nombres entiers
négatifs de cinq chiffres (un chiffre est utilisé
pour le signe négatif). Les valeurs
exponentielles sont indiquées avec au plus
deux chiffres pour l’exposant. Les valeurs
fractionnaires ne sont pas affichées.
# Vous pouvez voir la valeur complète affectée à un
élément en utilisant les touches de curseur pour
déplacer la surbrillance sur l’élément dont vous
voulez voir la valeur.
# Chaque élément d’une matrice nécessite 9 octets
de mémoire. Cela signifie qu’une matrice de 3 × 3
exige une mémoire de 81 octets (3 × 3 × 9 = 81).
L’introduction de nombres complexes dans une
matrice double la quantité de mémoire utilisée.
2-8-3
Calculs matriciels
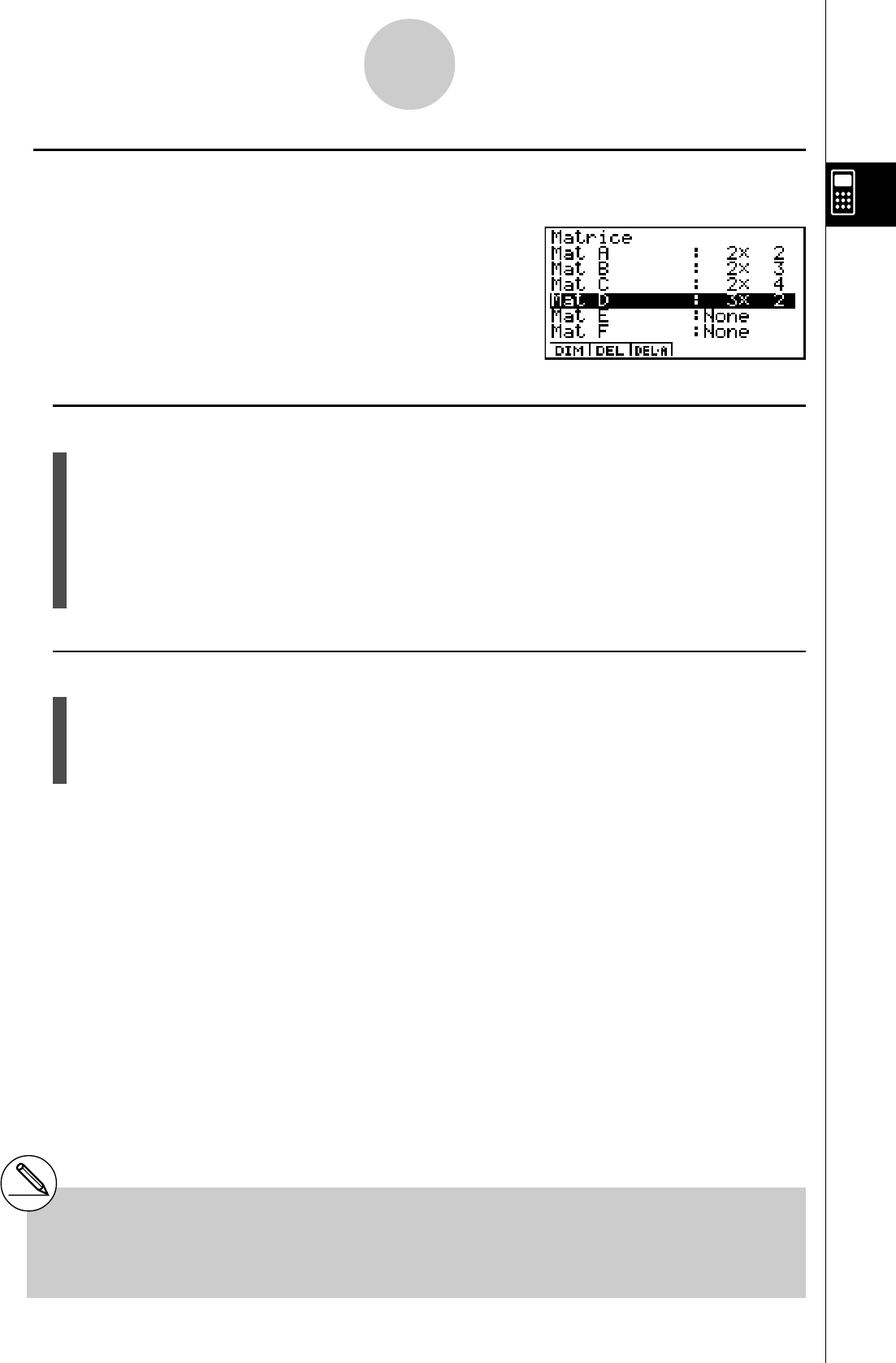
19990401
uSuppression d’une matrice
Vous pouvez supprimer une matrice particulière ou toutes les matrices en mémoire.
u Pour supprimer une matrice particulière
1. Quand la liste de matrices est à l’écran, utilisez f et c pour mettre la matrice que
vous voulez supprimer en surbrillance.
2. Appuyez sur 2(DEL).
3. Appuyez sur w(Oui) pour effacer la matrice ou sur i(Non) pour abandonner
l’opération en cours sans rien supprimer.
u Pour supprimer toutes les matrices
1. Quand la liste de matrices est à l’écran, appuyez sur 3(DEL·A).
2. Appuyez sur w(Oui) pour supprimer toutes les matrices en mémoire ou sur i(Non)
pour abandonner l’opération en cours sans rien supprimer.
2-8-4
Calculs matriciels
# L’indication “None” apparaît à la place des
dimensions de la matrice que vous avez
supprimée.
# La saisie du format ou le changement de
dimensions d’une matrice aura pour effet d’en
supprimer le contenu.

19990401
kOpérations sur les éléments d’une matrice
Procédez de la manière suivante pour préparer une matrice avant d’effectuer une opération.
1. Quand la liste de matrices est à l’écran, utilisez f et c pour mettre le nom de la
matrice que vous voulez utiliser en surbrillance.
Vous pouvez sauter à une matrice particulière en indiquant la lettre du nom de la
matrice. Si vous indiquez ai(N), par exemple, vous sauterez à la matrice N.
Pour accéder la mémoire de matrice, appuyez sur !-(Ans).
2. Appuyez sur w pour faire apparaître le menu de fonctions contenant les paramètres
suivants.
• {EDIT} ... {écran d’édition d’éléments}
• {R-OP} ... {menu d’opérations sur les lignes}
• {R • DEL}/{R • INS}/{R • ADD} ... {suppression}/{insertion}/{addition} de lignes
• {C • DEL}/{C • INS}/{C • ADD} ... {suppression}/{insertion}/{addition} de colonnes
Tous les exemples précédents utilisent la matrice A.
u Calculs sur les lignes
Le menu suivant apparaît si vous appuyez sur 2(R-OP) quand une matrice que vous avez
rappelée est à l’écran.
• {Swap} ... {échange de lignes}
• {×Row} ... {produit scalaire d’une ligne donnée}
• {×Row+} ... {addition du produit scalaire d’une ligne donnée et d’une autre ligne}
• {Row+} ... {addition d’une ligne désignée et d’une autre ligne}
u Pour échanger deux lignes
Exemple Échanger les lignes deux et trois de la matrice suivante:
12
Matrice A = 34
56
2(R-OP)b(Swap)
Indiquez le numéro des lignes que vous voulez échanger.
cwdw
6(EXE) (ouw)
2-8-5
Calculs matriciels
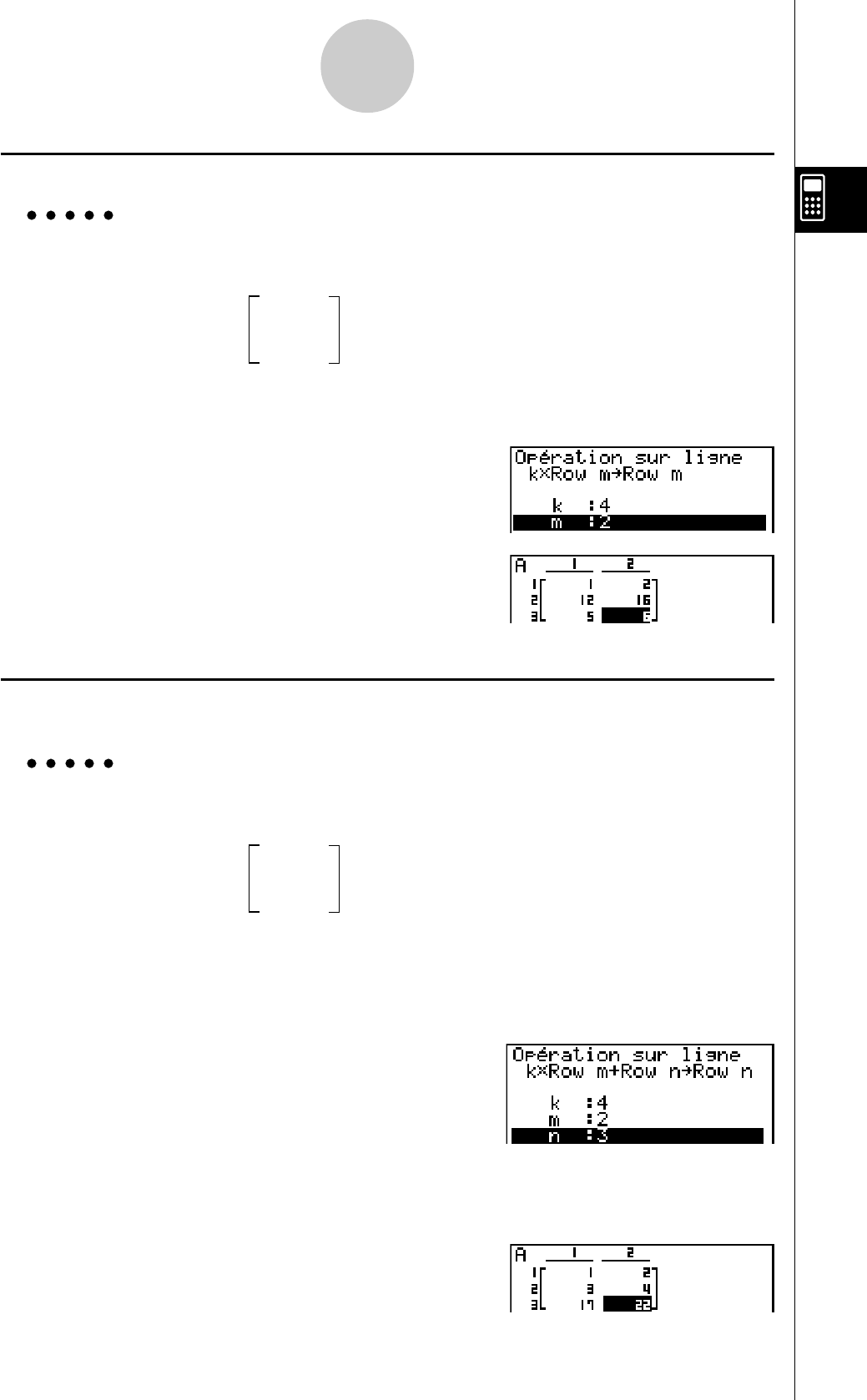
19990401
uu
uu
u Pour calculer le produit scalaire d’une ligne
Exemple Calculer le produit scalaire de la ligne 2 de la matrice suivante en la
multipliant par 4:
12
Matrice A = 34
56
2(R-OP)c(×Row)
Indiquez la valeur du multiplicateur.
ew
Désignez le numéro de la ligne.
cw
6(EXE) (ouw)
uu
uu
u Pour calculer le produit scalaire d’une ligne et ajouter le résultat à une
autre ligne
Exemple Calculer le produit scalaire de la ligne 2 de la matrice suivante en la
multipliant par 4 et ajouter le résultat à ligne 3:
12
Matrice A = 34
56
2(R-OP)d(×Row+)
Indiquez la valeur du multiplicateur.
ew
Désignez le numéro de la ligne dont le produit scalaire
doit être calculé.
cw
Désignez le numéro de la ligne dont le résultat doit
être ajouté.
dw
6(EXE) (ouw)
2-8-6
Calculs matriciels
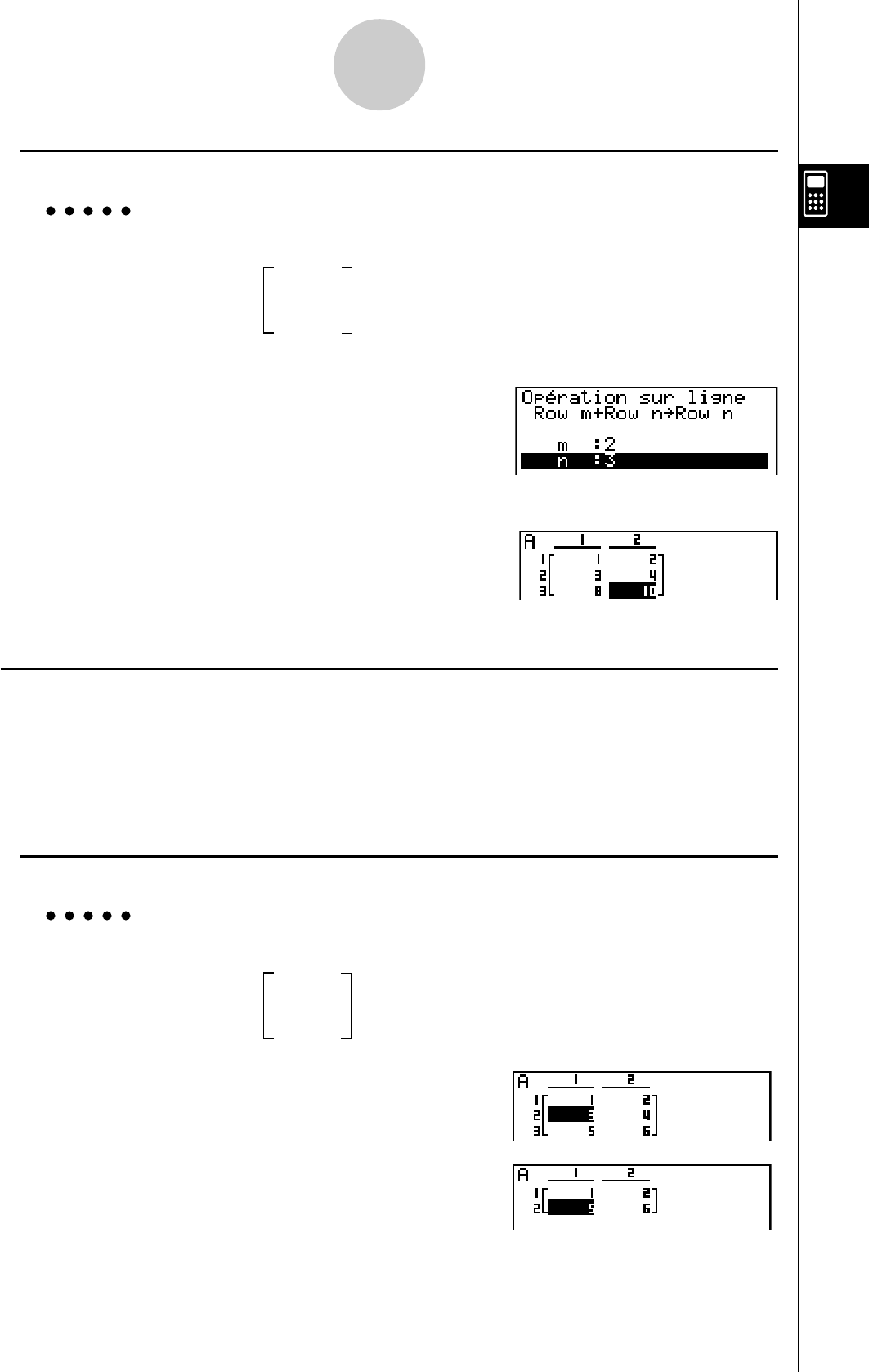
19990401
u Pour additionner deux lignes
Exemple Ajouter la ligne 2 à la ligne 3 de la matrice suivante:
12
Matrice A = 34
56
2(R-OP)e(Row+)
Désignez le numéro de la ligne que vous ajoutez.
cw
Désignez le numéro de la ligne à laquelle vous ajoutez
la première ligne.
dw
6(EXE) (ouw)
u Opérations sur les lignes
• {R • DEL} ... {suppression d’une ligne}
• {R • INS} ... {insertion d’une ligne}
• {R • ADD} ... {addition d’une ligne}
u Pour supprimer une ligne
Exemple Supprimer la ligne 2 de la matrice suivante:
12
Matrice A = 34
56
c
3(R • DEL)
2-8-7
Calculs matriciels
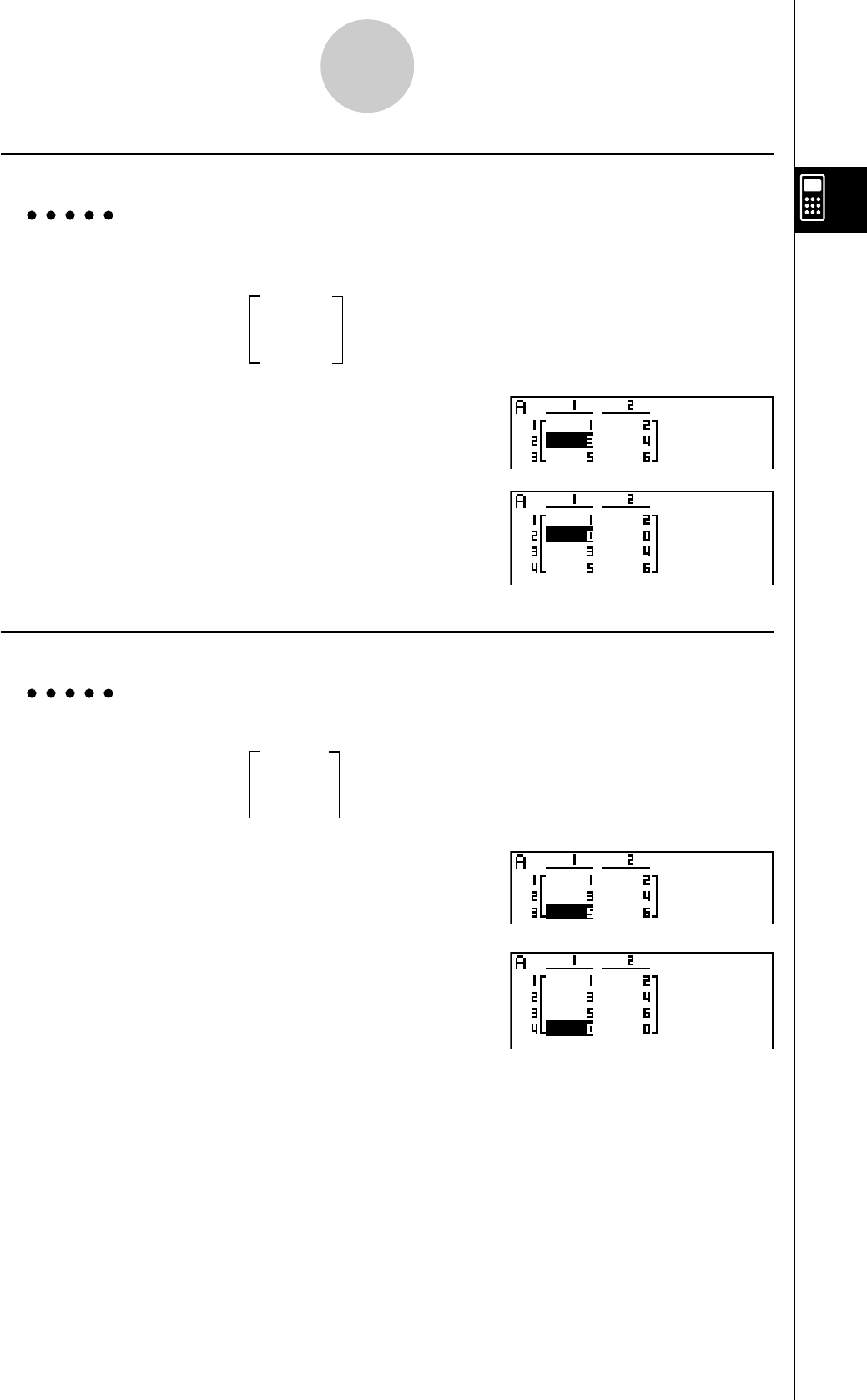
19990401
u Pour insérer une ligne
Exemple Insérer une nouvelle ligne entre les lignes une et deux de la matrice
suivante:
12
Matrice A = 34
56
c
4(R • INS)
u Pour ajouter une ligne
Exemple Ajouter une nouvelle ligne sous la ligne 3 de la matrice suivante:
12
Matrice A = 34
56
cc
5(R • ADD)
2-8-8
Calculs matriciels
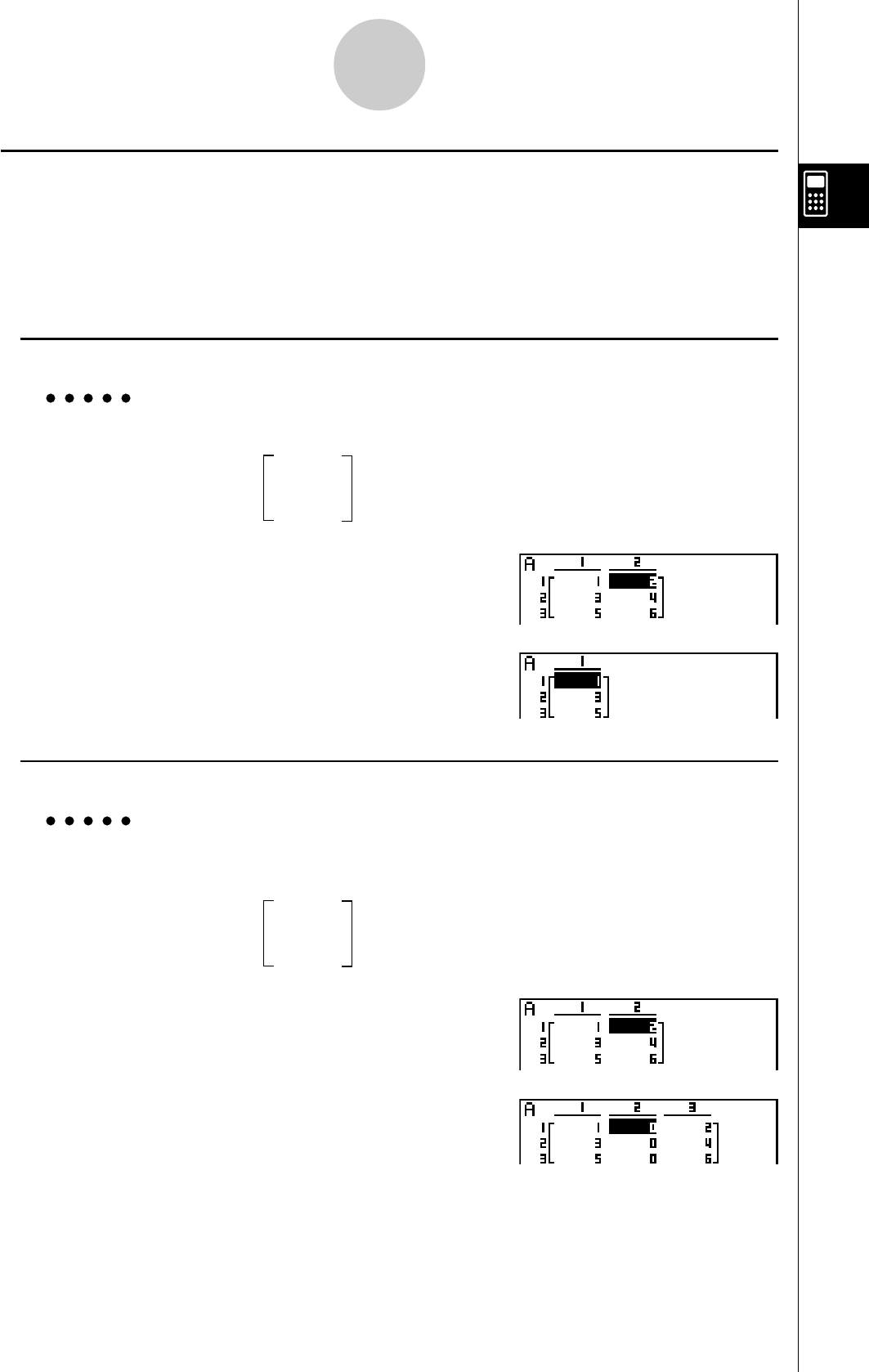
19990401
2-8-9
Calculs matriciels
uOpérations sur les colonnes
• {C • DEL} ... {suppression d’une colonne}
• {C • INS} ... {insertion d’une colonne}
• {C • ADD} ... {addition d’une colonne}
u Pour supprimer une colonne
Exemple Supprimer la colonne 2 de la matrice suivante:
12
Matrice A = 34
56
e
6(g)1(C • DEL)
u Pour insérer une colonne
Exemple Insérer une nouvelle colonne entre les colonnes une et deux de la
matrice suivante:
12
Matrice A = 34
56
e
6(g)2(C • INS)
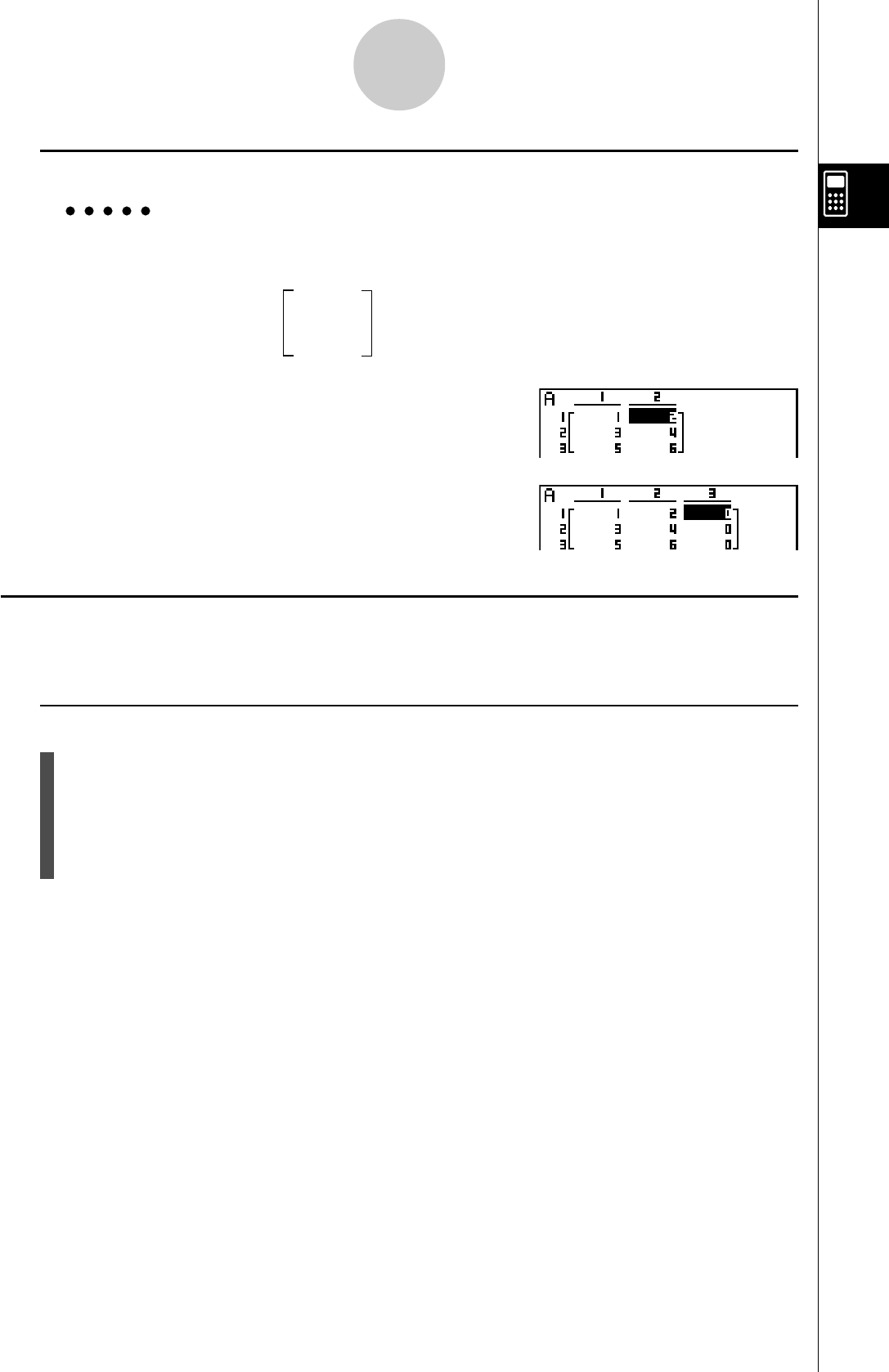
19990401
u Pour ajouter une colonne
Exemple Ajouter une nouvelle colonne à droite de la colonne 2 de la matrice
suivante:
12
Matrice A = 34
56
e
6(g)3(C • ADD)
kModification de matrices à l’aide des commandes de matrice
[OPTN]-[MAT]
u Pour afficher les commandes de matrice
1. A partir du menu principal, accédez au mode RUN • MAT.
2. Appuyez sur K pour afficher le menu d’options.
3. Appuyez sur 2(MAT) pour afficher le menu de commandes de matrice.
Vous trouverez ici seulement les paramètres du menu de commandes qui sont utilisés pour
la création d’une matrice et pour l’introduction de données dans cette matrice.
• {Mat} ... {commande Mat (désignation de la matrice)}
• {Dim} ... {commande Dim (contrôle de dimensions)}
• {Augmnt} ... {commande Augment (liaison de deux matrices)}
• {Ident} ... {commande Identity (introduction de matrice unité)}
• {Fill} ... {commande Fill (valeurs d’éléments identiques)}
• {M→List} ... {commande Mat→List (affectation du contenu de la colonne sélectionnée à
une liste)}
2-8-10
Calculs matriciels
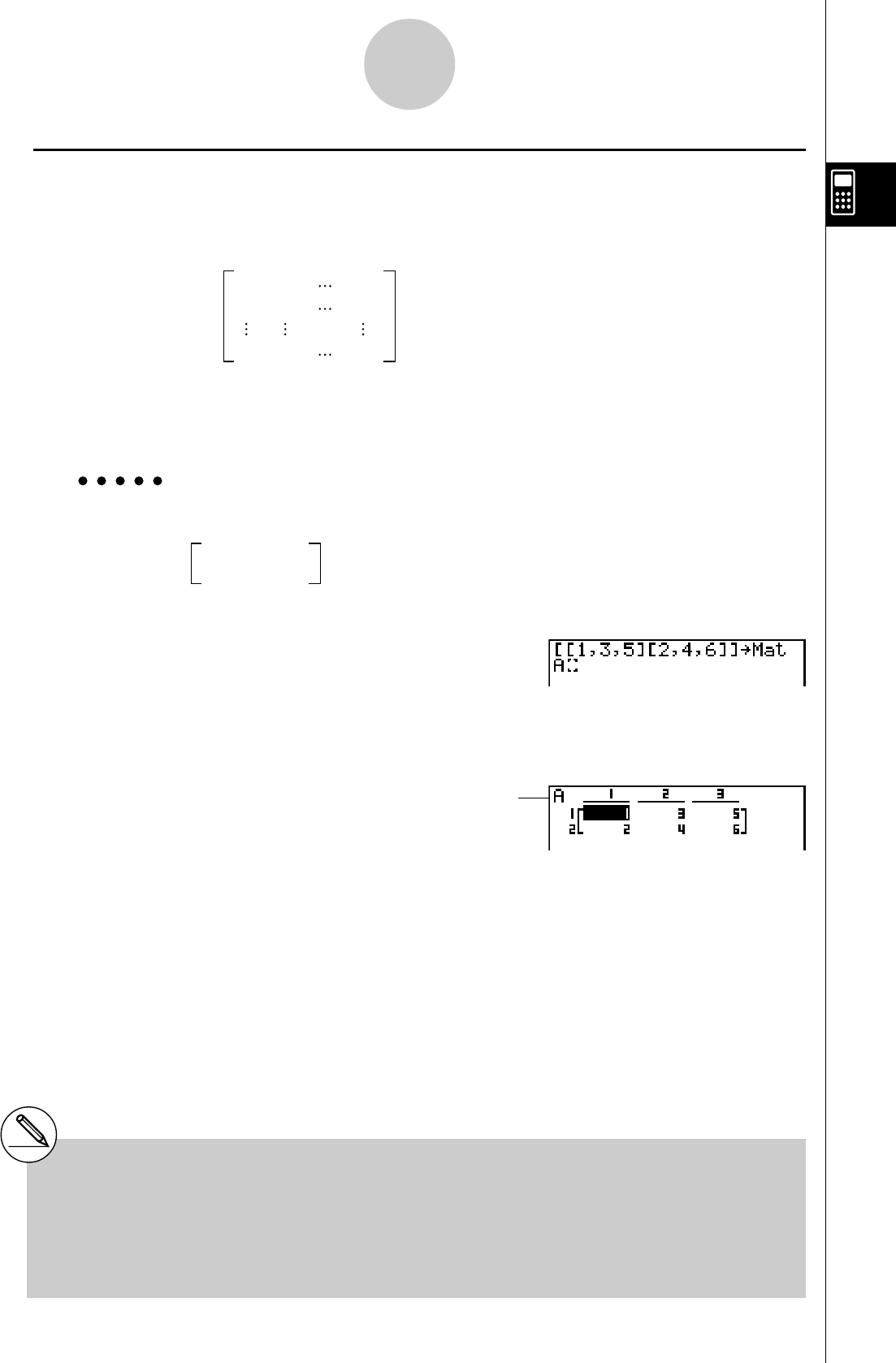
19990401
u Format d’introduction des données dans une matrice [OPTN]-[MAT]-[Mat]
Voici le format que vous devez utiliser quand vous introduisez des données pour créer une
matrice à l’aide de la commande Mat.
a11 a12 a1n
a21 a22 a2n
am1am2amn
= [ [a11, a12, ..., a1n] [a21, a22, ..., a2n] .... [am1, am2, ..., amn] ]
→ Mat [lettre de A à Z]
Exemple 1 Introduisez les données suivantes comme matrice A:
135
246
!+( [ )!+( [ )b,d,f
!-( ] )!+( [ )c,e,g
!-( ] )!-( ] )aK2(MAT)
b(Mat)av(A)
w
2-8-11
Calculs matriciels
# Vous pouvez aussi utiliser !c(Mat) au
lieu de K2 (MAT)b(Mat).
# La valeur maximale de m et n est 255.
# Une erreur se produit si la mémoire est pleine
quand vous introduisez des données.
# Vous pouvez aussi utiliser le format précédent
à l’intérieur d’un programme qui introduit des
données de matrice.
Nom de la matrice
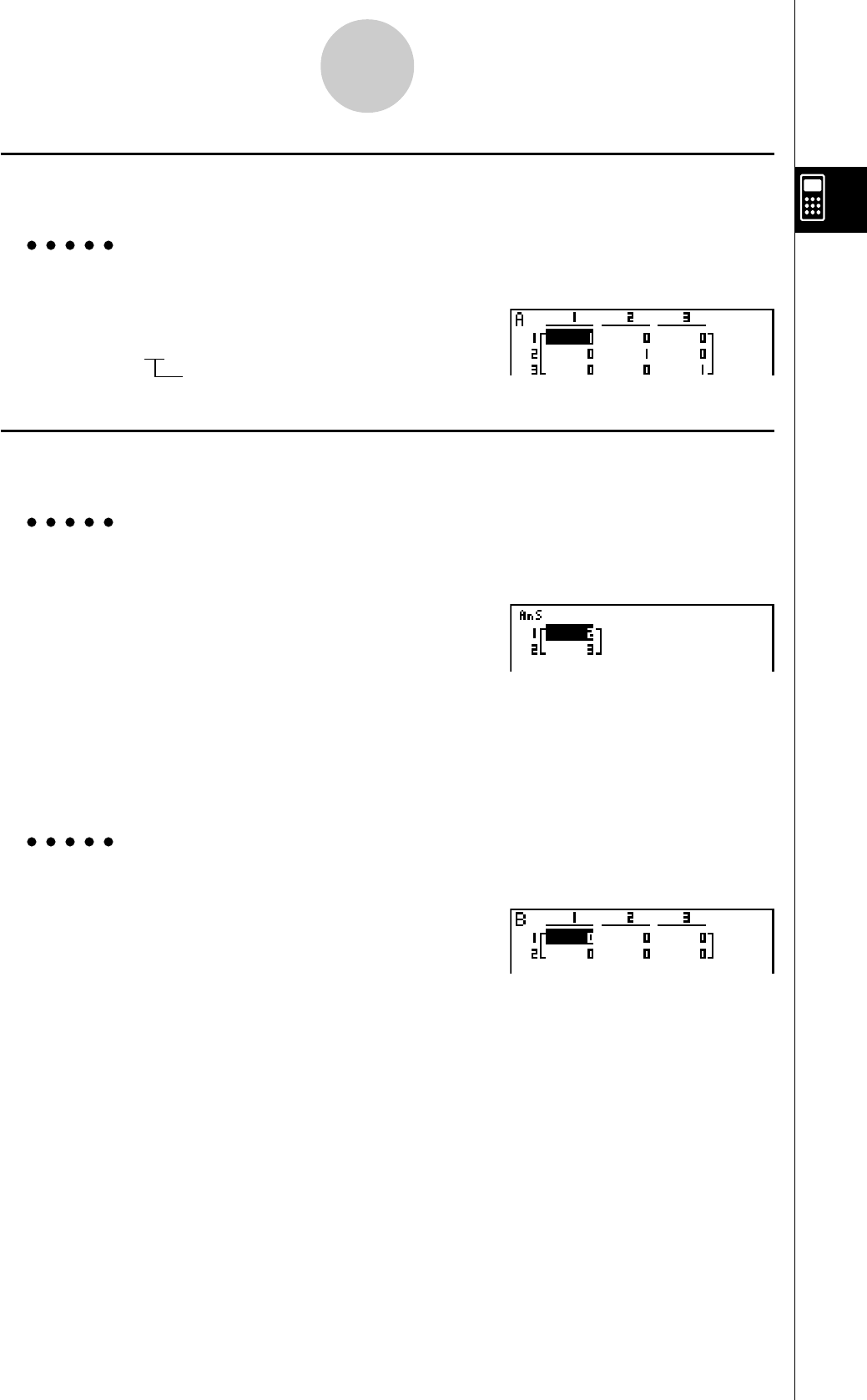
19990401
u Pour introduire une matrice unité [OPTN]-[MAT]-[Ident]
Utilisez la commande Identity pour créer une matrice unité.
Exemple 2 Créer une matrice unité 3 × 3 comme matrice A
K2(MAT)g(Ident)
da2(MAT)b(Mat)av(A)w
Nombre de lignes et colonnes
u Pour contrôler les dimensions d’une matrice [OPTN]-[MAT]-[Dim]
Utilisez la commande Dim pour contrôler les dimensions d’une matrice existante.
Exemple 3 Contrôler les dimensions de la matrice A qui a été introduite dans
l’exemple 1
K2(MAT)c(Dim)
2(MAT)b(Mat)av(A)w
L’affichage indique que la matrice A comprend deux lignes et trois colonnes.
Vous pouvez aussi utiliser {Dim} pour définir les dimensions d’une matrice.
Exemple 4 Définir une matrice de 2 lignes et de 3 colonnes pour la matrice B
!*( )c,d!/( )a
K2(MAT)c(Dim)
2(MAT)b(Mat)al(B)w
2-8-12
Calculs matriciels
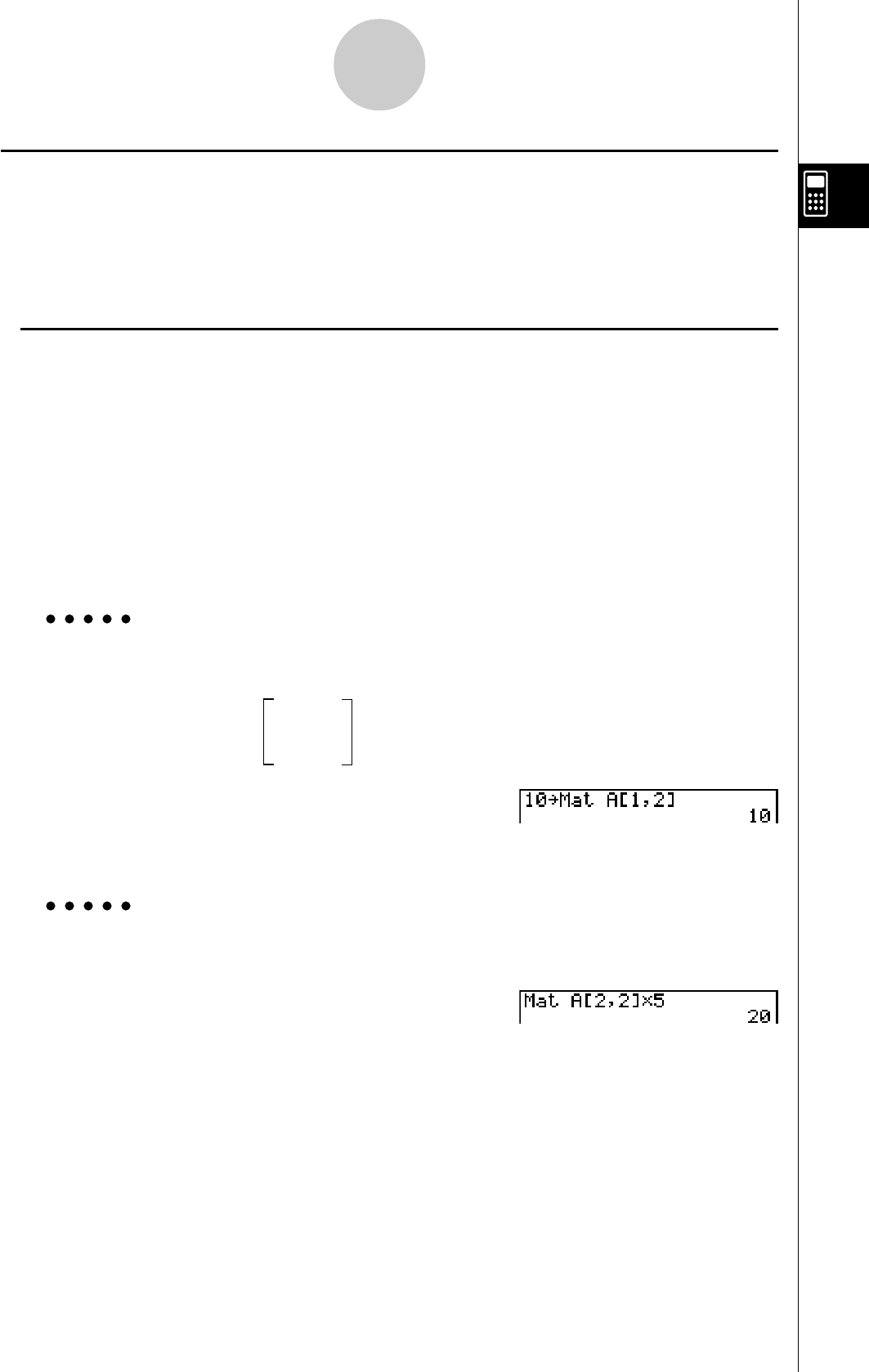
19990401
uModification d’une matrice à l’aide des commandes de matrice
Vous pouvez aussi utiliser les commandes de matrice pour affecter des valeurs à une
matrice et rappeler des valeurs d’une matrice existante, remplir tous les éléments d’une
matrice existante par la même valeur, combiner deux matrices en une seule matrice et
affecter le contenu d’une matrice à une liste.
u Pour affecter ou rappeler des valeurs d’une matrice existante
[OPTN]-[MAT]-[Mat]
Utilisez le format suivant avec la commande Mat pour désigner l’élément auquel ou duquel
une valeur sera affectée ou rappelée.
Mat X [m, n]
X .................................. nom de la matrice (A à Z, ou Ans)
m................................. numéro de la ligne
n.................................. numéro de la colonne
Exemple 1 Affecter 10 à l’élément correspondant à la ligne 1 et à la colonne 2 de
la matrice suivante:
12
Matrice A = 34
56
baaK2(MAT)b(Mat)
av(A)!+( )b,c
!-( )w
Exemple 2 Multiplier par 5 la valeur de l’élément correspond à la ligne 2 et à la
colonne 2 de la matrice précédente
K2(MAT)b(Mat)
av(A)!+( )c,c
!-( )*fw
2-8-13
Calculs matriciels
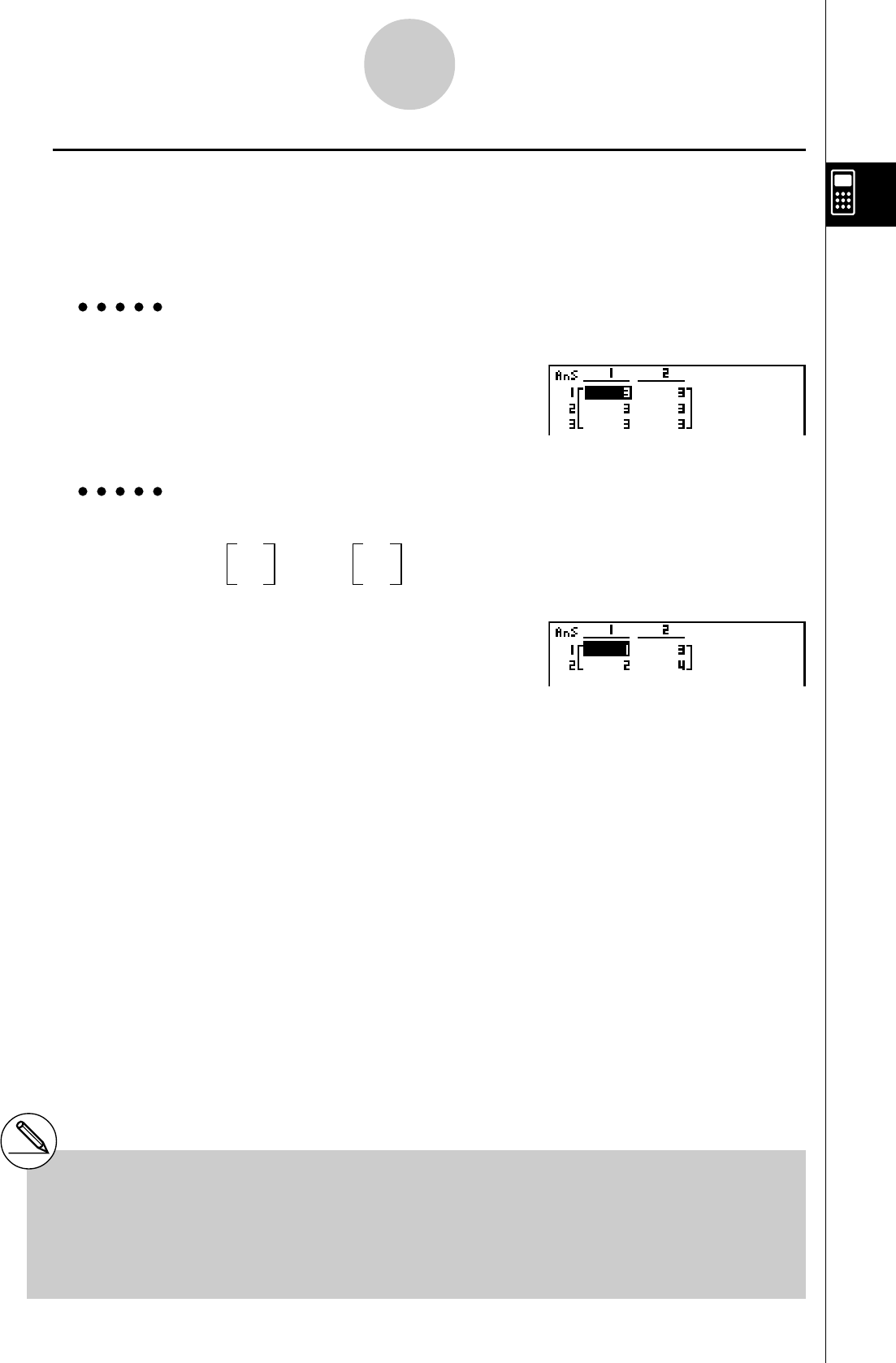
19990401
uu
uu
uPour remplir une matrice par des valeurs identiques et combiner deux
matrices en une seule [OPTN]-[MAT]-[Fill]/[Augmnt]
Utilisez la commande Fill pour remplir tous les éléments d’une matrice existante par une
valeur identique et la commande Augment pour combiner deux matrices existantes en une
seule.
Exemple 1 Remplir tous les éléments de la matrice A par la valeur 3
K2(MAT)h(Fill)
d,2(MAT)b(Mat)av(A)w
2(MAT)b(Mat)av(A)w
Exemple 2 Combiner les deux matrices suivantes:
A = 1B = 3
24
K2(MAT)f(Augmnt)
2(MAT)b(Mat)av(A),
2(MAT)b(Mat)al(B)w
2-8-14
Calculs matriciels
# Les deux matrices que vous combinez
doivent avoir le même nombre de lignes. Une
erreur se produit si vous essayez de
combiner deux matrices qui ont deux
nombres de lignes différents.
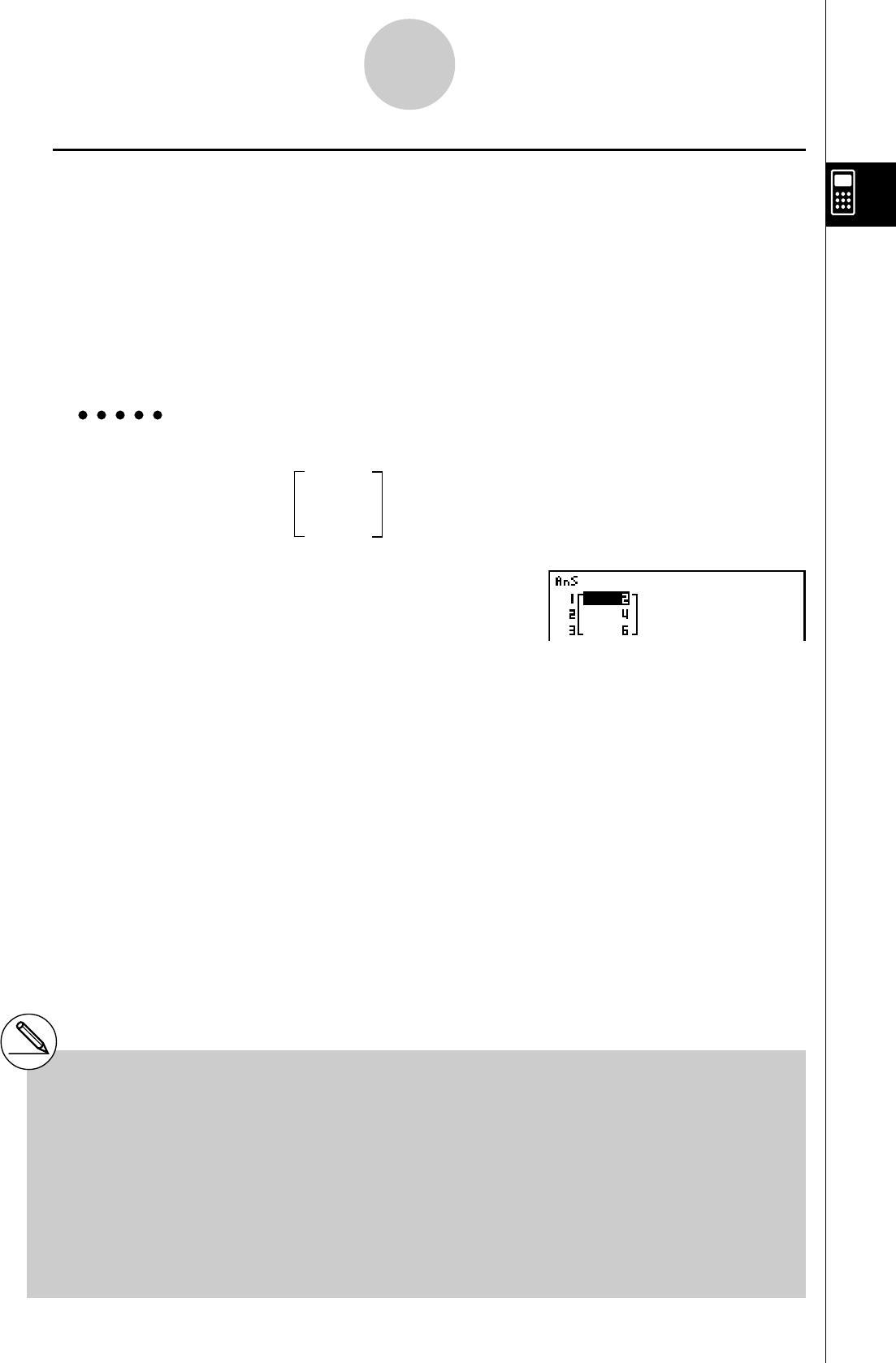
19990401
uu
uu
uPour affecter le contenu d’une colonne à une liste
[OPTN]-[MAT]-[M→List]
Utilisez le format suivant avec la commande Mat→List pour affecter une colonne et une liste.
Mat → List (Mat X, m) → List n
X = nom de la matrice (A à Z, ou Ans)
m = numéro de la colonne
n = numéro de la liste
Exemple Affecter le contenu de la colonne 2 de la matrice suivante à la liste 1:
12
Matrice A = 34
56
K2(MAT)i(M→List)
2(MAT)b(Mat)av(A),c)
aK1(LIST)b(List)bw
K1(LIST)b(List)w
# Vous pouvez aussi utiliser !b(List) au lieu
de K1(LIST)b(List).
# Vous pouvez utiliser la mémoire matricielle de
dernier résultat pour affecter les résultats de
l’entrée précédente et effectuer des
changements sur une variable de matrice.
Pour ce faire, utilisez la syntaxe suivante.
• Fill (n, Mat
α
) → Mat
β
• Augment (Mat
α
, Mat
β
) → Mat
γ
2-8-15
Calculs matriciels
Ici,
α
,
β
, et
γ
sont des noms de variables A à Z
et n est une valeur quelconque.
L’opération précédente n’affecte pas le contenu
de la mémoire matricielle de dernier résultat.

19990401
kCalculs matriciels [OPTN]-[MAT]
Utilisez le menu de commandes de matrice pour effectuer des calculs matriciels.
u Pour afficher les commandes de matrice
1. A partir du menu principal, accédez au mode RUN • MAT.
2. Appuyez sur K pour afficher le menu d’options.
3. Appuyez sur 2(MAT) pour afficher le menu de commandes de matrice.
Seules les commandes de matrice qui sont utilisées pour les opérations arithmétiques sont
décrites ici.
• {Mat} ... {commande Mat (désignation de la matrice)}
• {Det} ... {commande Det (commande de déterminant)}
• {Trn} ... {commande Trn (commande de transposition de matrice)}
• {Ident} ... {commande Identity (entrée de matrice unité)}
Tous les exemples suivants présupposent que les données matricielles sont déjà
enregistrées dans la mémoire.
2-8-16
Calculs matriciels
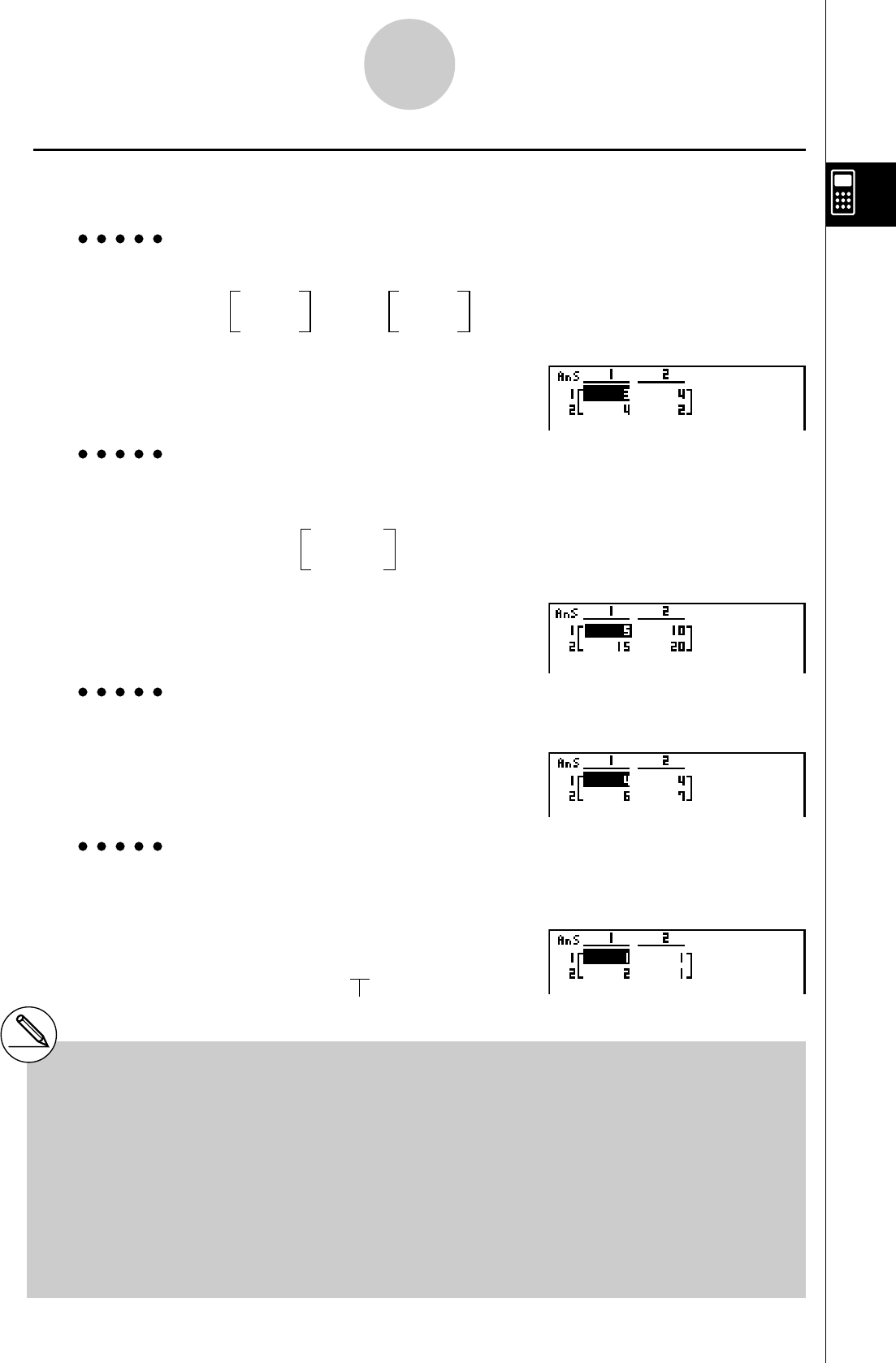
19990401
uOpérations arithmétiques sur une matrice [OPTN]-[MAT]-[Mat]
Exemple 1 Additionner les deux matrices suivantes (matrice A + matrice B) :
A = 11 B = 23
21 21
AK2(MAT)b(Mat)av(A)+
2(MAT)b(Mat)al(B)w
Exemple 2 Calculer le produit scalaire de la matrice suivante en utilisant le
multiplicateur 5:
Matrice A = 12
34
AfK2(MAT)b(Mat)
av(A)w
Exemple 3 Multiplier les deux matrices de l’exemple 1 (matrice A × matrice B)
AK2(MAT)b(Mat)av(A)*
2(MAT)b(Mat)al(B)w
Exemple 4 Multiplier la matrice A (de l’exemple 1) par une matrice unité de
dimensions 2 × 2
AK2(MAT)b(Mat)av(A)*
2(MAT)g(Ident)cw
Nombre de lignes et de colonnes
# Les deux matrices doivent avoir les
mêmes dimensions pour que vous
puissiez les additionner ou les soustraire.
Une erreur se produit si vous essayez
d’additionner ou de soustraire des
matrices de dimensions différentes.
# Pour la multiplication (matrice 1 × matrice 2)
le nombre de colonnes de la matrice 1 doit
être égal au nombre de lignes de la matrice 2,
sinon une erreur se produit.
2-8-17
Calculs matriciels
# Lorsque vous effectuez des opérations
arithmétiques sur une matrice, la saisie de la
commande d’unité à l’emplacement de la
commande de la matrice (comme MAT A) permet
d’effectuer des calculs de matrice unité.
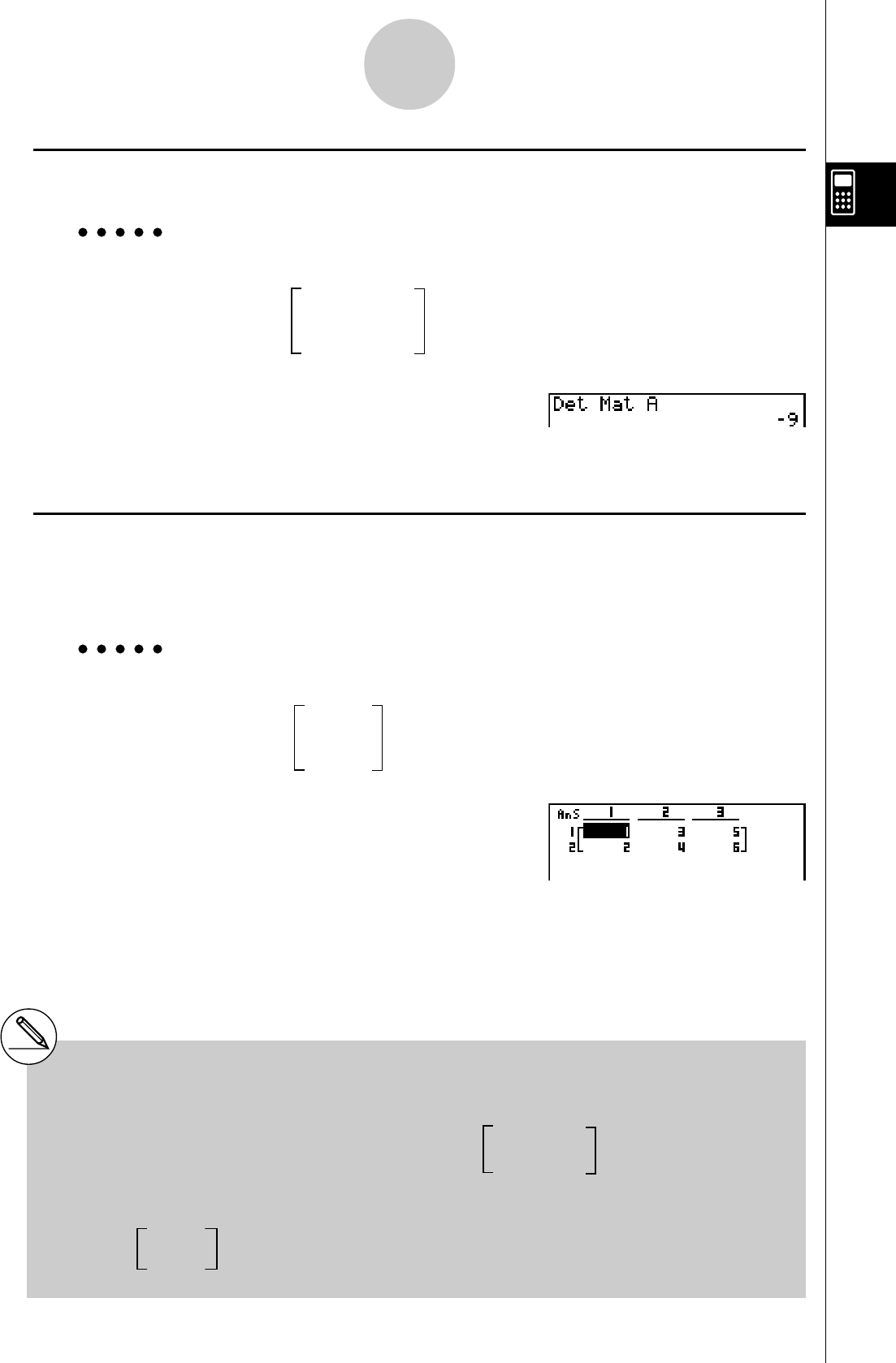
19990401
uDéterminant [OPTN]-[MAT]-[Det]
Exemple Obtenir le déterminant de la matrice suivante:
123
Matrice A = 456
–1 –2 0
K2(MAT)d(Det)2(MAT)b(Mat)
av(A)w
uTransposition de matrice [OPTN]-[MAT]-[Trn]
Une matrice est transposée quand ses lignes deviennent les colonnes et ses colonnes
deviennent les lignes.
Exemple Transposer la matrice suivante:
12
Matrice A = 34
56
K2(MAT)e(Trn)2(MAT)b(Mat)
av(A)w
2-8-18
Calculs matriciels
# Les déterminants ne peuvent être obtenus
que pour les matrices carrées (même nombre
de lignes et de colonnes). Si vous essayez
d’obtenir un déterminant pour une matrice qui
n’est pas carrée, une erreur se produira.
# Le déterminant de la matrice 2 × 2 est calculé
comme indiqué ci-dessous.
# Le déterminant de la matrice 3 × 3 est calculé
comme indiqué ci-dessous.
| A | = a11 a12 = a11a22 – a12a21
a21 a22
= a11a22a33 + a12a23a31 + a13a21a32
– a11a23a32 – a12a21a33 – a13a22a31
a11 a12 a13
a21 a22 a23
a31 a32 a33
| A | =
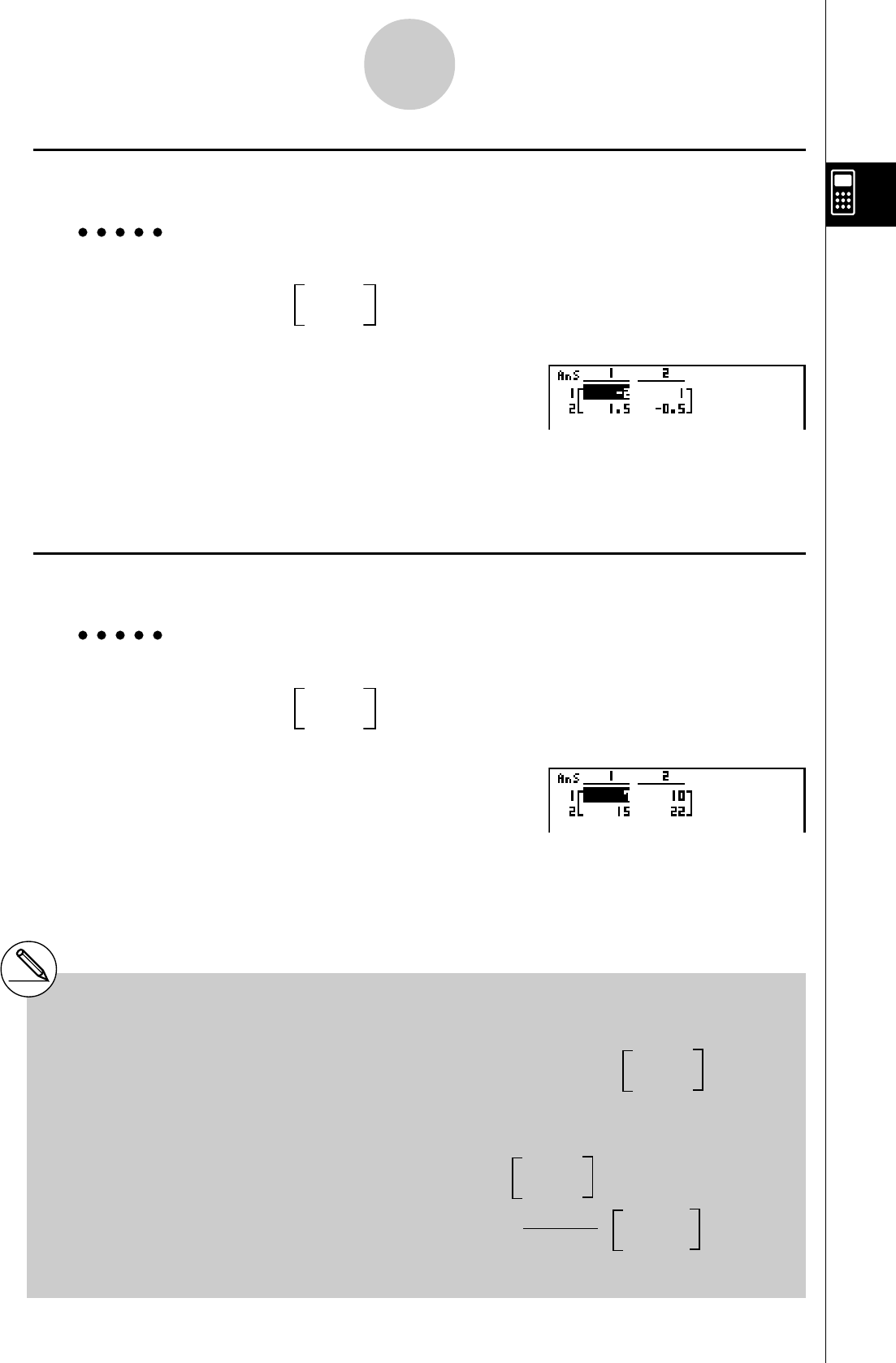
19990401
uInversion d’une matrice [OPTN]-[MAT]-[x–1]
Exemple Inverser la matrice suivante:
Matrice A = 12
34
K2(MAT)b(Mat)
av(A)!) (x–1) w
uÉlévation d’une matrice au carré [OPTN]-[MAT]-[x2]
Exemple Élever la matrice suivante au carré:
Matrice A = 12
34
K2(MAT)b(Mat)av(A)xw
2-8-19
Calculs matriciels
# Seules les matrices carrées (même nombre
de lignes et de colonnes) peuvent être
inversées. Si vous essayez d’inverser une
matrice qui n’est pas carrée, une erreur se
produira.
# Une matrice dont le déterminant est égale à
zéro ne peut pas être inversée. Si vous
essayez d’inverser une matrice dont le
déterminant est égale à zéro, une erreur se
produira.
# La précision du calcul est affectée pour les
matrices dont le déterminant est proche de
zéro.
# Une matrice inversée doit remplir les
conditions suivantes.
Voici la formule utilisée pour inverser la
matrice A en matrice inverse A–1.
A A–1 = A–1 A = E = 1 0
0 1
A = a b
c d
Notez que ad – bc G 0.
A–1=1
ad – bc
d–b
–c a
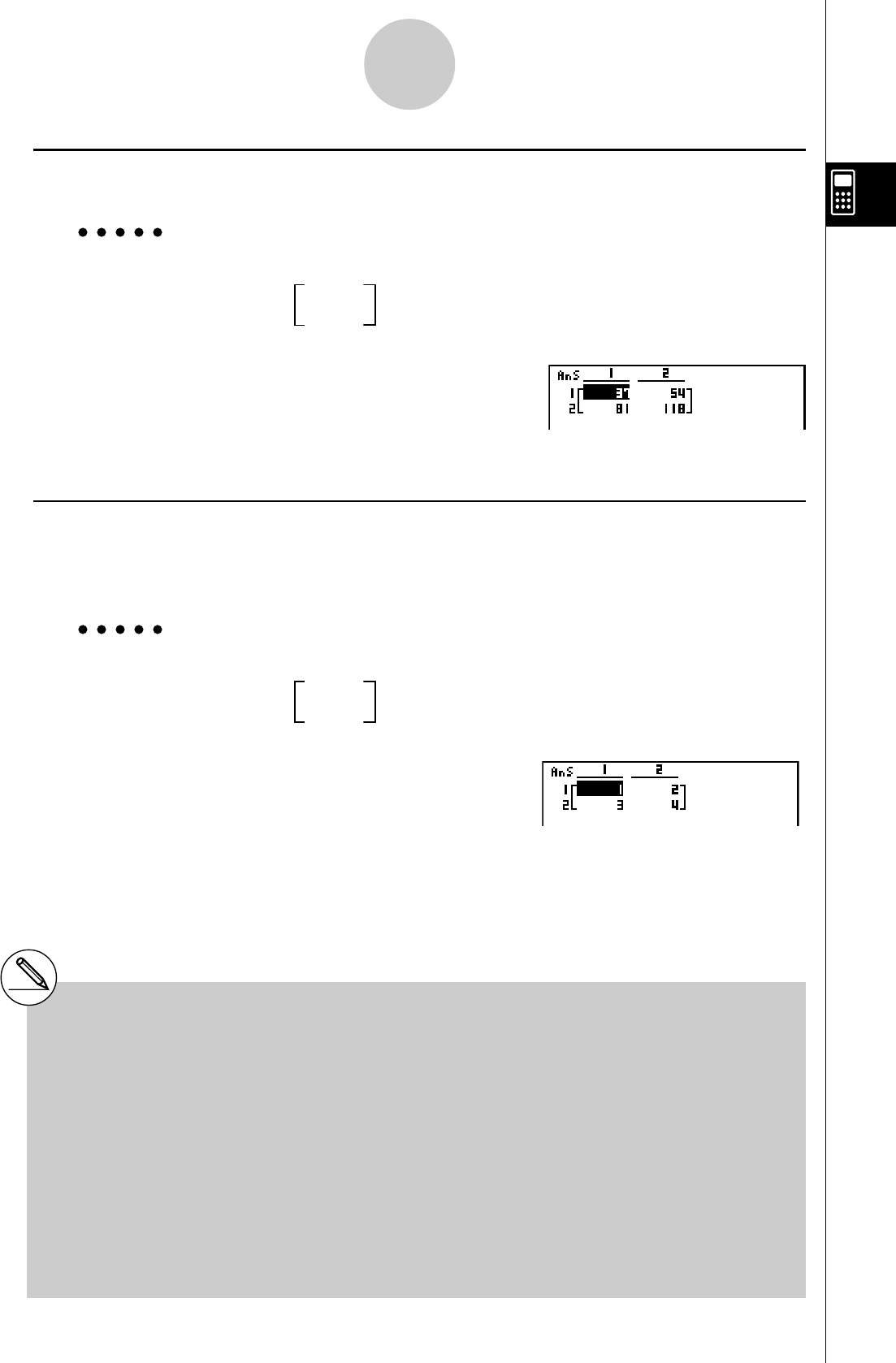
19990401
uÉlévation d’une matrice à une puissance [OPTN]-[MAT]-[
]
Exemple Élever la matrice suivante à la puissance 3:
Matrice A = 12
34
K2(MAT)b(Mat)av(A)
Mdw
uDétermination de la valeur absolue, de la partie entière, de la partie
fractionnaire et de l’entier maximal d’une matrice
[OPTN]-[NUM]-[Abs]/[Frac]/[Int]/[Intg]
Exemple Déterminer la valeur absolue de la matrice suivante:
Matrice A = 1–2
–3 4
K5(NUM)b(Abs)
K2(MAT)b(Mat)av(A)w
2-8-20
Calculs matriciels
^
# Les déterminants et les matrices inverses
sont sujets à erreur à cause des chiffres
tronqués.
# Les opérations sur une matrice sont
effectuées séparément pour chaque
élément, si bien que les calculs peuvent
prendre un temps considérable pour
aboutir au résultat.
# La précision de calcul des résultats
affichés pour les calculs matriciels est de
±1 au chiffre le moins significatif.
# Si le résultat d’un calcul matriciel est trop long
pour entrer dans la mémoire matricielle de
dernier résultat, une erreur se produira.
# Vous pouvez utiliser l’opération suivante pour
transférer le contenu de la mémoire matricielle
de dernier résultat dans une autre matrice (ou
quand la mémoire de réponse matricielle
contient un déterminant pour une variable).
MatAns → Mat
α
Ici,
α
est un nom de variable de A à Z.
L’opération précédente n’affecte pas le contenu
de la mémoire matricielle de dernier résultat.
19990401
Chapitre
Listes
Une liste est un lieu de stockage de données multiples.
Cette calculatrice peut contenir au maximum 6 fichiers de 20
listes chacun. Les listes pourront être utilisées dans des calculs
arithmétiques et statistiques ou pour le graphisme.
3-1 Saisie et édition d’une liste (Menu STAT)
3-2 Traitement des données d’une liste (Menu RUN
•
MAT)
3-3 Calculs arithmétiques à partir de listes (Menu RUN
•
MAT)
3-4 Changement de fichiers de listes
3
List 1 List 2 List 3 List 4 List 5 List 20
1 56 1 107 3.5 4 0
2 37 2 75 6 0 0
3 21 4 122 2.1 0 0
4 69 8 87 4.4 2 0
5 40 16 298 3 0 0
64832486.8 3 0
7 93 64 338 2 9 0
8 30 128 49 8.7 0 0
••••••
••••••
••••••
••••••
Numéro d’élément Plage d’affichage Élément
Ligne
Nom de la
liste
Colonne
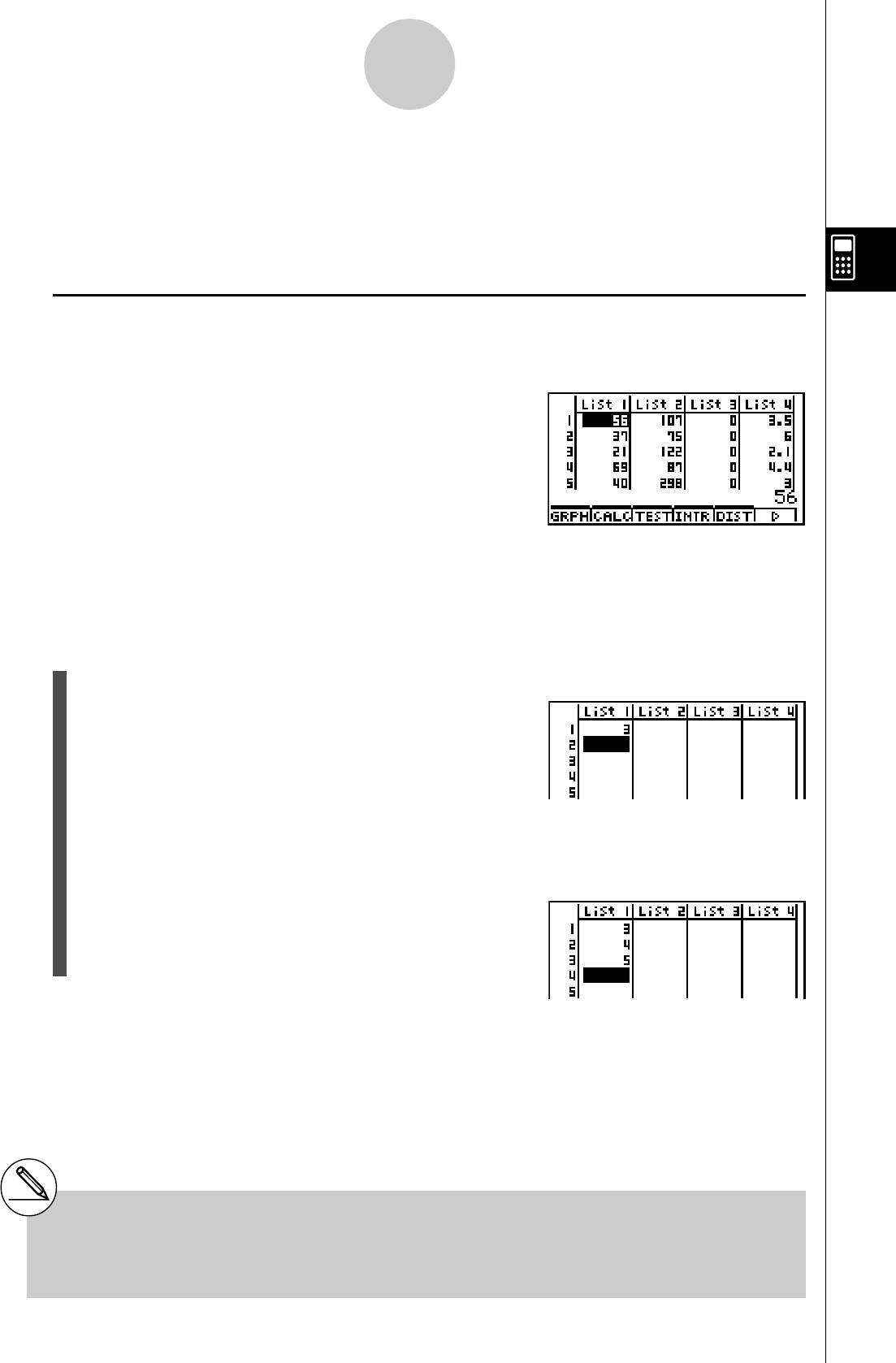
1999040120001202
3-1 Saisie et édition d’une liste (Menu STAT)
Accédez au mode STAT depuis le menu principal pour saisir des données dans une liste et
utiliser ensuite cette liste pour diverses opérations.
uu
uu
u Pour introduire des valeurs une à une
Utilisez les touches de curseur pour mettre la surbrillance sur le nom ou l’élément de la liste
que vous voulez sélectionner.
L’écran défile automatiquement quand la surbrillance atteint l’une ou l’autre extrémité de
l’écran.
Dans l’opération suivante, on part de l’élément 1 de la liste 1, qui a été mis en surbrillance.
1. Saisissez une valeur et appuyez sur w pour la stocker dans la liste.
dw
• La surbrillance va automatiquement sur l’élément
suivant.
2. Saisissez la valeur 4 dans le second élément, puis le résultat de 2 + 3 dans l’élément
suivant.
ewc+dw
3-1-1
Saisie et édition d’une liste (Menu STAT)
# Vous pouvez aussi introduire le résultat
d’une expression ou un nombre complexe
dans un élément.
# Des valeurs peuvent être écrites dans 255 éléments
d’une seule liste au maximum.

1999040120001202
uu
uu
u Pour introduire une série de valeurs
1. Utilisez les touches de curseur pour amener la surbrillance sur une autre liste.
2. Appuyez sur !*( { ), puis saisissez les valeurs souhaitées en appuyant sur ,
entre chaque valeur. Appuyez finalement sur !/( } ) après avoir saisi la dernière
valeur.
!*( { )g,h,i!/( } )
3. Appuyez sur w pour stocker toutes les valeurs dans votre liste.
w
Vous pouvez aussi utiliser des noms de listes dans une expression mathématique pour
introduire des valeurs dans un autre élément. L’exemple suivant indique comment ajouter
des valeurs sur chaque ligne des listes 1 et 2, et comment transférer le résultat dans la liste
3.
1. Utilisez les touches de curseur pour amener la surbrillance sur le nom de la liste où
vous voulez introduire le résultat du calcul.
2. Appuyez sur la touche K et introduisez l’expression.
K1(LIST)b(List)b+
K1(LIST)b(List)cw
3-1-2
Saisie et édition d’une liste (Menu STAT)
# Vous pouvez aussi utiliser !b(List) au lieu
de K1(LIST)b(List).
# Souvenez-vous qu’une virgule sépare des valeurs.
Il ne faut donc pas mettre de virgule après la
dernière valeur.
Bon: {34, 53, 78}
Mauvais: {34, 53, 78,}

1999040120001202
kk
kk
kÉdition des valeurs d’une liste
uu
uu
u Pour changer la valeur d’un élément
Utilisez d ou e pour amener la surbrillance sur l’élément dont vous voulez changer la
valeur. Introduisez la nouvelle valeur et appuyez sur w pour remplacer l’ancienne valeur
par la nouvelle.
uu
uu
u Pour éditer le contenu d’un élément
1. Utilisez les touches de curseur pour amener la surbrillance sur l’élément dont vous
voulez changer le contenu.
2. Appuyez sur 6(䉯)2(EDIT) pour afficher le contenu de l’élément au bas de l’écran.
3. Changez les données souhaitées.
uu
uu
u Pour supprimer un élément
1. Utilisez les touches de curseur pour amener la surbrillance sur l’élément que vous
voulez effacer.
2. Appuyez sur 6(䉯)3(DEL) pour supprimer l’élément sélectionné et faire remonter
toutes les valeurs qui se trouvent en dessous.
3-1-3
Saisie et édition d’une liste (Menu STAT)
# La suppression d’un élément n’affecte pas les
éléments des autres listes. Si la donnée de la
liste dont vous avez supprimé un élément est
en relation avec des données de listes voisines,
la suppression d’un élément peut causer un
mauvais alignement des valeurs
correspondantes.
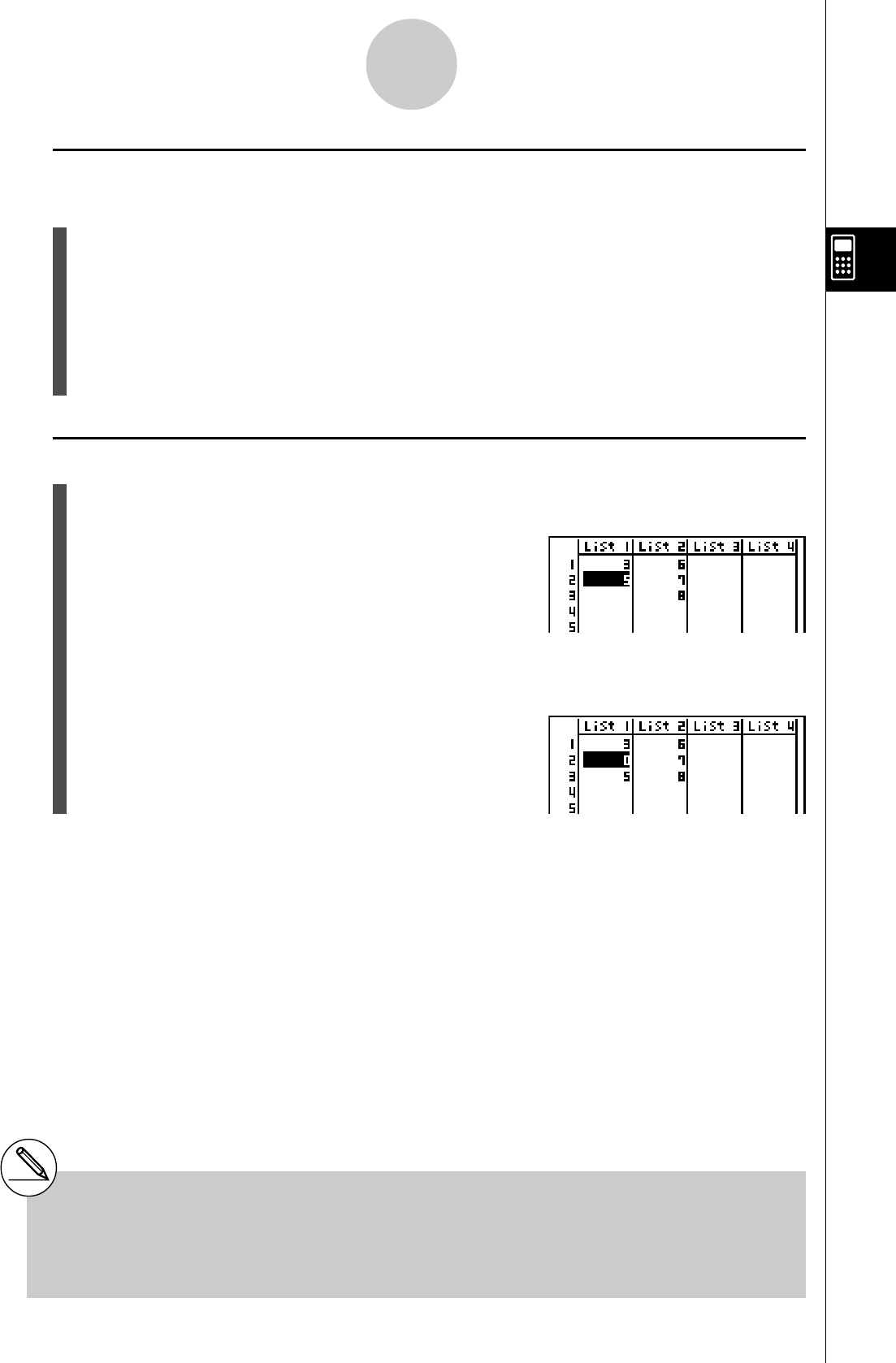
1999040120001202
uu
uu
u Pour supprimer tous les éléments d’une liste
Procédez comme suit pour supprimer toutes les données d’une liste.
1. Utilisez les touches de curseur pour amener la surbrillance sur un élément quelconque
de la liste dont vous voulez supprimer les données.
2. Lorsque vous appuyez sur 6(䉯)4(DEL
•
A), un message de confirmation apparaît.
3. Appuyez sur w(Oui) pour supprimer tous les éléments de la liste sélectionnée ou sur
i(Non) pour abandonner l’opération sans rien supprimer.
uu
uu
uPour insérer un nouvel élément
1. Utilisez les touches de curseur pour amener la surbrillance à l’endroit où vous voulez
insérer un nouvel élément.
2. Appuyez sur 6(䉯)5(INS) pour insérer un nouvel élément, qui contient la valeur 0.
Tout ce qui se trouve en dessous est décalé vers le bas.
# L’insertion d’un élément n’affecte pas les
éléments des autres listes. Si la donnée de la
liste où vous avez inséré un élément est en
relation avec des données de listes voisines,
3-1-4
Saisie et édition d’une liste (Menu STAT)
l’insertion d’un élément peut être à l’origine d’un
mauvais alignement des valeurs
correspondantes.

1999040120001202
kk
kk
kClassement des valeurs d’une liste
Les valeurs d’une liste peuvent être classées par ordre ascendant ou descendant.
La surbrillance peut se trouver dans n’importe quel élément de la liste.
uu
uu
u Pour classer une seule liste
Ordre ascendant
1. Quand les listes sont à l’écran, appuyez sur 6(䉯)1(TOOL)b(SortA).
2. Le message “Combien de listes?: ” apparaît pour vous demander combien de listes
vous voulez classer. Nous indiquons ici 1 car une seule liste doit être classée.
bw
3. Pour répondre au message “Sélectionner la liste List No: ” indiquez le numéro de la
liste qui doit être classée. Nous indiquons ici 2 pour désigner la liste 2.
bw
Ordre descendant
Procédez de même que pour le classement dans l’ordre ascendant. Vous devez
seulement appuyer sur c(SortD) au lieu de b(SortA).
3-1-5
Saisie et édition d’une liste (Menu STAT)
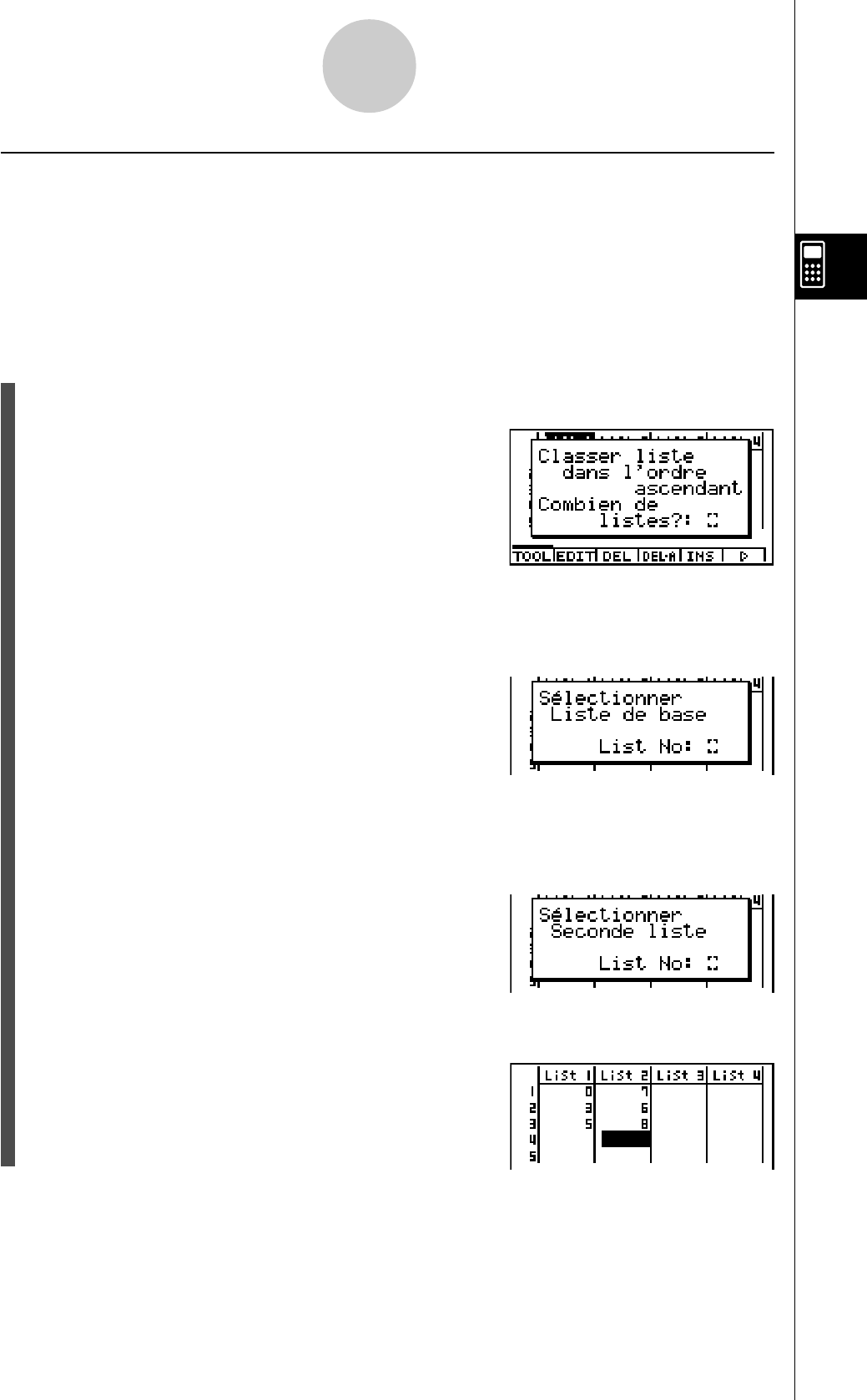
1999040120001202
uu
uu
u Pour classer plusieurs listes
Vous pouvez mettre en relation plusieurs listes pour les classer de sorte que tous leurs
éléments soient arrangés en fonction d’une liste servant de référence. La liste de référence
est classée dans l’ordre ascendant ou descendant, et les éléments des listes qui sont en
relation sont mis en ordre mais de manière à maintenir le lien qui existe entre toutes les
lignes.
Ordre ascendant
1. Quand les listes sont à l’écran, appuyez sur 6(䉯)1(TOOL)b(SortA).
2. Le message “Combien de listes?: ” apparaît pour vous demander combien de listes
vous voulez classer. Nous allons classer une liste de référence en relation avec une
autre liste, donc nous indiquons 2.
cw
3. Pour répondre au message “Sélectionner Liste de base List No: ”, indiquez le numéro
de la liste de référence pour la classer dans l’ordre ascendant. Ici nous désignons la liste
1.
bw
4. Pour répondre au message “Sélectionner Seconde liste List No: ”, indiquez le numéro
de la liste que vous voulez mettre en relation. Ici nous désignons la liste 2.
cw
3-1-6
Saisie et édition d’une liste (Menu STAT)
19990401
3-1-7
Saisie et édition d’une liste (Menu STAT)
Ordre descendant
Procédez de la même façon que pour le classement dans l’ordre ascendant. Mais vous
devez appuyer sur c(SortD) à la place de b(SortA).
# Vous pouvez désigner une valeur de 1 à 6 pour
le nombre de listes à classer.
# Si vous désignez plus d’une fois une liste pour un
seul classement, une erreur se produira.
Une erreur se produira également si les listes
devant être classées n'ont pas le même nombre
de valeurs (lignes).
# Si vous désignez la valeur 0 comme nombre de
listes, toutes les listes du fichier seront
classées. Dans ce cas, vous désignez une liste
de base d’après laquelle toutes les autres listes
du fichier seront classées.

19990401
3-2 Traitement des données d’une liste
(Menu RUN
•
MAT)
Les données des listes peuvent être utilisées dans les calculs arithmétiques et de fonctions.
Différentes fonctions permettent de traiter facilement et rapidement les données des listes.
Vous pouvez utiliser les fonctions de traitement de données dans les modes RUN
•
MAT,
STAT
,
GRPH
•
TBL
,
EQUA de traitement des données de listes et PRGM.
kk
kk
k Accès au menu de fonctions
Tous les exemples suivants sont exécutés à partir du mode RUN
•
MAT.
Appuyez sur K puis sur 1(LIST) pour afficher le menu de traitement des données de
listes qui contient les paramètres suivants.
•{List}/{Dim}/{Seq}/{Min}/{Max}/{Mean}/{Median}/{Sum}/{Prod}/{Cuml}/{%}/{AA
AA
AList}/
{Augmnt}/{Fill}/{L→Mat}
Notez que toutes les fermetures de parenthèses à la fin des opérations suivantes peuvent
être omises.
u Pour compter le nombre de paramètres de données dans une liste
[OPTN]-[LIST]-[Dim]
K1(LIST)c(Dim)1(LIST)b(List) <numéro de liste 1-20> w
• La dimension d’une liste désigne le nombre d’éléments de cette liste.
Exemple Compter le nombre de valeurs dans la liste 1 (36, 16, 58, 46, 56)
AK1(LIST)c(Dim)
1(LIST)b(List)bw
u Pour créer une liste ou une matrice en désignant le nombre de données
[OPTN]-[LIST]-[Dim]
Procédez de la façon suivante pour désigner le nombre de données dans l’instruction
d’affectation et créer une liste.
<nombre de données n>aK1(LIST)c(Dim)1(LIST)b(List)
<numéro de liste 1-20>w
n = 1 ~ 255
3-2-1
Traitement des données d’une liste (Menu RUN
•
MAT)
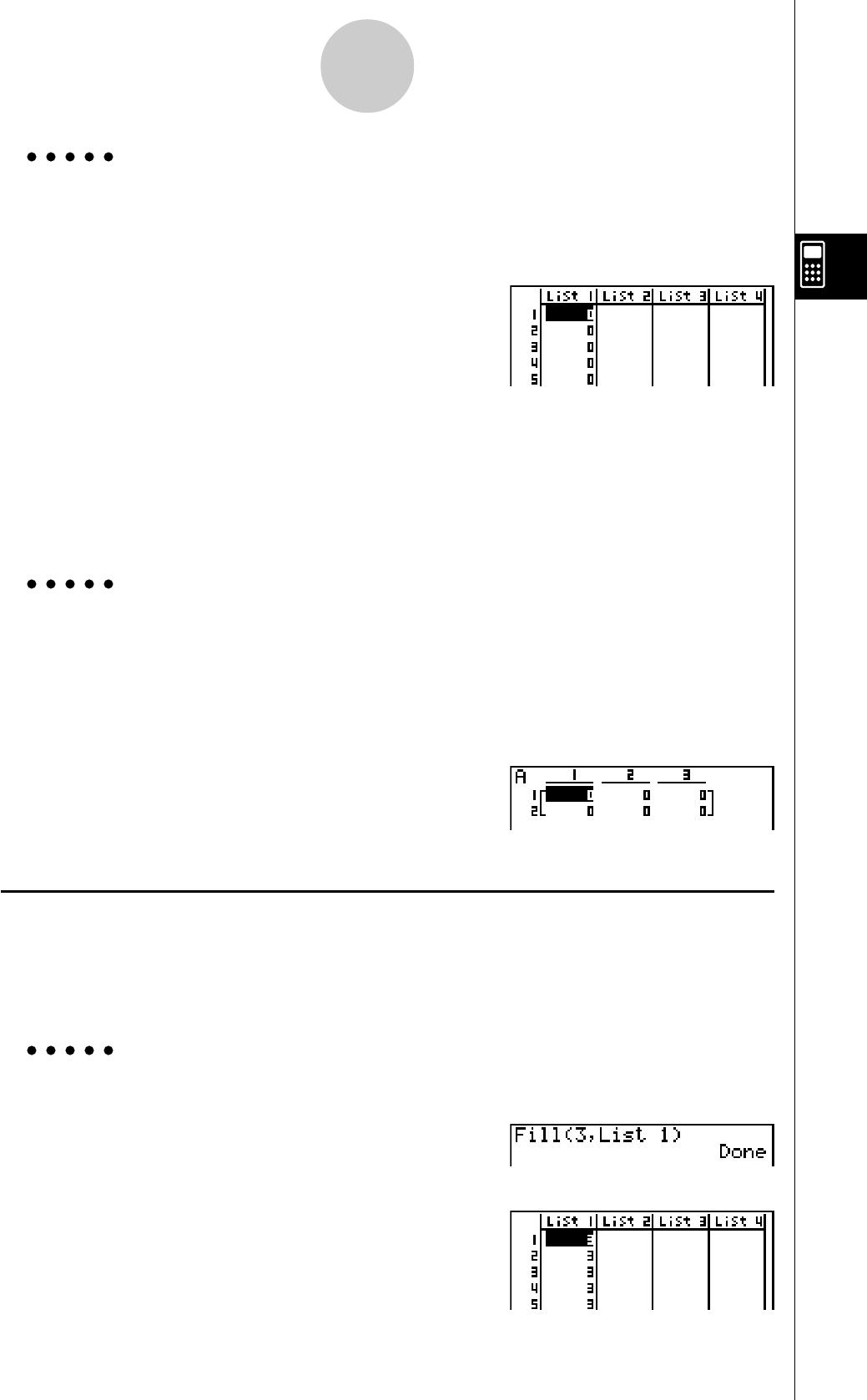
19990401
Exemple Créer cinq données (chacune d’elles contenant 0) dans la liste 1
AfaK1(LIST)c(Dim)
1(LIST)b(List) bw
Vous pouvez voir la liste créée en accédant au
mode STAT.
Procédez de la façon suivante pour désigner le nombre de lignes et de colonnes de données
et le nom de la matrice dans l’instruction d’affectation puis créer une matrice.
!*( { )<nombre de lignes m> ,<nombre de colonnes n> !/( } )a
K1(LIST)c(Dim)2(MAT)b(Mat)a<nom de matrice>w
m, n = 1 ~ 255, nom de matrice; A ~ Z
Exemple Créer une matrice de 2 lignes et 3 colonnes (chacun des éléments
contenant 0) dans la matrice A
A!*( { )c,d!/( } )a
K1(LIST)c(Dim)
2(MAT)b(Mat)av(A)w
L’illustration ci-contre indique le contenu de Mat A.
u Pour remplacer toutes les données par la même valeur
[OPTN]-[LIST]-[Fill]
K1(LIST)c(Fill) <valeur>,1(LIST)b(List) <numéro de liste 1-20>
)w
Exemple Remplacer toutes les données de la liste 1 par 3
AK1(LIST)c(Fill)
d,1(LIST)b(List)b)w
Voici le nouveau contenu de la liste 1.
3-2-2
Traitement des données d’une liste (Menu RUN
•
MAT)
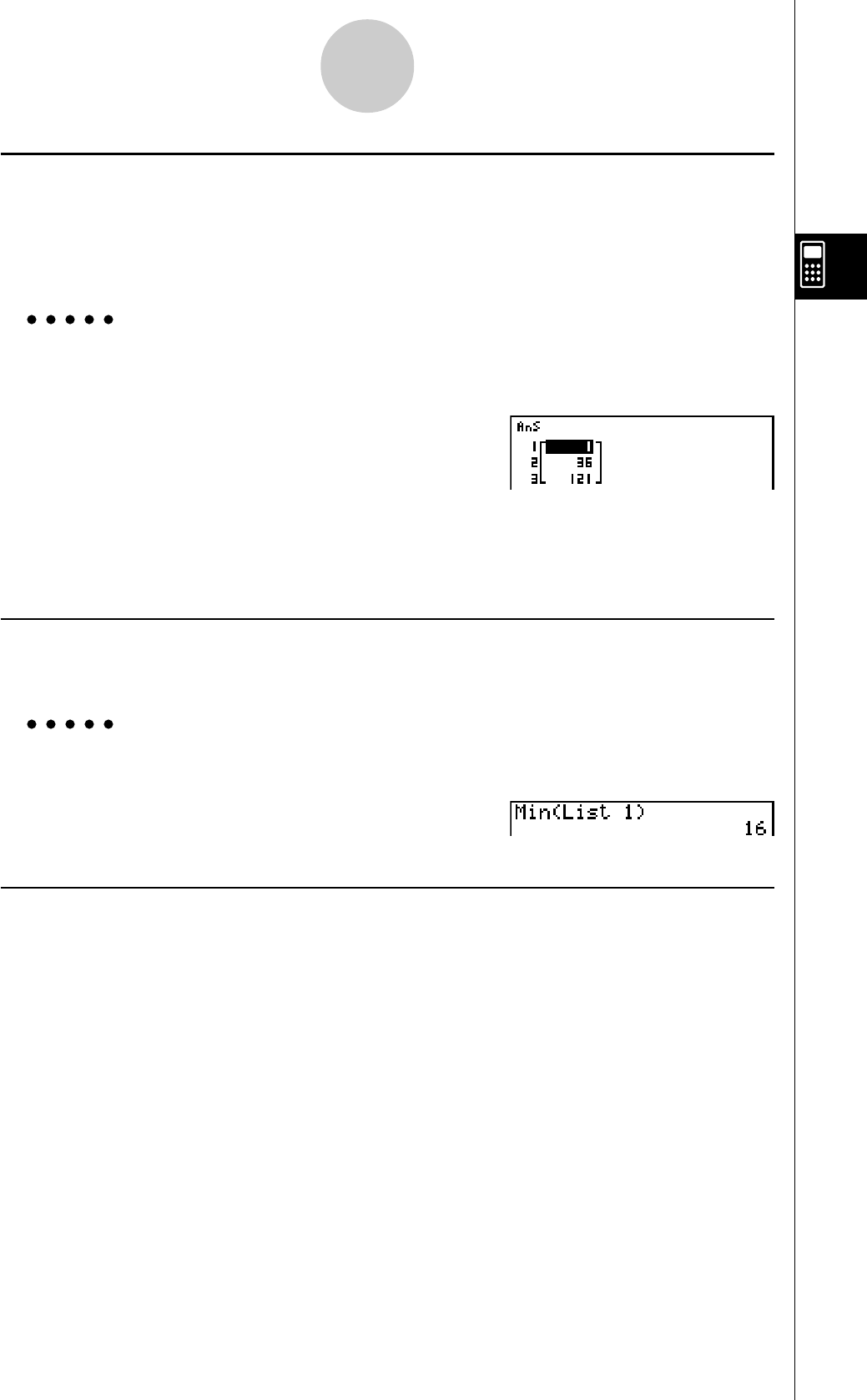
19990401
3-2-3
Traitement des données d’une liste (Menu RUN
•
MAT)
u Pour créer une suite de nombres [OPTN]-[LIST]-[Seq]
K1(LIST)d(Seq) <expression> , <nom de variable> , <valeur initiale>
, <valeur finale> , <incrément> ) w
• Le résultat de cette opération est sauvegardé dans la mémoire ListAns.
Exemple Introduire la séquence numérique 12, 62, 112 dans une liste en utilisant
la fonction f(x) = X2. Utiliser 1 comme valeur initiale, 11 comme valeur
finale et 5 comme incrément
AK1(LIST)d(Seq)vx,
v,b,bb,f)w
Si vous définissez 12, 13, 14 ou 15 comme valeur finale, le résultat sera le même que celui
indiqué ci-dessus, car toutes les valeurs sont inférieures à la valeur produite par l’incrément
suivant (16).
u Pour trouver la valeur minimale d’une liste [OPTN]-[LIST]-[Min]
K1(LIST)e(Min)1(LIST)b(List) <numéro de liste 1-20> )w
Exemple Trouver la valeur minimale dans la liste 1 (36, 16, 58, 46, 56)
AK1(LIST)e(Min)
1(LIST)b(List)b)w
u Pour trouver la valeur maximale d'une liste [OPTN]-[LIST]-[Max]
Procédez de la même façon que pour trouver la valeur minimale (Min), mais appuyez sur
f(Max) au lieu de e(Min).

19990401
3-2-4
Traitement des données d’une liste (Menu RUN
•
MAT)
u Pour trouver parmi deux listes celle qui contient la plus petite valeur
[OPTN]-[LIST]-[Min]
K1(LIST)e(Min)1(LIST)b(List) <numéro de liste 1-20>
,1(LIST)b (List) <numéro de liste 1-20>)w
• Les deux listes doivent contenir le même nombre de données, sinon une erreur se
produira.
• Le résultat de cette opération est sauvegardé dans la mémoire ListAns.
Exemple Trouver si la liste 1 (75, 16, 98, 46, 56) ou la liste 2 (35, 59, 58, 72, 67)
contient la plus petite valeur
K1(LIST)e(Min)
1(LIST)b(List)b,
1(LIST)b(List)c)w
u Pour trouver parmi deux listes celle qui contient la plus grande valeur
[OPTN]-[LIST]-[Max]
Procédez de la même façon que pour trouver la liste avec la plus petite valeur, mais
appuyez sur f(Max) au lieu de e(Min).
• Les deux listes doivent contenir le même nombre de données, sinon une erreur se
produira.
u Pour calculer la moyenne des données d’une liste
[OPTN]-[LIST]-[Mean]
K1(LIST)g(Mean)1(LIST)b(List) <numéro de liste 1-20>)w
Exemple Calculer la moyenne des données de la liste 1 (36, 16, 58, 46, 56)
AK1(LIST)g(Mean)
1(LIST)b(List)b)w
u Pour calculer la moyenne des données d’une fréquence donnée
[OPTN]-[LIST]-[Mean]
Cette opération utilise deux listes: une qui contient des valeurs et l’autre qui indique la
fréquence de chaque valeur (nombre d’occurences). La fréquence des données de l’élément
1 de la première liste est indiquée par la valeur de l’élément 1 de la seconde liste.
• Les deux listes doivent contenir le même nombre de données, sinon une erreur de
dimension se produira.
K1(LIST)g(Mean)1(LIST)b(List)<numéro de liste 1-20 (donnée)>
,1(LIST)b(List)<numéro de liste 1-20 (fréquence)>)w

19990401
Exemple Calculer la moyenne des données de la liste 1 (36, 16, 58, 46, 56), dont la
fréquence est indiquée dans la liste 2 (75, 89, 98, 72, 67)
AK1(LIST)g(Mean)
1(LIST)b(List)b,
1(LIST)b(List)c)w
u Pour calculer la médiane des données d’une liste
[OPTN]-[LIST]-[Med]
K1(LIST)h(Median)1(LIST)b(List)<numéro de liste 1-20>)w
Exemple Calculer la médiane des données de la liste 1 (36, 16, 58, 46, 56)
AK1(LIST)h(Median)
1(LIST)b(List)b)w
u Pour calculer la médiane des données d’une fréquence particulière
[OPTN]-[LIST]-[Med]
Cette opération utilise deux listes: une qui contient des valeurs et l’autre qui indique la
fréquence de chaque valeur (nombre d’occurences). La fréquence des données de l’élément
1 de la première liste est indiquée par la valeur de l’élément 1 de la seconde liste.
• Les deux listes doivent contenir le même nombre de données, sinon une erreur se
produira.
K1(LIST)h(Median)1(LIST)b(List) <numéro de liste 1-20 (donnée)>
,1(LIST)b(List) <numéro de liste 1-20 (fréquence)>)w
Exemple Calculer la médiane des données de la liste 1 (36, 16, 58, 46, 56), dont
la fréquence est indiquée dans la liste 2 (75, 89, 98, 72, 67)
AK1(LIST)h(Median)
1(LIST)b(List)b,
1(LIST)b(List)c)w
3-2-5
Traitement des données d’une liste (Menu RUN
•
MAT)
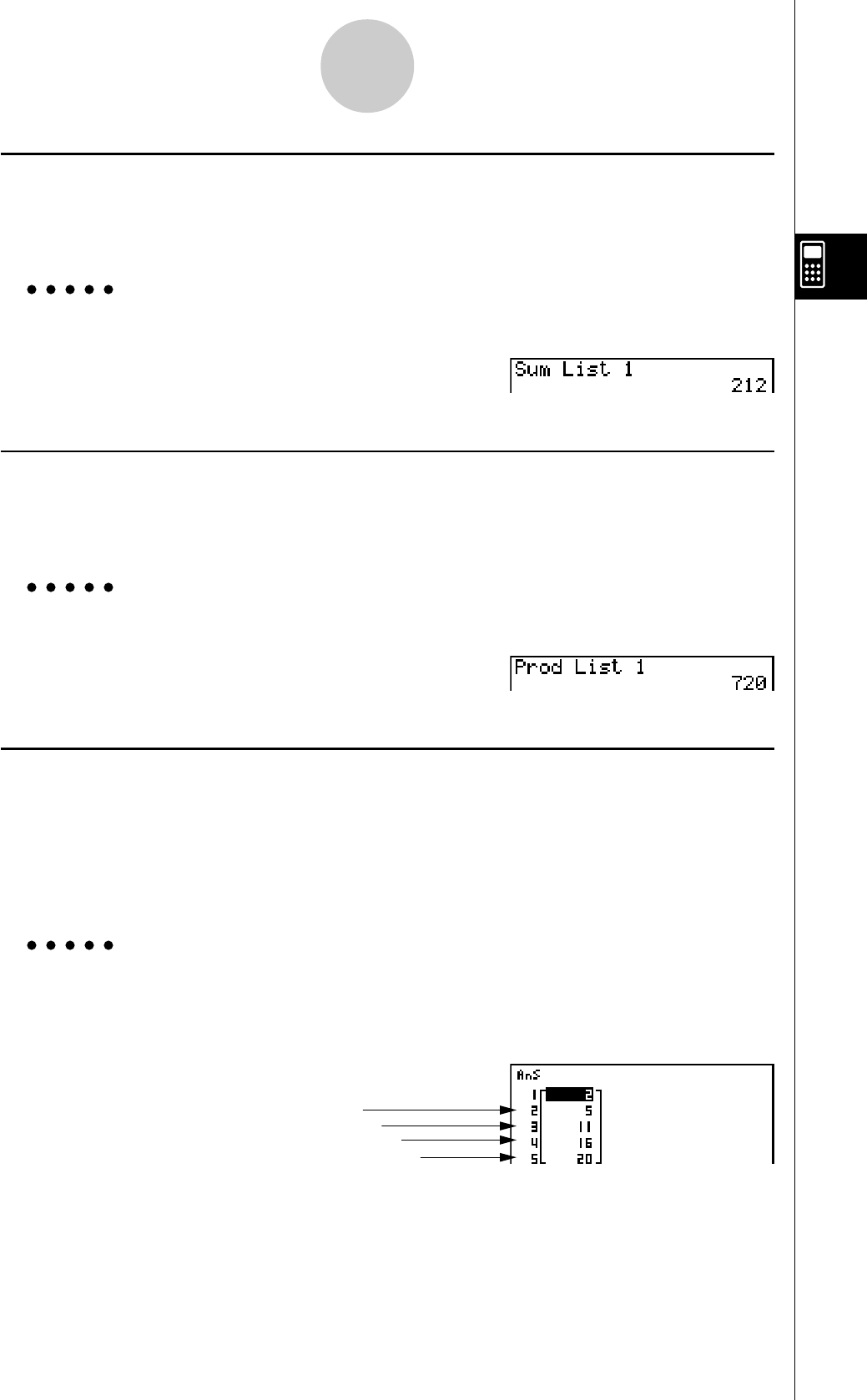
19990401
u Pour calculer la somme des données d’une liste
[OPTN]-[LIST]-[Sum]
K1(LIST)i(Sum)1(LIST)b(List)<numéro de liste 1-20>w
Exemple Calculer la somme des données de la liste 1 (36, 16, 58, 46, 56)
AK1(LIST)i(Sum)
1(LIST)b(List)bw
u Pour calculer le porduit cumulé d’une liste
[OPTN]-[LIST]-[Prod]
K1(LIST)j(Prod)1(LIST)b(List)<numéro de liste 1-20>w
Exemple Calculer le porduit cumulé des données de la liste 1 (2, 3, 6, 5, 4)
AK1(LIST)j(Prod)
1(LIST)b(List)bw
u Pour calculer la fréquence cumulative de chaque donnée
[OPTN]-[LIST]-[Cuml]
K1(LIST)v(Cuml)1(LIST)b(List) <numéro de liste 1-20>w
• Le résultat de cette opération est sauvegardé dans la mémoire ListAns.
Exemple Calculer la fréquence cumulative de chaque donnée de la liste 1 (2, 3,
6, 5, 4)
AK1(LIST)v(Cuml)
1(LIST)b(List)bw
3-2-6
Traitement des données d’une liste (Menu RUN
•
MAT)
2+3=
2+3+6=
2+3+6+5=
2+3+6+5+4=
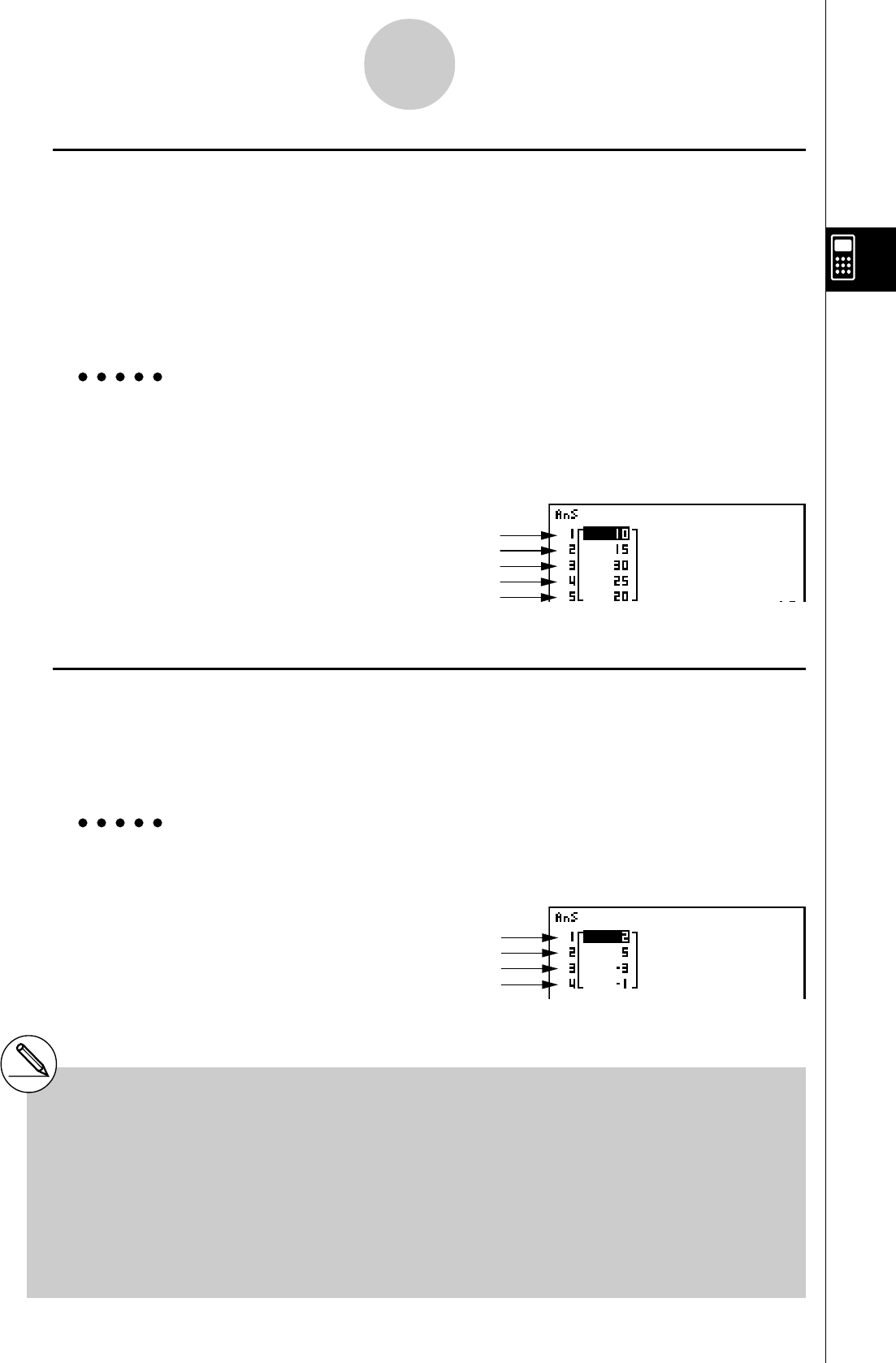
19990401
u Pour calculer le pourcentage représenté par chaque donnée
[OPTN]-[LIST]-[%]
K1(LIST)l(%)1(LIST)b(List)<numéro de liste 1-20>w
• L’opération précédente calcule le pourcentage de chaque donnée par rapport au total de
la liste.
• Le résultat de cette opération est sauvegardé dans la mémoire ListAns.
Exemple Calculer le pourcentage représenté par chaque donnée de la liste 1
(2, 3, 6, 5, 4)
AK1(LIST)l(%)
1(LIST)b(List)bw
u Pour calculer les différences entre des données voisines à l’intérieur d’une
liste [OPTN]-[LIST]-[AA
AA
AList]
K1(LIST)I(AList)<numéro de liste 1-20>w
• Le résultat de cette opération est sauvegardé dans la mémoire ListAns.
Exemple Calculer la différence entre les données de la liste 1
(1, 3, 8, 5, 4)
AK1(LIST)I(AList)
bw
3-2-7
Traitement des données d’une liste (Menu RUN
•
MAT)
# Vous pouvez désigner l’emplacement de la
nouvelle liste (Liste 1 à Liste 20) par une
instruction du type: AList 1 → List 2. Vous ne
pouvez pas désigner une autre mémoire ou la
mémoire de dernier résultat (ListAns) comme
destination de l’opération AList. Une erreur se
produira si vous désignez AList comme
destination des résultats d’une autre opération
AList.
# La nouvelle liste contient un élément de moins
que la liste originale.
# Une erreur se produit si vous exécutez AList
pour une liste qui ne contient aucune donnée
ou une seule donnée.
2/(2+3+6+5+4)
×
100 =
3/(2+3+6+5+4)
×
100 =
6/(2+3+6+5+4)
×
100 =
5/(2+3+6+5+4)
×
100 =
4/(2+3+6+5+4)
×
100 =
3 – 1 =
8 – 3 =
5 – 8 =
4 – 5 =
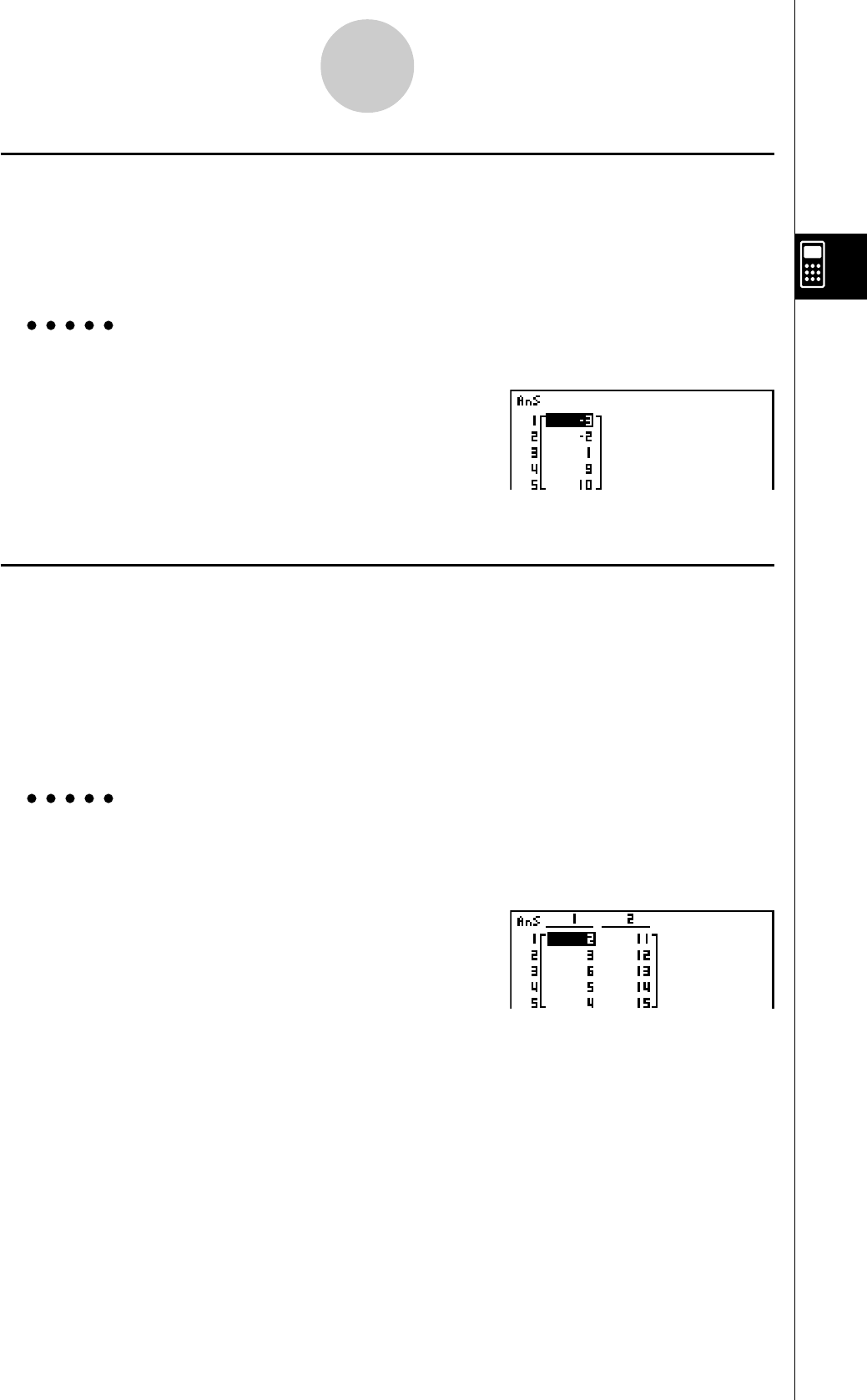
19990401
uu
uu
u Pour combiner des listes [OPTN]-[LIST]-[Augmnt]
• Vous pouvez combiner différentes listes en une seule liste. La liste obtenue sera
stockée dans la mémoire ListAns.
K1(LIST)s(Augmnt)1(LIST)b(List) <numéro de liste 1-20>
,1(LIST)b(List) <numéro de liste 1-20> )w
Exemple Combiner la liste 1 (–3, –2) et la liste 2 (1, 9, 10)
AK1(LIST)s(Augmnt)
1(LIST)b(List)b,
1(LIST)b(List)c)w
u Pour transférer le contenu de la liste dans la mémoire matricielle de
dernier résultat [OPTN]-[LIST]-[L→Mat]
K1(LIST)t(L→Mat)1(LIST)b(List) <numéro de liste 1-20>
,1(LIST)b(List) <numéro de liste 1-20> )w
• Vous pouvez omettre 1(LIST)b(List) dans la partie de l’opération précédente.
Exemple: List → Mat (1, 2)w
Exemple Transférer le contenu de la liste 1 (2, 3, 6, 5, 4) dans la colonne 1 et le
contenu de la liste 2 (11, 12, 13, 14, 15) dans la colonne 2 de la
mémoire de rappel de matrice
AK1(LIST)t(L→Mat)
1(LIST)b(List)b,
1(LIST)b(List)c)w
3-2-8
Traitement des données d’une liste (Menu RUN
•
MAT)

19990401
3-3 Calculs arithmétiques à partir de listes
(Menu RUN
•
MAT)
Vous pouvez effectuer des calculs arithmétiques à partir d’une ou deux listes et d’une valeur
numérique.
kMessages d’erreur
• Un calcul impliquant deux listes exécute l’opération entre les éléments correspondants.
Par conséquent, si les deux listes ne contiennent pas le même nombre de valeurs (donc
si leurs dimensions sont différentes), une erreur se produira.
• Une erreur se produit quand une opération impliquant deux éléments quelconques
aboutit à une erreur mathématique.
kIntroduction d’une liste dans un calcul
Il existe deux méthodes pour introduire une liste dans un calcul.
u Pour introduire une liste par le nom
1. Appuyez sur K pour afficher le premier menu d’opération.
•En mode RUN
•
MAT, voici le menu de fonctions qui apparaît quand vous appuyez sur
K.
2. Appuyez sur 1(LIST) pour afficher le menu de traitement des données d’une liste.
3. Appuyez sur b(List) pour afficher la commande “List” et indiquer le numéro de liste
souhaité.
Liste
Valeur numérique
Liste
Valeur numérique
+
−
×
÷
=
Liste
Mémoire de dernier
résultat (ListAns)
3-3-1
Calculs arithmétiques à partir de listes (Menu RUN
•
MAT)
Les résultats du calcul sont
stockés dans la mémoire de
dernier résultat (ListAns).
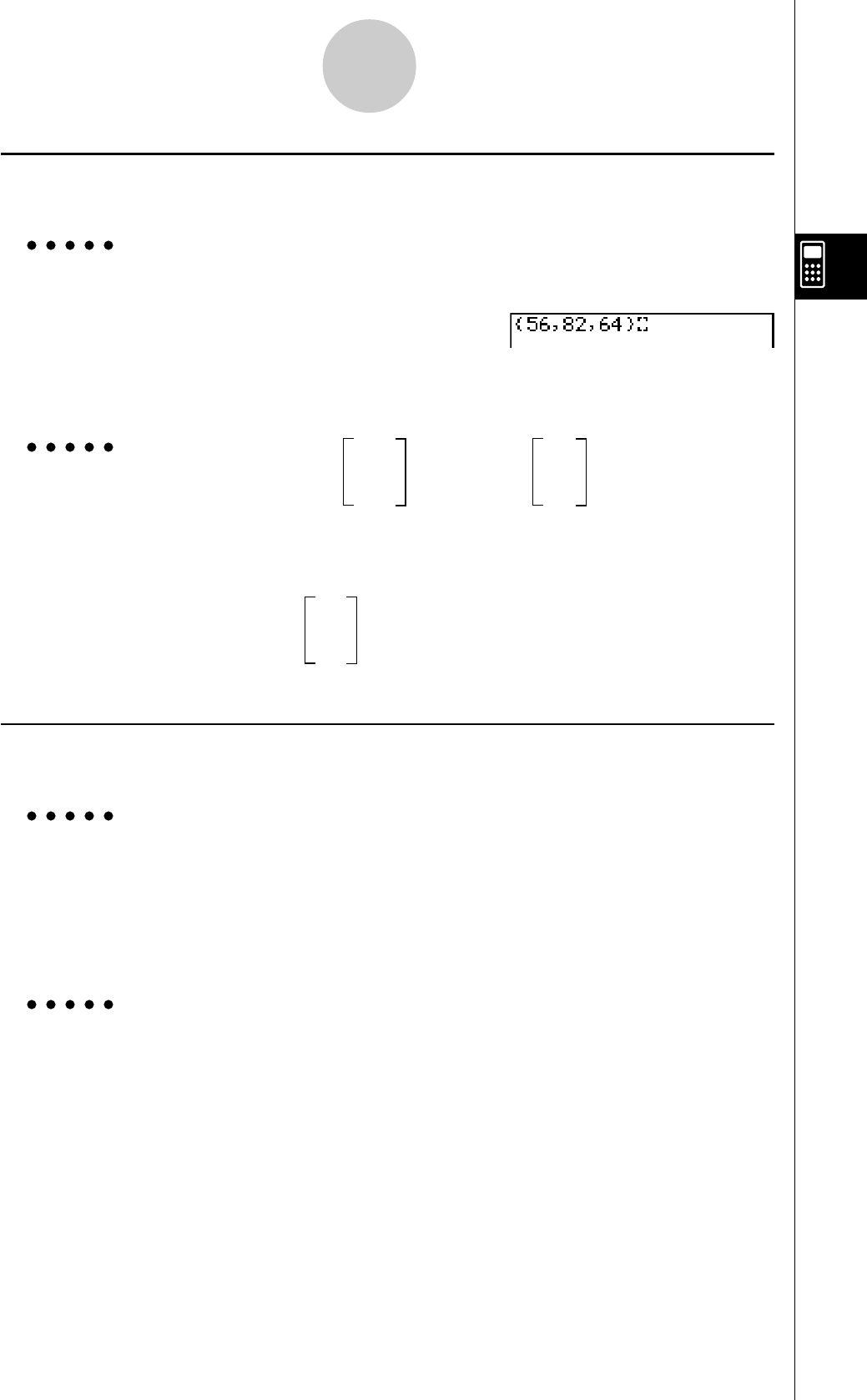
19990401
u Pour introduire directement une liste de valeurs
Vous pouvez aussi introduire directement une liste de valeurs avec {, } et ,.
Exemple 1 Introduire la liste: 56, 82, 64
!*( { )fg,ic,
ge!/( } )
w: Le résultat est mis dans ListAns.
41 6
Exemple 2 Multiplier la liste 3
(
= 65
)
par la liste 0
22 4
K1(LIST)b(List)d*!*( { )g,a,e!/( } )w
246
La liste qui en résulte 0 est stockée dans la mémoire de dernier résultat
88
(ListAns).
uPour affecter le contenu d’une liste à une autre liste
Utilisez a pour affecter le contenu d’une liste à une autre liste.
Exemple 1 Affecter le contenu de la liste 3 à la liste 1
K1(LIST)b(List)da1(LIST)b(List)bw
Au lieu d’appuyer sur K1(LIST)b(List)d dans l’opération précédente, vous pouvez
introduire !*( { )eb,gf,cc!/( } ).
Exemple 2 Affecter la liste dans la mémoire de dernier résultat (ListAns) à la liste 1
K1(LIST)b(List)!-(Ans)a1(LIST)b(List)bw
3-3-2
Calculs arithmétiques à partir de listes (Menu RUN
•
MAT)

19990401
u Pour rappeler la valeur d’un élément particulier de la liste
Vous pouvez rappeler la valeur d’un élément particulier d’une liste et l’utiliser dans un calcul.
Désignez le numéro d’élément en le mettant entre crochets.
Exemple Calculer le sinus de la valeur stockée dans l’élément 3 de la liste 2
sK1(LIST)b(List)c!+( [ )d!-( ] )w
u Pour introduire une valeur dans un élément particulier de la liste
Vous pouvez entrer une valeur dans un élément particulier d'une liste. La valeur qui était
inscrite dans cet élément est remplacée par la nouvelle valeur.
Exemple Introduire la valeur 25 dans l’élément 2 de la liste 3
cfaK1(LIST)b(List)d!+( [ )c!-( ] )w
kRappel du contenu d’une liste
Exemple Rappeler le contenu de la liste 1
K1(LIST)b(List)bw
• L'opération précédente affiche le contenu de la liste désignée et le stocke dans la
mémoire de dernier résultat (ListAns). Vous pouvez utiliser le contenu de la mémoire
dans un calcul.
u Pour utiliser dans un calcul le contenu d’une liste stockée dans la
mémoire de dernier résultat (ListAns)
Exemple Multiplier le contenu de la liste stockée dans la mémoire de dernier
résultat par 36
K1(LIST)b(List)!-(Ans)*dgw
• L’opération K1(LIST)b(List)!-(Ans) rappelle le contenu de la mémoire de
dernier résultat.
• Cette opération remplace le contenu de la mémoire de dernier résultat actuel par le
résultat du calcul précédent.
u Pour rappeler un élément d’une liste
Exemple Rappeler le 3ème élément de la liste 1: List 1 [3]
Pour rappeler le Nème élément: List 1 [N]
3-3-3
Calculs arithmétiques à partir de listes (Menu RUN
•
MAT)
19990401
kReprésentation graphique d’une fonction à partir d’une liste
Quand vous utilisez les fonctions graphiques de la calculatrice, vous pouvez introduire une
fonction du type: Y1 = XList 1. Si la liste 1 contient les valeurs 1, 2, 3, cette fonction produira
trois graphes: Y = X, Y = 2X, Y = 3X.
Il existe certaines restrictions quand les listes sont utilisées avec les fonctions graphiques.
kIntroduction de calculs scientifiques dans une liste
Vous pouvez utiliser les fonctions de génération de table numérique dans le menu Table et
Graphe pour introduire des valeurs résultant de certains calculs scientifiques dans une liste.
Créez auparavant une table, puis utilisez la fonction de copie de liste pour copier les valeurs
de la table dans la liste.
kCalculs de fonctions scientifiques à partir d’une liste
Les listes peuvent être utilisées au même titre que les valeurs numériques pour le calcul de
fonctions scientifiques. Quand le résultat d’un calcul est une liste, la liste est stockée dans la
mémoire de dernier résultat (ListAns).
41
Exemple Utiliser la liste 3 65 pour calculer le sinus (Liste 3)
22
Utilisez les radians comme unité d’angle.
sK1(LIST)b(List)dw
–0.158
La liste qui en résulte 0.8268 est stockée dans la mémoire de dernier
–8E–3
résultat (ListAns).
Au lieu d’effectuer l’opération précédente K1(LIST)b(List)d vous pouvez aussi
introduire !*( { ) eb,gf,cc!/( } ).
3-3-4
Calculs arithmétiques à partir de listes (Menu RUN
•
MAT)

19990401
14
Exemple Utiliser la liste 1 2et la liste 2 5pour effectuer Liste 1Liste 2
36
Une liste est créée avec les résultats 14, 25, 36.
K1(LIST)b(List)bM1(LIST)b(List)cw
1
La liste qui en résulte 32 est stockée dans la mémoire de dernier
729
résultat (ListAns).
3-3-5
Calculs arithmétiques à partir de listes (Menu RUN
•
MAT)

19990401
3-4-1
Changement de fichiers de listes
3-4 Changement de fichiers de listes
Vous pouvez stocker jusqu’à 20 listes (liste 1 à liste 20) dans chaque fichier (fichier 1 à fichier
6) après quoi une opération simple vous permettra de passer d’un fichier à l’autre.
u Pour passer d’un fichier de listes à un autre
1. A partir du menu principal, accédez au mode STAT.
Appuyez sur u3(SET UP) pour afficher l’écran de configuration du mode STAT.
2. Appuyez sur 1(FILE) et indiquez le numéro du fichier de listes que vous voulez
utiliser.
Exemple Sélectionner le fichier 3
1(FILE)d
w
Toutes les opérations de listes suivantes s’appliquent aux listes contenues dans le fichier que
vous sélectionnez (Fichier 3 dans l’exemple ci-dessus).

19990401
Chapitre
Calcul d’équations
La calculatrice graphique scientifique peut effectuer les trois
types de calculs suivants:
• Equations linéaires simultanées
• Equations de degré élevé
• Calculs avec résolution
A partir du menu principal, accédez au mode EQUA.
• {SIML} ... {équation linéaire de 2 à 30 inconnues}
• {POLY} ... {équations du 2e au 30e degré}
• {SOLV} ... {calcul avec résolution}
4-1 Equations linéaires simultanées
4-2 Equations de degré élevé
4-3 Calculs avec résolution
4-4 Que faire quand une erreur se produit ?
4

19990401
4-1-1
Equations linéaires simultanées
4-1 Equations linéaires simultanées
Description
Vous pouvez résoudre des équations linéaires simultanées de 2 à 30 inconnues.
• Equations linéaires simultanées à deux inconnues:
a1x1 + b1x2 = c1
a2x1 + b2x2 = c2
• Equations linéaires simultanées à trois inconnues:
a1x1 + b1x2 + c1x3 = d1
a2x1 + b2x2 + c2x3 = d2
a3x1 + b3x2 + c3x3 = d3
Réglage
1. A partir du menu principal, accédez au mode EQUA.
Exécution
2. Sélectionnez le mode SIML (équation simultanée) et désignez le nombre d’inconnues
(variables).
Il est possible de désigner de 2 à 30 inconnues. Pour désigner plus de six inconnues,
appuyez sur 6(n) puis indiquez une valeur.
3. Saisissez les coefficients l’un après l’autre.
L’élément actuellement sélectionné est en surbrillance. Chaque fois que vous
introduisez un coefficient, l’élément suivant est sélectionné dans l’ordre de:
a1 → b1 → c1 → … an → bn → cn → (n = 2 à 30)
Vous pouvez aussi introduire des fractions, des nombres complexes et des valeurs
affectées aux variables comme coefficients.
La valeur qui vient d’être saisie comme coefficient peut être annulée par une pression
sur i dans la mesure où elle n’a pas été validée par la touche w. Le coefficient
antérieur réapparaît. Vous pouvez alors saisir le coefficient souhaité.
Pour changer la valeur d’un coefficient déjà validé par la touche w, amenez le curseur
sur le coefficient que vous voulez changer. Saisissez ensuite la valeur que vous voulez
changer ou appuyez sur 1(EDIT).
Appuyez sur 3(CLR) pour supprimer tous les coefficients.
4. Résolvez les équations.
…

19990401
4-1-2
Equations linéaires simultanées
Exemple Résoudre les équations linéaires simultanées suivantes pour x, y, et z
4x+y–2z=– 1
x+6y+3z= 1
– 5x+4y+z=– 7
Procédure
1m EQUA
21(SIML)
2(3)
3ewbw-cw-bw
bwgwdwbw
-fwewbw-hw
46(SOLV)
Ecran de résultat
# Les calculs internes utilisent une mantisse de
15 chiffres mais le résultat est affiché sous
forme d’une mantisse de 10 chiffres et d’un
exposant de 2 chiffres.
# Les équations linéaires simultanées sont
résolues par inversion de la matrice qui
contient les coefficients des équations.
L’exemple suivant montre la solution (x1, x2, x3)
d’une équation linéaire simultanée à trois
inconnus.
x1a1b1c1–1 d1
x2=a2b2c2d2
x3a3b3c3d3
C’est la raison pour laquelle la précision diminue
lorsque la valeur du déterminant se rapproche
de zéro. Par ailleurs, à partir de trois inconnues,
il faut un temps considérable pour résoudre les
équations.
# Une erreur se produira si la calculatrice est
incapable de trouver une solution.
# Lorsque le calcul est terminé, vous pouvez
appuyer sur 1(REPT), changer de coefficient
et réexécuter le calcul.

19990401
4-2-1
Equations de degré élevé
# Les calculs internes utilisent une mantisse de
15 chiffres mais le résultat est affiché sous
forme d’une mantisse de 10 chiffres et d’un
exposant de 2 chiffres.
# A partir du troisième degré, il faut un temps
considérable pour résoudre les équations de
troisième degré ou d’un degré supérieur.
# Une erreur se produit si la calculatrice est
incapable de trouver une solution.
# Lorsque le calcul est terminé, vous pouvez
appuyer sur 1(REPT), changer de coefficient
et réexécuter le calcul.
4-2 Equations de degré élevé
Description
Vous pouvez utiliser cette calculatrice pour résoudre des équations de degré élevé, telles
que les équations quadratiques et les équations cubiques.
•Equation quadratique:
ax2 + bx + c = 0 (a ≠ 0)
•Equation cubique:
ax3 + bx2 + cx + d = 0 (a ≠ 0)
Réglage
1. A partir du menu principal, accédez au mode EQUA.
Exécution
2. Sélectionnez le mode POLY (équation de degré élevé) et désignez le degré de
l’équation.
Vous pouvez désigner un degré de 2 à 30. Pour désigner un degré supérieur à trois,
appuyez sur 3(n) et indiquez la valeur.
3. Introduisez les coefficients l’un après l’autre.
L’élément actuellement sélectionné est en surbrillance. Chaque fois que vous
introduisez un coefficient, l’élément suivant est sélectionné dans l’ordre de:
a → b → c → …
Vous pouvez aussi écrire des fractions, des nombres complexes et des valeurs
affectées aux variables comme coefficients.
La valeur qui vient d’être saisie comme coefficient peut être annulée par une pression
sur i dans la mesure où elle n’a pas été validée par la touche w. Le coefficient
antérieur à la saisie réapparaît. Vous pouvez alors saisir le coefficient souhaité.
Pour changer la valeur d’un coefficient déjà validé par la touche w, amenez le curseur
sur le coefficient que vous voulez changer. Saisissez ensuite la valeur que vous voulez
changer ou appuyez sur 1(EDIT).
Appuyez sur 3(CLR) pour supprimer tous les coefficients.
4. Résolvez les équations.
…
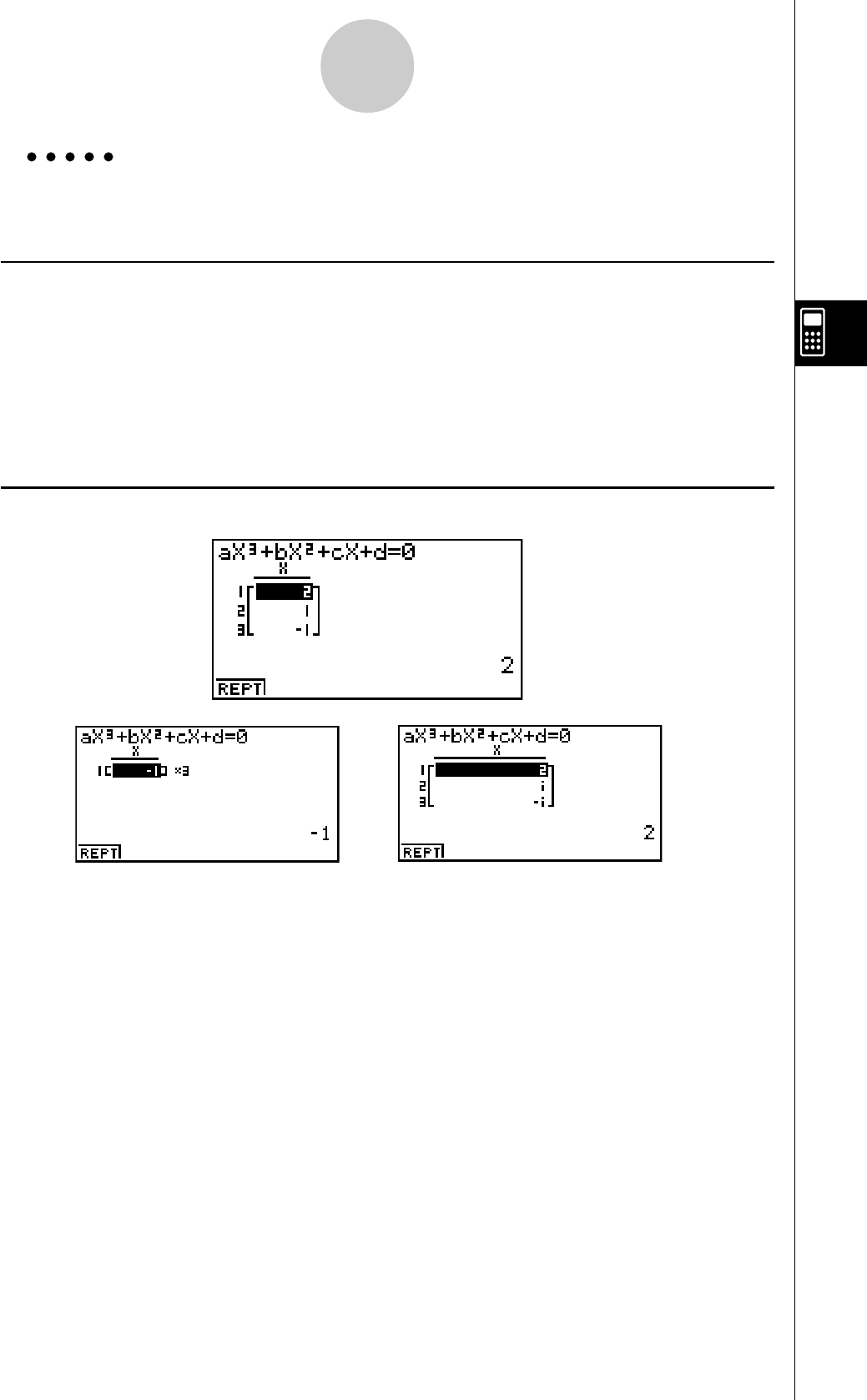
19990401
4-2-2
Equations de degré élevé
Exemple Résoudre l’équation cubique
x3 – 2x2 – x + 2 = 0
Procédure
1m EQUA
22(POLY)
2(3)
3bw-cw-bwcw
46(SOLV)
Ecran de résultat
(Solutions multiples) (Solution avec nombre complexe)

19990401
4-3-1
Calculs avec résolution
4-3 Calculs avec résolution
Description
Le mode de calcul Solve permet de déterminer la valeur d’une variable dans une formule,
sans avoir à effectuer tout le calcul de résolution d’équation.
Réglage
1. A partir du menu principal, accédez au mode EQUA.
Exécution
2. Sélectionnez le mode SOLV (résolution) et saisissez l’équation telle qu’elle est écrite.
Si vous n’écrivez pas de signe égal, la calculatrice présume que l’expression est à
gauche du signe égal et que la valeur à sa droite est zéro. *1
3. Dans la table de variables qui apparaît sur l’écran, indiquez les valeurs de chaque
variable.
Vous pouvez aussi désigner des valeurs dans Upper et Lower pour définir les limites
supérieures et inférieures de la plage de solutions. *2
4. Sélectionnez la variable que vous voulez résoudre pour obtenir la solution.
“Lft” et “Rgt” indiquent les côtés gauche et droit qui sont calculés à partir de la
solution.*3
*1Une erreur se produit si vous écrivez plus d’un
signe égal.
*2Une erreur se produit si la solution sort du
domaine de définition.
*3Les solutions sont approximatives lorsque la
méthode de Newton est utilisée. Les valeurs
Lft et Rgt sont affichées pour être vérifiées car
cette méthode peut produire la solution réelle
comme résultat.
Le degré d’erreur sera d’autant plus faible que la
différence entre les valeurs Lft et Rgt se
rapprochent de zéro.
# Le message “Réessayer” apparaît si la
calculatrice estime que la convergence n’est
pas suffisante pour les résultats affichés.

19990401
4-3-2
Calculs avec résolution
Exemple Un objet lancé en l’air à une vitesse initiale V met le temps T à
atteindre la hauteur H. Utiliser la formule suivante pour résoudre la
vitesse initiale V lorsque H = 14 (mètres), T = 2 (secondes) et
l’accélération terrestre est G = 9,8 (m/s2).
H = VT – 1/2 GT2
Procédure
1m EQUA
23(SOLV)
ax(H)!.(=)ac(V)a/(T)-(b/c)
aN(G)a/(T)xw
3bew(H = 14)
aw(V = 0)
cw(T = 2)
j.iw(G = 9,8)
4Appuyez sur f pour mettre V = 0 en surbrillance, puis sur 6(SOLV).
Ecran de résultat
19990401
4-4 Que faire quand une erreur se produit ?
uErreur pendant la saisie de la valeur du coefficient
Appuyez sur la touche i pour effacer l’erreur et revenir à la valeur enregistrée comme
coefficient avant que l’erreur ne se produise. Essayez de saisir une nouvelle valeur.
uErreur pendant un calcul
Appuyez sur la touche i pour effacer l’erreur et afficher le coefficient. Essayez de saisir de
nouvelles valeurs de coefficients.
4-4-1
Que faire quand une erreur se produit ?
kk
kk
kPour vider les mémoires d’équations
1. Accédez au mode de calcul d'équation (SIML ou POLY) que vous voulez utiliser
et effectuez l’opération de touches nécessaires pour ce mode.
• Dans le cas du mode SIML (1), utilisez les touches numériques pour désigner
le nombre d’inconnues.
• Dans le cas du mode POLY (2), utilisez les touches numériques pour désigner
le degré du polynôme.
• Si vous appuyez sur 3(SOLV), passez directement à l’étape 2.
2. Appuyez sur 2(DEL • A).
3. Appuyez sur w(Oui) pour vider les mémoires d'équation appropriées ou
i(Non) pour abandonner l’opération sans rien effacer.

19990401
Représentation
graphique de fonctions
Les sections 5-1 et 5-2 de ce chapitre donnent les informations de base
pour tracer un graphe. Les sections suivantes décrivent d’autres fonctions
et caractéristiques plus avancées de la représentation graphique.
Sur le menu principal sélectionnez l’icône qui correspond au type de
graphe que vous voulez tracer ou au type de table que vous voulez
générer.
•GRPH
·
TBL … Représentation graphique de fonctions générales ou génération de
tables numériques
•CONICS … Représentation graphique de fonctions implicites
(5-1-5 ~ 5-1-6, 5-11-17 ~ 5-11-21)
•RUN
·
MAT … Représentation graphique manuelle (5-6-1 ~ 5-6-4)
•DYNA … Graphe dynamique (5-8-1 ~ 5-8-6)
•RECUR … Représentation graphique de récurrences ou génération de tables
numériques (5-9-1 ~ 5-9-8)
5-1 Exemples de graphes
5-2 Contrôle des paramètres apparaissant sur un écran
graphique
5-3 Tracé d’un graphe
5-4 Stockage d’un graphe dans la mémoire d’images
5-5 Tracé de deux graphes sur le même écran
5-6 Représentation graphique manuelle
5-7 Utilisation de tables
5-8Représentation graphique dynamique
5-9 Représentation graphique d’une formule de récurrence
5-10 Changement de l’aspect d’un graphe
5-11 Analyse de fonctions
Chapitre
5

19990401
5-1-1
Exemples de graphes
5-1 Exemples de graphes
kk
kk
kComment tracer un graphe simple (1)
Description
Pour tracer un graphe, saisissez simplement la fonction appropriée.
Réglage
1. Depuis le menu principal, accédez au mode GRPH • TBL.
Exécution
2. Saisissez la fonction que vous voulez représenter.
Vous pouvez ici utiliser la fenêtre d’affichage pour définir la plage et d’autres
paramètres du graphe. Voir 5-2-1.
3. Tracez le graphe.
19990401
5-1-2
Exemples de graphes
Exemple Représenter graphiquement la fonction y = 3x2
Procédure
1m GRPH • TBL
2dvxw
35(DRAW) (ou w)
Ecran de résultat

19990401
5-1-3
Exemples de graphes
kk
kk
kComment tracer un graphe simple (2)
Description
Vous pouvez sauvegarder jusqu’à 20 fonctions dans la mémoire et en sélectionner une pour
la représenter.
Réglage
1. Depuis le menu principal, accédez au mode GRPH • TBL.
Exécution
2. Désignez le type de fonction et saisissez la fonction dont vous voulez tracer le graphe.
Vous pouvez utiliser le mode GRPH • TBL pour tracer un graphe pour les types
d’expressions suivantes: expression à coordonnées rectangulaires, expression à
coordonnées polaires, fonction paramétrique, expression X = constante, inéquation.
3(TYPE) b(Y =) ... coordonnées rectangulaires
c(r =) ... coordonnées polaires
d(Param) ... fonction paramétrique
e(X = c) ... fonction X = constante
f(INEQUA)b(Y>)~e(Y<) ... inéquation
Répétez cette étape le nombre de fois nécessaires pour enregistrer toutes les
fonctions souhaitées.
Vous devez ensuite indiquer la fonction que vous voulez représenter parmi celles qui
ont été stockées dans la mémoire (voir 5-3-6). Si vous ne sélectionnez pas de
fonctions particulières ici, les graphes de toutes les fonctions stockées dans la
mémoire seront tracés.
3. Tracez le graphe.
20001202
19990401
5-1-4
Exemples de graphes
Exemple Saisir les fonctions indiquées ci-dessous et tracer leurs graphes
Y1 = 2x2 – 3, r2 = 3sin2
θ
Procédure
1m GRPH • TBL
23(TYPE)b(Y=)cvx-dw
3(TYPE)c(r=)dscvw
35(DRAW)
Ecran de résultat
(Paramétrique) (Inéquation) (Marquage)
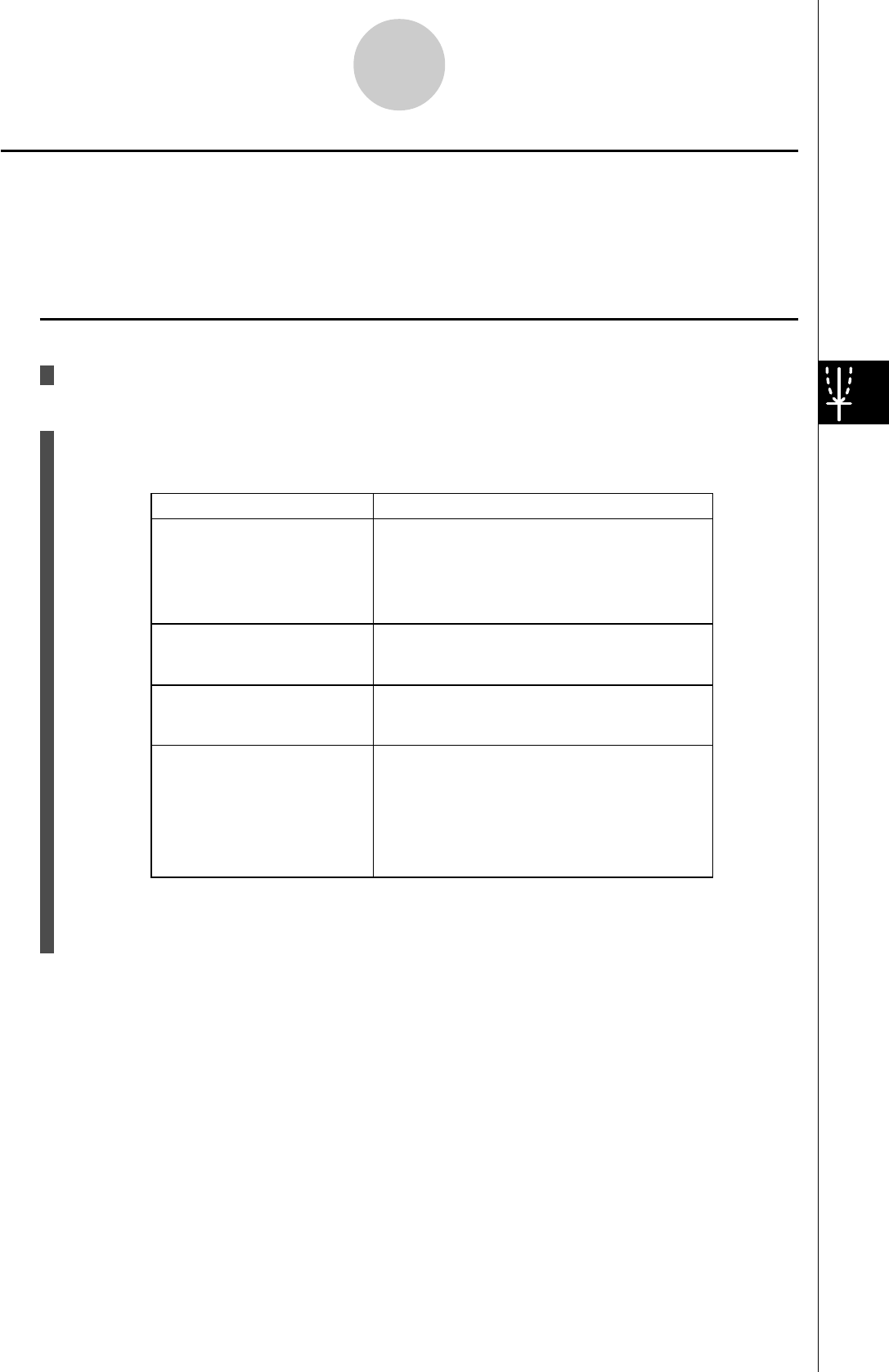
19990401
5-1-5
Exemples de graphes
kk
kk
kComment tracer un graphe simple (3)
Description
Procédez de la façon suivante pour représenter graphiquement la fonction d’une parabole,
d’un cercle, d’une ellipse ou d’une hyperbole.
Réglage
1. Depuis le menu principal, accédez au mode CONICS.
Exécution
2. Utilisez les touches de curseur fc pour désigner un des types de fonctions
suivants.
3. Indiquez des valeurs pour les variables.
4. Représentez graphiquement la fonction.
Type de graphe Fonction
Parabole X = A (Y – K)2 + H
X = AY2 + BY + C
Y = A (X – H)2 + K
Y = AX2 + BX + C
Cercle (X – H)2 + (Y – K)2 = R2
AX2 + AY2 + BX + CY + D = 0
Ellipse (X – H)2(Y – K)2
–––––––– + –––––––– = 1
A2B2
Hyperbole (X – H)2(Y – K)2
–––––––– – –––––––– = 1
A2B2
(Y – K)2(X – H)2
–––––––– – –––––––– = 1
A2B2
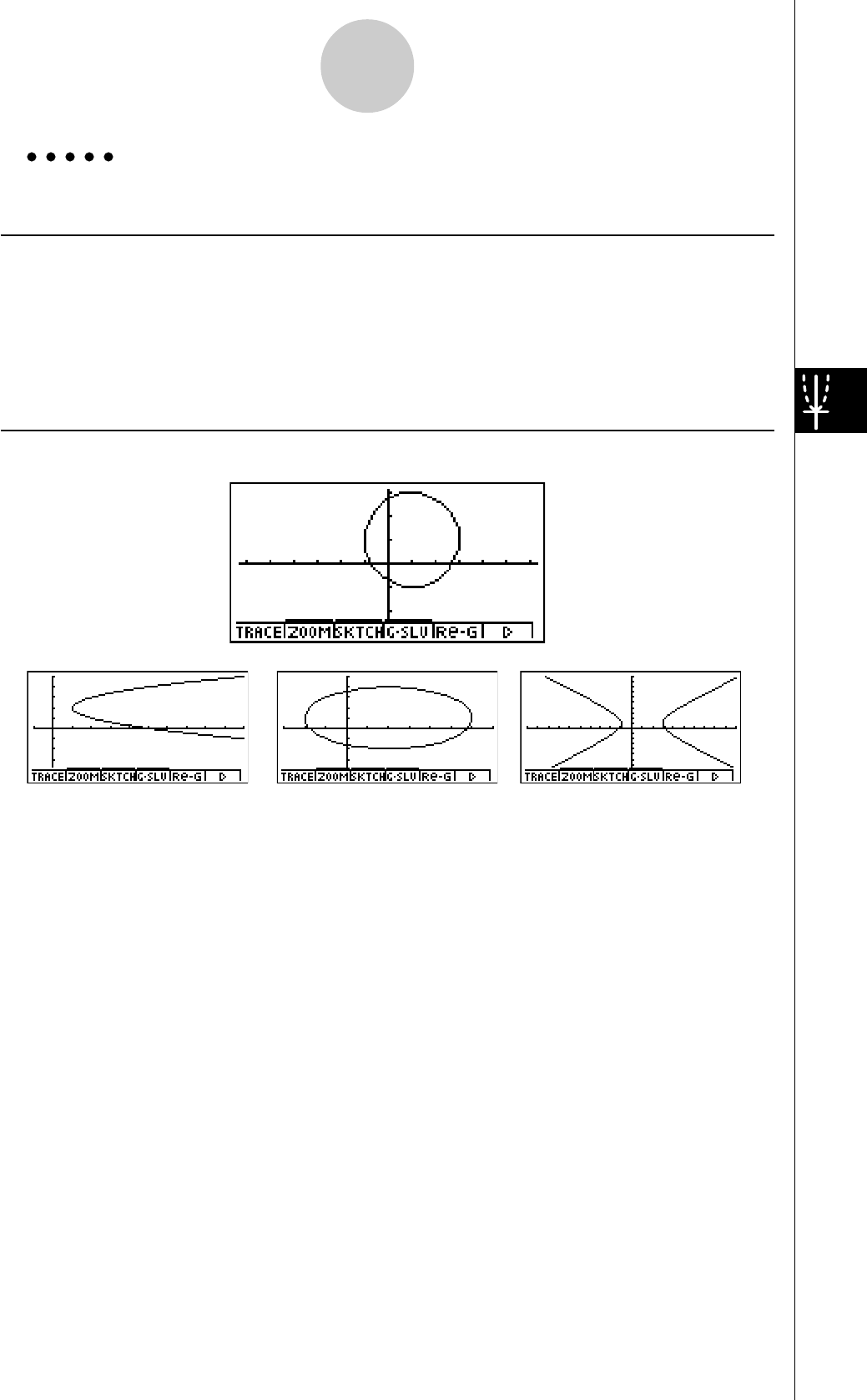
19990401
5-1-6
Exemples de graphes
Exemple Représenter graphiquement le cercle (X–1)2 + (Y–1)2 = 22
Procédure
1m CONICS
2ccccw
3bwbwcw
46(DRAW)
Ecran de résultat
(Parabole) (Ellipse) (Hyperbole)

19990401
5-2 Contrôle des paramètres apparaissant sur un
écran graphique
kk
kk
kRéglages de fenêtre d’affichage (V-Window)
Utilisez la fenêtre d’affichage pour définir la plage des axes x et y ainsi que l’espacement de
l’échelle des axes. Les paramètres de la fenêtre d’affichage que vous voulez utiliser doivent
toujours être définis avant le tracé du graphe.
uPour effectuer les réglages de la fenêtre d’affichage
1. Depuis le menu principal, accédez au mode GRPH • TBL.
2. Appuyez sur !K(V-Window) pour afficher l’écran de réglage de la fenêtre
d’affichage.
Paramètre des coordonnées rectangulaires
Xmin … Abscisse minimale
Xmax … Abscisse maximale
Xscale … Échelle de l’axe x
Xdot … Pas de variation de l’axe x
Ymin … Ordonnée minimale
Ymax … Ordonnée maximale
Yscale … Échelle de l’axe y
Paramètre des coordonnées polaires
T
θ
min ... Valeurs minimales de T,
θ
T
θ
max ... Valeurs maximales de T,
θ
T
θ
ptch ... Pas de T,
θ
3. Appuyez sur c pour déplacer la surbrillance et saisissez la valeur appropriée pour
chaque paramètre en appuyant sur w après chacun d’eux.
• {INIT}/{TRIG}/{STD} … {réglages initiaux}/{réglages initiaux avec l’unité d’angle désignée}/
{réglages standard} de la fenêtre d’affichage
•{STO}/{RCL} … {sauvegarde}/{rappel} des réglages de la fenêtre d’affichage
Lorsque les réglages sont comme vous voulez, appuyez sur i ou !i(QUIT) pour
sortir de l’écran de réglage de la fenêtre d’affichage*1
5-2-1
Contrôle des paramètres apparaissant sur un écran graphique
*1L’écran de réglage de la fenêtre d’affichage se
ferme si vous appuyez sur w sans rien saisir
lorsque k est affiché.

19990401
5-2-2
Contrôle des paramètres apparaissant sur un écran graphique
uPrécautions concernant les réglages de la fenêtre d’affichage
• La saisie de zéro pour T
θ
ptch entraîne une erreur.
• Toute saisie interdite (nombre hors du domaine de définition, signe négatif sans
valeur, etc.) cause une erreur.
• Une erreur se produira si Xmax (Ymax) est inférieur à Xmin (Ymin). Si T
θ
max est
inférieur à T
θ
min, T
θ
ptch sera négatif.
• Vous pouvez saisir des expressions (telles que 2π) comme paramètres de fenêtre
d’affichage.
• Si le réglage de la fenêtre d’affichage produit un axe qui ne rentre pas dans l’écran,
l’échelle de l’axe sera indiquée au bord de l’écran le plus près possible de l’origine.
• Le changement de réglage de la fenêtre d’affichage supprime le graphe affiché et le
remplace par les nouveaux axes seulement.
• Le changement de la valeur de Xmin ou Xmax entraîne automatiquement un
ajustement de la valeur Xdot. Le changement de la valeur Xdot entraîne
automatiquement un ajustement de la valeur Xmax.
• Un graphe à coordonnées polaires (r =) ou paramétrique apparaîtra grossier si les
réglages effectués dans la fenêtre d’affichage donne une valeur de pas T,
θ
trop
grande par rapport à l’écart entre les réglages T,
θ
min et T,
θ
max. D’autre part, si les
réglages effectués donnent une valeur de pas T,
θ
trop petite par rapport à l’écart
entre les réglages T,
θ
min et T,
θ
max, le tracé du graphe durera trop longtemps.
• La plage de saisie des paramètres de la fenêtre d’affichage est la suivante.
–9,999999999E 97 à 9,999999999E 97

19990401
kk
kk
kInitialisation et standardisation de la fenêtre d’affichage
uPour initialiser la fenêtre d’affichage
1. Depuis le menu principal, accédez au mode GRPH • TBL.
2. Appuyez sur !K(V-Window).
L’écran de réglage de la fenêtre d’affichage apparaît.
3. Appuyez su 1(INIT) pour initialiser la fenêtre d’affichage.
Xmin = –6.3, Xmax = 6.3, Xscale = 1, Xdot = 0.1,
Ymin = –3.1, Ymax = 3.1, Yscale = 1,
T
θ
min = 0, T
θ
max = 2π (rad), T
θ
ptch = 2π /60 (rad)
uPour initialiser la fenêtre d’affichage en fonction d’une unité d’angle
A l’étape 3 de la procédure de “Pour initialiser la fenêtre d’affichage” ci-dessus, appuyez sur
2(TRIG) pour initialiser la fenêtre d’affichage en fonction d’une unité d’angle.
Xmin = –3π (rad), Xmax = 3π (rad), Xscale = π /2 (rad), Xdot = π /21 (rad),
Ymin = –1.6, Ymax = 1.6, Yscale = 0.5
uPour standardiser la fenêtre d’affichage
Les réglages standard de la fenêtre d’affichage sont les suivants.
Xmin = –10, Xmax = 10, Xscale = 1, Xdot = 0.15873015,
Ymin = –10, Ymax = 10, Yscale = 1,
T
θ
min = 0, T
θ
max = 2π (rad), T
θ
ptch = 2π /60 (rad)
A l’étape 3 de “Pour initialiser la fenêtre d’affichage” ci-dessus, appuyez sur 3(STD) pour
standardiser les réglages de fenêtre d’affichage.
5-2-3
Contrôle des paramètres apparaissant sur un écran graphique
# L’initialisation et la standardisation entraînent
automatiquement un changement des valeurs
T
θ
min, T
θ
max, T
θ
ptch en fonction du
réglage d’unité d’angle actuel, comme indiqué
ci-dessous.
Mode Deg:
T
θ
min = 0, T
θ
max = 360, T
θ
ptch = 6
Mode Gra:
T
θ
min = 0, T
θ
max = 400, T
θ
ptch = 400/60

19990401
kk
kk
kMémoire de fenêtre d’affichage
Vous pouvez mémoriser six ensembles de réglages de fenêtre d’affichage dans la mémoire
de fenêtre d’affichage pour les rappeler lorsque vous en aurez besoin.
uPour stocker les réglages de fenêtre d’affichage
1. Depuis le menu principal, accédez au mode GRPH • TBL.
2. Appuyez sur !K(V-Window) pour afficher l’écran de réglage de la fenêtre
d’affichage et indiquez les valeurs souhaitées.
3. Appuyez sur 4(STO) pour afficher le menu déroulant.
4. Appuyez sur une touche numérique pour désigner la mémoire de fenêtre d’affichage
où vous voulez sauvegarder les réglages, puis appuyez sur w. Une pression sur
bw stocke les réglages dans la mémoire de fenêtre d’affichage 1 (V-Win1).
uPour rappeler les réglages de fenêtre d’affichage de la mémoire
1. Depuis le menu principal, accédez au mode GRPH • TBL.
2. Appuyez sur !K(V-Window) pour afficher l’écran de réglage de fenêtre
d’affichage.
3. Appuyez sur 5(RCL) pour afficher le menu déroulant.
4. Appuyez sur une touche numérique pour désigner le numéro de mémoire de fenêtre
d’affichage où se trouvent les réglages que vous voulez rappeler, puis appuyez sur w.
Une pression sur bw rappelle les réglages de la mémoire de fenêtre d’affichage 1
(V-Win1).
5-2-4
Contrôle des paramètres apparaissant sur un écran graphique
# Le stockage des réglages de la fenêtre
d’affichage dans une mémoire contenant déjà
des données remplace ces données par les
nouveaux réglages.
# Le rappel de réglages entraîne un remplacement
des réglages actuels de la fenêtre d’affichage par
ceux qui ont été rappelés de la mémoire.

19990401
kk
kk
kSpécification de la plage du graphe
Description
Vous pouvez définir une plage (point initial, point final) d’une fonction avant d’en tracer le
graphe.
Réglage
1. Depuis le menu principal, accédez au mode GRPH • TBL.
2. Effectuez les réglages de fenêtre d’affichage.
Exécution
3. Désignez le type de fonction et saisissez la fonction. La syntaxe pour la saisie de la
fonction est la suivante.
Fonction ,!+( [ )Point initial , Point final !-( ] )
4. Tracez le graphe.
5-2-5
Contrôle des paramètres apparaissant sur un écran graphique
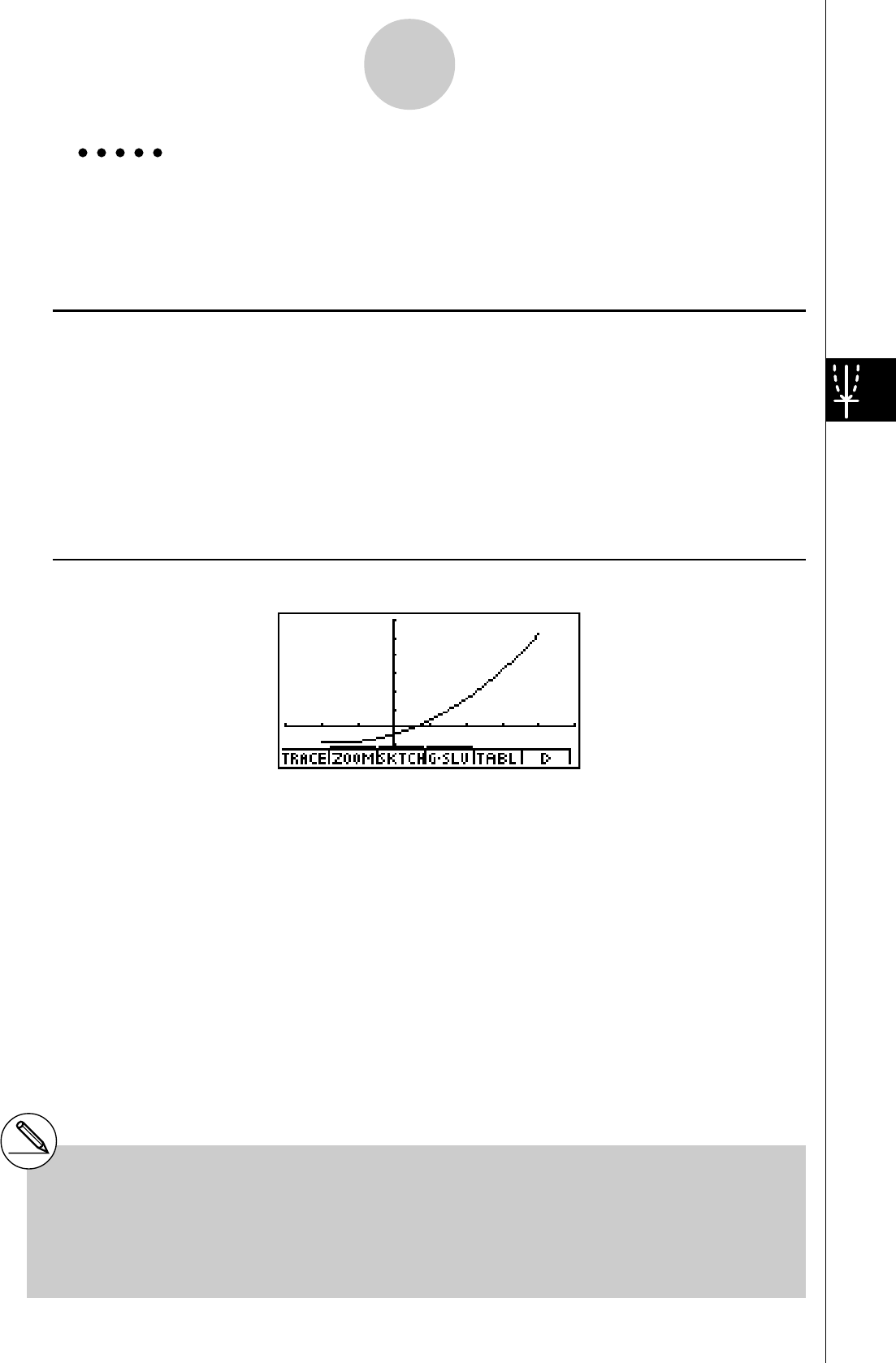
19990401
5-2-6
Contrôle des paramètres apparaissant sur un écran graphique
Exemple Représentez graphiquement y = x2 + 3x – 2 dans la plage de – 2 < x < 4
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –3, Xmax = 5, Xscale = 1
Ymin = –10, Ymax = 30, Yscale = 5
Procédure
1m
GRPH • TBL
2!K(V-Window) -dwfwbwc
-bawdawfwi
33(TYPE)b(Y=)vx+dv-c,
!+( [ )-c,e!-( ] )w
45(DRAW)
Ecran de résultat
# Vous pouvez définir une plage pour la
représentation graphique d’expressions à
coordonnées rectangulaires, d’expressions à
coordonnées polaires, de fonctions
paramétriques et d’inéquations.

19990401
5-2-7
Contrôle des paramètres apparaissant sur un écran graphique
kk
kk
kZoom
Description
Cette fonction sert à agrandir ou réduire le graphe affiché à l’écran.
Réglage
1. Tracez le graphe.
Exécution
2. Désignez le type de zoom.
2(ZOOM)b(Box) ... Zoom sur cadre
Trace un cadre autour d’une partie de l’affichage et agrandit
cette partie de manière à ce qu’elle remplisse tout l’écran.
c(Factor)
d(In)/e(Out) ... Zoom avec facteur
Le graphe est agrandi ou réduit à la position actuelle du
curseur, en fonction du facteur désigné.
f(Auto)
...Zoom automatique
Les réglages de l’axe y de la fenêtre d’affichage sont
automatiquement ajustés pour que le graphe remplisse tout
l’écran sur l’axe y.
g(Orig) ...Taille originale
Rétablit la taille originale du graphe après un zoom.
h(Square) ... Correction de graphe
Les valeurs de l’axe x de la fenêtre d’affichage sont corrigées
de manière à être identiques aux valeurs de l’axe y.
i(Rnd) ... Arrondi de coordonnées
Arrondit les valeurs des coordonnées à la position actuelle du
curseur.
j(Intg) ... Entier
Chaque point reçoit une largeur de 1 pour que les valeurs des
coordonnées soit des entiers.
v(Pre)
... Précédent
Les paramètres de la fenêtre d’affichage précédant le dernier
zoom sont rétablis.
l(QUICK) ... Zoom rapide
Retrace le graphe en fonction des réglages stockés dans la
mémoire de fenêtre d’affichage sélectionnée.
Définition de la plage du zoom sur cadre
3. Utilisez les touches de curseur pour amener le pointeur ( ) au centre de l’écran à
l’endroit où doit se trouver un angle du cadre, puis appuyez sur w.
4. Utilisez les touches de curseur pour déplacer le pointeur. Un cadre apparaît sur l’écran.
Déplacez le curseur jusqu’à ce que la zone que vous voulez agrandir se trouve dans le
cadre, puis appuyez sur w pour l’agrandir.
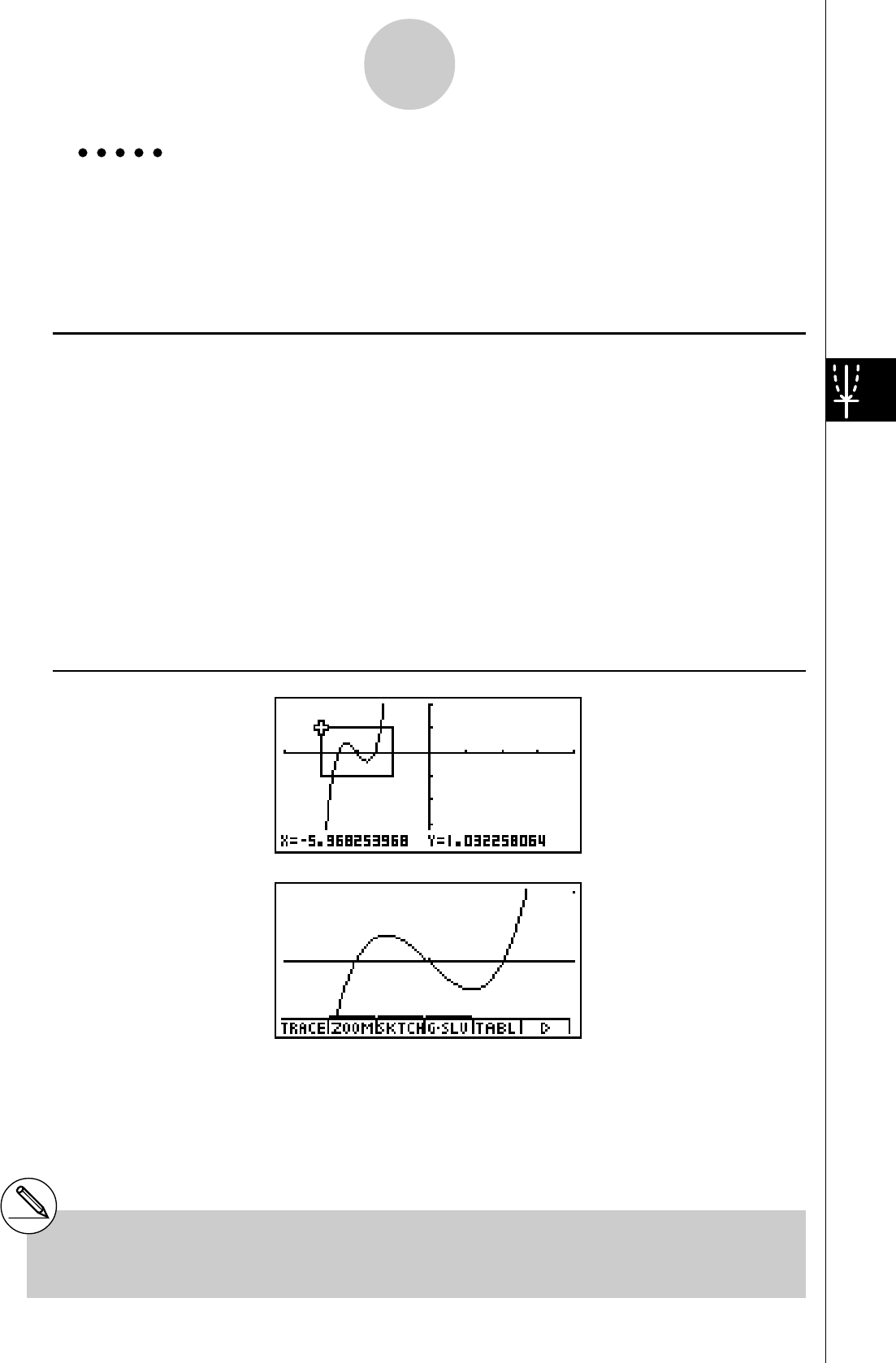
19990401
5-2-8
Contrôle des paramètres apparaissant sur un écran graphique
# Vous ne pouvez pas désigner le même point
ni une ligne pour le cadre du zoom sur cadre.
Exemple Représenter graphiquement y = (x + 5)(x + 4)(x + 3) et effectuer un
zoom sur cadre
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –8, Xmax = 8, Xscale = 2
Ymin = –4, Ymax = 2, Yscale = 1
Procédure
1m
GRPH • TBL
!K(V-Window) -iwiwcwc
-ewcwbwi
3(TYPE)b(Y=)(v+f)(v+e)
(v+d)w
5(DRAW)
22(ZOOM)b(Box)
3d~dw
4d~d,f~fw
Ecran de résultat

19990401
5-2-9
Contrôle des paramètres apparaissant sur un écran graphique
kk
kk
kZoom avec facteur
Description
Le zoom avec facteur permet d’agrandir ou de réduire un graphe depuis la position actuelle
du curseur.
Réglage
1. Tracez le graphe.
Exécution
2. Appuyez sur 2(ZOOM)c(Factor) pour ouvrir une fenêtre déroulante et désigner le
facteur du zoom pour l’axe x et l’axe y. Indiquez les valeurs souhaitées et appuyez sur
i.
3. Appuyez sur 2(ZOOM)d(In) pour agrandir le graphe ou sur 2(ZOOM)e(Out)
pour le réduire. Le graphe est agrandi ou réduit à partir de la position actuelle du
curseur.
4. Utilisez les touches de curseur pour amener le curseur à l’endroit qui sera le point de
départ de l’opération de zoom, puis appuyez sur w pour effectuer le zoom.
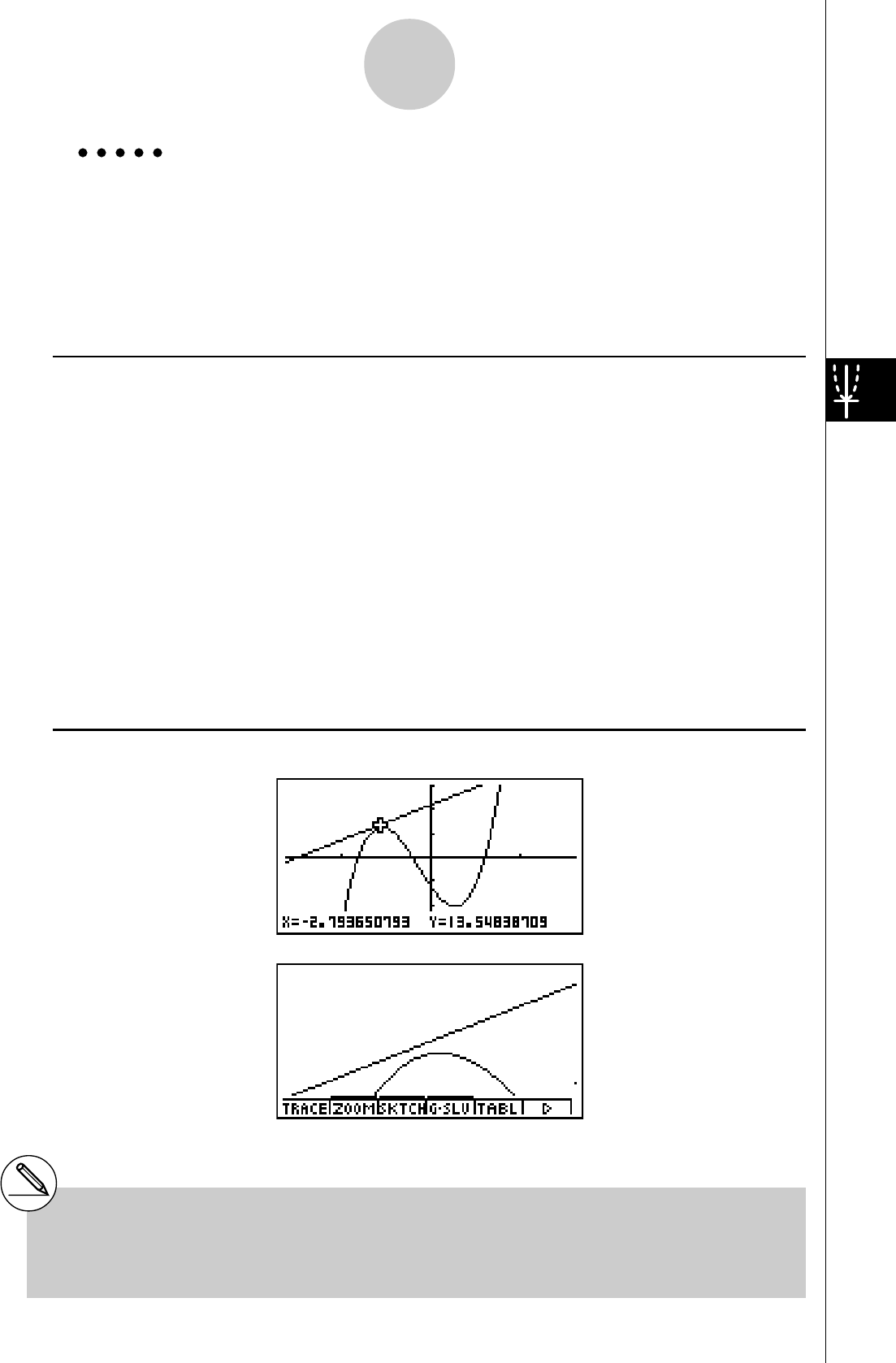
19990401
5-2-10
Contrôle des paramètres apparaissant sur un écran graphique
Exemple Agrandir cinq fois les graphes des deux expressions indiquées ci-
dessous sur les axes x et y pour voir s’ils sont tangents.
Y1 = (x + 4)(x + 1)(x – 3), Y2 = 3x + 22
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –8, Xmax = 8, Xscale = 1
Ymin = –30, Ymax = 30, Yscale = 5
Procédure
1m
GRPH • TBL
!K(V-Window) -iwiwbwc
-dawdawfwi
3(TYPE)b(Y=)(v+e)(v+b)
(v-d)w
dv+ccw
5(DRAW)
22(ZOOM)c(Factor)fwfwi
32(ZOOM)d(In)
4f~f,d~dw
Ecran de résultat
# Vous pouvez répéter le zoom avec facteur
pour agrandir ou réduire encore plus le
graphe.
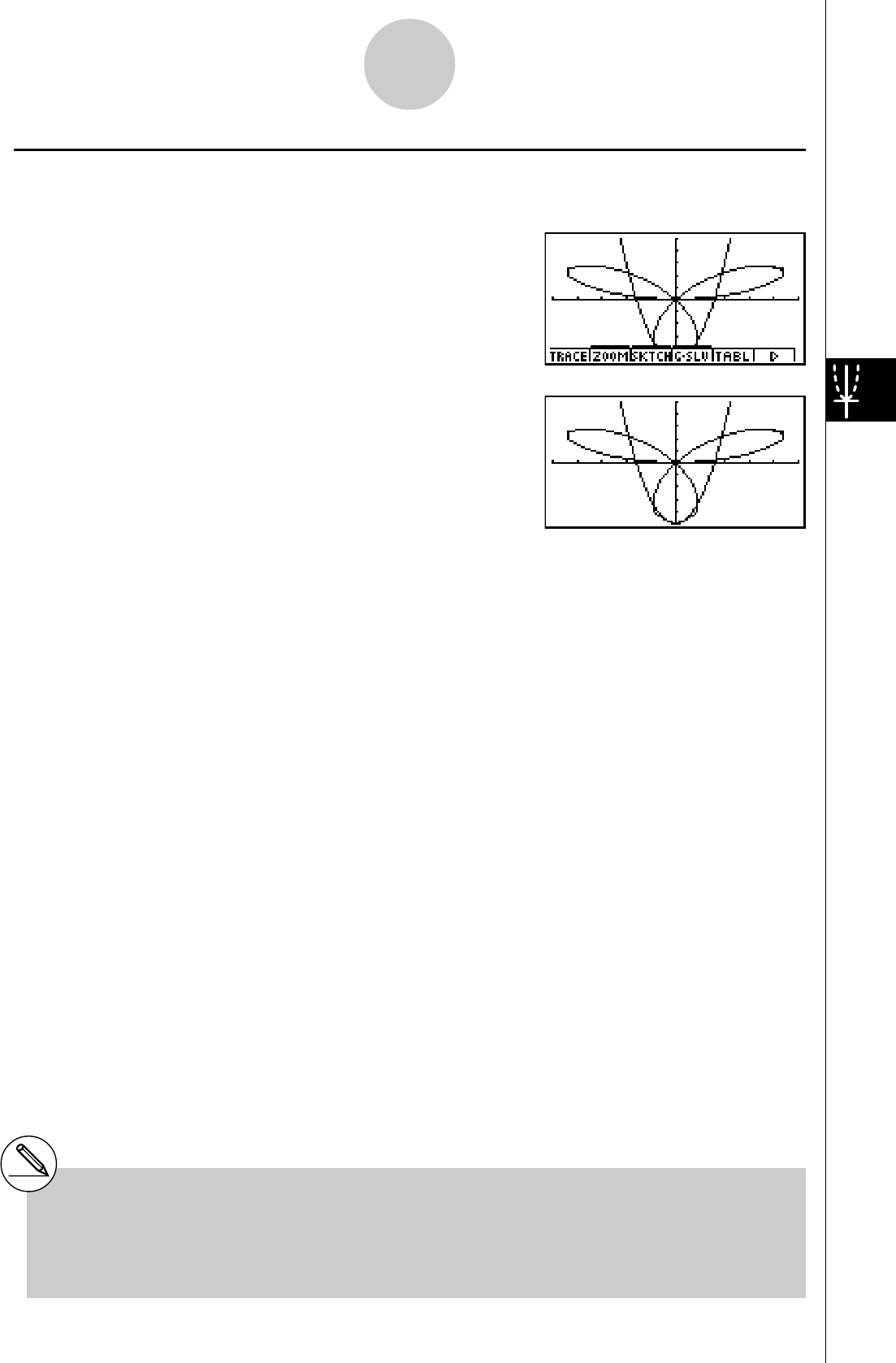
19990401
kk
kk
kAffichage ou non du menu de fonctions
Appuyez sur ua pour afficher ou non le menu au bas de l’écran.
Il est possible de voir une partie du graphe caché par le menu si celui-ci n’est pas affiché.
Lorsque vous utilisez la fonction d’affichage des coordonnées (TRACE) ou d’autres fonctions
pendant lesquelles le menu n’est normalement pas affiché, vous pouvez afficher le menu
pour exécuter une commande du menu.
5-2-11
Contrôle des paramètres apparaissant sur un écran graphique
# Si un menu déroulant est ouvert lorsque vous
appuyez sur ua pour désactiver
l’affichage du menu de fonctions, le menu
déroulant restera à l’écran.
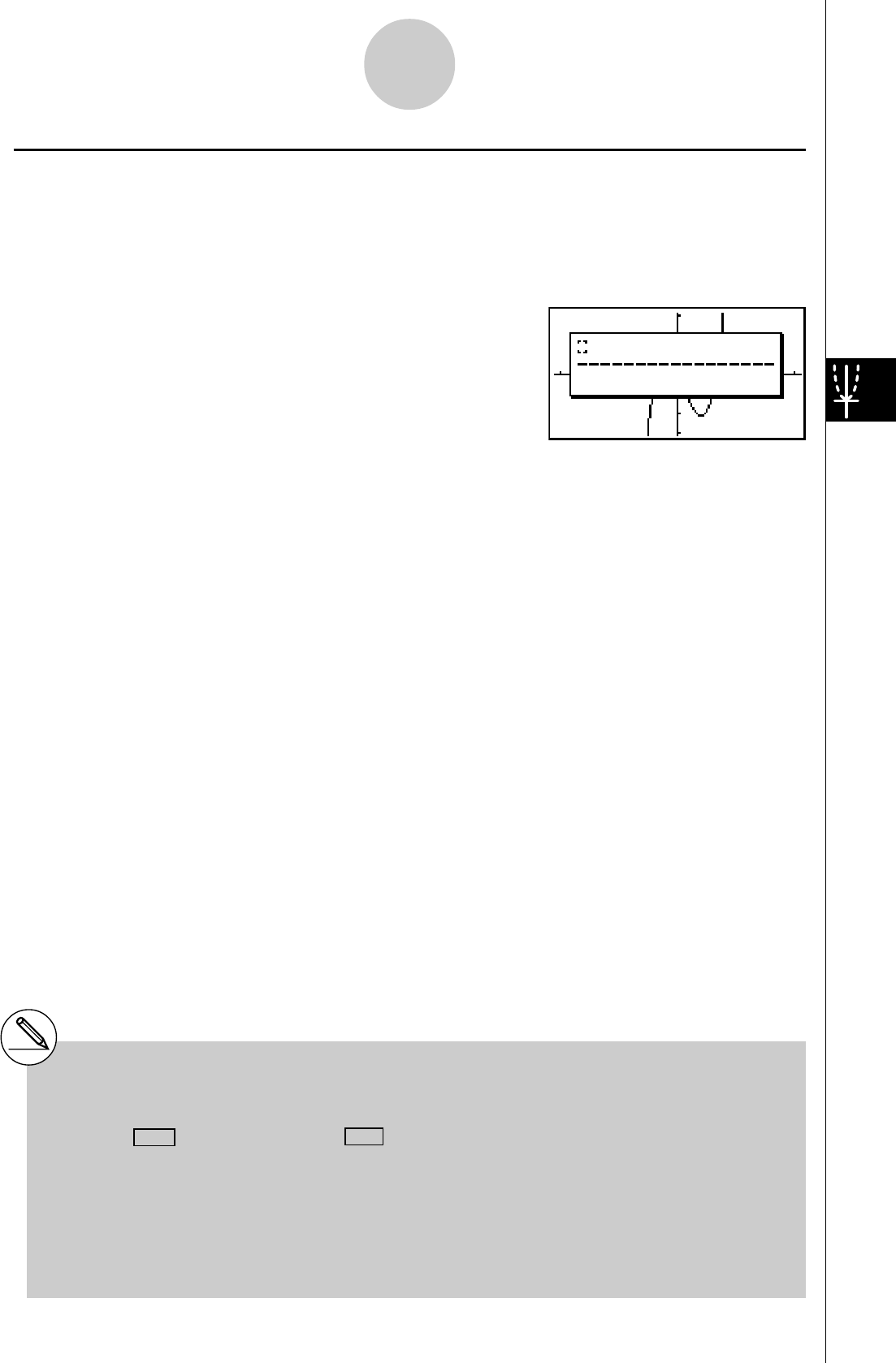
19990401
kk
kk
kA propos de la fenêtre Calc
La fenêtre Calc s’ouvre par une pression sur u4(CAT/CAL) lorsqu’un graphe ou une
table numérique est affiché. Vous pouvez utiliser la fenêtre Calc pour effectuer des calculs à
partir des valeurs obtenues lors de l’analyse de graphes, ou pour changer la valeur affectée
à la variable A dans Y = AX et d’autres expressions et pour retracer ensuite le graphe.
Appuyez sur i pour fermer la fenêtre Calc.
5-2-12
Contrôle des paramètres apparaissant sur un écran graphique
# Après avoir utilisé la fenêtre Calc pour
changer la valeur d’une variable reliée à un
graphe ou une table, veillez à toujours
exécuter Re-G (retracer le graphe) ou Re-T
(recalculer la table) pour que le graphe ou la
table soit actualisé.
# La fenêtre Calc ne peut pas être utilisée dans
le mode RUN • MAT, lorsqu’un programme
tourne ni en combinaison avec un graphe
dynamique.
# La fenêtre Calc ne peut pas être utilisée en
combinaison avec la fenêtre d’affichage ou l’écran
de réglage de la plage de la table.
# Les calculs de nombres complexes ne peuvent
pas être effectués sur la fenêtre Calc.

19990401
5-3-1
Tracé d’un graphe
5-3 Tracé d’un graphe
Vous pouvez stocker 20 fonctions au maximum dans la mémoire. Ces fonctions pourront être
éditées, rappelées et représentées graphiquement.
kk
kk
kSpécification du type de graphe
Avant de stocker une fonction de graphe en mémoire, vous devez spécifier le type de graphe.
1. Lorsque la liste des fonctions de graphes est affichée, appuyez sur 6(g)3(TYPE)
pour afficher le menu de types de graphes, qui contient les paramètres suivants.
•{Y=}/{r=}/{Param}/{X=c} ... graphe {à coordonnées rectangulaires}/{à coordonnées
polaires}/{paramétriques}/{X=constante}*1
•{INEQUA}
•{Y>}/{Y<}/{Ytt
tt
t}/{Yss
ss
s} ... graphe d’inéquation {Y>f(x)}/{Y<f(x)}/{Y>f(x)}/{Y<f(x)}
2. Appuyez sur la touche numérique correspondant au graphe que vous voulez spécifier.
kk
kk
kStockage de fonctions de graphes
uPour stocker une fonction à coordonnées rectangulaires (Y =) *2
Exemple Stocker l’expression suivante dans la zone de mémoire Y1 : y = 2x2 – 5
3(TYPE)b(Y =) (Désigne une expression à coordonnées rectangulaires.)
cvx-f(Saisit l’expression.)
w (Stocke l’expression.)
uPour stocker une fonction à coordonnées polaires (r =) *2
Exemple Stocker l’expression suivante dans la zone de mémoire r2 :
r = 5 sin3
θ
3(TYPE)c(r =) (Désigne une expression à coordonnées polaires.)
fsdv(Saisit l’expression.)
w(Stocke l’expression.)
*1 Une erreur se produira si vous essayez de
tracer le graphe d’une expression où X est
saisi pour une expression avec X= constante.
*2Il n’est pas possible de stocker une fonction dans
une zone de la mémoire contenant déjà une
fonction de type différent de celle que vous
essayez de stocker. Sélectionnez une zone de
mémoire contenant une fonction de même type
que celle que vous voulez stocker, ou supprimez la
fonction de la zone de mémoire avant de stocker la
nouvelle fonction.
19990401
5-3-2
Tracé d’un graphe
uPour stocker une fonction paramétrique *1
Exemple Stocker les fonctions suivantes dans les zones de mémoire Xt3 et Yt3 :
x = 3 sin T
y = 3 cos T
3(TYPE)d(Param) (Désigne une expression paramétrique.)
dsvw(Saisit et stocke l’expression x.)
dcvw(Saisit et stocke l’expression y.)
uPour stocker une expression avec X = constante *2
Exemple Stocker l’expression suivante dans la zone de mémoire X4 :
X = 3
3(TYPE)e(X = c) (Désigne l’expression avec X = constante.)
d(Saisit l’expression.)
w(Stocke l’expression.)
• On peut utiliser des valeurs de A, B, C... comme constante, sauf X, Y, T, r, ou
θ
qui
provoquent une erreur.
uPour stocker une inéquation *2
Exemple Stocker l’inéquation suivante dans la zone de mémoire Y5 :
y > x2 – 2x – 6
3(TYPE)f(INEQUA)b(Y>) (Désigne une inéquation.)
vx-cv-g(Saisie l’expression.)
w(Stocke l’expression.)
*1Il n’est pas possible de stocker l’expression
dans une zone qui contient déjà une
expression à coordonnées rectangulaires, une
expression à coordonnées polaires, une
expression avec X = constante ou une
inéquation. Sélectionnez une autre zone pour
stocker votre expression ou supprimez d’abord
l’expression existante.
*2Il n’est pas possible de stocker une fonction dans
une zone de la mémoire contenant déjà une
fonction de type différent de celle que vous
essayez de stocker. Sélectionnez une zone de
mémoire contenant une fonction de même type
que celle que vous voulez stocker, ou supprimez
la fonction de la zone de mémoire avant de
stocker la nouvelle fonction.

19990401
uPour créer une fonction composite
Exemple Enregistrer les fonctions suivantes en tant que fonction composite:
Y1= (X + 1), Y2 = X2 + 3
Affectez Y1°Y2 à Y3 et Y2°Y1 à Y4.
(Y1°Y2 = ((x2 + 3) +1) = (x2 + 4) Y2°Y1 = ( X + 12 + 3 = X + 4 (X ⭌ –1))
3(TYPE)b(Y=)
J4(GRPH)b(Yn)b
(1(Yn)c)w
4(GRPH)b(Yn)c
(1(Yn)b)w
• Une fonction composite peut comprendre cinq fonctions.
uPour affecter des valeurs aux coefficients et variables d’une fonction
graphique
Après avoir combiné les fonctions ou inégalités en une fonction composite, vous pouvez
attribuer des valeurs aux coefficients et variables de l’expression et tracer un graphe.
Exemple Affectez les valeurs –1, 0 et 1, au coefficient A, de l’expression
Y = AX2 –1.
3(TYPE)b(Y=)
av(A)vx-bw
J4(GRPH)b(Yn)b
(av(A)!.(=)-b)w
4(GRPH)b(Yn)b
(av(A)!.(=)a)w
4(GRPH)b(Yn)b
(av(A)!.(=)b)w
5-3-3
Tracé d’un graphe
20001202
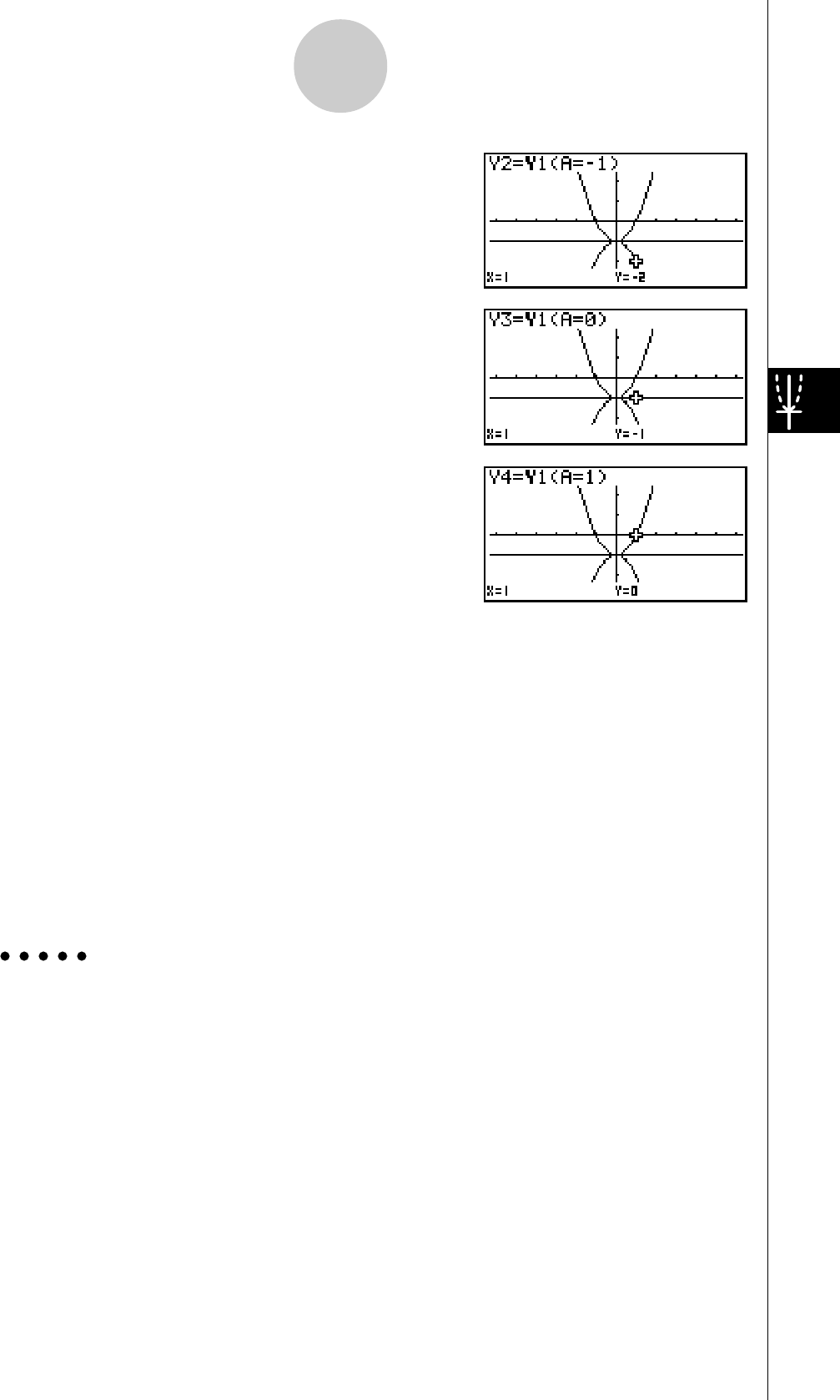
19990401
ffffi1(SEL)5(DRAW)
Les trois écrans ci-dessus s’obtiennent avec la fonction Trace.
Voir “5-11 Analyse de fonctions” pour de plus amples informations.
• Si vous ne désignez pas de nom de variable (variable A ci-dessus), la calculatrice utilisera
les variables par défaut, figurant dans la liste suivante. La variable par défaut utilisée
dépend du type de mémoire où vous avez sauvegardé la fonction graphique.
Type de mémoire Variable par défaut
YnX
rn
θ
Xtn T
Ytn T
fn X
Exemple Y1 (3) et Y1 (X = 3) sont des valeurs identiques.
• Vous pouvez aussi utiliser le graphe dynamique pour voir comment les changements de
coefficients modifient le graphe. Voir “5-8 Représentation graphique dynamique” pour de
plus amples informations.
5-3-4
Tracé d’un graphe
20001202
1999040120001202
kk
kk
kEdition et suppression de fonctions
uPour éditer une fonction en mémoire
Exemple Remplacer l’expression y = 2x2 – 5 stockée dans la zone de mémoire
Y1 par y = 2x2 – 3
e (Affiche le curseur.)
eeeeDd(Change le contenu.)
w(Stocke la nouvelle fonction de graphe.)
uPour changer le type d’une fonction *1
1. Lorsque la liste des fonctions de graphes est affichée, appuyez sur f ou c pour
amener la surbrillance sur la zone contenant la fonction dont vous voulez changer le
type.
2. Appuyez sur 3(TYPE)g(CONV).
3. Sélectionnez le type de fonction que vous voulez changer.
Exemple Remplacer la fonction y = 2x2 – 3 dans la zone de mémoire Y1 par
y < 2x2 – 3
3(TYPE)g(CONV)d(''
''
'Y<) (Remplace le type de fonction par “Y<”.)
uPour supprimer une fonction
1. Lorsque la liste des fonctions de graphes est affichée, appuyez sur f ou c pour
amener la surbrillance sur la zone contenant la fonction que vous voulez supprimer.
2. Appuyez sur 2(DEL) ou sur D.
3. Appuyez sur w(Oui) pour supprimer la fonction ou sur i(Non) pour abandonner la
procédure sans rien supprimer.
*1Le type de fonction ne peut être changé que
pour les fonctions à coordonnées
rectangulaires et les inéquations.
# Les fonctions paramétrique apparaissent sous
forme de paires (Xt et Yt).
Lors de l’édition d’une fonction paramétrique,
supprimez les fonctions de graphes et
saisissez-les un nouvelle fois depuis le début.
5-3-5
Tracé d’un graphe
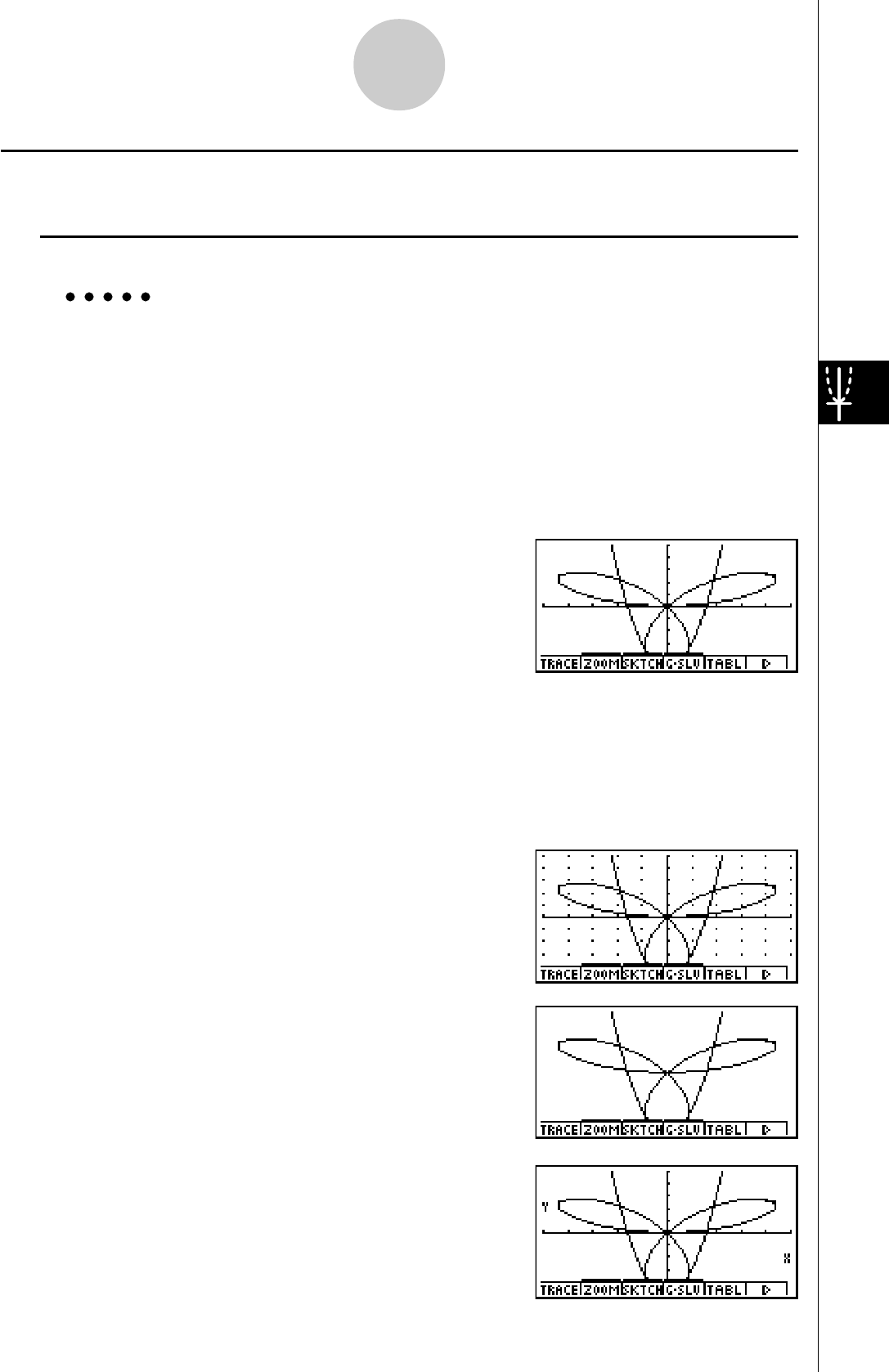
1999040120001202
kk
kk
kSélection de fonctions pour la représentation graphique
uPour définir le statut avec tracé ou sans tracé de graphe
Exemple Sélectionner les fonctions suivantes pour le tracé :
Y1 = 2x2 – 5, r2 = 5 sin3
θ
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –5, Xmax = 5, Xscale = 1
Ymin = –5, Ymax = 5, Yscale = 1
T
θ
min = 0, T
θ
max =
π
,T
θ
ptch = 2
π
/ 60
cc (Sélectionnez une zone de mémoire contenant une fonction pour
laquelle vous devez désigner le statut sans tracé.)
1(SEL) (Désigne le statut sans tracé.)
5(DRAW) ou w (Trace les graphes.)
• A chaque pression de 1(SEL), le statut du graphe change.
• La liste des fonctions de graphes se rétablit par une pression sur u5(G↔T) ou i.
• Vous pouvez utiliser les réglages d’écran de configuration pour changer l’aspect de
l’écran graphique, comme ci-dessous.
• Grid: On (Trame: Activé)
Ce réglage fait apparaître des points aux intersections
de la trame.
• Axes: Off (Axes: Désactivé)
Ce réglage supprime les axes de l’écran.
• Label: On (Nom: Activé)
Ce réglage affiche les noms des axes x et y.
5-3-6
Tracé d’un graphe
1999040120001202
kk
kk
kMémoire de graphes
Vous pouvez stocker jusqu’à 20 ensembles de données de fonctions de graphes dans la
mémoire de graphes pour les rappeler ultérieurement.
Les données suivantes sont sauvegardées dans la mémoire de graphes.
• Toutes les fonctions de graphes actuellement dans la liste de fonctions de graphes
affichée (20 au maximum)
• Types de graphes
• Statut avec tracé ou sans tracé de graphe
• Réglages de fenêtre d’affichage (1 ensemble)
uPour stocker une fonction de graphe dans la mémoire de graphes
1. Appuyez sur 4(GMEM)b(Store) pour afficher le menu déroulant.
2. Appuyez sur une touche numérique pour désigner la mémoire de graphes où vous
voulez sauvegarder la fonction, puis appuyez sur w. Si vous appuyez sur bw, par
exemple, la fonction du graphe sera stockée dans la mémoire de graphes 1 (G-Mem1).
• Il y a 20 mémoires de graphes, numérotées de G-Mem1 à G-Mem20.
uPour rappeler une fonction de graphe
1. Appuyez sur 4(GMEM)c(Recall) pour afficher le menu déroulant.
2. Appuyez sur une touche numérique pour désigner la mémoire de graphes où se trouve
la fonction que vous voulez rappeler, puis appuyez sur w. Si vous appuyez sur
bw, par exemple, la fonction de graphe se trouvant dans la mémoire de graphes 1
(G-Mem1) sera rappelée.
5-3-7
Tracé d’un graphe
# Le stockage d’une fonction dans une zone de
la mémoire contenant déjà une fonction
remplace la fonction existante par la nouvelle.
# Si les données dépassent la capacité restante
de la mémoire, une erreur se produira.
# Le rappel de données de la mémoire de graphes
supprime toutes les données actuellement dans la
liste de fonctions de graphes.
19990401
5-4 Stockage d’un graphe dans la mémoire
d’images
Vous pouvez stocker 20 images dans la mémoire d’images pour les rappeler ultérieurement.
Vous pourrez alors superposer un de ces graphes à celui qui est affiché à l’écran.
uPour stocker un graphe dans la mémoire d’images
1. Après avoir tracé un graphe dans le mode GRPH
•
TBL, appuyez sur
6(g)1(PICT)b(Store) pour afficher la fenêtre déroulante.
2. Appuyez sur une touche numérique pour désigner la mémoire d’images où vous voulez
sauvegarder l’image du graphe et appuyez sur w. Pour stocker la fonction dans la
mémoire d’images 1 (Pict 1), par exemple, appuyez sur bw.
• Il y a 20 mémoires d’images, numérotées Pict 1 à Pict 20.
uPour rappeler un graphe
• Dans le mode RUN
•
MAT:
K663 (PICT) c (Recall) b w
1. Après le tracé d’un graphe dans le mode GRPH
•
TBL, appuyez sur
6(g)1(PICT)c(Recall) pour afficher la fenêtre déroulante.
2. Appuyez sur une touche numérique pour désigner la mémoire de l’image que vous
voulez rappeler, puis appuyez sur w. Pour rappeler l’image stockée dans la mémoire
d’image 1 (Pict 1), par exemple, appuyez sur bw.
5-4-1
Stockage d’un graphe dans la mémoire d’images
# Le stockage d’une image dans une zone de la
mémoire contenant déjà une image remplace
l’image existante par la nouvelle.
# Il n’est pas possible de stocker l’écran d’un
double graphe ni aucun autre graphe utilisant un
écran divisé dans la mémoire d’images.

19990401
5-5 Tracé de deux graphes sur le même écran
kk
kk
kCopie du graphe sur l’écran secondaire
Description
Le double graphe permet de diviser l’écran en deux parties. Vous pouvez alors représenter
deux fonctions différentes de chaque côté pour les comparer, ou bien tracer un graphe de
taille normale sur un côté et un agrandissement du graphe sur l’autre côté. Le double graphe
est donc un instrument d’analyse précieux.
Le côté gauche de l’écran d’un double graphe est appelé “écran principal”, tandis que le côté
droit est appelé “écran secondaire.”
uu
uu
uEcran principal
Le graphe sur l’écran principal est directement tracé à partir de la fonction.
uu
uu
uEcran secondaire
Le graphe sur l’écran secondaire est une copie ou un agrandissement du graphe tracé sur
l’écran principal. Vous pouvez faire des réglages différents de fenêtre d’affichage pour
l’écran principal et l’écran secondaire.
Réglage
1. Depuis le menu principal, accédez au mode GRPH • TBL.
2. Sur l’écran de configuration, sélectionnez G+G pour Dual Screen.
3. Effectuez les réglages de fenêtre d’affichage pour l’écran principal.
Appuyez sur 6(RIGHT) pour afficher l’écran de réglages de graphe secondaire. Pour
revenir à l’écran de réglage de l’écran principal, appuyez sur 6(LEFT).
Exécution
4. Stockez la fonction et tracez le graphe sur l’écran principal.
5. Effectuez l’opération de double graphe souhaitée.
4(COPY) ... Copie le graphe de l’écran principal sur l’écran secondaire
5(SWAP) ... Echange le contenu de l’écran principal et celui de l’écran secondaire
5-5-1
Tracé de deux graphes sur le même écran
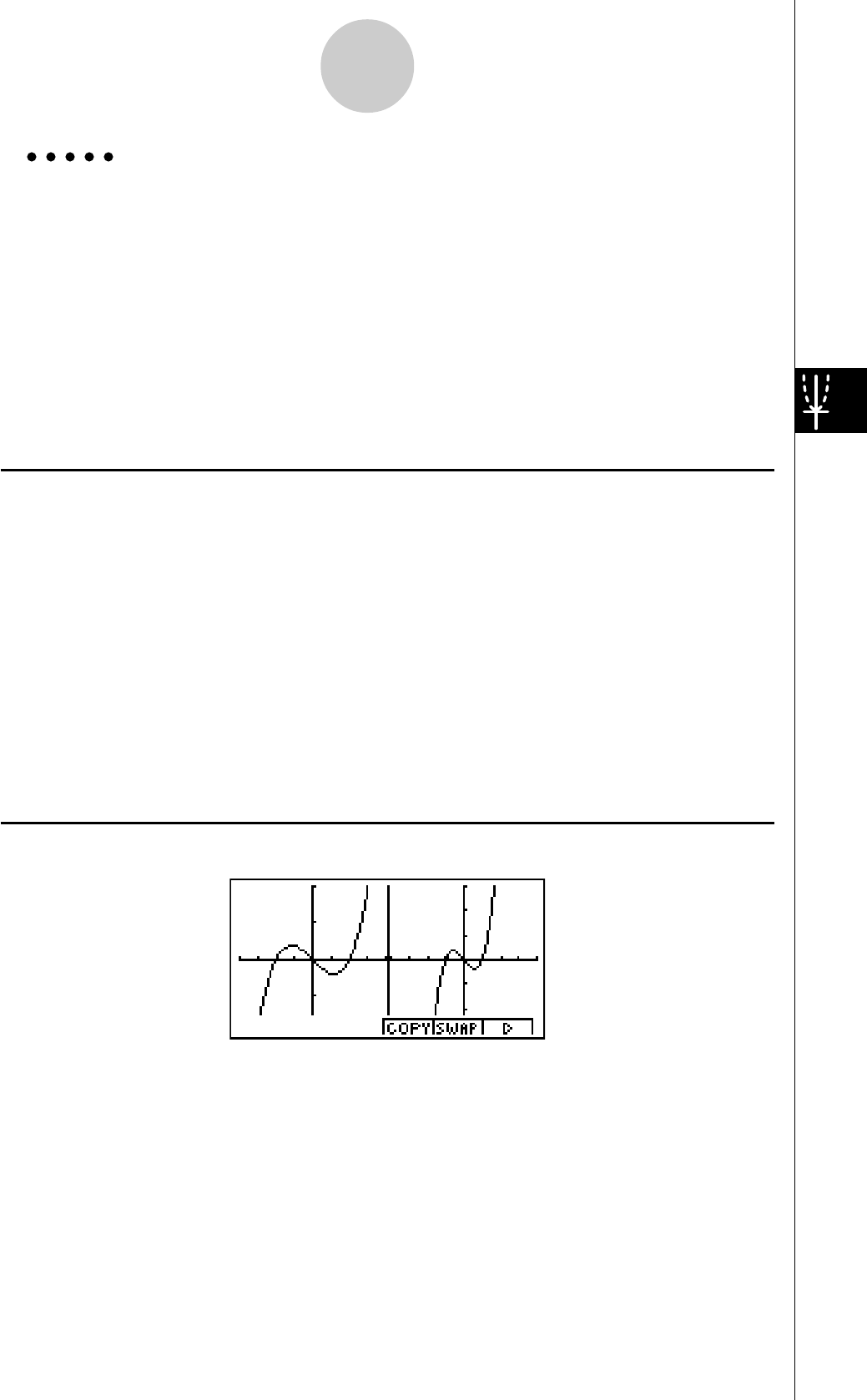
19990401
Exemple Représenter graphiquement y = x(x + 1)(x – 1) sur l’écran principal et
l’écran secondaire.
Utilisez les réglages de fenêtre d’affichage suivants.
(Ecran principal)
Xmin = –2, Xmax = 2, Xscale = 0.5
Ymin = –2, Ymax = 2, Yscale = 1
(Ecran secondaire)
Xmin = –4, Xmax = 4, Xscale = 1
Ymin = –3, Ymax = 3, Yscale = 1
Procédure
1m GRPH • TBL
2u3(SET UP)ccc2(G+G)i
3!K(V-Window) -cwcwa.fwc
-cwcwbw
6(RIGHT)-ewewbwc
-dwdwbwi
43(TYPE)b(Y=)v(v+b)(v-b)w
5(DRAW)
56(g)4(COPY)
Ecran de résultat
5-5-2
Tracé de deux graphes sur le même écran

19990401
kk
kk
kReprésentation graphique de deux fonctions différentes
Description
Procédez de la façon suivante pour représenter deux fonctions différentes sur l’écran
principal et l’écran secondaire.
Réglage
1. Depuis le menu principal, accédez au mode GRPH • TBL.
2. Sur l’écran de configuration, sélectionnez G+G pour Dual Screen.
3. Effectuez les réglages de fenêtre d’affichage pour l’écran principal.
Appuyez sur 6(RIGHT) pour afficher l’écran de réglages de graphe secondaire. Pour
revenir à l’écran de réglage de l’écran principal, appuyez sur 6(LEFT).
Exécution
4. Stockez les fonctions pour l’écran principal et l’écran secondaire.
5. Sélectionnez la fonction du graphe que vous voulez avoir sur l’écran secondaire.
6. Tracez le graphe sur l’écran principal.
7. Echangez le contenu de l’écran principal et celui de l’écran secondaire.
8. Revenez à l’écran de la fonction.
9. Sélectionnez la fonction du graphe suivant que vous voulez tracer sur l’écran principal.
10. Tracez le graphe sur l’écran principal.
5-5-3
Tracé de deux graphes sur le même écran
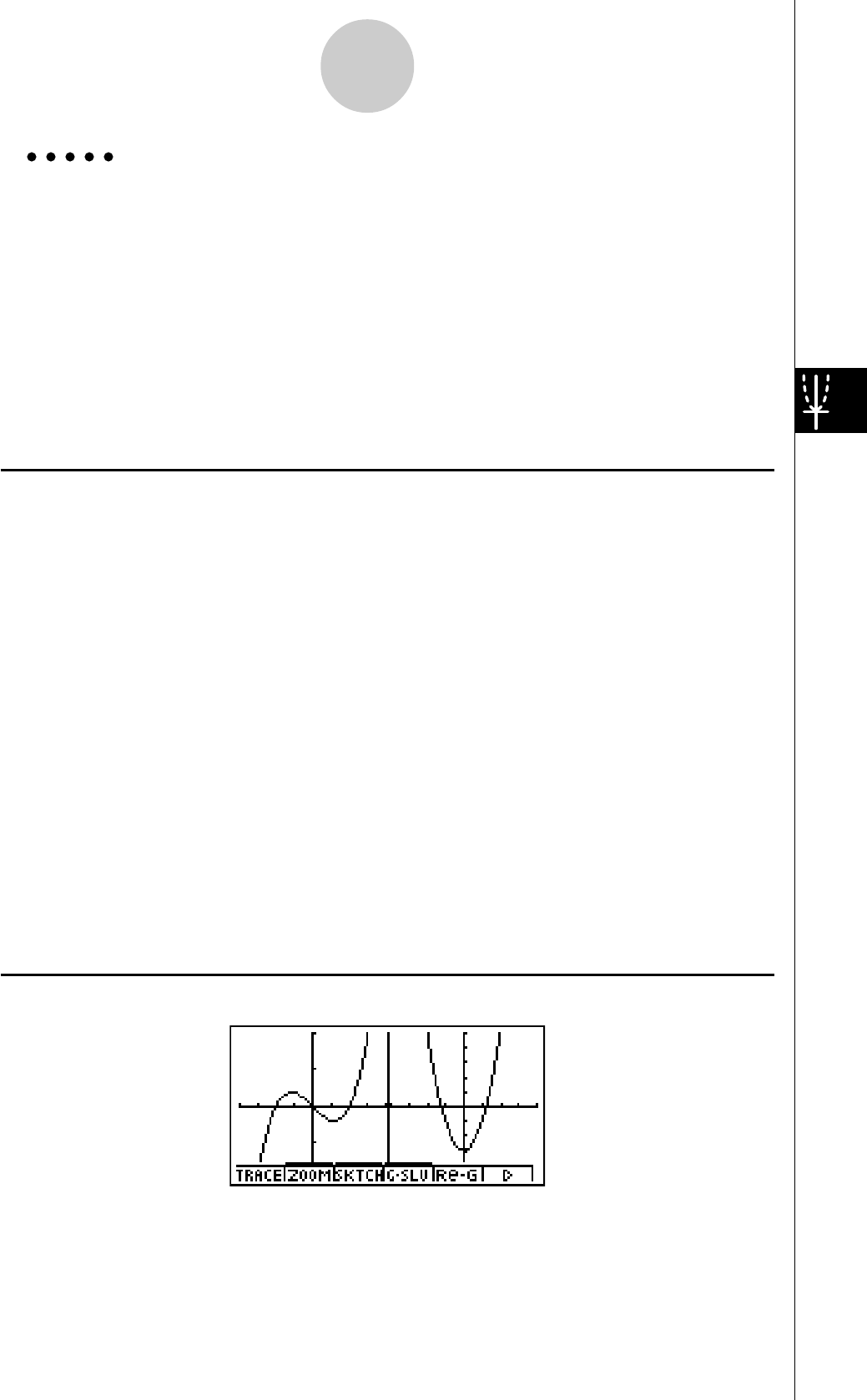
19990401
Exemple Représenter graphiquement y = x(x + 1)(x – 1) sur l’écran principal et
y = 2x2 – 3 sur l’écran secondaire.
Utilisez les réglages de fenêtre d’affichage suivants.
(Ecran principal)
Xmin = –4, Xmax = 4, Xscale = 1
Ymin = –5, Ymax = 5, Yscale = 1
(Ecran secondaire)
Xmin = –2, Xmax = 2, Xscale = 0.5
Ymin = –2, Ymax = 2, Yscale = 1
Procédure
1m GRPH • TBL
2u3(SET UP)ccc2(G+G)i
3!K(V-Window) -ewewbwc
-fwfwbw
6(RIGHT)-cwcwa.fwc
-cwcwbwi
43(TYPE)b(Y=)v(v+b)(v-b)w
cvx-dw
5ff1(SEL)
65(DRAW)
76(g)5(SWAP)
8i
91(SEL)
05(DRAW)
Ecran de résultat
5-5-4
Tracé de deux graphes sur le même écran

19990401
kk
kk
kUtilisation du zoom pour agrandir l’écran secondaire
Description
Procédez de la façon suivante pour agrandir le graphe de l’écran principal et l’afficher sur
l’écran secondaire.
Réglage
1. Depuis le menu principal, accédez au mode GRPH • TBL.
2. Sur l’écran de configuration, sélectionnez G+G pour Dual Screen.
3. Effectuez les réglages de fenêtre d’affichage pour l’écran principal.
Exécution
4. Saisissez la fonction et tracez le graphe sur l’écran principal.
5. Utilisez le zoom pour agrandir le graphe, puis affichez-le sur l’écran secondaire.
5-5-5
Tracé de deux graphes sur le même écran
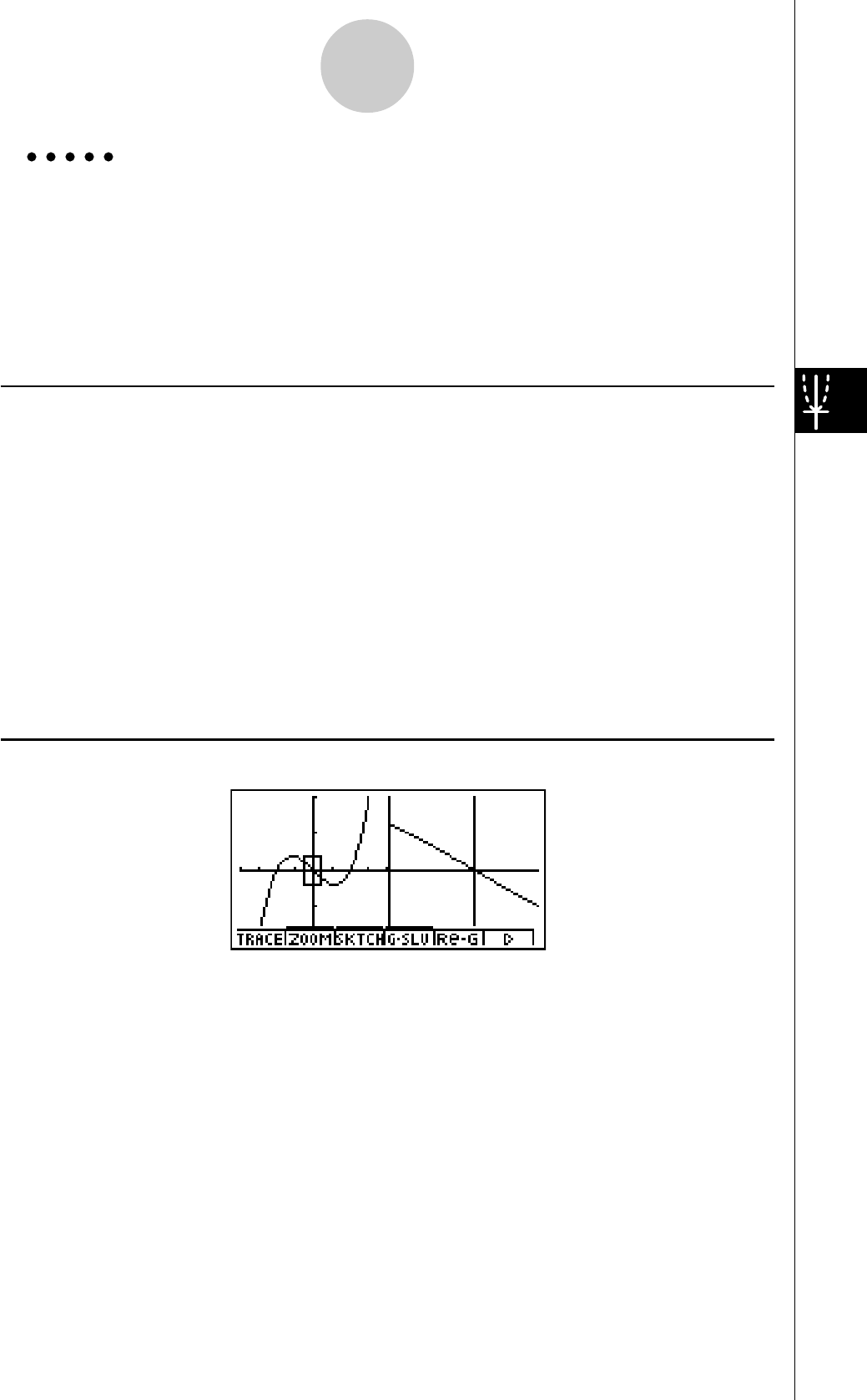
19990401
Exemple Représentez graphiquement y = x(x + 1)(x – 1) sur l’écran principal,
puis utilisez le zoom sur cadre pour l’agrandir.
Utilisez les réglages de fenêtre d’affichage suivants.
(Ecran principal)
Xmin = –2, Xmax = 2, Xscale = 0.5
Ymin = –2, Ymax = 2, Yscale = 1
Procédure
1m GRPH • TBL
2u3(SET UP)ccc2(G+G)i
3!K(V-Window) -cwcwa.fwc
-cwcwbwi
43(TYPE)b(Y=)v(v+b)(v-b)w
5(DRAW)
52(ZOOM)b(BOX)
c~ce~ew
f~fd~dw
Ecran de résultat
5-5-6
Tracé de deux graphes sur le même écran

19990401
5-6-1
Représentation graphique manuelle
5-6 Représentation graphique manuelle
kk
kk
kGraphe à coordonnées rectangulaires
Description
La saisie de la commande de graphe dans le mode RUN • MAT permet de tracer des
graphes à coordonnées rectangulaires.
Réglage
1. Depuis le menu principal, accédez au mode RUN • MAT.
2. Effectuez les réglages de fenêtre d’affichage.
Exécution
3. Validez les commandes pour le tracé de graphe à coordonnées rectangulaires.
4. Saisissez la fonction.
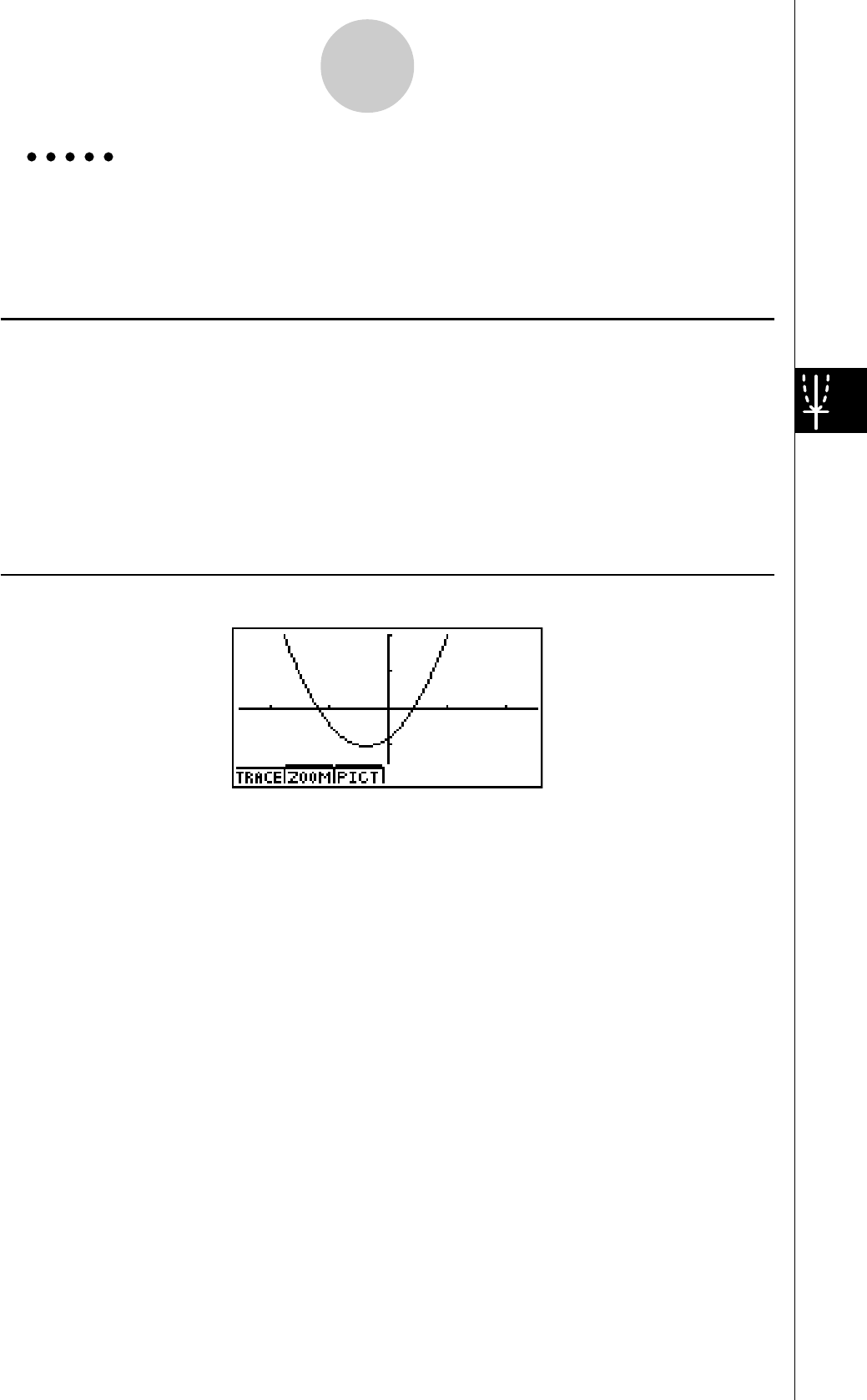
19990401
5-6-2
Représentation graphique manuelle
Exemple Représentez graphiquement y = 2x2 + 3x – 4
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = – 5, Xmax = 5, Xscale = 2
Ymin = –10, Ymax = 10, Yscale = 2
Procédure
1m
RUN • MAT
2!K(V-Window)-fwfwcwc
-bawbawfwi
3K6(g)6(g)2(SKTCH)b(Cls)w
2(SKTCH)e(GRAPH)b(Y=)
4cvx+dv-ew
Ecran de résultat

19990401
5-6-3
Représentation graphique manuelle
kk
kk
kGraphe d’intégration
Description
La validation de la commande de graphe dans le mode RUN • MAT permet de tracer le
graphe des fonctions produites par un calcul d’intégration.
Le résultat du calcul est affiché dans la partie inférieure gauche de l’écran et la plage du
calcul apparaît en noir sur le graphe.
Réglage
1. Depuis le menu principal, accédez au mode RUN • MAT.
2. Effectuez les réglages de fenêtre d’affichage.
Exécution
3. Validez les commandes de graphe pour le graphe d’intégration.
4. Saisissez la fonction.
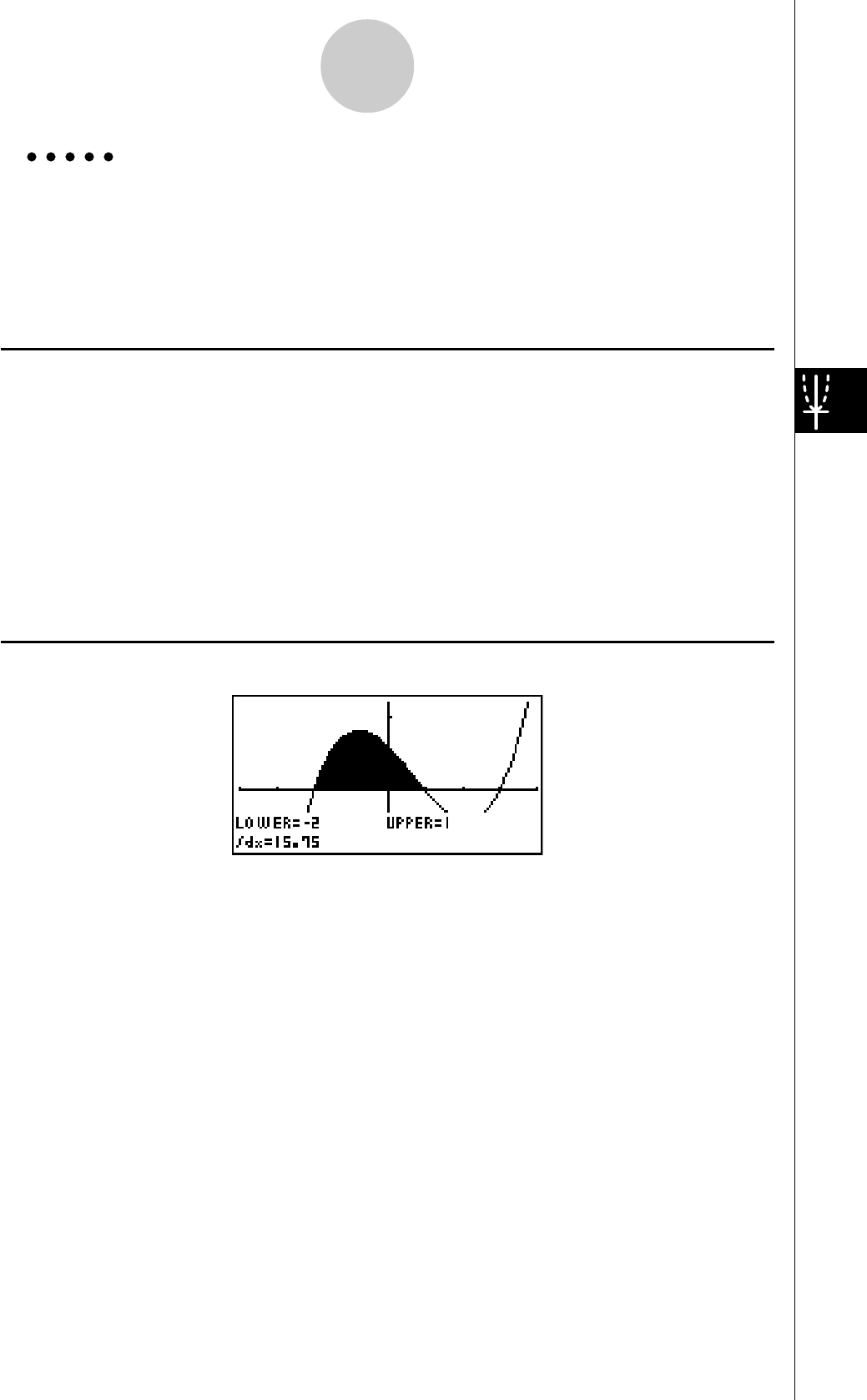
19990401
5-6-4
Représentation graphique manuelle
Exemple Tracez le graphe pour l’intégrale y =
∫
(x + 2)(x – 1)(x – 3) dx,
en utilisant 10 comme nombre de divisions.
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –4, Xmax = 4, Xscale = 1
Ymin = –8, Ymax = 12, Yscale = 5
Procédure
1m
RUN • MAT
2!K(V-Window)-ewewbwc
-iwbcwfwi
3K6(g)6(g)2(SKTCH)b(Cls)w
2(SKTCH)e(GRAPH)c(∫ dx)
4(v+c)(v-b)(v-d),
-c,b,baw
Ecran de résultat
1
–2

19990401
5-6-5
Représentation graphique manuelle
kk
kk
kTracé de graphes multiples sur le même écran
Description
Procédez de la façon suivante pour affecter différentes valeurs à une variable contenue dans
une expression et superposer les graphes qui en résultent sur l’écran.
Réglage
1. Depuis le menu principal, accédez au mode GRPH • TBL.
2. Effectuez les réglages de fenêtre d’affichage.
Exécution
3. Désignez le type de fonction et saisissez la fonction. La syntaxe pour la saisie de la
fonction est la suivante.
Expression contenant une variable ,!+( [ ) variable !.(=)
valeur , valeur , ... , valeur !-( ] )
4. Tracez le graphe.
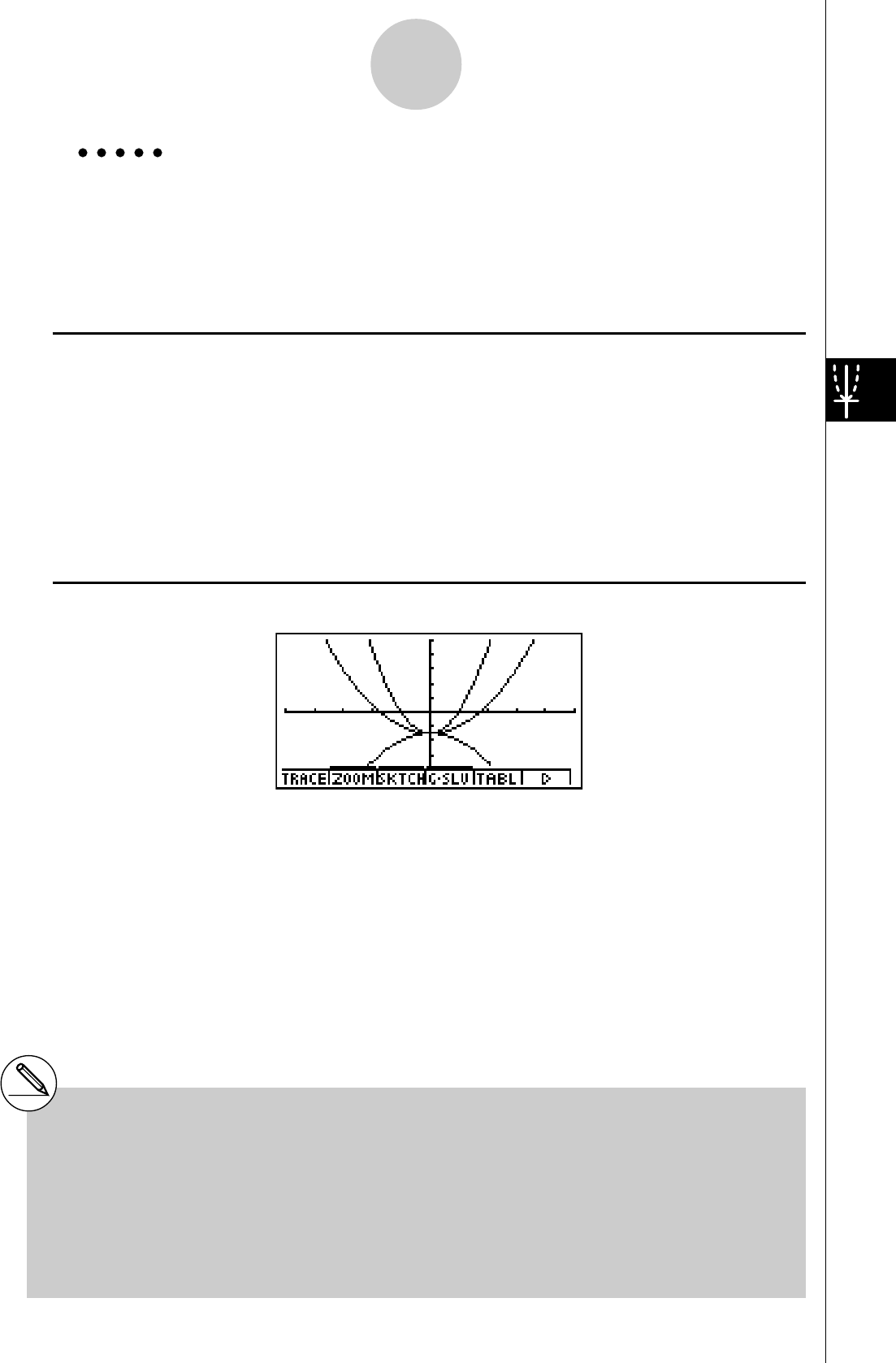
19990401
5-6-6
Représentation graphique manuelle
Exemple Représenter graphiquement y = Ax2 – 3 lorsque la valeur de A change
dans l’ordre de 3, 1, –1.
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –5, Xmax = 5, Xscale = 1
Ymin = –10, Ymax = 10, Yscale = 2
Procédure
1m
GRPH • TBL
2!K(V-Window)-fwfwbwc
-bawbawcwi
33(TYPE)b(Y=)av(A)vx-d,
!+( [ )av(A)!.(=)d,b,-b!-( ] )w
45(DRAW)
Ecran de résultat
# La valeur d’une variable seulement de
l’expression peut changer.
# X, Y, r,
θ
, T. ne peuvent pas être utilisés
comme nom de variable.
# Vous ne pouvez pas affecter de variable à la
variable à l’intérieur de la fonction.
# Lorsque le graphe simultané est activé, les
graphes sont tracés simultanément pour toutes
les variables spécifiées.
# La superposition de graphes peut être utilisée
pour la représentation graphique d’expressions
rectangulaires, d’expressions polaires, de
fonctions paramétriques, de fonctions avec X =
constante et d’inéquations.

19990401
5-7 Utilisation de tables
kk
kk
kStockage d’une fonction et génération d’une table numérique
uPour stocker une fonction
Exemple Stocker la fonction y = 3x2 – 2 dans la zone de mémoire Y1
Utilisez f et c pour amener la surbrillance dans la liste des fonctions de graphes sur la
zone de mémoire où vous voulez stocker la fonction. Saisissez ensuite la fonction et
appuyez sur w pour la stocker.
uSpécifications de la variable
Il existe deux méthodes pour spécifier la valeur de la variable x lors de la génération
d’une table numérique.
• Spécification de la plage de la table
Avec cette méthode, vous spécifiez les conditions de changement de la valeur de la
variable.
• Liste
Avec cette méthode, les données de la liste spécifiée se substituent à la variable x pour
générer une table numérique.
uPour générer une table à partir d’une plage numérique
Exemple Générer une table lorsque la valeur de la variable x change de –3 à 3,
par incréments de 1
6(g)2(RANG)
-dwdwbw
La plage de la table numérique définit les conditions dans lesquelles la valeur de la variable
x change pendant le calcul de la fonction.
Start ............ Valeur initiale de la variable x
End ............. Valeur finale de la variable x
pitch ............ Changement (intervalle) de la valeur de la variable x
Après avoir défini la plage de la table, appuyez sur i pour revenir à la liste des fonctions de
graphes.
5-7-1
Utilisation de tables

19990401
uPour générer une table à partir d’une liste
1. Lorsque la liste de fonctions de graphes est à l’écran, affichez l’écran de configuration.
2. Mettez Variable en surbrillance et appuyez sur 2(LIST) pour afficher la fenêtre
déroulante.
3. Sélectionnez la liste contenant les valeurs que vous voulez affecter à la variable x.
• Pour sélectionner la liste 6, par exemple, appuyez sur gw. Le paramètre Variable
sur l’écran de configuration se règle sur List 6.
4. Après avoir spécifié la liste que vous voulez utiliser, appuyez sur i pour revenir à
l’écran précédent.
• Notez que le paramètre {RANG} n’apparaît pas lorsqu’un nom de liste est spécifié pour le
paramètre Variable de l’écran de configuration.
• Les valeurs de la variable seront celles trouvées dans la liste 6.
uGénération d’une table
Exemple Générer une table de valeurs pour les fonctions stockées dans les
zones de mémoire Y1 et Y3 de la liste de fonctions de graphes
Utilisez f et c pour amener la surbrillance sur la fonction que vous voulez sélectionner
pour la génération de la table et appuyez sur 1(SEL) pour la sélectionner.
Le signe “=” des fonctions sélectionnées est en surbrillance. Pour ne pas sélectionner une
fonction, amenez le curseur dessus et appuyez une nouvelle fois sur 1(SEL).
Appuyez sur 5(TABL) pour générer une table numérique à partir des fonctions
sélectionnées. La valeur de la variable x change en fonction de la plage ou du contenu de la
liste que vous avez spécifiée.
L’exemple ci-contre montre les résultats obtenus pour
la liste 6 (– 3, –2, –1, 0, 1, 2, 3).
Chaque élément peut contenir jusqu’à six chiffres, signe négatif compris.
5-7-2
Utilisation de tables

19990401
Vous pouvez utiliser les touches de curseur pour déplacer la surbrillance sur la table et
effectuer les opérations suivantes.
• Afficher la valeur de l’élément sélectionné au bas de l’écran, en utilisant le nombre de
décimales, le nombre de chiffres significatifs et les réglages de plage d’affichage
exponentiel actuellement définis.
• Faire défiler l’affichage et voir les parties d’une table qui n’apparaissent pas sur l’écran.
• Afficher dans la partie supérieure de l’écran la fonction scientifique qui produit la valeur
dans l’élément sélectionné (dans les colonnes Y1, Y2, etc.).
• Changer les valeurs de la variable x en remplaçant les valeurs dans la colonne X.
Appuyez sur i pour revenir à la liste des fonctions de graphes.
uPour générer une table numérique différentielle *1
La validation du paramètre Derivative sur l’écran de configuration permet d’afficher une table
numérique avec la dérivée à chaque génération d’une table numérique.
uDésignation du type de fonction
Vous pouvez désigner un des trois types de fonctions suivants.*2
• A coordonnées rectangulaires (Y=)
• A coordonnées polaires (r
=)
• Paramétriques (Param)
1. Appuyez sur 3(TYPE) lorsque la liste des fonctions est à l’écran.
2. Appuyez sur la touche numérique correspondant au type de fonction que vous voulez
spécifier.
• Vous pouves créer plusieurs tables en sélectionnant plusieurs fonctions
(1(SEL)).
5-7-3
Utilisation de tables
*1Une erreur se produira si les expressions du
graphe contiennent un graphe pour lequel une
plage est définie ou un graphe de surécriture.
*2La table numérique n’est générée que pour le
type de fonctions spécifié dans la liste de
fonctions (Graph Func). Vous ne pouvez pas
générer une table numérique pour un groupe de
fonctions de différents types.
“
dy
/
dx
” apparaît en haut de l’écran pour
indiquer une différentielle lorsque le
curseur est positionné sur un coefficient
différentiel.

19990401
kk
kk
kEdition et suppression de fonctions
uPour éditer une fonction
Exemple Remplacer la fonction y = 3x2 – 2 dans la zone de mémoire Y1 par
y = 3x2 – 5
Utilisez f et c pour amener la surbrillance sur la fonction que vous
voulez éditer.
Utilisez d et e pour amener le curseur à la position qui doit être changée.
eeeeeDf
w
6(g)5(TABL)
• Les changements effectués sur les fonctions se répercutent automatiquement dans la
liste du mode GRPH • TBL et dans la liste du mode DYNA grâce à la fonction de liaison
des fonctions.
uPour supprimer une fonction
1. Utilisez f et c pour amener la surbrillance sur la fonction que vous voulez
supprimer puis appuyez sur 2(DEL) ou sur D.
2. Appuyez sur w(Oui) pour supprimer la fonction ou sur i(Non) pour abandonner
l’opération sans rien supprimer.
5-7-4
Utilisation de tables
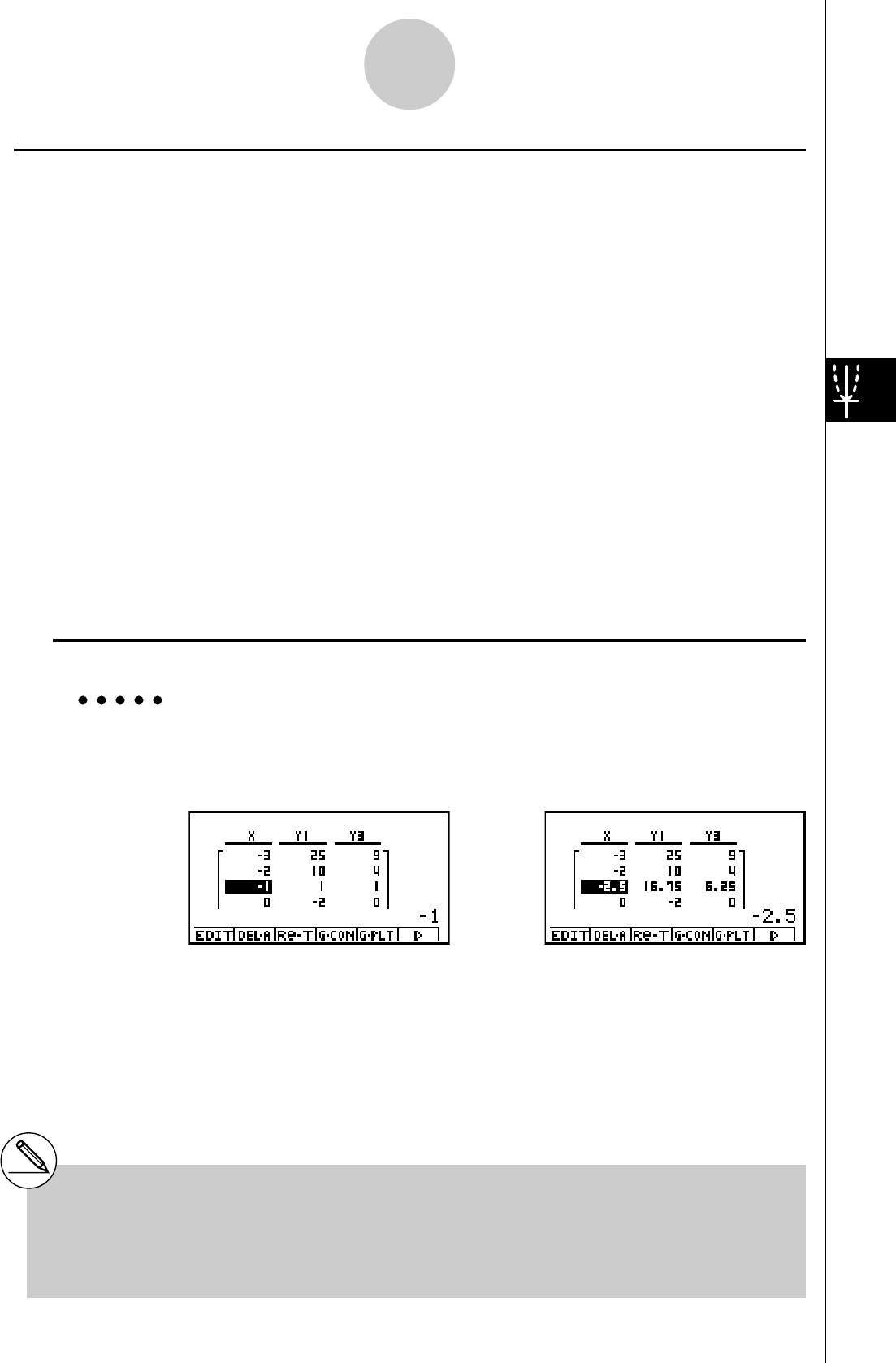
19990401
5-7-5
Utilisation de tables
kk
kk
kEdition de tables
Vous pouvez utiliser le menu de table pour effectuer les opérations suivantes après avoir
généré une table.
• Changer les valeurs de la variable x
• Editer (supprimer, insérer et ajouter) des lignes
• Supprimer une table et regénérer une table
• Tracer un graphe à points connectés
• Tracer un graphe à points séparés
Lorsque le menu Table & Graph est affiché, appuyez sur 5(TABL) pour afficher le menu.
• {EDIT} ... {édition de la valeur d’une variable x}
• {DEL·A} ... {suppression d’une table}
•{Re-T} ... {regénération d’une table à partir d’une fonction}
•{G·CON}/{G·PLT} ... tracé de graphe {à points connectés}/{à points séparés}
•{R·DEL}/{R·INS}/{R·ADD} ... {suppression}/{insertion}/{addition} d’une ligne
uPour changer les valeurs de la variable dans une table
Exemple Changer de –1 à –2,5 la valeur dans la colonne x, ligne 3 de la table
générée page 5-7-2
cc -c.fw
• Lorsque vous changez une valeur de la variable dans la colonne x, toutes les valeurs
dans les colonnes de droite sont recalculées et affichées.
# Si vous essayez de remplacer une valeur par
une opération interdite (par exemple une
division par zéro), une erreur se produira et la
valeur originale ne changera pas.
# Vous ne pouvez pas changer directement les
valeurs dans les autres colonnes (autres que x)
de la table.
20040901
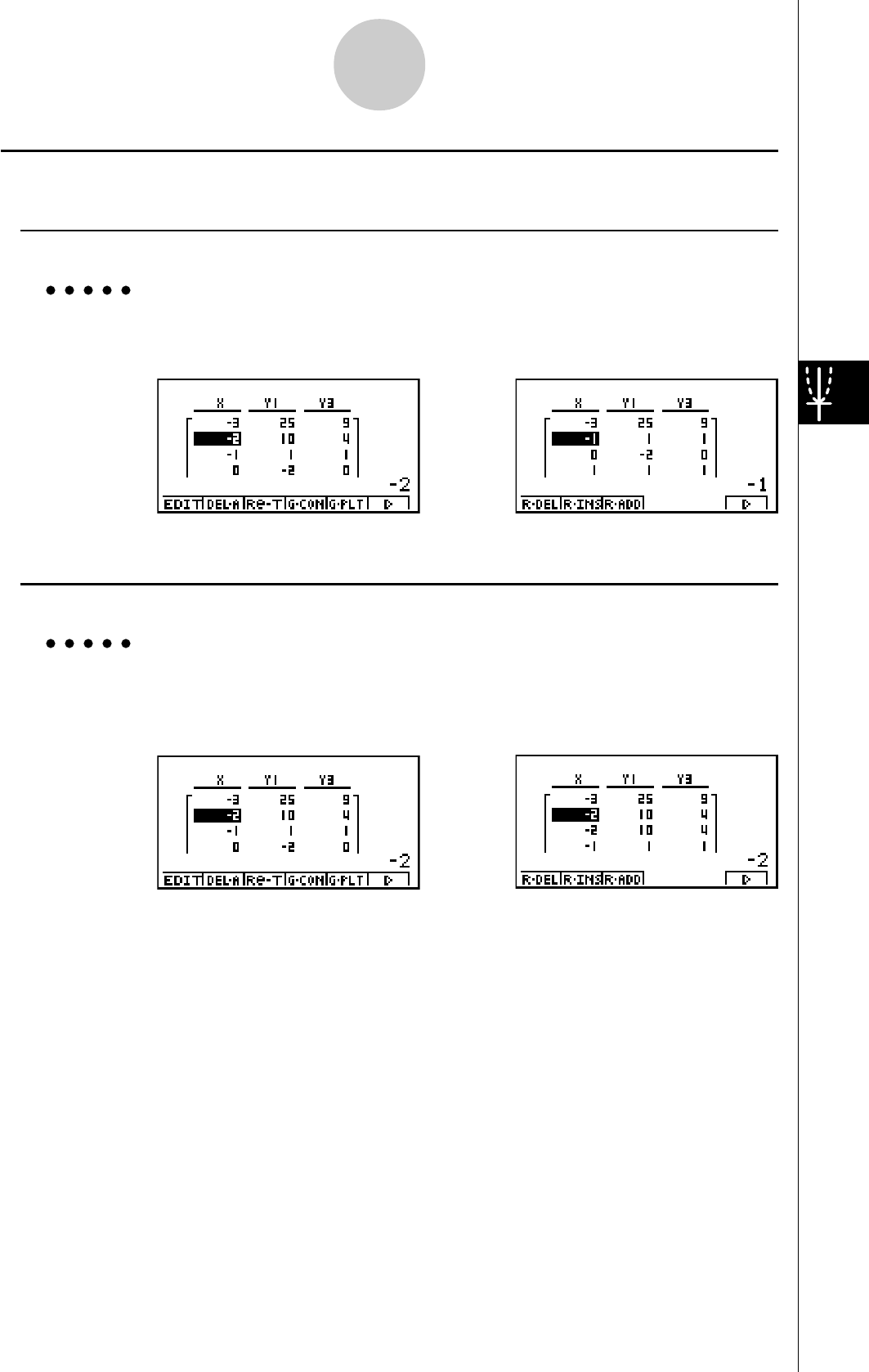
19990401
5-7-6
Utilisation de tables
uOpérations sur les lignes
uPour supprimer une ligne
Exemple Supprimer la ligne 2 de la table générée page 5-7-2
c6(g)1(R·DEL)
uPour insérer une ligne
Exemple Insérer une nouvelle ligne entre les lignes 1 et 2 dans la table générée
page 5-7-2
c6(g)2(R·INS)
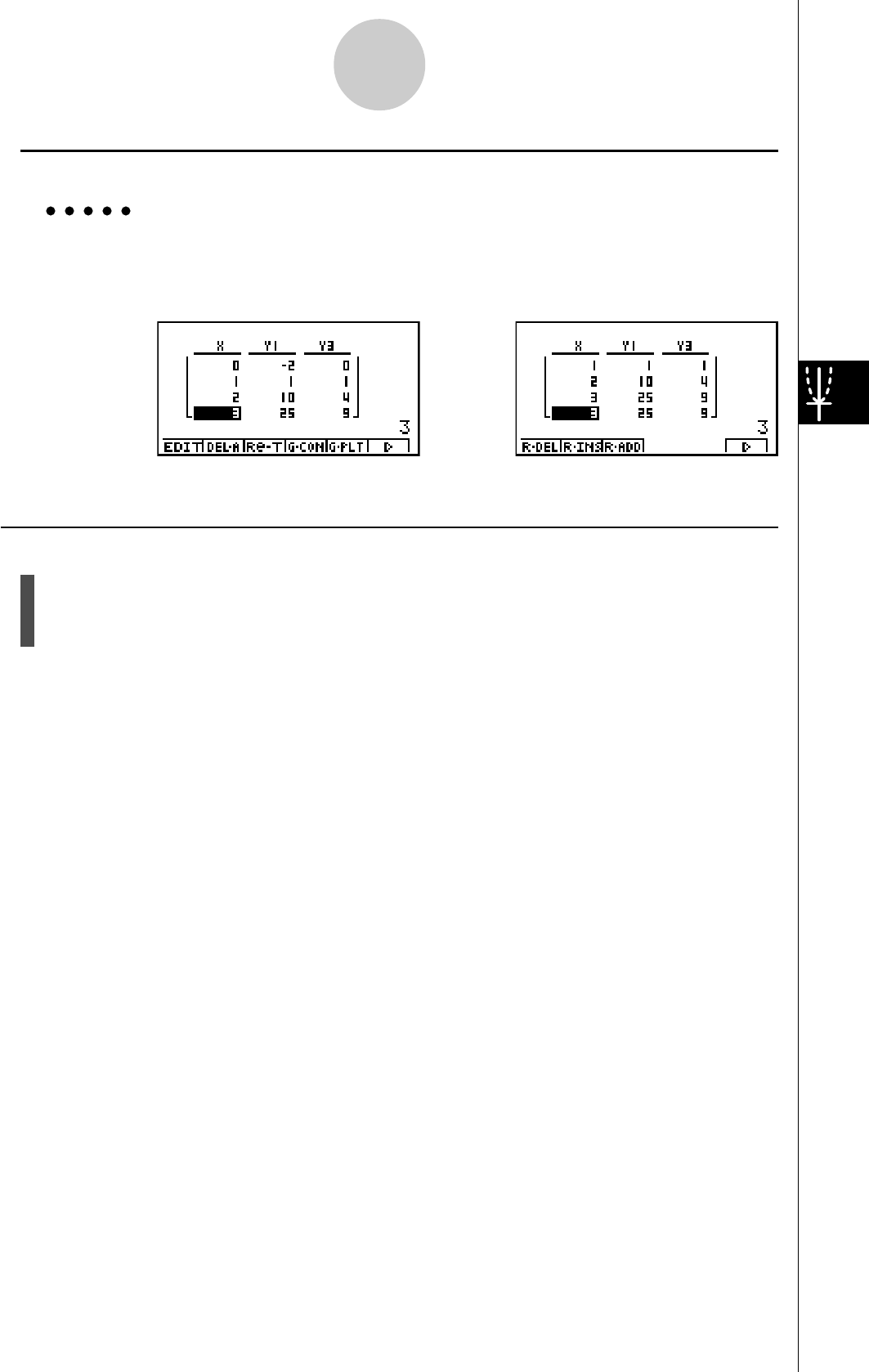
19990401
5-7-7
Utilisation de tables
uPour ajouter une ligne
Exemple Ajouter une nouvelle ligne en dessous de la ligne 7 dans la table
générée page 5-7-2
cccccc 6(g)3(R·ADD)
uSuppression d’une table
1. Affichez la table et appuyez sur 2(DEL·A).
2. Appuyez sur w(Oui) pour supprimer la table ou sur i(Non) pour abandonner
l’opération sans rien supprimer.
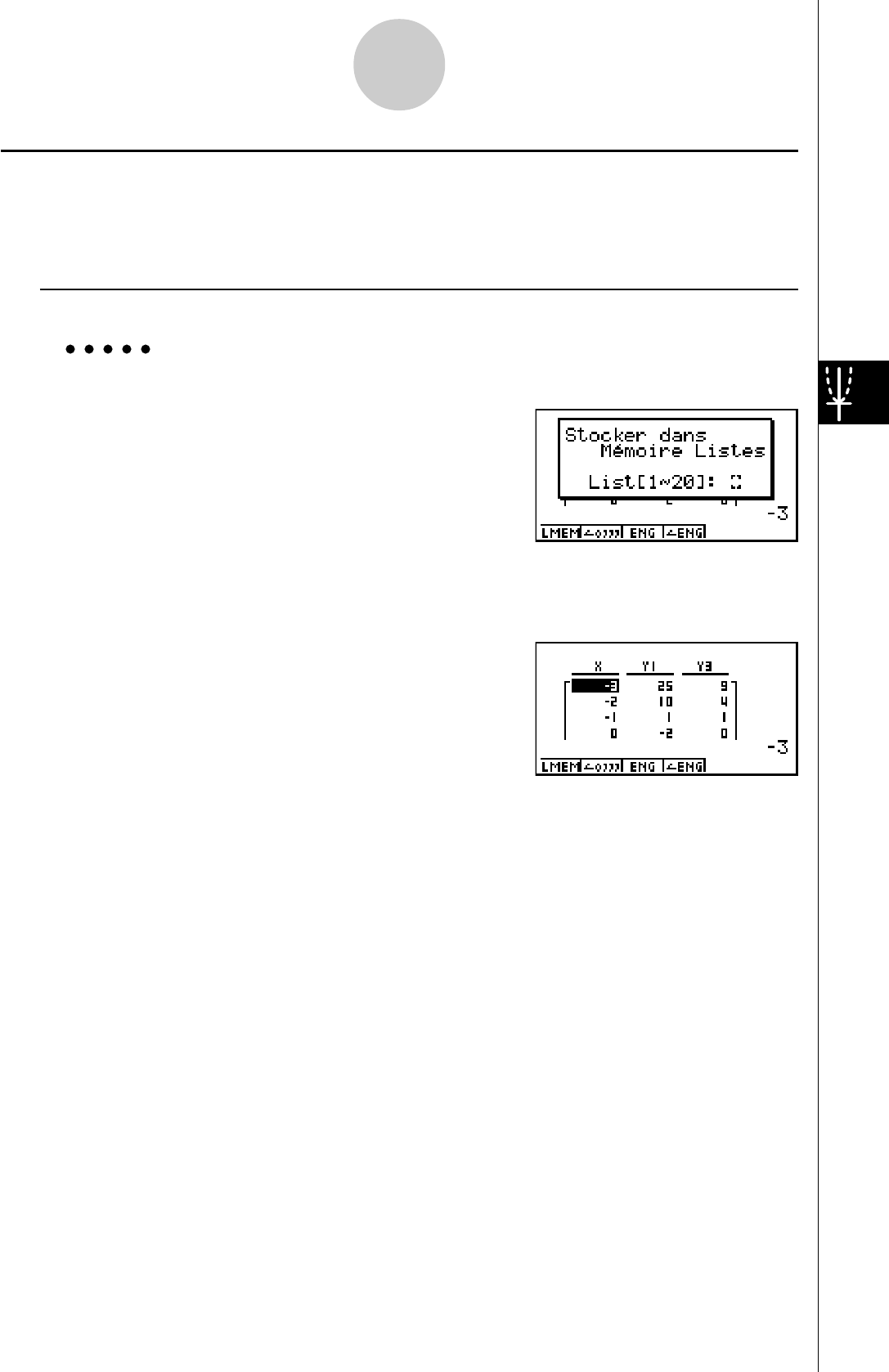
19990401
kk
kk
kCopie d’une colonne d’une table dans une liste
En effectuant une opération simple, vous pourrez copier le contenu d’une colonne d’une
table numérique dans une liste.
uPour copier une table dans une liste
Exemple Copier le contenu de la colonne x dans la liste 1
K1(LMEM)
• Vous pouvez sélectionner n’importe quelle ligne de la colonne que vous voulez copier.
Indiquez le numéro de la liste que vous voulez copier et appuyez sur w.
bw
5-7-8
Utilisation de tables

19990401
kk
kk
kTracé d’un graphe depuis une table numérique
Description
Procédez de la façon suivante pour générer une table numérique et tracer un graphe à partir
des valeurs de la table.
Réglage
1. Depuis le menu principal, accédez au mode GRPH • TBL.
2. Effectuez les réglages de fenêtre d’affichage.
Exécution
3. Stockez les fonctions.
4. Définissez la plage de la table.
5. Générez la table.
6. Sélectionnez le type de graphe et tracez-le.
4(G • CON) ... graphe linéaire*1
5(G • PLT) ... graphe à points séparés*1*2
5-7-9
Utilisation de tables
*1Après le tracé du graphe, appuyez sur u
5(G ↔ T) ou i pour revenir à l’écran de
stockage des fonctions. Pour revenir à l’écran
de la table numérique, appuyez sur
5(TABL).
*2Une pression sur (6(g) 4(G • PLT)) sur
l’écran de stockage des fonctions génère la
table numérique et trace simultanément un
graphe à points séparés.

19990401
Exemple Stocker les deux fonctions suivantes, générer une table numérique et
tracer ensuite un graphe linéaire. Définir une plage de –3 à 3 et 1
comme incrément.
Y1 = 3x2 – 2, Y2 = x2
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = 0, Xmax = 6, Xscale = 1
Ymin = –2, Ymax = 10, Yscale = 2
Procédure
1m GRPH • TBL
2!K(V-Window)awgwbwc
-cwbawcwi
33(TYPE)b(Y=) dvx-cw
vxw
46(g)2(RANG)-dwdwbwi
55(TABL)
64(G • CON)
Ecran de résultat
5-7-10
Utilisation de tables
# Vous pouvez utiliser les fonctions Trace,
Zoom et Sketch après le tracé du graphe.

19990401
kk
kk
kDéfinition d’une plage pour la génération d’une table numérique
Description
Procédez de la façon suivante pour définir une plage de table numérique lors du calcul de
données dispersées à partir d’une fonction.
Réglage
1. Depuis le menu principal, accédez au mode GRPH • TBL.
Exécution
2. Stockez les fonctions.
3. Définissez la plage de la table.
4. Sélectionnez les fonctions pour lesquelles vous voulez générer une table.
Le signe “=” des fonctions sélectionnées apparaît en surbrillance à l’écran.
5. Générez la table.
5-7-11
Utilisation de tables
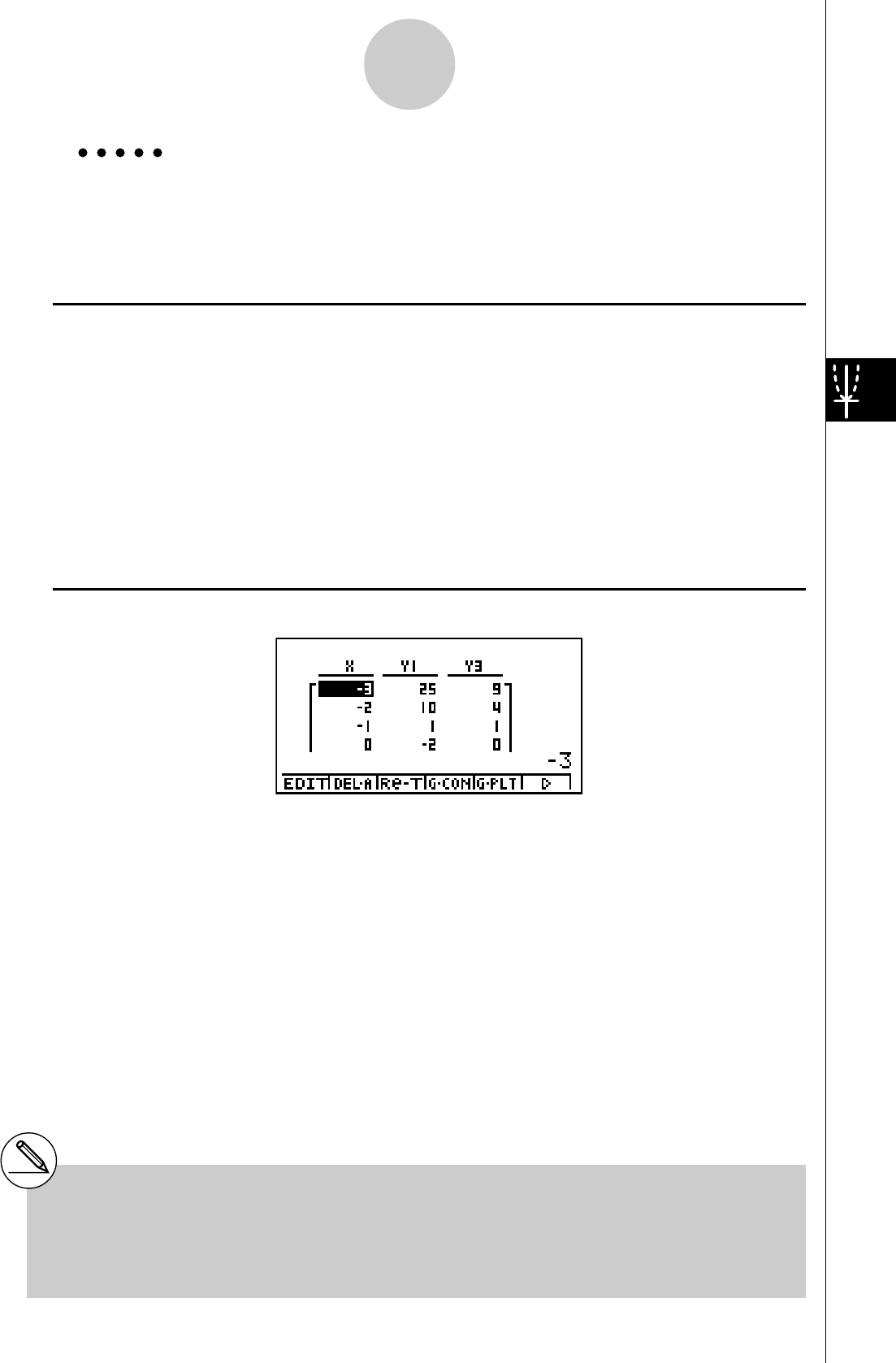
19990401
Exemple Stocker les trois fonctions suivantes et générer une table numérique
pour les fonctions Y1 et Y3. Définir une plage de –3 à 3 et 1 comme
incrément.
Y1 = 3x2 – 2, Y2 = x + 4, Y3 = x2
Procédure
1m GRPH • TBL
23(TYPE)b(Y=)dvx-cw
v+ew
vxw
36(g)2(RANG)-dwdwbwi
4ff1(SEL)
55(TABL)
Ecran de résultat
5-7-12
Utilisation de tables
# Vous pouvez générer des tables numériques à
partir de fonctions à coordonnées
rectangulaires, à coordonnées polaires et de
fonctions paramétriques.
# Vous pouvez inclure des dérivées dans les
tables numériques générées en validant (On) le
paramètre Derivative sur l’écran de
configuration.

19990401
kk
kk
kAffichage simultané d’une table numérique et d’un graphe
Description
En spécifiant T+G pour Dual Screen sur l’écran de configuration, vous pourrez afficher en
même temps une table numérique et un graphe.
Réglage
1. Depuis le menu principal, accédez au mode GRPH • TBL.
2. Effectuez les réglages de fenêtre d’affichage.
3. Sur l’écran de configuration, sélectionnez T+G pour Dual Screen.
Exécution
4. Saisissez la fonction.
5. Définissez la plage de la table.
6. La table numérique est affichée sur l’écran secondaire sur la droite.
7. Désignez le type de graphe et tracez le graphe.
4(G • CON) ... graphe linéaire
5(G • PLT) ... graphe à points séparés*1
5-7-13
Utilisation de tables
*1Une pression sur (6(g) 4(G • PLT)) sur
l’écran de stockage des fonctions génère la
table numérique et trace simultanément un
graphe à points séparés.
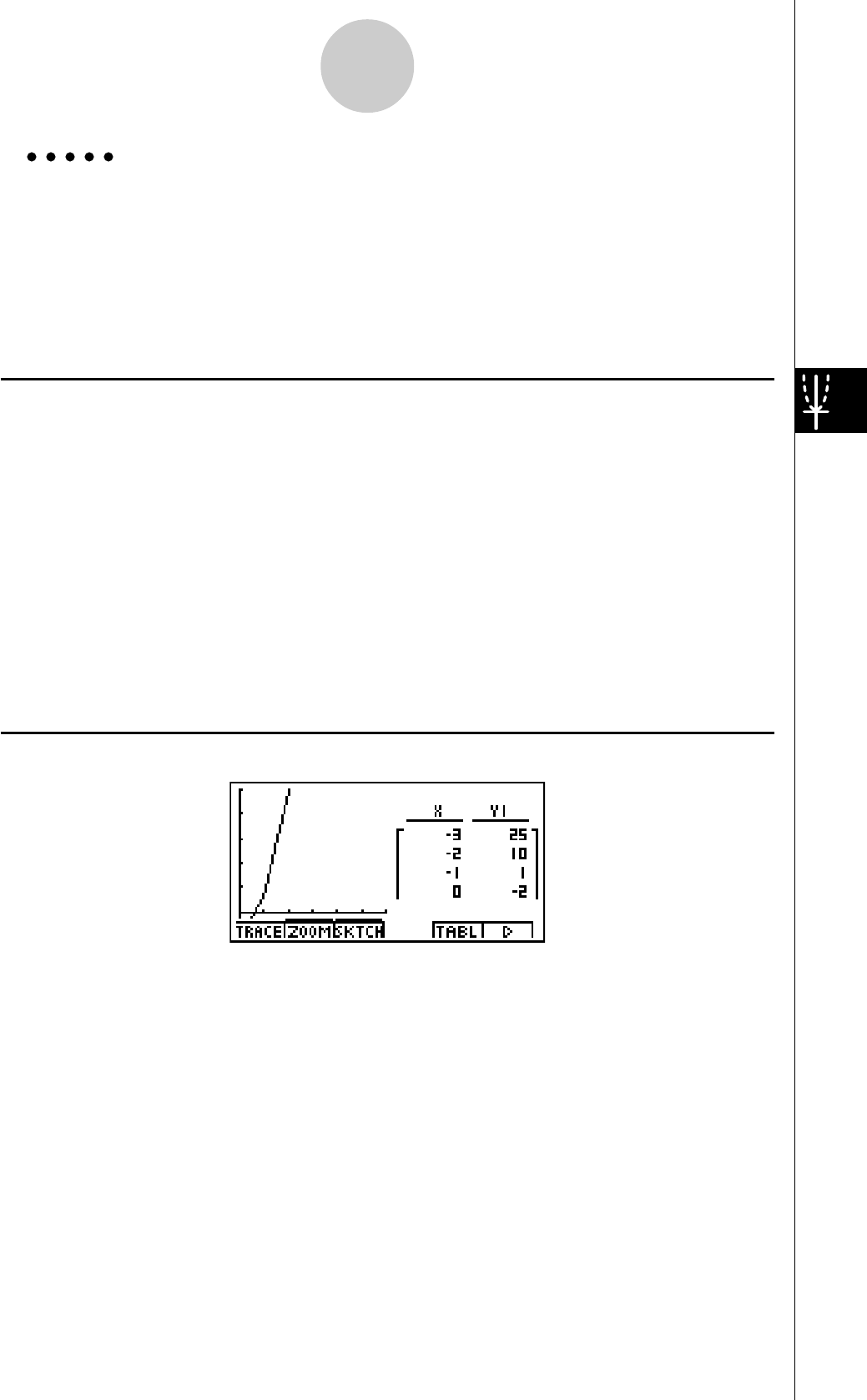
19990401
Exemple Stocker la fonction Y1 = 3x2 – 2 et afficher simultanément sa table
numérique et son graphe linéaire. Définir une plage de –3 à 3 et 1
comme incrément.
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = 0, Xmax = 6, Xscale = 1
Ymin = –2, Ymax = 10, Yscale = 2
Procédure
1m GRPH • TBL
2!K(V-Window)awgwbwc
-cwbawcwi
3u3(SET UP)ccc1(T+G)i
43(TYPE)b(Y=)dvx-cw
56(g)2(RANG)
-dwdwbwi
65(TABL)
74(G • CON)
Ecran de résultat
5-7-14
Utilisation de tables
19990401
5-7-15
Utilisation de tables
kk
kk
kUtilisation de la liaison Graphe-Table
Description
Avec le double graphe, vous pouvez procéder de la façon suivante pour relier les écrans de
graphe et de table pour que le pointeur sur l’écran graphique saute à la position de la valeur
actuellement sélectionnée sur la table.
Réglage
1. Depuis le menu principal, accédez au mode GRPH • TBL.
2. Effectuez les réglages de fenêtre d’affichage nécessaires.
Affichez l’écran de configuration, sélectionnez Dual Screen et validez le réglage “T+G”.
Exécution
3. Saisissez la fonction du graphe et effectuez les réglages nécessaires pour la plage de
la table.
4. Après avoir affiché la table numérique sur le côté droit de l’écran, tracez le graphe sur
le côté gauche.
4(G • CON) ... graphe à points connectés
5(G • PLT) ... graphe à points séparés
5. Validez G • Link.
6. Vous pouvez maintenant utiliser c et f pour déplacer la surbrillance sur les
éléments de la table. Le pointeur se positionne au point correspondant sur l’écran du
graphe.
Si plusieurs graphes sont affichés, le pointeur passe de l’un à l’autre à chaque pression
de d et e.
Pour invalider G • Link, appuyez sur i ou !i(QUIT).
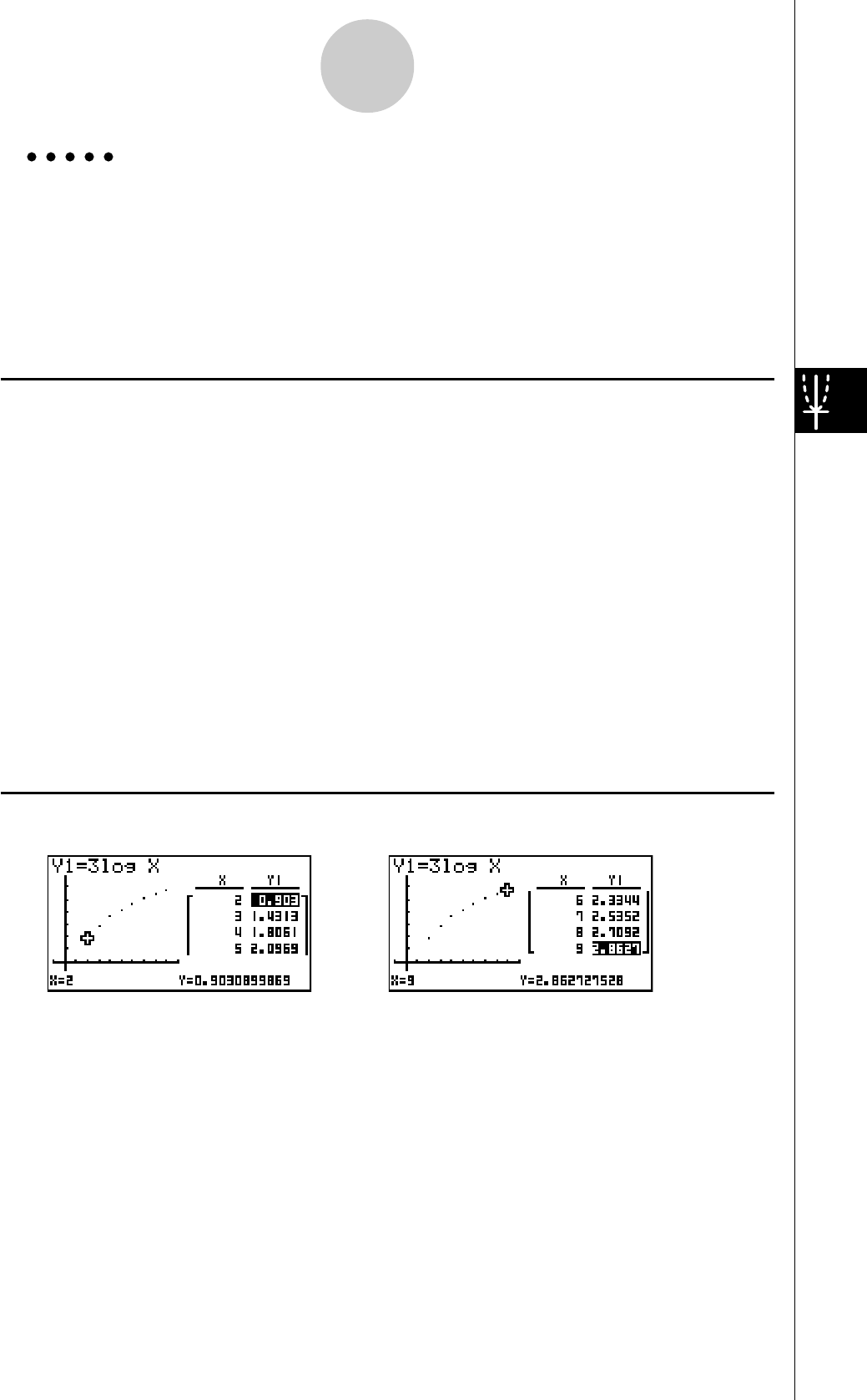
19990401
5-7-16
Utilisation de tables
Exemple Stocker la fonction Y1 = 3logx et afficher simultanément sa table
numérique et son graphe à points séparés. Utiliser une plage de table
comprise entre 2 et 9, avec 1 comme incrément.
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –1, Xmax = 10, Xscale = 1
Ymin = –1, Ymax = 4, Yscale = 1
Procédure
1m GRPH • TBL
2!K(V-Window)-bwbawbwc
-bwewbwi
u3(SET UP)ccc1(T+G)i
33(TYPE)b(Y=)dlvw
6(g)2(RANG)
cwjwbwi
45(TABL)
5(G • PLT)
56(g)4(G • Link)
6c ~ c, f ~ f
Ecran de résultat
…→
←…
19990401
5-8Représentation graphique dynamique
kk
kk
kUtilisation du graphe dynamique
Description
Le graphe dynamique permet de définir une plage de valeurs pour les coefficients d’une
fonction et d’observer comment un graphe est affecté par les changements de la valeur du
coefficient. Il permet ainsi de voir comment les coefficients et les termes d’une fonction
influencent la forme et la position d’un graphe.
Réglage
1. Depuis le menu principal, accédez au mode DYNA.
2. Effectuez les réglages de fenêtre d’affichage.
Exécution
3. Sur l’écran de configuration, désignez le type de graphe dynamique.
1(Cont) ... Continu
2(Stop) ... Arrêt automatique après 10 tracés
4. Utilisez les touches de curseur pour sélectionner le type de fonction sur la liste des
types de fonctions programmés.*1
5. Saisissez les valeurs des coefficients et désignez le coefficient qui sera la variable
dynamique.*2
6. Définissez la valeur initiale, la valeur finale et l’incrément.
7. Définissez la vitesse du tracé.
3(SPEED)1() ..... Pause après chaque tracé (arrêt et marche)
2() .......Moitié de la vitesse normale (lent)
3() .......Vitesse normale (normal)
4() ......Deux fois la vitesse normale (rapide)
8. Tracez le graphe dynamique.
5-8-1
Représentation graphique dynamique
*1Les sept types de fonctions programmés sont
les suivants:
•Y=AX+B
•Y=A(X–B)2+C
•Y=AX2+BX+C
•Y=AX^3+BX2+CX+D
•Y=Asin(BX+C)
•Y=Acos(BX+C)
•Y=Atan(BX+C)
Après une pression sur 3(TYPE) et la
sélection du type de fonction, vous pouvez
saisir la fonction proprement dite.
b ... expression à coordonnées
rectangulaires
c ... expression à coordonnées polaires
d ... fonction paramétrique
*2Vous pouvez aussi appuyer sur w et afficher le
menu de réglage de paramètres.
# Le message “Trop de fonctions” apparaît si plus
d’une fonction est sélectionnée pour le tracé
dynamique de graphe.
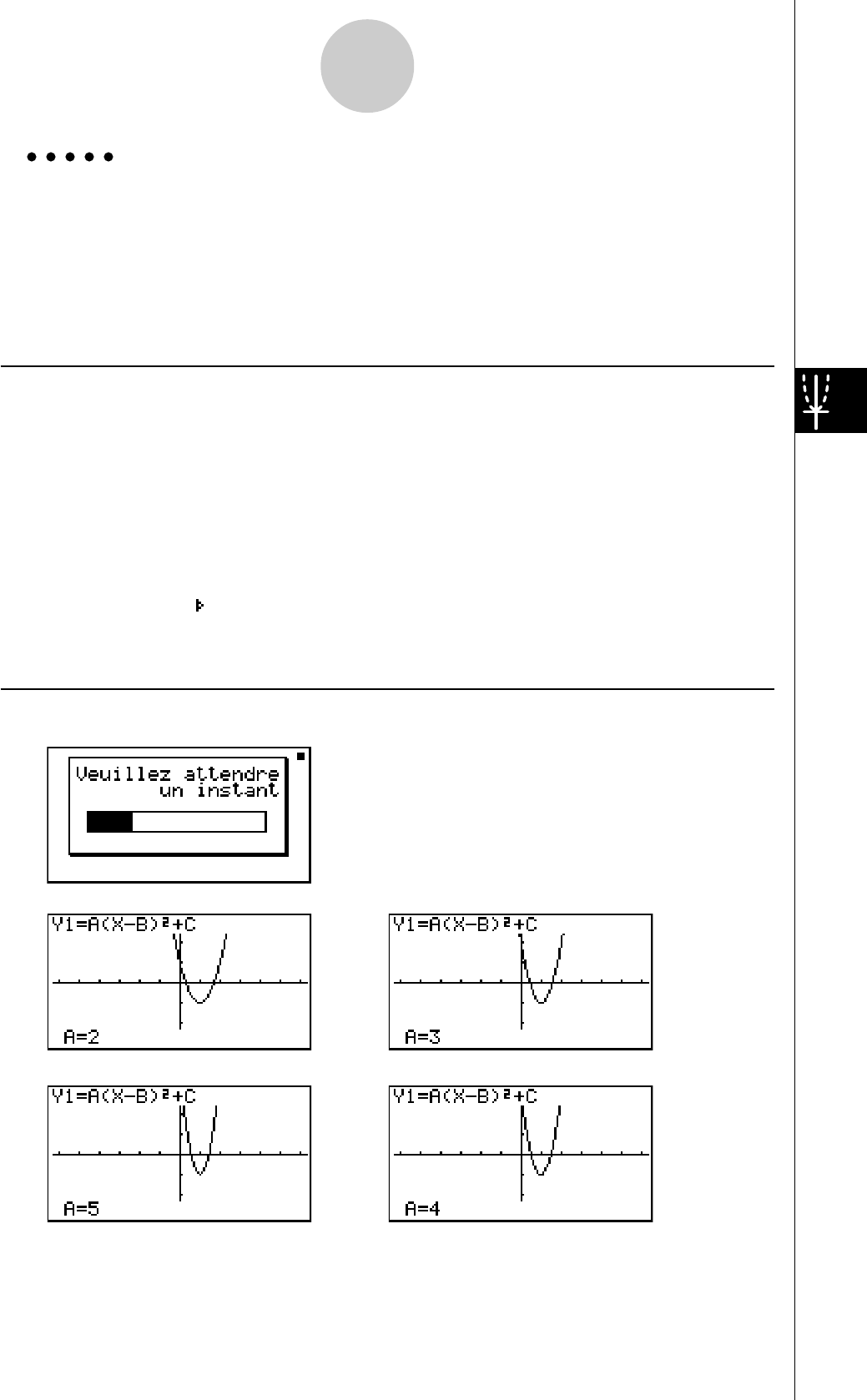
19990401
Exemple Utilisez le graphe dynamique pour tracer y = A (x – 1)2 – 1, lorsque le
coefficient A change de 2 à 5 par incréments de 1. Le graphe doit être
tracé 10 fois.
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –6.3, Xmax = 6.3, Xscale = 1
Ymin = –3.1, Ymax = 3.1, Yscale = 1 (réglages initiaux)
Procédure
1m
DYNA
2!K(V-Window)1(INIT)i
3u3(SET UP)2(Stop)i
46(g)3(B-IN)c1(SEL)
56(g)4(VAR)cwbw-bw
62(RANG)cwfwbwi
73(SPEED)3( ) i
86(DYNA)
Ecran de résultat
↓
→
←
↓↑
→
←
5-8-2
Représentation graphique dynamique
1
4
2
3
Se répète de 1 à 4.

19990401
kk
kk
kExemples d’applications de graphe dynamique
Description
Vous pouvez aussi utiliser le graphe dynamique pour simuler des phénomènes physiques
simples.
Réglage
1. Depuis le menu principal, accédez au mode DYNA.
2. Effectuez les réglages de fenêtre d’affichage.
Exécution
3. Sur l’écran de configuration, désignez Stop (tracé avec pause) pour Dynamic Type et
Deg (degré) pour Angle.
4. Désignez Param (paramétrique) comme type de fonction et saisissez une fonction
contenant une variable dynamique.
5. Désignez le coefficient dynamique.
6. Désignez la valeur initiale, la valeur finale et l’incrément.
7. Désignez Normal comme vitesse de tracé.
8. Commencez le tracé de graphe dynamique.
5-8-3
Représentation graphique dynamique

19990401
Exemple Calculer le parcours dans le temps T d’un ballon lancé en l’air à une
vitesse initiale V et à un angle de
θ
degrés de l’horizontale de la façon
suivante.
X = (Vcos
θ
)T, Y = (Vsin
θ
)T – (1/2)gT2 (g = 9,8m/s2)
Utiliser le graphe dynamique pour marquer le chemin du ballon lancé
à une vitesse initiale de 20 mètres par seconde, à un angle de 30, 45 et
60 degrés de l’horizontale (Angle: Deg).
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –1, Xmax = 42, Xscale = 5
Ymin = –1, Ymax = 16, Yscale = 2
T
θ
min = 0, T
θ
max = 6, Pitch = 0.1
Procédure
1m DYNA
2!K(V-Window)-bwecwfwc
-bwbgwcw
awgwa.bwi
3u3(SET UP)2(Stop)
cccc1(Deg)i
43(TYPE)d(Param)
(cacav(A))vw
(casav(A))v-e.jvxw
54(VAR)
62(RANG)dawgawbfwi
73(SPEED)3( ) i
86(DYNA)
Ecran de résultat
5-8-4
Représentation graphique dynamique
20011001
···→
←···

19990401
kRéglage de la vitesse du graphe dynamique
Vous pouvez procéder de la façon suivante pour ajuster la vitesse du graphe dynamique
pendant le tracé.
1. Pendant le tracé d’un graphe dynamique, appuyez sur A pour passer au menu de
réglage de la vitesse.
•{ } ... {Chaque étape du tracé du graphe dynamique est effectuée chaque fois que
vous appuyez sur w.}
•{ }/{ }/{} ... {ralenti (demi-vitesse)}/{normale (réglage par défaut}/{rapide (double
vitesse)}
•{STO} ... {stocke les conditions de tracé du graphe et les données d’écran dans
la mémoire de graphe dynamique}
2. Appuyez sur la touche de fonction (1 à 4) correspondant à la vitesse que vous
voulez.
5-8-5
Représentation graphique dynamique
# Pour annuler le menu de réglage de la vitesse
sans rien changer, appuyez sur w.
# Appuyez sur u5(G↔T) pour revenir à
l’écran du graphe.

19990401
kk
kk
kUtilisation de la mémoire de graphe dynamique
Vous pouvez stocker les conditions de tracé d’un graphe dynamique et les données d’écran
dans la mémoire de graphe dynamique pour les rappeler ultérieurement lorsque vous en
aurez besoin. Vous gagnerez du temps en rappelant simplement les données pour tracer le
graphe. Vous ne pouvez stocker qu’un seul ensemble de données à la fois.
Un ensemble contient les données suivantes.
• Fonctions de graphes (20 au maximum)
• Conditions de tracé du graphe dynamique
• Réglages de l’écran de configuration
• Contenu de la fenêtre d’affichage
• Ecran de graphe dynamique
uu
uu
uPour sauvegarder des données dans la mémoire de graphe dynamique
1. Pendant le tracé d’un graphe dynamique, appuyez sur A pour passer au menu de
réglage de la vitesse.
2. Appuyez sur 6(STO). En réponse à la boîte de dialogue de confirmation qui apparaît,
appuyez sur w(Oui) pour sauvegarder les données.
uu
uu
uPour rappeler les données de la mémoire de graphe dynamique
1. Affichez la liste de fonctions de graphe dynamique.
2. Appuyez sur 6(RCL) pour rappeler toutes les données stockées dans la mémoire de
graphe dynamique.
5-8-6
Représentation graphique dynamique
# Si des données se trouvent déjà dans la
mémoire de graphe dynamique, elles seront
remplacées par les nouvelles données.
# Les données rappelées de la mémoire de
graphe dynamique remplacent les fonctions de
graphes actuelles, les conditions du tracé et les
données d’écran de la calculatrice. Les données
précédentes sont perdues lorsqu’elles sont
remplacées.
20040901
19990401
5-9 Représentation graphique d’une formule
de récurrence
kk
kk
kGénération d’une table numérique depuis une formule de récurrence
Description
Vous pouvez saisir jusqu’à trois des formules de récurrence suivantes et générer une table
numérique.
• Terme général de la séquence {an}, composée de an, n
• Récurrence linéaire à deux termes, composée de an+1, an, n
• Récurrence linéaire à trois termes, composée de an+2, an+1, an, n
Réglage
1. Depuis le menu principal, accédez au mode RECUR.
Exécution
2. Définissez le type de récurrence.
3(TYPE)b(an=) ... {terme général de la séquence an}
c(an+1=) ... {récurrence linéaire à deux termes}
d(an+2=) ... {récurrence linéaire à trois termes}
3. Saisissez la formule de récurrence.
4. Définissez la plage de la table. Indiquez le point initial et le point final pour n.
Au besoin, définissez une valeur pour le terme initial et la valeur initiale pour le point de
départ du pointeur si vous avez l’ intention de tracer le graphe de la formule.
5. Affichez la table numérique de la formule de récurrence.
5-9-1
Représentation graphique d’une formule de récurrence
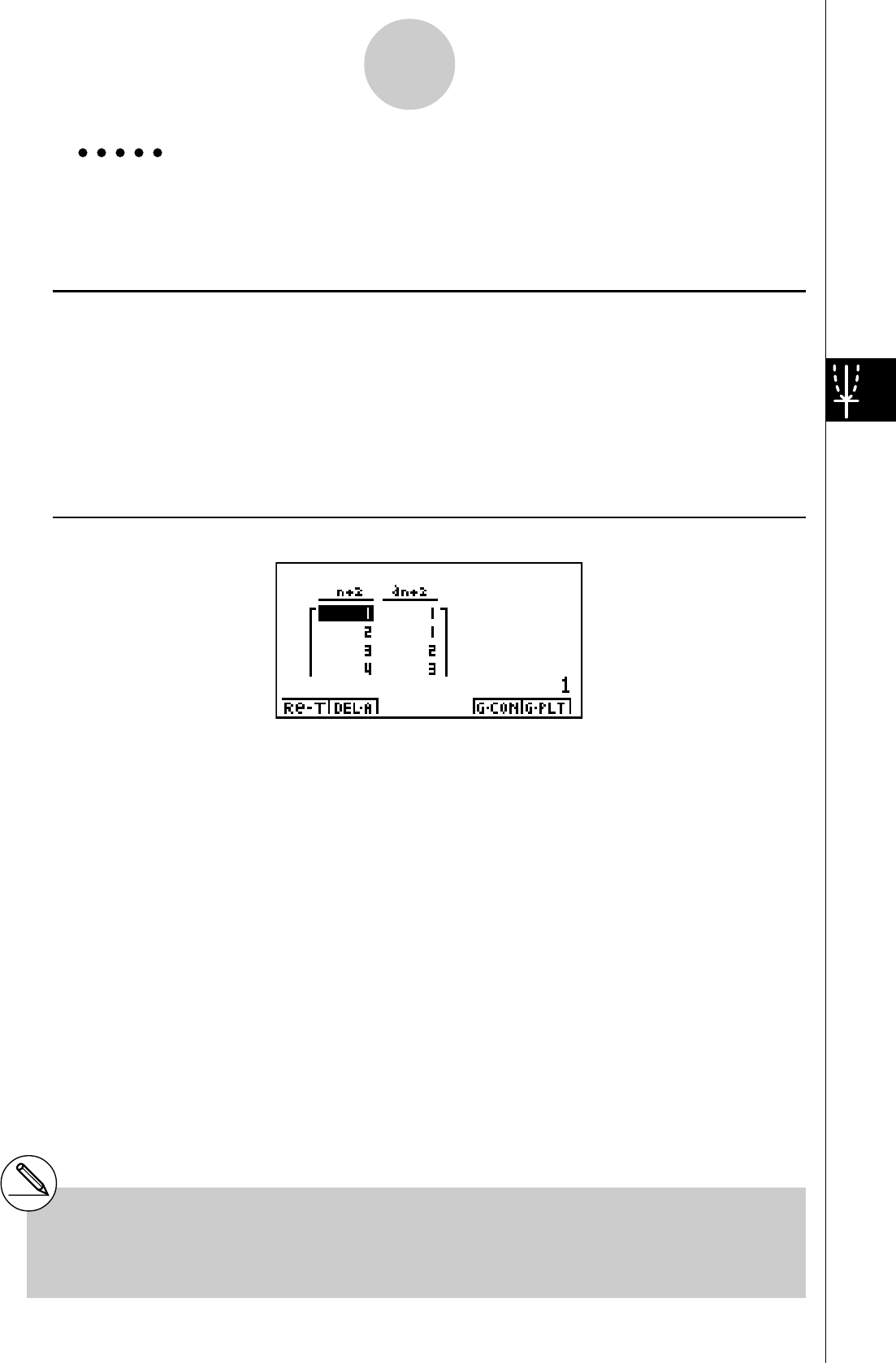
19990401
Exemple Générer une table numérique à partir de la récurrence entre trois
termes, telle qu’exprimée par an+2 = an+1 + an, avec a1 = 1, a2 = 1
(séquence de Fibonaci) comme termes initiaux, lorsque la valeur
de n change de 1 à 6.
Procédure
1m RECUR
23(TYPE)d(an+2=)
34(n. an ··)d(an+1)+2(an)w
45(RANG)2(a1)bwgwbwbwi
56(TABL)
Ecran de résultat
5-9-2
Représentation graphique d’une formule de récurrence
# La validation de l’affichage Σ sur l’écran de
configuration permet d’inclure la somme de
chaque terme dans la table.

19990401
kk
kk
kReprésentation graphique d’une formule de récurrence (1)
Description
Après avoir généré une table numérique à partir d’une formule de récurrence, vous pouvez
représenter les valeurs sur un graphe linéaire ou un graphe à points séparés.
Réglage
1. Depuis le menu principal, accédez au mode RECUR.
2. Effectuez les réglages de fenêtre d’affichage.
Exécution
3. Désignez le type de formule de récurrence et saisissez la formule.
4. Définissez la plage de la table et les valeurs initiale et finale pour n. Au besoin,
définissez la valeur initiale du terme et le point de départ du pointeur.
5. Affichez la table numérique de la formule de récurrence.
6. Définissez le type de graphe et tracez le graphe.
5(G • CON) ... graphe linéaire
6(G • PLT) ... graphe à points séparés
5-9-3
Représentation graphique d’une formule de récurrence
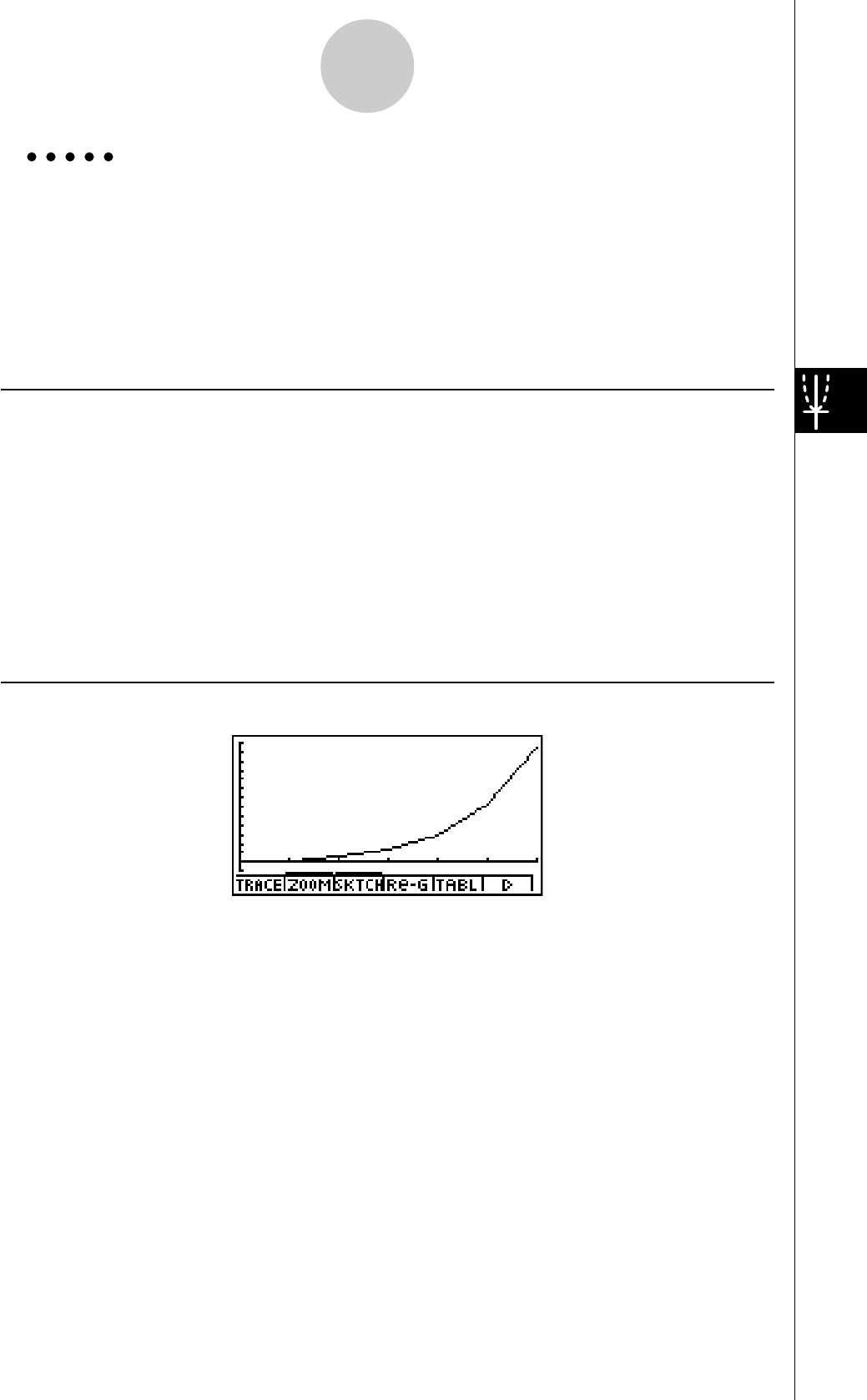
19990401
Exemple Générer une table numérique à partir d’une récurrence entre deux
termes telle qu’exprimée par an+1 = 2an+1, avec a1 = 1 comme terme
initial, lorsque la valeur de n change de 1 à 6. Utiliser les valeurs de la
table pour tracer un graphe linéaire.
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = 0, Xmax = 6, Xscale = 1
Ymin = –15, Ymax = 65, Yscale = 5
Procédure
1m
RECUR
2!K(V-Window)awgwbwc
-bfwgfwfwi
33(TYPE)c(an+1=)c2(an)+bw
45(RANG)2(a1)bwgwbwi
56(TABL)
65(G • CON)
Ecran de résultat
5-9-4
Représentation graphique d’une formule de récurrence
19990401
kk
kk
kReprésentation graphique d’une formule de récurrence (2)
Description
La génération d’une table numérique à partir d’une formule de récurrence et la
représentation graphique de ses valeurs lorsque Σ Display (affichage de Σ) est validé (On)
s’effectuent de la façon suivante.
Réglage
1. Depuis le menu principal, accédez au mode RECUR.
2. Sur l’écran de configuration, désignez On pour Σ Display.
3. Faites les réglages de fenêtre d’affichage.
Exécution
4. Désignez le type de formule de récurrence et saisissez la formule de récurrence.
5. Définissez la plage de la table et les valeurs initiale et finale pour n. Au besoin,
définissez la valeur initiale du terme et le point de départ du pointeur.
6. Affichez la table numérique de la formule de récurrence.
7. Définissez le type de graphe et tracez le graphe.
5(G • CON)b(an) ... graphe linéaire avec ordonnée an et abscisse n
c(Σan) ... graphe linéaire avec ordonnée Σan et abscisse n
6(G • PLT) b(an) ... graphe à points séparés avec ordonnée an et abscisse n
c(Σan) ... graphe à points séparés avec ordonnée Σan et abscisse n
5-9-5
Représentation graphique d’une formule de récurrence

19990401
Exemple Générer une table numérique à partir d’une récurrence entre deux
termes telle qu’exprimée par an+1 = 2an+1, avec a1 = 1 comme terme
initial, lorsque la valeur de n change de 1 à 6. Utiliser les valeurs de la
table pour tracer un graphe linéaire à points séparés avec l’ordonnée
Σan et l’abscisse n.
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = 0, Xmax = 6, Xscale = 1
Ymin = –15, Ymax = 65, Yscale = 5
Procédure
1m
RECUR
2u3(SET UP)1(On)i
3!K(V-Window)awgwbwc
-bfwgfwfwi
43(TYPE)c(an+1=)c2(an)+bw
55(RANG)2(a1)bwgwbwi
66(TABL)
76(G • PLT)c(Σan)
Ecran de résultat
5-9-6
Représentation graphique d’une formule de récurrence
19990401
kk
kk
kGraphe WEB (Convergence, Divergence)
Description
y = f(x) est représenté graphiquement à supposé que an+1 = y, an = x pour la régression
linéaire à deux termes an+1 = f(an), composée de an+1, an. On peut ensuite déterminer si la
fonction est convergente ou divergente.
Réglage
1. Depuis le menu principal, accédez au mode RECUR.
2. Effectuez les réglages de fenêtre d’affichage.
Exécution
3. Sélectionnez une récurrence à 2 termes comme type de formule de récurrence et
saisissez la formule.
4. Définissez la plage de la table, les points initial et final de n, la valeur du terme initial et
le point de départ du pointeur.
5. Affichez la table numérique de la formule de récurrence.
6. Tracez le graphe.
7. Appuyez sur w pour faire apparaître le pointeur au point initial défini.
Appuyez plusieurs fois de suite sur w.
S’il existe une convergence, des lignes en toile d’araignée seront tracées. Si aucune
toile d’araignée n’apparaît, c’est qu’il existe une divergence ou que le graphe est hors
de l’écran. Le cas échéant, sélectionnez des valeurs de fenêtre d’affichage plus
grandes et recommencez.
Vous pouvez utiliser les touches de curseur f c pour sélectionner le graphe.
5-9-7
Représentation graphique d’une formule de récurrence
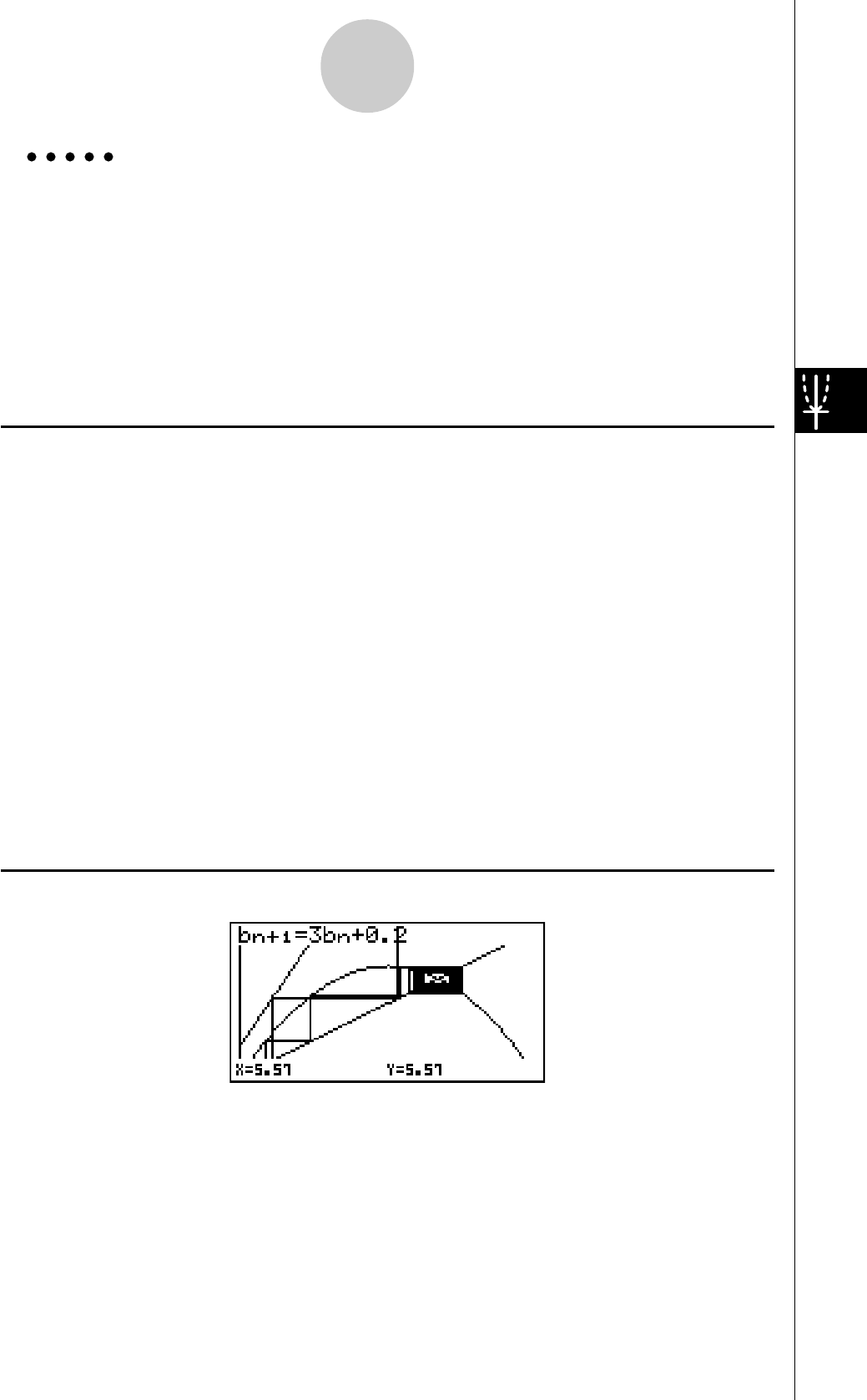
19990401
Exemple Tracer le graphe WEB de la formule de récurrence an+1 = –3(an)2 + 3an,
bn+1 = 3bn + 0,2 et vérifier s’il y a convergence ou divergence. Utiliser
la plage de table et les réglages de fenêtre d’affichage suivants.
Plage de table
Start = 0, End = 6, a0 = 0,01, anStr = 0,01, b0 = 0,11, bnStr = 0,11
Réglages de fenêtre d’affichage
Xmin = 0, Xmax = 1, Xscale = 1
Ymin = 0, Ymax = 1, Yscale = 1
Procedure
1m RECUR
2!K(V-Window)awbwbwc
awbwbwi
33(TYPE)c(an+1=)-d2(an)x+d2(an)w
d3(bn)+a.cw
45(RANG)1(a0)
awgwa.abwa.bbwc
a.abwa.bbwi
56(TABL)
64(WEB)
71(TRACE)w~w(an est convergeant)
cw~w(bn est divergeant)
Ecran de résultat
5-9-8
Représentation graphique d’une formule de récurrence
19990401
5-10-1
Changement de l’aspect d’un graphe
5-10 Changement de l’aspect d’un graphe
kk
kk
kTracé d’une ligne
Description
La fonction de dessin (Sketch) vous permet de tracer des points et des lignes à l’intérieur de
graphes.
Réglage
1. Tracez un graphe.
Exécution
2. Sélectionnez la fonction de dessin que vous voulez utiliser.*1
3(SKTCH)b(Cls) ... Annulation d’écran
c(PLOT)
{On}/{Off}/{Change}/{Plot} ... {Validation}/{Invalidation}/{Changement}/
{Tracé par point séparés} de points
d(LINE)
{F-Line}/{Line} ... {Ligne à main levée}/{Ligne}
e(Text) ... Saisie de texte
f(Pen) ... Main levée
g(Tangnt) ... Tangente
h(Normal) ... Normale à une courbe
i(Invrse) ... Fonction inverse*2
j(Circle) ... Cercle
v(Vert) ... Verticale
l(Horz) ... Horizontale
3. Utilisez les touches de curseur pour placer le pointeur ( ) à l’endroit où vous voulez
dessiner et appuyez sur w.*3
*1Le menu de fonctions qui apparaît dans le
mode GRPH • TBL est indiqué ci-dessus. Les
paramètres du menu peuvent être différents
dans d’autres modes.
*2Dans le cas d’un graphe de fonction inverse,
le tracé commence dès que vous sélectionnez
cette option.
*3Certaines fonctions de dessin exigent la
définition de deux points. Après avoir appuyé
sur w pour désigner le premier point,
utilisez les touches de curseur pour placer le
pointeur à la position du second point et
appuyez sur w.
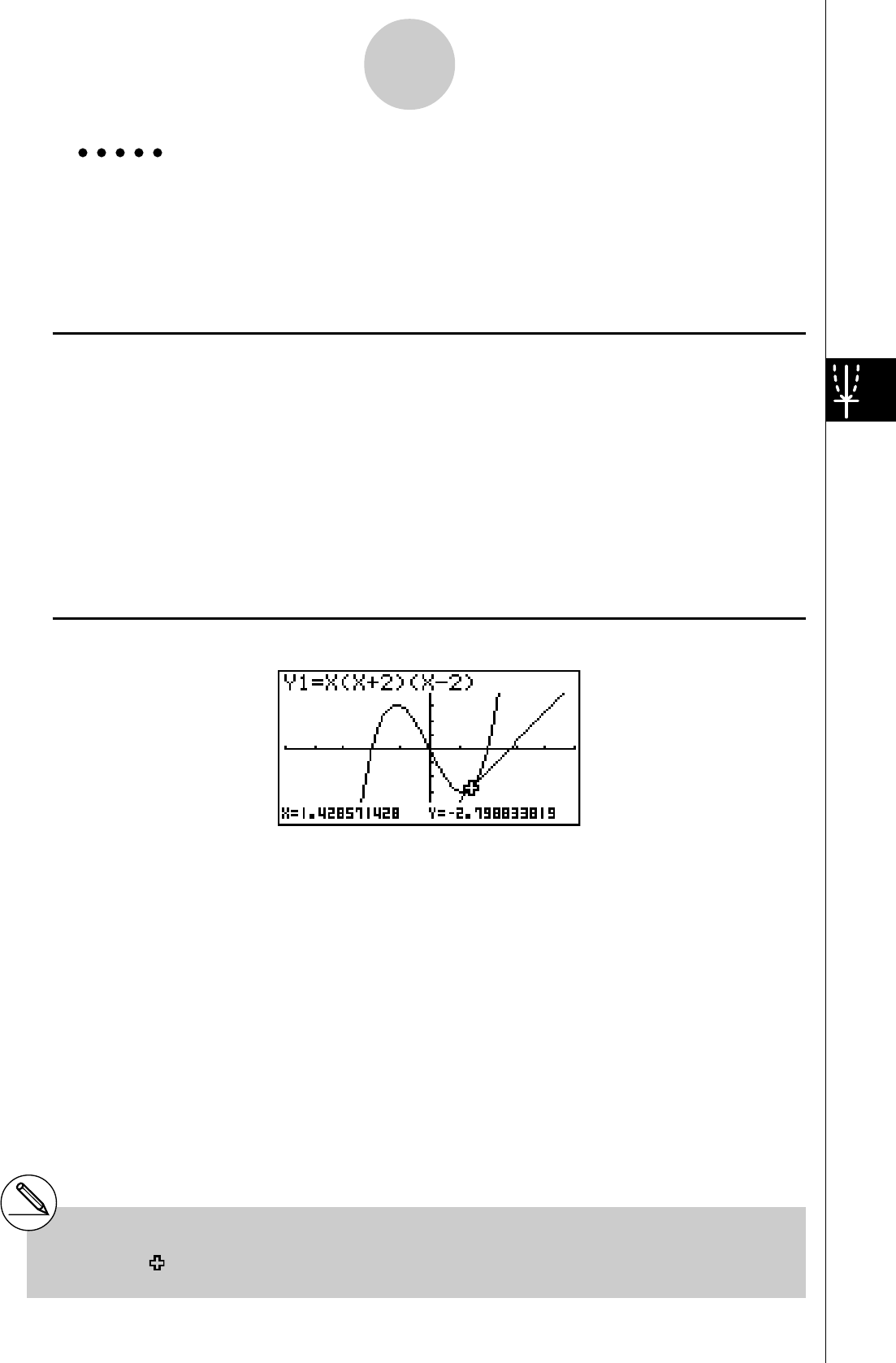
19990401
Exemple Tracer une ligne qui est tangente au point (2, 0) sur le graphe de
y = x (x + 2)(x – 2).
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –5, Xmax = 5, Xscale = 1
Ymin = –5, Ymax = 5, Yscale = 1
Procédure
1m
GRPH • TBL
!K(V-Window) -fwfwbwc
-fwfwbwi
3(TYPE)b(Y=)v(v+c)(v-c)w
5(DRAW)
23(SKTCH)g(Tangnt)
3e~ew*1
Ecran de résultat
5-10-2
Changement de l’aspect d’un graphe
*1Vous pouvez tracer une tangente en déplaçant
le pointeur “ ” et appuyant sur w.

19990401
kk
kk
kInsertion de commentaires
Description
Vous pouvez insérer des commentaires où vous voulez dans un graphe.
Réglage
1. Tracez le graphe.
Exécution
2. Appuyez sur 3(SKTCH)e(Text) pour faire apparaître un pointeur au centre de
l’écran.
3. Utilisez les touches de curseur pour placer le pointeur à l’endroit où le texte doit être
inséré et écrivez le texte.
5-10-3
Changement de l’aspect d’un graphe
# Le commentaire peut contenir les caractères
suivants: A~Z, r,
θ
, espace, 0~9, ., +, –, ×, ÷,
(–), ×10x, π, Ans, (, ), [, ], {, }, virgule, →,
x2, ^, log, In, , x, 10x, ex, 3, x–1, sin, cos,
tan, Asn, Acs, Atn, i, List, Mat
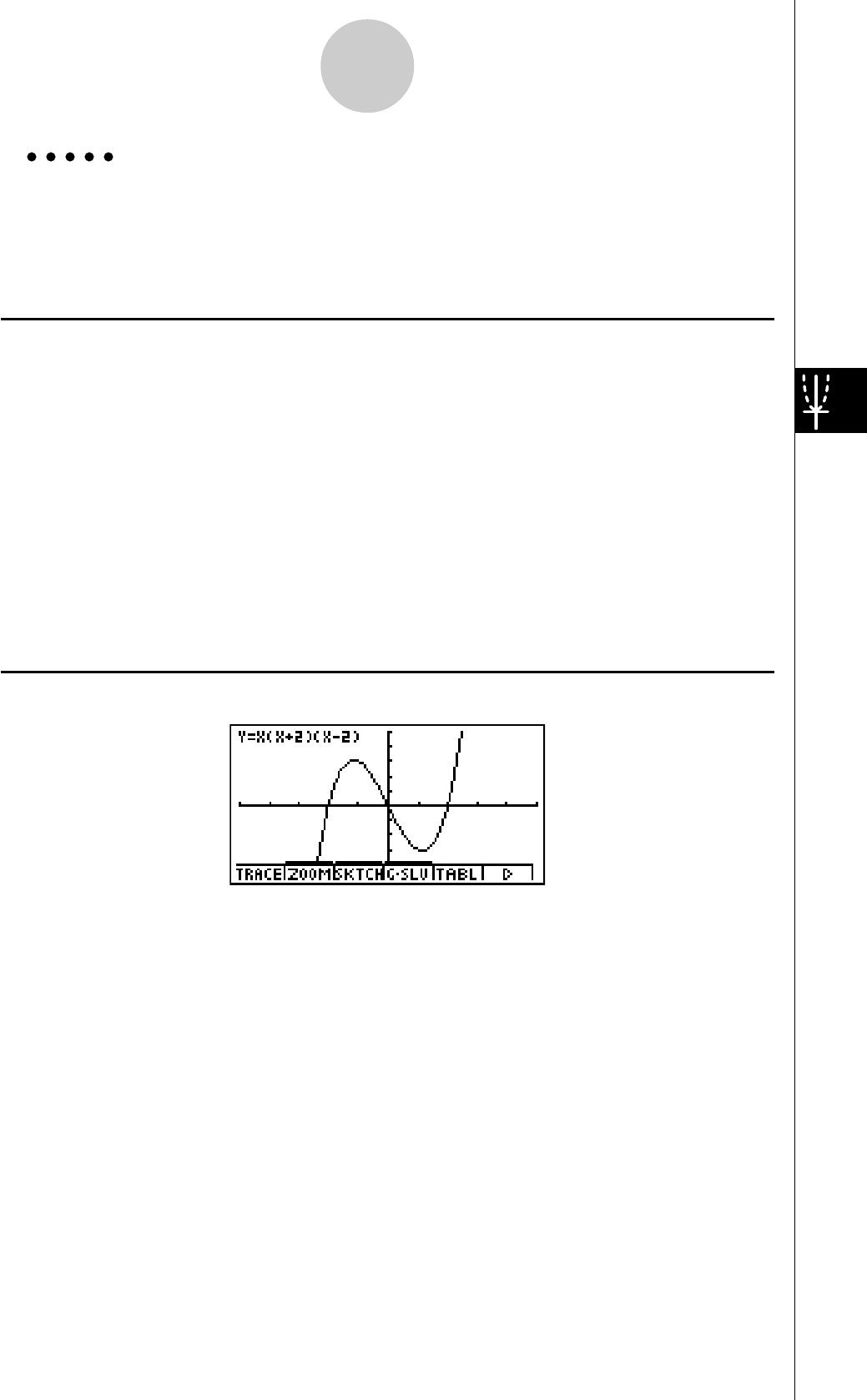
19990401
Exemple Insérer du texte dans le graphe de y = x (x + 2)(x – 2).
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –5, Xmax = 5, Xscale = 1
Ymin = –5, Ymax = 5, Yscale = 1
Procédure
1m
GRPH • TBL
!K(V-Window) -fwfwbwc
-fwfwbwi
3(TYPE)b(Y=)v(v+c)(v-c)w
5(DRAW)
23(SKTCH)e(Text)
3fcee
a-(Y)!.(=)v(v+c)(v-c)
i
Ecran de résultat
5-10-4
Changement de l’aspect d’un graphe

19990401
kk
kk
kDessin à main levée
Description
Vous pouvez utiliser l’option crayon pour tracer un graphe à main levée.
Réglage
1. Tracez le graphe.
Exécution
2. Appuyez sur 3(SKTCH)f(Pen) pour faire apparaître un pointeur au centre de
l’écran.
3. Utilisez les touches de curseur pour amener le pointeur à l’endroit où vous voulez
commencer à dessiner, puis appuyez sur w.
4. Utilisez les touches de curseur pour déplacer le pointeur. Une ligne est tracée lorsque
vous déplacez le pointeur.
Pour arrêter la ligne, appuyez sur w.
Répétez les étapes 3 et 4 pour tracer d’autres lignes.
Lorsque vous avez fini de dessiner, appuyez sur i.
5-10-5
Changement de l’aspect d’un graphe
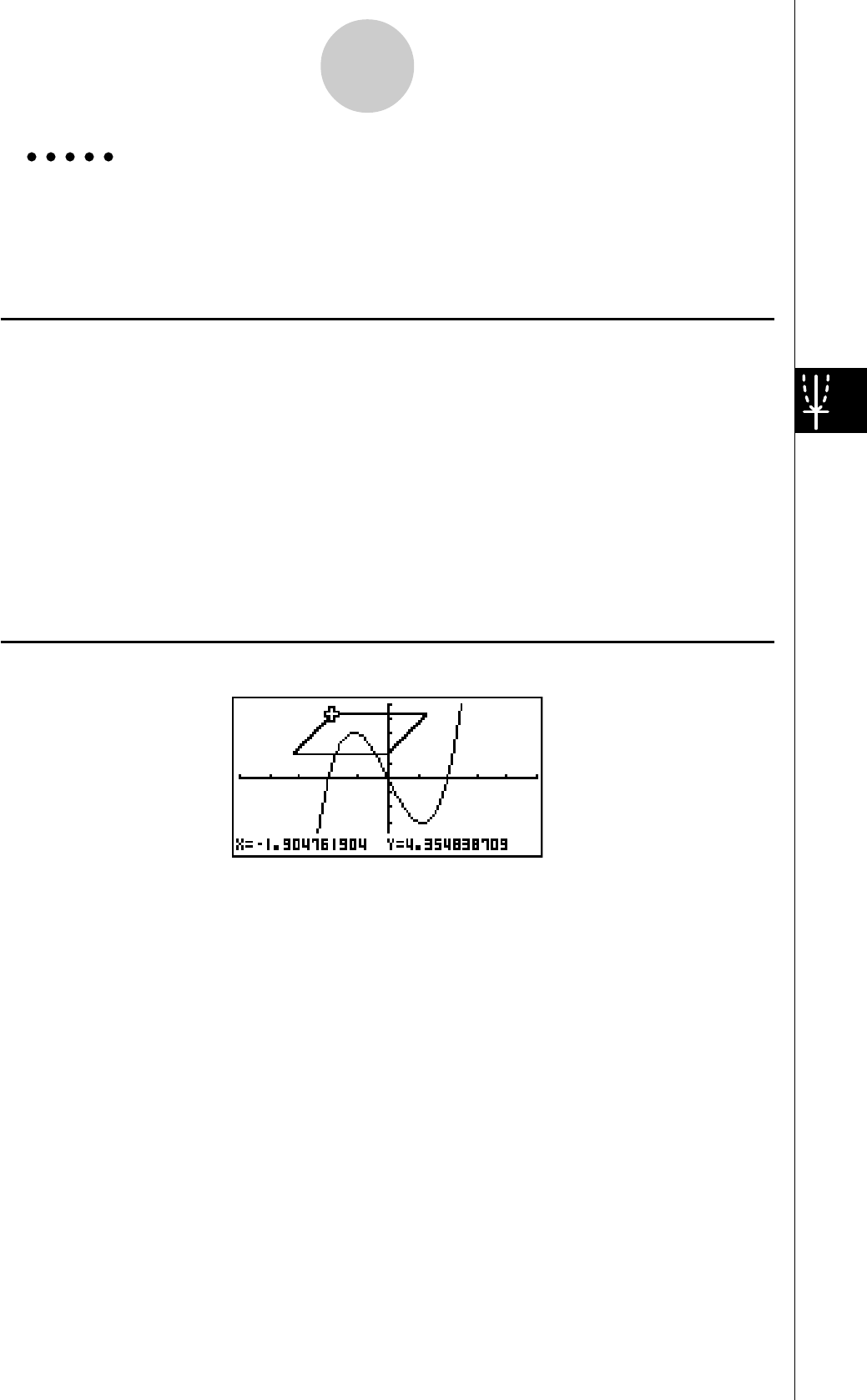
19990401
Exemple Utiliser le crayon pour tracer le graphe de y = x (x + 2)(x – 2).
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –5, Xmax = 5, Xscale = 1
Ymin = –5, Ymax = 5, Yscale = 1
Procédure
1m
GRPH • TBL
!K(V-Window) -fwfwbwc
-fwfwbwi
3(TYPE)b(Y=)v(v+c)(v-c)w
5(DRAW)
23(SKTCH)f(Pen)
3fceew
4fceew
Ecran de résultat
5-10-6
Changement de l’aspect d’un graphe
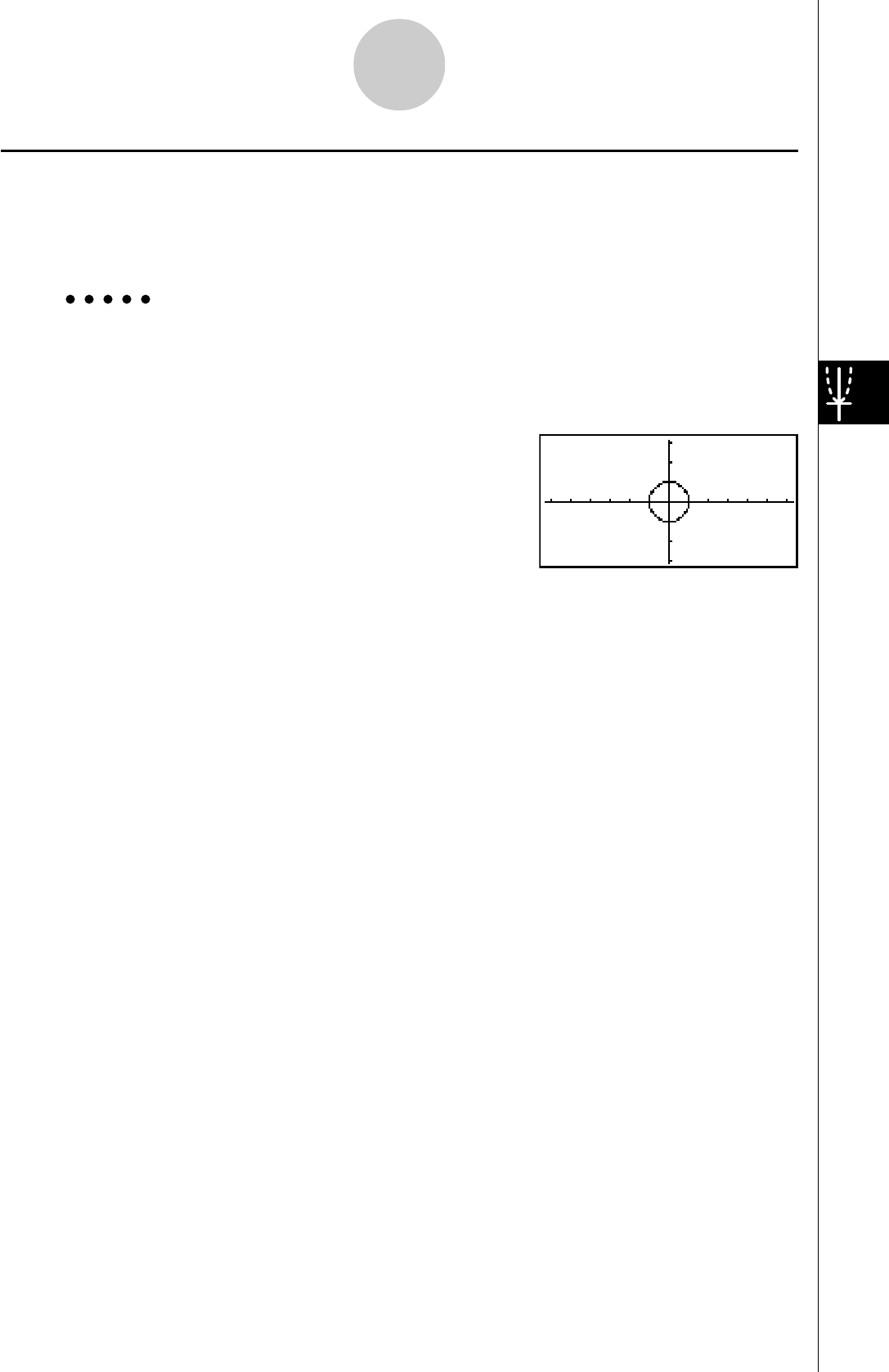
19990401
5-10-7
Changement de l’aspect d’un graphe
kk
kk
kChangement de l’arrière-plan d’un graphe
Vous pouvez utiliser l’écran de configuration pour spécifier le contenu d’une zone de la
mémoire d’images (Pict 1 à Pict 20) comme fond d’écran graphique.
Exemple 1 En utilisant le cercle X2 + Y2 = 1 comme fond, utiliser le graphe
dynamique pour tracer le graphe de Y = X2 + A lorsque la variable A
change de –1 à 1 par incréments de 1.
Rappelez le graphe qui servira de fond.
(X2 + Y2 = 1)
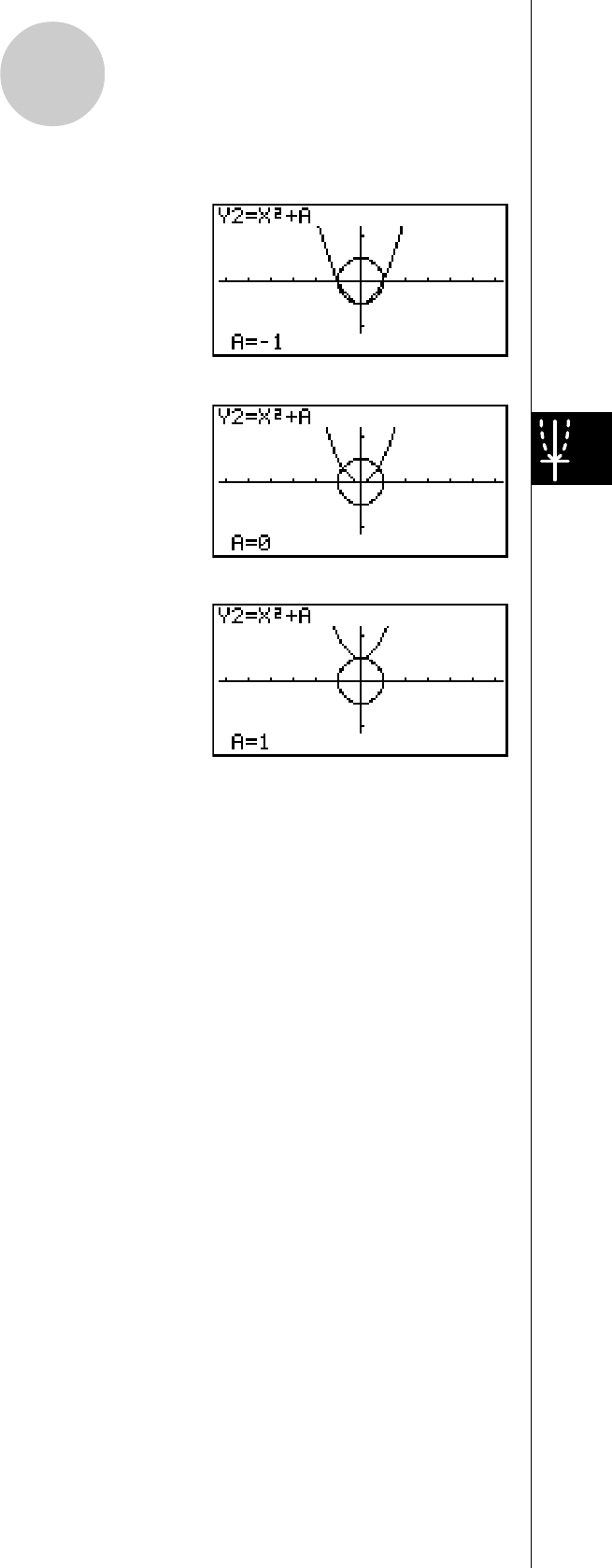
19990401
5-10-8
Changement de l’aspect d’un graphe
Tracez le graphe dynamique.
(Y = X2 – 1)
↓↑
(Y = X2)
↓↑
(Y = X2 + 1)
• Voir “5-8-1 Représentation graphique dynamique” pour les détails sur la fonction de
graphe dynamique.

19990401
5-11 Analyse de fonctions
kk
kk
kLecture des coordonnées sur une ligne du graphe
Description
La fonction Trace permet de déplacer un pointeur sur un graphe et de lire les coordonnées à
la position du pointeur.
Réglage
1. Tracez le graphe.
Exécution
2. Appuyez sur 1(TRACE) pour faire apparaître un pointeur au centre du graphe.*1
3. Utilisez d et e pour déplacer le pointeur le long du graphe jusqu’à l’endroit où vous
voulez afficher la dérivée.
Lorsqu’il y a plusieurs graphes sur l’écran, appuyez sur f et c pour passer de l’un
à l’autre sur l’axe x de l’emplacement actuel du pointeur.
4. Vous pouvez aussi déplacer le pointeur en appuyant sur v pour afficher la fenêtre
déroulante et en saisissant ensuite les coordonnées.
Pour arrêter l’opération Trace, appuyez i.
5-11-1
Analyse de fonctions
*1Le pointeur n’est pas visible sur le graphe
lorsqu’il se trouve à un point hors de la
zone d’affichage du graphe ou lorsqu’une
erreur se produit.
# Vous pouvez invalider l’affichage des
coordonnées à la position du pointeur en
spécifiant “Off” pour le paramètre “Coord” de
l’écran de configuration.
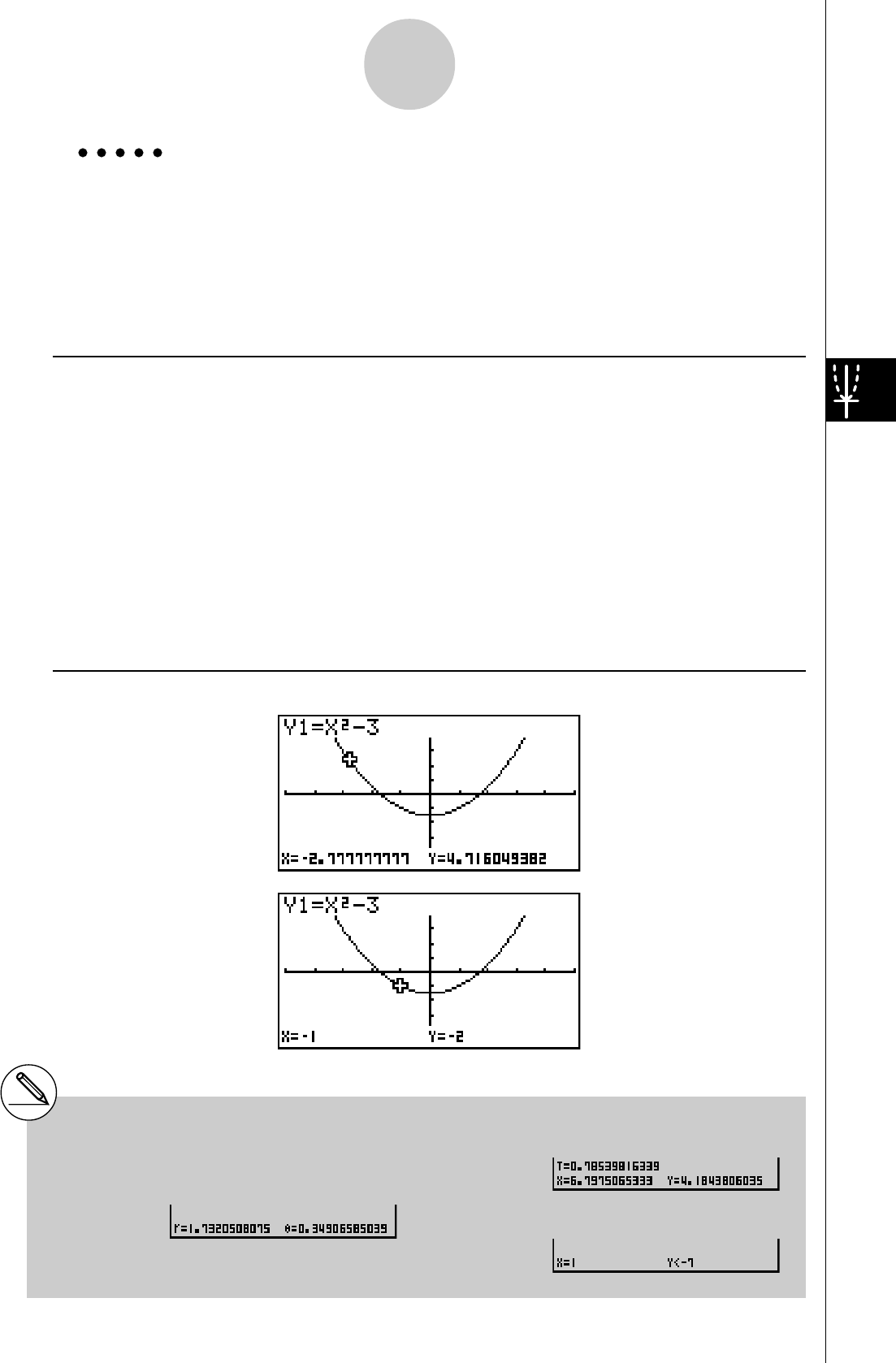
19990401
Exemple Lire les coordonnées le long du graphe de la fonction indiquée
ci-dessous.
Y1 = x2 – 3
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –5, Xmax = 5, Xscale = 1
Ymin = –10, Ymax = 10, Yscale = 2
Procédure
1m GRPH • TBL
!K(V-Window) -fwfwbwc
-bawbawcwi
3(TYPE)b(Y=)vx-dw
5(DRAW)
21(TRACE)
3d~d
4v-bw
Ecran de résultat
5-11-2
Analyse de fonctions
# Les coordonnées sont affichées de la façon
suivante pour chaque type de fonction.
• Graphe à coordonnées polaires
• Graphe paramétrique
• Graphe d’inéquation

19990401
kk
kk
kAffichage de la dérivée
Description
Vous pouvez utiliser la fonction Trace non seulement pour afficher les coordonnées mais
aussi pour afficher la dérivée à la position actuelle du pointeur.
Réglage
1. Sur l’écran de configuration, désignez On pour Derivative (dérivée).
2. Tracez le graphe.
Exécution
3. Appuyez sur 1(TRACE) pour faire apparaître le pointeur au centre du graphe. Les
coordonnées actuelles et la dérivée apparaissent à ce moment à l’écran.
4. Utilisez d et e pour déplacer le pointeur le long du graphe jusqu’au point où vous
voulez afficher la dérivée.
Si plusieurs graphes sont affichés, appuyez sur f et c pour passer de l’un à l’autre
le long de l’axe x de la position actuelle du pointeur.
5. Vous pouvez aussi déplacer le pointeur en appuyant sur v pour afficher la fenêtre
déroulante puis en saisissant des coordonnées.
5-11-3
Analyse de fonctions
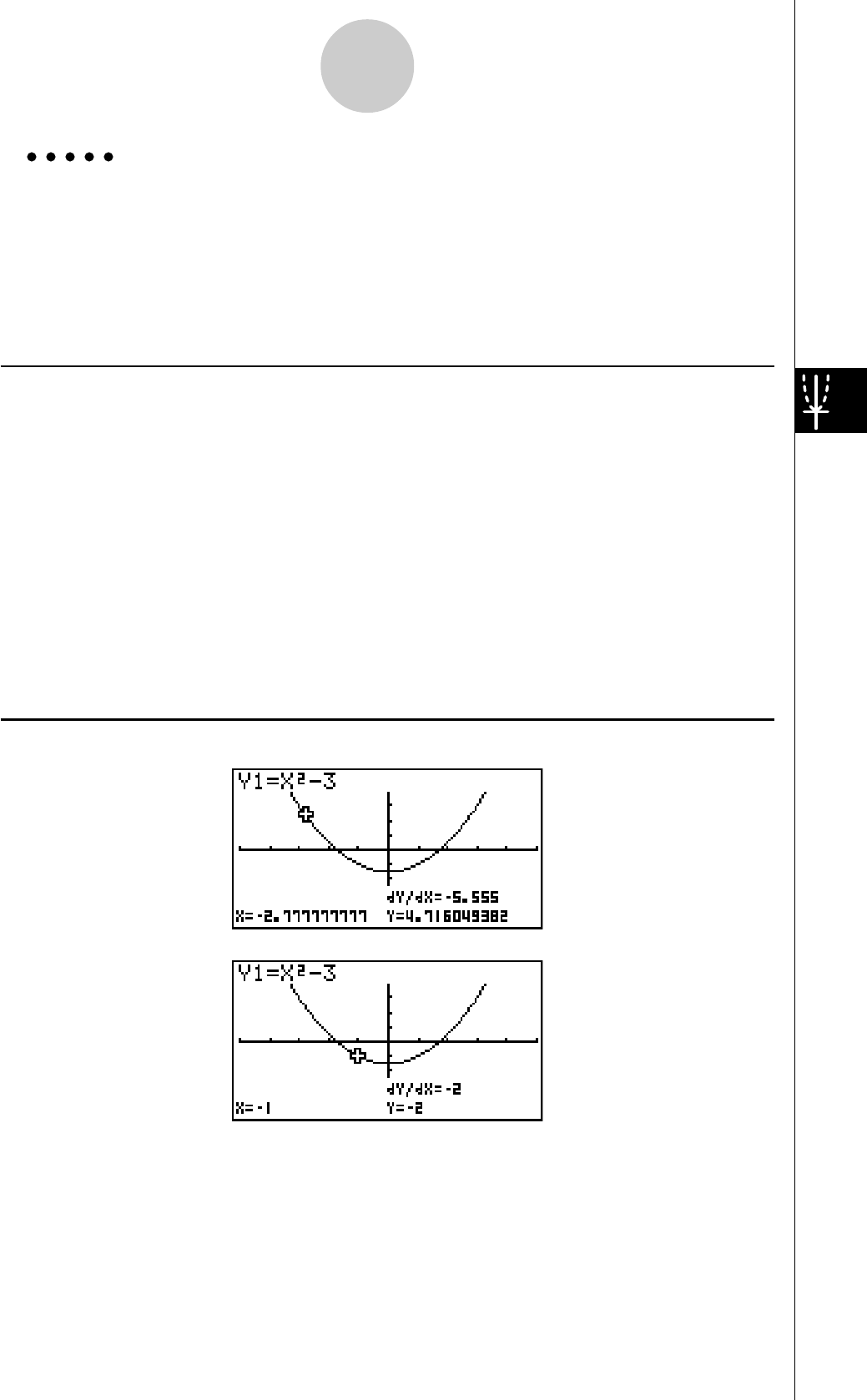
19990401
Exemple Lire les coordonnées et les dérivées le long du graphe de la fonction
indiquée ci-dessous.
Y1 = x2 – 3
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –5, Xmax = 5, Xscale = 1
Ymin = –10, Ymax = 10, Yscale = 2
Procédure
1m
GRPH • TBL
u3(SET UP)ccccc1(On)i
2!K(V-Window) -fwfwbwc
-bawbawcwi
3(TYPE)b(Y=)vx-dw
5(DRAW)
31(TRACE)
4d~d
5v-bw
Ecran de résultat
5-11-4
Analyse de fonctions
19990401
kk
kk
kGraphe à table
Description
Vous pouvez utiliser la fonction Trace pour lire les coordonnées d’un graphe et les stocker
dans une table numérique. Vous pouvez aussi utiliser le double graphe pour stocker
simultanément le graphe et la table numérique. Vous aurez ainsi à votre disposition un outil
d’analyse important.
Réglage
1. Depuis le menu principal, accédez au mode GRPH • TBL.
2. Sur l’écran de configuration, désignez GtoT pour Dual Screen (double écran).
3. Effectuez les réglages de fenêtre d’affichage.
Exécution
4. Sauvegardez la fonction et tracez le graphe sur l’écran actif (gauche).
5. Validez la fonction Trace. S’il y a plusieurs graphes à l’écran, appuyez sur f ou c
pour sélectionner le graphe souhaité.
6. Utilisez d pour déplacer le pointeur et appuyez sur w pour stocker les coordonnées
dans la table numérique.
Répétez cette étape pour stocker le nombre de valeurs souhaitées.
7. Appuyez sur 6(CHNG) pour passer à la table numérique.
8. Sur la fenêtre déroulante, saisissez le numéro de la liste que vous voulez sauvegarder.
5-11-5
Analyse de fonctions
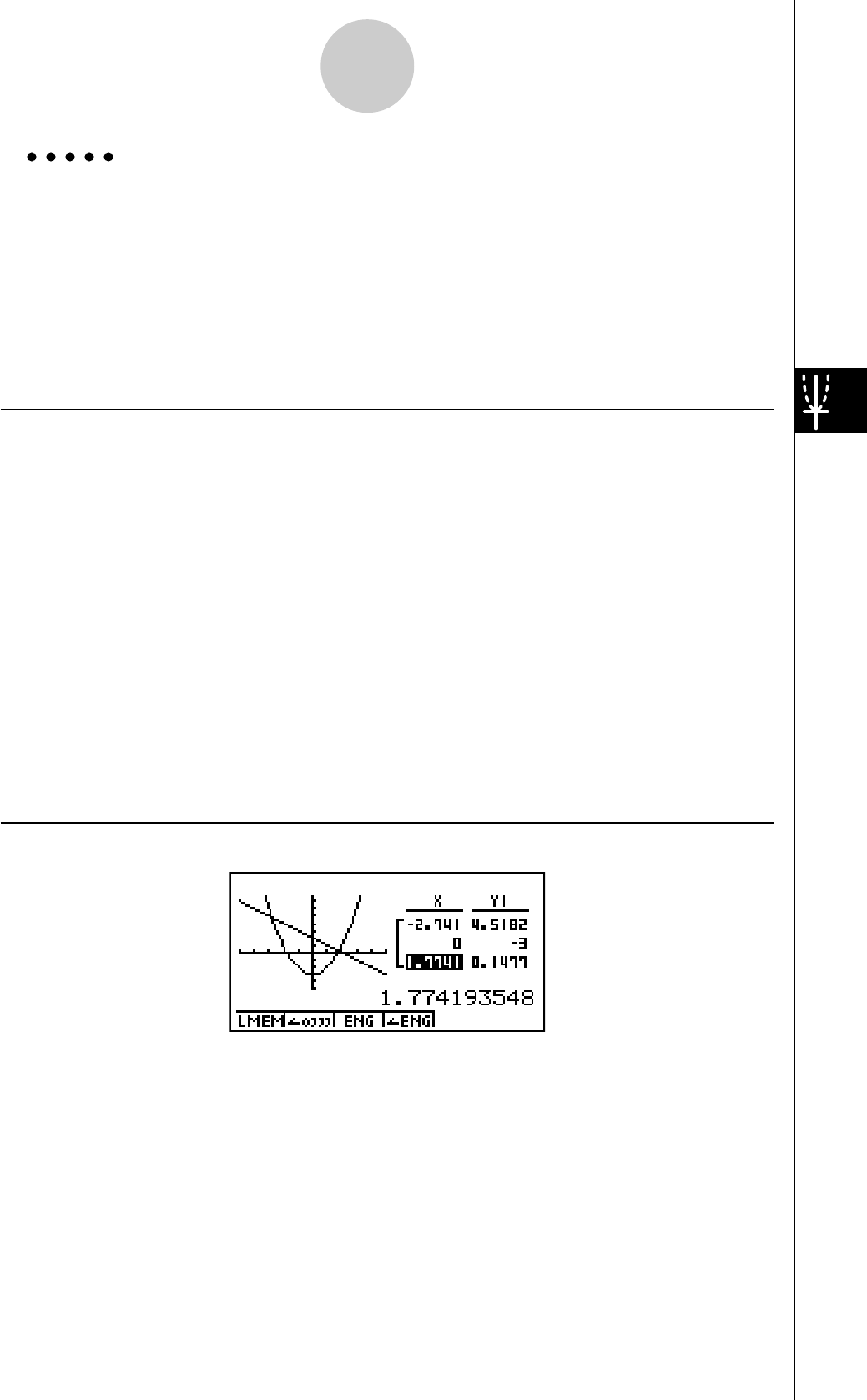
19990401
Exemple Sauvegarder dans une table les coordonnées proches des points
d’intersection à X = 0 des deux graphes montrés ci-dessous et stocker
le contenu de la table dans la liste 1.
Y1 = x2 – 3, Y2 = – x + 2
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –5, Xmax = 5, Xscale = 1
Ymin = –10, Ymax = 10, Yscale = 2
Procédure
1m GRPH • TBL
2u3(SET UP)ccc3(GtoT)i
3!K(V-Window) -fwfwbwc
-bawbawcwi
43(TYPE)b(Y=) vx-dw
-v+cw
5(DRAW)
51(TRACE)
6d~dwe~ewi
76(CHNG)
8K1(LMEM)bw
Ecran de résultat
5-11-6
Analyse de fonctions

19990401
kk
kk
kArrondi de coordonnées
Description
Cette fonction sert à arrondir les valeurs des coordonnées affichées par la fonction Trace.
Réglage
1. Tracez le graphe.
Exécution
2. Appuyez sur 2(ZOOM)i(Rnd). Les valeurs de la fenêtre d’affichage changent
automatiquement en fonction de la valeur Rnd.
3. Appuyez sur 1(TRACE) et utilisez ensuite les touches de curseur pour déplacer le
pointeur le long du graphe. Les coordonnées qui apparaissent maintenant sont
arrondies.
5-11-7
Analyse de fonctions
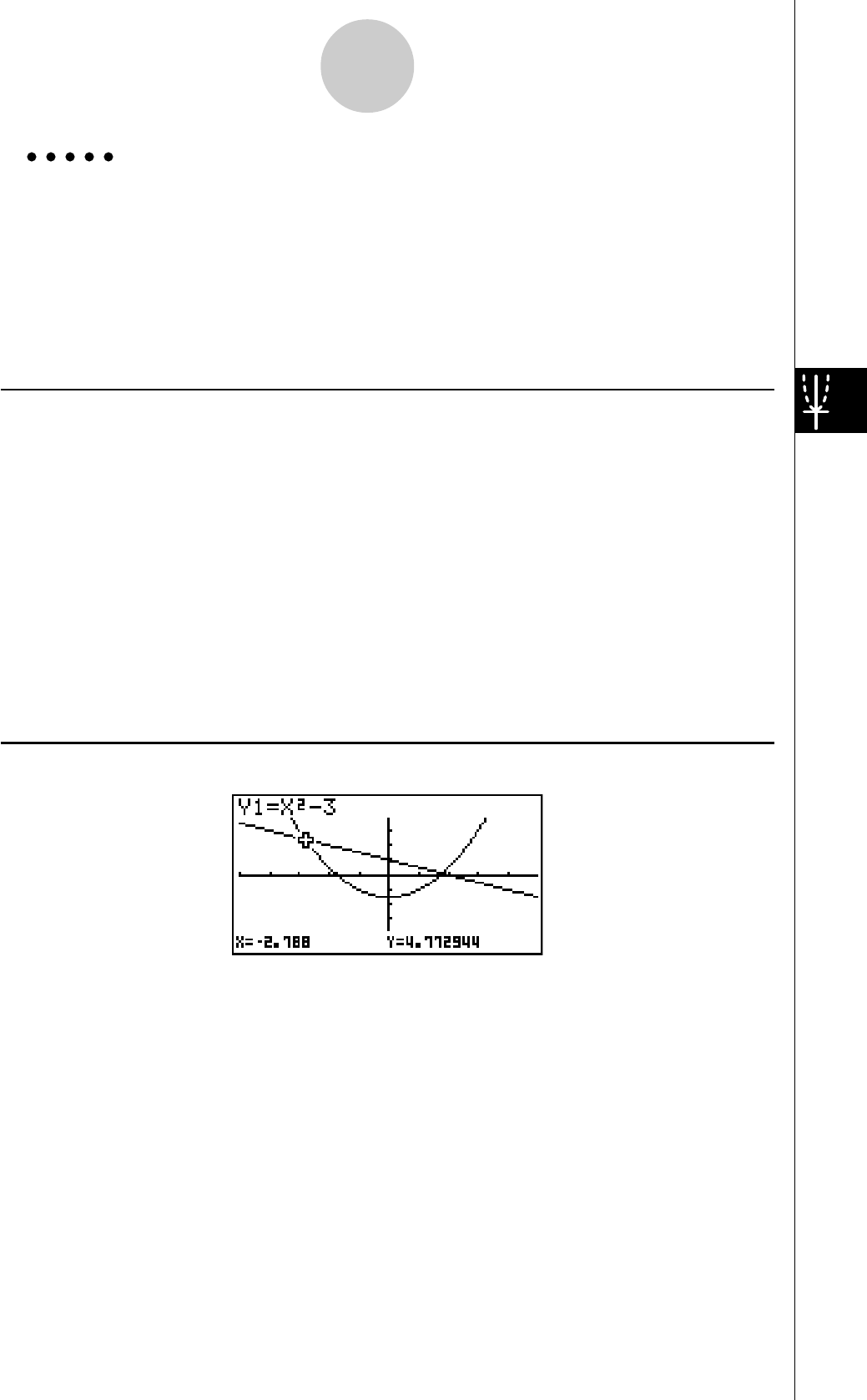
19990401
Exemple Utiliser l’arrondi de coordonnées et afficher les coordonnées proches
du point d’intersection des deux graphes produits par les fonctions
suivantes.
Y1 = x2 – 3, Y2 = – x + 2
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –5, Xmax = 5, Xscale = 1
Ymin = –10, Ymax = 10, Yscale = 2
Procédure
1m
GRPH • TBL
!K(V-Window) -fwfwbwc
-bawbawcwi
3(TYPE)b(Y=)vx-dw
-v+cw
5(DRAW)
22(ZOOM)i(Rnd)
31(TRACE)
d~d
Ecran de résultat
5-11-8
Analyse de fonctions

19990401
kk
kk
kCalcul de la racine
Description
Cette fonction fournit plusieurs méthodes pour l’analyse de graphes.
Réglage
1. Tracez les graphes.
Exécution
2. Sélectionnez la fonction d’analyse.
4(G-SLV) b(Root) ... Calcul de la racine
c(Max) ... Valeur maximale
d(Min) ... Valeur minimale
e(Y-lcpt) ... Intersection en y
f(Isect) ... Intersection de deux graphes
g(Y-Cal) ... Ordonnée y pour une abscisse x donnée
h(X-Cal) ... Abscisse x pour une ordonnée y donnée
i(∫dx) ... Valeur de l’intégrale pour une plage donnée
3. Lorsque plusieurs graphes sont affichés, le curseur de sélection (k) se trouve sur le
graphe au numéro inférieur. Utilisez les touches de curseur pour amener le curseur sur
le graphe que vous voulez sélectionner.
4. Appuyez sur w pour sélectionner le graphe où se trouve le curseur et afficher la
valeur produite par l’analyse.
Si une analyse produit plusieurs valeurs, appuyez sur e pour calculer la valeur
suivante. Appuyez sur d pour revenir à la valeur précédente.
5-11-9
Analyse de fonctions
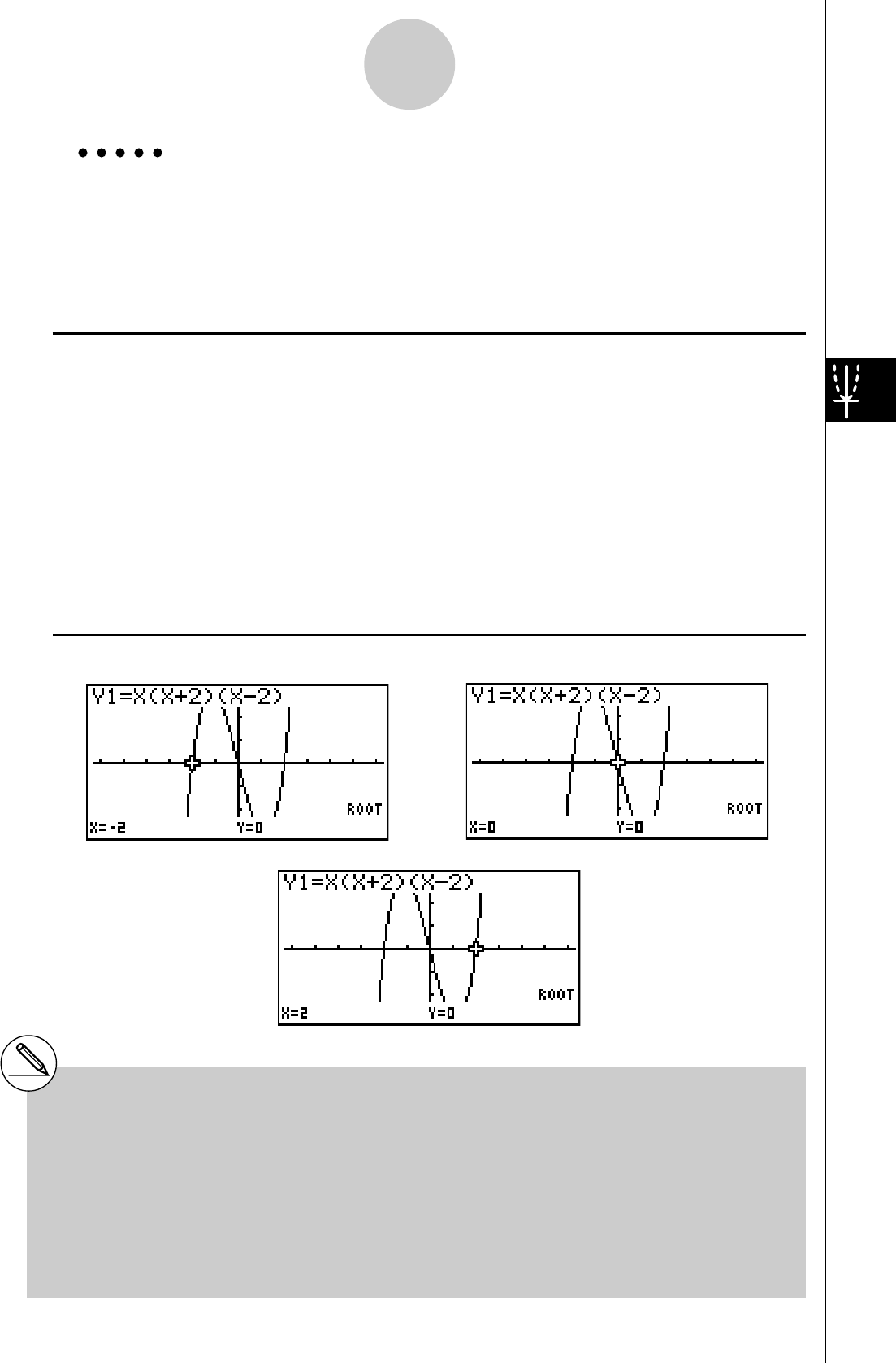
19990401
Exemple Tracer le graphe indiqué ci-dessous et calculer la racine pour Y1
Y1 = x(x + 2)(x – 2)
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –6.3, Xmax = 6.3, Xscale = 1
Ymin = –3.1, Ymax = 3.1, Yscale = 1 (réglages initiaux)
Procédure
1m GRPH • TBL
!K(V-Window) 1(INIT)i
3(TYPE)b(Y=)v(v+c)(v-c)w
5(DRAW)
24(G-SLV)b(Root)
4e
e
Ecran de résultat
5-11-10
Analyse de fonctions
# Lors de l’analyse d’un seul graphe, les
résultats apparaissent dès que vous
sélectionnez une fonction d’analyse à l’étape
2, si bien que l’étape 3 n’est pas nécessaire.
# La racine, la valeur maximale, la valeur
minimale et l’intersection en y peuvent être
calculées pour les graphes à coordonnées
rectangulaires et les graphes d’inéquations
seulement.
# L’intersection en y est le point où le graphe
traverse l’axe y.
…

19990401
kk
kk
kCalcul du point d’intersection de deux graphes
Description
Procédez de la façon suivante pour calculer le point d’intersection de deux graphes.
Réglage
1. Tracez les graphes.
Exécution
2. Appuyez sur 4(G-SLV)5(Isect). Si trois graphes ou plus sont affichés, le curseur de
sélection (k) apparaîtra sur le graphe au numéro inférieur.
3. Utilisez les touches de curseur pour amener le curseur sur le graphe que vous voulez
sélectionner.
4. Appuyez sur w pour sélectionner le premier graphe. Le curseur k prend la forme 쏆.
5. Utilisez les touches de curseur pour amener le curseur sur le second graphe.
6. Appuyez sur w pour calculer le point d’intersection des deux graphes.
Si une analyse produit plusieurs valeurs, appuyez sur e pour calculer la valeur
suivante. Appuyez sur d pour revenir à la valeur précédente.
5-11-11
Analyse de fonctions
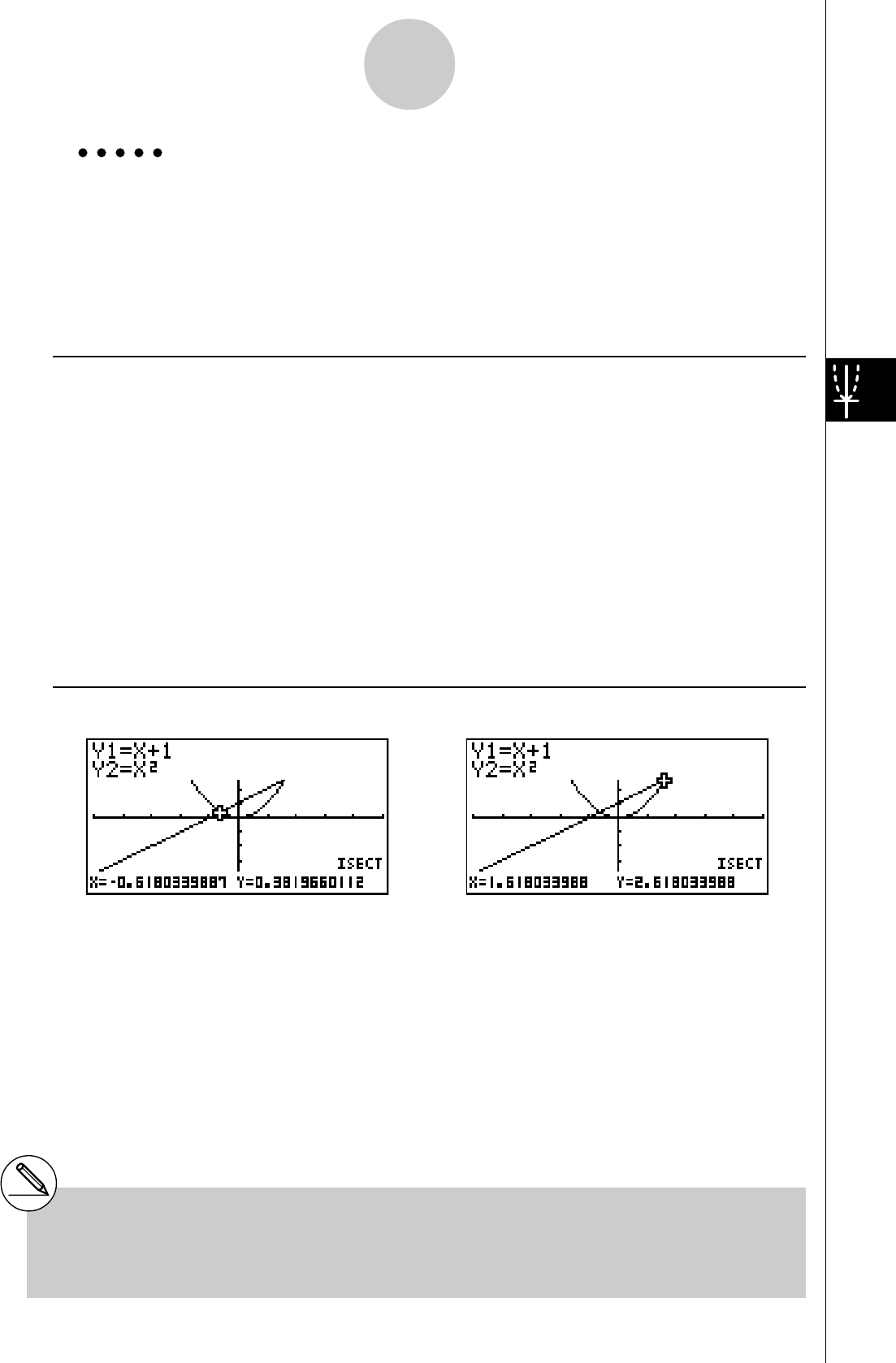
19990401
Exemple Tracer les deux fonctions indiquées ci-dessous et déterminer le point
d’intersection entre Y1 et Y2.
Y1 = x + 1, Y2 = x2
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –5, Xmax = 5, Xscale = 1
Ymin = –5, Ymax = 5, Yscale = 1
Procédure
1m
GRPH • TBL
!K(V-Window) -fwfwbwc
-fwfwbwi
3(TYPE)b(Y=)v+bw
vxw
5(DRAW)
24(G-SLV)f(Isect)
6e
Ecran de résultat
5-11-12
Analyse de fonctions
# Dans le cas de deux graphes, le point
d’intersection est calculé dès que vous
appuyez sur 4f à l’étape 2.
# Vous pouvez calculer le point d’intersection de
graphes à coordonnées rectangulaires et de
graphes d’inéquations seulement.
…

19990401
kDétermination des coordonnées de points donnés
Description
La procédure suivante décrit comment déterminer l’ordonnée y pour un point x donné et
l’abscisse x pour un point y donné.
Réglage
1. Tracez le graphe.
Exécution
2. Sélectionnez la fonction que vous voulez effectuer. Si plusieurs graphes sont affichés,
le curseur de sélection (k) apparaîtra sur le graphe au numéro inférieur.
4(G-SLV)g(Y-Cal) ... ordonnée y pour un x donné
h(X-Cal) ... abscisse x pour un y donné
3. Utilisez f et c pour amener le curseur (k) sur le graphe souhaité et appuyez sur
w pour le sélectionner.
4. Indiquez la valeur de l’abscisse x ou de l’ordonnée y donnée.
Appuyez sur w pour calculer la valeur de l’ordonnée y ou l’abscisse x
correspondante.
5-11-13
Analyse de fonctions
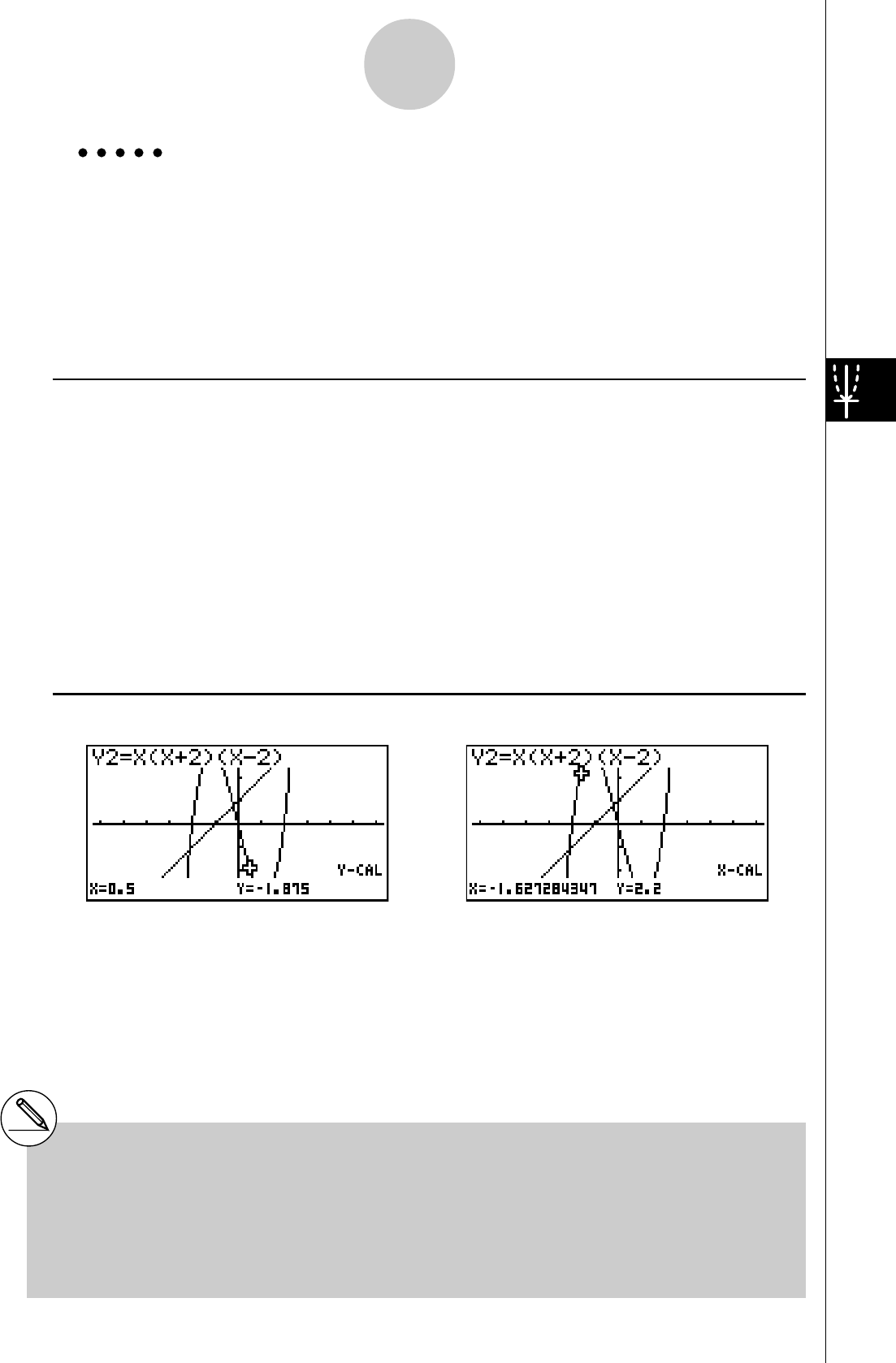
19990401
Exemple Tracer le graphe des deux fonctions indiquées ci-dessous et
déterminer l’ordonnée y pour x = 0,5 et l’abscisse x pour y = 2,2 sur le
graphe Y2.
Y1 = x + 1, Y2 = x(x + 2)(x – 2)
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –6.3, Xmax = 6.3, Xscale = 1
Ymin = –3.1, Ymax = 3.1, Yscale = 1 (réglages initiaux)
Procédure
1m GRPH • TBL
!K(V-Window) 1(INIT)i
3(TYPE)b(Y=)v+bw
v(v+c)(v-c)w
5(DRAW)
24(G-SLV)g(Y-Cal) 24(G-SLV)h(X-Cal)
3cw3cw
4 a.fw4 c.cw
Ecran de résultat
5-11-14
Analyse de fonctions
# S’il y a plusieurs résultats pour la procédure
précédente, appuyez sur e pour calculer la
valeur suivante. Appuyez sur d pour revenir
à la valeur précédente.
# L’étape 3 de la procédure précédente est
ignorée si un seul graphe est affiché.
# La valeur X-Cal ne peut pas être obtenue pour
un graphe de fonction paramétrique.
# Après avoir obtenu les coordonnées avec la
procédure précédente, vous pouvez saisir
d’autres coordonnées en appuyant d’abord sur
v.

19990401
kk
kk
kCalcul de la valeur de l’intégrale pour une plage donnée
Description
Procédez de la façon suivante pour obtenir les valeurs d’intégration pour une plage donnée.
Réglage
1. Tracez le graphe.
Exécution
2. Appuyez sur 4(G-SLV)i(∫dx). Si plusieurs graphes sont affichés, le curseur de
sélection (k) apparaîtra sur le graphe au numéro inférieur.
3. Utilisez f et c pour amener le curseur (k) sur le graphe souhaité et appuyez sur
w pour le sélectionner.
4. Utilisez d pour amener le pointeur de la limite inférieure à l’endroit voulu et appuyez
sur w.
Vous pouvez aussi déplacer le pointeur en appuyant sur v pour afficher la fenêtre
déroulante puis en saisissant les coordonnées.
5. Utilisez e pour déplacer le pointeur de la limite supérieure à l’endroit voulu.
Vous pouvez aussi déplacer le pointeur en appuyant sur v pour afficher la fenêtre
déroulante puis en saisissant les valeurs des limites supérieure et inférieure de la
plage d’intégration.
6. Appuyez sur w pour calculer la valeur de l’intégrale.
5-11-15
Analyse de fonctions
# Lorsque vous définissez la plage, assurez-
vous que la limite inférieure est inférieure à la
limite supérieure.
# Les valeurs de l’intégrale peuvent être calculées
pour les graphes à coordonnées rectangulaires
seulement.
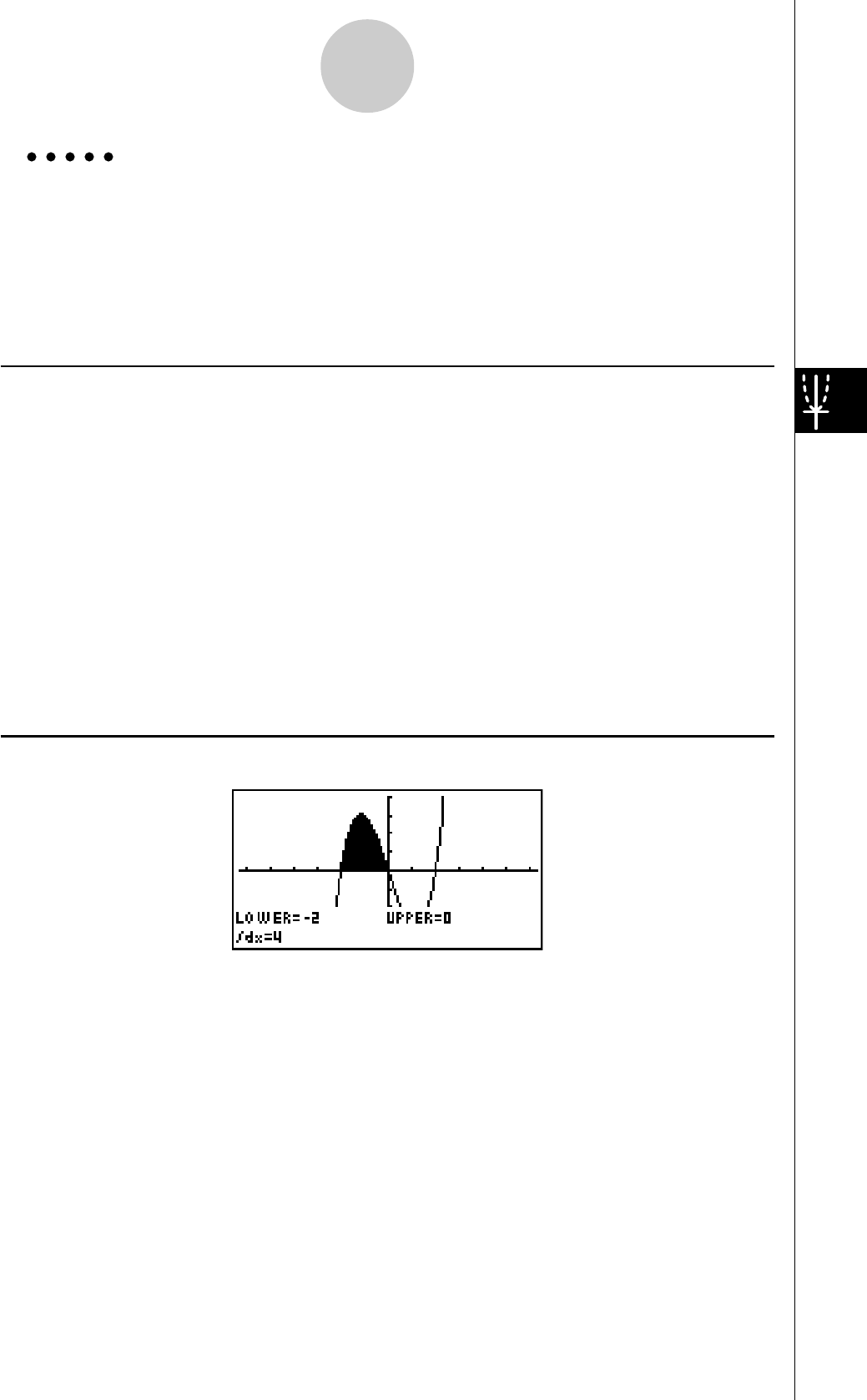
19990401
Exemple Tracer le graphe de la fonction indiquée ci-dessous et déterminer la
valeur de l’intégrale à (–2, 0).
Y1 = x(x + 2)(x – 2)
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –6.3, Xmax = 6.3, Xscale = 1
Ymin = –4, Ymax = 4, Yscale = 1
Procédure
1m
GRPH • TBL
!K(V-Window) -g.dwg.dwbwc
-ewewbwi
3(TYPE)b(Y=)v(v+c)(v-c)w
5(DRAW)
24(G-SLV)i(∫dx)
4d~dw
5e~e(Limite supérieure; x = 0)
6w
Ecran de résultat
5-11-16
Analyse de fonctions
…

19990401
kk
kk
kAnalyse des graphes de fonctions implicites
Vous pouvez déterminer les approximations des résultats analytiques suivants à partir des
graphes de fonctions implicites.
• Foyer/sommet/excentricité
• Latus rectum
• Centre/rayon
• Intersection de x/y
• Tracé et analyse de la directrice/axe de symétrie
• Tracé et analyse de l’asymptote
Après avoir tracé le graphe d’une fonction implicite, appuyez sur 4(G-SLV) pour afficher les
menus d’analyse de graphes suivants.
uAnalyse de graphe parabolique
•{Focus}/{Vertex}/{Length}/{e} ... {foyer}/{sommet}/{latus rectum}/{excentricité}
•{Dirtrx}/{Sym} ... {directrice}/{axe de symétrie}
•{X-Icpt}/{Y-Icpt} ... {intersection de x}/{intersection de y}
uAnalyse de graphe circulaire
•{Center}/{Radius} ... {centre}/{rayon}
•{X-Icpt}/{Y-Icpt} ... {intersection de x}/{intersection de y}
uAnalyse de graphe elliptique
•{Focus}/{Vertex}/{Center}/{e} ... {foyer}/{sommet}/{centre}/{excentricité}
•{X-Icpt}/{Y-Icpt} ... {intersection de x}/{intersection de y}
uAnalyse de graphe hyperbolique
•{Focus}/{Vertex}/{Center}/{e} ... {foyer}/{sommet}/{centre}/{excentricité}
•{Asympt} ... {asymptote}
•{X-Icpt}/{Y-Icpt} ... {intersection de x}/{intersection de y}
Les exemples suivants montrent comment utiliser les menus précédents avec divers types
de graphes de fonctions implicites.
5-11-17
Analyse de fonctions
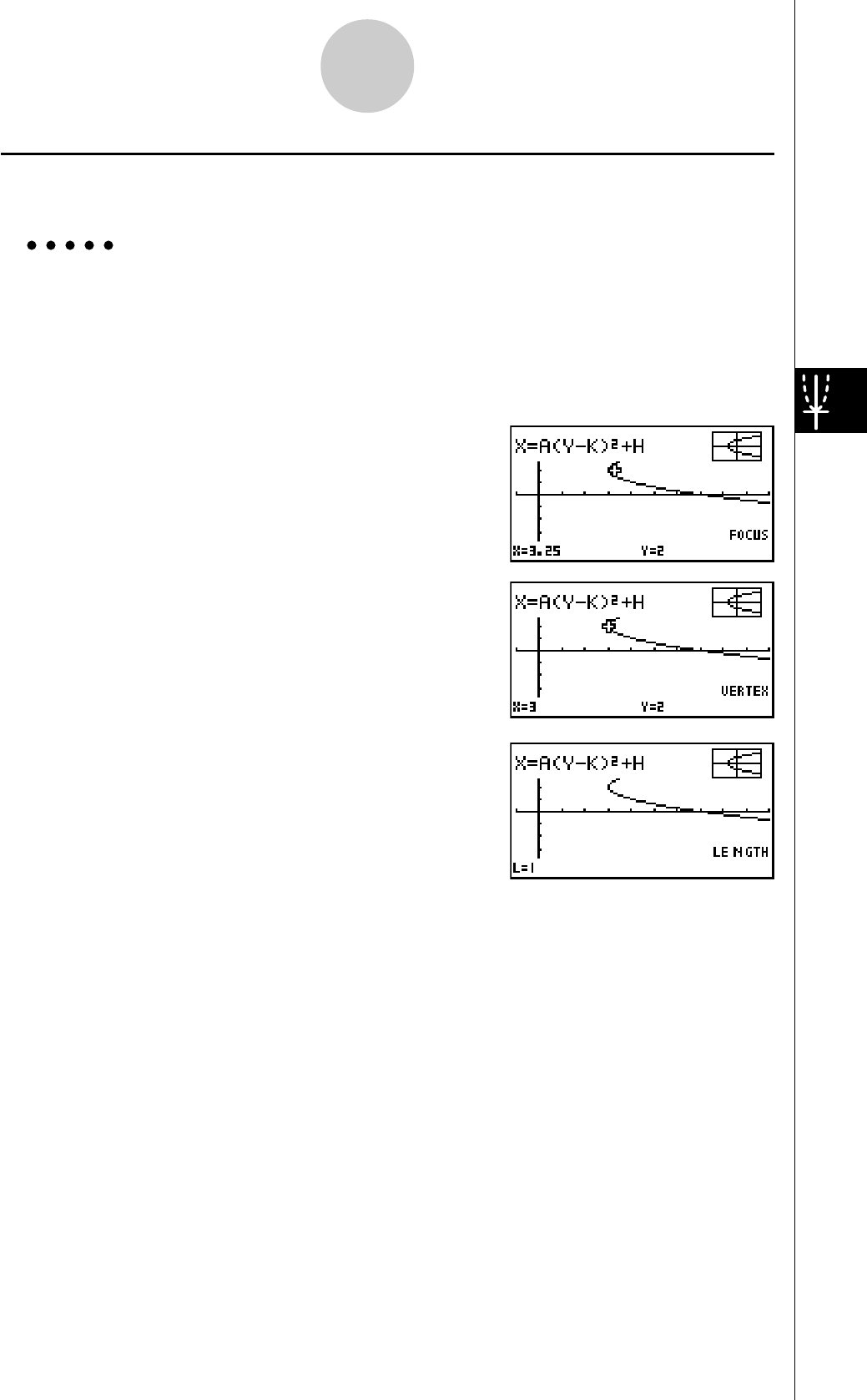
19990401
uPour calculer le foyer, le sommet et le latus rectum
[G-SLV]-[Focus]/[Vertex]/[Length]
Exemple Déterminer le foyer, le sommet et le latus rectum de la parabole
X = (Y – 2)2 + 3
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –1, Xmax = 10, Xscale = 1
Ymin = –5, Ymax = 5, Yscale = 1
4(G-SLV)
b(Focus)
(Calcule le foyer.)
i
4(G-SLV)
d(Vertex)
(Calcule le sommet.)
i
4(G-SLV)
f(Length)
(Calcule le latus rectum.)
• Lors du calcul de deux foyers d’une ellipse ou d’un graphe hyperbolique, appuyez sur e
pour calculer le second foyer. Appuyez sur d pour revenir ensuite au premier foyer.
• Lors du calcul de deux sommets d’une ellipse ou d’un graphe hyperbolique, appuyez sur
e pour calculer le second sommet. Appuyez sur d pour revenir ensuite au premier
sommet.
5-11-18
Analyse de fonctions
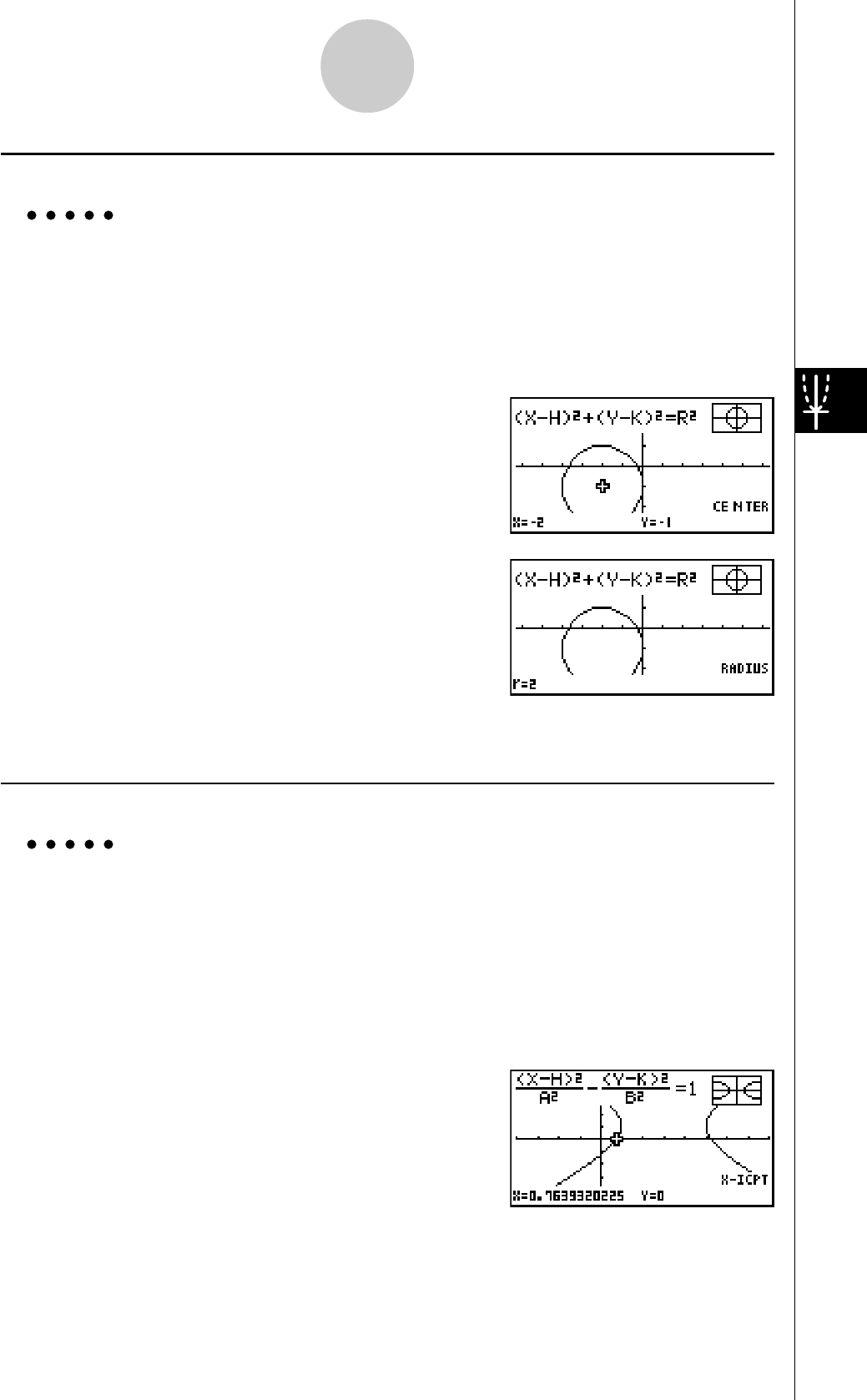
19990401
uPour calculer le centre et le rayon [G-SLV]-[Center]/[Radius]
Exemple Déterminer le centre et le rayon du cercle
(X + 2)2 + (Y + 1)2 = 22
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –6.3, Xmax = 6.3, Xscale = 1
Ymin = –3.1, Ymax = 3.1, Yscale = 1
4(G-SLV)
b(Center)
(Calcule le centre.)
i
4(G-SLV)
c(Radius)
(Calcule le rayon.)
uPour calculer les intersections de x et y[G-SLV]-[X-Icpt]/[Y-Icpt]
Exemple Déterminer les intersections de x et y pour l’hyperbole
(X – 3)2(Y – 1)2
–––––––– – –––––––– = 1
2222
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –4, Xmax = 8, Xscale = 1
Ymin = –5, Ymax = 5, Yscale = 1
4(G-SLV)
g(X-Icpt)
(Calcule l’intersection de x.)
5-11-19
Analyse de fonctions

19990401
i
4(G-SLV)
h(Y-Icpt)
(Calcule l’intersection de y.)
• Appuyez sur e pour calculer la seconde paire d’intersections x/y. Appuyez sur d pour
revenir à la première paire d’intersections.
uPour tracer et analyser l’axe de symétrie et la directrice
[G-SLV]-[Sym]/[Dirtrx]
Exemple Tracer l’axe de symétrie et la directrice de la parabole
X = 2(Y – 1)2 + 1
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –6.3, Xmax = 6.3, Xscale = 1
Ymin = –3.1, Ymax = 3.1, Yscale = 1
4(G-SLV)
e(Sym)
(Trace l’axe de symétrie.)
i
4(G-SLV)
c(Dirtrx)
(Trace la directrice.)
5-11-20
Analyse de fonctions
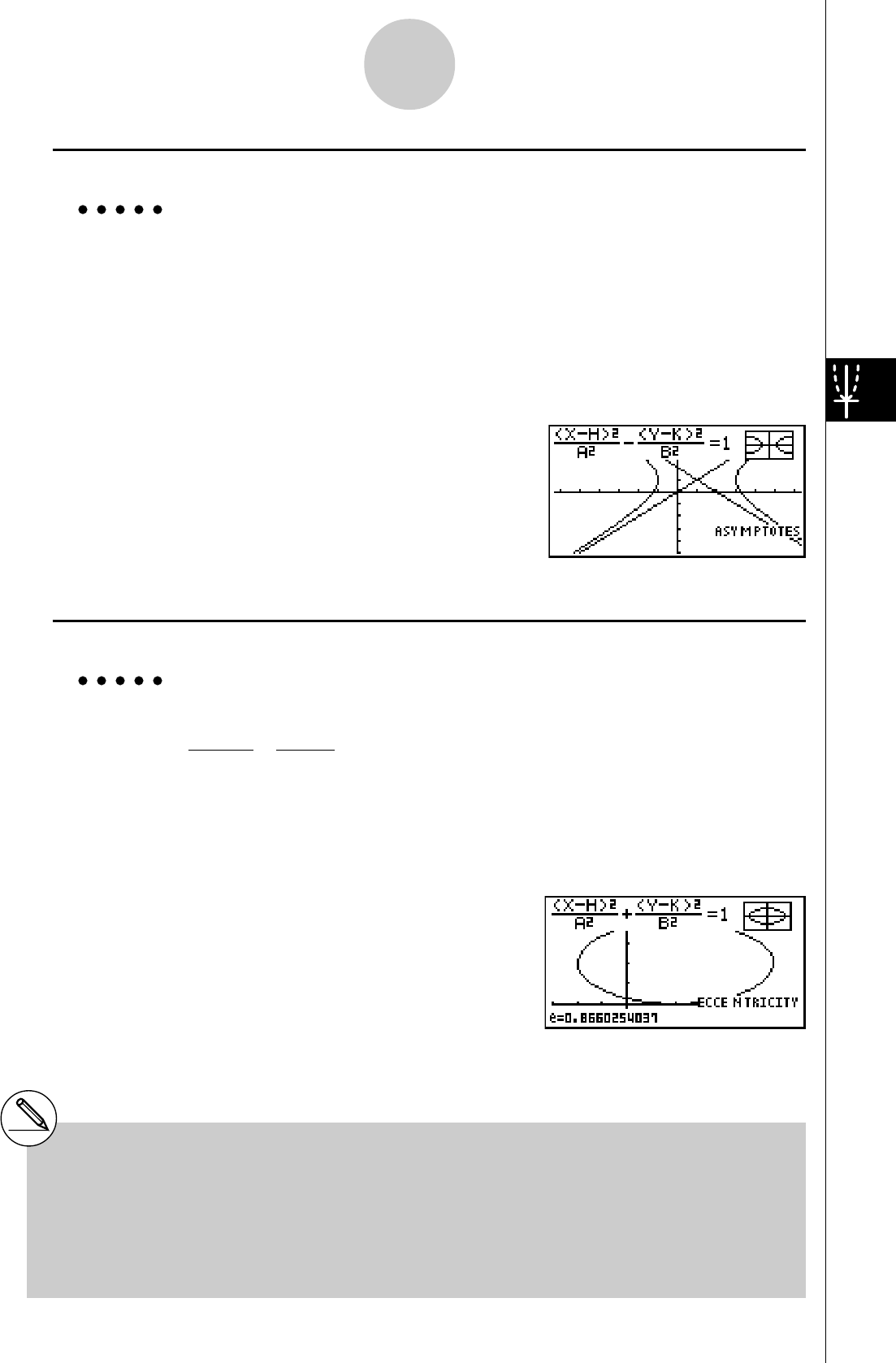
19990401
uPour tracer et analyser les asymptotes [G-SLV]-[Asympt]
Exemple Tracer l’axe les asymptotes de l’hyperbole
(X – 1)2(Y – 1)2
–––––––– – –––––––– = 1
2222
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –6.3, Xmax = 6.3, Xscale = 1
Ymin = –5, Ymax = 5, Yscale = 1
4(G-SLV)
e(Asympt)
(Trace les asymptotes.)
uPour calculer l’excentricité [G-SLV]-[e]
Exemple Déterminer l’excentricité du graphe pour l’ellipse
(X – 2)2 + (Y – 2)2 = 1
4222
Utilisez les réglages de fenêtre d’affichage suivants.
Xmin = –3, Xmax = 7, Xscale = 1
Ymin = –1, Ymax = 5, Yscale = 1
4(G-SLV)
e(e)
(Calcule l’excentricité.)
5-11-21
Analyse de fonctions
# Certains paramètres de fenêtre d’affichage
peuvent produire des valeurs erronées dans
les résultats d’analyse de graphe.
# Le message “Non trouvé” apparaît à l’écran
quand l’analyse d’un graphe ne peut pas
produire de résultat.
# Dans les cas suivants, les résultats d’analyse
peuvent être imprécis, ou il peut être impossible
d’obtenir une solution.
— Quand la solution est tangente à l’axe x.
— Quand la solution est un point de tangence
entre deux graphes.

19990401
Chapitre
Graphes et calculs
statistiques
Ce chapitre explique comment entrer des données statistiques
dans des listes et calculer la moyenne, le maximum ou d’autres
valeurs statistiques. Il indique aussi comment effectuer des
calculs de régression.
6-1 Avant d’effectuer des calculs statistiques
6-2 Calcul et représentation graphique de données
statistiques à variable unique
6-3 Calcul et représentation graphique de données
statistiques à variable double
6-4 Exécution de calculs statistiques
6-5 Distribution
Important!
• Ce chapitre contient un certain nombre d’illustrations d’écrans graphiques.
Dans chaque cas, de nouvelles données ont été entrées afin de mieux faire
ressortir les caractéristiques du graphe tracé. Notez que lorsque vous essayez
de tracer un graphe similaire, la machine utilise les données que vous avez
entrées en utilisant les listes. Par conséquent, les graphes qui apparaîtront à
l’écran quand vous effectuerez une opération graphique, seront probablement
un peu différents de ceux indiqués dans ce manuel.
6
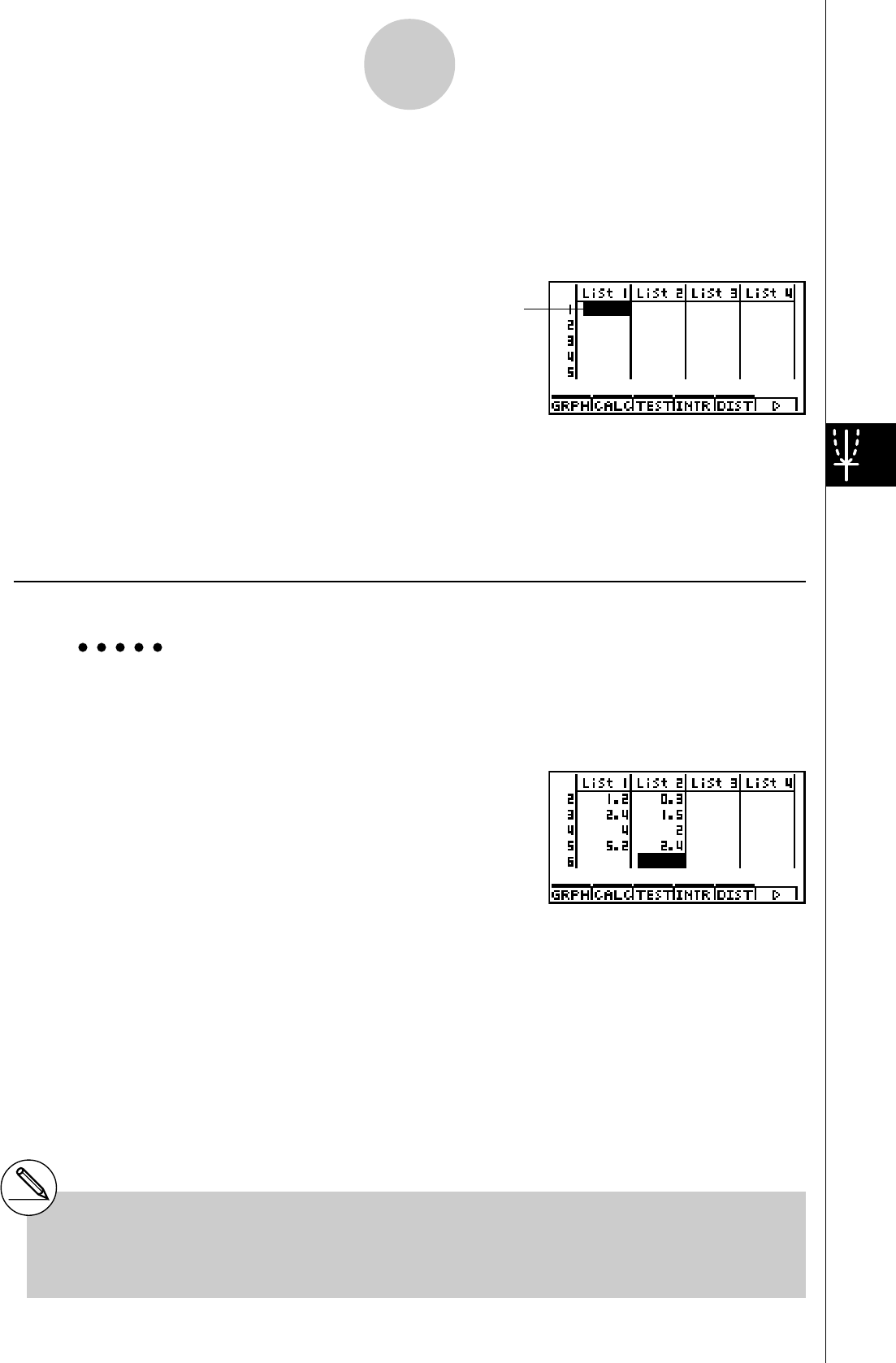
19990401
6-1 Avant d’effectuer des calculs statistiques
A partir du menu principal, accédez au mode STAT et affichez les listes de données statistiques.
Utilisez ces listes pour introduire des données et effectuer des calculs statistiques.
Utilisez
f, c, d
et
e
pour
déplacer la surbrillance sur les
listes.
Une fois que vous avez introduit des données, vous pouvez les utiliser pour produire un
graphe et en vérifier les tendances. Vous pouvez aussi utiliser tout un éventail de calculs de
régression pour analyser les données.
kIntroduction de données dans les listes
Exemple Introduisez les deux groupes de données suivants
0,5, 1,2, 2,4, 4,0, 5,2
–2,1, 0,3, 1,5, 2,0, 2,4
a.fwb.cw
c.ewewf.cw
e
-c.bwa.dw
b.fwcwc.ew
Après avoir introduit les données, vous pouvez les utiliser pour tracer des graphes ou faire des
calculs statistiques.
6-1-1
Avant d’effectuer des calculs statistiques
# A l’exception des nombres complexes, les
résultats de calculs peuvent être saisis
comme données statistiques.
# Vous pouvez utiliser les touches f, c, d
et e pour amener la surbrillance sur un
élément de la liste et entrer des données.
20001202

19990401
kChangement des paramètres d’un graphe
Vous pouvez changer les paramètres de tracé de graphe comme nécessaire (SET).
Vous pouvez aussi sauvegarder trois ensembles de paramètres et les rappeler lorsque vous
en avez besoin (SEL).
SET et SEL sont des options pratiques qui éliminent les réglages complexes à chaque tracé
de graphe.
Quand la liste de données statistiques est à l’écran, appuyez sur 1(GRPH) pour afficher
le menu de graphes, qui contient les paramètres suivants.
•{S-Gph1}/{S-Gph2}/{S-Gph3} ... tracé de graphe {1}/{2}/{3}*1
•{Select} ... {sélection (GPH1, GPH2, GPH3) comme graphe simultané} (Vous pouvez
spécifier plusieurs graphes.)
•{Set} ... {réglages de graphe (type de graphe, affectation aux listes)}
kTypes de représentations graphiques
Il est possible de représenter trois types de graphiques différents - Graph 1, Graph 2 et Graph
3 - en utilisant les données de listes.
• Les caractéristiques définissant le type de graphique sont mémorisées par la fonction SET.
Exemple Graph 1: Ce graphe utilisera les données de la liste 1 comme
variable X, celles de la liste 3 comme variable Y. La fréquence sera 1.
Graph 2: Ce graphe représentera des histogrammes avec en abscisses
les données de la liste 2.
• Pour utiliser un des graphes, il faudra le sélectionner avec la fonction SEL.
• Vous pouvez appuyer sur une des touches de fonction (1,2,3) pour tracer un
graphe quelle que soit la liste de données statistiques mise en surbrillance.
6-1-2
Avant d’effectuer des calculs statistiques
*1 Le type de graphe défini par défaut pour
tous les graphes (graphe 1 à graphe 3) est
le diagramme de dispersion, mais vous
pouvez choisir un autre type.

19990401
kk
kk
kDéfinition des paramètres de la représentation graphique
1. Réglages généraux de graphe [GRPH]-[Set]
Ce paragraphe explique comment utiliser l’écran de réglages généraux pour effectuer les
réglages suivants pour chaque graphe (GPH1, GPH2, GPH3).
• Type de graphe
Le type de graphe par défaut pour tous les graphes est un diagramme de dispersion, mais
vous avez un grand choix d’autres diagrammes statistiques.
• Liste
La liste 1 de données statistiques a été définie par défaut pour les données à variable
unique et la liste 1 et la liste 2 pour les données à variable double. Vous pouvez définir la
liste de données statistiques que vous souhaitez utiliser pour les données x et les données y.
• Fréquence
En principe, chaque donnée ou paire de données de la liste de données statistiques est
représentée sur le diagramme par un point. Lorsque vous travaillez avec un grand nombre
de données, le nombre de points marqués peut devenir trop important. Dans ce cas, vous
pouvez définir une liste de fréquences qui contient les valeurs indiquant le nombre
d’occurrences (la fréquence) des données dans les éléments correspondants des listes que
vous utilisez pour les données x et les données y. Un seul point représentera alors plusieurs
données et le diagramme sera mieux compréhensible.
• Type de points
Ce réglage permet de varier la forme des points sur le diagramme.
6-1-3
Avant d’effectuer des calculs statistiques

19990401
uPour afficher l’écran de réglages généraux de graphe [GRPH]-[Set]
Appuyez sur 1(GRPH)f(Set) pour afficher l’écran de réglages généraux de graphe.
• Les réglages indiqués ici ne servent qu’à titre d’exemples. Les réglages de votre écran
peuvent être différents.
• StatGraph (désignation d’un graphe statistique)
•{GPH1}/{GPH2}/{GPH3} ... graphe {1}/{2}/{3}
• Graph Type (désignation du type de graphe)
•{Scat}/{xy}/{NPP} ... {diagramme de dispersion}/{graphe linéaire xy}/{marquage de
probabilité normale}
•{Hist}/{Box}/{ModB}/{N·Dis}/{Brkn} ... {histogramme}/{graphe med-box}/{graphe en
boîte modifiée}/{courbe de répartition normale}/{graphe linéaire}
•{X}/{Med}/{X^2}/{X^3}/{X^4} ... {graphe de régression linéaire}/{graphe Med-Med}/
{graphe de régression quadratique}/{graphe de régression cubique}/{graphe de
régression quartique}
•{Log}/{Exp}/{Pwr}/{Sin}/{Lgst} ... {graphe de régression logarithmique}/{graphe de
régression exponentielle}/{graphe de régression de puissance}/{graphe de
régression sinusoïdale}/{graphe de régression logistique}
• XList (liste de données pour l’axe x)
•{LIST} ... {Liste 1 à 20}
• YList (liste de données pour l’axe y)
•{LIST} ... {Liste 1 à 20}
• Frequency (nombre d’occurences d’une valeur)
•{1} ... {marquage 1 à 1}
•{LIST} ... le contenu de ces listes indique la fréquence des données de XList et de YList
• Mark Type (type de point)
•{ }/{×}/{•} ... types de points d’un diagramme dispersé
6-1-4
Avant d’effectuer des calculs statistiques

19990401
2. Statut avec ou sans tracé de graphe [GRPH]-[Select]
L’opération suivante peut être utilisée pour définir le statut avec ou sans tracé de graphe
(On/Off) de chaque graphe sur le menu.
uPour définir le statut avec ou sans tracé de graphe
1. Appuyez sur 1(GRPH)e(Select) pour afficher l’écran de statut de graphe (avec ou
sans tracé).
• Notez que le réglage StatGraph1 est pour le graphe 1 (GPH1 du menu), StatGraph2
pour le graphe 2 et StatGraph3 pour le graphe 3.
2. Utilisez les touches de curseur pour amener la surbrillance sur le graphe dont vous
voulez changer le statut et appuyez sur la touche de fonction correspondante pour
changer le statut.
•{On}/{Off} ... {On (tracé)}/{Off (sans tracé)}
•{DRAW} ... {tracé de tous les graphes}
3. Pour revenir au menu de graphes, appuyez sur i.
6-1-5
Avant d’effectuer des calculs statistiques
# Les paramètres de la fenêtre d’affichage sont
normalement automatiquement définis pour
les graphes statistiques. Si vous voulez
définir vous-même les paramètres de la
fenêtre d’affichage, vous devez régler Stat
Wind sur “Manual”.
Quand la liste de données statistiques est à
l’écran, effectuez l’opération suivante.
u3(SET UP)2(Man)
i(Retour au menu précédent.)
# La liste de données 1 est automatiquement
utilisée pour l’axe x (horizontal) et la liste de
données 2 pour l’axe y (vertical). Chaque
ensemble de données x/y est représenté par
un point sur le diagramme de dispersion.
# Une pression sur ua ne cache pas le menu
lorsqu’un graphe statistique est affiché.

1999040120001202
6-2 Calcul et représentation graphique de
données statistiques à variable unique
Les données à variable unique sont des données ne comprenant qu’une seule variable. Si
vous calculez la grandeur moyenne des élèves d’une classe, par exemple, il n’y a qu’une
variable, la grandeur.
Les statistiques à variable unique comprennent la répartition et la somme. Les types de
graphes suivants sont disponibles pour les statistiques à variable unique.
Vous pouvez aussi procéder comme indiqué dans “Changement des paramètres d’un graphe”
à la page 6-1-2 pour effectuer les réglages que vous voulez avant de tracer chaque graphe.
kk
kk
kPoint de probabilité normale (NPP)
Cette fonction compare le taux d’accumulation de données avec le taux d’accumulation
d’une distribution normale. XList désigne la liste où les données sont saisies et Mark Type
sert à sélectionner le type de point que vous voulez marquer { / × / •}.
Appuyez sur i ou !i(QUIT) pour revenir à la liste de données statistiques.
kk
kk
kHistogramme (diagramme à barres) (Hist)
XList désigne la liste où les données sont saisies tandis que Freq désigne la liste où la
fréquence est saisie. 1 est spécifié pour la Freq lorsqu’aucune autre fréquence n’est
spécifiée.
6-2-1
Calcul et représentation graphique de données statistiques à variable unique
⇒
w(Dessin)
L’écran indiqué ci-dessus apparaît avant que le graphe soit tracé. A ce moment, vous pouvez
changer la valeur initiale et le pas.
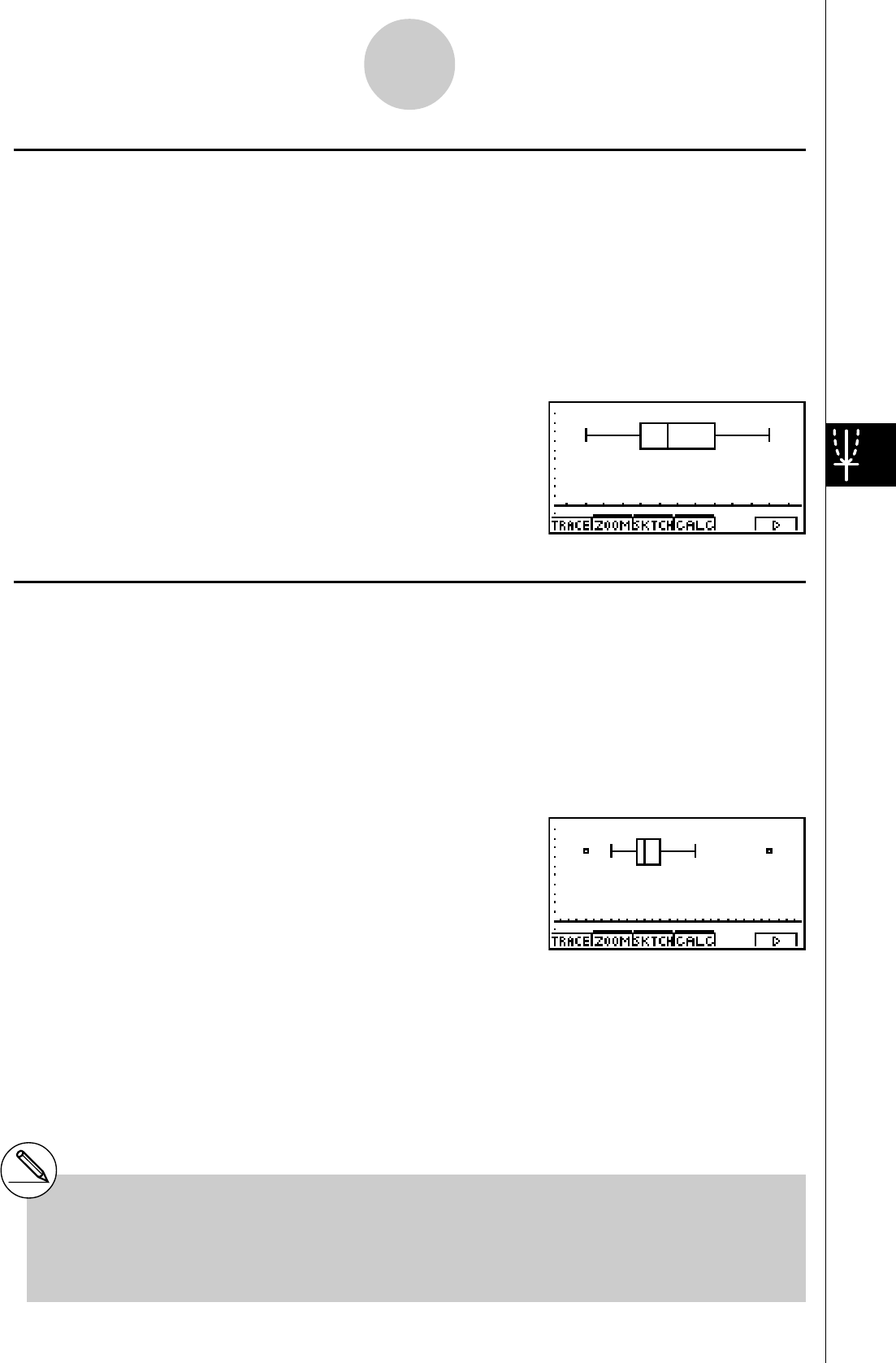
19990401
kGraphe en boîte-médiane (Box)
Ce type de graphe vous permet de voir de quelle manière un grand nombre de données sont
regroupées dans des plages particulières. Un boîte comprend toutes les données dans une
zone du 25e percentile au 75e percentile, avec une ligne tracée au 50e percentile. Des lignes
(appelées barbes) s’étendent de chaque extrémité de la boîte jusqu’au minimum et maxi-
mum des données.
XList désigne la liste où les données sont saisies tandis que Freq désigne la liste où la
fréquence est saisie. 1 est spécifié pour Freq lorsqu’aucune autre fréquence n’est spécifiée.
kGraphe en boîte modifiée (ModB)
Le graphe à boîte modifiée omet tout ce qui est dans la plage au-delà de 1,5 × IQR (IQR =
Q3 – Q1, Q3 : 3e quartile, Q1 : 1er quartile) depuis le 4e quartile de la boîte médiane et trace
des barbes.
Les points aberrants sont indiqués comme points.
XList désigne la liste où les données sont saisies tandis que Freq désigne la liste où la
fréquence est saisie. 1 est spécifié pour Freq lorsqu’aucune autre fréquence n’est spécifiée.
6-2-2
Calcul et représentation graphique de données statistiques à variable unique
# Saisissez un entier positif pour les données de
fréquence.
Les autres types de valeurs (décimales, etc.)
causent une erreur.
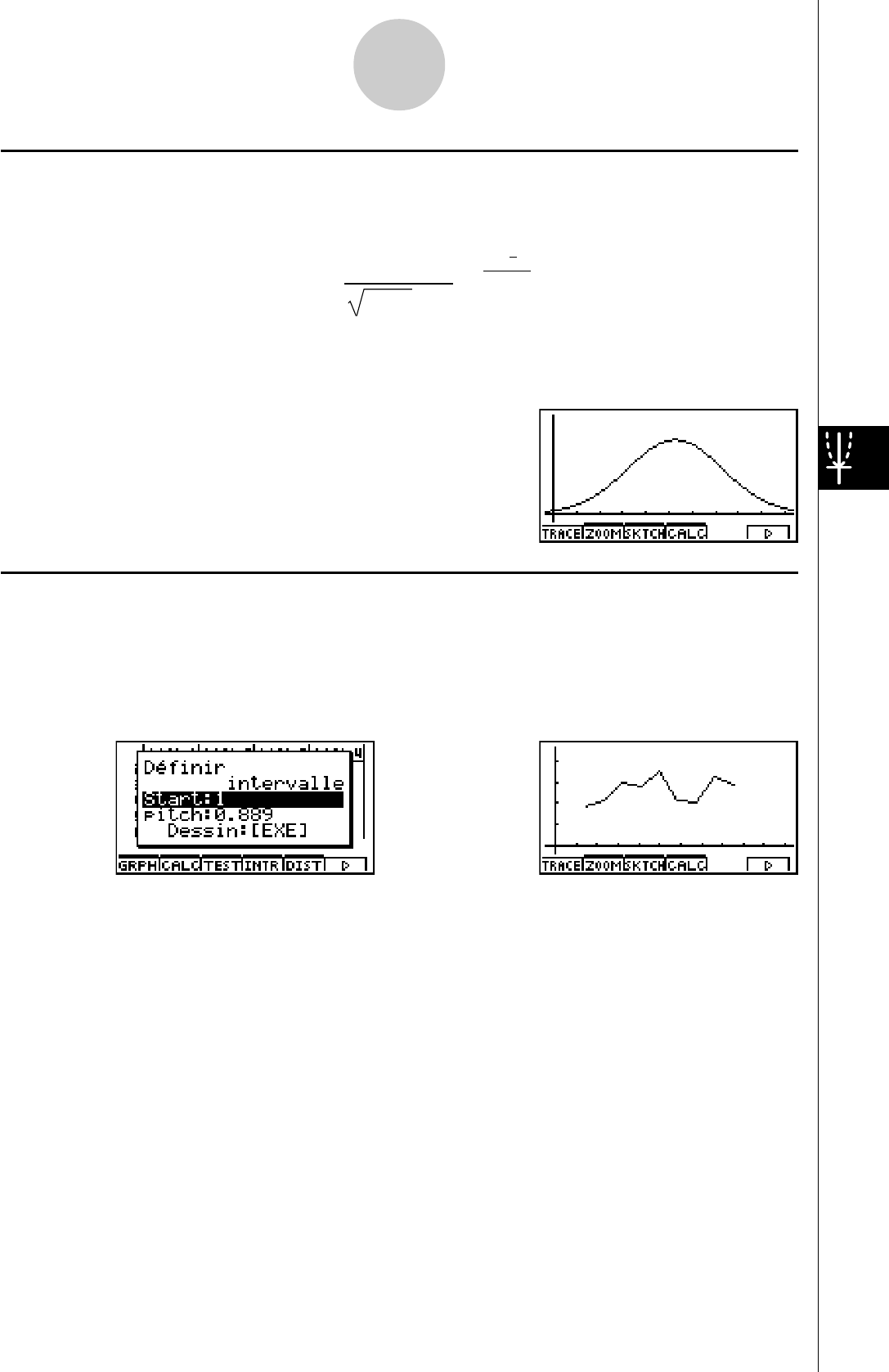
1999040120001202
kCourbe de répartition normale (N•Dis)
La courbe de répartition normale est tracée à l’aide de la fonction de répartition normale
suivante.
y
= 1
(2 π)xσ
n
e
–2xσ
n
2
(x–x)
2
XList désigne la liste où les données sont saisies tandis que Freq désigne la liste où la
fréquence est saisie. 1 est spécifié pour Freq lorsqu’aucune autre fréquence n’est spécifiée.
kGraphe linéaire (Brkn)
Les lignes relient les points centraux d’un histogramme.
XList désigne la liste où les données sont saisies tandis que Freq désigne la liste où la
fréquence est saisie. 1 est spécifié pour Freq lorsqu’aucune autre fréquence n’est spécifiée.
6-2-3
Calcul et représentation graphique de données statistiques à variable unique
⇒
w(Dessin)
L’écran indiqué ci-dessus apparaît avant que le graphe soit tracé. A ce moment, vous pouvez
changer la valeur initiale et le pas.

19990401
kAffichage des résultats du calcul d’un graphe à variable unique
Les statistiques à variable unique peuvent être exprimées sous forme de graphes et de
paramètres. Lorsque des graphes sont affichés, les résultats du calcul à variable unique
apparaissent de la façon suivante lorsque vous appuyez sur 4(CALC)b(1VAR).
• Utilisez c pour faire défiler la liste et voir les paramètres qui défilent au bas de l’écran.
Voici la signification de chacun des paramètres.
o............. moyenne
Σx........... somme
Σx2.......... somme des carrés
xσn.......... écart-type d’une population
xσn–1 ........ écart-type d’un échantillon
n............. nombre de données
minX ....... minimum
Q1 .......... premier quartile
Med ........ médiane
Q3 .......... troisième quartile
maxX ...... maximum
Mod ........ mode
Mod : n ... nombre de paramètres du mode de données
Mod : F ... fréquence du mode de données
• Appuyez sur 6(DRAW) pour revenir au graphe statistique original à variable unique.
# Lorsque Mod a plusieurs solutions, celles-ci
sont toutes affichées.
6-2-4
Calcul et représentation graphique de données statistiques à variable unique

19990401
kTracé d’histogramme
Exemple Représenter l’histogramme correspondant au classement des
données suivantes en 5 classes d’amplitude identique.
• Définissez la fenêtre !K(V-Window)
en choisissant Xmin = 0, Xmax = 50
Ymin = –2, Ymax = 10
• Revenez aux listes, appuyez sur 1(GRPH)b(S-Gph1) et choisissez Graphe 1.
Attention: On avait au préalable fixé les caractéristiques de Graphe 1 comme histogramme.
• Choisissez l’amplitude des classes.
Puisqu’il faut 5 classes égales et que Xmax - X min = 50, nous fixerons Start = 0 et pitch = 10.
Les 5 classes regrouperont les valeurs:
Classe 1 valeurs de 0 à 9, Classe 2 valeurs de 10 à 19
Classe 3 valeurs de 20 à 29, Classe 4 valeurs de 30 à 39
Classe 5 valeurs de 40 à 49
• Tracez l’histogramme avec w(DRAW).
• Si on ne souhaite pas regrouper les valeurs par classes mais les représenter réellement, il
faut choisir pitch = 1.
Liste 1
2
35
39
40
Liste 2
3
2
3
6
6-2-5
Calcul et représentation graphique de données statistiques à variable unique

19990401
6-3-1
Calcul et représentation graphique de données statistiques à variable double
6-3 Calcul et représentation graphique de
données statistiques à variable double
k Représentation d’un diagramme de dispersion et d’un graphe linéaire xy
Description
La procédure suivante permet de marquer les points d’un diagramme et de les relier pour
produire un graphe linéaire xy.
Réglage
1. Depuis le menu principal, accédez au mode STAT.
Exécution
2. Saisissez les données dans la liste.
3. Désignez Scat (diagramme de dispersion) ou xy (graphe linéaire xy) comme type de
graphe et exécutez l’opération.
Appuyez sur i ou !i(QUIT) pour revenir à la liste de données statistiques.

19990401
Exemple Saisir les deux groupes de données suivants. Marquer ensuite les
données sur un diagramme de dispersion et relier les points pour
produire un graphe linéaire xy.
0,5, 1,2, 2,4, 4,0, 5,2,
–2,1, 0,3, 1,5, 2,0, 2,4
Procédure
1m STAT
2 a.fwb.cw
c.ewewf.cw
e
-c.bwa.dw
b.fwcwc.ew
3(Diagramme de dispersion)1(GRPH)f(Set)c1(Scat)i
1(GRPH)b(S-Gph1)
3(Graphe linéaire xy)1(GRPH)f(Set)c2(xy)i
1(GRPH)b(S-Gph1)
Ecran de résultat
(Diagramme de dispersion)
(Graphe linéaire xy)
6-3-2
Calcul et représentation graphique de données statistiques à variable double

19990401
k Tracé d’un graphe de régression
Description
Procédez de la façon suivante pour saisir des données statistiques à variable double,
effectuer un calcul de régression en utilisant ces données puis représenter graphiquement
les résultats obtenus.
Réglage
1. Depuis le menu principal, accédez au mode STAT.
Exécution
2. Saisissez les données dans une liste et marquez les points du diagramme de disper-
sion.
3. Sélectionnez le type de régression, exécutez le calcul et affichez les paramètres de
régression.
4. Tracez le graphe de régression.
6-3-3
Calcul et représentation graphique de données statistiques à variable double
# Vous pouvez utiliser la fonction Trace sur un
graphe de régression mais vous ne pouvez
pas utiliser la fonction Trace Scroll.
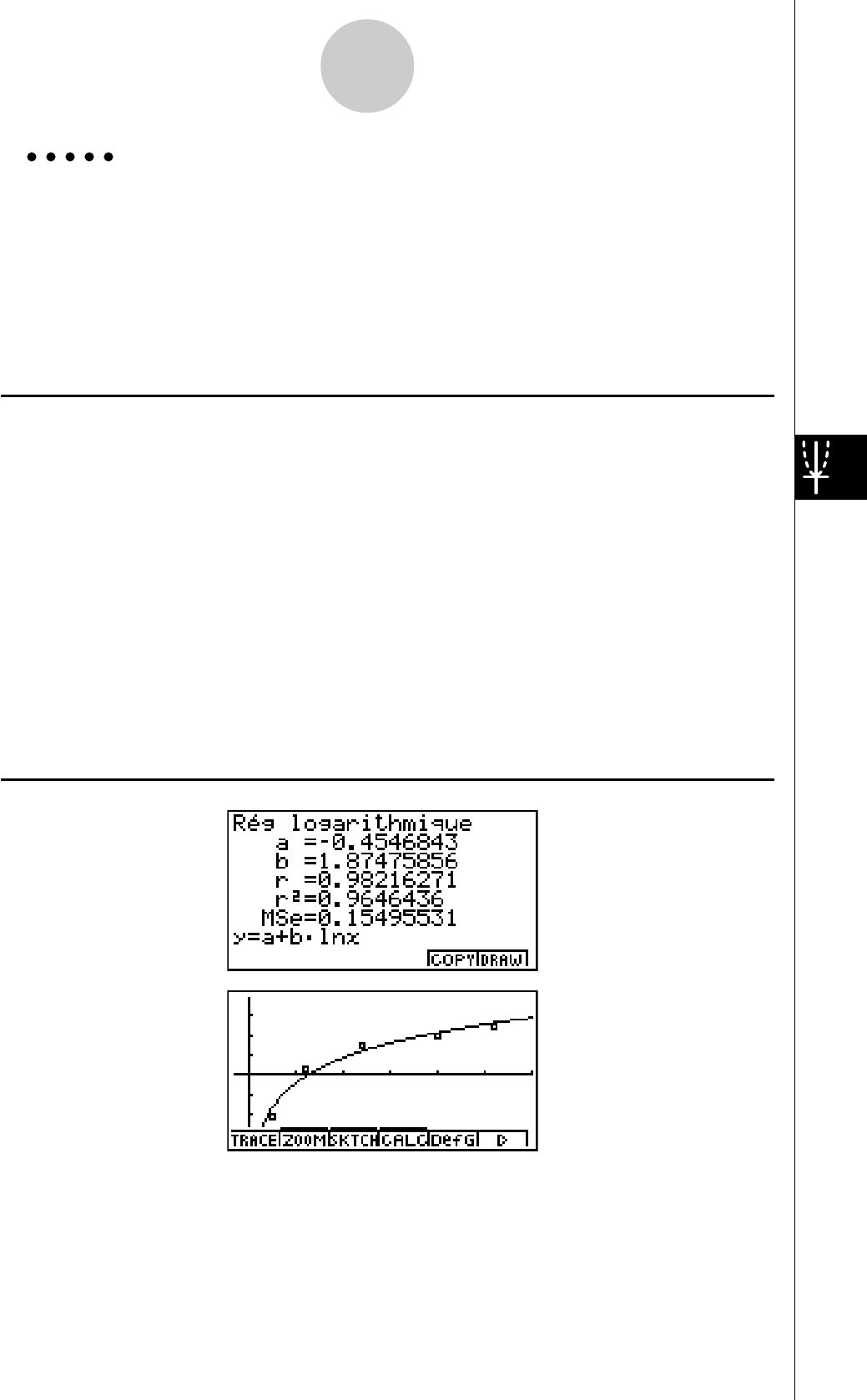
1999040120001202
Exemple Saisir les deux groupes de données indiqués ci-dessous et marquer
les données sur un diagramme de dispersion. Effectuer ensuite une
régression logarithmique sur les données pour afficher les paramètres
de régression logarithmique, puis tracer le graphe de régression
correspondant.
0,5, 1,2, 2,4, 4,0, 5,2,
–2,1, 0,3, 1,5, 2,0, 2,4
Procédure
1m STAT
2 a.fwb.cw
c.ewewf.cw
e
-c.bwa.dw
b.fwcwc.ew
1(GRPH)f(Set)c1(Scat)i
1(GRPH)b(S-Gph1)
34(CALC)h(Log)
46(DRAW)
Ecran de résultat
6-3-4
Calcul et représentation graphique de données statistiques à variable double

19990401
kk
kk
kSélection du type de régression
Après avoir représenté graphiquement des données statistiques à double variable, appuyez
sur 4(CALC). Vous pouvez ensuite utiliser le menu de fonctions au bas de l’écran pour
sélectionner un type de régression.
•{2VAR} ... {résultat stastistique à variable double}
•{Linear}/{MedMed}/{Quad}/{Cubic}/{Quart}/{Log}/{Exp}/{Power}/{Sin}/{Lgstic}
... calcul et représentation graphique de {régression linéaire}/{Med-Med}/
{régression quadratique}/{régression cubique}/{régression quartique}/{régression
logarithmique}/{régression exponentielle}/{régression de puissance}/{régression
sinusoïdale}/{régression logistique}
kk
kk
kAffichage des résultats de calculs statistiques
Quand vous effectuez un calcul de régression, les résultats du calcul des paramètres de la
formule de régression (comme a et b dans la régression linéaire y = ax + b) apparaissent à
l’écran. Vous pouvez les utiliser pour obtenir les résultats de calculs statistiques.
Les paramètres de régression sont calculés dès que vous appuyez sur une touche de
fonction pour sélectionner le type de régression quand un graphe est affiché.
kk
kk
kReprésentation graphique des résultats de calculs statistiques
Lorsque le résultat d’un calcul de paramètres est affiché, vous pouvez représenter
graphiquement la formule de régression affichée en appuyant sur 6(DRAW).
6-3-5
Calcul et représentation graphique de données statistiques à variable double
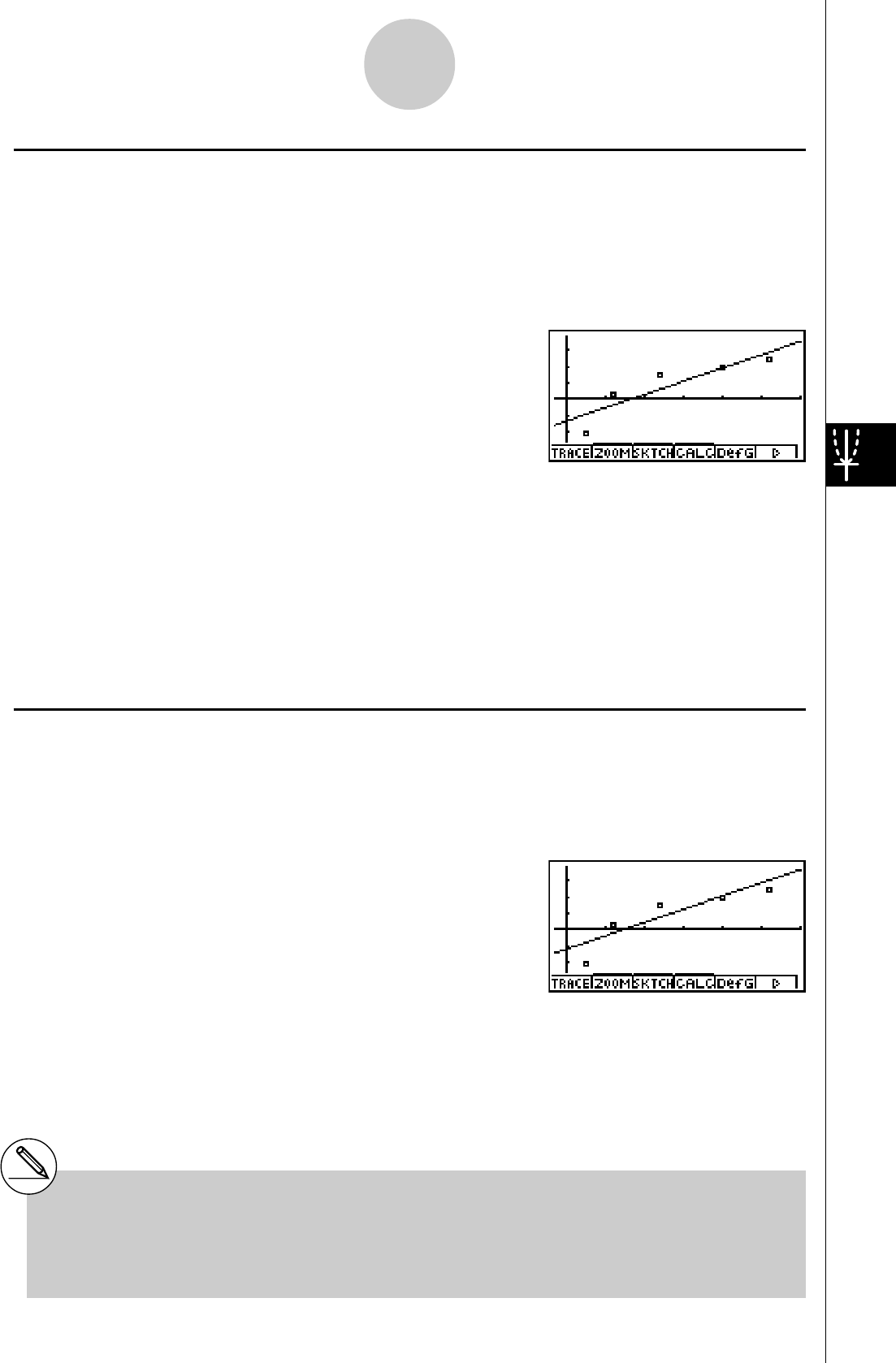
1999040120001202
kk
kk
kGraphe de régression linéaire
La régression linéaire utilise la méthode des moindres carrés pour marquer une ligne droite
qui passe près du plus grand nombre de points possible et renvoie les valeurs pour la pente
et l’intersection y (ordonnée y lorsque x = 0) de la ligne.
La représentation graphique de la relation est un graphe de régression linéaire.
4(CALC)c(Linear)
6(DRAW)
Voici la formule du modèle de régression linéaire.
y = ax + b
a............. coefficient de régression (pente)
b............. terme constant de la régression (intersection)
r............. coefficient de corrélation
r2............ coefficient de détermination
MSe ........ carrés des moyennes des erreurs
kk
kk
kGraphe Med-Med
Si l’on suspecte un certain nombre de valeurs extrêmes, un graphe Med-Med peut être
utilisé au lieu de la méthode des moindres carrés. Le résultat est similaire à la régression
linéaire mais l’effet des valeurs extrêmes est réduit.
4(CALC)d(MedMed)
6(DRAW)
Voici la formule du modèle de graphe Med-Med.
y = ax + b
a ............. pente de graphe Med-Med
b ............. intersection de graphe Med-Med
6-3-6
Calcul et représentation graphique de données statistiques à variable double
# Saisissez un entier positif pour les données de
fréquence.
Les autres types de valeurs (décimales, etc.)
causent une erreur.
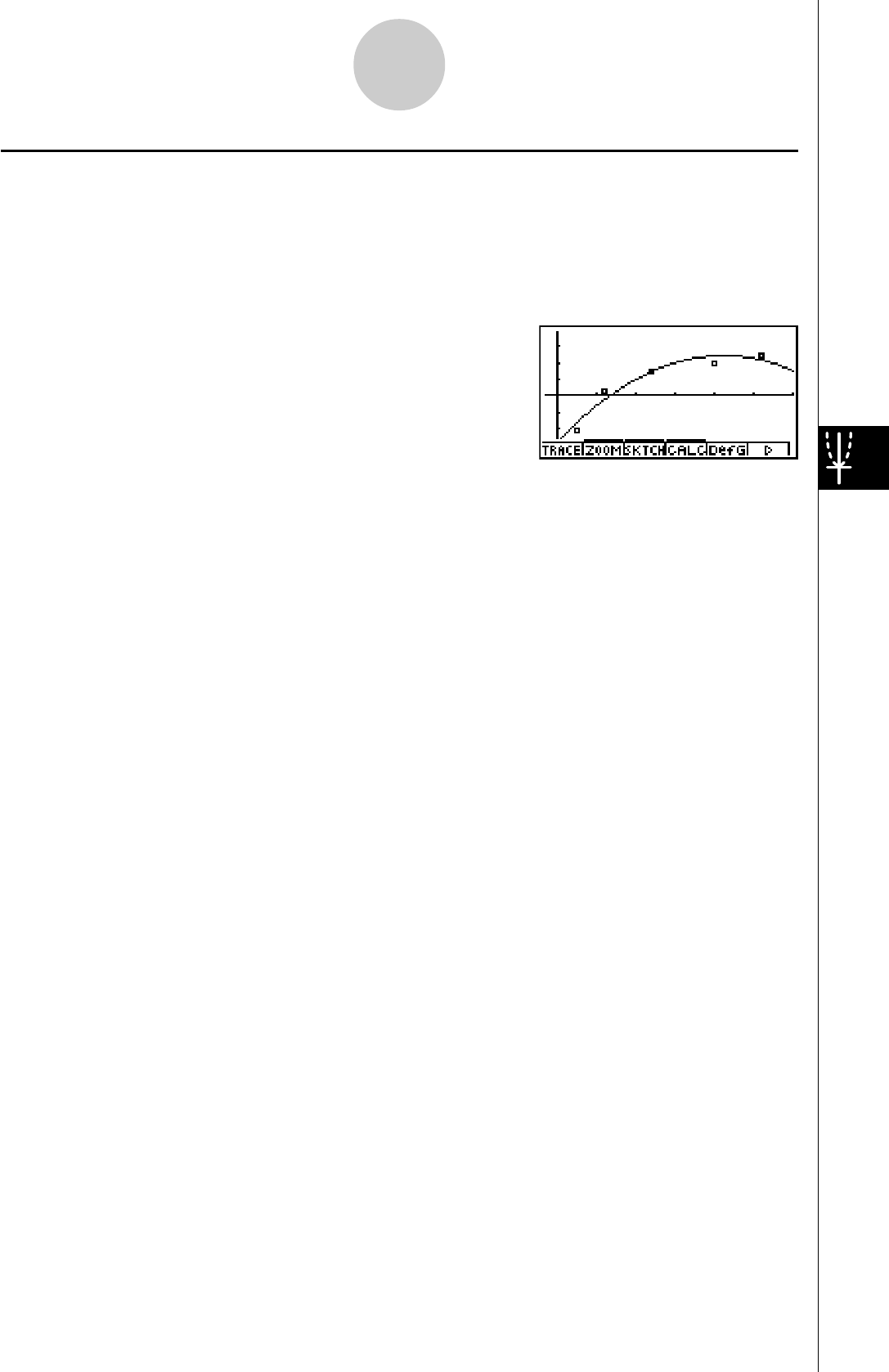
19990401
kk
kk
kGraphe de régression quadratique/cubique/quartique
Un graphe de régression quadratique/cubique/quartique représente la connexion des points
d’un diagramme de dispersion. Il utilise la méthode des moindres carrés pour tracer une
courbe qui passe près du plus grand nombre de points possible; il est représenté par la
formule de régression quadratique/cubique/quartique.
Ex. Régression quadratique
4(CALC)e(Quad)
6(DRAW)
Régression quadratique
formule du modèle …… y = ax2 + bx + c
a ............. second coefficient de régression
b ............. premier coefficient de régression
c ............. terme constant de régression (intersection)
r2............ coefficient de détermination
MSe ........ carrés des moyennes des erreurs
Régression cubique
formule du modèle …… y = ax3 + bx2 + cx + d
a ............. troisième coefficient de régression
b ............. second coefficient de régression
c ............. premier coefficient de régression
d ............. terme constant de régression (intersection)
r2............ coefficient de détermination
MSe ........ carrés des moyennes des erreurs
Régression quartique
formule du modèle …… y = ax4 + bx3 + cx2 + dx + e
a ............. quatrième coefficient de régression
b ............. troisième coefficient de régression
c ............. second coefficient de régression
d ............. premier coefficient de régression
e ............. terme constant de régression (intersection)
r2............ coefficient de détermination
MSe ........ carrés des moyennes des erreurs
6-3-7
Calcul et représentation graphique de données statistiques à variable double
20001202
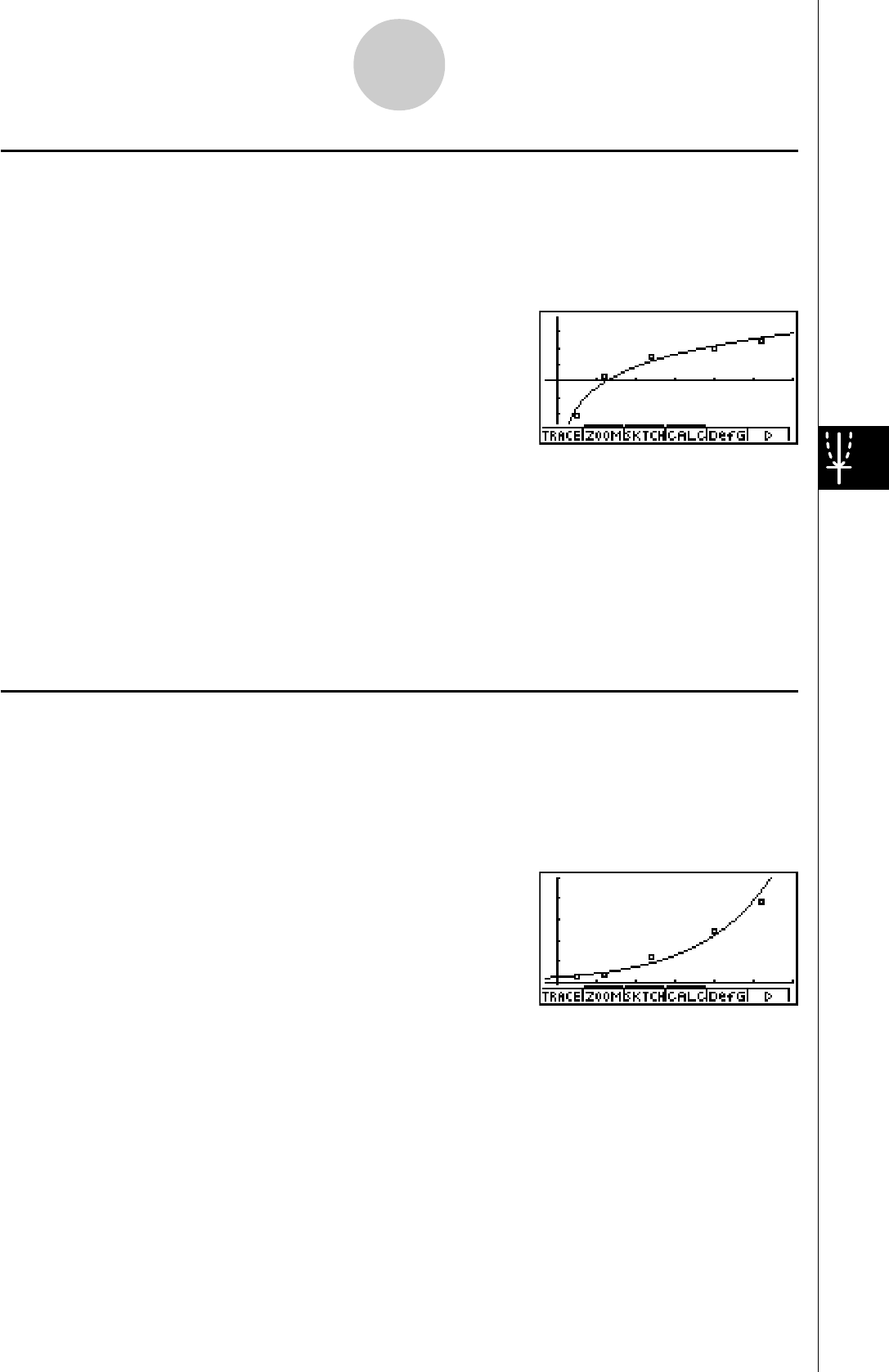
19990401
kGraphe de régression logarithmique
La régression logarithmique exprime y comme fonction logarithmique de x. La formule de
régression logarithmique standard est y = a + b × ln x, et si l’on suppose que X = ln x, la
formule correspond à la formule de régression y = a + bX.
4(CALC)h(Log)
6(DRAW)
Voici la formule du modèle de régression logarithmique.
y = a + b • ln x
a ............. terme constant de la régression
b ............. coefficient de régression
r .............. coefficient de corrélation
r2............ coefficient de détermination
MSe ........ carrés des moyennes des erreurs
kGraphe de régression exponentielle
La régression exponentielle exprime y comme proportion de la fonction exponentielle de x.
La formule de régression exponentielle standard est y = a × ebx, et si l’on prend les
logarithmes des deux côtés, on obtient ln y = ln a + bx. Ensuite, si l’on suppose que Y = ln y
et a = ln a, la formule correspond à la formule de régression linéaire Y = a + bx.
4(CALC)i(Exp)
6(DRAW)
Voici la formule du modèle de régression exponentielle.
y = a • ebx
a ............. coefficient de régression
b ............. terme constant de la régression
r .............. coefficient de corrélation
r2............ coefficient de détermination
MSe ........ carrés des moyennes des erreurs
6-3-8
Calcul et représentation graphique de données statistiques à variable double
20001202
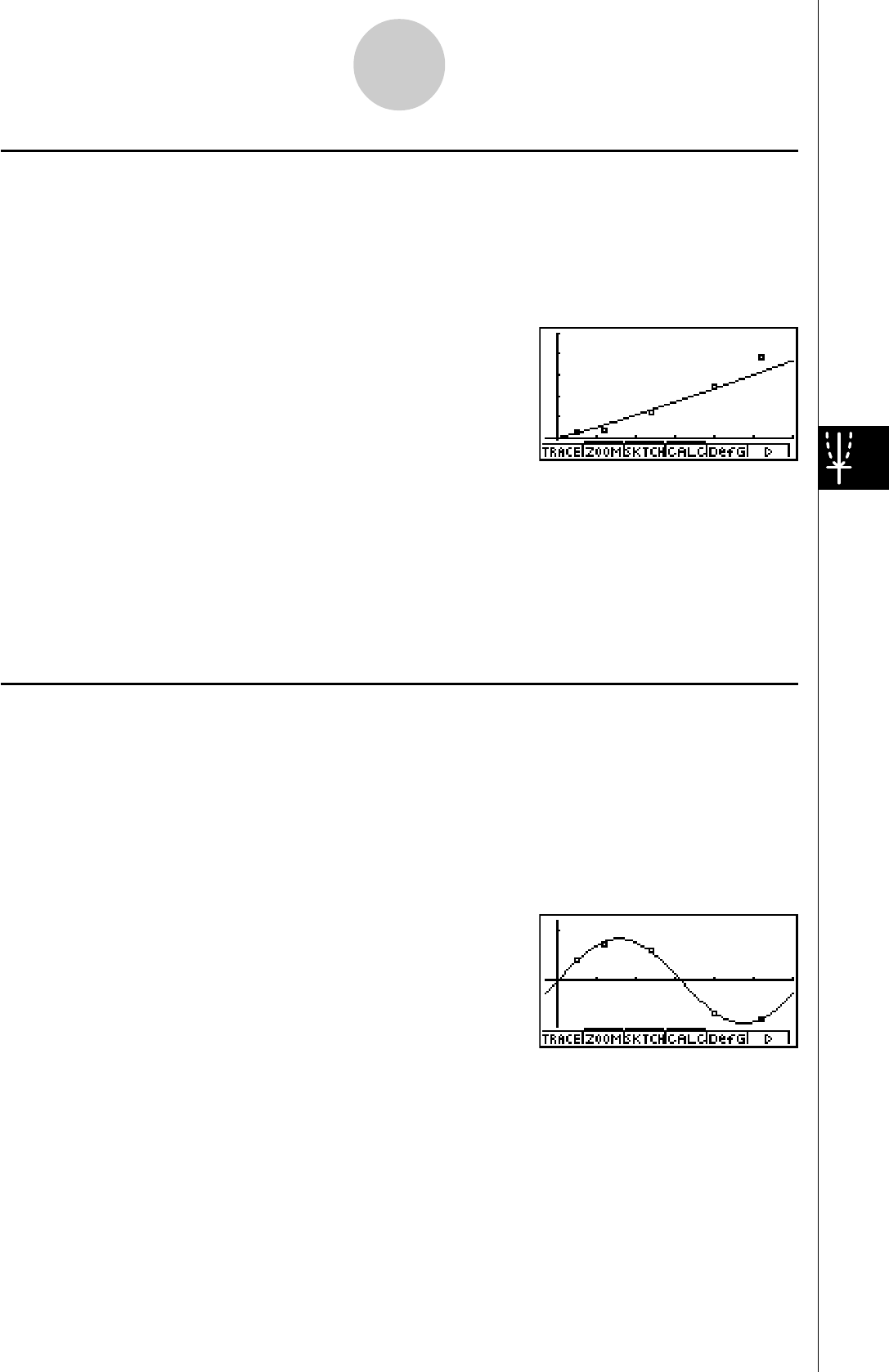
19990401
kk
kk
kGraphe de régression de puissance
La régression de puissance exprime y comme proportion de la puissance de x. La formule
de régression de puissance standard est y = a × xb, et si l’on prend les logarithmes des deux
côtés, on obtient ln y = ln a + b × ln x. Ensuite, si l’on suppose que X = ln x, Y = ln y et
a = ln a, la formule correspond à la formule de régression linéaire Y = a + bX.
4(CALC)j(Power)
6(DRAW)
Voici la formule du modèle de régression de puissance.
y = a • xb
a ............. coefficient de régression
b ............. puissance de régression
r .............. coefficient de corrélation
r2............ coefficient de détermination
MSe ........ carrés des moyennes des erreurs
kk
kk
kGraphe de régression sinusoïdale
La régression sinusoïdale est idéale pour les données cycliques.
Voici la formule du modèle de régression sinusoïdale.
y = a·sin(bx + c) + d
Quand la liste de données statistiques est à l’écran, effectuez l’opération de touches
suivante.
4(CALC)v(Sin)
6(DRAW)
Lors de la représentation d’un graphe de régression sinusoïdale, l’unité d’angle se règle
automatiquement sur les radians (Rad). L’unité d’angle ne change pas quand vous
effectuez un calcul de régression sinusoïdale sans tracer de graphe.
• Le calcul de certains types de données peut durer assez longtemps. C’est normal.
6-3-9
Calcul et représentation graphique de données statistiques à variable double
20001202
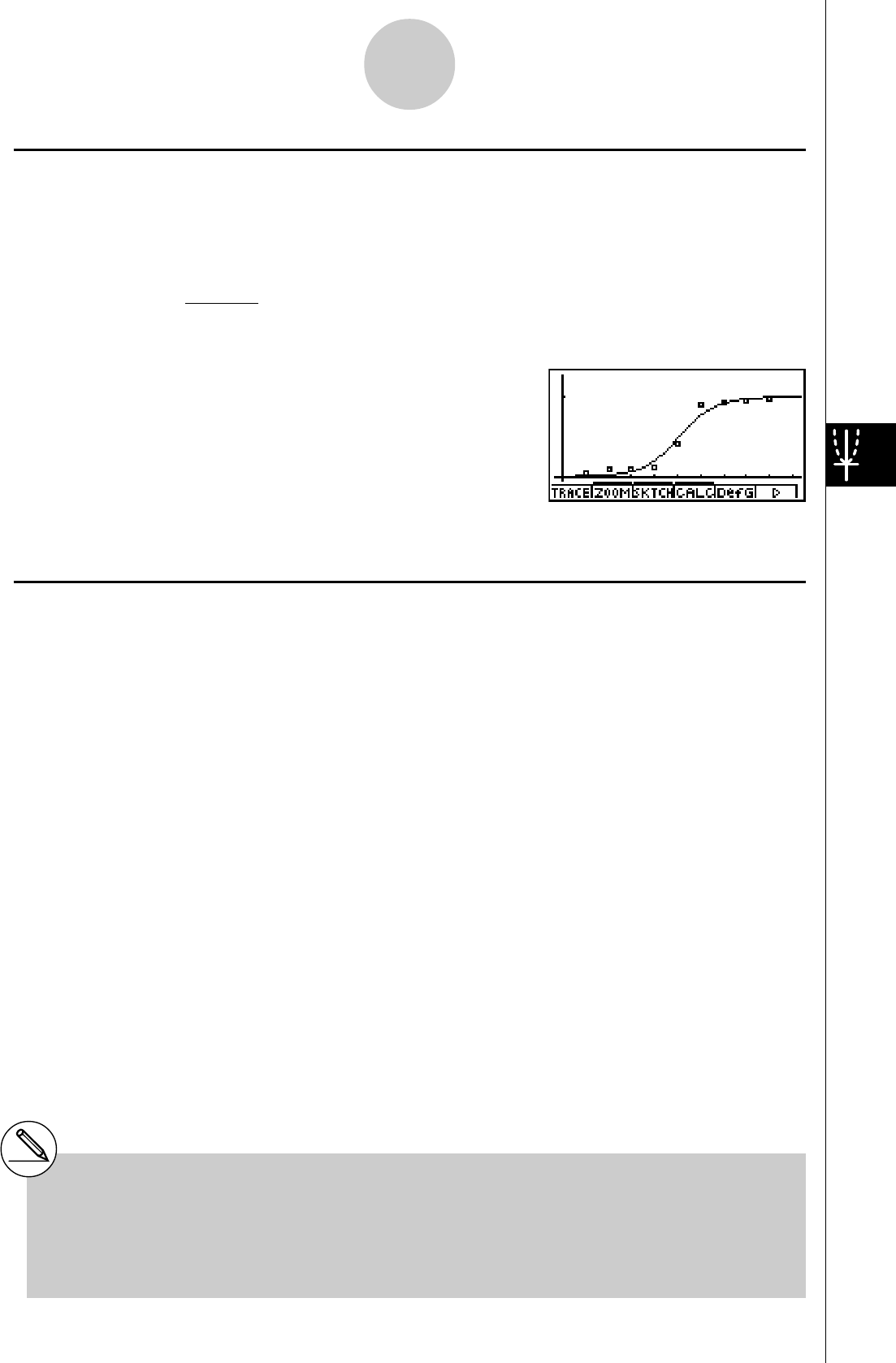
19990401
kk
kk
kGraphe de régression logistique
La régression logistique convient aux phénomènes liés au temps, où il y a un accroissement
continu jusqu’à un point de saturation.
Voici la formule du modèle de régression logistique.
y = c
1 + ae
–bx
4(CALC)l(Lgstic)
6(DRAW)
• Le calcul de certains types de données peut durer assez longtemps. C’est normal.
kk
kk
kCalcul résiduel
Les points actuellement marqués (ordonnées y) et la distance au modèle de régression
peuvent être calculés pendant le calcul de régression.
Quand la liste de données statistiques est à l’écran, rappelez l’écran de configuration pour
désigner LIST (“List 1” à “List 20”) pour “Resid List”. Les données résiduel les calculées sont
enregistrées dans la liste sélectionnée.
La distance verticale des points marqués au modèle de régression est mémorisée dans la
liste.
Les points supérieurs au modèle de régression sont positifs tandis que les points inférieurs
sont négatifs.
Le calcul résiduel peut être effectué et sauvegardé pour tous les modèles de régression.
6-3-10
Calcul et représentation graphique de données statistiques à variable double
# Toutes les données existantes dans la liste
sélectionnée sont supprimées. Les points
résiduels sont mémorisés dans le même
ordre de priorité que les données utilisées
comme modèle.
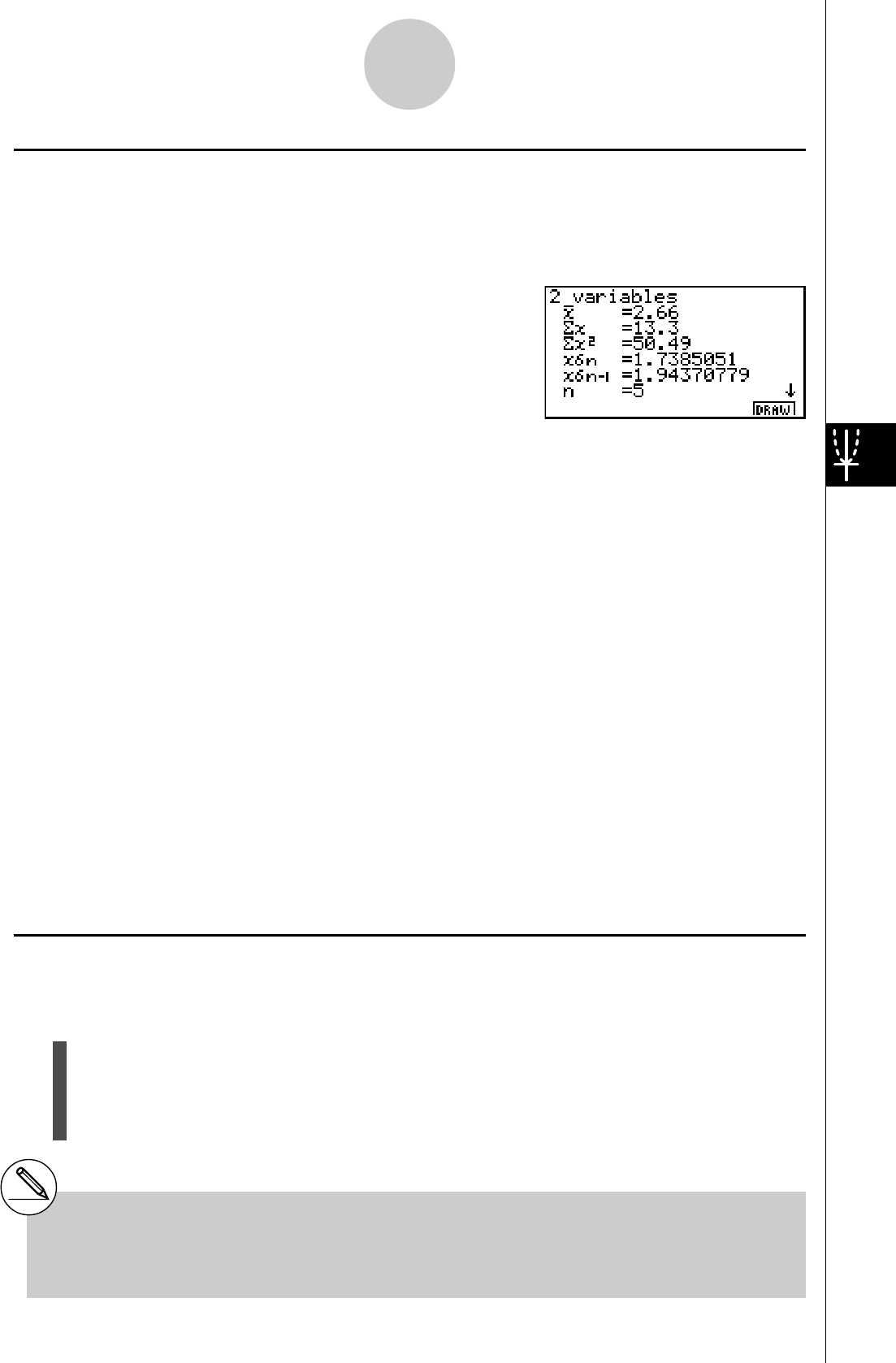
19990401
kk
kk
kAffichage des résultats du calcul d’un graphe à variable double
Les statistiques à variable double peuvent être exprimées sous forme de graphes et de
valeurs paramétriques. Lorsque ces graphes sont affichés, les résultats des calculs à
variable double apparaissent de la façon suivante lorsque vous appuyez sur 4(CALC)
b(2VAR).
• Utilisez c pour faire défiler la liste et voir les paramètres qui défilent au bas de l’écran.
o.............. Moyenne des données
stockées dans xList
Σx............ Somme des données
stockées dans xList
Σx2.......... Somme des carrés des
données stockées dans
xList
xσn........... Ecart-type sur une popula-
tion des données stockées
dans xList
xσn-1 ......... Ecart-type sur un échantillon
des données stockées dans
xList
n.............. Nombre de données
_
y.............. Moyenne des données
stockées dans yList
Σy............ Somme des données
stockées dans yList
kk
kk
kCopie d’une formule de graphe de régression dans le mode GRPH • TBL
Vous pouvez copier les résultats des calculs d’une formule de régression dans la zone de
formules de graphes du mode GRPH • TBL, les stocker et les comparer.
1. Appuyez sur 5(COPY) pour copier la formule de régression qui produit les données
affichées dans la zone de formules de graphes du mode GRPH • TBL*1.
2. Appuyez sur w pour stocker la formule graphique copiée et revenir à l’affichage
précédent du résultat de calculs de régression.
6-3-11
Calcul et représentation graphique de données statistiques à variable double
Σy2...... Somme des carrés des données
stockées dans yList
yσn...... Ecart-type sur une population des
données stockées dans yList
yσn-1 .... Ecart-type sur un échantillon des
données stockées dans yList
Σxy ..... Somme des données stockées dans
xList et yList
minX ... Minimum des données stockées
dans xList
maxX .. Maximum des données stockées
dans xList
minY ... Minimum des données stockées
dans yList
maxY .. Maximum des données stockées
dans yList
*1Vous ne pouvez pas modifier les formules de
régression de formules graphiques dans le
mode GRPH • TBL.
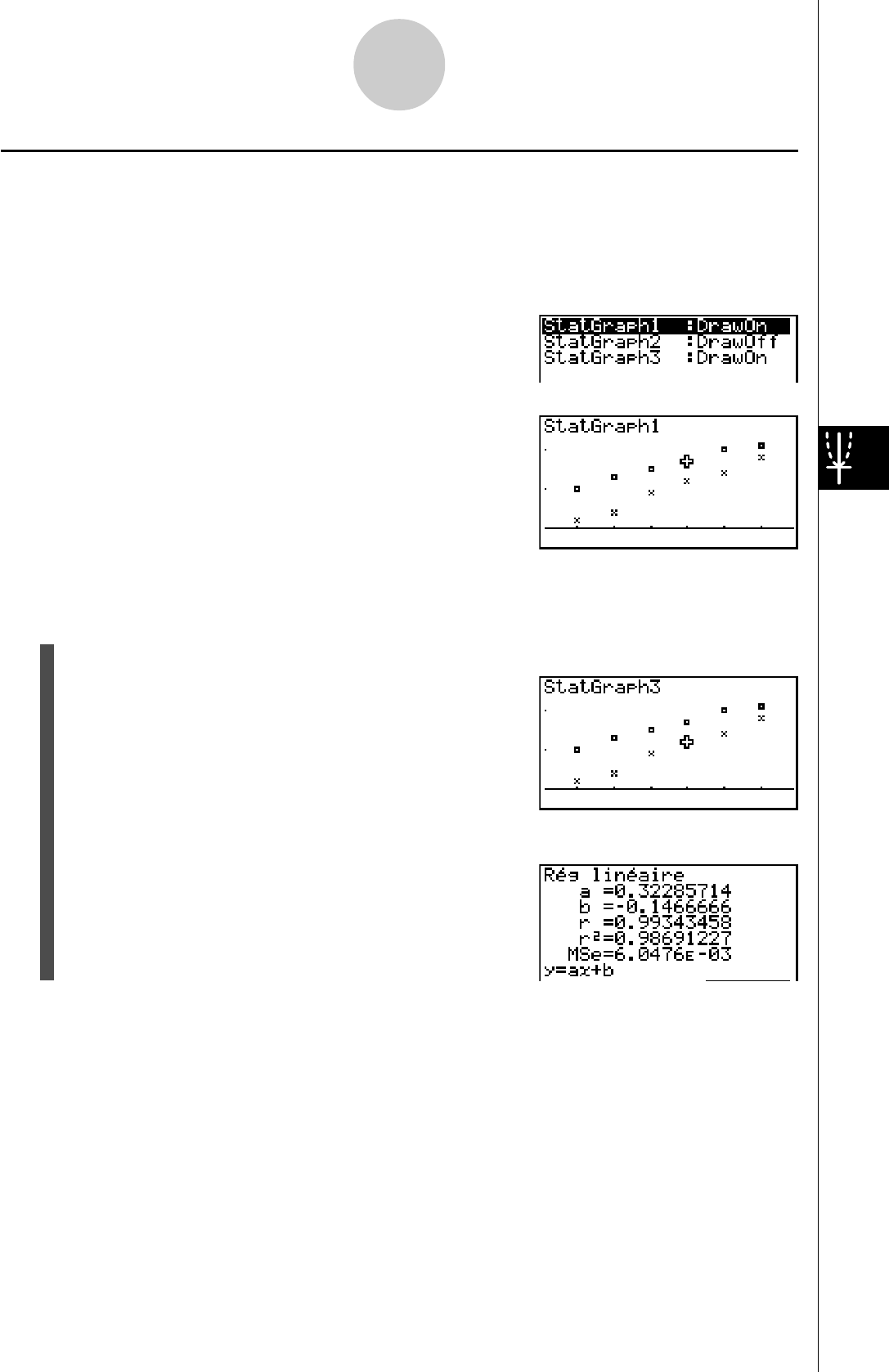
19990401
kk
kk
kGraphes multiples
Vous pouvez tracer plus d’un graphe sur le même écran en procédant comme indiqué dans
“Changement des paramètres d’un graphe” pour définir le statut avec ou sans tracé de deux
ou des trois graphes, puis appuyez sur 6(DRAW) (voir page 6-1-5). Quand les graphes ont
été tracés, vous pouvez sélectionner la formule à utiliser pour l’exécution des calculs de
statistiques à variable unique ou de régression.
4(CALC)
c(Linear)
• Le texte en haut de l’écran indique le graphe actuellement sélectionné (StatGraph1 =
Graphe 1, StatGraph2 = Graphe 2, StatGraph3 = Graphe 3).
1. Appuyez sur c. Le nom du graphe en haut de l’écran change.
2. Quand le graphe souhaité est sélectionné, appuyez sur w.
Maintenant vous pouvez procéder comme dans “Affichage des résultats du calcul d’un
graphe à variable double” à la page 6-3-11 pour effectuer des calculs statistiques.
6-3-12
Calcul et représentation graphique de données statistiques à variable double
20001202

19990401
k Superposition d’un graphe de fonction à un graphe de statistiques
Description
Vous pouvez superposer un graphe de statistique à variable double sur n’importe quel type
de graphe de fonction.
Réglage
1. Depuis le menu principal, accédez au mode STAT.
Exécution
2. Saisissez les données dans une liste et tracez le graphe de statistiques.
3. Affichez le menu de fonctions graphiques et indiquez la fonction que vous voulez
superposer au graphe statistique.
4. Tracez la fonction.
6-3-13
Calcul et représentation graphique de données statistiques à variable double

19990401
6-3-14
Calcul et représentation graphique de données statistiques à variable double
Exemple Saisir les deux groupes de données indiqués ci-dessous. Marquer
ensuite les données sur un diagramme de dispersion et superposer le
graphe de fonction y = 2ln x.
0,5, 1,2, 2,4, 4,0, 5,2,
–2,1, 0,3, 1,5, 2,0, 2,4
Procédure
1m STAT
2 a.fwb.cw
c.ewewf.cw
e
-c.bwa.dw
b.fwcwc.ew
1(GRPH)b(S-Gph1)
35(DefG)
cIvw(Enregistrez Y1 = 2In x)
46(DRAW)
Ecran de résultat
# Vous pouvez aussi utiliser la fonction Trace,
etc. pour la représentation graphique de
fonctions.
# Les graphes qui ne sont pas de type
rectangulaire ne peuvent pas être tracés.
# Si vous appuyez sur i lorsque vous
introduisez la fonction, l’expression précédente
sera rétablie.
Si vous appuyez sur !i(QUIT) ,
l’expression introduite sera effacée et la liste de
donnée statistiques réapparaîtra.

19990401
6-4 Exécution de calculs statistiques
Tous les calculs statistiques étaient effectués jusqu’à présent après l’affichage d’un graphe.
Voici maintenant comment utiliser seulement les calculs statistiques.
uu
uu
uPour définir les listes de données pour les calculs statistiques
Vous devez entrer les données statistiques pour le calcul que vous voulez effectuer et
désigner où elles se trouvent avant de commencer un calcul. Affichez les données
statistiques puis appuyez sur 2(CALC)e(Set).
Voici la signification de chaque paramètre.
1Var XList ............ emplacement des valeurs statistiques x à variable unique (XList)
1Var Freq ............ emplacement des valeurs de fréquence à variable unique
(Fréquence)
2Var XList ............ emplacement des valeurs statistiques x à variable double (XList)
2Var YList ............ emplacement des valeurs statistiques y à variable double (YList)
2Var Freq ............ emplacement des valeurs de fréquence à variable double
(Fréquence)
• Les calculs effectués dans cette partie utilisent les spécifications précédentes.
6-4-1
Exécution de calculs statistiques
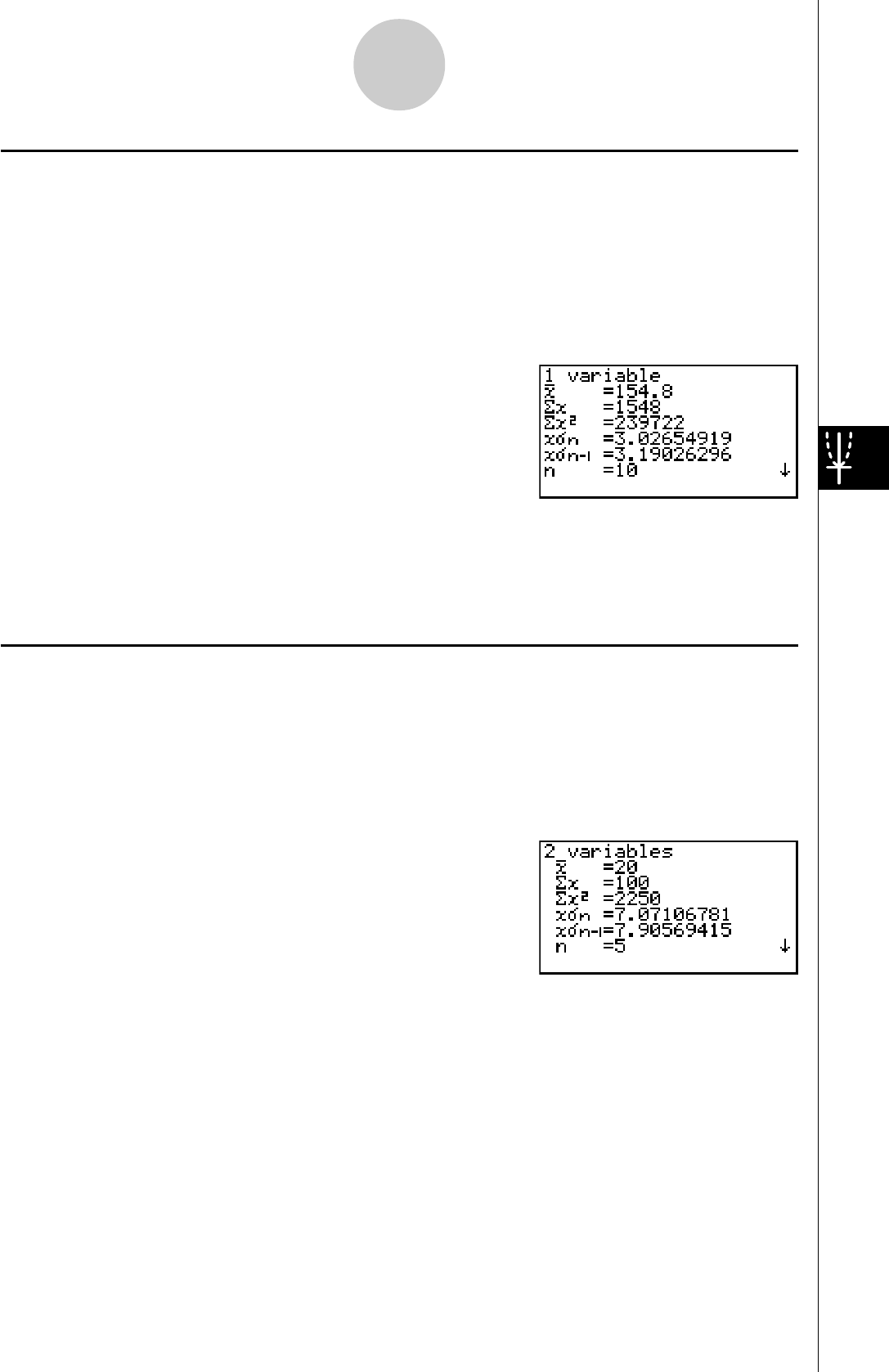
19990401
kk
kk
kCalculs statistiques à variable unique
Dans les exemples précédents de “Marquage d’un point de probabilité normale” et
“Histogramme (diagramme à barres)” à “Graphe linéaire”, les résultats des calculs
statistiques étaient affichés après le tracé du graphe. Il s’agissait d’expressions
numériques des caractéristiques des variables utilisées pour la représentation graphique.
Ces valeurs peuvent aussi être obtenues directement en affichant la liste de données
statistiques et en appuyant sur 2(CALC)b(1VAR).
Ensuite, appuyez sur f ou c pour faire défiler les résultats de calculs statistiques et voir
les caractéristiques des variables.
Pour les détails sur la signification des valeurs statistiques, voir “Affichage des résultats du
calcul d’un graphe à variable unique” (page 6-2-4).
kk
kk
kCalculs statistiques à variable double
Dans les exemples précédents de “Graphe de régression linéaire” à “Graphe de
régression logistique”, les résultats des calculs statistiques étaient affichés après le tracé
du graphe. Il s’agissait d’expressions numériques des caractéristiques de variables
utilisées pour la représentation graphique.
Ces valeurs peuvent aussi être obtenues directement en affichant la liste de données
statistiques et en appuyant sur 2(CALC)c(2VAR).
Ensuite, appuyez sur f ou c pour faire défiler les résultats de calculs statistiques et voir
les caractéristiques des variables.
Pour les détails sur la signification des valeurs statistiques, voir “Affichage des résultats du
calcul d’un graphe à variable double” (page 6-3-11).
6-4-2
Exécution de calculs statistiques

19990401
kCalculs de régression
Dans “Graphe de régression linéaire” à “Graphe de régression logistique”, les résultats des
calculs de régression étaient affichés après le tracé du graphe. Ici, chaque coefficient de la
ligne de régression et de la courbe de régression est exprimé sous forme d’un nombre.
Vous pouvez déterminer directement la même expression à partir de l’écran de saisie de
données.
Appuyez sur 2(CALC)d(REG) pour afficher le menu déroulant qui contient les
paramètres suivants.
•{Linear}/{MedMed}/{Quad}/{Cubic}/{Quart}/{Log}/{Exp}/{Power}/{Sin}/{Lgstic} ...
paramètres de {régression linéaire}/{Med-Med}/{régression quadratique}/{régression
cubique}/{régression quartique}/{régression logarithmique}/{régression exponentielle}/
{régression de puissance}/{régression sinusoïdale}/{régression logistique}
Exemple Afficher des paramètres de régression à variable unique
2(CALC)d(REG)b(Linear)
La signification des paramètres qui apparaissent à l’écran est la même que celle indiquée
pour “Graphe de régression linéaire” à “Graphe de régression logistique”.
6-4-3
Exécution de calculs statistiques
20001202
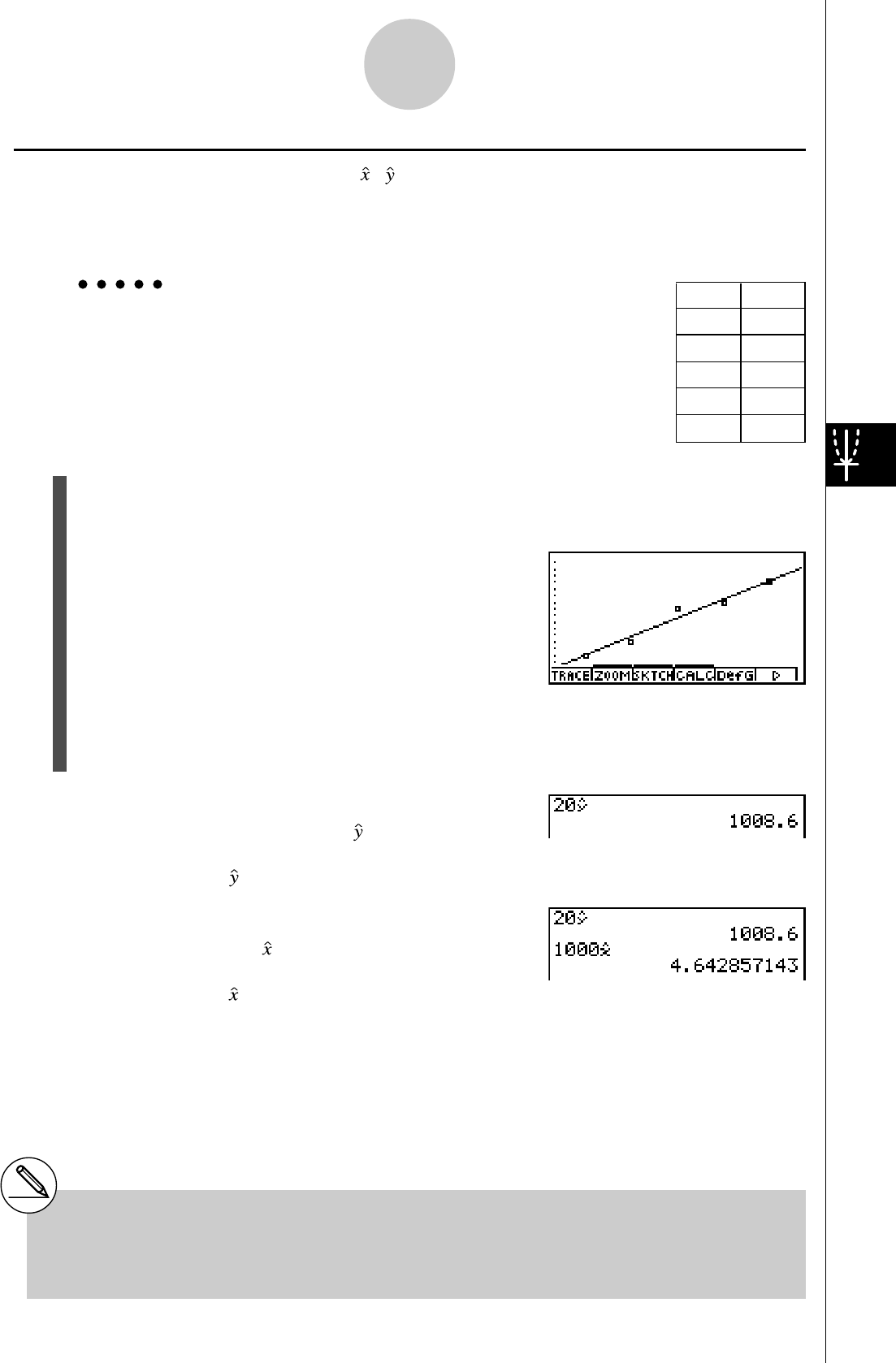
19990401
kCalcul des valeurs estimées ( , )
Après avoir tracé un graphe de régression dans le mode STAT, vous pouvez utiliser le mode
RUN • MAT pour calculer les valeurs estimées des paramètres x et y du graphe de
régression.
Exemple Effectuer la régression de puissance en utilisant les
données ci-contre et estimer les valeurs de nn
nn
n et mm
mm
m
quand xi = 20 et yi = 1000
1. Depuis le menu principal, accédez au mode STAT.
2. Introduisez les données dans la liste et tracez le graphe de régression de linéaire.
3. Depuis le menu principal, accédez au mode RUN • MAT.
4. Appuyez sur les touches suivantes.
ca(valeur de xi)
K6(g)4(STAT)c( )w
La valeur estimée est affichée pour xi = 20.
baaa(valeur de yi)
4(STAT)b( )w
La valeur estimée est affichée pour yi = 1000.
6-4-4
Exécution de calculs statistiques
xi yi
10 1003
15 1005
20 1010
25 1011
30 1014
# Vous ne pouvez pas obtenir une valeur
estimée pour le graphe Med-Med, de
régression quadratique, régression cubique,
régression quartique, régression sinusoïdale
ou régression logistique.
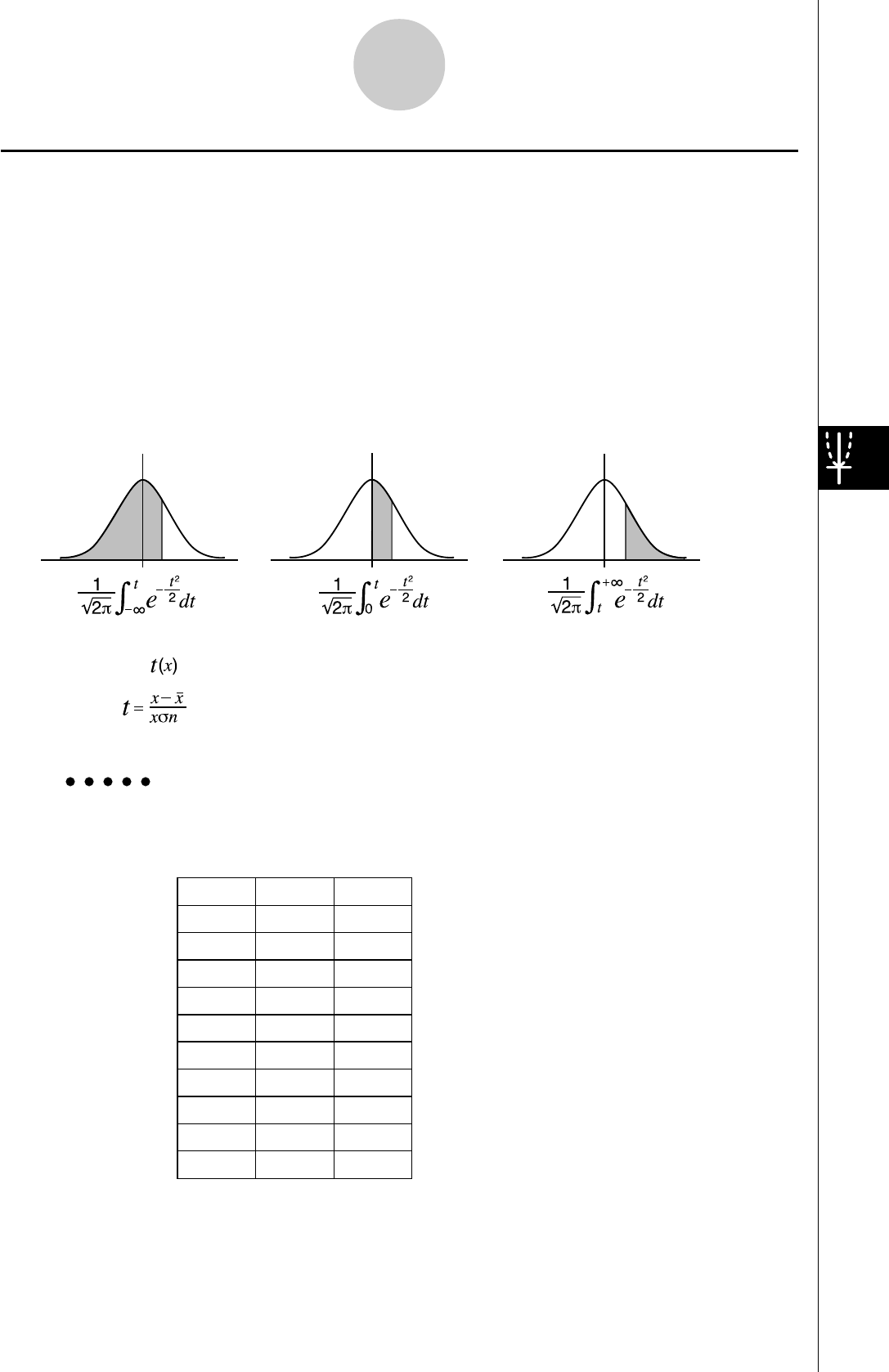
19990401
kCalcul de distributions de probabilité
Vous pouvez calculer les distributions de probabilité pour des statistiques à variable unique
avec le mode RUN • MAT.
Appuyez sur K6(g)1(PROB) pour afficher un menu de fonctions contenant les
paramètres suivants.
•{P(}/{Q(}/{R(} ... calcul de la valeur {P(t)}/{Q(t)}/{R(t)} de probabilité
•{t(} ... {calcul la valeur t(x) de la variante réduite}
• La probabilité P(t), Q(t) et R(t) et la variante réduite t(x) sont calculées à l’aide des
formules suivantes.
Exemple Le tableau suivant indique le résultat de la mesure de 20 étudiants.
Déterminer quel pourcentage d’étudiants a entre 160,5 cm et 175,5 cm
et dans quel percentile rentre l’étudiant de 175,5 cm.
Classement Grandeur (cm) Fréquence
1 158,5 1
2 160,5 1
3 163,3 2
4 167,5 2
5 170,2 3
6 173,3 4
7 175,5 2
8 178,6 2
9 180,4 2
10 186,7 1
6-4-5
Exécution de calculs statistiques
P
(
t
)Q
(
t
)R
(
t
)

19990401
1. Introduisez les grandeurs dans la liste 1 et la fréquence dans la liste 2.
2. Effectuer des calculs statistiques à variable unique*1.
2(CALC)e(Set)
c2(LIST)cwi
2(CALC)b(1VAR)
3. Appuyez sur m, sélectionnez le menu RUN • MAT, appuyez sur
K6(g)1(PROB) et rappelez le menu (PROB) du calcul de probabilité.
1(PROB)i(t() bga.f)w
(Variante réduite t pour 160,5 cm) Résultat: –1,633855948
( –1,634)
1(PROB)i(t() bhf.f)w
(Variante réduite t pour 175,5 cm) Résultat: 0,4963343361
( 0,496)
1(PROB)f(P()a.ejg)-
1(PROB)f(P()-b.gde)w
(Pourcentage du total) Résultat: 0,638921
(63,9% de l’ensemble)
1(PROB)h(R()a.ejg)w
(Percentile) Résultat: 0,30995
(31,0 percentile)
6-4-6
Exécution de calculs statistiques
*1 Vous pouvez obtenir la variante réduite
immédiatement après avoir effectué des calculs
statistiques à variable unique seulement.

19990401
k Représentation graphique d’une distribution de probabilité
Description
Vous pouvez représenter graphiquement une distribution de probabilité en utilisant le graphe
manuel du mode RUN • MAT.
Réglage
1. Depuis le menu principal, accédez au mode RUN • MAT.
Exécution
2. Entrez les commandes pour tracer un graphe à coordonnées rectangulaires.
3. Indiquez la valeur de probabilité.
6-4-7
Exécution de calculs statistiques
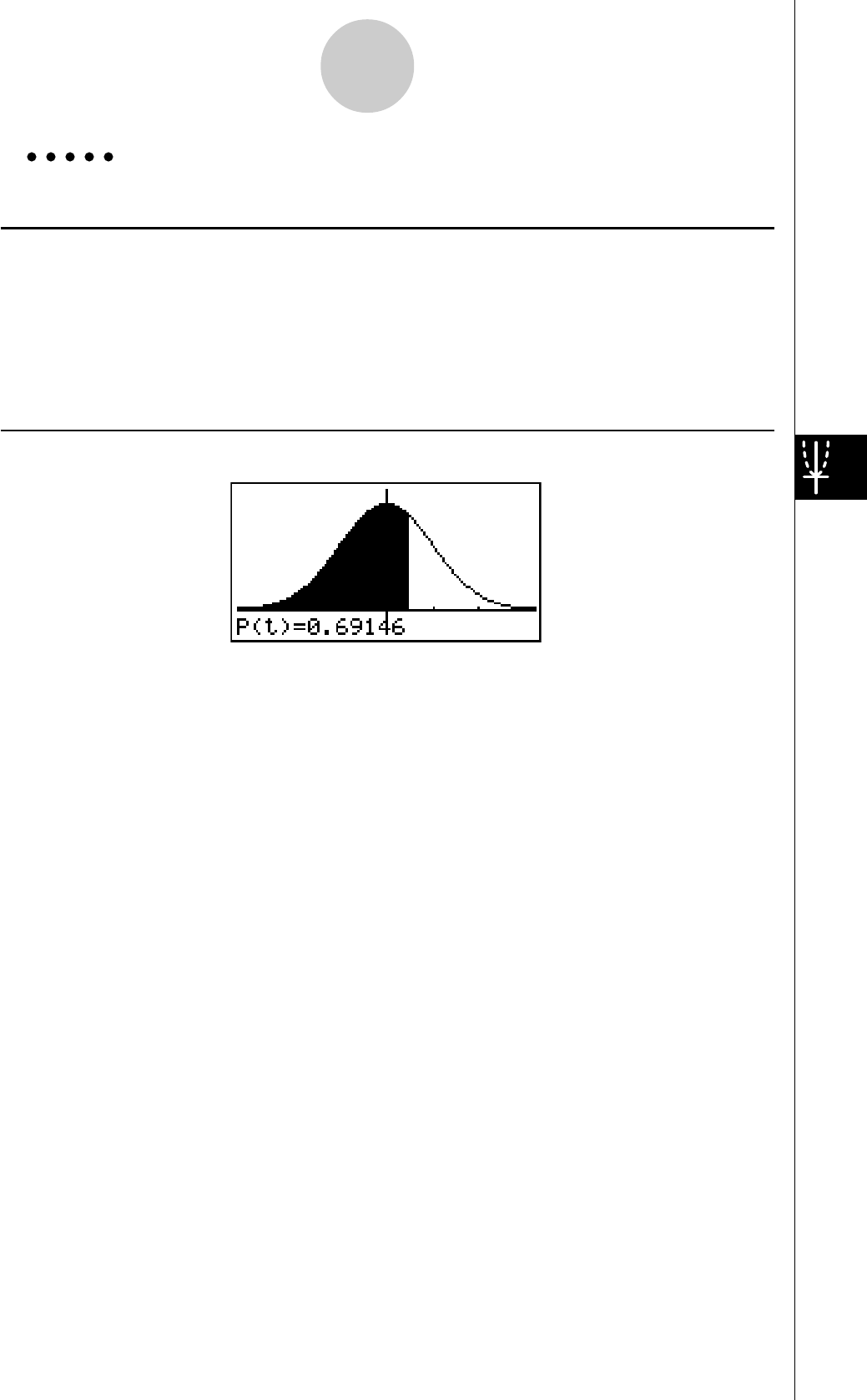
19990401
Exemple Tracer le graphe de probabilité P (0,5)
Procédure
1m RUN • MAT
2K6(g)6(g)2(SKTCH)b(Cls)w
2(SKTCH)e(GRPH)b(Y=)
3K6(g)1(PROB)f(P()a.fw
Ecran de résultat
6-4-8
Exécution de calculs statistiques
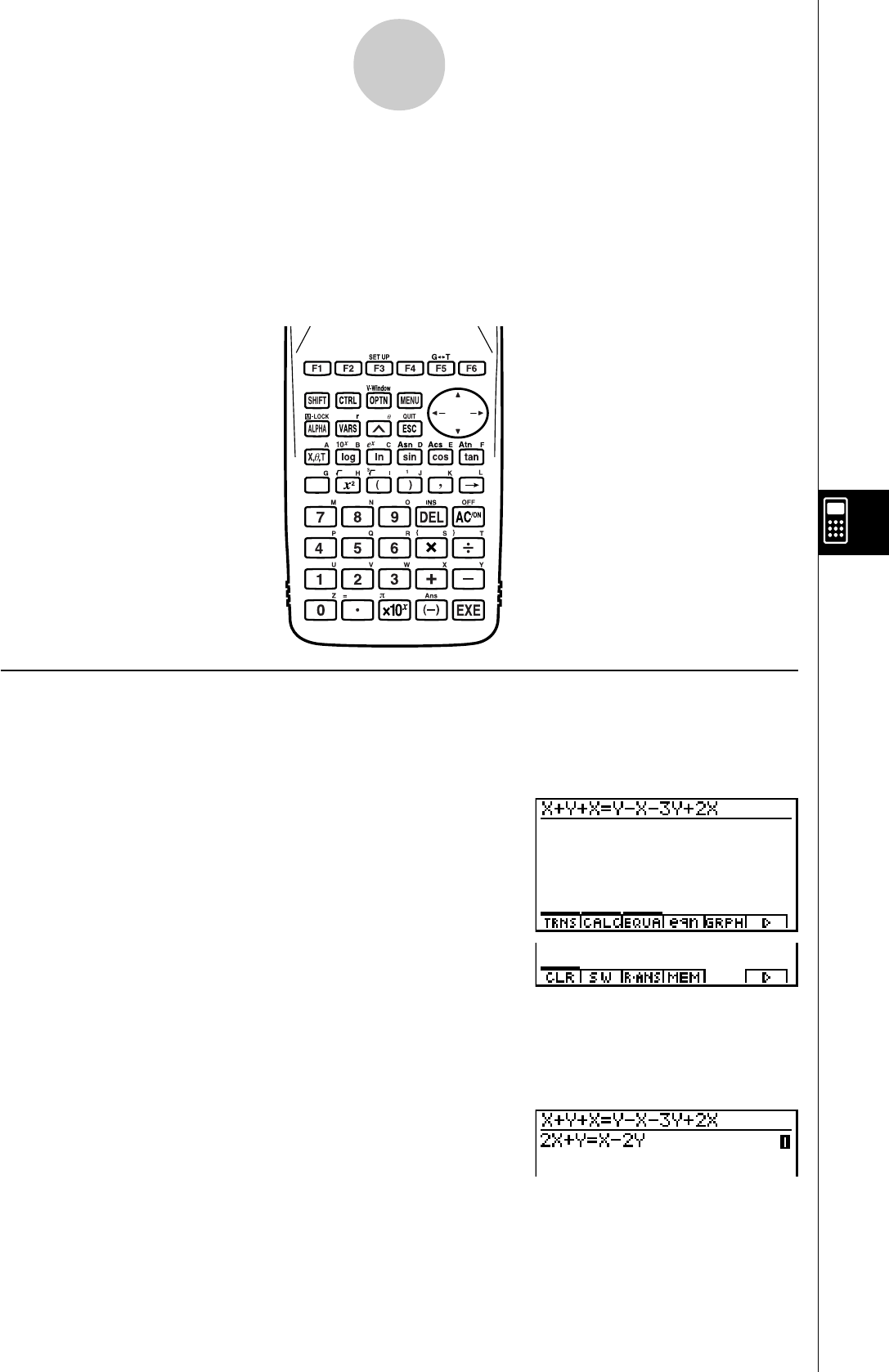
20001202
REPLAY
COPY PASTE
H-COPY
i
7-1-1
Utilisation du mode CAS (Système d’algèbre informatique)
7-1 Utilisation du mode CAS (Système d’algèbre
informatique)
Sur le menu principal, sélectionnez l’icône CAS pour accéder au mode CAS.
L’illustration suivante montre les touches qui peuvent être utilisées dans le mode CAS.
kk
kk
k Saisie et affichage de données
La saisie de données dans le mode Algèbre s’effectue dans la partie supérieure de l’écran,
qui est appelée “zone d’entrée”. Vous pouvez saisir des commandes et des expressions à la
position actuelle du curseur.
Les résultats des calculs apparaissent dans la partie inférieure de l’écran, qui est appelée
“zone de sortie”. Si un calcul produit une équation ou une inéquation, la partie inférieure de
l’écran se divisera en une “zone d’affichage de résultat naturel” pour le résultat et une “zone
de numéro de formule” pour le numéro de formule, comme indiqué ci-dessous.

20001202
Si tout le résultat ne rentre pas dans l’écran, utilisez les touches de curseur pour le faire
défiler.
k Saisie des données de listes
Liste: {élément, élément, … , élément}
• Les éléments doivent être séparés par des virgules et l’ensemble des éléments doit être à
l’intérieur {d’accolades}.
• Vous pouvez saisir des valeurs numériques et des expressions, des équations et des
inégalités comme éléments d’une liste.
Exemple Pour saisir la liste {1, 2, 3}
!*( { )b,c,d
!/( } )w
kSaisie des données de matrices
Matrice (m × n): [[saisie de (1,1), saisie de (1,2), ..., saisie de (1,m)] [saisie de (2,1), ......,
saisie de (2,n)]... [saisie de (m,n), ..., saisie de (m,n)]
• Les données saisies sont indiquées de manière à montrer la position relative de chaque
donnée dans la matrice. En fait, la ligne est continue de gauche à droite.
• Les données saisies doivent être séparées par des virgules et l’ensemble des éléments doit
être à l’intérieur de [crochets]. Chaque ligne doit également être à l’intérieur de [crochets].
• Vous pouvez saisir des valeurs numériques et des expression dans la matrice.
Exemple Saisir la matrice suivante. 1 2 3
4 5 6
7 8 9
!+( [ )!+( [ )b,c,d
!-( ] )!+( [ )e,f,g
!-( ] )!+( [ )h,i,j
!-( ] )!-( ] )w
7-1-2
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
kSaisie des données de vecteurs
Vecteur: [composante, composante, …, composante]
• Les composantes doivent être séparées par des virgules, et l’ensemble des composantes
doit être à l’intérieur de [crochets].
• Vous pouvez saisir des valeurs numériques et des expressions comme composantes des
vecteurs.
Exemple Saisir le vecteur (1, 2, 3).
!+( [ )b,c,d
!-( ] )w
kk
kk
k Opération dans le mode Algèbre
Vous pouvez utiliser deux méthodes pour la saisie d’opérations dans le mode Algèbre.
• Saisie à l’aide des commandes du menu de fonctions
• Saisie manuelle de formules et de paramètres
kk
kk
k Saisie à l’aide des commandes du menu de fonctions
Appuyez sur une touche du menu de fonctions pour afficher le menu de fonctions pour le
type d’opérations que vous essayez d’effectuer.
•TRNS ... {menu de transformation de formules}
•CALC ... {menu de calcul de formules}
•EQUA ... {menu d’équations, d’inéquations}
•eqn ... {rappel d’une équation stockée dans la mémoire d’équations en fonction de la
valeur spécifiée}
•CLR ... {menu de suppression de variables/formules}
Le menu suivant s’affiche par une pression de la touche K.
•LIST ... {menu de calculs avec listes}
•MAT ... {menu de calculs matriciels}
•VECT ... {menu de calculs vectoriels}
Pour les détails sur les commandes et leurs formats, voir “Liste des commandes
algébriques” à la page 7-1-11.
7-1-3
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
kk
kk
k Saisie manuelle de formules et de paramètres
Vous pouvez utiliser ensemble les menus de fonctions, la touche K et la touche J pour
saisir des formules et des paramètres, comme indiqué ci-dessous.
•3(EQUA)b(INEQUA)
•{>}/{<}/{tt
tt
t}/{ss
ss
s} ... {inéquation}
• Touche K
•{∞}/{Abs}/{x!}/{sign} ... {infini}/{valeur absolue}/{factoriellel}/{fonction signum*1}
•{HYP} ... fonctions {hyperboliques}/{hyperboliques inverses}
•{sinh}/{cosh}/{tanh}/{sinh–1}/{cosh–1}/{tanh–1}
• Touche J
•{Y}/{r}/{Xt}/{Yt}/{X} ... saisie de la mémoire de graphes {Y}/{r}/{Xt}/{Yt}/{X}
k Mémoire de formules
Le mode CAS a 28 variables de formules. Les variables sont indiquées par les noms A à Z, r
et
θ
. Les variables des formules du mode CAS sont indépendantes des variables ordinaires.
Exemple Affecter à la variable A la dérivée de sin(X) pour X
2(CALC)b(diff)sv,
v)aav(A)w
7-1-4
Utilisation du mode CAS (Système d’algèbre informatique)
1 (nombre réel, A > 0)
–1 (nombre réel, A < 0)
*1signum (A) A (A= nombre imaginaire)
|A|
Non défini (A = 0)
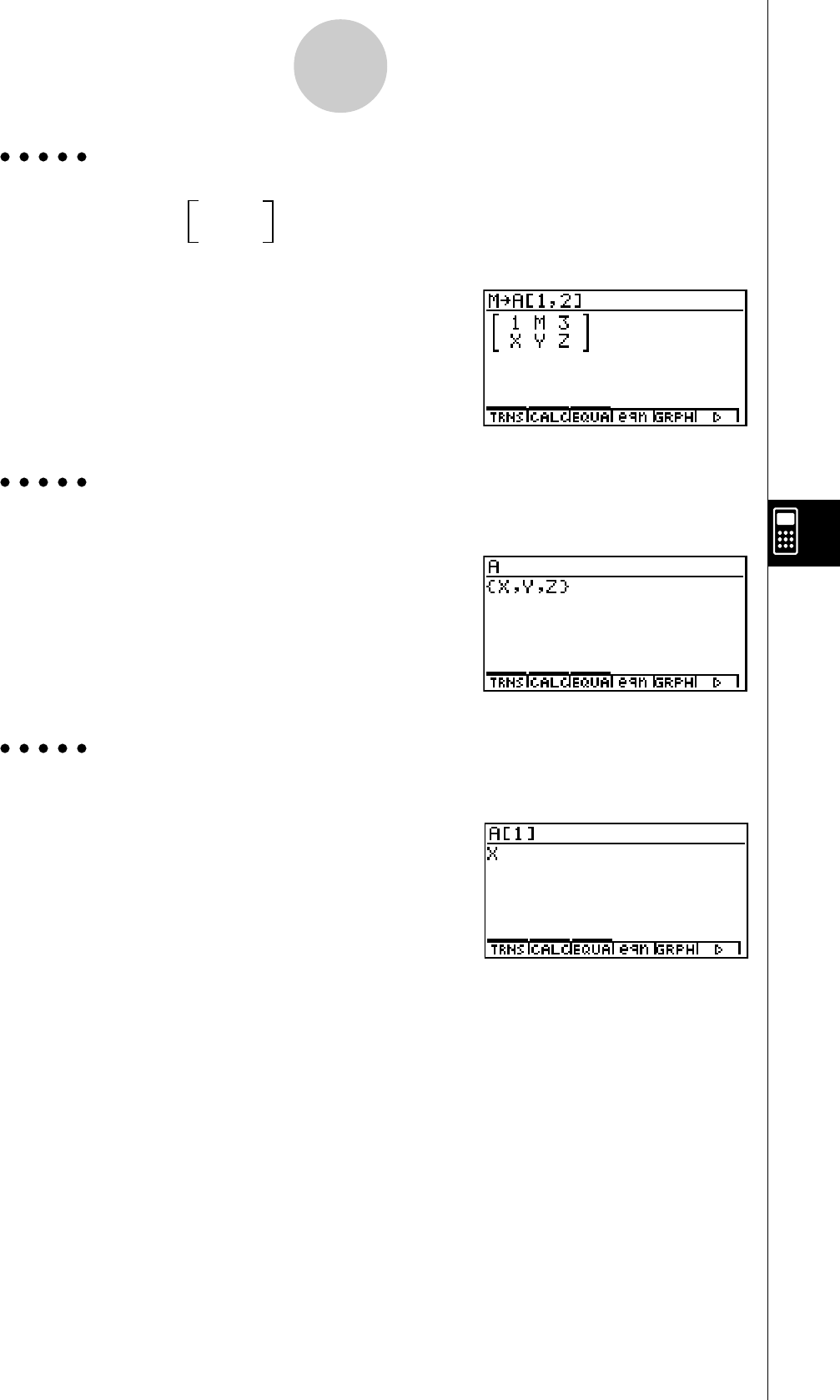
20001202
Exemple Affecter M à la ligne 1 et la colonne 2 de la variable A lorsque la
matrice lui est affectée.
ah(M)aav(A)
!+( [ )b,c!-( ] )w
Exemple Rappeler la valeur de la variable A lorsque la liste {X, Y, Z} lui est
affectée.
av(A)w
Exemple Rappeler la première composante (A[1]) de la variable A lorsque le
vecteur (X Y Z) lui est affecté.
av(A)!+( [ )b
!-( ] )w
7-1-5
Utilisation du mode CAS (Système d’algèbre informatique)
123
XYZ
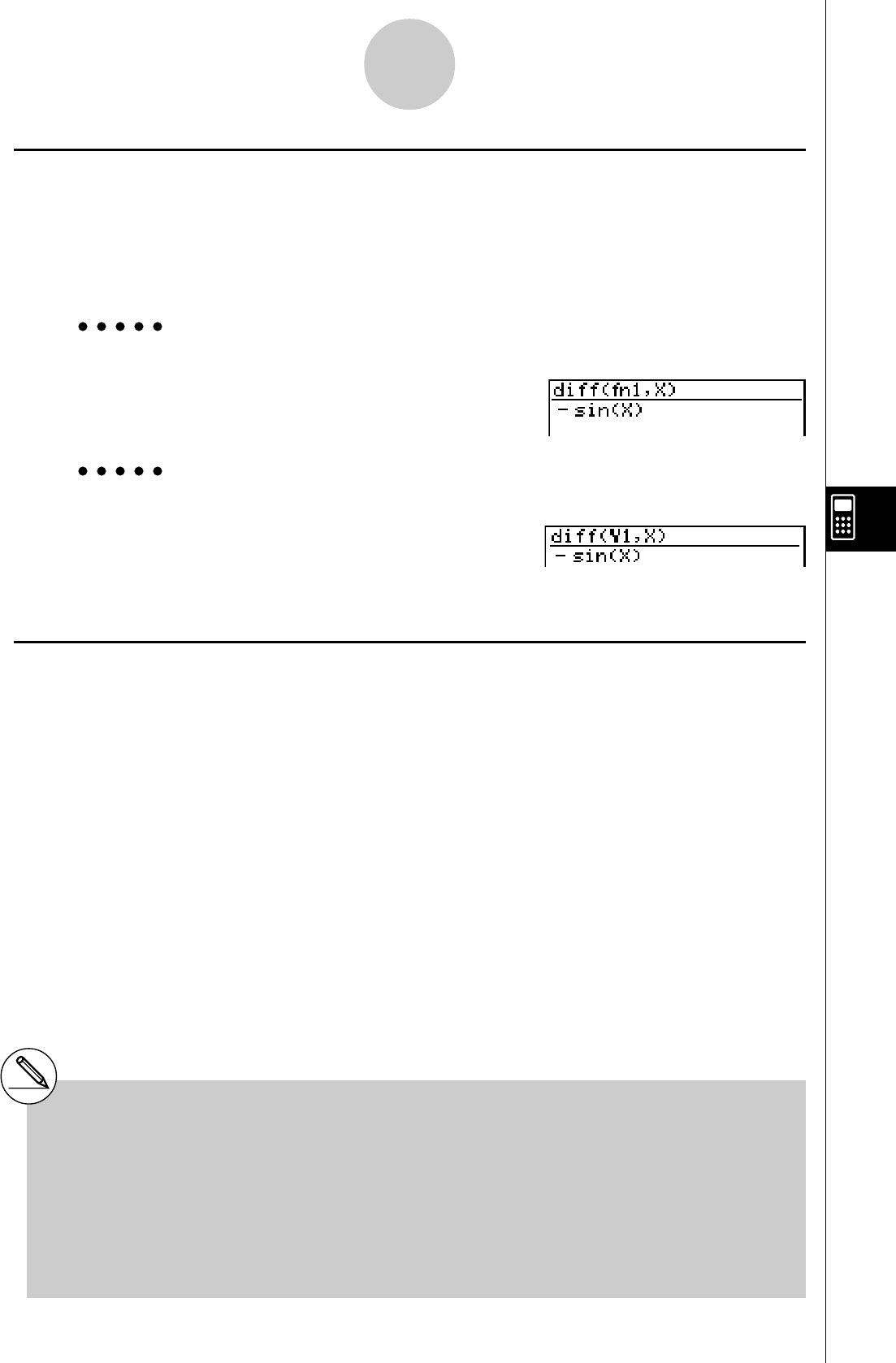
20001202
k Mémoire de fonctions et mémoire de graphes
La mémoire de fonctions permet de stocker des fonctions pour un rappel ultérieur.
La mémoire de graphes permet de stocker des graphes dans la mémoire. Appuyez sur la
touche J et indiquez le nom du graphe.
Exemple Dériver la mémoire de fonction f1 qui contient cos(X)
2(CALC)b(diff)K6(g)4(FMEM)
d(fn)b,v)w
Exemple Dériver la mémoire de graphe Y1 qui contient cos(X)
2(CALC)b(diff)
J1(Y) b,v)w
k Mémoire d’équations
Si le résultat d’un calcul est une équation ou une inéquation, son numéro de formule sera
affiché dans la zone de numéro de formule et l’équation sera stockée dans la mémoire
Eqn*1. Les équations stockées peuvent être rappelées avec la commande eqn, la
commande rclEqn ou rclAllEqn.
7-1-6
Utilisation du mode CAS (Système d’algèbre informatique)
*199 formules peuvent être stockées dans la
mémoire Eqn.
Le message d’erreur “Erreur mémoire”
apparaît lorsque vous essayez de stocker
une équation si 99 équations se trouvent déjà
dans la mémoire Eqn. Si c’est le cas,
exécutez ALLEQU (suppression de toutes les
équations) depuis le menu CLR.

20001202
k Mémoire de dernier résultat (Ans) et calcul continu
La mémoire de dernier résultat (Ans) et le calcul continu peuvent être utilisés comme pour
les calculs standard. Dans le mode Algèbre, vous pouvez même stocker des formules dans
la mémoire de dernier résultat.
Exemple Développer (X+1)2 et ajouter le résultat à 2X
1(TRNS)b(expand)
(v+b)x)w
En continuant:
+cvw
k Contenu de la mémoire de rappel
La mémoire de rappel peut être utilisée dans la zone d’entrée. Lorsqu’un calcul est terminé,
une pression sur d ou e dans la zone d’entrée rappelle la formule du dernier calcul
effectué. Après un calcul ou après une pression sur A, vous pouvez appuyer sur f ou
c pour rappeler les formules antérieures.
k Déplacement du curseur entre les zones d’affichage
Lorsque ] ' ` $ indiquent un résultat de calcul ne rentrant pas dans l’écran, les touches
de curseur servent à faire défiler la zone de sortie. Pour utiliser la fonction de rappel dans
ces conditions, appuyez sur 6(g)2(SW). ] ' ` $ se transforment en une ligne
pointillée pour indiquer que les touches de curseur contrôlent la zone de sortie.
Une nouvelle pression sur 2(SW) faire revenir le curseur dans la zone de sortie.
7-1-7
Utilisation du mode CAS (Système d’algèbre informatique)
# Le contenu de la mémoire Eqn, de la
mémoire Ans et de la mémoire de rappel se
supprime par une pression sur
6(g)1(CLR)d(ALLEQU) .
# Vous pouvez saisir jusqu’à 255 octets de données
dans la zone d’entrée.

20001202
Paramètres SET UP
uu
uu
uAngle ... Définition de l’unité d’angle
•{Deg}/{Rad} ... {degré}/{radian}
uu
uu
uAnswer Type ... Définition de la plage de résultat
•{Real}/{Cplx} ... {nombre réel}/{nombre complexe}
uu
uu
uDisplay ... Définition du format d’affichage (pour approx seulement)
•{Fix}/{Sci}/{Norm} ... {nombre de décimales}/{nombre de chiffres significatifs}/
{format d’affichage normal}
k Fonction de graphe
L’écran de formules graphiques s’affiche par une pression de 5(GRPH). Sur cet écran
vous pouvez saisir vos formules graphiques. Appuyez sur 4(G
•
VAR) si vous voulez saisir
une mémoire de graphe.
Vous pouvez aussi utiliser les fonctions 1(SEL), 2(DEL) et 3(TYPE) quand l’écran de
formules graphiques est affiché.
Appuyez sur 6(DRAW) pour tracer un graphe.
k Fonction RECALL ANS
Le contenu de la mémoire Ans se rappelle par une pression sur 6(g)3(R
•
ANS).
k Mémoire de solutions
Dans le mode CAS, vous pouvez sauvegarder l’historique d’un calcul (contenu de la
mémoire d’expressions) dans la mémoire de solutions. Cette partie du manuel décrit
comment accéder et travailler avec le contenu de la mémoire de solutions. L’écran initial de
la mémoire de solutions suivant s’affiche par une pression de 6(g)4(MEM) sur le menu
principal du mode CAS.
7-1-8
Utilisation du mode CAS (Système d’algèbre informatique)
•{SAVE
}... {sauvegarde de l’historique d’un calcul dans la mémoire de solution}
•{DEL
•
A
}... {vidage de la mémoire de solutions}
•{OPT
} ... {optimisation de la mémoire de solutions}
•{DISP
} ... {affichage du contenu de la mémoire de solutions}

20001202
u Pour sauvegarder l’historique d’un calcul dans la mémoire de solutions
(Sauvegarde)
Sur l’écran de mémoire de solutions initial, appuyez sur 1(SAVE).
Appuyez sur 1(YES) pour sauvegarder l’historique du calcul dans la mémoire de solutions.
L’écran de mémoire de solutions initial se rétablit par une pression de i.
• L’écran de mémoire de solutions initial se rétablit sans que la solution soit sauvegardée, par
une pression de 6(NO) au lieu de 1(YES).
u Pour vider la mémoire de solutions (Effacer mémoire)
Sur l’écran de mémoire de solutions initial, appuyez sur 2(DEL
•
A).
Appuyez sur 1(YES) pour vider la mémoire de solutions.
L’écran de mémoire de solutions initial se rétablit par une pression de i.
• L’écran de mémoire de solutions initial se rétablit sans que la solution soit sauvegardée, par
une pression de 6(NO) au lieu de 1(YES).
7-1-9
Utilisation du mode CAS (Système d’algèbre informatique)
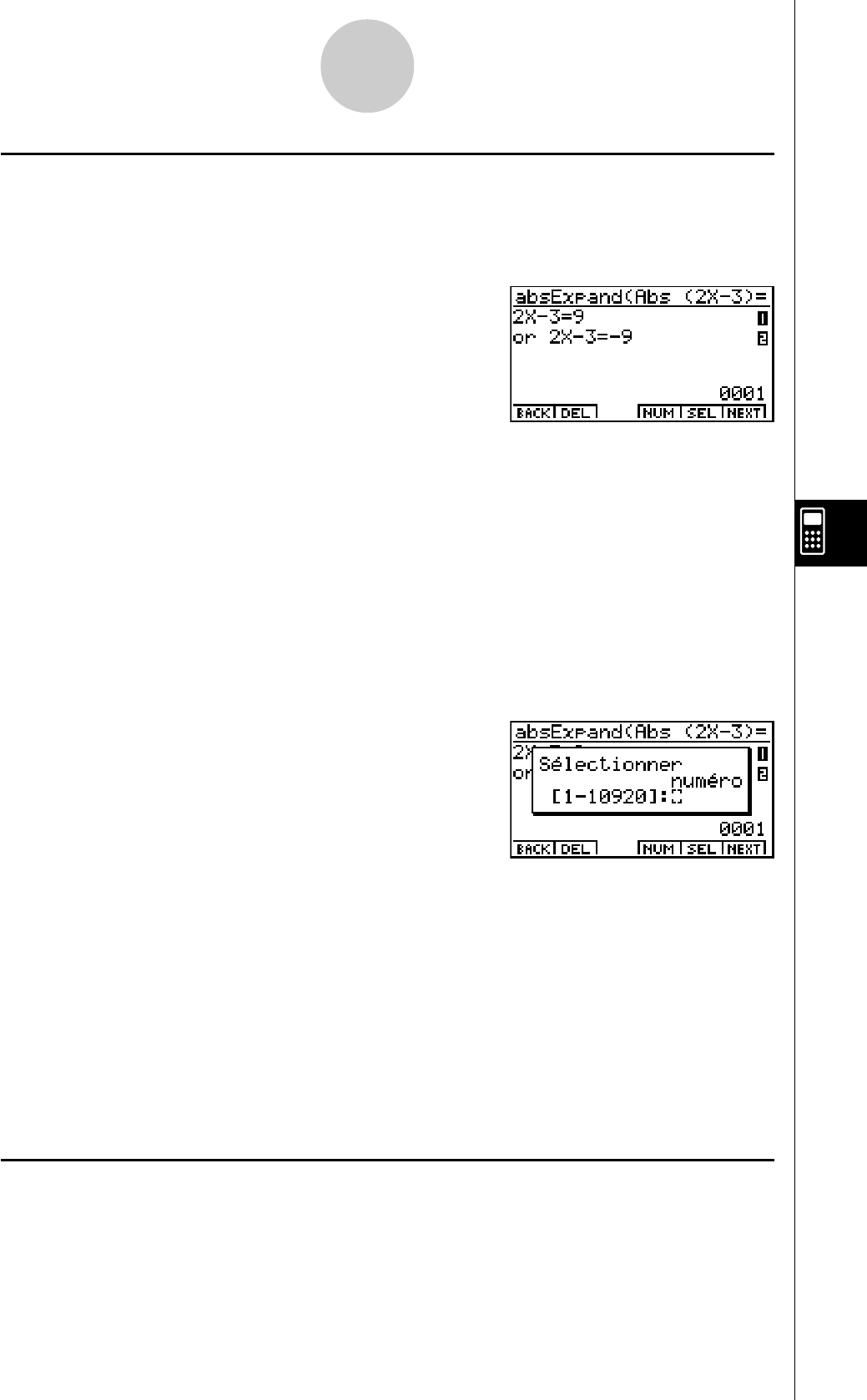
20001202
•6(DISP) est désactivé si la mémoire ne contient plus aucune solution.
• Pour afficher la solution suivante
Appuyez sur 6(NEXT).
• Pour afficher la solution précédente
Appuyez sur 1(BACK).
• Lorsque la solution la plus ancienne est affichée, l’écran de mémoire de solutions initial se
rétablit par une pression de 1(BACK).
• Pour afficher une solution particulière
Appuyez sur 5(SEL) et désignez le numéro de la solution que vous voulez afficher.
La solution dont vous avez indiqué le numéro s’affiche ensuite par une pression de w.
• Pour supprimer une seule solution de la mémoire
Affichez la solution que vous voulez supprimer, puis appuyez sur 2(DEL).
En réponse au message de confirmation qui apparaît, appuyez sur w(Oui) pour supprimer
la solution affichée.
Pour dégager cet écran sans rien supprimer, appuyez sur i(Non).
• Pour activer ou désactiver le numéro de solution
Appuyez sur 4(NUM).
uPour optimiser la mémoire de solutions (Optimisation)
Sur l’écran de mémoire de solutions initial, appuyez sur 3(OPT).
L’écran de mémoire de solutions initial se rétablit par une pression de i.
Lorsque vous optimisez la mémoire de solutions, les données sont réarrangées pour libérer
de l’espace. Effectuez cette procédure lorsque la capacité de la mémoire est réduite.
7-1-10
Utilisation du mode CAS (Système d’algèbre informatique)
u Pour afficher le contenu de la mémoire de solutions (Afficher mémoire)
Sur l’écran de mémoire de solutions initial, appuyez sur 6(DISP).
L’expression et le résultat les plus anciens s’affichent. La ligne inférieure indique le nombre
de solutions enregistrées.

20001202
7-1-11
Utilisation du mode CAS (Système d’algèbre informatique)
Liste des commandes algébriques
Les abréviations utilisées dans cette section sont les suivantes.
•Exp ... Expression (valeur, formule, variable, etc.)
•Eq ... Equation
•Ineq ... Inéquation
•List ... Liste
•Mat ... Matrice
•Vect ... Vecteur
Tout ce qui se trouve entre crochets carrés peut être omis.
u expand
Fonction: Développe une expression.
Syntaxe: expand (
{Exp/Eq/Ineq/List/Mat/Vect} [ ) ]
Exemple Développer (X+2)2
1(TRNS)b(expand)(v+c)xw X2 + 4X + 4
expand( (X + 2)(X – 3 2) ) X2 – 2 2 X – 6
u rFactor (rFctor)
Fonction: Factorise une expression jusqu’à sa racine.
Syntaxe: rFactor (
{Exp/Eq/Ineq/List/Mat/Vect} [ ) ]
Exemple Factoriser X2– 3
1(TRNS)c(rFctor)vx-dw(X – 3) (X + 3)
rFactor( 2X2 – 1 ) ( 2 X – 1) ( 2 X + 1)
rFactor( X2 + 2 ) (X – 2 i) (X + 2 i)
... Answer Type: Complex
u factor
Fonction: Factorise une expression.
Syntaxe: factor (
{Exp/Eq/Ineq/List/Mat/Vect} [ ) ]
Exemple Factoriser X2– 4X + 4
1(TRNS)d(factor)vx-ev+ew (X – 2)2
factor( 8/9 ) 23/32
factor( X2 + 1 ) (X – i) (X + i)
... Answer Type: Complex

20001202
usolve
Fonction: Résout une équation.
Syntaxe: solve( Exp [,variable] [ ) ]
solve( {Exp-1,..., Exp-n}, {variable-1,...,variable-n} [ ) ]
Exemple Résoudre AX + B = 0 pour X
1(TRNS)e(solve)av(A)v+
al(B)!.(=)aw
Exemple Résoudre l’équation linéaire simultanée 3X + 4Y = 5, 2X – 3Y = – 8
1(TRNS)e(solve)!*( { )
da+(X)+ea-(Y)!.(=)f,
ca+(X)-da-(Y)!.(=)-i
!/( } ),!*( { )a+(X),X = – 1
a-(Y)!/( } )wY = 2
• X est la variable par défaut lorsqu’aucune variable n’est spécifiée.
utExpand (tExpnd)
Fonction: Emploie le théorème de l’addition pour développer une fonction trigonométrique.
Syntaxe: tExpand( {Exp/List/Mat/Vect} [ ) ]
Exemple Employer le théorème de l’addition pour développer sin(A+B)
1(TRNS)f(TRIG)b(tExpnd)
s(av(A)+al(B)wcos(B) • sin(A) + sin(B) • cos(A)
utCollect (tCollc)
Fonction: Emploie le théorème de l’addition pour transformer le produit d’une fonction
trigonométrique en une somme.
Syntaxe: tCollect( {Exp/List/Mat/Vect} [ ) ]
Exemple Employer le théorème de l’addition pour transformer sin(A)cos(B) en
somme trigonométrique
1(TRNS)f(TRIG)c(tCollc)
sav(A)cal(B)w
7-1-12
Utilisation du mode CAS (Système d’algèbre informatique)
sin (A + B)
2
sin (A – B)
2
+
– B
A
X =

20001202
7-1-13
Utilisation du mode CAS (Système d’algèbre informatique)
u trigToExp (trigToE)
Fonction: Transforme une fonction trigonométrique ou hyperbolique en une fonction
exponentielle.
Syntaxe: trigToExp( {Exp/List/Mat/Vect} [ ) ]
Exemple Convertir cos(iX) en fonction exponentielle
1(TRNS)f(TRIG)d(trigToE)c!a(i)vw
trigToExp( sinh X ) (eX – e–X) / 2
uexpToTrig (expToT)
Fonction: Convertit une fonction exponentielle en une fonction trigonométrique ou
hyperbolique.
Syntaxe: expToTrig( {Exp/List/Mat/Vect} [ ) ]
Exemple Convertir eix en une fonction trigonométrique
1(TRNS)f(TRIG)e(expToT)
!I(ex)(!a(i)vw cos(X) + sin(X) • i
u simplify (smplfy)
Fonction: Simplifie une expression.
Syntaxe: simplify( {Exp/Eq/Ineq/List/Mat/Vect} [ ) ]
Exemple Simplifier 2X + 3Y – X + 3 = Y + X – 3Y + 3 – X
1(TRNS)g(smplfy)ca+(X)+da-(Y)
-a+(X)+d!.(=)a-(Y)
+a+(X)-da-(Y)+d-
a+(X)wX + 3Y + 3 = –2Y + 3
simplify( ln 5 + ln 3 ) ln (15)
simplify( (sin X)2 + (cos X)2 )1
simplify( sin X/cos X ) tan(X)
ex+ e
—
x
2

20001202
u combine (combin)
Fonction: Réduit une fraction.
Syntaxe: combine( {Exp/Eq/Ineq/List/Mat/Vect} [ ) ]
Exemple Réduire la fraction (X + 1)
/
(X + 2) + X (X + 3)
1(TRNS)h(combin)(v+b)/
(v+c)+v(v+dw
combine( 1/2 + 1/3 ) 5/6
combine( 1/(X + 1) + 2/(X + 2) ) (3X+4)/((X+1)(X+2))
ucollect (collct)
Fonction: Réarrange une expression autour d’une variable particulière.
Syntaxe: collect( {Exp/Eq/Ineq/List/Mat/Vect} [,{Exp/variable}] [ ) ]
Exemple Réarranger X2 + AX + BX, autour de la variable X
1(TRNS)i(collct)vx+av(A)v+
al(B)vw X2 + (A + B)X
collect( X2 + 6X – 7 , X + 3 ) (X+3)2 – 16
collect( X2 + 6X – 7 , X + 5 ) (X + 1)(X + 5) – 12
• X est la valeur par défaut lorsque rien n’est spécifié pour [,Exp-1/, variable].
u substitute (sbstit)
Fonction: Affecte une expression à une variable.
Syntaxe: substitute( {Exp/Eq/Ineq/List/Mat/Vect}, variable=expression
[,..., variable=expression] [ ) ]
Exemple Affecter 5 à X dans 2X – 1
1(TRNS)j(sbstit)cv-b,
v!.(=)fw9
substitute( 2A + 1 , A = X – 3 ) 2X – 5
substitute( 2A + 3B , A = 5 , B = 7 ) 31
7-1-14
Utilisation du mode CAS (Système d’algèbre informatique)
X3 + 5X2 + 7X + 1
X + 2

20001202
ucExpand (cExpnd)
Fonction: Développe la racine Xe du nombre imaginaire.
Syntaxe: cExpand( {Exp/Eq/Ineq/List/Mat/Vect} [ ) ]
Exemple Développer 2i
1(TRNS)v(cExpnd)!x( )c!a(i)w1 + i
uapprox
Fonction: Produit une approximation numérique pour une expression
Syntaxe: approx( {Exp/Eq/Ineq/List/Mat/Vect} [ ) ]
Exemple Obtenir une valeur numérique pour 2
1(TRNS)l(approx)!x( )cw1.414213562
Exemple 920
Normal:jMcaw12157665459056928801
approx: 1(TRNS)l(approx)jMcaw1. 215766546E+19 (Affichage: Norm1)
7-1-15
Utilisation du mode CAS (Système d’algèbre informatique)
#A propos d’approx
Avec les calculs ordinaires, (lorsque approx
n’est pas utilisé) dans le mode CAS, les
résultats des calculs sont entièrement
affichés, sans exposants. Par contre, lorsque
vous utilisez approx dans le mode CAS, les
résultats sont affichés en fonction de la plage
exponentielle définie dans le paramètre Display de
l’écran de configuration.
C’est-à-dire que dans le mode CAS, approx affiche
les résultats tels qu’ils sont affichés dans le mode
RUN •MAT.

20001202
u diff
Fonction: Différentie un expression.
Syntaxe:diff( {Exp/List} [, variable, ordre, dérivée ] [ ) ]
diff( {Exp/List}, variable [, ordre, dérivée ] [ ) ]
diff( {Exp/List}, variable, ordre [, dérivée ] [ ) ]
Exemple Différentier X6 par rapport à X
2(CALC)b(diff)vMgw6X5
diff( 2X2 + 3X , X , 1 , 10 ) 43
diff( X^4 + X^3 + X^2 , X , 2 ) 12X2 + 6X + 2
• X est la variable par défaut quand aucune autre variable n’est définie.
• 1 est la variable par défaut quand aucun ordre n’est défini.
u∫
Fonction: Intègre une expression.
Syntaxe:∫( {Exp/List} [, variable, constante d’intégration ] [ ) ]
∫( {Exp/List}, variable [, constante d’intégration ] [ ) ]
∫( {Exp/List}, variable, limite inférieure, limite supérieure [ ) ]
Exemple Intégrer X2 par rapport à X
2(CALC)c( ∫ )vxw
∫ ( eX sin X , X ) (– eX cos(X))/2 + (eX sin(X))/2
∫ ( X2 + X , X , C ) X3/3 + X2/2 + C
∫ ( X2 – 4 , X , – 2 , 2 ) –32/3
• X est la variable par défaut quand aucune autre variable n’est définie.
u lim
Fonction: Détermine les limites de l’expression d’une fonction.
Syntaxe: lim( {Exp/List}, variable, point [, direction ] [ ) ]
Exemple Déterminer les limites de sin(X)/X lorsque X = 0
2(CALC)d(lim)sv/v,v,aw1
• La direction peut être positive (de droite) ou négative (de gauche).
7-1-16
Utilisation du mode CAS (Système d’algèbre informatique)
X3
3

20001202
uΣ
Fonction: Calcule une somme.
Syntaxe: Σ( {Exp/List}, variable, valeur initiale, valeur finale [ ) ]
Exemple Calculer la somme lorsque la valeur de X dans X2 change de X = 1 à
X = 10
2(CALC)e(Σ)vx,v,b,baw385
uΠ
Fonction: Calcule un produit.
Syntaxe: Π( {Exp/List}, variable, valeur initiale, valeur finale [ ) ]
Exemple Calculer le produit lorsque la valeur de X dans X2 change de X = 1 à
X = 5
2(CALC)f(Π)vx,v,b,fw14400
u taylor
Fonction: Trouve un polynôme de Taylor.
Syntaxe: taylor( {Exp/List}, variable, ordre [, point central ] [ ) ]
Exemple Trouver un polynome de Taylor de 5e ordre pour sin(X) par rapport à
X = 0
2(CALC)g(taylor)sv,v,f,aw
• Le point central par défaut est zéro.
u arcLen
Fonction: Renvoie la longueur de l’arc.
Syntaxe: arcLen( {Exp/List}, variable, valeur initiale, valeur finale [ ) ]
Exemple Déterminer la longueur de l’arc pour X2 de X = 0 à X = 1
2(CALC)h(arcLen)
vx,v,a,bw
7-1-17
Utilisation du mode CAS (Système d’algèbre informatique)
X5–X3+ X
120 6
In (4
5 + 8)–In(2) + 5
422

20001202
u tanLine (tanLin)
Fonction: renvoie l’expression pour une tangente.
Syntaxe: tanLine( {Exp/List}, variable, valeur de la variable au point de tangence [ ) ]
Exemple Déterminer l’expression pour la tangente à X3 lorsque X = 2
2(CALC)i(tanLin)vMd,v,cw12X – 16
u denominator (den)
Fonction: Extraie le dénominateur d’une fraction.
Syntaxe: denominator( {Exp/List} [ ) ]
Exemple Extraire le dénominateur de la fraction (X + 2)/(Y – 1)
2(CALC)j(EXTRCT)b(den)
(a+(X)+c)/(a-(Y)-bwY – 1
u numerator (num)
Fonction: Extraie le numérateur d’une fraction.
Syntaxe: numerator( {Exp/List} [ ) ]
Exemple Extraire le numérateur de la fraction (X + 2)/(Y – 1)
2(CALC)j(EXTRCT)c(num)
(a+(X)+c)/(a-(Y)-bwX + 2
u gcd
Fonction: Renvoie le plus grand dénominateur commun.
Syntaxe: gcd( {Exp/List}, {Exp/List} [ ) ]
Exemple Déterminer le plus grand dénominateur commun de X + 1 et
X2 – 3X – 4
2(CALC)v(gcd)v+b,vx-
dv-ewX + 1
gcd( 144 , 80 ) 16
7-1-18
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
u lcm
Fonction: Calcule le plus petit commun multiple de deux expressions.
Syntaxe: lcm( {Exp/List}, {Exp/List} [ ) ]
Exemple Obtenir le plus petit commun multiple de X2 – 1 et X2 + 2X – 3
2(CALC)l(lcm)vx-b,
vx+cv-dwX3 + 3X2 – X – 3
u rclEqn
Fonction: Rappelle le contenu de plusieurs mémoires d’équations
Syntaxe: rclEqn( numéro de mémoire [, ..., numéro de mémoire] [ ) ]
Exemple Rappeler le contenu des mémoires d’équation 2 et 3
3(EQUA)c(rclEqn)c,dw3X – Y = 7
3X + 6Y = 63
• Les numéros de mémoire des équations résultant d’un rappel ne sont pas mis à jour.
u rclAllEqn (rclAll)
Fonction: Rappelle le contenu de toutes les mémoires.
Syntaxe: rclAllEqn
• Les numéros de mémoire des équations résultant d’un rappel ne sont pas mis à jour.
u rewrite (rewrit)
Fonction: Déplace l’élément de droite vers la gauche.
Syntaxe: rewrite( {Eq/Ineq/List} [ ) ]
Exemple Déplacer l’élément de droite de X + 3 = 5X – X2 vers la gauche
3(EQUA)e(rewrit)v+d!.(=)
fv-vxw X2 – 4X + 3 = 0
7-1-19
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
u exchange (exchng)
Fonction: Echange les éléments des côtés droit et gauche.
Syntaxe: exchange( {Eq/Ineq/List} [ ) ]
Exemple Echanger les éléments gauche et droit de 3 > 5X – 2Y
3(EQUA)f(exchng)d3(EQUA)b(INEQUA)b(>)
fa+(X)-ca-(Y)w5X – 2Y < 3
u eliminate (elim)
Fonction: Affecte une expression à une variable.
Syntaxe: eliminate( {Eq/Ineq/List} -1, variable, Eq-2 [ ) ]
Exemple Dans 2X + 3Y = 5 remplacer X par sa valeur donnée par Y = 2X + 3
3(EQUA)g(elim)ca+(X)+da-(Y)!.(=)
f,a+(X),a-(Y)!.(=)
ca+(X)+dw4Y – 3 = 5
u getRight (getRgt)
Fonction: Obtient l’élément du côté droit.
Syntaxe: getRight( {Eq/Ineq/List} [ ) ]
Exemple Extraire l’élément du côté droit de Y = 2X2 + 3X + 5
3(EQUA)h(getRgt)a-(Y)!.(=)
ca+(X)x+da+(X)+fw2X2 + 3X + 5
u invert
Fonction: Inverse deux variables.
Syntaxe: invert( {Exp/Eq/Ineq/List} [,nom de la variable 1, nom de la variable 2 ] [ ) ]
Si vous omettez les noms de variables, les variables X et Y seront inversées.
Exemple Inverser X et Y dans l’expression 2X = Y
3(EQUA)i(invert)cv!.(=)a-(Y)w2Y = X
7-1-20
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
u absExpand (absExp)
Fonction: Divise une expression contenant une valeur absolue en deux expressions.
Syntaxe: absExpand( {Eq/Ineq} [ ) ]
Exemple Décomposer la valeur absolue de | 2X – 3 | = 9
3(EQUA)j(absExp)K5(Abs)(
cv-d)!.(=)jw
u andConnect (andCon)
Fonction: Combine deux inégalités en une seule expression.
Syntaxe: andConnect( Ineq-1, Ineq-2 [ ) ]
Exemple Combiner X > – 1 et X < 3 en une seule inégalité.
3(EQUA)v(andCon)v3(EQUA)b(INEQUA)b(>)
-b,v3(EQUA)b(INEQUA)c(<)dw–1 < X < 3
u eqn
Fonction: Rappelle le contenu de la mémoire d’équations.
Syntaxe: eqn( numéro de mémoire [ ) ]
Exemple Ajouter 15 aux deux côtés de l’équation 6X – 15 = X – 7, qui est
stockée dans la mémoire d’équations 3
4(eqn)d)+bfw6X = X + 8
7-1-21
Utilisation du mode CAS (Système d’algèbre informatique)
2X – 3 = 9
or 2X – 3 = – 9 2
1

20001202
uclear (clrVar)
Fonction: Supprime le contenu d’une équation particulière (A à Z, r,
θ
).*1
Syntaxe: clear( variable [ ) ]
clear( {liste de variables} [ ) ]
Exemple Supprimer le contenu de la variable A
6(g)1(CLR)b(clrVar)av(A)w{ }
Exemple Supprimer le contenu des variables X, Y et Z
6(g)1(CLR)b(clrVar)!*( { )a+(X),
a-(Y),aa(Z)!/( } )w{ }
uclearVarAll (VarAll)
Fonction: Supprime le contenu des 28 variables (A à Z, r,
θ
).
Syntaxe: clearVarAll { }
*1Lorsque vous commencez par les mémoires
A, B, C et D, par exemple, et supprimez les
mémoires A et B, seulement C, D seront
affichés parce que ce sont les seules
mémoires restantes.
7-1-22
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
kCommandes de calculs avec listes [OPTN]-[LIST]
uDim
Fonction: Donne la dimension d’une liste.
Syntaxe: Dim List
Exemple Déterminer la dimension de la liste {1, 2, 3}.
K1(LIST)b(CALC)b(Dim)!*( { )b,c,d
!/( } )w3
uMin
Fonction: Donne la valeur minimale d’une expression ou les éléments d’une liste.
Syntaxe: Min( {List/Exp} [ ) ]
Min( {List/Exp}, {List/Exp} [ ) ]
Exemple Déterminer la valeur minimale des éléments de la liste {1, 2, 3}.
K1(LIST)b(CALC)c(Min)!*( { )b,c,d
!/( } )w1
Exemple Comparer chaque élément de la liste {1, 2, 3} avec la valeur 2 et
produire une liste dont les éléments sont la valeur minimale résultant
de chaque comparaison.
K1(LIST)b(CALC)c(Min)!*( { )b,c,d
!/( } ),cw{
1, 2, 2
}
Exemple Comparer les éléments d’une liste {1, 2, 3} et de la liste {3, 1, 2} et
produire une liste dont les éléments sont la valeur minimale résultant
de chaque comparaison.
K1(LIST)b(CALC)c(Min)!*( { )b,c,d
!/( } ),!*( { )d,b,c!/( } )w{1, 1, 2
}
7-1-23
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
7-1-24
Utilisation du mode CAS (Système d’algèbre informatique)
uMax
Fonction: Donne la valeur maximale d’une expression ou les éléments d’une liste.
Syntaxe: Max( {List/Exp} [ ) ]
Max( {List|Exp}, {List/Exp} [ ) ]
Exemple Déterminer la valeur maximale des éléments de la liste {1, 2, 3}.
K1(LIST)b(CALC)d(Max)!*( { )b,c,d
!/( } )w3
Exemple Comparer chaque élément de la liste {1, 2, 3} avec la valeur 2 et
produire une liste dont les éléments sont la valeur maximale résultant
de chaque comparaison.
K1(LIST)b(CALC)d(Max)!*( { )b,c,d
!/( } ),cw{
2, 2, 3
}
Exemple Comparer les éléments de la liste {1, 2, 3} et de la liste {3, 1, 2} et
produire une liste dont les éléments sont la valeur maximale résultant
de chaque comparaison.
K1(LIST)b(CALC)d(Max)!*( { )b,c,d
!/( } ),!*( { )d,b,c!/( } )w{
3, 2, 3
}
u Mean
Fonction: Donne la moyenne des éléments d’une liste.
Syntaxe: Mean( List [ ) ]
Mean( List, List [ ) ]
La liste doit contenir des valeurs ou des expressions mathématiques seulement. Les
équations et les inégalités ne sont pas autorisées.
Exemple Déterminer la moyenne des éléments de la liste {1, 2, 3}.
K1(LIST)b(CALC)e(Mean)!*( { )b,c,d
!/( } )w2

20001202
Exemple Déterminer la moyenne des éléments de la liste {1, 2, 3} lorsque leurs
fréquences sont {3, 2, 1}.
K1(LIST)b(CALC)e(Mean)!*( { )b,c,d
!/( } ),!*( { )d,c,b!/( } )w
uMedian
Fonction: Donne la médiane des éléments d’une liste.
Syntaxe: Median( List [ ) ]
Median( List, List [ ) ]
La liste doit contenir des valeurs ou des expressions mathématiques seulement. Les
équations et les inégalités ne sont pas autorisées.
Exemple Déterminer la médiane des éléments de la liste {1, 2, 3}.
K1(LIST)b(CALC)f(Median)!*( { )b,c,d
!/( } )w2
Exemple Déterminer la médiane des éléments de la liste {1, 2, 3} lorsque leurs
fréquences sont {3, 2, 1}.
K1(LIST)b(CALC)f(Median)!*( { )b,c,d
!/( } ),!*( { )d,c,b!/( } )w
u Sum
Fonction: Donne la somme des éléments d’une liste.
Syntaxe: Sum List
La liste doit contenir des valeurs ou des expressions mathématiques seulement. Les
équations et les inégalités ne sont pas autorisées.
Exemple Déterminer la somme des éléments de la liste {1, 2, 3}.
K1(LIST)b(CALC)g(Sum)!*( { )b,c,d
!/( } )w6
7-1-25
Utilisation du mode CAS (Système d’algèbre informatique)
5
3
3
2
20001202
u Prod
Fonction: Donne le produit des éléments d’une liste.
Syntaxe: Prod List
La liste doit contenir des valeurs ou des expressions mathématiques seulement. Les
équations et les inégalités ne sont pas autorisées.
Exemple Déterminer le produit des éléments de la liste {2, 3, 4}.
K1(LIST)b(CALC)h(Prod)!*( { )c,d,e
!/( } )w24
uCuml
Fonction: Donne la fréquence cumulée des éléments d’une liste.
Syntaxe: Cuml List
La liste doit contenir des valeurs ou des expressions mathématiques seulement. Les
équations et les inégalités ne sont pas autorisées.
Exemple Déterminer la fréquence cumulée des éléments de la liste {1, 2, 3}.
K1(LIST)b(CALC)i(Cuml)!*( { )b,c,d
!/( } )w{
1, 3, 6
}
u Percent (%)
Fonction: Donne le pourcentage de chaque élément d’une liste dont la somme est
supposée être 100.
Syntaxe: Percent List
La liste doit contenir des valeurs ou des expressions mathématiques seulement. Les
équations et les inégalités ne sont pas autorisées.
Exemple Déterminer le pourcentage de chaque élément de la liste {1, 2, 3}.
K1(LIST)b(CALC)j(%)!*( { )b,c,d
!/( } )w
7-1-26
Utilisation du mode CAS (Système d’algèbre informatique)
3
50
3
100 50
,,
{
{

20001202
uA List
Fonction: Donne la liste dont les éléments sont la différence entre les éléments d’une
autre liste.
Syntaxe: AA
AA
A List List
La liste doit contenir des valeurs ou des expressions mathématiques seulement. Les
équations et les inégalités ne sont pas autorisées.
Exemple Générer la liste dont les éléments sont les différences entre les
éléments de la liste {1, 2, 4}.
K1(LIST)b(CALC)v(AList)!*( { )b,c,e
!/( } )w{
1, 2
}
uStdDev
Fonction: Donne l’écart-type des éléments d’une liste.
Syntaxe: StdDev List
La liste doit contenir des valeurs ou des expressions mathématiques seulement. Les
équations et les inégalités ne sont pas autorisées.
Exemple Déterminer l’écart-type des éléments de la liste {1, 2, 4}.
K1(LIST)b(CALC)l(StdDev)!*( { )b,c,e
!/( } )w
u Variance (Vari)
Fonction: Donne la variance des éléments d’une liste.
Syntaxe: Variance List
La liste doit contenir des valeurs ou des expressions mathématiques seulement. Les
équations et les inégalités ne sont pas autorisées.
Exemple Déterminer la variance des éléments de la liste {1, 2, 4}.
K1(LIST)b(CALC)I(Vari)!*( { )b,c,e
!/( } )w
7-1-27
Utilisation du mode CAS (Système d’algèbre informatique)
7
3
3
21

20001202
uSeq
Fonction: Génère une liste à partir d’une expression contenant une suite numérique.
Syntaxe: Seq( Exp, variable, valeur initiale, valeur finale, [incrément] [ ) ].
Si vous ne spécifiez pas d’incrément, l’incrément 1 sera utilisé.
Exemple Générer une liste en fonction de l’expression : valeur A, valeur finale
3A, incrément A.
K1(LIST)c(CREATE)b(Seq)v,v,av(A),d
av(A),av(A)w{
A, 2A, 3A
}
u Augment (Augmnt)
Fonction: Combine deux listes.
Syntaxe: Augment( List, List [ ) ]
Exemple Combiner la liste {1, 2} et la liste {3, 4}.
K1(LIST)c(CREATE)c(Augmnt)!*( { )b,c
!/( } ),!*( { )d,e!/( } )w{
1, 2, 3, 4
}
uFill
Fonction: Remplace les éléments d’une liste par la valeur ou l’expression spécifiée.
Cette commande peut aussi être utilisée pour créer une nouvelle liste dont les
éléments contiennent tous la même valeur ou expression.
Syntaxe: Fill( {Exp/Eq/Ineq}, List [ ) ]
Fill( Exp, valeur numérique [ ) ]
Exemple Remplacer les éléments de la liste {3, 4} par X.
K1(LIST)c(CREATE)d(Fill)v,!*( { )
d,e!/( } )w{
X, X
}
Exemple Créer une liste à partir de huit éléments, chacun d’eux étant X.
K1(LIST)c(CREATE)d(Fill)v,iw{
X, X, X, X, X, X, X, X
}
7-1-28
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
uSortA
Fonction: Trie les éléments d’une liste dans l’ordre ascendant.
Syntaxe: SortA( List [ ) ]
La liste doit contenir des valeurs ou des expressions mathématiques seulement. Les
équations et les inégalités ne sont pas autorisées.
Exemple Trier les éléments de la liste {1, 5, 3} dans l’ordre ascendant.
K1(LIST)c(CREATE)e(SortA)!*( { )b,f,d
!/( } )w{
1, 3, 5
}
u SortD
Fonction: Trie les éléments d’une liste dans l’ordre descendant.
Syntaxe: SortD( List [ ) ]
La liste doit contenir des valeurs ou des expressions mathématiques seulement. Les
équations et les inégalités ne sont pas autorisées.
Exemple Trier les éléments de la liste {1, 5, 3} dans l’ordre descendant.
K1(LIST)c(CREATE)f(SortD)!*( { )b,f,d
!/( } )w{
5, 3, 1
}
u SubList (SubLst)
Fonction: Extraie une partie particulière d’une liste pour la mettre dans une nouvelle liste.
Syntaxe: SubList( List, premier nombre [, dernier nombre] [ ) ]
Exemple Extraire les éléments 2 à 3 de la liste {1, 2, 3, 4}.
K1(LIST)c(CREATE)g(SubLst)!*( { )b,c,d
,e!/( } ),c,dw{
2, 3
}
• Si vous ne désignez pas un dernier nombre, tous les éléments seront extraits, du premier
nombre au dernier.
7-1-29
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
u List→Mat (L→Mat)
Fonction: Convertit les listes en matrice.
Syntaxe: List→Mat( List [, ... ,List ] [ ) ]
Exemple Convertir la liste {3, 5} et la liste {2, 4} en une matrice.
K1(LIST)d(LIST→)b(L→Mat)!*( { )d,f 32
!/( } ),!*( { )c,e!/( } )w54
u List→Vect (L→Vect)
Fonction: Convertit une liste en vecteur.
Syntaxe: List→Vect List
Exemple Convertir la liste {3, 2} en vecteur.
K1(LIST)d(LIST→)c(L→Vect)!*( { )d,c
!/( } )w[
3, 2
]
7-1-30
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
kCommandes de calculs matriciels [OPTN]-[MAT]
uDim
Fonction: Donne la dimension d’une matrice.
Syntaxe: Dim Mat
Exemple Déterminer la dimension de la matrice suivante.
123
456
K2(MAT)b(CALC)b(Dim)!+( [ )!+( [ )
b,c,d!-( ] )!+( [ )e,f,g
!-( ] )!-( ] )w{
2, 3
}
u Det
Fonction: Donne le déterminant d’une matrice.
Syntaxe: Det Mat
Exemple Déterminer le déterminant de la matrice suivante.
12
45
K2(MAT)b(CALC)c(Det)!+( [ )!+( [ )
b,c!-( ] )!+( [ )e,f
!-( ] )!-( ] )w– 3
u Norm
Fonction: Donne la norme d’une matrice.
Syntaxe: Norm Mat
Exemple Déterminer la norme de la matrice suivante.
12
45
K2(MAT)b(CALC)d(Norm)!+( [ )!+( [ )
b,c!-( ] )!+( [ )e,f
!-( ] )!-( ] )w 46
7-1-31
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
u EigVc
Fonction: Donne le vecteur propre d’une matrice.
Syntaxe: EigVc Mat
Exemple Déterminer le vecteur propre de la matrice suivante.
34
13
K2(MAT)b(CALC)e(EigVc)
!+( [ )!+( [ )d,e
!-( ] )!+( [ ) [
0.894427191 – 0.894427191
]
b,d!-( ] )!-( ] )w[
0.4472135955 0.4472135955
]
Les vecteurs propres sont empilés verticalement sur l’écran.
Dans cet exemple, (0,894427191 0,4472135955) sont les vecteurs propres correspondant
à 5, tandis que (–0,894427191 0,4472135955) sont les vecteurs propres correspondant à
1.
Un vecteur propre a un nombre infini de solutions. Le vecteur propre indiqué par cette
commande est un vecteur de taille 1.
u EigVl
Fonction: Donne la valeur propre d’une matrice.
Syntaxe: EigVl Mat
Exemple Déterminer la valeur propre de la matrice suivante.
34
13
K2(MAT)b(CALC)f(EigVl)!+( [ )!+( [ )
d,e!-( ] )!+( [ )b,d
!-( ] )!-( ] )w{
5, 1
}
7-1-32
Utilisation du mode CAS (Système d’algèbre informatique)
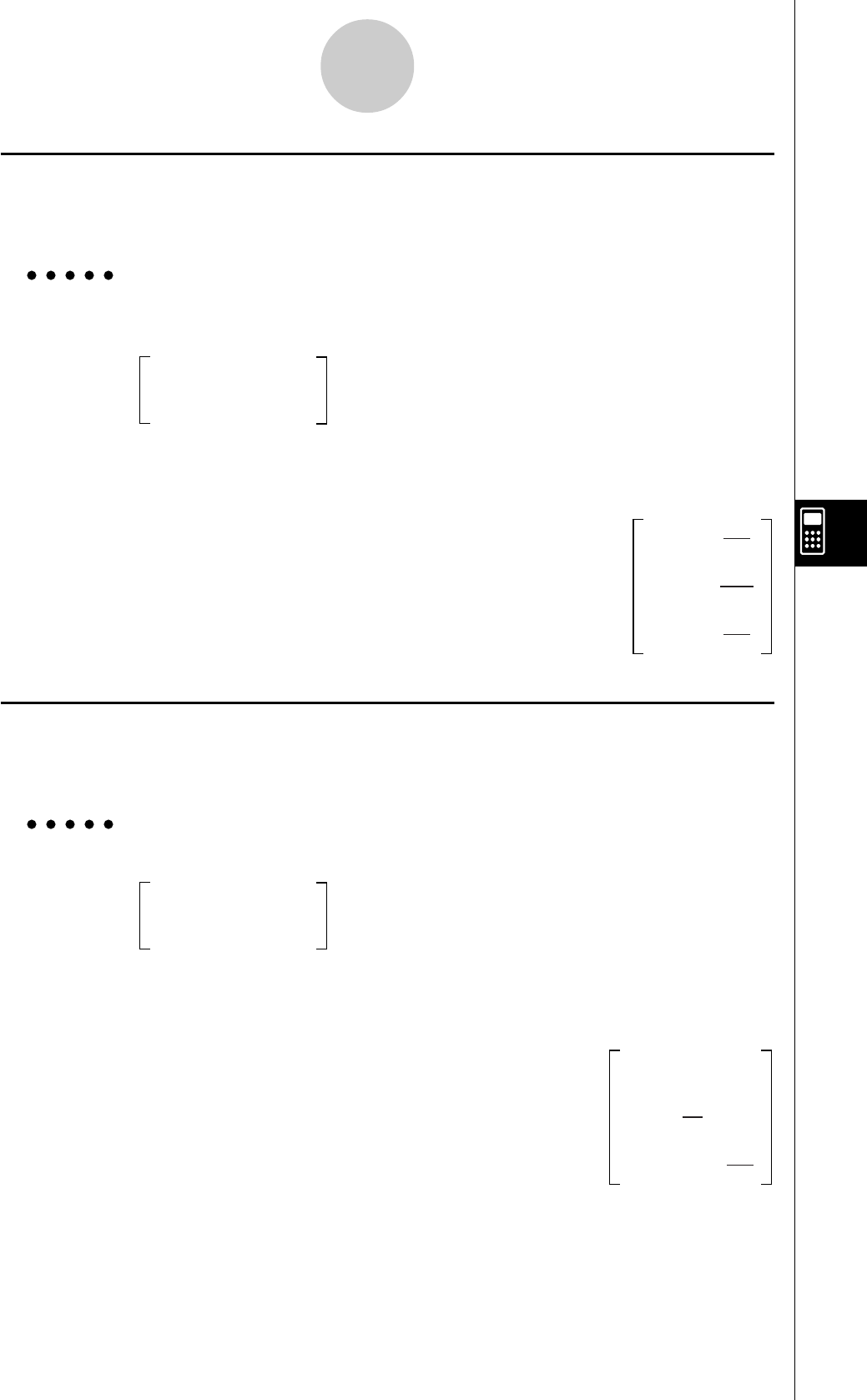
20001202
u Rref
Fonction: Donne la forme échelonnée réduite des lignes d’une matrice.
Syntaxe: Rref Mat
Exemple Déterminer la forme échelonnée réduite des lignes de la matrice
suivante.
–
2–
20–
6
1–
19–
9
–
5 24–
4
K2(MAT)b(CALC)g(Rref)!+( [ )!+( [ )
-c,-c,a,-g!-( ] )!+( [ )
b,-b,j,-j!-( ] )
!+( [ )-f,c,e,-e
!-( ] )!-( ] )w
u Ref
Fonction: Donne la forme échelonnée des lignes d’une matrice.
Syntaxe: Ref Mat
Exemple Déterminer la forme échelonnée des lignes de la matrice suivante.
–
2–
20–
6
1–
19–
9
–
5 24–
4
K2(MAT)b(CALC)h(Ref)!+( [ )!+( [ )
-c,-c,a,-g!-( ] )!+( [ )
b,-b,j,-j!-( ] )
!+( [ )-f,c,e,-e
!-( ] )!-( ] )w
7-1-33
Utilisation du mode CAS (Système d’algèbre informatique)
71
66
71
147
71
62
–
1 0 0
0 1 0
0 0 1
71
62
–
1 1 0
0 1
3
6
0 0 1
2
9
–
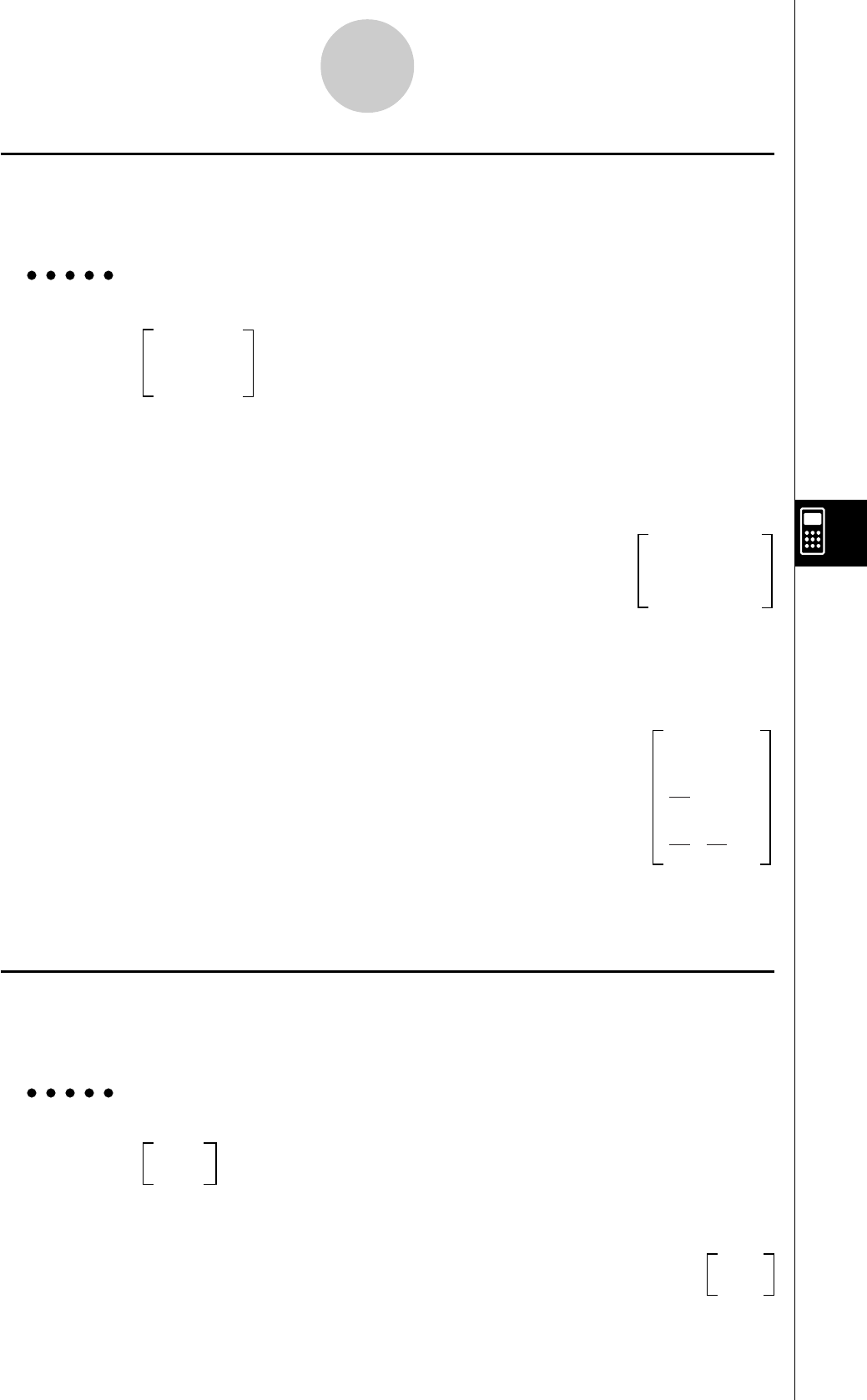
20001202
u LU
Fonction: Donne la résolution LU d’une matrice.
Syntaxe: LU (Mat, mémoire inférieure, mémoire supérieure)
Exemple Déterminer la résolution LU de la matrice suivante.
61218
51431
3818
La matrice inférieure est affectée à la variable A, tandis que la matrice supérieure est affectée
à la variable B.
K2(MAT)b(CALC)i(LU)!+( [ )!+( [ )
g,bc,bi!-( ] )!+( [ )
f,be,db!-( ] ),!+( [ ) 61218
d,i,bi!-( ] )!-( ] ),04 16
av(A),al(B)w00 1
Le résultat du calcul indique la matrice supérieure.
Pour afficher la matrice inférieure, rappelez la variable de la matrice inférieure (A dans cet
exemple) spécifiée par la commande.
av(A)w
Pour afficher la matrice supérieure, rappelez la variable de la matrice supérieure (B dans
cet exemple) spécifiée par la commande.
u Trn
Fonction: Transpose une matrice.
Syntaxe: Trn Mat
Exemple Transposer la matrice suivante.
12
34
K2(MAT)c(CREATE)b(Trn)!+( [ )!+( [ )
b,c!-( ] )!+( [ )d,e 13
!-( ] )!-( ] )w24
7-1-34
Utilisation du mode CAS (Système d’algèbre informatique)
100
01
1
6
5
2
1
2
1

20001202
u Augment (Augmnt)
Fonction: Combine deux matrices.
Syntaxe: Augment( Mat, Mat [ ) ]
Exemple Combinez les deux matrices suivantes.
12 56
34 78
K2(MAT)c(CREATE)c(Augmnt)!+( [ )!+( [ )
b,c!-( ] )!+( [ )d,e
!-( ] )!-( ] ),!+( [ )!+( [ )
f,g!-( ] )!+( [ )h,i 1256
!-( ] )!-( ] )w3478
u Identify (Ident)
Fonction: Crée une matrice unité.
Syntaxe: Ident
valeur numérique
Exemple Créer une matrice unité 2 × 2.
K2(MAT)c(CREATE)d(Ident)cw10
01
u Fill
Fonction: Remplace les éléments d’une matrice par la valeur ou l’expression spécifiée.
Cette commande peut aussi être utilisée pour créer une nouvelle matrice dont
les éléments contiennent tous la même valeur ou expression.
Syntaxe: Fill( Exp, Mat [ ) ]
Fill( Exp, nombre de lignes, nombre de colonnes [ ) ]
Exemple Remplacer les éléments de la matrice suivante par X.
34
12
K2(MAT)c(CREATE)e(Fill)v,!+( [ )
!+( [ )d,e!-( ] )!+( [ ) XX
b,c!-( ] )!-( ] )wXX
7-1-35
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
Exemple Créer un matrice 2 × 3 dont toutes les entrées sont X.
K2(MAT)c(CREATE)e(Fill)v,c,dwXXX
XXX
u SubMat
Fonction: Extraie une partie spécifique d’une matrice pour la mettre dans une autre
matrice.
Syntaxe: SubMat( Mat [, première ligne] [, première colonne] [, dernière ligne]
[, dernière colonne] [ ) ]
Exemple Extraire la partie comprise entre la ligne 2, colonne 2 et la ligne 3
colonne 3 de la matrice suivante.
123
456
789
K2(MAT)c(CREATE)f(SubMat)!+( [ )!+( [ )
b,c,d!-( ] )!+( [ )e,f,g
!-( ] )!+( [ )h,i,j!-( ] ) 56
!-( ] ),c,c,d,dw89
• Si vous ne spécifiez pas les dernières lignes et colonnes, toutes les entrées de la première
ligne/colonne à la dernière de la matrice seront extraites.
7-1-36
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
uDiag
Fonction: Extraie les éléments en diagonale d’une matrice.
Syntaxe: Diag Mat
Exemple Extraire les éléments en diagonale de la matrice suivante.
12
34
K2(MAT)c(CREATE)g(Diag)!+( [ )!+( [ )
b,c!-( ] )!+( [ )d,e
!-( ] )!-( ] )w[
1 4
]
uMat→List (M→List)
Fonction: Convertit une colonne spécifique d’une matrice en une liste.
Syntaxe: Mat→List( Mat, numéro de colonne [ ) ]
Exemple Convertir la colonne 2 de la matrice suivante en un liste.
12
34
K2(MAT)d(MAT→)b(M→List)!+( [ )!+( [ )
b,c!-( ] )!+( [ )d,e
!-( ] )!-( ] ),cw{
2 4
}
uMat→Vect (M→Vect)
Fonction: Convertit une colonne spécifique d’une matrice en vecteur.
Syntaxe: Mat→Vect( Mat, numéro de colonne [ ) ]
Exemple Convertir la colonne 2 de la matrice suivante en vecteur.
12
34
K2(MAT)d(MAT→)c(M→Vect)!+( [ )!+( [ )
b,c!-( ] )!+( [ )d,e
!-( ] )!-( ] ),cw[
2, 4
]
7-1-37
Utilisation du mode CAS (Système d’algèbre informatique)
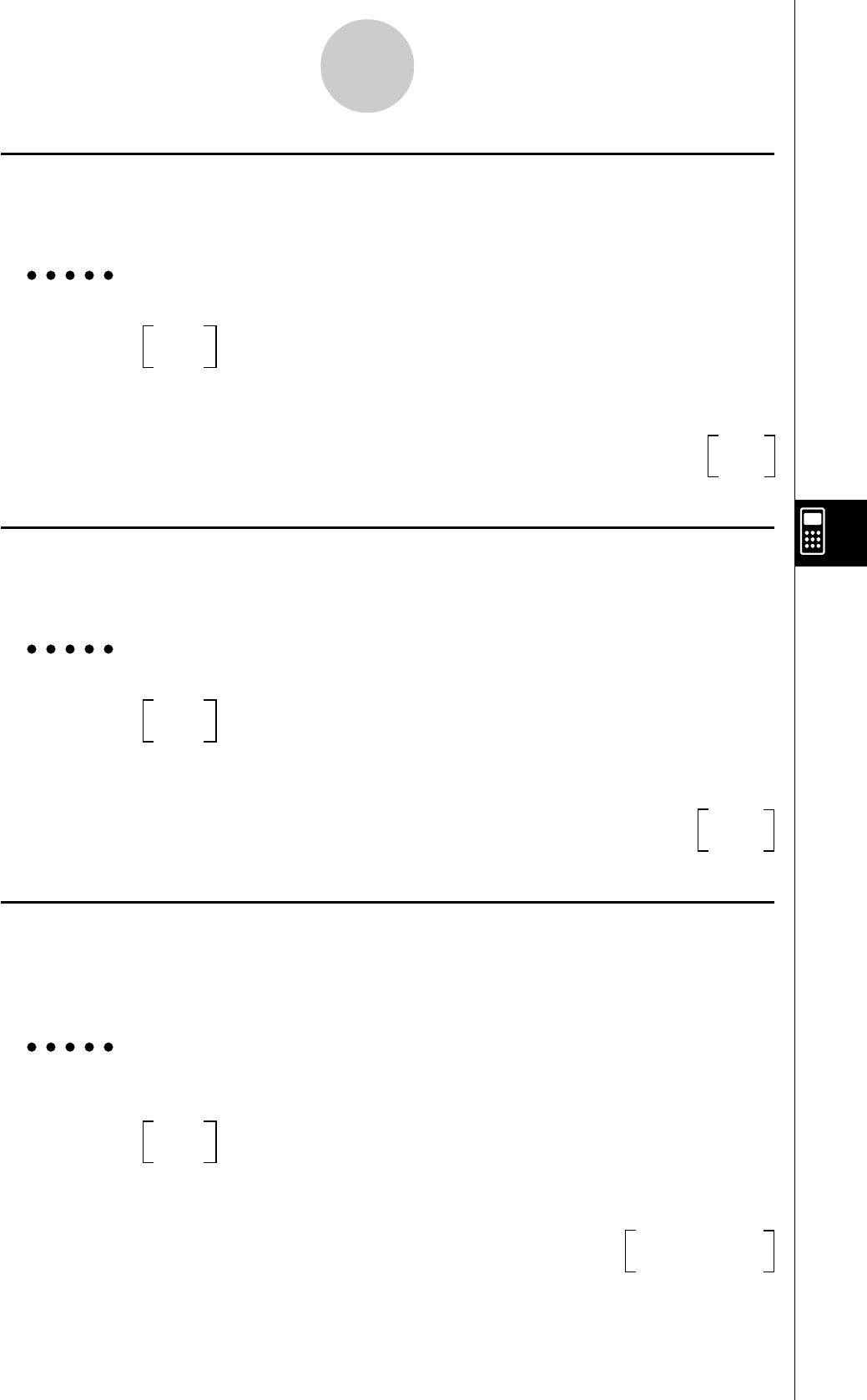
20001202
uSwap
Fonction: Echange deux rangées en un matrice.
Syntaxe: Swap Mat, numéro de ligne 1, numéro de ligne 2
Exemple Echanger la ligne 1 et la ligne 2 de la matrice suivante.
12
34
K2(MAT)e(ROW)b(Swap)!+( [ )!+( [ )
b,c!-( ] )!+( [ )d,e 34
!-( ] )!-( ] ),b,cw12
u`Row
Fonction: Donne le produit scalaire d’une ligne d’une matrice.
Syntaxe: `Row( Exp, Mat, numéro de ligne [ ) ]
Exemple Multiplier la ligne 1 de la matrice suivante par X.
12
34
K2(MAT)e(ROW)c(`Row)v,!+( [ )
!+( [ )b,c!-( ] )!+( [ ) X2X
d,e!-( ] )!-( ] ),bw34
u`Row+
Fonction: Calcule le produit scalaire d’une ligne d’une matrice et ajoute le résultat à une
autre ligne.
Syntaxe: `Row+( Exp, Mat, numéro de ligne 1, numéro de ligne 2 [ ) ]
Exemple Multiplier la ligne 1 de la matrice suivante par X et ajouter le résultat à
la ligne 2.
12
34
K2(MAT)e(ROW)d(`Row+)v,!+( [ )
!+( [ )b,c!-( ] )!+( [ ) 12
d,e!-( ] )!-( ] ),b,cwX + 3 2X + 4
7-1-38
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
uRow+
Fonction: Ajoute une ligne d’une matrice à une autre ligne.
Syntaxe: Row+( Mat, numéro de ligne 1, numéro de ligne 2 [ ) ]
Exemple Ajouter la ligne 1 de la matrice suivante à la ligne 2.
12
34
K2(MAT)e(ROW)e(Row+)!+( [ )
!+( [ )b,c!-( ] )!+( [ ) 12
d,e!-( ] )!-( ] ),b,cw46
7-1-39
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
kCommandes de calculs vectoriels [OPTN]-[VECT]
uDim
Fonction: Donne la dimension d’un vecteur.
Syntaxe: Dim Vect
Exemple Déterminer la dimension du vecteur (1 2 3).
K3(VECT)b(CALC)b(Dim)!+( [ )b,c,d
!-( ] )w3
uCrossP
Fonction: Donne le produit externe de deux vecteurs.
Syntaxe: CrossP( Vect, Vect [ ) ]
Exemple Déterminer le produit externe du vecteur (1 2 3) et du vecteur (4 5 6).
K3(VECT)b(CALC)c(CrossP)!+( [ )b,c,d
!-( ] ),!+( [ )e,f,g!-( ] )w[ – 3, 6, – 3 ]
uDotP
Fonction: Donne le produit interne de deux vecteurs.
Syntaxe: DotP( Vect, Vect [ ) ]
Exemple Déterminer le produit interne du vecteur (1 2 3) et du vecteur (4 5 6).
K3(VECT)b(CALC)d(DotP)!+( [ )b,c,d
!-( ] ),!+( [ )e,f,g!-( ] )w32
uNorm
Fonction: Donne la norme d’un vecteur.
Syntaxe: Norm Vect
Exemple Déterminer la norme du vecteur (1 2 3).
K3(VECT)b(CALC)e(Norm)!+( [ )b,c,d
!-( ] )w 14
7-1-40
Utilisation du mode CAS (Système d’algèbre informatique)
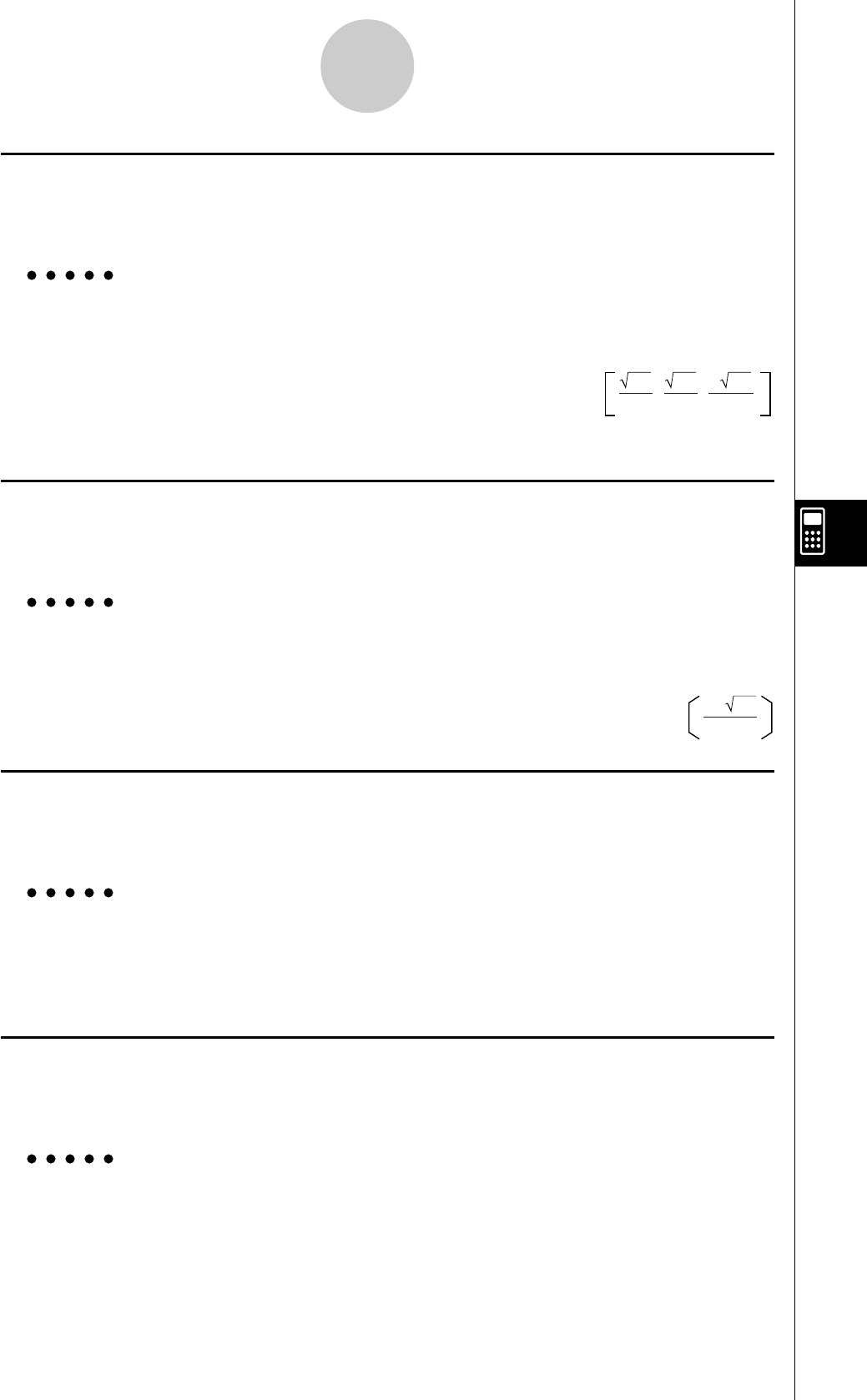
20001202
uUnitV
Fonction: Donne la taille 1 à un vecteur.
Syntaxe: UnitV Vect
Exemple Donner la taille 1 au vecteur (1 2 3).
K3(VECT)b(CALC)f(UnitV)
!+( [ )b,c,d
!-( ] )w
uAngle
Fonction: Donne l’angle formé par deux vecteurs.
Syntaxe: Angle( Vect, Vect [ ) ]
Exemple Déterminer l’angle formé par le vecteur (1 2) et le vecteur (3 4).
(Unité d’angle : Rad)
K3(VECT)b(CALC)g(Angle)!+( [ )b,c
!-( ] ),!+( [ )d,e!-( ] )w
uAugment (Augmnt)
Fonction: Combine deux vecteurs.
Syntaxe: Angle( Vect, Vect [ ) ]
Exemple Combiner le vecteur (1 2) et le vecteur (3 4).
K3(VECT)c(CREATE)b(Augmnt)!+( [ )b,c
!-( ] ),!+( [ )d,e!-( ] )w[
1, 2, 3, 4
]
uFill
Fonction: Remplace les éléments d’un vecteur par la valeur ou l’expression spécifiée.
Syntaxe: Fill( Exp, Vect [ ) ]
Exemple Remplacer les éléments du vecteur suivant par X.
K3(VECT)c(CREATE)c(Fill)v,!+( [ )
d,e!-( ] )w[
X, X
]
7-1-41
Utilisation du mode CAS (Système d’algèbre informatique)
,, 14
3 14
14
14
7
14
25
11 5
cos
–1

20001202
uVect→List (V→List)
Fonction: Convertit un vecteur en une liste.
Syntaxe: Vect→List Vect
Exemple Convertir le vecteur (3 2) en une liste.
K3(VECT)d(VECT→)b(V→List)!+( [ )d,c
!-( ] )w{
3, 2
}
uVect→Mat (V→Mat)
Fonction: Convertit les vecteurs en une matrice.
Syntaxe: Vect→Mat( Vect [, ... ,Vect ] ( ] )
Exemple Convertir les vecteurs (3 5) et (2 4) en une matrice.
K3(VECT)d(VECT→)c(V→Mat)!+( [ )d,f 32
!-( ] ),!+( [ )c,e!-( ] )w54
7-1-42
Utilisation du mode CAS (Système d’algèbre informatique)

20001202
∫
a
b f(x)dx = F(b) – F(a)
7-2-1
Précautions concernant le mode CAS
7-2 Précautions concernant le mode CAS
• Si une opération algébrique ne peut pas être effectuée pour une raison ou une autre,
l’expression originale restera affichée.
• L’exécution d’une opération algébrique peut durer très longtemps. L’absence
d’affichage immédiat du résultat ne signifie pas obligatoirement que la calculatrice
fonctionne mal.
• Les expressions peuvent être affichées dans différents formats. Une expression n’est
donc pas forcément fausse parce qu’elle n’apparaît pas sous le format attendu.
• La calculatrice effectue des calculs d’intégration en supposant que les intégrales sont
toujours positives même lorsque qu’elles sont discontinues (en raison d’une
commutation entre positif et négatif).
f(x)
F(x): fonction primitive de f(x)

19990401
Programmation
8-1 Etapes de la programmation de base
8-2 Touches de fonction du mode de programmation
8-3 Edition du contenu d’un programme
8-4 Gestion de fichiers
8-5 Guide des commandes
8-6 Utilisation des fonctions de la calculatrice dans
un programme
8-7 Liste des commandes de programmation
8-8Bibliothèque de programmes
Chapitre
Cette calculatrice a environ 144 koctets de mémoire.
• Vous pouvez vérifier la quantité de mémoire utilisée et la quantité de
mémoire restante en accédant au mode SYSTEM depuis le menu principal,
puis en appuyant sur 1(Mem). Voir “ 9-2 Opérations concernant la
mémoire” pour les détails.
8
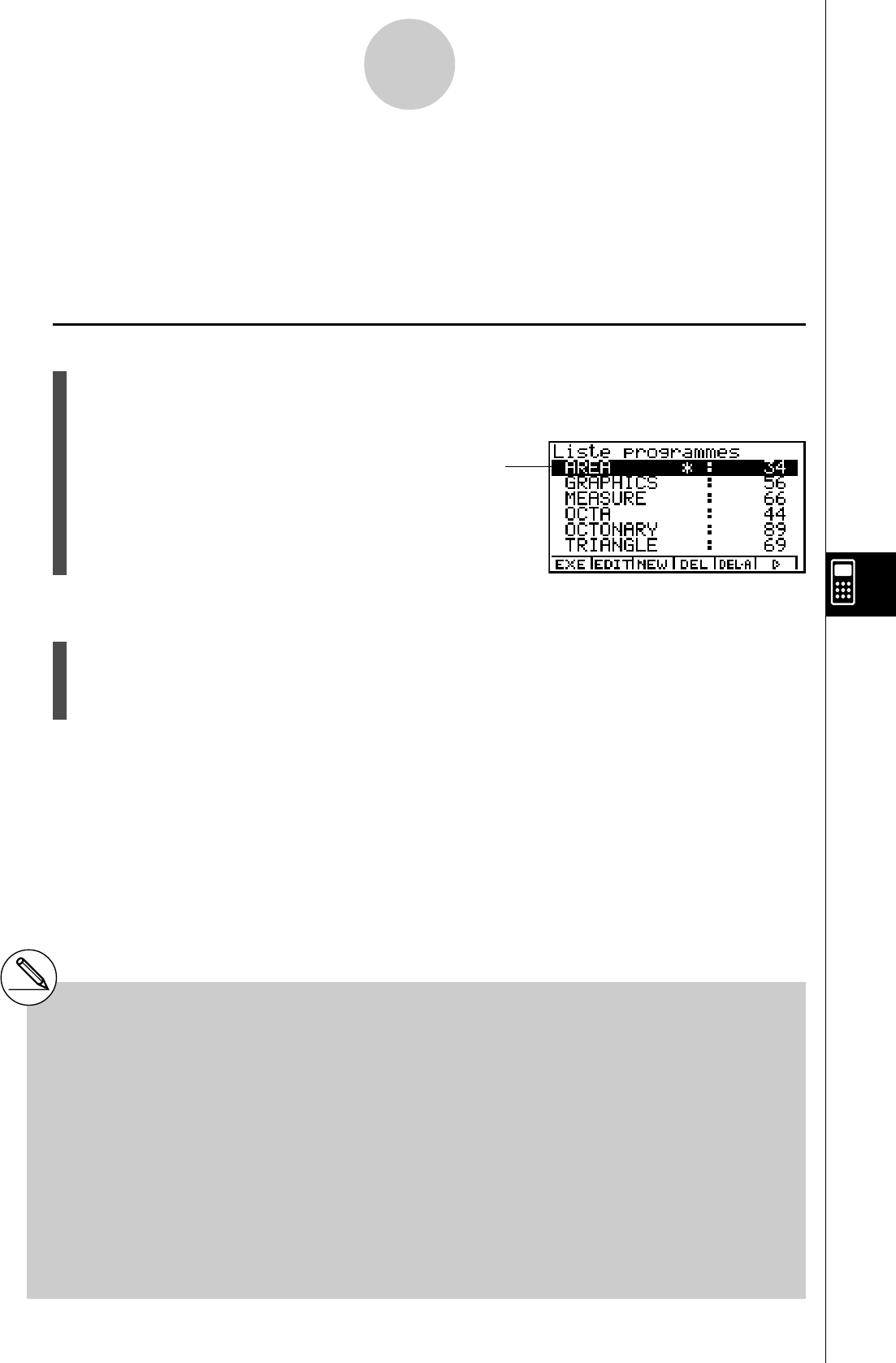
19990401
8-1 Etapes de la programmation de base
Description
Les commandes et les calculs sont exécutés dans l’ordre, tout comme les instructions
multiples d’un calcul manuel.
Réglage
1. Depuis le menu principal, accédez au mode PRGM. A ce moment, une liste de
programmes apparaît.
Zone de programme sélectionnée
(utilisez
f
et
c
pour changer de zone)
Les fichiers sont classés dans l’ordre alphabétique
de leurs noms.
Exécution
2. Enregistrez un nom de fichier.
3. Ecrivez le programme.
4. Lancez le programme.
8-1-1
Etapes de la programmation de base
# Si aucun programme ne se trouve en
mémoire lorsque vous accédez au mode
PRGM, le message “Aucun programme”
apparaîtra et seul le paramètre NEW (3)
sera présent dans le menu de fonctions.
# Les valeurs à droite dans la liste de
programmes indiquent le nombre d’octets
utilisés par chaque programme.
# Un nom de fichier peut contenir jusqu’à huit
caractères.
# Vous pouvez utiliser les caractères suivants
pour les noms de fichier :
A à Z, r,
θ
, espace, [, ], {, }, ’, ”, ~,
0 à 9, ., +, –, ×, ÷
# L’enregistrement d’un nom de fichier utilise 24
octets de mémoire.
# L’écran d’enregistrement de nom de fichier reste
affiché si vous appuyez sur w sans indiquer de
nom de fichier.
# Pour sortir de l’écran d’enregistrement de nom
de fichier et revenir à la liste de programmes
sans enregistrer de nom de fichier, appuyez sur
i.
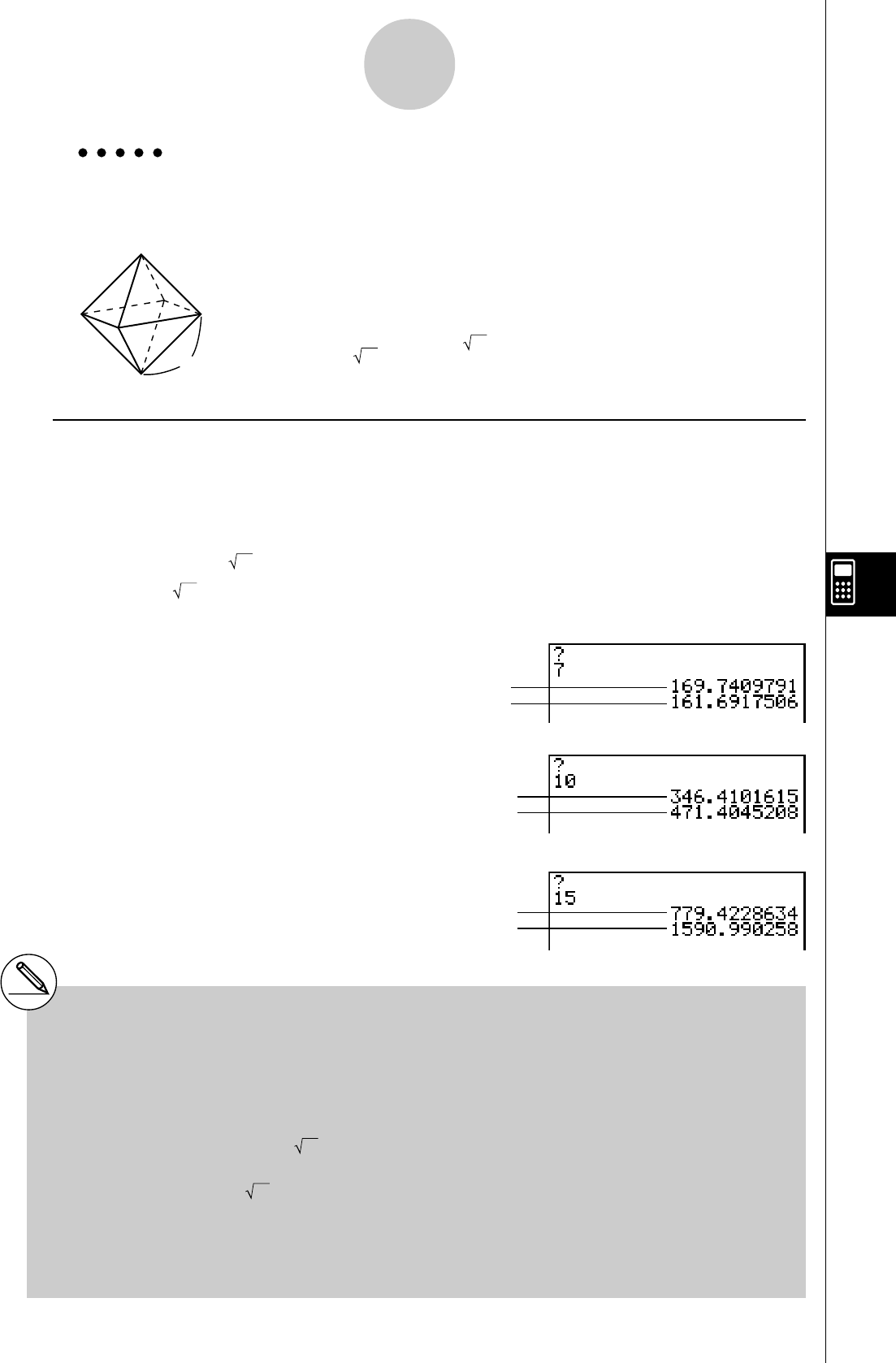
19990401
Exemple 1 Calculer l’aire (cm2) et le volume (cm3) de trois octaèdres dont les
côtés mesurent 7, 10 et 15 cm
Stockez la formule sous le nom de fichier OCTA.
A
Les formules utilisées pour le calcul de l’aire S et du volume V d’un
octaèdre régulier dont la longueur d’un côté A est connue sont les
suivants.
Procédure
1m PRGM
23(NEW)OCTAw*1
3!J(PRGM)3(?)aav(A)6(g)6(g)3(:)*2
c*!x( )d*av(A)x6(g)4(^)
!x( )c/d*av(A)Md
ii
41(EXE) ou w
hw(Valeur de A)
w
w
wbaw
w
w
wbfw
w*3
8-1-2
Etapes de la programmation de base
2
S = 2 3 A2, V = –––– A3
3
*1Appuyez sur 3(NEW) pour faire changer de
forme le curseur et pouvoir saisir des
caractères alphabétiques.
*2Le calcul de la surface et du volume d’un
octaèdre régulier s’effectue de la façon
suivante lors d’un calcul manuel.
Surface S ...... c*!x()d*
<valeur de A> xw
Volume V ....... !x()c/d*
<valeur de A> Mdw
*3Lorsque le résultat final d’un programme est
affiché, une pression sur w affiche la liste de
programmes.
# Vous pouvez lancer un programme dans le
mode RUN
•
MAT en entrant: Prog “<nom de
fichier>” w.
# Lorsque le résultat final d’un programme
exécuté au moyen de cette méthode est affiché,
une pression sur w réexécute le programme.
# Une erreur se produit si le programme désigné
par Prog “<nom de fichier>” ne peut pas être
trouvé.
S lorsque A = 7
V lorsque A = 7
S lorsque A = 10
V lorsque A = 10
S lorsque A = 15
V lorsque A = 15

19990401
8-2 Touches de fonction du mode de
programmation
•{NEW} ... {nouveau programme}
u Lorsque vous enregistrez un nom de fichier
•{RUN}/{BASE} ... entrée de programme {calcul général}/{base numérique}
•{
QQ
QQ
Q} ... {enregistrement d’un mot de passe}
•{SYBL} ... {menu de symboles}
uLorsque vous écrivez un programme —— 1(RUN) … défaut
•{JUMP} ... {haut}/{bas} du programme
•{SRC} ... {recherche}
•{MAT}/{STAT}/{LIST}/{GRPH}/{DYNA}/{RECR}
... menu {matrice}/{statistiques}/{liste}/{graphe}/{graphe dynamique}/{récurrence}
• Lorsque vous appuyez sur !J(PRGM), le menu PRGM (PROGRAM) suivant apparaît.
•{Prog} ... {rappel de programme}
•{JUMP} ... {menu de commande de saut}
•{?}/{^^
^^
^} ... commande {d’entrée}/{sortie}
•{I/O} ... menu de commande {de contrôle/transfert d’entrée/sortie}
•{IF}/{FOR}/{WHLE}/{CTRL}/{LOGIC}
... menu de commande de {saut conditionnel}/{contrôle de boucle}/{contrôle de
boucle conditionnelle}/{contrôle de programme)/{opération logique}
•{CLR}/{DISP} ... menu de commande de {suppression/affichage}
•{
:} ......... {séparateur pour les expressions et commandes}
Voir “8-5 Guide des commandes” pour tous les détails sur ces commandes.
• Lorsque vous appuyez sur u3(SET UP) le menu de commandes de mode suivant
apparaît.
•{ANGL}/{DISP}/{CPLX}/{GRPH}/{STAT}/{DERIV}/{T-VAR }/{Σ DSP}
Voir “Menus de touches de fonction sur l’écran de configuration” à la page 1-7-1 pour les
détails au sujet de chaque commande.
8-2-1
Touches de fonction du mode de programmation

19990401
u Lorsque vous écrivez un programme —— 2(BASE)*1
•{JUMP}/{SRC}
•{d~o} ... saisie de valeurs {décimales}/{hexadécimales}/{binaires}/{octales}
•{LOG} ... {opérateurs logiques}
•{DISP} ... conversion de la valeur affichée en valeur {décimale}/{hexadécimale}/{binaire}/
{octale}
•{SYBL} ... {menu de symboles}
• Lorsque vous appuyez sur !J(PRGM), le menu PRGM (PROGRAM) suivant apparaît.
•{Prog}/{JUMP}/{?}/{^^
^^
^}
•{= ≠ <} ... {menu d’opérateurs logiques}
•{
:} ......... {séparateur pour les expressions et commandes}
• Lorsque vous appuyez sur u3(SET UP), le menu de commandes de mode ci-dessous
apparaît.
•{Dec}/{Hex}/{Bin}/{Oct}
•{EXE}/{EDIT}
... {exécution}/{édition} de programme
•{NEW} ... {nouveau programme}
•{DEL}/{DEL·A}
... suppression de {programme particulier}/{tous les programmes}
•{SRC}/{REN}
... {recherche}/{changement} de nom de fichier
8-2-2
Touches de fonction du mode de programmation
*1Les programmes écrits après une pression sur
2(BASE) sont indiqués par
B
à la droite du
nom de fichier.

19990401
8-3-1
Edition du contenu d’un programme
8-3 Edition du contenu d’un programme
kMise au point d’un programme (débogage)
Un problème apparaissant dans un programme et l’empêchant de se dérouler normalement
est appelé un “bogue” et l’élimination de ce problème est appelé “débogage”. Les
symptômes suivants indiquent que votre programme contient une erreur (un bogue) et
qu’une mise au point est nécessaire.
• Messages d’erreur apparaissant quand le programme est en route
• Résultats qui ne correspondent pas aux prévisions
uu
uu
uPour éliminer une erreur à l’origine d’un message
Un message d’erreur comparable au message suivant apparaît quand un problème se
présente pendant l’exécution d’un programme.
Quand ce type de message apparaît, appuyez sur i pour afficher le point du programme
où l’erreur s’est produite. Le curseur clignote à l’endroit où se trouve le problème. Contrôlez
le “Tableau des messages d’erreur” (page
α
-1-1) pour savoir quelles dispositions prendre
pour corriger le problème.
• Notez que la position de l’erreur ne sera pas indiquée lorsque vous appuyez sur i si
le programme est protégé par un code. La liste de programmes sera affichée à la place.
uu
uu
uPour éliminer les erreurs à l’origine de mauvais résultats
Si le programme aboutit à un résultat qui ne correspond pas à vos attentes, vérifiez le
contenu du programme et effectuez les modifications nécessaires.
La touche 1(JUMP) est aussi utile lors de l’édition du contenu d’un programme.
1(JUMP)b(Top) ......
Positionne le curseur en
début de programme
1(JUMP)c(Bottom)...
Positionne le curseur en
fin de programme

19990401
kUtilisation d’un programme existant pour la création d’un nouveau
programme
Vous pouvez écrire un nouveau programme à partir d’un programme déjà existant.
Rappelez simplement ce programme, effectuez les changements nécessaires puis
exécutez le programme.
Exemple 2 Utiliser le programme OCTA (page 8-1-2) pour créer un programme qui
calcule l’aire (cm2) et le volume (cm3) d’un tétraèdre régulier quand la
longueur d’une face est 7, 10 et 15 cm
Utiliser TETRA comme nom de fichier.
Les formules utilisées pour le calcul de l’aire S et du volume V d’un
tétraèdre régulier dont la longueur d’une face A est connue sont les
suivantes.
Faites les opérations suivantes pour introduire le programme.
Longueur d’une face A .... !J(PRGM)3(?)aav(A)6(g)6(g)3(:)
Aire S ............................... !x( )d*av(A)x6(g)4(^)
Volume V .......................... !x( )c/bc*av(A)Md
Comparez ce programme à celui effectué pour le calcul de l’aire et du volume d’un
octaèdre régulier.
Longueur d’une face A .... !J(PRGM)3(?)aav(A)6(g)6(g)3(:)
Aire S ............................... c*!x( )d*av(A)x6(g)4(^)
Volume V .......................... !x( )c/d*av(A)Md
Vous pouvez donc créer le programme TETRA en effectuant les changements suivants
dans le programme OCTA.
• Vous supprimez c * (signalé par un trait ondulé)
• Vous remplacez d par b c (signalé par un trait continu)
A
8-3-2
Edition du contenu d’un programme
2
S = 3 A2, V = –––– A3
12

19990401
8-3-3
Edition du contenu d’un programme
Modifions maintenant OCTA pour obtenir le programme TETRA.
1. Changez d’abord le nom.
6(g)2(REN)ATETRAw
2. Changez ensuite le contenu.
2(EDIT)
eeeeDD
cdDbc
i
3. Mettons maintenant le programme en route.
1(EXE) ou w
hw(Valeur de A)
w
w
wbaw
w
w
wbfw
w

19990401
8-3-4
Edition du contenu d’un programme
kRecherche de données à l’intérieur d’un programme
Exemple Rechercher la lettre “A” dans le programme nommé OCTA
1. Rappeler le programme.
2. Appuyez sur 2(SRC) ou w et saisissez les données que vous recherchez.
2(SRC)
av(A)
3. Appuyez sur w pour commencer la recherche. Le contenu du programme
apparaît à l’écran avec le curseur sur la première occurrence de la donnée désignée.*1
4. A chaque pression de w ou 1 (SRC), le curseur
saute à la prochaine occurrence de la donnée
désignée.*2
*1Le message “Non trouvé” apparaîtra si la
donnée recherchée ne pourra pas être
localisée dans le programme.
*2S’il n’y a plus aucune occurrence de la
donnée désignée, la recherche s’arrêtera et
le curseur reviendra au point où la recherche
a commencé.
# Vous ne pouvez pas spécifier le retour à la
ligne (_) ni la commande d’affichage (^)
pour la donnée recherchée.
# Lorsque le contenu du programme est affiché,
vous pouvez utiliser les touches de curseur pour
placer le curseur à un autre endroit avant de
chercher la prochaine occurrence de la donnée.
La recherche ne s’effectuera que sur la partie
du programme débutant à la position du curseur
lorsque vous appuierez sur w.
# Lorsque la donnée recherchée est localisée, la
recherche s’arrête si vous saisissez des
données ou déplacez le curseur.
# Si vous faites une erreur lors de la saisie de
caractères, appuyez sur A pour annuler la
saisie et recommencez depuis le début.

19990401
8-4-1
Gestion de fichiers
8-4 Gestion de fichiers
kRecherche d’un fichier
uPour localiser un fichier par ses initiales
Exemple Faire une recherche par initiales pour rappeler le programme nommé
OCTA
1. Quand la liste de programmes est à l’écran, appuyez sur 6(g)1(SRC) et
saisissez les premiers caractères du fichier souhaité.
6(g)1(SRC)
OCT
2. Appuyez sur w pour commencer la recherche.
• Le nom commençant par les caractères que vous avez saisis est mis en surbrillance.
# Si aucun programme ne commence par les
caractères que vous avez saisis, le message
“Non trouvé” apparaitra à l’écran. Dans ce
cas, appuyez sur i pour annuler le message
d’erreur.

19990401
8-4-2
Gestion de fichiers
kk
kk
kEdition d’un nom de fichier
Exemple Remplacer le nom de fichier TRIANGLE par ANGLE
1. Quand la liste de programmes est à l’écran, utilisez f et c pour amener la
surbrillance sur le fichier dont vous voulez changer le nom, puis appuyez sur
6(g)2(REN).
2. Effectuez les changements souhaités.
DDD
3. Appuyez sur w pour enregistrer le nouveau nom et revenir à la liste de
programmes.
La liste de programmes est reclassée selon les changements effectués dans le nom de
fichier.
kk
kk
kEffacement d’un programme
uPour supprimer un programme précis
1. Quand la liste de programmes est à l’écran, utilisez f et c pour amener la
surbrillance sur le nom du programme que vous voulez supprimer.
2. Appuyez sur 4(DEL).
3. Appuyez sur w(Oui) pour supprimer le programme sélectionné ou sur i(Non)
pour abandonner l’opération sans rien supprimer.
# Si, après modification, le nouveau nom de
fichier est identique à un nom de programme
stocké en mémoire, le message “Existe déjà”
apparaitra. Dans ce cas, vous pouvez
effectuer une des deux opérations suivantes
pour corriger le problème.
• Appuyez sur i pour annuler l’erreur et revenir
à l'écran d’édition du nom de fichier.
• Appuyez sur A pour annuler le nom du fichier
et entrer un nouveau nom.

19990401
8-4-3
Gestion de fichiers
uPour supprimer tous les programmes
1. Quand la liste de programmes est à l’écran, appuyez sur 5(DEL·A).
2. Appuyez sur w(Oui) pour supprimer tous les programmes ou sur i(Non) pour
abandonner l’opération sans rien supprimer.
• Vous pouvez aussi effacer tous les programmes en accédant au mode SYSTEM depuis le
menu principal et en appuyant sur 1(Mem) pour afficher l’écran de gestion de la
mémoire.
Voir “9-2 Opérations concernant la mémoire” pour les détails.
kk
kk
kEnregistrement d’un code d’accès
Lorsque vous écrivez un programme, vous pouvez le protéger par un code sans lequel il ne
sera pas possible d’accéder au contenu de ce programme.
• Il n’est pas nécessaire d’indiquer le code d’accès pour lancer un programme.
Exemple Créer un fichier de programme sous le nom AREA et le protéger par
le code CASIO
1. Quand la liste de programmes est à l’écran, appuyez sur 3(NEW) pour enregistrer
le nom de fichier du nouveau programme.
3(NEW)
AREA
2. Appuyez sur 5(Q) puis saisissez le code d’accès.
5(Q)
CASIO
# La saisie d’un code d’accès est identique à la
saisie d’un nom de fichier.

19990401
8-4-4
Gestion de fichiers
3. Appuyez sur w pour enregistrer le nom de fichier et le code. Vous pouvez
maintenant introduire le contenu du programme.
4. Une fois que vous avez introduit le programme, appuyez sur !i(QUIT) pour
sortir du fichier et revenir à la liste de programmes. Les fichiers qui sont protégés par
un code sont indiqués par un astérisque à la droite du nom de fichier.
kk
kk
kRappel d’un programme protégé par un code d’accès
Exemple Rappeler le fichier nommé AREA qui est protégé par le code d’accès
CASIO
1. Dans la liste de programmes, utilisez f et c pour amener la surbrillance sur le
nom du programme que vous voulez rappeler.
2. Appuyez sur 2(EDIT).
3. Entrez le code d’accès et appuyez sur w pour rappeler le programme.
# Le fichier de sauvegarde du nouveau
programme n’aura pas de code si vous
appuyez sur w sans indiquer un code
d’accès. Seul le nom de fichier est enregistré,
sans code, lorsque vous appuyez sur w.
# Le message d’erreur “Incompatibilité”
apparaîtra si vous indiquez le mauvais code
d’accès lors du rappel d’un programme protégé
par un code. Appuyez sur i pour revenir à
l'écran de saisie du code d’accès.

19990401
8-5-1
Guide des commandes
8-5 Guide des commandes
kIndex des commandes
Break ...............................................................................................................8-5-6
ClrGraph ....................................................................................................... 8-5-11
ClrList ............................................................................................................8-5-11
ClrText ...........................................................................................................8-5-12
ClrMat ............................................................................................................8-5-12
DispF-Tbl, DispR-Tbl .....................................................................................8-5-12
Do~LpWhile .....................................................................................................8-5-5
DrawDyna ..................................................................................................... 8-5-12
DrawFTG-Con, DrawFTG-Plt ........................................................................8-5-13
DrawGraph ................................................................................................... 8-5-13
DrawR-Con, DrawR-Plt .................................................................................8-5-13
DrawRΣ-Con, DrawRΣ-Plt .............................................................................8-5-14
DrawStat ....................................................................................................... 8-5-14
DrawWeb .......................................................................................................8-5-14
Dsz ..................................................................................................................8-5-9
For~To~(Step~)Next ........................................................................................8-5-4
Getkey ...........................................................................................................8-5-15
Goto~Lbl ....................................................................................................... 8-5-10
If~Then~(Else~)IfEnd ......................................................................................8-5-4
Isz ..................................................................................................................8-5-11
Locate............................................................................................................8-5-16
Prog ................................................................................................................ 8-5-7
Receive ( / Send ( ..........................................................................................8-5-17
Return .............................................................................................................8-5-8
Stop ................................................................................................................ 8-5-8
While~WhileEnd ..............................................................................................8-5-6
? (Commande d’entrée) ................................................................................. 8-5-2
^ (Commande de sortie) ...............................................................................8-5-3
: (Commande d’instructions multiples) ........................................................... 8-5-3
_ (Retour) ..................................................................................................... 8-5-3
’ (Délimiteur de commentaire) ........................................................................ 8-5-3
=,
GG
GG
G
, >, <, ≥, ≤ (Opérateurs relationnels) ......................................................8-5-18

19990401
8-5-2
Guide des commandes
Les conventions utilisées dans cette section pour la description des différentes
commandes sont les suivantes.
Texte en caractères gras ...... Les commandes et autres paramètres qui doivent
toujours être saisis sont en caractères gras.
{Accolades} .......................... Les accolades sont utilisées pour indiquer un
certain nombre de paramètres dont un doit être
sélectionné lorsqu’une commande est utilisée.
N’insérez pas d’accolades quand vous introduisez
une commande.
[Crochets] ............................. Les crochets doivent être utilisés pour indiquer des
paramètres qui sont optionnels. N’insérez pas de
crochets quand vous introduisez une commande.
Expressions numériques ..... Les expressions numériques, telles que 10, 10 +
20, A, indiquent des constantes, des calculs, des
constantes numériques, ou autres.
Caractères alphabétiques .... Les caractères alphabétiques indiquent des
chaînes, telles AB.
kk
kk
kCommandes de base
Commande d’entrée (?)
Fonction: Demande de saisir une valeur devant être affectée à une variable pendant la
programmation.
Syntaxe: ? → <nom de la variable>, ”<prompt> ” ? → <nom de variable>
Exemple: ? → A
Description:
• Cette commande interrompt momentanément l’exécution du programme et demande de
saisir une valeur ou une expression à affecter à une variable. Si vous ne spécifiez pas de
prompt, l’exécution de cette commande fera apparaître “?” pour indiquer que la calculatrice
attend que vous saisissiez une valeur. Si vous spécifiez le prompt, “<prompt> ?” apparaîtra
pour demander de saisir une valeur. Il n’y a pas de limite au nombre de caractères pouvant
être spécifiés pour un prompt.
• La réponse à cette commande doit être une valeur ou une expression, mais l’expression
ne peut pas être une instruction multiple.

19990401
8-5-3
Guide des commandes
Commande de sortie (^^
^^
^)
Fonction: Affiche un résultat intermédiaire pendant l’exécution d’un programme.
Description:
• Cette commande interrompt momentanément l’exécution d’un programme et affiche un
texte en caractères alphabétiques ou le résultat du calcul précédant immédiatement cette
commande.
• La commande de sortie doit être utilisée aux endroits où vous appuieriez normalement
sur la touche w pendant un calcul manuel.
Commande d’instructions multiples (:)
Fonction: Relie deux instructions pour qu’elles soient exécutées dans l’ordre sans
interruption.
Description:
• Contrairement à la commande de sortie (^), les instructions reliées par cette commande
sont exécutées sans interruption.
• La commande d’instructions multiples peut être utilisée pour mettre en relation deux
expressions d’un calcul ou deux commandes.
• Vous pouvez utiliser un retour indiqué par _ au lieu de la commande d’instructions
multiples.
Retour (__
__
_)
Fonction: Relie deux instructions pour qu’elles soient exécutées dans l’ordre sans
interruption.
Description:
• Le retour fonctionne de la même façon que la commande d’instructions multiples.
• L’utilisation du retour à la place de la commande d’instructions multiples facilite la lecture
du programme affiché.
Délimiteur de commentaire ( ’ )
Fonction: Indique un commentaire inséré à l’intérieur d’un programme.
Description: Tout ce qui suit une apostrophe est traité comme commentaire et n’est pas
exécutable.

19990401
kCommandes de boucles et branchements conditionnels (COM)
• Définissons a, b, c, d, e... comme étant des instructions.
• Les séparations entre les instructions peuvent être “_”, “:” ou “^”.
Dans les exemples ci-dessous nous utiliserons “:”.
• Nous dirons qu’un test est vrai s’il est vérifié et qu’il est faux dans le cas contraire.
Exemple: Si A>3 est vrai pour A = 5.
If~Then~(Else~)IfEnd
Syntaxe: If <condition> : Then a : b : c : Else d : e : If End : f : g : etc...
Si le test est vrai, a, b, c, f, g sont exécutées.
Si le test est faux, d, e, f, g sont exécutées.
Description:
(1) If ~ Then ~ IfEnd
• Lorsque la condition est vraie, l’exécution passe à l’instruction Then puis continue par
l’instruction suivant IfEnd.
• Lorsque la condition est fausse, l’exécution saute l’instruction suivant IfEnd.
(2) If ~ Then ~ Else ~ IfEnd
• Lorsque la condition est vraie, l’exécution passe à l’instruction Then puis saute à
l’instruction suivant IfEnd.
• Lorsque la condition est fausse, l’exécution saute à l’instruction Else et continue par
l’instruction suivant IfEnd.
For~To~(Step~)Next
Fonction: Cette commande répète tout ce qui se trouve entre l’instruction For et
l’instruction Next. La valeur initiale est affectée à la variable de référence à la première
exécution, puis la valeur de la variable de référence change en fonction de la valeur de
l’incrément à chaque exécution. L’exécution continue jusqu’à ce que la valeur de la variable
de référence dépasse la valeur finale.
Syntaxe:
Paramètres:
• Nom de la variable de référence: A à Z
• Valeur initiale: valeur ou expression qui produit une valeur (i.e. sin x, A, etc.)
• Valeur finale: valeur ou expression qui produit une valeur (i.e. sin x, A, etc.)
• Valeur de l’incrément: valeur numérique (défaut : 1)
8-5-4
Guide des commandes
_
:
^
For <
valeur initiale
> → <
nom de la variable de référence
>To <
valeur finale
>
Step <
valeur de l'incrément
> Next

19990401
8-5-5
Guide des commandes
Description:
• La valeur par défaut de l’incrément est 1.
• La définition d’une valeur initiale inférieure à la valeur finale et d’un incrément positif
incrémente la variable de référence à chaque exécution. La définition d’une valeur initiale
supérieure à la valeur finale et d’un incrément négatif décrémente la valeur de la variable
de référence à chaque exécution.
Do~LpWhile
Fonction: Cette commande répète des commandes particulières entre Do et LpWhile tant
que sa condition est vraie. Le test est réalisé après les instructions.
Syntaxe:
Paramètres: expression
Description:
• Cette commande répète les commandes contenues dans la boucle tant que sa condition
est vraie. Quand la condition devient fausse, l’exécution continue à partir de l’instruction
suivant l’instruction LpWhile.
• Comme la condition vient après l’instruction LpWhile, la condition est testée (vérifiée)
après que toutes les commandes à l’intérieur de la boucle ont été exécutées.
__
Do : <instruction> : LpWhile <condition>
^^
expression numérique

19990401
_
:
^
_
:
^
8-5-6
Guide des commandes
While~WhileEnd
Fonction: Cette commande répète des commandes particulières entre While et WhileEnd
tant que sa condition est vraie. Le test est réallsé avant les instructions.
Syntaxe:
Paramètres: expression
Description:
• Cette commande répète les commandes contenues dans la boucle tant que sa condition
est vraie. Quand la condition devient fausse, l’exécution se poursuit à partir de
l’instruction suivant l’instruction WhileEnd.
• Comme la condition vient après l’instruction While, elle est testée (vérifiée) avant que les
commandes à l’intérieur de la boucle soient exécutées.
kk
kk
kCommandes de contrôle de la programmation (CTL)
Break
Fonction: Cette commande interrompt l’exécution d’une boucle et continue à partir de la
commande suivante après la boucle.
Syntaxe: Break
Description:
• Cette commande interrompt l’exécution d’une boucle et continue à partir de la
commande suivante, après la boucle.
• Cette commande peut être utilisée pour interrompre l’exécution des instructions For, Do
et While.
While <condition> <instruction> WhileEnd
expression numérique
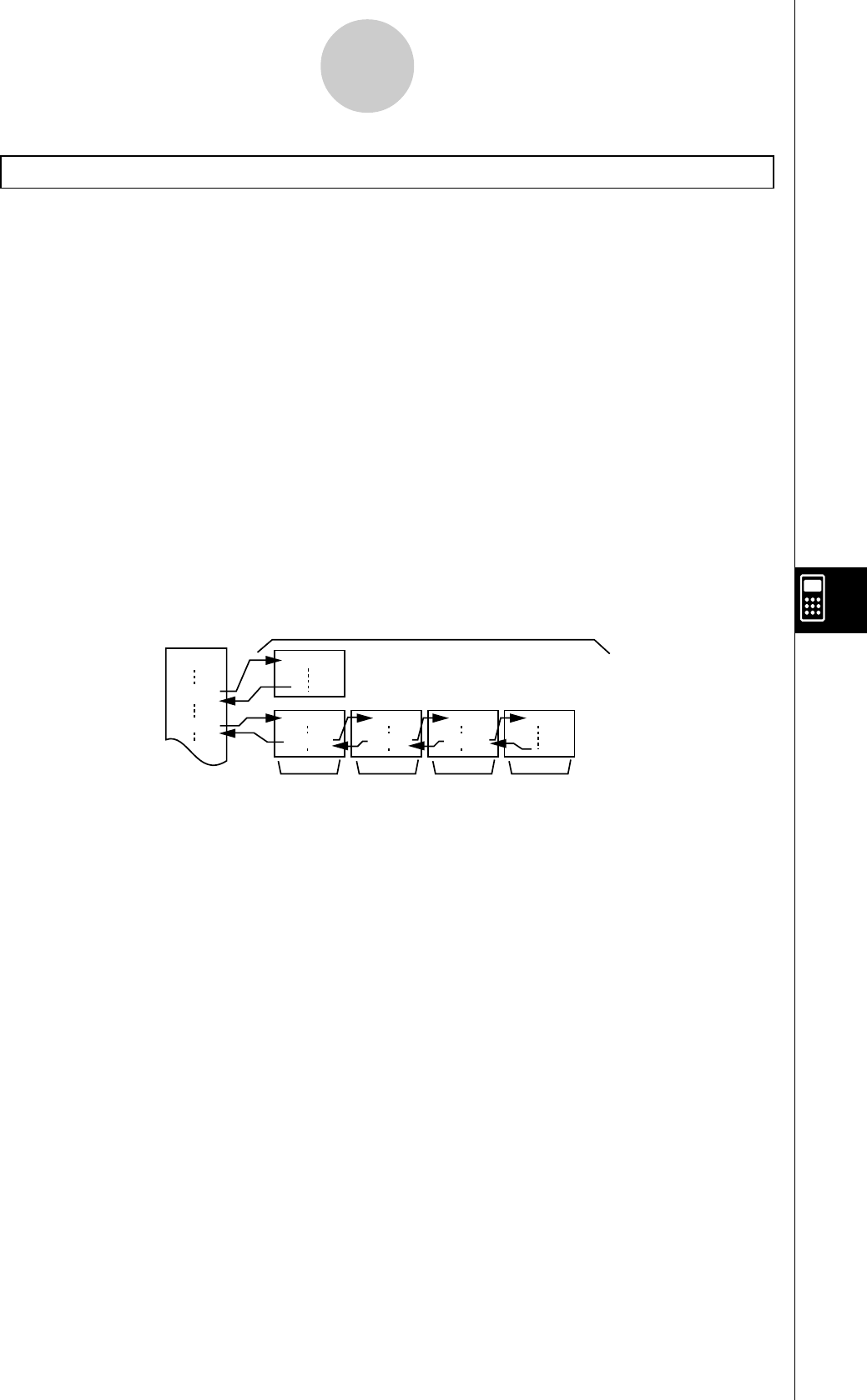
19990401
8-5-7
Guide des commandes
Prog
Fonction: Cette commande définit l’exécution d’un autre programme en tant que sous-
programme. Dans le mode RUN
•
MAT, cette commande exécute un nouveau programme.
Syntaxe: Prog ”nom de fichier”
Exemple: Prog ”ABC”
Description:
• Même quand cette commande se trouve à l’intérieur d’une boucle, elle interrompt
immédiatement la boucle et démarre le sous-programme.
• Cette commande peut être utilisée autant de fois que nécessaire à l’intérieur d’un
programme principal pour faire appel à des sous-programmes qui exécutent des tâches
particulières.
• Un sous-programme peut être utilisé à plusieurs endroits à l’intérieur d’un même
programme principal, ou il peut être appelé par un certain nombre de programmes
principaux.
Programme principal Sous-programmes
D
CEIJ
Prog ”E” Prog ”I” Prog ”J”
A
Prog ”D”
Prog ”C”
Niveau 1 Niveau 2 Niveau 3 Niveau 4
• L’appel d’un sous-programme exécute celui-ci à partir du début. Quand l’exécution du
sous-programme est terminée, on revient au programme principal et continue à partir de
l’instruction suivant la commande Prog.
• Une commande Goto~Lbl à l’intérieur d’un sous-programme est valide à l’intérieur de ce
sous-programme seulement. Elle ne peut pas être utilisée pour sauter à un label hors du
sous-programme.
• Si le sous-programme correspondant au nom de fichier défini par la commande Prog
n’existe pas, une erreur se produira.
• Dans le mode RUN
•
MAT, la saisie de la commande Prog et sa validation par w mettent
en route le programme désigné par la commande.
19990401
8-5-8
Guide des commandes
Return
Fonction: Cette commande fait revenir d’un sous-programme au programme d’origine.
Syntaxe: Return
Description:
L’exécution de la commande de retour à l’intérieur du programme principal interrompt
l’exécution du programme. L’exécution de la commande de retour à l’intérieur d’un sous-
programme interrompt le sous-programme et fait revenir au programme principal, à l’endroit
où le sous-programme a commencé.
Stop
Fonction: Cette commande termine l’exécution d’un programme.
Syntaxe: Stop
Description:
• Cette commande termine l’exécution du programme.
• L’exécution de cette commande à l’intérieur d’une boucle achève l’exécution du
programme sans qu’aucune erreur ne se produise.

19990401
8-5-9
Guide des commandes
kCommandes de saut (JUMP)
Dsz
Fonction: Cette commande est un saut avec compteur qui décrémente la valeur d’une
variable de référence d’une unité, puis saute quand la valeur de la variable est égale à
zéro.
Syntaxe:
Paramètres: nom de la variable: A à Z, r,
θ
[Exemple] Dsz B : Décrémente la valeur affectée à la variable B d’une unité.
Description:
Cette commande décrémente la valeur d’une variable de référence d’une unité, puis la
teste (vérifie). Si la valeur actuelle n’est pas zéro, l’exécution continue avec l’instruction
suivante. Si la valeur est égale à zéro, l’exécution saute à l’instruction suivant la
commande d’instruction multiple (:), la commande d’affichage de résultat (^) ou la
commande de retour (_).
Valeur de la variable
GG
GG
G 0 _
Dsz <
nom de la variable
> : <
instruction
> : <
instruction
>
^
Valeur de la variable
= 0

19990401
8-5-10
Guide des commandes
Goto~Lbl
Fonction: Cette commande effectue un saut inconditionnel à un endroit défini.
Syntaxe: Goto <nom de label> ~ Lbl <nom de label>
Paramètres: nom de label : valeur (0 à 9) variable (A à Z, r,
θ
)
Description:
• Cette commande comprend deux parties : Goto n (n étant un paramètre comme décrit plus
haut) et Lbl n (n étant un paramètre référencée par Goto n). Cette commande fait sauter
l’exécution du programme à l’instruction Lbl dont le paramètre n correspond à celui qui a
été spécifié par l’instruction Goto.
• Cette commande peut être utilisée pour revenir au début d’un programme ou pour sauter
à un endroit quelconque du programme.
• Cette commande peut être combinée aux sauts conditionnels et aux sauts avec
compteurs.
• S’il n’y a aucune instruction Lbl dont la valeur correspond à celle définie par l’instruction
Goto, une erreur se produira.

19990401
Isz
Fonction: Cette commande est un saut avec compteur qui incrémente la valeur de la
variable de référence d’une unité, puis saute quand la valeur de la variable est égale à zéro.
Syntaxe:
Paramètres: nom de la variable: A à Z, r,
θ
[Exemple] Isz A : Incrémente la valeur affectée à la variable A d’une unité.
Description:
Cette commande incrémente la valeur d’une variable de référence d’une unité, puis la teste
(vérifie). Si la valeur actuelle n’est pas égale à zéro, l’exécution continue avec l’instruction
suivante. Si la valeur est égale à zéro, l’exécution saute à l’instruction suivant la commande
d’instructions multiples (:), la commande d’affichage de résultat (^) ou la commande de
retour (_).
kk
kk
kCommandes d’effacement (CLR)
ClrGraph
Fonction: Cette commande annule l’écran de graphe et rétablit les réglages initiaux (INIT)
de la fenêtre d’affichage.
Syntaxe: ClrGraph
Description: Cette commande efface l’écran graphique pendant l’exécution du
programme.
ClrList
Fonction: Cette commande supprime les données d’une liste.
Syntaxe: ClrList <nom de liste>
ClrList
Paramètres: nom de liste : 1 à 20, Ans
Description: Cette commande supprime les données de la liste désignée par “nom de liste”.
Toutes les données de la liste sont supprimées si rien n’est spécifié pour le “nom de liste”.
8-5-11
Guide des commandes
Valeur de la variable
GG
GG
G 0 _
Isz <
nom de la variable
> : <instruction> :<instruction>
^
Valeur de la variable
= 0

19990401
8-5-12
Guide des commandes
ClrText
Fonction: Cette commande efface le texte de l’écran.
Syntaxe: ClrText
Description: Cette commande efface le texte de l’écran pendant l’exécution du
programme.
ClrMat
Fonction: Cette commande supprime les données de matrice.
Syntaxe: ClrMat <nom de matrice>
ClrMat
Paramètres: nom de matrice : A à Z, Ans
Description: Cette commande supprime les données de la matrice désignée par “nom de
matrice”. Toutes les données de la matrice sont supprimées si aucun “nom de matrice” n’est
désigné.
kk
kk
kCommandes d’affichage (DISP)
DispF-Tbl, DispR-Tbl Aucun paramètre
Fonction: Ces commandes affichent des tables numériques.
Description:
• Ces commandes créent des tables numériques pendant l’exécution d’un programme en
fonction des conditions définies dans le programme.
• DispF-Tbl crée une table de fonctions, tandis que DispR-Tbl crée une table de
récurrence.
DrawDyna Aucun paramètre
Fonction: Cette commande exécute un tracé de graphe dynamique.
Description: Cette commande trace un graphe dynamique pendant l’exécution d’un
programme en fonction des paramètres de graphe dynamique actuels.
19990401
8-5-13
Guide des commandes
DrawFTG-Con, DrawFTG-Plt Aucun paramètre
Fonction: Cette commande utilise les valeurs d’une table pour représenter graphiquement
une fonction.
Description:
• Cette commande trace un graphe en fonction des conditions actuelles.
• DrawFTG-Con produit un graphe à points connectés, tandis que DrawFTG-Plt produit un
graphe à points séparés.
DrawGraph Aucun paramètre
Fonction: Cette commande trace un graphe.
Description:
• Cette commande trace un graphe en fonction des conditions actuelles.
DrawR-Con, DrawR-Plt Aucun paramètre
Fonction: Ces commandes utilisent les valeurs d’une table pour représenter graphiquement
une expression de récurrence avec an(bn ou cn) connecteur comme ordonnée et n comme
abscisse.
Description:
• Ces commandes tracent les graphes des expressions de récurrence en fonction des
conditions actuelles, avec an(bn ou cn) comme ordonnée et n comme abscisse.
• DrawR-Con produit un graphe à points connectés, tandis que DrawR-Plt produit un graphe
à points séparés.
19990401
8-5-14
Guide des commandes
DrawRΣ-Con, DrawRΣ-Plt Aucun paramètre
Fonction: Ces commandes utilisent les valeurs d’une table pour représenter graphiquement
une expression de récurrence avec Σan(Σbn ou Σcn) connecteur comme ordonnée et n
comme abscisse.
Description:
• Ces commandes représentent graphiquement des expressions récurrentes avec Σan(Σbn
ou Σcn) comme ordonnée et n comme abscisse.
•DrawRΣ-Con produit un graphe à points connectés tandis que DrawRΣ-Plt produit un
graphe à points séparés.
DrawStat
Fonction: Trace un graphe statistique.
Syntaxe: Voir “8-6-9 Utilisation de calculs et de graphes statistiques dans un programme”.
Description:
Cette commande trace un graphe statistique en fonction des conditions de graphe statistique
actuelles.
DrawWeb
Fonction: Cette commande représente graphiquement la convergence/divergence d’une
expression récurrente (graphe WEB).
Syntaxe: DrawWeb <type de récurrence>, <nombre de lignes>
Exemple: DrawWeb an+1 (bn+1 ou cn+1), 5
Description:
• Cette commande représente graphiquement la convergence/divergence d’une
expression récurrente (graphe WEB).
• L’omission de la définition du nombre de lignes impose automatiquement 30, la valeur
par défaut.
19990401
8-5-15
Guide des commandes
kCommandes d’entrée/sortie (I/O)
Getkey
Fonction: Cette commande se comporte comme une variable qui prend la valeur
correspondant au code de la dernière touche activée.
Syntaxe: Getkey
Exemple: Se brancher sur les Lbl 1, Lbl 2 ou Lbl
3, dans une boucle en appuyant sur
les touches 1, 2 ou 3
Lbl 0
If Getkey = 72
Then Goto 1
IfEnd
If Getkey = 62
Then Goto 2
IfEnd
If Getkey = 52
Then Goto 3
IfEnd
Goto 0
• La boucle tournera sur elle-même tant qu’il n’y
aura pas d’appui sur une touche.
64
79
78 68 58 48
77 67 57 47
76 66 56 46
75
74 54 44
6373 53 43 33
6272 52 42 32
6171 51 41 31
65 55 45
36
35
26
25
69 59 49 39 29
28
38 27
37
19990401
8-5-16
Guide des commandes
Locate
Fonction: Cette commande affiche des caractères alphanumériques à une position précise
de l’écran de texte.
Syntaxe: Locate <numéro de colonne>, <numéro de ligne>, <valeur>
Locate <numéro de colonne>, <numéro de ligne>, <expression numérique>
Locate <numéro de colonne>, <numéro de ligne>, ”<chaîne>”
[Exemple] Locate 1, 1, ”AB”_
Paramètres:
• Numéro de ligne: numéro de 1 à 7
• Numéro de colonne: numéro de 1 à 21
• Valeur et expression numérique
• Chaîne: chaîne de caractères
Description:
• Cette commande affiche des valeurs (y compris le contenu des variables) ou du texte à
une position précise de l’écran de texte. Si un calcul est introduit, le résultat de ce calcul
sera affiché.
• La ligne est désignée par une valeur de 1 à 7 et la colonne est désignée par une valeur
de 1 à 21.
(1, 1) → ← (21, 1)
(1, 7) → ← (21, 7)
Exemple: Cls_
Locate 7, 1, ”CASIO FX”
Ce programme affiche le texte “CASIO FX” au centre de l’écran.
• Dans certains cas, la commande ClrText doit être exécutée avant de mettre le programme
précédent en route.
19990401
8-5-17
Guide des commandes
kCommandes entrées/sorties avec un analyseur (CASIO Data Analyzer)
Receive ( / Send (
Fonction: Cette commande reçoit les données d’un analyseur (CASIO Data Analyzer) et
envoie des données à un analyseur (CASIO Data Analyzer).
Syntaxe: Recevoir (<données>) / Envoyer (<données>)
Description:
• Cette commande reçoit des données et envoie des données à un analyseur (CASIO Data
Analyzer).
• Les types de données suivantes peuvent être reçues (envoyées) par cette commande.
• Valeurs individuelles affectées aux variables
• Données de matrices (toutes les valeurs - des valeurs individuelles ne peuvent pas être
désignées)
• Données de listes (toutes les valeurs - des valeurs individuelles ne peuvent pas être
désignées)
19990401
8-5-18
Guide des commandes
kOpérateurs relationnels avec saut conditionnel (REL)
=,
GG
GG
G
, >, <, ≥, ≤
Fonction: Les opérateurs relationnels sont utilisés communément avec la commande de
saut conditionnel.
Syntaxe:
Paramètres:
Côté gauche/côté droit: variable (A à Z, r,
θ
), constante numérique, expression avec
variable (comme: A × 2)
opérateur relationnel: =,
GG
GG
G
, >, <, ≥, ≤
<côté gauche> <opérateur relationnel> <côté droit>

19990401
8-6-1
Utilisation des fonctions de la calculatrice dans un programme
8-6 Utilisation des fonctions de la calculatrice
dans un programme
kAffichage de texte
Il suffit de mettre un texte entre guillemets pour l’inclure dans un programme. Ce texte sera
affiché pendant l’exécution du programme, ce qui signifie que vous pouvez ajouter des
labels pour entrer des messages et résultats.
Programme Affichage
”CASIO” CASIO
? → X?
”X =” ? → X X = ?
• Si le texte est suivi d’une formule de calcul, n’oubliez pas d’insérer une commande
d’affichage (^) entre le texte et le calcul.
• La saisie de plus de 21 caractères fait passer à la ligne suivante. L’écran défile
automatiquement si le texte remplit tout l’écran.
kUtilisation d’opérations sur les lignes d’une matrice dans un
programme
Ces commandes vous permettent de travailler sur les lignes d’une matrice dans un
programme.
• Pour ce programme, accédez au mode RUN • MAT et utilisez l’éditeur MAT pour
indiquer la matrice, puis accédez au mode PRGM pour écrire le programme.
• Appuyez sur 3(MAT).
uPour échanger le contenu de deux lignes (Swap)
Exemple 1 Échanger les valeurs de la ligne 2 et de la ligne 3 dans la matrice
suivante:
12
Matrice A = 34
56
La syntaxe utilisée pour ce programme est la suivante.
Swap A, 2, 3_
Nom de la matrice
L’exécution de ce programme produit le résultat suivant.
Lignes à échanger
Mat A
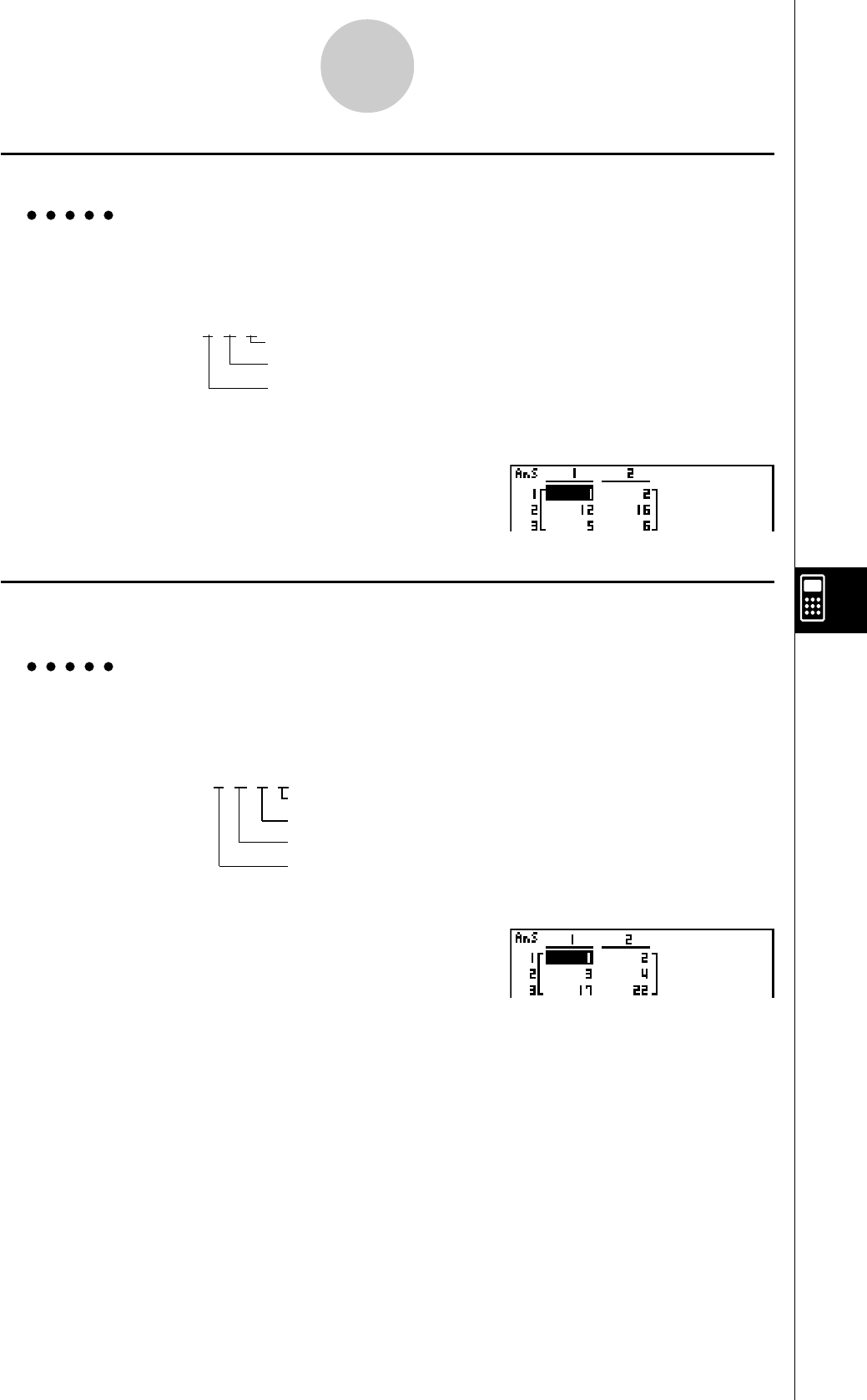
19990401
uPour calculer un produit scalaire (``
``
`Row)
Exemple 2 Calculer le produit scalaire de la ligne 2 de la matrice dans l’exemple
1, en le multipliant par 4
La syntaxe utilisée pour ce programme est la suivante.
`Row 4, A, 2_
L’exécution de ce programme produit le résultat suivant.
uPour calculer le produit scalaire et ajouter le résultat à une autre ligne
(``
``
`Row+)
Exemple 3 Calculer le produit scalaire de la ligne 2 de la matrice citée dans
l’exemple 1, en le multipliant par 4, et ajouter le résultat à la ligne 3
La syntaxe utilisée pour ce programme est la suivante.
`Row+ 4, A, 2, 3_
L’exécution de ce programme produit le résultat suivant.
8-6-2
Utilisation des fonctions de la calculatrice dans un programme
Ligne
Nom de la matrice
Multiplicateur
Mat A
Mat A
Nom de la matrice
Multiplicateur
Lignes à ajouter
Ligne pour laquelle le produit scalaire doit être calculé.
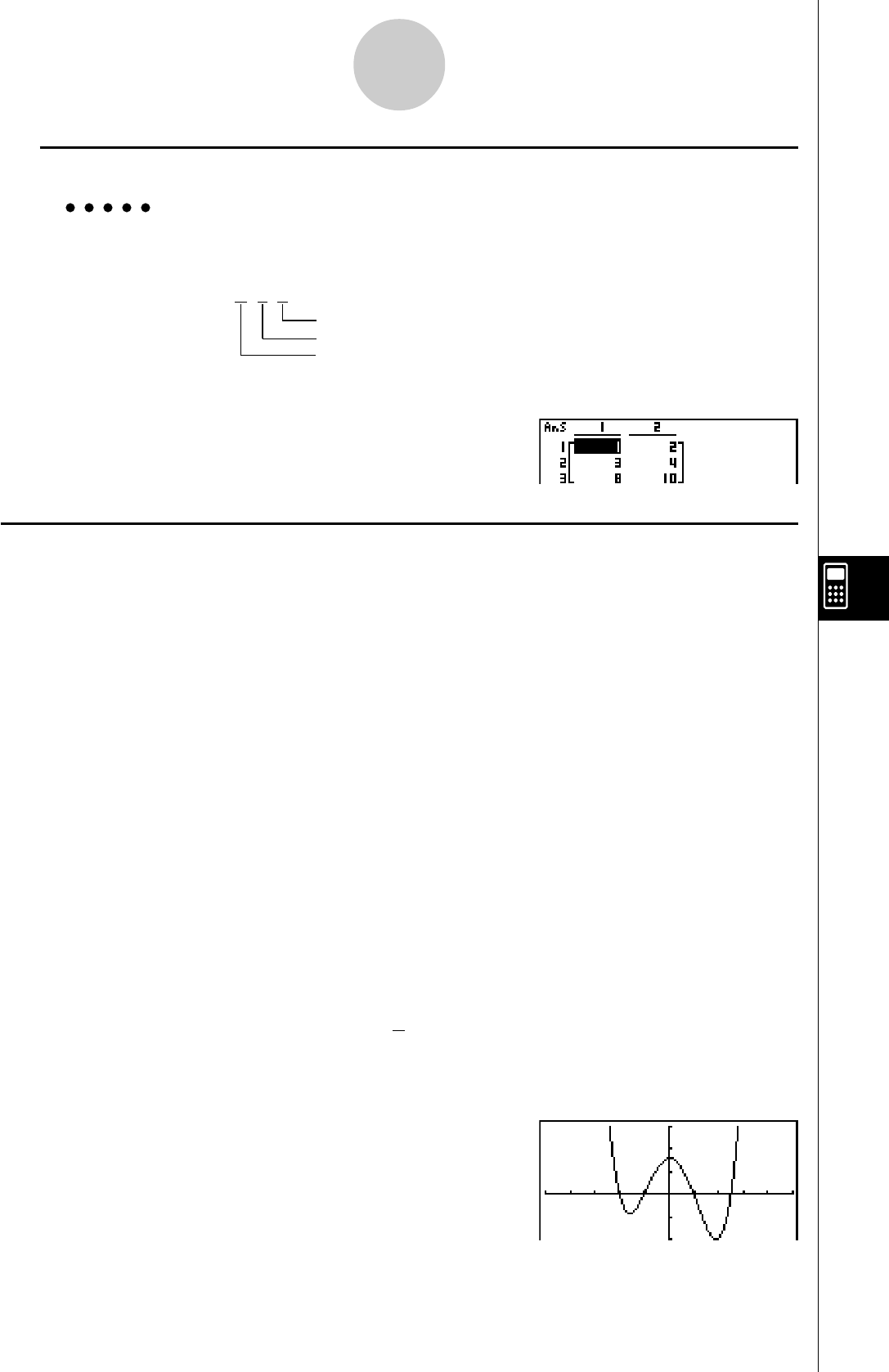
19990401
uPour additionner deux lignes (Row+)
Exemple 4 Additionner la ligne 2 et la ligne 3 de la matrice citée dans l’exemple 1
La syntaxe utilisée pour ce programme est la suivante.
Row+ A, 2, 3_
L’exécution de ce programme produit le résultat suivant.
kk
kk
kUtilisation de fonctions graphiques dans un programme
• m PRGM w6(g)1(GRPH)
Vous pouvez intégrer des fonctions graphiques dans un programme pour tracer des graphes
complexes, puis superposer plusieurs graphes. Les différentes syntaxes nécessaires pour la
programmation de fonctions graphiques sont les suivantes.
• Fenêtre d’affichage
View Window –5, 5, 1, –5, 5, 1_
• Saisie de la fonction graphique
Y = Type_............... Définit le type de graphe.
”X2 – 3” → Y1_
• Tracé de graphe
DrawGraph_
Exemple de programme
1ClrGraph_1 !J661ci
2View Window –10, 10, 2, –120, 150, 50_2 !K1i
3Y = Type_3 61db
”X^4–X^3–24X2 + 4X + 80” @ Y1_4 J4bi
4
5G SelOn 1_5 61b
6DrawGraph 6 !J662c
L’exécution du programme produit le résultat indiqué ici.
8-6-3
Utilisation des fonctions de la calculatrice dans un programme
Nom de la matrice
Lignes à ajouter
Ligne pour laquelle le produit scalaire doit être calculé.
• Les commandes soulignées
sont obtenues par l’appui sur les
touches suivant le numéro
correspondant, par exemple 2.
Mat A

19990401
8-6-4
Utilisation des fonctions de la calculatrice dans un programme
uSyntaxe d’autres fonctions de représentation graphique
• V-Window
View Window <Xmin>, <Xmax>, <Xscale>, <Ymin>, <Ymax>, <Yscale>,
<T
θ
min>, <T
θ
max>, <T
θ
pitch>
StoV-Win <zone de V-Win> ............ zone: 1 à 6
RclV-Win <zone de V-Win>............. zone: 1 à 6
• Zoom
Factor <facteur X>, <facteur Y>
ZoomAuto ........... Aucun paramètre
• Pict
StoPict <zone de l’image> .............. zone: 1 à 20
RclPict <zone de l’image> .............. zone: 1 à 20
• Sketch
PlotOn <abscisse X>, <ordonnée Y>
PlotOff <abscisse X>, <ordonnée Y>
PlotChg <abscisse X>, <ordonnée Y>
PxlOn<numéro de ligne>, <numéro de colonne>
PxlOff<numéro de ligne>, <numéro de colonne>
PxlChg<numéro de ligne>, <numéro de colonne>
PxlTest( <numéro de ligne>, <numéro de colonne>[)]
F-Line <abscisse X 1>, <ordonnée Y 1>, <abscisse X 2>, <ordonnée Y 2>
Text <numéro de ligne>, <numéro de colonne>, ”<texte>”
Text <numéro de ligne>, <numéro de colonne>, <expression>
Tangent <fonction>, <abscisse X>
Normal <fonction>, <abscisse X>
Inverse <fonction>
Circle <abscisse X du point central>, <ordonnée Y du point central>,
<valeur R du rayon>
Vertical <abscisse X>
Horizontal <ordonnée Y>
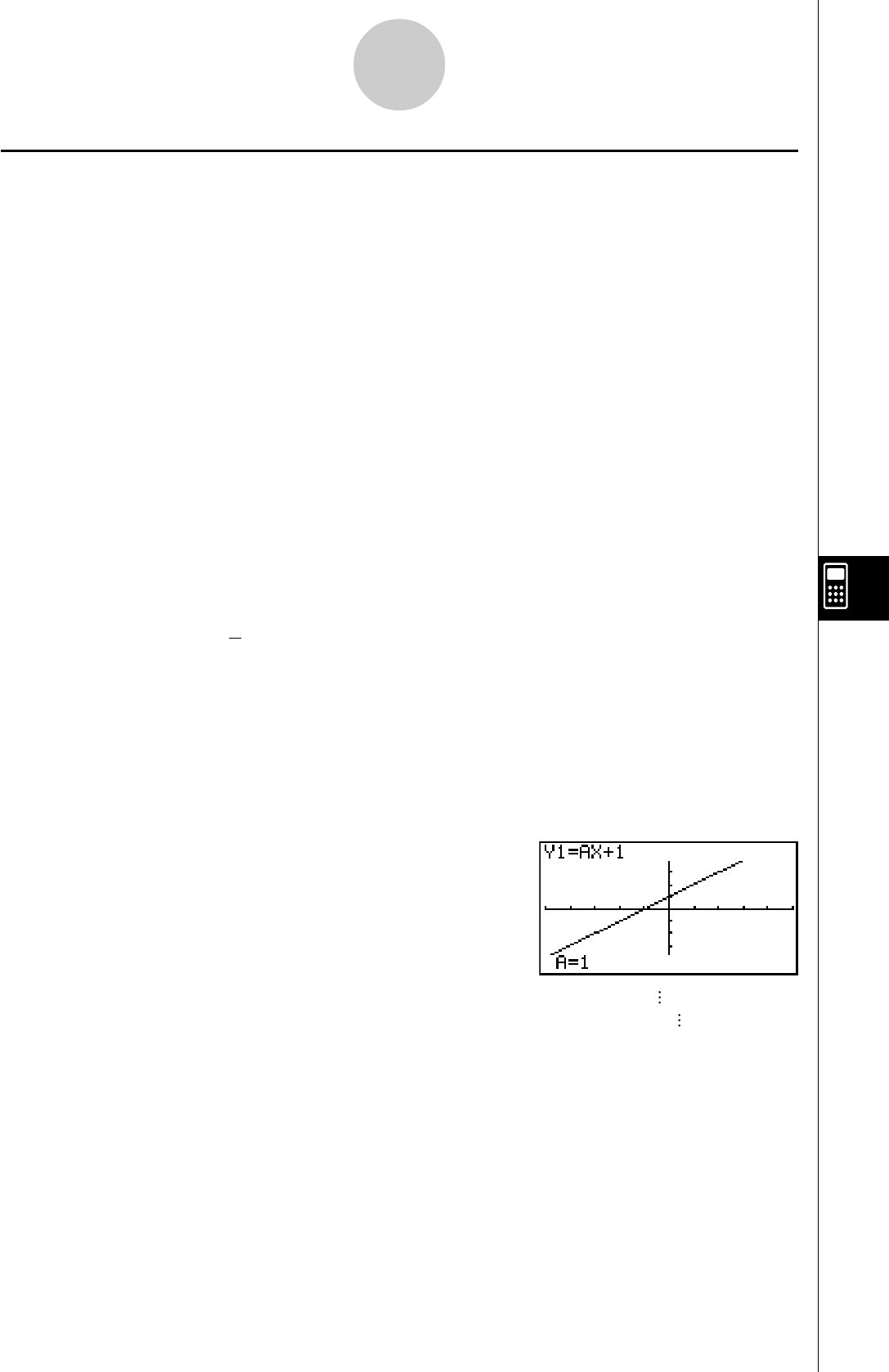
19990401
kk
kk
kUtilisation des fonctions de graphe dynamique dans un programme
L’utilisation des fonctions de graphe dynamique dans un programme permet de répéter les
tracés d’un graphe dynamique. La définition de la plage du graphe dynamique à l’intérieur
d’un programme s’effectue de la façon suivante.
• m PRGM w6(g)2(DYNA)
• Plage du graphe dynamique
1 → D Start_
5 → D End_
1 → D pitch_
Exemple du programme
ClrGraph_
View Window –5, 5, 1, –5, 5, 1_
Y = Type_
”AX + 1” → Y1_1 J4bi
1
2D SelOn 1_2 62b
3D Var A_3 2d
1 → 4 D Start_4 J5b
5 → 5 D End_5 5c
1 → 6 D pitch_6 5d
7DrawDyna 7 !J662d
L’exécution du programme produit le résultat indiqué ici.
↑
↓
8-6-5
Utilisation des fonctions de la calculatrice dans un programme
• Les commandes soulignées sont
obtenues par l’appui sur les
touches suivant le numéro
correspondant, par exemple 2.
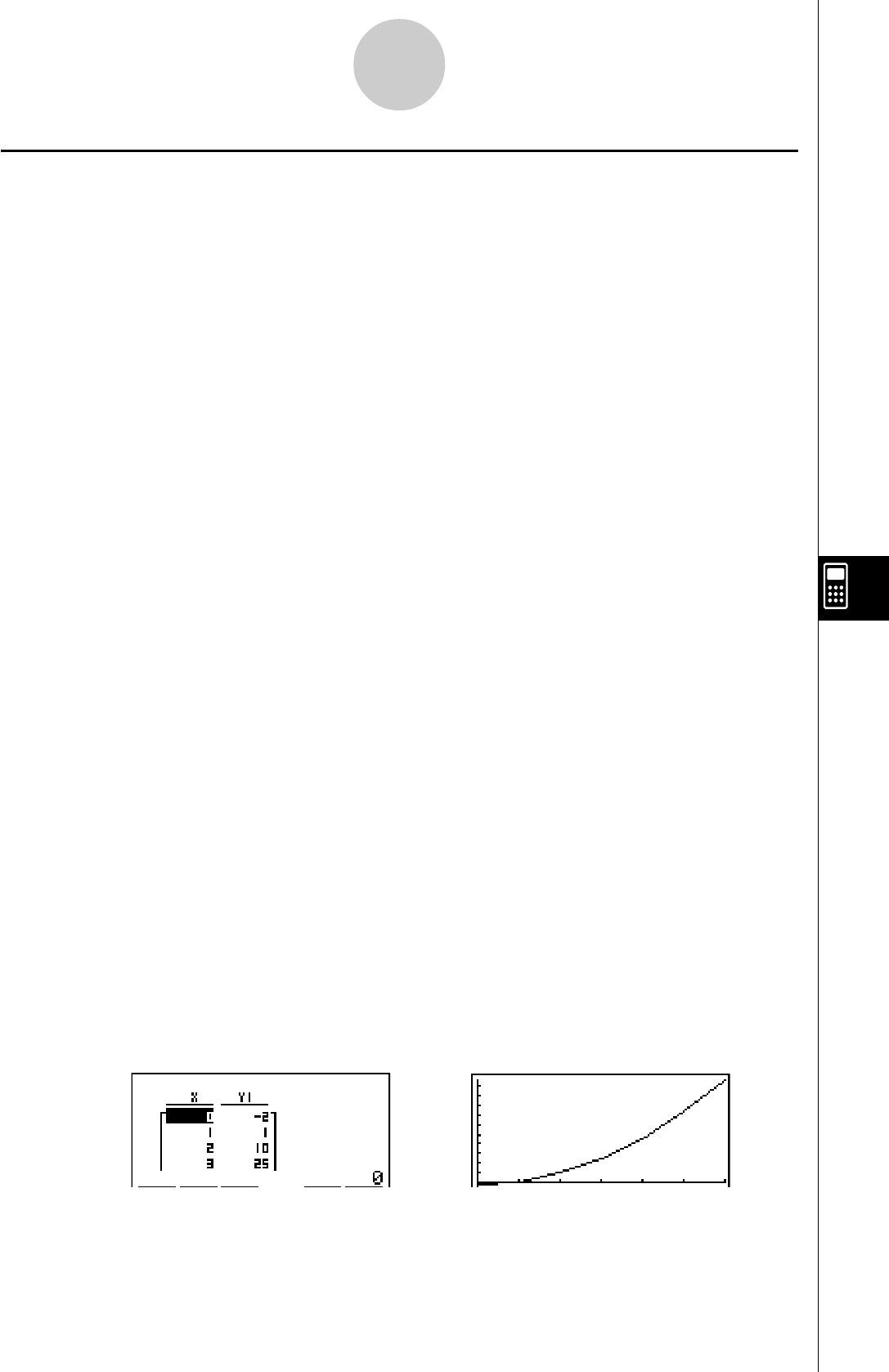
19990401
kk
kk
kUtilisation des fonctions de table et graphe dans un programme
• m PRGM w6(g)1(GRPH)
L’utilisation des fonctions de table et graphe dans un programme permet de créer des
tables numériques et d’effectuer des opérations graphiques. Les différentes syntaxes
nécessaires lors de la programmation de fonctions avec table et graphe sont les suivantes.
• Définition de la plage de la table
1 → F Start_
5 → F End_
1 → F pitch_
• Génération d’une table numérique
DispF-Tbl_
• Tracé de graphe
Graphe à points connectés: DrawFTG-Con_
Graphe à points séparés: DrawFTG-Plt_
Exemple de programme
ClrGraph_
ClrText_
View Window 0, 6, 1, –20, 106, 10_
Y = Type_
”3X2 – 2” → Y1_
1G SelOn 1_1 61b
0 → 2 F Start_2 J61b
6 → 3 F End_3 1c
1 → 4 F pitch_4 1d
5DispF-Tbl^5 !J662eb
6DrawFTG-Con 6 !J662ec
L’exécution du programme produit le résultat indiqué ici.
Table numérique Graphe
8-6-6
Utilisation des fonctions de la calculatrice dans un programme

19990401
kk
kk
kUtilisation des fonctions de table et graphe de récurrence dans un
programme
• m PRGM w6(g)3(RECR)
L’intégration de fonctions de table et graphe de récurrence dans un programme permet de
créer des tables numériques et d’effectuer des opérations graphiques. Les différentes
syntaxes nécessaires lors de la programmation de fonctions avec table et graphe de
récurrence sont les suivantes.
• Saisie de la formule de récurrence
an+1 Type_..... Définit le type de récurrence.
”3an + 2” → an+1_
”4bn + 6” → bn+1_
• Définition de la plage de la table
1 → R Start_
5 → R End_
1 → a0_
2 → b0_
1 → an Start_
3 → bn Start_
• Génération d’une table numérique
DispR-Tbl_
• Tracé de graphe
Graphe à points connectés: DrawR-Con_, DrawRΣ-Con_
Graphe à points séparés: DrawR-Plt_, DrawRΣ-Plt_
• Graphe statistique de convergence/divergence (graphe WEB)
DrawWeb an+1, 10_
8-6-7
Utilisation des fonctions de la calculatrice dans un programme
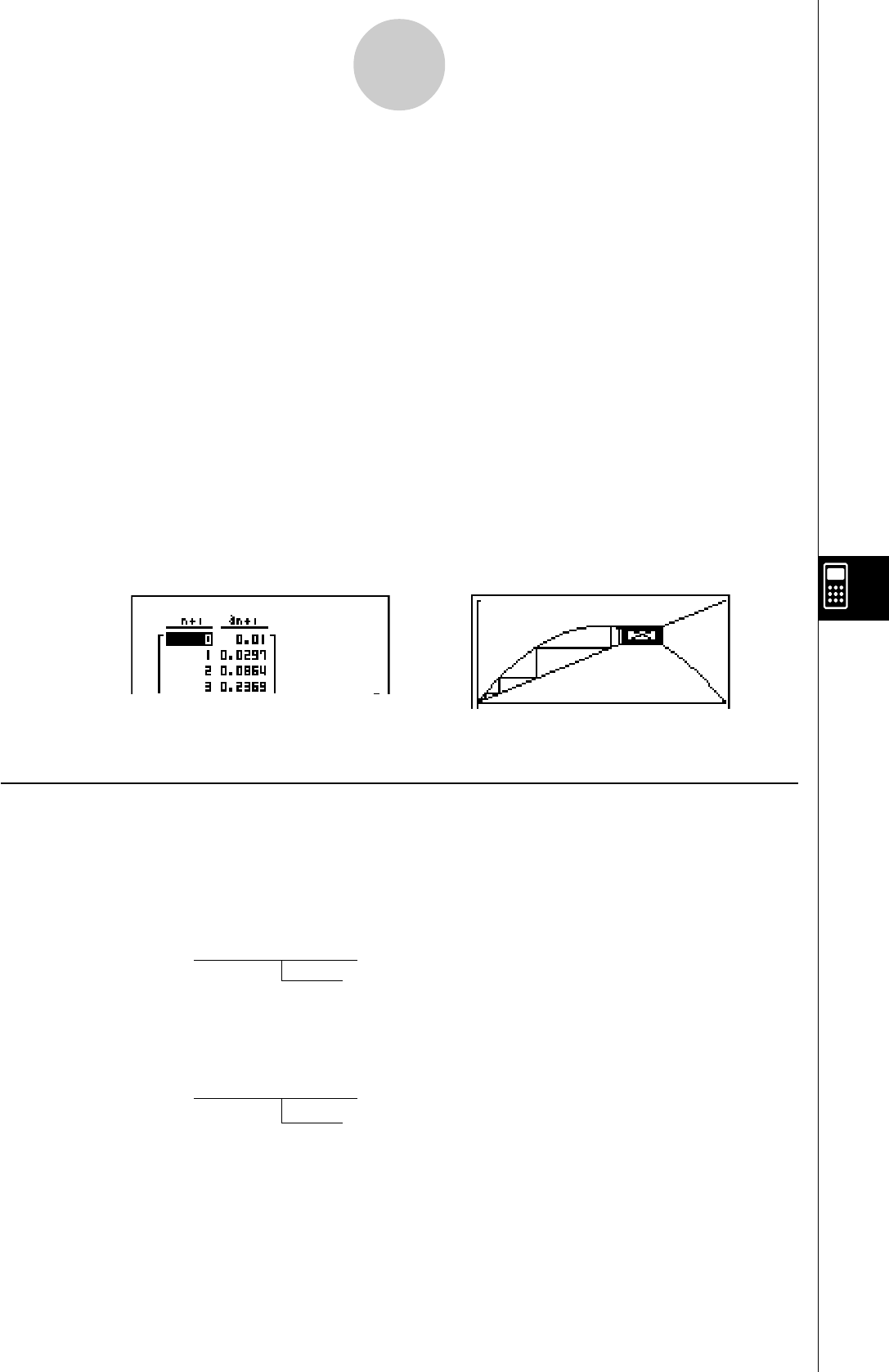
19990401
8-6-8
Utilisation des fonctions de la calculatrice dans un programme
Exemple de programme
View Window 0, 1, 1, –0.2, 1, 1_
1an+1 Type_
23
”–3an2 + 3an” → an+1_
0 → R Start_
6 → R End_
0.01 → a0_
0.01 → an Start_
8DispR-Tbl^
0
9DrawWeb an+1, 30
L’exécution du programme produit le résultat indiqué ici.
Table numérique Graphe de récurrence
kk
kk
kUtilisation des fonctions de classement de listes dans un programme
Cette commande vous permet de classer les données de listes dans un ordre ascendant
ou descendant.
• Ordre ascendant
12
SortA (List 1, List 2, List 3)
Listes à classer (six listes au maximum)
1 5b 2 4e
• Ordre descendant
3
SortD (List 1, List 2, List 3)
Listes à classer (six listes au maximum)
3 5c
4
5
6
1 63gc
2 3bc
3 3bd
4 J62cb
5 2cc
6 2cd
7 2cC
8 !J662fb
9 2fci
0 63bd
7

19990401
kk
kk
kUtilisation de la fonction de résolution dans un programme
La syntaxe requise pour l’utilisation de la fonction de résolution dans un programme est la
suivante.
Solve( f(x), n, a, b)
Limite supérieure
Limite inférieure
Valeur initiale estimée
Exemple de programme
1Solve( 2X2 + 7X – 9, 1, 0, 1) 1K4h
• Dans la fonction f(x), seul X peut être utilisé comme variable dans les expressions. Les
autres variables (A à Z, r,
θ
) sont traitées comme constantes, et la valeur actuellement
affectée à la variable est appliquée pendant le calcul.
• La saisie de la fermeture de parenthèses, de la limite inférieure a et de la limite supérieure
b peut être omise.
kk
kk
kUtilisation de calculs et de graphes statistiques dans un programme
L’insertion de calculs et de graphes statistiques dans un programme vous permet de
calculer et de représenter graphiquement des données statistiques.
u Pour définir les conditions et tracer un graphe statistique
Après “StatGraph”, vous devez définir les conditions suivantes:
• Statut avec tracé ou sans tracé de graphe (DrawOn/DrawOff)
• Type de graphe
• Emplacement des données sur l’axe x (nom de liste)
• Emplacement des données sur l’axe y (nom de liste)
• Emplacement des données de fréquence (nom de liste)
• Type de point
8-6-9
Utilisation des fonctions de la calculatrice dans un programme
# Les solutions obtenues lorsqu'on utilise la
résolution peuvent contenir des erreurs.
# Vous ne pouvez pas utiliser une valeur de
différentielle, différentielle quadratique,
intégration, Σ, valeur maximale/minimale ou
une expression de calcul de résolution dans
un terme du calcul avec résolution.

19990401
Les conditions de tracé du graphe dépendent du type de graphe. Voir “Changement des
paramètres d’un graphe” (page 6-1-2).
• La définition typique d’un diagramme de dispersion ou d’un graphe linéaire xy est la
suivante.
S-Gph1 DrawOn, Scatter, List 1, List 2, 1, Square _
Dans le cas d’un graphe linéaire xy, remplacez “Scatter” dans la définition précédente par
“xyLine”.
• La définition typique d’un graphe de probabilité normale est la suivante.
S-Gph1 DrawOn, NPPlot, List 1, Square _
• La définition typique d’un graphe à variable unique est la suivante.
S-Gph1 DrawOn, Hist, List 1, List 2 _
Le même format peut être utilisé pour les types de graphes suivants en remplaçant
simplement “Hist” de la définition précédente par le type de graphe applicable.
Histogramme: ................................ Hist
Boîte-médiane: .............................. MedBox
Boîte modifiée:............................... Modified
Distribution normale: ..................... N-Dist
Ligne brisée: .................................. Broken
• La définition typique d’un graphe de régression est la suivante.
S-Gph1 DrawOn, Linear, List 1, List 2, List 3 _
Le même format peut être utilisé pour les types de graphes suivants en remplaçant
simplement “Linear ” de la définition précédente par le type de graphe applicable.
Régression linéaire: ....................... Linear
Med-Med: ...................................... Med-Med
Régression quadratique: ............... Quad
Régression cubique: ...................... Cubic
Régression quartique: ................... Quart
Régression logarithmique: ............. Log
Régression exponentielle: ............. Exp
Régression de puissance: ............. Power
8-6-10
Utilisation des fonctions de la calculatrice dans un programme
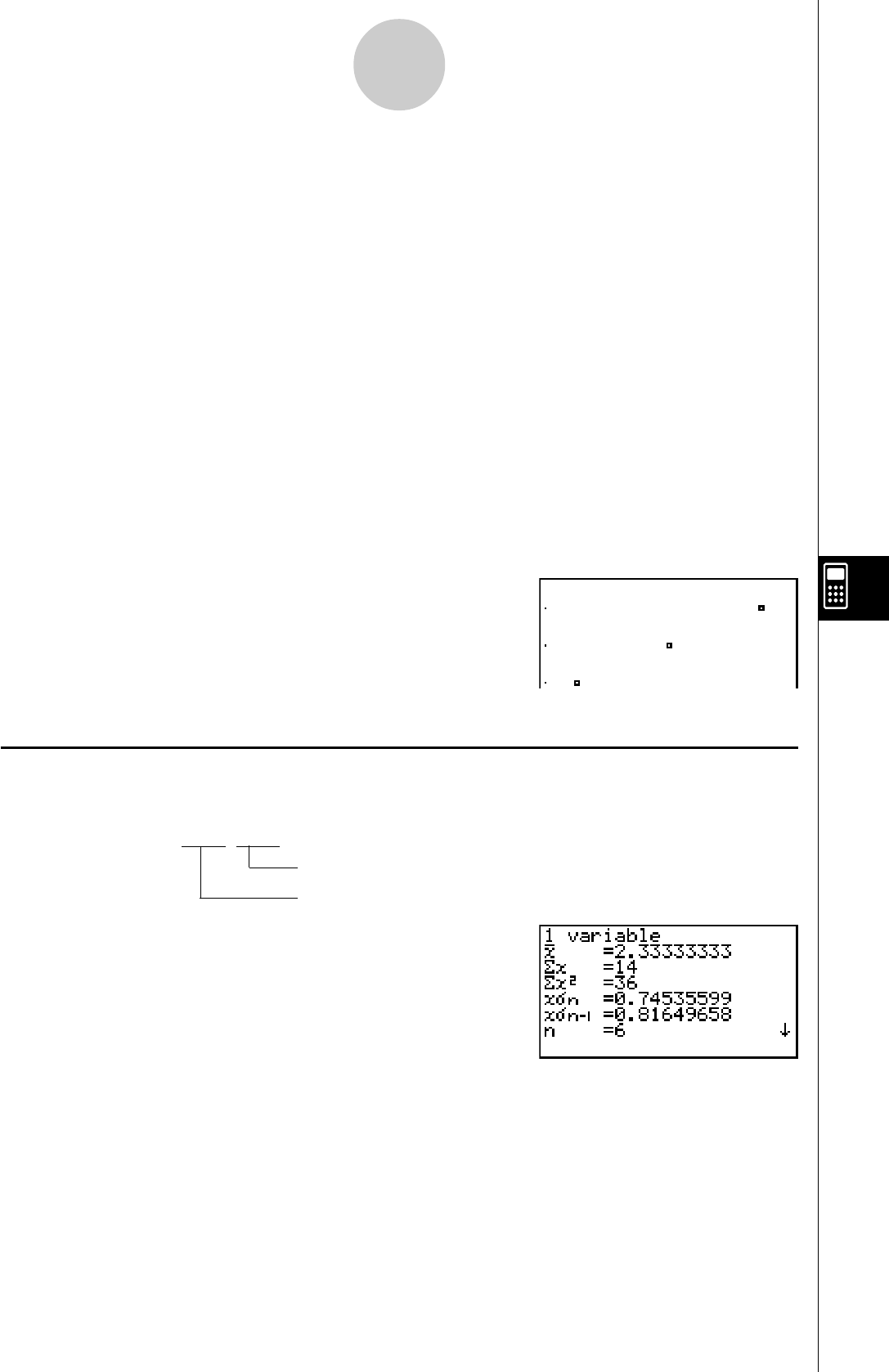
19990401
• La définition typique d’un graphe de régression sinusoïdale est la suivante.
S-Gph1 DrawOn, Sinusoidal, List 1, List 2 _
• La définition typique d’un graphe de régression logistique est la suivante.
S-Gph1 DrawOn, Logistic, List 1, List 2 _
Exemple de programme
ClrGraph_
1
S-Wind Auto_
{1, 2, 3} → List 1_
{1, 2, 3} → List 2_
23 4 5
S-Gph1 DrawOn, Scatter, List 1, List 2, 1, Square _
6
DrawStat
L’exécution de ce programme produit le diagramme
de dispersion indiqué ici.
kExécution de calculs statistiques
• Calcul statistique à variable unique
11-Variable List 1, List 2
Données de fréquence (Frequency)
Données de l’axe
x
(XList)
14gb
8-6-11
Utilisation des fonctions de la calculatrice dans un programme
1u35bbi
24bb
34cb
44db
54fb
6!J662b
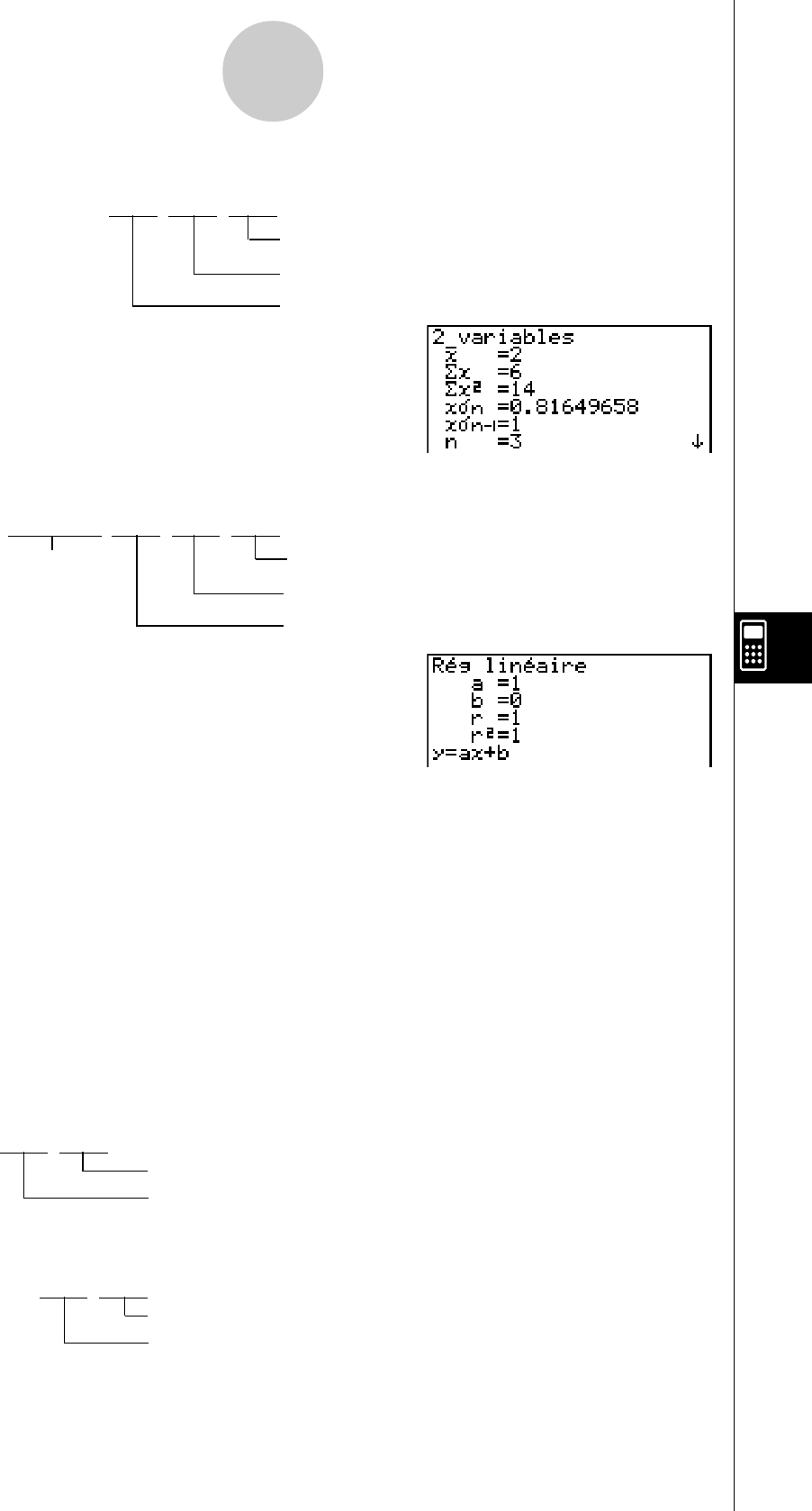
19990401
• Calcul statistique à variable double
12-Variable List 1, List 2, List 3
Données de fréquence (Frequency)
Données de l’axe
y
(YList)
Données de l’axe
x
(XList)
14gc
• Calcul statistique de régression
1LinearReg List 1, List 2, List 3
Type de Données de fréquence (Frequency)
calcul*Données de l’axe
y
(YList)
Données de l’axe
x
(XList)
14gd
* Vous pouvez définir comme type de calcul les paramètres suivants.
LinearReg .......... régression linéaire
Med-MedLine .... calcul Med-Med
QuadReg ........... régression quadratique
CubicReg........... régression cubique
QuartReg ........... régression quartique
LogReg .............. régression logarithmique
ExpReg ............. régression exponentielle
PowerReg .......... régression de puissance
8-6-12
Utilisation des fonctions de la calculatrice dans un programme
• Calcul statistique de régression sinusoïdale
SinReg List 1, List 2
• Calcul statistique de régression logistique
LogisticReg List 1, List 2
Données de l’axe
y
(YList)
Données de l’axe
x
(XList)
Données de l’axe
y
(YList)
Données de l’axe
x
(XList)

19990401
8-7-1
Liste des commandes de programmation
8-7 Liste des commandes de programmation
G_SelOn_
G_SelOff_
Y=TYPE
r=TYPE
ParamTYPE
X=cTYPE
Y>Type
Y<Type
Y
≥
Type
Y
≤
Type
StoGMEM
RclGMEM
D_SelOn_
D_SelOff_
D_Var_
Y=Type
r=Type
ParamType
n
an
an+
1
bn
bn+
1
cn
cn+
1
R_SelOn_
R_SelOff_
Sel_a
0
Sel_a
1
anType
an+
1
Type
an+
2
Type
SelOn
SelOff
TYPE
GMEM
SelOn
SelOff
Var
TYPE
n,an..
SelOn
SelOff
Sel a
0
Sel a
1
TYPE
Y=
r=
Param
X=c
Y>
Y<
Y>
Y<
Store
Recall
Y=
r=
Param
n
an
an+
1
bn
bn+
1
cn
cn+
1
an
an+
1
an+
2
Niveau 1
Niveau 2 Niveau 3
Commande
θθ
MAT
STAT
LIST
Swap
*Row
*Row+
Row+
S-GPH
DRAW
GRAPH
List
MARK
CALC
SortA
SortD
Swap_
*Row_
*Row+_
Row+_
S-Gph1_
S-Gph2_
S-Gph3_
DrawOn
DrawOff
Scatter
xyLine
NPPlot
Hist
MedBox
ModifiedBox
N-Dist
Broken
Linear
Med-Med
Quad
Cubic
Quart
Log
Exp
Power
Sinusoidal
Logistic
List_
Square
Cross
Dot
1-Variable_
2-Variable_
LinearReg_
Med-MedLine_
QuadReg_
CubicReg_
QuartReg_
LogReg_
ExpReg_
PowerReg_
SinReg_
LogisticReg_
SortA(
SortD(
S-Gph1
S-Gph2
S-Gph3
On
Off
Scat
xyLine
NPPlot
Hist
Box
ModBox
N-Dist
Broken
Linear
MedMed
Quad
Cubic
Quart
Log
Exp
Power
Sin
Lgstic
•
1VAR
2VAR
Linear
MedMed
Quad
Cubic
Quart
Log
Exp
Power
Sin
Lgstic
x!
nPr
nCr
Ran#
P(
Q(
R(
t(
sinh
cosh
tanh
sinh
–1
cosh
–1
tanh
–1
°
r
g
° ’ ”
'
DMS
Pol(
Rec(
m
n
fn
Factor
Auto
Cls
PLOT
LINE
GRAPH
Text
PIXEL
Tangnt
Normal
Invrse
Circle
Vert
Horz
Store
Recall
’
”
~
*
#
On
Off
Change
Plot
F-Line
Line
Y=
dx
On
Off
Change
Test
!
P
C
Ran#_
P(
Q(
R(
t(
sinh_
cosh_
tanh_
sinh
–1
_
cosh
–1
_
tanh
–1
_
°
r
g
° ’ ”
'
DMS
Pol(
Rec(
m
n
fn
Factor_
ZoomAuto
Cls
PlotOn_
PlotOff_
PlotChg_
Plot_
F-Line_
Line
Graph_Y=
Graph_
Text_
PxlOn_
PxlOff_
PxlChg_
PxlTest(
Tangent_
Normal_
Inverse_
Circle_
Vertical_
Horizontal_
StoPict_
RclPict_
’
”
~
*
#
Niveau 1
Niveau 2 Niveau 3
Commande
Touche [OPTN]
PROB
HYP
ANGL
STAT
FMEM
ZOOM
SKTCH
PICT
SYBL
° ’ ”
LIST
MAT
CPLX
CALC
NUM
List
Dim
Seq
Min
Max
Mean
Median
Sum
Prod
Cuml
%
AList
Augmnt
Fill
L→Mat
Mat
Dim
Det
Trn
Augmnt
Ident
Fill
M→List
Abs
Arg
Conjg
ReP
ImP
'
re^
i
'
a+bi
d/dx
d
2
/dx
2
dx
Σ
FMin
FMax
Solve
Abs
Int
Frac
Rnd
Intg
E-SYM
List_
Dim_
Seq(
Min(
Max(
Mean(
Median(
Sum_
Prod_
Cuml_
Percent_
AList_
Augment(
Fill(
List→Mat(
Mat_
Dim_
Det_
Trn_
Augment(
Identity_
Fill(
Mat→List(
Abs_
Arg_
Conjg_
ReP_
ImP_
'
re^ i
'
a+bi
d/dx(
d
2
/dx
2
(
(
Σ
(
FMin(
FMax(
Solve(
Abs_
Int_
Frac_
Rnd
Intg_
m
n
p
f
k
M
G
T
P
E
m
n
p
f
k
M
G
T
P
E
Programme RUN
∫∫
∫
∫
∫
μμ
GRPH
DYNA
RECR

19990401
Niveau 1
V-WIN
FACT
STAT
Niveau 2
Xmin
Xmax
Xscale
Xdot
Ymin
Ymax
Yscale
T min
T max
T ptch
R-Xmin
R-Xmax
R-Xscl
R-Xdot
R-Ymin
R-Ymax
R-Yscl
R-Tmin
R-Tmax
R-Tpch
Xfact
Yfact
n
X
Y
GRAPH
Niveau 3
x
Σx
Σx2
xσn
xσn–
1
minX
maxX
y
Σy
Σy2
Σxy
y
σ
n
y
σ
n–
1
minY
maxY
a
b
c
d
e
r
r2
Q1
Med
Q3
Mod
H-Strt
H-ptch
Commande
Touche [VARS]
GRPH
DYNA
TABL
RECR
EQUA
PTS
Yn
rn
Xtn
Ytn
Xn
Start
End
Pitch
Start
End
Pitch
Result
FORM
RANGE
Result
S-Rslt
S-Coef
P-Rslt
P-Coef
x1
y1
x2
y2
x3
y3
an
an+
1
an+
2
bn
bn+
1
bn+
2
cn
cn+
1
cn+
2
R-Strt
R-End
a0
a1
a2
b0
b1
b2
c0
c1
c2
anStrt
bnstrt
cnStrt
x1
y1
x2
y2
x3
y3
Y
r
Xt
Yt
X
D_Start
D_End
D_pitch
F_Start
F_End
F_pitch
F_Result
an
an+
1
an+
2
bn
bn+
1
bn+
2
cn
cn+
1
cn+
2
R_Start
R_End
a0
a1
a2
b0
b1
b2
c0
c1
c2
anStart
bnStart
cnStart
R_Result
Sim_Result
Sim_Coef
Ply_Result
Ply_Coef
Niveau 1
Prog
JUMP
?
^
I/O
IF
FOR
WHLE
CTRL
LOGIC
CLR
DISP
:
Niveau 2
Lbl
Goto
lsz
Dsz
Locate
Getkey
Send
Receiv
If
Then
Else
IfEnd
For
To
Step
Next
While
WhlEnd
Do
LpWhle
Prog
Return
Break
Stop
= G <
And
Or
Not
Text
Graph
List
Matrix
Stat
Graph
Dyna
F-TBL
R-TBL
Niveau 3
=
G
>
<
>
<
Table
G-Con
G-Plot
Table
Web
R-Con
RΣ-Con
R-Plot
RΣ-Plt
Commande
Prog_
Lbl_
Goto_
lsz_
Dsz_
?
^
Locate_
Getkey
Send(
Receive(
If_
Then_
Else_
IfEnd
For_
_To_
_Step_
Next
While_
WhileEnd
Do
LpWhile_
Prog_
Return
Break
Stop
=
G
>
<
>
<
_And_
_Or_
Not_
ClrText
ClrGraph
ClrList_
ClrMat_
DrawStat
DrawGraph
DrawDyna
DispF-Tbl
DrawFTG-Con
DrawFTG-Plt
DispR-Tbl
DrawWeb_
DrawR-Con
DrawR
Σ
-Con
DrawR-Plt
DrawR
Σ
-Plt
:
Touches [SHIFT] [VARS] (PRGM)
θ
θ
θ
θ
θ
θ
Xmin
Xmax
Xscl
Xdot
Ymin
Ymax
Yscl
T min
T max
T ptch
RightXmin
RightXmax
RightXscl
RightXdot
RightYmin
RightYmax
RightYscl
RightT min
RightT max
RightT ptch
Xfct
Yfct
n
x
Σ
x
Σ
x2
x
σ
n
x
σ
n–
1
minX
maxX
y
Σ
y
Σ
y2
Σ
xy
y
σ
n
y
σ
n–
1
minY
maxY
a
b
c
d
e
r
r2
Q1
Med
Q3
Mod
H_Start
H_pitch
θ
θ
θ
Niveau 1
ANGL
DISP
CPLX
GRPH
STAT
DERIV
T-VAR
Σ•DSP
Niveau 2
Deg
Rad
Gra
Fix
Sci
Norm
EngOn
EngOff
Real
a+bi
re^ i
G-FUNC
D-TYPE
BG
SIMUL
COORD
GRID
AXES
LABEL
S-WIN
File
RESID
On
Off
Range
List
On
Off
Niveau 3
On
Off
G-Con
G-Plot
None
Pict
On
Off
On
Off
On
Off
On
Off
On
Off
Auto
Manual
None
List
Commande
Deg
Rad
Gra
Fix_
Sci_
Norm
EngOn
EngOff
Real
a+bi
re^ i
FuncOn
FuncOff
G-Connect
G-Plot
BG-None
BG-Pict_
SimulOn
SimulOff
CoordOn
CoordOff
GridOn
GridOff
AxesOn
AxesOff
LabelOn
LabelOff
S-WindAuto
S-WindMan
File_
Resid-None
Resid-List_
DerivOn
DerivOff
VarRange
VarList_
Σ
dispOn
Σ
dispOff
Touches [CTRL][F3](SET UP)
θθ
θ
8-7-2
Liste des commandes de programmation
19990401
Niveau 1
d~o
LOG
DISP
Niveau 2
d
h
b
o
Neg
Not
and
or
xor
xnor
'
Dec
'
Hex
'
Bin
'
Oct
Niveau 3
Commande
d
h
b
o
Neg_
Not_
and
or
xor
xnor
'
Dec
'
Hex
'
Bin
'
Oct
Niveau 1
Dec
Hex
Bin
Oct
Niveau 2 Niveau 3
Commande
Dec
Hex
Bin
Oct
Touches [CTRL][F3](SETUP)
Niveau 1
V-Win
Sto
Rcl
Niveau 2 Niveau 3
Commande
ViewWindow_
StoV-Win_
RclV-Win_
Touche [SHIFT][OPTN](V-Window)
Programme BASE
Level 1
Prog
JUMP
?
^
= G <
:
Level 2
Lbl
Goto
lsz
Dsz
=
G
>
<
>
<
Level 3 Command
Prog_
Lbl_
Goto_
lsz_
Dsz_
?
^
=
G
>
<
>
<
:
[SHIFT][VARS](PRGM) key
8-7-3
Liste des commandes de programmation
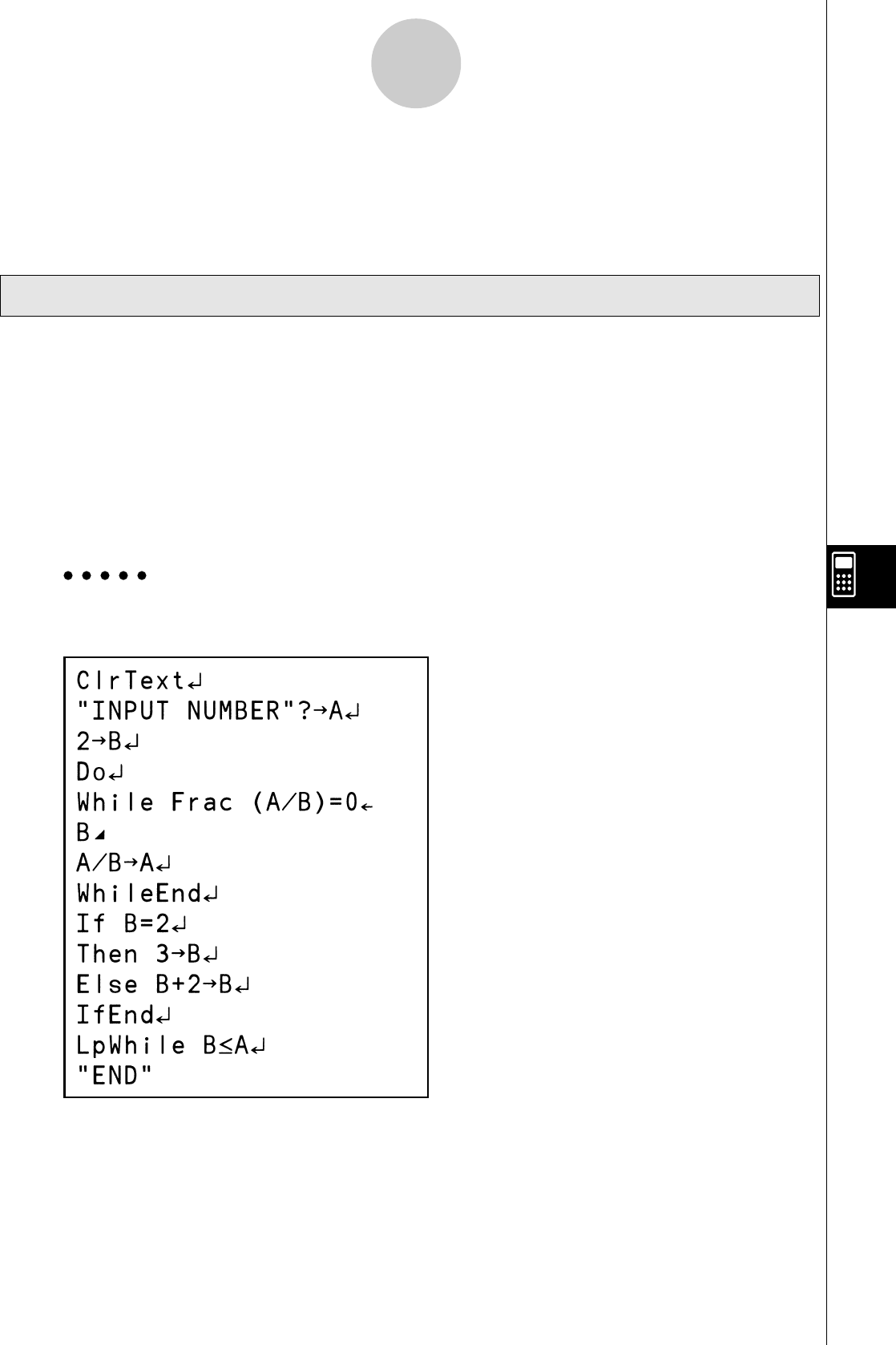
19990401
8-8-1
Bibliothèque de programmes
8-8Bibliothèque de programmes
• Vérifiez le nombre d’octets libres dans la mémoire avant d’essayer d’utiliser un
programme.
Description
Ce programme divise continuellement un nombre naturel par des facteurs jusqu’à ce que
tous ses facteurs premiers soient produits.
But
Ce programme accepte la saisie d’un nombre naturel A et le divise par B (2, 3, 5, 7…) pour
trouver les facteurs premiers de A.
• Si une division ne produit pas de reste, le résultat de l’opération sera affecté à A.
• L’opération précédente se répète jusqu’à ce que B > A.
Exemple
440730 = 2 × 3 × 3 × 5 × 59 × 83
Nom du programme Décomposition en facteurs premiers
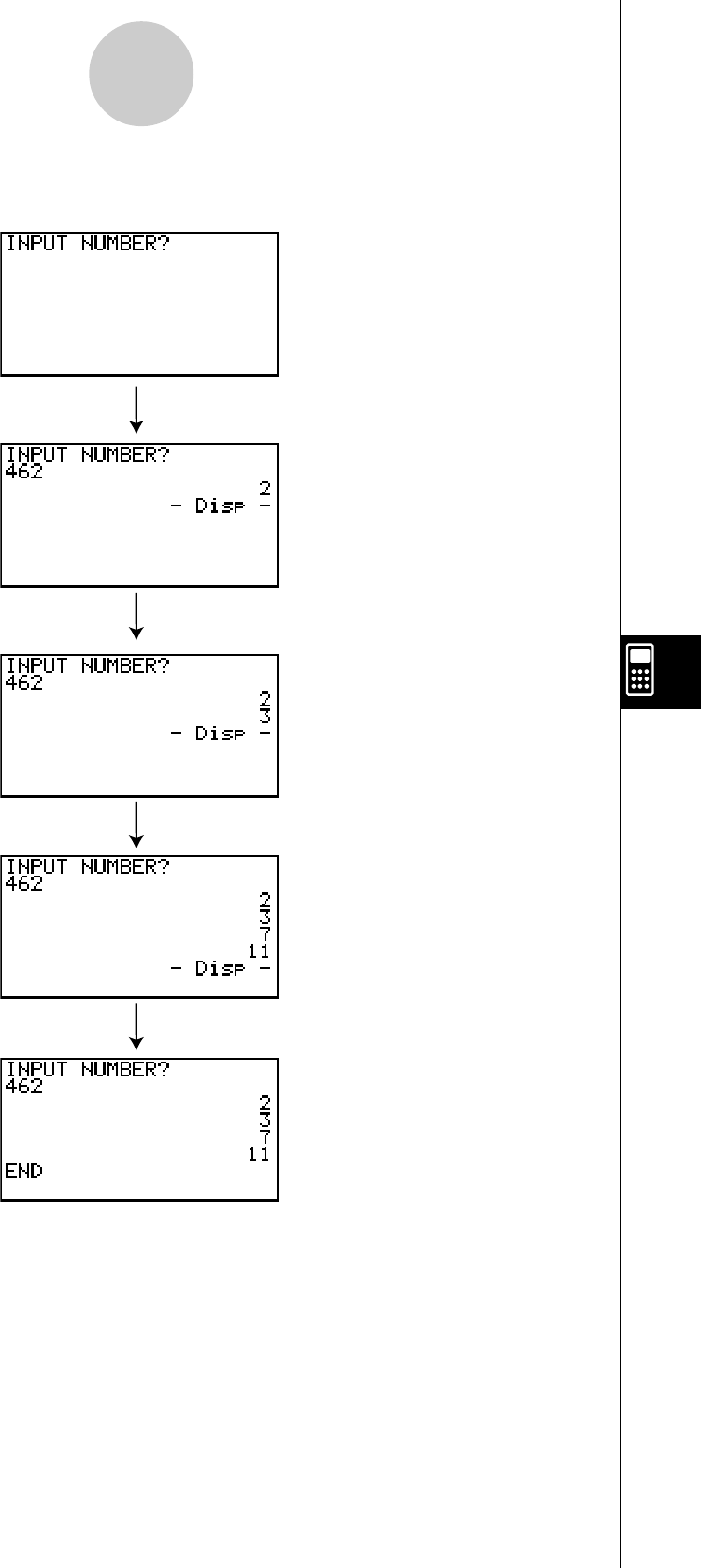
19990401
8-8-2
Bibliothèque de programmes
egcw
w
ww
w

19990401
Description
Après avoir saisi les termes d’une séquence 1, 2 et 3, ce programme détermine s’il s’agit
d’une séquence arithmétique ou géométrique en se fondant sur les différences et taux des
termes.
But
Ce programme détermine si une séquence particulière est une séquence arithmétique ou
géométrique.
Exemple 1 5, 10, 15, ... Séquence arithmétique
Exemple 2 5, 10, 20, ... Séquence géométrique
Nom du programme Différentiation arithmétique-géométrique d’une séquence
8-8-3
Bibliothèque de programmes
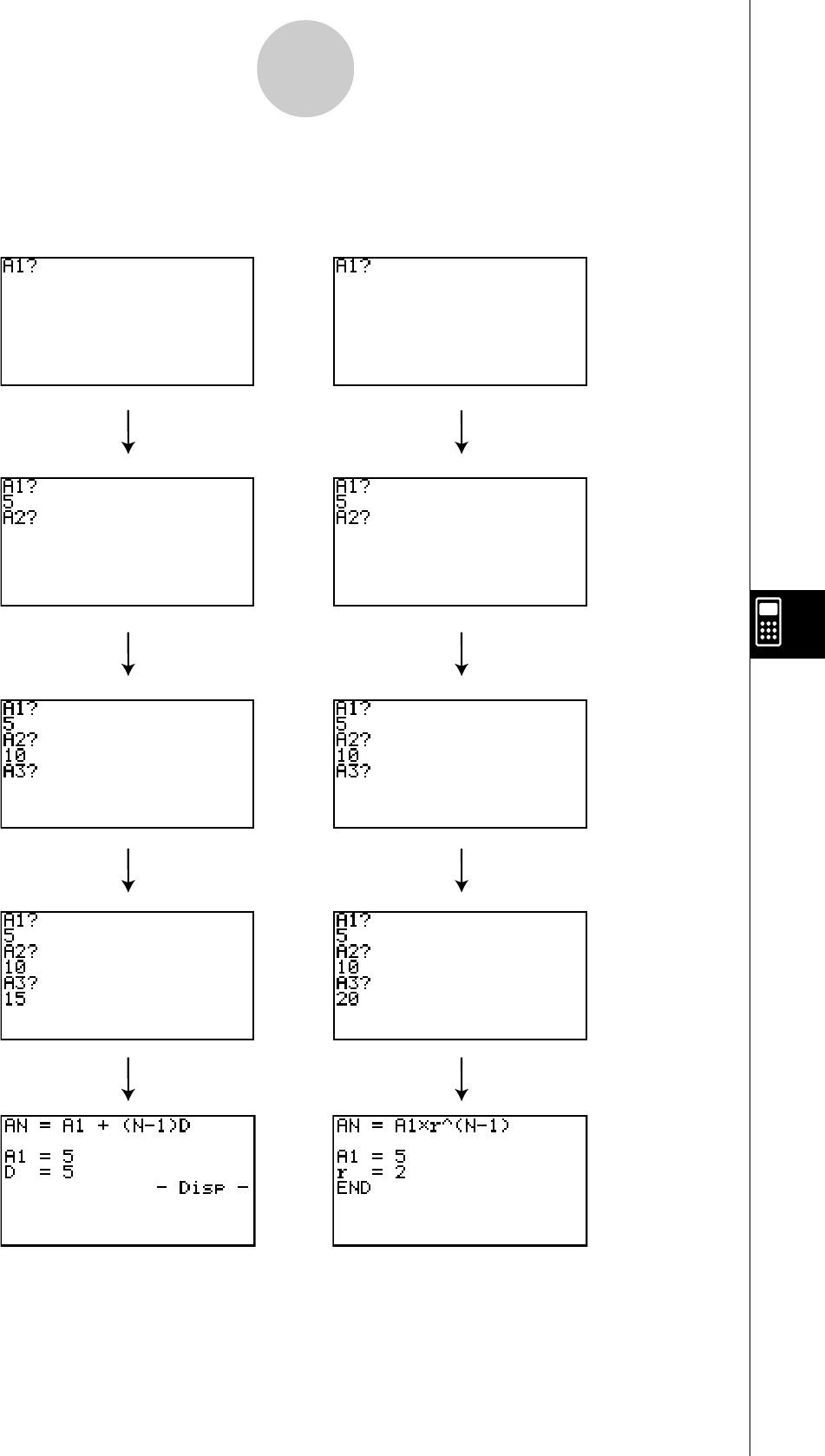
19990401
8-8-4
Bibliothèque de programmes
Exemple 1 Exemple 2
fw
baw
bf
w
fw
baw
ca
w

19990401
8-8-5
Bibliothèque de programmes
Description
Ce programme affiche une table des valeurs suivantes, basée sur la saisie des foyers d’une
ellipse, la somme de la distance entre les losi et les foyers et l’échelle (pas) de X.
Y1: Valeurs des coordonnées de la partie supérieure de l’ellipse
Y2: Valeurs des coordonnées de la partie inférieure de l’ellipse
Y3: Distance entre le foyer et loci droits
Y4: Distance entre le foyer et loci gauches
Y5: Somme de Y3 et Y4
Le programme place ensuite les loci et les valeurs dans Y1 et Y2.
But
Ce programme montre que les sommes des
distances entre les loci et deux foyers d’une
ellipse sont égales.
Nom du programme Ellipse
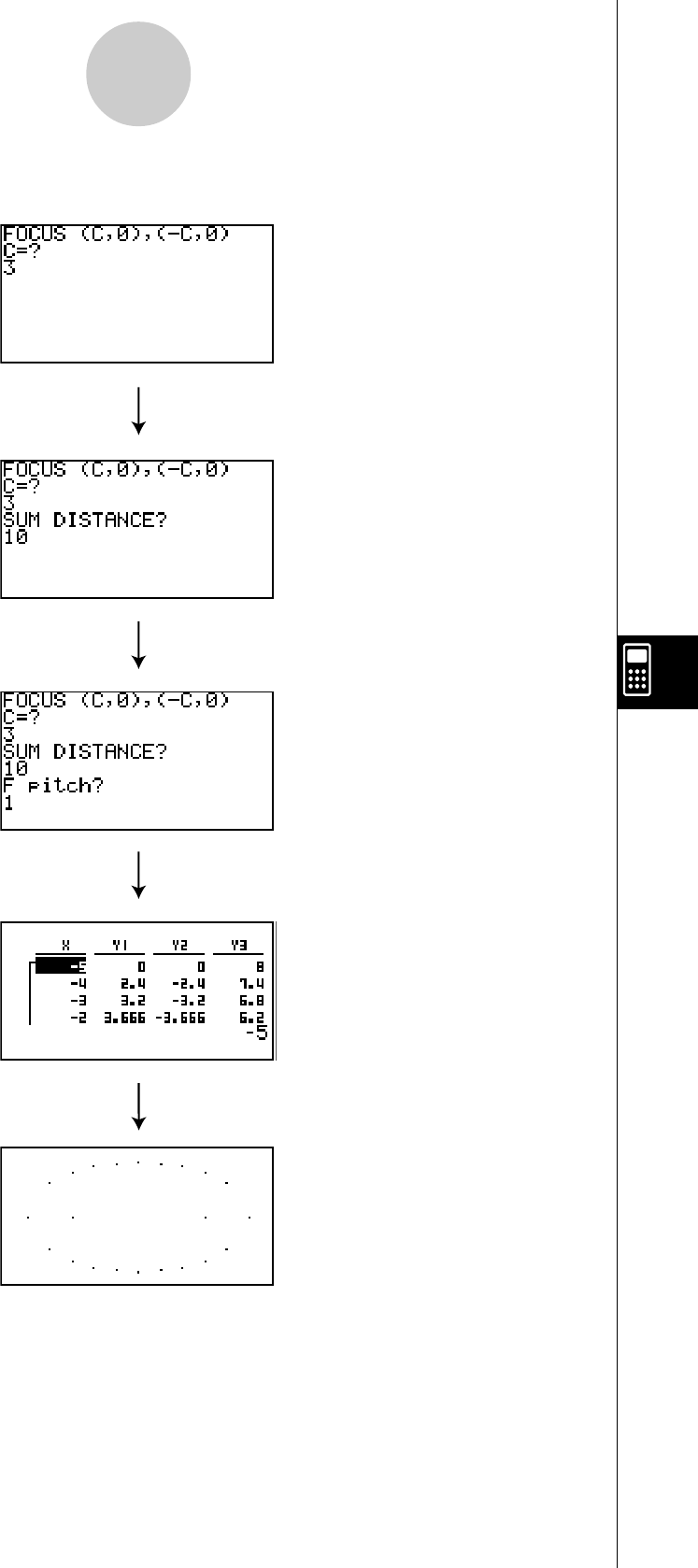
19990401
8-8-6
Bibliothèque de programmes

19990401
Description
Ce programme trace un angle à la coordonnée définie par le sommet indiqué et le fait
tourner à un angle particulier autour de ce sommet.
But
Ce programme démontre la transformation de coordonnées à partir d’une matrice.
Important!
Le degré doit être utilisé comme unité d’angle pour ce programme.
Nom du programme Rotation
8-8-7
Bibliothèque de programmes
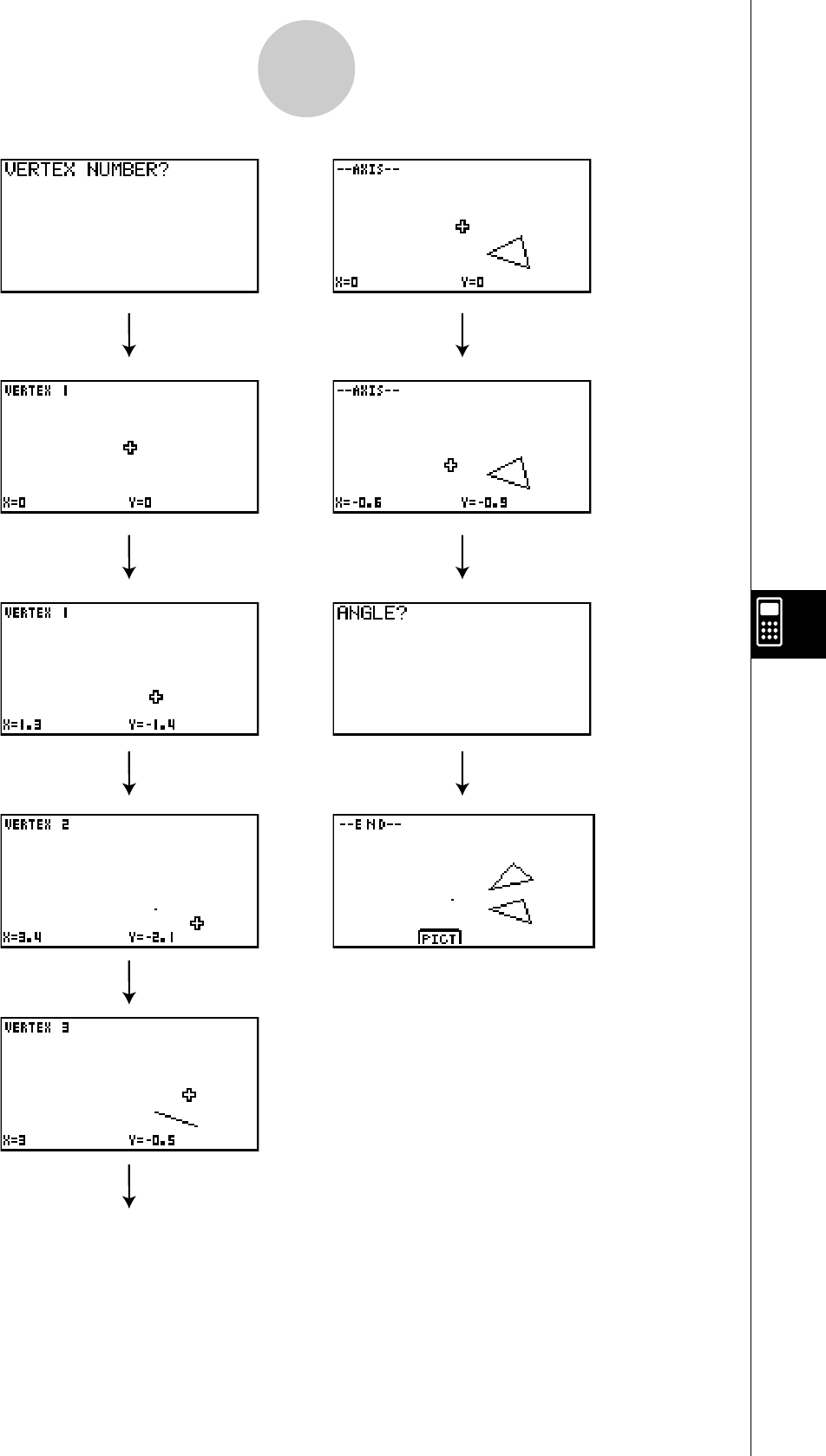
19990401
8-8-8
Bibliothèque de programmes
dw
fcde
wfcde
wfcde
fcde
w
daw
w

19990401
Description
Ce programme calcule les angles intérieurs et l’aire d’un triangle défini par les coordonnées
indiquées pour les angles A, B et C.
But
Ce programme calcule les angles intérieurs et l’aire d’un triangle défini par les coordonnées
des angles A, B et C.
Important!
La saisie de coordonnées identiques pour deux angles (A, B, C) entraîne une erreur.
Nom du programme Angles intérieurs et surface d’un triangle
8-8-9
Bibliothèque de programmes
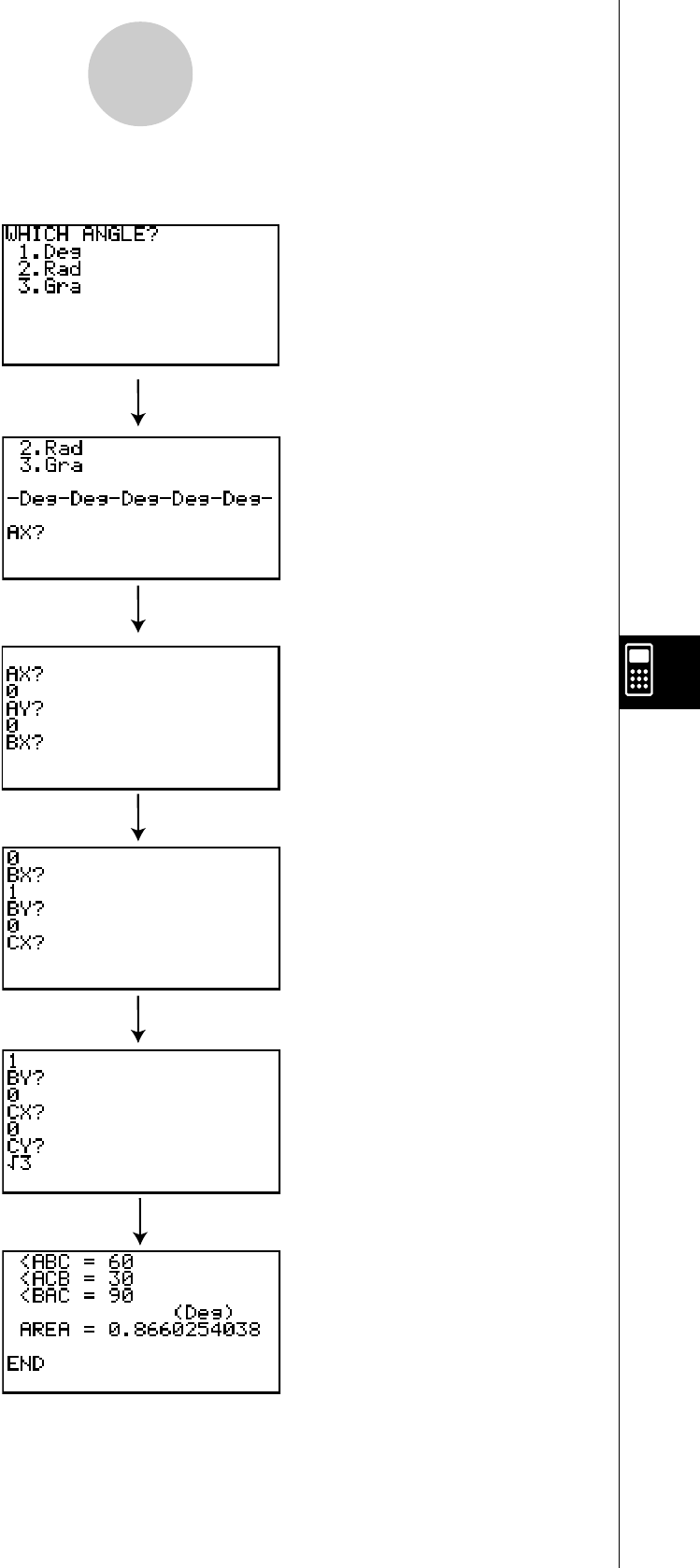
19990401
8-8-10
Bibliothèque de programmes
b
awaw
bwaw
aw9d
w

19990401
Chapitre
Menu de réglages du
système
Utilisez le menu de réglages du système pour voir les informa-
tions concernant le système et effectuer des réglages. Le menu
de réglages du système permet d’effectuer les réglages suivants.
• Afficher les informations concernant l’emploi de la mémoire
• Effectuer le réglage de contraste
• Effectuer le réglage de mise hors tension automatique
• Désigner la langue du système
• Initialiser la calculatrice
9-1 Utilisation du menu de réglages du système
9-2 Opérations concernant la mémoire
9-3 Réglages du système
9-4 Initialisation
9

19990401
9-1-1
Utilisation du menu de réglages du système
9-1 Utilisation du menu de réglages du système
A partir du menu principal, accédez au mode SYSTEM et afficher les paramètres de menu
suivants.
• 1(Mem) ... {affichage de l’état actuel de la mémoire et suppression des données
stockées dans la mémoire}
• 2() ... {réglage du contraste de l’affichage}
• 3(APO) ... {réglage du délai de mise hors tension automatique}
• 4(Lang) ... {langue du système}
• 5(Reset) ... {opérations d’inialisation du système}

19990401
9-2 Opérations concernant la mémoire
Utilisez le paramètre Mem (Utilisation mémoire) pour voir l’état actuel de la mémoire et
supprimer certaines données mémorisées.
Lorsque l’écran du mode de réglages du système est affiché, appuyez sur 1(Mem) pour
faire apparaître l’écran d’utilisation de la mémoire.
• 1(Main) ... {affichage de l’écran des mémoires principales}
• 2(Strg) ... {affichage de l’écran des mémoires de stockage}
1(Main) permet d’afficher les données actuellement stockées dans les mémoires
principales.
• Pour supprimer des données
1. Utilisez les touches de curseur f et c pour amener la surbrillance sur le type de
mémoire dont vous voulez supprimer les données.
2. Selon l’écran affiché, appuyez sur la touche de fonction affectée à la fonction DEL.
• Sur l’écran de mémoires principales, appuyez sur 1(DEL).*1
• Sur l’écran de mémoires de stockage, appuyez sur 6(DEL).
3. Si vous avez sélectionné List File, Graph Memory, V-Win Memory, Picture ou H-Copy
Memory à l’étape 1, le menu apparaîtra et vous pourrez sélectionner les données que
vous voulez supprimer.
Indiquez un numéro pour spécifier les données et appuyez sur w.
4. En réponse au message de confirmation qui apparaît, appuyez sur w(Oui) pour
supprimer les données désignées, ou sur i(Non) pour annuler l’opération.
Pour revenir à l’écran initial du mode de réglages du système appuyez sur i ou
!i(QUIT).
9-2-1
Opérations concernant la mémoire
*1Une pression sur 6(DEL • A) supprime toutes
les données de la mémoire sélectionnée.
# Il n’est pas possible de supprimer une seule
application ajoutée. Toutes les applications
ajoutées sont supprimées lorsque vous
effectuez la procédure.
20001202

19990401
• Pour afficher les informations concernant l’utilisation de la mémoire
Utilisez f et c pour sélectionner chaque type de données et voir la quantité de mémoire
(en octets) utilisée.
Le tableau suivant indique tous les types de données qui apparaissent sur l’écran d’état de
la mémoire.
Mémoires principales
Type de données Signification
Program Données de programmation
Matrix Données de la mémoire matricielle
Statistics Calculs et graphiques statistiques
List File Données de listes
Y=Data Fonctions graphiques
Draw Memory Condition de tracé de graphes (fenêtre d’affichage,
facteur d’agrandissement/réduction)
Graph Memory Données de la mémoire de graphes
V-Win Memory Données de la mémoire de la fenêtre d’affichage
Picture Données de la mémoire d’image
Table Données de la fonction Table & Graphe
Dynamic Graph Données de graphes dynamiques
Recursion Données de Table & Graphe de récurrence
Equation Données de calcul d’équations
Algebra Données de variables algébriques
Financial Données financières
Diff Eq Equation différentielle et conditions de la
représentation graphique
E-Con Mémoire de réglage E-CON, liste de sondes
particulières
Alpha Memory Données de la mémoire alphabétique
Function Mem Données de la mémoire de fonctions
H-Copy Memory Mémoire de transfert d’image d’écran
System Données de variables du système
Others Autres données
Mémoires de stockage*1
Type de données Signification
ADD-IN APP. Applications ajoutées
[B]~ Données de sauvegarde
Pour afficher les noms des applications et les versions de toutes les applications ajoutées et
appuyez sur 1(Ver).
9-2-2
Opérations concernant la mémoire
20001202
*1Les options ne contenant pas de données
n’apparaissent pas à l’écran.

19990401
9-3 Réglages du système
kk
kk
kRéglage du contraste
Utilisez le paramètre (contraste) pour ajuster le contraste de l’affichage.
Lorsque l’écran initial du mode de réglages du système est affiché, appuyez sur 2( )
pour afficher l’écran de réglage du contraste.
• La touche de curseur e assombrit l’affichage.
• La touche de curseur d éclaircit l’affichage.
• 1(INIT) rétablit le contraste initial.
Pour revenir à l’écran initial du mode de réglages du système appuyez sur iou
!i(QUIT).
Vous pouvez ajuster le contraste sur n’importe quel écran sauf sur le menu principal en
appuyant sur ! puis sur e ou d. Pour sortir de l’écran de réglage du contraste,
appuyez une nouvelle fois sur !.
kk
kk
kRéglages APO
Vous pouvez spécifier six minutes ou 60 minutes comme délai de mise hors tension
automatique. Le réglage initial est de six minutes.
Lorsque l’écran initial du mode de réglages du système est affiché, appuyez sur 3(APO)
pour afficher l’écran de réglage APO.
• 1(6) ... 6 minutes
• 2(60) ... 60 minutes
Pour revenir à l’écran initial du mode de réglages du système appuyez sur i ou
!i(QUIT).
9-3-1
Réglages du système

19990401
kk
kk
kRéglage de la langue du système
Utilisez le paramètre Lang pour sélectionner la langue d’affichage pour les applications
intégrées. Vous pouvez aussi utiliser ajouter d’autres langues.
1. Lorsque l’écran initial du mode de réglages du système est affiché, appuyez sur
4(Lang) pour afficher l’écran de réglage de la langue.
2. Utilisez les touches de curseur f et c pour sélectionner la langue souhaitée, puis
appuyez sur 1(Sel).
3. La fenêtre apparaît avec la langue sélectionnée. Vérifiez-en le contenu et appuyez sur
i.
Pour revenir à l’écran initial du mode de réglages du système appuyez sur i ou
!i(QUIT).
9-3-2
Réglages du système
20001202
# Lorsque vous installez une nouvelle langue,
celle-ci est automatiquement sélectionnée
comme la langue du système. Lorsque vous
changez de langue pour revenir à une langue
préprogrammée, la langue installée est
automatiquement supprimée.
# L’affichage est en anglais pour les fonctions
E-CON.
C’est-à-dire que tous les affichages sont en
anglais, même si vous avez sélectionné une
autre langue.

19990401
9-4 Initialisation
1. Lorsque l’écran initial du mode de réglages du système est affiché, appuyez sur
5(Reset) pour afficher l’écran d’initialisation.
• 1(S/U) ... {initialisation de la configuration}
• 2(Main) ... {suppression des données de la mémoire principale}
• 4(Init) ... {suppression de toutes les mémoires}
L’écran de mémoires de stockage suivant s’affiche par une pression de 3(Strg) sur
l’écran précédent.
·• 1(A&B) ... {suppression des applications ajoutées et des données de sauvegarde}
·• 2(ADDIN) ... {suppression des applications ajoutées}
·• 3(BACK) ... {suppression des données de sauvegarde}
• 4(B&M) ... {suppression des données de sauvegarde et des données des
mémoires principales}
2. Appuyez sur la touche de fonction correspondant à l’opération d’initialisation que vous
voulez effectuer.
3. En réponse au message de confirmation qui apparaît, appuyez sur w(Oui) pour
effectuer l’opération désignée ou sur i(Non) pour annuler l’opération.
4. Un message vous avertissant que l’initialisation est terminée apparaît.
Appuyez sur m pour revenir au menu principal.
9-4-1
Initialisation
20001202

19990401
Communication de
données
Ce chapitre contient tout ce qu’il faut savoir pour le transfert de
programmes entre deux calculatrices graphiques scientifiques
CASIO reliées par le câble fourni en standard.
Vous pouvez aussi utiliser le câble pour relier la calculatrice à
une imprimante d’étiquettes CASIO.
Pour le transfert de données entre une calculatrice et un
ordinateur, vous devrez vous procurer le kit de connexion CASIO
proposée en option.
10-1 Connexion de deux calculatrices
10-2 Connexion de la calculatrice à une imprimante
d’étiquettes CASIO
10-3 Connexion de la calculatrice à un ordinateur
10-4 Communication des données
10-5 Précautions lors la communication de données
10-6 Envoi d’une copie d’écran
10-7 Ajouts
10-8Mode MEMORY
Chapitre
10
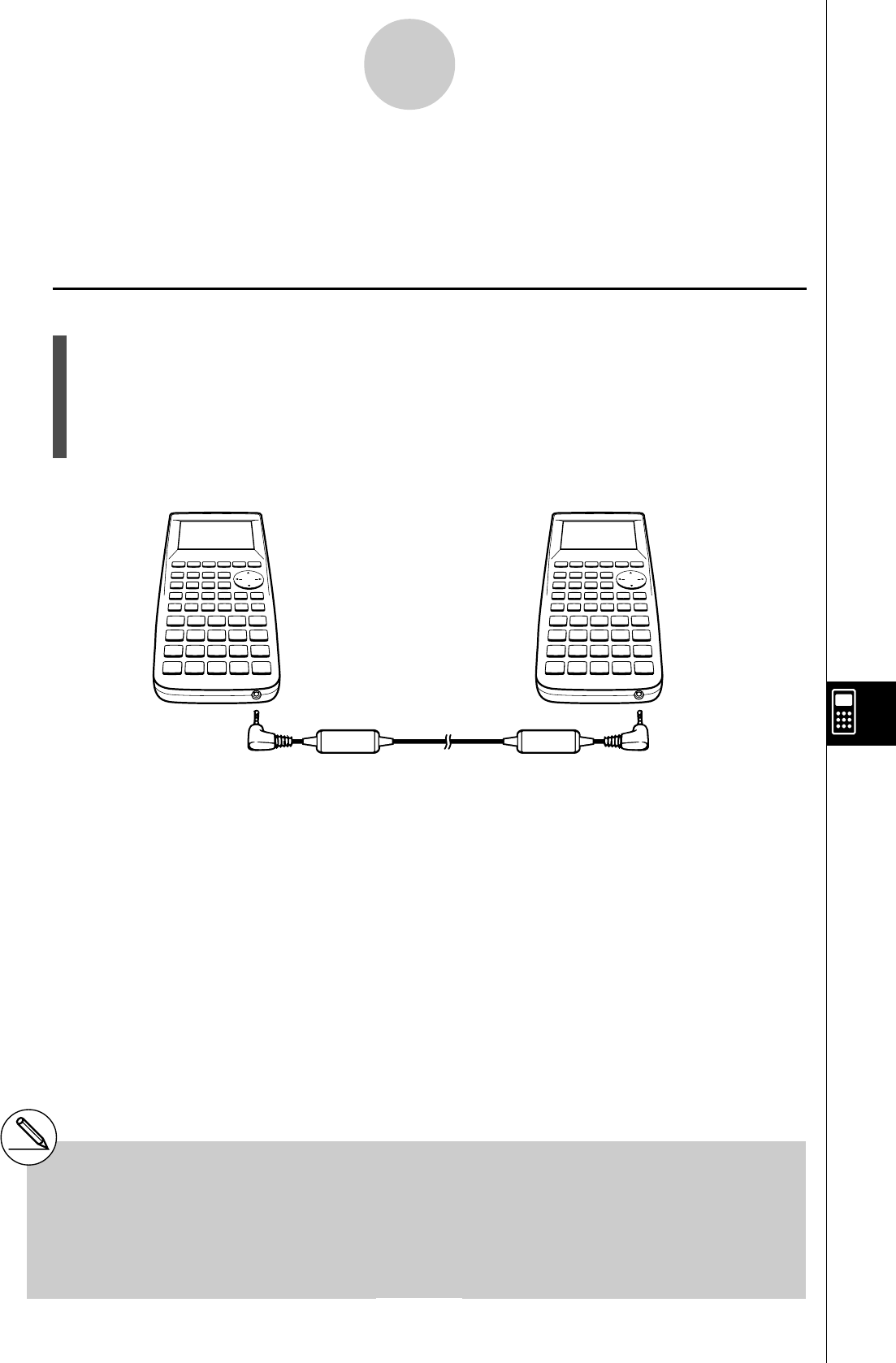
19990401
10-1-1
Connexion de deux calculatrices
10-1 Connexion de deux calculatrices
Les opérations suivantes expliquent comment raccorder deux calculatrices avec le câble de
liaison fourni comme accessoire standard.
uu
uu
uPour raccorder deux calculatrices
1. Vérifiez que les deux calculatrices sont éteintes.
2. Enlevez les caches des connecteurs des deux calculatrices.
3. Raccordez les deux calculatrices en utilisant le câble.
# Les modèles supportés par cette
configuration sont mentionnés ci-dessous.
ALGEBRA FX 2.0/FX 2.0 PLUS
FX 1.0/FX 1.0 PLUS
GRAPH 100+
# Les connecteurs doivent rester couverts lorsqu’ils
ne sont pas utilisés.
# Gardez les caches en lieu sûr, car vous devrez
les remettre en place dès que vous aurez terminé
la communication de données.
Câble
20011001
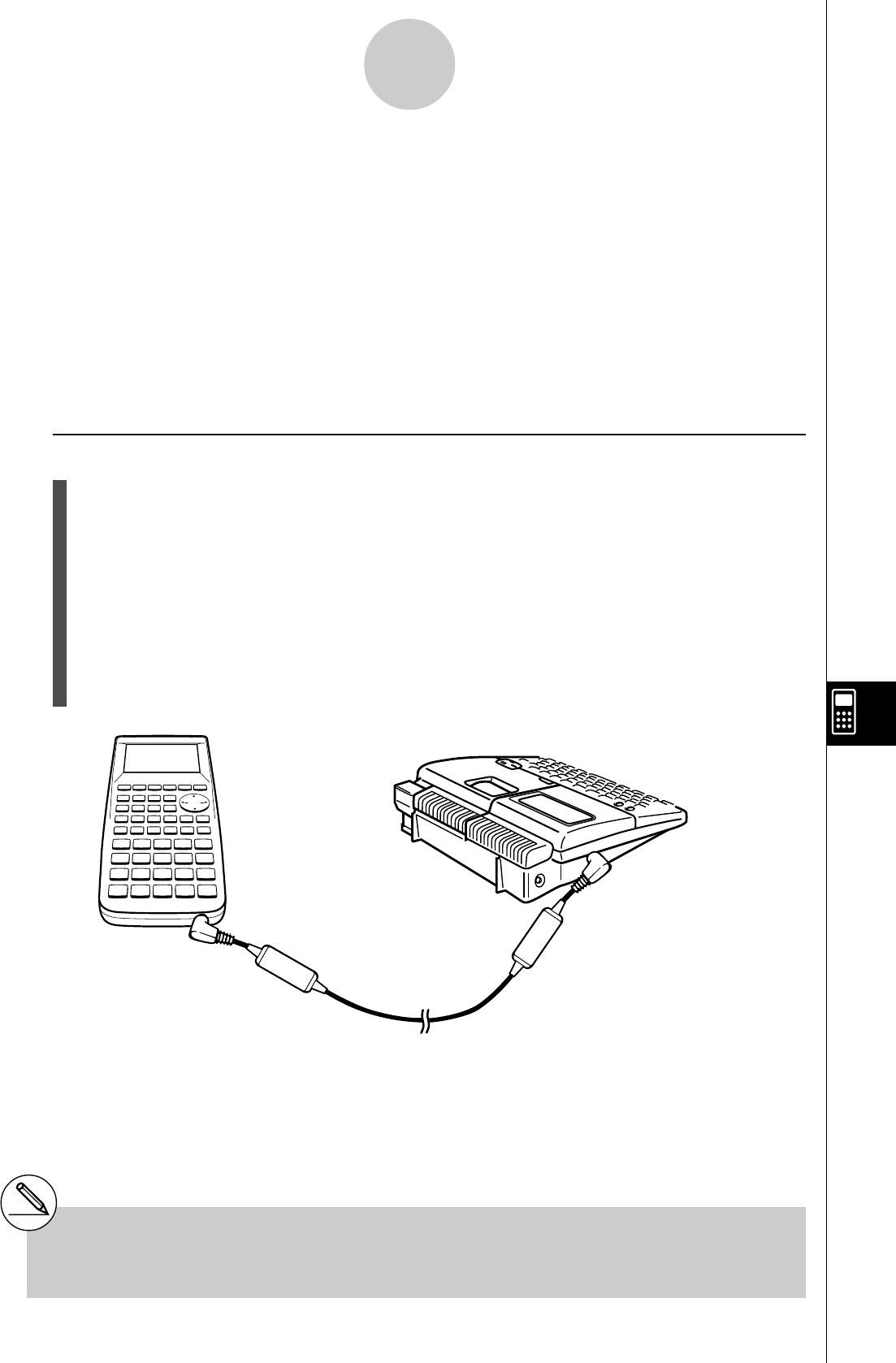
19990401
10-2-1
Connexion de la calculatrice à une imprimante d’étiquettes CASIO
10-2 Connexion de la calculatrice à une
imprimante d’étiquettes CASIO
Après avoir raccordé la calculatrice à une imprimante d’étiquettes CASIO avec un câble,
vous pouvez utiliser l’imprimante d’étiquettes pour imprimer les données figurant sur l’écran
de la calculatrice (Voir 10-6 Envoi d’une copie d’écran). Voir le mode d’emploi de l’imprimante
d’étiquettes pour les détails à ce sujet.
• L’opération décrite ci-dessus peut être réalisée en utilisant les modèles d’imprimante
d’étiquettes suivants : KL-2000, KL-8200.
uPour raccorder la calculatrice à une imprimante d’étiquettes
1. Vérifiez que la calculatrice et l’imprimante d’étiquettes sont éteintes.
2. Raccordez le câble à l’imprimante d’étiquettes.
3. Retirez le cache du connecteur de la calculatrice.
4. Raccordez l’autre extrémité du câble à la calculatrice.
5. Mettez la calculatrice, puis l’imprimante d’étiquettes sous tension.
• Quand la transmission de données est terminée, mettez en premier la calculatrice puis
l’imprimante d’étiquettes hors tension. Enlevez ensuite le câble reliant les deux appareils.
Imprimante d’étiquettes
Câble
# Conservez le cache de connecteur en lieu
sûr pour le remettre en place lorsque vous
aurez terminé la communication de données.
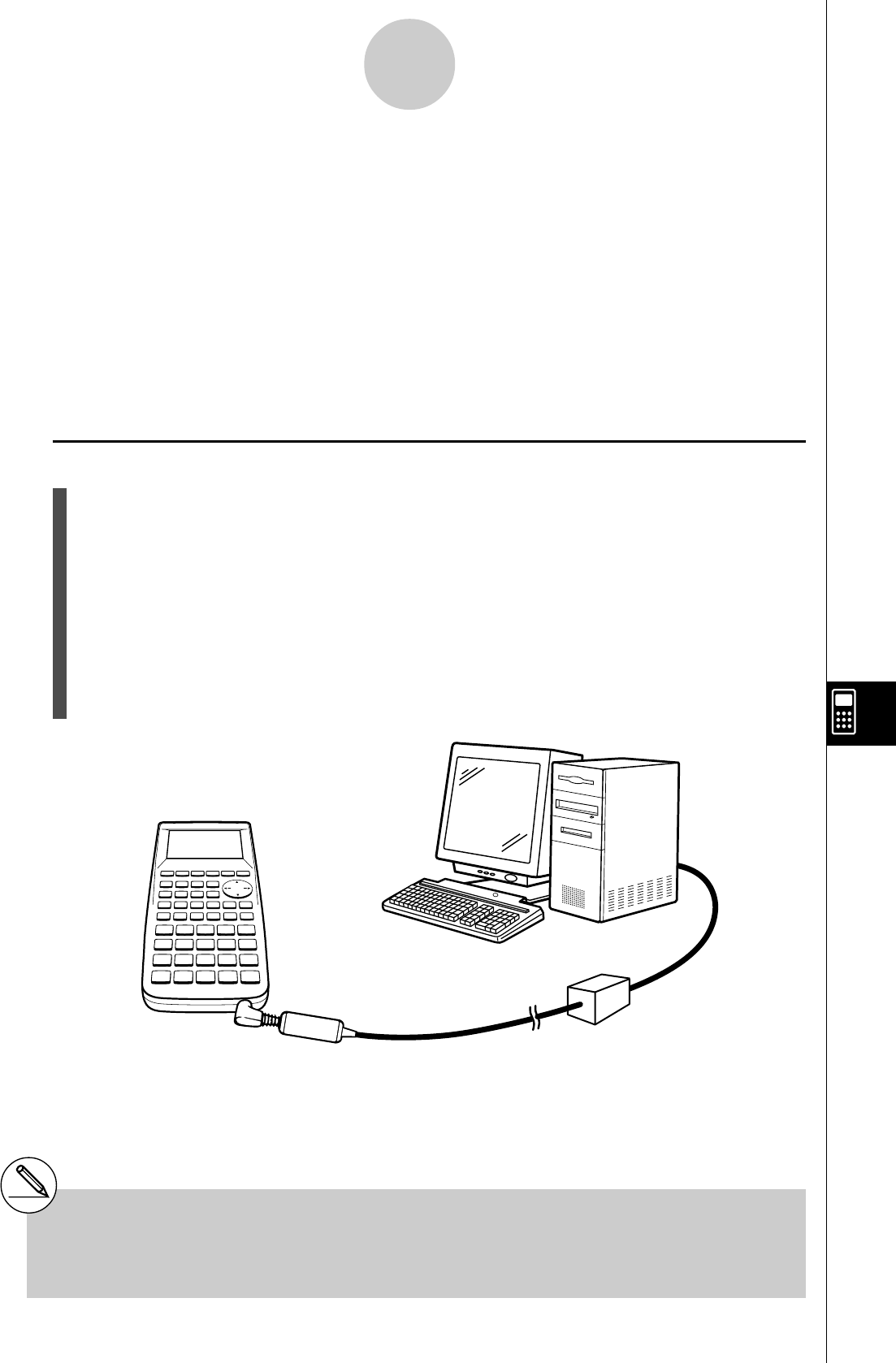
1999040120011001
10-3 Connexion de la calculatrice à un
ordinateur
Pour transférer des données et des images d’écran entre l’appareil et un ordinateur, vous
devez les raccorder à l’aide d’un kit de connexion optionnel CASIO.
Pour les détails sur le fonctionnement, les types d’ordinateurs pouvant être connectés et les
restrictions concernant le matériel, voir le mode d’emploi fourni avec kit de connexion.
Certains types de données ne peuvent pas être échangés avec un ordinateur.
uPour raccorder la calculatrice à un ordinateur personnel
1. Vérifiez que l’alimentation de la calculatrice et de l’ordinateur personnel est coupée.
2. Raccordez l’ordinateur personnel au kit de connexion.
3. Enlevez le cache du connecteur de la calculatrice.
4. Raccordez la calculatrice au kit de connexion.
5. Mettez la calculatrice sous tension puis l’ordinateur.
• Lorsque la communication des données est terminée, mettez la calculatrice puis
l’ordinateur personnel hors tension et débranchez les deux appareils.
10-3-1
Connexion de la calculatrice à un ordinateur
# Les programmes créés avec les calculatrices
de la série CFX-9850 peuvent être
transférés.
# Gardez le cache en lieu sûr, car vous devrez le
remettre en place dès que vous aurez terminé la
communication de données.

19990401
10-4 Communication des données
A partir du menu principal, accédez au mode LINK. Le menu principal servant à la
communication de données apparaît à l’écran.
•{TRNS}/{Recv} ... menu de {réglages d’émission}/{réglages de réception}
Les paramètres de communication sont déterminés par les réglages suivants.
• Vitesse (BPS): 38,4 kbps (envoi de données)
9.600 bps (envoi d’images d’écran)
• Parité (PARITY): NONE
kk
kk
kExécution d’un transfert de données
Raccordez les deux machines, puis effectuez les opérations suivantes.
Machine réceptrice
Pour configurer la calculatrice pour la réception de données, appuyez sur 2(Recv) quand
le menu de communication de données est affiché.
La calculatrice se met dans le mode d’attente, prête pour la réception des données. La
réception commence dès que les données sont envoyées par l’autre machine.
10-4-1
Communication des données

19990401
Machine émettrice
Pour configurer la calculatrice pour la transmission de données, appuyez sur 1(TRNS)
quand le menu principal destiné à la communication de données est affiché.
Appuyez sur la touche de nombre qui correspond au type de données que vous voulez
envoyer.
• {Select} ... {sélectionne les types de données et les envoie}
• {Currnt} ... {sélectionne les types de données parmi des données sélectionnées au
préalable et les envoie}
• {Backup} ... {envoie tous les types de données avec les réglages de modes}
• {H-Copy} ... {sélectionne les données d’image d’écran et les envoie}
uPour envoyer les types de données sélectionnés
Appuyez sur b(Select) ou c(Currnt) pour afficher l’écran de sélection de types de
données.
• {Sel} ... {sélectionne le type de données où se trouve le curseur}
• {All} ... {sélectionne toutes les données}
• {Trns} ... {envoie le type de données sélectionné}
Utilisez les touches de curseur f et c pour amener le curseur sur le type de données
que vous voulez sélectionner, puis appuyez sur 1(Sel) pour valider votre sélection. Les
types de données sélectionnés sont marqués du signe “'”. Appuyez maintenant sur
6(Trns) pour les envoyer.
• Pour invalider une sélection, amener le curseur dessus et appuyez une nouvelle fois sur
1(Sel) .
Seuls les types qui contiennent des données apparaissent à l’écran de sélection. Si tous les
types de données ne rentrent pas sur un seul écran, la liste défile quand vous mettez le
curseur sur la dernière ligne de la liste affichée.
10-4-2
Communication des données
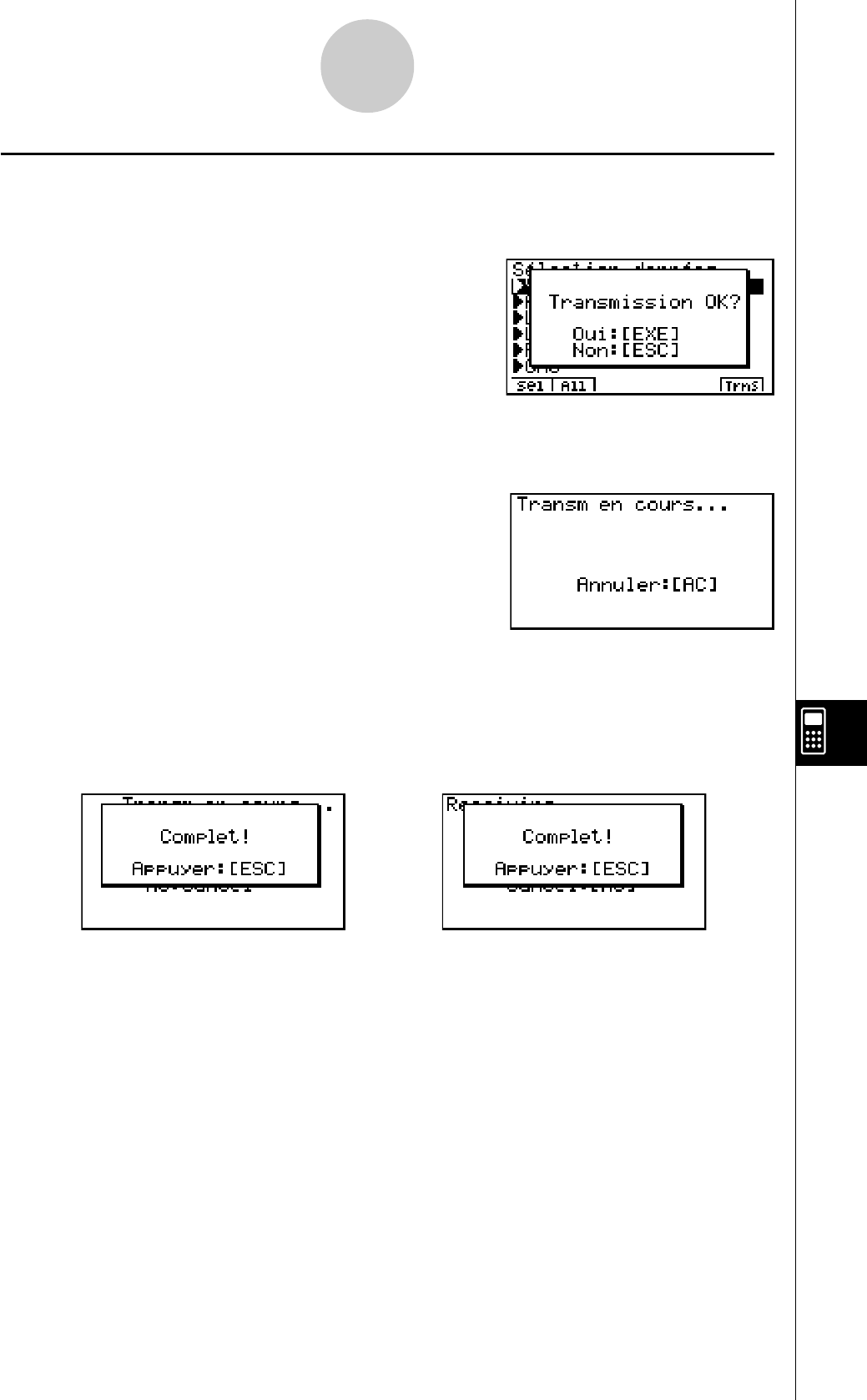
19990401
uPour exécuter une transmission
Après avoir sélectionné le type de données à envoyer, appuyez sur 6(Trns). Un message
apparaît vous demandant de confirmer l’opération.
•w(Oui) ... envoie des données
•i(Non) ... retour à l’écran de sélection
Appuyez sur w(Oui) pour envoyer les données.
• Vous pouvez interrompre la transmission en appuyant sur A.
L’écran de la machine émettrice et celui de la machine réceptrice qui apparaissent après le
transfert de données affichent les messages suivants.
Machine émettrice Machine réceptrice
Appuyez sur i pour revenir au menu principal de communication de données.
10-4-3
Communication des données
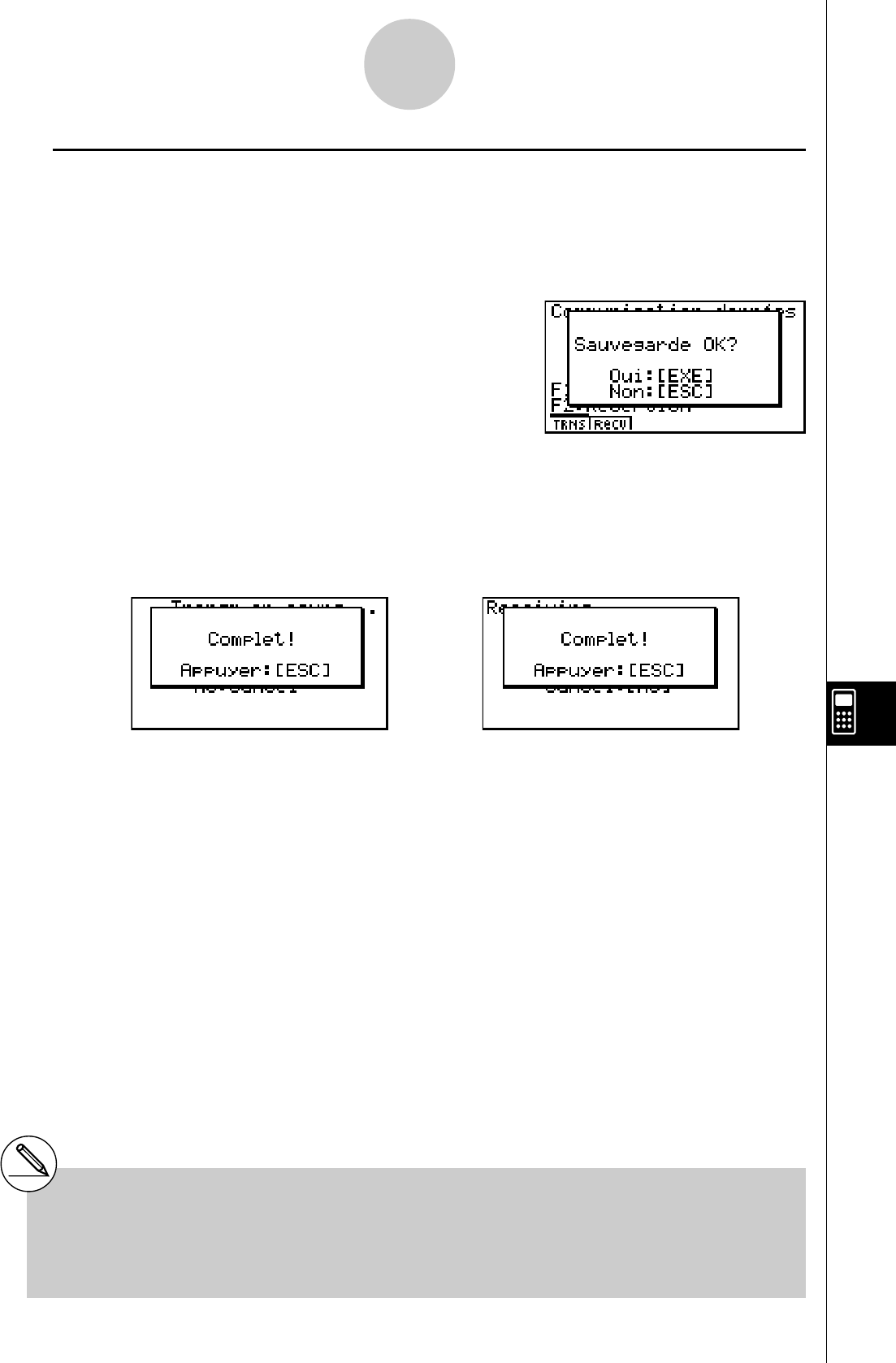
19990401
uPour transmettre des données de sauvegarde
Cette opération permet de transmettre tout le contenu de la mémoire, réglages de modes
compris.
Lorsque le menu de sélection du type de données à transmettre est à l’écran, appuyez sur
d(Backup) pour afficher l’écran suivant.
Appuyez sur w(Oui) pour envoyer les données.
L’écran de la machine émettrice et celui de la machine réceptrice qui apparaissent après le
transfert de données affichent les messages suivants.
Machine émettrice Machine réceptrice
Appuyez sur i pour revenir au menu principal de communication de données.
10-4-4
Communication des données
# Les données peuvent être altérées,
nécessitant une initialisation de la machine
réceptrice, si le câble de liaison se débranche
pendant la transmission. Assurez-vous que le
câble est bien branché sur les deux
machines avant d’effectuer une
communication de données.

19990401
10-5-1
Précautions lors la communication de données
*1Sans contrôle: Si la machine réceptrice contient déjà des données de même type, les
données existantes seront écrasées et remplacées par les nouvelles.
Avec contrôle: Si la machine réceptrice contient déjà des données de même type, un
message apparaît pour demander si les données existantes peuvent être écrasées et
remplacées par les nouvelles.
20001202
10-5 Précautions lors la communication de
données
Les types de données que vous pouvez envoyer sont les suivants.
Type de données Contenu
Contrôle
Contrôle du
d’écrasement*
1
code d’accès
*
2
Noms de Contenu du programme Oui Oui
programme (Tous les programmes sont listés.)
Mat nContenu des mémoires matricielles Oui
(A à Z)
List n
Contenu des mémoires de listes (1 à 20)
Oui
File n
Contenu des mémoires de fichiers de listes (1 à 20)
Oui
Y=Data
Expressions graphiques, statut avec
ou sans graphe, fenêtre d’affichage, Non
facteurs de zoom
G-Mem n
Contenu des mémoires de graphes (1 à 20)
Oui
V-Win n
Contenu des mémoires de fenêtres d’affichage
Non
Picture nDonnées de mémoires d’images (graphes)
(1 à 20)
Non
DynaMen Fonctions de graphe dynamique Oui
Equation Valeurs des coefficients de calcul Non
d’équations
Alpha Memory Contenu de la mémoire de variable Non
F-Mem nContenu de la mémoire de fonctions Non
CAS Contenu des données de formules CAS Non
DIFF Equation Données de équations différentielles Non
E-CON Data Données E-CON Non
Noms Données des applications ajoutées Non
d’applications
(Toutes les applications ajoutées sont listées.)
ajoutées
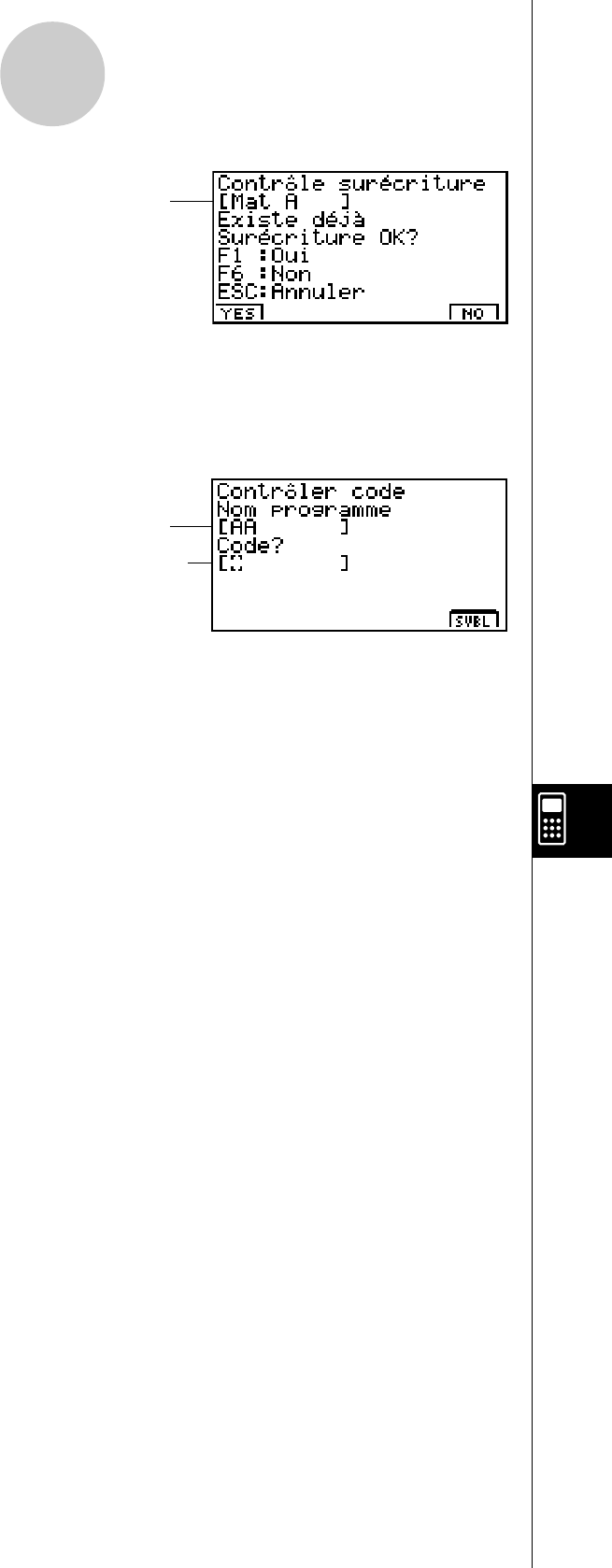
19990401
•1(YES)... {remplace les données existantes de la machine réceptrice par les nouvelles}
•6(NO) ... {passe au type de données suivant}
*2Avec contrôle du code d’accès: Si un fichier est protégé, un message apparaîtra pour vous
demander d’entrer le code d’accès.
2
Après avoir indiqué le code d’accès, appuyez sur w.
Respectez les précautions suivantes lorsque vous effectuez une communication de
données.
• Une erreur se produit quand vous essayez d’envoyer des données à une machine
réceptrice qui n’est pas en attente de réception. Dans ce cas, appuyez sur i pour
effacer l’erreur et recommencez l’opération, après avoir réglé la machine réceptrice pour
la réception de données.
• Une erreur se produit si la machine réceptrice ne reçoit aucune donnée dans les six
minutes environ qui suivent le réglage de réception de données. Dans ce cas, appuyez
sur i pour effacer l’erreur.
• Une erreur se produit durant la communication des données si le câble est débranché,
si les paramètres des deux machines ne correspondent pas ou si un autre problème de
communication se produit. Dans ce cas, appuyez sur i pour effacer l’erreur et corriger
le problème avant d’essayer de communiquer à nouveau. Si la communication de
données est interrompue par une pression sur la touche i ou une erreur, toutes les
données reçues avec succès jusqu’à l’interruption de la communication se trouveront
dans la mémoire de la machine réceptrice.
• Une erreur se produit si la mémoire de la machine de réception devient pleine durant la
communication des données. Dans ce cas, appuyez sur i pour effacer l’erreur et
annuler les données inutiles dans la machine réceptrice afin de faire de la place pour les
nouvelles données, puis essayez une fois de plus.
• L’option E-CON contient les données suivantes :
1. Données de la configuration actuelle
2. Données de la mémoire de configurations
3. Données de la mémoire de sondes particulières
Les données correspondantes remplacent celles du récepteur. Les données de mémoire
de configurations et les données de la mémoire de sondes particulières se substituent
aux données de la mémoire ayant le même numéro sur le récepteur. Si vous voulez
conserver ces données sur le récepteur, changez le numéro de mémoire.
10-5-2
Précautions lors la communication de données
20001202
Nom du type de données
Nom du fichier protégé
Champ d’entrée du code
19990401
10-6 Envoi d’une copie d’écran
Procédez de la façon suivante pour envoyer la copie d’un écran directement à l’ordinateur
raccordé (ou à une imprimante d’étiquettes CASIO) ou pour sauvegarder un écran dans la
mémoire et l’envoyer plus tard. Les copies d’écran peuvent aussi être envoyées à une
imprimante d’étiquettes CASIO.
Utilisez le réglage du mode LINK (u3(SET UP)) pour indiquer si vous voulez envoyer la
copie d’écran maintenant ou d’abord la sauvegarder.
u H-Copy
•{Dirct}/{Mem} ............. {envoi direct}/{sauvegarde}
uu
uu
uPour envoyer une copie d’écran directement à l’ordinateur raccordé (ou à
une imprimante d’étiquettes CASIO) (Direct)
1. Raccordez l’appareil à l’ordinateur (ou à l’imprimante d’étiquettes CASIO).
Sur l’ordinateur (ou l’imprimante d’étiquettes CASIO), effectuez les opérations
nécessaires pour la réception de données.
2. Affichez l’écran dont vous voulez envoyer une copie.
3. Appuyez sur u6(H-COPY).
uu
uu
uPour sauvegarder une copie d’écran (Memory)
1. Affichez l’écran que vous voulez sauvegarder.
2. Appuyez sur u6(H-COPY).
• Vous pouvez sauvegarder jusqu’à 20 copies d’écran. Les copies d’écran
sauvegardées reçoivent automatiquement les noms de fichiers Hcopy1 à Hcopy20.
10-6-1
Envoi d’une copie d’écran
# Vous ne pouvez pas envoyer les types
d’écrans suivants à un ordinateur ou une
imprimante.
• L’écran qui apparaît pendant la communica-
tion des données.
• L’écran qui apparaît pendant le déroulement
d’un calcul.
• L’écran qui apparaît à la suite de
l’initialisation.
• Le message de faible tension des piles.
# Le curseur clignotant n’est pas compris dans
l’image d’écran qui est envoyée par la
calculatrice.
# Vous ne pouvez pas utiliser une bande de 6 mm
pour imprimer un graphe affiché.

19990401
uu
uu
uPour envoyer une copie d’écran à un ordinateur ou une imprimante
d’étiquettes CASIO
1. Raccordez l’appareil à l’ordinateur (ou à l’imprimante d’étiquettes CASIO).
Sur l’ordinateur (ou l’imprimante d’étiquettes CASIO), effectuez les opérations
nécessaires pour la réception de données.
2. Dans le mode LINK, appuyez sur 1(TRNS)e(H-Copy) pour afficher la liste des
copies d’écran sauvegardées.
3. Utilisez les touches de curseur f et c pour mettre le nom de la copie d’écran que
vous voulez transférer en surbrillance et appuyez sur 6(Trns).
10-6-2
Envoi d’une copie d’écran

19990401
10-7-1
Ajouts
10-7 Ajouts
La capacité d’ajout permet d’installer d’autres applications et logiciels pour adapter la
calculatrice à vos besoins particuliers.
Les ajouts s’installent à partir d’un ordinateur par la communication de données décrite à la
page 10-4-1.
Les types de logiciels qui peuvent être ajoutés à la calculatrice sont les suivants.
uu
uu
uApplication ajoutée
Aprés avoir installé une application, son icône apparaît sur le menu principal. Elle peut alors
être lancée comme toute autre application intégrée.
uu
uu
uNouvelles versions d’applications intégrées
Ce sont de nouvelles versions destinées aux applications préprogrammées dans la ROM de
la calculatrice.
uu
uu
uDonnées de langue pour affichage de messages
Ces données sont nécessaires pour l’affichage des messages dans d’autres langues. Après
l’installation de ces données, les messages sont affichés dans la langue correspondante.
20001202

19990401
10-8-1
Mode MEMORY
10-8Mode MEMORY
Cette calculatrice a deux zones mémoire séparées: une “zone active” et une “zone de
stockage”. La zone active est une zone de travail où vous pouvez saisir des données,
effectuer des calculs et lancer des programmes. Les données dans la zone active sont
relativement protégées, mais elles peuvent être détruites lorsque les piles sont vides et
lorsque vous effectuez une réinitialisation complète.
La zone de stockage utilise la “mémoire flash” et les données sont protégées même en cas
d’interruption d’alimentation.
Normalement, vous utilisez la zone de stockage pour sauvegarder les données que vous
voulez conserver et vous chargez les données dans la zone active lorsque vous en avez
besoin.
Utilisez le mode MEMORY pour transférer des données entre la zone active et la zone de
stockage ainsi que pour effectuer d’autres opérations de gestion de la mémoire.
Sur le menu principal, sélectionnez l’icône MEMORY pour accéder au mode MEMORY et
afficher l’écran initial.
•{PROG} ...... {sauvegarde, chargement, suppression, recherche de fichiers de programme}
•{BACK} ...... {sauvegarde et restauration de données de la zone active}
•{OPT} ......... {optimisation de la zone de stockage}
kStockage et chargement de fichiers de programme
Procédez de la façon suivante pour sauvegarder dans la zone de stockage un fichier de
programme se trouvant dans la zone active et charger dans la zone active un fichier de
programme se trouvant dans la zone de stockage.
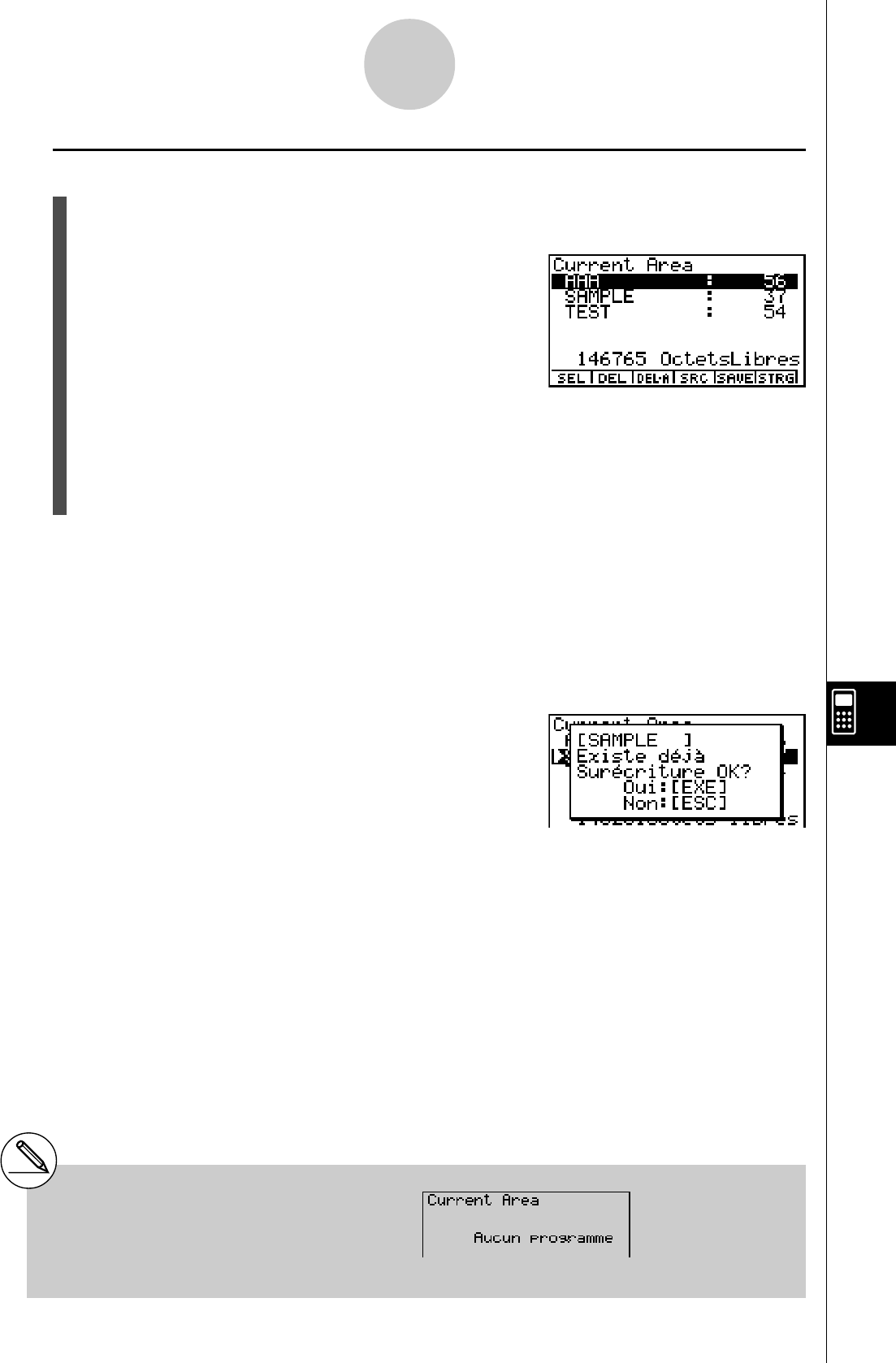
19990401
uPour stocker un fichier de programme dans la zone de stockage
1. Sur l’écran initial du mode MEMORY, appuyez sur 1(PROG).
• Une liste des fichiers de programme se trouvant dans la zone active apparaît.*1
2. Sélectionnez le fichier de programme que vous voulez stocker.
• Utilisez les touches de curseur f et c pour mettre le nom du fichier de pro-
gramme que vous voulez sauvegarder en surbrillance, puis appuyez sur 1(SEL).
3. Appuyez sur 5(SAVE).
Le message “Complet!” apparaît lorsque l’opération est terminée.
Appuyez sur i pour revenir à l’écran affiché à l’étape 1.
Une “Erreur de mémoire” se produit et le stockage est interrompu si la zone de stockage est
pleine.
Le message suivant apparaît s’il existe déjà un fichier de programme de même nom dans la
zone.
Appuyez sur w(Oui) pour sauvegarder le nouveau fichier de programme ou sur i(Non)
pour annuler la sauvegarde.
10-8-2
Mode MEMORY
*1L’écran suivant apparaît si la zone active ne
contient pas de fichiers lorsque vous
effectuer la sauvegarde.

19990401
u Pour charger un fichier de programme depuis la zone de stockage
1. Sur l’écran initial du mode MEMORY, appuyez sur 1(PROG).
2. Appuyez sur 6(STRG).
• Une liste des fichiers de programme se trouvant dans la zone de stockage apparaît. *1
3. Sélectionnez le fichier de programme que vous voulez charger.
• Utilisez les touches de curseur f et c pour mettre le nom du fichier de pro-
gramme que vous voulez sauvegarder en surbrillance, puis appuyez sur 1(SEL).
4. Appuyez sur 5(LOAD).
Le message “Complet!” apparaît lorsque l’opération est terminée.
Appuyez sur i pour revenir à l’écran affiché à l’étape 1.
Une “Erreur de mémoire” se produit et le chargement est interrompu si la zone active est
pleine.
Le message suivant apparaît s’il existe déjà un fichier de programme de même nom dans la
zone active.
Appuyez sur w(Oui) pour charger le nouveau fichier de programme ou sur i(Non) pour
annuler le chargement.
*1L’écran suivant apparaît s’il n’y a pas de
fichier de programme dans la zone de
stockage lorsque vous effectuez le
chargement.
10-8-3
Mode MEMORY
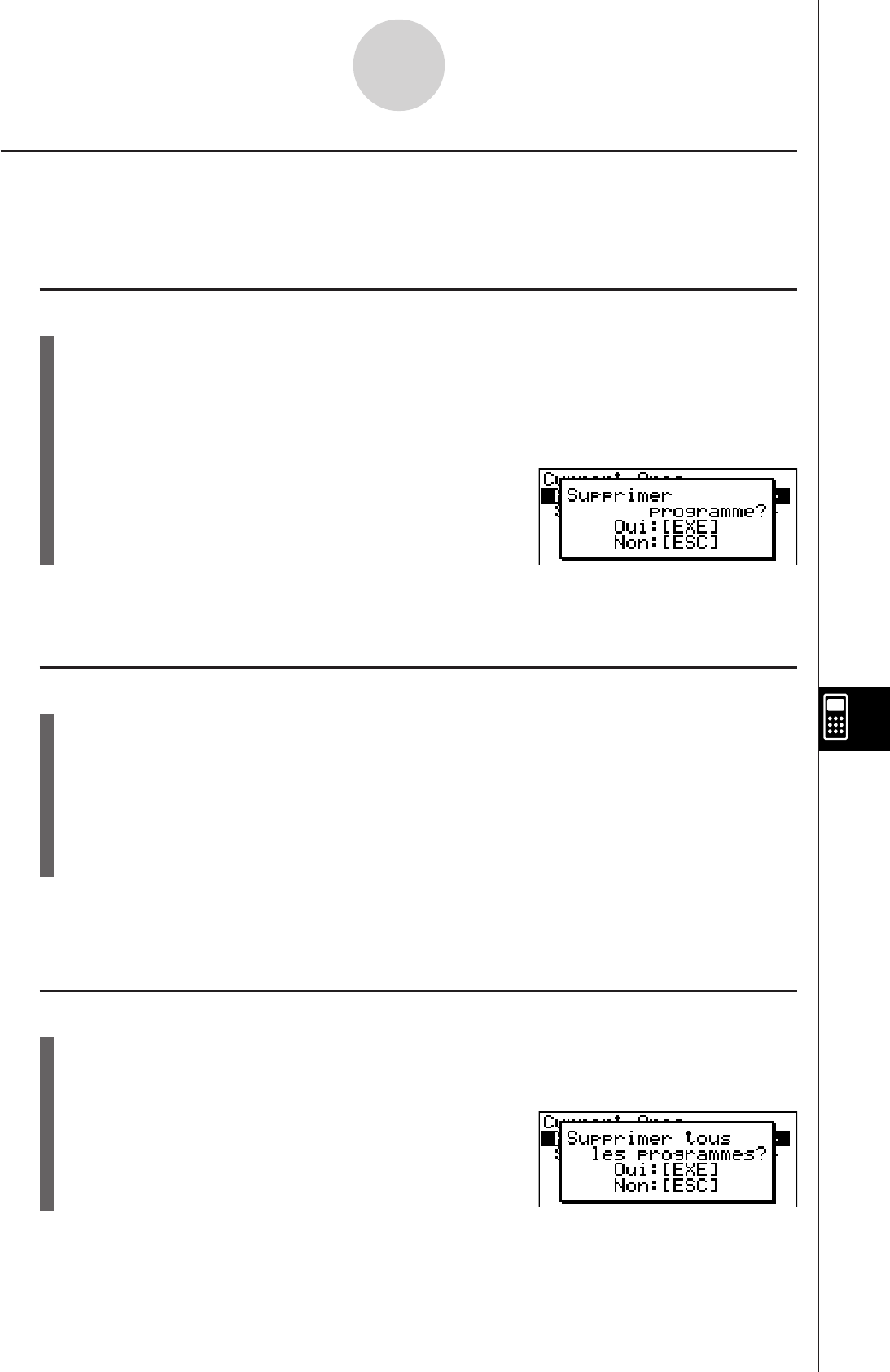
19990401
kSuppression de fichiers de programme
Procédez de la façon suivante pour supprimer certains fichiers ou tous les fichiers se
trouvant dans la zone active ou dans la zone de stockage.
uPour supprimer un fichier de programme de la zone active
1. Sur l’écran initial du mode MEMORY, appuyez sur 1(PROG).
•Une liste des fichiers de programme se trouvant dans la zone active apparaît.
2. Utilisez les touches de curseur f et c pour mettre le nom du fichier de programme
que vous voulez supprimer en surbrillance, puis appuyez sur 2(DEL).
•Appuyez sur w(Oui) pour supprimer le fichier de programme.
•Appuyez sur i(Non) pour annuler la suppression.
uPour supprimer un fichier de programme de la zone de stockage
1. Sur l’écran initial du mode MEMORY, appuyez sur 1(PROG).
2. Appuyez sur 6(STRG).
•Une liste des fichiers de programme dans la zone de stockage apparaît.
3. Utilisez les touches de curseur f et c pour mettre en surbrillance le nom du fichier
de programme que vous voulez supprimer, puis appuyez sur 2(DEL).
•Appuyez sur w(Oui) pour supprimer le fichier de programme.
•Appuyez sur i(Non) pour annuler la suppression.
uPour supprimer tous les fichiers de programme de la zone active
1. Sur l’écran initial du mode MEMORY, appuyez sur 1(PROG).
•Une liste des fichiers de programme se trouvant dans la zone active apparaît.
2. Appuyez sur 3(DEL•A).
•Appuyez sur w(Oui) pour supprimer tous les fichiers de programme se trouvant dans
la zone active.
•Appuyez sur i(Non) pour annuler la suppression.
10-8-4
Mode MEMORY

19990401
uPour supprimer tous les fichiers de programme de la zone de stockage
1. Sur l’écran initial du mode MEMORY, appuyez sur 1(PROG).
2. Appuyez sur 6(STRG).
• Une liste des fichiers de programme se trouvant dans la zone de stockage apparaît.
3. Appuyez sur 3(DEL•A).
• Appuyez sur w(Oui) pour supprimer tous les fichiers de la zone de stockage.
• Appuyez sur i(Non) pour annuler la suppression.
kRecherche d’un fichier de programme
Procédez de la façon suivante pour rechercher un fichier de programme donné dans la zone
active ou dans la zone de stockage.
u Pour rechercher un fichier de programme dans la zone active *1
Exemple Rechercher tous les fichiers de programme dans la zone active dont le
nom commence par la lettre “C”
1. Sur l’écran initial du mode MEMORY, appuyez sur 1(PROG).
• Une liste de tous les fichiers de programme se trouvant dans la zone active apparaît.
2. Appuyez sur 4(SRC).
• Saisissez la lettre “C” au clavier.
• Le premier nom de fichier commençant par la lettre “C” est mis en surbrillance.
10-8-5
Mode MEMORY
*1 Vous pouvez saisir un nom de huit
caractères au maximum.
Le message “Non trouvé” apparaît si aucun
nom de fichier de programme correspond au
nom saisi.
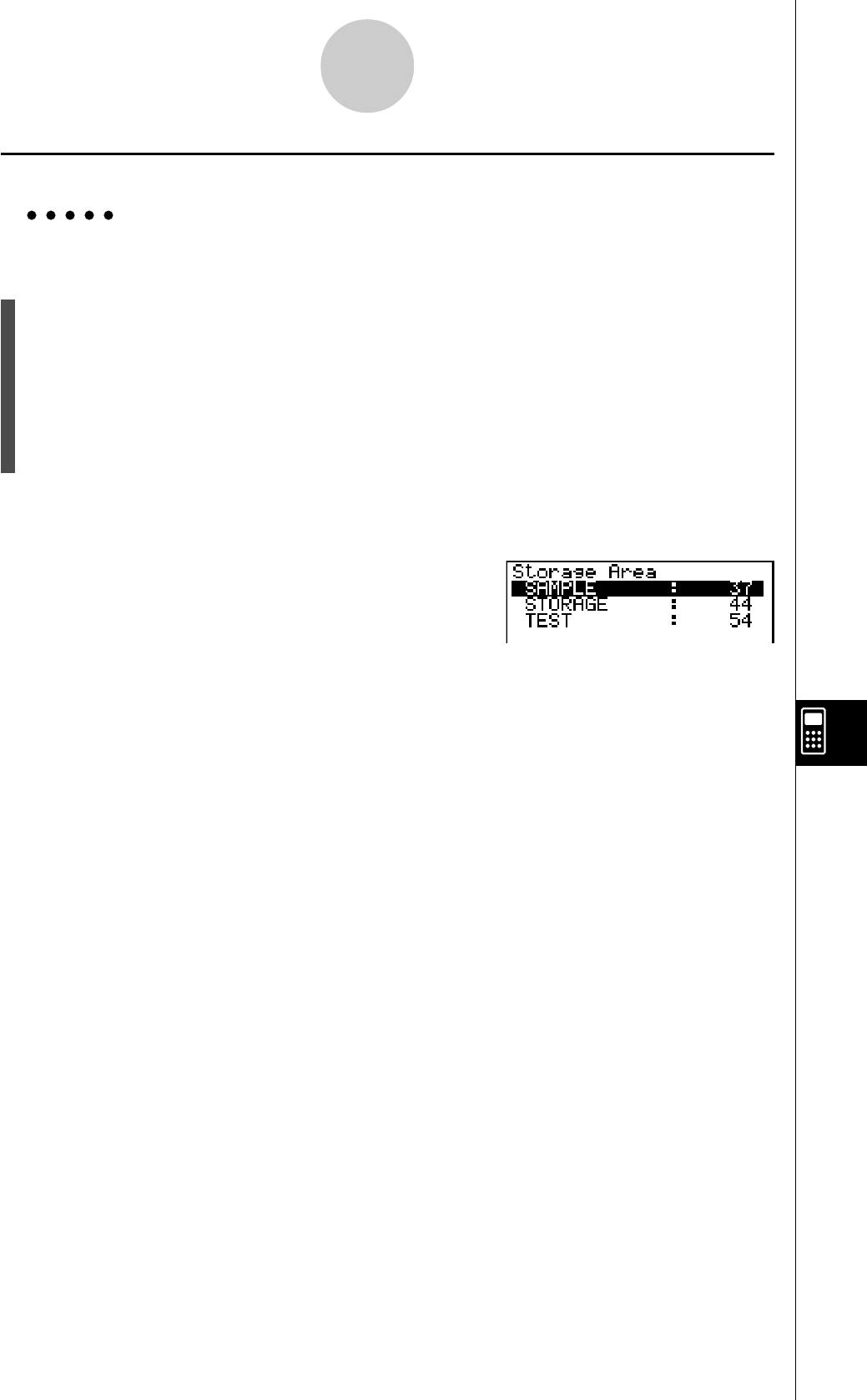
19990401
uPour rechercher un fichier de programme dans la zone de stockage
Exemple Rechercher tous les fichiers de programme dans la zone de stockage
dont le nom commence par la lettre “S”
1. Sur l’écran initial du mode MEMORY, appuyez sur 1(PROG).
2. Appuyez sur 6(STRG).
• Une liste des fichiers de programme se trouvant dans la zone de stockage apparaît.
3. Appuyez sur 4(SRC).
• Saisissez la lettre “S” au clavier.
• Le premier nom de fichier de programme commençant par la lettre “S” est mis en
surbrillance.
Appuyez sur c ou 1(SRC) pour mettre le nom de fichier suivant en surbrillance.
Appuyez sur f pour mettre le nom de fichier précédent en surbrillance.
Le message “Non trouvé” apparaît s’il n’existe pas de programme correspondant à la lettre.
Appuyez sur i pour abandonner la recherche.
10-8-6
Mode MEMORY
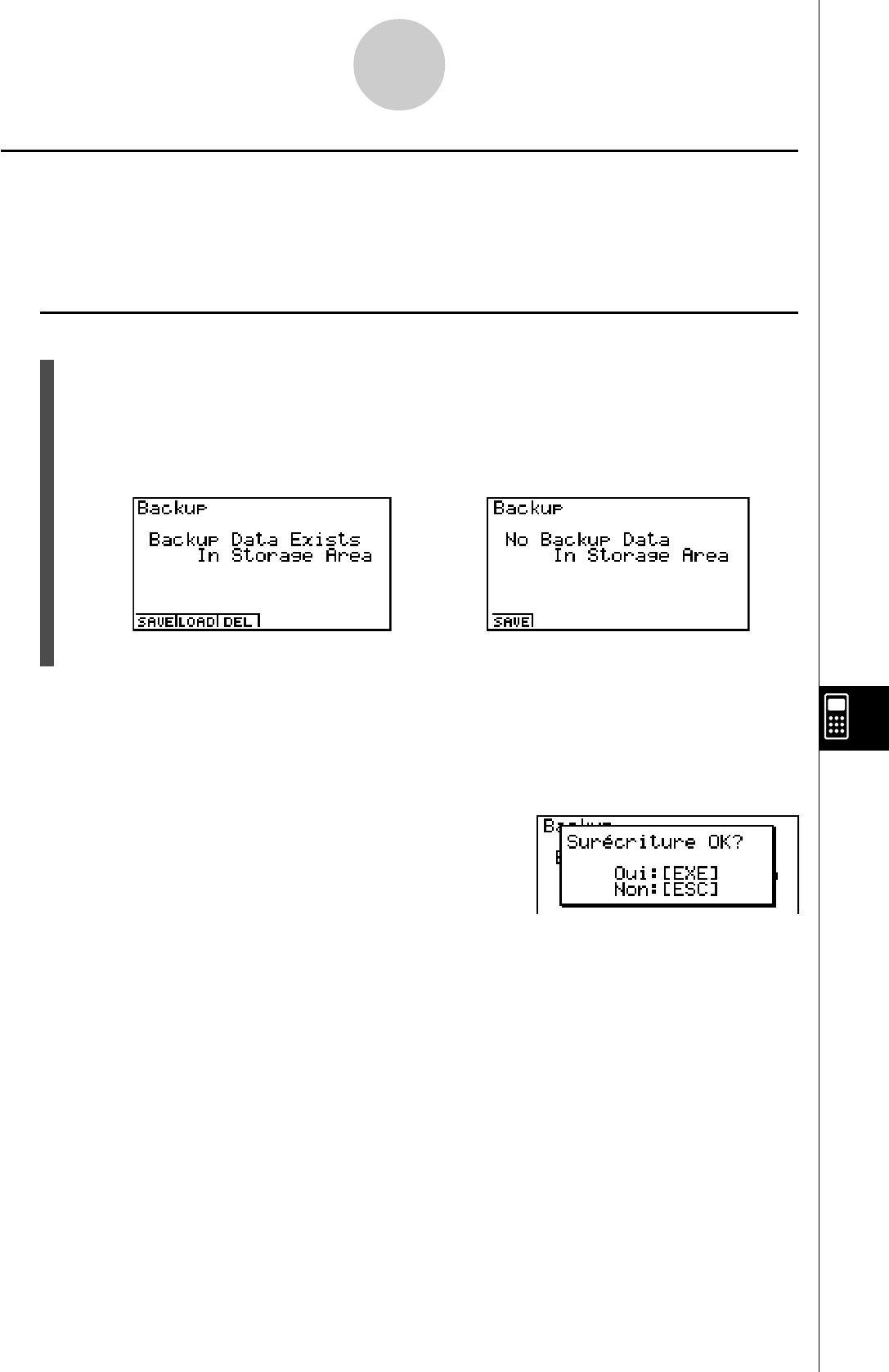
19990401
kSauvegarde des données de la zone active
Vous pouvez faire une sauvegarde de toutes les données se trouvant dans la zone active
pour les mettre dans la zone de stockage. Vous pourrez les transférer à nouveau dans la
zone active lorsque vous en aurez besoin.
uPour sauvegarder les données de la zone active
1. Sur l’écran initial du mode MEMORY, appuyez sur 2(BACK).
• L’écran A apparaît s’il existe déjà des données de sauvegarde dans la zone de
stockage. L’écran B apparaît s’il n’y a pas de données de sauvegarde dans la zone
de stockage.
Ecran A Ecran B
2. Appuyez sur 1(SAVE) pour sauvegarder les données.
Le message “Complet!” apparaît lorsque l’opération est terminée.
Appuyez sur i pour revenir à l’écran affiché à l’étape 1.
Le message suivant apparaît s’il y a déjà des données de sauvegarde dans la zone de
stockage.
Appuyez sur w(Oui) pour sauvegarder les données ou sur i(Non) pour abandonner
l’opération.
Une “Erreur de mémoire” se produit si l’espace disponible dans la zone de stockage est
insuffisant pour une sauvegarde complète des données.
10-8-7
Mode MEMORY
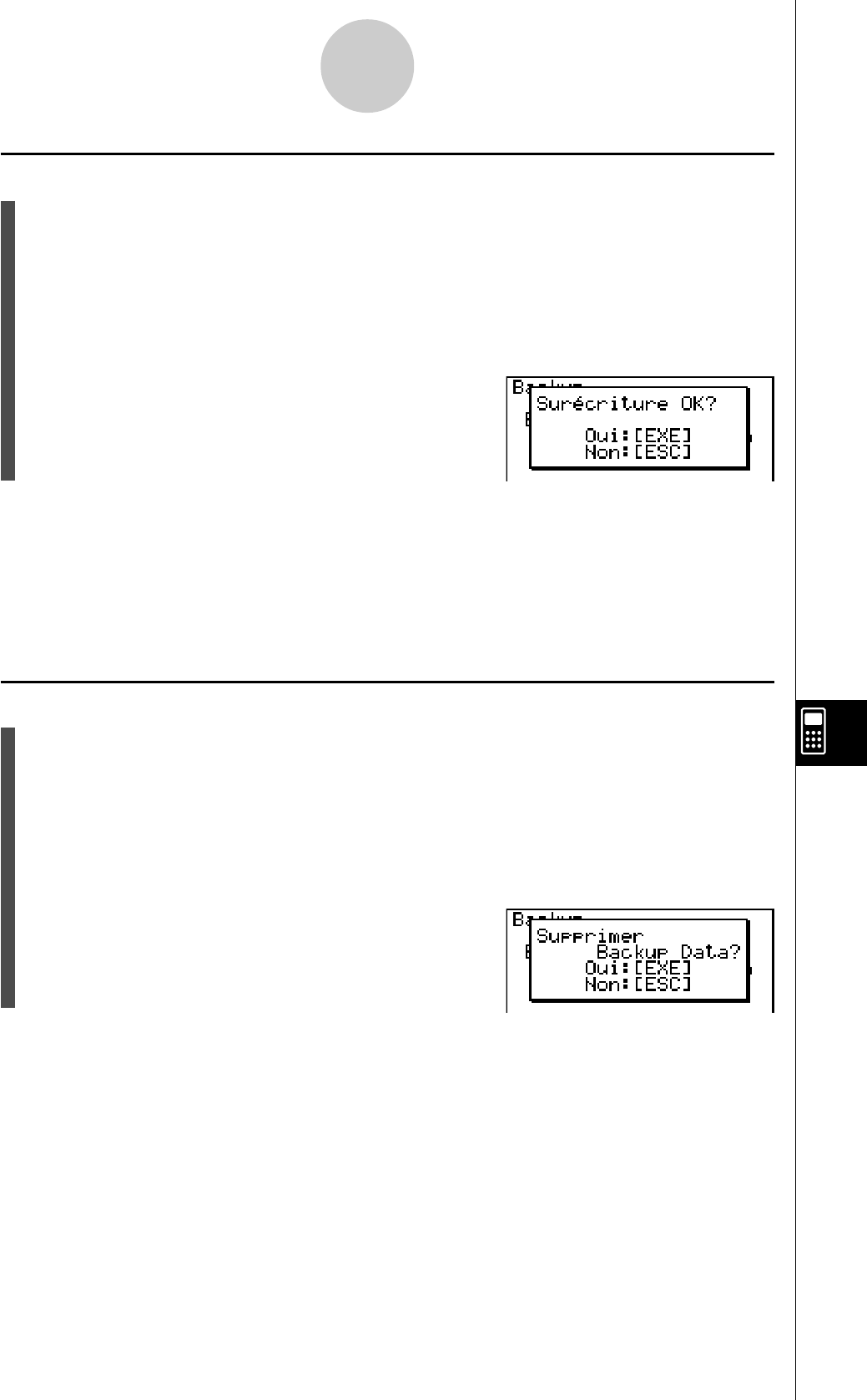
19990401
uPour rétablir les données de sauvegarde dans la zone active
1. Sur l’écran initial du mode MEMORY, appuyez sur 2(BACK).
• Sur l’écran qui apparaît vous pouvez vérifier s’il y a ou non des données de
sauvegarde dans la zone de stockage.
2. Appuyez sur 2(LOAD).
• Un message apparaît vous demandant de confirmer le rétablissement des données
de sauvegarde.
Appuyez sur w(Oui) pour rétablir les données et supprimer les données actuellement dans
la zone active.
Appuyez sur i(Non) pour annuler l’opération.
Le message “Complet!” apparaît lorsque l’opération est terminée.
Appuyez sur i pour revenir à l’écran affiché à l’étape 1.
uPour supprimer les données de sauvegarde de la zone de stockage
1. Sur l’écran initial du mode MEMORY, appuyez sur 2(BACK).
• Sur l’écran qui apparaît vous pouvez vérifier s’il y a ou non des données de
sauvegarde dans la zone de stockage.
2. Appuyez sur 3(DEL).
• Un message apparaît vous demandant de confirmer la suppression des données de
sauvegarde.
Appuyez sur w(Oui) pour supprimer les données de sauvegarde de la zone de stockage.
Appuyez sur i(Non) pour annuler l’opération.
Le message “Complet!” apparaît lorsque l’opération est terminée.
Appuyez sur i pour revenir à l’écran affiché à l’étape 1 qui contient maintenant le
message “No Backup Data.”
10-8-8
Mode MEMORY

19990401
kOptimisation de la zone de stockage
La zone de stockage est fragmentée après plusieurs opérations de stockage et de
chargement.
La fragmentation peut entraîner une indisponibilité de certains blocs de mémoire.
C’est pourquoi il est conseillé d’effectuer régulièrement l’opération suivante pour optimiser la
zone de stockage. Les données seront réarrangées et l’emploi de la mémoire sera plus
économique.
uPour optimiser la zone de stockage
Sur l’écran initial du mode MEMORY, appuyez sur 3(OPT) pour optimiser la zone de
stockage.
Le message “Complet!” apparaît lorsque l’opération est terminée.
Appuyez sur i pour revenir à l’écran initial du mode MEMORY.
10-8-9
Mode MEMORY

19990401
Signification
• Syntaxe incorrecte
• Saisie d’une commande
incorrecte
• Le résultat du calcul dépasse la
plage d’affichage.
• Le calcul est hors de la plage
d’introductión d’une fonction.
• Erreur mathématique (division
par zéro, etc.)
• Impossible d’obtenir une
précision suffisante pour le calcul
de Σ, de différentielles, etc.
• Impossible d’obtenir une solution
pour le calcul d’équations, etc.
1Pas de ”Lbl n” correspondant à
“Goto n”.
2Aucun programme enregistré
dans la zone de programme Prog
”nom de fichier”.
• Le branchement de sous-
programmes par Prog ”nom de
fichier” dépasse les 10 niveaux.
Message
Erreur syntaxe
Erreur math
Erreur saut
Erreur branch
Mesure corrective
• Appuyer sur i pour afficher
l’erreur et effectuer les rectifica-
tions nécessaires.
• Vérifiez les valeurs saisies et
effectuez les rectifications
nécessaires pour que les
valeurs soient dans les limites
permises.
1Introdui la commande “Lbl n”
qui correspond au “Goto n”, ou
supprimer le “Goto n” s’il n’est
pas nécessaire.
2Stocker un programme dans la
zone Prog ”nom de fichier”, ou
effacer l’instruction Prog ”nom
de fichier”, si elle est inutile.
• S’assurer que Prog ”nom de
fichier” n’est pas utilisé pour
revenir d’un sous-programme
au programme principal. Le cas
échéant, supprimer tout Prog
”nom de fichier” inutile.
• Rechercher les destinations des
sauts aux sous-programmes et
s’assurer qu’aucun saut n’est
effectué vers la zone de
programme original. Vérifier si
les retours sont exacts.
α
-1-1
Tableau des messages d’erreur
1 Tableau des messages d’erreur

19990401
Signification
Message Mesure corrective
α
-1-2
Tableau des messages d’erreur
Erreur pile
Erreur mémoire
Erreur
argument
Erreur
dimension
Erreur plage
Condition
ERROR
(Erreur de
condition)
• L’exécution des calculs dépasse
la capacité de la pile de valeurs
numériques ou de celle de
commandes.
• L’opération ou le stockage en
mémoire dépasse la capacité de
la mémoire restante.
• Spécification d’argument
incorrecte pour une commande
nécessitant un argument.
• Dimension ou liste incorrecte
utilisée pendant les calculs
matriciels.
1Saisie d’une valeur inadaptée
pour la fenêtre d’affichage.
2Réglages de plage de fenêtre
d’affichage dépassés lorsqu’un
graphe est retracé.
3Saisie d’une valeur inadaptée sur
l’écran de plage et utilisation de
cette valeur pour l’exécution.
• Exécution d’un calcul ou d’une
fonction avant que toutes les
conditions requises soient
remplies.
• Simplifier les formules pour
que la pile de valeurs
numériques ne comporte que
10 niveaux au maximum et que
celle de commandes ne
comporte que 26 niveaux au
maximum.
• Diviser la formule en au moins
deux parties.
• Le nombre de variables
utilisées pour l’opération ne
doit pas dépasser le nombre
de variables actuellement
disponibles.
• Simplifier les données pour
pouvoir les stocker dans la
mémoire disponible.
• Supprimer les données inutiles
pour libérer de l’espace pour
de nouvelles données.
• Corriger l’argument.
• Contrôler la dimension de la
matrice ou de la liste.
1Changer la valeur de la fenêtre
d’affichage pour qu’elle soit
dans la plage.
2Retracer le graphe en utilisant
les réglages appropriés.
3Saisir une valeur appropriée.
• Vérifier les conditions et
effectuer les rectifications
nécessaires.
19990401
α
-1-3
Tableau des messages d’erreur
Signification
Message Mesure corrective
Erreur non réel
Nombre
complexe dans
la liste
Nombre
complexe dans
la matrice
Résol
impossible!
Définir val init ou
limites et
réssayer.
Pas de variable
Erreur itération
Erreur com
1Calcul produisant un nombre
complexe lorsque Real est
spécifié pour le réglage de
Complex Mode sur l’écran de
configuration, bien que
l’argument soit un nombre réel.
2Calcul produisant une nombre
complexe lorsque Real est
spécifié pour le réglage de
Answer Type sur l’écran de
configuration bien que
l’argument soit un nombre réel.
• Utilisation d’une liste contenant
des nombres complexes dans
un calcul avec nombres réels.
• Utilisation d’une matrice
contenant des nombres
complexes dans un calcul avec
nombres réels.
• Impossible d’obtenir une
solution avec la plage définie.
• Aucune variable désignée dans
la fonction de graphe utilisée
pour le graphe dynamique.
• Pas de variable dans une
équation à résoudre.
1Pas de convergence des
solutions.
2Pas de solution du calculle
d’intégration ou de différentielle
satisfaisant la condition de la fin
de l’opération (valeur tol).
• Problème de liaison ou de
réglage de paramètre lors de la
communication d’un programme.
1Sélectionner autre chose que
Real comme réglage de
Complex Mode.
2Sélectionner autre chose que
Real comme réglage de
Answer Type.
• Remplacer toutes les données
dans la liste par des nombres
réels.
• Remplacer toutes les données
dans la matrice par des
nombres réels.
• Changez la plage.
• Corrigez l’expression saisie.
• Définissez une variable pour la
fonction de graphe.
1Remplacer la valeur estimée
initiale par celle qui est la plus
proche de la solution.
2Augmenter la valeur tol pour
réduire la précision.
• Vérifier le raccordement du
câble.

19990401
α
-1-4
Tableau des messages d’erreur
Erreur transm
Erreur
réception
Mémoire
pleine
Erreur de
téléchargement
Incompatibilité
Erreur
dépassement
capacité
Erreur
domaine
• Problème de raccordement de
câble ou de spécification d’un
paramètre pendant la communi-
cation de données.
• Problème de raccordement de
câble ou de spécification d’un
paramètre pendant la communi-
cation de données.
• La mémoire de la machine
réceptrice est saturée pendant
la communication des données
de programme.
• Câble de communication de
données débranché pendant
l’installation du nouveau logiciel
ou conditions de transfert de
données incorrectes.
• Tentative de sauvegarde entre
deux modèles différents.
• Dépassement de la plage de
calcul dans le mode Algèbre.
• Dépassement de la plage
d’éléments saisie dans le mode
Algèbre.
• Vérifier le raccordement du
câble.
• Vérifier le raccordement du
câble.
• Effacer quelques données
mémorisées dans la machine
réceptrice et essayer à nouveau.
• Appuyer sur w pour essayer
une nouvelle fois.
• Appuyer sur i pour essayer
une nouvelle fois.
• Utiliser des modèles identiques.
• Corriger l’expression saisie.
• Corriger l’expression saisie.
SignificationMessage Mesure corrective

19990401
α
-2-1
Plages d’introduction
sinx
cosx
tanx
Asn(sin–1)x
Acs(cos–1)x
Atn(tan–1)x
sinhx
coshx
tanhx
sinh–1x
cosh–1x
tanh–1x
logx
Inx
10x
ex
x
x2
1/x
3x
x
!
nPr
nCr
Pol (x, y)
En règle
générale, la
précision est
de ±1 au 10e
chiffre.
"
"
"
"
"
"
"
"
"
"
Cependant, pour tanx:
|x|
GG
GG
G
90(2n+1):DEG
|x|
GG
GG
G
π/2(2n+1):RAD
|x|
GG
GG
G
100(2n+1):GRA
*
Des nombres complexes peuvent
être utilisés comme arguments.
*
Des nombres complexes peuvent
être utilisés comme arguments.
Pour sinh et tanh, lorsque
x = 0, les erreurs sont
cumulatives et la précision
en est affectée à un
certain point.
*
Des nombres complexes peuvent
être utilisés comme arguments.
(DEG) |x| < 9 × (109)°
(RAD) |x| < 5 × 107π rad
(GRA) |x| < 1 × 1010grad
|x| < 1
|x| < 1 × 10100
|x| < 230,2585092
|x| < 1 ×10100
|x| < 5 × 1099
1< x < 5 × 1099
|x| < 1
1 × 10–99 < x < 1 × 10100
–1 × 10100 < x < 100
–1 × 10100
< x < 230,2585092
0 < x < 1 × 10100
|x| <1 × 1050
|x| < 1 × 10100, x
GG
GG
G
0
|x| < 1 × 10100
0 < x < 69
(x est un nombre entier)
Résultat < 1 × 10100
n, r (n et r sont des nombres
entiers)
0 < r < n, n < 1 × 1010
< 1 × 10100
x2 + y2
2 Plages d’introduction
15
chiffres
"
"
"
"
"
"
"
"
"
"
Plage d’introduction pour les
solutions à nombres réels
Fonction Chiffres
internes Précision Notes
*
Des nombres complexes peuvent
être utilisés comme arguments.
*
Des nombres complexes peuvent
être utilisés comme arguments.
*
Des nombres complexes peuvent
être utilisés comme arguments.
*
Des nombres complexes peuvent
être utilisés comme arguments.
*
Des nombres complexes peuvent
être utilisés comme arguments.

19990401
α
-2-2
Plages d’introduction
Rec
(r ,
θ
)
° ’ ”
←⎯
° ’ ”
^(xy)
xy
a+ b/c
15 chiffres
"
"
"
"
En règle
générale, la
précision est
de ±1 au 10e
chiffre.
"
"
"
"
Cependant, pour tan
θ
:
|
θ
|
GG
GG
G
90(2n+1):DEG
|
θ
|
GG
GG
G
π/2(2n+1):RAD
|
θ
|
GG
GG
G
100(2n+1):GRA
|r| < 1 × 10100
(DEG) |
θ
| < 9 × (109)°
(RAD) |
θ
| < 5 × 107π rad
(GRA) |
θ
| < 1 × 1010grad
|a|, b, c < 1 × 10100
0 < b, c
|x| < 1 × 10100
Affichage sexagésimal:
|x| < 1 × 107
y > 0 : x
GG
GG
G
0 1
–1 × 10100 < –– log y < 100
x
y = 0 : x > 0 1
y < 0 : x = 2n +1, ––
n
(n
GG
GG
G
0, n est un nombre
entier ou une fraction)
Cependant; 1
–1 × 10100 < –– log |y| < 100
x
Le total de l’entier, du
numérateur et du
dénominateur ne doit pas
dépasser 10 chiffres
(signes de division
compris).
x > 0:
–1 × 10100 < y log x < 100
x = 0 : y > 0
x < 0 :
y = n,
(n est un nombre entier ou
une fraction)
Cependant;
–1 × 10100 < log |x| < 100
1
––
y
1
––––
2n+1
*Les erreurs peuvent être cumulatives et la précision peut être affectée par ^ (xy), xy, x!, 3x et
par d’autres fonctions exigeant des calculs continus internes ainsi que par les calculs impliquant
des nombres complexes.
Plage d’introduction pour les
solutions à nombres réels
Fonction Chiffres
internes Précision Notes
*
Des nombres complexes
peuvent être utilisés comme
arguments.
*
Des nombres complexes
peuvent être utilisés comme
arguments.

19990401
α
-2-3
Plages d’introduction
Fonction
Calcul
binaire,
octal,
décimal,
hexadécimal
Plage d’introduction
Les valeurs rentrent dans les plages suivantes après la conversion:
DEC: –2147483648 < x < 2147483647
BIN: 1000000000000000 < x
< 1111111111111111 (négative)
0 < x < 0111111111111111 (0, positive)
OCT: 20000000000 < x < 37777777777 (négative)
0 < x < 17777777777 (0, positive)
HEX: 80000000 < x < FFFFFFFF (négative)
0 < x < 7FFFFFFF (0, positive)

19990401
α
-3-1
Spécifications
3 Spécifications
Variables: 28
Plage de calculs:
±1 × 10–99 à
±9,999999999 × 1099 et 0. Les opérations internes utilisent une mantisse de 15
chiffres.
Plage d’affichage exponentiel: Norm 1: 10–2 > |x|, |x| > 1010
Norm 2: 10–9 > |x|, |x| > 1010
Capacité de programmation:
Mémoire active : 144K octets maximum
Capacité de stockage annexe : 768K octets maximum
Alimentation:
Principale: Quatre piles de taille AAA (LR03 (AM4) ou R03(UM-4))
Sauvegarde: Une pile au lithium CR2032
Consommation: 0,2 W
Autonomie des piles environ
Principale:
LR03 (AM4): 230 heures (affichage continu du menu principal)
150 heures de fonctionnement continu (5 minutes de calcul, 55 minutes
d’affichage)
R03 (UM-4): 140 heures (affichage continu du menu principal)
90 heures de fonctionnement continu (5 minutes de calcul, 55 minutes
d’affichage)
Pile de sauvegarde : 2 ans
Extinction automatique :
La calculatrice s’éteint automatiquement six minutes ou 60 minutes environ après la dernière
opération.
Plage de température ambiante: 0 °C à 40 °C
Dimensions: 19,5 mm (E) × 82 mm (L) × 178 mm (L)
Poids: Environ 213 g (avec les piles)

19990401
α
-3-2
Spécifications
Communication de données
Méthode: Start-stop (asynchrone), semi-duplex
Vitesse de transmission (BPS): 38400 bits/seconde (normal)
9600 bits/seconde (H-Copy & Send/Receive)
Parité: NONE
Longueur de bit: 8 bits
Bit d’arrêt:
Émission: 3 bits
Réception: 2 bits
Comprend parité (NONE) 1 bit
Commande X ON/X OFF: Sans

1999040120001202
Symboles
AList .................................................. 3-2-7
Σ.......................................................2-5-10
A
Affichage de texte ..............................8-6-1
Affichage normal ........... 1-2-4, 2-1-2, 2-3-2
Ajouts ...............................................10-7-1
Alimentation ...................................... α-7-1
Analyse de fonctions ....................... 5-11-1
Ans ................................................... 2-2-5
APO .................................................. 9-3-1
Argument ...........................................2-6-2
Arrière-plan d’un graphe ................. 5-10-7
Arrondi de coordonnées .................. 5-11-7
Asymptotes .................................... 5-11-21
Axe de la directrice ........................ 5-11-20
Axe de symétrie ............................. 5-11-20
B
Bibliothèque de programmes ............ 8-8-1
Binaire ...............................................2-7-1
Bouton P ........................................... α-6-1
C
Calculs arithmétiques ....................... 2-1-1
Calculs continus ..................... 2-2-5, 7-1-7
Calculs de régression ....................... 6-4-3
Calculs et de graphes statistiques dans un
programme ..................................8-6-9
Capacité de la mémoire .................... 2-1-6
CAS .................................................. 7-1-1
Catalogue ......................................... 1-3-5
Centre ............................................ 5-11-19
Cercle ............................................... 5-1-5
Chiffres significatifs ................. 2-1-2, 2-3-2
Classement de listes dans un programme
.................................................... 8-6-8
Classement des valeurs d’une liste .. 3-1-5
Code d’accès .................................... 8-4-3
Collage du texte ................................ 1-3-5
Colonne, matrice .............................. 2-8-9
Combinaison ..................................... 2-4-9
Commande dans la barre de menu .. 1-2-3
Commandes de programmation ....... 8-7-1
Commentaire .................................. 5-10-3
Communication de données ............10-4-1
Configuration d’un mode .................. 1-7-1
CONICS ............................................ 5-1-5
Connexion de deux calculatrices .... 10-1-1
Connexion de la calculatrice à un
ordinateur ..................................10-3-1
Connexion de la calculatrice à une
imprimante d’étiquettes CASIO
...................................................10-2-1
Contraste ...........................................9-3-1
Conversion de coordonnées ... 2-4-2, 2-4-8
Coordonnées de points donnés ..... 5-11-13
Coordonnées sur une ligne du graphe
................................................... 5-11-1
Copie d’écran, envoi ........................10-6-1
Copie d’écran, sauvegarder ............10-6-1
Copie d’une colonne d’une table dans une
liste ............................................. 5-7-8
Copie d’une formule de graphe de
régression .................................. 6-3-11
Copier ............................................... 1-3-4
Correction ......................................... 1-3-4
Courbe de répartition normale .......... 6-2-3
α
-4-1
Index
4 Index

1999040120001202
α
-4-2
Index
D
Débogage ......................................... 8-3-1
Décimale ........................................... 2-7-1
Degrés/minutes/secondes ...... 1-2-5, 2-4-2
Dépassement ................................... 2-1-5
Dessin ..............................................5-10-1
Dessin à main levée ........................5-10-5
Déterminant .....................................2-8-18
Diagramme à barres ......................... 6-2-1
Diagramme de dispersion ................. 6-3-1
Différentielles .................................... 2-5-2
Différentielles quadratiques .............. 2-5-5
Données de sauvegarde, émettrice
...................................................10-4-4
Données d’une liste, traitement ........ 3-2-1
Double graphe .................................. 5-5-1
DYNA ................................................ 5-8-1
E
Ecran de configuration ...................... 1-7-1
Ecran de texte .................................. 1-2-3
Ecran graphique ............................... 1-2-3
Ecran principal .................................. 5-5-1
Ecran secondaire .............................. 5-5-1
Ecrans ...............................................1-2-3
Edition de calculs .............................. 1-3-1
Elément, edition ................................ 3-1-3
Ellipse ............................................... 5-1-5
Eng ................................................... 2-3-2
EQUA ................................................ 4-1-1
Equations de degré élevé ................. 4-2-1
Equations linéaires simultanées ....... 4-1-1
Excentricité .................................... 5-11-21
Exponentielle .................................... 2-4-4
Expressions X = constante ............... 5-3-2
F
Faible tension des piles .................... 1-8-2
Fenêtre calc .....................................5-2-12
Fenêtre d’affichage ........................... 5-2-1
Fichier de programme, charger .......10-8-3
Fichier de programme, recherche
........................................ 8-4-1, 10-8-5
Fichier de programme, stocker ........10-8-2
Fichiers de listes, changement ......... 3-4-1
Fichiers de programme, suppression
...................................................10-8-4
FMEM ............................................... 2-2-2
Fonction à coordonnées polaires ..... 5-3-1
Fonction à coordonnées rectangulaires
.................................................... 5-3-1
Fonction composite ................ 2-1-3, 5-3-3
Fonction de graphs, stocker/rappeler 5-3-7
Fonction de résolution dans un programme
.................................................... 8-6-9
Fonction paramétrique ...................... 5-3-2
Fonction, éditer/changer/supprimer .. 5-3-5
Fonctions graphiques dans un programme
.................................................... 8-6-3
Format d’affichage ............................ 2-3-1
Forme polaire ................................... 2-6-4
Forme rectangulaire ......................... 2-6-4
Foyer ............................................. 5-11-18
Fractions ..........................................5-4-10
G
Génération d’une table ..................... 5-7-2
Graphe à table ................................. 5-11-5
Graphe de régression ....................... 6-3-3
Graphe de régression de puissance
.................................................... 6-3-9
Graphe de régression exponentielle
.................................................... 6-3-8

1999040120001202
α
-4-3
Index
Graphe de régression linéaire .......... 6-3-6
Graphe de régression logarithmique
.................................................... 6-3-8
Graphe de régression logistique ..... 6-3-10
Graphe de régression sinusoïdale .... 6-3-9
Graphe dynamique dans un programme
.................................................... 8-6-5
Graphe d’intégration ......................... 5-6-3
Graphe en boîte modifiée ................. 6-2-2
Graphe en boîte-médiane ................. 6-2-2
Graphe linéaire ..................................6-2-3
Graphe linéaire xy ............................ 6-3-1
Graphe Med-Med ..............................6-3-6
Graphe statistiques à variable double
.................................................... 6-3-1
Graphe statistiques à variable unique
.................................................... 6-2-1
Graphe WEB .................................... 5-9-7
Graphe, stocker/rappeler .................. 5-4-1
Graphes multiples ............................6-3-12
Graphique dynamique ...................... 5-8-1
Graphique d’une distribution de probabilité
.................................................... 6-4-7
Graphique manuelle ......................... 5-6-1
GRPH
•
TBL ....................................... 5-1-1
H
Hexadécimale ......................... 1-2-5, 2-7-1
Histogramme .................................... 6-2-1
Hyperbole ......................................... 5-1-5
Hyperbolique inverse .............. 2-4-2, 2-4-5
Hyperboliques (HYP) .............. 2-4-2, 2-4-5
I
Icône ................................................. 1-2-1
Implicite ......................................... 5-11-17
Indicateur d’exécution de calcul ....... 1-2-5
Inéquation ......................................... 5-3-2
Ingénieur ............................... 2-3-2, 2-4-11
Initialisation ....................................... 9-4-1
Inscriptions sur le clavier .................. 1-1-3
Instructions multiples ........................ 2-2-7
Intégration ......................................... 2-5-7
Intersections .................................. 5-11-19
L
Langue du système .......................... 9-3-2
Latus rectum .................................. 5-11-18
Liaison Graphe-Table ..................... 5-7-15
Ligne, matrice ................................... 2-8-5
LINK ................................................ 10-4-1
Liste des données statistiques ......... 6-1-1
Liste, calculs arithmétiques .............. 3-3-1
Liste, saisie ....................................... 3-1-1
Listes dans le mode CAS ................. 7-1-2
Listes de données pour les calculs
statistiques .................................. 6-4-1
Logarithmique ................................... 2-4-4
M
Marquage ......................................... 5-1-4
MatAns ............................................. 2-8-1
Matrice, dimensions .............. 2-8-2, 2-8-12
Matrice, élévation à une puissance
...................................................2-8-20
Matrice, élévation au carré ............. 2-8-19
Matrice, inversion ............................2-8-19
Matrice, opérations arithmétiques ...2-8-17
Matrice, saisie et édition ................... 2-8-2
Matrice, transposition ..................... 2-8-18
Matrices à l’aide des commandes de
matrice .......................... 2-8-10, 2-8-13
Matrices dans le mode CAS ............. 7-1-2
Mémoire ............................................ 2-2-1

1999040120001202
α
-4-4
Index
Mémoire de dernier résultat .... 2-2-5, 7-1-7
Mémoire de fenêtre d’affichage ........ 5-2-4
Mémoire de fonctions ............. 2-2-2, 7-1-6
Mémoire de formules ........................ 7-1-4
Mémoire de graphe dynamique ........ 5-8-6
Mémoire de graphes ............... 5-3-7, 7-1-6
Mémorie de solutions ....................... 7-1-8
Mémoire d’équations ........................ 7-1-6
Mémoire d’images ............................ 5-4-1
Mémoire flash ..................................10-8-1
Mémoires de stockage ..................... 9-2-1
Mémoires principales ........................ 9-2-1
MEMORY .........................................10-8-1
Menu de données de variables (VARS)
.................................................... 1-5-1
Menu de fonction .................. 1-2-3, 5-2-11
Menu de programmation (PRGM) .... 1-6-1
Menu de réglages du système ......... 9-1-1
Menu déroulant ..................................1-2-3
Menu d’options (OPTN) .................... 1-4-1
Message Erreur de données ............ α-6-1
Messages d’erreur .................. 2-1-5, α-1-1
Mise hors tension automatique
.......................................... 9-3-1, α-7-5
Mode Algèbre, opération .................. 7-1-3
Multi-répétitions ................................ 1-3-3
N
Nom de fichier, edition ...................... 8-4-2
Nom de fichier, enregistrement
.......................................... 8-1-1, 8-2-1
Nombre de ciffres ................... 2-1-2, 2-3-1
Nombres aléatoires .......................... 2-4-7
Nombres complexes ......................... 2-6-1
Nombres complexes conjugués ....... 2-6-3
Norm 1/2 ................................. 1-2-4, 2-3-2
Numeriques (NUM) ........................... 2-4-1
O
Octale ............................................... 2-7-1
Opérations concernant la mémoire .. 9-2-1
Opérations logiques .......................... 2-7-4
Opérations sur les lignes d’une matrice
dans un programme ................... 8-6-1
Optimisation de la zone de stockage
...................................................10-8-9
OPTN ................................................ 1-4-1
P
Parabole ........................................... 5-1-5
Paramètre derivative ............ 5-7-3, 5-11-3
Paramètres d’un graphe, changement
.................................................... 6-1-2
Parenthèses ..................................... 2-1-1
Partie imaginaire ............................... 2-6-3
Partie réelle ...................................... 2-6-3
Permutation ...................................... 2-4-9
Piles .................................................. 2-2-6
Plage de la table ............................... 5-7-1
Plages d’introduction ........................ α-2-1
Point de probabilité normale ............. 6-2-1
Point d’intersection de deux graphes
................................................. 5-11-11
POLY ................................................ 4-2-1
Presse-papiers ..................................1-3-4
PRGM ............................................... 8-1-1
Priorité de calcul ............................... 2-1-3
Probabilité/répartition (PROB)
.......................................... 2-4-1, 6-4-5
Produit scalaire ................................2-8-17
Programme, écrire ............................ 8-2-1
Programme, edition .......................... 8-3-1
Programme, effacement ................... 8-4-2
Programme, lancer ........................... 8-1-1
Programme, mode BASE ................. 8-2-2

1999040120001202
α
-4-5
Index
Programme, recherche de données
.................................................... 8-3-4
R
Racine ............................................. 5-11-9
Rayon ............................................ 5-11-19
RECUR ............................................. 5-9-1
Régression cubique .......................... 6-3-7
Régression quadratique ................... 6-3-7
Régression quartique ....................... 6-3-7
Répétition ............................... 1-3-3, 7-1-7
Réponse ........................................... 2-2-5
Résiduel ...........................................6-3-10
Résolution ............................... 2-5-1, 4-3-1
Résultats du calcul d’un graphe à variable
double ............................. 6-3-11, 6-4-2
Résultats du calcul d’un graphe à variable
unique ............................... 6-2-4, 6-4-2
RUN
•
MAT ......................................... 2-1-1
S
Saisie de calculs ............................... 1-3-1
Sauvegarde des données ................10-8-7
Sexagécimale ......................... 1-2-5, 2-4-2
Signe de multiplication ...................... 2-1-5
SIML ................................................. 4-1-1
Sommet ......................................... 5-11-18
Sous-menu ....................................... 1-2-3
STAT ................................................. 6-1-1
Superposer les graphes ................... 5-6-5
SYSTEM ........................................... 9-1-1
Système numérique .......................... 2-7-3
T
Table et graphe dans un programme
.................................................... 8-6-6
Table et graphe de récurrence dans un
programme ..................................8-6-7
Table numérique de la formule de
récurrence .................................. 5-9-1
Table, suppression ............................ 5-7-7
Tableau des touches ......................... 1-1-2
Tables ............................................... 5-7-1
Tables, edition ................................... 5-7-5
Trace ................................................ 5-11-1
Tracé d’une ligne .............................5-10-1
Tracé ou sans tracé de graphe ......... 5-3-6
Transformation du système numérique
.................................................... 2-7-5
Trigonométrique ................................ 2-4-3
Trigonométrique inverse ................... 2-4-3
Type de graphe, spécification ........... 5-3-1
U
Unité d’angle .......................... 2-3-1, 2-4-2
Utilisation mémoire........................... 9-2-1
V
Valeur absolue ...................... 2-6-2, 2-8-20
Valeur de l’intégrale pour une plage
donnée ..................................... 5-11-15
Valeurs estimées .............................. 6-4-4
Valeurs maximale/minimale ............ 2-5-12
Valeurs négatives ..............................2-7-4
Variable(s)......................................... 2-2-1
VARS ................................................ 1-5-1
Vecteurs dans le mode CAS ............. 7-1-3
Z
Zone active ......................................10-8-1
Zone de numéro de formule ............. 7-1-1
Zone de sortie ................................... 7-1-1

1999040120001202
Zone de stockage ............................10-8-1
Zone d’affichage de résultat naturel . 7-1-1
Zone d’entrée ................................... 7-1-1
Zoom ................................................ 5-2-7
Zoom avec facteur ............................ 5-2-9
Zoom sur cadre ................................ 5-2-7
α
-4-6
Index

1999040120001202
α
-4-7
Index
Index des commandes
algébriques
∫
........................................................7-1-16
Σ.......................................................7-1-17
Π......................................................7-1-17
absExpand ...................................... 7-1-21
andConnect .....................................7-1-21
approx ..............................................7-1-15
arcLen ..............................................7-1-17
cExpand ...........................................7-1-15
clear ................................................ 7-1-22
clearVarAll....................................... 7-1-22
collect ..............................................7-1-14
combine ...........................................7-1-14
denominator .....................................7-1-18
diff ................................................... 7-1-16
eliminate ..........................................7-1-20
eqn ...................................................7-1-21
exchange .........................................7-1-20
expand ............................................. 7-1-11
expToTrig .........................................7-1-13
factor ................................................ 7-1-11
gcd ...................................................7-1-18
getRight ...........................................7-1-20
invert ............................................... 7-1-20
lcm ...................................................7-1-19
lim ................................................... 7-1-16
numerator ....................................... 7-1-18
rclAllEqn ..........................................7-1-19
rclEqn ..............................................7-1-19
rewrite ..............................................7-1-19
rFactor ............................................. 7-1-11
simplify .............................................7-1-13
solve ............................................... 7-1-12
substitute .........................................7-1-14
tanLine .............................................7-1-18
taylor ............................................... 7-1-17
tCollect .............................................7-1-12
tExpand ...........................................7-1-12
trigToExp ..........................................7-1-13
(Commandes de calculs avec listes)
AList .................................................... 7-1-27
Augment .............................................. 7-1-28
Cuml .................................................... 7-1-26
Dim ...................................................... 7-1-23
Fill ........................................................ 7-1-28
List → Mat ........................................... 7-1-30
List → Vect .......................................... 7-1-30
Max ...................................................... 7-1-24
Mean.................................................... 7-1-24
Median ................................................. 7-1-25
Min ....................................................... 7-1-23
Percent ................................................ 7-1-26
Prod ..................................................... 7-1-26
Seq ...................................................... 7-1-28
SortA.................................................... 7-1-29
SortD ................................................... 7-1-29
StdDev ................................................. 7-1-27
SubList ................................................ 7-1-29
Sum ..................................................... 7-1-25
Variance ............................................... 7-1-27
(Commandes de calculs matriciels)
`Row .................................................. 7-1-38
`Row+................................................ 7-1-38
Augment .............................................. 7-1-35
Det ....................................................... 7-1-31
Diag ..................................................... 7-1-37
Dim ...................................................... 7-1-31
EigVc ................................................... 7-1-32

1999040120001202
EigVl .................................................... 7-1-32
Fill ........................................................ 7-1-35
Identify ................................................. 7-1-35
LU ........................................................ 7-1-34
Mat → List ........................................... 7-1-37
Mat → Vect .......................................... 7-1-37
Norm .................................................... 7-1-31
Ref ....................................................... 7-1-33
Row+ ................................................... 7-1-39
Rref ...................................................... 7-1-33
SubMat ................................................ 7-1-36
Swap.................................................... 7-1-38
Trn ....................................................... 7-1-34
(Commandes de calculs vectoriels)
Angle ................................................... 7-1-41
Augment .............................................. 7-1-41
CrossP ................................................. 7-1-40
Dim ...................................................... 7-1-40
DotP .................................................... 7-1-40
Fill ........................................................ 7-1-41
Norm .................................................... 7-1-40
UnitV .................................................... 7-1-41
Vect → List .......................................... 7-1-42
Vect → Mat .......................................... 7-1-42
α
-4-8
Index

19990401
α
-4-9
Index
Index des commandes
PRGM
Break ................................................ 8-5-6
ClrGraph .......................................... 8-5-11
ClrList............................................... 8-5-11
ClrMat ..............................................8-5-12
ClrText .............................................8-5-12
DispF-Tbl, DispR-Tbl ...................... 8-5-12
Do~LpWhile ...................................... 8-5-5
DrawDyna ....................................... 8-5-12
DrawFTG-Con, DrawFTG-Plt ......... 8-5-13
DrawGraph ......................................8-5-13
DrawR-Con, DrawR-Plt....................8-5-13
DrawRΣ-Con, DrawRΣ-Plt ...............8-5-14
DrawStat ..........................................8-5-14
DrawWeb .........................................8-5-14
Dsz ................................................... 8-5-9
For~To~(Step~)Next ......................... 8-5-4
Getkey .............................................8-5-15
Goto~Lbl ..........................................8-5-10
If~Then~(Else~)IfEnd ....................... 8-5-4
Isz .................................................... 8-5-11
Locate ..............................................8-5-16
Prog .................................................. 8-5-7
Receive ( / Send ( ............................8-5-17
Return ............................................... 8-5-8
Stop .................................................. 8-5-8
While~WhileEnd ............................... 8-5-6
? (Commande d’entrée) .................... 8-5-2
^ (Commande de sortie) ................. 8-5-3
: (Commande d’instructions multiples) 8-5-3
_ (Retour) ....................................... 8-5-3
’ (Délimiteur de commentaire)........... 8-5-3
=,
GG
GG
G
, >, <, ≥, ≤
(Opérateurs relationnels) .................8-5-18
20001202

19990401
α
-5-1
Index des touches
5 Index des touches
H-COPY
6
a
Touche
Touche
Fonction primaire Combinée avecu
Combinée avec
Fonction primaire Combinée avec
Combinée avec
a
!a
COPY
1
PASTE
2
SET UP
CAT/CAL
3
Entre le chiffre 0.
4
G ↔ T
5
!
u
V-Window
K
PRGM
J
Affiche le menu d’options.
m
Revient au menu principal.
A -LOCK
a
r
x
θ
M
QUIT
i
Ramène à l’écran précédent sans
aucun changement.
Opération de copie.
Opération de collage.
Sélectionne le 1
er
paramètre du menu
de fonctions.
Sélectionne le 2
e
paramètre du menu
de fonctions.
Sélectionne le 3
e
paramètre du menu
de fonctions.
Sélectionne le 4
e
paramètre du menu
de fonctions. Affichage du catalogue ou
ouverture de la fenêtre Calc.
Commutation des affichages
de graphe et de texte.
Envoi d’une copie de l’écran
actuel à l’appareil raccordé.
Activation ou désactivation de
l’affichage du menu de fonctions.
Affichage de l’écran de
configuration.
Affichage de l’écran de saisie
des paramètres de la fenêtre
d’affichage.
Saisit le
caractère r.
Saisit le
caractère
.
Bloquage/débloquage de la
saisie de caractères
alphanumériques.
Affichage du menu de com-
mandes de programmation.
Sélectionne le 5
e
paramètre du menu
de fonctions.
Sélectionne le 6
e
paramètre du menu
de fonctions.
Active les fonctions décalées d’autres
menus de fonctions et de touches.
Active les fonctions marquées
au-dessus des touches de fonction.
Permet la saisie de caractères
alphanumériques en rouge.
Affiche le menu de données de
variables.
Appuyer entre deux valeurs pour faire
de la seconde valeur l’exposant de la
première.
Appuyer entre la saisie de
deux valeurs X et Y pour
indiquer la racine
x
e
de
y
.
Retour à l’écran initial du
mode.
θ

19990401
α
-5-2
Index des touches
H
x
e
A
v
Saisit la lettre A.
10
x
B
l
Saisit la lettre B.
e
x
C
I
Saisit la lettre C.
Asn
D
s
Saisit la lettre D.
Acs
E
c
Saisit la lettre E.
Atn
F
t
Saisit la lettre F.
d/c
G
N
Saisit la lettre G.
Saisit la lettre H.
Saisit la lettre I.
x
–1
J
)
Saisit la lettre J.
K
,
Saisit une virgule.
Saisit la lettre K.
L
a
Saisit la lettre L.
M
h
Saisit le chiffre 7.
Saisit la lettre M.
N
i
Saisit le chiffre 8.
Saisit la lettre N.
I
(
3
d
f
c
Touche
Fonction primaire Combinée avec
Combinée avec
!a
Déplace le curseur vers la gauche.
Fait défiler l’écran. Appuyer après w
pour afficher le calcul à partir de la fin.
Déplace le curseur vers le haut.
Fait défiler l’écran. Retour à la fonc-
tion précédente dans le mode de lec-
ture des coordonnées.
Déplace le curseur vers le bas.
Fait défiler l’écran. Passage à la
fonction suivante dans le mode de
lecture des coordonnées.
Déplace le curseur vers la droite.
Fait défiler l’écran. Appuyer après
w
pour afficher le calcul à partir du début.
θ
Permet l’entrée des variables X, et
T.
Appuyer avant de saisir une valeur
pour calculer le logarithme décimal. Appuyer avant de saisir
l’exposant 10.
Appuyer avant de saisir une valeur
pour calculer le logarithme népérien. Appuyer avant de saisir
l’exposant e.
Appuyer avant de saisir une valeur
pour calculer le sinus.
Appuyer avant de saisir une
valeur pour calculer le sinus
inverse.
Appuyer avant de saisir une
valeur pour calculer le cosinus
inverse.
Appuyer avant de saisir une valeur
pour calculer la tangente.
Appuyer avant de saisir une
valeur pour calculer la tangente
inverse.
Appuyer entre de saisir des valeurs
fractionnaires.
Convertit une fraction en décimale.
Affichage d’une fraction
supérieure à l’unité.
Appuyer avant de saisir une valeur
pour calculer le cosinus.
Appuyer après la saisie d’une valeur
pour calculer le carré.
Appuyer avant de saisir une
valeur pour calculer la racine
carrée.
Saisit une ouverture de parenthèse
dans la formule.
Appuyer avant de saisir une
valeur pour calculer la racine
cubique.
Saisit une fermeture de parenthèse
dans la formule.
Affecte une valeur à un nom de
variable.
Appuyer après la saisie d’une
valeur pour calculer la
réciproque.

19990401
α
-5-3
Index des touches
INS
D
OFF
o
P
e
Saisit le chiffre 4. Saisit la lettre P.
Q
f
Saisit le chiffre 5. Saisit la lettre Q.
R
g
Saisit le chiffre 6. Saisit la lettre R.
{ S
*
Fonction de multiplication. Saisit la lettre S.
} T
/
Fonction de division. Saisit la lettre T.
UList
Mat
b
Saisit le chiffre 1. Saisit la lettre U.
V
c
Saisit le chiffre 2. Saisit la lettre V.
W
d
Saisit le chiffre 3. Saisit la lettre W.
[ X
+
Saisit une ouverture de crochet. Saisit la lettre X.
] Y
-
Saisit la lettre Y.
i Z
a
Saisit le chiffre 0. Saisit la lettre Z.
=SPACE
.
Saisit la virgule décimale. Saisit le caractère =.
π”
Z
Permet la saisie d’un exposant.
Ans
-
_
w
O
j
Saisit le chiffre 9. Saisit la lettre O.
Touche
Fonction primaire Combinée avec !
Combinée avec
a
Efface le caractère à la actuelle du
curseur. Permet l’insertion de carac-
tères à position du curseur.
Saisit une ouverture
d’accolades.
Saisit une fermeture
d’accolades.
Saisit des
guillemets.
Fonction d’addition. Spécifie une
valeur positive.
Saisit une fermeture de crochet.
Fonction de soustraction. Spécifie
une valeur négative.
Saisit une commande List.
Saisit une commande Mat.
Met sous tension. Efface l’affichage. Met hors tension.
Saisit un espace.
Saisit la valeur de pi. Saisit le
symbole pi.
Saisit l’unité d’un nombre
imaginaire.
Rappelle le résultat du dernier
calcul.
Saisir avant la valeur pour spécifier
une valeur négative.
Saisit une nouvelle ligne.
Affiche le résultat du calcul.
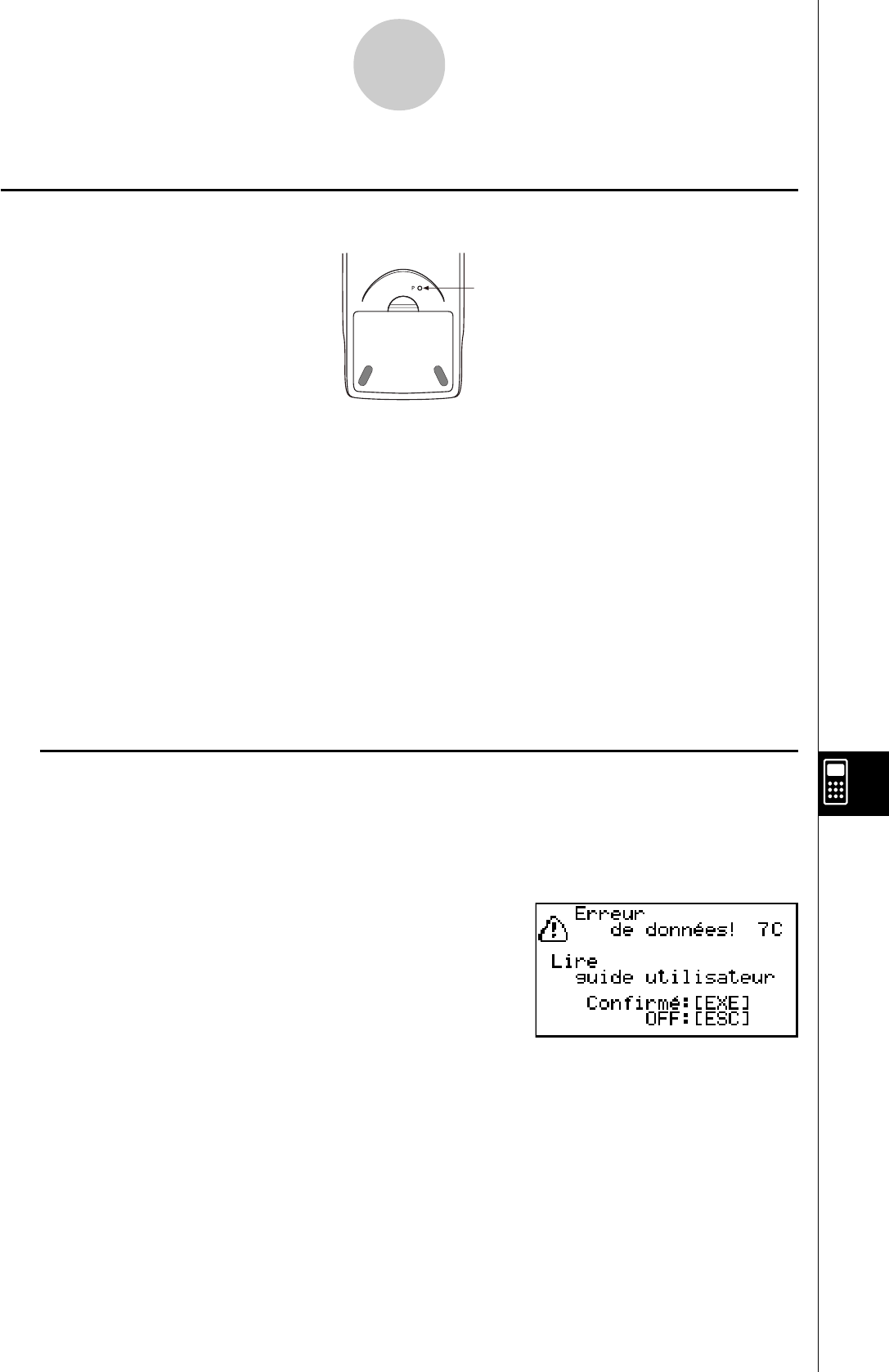
19990401
α
-6-1
Bouton P (en cas de blocage)
6 Bouton P (en cas de blocage)
Appuyez sur le bouton P pour réinitialiser la calculatrice en cas de blocage.
Avertissement !
N’effectuez jamais cette opération à moins de vouloir effacer totalement la mémoire de la
calculatrice. Si vous avez besoin des données actuellement en mémoire, écrivez-les
quelque part avant d’effectuer cette opération.
• Une pression sur le bouton P pendant l’exécution d’un calcul (pendant le calcul interne)
supprime toutes les données mémorisées.
• Vous pouvez aussi réinitialiser la calculatrice en utilisant les touches de la face avant de
la calculatrice (voir 9-4 Initialisation). Utilisez le bouton P pour réinitialiser la calculatrice
uniquement si les touches de la face avant de la calculatrice sont bloquées pour une
raison quelconque.
uMessage Erreur de données
Une erreur de données indique que les données dans la calculatrice sont sérieusement
altérées. Une altération des données peut provenir d’une charge électrostatique puissante,
de températures extrêmes, d’une humidité élevée, etc. Une erreur de données est
indiquée de la façon suivante à l’écran.
Appuyez sur la touche w pour réinitialiser la calculatrice.
• L’écran d’erreur de données apparaît lorsque vous appuyez sur le bouton P pour
réinitialiser la calculatrice ou lorsque vous mettez la calculatrice sous tension.
Avertissement !
Lorsque vous appuyez sur w toutes les données mémorisées sont supprimées.
Si une erreur de données se produit lorsque vous appuyez sur w, il se peut que la calculatrice
fonctionne mal. Si l’écran d’erreur de données reste affiché, appuyez sur i pour éteindre la
calculatrice. Apportez ensuite la calculatrice à votre revendeur ou à un service après-vente
CASIO.
Bouton P

19990401
α
-7-1
Alimentation
7 Alimentation
Cette machine est alimentée par quatre piles de taille AAA (LR03 (AM4) ou R03 (UM-4)). En
plus, une pile au lithium CR2032 fournit l’alimentation de sauvegarde permettant de
préserver la mémoire.
Si un des messages suivants apparaît à l’écran, éteignez immédiatement la calculatrice et
remplacez les piles principales ou la pile de sauvegarde de la mémoire de la façon indiquée.
Si vous continuez votre calcul, la machine se mettra d’elle-même hors tension afin de
protéger les données qu’elle contient, et vous ne pourrez pas la remettre sous tension tant
que vous n’aurez pas remplacé les piles.
N’oubliez pas de remplacer les piles principales au moins une fois tous les deux ans, même
si vous avez peu utilisé la calculatrice.
Les piles fournies avec cette machine se déchargent lentement durant l’expédition et le
stockage. Elles devront éventuellement être remplacées plus rapidement car leur autonomie
peut être inférieure à la normale.
Avertissement !
Si vous enlevez en même temps les piles principales et la pile de sauvegarde, tout le
contenu de la mémoire sera supprimé. Si vous devez remplacer toutes les piles, réinitialisez
la calculatrice après avoir remis les piles correctement en place.

19990401
kRemplacement des piles
Précautions:
L’utilisation incorrecte de piles peut entraîner une fuite ou une explosion et risque
d’endommager la calculatrice. Suivez les précautions suivantes:
• S’assurer que la polarité (+)/(–) de chaque pile est correcte.
• Ne pas mélanger les marques de piles.
• Ne pas mélanger des piles neuves avec
des piles usées.
• Ne jamais laisser de piles mortes dans le
logement des piles.
• Retirer les piles lorsque la calculatrice
n’est pas utilisée pendant un certain temps.
• Ne pas recharger les piles fournies avec
l’appareil.
• Ne pas exposer les piles à une chaleur
directe, les court-circuiter ou essayer de
les démonter.
(Si une pile fuit, nettoyez immédiatement le logement des piles, en évitant de toucher
l’électrolyte de la pile.)
Gardez les piles hors de portée des enfants. Si une pile est avalée, consultez
immédiatement un médecin.
uPour remplacer les piles principales
* Avant de remplacer les piles principales, allumez la calculatrice et vérifiez si le message
“Pile sauvegarde faible!” apparaît à l’écran. Le cas échéant, remplacez la pile de
sauvegarde avant de remplacer les piles principales.
* N’enlevez jamais les piles principales et la pile de sauvegarde en même temps.
* Ne mettez pas la calculatrice sous tension lorsque les piles principales ont été enlevées de
la calculatrice, ou lorsqu’elles ne sont pas insérées correctement. Sinon, toutes les
données mémorisées seront effacées et la calculatrice fonctionnera mal. En cas de
problèmes provenant d’une mauvaise manipulation lors du remplacement de piles, insérez
correctemment les piles neuves, puis réinitialisez la calculatrice pour qu’elle fonctionne
normalement.
* Remplacez toutes les quatre piles par des neuves.
α
-7-2
Alimentation
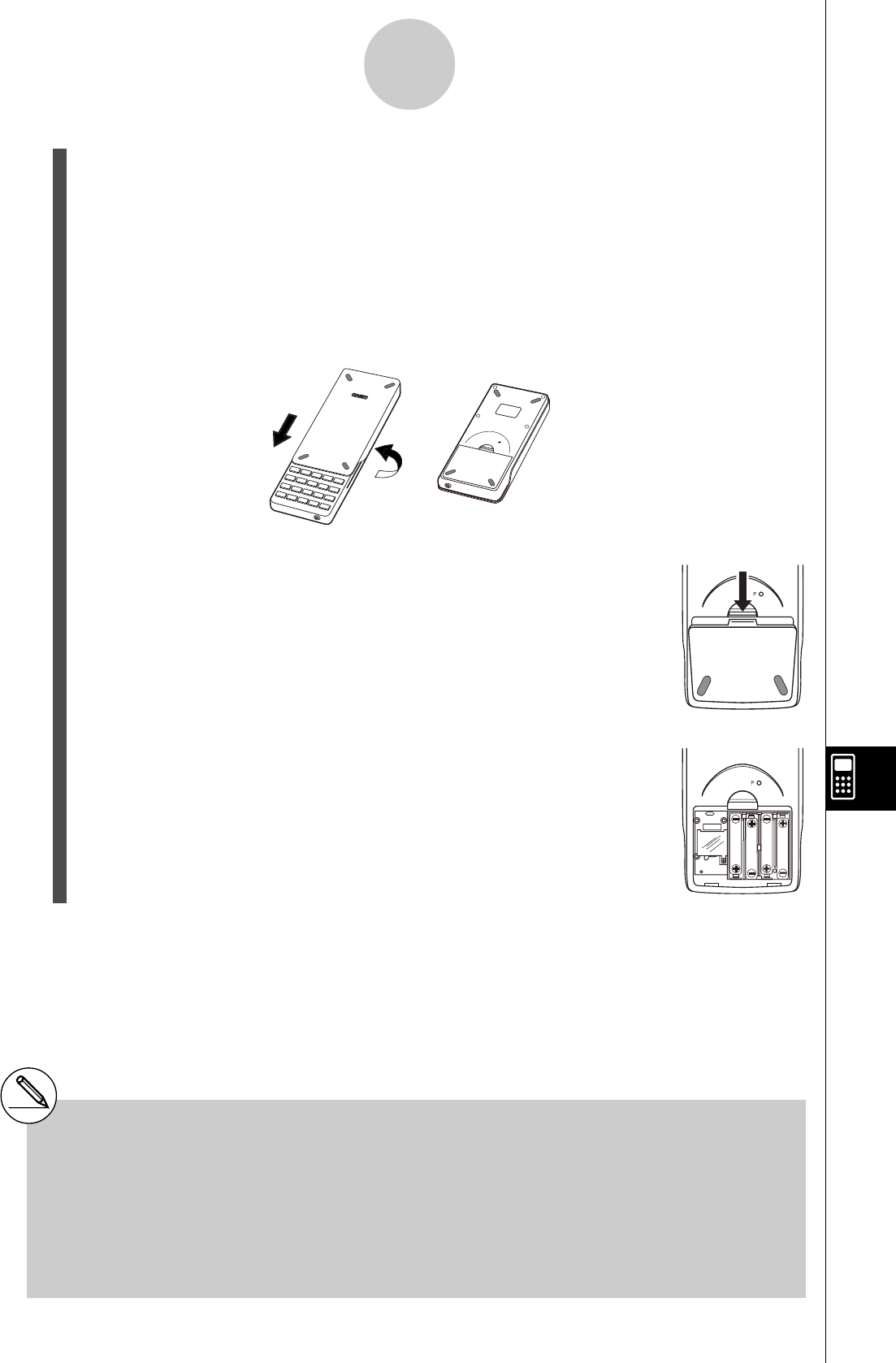
19990401
1. Appuyez sur !o(OFF) pour mettre la calculatrice hors tension.
Avertissement !
* Mettez la calculatrice hors tension avant de remplacer les piles. Si vous remplacez
les piles lorsqu’elle est sous tension, les données mémorisées seront effacées.
2. En veillant à ne pas appuyer accidentellement sur la touche o, insérez l’étui sur la
calculatrice et retournez la calculatrice.
P
3. Enlevez le convercle de la calculatrica en tirant
avec le doigt à l’endroit indiqué par 1.
4. Enlevez les quatre piles usées.
5. Remettez quatre piles neuves, en vous assurant
que les pôles positifs (+) et négatifs (–) sont dirigés
dans le bon sens.
BACK UP
6. Remettez le couvercle en place.
7. Retournez la calculatrice, face vers le haut, et
enlevez l’étui. Appuyez ensuite sur o pour la
mettre sous tension.
α
-7-3
Alimentation
# Grâce à la pile de sauvegarde, le contenu de
la mémoire est préservé pendant le
remplacement des quatre piles principales.
# Ne laissez pas la machine sans piles principales
pendant un période prolongée. Les données
mémorisées risqueraient d’être effacées.
# Si les caractères à l’écran apparaissent trop
légers ou sont à peine visibles, après la mise
sous tension, réglez la teinte.
1
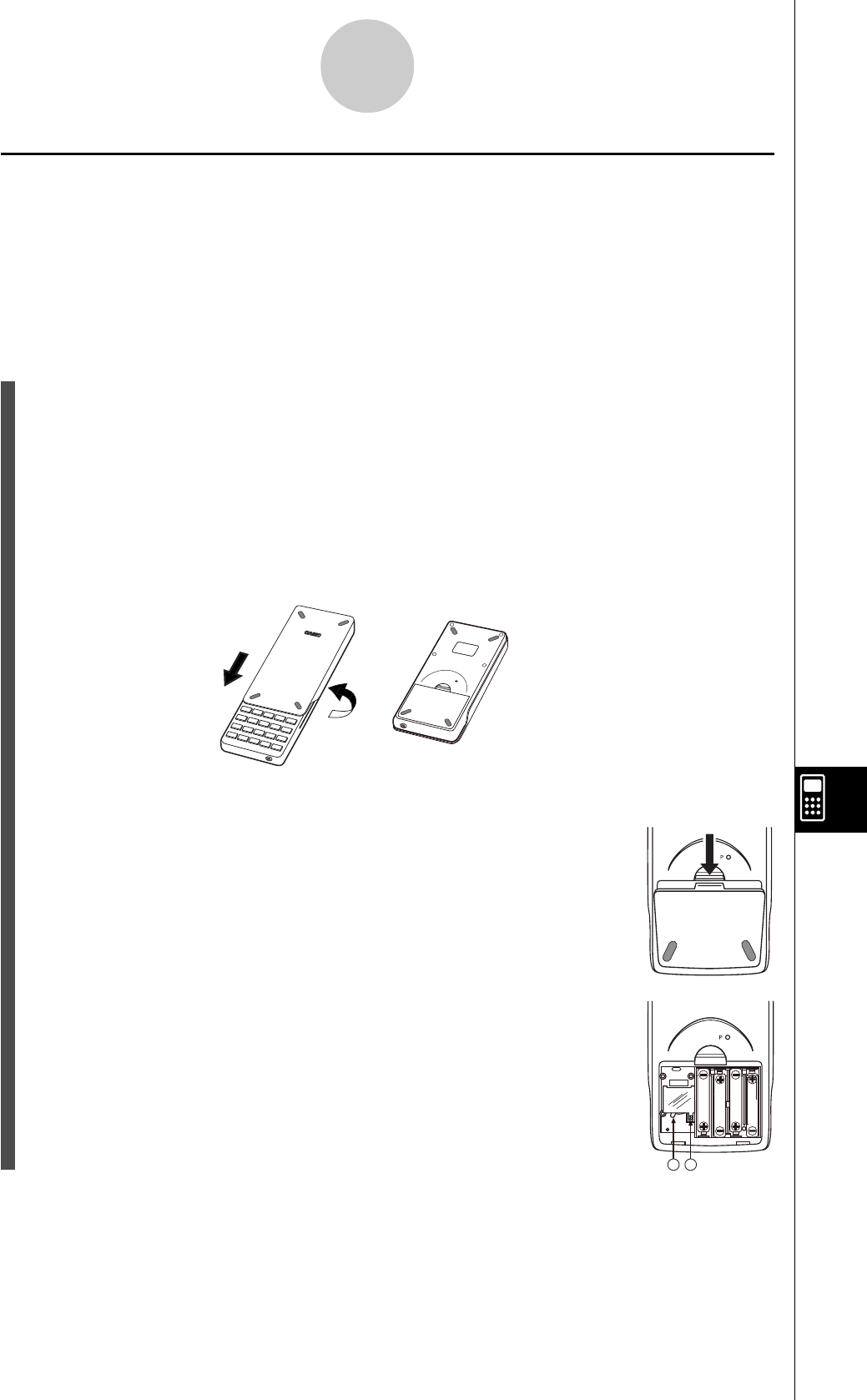
19990401
uPour remplacer la pile de sauvegarde
* Avant de remplacer la pile de sauvegarde, assurez-vous que les piles principales ne
sont pas épuisées.
* N’enlevez jamais les piles d’alimentation principales et la pile de sauvegarde en même
temps.
* Remplacez la pile de sauvegarde une fois tous les 2 ans, même si vous utilisez peu la
calculatrice, sinon les données mémorisées seront perdues.
1. Appuyez sur !o(OFF) pour mettre la calculatrice hors tension.
Avertissement !
* Mettez la calculatrice hors tension avant de remplacer la pile. Si vous remplacez
la pile lorsqu’elle est sous tension, les données mémorisées seront effacées.
2. En veillant à ne pas appuyer accidentellement sur la touche o, insérez l’étui sur la
calculatrice et retournez la calculatrice.
3. Enlevez le couvercle de la calculatrice en tirant
avec le doigt à l’endroit indiqué par 1.
4. Enlevez la vis i à l’arrière de la calculatrice et
enlevez le couvercle du logement de la pile de
sauvegarde.
5. Insérez un objet fin et pointu mais pas en métal
(ex. un cure-dent) dans l’orifice j et retirez la pile
usée.
α
-7-4
Alimentation
P
A
B
BACK UP
1

19990401
6. Essuyez les deux faces de la nouvelle pile avec un
chiffon sec et doux. Mettez la pile dans la
calculatrice en vous assurant que la face positive
(+) est dirigée vers le haut.
7. Remettez le couvercle du logement de la pile de
sauvegarde en place sur la calculatrice et fixez-le
avec la vis. Remettez ensuite le couvercle arrière.
8. Retournez la calculatrice, face vers le haut, et
enlevez l’étui. Appuyez ensuite sur o pour la
mettre sous tension.
kMise hors tension automatique
La calculatrice s’éteint automatiquement si vous n’effectuez aucune opération pendant le
délai fixé. Vous pouvez choisir six minutes ou 60 minutes comme délai d’arrêt automatique
(voir “Réglages APO” à la page 9-3-1). Pour rétablir l’alimentation, appuyez sur o.
α
-7-5
Alimentation
BACK UP
ATTENTION
COMMUNICATION ENTRE MODELES DIFFERENTS
Toutes les calculatrices Graphiques Connectables CASIO
peuvent échanger des données entre elles.Toutefois les
procédures et moyens de liaison peuvent être différents.
Il y a des limitations de transfert suivant les familles de
modèles,les capacités mémoire,et les types de données.
FAMILLES de MODELES:
A : FX-7900GC,FX-9900GC,CFX-9900GC
B : FX-8930GT,CFX-9930GT/9940GT+/9960GT/9990GT
GRAPH 25,GRAPH 30,GRAPH 35,GRAPH 60,GRAPH 65,GRAPH 80
C : GRAPH 100,100+
PROCEDURES de COMMUNICATION
1-AVEC CABLE SB-62
Famille de Modèles Types de données
Emetteur Récepteur transmissibles
A A TOUTES
B B TOUTES
C C TOUTES
B* C* PROGRAMMES *
* Dans ce cas il faut utiliser la manipulation spéciale
suivante,non décrite dans le Manuel
1-Relier les 2 produits B et C avec le câble SB-62
et, appuyer sur ON
2-Sur la calculatrice C(GRAPH 100,100+) choisir le Menu
LINK et appuyer successivement sur les touches
[F4],[F5],[F6], l'écran affichera : "Réception en cours"
3-Sur la calculatrice B,choisir le Menu LINK ,
et respecter la procédure décrite dans le Manuel de B,
pour envoyer les programmes(Send)
4-N'interrompre le transfert que lorsque celui-ci est
complètement terminé
2-AVEC un P.C. et une INTERFACE FX
Famille de Modèles Types de données
Emetteur Récepteur transmissibles
A ou B ou C A ou B ou C TOUTES

CASIO COMPUTER CO., LTD.
6-2, Hon-machi 1-chome
Shibuya-ku, Tokyo 151-8543, Japan
G351-11
Agent : DEXXON DATAMEDIA / 79 av Louis Roche 92238 Gennevilliers
SA0910-A




