Casio ALGEBRA FX 2.0 PLUS_FX 1.0_PLUS_Po_Ch07 Capítulo 7 GY350 Users Guide Ch07 PT
User Manual: Casio Capítulo 7 ALGEBRA FX 2.0 PLUS, ALGEBRA FX 1.0 PLUS | Calculadoras | Manuais | CASIO
Open the PDF directly: View PDF ![]() .
.
Page Count: 53

20010102
Modos tutor e de
sistema de álgebra
computacional
(Apenas ALGEBRA FX 2.0 PLUS)
7-1 Utilizar o modo CAS
(Sistema de álgebra computacional)
7-2 Modo de álgebra
7-3 Modo tutor
7-4 Precauções com o sistema de álgebra
Capítulo
7

20010102
7-1-1
Utilizar o modo CAS (Sistema de álgebra computacional)
7-1 Utilizar o modo CAS (Sistema de álgebra
computacional)
No menu principal,. seleccione o icon CAS para entrar no modo CAS.
A tabela seguinte mostra as teclas que podem ser utilizadas no modo CAS.
kk
kk
k Introduzir e visualizar dados
A introdução no modo de álgerbra é realizada no topo do ecrã, designado por "área de
introdução", sendo possivel introduzir comandos e expressões no actual localização do
cursor.
Os reultados dos cálculos surgem no fundo do ecrã, designado por "área de saída". Quando
um cálculo produz uma equação ou desigualdade, a parte de baixo do ecrã é dividido entre
uma "área de visualização do resultado natural" para o resultado e a "área de número de
fórmula" para o número de fórmula, tal como é demonstrado a seguir.
REPLAY
COPY PASTE
H-COPY
i

20010102
Se o resultado não cabe todo no ecrã, utilize as teclas de cursor para o visualizar.
k Introdução de dados numa lista
Lista: {elemento, elemento, ..., elemento}
•Os elementos devem serseparados por vírgulas, e o conjunto inteiro de elementos deve
ser encerrado dentro de {chaves}.
•Pode introduzir valores numéricos e expressões, equações e desigualdades como
elementos da lista.
Exemplo Para introduzir a lista {1, 2, 3}
!*( { )b,c,d
!/( } )w
kIntrodução de dados matriciais
Matriz (m × n): [[(1, 1) entrada, (1, 2) entrada, ..., (1, m) entrada] [(2, 1) entrada, ......,
(2, n) entrada]... [(m, n) entrada, ..., (m, n) entrada]]
•A introdução acima foi arranjada para mostrar as posições relativas das entradas na matriz.
A introdução real é feita em uma linha contínua, da esquerda para a direita.
•As entradas devem ser separadas por vírgulas, e o conjunto inteiro de elementos deve ser
encerrado dentro de [colchetes]. E cada linha também deve ser encerrada dentro de
[colchetes].
•Pode introduzir valores numéricos e expressões como entradas matriciais.
Exemplo Para introduzir a matriz apresentada a seguir 1 2 3
4 5 6
7 8 9
!+( [ )!+( [ )b,c,d
!-( ] )!+( [ )e,f,g
!-( ] )!+( [ )h,i,j
!-( ] )!-( ] )w
7-1-2
Utilizar o modo CAS (Sistema de álgebra computacional)

20010102
kIntrodução de dados vectoriais
Vector: [componente, componente, ..., componente]
•Os componentes devem ser separados por vírgulas, e o conjunto inteiro dos componentes
deve ser encerrado dentro de [colchetes].
•Pode introduzir valores numéricos e expressões como entradas de componentes vectoriais.
Exemplo Para introduzir o vector (1 2 3)
!+( [ )b,c,d
!-( ] )w
kk
kk
k Realizar uma operação no modo de álgebra
Existem dois métodos que pode utilizar para introduzir o modo de álgebra.
•Introdução do comando do menu de funções
• Introdução manual da fórmula e do parâmetro
kk
kk
k Introdução do comando de menu
Pressione uma tecla do menu de funções para visualizar o menu de funções para o tipo de
operação que pretende realizar.
•TRNS ... {menu de transformação de fórmula}
•CALC ... {menu de cálculo de fórmula}
•EQUA ... {menu de equação, desigualdade}
•eqn ... {Chama uma equação armazenada na memória de equações de acordo com um
valor de introdução especificado}
•CLR ... {menu para apagar a variável/fórmula}
Pressionar a tecla K visualiza o menu apresentado abaixo.
•LIST ... {menu de cálculos de listas}
•MAT ... {menu de cálculos matriciais}
•VECT ... {menu de cálculos vectoriais}
Para mais detalhes sobre comandos e os seus formatos consulte a secção "Referência de
comandos de álgebra" na página 7-1-11.
7-1-3
Utilizar o modo CAS (Sistema de álgebra computacional)

20010102
kk
kk
k Introdução de parâmetro e de fórmula manual
Pode utilizar os menus de funções, a teclaK e a tecla J em conjunto para introduzir
parâmetro e fórmulas, tal como se descreve a seguir.
•3(EQUA)b(INEQUA)
•{>}/{<}/{tt
tt
t}/{ss
ss
s} ... {desigualdade}
• teclaK
•{∞}/{Abs}/{x!}/{sign} ... {infinito}/{valor absoluto}/{factorial}/{função de signo*1}
•{HYP} ... funções {hiperbolica}/{hiperbolica inversa}
•{sinh}/{cosh}/{tanh}/{sinh–1}/{cosh–1}/{tanh–1}
• teclaJ
•{Y}/{r}/{Xt}/{Yt}/{X} ... introdução da memória gráfica{Y}/{r}/{Xt}/{Yt}/{X}
k Memória de fórmula
O modo CAS tem cerca de 28 variáveis de fórmula. Os nomes das variáveis são
constituidos pelas letras de A a Z, por r e
θ
. As variáveis de fórmula do modo CAS são
independentes das variáveis de valor standart.
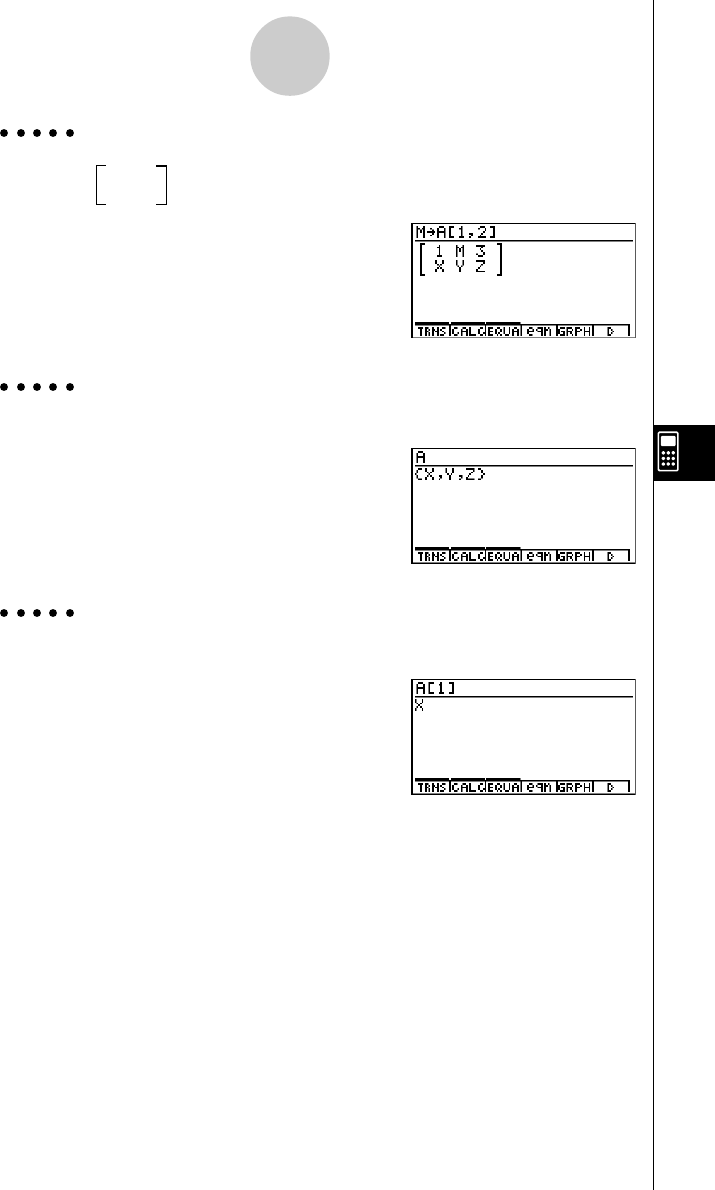
Exemplo Especificar a fórmula que diferencia sen(X) em X (cos(X)) à variável A
2(CALC)b(diff)sv,
v)aav(A)w
7-1-4
Utilizar o modo CAS (Sistema de álgebra computacional)
1 (número real, A > 0)
–1 (número real, A < 0)
*1signo (A) A (A=número imaginário)
|A|
Indefinido(A = 0)
20010102
7-1-5
Utilizar o modo CAS (Sistema de álgebra computacional)
Exemplo Para designar M para a fila 1, coluna 2 da variável A quando a matriz
é designada para ela.
ah(M)aav(A)
!+( [ )b,c!-( ] )w
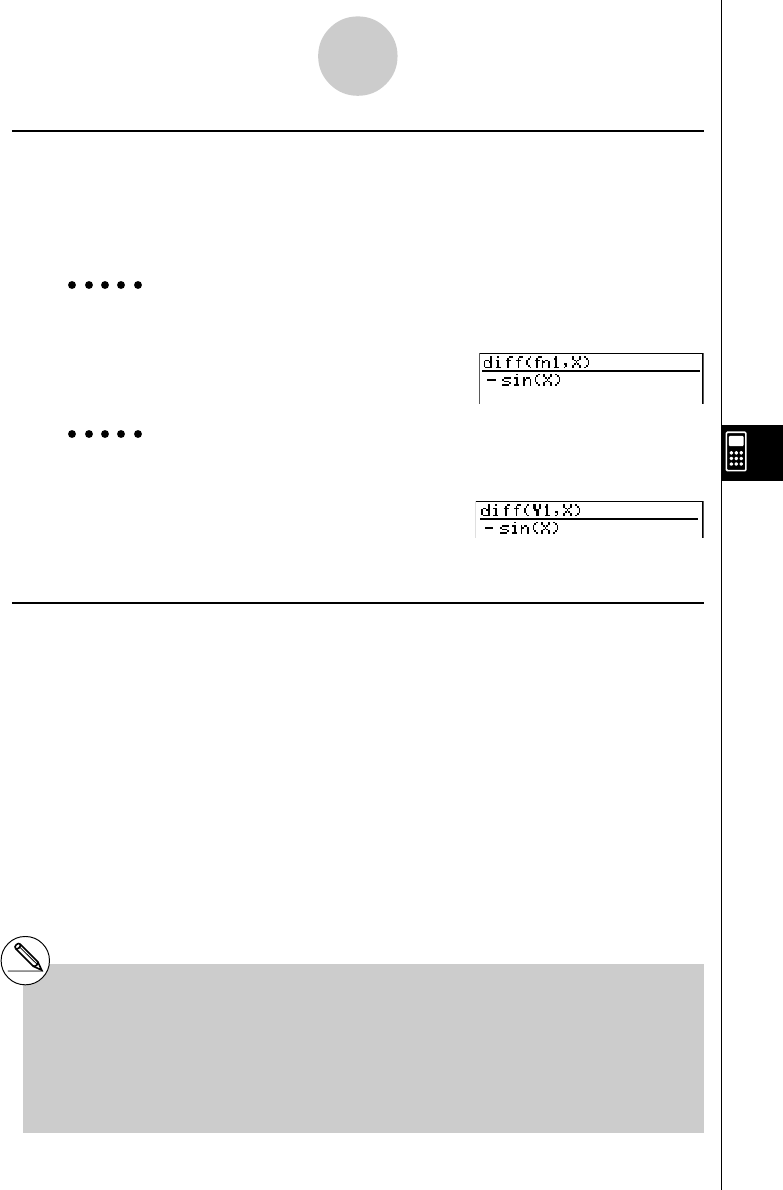
Exemplo Para chamar o valor da variável A quando a lista {X, Y, Z} é designada
para ela.
av(A)w
Exemplo Para chamar o primeiro componente (A [1]) da variável A quando o
vector (X Y Z) é designado para ela.
av(A)!+( [ )b
!-( ] )w
123
XYZ
20010102
k Memória gráfica e memória de funções
A memória de funções permite armazenar funções para serem utilizadas mais tarde.
Com a memória gráfica pode armazenar gráficos em memória. Pressione a tecla J e introduza
o nome do gráfico.
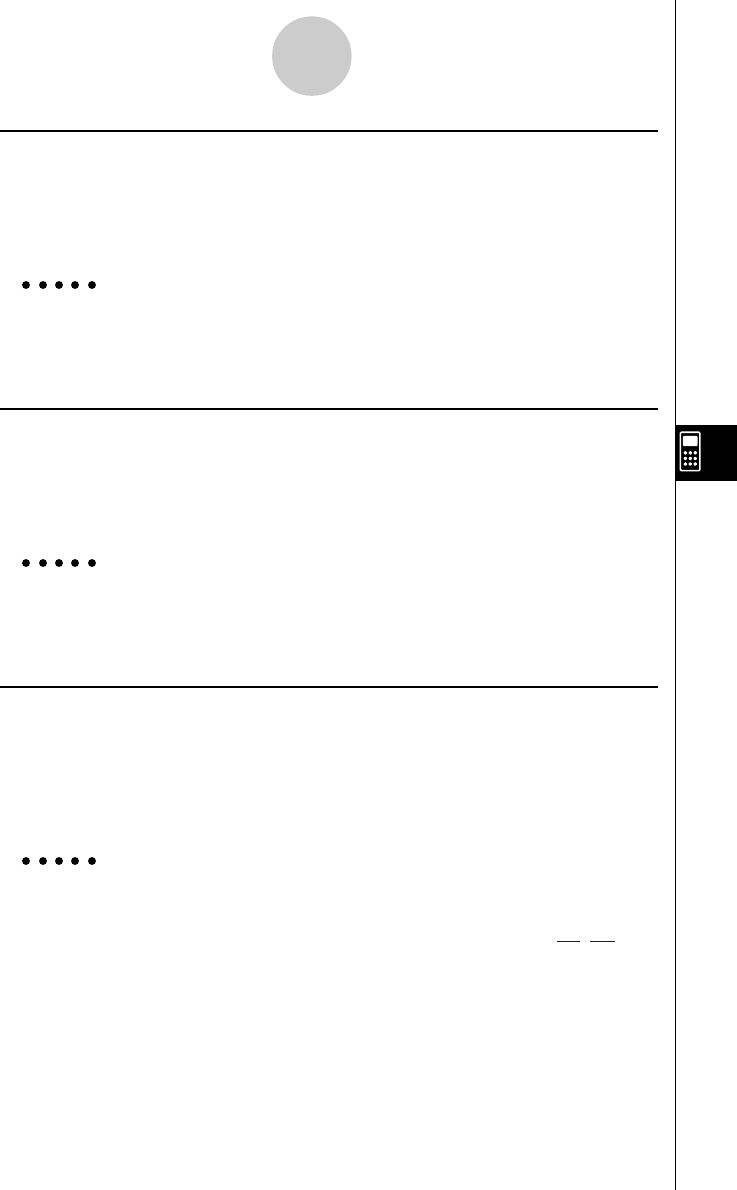
Exemplo Diferenciar f1 = cos(X), que está especificado à memória de funções f1,
em X
2(CALC)b(diff)K6(g)4(FMEM)
d(fn)b,v)w
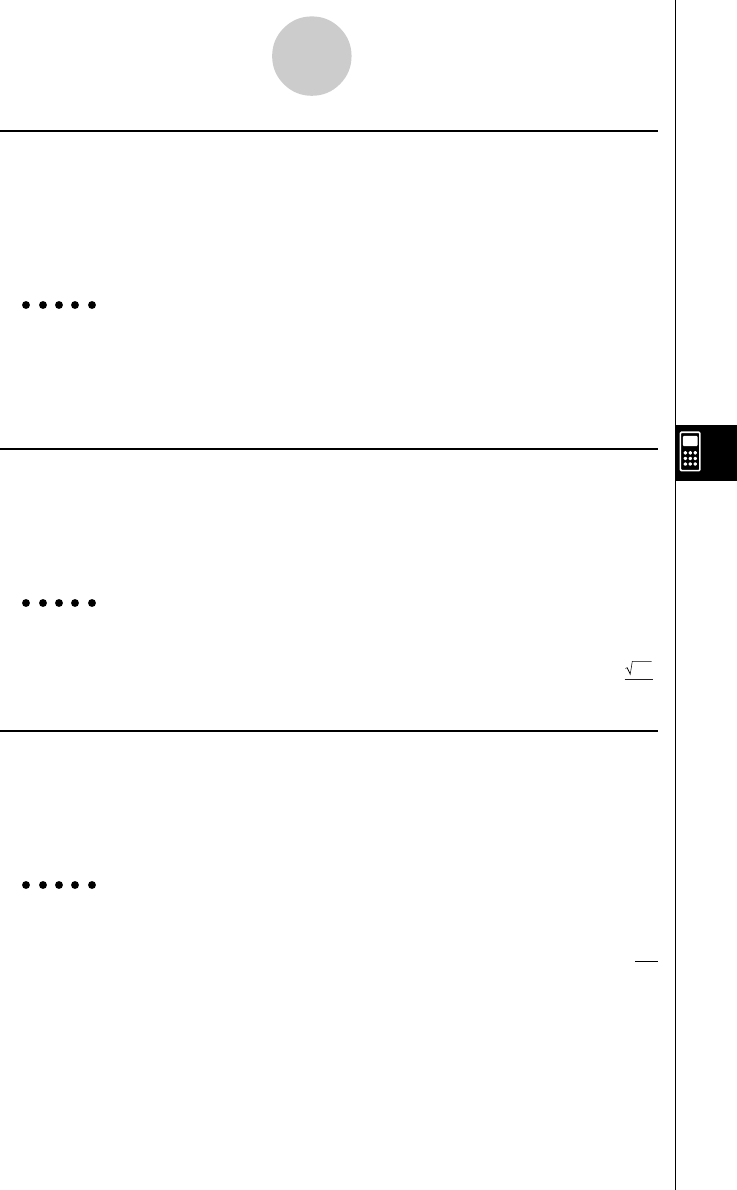
Exemplo Diferenciar Y1 = cos(X), que está especificado à memória gráfica Y1,
em X
2(CALC)b(diff)
J1(Y) b,v)w
kMemória de equações (Eqn)
Quando um resultado de cálculo é uma equação ou uma desigualdade, o seu número de
fórmula é visualizado na área numérica de fórmula e a equação armazenada na memória
Eqn.*1 Equações armazenadas podem ser chamadas através do comando eqn, rclEqn ou
rclAllEqn.
7-1-6
Utilizar o modo CAS (Sistema de álgebra computacional)
*1Podem ser armazenadas cerca de 99
fórmulas na memória Eqn.
A mensagem "Memory ERROR" surge ao
tentar armazenar uma equação quando já
existem 99 fórmulas na memória Eqn.
Quando isto acontecer, execute o comando
ALLEQU (apagar todas as equações) apartir
do menu CLR.

20010102
k Memória de resposta (Ans) e função de cálculos contínuos
A memória de resposta (Ans) e a função de cálculos contínuos podem ser utilizados tal
comoos cálculos standart. No modo de álgebra, pode, inclusive, armazenar fórmulas na
memória Ans.
Exemplo Expandir (X+1)2 e adicionar o resultado a 2X
1(TRNS)b(expand)
(v+b)x)w
Continuando:
+cvw
k Conteúdos de repetição
A memória de repetição pode ser utilizada na área de introdução. Após completar um
cálculo, se pressionard ou e na área de introdução chama a fórmula do último cálculo
realizado. Após um cálculo ou depois de pressionar A pode pressionar f ou c para
chamar as fórmulas anteriores.
k Mover o cursor entre áreas de ecrã
Quando ] ' ` $ indicam que o resultado de um cálculo não cabe no ecrã, as teclas de
cursor permitem navegar pelo ecrã. Para utilizar a função de repetição a partir desta
condição, pressione 6(g)2(SW). ] ' ` $ mudam para uam linha tracejada para
indicar que as operações das teclas de cursor controlam a área de introdução.
Pressionar novamente 2(SW) move o cursor de novo para a área de saida.
7-1-7
Utilizar o modo CAS (Sistema de álgebra computacional)
# Pressionar 6(g)1(CLR)d(ALLEQU) o
conteúdo da memória Eqn, da memória Ans
e da memória de repetição.
#Pode introduzir até 255 bytes de dados na área
de introdução.

20010102
Itens SET UP
uu
uu
uAngle ...Especificação da medida da unidade angular
•{Deg}/{Rad} ... {graus}/{radianos}
uu
uu
uAnswer Type ...Especificação do limite de resultado
•{Real}/{Cplx} ... {número real}/{número complexo}
uu
uu
uDisplay ...Especificação do formato de apresentação (apenas para approx)
•{Fix}/{Sci}/{Norm} ... {número de casas decimais}/{número de dígitos significantes}/
{formato normal de ecrã}
k Função de gráfico
Pressionar 5(GRPH) visualiza o ecrã de fórmula gráfica, que pode usar para introduzir
uma fórmula gráfica. Pressione 4(G•VAR) se quiser introduzir uma memória gráfica.
Também pode usar as funções 1(SEL), 2(DEL) e 3(TYPE) enquanto o ecrã de
fórmula gráfica está no mostrador.
Pressione 6(DRAW) para desenhar um gráfico.
k Função RECALL ANS
Pressiopnar 6(g)3(R
•
ANS) chama o conteúdo da memória Ans.
k Memória de solução
No modo CAS ou modo ALGEBRA, pode armazenar a história de um cálculo executado
(conteúdo da memória de repetição) na memória de solução. Esta secção descreve como
pode ter acesso e trabalhar com o conteúdo da memória de solução. Pressionar
6(g)4(MEM) no menu principal do modo CAS ou modo ALGEBRA visualiza o ecrã da
memória de solução apresentada abaixo.
•{SAVE} ... {armazena a história do cálculo na memória de solução}
•{DEL
•
A}... {apaga o conteúdo da memória de solução}
•{OPT} ... {optimiza a memória de solução}
•{DISP} ... {visualiza o conteúdo da memória de solução}
7-1-8
Utilizar o modo CAS (Sistema de álgebra computacional)

20010102
7-1-9
Utilizar o modo CAS (Sistema de álgebra computacional)
u Para armazenar a história de um cálculo na memória de solução (Save)
No ecrã inicial da memória de solução, pressione 1(SAVE).
Pressione 1(YES) para armazenar a história do cálculo na memória de solução.
Pressionar i retorna-o ao ecrã inicial da memória de solução.
• Pressionar 6(NO) no lugar de 1(YES) retorna-o ao ecrã inicial da memória de solução
sem armazenar nada.
u Para apagar o conteúdo da memória de solução (Clear Memory)
No ecrã inicial da memória de solução, pressione 2(DEL
•
A).
Pressione 1(YES) para apagar o conteúdo da memória de solução.
Pressionar i retorna-o ao ecrã inicial da memória de solução.
• Pressionar 6(NO) no lugar de 1(YES) retorna-o ao ecrã inicial da memória de solução
sem apagar nada.
•Isso apaga os conteúdos da memória tanto do modo CAS como do modo ALGEBRA. Não
é possível seleccionar o modo que deseja apagar.

20010102
7-1-10
Utilizar o modo CAS (Sistema de álgebra computacional)
u Para visualizar o conteúdo da memória de solução (Display Memory)
No ecrã inicial da memória de solução, pressione 6(DISP).
Isso visualiza a expressão mais antiga e o seu resultado na memória de solução. A linha
inferior mostra o número do registo.
•6(DISP) é desactivado quando não há dados na memória de solução.
•Para visualizar o próximo registo
Pressione 6(NEXT).
•Para visualizar o registo anterior
Pressione 1(BACK).
• Pressionar 1(BACK) enquanto o registo mais antigo está no mostrador retorna-o ao ecrã
inicial da memória de solução.
•Para visualizar um registo particular
Pressione 5(SEL) e de seguida introduza o número do registo que deseja visualizar.
Pressionar w visualiza o registo cujo número introduziu.
•Para apagar um único registo da memória de solução
Exiba o registo que deseja apagar, e de seguida pressione 2(DEL).
Em resposta à mensagem de confirmação que aparece, pressione w(Yes) para apagar o
registo visualizado.
Para apagar o ecrã acima sem apagar nada, pressione i(No).
•Para activar e desactivar a visualização do número do registo
Pressione 4(NUM) para activar ou desactivar a visualização do número do registo.
uPara optimizar a memória de solução (Optimization)
No ecrã inicial da memória de solução, pressione 3(OPT).
Pressionar i retorna-o ao ecrã inicial da memória de solução.
Optimizar a memória de solução rearranja os dados e pode criar mais espaço para
armazenamento. Realize o procedimento acima quando a capacidade da memória de
solução começar a ficar cheia.

20010102
Referência de comandos de álgebra
As abreviações utilizadas nesta secção são as seguintes:
•Exp ... Expressão (valor, fórmula, variável, etc.)
•Eq ... Equação
•Ineq ... Desigualdade
•List ... Lista
•Mat ... Matriz
•Vect ... Vector
Tudo o que estiver dentro de parênteses rectos pode ser omitido.
u expand
Função: Expande uma expressão.
Sintaxe: expand (
{Exp/Eq/Ineq/List/Mat/Vect} [ ) ]
Exemplo Expandir (X+2)2
1(TRNS)b(expand)(v+c)xw X2 + 4X + 4
u rFactor (rFctor)
Função: Decompõe uma expressão até à sua raiz.
Sintaxe: rFactor (
{Exp/Eq/Ineq/List/Mat/Vect} [ ) ]
Exemplo Decompor em factores X2– 3
1(TRNS)c(rFctor)vx-dw(X – 3) (X + 3)
u factor
Função: Decompõe uma expressão.
Sintaxe: factor (
{Exp/Eq/Ineq/List/Mat/Vect} [ ) ]
Exemplo Decompor em factores X2– 4X + 4
1(TRNS)d(factor)vx-ev+ew (X – 2)2
7-1-11
Utilizar o modo CAS (Sistema de álgebra computacional)

20010102
usolve
Função: Resolve uma equação.
Sintaxe: solve( Exp [,variável] [ ) ]
solve( {Exp-1,..., Exp-n}, {variável-1,...,variável-n} [ ) ]
Exemplo Resolver AX + B = 0 para X
1(TRNS)e(solve)av(A)v+
al(B)!.(=)aw
Exemplo Resolver a equação linear simultânea 3X + 4Y = 5, 2X – 3Y = – 8
1(TRNS)e(solve)!*( { )
da+(X)+ea-(Y)!.(=)f,
ca+(X)-da-(Y)!.(=)-i
!/( } ),!*( { )a+(X),X = – 1
a-(Y)!/( } )wY = 2
• Se não é especificada nenhuma variável, X é o ajuste por defeito.
utExpand (tExpnd)
Função: Emprega o teorema da soma para expandir uma função trigonométrica
Sintaxe: tExpand( {Exp/List/Mat/Vect} [ ) ]
Exemplo Empregar po teorema da soma para expandir sen(A+B)
1(TRNS)f(TRIG)b(tExpnd)
s(av(A)+al(B)wcos(B) • sin(A) + sin(B) • cos(A)
utCollect (tCollc)
Função: Aplica o teorema da soma para transaformar o produto de uma função
trigonométrica numa soma.
Sintaxe: tCollect( {Exp/List/Mat/Vect} [ ) ]
Exemplo Empregar o teorema da soma para transformar sen(A)cos(B) numa
soma trigonométrica.
1(TRNS)f(TRIG)c(tCollc)
sav(A)cal(B)w
7-1-12
Utilizar o modo CAS (Sistema de álgebra computacional)
sin (A + B)
2
sin (A – B)
2
+
– B
A
X =

20010102
7-1-13
Utilizar o modo CAS (Sistema de álgebra computacional)
u trigToExp (trigToE)
Função: Transforma uma função hiperbólica ou trigonométrica numa função
exponencial.
Sintaxe: trigToExp( {Exp/List/Mat/Vect} [ ) ]
Exemplo Converter cos(iX) numa função exponencial
1(TRNS)f(TRIG)d(trigToE)c!a(i)vw
uexpToTrig (expToT)
Função: Converte uma função exponencial numa função hiperebólica ou trignométrica
Sintaxe: expToTrig( {Exp/List/Mat/Vect} [ ) ]
Exemplo Converter eix numa função trignométrica
1(TRNS)f(TRIG)e(expToT)
!I(ex)(!a(i)vw cos(X) + sin(X) • i
u simplify (smplfy)
Função: Simplifica uma expressão
Sintaxe: simplify( {Exp/Eq/Ineq/List/Mat/Vect} [ ) ]
Exemplo Simplificar 2X + 3Y – X + 3 = Y + X – 3Y + 3 – X
1(TRNS)g(smplfy)ca+(X)+da-(Y)
-a+(X)+d!.(=)a-(Y)
+a+(X)-da-(Y)+d-
a+(X)wX + 3Y + 3 = –2Y + 3
ex+ e
—
x
2

20010102
u combine (combin)
Função: Reduz uma fracção.
Sintaxe: combine( {Exp/Eq/Ineq/List/Mat/Vect} [ ) ]
Exemplo Reduzir a fracção (X + 1)
/
(X + 2) + X (X + 3)
1(TRNS)h(combin)(v+b)/
(v+c)+v(v+dw
ucollect (collct)
Função: Reorganiza uma expressão, com base numa determinada variável.
Sintaxe: collect( {Exp/Eq/Ineq/List/Mat/Vect} [,{Exp/variável}] [ ) ]
Exemplo Reorganizar X2 + AX + BX, com base na variável X
1(TRNS)i(collct)vx+av(A)v+
al(B)vw X2 + (A + B)X
• Se não for especificado nada para [,{Exp/variável}], X é o ajuste por defeito.
u substitute (sbstit)
Função: Específica uma expressão a uma variável.
Sintaxe: substitute( {Exp/Eq/Ineq/List/Mat/Vect}, variável=expressão
[,..., variável=expressão] [ ) ]
Exemplo Especificar 5 a X in 2X – 1
1(TRNS)j(sbstit)cv-b,
v!.(=)fw9
7-1-14
Utilizar o modo CAS (Sistema de álgebra computacional)
X3 + 5X2 + 7X + 1
X + 2

20010102
ucExpand (cExpnd)
Função: Expande a raiz enésima de um número imaginário.
Sintaxe: cExpand( {Exp/Eq/Ineq/List/Mat/Vect} [ ) ]
Exemplo Expandir 2i
1(TRNS)v(cExpnd)!x( )c!a(i)w1 + i
uapprox
Função: Produz uma aproximação numérica para uma expressão.
Sintaxe: approx ( {Exp/Eq/Ineq/List/Mat/Vect} [ ) ]
Exemplo Obter o valor numérico para 2
1(TRNS)l(approx)!x( )cw1.414213562
Exemplo 920
Normal:jMcaw12157665459056928801
approx: 1(TRNS)l(approx)jMcaw1. 215766546E+19 (Display: Norm1)
7-1-15
Utilizar o modo CAS (Sistema de álgebra computacional)
#Sobre o comando approx (aproximação)
Com os cálculos normais no modo CAS
(quando não se utiliza o comando approx), os
resultados dos cálculos são visualizados na
sua totalidade, sem se utilizar expoentes.
No entanto, quando se utiliza o comando
approx no modo CAS, os resultados são
visualizados utilizando o limite do formato
exponêncial especificado no item Ecrã dos
ajustes básicos.
O que quer dizer que o comando approx visualiza os
resultados no modo CAS da mesma forma que são
visualizado no modo RUN•MAT.

20010102
u diff
Função: Diferencia uma expressão
Sintaxe: diff( {Exp/List} [, variável, ordem, dertivada] [ ) ]
diff( {Exp/List}, variável [, ordem, derivada] [ ) ]
diff( {Exp/List}, variável, ordem [, derivada] [ ) ]
Exemplo Diferenciar X6 com respeito a X
2(CALC)b(diff)vMgw6X5
• Se não é especificada nenhuma variável, X é o ajuste por defeito.
• Se não é especificada nenhuma ordem, 1 é o ajuste por defeito.
u∫
Função: Integra uma expressão
Sintaxe: ∫( {Exp/List} [, variável, constante de integração] [ ) ]
∫( {Exp/List}, variável [, constante de integração] [ ) ]
∫( {Exp/List}, variável, limite inferior, limite superior [ ) ]
Exemplo Integrar X2 com respeito a X
2(CALC)c( ∫ )vxw
• Se não é especificada nenhuma variável, X é o ajuste por defeito.
u lim
Função: Determina os limites de uma expressão de função.
Sintaxe: lim( {Exp/List}, variável, ponto [, direcção] [ ) ]
Exemplo Determinar os limites de sen(X)/X quando X = 0
2(CALC)d(lim)sv/v,v,aw1
• A direcção pode ser positiva (da direicta) ou negativa (da esquerda).
7-1-16
Utilizar o modo CAS (Sistema de álgebra computacional)
X3
3

20010102
uΣ
Função: Cálcula uma soma
Sintaxe: Σ( {Exp/List}, variável, valor de inicial, valor final [ ) ]
Exemplo Calcular a soma à medida que o valor de X em X2 muda de X = 1 até
X = 10
2(CALC)e(Σ)vx,v,b,baw385
uΠ
Função: Cálcula um produto.
Sintaxe: Π( {Exp/List}, variável, valor inicial, valor final [ ) ]
Exemplo Calcular o produtio à medida que o valor de X em X2 muda de X = 1 a
X = 5
2(CALC)f(Π)vx,v,b,fw14400
u taylor
Função: Procura o polinómio de Taylor.
Sintaxe: taylor( {Exp/List}, variável, ordem [, ponto central] [ ) ]
Exemplo Encontrar um polinómio de Taylor de 5ª ordem para sen(X) com
respeito a X = 0
2(CALC)g(taylor)sv,v,f,aw
• O ponto central por defeito é zero.
u arcLen
Função: Obtem a longitude do arco.
Sintaxe: arcLen( {Exp/List}, variável, valor inicial, valor final [ ) ]
Exemplo Determinar a longitude do arco para X2 desde X = 0 a X = 1
2(CALC)h(arcLen)
vx,v,a,bw
7-1-17
Utilizar o modo CAS (Sistema de álgebra computacional)
X5
–X3+ X
120 6
In (4
5 + 8) –In(2) + 5
422

20010102
u tanLine (tanLin)
Função: Obtem a expressão para a linha tangente.
Sintaxe: tanLine( {Exp/List}, variável, valor de variável no ponto da tangente [ ) ]
Exemplo Determinar a expressão para uma linha tangente com X3 quando X = 2
2(CALC)i(tanLin)vMd,v,cw12X – 16
u denominator (den)
Função: Extrai o denominador de uma fracção.
Sintaxe: denominator( {Exp/List} [ ) ]
Exemplo Extrair o denominador da extracção (X + 2)/(Y – 1)
2(CALC)j(EXTRCT)b(den)
(a+(X)+c)/(a-(Y)-bwY – 1
u numerator (num)
Função: Extrai o denominador de uma fracção.
Sintaxe: numerator( {Exp/List} [ ) ]
Exemplo Extrair o denominador da fracção (X + 2)/(Y – 1)
2(CALC)j(EXTRCT)c(num)
(a+(X)+c)/(a-(Y)-bwX + 2
u gcd
Função: Obtem o maior denominador comum.
Sintaxe: gcd( {Exp/List}, {Exp/List} [ ) ]
Exemplo Determinar o maior denominador comum de X + 1 e X2 – 3X – 4
2(CALC)v(gcd)v+b,vx-
dv-ewX + 1
7-1-18
Utilizar o modo CAS (Sistema de álgebra computacional)

20010102
u lcm
Função: Obtém o mínimo múltiplo comum de duas expressões.
Sintaxe: lcm({Exp/List},{Exp/List} [ ) ]
Exemplo Para obter o mínimo múltiplo comum de X2 – 1 e X2 + 2X – 3
2(CALC)l(lcm)vx-b,
vx+cv-dwX3 + 3X2 – X – 3
u rclEqn
Função: Obtem múltiplos conteúdos da memória eqn.
Sintaxe: rclEqn( número de memória [ , ..., número de memória] [ ) ]
Exemplo Chamar os conteúdos das memória de equações 2 e 3
3(EQUA)c(rclEqn)c,dw3X – Y = 7
3X + 6Y = 63
•Os números das memórias de equação produzidos como resultado de uma chamada de
memória não são actualizados.
u rclAllEqn (rclAll)
Função: Chamar todos os conteúdos da memória de equações.
Syntaxe: rclAllEqn
•Os números das memórias de equação produzidos como resultado de uma chamada de
memória não são actualizados.
u rewrite (rewrit)
Função: Move o elemento do lado direito para o lado esquerdo.
Sintaxe: rewrite( {Eq/Ineq/List} [ ) ]
Exemplo Mover o lemento do lado direito de X + 3 = 5X – X2 para o lado
esquerdo
3(EQUA)e(rewrit)v+d!.(=)
fv-vxw X2 – 4X + 3 = 0
7-1-19
Utilizar o modo CAS (Sistema de álgebra computacional)

20010102
u exchange (exchng)
Função: Troca os elemtentos do lado direito e do lado esuqerdo.
Sintaxe: exchange( {Eq/Ineq/List} [ ) ]
Exemplo Trocar os elementos do lado direito e do lado esquerdo de 3 > 5X – 2Y
3(EQUA)f(exchng)d3(EQUA)b(INEQUA)b(>)
fa+(X)-ca-(Y)w5X – 2Y < 3
u eliminate (elim)
Função: Especifica uma expressão a uma variável.
Sintaxe: eliminate( {Eq/Ineq/List} -1, variável, Eq-2 [ ) ]
Exemplo Transformar Y = 2X + 3 em X= e de seguida substituir 2X + 3Y = 5
3(EQUA)g(elim)ca+(X)+da-(Y)!.(=)
f,a+(X),a-(Y)!.(=)
ca+(X)+dw4Y – 3 = 5
u getRight (getRgt)
Função: Obtem o elemento do lado direito.
Sintaxe: getRight( {Eq/Ineq/List} [ ) ]
Exemplo Extrair o elemento do lado direito de Y = 2X2 + 3X + 5
3(EQUA)h(getRgt)a-(Y)!.(=)
ca+(X)x+da+(X)+fw2X2 + 3X + 5
u invert
Função: Inverte duas variáveis.
Sintaxe: invert( {Exp/Eq/Ineq/List} [,nome da variável 1, nome da variável 2] [ ) ]
Se omitir os nomes das variáveis, as variáveis X e Y são invertidas.
Exemplo Para inverter X e Y na expressão 2X = Y
3(EQUA)i(invert)cv!.(=)a-(Y)w2Y = X
7-1-20
Utilizar o modo CAS (Sistema de álgebra computacional)

20010102
u absExpand (absExp)
Função: Divide uma expressão que contem um valor absoluto em duas expressões.
Sintaxe: absExpand( {Eq/Ineq} [ ) ]
Exemplo Eliminar o valor absoluto de | 2X – 3 | = 9
3(EQUA)j(absExp)K5(Abs)(
cv-d)!.(=)jw
u andConnect (andCon)
Função: Liga duas desigualdades numa única expressão.
Sintaxe: andConnect( Ineq-1, Ineq-2 [ ) ]
Exemplo Combinar X > – 1 e X < 3 numa única desigualdade
3(EQUA)v(andCon)v3(EQUA)b(INEQUA)b(>)
-b,v3(EQUA)b(INEQUA)c(<)dw–1 < X < 3
u eqn
Função: Chama o conteúdo da memória eqn.
Sintaxe: eqn( número de memória [ ) ]
Exemplo Adicionar15 a ambos os lados da equação 6X – 15 = X – 7,
armazenada na memória de equação 3
4(eqn)d)+bfw6X = X + 8
7-1-21
Utilizar o modo CAS (Sistema de álgebra computacional)
2X – 3 = 9
or 2X – 3 = – 9 2
1

20010102
uclear (clrVar)
Função: Limpa o conteúdo de uma equação especifica (A a Z, r,
θ
).*1
Sintaxe: clear( variável [ ) ]
clear( {lista de variáveis} [ ) ]
Exemplo Limpar o conteúdo da variável A
6(g)1(CLR)b(clrVar)av(A)w
Exemplo Limpar o conteúdo das variáveis X, Y e Z
6(g)1(CLR)b(clrVar)!*( { )a+(X),
a-(Y),aa(Z)!/( } )w
uclearVarAll (VarAll)
Função:Limpa o conteúdo de todas as 28 variáveis (A a Z, r,
θ
).
Sintaxe: clearVarAll
7-1-22
Utilizar o modo CAS (Sistema de álgebra computacional)
{ }
{ }
{ }
*1Quando começa com as memórias A, B, C e
D, por exemplo e apaga as memórias A e B,
o ecrã mostra apenas C e D porque são as
únicas memórias que restam.

20010102
7-1-23
Utilizar o modo CAS (Sistema de álgebra computacional)
kLista dos comandos de um cálculo [OPTN]-[LIST]
uDim
Função: Retorna a dimensão de uma lista.
Sintaxe: Dim List
Exemplo Para determinar a dimensão da lista {1, 2, 3}
K1(LIST)b(CALC)b(Dim)!*( { )b,c,d
!/( } )w3
uMin
Função: Retorna o valor mínimo de uma expressão ou os elementos numa lista.
Sintaxe: Min( {List/Exp} [ ) ]
Min( {List/Exp}, {List/Exp} [ ) ]
Exemplo Para determinar o valor mínimo dos elementos na lista {1, 2, 3}
K1(LIST)b(CALC)c(Min)!*( { )b,c,d
!/( } )w1
Exemplo Para comparar cada elemento da lista {1, 2, 3} com o valor 2, e
produzir uma lista cujos elementos são o valor mínimo resultante de
cada comparação
K1(LIST)b(CALC)c(Min)!*( { )b,c,d
!/( } ),cw{
1, 2, 2
}
Exemplo Para comparar os elementos da lista {1, 2, 3} e lista {3, 1, 2}, e produzir
uma lista cujos elementos são o valor mínimo resultante de cada
comparação
K1(LIST)b(CALC)c(Min)!*( { )b,c,d
!/( } ),!*( { )d,b,c!/( } )w{1, 1, 2
}

20010102
7-1-24
Utilizar o modo CAS (Sistema de álgebra computacional)
uMax
Função: Retorna o valor máximo de uma expressão ou os elementos duma lista.
Sintaxe: Max( {List/Exp} [ ) ]
Max( {List/Exp}, {List/Exp} [ ) ]
Exemplo Para determinar o valor máximo dos elementos na lista {1, 2, 3}
K1(LIST)b(CALC)d(Max)!*( { )b,c,d
!/( } )w3
Exemplo Para comparar cada elemento da lista {1, 2, 3} com o valor 2, e
produzir uma lista cujos elementos são o valor máximo resultante de
cada comparação
K1(LIST)b(CALC)d(Max)!*( { )b,c,d
!/( } ),cw{
2, 2, 3
}
Exemplo Para comparar os elementos da lista {1, 2, 3} e lista {3, 1, 2}, e produzir
uma lista cujos elementos são o valor máximo resultante de cada
comparação
K1(LIST)b(CALC)d(Max)!*( { )b,c,d
!/( } ),!*( { )d,b,c!/( } )w{
3, 2, 3
}
u Mean
Função: Retorna a média dos elementos numa lista.
Sintaxe: Mean( List [ ) ]
Mean( List, List [ ) ]
A lista deve conter apenas valores ou expressões matemáticas. Equações e
desigualdades não são permitidas.
Exemplo Para determinar a média dos elementos na lista {1, 2, 3}
K1(LIST)b(CALC)e(Mean)!*( { )b,c,d
!/( } )w2

20010102
7-1-25
Utilizar o modo CAS (Sistema de álgebra computacional)
Exemplo Para determinar a média dos elementos na lista {1, 2, 3} quando suas
frequências são {3, 2, 1}
K1(LIST)b(CALC)e(Mean)!*( { )b,c,d
!/( } ),!*( { )d,c,b!/( } )w
uMedian
Função: Retorna a mediana dos elementos numa lista.
Sintaxe: Median( List [ ) ]
Median( List, List [ ) ]
A lista deve conter apenas valores ou expressões matemáticas. Equações e
desigualdades não são permitidas.
Exemplo Para determinar a mediana dos elementos na lista {1, 2, 3}
K1(LIST)b(CALC)f(Median)!*( { )b,c,d
!/( } )w2
Exemplo Para determinar a mediana dos elementos na lista {1, 2, 3} quando
suas frequências são {3, 2, 1}
K1(LIST)b(CALC)f(Median)!*( { )b,c,d
!/( } ),!*( { )d,c,b!/( } )w
u Sum
Função: Retorna a soma dos elementos numa lista.
Sintaxe: Sum List
A lista deve conter apenas valores ou expressões matemáticas. Equações e
desigualdades não são permitidas.
Exemplo Para determinar a soma dos elementos na lista {1, 2, 3}
K1(LIST)b(CALC)g(Sum)!*( { )b,c,d
!/( } )w6
5
3
3
2
20010102
7-1-26
Utilizar o modo CAS (Sistema de álgebra computacional)
u Prod
Função: Retorna o produto dos elementos numa lista.
Sintaxe: Prod List
A lista deve conter apenas valores ou expressões matemáticas. Equações e
desigualdades não são permitidas.
Exemplo Para determinar o produto dos elementos na lista {2, 3, 4}
K1(LIST)b(CALC)h(Prod)!*( { )c,d,e
!/( } )w24
uCuml
Função: Retorna a frequência cumulativa dos elementos numa lista.
Sintaxe: Cuml List
A lista deve conter apenas valores ou expressões matemáticas. Equações e
desigualdades não são permitidas.
Exemplo Para determinar a frequência cumulativa dos elementos na lista {1, 2, 3}
K1(LIST)b(CALC)i(Cuml)!*( { )b,c,d
!/( } )w{
1, 3, 6
}
u Percent (%)
Função: Retorna a porcentagem de cada elemento numa lista, a soma dos quais é
assumida como sendo 100.
Sintaxe: Percent List
A lista deve conter apenas valores ou expressões matemáticas. Equações e
desigualdades não são permitidas.
Exemplo Para determinar a porcentagem de cada elemento na lista {1, 2, 3}
K1(LIST)b(CALC)j(%)!*( { )b,c,d
!/( } )w
3
50
3
100 50
,,
{
{
20010102
7-1-27
Utilizar o modo CAS (Sistema de álgebra computacional)
uA List
Função: Retorna uma lista cujos elementos são as diferenças entre os elementos duma
outra lista.
Sintaxe: AA
AA
A List List
A lista deve conter apenas valores ou expressões matemáticas. Equações e
desigualdades não são permitidas.
Exemplo Para gerar uma lista cujos elementos são as diferenças entre os
elementos da lista {1, 2, 4}
K1(LIST)b(CALC)v(AList)!*( { )b,c,e
!/( } )w{
1, 2
}
uStdDev
Função: Retorna o desvio padrão dos elementos numa lista.
Sintaxe: StdDev List
A lista deve conter apenas valores ou expressões matemáticas. Equações e
desigualdades não são permitidas.
Exemplo Para determinar o desvio padrão dos elementos na lista {1, 2, 4}
K1(LIST)b(CALC)l(StdDev)!*( { )b,c,e
!/( } )w
u Variance (Vari)
Função: Retorna a variância dos elementos numa lista.
Sintaxe: Variance List
A lista deve conter apenas valores ou expressões matemáticas. Equações e
desigualdades não são permitidas.
Exemplo Para determinar a variância dos elementos na lista {1, 2, 4}
K1(LIST)b(CALC)I(Vari)!*( { )b,c,e
!/( } )w
3
21
7
3

20010102
7-1-28
Utilizar o modo CAS (Sistema de álgebra computacional)
uSeq
Função: Gera uma lista de acordo com uma expressão de sequência numérica.
Sintaxe: Seq( Exp, variável, valor inicial, valor final, [incremento] [ ) ]
Se não especificar um incremento, um incremento de 1 é usado.
Exemplo Para gerar uma lista de acordo com a expressão: valor A, valor final
3A, incremento A
K1(LIST)c(CREATE)b(Seq)v,v,av(A),d
av(A),av(A)w{
A, 2A, 3A
}
u Augment (Augmnt)
Função: Combina duas listas.
Sintaxe: Augment( List, List [ ) ]
Exemplo Para combinar a lista {1, 2} e lista {3, 4}
K1(LIST)c(CREATE)c(Augmnt)!*( { )b,c
!/( } ),!*( { )d,e!/( } )w{
1, 2, 3, 4
}
uFill
Função: Substitui os elementos de uma lista por um valor ou expressão especificado(a).
Este comando também pode ser usado para criar uma nova lista em que todos
os elementos contêm o mesmo valor ou expressão.
Sintaxe: Fill( Exp/Eq/Ineq), List [ ) ]
Fill( Exp, valor numérico [ ) ]
Exemplo Para substituir os elementos da lista {3, 4} por X
K1(LIST)c(CREATE)d(Fill)v,!*( { )
d,e!/( } )w{
X, X
}
Exemplo Para criar uma lista com oito elementos, todos os quais são X
K1(LIST)c(CREATE)d(Fill)v,iw{
X, X, X, X, X, X, X, X
}

20010102
7-1-29
Utilizar o modo CAS (Sistema de álgebra computacional)
uSortA
Função: Classifica os elementos de uma lista em ordem ascendente.
Sintaxe: SortA( List [ ) ]
A lista deve conter apenas valores ou expressões matemáticas. Equações e
desigualdades não são permitidas.
Exemplo Para classificar os elementos da lista {1, 5, 3} em ordem ascendente
K1(LIST)c(CREATE)e(SortA)!*( { )b,f,d
!/( } )w{
1, 3, 5
}
u SortD
Função: Classifica os elementos de uma lista em ordem descendente.
Sintaxe: SortD( List [ ) ]
A lista deve conter apenas valores ou expressões matemáticas. Equações e
desigualdades não são permitidas.
Exemplo Para classificar os elementos da lista {1, 5, 3} em ordem descendente
K1(LIST)c(CREATE)f(SortD)!*( { )b,f,d
!/( } )w{
5, 3, 1
}
u SubList (SubLst)
Função: Extrai uma secção específica de uma lista para uma nova lista.
Sintaxe: SubList( List, número inicial [, número final ] [ ) ]
Exemplo Para extrair o elemento 2 ao elemento 3 da lista {1, 2, 3, 4}
K1(LIST)c(CREATE)g(SubLst)!*( { )b,c,d
,e!/( } ),c,dw{
2, 3
}
• Se não especificar um número final, todos os elementos, desde o número inicial até ao fim
da lista, são extraídos.

20010102
7-1-30
Utilizar o modo CAS (Sistema de álgebra computacional)
u List→Mat (L→Mat)
Função: Converte listas para uma matriz.
Sintaxe: List→Mat( List [ , ... ,List ] [ ) ]
Exemplo Para converter a lista {3, 5} e a lista {2, 4} para uma matriz
K1(LIST)d(LIST→)b(L→Mat)!*( { )d,f 32
!/( } ),!*( { )c,e!/( } )w54
u List→Vect (L→Vect)
Função: Converte uma lista para um vector.
Sintaxe: List→Vect List
Exemplo Para converter a lista {3, 2} para um vector
K1(LIST)d(LIST→)c(L→Vect)!*( { )d,c
!/( } )w[
3, 2
]

20010102
7-1-31
Utilizar o modo CAS (Sistema de álgebra computacional)
kComandos de cálculos matriciais [OPTN]-[MAT]
uDim
Função: Retorna a dimensão de uma matriz.
Sintaxe: Dim Mat
Exemplo Para determinar a dimensão da matriz abaixo
123
456
K2(MAT)b(CALC)b(Dim)!+( [ )!+( [ )
b,c,d!-( ] )!+( [ )e,f,g
!-( ] )!-( ] )w{
2, 3
}
u Det
Função: Retorna o determinante de uma matriz.
Sintaxe: Det Mat
Exemplo Para determinar o determinante da matriz abaixo
12
45
K2(MAT)b(CALC)c(Det)!+( [ )!+( [ )
b,c!-( ] )!+( [ )e,f
!-( ] )!-( ] )w– 3
u Norm
Função: Retorna o valor normal de uma matriz.
Sintaxe: Norm Mat
Exemplo Para determinar o valor normal da matriz abaixo
12
45
K2(MAT)b(CALC)d(Norm)!+( [ )!+( [ )
b,c!-( ] )!+( [ )e,f
!-( ] )!-( ] )w 46

20010102
7-1-32
Utilizar o modo CAS (Sistema de álgebra computacional)
u EigVc
Função: Retorna o eigenvector de uma matriz.
Sintaxe: EigVc Mat
Exemplo Para determinar o eigenvector da matriz abaixo
34
13
K2(MAT)b(CALC)e(EigVc)
!+( [ )!+( [ )d,e
!-( ] )!+( [ ) [
0.894427191 – 0.894427191
]
b,d!-( ] )!-( ] )w[
0.4472135955 0.4472135955
]
Os eigenvectores são empilhados verticalmente no mostrador.
Neste exemplo, (0.894427191 0.4472135955) são os eigenvectores que correspondem a 5,
enquanto que (–0.894427191 0.4472135955) são os eigenvectores que correspondem a 1.
Um eigenvector tem um número infinito de soluções. O eigenvector visualizado por este
comando é um eigenvector com um tamanho de 1.
u EigVl
Função: Retorna o eigenvalor de uma matriz.
Sintaxe: EigVI Mat
Exemplo Para determinar o eigenvalor da matriz abaixo
34
13
K2(MAT)b(CALC)f(EigVl)!+( [ )!+( [ )
d,e!-( ] )!+( [ )b,d
!-( ] )!-( ] )w{
5, 1
}

20010102
7-1-33
Utilizar o modo CAS (Sistema de álgebra computacional)
u Rref
Função: Retorna a forma do escalão da fila reduzida de uma matriz.
Sintaxe: Rref Mat
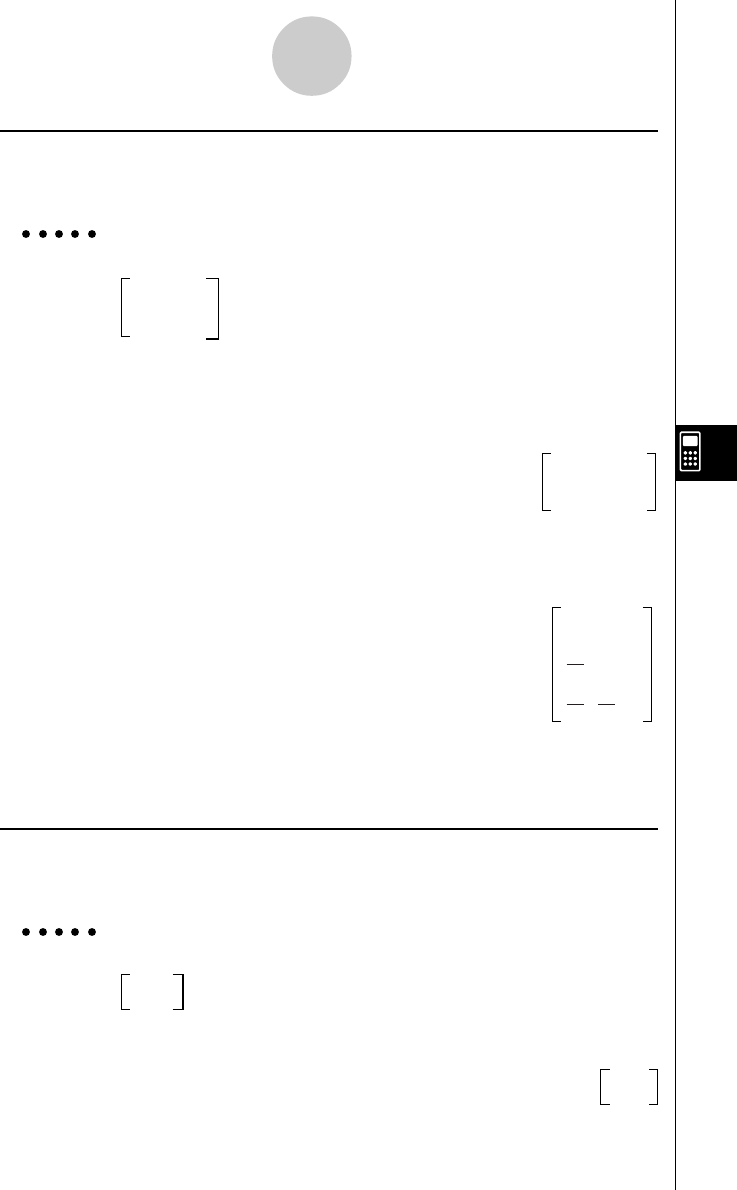
Exemplo Para determinar a forma do escalão da fila reduzida da matriz abaixo
–
2–
20–
6
1–
19–
9
–
524–
4
K2(MAT)b(CALC)g(Rref)!+( [ )!+( [ )
-c,-c,a,-g!-( ] )!+( [ )
b,-b,j,-j!-( ] )
!+( [ )-f,c,e,-e
!-( ] )!-( ] )w
u Ref
Função: Retorna a forma do escalão da fila de uma matriz.
Sintaxe: Ref Mat
Exemplo Para determinar a forma do escalão da fila da matriz abaixo
–
2–
20–
6
1–
19–
9
–
524–
4
K2(MAT)b(CALC)h(Ref)!+( [ )!+( [ )
-c,-c,a,-g!-( ] )!+( [ )
b,-b,j,-j!-( ] )
!+( [ )-f,c,e,-e
!-( ] )!-( ] )w
71
66
71
147
71
62
–
1 0 0
0 1 0
0 0 1
71
62
–
1 1 0
0 1
3
6
0 0 1
2
9
–
20010102
7-1-34
Utilizar o modo CAS (Sistema de álgebra computacional)
u LU
Função: Retorna a resolução LU de uma matriz.
Sintaxe: LU( Mat, memória inferior, memória superior)
Exemplo Para determinar a resolução LU da matriz abaixo
61218
51431
3818
A matriz inferior é designada para a variável A, enquanto que a matriz superior é designada
para a variável B.
K2(MAT)b(CALC)i(LU)!+( [ )!+( [ )
g,bc,bi!-( ] )!+( [ )
f,be,db!-( ] )!+( [ ) 61218
d,i,bi!-( ] )!-( ] ),04 16
av(A),al(B)w00 1
A matriz superior é exibida como o resultado do cálculo.
Para visualizar a matriz inferior, chame a variável da matriz inferior (A, neste exemplo)
especificada pelo comando.
av(A)w
Para visualizar a matriz superior, chame a variável da matriz superior (B, neste exemplo)
especificada pelo comando.
u Trn
Função: Transpõe uma matriz.
Sintaxe: Trn Mat
Exemplo Para transpor a matriz abaixo
12
34
K2(MAT)c(CREATE)b(Trn)!+( [ )!+( [ )
b,c!-( ] )!+( [ )d,e 13
!-( ] )!-( ] )w24
100
01
1
6
5
2
1
2
1

20010102
7-1-35
Utilizar o modo CAS (Sistema de álgebra computacional)
u Augment (Augmnt)
Função: Combina duas matrizes.
Sintaxe: Augment( Mat, Mat [ ) ]
Exemplo Para combinas as duas matrizes abaixo
12 56
34 78
K2(MAT)c(CREATE)c(Augmnt)!+( [ )!+( [ )
b,c!-( ] )!+( [ )d,e
!-( ] )!-( ] ),!+( [ )!+( [ )
f,g!-( ] )!+( [ )h,i 1256
!-( ] )!-( ] )w3478
u Identify (Ident)
Função: Cria uma matriz de identidade.
Sintaxe: Ident valor numérico
Exemplo Para criar uma matriz de identidade 2 × 2
K2(MAT)c(CREATE)d(Ident)cw10
01
u Fill
Função: Substitui os elementos de uma matriz por um valor ou expressão
especificado(a).
Este comando também pode ser usado para criar uma nova matriz em que
todos os elementos contêm o mesmo valor ou expressão.
Sintaxe: Fill( Exp, Mat [ ) ]
Fill( Exp, número de linhas, número de filas [ ) ]
Exemplo Para substituir os elementos da matriz abaixo por X
34
12
K2(MAT)c(CREATE)e(Fill)v,!+( [ )
!+( [ )d,e!-( ] )!+( [ ) XX
b,c!-( ] )!-( ] )wXX

20010102
7-1-36
Utilizar o modo CAS (Sistema de álgebra computacional)
Exemplo Para criar uma matriz 2 × 3, em que todos as entradas são X
K2(MAT)c(CREATE)e(Fill)v,c,dwXXX
XXX
u SubMat
Função: Extrai uma secção específica de uma matriz para uma nova matriz.
Sintaxe: SubMat( Mat [,fila inicial] [,coluna inicial], [,fila final] [,coluna final] [ ) ]
Exemplo Para extrair a secção da fila 2, coluna 2 para fila 3, coluna 3 da matriz
abaixo
123
456
789
K2(MAT)c(CREATE)f(SubMat)!+( [ )!+( [ )
b,c,d!-( ] )!+( [ )e,f,g
!-( ] )!+( [ )h,i,j!-( ] ) 56
!-( ] ),c,c,d,dw89
•Se não especificar uma fila e coluna final, todas as entradas desde a fila/coluna inicial até
a fila/coluna final da matriz são extraídas.

20010102
7-1-37
Utilizar o modo CAS (Sistema de álgebra computacional)
uDiag
Função: Extrai os elementos diagonais de uma matriz.
Sintaxe: Diag Mat
Exemplo Para extrair os elementos diagonais da matriz abaixo
12
34
K2(MAT)c(CREATE)g(Diag)!+( [ )!+( [ )
b,c!-( ] )!+( [ )d,e
!-( ] )!-( ] )w[
1 4
]
uMat→List (M→List)
Função: Converte uma coluna específica de uma matriz para uma lista.
Sintaxe: Mat→List( Mat, número da coluna [ ) ]
Exemplo Para converter a coluna 2 da matriz abaixo para uma lista
12
34
K2(MAT)d(MAT→)b(M→List)!+( [ )!+( [ )
b,c!-( ] )!+( [ )d,e
!-( ] )!-( ] ),cw{
2 4
}
uMat→Vect (M→Vect)
Função: Converte uma coluna específica de uma matriz para um vector.
Sintaxe: Mat→Vect( Mat, número da coluna [ ) ]
Exemplo Para converter a coluna 2 da matriz abaixo para um vector
12
34
K2(MAT)d(MAT→)c(M→Vect)!+( [ )!+( [ )
b,c!-( ] )!+( [ )d,e
!-( ] )!-( ] ),cw[
2, 4
]
20010102
7-1-38
Utilizar o modo CAS (Sistema de álgebra computacional)
uSwap
Função: Troca duas filas de uma matriz.
Sintaxe: Swap Mat, fila número 1, fila número 2
Exemplo Para trocar a fila 1 com a fila 2 da matriz abaixo
12
34
K2(MAT)e(ROW)b(Swap)!+( [ )!+( [ )
b,c!-( ] )!+( [ )d,e 34
!-( ] )!-( ] ),b,cw12
u`Row
Função: Retorna o produto escalar da fila de uma matriz.
Sintaxe: *Row( Exp, Mat, número da fila [ ) ]
Exemplo Para multiplicar a fila 1 da matriz abaixo por X
12
34
K2(MAT)e(ROW)c(`Row)v,!+( [ )
!+( [ )b,c!-( ] )!+( [ ) X2X
d,e!-( ] )!-( ] ),bw34
u`Row+
Função: Calcula o produto escalar de uma fila de uma matriz e adiciona o resultado para
uma outra fila.
Sintaxe: `Row+( Exp, Mat, linha número 1, linha número 2 [ ) ]
Exemplo Para multiplicar a fila 1 da matriz abaixo por X, e adicionar o resultado
para a fila 2
12
34
K2(MAT)e(ROW)d(`Row+)v,!+( [ )
!+( [ )b,c!-( ] )!+( [ ) 12
d,e!-( ] )!-( ] ),b,cwX + 3 2X + 4

20010102
7-1-39
Utilizar o modo CAS (Sistema de álgebra computacional)
uRow+
Função: Adiciona uma fila de uma matriz para uma outra fila.
Sintaxe: Row+( Mat, fila número 1, fila número 2 [ ) ]
Exemplo Para adicionar a fila 1 da matriz abaixo para a fila 2
12
34
K2(MAT)e(ROW)e(Row+)!+( [ )
!+( [ )b,c!-( ] )!+( [ ) 12
d,e!-( ] )!-( ] ),b,cw46

20010102
7-1-40
Utilizar o modo CAS (Sistema de álgebra computacional)
kComandos de cálculos vectoriais [OPTN]-[VECT]
uDim
Função: Retorna a dimensão de um vector.
Sintaxe: Dim Vect
Exemplo Para determinar a dimensão do vector (1 2 3)
K3(VECT)b(CALC)b(Dim)!+( [ )b,c,d
!-( ] )w3
uCrossP
Função: Retorna o produto externo de dois vectores.
Sintaxe: CrossP( Vect, Vect [ ) ]
Exemplo Para determinar o produto externo do vector (1 2 3) e vector (4 5 6)
K3(VECT)b(CALC)c(CrossP)!+( [ )b,c,d
!-( ] ),!+( [ )e,f,g!-( ] )w[ – 3, 6, – 3 ]
uDotP
Função: Retorna o produto interno de dois vectores.
Sintaxe: DotP( Vect, Vect [ ) ]
Exemplo Para determinar o produto interno do vector (1 2 3) e vector (4 5 6)
K3(VECT)b(CALC)d(DotP)!+( [ )b,c,d
!-( ] ),!+( [ )e,f,g!-( ] )w32
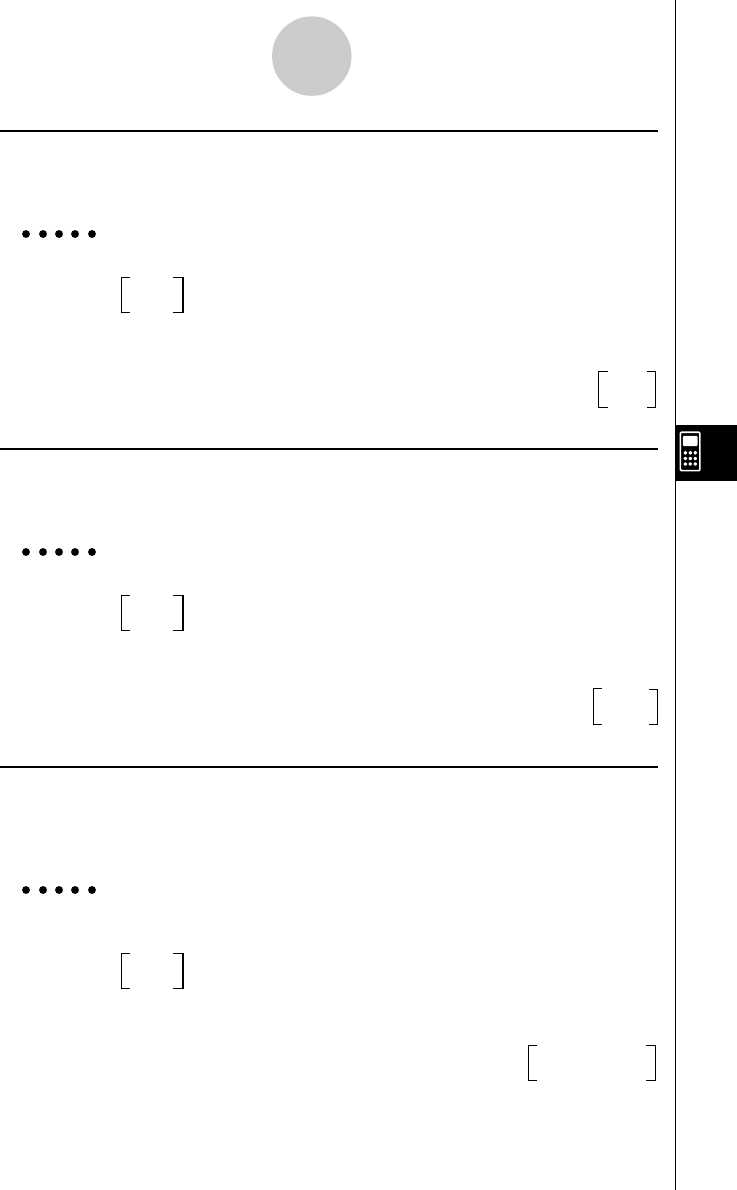
uNorm
Função: Retorna o valor normal de um vector.
Sintaxe: Norm Vect
Exemplo Para determinar o valor normal do vector (1 2 3)
K3(VECT)b(CALC)e(Norm)!+( [ )b,c,d
!-( ] )w 14
20010102
7-1-41
Utilizar o modo CAS (Sistema de álgebra computacional)
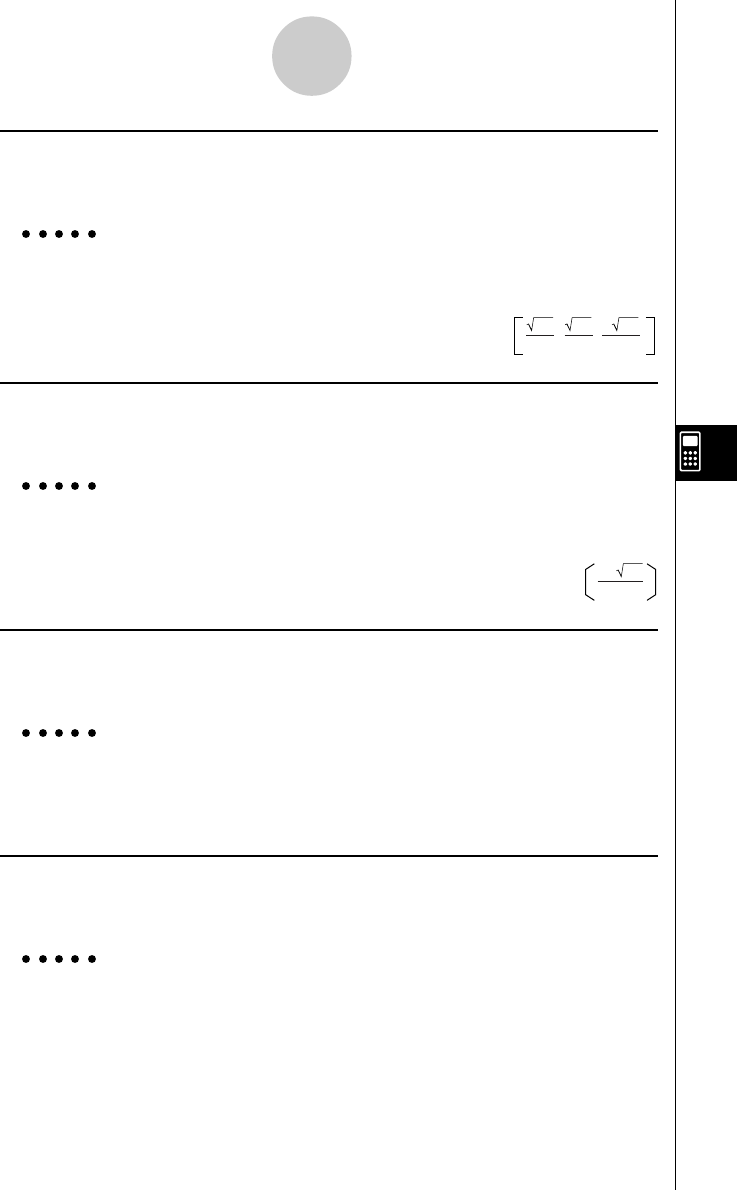
uUnitV
Função: Faz o tamanho de um vector 1.
Sintaxe: UnitV Vect
Exemplo Para fazer o tamanho do vector (1 2 3) 1
K3(VECT)b(CALC)f(UnitV)
!+( [ )b,c,d
!-( ] )w
uAngle
Função: Retorna o ângulo formado por dois vectores.
Sintaxe: Angle( Vect, Vect [ ) ]
Exemplo Para determinar o ângulo formado pelo vector (1 2) e vector (3 4)
(Unidade angular: Rad)
K3(VECT)b(CALC)g(Angle)!+( [ )b,c
!-( ] ),!+( [ )d,e!-( ] )w
uAugment (Augmnt)
Função: Combina dois vectores.
Sintaxe: Angle( Vect, Vect [ ) ]
Exemplo Para combinar o vector (1 2) e vector (3 4)
K3(VECT)c(CREATE)b(Augmnt)!+( [ )b,c
!-( ] ),!+( [ )d,e!-( ] )w[
1, 2, 3, 4
]
uFill
Função: Substitui os elementos de um vector por um valor ou expressão especificado(a).
Sintaxe: Fill( Exp, Vect [ ) ]
Exemplo Para substituir os componentes do vector abaixo por X
K3(VECT)c(CREATE)c(Fill)v,!+( [ )
d,e!-( ] )w[
X, X
]
,, 14
3 14
14
14
7
14
25
11 5
cos
–1

20010102
7-1-42
Utilizar o modo CAS (Sistema de álgebra computacional)
uVect→List (V→List)
Função: Converte um vector para uma lista.
Sintaxe: Vect→List Vect
Exemplo Para converter (3 2) para uma lista
K3(VECT)d(VECT→)b(V→List)!+( [ )d,c
!-( ] )w{
3, 2
}
uVect→Mat (V→Mat)
Função: Converte vectores para uma matriz.
Sintaxe: Vect→Mat( Vect [, ... ,Vect ] ( ] )
Exemplo Para converter os vectores (3 5) e (2 4) para uma matriz
K3(VECT)d(VECT→)c(V→Mat)!+( [ )d,f 32
!-( ] ),!+( [ )c,e!-( ] )w54

20000501
7-2 Modo de álgebra
No modo CAS o resultado final surge automáticamente no ecrã, enquanto no modo de
álgebra é possivel obter os resultados intermédios.
No menu principal, seleccione o icon ALGEBRA para entrar o modo de álgebra. Os ecrã
neste modo são iguais aos do modo CAS.
As operações no modo de álgebra são identicas às do modo CAS, com a excepção de
algumas limitações. Para além disso, os comandos seguintes estão apenas dísponiveis no
modo de álgebra:
u arrange (arrang)
Função: Arranja os termos na sequência das suas variáveis.
Sintaxe: arrange( {Exp/Eq/Ineq} [ ) ]
Exemplo Arranjar 2X + 3 – 5X + 8Yna sequência das suas variáveis
1(TRNS)j(arrang)ca+(X)+d-
fa+(X)+ia-(Y)w – 5X + 2X + 8Y + 3
u replace (replac)
Função: Substitui a variável pela expressão especificada à variável correspondente.
Sintaxe: replace( {Exp/Eq/Ineq} [ ) ]
Exemplo Substitui S na expressão 3X + 2S,quando a expressão 2X + 1 está
especificada a S
1(TRNS)v(replac)dv+ca*(S)w3X + 2 (2X + 1)
7-2-1
Modo de álgebra

20000501
7-3 Modo tutor
No menu principal seleccione o icon TUTOR para entrar o modo tutor.
k Fluxoi do modo tutor
1. Especidique o tipo de expressão.
2. Defina a expressão.
3. Especifique o modo de resolução.
k Especificar o tipo de expressão
Entrar no modo tutor visualiza um menu com os seguintes tipos de expressões:
•Linear Equation (equação linear)
•Linear Inequality (equação de desigualdade)
•Quadratic Equation (equação quadrática)
•Simul Equation (equação simultânea)
Utilize as teclas de cursor para seleccionar o tipo de expressão que pretende e de seguida
pressione w.
Visualiza, assim, uma listas de fórmulas para o tipo de expressão que seleccionou. Mova o
cursor para a fórmula que pretende utilizar.
No caso da desigualdade linear, pressione 4(TYPE) para seleccionar o tipo de
desigualdade.
7-3-1
Modo tutor

20000501
As fórmulas dísponiveis para cada tipo de expressão são as seguintes:
Linear Equation — 6 tipos
• AX = B • X + A = B
• AX + B = C • AX + B = CX + D
• A(BX + C) = D(EX + F) •AX + B= C
Linear Inequality — 6 × 4 tipos
• AX { > < ><} B • X + A { > < ><} B
• AX + B { > < ><} C • AX + B { > < ><} CX + D
• A(BX + C) { > < ><} D(EX + F) •AX + B{ > < ><} C
Quadratic Equation — 5 tipos
• AX2 = B • (AX + B)2 = C
• AX2 + BX + C = 0 • AX2 + BX + C = D
• AX2 + BX + C = DX2 + EX + F
Simul Equation — 10 tipos
•AX + BY = C • Y = AX + B
DX + EY = F Y = CX + D
•AX + BY + C = 0 • AX + BY + C = DX + EY + F
DX + EY + F = 0 GX + HY + I = JX + KY + L
•AX + BY = C • AX + BY = C
Y = DX + E DX + EY + F = 0
•AX + BY = C • AX + BY + C = 0
DX + EY + F = GX + HY + I Y = DX + E
•AX + BY + C = DX + EY + F • AX + BY + C = 0
Y = GX + H DX + EY + F = GX + HY + I
Pressionar6(EXCH) inverte os elementos do lado esquerdo e do lado direito da expressão.
7-3-2
Modo tutor

20000501
kDefinir as expressões
Neste passo, especifica coeficientes e define a expressão. Pode seleccionar um dos três
metodos seguintes para especificar coeficientes:
•{RAND} ... {criação aleatória de coeficientes}
•{INPUT} ... {introdução de coeficientes por tecla}
•{SMPL} ... {selecção de coeficientes por amostras}
•{SEED} ... {selecção de um número de 1 a 99 (especificação do mesmo número
visualiza a mesma expressão)}
1(RAND) ou w cria coeficientes aleatórios e define a expressão.
2(INPUT)visualiza o ecrã de introdução de coeficiente. Introduza os coeficientes,
pressionando w depois de cada um. Depois de introduzir todos os coeficientes, pressione
6(EXE) para definir o coeficiente.
3(SMPL) visualiza um conjunto de expressões de amostra pré-ajustadas, Seleccione a
que pretende e de seguida pressione w para a definir.
Pressionar4(SEED) visualiza o ecrã de selecção de número. Quando quiser criar o
mesmo problema noutra calculadora, especifique um número de sincronização adequado e
pressione w.
Independentemente do método que utiliza, a expressão que definir é visualizada na área de
saida.
Pode copiar uma expressão para o modo gráfico como uma função gráfica*1.
•{L•COP}/{R•COP} ... copia o {elemento do lado esquerdo}/{elemento do lado direito}
como uma função gráfica.
(Modo de equação simultânea*2)
•{1•COP}/{2•COP} ... copia a {primiera}/{segunda} expressão como uma função gráfica
7-3-3
Modo tutor
*1No caso da desigualdade, os símbolos de
desigualdade são copiados.
*2As equações simultâneas quando são copiadas
são transformadas no formatoY = AX + B.

20000501
k Especificar o modo de resolução
Pode seleccionar um dos três modos de resolução seguintes para a expressão visualizada.
•{VRFY} ... {modo de verificação}
Neste modo, introduz a solução para verificar se está correcta ou não. Proporciona uma
boa forma para verificar soluções a que chegou manualmente.
•{MANU} ... {Modo manual}
Neste modo, introduz manualmente os comandos de álgebra, transforma a expressão e
calcula o resultado.
•{AUTO} ... {Modo automático}
Neste modo, a solução é produzida automáticamente, um passo de cada vez.
kModo de verificação
Pressione 4(VRFY) para entrar o modo de verificação.
A expressão é visualizada na linha de topo do ecrã. Introduza a solução por baixo e de
seguida pressione6(JUDG) para determiniar se a solução está correcta.
O ecrã de resultado da verificação mostra o resultado da verificação do lado esquerdo e do
lado direito (excepto para a equação linear).
•No entanto, no caso de uma equação linear ou quadrática tiverem duas soluções, o lado
esquerdo e o lado direito são obtidos para o valor onde estiver localizado o ponteiro.
•No caso das equações simultâneas onde o lado esquerdo e o lado direito da segunda
equação não são coincidentes mesmo no caso de coincidirem na primeira equação,
apenas o lado esquerdo e o lado direito da segunda equação são obtidos. Nos outros
casos, o lado esquerdo e o lado direito da primeira equação são obtidos.
O tipo de ecrã de introdução de solução que surge é seleccionado de acordo com o tipo de
expressão. Para introduzir um tipo diferente, pressione 1(TYPE) e de seguida seleccione
o tipo de selecção que pretende. Os tipo de soluções disponíveis dependem do modo.
•{X = a} ... X tem uma solução (X = a) (equação linear dpor defeito)
•{X = a, b} ... X tem duas soluções (X = a, X = b) (equação quadrática por defeito)
•{X = a,
Y=} ... X e Y têm uma solução cada (X = a, Y = b) (equação simultânea por
defeito)
•{X > a} ... X { > < ><} a (desigualdade linear por defeito)
•{X < a, b <} ... X < a, b < X ou X < a, b < X
•{a < X < b} ... a < X< b, a < X < b ou X = a
•{Identi} (Identity) ...identidade do lado esquerdo e do lado direito
•{Many} (Many Solutions) ... muitas soluções
•{No sol} (No Solution) ...sem solução
7-3-4
Modo tutor
20000501
7-3-5
Modo tutor
Pode pressionar 4(MANU) para mudar para o modo manual ou 5(AUTO) para mudar
para o modo automático.
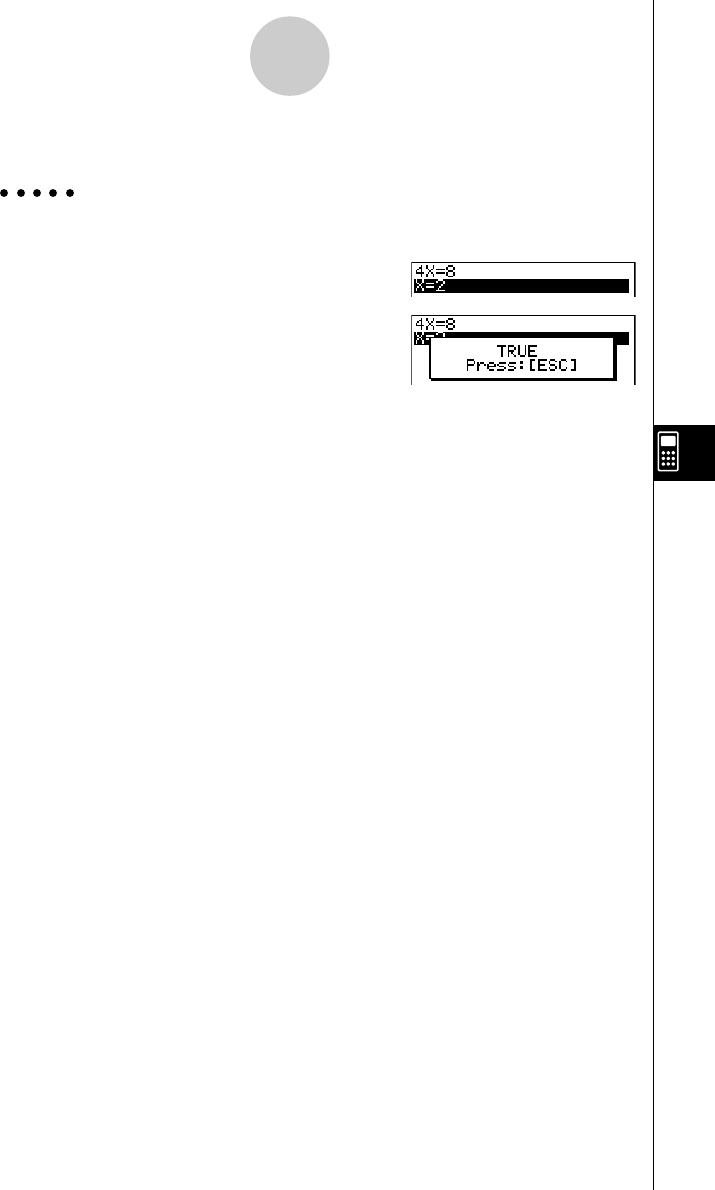
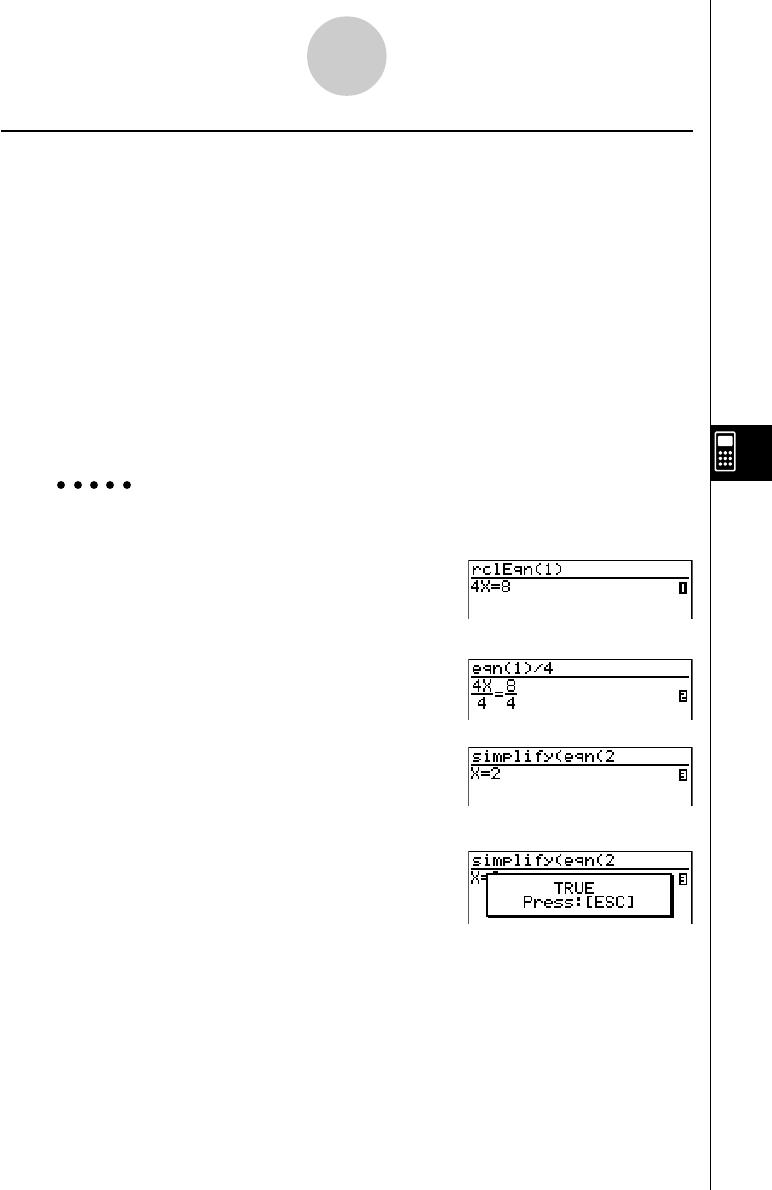
Exemplo Resolver 4X = 8 no modo de verificação
(Linear Equation)(AX = B)
2(INPUT)ewiw6(EXE)
4(VRFY)cw
6(JUDG)
20000501
7-3-6
Modo tutor
k Modo manual
Pressione 5(MANU) para entrar no modo manual.
Tal como no modo de álgebra, o ecrã é dividido entre uma área de introdução e uma área
de visualização. O que quer dizer que pode seleccionar comandos do modo de álgebra a
partir do modo do menu de funções, transformar a expressão e resolve-la.
a operação é igual à do modo de álgebra.
Depois de obter um resultado, pode pressionar 5(JUDG) para determinar se está ou não
correcta.
•{DISP} ... Determina se a expressão na área de visualização é uma solução correcta.
•{Identi} ...Identidade do lado esuqerod e do lado direito.
•{Many} ... muitas soluções
•{No sol} ...sem solução
Pode pressionar 6(AUTO) para mudar para o modo automático.
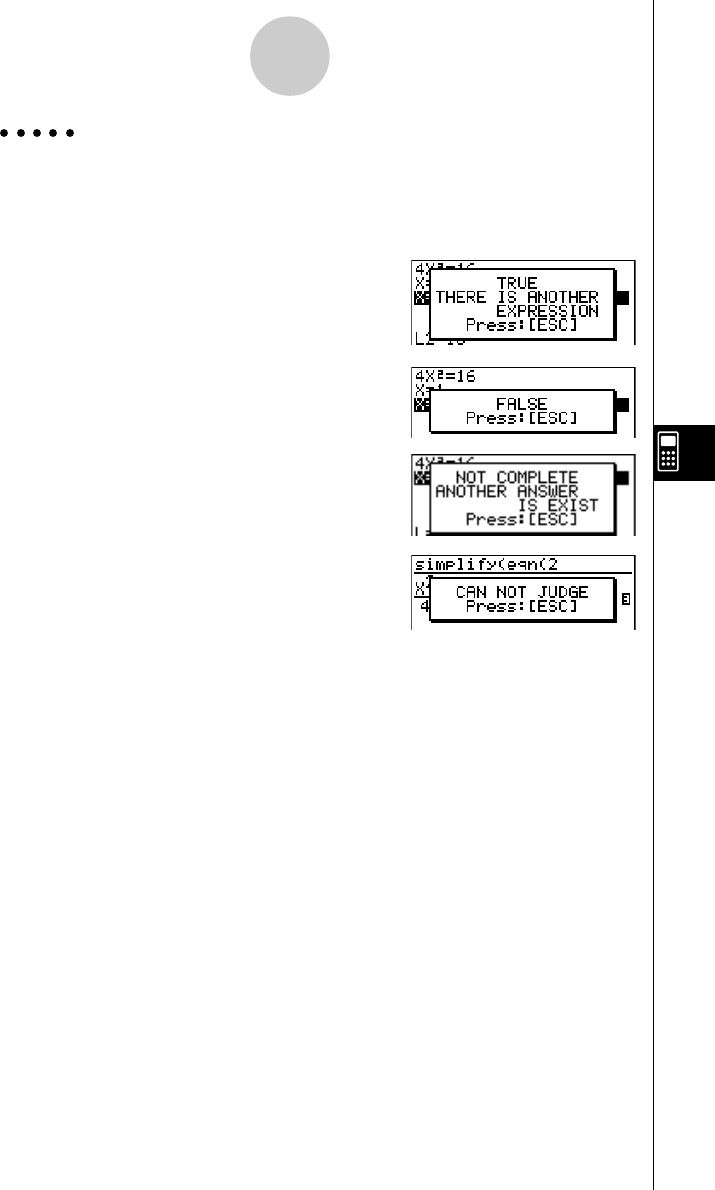
Exemplo resolver 4X = 8 no modo manual
(Linear Equation)(AX=B)
2(INPUT)ewiw6(EXE)
5(MANU)
4(eqn)b)/e
w
1(TRNS)b(smplfy)
4(eqn)c
w
5(JUDG)b(DISP)
20010102
7-3-7
Modo tutor
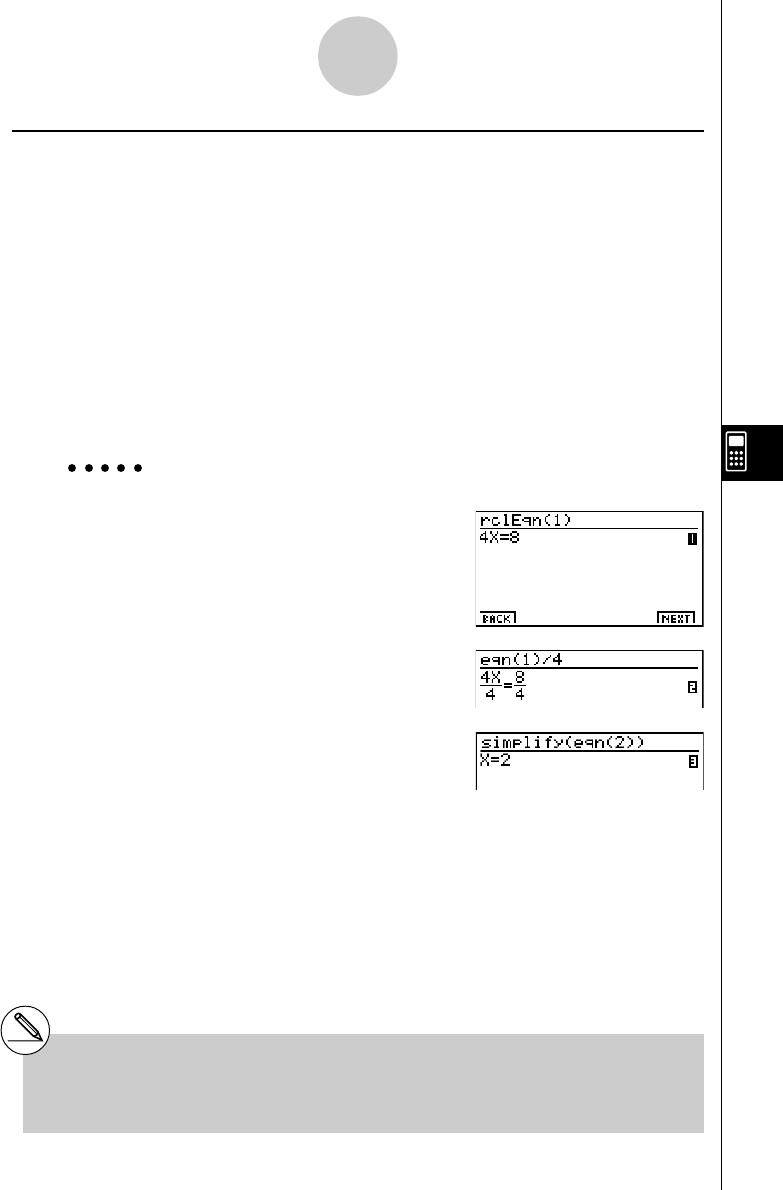
Exemplo 4X2 = 16
True (X = 2, X = – 2)
Também pode surgir a mensagem do exemplo em baixo como resultado de uma verificação.
A mensagem “CAN NOT JUDGE” surge no modo manual enquanto as outras mensagens
surgem, quer no modo de verificação, quer no modo manual.
20010102
7-3-8
Modo tutor
k Modo automático
Pressione 6(AUTO) para entrar no modo automático.
No modo de equação simultânea, deve também seleccionar SBSTIT (método de
sunstituição) ou ADD-SU (método de soma/subtracção).
O método de substituição primiero transforma a equação para o formato Y = aX + b e
substitui a outra expressão para Y.*1
O método de soma/subtracção multiplica ambos os lados da expressão pelo mesmo valor
para isolar o coeficiente X (ou Y).
tal como no modo de álgebra, o ecrã é dividido entre área de introdução e área de
visualização.
Cada vez que pressiona 6(NEXT) avança para o próximo passo. 6(NEXT) só é
mostrado depois de ser obtida a solução.
Pode voltar atrás nos passos, pressionando 1(BACK).
Exemplo Resolver 4X = 8 no modo automático
(Linear Equation)(AX = B)
2(INPUT)ewiw6(EXE)
6(AUTO)
6(NEXT)
6(NEXT)
*1Pode pressionar 5(ADD SU) em qualquer
altura para alternar entre o método de
substituição e o método de soma/subtracção.
#Consulte a página 7-1-8 para informação sobre
funções gráficas.

20000501
∫
a
b f(x)dx = F(b) – F(a)
7-4-1
Precauções com o sistema de álgebra
7-4 Precauções com o sistema de álgebra
•Se uma operação algebraica não poder ser realizada por alguma razão, a expressão
original mantem-se no ecrã.
•Uma operação algebraica pode levar algum tempo a ser realizada. Se um reultado não
surgir imediatamente no ecrã, isso não quer dizer que a calculadora está estragada.
•Qualquer expressão pode ser visualizada em diferentes formatos. Por isso, não deve
assumir que uma expressão está errada só porque não surge como esperava.
•Esta calculadora realiza cálculos de integração assumindo que os integrais são sempre
positivos, mesmo quamdo os integrais são descontinuos (devido á alternancia entre
positivo e negativo).
f(x)
F(x): função primitiva de f(x)