BA 13 X 0613geans

GEOMETRY

The

University

of

the

State

of

New

York

REGENTS

HIGH

SCHOOL

EXAMINATION

GEOMETRY

Wednesday, June

19,

2013-9:15

a.m. to 12:15 p.m., only

Student

Name:

fY}

(,

c;;

b()}

SchooiName:

____

~~fl1--~~--;0---------------------------------

The

possession

or

use

of

any

communications

device

is strictly

prohibited

when

taking

this

examination.

If

you

have

or

use

any

communications

device,

no

matter

how

briefly,

your

examination

will

be

invalidated

and

no

score

will

be

calculated

for

you.

Print

your

name

and

the

name

of

your

school

on

the

lines

above.

A

separate

answer

sheet

for

Part

I

h~s

been

provided

to

you. Follow

the

instructions

from

the

proctor

for

completing

the

student

information

on

your

answer

sheet.

This

examination

has

four

parts,

with

a

total

of

38

questions.

You

must

answer

all

questions

in

this

examination.

Record

your

answers

to

the

Part

I

multiple-choice

questions

on

the

separate

answer

sheet.

Write

your

answers

to

the

questions

in

Parts

II,

III,

and

IV

directly

in

this

booklet.

All

work

should

be

written

in

pen,

except

for

graphs

and

drawings,

which

should

be

done

in

pencil.

Clearly

indicate

the

necessary

steps,

including

appropriate

formula

substitutions,

diagrams,

graphs,

charts,

etc.

The

formulas

that

you

may

need

to

answer

some

questions

in

this

examination

are

found

at

the

end

of

the

examination.

This

sheet

is

perforated

so

you

may

remove

it

from

this

booklet.

Scrap

paper

is

not

permitted

for

any

part

of

this

examination,

but

you

may

use

the

blank

spa~es

in

this

booklet

as

scrap

paper.

A

perforated

sheet

of

scrap

graph

paper

is

provided

.at,,the

end

of

this

booklet

for

any

question

for

which

graphing

may

be

helpful-but

is_Jlot

required.

You

may

remove

this

sheet

from

this

booklet.

Any

work

done

on

this

sheet

of

scrap

graph

paper

will

not

be

scored.

\

When

yoti~ave

completed

the

examination,

you

must

sign

the

statement

printed

at

the

end

of

the

a'swer

sheet,

indicating

that

you

had

no

unlawful

knowledge

of

the

questi6'ns

or

ap:swers

prior

to

the

examination

and

that

you

have

neither

given

nor

received

assiltance

in

answering

any

of

the

questions

during

the

examination.

Your

answer

sheet

cannot

be

accepted

if

you

fail

to

sign

this

declaration.

Notice

...

A

graphing

calculator, a

straightedge

(ruler),

and

a

compass

must

be

available

for

you

to

use

while

taking

this

examination.

,,

DO

NOT

OPEN

THIS EXAMINATION BOOKLET UNTIL

TilE

SIGNAL IS GIVEN.

Al::IJ.3V\103E>

Part

I

Answer

all

28

questions

in

this

part.

Each

correct

answer

will

receive

2

credits.

For

each

statement

or

question,

choose

the

word

or

expression

that,

of

those

given,

best

completes

the

statement

or

answers

the

question.

Record

your

answers

on

your

separate

answer

sheet.

[56]

I

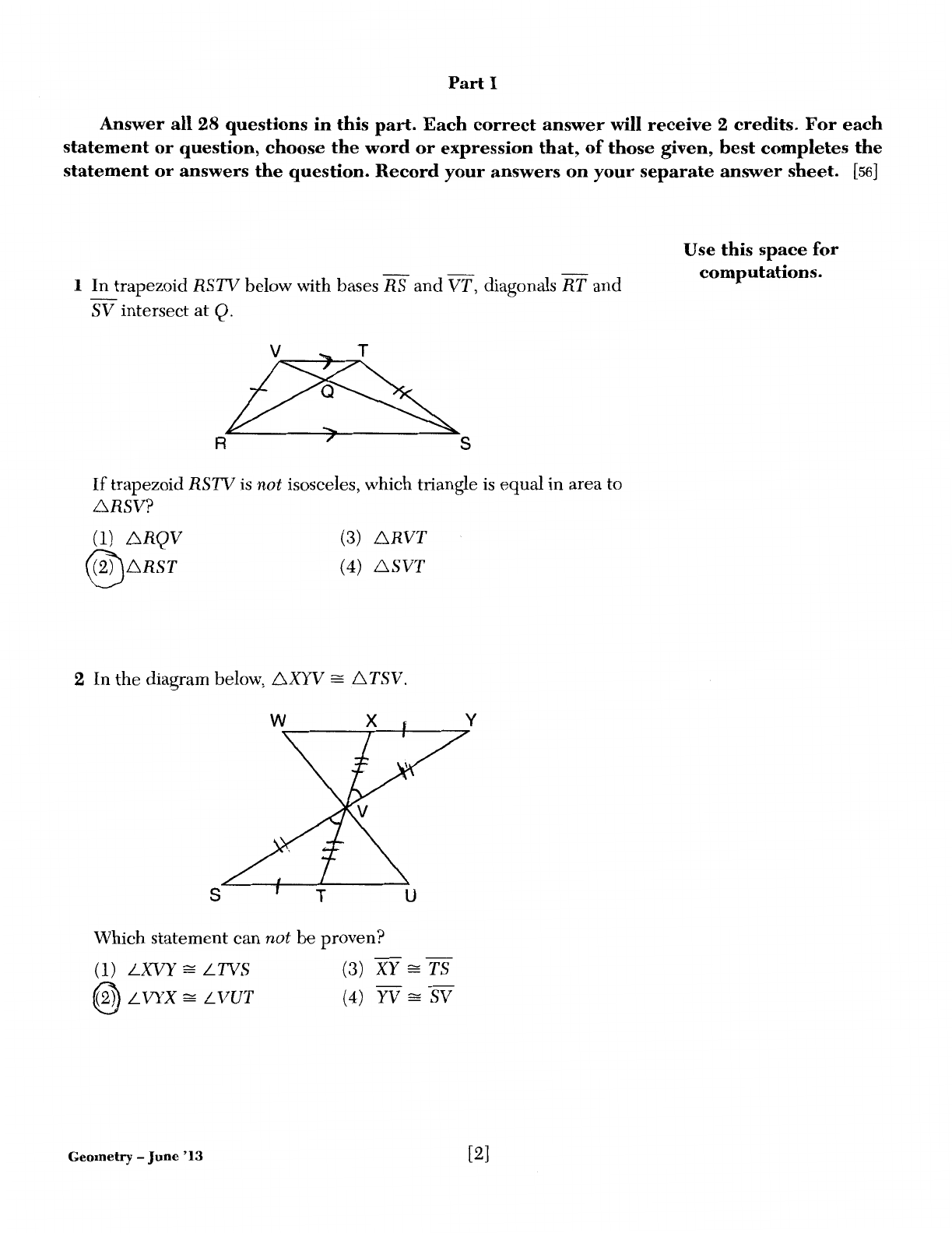
In

trapezoid

RSTV

below with bases

RS

and

VT,

diagonals

RT

and

SV

intersect at

Q.

~

R S

If

trapezoid

RSTV

is

not isosceles, which triangle

is

equal in area to

6RSV?

(1)

6RQV

@)6RST

(3)

6RVT

(4)

6SVT

2

In

the

diagram below,

6XYV

::::::

6 TSV.

8

Which statement can not

be

proven?

(1)

LXVY::::::

LTVS

@

LVYX::::::

LVUT

Geometry-

June

'13

(3)

XY::::::

TS

(4)

YV::::::

SV

[2]

Use

this

space

for

computations.

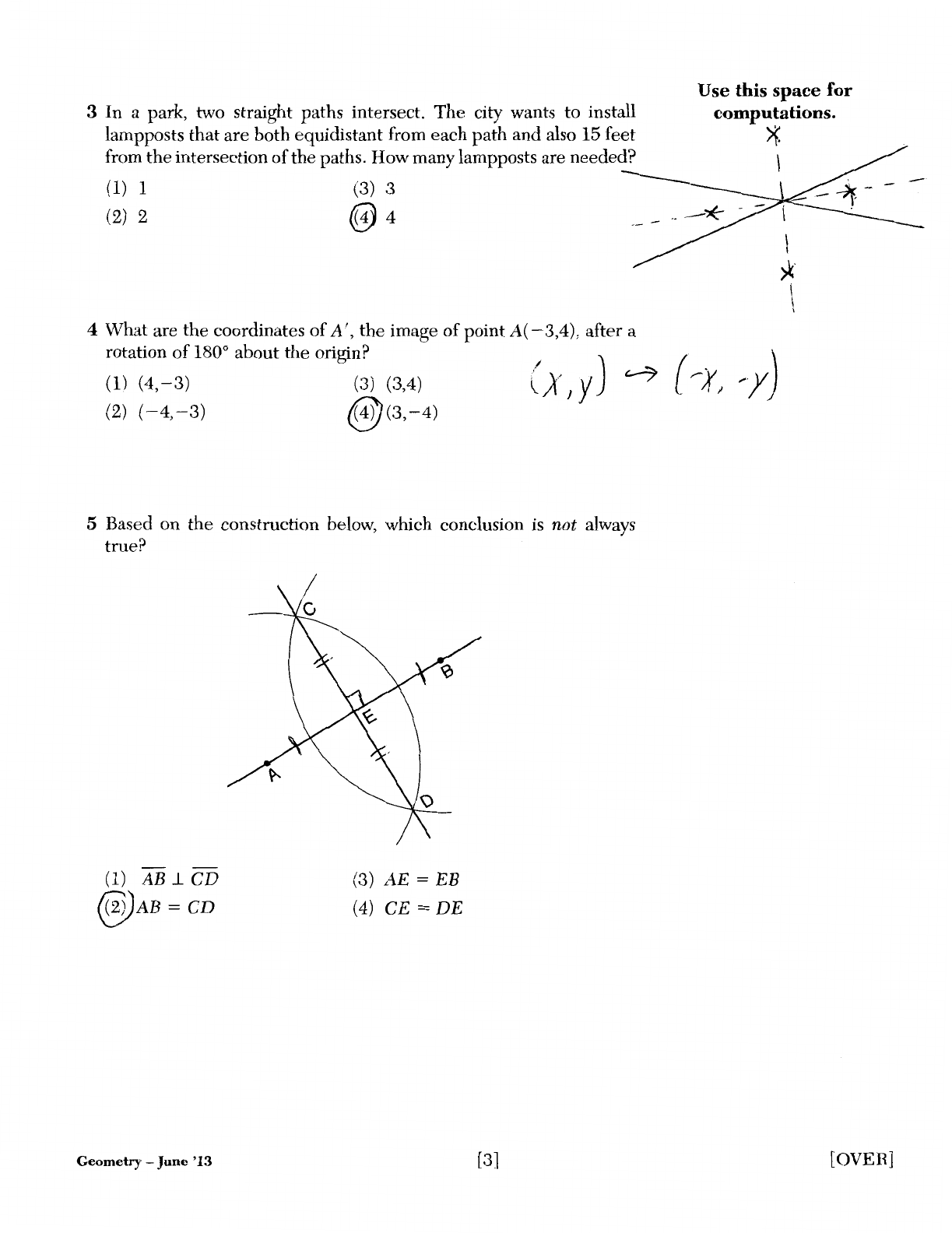
Use

this

space

for

3

In

a park, two straight paths intersect.

The

city

wants to install computations.

lampposts that are both equidistant from each

path

and

also 15 feet ~

from the intersection

of

the paths. How many lampposts are needed? \

------·--

-~

-

~

--

(1) 1

(2) 2

(3) 3

@4

.....L-

•

--

---..,:..__

4

vVhat

are the coordinates

of

A',

the

image

of

point

A(

-3,4),

after a

rotation

of

180° about

the

origin?

.-

-

---"\,

~

---------

\

~-

\

(l)

(4,

-3)

(2) (

-4,

-3)

(3) (3,4)

@(3,

-4)

/ )

()'

J y c.-7

5 Based on the construction below, which conclusion

is

not always

tme?

(1) AB

.1

CD

@)AB

=CD

Geometry-

June

'13

(3) AE = EB

(4)

CE

=DE

[3]

[OVER]

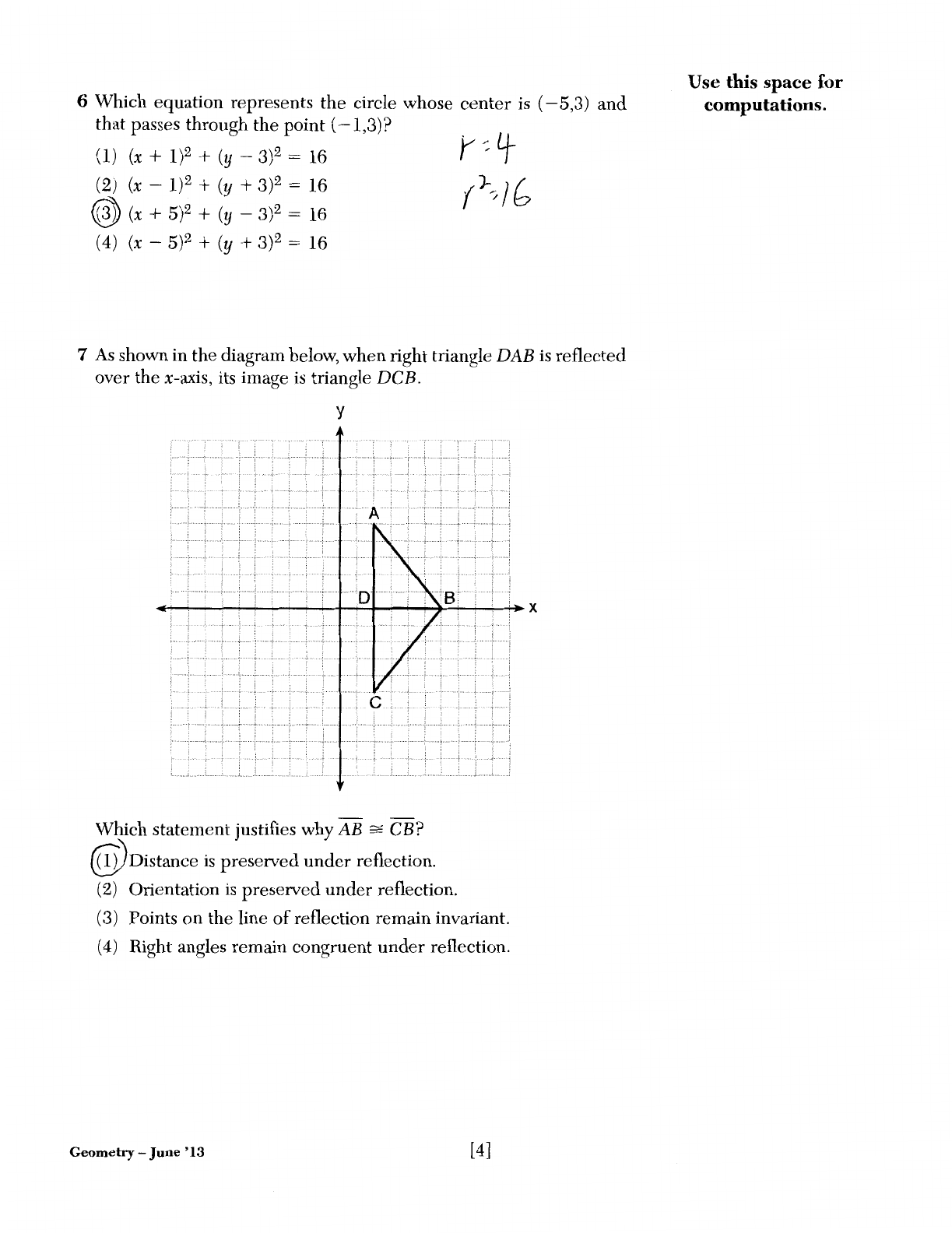
6 Which equation represents

the

circle whose

center

is

(-

5,.3)

and

that

passes through

the

point ( -1,.3)?

(I)

(x

+ 1)2 + (y -

.3)

2 = 16

(2)

(x

-1)2 + (y +

.3)

2 = 16

<[~

(x

+ 5)2 +

(y

-

.3)

2 = 16

(4)

(x

-5)2 + (y +

.3)

2 = 16

7

As

shown in

the

diagram below, when right triangle

DAB

is

reflected

over

the

x-axis, its image

is

triangle DCB.

y

Which statement justifles why

AB

:::::

CB?

@Distance

is

preserved

under

reflection.

(2) Orientation

is

preserved

under

reflection.

(,3)

Points

on

the

line

of

reflection remain invariant.

(4) Right angles remain congruent

under

reflection.

Geometry

-

June

'13

[4]

Use

this

space

for

computations.

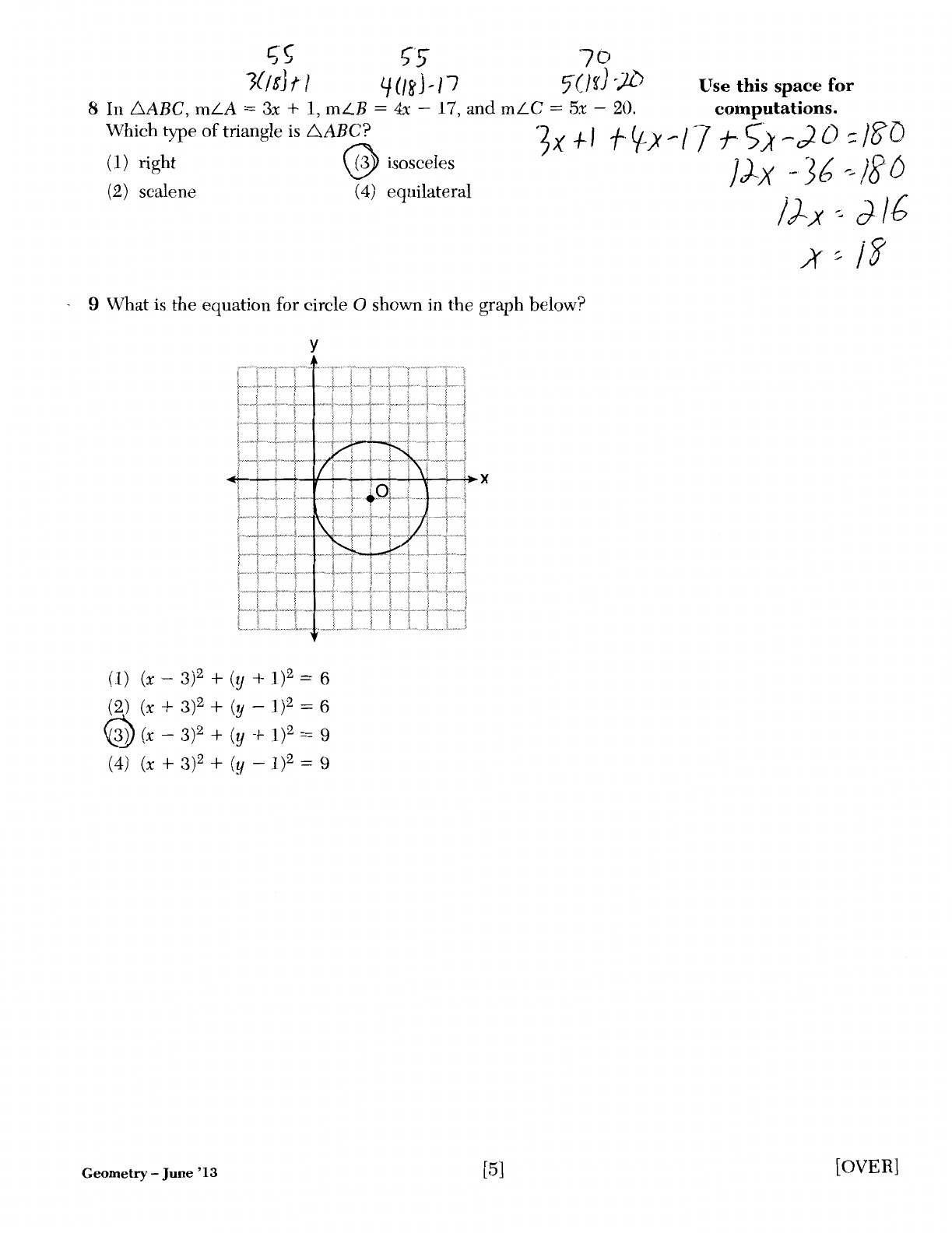
s~

~5

70

3(/c]r I

~(/g)-(1

r;(ig)

)b

Use

this

space

for

8

In

.6.ABC,

mLA

= 3x +

1,

mLB

=

4x

-17, and

mLC

=

.Sx

-20.

computations.

\:Vhich

type of triangle

is

D.ABC?

'3

X

+I

f·

Cf)

-·/7

-j-·

S")

-J 0

::

/8'

0

(1) right @

isos~eles

}J.-x

_

36

~/

/86

(2)

scalene

(4)

eqmlateral / . / {

d--.x

-:;

d b

9 What

is

the

equation for circle 0 shown in

the

graph below?

y

(

1)

(x

-3 )2 + (y + l )2 = 6

(2)

(x

+ 3)2 + (y -1)2 = 6

@

(x

-3 )2 + (y + 1 )2 = 9

(4) (x + 3)2 + (y -1)2 = 9

Geometry-

June

'13

X

[5]

){:,

!8

[OVER]

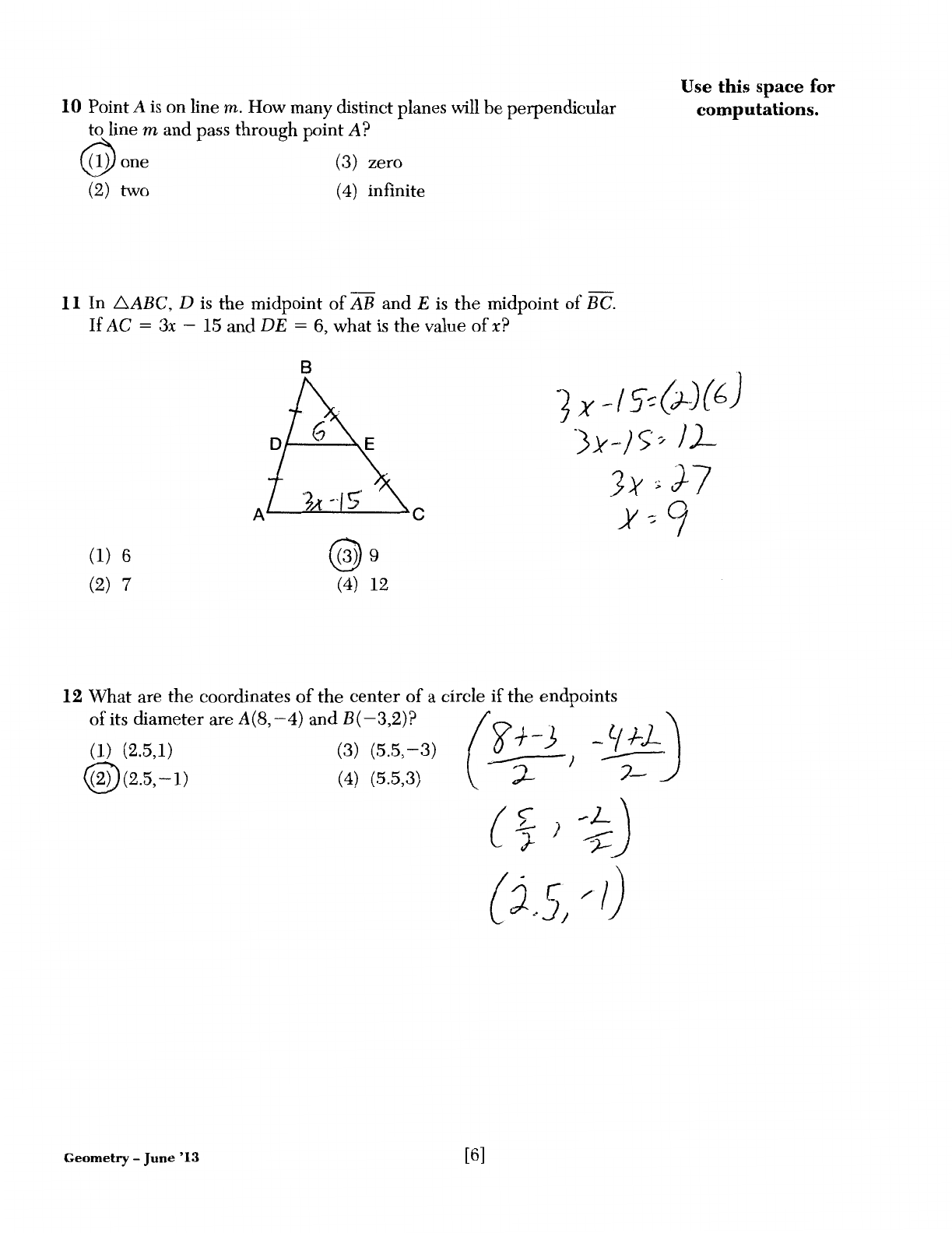
10 Point A

is

on line m. How many distinct planes will be perpendicular

to line m and pass through point

A?

@one

(3) zero

(2)

two (4) infinite

11 In

6ABC,

Dis

the

midpoint

of

AB

and E

is

the

midpoint

of

BC.

If

AC

= 3x -

15

and

DE

= 6, what

is

the

value

of

x?

Use

this

space

for

computations.

8

] X

-15~(J-.){b)

)x-)(;:/

J)_

(1) 6

(2) 7

@9

(4)

12

3x

>

),7

.Y~

9

12 What are

the

coordinates

of

the

center

of

a circle

if

the

endpoints

(1) (2.5,1) (3) (5.5,

-3)

f!_!__!_,

-~

of

its diameter are

A(8,

-4)

and B(

-3,2)?

(Q

. _

1 (

..

··

).

J

@(2.5,

-1)

(4) (5.5,3) )._.

?-

{

£.

J

-LJ

;)-

~

.

(),51

r/)

Geometry-

June

'13

[6]

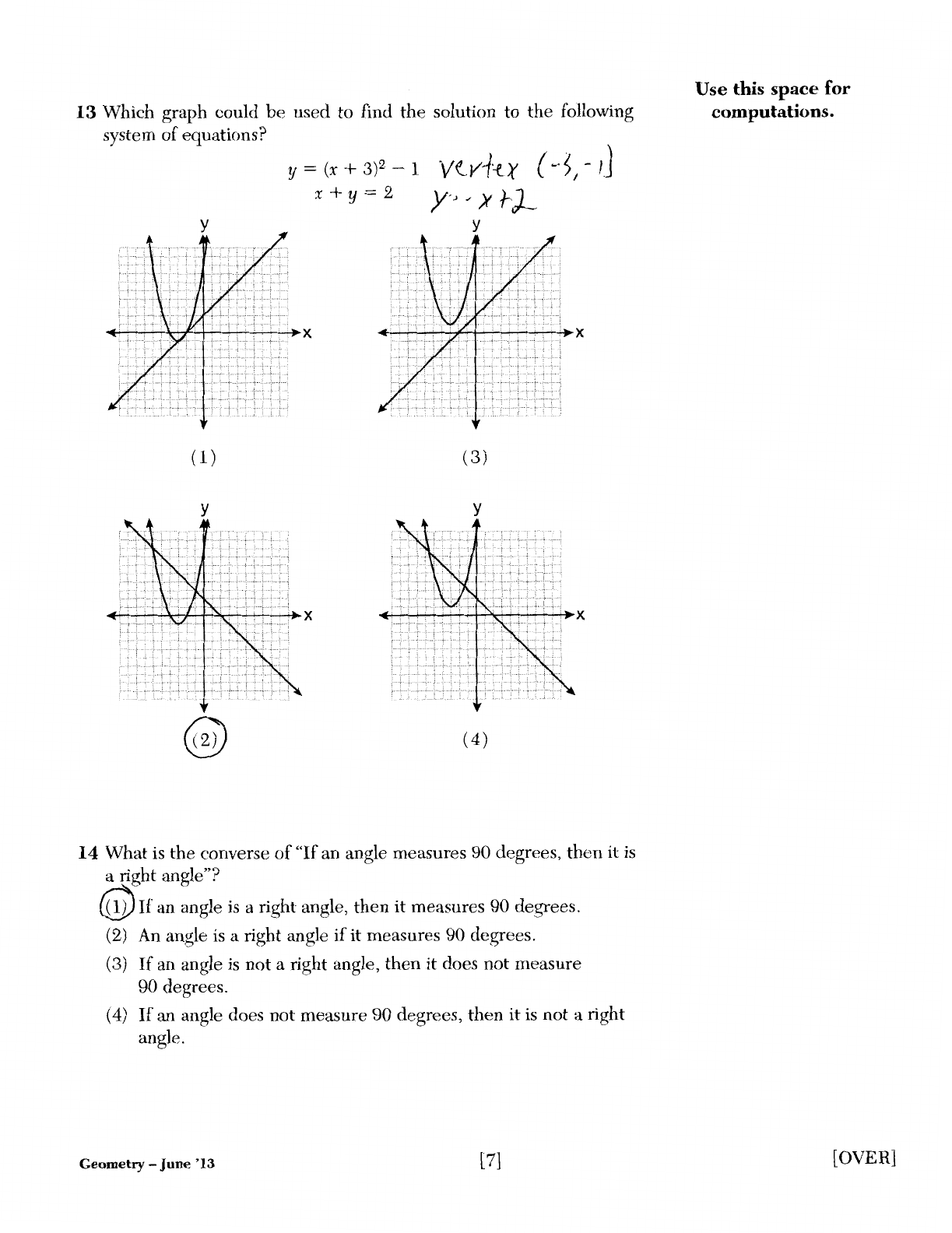
13 Which graph could

be

used to find

the

solution to the following

system

of

equations?

(1)

y

y =

(x

+ 3)2-1

x+y=2

X

VtV1-f-'¥

(

...

~I

-d

y~)--

x

rJ.-

y

(3)

y

X

(4)

14 What

is

the converse

of

..

If

an angle measures 90 degrees,

then

it

is

a right angle"?

~If

an angle

is

a right angle, then it measures 90 degrees.

(2)

An

angle

is

a right angle

if

it measures 90 degrees.

(3)

If

an angle

is

not a right angle,

then

it does not measure

90 degrees.

( 4)

If

an angle does not measure 90 degrees,

then

it

is

not a right

angle.

Geometry

-June

'13

[7]

Use

this

space

for

computations.

[OVER]

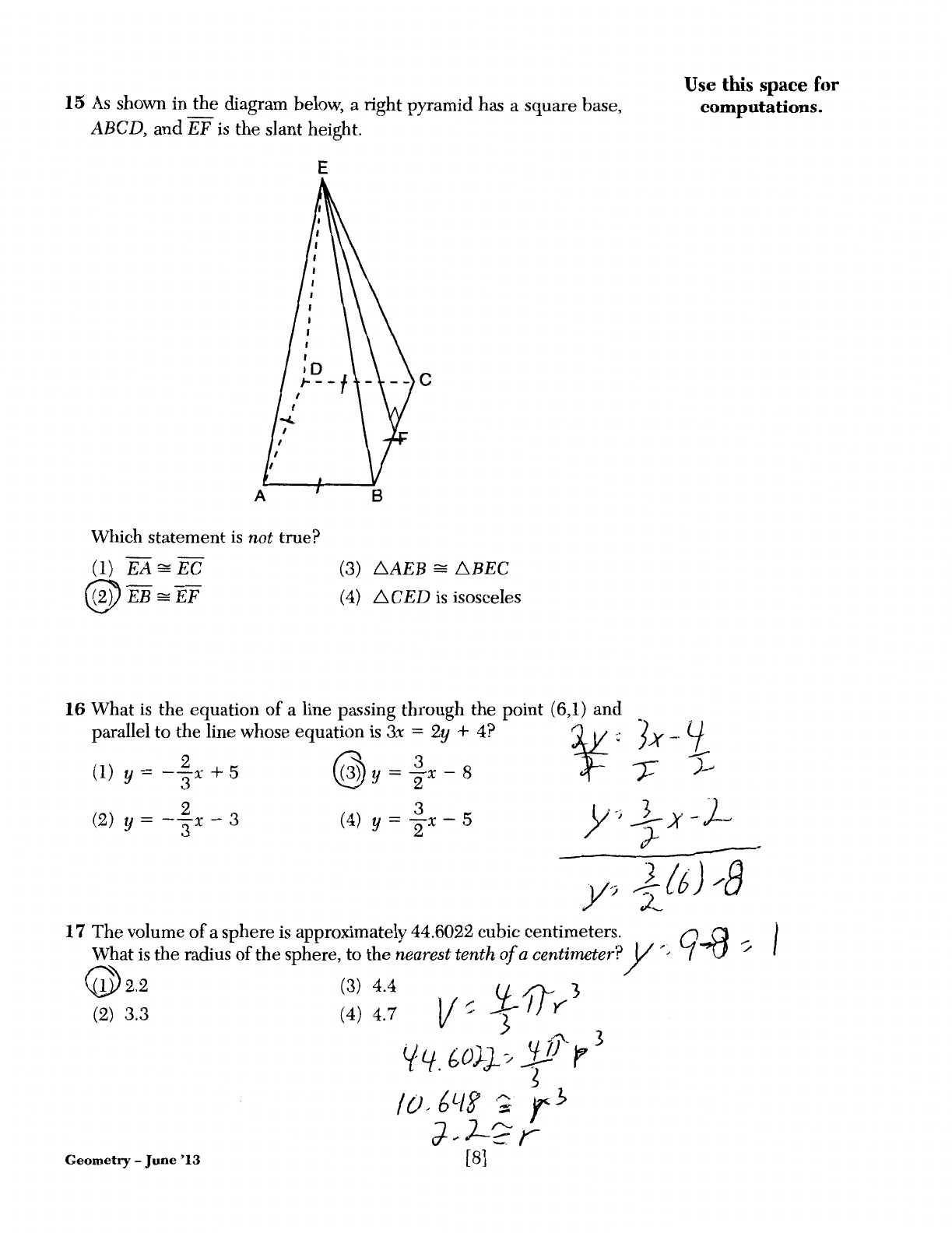
15

As

shown in

the

diagram below, a right pyramid has a square base,

ABCD, and

EF

is

the slant height.

E

Which statement

is

not

true?

(1)

EA:::::

EC

@EB:::::EF

(3) D.AEB

:::::

D.BEC

(4)

6CED

is

isosceles

Use this space for

computations.

16 What

is

the equation

of

a line passing through the point (6,1) and _

~

parallel to the line whose equation

is

3x = 2y +

4?

¥

~

J X _

LJ

2

~

3 .

_.:.-

(1) y =

-3x

+ 5 @ y =

2x

-8

-;::

J_.-

2 3

y·

·- 3

~

')

(2) y =

-3x

-3 (4) y =

2x

-5 '

-;:

:x

-

~

Y'

{t6rB

17

The volume

of

a sphere

is

approximately 44.6022 cubic centimeters. . 0-fj / J

What

is

the radius

of

the sphere, to the nearest

tenth

of

a centimeter? y

';

1

cw2.2

(3) 4.4

..

u

~

3

(2) 3.3 ( 4) 4.1 V

~

-t

I I

v-

I(

4.

&o

)-:J

..

,

f"'r

3

/0,

6L!§'

~·

r!>

J

..

J-2r

Geometry-

June

'13

[8]

f---t

18 Points A(5,3)

and

B(7,6) lie on

AB

. Points C(6,4)

and

D(9,0) lie on

CD.

Which statement

is

true?

1'1

~

~·

(; "]

1..

(1)

AB)

II

CD

'-flt'

7-)

'/

~

f---t f---t

(2)

AB

l.

CD

lf-6

'f

f---t

d

f---t

1

fl1

~

,::;

c;

-

(3)ABan

CDarethesameine.

CIS

6-a

-1

~~

f---t

) 1 >

~~B

and

CD

intersect,

but

are not perpendicular.

19

Which set

of

equations represents two circles that have

the

same

center?

(1)

x2 +

(y

+ 4)2 = 16 and

(x

+ 4)2 + y2 = 16

(2)

(x

+ 3)2 +

(y

-3)2 = 16 and

(x

-3)2 + (y + 3)2 = 25

(3)

(x

-

7)

2 +

(y

-

2)

2 = 16

and

(x

+

7)

2 +

(y

+

2)

2 = 25

@

(x

-

2)

2 + (y -5)2 = 16 and

(x

-

2)

2 + (y -

.5)

2 = 25

t;-:;::7

f---t

20

Transversal t./1 intersects

AB

and

CD,

as

shown in

the

diagram

below.

A B

c D

Which statement could always

be

used

to

prove

AB

II

CD?

(1) L2::::

L4

@

L3

and

L6

are supplementary

(2)

L1::::

L8

(4)

L1

and

L5

are supplementary

Geometry-

June

'13

[9]

Use

this

space

for

computations.

[OVER]

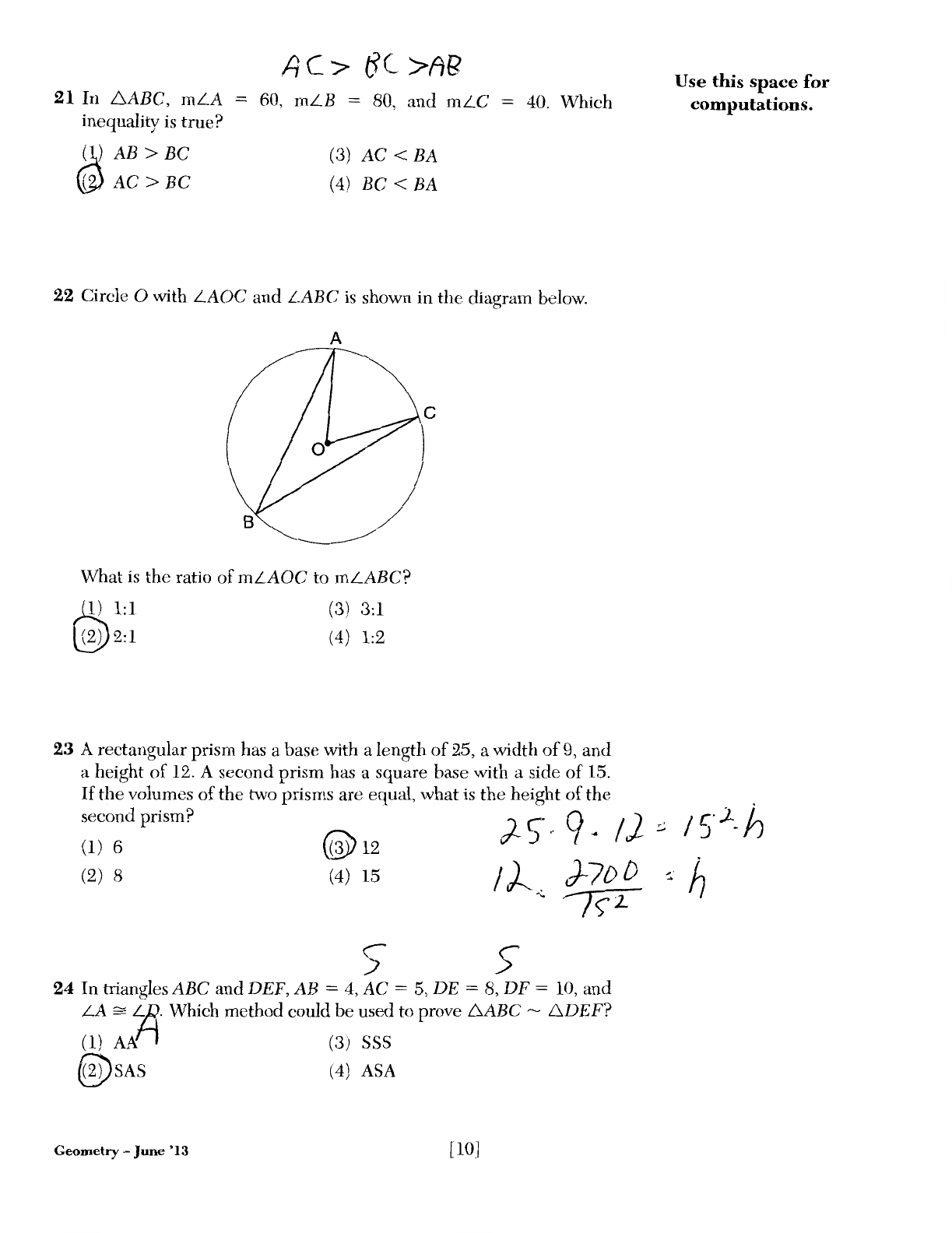
AC>

6C

>AB

21 In LiABC,

mLA

= 60,

mLB

= 80, and

mLC

= 40. \Vhich

inequality

is

true?

~

A.B

> BC

(ij.}

AC

> BC

(3)

AC

< BA

(4) BC <

B1\

22

Circle 0 with

LAOC

and

LABC

is

shown in

the

diagram below.

A

What

is

the ratio

of

mLAOC

to

mLABC?

).!(

1:1

\J.:V

2:1

(3)

.3:1

(4)

1:2

23

A rectangular prism has a base

\Vith

a length

of

25, a width

of

9, and

a height

of

12. A second prism has a square base with a side

of

15.

Use this

space

for

computations.

If

the volumes

of

the two prisms are equal, what

is

the height

of

the ,

second prism? lS"

..

9

..

I)

.:::.:

1

5.

J~~

h

(1) 6

~

12

(2) 8 (4)

15

1

),

J-7o

D

-::

h

-~

~

I

) >

24

In triangles

ABC

and DEF,

AB

=

4,

AC

= 5, DE = 8, DF = 10, and

LA

:::::::

fi·

Which method could

be

used to prove LiABC

~

LiDEF?

(1)

AN.

(3)

SSS

@sAS

(4) ASA

Geometry

-June

'13

[10]

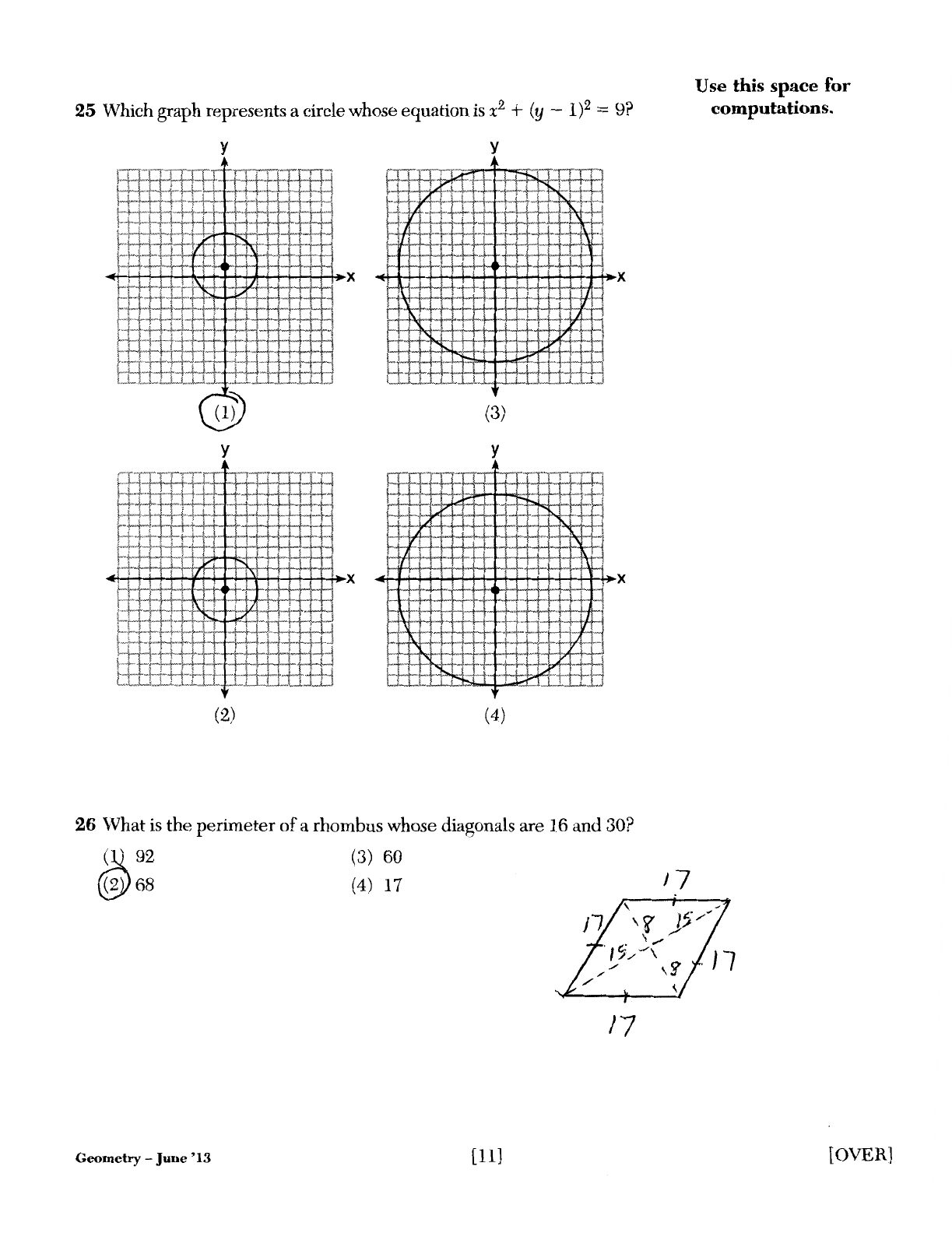
25

\Vhich graph represents a circle whose equation

is

x2 +

(y

-

1)

2 = 9?

y y

X X

(3)

y y

X

(2)

(4)

26

\Vhat

is

the

perimeter

of

a rhombus whose diagonals are 16

and

30?

~

92

(3)

60

~68

(4)

17

Geometry-

June

'13

(11]

J]

Use this

space

for

computations.

[OVER]

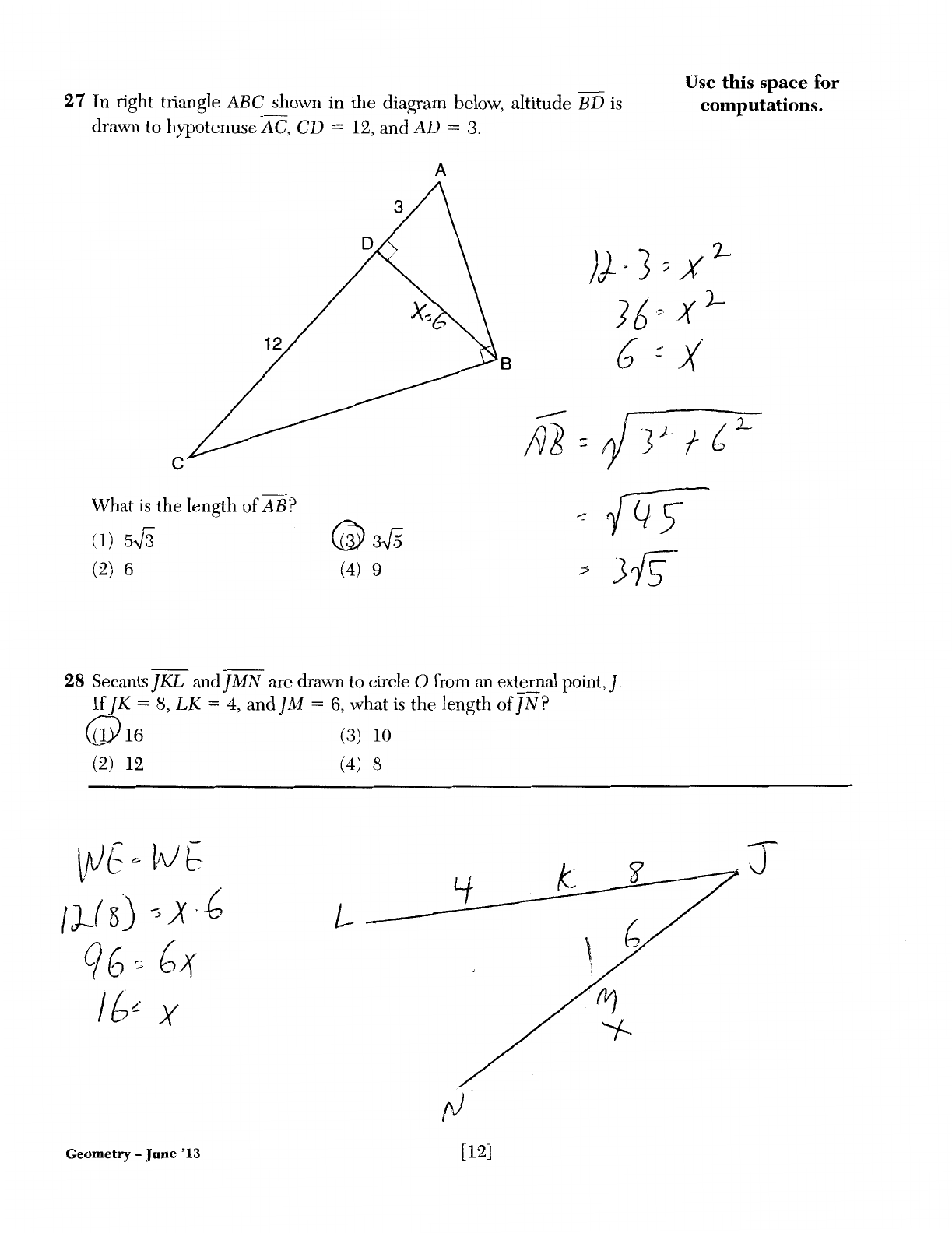
27

In right triangle

ABC

shown in the diagram below, altitude

BD

is

drawn to hypotenuse AC,

CD

= 12, and

AD

=

3.

Use

this

space

for

computations.

c

What

is

the length

of

AB?

(1)

sJ3

(2) 6

@315

(4) 9

A

8

})

· 3

~X

'L

](;·~XJ

(;::X

!fi~J>~f{,'

~{f(S

~

315

28

Secants JKL and JMN are drawn to circle 0 from an external point,].

If

JK = 8,

LK

= 4, and

JM

=

6,

what

is

the length

of

JN?

((iY

16 (3) 10

(2)

12 (4) 8

V'}b

~

lAJb

f)-(B)

>)·b

qG

~

G~

I&~

X

Geometry

-June

'13

[12]

Part

II

Answer

all

6

questions

in

this

part.

Each

correct

answer

will

receive

2

credits.

Clearly

indicate

the

necessary

steps,

including

appropriate

formula

substitutions,

diagrams,

graphs,

charts,

etc.

For

all

questions

in

this

part,

a

correct

numerical

answer

with

no

work

shown

will

receive

only

1

credit.

All

answers

should

be

written

in

pen,

except

for

graphs

and

drawings,

which

should

be

done

in

pencil.

[12]

29 A right circular cylinder has a height

of

7 inches and the base has a diameter

of

6 inches.

Determine the lateral area, in square inches,

of

the cylinder in terms

of

'1T.

Geometry-

June

'13

L~

:JJJrh

--J-1TOJL7)

:>

LfJ-11

[13] [OVER]

30

Determine, in degrees,

the

measure

of

each interior angle

of

a regular octagon.

Geometry

-June

•13

~h

(?-~

/'10

---

~

I~

5

[14]

31 Triangle

ABC

has vertices at A(3,0), B(9,

-5),

and G(7,

-8).

Find the length

of

AC

in simplest

radical form.

Geometry-

June

'13

----;-:--:--

1{7-3))-

-1

C'i-v?

{/6+6y-

1f0

4:{5

[15] [OVER]

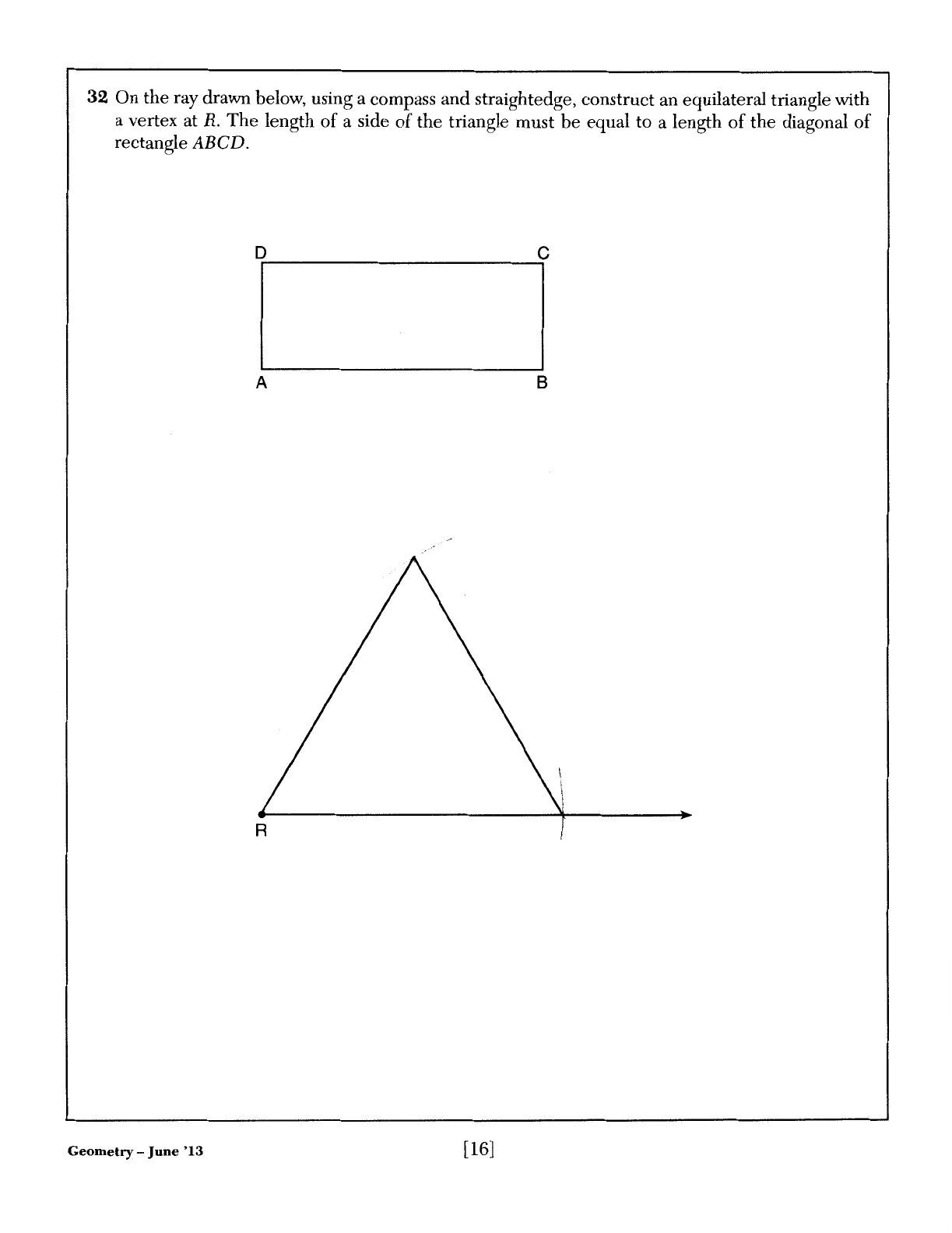
32

On

the

ray drawn below, using a compass

and

straightedge, construct an equilateral triangle with

a vertex at

R.

The

length

of

a side

of

the

triangle must

be

equal to a length

of

the

diagonal

of

rectangle ABCD.

D c

A B

R

Geometry-

June

'13

[16]

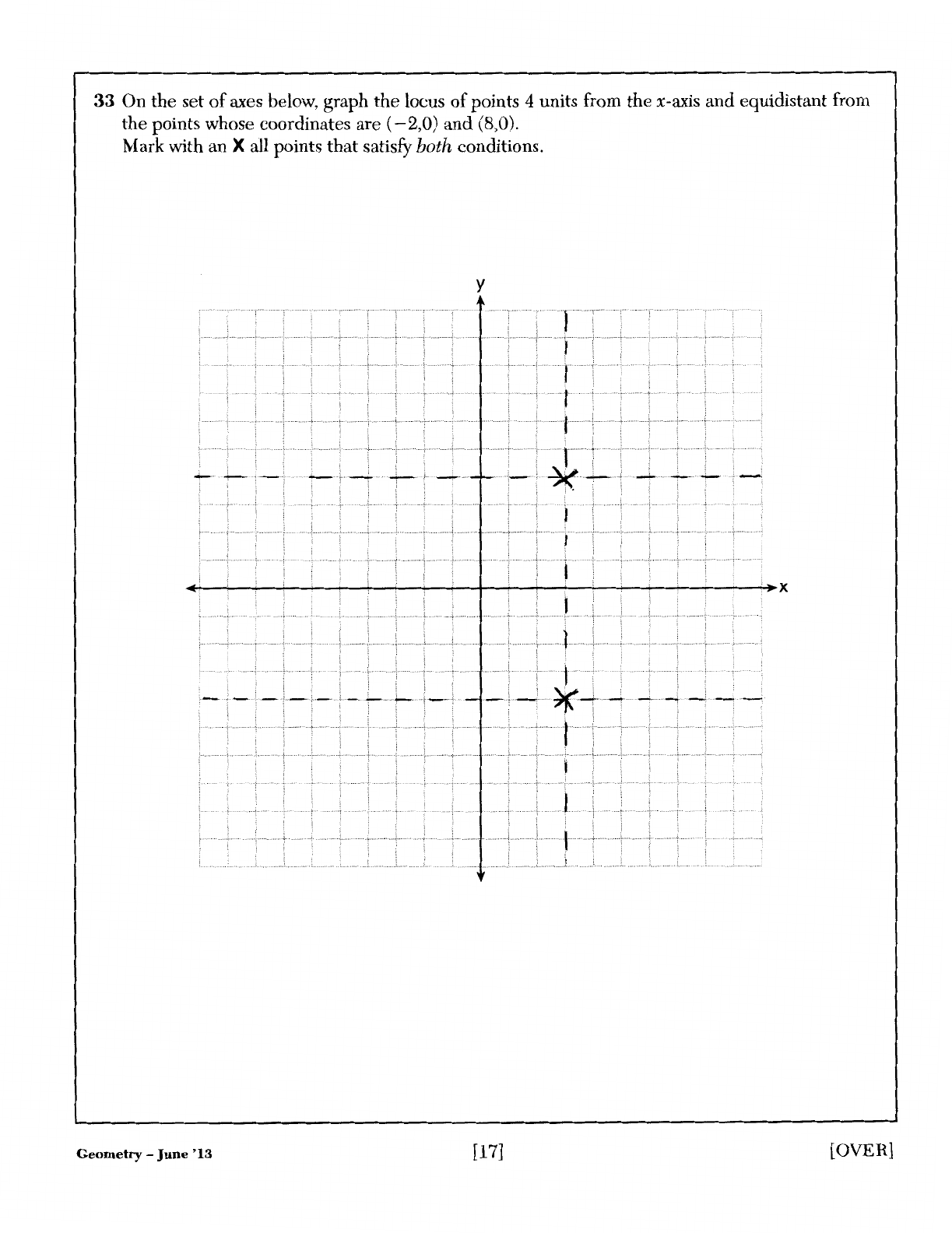
33

On

the

set

of

axes below, graph

the

locus

of

points 4 units from

the

x-axis

and

equidistant from

the

points whose coordinates are (

-2,0)

and

(8,0).

Mark with an X all points

that

satisfy both conditions.

y

r I I

I

·+·············t··············+·············-+············1·········~··:-···············-~·············-t

····ll···········l··········-1

·········!······+

!················f·············i··············+·············l··············+··········-·+················1··············4

..

1

......

'\.~

Rf·

I

+-:.....:.

~

.

-·-+.-~~+!~

i

·-+-f.-f--i

.........j-. i .

~-

1

r-·--+--1....--t----+'........-..J

i--t=+·············t··············+--···-·=~

==

-~

i-······+·········+···········

..•

··.·············

···+·!-~·

.•

·:·.··::.·:

..

:~::·::·:.·~

Geometry-

June

'13

[17] [OVER]

34

The

coordinates

of

two vertices

of

square ABCD

are

A(2,1)

and

B(4,4).

Determine

the

slope

of

side

BC.

4

-1

~J-

'"--

-

~-;;..,

:L

AS

(V}JO

~)-

.,

----

.;

3

Geometry

-June

'13

[18]

Part

III

Answer

all

3

questions

in

this

part.

Each

correct

answer

will

receive

4

credits.

Clearly

indicate

the

necessary

steps,

including

appropriate

formula

substitutions,

diagrams,

graphs,

charts,

etc.

For

all

questions

in

this

part,

a

correct

numerical

answer

with

no

work

shown

will

receive

only

1

credit.

All

answers

should

be

written

in

pen,

except

for

graphs

and

drawings,

which

should

be

done

in

pencil.

[ 12]

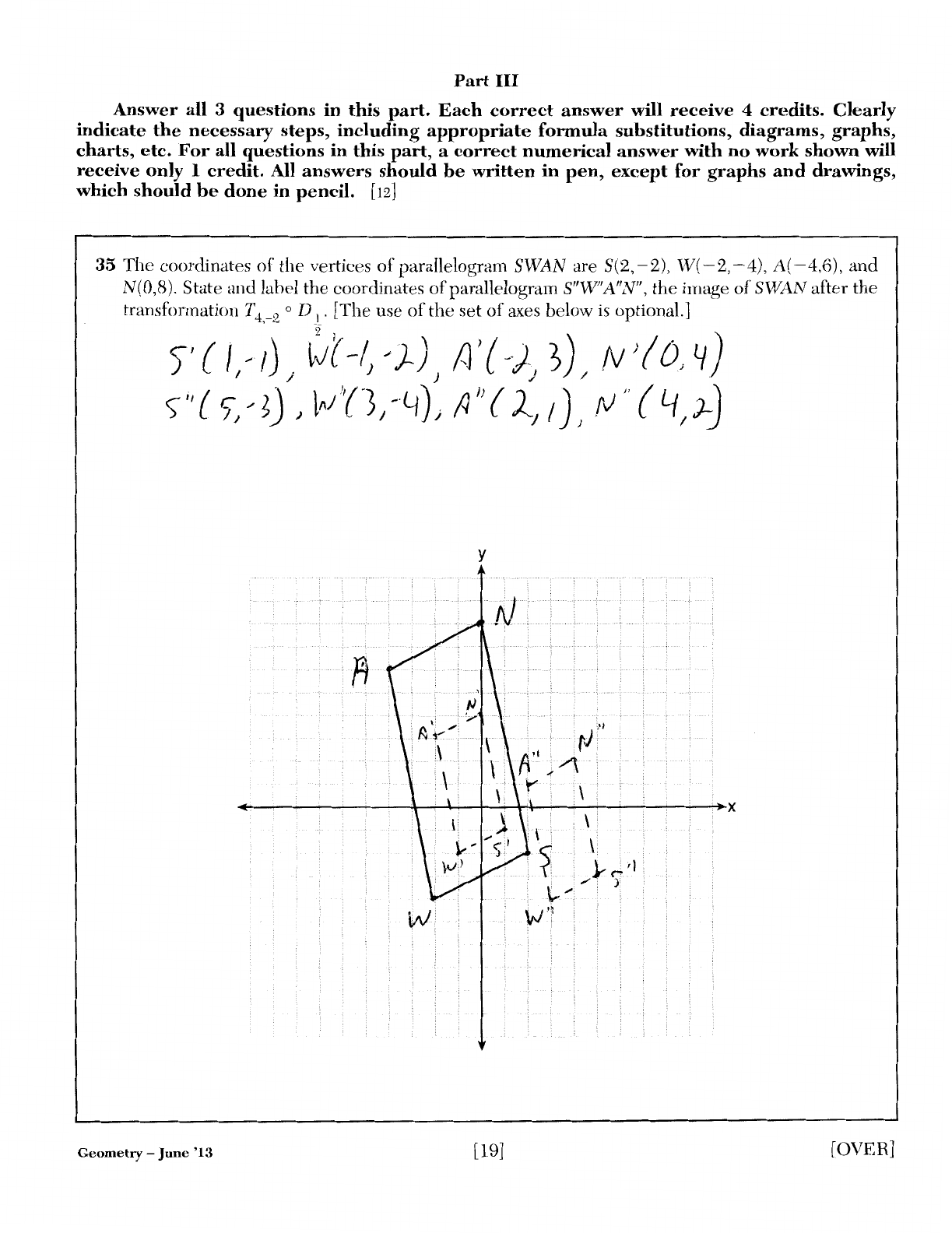
35

The coordinates

of

the

vertices

of

parallelogram SWAN are S(2,

-2),

W(

-2,

-4),

A(

-4,6),

and

N(0,8). State and label

the

coordinates

of

parallelogram S"W'A"N",

the

image

of

SWAN after

the

transformation T4 _2 o D 1. [The use

of

the

set

of

axes below

is

optional.]

)'

( I ,

~'

~t

-I)

;)-) A'{-J

3)

N > (

6/

~)

I

))

) ) I

<;''(_

s-,.,$))

~/'{11-y))

~}J{

~!))

tJ"{41Jj

y

X

Geometry

-June

'13

[19] [OVER]

36

In

circle 0 shown below, chords AB and

CD

and radius OA are drawn, such that AB:::: CD,

OE

l.

AB,

OF

l.

CD, OF = 16, CF = y + 10, and

CD

= 4y -20.

Determine

the

length

of

DF.

J_{yrlo)

~

9

y-Jo

:J-y+)o

~

Lfy

.,)o

lfD "

J-y

J-0

~y

Determine the length

of

OA.

6A

~DD

~

f;t]--+

;t/

~]

lf

Geometry-

June

'13

[20]

c

6fs

yf/()

~

d-0

1-)

0

~

3 0

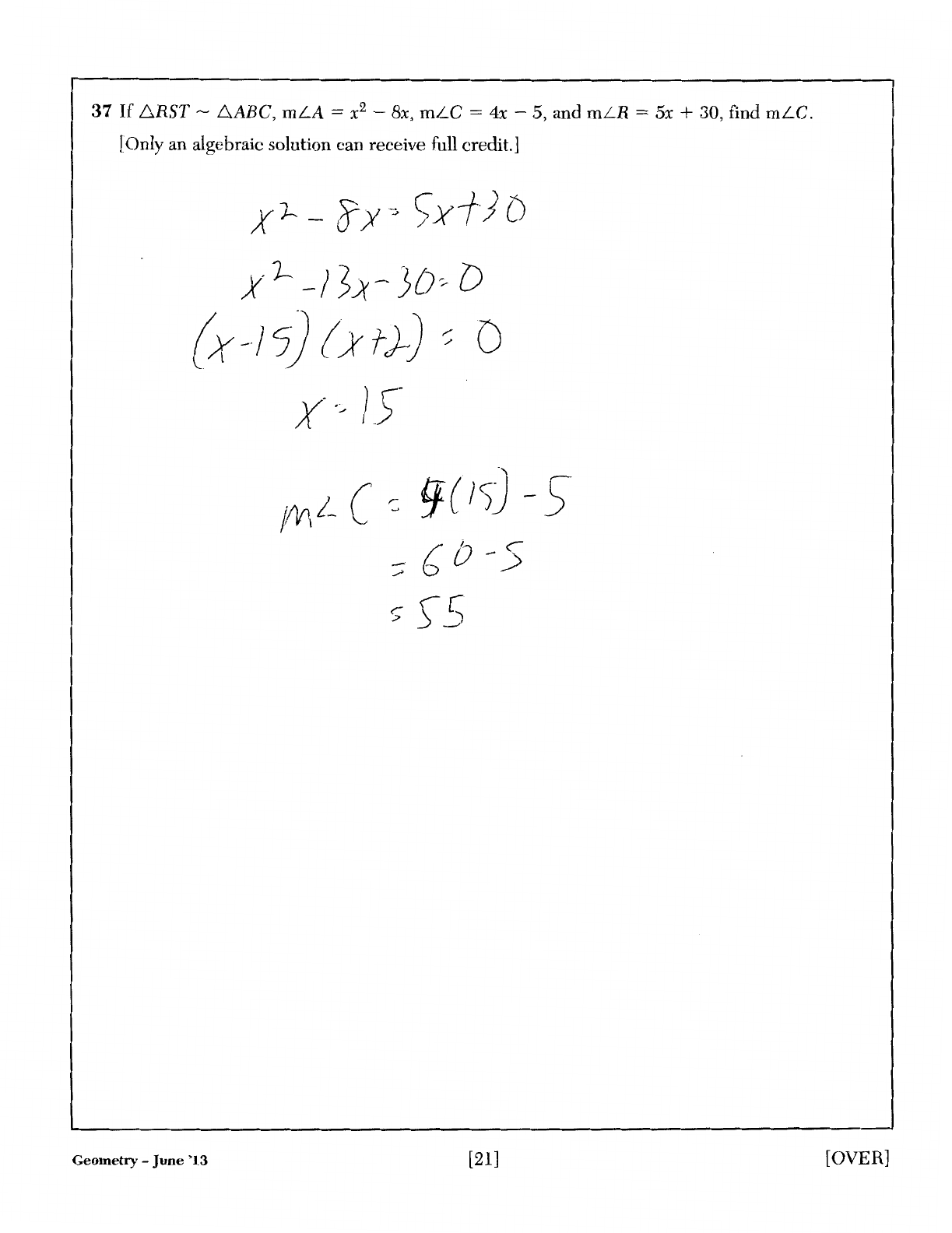
37

If

.6.RST-

6ABC,

mLA

= x2 -

8x,

mLC

=

4x

-5, and

mLR

=

5x

+ 30, find

mLC.

(Only an algebraic solution can receive

full

credit.]

X~--

? Y

-~

>x-f')

()

X

7-.

-.J

3~-

]()/

u

(x-!5)

fyr))

; o

Geometry

-June

'13

::

r;

{)

---s

s-

s-s

[21] [OVER]

Part

IV

Answer

the

question

in

this

part.

A

correct

answer

will

receive

6

credits.

Clearly

indicate

the

necessary

steps,

including

appropriate

formula

substitutions,

diagrams,

graphs,

charts,

etc.

A

correct

numerical

answer

with

no

work

shown

will

receive

only

1

credit.

The

answer

should

be

written

in

pen,

except

for

graphs

and

drawings,

which

should

be

done

in

pencil. [

6]

38

In

the

diagram

of

./:').MAH

below,

MH

::::.::

AH

and

medians

AB

and

MT

are drawn.

Prove:

LMBA

::::.::

LATM

Geometry-

June

'13

1

Cl

ve

">

:h

~-(!Qt.;

vl-

/Yof

er

ty

3

/}

-ef

J

'II

i-Ho

h

t)

( ; s

oy_e)

QS.

fritJ)t<~

/,cr;cJ-<s.

-lrlAhJJe

J).wvU>~

OefJ~J,;

}rtJn

()

r Mol

/tt~

!JefJ'hl~tjO-;,

of" /nJdttn'hf

1'1

u

lh(

}j

($-/J/o}..l'-'

lu

1~--k

S'AS

C?CTG

[22]

BA 13 X 0613geans

Navigation menu

Versions of this User Manual:

Views

Navigation