06 Gradient Descent For Linear Regression Instructionsl

User Manual:

Open the PDF directly: View PDF .
Page Count: 2

Gradient Descent For Linear

Regression

Note: [At 6:15 "h(x) = -900 - 0.1x" should be "h(x) = 900 - 0.1x"]

When specifically applied to the case of linear regression, a new form of the

gradient descent equation can be derived. We can substitute our actual cost

function and our actual hypothesis function and modify the equation to :

where m is the size of the training set, a constant that will be changing

simultaneously with and

are values of the given training set (data).

Note that we have separated out the two cases for into separate equations for

and ; and that for we are multiplying at the end due to the derivative. The

following is a derivation of for a single example :

The point of all this is that if we start with a guess for our hypothesis and then

repeatedly apply these gradient descent equations, our hypothesis will become

more and more accurate.

So, this is simply gradient descent on the original cost function J. This method

looks at every example in the entire training set on every step, and is called batch

gradient descent . Note that, while gradient descent can be susceptible to local

minima in general, the optimization problem we have posed here for linear

regression has only one global, and no other local, optima; thus gradient descent

always converges (assuming the learning rate α is not too large) to the global

minimum. Indeed, J is a convex quadratic function. Here is an example of gradient

descent as it is run to minimize a quadratic function.

Gradient Descent for

Linear Regression

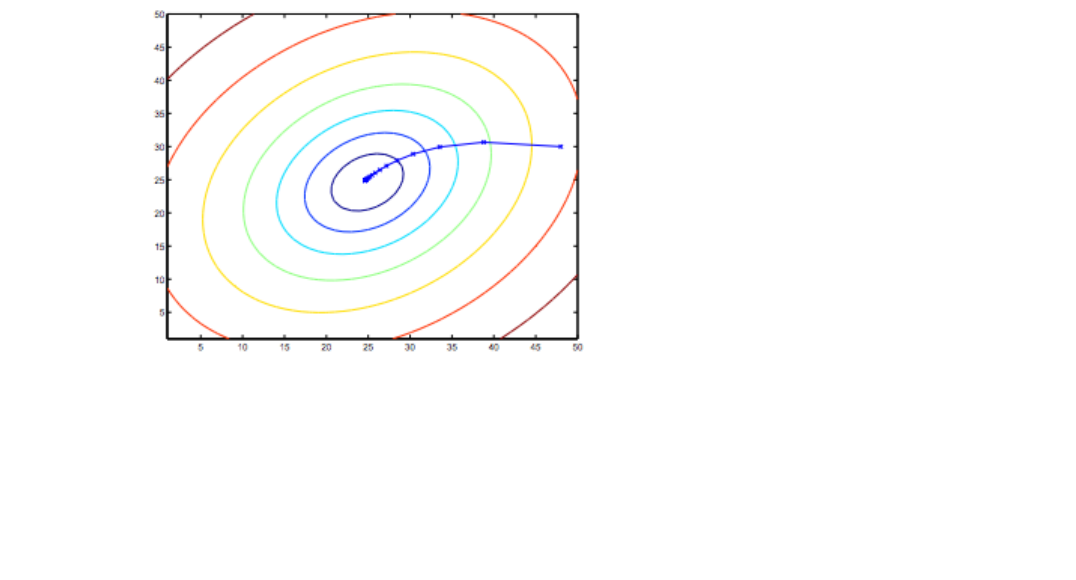
The ellipses shown above are the contours of a quadratic function. Also shown is

the trajectory taken by gradient descent, which was initialized at (48,30). The x’s

in the figure (joined by straight lines) mark the successive values of θ that gradient

descent went through as it converged to its minimum.

Navigation menu