KH 3900 1538 3881 128 3 1265

User Manual: KH 3900

Open the PDF directly: View PDF .
Page Count: 8

KH 15D: A SPECTROSCOPIC BINARY

John Asher Johnson,

Geoffrey W. Marcy,

Catrina M. Hamilton,

3, 4

William Herbst,

and Christopher M. Johns-Krull

3, 4

Received 2004 March 3; accepted 2004 May 19

ABSTRACT

We present the results of a high-resolution spectroscopic monitoring program of the eclipsing pre–main-

sequence star KH 15D that reveal it to be a single-lined spectroscopic binary. We ﬁnd that the best-ﬁt Keplerian

model has a period P¼48:38 days, which is nearly identical to the photometric period. Thus, we ﬁnd the best

explanation for the periodic dimming of KH 15D is that the binary motion carries the currently visible star

alternately above and behind the edge of an obscuring cloud. The data are consistent with the models involving

an inclined circumstellar disk, as recently proposed by Winn et al. and Chiang & Murray-Clay. We show that

the mass ratio expected from models of pre–main-sequence evolution, together with the mass constraints for

the visible star, restrict the orbital eccentricity to 0:68 e0:80andthemassfunctionto0:125 M

FM=sin3i0:5M.

Key words: binaries: spectroscopic — circumstellar matter — stars: individual (KH 15D) —

stars: pre–main-sequence — techniques: radial velocities

1. INTRODUCTION

KH 15D is a K6–K7 pre–main-sequence star that exhibits

dramatic photometric variability ( Kearns & Herbst 1998).

Every 48.35 days, the star’s brightness dims by 3.5 mag and

remains in this faint state for nearly half of the photometric

period. These deep brightness minima are accompanied by a

slight blueing of the star’s color indexes (Herbst et al. 2002,

hereafter He02), little or no change in spectral type (Hamilton

et al. 2001), and an increase in linear polarization (Agol et al.

2004). This implies that the star is completely eclipsed by an

optically thick, extended collection of dust grains, possibly in

the form of a circumstellar disk. If this is the case, the ser-

endipitous alignment of the KH 15D star-disk system may

provide insights into the evolution of young stars and their

interactions with their circumstellar environments.

While KH 15D has periodic eclipses, it cannot be an ordi-

nary eclipsing binary, because of the long duration of mini-

mum light. Recent theories postulate that there is, nonetheless,

a currently unseen binary companion to the visible star. In a

study of archival photographic plates, Johnson & Winn (2004,

hereafter JW04) discovered that the historical light curve of

KH 15D is similar to the modern light curve but appears to be

diluted by light from a second star. Motivated by these ﬁnd-

ings, Winn et al. (2004, hereafter W04) constructed a model

composed of a binary system with the orbital plane inclined

with respect to the edge of an optically thick screen. As the

two stars orbit one another, the reﬂex motion carries one star

alternately above and behind the edge of an opaque screen,

causing the eclipses. The long-term evolution of the light

curve is reproduced by allowing the screen to move slowly

across the binary orbit—a feature of the model that led the

authors to envision the screen as a precessing, circumbinary

disk. A similar model is proposed by Chiang & Murray-Clay

(2004, hereafter CM04), who also envision the opaque screen

as an inclined, precessing circumbinary disk, or ‘‘ring,’’ with

an inner edge truncated by tidal interactions with the binary

and an outer edge possibly shepherded by a planetary com-

panion. Both models provide explanations of the unique

features of KH 15D’s light curve. The W04 model makes

quantitative predictions about the orbital parameters of the

binary system, while the CM04 model provides a physical

description of the circumbinary ring.

A fundamental question that has not yet been answered is

whether KH 15D is a single or multiple stellar system. He02

(see also Hamilton et al. 2003, hereafter Ha03) ﬁrst searched

for evidence of orbital companions using high-resolution VLT

spectra and reported a radial velocity change of þ3:3

0:6kms

1over two widely spaced epochs. However, one of

the measurements was made during egress, when there was a

strong possibility of contamination from scattered light or line

proﬁle distortions from a sharp-edged cloud only partially

occulting the stellar disk.

Over the past 2 years, we have conducted a high-resolution,

multisite spectroscopic monitoring campaign to determine

whether or not KH 15D exhibits orbital motion indicative of a

multiple system. Here we present the results of our study,

which show that KH 15D undergoes signiﬁcant radial velocity

variations. The variations are consistent with a binary com-

panion with an orbital period equal to the 48 day photometric

period. In x2, we summarize our observations and reduction

procedures. The radial velocity measurements and best-ﬁt

Keplerian orbital parameters are presented in x3. We conclude

in x4 with a discussion of our ﬁndings and implications for

existing models of the KH 15D eclipse mechanism.

2. DATA

During the 2002–2003 and 2003–2004 observing seasons,

we made 16 observations of KH 15D at maximum light,

Based on observations obtained at the W. M. Keck Observatory, which

is operated as a scientiﬁc partnership among the California Institute of Tech-

nology, the University of California, and the Naional Aeronautics and Space

Administration; at Las Campanas Observatory of the Carnegie Institution with

the Magellan II Clay Telescope; and at McDonald Observatory of the Uni-

versity of Texas at Austin.

Department of Astronomy, University of California at Berkeley, Berkeley,

CA 94720-3411; johnjohn@astron.berkeley.edu, gmarcy@astron.berkeley.edu.

Visiting Astronomer, McDonald Observatory, which is operated by the

University of Texas at Austin.

Department of Physics and Astronomy, Rice University, 6100 Main

Street, Houston, TX 77005; cmham@rice.edu, cmj@rice.edu.

Van Vleck Observatory, Wesleyan University, Middletown, CT 06459;

wherbst@wesleyan.edu.

1265

The Astronomical Journal, 128:1265–1272, 2004 September

including 11 spectra with the 10 m Keck I Telescope and

HIRES echelle spectrometer, two spectra with the 6.5 m

Magellan II (Clay) telescope and the MIKE echelle spectrom-

eter, and three spectra with the 2.1 m Otto Struve Telescope

at McDonald Observatory with the Sandiford Cassegrain

Echelle Spectrometer (CE). The observations are summarized

in Table 1. Additional Keck HIRES spectra were obtained

during minimum light. However, since it is unlikely that the

star’s photosphere is visible through the obscuring material,

we decided to exclude from our analysis spectra that were

obtained within 10 days of mid-eclipse. In addition to our own

measurements, we also include the out-of-eclipse radial ve-

locity measurement, vr¼9:00:2kms

1, reported by Ha03

based on their observations with the VLT UV-Visual Echelle

Spectrograph.

Most of the HIRES observations were made as part of the

California and Carnegie Planet Search.

For these observations,

the relatively faint apparent magnitude of KH 15D (V¼16) at

maximum light precluded the use of the iodine cell to establish

a wavelength scale. The cell was therefore removed from the

light path during observations of KH 15D to increase the

throughput of the spectrometer. The raw CCD frames from all

telescopes were reduced using reduction packages written in

IDL. The details of the reduction procedures are fundamen-

tally identical to the algorithm presented by Valenti (1994).

After bias subtraction, each echelle frame is divided by a

normalized median ﬂat-ﬁeld image. Order deﬁnition is per-

formed using a bright star or ﬂat-ﬁeld exposure, and scattered

light is removed by ﬁtting a two-dimensional B-spline to the

interorder regions and interpolating across each spectral order.

After the scattered light is subtracted, each order is rectiﬁed,

sky-subtracted, and summed in the cross-dispersion direction

to form the ﬁnal one-dimensional spectrum.

Instead of a summation in the cross-dispersion direction,

the rectiﬁed orders of the McDonald spectra are reduced to

one-dimensional spectra using the optimal extraction algo-

rithm described by Hinkle et al. (2000). In the case of the

MIKE reductions, the standard code is modiﬁed to correct for

the tilt of the spectrometer entrance slit with respect to the

CCD columns. The correction of the slit tilt is necessary be-

cause the sky subtraction algorithm we employ requires that

the projected slit image lie parallel to the detector columns.

The radial velocity of KH 15D relative to the solar system

barycenter is measured from each spectral observation by

means of a cross-correlation analysis. For the spectra of

KH 15D obtained as part of the Planet Search observing

program, the program stars observed on each night provided

an extensive selection of reference stars with known bary-

centric radial velocities, listed in Nidever et al. (2002). We

selected reference stars that were observed within 30 minutes

of KH 15D and with spectral types ranging from M0 to G5.

Since the Planet Search target stars are observed through an

iodine cell, orders containing iodine absorption lines are

avoided in the analysis. For KH 15D observations obtained as

part of programs other than the Planet Search, a single K-type

reference star observed either before or after KH 15D is used

as the reference star.

The cross-correlation of each KH 15D spectrum with

respect to the reference spectra is performed using custom

routines written in IDL. The procedure involves ﬁrst rebinning

each one-dimensional spectral order onto a new wavelength

scale that is linear in log k. This ensures that each pixel in the

rebinned spectrum represents a velocity interval that is uni-

form over the entire spectral order (Tonry & Davis 1979).

Regions containing telluric lines, strong emission features,

and CCD defects are masked out, and each spectral order is

cross-correlated with respect to the corresponding order of

the reference spectrum. Each spectral order thus yields an

independent measurement of the radial velocity of KH 15D

relative to the reference star. The average of the ensemble set

of velocities from all orders is then adopted as the relative

radial velocity of KH 15D for a given epoch.

TABLE 1

Spectroscopic Observations of KH 15D

UT Date

Telescope and

Instrument

k

(8)R

(2,400,000+)

(km s1)

2002 Oct 25 ......... Keck / HIRES 3900–6200 70,000 52,572.574 1.7 0.2

2002 Oct 28 ......... Keck / HIRES 3900–6200 70,000 52,575.511 3.0 0.3

2002 Dec 16 ........ Magellan / MIKE 4500–6800 45,000 52,624.738 3.1 0.2

2003 Jan 14.......... Keck / HIRES 3900–6200 70,000 52,653.468 3.3 0.2

2003 Feb 8 ........... Keck / HIRES 4200–6600 70,000 52,678.400 9.0 0.5

2003 Feb 9 ........... Keck / HIRES 4200–6600 70,000 52,679.410 11.5 0.5

2003 Mar 9 .......... Magellan / MIKE 4900–8700 22,000 52,707.511 0.8 0.2

2003 Nov 3 .......... Keck / HIRES 4200–6600 30,000 52,946.584 1.2 0.4

2003 Nov 4 .......... Keck / HIRES 4200–6600 30,000 52,947.594 1.8 0.3

2004 Jan 4............ McDonald /CE 5600–6900 30,000 53,008.762 1.4 0.6

2004 Jan 5............ McDonald /CE 5600–6900 30,000 53,009.852 1.7 0.4

2004 Jan 10.......... Keck / HIRES 3900–6200 70,000 53,014.320 5.4 0.3

McDonald /CE 5600–6900 30,000 53,014.760 5.8 0.4

2004 Jan 11.......... Keck / HIRES 3900–6200 70,000 53,015.506 7.0 0.2

2004 Feb 9 ........... Keck / HIRES 3900–6200 70,000 53,044.834 1.8 0.2

2004 Feb 10 ......... Keck / HIRES 3900–6200 70,000 53,045.828 1.3 0.2

Multiple reference stars were used to calculate the radial velocity. The reported velocity is the mean velocity

measured from the various target-reference star pairs. The estimated uncertainty is the standard deviation of the

mean velocity. See Table 2 for a listing of individual reference stars and radial velocity measurements for each

target-reference star pair.

Only one reference star was used in the radial velocity measurement. The reported velocity is the mean velocity

from all echelle orders. The estimated uncertainty is the standard deviation of the mean velocity.

See http://www.exoplanets.org.

JOHNSON ET AL.1266 Vol. 128

The relative radial velocities from each night are converted

into absolute barycentric radial velocities using the relation

vrad ¼vþ(BCkh BCref )þvref :ð1Þ

In equation (1), vis the relative velocity from the cross-

correlation analysis; BCkh and BCref are the barycentric cor-

rections for KH 15D and the reference star, respectively; and

vref is the absolute barycentric radial velocity of the reference

star as listed in Nidever et al. (2002). The mean measured

velocities from each epoch are listed in the ﬁnal column of

Table 1. Table 2 lists the velocities obtained from our cross-

correlation analysis for each individual reference star on each

night.

For nights when only one reference spectrum is available,

the uncertainty is estimated using the standard deviation of

the mean radial velocity measured from all echelle orders.

For nights with multiple reference spectra, the standard de-

viation of the velocities computed from each target-reference

pair is adopted as the uncertainty. This latter method of error

estimation typically yields a larger value than the order-to-

order scatter seen for an individual observation (0.2 km s1

v0.6 km s1compared with 0:1v0:3). The larger

scatter in velocity measurements among the target-reference

star combinations is likely due to external systematic effects

such as small shifts in the position of the CCD throughout the

night caused by thermal relaxation of the detector mount.

Thus, the standard deviation measured from the echelle orders

in a single observation likely underestimates the true uncer-

tainty by approximately a factor of 2.

3. RESULTS

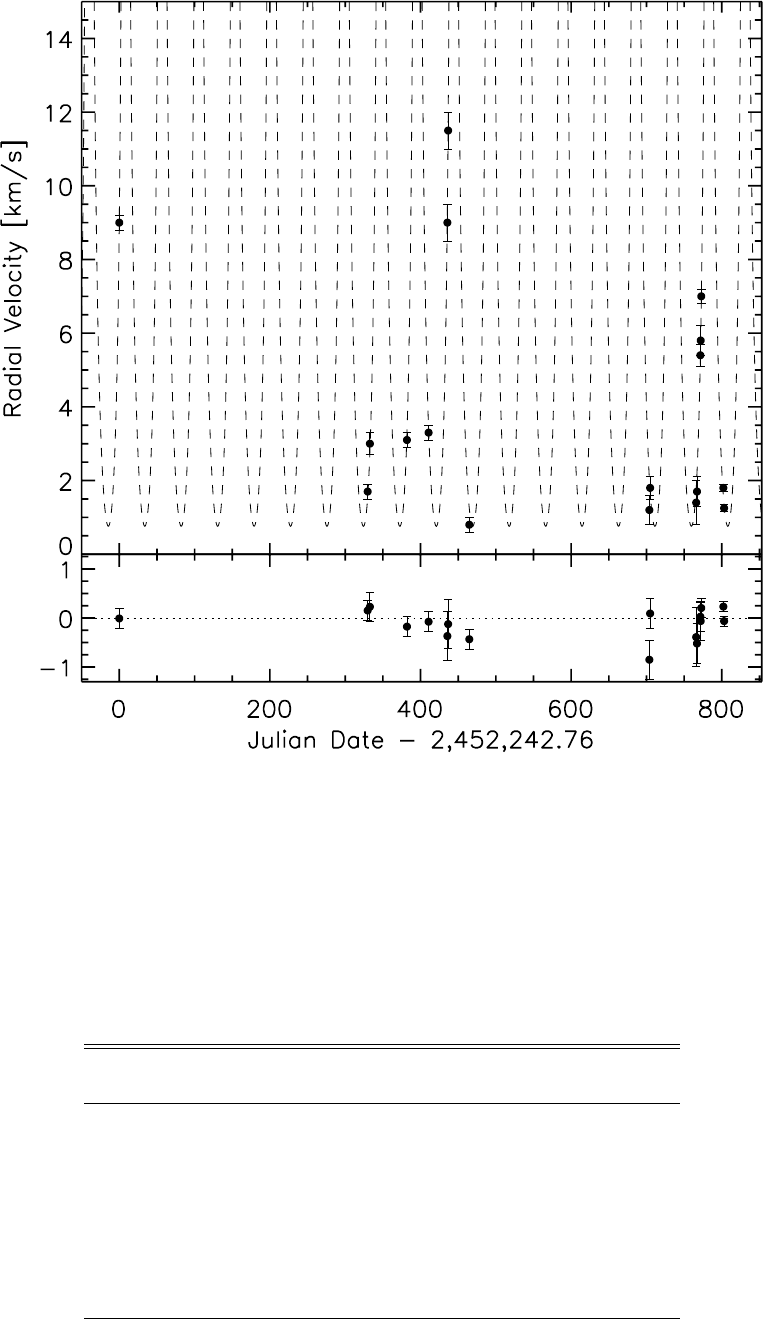
Figure 1 illustrates how the radial velocity of KH 15D

varies temporally out of eclipse over a range of 10.7 km s1.

These data indicate that there must be an unseen star in the

system, as had previously been inferred from the analysis of

the historical light curve (JW04). Hereafter we will adopt the

naming convention of W04 and refer to the currently visible

star as A and the hidden companion as B.

3.1. Orbit Solution

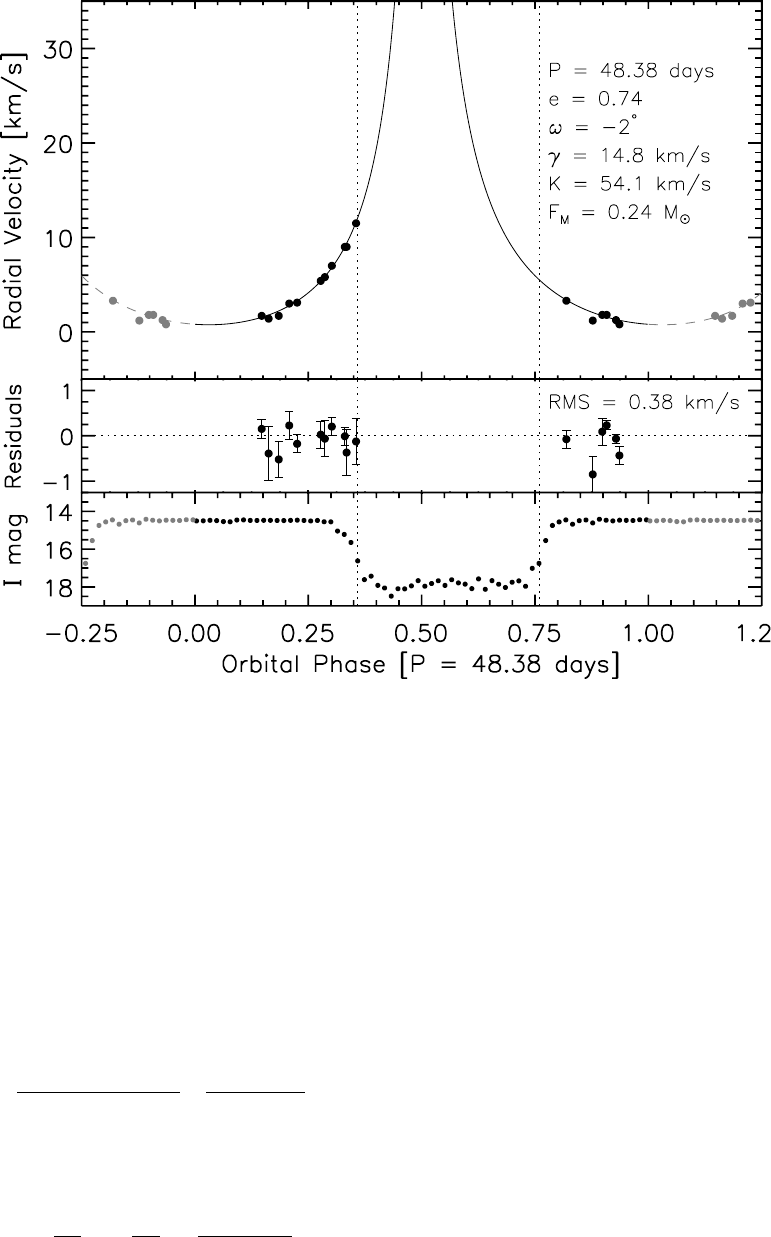
Using a nonlinear least-squares algorithm, we found a best-

ﬁt model orbit with a period P¼48:38 days, eccentricity

e0:27, and velocity semiamplitude K8:15 km s1.The

other orbit parameters are listed in Table 3. Figure 2 shows a

plot of radial velocity versus orbital phase for P¼48:38 days.

The rms scatter of the ﬁt residuals is 0.38 km s1and the

reduced ﬃﬃﬃﬃﬃﬃ

2



p¼1:5. The vertical lines at ¼0:33 and

¼0:73 denote the approximate phases of ingress and egress,

respectively, based on the He02 ephemeris. We have no radial

velocity measurements between these phases because of the

eclipse of star A.

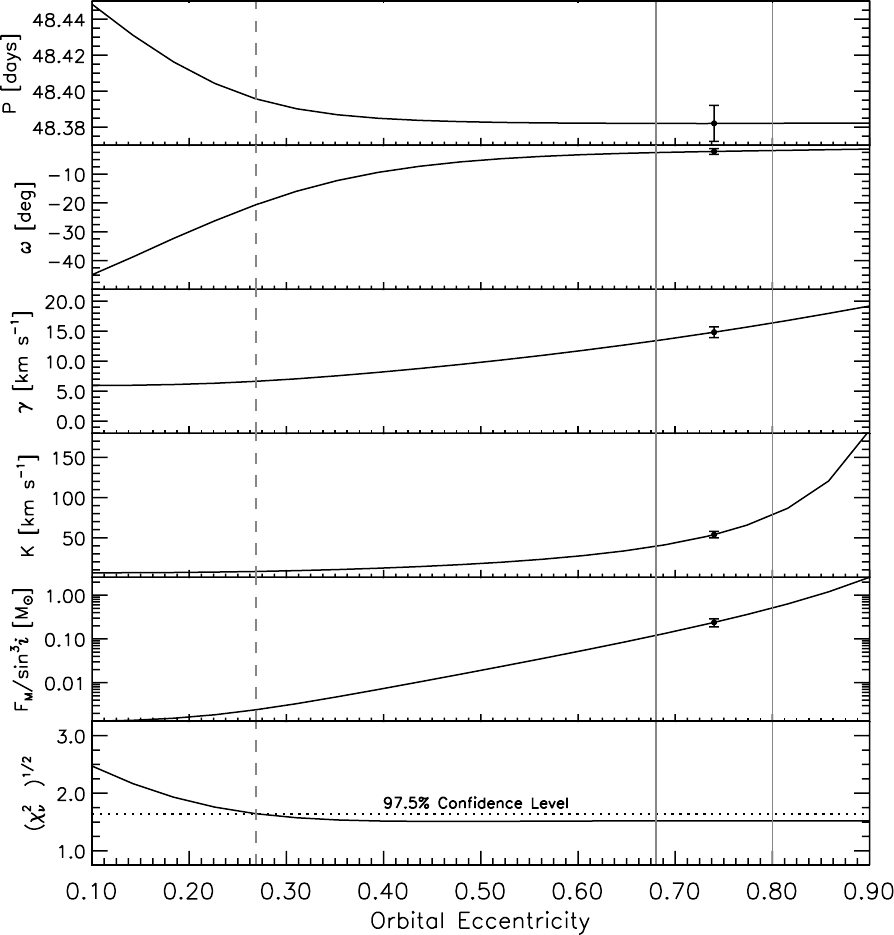
We ﬁnd that the orbit solution is not well constrained as a

consequence of the lack of data near periapse, which allows

the velocity semiamplitude of the orbit solution to compensate

for changes in the eccentricity. As such, we were able to ob-

tain reasonable ﬁts by ﬁxing the eccentricity at values e>

0:27, with each solution yielding different values of the orbit

parameters and values of ﬃﬃﬃﬃﬃﬃ

2



pthat are equivalent at the 97.5%

conﬁdence level (based on the 9 degrees of freedom in the ﬁt).

Figure 3 shows how ﬃﬃﬃﬃﬃﬃ

2



pand the orbit parameters vary

as a function of eccentricity. While the period varies little

over a wide range of eccentricities, it is apparent that the

radial velocity data alone provide poor constraints for the

other orbit parameters. However, the implied mass ratio from

other KH 15D observations, together with the measured mass

limits of star A, can be used to place limits on the orbital

eccentricity, as we now show.

3.2. Orbit Parameter Constraints

JW04 determined from photometric measurements of ar-

chival plates that the out-of-eclipse magnitude of KH 15D was

0.9 mag brighter (at Iband)40yearsagocomparedwiththe

modern bright state. The two most probable explanations for

the brighter apparent magnitude in the past are that either

both stars were visible or star B alone was visible. If both stars

were visible, then LB=LA¼1:3. If only B were visible, then

LB=LA¼2:3. In either case, the condition LB=LA>1must

hold.

Multicolor photometric measurements obtained during

minimum light show a slight blueing of the color indexes

(Ha03) compared with the colors at maximum light. Similarly,

Agol et al. (2004) measure slightly bluer colors during eclipse

TABLE 2

Absolute Radial Velocity Measurements of

KH 15D from Each Reference Star

(2,400,000+)

Reference Star

HD No.

(km s1)

52,572.574...... 40979 1.6 0.1

56274 2.1 0.1

52265 2.1 0.08

49674 1.3 0.09

66171 1.2 0.2

52,575.511...... 31966 2.9 0.2

36395 4.0 0.08

47157 3.2 0.2

37124 2.2 0.1

40979 2.7 0.3

52,624.738...... 10700 3.1 0.2

52,653.468...... 31966 3.6 0.1

42618 2.7 0.1

47157 3.1 0.07

99109 3.6 0.09

99492 3.4 0.1

52,678.400...... 36006 9.0 0.5

52,679.410...... 36006 11.5 0.5

52,707.511...... 36006 0.8 0.2

52,946.584...... 36006 1.2 0.4

52,947.594...... 36006 1.8 0.3

53,008.762...... 36006 1.4 0.6

53,009.852...... 17660 1.7 0.4

53,014.320...... 45350 5.1 0.2

18830 5.6 0.3

53,014.760...... 17660 5.8 0.4

53,015.506...... 45350 7.0 0.2

53,044.834...... 50499 2.0 0.2

46375 1.7 0.1

50281 1.8 0.2

46375 1.9 0.2

53,045.828...... 50499 1.6 0.1

76909 1.3 0.1

73667 0.9 0.1

72673 1.2 0.1

Velocities are the mean value from all echelle

orders used in the cross-correlation analysis. Estimated

uncertainties are the standard deviation of the mean

velocity from all echelle orders.

SPECTROSCOPIC BINARY KH 15D 1267No. 3, 2004

from their low-resolution spectropolarimetric observations

compared with their out-of-eclipse observations. One possi-

bility for the bluer color indexes during eclipse is that the

scattered light is dominated by Rayleigh scattering. However,

He02 show that there is no reddening of the light from star A

during ingress and egress. This suggests that the opacity of the

occulting material is wavelength independent and that the

bluer colors are due to a bluer object. Therefore the temper-

ature of B must be hotter than the temperature of A, assuming

both stars contribute nearly equally to the scattered component

Fig. 1.—Radial velocity of KH 15D as a function of time. The dashed curve is the best-ﬁt Keplerian orbit with the eccentricity ﬁxed at e¼0:74, the mean value

allowed by our orbit constraints (see x3.2).

TABLE 3

Optimized Model Parameters

Parameter

Acceptable Fit

to Velocities

Acceptable Fit

with e= 0.74

W04

Model 1

P(days)...................... 48.38 to 48.40 48.38 (0.01) 48.35 (Bﬁxed)

e.................................. 0.27 0.74 (Bﬁxed) 0.7

!(deg) ....................... 20 to 1 2 (1) 7.2



(km s

1)................ +6.9 to +22.5 +14.7 (0.9) +15.5

asin i(AU) ............... 0.29 0.21 (0.5) 0.18

K(km s

1)................. 8 53 (4) 27.5

FM/sin3i..................... 2.4 ;103to 2.2 0.24 (0.05) 3.8 ;102

(JD) ...................... ... 2,452,251.0 (0.6) ...

Fit rms ( km s1)........ 0.38 0.38 ...

Reduced ﬃﬃﬃﬃﬃﬃ

2



p............ 1.5 1.5 ...

The limits on the ﬁt parameters correspond to the 97.5% conﬁdence upper limit on ﬃﬃﬃﬃﬃﬃ

2



(see Fig. 3) and the condition e<1.

Radial velocity of the binary center of mass with respect to the solar system barycenter.

Time of periastron passage.

JOHNSON ET AL.1268 Vol. 128

of the light observed during the eclipse of A. However, since

the colors are only 0.1 mag bluer at minimum light ( He02),

TBcannot be much larger than TA.

For most low-mass (M<1:0M) pre–main-sequence evo-

lutionary models (e.g., Chabrier & Baraffe 1997; D’Antona &

Mazzitelli 1997), the stellar mass is monotonic with both lu-

minosity and temperature. For coeval stars on their Hayashi

tracks, TBkTAand LB=LA>1 imply that MBkMAor, in

terms of the mass ratio, MA=MBP1.

ThemassfunctionofaKeplerianorbitcanbeexpressedas

FM(e;K;P)¼K3P(1 e2)3=2sin3i

2G¼M3

Bsin3i

(MAþMB)2;ð2Þ

where Pis the orbital period and Kis the velocity semi-

amplitude. Solving equation (2) for MAyields

MA(e;MA=MB)¼MA

MB1þMA

MB2FM(e;K;P)

sin3i:ð3Þ

The mass function FM=sin3iin equation (3) is calculated from

the parameters of the best-ﬁt orbit to the radial velocity data

with the value of eﬁxed in the ﬁtting procedure. Figure 4

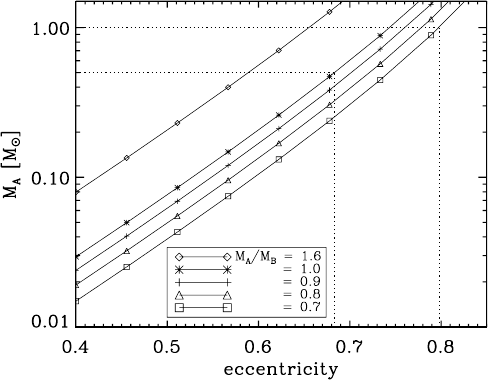
shows plots of MAversus efor MA=MBMA/MB

=0.7,0.8,0.9and1.0.

Also shown is the value of MA=MB¼1:6 obtained by W04

based on their model ﬁt to the KH 15D light curve (see x4).

Since the mass of the visible star is known to fall within the

limits 0:5MMA1:0M(Flaccomio et al. 1999; Park

et al. 2000), it can be seen by inspection of Figure 4 that

acceptable choices of the eccentricity fall within the range

0:68 e0:80.

The resulting range of acceptable orbit parameter values is

shown in Figure 3 between the solid vertical lines in each

panel. The third column of Table 3 lists the best-ﬁt parameter

values obtained using the mean acceptable value of the ec-

centricity, e¼0:74 (see also Fig. 2). The uncertainties in the

ﬁt parameters were estimated using a Monte Carlo simulation.

We generated 103statistical realizations of the velocity time

series assuming the errors are normally distributed with

standard deviations equal to the measurement uncertainties.

The estimated uncertainties are also displayed in Figure 3, as

error bars on the points located at e¼0:74.

3.3. Periodicity

As discussed in x3.1, we ﬁnd the best-ﬁt Keplerian has an

orbital period of P¼48:38 0:01 days. He02 report a period

of P¼48:35 0:02 days from their photometric monitoring,

andJW04reportP¼48:42 0:02 days from a periodogram

analysis of archival photographic plates photometry. Thus, our

measured orbital period differs by 1.5 and 2 from the

modern and historical photometric periods, respectively. Since

Fig. 2.—Radial velocity of KH 15D as a function of orbital phase. The solid curve is the best-ﬁt Keplerian orbit with the eccentricity ﬁxed at e¼0:74, the mean

value allowed by our orbit constraints (see x3.2). The ﬁt has reduced chi-square ﬃﬃﬃﬃﬃﬃ

2



p¼1:5. The vertical dotted lines represent the approximate phases of ingress

(left) and egress (right) based on the He02 ephemeris. The bottom panel shows the 2001–2002 I-band light curve. The phased photometric measurements have been

binned for clarity using phase intervals of ¼0:015.

SPECTROSCOPIC BINARY KH 15D 1269No. 3, 2004

the evolving shape of the light curve may complicate the ac-

curate determination of the photometric period, we conclude

that the orbital period and photometric period of KH 15D are

indistinguishable within measurement errors.

He02 noted that the shape of the light curve varies from

eclipsetoeclipseinsuchawayastosuggesta96dayperiod

for the system, with each cycle containing two brightness

minima. In order to investigate this alternative periodicity,

we ﬁxed the period in our ﬁt at P¼96:76 days and obtained a

reduced ﬃﬃﬃﬃﬃﬃ

2



pof 47.5. Based on this poor quality of ﬁt, we ﬁnd

that a 96 day period is incompatible with our radial velocity

measurements.

4. DISCUSSION

The results of our spectroscopic monitoring campaign show

that KH 15D is a spectroscopic binary system. The observed

radial velocities are consonant with a stellar companion with

an orbital period equal to the photometric period. We now

discuss the implications of the binarity of KH 15D for current

models of the photometric variability mechanism.

Existing models of the KH 15D eclipse mechanism fall into

two classes differentiated by whether it is the orbital motion of

thestarorafeatureofacircumstellardiskthatcausesthe

photometric variability. The ﬁrst class of models posits the

existence of a single star surrounded by a circumstellar disk

containing a nonaxisymmetric density enhancement or, alter-

natively, a warp. As the disk feature orbits the star with a

48 day period, it periodically blocks the line of sight to the

stellar surface. Based on their spectropolarimetric observa-

tions, which showed an increase in polarization during mini-

mum light, Agol et al. (2004) developed a model of a warped

disk with an extended atmosphere and obtained a reasonable

Fig. 3.—Dependence of the best-ﬁt orbit parameters (top ﬁvepanels) and reduced 2(bottom) on the orbital eccentricity. The ordinate values are generated by

ﬁxing the orbital eccentricity in the least-squares ﬁt to the radial velocity data. The vertical dashed line indicates the lower limits placed on the ﬁtparametersbased

on the 97.5% conﬁdence level for ﬃﬃﬃﬃﬃﬃ

2



pwith 9 degrees of freedom. The solid vertical lines denote the upper and lower limits placed on the eccentricity as discussed

in x3.2 (see also Fig. 4), and the ﬁts generated for e¼0:74 are denoted by circles with error bars.

JOHNSON ET AL.1270 Vol. 128

ﬁt to the 2001–2002 light curve. A similar analysis was per-

formed by Barge & Viton (2003) using a model involving a

large dusty vortex.

While these single-star models are able to match the light

curve of KH 15D at one point in time, they do not adequately

explain the temporal changes in the observed light curve. Per-

haps more importantly, it is not clear if a binary companion to

KH 15D is compatible with an eclipsing disk feature. If a

density enhancement in a circumstellar disk is responsible for

the 48 day photometric period, the feature must orbit the central

star at a distance of 0.22 AU, assuming a Keplerian orbit. This

geometry would restrict the stellar companion to orbit either at a

distance less than 0.22 AU or beyond the outer extent of the

circumstellar disk. However, since our best-ﬁt orbit yields a

period of 48:38 0:01 days and asin i¼0:21 AU (assuming

e¼0:74; see x3.2) for the binary companion, neither of these

scenarios seems plausible. Thus, it does not seem possible for

both an eclipsing disk feature and a stellar-mass companion to

coexist with the same orbital period.

In the second class of models, proposed by W04 and CM04,

there exists an unseen binary companion of comparable mass to

the visible K-type star seen today. Surrounding the two stars is a

circumbinary disk viewed nearly edge-on. The orbital plane of

the two stars is tilted at a small angle with respect to the disk

plane and the present-day light curve is produced as the reﬂex

motion of star A carries it above and behind the disk plane.

Independent evidence for the binary nature of KH 15D has

emerged from studies of archival photographic plates. In a

study of photographic plates obtained from Asiago Observa-

tory, JW04 show that the apparent magnitude of KH 15D was

variable from 1968 to 1983 but the light curve from this epoch

was markedly different from the one observed today. The

bright state was nearly a factor of 2 brighter in the past and the

eclipse depth was a factor of 5 shallower. These ﬁndings can

be explained by invoking the presence of a second star that

was visible in the past but is unseen today (JW04).

Motivated by these ﬁndings, W04 constructed a model of

an eccentric binary with a fraction of the orbital plane ob-

scured by an opaque screen (or circumbinary disk) and found

a quantitative orbital solution by ﬁtting simultaneously to the

2001–2002 photometry of He02, the historical photometry of

JW04 and the radial velocity measurements of Ha03. Based on

a preliminary investigation of the radial velocities presented

here, CM04 independently used physical arguments to pro-

pose a similar model of an eccentric binary surrounded by a

nodally precessing circumbinary ring. As the ring precesses,

the light curve gradually changes from the one recovered from

the archival plates to the shape seen today. Perhaps the

greatest advantage of the two-star models is their ability to

explain not only the present-day light curve, but also its

evolution over the past half-century.

In addition to explaining the photometric phenomenology

of KH 15D, the two-star models make predictions about the

nature of the binary orbit. Both CM04 and W04 predict that

(1) periastron passage occurs during minimum light, (2) the

orbital companion has a mass comparable to the currently

visible star, and (3) the binary orbit is highly eccentric. These

predictions are precisely what we ﬁnd from our orbit solution.

The W04 model makes additional, quantitative predictions

about the orbital parameters of the binary. For an assumed

ﬁxed period of 48.35 days, the model produces a velocity

semiamplitude of 27.5 km s1, eccentricity e¼0:7, a mass

ratio MA=MB¼1:6, argument of pericenter !¼7N2, and a

center-of-mass radial velocity ¼þ15:5kms

1. As can be

seen in Table 3, the predictions of W04 model 1 agree well

with our orbital solution with ﬁxed eccentricity, e¼0:74 (see

x3.2). We note here that our center-of-mass velocity for the

binary system of ¼þ14:70:9kms

1clearly rules out

W04 model 2, which predicts ¼þ5:7kms

1and negative

velocity at periapse.

The W04 model also predicts the inclination of the binary

orbit, a property of the system that our radial velocities do not.

W04 model 1 predicts i¼84N6, or sin i¼0:996. Similarly,

using the geometry of the circumbinary ring proposed by

CM04, an upper limit on the inclination of i<80can be

assigned to the binary orbit based on the time lag between

periastron passage and mid-eclipse (E. Chiang 2004, private

communication).

We note that the W04 model has the peculiar feature that the

less massive star is the more luminous. Using equation (3), the

values of P,K,andeproduced by the W04 model lead to a

mass function FM¼0:038 Mand MA¼0:41 M.Thismass

is signiﬁcantly less than the lower limit of 0.5 Mmeasured

by Park et al. (2000) and the value of 0.6 Mmeasured by

Flaccomio et al. (1999). Figure 4 shows a plot of MAas a

function of efor the W04 mass ratio MB=MA¼1:6. For our

best-ﬁtting model parameters, only eccentricities between 0.58

and 0.65 yield a mass of A between 0.5 and 1.0 M.There-

fore, for a mass ratio of 1.6, the eccentricity reported by W04

(e¼0:7) is larger than the value allowed by our radial velocity

measurements, assuming 0:5MMA1:0M.However,

this discrepancy is not too surprising, since the W04 model

used only two radial velocity measurements. It is also im-

portant to note that the mass limits on star A are derived by

placing KH 15D on a theoretical H-R diagram and are

therefore subject to the accuracy of the pre–main-sequence

evolutionary model employed. In all other features of the

KH 15D binary system, there is a remarkable agreement be-

tween the W04 model and the orbital solution calculated from

the radial velocities. Because of the strong evidence of a

second star from our radial velocity measurements and the

historical photometry, we ﬁnd the two-star class of model to

be the most compelling explanation of the KH 15D photo-

metric variability mechanism.

Fig. 4.—Mass of the visible component of KH 15D, MA, vs. orbital ec-

centricity for ﬁve choices of the mass ratio MA=MBMA/MB

. The dotted lines show that

for 0:5M<MA<1:0Mand MA=MBP1:0, acceptable values of the ec-

centricity fall within the range 0:68 e0:80. The inclination is assumed to

be i¼90(sin3i¼0).

SPECTROSCOPIC BINARY KH 15D 1271No. 3, 2004

However, the case of the ‘‘winking star’’ is still far from

closed. A key missing aspect of the two-star models is direct

detection of a circumbinary disk around KH 15D. He02 report a

lack of near-infrared excess and a null detection at millimeter

wavelengths. CM04 state that such ﬁndings are consistent with

a circumbinary ring having an inner radius of 1AUthatis

tidally truncated by the central binary, and an outer radius of

5 AU that is possibly shepherded by an as yet unseen planet.

They predict mid-infrared ﬂuxes that are observable with the

Spitzer Space Telescope. Clearly such observations will be vital

in further development of models of the KH 15D system.

We would like to thank Gibor Basri, Paul Butler, Debra

Fischer, and Subanjoy Mohanty for generously lending por-

tions of their observing time for our project. Many thanks to

Eugene Chiang, Ruth Murray-Clay, Steve Dawson, and Josh

Winn for their helpful conversations and suggestions. We

acknowledge support by NASA grant NAG 5-8299 and NSF

grant AST 95-20443 (to G. W. M.), NASA grant NAG

5-12502 (to W. H.), and Sun Microsystems. We thank the

NASA, University of California, and McDonald Observatory

telescope assignment committees for allocations of telescope

time.

REFERENCES

Agol, E., Barth, A. J., Wolf, S., & Charbonneau, D. 2004, ApJ, 600, 781

Barge, P., & Viton, M. 2003, ApJ, 593, L117

Chabrier, G., & Baraffe, I. 1997, A&A, 327, 1039

Chiang, E. I., & Murray-Clay, R. A. 2004, ApJ, 607, 913 (CM04)

D’Antona, F., & Mazzitelli, I. 1997, Mem. Soc. Astron. Italiana, 68, 807

Flaccomio, E., Micela, G., Sciortino, S., Favata, F., Corbally, C., &

Tomaney, A. 1999, A&A, 345, 521

Hamilton, C. M., Herbst, W., Mundt, R., Bailer-Jones, C. A. L., & Johns-Krull,

C. M. 2003, ApJ, 591, L45 ( Ha03)

Hamilton, C. M., Herbst, W., Shih, C., & Ferro, A. J. 2001, ApJ, 554, L201

Herbst, W., et al. 2002, PASP, 114, 1167 ( He02)

Hinkle, K., Wallace, L., Valenti, J., & Harmer, D. 2000, Visible and Near

Infrared Atlas of the Arcturus Spectrum, 3727–9300 8(San Francisco: ASP)

Johnson, J. A., & Winn, J. N. 2004, AJ, 127, 2344 (JW04)

Kearns, K. E., & Herbst, W. H. 1998, AJ, 116, 261

Nidever, D. L., Marcy, G. W., Butler, R. P., Fischer, D. A., & Vogt, S. S. 2002,

ApJS, 141, 503

Park, B.-G., Sung, H., Bessell, M. S., & Kang, Y. H. 2000, AJ, 120, 894

Tonry, J., & Davis, M. 1979, AJ, 84, 1511

Valenti, J. A. 1994, Ph.D. thesis, Univ. California, Berkeley

Winn, J. N., Holman, M. J., Johnson, J. A., Stanek, K. Z., & Garnavich, P. M.

2004, ApJ, 603, L45 ( W04)

JOHNSON ET AL.1272

KH 3900 1538 3881 128 3 1265

Navigation menu

Versions of this User Manual:

Views

Navigation