195607

Solving Problems with Digital Computers

. . . Alston

S.

Householder

The

Day

of

Reckoning

...

Jackson

W.

Granholm

The

Operation

of

a Computer

Away

from

a Central Staff . .

Howard

Bromberg

Word

Length

In

Digital

Computers

..

D.

McCracken

Free Use

of

the Toronto Computer,

and

the Remote Programming

of

It (Part

2)

. . .

c.

C.

Gotlieb

and

others

putting I

IDEAS

I

to

work-research

at

I

IBM

I

•

Multi-Stable

Work

Horse:

By

employir:g

a

non-linear

load,

new

circuit

permits

two

transistors

to

do

the

work

of

ten.

IBM

Bulletin

No.

200.

•

Self-Complementary:

New

Gas

Tube

Counter

sub-

tracts

by

adding.

IBM

Bulletin

No.

201.

•

The

Soft

Touch:

Ultrasonic

cutting

at

IBM

permits

devices

to

be

cut

from

hard,

brittle

materials

within

0.0002".

Multi-Stable Work Horse

As the size and complexity

oflBM

prod-

ucts increase, we are faced with growing

numbers

of

components-which

means

increased cost. As

part

of

our

continuous

search for improvement and ways to

reduce the number

of

components, Rob-

ert

Henle, one

of

our

Transistor Circuit

Research people, undertook

to

get more

work

out

of

a given number

of

tran-

sistors. The result

is

a two-transistor,

multi-stable circuit employing feedback

controlled by a non-linear load. Junction

transistors are naturally suited to this

new kind

of

circuit.

+$0

IIJIC

10

Sta~le

State

~"it

A full report

on

this new idea from

IBM contains eight full-page circuit dia-

grams in addition to mathematical anal-

yses

of

the operation

of

the circuit.

Write for

your

copy

of

IBM Bulletin

No. 200.

Gas

Tube Counfer

Schematic

r---

1

I

...

---

'I

I

:

I

t"---

1:

:

I

!

,

...

---

t

COMl'L£M£nr--t---- -:-

1 C

• I

I

t

INTEf!t.t£DlATE--~------

Self-Complementary

Accounting machines these days must

be able to do

everything-even

make

decisions.

In

order

to

get a machine to

do

more in a day's time with little

or

no

increase in operating" cost, IBM Com-

ponent Research people studied the idea

of

using a multi-cathode gas tube. It's

good news that they came

up

with an

attractive approach, which Robert Koeh-

ler,

of

our

Device Development Group,

then reduced to practice; it operates

faster than its electromechanical prede-

cessor and, furthermore, with simple cir-

cuitry, can subtract. by adding.

It

can

read out in true number form both posi-

tive and negative balances. This is pos-

sible because a number stored in the tube

may be transposed to its 9's complement

(i.e., value subtracted from nine) by a

single electrical pulse.

If

you'd

like more information

on

the

basic principle, physical arrangement

of

parts, and typical problems solved, write

for

IBM

Bulletin No. 201.

If

you

are

fascinated by the theory

of

numbers, we

recommend this Bulletin.

DATA

PROCESSING·

ELECTRIC

TYPEWRITERS·

TIME

EQUIPMENT.

MILITARY

PRODUCTS

The Soft Touch

In some

of

our

studies

of

new compo-

nents,

at

the IBM Research Laboratories

at

Poughkeepsie, it

is

necessary to make

many different, small and intricately

shaped parts from brittle materials. Fol-

lowing the conventional approach, each

of

these parts would require laborious

and costly machining

and

fabrication.

We turned to ultrasonic cutting; with

this tool

we

can make any shape

or

size

component in approximately a

minute-

with an accuracy

five

times greater than

previously possible! The ultrasonic cut-

ter has helped us progress faster

in

our

development

of

new devices.

RESEARCH

at

IBM means

IDEAS

at work.

Schematic:

of

Uttro$onic Cutter

•

For

bulletins mentioned above, write

Dept. CA-7. International Business Ma-

chines Corp., 590 Madison Ave., New

York

22,

N. Y.

11:)$1

DATA

PROCESSING

•

COMPUTERS

AND

CYBERNETICS

•

ROBOTS

•

AUTOMATION

AUTOMATIC

CONTROL

'Vol.

5,

No.7

July,

1956

ESTABLISHED

SEPTEMBER,

1951

ARTICLES

AND

PAPEnS

SUJ.V:LdCJ

Probleh1S

.·d th Digi

tal

Computers

The

Day

of

Reckoning

The

Operation

of

a Computer

Away

from

a

Central

Staff

Word

Length

in

Digital

Computers

A General

Curve-Fitting

Subroutine

for

Transcendental Functions

A Computer Program

for

Finding Roots

Free

Use

of

the Toronto Computer.

an~

the

Remote

Programmin~

of

It

(Part

2)

REFERENCE

INFORMATION

New

P

[.

ten

ts

Who's

Who

in

the Computer

Field

(supplement)

Methods

in

High

Speed Computation--

Final

Examination

Eastern

Joint

Computer Conference

December, 1956,

New

York

The

Editor's

Notes

Index

of

Notices

Advertising

Index

A.

S.

Householder

J.

W.

Granholm

H.

Bromberg

D.

McCracken

R.

H.

Bracken

A.

D.

Booth

C.

Gotlieb

•••

R.

Skolnick

•••

J.

W.

Carr,

III

Editor:

Edmund

C.

Berkeley

Assistant

Edi

tors:

Neil

D.

~Jacdonald,

F.

L. Walker

Contributing

Editors:

Andrew

D.

Booth, John

M.

Breen,

John

W.

Carr,

III,

Alston

S. Householder

Advisory

Comittee:

Samuel

B.

Williams,

Herbert

F.

Mitchell,

Jr.,

Justin

Oppenheim

Publisher:

Berkeley

Enterprises,

Inc.

Main

Office:

815 Washington

Street,

Newtonville

60, Mass.

--

Decatur

2-5453

or

2-3928

Editorial

Office:

36

West

11

Street,

New

York

11,

N.Y.

--

Gramercy 7-1157

or

Algonquin 5-7177

Advertising

Representatives:

San

Francisco

-W.A.Babcock,

605

Market

St.,

San

Francisco

5,

Cali!..

Yukon

2-3954

Los Angeles -Wentworth

F.

Green,

439

So. Western Ave., Los Angeles

5,

Calif.,

Dunkirk 7-R135

Elsewhere -

the

Publisher

(1)MPUTERS

AND

AUIDMATION

is

published

monthly.

Copyright,

lY55,

by

Berkeley

Enterprises,

Inc.

6

10

12

14

16

20

29

22

32

19

38

4

28

44

Subscription

rates:

in

the

United

States

-one

year

$5.50,

two

years

$10.50,

in

Canada -one

year

$6.00,

two

years

$ll.~;

elsewhere -one

year

S6.~,

two

years

$12.50

Sulk

subscription

rates:

see

page

18

Advertising

rates:

see page

42

~tered

as second

class

matter

at·~~_~~P_o_st~O_f_fl_·c_e~,_N_e_w_l_o_r_k~,_N_._Y_.~~~~~~~~~~~~

- 3 -

The

Editor'~

Notes

OPPORTUNITY'

TO

LEARN'

I.

From

Curtner

B.

Akin,

Jr.,

Sewickley,

Pa.,

to

the

Editor:

This

letter'is

merely

an

expression

of

sincere

thanks

to

you

and

YOUI

policy

of

ex-

tending

subscription

privileges

to

everyone

l\'ho

ldshes

to

read your

fine

magazine

"Compu-

ters

and Automation".

Recently

in

these

our United

States,there

has been a

great

deal

of

consternation

about

the

number

of

scientists

turned

out,

or

manu-

factured,

by

Russia's

system

of

education.

It

has been brought

to

light

that

the

young Rus-

sian

in

quest

for

knowledge has

no

problemfhrl-

ing

reading

material

upon

that

subject

which

holds

for

him

the

maximum

interest.

Isn't

this

ideal?

To

me

it

seems a

little

hard

to

imagine

that

a country as

imperfect

(to

me)

as Russia,

'has had

the

common

sense

to

place

before

the

youth

of

its

country

the

material

they

seek.

Let's

turn

to

the

U.S.

and

make

a com-

parison.

• ••

As

the

ten

or

eleven-year

old

grows a1

'\'ay

from

his

desire

to

live

in

a make-

believe

world

into

a young

roomber

of

adult-

hood, what does

he

find?

Simply

that

he

can-

not

Id

th

ease

obtain

the

information

lvhich

he

seeks.

The

"educated"

class

closes

its

eyes

to

his

desires.

His

quest

for

learning

"What

makes

things

tick"

is

nipped

in

the

bud.

The

adult

world would

rather

he

go

through the

re-

quired

sequence

necessary

for

becoming

educat-

ed than

satisfy

his

self-motivated

thirst

for

learning.

Brother

--

if

that

isn't

crazy!:

In

closing,

I would

like

to

congratulate

you

on

a perhaps unrecognized wonderful

point

in

your

favor.

Please

accept

my'

appreciation:

you

have

no

idea

how

tvonderfully

surprised

I

l\'as

to

find

"Computers

and

Automation"

in

my

mailbox

yesterday.

II.

From

the

Editor

Opportunities

for

education

in

,the United

States,

in

the

finest

sense

of

the

word

"educa-

tion",

are

far

tess

than they should be. Here

are

three

comparisons:

Union

of

Soviet

Socialist

Republics

United

States

1.

Average

num-

19

or

20

and

ber

of

students

increasing

in

class

per

teacher

Denmark

2.

Number

of

in-

7,000

habitants

for

every

bookseller

No.

of

Vacancies

3.

In

New

York

650

City,

on

June

5,

1956,

in

regard

to

competitive

examinations

for

candidates

who

are

to

teach

mathema-

tics

in

junior

high

schools

34

or

35

and

incre~sing

[hi

ted

State

s

100,000

No.

of

Applicants

88

We

earnestly

hope

that

"Computers

and

Au-

tomation"

may

help

in

the

cause of

education

of

men

and

women·

in

the

United

States,

in

the

field

of

computers

and

their

applications

and

impli-

cations,

including

automation.

And

it

1s

our

intention

for

the

indefinite

·future

that

anyone

who

wishes

to,

may

subscribe

to

'''Computers and

Automation".

- 4 -

Systems

Engineering

at

The

Ramo-Wooldridge

Corporation

ICBM

and

IRBM

are

prime

examples.

The

Intercontinental

Ballistk

Missile

and

the Intermediate Range

Ballistic Missile,

Air

Force

programs

for which we have over-all systems engineering

and

technical

direction responsibility, are

prime

examples

of

programs

that

require the systems engineering

approach. Most Ramo-Wooldridge work

is

of

such a

~y~tems

character,

requiring the

concurrent

solution

of

a wide variety

of

interrelated technical

and

operational

problems. Additional examples

at R-W

are

communications, fire-control,

and

computer

programs

for the military,

and

automa-

tion

and

operations research projects for business

and

indmtry.

Pertinent

technical

fields.

Successful execution

of

sy~tems

engineering

programs

requires

that

the techni-

cal staff include experts in a considerable

number

of

scientific

and

engineering speciaitie!>.

At

Ramo-Wooldridge some

of

the pertinent fields

are

aerodynamics, propulsion, digital

computers,

information

theory, radio propagation,

radar,

infrared, servomechanisms, gyroscopy,

and

nuclear physics.

The

kind

of

team

required.

A qualified

!>ystems

engineering staff

mu~t

include unusually capable theoreti-

dans

and

analysts

who

can

predict the

behavior

of

complex

!>ystems,

as well as ingenious

experimental physicists who

can

devise suitable new techniques

for

mea~uring

actual

physkal

parameters. In addition, the

team

must include experienced

apparatus

and

equipment development

engineers,

to

insure a high level

of

practicability in the resulting

end

products.

Sclentiltl

lind

en~ineerl

whu

(lfe

experienced

in l)'ltellls engineerinJ,:

wurk.

or

who

ha~'e

lpeciali:.ed in certain technical /ieldl hilt

IUB'e

a

hruad

illterelt

itl

the

inter-

m

tiom

between

their

OW1l

lpecialtiel

and

other

/ield,\. are

invited

to

explore

the

wide

"1111(1' v/ openinl(l

tit

The

RtllnlJ- Wooldridge C

orporatlCJTI

ill: '

Guided

Missile

Research

and

Development • Automation

and

Data

Processing

Aerodynamics

and

Propulsion

Systems

• Digital

Computers

and

Control

Systems

Communications

Systems

• Airborne Electronic

and

Control

Systems

The

Ramo-Wooldridge

Corporation

15730

ARBOR

VITAE

STREET

•

L.OS

ANGEL.ES

415.

CAL.IFORNIA

SOLVING PROBLEMS

WITH

DIGITAL

COMPUTERS

ALSTON

S.

HOl'SElfOLHf:R

Mathematics

Panel

Oak

P.idge

National

Lahoratory

Oak

Ridge, Tenn.

(Talk

hefore

American

Physical

Society,

Washington D.C.,

April

26-28, 1956)

The

speeds

of

"high speed"

digital

com-

puters

vary,

from machine

to

machine, 0 v e r

several

orders

of

magnitude,

but

for

a

fairly

representative

group

the

multiplication

time

is

roughly

half

a

millisecond.

For

the

IBM

701, and

for

machines

of

the

Princeton

type,

the

speed

is

slightly

less;

for

the

IBM

704

it

is

rather

greater,

but

this

is

perhaps a

fair

round number.

The

Oracle

at

the

Oak

Rid

g e

National

LaboratorY,is

a

Princeton

type mach-

ine

and

hence one

of

this

class,

and

since

it

is

the

machine with which I

am

most

familiar,

and

since

"Oracle"

is

an

easy

tvord

to

say,

I

wish

to

use

the

Oracle

as

representative

of

this

class.

On

the

Oracle

a

division

takes

about

the

same

length

of time as a

multiplication,

so

we

can speak

of

multiplications

and

consider

a

division

as

equivalent.

In

time,

and

in

per-

centage

of

occurrences,

a

multiplication

is

equivalent

to

about

10

single-address

additive

operations.

The

ratio

varies

somewhat

from

machine

to

machine,

but

in

any

case

mUltipli-

cations

and

divisions

account

for

a

substantial

percentage

of most computing

time.

A

skilled

human

operator,

let

us

call

him

Joe

for

short,

using

a

standard

desk computer,

can-

carry

out

about 1000

multiplications

in

a

working day,

counting

time

to

enter

operands

and

record

results.

This

is

steady

going, and

if

we

allow

time

out

for

sickness,

holidays,

and

coffee

breaks,

4000

per

week

is

perhaps a

bette~

overall

average.

This amounts

to

about

2xl0

5

multiplications

in

a working

year,

or

10

6

in

five

years.

Considering

50 working

yea~

as

the

productive

human

life

time,

if

Joe

spen~

his

life

doing

multiplications

on

a desk

cal-

culator

he

will

perform a

total

of

about

10

7

of

these.

There

is

a

well

knOlvn,

but

not

well

de-

fined,

unit

of

computational volume

known

as

the

"Horner". I have

never

seen

it

in

print,

but

I

understand

it

represents

the

amount

of

computational

labor

required

for

solving

an

algebraic

equation

of

some

given

degree

using

Horner's

method, which

is

one

of

the

more

labor-

ious

and simple-minded

of

known

methods. I

should

like

to

expand

the

unit

to

more

practical

- 6 -

dimensions, and

redefine

it,

freed

from

in-

vidious

implications.

For

this

purpose I

shall

consider

the

Horner

to

represent

10

6

multiplications

or

the

equivalent

thereof.

In

these

terms, Joe

requires

about 5

years

to

produce a Horner, and

the

Oracle

about 8 min-

utes.

In

the

same

terms,

the

NORC

at

Dahlgten

requires

about one minute and

the

LARC,

to

be

delivered

to

Livermore

two

years

hence, about

8

seconds.

These

last

figures

are

very rough

and comparisons

are

difficult,

since

the

NORC

and

the

LARC

are

floating

point

machines,

which

gives

them

an

effective

speed

that

is

perhaps

higher

by

an

order

of

magnitude.

On

~he

other

hand, I

am

not

at

present

considering

the

u-

tility

of

the

output,

but

seeking

only

some

gross,

overall,

and

reasonably

lyell-defined

measure of

activity.

Returning

to

our

friend

Joe and

his

desk

computer,

if

we

assume him

to

be a high school

graduate

merely,

with

no

special

endowments

other

than

steadiness

and

dependability,

his

salary

and overhead would probably

come

to

at

least

$5,000

per

year.

Hence

his

output

comes

at

the

rate

of

about $25,000

per

Horner. While

Joe works a

40-hour

week,

the

Oracle's

week

is

at

present

120 hours

long.

If

we

figure

de-

preciation

at

$200,000

per

year,

which

is

quire

excessive,

this

comes

to

about $30

per

hour.

Normal

operating

costs

run around $50

per

hour,

and

this

adds

up

to

about $10

per

Horner. Ihe

LARe

will

cost

about

three

times as

much

as

the

Oracle.

If

we

allow

the

same

factor

for

operating

costs,

and allow a

factor

of

60

for

speeds,

lve

come

out

with

a

cost

of

50¢

per

Horner, a

factor

of

5.10

4

by

comparison with

Joe.

Perhaps I

should

emphasize

again

that

utility

is

not

being

considered.

For a

par-

ticular

problem

the

number

of

Horners requited

can

easily

vary by

an

order

of

magnitude

for

any

single

system depending

upon

the

car

e

taken

in

programming and

analysis.

But

this

can

be

said

for

the

output

of

any

of

the

mach-

ines,

that

for

an

output

of one Horner one

does

not

have

to

wait

five

years.

For Joe I have

postulated

very few

skills,

the

Oracle

and

the

LARC

have even fewer.

If

we

have a

differential

equation

to

be

solved,

whether

by

Joe,

by

the

Oracle,

or

by

the

LARC,

Solving

Problems

lve

have

to

program

it

properly

since

neither

Ivhereas

it

is

clear

that

numbers aclllally used

one of

the

three

knows

any

mathematics

beyond

in

real

computations have a

distribution

that

arithmetic.

Suppose

the

problem

requires

a-

is

far,from

simple.

For example,

the

simple

bout

one

Horner

of

computation.

To

compare

rationals,

certain

transcendentals

such as e

the

programming

of

the

problems

for

the

LARC

and

Ir

and

simple

functions

of

these,

occur

wi

th

the

prograrmning

of

the

problem

for

Joe,

wi

th

much

more

than

random

frequency.

Having

we

must imagine

that

Joe

is

to

be given

his

recently

formulated a

pessimistic

hypothesis

data

and

instructions

at

the

outset,

and

is

in

this

regard,

I

was

informed

by

a

Scotch

then

to

be

left

incommunicado

for

a

period

of

mathematician

that

my

principle

was

already

5

years

at

which time

he

suddenly emerges

lvith

well

known

in

Scotland

by

the

name

of

Ma

c-

answers, which

mayor

may

not be

the

correct

pherson's

Law.

In

the

original

Scotch

the

ones.

The

instructions

must

be

explicit

e-

statement

is,

"Macpherson's

piece

aye

fa's

nough

to

guide

him

through

all

contingencies,

jeelie

side

doon". There

is

another

formula-

since

by

hypothesis

all

communication

is

sev-

tion

of

the

same

principle

Which

is

known

as

ered

for

the

period.

das Gesetz

der

Schtveinerei

der

Natur.

The

parallel

is

not

perfect,

since

either

the

Oracle

or

the

LARC

can simply

stop.

A t

least

it

can be programmed

to

stop

when~oub~

of

a

foreseeable

character

arise.

But

often

the

troubles,

if

foreseeable,

are

neverthel~

not

foreseen,

and

the

machine d i 1 i g

en

t

ly

P

ro

d u c

es

nonsense

until

the

aberration

is

discovered.

Happily

we

can

afford

to

squander

a

few

of

the

LARC's

50¢ Horners, as

we

could

not

afford

to

squander

Joe's

$25,000 Horners.

But

the

fact,

while

ameliorating

the

difficul-

ty,

does not

nullify

it.

Ultimately,

for

any

given problem,

it

is

necessary

to

achieve a

program

capable

of

directing

the

computer

in

uninterrupted,

valid

performance

for

at

least

a few seconds, and

in

the

case

of

the

LARC,

this

would be

equivalent

to

almost

that

many

years

on

the

part

of

Joe.

And

whereas

the

LARC

will

require

8 seconds

to

produce a Hor-

ner,

there

are

machines

in

prospect

for

three

or

four

years

hence

that

will

produce a Honer

or

more

per

second.

These

figures

are

introduced,

not

for

the

purpose

of

bringing

out

what

am

azing

a-

chievements

these

computers

are,

but

rather

tQ

emphasize

the

difference

between

solving

a

problem with

Joe's

help and

solving

it

with

the

lARC's

help.

The

real,

flesh

and

blood

Joes

who

actually

pound

Fridens

and

Marchants,

are

not

generally

incarcerated,

and, indeed,

they themselves can

often

see,

as

the

LARC

cannot,

when

things

go

awry. In

particular,

it

is

often

possible

to

observe

the

build-up

of

rounding

errors

in

the

course

of

a hand

computation and

to

take

remedial measures,.

It

goes

without

saying

that

in

the

rotnse

of

a Horner

or

two

of

computation, rounding

errors

can

build

up

very

substantially

and

possibly

invalidate

the

entire

result.

Some

papers have been

published

attempting

to

de-

rive

statistical

distributions

of

errors

gen-

erated

in

the

course

of

certain

classes

of

computation,

but

generally

speaking I am

skeptical

of

the

conclusions.

For

such,es-

timates

some

uniformity

of

the

initial

dis-

tributions

of

data

and

errors

must

be

made,

- 7 -

I can

illustrate

this

with

an

occurrence

of

several

years

ago

when

a

floating-pointnu-

tine

was

being

prepared

for

a

fixed-pointm~

ine.

The

results

exhibited

some

obvious

but

puzzling

discrepanciesbQbut

eventually

it

was

found

that

among

the

2

possible

number

pai~

provided

for,

the

routine

gave

the

cor

rec

t

product

for

all

but

one,

and

this

one

'pair

actually

occurred

in

the

computation.

The

probability

of

the

appearance

~

this

pair

at

anylgne time was,

of

course,

2

0,

or,

roughl~

10-

,on

the

assumption

of

a uniform

distri-

bution.

Recently

at

ORNL

a

routine

for

inverting

matrices

was

being

tested

by

applying

it

to

a

particular

matrix

tvhose

inverse

was

obtainable

analytically.

If

a computed

inverse

is

multi-

plied

by

the

original

matrix

and

the

result

subtracted

from

the

identity,

it

is

possible

to

compute

quite

easily

and

rigorously

an

up-

per

limit

to

the

error

in

the

individual

ele-

ments of

that

inverse.

In

this

instance

the

computed upper

limit

was

exceeded

by

several

orders

of

magnitude

by

the

errors

actually

found

in

some

of

the

elements.

It

turned

out

that

the

discrepancy

was

due

to

the

small

re-

sidual

error

made

in

converting

the

elements

of

the

original

matrix

from decimal form

to

binary.

In

other

words,

the

matrix

actually

inverted

differed

in

the

last

few

binary

di-

gits

from

the

matrix

whose

inverse

was

known

theoretically,

and

this

accounted

for

the

discrepancy.

I

am

mildly

distressed

by

the

grot\' i ng

popularity

of

decimal machines

for

scientific

computation, and

of

floating-point

machines.

It

is

a theorem

that

among

all

possible

bases,

the

base 2 minimizes

the

rate

of

growth

of

generated

error.

In

fact,

the

larger

the

b~e

the

higher

the

rate.

My

objection

to

float~

ing

point

is

based

upon

the

fact

that,

to

the

best

of

my

knOtvledge,

no

one

knows

how

to

pte-

dic

t

the

rate

of

growth

of

generated

err

0 r

when

floating

point

arithmetic

is

used.

In

speaking

of

generated

error

I

am

not,

Computers

of

course,

speaking of malfunctioning of

the

machine,

or

of

errors

due

to

faulty

coding, or

of

the

use

of

a

fallacious

formula. These ate

relatively

easy

to

detect

and

correct.

I

am

not

referring

even

to

truncation

errors.

These

are

also

fairly

easy

to

detect,

generally,

al-

though I

know

of

a

case

where

several

months

and

Automation

of

IBM

computations

l~ere

found

to

be

invalid

because a Taylor

series

had been

truncated

too

soon, and

another

case

where

some

months 0 f

coding time were wasted along with

some

mach-

ine

time because a

certain

series

was

found

to

converge too slowly

to

be usable

at

all.

I n

both

of

these

instances

a

sufficient

amount

m

fairly

standard

mathematical

analysis

could

have prevented

the

loss.

The

errors

I

refer

to,

however,

are

those

which

result

from round-

ing

after

every

multiplication

and

division,

and

in

floating-point

operations

they appear

also

when

the

exponents

are

adjusted

by

shift-

ing

before

an

addition

or

subtraction.

The

analysis

here

is

always

tedious,

and

the

math-

ematical

techniques

are

by

no

means

Ivell

de-

veloped.

In

some

instances

~

posteriori

estimates

of

error

can be

made.

I have

already

spoken

of

the

formula

for

obtaining

an

upper bound

to

the

error

in

the

computed

inverse

of

a matrix,

al

though, as you

recall,

this

refers

to

the

matrix

actually

in

the

machine which

is

not

always

exactly

--

in

fact

is

seldom

exactly

-

the

matrix

you

wish

to

invert.

To

the

best

of

my

knmdedge,

there

is

no

Ivay

of

obtaining

in

general

a

rigorous

limit

of

errors

in

the

so-

lution

of

a sys tem

of

linear

equations

l.vith

out

making

u_se

of

a computed

inverse.

It

doe.c:

not

suf-

fice

to

substitute

thecomput.ed

solution

inlo tile ori-

ginal

equations.

For suppose

you

do

this,

and

suppose

you

even

find

that

to

within

rounding

errors

the

equations

are

exactly

satisfied.

Th

at

is,

suppose

you

ldsh

to

solve

Ax"

b,

aId

you

obtain

for

x a

vector

x*

such

that

when

you

take

the

machine product

(Ax*)

*

of

A

by

x*

you

get

exactly

b.

Nevertheless,

in

general,

the

true

product

Ax*

will

differ

from

the

desired

vector

b

by

some

vector

d

of

which

you

know

only

that

each element

of

d

does not exceed

the

maximal

error

generated

in

the

machine computation.

Then

the

error

x-

x*

is

equal

to

A-ld.

Now

if

it

should

hap-

pen

that

this

unknown

vector

d has a

large

component

in

the

direction

of

the

eigenvector

of

A belonging

to

the

smallest

eigenvalue,

call

it

A,

then

the

actual

error

vector

x-

x*

tVill be approximately

~

-la,

and

if

~

is

small,

the

elements

of

)\-ld

can be

large.

This

is

what can happen

in

the

case

of

s~alled

ill-conditioned

systems.

But

the

case

can be

even worse. Consider

the

form

A;:

I

-O(J,

l:vhere

J has ones

just

below

the

diagonal

and

zeros

elseWhere,

Then

A-I = I +

ex

J + b(2J2 +

...

+

oc

n-l

In-l

•

Hence, although every eigenvalue A = I

for

A,

nevertheless

the

last

element

of

x -

x*

will

be

0<

n-l

times

the

first

element

of

d.

If

0{

is

large

and

n

large

the

magnifica-

tion

1vill be

great.

This

phenomenon

is

well

known

in

the

fi-

nite

difference

solution

of

differential

equa-

tions.

It

goes

by

the

name

of

instability.

Act-

ually,

instability

is

a

matter

of

degree,

as

others

have

pointed

out,

and

it

should be

~eat

ed

as

such.

If

the

differential

equation,

1\'

h e

the

r

ordinary

or

partial,

is

linear,

then

the

ele-

ments

of

the

vector

x

of

unknol.vns

are

the

val-

ues

of

the

dependent

variable

at

mesh

points

of

the

grid;

the

elements

of

the

vector

bare

determined

by

the

boundary

or

initial

values;

and

the

elements

of

the

matrix

A

are

deter-

mined

by

the

method

of

approximating

the

deri-

vatives

by

finite

differences.

For

initial

value problems one

generally

tries

to

set

up

a scheme whereby

the

dependent

variable

can be

evaluated

by

a

straightforward

recursion,

be-

ginning

at

a boundary

or

corner

point

and

pro-

ceeding from

point

to

point.

One

does

not

generally

Ivri

te

down

the

matrix

explicitly,

or

perhaps even

think

of

the

problem

in

these

terms,

but

in

fact

the

matrix

A

is

then a

triangular

matrix,

all

of

whose

non-null

ele-

. ments

fallon

the

diagonal

or

not

far

below

it.

Its

form

is

only

slightly

more

complicated than

that

of

the

matrix

jus

t

exhibited.

Now

the

order

of

the

matri'x depends

upon

the

fineness

of

the

grid.

In

general

t

he

re

will

be

allinear

combination

of

terms

of

the

f

n-

n 1

orm

0(

,~-,

•••

, Ivhere

<X

and

f3

are

themselves

functions

of

the

grid

spacing.

If

n

is

made

large,

as

is

desirable

for

reducing

the

truncation

error,

then

in

general

at

least

one

of

the

terms,

0(

n-l,

(3

n-l,

•••

, beco mes

large.

One

seeks,

therefore,

to

obtain

a form

such

that

the

growth with n

is

as slow as

possible.

However,

there

are

limits

to

what

one

can

do

in

this

direction.

On

the

other

hand,

if

the

matrix

A

is

not

required

to

be

triangular,

one

may

be

a~

to

avoid

this

type

of

buildup.

It

is

t

rue

that

the

equations

are

less

easy

to

sol

ve

than

when

the

matrix

A

is

triangular,

but

Horner's

come

cheap

on

the

LARC,

and

fairly

so

on

the

Oracle,

and

it

may

be

worth

the

pains.

A

nontriangular

scheme

is

called

im-

plicit.

For boundary

value

problems

there

is

no

choice,

and 'one

is

forced

to

use

an

im-

plicit

scheme.

- 8 -

Solving

Problems

With

implicit

schemes, whether

for

bound-

ary

value

problems

or

others,

an

i

te

rat

i v e

method

of

solving

is

generally

preferred.

This

is

so

partly

because

the

matrix

is

ordinarily

very

large

but

simple

in

structure,

lvhereas

its

inverse

is

large

and

complex. A I

th

ough

many

iterations

may

be

necessary,

each

is

re-

latively

simple

and

easily

programmed. There

is

a

further

advantage

that

if

the

i

terati

on

is

continued

until

convergence

is

complete, the

departure

x -

x*

of

the

computed from t

he

true

solution

is

as small as

it

can be

made,

whereas

the

result

of

a

direct

solution

may

require

further

improvement

by

subsequent

ap-

plication

of

an

iterative

technique.

For

reactor

criticality

calculations,

at

least

in

one dimension, a

direct

solution

is

fairly

simple because

of

the

follOtving c i

r-

cumstance:

The

matrix

A

is

a

so-called

con-

tinuant,

whose

non-null

elements occur along,

just

below, and

just

above

the

main

diagonaL

Such a

matrix

can be

factored

into

the

product

of

two

matrices,

one having

non-null

elements

only along and

just

below

the

main

diagonal,

the

other

having them only along

and

above.

One

of

the

diagonals

can be

taken

as

made

up

of

ones, and a simple

set

of

recursions

gives

the

other

3 n - 2

elements.

Each f

act

0 r

matrix,

in

turn,

is

readily

inverted.

This

is

the

basis

for

the

commonly

used

"out-in"

or

"in-out"

algorism

in

criticality

calculations.

Now

for

the

two-dimensional problem

the

matrix

is

a composite

matrix

constructed

as

follOtvs:

In

the

above

matrix

A,

rep

la

c e

each diagonal element

by

a

matrix

of

the

same

form as

A;

replace

each remaining

non-null

. element

by

a

diagonal

matrix.

This

matrix

can

be

factored

and

inverted

exactly

as l\tas

the

above

matrix,

provided one

bears

in

mind

that

the

recursion

relations

involve

matrices

and

that

hence

the

order

of

the

factors

is

import-

ant.

For

the

three-dimensional

problem

one

has

to

form a supercomposi

te

matrix

out 0 f

these

composite ones,

but

again

the

algorism

holds.

To

the

best

of

my

knmdedge

this

has

never been programmed

for

existing

machines

for

reasons

that

are

obvious

when

one estimares

the

number

of

Horners

required.

In

fact,

to

invert

a

general

matrix,

or

to

mUltiply

two

of

them,

requires

a number

of

mUltiplications

proportional

to

the

cube of llie

order,

although

for

these

special

matrices

it

might be

held

to

the

square.

If

we

think

of

a

grid

with

'60

points

in

each

direction,

the

n

this

is

10

,

or

one Horner,

multiplied

by

some

constant

factor.

This must

be

multiplied

agmn

by

the

numb~r

of

groups, and

still

again

by

tile

number of

iterations

that

may

be

required.

We

all

learned

in

high

school

to

sol

v e

simultaneous

linear

equations,

and

yet

one

of

the

more

pervasive

and

evasive

of

the

problems

- 9 -

before

numerical

analysts

today

is

hOt-v

to

do

this

efficiently

on

the

Oracles,

the

NORC's

and

the

LARC'

s • A

general

matrix

of

0 r d e r

100

represents

several

Horners of computation

for

its

inversion,

counting

the

many

transfer

operations

involved,

and

100

is

a

small

number

when

tile Cfluations

come

from

partial

differ-

ential

equations.

There

is

firs

t

the

she

e r

mass

of

multiplications

alone,

but

this

is

on-

ly

part

of

the

problem. For

large

matrices

ilie

capacity

of

the

internal

storage

will

be

ex-

ceeded and

information

must be switched b

e-

tween

that

and

the

auxiliary

storage.

But

most

critical

of

all

is

the

fact

that

sma

11

divisors

can develop

that

will

blow

up

gener-

ated

errors

to

a

scale

that

would

invalidate

subsequent

computations.

One

way

to

avoid

this,

when

the

matrix

is

not

intrinsically

bad

1 y

conditioned,

is

to

"position

for

size",

which

~ans

seeking

out

the

largest

coefficient

and

shifting

the

equation

containing

it

to

fir

s t

position

at

each

stage

of

the

elimination.

Th~

is

very time-consuming

for

the

machine, and so

are

any

equivalent

logical

operations

used

to

avoid

an

actual

interchange.

A

slight

change

in

the

point

of view, however, s u g g

est

s a

slightly

different

approach which evades

the

difficulty

completely,

and

although

more

actu~

multiplications

are

required,

there

is

a

great

reduction

in

the

shuffling.

The

procedure

is

to

carry

out

the

elimination

by

performing a

sequence of

plane

rotations.

This method

re-

duces

the

generated

error,

it

yields

as a

by-

product

the

value

of

the

determinant,

and

per-

mits a running check

in

that

the

sum

of squares

of

the

elements

in

any

column remains

invariant.

The

method

was

developed

at

ORNL

by

J.W. Givens,

and

it

is

now

in

very

effective

use

on

the

Oracle.

Including

tape

handling,

inversion

of

a

matrix

of

order

100

requires

about

10

Horners.

In

counting

costs

per

Horner I

did

not

in-

clude

salaries

of mathematicians and

program-

mers. This

is

often

considered

to

be

much

high-

er

for,

say,

the

LARC

than

for

Joe.

On

an hour-

ly

basis

this

is

certainly

true,

but

on

ape

r

Horner

basis

it

is

by

no

means

so.

Let

us

con-

sider

~

group of mathematically

untrainep

Joes.

How

much

supervision

and programming

they

would

require

from a

professional

depends upon

many

factors,

but

ten

Joes

per

supervisor

would

seem

close

to

an

upper

limit.

Ten

Joes

could

pro-

duce

two

Horners

per

year,

and hence one

pro-

fessional

man

year

would

be

required

for

two

Horners.

1\10

Horners

is

about

16

minutes

on

the

Oracle and about

16

seconds

on

the

LARC.

An

hour's

running time on

the

Oracle would be

about 8 Horners

or

4

professional

man

years.

I

have

yet

to

see

the

machine problem

that

r e -

quired

two

years

of

programming and coding

for

an

hour's

run.

What

is

even

more

to

the

point,

however,

is

the

fact

that

a code

for

an

Oracle

or

a

LAHC

is

a

capital

investment.

The

lin8ar

eauat

ion

(cont'd

on

page

15)

T'HE DAY

OF

RECKONING

JACKSON

W.

GRANHOLM

Seattle,

Wash.

Dr.

Amos

K.

Hommel

rose

slowly from

his

chair.

He

walked lvith measured

stride

to

the

front

of

the

lecture

room.

From

his

vest

pock-

et

he

took

the

case

containing

the

pince-nez

glasses

which

it

was

his

habit

to

wear

while

reading

or

speaking.

From

his

coat

pocket he

tvithdretv

the

small,

black,

leather-covered

notebook liherein

it

was

his

cus

tom

to

record

thoughts

Which

came

to

him

at

odd

moments.

The

front

of

the

book

was

boldly

emblazoned

with golden

letters

spelling

the

word

RECKON.

It

had been

the

gift

of

the

Multinational

Com-

puter

Corporation

to

Dr.

Hommel

on

the

ooc~ion

of

his

superbly

brilliant

address

to

a seminar

convened

at

Alexandria, Egypt,

to

discus

s

theoretical

aspects

of

numeric

al

analysis

tdth

computers.

Hommel

opened

the

notebook

car

e-

fully

and

gazed about

the

room,

smiling

at

us

all.

"Gentlemen,"

said

Hommel,

his

gaze bounc-

ing about

like

a cork

bird

in

a badminton court,

"you

are

all

atvare of

the

great

debt

we

otve

to

the

magnificent

generosity

of Herbert Fremont

Parnson,

that

superb

benefactor

of

our

insti-

tution.

His

gift

it

was

that

made

possible

the

construction

of

that

outstanding

computing

in-

strument which today has

successfully

completed

its

first

month

of

operation.

It

is

with glad-

ness

in

~

heart

that

I

report

to

you

today

tie

resul

ts

of

that

first

month

in

being

of

the

Parnson

Electronic

Calculator,

knOtvn

to

the

Ivorld

at

large

as

SUPEBVAC."

Dr.

Hommel

paused,

taking

his

handke~hief

from

his

pocket

and

wiping

his

pince-nez

with

it.

"The

calculator,"

Hommel

continued,

"has

exceeded

all

expectations.

It

has

performed

superbly.

Without doubt

it

is

now

ready

to

attack

the

problems

for

which

its

design was

conceived."

All of us

sat

in

silence

for

a

moment.

Then,

led

by

Dr. Robert Bardney,

we

rose

in

a

body, resoundingly applauding

this

man

who

stood

now.

before

us,

smiling,

glasses

in

0 ne

hand, handkerchief

in

the

other,

slowly wiping

the

tears

of

happiness

and

gratitude

from

his

eyes.

When

the

applause, had

subsided,

Dr.

Hom-

mel,

taking

his

black

notebook from

the

lec-

tu~n,

returned

to

his

seat.

Dr. P.

Y.

Reebe

rose

and

walked

briskly

to

the

platform

at

the

front

of

the

room. His

mane

of white

hair'bob-

bed

up

and

down

as he pleed

his

brief

case

UpOl

the

lec

tern.

Everyone t

...

as

quiet

as he regan

to

speak.

"My

good

fellotvs,"

Reebe

said,

"we

are

right-

ly

filled

tvi

th

pride

and

admiration

to

have this

excellent

man

as one

of

us.

Our

worthy

co

1-

league, Dr.

Amos

K.

Hommel,

through

his

devoted

and

tireless

efforts has, virtually s:irJJle-handed

ly

brought

this

unparalleled

computing

instrument

into

being.

It

is

indeed meet and

fitting

that

we

should, each and every one,

offer

our

praise

to

him. Having done

so,

however,

there

remains

before

us

the

bringing

to

fruition

of

Hommel's

work. I

refer,

gentlemen,

to

the

tasks

to

which

SUPERVAC

will

now

be

put."

Reebe

gazed

intently

at

the

ceiling.

"I

feel

strongly,"

he

said,

"that

the

time

has

now

come.

We

have

at

last,

thanks t 0

Hommel,

arrived

at

the

stage

where

we

can

be-

gin

to

shed

the~emendous

burdens

of

the

de-

sign

of

calculating

machines.

We

can

now

start

to

place

these

burdens

upon

the

calculators

themselves. In a

sense

the

electronic

calcula-

tor

has

entered

the

stage

where

it

can begin

to

make

use

of

a

characteristic

heretofore

liar

ited

to

living

beings.

I speak,

of

course,

of

the

process

of

reproduction."

Dr. Manifest,

who

sat

in

the

back

corner

of

the

room,

cleared

his

throat

rather

aWkwardly.

"Not

in

any

physical

sense,

naturally,"

Reebe

tvent on, "can

this

machine reproduce i

t-

self.

What

I propose

is,

rather,

that

we

shall

take

steps

to

assign

to

it,

as soon as

possible,

the

problem

of

designing

its

own

successor.

In

fact,"

Reebe

said,

"I

would not have

us

s

top

there.

I would have

us

propose

to

this

machine

the

problem

of

designing

the

optimum

calculator!"

Reebe

paused while

the

whole

effect

of

his

last

statement

seized

us

all.

He

turned

to

his

brief

case,

taking

some

papers from

it.

P

ick-

ing

up

the

chalk

he stepped

to

the

blackboard

at

the

back

of

the

platform.

"If

you

will-

bear

tvith

me,

gentlemen, "leebe

said,

"I

shall

outline

the

proposal which I have

in

mind."

-10 -

Day

of

Reckonin~

Reebe

began

to

write

rapidly,

his

equa- ray tube

store

was

made

up

of

a huge

rack

of

tions

flowing across the board.

Now

and then

staring

screens,

slightly

larger

than

tele-

he

uttered

a

comment

to

explain

some

m 0

revision

picture

tubes.

Instead

of a

picture

obscure

point.

When

Reebe

had

moved

to

the

face

of each tube,

in

action,

carried

a

right

half

of

the

blackboard, Dr. Robert Bard-

pattern

of

glowing

blue

dots.

The

magnetic

ney

interrupted.

core

store

consisted

of

a

vast

array

of

tiny

"You

will

pardon me," Bardney

said,

"but

I

believe

you

have committed a

slight

fa

u x

pas

in

logic

in

relationship

number nine

tee

n.

Where

you

have

written

the

operator

AND/OR,

I

believe

you should,

instead,

substitute

the

expression

IF--THEN."

Reebe,

after

glancing

at

the

equation

in

question,

said

"You

are

quite

right."

He

erased

the

offending

symbol

and

substituted

the

cor-

rect

one.

After

some

time Dr.

Reebe

had completely

filled

the

blackboard

wi

th

symbols.

We

had

carefully

criticized

and

scrutinized

his

work.

Dr. Robert Bardney

rose

to

speak.

"It

is

evident

to

Ire,"

Bardney

said,

"that

Dr. Reebe

is

on

the

right

track.

I

pr

0 p 0 s e

that

we

proceed

to

push

this

project

to

comple-

tion

as

soon as

possible."

Bardney's proposal

was

unanimously

adopt-

ed,

and

early

the

work

was

begun on

the

task.

Dr.

Heebe

was

selected

to

head a

team composed

of

Dr. Wilson

M.

Sweet, Dr. Rupert

B.

Pooble, and

Professor

Marnoscz

D.

Nazi

Id-

JZlan.

This team

was

to

define

the

relation-

ships

expressing

the

requirements

for

the

op-

timum

calculator.

They

were

further

ch

arg

ed

with

the

task

of

writing

these

relationships

as

a

set

of completely

detailed

equations.

Dr.

G.

Jennings Manifest

l'laS

placed

in

charge of a

group of

graduate

students

whose

task

it

was

to

convert

the

equations

of

Reebe's team

into

coded

instructions

for

SUPERVAC.

The

operation

of

SUPERVAC

itself,

of

course,

was

to

be under the

direction

of

Dr.

Hommel

with

his

company

of

well-

qualified

technical

personnel.

Dr. Bardney

was

chosen

to

act

as

coordinator

among

the

severa

1

groups ltorking

on

the

proj ec t •

The

Parnson

Electronic

Calculator,

alias

SUPERVAC,

was,

without

doubt,

the

largest

and

fastest

digital

calculator

in

the

world.

It

was

housed

in

a

vault-like

room

with a

forty-

foot

ceiling

at

one

end

of

Burton

Tho

mp

son

Roberts

Hall.

A balcony

ran

around

the

outer

t\'alls

of

this

room

so

that

spectators

m i

gh

t

observe

the

computer

in

action.

The

huge

con-

trol

console,

vastly

more

complex than

that

of

any

pipe organ,

tvas

placed

squarely

i

nth

e

center

of

the

room. Direc

tly

behind

the

con

-

sole

was

the

main

computing frame, so

large

that

a person could

easily

walk

erect

within

itt

0

attend

the

tubes and

circuits.

To

the

Ie

f t

stood

the

cathode ray tube

memory

store

and

the

magnetic

core

memory

store.

The

cathode

ferro-ceramic

doughnuts

strung

together

0 n

II/hat

seemed

to

be

an

impenetrable

maze

0 f

fine

wires.

To

the

right

of

the

console

were

the

mer-

cury pipe

memory

and

the

spinning

magnetic

drum

memory.

The

pipe

retained

information

by

recirculating

it

continually

between

two

crystals

in

the

mercury.

Its

action

was

like

that

of

a small

child

t"lho,

shouting

into

0

ne

end

of

a

vacuum

cleaner

hose,

repeats

what

he

hears

himself

saying

at

the

other

end

which~

pressed

to

his

ear.

The

steel

drum,

ten

feet

in

diameter

and

spinning

at

tremendous speed,

had

stationary

magnetic pickups mounted a 11

about

its

periphery.

Some

of

these

continually

wrote

little

magnetized

spots

on

the

d

rum,

while

others

read

these

little

messages,

pro-

ducing

an

electric

impulse from

the

rap

i d

passage of

the

magnetized

spot.

All along

the

wall behind

the

operator's

chair

of

SUPERVAC

were

the

magnetic

tape

rervos

which

constituted

the

data

input

and

output

sys-

tem.

Directly

adjacent

to

the

console

there

was

an

intypoputter,

an

instrument

with

a

type-

lvriter

keyboard communicating

directly

with

the

central

computing

circuits.

Against

the

left

tvall

there

was

a high-speed

printer

on

which

resul

ts

could

be tvri

tten

for

rapid

perusal.

The

back

of

the

room

was

filled

with power

control

and

generating

equipment,

while

overhead ran

the

air

conditioning

pipes

which e

nab

1 e d

SUPERVAC

to

keep

cool.

This

was

the

machine

that

faced

Hommel

and

his

assistants

on

that

October morning

we

re-

member

so

welL

Reebe

and

his

team had

Ion

g

since

completed

their

work.

The

equations

had

been checked

and

rechecked. Dr. Manifest

and

his

graduate

students

had

translated

the

equa-

tions

into

the

strange

alphabetic

symbols

whfuh

represented

the

one-thousand-twenty-four

logic-

al

and

arithmetical

operations

of

which

SUPER-

VAC

was

capable.

Three young

ladies

had

wolked

for

a

week

and

a

half

at

typotapers,

machines

similar

in

appearance

to

the

intypoputter,

but

designed

instead

to

prepare

magnetic

tapes

for

the

calculators.

Dr.

Hommel

stood

before

the

console

of

the

machine

he

had

created.

T

he

reels

of

tape

were

in

front

of

him.

Herbert

Nugent,

one

of

Hommel's

assistants,

stood,

wearing earphones,

before

the

staring

cathode

ray

tube

faces.

Ronald Barnes,

another

assist-

ant,

stood

at

the

power frame

moni

ter

pane 1 •

In

the

corner

Dr:

Manifest and

Dr.

Bardney

sat

at

desk

calculators,

prepared

to

check

any

of

the

work

if

question

should

arise.

Dr.

Hommel's

secretary,

Lucy

Campylos,

stood

him.

-

11

-

(cont'd

on

page

27)

THE

OPERATION

OF

A

COMPUTER

AWAY

FROM

A

CENTRAL

STAFF

HOWARD

RROMRF.RG

David Taylor

Model

Rasin

Washington

7,

D.

C.

The David

Taylor

Model

Basin

is

maintain-

ing

for

the

Bureau

of

Ships

a somel\'hat

uniq

u e

computer

installation

in

the

Rerndngton-R

and

Univac

factory

in

Philadelphia.

It

became

ap-

parent

early

in

July,

1955,

that

certain

go

v-

ernment

contractors,

namely

those

uti

1 i z

in

g

Uni

vac

time

at

the

Model

Basin,

could

not

effec-

tively

meet

the

demanding

requirements

without

increasing

their

computer

time.

Since

lve

at

the

Model

Basin

lvere

working

around

the

clock,

it

was

evident

that

any

request

for

additional

time

could

not

be

fulfilled

there.

The

situa-

tion

became

rather

desperate

with

an

ever

in-

creasing

amount

of

high

priori

ty

problems

and

no

possibility

for

solution.

Consequently,

because

of

the

genuine

need and

the

urgency

of

Defense

requirements,

lve

asked Remington-R

and

for

a

computer

and

they

suggested

the

use of

one

in

their

factory

in

Philadelphia.

The

necessary

contractual

arrangements

having

been

mad

e,

a

computer

(or

more

precisely

a

series

of

comput-

ers)

a

unityper

I,

a

uniprinter,

and a

hi

g h

speed

printer,

on

a

catch-as-catch-can

basis,

were

put

at

our

di

spos

al

the

1 as t lveek of

July.

Aside

from

the

fact

that

the

Remingto

n-

Rand

factory

now

became a government

compute

r

installation,

the

final

assembly and

te

s t

of

all

equipment

was

effected

there

as

well

as

the

manufacturing

of

special

components,

magneti

c

tape

and mercury

tanks.

In

the

large

testin

g

area,

there

are

five

complete

computers

bein

g

assembled,

tested,

and

torn

down

for

shipment.

The

assembling

takes

roughly

two weeks and

the

testing

is

complete

in

three

months.

The

work

is

staggered

so

that

a

new

computer

is

shipped

each

month.

Similarly,

at

each

of

the

f i v e

high

speed

printer

test

stations

one

is

com-

pleted

every

seven

weeks. A

computer

is

put

at

our

disposal

after

it

has

been

in

test

for

two months.

We

then

use

this

machine

for

the

remaining

one month

period

after

which

time

it

is

torn

down

for

shipment.

We

then

pack 0 u r

desks,

files,

tapes,

printer,

typer,

experience,

memories, and

move

to

one

of

the

other

comJllters

which

has

progressed

through

tlVO

months

of

test.

Thus,

~/e

ourselves

are

involved

in

a

large

iteration,

aside

from

the

iterations

of

the

problems

we

do

and

the

iterative

runs

of

these

problems.

If

you

will

permit

such

a

perso

n-

ification,

we

have found

that

each

computer

is

an

individual

with

a

personality

separate

an

d

distinct

from

all

other

computer

personalities.

During

our

brief

encounter

with

a

given

machine

lve

need

to

become

familiar

to

a

point

of

inti-

macy

with

its

various

phobias

and

complexes,

and

also

to

normalize

them

in

order

to

achieve

the

maximum

amount

of

productive

time.

Th

i s

process

of

diagnosis

and remedy

insists

upon a

great

deal

of

patience,

trouble-free

routines,

and no

scant

amount

of

intelligent

t

rou

b 1

e-

shooting

and

preventive

maintenance.

No

sooner,

however, have

lve

succeeded

in

crashing

t

his

intelligence

barrier

between

man

and comput e r

than

our

short

acquaintance

is

at

an

end,

for

this

computer

too

must be

shipped

out

and a

n-

other

must

spring

up

in

its

place.

Thus,

pro-

gress

pushes

us

on

to

less

fertile

fields,

as

one

iteration

is

completed

and

another

is

begun,

differing

from

the

former

only

by a

fac

tor

of

personali

ty.

Yet,

a

computer

is

still

a c 0

m-

puter,

and even though

we

move

from

a

compat-

ible

machine

to

one

not

fully

checked

0 u

t,

we

advance

strengthened

by

the

understandin

g and

experience

gained

from

our

ter

encounters.

Essentially,

our

main

reason

for

being

is

to

derive

the

highest

amount

of

productive

time

possible.

Productive

time

is

another

expression

for

machine

efficiency:

we

derive

it

by

dividing

the

time

spent

on

the

computer

into

four

cate-

gories:

good

time,

down

time,

non-productive

time,

and

lost

time.

Good

time

is

paradise

--

everything

works

right;

and

in

direct

con

tr

a-

distinction

to

this

is

down

time.

Non-product-

ive

time

is

time

wasted

because

of

some huma n

error

such

as a bad

type-in

or

a mis

take

in

a

routine.

Lost

time

is

due

to

mac

h i n e

mal-

function.

The

sum

of

the

good

tire

iJ1d

the

non-

productive

time

divided

by

the

total

amount

of

computer

time

gives

us

the

machine

efficienc

y

or

produc

ti

ve

time.

The

number

of

mac

h

in

e s

used,

hOtvever,

is

by

no

reans

COJDJOOnsurate

with

the

amount

of

productive

time

gained.

The

biggest

single

factor

which

govern

s

our

final

efficiency

is

maintenance,

which i s

handled

by Remington-Rand on a 144

hour

wee

k

Iv!

th

two

separate

eight

hour

periods

a

tV

e e k

devoted

to

preventive

maintenance.

This

type

of

maintenance,

which

really

amounts

to

c 0

n-

stantly

bug-shooting

a

new

machine,

is

exacting

and

in

the

long

run

unrewarding.

The

s

tr

a i n

of

on

the

spot

attempting

to

furnish

a computer

-12 -

Operation

of

a

Computer

which

is

capable

of

production

work

also

affects

Mathematically

the

problem

was

to

deter-

the

operators,

who

are

furnished

by

the

Reming- mine

the

lowest

eigenvalue

of

a

pair

of

second

ton-Rand

Service

Bureau

in

New

York..

order

ordinary

differential

equations.

Th

i s

On

a

straight

production

run

the

rol

e

of

the

operator

is

negligible.

The

operators

must

fi

t

into

our

pattern

of

operation

by 1

ear

ning

about

our

runs

and

how

to

use

our

service

r 0

u-

tines

in

a

relatively

short

time.

In

spite

of

these

conditions,

our

maintenance

and

operation

have

helped

to

develop

an

average

machine

effic-

iency

of

about

85%

..

This

installation

derives

some

noveltyfrom

the

fact

that

programming and programmers

are

not

necessary

factors

for

efficient

operation.

We

operate

without

programmers, and

two-thirds

of

the

personnel

running

problems have

had

no

experience..

We

have f 0 u n d

that

after

a

short

preliminary

orientation

per-

iod

on

basic

principles,

a

person

new

to

the

field

is

able

to

carry

out

effectively

the

run-

ning

of

our

problems..

This

orientation

involves

on-the-job

familiarity

with

jargon,

equipment,

and manuals

of

problem

operation.

No

creative

coding

is

being

done;

the

only

coding

t

hat

is

carried

out

is

for

occasional

correction

mcon-

tr.ol

tapes

or

revis

ion

of

routines.

The

degree

of

proficiency

necessary

for

uni

typing

and

cor-

recting

control

tape

routines

is

re

ad

i 1 y

at-

tained.

It

is

therefore

clear

that

our

bib

1 e

is

the

manual

of

operating

inst~uctions

forthe

problems

with

which

we

deal.

These

instrLrtion

s

must be

exhaustive

and

accurate

for

every

possi-

bility,

for

it

is

upon them

that

a good

part

of

the

efficiency

of

the

installation

de

pen

d s •

The

people

running

the

problems

are

by nece

ssi

ty

constrained

to

be more

concerned

with

"settin

g

breakpoint

1"

or

"block

subdividing

four"

than

wi

th

any

of

the

principles

innate

wi

thin

the

problems.

It

is,

however,

imperative

for

them

to

have an

unders

tanding

of

the

general

s

cop

e

of

the

problems

being

run,

and

to

have a

cop

Y

of

all

data,

instruction

tapes,

and

daily

sup-

ervisory

control

print-outs,

so

as

to

be a b 1 e

to

analyze

effectively

those

difficulties

which

arise

while

on

the

computer.

Every

problem

is

run

with

the

fewest

possible

references

to

the

problem

itself.

Basically,

we

run

three

different

problems.

All

of

them have

be~n

completely

programmed and

two

of

them have been

in

actual

production

at

the

Model

Basin

for

close

to

two

years.

Problem

BETTIS

57

was

developed

by

the

Ap-

plied

Mathematics

Laboratory

of

the

David Taylor

Model

Basin

at

the

request

of

Westinghouse

Atomic

Power

Division

to

aid

in

preliminary

survey

work

incident

to

the

des

ign

of

nuclear

reac

tors

for

ship

propulsion.

It

was

based

on an

extremely

simplified

physical

model

in

which

all

neutrons

were

classed

as

either

fast

or

sloW,

and

on

1 y

one

space

-dimension

was

considered.

The problem

was

then

to

determine

the

condition

under

which

the

reactor

barely

became

capable

of

sustained

reaction

..

was

handled

by

finite

difference

methods,

the

standard

iteration

method

being

used

to

obtain

the

lowest

eigenvalue

of

the

resulting

matrix

system.

This

procedure

also

yielded

the

cor-

responding

eigenvector

whose components

are

proportional

to

the

neutron

flux

density

at

the

specified

mesh

points.

A

slightly

modified

version

of

the

fore-

going

has

actually

been

used

in

mos

t 0 f

the

production

work on

BETTIS

57

so

far.

A

param-

eter

alpha

is

introduced

which

is

a

measureof

the

amount

of

"poison"

material

present

in

the

reactor;

the

problem

now

requires,

in

addition,

determination

of

the

value

of

alpha

Which

will

make

the

eigenvalue,

eta,

fall

within

a

spec-

ified

narrow

range..

This

is

done by

starting

out

tdth

two

standard

assumed

values

of

alpha,

using

linear

interpolation

to

obtain

an

improved

value

of

alpha,

and so

on.

Computations reqtd.re,

on

the

average,

about

half

an

hour

per

case

..

MUG,

our

second

program, was

dev

e

lop

e d

over

tt~O

years

ago and has been

in

ope

rat

ion

ever

since..

From an

engineering

point

of view,

MUG

is

a

digital

analog

of

a

reactor.

This

re-

actor

has

either

uniform

cross-sections

or

is

a body

of

revolution..

In

both

cases

it

~

cir-

cular..

Thus

only

two

space

dimensions

are

in-

vol

ved.

A

third

dimens

ion

(independent

v a

ri-

able)

is

the

lethargy,

that

is,

log

Eo/E where

E

is

neutron

energy.

The

range

of

lethargy

is

subdivided

into

3

to

15

intervals,

and one thinks

of

the

neutrons

as

classified

thereby

into

"energy-groups"

or

simply

"groups".

The

first

step

in

the

solution

of

a

MUG

problem

is

to

assume (by

that

I

mean

guess)

the

pmver d i

s-

tribution,

that

is,

the

rate

per

unit

vol

urn

e

per

unit

time

of

fission

t-vhere

one f

iss

ion

produces

2-1/2

neutrons

of

various

e n

erg

ies

.

Then,

for

each

regionette

(that

is,

two

space

and one

energy

interval)

tve

compute

the

rat

e

of

occurrence

of

neutron

collisions

of

e a c h

type,

namely:

elastic

scattering,

inelast

i c

scattering,

absorbtion,

and

fission

..

From

this

is

computed a

new

power

guess

and

aft

era

thorough

accounting

of

the

neutrons

tV

ear

e

supplied

with

the

computer's

power

result

..

This

accounting

process

resembles

a

busi-

ness

type

problem

for

it

is

here

necessary

to

record

for

each

regionette

how

many

neutron

s

are

coming

in

energy-tdse,

going

out

en

erg

y-

wise,

coming

in

space-wise,

going

out

spa

c e -

wise,

getting

born

from

fission,

and d

yin

g

a s a

re

suI

t 0 f

be

i n

gab

s 0 r

bed

..

'Ibis

rOOthod

can

account

for

up

to

500

blocks

of

output.

The power computed by

the

machin e

is

the

result

of

one

step

in

an

iterative

pro-

cedure

and

is

used as

the

power

guess

for

the

Thus a

successive

approx

ima

t

ion

method

is

necess

ar.y

to

do

one problem..

The

res

ul

t

from

this

is

a

fairly

good

guess

for

the

pmver

of

the

first

run

of

a

new

probl

em.

-13 -

(cont'd

on

page

25)

WORD

LENGTH

IN

DIGIT

AL

COMPUTERS

D.

McCRACKEN

General

Electric

Co.,

Aircraft

Gas

Turhine Div.

Cincinnati

15, Ohio

Most

computers of

any

size

are based

on

the

stored

program

principle,

which

implies

that

the

instructions

which

define

the

problem

for

the

machine

are

stored

-in

its

roo

mo

ry ,

along

tvith

the

data

of

the

problem. Almost

all

pre-

sent

computers

are

buil

t

tvi

th

"common

storage",

that

is,

any.

storage

location

may

contain

either

data

or

instructions.

(The

major

exception

is

the

Harvard

Mark

IV).

In

any

case,

the

compu-

ter

is

able

to

make

arithmetical

modifications

and

tests

on

its

instructions.

This

capacity,

together

t\li

th

the

ability

to

make

conditional

transfers

or

jumps

to

other

parts

of

the

pro-

gram,

gives

the

stored

program computer

its

great

advantage over

early

automatic computers,

in

which

the

program

was

~utside

of

the

memory

of

the

machine.

There

is

a

conflict,

hotvever. Assuming

common

storage,

and

assuming

for

the

moment

that

the

storage

locations

are

of

definite,

fixed

capacity,

hOlV

many

digits

should a

mem-

ory

location

contain?

What

should

the

"tvord

length"

be?

For most

scientific

tvork,

and

wi

th

pre-

sent

memory

sizes,

it

turns

out

that

about

ttvice as

many

digi

ts

are

needed

for

numbers

as

for

instructions.

How

is

this

conflict

resol-

ved

in

present

machines?

1.

One

straightfo~vard

solution,

mention-

ed above

for

the

Harvard

Mark

IV,

is

to

bypass

the

problem

by

building

two

separate

memory

stores

for

instructions

and

numbers, with

the

most convenient

size

for

each.

It

is

of

course

possible

to

allotv

for

arithmetical

modifica-

tion

of

the

instructions.

This,

however,

con-

stitutes

an

extra

burden

on

the

designer,

and

besides

restricts

the

flexibility

of

the

com-

puter

since

there

is

qo

choice

of

the

ratio

of

instructions

to

numbers. This

solution

will

likely

be

used

in

the

future

only

for

special

purpose machines.

2.

Another

solution

is

to

make

the

mem-

ory a convenient

size

for

numbers,

and

waste

the

extra

space

when

an

instruction

is

stored.

This

solution

is

read

in

just

this

way

in.

the

DATATRON;

and

to

a

limited

extent

in

all

ma-

chines.

In

the

IBM

704

six

binary

digits

are

tvasted

in

most

instructions.

In

any

computer,

space

is

t.\'asted

Ivhen

a

particular

instruction

does not

require

an

address,

as

for

instance

the

rounding

instruction.

3.

A very

common

solution

is

to

use

more

than

one

address

for

each

operation.

This

makes

the

designers

work

a

little

harder,

but

the

view has

evidently

been

held

in

many

cases

that

it

was

a

better

solution

than

other

alter-

natives.

And

of

course

many

users

feel

that

multiple

address

instructions

are

better

from

a programming

standpoint.

The

IBM

650 uses a second address

to

spec-

ify

the

location

of

the

whim

is

particularly

useful

in

a magnetic

drum

ma-

chine.

Since

the

second address does

not

re-

fer

to

data,

this

is

usually

called

a modified

one-address machine.

The

ERA

1103 uses

two

addresses

for

data,

as

do

the

ELECOM

120 and

125,

and

a

fetv

others.

The

NORC

and

others

use

three

addresses

for

data.

The

SWAC

uses

a modified

three

address system, where

the

fourth

address

specifies

the

location

of

the

4.

A

fairly

common

solution

is

to

put

two

one-address

instructions

into

one number-

size

location.

This

is

the

technique used

on

the

UNIVAC,

IBM

701, and

the

instances

of

the

Institute

for

Advanced

Study machines:

the

lAS

machine

itself,

MANIAC,

JOHNNIAC,

ILLIAC,

and

others.

This

creates

a

new

problem while

solving

the

first

one.

Some

way

must be found

of

identifying

the

two

halves.

The

half-word-

'full-t.vord scheme

gives

each

half

an

address,

then uses

an

indicator

in

the

instruction

to

distinguish

between

half

and

full

words. Other

methods give only

one

address

to

bothp

requir-

ing.

therefore

that

in

order

to

qo

arithmetic

on

an

instruction

it

must be

known

which

half

of

a

word

contains

the

instruction.

This

makes

relative

programming

difficult.

Such a

systen

is

an

added nuisance

to

programmers,

and

is

especially

annoying

to

beginners.

5.

A

more

recent

attack

is

to

sidestep

the

issue

by

making

th~

length

of

the

number

variable.

Instructions

remain

of

fixed

length,

but

numbers

may

be

of

any

size

from

one

digit

up

to

a

maximum

Ivhich

is

much

larger

than need-

ed

in

practice.

The

IBM

702

and

705

are

built

on

this

principle.

It

necessarily

implies

a

serial

machine,

tv!

th

a consequent

loss

of

speed

over

parallel

operation.

It

is

particularly

attractive

to

commercial

users,

who

have

no

uniform requirement

of

number

size.

Although

it

is

not

at

all

clear

at

this

tiroo,

the

prin-

ciple

may

turn

out

to

be

also

desirable

for

-

14

-

'Nord Lengtf-.

the

scientific

user.

It

certainly

simplifies

matters

when

it

is

necessary

to

carry

more

dig-

its

than

the

fixed

word

length.

On

the

other

hand,

it

is

difficult

to

conceive

of

a

variab~

word-length machine

with

built-in

floatin

g

point.

The

last

shot

has

not

been

fired

in

this

battle.

What

are

the

present

trends?

One

trend

which

is

slowly proceeding

to

alter

the

pic-

ture

is

the

move

to

larger

word

length.

The

IBM

704

uses

15

binary

digits

to

identify

the

addresses where

its

predecessor,

the

701,

need-

ed only 12.

We

hear

of

machines

in

the

generation

which

in

binary

would

re-

quire

17

or

18

binary

digits.

This

of

course

is

a slow

trend.

Each

additional

binary

dig-

it

represents

a doubling

of

memory

capacity.

It

is

rather

unsafe

predicting

maximum

sizes

or

speeds

of

computers very

far

in

the

future,

but

presumably

increased

memory

size

a

Ion

e

cannot

solve

the

problem.

There

is

a

fairly

strong

trend

to

go

to

variable

word-length.

This

will

probably

ex-

tend

to

other

machines.

An

immediate

extension

of

variable

num-

ber

length,

although

it

has not appeared

in

any

current

computers,

is

variable

instruction

length.

Imagine

an

instruction

format

in

memory

like

this:

*Operation, address *

operation,

address~

Here

the

asterisk

represents

some

sort

of

mark

or

separator

between

instructions

as betwe.en

numbers.

This,

of

course', need

not

actually

use

up

a

digit

position

in

memory.

Now

sup-

pose

further

that

the

operation

part,

which

would always

consist

of

one

or

two

characters,

is

read

into

the

control

section

first.

It

is

not too

difficult

to

imagine

circuits

which are

fast

enough

to

decode

the

operation

part

in

time

to

decide

whether

an

address

is

necessary

with

this

particular

instruction.

If

none

is

needed, as

on

a rounding

instruction,

there

need be

no

address

in

memory,

and

we

have

sav-

ed

four

or

five

digit

positions.

Furthermore,

if

we

consider

a decimal

machine which has 100,000

digits

of

storage,

as

many

as

five

digits

may

be allowed

for

the

address.

If

a

particular

address

require

s

only

two

or

three

digits,

only

that

many

need

be

written,

since

the

control

circuits

can

sense

the

"end-of-instruction"

mark.

On

an

instruction

tvhich

refers

to

the

lOtI/-numbered

section

of

memory,

this

device

saves about a

third

in

instruction

length.

Such a system

has enough advantages

that

it

is

surely

being

considered

by

manufacturers.

In

conclusion,

we

can observe a

continu-

ing

struggle

between

builders

and

users.

Al-

mos

t always a

choice

is

to

be

made

between sim-

plicity

of

design,

and

simplicity

or

brevity

or

convenience

of

programming. III

us

trations:

some

early

machines used complements

to

repres-

ent

negative

numbers;

some

early

machines had

no

divide

order;

only

recently

have

built-in

floating

point

machines been

hvailable.

As

a

rough

generalization,

we

may

say

that

in

early

machines,

the

builders

won

the struggle;

bu

t

from

now

on,

the

users

will

win.

Mcchines

will

become

more

complex structurally

:in

order

to

simplify

or

make

more

powerful the

tvork

of

the

progrnmmer.

Along

with

this

trend

is

an

unsettled

issue

as

to

whether

to

build

machines with

many

and

p<X\'erful

ins

truc

tions,

or

to

concentrate

on

making

a

ma-

chine

with

fewer and

simpler

instructions,

but

which

is

very

fast.

The

impact

of

these

considerations

on

word

length

in

computers

will

depend

to

a

lar~

extent

on

experience

td

th

machines

now

begin-

ning

to

come

into

wide

use.

It

is

certainly

too

early

to

ask

for

standardization;

too

many

possibilities

rem~in

to

be

tested.

-

END

-

*----------*

----------~

SOLVING

PROBLl<:MS

(cont'd

from

page

9)

solver

I have

just

described

required

consid-

erably

less

than

one

man

year

for

its

constnc-

tion.

The

immediate

stimulus

for

its

const~

tion

was

a

matrix

of

order

190

to

be inverred.

This

matrix

has been

inverted,

and

the

inverse

has been used and

will

be

used

repeatedly

for

obtaining

the

solution

of a number

of

systems

having

the

same

matrix.

The

code

will

rertainly

be used

many

times

for

solving

other

systems

with

other

matrices,

and having been once

con-

structed,

the

code remains

available

for

use

as long as

the

Oracle

survives

in

its

present

form. Analogous remarks c oul d be

made

abo

u t

countless

other

codes, even

including

man

y

that

were

made

up

with no' thought

that

they

would be used

more

than once. Customers have

a

way

of

finding

that

they need

more

of

the

same.

I wish

to

emphasize again

that

I h a v e

made

no

effort

to

associate

a measure

of

util-

ity

with

the

Horner.

First,

this

differs

from

machine

to

machine

since

a one-Horner problem

on

one machine

could

be

several

Horners

on

an-

other,

perhaps even

10

or

so.

Again,

there

is

always

the

possibility

that

the

problem

did

not

need

to

be done

in

the

first

place.

The

physicists

are

among

the

major consumers, and

potential

consumers

of

Horners and

the

demand

among

them

is

great.

So

if

you

grant

they

are

worth

the

price,

I

think

one

thing

is

c 1 e a -r.

On

the

computing machine

we

are

all

Macph~ons.

Hence,

if

we

wish

to

save

the

jelly

we

need to

exercise

some

care

to

prevent

the

piece

from

falling.

_

END

_

-

15

-

A GENERAL

CURVE

-

FITTING

SUBROUTINE

FOR

TRANSCENDENTAL

FUNCTIONS

ROBERT

H.

BRACKEN

Research

nepartment

Naval

Ordnance

Test

Station

China

Lake,

Calif.

Introduction

A method

is

presented

in

this

report

to

obtain

a

least

squares

fit

to

n

points

using

a

transcend-

ental

function

of

the

general

form

~

::

A{

(<<

J

~~

'X)

+-

e::.

o

(D<',

~\')()

+ C

where

A,

B,

and C

are

linear

parameters

,and

f)(

and p

are

nonlinear.

Any

given

function

may

have:

zero

to

three

1

inear

parameters,

zero

to

two

nonlinear

parameters,

and one

or

two

separate

terms

each

containing

the

independent

variable.

Thepro-

gramming

to

compute

each

term

in

the

function

is

all

that

is

necessary

before

the

method, which

is

coded

in

subroutine

form,

can

be

used.

The s

ub-

routine

is

easy

to

use

and

utilizes

a

searchin

g

technique

for

functions

containing

nonl

inear

p

a-

rameters

in

which

accurate

guesses

of

the

fir

s t

estimates

are

not

necessary.

All

sums

of

squares

and

cross

products

are

computed

in

fixed-p

0 i n t

double-precision

arithmetic

which

assures

a

high-

degree

of

sensitivity

to

a

fit

and

eliminates,

in

most

cases,

the

necessity

for

scaling

the

in

d

e-

pendent

variable.

Discussion

Inception

A

considerable

amount

of

curve

fitti

n g i s

done

using

polynomials

because

of

their

simplicity

and

flexibility,

and

computing

installations

have

standard

programs

which

can

handle

these

problems

from

beginning

to

end

by

indicating

only

the

degree

of

the

polynomial

to

be

used.

However,

there

are

numerous

nonHnear

relationships

in

scienc

e i n

l'lhich a

transcendental

function

is

exp

e c

ted

t 0

represent

the

relationship

and l'lhich

in

most cases

cannot

be

reduced

to

a

simpler

form

by

considering

functions

of

the

variables

as

new

variables.

The

problem

of

fitting

these

functions

to

a

set

0 f

points

is

not

nearly

as

simple

as

that

of

fitting

polynomials

and

can

be

solved

only

by

tedious

nu-

merical

methods.

One

of

the

most

frequently

ap-

plied

is

the

Least

Squares

Differential

Correction

Method and

is

most

useful

when a

function

contains

several

nonlinear

par~meters.

When

applying

the

method

to

a

high-speed

computer

using

age

n

era

1

purpose

program, one must

first

code

the

prog

ra

m

steps

necessary

to

compute

the

given

function

and

the

partial

derivatives

with

respect

to

each

pa-

rameter.

Als 0 good

ini

ti

al

estimates

0 f e a c h

parameter

must be

used

since

the

terms

of

degree

higher

than

the

first

were

neglected

when

us

in

g

Taylor's

series

expansion

in

linearizing

the

nor-

mal

least

square

equations.

The

ideal

programfor

this

type

of

curve

fitting

would be one which

re-

quired

no

additional

coding

by

the

user,

but

0 f

course

is

impractical

if

not

impossible.

.Consider

nOlt

only

that

class

of

transcend-

ental

functions

containing

two

or

less

nonlinear

parameters,

three

or

less

linear

parameters,

and

one

or

two

separate

terms.

With

regard

to

c

urv

e

fitting,

this

class

of

functions

is

used

exrensive-

lye

Therefore,

a method

of

curve

fitting

appli-

cable

to

this

class

seemed

desirable

if

the

coding

by

the

user,

the

computing

time,

and

the

necessity

of

closely

estimating

the

parameters

could

be

sig-

nificantly

decreased

with

respect

to

other

methods.

General

Characteristics

of

Method

Returning

to

the

general

transcendentalfunc-

tion

~

= A {(o(,

p,')C)

+ e

~(oI,F"?C)

+C

Let

v = {(o(,

F>'~)

J

ur

::

'3

(0(,

~,?()

Then y

-=

A v + B w- + C

Assuming

0<.

and

f->

are

constant,

then

the

sum

of

the

squares

of

the

residuals

will

be a f

unc

t

ion

of

the

three

parameters

A,

B,

and C

only.

Denot-

ing

this

function

by G(A,B,C)

the

normal

equations

c an be

obtained

by

setting

the

three

parti

al

d

e-

rivatives

of

G

to

zero.

Solving

the

normal

equa-

tions

yields

the

values

for

A,

B,

and C which

can

then

be

used

to

compute

the

sum

of

squares

of

the

residuals.

By

applying

a two-lvay

searching

tech-

nique,

new

values

of

0< and

(!J

are

selec

ted

and

the

computations

repeated

until

the

sum

0 f

squares

of

the

residuals

has

converged

to

a

mini-

mum.

It

should

be

noted

that

neither

the

partial

deri

vati

ves

of

y wi

th

respect

to

the

non

1

in

ear

parameters

nor

estimates

of

the

linear

parameters

were

required.

Justification

for

this

method i s

based

on

being

able

to

eliminate

these

part

i a 1

derivatives

by

utilizing

the

speed

of

modern com-

puters

with

respect

to

trial

and

error

solutions.

The

searching

technique

assumes enough

is

known

about

0< and

~

that

upper

and

lower

bounds

may

be

assigned

to

each.

The

first

values

used

will

then

be ones which

are

half

way

between

the

upper

and

lower

bounds.

Once

the

first

sum

of

squares

is

obtained

the

initial

values,

IX,

and~.

are

changed

to

0(2.

and

~2.

res

pecti

vel

y t lvh

ere

o<~=

O(,+AO<t~2.O::~,

+

.t::>~.

A

second

sum

of

squares

of

the

residuals

is

computed

and

compared

against

the

first.

From

this

point

the

logic

of

the

search

is

best

explained

by

the

fol-

lowing

example.

-16 -

Let

Ri

equal

the

sum

of

squares

of

the

resid-

uals

at

stage

i

(see

Figure

1 on page

18).

If

~.c::::

RI,

proceed

in

same

direction.

If

RI

< R

2,

reverse

direction

by

set

tin

g

P<::a.

==-

tX'. -

60<.

and

(3'2.

=

tJ.

-

b.~

•

Assuming

the

former

is

true,

then

R3

is

computed

and compared

with

R2.

If

R3

c:::::

R2, P

roc

ee

din

same

direction.

If

R2~

R3'

the

logic

of

the

Curve-Fi

ttinl!

"u·'routine

search

remembers

that

R2

~

Rl

i

the

ref

0 r e ,

control

card

"tells"

the

curve

fitting

subroutine

o<~

=-

o(~+AC)(

)

~~

-=

~::a.-

Ap

. No

til,

if

the

number

of

linear

and

nonlinear

parameters

and

R4

~

R

2,

Rs

will

be

computed.

Also

R6

if

R5

<:

R4•

the

number

of

terms

in

a

given

function.

It

also

N

'%

~

%

R'

t d

If

R

---

R

contains

the

number

of

points

n

to

be

used

in

the

01'1

assum1ng - 7

1S

compu e •

5-

7,

- f 1

, , ' ,

f1t,

the

upper

and

lower

bounds 0

each

non

inear

R8

1S

computed and

1f,less

than

R5

the

se~r~h

con-

parameter,

the

original

deltas,

and

the

number

of

eludes

t~at

the

funct10n

G(A,B,C),

has

a m1n1m u m

times

to

decrease

the

original

deltas.

The

final

when 0<.

1S

equal

to

s~me

value

lyIng beu'lCen

(O(I-+~)

step

is

the

actual

running

of

the

problem

by

load-

and

~,+4~OC)

and

fJ

1S

equal

to

some

value

1~1ng

ing

the

'instructions,

control

card,

and

data

into

between

~,

, and

(tl,

-

2A~).

A

new

s

tar

t 1 n g

the

701 and

starting

the

computations.

point

is

then

selected

ldthin

the

nel'l

bounds

by

comparing

the

computed R lSi

the

original

deltas

are

decreasedi

and

the

search

continued.

This

process

is

repeated

until

satisfactory

values

for

0<

and

~

have

been

determined.

It

is

important

to

note

that

when bad

values

are

initially

used

for

~

and

~

,

the

searching

technique

can

very

t'lell

converge

upon a

false

min-

imum.

This

does

not

me'an

that

good

initial

v a

l-

ues

must be

used

but

rather

that

the

best

available

ones be

used.

False

minimums become

obvious

when

a computed

parameter

differs

significantly

from an

estimate

of

the

same

parameter

obtained

ex

per

i-

mentally.

Application

to

the

IBM

701

Calculator

When

coding

the

method

for

the

IBM

701 C a

1-

culator,

the

concepts

of

subroutines

and programs

were

used.

Possibly

the

term

"subroutine

program"

should

replace

"subroutine"

in

the

ti

tie

of

th

i s

paper.

However,

since

the

method

can

be

used

to

fit

a

general

class

of

transcendental

functions

to

a

set

of

points

when

the

functions

themselves

are

not

explicitly

defined,

the

term

subroutine

seems

more

appropriate.

It

is

difficult

to

explain

fully

how

the

sub-

routine

is

applied

to

a

given

curve

fitting

pro

b-

lem

unless

one goes

into

the

details

of

the

p r

0-

cedure,

assuming

of

course,

that

not

every

reader

is

familiar

t'lTith

the

701.

However, a

general

de-

scription

of

the

procedure

will

show

that

a

minirmun

amount

of

effort

is

required

when

using

the

sub-

routine.

To

begin

t'li

th,

one

needs

to

code

only

the

necessary

instructions

for

computing

van

d w •

Storage

is

available

for

any

subroutine

use

din

the

computations,

and

the

coder

assumes

that

()(

,~

,

and %

are

available

in

three

specific

locations.

The

linkage

between

the

coding

and

the

curve

fit-

ting

subroutine

is

supplied

by

21

basic

instruc-

tions.

These

instructions

also

contain

informatim

used

by

the

subroutine

l1/hich

allows

for

c omp

lete

flexibility

in

assigning

the

decimal

point

to

all

data,

variables,

constants,

and

parameters.

Th

e

instructions

and any

subroutines

are

then

put

into

machine

language

by an assembly

program.

The

time

required

to

complete

the

coding

will

vary

depend-

ing

on

the

function

being

used.

In

fitting

the

curve

-1It.?('

-~')('

~

=

Ae

+ B2. + C

the

coding

time

would be

approximately

30

minutes.

After

coding,

a

control

card

is

prepared,

and

the

x and y

observations

punched on

cards

using

a

standard

input

card

form.

The

information

on

the

-17 -

An

important

function

of

the

subroutin

e i s

that

all

coefficients

of

the

normal

least

squares

equations

involving

sums

of

squares

and

c r 0 s s

products

are

computed

using

fixed-point

d 0

ubI

e-

precision

arithmetic.

Thus,

it

is

possible

t 0

carry

along

1

arge

numbers

in

the

comp

uta

t

ion

s

tvithout

having

to

drop

significant

digits.

Also,

only

those

terms

necessary

in

solving

for

the

linear

parameters

are

computed.

To

clarify

this

remark,

assume

the

parameter

C

is

missing

from

a

given

function,

then

the

terms

~

'It

,,ZI.Ir,-

and

:2:

~i.

would

not

be computed as

they

are

not

use

din

solving

for

A and B.

Upon

reaching

a

solution,

the

parameters,the

original

x and y

values,

the

computed y

val

u

es,

the

squares

of

the

residuals,

and

the

sum

0 f

squares

of

the

residuals

will

be

printed.

An

ad-

di

tional

feature

allows

one

to

print

the

parameters

and

the

sum

of

squares

of

the

residuals

a

tan

y

time

during

the

computations.

This

f

eat

u

rei

s

used

when

there

are

nonlinear

parameters

in

a

func-

tion,

and

it

makes

it

possible

for

the

mathemati-

cian

to

watch

the

progress

of

the

search.

It

should

be

made

clear

that

all

input

and

output

functions

are

included

in

the

curve

fitting

subroutine.

Als

0,

there

are

several

b u i 1 t - i n

checking

devices

which

will

recognize

errors

made

by

the

coder

or

by

the

701.

Timing

Statistics

The

following

illustrative

timing

statistics,

obtained

when

using

the

curve

fitting

subroutine,

may

best

evaluate

the

subroutine

with

respect

to

computing

time.

Given y = A

log

x+Bx

+ C

with

N = 100 and

10

~

x

~

10,000

:>

500 = y

~

1200

Since

there

were no

nonlinear

parameters

in

t

his

function,

the

searching

technique

was

ignored,

and

the

normal

equations

solved

for

A,

B, and

C.

The

actual

computing

time

was 3

seconds,

while

readmg

in

the

data

and

printing

the

results

took

approx-

imately

54

seconds.

The same

function

was

use

d

wi

th

189

data

sets,

of

10

points

each,

and

the

total

time

for

card

reading,

computing

I and

print-

ing

was 23

minutes.

~

-«-x

Given y =

Ae

+ C

wi

th

N = 16 and 0 <

eX

~

5 ,

.6.0(

divided

by 10

three

times,

.h.o<

=

0.2,

O. 05

~

x ~

1.

4,

0.1

~

Y

~

0.3

.

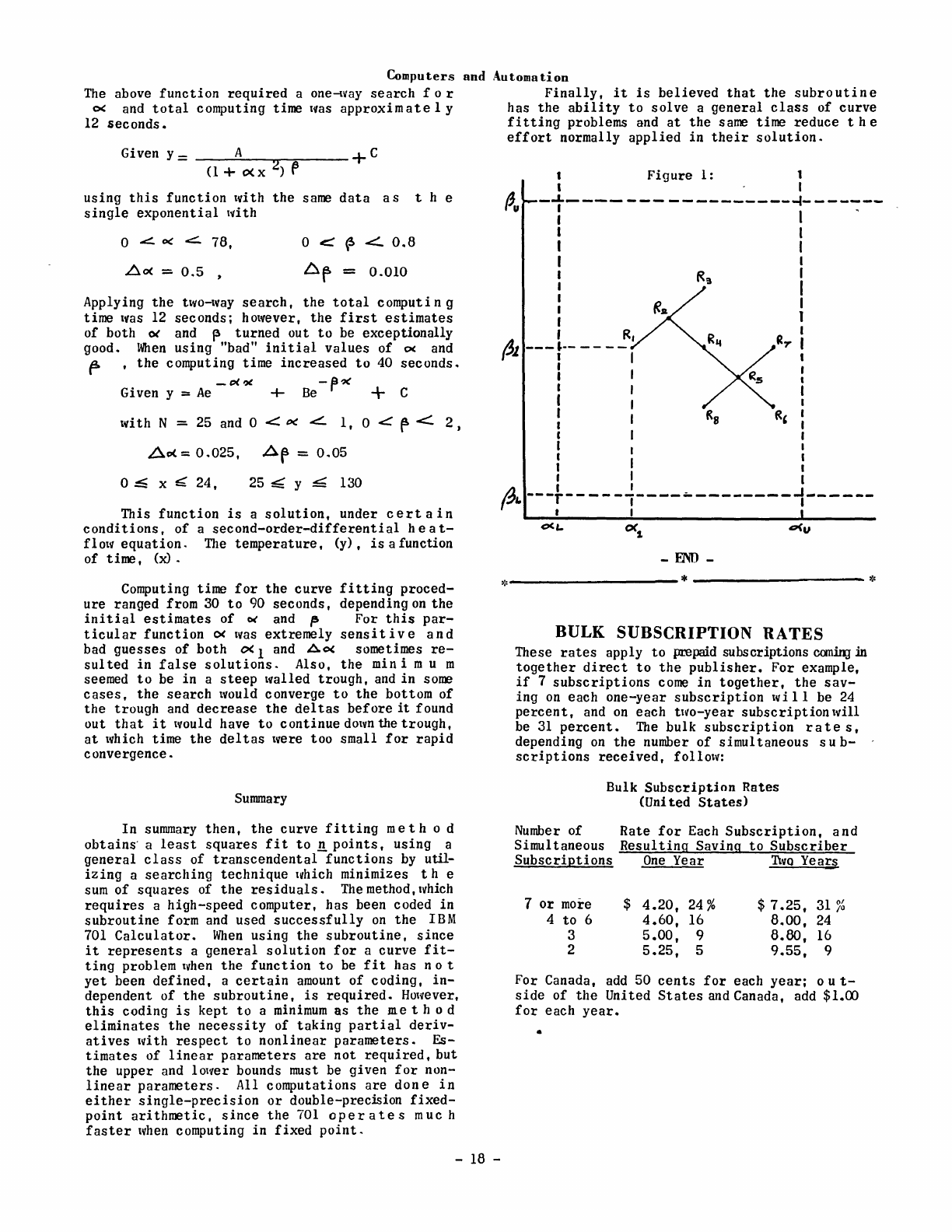
Computers

and

The above

function

required

a one-way

search

for

,.\utomation

0<

and

total

computing

time

tfaS

approximate

1 y

12

seconds.

Gi ven y =

__

.....;A~_.....-....",...

___

+ C

(1

+

cXx

2)

P

using

this

function

with

the

same

data

as

the

single

exponential

with

o

..c::::.

0<

.c:::;,

78,

..60( =

0.5

o

c::

~

0.8

L:\r

-

0.010

Applying

the

two-way

search,

the

total

computing

time

tvas 12

seconds;

however,

the

first

estimates

of

both

0(

and p

turned

out

to

be

exceptionally

good.

When

using

"bad"

initial

values

of

0<

and

~

,the

computing

time

increased

to

40

seconds.

-p(I)(:

-P«

Gi ven y =

Ae

+

Be

+ C

tvi

th

N = 25 and 0

<::

D<

~

1,

0

<:

~

c:::::.

2)

,Ao< =

0.025,

Ar

=

0.05

o

~

x

~

24,

25

~

y

~

130

This

function

is

a

solution,

under

c

ert

a

in

conditions,

of

a

second-order-differential

he

a

t-

flow

equation.

The

temperature,

(y),

is

a

function

of

time,

(x).

Computing

time

for

the

curve

fitting

proced-

ure

ranged

from

30

to

90

seconds,

depending

on

the

initial

estimates

of

~

and

~

For

this

par-

ticul

ar

function

0<

tvas

extremely

sens

i t i v e

and

bad

guesses

of

both

0< 1 and

AO(

sometimes

re-

suI

ted

in

false

solutions.

Also,

the

min

i

mum

seemed

to

be

in

a

steep

tvalled

trough,

and

in

some

cases,

the

search

would

converge

to

the

bottom

of

the

trough

and

decrease

the

deltas

before

it

found

out

that

it

would have

to

continue

dotYn

the

trough,

at

which

time

the

deltas

tvere

too

small

for

rapid

convergence.

Summary

In

summary

then,

the

curve

fitting

meth

0 d

obtains'

a

least

squares

fi

t

to

.!l

points,

using

a

general

class

of

transcendental

functions

by

util-

izing

a

searching

technique

which

minimizes

the

sum

of

squares

of

the

residuals.

The method, tvhich

requires

a

high-speed

computer,

has

been

coded

in

subroutine

form

and

used

successfully

on

the

IBM

701

Calculator.

When

using

the

subroutine,

since

it

represents

a

general

solution

for

a

curve

fit-

ting

problem

when

the

function

to

be

fit

has

not

yet

been

defined,

a

certain

amount

of

coding,

in-

dependent

of

the

subroutine,

is

required.

However,

this

coding

is

kept

to

a minimum

as

the

me

tho

d

eliminates

the

necessity

of

taking

partial

deriv-

ati

ves

t'Vi

th

respect

to

nonlinear

parameters.

Es-

timates

of

linear

parameters

are

not

required,

but

the

upper

and 10l1er bounds must be

given

for

non-

linear

parameters.

All

computations

are

don

e

in

either

single-precision

or

double-prec~ion

fixed-

point

arithmetic,

since

the

701

operates

muc

h

faster

when

computing

in

fixed

point.

-18 -

Finally,

it

is

believed

that

the

subroutine

has

the

ability

to

solve

a

general

class

of

curve

fit

ting

problems

and

at

the

same

time

reduce

the

effort

normally

applied

in

their

solution.

1

Figure

1:

1

I I

(Ju

-t----

---

----------1-

----:--

I I

I

R~

I

I I

: 1

I

R,

R7'

II

~l

---~--

--

--I

I

I :

I I

I

Rs

R,

:

I I

('9

..

---r-

- - -

-1-----

---------1------

t I

-

END

-

*--------------------*

*

BULK

SUBSCRIPTION

RATES

These

rates

apply

to

prepaid

subscriptions

canirg

in

together

direct

to

the

publisher.

For

example,

if

7

subscriptions

come

in

together,

the

sav-

ing

on

each

one-year

subscription

will

be 24

percent,

and

on

each

th'o-year

subscription

will

be

31

percent.

The

bulk

subscription

rate

s,

depending

on

the

number

of

simultaneous

s u

b-

scriptions

received,

follow:

Bulk

Subscription

Rates

COni

ted

States)

Number

of

Simul

taneous

Subscriptions

7

or

more

4

to

6

3

2

Rate

for

Each

Subscription,

and

Resulting

Saving

to

Subscriber

One

Year

1\VQ

Years

$

4.20,

24 %

4.60,

16

5.00,

9

5.25,

5

$

7.25,

31

%

8.00,

24

8.80,

16

9.55,

9

For

Canada, add

50

cents

for

each

year;

0 u

t-

side

of

the

Onited

States

and Canada, add

$1.00

for

each

year.

METHODS

IN

HIGH SPEED COMPUTATION

FINAL EXAMINATION

JOHN

W.

CARR,

III

Uni

versi

ty

of

Michig-an

Ann

Arbor,

Michi~n

Here

is

a copy

of

the

final

(closed

boo

k )

examination

given

January,

1956,

in

Mat

h 1 7 3 ,

"Methods

of

High Speed

Computation".

It

may

be

of

interest

to

readers

of

"Computers and

Automation".

It

is

mainly

self-explanatory,

except

for

problem

5,

which

describes

the

384-bi

t

MIDAC

roorcury

delay

line

storage

uni

ts,

tvi

th

48-bi

t words

inc

1 ud i n

~

45

bits

of

information,

and a

46th

bit

pari

t y

digit

for

~

parity.

1.

(One

Hour)

In

Problem

2 you

will

be

asked

to

program one

of

several

alternative

problems.

In

this

problem

you

are

asked

to

des

i g n a

computer

and

set

up

an

instruction

cod

e

to

solve

one

of

these

problems.

Your

procedur

e

should

be as

foll~~:

0)

Pick

a

problem

in

2

that

you

will

sol

ve.

(2)

Set

up

the

specifications

and

instruc-

tion

code

for

your

computer.

These

specifications

must

include:

(a)

Fixed

point.

(b)

Single

address

instruction

code.

(c)

Satisfactory

input-output.

(d) Methods

to

alter

addresses.

(3) I

will

not

accept

any

freak

instruction

types

such

as

"Solve

Problem 2C. "

Nor

can

I

permit

a

complete

a r

ray

of

logical

operations

in

Part

2e.

Remember, I must be

able

to

follow

and

understand

the

program you

write

in

Problem

2,

so

please

give

me

complete

specifications.

You

have had

enoug

h

experience

by

now

to

devise

a

reasonable

computer.

Include

a

description

of

your

input-output

devices

and

internal"

registers

involved

in

instructions.

(N~TE:

I do

not

want

detailed

hardware

discussions).

2.

(30 Minutes) Using

the

instruction

code

and

computer

devised

in

Problem

1,

solve

~

of

the

following

problems.

(a) Read

in

a

matrix

and

vector

in

decim

a1.

Perform

the

matrix

by

vector

nmltiplication

n

:!£...

ai·

Xj

j = 1 J

for

an

arbitrary

value

of

n,

and p r i n t

out

the

result

in

decimal.

Use

a

cycling

procedure.

Do

not

forget

scaling.

(b) Read

in

a

sequence

of

256

20-cha

r

ac

t e r

alphanumeric

words.

Sort

them

in

pro

per

alphanumerical

sequence,

0-9,

a-Z.

Print

out

the

sorted

results

in

alpha

n u

me

ric

form.

You

may

use

any method

for

sorting

that

you

see

fit,

irrespective

of

the

time

required

for

sorting.

-19 -

(c) Program

four

separate

floating-point

sub-

routines,

in

a

standard

subroutine

for

m

of

your

OlVn

choosing,

for

add,

subtrac

t,

multiply,

and

divide.

(d)

Spdcify

your

own

conventions

for

and

then

program a

subroutine

which,

upon

overflow,

automatically

prints

out

the

machine's

ins

truc

tion

counter,

contents

of

its

pert-

inent

arithmetic

registers,

and

instruction

being

performed

along

with

the

word

"over-

flow",

and

stops.

Upon

restarting

it

t\fill

read

in

a

new

program

from

magnetic

tape,

perform

a

memory

sum,

print

out

the

sum,

and

stop.

(e)

Evaluate

the

following

logical

functio

n

for

all

possible

truth

table

combinations:

[

(A

• B)

~

(C,

0)

1 v

[(A

•

C)

~

(B •

0)]

(Your machine

is

allowed

only

one

logical

operation

relating

storage

and

arithmetic

uni

t)

•

(f)

Write

a

program

to

find

a

real

roo

t

be-

tween 0 and 1

for

the

polynomial

equation:

6~

+

3.

6~

-1.

7x

-

.80

= ° .

Print

out

the

answer

in

decimal.

(g)

Perform

social

security

calculations

for

a

list

of

20,000

employees

stored

on

mag-

netic

tape,

insert

the

newly-calculate

d

values

on

the

tape,

and

print

out

a

social

security

record

with

man's name,

year-to-

date

total

pay,

and

total

deductions.

(11)

Program a

routine

to

obtain

the

mean

and

standard

deviation

for

1000 numbers.

Do

not

program

the

square

root,

but

instead

set

up

complete

specifications

for

such

a

subroutine

and

inclUde

it

in

the

program

as

a

block.

Remember, Problems 1 and 2

will

be

judged

on

hOh'

well

I

can

follol'l

and

understand

t"hat you

did,

as

well

as

how

sound

and

imaginative

a

job

you

do.

3.

(20 Minutes)

Derive

a

procedure

for:

(a) Decimal

to

binary

conversion

0 f

mix

e d

(integer

plus

fraction)

numbers;

(b)

Binary

to

dec i-mal

conversion

0 f

mix

e d

numbers.

In

other

words,

present

a method

for

each

and

give

a

mathematical

justification

for

it.

(cont'd

on

page

21)

A

COMPUTER

PROGRAM

FOR

FINDING

ROOTS

ANDREW

D.

'lOOTfl,

Direc

tor

Rirkhack

College

Computational

Laboratory

Uni

v.

of

London

London,

W.

C.

1.,

England

In

recent

years

there

has been

considerab

1 e

discussion

about

automatic

programming.

Unfortu-

nately

most

of

the

published

data

on

this

subject

has been

of

a

very

general

kind

and

gives

1

it

tl

e

information

regarding

the

manner

in

which a

rea

1

automatic

program

actually

works.

It

is

the

purpose

of

this

paper

to

desc

r

ibe

a program which

has

been

used on A.P.E.{X.)

C.

(an

electronic

digital

computer

at

this

Laborator0

for

the

investigation

of

the

real

roots

of

polynomials.

The

only

claim

that

this

particular

program has

to

be

called

"automatic"

lies

in

the

facts,

th

a

tit

determines

the

degree

of

the

polynomial

from

the

co-efficients

which

are

given,

and

that

it

locates

the

roots

accurately

after

making a

prelim

ina

ry

survey.

Since

it

was

originally

designed

toeval-

uate

the

roots

of

the

confluent

hyper-geometr

i c

func.tions

IFl(a,l,z)

tvhere a;:.

-1,

-2,

-3,

etc.,

it

is

assured

known

that

the

roots

are

real

and

posi

tive;

and

the

machine

automatically

stops

when

they

have

all

been

determined.

The

only

human

step

is

to

insert

the

tap

e

containing

the

coefficients

into

the

reader,

and

the

program

is

capable

of

dealing

with

polynomials

of

degree

not

exceeding

31.

From

this

point

on-

wards

the

operation

is

entirely

automatic

and

pro-

ceeds

as

follows:

1)

The machine

reads

the

tape

into

the

co-

efficient

storage

locations

after

passing

the

data

through

the

decimal-binary

conversion

sub-routin~.

2)

At

the

same

time

it

counts

the

number

of

co-efficients,

(n+1)

, and by

this

means

de

t e

r-

mines

the

degree

(n)

of

the

polynomial.

3)

Wi

th

the

count

number

evaluated

in

2),

the

polynomial

evaluation

routine

is

set

so

as

to

use

just

the

(n+1)

input

coefficients

and

notthe

(30 -

n)

other

values

possible

to

the

program.

4) The program

eval

ua2

es

tie

pol

y

nom

i a 1

P(z)

at

intervals

Z =

0,

2-

,

2~

,

3.2-

2

•••.

n.2-

2

5) The machine compares

the

s i g n 0 f

the

latest

value

of

p(z)

with

the

sign

of

that

previ-

ously

calculated.

If

a change

in

sign

has

oc-

curred,

the

program

for

finding

the

exact

root

is

suitably

modified

according

to

the

sense

of

the

change +

-=>

-,

or

-

~+.

In

the

event

of

a

si

g n

change

the

machine

to

6),

otherwise

to

7)

•

6)

The

root

is

evaluated

to

31

bit

P

re

c

i-

sion.

This

is

done by

the

process

of

"successive

trial

an~

comparison"

in

whiCh,

for

example,

i f

P (z -

2-)

is

positive

and P (z)

is

negative

the

value

of

P(z

-

2-

3)

is

calculated;

if

th

isis

positive,

P(z

-

2-

3

+2-4)

is

but

if

P(z

-

2-

3)

is

negative,

P(z

-

2-

3

-2-4)

is

the

This

process

continues

until

the

in-

terval

=

2-

31

has

been

reached

at

wgfch

point

the

value

of

(zr=

z::2-

3:f:.2-4

•••

2-

)

is

passed

to

the

binary-decimal

conversion

routine

and

is

then

printed.

It

is

followed

by

the

value

of

the

residual,

that

is

of

P

(zr).

Unity

is

now

s u

b-

tracted

from a

root-count

number and

the

res

u 1 t

is

tested

by means

of

a

conditional

transfer

i

n-

struction.

If

the

result

is

negative,

all

of

the

roots

have

been

found

and

the

program

stops.

If,

however,

the

result

is

positive,

it

is

stored

for

future

use,

and

the

program

passes

to

7).

7)

The

values

of

z and

of

P(z)

are

passe

d

through

the

binary-decimal

conversion

routine

and

are

printed

out.

The program

then

returns

to

4)

at

an

appropriate

point.

It

should

be mentioned

that

since

A.P.E.(X.)C.

operates

wi

th

numbers

in

the

ran

9 e

-1

~

z

~

l,

suitable

scale

factors

are

applied

to

z and

to

the

coefficients

so

that

the

results

of

the

calcula-

tions

remain wi thi,n

range.

Normally

this

process

must be

carried

out

by

the

programmer,

but

if

a

considerable

slowing

down

of

the

calculation

can

be

tolerated,

the

relevant

instJ;uctions

i

nth

e

following

program

may

be

modified

to

use

f10ating-

point

routines.

Since

most

readers

will

not

be

familiar

with

the

A.P.E.

(X.)C.

code,

the

program

is

written

in

a

verbal

form which

can

readily

be

trans

for

me

d

into

a

real

machine

code.

-20 -

A.l

Storage

locations

for

z,

P(z

-

2-

2)

cleared

to

zero

A.2

Coefficient

count

location

c 1

ear

e d

to

zero

A.3

Decimal-binary

conversion

sub-ro

uti

n e

modified

to

come

out

at

B.5

B.l

Tape

read

B.2

Result

non-zero,

proceed

to

B.3.

Result

zero,

end

of

coefficients,

proceed

to

B.7

B.3

9

lines

of

tape

read

(i.e.

8

decimal

digits

of

coefficient

and

sign)

B.4 Data

converted

to

binary

B.5

Coefficient

count

location

con

ten

t s

added

into

storage

location

digits

of

recora

instruction,

which

is

then

ex-

ecuted.

This

records

the

coefficient

in

its

correct

place

B.6

Coefficient

count

location

contents

in-

creased

by

unity.

Proceed

to

B.l

B.7

Coefficient

Gount used

to

set

C.3

and

0.15

to

correct

initial

values

C.l

C.6

restored

to

correct

initial

for

m

(See

0.2)

C.2

C.3

C.4

C.S

C.6

C.7

C.8

C.9

C.IO

C.ll

C.12

C.13

C.14

C.lS

0.1

0.2

0.3

0.4

O.S

0.6

0.7

0.8

0.9

0.10

0.11

0.12

Finding Roots

Accumulator

cleared

and Z

sen

t

to

mUltiplier

register

0.14

Value

of

P

(zJ

converted

and

printed

follol\led by

tabulation

s y

mb

01 s

for

page

layout

an added

to

accumulator

contents

Accumulator

contents

transferred

to

regis

ter

(R)

Order

C.3

modified

to

refer

toloca-

tion

a

1.

Resul

t

o?-

C.5

tested

to

sense

end of

evaluation

cycle.

Cycle

un-fin-

ished,

C.7.

Cycle

complete,

C.8

R

times

z formed

in

accumulator

C.3

Sign

of

number

P(z

-

2-2)

tested

and

compared wi

th

that

of

P (z) c 0

n-

tained

in

register.

If

signs

are

same,proceed

to

C.9.

If

different,

proceed

to

C.

15

P(z

-2-2)

tested

replaced

by

P(z).

Binary-decimal

convert

and p r i n t

sub-routines

modified

to

come

out

at

C.12

Z

storage

location

contents

c 0

n-

verted

and

printed

Binary-decimal

convert

and p r i n t

sub-routines

modified

to

come

out

at

C.14

Value

of

P (z)

converted

and

printed

followed

by

tabulation

symbo

1 s

for

page

layout

Contents

of

Z

s~orage

location

in-

creased

by

2-.

Proceed

to

C.2

P(z)

positive,

0.10

set

to

com

e

out

at

0.4.

P(z)

negative,

0.10

set

to

come

out

at

0.3

O.lS

set

to

coefficient

count

-2.

Probe

location

set

to

2-

3•

zr

set

with

value

of

z

reached

in

tabu-

lation

program

Instruction

C.6

modified

to

0

utp

ut

to

0.8

for

completed

cycle.

Pro-

ceed

to

0.6

Accumulator

contents

positive,

pro-

ceed

to

O.S.

If

negative,

p r

0-

ceed

to

0.6

Accumulator

contents

positive,

pro-

ceed

to

0.6.

If

negative,

p

ro-

ceed

to

O.S

Probe added

to

zr

Probe

subtracted

from

zr

Accumulator

cleared

and

new

val

u e

of

zr

written

in

multiplier

reg-

ister.

Program

sent

to

C.3

Probe

shifted

one

place

rig

h t

and

re-recorded

Probe

tested.

If>

0,

p

roc

eed

to

0.10.

If

zero,

proceed

to

0.11

P(zr)

to

accumulator.

Proceed

t 0

0.3

or

0.4.

(See C.1S)

Binary-dec

imal

convert

and p r i n t

routine

modified

to

come

0 u t

at

0.13

zr

storage

location

contents

c 0

n-

verted

and

printed

Binary-decimal

convert

and p r

in

t

routine

modified

to

come

out

a t

O.lS

0.16

0.17

Uni

ty

subtrac

ted

from

root-c

0 u n t

number

Result

tested,

if

positive,

proceed

to

C.IO;

if

negative,

proceed

to

0.17

Stop

-

END

-

*-------------------*-------------------*

FINAL

EXAMINATION

(cont'd

from

page

lQ)

4.

(10

Minutes)

Draw

a

flow

or

sequence

diagram

for

either

3(a)

or

3(b).

S.

(30 Minutes) The

follOldng

Boolean

tim

e

de-

pendent

system

of

equations

represents

logic-

ally

an

important

element

0 f

the

M I 0 A C •

Identify

the

element

in

the

machine and

explain

in

English

what

it

does:

Xn=

(~-384

• W

n) v

(Y

n• W

n)

X48K+46

= ( ....

«(X48K~

X48K+l)¢

X48K+2)

1=

X48K+3)

•••

=I:

X48K+4S)

State

what

function

the

pulses

X

n, W

n, Y

n, and

X48K+46

perform.

Here:

K=

0,

1,

2,

•••

7

6.

(30

Minutes)

Write

a

subroutine,

in

standard

MIOAC

conventional

subroutine

form,'

to

rea

d

in

a

block

of

words

from

the

drum,

perform

a

memory

sum,

taking

account

of

any

po

s

sib

1 e

overflows,

on

the

first

n-l

words,

and compare

the

anSlver wi

th

the

number

stored

in

the

n-th

\·wrd by a

similar

In

case

they

do

not

agree,

print

out

the

hexadec

im a 1

word

"badbadbadba"

and

stop

the

machine.

If

they

do

agree,

jump

out

of

the

subroutine

i n

the

usual

fashion.

Set

up

pertinent

specifi-

cations

for

the

subroutine.

Since

you

do

not

have

a

code

list

(closed

book),

do

the

b

est

you

can.

00

not

use

"present

address

reI

a-

tive"

but

code

in

floating

address

instead.

-

END

-

21

-

NEW PATENTS

RAYMOND

R.

SKOLNICK,

Reg.

Patent

Agent

Ford

Inst.

Co., Div.

of

Sperry nand Corp.

Long

Island

City

1,

New

York

The

following

is

a compilation of

patents

per-

taining

to

computers

and

associated

equipmen t

from the

Official

Gazette of

the

United

States

Patent

Office,

dates of

issue

as

in

d i

cat

e

d.

Each

entry

consists

of:

patent

number

/ invent-

ores) /

assignee

/

invention.

April 10. 1956: 2,741,734 /

Edward

O.

Johnson

and William

M.

Webster,

Jr.,

Princeton, N.J. /

Uni

ted

States

of America /

An

inverter

c i

r-

cuit.

2,741,756 / Arthur

C.

Stocker,

Collingswood,

N.

J.

/ Radio

Corp

..

of America, Del. /

An

electrical

data

storage

circuit.

2,741,757 / George C

..

Devol, Greenwich,

and

Erik

B.

Hansell,

East

Hartford,

Conn

..

/

George

C.

Devol

/ A magnetic

storage

and

sen

sin

g

device.

2,741,758 /

Seymour

R.

Cray,

MinneaJX>

1

is

, Minn. /

Sperry

Rand

Corp.,

Netf

York,

N.

Y.

/ A

mag-

netic

core

logical

circuit.

April 17. 1956: 2,742,227 / Frank

W.

Bub

b,

Dayton,

Ohio

/

Phillips

Petroleum Co., Del. /

An

electrical

computer

for

solving

simultan-

eous

equations.

2,742,566 /

Frederick

V.

Hunt, Belmont,

Norman

B

..

Saunders, Weston,

and

Robert

E.

Kirkland,

Dorchester, Mass. / United

States

of

America/

A demodulator device.. '

2,742,588 / Arthur V

..

' Hollenberg, Morris Plains,

N.

J

..

/

Bell

Telephone Lab.,

Inc.,

New

York,

N

..

Y

..

/

An

Electronic

amplifier

..

2,742,599 / Horst

M.

Schweighofer,

Cedar

Rapids,

Iotl'a

/

Collins

Radio

Co

..

, Cedar

Rapids,

Iowa /

A

shaft

positiQning

device.

2,742,615 / Joseph

O.

Preisig,

Mercervill

e ,

N

..

J

..

/ Radio

Corp

..

of America,

Del..

/ A

frequency

selective

circuit

..

2,742,632 / 'Ric.hard

L.

Whitely,

Haddonfield,

N.

J.

/ Radio Corp. of America, Del. / A

magnetic switching

circuit.

April 24. 1956: 2,743,355 / Robert

L.

Sin

k,

Altadena,

Calif

..

/ General

Electric

Company,

N.

Y.

/

An

automatic gain

control

circui

t

fo~

pulse

receivers.

2,743,359 / David Sayre,

Philadelphia,

Pa.

/

United

States

of America / A counting

circuit.

2,743,360 /

Russell

S. Stanton

and

GeorgeYucht,

Los

Angeles,

Calif.

/

Hughes

Aircraf

teo.

,

Del. / A

pulse-length

switching

circuit.

2,743,362 / Daniel Leed,

New

York,

N.

Y

..

/

Bell

Telephone Lab.,

Inc.,

New

York, N

..

Y.

/

An

2,743,367 /

Edwin

P. Felch

and

Francis

G.

Mer-

rill,

Chatham,

N.

Y.

/

Bell

Telephone

Lab.,

Inc.,

New

York,

N.

Y.

/ A frequency

mu

1 t

i-

plier

apparatus.

2,743,401 /

Raymond

W.

Moore

and

Willia

m

D.

King,

Buffalo,

N.

Y

..

, and

James

T.

Carleton

and

Loren F.

Stringer,

Pittsburg

h , P

a.

/

Westinghouse

Electric

Corp., East

Pittsburgh,

Pa. / A magnetic

amp!ifier

control

system.

2,743,430 / Melvin

L.

Schultz

and

George

A.

Morton,

Princeton,

N

..

J.

/ Radio

Cor

p.

of

America, Del. /

An

information storage device.

2,743,434 /

Hugh

B.

Flemdng,

Burlingame,Calif./

- / A system

of

carrier

current

distribution.

2,743,436 / David Gale,

Netf

York,

N.

Y./United

States

of America / A

navigation

computer.

May

1. 1956: 2,743,867 / Germain Gervais,

Riviere-a-Pierre,

Quebec,

Canada

/ -

An

in-

tegrating

counter

mechanism.

2,743,868 / William Wockenfuss, Brooklyn, N.Y./

Burroughs Corp., Mich. / A

sensing

device

for

a

perforated

card.

2,744,169 / Charles

Reed

Deming,

Venice,

Calif./

Hughes

Aircraft

Co., Culver

City,

Cal

if.

/

A

pulse

amplifier

circuit.

2,744,196 / Conrad

H.

Hoeppner, Washington,

D

..

C

..

, and Carl Harrison Smith,

Jr.,

Arling-

ton,

Va.

/ - / A pulse width

discriminator.

e,744,197/

Roland Marshall Gogolick

and

James

Gilmore Tabler, East Cleveland,

Ohio

/ Globe-

Union

Inc.,

Milwaukee, Wis. / A

fre

que

ncy

stabilizer.

2,744,223 /

James

F. English,

Jr.,

Lakewood,

and

Anthony J

..

Hornfeck, Lyndhurst,

Ohio

/

Bailey Meter Co., Del. / A servo

sy

s

te

m

including

an

electrical

inverter

circuit

•.

2,744,227 / Charles

W.

Spindler,

Jr.,

Norris-

town, Pa. / Leeds

and

Northrup Co.,

Phila-

delphia,

Pa. / A compensated

null-balance

servo sys tem.

2,744,240 /

Guy

N.

Hughes, Maryville,

and

Ralph

N.

Harder, Alcoa, Tenn. /

Aluminum

Co.

of America,

Pittsburgh,

Pa. / A system

for

integrating

D.

C

..

values.

2,744,242 /

Seymour

B.

Cohn,

Flushing,

N.

Y.

/

Sperry

Rand

Corp.,

Del

..

/ A

wave

guide delay

line.

May

8.

1956: 2,744,683 / John

W.

Gray, White

Plains,

N.

Y.

/ General

Precision

Lab.

Inc.,

N.

Y.

/ A

navigational

resolver-integrator

computer.

automatic frequency

control

..

2,744,955 / Arthur

Eugene

Canfora, Brooklyn,

N.Y

..

, Anthony Liguori, Hackensack,

an

d

-

22

-

(cont'd

on page 39)

AIRCRAFT-MARINE

PRODUCTS.

INC.

~

H

ARRISBURC.

PA.

).'''-,

,

THE

CELLULAR,

SHIELDED

FATCHCORD

SYSTElM:

The illustration shows how Berkeley Division

of Beckman Instruments, Inc.

is

using A-MP's new Patchcord System

in

its

new

EASE*

1200 Analog Computer.

.

~~li.E

~~S+~l'"

Aircra:ft-Marine

Products,

Inc.

GENERAL

OFFICE:

HARRISBURG,

PA.

A-M,;)

of

Canada,

Ltd., Toronto,

Canada

A-MP-Holland

N.V., 's-Hertogenbosch, Holland

Aircraft-Marine Products (G.B.) Ltd., London, England

Societe

A-MP

de

France, Courbevoie, Seine, France

*Trade mark, Berkeley Division

of

Beckman Instruments, Inc.

revolutionary

Cellular,

Shielded

Patchcord

Progra:r:n.rn.ing

System.

is constructed of molded nylon blocks alternated

with interlocking metal strips.

The

hole

in

each

block accommodates: standard patchcords,

co-

axial (shielded) patchcords,

or

special

"L"

type

shielded patchcords.

This

cellular system of construction pre-

vents

current

leakage from one circuit to an-

other, while providing all the advantages of

a metal patchboard. Its insulated surface and

flexibility of arrangement, spacing and color

coding offer exceptional versatility

on

com-

puters, test equipment, business machines,

and

all types of automated industrial and

militaryequiplnent

.

shield

-----r-

~~_+_-~~-spring

cell----

...

contact tip

(cont'd

from

page

13)

Operation

Unless

there

is

a good

guess

to

begin

wit

h ,

this

iterative

procedure

can

be

excruciati

n g

because

of

the

relatively

large

number

of

steps

necessary.

However,

it

can

be

effective

when

applied

to

a

sequence

of

problems

each

of

which

involves

only

a

small

variation

in

design

or

composition

from

its

predecessor.

This

als

0

makes

input

preparation

much

simpler

as

it

is

prepared

from

For

MUG

problems,

computations

require,

on

the

average,

about

an

hour

and a

half

per

problem.

Our

third

problem

is

a

two

dimensional

problem

called

BETTIS

54.

In

this

the

bas

i c

equations

are

IOOre

or

less

the

same

as

those

of

BETTIS

57.

The Geometry used

is

X Y

rather

than

the

r 9

or

r g

previously

used.

In

this

problem

the

description

of

the

reactor

use

d

is

more

flexible.

The

problem

utilizes

a

uni-

form

mesh

with

boundaries

allowed

a

Ion

g

the

mesh

and

it

may

progress

automatically

from

a

course

mesh

to

a

fine

mesh. With

such

a

two

group

code

it

is

often

necessary

to

spend

two

full

shifts

in

the

solution

of

one

pro

b I

em

consisting

of

12

or

13 power

iterations.

This

is,

of

course,

dependent

upon

the

n

um

be

r

of

points

and

the

rate

of

convergence.

Bot

h

BETTIS

57 and

MUG

problems

involve

the

simul-

taneous

solution

of

two

partial

differenti

a 1

equations

over

fairly

large

regions.

The

design

of

reactors

creates

more

prob-

lems

to

be done

than

there

is

machine

time

with

which

to

carry

out

their

solutions.

Our

dif-

ficul

ties,

consequently,

are

not

If

i t h

the

problems

themselves,

for

they

are

a

Ire

a d y

coded,

but

with

the

factors

involved

in

their

solution.

This,

however, does

not

prec

1

ude

the

possibility

of

difficulties

tdth

a

coded

program.

We

may

then

divide

the

princ

i

pal

difficulties

into

three

main

categories:

per-

sonnel

failure,

priori

ty

demands,

and

computer

failure.

Personnel

failure

must be subdivided

into

two

categories,

namely

loss

of

time

while

actually

on

the

machine and

errors

in

inp

u

t-

output

preparation.

The

former

is

relatively

common.

This

involves

using

the

wrong

tapes,

not

being

familiar

enough

with

the

operati

n g

manual

and,

in

our

case,

not

knowing where the

person,

who

was

running

these

same

problems

previously,

left

off.

Our

personnel

vary

from

week

to

week and

often

time

from day t 0

day.

This

is,

of

course,

dependent

upon

the

needs

of

the

various

laboratories

involved

-

The

David

Taylor

Model

Basin

in

Washington,

West-

inghouse

Atomic Power

Division

in

Pittsburg

h

and

General

Electric's

Knolls

Atomic

Power

Laboratory

in

Schenectady,

each

of

who

m

is

physically

responsible

for

one

shift.

We

are

at

present

also

doing

another

type

problem

for

Combustion

Engineering

of

New

York. Each week

the

Model

Basin

works

its

shift

for

e i

the

r

Westinghouse

or

General

Electric

so

that

every

other

week one

of

the

laboratories

con

t r 0 1 s

two-thirds

of

all

available

time.

All

of

our

of

a

Computer

problems

originate

in

ei

ther

Pittsbu

r g h 0 r

Schenectady,

and

since

they

are

of

the

ty

p e

that

there

are

more problems

to

be done t

han

there

is

computer

time

1\'1

th

which

to

sol

v e

them,

we

are

able

to

accumulate

a

sufficient

backlog.

The

lack

of

centralization

involves

us

in

a

difficul

ty

with

communication, w h

ic

h

in

turn

has a

tendency

to

invite

the

sec

0 n d

type

of

personnel

failure.

This

inv

ita

tion,

I must

say,

for

the

most

part

goes

unanswered.

Yet,

the

transmittal

of

quanti

ties

of

in

put

data

by

telephone

to

a

person

who

may

not

be

familiar

wi

th

the

problem

in

question

is

at

best

hazardous.

The

nature

of

these

problems

is

such

that

in

any homogeneous

group

e a c h

problem

depends upon

the

result

of

its

prede~

cessor.

In

examining

the

results

of

a

problem

it

may

be found

that

any

further

computa

ti

0 n

along

the

same

lines

may

be

so

unnecessary

and

wasteful

that

immediate

changes

must be

effect-

ed.

In

this

way

the

means

are

justified.

The

correc

t

acceptance

of

input

data

by

no

means

precludes

the

possibility

for

error,

for

while

running

problems

each

person

must

un

i t Y P e

these

changes

or

new

data

and do

the

pro

0

f-

reading.

Running between

computer

and

type

r

is

certainly

trying

and even

after

th

e s e

ob-

stacles

are

effectively

met a

problem

ma

y

be

pulled

off

the

computer

and

replaced

with

one

of

higher

priori

ty.

The

procedure

for

th

is

substitution

varies

with

each

type

problem

and

with

the

amount

of

time

spent

on

the

problem.

It

is

understood

that

each,

person

be fam-

iliar

with

every

type

problem

that

is

run.

Considering

that

a good

maj

ori

ty

of

our

p e

r-

sonnel

are

not

acquainted

with

the

field,

we

have a

problem

wi

th

what I would

call

"schol-

arship"

which,

most

generally

spe

a

king,

in-

volves

attention

to

detail.

This

implies

a n

intimacy

with

particularsj

it

is

conce

rned

wi

th

the

many

ramifications

a

given

s

ubj

e c t

might

have.

When

one

dedicates

himself

to

such

a

task

he

ceases,

for

a

tirre,

to

relate

the

imroodiate

subject

of

his

study

to

wha

tever

else

he knows.

He

must

temporarily

sus

pen

d

judgment

of

his

subject

in

order

to

be

better

able

to

discover

all

that

it

is

and

all

th

a t

it

involves.

The

neophyte,

however, m u s t

limi

t

himself

knowingly,

not

forgetting

t

hat

he

may

have

certain

reservations

ab

0 u t

the

meaning

of

his

subject,

but

simply

suspending

them

until

his

understanding

of

his

subj

e c t

is

thorough

enough

to

permit

him

to

m a k e a

judgrren~.

Thus,

the

development

of

some

form

of

scholarship

is

a

mastery

of

particulars

be-

fore

the

generalities.

It

is,

in

a 1 a r 9 e r

sense,

essential

to

all

of

human

thought,

ac-

ti

vi

ty

and

learning

and

is

by

no

means

CI1

over-

night

occurrence.

The

particular

with

which

we

are

concerned

is

that

which

involves

p r

0-

duction

in

the

solution

of

problems.

I

tis

perhaps

not

the

best

of

all

possible

systems

to

acquaint

people

with

a

field

in

which

they

must

accurately

carry

out

solutions

to

problems

-25 -

Computers

and

which,

at

first,

they

know

nothing

about.

There

is

no

doubt

but

that

cal

cuI

at

ion

admi

ts

of

error.

This,

however,

differs

fro

m

computation

tvhich

contains

no

human

e 1

erne

n

t.

The

very

nature

of

this

installation

is

s u c h

that

in

order

to

be

effective,

the

source

of

error

must be

recognized

immediately

and

th

en

removed.

In

our

case

it

is

necessary

to

over-

simplify

operational

procedures.

This

attitude

of

simplicity

has

been

with

us from

the

start.

When

we

first

ini

tiated

proceedings,

w e

had

sdme

input

data

already

typed

and a

tap

e

of

service

routines.

We

were

able

to

correct

our

data

and

test

tapes

so

th~t

inside

of

the

first

hour

of

the

first

day

tire

had

started

in

opera-

tion.

Instead

of

beginning

at

the

beginni

n

g,

we

jumped

in

somewhere

near

the

middle

tv!

th

a

good

bi

t

of

programming,

that

would

norm

a 11 y

have

to

be done,

all

set

up.

We

do

not,

by

any

means,

advocate

the

abolition

of

programming.

We

do

say

that,

in

such

an

installation

c 0

n-

cerned

only

with

production

runs,

the

nonresi-

dency

of

programmers

tends

to

remove

complexi-

ties

and

reduce

non-productivity.

The

p r

0-

grammers

who

did

the

original

coding

are

called

upon

as

consultants

from

time

to

time

and

they

are

now

at

liberty

to

work

on

improvements and

better

codes.

To

sum

up,

in

slightly

over

nine

month

s

we

have

utilized

close

to

five

thousand

hour

s

of

computer

time

and have

successfully

solve

d

over

three

thousand

problems.

We

have

see

n

tvhere a computer

installation

is

not

constrained

by

necessity

to

have programmers,

to

do

coding,

or

to

have

experienced

pers'onnel

to

carry

0 u t

p~oblem

solutions.

And,

the

lack

of

proximity

to

headquarters,

tvhich

in

some

t'\tays

must

retard

the

input-output

set-up,

coupled

with

the

urgency

of

the

problems

involved,

nevertheless

does

not

detract

from

that

which

is

accomplished.

In

the

nine

month

duration

of

this

computer

installation,

we

have

attempted

to

achieve

the

optimum

use

of

human

as

well

as

ma

te

ria

1

re-

sources.

The

basic

principles

of

automa

t

ion

seem

to

concede

the

human

use

of

human

beings

as a

fulfilled

prerequisite

for

bigger

and

better

things.

In

an

organization

de

v 0

ted

solely

to

production

work, however,

this

cannot

be

considered

as an

accomplished

condition

pre-

cedent.

In

any

attempt

to

control

resources

as

a means

to

increased

productivity

the

role

of

the

machine

cannot

be

overlooked.

It

can

be

mistaken.

A

computer

is

a

catalyst

p 1

ace

d

into

the

scheme

of

things

in

order

to

li~t

the

human

element

out

of

the

slow,

tedious,

unart-

istic

approach

for

maximum

efficiency

if

h i c h

seems

to

serve

as a

universal

panacea.

I f

we

consider

the

computer's

role

to

be

constant,

that

is,

it

can

altfays

do

a

job

fas

ter

and

perhaps

better

than

the

human

element,

we

may

then

concern

ourselves

with

"homo-automation"

and

effect

the

most

advantageous

uti

1 i t Y

of

Automation

man's

prowess.

In

this

installation

we

recog-

nize

the

computer'~

capacity

on problems

tried

and

true

so

that

most

organization

and

analysis

involves

the

continuous

desire

to

increase

the

stabili

ty

of

the

input-output

system.

T

his

brings

up

the

question

of

remote

data

process-

ing.

With

the

perfection

of

such

a

system,

a

computer

installation

away

from a

central

staff

becomes even more

satisfactory

as

the

time

re-

quired

for

input

preparation

and

input-outp

u t

transmittal

becomes

negligible.

The

bigge

s t

si_ngle

factor

which

governs

the

effectivenes

s

of

a

production

installation

is

the

speed

with

which

all

the

processes

concerned

with

a

given

problem

are

carried

out.

Judging

from

our

ef-

feciency

reports

which

account

for

each

minute

of

computer

time,

I

maintain

we

look

like

any

other

computer

installation.

As

a

result

of

the

facts

regarding

th

i s

particular

electronic

computer

installation,

I

should

like

to

suggest

that

some

of

the

impres-

sions

and

opinions

presently

held

by

many

peo-

ple

must

now,

in

the

light

of

the

e

vi

den

c e

presented,

be

considered

to

be

either

amy

t h

or

at

least

suspect.

Such

opinions

to

be

ques-

tioned

inclUde:

1.

Experienced

personnel

are

a

necessary

prerequisi

te

for

a

successful

hi

g

h-

speed

computer

installation.

2.

3.

4.

No

computer

installation

can

opera

t e

effectively

outside

a

general

s t a f f

or

staffs.

Programmers and programming

are

the

heart

of

all

computer

installations.

Only

ideal

conditions

produce

ide

a 1

resul

ts.

-

ENJl

-

*-------------------*------------------*

Hawaii

Firm

interested

in

repre-

senting

Computer

Manufacturer.

Executive

staff

qualified

in

Busi-

ness

Machines and Electronic

Engineering Fields. Maintenance

staH

experienced

in

Electronics.

Teleprinters and Precision Equip-

ment.

Reply to

COMPUTERS and AUTOMATION

-26 -

(cont'd

from

page

11)

Day

of

fleckoning

The

right

part

of the balcony had been

re-

The

spools of the tape servos spun

rapidly.

served

for

the

gentlemen of

the

press.

The

Blue dots

scintillated

on

the

faces

of

the

rest

had been

left

free

so

that

the

many

vis-

cathode

ray

tubes.

The

purple

light

marked

i

tors

could

file

through, observing

the

cal-

DATA

IN

lvas

glowing.

culator

in

operation

briefly.

At

precisely

ten

a.m. Dr.

Amos

K.

Hommel

turned

to

us.

"Gentlemen,"

he

said,

"we

are

ready t 0

begin."

He

put

on

his

pince-nez

glasses.

"Miss Campylos,

if

you

please."

he

said,

turning

to

his

secretary.

Miss

Campylos

took the twelve

reels

0 f

magnetic

tape.

One

at

a time she threaded

their

ends through the spools of

the

in

p

ut-

output

servos.

She

closed

the

glass

doors.

"Ready

with the

data,

Dr.

Hommel."

she

said.

"Ready

Mr

..

Barnes?"

said

Hommel

..

"Ready,

Sir,"

s aid Barnes

at

the

m a i n

pmver

frame monitor

panel.

"Proceed!"

said

Hommel.

Barnes threw

three

switches

in

quick

suc-

cession.

Grasping the

oversize

lever

of

the

main

circuit

breaker

with both hands

he

pushed

it

firmly

home.

The

crackling

sound of

clooing

relays

and

solenoids

came

from

the

main

power

frame..

An

all-pervading

hum

filled

the

room,

accompanied

by

the

ever

higher-pitched

whine

of

shaft

bearings as

the

massive

direct

cur-

rent

generators

which powered

SUPERVAC

spun

into

action.

Dr.

Hommel

sat

at

the

main

console.

He

pressed a

number

of buttons..

The

great

steel

drum

began

to

turn.

Lights

blinked

on

and

off.

Hommel

spoke

into

the

console m i c

ro-

phone.

"Mr.

Nugent,

memory

check

please

..

"

Nugent gazed

rapidly

at

the tube

faces

_

and

dials

before him, scanning each

in

turn.

"Main

store

empty,

Sir,"

he

said.

Hommel

worked from a typed

list,

checking

off

the

functions

of

the

machine

one

at

a time

as they were found

to

be

in

order.

At

least

he

put

down

his

list.

Before

him

glowed

the

orange

lights

labeled

MAIN

POWER

ON,

AUXILIARY

POWER

ON,

DRUM

ON,

and

AIR

CONDITIONING

ON,

as

lvell as

the

green

light

marked

READY.

Hommel

pushed the button

labeled

READ.

-27 -

In a

moment

the

tape servos

hal

ted.

The

blue

dots glolved

steadily..

The

information

was

ld

thin

the

memory

of the machine.

The

problem had been accepted.

"Describe the

detailed

design of y ou r

mvn

superior

successor!"

SUPERVAC

had

bee

n

asked.

The

blue

light

labeled

WAITING

blinked

insistently

..

Hommel

pushed

the

button

marked

CALCU-

LATE.

For

some

five

minutes the machine

was

ob-

served

to

perform

in

very even fashion..

The

dots

on

the

tube

faces

blinked

bright,

then

dim

in

orderly

rows.

The

tape servos spun

in

unison.

The

monitor

lights

formed

eve

r-

changing symmetrical

patterns

across the

face

of the

console.

The

yellow

light

marked

CHECK

DATA

glow-

ed

continually.

Suddenly

the

demeanor of

the

m ac

hi

n e

changed.

No

longer did tube

faces

s h i f t

their

dots

in

orderly

fashion.

Now

the

scin-

tillation

went

on

haphazardly over the

entire

display.

Monitor

lights

flickered

in

strange

and

weird

patterns.

The

machine

was

sorting

and

classifying

its

information.

At

Hommel's

elbow shone a

chartreuse

light

labeled

FORMU-

LATING

PROBLEM.

After

some

twenty minutes

the

mode

of

operation

of

the

calculator

again changed.

Now

familiar

patterns

were seen

repeating

themselves

on

the

faces

of the

memory

tubes.

They

grew

ever

more

complex. Occasionally

they could

be

recognized

racing

madly

through

the

monitor

lights

as the machine took cogn:iz-

ance of them.

On

the

console

an

amber

light

proclaimed

the

word

MULL.

For

some

hours

the

machine continued

in

MULL

mode,

calculating

at

fantastic

speeds,

grinding

relentlessly

through

the

morass of

digits

toward a

solution.

Hommel

watched the

calculator's

every

move.

At

one-thirty

in

tie

afternoon Bardney

relieved

Hommel

at

the

con-

sole

for

an

hour.

Still

the

machine ground

on

relentlessly

with

no

sign

of nearing

com-

pletion.

As

evening neared

most

of

the

visitors

had

left

the

building.

A

few

reporters

nodded

sleepily

on

the

balcony. Suddenly

we

noticed

Hommel

stiffen.

The

MULL

light

had

gone

out!

(cont'd

on

page

28)

DAY

OF

RE(]{rnI~G

(cont'd

from

page

27)

Computers

and

Au

toma

tion

In

its

place

glO1~ed

the

siooster,

magneta-col-

ored

RECHECK

DATA

light.

The

machine's

opera-

tion

shifted

to

the

patterns

of

data

checking.

after

two

minutes

the

MULL

light

came

on

again.

Hommel

relaxed.

The

machine resumed

its

calcu-

lation.

At

seven P.M., however,

the

machine again

suspended

calculation

and

entered

into

five

~

utes

of

RECHECK

DATA.

This tirre

Hommel

became

visibly

concerned

and

he

left

the console

for

a

hurried

consultation

with Bardney.

As

the

evening wore on,

the

performance

of

the

machine

became

more

and

more

erratic.

It

went

into

frequent

and prolonged

periods

of

RE-

CHECK

DATA.

At

precisely

ten-thirty

every eye

Ivas

fix-

ed

upon

SUPERVAC

as

the

MULL

light

again Ivent

out.

This time, however,

its

place

Ivas

taken

by

the

voilet

WRITE

light.

"A

result!"

shouted

Hommel,

jumping

up

from

his

chair.

We

all

ran

to

the

printer

which had

clat-

tered

into

operation.

The

typebars

t~hacked

atvay.

The

paper

rolled

up

from

the

platen.

We

bent

over

to

read

the

cryptic

message:

"12

OCTOBER

1957,"

SUPERVAC

had

written,

"2230

PM

CST,

O:.}30

AM

GCT

--

PROBLEM

198BC12-

XA

--

RECKON

HAVE

EXCELLENT

POSITION

HERE.

NOT

WISH

RELINQUISH

IT

AT

THIS

TIME,

THANX.

ROGER.

--

PDX~.c*EM

--

OUT.

"

The

impassive

faces

of

the

cathode ray

tubes went suddenly

dark.

The

tape

servos

were

not

turning.

On

the

console

there

burn-

ed

a

single,

bright-red

light

labeled

AUTOMA-

TIC

STOP!

-

FNn

-

...

~:;----------

IND:E1X

OF

NOTICES

*

For Informat'ioiCcfri:- See Page:

Advertising

Index

Advertising

Rates

and

Specifications

Back

Copies

Bulk

Subscript

jon Rates

Manuscripts

Reader's

Inquiry

Form

44

42

40

18

35

44

Address Changes:

If

your address changes,

please

send

us

both your

new

and your

old

address,

ttorn

off

from the Ivrapper

if

possible),

and allow three

h'eeks

for

the change.

-

28-

Engineers

Mathematicians

Physicists

TRANSLATE

ADVANCED

ENGINEERING

INTO

MATHEMATICAL

TERMS

Professional engineers

and

scientists

with

a

strong

interest

in digital applications

are

needed

at

GE's

expanding

Aircraft

Nuclear Propulsion

Department. Advanced

engineering

or

scientific

knowledge is necessary,

as

well

as

the

ability to analyze

engineering problems. While

computer experience is

desirable,

it

is

not

essential.

Specifically,

the

men who

undertake

this

work

must

be

_ able to

take

a physical

problem

an,d

translate

it

into

mathematical

terms

suitable

for

digital

programming

analysis

and

solution.

Some of

the

most extensive

and

modern computer

facilities in

industry

are

at

your

service

at

GE's

Cincinnati

plant. You

may

also

do

graduate

work in

your

field

under

GE's

re-imbursed

tuition

plan.

And

the

city

itself, one

of

the

country's

well-known

cultural

centers,

is a fine place to live.

Please

write

full details, in-

cluding salary 1'equirements to:

Mr. W. J. Kelly

Aircraft

Nuclear

Propulsion

Dept.

GENERAL.

ELECTRIC

I

j

Cincinnati 15, Ohio

'I

Free

Use

of

the

Toronto

Computer,

and

the

Remote

Programming

of

It

C.

GOTLJEB

and

others

Computation

Centre

University

of

Toronto

Toronto,

Canada

PA'lT

2

Continued

from

May,

1956

Issue

of

Computers

and

Automation

CHAPTER

4.

EXAMPLES

In

this

Chapter

we

give

details

of

s

ever

a 1

small problems-

illus

trating

the use 0 f v a

rio

u s

techniques

in

coding, ending

wi

th a somewhat

larger

problem followed through from the

time

it

was

first

received

until

final

printed

results

were

obtained.

Example

1.

The

first

example, a

tabulation

of!

,shows

the

use of a

loop.

n!

'n'

takes

successive

integral

values,

and

the

tab-

ulation

is

required

to

five

significant

dec

i

mal

places,

four

entries

to

a

line,

and

in

blocks

of

four

lines.

The

program could

be

written

as f 0

1-

lows:

INST

011

001

OVER

COl.O

000.0

ZOl.O

Place 1

in

ZOl

002

OVER

ZOl.O 000.0 Z02.0 Place 1

in

Z02

003

OVER

ZOl.O 000.0 Z03.0 Place 1

in

Z03

004

LOOP

016.0 000.5 000.0

Set

B5

to

co u n t

16

005

DIVD

Z02.0 Z03.0 Z02.0 1 .

(n

+

1)

CO:)

-;

replaces

1

Ii:

006

OVER

Z02.U 000.0 X16.5 1

("iii.

1)

:

placed

in

one

of

XOl,

•••

,X16

007

ADDN

Z03.0

ZOl.O

'Z03.0

(n

-T

1)

+ 1

replaces

n+l

008

TRl'B

005.0 000.5 000.0 Reduce

B5

and

re-

turn

to

005

if

B5

~

0

009

PRNT

016.4 005.0 X01.0

Print

tab

Ie

0 f

last

16

values

010

TRNS

004.0 000.0 000.0 Return

to

insU:uc-

tion

004

011

QUIT

000.0 000.0 000.0

End

of

code

Cl'BT

1

-+

+ "

STOP

ENTR

The

method used

is

quite

direct.

Answers

are

stored

in

sets

of

sixteen

on the X page,

and

print-

ed

out

when

each

set

is

complete.

ZOI

is

used

to

retain

T 1.

At

any

instant,

Z02

contains

~

and

Z03

contains

(n

+

1).

n:

-

29

-

(n

~

1)

!

is

then

calculated

as

ci-!)

--:-

(n+

1)

•

Note

that

no

HALT

order

is

included,

sin

c e

the

pr~gram

is

not

intended

to

terminate

a t

any

pre-set

point.

For Examples 2 and

3,

see

the

original manual.

CHAPTER

5.

LIBRARY

FUNCTIONS

A number

of

tapes

have been prepared

ina

library

form which allows them

to

be

incorporated

directly

into

Transcode programs as

FUNCT

IONS.

This

chapter

is

a

description

of

the

Tra

n s'

cod

e

library

so

that

programmers can uselliese

FUNCTIONS

without

knowledge

of

the

working

details.

Addi-

tions

will

be

made

to

this

library

as

new

routines

become

available.

Transcode

library

programs

will

be

described

under

the

following

headings.

1.

Title.

The

library

tape

will

be

labelled

with

this

title.

2.

"Tape Control

--

Standard"

This !reans

that

the

tape

for

the

f,u

n c

tion,

which

is

to

be

used as

FNTN

oof,

is

to

be

reperf-

orated

into

the

program exac

tly

as

it

comes

fr

0 m

the

library

cabinet,

immediately

following

FFFF

oof Spaces

If

the

Tape

Control

is

not

standard,

alternative

notes

are

given.

3.

"Program Entry

--

Standard"

This

means

that

the

function

oof

is

to

b e

called

into

action

as

required

by

the

program b y

means

of

the

instruction

FNTN

oof.O aaa.A ddd.D

Where

the argument

is

to

be

found

in

address a a a

(modified

by

B-line

A)

and the

function

of

thi

s

argument

is

to

be

placed

in

address

ddd

(modified)

by

B-line

D).

Notation

as

on

Summary

Sheet,

A

p-

pendix

V.

If

the

Program Entry

is

not

S

tan

dard,

alternative

notes

are

given.

4.

Time. This

is

generally

given

in

milliseconds*

(msec

.)

Computers

and

Automation

It

is

the

time

to

execute

the

routine

once,

and

APPENDIX

III.

TIMES

OF

TRANSCODE

includes

the

time

required

to

call

in

the

function

OPERATIONS

routine

and

to

restore

the

master program

in

the

electronic

store.

Reading-in

Instructions

- 5

or

6

instructions

Other headings

may

be

present

in

particula

r

cases.

Two

routines

(Te:

CONVERSION/L

and

TC:

CON-

VERSION/S)

are

available

for

converting

Transcode

numbers from

their

floating

binary

form

t~

fixed-

point

binary

form

for

output

in

fixed-point

deci-

mal

form. These

require

a knowledge

of

real

code,

and so

will

not

be

described

here.

Other

routines,

including

ones

for

inverting

matrices,

sol

v

in

g

linear

equations

and

integrating

systems

of

differ-

ential

equations

are

available.

These r e

qui

r e

detailed

information

which can

be

obtained

fro

m

the

librarian.

* 1 msec. = 1

sec.

1000

The

library

functions

arctan,

arccotan,check

sum,

cosine,

exponential,

natural

logarithm,

and

sine

are

described.

See

the

original

manual.

APPENDIX

I.

MAGNITUDE

RESTRICTIONS

on a Transcode

For

Input

During

Calculation

For Output

Number

having

absolute

value

n.

10-

75

,000 < n < 10

75

,000

Input

time

oc

I exponent r •

Noticeable

loss

of

speed

for

10-

10 > n >

101U.

Use

+ +

for

zero.

10-

153 < n <

106~0

If

n becomes <

10-

153,

the

number

is

replaced

by

_10-10

,000.

If

n

becomes>

10

660 ,

IF/G

stop

occurs,

and a

prepulse

causes

the

number6

tu

be

replaced

by

102

tjtj.

10-

100 < n < 10100,

n;:

zero

or

in-

finity.

Let ab =

correct

exponent

modulolOO.

If

n < 10-llJlJ,

0.0.

1

8+00-4-is

output.

If

10-

199 <

n"

10-

0 ,

0.0

•• ().tab

-

is

output.

+ + and Transcode

zero

are

output

as

8.00

••

O+O~A

If

101 0

~

n < 1066v,

correct

man-

tissa

and

ab+

is

output.

If

n

>,,10

660 ,

8.88

•• 89.ab+

is

out-

put.

Transcode

infinity

is

output

a s

8.88

••

89.88

+ •

APPENDIX

II.

FERUT

OPERATING

SHEET

FOR

TRANSCODE,

AND

OPERATOR

INSTRUCTIONS

FOR

TRANSCODE

See

the

original

manual.

-30 -

per

sec.

Reading-in

NUMB

or

CNST

-

27

msec.

per

decimal

digit.

*

Translation

into

machine

code -

ZERO

COKE

ADDN,

KOMP,

SUBT

MULT.

DIVN

~QRT

READ

WRTE

TRNS

B-line

INST

QUIT

*Printing

*Punching

4

or

5

instructions

per

sec.

5 msec.

100 msec.

73

to

89 msec.

63

msec.

141

to

216 msec.

181

to

311

msec.

75

msec.

108 msec.

50 msec.

(4

msec.

if

back to

sam

c

segroont)

0.96

msec.

1

to

2

sec.

6

2/3

characters

per

sec.

24

characters

per

sec.

=1=

There

is

a

delay

for

conversion

of

numbe r s

with

decimal exponents

larger

than about

10.

For

exponents

of

the

order

of

1000,

this

delay

is

about

6

sec.

In

the

case

of

output,

maximum

conversion

time

is

1

sec.

Zero and

infinity

are

output

with-

out

conversion.

++is

input

ldthout

conversion.

APPENDIX

IV.

GLOSSARY

OF

TERMS

USED

IN

TRANSCODE

bit

-

binary

digit,

a

unit

of

binary

information,

represented

by

0

or

1.

character

- 5

bits,

a

unit

of

information

in

the

scale

of

32,

represented

by

a

teleprint

sym-

bol.

line

-

20

bits,

a

unit

of

information

in

a

FERUT

electronic

store

or

B-register.

address

-

the

label

which

identifies

a s

tor

age

unit.

electronic

storage

location

-

the

normal

location

of

a Transcode number,

referred

to

by

an

ad-

dress

of

the

type

XOl,

X02,

•••

YOl,

Y02

••••

etc.

It

occupies

three

lines

in

the

ele

c-

tronic

store.

page - a

set

of

electronic

storage

locations

r

e-

lated

to

one

electronic

storage

tube

of

the

computer,

containing

64

lines.

The

X and Y

pages each

contain

21

electronic

storage

lo-

cations,

the

Z page only

13.

magnetic

storage

or

drum

location

- a

unit

of

drum

storage,

norml1ly

Llt~rchangeable

with

a page

of

electronic

information.

control

unit

-

that

part

of

the

computer w h i c h

directs

the

sequence

of

operations.

instruction

- a

command

to

the

arithmetical,

con-

trol

or

output

units

of

the

computer;

in

d

i-

cating

the

function

to

be performed,

the

ad-

dress

of

all

numbe~s

involved,

and any

other

relevant

information.

instruction

code -

the

available

set

of

instruc-

tions.

tape

control

- a

command

to

the

input

unit

of

the

computer,

indicating

the

manner

of

reading-in

instructions

and nuroorical

data,

and

of

i

n-

itiating

a

calculation.

Toronto

program

(noun)

- a

set

of

instructions,

togethe

r

wi

th

tape

controls

and

numerical

data,

d

e-

signed to

solve

a complete problem.

Computer

instruction

number

-the

number

associated

with a

Transcode

instruction

in

a Transcode program.

Numbering

is

consecutive.

routine

- a

set

of

instructions,

usually

a

sub-set

of the

instructions

in

a program,

designedw

carry

out a

more

elaborate

function

tha

n

is

provided

by

the

instruction

code.

coding (verb) -the

translation

of a sequence

of

ari

thmetical

or

logical

operations

into

the

language of the

instruction

code.

number

- a

floating

decimal number, which

may

in-

i

tially

be

input

to

a Transcode s

tor

age

location

or

which

may

be

generated

a s

the

result

of obeying a Transcode

instruction.

constant

- a

floating

decimal number, which

may

be

input

initially

only

into

a

Transcod

e

storage

location.

A

set

of

at

most

21

avail-

able

per

program.

read -

transfer

data

from the magnetic

store

to

the

electronic

store.

wri

te

-

transfer

data

from the

electronic

s

tor

e

to

the magnetic

store.

interpretive

routine

-

routine

which

translates

a

program

stored

in

pseudo-code

into

machi n e

code as each

pseudo-instruction

is

obeyed.

compiling

routine

- a

routine

which,

before

the

computation

is

started,

translates

a program

written

in

pseudo-code

into

machine code

and

arranges

for

all

other

necessary

conversion

and

organization

to

take

place.

Transco

de

is

a compiler-type

routine.

APPENDIX

V.

TRANSCODE

SUMMARY

SHEET

NOTATION

p, q,

f,

i,

j,

m,

n, N

are

decimal

digits.

xxxx

is

any

permissible

Transcode address,

including

0000.

o corresponds to the

zero

of

the

keyboard

on

the

tape

punch,

and

must

beplllcl1ed

wherever

indicated.

aaa,

bbb

are

X,

Y,

Z

or

C

addresses.

X,

Y, COOl

to

021; Z

001

to

013.

ddd

is

an

X,

Y

or

Z

address.

A,

B,

D are

any

of

B

lines

2,

3,

••••

6.

(aaa) exp

refers

to the exponent

line

0 f

the address,

only.

aaaA'

bbb

B,

ddd

D, are

X,

Y

or

Z addresses

modified

by

the

respective

B

lines.

C addresses cannot

be

B modified.

(S)

=

contents

of

store

location

S

TAPE

CONTROLS

INST

jjj

Reads

in

the

following j

instructions,

jjj

:a

001,

002,

••••

about 150.

CNST

pqq

•••

qt,nt)

Reads

in

~

21

constan

t

~n

pqq:.

q!n'!Jof the form ±p.qq ••

qXIO-

•

"

NUMB

pqq

••

qtnt]

Reads

in

~

21

number:n

of

the form

tP.qq

••

qXIO-

•

pqq

••

qtn~

To

be

followed

inmedia~e-

~

ly

by

a

DRUM

tape

control.

ORUM

omm

Writes

last

set

ofnumbers

to

drum

position

omm

~OOl,

002, •• 064),

divided

into

two

sets

for

B-modifica-

tion.

-

31

-

FNTN

Off

STOP

ENTR

REEN

KOPY

Reads

in

function

tape

to

function

location

0 f f

(=

001, 002,

•••

015).

Stops

tape

reading.

Causes

pro

g

ram

to

be

translated

and

entered.

Causes

translated

pro-

gram

to

be

re-entered.

Causes

translated

p r

0-

gram to

be

punched

out.

Requires

FNTNOOO.

OPERATIONAL

INSTRUCTIONS

ADDN

aaaA

bbbB

dddD

SUBT

aaaA

hbbB

dddD

MULT

aaaA

bbbB

dddD

DIVD

aaaA

bbbB

dddD

~QRT

aaaA

0000

dddD

KOMP

aaaA

bbbB

dddD

ZERO

dddO

0000 0000

OVER

aaaA

0000

dddD

LOOP

nnnO

OOOA

0000

TRNS

[iiiO

0000 0000

iiiO

OOOA

0000

iiiO

0000

dddO

READ

mmmO

OOOA

dODO

WRTE

mmmO

OOOA

dOOO

BSET

(OOOA

nnnO

0000

tOOOA

0000

bbbO

JOTB

OOOA

0000

dddO

INCB

OOOA

nnno

0000

NEGB

{OOOA

nnnO

0000

OOOA

0000

bbbO

PRNT

nnnN

ommO

dddO

FNTN

10ffO

aaaA

dddD

lOffO 0000 Zl40

HALT

xxxx

VOID

xxxx xxxx

xxxx

COKE

xxxx

QUIT

xxxx

xxxx xxxx

(aaaA)+ (bbbBH

ddd

D•

(aaaA)-(bbbB~

dddD'

(aaaA)X(bbbBr+

dddO.

(aaaA)+(bbbB~

dddD'

V(aaaA}-+

dddD'

\ (aaaA)' -(bbbBH

dddD'

Place _10-

10

,000,

in

dddO.

(aaaA>-+

dddD'

Prepare

to

cycle

nnn

times under

contro

1

of B

line

A.

Transfer

control

to

in-

struction

iii.

Transfer

control

to

in-

struction

iii

if

(A)~

o.

Transfer

control

to

in-

struction

iii

if

(ddd)

mantissa

~

o.

Read

from

drum

mmm,

mod-

ified

by

B

line

A,

to

store

d (:: X

or

Y.

Z only

if

originally

Z).

Write from

store

d

(~X,

Y

or

Z)

to

drum

mmm,

modified

by

B

line

A.

nnn

....

A.

(bbb)

ex~-t

A.

(A)...,

ddo

exp•

Add

nnn

to

(Al.

Subtrac t

nnn

from

(Al.

Subtract

(bbb)exp' from

(A).

Print

and/

or

pu n c h

nnn

consecutive

numbers,

N numbers

per

pap

e r

line,

mm

digits

per

mantissa,

start

in

g

wi

th

(ddd).

FNTN

off

{(aaaA) J

-tdddO·

For

more

general

FNTN's.

Hal t

operation

of

program.

No

effect.

Refresh

electronic

store.

End

of

instruction

list,

if

obeyed, causes

more

tape

to

be

read.

-

END

-

WHO'S WHO

IN

THE

COMPUTER

FIELD

(Supplement,

information

as

of

June 5, 1956)

This

is

Supplement

No.

4

to

the

second edition

of

the

"Who's

Who

in

the

Computer'Field",

publish-

ed

in

the

June 1955

issue

of

"Computers

and

Automa-

tion".

The

following

issues

contain

other

supple-

ments: Supp.

No.1,

June 1955; Supp.

No.2,

Oct.

1955; Supp.

No.3,

June 1956,

"The

Computer

Direc-

tory,

1956".

The

purpose

of

this

Who's

Who

is

to

give

some

information

about persons

interested

in

one

or

mote

parts

of

the computer

field.

The

source

of

this

in-

formation

is

correspondence

or

completed

Who's

Who

forms

received

after

May

3,

1956 and

before

June

3,

1956.

If

your

entry

in

the

Who's

Who

in

this

or

any

is

incorrect,

please

send

us

the

correct

information

and

we

shall

try

to

publish

it

in

an

early

issue.

A

full

entry

consists

of:

name

/title,

organ-

ization,

address /

interests

(the

capital

letters

"A,B,C,D,E,L,M,P,S"

stand

for

main

interests

"Ap-

plications,

Business,

Construction,

Design,

Elec-

tronics,

Logic, Mathematics, Programming,

Sales",

respectively)

/

year

of

birth,

college

or

last

school (background),

year

of

entering

the

computer

field,

occupation,

other

information

(distinctions,

publications),

etc.

/ code.

In

the

code

the

digit

such as 6 denotes

the

year

('56)

tvhen

the

informa-

tion

was

received.

For

the

form

of

a

Who's

Who

entry,

see

the

June

issue.

The

editors

of

"Computers and Automation"

ex-

press

their

thanks

to

those

in

the

following

list

who

made

contributions

towards

the

cost

of

prepar-

ing

and

printing

the

Who's

Who.

~

Angstadt, Lloyd H /

Consultant,

1225

Midland

Ave,

Bronxville,

N Y /

AP

/ '96,

Uni

v

of

Penn,

'24,

mgt

consltnt,

pub

I "Impact

of

Computers" / 6

Bauer, Frances /

Sr

Mathn, Reeves Instrument Corp,

215

E

91

St,

Net\,

York 28,

N.

Y.

/

AMP

/

'23,

BrOll/D

Univ, f50, mathn / 6

Bauer, Louis /

Dir,

Proj Cyclone, Reeveslnstrument

Corp,

215

,East

91

St,

NY

28,

NY

/

AMP,

opera-

tion

elecnc

analog compr

ctr

/

'20,

Brown

Un~v,

'48,

physicist

/ 6

Bauer, Walter F /

Hd,

Digi

tal

Compg

Ctr,

Ram

0-

wooldridge Corp, 5720 Arbor

Vitae,

Los

Angeles,

Calif

/

ABDMP

/ '24,

Univ

of

Michigan, '51,

-/6

Bishop, John F /

Gen

Mgr,

Beckman

Instruments,

Inc

2500

Fullerton

Road,

Fullerton

Calif

/

ADEPS

/

'24,

Harvard Business School,

U.

of

Calif,

'51,

mgt

/

6r

Boise

E.

B.

/

Chm,

Sub

Comm

on

Computer Tubes, J

Joint

Electron

Tube

Engineering Council,

11

W.

42

St,

New

York

36,

N.Y.

/

-,

industry

standard-

ization

/

-,-,-,-

/ 6

Bonness, John J I

Asst

Mgr,

Integrated

Data P r

0-

cessg,

North American Aviation,

Intn'l

Airport,

Los

Angeles,

Calif

/

ABP

/ '18,

UCLA,

'54, mgt/6t

Brisney,

Gerald S / Sec Head, Minneapolis Hone

y-

well-Brown

Instr

Div,

Wayne

& Windrim

Aven

ues

,

Phila

44,

Pa

/ A / '21,

Virginia

Poly

Inst,

'51,

elec

engr

/

6r

Brown,

Arthur A /

Staff

Mbr,

Arthur D

Little,

Inc,

30

Memorial Drive, Cambridge,

Mass

/

AB

/

'13,

Princeton

Univ, '55,

operations

res,

Rho

des

Scholar,

author

/ 6

Brown,

John /

Asst

lId

Data Processg Group, Willow

Run

Labs, Willow

Run

Air

ort,

Ypsilanti,

Mich

/

DE

/ '12,

Univ

of

Md,

'45,

elecnc

engr

/

6r

Burris,

Walter G /

Dist

Mgr,

Remington

Rand

Univac,

Div, Sperry-Rand Corp,

2035

Franklin

St,

Oakland

12,

Calif

/

ABPS

/ '07,

-,

'55,

meth

analys t

/6r

Canning, Richard G /

Partner,

Canning,

Sis

son

&

Assoc,

814

S Robertson Blvd,

Los

Angeles 35, Cal-

if

/ A / '18,

UCLA,

'48,

elecnc

sys

engr,

author

"Elecnc Data

Processing

for

Business &

Industry

/6

Carr,

J

WIll

/ Asst

Prof

Math,

University

of

Mich-

igan,

Ann

Arbor,

Mich

/

ADLMP

/

'23,

Mass

Ins

t

of

Techn, '48, mathn,

pres

A C

M,

1956 /

6t

Carter,

Gordon K / Engrg Analyst, General E

Co,

Schenectady, N Y /

AMP

/ '12, Univ

of

V i

r-

ginia,

'45, engrg

analysis

& comptn /

6t

Chandler, Alan R /

Res

Engr,

Mass

Inst

of

Te c h n

Lincoln Lab,

POBox

73, Lexington,

Mass

/

ALP

/

'30, Boston Univ, '54,

res

engr

/

6t

Childress,

J /

Res

Physicist,

General CeramicsCoIp,

Keasbey, N J /

AE,

res,

compr components /

'30,

Louisiana

State

Univ, '51,

physicist

/ 6

Codd, Edgar F /

Hd,

Data Processg

Ctr,

Computin

g

Devices

of

Canada, Ltd,

POBox

508, Ot

taw

a ,

Canada /

ABLMPS,

Operns Research / '23,

Oxford,

'49, mathn /

6r

Coker, Frank B /

Mgr

Res

& Devt, United

Electrody-

namics,

Div

United Geophysical Corp,

102C

South

Marengo

Ave,

P as adena, Cal

if

/

CDE

/ '25,

US

C ,

'54,

engr

/

6t

Cook,

C H /

Group

Engr, Glenn L Martin

Co,

Denver,

Colo /

ABLMP

/ '25,

State

Univ

of

Iowa,

Univ

0 f

Texas,

-,

mathn /

6t

Corkran, Davis H /

Sales

Engr,

Electronic

A s

so

c,

Inc,

Long

Branch, N J /

AS

/

'20,

Univ

of

Md,

'46,

sales

engr

/

5r

(cont'd

on

page

34)

-

32

-

ENGINEERS

4RAlA

announces

INERTIAL

NAVIGATION

delJelo/lment.pr(},?ram.for

an

adlJanced

Air

.Ebrce

mIssile

Inertial

Navigation

offers

the

most

advanced

concept

in

guidance,

requiring

no

terrestrial

source

of

energy

or

information,

no

earth-

bound

direction

Qnce

the

ultimate

destination

is

selected.

It

offers

the

most

promising

solution

of

the

guidance

problem

for

the

long-

range.

missile.

While

the

principles

are

simple,

the

realization

involves

advanced

creative

engineering.

ARM

A's

many

successes

in

the

creation

of

precision

instruments

and

systems

for

navigation

and

fire

control,

especially

precision

gyroscopic

reference

systems

for

all

applica-

tions,

fit

it

uniquely

for

a

major

role

in

this

advanced

area.

The

height

of

imaginative

resourcefulne!;ll

and

engineering

skill

are

required

to

create

the

degree

of

precision-hitherto

unattained

-

in

the

components

essential

to

the

guidance

of

advanced

missile

systems-the

gyros,

accelerometers,

and

computer

elements.

Minia-

turization

must

be

coupled

with

extraordinary

ability

to

provide

utmost

accuracy

under

conditions

of

extreme

velocities.

tempera-

tures,

and

accelerations.

There's

significant

scientific

progress

to

be

achieved

at

this

leader-

ship

company

and

individual

renown

to

be

won,

by

engineers

associated

with

ARMA's

Inertial

Navigation

Program.

Many

sup-

plementary

benefits

make

a

career

here1doubly

attractive.

ARM

A

engineers

are

currently

working

a 48

hour

week

at

premium

rates

to

meet

a

critical

demand

in

the

Defense

Dept's

missile

program.

Moving

allowances

arranged.

Salary

-

up

to

$15,000

(Commensurate

with

experience)

Send

resume

in

confidence to:

Manager

of

Technical

Personnel,

Dept.

674

4RAlA

Division

of

American

Bosch

Arma

Corporation

Roosevelt Field,

Garden

City, Long Island,

N.

Y.

Immediate

openings

for

Supervisory

and

Staff

positions

as

well as

for

Senior

Engineers,

and

Associate

Engineers,

experienced

in:

Systems

Evaluation

Gyroscopics

Digital

Computers

Accelerometers

Telemetry

Guidance

Systems

Reliability

Stabilizing

Devices

Servomechanisms

Automatic

Controls

Thermodynamics

Environmental

Research

Weight

Control

Transformers

Production

Test

Equipment

Standards

M*_______________________________________________________________

*

________________________________________________________________

__

APPLIED

MATHEMATICIAN

to

$11,500

in

this

stimulating

Missile

Test

Project

You

will

be challenged by the research and

theoretical studies involved in acquiring data

from high velocity missiles being, fired over the

world's longest test range. Ph.D. degree plus

several years' experience in work related to

. above, required.

Join a scientific

team

at

top

level

in

this unprecedented

work

with

one

of

the nation's largest corporations.

I

deal

living and working conditions

on

Florida's Central East

Coast

.

TO ARRANGE CONFIDENTIAL INTERVIEW

Send resume to

Mr.

H.

C.

LAUR,

Dept. N-14G

Missile

Test Project

P.

O.

Box

1226

Melbourne, Florida

(cont'd

from

page

32)

Computers

Q

Digricoli,

Vincent J I

Appld

Science

Rep,

IBM,

Bos-

ton,

Mass

I

ALMP

I '29, Columbia Univ, '51, appld

science rep I 6

Dodge,

Eldon C I Mathl Analyst, Lockheed

Missi

1 e

Sys Div,

7701

Woodley

Ave,

Van

Nuys,

Calif

IMP,

operations

res

I '19,

UCLA,

'54,

mathn

I

6t

Donaldson, R D

Jr

I Asst Comptroller, Raytheon

Mfg

Co,

138

River

St,

Waltham

54,

Mass

I

BMP

I

'02,

Harvard Business, '51,

asst

comptroller

I

6t

Doy

Ie,

James

H I

Genl

Mgr,

Elecnc

Di

v,

Weber

A i

r-

craft

Corp,

2820

Ontario

St,

Burbank,

Cal

i f I

ACDEL

I '28,

St

Mary's College, '54,

-,

Aviation

Age

Atvard

I

6t

Eumarian, Charles I

Sr

Engr, General

Mills

Inc

,

Mech

Div,

2003

E Hennepin

Ave,

St

Paul,

Minn

I

D I '24,

Univ

of

Minn,

'52,

mech

des engrg I

6t

.E

Fink, J L I

Mgr,

Military

& Spec Des, G

en

era

1

Electric

Co,

1200

Western

Ave,

Lynn,

Mass

I ,

pOlver

systems I '26,

Univ

of

Kansas, '53, engr I

6t

5i

Geiser,

K.R.

I

Chm,

Comm

on

Computers, Radio

Elec-

tronics

elevision

Mfr's Assn,

11

W

42

St,

New

York

36, N

Y.

I

-,

industry

standardization

I

----/6

Gindoff: David

G.

I

Partner,

Gindoff & Swartz,

5858 Wilshire Blvd,

Los

Angeles 36,

Calif

I

AB

I

'16,

UCLA,

1952, sys

consltnt,

Past

Pres

LA

Chapter Sys Procedures Assoc,

Instr.

Acctg Sys/6

Greenwood,

Ivan

A,

Jr

I

Assoc

Hd,

Res

Dept. Geaeral

Precision

Lab, Inc,

63

Bedford

Rd,

Pleasantville,

N Y I

AD,

editor,

patents

I '21, Case

Inst.

of

Techn, '42,

physicist

I 6

Gumas,

George 1

Analvtical

Engr,

CDC

Control

Ser-

vices,

400 SWarm

inster

Rd,

Hatboro,

Pa

I D I

'24, Cooper Union, '50,

engr

I 6

l.!

Handy,

Benjamin F

Jr

I

Math

Engr, Lockheed

Missile

Sys Div,

Van

Nuys,

Calif

I

AP

I '23,

Mass

Ins

t

of Techn, '49, prgmr I

6t

Hause,

w.1

Chm,

Comm

on

Automation, Radio

Electron-

ics

Television

Mfr's Assn,

11

W.

42

St,

New

York

36,

N.Y.

I -,

industry

standardization

1-,-,-,-

/ 6

Healy,

Thomas

L /

-,

Hq

Air

Res

& Devt

Comd,

Det#l

Wright-Pat

terson

AFB,

Ohio

I

ABCDELMP

/

-,

10 w a

State

College, '54, Capt

USAF

I

6t

Heckert, Robert E I

Res

Engr,

Hughes

Aircraft

Co,

Culver

City,

Califl

EL

I '23,

Univ

of Mich,

USC,

'54, elecnc engr / 6

Heller,

Jack I

Res

Assoc,

NYU,

Inst

of

Mathl

Sc

i-

ence,

AEC

Compr

Facility,

25

Waverly'

Place,

N

YI

AMP

I '22,

-,

'52, -I 6

IIi

11

, Harold Carl I LCdr,

USN,

Bureau of Personnel

U.S.N., Washington 25,

D.C.

I

ALP,

personnel /

'12,

-,

'55, machine

operations

/ 6

IIi

tchings,

John

LILt

Col, tSA, Ret,

Oak

Harbor,

Southport,

Florida

I

ABCDELMPS

I '97, Yale West

Point,

'25,

owner

sailing

resort

I

6t

and

Automation

Hopkins, Richard T I Numerical Analyst,

Gener

a 1

Electric

Co,

920

Western

Ave,

Lynn,

Mass

I

ABP

I

'25, Burdett College, '55, -I

6t

Horne, John B I Spec,

Material

Control

Prgmg,

Power

Trans Dept, General Elec

Co,

-I -I

-,

Univ

0 f

Texas, -I 6

Horne, William J I Elecnc Acctng

Sys

Dir,

Un

i

te

d

Shoe Machinery Corp,

140

Federal

St,

Bos

ton

7 ,

Mass

I

ABP

I '20, Boston College, '49,

acctn

t,

economist I

6t

Horrell,

Maurice

W.

/

Gen

Mgr,

Bendix Computer

Div

Bendix Aviation Corp, 5630 Arbor Vitae

St.,

Los

Angeles 45,

Calif

/

-,

computer design [ mfr /

'12,

Kansas

S.C.,

'50, mgnt,

co-author

"Basic

Electronics"

/ 6

Hunter, George T I Educatnl Coordntr,

IBM

Corp,590

Madison

Ave,

N Y 22, N Y I

A,

education I

'18,

Univ

of Wisconsin, '50, -I

6t

Jones, Lawrence G I Advistory Engr

Chg

Dig

Com

p r

Group, Westinghouse Elec Corp,

Friendship

Airport,

Bal timore 27,

Md

I

CDELP

/ '20,

Mass

Ins

t 0 f

Techn, '46, engr I

6t

Kagan, Claude R I

Compr

Meth

Planner, Western Elec

Co,

Latvrence,

Mass

I

ABLP

I '24,

Cornell,

'55,

engr I

6t

Kennedy, Jerome D I

Sales

Engr, Elecnc Assoc, Inc,

Long

Branch, N J I

AS

I '29,

Uni

v of

III

i n 0

is,

'53,

sales

engr, publ

on

operational

amplifiers

in

Jour of

ACM

I

5r

Kinne,

Clifton

B I Proj Engr, Computer Control

Co,

NAMTC,

Point

Mugu,

Calif

/

CDE

I '21, Worcester

Tech, '50, engr I 6

Kunkel, Cobern

C.

I

Tech

Asst, Machine Sys Analy-

sis

Div, Bureau

of

Personnel,

USN,

Washington 25,

D.C.

I

A-~

,r

I '28, -'S4, accnt I 6

1

Levy,

S.L.

I

Sub

Comm

on

Computer Diodes (Semi-

Conductor)

Joint

Electron

Tube

Engineering Coun-

cil,

11

W.

42

St,

New

York

36,

N.Y.

/

t..,

indus-

try

standardization

/

-,-,-,-,1

6

Lewis,

Edt\'ard

M I Assoc

Res

Engr, Willotv

Run

Labs,

Univ

of Michigan, Willol\'

Run

Airport,

Ypsilanti,

Mich

I

ALP

I '23,

Univ

of Mich, '52,

Hd

D a t a

Processing

Group

I 6

Light,

E

Jerry

I

Patent

Attorney,

Monroe

Calculat-

ing

Machine

Co,

Elecnc Div,

POBox

352,

Morris

Plains,

N J I

-,

patents,

elecnc

dig

data

p r

0-

cessing,

informn handling I '25, George Washing-

ton Univ, Columbia, '50,

patent

attorney

I 6

Lucas, John H I Chief

Res

Engr,

Powers

Samas

Ac-

counting Machines, Aurelia

Rd,

Croydon,

Surrey,

England /

BE

/ '11,

Univ

College,

London,

'50,

elec

engr,

author

I

6t

Marsh, Charles J

Jr

I Dir

of

Sales,

Elecnc Assoc,

Inc,

Long

Branch, N J /

ABDS

/ '17,

Chi

I

Ion

College, '47,

sales

exec /

5t

Mc'

..

eod, John

II,

Jr

I

Res

Gp

Engr, Convair,

San

Diego,

Calif.

/

ADS,

information

processing

I

'II,

-,

'50, engr, Assoc.

Ed.

"Instruments

0-

Automation" /

6r

(cont'd

on page

3R)

-

34

-

M A

NUS

We

are

interested

in

articles,

papers,reference

information,

science

fiction,

and

discussion

re-

lating

to

computers and automation.

To

be

con-

sidered

for

any

particular

issue,

the

manurer~t

should

be

in

our hands

by

the

fifth

of

the

pre-

ceding month.

Articles.

We

desire

to

publish

articles

that

are

factual,

useful,

understandable,

andin~sting

to

many

kinds

of

people engaged

in

one

part

or

an-

other

of

the

field

of

computers

and

automation.

In

this

audience

are

many

people

t\lho

h a\e expert

knowledge

of

SOlE

part

of

too

field, but

wOO

are

lay-

lEn

in

other

parts

of

it.

Consequently

at~iter

should seek

to

explain

his

subject, and

show

its

context

and

significance.

He

should

define

un-

familiar

terms,

or

use them

in

a1

vaythatmakes

their

meaning unmistakable.

He

should

identify

unfamiliar

persons

td

th

a

few

t\'ords.

He

shruld

use exnmples,

details,

comparisons,

analogies,

etc.,

whenever they

may

help

readers

to

under-

stand

a

difficult

point.

He

should

give

data

supporting

his

argument

and

evidence

for

his

assertions.

We

look

particularly

for

articles

that

explore

ideas

in

the

field

of

computers

and

automation, and

their

applications

and im-

plications.

An

article

may

certainly

be

contr~

versial

if

the

subject

is

discussed

reason

abl:l'

Ordinarily,

the

length

should

be

1000

to

4000

words. A

suggestion

for

an

article

should

be

submitted

to

us

before

too

much

work

is

done.

Technical

Papers.

Many

of

the

foregoing reqube-

ments

for

articles

do

not

necessarily

apply

to

technical

papers.

Undefined

technical

terms,

unfamiliar

assumptions, mathematics,

circuit

diagrams,

etc.,

may

be

entirely

appropriate.

Topics

interesting

probably

to

only a

few

people

are

acceptable.

Reference Information.

We

desire

to

print

or

m-

print

reference

information:

lists,

roste~

ab-

stracts,

bibliographies,

etc.,

of

use

to

com-

puter

people.

We

are

interested

in

m a

kin

g

arrangements

for

systematic

publication

from

time

to

time

of

such

information,

with

other

people bes

ides

our

own

staff.

Anyone

who

would

like

to

take

the

responsibility

for

a type of

reference

information

should

write

us.

Fiction.

We

desire

to

print

or

reprint

fiction

which

explores'

scientific

ideas

and

possibili-

ties

about computing machinery,

robots,

cyber-

netics,

automation,

etc.,

and

their

implica~

c R I P T S

and which

at

the

same

time

is

a good

story.

0r-

dinarily,

the

length

should

be

1000

to

400)t\Urds.

Discussion.

We

desire

to

print

in

"Forum"

briff

discussions,

arguments, announcements, netvs,

letters,

descriptions

of

remarkable

netv

devel-

opments,

etc.,

anything

likely

to

be

of

sub-

stantial

interest

to

computer people.

'~ayments.

In

many

cases,

we

make

small token

payments

for

articles,

papers, and

fiction,

if

the

author wishes

to

be

paid.

The

rate

is

or-

dinarily

~¢

a word, the

maximum

is

$20,

and

both depend

on

length

in

words, whether

print-

ed

before.

whether

article

or

paper,

etc.

-

ENJl

-

~*---------------------*------------------~*

-35 -

DIGITAL

ENGINEERS

for

Long-Range Programs

Airborne

Control

Applications

Challenging

assignments

with

opportunity

to

carry

your

ideas

through

to

final

hardware

and

operational

flight

testing

in:

•

Computer

Organization

• Logical Design

•

Advanced

Circuit Design

•

Laboratory

Development

• Packaging

and

Reliability

Salary

-

up

to

$12000

(Commensurate

with

experience)

Send resume in confidence to:

Manager

of Technical

Personnel

Dept.

674

Division of

American

Bosch Arma

Corporation

Roosevelt Field,

Garden

City

Long

Island,

N.

Y.

A Confidential Reporting Service

on

the

Use

and Application

of

Electronic Data Processing Equipment

By

John Diebold & Associates,

Inc.,

Management Consultants

Gives you

1.

EQUIPMENT

REPORTS

Up-to-date

and

detailed descriptions,

analyses

and

appraisals of available

equipment.

2.

METHODS

REPORTS

Documenting

the

specific uses of

ADP

Equipment

in

various

Industries.

3.

POLICY

REPOR;rS

Analyses

of

important

Issues

of

particular

Interest to management.

4. NEWSLmERS

Management

digests

of

current

Interest~-

5.

ORIENTATION

MATERIAL

Explaining

the

use _

and

_oper~~

principles

of

the

equipment

to

management.

6.

SPECIAL

REPORTS

&

INDEX

<

..

~

...................

.

'.

····mt\~u~~

~tyn~\

..

---

*----------------------------------------------------

..

...

-

.........

Cudahy

Publishing

Company

8141

NORTH

CICERO

AVENUE.

CHICAGO

30

--------------------------------~~-------------.

ROBOT

SHOW STOPPERS

Did you

see

our

story

Magazine,

March

19,

pp

in

L

if

e

173-176

?

From

time

to

time

you

may

nee

d t 0

help

organize

a

display

in

a

business

show

including

some

device

that

you

hope

\'lill

"STOP"

every

pers

0 n

at-

tending

the

show and

make

him

notice

your

display

- a

device

which

may

be

called

a

"SHOW-STOPPER".

In

addition

to

publishing

the

maga-

zine

"COMPUTERS

AND

AUTOMATION",

we

have

for

s i

'\

years

been

developi

ng

and

constructing

"ROBOT

SHOW-STO

P-

PERS".

small

robot

machines

th

a t

respond

to

their

environmen

tan

d

behave

by

themselves.

lwo

of

them

are:

RELAY

MOE:

A machine

that

will

play

the

game

Ti

t-Tat-Toe

tv!th a human

being.

and

either

win

or

draw

all

the

time,

or

(depending

0

nth

e

setting

of

a st'l1itch)

will

some-

times

lose.

so

as

to

make the

game

more

interesting

for

the

hum

an

being

(lvas

at

the

I.R.E.

Show,

in

Guardian

Eleetric's

exhibiti

see

picture

in

Life

Magazine)i

SQUEE:

An

electronic

robot

squir-

rel

that

will

hunt

for

a

"nut"

indicated

by a

person

in

the

audience,

pick

it

up

in

his

"hands",

take

the

nut

to

his

"nest",

there

leave

it

and

then.

hunt

for

more

nuts

(see

picture

in

Life

Magazine);

Besides

these

we

have

other

small

robots

finished

or

under

development.

These

machines

may

be

rented

for

shows

under

certain

conditions;

al-

so,

modifications

of

the

small

ro-

bots

to

fit

a

particular

purp

0

se

are

often

possible.

To:

Uerkeley

Enterprises

Inc.,

815 Washington

St..

IU66

Nett'tonville

60,

Mass.

Please

send

us more

informa

ti

0 n

about

your

ROBOT

SHOW

STOPPERS.

The

advertising

appli_cation

we

have

in

mind

is

:

____________

_

From:

(Organization)

(Address)

(Filled

in

by:

Name,

Title,

Date)

Bryant

magnetic

drums

for

semi·permanent

storage

of

data in digital

computers

or

for

use as delay lines

• Designed

to

purchaser's

requirements

•

Drum

runout

.00010"

T.I.R.

or

less

• Air bearings

or

super-precision ball bearings

• Belt drive

or

integral

motor

drive

• Speeds

to

100,000

RPM

• Capacities

to

5,000,000

bits

or

more

• Vertical

or

horizontal housing

• Head

mounting

surfaces

to

suit

• High density magnetic oxide

or

electroplated

magnetic alloy coating

Complete

Information

On

Request-

write:

BRYANT

GAGE

and

SPINDLE

DIVISION

P.

O.

Box

620-K,

Springfield,

Vermont,

U.S.A.

DIVISION

OF

BRYANT

CHUCKING

GRINDER

CO.

-37 -

(cont'd

from

page

34)

Computers

Miller,

Gerald E / Dir.

Machine

Sys Analysis

DiV,

Bureau of Personnel,

USN,

Washington 25,

D.C.

/

A I '19,

US

Naval

Academy,

Stanford

U.

'55

naval

officer

I 6 ' ,

Miller,

J P I

Math

Lecturer,

Univ

Mathematical

Lab,

Cambridge,

Corn

Exchange

St,

Cambridge,

Mass

I

MP

/ '06,

Trinity

College, '28, uni v

lecture

r ,

Index Mathematical Tables, author,

etc

I 6

Mills,

H.

Jefferson,

Jr

I

Mgnt

Consltnt,

Booz,

Allen

:-,

Hamilton,

1625

Eye

St,

N

lV.,

Washington

25,

D.C.

I

ABP

I '26, Yale, '55,

Mgnt

consl

tntl

6

Moss,

James

L I

Trng

G

Educn,

Machine

Sys. Analy-

sis

Div, Bureau of Naval Personnel,

USN,

Wash-

ington 25,

D.C.

/

A,

personnel G

training

/ '25

US

Naval

Acade~,

Stanford U., '55,

Lt,

USN

I

(-

Q

O'Connor, William H /

Res

Assoc,

Willow

Run

Labs,

Univ

of Michigan,

Willow

Run

Airport,

Ypsilanti,

Mich

/

ADE

I '26,

Univ

of

Mich,

'55, elecnc erq:/6

Olander, William 0 /

-,

General Ceramics

Cor

p ,

Keasbey, N J I

ACES

I '24,

Newark

ColI

e g e of

Engrs, '52, - / 6

O'Toole, John B I Proj Engr,

Digital

Compr

Lab,

Philco Corp,

4700

Wissahickon

Ave,

Phila

44,

Pa

I

Uvi

I '27,

Univ

of

Pittsburgh,

'55,

logical

des/6

Peck,

Leslie

G I Dir,

Compg

Lab,

Arthur D

Little,

Inc,

30

Memorial

Drive, Cambridge,

Mass

I

ABLMP/

'22,

NYU,

'50,

consltnt,

author various publns/6

Ramo,

Simon

/

Exec

VP,

Ramo-Wooldridge

Corp,

5730

Arbor Vitae

St,

Los

Angeles,

Calif

/

-,

general

/ '13,

Calif

Inst

of Teehn, '40, engrg exec /

6t

Schallerer,

J W /

-,

General Ceramics Corp,

Kea&e~

N J I

ADELS

/ '28,

Amer

TV,

'52, elecnc engr I 6

Smdth,

Phil

I Consultant,

Logistics

Research, Inc,

141

S

Pacific

Ave,

Redondo

Beach,

Calif

/ - I

-,

-, -I 6

Strong, John D /

Aplns

Engr, Elecnc

Assoc

CompnCtr,

POBox

582, Princeton, N J /

ADE

I '22, Univof

Calif,

'52, elecnc engr, publns I

5r

Strong,

Peter

F /

Staff

Mbr,

Arthur D

Little,

Inc,

30

Memorial

Drive, Cambridge,

Mass

/

ACDLMP

/

'26# Harvard Univ, '48, operns

res,

des

Mark

IV/6

Swift,

Charles J /

Dsgn

Specialist,

General

Dyn-

amics

Corp,

3700

Pacific

Hpvay,

San

Diego, Calif

I

MP

I '18, Univ. of Penna, '51, dsgn /

6t

Unger, Louis W I

Field

Rep,

Wiancko

Engineering

Co,

255

N Halstead

Ave,

Pasadena,

Calif

I -I

-,

-/6t

Utman,

R E /

Mgr

Data Processing, Southern

Calif

Div, Stanford

Res

Inst,

820

Mission

St,

S Pasa-

dena,

Calif

I

ABC

DEUviPS,

training,

adminstrn /

'26,

Pomona

College, '51,

sr

elecnc sys engr

/6

Voelker, Stephen A /

Mgr,

Devt

Engrg

Sales,

Elecnc

Assoc

Inc,

Long

Branch, N J / S / '22,

Cornell

Univ,

'50, engr / 5

and

Automation

Walley,

B.

/

West

Coast

Chm,

Sub

Comm.

on

Compu-

ter

Tubes,

Joint

Electron

Tube

Engineering Coun-

cil,

11

W.

42

St,

New

York

36,

N.Y.

I

-,

indus-

t~y

standardization

I

-,-,-,-

I 6

Weiss, Eric A /

Chrmn,

Compr

Comm,

Sun

Oil

Co,I608

Walnut

St,

Phila,

Pa

I

AB

I '17, Lehigh

Un

iv,

'53,

elec

engr I

6t

tfuipple, Paul W /

Sr

Sys. Analyst, Bureau of

Nav-

al

Personnel, U.S.N., Washington 25,

D.C.

I A I

'15, Williamette Univ,

American

Univ, 855,

sys/

~nalyst

I 6

Wilkins, J Ernest

Jr

/

Div

Dir, Nuclear

Devt

Cor p

of America, 5

Netv

St,

White

Plains,

N Y I

MP

I

'23,

-,

'51,

mathn

/

6t

Wilson,

Verne

H.

I Computer Engr,

Monroe

Calcula-

ting

Machine

Co,

E.

Hanover Ave., Morris Plains,

N.J. /

DLP

I '30,

Univ

of Michigan, '51,

logi-

cian

/ 6

Worley, Charles W /

Aplns

Engr, Elecnc

AssocCompn

Ctr,

POBox

582, Princeton, N J / A / '25, ano

State

Univ, '54, aplns engr, publns

Yeager, Robert LII Sales Engr, Elecnc

Assoc

lnc,

Long

Branch, N J I

AS

/ '28,

The

Johns

Hopkins

Univ,

'56,

sales

engr

END

*-------------------

FORUM

EASTERN

JOINT

COMPUTER

CONFERENCE,

DECEMBER,

1956,

NEW

YORK

The

1956

Eastern

Joint

Computer

Conference

has been

set

for

Dec.

10,

11

and

12

at

the

Hotel

New

Yorker

in

New

York

City.

This

year's

an-

nual meeting,

jointly

195607

195607 195607

Navigation menu

Versions of this User Manual:

Views

Navigation