Contents ACI 318 11 Example 001
User Manual: ACI 318-11 Example 001
Open the PDF directly: View PDF ![]() .
.
Page Count: 5
Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
0
ACI 318-11 Example 001
SHEAR AND FLEXURAL REINFORCEMENT DESIGN OF A SINGLY REINFORCED RECTANGLE
EXAMPLE DESCRIPTION
The flexural and shear design of a rectangular concrete beam is calculated in this
example.
A simply supported beam is subjected to an ultimate uniform load of 9.736 k/ft.
This example is tested using the ACI 318-11 concrete design code. The flexural
and shear reinforcing computed is compared with independent hand calculated
results.
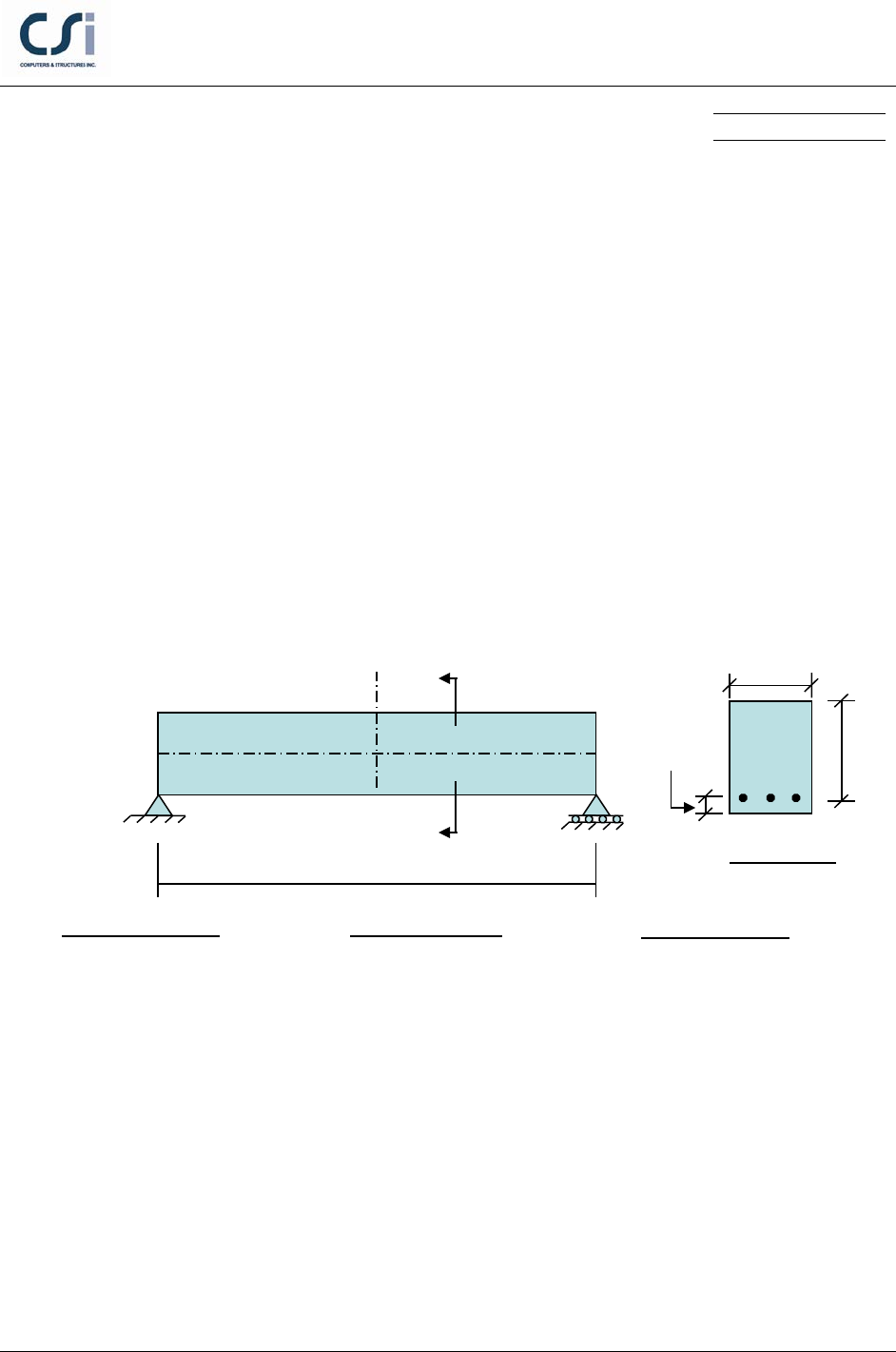
GEOMETRY, PROPERTIES AND LOADING
TECHNICAL FEATURES TESTED
Calculation of Flexural reinforcement, As
Enforcement of Minimum tension reinforcement, As,min
Calculation of Shear reinforcement, Av
Enforcement of Minimum shear reinforcing, Av,min
Section A-A
C
L
10' = 120"
Material Properties
E = 3600 k/in2
ν = 0.2
G = 1500 k/in
2
Section Properties
A
A
d = 13.5 in
b = 10.0 in
I = 3,413 in4
13.5"
10"
2.5"
Design Properties
f’
c
= 4 k/in2
fy = 60 k/in2
ACI 318-11 Example 001 - 1
Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
0
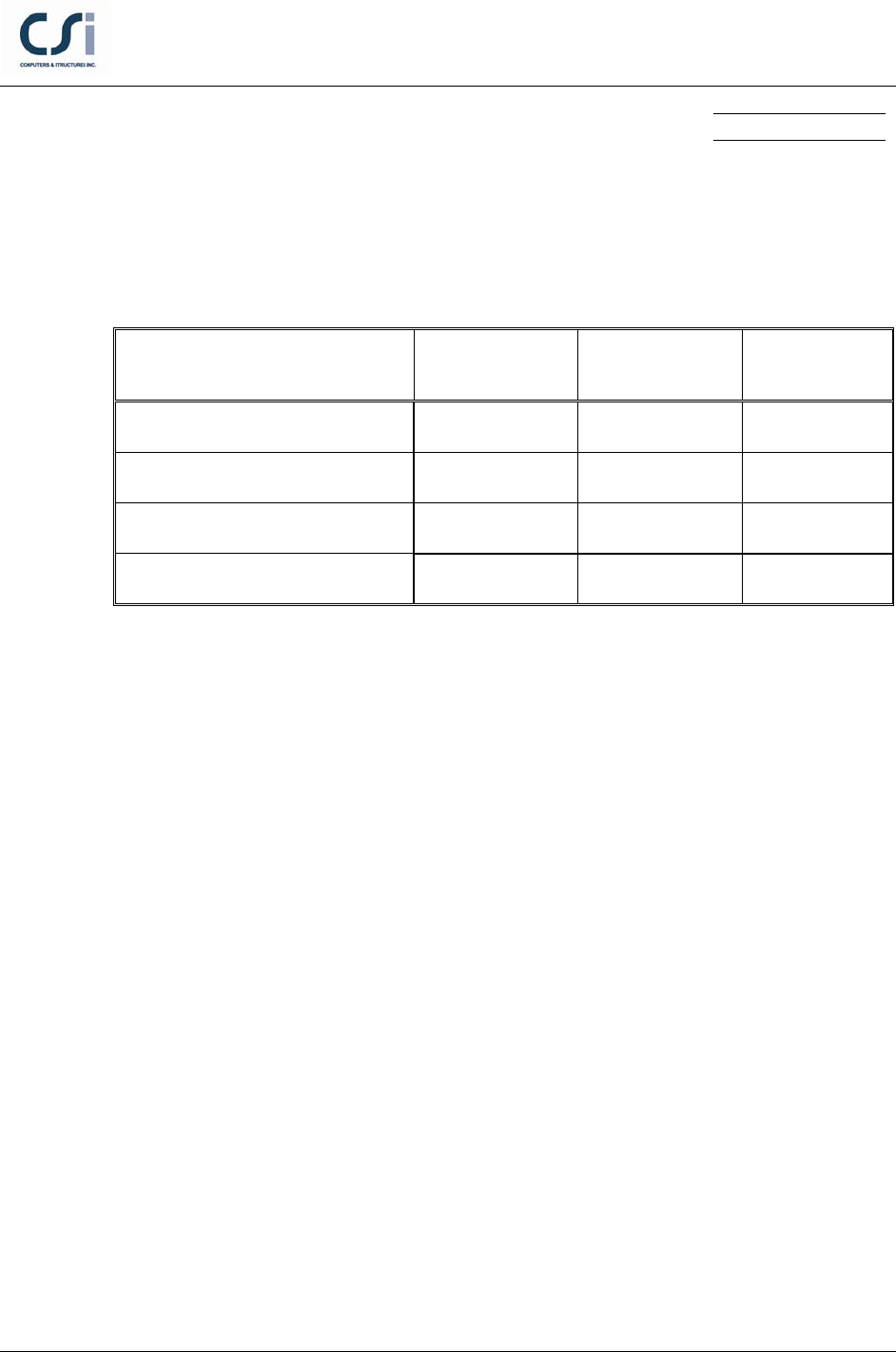
RESULTS COMPARISON
Independent results are hand calculated based on the equivalent rectangular stress
distribution described in Example 6.1 in Notes on ACI 318-11 Building Code.
Output Parameter ETABS Independent Percent
Difference
Design Moment, Mu (k-in) 1460.4 1460.4 0.00%
Tension Reinf, As (in2) 2.37 2.37 0.00%
Design Shear Force, Vu 37.73 37.73 0.00%
Shear Reinf, Av/s (in2/in) 0.041 0.041 0.00%
COMPUTER FILE: ACI 318-11 Ex001
CONCLUSION
The computed results show an exact match for the flexural and the shear
reinforcing.
ACI 318-11 Example 001 - 2

Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
0
HAND CALCULATION
Flexural Design
The following quantities are computed for all the load combinations:
ϕ = 0.9, Ag = 160 sq-in
As,min =
db
f
w
y
200
= 0.450 sq-in (Govern)
=
db
f
f
w
y
c'
3
= 0.427 sq-in
14000
0.85 0.05 0.85
1000
c
f
β
′−
=−=
max
0.003
0.003 0.005
cd= =
+
5.0625 in
max 1 max
ac
β
=
= 4.303 in
Combo1
wu = (1.2wd + 1.6wl) = 9.736 k/ft
8
2
lw
Mu
u=
= 9.736∙102/8 = 121.7 k-ft = 1460.4 k-in
The depth of the compression block is given by:
bf
M
dda
c
u
ϕ
'
2
85.0
2
−−=
= 4.183 in (a < amax)
The area of tensile steel reinforcement is given by:
As =
−2
a
df
M
y
u
ϕ
=
( )
2/183.45.13609.0
4.1460
−••
As = 2.37 sq-in
ACI 318-11 Example 001 - 3

Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
0
Shear Design
The following quantities are computed for all of the load combinations:
ϕ = 0.75
Check the limit of
c
f′
:
c
f′
= 63.246 psi < 100 psi
The concrete shear capacity is given by:
ϕ Vc = ϕ 2
c
f′
bd = 12.807 k
The maximum shear that can be carried by reinforcement is given by:
ϕ Vs = ϕ 8
c
f′
bd = 51.229 k
The following limits are required in the determination of the reinforcement:
(ϕ Vc/2) = 6.4035 k
(ϕ Vc + ϕ 50 bd) = 11.466 k
ϕ Vmax = ϕ Vc + ϕ Vs = 64.036 k
Given Vu, Vc and Vmax, the required shear reinforcement in area/unit length for
any load combination is calculated as follows:
If Vu ≤ ϕ (Vc/2),
s
A
v
= 0,
else if ϕ (Vc/2) < Vu ≤ ϕ Vmax
s
A
v
=
min
()
uc v
ys
VV A
fd s
φ
φ
−
≥
where:
min
3
max 50 , 4
v ww c
yt yt
A bb f
s ff
′
=
else if Vu > ϕ Vmax,
a failure condition is declared.
ACI 318-11 Example 001 - 4

Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
0
Combo1
Vu = 9.736∙(5-13.5/12) = 37.727 k
( )
max
/ 2 6.4035 37.727 64.036
cu
V kV k V k
φφ
= ≤= ≤ =
min
10 10 3
max 50 , 4,000
60,000 60,000 4
v
A
s
=
{ }
2
min
max 0.0083, 0.0079 0.0083
v
Ain
s in
= =
s
A
v
=
22
()
0.041 0.492
uc
ys
VV in in
f d in ft
φ
φ
−= =
ACI 318-11 Example 001 - 5