ACI 318 14 PT SL Example 001
User Manual: ACI 318-14 PT-SL Example 001
Open the PDF directly: View PDF ![]() .
.
Page Count: 7
Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
ACI 318-14 PT-SL EXAMPLE 001 - 1
ACI 318-14 PT-SL EXAMPLE 001
Design Verification of Post-Tensioned Slab using the ACI 318-14 code
PROBLEM DESCRIPTION
The purpose of this example is to verify the slab stresses and the required area of
mild steel strength reinforcing for a post-tensioned slab.
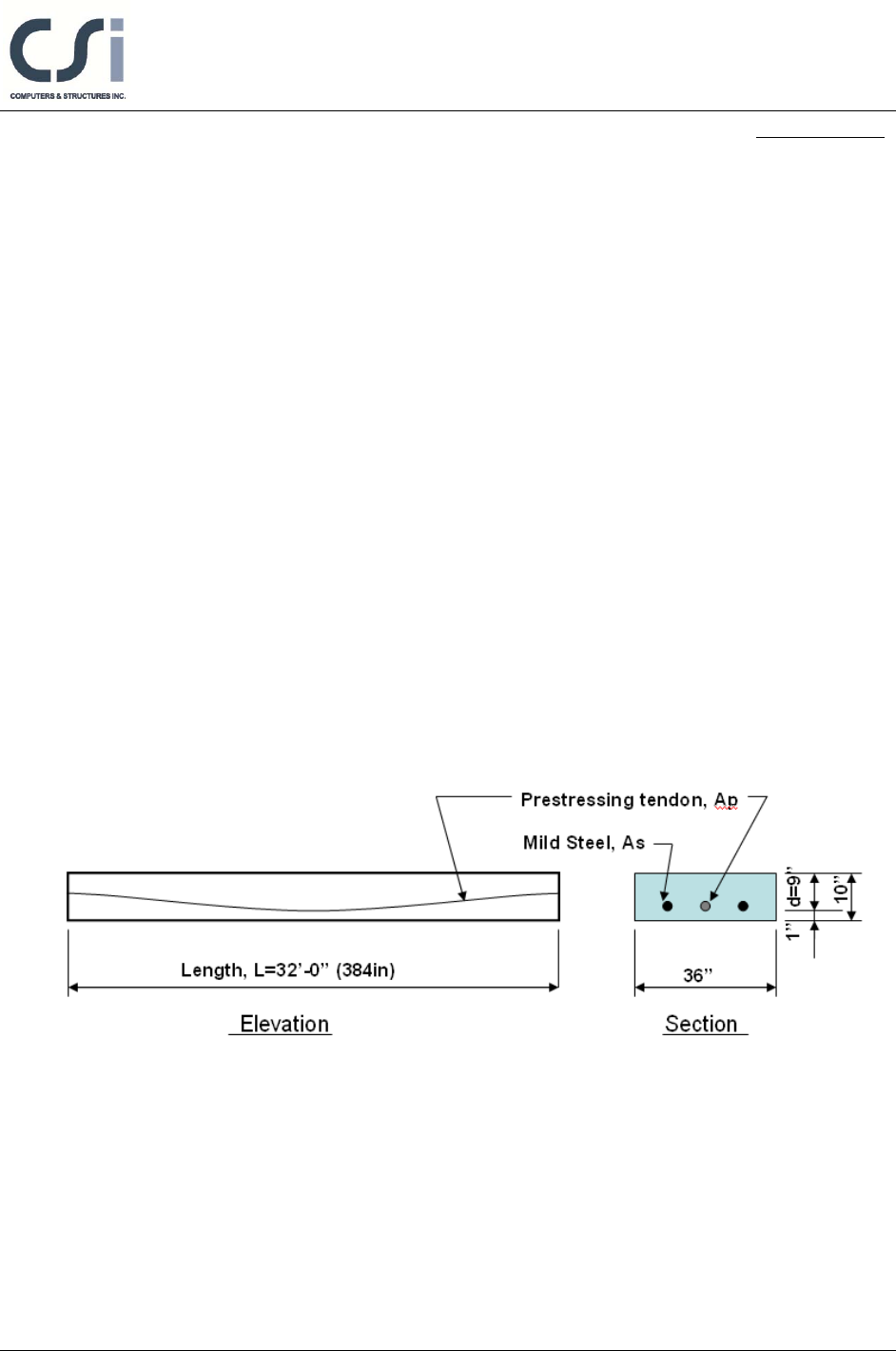
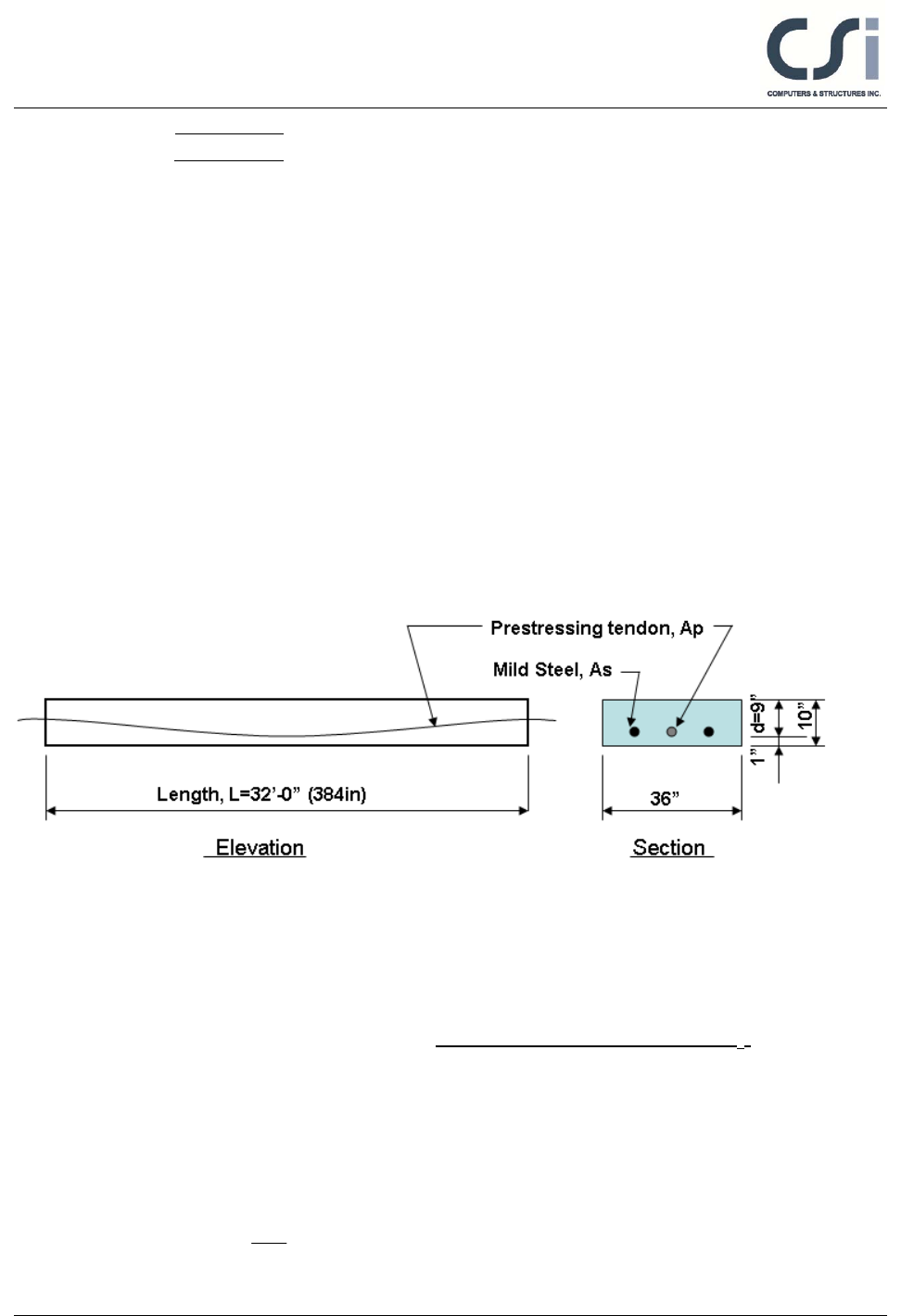
A one-way, simply supported slab is modeled in ETABS. The modeled slab is 10
inches thick by 36 inches wide and spans 32 feet, as shown in shown in Figure 1.
A 36-inch-wide design strip was centered along the length of the slab and was
defined as an A-Strip. B-strips were placed at each end of the span perpendicular
to the Strip-A (the B-Strips are necessary to define the tendon profile). A tendon,
with two strands having an area of 0.153 square inches each, was added to the A-
Strip. The self weight and live loads were added to the slab. The loads and post-
tensioning forces are shown below. The total factored strip moments, required
area of mild steel reinforcement, and slab stresses are reported at the mid-span of
the slab. Independent hand calculations were compared with the ETABS results
and summarized for verification and validation of the ETABS results.
Loads: Dead = self weight, Live = 100psf

Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
ACI 318-14 PT-SL EXAMPLE 001 - 2
Figure 1 One-Way Slab
GEOMETRY, PROPERTIES AND LOADING
Thickness, T, h = 10 in
Effective depth, d = 9 in
Clear span, L = 384 in
Concrete strength, C
f
' = 4,000 psi
Yield strength of steel, y
f
= 60,000 psi
Prestressing, ultimate pu
f
= 270,000 psi
Prestressing, effective e
f
= 175,500 psi
Area of Prestress (single strand), P
A
= 0.153 sq in
Concrete unit weight, wc = 0.150 pcf
Modulus of elasticity, Ec = 3,600 ksi
Modulus of elasticity, Es = 29,000 ksi
Poisson’s ratio, = 0
Dead load, wd = self psf
Live load, wl = 100 psf
TECHNICAL FEATURES OF ETABS TESTED
Calculation of the required flexural reinforcement
Check of slab stresses due to the application of dead, live and post-tensioning
loads.
Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
ACI 318-14 PT-SL EXAMPLE 001 - 3
RESULTS COMPARISON
The ETABS total factored moments, required mild steel reinforcing and slab
stresses are compared to the independent hand calculations in Table 1.
Table 1 Comparison of Results
FEATURE TESTED INDEPENDENT
RESULTS ETABS
RESULTS DIFFERENCE
Factored moment,
Mu (Ultimate) (k-in) 1429.0 1428.3 -0.05%
Area of Mild Steel req’d,
As (sq-in) 2.21 2.21 0.00%
Transfer Conc. Stress, top
(D+PTI), ksi 0.734 0.735 0.14%
Transfer Conc. Stress, bot
(D+PTI), ksi 0.414 0.414 0.00%
Normal Conc. Stress, top
(D+L+PTF), ksi 1.518 1.519 0.07%
Normal Conc. Stress, bot
(D+L+PTF), ksi 1.220 1.221 0.08%
Long-Term Conc. Stress,
top (D+0.5L+PTF(L)), ksi 1.134 1.135 0.09%
Long-Term Conc. Stress,
bot (D+0.5L+PTF(L)), ksi 0.836 0.837 0.12%
COMPUTER FILE: ACI 318-14 PT-SL EX001.EDB
CONCLUSION
The ETABS results show an acceptable comparison with the independent results.
Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
ACI 318-14 PT-SL EXAMPLE 001 - 4
CALCULATIONS:
Design Parameters:
=0.9
Mild Steel Reinforcing Post-Tensioning
f
c = 4000 psi fj = 216.0 ksi
fy = 60,000 psi Stressing Loss = 27.0 ksi
Long-Term Loss = 13.5 ksi
fi = 189.0 ksi
fe = 175.5 ksi
Loads: Dead, self-wt = 10 12
/
ft 0.150 kcf = 0.125 ksf (D) 1.2 = 0.150 ksf (Du)
Live, 0.100 ksf (L) 1.6 = 0.160 ksf (Lu)
Total =0.225 ksf (D+L) 0.310 ksf (D+L)ult
=0.225 ksf 3 ft = 0.675 klf,
u
= 0.310 ksf 3ft = 0.930 klf
Ultimate Moment, 2
1
8
U
wl
M= 0.310 klf 322/8 = 119.0 k-ft = 1429.0 k-in

Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
ACI 318-14 PT-SL EXAMPLE 001 - 5
Ultimate Stress in strand, 10000 300
PS SE
P
f
'c
ff
(span-to-depth ratio > 35)
4,000
175,500 10,000 300 0.000944
199,624 psi 205,500 psi
Ultimate force in PT,
,2 0.153 199.62 61.08 kips
ult PT P PS
FAf
Ultimate force in RC,
,2.00(assumed) 60.0 120.0 kips
ult RC s y
FAf
Total Ultimate force, ,61.08 120.0 181.08 kips
ult Total
F
Stress block depth,
,181.08 1.48 in
0.85 ' 0.85 4 36
ult Total
F
afcb
Ultimate moment due to PT,
,,
1.48
61.08 9 0.9 454.1k-in
22
ult PT ult PT
a
MFd
Net ultimate moment, ,1429.0 454.1 974.9 k-in
net U ult PT
MMM
Required area of mild steel reinforcing,
2
974.9 2.18 in
1.48
0.9 60 9
22
net
S
y
M
Aa
fd
Note: The required area of mild steel reinforcing was calculated from an assumed amount of
steel. Since the assumed value and the calculated value are not the same a second iteration can be
performed. The second iteration changes the depth of the stress block and the calculated area of
steel value. Upon completion of the second iteration the area of steel was found to be 2.21in2

Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
ACI 318-14 PT-SL EXAMPLE 001 - 6
Check of Concrete Stresses at Mid-Span:
Initial Condition (Transfer), load combination (D + L + PTi) = 1.0D + 1.0PTI
The stress in the tendon at transfer = jacking stress stressing losses = 216.0 27.0
= 189.0 ksi
The force in the tendon at transfer, =
189.0 2 0.153 57.83kips
Moment due to dead load,
2
0.125 3 32 8 48.0 k-ft 576 k-in
D
M
Moment due to PT,
(sag) 57.83 4 in 231.3 k-in
PT PTI
MF
Stress in concrete,
57.83 576.0 231.3
10 36 600
PTI D PT
FMM
fAS , where S = 600 in3
0 161 0 5745 f. .
0.735(Comp)max,0.414(Tension)maxf=-
Normal Condition, load combinations: (D + L + PTF) = 1.0D + 1.0L + 1.0PTF
Tendon stress at normal = jacking stressing long-term = 216.0 27.0 13.5 = 175.5 ksi
The force in tendon at Normal, =
175.5 2 0.153 53.70kips
Moment due to dead load,
2
0.125 3 32 8 48.0 k-ft 576 k-in
D
M
Moment due to dead load,
2
0.100 3 32 8 38.4 k-ft 461k-in
L
M
Moment due to PT,
(sag) 53.70 4 in 214.8 k-in
PT PTI
MF
Stress in concrete for (D + L+ PTF),
53.70 1037.0 214.8
10 36 600
PTI D L PT
FM M
fAS
0 149 1 727 0 358
f
...
1.518(Comp)max,1.220(Tension)max
f
Long-Term Condition, load combinations: (D + 0.5L + PTF(L)) = 1.0D + 0.5L + 1.0PTF
Tendon stress at normal = jacking stressing long-term = 216.0 27.0 13.5 = 175.5 ksi
The force in tendon at Normal, =
175.5 2 0.153 53.70kips
Moment due to dead load,
2
0.125 3 32 8 48.0 k-ft 576 k-in
D
M
Moment due to dead load,
2
0.100 3 32 8 38.4 k-ft 460 k-in
L
M
Moment due to PT,
(sag) 53.70 4 in 214.8 k-in
PT PTI
MF

Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
ACI 318-14 PT-SL EXAMPLE 001 - 7
Stress in concrete for (D + 0.5L + PTF(L)),
0.5 53.70 806.0 214.8
10 36 600
DL PT
PTI MM
F
fAS
0 149 0 985
f
..
1.134(Comp)max,0.836(Tension)maxf