Contents AISC 360 05 Example 001
User Manual: AISC 360-05 Example 001
Open the PDF directly: View PDF ![]() .
.
Page Count: 7
Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
0
AISC 360-05 Example 001
WIDE FLANGE MEMBER UNDER BENDING
EXAMPLE DESCRIPTION
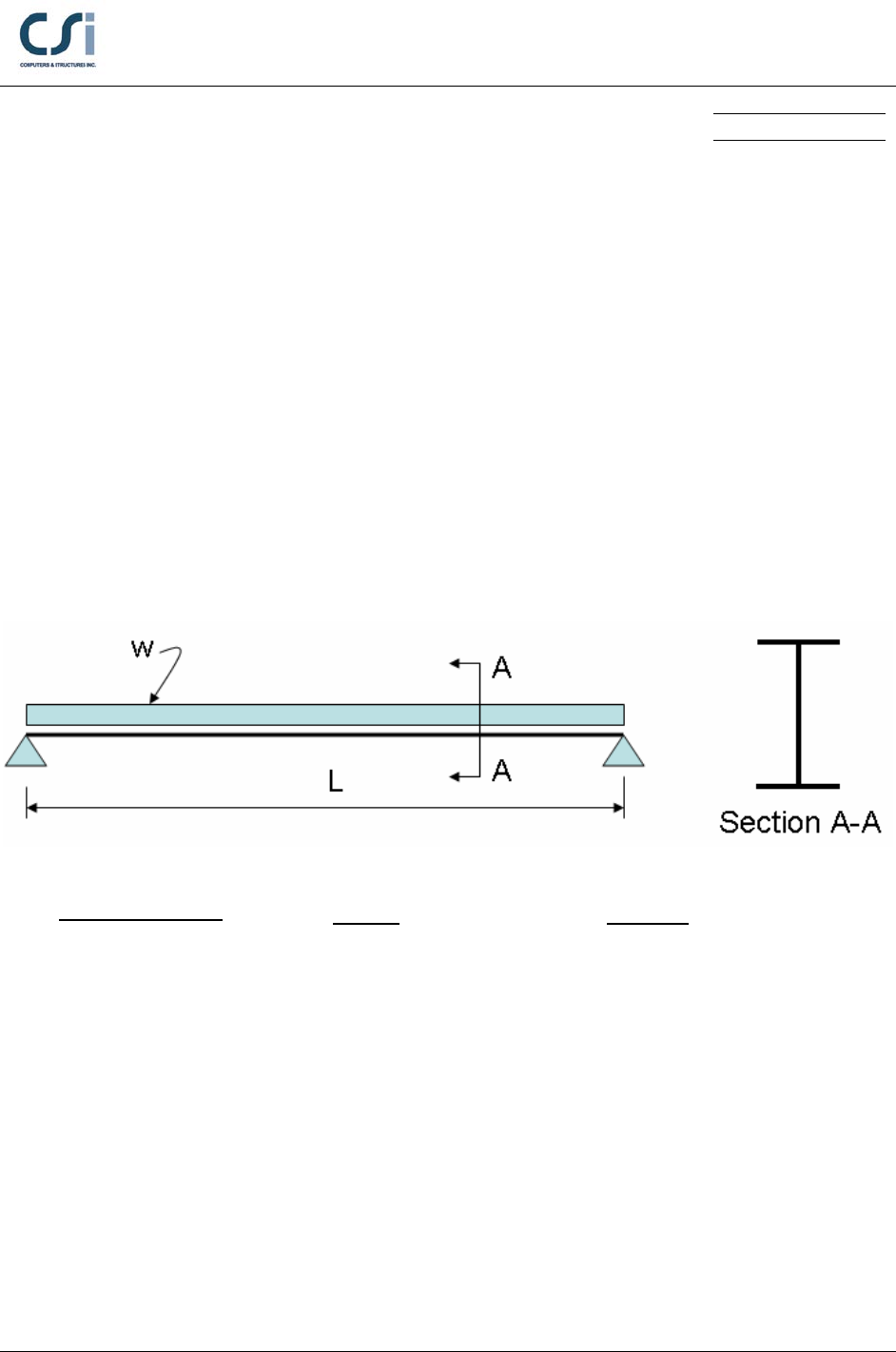
The design flexural strengths are checked for the beam shown below. The beam
is loaded with a uniform load of 0.45 klf (D) and 0.75 klf (L). The flexural
moment capacity is checked for three unsupported lengths in the weak direction,
Lb = 5 ft, 11.667 ft and 35 ft.
GEOMETRY, PROPERTIES AND LOADING
TECHNICAL FEATURES TESTED
Section Compactness Check (Bending)
Member Bending Capacities
Unsupported length factors
Member Properties
W18X50
E = 29000 ksi
Fy = 50 ksi
Loading
w = 0.45 klf (D)
w = 0.75 klf (L)
Geometry
Span, L = 35 ft
AISC 360-05 Example 001 - 1
Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
0
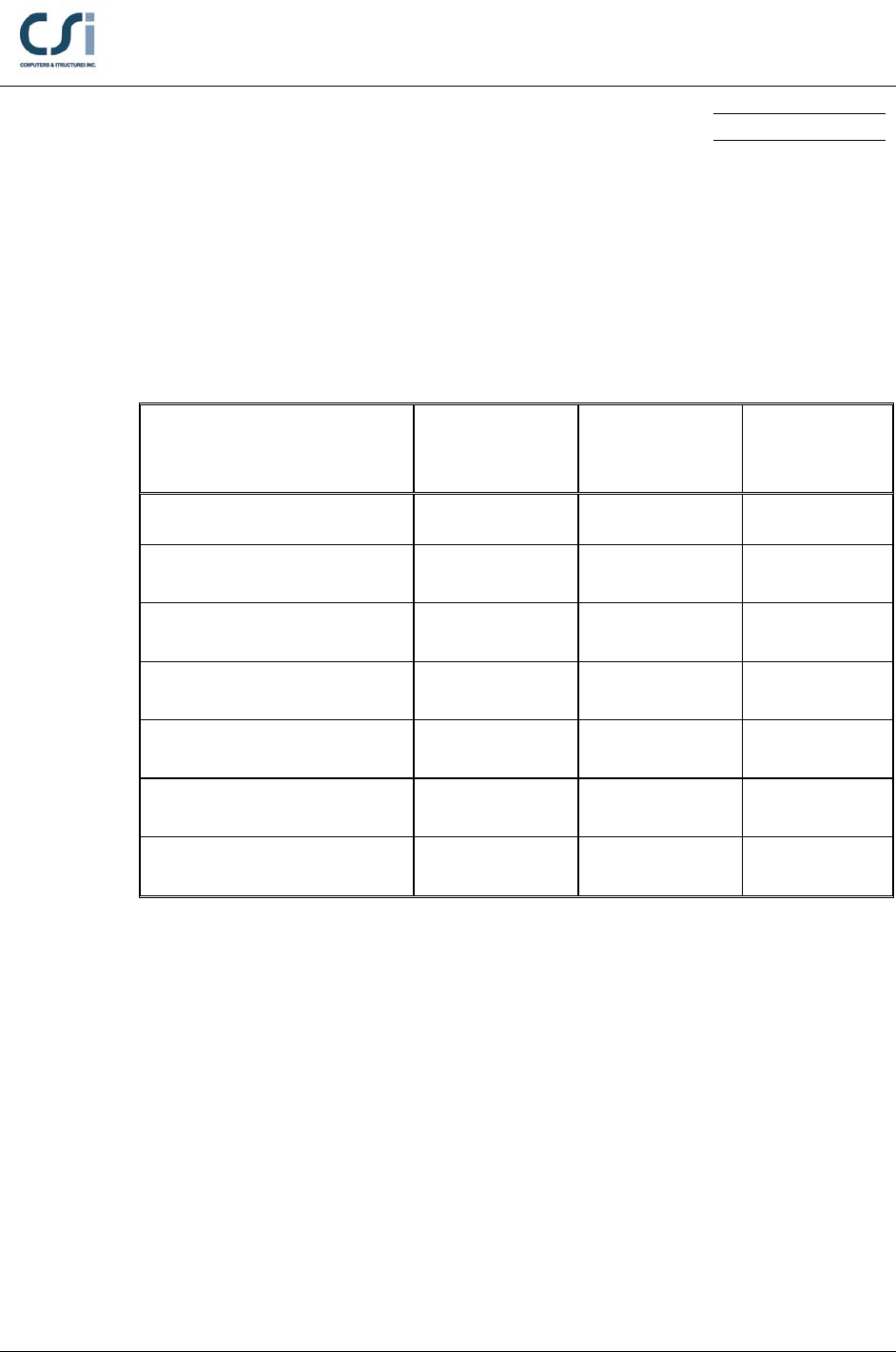
RESULTS COMPARISON
Independent results are comparing with the results of Example F.1-2a from the
AISC Design Examples, Volume 13 on the application of the 2005 AISC
Specification for Structural Steel Buildings (ANSI/AISC 360-05).
Output Parameter
ETABS Independent Percent
Difference
Compactness Compact Compact 0.00%
Cb (
b
L
=5ft) 1.004 1.002 0.20%
bn
M
φ
(
b
L
=5ft) (k-ft) 378.750 378.750 0.00%
Cb (
b
L
=11.67ft) 1.015 1.014 0.10%
bn
M
φ
(
b
L
=11.67ft) (k-ft) 307.124 306.657 0.15%
Cb (
b
L
=35ft) 1.138 1.136 0.18%
bn
M
φ
(
b
L
=35ft) (k-ft) 94.377 94.218 0.17%
COMPUTER FILE: AISC 360-05 EX001
CONCLUSION
The results show an acceptable comparison with the independent results.
AISC 360-05 Example 001 - 2
Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
0
HAND CALCULATION
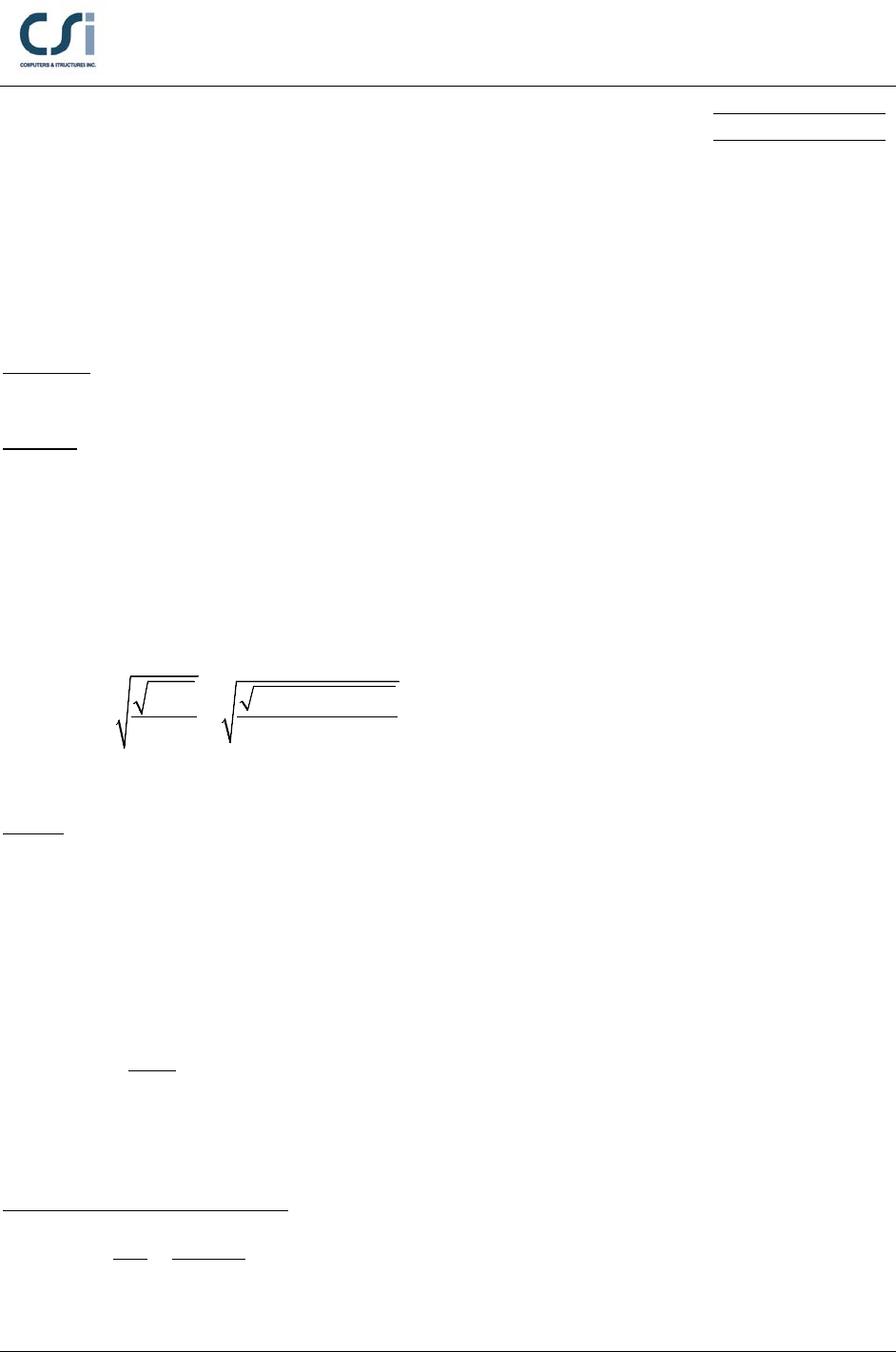
Properties:
Material: ASTM A572 Grade 50 Steel
E = 29,000 ksi, Fy = 50 ksi
Section: W18x50
bf = 7.5 in, tf = 0.57 in, d = 18 in, tw = 0.355 in
2 18 2 0.57 16.86
f
h d t in= − = −• =
018 0.57 17.43
f
h d t in
=−=− =
S33 = 88.9 in3, Z33 = 101 in3
Iy =40.1 in4, ry = 1.652 in, Cw = 3045.644 in6, J = 1.240 in4
33
40.1 3045.644 1.98
88.889
yw
ts
IC
r in
S
•
= = =
0.1=
m
R
for doubly-symmetric sections
Other:
c = 1.0
L = 35 ft
Loadings:
wu = (1.2wd + 1.6wl) = 1.2(0.45) + 1.6(0.75) = 1.74 k/ft
2
8
u
u
wL
M=
= 1.74∙352/8 = 266.4375 k-ft
Section Compactness:
Localized Buckling for Flange:
579.
6
57.02
50.7
2=
•
==
f
f
t
b
λ
AISC 360-05 Example 001 - 3
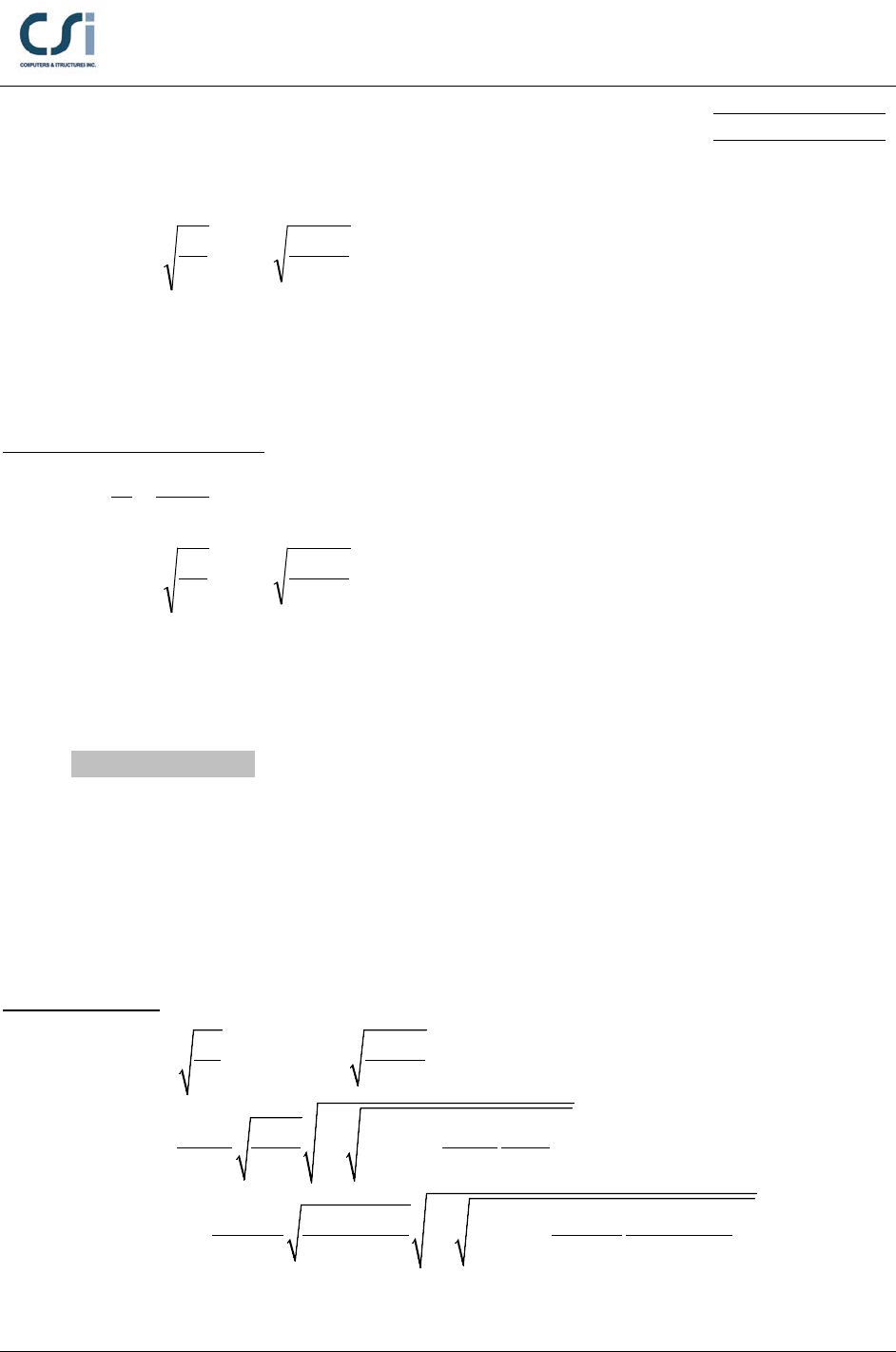
Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
0
152
.
9
50
29000
38.038.0 ===
y
pF
E
λ
p
λλ
<
, No localized flange buckling
Flange is Compact.
Localized Buckling for Web:
16.86 47.49
0.355
w
h
t
λ
= = =
553.90
50
29000
76.3
76.3 =
==
y
pF
E
λ
p
λλ
<
, No localized web buckling
Web is Compact.
Section is Compact.
Section Bending Capacity:
33
50 101 5050
py
M F Z k in= =•= −
Lateral-Torsional Buckling Parameters:
Critical Lengths:
29000
1.76 1.76 1.652 70.022 5.835
50
py
y
E
L r in ft
F
==•==
2
33
33
0.7
1.95 1 1 6.76
0.7
yo
r ts
yo
FSh
E Jc
Lr
F S h E Jc
= ++
2
29000 1.240 1.0 0.7 50 88.9 17.43
1.95 1.98 1 1 6.76
0.7 50 88.9 17.43 29000 1.240 1.0
r
L• ••
= • ++
•• •
AISC 360-05 Example 001 - 4

Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
0
16.966
r
L ft=
Non-Uniform Moment Magnification Factor:
For the lateral-torsional buckling limit state, the non-uniform moment magnification factor is
calculated using the following equation:
0.3
3
435.2
5.12
max
max
≤
+++
=
m
CBA
b
R
M
MMM
M
C
Eqn. 1
Where MA = first quarter-span moment, MB = mid-span moment, MC = second quarter-span
moment.
The required moments for Eqn. 1 can be calculated as a percentage of the maximum mid-span
moment. Since the loading is uniform and the resulting moment is symmetric:
2
1
14
b
AC
L
MM L
= = −
Member Bending Capacity for Lb = 5 ft:
max 1.00
B
MM= =
22
1 15
1 1 0.995
4 4 35
b
AC
L
MM L
==−=−=
()
( ) ( ) ( ) ( )
12.5 1.00
2.5 1.00 3 0.995 4 1.00 3 0.995
b
C=+ ++
1.002
b
C=
pb
LL <
, Lateral-Torsional buckling capacity is as follows:
5050
np
M M k in= = −
0.9 5050 /12
bn
M
ϕ
= •
378.75
bn
M k ft
ϕ
= −
AISC 360-05 Example 001 - 5

Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
0
Member Bending Capacity for Lb = 11.667 ft:
max 1.00
B
MM= =
22
1 1 11.667
1 1 0.972
4 4 35
b
AC
L
MM L
==−=− =
( )
() ( ) ( ) ( )
12.5 1.00
2.5 1.00 3 0.972 4 1.00 3 0.972
b
C=+ ++
1.014
b
C=
r
bp
L
LL <<
, Lateral-Torsional buckling capacity is as follows:
( )
p
pr
pb
yppbn M
LL
LL
SFMMCM ≤
−
−
−−= 33
7.0
( )
11.667 5.835
1.014 5050 5050 0.7 50 88.889 4088.733
16.966 5.835
n
M k in
−
= − − •• = −
−
0.9 4088.733/12
bn
M
ϕ
= •
306.657
bn
M k ft
ϕ
= −
Member Bending Capacity for Lb = 35 ft:
max 1.00
B
MM= =
22
1 1 35
1 1 0.750
4 4 35
b
AC
L
MM L
==−=−=
.
( )
( ) ( ) ( ) ( ) ( )
12.5 1.00 1.00
2.5 1.00 3 0.750 4 1.00 3 0.750
b
C=+ ++
1.136
b
C=
rb LL >
, Lateral-Torsional buckling capacity is as follows:
AISC 360-05 Example 001 - 6

Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
0
2
33
2
2078
.0
1
+
=
ts
b
o
ts
b
b
cr r
L
h
S
Jc
r
L
E
C
F
π
2
2
2
1.136 29000 1.24 1 420
1 0.078 14.133
88.889 17.4 1.983
420
1.983
cr
F ksi
π
•• •
=+=
•
p
crnM
SF
M≤
=33
14.133 88.9 1256.245
n
M k in= •= −
0.9 1256.245/12
bn
M
ϕ
= •
94.218
bn
M k ft
ϕ
= −
AISC 360-05 Example 001 - 7