Contents AISC 360 10 Example 002
User Manual: AISC-360-10 Example 002
Open the PDF directly: View PDF ![]() .
.
Page Count: 8
Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
3
AISC-360-10 Example 002
COMPOSITE GIRDER DESIGN
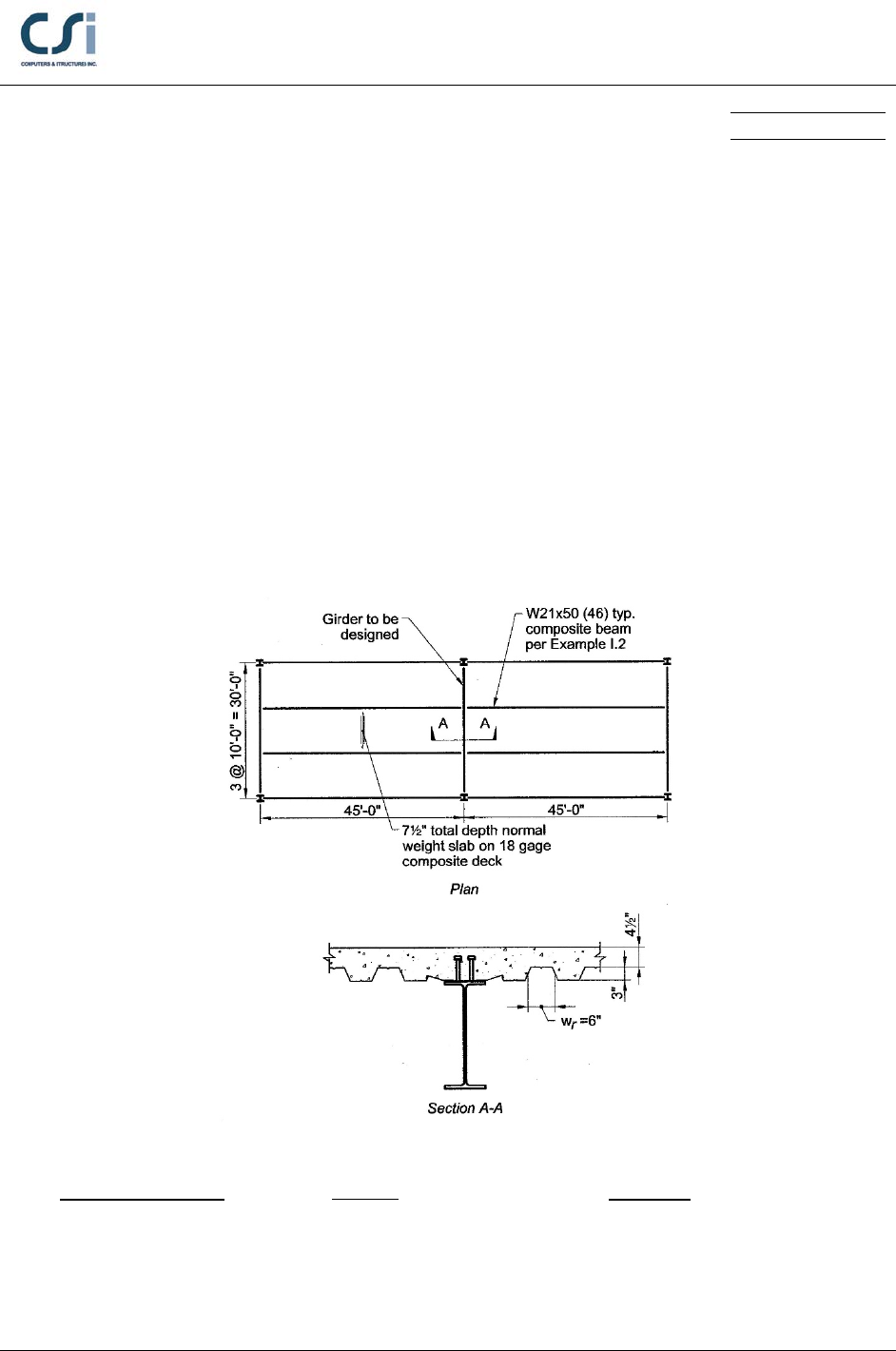
EXAMPLE DESCRIPTION
The design is checked for the composite girder shown below. The deck is 3 in.
deep with 4 ½″ normal weight (145 pcf) concrete cover with a compressive
strength of 4 ksi. The girder will not be shored during construction. The applied
loads are the weight of the structure, a 25 psf construction live load, a 10 psf
superimposed dead load and a 100 psf non-reducible service line load.
GEOMETRY, PROPERTIES AND LOADING
Member Properties
W24x76
E = 29000 ksi
F
y
= 50 ksi
Loading
P = 36K (Dead Load)
P = 4.5K (SDL)
P = 45K (Live Load)
Geometry
Span, L = 45 ft
AISC-360-10 Example 002 - 1

Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
3
TECHNICAL FEATURES OF ETABS TESTED
Composite beam design, including:
Selection of steel section, camber and shear stud distribution
Member bending capacities, at construction and in service
Member deflections, at construction and in service
RESULTS COMPARISON
Independent results are referenced from Example I.2 from the AISC Design
Examples, Version 14.0.
Output Parameter ETABS Independent Percent
Difference
Pre-composite Mu (k-ft) 622.3 622.3 0.00%
Pre-composite ΦbMn (k-ft) 677.2 677.2 0.00%
Pre-composite Deflection (in.) 1.0 1.0 0.00%
Required Strength Mu (k-ft) 1216.3 1216.3 0.00%
Full Composite ΦbMn (k-ft) 1480.1 1480.1 0.00%
Partial Composite ΦbMn (k-ft) 1267.3 1267.3 0.00%
Shear Stud Capacity Qn 21.54 21.54 0.00%
Shear Stud Distribution 26, 3, 26 26, 3, 26 0.00%
Live Load Deflection (in.) 0.63 0.55 12.7%
Required Strength Vu (kip) 122.0 122.0 0.00%
ΦVn (k) 315.5 315.5 0.00%
AISC-360-10 Example 002 - 2

Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
3
COMPUTER FILE: AISC-360-10 EXAMPLE 002.EDB
CONCLUSION
The ETABS results show an acceptable comparison with the independent results.
The live load deflection differs more markedly because of a difference in
methodology. In the AISC example, the live load deflection is computed based
on a lower bound value of the beam moment of inertia, whereas in ETABS, it is
computed based on the approximate value of the beam moment of inertia derived
from Equation (C-I3-6) from the Commentary on the AISC Load and Resistance
Factor Design Specification – Second Edition.
AISC-360-10 Example 002 - 3

Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
3
HAND CALCULATION
Properties:
Materials:
ASTM A572 Grade 50 Steel
E = 29,000 ksi, Fy = 50 ksi, wsteel = 490 pcf
4000 psi normal weight concrete
Ec = 3,644 ksi,
4 ksi,
′=
c
f
wconcrete = 145 pcf
Section:
W24x76
d = 23.9 in, bf = 8.99 in, tf = 0.68 in, tw = 0.44 in
Asteel = 22.4 in2, Isteel = 2100 in4
Deck:
tc =4 ½ in., hr = 3 in., sr =12 in., wr = 6 in.
Shear Connectors:
d = ¾ in, h =4 ½ in, Fu = 65 ksi
Design for Pre-Composite Condition:
Construction Required Flexural Strength:
22.4
• sq.ft. 490 pcf 76.2 plf
steel steel 144
= = •=
wA w
[ ]
(45 ft)(10 ft)(75 psf ) (50 plf)(45 ft) (0.001 kip / lb) 36 kips
D
P=+=
[ ]
(45 ft)(10 ft)(25 psf ) (0.001 kip/lb) 11.25 kips
L
P= =
( )
( )
2
2
1.2 1.2 1.6
83
76.2 30 30
1.2 1.2 36 +1.6 11.25 622.3 kip-ft
83
= ++
•
= +• • =
u DL
wL L
M PP
AISC-360-10 Example 002 - 4

Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
3
Moment Capacity:
Lb = 10 ft
Lp = 6.78 ft
Lr = 19.5 ft
ΦbBF = 22.6 kips
ΦbMpx = 750 kip-ft
Cb = 1.0
( )
()
1.0 750 22.6 • 10 6.78 677.2 kip-ft
Φ = Φ −Φ −
=−− =
b n b b px b b p
M C M BF L L
Pre-Composite Deflection:
4
34 3
0.0762
5 360
536.0 360 12 1.0
28 384 28 29,000 2,100 384 29,000 2,100
DD
nc
PL wL
EI EI
••
•
∆= + = + =
•• ••
Camber 0.8 0.8 in.
nc
= •∆ =
which is rounded down to ¾ in.
Design for Composite Flexural Strength:
Required Flexural Strength:
[ ]
(45 ft)(10 ft)(75 +10psf) (50 plf)(45 ft) (0.001 kip/lb) 40.5kips=+=
PD
[ ]
(45 ft)(10 ft)(100 psf ) (0.001 kip/lb) 45 kips= =
PL
2
2
1.2 (1.2 1.6 )
83
1.2 76.22 30 30
(1.2 40.5 +1.6 45) 1216.3 kip-ft
83
u DL
wL L
M PP= ++
••
= +• • =
Full Composite Action Available Flexural Strength:
Effective width of slab:
30.0 ft 7.5 ft 90 in.
eff 8
= = =b
AISC-360-10 Example 002 - 5

Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
3
Resistance of steel in tension:
22.4 50 1,120 kips
y sy
CP AF==•= •=
controls
Resistance of slab in compression
2
eff eff
7.5 12
( 2) (7.5 12) 4.5 3 540 in
2
•
= • + • = • • + •=
r
cc
Ab t b h
0.85 ' 0.85 4 540 1836 kips
cc
C fA= • = •• =
Depth of compression block within slab:
1,120 3.66 in.
0.85 ' 0.85 (7.5 12) 4
eff c
C
abf
= = =
•• • ••
Moment resistance of composite beam for full composite action:
1
3.66
( ) (4.5 3) 5.67 in.
22
cr
a
d th= + −= +− =
12
23.9 12
0.9 1,120 5.67 /12 1,120 1480.1 kip-ft
2
d
M Cd P
ny
Φ =Φ •+ •
=• • +• =
Partial Composite Action Available Flexural Strength:
Assume 50% composite action:
0.5 560 kips
y
CP= •=
Depth of compression block within slab
560 1.83 in.
0.85 ' 0.85 (7.5 12) 4
eff c
C
abf
= = =
•• • ••
1
1.83
( ) (4.5 3) 6.58 in.
22
cr
a
d th= + −= +− =
Depth of compression block within steel section flange
1,120 560 0.623 in.
2 2 8.99 50
y
fy
PC
xbF
−−
= = =
•• • •
2
/ 2 0.311 in.dx= =
AISC-360-10 Example 002 - 6

Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
3
12 32
()( )
23.9
560 (6.58 0.312) 1,120 0.312 12 1,408 kip-ft
2
=• + +• −
=•+ +• − =
ny
M Cdd P dd
0.9 0.9 1,408 1,267.3 kip-ft
nn
MMΦ= =• =
Shear Stud Strength:
0.5 '= ≤
n sa c c g p sa u
Q A f E RRAF
22 2
4 (0.75) 4 0.442 in
=π=π =
sa sa
Ad
' 4 ksi
c
f=
1.5 1.5
' 145 4 3,490 ksi
cc
Ew f= = =
Rg = 1.0 Studs welded directly to the steel shape with the slab haunch
Rp = 0.75 Studs welded directly to the steel shape
Fu = 65 ksi
22
0.5 0.442 4 3,490 1.0 0.75 0.442 65
26.1 kips 21.54 kips controls
n
Q=• • ≤• • •
= ≥
Shear Stud Distribution:
560 26 studs from each end to nearest concentrated load point
21.54
Σ
=
= =
n
n
Q
nQ
Add 3 studs between load points to satisfy maximum stud spacing requirement.
Live Load Deflection:
Modulus of elasticity ratio:
/ 29,000 / 3,644 8.0= = =
c
n EE
AISC-360-10 Example 002 - 7

Software Verification
PROGRAM NAME:
ETABS
REVISION NO.:
3
Transformed elastic moment of inertia assuming full composite action:
Element
Transformed
Area
A (in2)
Moment Arm
from
Centroid
y (in.) Ay
(in.3) Ay2
(in,4) I0
(in.4)
Slab
50.9
17.2
875
15,055
86
Deck ribs
17.0
13.45
228
3,069
13
W21x50
22.4
0
0
0
2,100
89.5
1,103
18,124
2,199
24
02,199 18,124 20,323 in.
x
I I Ay=+= + =
1,092 12.2 in.
89.5
y= =
224
20,323 90.3 12.2 6,831 in
tr x
I I Ay
= −• = − • =
Effective moment of inertia assuming partial composite action:
()( )
4
equiv 2,100 0.5 6,831 2,100 5,446 in
= +Σ − = + − =
s n y tr s
I I QPI I
4
eff equiv
0.75 0.75 5,446 4,084 in=•=• =II
33
45.0 (30 12) 0.633 in.
28 28 29,000 4,084
L
LL
eff
PL
EI
••
∆= = =
••
Design for Shear Strength:
Required Shear Strength:
1.2 1.6 1.2 40.5 1.6 45 120.6 kip
u DL
PPP= •+•= • +•=
1.2 1.2 0.076 30 120.6 121.2 kip-ft
22
uu
wL
VP
•• • •
= += + =
Available Shear Strength:
0.6 1.0 0.6 23.9 0.44 50 315.5 kips
n wy
V dt FΦ=Φ••••=•• • •=
AISC-360-10 Example 002 - 8