Introduction To Power MOSFETs And Their Applications AN 0558

User Manual: AN-0558

Open the PDF directly: View PDF .
Page Count: 16

TL/G/10063

Introduction to Power MOSFETs and Their Applications AN-558

National Semiconductor

Application Note 558

Ralph Locher

December 1988

Introduction to Power

MOSFETs

and Their Applications

INTRODUCTION

The high voltage power MOSFETs that are available today

are N-channel, enhancement-mode, double diffused, Metal-

Oxide-Silicon, Field Effect Transistors. They perform the

same function as NPN, bipolar junction transistors except

the former are voltage controlled in contrast to the current

controlled bi-polar devices. Today MOSFETs owe their

ever-increasing popularity to their high input impedance and

to the fact that being a majority carrier device, they do not

suffer from minority carrier storage time effects, thermal run-

away, or second breakdown.

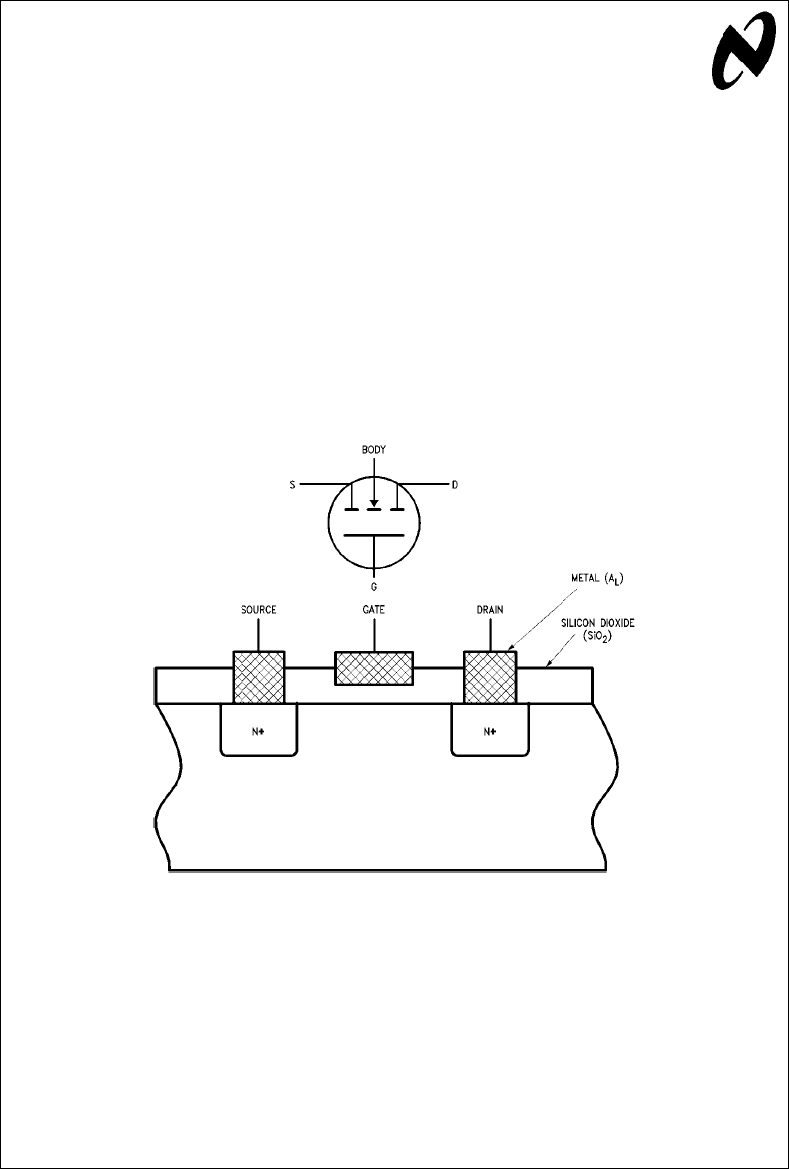
MOSFET OPERATION

An understanding of the operation of MOSFETs can best be

gleaned by first considering the later MOSFET shown in

Figure 1

With no electrical bias applied to the gate G, no current can

flow in either direction underneath the gate because there

will always be a blocking PN junction. When the gate is

forward biased with respect to the source S, as shown in

Figure 2

, the free hole carriers in the p-epitaxial layer are

repelled away from the gate area creating a channel, which

allows electrons to flow from the source to the drain. Note

that since the holes have been repelled from the gate chan-

nel, the electrons are the ‘‘majority carriers’’ by default. This

mode of operation is called ‘‘enhancement’’ but it is easier

to think of enhancement mode of operation as the device

being ‘‘normally off’’, i.e., the switch blocks current until it

receives a signal to turn on. The opposite is depletion mode,

which is a normally ‘‘on’’ device.

TL/G/10063–1

FIGURE 1. Lateral N-Channel MOSFET Cross-Section

C1995 National Semiconductor Corporation RRD-B30M115/Printed in U. S. A.

The advantages of the lateral MOSFET are:

1. Low gate signal power requirement. No gate current can

flow into the gate after the small gate oxide capacitance

has been charged.

2. Fast switching speeds because electrons can start to

flow from drain to source as soon as the channel opens.

The channel depth is proportional to the gate volage and

pinches closed as soon as the gate voltage is removed,

so there is no storage time effect as occurs in bipolar

transistors.

The major disadvantages are:

1. High resistance channels. In normal operation, the

source is electrically connected to the substrate. With no

gate bias, the depletion region extends out from the Na

drain in a pseudo-hemispherical shape. The channel

length L cannot be made shorter than the minimum de-

pletion width required to support the rated voltage of the

device.

2. Channel resistance may be decreased by creating wider

channels but this is costly since it uses up valuable silicon

real estate. It also slows down the switching speed of the

device by increasing its gate capacitance.

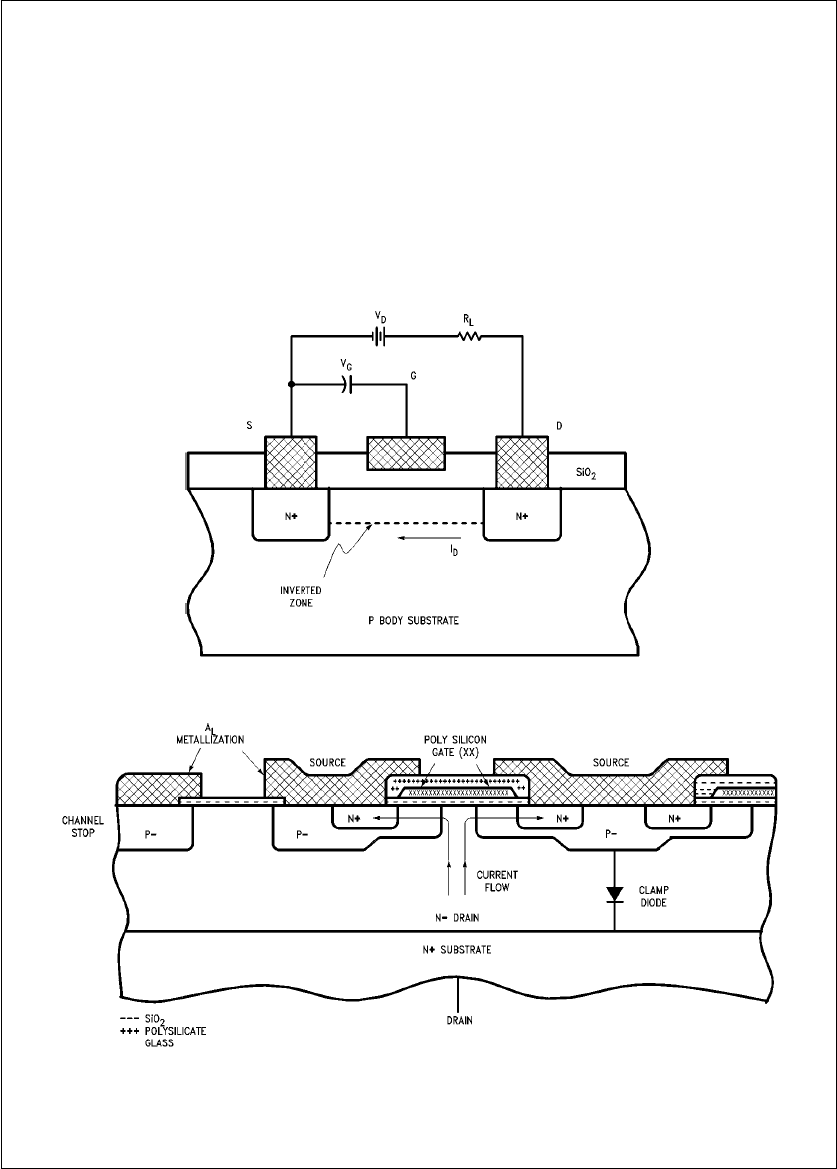
Enter vertical MOSFETs!

The high voltage MOSFET structure (also known as DMOS)

is shown in

Figure 3

TL/G/10063–2

FIGURE 2. Lateral MOSFET Transistor Biased for Forward Current Conduction

TL/G/10063–3

FIGURE 3. Vertical DMOS Cross-Sectional View

The current path is created by inverting the p-layer under-

neath the gate by the identical method in the lateral FETs.

Source current flows underneath this gate area and then

vertically through the drain, spreading out as it flows down.

A typical MOSFET consists of many thousands of Na

sources conducting in parallel. This vertical geometry

makes possible lower on-state resistances (RDS(on)) for the

same blocking voltage and faster switching than the lateral

FET.

There are many vertical construction designs possible, e.g.,

V-groove and U-groove, and many source geometries, e.g.,

squares, triangles, hexagons, etc. All commercially available

power MOSFETs with blocking voltages greater than 300V

are manufactured similarly to

Figure 3

. The many considera-

tions that determine the source geometry are RDS(on), input

capacitance, switching times and transconductance.

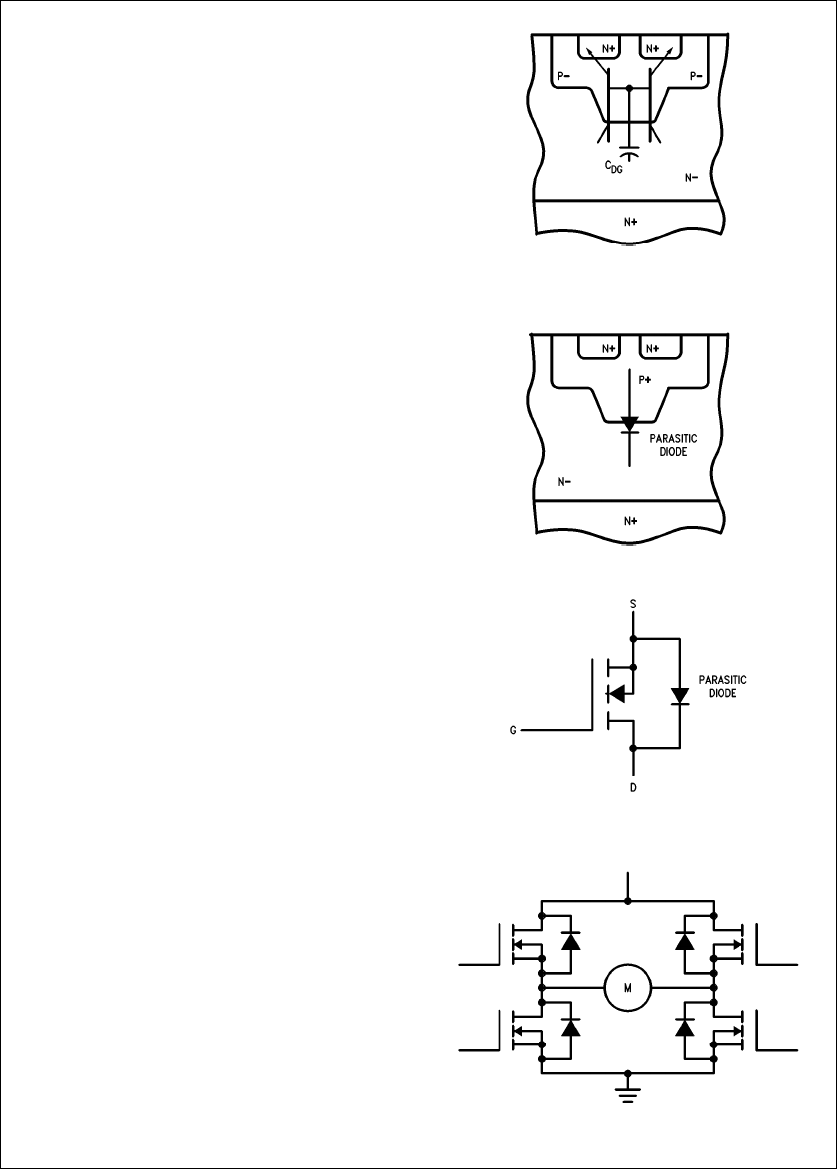
PARASITIC DIODE

Early versions of MOSFETs were very susceptible to volt-

age breakdown due to voltage transients and also had a

tendency to turn on under high rates of rise of drain-to-

source voltage (dV/dt), both resulting in catastrophic fail-

ures. The dV/dt turn-on was due to the inherent parasitic

NPN transistor incorporated within the MOSFET, shown

schematically in

Figure 4a

. Current flow needed to charge

up junction capacitance CDG acts like base current to turn

on the parasitic NPN.

The parasitic NPN action is suppressed by shorting the Na

source to the Pabody using the source metallization. This

now creates an inherent PN diode in anti-parallel to the

MOSFET transistor (see

Figure 4b

). Because of its exten-

sive junction area, the current ratings and thermal resist-

ance of this diode are the same as the power MOSFET.

This parasitic diode does exhibit a very long reverse recov-

ery time and large reverse recovery current due to the long

minority carrier lifetimes in the N-drain layer, which pre-

cludes the use of this diode except for very low frequency

applications, e.g., motor control circuit shown in

Figure 5

However in high frequency applications, the parasitic diode

must be paralleled externally by an ultra-fast rectifier to en-

sure that the parasitic diode does not turn on. Allowing it to

turn on will substantially increase the device power dissipa-

tion due to the reverse recovery losses within the diode and

also leads to higher voltage transients due to the larger re-

verse recovery current.

CONTROLLING THE MOSFET

A major advantage of the power MOSFET is its very fast

switching speeds. The drain current is strictly proportional to

gate voltage so that the theoretically perfect device could

switch in 50 ps– 200 ps, the time it takes the carriers to flow

from source to drain. Since the MOSFET is a majority carrier

device, a second reason why it can outperform the bipolar

junction transistor is that its turn-off is not delayed by minori-

ty carrier storage time in the base. A MOSFET begins to

turn off as soon as its gate voltage drops down to its thresh-

old voltage.

TL/G/10063–41

a. MOSFET Transistor Construction

Showing Location of the

Parasitic NPN Transistor

TL/G/10063–42

b. Parastic Diode

TL/G/10063–43

c. Circuit Symbol

FIGURE 4

TL/G/10063–4

FIGURE 5. Full-Wave Motor Control Circuit

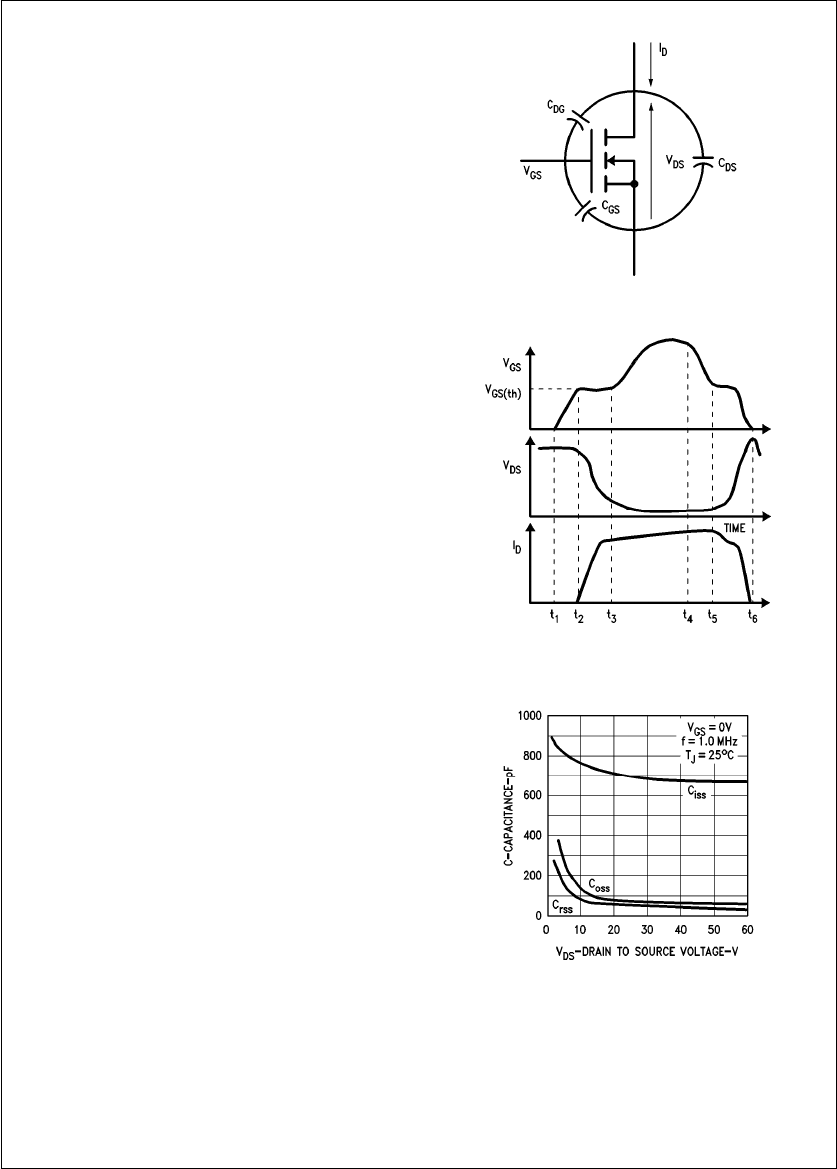
SWITCHING BEHAVIOR

Figure 6

illustrates a simplified model for the parasitic ca-

pacitances of a power MOSFET and switching voltage

waveforms with a resistive load.

There are several different phenomena occurring during

turn-on. Referring to the same figure:

Time interval t1ktkt2:

The initial turn-on delay time td(on) is due to the length of

time it takes VGS to rise exponentially to the threshold volt-

age VGS(th). From

Figure 6

, the time constant can be seen

to be RSxC

GS. Typical turn-on delay times for the National

Semiconductor IRF330 are:

td(on) eRScCGS cIn (1 bVGS(th)/VPK)

For an assumed gate signal generator impedance of RSof

50Xand CGS of 600 pF, tdcomes to 11 ns. Note that since

the signal source impedance appears in the tdequation, it is

very important to pay attention to the test conditions used in

measuring switching times.

Physically one can only measure input capacitance Ciss,

which consists of CGS in parallel with CDG. Even though

CGS ll CDG, the latter capacitance undergoes a much

larger voltage excursion so its effect on switching time can-

not be neglected.

Plots of Ciss,C

rss and Coss for the National Semiconductor

IRF330 are shown in

Figure 7

below. The charging and dis-

charging of CDG is analogous to the ‘‘Miller’’ effect that was

first discovered with electron tubes and dominates the next

switching interval.

Time interval t2ktkt3:

Since VGS has now achieved the threshold value, the

MOSFET begins to draw increasing load current and VDS

decreases. CDG must not only discharge but its capacitance

value also increases since it is inversely proportional to

VDG, namely:

CDG eCDG(0)/(VDG)n(2)

Unless the gate driver can quickly supply the current re-

quired to discharge CDG, voltage fall will be slowed with the

attendant increase in turn-on time.

Time interval t3ktkt4:

The MOSFET is now on so the gate voltage can rise to the

overdrive level.

Turn-off interval t4ktkt6:

Turn-off occurs in reverse order. VGS must drop back close

to the threshold value before RDS(on) will start to increase.

As VDS starts to rise, the Miller effect due to CDG re-occurs

and impedes the rise of VDS as CDG recharges to VCC.

Specific gate drive circuits for different applications are dis-

cussed and illustrated below.

TL/G/10063–5

a. MOSFET Capacitance Model for Power MOSFET

TL/G/10063–6

b. Switching Waveforms for Resistive Load

FIGURE 6

TL/G/10063–7

FIGURE 7. Typical Capacitances of the National IRF330

MOSFET CHARACTERIZATION

The output characteristics (IDvs VDS) of the National Semi-

conductor IRF330 are illustrated in

Figures 8

and

The two distinct regions of operation in

Figure 8

have been

labeled ‘‘linear’’ and ‘‘saturated’’. To understand the differ-

ence, recall that the actual current path in a MOSFET is

horizontal through the channel created under the gate oxide

and then vertical through the drain. In the linear region of

operation, the voltage across the MOSFET channel is not

sufficient for the carriers to reach their maximum drift veloci-

ty or their maximum current density. The static RDS(on), de-

fined simply as VDS/IDS, is a constant.

As VDS is increased, the carriers reach their maximum drift

velocity and the current amplitude cannot increase. Since

the device is behaving like a current generator, it is said to

have high output impedance. This is the so-called ‘‘satura-

tion’’ region. One should also note that in comparing

MOSFET operation to a bipolar transistor, the linear and

saturated regions of the bipolar are just the opposite to the

MOSFET. The equal spacing between the output IDcurves

for constant steps in VGS indicates that the transfer charac-

teristic in

Figure 9

will be linear in the saturated region.

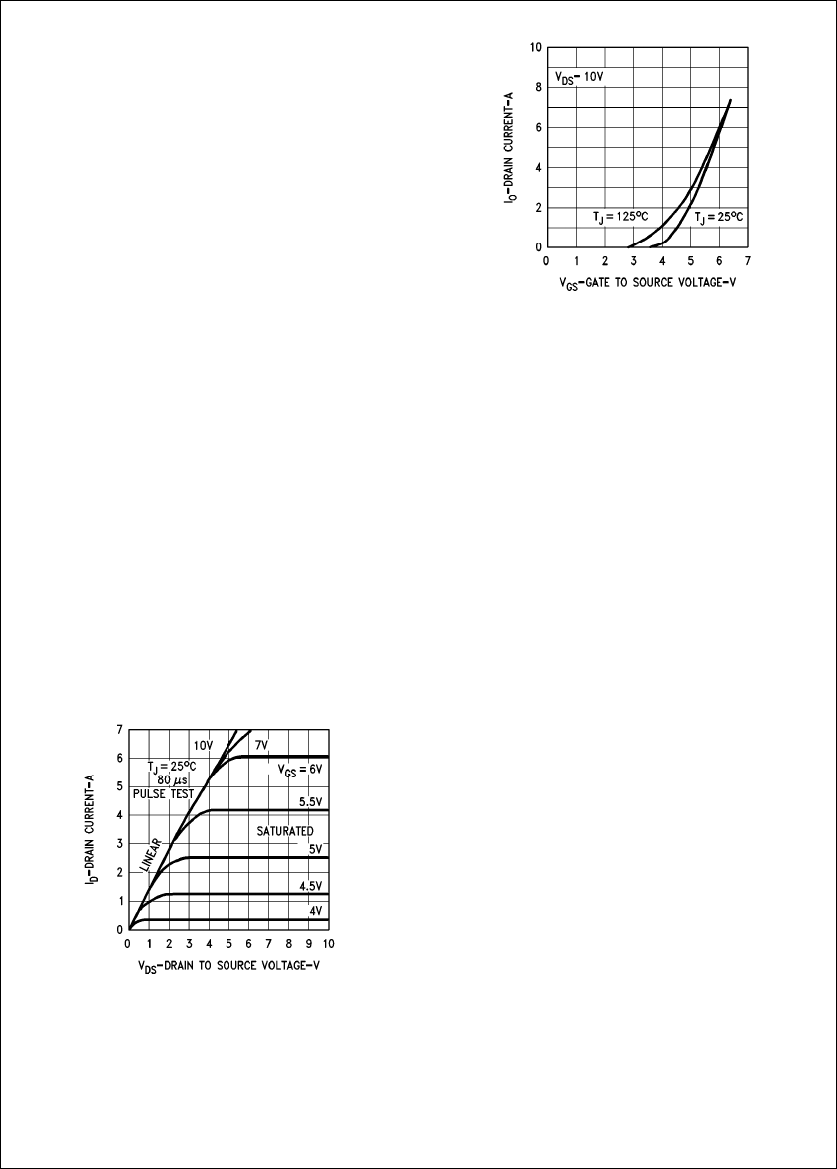
IMPORTANCE OF THRESHOLD VOLTAGE

Threshold voltage VGS(th) is the minimum gate voltage that

initiates drain current flow. VGS(th) can be easily measured

on a Tektronix 576 curve tracer by connecting the gate to

the drain and recording the required drain voltage for a

specified drain current, typically 250 mA or 1 mA. (VGS(th) in

Figure 9

is 3.5V. While a high value of VGS(th), can appar-

ently lengthen turn-on delay time, a low value for power

MOSFET is undesirable for the following reasons:

1. VGS(th) has a negative temperature coefficient

b7 mV/§C.

2. The high gate impedance of a MOSFET makes it suscep-

tible to spurious turn-on due to gate noise.

3. One of the more common modes of failure is gate-oxide

voltage punch-through. Low VGS(th) requires thinner ox-

ides, which lowers the gate oxide voltage rating.

TL/G/10063–8

FIGURE 8. Output Characteristics

TL/G/10063–9

FIGURE 9. Transfer Characteristics

POWER MOSFET THERMAL MODEL

Like all other power semiconductor devices, MOSFETs op-

erate at elevated junction temperatures. It is important to

observe their thermal limitations in order to achieve accept-

able performance and reliability. Specification sheets con-

tain information on maximum junction temperature (TJ(max)),

safe areas of operation, current ratings and electrical char-

acteristics as a function of TJwhere appropriate. However,

since it is still not possible to cover all contingencies, it is

still important that the designer perform some junction cal-

culations to ensure that the device operate within its specifi-

cations.

Figure 10

shows an elementary, stead-state, thermal model

for any power semiconductor and the electrical analogue.

The heat generated at the junction flows through the silicon

pellet to the case or tab and then to the heat sink. The

junction temperature rise above the surrounding environ-

ment is directly proportional to this heat flow and the junc-

tion-to-ambient thermal resistance. The following equation

defines the steady state thermal resistance R(th)JC between

any two points x and y:

R(th)JC e(TybTx)/P (3)

where:

Txeaverage temperature at point x (§C)

Tyeaverage temperature at point y (§C)

Peaverage heat flow in watts.

Note that for thermal resistance to be meaningful, two tem-

perature reference points must be specified. Units for

R(th)JC are §C/W.

The thermal model show symbolically the locations for the

reference points of junction temperature, case temperature,

sink temperature and ambient temperature. These tempera-

ture reference define the following thermal references:

R(th)JC: Junction-to-Case thermal resistance.

R(th)CS: Case-to-Sink thermal resistance.

R(th)SA: Sink-to-Ambient thermal resistance.

Since the thermal resistances are in series:

R(th)JA eR(th)JC aR(th)CS aR(th)SA. (4)

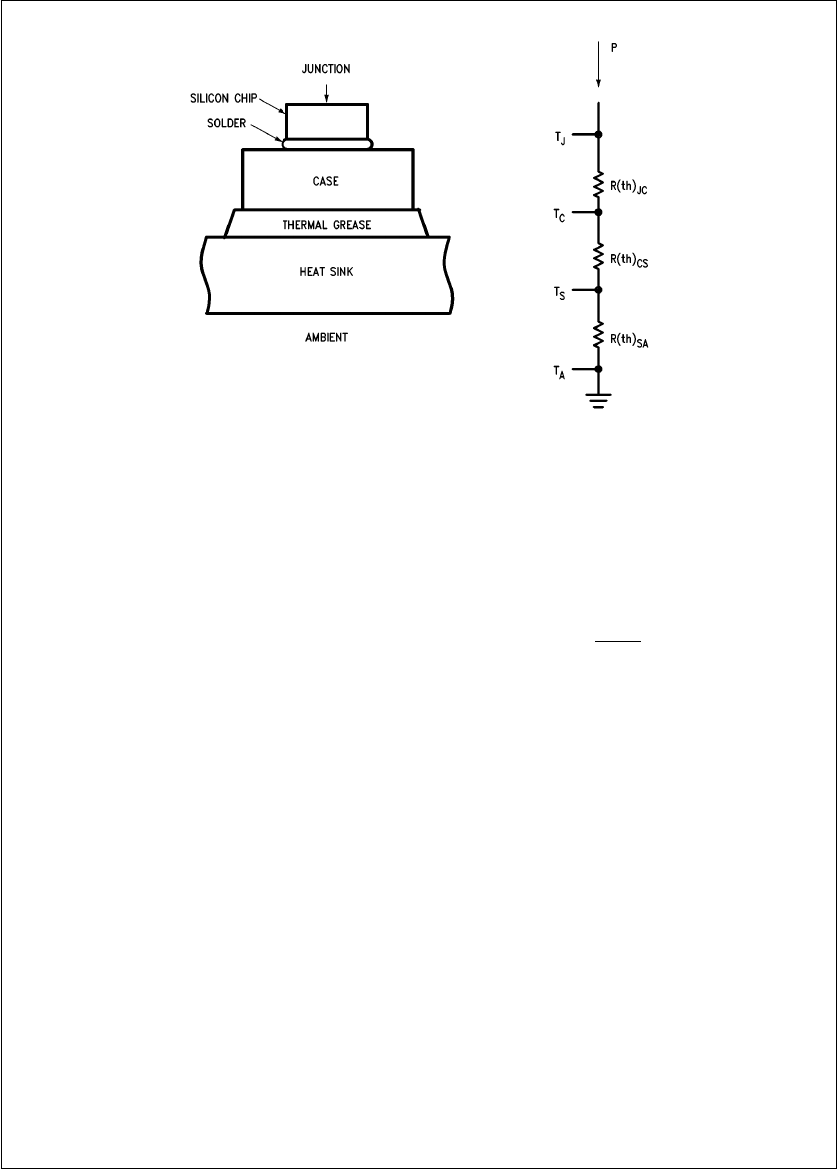
TL/G/10063–10

FIGURE 10. MOSFET Steady State Thermal Resistance Model

The design and manufacture of the device determines

R(th)JC so that while R(th)JC will vary somewhat from device

to device, it is the sole responsibility of the manufacturer to

guarantee a maximum value for R(th)JC. Both the user and

manufacturer must cooperate in keeping R(th)CS to an ac-

ceptable maximum and finally the user has sole responsibili-

ty for the external heat sinking.

By inspection of

Figure 10

, one can write an expression for

TJ:

TJeTAaPx [R(th)JC aR(th)CS aR(th)SA](5)

While this appears to be a very simple formula, the major

problem in using it is due to the fact that the power dissipat-

ed by the MOSFET depends upon TJ. Consequently one

must use either an iterative or graphical solution to find the

maximum R(th)SA to ensure stability. But an explanation of

transient thermal resistance is in order to handle the case of

pulsed applications.

Use of steady state thermal resistance is not satisfactory for

finding peak junction temperatures for pulsed applications.

Plugging in the peak power value results in overestimating

the actual junction temperature while using the average

power value underestimates the peak junction temperature

value at the end of the power pulse. The reason for the

discrepancy lies in the thermal capacity of the semiconduc-

tor and its housing, i.e., its ability to store heat and to cool

down before the next pulse.

The modified thermal model for the MOSFET is shown in

Figure 11

. The normally distributed thermal capacitances

have been lumped into single capacitors labeled CJ,C

and CS. This simplification assumes current is evenly distrib-

uted across the silicon chip and that the only significant

power losses occur in the junction. When a step pulse of

heating power P is introduced at the junction,

Figure 12a

shows that TJwill rise at an exponential rate to some steady

state value dependent upon the response of the thermal

network. When the power input is terminated at time t2,T

will decrease along the curve indicated by Tcool in

Figure

12a

back to its initial value. Transient thermal resistance at

time t is thus defined as:

Z(th)JC eDTJC(t)

P(6)

The transient thermal resistance curve approaches the

steady state vaule at long times and the slope of the curve

for short times is inversely proportional to CJ. In order that

this curve can be used with confidence, it must represent

the highest values of Z(th)JC for each time interval that can

be expected from the manufacturing distribution of prod-

ucts.

While predicting TJin response to a series of power pulses

becomes very complex, superposition of power pulses of-

fers a rigorous numerical method of using the transient ther-

mal resistance curve to secure a solution. Superposition

tests the response of a network to any input function by

replacing the input with an equivalent series of superim-

posed positive and negative step functions. Each step func-

tion must start from zero and continue to the time for which

TJis to be computed. For example,

Figure 13

illustrates a

typical train of heating pulses.

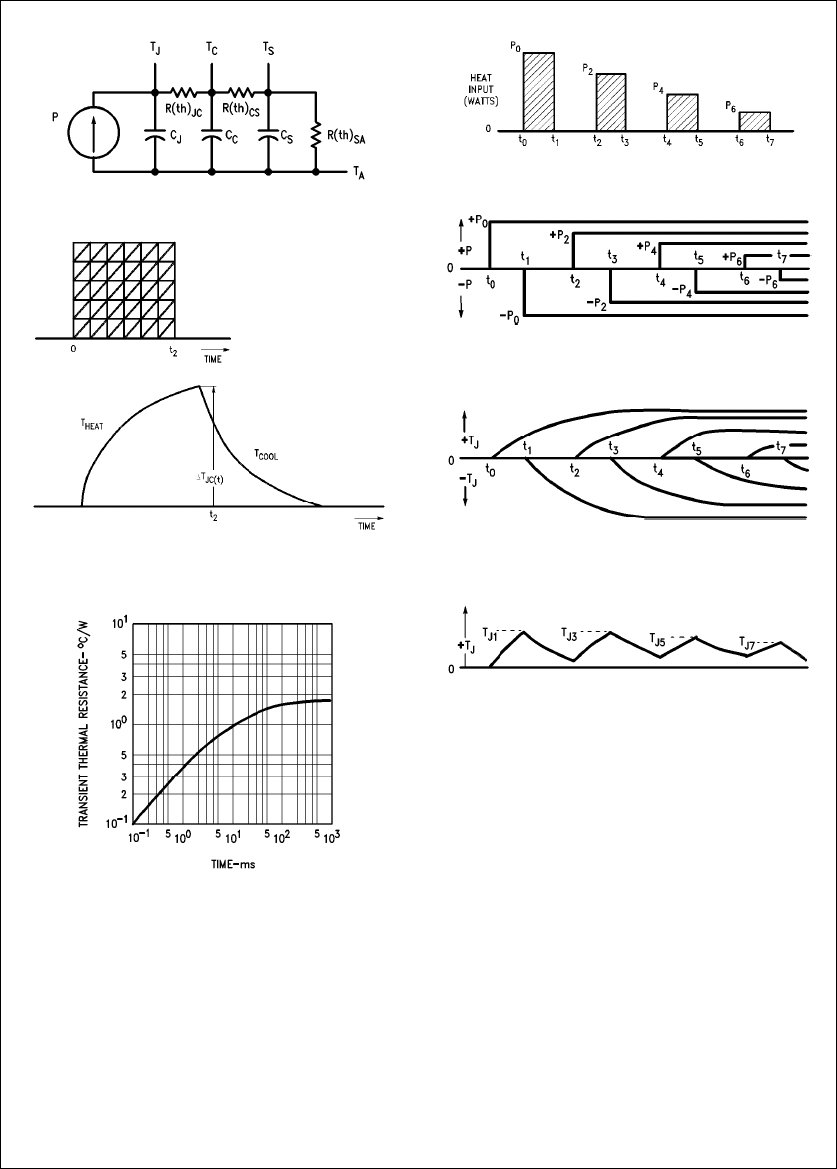
TL/G/10063–11

FIGURE 11. Transient Thermal Resistance Model

TL/G/10063–12

a. Junction Temperature Response to a

Step Pulse of Heating Power

TL/G/10063–13

b. Transient Thermal Resistance Curve

for National Semiconductor IRF330 MOSFET

FIGURE 12

TL/G/10063–14

a. Heat Input

TL/G/10063–15

b. Equivalent Heat Input by

Superposition of Power Pulses

TL/G/10063–16

c. Junction Temperature Response

to Individual Power Pulses of b

TL/G/10063–17

d. Actual TJ

FIGURE 13. Use of Superposition to Determine Peak TJ

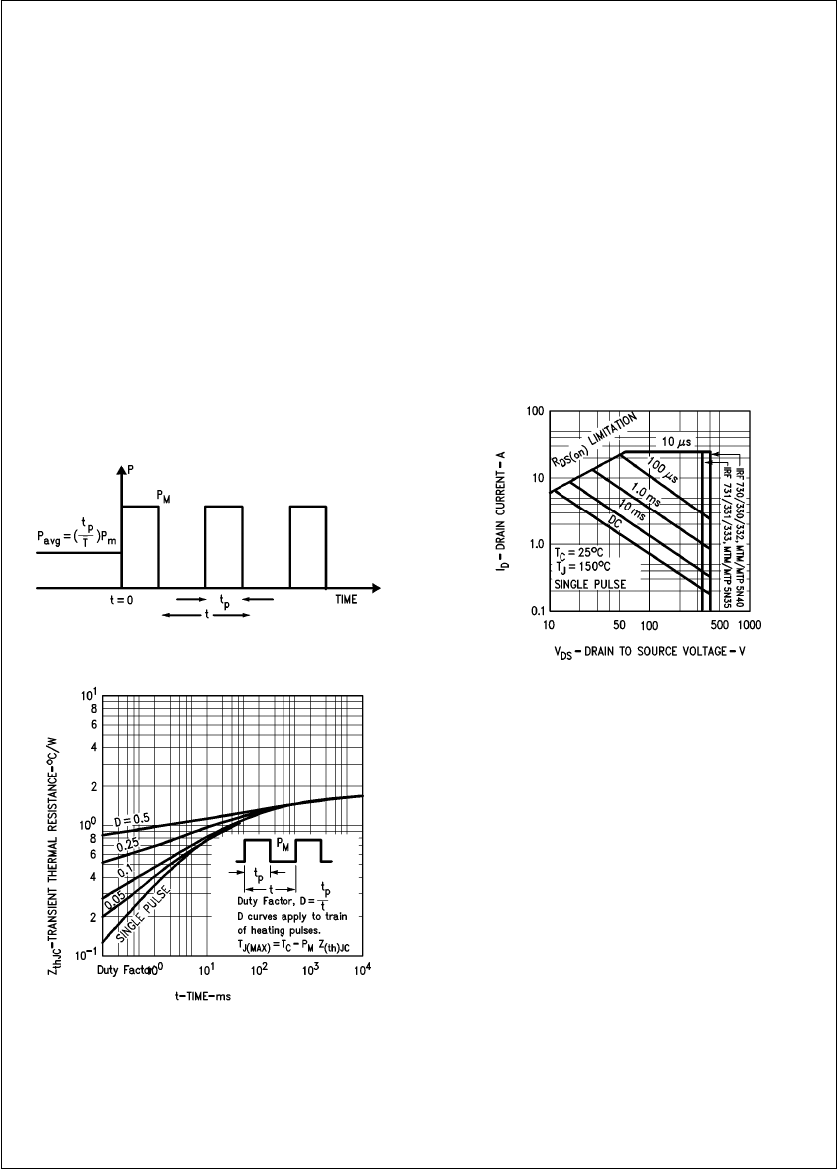
TJat time t is given by:

TJ(t) eTJ(0) a&

ie0

Pi (7)

[Z(th)JC (tnbti)bZ(th)JC (tnbtia1)]

The usual use condition is to compute the peak junction

temperature at thermal equilibrium for a train of equal ampli-

tude power pulses as shown in

Figure 14

To further simplify this calculation, the bracketed expression

in equation (G) has been plotted for all National Semicon-

ductor power MOSFETs, as exemplified by the plot of

Z(th)JC in

Figure 14b

. From this curve, one can readily calcu-

late TJif one knows PM,Z

(th)JC and TCusing the expres-

sion:

(8)TJeTCaPMcZ(th)JC

Example: Compute the maximum junction temperature for a

train of 25W, 200 ms wide heating pulses repeated every

2 ms. Assume a case temperature of 95§C.

Duty factor e0.1

From

Figure 14b:

Z(th)JC e0.55§C/W

Substituting into Equation (H):

TJ(Max) e95 a25 c0.55 e108.75 §C

TL/G/10063–18

a. Train of Power Pulses

TL/G/10063–19

b. Normalized Z(th)JC for National Semiconductor

IRF330 for Power Pulses Typified in

Figure 14a

FIGURE 14

SAFE AREA OF OPERATION

The power MOSFET is not subject to forward or reverse

bias second breakdown, which can easily occur in bipolar

junction transistors. Second breakdown is a potentially cata-

strophic condition in bi-polar transistors caused by thermal

hot spots in the silicon as the transistor turns on or off.

However in the MOSFET, the carriers travel through the

device much as if it were a bulk semiconductor, which ex-

hibits a positive temperature coefficient of 0.6%/§C. If cur-

rent attempts to self-constrict to a localized area, the in-

creasing temperature of the spot will raise the spot resist-

ance due to the positive temperature coefficient of the bulk

silicon. The ensuing higher voltage drop will tend to redis-

tribute the current away from the hot spot.

Figure 15

deline-

ates the safe areas of operation of the National Semicon-

ductor IRF330 device.

Note that the safe area boundaries are only thermally limit-

ed and exhibit no derating for second breakdown. This

shows that while the MOSFET transistor is very rugged, it

may still be destroyed thermally by forcing it to dissipate too

much power.

TL/G/10063–20

FIGURE 15. Safe Area of Operation of the

National Semiconductor IRF330 MOSFET Transistor

ON-RESISTANCE RDS(on)

The on-resistance of a power MOSFET is a very important

parameter because it determines how much current the de-

vice can carry for low to medium frequency (less than

200 kHz) applications. After being turned on, the on-state

voltage of the MOSFET falls to a low value and its RDS(on)

is defined simply as its on-state voltage divided by on-state

current. When conducting current as a switch, the conduc-

tion losses PCare:

PCeI2D(RMS) xR

DS(on) (9)

To minimize RDS(on), the applied gate signal should be large

enough to maintain operation in the linear or ohmic region

as shown in

Figure 8

. All National Semiconductor MOSFETs

will conduct their rated current for VGS e10V, which is also

the value used to generate the curves of RDS(on) vs IDand

TJthat are shown in

Figure 16

for the National Semiconduc-

tor IRF330. Since RDS(on) increases with TJ,

Figure 16

plots

this parameter as a function of current for room ambient and

elevated temperatures.

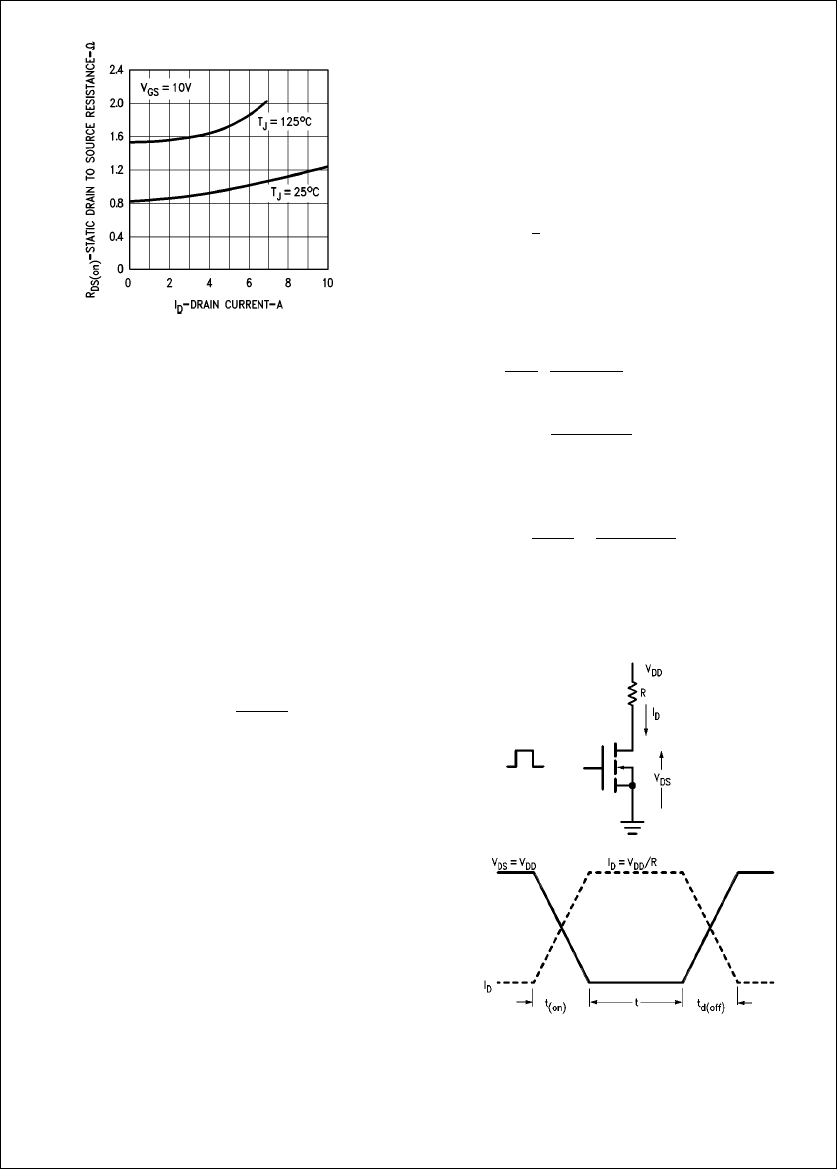
TL/G/10063–21

FIGURE 16. RDS(on) of the

National Semiconductor IRF330

Note that as the drain current rises, RDS(on) increases once

IDexceeds the rated current value. Because the MOSFET is

a majority carrier device, the component of RDS(on) due to

the bulk resistance of the Nbsilicon in the drain region

increases with temperature as well. While this must be tak-

en into account to avoid thermal runaway, it does facilitate

parallel operation of MOSFETs. Any inbalance between

MOSFETs does not result in current hogging because the

device with the most current will heat up and the ensuing

higher on-voltage will divert some current to the other devic-

es in parallel.

TRANSCONDUCTANCE

Since MOSFETs are voltage controlled, it has become nec-

essary to resurrect the term transconductance gfs, com-

monly used in the past with electron tubes. Referring to

Fig-

ure 8

fs equals the change in drain current divided by the

change in gate voltage for a constant drain voltage. Mathe-

matically:

gfs (Siemens) edID(A)

dVGS(V) (10)

Transconductance varies with operating conditions, starting

at 0 for VGS kVGS(th) and peaking at a finite value when

the device is fully saturated. It is very small in the ohmic

region because the device cannot conduct any more cur-

rent. Typically gfs is specified at half the rated current and

for VDS e20V. Transconductance is useful in designing

linear amplifiers and does not have any significance in

switching power supplies.

GATE DRIVE CIRCUITS FOR POWER MOSFETs

The drive circuit for a power MOSFET will affect its switch-

ing behavior and its power dissipation. Consequently the

type of drive circuitry depends upon the application. If on-

state power losses due to RDS(on), will predominate, there is

little point in designing a costly drive circuit. This power dis-

sipation is relatively independent of gate drive as long as

the gate-source voltage exceeds the threshold voltage by

several volts and an elaborate drive circuit to decrease

switching times will only create additional EMI and voltage

ringing. In contrast, the drive circuit for a device switching at

200 kHz or more will affect the power dissipation since

switching losses are a significant part of the total power

dissipation.

Compare to a bi-polar junction transistor, the switching loss-

es in a MOSFET can be made much smaller but these loss-

es must still be taken into consideration. Examples of sever-

al typical loads along with the idealized switching wave-

forms and expressions for power dissipation are given in

Figures 17

Their power losses can be calculated from the general ex-

pression:

PDe#1

u#u

oID(t) #VDS(t)dt J#fs(11)

where: fseSwitching frequency.

For the idealized waveforms shown in the figures, the inte-

gration can be approximated by the calculating areas of tri-

angles:

Resistive load:

PDeV2DD

RÐt(on) at(off)

6aRDS(on) #T(#fs

Inductive load:

PDeVCL Imt(off)fs

2aPc

where:

PCeconduction loss during period T.

Capacitive load:

PDe#CV2DD

2aV2DDRDS(on)

R2TJfs

Gate losses and blocking losses can usually be neglected.

Using these equations, the circuit designer is able to esti-

mate the required heat sink. A final heat run in a controlled

temperature environment is necessary to ensure thermal

stability.

TL/G/10063–23

FIGURE 17. Resistive Load Switching Waveforms

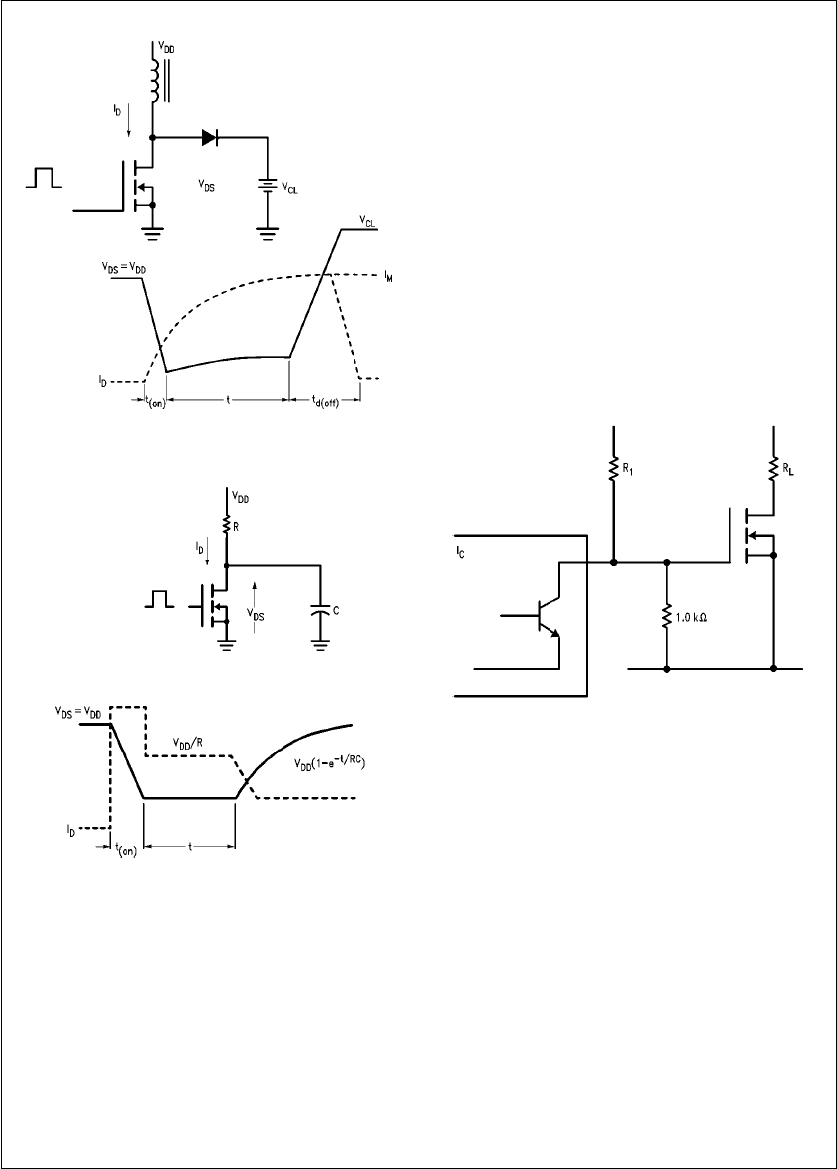
TL/G/10063–24

FIGURE 18. Clamped Inductive

Load Switching Waveforms

TL/G/10063–25

FIGURE 19. Capacitive Load Switching Waveforms

Since a MOSFET is essentially voltage controlled, the only

gate current required is that necessary to charge the input

capacitance Ciss. In contrast to a 10A bipolar transistor,

which may require a base current of 2A to ensure saturation,

a power MOSFET can be driven directly by CMOS or open-

collector TTL logic circuit similar to that in

Figure 20

Turn-on speed depends upon the selection of resistor R1,

whose minimum value will be determined by the current

sinking rating of the IC. It is essential that an open collector

TTL buffer be used since the voltage applied to the gate

must exceed the MOSFET threshold voltage of 5V. CMOS

devices can be used to drive the power device directly since

they are capable of operating off 15V supplies.

Interface ICs, originally intended for other applications, can

also be used to drive power MOSFETs, as shown below in

Figure 21

Most frequently switching power supply applications employ

a pulse width modulator IC with an NPN transistor output

stage. This output transistor is ON when the MOSFET

should be ON, hence the type of drive used with open-col-

lector TTL devices cannot be used.

Figures 22

and

give

examples of typical drive circuits used with PWM ICs.

TL/G/10063–26

FIGURE 20. Open Collector TTL Drive Circuit

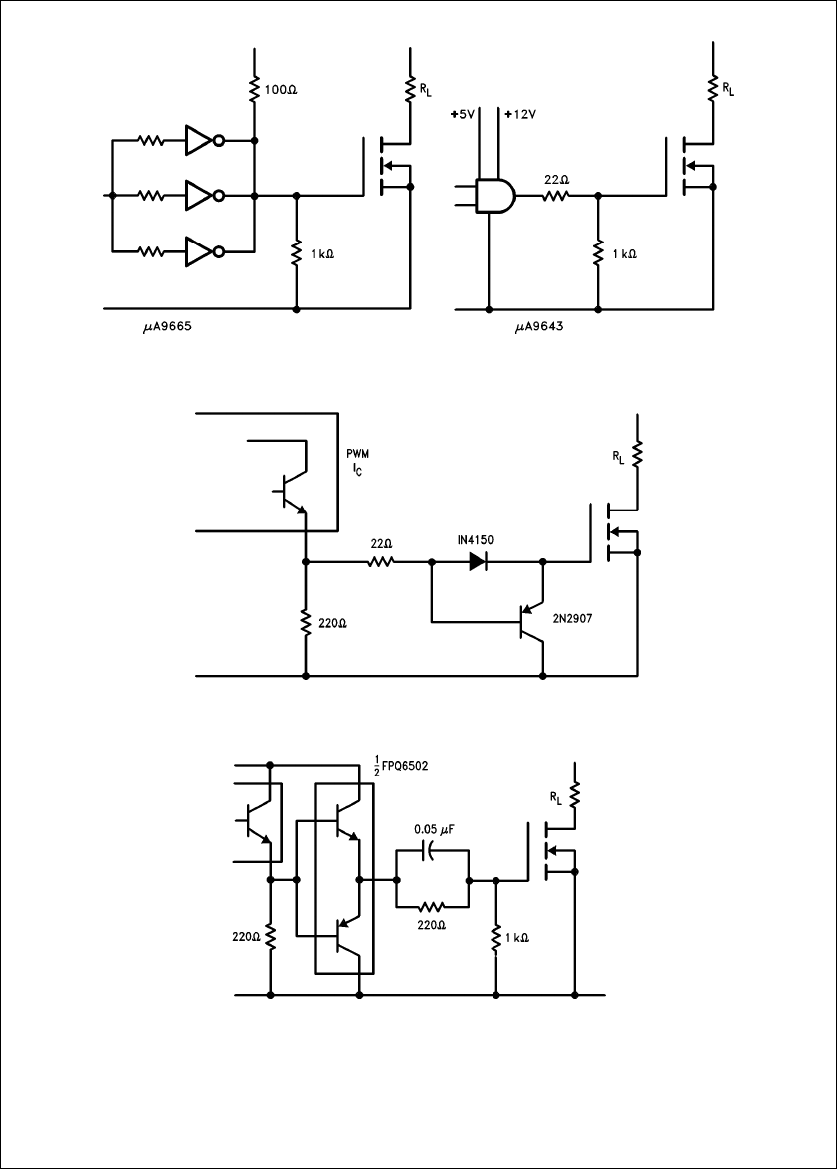
TL/G/10063–27

FIGURE 21. Interface ICs Used to

Drive Power MOSFETs

TL/G/10063–28

FIGURE 22. Circuit for PWM IC Driving MOSFET.

The PNP Transistor Speeds Up Turn-Off

TL/G/10063–29

FIGURE 23. Emitter Follower with Speed-Up Capacitor

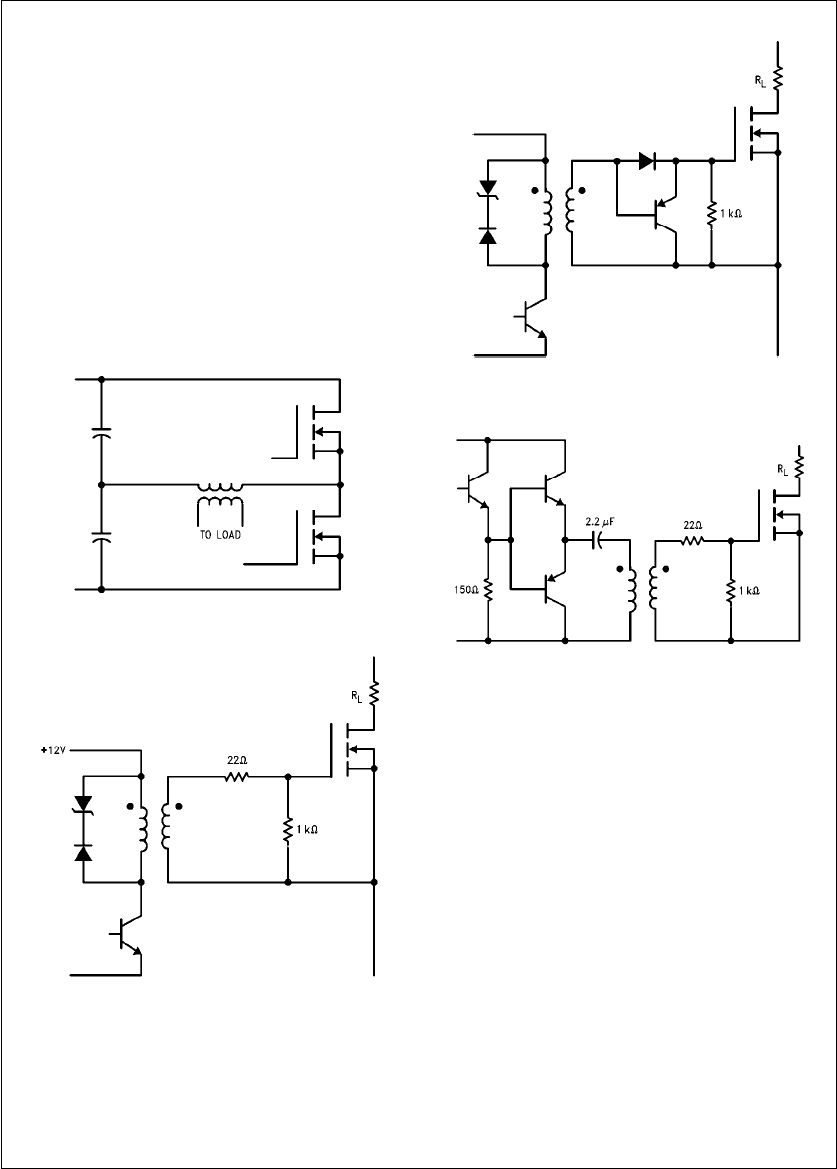
Isolation: Off-line switching power supplies use power MOS-

FETs in a half-bridge configuration because inexpensive,

high voltage devices with low RDS(on) are not available.

Since one of the power devices is connected to the positive

rail, its drive circuitry is also floating at a high potential. The

most versatile method of coupling the drive circuitry is to

use a pulse transformer. Pulse transformers are also nor-

mally used to isolate the logic circuitry from the MOSFETs

operating at high voltage to protect it from a MOSFET fail-

ure.

The zener diode shown in

Figure 25

is included to reset the

pulse transformer quickly. The duty cycle can approach

50% with a 12V zener diode. For better performance at

turn-off, a PNP transistor can be added as shown in

Figure

Figure 27

illustrates an alternate method to reverse bias the

MOSFET during turn-off by inserting a capacitor in series

with the pulse transformer. The capacitor also ensures that

the pulse transformer will not saturate due to DC bias.

TL/G/10063–30

FIGURE 24. Half-Bridge Configuration

TL/G/10063–31

FIGURE 25. Simple Pulse Transformer Drive

Circuit. The Transistor May Be a

Part of a PWM IC if Applicable.

TL/G/10063–32

FIGURE 26. Improved Performance at Turn-Off

with a Transistor

TL/G/10063–33

FIGURE 27. Emitter Follower Driver

with Speed-Up Capacitor

Opto-isolators may also be used to drive power MOSFETs

but their long switching times make them suitable only for

low frequency applications.

SELECTING A DRIVE CIRCUIT

Any of the circuits shown are capable of turning a power

MOSFET on and off. The type of circuit depends upon the

application. The current sinking and sourcing capabilities of

the drive circuit will determine the switching time and switch-

ing losses of the power device. As a rule, the higher the

gate current at turn-on and turn-off, the lower the switching

losses will be. However, fast drive circuits may produce ring-

ing in the gate and drain circuits. At turn-on, ringing in the

gate circuit may produce a voltage transient in excess of the

maximum VGS rating, which will puncture the gate oxide and

destroy it. To prevent this occurrence, a zener diode of the

appropriate value may be added to the circuit as shown in

Figure 28

. Note that the zener should be mounted as close

as possible to the device.

At turn-off, the gate voltage may ring back up to the thresh-

old voltage and turn on the device for a short period. There

is also the possibility that the drain-source voltage will ex-

ceed its maximum rated voltage due to ringing in the drain

circuit. A protective RC snubber circuit or zener diode may

be added to limit drain voltage to a safe level.

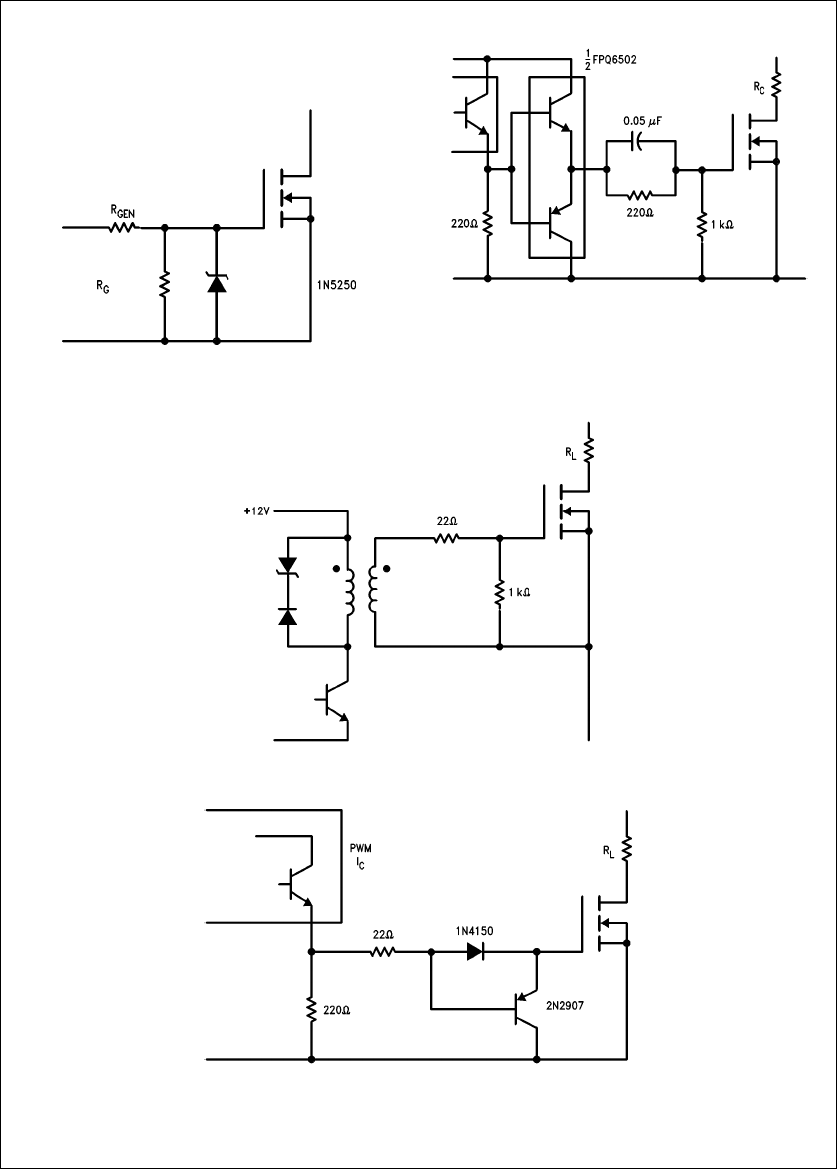
Figures 29– 34

give typical turn-on and turn-off times of vari-

ous drive circuits for the following test circuit:

Device: National Semiconductor IRF450, VDD e200V,

Load e33Xresistor.

TL/G/10063–34

FIGURE 28. Zener Diode to Prevent Excessive

Gate-Source Voltages

DRIVE CIRCUIT TURN-ON/TURN-OFF TIMES

TL/G/10063–35

Note: Voltage Fall Time e17 ns, Voltage Rise Time e20 ns

FIGURE 29. Emitter Follower PWM

TL/G/10063–36

Note: Voltage Fall Time e50 ns, Voltage Rise Time e112 ns

FIGURE 30. Simple Pulse Transformer

TL/G/10063–37

Note: Voltage Fall Time e50 ns, Voltage Rise Time e16 ns

FIGURE 31. Pulse Width Modulator

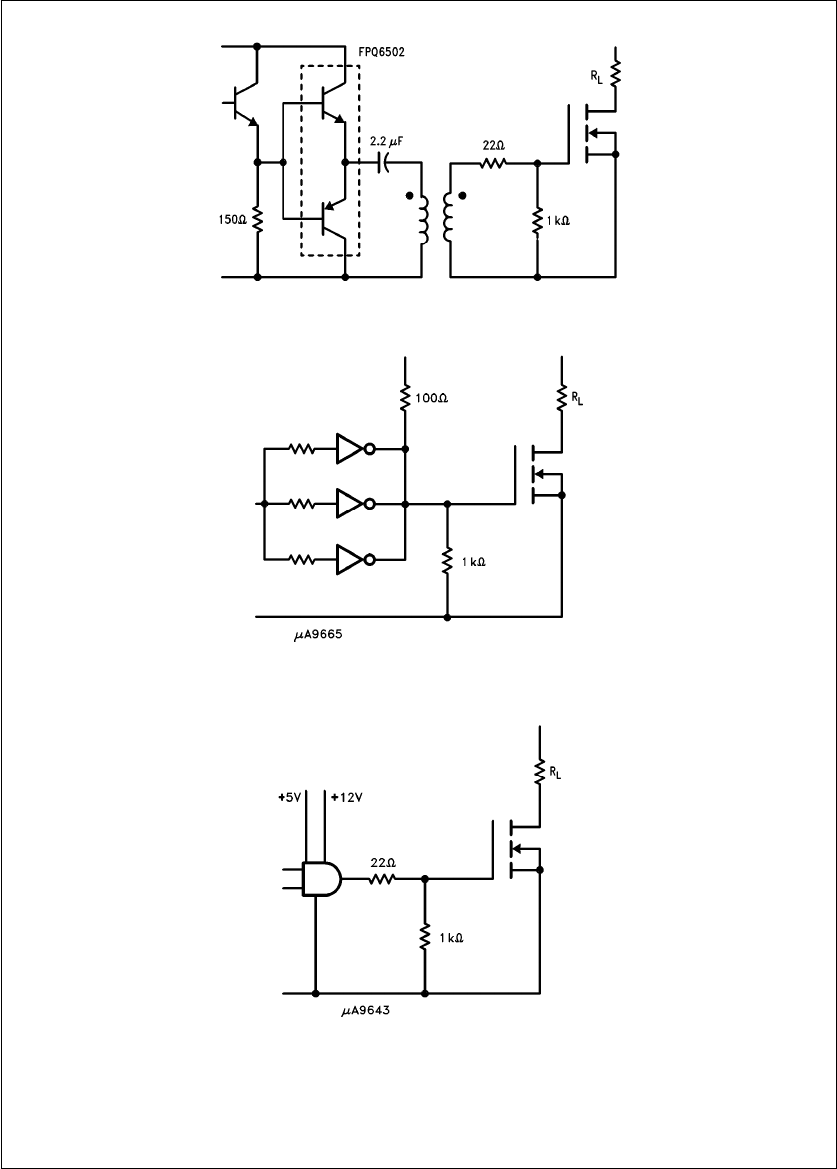
TL/G/10063–38

Note: Voltage Fall Time e63 ns, Voltage Rise Time e74 ns

FIGURE 32. Pulse Transformer with Speed-Up Capacitor

TL/G/10063–39

Note: Voltage Fall Time e200 ns, Voltage Rise Time e84 ns

FIGURE 33. Interface Drive

TL/G/10063–40

Note: Voltage Fall Time e70 ns, Voltage Rise Time e30 ns

FIGURE 34. Interface Drive

AN-558 Introduction to Power MOSFETs and Their Applications

LIFE SUPPORT POLICY

NATIONAL’S PRODUCTS ARE NOT AUTHORIZED FOR USE AS CRITICAL COMPONENTS IN LIFE SUPPORT

DEVICES OR SYSTEMS WITHOUT THE EXPRESS WRITTEN APPROVAL OF THE PRESIDENT OF NATIONAL

SEMICONDUCTOR CORPORATION. As used herein:

1. Life support devices or systems are devices or 2. A critical component is any component of a life

systems which, (a) are intended for surgical implant support device or system whose failure to perform can

into the body, or (b) support or sustain life, and whose be reasonably expected to cause the failure of the life

failure to perform, when properly used in accordance support device or system, or to affect its safety or

with instructions for use provided in the labeling, can effectiveness.

be reasonably expected to result in a significant injury

to the user.

National Semiconductor National Semiconductor National Semiconductor National Semiconductor

Corporation Europe Hong Kong Ltd. Japan Ltd.

1111 West Bardin Road Fax: (

49) 0-180-530 85 86 13th Floor, Straight Block, Tel: 81-043-299-2309

Arlington, TX 76017 Email: cnjwge

tevm2.nsc.com Ocean Centre, 5 Canton Rd. Fax: 81-043-299-2408

Tel: 1(800) 272-9959 Deutsch Tel: (

49) 0-180-530 85 85 Tsimshatsui, Kowloon

Fax: 1(800) 737-7018 English Tel: (

49) 0-180-532 78 32 Hong Kong

Fran3ais Tel: (

49) 0-180-532 93 58 Tel: (852) 2737-1600

Italiano Tel: (

49) 0-180-534 16 80 Fax: (852) 2736-9960

National does not assume any responsibility for use of any circuitry described, no circuit patent licenses are implied and National reserves the right at any time without notice to change said circuitry and specifications.

Introduction To Power MOSFETs And Their Applications AN 0558

Navigation menu

Versions of this User Manual:

Views

Navigation