A COVER 1 Portfolio Managers Guide To Multi Factor Fixed Income Risk S And Their Ap

A_Portfolio_Managers_Guide_to_Multi-Factor_Fixed_Income_Risk_s_and_Their_Ap

User Manual:

Open the PDF directly: View PDF .
Page Count: 33

INDEX, PORTFOLIO & RISK SOLUTIONS 24 June 2011

PLEASE SEE ANALYST CERTIFICATIONS AND IMPORTANT DISCLOSURES STARTING AFTER PAGE 31

A Portfolio Manager’s Guide to

Multi-Factor Fixed Income Risk

Models and Their Applications1

Risk management is an integral part of the portfolio management process. Risk models

are central to this practice, allowing managers to quantify and analyze the risk

embedded in their portfolios. Risk models provide managers with insight into the major

sources of risk in a portfolio, helping them to control their exposures and understand

the contributions of different portfolio components to total risk. They help portfolio

managers in their decision-making process by providing answers to important

questions such as: How does my short duration position affect portfolio risk? Does my

underweight in diversified financials hedge my overweight in banks? Risk models are

also widely used in other areas, including portfolio construction, performance

attribution and scenario analysis.

We discuss the structure of multi-factor fixed income risk models, the types of factors

used in these models, and describe estimation techniques used in this context. We also

illustrate the use of fixed income risk factor models in various applications, namely the

analysis of portfolio risk, portfolio construction and scenario analysis. Throughout this

paper, we use the Barclays Capital Global Risk Model2 for illustration purposes. For

completeness, we also refer to other possible approaches to constructing such a model.

1 The authors would like to thank Dev Joneja, Lev Dynkin, Albert Desclee, Jay Hyman, Bruce Phelps and Andy

Sparks for continuous conversations and feedback over the years on this topic and for their comments on

previous drafts of this paper.

2 The Barclays Capital Global Risk Model is available through POINT®, Barclays Capital portfolio management

tool. It is a multi-currency cross-asset model that covers many different asset classes across the fixed income

and equity markets, including derivatives in these markets. At the heart of the model is a covariance matrix of

risk factors. The model has more than 500 factors, many specific to a particular asset class. The asset class

models are periodically reviewed. Structure is imposed to increase the robustness of the estimation of such large

covariance matrix. The model is estimated from historical data. It is calibrated using extensive security-level

historical data and is updated on a monthly basis.

Anthony Lazanas

+ 1 212 526 3127

alazanas@barcap.com

Antonio Silva

+1 212 526 8880

antonio.silva@barcap.com

Radu Gabudean

+1 212 526 5199

radu.gabudean@barcap.com

Arne D. Staal

+44 (0)20 3134 7602

arne.staal@barcap.com

www.barcap.com

Contents

Quantifying Risk 2

Approaches Used to Analyze Risk 5

Applications of Risk Modeling 25

Conclusion 31

References 31

A version of this paper will be published in the Handbook of Fixed Income Securities,

b

y

Frank J. Fabozzi, McGraw Hill, 2011

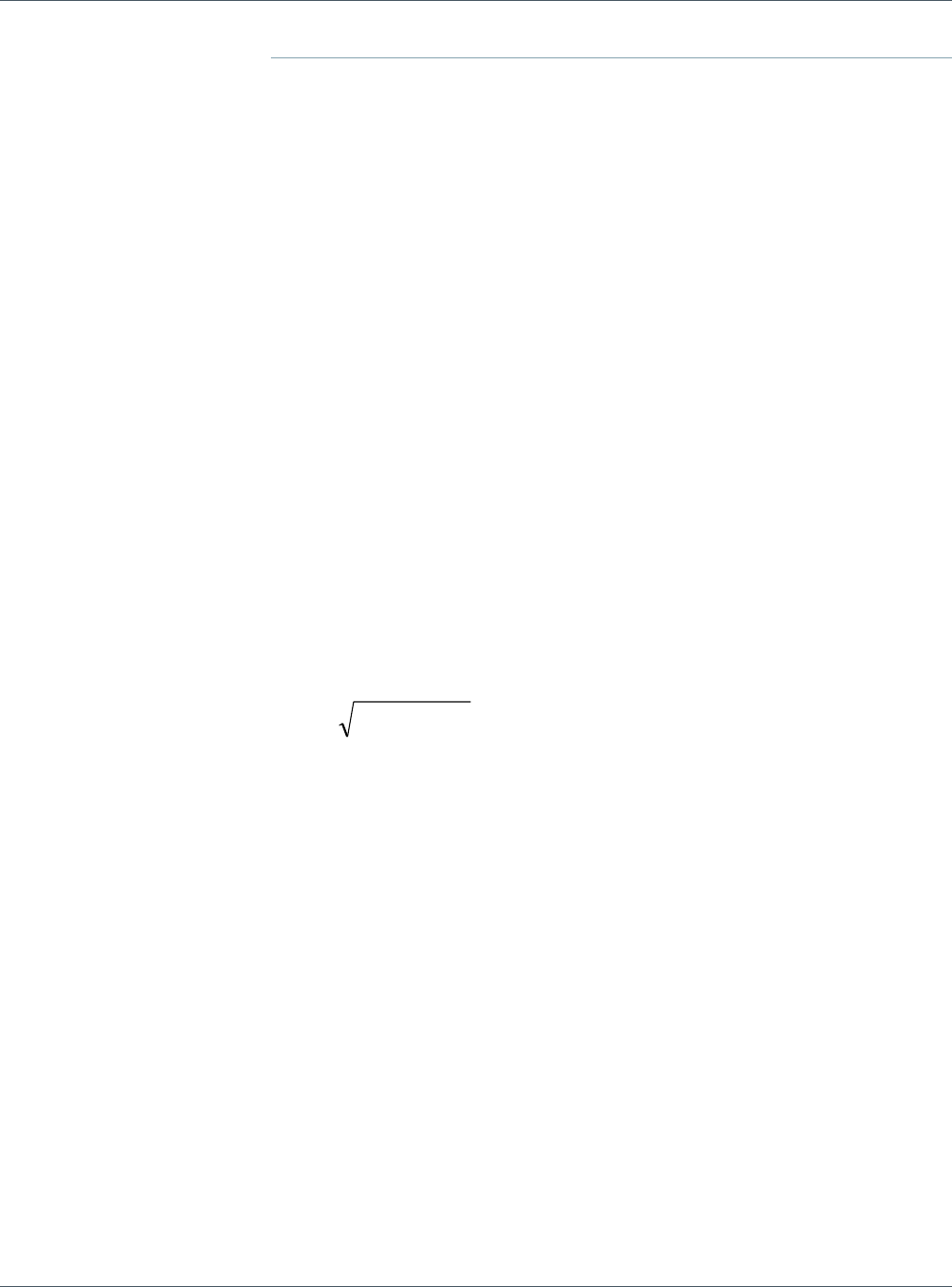
Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 2

Quantifying Risk

Portfolio managers constantly monitor their exposures, typically net of a benchmark and

routinely ask themselves: What is the portfolio duration? How risky is the overweight to

credit? How does it relate to the exposure to mortgages? What is the exposure to specific

issuers? Even when portfolio holdings and exposures are well known, portfolio managers

increasingly rely on quantitative techniques to translate this information into a common risk

language. Risk models can present a coherent view of the portfolio, its exposures, and how

they correlate to each other. They can quantify the risk of each exposure and its

contribution to the overall risk of the portfolio.

To start illustrating the motivation behind the risk models, let us assume that a portfolio

manager wants to estimate and analyze the volatility of a large portfolio of fixed-income

instruments. A straightforward idea would be to compute the volatility of the historical

returns of the portfolio and use this measure to forecast future volatility. However, this

framework does not provide insight into the relationships among different securities in the

portfolio or among the major sources of risk. For instance, it does not assist a portfolio

manager interested in diversifying a portfolio or constructing a portfolio that has better risk-

adjusted performance. Additionally, the characteristics of a fixed-income portfolio change

substantially over time (for instance, as instruments mature or are subject to credit events).

Instead of estimating the portfolio volatility using historical portfolio returns, a portfolio

manager could use a different strategy. The portfolio return is a function of individual

instrument returns (eg, Treasury securities, corporate bonds, credit derivatives, municipal

bonds, interest rate swaps, etc) and the market weights of these securities in the portfolio.

Using this, the forecast volatility of the portfolio ( f

P

σ

) can be computed as a function of the

weights (w) and the covariance matrix ( S

∑

) of the instrument returns in the portfolio:

ww S

Tf

P ×∑×=

σ

where the superscript T denotes a matrix transpose. This covariance matrix can be broken

down into individual instrument volatilities and the correlations between returns.

Volatilities measure the riskiness of individual instrument returns and correlations represent

the relationships between the returns of different instruments. By measuring these

correlations and volatilities, the portfolio manager can gain insight into her portfolio related

to the riskiness of its different parts or how the portfolio can be diversified. As outlined

above, to estimate the portfolio volatility we need to estimate the correlation between each

pair of instruments. Unfortunately, this means that the number of parameters to be

estimated grows quadratically with the number of instrument in the portfolio. For most

practical portfolios, the relatively large number of constituents makes it difficult to estimate

the relationship between instrument returns in a robust way. Moreover, this framework

uses the history of individual instrument returns to forecast future security return volatility.

However, instrument characteristics are dynamic; hence, using returns from different

periods may not produce good forecasts. These drawbacks constitute the motivation for

multi-factor risk models discussed in this paper.

A major characteristic of multi-factor models is their ability to describe the return of a

portfolio using a relatively small set of variables, called factors. These factors should be

designed to capture broad (systematic) market fluctuations, but should also be able to

capture specific nuances of individual portfolios. For instance, a broad fixed-income market

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 3

factor would capture the general movement in the fixed-income markets, but not the varying

behavior across types of instruments. If, for example, a portfolio is heavily biased towards the

long end of the US Treasury yield curve, or is tilted towards credit bonds of particular

industries, the broad market factor may not allow for a good representation of the portfolio’s

return. Other factors might be needed to capture these more specific sources of risk.

Most factor models are linear and the total return is broken down into the sum of the

contributions of the factors (referred to as the systematic return) and an idiosyncratic

component. Systematic return is the component of total return due to movements in the

common (market-wide) risk factors. On the other hand, idiosyncratic return can be

described as the residual component that cannot be explained by the systematic factors.

Under most factor models, idiosyncratic returns are uncorrelated across issuers. Therefore,

correlations across securities of different issuers are driven by their exposures to the

systematic risk factors, and the correlation between those factors.

The following equation demonstrates the systematic and the idiosyncratic components of

total return for security s:

sss FLr

ε

+×=

The systematic return is the product of the instrument’s loadings (L, also called sensitivities)

to the systematic risk factors and the returns of these factors (F). The idiosyncratic return is

given by s

ε

. Under this representation, the return is linear on the risk factors; therefore, we

call these linear factor models.

Under these models, the portfolio volatility can be estimated as

wwLL T

pF

T

p

f

p×Ω×+×∑×=

σ

Here p

Lare the loadings of the portfolio to the risk factors (determined as the weighted

average of individual instrument loadings) and F

∑

is the covariance matrix of factor

returns. Ω is the covariance matrix of the idiosyncratic security returns. Typically, the

idiosyncratic return of securities is assumed uncorrelated. Therefore, this covariance matrix

is diagonal, with all elements outside its diagonal being zero. As a result, the idiosyncratic

risk of the portfolio is diversified away as the number of securities in the portfolio increases.

This is the diversification benefit attained when combining uncorrelated exposures.

For most practical portfolios, the number of factors is significantly smaller than the number

of instruments in the portfolio. Therefore, the number of parameters in F

∑ is much smaller

than in S

∑, leading to a generally more robust estimation. Moreover, the factors can be

designed in such a way that they are more stable than individual stock returns, leading to

models with potentially better predictability. In this setting, the changing nature of each

particular instrument can be captured through its loadings to the different risk factors.

Another very important advantage of using factor models is the detailed insight they can

provide into the structure and properties of portfolios. These models characterize

instrument returns in terms of systematic factors that (can) have intuitive economic

interpretations. Linear factor models can provide important insights regarding the major

systematic and idiosyncratic sources of risk and return. This analysis can help managers to

better understand their portfolios and can guide them through the different tasks they

perform, such as rebalancing, hedging or tilting of their portfolios.

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 4

Naturally, the success of a risk model depends on its ability to interpret historical and current

data in order to formulate estimates of future portfolio risk. It should therefore seek to

discover properties of the data that are quasi-predictable; that is, that the error in the estimate

of future realizations — given all information known today — is relatively small. For example, it

is notoriously difficult to predict the expected return of a financial asset. On the other hand,

historical data contain sufficient information to allow risk models to provide good estimates of

the volatility of future returns. Nevertheless, one should not forget that even the most

sophisticated risk model can provide only an estimate of risk. It is well known that financial

markets are subject to event risk (ie, a sudden change in market conditions cause by geo-

political or financial events). Such events are usually followed by a period of large negative

returns on risky assets, large positive returns on assets considered to be safe havens,

significantly higher volatility and very high (positive or negative) correlations. It is impossible

for a risk model to predict when such events will occur. Therefore, it is useful to complement

model-based risk management and portfolio construction with what-if analysis, which

estimates portfolio return and risk under stressed conditions; that is, scenarios with extreme

realizations of market returns and a covariance matrix with much higher volatilities and

absolute correlations.

Fixed-Income Risk Models3

Fixed-income securities are exposed to many different types of risk. Multi-factor risk models

in this area capture these risks by first identifying common sources along different

dimensions, the systematic fixed-income risk factors. All risk not captured by these

systematic factors is considered idiosyncratic and is determined by the choice of systematic

risk factors. Typically, fixed-income systematic risk factors are divided into two sets: those

that influence securities across asset classes (eg, yield curve risk) and those specific to a

particular asset class (eg, prepayment risk in securitized products).

There are many ways to define systematic risk factors. For instance, they can be defined

purely by statistical methods, observed in the markets (eg, a yield curve), or estimated from

asset returns. In fixed-income, the standard approach is to use pricing models to calculate

the analytics that are the natural candidates for risk factor loadings (L in the notation

presented earlier). In this setting, the risk factors are either observable (eg, the movements

in the yield curve) or estimated from regressing cross-sectional asset returns on instrument

sensitivities. This is the approach taken in the Barclays Capital Global Risk Model, which is

used for illustration throughout this paper4.

In this risk model, the forecast risk of the portfolio is driven by a systematic and an

idiosyncratic (also called specific, non-systematic, or concentration) component. The

forecast systematic risk is a function of the mismatch between the portfolio and the

benchmark in the exposures to the risk factors, such as yield curve or spreads. The (net)

portfolio exposures are aggregated from security-level analytics. The systematic risk is also a

function of the volatility of the risk factors, as well as of the correlations among risk factors.

In this setting, the correlation of returns across securities is driven by the correlation of

systematic risk factors these securities load on. Because the model uses security-level returns

and analytics to estimate the factors, we can recover the idiosyncratic return for each

security. This is the return net of all systematic factors. The use of detailed level analysis of

idiosyncratic returns allows for the estimation of rich specifications of idiosyncratic risk.

3 For a discussion of linear risk factor models in equity markets, please refer to Lazanas et al. (2011)

4 See, for instance, Silva (2009).

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 5

Approaches to Analyzing Risk

Throughout this paper we analyze the risk of a particular bond portfolio, going through the

various aspects of risk typically looked at by a manager. We assume the following:

 The Barclays Capital US Aggregate Index is the portfolio manager’s benchmark.

 The portfolio manager believes interest rates are coming down. To capitalize on this view,

she seeks to create a portfolio with interest-rate duration longer than the interest-rate

duration of the benchmark. A portfolio with interest-rate duration that exceeds that of the

benchmark is referred to as being “long duration” and it outperforms the benchmark

when interest rates fall and all other market factors remain unchanged.

 The manager seeks a portfolio with a yield higher than that of the benchmark. Such a

portfolio creates superior carry return (also known as income) relative to the benchmark

but is subject to higher risks. The total yield of a portfolio can be broken down into a risk-

free yield and a spread over the risk-free yield. Because the portfolio is expected to

contain securities with longer maturities to satisfy the long duration target, it will earn a

risk-free yield that differs from the risk-free yield of the benchmark (higher most of the

time given that interest-rate curves are typically upward-sloping). To further enhance the

portfolio yield, the manager wants to target a portfolio spread that is also higher than the

benchmark spread. Higher spread typically exposes the portfolio to liquidity and issuer

default risks. If defaults occur, or if the portfolio manager is forced to sell securities at a

significant discount because of a lack of liquidity, the incurred losses may cancel out the

higher yield advantage and could lead to portfolio underperformance relative to the

benchmark. The manager must be comfortable that such risks are sufficiently

compensated by the higher carry return associated with higher portfolio spread.

 The portfolio manager is required to maintain the difference between the returns of the

portfolio and the benchmark at around 15bp, on a monthly basis. Thus, she must

calibrate the long duration and high yield portfolio positions to abide by this constraint.

To summarize, the portfolio manager has the mandate to track the benchmark, but is allowed

to deviate from it up to a point to express views that may lead to superior returns. A portfolio

manager with such a mandate is called an enhanced indexer. The amount of deviation

allowed is called the risk budget (15bp in our example) and can be quantified using a risk

model. The risk model produces an estimate of the volatility of the difference between the

portfolio and the benchmark returns, called tracking error volatility (TEV). TEV gives the

forecast magnitude of the typical tracking error. The manager should keep the portfolio’s TEV

at a level equal to or less than that specified in the risk budget. The final portfolio, which we

will analyze, contains 50 securities and is consistent with the manager’s views and risk budget.

Market Structure and Exposure Contributions

The first level of analysis that any portfolio manager usually performs is to compare the

portfolio holdings in terms of market value with the holdings from the benchmark. For

instance, Figure 1 shows that the composition of the portfolio has several important

mismatches when compared with the benchmark. The portfolio is underweighted in

Treasuries and government-related securities by 8.4%. This is offset by an overweight of

12.3% in corporates, especially in the financials sector. Other mismatches include an

underweight in mortgage-backed securities (MBS) (-5.8%) and an overweight in

commercial mortgage-backed securities (CMBS) (+2.1%).

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 6

Figure 1: Market Weights for Portfolio and Benchmark

Asset Class Portfolio Benchmark Difference

Total 100.0 100.0 0.0

Treasury 30.2 32.1 -1.9

Government-related 5.8 12.3 -6.5

Corporate Industrials 9.0 9.7 -0.7

Corporate Utilities 2.9 2.1 0.8

Corporate Financials 18.6 6.4 12.2

MBS Agency 28.4 34.1 -5.8

ABS 0.0 0.3 -0.3

CMBS 5.2 3.1 2.1

Source: POINT, Barclays Capital

Interestingly, for an equity manager, this kind of information (applied, for example, to the

various industries or sectors of the portfolio) would be key to the analysis of portfolio risk.

For a fixed income portfolio, this is not the case. Although important, this analysis tells us

very little about the true active exposures of a fixed income portfolio. What if the Treasuries

in the portfolio have significantly longer duration than those in the benchmark – would we

be really “short” in this asset class? What if the spreads from Financials in the portfolio are

much smaller than those in the benchmark – is the weight mismatch that important?

To answer these questions, we turn to another aspect of our analysis: the exposure of the

portfolio to major sources of risk. An example of such exposure is the duration of the portfolio.

Other exposures typically monitored are spread duration, convexity, spread level and vega (if

the portfolio has many securities with optionality, eg, mortgages or callable bonds). Figure 2

shows these analytics at the aggregate level for our portfolio, benchmark and the difference

between them:

 The portfolio is long duration (+0.25 year), consistent with the manager’s view on the

direction of interest rate moves.

 In terms of spread duration, the mismatch is smaller (+0.11 year). The manager wants to

minimize the exposure to spread changes as much as possible given the manager has no

view on this source of risk. However, the spread duration mismatch cannot be zero

because spread risk is related to other risks on which she does have a view, such as rates.

 The portfolio has significantly milder negative convexity than the benchmark (-0.15 vs

-0.29). This is attributable to the smaller weight that MBS have in the portfolio.

 The portfolio has more negative vega, but the number is fairly small for both universes.

 Finally, the portfolio has significantly higher spreads (100bp) than the benchmark. This

mismatch is consistent with the manager’s goal of having a higher yield in her portfolio,

when compared with the benchmark.

Figure 2: Aggregate Analytics

Analytics Portfolio Benchmark Difference

Duration 4.55 4.30 0.25

Spread Duration 4.67 4.56 0.11

Convexity -0.15 -0.29 0.13

Vega -0.02 -0.01 -0.01

Spread 157 57 100

Source: POINT, Barclays Capital

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 7

The analysis in Figures 1 and 2 can be combined to deliver a more detailed picture of where

the different exposures are coming from. Figure 3 shows this analysis for the duration of the

portfolio, demonstrating that most of the mismatch in duration contribution (market

weighted duration exposures) stems from the Treasury component of our portfolio (+0.21).

Interestingly, even though we are short in Treasuries, we are long in duration for that asset

class. This means that our Treasury portfolio would be negatively affected, when compared

with the benchmark, by a rise in interest rates. Because we are short in Treasuries, this result

must mean that our Treasury portfolio is longer in duration than the Treasury component of

the benchmark. Conversely, a relatively small contribution to excess duration comes from our

very large over-exposure to corporates. This means that, on average, the corporate bonds in

the portfolio are significantly shorter in duration than those in the benchmark.

Figure 3: Duration Contribution per Asset Class

Duration Contribution Portfolio Benchmark Difference

Total 4.55 4.30 0.25

Treasury 1.92 1.71 0.21

Government-Related 0.40 0.49 -0.09

Corporate 1.31 1.19 0.11

Securitized 0.92 0.90 0.02

Source: POINT, Barclays Capital

Adding Volatility and Correlations to the Analysis

The analysis above gives us some basic understanding of our exposures to different kinds of

risk. However, it is still hard to understand how we can compare the level of risk across

these different exposures. What is more risky, my long duration exposure of 0.25 years, or

my extra spread of 100bp? How can I quantify the seriousness of the vega mismatch on my

portfolio? Specifically, the risk of the portfolio is a function of the exposures to the risk

factors, but also of how volatile (how “risky”) each of the factors is.

To enhance the analysis, we bring volatilities into the picture. Figure 4 shows the outcome of

this addition to our example. In particular, it displays the risk of the different exposures of the

portfolio in isolation (that is, if the only active imbalances were those from that particular set

of risk factors). For example, in this figure one can see that if the only active weight in the

portfolio were the mismatch in the yield curve exposures, the risk of the portfolio would be

8.5bp per month. By adding volatilities to the analysis, we can now quantify that the

mismatch of +0.25 years in duration “costs” the portfolio 8.5bp per month of extra volatility,

when taken in isolation5. Similarly, if the only mismatch were the exposure to corporate

spreads, the risk of the portfolio would be 5.1bp. Interestingly, we also see that both

government-related and securitized sectors have non-trivial risk, despite having smaller

imbalances in terms of market weights relative to corporates. By bringing volatilities into the

analysis, we can compare and quantify the impact of each imbalance in the portfolio.

5 Later in this paper we refer to this risk number as Isolated TEV.

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 8

Figure 4: Isolated Risk per Category

Risk Factors Categories Risk

Curve 8.5

Volatility 1.7

Spread Government-Related 3.0

Spread Corporate 5.1

Spread Securitized 3.0

Source: POINT, Barclays Capital

For future reference, consider the volatility of the portfolio if all these sources of risk were

independent (eg, correlations were zero). That number would be 10.9bp per month6. Of

course, this scenario is unrealistic, as these sources of risk are not independent. Also, this

analysis does not allow us to understand the interplay among imbalances. For instance, we

know that the isolated risk associated with the curve is 8.5. But this value can be achieved by

being long or short duration. So the isolated number does not allow us to understand the

impact of the curve imbalance on the total risk of the portfolio. The net impact certainly

depends on the sign of the imbalance. For instance, if the long exposure in the curve is

diversified away by a long exposure in credit (due, for instance, to negative correlation

between rates and credit spreads), a symmetric (short) curve exposure would add to the risk

of the long exposure in credit. The risk is clearly smaller in the first case.

To alleviate these shortcomings, we bring correlations into the picture. They allow us to

understand the net impact of the different exposures to the portfolio’s total risk and to detect

potential sources of diversification among the imbalances in the portfolio. Figure 5 reports the

contribution of each of the risk factor groups to the total risk, once all correlations are taken

into account. The total risk (9.3bp/month) is smaller than the zero-correlation risk calculated

previously (10.9bp/month), indicating that the net imbalances of our portfolio are generally

negatively correlated. The figure also allows us to isolate the main sources of risk as being

curve (5.9bp/month) and credit spreads (2.4bp/month), in line with the evidence from the

earlier analysis. In particular, the risk of the government-related and securitized spreads is

significantly smaller once correlations are taken into account.

Figure 5: Correlated Risk per Category

Risk Factors Categories Risk

Total 9.3

Curve 5.9

Volatility 0.1

Spread Government-Related 0.1

Spread Corporate 2.4

Spread Securitized 0.7

Source: POINT, Barclays Capital

The difference in analysis between the isolated and correlated risks reported in Figures 4

and 5 deserves more discussion. For simplicity, assume there are only two sources of risk in

the portfolio – yield curve (Y) and spreads (S). The total systematic variance of the portfolio

(P) can be calculated as follows:

6 We calculate this number by taking the square root of the sum of squares of all the numbers in the table; 10.9 =

(8.5^2+1.7^2+3.0^2+5.1^2+3.0^2)^0.5. Moreover, this number would represent the total systematic risk of the

portfolio. This definition will be developed later in the paper.

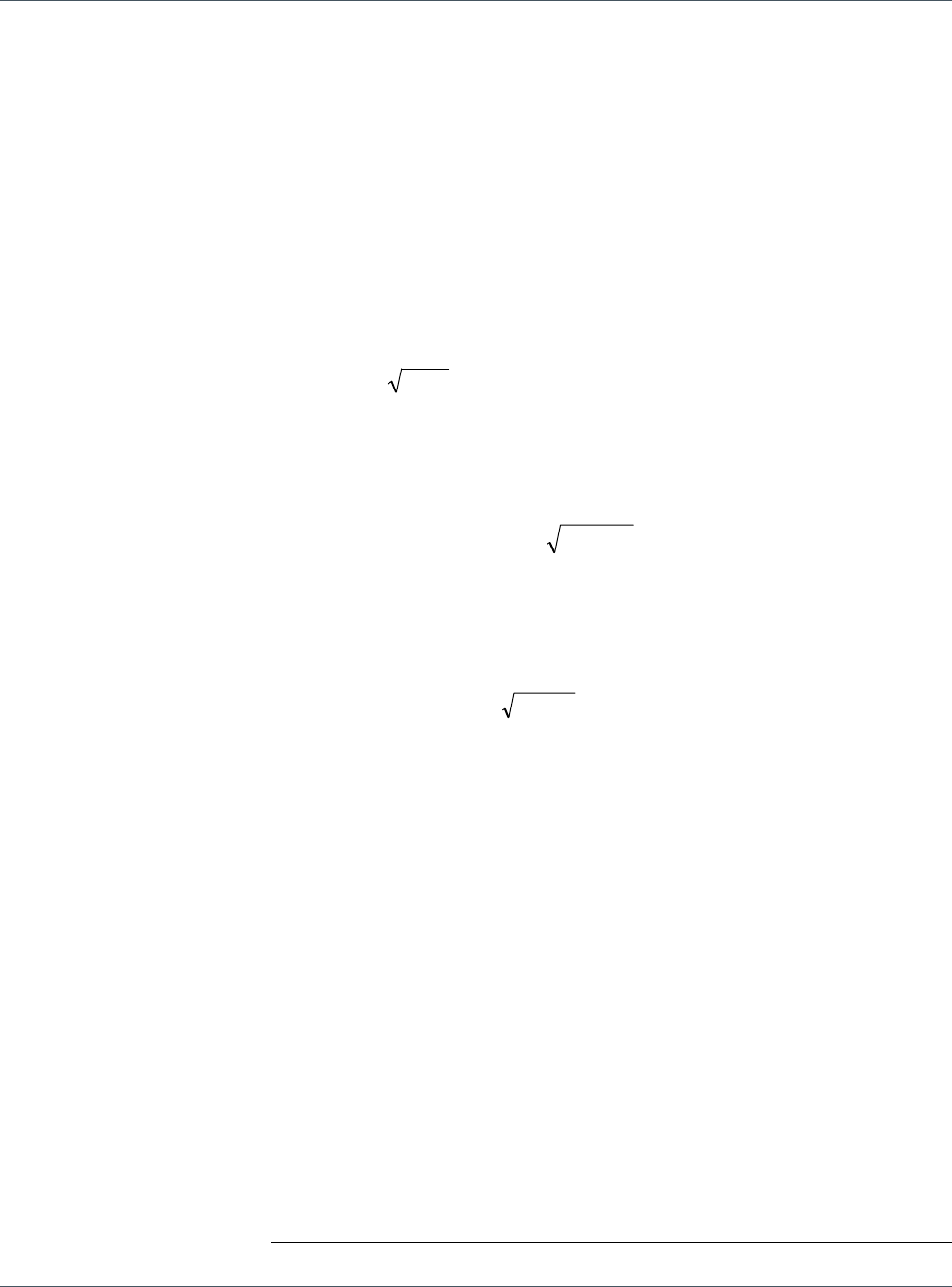
Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 9

VAR(

P

)=VAR(

Y

+

S

)=VAR(

Y

)+VAR(

S

)+2CO

V

(

Y

,

S

)=

=Y×Y+S×S+2(Y×S)

where we use the product X to represent variances and covariances. Another way to

represent this summation is using the following matrix:

⎥

⎦

⎤

⎢

⎣

⎡

××

××

SSSY

SYYY

The sum of the four elements in the matrix is the variance of the portfolio. The isolated risk

(in standard deviation units) reported in Figure 4 is the square root of the diagonal terms. So

the isolated risk due to spreads is represented as:

RiskSpreads

Isolated =S×S.

It would be a function of the exposure to all spread factors, the volatilities of all these factors

and the correlations among them.

The correlated risk reported in Figure 5 is:

)(/][ PVARSSSYRiskcorrelated

Spreads ×+×=

that is, we sum all elements in the row of interest (row 1 for Y, row 2 for S) from the matrix

above, and normalize it by the standard deviation of the portfolio. This statistic (1) takes

into account correlations across groups of risk factors and (2) ensures that the correlated

risks of all factors add up to the total risk of the portfolio given by7

)()( PSTDPVARRiskRisk correlated

Spreads

correlated

Curve ==+

The difference between isolated and contribution to risk, given the interplay of the two

sources ( )(2 SY ×), is allocated equally to each source of risk. In cases when one type of risk

on isolated basis is much smaller in magnitude than the other, the term may have an outsized

effect. In sum, isolated risk takes into account only the individual behavior of each source of

risk, while the contribution to correlated risk looks at the joint behavior of various risk sources.

The generic analysis just performed constitutes the first step in the description of the risk

associated with a portfolio. The analysis refers to categories of risk factors (such as “curve” or

“spreads”). However, a factor based risk model allows for a significantly deeper analysis of the

imbalances the portfolio may have. Each of the risk categories referred to above can be

described with a rich set of detailed risk factors. Typically, in a fixed income factor model, each

asset class has a specific set of risk factors in addition to the potential set of factors common

to all (eg, curve factors). These asset-specific risk factors are designed to capture the

particular sources of risk the asset class is exposed to. In the following section, we go through

a risk report built in such a way, emphasizing risk factors that are common or particular to the

different asset classes. Along the way, we demonstrate how the report offers insights from

both a risk management and a portfolio construction perspective.

7 In this example we focus only on the systematic component of risk. Later, the normalization is with respect to the

total risk of the portfolio, including idiosyncratic risk.

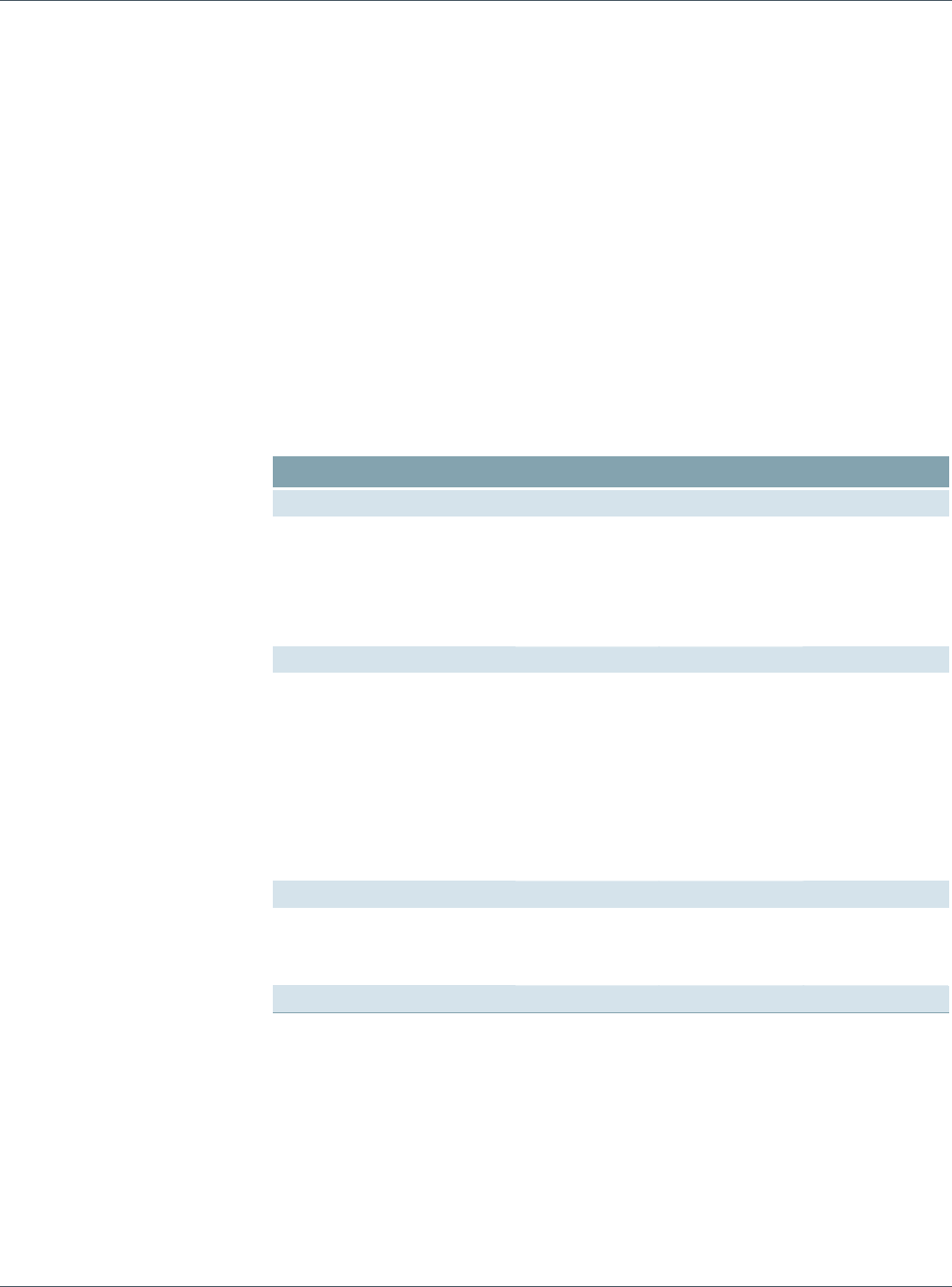
Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 10

A Detailed Risk Report

In this section, we continue the analysis of the portfolio introduced previously, a 50-bond

portfolio benchmarked against the Barclays Capital US Aggregate Index. The report package

we present was generated using POINT®, Barclays Capital’s cross-asset portfolio analysis

and construction tool, and gives a very detailed picture of the risk embedded in the

portfolio. The package is divided into four types of reports: summary reports, factor

exposure reports, issue/issuer level reports and scenario analysis reports. Some of the

information we reviewed earlier can be thought of as summary reports.

Summary Report

Figure 6 illustrates a typical risk summary statistics report. It shows that the portfolio has 50

positions from only 27 issuers. This implies limited ability to diversify idiosyncratic risk, as

we will see below. The report confirms that the portfolio is long duration (OAD of 4.55 years

versus 4.30 years for the benchmark) and has higher yield (yield to worst of 3.71% versus

2.83% for the benchmark) and coupon (4.73% versus 4.46% for the benchmark).

Figure 6: Summary Statistics Report

Portfolio Benchmark

A. Parameters

Positions 50 8191

Issuers 27 787

Currencies 1 1

Market Value ($mn) 200 14,762

Notional ($mn) 187 13,750

B. Analytics Difference

Coupon 4.73 4.46 0.27

Average Life 6.63 6.35 0.27

Yield to Worst 3.71 2.83 0.88

Spread 157 57 100

Duration 4.55 4.30 0.25

Vega -0.02 -0.01 -0.01

Spread Duration 4.67 4.56 0.11

Convexity -0.15 -0.29 0.13

C. Volatility TEV

Systematic 162.9 158.0 9.3

Idiosyncratic 11.1 5.6 10.1

Total 163.3 158.1 13.7

D. Portfolio Beta 1.03

Source: POINT, Barclays Capital

Figure 6 also reports that the total volatility of the portfolio (163.3bp/month) is higher than

that of the benchmark (158.1bp/month). This is not surprising: longer duration, higher

spread and less diversification all tend to increase the volatility of a portfolio. Because of its

higher volatility, we consider the portfolio to be riskier than the benchmark. Looking into the

different components of the portfolio volatility, the figure reports that the idiosyncratic

volatility of the portfolio is significantly smaller than that of the systematic (11.1bp/month

versus 162.9bp/month, respectively). This is also expected from a portfolio of investment

grade bonds. Given the fact that, by construction, the systematic and idiosyncratic

components of risk are independent, we can calculate the total volatility of the portfolio as

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 11

3.1631.119.162 22 =+=

PTF

TEV

There are two interesting observations regarding this number: first, the total volatility is

smaller than the sum of the volatilities of the two components. This is the diversification

benefit that comes from combining independent sources of risk. Second, the total volatility

is very close to the systematic one. This may suggest that the idiosyncratic risk is irrelevant.

That is an erroneous and dangerous conclusion. In particular, when managing against a

benchmark, the focus should be on the net exposures and risk, not on their absolute

counterparts. In Figure 6, the total TEV is reported as 13.7bp/month. This means that the

model forecasts the portfolio monthly return to be typically no more than 14bp/month

higher or lower than the return of the benchmark. This number is in line with the risk

budget of our manager. The figure also reports idiosyncratic TEV of 10.1bp/month, which is

greater than the systematic TEV (9.3). When measured against the benchmark, our major

source of risk is idiosyncratic, contrary to the conclusion one could draw by looking only at

the portfolio’s volatility. The TEV of the portfolio is also greater than the difference between

the volatilities of the portfolio and benchmark. It would be equal to the difference only if the

portfolio and benchmark were perfectly correlated.

Finally, the report estimates the portfolio to have a beta of 1.03 to the benchmark. This

statistic measures the co-movement between the portfolio and the benchmark. We can

read it as follows: the model forecasts that a movement of 100bp in the benchmark leads to

a movement of 103bp in the portfolio in the same direction. Note that a beta of less than

one does not mean that the portfolio is less risky than the benchmark; it just means that the

portfolio is less sensitive to movements in the benchmark. To see this more clearly, consider

the limit case when the portfolio and benchmark are uncorrelated. The portfolio beta in this

case is zero, but this does not mean that the portfolio has zero risk. Finally, one can

compute many different “betas” for the portfolio or subcomponents of it8. A simple and

widely used one is the “interest-rate duration beta”, given by the ratio of the portfolio

duration to that of the benchmark. In our case, the ratio is 4.55/4.30 = 1.06. This implies

that the portfolio has a return from yield curve movements around 1.06 times larger than

that of the benchmark. This beta is larger than the portfolio beta (1.03), meaning that net

exposures to other factors (eg, spreads) “hedge” the portfolio’s net curve risk.

This first summary report (Figure 6) gives us a glimpse into the risk of the portfolio.

However, the manager wants to know in more detail what the sources of this risk are. Risk

can be broken down along various dimensions, two of which we looked at briefly above:

security groups (asset classes) and risk factors. The next two summary reports present the

detailed risk breakdown along these two dimensions. In the first, risk is partitioned across

different groups of risk factors. In the second, the partition is across groups of securities.

Figure 7 shows four different statistics associated with each set of risk factors. The first two

were explored to an extent in Figure 4 and Figure 59. The figure reports in the first column

the isolated TEV, that is, the risk associated with that particular set of risk factors only. We

see that in an isolated analysis, the systematic and idiosyncratic risks are balanced, at 9.3

and 10.1 respectively. The report also shows the isolated risk associated with the major

components of systematic risk. As discussed before, all components of systematic risk have

non-trivial isolated risk, but only curve and credit spreads are significant when we look into

the contributions to TEV. If we look across factors, the major contributors are idiosyncratic

risk, curve and credit spreads. Other systematic exposures are relatively small.

8 For example, see Figure 13 later in this paper.

9 Note that the contribution numbers are different than those from Figure 5, because there we reported the

contribution to systematic—not total—risk.

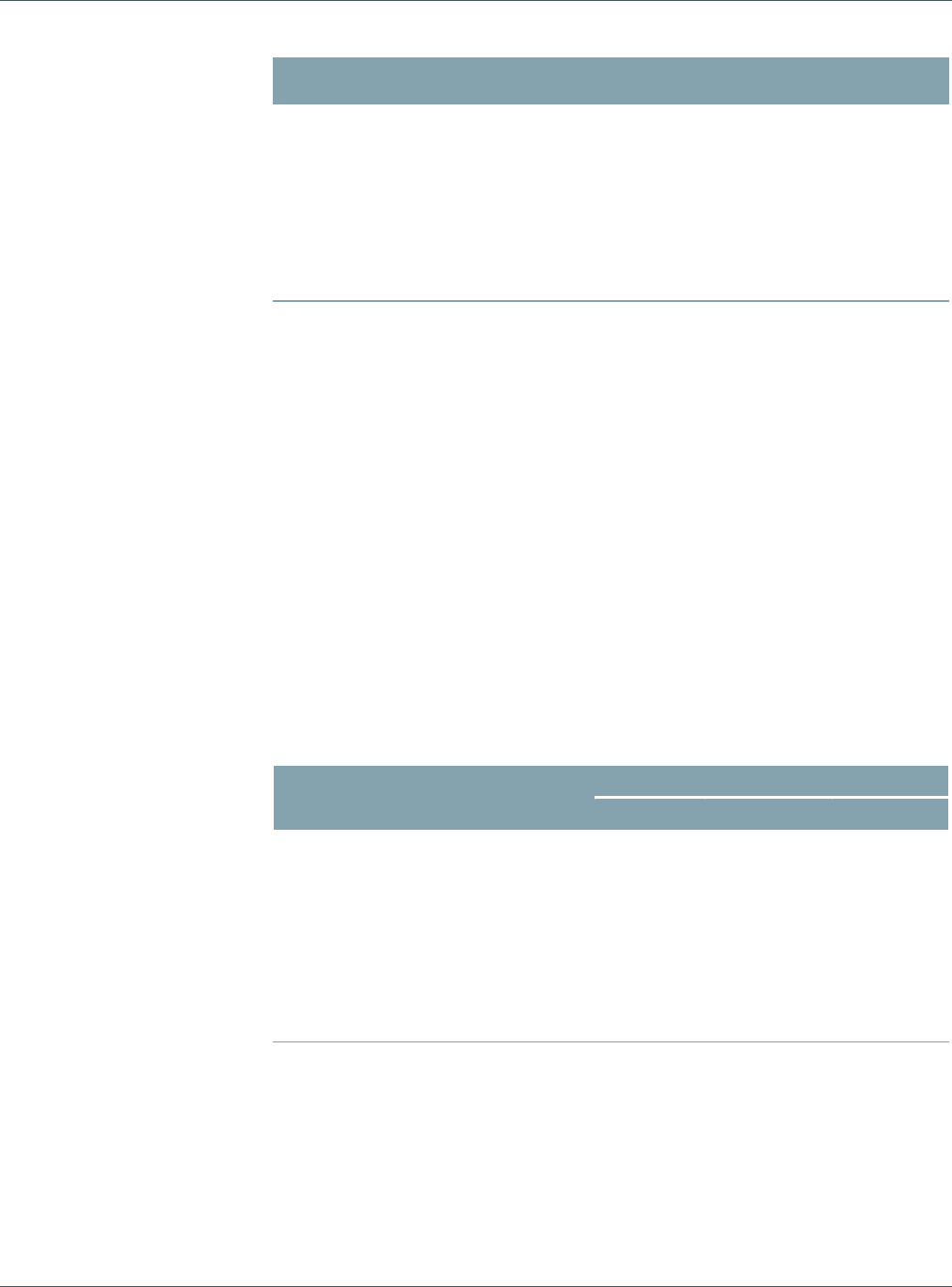
Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 12

Figure 7: Factor Partition – Risk Analysis

Risk Factor Group Isolated TEV

Contribution to

TEV

Liquidation Effect

on TEV

T

EV Elasticity

(%)

Total 13.7 13.7 -13.7 1.0

Systematic Risk 9.3 6.3 -3.6 0.5

Curve 8.5 4.0 -1.5 0.3

Volatility 1.7 0.1 0.0 0.0

Government-Related Spreads 3.0 0.1 0.2 0.0

Corporate Spreads 5.1 1.6 -0.7 0.1

Securitized Spreads 3.0 0.5 -0.2 0.0

Idiosyncratic Risk 10.1 7.4 -4.4 0.5

Source: POINT, Barclays Capital

Another look into the correlation comes when we analyze the liquidation effect reported on

the table. This number represents the change in TEV when we completely hedge that

particular group of risk factors. For instance, if we hedge the curve component of our

portfolio, our TEV drops by 1.5bp/month: from 13.7bp to 12.2bp. One may think that the

drop is rather small, given the magnitude of isolated risk the curve represents. However, if

we hedge the curve, we also eliminate the beneficial effect the negative correlation between

curve and spreads has on the overall risk of the portfolio. Therefore, we have a more limited

impact when hedging the curve risk. In fact, for this portfolio we see that hedging any

particular set of risk factors has a limited effect on the overall risk.

The TEV elasticity reported in the last column gives further insight into how the TEV in

the portfolio changes when the risk loadings are changed. Specifically, it tells us what the

percentage change in TEV would be if we changed our exposure to that particular set of

factors by 1%. If we reduce our exposure to corporate spreads by 1%, our TEV would fall

by 0.1%.

Figure 8: Security Partition – Risk Analysis I

Contribution to TEV

Security Partition Bucket

NMW (%) Systematic Idiosyncratic Total

Total 0.0 6.3 7.4 13.7

Treasuries -2.0 2.9 0.2 3.1

Government Agencies -5.4 0.5 0.4 0.9

Government Non-Agencies -1.0 -1.4 0.1 -1.3

Corporates 12.4 3.4 4.3 7.7

MBS -5.8 0.9 0.8 1.7

ABS -0.3 0.0 0.0 0.0

CMBS 2.1 0.0 1.6 1.6

Source: POINT, Barclays Capital

We perform a similar analysis in Figure 8, but applied to a security partition. That is, instead

of looking at individual sources of risk (eg, curve) across all securities, we now aggregate all

sources of risk within a security and report analytics for different groups of these securities

(eg, sub-portfolios). Figure 8 reports results when securities are grouped by asset class. It

shows that the majority of risk (7.7bp/month) comes from the corporate component of the

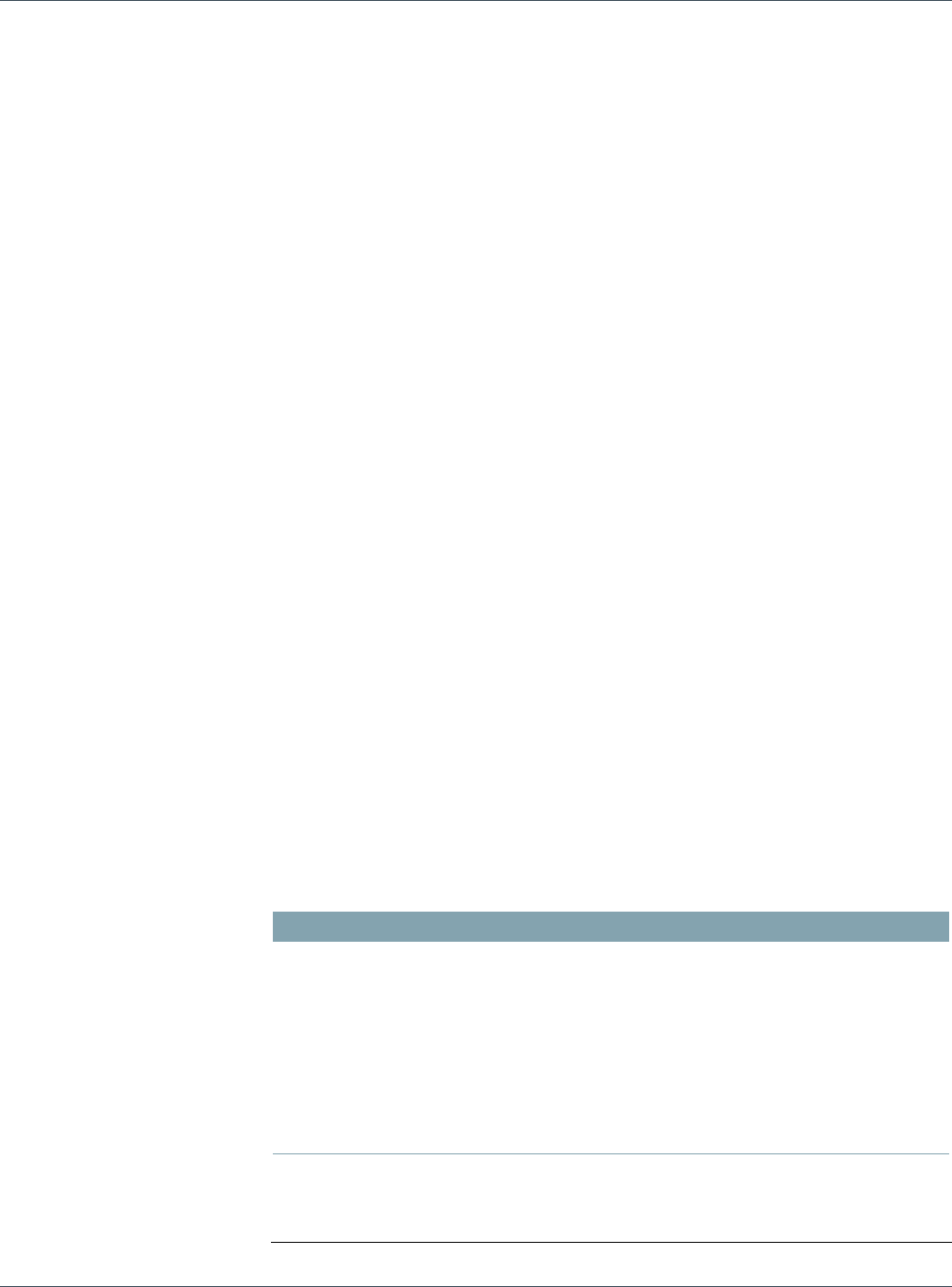
Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 13

portfolio10. This sector is the primary contributor to both the portfolio’s systematic and

idiosyncratic components of risk. This is not surprising, given the portfolio’s large net

market weight (NMW) to this sector. There are two other important sources of risk. The first

is the Treasuries sub-portfolio, with 3.1bp/month of risk. This risk comes mainly from the

mismatch in duration. The second comes from the idiosyncratic risk of the CMBS

component of the portfolio. Even though the NMW and systematic risk are not significant

for this asset class, the relatively small number of (risky) CMBS positions in the portfolio

causes it to have significant idiosyncratic risk (three securities in the portfolio versus 1,735

in the index). Since the portfolio manager is trying to replicate a very large benchmark with

only 50 positions, she has to be very confident in the issuers selected. This report highlights

the significant name risk to which the portfolio is exposed.

Figure 9 completes the analysis, reporting other important risk statistics about the different

asset classes within the portfolio. These statistics mimic the analysis done in terms of risk

factor partitions in Figure 7, so we will not repeat their definitions. We focus on the

numbers. In particular, the isolated TEV from the corporate sector is 15.2bp/month, higher

than the total risk of the portfolio. This means that the exposures to the other asset classes,

on average, hedge our credit portfolio. The figure also reports that the agencies’ isolated

risk is very large. This is because of our large negative net exposure (-5.4%) to this asset

class. But the risk is fully hedged by the other exposures of the portfolio (eg, long exposure

to credit or long duration on Treasuries), so, overall, the risk contribution of this asset class

is small, as previously discussed. We can even take the analysis a bit further: Figure 9 shows

us, via the liquidation effect, that if we eliminate the imbalance that the portfolio has on

agencies, we actually would raise the total risk of the portfolio by 2.0bp/month. In short, we

would be eliminating the hedge this asset class provides to the global portfolio, therefore

increasing its risk. The exposures to this asset class were clearly built to counteract other

exposures in the portfolio. Finally, Figure 9 also reports the TEV elasticity of the different

components of the portfolio. This number represents the percentage change in TEV if the

NMW to that sub-portfolio changes by 1%, so we need to read the numbers with an

opposite sign if the NMW is negative. In particular, if we increase the weight of the agency

portfolio in absolute value (making it “more short”) by 1%, we would actually increase the

TEV by 0.1%. This result shows that the position in agencies provides hedging “on average”,

but further increasing the exposure to this sector would actually increase the risk of the

portfolio. In other words, the hedging went beyond its optimal value.

Figure 9: Security Partition – Risk Analysis II

Security Partition Bucket Isolated TEV Liquidation Effect on TEV TEV Elasticity (%)

Total 13.7 -13.7 1.0

Treasuries 7.4 -1.1 0.2

Government Agencies 9.1 2.0 0.1

Government Non-Agencies 6.7 2.7 -0.1

Corporates 15.2 0.6 0.6

MBS 5.8 -0.5 0.1

ABS 1.1 0.1 0.0

CMBS 5.1 -0.7 0.1

Source: POINT, Barclays Capital

10 This result does not contradict the findings in Figure 7, where we see that curve is the major source of risk.

Remember that the curve risk can come from our corporate sub-portfolio.

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 14

The summary reports give a very clear picture of the major sources of risk and how they

relate to each other. Below, we give a more detailed analysis of individual systematic

sources of risk.

Factor Exposure reports

At the heart of a multi factor risk model is the definition of the set of systematic factors that

drive risk across the portfolio. As described above, a fixed income portfolio is exposed to

different sorts of risk. In what follows, we focus on the three major types: curve, credit and

prepayment risk. Specifically as regards the latter two, we use the credit and MBS

component of the portfolio, respectively, to illustrate how to measure risks along these

dimensions. Moreover, to keep the example simple, we show only a partial view of all

relevant factors for these sources of risk. Later in this section we refer briefly to the other

sources of risk to which a fixed-income portfolio may be exposed.

 Curve Risk

Curve risk is the major source of risk across fixed-income instruments. This kind of risk is

embedded in virtually all fixed-income securities11; therefore, mismatches in curve profiles

relative to a benchmark are often the main drivers of portfolio risk. As the previous analysis

shows (eg, Figure 7), curve is the major source of risk in our particular portfolio.

When analyzing curve risk, we should use the curve of reference we are interested in.

Depending on the portfolio and circumstances, this is typically the government or swap

curve12. In calm periods, the behavior of the swap curve tends to match that of the

government curve. However, during liquidity crises (eg, the Russian crisis of 1998 or the

credit crisis of 2008), they can diverge significantly. To capture these different behaviors

adequately, we analyze curve risk using the following breakdown: for government products,

the curve risk is assessed using the government curve; for all other products in our portfolio

(that usually trade off the swap curve), this risk is measured using both the Treasury curve

and swap spreads (ie, the spreads between the swap and the government curve). Other

decompositions are also possible.

The risk associated with each of these curves can be described by the portfolio’s exposure

to different points along the curve and a convexity term, and by how volatile and correlated

the movement in these points of the curve is. For a typical portfolio, a good description of

the curve can be achieved by looking at a relatively small number of points along the curve

(called key rates), eg, 6-month, 2-year, 5-year, 10-year, 20-year, and 30-year. An alternative

set of factors used to capture yield curve risk can be defined using statistical analysis of the

historical realizations of the various yield curve points. The statistical method used most

often is called principal component analysis (PCA). This method defines factors that are

statistically independent of each other. Typically, three or four such factors are sufficient to

explain the risk associated with changes of yields across the yield curve. PCA analysis has

several shortcomings and must be used with caution. Using a larger set of economic

factors, like the key-rate points described above, is more intuitive and captures the risk of

specialized portfolios better. For these reasons, many portfolio managers favor the key-rates

approach for most risk analysis problems.

Figure 10 details the risk in our portfolio associated with the US Treasury curve. It starts by

describing all risk factors our portfolio or benchmark load on. As discussed above, we identify

the six key-rate (KR) points in the curve plus the convexity term as the risk factors associated

11 Exceptions are for instance floaters or distressed securities.

12 Other curves that can be used are for instance the municipals (tax free) curve, derivatives-based curves, etc.

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 15

with US Treasury risk. They are described in the first column of panel A in the figure. They

measure the risk associated with moves in that particular point in the curve. Exposure to these

risk factors is measured by the key rate durations (KRD) for each of the six points. The

description of the loading is in the second column of the figure, while values for the portfolio,

benchmark and the difference are displayed in subsequent columns. Key-rate durations are

also called partial durations, as they add up to approximately the duration of the portfolio.

Their loadings are constructed by aggregating partial durations across (virtually) all the

securities. For instance, for our portfolio, the sum of the key rate durations is 0.14 + 0.86 + 1.3

+ 0.77 + 1.02 + 0.47 = 4.56, very close to the total duration of our portfolio. Their loadings are

constructed by aggregating partial durations across all the securities.

Figure 10 shows significant mismatches in the duration profiles of our portfolio and its

benchmark, namely at the 10-year and 20-year points on the curve. Specifically, we are short

0.36 years at the 10-year point and long 0.49 years at the 20-year point. How serious is this

mismatch? Looking at the factor volatility column, it can be seen that these points on the

curve have been very volatile, at around 40bp/month. If we interpret this volatility as a typical

move, the first two columns of panel B show us the potential impact of such a movement in

the return of our portfolio, net of benchmark. For instance, a typical move up

(+44.2bp/month) in the 10-year point of the Treasury curve, when considered in isolation, will

deliver a positive net return of 15.9bp13. In isolation, the positive impact is expected because

we are short that point of the curve. More interesting may be the correlated number in the

figure. It states the return impact but in a correlated fashion. In the scenario under analysis, a

movement in the 10-year point will almost certainly involve a movement of the neighboring

points in the curve. So, contrary to the positive isolated effect documented above, the

correlated impact of a change up in the 10-year point is actually negative, at -5.0bp. This result

is in line with the overall positive duration exposure of the portfolio: general (correlated)

movements up in the curve have a negative impact on the portfolio’s performance14.

Moreover, and broadly speaking, the ratio of the correlated impact to the factor volatility gives

us the model-implied partial empirical duration of the portfolio. For instance, if we focus on

the 10-year point, we get 5.0/44.2 = 0.11. This smaller empirical duration is typical in

portfolios with spread exposure. The spread exposure tends to empirically hedge some of the

curve exposure, given the negative correlation between these two sources of risk. Finally, the

figure shows the risk associated with convexity. We can see that the benchmark is significantly

more negatively convex, so the portfolio is more protected than the benchmark from higher-

order changes in the yield curve.

One can analyze many other statistics of interest with regard to the Treasury curve risk of the

portfolio. Portfolio managers frequently want to know: If I want to reduce the risk of my

portfolio by manipulating my Treasury curve exposure, what should I change? What is the

most effective move? By how much would my risk actually change? The statistics reported in

the columns “Marginal Contribution to TEV” and “TEV Elasticity (%)” of panel B are typically

used to answer these questions. Regarding the marginal contributions, the 10-year point has

the largest value, showing us that an increase (reduction) of one unit of exposure (in this case

one year of duration) to the 10-year point leads to an increase (reduction) of around 16bp in

13 This number is obtained by simply multiplying the net exposure by the factor volatility. The sign of the move depends on

the interpretation of the factor. In the case of the yield curve movements we know that KRKRDR

Δ

×−= , where KRD is

the duration associated with the KR point. In our example –(-0.36) x 44.2 = 15.9.

14 This reversal is clearly related to the fact that the 10-year and the 20-year points in the curve are usually highly

correlated. In our case our short position on the 10-year point is more than compensated by the positive exposure in the

20-year. Netting out, the 20-year effect (long duration) dominates when all changes are taken in a correlated fashion.

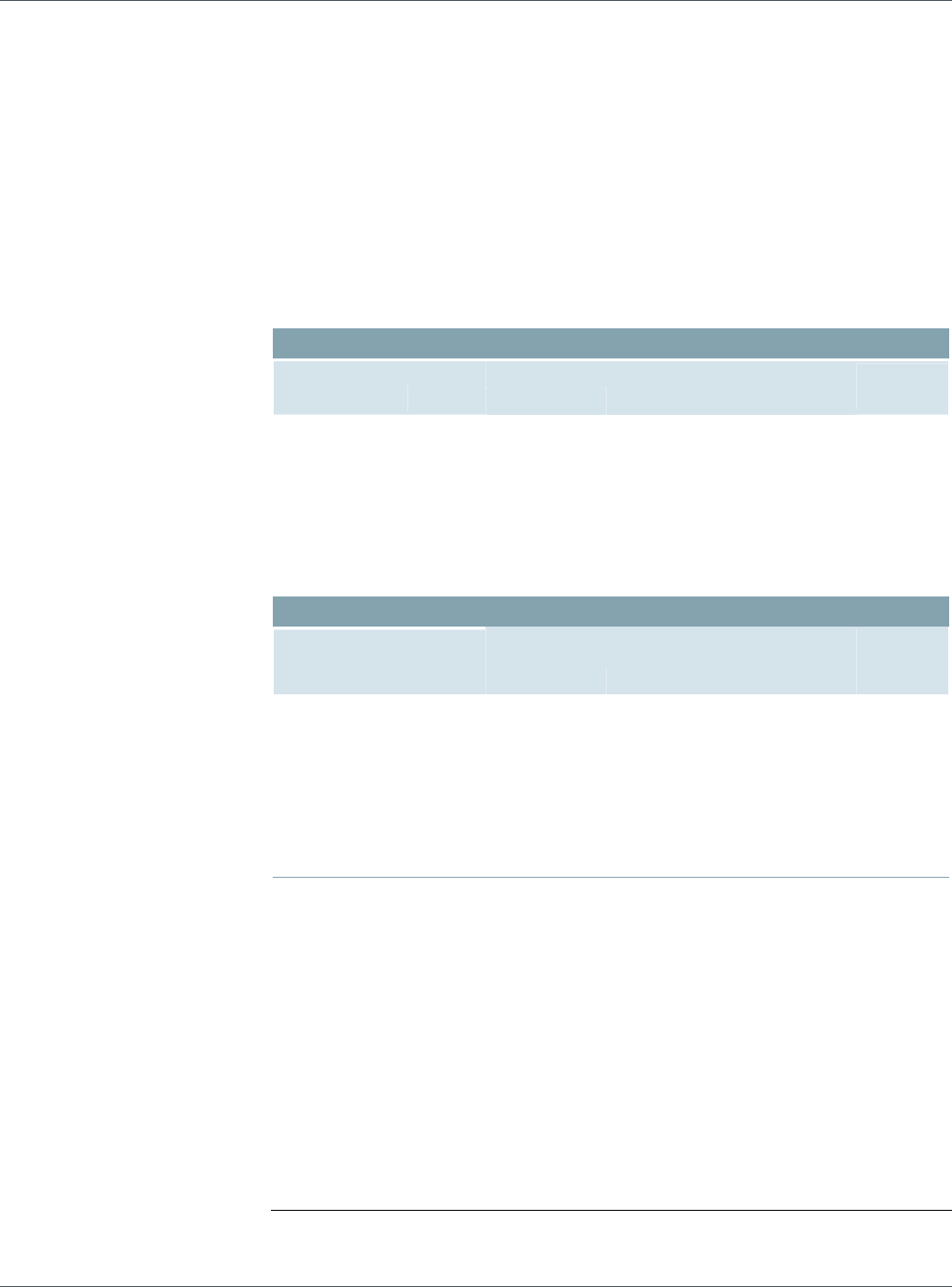
Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 16

our TEV15. In other words, if we want to reduce risk by manipulating our exposure to the yield

curve, the 10-year point seems to present the fastest track. In addition, the figure shows that

all Treasury risk factors are associated with positive marginal contributions. This means that a

rise in exposure to any of these factors increases the risk (TEV) of the portfolio. This

conclusion holds, even for factors for which we have negative exposure (eg, the 10-year key-

rate). The reason behind this result is our overall long duration exposure. If we add exposure

to it, regardless of the specific point where we add it, we extend our duration even further,

increasing the mismatch our portfolio has in terms of duration, and so increasing its risk16.

This result holds because we take into consideration the correlations between the different

points in the Treasury curve. Without correlations, the analysis would be much less clear.

Figure 10: Treasury Curve Risk

A. Exposures and Factor Volatility

Exposure

Factor name Units Portfolio Benchmark Net

Factor

Volatility

USD 6M key rate KRD (Yr) 0.14 0.15 -0.01 36.0

USD 2Y key rate KRD (Yr) 0.86 0.70 0.15 38.0

USD 5Y key rate KRD (Yr) 1.30 1.25 0.05 44.3

USD 10Y key rate KRD (Yr) 0.77 1.13 -0.36 44.2

USD 20Y key rate KRD (Yr) 1.02 0.53 0.49 39.6

USD 30Y key rate KRD (Yr) 0.47 0.53 -0.06 39.7

USD Convexity OAC -0.15 -0.29 0.13 8.4

B. Other Risk Statistics

Return Impact of a Typical Move

Factor name Isolated Correlated

Marginal

Contribution to

TEV

TEV

Elasticity

(%)

USD 6M key rate 0.5 -2.4 6.3 0.0

USD 2Y key rate -5.8 -4.5 12.2 0.1

USD 5Y key rate -2.0 -4.5 14.5 0.0

USD 10Y key rate 15.9 -5.0 15.9 -0.4

USD 20Y key rate -19.5 -5.2 14.9 0.5

USD 30Y key rate 2.5 -5.2 14.8 -0.1

USD Convexity 1.1 2.0 1.2 0.0

Source: POINT, Barclays Capital

Figure 10 also reports the TEV elasticity of each of the risk factors, a concept introduced

earlier. The interpretation is similar to the marginal contribution, but with normalized

changes (percentage changes). This normalization makes the numbers more comparable

across different risk factors. It is also useful when considering leveraging the entire portfolio

proportionally. In our case, if we increase the exposure to the 10-year key rate point by

10%, from -0.36 to something around -0.40 (effectively reducing our long duration

exposure), our TEV would be reduced by 4% (from 13.7 to 13.2bp/month).

We now turn the analysis to the other component of the curve risk described above: the risk

embedded into the portfolio exposure to swap spreads; that is, the differences between the

swap and Treasury curves. Many securities trade against the swap curve, making it the

15 The marginal contribution is the derivative of the TEV with respect to the loading of each factor, so its interpretation

holds only locally. Therefore a more realistic reading may be that if we reduce the exposure to the 10-year by 0.1

years, the TEV would be reduced by around 1.6bp.

16 This is a rationale very similar to the one used before, where we see all correlated impact with the same signal.

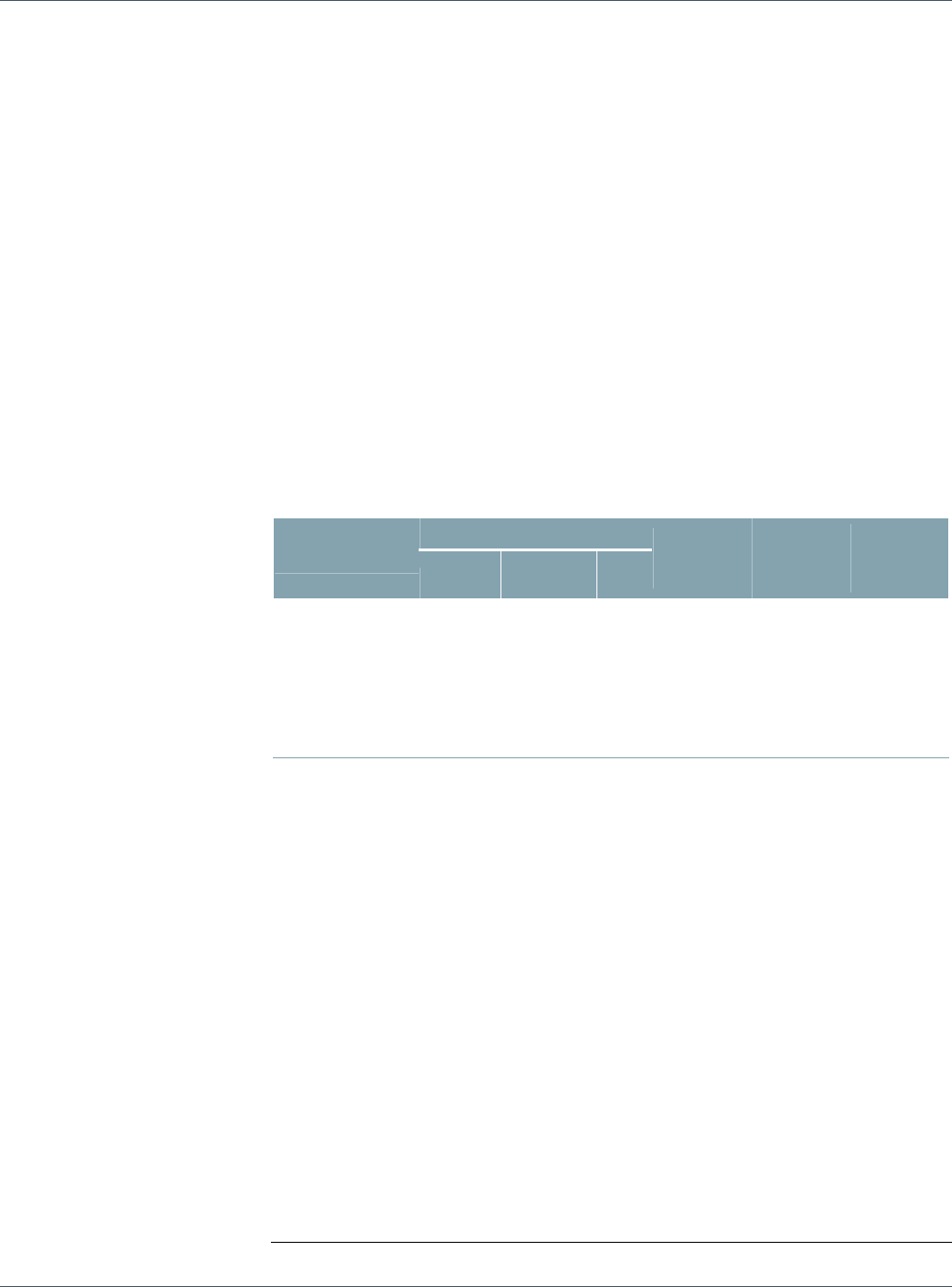
Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 17

natural choice as the base risk curve for those markets. To unify the analysis with markets

that use Treasuries as the base curve, we break the swap curve into the Treasury curve

(analyzed in Figure 10) and excess over the Treasury — the swap spread.

In our approach, all securities that trade against the swap curve (eg, all typical credit and

securitized bonds) are exposed to both Treasury and swap spread (SS) risk. The analysis of the

latter follows very closely that of the Treasury curve, so we highlight only the major risk

characteristics of the portfolio along this dimension. Figure 11 shows that, in general, our

exposure to the swap spreads is smaller than that of the Treasury curve. Remember that

Treasuries do not load on this set of risk factors, so the market-weighted exposures are

smaller. Looking at the profile of factor volatilities, it is clear that its term structure of volatilities

is U-shaped, with the short end extremely volatile and the five-year point having the least

volatility. When comparing with the Treasury curve volatility profile (Figure 10), we can see

significant differences, the aftermath of a strong liquidity crisis. Regarding net exposures,

Figure 11 shows that our largest mismatch is at the 30-year point, where we are short by 0.15

year. Interestingly, this is not the most expensive mismatch in terms of risk: when looking at

the last column, we see that we would be able to change risk the most by manipulating the

short end of our exposure to the swap spread curve, namely the six-month point.

Figure 11: Swap Spread (SS) Risk

Exposure (SS-KRD)

Factor name

Portfolio Benchmark Net

Factor

Volatility

Return

Impact

Correlated

Marginal

Contribution

to TEV

6M SS 0.14 0.13 0.01 39.1 -2.1 5.8

2Y SS 0.52 0.47 0.04 20.4 -2.1 3.0

5Y SS 0.84 0.75 0.09 9.6 -2.0 1.4

10Y SS 0.71 0.68 0.03 14.1 1.7 -1.8

20Y SS 0.34 0.33 0.01 17.0 2.2 -2.7

30Y SS 0.06 0.20 -0.15 20.1 2.4 -3.5

Source: POINT, Barclays Capital

The previous figures help us to understand our exposures to the different types of curve risk

and their impact on the return and risk of our portfolios. They also guide us as to changes

we might introduce to modify the risk profile of the portfolio. We now turn to sources of risk

that are more specific to particular asset classes. We start with the analysis of credit risk.

 Credit Risk

Instruments issued by corporations or entities that may default are said to have credit risk.

Holders of these securities demand some extra yield – on top of the risk-free yield – to

compensate for that risk. The extra yield is usually measured as a spread to a reference

curve. For instance, for corporate bonds, the reference curve is usually the swap curve, so

spread is typically quoted relative of this curve. The level of credit spreads determines to a

large extent the portfolio’s exposure to credit risk17.

Several characteristics of credit bonds are naturally associated with systematic sources of

credit spread risk. For instance, depending on the business cycle, particular industries may be

going through especially tough times. So industry membership is a natural systematic source

of risk. Similarly, bonds with different credit ratings are usually treated as having different

17 Spreads are also compensation for sources of risk other than credit (eg, liquidity), but for the sake of our argument,

we treat them as major indicators of credit risk.

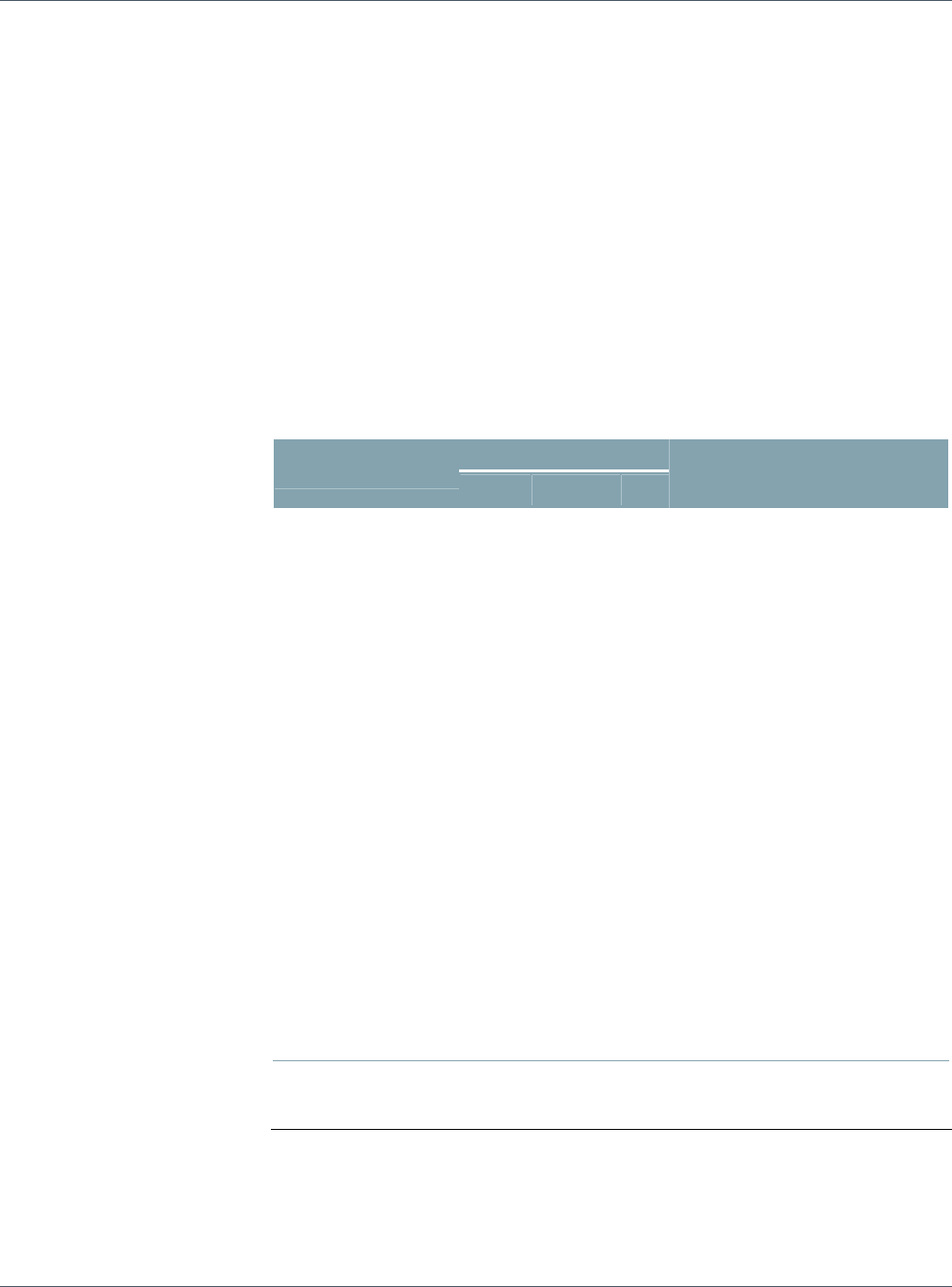
Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 18

levels of credit risk. Credit rating could also be used to measure systematic exposure to credit

risk. Given these observations, it is common to see factor models for credit risk using industry

and ratings as the major systematic risk factors. Recent research suggests that risk models

that directly use the spreads of the bonds instead of their ratings to asses risk perform better

for relatively short/medium horizons of analysis18. Under this approach, the loading of a

particular bond to a credit risk factor would be the commonly used spread duration, but now

multiplied by the bond’s spread (the loading is termed DTS = Duration Times Spread = OASD

× OAS). By directly using the spread of the bond in the definition of the loading to the credit

risk factors, we do not need to assign specific risk factors to capture the rating or any similar

quality-like effect. It will be automatically captured by the bond’s loading to the credit risk

factor, and will adjust as the spread of the bond changes. We use different systematic risk

factors only to distinguish among credit risks coming from different industries.19

The results of this approach to the analysis of our portfolio are displayed in Figure 12, which

shows the typical industry risk factors associated with credit risk.

Figure 12: Credit Spread Risk

Exposure (DTS)

Factor name Portfolio Benchmark Net

Factor

Volatility

Return Impact

Correlated

Marginal

Contribution

to TEV

IND Chemicals 0.00 0.03 -0.03 15.01 -0.39 0.43

IND Metals 0.00 0.06 -0.06 20.01 -0.16 0.23

IND Paper 0.00 0.01 -0.01 17.04 -0.40 0.49

IND Capital Goods 0.00 0.05 -0.05 14.98 -0.02 0.02

IND Div. Manufacturing 0.00 0.03 -0.03 14.21 -0.62 0.64

IND Auto 0.00 0.01 -0.01 22.18 -0.53 0.85

IND Consumer Cyclical 0.10 0.05 0.06 17.05 -0.26 0.32

IND Retail 0.00 0.05 -0.05 16.95 0.14 -0.17

IND Cons. Non-cyclical 0.00 0.13 -0.13 14.62 -0.22 0.24

IND Health Care 0.00 0.02 -0.02 14.07 0.13 -0.13

IND Pharmaceuticals 0.19 0.06 0.12 15.13 -0.34 0.37

IND Energy 0.12 0.20 -0.07 16.39 -0.29 0.34

IND Technology 0.00 0.06 -0.06 15.52 -0.11 0.12

IND Transportation 0.00 0.05 -0.05 15.09 -0.26 0.29

IND Media Cable 0.24 0.06 0.18 15.83 0.51 -0.58

IND Media Non-cable 0.00 0.04 -0.04 15.94 0.20 -0.23

IND Wirelines 0.09 0.17 -0.08 15.26 0.41 -0.45

IND Wireless 0.00 0.03 -0.03 14.87 1.06 -1.13

UTI Electric 0.28 0.20 0.08 15.79 -0.16 0.18

UTI Gas 0.09 0.10 -0.01 18.51 -0.41 0.55

FIN Banking 0.88 0.56 0.32 18.61 1.19 -1.59

FIN Brokerage 0.00 0.02 -0.02 15.90 1.47 -1.68

FIN Finance Companies 0.08 0.10 -0.02 20.64 0.68 -1.01

FIN Life & Health Insurance 0.12 0.11 0.01 19.96 0.58 -0.84

FIN P&C Insurance 0.00 0.06 -0.06 11.76 0.34 -0.29

FIN Reits 0.14 0.04 0.10 17.68 0.80 -1.02

Non Corporate 0.06 0.23 -0.17 25.27 0.28 -0.50

Source: POINT, Barclays Capital

18 For details, please refer to Ben Dor et al. (2010).

19 The general principle of a risk model is that the historical returns of assets contain information that can be used to

estimate the future volatility of portfolio returns. However, good risk models must have the ability to translate the

historical asset returns to the context of the current environment. This translation is made when designing a particular

risk model/factor and delivers risk factors that are as invariant as possible. This invariance makes the estimation of the

factor distribution much more robust. In the particular case of the DTS, by including the spread in the loading (instead

of using only the typical spread duration), we change the nature of the risk factor being estimated. The factor now

represents percentage change in spreads, instead of absolute changes in spreads. The former has a significantly more

invariant distribution. For more details, please refer to Silva (2009a).

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 19

The portfolio has net positions in 27 industries, spanning all three major sectors: Industrials

(IND), Utilities (UTI) and Financials (FIN). We saw before that we have a significant net

exposure to financials in terms of market weights (12.2%; Figure 1). In terms of risk exposure,

Figure 12 shows that the net DTS attached to the Banking industry is 0.32, clearly the highest

across all sectors.20 However, the marginal contribution to TEV that comes from that industry,

although high, is comparable to other industries, namely Brokerage, for which the net

exposure is close to zero. This means that these two industries are close substitutes in terms

of the current portfolio holdings.

Another interesting point is highlighted by the fact that the marginal contribution is

negative for all industries, even though some (such as Banking or Media Cable) are

significantly overweighted. The analysis suggests that if we increase our risk exposure to

Banking, our risk would actually decrease. This result is again driven by the strong negative

correlation between spreads in financials and the yield curve. Therefore, the exposure in

banking is actually helping hedge out our (more risky) long duration position. This kind of

analysis is possible only when you account for the correlations across factors. It is also

dependent on the quality of the model’s correlation estimates.

Although the risk factors used to measure risk are predetermined in a linear factor model,

there is extreme flexibility on the way the risk numbers can be aggregated and reported21. For

example, as explained above, the risk model we use to generate the current risk reports does

not use credit ratings as drivers of systematic credit risk. Instead, it relies on the DTS concept.

However, once generated, the risk numbers can be reported using any portfolio partition.

As an example, Figure 13 shows the risk breakdown by rating, indicating that the majority of

risk is coming from our AAA exposure (10.9bp/month), the bucket with the biggest mismatch

in terms of net weight (-7.2%). This bucket includes Treasury and government-related

securities, sectors that are underweighted in the portfolio leading to significant risk. This is

clearer when we look into the isolated TEV numbers. If we had mismatches only on AAAs, the

risk of our portfolio would be 37.4bp/month, instead of the actual 13.7bp; the other exposures

(namely the one to single-As) hedge the risk from AAAs.

Figure 13: Risk per Rating

TEV

Rating NMW (%) Contribution Isolated Liquidation Elasticity (%)

Systematic

Beta

Total 0.0 13.7 13.7 -13.7 1.0 1.03

AAA -7.2 10.9 37.4 22.2 0.8 1.12

AA1 -0.3 -0.2 1.0 0.2 0.0 0.00

AA2 0.2 0.3 3.3 0.1 0.0 1.10

AA3 -2.3 -1.3 6.7 2.6 -0.1 0.00

A1 -0.5 0.3 4.2 0.4 0.0 1.51

A2 7.1 3.6 11.2 1.0 0.3 0.77

A3 4.7 1.7 5.8 -0.5 0.1 0.65

BAA1 -0.1 0.3 3.7 0.2 0.0 1.51

BAA2 -3.3 -2.3 11.5 5.9 -0.2 0.00

BAA3 1.7 0.3 7.7 1.7 0.0 0.37

Source: POINT, Barclays Capital

20 The DTS units used in the report are based on a OASD stated in years and an OAS in percentage points. Thus, a

bond with an OASD = 5 and an OAS = 200bp would have a DTS of 5 × 2 =10. The DTS industry exposures are the

market-weighted sum of the DTS of each of the securities in that industry.

21 For a detailed methodology on how to performed this customized analysis, please see Silva (2009b).

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 20

Figure 13 also indicates the systematic betas associated with each of the rating sub-portfolios.

These betas add up to the portfolio beta, when we use the portfolio weights (not NMW) as

weights in the summation. For example, the figure allows us to infer that a movement of 10bp

in the benchmark leads to an 11.2bp return in the AAA sub-component of the portfolio. On

the other hand, the beta of 0.37 for the BAA3 component of the portfolio does not signal low

volatility for this sub-portfolio. It mainly indicates low correlation with the benchmark, possibly

a result of the significant role of idiosyncratic risk for this set of bonds. Systematic betas of

zero identify buckets for which the portfolio has (close to) no holdings.

 Prepayment Risk

Securitized products are generally exposed to prepayment risk. The most common of the

securitized products are the residential MBS (RMBS or simply MBS). These securities

represent pools of deals that allow the borrower to prepay their debt before the maturity of

the loan/deal, typically when prevailing lending rates are lower. This option means an extra

risk to the holder of the security: the risk of holding cash exactly when reinvestment rates

are low. Therefore, these securities have two major sources of risk: interest rates (including

convexity) and prepayment risk.

Some part of the prepayment risk can be expressed as a function of interest rates via a

prepayment model. This risk will be captured as part of interest-rate risk using the key-rate

durations and the convexity. Convexity, which is usually negative for these instruments, is a

significant source of risk. Negative convexity has a detrimental effect on the market value of

an instrument – compared with one with positive or zero convexity – when interest rates

move significantly in either direction. Indeed, decreasing interest rates cause prepayments

to increase thereby reducing the price appreciation because of the falling rates. Conversely,

rising interest rates intensify the price depreciation the instrument suffers with higher rates.

The remaining part of prepayment risk – that is not captured by the prepayment model –

must be modeled with additional systematic risk factors. Typically, the volatility of

prepayment speeds (and therefore of risk) on MBS securities depends on three

characteristics: program/term of the deal, if the bond is priced at discount or premium (eg,

if the coupon on the bond is bigger than the current mortgage rates) and how seasoned the

bond is. This analysis suggests that the systematic risk factors in a risk model should span

these three characteristics of the securities.

Figure 14: MBS (Spread) Prepayment Risk

Exposure (OASD)

Factor name Portfolio Benchmark Net

Factor

Volatility

Return

Impact

Correlated

Marginal

Contribution

to TEV

MBS New Discount 0.00 0.00 0.00 36.8 -1.2 3.3

MBS New Current 0.00 0.04 -0.04 24.5 -0.3 0.6

MBS New Premium 0.38 0.59 -0.21 29.7 -0.1 0.3

MBS Seasoned Current 0.00 0.00 0.00 25.5 -0.6 1.2

MBS Seasoned Premium 0.65 0.46 0.19 29.8 0.1 -0.2

MBS Ginnie Mae 30Y 0.31 0.21 0.10 6.1 -0.1 0.0

MBS Fannie Mae 15Y 0.00 0.11 -0.11 15.7 0.4 -0.4

MBS Ginnie Mae 15Y 0.00 0.01 -0.01 12.3 0.5 -0.4

Source: POINT, Barclays Capital

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 21

Figure 14 shows a potential set of risk factors that capture the three characteristics

discussed above. Programs identified as having different pre-payment characteristics are

the conventional (Fannie Mae) 30-year bonds (the base case used for the analysis), the 15-

year conventional (Fannie Mae) bonds, as well as the Ginnie Mae 30- and 15-year bonds.

The age of bonds is captured by factors distinguishing between new and aged deals. Finally,

each bond is also classified by the price of the security – discount, current or premium. In

this example there are no seasoned discounted bonds, given the current unprecedented

level of mortgage rates. In terms of risk exposures, the figure shows that we are currently

underweighting 15-year conventional bonds, and overweighting 30-year Ginnie Mae bonds.

 Interaction between Sources of Risk

So far we analyzed the major sources of spread risk: credit and prepayment. To do this, we

conveniently used two asset classes – credit and agency RMBS, respectively – where one

can argue that these sources of risk appear relatively isolated. However, recent

developments have made very clear that these sources of risk appear simultaneously in

other major asset classes, including non-agency RMBS, home equity loans and CMBS22.

When designing a risk model for a particular asset class, one should be able to anticipate

the nature of the risks the asset class exhibits currently or may encounter in the future. The

design and ability to segregate between these two kinds of risk depends also on the

richness of the bond indicatives and analytics available to the researcher. For this last point,

it is imperative that the researcher understands well the pricing model and assumptions

made to generate the analytics typically used as inputs in a risk model. This allows the user

to fully understand the output of the model, as well as its applicability and shortcomings.

 Other Sources of Risk

There are other sources of systematic risk that may be important sources of risk for

particular portfolios. Specific risk models can be designed to address them. We now

mention some of them briefly.

Implied Volatility Risk: Many fixed income securities have embedded options (eg, callable

bonds). This means that the expected future volatility (implied volatility23) of the interest

rate or other discount curves used to price the security plays a role in the value of that

option. If expected volatility increases, options generally become more expensive affecting

the prices of bonds with embedded options. For example, callable bonds will become

cheaper with increasing implied volatility because the bond holder is short optionality (the

right of the issuer to call the bond). Therefore, the exposure of the portfolio to the implied

volatility of the yield curve is also a source of risk that should be accounted for. The

sensitivity of securities to changes of implied volatilities is measured by vega, which is

calculated using the security pricing model. Implied volatility factors can be either calculated

by the market prices of liquid fixed-income options (caps, floors and swaptions), or implied

by the returns of bonds with embedded options within each asset class.

Liquidity Risk: Many fixed income securities are traded over-the-counter, in decentralized

markets. Some trade infrequently, making them illiquid. It is therefore hard to establish their

fair price, These bonds are exposed to liquidity risk. The holder of illiquid bonds would have

to pay a higher price to liquidate its position, usually meaning selling at a discount. This

discount is uncertain and varies across the business cycle. For instance, the discount can be

significant in a liquidity crisis, such as the one of 2008. The uncertainty about this discount

22 For more discussion, please refer to Gabudean (2009).

23 The volatility is called implied because it is calculated from the market prices of liquid options with the help of an

option-pricing model.

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 22

means that, everything equal, a more illiquid bond will be riskier. This extra risk can be

captured through liquidity risk factors. For instance, in the Treasury markets, one generally

refers to the difference in volatility between an on-the-run and an off-the-run Treasury

bond as liquidity risk.

Inflation risk: Inflation-linked securities are priced based on the expectation of future inflation.

Uncertainty about this variable adds to the volatility of the bond over and above the volatility

from other sources of risk, such as the nominal interest rates. Expected inflation is not an

observed variable in the marketplace but can be extracted from the prices on inflation-linked

government bonds and inflation swaps. Expected inflation risk factors can be constructed by

summarizing this information. The sensitivity of securities to expected inflation is calculated

using a specialized pricing model and is usually called inflation duration.

Tax-Policy Risk: Many municipal securities are currently tax-exempt. This results in added

benefit to their holders. This benefit – incorporated in the price of the security – depends on

the level of exemption allowed. Uncertainty regarding tax policy – tax-policy risk – adds to

the risk of these securities. Once again, tax-policy risk factors cannot be observed in the

marketplace and must be extracted from the prices of municipal securities. The return of

municipal securities in excess of interest rates is driven partially by tax-policy expectations

changes. However, it is also driven by changes in the creditworthiness of the municipal

issuers as well as other factors. In this case it is difficult to separate tax-policy risk factors

from other factors driving municipal bond spreads. Therefore, instead of specific tax-policy

factors we usually extract factors representing the overall spread risk of municipal

securities. This exercise is performed in a similar way to the credit risk model, where

securities are partitioned into groups of “similar” risk by geography, bond-type (general

obligation vs. revenue), tax-status, etc24.

Issue-Level Reports

The previous analysis focused on the systematic sources of risk. We now turn our attention

to the idiosyncratic or security-specific risk embedded in our portfolio. This risk measures

the volatility the portfolio has as a result of news specific to the individual issues/issuers it

holds. Therefore, the idiosyncratic risk is independent across issuers and diversifies away as

the number of issues in the portfolio increases: negative news about some issuers is

canceled by positive news about others. For relatively small portfolios, the idiosyncratic risk

may be a substantial component of the total risk. This can be seen in our example, as our

portfolio has only 27 issuers. Figure 6 shows that the idiosyncratic volatility of our portfolio

is 11.1bp/month, almost twice the idiosyncratic volatility of the benchmark (5.6bp/month).

When looking at the tracking error volatility net of benchmark, Figure 7 shows that our

specific risk is 10.1 bp/month and larger than the systematic component (9.3 bp/month).

This means that, typically, a major component of the monthly net return is driven by events

affecting only individual issues or issuers. Therefore, monitoring these individual exposures

is of paramount importance.

The idiosyncratic risk of each bond is a function of two variables: its net market weight and

its idiosyncratic volatility. This last parameter depends on the nature of the bond issuer. For

instance, a bond from a distressed firm has much higher idiosyncratic volatility than one

from a government-related agency.

Figure 15 provides a summary of the idiosyncratic risk for the top ten positions by market

weight in our portfolio. Unsurprisingly, our top seven holdings are Treasuries and MBS

24 For more discussion, please refer to Staal (2009).

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 23

securities, in line with the constitution of the index we are using as benchmark. Moreover,

these positions have significant market weights, given that our portfolio contains only 50

securities. Although we see large concentrations, the idiosyncratic TEV for the top holdings

is small, as they are not exposed to significant name risk. The last column of the table

shows that from this group the largest idiosyncratic risk comes from two corporate bonds

(issued by Comcast Cable Communication “CMCSA” and Merrill Lynch “BAC”). This is not

surprising, as these are the type of securities with larger event risk. Even within corporates,

idiosyncratic risk can be quite diverse, depending on the industry, duration and level of

distress of the issuer (usually proxied by rating, in our model by the spread of the bond). For

instance, the net positions of the CMCSA and BAC bonds are similar (2.2% and 2.1%,

respectively), but even though the maturity of the BAC bond is significantly shorter, its

spread is higher, delivering a higher idiosyncratic risk (2.9 versus 2.4bp/month). The fact

that BAC is a firm from an industry (Financials) that experienced significant volatility in the

recent past also contributes to higher idiosyncratic volatility. To manage the idiosyncratic

risk in the portfolio one should pay particular attention to mismatches between the portfolio

and benchmark for bonds with large spreads or long durations. These would tend to affect

disproportionably the idiosyncratic risk of the portfolio.

Figure 15: Issue-Specific Risk

Market Weight (%)

Identifier Ticker Description Maturity Spread (bp) Portfolio Net

Idiosyncratic

TEV

912828KF US/T US TREASURY NOTES 2/28/2014 4 5.4 5.2 0.4

912828KJ US/T US TREASURY NOTES 3/31/2014 3 5.0 4.8 0.4

912828JW US/T US TREASURY NOTES 12/31/2013 1 4.7 4.5 0.4

912828KN US/T US TREASURY NOTES 4/30/2014 2 3.8 3.6 0.3

FNA04409 FNMA FNMA Conventional Long T. 30yr 3/1/2039 20 3.2 1.1 0.4

FGB04409 FHLMC FHLM Gold Guar Single F. 30yr 3/1/2039 25 2.7 1.1 0.4

912810FT US/T US TREASURY BONDS 2/15/2036 -1 2.3 2.1 0.7

20029PAG CMCSA COMCAST CABLE COMMUNICATION 5/1/2017 222 2.2 2.2 2.4

59018YSU BAC MERRILL LYNCH & CO. 2/3/2014 300 2.1 2.1 2.9

912828KV US/T US TREASURY NOTES 5/31/2014 1 2.1 1.9 0.2

Source: POINT, Barclays Capital

Although important, the information in Figure 15 is not enough to assess fully the

idiosyncratic risk embedded in the portfolio. For instance, a portfolio manager could buy

credit protection on CMCSA through a credit default swap (CDS), thereby significantly

reducing the net exposure to this issuer’s bond. The position reported in this exhibit would

still look significant because the CDS protection would not be reflected in it.

A better way is to look at idiosyncratic risk at the issuer rather than at the issue level.

Although idiosyncratic risk is usually independent across issuers, one should not assume that

the idiosyncratic risk of securities of the same issuer is uncorrelated because they are all

subject to the same company-specific events. A good risk model should account for such

correlation and try to quantify it for different issuer and security types. For example, all types

of securities (bonds, equities, convertibles, etc) of an issuer in financial distress tend to move

in a correlated fashion because they all represent claims to the same distressed assets.

Adding more securities from such an issuer to a portfolio does not generally deliver

additional diversification. On the other hand, securities from issuers in strong financial health

can move quite differently from each other, driven mainly by liquidity or capital structure

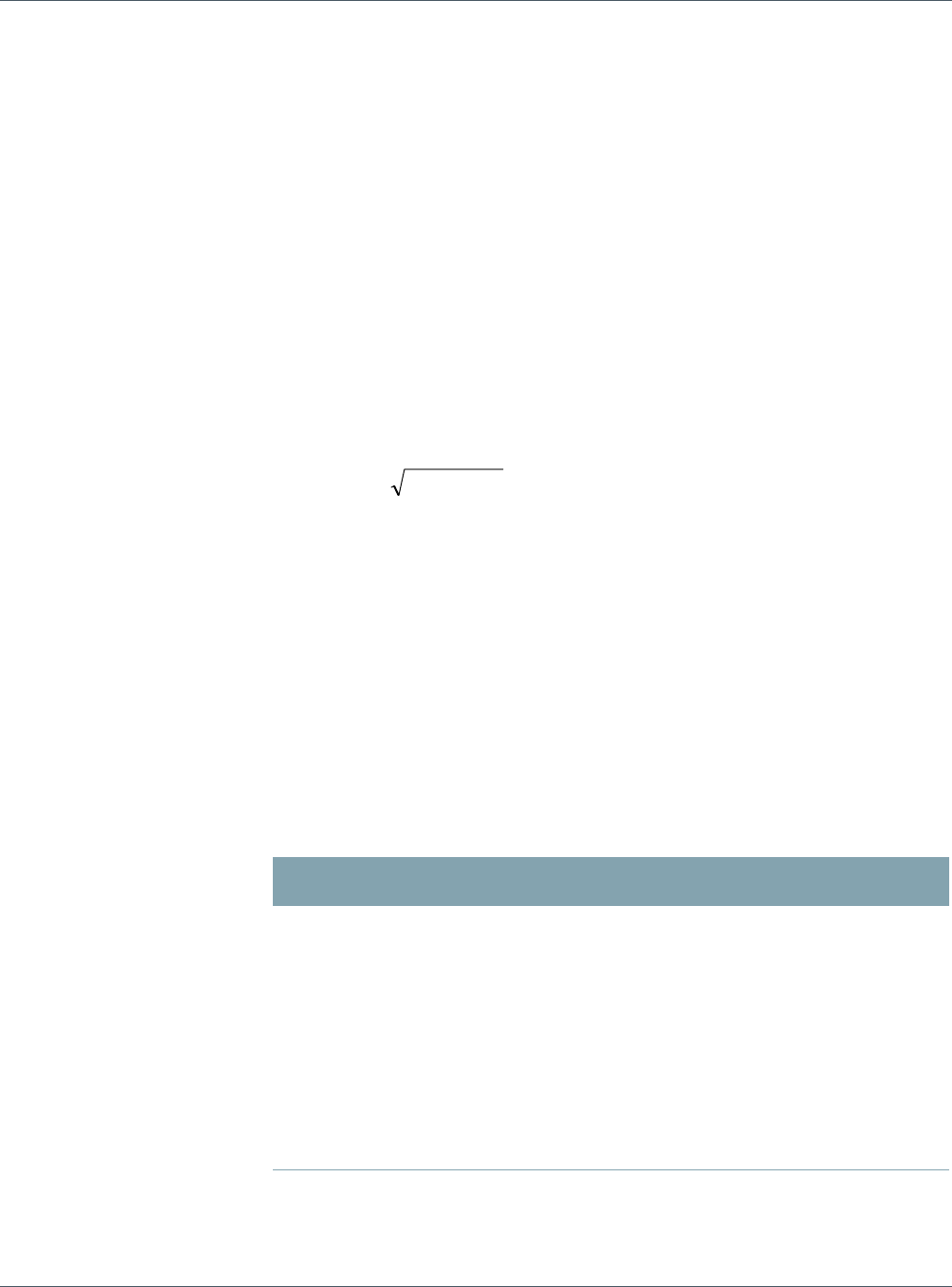
Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 24

effects rather than credit. In this case, a portfolio manager can achieve some diversification

of idiosyncratic risk (although limited) even when adding issues from that same issuer into

the portfolio.

To help us understand the net effect of all these points, it is useful to look at the

idiosyncratic risk at the issuer level. When aggregating risk from the issue (as shown in

Figure 15) to the issuer level, the correlations referred to above should be fully taken into

account. Figure 16 shows the results of this exercise, for the ten issuers in our portfolio with

the highest idiosyncratic TEV. Our riskiest exposure comes from Johnson & Johnson (“JNJ”),

with 3.7bp/month of issuer risk. We can also observe that idiosyncratic TEV is not

monotonic in the NMW: we have JNJ and President & Fellows of Harvard (“HARVRD”) with

the same NMW, but the former is significantly more risky (3.7 versus 2.0bp/month). It is

possible to have important issuer risk even for names we do not have in our portfolio, if they

have significant market weight in the benchmark.

Finally, note that because the idiosyncratic risk across issuers is independent, we can easily

calculate the cumulative risk of several issuers. For example, the total idiosyncratic risk of

the first two issuers is given by:

6.48.27.3 22 =+=

+DJNJ

idio

TEV

As is the case w ith most portfolios tracking a benchmark, most issuers present in the portfolio

are overweighted relative to the benchmark. This is a natural consequence of the fact that, in

practice, portfolios hold far fewer positions than the benchmark. It may be difficult for the

manager to hold positive views on all issuers selected in the portfolio. In fact, some of these

positions may be selected to build exposure to specific systematic factors, eg, a particular

industry or asset class, and not to a particular issuer. However, it is important that the

manager hold positive views for the issuers with the largest contribution to idiosyncratic risk. If

this is not the case, the manager is assuming a significant unintended name risk that should

be promptly taken out of the portfolio, in favor of another issuer with similar characteristics on

which the manager does have a positive view. This interactive exercise can easily be

performed with a flexible portfolio construction tool and the help of an optimizer.

Figure 16: Issuer Specific Risk

Ticker Name Sector NMW

(%) Idiosyncratic

TEV

JNJ JOHNSON & JOHNSON PHARMACEUTICALS 2.0 3.7

D DOMINION RESOURCES INC ELECTRIC 1.8 2.8

CMCSA COMCAST CABLE COMMUNICATION MEDIA_CABLE 2.0 2.1

BBT BB&T CORPORATION BANKING 2.0 2.1

HARVRD PRES&FELLOWS OF HARVARD INDUSTRIAL_OTHER 2.0 2.0

AXP AMERICAN EXPRESS CREDIT BANKING 1.7 1.8

MS MORGAN STANLEY DEAN WITTER BANKING 1.3 1.7

C CITIGROUP INC BANKING 1.5 1.7

BAC MERRILL LYNCH & CO. BANKING 1.6 1.6

RBS CHARTER ONE BANK FSB BANKING 1.6 1.4

Source: POINT, Barclays Capital

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 25

Scenario Analysis Report

Scenario analysis provides additional perspective on the portfolio’s risk. This exercise can be

performed in several ways. For instance, a manager may want to re-price the whole

portfolio under a particular scenario on risk factors, such as interest rates or spreads, and

look at the hypothetical return under that scenario. Alternatively, a portfolio manager may

wish to evaluate how the portfolio would have performed under particular historical

scenarios (eg, the 1987 equity crash or the 1997 Asian crisis). One problem with this

approach is the fact that, given the dynamic nature of the securities, the current portfolio

with its current characteristics did not exist during such historical episodes. Some of the

portfolio securities may have not even been issued during such periods. A solution might be

to price the current securities with the market variables at the time. While a valid solution, it

is difficult to implement because pricing models require inputs possibly not available during

that period.

An alternative is to represent the current portfolio as the set of loadings to all systematic

risk factors in a linear factor risk model. We can then multiply these loadings by the

historical realizations of the risk factors. The result is a set of historical simulated systematic

returns. Figure 17 presents these returns for our portfolio for five years finishing in June

2010. The dark line represents the portfolio returns and the lighter line represents the

portfolio’s return net of the benchmark. Note that this analysis uses only one set of static

portfolio loadings. Therefore, these simulated returns can be interpreted as the hypothetical

returns a portfolio with these characteristics would have, if submitted to the historical

episodes. As expected, the largest volatility came with the crisis of 2008, when the portfolio

registered returns between -200 and +300bp. The largest underperformance against the

benchmark appeared in September 2008, followed by the largest outperformance two

months after, both at about 20bp.

Figure 17: Historical Systematic Simulated Returns (basis points)

-300

-200

-100

0

100

200

300

400

Jul-05 Jan-06 Jul-06 Jan-07 Jul-07 Jan-08 Jul-08 Jan-09 Jul-09 Jan-10

-20

-15

-10

-5

0

5

10

15

20

25

Portoflio Return Net Return (right axis)

Source POINT, Barclays Capital

This analysis has some limitations, especially for the portfolio under consideration, where

idiosyncratic exposure is a major source of risk. This kind of risk is always very hard to pin

down and obviously less relevant from an historical perspective, as the issuers in our current

portfolio may not have witnessed any particular major idiosyncratic event in the past.

However, these and other kinds of historical scenario analysis are very important, as they

give us some indication of the magnitude of historical returns our portfolio might have

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 26

encountered. They are usually the starting point for any scenario analysis. The manager

should always complement them with other non-historical scenarios relevant for the

particular portfolio under analysis. In particular, the risk model can be used to express such

scenarios, as discussed in the following section.

Applications of Risk Modeling

In this section we illustrate several risk model applications typically used for portfolio

management. All applications make use of the fact that the risk model translates into a

common, comparable set of numbers the imbalances the portfolio may have across many

different dimensions. In some of applications – risk budgeting and portfolio rebalancing – an

optimizer that uses the risk model as an input is the optimal setting to perform the exercise.

Portfolio Construction and Risk Budgeting

Portfolio managers can be divided broadly into indexers (those who measure their returns

relative to a benchmark index) and absolute return managers (typically hedge fund

managers). In between stand the enhanced indexers that we introduced previously in this

report. All are typically subject to a risk budget that prescribes how much risk they are

allowed to take to achieve their objectives: minimize transaction costs and match the index

returns for the pure indexers, maximize the net return for the enhanced indexers, or

maximize absolute returns for absolute return managers. In any of these cases, the manager

has to merge all her views and constraints into a final portfolio. When constructing the

portfolio, how can she manage the competing views, while respecting the risk budget? How

can the views be combined to minimize the risk? What trade-offs can be made? Many

different techniques can be used to structure portfolios in accordance to the manager

views. In particular, risk models are widely used to perform this exercise. They perform this

task in a simple and objective manner: they can measure how risky each view is and how

correlated they are. The manager can then compare the risk with the expected return of

each of the views and decide on the optimal allocation across her views.

An example of a portfolio construction exercise using the risk model is the one we performed

to construct the portfolio analyzed in the previous section25. Figure 18 shows the exact

problem we asked the optimizer to solve. We start the problem by defining an initial portfolio

(empty in our case) and a tradable universe – the set of securities we allow the optimizer to

buy or sell from. In our case, this is the Barclays Capital US Aggregate index with issues

having at least $300mn of amount outstanding (first panel in the figure). The selection of this

universe allows us to avoid having small issues in our portfolio, potentially increasing its

liquidity. Pertaining to the risk model use, the second panel on the figure shows that the

objective function used in the problem is to minimize Total TEV. This means we are giving

leeway to the risk model to choose a portfolio from the tradable universe that minimizes the

risk relative to the benchmark, in our case the Barclays Capital US Aggregate index. The third

panel shows additional generic constraints we impose: we want a $100mn final portfolio

with a maximum number of 50 securities. The fourth panel shows how we force the

optimizer to tilt our portfolio to respect the portfolio manager’s views: long duration against

the benchmark between 0.25 and 0.30 year and spreads 100-150bp higher than the

benchmark. The last panel imposes a maximum under/overweight of 2% per issuer, to

25 The example is constructed using the POINT® Optimizer. For more details, please refer to Kumar (2010).

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 27

ensure proper diversification26. The characteristics of the portfolio resulting from this

optimization problem were extensively analyzed in the previous section.

Figure 18: Portfolio Construction Optimization Set-up

Source: POINT, Barclays Capital

26 Another way to ensure diversification would be to include the minimization of the idiosyncratic TEV as a specific

goal in the objective function.

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 28

Portfolio Rebalancing

Most managers rebalance their portfolios at regular intervals to reflect changing views and

market circumstances. For instance, as time goes by, the characteristics of the portfolio may

drift away from targeted levels. This may be due to the aging of its holdings, market moves,

or issuer-specific events such as downgrades or defaults. The periodic re-alignment of a

portfolio to its investment guidelines is called portfolio rebalancing. Similar needs arise in

many different contexts: when managers receive extra cash to invest, get small changes to

their mandates, want to tilt positions towards their views, etc. Similar to portfolio

construction, a risk model is very useful in the rebalancing exercise. During rebalancing, the

portfolio manager typically seeks to sell bonds currently held and replace them with others

having properties more consistent with the overall portfolio goals. Such buy-and-sell

transactions are costly and their cost must be weighted against the benefit from moving the

portfolio closer to its desired profile. A risk model can tell the managers how much risk

reduction (or increase) a particular set of transactions can achieve so that they can evaluate

the risk adjustment benefits relative to the transaction cost.

As an example, suppose a portfolio manager wants to tone down her heavy overweight on

banking. She wants to cap that overweight at 5% and to do it with no more than 10 trades.

Each trade should be larger than $1mn. Finally, assume she wants no change to the market

value of the final portfolio. We can use a setup similar to that of Figure 18, but adjusting some

of the constraints. Figure 19 shows the third and fourth panel from Figure 18, changed to

allow for the new constraints. Specifically, in the first panel we allow for 10 trades (with a

minimum of $1mn); in the second we include the extra constraint for the banking industry.

Figure 19: Portfolio Rebalancing Optimization Set-up

Source: POINT, Barclays Capital

Figure 20 shows the trading list suggested by the optimizer. Not surprisingly, the biggest

sells are of financial companies. To replace them, the optimizer – using the risk model –

recommends more holdings of Treasury and corporate bonds (we need these last to keep

the net yield of the portfolio high). Remember that we concluded that our financial holdings

were highly correlated with Treasuries, so the proposed swap is not surprising.

Interestingly, the extra constraint imposed on the optimization problem did not materially

change the portfolio’s risk. In fact, risk decreased to about 13bp/month. This is because of

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 29

the extra three positions added to the portfolio, which now has 53 securities. The extra

securities allowed the portfolio to reduce its systematic and idiosyncratic risk.

Figure 20: Proposed Trading List

BUYS

Identifier Description Position Amount Market Value

912828KV US TREASURY NOTES 967,403 1,000,000

126650BK CVS CORP-GLOBAL 1,696,069 1,518,408

98385XAJ XTO ENERGY INC 2,097,746 2,508,567

FNA05009 FNMA Conventional Long T. 30yr 2,547,359 2,708,258

912828KF US TREASURY NOTES 3,786,070 3,882,263

Total 11,617,497

SELLS

Identifier Description Position Amount Market Value

16132NAV CHARTER ONE BANK FSB -3,229,847 -3,370,981

05531FAF BB&T CORPORATION -2,425,413 -2,499,505

0258M0BZ AMERICAN EXPRESS CREDIT -2,021,013 -2,208,231

3133XN4B FEDERAL HOME LOAN BANK -1,818,417 -2,085,812

740816AB PRES&FELLOWS OF HARVARD -1,281,616 -1,452,968

Total -11,617,497

Source: POINT, Barclays Capital

Scenario Analysis

Scenario analysis is a popular tool for risk management and portfolio construction. In this

section, we illustrate a way to construct scenarios based on factor models. In this context,

users express views on the returns of particular financial variables, indices, securities or risk

factors and the scenario analysis tool (using the risk model) calculates their effect on the

portfolio’s (net) return.

Typically in this kind of scenario analysis, views are only partial. This means one can have

specific views on how particular macro variables, asset classes, or risk factors will behave, but it

is unlikely to have views on all risk factors the portfolio under analysis is exposed to. This is

when risk models may be useful. At the heart of the linear factor models described in this paper

is a set of risk factors and the covariance matrix between them. Under certain statistical

assumptions, the covariance matrix can be used to “complete” specific partial views or

scenarios and deliver a complete picture of the effect of the scenario in the return of the

portfolio. Mechanically, what happens is the following: first, the manager translates the views

into realizations of a subset of risk factors. Then the scenario is completed – using the risk

model covariance matrix - to get the realizations of all risk factors. Finally, the portfolio’s (net)

loadings to all risk factors are used to get its (net) return under that scenario (by multiplying the

loadings by the factor realizations under the scenario). This construction implies a set of

assumptions that should be carefully understood. For instance, it is assumed that the manager

can represent or translate views as risk factor returns. So a view about the unemployment rate,

which is typically not used as a risk factor27, cannot be used in this context. Also, to “complete”

the scenario, we generally assume a stationary and normal multivariate distribution between all

factors. These assumptions make this analysis less appropriate when looking at extreme events

or regime shifts, for instance. However, it can be very useful in many other circumstances.

27 Unemployment rate is not used as a factor in most short- and medium-term risk models.

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 30

As an example, consider using the scenario analysis to compute the model-implied scenario

durations of the portfolio already analyzed in detail. To do this, we express our views as

changes in the curve factors. In our risk model, these are represented by the six key-rate

factors shown in Figure 10. In particular, to calculate the model-implied empirical duration,

we assume that all six decrease by 25bp/month, broadly in line with our managers’ views.

Figure 21 shows that under this scenario, the portfolio returns 99bp, against 93bp for the

benchmark. As expected given the longer duration, the portfolio outperformed the

benchmark. Because of the other exposures present in the portfolio and benchmark and

their average negative correlation with the curve factors (eg, spreads), the duration implied

by the scenario for our portfolio is only 3.96 (= 99 / 25), against the analytical 4.55

(Figure 2). The scenario shows a similar decrease in the benchmark’s duration.

Figure 21: Scenario Analysis: Analytical and Model-Implied Durations

Durations

Universe Return under

scenario (bp) Scenario (Model-Implied) Analytical

Portfolio 99 3.96 4.55

Benchmark 93 3.72 4.30

Source: POINT, Barclays Capital

Another characteristic imposed while constructing the portfolio was a targeted higher

spread. As Figure 2 shows, this resulted in an OAS for the portfolio of 157bp, against the

57bp of the benchmark. It would be interesting to evaluate the impact on the portfolio (net)

return of a credit spread contraction of 10%. The portfolio is long spread duration (net OASD

= 0.11, see Figure 2), so we may expect our portfolio to outperform in this scenario. To

evaluate this episode, we analyze the results under two spread contraction scenarios:

imposing no change in the yield curve (that is, an unchanged yield curve is part of the view)

or allowing this change to be “completed” by the correlation matrix (that is, the change in

the yield curve is not part of the scenario, we have no views about it, but we allow it to

change in a way historically consistent with our spread view). Contrary to what one might

expect, Figure 22 shows that the effect in the net return is minimal in both scenarios – our

portfolio does not benefit from the spread contraction, when compared with the benchmark.

The higher spread duration delivers no return advantage under this scenario. This is due to

the many other exposures our portfolio has and that cannot be summarized by a small set of

portfolio level analytics. The figure also shows that the absolute returns are quite different

across the two scenarios. When one allows the rates to move in a correlated fashion with

spreads, the net return drops to zero: all positive return from the spread contraction is

cancelled by the probable increase in the level of the curve and our long duration exposure.

Figure 22: Scenario Analysis: Spread Contraction of 10%

Restriction on YC movement

Universe No movement Correlated

Portfolio 31 -3

Benchmark 32 0

Net -1 -3

Source: POINT, Barclays Capital

Barclays Capital | A Portfolio Manager’s Guide to Multi-Factor Fixed Income Risk Models and Their Applications

24 June 2011 31

These simple examples show how one can use reasonable scenarios to study the behavior of a

portfolio or benchmark in different environments. This type of factor-based scenario analysis

can significantly raise the intuition that a portfolio manager can gain from a risk model report.

Conclusion

Risk models describe the different imbalances of a portfolio using a common language. The

imbalances are combined into a consistent and coherent analysis reported by the risk

model. Risk models provide important insights regarding the different trade-offs existing in

the portfolio. They provide guidance regarding how to balance them.

Risk models in fixed income are unique in two ways: First, the existence of good pricing

models allows us to robustly calculate important analytics regarding the securities. These

analytics can be used confidently as inputs into a risk model. Second, returns are not

typically used directly to calibrate risk factors. Instead returns are first normalized into more

invariant series (eg, returns normalized by the duration of the bond).

The fundamental systematic risk of all fixed income securities is interest rate and term

structure risk. This is captured by factors representing risk-free rates and swap spreads of

various maturities. Excess (of interest rates) systematic risk is captured by factors specific to

each asset class. The most important components of such risk are credit risk and

prepayment risk. Other important potential risks are volatility, liquidity, inflation or tax-

policy. Idiosyncratic risk is diversified away in large portfolios and indices but can become a

very significant component of total risk in small portfolios. The correlation of idiosyncratic

risk of securities of the same issuer is non-zero and should be modeled carefully.

A good risk model provides detailed information about the exposures of a complex portfolio

and can be a valuable tool for portfolio construction and management. It can help

managers construct portfolios tracking a particular benchmark, express views subject to a

given risk budget, and rebalance a portfolio while avoiding excessive transaction costs.

Furthermore, by identifying the exposures where the portfolio has the highest risk sensitivity

it can help a portfolio manager reduce (or increase) risk in the most effective way. The

analysis can be significantly enhanced by using scenario analysis tools.

References

Ben Dor, A. Dynkin, L. Houweling, P. Hyman, J. Leeuwen, E. and Olaf Penninga, “A New

Measure of Spread Exposure in Credit Portfolios,” Barclays Capital, February 2010

Gabudean, R., “US Home Equity ABS Risk Model”, Barclays Capital, October 2009

Kumar, A. , “The POINT Optimizer”, Barclays Capital, June 2010

Lazanas, A. Silva, A. Staal, A. Cenk Ural, “Multi-Factor Equity Risk Models and Their

Applications”, in Equity Valuation and Portfolio Management, by Frank J. Fabozzi and Harry

M. Markowitz, John Wiley & Sons, 2011

Silva, A., “Emerging Markets Risk Model: G4-Denominated Fixed Income Securities”,

Barclays Capital, December 2009

Silva, A. (a), “A Note on the New Approach to Credit in the Barclays Capital Global Risk

Model”, Barclays Capital, September 2009

Silva, A. (b), “Risk Attribution with Custom-Defined Risk Factors,” Barclays Capital, August 2009

Staal, A., “US Municipal Bond Risk Model”, Barclays Capital, July 2009

Analyst Certification(s)

We, Anthony Lazanas, Antonio Silva, Radu Gabudean and Arne D. Staal, hereby certify (1) that the views expressed in this research report accurately

reflect our personal views about any or all of the subject securities or issuers referred to in this research report and (2) no part of our compensation

was, is or will be directly or indirectly related to the specific recommendations or views expressed in this research report.

Important Disclosures

For current important disclosures regarding companies that are the subject of this research report, please send a written request to: Barclays Capital

Research Compliance, 745 Seventh Avenue, 17th Floor, New York, NY 10019 or refer to https://ecommerce.barcap.com/research/cgi-

bin/all/disclosuresSearch.pl or call 212-526-1072.

Barclays Capital does and seeks to do business with companies covered in its research reports. As a result, investors should be aware that Barclays

Capital may have a conflict of interest that could affect the objectivity of this report. Any reference to Barclays Capital includes its affiliates. Barclays

Capital and/or an affiliate thereof (the "firm") regularly trades, generally deals as principal and generally provides liquidity (as market maker or

otherwise) in the debt securities that are the subject of this research report (and related derivatives thereof). The firm's proprietary trading accounts

may have either a long and / or short position in such securities and / or derivative instruments, which may pose a conflict with the interests of

investing customers. Where permitted and subject to appropriate information barrier restrictions, the firm's fixed income research analysts regularly

interact with its trading desk personnel to determine current prices of fixed income securities. The firm's fixed income research analyst(s) receive

compensation based on various factors including, but not limited to, the quality of their work, the overall performance of the firm (including the

profitability of the investment banking department), the profitability and revenues of the Fixed Income Division and the outstanding principal

amount and trading value of, the profitability of, and the potential interest of the firms investing clients in research with respect to, the asset class

covered by the analyst. To the extent that any historical pricing information was obtained from Barclays Capital trading desks, the firm makes no

representation that it is accurate or complete. All levels, prices and spreads are historical and do not represent current market levels, prices or

spreads, some or all of which may have changed since the publication of this document. Barclays Capital produces a variety of research products

including, but not limited to, fundamental analysis, equity-linked analysis, quantitative analysis, and trade ideas. Recommendations contained in one

type of research product may differ from recommendations contained in other types of research products, whether as a result of differing time

horizons, methodologies, or otherwise.

This publication has been prepared by Barclays Capital, the investment banking division of Barclays Bank PLC, and/or one or more of its affiliates as

provided below. It is provided to our clients for information purposes only, and Barclays Capital makes no express or implied warranties, and

expressly disclaims all warranties of merchantability or fitness for a particular purpose or use with respect to any data included in this publication.

Barclays Capital will not treat unauthorized recipients of this report as its clients. Prices shown are indicative and Barclays Capital is not offering to

buy or sell or soliciting offers to buy or sell any financial instrument.

Without limiting any of the foregoing and to the extent permitted by law, in no event shall Barclays Capital, nor any affiliate, nor any of their

respective officers, directors, partners, or employees have any liability for (a) any special, punitive, indirect, or consequential damages; or (b) any lost

profits, lost revenue, loss of anticipated savings or loss of opportunity or other financial loss, even if notified of the possibility of such damages,

arising from any use of this publication or its contents.

Other than disclosures relating to Barclays Capital, the information contained in this publication has been obtained from sources that Barclays

Capital believes to be reliable, but Barclays Capital does not represent or warrant that it is accurate or complete. The views in this publication are

those of Barclays Capital and are subject to change, and Barclays Capital has no obligation to update its opinions or the information in this

publication.

The analyst recommendations in this publication reflect solely and exclusively those of the author(s), and such opinions were prepared

independently of any other interests, including those of Barclays Capital and/or its affiliates. This publication does not constitute personal

investment advice or take into account the individual financial circumstances or objectives of the clients who receive it. The securities discussed

herein may not be suitable for all investors. Barclays Capital recommends that investors independently evaluate each issuer, security or instrument

discussed herein and consult any independent advisors they believe necessary. The value of and income from any investment may fluctuate from

day to day as a result of changes in relevant economic markets (including changes in market liquidity). The information herein is not intended to

predict actual results, which may differ substantially from those reflected. Past performance is not necessarily indicative of future results.

This communication is being made available in the UK and Europe primarily to persons who are investment professionals as that term is defined in

Article 19 of the Financial Services and Markets Act 2000 (Financial Promotion Order) 2005. It is directed at, and therefore should only be relied

upon by, persons who have professional experience in matters relating to investments. The investments to which it relates are available only to such

persons and will be entered into only with such persons. Barclays Capital is authorized and regulated by the Financial Services Authority ('FSA') and

member of the London Stock Exchange.

Barclays Capital Inc., U.S. registered broker/dealer and member of FINRA (www.finra.org), is distributing this material in the United States and, in

connection therewith accepts responsibility for its contents. Any U.S. person wishing to effect a transaction in any security discussed herein should

do so only by contacting a representative of Barclays Capital Inc. in the U.S. at 745 Seventh Avenue, New York, New York 10019.

Non-U.S. persons should contact and execute transactions through a Barclays Bank PLC branch or affiliate in their home jurisdiction unless local

regulations permit otherwise.

This material is distributed in Canada by Barclays Capital Canada Inc., a registered investment dealer and member of IIROC (www.iiroc.ca). Subject to

the conditions of this publication as set out above, Absa Capital, the Investment Banking Division of Absa Bank Limited, an authorised financial

services provider (Registration No.: 1986/004794/06), is distributing this material in South Africa. Absa Bank Limited is regulated by the South

African Reserve Bank. This publication is not, nor is it intended to be, advice as defined and/or contemplated in the (South African) Financial

Advisory and Intermediary Services Act, 37 of 2002, or any other financial, investment, trading, tax, legal, accounting, retirement, actuarial or other

professional advice or service whatsoever. Any South African person or entity wishing to effect a transaction in any security discussed herein should

do so only by contacting a representative of Absa Capital in South Africa, 15 Alice Lane, Sandton, Johannesburg, Gauteng 2196. Absa Capital is an

affiliate of Barclays Capital. In Japan, foreign exchange research reports are prepared and distributed by Barclays Bank PLC Tokyo Branch. Other

research reports are distributed to institutional investors in Japan by Barclays Capital Japan Limited. Barclays Capital Japan Limited is a joint-stock

company incorporated in Japan with registered office of 6-10-1 Roppongi, Minato-ku, Tokyo 106-6131, Japan. It is a subsidiary of Barclays Bank PLC

and a registered financial instruments firm regulated by the Financial Services Agency of Japan. Registered Number: Kanto Zaimukyokucho (kinsho)

No. 143. Barclays Bank PLC, Hong Kong Branch is distributing this material in Hong Kong as an authorised institution regulated by the Hong Kong

Monetary Authority. Registered Office: 41/F, Cheung Kong Center, 2 Queen's Road Central, Hong Kong. Barclays Bank PLC Frankfurt Branch

distributes this material in Germany under the supervision of Bundesanstalt für Finanzdienstleistungsaufsicht (BaFin). This material is distributed in

Malaysia by Barclays Capital Markets Malaysia Sdn Bhd. This material is distributed in Brazil by Banco Barclays S.A. This material is distributed in

Mexico by Barclays Bank Mexico, S.A. Barclays Bank PLC in the Dubai International Financial Centre (Registered No. 0060) is regulated by the Dubai

Financial Services Authority (DFSA). Barclays Bank PLC-DIFC Branch, may only undertake the financial services activities that fall within the scope of

its existing DFSA licence. Barclays Bank PLC in the UAE is regulated by the Central Bank of the UAE and is licensed to conduct business activities as a

branch of a commercial bank incorporated outside the UAE in Dubai (Licence No.: 13/1844/2008, Registered Office: Building No. 6, Burj Dubai

Business Hub, Sheikh Zayed Road, Dubai City) and Abu Dhabi (Licence No.: 13/952/2008, Registered Office: Al Jazira Towers, Hamdan Street, PO

Box 2734, Abu Dhabi). Barclays Bank PLC in the Qatar Financial Centre (Registered No. 00018) is authorised by the Qatar Financial Centre

Regulatory Authority (QFCRA). Barclays Bank PLC-QFC Branch may only undertake the regulated activities that fall within the scope of its existing

QFCRA licence. Principal place of business in Qatar: Qatar Financial Centre, Office 1002, 10th Floor, QFC Tower, Diplomatic Area, West Bay, PO Box

15891, Doha, Qatar. This material is distributed in Dubai, the UAE and Qatar by Barclays Bank PLC. Related financial products or services are only

available to Professional Clients as defined by the DFSA, and Business Customers as defined by the QFCRA. This material is distributed in Saudi

Arabia by Barclays Saudi Arabia ('BSA'). It is not the intention of the Publication to be used or deemed as recommendation, option or advice for any

action (s) that may take place in future. Barclays Saudi Arabia is a Closed Joint Stock Company, (CMA License No. 09141-37). Registered office Al

Faisaliah Tower | Level 18 | Riyadh 11311 | Kingdom of Saudi Arabia. Authorised and regulated by the Capital Market Authority, Commercial

Registration Number: 1010283024. This material is distributed in Russia by OOO Barclays Capital, affiliated company of Barclays Bank PLC,

registered and regulated in Russia by the FSFM. Broker License #177-11850-100000; Dealer License #177-11855-010000. Registered address in

Russia: 125047 Moscow, 1st Tverskaya-Yamskaya str. 21. This material is distributed in India by Barclays Bank PLC, India Branch. This material is

distributed in Singapore by the Singapore branch of Barclays Bank PLC, a bank licensed in Singapore by the Monetary Authority of Singapore. For

matters in connection with this report, recipients in Singapore may contact the Singapore branch of Barclays Bank PLC, whose registered address is

One Raffles Quay Level 28, South Tower, Singapore 048583. Barclays Bank PLC, Australia Branch (ARBN 062 449 585, AFSL 246617) is distributing

this material in Australia. It is directed at 'wholesale clients' as defined by Australian Corporations Act 2001.

IRS Circular 230 Prepared Materials Disclaimer: Barclays Capital and its affiliates do not provide tax advice and nothing contained herein should be

construed to be tax advice. Please be advised that any discussion of U.S. tax matters contained herein (including any attachments) (i) is not intended

or written to be used, and cannot be used, by you for the purpose of avoiding U.S. tax-related penalties; and (ii) was written to support the promotion

or marketing of the transactions or other matters addressed herein. Accordingly, you should seek advice based on your particular circumstances

from an independent tax advisor.

Barclays Capital is not responsible for, and makes no warranties whatsoever as to, the content of any third-party web site accessed via a hyperlink in

this publication and such information is not incorporated by reference.

© Copyright Barclays Bank PLC (2011). All rights reserved. No part of this publication may be reproduced in any manner without the prior written

permission of Barclays Capital or any of its affiliates. Barclays Bank PLC is registered in England No. 1026167. Registered office 1 Churchill Place,

London, E14 5HP. Additional information re

g

ardin

g

this

p

ublication will be furnished u

p

on re

q

uest.

US18761