14_Petrucci10e_CSM K 6.85 M All 1B CSM
User Manual: K 6.85 M
Open the PDF directly: View PDF ![]() .
.
Page Count: 486 [warning: Documents this large are best viewed by clicking the View PDF Link!]

611
CHAPTER 14
CHEMICAL KINETICS
PRACTICE EXAMPLES
1A (E) The rate of consumption for a reactant is expressed as the negative of the change in molarity
divided by the time interval. The rate of reaction is expressed as the rate of consumption of a
reactant or production of a product divided by its stoichiometric coefficient.
rate of consumption of A
51
A0.3187 M 0.3629 M 1min
= = = 8.93 10 M s
8.25 min 60 st
rate of reaction = rate of consumption of A2 = 51 51
8.93 10 M s 4.46 10 M s
2
1B (E) We use the rate of reaction of A to determine the rate of formation of B, noting from the
balanced equation that 3 moles of B form (+3 moles B) when 2 moles of A react (–2 moles A).
(Recall that “M” means “moles per liter.”)
41
0.5522M A 0.5684M A 3moles B
rateof B formation= 1.62 10 M s
60s 2moles A
2.50min 1min
2A (M)
(a) The 2400-s tangent line intersects the 1200-s vertical line at 0.75 M and reaches 0 M at
3500 s. The slope of that tangent line is thus
41
0 M 0.75 M
slope = = 3.3 10 M s = instantaneous rate
3500 s 1200 s
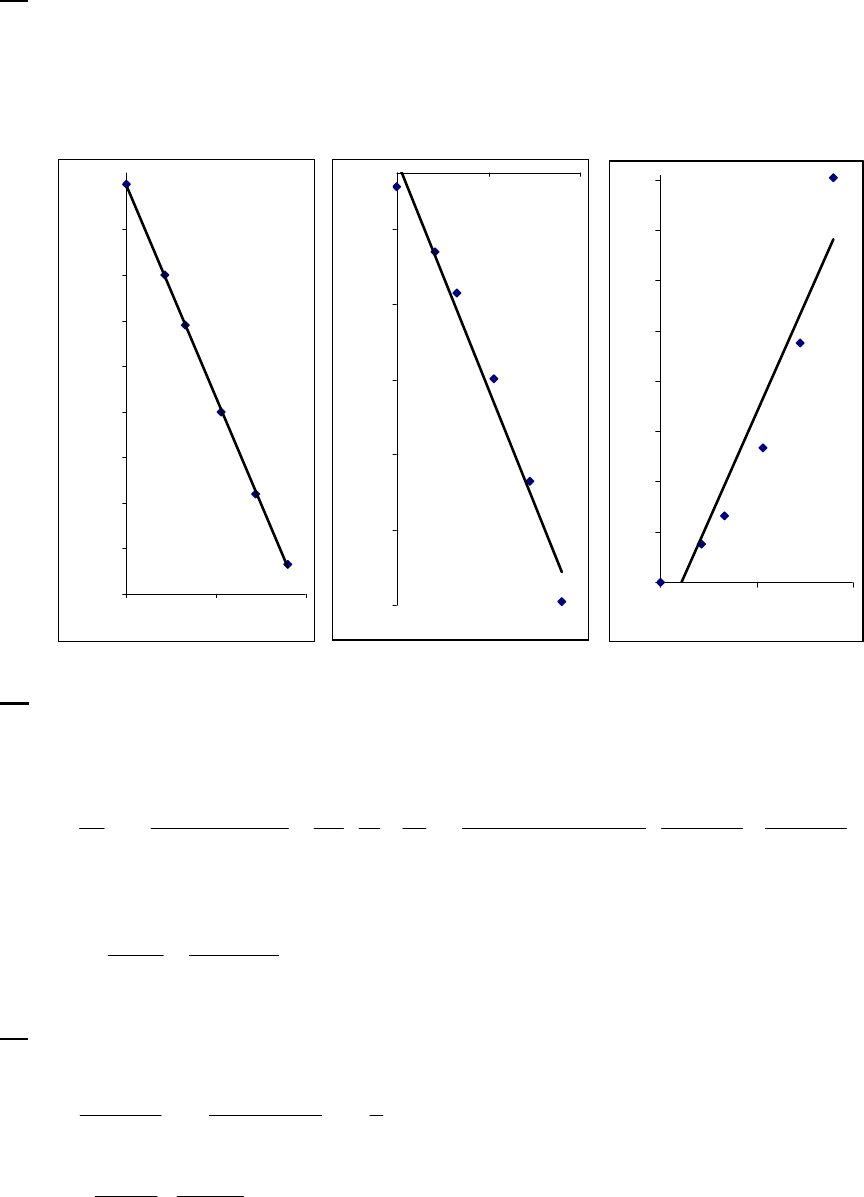
of reaction
The instantaneous rate of 41
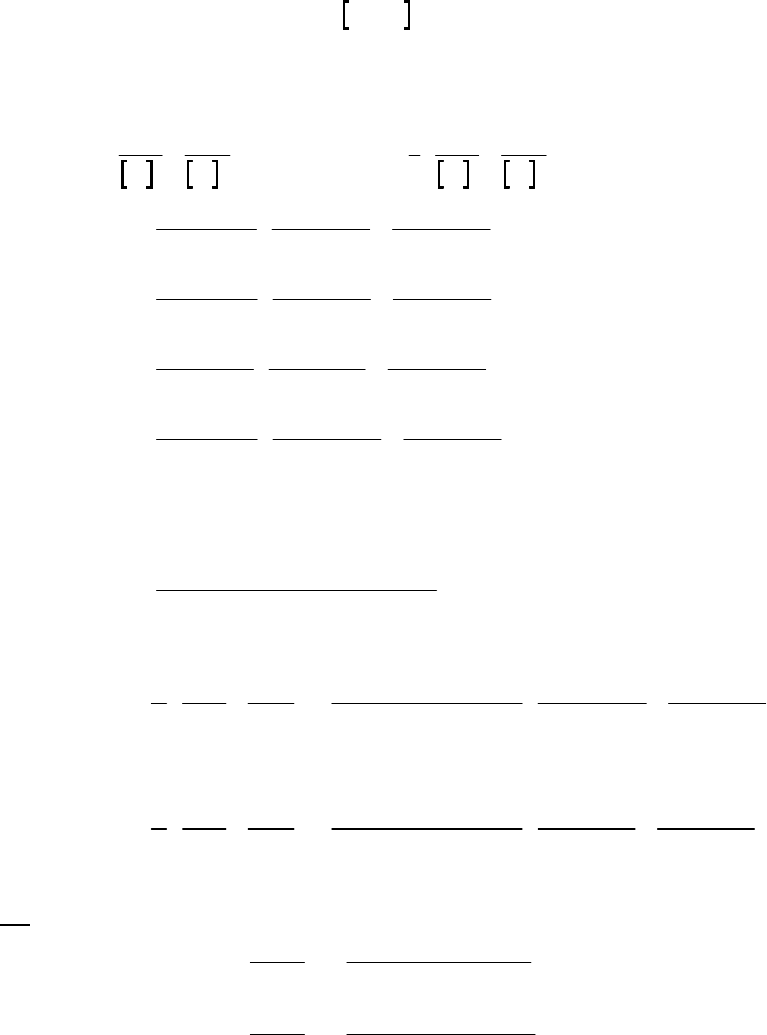
reaction = 3.3 10 M s
.
(b)
22 22
At 2400 s, H O = 0.39 M. At 2450 s, H O = 0.39 M + rate t
411
22 22
At 2450 s, H O = 0.39 M + 3.3 10 mol H O L s 50s
= 0.39 M 0.017 M = 0.37 M
2B (M) With only the data of Table 14.2 we can use only the reaction rate during the first 400 s,
41
22
H O / =15.0 10 M st
, and the initial concentration,
22
0
HO =2.32M.
We calculate the change in
22
HO and add it to
22
0
HO to determine
22
100
HO .
41
22 22
H O = rate of reaction of H O = 15.0 10 M s 100 s = 0.15 Mt
22 22 22
100 0
H O = H O + H O = 2.32 M + 0.15 M = 2.17 M
This value differs from the value of 2.15 M determined in text Example 14-2b because
the text used the initial rate of reaction
41
17.1 10 M s
, which is a bit faster than the average
rate over the first 400 seconds.
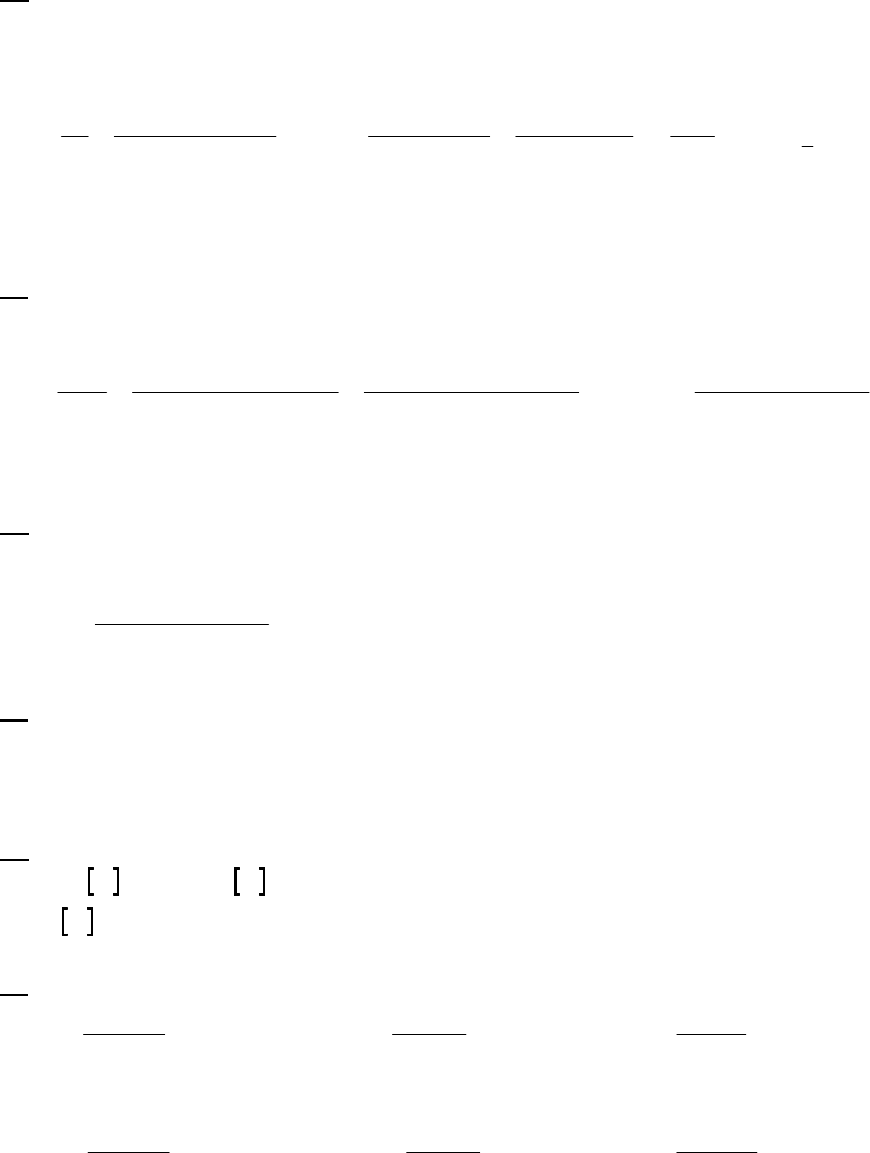
Chapter 14: Chemical Kinetics
612
3A (M) We write the equation for each rate, divide them into each other, and solve for n.
51
125
1
51
225
2
= N O = 5.45 10 M s = 3.15 M
= N O = 1.35 10 M s = 0.78 M
n
n
n
n
Rk k
Rk k
51 25
11
51
225
2
NO 3.15 M
5.45 10 M s 3.15
= = 4.04 = = = = 4.04
1.35 10 M s 0.78
0.78 MNO
nnnn
nn
kk
R
Rkk
We kept an extra significant figure (4) to emphasize that the value of n= 1. Thus, the reaction is
first-order in 25
N O .
3B (E) For the reaction, we know that
2
12
224
rate = HgCl C Ok
. Here we will compare Expt. 4 to
Expt. 1 to find the rate.
2
122
224
4 4
22
51
12
1224
HgCl C O 0.025 M 0.045 M
rate rate
= = = 0.0214 =
rate 1.8 10 Mmin
0.105 M 0.150 M
HgCl C O
k
k
The desired rate is 51 71
4
rate = 0.0214 1.8 10 M min = 3.9 10 M min
.
4A (E) We place the initial concentrations and the initial rates into the rate law and solve for
k
.
22
21
rate = A B = 4.78 10 M s = 1.12 M 0.87 Mkk
21 221
2
4.78 10 M s
==4.410 M s
1.12 M 0.87 M
k
4B (E) We know that 2
12
224
rate = HgCl C Ok
and
k
=7.6 1032 1
Mmin.
Thus, insertion of the starting concentrations and the k value into the rate law yields:
12
32 1 7 1
Rate = 7.6 10 M min 0.050 M 0.025 M = 2.4 10 M min
5A (E) Here we substitute directly into the integrated rate law equation.
ln A ln A s s ln
tkt= + = 3.02 10 325 + 2.80 = 0.982 +1.030 = 0.048
0
31
bg
A e M
t==1.0
0.048
5B (M) This time we substitute the provided values into text Equation 14.13.
22 41
22
0
HO 1.49 M 0.443
ln = = 600 s = ln = 0.443 = = 7.38 10 s
H O 2.32 M 600 s
tkt k k
22 22
0
Now we choose H O =1.49 M, H O = 0.62, =1800 s 600 s =1200 s
tt
22 41
22
0
HO 0.62 M 0.88
ln = = 1200 s = ln = 0.88 = = 7.3 10 s
H O 1.49 M 1200 s
tkt k k
These two values agree within the limits of the experimental error and thus, the reaction is first-
order in [H2O2].
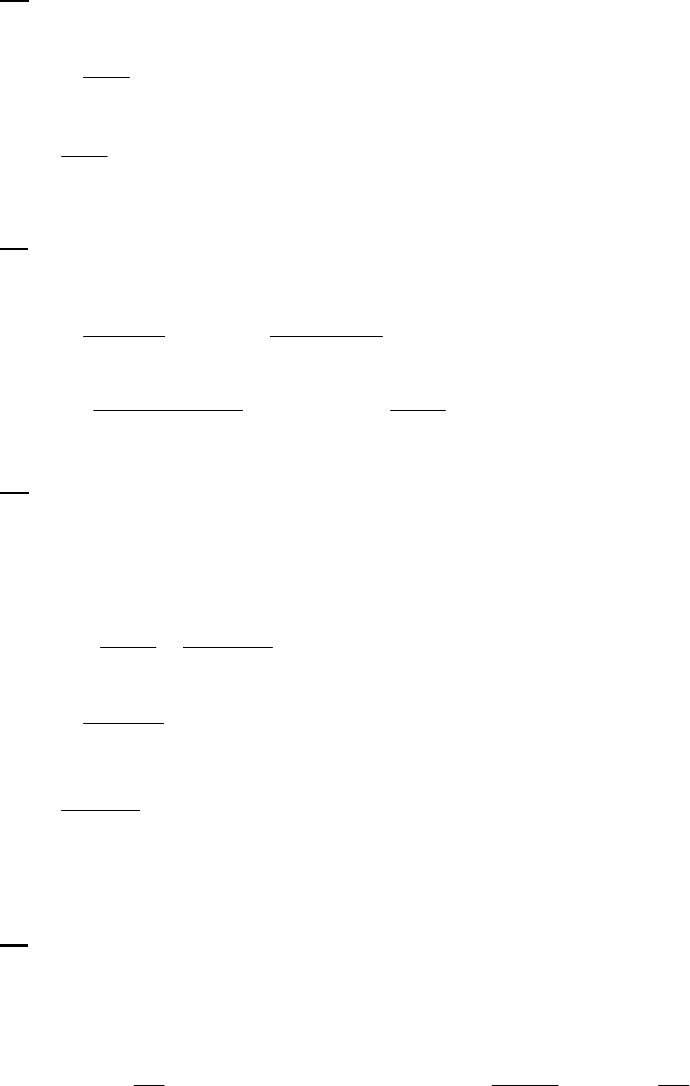
Chapter 14: Chemical Kinetics
613
6A (M) We can use the integrated rate equation to find the ratio of the final and initial
concentrations. This ratio equals the fraction of the initial concentration that remains at time t.
31
0
0.443
0
0
A
ln = = 2.95 10 s 150 s = 0.443
A
A= = 0.642; 64.2% of A remains.
A
t
t
kt
e
6B (M) After two-thirds of the sample has decomposed, one-third of the sample remains.
Thus 22 22
0
HO = HO 3
t
, and we have
22 22 41
0
22 22
00
3
41
HO HO 3
ln = = ln = ln 1/ 3 = 1.099 = 7.30 10 s
HO HO
1.099 1 min
= =1.51 10 s = 25.1 min
7.30 10 s 60 s
tkt t
t
7A (M) At the end of one half-life the pressure of DTBP will have been halved, to 400 mmHg. At the
end of another half-life, at 160 min, the pressure of DTBP will have halved again, to 200 mmHg.
Thus, the pressure of DTBP at 125 min will be intermediate between the pressure at
80.0 min (400 mmHg) and that at 160 min (200 mmHg). To obtain an exact answer, first we
determine the value of the rate constant from the half-life.
1
1/2
DTBP 1
DTBP 0
0.693 0.693
= = = 0.00866 min
80.0 min
ln = = 0.00866 min 125 min = 1.08
t
kt
Pkt
P
DTBP 1.08
DTBP 0
DTBP DTBP 0
= = 0.340
= 0.340 = 0.340 800 mmHg = 272 mmHg
t
t
Pe
P
PP
7B (M)
(a)
We use partial pressures in place of concentrations in the integrated first-order rate
equation. Notice first that more than 30 half-lives have elapsed, and thus the ethylene oxide
pressure has declined to at most 0.5 = 9 10
30 10
bg of its initial value.
4 1 22.1 10
30 30
0 0
3600 s
ln = = 2.05 10 s 30.0 h = 22.1 = = 2.4 10
1 h
PP
kt e
PP
10 10 7
30 0
= 2.4 10 = 2.4 10 782 mmHg = 1.9 10 mmHgPP

Chapter 14: Chemical Kinetics
614
(b) P
ethylene oxide initially 782 mmHg 1.9 107 mmHg (~ 0). Essentially all of the ethylene
oxide is converted to CH4 and CO. Since pressure is proportional to moles, the final
pressure will be twice the initial pressure (1 mole gas 2 moles gas;
782 mmHg 1564 mmHg). The final pressure will be 1.56 103 mmHg.
8A (D) We first begin by looking for a constant rate, indicative of a zero-order reaction. If the rate is
constant, the concentration will decrease by the same quantity during the same time period. If we
choose a 25-s time period, we note that the concentration decreases
0.88 M 0.74 M = 0.14 M
during the first 25 s,
0.74 M 0.62 M = 0.12 Mduring the second 25 s,
0.62 M 0.52 M = 0.10 Mduring the third 25 s, and
0.52 M 0.44 M = 0.08 M during the
fourth 25-s period. This is hardly a constant rate and we thus conclude that the reaction is not
zero-order.
We next look for a constant half-life, indicative of a first-order reaction. The initial concentration
of 0.88 M decreases to one half of that value, 0.44 M, during the first 100 s, indicating a 100-s
half-life. The concentration halves again to 0.22 M in the second 100 s, another 100-s half-life.
Finally, we note that the concentration halves also from 0.62 M at 50 s to 0.31 M at 150 s, yet
another 100-s half-life. The rate is established as first-order. The rate constant is
kt
=0.693 =0.693
100 =6.93 10
1/2
31
s s
.
That the reaction is first-order is made apparent by the fact that the ln[B] vs time plot is a straight
line with slope = -k (k = 6.85 103 s1).
Plot of [B]
versus Time
0.15
0.25
0.35
0.45
0.55
0.65
0.75
0.85
0 100 200 300
Time(s)
[B] (M)
Plot of ln([B]) versus
Time
-2
-1.8
-1.6
-1.4
-1.2
-1
-0.8
-0.6
-0.4
-0.2
0
0 200 400
Time(s)
ln([B])
Plot of 1/[B] versus
Time
1
2
3
4
5
6
7
0 100 200 300
Time (s)
1/[B] (M
-1
)
Chapter 14: Chemical Kinetics
615
8B (D) We plot the data in three ways to determine the order. (1) A plot of [A] vs. time is linear if
the reaction is zero-order. (2) A plot of ln [A] vs. time will be linear if the reaction is first-order.
(3) A plot of 1/[A] vs. time will be linear if the reaction is second-order. It is obvious from the
plots below that the reaction is zero-order. The negative of the slope of the line equals
3
= 0.083 M 0.250 M 18.00 min = 9.28 10 M/mink
(k = 9.30 103 M/min using a
graphical approach).
9A (M) First we compute the value of the rate constant at 75.0 C with the Arrhenius equation. We
know that the activation energy is Ea=1.06 10
5
J/mol, and that
k
=3.46 1051
s at 298 K.
The temperature of o
75.0 C = 348.2 K.
ln ln s
J/mol
J mol K K K
k
k
kE
RT T
a2
1
2
51 12
5
11
=3.46 10 =11
=1.06 10
8.3145
1
298.2
1
348.2 = 6.14
F
H
GI
K
J
F
H
GI
K
J
51 +6.14 51 2 1
2= 3.46 10 s = 3.46 10 s 4.6 10 = 0.016 ske
1/2 1
0.693 0.693
= = = 43 s at 75 C
0.016 s
tk
9B (M) We use the integrated rate equation to determine the rate constant, realizing that one-third
remains when two-thirds have decomposed.
25 25
0
25 25
00
NO NO 3 1
ln = ln = ln = = 1.50 h = 1.099
NO NO 3
tkt k
41
1.099 1 h
= = 2.03 10 s
1.50 h 3600 s
k
Plot of [A]
versus Time
y = -0.00930x + 0.2494
0.07
0.09
0.11
0.13
0.15
0.17
0.19
0.21
0.23
0.25
01020
Time (min)
[A] (M)
Plot of ln([A])
versus Time
-2.5
-2.3
-2.1
-1.9
-1.7
-1.5
01020
Time (min)
ln([A])
Plot of 1/[A]
versus Time
4
5
6
7
8
9
10
11
12
01020
Time (min)
1/[A] (M
-1
)

Chapter 14: Chemical Kinetics
616
Now use the Arrhenius equation to determine the temperature at which the rate constant is 2.04
104 s1.
ln ln s
s
J/mol
J mol K K
k
k
E
RT T T
a2
1
41
51 12
5
11 2
=2.04 10
3.46 10 =1.77= 11
=1.06 10
8.3145
1
298
1
F
H
GI
K
J
F
H
GI
K
J
1=1
298
1.77 8.3145
1.06 10 = 3.22 10 = 311
2
1
5
31 2
TT
K
K K K
10A (M) The two steps of the mechanism must add, in a Hess's law fashion, to produce the overall
reaction.
22 22
Overall reaction: CO + NO CO + NO or CO + NO CO + NO
322223
Second step: NO + CO NO + CO or + NO + CO NO + CO
First step: 2 +
23
NO NO NO
If the first step is the slow step, then it will be the rate-determining step, and the rate of that step
will be the rate of the reaction, namely, rate of
2
12
reaction = NOk.
10B (M)
(1) The steps of the mechanism must add, in a Hess's law fashion, to produce the overall reaction.
This is done below. The two intermediates, NO F g
22
bgand F(g), are each produced in one step
and consumed in the next one.
Fast:
22 22
NO g + F g NO F g
Slow: NO F g NO F g F g
22 2 +
bgbgbg
Fast: F g NO g NO F g
bgbgbg
+22
Net: 2 + 2
22 2
NO g F g NO F g
bgbgbg
(2) The proposed mechanism must agree with the rate law. We expect the rate-determining step
to determine the reaction rate:
322
Rate = NO Fk. To eliminate NO F
22, we recognize that
the first elementary reaction is very fast and will have the same rate forward as
reverse:
122222
=NOF=NOF=
f
r
R
kkR. We solve for the concentration of
intermediate:
22 1 2 2 2
NO F = NO F /kk
. We now substitute this expression for NO F
22
into the rate equation:
13 2 2 2
Rate = / NO Fkk k . Thus the predicted rate law agrees with
the experimental rate law.
Chapter 14: Chemical Kinetics
617
INTEGRATIVE EXAMPLE
A. (M)
(a) The time required for the fixed (c) process of souring is three times as long at 3 °C refrigerator
temperature (276 K) as at 20 °C room temperature (293 K).
4
aa a
21
12 12
11 4
a41 41
/ 64 h 1 1 1 1
ln ln ln 1.10 ( 2.10 10 )
/ 3 64 h 293 K 276 K
1.10 1.10 8.3145 J mol K 4.4 10 J/mol 44 kJ/mol
2.10 10 K 2.10 10 K
EE E
ct t
ct t R T T R R
R
E
(b) Use the Ea determined in part (a) to calculate the souring time at 40 °C = 313 K.
4
a
1 1
11
212
1.15
11
1 1 4.4 10 J/mol 1 1
ln 1.15 ln
8.3145 J mol K 313 K 293 K 64 h
0.317 0.317 64 h 20. h
64 h
E
tt
tRTT
tet
B. (M) The species A* is a reactive intermediate. Let’s deal with this species by using a steady state
approximation.
d[A*]/dt = 0 = k1[A]2 – k-1[A*][A] – k2[A*]. Solve for [A*]. k-1[A*][A] + k2[A*] = k1[A]2
2
1
-1 2
k[A]
[A*] = k[A] k The rate of reaction is: Rate = k2[A*] =
2
21
-1 2
kk[A]
k[A] k
At low pressures ([A] ~ 0 and hence k2 >> k-1[A]), the denominator becomes ~ k2 and the rate law is
22
21 1
2
kk[A]
Rate = = k [A]
k Second-order with respect to [A]
At high pressures ([A] is large and k-1[A] >> K2), the denominator becomes ~ k-1[A] and the rate law
is
2
21 21
-1 -1
kk[A] kk[A]
Rate = =
k[A] k First-order with respect to [A]
EXERCISES
Rates of Reactions
1. (M) 2A + B C + 3D [A]
t
= 6.2 104 M s1
(a) Rate = 1[A]
2t
= 1/2(6.2 104 M s1) = 3.1 104 Ms1
(b) Rate of disappearance of B = 1[A]
2t
= 1/2(6.2 104 M s1) = 3.1 104 Ms1
(c) Rate of appearance of D = 3[A]
2t
= 3(6.2 104 M s1) = 9.3 104 Ms1
Chapter 14: Chemical Kinetics
618
2. (M) In each case, we draw the tangent line to the plotted curve.
(a) The slope of the line is
22 41
HO 1.7 M 0.6 M
==9.210 M s
400 s 1600 st
22 41
HO
reaction rate = = 9.2 10 M s
t
(b) Read the value where the horizontal line [H2O2] = 0.50 M intersects the curve,
2150 s or 36 minutes
3. (E)
31
A0.474 M 0.485 M
Rate = = =1.0 10 M s
82.4 s 71.5 st
4. (M)
(a)
Rate A M M
min min Mmin==
0.1498 0.1565
1.00 0.00 = 0.0067 1
t
Rate A M M
min min Mmin==
0.1433 0.1498
2.00 1.00 = 0.0065 1
t
(b) The rates are not equal because, in all except zero-order reactions, the rate depends on the
concentration of reactant. And, of course, as the reaction proceeds, reactant is consumed
and its concentration decreases, so the rate of the reaction decreases.
5. (M)
(a) AA A M M M= + = 0.588 0.013 = 0.575
i
(b)
A M M M= 0.565 0.588 = 0.023
2
0.023 M
= A = =1.0 min
A 2.2 10 M/min
time = + = 4.40 +1.0 min = 5.4 min
t
t
tt
6. (M)
Initial concentrations are HgCl2= 0.105 M and CO
24
2= 0.300
M.
The initial rate of the reaction is7.1 10 51
M min . Recall that the reaction is:
2
224 2 22
2 HgCl (aq) + C O (aq) 2 Cl (aq) + 2 CO (g) + Hg Cl (aq)
.
The rate of reaction equals the rate of disappearance ofC O4
2
2
. Then, after 1 hour, assuming that
the rate is the same as the initial rate,
(a)
2
524 2
22
24
mol C O 2 mol HgCl 60min
HgCl = 0.105 M 7.1 10 1 h 0.096 M
L s 1 h
1 mol C O
(b) CO M mol
Lmin h min
h M
4
2
25
= 0.300 7.1 10 1 60
1= 0.296
F
H
G
I
K
J

Chapter 14: Chemical Kinetics
619
7. (M)
(a)
51
51 5
AC
Rate = = = 1.76 10 M s
2
C= 2 1.76 10 M s = 3.52 10 M/s
tt
t
(b)
AC M s Assume this rate is constant
tt
=2= 1.76 10 .
51
51 60 s
A = 0.3580 M + 1.76 10 M s 1.00min = 0.357 M
1min
(c)
51
2
55
A=1.7610 M s
A0.3500 M 0.3580 M
= = = 4.5 10 s
1.76 10 M/s 1.76 10 M/s
t
t
8. (M)
(a)
4
24
22 2 2
22
O5.7 10 mol H O 1 mol O
=1.00 L soln = 2.9 10 mol O /s
1 L soln s 2 mol H O
n
t
(b)
n
t
O mol O
s
s
min mol O min
24222
= 2.9 10 60
1= 1.7 10 /
(c)
V
t
O mol O
min
mL O at STP
mol O
mL O at STP
min
2222
2
22
= 1.7 10 22,414
1=3.8 10
9. (M) Notice that, for every 1000 mmHg drop in the pressure of A(g), there will be a corresponding
2000 mmHg rise in the pressure of B(g) plus a 1000 mmHg rise in the pressure of C(g).
(a) We set up the calculation with three lines of information below the balanced equation: (1)
the initial conditions, (2) the changes that occur, which are related to each other by reaction
stoichiometry, and (3) the final conditions, which simply are initial conditions + changes.
A(g) 2B(g) + C(g)
Initial 1000. mmHg 0. mmHg 0. mmHg
Changes –1000. mmHg +2000. mmHg +1000. mmHg
Final 0. mmHg 2000. MmHg 1000. mmHg
Total final pressure mmH
g
mmH
g
mmH
g
mmH
g
= 0. + 2000. +1000. = 3000.
(b) A(g) 2B(g) + C(g)
Initial 1000. mmHg 0. mmHg 0. mmHg
Changes –200. mmHg +400. mmHg +200. mmHg
Final 800 mmHg 400. mmHg 200. mmHg
Total pressure mmH
g
mmH
g
mmH
g
mmH
g
= 800. +400. +200. =1400.

Chapter 14: Chemical Kinetics
620
10. (M)
(a) We will use the ideal gas law to determine N O
25
pressure
25
25
1molNO L atm
1.00 g× ×0.08206 × 273 + 65 K
108.0g mol K
nRT 760 mmHg
P{N O } = = × = 13 mmHg
V 15 L 1 atm
(b) After 2.38 min, one half-life passes. The initial pressure of NO
25
decreases by half to 6.5
mmHg.
(c) From the balanced chemical equation, the reaction of 2 mol N O g
25
bg produces 4 mol
NO g
2bg and 1 molO g
2bg. That is, the consumption of 2 mol of reactant gas produces 5
mol of product gas. When measured at the same temperature and confined to the same
volume, pressures will behave as amounts: the reaction of 2 mmHg of reactant produces 5
mmHg of product.
total 2 5 2 5
(product)
initially) reactant) (reactant)
(reactant)
(( 5 mmHg
= 13 mmHg N O 6.5 mmHg N O + 6.5 mmHg 2 mmHg
P
(13 6.5 16) mmHg 23 mmHg
Method of Initial Rates
11. (M)
(a) From Expt. 1 to Expt. 3, [A] is doubled, while [B] remains fixed. This causes the rate to
increases by a factor of 6.75 10
3.35 10 =2.01 2
41
41
M s
M s .
Thus, the reaction is first-order with respect to A.
From Expt. 1 to Expt. 2, [B] doubles, while [A] remains fixed. This causes the rate to
increases by a factor of 1.35 10
3.35 10 =4.03 4
31
41
M s
M s .
Thus, the reaction is second-order with respect to B.
(b) Overall reaction order order with respect to A order with respect to B = 1 2 = 3. The
reaction is third-order overall.
(c) Rate M s M M= 3.35 10 = 0.185 0.133
41 2
kbgbg
k=3.35 10
0.185 0.133 = 0.102
41
2
21
M s
M M M s
bgbg
12. (M) From Expt. 1 and Expt. 2 we see that [B] remains fixed while [A] triples. As a result, the
initial rate increases from 4.2 10 3
M/min to 1.3 10 2
M/min, that is, the initial reaction rate
triples. Therefore, the reaction is first-order in [A]. Between Expt. 2 and Expt. 3, we see that [A]
doubles, which would double the rate, and [B] doubles. As a consequence, the initial rate goes
from 1.3 10 2
M/min to 5.2 10 2
M/min, that is, the rate quadruples. Since an additional
doubling of the rate is due to the change in [B], the reaction is first-order in [B]. Now we
determine the value of the rate constant.
Chapter 14: Chemical Kinetics
621
Rate A B Rate
AB
Mmin
M M L mol min===
5.2 10 /
3.00 3.00 =5.8 10
11 2311
kk
The rate law is Rate L mol min A B=5.8 10
311
11
ch
.
13. (M) From Experiment 1 to 2, [NO] remains constant while [Cl2] is doubled. At the same time the
initial rate of reaction is found to double. Thus, the reaction is first-order with respect to [Cl2],
since dividing reaction 2 by reaction 1 gives 2 = 2x when x = 1. From Experiment 1 to 3, [Cl2]
remains constant, while [NO] is doubled, resulting in a quadrupling of the initial rate of reaction.
Thus, the reaction must be second-order in [NO], since dividing reaction 3 by reaction 1 gives
4 = 2x when x = 2. Overall the reaction is third-order: Rate = k [NO]2[Cl2]. The rate constant
may be calculated from any one of the experiments. Using data from Exp. 1,
k = 51
22
2
Rate 2.27 10 M s
=
[NO] [Cl ] (0.0125 M) (0.0255M)
= 5.70 M2 s1
14. (M)
(a) From Expt. 1 to Expt. 2, [B] remains constant at 1.40 M and [C] remains constant at
1.00 M, but [A] is halved
0.50
bg. At the same time the rate is halved 0.50
bg. Thus, the
reaction is first-order with respect to A, since 0.50 = 0.50
x when
x
=1.
From Expt. 2 to Expt. 3, [A] remains constant at 0.70 M and [C] remains constant at
1.00 M, but [B] is halved
0.50
bg, from 1.40 M to 0.70 M. At the same time, the rate is
quartered 0.25
bg. Thus, the reaction is second-order with respect to B, since 0.50 = 0.25
y
when
y
=2.
From Expt. 1 to Expt. 4, [A] remains constant at 1.40 M and [B] remains constant at
1.40 M, but [C] is halved
0.50, from 1.00 M to 0.50 M. At the same time, the rate is
increased by a factor of 2.0.
43 22 11
11
Rate =16 Rate =16 Rate = 4 Rate = 4 Rate = 2 Rate .
42
Thus, the order of the reaction with respect to C is
1, since 0.5 = 2.0
z when z=1
.
(b)
12 1
12 1
5
1+2 1 2
12 1
12 1
11 1 1
111
22 2 4
1.40 M 1.40 M 1.00 M
rate = 0.70 M 0.70 M 0.50 M = 222
11
1.40 M 1.40 M 1.00 M = rate = rate = rate
22
kk
k
This is based on
12 1
1
rate = 1.40 M 1.40 M 1.00 Mk

Chapter 14: Chemical Kinetics
622
First-Order Reactions
15. (E)
(a) TRUE The rate of the reaction does decrease as more and more of B and C are formed,
but not because more and more of B and C are formed. Rather, the rate decreases
because the concentration of A must decrease to form more and more of B and
C.
(b) FALSE The time required for one half of substance A to react—the half-life—is
independent of the quantity of A present.
16. (E)
(a) FALSE For first-order reactions, a plot of ln [A] or log [A] vs. time yields a straight line.
A graph of [A] vs. time yields a curved line.
(b) TRUE The rate of formation of C is related to the rate of disappearance of A by the
stoichiometry of the reaction.
17. (M)
(a) Since the half-life is 180 s, after 900 s five half-lives have elapsed, and the original quantity
of A has been cut in half five times.
final quantity of A initial=0.5
5
bg quantity of
A
initial= 0.03125
quantity of A
About 3.13% of the original quantity of A remains unreacted after 900 s.
or
More generally, we would calculate the value of the rate constant, k, using
1
1/2
ln 2 0.693
= = = 0.00385 s
180 s
kt
Now ln(% unreacted) = -kt = -0.00385 s-1×(900s) = -
3.465
(% unreacted) = 0.0313 × 100% = 3.13% of the original quantity.
(b) Rate A s M M / s= = 0.00385 0.50 = 0.00193
1
k
18. (M)
(a)
The reaction is first-order, thus
1
0
A0.100 M 2.08
ln = = ln = 54min( ) = = 0.0385 min
A 0.800 M 54 min
tkt k k
We may now determine the time required to achieve a concentration of 0.025 M
1
1
0
A0.025 M 3.47
ln = = ln = 0.0385 min ( ) = = 90. min
A 0.800 M 0.0385 min
tkt t t
(b) Since we know the rate constant for this reaction (see above),
114
Rate = A = 0.0385 min 0.025 M = 9.6 10k
M/min
Chapter 14: Chemical Kinetics
623
19. (M)
(a) The mass of A has decreased to one fourth of its original value, from 1.60 g to
0.40 g. Since 1
4=1
2
1
2
, we see that two half-lives have elapsed.
Thus, 2 = 38
1/2
tmin, or t1/2 =19 min.
(b)
11
1/2
0
A
0.693
= 0.693/ = = 0.036min ln = = 0.036 min 60min = 2.2
19min A
t
kt kt
2.2
0
0
A= e = 0.11 or A = A = 1.60 g A 0.11= 0.18 g A
A
kt
t
te
20. (M)
(a)
1
0
A0.632 M 0.256
ln = = ln = 0.256 = = 0.0160 min
A 0.816 M 16.0 min
tkt k
(b) 1/2 1
0.693 0.693
= = = 43.3 min
0.0160 min
tk
(c) We need to solve the integrated rate equation to find the elapsed time.
1
0
A0.235 M
ln = = ln = 1.245 = 0.0160min
A0.816 M
tkt t
1
1.245
= = 77.8min
0.0160min
t
(d) ln A
A0
=kt becomes
0
A=
A
kt
e
which in turn becomes
1
0
60min
A = A = 0.816 M exp 0.0160min 2.5 h = 0.816 0.0907 = 0.074 M
1 h
kt
e
21. (M) We determine the value of the first-order rate constant and from that we can calculate the
half-life. If the reactant is 99% decomposed in 137 min, then only 1% (0.010) of the initial
concentration remains.
1
0
A0.010 4.61
ln = = ln = 4.61 = 137min = = 0.0336 min
A 1.000 137 min
tkt k k
tk
1/2 1
=0.0693 =0.693
0.0336 = 20.6
min min
Chapter 14: Chemical Kinetics
624
22. (E) If 99% of the radioactivity of 32 P is lost, 1% (0.010) of that radioactivity remains. First we
compute the value of the rate constant from the half-life. kt
=0.693 =0.693
14.3 = 0.0485
1/2
1
d d
Then we use the integrated rate equation to determine the elapsed time.
ln A
Aln A
A d
ln days
tt
kt t k
00
1
==
1=1
0.0485
0.010
1.000 =95
23. (D)
(a) 0
0
35 [A]
100
ln [A]
= ln(0.35) = kt = (4.81 103 min1)t t = 218 min.
Note: We did not need to know the initial concentration of acetoacetic acid to answer the
question.
(b) Let’s assume that the reaction takes place in a 1.00L container.
10.0 g acetoacetic acid 1 mol acetoacetic acid
102.090 g acetoacetic acid = 0.09795 mol acetoacetic acid.
After 575 min. (~ 4 half lives, hence, we expect ~ 6.25% remains as a rough
approximation), use integrated form of the rate law to find [A]t = 575 min.
0
[A]
ln [A]
t
= kt = (4.81 103 min1)(575 min) = 2.766
0
[A]
[A]
t= e2.766 = 0.06293 (~ 6.3% remains) [A]
0.09795moles
t= 0.063 [A]t = 6.2 103
moles.
[A]reacted = [A]o [A]t = (0.098 6.2 103) moles = 0.092 moles acetoacetic acid. The
stoichiometry is such that for every mole of acetoacetic acid consumed, one mole of CO2
forms. Hence, we need to determine the volume of 0.0918 moles CO2 at 24.5 C (297.65
K) and 748 torr (0.984 atm) by using the Ideal Gas law.
V =
Latm
0.0918mol 0.08206 297.65K
Kmol
=0.984atm
nRT
P
= 2.3 L CO2
24. (M)
(a)
41
0
3
41
A2.5 g
ln = = ln = 3.47 = 6.2 10 s
A 80.0 g
3.47
= = 5.6 10 s 93 min
6.2 10 s
tkt t
t
We substituted masses for concentrations, because the same substance (with the same
molar mass) is present initially at time ,t and because it is a closed system.
Chapter 14: Chemical Kinetics
625
(b) amount O g N O mol N O
g N O
mol O
mol N O mol O
22525
25
2
25
2
= 77.5 1
108.0
1
2= 0.359
2
2
Latm
0.359 mol O 0.08206 (45 273) K
mol K 9.56 L O
1atm
745 mmHg 760 mmHg
nRT
VP
25. (D)
(a) If the reaction is first-order, we will obtain the same value of the rate constant from several
sets of data.
31
0
A0.497 M 0.188
ln = = ln = 100 s = 0.188, = =1.88 10 s
A 0.600 M 100 s
tkt k k
31
0
A0.344 M 0.556
ln = = ln = 300 s = 0.556, = =1.85 10 s
A 0.600 M 300 s
tkt k k
31
0
A0.285 M 0.744
ln = = ln = 400 s = 0.744, = =1.86 10 s
A 0.600 M 400 s
tkt k k
31
0
A0.198 M 1.109
ln = = ln = 600 s = 1.109, = =1.85 10 s
A 0.600 M 600 s
tkt k k
31
0
A0.094 M 1.854
ln = = ln = 1000 s = 1.854, = =1.85 10 s
A 0.600 M 1000 s
tkt k k
The virtual constancy of the rate constant throughout the time of the reaction confirms that
the reaction is first-order.
(b) For this part, we assume that the rate constant equals the average of the values obtained in
part (a).
k=1.88 +1.85+1.86 +1.85
410 = 1.86 10
31 31
s s
(c) We use the integrated first-order rate equation:
31
750 0
1.40
750
A = A exp = 0.600 M exp 1.86 10 s 750 s
A = 0.600 M e = 0.148 M
kt
26. (D)
(a)
If the reaction is first-order, we will obtain the same value of the rate constant from several
sets of data.
0
264 mmHg
ln = = ln = 390 s = 0.167
312 mmHg
t
Pkt k
P
, k=0.167
390 =4.28 1041
s s
0
224 mmHg
ln = = ln = 777 s = 0.331
312 mmHg
t
Pkt k
P, k=0.331
777 =4.26 1041
s s
0
187 mmHg
ln = = ln = 1195 s = 0.512
312 mmHg
t
Pkt k
P, k=0.512
1195 =4.28 1041
s s

Chapter 14: Chemical Kinetics
626
0
78.5 mmHg
ln = = ln = 3155 s = 1.38
312 mmHg
t
Pkt k
P, 41
1.38
= = 4.37 10 s
3155 s
k
The virtual constancy of the rate constant confirms that the reaction is first-order.
(b) For this part we assume the rate constant is the average of the values in part
(a):4.3 10 41
s.
(c) At 390 s, the pressure of dimethyl ether has dropped to 264 mmHg. Thus, an amount of
dimethyl ether equivalent to a pressure of 312 264 = mmHg mmHg
bg 48 mmHg has
decomposed. For each 1 mmHg pressure of dimethyl ether that decomposes, 3 mmHg of
pressure from the products is produced. Thus, the increase in the pressure of the products is
348=144 mmHg. The total pressure at this point is 264 +144 = 408mmH
g
mmH
g
mmHg. Below, this calculation is done in a more systematic fashion:
CH O g
32
bgbg CH g
4bg + H g
2bg + CO g
bg
Initial 312 mmHg 0 mmHg 0 mmHg 0 mmHg
Changes – 48 mmHg + 48 mmHg + 48 mmHg + 48 mmHg
Final 264 mmHg 48 mmHg 48 mmHg 48 mmHg
PP P P P
total DME methane hydrogen CO
+
mmHg 48 mmHg 48 mmHg 48 mmHg 408 mmHg
=+ +
264
(d) This question is solved in the same manner as part (c). The results are summarized below.
CH O g CH g H g CO g
Initial 312 mmHg 0 mmHg 0 mmHg 0 mmHg
Changes mmHg mmHg mmHg + 312 mmHg
Final mmHg mmHg mmHg mmHg
+
mmHg mmHg mmHg mmHg mmHg
total DME methane hydrogen CO
3242
+
312 312 312
0 312 312 312
=+ +
0 312 312 312 936
b g bg bg bg bg
PP P P P
(e) We first determine PDME at 1000 s. ln s s
P
Pkt
1000
0
41
= = 4.3 10 1000 = 0.43
0.43
1000 1000
0
= = 0.65 = 312 mmHg 0.65 = 203 mmHg
PeP
P
Then we use the same approach as was used for parts (c) and (d)
342
2
total DME methane hydrogen CO
CH O g CH g + H g + CO g
Initial 312 mmHg 0 mmHg 0 mmHg 0 mmHg
Changes 109 mmHg 109 mmHg 109 mmHg 109 mmHg
Final 203 mmHg 109 mmHg 109 mmHg 109 mmHg
=+ + +
= 203 mmHg +109 mmHg +109 mmH
PPP P P
g +109 mmHg = 530. mmHg

Chapter 14: Chemical Kinetics
627
Reactions of Various Orders
27. (M)
(a) Set II is data from a zero-order reaction. We know this because the rate of set II is constant.
0.25 M/25 s M s= 0.010 1. Zero-order reactions have constant rates of reaction.
(b) A first-order reaction has a constant half-life. In set I, the first half-life is slightly less than
75 sec, since the concentration decreases by slightly more than half (from 1.00 M to 0.47 M)
in 75 s. Again, from 75 s to 150 s the concentration decreases from 0.47 M to 0.22 M, again
by slightly more than half, in a time of 75 s. Finally, two half-lives should see the
concentration decrease to one-fourth of its initial value. This, in fact, is what we see. From
100 s to 250 s, 150 s of elapsed time, the concentration decreases from 0.37 M to 0.08 M,
i.e., to slightly less than one-fourth of its initial value. Notice that we cannot make the same
statement of constancy of half-life for set III. The first half-life is 100 s, but it takes more
than 150 s (from 100 s to 250 s) for [A] to again decrease by half.
(c) For a second-order reaction,1/ 1/ =
0
AA
tkt
. For the initial 100 s in set III, we have
111
11
=1.0 L mol = 100 s, = 0.010 L mol s
0.50 M 1.00 M kk
For the initial 200 s, we have
111
11
= 2.0 L mol = 200 s, = 0.010 L mol s
0.33 M 1.00 M kk
Since we obtain the same value of the rate constant using the equation for second-order
kinetics, set III must be second-order.
28. (E) For a zero-order reaction (set II), the slope equals the rate constant:
= A / = 1.00 M/100 s = 0.0100 M/skt
29. (M) Set I is the data for a first-order reaction; we can analyze those items of data to determine the
half-life. In the first 75 s, the concentration decreases by a bit more than half. This implies a half-
life slightly less than 75 s, perhaps 70 s. This is consistent with the other time periods noted in the
answer to Review Question 18 (b) and also to the fact that in the 150-s interval from 50 s to 200 s,
the concentration decreases from 0.61 M to 0.14 M, which is a bit more than a factor-of-four
decrease. The factor-of-four decrease, to one-fourth of the initial value, is what we would expect
for two successive half-lives. We can determine the half-life more accurately, by obtaining a
value of
k
from the relation
0
ln A / A =
tkt
followed by tk
1/2 = 0.693/ For instance,
ln(0.78/1.00) = -k (25 s);
k = 9.94 ×10-3 s-1. Thus, t1/2 = 0.693/9.94 ×10-3 s-1 = 70 s.
30. (E)
We can determine an approximate initial rate by using data from the first 25 s.
1
A0.80 M 1.00 M
Rate = = = 0.0080 M s
25 s 0 st
Chapter 14: Chemical Kinetics
628
31. (M) The approximate rate at 75 s can be taken as the rate over the time period from 50 s to 100 s.
(a) Rate A M M
s s M s
II ==
0.00 0.50
100 50 = 0.010 1
t
(b) Rate A M M
s s M s
I==
0.37 0.61
100 50 = 0.0048 1
t
(c) Rate A M M
s s M s
III ==
0.50 0.67
100 50 = 0.0034 1
t
Alternatively we can use [A] at 75 s (the values given in the table) in the
relationship Rate A=km, where m= 0 , 1, or 2.
(a)
0
11
II
Rate = 0.010 M s 0.25 mol/L = 0.010 M s
(b) 1
1/2
Since 70s, 0.693/ 70s 0.0099stk
111
I
Rate 0.0099 (0.47 mol/L) 0.0047Mss
(c)
2
11 1
III
Rate = 0.010 L mol s 0.57 mol/L = 0.0032 M s
32. (M) We can combine the approximate rates from Exercise 31, with the fact that 10 s have
elapsed, and the concentration at 100 s.
(a)
II
A = 0.00 M There is no reactant left after 100 s.
(b) AA s rate M s M s M
I= 10 = 0.37 10 0.0047 = 0.32
100
1
bg ch
(c) AA s rate M s M s M
III = 10 = 0.50 10 0.0032 = 0.47
100
1
bg ch
33. (E) Substitute the given values into the rate equation to obtain the rate of reaction.
Rate A B M min M M M min= = 0.0103 0.116 3.83 = 1.39 10 /
20 11 20 4
k
ch
bgbg
34. (M)
(a) A first-order reaction has a constant half-life. Thus, half of the initial concentration remains
after 30.0 minutes, and at the end of another half-life—60.0 minutes total—half of the
concentration present at 30.0 minutes will have reacted: the concentration has decreased to
one-quarter of its initial value. Or, we could say that the reaction is 75% complete after two
half-lives—60.0 minutes.
(b) A zero-order reaction proceeds at a constant rate. Thus, if the reaction is 50% complete in
30.0 minutes, in twice the time—60.0 minutes—the reaction will be 100% complete. (And
in one-fifth the time—6.0 minutes—the reaction will be 10% complete. Alternatively, we
can say that the rate of reaction is 10%/6.0 min.) Therefore, the time required for the
reaction to be 75% 60.0 min
complete = 75% = 45 min.
100%
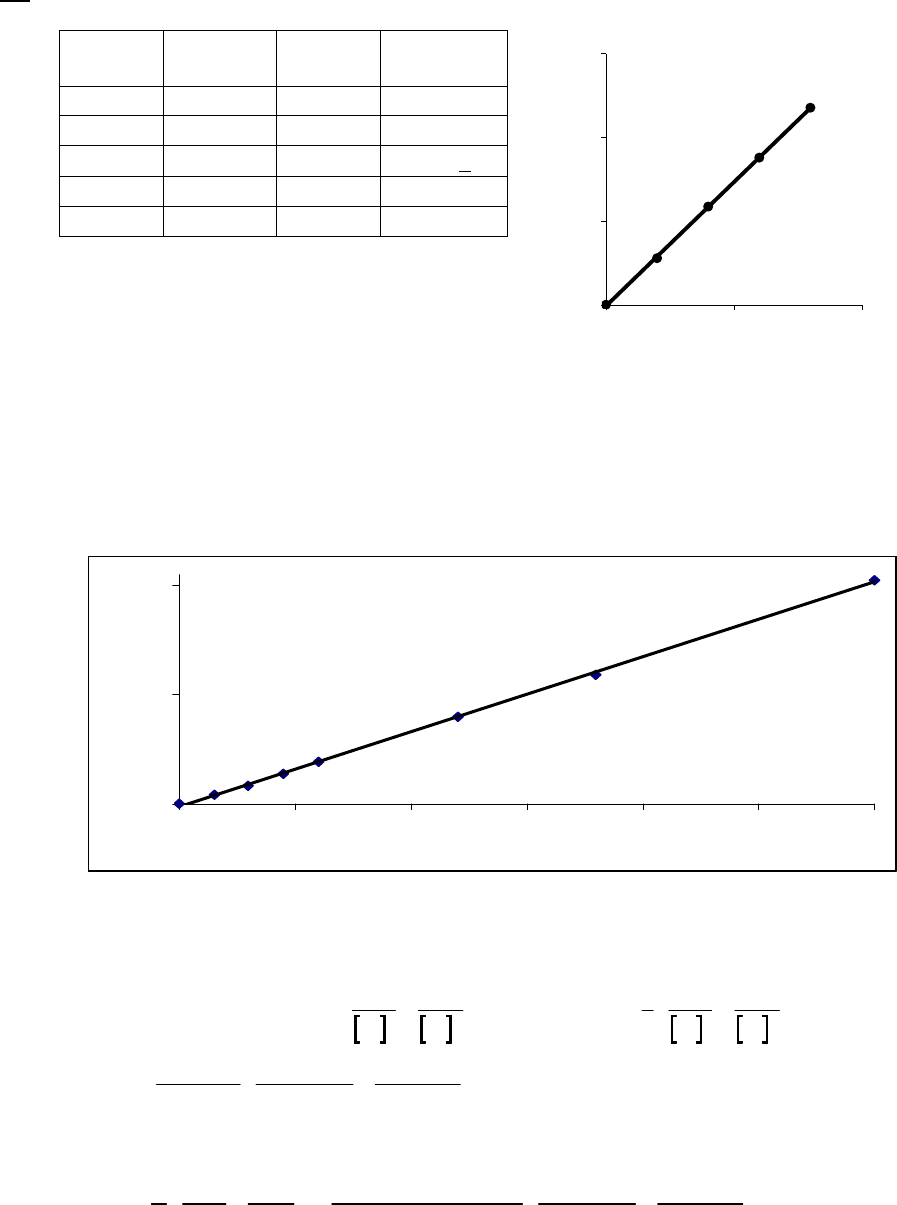
Chapter 14: Chemical Kinetics
629
35. (M) For reaction: HI(g) 1/2 H2(g) 1/2 I2(g) (700 K)
Time
(s) [HI] (M) ln[HI] 1/[HI](M1)
0 1.00 0 1.00
100 0.90
0.105 1.11
200 0.81
0.211 1.235
300 0.74
0.301 1.35
400 0.68
0.386 1.47
From data above, a plot of 1/[HI] vs. t yields
a straight line. The reaction is second-order
in HI at 700 K. Rate = k[HI]2. The slope of
the line = k = 0.00118 M1s1
Plot of 1/[HI] vs time
y = 0.00118x + 0.997
1.00
1.20
1.40
1.60
0 250 500
Time(s)
1/[HI] (M-1)
36. (D)
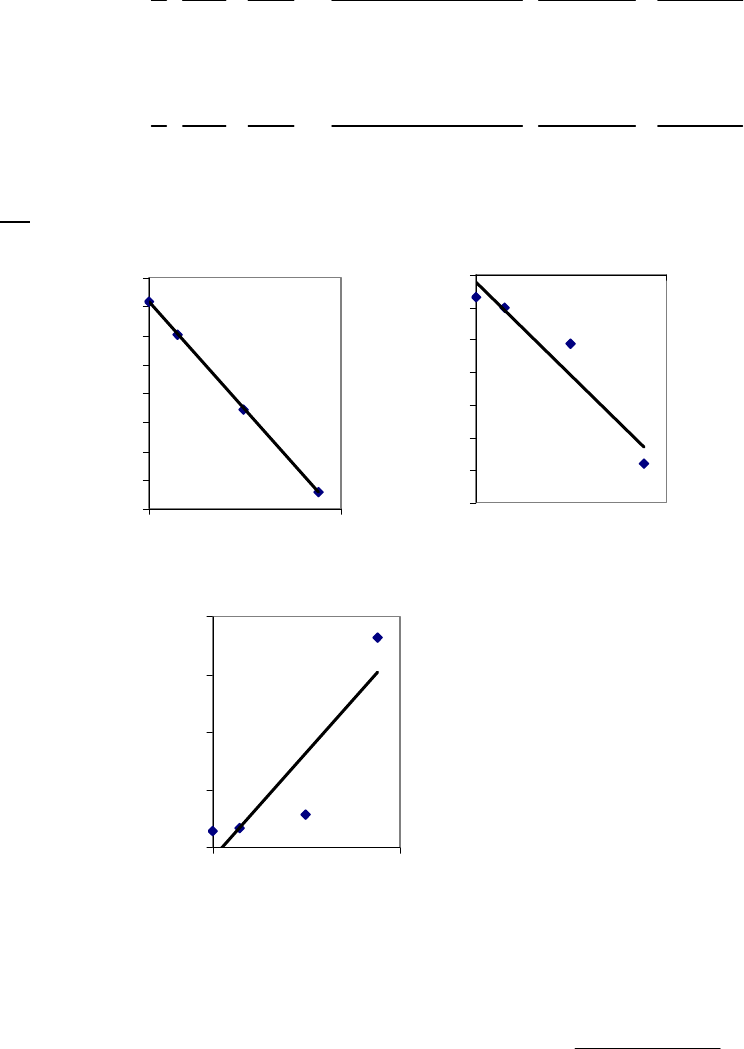
(a) We can graph 1/[ArSO2H] vs. time and obtain a straight line. We can also graph [ArSO2H]
vs. time and ln([ArSO2H]) vs. time to demonstrate that they do not yield a straight line.
Only the plot of 1/[ArSO2H] versus time is shown.
The linearity of the line indicates that the reaction is second-order.
(b) We solve the rearranged integrated second-order rate law for the rate constant, using the
longest time interval. 11
=11 1=
00
AA AA
tt
kt tk
F
H
G
I
K
J
11
11 1
= = 0.137 L mol min
300 min 0.0196 M 0.100 M
k
(c) We use the same equation as in part (b), but solved fort, rather than k.
11
0
11 1 1 1 1
= = = 73.0 min
A A 0.137 L mol min 0.0500 M 0.100 M
t
tk
Plot of 1/[ArSO
2
H] versus Time
y = 0.137x + 9.464
10
30
50
0 50 100 150 200 250 300
Time (min)
1/[ArSO
2
H] (M
-1
)
1/[ArSO2H] (M-1)
Plot of 1/[ArSO2H] versus Time
Chapter 14: Chemical Kinetics
630
(d) We use the same equation as in part (b), but solve fort, rather than k.
11
0
11 1 1 1 1
= = = 219 min
A A 0.137 L mol min 0.0250 M 0.100 M
t
tk
(e) We use the same equation as in part (b), but solve fort, rather than k.
11
0
11 1 1 1 1
= = =136 min
A A 0.137 L mol min 0.0350 M 0.100 M
t
tk
37. (M)
(a) Plot [A] vs t, ln[A] vs t, and 1/[A] vs t and see which yields a straight line.
y = -0.0050x + 0.7150
R
2
= 1.0000
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0150
Time(s)
[A] (mol/L)
y = -0.0191x
- 0.1092
R
2
= 0.9192
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0
0150
Time(s)
ln[A]
y = 0.1228x
- 0.9650
R
2
= 0.7905
0
5
10
15
20
0150
Time(s)
1/[A]
Clearly we can see that the reaction is zero-order in reactant A with a rate constant of 5.0 ×10-3.
(b) The half-life of this reaction is the time needed for one half of the initial [A] to react.
Thus,
A = 0.715 M 2 = 0.358
M and t1/2 3
=0.358
5.0 10 =72
M
M/s s.
Chapter 14: Chemical Kinetics
631
38. (D)
(a)
We can either graph 1/ 46
C H vs. time and obtain a straight line, or we can determine the
second-order rate constant from several data points. Then, if
k
indeed is a constant, the
reaction is demonstrated to be second-order. We shall use the second technique in this case.
First we do a bit of algebra.
11
=11 1=
00
AA AA
tt
kt tk
F
H
G
I
K
J
k=1
12.18
1
0.0144
1
0.0169 = 0.843 11
min M M L mol min
F
H
GI
K
J
k=1
24.55
1
0.0124
1
0.0169 = 0.875 11
min M M L mol min
F
H
GI
K
J
k=1
42.50
1
0.0103
1
0.0169 = 0.892 11
min M M L mol min
F
H
GI
K
J
k=1
68.05
1
0.00845
1
0.0169 = 0.870 11
min M M L mol min
F
H
GI
K
J
The fact that each calculation generates similar values for the rate constant indicates that
the reaction is second-order.
(b) The rate constant is the average of the values obtained in part (a).
11 11
0.843+ 0.875 + 0.892 + 0.870
= L mol min = 0.87 L mol min
4
k
(c) We use the same equation as in part (a), but solve fort, rather than
k
.
2
11
0
11 1 1 1 1
== =2.010min
A A 0.870 L mol min 0.00423 M 0.0169 M
t
tk
(d) We use the same equation as in part (a), but solve fort, rather than
k
.
2
11
0
11 1 1 1 1
== =1.610min
A A 0.870 L mol min 0.0050 M 0.0169 M
t
tk
39. (E)
(a)
A1.490 M 1.512 M
initial rate = = = +0.022 M / min
1.0 min 0.0 mint
A2.935 M 3.024 M
initial rate = = = +0.089 M / min
1.0 min 0.0 mint
(b) When the initial concentration is doubled
2.0
bg, from 1.512 M to 3.024 M, the initial rate
quadruples 4.0
bg. Thus, the reaction is second-order in A (since 2.0 = 4.0
x when
x
=2).
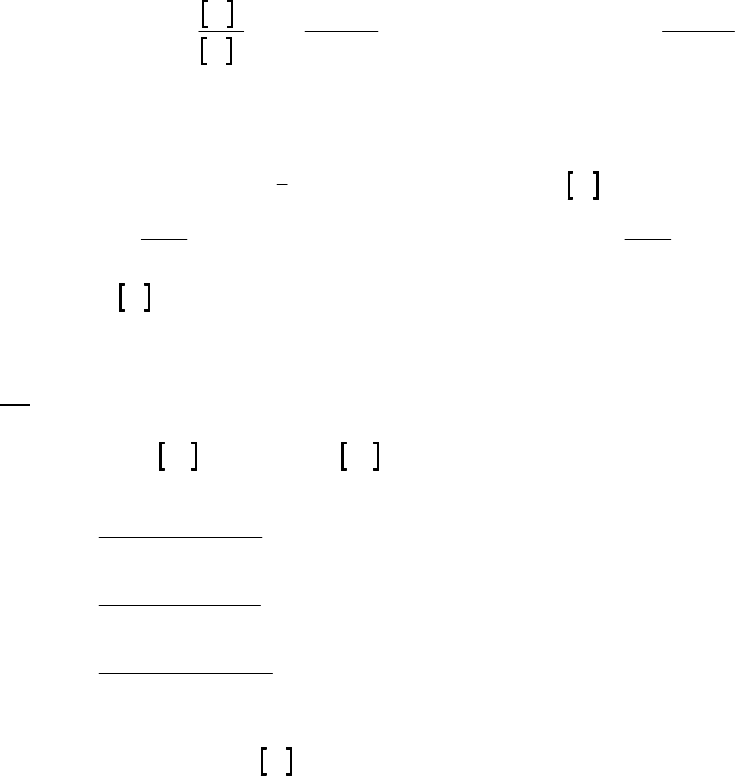
Chapter 14: Chemical Kinetics
632
40. (M)
(a) Let us assess the possibilities. If the reaction is zero-order, its rate will be constant. During
the first 8 min, the rate is
0.60 M 0.80 M /8 min = 0.03 M/min . Then, during the first
24 min, the rate is
0.35 M 0.80 M /24 min = 0.019 M/min . Thus, the reaction is not
zero-order. If the reaction is first-order, it will have a constant half-life that is consistent
with its rate constant. The half-life can be assessed from the fact that 40 min elapse while
the concentration drops from 0.80 M to 0.20 M, that is, to one-fourth of its initial value.
Thus, 40 min equals two half-lives and 1/2 =20 mint.
This gives kt= 0.693/ = 0.693/ 20 = 0.035
1/2 1
min min. Also
kt k k
t
==
0.35
0.80 = 0.827 = 24 = 0.827
24 = 0.034
0
1
ln A
Aln M
M min min min
The constancy of the value of
k
indicates that the reaction is first-order.
(b) The value of the rate constant is k= 0.034 1
min.
(c) Reaction rate = 1
2 (rate of formation of B) =1
kA First we need [A] at t=30. min
11.02
2
0 0
AA
ln = = 0.034 min 30. min = 1.0 = = 0.36
AA
kt e
A M M= 0.36 0.80 = 0.29
rate of formation of B min M M min= 2 0.034 0.29 = 2.0 10
121
41. (M) The half-life of the reaction depends on the concentration of A and, thus, this reaction cannot
be first-order. For a second-order reaction, the half-life varies inversely with the reaction rate:
tk
1/2 0
=1/ A
chor kt=1/ 1/2 0
A
ch. Let us attempt to verify the second-order nature of this
reaction by seeing if the rate constant is fixed.
11
1
= = 0.020 L mol min
1.00 M 50 min
k
11
1
= = 0.020 L mol min
2.00 M 25 min
k
k=1
0.50 100 = 0.020 11
Mmin L mol min
The constancy of the rate constant demonstrates that this reaction indeed is second-order. The rate
equation is Rate A=2
k and
k
= 0.020 11
L mol mi
n
.
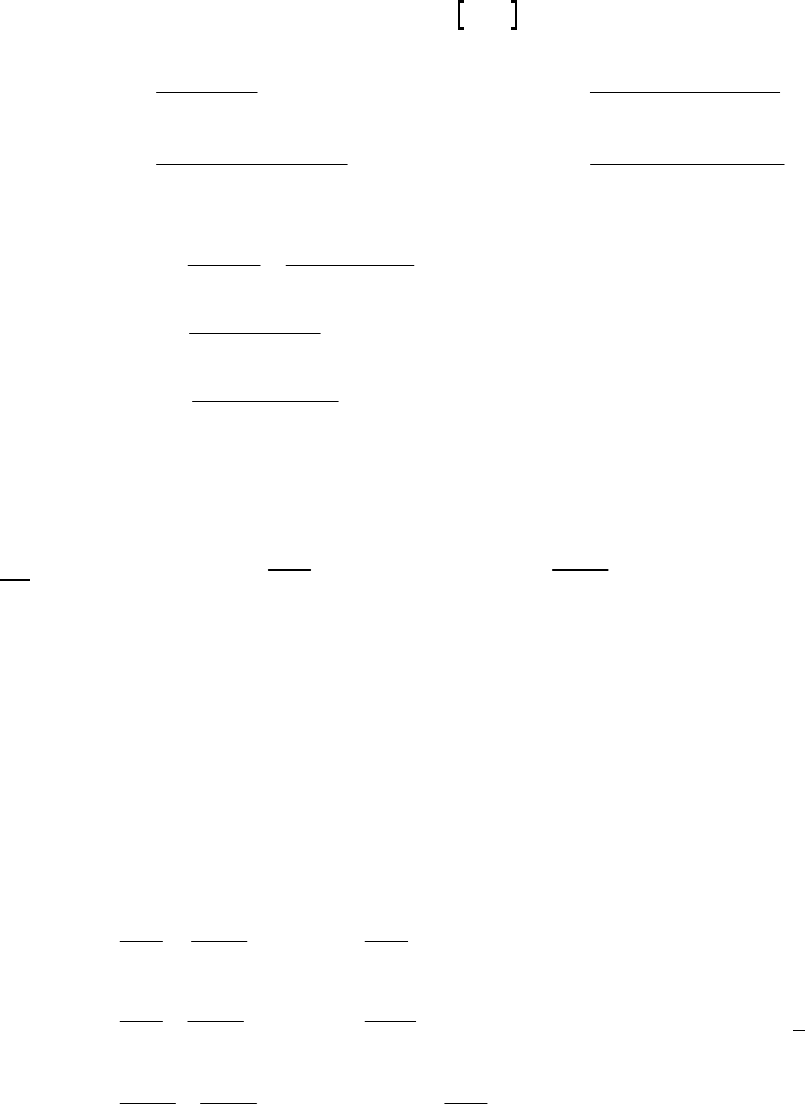
Chapter 14: Chemical Kinetics
633
42. (M)
(a)
The half-life depends on the initial NH3 and, thus, the reaction cannot be first-order. Let
us attempt to verify second-order kinetics.
11
31/2
0
11
= for a second-order reaction = = 42 M min
NH 0.0031 M 7.6 min
kk
t
11 11
11
= =180 M min = = 865 M min
0.0015 M 3.7 min 0.00068 M 1.7min
kk
The reaction is not second-order. But, if the reaction is zero-order, its rate will be constant.
4
0
1/2
A/2 0.0031 M 2
Rate = = = 2.0 10 M/min
7.6 mint
4
0.0015 M 2
Rate = = 2.0 10 M/min
3.7 min
4
0.00068 M 2
Rate = 2.0 10 M / min
1.7 min
Zero-order reaction
(b) The constancy of the rate indicates that the decomposition of ammonia under these
conditions is zero-order, and the rate constant is
k
=2.0 104
M/min.
43. (M) Zero-order: t1/2 = 0
[A]
2k Second-order: t1/2 =
0
1
[A]k
A zero-order reaction has a half life that varies proportionally to [A]0, therefore, increasing [A]0
increases the half-life for the reaction. A second-order reaction's half-life varies inversely
proportional to [A]0, that is, as [A]0 increases, the half-life decreases. The reason for the
difference is that a zero-order reaction has a constant rate of reaction (independent of [A]0). The
larger the value of [A]0, the longer it will take to react. In a second-order reaction, the rate of
reaction increases as the square of the [A]0, hence, for high [A]0, the rate of reaction is large and
for very low [A]0, the rate of reaction is very slow. If we consider a bimolecular elementary
reaction, we can easily see that a reaction will not take place unless two molecules of reactants
collide. This is more likely when the [A]0 is large than when it is small.
44. (M)
(a) 0
[A]
2k= 0.693
k Hence, 0
[A]
2= 0.693 or [A]0 = 1.39 M
(b) 0
0
[A] 1
2[A]kk
, Hence,
2
0
[A]
2= 1 or [A]02 = 2.00 M [A]0 = 1.414 M
(c)
o
0.693 1
[A]kk
, Hence, 0.693 =
0
1
[A] or [A]0 = 1.44 M

Chapter 14: Chemical Kinetics
634
Collision Theory; Activation Energy
45. (M)
(a) The rate of a reaction depends on at least two factors other than the frequency of collisions.
The first of these is whether each collision possesses sufficient energy to get over the
energy barrier to products. This depends on the activation energy of the reaction; the higher
it is, the smaller will be the fraction of successful collisions. The second factor is whether
the molecules in a given collision are properly oriented for a successful reaction. The more
complex the molecules are, or the more freedom of motion the molecules have, the smaller
will be the fraction of collisions that are correctly oriented.
(b) Although the collision frequency increases relatively slowly with temperature, the fraction
of those collisions that have sufficient energy to overcome the activation energy increases
much more rapidly. Therefore, the rate of reaction will increase dramatically with
temperature.
(c) The addition of a catalyst has the net effect of decreasing the activation energy of the
overall reaction, by enabling an alternative mechanism. The lower activation energy of the
alternative mechanism, (compared to the uncatalyzed mechanism), means that a larger
fraction of molecules have sufficient energy to react. Thus the rate increases, even though
the temperature does not.
46. (M)
(a) The activation energy for the reaction of hydrogen with oxygen is quite high, too high, in
fact, to be supplied by the energy ordinarily available in a mixture of the two gases at
ambient temperatures. However, the spark supplies a suitably concentrated form of energy
to initiate the reaction of at least a few molecules. Since the reaction is highly exothermic,
the reaction of these first few molecules supplies sufficient energy for yet other molecules
to react and the reaction proceeds to completion or to the elimination of the limiting
reactant.
(b) A larger spark simply means that a larger number of molecules react initially. But the
eventual course of the reaction remains the same, with the initial reaction producing enough
energy to initiate still more molecules, and so on.
47. (M)
(a)
The products are 21 kJ/mol closer in energy to the energy activated complex than are the
reactants. Thus, the activation energy for the reverse reaction is
84 21 = 63 . kJ / mol kJ / mol kJ / mol
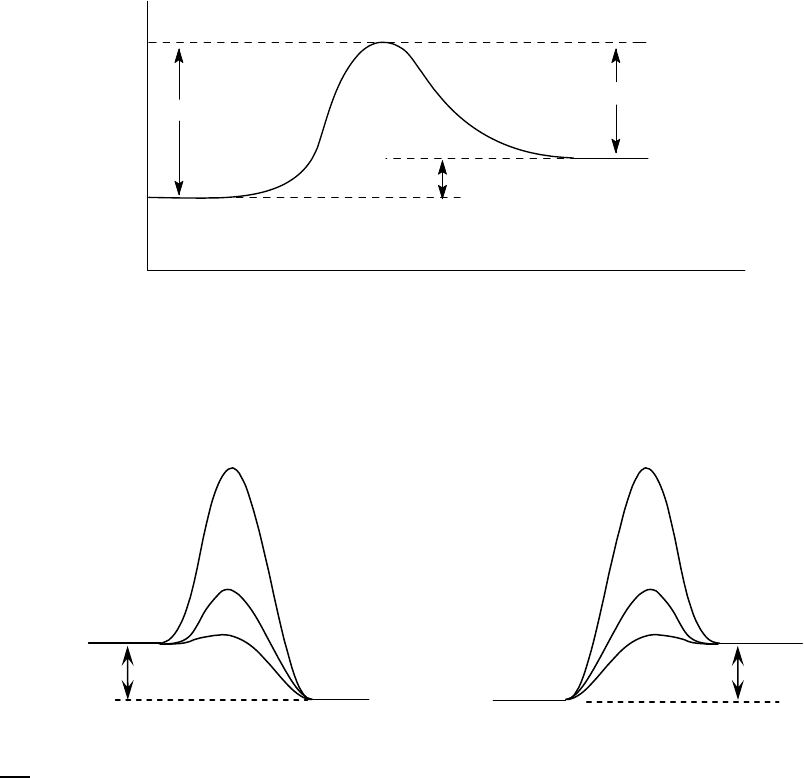
Chapter 14: Chemical Kinetics
635
(b) The reaction profile for the reaction in Figure 14-10 is sketched below.
48. (M)
In an endothermic reaction (right), Eamust be larger than the
H
for the reaction. For an
exothermic reaction (left), the magnitude of Ea may be either larger or smaller than that of
H
.
In other words, a small activation energy can be associated with a large decrease in the enthalpy,
or a large Ea can be connected to a small decrease in enthalpy.
49. (E)
(a) There are two intermediates (B and C).
(b) There are three transition states (peaks/maxima) in the energy diagram.
(c) The fastest step has the smallest Ea, hence, step 3 is the fastest step in the reaction with
step 2 a close second.
(d) Reactant A (step 1) has the highest Ea, and therefore the slowest smallest constant
(e) Endothermic; energy is needed to go from A to B.
(f) Exothermic; energy is released moving from A to D.
reactants
products
ΔH<0 reactants
products
ΔH>0
Transiton State
Ea(forward) = 84 kJ Ea(reverse) = 63 kJ
H = +21 kJ
A + B
C + D
A . . . . B
Reactants
Products
Potential Energy (kJ)
Progress of Reaction

Chapter 14: Chemical Kinetics
636
50. (E)
(a) There are two intermediates (B and C).
(b) There are three transition states (peaks/maxima) in the energy diagram.
(c) The fastest step has the smallest Ea, hence, step 2 is the fastest step in the reaction.
(d) Reactant A (step 1) has the highest Ea, and therefore the slowest smallest constant
(e) Endothermic; energy is needed to go from A to B.
(f) Endothermic, energy is needed to go from A to D.
Effect of Temperature on Rates of Reaction
51. (M)
ln ln L mol s
L mol s K K
k
k
E
RT T
E
R
aa1
221
411
211
=11
=5.4 10
2.8 10 =1
683
1
599
F
H
GI
K
J
F
H
GI
K
J
3.95 = 2.05 10 4
RE
a
ER
a=3.95
2.05 10 = 1.93 10 8.3145 = 1.60 10 = 160
4
41 11 5
K J mol K J / mol kJ / mol
52. (M)
311 5
1
211 11
221
1 1 5.0 10 L mol s 1.60 10 J/mol 1 1
ln = = ln = 683 K
2.8 10 L mol s 8.3145 J mol K
a
E
k
kRTT T
4 5
4
1 1 1 1 1.72
1.72 = 1.92 10 = = 8.96 10
683 K 683 K 1.92 10TT
53 3
1= 8.96 10 +1.46 10 =1.55 10 = 645 KT
T
53. (D)
(a)
First we need to compute values of ln
k
and 1/
T
. Then we plot the graph of ln k versus
1/T.
,CT 0 C 10 C 20 C 30 C
T
, K 273 K 283 K 293 K 303 K
1/ , 1
T K 0.00366 0.00353 0.00341 0.00330
1
, sk 5.6 10 6
3.2 10 5
1.6 10 4
7.6 10 4
ln
k
12.09
10.35
8.74
7.18

Chapter 14: Chemical Kinetics
637
(b) The slope = ER
a/.
4
a2
J 1 kJ kJ
= slope = 8.3145 1.35 10 K = 112
mol K 1000 J mol
ER
(c) We apply the Arrhenius equation, with
k
=5.6 10 61
s at 0C (273 K),
k
=? at 40C
(313 K), and Ea= 113 103
J/mol.
3
a
61 1 1
12
1 1 112 10 J/mol 1 1
ln = = = 6.306
273 K 313 K
5.6 10 s 8.3145 J mol K
E
k
RT T
6.306 61 31
61
= 548 = = 548 5.6 10 s = 3.07 10 s
5.6 10 s
k
ek
54. (D)
(a) Here we plot ln
k
vs.1/
T
. The slope of the straight line equals ER
a/. First we tabulate
the data to plot. (the plot is shown below).
,T C 15.83 32.02 59.75 90.61
T
, K 288.98 305.17 332.90 363.76
1/
T
, K1 0.0034604 0.0032769 0.0030039 0.0027491
k
, M1s1 5.03 10 5
3.68 10 4
6.71 10 3
0.119
ln
k
9.898
7.907
5.004 2.129
Plot of ln k versus 1/T
y = -13520x + 37.4
-12.1
-11.1
-10.1
-9.1
-8.1
-7.1
0.00325 0.00345 0.00365
1/T (K
-1
)
ln k
Plot of ln k versus 1/T
y = -10890x + 27.77
-12
-10
-8
-6
-4
-2
0
0.0027 0.0029 0.0031 0.0033 0.0035
1/T (K-1)
ln k
2
1/2 31
0.693 0.693
= = = 2.3 10 s
3.07 10 s
tk
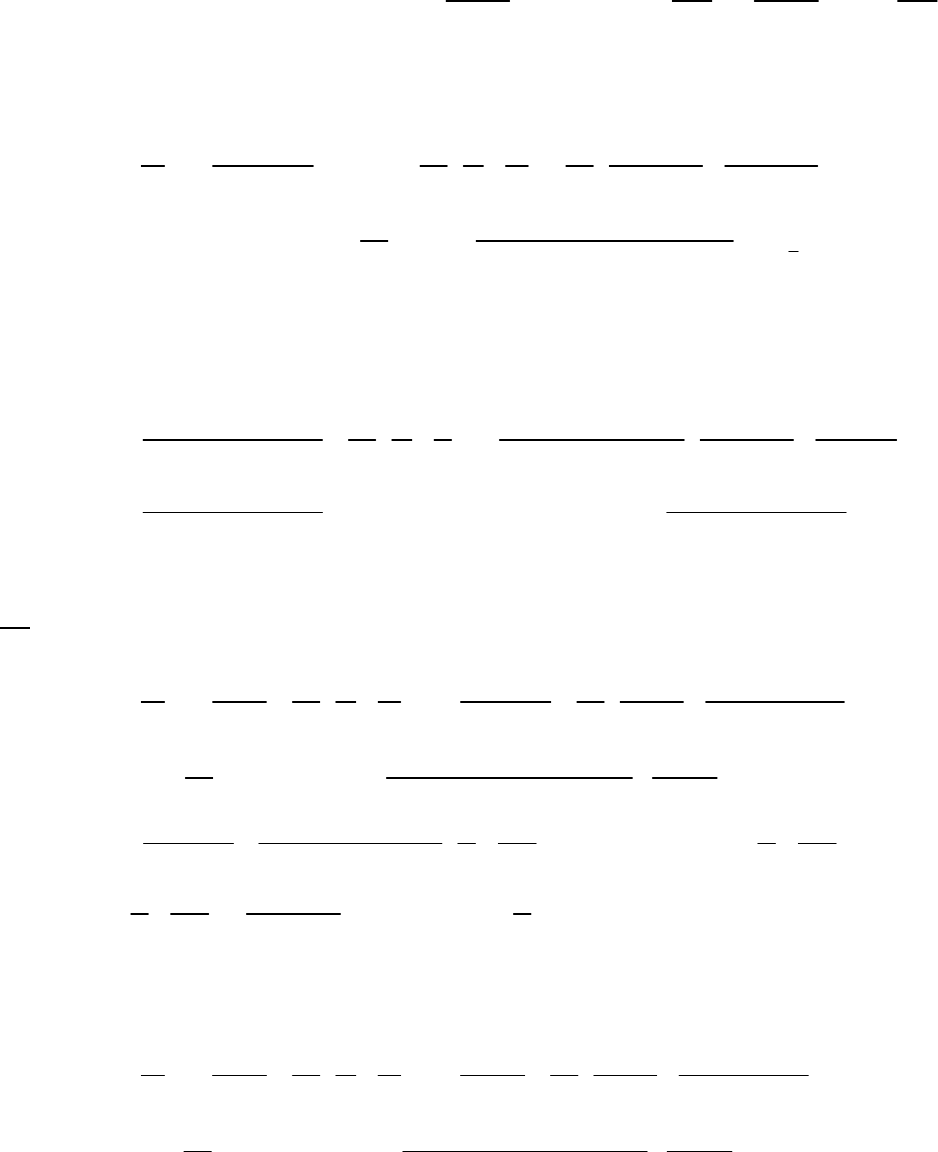
Chapter 14: Chemical Kinetics
638
The slope of this graph K a
=1.0910 = /
4
ER
44
a
J J 1 kJ kJ
= 1.089 10 K 8.3145 = 9.054 10 = 90.5
mol K mol 1000 J mol
E
(b) We calculate the activation energy with the Arrhenius equation using the two extreme data
points.
aa
2
5
112
11
41 4
aa41
0.119 1 1 1 1
ln = ln = +7.77 = =
5.03 10 288.98 K 363.76 K
7.769 8.3145 J mol K
= 7.1138 10 K = = 9.08 10 J/mol
7.1138 10 K
EE
k
kRTTR
EE
R
a=91EkJ/mol. The two Ea values are in quite good agreement, within experimental limits.
(c) We apply the Arrhenius equation, with Ea= 9.080 104
J/mol,
k
=5.03 10 511
M sat 15.83 C (288.98 K), and
k
=? at 100.0 C (373.2 K).
3
a
511 11
2
1
8.528 3
511 511
1 1 90.80 10 J/mol 1 1
ln = =
5.03 10 M s 8.3145 J mol K 288.98 K 373.2 K
ln = 8.528 = 5.05 10 =
5.03 10 M s 5.03 10 M s
E
k
RT T
kk
e
3511 11
= 5.05 10 5.03 10 M s = 0.254 M sk
55. (M) The half-life of a first-order reaction is inversely proportional to its rate constant:
kt= 0.693/ 1/2 . Thus we can apply a modified version of the Arrhenius equation to find Ea.
(a)
1/2 aa21
11/2 12
2
1 1 46.2 min 1 1
ln = ln = = ln =
2.6 min 298 K 102 + 273 K
tEEk
kt RTT R
11
4
aa41
2.88 8.3145 J mol K 1 kJ
2.88 = 6.89 10 = = 34.8 kJ/mol
6.89 10 K 1000 J
EE
R
(b) 10.0
46.2 =34.8 10
8.3145
11
298 = 1.53 = 4.19 10 11
298
3
11
3
ln min
min
J/mol
J mol K
F
H
G
I
K
J
F
H
G
I
K
J
TT
43 o
3
1 1 1.53 1
= = 3.65 10 = 2.99 10 = 334 K = 61 C
298 4.19 10 T
TT
56. (M)
The half-life of a first-order reaction is inversely proportional to its rate
constant: kt= 0.693/ 1/2 . Thus, we can apply a modified version of the Arrhenius equation.
(a)
1/2 aa21
11/2 12
2
1 1 22.5 h 1 1
ln = ln = = ln =
1.5 h 293 K 40 + 273 K
tEEk
kt RTT R
11
4
aa41
2.71 8.3145 J mol K 1 kJ
2.71= 2.18 10 , = =103 kJ/mol
2.18 10 K 1000 J
EE
R
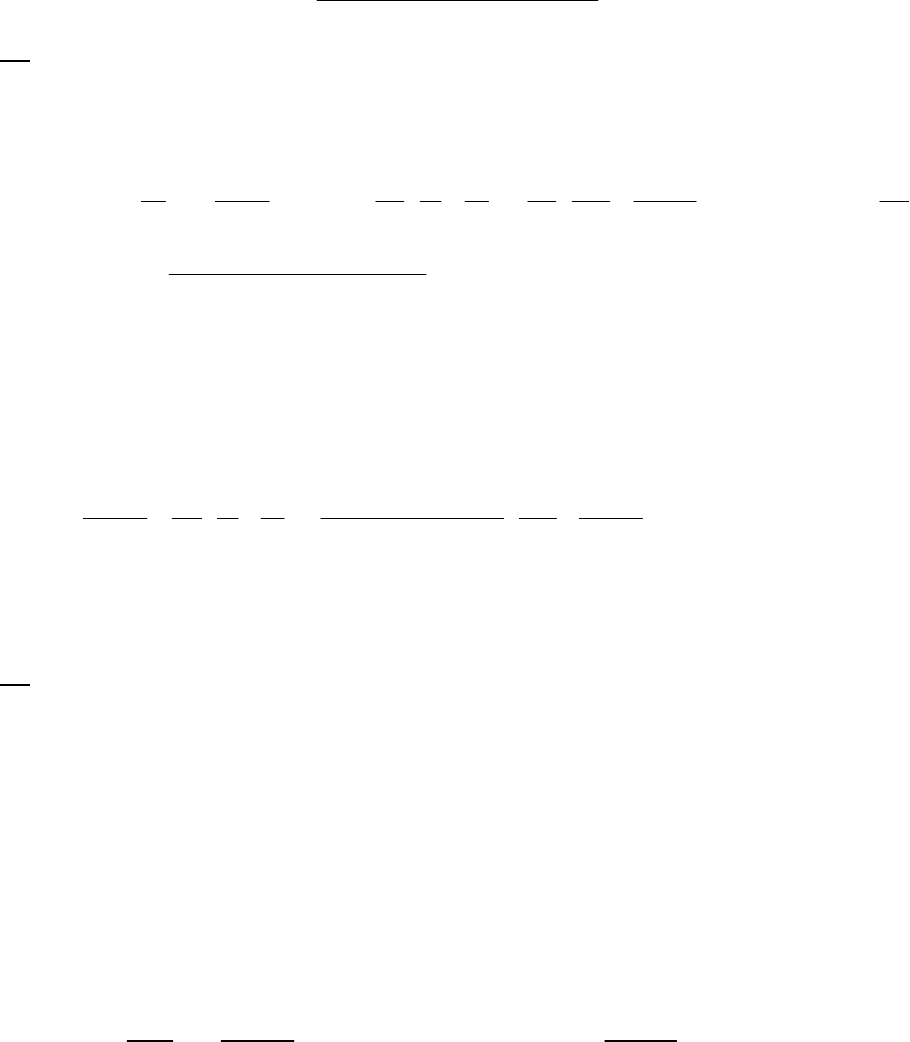
Chapter 14: Chemical Kinetics
639
(b) The relationship is kA ERT=/exp a
bg
31
11
13 1 13 1 40.9 5 1
103 10 J mol
8.3145 J mol K 273+ 30 K
=2.05 10 s exp =2.05 10 s 3.5 10 ske
57. (M)
(a) It is the change in the value of the rate constant that causes the reaction to go faster. Let k1
be the rate constant at room temperature, 20 C
(293 K). Then, ten degrees higher (30° C
or 303 K), the rate constant 21
=2kk
.
41
aa
21
11 12
211 1 1
ln = ln = 0.693 = = = 1.13 10 K
293 303 K
a
EE E
kk
kk RTTR R
Ea
J mol K
K J / mol kJ / mol=0.693 8.3145
1.13 10 =5.1 10 =51
11
41
4
(b) Since the activation energy for the depicted reaction (i.e., N2O + NO N2 + NO2) is 209
kJ/mol, we would not expect this reaction to follow the rule of thumb.
58. (M) Under a pressure of 2.00 atm, the boiling point of water is approximately 121 C or 394 K.
Under a pressure of 1 atm, the boiling point of water is 100C or 373 K. We assume an
activation energy of 5.1 104
J / mol and compute the ratio of the two rates.
ln Rate
Rate
J/mol
J mol K K
2
112
4
11
=11
=5.1 10
8.3145
1
373
1
394 = 0.88
E
RT T
a
F
H
GI
K
J
F
H
GI
K
J
0.88
211
Rate = Rate = 2.4 Rate .e Cooking will occur 2.4 times faster in the pressure cooker.
Catalysis
59. (E)
(a) Although a catalyst is recovered unchanged from the reaction mixture, it does “take part in
the reaction.” Some catalysts actually slow down the rate of a reaction. Usually, however,
these negative catalysts are called inhibitors.
(b) The function of a catalyst is to change the mechanism of a reaction. The new mechanism is
one that has a different (lower) activation energy (and frequently a different A value), than
the original reaction.
60. (M) If the reaction is first-order, its half-life is 100 min, for in this time period [S] decreases from
1.00 M to 0.50 M, that is, by one half. This gives a rate constant of
kt= 0.693/ = 0.693/100 = 0.00693
1/2 1
min min.
The rate constant also can be determined from any two of the other sets of data.
1
0
A1.00 M 0.357
= ln = ln = 0.357 = 60 min = = 0.00595 min
A0.70 M 60min
t
kt k k
This is not a very good agreement between the two k values, so the reaction is probably not first-
order in [A]. Let's try zero-order, where the rate should be constant.
Chapter 14: Chemical Kinetics
640
0.90 M 1.00 M 0.50 M 1.00 M
Rate = = 0.0050 M/min Rate = = 0.0050 M/min
20 min 100 min
0.20 M 0.90 M 0.50 M 0.90 M
Rate = = 0.0050 M/min Rate = = 0.0050 M/min
160 min 20 min 100 min 20 min
Thus, this reaction is zero-order with respect to [S].
61. (E) Both platinum and an enzyme have a metal center that acts as the active site. Generally
speaking, platinum is not dissolved in the reaction solution (heterogeneous), whereas enzymes are
generally soluble in the reaction media (homogeneous). The most important difference, however,
is one of specificity. Platinum is rather nonspecific, catalyzing many different reactions. An
enzyme, however, is quite specific, usually catalyzing only one reaction rather than all reactions
of a given class.
62. (E) In both the enzyme and the metal surface cases, the reaction occurs in a specialized location:
either within the enzyme pocket or on the surface of the catalyst. At high concentrations of
reactant, the limiting factor in determining the rate is not the concentration of reactant present but
how rapidly active sites become available for reaction to occur. Thus, the rate of the reaction
depends on either the quantity of enzyme present or the surface area of the catalyst, rather than on
how much reactant is present (i.e., the reaction is zero-order). At low concentrations or gas
pressures the reaction rate depends on how rapidly molecules can reach the available active sites.
Thus, the rate depends on concentration or pressure of reactant and is first-order.
63. (E) For the straight-line graph of Rate versus [Enzyme], an excess of substrate must be present.
64. (E) For human enzymes, we would expect the maximum in the curve to appear around 37C, i.e.,
normal body temperature (or possibly at slightly elevated temperatures to aid in the control of
diseases (37 - 41 C). At lower temperatures, the reaction rate of enzyme-activated reactions
decreases with decreasing temperature, following the Arrhenius equation. However, at higher
temperatures, these temperature sensitive biochemical processes become inhibited, probably by
temperature-induced structural modifications to the enzyme or the substrate, which prevent
formation of the enzyme-substrate complex.
Reaction Mechanisms
65. (E) The molecularity of an elementary process is the number of reactant molecules in the process.
This molecularity is equal to the order of the overall reaction only if the elementary process in
question is the slowest and, thus, the rate-determining step of the overall reaction. In addition, the
elementary process in question should be the only elementary step that influences the rate of the
reaction.
66. (E) If the type of molecule that is expressed in the rate law as being first-order collides with other
molecules that are present in much larger concentrations, the reaction will seem to depend only
on the amount of those types of molecules present in smaller concentration, since the larger
concentration will be essentially unchanged during the course of the reaction. Such a situation is
quite common, and has been given the name pseudo first-order. It is also possible to have
molecules which, do not participate directly in the reaction— including product molecules—
Chapter 14: Chemical Kinetics
641
strike the reactant molecules and impart to them sufficient energy to react. Finally, collisions of
the reactant molecules with the container walls may also impart adequate energy for reaction to
occur.
67. (M) The three elementary steps must sum to give the overall reaction. That is, the overall reaction
is the sum of step 1 step 2 step 3. Hence, step 2 = overall reaction step 1 step 3. Note that
all species in the equations below are gases.
Overall: 222 222
2 NO + 2H N + 2 H O 2 NO + 2 H N + 2 H O
First:
22 22
2 NO N O N O 2NO
Third
2 2 22 22 2 2
NO+H N +HO or N +HO NO+H
The result is the second step, which is slow: H NO HO NO
222 2 2
++
The rate of this rate-determining step is: Rate =
22 22
HNOk
Since N O
22
does not appear in the overall reaction, we need to replace its concentration with the
concentrations of species that do appear in the overall reaction. To do this, recall that the first step
is rapid, with the forward reaction occurring at the same rate as the reverse reaction.
kk
1
2
122
===NO forward rate reverse rate N O
. This expression is solved for NO
22
,
which then is substituted into the rate equation for the overall reaction.
NO NO Rate H NO
22 1
2
1
21
1
2
2
==
k
k
kk
k
The reaction is first-order in H2 and second-order in [NO]. This result conforms to the
experimentally determined reaction order.
68. (M) Proposed mechanism: 1
-1
2
I(g) 2I(g)
k
k
Observed rate law:
2
2
2 I(g) + H (g) 2 HI(g)
k
Rate = k[I2][H2]
I2(g) + H2(g) 2 HI(g)
The first step is a fast equilibrium reaction and step 2 is slow. Thus, the predicted rate law is
Rate = k2[I]2[H2]. In the first step, set the rate in the forward direction for the equilibrium equal
to the rate in the reverse direction. Then solve for [I]2.
Rateforward = Ratereverse Use: Rateforward = k1[I2] and Ratereverse = k-1[I]2
From this we see: k1[I2] = k-1[I]2. Rearranging (solving for [I]2)
[I]2 = 12
-1
[I ]k
k Substitute into Rate = k2[I]2[H2] = k212
-1
[I ]k
k [H2] = kobs[I2][H2]
Since the predicted rate law is the same as the experimental rate law, this mechanism is
plausible.

Chapter 14: Chemical Kinetics
642
69. (M) Proposed mechanism: 1
-1
2
Cl (g) 2Cl(g)
k
k
Observed rate law:
2
2 Cl(g) + 2 NO(g) 2 NOCl(g)
k
Rate = k[Cl2][NO]2
Cl2(g) + 2NO(g) 2 NOCl(g)
The first step is a fast equilibrium reaction and step 2 is slow. Thus, the predicted rate law is
Rate = k2[Cl]2[NO]2 In the first step, set the rate in the forward direction for the equilibrium equal
to the rate in the reverse direction. Then express [Cl]2 in terms of k1, k-1 and [Cl2]. This
mechanism is almost certainly not correct because it involves a tetra molecular second step.
Rateforward = Ratereverse Use: Rateforward = k1[Cl2] and Ratereverse = k-1[Cl]2
From this we see: k1[Cl2] = k-1[Cl]2. Rearranging (solving for [Cl]2)
[Cl]2 = 12
-1
[Cl ]k
k Substitute into Rate = k2[Cl]2[NO]2 = k212
-1
[Cl ]k
k [NO]2 = kobs[Cl2][NO2]2
There is another plausible mechanism. 1
-1
2
Cl (g) + NO(g) NOCl(g) + Cl(g)
k
k
1
-1
Cl(g) + NO(g) NOCl(g)
k
k
Cl2(g) + 2NO(g) 2 NOCl(g)
Rateforward = Ratereverse Use: Rateforward = k1[Cl2][NO] and Ratereverse = k-1[Cl][NOCl]
From this we see: k1[Cl2][NO] = k-1[Cl][NOCl]. Rearranging (solving for [Cl])
[Cl] = 12
-1
k[Cl][NO]
k[NOCl] Substitute into Rate = k2[Cl][NO] =
2
21 2
-1
[Cl ][NO]
[NOCl]
kk
k
If [NOCl], the product is assumed to be constant (~ 0 M using method of initial rates), then
21 obs
-1
constant = k
[NOCl]
kk
k Hence, the predicted rate law is 2
2
[Cl ][NO]
obs
kwhich agrees with
the experimental rate law. Since the predicted rate law agrees with the experimental rate law,
both this and the previous mechanism are plausible, however, the first is dismissed as it has a
tetramolecular elementary reaction (extremely unlikely to have four molecules simultaneously
collide).
70. (M) A possible mechanism is: Step 1:
32
OO+ Ofast
Step 2:
32
3
O+ O 2 O slow
k
The overall rate is that of the slow step:Rate O O=33
k. But O is a reaction intermediate, whose
concentration is difficult to determine. An expression for [O] can be found by assuming that the
forward and reverse “fast” steps proceed with equal speed.
13
121322
22
O
Rate = Rate O = O O O = O
k
kk k
2
13 3
31
33
22 2 2
OO
Rate = O =
OO
kkk
kkk
Then substitute this expression into the rate law for the reaction. This rate equation has the same
form as the experimentally determined rate law and thus the proposed mechanism is plausible.

Chapter 14: Chemical Kinetics
643
71. (M)
1
1
2
k
12 12
k
k
12 12
SS S:S
S:S S:S
12
11 2 11 2 2 1 2
11 2 1 2 1 2
1
12 1 2
12
211 2
12
21 2
12
dS:S kS S k S:S k S:S
dt
kS S k k S:S
k
S:S S S
kk
kkSS
dS:S kS:S
dt k k
72. (M)
1
1
2
k
3322
2k
k
32 3
2
CH CO (aq) + OH CH C O CH (aq) + H O (l)
CH C O CH (aq) + CH CO (aq) Prod
We note that CH3C(O)CH2– is an intermediate species. Using the steady state approximation,
while its concentration is not known during the reaction, the rate of change of its concentration is
zero, except for the very beginning and towards the end of the reaction. Therefore,
32
13 13 22
2
23 2 3
2
dCHCOCH k CH CO OH k CH C O CH H O
dt
kCHCOCH CH CO 0
Rearranging the above expression to solve for CH3C(O)CH2– gives the following expression
13
2
32
12 2 3
2
kCHCOOH
CH C O CH k H O k CH CO
The rate of formation of product, therefore, is:
23 2 3
2
13
2
23
2
12 2 3
2
2
21 32
12 2 3
2
dProd kCHCOCH CH CO
dt
kCHCOOH
kCHCO
k H O k CH CO
kk CH CO OH
k H O k CH CO

Chapter 14: Chemical Kinetics
644
INTEGRATIVE AND ADVANCED EXERCISES
73. (M) The data for the reaction starting with 1.00 M being first-order or second-order as well as that
for the first-order reaction using 2.00 M is shown below
Time
(min) [A]o = 1.00 M
(second order) [A]o = 1.00 M
(first order) [A]o = 2.00 M
(second order) [A]o = 2.00 M
(first order)
0 1.00 1.00 2.00 2.00
5 0.63 0.55 0.91 1.10
10 0.46 0.30 0.59 0.60
15 0.36 0.165 0.435 0.33
25 0.25 0.05 0.286 0.10
Clearly we can see that when [A]o = 1.00 M, the first-order reaction concentrations will always be
lower than that for the second-order case (assumes magnitude of the rate constant is the same). If,
on the other hand, the concentration is above 1.00 M, the second-order reaction decreases faster
than the first-order reaction (remember that the half-life shortens for a second-order reaction as
the concentration increases, whereas for a first-order reaction, the half-life is constant).
From the data, it appears that the crossover occurs in the case where [A]0 = 2.00 M at just over 10
minutes.
1 1 0.12
Second-order at 11 minutes: (11 min) [A] = 0.549 M
[A] 2 M min
0.12
First-order at 11 minutes: ln[A] ln(2) (11 min) [A] = 0.534 M
min
A quick check at 10.5 minutes reveals,
1 1 0.12(10.5 min)
Second-order at 10.5 minutes: [A] = 0.568 M
[A] 2 M min
0.12(10.5 min)
First-order at 10.5 minutes: ln[A] ln(2) [A] = 0.567 M
M min
Hence, at approximately 10.5 minutes, these two plots will share a common point (point at which
the concentration versus time curves overlap).
74. (M)
(a) The concentration vs. time graph is not linear. Thus, the reaction is obviously not zero-order
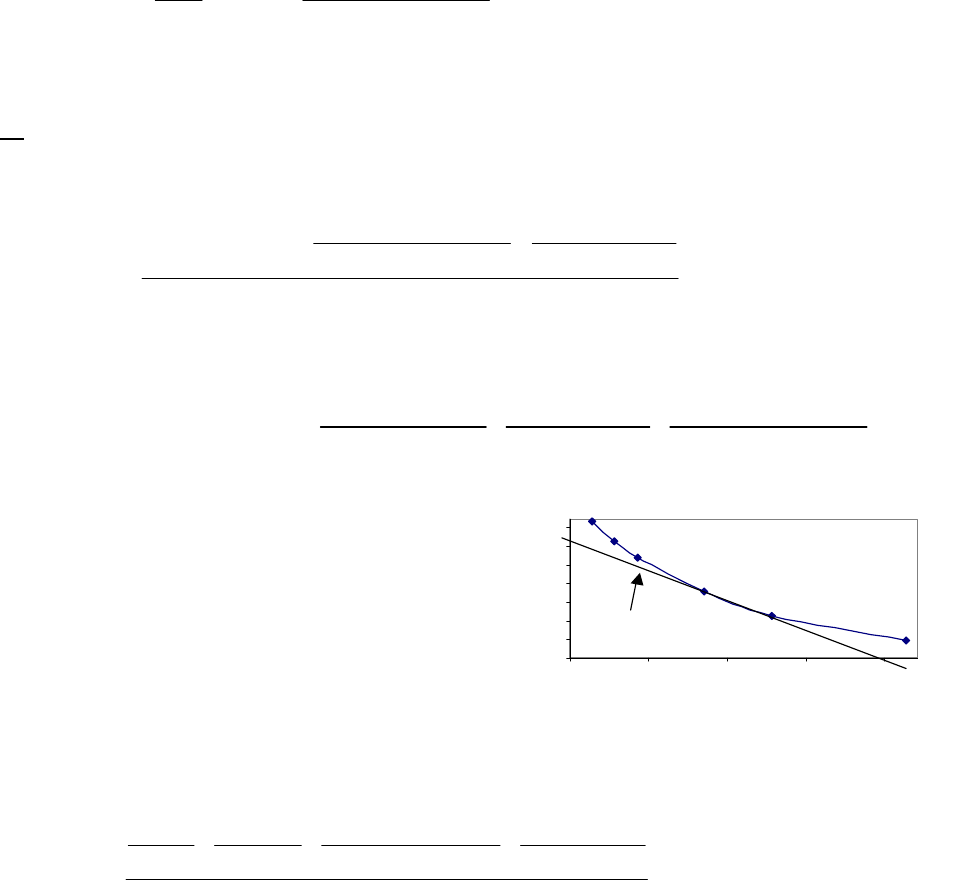
(the rate is not constant with time). A quick look at various half lives for this reaction shows
the ~2.37 min (1.000 M to 0.5 M), ~2.32 min (0.800 M to 0.400 M), and ~2.38 min(0.400 M
to 0.200 M). Since the half-life is constant, the reaction is probably first-order.
(b) average 1
1/2
1/2
(2.37 2.32 2.38) 0.693 0.693
2.36 min 0.294min
3 t 2.36 min
tk
or perhaps better expressed as k = 0.29 min–1 due to imprecision.
Chapter 14: Chemical Kinetics
645
(c) When M. 0.352 [A] min, .53t Then, rate = k[A] = –1
0.294 min 0.352 M 0.103 M/min.
(d) [A] 0.1480 M 0.339 M
Slope Rate 0.0637 M / min Rate 0.064 M/min.
6.00 min 3.00 mint
(e) Rate = k[A] = 0.294 min–1 × 1.000 M = 0.294 M/min.
75. (M) The reaction being investigated is:
-+2+
422 22
2MnO (aq)+5H O (aq)+6H (aq) 2Mn (aq)+8H O(l)+5O (g)
We use the stoichiometric coefficients in this balanced reaction to determine [H2O2].
-
422
-
4
22
0.1000 mmol MnO 5 mmol H O
37.1 mL titrant 1 mL titrant 2 mmol MnO
[H O ] 1.86 M
5.00 mL
76. (D) We assume in each case that 5.00 mL of reacting solution is titrated.
-
-22 4
4-
22 4
-
22 4
2.32 mmol H O 2 mmol MnO 1 mL titrant
volume MnO 5.00 mL 1 mL 5 mmol H O 0.1000 mmol MnO
20.0 2.32 M H O 46.4 mL 0.1000 M MnO titrant at 0 s
At 200 s Vtitrant = 20.0 × 2.01 M H2O2 = 40.2 mL
At 400 s Vtitrant = 20.0 × 1.72 M H2O2 = 34.4 mL
At 600 s Vtitrant = 20.0 × 1.49 M H2O2 = 29.8 mL
At 1200 s Vtitrant = 20.0 × 0.98 M H2O2 = 19.6 mL
At 1800 s Vtitrant = 20.0 × 0.62 M H2O2 = 12.4 mL
At 3000 s Vtitrant = 20.0 × 0.25 M H2O2 = 5.00 mL
The graph of volume of titrant vs. elapsed time is given above. This graph is of approximately the
same shape as Figure 14-2, in which [H2O2] is plotted against time. In order to determine the rate,
the tangent line at 1400 s has been drawn on the graph. The intercepts of the tangent line are at 34
mL of titrant and 2800 s. From this information we determine the rate of the reaction.
-
422
-4
4
0.1000 mol MnO 5 mol H O34 mL 1 L
2800 s 1000 mL 1 L titrant 2 mol MnO
Rate 6.1 10 M/s
0.00500 L sample
This is the same as the value of 6.1 × 10–4 obtained in Figure 14-2 for 1400 s. The discrepancy is
due, no doubt, to the coarse nature of our plot.
0
5.5
11
16.5
22
27.5
33
38.5
0 700 1400 2100 2800
Tangent line

Chapter 14: Chemical Kinetics
646
77. (M) First we compute the change in [H2O2]. This is then used to determine the amount, and
ultimately the volume, of oxygen evolved from the given quantity of solution. Assume the O2(g)
is dry.
3
22
22
22 2
2 2
22
[H O ] 60 s
[H O ] 1.7 10 M/s 1.00 min 0.102 M
1 min
0.102 mol H O 1 mol O
amount O 0.175 L soln 0.00892 mol O
1 L 2 mol H O
t
t
2
2 2
Latm
0.00892 mol O 0.08206 (273 24) K
mol K
Volume O 0.22 L O
1 atm
757 mmHg 760 mmHg
nRT
P
78. (M) We know that rate has the units of M/s, and also that concentration has the units of M. The
generalized rate equation is
0
Rate Ak. In terms of units, this becomes
M/s = {units of k} M0. Therefore 1
10
0
M/s
{Units of } M s
M
k
79. (M)
(a) Comparing the third and the first lines of data, [I-] and [OH-]stay fixed, while [OCl–]
doubles. Also the rate for the third kinetics run is one half of the rate found for the first run.
Thus, the reaction is first-order in [OCl-]. Comparing the fourth and fifth lines, [OCl–] and
[I-] stay fixed, while [OH-] is halved. Also, the fifth run has a reaction rate that is twice that
of the fourth run. Thus, the reaction is minus first-order in [OH-]. Comparing the third and
second lines of data, [OCl-] and [OH-] stay fixed, while the [I-] doubles. Also, the second
run has a reaction rate that is double that found for the third run. Thus, the reaction is first-
order in [I-].
(b) The reaction is first-order in [OCl-] and [I-] and minus first-order in [OH-]. Thus, the overall
order = 1 + 1 – 1 = 1. The reaction is first-order overall.
(c) 41
[OCl ][I ]
Rate [OH ]
Rate [OH ] 4.8 10 M/s 1.00 M
using data from first run: 60. s
[OCl ][I ] 0.0040 M 0.0020 M
k
80. (M) We first determine the number of moles of N2O produced. The partial pressure of N2O(g) in
the “wet” N2O is 756 mmHg – 12.8 mmHg = 743 mmHg.
ON mol 00207.0
K )15273(K mol atm L 0.08206
L 0500.0
mmHg 760
atm 1
mmHg 743
ONamount 2
11
2
RT
PV
Now we determine the change in [NH2NO2].

Chapter 14: Chemical Kinetics
647
22
2
2
22
1
22final
1
0
1 mol NH NO
0.00207 mol N O 1 mol N O
[NH NO ] 0.0125 M
0.165 L soln
0.693
[NH NO ] 0.105 M–0.0125 M 0.093 M 0.00563 min
123 min
[A]
1 1 0.093 M
ln ln 22 min elapsed t
[A] 0.00563 min 0.105 M
t
k
tk
ime
81. (D) We need to determine the partial pressure of ethylene oxide at each time in order to determine
the order of the reaction. First, we need the initial pressure of ethylene oxide. The pressure at
infinite time is the pressure that results when all of the ethylene oxide has decomposed. Because
two moles of product gas are produced for every mole of reactant gas, this infinite pressure is twice
the initial pressure of ethylene oxide. Pinitial = 249.88 mmHg 2 = 124.94 mmHg. Now, at each
time we have the following. 22 4
(CH ) O(g) CH (g) CO(g)
Initial: 124.94 mmHg Changes: –x mmHg +x mmHg +x mmHg Final: 124.94 + x mmHg
Thus, x = Ptot – 124.94 and PEtO = 124.94 – x = 124.94 – (Ptot – 124.94) = 249.88 – Ptot
Hence, we have, the following values for the partial pressure of ethylene oxide.
t, min 0 10 20 40 60 100 200
PEtO, mmHg 124.94 110.74 98.21 77.23 60.73 37.54 11.22
For the reaction to be zero-order, its rate will be constant.
The rate in the first 10 min is: mmHg/min 42.1
mi
n
10
mmHg )94.12474.110(
Rate
The rate in the first 40 min is: mmHg/min 19.1
mi
n
40
mmHg )94.12423.77(
Rate
We conclude from the non-constant rate that the reaction is not zero-order. For the reaction to be
first-order, its half-life must be constant. From 40 min to 100 min—a period of 60 min—the partial
pressure of ethylene oxide is approximately halved, giving an approximate half-life of 60 min.
And, in the first 60 min, the partial pressure of ethylene oxide is approximately halved. Thus, the
reaction appears to be first-order. To verify this tentative conclusion, we use the integrated first-
order rate equation to calculate some values of the rate constant.
1
0
1 1
1 1 110.74 mmHg
ln ln 0.0121 min
10 min 124.94 mmHg
1 37.54 mmHg 1 60.73 mmHg
ln 0.0120 min ln 0.0120 min
100 min 124.94 mmHg 60 min 124.94 mmHg
P
ktP
kk
The constancy of the first-order rate constant suggests that the reaction is first-order.
82. (M) For this first-order reaction kt
P
Pt
0
ln Elapsed time is computed as:
0
ln
1
P
P
k
tt
We first determine the pressure of DTBP when the total pressure equals 2100 mmHg.
Chapter 14: Chemical Kinetics
648
8182 36 26
Reaction: C H O (g) 2C H O(g) C H (g) [Equation 15.16]
Initial: 800.0 mmHg
Changes: – mmHg 2 mmHg mmHg
Final: (800.0 ) mmHg 2 mmHg
xxx
xx
8182
2
2
31
0
mmHg
Total pressure (800.0– ) 2 800.0 2 2100.
650. mmHg {C H O (g)} 800. mmHg 650. mmHg 150. mmHg
1 1 150. mmHg
ln ln 19 min 1.9 10 min
8.7 10 min 800. mmHg
t
x
xxx x
xP
P
tkP
83. (D) If we compare Experiment 1 with Experiment 2, we notice that [B] has been halved, and also
that the rate, expressed as [A]/ t
, has been halved. This is most evident for the times 5 min,
10 min, and 20 min. In Experiment 1, [A] decreases from 1.000 × 10–3 M to 0.779 × 10–3 M in 5
min, while in Experiment 2 this same decrease in [A] requires 10 min. Likewise in Experiment 1,
[A] decreases from 1.000 × 10–3 M to 0.607 M× 10–3 in 10 min, while in Experiment 2 the same
decrease in [A] requires 20 min. This dependence of rate on the first power of concentration is
characteristic of a first-order reaction. This reaction is first-order in [B]. We now turn to the order
of the reaction with respect to [A]. A zero-order reaction will have a constant rate. Determine the
rate
After over the first minute: M/min 109.4
mi
n
1
M 10)000.1951.0(
Rate 5
3
After over the first five minutes: M/min 104.4
mi
n
5
M 10)000.1779.0(
Rate 5
3
After over the first twenty minutes: M/min 102.3
mi
n
20
M 10)000.1368.0(
Rate 5
3
This is not a very constant rate; we conclude that the reaction is not zero-order. There are no clear
half-lives in the data with which we could judge the reaction to be first-order. But we can
determine the value of the first-order rate constant for a few data.
1
0
1 1
1 [A] 1 0.951 mM
ln ln 0.0502 min
[A] 1 min 1.000 mM
1 0.607 mM 1 0.368 mM
ln 0.0499 min ln 0.0500 min
10 min 1.000 mM 20 min 1.000 mM
kt
kk
The constancy of the first-order rate constant indicates that the reaction indeed is first-order in [A].
(As a point of interest, notice that the concentrations chosen in this experiment are such that the
reaction is pseudo-zero-order in [B]. Here, then it is not necessary to consider the variation of [B]
with time as the reaction proceeds when determining the kinetic dependence on [A].)

Chapter 14: Chemical Kinetics
649
84. (M) In Exercise 79 we established the rate law for the iodine-hypochlorite ion reaction:
1
Rate [OCl ][I ][OH ]k
. In the mechanism, the slow step gives the rate law;
3
Rate [I ][HOCl]k
. We use the initial fast equilibrium step to substitute for [HOCl] in this rate
equation. We assume in this fast step that the forward rate equals the reverse rate.
12
121
1
[OCl ][H O]
[OCl ][H O] [HOCl][OH ] [HOCl] [OH ]
k
kk k
12212
2
11
[OCl][HO] [HO]
[OCl ][I ] [OCl ][I ]
Rate [I ] [OH ] [OH ] [OH ]
kkk
kk
kk
This is the same rate law that we established in Exercise 79. We have incorporated [H2O] in the
rate constant for the reaction because, in an aqueous solution, [H2O] remains effectively constant
during the course of the reaction. (The final fast step simply involves the neutralization of the acid
HOI by the base hydroxide ion, OH–.)
85. (M) It is more likely that the cis-isomer, compound (I), would be formed than the trans-isomer,
compound (II). The reason for this is that the reaction will involve the adsorption of both
CH3CCCH3 and H2 onto the surface of the catalyst. These two molecules will eventually be
adjacent to each other. At some point, one of the
bonds in the CC bond will break, the H–H
bond will break, and two C–H bonds will form. Since these two C–H bonds form on the same side
of the carbon chain, compound (I) will be produced. In the sketches below, dotted lines (…)
indicate bonds forming or breaking.
CCCH
3
CH3
HH
CCCH
3
CH3
HH
···
···
···
···
CCCH
3
CH3
HH
86. (D) Hg22+ + Tl3+ 2 Hg2+ + Tl+
2+ 3+
2
2+
[Hg ][Tl ]
Experimental rate law = k [Hg ]
Possible mechanism: Hg22+ + Tl3+ 1
1
k
k
Hg2+ + HgTl3+ (fast)
HgTl
3+ 2
k
Hg2+ + Tl3+ (slow)
Hg
22+ + Tl3+ 2 Hg2+ + Tl+ Rate = k2[HgTl3+]
k1[Hg22+][Tl3+] = -1
k [Hg2+][HgTl3+] rearrange 2+ 3+
3+ 12
2+
-1
[Hg ][Tl ]
[HgTl ] = [Hg ]
k
k
Rate = k2[HgTl3+]2+ 3+ 2+ 3+
21 2 2
obs
2+ 2+
-1
[Hg ][Tl ] [Hg ][Tl ]
= =
[Hg] [Hg]
kk k
k

Chapter 14: Chemical Kinetics
650
87. (M)
3formation disappearance formation decomposition
2
2333 3 3
3
2
33 3 3
3
ΔCCl rate rate 0 so rate rate
Δt
[Cl(g)][CHCl ] [CCl ][[Cl(g)] and, simplifying, [CCl ] [CHCl ]
since rate [CCl ][Cl(g)] [CHCl ]
k
kk k
k
kk
k
23
[Cl(g)] [CHCl ][Cl(g)] k
1/2 1/2
11
2overall232
-1 -1
1/2 1/2
3
2
1
23
-1
We know: [Cl(g)] [Cl (g)] then rate = [CHCl ] [Cl (g)]
4.8 10
and the rate constant will be: (1.3 10 ) 0.015
3.6 10
kk
k
kk
k
kkk
k
88. (D)
t
o
3
3
0t
[A]
t
322
to
0[A]
2
t
d[A] d[A]
Rate = [A] - Rearrange: - t =
dt [A]
Integrate using the limits time (0 to t) and concentration ([A] to [A] )
d[A] 1 1 1 1
-t= t((0))
[A] 2 [A] 2 [A]
11
Simplify: t 2[A] 2[
kk
kkk
k
222
ot0
11
Rearrange : t
A] 2[A] 2[A]
k
22
to
o
12 12 t
12
22
22
oo
o
0
12
11
Multiply through by 2 to give the integrated rate law: 2 t
[A] [A]
[A]
To derive the half life(t ) substitute t =t and [A] = 2
1114
2 t Collect terms
[A] [A]
[A]
[A]
4
2
4
2t
k
k
k
12 12
22 2 2
oo o o
13 3
Solve for t t
[A] [A] [A] 2 [A]k
89. (D) Consider the reaction: A + B products (first-order in A, first-order in B). The initial
concentration of each reactant can be defined as [A]0 and [B]0 Since the stoichiometry is 1:1, we
can define x as the concentration of reactant A and reactant B that is removed (a variable that
changes with time).
The [A]t = ([A]o – x) and [B]t = ([B]o – x).
Algebra note: [A]o – x = – (x – [A]o) and [B]o – x = – (x – [B]o).
Chapter 14: Chemical Kinetics
651
As well, the calculus requires that we use the absolute value of |x – [A]o| and |x – [B]o| when taking
the integral of the reciprocal of |x – [A]o| and |x – [B]o|
tt o o
oo
oo
Note: this i
d[A] d[B] dx dx
Rate = - =- = [A] [B] = ([A] -x)([B] -x) or =
([A] -x)([B] -x)
further ease integration:
1
([B] -[A] )
In order to solve this, partial fraction decomposition is required to
kk kdt
dt
dx
dt dt
oo
s a constant
11
-
([A] -x) ([B] -x) kdt
oo
too
From the point of view of integration, a further rearrangement is desirable (See algebra note above).
1-1-1
x-
([B] -[A] ) x-[A] x-[B]
dkdt
oo
oo
o
oo o
oo
oo
1
Integrate both sides -ln - (-ln ) = t + C
([B] -[A] )
[A] -x and [B] -x Substitute and simplify
([B] -x)
1ln = t + C Determine C by setting = 0
([B] -[A] ) [A] -x
x-[A] x-[B]
x-[A] = x-[B] =
k
kx
at t = 0
o
oo oo o oo
o o
o o
([B] -x)
11 1
C= ln Hence: ln = t + ln
([B] -[A] ) ([B] -[A] ) ([A] -x) ([B] -[A] )
[B] [B]
[A] [A]
k
o
o
o
o
ooo
ooo
o
oo oo
o
ooo o
o
o
([B] -x)
ln = t + ln
([A] -x)
([B] -x)
([A] -x)
([B] -x) [A] ([B] -x)
ln -ln = t = ln = ln
([A] -x) [B] ([A] -x)
[B]
Multiply both sides by([B] -[A] ), hence, ([B] -[A] )× [A]
[B] ([B] -[A] )× [B]
[A]
[A]
k
k
ot
ot
ot ot oo
[A] [B]
Set ln = t
[B] [A]
×
([A] -x)=[A] and ([B] -x)=[B] togive ([B] -[A] )×
×k
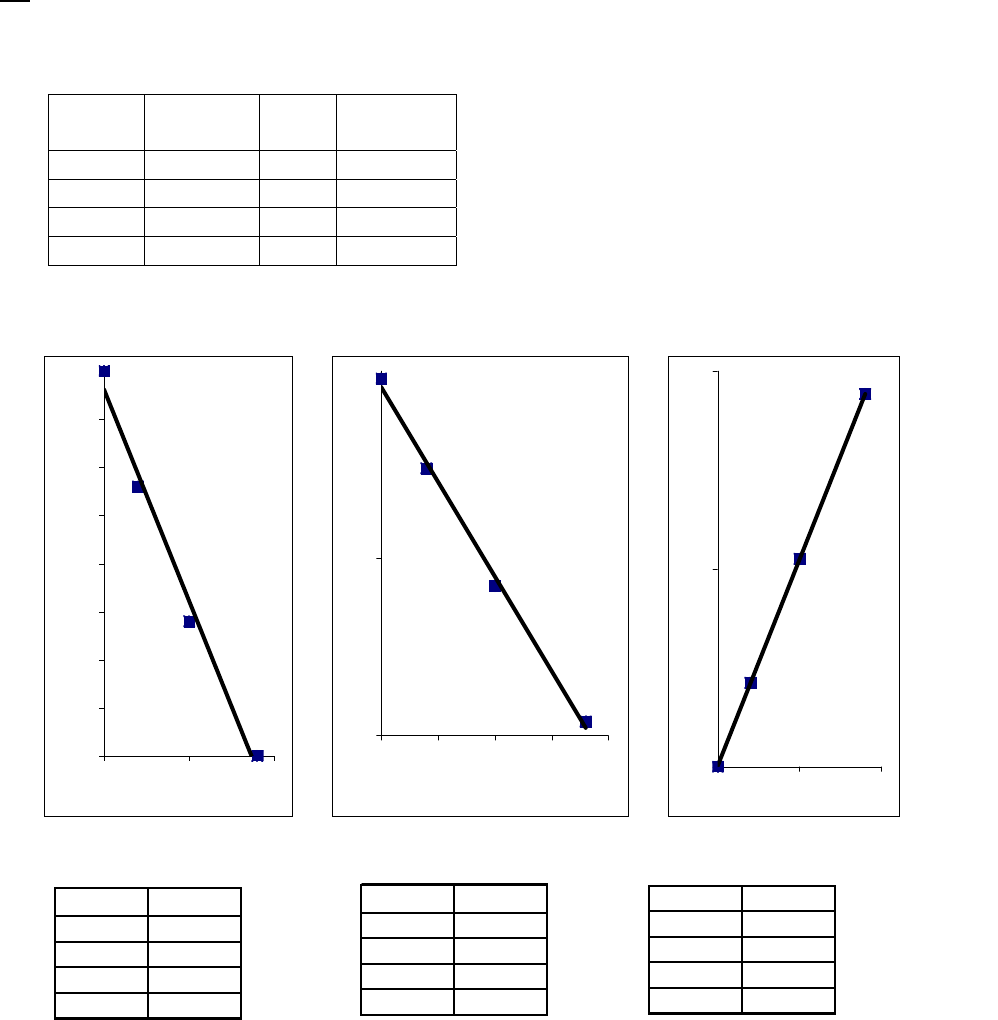
Chapter 14: Chemical Kinetics
652
90. (D) Let 250-2x equal the partial pressure of CO(g) and x be the partial pressure of CO2(g).
2
2CO CO C(s)
250-2
x
x
Ptot =PCO + PCO2 = 250 – 2x +x = 250 – x
Ptot
[torr] Time
[sec] PCO2 P
CO [torr]
250 0 0 250
238 398 12 226
224 1002 26 198
210 1801 40 170
The plots that follow show that the reaction appears to obey a second-order rate law.
Rate = k[CO]2
R2 = 0.9867
170
180
190
200
210
220
230
240
250
0 1000 2000
time (S)
PCO (mmHg)
R2 = 0.9965
5.12
5.32
5.52
0 500 1000 1500 2000
time (S)
ln PCO
R2 = 1
0.004
0.005
0.006
0 1000 2000
time (S)
1/PCO (mmHg-1)
ZERO ORDER PLOT 1st ORDER PLOT 2nd ORDER PLOT
TP
CO
0 250
398 226
1002 198
1801 170
TlnP
CO
0 5.521461
398 5.420535
1002 5.288267
1801 5.135798
T1/CO
00.004
398 0.004425
1002 0.005051
1801 0.005882
(Best
correlation
coefficient)
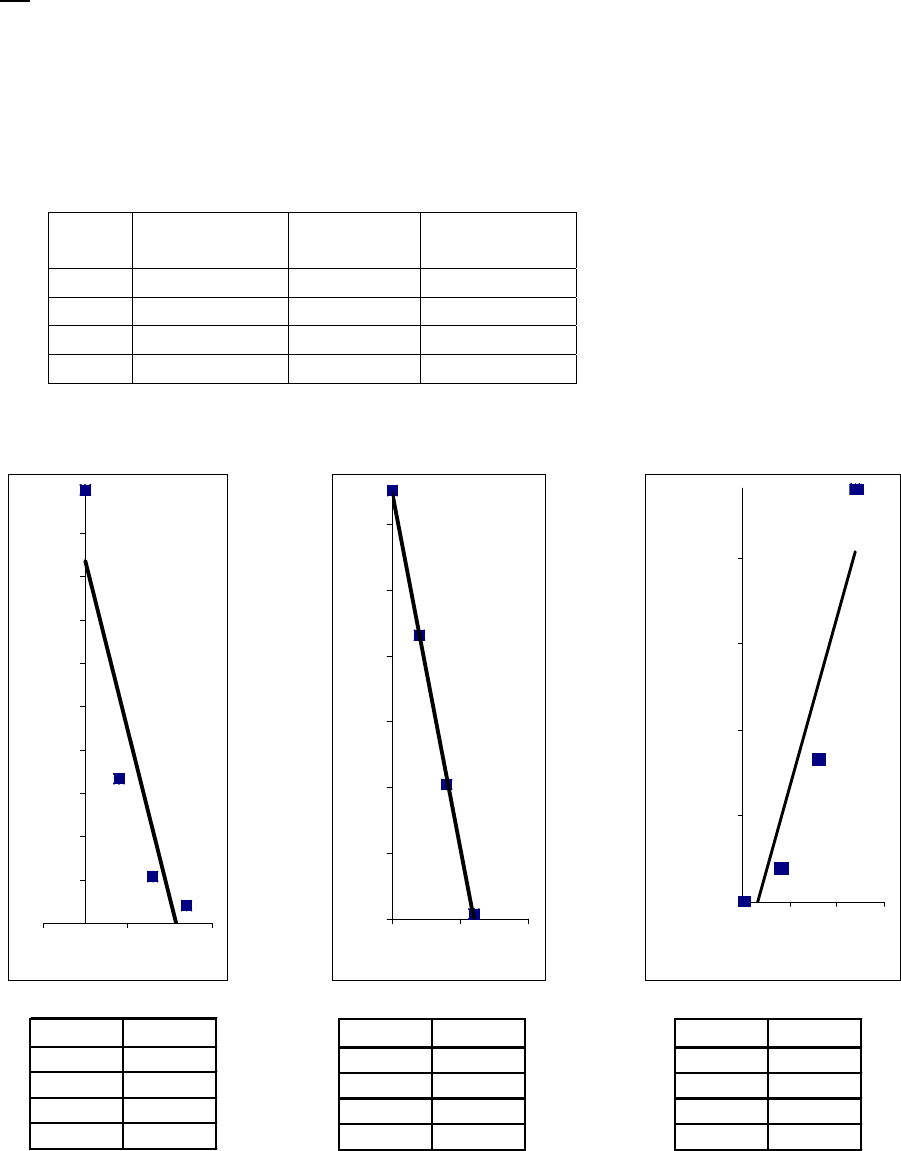
Chapter 14: Chemical Kinetics
653
91. (D) Let 100-4x equal the partial pressure of PH3(g), x be the partial pressure of P4(g)and 6x be the
partial pressure of H2 (g)
34 2
4 PH (g) P ( ) 6 H (g)
100 4 6
g
x
xx
Ptot =PPH3 + PP4 + PH2 = 100 4
x
+ x + 6x = 100+ 3x
Ptot
[torr] Time [sec] PP4 [torr] PPH3 [torr]
100 0 0 100
150 40 50/3 100-(4)(50/3)
167 80 67/3 100-(4)(67/3)
172 120 72/3 100-(4)(72/3)
The plots to follow show that the reaction appears to obey a first-order rate law.
Rate = k[PH3]
R2 = 0.8369
0
10
20
30
40
50
60
70
80
90
100
-50 50 150
time (S)
PPH3 (mmHg)
R2 = 0.9991
1.35
1.85
2.35
2.85
3.35
3.85
4.35
0 100 200
time (S)
ln PPH3
ZERO ORDER PLOT 1st ORDER PLOT 2nd ORDER PLOT
TP
PH3
0 100
40 33.3
80 10.7
120 4
TlnP
PH3
04.61
40 3.51
80 2.37
120 1.39
T1/P
PH3
00.010
40 0.030
80 0.093
120 0.250
R
2
= 0.8652
0.010
0.060
0.110
0.160
0.210
0 50 100 150
time (S)
1/P
PH3
(mmHg
-1
)
Chapter 14: Chemical Kinetics
654
92. (D) Consider the following equilibria.
1 I
2
-1
kK
k
k
2
1-121 -12
E + S ES E + P E + I EI
d[P]
Product production = k [ES] Use the steady state approximation for [ES]
dt
d[ES] = k [E][S] k [ES] k [ES] = k [E][S] [ES] k k = 0
dt
solve f
-1 2 1
M
1-12M
I
I
o
MI
kk k[E][S]
[E][S]
or [ES] Keep in mind K = [ES] = =
kkkK
[E][I] [E][I]
Formation of EI: K = [EI] =
[EI] K
[E][S] [E][I]
[E ] = [E] + [ES] + [EI] = [E] + +
KK
o
o
MI
MI
[E ]
[S] [I]
[E ] = [E] 1 + + Solve for [E] [E] =
KK [S] [I]
1 + +
KK
o
MM
M M
MI
oo
M
MM
II
[S]
[E ] KK
[E][S]
From above: [ES] = [ES] = multiplication by affords
KK
[S] [I]
1 + +
KK
[E ][S] [E ][S]
[ES] = =
[I]K [I]
K + [S] + K 1 + + [S]
KK
d[P]
Remember dt
2o
2
M
I
max
2o max
M
I
k[E][S]
= k [ES] =
[I]
K1 + + [S]
K
V[S]
d[P]
If we substitute k [E ] = V then =
dt [I]
K1 + + [S]
K
Thus, as [I] increases, the ratio max
M
I
V[S]
[I]
K1 + + [S]
K
decreases;
i.e., the rate of product formation decreases as [I] increases.
Chapter 14: Chemical Kinetics
655
93. (D) In order to determine a value for KM, we need to rearrange the equation so that we may obtain
a linear plot and extract parameters from the slope and intercepts.
2o MM
M 2o2o2o
M
2o 2o
k[E][S] K+[S] K
1[S]
V = = = +
K +[S] V k [E ][S] k [E ][S] k [E ][S]
K
11
= + We need to have this in the form of y = mx+b
Vk[E][S]k[E]
11
Plot on the y-axis and on the x-axis. See result below:
V[S]
x-intercept
= -1 y-intercept
=
KM
k2[Eo]
1
1
[S]
[V]
1
K
M
k
2
[E
o
]
slope =
The plot of 1/V vs 1/[S] should yield a slope of M
2o
K
k[E]
and a
y-intercept of
2o
1
k[E]
. The x-intercept = -1/KM
2o
M
2o 2o 2o M M
-k [E ]
K11 1 -1
0 = =
k[E] [S] k[E] [S] k[E] K K
To find the value of KM take the negative inverse of x-intercept.
To find k2, invert the y-intercept and divide by the [Eo].
94. (M)
a) The first elementary step HOOBrOHBr k1
2 is rate-determining if the reaction obeys
reaction rate = k [HBr][O2] since the rate of this step is identical to that of the experimental rate
law.
b) No, mechanisms cannot be shown to be absolutely correct, only consistent with experimental
observations.
c) Yes; the sum of the elementary steps (3 HBr + O2 HOBr + Br2 + H2O) is not consistent with
the overall stoichiometry (since HOBr is not detected as a product) of the reaction and
therefore cannot be considered a valid mechanism.
95. (M)
(a) Both reactions are first-order, because they involve the decomposition of one molecule.
(b) k2 is the slow reaction.
(c) To determine the concentration of the product, N2, we must first determine how much reactant
remains at the end of the given time period, from which we can calculate the amount of
reactant consumed and therefore the amount of product produced. Since this is a first-order
reaction, the concentration of the reactant, N2O after time t is determined as follows:
kt
t0
1
2 2
0.1
AAe
N O 2.0 M exp 25.7 s 0.1s 0.153 M N O remaining
Chapter 14: Chemical Kinetics
656
The amount of N2O consumed = 2.0 M – 0.153 M =1.847 M
2
22
1MN
[N ] 1.847 M NO 0.9235 M N
2M NO
(d) The process is identical to step (c).
1
2 2
0.1
N O 4.0 M exp 18.2 s 0.025 s 2.538 M N O remaining
The amount of N2O consumed = 4.0 M – 2.538 M =1.462 M
2
22
1MN O
[N O] 1.462 M NO 0.731M N O
2M NO
FEATURE PROBLEMS
96. (D)
(a) To determine the order of the reaction, we need CHNCl
652 at each time. To determine
this value, note that 58.3 mL
2
Ng evolved corresponds to total depletion of C H N Cl
652 ,
to CHNCl M
652 = 0.000 .
Thus, at any point in time, C H N Cl M volume N g M C H N Cl
mL N g
652 2 652
2
= 0.071 0.071
58.3
F
H
G
I
K
J
bgbg
Consider 21 min:
652
652 2
2
0.071 M C H N Cl
C H N Cl = 0.071 M 44.3 mL N = 0.017 M
58.3 mL N g
The numbers in the following table are determined with this method.
Time, min 0 3 6 9 12 15 18 21 24 27 30
2
N
V, mL 0 10.8 19.3 26.3 32.4 37.3 41.3 44.3 46.5 48.4 50.4 58.3
652
CHNCl, mM 71 58 47 39 32 26 21 17 14 12 10 0
[The concentration is given in thousandths of a mole per liter (mM).]
(b)
time(min) 0 3 6 9 12 15 18 21 24 27 30
T(min) 3 3 3 3 3 3 3 3 3 3
[C
6
H
5
N
2
Cl](mM) 71 58 47 39 32 26 21 17 14 12 10
[C
6
H
5
N
2
Cl](mM) -13 -11 -8 -7 -6 -5 -4 -3 -2 -2
Reaction Rate (mM min
-1
) 4.3 3.7 2.7 2.3 2.0 1.7 1.3 1.0 0.7 0.7
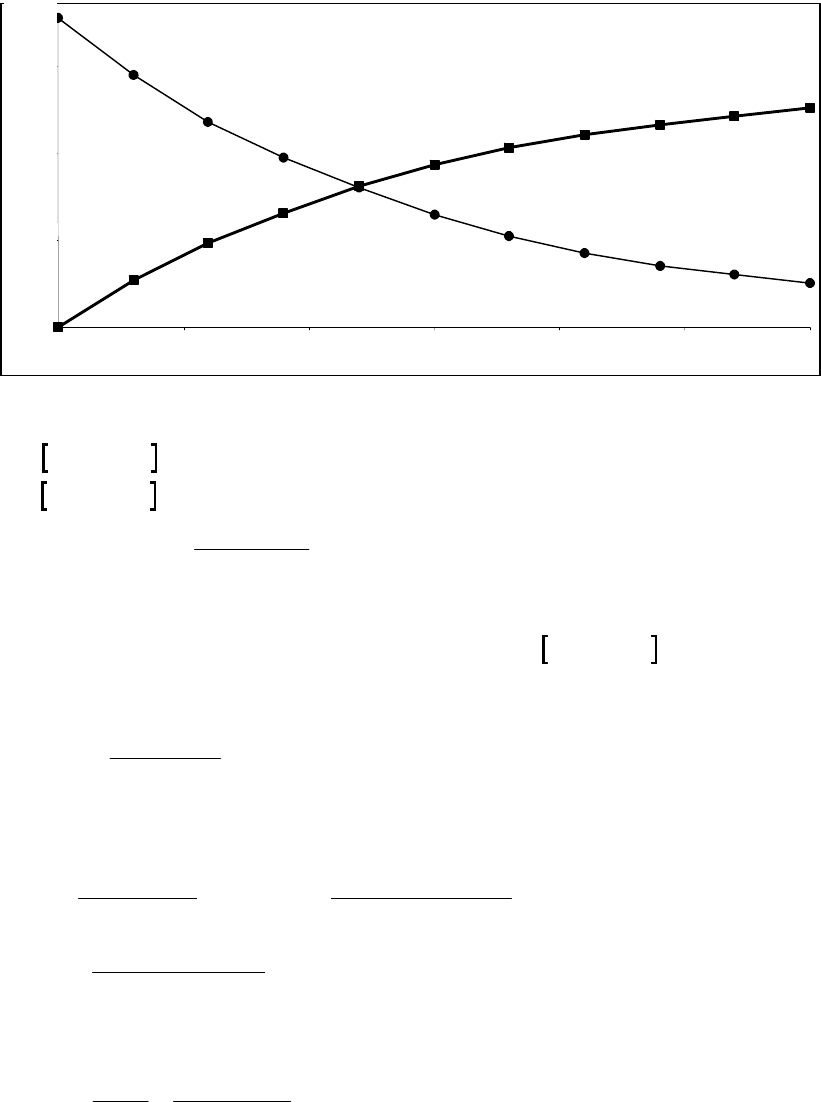
Chapter 14: Chemical Kinetics
657
(c) The two graphs are drawn on the same axes.
(d) The rate of the reaction at t= 21 min is the slope of the tangent line to the
CHNCl
652 curve. The tangent line intercepts the vertical axis at about
CHNCl mM
652 = 39 and the horizontal axis at about 37 min
331 31
5
39 10 M
Reaction rate = = 1.0 10 M min = 1.1 10 M min
37 min
The agreement with the reported value is very good.
(e) The initial rate is the slope of the tangent line to the CHNCl
652 curve at t=0. The
intercept with the vertical axis is 71 mM, of course. That with the horizontal axis is about
13 min.
331
71 10 M
Rate = = 5.5 10 M min
13 min
(f) The first-order rate law is
652
Rate = C H N Clk, which we solve for k:
652
Rate
=CHNCl
k 31 1
03
5.5 10 M min
= = 0.077 min
71 10 M
k
31 1
21 3
1.1 10 Mmin
= = 0.065 min
17 10 M
k
An average value would be a reasonable estimate: kavg min= 0.071 1
(g) The estimated rate constant gives one value of the half-life:
tk
1/2 1
=0.693 =0.693
0.071 =9.8
min min
The first half-life occurs when
652
CHNCl drops from 0.071 M to 0.0355 M. This occurs
at about 10.5 min.
(h) The reaction should be three-fourths complete in two half-lives, or about 20 minutes.
Plot of [C6H5N2Cl] and VN versus time
0
20
40
60
0 5 10 15 20 25 30
time (min)
[C
6
H
5
N
2
Cl]
(m
M)
or
V
N
2
(m
L)
2
mL of N
2
[C
6
H
5
N
2
Cl]
[C6H5N2Cl (mM) or VN
2
(
mL
)
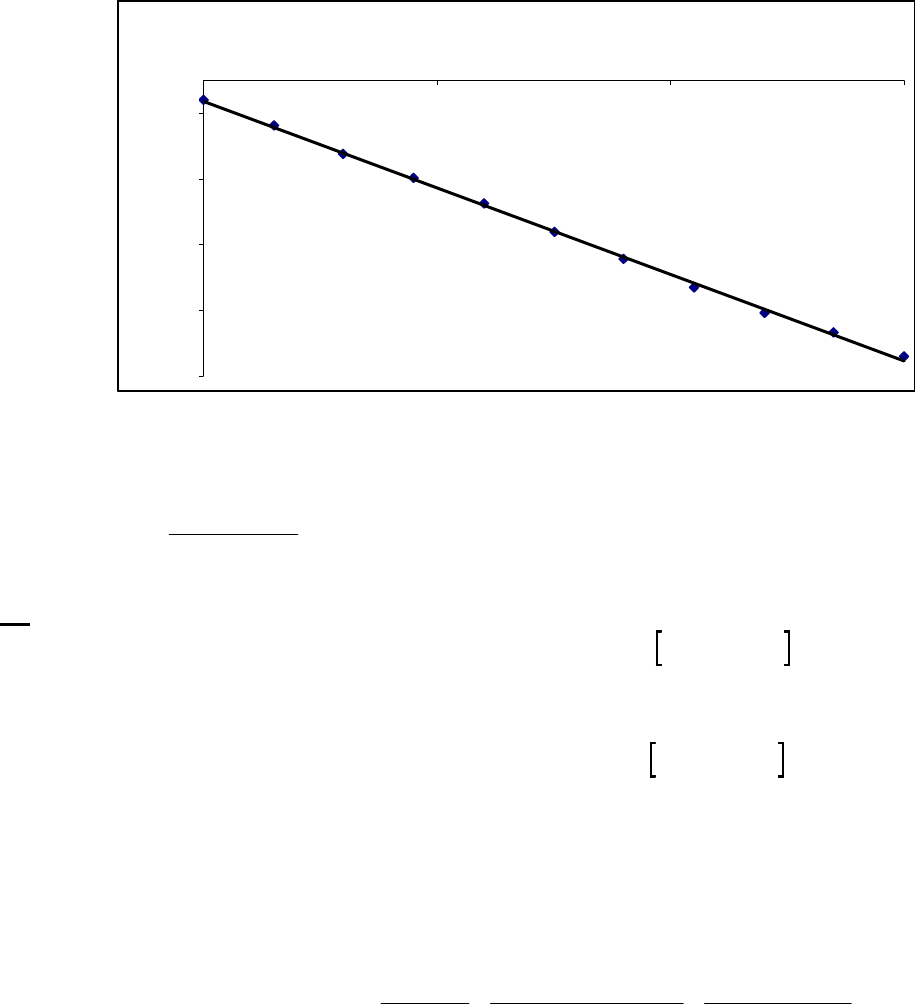
Chapter 14: Chemical Kinetics
658
(i) The graph plots ln
652
CHNCl (in millimoles/L) vs. time in minutes.
The linearity of the graph demonstrates that the reaction is first-order.
(j)
21 1
= slope = 6.61 10 min = 0.0661 mink
1/2 1
0.693
= =10.5 min
0.0661 min
t, in good agreement with our previously determined values.
97. (D)
(a) In Experiments 1 & 2, [KI] is the same (0.20 M), while NH S O
4228
bg is halved, from 0.20
M to 0.10 M. As a consequence, the time to produce a color change doubles (i.e., the rate is
halved). This indicates that reaction (a) is first-order in 2
28
SO
. Experiments 2 and 3
produce a similar conclusion. In Experiments 4 and 5, NH S O
4228
bgis the same (0.20 M)
while [KI] is halved, from 0.10 to 0.050 M. As a consequence, the time to produce a color
change nearly doubles, that is, the rate is halved. This indicates that reaction (a) is also first-
order in I. Reaction (a) is (1 + 1) second-order overall.
(b) The blue color appears when all the S O3
2
2
has been consumed, for only then does reaction
(b) cease. The same amount of S O32 2 is placed in each reaction mixture.
2
2 4
22 3 2 3
23
22 3
0.010 mol Na S O 1 mol S O
1 L
amount S O = 10.0 mL = 1.0 10 mol
1000 mL 1 L 1 mol Na S O
Through stoichiometry, we determine the amount of each reactant that reacts before this
amount of 2
23
SO will be consumed.
Plot of ln[C
6
H
5
N
2
Cl] versus time
y = -0.0661x - 2.66
-4.75
-4.25
-3.75
-3.25
-2.75
0102030
Time (min)
ln[C
6
H
5
N
2
Cl]
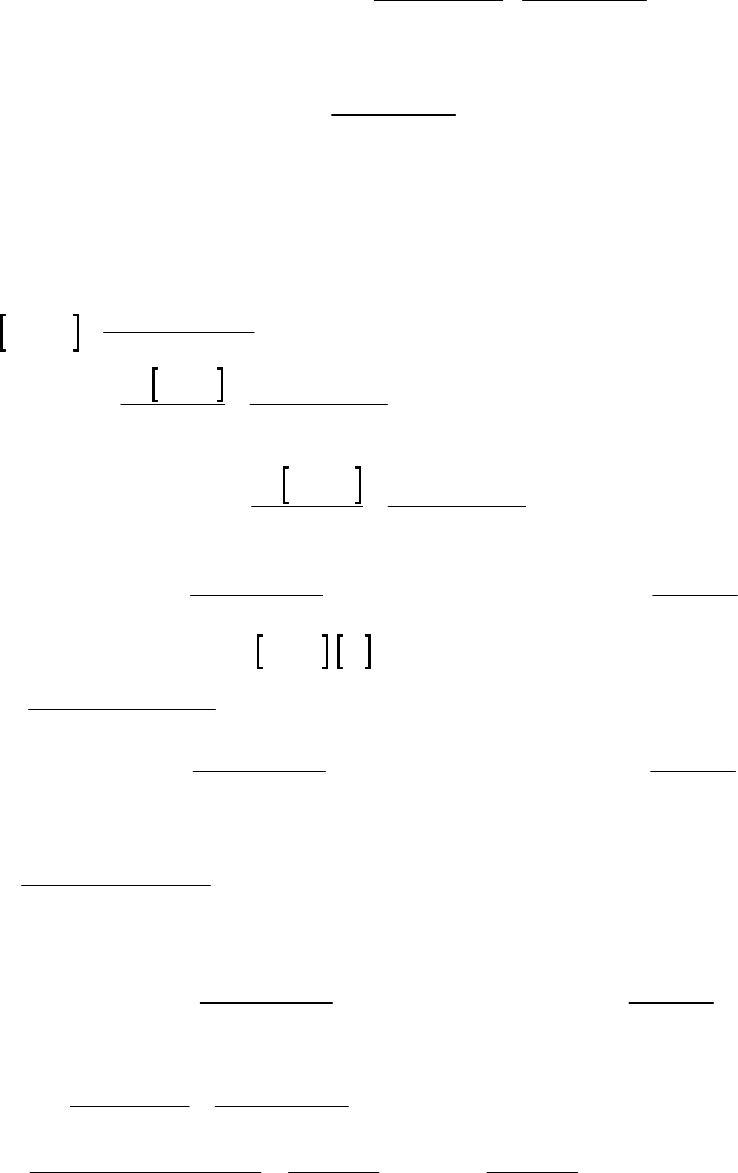
Chapter 14: Chemical Kinetics
659
2
22
4328
28 23 2
23 3
2
5
28
1 mol I 1 mol S O
amount S O 1.0 10 mol S O 2 mol S O 1 mol I
= 5.0 10 mol S O
2
54
28 2
28
2 mol I
amount I = 5.0 10 mol S O =1.0 10 mol I
1 mol S O
Note that we do not use “3 mol I
” from equation (a) since one mole has not been
oxidized; it simply complexes with the product I2. The total volume of each solution
is
25.0 mL + 25.0 mL +10.0 mL +5.0 mL = 65.0 mL , or 0.0650 L.
The amount of 2
28
SO that reacts in each case is 5.0 10 5
mol and thus
SO mol
L M
28
254
=5.0 10
0.0650 =7.710
Thus, Rate SO M
s M s
8
1
22451
==
+7.7 10
21 =3.7 10
t
(c) For Experiment 2, Rate SO M
s M s
2
28
2451
==
+7.7 10
42 =1.8 10
t
To determine the value of
k
, we need initial concentrations, as altered by dilution.
2
28 1 1
25.0 mL 25.0 mL
S O = 0.20 M = 0.077 M I = 0.20 M = 0.077 M
65.0 mL total 65.0 mL
Rate M s S O I M M
8
2
151 2
11 11
= 3.7 10 = = 0.077 0.077
kk
bgbg
51 311
3.7 10 M s
==6.210 M s
0.077 M 0.077 M
k
2
28 2 2
25.0 mL 25.0 mL
S O = 0.10 M = 0.038 M I = 0.20 M = 0.077 M
65.0 mL total 65.0 mL
11 11
51 2
228
Rate = 1.8 10 M s = S O I = 0.038 M 0.077 Mkk
k=1.8 10
0.038 0.077 =6.2 10
51 311
M s
M M M s
(d) First we determine concentrations for Experiment 4.
2
28 4
4
25.0 mL 25.0 mL
S O = 0.20 M = 0.077 M I = 0.10 = 0.038 M
65.0 mL total 65.0 mL
We have two expressions for Rate; let us equate them and solve for the rate constant.
2411
28 2
428
4
4
SO +7.7 10 M
Rate = = = S O I = 0.077 M 0.038 Mkk
tt
411
11
3
7.7 10 M 0.26 M 0.26 M
= = = = 0.0014 M s
0.077 M 0.038 M 189 s
kk
tt
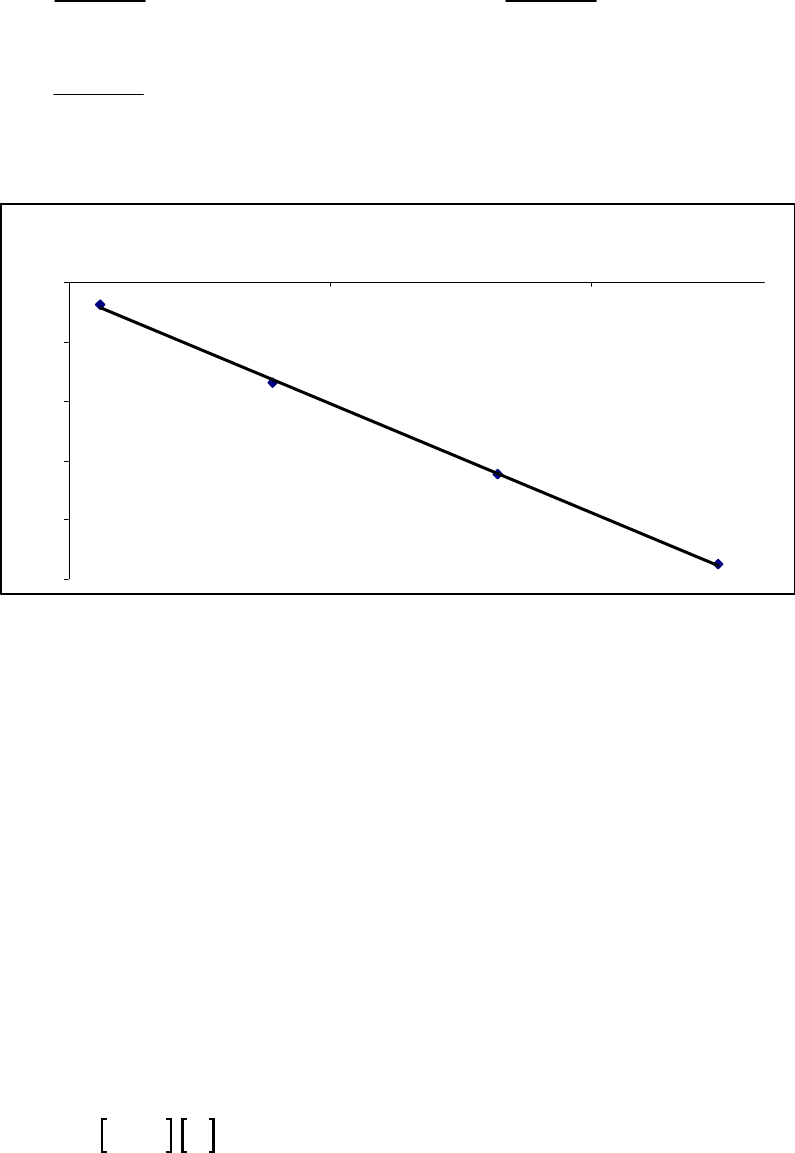
Chapter 14: Chemical Kinetics
660
11
11 11
13 24
0.26 M 0.26 M
= = 0.0030 M s = = 0.0062 M s
88 s 42 s
kk
111
33
0.26 M
= = 0.012 M s
21 s
k
(e) We plot l
n
k vs. 1/
T
The slope of the line = /
ER
a.
11 3
a= +6135 K 8.3145 J mol K = 51.0 10 J/mol = 51.0 kJ/molE
The scatter of the data permits only a two significant figure result: 51 kJ/mol
(f) For the mechanism to agree with the reaction stoichiometry, the steps of the mechanism
must sum to the overall reaction, in the manner of Hess's law.
(slow) I +S O IS O
88
3
222
(fast) IS O SO I
8
34
2
2+
2+
(fast) I I I
+2
+
(fast) I I I32 +
(net) 3 + 2 +
2
ISO SO I
8
24
23
Each of the intermediates cancels: IS O8
3
2
is produced in the first step and consumed in the
second, I+is produced in the second step and consumed in the third, 2
Iis produced in the
third step and consumed in the fourth. The mechanism is consistent with the stoichiometry.
The rate of the slow step of the mechanism is
Rate S O I
8
2
112
11
=k
This is exactly the same as the experimental rate law. It is reasonable that the first step be
slow since it involves two negatively charged species coming together. We know that like
charges repel, and thus this should not be an easy or rapid process.
Plot of ln k versus 1/T
y = -6135x + 16
-6
-5.5
-5
-4.5
-4
-3.5
0.00325 0.0034 0.00355
1/T (K
-1
)
ln k

Chapter 14: Chemical Kinetics
661
SELF-ASSESSMENT EXERCISES
98. (E)
(a) [A]0: Initial concentration of reactant A
(b) k: Reaction rate constant, which is the proportionality constant between reaction rate and
reactant concentration
(c) t1/2: Half-life of the reaction, the amount of time that the concentration of a certain reactant is
reduced by half
(d) Zero-order reaction: A reaction in which the rate is not dependent on the concentration of the
reactant
(e) Catalyst: A substance which speeds up the reaction by lowering the activation energy, but it
does not itself get consumed
99. (E)
(a) Method of initial rates: A study of the kinetics of the reaction by measuring the initial reaction
rates, used to determine the reaction order
(b) Activated complex: Species that exist in a transitory state between the reactants and the
products
(c) Reaction mechanism: Sequential elementary steps that show the conversion of reactant(s) to
final product(s)
(d) Heterogeneous Catalyst: A catalyst which is in a different physical phase than the reaction
medium
(e) Rate-determining step: A reaction which occurs more slowly than other reactions in a
mechanism and therefore usually controls the overall rate of the reaction
100. (E)
(a) First-order and second-order reactions: In a first-order reaction, the rate of the reaction
depends on the concentration of only one substrate and in a 1-to-1 manner (doubling the
concentration of the reactant doubles the rate of the reaction). In a second-order reaction, the
rate depends on two molecules reacting with each other at the elementary level.
(b) Rate law and integrated rate law: Rate law describes how the rate relates to the concentration
of the reactants and the overall rate of a reaction, whereas the integrated rate law expresses the
concentration of a reactant as a function of time
(c) Activation energy and enthalpy of reaction: Activation energy is the minimum energy
required for a particular reaction to take place, whereas enthalpy of reaction is the amount of
heat generated (or consumed) by a reaction when it happens
(d) Elementary process and overall reaction: Individual steps of a reaction mechanism, which
describes any molecular event that significantly alters a molecule’s energy or geometry or
produces a new molecule
(e) Enzyme and substrate: An enzyme is a protein that acts as a catalyst for a biological reaction.
A substrate is the reactant that is transformed in the reaction (in this context, by the enzyme).
101. (E) The answer is (c). The rate constant k is only dependent on temperature, not on the
concentration of the reactants
Chapter 14: Chemical Kinetics
662
102. (E) The answers are (b) and (e). Because half-life is 75 seconds, the quantity of reactant left at
two half-lives (75 + 75 = 150) equals one-half of the level at 75 seconds. Also, if the initial
concentration is doubled, after one half-life the remaining concentration would have to be twice
as much as the original concentration.
103. (E) The answer is (a). Half-life t½ = 13.9 min, k = ln 2/t½ = 0.050 min-1. Rate of a first-order
reaction is as follows:
11
dA k A 0.050 min 0.40 M 0.020 M min
dt
104. (E) The answer is (d). A second-order reaction is expressed as follows:
2
dA kA
dt
If the rate of the reaction when [A] =0.50 is k(0.50)2 = k(0.25). If [A] = 0.25 M, then the rate is
k(0.0625), which is ¼ of the rate at [A] =0.50.
105. (M) The answer is (b). Going to slightly higher temperatures broadens the molecular speed
distribution, which in turn increases the fraction of molecules at the high kinetic energy range
(which are those sufficiently energetic to make a reaction happen).
106. (E) The answer is (c). Since the reaction at hand is described as an elementary one, the rate of the
reaction is k[A][B].
107. (E) We note that from the given data, the half-life of the reaction is 100 seconds (at t = 0, [A] =
0.88 M/s, whereas at t = 100, [A] = 0.44 M/s). Therefore, the rate constant k is:
k = ln 2/100 s = 0.00693 s-1. We can now calculate instantaneous rate of the reaction:
d[A]/dt = (0.00693 s-1)(0.44 M) = 3.0×10-3 M·s-1
108. (M)
(a) For a first-order reaction,
1
1/2
t0
t0
1
ln 2 0.693
k 0.0231min
t30
ln[A] ln[A] kt
ln 0.25 0
ln[A] ln[A]
t 60.0 min
k 0.0231min
(b) For a zero-order reaction,
1
1/2
t0
t0
1
0.5 0.5
k 0.0167 min
t30
[A] [A] kt
[A] [A] 0.25 1.00
t 45.0 min
k 0.0167 min
Chapter 14: Chemical Kinetics
663
109. (M) The reaction is second-order, because the half-life doubles with each successive half-life
period.
110. (M)
(a) The initial rate = ΔM/Δt = (1.204 M – 1.180 M)/(1.0 min) = 0.024 M/min
(b) In experiment 2, the initial concentration is twice that of experiment A. For a second-order
reaction:
Rate = k [Aexp 2]2 = k [2×Aexp 1]2 = 4 k [Aexp 1]2
This means that if the reaction is second order, its initial rate of experiment 2 will be 4 times that
of experiment 1 (that is, 4 times as many moles of A will be consumed in a given amount of
time). The initial rate is 4×0.024 M/min = 0.096 M/s. Therefore, at 1 minute, [A] = 2.408 –
0.0960 = 2.312 M.
(c) The half-life of the reaction, obtained from experiment 1, is 35 minutes. If the reaction is
first-order, then k = ln 2/35 min = 0.0198 min-1.
For a first-order reaction,
kt
t0
-1
35min
AAe
A 2.408 exp 0.0198 min 30 min 1.33 M
111. (D) The overall stoichiometry of the reaction is determined by adding the two reactions with each
other: A + 2B C + D
(a) Since I is made slowly but is used very quickly, its rate of formation is essentially zero. The
amount of I at any given time during the reaction can be expressed as follows:
12
1
2
dI 0kAB kBI
dt
k
IA
k
Using the above expression for [I], we can now determine the overall reaction rate law:
1
22 1
2
dC k
kIB k A B kAB
dt k
(b) Adding the two reactions given, we still get the same overall stoichiometry as part (a).
However, with the given proposed reaction mechanisms, the rate law for the product(s) is given
as follows:
Chapter 14: Chemical Kinetics
664
2
2
1122
2
1
2
12
2
21
22
12
dB kB k B kAB 0
dt
kB
BkkA
Therefore,
dC kk A B
kAB
dt k k A
which does not agree with the observed reaction rate law.
112. (M) The answer is (b), first-order, because only in a first-order reaction is the half-life
independent of the concentration of the reacting species.
113. (E) The answer is (a), zero-order, because in a zero-order reaction the relationship between
concentration and time is: [A]t = kt + [A]0
114. (M) The answer is (d). The relationship between rate constant (and thus rate) between two
reactions can be expressed as follows:
2
112
kEa11
exp
kRTT
If T2 is twice T1, the above expression gets modified as follows:
a
2
111
21
a1 1
R
E
21
11
kEa11
ln kRT2T
kT1
Rln ,
Ek2T
kT1
ln k2T
a
a
R
E
21
11
R
E1/2
2
1
For reasonably high temperatures,
kT1
ln k2T2
Therefore,
ke 1.64
k

Chapter 14: Chemical Kinetics
665
115. (E) The answer is (c), remain the same. This is because for a zero-order reaction,
d[A]/dt = k[A]0 = k. Therefore, the reaction rate is independent of the concentration of the
reactant.
116. (M) The overarching concept for this concept map is kinetics as a result of successful collision.
The subtopics are collision theory, molecular transition theory. Molecular speed and orientation
derive from collision theory. Transition complexes and partial bonds fall under the molecular
transition theory heading. Deriving from the collision theory is another major topic, the
Arrhenius relationship. The Arrhenius relationship encompasses the ideas of activation energy,
Arrhenius collision factor, and exponential relationship between temperature and rate constant.
666
CHAPTER 15
PRINCIPLES OF CHEMICAL EQUILIBRIUM
PRACTICE EXAMPLES
1A (E) The reaction is as follows:
22 4
2Cu(aq)Sn(aq) 2Cu(aq)Sn(aq)
Therefore, the equilibrium expression is as follows:
24
2
22
Cu Sn
KCu Sn
Rearranging and solving for Cu2+, the following expression is obtained:
1/2
21/2
+4+ 2
2+
2+
Cu Sn
Cu = 1.48 1.22
KSn
x
xx
x
1B (E) The reaction is as follows:
32 2 2
2
2Fe (aq) Hg (aq) 2Fe (aq) 2Hg (aq)
Therefore, the equilibrium expression is as follows:
22 22
22
6
22
32
2
Fe Hg 0.0025 0.0018
K9.1410
0.015 x
Fe Hg
Rearranging and solving for Hg22+, the following expression is obtained:
22 22
22
2
222
6
3
Fe Hg 0.0025 0.0018
Hg 0.009847 0.0098 M
0.015 9.14 10
Fe K
2A (E) The example gives Kc = 5.8×105 for the reaction
22 3
Ng+3 Hg 2 NHg
.
The reaction we are considering is one-third of this reaction. If we divide the reaction by
3, we should take the cube root of the equilibrium constant to obtain the value of the
equilibrium constant for the “divided” reaction: 35 2
3
c3 c 5.8 10 8.3 10KK
2B (E) First we reverse the given reaction to put NO g
2bg on the reactant side. The new
equilibrium constant is the inverse of the given one.
2
1
22c
2
NO g NO g + O g ' = 1/ (1.2 10 ) = 0.0083K
Then we double the reaction to obtain 2 moles of NO g
2bg as reactant. The equilibrium
constant is then raised to the second power.
25
22c
2 NO g 2 NO g +O g = 0.00833 = 6.9 10
K
Chapter15: Principles of Chemical Equilibrium
667
3A (E) We use the expression
pc
=
g
as
n
KKRT
. In this case,
ngas = 3+1 2 = 2 and thus we
have
22
96
pc
= = 2.8 10 0.08314 298 = 1.7 10KKRT
3B (M) We begin by writing the Kp expression. We then substitute
/=[ ]P n V RT concentration RT for each pressure. We collect terms to obtain an expression
relating Kc and Kp, into which we substitute to find the value of Kc.
KPP
P
RT RT
RT RT K RT
p222
2
2
222
2
2
22
2
2c
H)} S
HS)}
H)
HS]
[H [S
[H S]
{( {( )}
{(
([ ] ([S ] )
([ )
]]
2
The same result can be obtained by using KKRT
n
pc
gas
=bg, since
ngas =2+1 2=+1.
2
p4
c
1.2 10
== =1.110
0.08314 1065 + 273
K
KRT
But the reaction has been reversed and halved. Thus Kfinal=4
11
9091 95
1.1 10
c
K
4A (E) We remember that neither solids, such as Ca PO OH(s)
543
() , nor liquids, such as 2
HO(l),
appear in the equilibrium constant expression. Concentrations of products appear in the
numerator, those of reactants in the denominator. Kc
Ca HPO
H
=
2+ 5
4
23
+4
4B (E) First we write the balanced chemical equation for the reaction. Then we write the
equilibrium constant expressions, remembering that gases and solutes in aqueous solution
appear in the Kc expression, but pure liquids and pure solids do not.
2342
3 Fes+4 HOg FeO s+4 H g
KP
PKnKK
pc gaspc
H
HO
H
HO Because == =44=0,=
24
24
2
4
2
4
{}
{}
bg
bg
5A (M) We compute the value of Qc. Each concentration equals the mass m
bg of the substance
divided by its molar mass (this quotient is the amount of the substance in moles) and further
divided by the volume of the container.
Chapter15: Principles of Chemical Equilibrium
668
22
22
c c
2
2
22
2
1 mol CO 1 mol H
1
44.0 g CO 2.0 g H
CO H 28.0 18.0
44.0 2.0
==5.71.00=
1 mol H O 1
1 mol CO
CO H O 44.0 2.0
18.0 g H O 28.0 18.0
28.0 g CO
mm
VV
Q K
m
m
VV
(In evaluating the expression above, we cancelled the equal values of V, and we also
cancelled the equal values of m.) Because the value of Qc is larger than the value of Kc,
the reaction will proceed to the left to reach a state of equilibrium. Thus, at equilibrium
there will be greater quantities of reactants, and smaller quantities of products than there
were initially.
5B (M) We compare the value of the reaction quotient,
p
Q, to that of
p
K.
32
p
5
{(PCl)}{(Cl)} 2.19 0.88
= = = 0.098
{ (PCl } 19.7
PP
QP
21 1 1
pc c
= = = 0.0454 0.08206 (261 273) =1.99KKRT KRT
Because QK
cc
, the net reaction will proceed to the right, forming products and consuming
reactants.
6A (E) Og
2bg is a reactant. The equilibrium system will shift right, forming product in an
attempt to consume some of the added O2(g) reactant. Looked at in another way, O2 is
increased above its equilibrium value by the addition of oxygen. This makes Qc smaller
than Kc. (The O2 is in the denominator of the expression.) And the system shifts right to
drive Qc back up to Kc, at which point equilibrium will have been achieved.
6B (M)
(a) The position of an equilibrium mixture is affected only by changing the concentration
of substances that appear in the equilibrium constant expression, Kc=2
CO . Since
CaO(s) is a pure solid, its concentration does not appear in the equilibrium constant
expression and thus adding extra CaO(s) will have no direct effect on the position of
equilibrium.
(b) The addition of CO g
2bg will increase CO2 above its equilibrium value. The reaction
will shift left to alleviate this increase, causing some CaCO s
3bg to form.
(c) Since CaCO3(s) is a pure solid like CaO(s), its concentration does not appear in the
equilibrium constant expression and thus the addition of any solid CaCO3 to an
equilibrium mixture will not have an effect upon the position of equilibrium.
Chapter15: Principles of Chemical Equilibrium
669
7A (E) We know that a decrease in volume or an increase in pressure of an equilibrium mixture
of gases causes a net reaction in the direction producing the smaller number of moles of gas.
In the reaction in question, that direction is to the left: one mole of N O g
24
bg is formed when
two moles of NO g
2bg combine. Thus, decreasing the cylinder volume would have the initial
effect of doubling both NO
24
and NO2. In order to reestablish equilibrium, some NO2
will then be converted into N2O4. Note, however, that the NO2 concentration will still
ultimately end up being higher than it was prior to pressurization.
7B (E) In the balanced chemical equation for the chemical reaction,
ngas =1+1 1+1=0
bgbg.
As a consequence, a change in overall volume or total gas pressure will have no effect on the
position of equilibrium. In the equilibrium constant expression, the two partial pressures in
the numerator will be affected to exactly the same degree, as will the two partial pressures in
the denominator, and, as a result, Qp will continue to equal Kp.
8A (E) The cited reaction is endothermic. Raising the temperature on an equilibrium mixture
favors the endothermic reaction. Thus, N O g
24
bg should decompose more completely at
higher temperatures and the amount of NO g
2bg formed from a given amount of N O g
24
bg
will be greater at high temperatures than at low ones.
8B (E) The NH3(g) formation reaction is
o
3
122 3
22
N g + H g NH g , = 46.11 kJ/mol.H
This reaction is an exothermic reaction. Lowering temperature causes a shift in the direction
of this exothermic reaction to the right toward products. Thus, the equilibrium NH g
3bg will
be greater at 100 C
.
9A (E) We write the expression for Kc and then substitute expressions for molar concentrations.
2
24
22
c22
2
0.22 0.11
[H ] [S ] 3.00 3.00 2.3 10
[H S] 2.78
3.00
K
9B (M) We write the equilibrium constant expression and solve for NO
24
.
222
22
3
c24
33
24
NO NO 0.0236
= 4.61 10 = N O = = = 0.121 M
NO 4.61 10 4.61 10
K
Then we determine the mass of NO
24
present in 2.26 L.
NO mass L mol N O
L
g N O
mol N O g N O
24 24 24
24
24
=2.26 0.121
1
92.01
1= 25.2
Chapter15: Principles of Chemical Equilibrium
670
10A (M) We use the initial-change-equilibrium setup to establish the amount of each substance
at equilibrium. We then label each entry in the table in the order of its determination (1st,
2nd, 3rd, 4th, 5th), to better illustrate the technique. We know the initial amounts of all
substances (1st). There are no products at the start.
Because ‘‘initial’’ ‘‘change’’ ‘‘equilibrium’’+= , the equilibrium amount (2nd) of
2
Br g
enables us to determine “change” (3rd) for Br g
2bg. We then use stoichiometry to write other
entries (4th) on the “change” line. And finally, we determine the remaining equilibrium
amounts (5th).
Reaction:
2
2 NOBr g 2 NO g + Br g
Initial: 1.86 mol (1st) 0.00 mol (1st) 0.00 mol (1st)
Change: 0.164 mol (4th) +0.164 mol (4th) +0.082 mol (3rd)
Equil.: 1.70 mol (5th) 0.164 mol (5th) 0.082 mol (2nd)
2
24
2
c22
0.164 0.082 mol
5.00 5.00
[NO] [Br ] 1.5 10
[NOBr] 1.70
5.00
K
Here, gas =2+1 2=+1.n
+1 43
pc
= =1.5 10 0.08314 298 = 3.7 10KKRT
10B (M) Use the amounts stated in the problem to determine the equilibrium concentration for
each substance.
Reaction:
322
2 SO g 2 SO g + O g
Initial: 0 mol 0.100 mol 0.100 mol
Changes: +0.0916 mol
0.0916 mol
0.0916 / 2 mol
Equil.: 0.0916 mol 0.0084 mol 0.0542 mol
Concentrations: 0.0916 mol
1.52 L 0.0084
1.52
mol
L 0.0542
1.52
mol
L
Concentrations: 0.0603 M 0.0055 M 0.0357 M
We use these values to compute Kc for the reaction and then the relationship
KKRT
n
pc
gas
=bg (with gas =2+1 2=+1)n to determine the value of Kp.
22
22 4
c22
3
4
p
SO O 0.0055 0.0357
== =3.010
0.0603
SO
= 3.0 10 (0.08314 900) 0.022
K
K

Chapter15: Principles of Chemical Equilibrium
671
11A (M) The equilibrium constant expression is KP P
pHO} CO= = 0.231
22
{ { } at 100 C. From
the balanced chemical equation, we see that one mole of H O g
2bg is formed for each mole of
CO g
2bg produced. Consequently, PP{{}HO} CO
22
= and KP
pCO=2
2
{}
bg. We solve this
expression for 2
{CO } :P 2
22p
{CO } ( {CO }) 0.231 0.481 atm.PP K
11B (M) The equation for the reaction is
432p
NH HS s NH g + H S g , = 0.108 at 25 C.K
The two partial pressures do not have to be equal at equilibrium. The only instance in which
they must be equal is when the two gases come solely from the decomposition of NH HS s
4bg.
In this case, some of the NH g
3bg has come from another source. We can obtain the pressure
of H S g
2bg by substitution into the equilibrium constant expression, since we are given the
equilibrium pressure of NH g
3bg.
p2 3 2 32
0.108
= {H S} {NH } = 0.108 = {H S} 0.500 atm NH {H S} = = 0.216 atm
0.500
KP P P P
So, Ptotal = 3
2NH
HS
PP= 0.216 atm + 0.500 atm = 0.716 atm
12A (M) We set up this problem in the same manner that we have previously employed, namely
designating the equilibrium amount of HI as 2
x
. (Note that we have used the same
multipliers for
x
as the stoichiometric coefficients.)
Equation:
22
Hg + Ig 2 HIg
Initial: 0.150 mol 0.200 mol 0 mol
Changes:
x
mol
x
mol +2
x
mol
Equil: 0.150 x
bg mol 0.200
x
bg mol 2
x
mol
2
2
c
2
2
15.0 = = 50.2
0.150 0.200 0.150 0.200
15.0 15.0
x
x
Kxx xx
We substitute these terms into the equilibrium constant expression and solve for x.
4 = 0.150 0.200 50.2 = 50.2 0.0300 0.350 + = 1.51 17.6 + 50.2
222
xxx xx xx
bgbg ch
2
0 = 46.2 17.6 +1.51 Now we use the quadratic equation to determine the value of .
x
xx
xbb ac
a
=4
2=17.6 (17.6) 4 46.2 1.51
2 46.2 =17.6 5.54
92.4 = 0.250 0.131
22
or
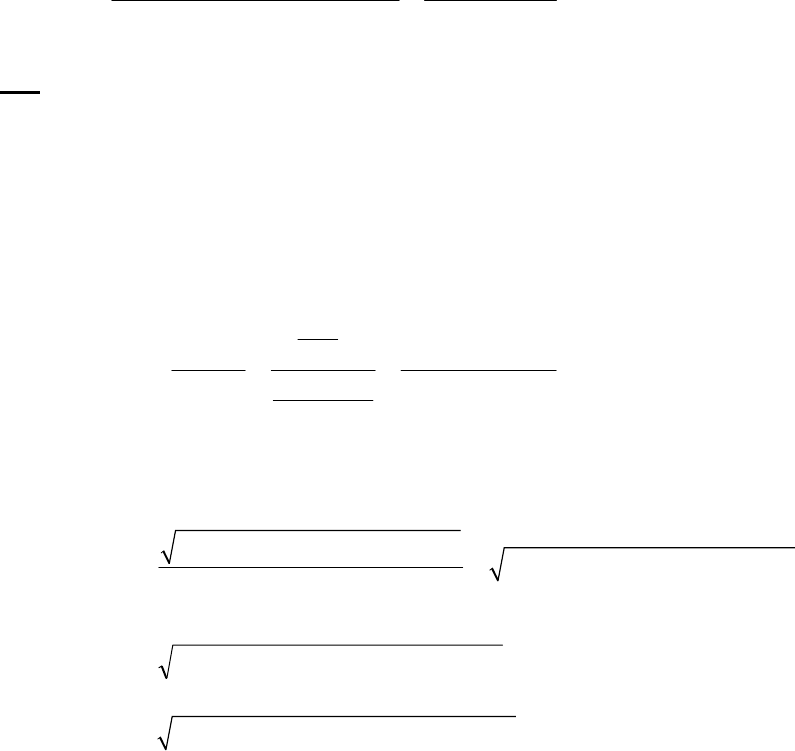
Chapter15: Principles of Chemical Equilibrium
672
The first root cannot be used because it would afford a negative amount of H2 (namely,
0.150-0.250 = -0.100). Thus, we have 2 0.131= 0.262
mol HI at equilibrium. We check
by substituting the amounts into the Kc expression. (Notice that the volumes cancel.) The
slight disagreement in the two values (52 compared to 50.2) is the result of rounding error.
Kc=0.262
0.150 0.131 0.200 0.131 =0.0686
0.019 0.069 =52
2
bg
bgbg
12B (D)
(a) The equation for the reaction is
3
24 2 c
N O g 2 NO g and = 4.61 10K
at 25C.
In the example, this reaction is conducted in a 0.372 L flask. The effect of moving the
mixture to the larger, 10.0 L container is that the reaction will be shifted to produce a
greater number of moles of gas. Thus, NO g
2bg will be produced and N O g
24
bg will
dissociate. Consequently, the amount of N O
24
will decrease.
(b) The equilibrium constant expression, substituting 10.0 L for 0.372 L, follows.
K
x
x
x
x
c2
24
NO
[N O
F
H
G
I
K
J
[]
]
.
.
.
.(. ) .
2
2
23
2
10 0
0 0240
10 0
4
10 0 0 0240 461 10
This can be solved with the quadratic equation, and the sensible result is
x
= 0.0118
moles. We can attempt the method of successive approximations. First, assume that
x
0.0240. We obtain:
3
3
4.61 10 10.0 (0.0240 0) 4.61 10 2.50 (0.0240 0) 0.0166
4
x
Clearly
x
is not much smaller than 0.0240. So, second, assume
x
0.0166 . We obtain:
x
4 61 10 2 50 0 0240 0 0166 0 00925
3
..(..).
This assumption is not valid either. So, third, assume
x
0.00925 . We obtain:
3
4.61 10 2.50(0.0240 0.00925) 0.0130x
Notice that after each cycle the value we obtain for
x
gets closer to the value obtained
from the roots of the equation. The values from the next several cycles follow.
Cycle 4th 5
th 6
th 7
th 8
th 9
th 10th 11th
x value 0.0112 0.0121 0.0117 0.0119 0.01181 0.01186 0.01183 0.01184
The amount of N O
24
at equilibrium is 0.0118 mol, less than the 0.0210 mol N O
24
at
equilibrium in the 0.372 L flask, as predicted.
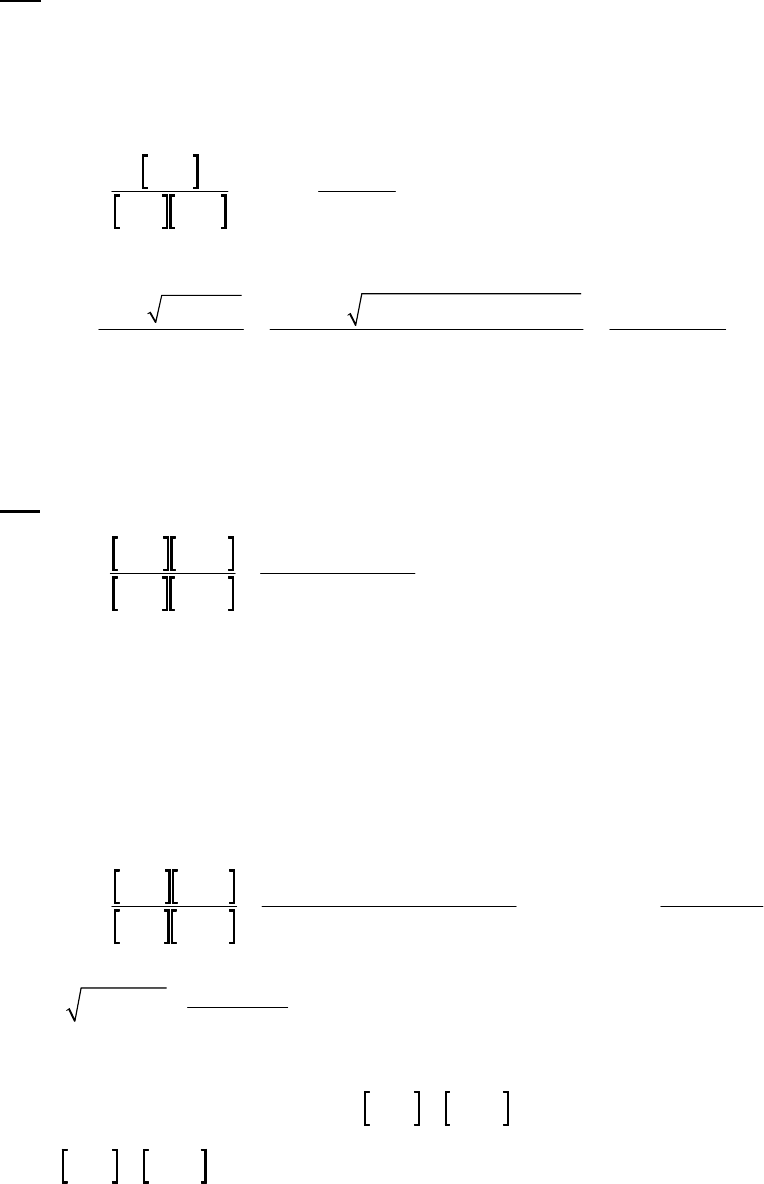
Chapter15: Principles of Chemical Equilibrium
673
13A (M) Again we base our solution on the balanced chemical equation.
Equation:
+2+ 3+ c
Ag aq + Fe aq Fe aq + Ag s = 2.98K
Initial: 0 M 0 M 1.20 M
Changes: +
x
M +
x
M
x
M
Equil:
x
M
x
M 1.20
x
bg M
Kx
xxx xx
c
Fe
Ag Fe
= = 2.98 = 1.20 2.98 = 1.20 0 = 2.98 + 1.20
3+
+2+ 2
22
We use the quadratic formula to obtain a solution.
2
21.00 (1.00) + 4 2.98 1.20
41.003.91
= = = = 0.488 M or 0.824 M
2 2 2.98 5.96
bb ac
xa
A negative root makes no physical sense. We obtain the equilibrium concentrations from x.
+2+ 3+
Ag = Fe = 0.488 M Fe =1.20 0.488 = 0.71 M
13B (M) We first calculate the value of Qc to determine the direction of the reaction.
QK
c c
V Cr
V Cr
==
0.150 0.150
0.0100 0.0100 = 225 7.2 10 =
2+ 3+
3+ 2+
2
Because the reaction quotient has a smaller value than the equilibrium constant, a net
reaction to the right will occur. We now set up this solution as we have others, heretofore,
based on the balanced chemical equation.
3+ 2+ 2+ 3+
V aq + Cr aq V aq + Cr aq
initial 0.0100 M 0.0100 M 0.150 M 0.150 M
changes –x M –x M +x M +x M
equil (0.0100 – x)M (0.0100 – x)M (0.150 + x)M (0.150 + x)M
Kxx
xx
x
x
c
V Cr
V Cr
==
0.150 + 0.150 +
0.0100 0.0100 =7.2 10 = 0.150 +
0.0100
2+ 3+
3+ 2+
2
2
bgbg
bgbg
F
H
G
I
K
J
If we take the square root of both sides of this expression, we obtain
20.150
7.2 10 27
0.0100
x
x
0.150 + x = 0.27 – 27x which becomes 28 = 0.12x and yields 0.0043 M. Then the
equilibrium concentrations are: V Cr M M M
3+ 2+
= = 0.0100 0.0043 = 0.0057
V Cr M M M
2+ 3+
= = 0.150 + 0.0043 = 0.154
Chapter15: Principles of Chemical Equilibrium
674
INTEGRATIVE EXAMPLE
A. (E) We will determine the concentration of F6P and the final enthalpy by adding the two
reactions:
6126
6126
CH O ATP G6P ADP
G6P F6P
CH O ATP ADP F6P
ΔHTOT = –19.74 kJ·mol-1 + 2.84 kJ·mol-1 = –16.9 kJ·mol-1
Since the overall reaction is obtained by adding the two individual reactions, then the overall
reaction equilibrium constant is the product of the two individual K values. That is,
12
K K K 1278
The equilibrium concentrations of the reactants and products is determined as follows:
C
6H12O6 + ATP ADP + F6P
Initial 1.20×10-6 1×10-4 1×10-2 0
Change -x -x +x +x
Equil 1.20×10-6-x 1×10-4-x 1×10-2+x x
6126
222
10 4 2
64
ADP F6P
CH O ATP
110 1.0 10
1278 1.2 10 1.012 10
1.20 10 1 10
K
xx xx
x
x
xx
Expanding and rearranging the above equation yields the following second-order polynomial:
1277 x2 – 0.1393 x + 1.534×10-7 = 0
Using the quadratic equation to solve for x, we obtain two roots: x = 1.113×10-6 and
1.080×10-4. Only the first one makes physical sense, because it is less than the initial value of
C6H12O6. Therefore, [F6P]eq = 1.113×10-6.
During a fever, the body generates heat. Since the net reaction above is exothermic,
Le Châtelier's principle would force the equilibrium to the left, reducing the amount of F6P
generated.

Chapter15: Principles of Chemical Equilibrium
675
B. (E)
(a) The ideal gas law can be used for this reaction, since we are relating vapor pressure and
concentration. Since K = 3.3×10-29 for decomposition of Br2 to Br (very small), then it can be
ignored.
1
0.100 mol 0.08206 L atm K 298.15 K
nRT
V8.47L
P 0.289 atm
(b) At 1000 K, there is much more Br being generated from the decomposition of Br2.
However, K is still rather small, and this decomposition does not notably affect the volume
needed.
EXERCISES
Writing Equilibrium Constants Expressions
1. (E)
(a)
24
224 c
2
2
CO CF
2 COF g CO g + CF g K = COF
(b)
2+
+2+
c2
+
Cu
Cu s + 2 Ag aq Cu aq + 2 Ag s K = Ag
(c)
22
23+
4
22
2+ 3+
28 4 c 2
22+
28
SO Fe
S O aq + 2 Fe aq 2 SO aq + 2 Fe aq = SO Fe
K
2. (E)
(a)
26
22
32 2 2 P 43
32
PN PHO
4 NH g +3 O g 2 N g + 6 H O g = PNH PO
K
(b)
24
32
22 32 P
72
22
PNH PHO
7 H g + 2 NO g 2 NH g + 4 H O g = PH PNO
K
(c)
3
223 c
2
CO
N g + Na CO s + 4 C s 2 NaCN s +3 CO g = N
K
3. (E)
(a)
2
2
c2
2
NO
=NO O
K (b) Kc
Zn
Ag
=
2+
+2 (c) Kc
OH
CO
=
2
3
2

Chapter15: Principles of Chemical Equilibrium
676
4. (E)
(a) KP
P
p
{CH }P{H S}
{CS }P{H
=42
2
22
4
} (b) KP
pO= 2
1/2
lq
(c) KP P
pCO H O}=22
{}{
5. (E) In each case we write the equation for the formation reaction and then the equilibrium
constant expression, Kc, for that reaction.
(a)
11
22 c
22 1/2 1/2
22
HF
Hg+ Fg HFg =
HF
K
(b)
2
3
22 3 c 3
22
NH
Ng+3 Hg 2 NHg =
NH
K
(c)
2
2
22 2 c
2
22
[N O]
2 N g + O g 2 N O g = [N ] [O ]
K
(d) 3
122 3 c
22 1/2 3/2
22
1
Cl (g)+ F (g) ClF (l) [Cl ] [F ]
K
6. (E) In each case we write the equation for the formation reaction and then the equilibrium
constant expression, Kp, for that reaction.
(a)
22 2
NOCl
111
22 2 P
222 1/2 1/2 1/2
NOCl
P
N g + O g + Cl g NOCl g = PPP
K
(b)
2
22 2
2
ClNO
222 2 P 2
NO Cl
P
Ng + 2 Og+ Clg 2 ClNOg =
PP P
K
(c)
24
22
NH
22 24 P 2
NH
P
Ng + 2 Hg NHg =
PP
K
(d)
222
11
22 2 4 P
22 1/2 2 1/2
NCl
1
N g + 2 H g + Cl g NH Cl s = PPP
H
K
7. (E) Since
pc
=
g
n
KKRT
, it is also true that
cp
=
g
n
KKRT
.
(a)
(1)
22 -2 -1
cp
22
SO [Cl ]
= = = 2.9 10 (0.08206 303) = 0.0012
SO Cl
KKRT
(b)
2
(1)
245
cp
2
2
NO
= = =1.48 10 (0.08206 303) = 5.55 10
NO [O ]
KKRT
(c)
3
0
2
cpp
3
2
HS
= = = = 0.429
H
KKRTK

Chapter15: Principles of Chemical Equilibrium
677
8. (E)
pc
=
g
n
KKRT
, with 11
= 0.08206 L atm mol KR
(a) 2+1 -3 1
2
pc
24
P{NO }
= (RT) = 4.61 × 10 (0.08206×298) 0.113
P{N O }
KK
(b) 3(2) 2 3
22 2
pc
2
4
P{C H }P{H } K (RT) (0.154)(0.08206 2000) 4.15 10
P{CH }
K
(c) 4(2) 8 2 4
22
pc
2
24
P{H } P{CS }
K K (RT) (5.27 10 )(0.08206 973) 3.36 10
P{H S} P{CH }
9. (E) The equilibrium reaction is
22
HOl HOg
with
ngas =+1.
pc
=
g
n
KKRT
gives
cp
=
g
n
KKRT
. KP
p2
= {H O} = 23.8 mmHg 1 atm
760 mmHg =0
.0313
1p-3
cp
K0.0313
= = = = 1.28 10
RT 0.08206 298
KKRT
10. (E) The equilibrium rxn is
66 66
CH l CH g
with
ngas =+1. Using
pc
=
g
n
KKRT
,
3
p
c66
= = 5.12 10 0.08206 298 = 0.125 = {C H }KKRT P
66
760 mmHg
{C H } = 0.125 atm = 95.0 mmHg
1 atm
P
11. (E) Add one-half of the reversed 1st reaction with the 2nd reaction to obtain the desired
reaction.
11
22 c
22 30
1
Ng+Og NOg =2.1 10
K
12 c
2
NO g + Br g NOBr g =1.4K
16
111
22 2 c
222 30
1.4
net : N g + O g + Br g NOBr g = = 9.7 10
2.1 10
K
12. (M) We combine the several given reactions to obtain the net reaction.
222c
2
18
1
2 N O g 2 N g O (g) = 2.7 10
K
224 c2
3
1
4 NO g 2 N O g = 4.6 10
K
94
22 2c
4
9
6
22 24() 22
18 3
2 N (g) + 4O (g) 4NO (g) (4.1 10 )
4.1 10
net : 2 N O g + 3 O g 2 N O g = = 1.8 10
2.7 10 4.6 10
cNet
K
K

Chapter15: Principles of Chemical Equilibrium
678
13. (M) We combine the Kc values to obtain the value of Kc for the overall reaction, and then
convert this to a value for Kp.
2
22 2 c
2 CO g+2H g 2 COg+2 HOg =1.4K
2
8
2
2 C graphite + O g 2 CO g = 1 10
c
K
22
1
4 CO g 2 C graphite + 2 CO g =
0.64
c
K
net: 282 6
22 2 c(Net) 2
(1.4) (1 10 )
2H (g)+O (g) 2H O(g) 5 10
(0.64)
K
16 14
pc
510
=== =510
0.08206 1200
nc
K
KKRT RT
14. (M) We combine the Kp values to obtain the value of Kp for the overall reaction, and then
convert this to a value for Kc.
2
22p
2
1
2 NO Cl g 2 NOCl g + O g = 1.1 10
K
2
22 2 p
2 NO g + Cl g 2 NO Cl g = 0.3K
92
22 2 p
N g + 2 O g 2 NO g = (1.0 10 )K
net: 292 24
222 p(Net) 22
(0.3) (1.0 10 )
N (g) + O (g) + Cl (g) 2 NOCl(g) 7.4 10
(1.1 10 )
K
24
p22
pc c 23
7.4 10
====210
0.08206 298
n
n
K
KKRT K RT
15. (E) 22 23
CO (g) H O(l) H CO (aq)
In terms of concentration, K = a(H2CO3)/a(CO2)
In terms of concentration and partial pressure,
2
23
CO
HCO c
KPP
16. (E) 223
2 Fe(s) 3 O (g) Fe O (s)
23
2
Fe O
Fe O
a
Kaa
. Since activity of solids and liquids is defined as 1, then the expression
simplifies to
2
O
1
Ka
Similarly, in terms of pressure and concentration,
2
O
K1P/P

Chapter15: Principles of Chemical Equilibrium
679
Experimental Determination of Equilibrium Constants
17. (M) First, we determine the concentration of PCl5 and of Cl2 present initially and at
equilibrium, respectively. Then we use the balanced equation to help us determine the
concentration of each species present at equilibrium.
34
52
5 2
1.00 10 mol PCl 9.65 10 mol Cl
PCl = = 0.00400 M Cl = = 0.00386 M
0.250 L 0.250 L
initial equil
Equation:
532
PCl g PCl (g) + Cl g
Initial: 0.00400M 0 M 0 M
Changes: –xM +xM +xM
Equil: 0.00400M-xM xM xM 0.00386 M (from above)
At equilibrium, [Cl2] = [PCl3] = 0.00386 M and [PCl5] = 0.00400M – xM = 0.00014 M
32
c
5
PCl Cl (0.00386M)(0.00386M)
PCl 0.00014M
K = 0.106
18. (M) First we determine the partial pressure of each gas.
2
2
2
initial 2
1molH 0.08206Latm
1.00g H 1670K
2.016g H molK
{H g }= = 136atm
0.500L
nRT
PV
2
2
2
initial 2
1molH S 0.08206Latm
1.06g H S 1670K
34.08g H S molK
{H S g }= = 8.52atm
0.500L
nRT
PV
6
2
3
equil 2
0.08206Latm
8.00 10 mol S 1670K
mol K
{S g }= = 2.19 10 atm
0.500L
nRT
PV
22 2
Equation: 2 H g + S g 2 H S g
Initial : 136 atm 0 atm 8.52 atm
Changes : +0.00438atm 0.00219 atm 0.00438 atm
Equil : 136 atm 0.00219 atm 8.52 atm
2
2
2
p22
22
{H S g } 8.52
===1.79
{H g } P{S (g)} 136 0.00219
P
KP

Chapter15: Principles of Chemical Equilibrium
680
19. (M)
(a) Kc
5
32
55
33 22
PCl
PCl Cl
gPCl
L
mol PCl
g
gPCl
L
mol PCl
g
gCl
L
molCl
g
==
0105
250
1
208 2
0 220
250
1
137 3
212
250
1
70 9
26 3
L
N
MO
Q
PL
N
MO
Q
P
F
H
GI
K
J
F
H
GI
K
J
.
..
.
..
.
..
.
(b) KKRT
n
pc
= = 26.3 0.08206 523 = 0.613
1
bgbg
20. (M)
-3
initial
1 mol ICl
0.682 g ICl×162.36 g ICl
[ICl] = = 6.72×10 M
0.625 L
Reaction: 2 ICl(g)
I2(g) + Cl2(g)
Initial: 6.72 × 10-3 M 0 M 0 M
Change -2x +x +x
Equilibrium 6.72 × 10-3 M -2x x x
2
2
-4
2
2 equil
1 mol I
0.0383 g I × 253.808 g I
[I ] = = 2.41×10 M
0.625L = x
42 6
c334
(2.41 10 )
9.31 10
(6.72 10 2 ) (6.72 10 2(2.41 10 ))
xx
Kx
21. (E)
33
3
33
7
318
Fe Fe
K 9.1 10
H1.0 10
Fe 9.1 10 M
22. (E)
33
3
9
3
NH (g) NH (g)
911
NH (g)
NH (aq) 510
K 57.5
PP
P 5 10 57.5 8.7 10

Chapter15: Principles of Chemical Equilibrium
681
Equilibrium Relationships
23. (M)
22
33 2
c22
3
22 2
SO SO SO
0.185 L 0.185
=281= = = = 0.516
0.00247 mol SO 0.00247 281
SO O SO
K
24. (M)
2
2
c2
2
0.37mol I
I10.14
0.011 0.14 13L
1.00molI
I 0.011
V
KV
V
V
25. (M)
(a) A possible equation for the oxidation of NH g
3bg to NO g
2bg follows.
73
32 2 2
42
NH g + O g NO g + H O g
(b) We obtain p
K for the reaction in part (a) by appropriately combining the values of
p
K given in the problem.
19
53
32 2
42
NH g + O g NO g + H O g = 2.11 10
p
K
122 p
2
1
NO g + O g NO g = 0.524
K
19 19
73
32 22
42
2.11 10
net: NH g + O g NO g + H O g = = 4.03 10
0.524
p
K
26. (D)
(a) We first determine [H2] and [CH4] and then [C2H2]. [CH4] = [H2] = 0.10 mol
1.0 L = 0.10 M
32
2
22 2 c 4
c22
23
3
42
CH H CH 0.154 0.10
= C H = = = 1.54 M
0.10
CH H
K
K
In a 1.00 L container, each concentration numerically equals the molar quantities of
the substance.
22
22
22 4 2
1.54 mol C H
{C H } = = 0.89
1.54 mol C H + 0.10 mol CH + 0.10 mol H
(b) The conversion of CH4(g) to C2H2(g) is favored at low pressures, since the conversion
reaction has a larger sum of the stoichiometric coefficients of gaseous products (4) than
of reactants (2).
(c) Initially, all concentrations are halved when the mixture is transferred to a flask that is
twice as large. To re-establish equilibrium, the system reacts to the right, forming more
moles of gas (to compensate for the drop in pressure). We base our solution on the
balanced chemical equation, in the manner we have used before.
Chapter15: Principles of Chemical Equilibrium
682
422 2
Equation: 2 CH (g) C H (g) + 3 H
0.10mol 1.5mol 0.10mol
Initial: 2.00L 2.00L 2.00L
= 0.050 M = 0.75 M = 0.050 M
Changes: 2 M + M +3 M
Equil: 0.050 2 M 0.0750 + M 0.050 + 3 M
xx x
xxx
33
22 2
c22
4
CH H 0.050 + 3 0.750 +
= = = 0.154
0.050 2
CH
xx
Kx
We can solve this 4th-order equation by successive approximations.
First guess:
x
= 0.010 M .
33
c22
0.050 + 3 0.010 0.750 + 0.010 0.080 0.760
= 0.010 = = = 0.433 0.154
0.030
0.050 2 0.010
xQ
33
c22
0.050 + 3 0.020 0.750 + 0.020 0.110 0.770
= 0.020 = = = 10.2 0.154
0.010
0.050 2 0.020
xQ
33
c22
0.050 + 3 0.005 0.750 + 0.005 0.065 0.755
= 0.005 = = = 0.129 0.154
0.040
0.050 2 0.005
xQ
33
c22
0.050 + 3 0.006 0.750 + 0.006 0.068 0.756
= 0.006 = = = 0.165 0.154
0.038
0.050 2 0.006
xQ
This is the maximum number of significant figures our system permits. We have
x
= 0.006 M .
4222
CH = 0.038 M; C H = 0.756 M; H = 0.068 M
Because the container volume is 2.00 L, the molar amounts are double the values of
molarities.
22
22
0.756 mol C H
2.00 L = 1.51 mol C H
1 L
4
4
0.038 mol CH
2.00 L = 0.076 mol CH
1 L
2.00 0.068
1=0.14
22
L mol H
L mol H
Thus, the increase in volume results in the production of some additional C2H2.
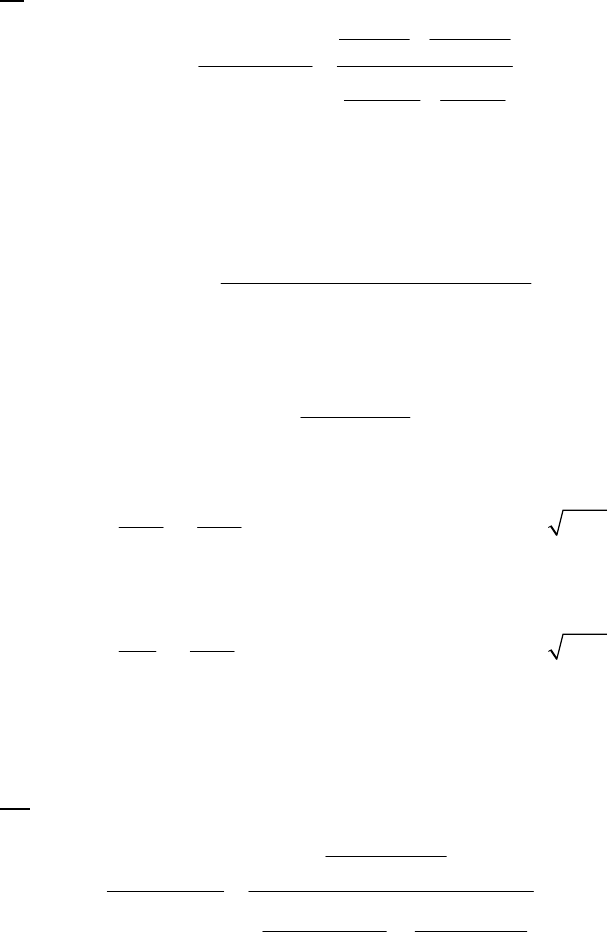
Chapter15: Principles of Chemical Equilibrium
683
27. (M)
(a)
2
2
c
2
22 2
CO H O
CO H O VV
H
CO H {CO }
VV
nn
Kn
n
Since V is present in both the denominator and the numerator, it can be stricken from
the expression. This happens here because ng = 0. Therefore, Kc is independent of V.
(b) Note that KK
pc
= for this reaction, since
ngas =0.
KK
cp
mol CO mol H O
mol CO mol H
==
0.224 0.224
0.276 0.276 = 0.659
2
22
28. (M) For the reaction CO(g) + H2O(g)
CO2(g) + H2(g) the value of Kp = 23.2
The expression for Qp is 22
2
[CO ][H ]
[CO][H O] . Consider each of the provided situations
(a) 22 2
CO H O H CO
P = P = P = P ; Qp = 1 Not an equilibrium position
(b) 22
2
HCO
HO CO
PP
= = ;
PP
x
Qp = x2 If x = 23.2 , this is an equilibrium position.
(c)
222
CO H O CO H
PP = P P; Qp = 1 Not an equilibrium position
(d) 22
2
HCO
CO H O
PP
= = ;
PP
x
Qp = x2 If x = 23.2 , this is an equilibrium position.
Direction and Extent of Chemical Change
29. (M) We compute the value of Qc for the given amounts of product and reactants.
Qc=
2
3
2
3
c
22
22 22
1.8mol SO
SO 7.2L 0.82 100
SO O 3.6mol SO 2.2mol O
7.2L 7.2L
K
The mixture described cannot be maintained indefinitely. In fact, because QK
cc
, the
reaction will proceed to the right, that is, toward products, until equilibrium is established.
We do not know how long it will take to reach equilibrium.
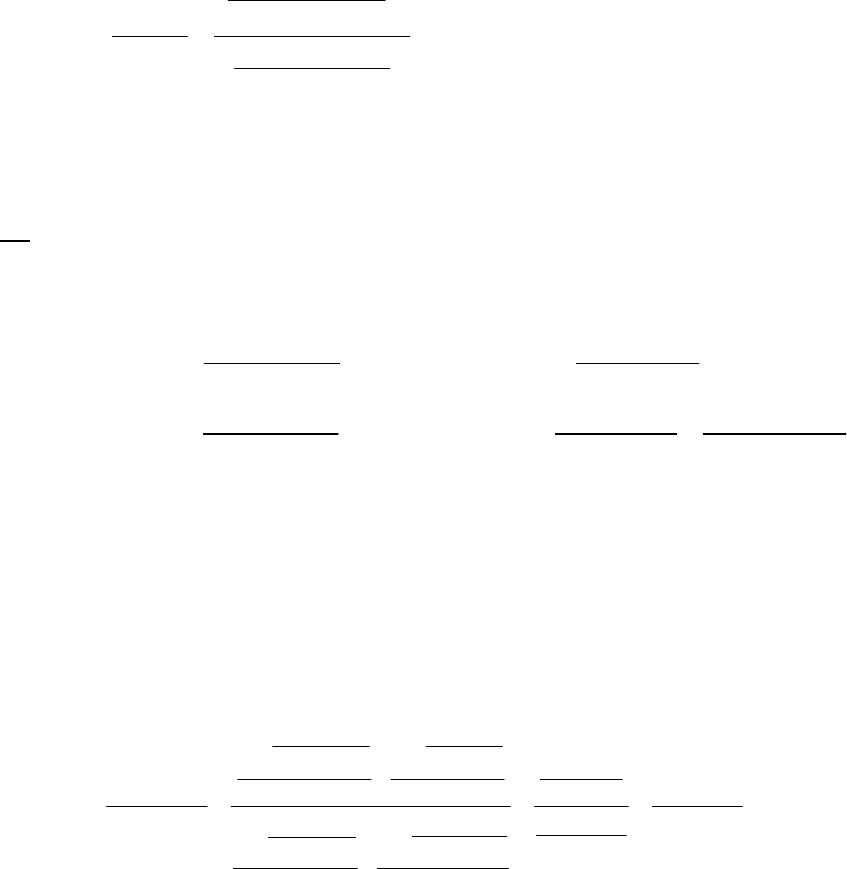
Chapter15: Principles of Chemical Equilibrium
684
30. (M) We compute the value of Qc for the given amounts of product and reactants.
2
2
2
243
c c
24
24
0.0205mol NO
NO 5.25L 1.07 10 K 4.61 10
0.750mol N O
NO
5.25L
Q
The mixture described cannot be maintained indefinitely. In fact, because Qc < Kc, the
reaction will proceed to the right, that is, toward products, until equilibrium is established.
If Ea is large, however, it may take some time to reach equilibrium.
31. (M)
(a) We determine the concentration of each species in the gaseous mixture, use these
concentrations to determine the value of the reaction quotient, and compare this value
of Qc with the value of Kc.
22
22
0.455 mol SO 0.183 mol O
SO = = 0.239 M O = = 0.0963 M
1.90 L 1.90 L
22
3
3
322
22
SO 0.299
0.568 mol SO
SO = = 0.299 M = = = 16.3
1.90 L SO O 0.239 0.0963
c
Q
SinceQK
cc
=16.3 2.8 10 =
2
, this mixture is not at equilibrium.
(b) Since the value of Qc is smaller than that of Kc, the reaction will proceed to the right,
forming product and consuming reactants to reach equilibrium.
32. (M) We compute the value of Qc. Each concentration equals the mass m
bg of the substance
divided by its molar mass and further divided by the volume of the container.
22
22
c c
2
2
22
2
1 mol CO 1 mol H
44.0 g CO 2.0 g H 1
CO H 28.0 18.0
44.0 2.0
= = 5.7 31.4(value of
1 mol H O 1
1 mol CO
CO H O 44.0 2.0
28.0 18.0
18.0 g H O
28.0 g CO
)
mm
VV
Q K
m
m
VV
(In evaluating the expression above, we cancelled the equal values of
V
, along with, the
equal values of m.) Because the value of Qc is smaller than the value of Kc, (a) the
reaction is not at equilibrium and (b) the reaction will proceed to the right (formation of
products) to reach a state of equilibrium.

Chapter15: Principles of Chemical Equilibrium
685
33. (M) The information for the calculation is organized around the chemical equation. Let
x=2
mol H (or I2) that reacts. Then use stoichiometry to determine the amount of HI
formed, in terms of
x
, and finally solve for
x
.
Equation: H g
2bg Ig
2bg
2 HI g
bg
Initial: 0.150 mol 0.150 mol 0.000 mol
Changes:
x
mol
x
mol +2
x
mol
Equil: 0.150
x
0.150
x
2
x
2
2
c
22
2
HI 3.25 L
0.150 0.150
HI
3.25L 3.25 L
x
K
x
x
Then take the square root of both sides: Kx
x
c
50 2 2
0150 709...
1.06
2 =1.06 7.09 = = 0.117 mol, amount HI = 2 = 2 0.117 mol = 0.234 mol HI
9.09
xxx x
amount
22 22
H = amount I = 0.150 mol = 0.150 0.117 mol = 0.033 mol H (or I )x
34. (M) We use the balanced chemical equation as a basis to organize the information
Equation:
532
SbCl g SbCl g + Cl g
Initial:
0.00
2.50
0.280
2.50
0.160
2.50
mol
L
mol
L
mol
L
Initial: 0.000 M 0.112 M 0.0640 M
Changes: + M M M
x
xx
Equil: xx x M M M0.112 0.0640
bgbg
2
32
c
5
SbCl Cl 0.112 0.0640 0.00717 0.176 +
= 0.025= = =
SbCl
xx
x
x
Kxx
22
0.025 = 0.00717 0.176 + 0.201 + 0.00717 = 0xxxxx
2
b b 4ac 0.201 0.0404 0.0287
= = = 0.0464 or 0.155
2a 2
x
The second of the two values for
x
gives a negative value of
2
Cl = 0.091 M, and thus is
physically meaningless in our universe. Thus, concentrations and amounts follow.
555
SbCl = = 0.0464 M amount SbCl = 2.50 L 0.0464 M = 0.116 mol SbClx
333
SbCl = 0.112 = 0.066 M amount SbCl = 2.50 L 0.066 M = 0.17 mol SbClx
222
Cl = 0.0640 = 0.0176 M amount Cl = 2.50 L 0.0176 M = 0.0440 mol Clx
Chapter15: Principles of Chemical Equilibrium
686
35. (M) We use the chemical equation as a basis to organize the information provided about the
reaction, and then determine the final number of moles of
2
Cl g present.
Equation:
22
CO g + Cl g COCl g
Initial: 0.3500 mol 0.0000 mol 0.05500 mol
Changes: + mol + mol molxx x
Equil.:
0.3500 + mol mol 0.05500 molxx x
2
3
c
2
(0.0550 )mol
COCl 3.050L
1.2 10 (0.3500 + )mol mol
CO Cl
3.050L 3.050 L
x
Kxx
3
1.2 10 0.05500
3.050 (0.3500 )
x
x
x
Assume
x
0.0550 This produces the following expression.
34
2
3
1.2 10 0.05500 3.050 0.05500
= = = 4.0 10 mol Cl
3.050 0.3500 0.3500 1.2 10
x
x
We use the first value we obtained, 4
4.0 10
(= 0.00040), to arrive at a second value.
4
2
3
3.050 0.0550 0.00040
==4.010 mol Cl
0.3500 + 0.00040 1.2 10
x
Because the value did not change on the second iteration, we have arrived at a solution.
36. (M) Compute the initial concentration of each species present. Then determine the equilibrium
concentrations of all species. Finally, compute the mass of CO2 present at equilibrium.
int
1.00 g 1 mol CO
CO = = 0.0253 M
1.41 L 28.01 g CO
2
2int 2
1.00 g 1 mol H O
H O = = 0.0394 M
1.41 L 18.02 g H O
2
2int 2
1.00 g 1 mol H
H = = 0.352 M
1.41 L 2.016 g H
222
Equation : CO g + H O g CO g + H g
Initial : 0.0253 M 0.0394 M 0.0000 M 0.352 M
Changes : M M + M + M
Equil : 0.0253 M 0.0394 M M 0.352 + M
xx x x
xxx x
2
22
c2
2
CO H 0.352 + 0.352 +
= = 23.2 = =
CO H O 0.0253 0.0394 0.000997 0.0647 +
xx xx
K
x
xxx
222
0.0231 1.50 + 23.2 = 0.352 + 22.2 1.852 + 0.0231 = 0xx xx x x

Chapter15: Principles of Chemical Equilibrium
687
24 1.852 3.430 2.051
= = = 0.0682 M, 0.0153 M
2 44.4
bb ac
xa
The first value of
x
gives negative concentrations for reactants ([CO] = -0.0429 M and [H2O]
= -0.0288 M). Thus, x= 0.0153 = 2
M CO . Now we can find the mass of CO2.
1.41 0.0153
1
44.01
1= 0.949
22
2
2
L mol CO
L mixture
g CO
mol CO g CO
37. (D) We base each of our solutions on the balanced chemical equation.
(a)
532
Equation : PCl g PCl g + Cl g
0.550 mol 0.550 mol 0 mol
Initial : 2.50 L 2.50 L 2.50 L
mol + mol + mol
Changes : 2.50 L 2.50 L 2.50 L
0.550 mol 0.550 + mol mol
Equil : 2.50 L 2.50 L 2.50 L
xxx
xx
x
2 2
32
c
5
0.550 mol mol
[PCl ][Cl ] (0.550 )
2.50L 2.50L
3.8 10 3.8 10
(0.550 )mol
[PCl ] 2.50(0.550 )
2.50L
xx
xx
Kxx
xx xxx
22
+ 0.550 = 0.052 0.095 + 0.645 0.052 = 0
24 0.645 0.416 + 0.208
= = = 0.0725 mol, 0.717 mol
22
bb ac
xa
The second answer gives a negative quantity. of Cl2, which makes no physical sense.
5
PCl
n = 0.550 0.0725 = 0.478 mol PCl5
3
PCl
n = 0.550 + 0.0725 = 0.623 mol PCl3
2
Cl
n==0.0725x mol Cl2
(b)
532
Equation : PCl g PCl g + Cl g
0.610 mol
Initial : 0 M 0 M
2.50 L
+ mol
mol + mol
Changes : 2.50 L 2.50 L 2.50 L
mol mol
0.610 mol
Equil : 2.50 L 2.50 L 2.50 L
x
xx
xx
x
Chapter15: Principles of Chemical Equilibrium
688
32 2
c
5
2
222
(mol) ( mol)
PCl Cl 2.50L 2.50 L
==3.810
0.610 mol
PCl
2.50 L
2.50 3.8 10 0.095 0.058 0.095 = + 0.095 0.058 = 0
0.610
xx
Kx
xxx x x
x
24 0.095 0.0090 + 0.23
= = = 0.20 mol, 0.29 mol
22
bb ac
xa
amount PCl mol amount Cl
32
= 0.20 = ; amount PCl mol
5= 0.610 0.20 = 0.41
38. (D)
(a) We use the balanced chemical equation as a basis to organize the information we have
about the reactants and products.
22 4
Equation: 2 COF g CO g + CF g
0.145 mol 0.262 mol 0.074 mol
Initial: 5.00 L 5.00 L 5.00 L
Initial: 0.0290 M 0.0524 M 0.0148 M
And we now compute a value of Qc and compare it to the given value of c
K.
24
c c
22
2
CO CF 0.0524 0.0148
= = = 0.922 2.00 =
0.0290
COF
QK
Because
c
Q is not equal to c
K, the mixture is not at equilibrium.
(b) Because c
Q is smaller than c
K, the reaction will shift right, that is, products will be
formed at the expense of COF2, to reach a state of equilibrium.
(c) We continue the organization of information about reactants and products.
22 4
Equation: 2 COF g CO g + CF g
Initial: 0.0290 M 0.0524 M 0.0148 M
Changes: 2 M + M + M
Equil: 0.0290 2 M 0.0524+ M 0.0148+ M
xx x
xxx

Chapter15: Principles of Chemical Equilibrium
689
2
24
c22 2
2
CO CF 0.0524 + 0.0148 + 0.000776 + 0.0672 +
== =2.00=
0.000841 0.1160 + 4
0.0290 2
COF
xx
x
x
K
x
x
x
0.00168 0.232 +8 = 0.000776 + 0.0672 + 7 0.299 + 0.000904 = 0
222
xx xx x x
xbb ac
a
=4
2=0.299 0.0894 0.0253
14 = 0.0033 ,0.0394
2
M M
The second of these values for
x
(0.0394) gives a negative
2
COF = 0.0498 M,
clearly a nonsensical result. We now compute the concentration of each species at
equilibrium, and check to ensure that the equilibrium constant is satisfied.
2
COF = 0.0290 2 = 0.0290 2 0.0033 = 0.0224 Mx
2
CO = 0.0524 + = 0.0524 + 0.0033 = 0.0557 Mx
4
CF = 0.0148 + = 0.0148 + 0.0033 = 0.0181 Mx
24
c22
2
CO CF 0.0557 M 0.0181 M
= = = 2.01
0.0224 M
COF
K
The agreement of this value of Kc with the cited value (2.00) indicates that this solution
is correct. Now we determine the number of moles of each species at equilibrium.
mol COF L M mol COF
22
= 5.00 0.0224 = 0.112
mol CO L M mol CO
22
= 5.00 0.0557 = 0.279
mol CF L M mol CF
44
= 5.00 0.0181 = 0.0905
But suppose we had incorrectly concluded, in part (b), that reactants would be formed
in reaching equilibrium. What result would we obtain? The set-up follows.
22 4
Equation : 2 COF g CO g + CF g
Initial : 0.0290M 0.0524 M 0.0148 M
Changes : +2 M M M
Equil : 0.0290 + 2 M 0.0524 M 0.0148 M
yy y
yy y
2
24
c22 2
2
CO CF 0.0524 0.0148 0.000776 0.0672 +
== =2.00=
0.000841+ 0.1160 + 4
0.0290 + 2COF
yy
y
y
K
y
y
y
0.00168 + 0.232 + 8 = 0.000776 0.0672 + 7 + 0.299 + 0.000904 = 0
222
yy yy y y
ybb ac
a
=4
2=0.299 0.0894 0.0253
14 = 0.0033 , 0.0394
2
M M
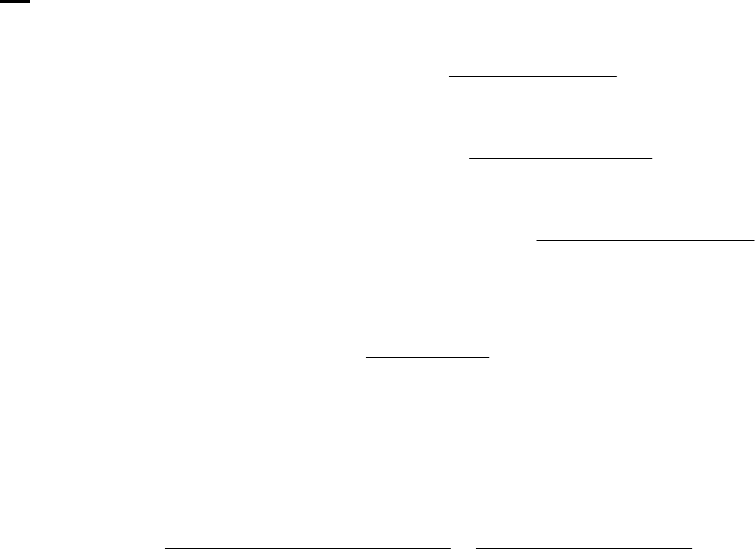
Chapter15: Principles of Chemical Equilibrium
690
The second of these values for x
0.0394
bg gives a negative
2
COF = 0.0498 M,
clearly a nonsensical result. We now compute the concentration of each species at
equilibrium, and check to ensure that the equilibrium constant is satisfied.
2
COF = 0.0290 + 2 = 0.0290 + 2 0.0033 = 0.0224 My
2
CO = 0.0524 = 0.0524 + 0.0033 = 0.0557 My
4
CF = 0.0148 = 0.0148 + 0.0033 = 0.0181 My
These are the same equilibrium concentrations that we obtained by making the correct
decision regarding the direction that the reaction would take. Thus, you can be assured
that, if you perform the algebra correctly, it will guide you even if you make the
incorrect decision about the direction of the reaction.
39. (D)
(a) We calculate the initial amount of each substance.
25
25 25 25
25
1 mol C H OH
{C H OH =17.2 g C H OH = 0.373 mol C H OH
46.07 g C H OH
n
32
32 32 32
32
1 mol CH CO H
{CH CO H = 23.8 g CH CO H = 0.396 mol CH CO H
60.05 g CH CO H
n
3225
3225 3225
3225
3225 3225
1 mol CH CO C H
{CH CO C H } = 48.6 g CH CO C H 88.11 g CH CO C H
{CHCOCH}=0.552 mol CHCOCH
n
n
2
22 2
2
1 mol H O
H O = 71.2 g H O = 3.95 mol H O
18.02 g H O
n
Since we would divide each amount by the total volume, and since there are the same
numbers of product and reactant stoichiometric coefficients, we can use moles rather
than concentrations in the c
Q expression.
3225 2
c c
25 3 2
{CH CO C H H O 0.552 mol 3.95 mol
= = =14.8 = 4.0
{C H OH CH CO H 0.373 mol 0.396 mol
nn
QK
nn
Since cc
QK the reaction will shift to the left, forming reactants, as it attains
equilibrium.
(b) 25 32 3225 2
Equation: C H OH + CH CO H CH CO C H + H O
Initial 0.373 mol 0.396 mol 0.552 mol 3.95 mol
Changes +x mol +x mol –x mol –x mol
Equil (0.373+x) mol (0.396+x) mol (0.552–x) mol (3.95–x) mol

Chapter15: Principles of Chemical Equilibrium
691
2
2
(0.552 )(3.95 ) 2.18 4.50 4.0
(0.373 )(0.396 ) 0.148 0.769
c
xx xx
Kxx xx
xx xx xx
22 2
4.50 + 2.18 = 4 + 3.08 + 0.59 3 + 7.58 1.59 = 0
247.5857+19
= = = 0.19 moles, 2.72 moles
26
bb ac
xa
Negative amounts do not make physical sense. We compute the equilibrium amount of each
substance with x = 0.19 moles.
25 25
{C H OH = 0.373 mol + 0.19 mol = 0.56 mol C H OHn
25
25 25 25
25
46.07g C H OH
mass C H OH = 0.56mol C H OH 26g C H OH
1 mol C H OH
32 32
{CH CO H = 0.396 mol + 0.19 mol = 0.59 mol CH CO Hn
32
32 32 32
32
60.05g CH CO H
mass CH CO H = 0.59mol CH CO H 35g CH CO H
1 mol CH CO H
3225 3225
{CH CO C H = 0.552 mol 0.19 mol = 0.36 CH CO C Hn
3225
3 225 3 225 3 225
3225
88.10g CH CO C H
mass CH CO C H = 0.36mol CH CO C H 32g CH CO C H
1 mol CH CO C H
22
{H O = 3.95 mol 0.19 mol = 3.76 mol H On
2
22 2
2
18.02g H O
mass H O = 3.76mol H O 68g H O
1 mol H O
3225 2
c
25 3 2
CH CO C H H O 0.36 mol 3.76 mol
To check = = = 4.1
C H OH CH CO H 0.56 mol 0.59 mol
nn
Knn
40. (M)
The final volume of the mixture is 0.750 + 2.25 = 3.00L L L. Then use the balanced
chemical equation to organize the data we have concerning the reaction. The reaction
should shift to the right, that is, form products in reaching a new equilibrium, since the
volume is greater.
24 2
Equation: N O g 2 NO g
0.971 mol 0.0580 mol
Initial: 3.00 L 3.00 L
Initial: 0.324M 0.0193M
Changes: M 2 M
Equil : (0.324 )M (0.0193 2 )M
xx
xx
Chapter15: Principles of Chemical Equilibrium
692
222
23
c
24
NO 0.0193 + 2 0.000372 + 0.0772 + 4
= = = = 4.61 10
N O 0.324 0.324
xxx
Kxx
0.000372 + 0.0772 + 4 = 0.00149 0.00461 4 + 0.0818 0.00112 = 0
22
xx x x x
24 0.0818 0.00669 + 0.0179
= = = 0.00938 M, 0.0298 M
28
bb ac
xa
2
22
NO = 0.0193 + 2 0.00938 = 0.0381 M
amount NO = 0.0381 M 3.00 L = 0.114 mol NO
24
24 24
N O = 0.324 0.00938 = 0.3146 M
amount N O = 0.3146 M 3.00 L = 0.944 mol N O
41. (M)
2init
0.186 mol
HCONH = = 0.0861 M
2.16 L
23
Equation: HCONH g NH g + CO g
Initial : 0.0861 M 0 M 0 M
Changes: M + M + M
Equil : (0.0861- )M M M
xxx
xx x
322
c
2
NH CO
= = = 4.84 = 0.417 4.84 0 = + 4.84 0.417
HCONH 0.0861
xx
Kxxxx
x
24 4.84 23.4 +1.67
= = = 0.084 M, 4.92 M
22
bb ac
xa
The negative concentration obviously is physically meaningless. We determine the total
concentration of all species, and then the total pressure with x = 0.084.
32
total = NH + CO + HCONH = + +0.0861 = 0.0861+ 0.084 = 0.170 Mxx x
111
tot = 0.170 mol L 0.08206 L atm mol K 400. K = 5.58 atmP
42. (E) Compare
p
Qto p
K. We assume that the added solids are of negligible volume so that the
initial partial pressures of CO2(g) and H2O(g) do not significantly change.
2 2
1 atm
{H O = 715 mmHg = 0.941 atm H O
760 mmHg
P
p22
= CO H O = 2.10QP P atm CO20.941
atm 2
H O = 1.98 0.23 = p
K
Because Qp is larger than Kp, the reaction will proceed left toward reactants to reach
equilibrium. Thus, the partial pressures of the two gases will decrease.

Chapter15: Principles of Chemical Equilibrium
693
43. (M)
We organize the solution around the balanced chemical equation.
3+ 2+ 2
Equation: 2 Cr aq + Cd(s) 2 Cr aq Cd aq
Initial : 1.00 M 0 M 0 M
Changes: 2 M 2
Equil: (1.00 2 ) M 2
xxx
xxx
2
2+ 2+ 2,
c22
3
Cr Cd (2 ) ( )
= = = 0.288 = 0.257M
1.00 2
Cr
Via successiveapproximations one obtains
xx
Kx
x
Therefore, at equilibrium, [Cd2+] = 0.257 M, [Cr2+] = 0.514 M and [Cr3+] = 0.486 M
Minimum mass of Cd(s) = 0.350L 0.257 M 112.41 g/mol = 10.1 g of Cd metal
44. (M) Again we base the set-up of the problem around the balanced chemical equation.
3+ 2+ 2+
10
c=3.2 10
Equation: Pb s + 2 Cr aq Pb aq + 2 Cr aq
Initial: 0.100M 0M 0M
Changes: 2 M M 2 M
Equil : (0.100 2 )M M 2 M
K
xxx
xxx
210
2
(2 )
==3.210
(0.100)
c
xx
K
32 10 12
4 (0.100) 3.2 10 3.2 10x
12
35
3.2 10 9.3 10 M
4
x
Assumption that 2 0.100
x
, is valid and thus
Pb M
2+ 5
==9.310x, [Cr2+] = 1.9 10-4 M and [Cr3+] = 0.100 M
45. (M) We are told in this question that the reaction SO2(g) + Cl2(g)
SO2Cl2(g) has
Kc = 4.0 at a certain temperature T. This means that at the temperature T, [SO2Cl2] = 4.0
[Cl2] [SO2]. Careful scrutiny of the three diagrams reveals that sketch (b) is the best
representation because it contains numbers of SO2Cl2, SO2, and Cl2 molecules that are
consistent with the Kc for the reaction. In other words, sketch (b) is the best choice because it
contains 12 SO2Cl2 molecules (per unit volume), 1 Cl2 molecule (per unit volume) and 3 SO2
molecules (per unit volume), which is the requisite number of each type of molecule needed
to generate the expected Kc value for the reaction at temperature T.
46. (M) In this question we are told that the reaction 2 NO(g) + Br2(g)
2 NOBr(g) has
Kc = 3.0 at a certain temperature T. This means that at the temperature T, [NOBr]2 = 3.0
[Br2][NO]2. Sketch (c) is the most accurate representation because it contains 18 NOBr
molecules (per unit volume), 6 NO molecules (per unit volume), and 3 Br2 molecules (per
unit volume), which is the requisite number of each type of molecule needed to generate the
expected Kc value for the reaction at temperature T.

Chapter15: Principles of Chemical Equilibrium
694
47. (E)
5
aconitate
Kcitrate
4.0 10
Q 0.031
0.00128
Since Q = K, the reaction is at equilibrium,
48. (E)
2red
ox
CO NAD oxoglut.
Kcitrate NAD
0.00868 0.00132 0.00868
Q 0.00895
0.00128 0.00868
Since Q < K, the reaction needs to proceed to the right (products).
Partial Pressure Equilibrium Constant, Kp
49. (M) The Is
2bg maintains the presence of I2 in the flask until it has all vaporized. Thus, if
enough HI(g) is produced to completely consume the I s
2bg, equilibrium will not be achieved.
2
1 atm
{H S} = 747.6 mmHg = 0.9837 atm
760 mmHg
P
Equation:
22
H S g + I s 2 HI g + S s
Initial: 0.9837 atm 0 atm
Changes:
x
atm +2
x
atm
Equil: 0.9837 x
bg atm 2
x
atm
2
22
5
2
2
{HI} 4
== =1.3410=
{H S} 0.9837 0.9837
p
x
Px
KPx
53
1.34 10 0.9837
= = 1.82 10 atm
4
x
The assumption that 0.9837
x
is valid. Now we verify that sufficient I2(s) is present by
computing the mass of I2 needed to produce the predicted pressure of HI(g). Initially, 1.85 g
I2 is present (given).
3
22
2 2
11 2
1.82 10 atm 0.725 L 1 mol I 253.8 g I
mass I = = 0.00613 g I
0.08206 L atm mol K 333 K 2 mol HI 1 mol I
tot 2
tot
= {H S}+ {HI} = 0.9837 + 2 = 0.9837 + = 0.9837 + 0.00182 = 0.9855 atm
= 749.0mmHg
PP P x x x
P

Chapter15: Principles of Chemical Equilibrium
695
50. (M) We first determine the initial pressure of NH3.
11
3
3
0.100 mol NH 0.08206 L atm mol K 298 K
{NH g }= = =0.948 atm
2.58 L
nRT
PV
Equation: NH4HS(s)
NH3(g) + H2S(g)
Initial: 0.948 atm 0 atm
Changes: +
x
atm +
x
atm
Equil:
0.948+ atmx
x
atm
KP P xx xx x x
p32
= {NH } {H S} = 0.108 = 0.948 +
bg
= 0.948 + 0 = + 0.948 0.108
22
24 0.948 0.899 + 0.432
= = = 0.103 atm, 1.05 atm
22
bb ac
xa
The negative root makes no physical sense. The total gas pressure is obtained as follows.
PP P xx x
tot NH H S} atm= + = 0.948 + + = 0.948 + 2 = 0.948 + 2 0.103 = 1.154
32
{}{ bg
51. (M) We substitute the given equilibrium pressure into the equilibrium constant expression
and solve for the other equilibrium pressure.
33
22
p2
2
22
{O } {O }
= = 28.5 =
{CO } 0.0721 atm CO
PP
KP
32
3
3
22 2
{O } {O } 28.5(0.0712 atm) 0.529atm OPP
total 2 2 2 2
= {CO }+ {O } = 0.0721 atm CO + 0.529 atm O = 0.601 atm totalPP P
52. (M) The composition of dry air is given in volume percent. Division of these percentages by
100 gives the volume fraction, which equals the mole fraction and also the partial pressure in
atmospheres, if the total pressure is 1.00 atm. Thus, we have 2
{O } = 0.20946P atm and
2
{CO } = 0.00036P atm. We substitute these two values into the expression for
p
Q.
3
324
2
p
2
2
22
0.20946 atm O
{O }
= = = 6.4 10 28.5 =
{CO } 0.00036 atm CO
p
P
QK
P
The value of p
Q is much larger than the value of p
K. Thus this reaction should be
spontaneous in the reverse direction until equilibrium is achieved. It will only be
spontaneous in the forward direction when the pressure of 2
O drops or that of 2
CO rises
(as would be the case in self-contained breathing devices).

Chapter15: Principles of Chemical Equilibrium
696
53. (M)
(a) We first determine the initial pressure of each gas.
PPnRT
V
{{}CO} Cl mol L atm mol K K
L atm===
1.00 0.08206 668
1.75 = 31.3
2
11
Then we calculate equilibrium partial pressures, organizing our calculation around
the balanced chemical equation. We see that the equilibrium constant is not very large,
meaning that we must solve the polynomial exactly (or by successive approximations).
Equation CO(g)
22
+ Cl g COCl g
Kp = 22.5
Initial: 31.3 atm 31.3 atm 0 atm
Changes:
x
atm
x
atm +
x
atm
Equil: 31.3
x
atm 31.3
x
atm
x
atm
2
p22
2
22
2
{COCl } 22.5
{CO} {Cl } (31.3 ) (979.7 62.6 )
22.5(979.7 62.6 ) 22043 1408.5 22.5
22043 1409.5 22.5 0 (Solve by using the quadratic equation)
Pxx
KPP xxx
xx x x x x
xx
2
2( 1409.5) ( 1409.5) 4(22.5)(22043)
4
==
2 2(22.5)
1409.5 2818
= 30.14, 32.5(too large)
45
bb ac
xa
x
2 2
{CO} = {Cl } = 31.3 atm 30.14 atm = 1.16 atm {COCl } = 30.14 atmPP P
(b) total 2 2
= {CO}+ {Cl }+ {COCl } =1.16 atm +1.16 atm +30.14 atm = 32.46 atmPP P P
54. (M) We first find the value of Kp for the reaction.
6
22c
2 NO g 2 NO g + O g , = 1.8 10 at 184 C = 457 KK
.
For this reactionngas =2+1 2=+1.
g
n
(RT)
pc
KK
= 1.8 10-6 (0.08206 457) 1
= 6.8 10-5
To obtain the required reaction
122
2
NO g + O g NO g
from the initial reaction,
that initial reaction must be reversed and then divided by two. Thus, in order to determine
the value of the equilibrium constant for the final reaction, the value of Kp for the initial
reaction must be inverted, and the square root taken of the result.
2
p, final 5
11.2 10
6.8 10
K

Chapter15: Principles of Chemical Equilibrium
697
Le Châtelier's Principle
55. (E) Continuous removal of the product, of course, has the effect of decreasing the
concentration of the products below their equilibrium values. Thus, the equilibrium system
is disturbed by removing the products and the system will attempt (in vain, as it turns out)
to re-establish the equilibrium by shifting toward the right, that is, to generate more
products.
56. (E) We notice that the density of the solid ice is smaller than is that of liquid water. This
means that the same mass of liquid water is present in a smaller volume than an equal mass
of ice. Thus, if pressure is placed on ice, attempting to force it into a smaller volume, the
ice will be transformed into the less-space-occupying water at 0C
. Thus, at 0C
under
pressure, H2O(s) will melt to form H2O(l). This behavior is not expected in most cases
because generally a solid is more dense than its liquid phase.
57. (M)
(a) This reaction is exothermic with
H
o= 150 . kJ. Thus, high temperatures favor the
reverse reaction (endothermic reaction). The amount of
2
Hg present at high
temperatures will be less than that present at low temperatures.
(b) HOg
2bg is one of the reactants involved. Introducing more will cause the equilibrium
position to shift to the right, favoring products. The amount of
2
Hg
will increase.
(c) Doubling the volume of the container will favor the side of the reaction with the
largest sum of gaseous stoichiometric coefficients. The sum of the stoichiometric
coefficients of gaseous species is the same (4) on both sides of this reaction.
Therefore, increasing the volume of the container will have no effect on the amount
of
2
Hg present at equilibrium.
(d) A catalyst merely speeds up the rate at which a reaction reaches the equilibrium position.
The addition of a catalyst has no effect on the amount of
2
Hg present at equilibrium.
58. (M)
(a)
This reaction is endothermic, with
H
o= +92.5 kJ. Thus, a higher temperature will
favor the forward reaction and increase the amount of HI(g) present at equilibrium.
(b) The introduction of more product will favor the reverse reaction and decrease the
amount of HI(g) present at equilibrium.
(c) The sum of the stoichiometric coefficients of gaseous products is larger than that for
gaseous reactants. Increasing the volume of the container will favor the forward
reaction and increase the amount of HI(g) present at equilibrium.
(d) A catalyst merely speeds up the rate at which a reaction reaches the equilibrium position.
The addition of a catalyst has no effect on the amount of HI(g) present at equilibrium.

Chapter15: Principles of Chemical Equilibrium
698
(e) The addition of an inert gas to the constant-volume reaction mixture will not change any
partial pressures. It will have no effect on the amount of HI(g) present at equilibrium.
59. (M)
(a)
The formation of NO(g) from its elements is an endothermic reaction (
H
o= +181
kJ/mol). Since the equilibrium position of endothermic reactions is shifted toward
products at higher temperatures, we expect more NO(g) to be formed from the
elements at higher temperatures.
(b) Reaction rates always are enhanced by higher temperatures, since a larger fraction of the
collisions will have an energy that surmounts the activation energy. This enhancement of
rates affects both the forward and the reverse reactions. Thus, the position of equilibrium is
reached more rapidly at higher temperatures than at lower temperatures.
60. (M) If the reaction is endothermic (H > 0), the forward reaction is favored at high
temperatures. If the reaction is exothermic (H < 0), the forward reaction is favored at
low temperatures.
(a)
oo o o
f5 f3 f2
= PCl g PCl g Cl gHH H H
o(favored at low temperatures)= 374.9 kJ 287.0 kJ 0.00 kJ = 87.9 kJ/molH
(b) HH H H H
of
o2f
of
o2f
o2
HO(g ) (g) HS(g)=2 3 2[ )] [S(rhombic ] [SO ] [ ]
o
o
= 2 241.8 kJ + 3 0.00 kJ 296.8 kJ 2 20.63 kJ
= 145.5 kJ/mol (favored at low temperatures)
H
H
(c)
oo o
ff2
=4 NOCl g +2 HO gHH H
ooo
f2 f2 f
2Ng3Og4HClgHHH
o
o(favored at higher temperatures)
4 51.71 kJ + 2 241.8 kJ 2 0.00 kJ 3 0.00 kJ 4 92.31 kJ
+92.5 kJ/mol
=
=
H
H
61. (E) If the total pressure of a mixture of gases at equilibrium is doubled by compression, the
equilibrium will shift to the side with fewer moles of gas to counteract the increase in
pressure. Thus, if the pressure of an equilibrium mixture of N2(g), H2(g), and NH3(g) is
doubled, the reaction involving these three gases, i.e., N2(g) + 3 H2(g)
2 NH3(g), will
proceed in the forward direction to produce a new equilibrium mixture that contains
additional ammonia and less molecular nitrogen and molecular hydrogen. In other words,
P{N2(g)} will have decreased when equilibrium is re-established. It is important to note,
however, that the final equilibrium partial pressure for the N2 will, nevertheless, be higher
than its original partial pressure prior to the doubling of the total pressure.

Chapter15: Principles of Chemical Equilibrium
699
62. (M)
(a) Because
H
o= 0 , the position of the equilibrium for this reaction will not be
affected by temperature. Since the equilibrium position is expressed by the value of
the equilibrium constant, we expect Kp to be unaffected by, or to remain constant
with, temperature.
(b) From part (a), we know that the value of Kp will not change when the temperature is
changed. The pressures of the gases, however, will change with temperature. (Recall
the ideal gas law: PnRT
V
=/
.) In fact, all pressures will increase. The
stoichiometric coefficients in the reaction are such that at higher pressures the
formation of more reactant will be favored (the reactant side has fewer moles of gas).
Thus, the amount of D(g) will be smaller when equilibrium is reestablished at the
higher temperature for the cited reaction.
1
As Bs+2 Cg+ Dg
2
63. (M) Increasing the volume of an equilibrium mixture causes that mixture to shift toward
the side (reactants or products) where the sum of the stoichiometric coefficients of the
gaseous species is the larger. That is: shifts to the right if
ngas 0, shifts to the left
if ngas 0, and does not shift if
ngas =0.
(a)
22gas
C s + H O g CO g + H g , 0, shift right, toward productsn
(b)
232gas
2
Ca OH s + CO g CaCO s + H O g , = 0,n
no shift, no change in
equilibrium position.
(c)
32 2 gas
4 NH g + 5 O g 4 NO g + 6 H O g , 0, shifts right, towards productsn
64. (M) The equilibrium position for a reaction that is exothermic shifts to the left (reactants
are favored) when the temperature is raised. For one that is endothermic, it shifts right
(products are favored) when the temperature is raised.
(a)
11
22
22
NO g N g + O g = 90.2 kJ shifts left, % dissociation
o
H
(b)
1
322
2
SO g SO g + O g = +98.9 kJ shifts right, % dissociation
o
H
(c)
24 2 2
N H g N g + 2 H g = 95.4 kJ shifts left, % dissociation
o
H
(d)
22
COCl g CO g + Cl g = +108.3 kJ shifts right, % dissociation
o
H
65. (E)
(a) Hb:O2 is reduced, because the reaction is exothermic and heat is like a product.
(b) No effect, because the equilibrium involves O2 (aq). Eventually it will reduce the Hb:O2
level because removing O2(g) from the atmosphere also reduces O2 (aq) in the blood.
(c) Hb:O2 level increases to use up the extra Hb.

Chapter15: Principles of Chemical Equilibrium
700
66. (E)
(a) CO2 (g) increases as the equilibrium is pushed toward the reactant side
(b) Increase CO2 (aq) levels, which then pushes the equilibrium to the product side
(c) It has no effect, but it helps establish the final equilibrium more quickly
(d) CO2 increases, as the equilibrium shifts to the reactants
67. (E) The pressure on N2O4 will initially increase as the crystal melts and then vaporizes, but
over time the new concentration decreases as the equilibrium is shifted toward NO2.
68. (E) If the equilibrium is shifted to the product side by increasing temperature, that means that
heat is a “reactant” (or being consumed). Therefore, HI decomposition is endothermic.
69. (E) Since ΔH is >0, the reaction is endothermic. If we increase the temperature of the
reaction, we are adding heat to the reaction, which shifts the reaction toward the
decomposition of calcium carbonate. While the amount of calcium carbonate will decrease,
its concentration will remain the same because it is a solid.
70. (E) The amount of N2 increases in the body. As the pressure on the body increases, the
equilibrium shifts from N2 gas to N2 (aq).
Integrative and Advanced Exercises
71. (E) In a reaction of the type I2(g) 2 I(g) the bond between two iodine atoms, the I—I
bond, must be broken. Since I2(g) is a stable molecule, this bond breaking process must be
endothermic. Hence, the reaction cited is an endothermic reaction. The equilibrium position
of endothermic reactions will be shifted toward products when the temperature is raised.
72. (M)
(a) In order to determine a value of Kc, we first must find the CO2 concentration in the gas phase.
Note, the total volume for the gas is 1.00 L (moles and molarity are numerically equal)
2
2
2 c
2
[CO (aq)]
1.00 atm 3.29 10 M
[CO ] 0.0409 M 0.804
Latm [CO (g)] 0.0409 M
0.08206 298 K
mol K
nP K
VRT
(b) It does not matter to which phase the radioactive 14CO2 is added. This is an example of
a Le Châtelier’s principle problem in which the stress is a change in concentration of the
reactant CO2(g). To find the new equilibrium concentrations, we must solve and I.C.E.
table. Since Qc < Kc, the reaction shifts to the product, CO2 (aq) side.
22
-3
Reaction: CO (g) CO (aq)
Initial: 0.0409 mol 3.29 10 mol
Stress +0.01000 mol
Changes: mol x
-3
mol
Equilibrium: (0.05090 ) mol 3.29 10 mol
x
xx

Chapter15: Principles of Chemical Equilibrium
701
-3
-2 4
2
C 2
2
3.29 10 mol
[CO (aq)] 3.29 10 10
0.1000 L 0.804 7.43 10 mol CO
(0.05090 ) mol
[CO (g)] 0.05090
1.000 L
x
x
Kx
xx
Total moles of CO2 in the aqueous phase (0.1000 L)(3.29×10-2 +7.43×10-3) = 4.03 ×10-3 moles
Total moles of CO2 in the gaseous phase (1.000 L)(5.090×10-2 7.43×10-4) = 5.02 ×10-2 moles
Total moles of CO2 = 5.02 ×10-2 moles + 4.03 ×10-3 moles = 5.42×10-2 moles
There is continuous mixing of the 12C and 14C such that the isotopic ratios in the two phases is
the same. This ratio is given by the mole fraction of the two isotopes.
For 2
14 CO in either phase its mole fraction is -2
0.01000 mol 100 18.45 %
5.419 10 mol
Moles of 2
14 CO in the gaseous phase = 5.02×10-2 moles×0.1845 = 0.00926 moles
Moles of 2
14 CO in the aqueous phase = 4.03 ×10-3 moles×0.1845 = 0.000744 moles
73. (M) Dilution makes Qc larger than Kc. Thus, the reaction mixture will shift left in order to
regain equilibrium. We organize our calculation around the balanced chemical equation.
23
Equation: Ag (aq) Fe (aq) Fe (aq) Ag(s) 2.98
Equil: 0.31 M 0.21 M 0.19 M
Dilution: 0.12 M 0.084 M
c
K
3
c2
0.076 M
Changes: M M M
New equil: (0.12 ) M (0.084 ) M (0.076 ) M
[Fe ] 0.076
2.98 2.9
[Ag ][Fe ] (0.12 ) (0.084 )
xx x
xx x
x
Kxx
22
8 (0.12 ) (0.084 ) 0.076
0.076 0.030 0.61 2.98 2.98 1.61 0.046 0
x
xx
xxxxx
57.0 ,027.0
96.5
0.55 59.261.1
x Note that the negative root makes no physical
sense; it gives M 49.057.0084.0]Fe[ 2
.
Thus, the new equilibrium concentrations are
2
3
[Fe ] 0.084 0.027 0.111 M [Ag ] 0.12 0.027 0.15 M
[Fe ] 0.076- 0.027 0.049 M We can check our answer by substitution.
0.049 M
c = = 2.94 2.98 (within precision limits)
0.111 M 0.15 M
K
74. (M) The percent dissociation should increase as the pressure is lowered, according to Le
Châtelier’s principle. Thus the total pressure in this instance should be more than in
Example 15-12, where the percent dissociation is 12.5%. The total pressure in Example
15-12 was computed starting from the total number of moles at equilibrium.
The total amount = (0.0240 – 0.00300) moles N2O4 + 2 × 0.00300 mol NO2 = 0.027 mol gas.

Chapter15: Principles of Chemical Equilibrium
702
-1 -1
total
0.0270mol × 0.08206LatmK mol × 298 K
nRT
P = = = 1.77atm (Example 15-12)
V 0.372 L
We base our solution on the balanced chemical equation. We designate the initial pressure
of N2O4 as P. The change in P{N2O4}is given as –0.10 P atm. to represent the 10.0 %
dissociation.
24 2
Equation: N O (g) 2 NO (g)
Initial: P atm 0 atm
Changes: 0.10P atm +2(0.10P atm)
Equil: 0.90 P atm
0.20P atm
22
2
p
24
P{NO } (0.20P) 0.040P 0.113 × 0.90
K = = = =0.113 P = = 2.54atm.
P{N O } 0.90P 0.90 0.040
Thus, the total pressure at equilibrium is 0.90 P + 0.20 P and 1.10 P (where P = 2.54 atm)
Therefore, total pressure at equilibrium = 2.79 atm.
75. (M) 322
Equation: 2 SO (g) 2 SO (g) O (g)
Initial: 1.00 atm 0atm 0 atm
Changes: 2 atm 2 atm atm
Equil: (1.00 2 )atm 2 atm atm
xxx
xx x
Because of the small value of the equilibrium constant, the reaction does not proceed very
far toward products in reaching equilibrium. Hence, we assume that x << 1.00 atm and
calculate an approximate value of x (small K problem).
22 3
5
22
22 2
3
{SO } {O } (2 ) 4
1.6 10 0.016 atm
{SO } (1.00 2 ) (1.00)
P
PP xx x
Kx
Px
A second cycle may get closer to the true value of x.
atm 016.0
)032.000.1(
4
106.1 2
3
5
x
x
Our initial value was sufficiently close. We now compute the total pressure at equilibrium.
atm 02.1016.000.100.12)200.1(}{O}SO{}SO{ 223total
xxxxPPPP
76. (M) Let us start with one mole of air, and let 2x be the amount in moles of NO formed.
22
Equation: N (g) O (g) 2 NO(g)
Initial: 0.79 mol 0.21 mol 0 mol
Changes: mol mol 2 mol
Equil:
xx x
(0.79 )mol (0.21 )mol 2 molxx x
Chapter15: Principles of Chemical Equilibrium
703
NO
22
2 2
{NO} 2 2
0.018
{N } {O } {NO} (0.79 ) (0.21 ) 2 1.00
0.0090 mol 0.79 0.78 mol N 0.21 0.20 mol O
2 0.018 mol NO
nxx
nnn x xx
xx x
x
2
222
total 3
p22
22 22
total total
{NO}
{NO} {NO} (0.018) 2.1 10
{N ) {O }
(N } {O } {N } {O } 0.78 0.20
nRT
V
Pn
KnRTnRT
PP nn
VV
77. (D) We organize the data around the balanced chemical equation. Note that the reaction is
stoichimoetrically balanced.
(a)
22 3
Equation: 2 SO (g) O (g) 2 SO (g)
M)2 (0.200 M M 2 :Equil
M2 M M 2 :Changes
M 0.200 M 0.000 M 0.000 :right To
M 0.168 M 0.016 M 0.032 :Initial
xxx
xxx
In setting up this problem, we note that solving this question exactly involves finding
the roots for a cubic equation. Thus, we assumed that all of the reactants have been
converted to products. This gives the results in the line labeled “To right.” We then
reach equilibrium from this position by converting some of the product back into
reactants. Now, we substitute these expressions into the equilibrium constant
expression, and we solve this expression approximately by assuming that 0.200 2 x.
033.0or
4
)200.0(
108.2
)2(
)2200.0(
]O[]SO[
]SO[
3
2
2
2
2
2
2
2
2
3
c
x
xxx
x
K
We then substitute this approximate value into the expression for Kc.
025.0 108.2
4
)066.0200.0( 2
3
2
c
xor
x
K
Let us try one more cycle. 027.0or 108.2
4
)050.0200.0( 2
3
2
c
x
x
K
L 10.0
mol 68.1
L 10.0
mol 0.16
L 10.0
mol 0.32
:Initial
mol 1.68 mol 0.16 mol 0.32 SO Add
mol 0.68 mol 0.16 mol 0.32 :Equil
3
Chapter15: Principles of Chemical Equilibrium
704
This gives the following concentrations and amounts of each species.
222
222
333
O mol 0.27M 0.027L 10.0Oamount M 0.027][O
SO mol 0.54M 0.054L 10.0SOamount M 0.0540.0272][SO
SO mol 1.46M 0.146L 10.0SOamount M 0.1460.027)(20.200][SO
(b) 22 3
Equation: 2 SO (g) O (g) 2 SO (g)
M)2 (1.00 M M 2 :Equil
M 2 M M 2 :Changes
M 1.00 M 0.00 M 0.00 :right To
M 0.68 M 0.16 M 32.0 : 0.10
M 0.068 M 0.016 M 0.032 :Equil
L 10.0
mol 68.0
L 10.0
mol 16.0
L 10.0
mol 0.32
:Equil
mol0.68 mol0.16 mol 0.32 :Equil
xxx
xxx
V
Again, notice that an exact solution involves finding the roots of a cubic. So we have
taken the reaction 100% in the forward direction and then sent it back in the reverse
direction to a small extent to reach equilibrium. We now solve the Kc expression for x,
obtaining first an approximate value by assuming 2x << 1.00.
096.0
4
)00.1(
108.2
)2(
)200.1(
]O[]SO[
]SO[
3
2
2
2
2
2
2
2
2
3
c
xor
xxx
x
K
We then use this approximate value of x to find a second approximation for x.
084.0or108.2
4
)19.000.1( 2
3
2
c
x
x
K
Another cycle gives 085.0or 108.2
4
)17.000.1( 2
3
2
c
x
x
K
Then we compute the equilibrium concentrations and amounts.
333
222
222
[SO ] 1.00 (2 0.085) 0.83 M amount SO 1.00 L 0.83 M 0.83 mol SO
[SO ] 2 0.085 0.17 M amount SO 1.00 L 0.17 M 0.17 mol SO
[O ] 0.085 M amount O 1.00 L 0.085 M 0.085 mol O
78. (M)
2
64 65 2
-3
co 2
Equation: HOC H COOH(g) C H OH(g) CO (g)
730mmHg 48.2 48.5 1 L
PV 760mmHg/atm 2 1000 mL
n 1.93 10 mol CO
RT 0.0821L atm/mol K 293K

Chapter15: Principles of Chemical Equilibrium
705
2
-3
salicylic acid
Note that moles of CO moles phenol
0.300 2.17 10 mol salicylic acid
138 /
g
ngmol
2
65 2
c
64
1.93 mmol
[C H OH ] [CO (g)] 50.0 mL
K 0.310
(2.17 1.93) mmol
[HOC H COOH]
50.0 mL
(2-1)
pc
L atm
K K (RT) (0.310) 0.08206 (473 K) 12.0
mol K
79. (D)
(a) This reaction is exothermic and thus, conversion of synthesis gas to methane is favored at
lower temperatures. Since 2)31()11(
gas
n, high pressure favors the products.
(b) The value of Kc is a large number, meaning that almost all of the reactants are converted
to products (note that the reaction is stoichiometrically balanced). Thus, after we set up
the initial conditions we force the reaction to products and then allow the system to
reach equilibrium.
242
Equation: 3 H (g) CO(g) CH (g) H O(g)
3.00 mol 1.00 mol
Initial: 0 M 0 M
15.0 L 15.0 L
Initial: 0.200 M 0.0667 M 0 M 0 M
To right: 0.000 M
0.000 M 0.0667 M 0.0667 M
Changes: 3 M M M M
Equil: 3 M M (0.0667 )M (0.0667 )M
xx x x
x
xxx
2
42
c33 2
2
222
2
[CH ][H O] (0.0667 ) 0.0667
190. 190.
[H ] [CO] (3 ) 27
190 27 0.0667 71.6 71.6 0.0667 0
4 1.00 1.00 19.1 0.0244 M
2 143
xx
Kxx x
xxx xx
bb ac
xa
42
2
[CH ] [H O] 0.0667 0.0244 0.0423 M
[H ] 3 0.0244 0.0732 M
[CO] 0.0244 M
We check our calculation by computing the value of the equilibrium constant.
187
0244.0)0732.0(
)0423.0(
CO][][H
O]H[][CH
3
2
3
2
24
c
K

Chapter15: Principles of Chemical Equilibrium
706
Now we compute the amount in moles of each component present at equilibrium, and
finally the mole fraction of CH4.
42
amount CH amount H O 0.0423 M 15.0 L 0.635 mol
2
amount H 0.0732 M 15.0 L 1.10 mol
amount CO 0.0244 M 15.0 L 0.366 mol
4
CH
0.635 mol 0.232
0.635 mol 0.635 mol 1.10 mol 0.366 mol
80. (M) We base our calculation on 1.00 mole of PCl5 being present initially.
532
Equation: PCl (g) PCl (g) Cl (g)
Initial: 1.00 mol 0 M 0 M
Changes: mol mol mol
Equil: (1.00 ) mol mol mol
total 1.00 1.00n
532
Equation: PCl (g) PCl (g) Cl (g)
1.00
Mol fract.
1.00 1.00 1.00
2
total 2 2
2 3 2 total 3 total total total
p2
5 5 total total
{Cl } {PCl } [ {Cl } ] [ {PCl } ]
1.00
1.00
{PCl } [ {PCl } ] (1.00 )(1.00 ) 1
P
1.00
P
P
PPP PP
KPP
81. (M) We assume that the entire 5.00 g is N2O4 and reach equilibrium from this starting point.
M 109.0
ON g01.92
ON mol 1
L 0.500
g 00.5
]ON[
42
42
42
i
Equation: N2O4 (g) 2 NO2 (g)
Initial: 0.109 0 M
Changes: –
x M + 2x M
Equil: (0.0109 –
x) M 2x M
22
3243
2
C
24
2
[NO ] (2 )
4.61 10 4 5.02 10 4.61 10
[N O ] 0.109
4 0.00461 0.000502 0
x
Kxx
x
x
x
253
4 0.00461 2.13 10 8.03 10 0.0106M, 0.0118 M
28
bb ac
xa
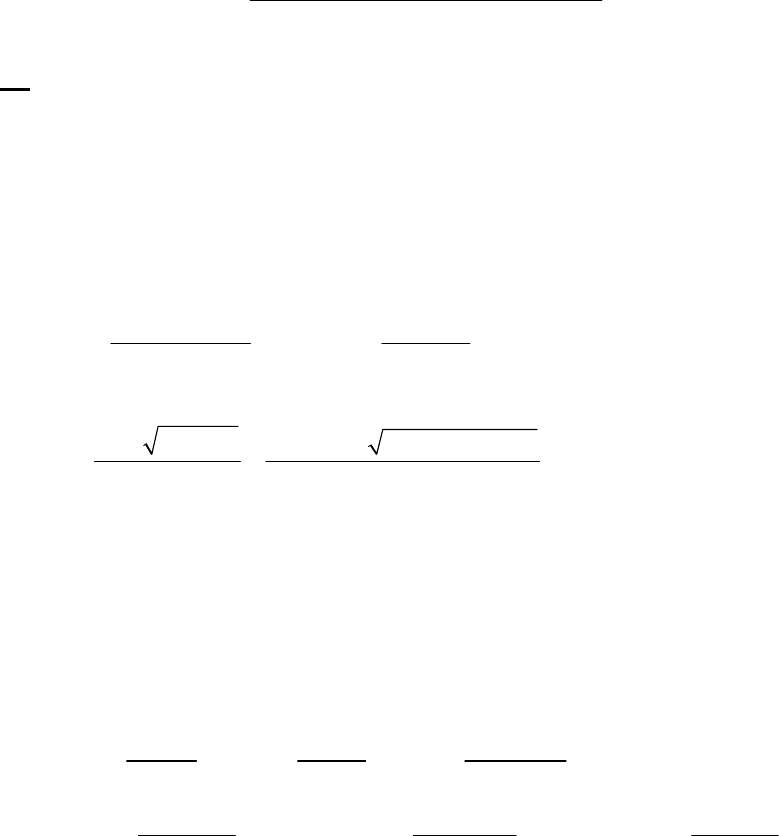
Chapter15: Principles of Chemical Equilibrium
707
24 24
22
2
(The method of successive approximations yields 0.0106 after two iterations)
amount N O 0.500 L (0.109 0.0106) M 0.0492 mol N O
amount NO 0.500 L 2 0.0106 M 0.0106 mol NO
0.0106 mo
mol fraction NO
2
224
l NO 0.177
0.0106 mol NO 0.0492 mol N O
82. (M) We let P be the initial pressure in atmospheres of COCl2(g).
22
Equation: COCl (g) CO(g) Cl (g)
Initial: P 0 M 0 M
Changes:
Equil: P
xxx
x
Total pressure 3.00 atm P P P 3.00
xx
x
xx x x
2
2
p
2
22
2
P{COCl } P 3.00 3.00 2
P{CO}P{Cl }
K 0.0444
P(COCl } 3.00 2
0.133 0.0888 0.0888 0.133 0
4 0.0888 0.00789 0.532 0.323, 0.421
22
xxx x
xx
x
xxxx
bb ac
xa
Since a negative pressure is physically meaningless, x = 0.323 atm.
(The method of successive approximations yields x = 0.323 after four iterations.)
2
2
{CO} {Cl } 0.323 atm
{COCl } 3.00 2 0.323 2.35 atm
PP
P
The mole fraction of each gas is its partial pressure divided by the total pressure. And the
contribution of each gas to the apparent molar mass of the mixture is the mole fraction of that
gas multiplied by the molar mass of that gas.
22
avg 2 2
tot tot tot
{Cl } {COCl }{CO} {CO} {Cl } {COCl }
0.323 atm 0.323 atm 2.32 atm
28.01 g/mol 70.91g/mol 98.92 g/mol
3.00 atm 3.00 atm 3.00 atm
87.1 g/mol
PPP
MM M M
PP P

Chapter15: Principles of Chemical Equilibrium
708
83. (M) Each mole fraction equals the partial pressure of the substance divided by the total
pressure. Thus tot33tot33 }NH{}NH{or /}NH{}NH{ PPPP
2
tot
3
22
2
3
4
tot
2
tot
3
22
2
3
3
tot2tot2
2
tot3
3
22
2
3
p
)(
1
}{H }N{
}NH{
)(
)(
}{H }N{
}NH{
)}{H( )}N{(
)}NH{(
}H{ }N{
}NH{
P
P
P
PP
P
PP
P
K
This is the expression we were asked to derive.
84. (D) Since the mole ratio of N2 to H2 is 1:3, }{N 3}H{ 22
. Since Ptot = 1.00 atm, it follows.
56.10906.03
}{N
}{NH
}N{
}{NH
}{N }{N
}{NH
0906.03
0906.01006.9
)00.1(
1
}){N (3 }N{
}{NH
3
2
2
3
4
2
2
3
3
22
2
33
2
23
22
2
3
p
K
We realize that }{N 3 }{N }{NH00.1}{H }{N }{NH 223223
This gives }{N 4 00.1}{NH 23
And we have
22
2
2
1.00 4 {N }
1.56 For ease of solving, we let {N }
{N } x
22
2
2
1.00 4
1.56 1.56 1.00 4 1.56 4 1.00 0
4 4.00 16.00 6.24 0.229, 2.794
23.12
xxxxx
x
bb ac
xa
Thus 229.0}{N 2
Mole % NH3 = (1.000 mol –(4 × 0.229 mol)) × 100% = 8.4%
85. (M) Since the initial mole ratio is 2 H2S(g) to 1 CH4(g), the reactants remain in their
stoichiometric ratio when equilibrium is reached. Also, the products are formed in their
stoichiometric ratio.
33
4
42 4
2
3 4
2
24 2
4
4
22
1 mol CH
amount CH 9.54 10 mol H S 4.77 10 mol CH
2 mol H S
1 mol CS
1 mol S
amount CS 1.42 10 mol BaSO 7.10 10 mol CS
1 mol BaSO 2 mol S
4 mol
amount H 7.10 10 mol CS
3
22
2
33 4 3
2422
3
H 2.84 10 mol H
1 mol CS
total amount 9.54 10 mol H S 4.77 10 mol CH 7.10 10 mol CS 2.84 10 mol H
17.86 10 mol
The partial pressure of each gas equals its mole fraction times the total pressure.
Chapter15: Principles of Chemical Equilibrium
709
3
2
23
3
4
43
9.54 10 mol H S
{H S} 1.00 atm 0.534 atm
17.86 10 mol total
4.77 10 mol CH
{CH } 1.00 atm 0.267 atm
17.86 10 mol total
P
P
4
2
23
3
2
23
444
22
p22
24
7.10 10 mol CS
{CS } 1.00 atm 0.0398 atm
17.86 10 mol total
2.84 10 mol H
{H } 1.00 atm 0.159 atm
17.86 10 mol total
{H } {CS } 0.159 0.0398 3.34 10
{H S} {CH } 0.534 0.267
P
P
PP
KPP
86. (D)
81. We base our calculation on an I.C.E. table, after we first determine
the direction of the reaction by computing :
6
2
22
2
2
23
2222
c1048.6
)5000.0()5000.0(
)03000.0()03000.0(
]Hg[]Fe[
]Hg[][Fe
Q
Because this value is smaller than Kc, the reaction will shift to the right to reach equilibrium.
Since the value of the equilibrium constant for the forward reaction is quite small, let us
assume that the reaction initially shifts all the way to the left (line labeled “to left:”), and then
reacts back in the forward direction to reach a position of equilibrium.
32 2 2
2
Equation: 2 Fe (aq) Hg (aq) 2 Fe (aq) 2 Hg (aq)
Initial: 0.5000 M 0.5000 M 0.03000 M 0.03000 M
0.03000 M
0.0150 M 0.03000 M 0.03000 M
To left: 0.5300 M 0.5150 M 0 M 0 M
Changes: 2 M M xx
22 22 2 2 2 2
6
c32 2 2
2
2 M 2 M
Equil: (0.5300 2 )M (0.5150 )M 2 M 2 M
[Fe ] [Hg ] (2 ) (2 ) 4 4
9.14 10
[Fe ] [Hg ] (0.5300 2 ) (0.5150 ) (0.530
xx
xxx x
xx xx
Kxx
2
0) 0.5150
Note that we have assumed that 5150.0 and 0.5300 2
xx
0170.01026.8
44
(0.5150) (0.5300) 1014.9 8
26
4
xx
Our assumption, that 0.5300 0.0340) ( 2
x, is reasonably good.
32
2
22
[Fe ] 0.5300 2 0.0170 0.4960 M [Hg ] 0.5150 0.0170 0.4980
[Fe ] [Hg ] 2 0.0170 0.0340 M

Chapter15: Principles of Chemical Equilibrium
710
c
22 22 2 2
6 6
c32 2 2
2
We check by substituting into the K expression.
[Fe ] [Hg ] (0.0340) (0.0340)
9.14 10 K 11 10 Not a substantial difference.
[Fe ] [Hg ] (0.4960) 0.4980
Mathematica (version 4.0, Wolfram Research, Champaign, IL) gives a root of 0.0163.
87. (D) Again we base our calculation on an I.C.E. table. In the course of solving the
Integrative Example, we found that we could obtain the desired equation by reversing
equation (2) and adding the result to equation (1)
24 2
222
42
(2) H O(g) CH (g) CO(g) 3 H (g) 1/190
(1) CO(g) H O(g) CO (g) H (g) 1.4
Equation:CH (g) 2 H O(g)
K
K
22
CO (g) 4 H (g) 1.4/190 0.0074K
24 2
222
42
(2) H O(g) CH (g) CO(g) 3 H (g) 1/190
(1) CO(g) H O(g) CO (g) H (g) 1.4
Equation: CH (g) 2 H O(g)
K
K
22
CO (g) 4 H (g) 1.4 /190 0.0074
Initial: 0.100 mol 0.100 mol 0.100 mol 0.100 mol
0.025 mol 0.050 mol 0.025 mol 0.100 mol
T
K
o left: 0.125 mol 0.150 mol 0.075 mol 0.000 mol
Concns: 0.0250 M 0.0300 M 0.015 M 0.000 M
Changes: M 2 mol xx mol 4 mol
Equil: (0.0250 ) M (0.0300 2 ) (0.015 ) M 4 mol
xx
xxxx
Notice that we have a fifth order polynomial to solve. Hence, we need to try to approximate
its final solution as closely as possible. The reaction favors the reactants because of the small
size of the equilibrium constant. Thus, we approach equilibrium from as far to the left as
possible.
M 014.0
2560150.0
0.0074 (0.0300) 0.0250
(0.0300) 0250.0
)(4 0150.0
)20300.0( )0250.0(
)4)(0150.0(
O]H][CH[
]H][CO[
0074.0
4
2
2
4
2
4
2
24
4
22
c
x
x
xx
xx
K
Our assumption is terrible. We substitute to continue successive approximations.
44
22
(0.0150 0.014) (4 ) (0.029)(4 )
0.0074
(0.0250 0.014) (0.0300 2 0.014) (0.011)(0.002)
xx
Next, try x2 = 0.0026
4
2
(0.0150 0.0026)(4 )
0.074 (0.0250 0.0026) (0.0300 2 0.0026)
x
Chapter15: Principles of Chemical Equilibrium
711
then, try x3 = 0.0123.
After 18 iterations, the x value converges to 0.0080.
Considering that the equilibrium constant is known to only two significant figures, this is a
pretty good result. Recall that the total volume is 5.00 L. We calculate amounts in moles.
4 4
2 2
2 2
2
CH (g) (0.0250 0.0080) 5.00 L 0.017 M 5.00 L 0.085 moles CH (g)
H O(g) (0.0300 2 0.0080) M 5.00 L 0.014 M 5.00 L 0.070 moles H O(g)
CO (g) (0.015 0.0080) M 5.00 L 0.023 M 5.00 L 0.12 mol CO
H(g) (4
2
0.0080) M 5.00 L 0.032 M 5.00 L 0.16 mol H
88. (M) The initial mole fraction of C2H2 is i0.88
. We use molar amounts at equilibrium to
compute the equilibrium mole fraction of C2H2, eq
. Because we have a 2.00-L container,
molar amounts are double the molar concentrations.
22
eq
22 4 2
(2 0.756) mol C H 0.877
(2 0.756) mol C H (2 0.038) mol CH (2 0.068) mol H
Thus, there has been only a slight decrease in mole fraction.
89. (M)
(a) Keq = 4.6×104 22
22
2
P{NOCl} (4.125)
=
P{NO} P{Cl } P{NO} (0.1125)
2
4
(4.125)
P{NO} = = 0.0573 atm
4.6 10 (0.1125)
(b) Ptotal = PNO+ PCl2 + PNOCl = 0.0573 atm + 0.1125 atm + 4.125 atm = 4.295 atm
90. (M) We base our calculation on an I.C.E. table.
22 3
Reaction: N (g) + 3H (g) 2NH (g)
0.424mol 1.272mol 0 mol
Initial: 10.0L 10.0L 10.0L
-3 mol +2 mol
- mol
Change 10.0L 10.0L 10.0L
(1.272-3 ) mol 2 mol
(0.424- ) mol
Equilibrium 10.0L 10.0L 10.0L
xx
x
xx
x
Chapter15: Principles of Chemical Equilibrium
712
2
2
3
c3
3
22
2mol
10.0L
[NH ]
K = =152=
[N ][H ] (0.424- ) mol (1.272-3 )mol
10.0L 10.0L
x
xx
2
c3
22
c44
3
100 2 mol
K=(0.424- ) mol 3 0.424- ) mol
100 2 mol 2 mol
K = = 152 = 41.04 Take root of both sides
3 0.424- ) mol 0.424- ) mol
x
xx
xx
xx
2
2
22 2
3
2mol = 6.41 6.41(0.424- ) = 2
0.424- ) mol
3.20(0.180 0.848 ) 3.20 2.71 0.576 3.20 3.71 0.576 0
Now solve using the quadratic equation: = 0.1846 mol or 0.9756 mol (too large)
amount of NH 2
xxx
x
xx x x x x x
x
22
2(0.1846mol) = 0.369mol in 10.0 L or 0.0369 M
([H ] = 0.0718 [ ] 0.0239 )
x
M and N M
91. (D)
23c
2
Δn 3
pc
Equation: 2 H (g) CO(g) CH OH(g) K 14.5 at 483 K
L-atm
K K (RT) 14.5 0.08206 483K 9.23 10
mol-K
2
CO
H
We know that mole percents equal pressure percents for ideal gases.
P 0.350 100 atm 35.0 atm
P 0.650 100 atm 65.0 atm
23
Equation: 2 H (g) CO(g) CH OH(g)
Initial: 65 atm 35 atm
Changes: 2P atm P atm P atm
Equi
3
2
2
3
CH OH 3
p2
H
CO
CH OH
l: 65-2P 35-P P
PP
K 9.23 10
(35.0 P)(65.0 2P)
P P
By successive approximations, P 24.6 atm = P at equilibrium.
Mathematica (version 4.0, Wolfram Research, Champaign, IL) gives a root of 24.5.

Chapter15: Principles of Chemical Equilibrium
713
FEATURE PROBLEMS
92. (M) We first determine the amount in moles of acetic acid in the equilibrium mixture.
32
2
32
2
32
0.1000 mol Ba OH 2 mol CH CO H1 L
amount CH CO H = 28.85 mL 1000 mL 1 L 1 mol Ba OH
complete equilibrium mixture = 0.5770 mol CH CO H
0.01 of equilibrium mixture
3225 2
c
25 3 2
0.423mol 0.423mol
CH CO C H H O 0.423 0.423
=4.0
0.077mol 0.577mol
C H OH CH CO H 0.077 0.577
VV
K
VV
93. (D) In order to determine whether or not equilibrium has been established in each bulb, we
need to calculate the concentrations for all three species at the time of opening. The results
from these calculations are tabulated below and a typical calculation is given beneath this table.
Bulb
No. Time
Bulb
Opened
(hours)
Initial
Amount
HI(g)
(in mmol)
Amount of I2(g)
and H2(g) at
Time of Opening
(in mmol)
Amount HI(g)
at Time of
Opening
(in mmol)
[HI]
(mM) [I2] &
[H2]
(mM)
2
22
[HI]
]][I[H
1 2 2.345 0.1572 2.03 5.08 0.393 0.00599
2 4 2.518 0.2093 2.10 5.25 0.523 0.00992
3 12 2.463 0.2423 1.98 4.95 0.606 0.0150
4 20 3.174 0.3113 2.55 6.38 0.778 0.0149
5 40 2.189 0.2151 1.76 4.40 0.538 0.0150
Consider, for instance, bulb #4 (opened after 20 hours).
Initial moles of HI(g) = 0.406 g HI(g) 1 mole HI
127.9 g HI = 0.003174 mol HI(g) or 3.174 mmol
moles of I2(g) present in bulb when opened.
= 0.04150 L Na2S2O3 22 3
22 3
0.0150 mol Na S O
1 L Na S O OSNa mol 2
Imol1
322
2= -4
2
3.113 10 mol I
millimoles of I2(g) present in bulb when opened = -4
2
3.113 10 mol I
moles of H2 present in bulb when opened = moles of I2(g) present in bulb when opened.
HI reacted = 3.113 10-4 mol I2
2
I mol 1
HI mole 2 = 6.226 10-4 mol HI (0.6226 mmol HI)
moles of HI(g) in bulb when opened= 3.174 mmol HI
0.6226 mmol HI = 2.55 mmol HI
Concentrations of HI, I2, and H2
Chapter15: Principles of Chemical Equilibrium
714
[HI] = 2.55 mmol HI 0.400 L = 6.38 mM
[I2] = [H2] = 0.3113 mmol 0.400 L = 0.778 mM
Ratio: 22
22
[H ][I ] (0.778 mM)(0.778 mM)
[HI] (6.38 mM)
= 0.0149
As the time increases, the ratio 2
22
[HI]
]][I[H initially climbs sharply, but then plateaus at
0.0150 somewhere between 4 and 12 hours. Consequently, it seems quite reasonable to
conclude that the reaction 2HI(g)
H2(g) + I2(g) has a Kc ~ 0.015 at 623 K.
94. (D) We first need to determine the number of moles of ammonia that were present in the
sample of gas that left the reactor. This will be accomplished by using the data from the
titrations involving HCl(aq).
Original number of moles of HCl(aq) in the 20.00 mL sample
= 0.01872 L of KOH 0.0523 mol KOH 1 mol HCl
1 L KOH 1 mol KOH
= 9.7906 10-4 moles of HCl(initially)
Moles of unreacted HCl(aq)
= 0.01542 L of KOH 0.0523 mol KOH 1 mol HCl
1 L KOH 1 mol KOH
=
8.0647 10-4 moles of HCl(unreacted)
Moles of HCl that reacted and /or moles of NH3 present in the sample of reactor gas
= 9.7906 10-4 moles 8.0647 10-4 moles = 1.73 10-4 mole of NH3 (or HCl).
The remaining gas, which is a mixture of N2(g) and H2(g) gases, was found to occupy 1.82 L
at 273.2 K and 1.00 atm. Thus, the total number of moles of N2 and H2 can be found via the
ideal gas law: 22
H
N
n= PV
R
T= (1.00 atm)(1.82 L)
L atm
(0.08206 )(273.2 K)
K mol
= 0.08118 moles of (N2 + H2)
According to the stoichiometry for the reaction, 2 parts NH3 decompose to give 3 parts H2
and 1 part N2. Thus the non-reacting mixture must be 75% H2 and 25% N2.
So, the number of moles of N2 = 0.25 0.08118 moles = 0.0203 moles N2 and the
number of moles of H2 = 0.75 0.08118 moles = 0.0609 moles H2.

Chapter15: Principles of Chemical Equilibrium
715
Before we can calculate Kc, we need to determine the volume that the NH3, N2, and H2
molecules occupied in the reactor. Once again, the ideal gas law (PV = nRT) will be
employed. ngas = 0.08118 moles (N2 + H2 ) + 1.73 10-4 moles NH3 = 0.08135 moles
Vgases = nRT
P =
L atm
(0.08135 mol)( 0.08206 )(1174.2 K)
K mol
30.0 atm = 0.2613 L
So, Kc =
-4 2
31
1.73 10 moles
0.2613 L
0.0609 moles 0.0203 moles
0.2613 L 0.2613 L
= 4.46 10-4
To calculate Kp at 901 C, we need to employ the equation
gas
n
pc gas
; 2KKRT n
Kp = 4.46 10-4 [(0.08206 L atm K-1mol-1)] (1174.2 K)]-2 = 4.80
10-8 at 901C for the
reaction N2(g) + 3 H2(g)
2 NH3(g)
95. (M) For step 1, rate of the forward reaction = rate of the reverse reaction, so,
k1[I2] = k-1[I]2 or 1
-1
k
k=][I
[I]
2
2
= Kc (step 1)
Like the first step, the rates for the forward and reverse reactions are equal in the second step
and thus,
k2[I]2[H2] = k-2[HI]2 or 2
-2
k
k=2
22
[HI]
[I] [H ] = Kc (step 2)
Now we combine the two elementary steps to obtain the overall equation and its associated
equilibrium constant.
I
2(g)
2 I(g) Kc = 1
-1
k
k=][I
[I]
2
2
(STEP 1)
and
H2(g) + 2 I(g)
2 HI(g) Kc = 2
-2
k
k=2
22
[HI]
[I] [H ] (STEP 2)
H2(g) + I2(g)
2 HI(g) Kc(overall) = Kc(step 1) Kc(step 2)
Kc(overall) = 1
-1
k
k
2-
2
k
k = ][I
[I]
2
2
2
22
[HI]
[I] [H ]
Kc(overall) = 12
-1 2
kk
kk
=
2
22
2
2
[I] [HI]
[I] [I ][H ] =
2
2
2
[HI]
[I ][H ]

Chapter15: Principles of Chemical Equilibrium
716
96. (M) The equilibrium expressions for the two reactions are:
2
33
12
23 3
HHCO HCO
K; K
HCO HCO
First, start with [H+] = 0.1 and [HCO3–] = 1. This means that [H+]/[HCO3–] = 0.1, which
means that [CO32–] = 10K2. By adding a small amount of H2CO3 we shift [H+] by 0.1 and
[HCO3–] by 0.1. This leads to [H+]/[HCO3–]
0.2, which means that [CO32–] = 5K2. Note that
[CO32–] has decreased as a result of adding H2CO3 to the solution.
97. (D) First, it is most important to get a general feel for the direction of the reaction by
determining the reaction quotient:
C(aq) 0.1
Q10
A(aq) B(aq) 0.1 0.1
Since Q>>K, the reaction proceeds toward the reactants. Looking at the reaction in the
aqueous phase only, the equilibrium can be expressed as follows:
A(aq) + B(aq)
C(aq)
Initial 0.1 0.1 0.1
Change -x -x +x
Equil. 0.1 - x 0.1 - x 0.1 + x
We will do part (b) first, which assumes the absence of an organic layer for extraction:
0.1 x
K0.01
0.1 x 0.1 x
Expanding the above equation and using the quadratic formula, x = -0.0996. Therefore, the
concentration of C(aq) and equilibrium is 0.1 + (-0.0996) = 4×10-4 M.
If the organic layer is present for extraction, we can add the two equations together, as shown
below:
A(aq) + B(aq) C(aq)
C(aq)
C(or)
A(aq) + B(aq) C(or)
K = K1 × K2 = 0.1 × 15 = 0.15.
Since the organic layer is present with the aqueous layer, and K2 is large, we can expect that
the vast portion of C initially placed in the aqueous phase will go into the organic phase.

Chapter15: Principles of Chemical Equilibrium
717
Therefore, the initial [C] = 0.1 can be assumed to be for C(or). The equilibrium can be
expressed as follows
A(aq) + B(aq)
C(or)
Initial 0.1 0.1 0.1
Change -x -x +x
Equil. 0.1 - x 0.1 - x 0.1 + x
We will do part (b) first, which assumes the absence of an organic layer for extraction:
0.1 x
K0.15
0.1 x 0.1 x
Expanding the above equation and using the quadratic formula, x = -0.0943. Therefore, the
concentration of C(or) and equilibrium is 0.1 + (-0.0943) = 6×10-4 M. This makes sense
because the K for the overall reaction is < 1, which means that the reaction favors the
reactants.
SELF-ASSESSMENT EXERCISES
98. (E)
(a) Kp: The equilibrium constant of a reaction where the pressures of gaseous reactants and
products are used instead of their concentrations
(b) Qc: The reaction quotient using the molarities of the reactants and products
(c) Δngas: The difference between the number of moles (as determined from a balanced
reaction) of product and reactant gases
99. (E)
(a) Dynamic equilibrium: In a dynamic equilibrium (which is to say, real equilibrium), the
forward and reverse reactions happen, but at a constant rate
(b) Direction of net chemical change: In a reversible reaction, if the reaction quotient Qc > Kc,
then the net reaction will go toward the reactants, and vice versa
(c) Le Châtelier’s principle: When a system at equilibrium is subjected to external change
(change in partial pressure of reactants/products, temperature or concentration), the
equilibrium shifts to a side to diminish the effects of that external change
(d) Effect of catalyst on equilibrium: A catalyst does not affect the final concentrations of the
reactants and products. However, since it speeds up the reaction, it allows for the
equilibrium concentrations to be established more quickly
100. (E)
(a) Reaction that goes to completion and reversible reaction: In a reversible reaction, the
products can revert back to the reactants in a dynamic equilibrium. In a reaction that goes
to completion, the formation of products is so highly favored that there is practically no
reverse reaction (or the reverse is practically impossible, such as a combustion reaction).
Chapter15: Principles of Chemical Equilibrium
718
(b) Kp and Kc: Kp is the equilibrium constant using pressures of products and reactants, while
Kc is the constant for reaction using concentrations.
(c) Reaction quotient (Q) and equilibrium constant expression (K): The reaction quotient Q is
the ratio of the concentrations of the reactants and products expressed in the same format
as the equilibrium expression. The equilibrium constant expression is the ratio of
concentrations at equilibrium.
(d) Homogeneous and heterogeneous reaction: In a homogeneous reaction, the reaction
happens within a single phase (either aqueous or gas). In a heterogeneous reaction, there
is more than one phase present in the reaction.
101. (E) The answer is (c). Because the limiting reagent is I2 at one mole, the theoretical yield of
HI is 2 moles. However, because there is an established equilibrium, there is a small amount
of HI which will decompose to yield H2 and I2. Therefore the total moles of HI created is
close, but less than 2.
102. (E) The answer is (d). The equilibrium expression is:
2
3
2
22
PSO
K 100
PSO PO
If equilibrium is established, moles of SO3 and SO2 cancel out of the equilibrium expression.
Therefore, if K = 100, the moles of O2 have to be 0.01 to make K = 100.
103. (E) The answer is (a). As the volume of the vessel is expanded (i.e., pressure is reduced), the
equilibrium shifts toward the side with more moles of gas.
104. (E) The answer is (b). At half the stoichiometric values, the equilibrium constant is K1/2. If
the equation is reversed, it is K-1. Therefore, the K’ = K-1/2 = (1.8×10-6)-1/2 = 7.5×10-2.
105. (E) The answer is (a). We know that Kp = Kc (RT)Δn. Since Δn = (3–2) = 1, Kp = Kc (RT).
Therefore, Kp > Kc.
106. (E) The answer is (c). Since the number of moles of gas of products is more than the
reactants, increasing the vessel volume will drive the equilibrium more toward the product
side. The other options: (a) has no effect, and (b) drives the equilibrium to the reactant side.
107. (E) The equilibrium expression is:
22
22
C0.43
K1.9
0.55 0.33
BA
108. (E)
(a) As more O2 (a reactant) is added, more Cl2 is produced.
(b) As HCl (a reactant) is removed, equilibrium shifts to the left and less Cl2 is made.
(c) Since there are more moles of reactants, equilibrium shifts to the left and less Cl2 is made.
(d) No change. However, the equilibrium is reached faster.
(e) Since the reaction is exothermic, increasing the temperature causes less Cl2 to be made.
Chapter15: Principles of Chemical Equilibrium
719
109. (E) SO2 (g) will be less than SO2 (aq), because K > 1, so the equilibrium lies to the product
side, SO2 (aq).
110. (E) Since K >>1, there will be much more product than reactant
111. (M) The equilibrium expression for this reaction is:
2
3
2
22
SO
K 35.5
SO O
(a) If [SO3]eq = [SO2]eq, then [O2] = 1/35.5 = 0.0282 M.
moles of O2 = 0.0282 × 2.05 L = 0.0578 moles
(b) Plugging in the new concentration values into the equilibrium expression:
22
32
22
2
22 22
SO 2 SO 4
K 35.5
O
SO O SO O
[O2] = 0.113 M
moles of O2 = 0.113 × 2.05 L = 0.232 moles
112. (M) This concept map involves the various conditions that affect equilibrium of a reaction,
and those that don’t. Under the category of conditions that do cause a change, there is
changing the partial pressure of gaseous products and reactants, which includes pressure and
vessel volume. The changes that do not affect partial pressure are changing the concentration
of reactants or products in an aqueous solution, through dilution or concentration. Changing
the temperature can affect both aqueous and gaseous reactions. Under the category of major
changes that don’t affect anything is the addition of a non-reactive gas.
720
CHAPTER 16
ACIDS AND BASES
PRACTICE EXAMPLES
1A (E)
(a) In the forward direction, HF is the acid (proton donor; forms F), and H2O is the base
(proton acceptor; forms H3O). In the reverse direction, F is the base (forms HF),
accepting a proton from H3O, which is the acid (forms H2O).
(b) In the forward direction, HSO4 is the acid (proton donor; forms SO42), and NH3 is
the base (proton acceptor; forms NH4). In the reverse direction, SO42 is the base
(forms HSO4), accepting a proton from NH4, which is the acid (forms NH3).
(c) In the forward direction, HCl is the acid (proton donor; forms Cl), and C2H3O2 is
the base (proton acceptor; forms HC2H3O2). In the reverse direction, Cl is the base
(forms HCl), accepting a proton from HC2H3O2, which is the acid (forms C2H3O2).
1B (E) We know that the formulas of most acids begin with H. Thus, we identify HNO2 and
HCO3
as acids.
+
22 2 3
2+
32 3 3
HNO aq + H O(l) NO aq + H O aq ;
HCO aq + H O(l) CO aq + H O aq
A negatively charged species will attract a positively charged proton and act as a base.
Thus PO4
3 and HCO3
can act as bases. We also know that PO4
3 must be a base
because it cannot act as an acid—it has no protons to donate—and we know that all three
species have acid-base properties.
32
42 4
32 23 22
PO aq + H O(l) HPO aq + OH aq ;
HCO aq + H O(l) H CO (aq) CO H O aq + OH aq
Notice that HCO3
is the amphiprotic species, acting as both an acid and a base.
2A (M) HO
3+ is readily computed from pH: HO HO
pH
3+3+2.85 3
=10 =10 =1.4 10
M.
OHcan be found in two ways: (1) from KwHO OH=3+, giving
14 12
w
3
+
3
1.0 10
OH = = = 7.1 10
1.4 10
HO
K
M, or (2) from pH pOH+ = 14.00 , giving
pOH pH= 14.00 = 14.00 2.85 = 11.15
, and then OH
p
OH 11.15 12
= 10 = 10 = 7.1 10
M.
Chapter 16: Acids and Bases
721
2B (M) HO
3+ is computed from pH in each case: HO pH
3+=10
HO M HO M
conc dil
3+
.
2.50 3 3+
.
3.10 4
= 10 = 3.2 10 = 10 = 7.9 10
All of the H O
3+ in the dilute solution comes from the concentrated solution.
3+
+3+
3
3 3
3.2 10 mol H O
amount H O =1.00 L conc. soln = 3.2 10 mol H O
1 L conc. soln
Next we calculate the volume of the dilute solution.
3+
34+
3
1 L dilute soln
volume of dilute solution = 3.2 10 mol H O = 4.1 L dilute soln
7.9 10 mol H O
Thus, the volume of water to be added is = 3.1 L.
Infinite dilution does not lead to infinitely small hydrogen ion concentrations. Since
dilution is done with water, the pH of an infinitely dilute solution will approach that of
pure water, namely pH = 7.
3A (E) pH is computed directly from the equation below.
++
33
H O , pH = log H O = log 0.0025 = 2.60
.
We know that HI is a strong acid and, thus, is completely dissociated into H O
3
+ and I.
The consequence is that IHO
= = 0.0025
3
+ M. OHis most readily computed from
pH:
p
OH 11.40 12
pOH =14.00 pH =14.00 2.60 =11.40; OH =10 =10 = 4.0 10
M
3B (M) The number of moles of HCl(g) is calculated from the ideal gas law. Then HO
3+ is
calculated, based on the fact that HCl(aq) is a strong acid (1 mol H O
3
+ is produced from
each mole of HCl).
+
3
+
3
1atm
747mmHg 0.535L
760mmHg
moles HCl(g) = 0.08206Latm (26.5 273.2)K
mol K
moles HCl(g) 0.0214molHCl(g) = 0.0214mol H O when dissolved in water
[H O ] 0.0214mol pH = -log(0.0214) = 1.670
4A (E) pH is most readily determined from pOH log OH=. Assume Mg OH
bg2 is a strong
base.
22
22
9.63 mg Mg OH 1 mol Mg OH
1000 mL 1g 2mol OH
OH = 100.0 mL soln 1 L 1000 mg 58.32g Mg OH 1 mol Mg OH
OH = 0.00330M; pOH = log 0.00330 = 2.481
pH =14.000 pOH =14.000 2.481=11.519
Chapter 16: Acids and Bases
722
4B (E) KOH is a strong base, which means that each mole of KOH that dissolves produces one
mole of dissolved OH aq
bg
. First we calculate OH and the pOH. We then use
pH pOH+ = 14.00 to determine pH.
OH g KOH
g soln
mol KOH
g KOH
mol OH
mol KOH
g soln
mL soln
mL
LM
=3.00
100.00
1
56.11
1
1
1.0242
1
1000
1= 0.548
pOH = log 0.548 = 0.261 pH =14.000 pOH =14.000 0.261= 13.739
5A (M) HO pH
3
+4.185
= 10 = 10 = 6.6 10
M.
Organize the solution using the balanced chemical equation.
Equation:
2
HOCl aq + H O(l)
HO aq
3+bg
+ OCl aq
bg
Initial: 0.150 M — 0 M
0 M
Changes: 5
6.6 10 M
— 5
+6.6 10 M
5
+6.6 10 M
Equil: ≈ 0.150 M — 5
6.6 10 M
5
6.6 10 M
55+
38
6.6 10 6.6 10
HO OCl =2.910
HOCl 0.150
a
K
5B (M) First, we use pH to determine OH. pOH pH= 14.00 = 14.00 10.08 = 3.92
.
OH pOH
= 10 = 10 = 1.2 10
3.92 4 M. We determine the initial concentration of cocaine
and then organize the solution around the balanced equation in the manner we have used
before.
17 21 4 17 21 4
17 21 4
17 21 4
0.17g C H O N 1mol C H O N
1000mL
[C H O N] = = 0.0056M
100mL soln 1L 303.36g C H O N
Equation: 17 21 4 2
CHON(aq)+ HO(l)
CHONH aq
17 21 4 +bg
+ OH aq
bg
Initial: 0.0056 M — 0 M 0 M
Changes: 4
1.2 10 M
— 4
+1.2 10 M
4
+1.2 10 M
Equil: ≈ 0.0055 M — 4
1.2 10 M
4
1.2 10 M
Kb
CHONH OH
CHON
17 21 4 +
17 21 4
44
6
1.2 10 1.2 10
0 0055 26 10
chch
..
Chapter 16: Acids and Bases
723
6A (M) Again we organize our solution around the balanced chemical equation.
Equation:
Initial: 22 2 2
HC H FO (aq) + H O(l)
0.100 M —
HO
3+(aq) +
0M
CHFO
22 2
(aq)
0 M
Changes:
x
M — +
x
M +
x
M
Equil: 0.100 x
bg M —
x
M
x
M
+
3222 3
a
22 2
HO CHFO
= ; therefore, 2.6 10 0.100
HC H FO
xx
K
x
We can use the 5% rule to ignore x in the denominator. Therefore, x = [H3O+] = 0.016 M,
and pH = –log (0.016) = 1.8. Thus, the calculated pH is considerably lower than 2.89
(Example 16-6).
6B (M) We first determine the concentration of undissociated acid. We then use this value in
a set-up that is based on the balanced chemical equation.
974 974
974
0.500 g HC H O 1 mol HC H O 1
2aspirin tablets× × × = 0.0171M
tablet 180.155g HC H O 0.325L
Equation:
Initial: 974
HC H O (aq) + H2O(l)
0.0171 M —
HO
3+(aq) +
0 M 974
CHO (aq)
0 M
Changes:
x
M — +
x
M +
x
M
Equil: 0.0171x
bg M —
x
M
x
M
+
3974 4
a
974
HO CHO
==3.310=
HC H O 0.0171
x
x
K
x
24 6
+3.3 10 5.64 10 = 0x
(find the physically reasonable roots of the quadratic equation)
475
3.3 10 1.1 10 2.3 10 0.0022M; pH log(0.0022) 2.66
2
x
7A (M) Again we organize our solution around the balanced chemical equation.
Equation:
Initial:
Changes
22 2 2
HC H FO (aq) + H O(l)
0.015 M —
x
M —
H3O+ (aq) +
0M
+
x
M
CHFO
22 2
(aq)
0 M
+
x
M
Equil: 0.015x
bg M —
x
M
x
M
+2
3222 3
a
22 2
HO CHFO
==2.610=
HC H FO 0.015 0.015
xx
x
Kx
xx= 0 015 2 6 10 0 0062
23
.. .M=[HO]
3+ Our assumption is invalid:

Chapter 16: Acids and Bases
724
0.0062 is not quite small enough compared to 0.015 for the 5% rule to hold. Thus we use
another cycle of successive approximations.
33+
a 3
33+
a 3
= = 2.6 10 = (0.015 0.0062) 2.6 10 0.0048 M = [H O ]
0.015 0.0062
= = 2.6 10 = (0.015 0.0048) 2.6 10 0.0051 M = [H O ]
0.015 0.0048
xx
Kx
xx
Kx
33+
a 3
= = 2.6 10 = (0.015 0.0051) 2.6 10 0.0051 M = [H O ]
0.015 0.0051
xx
Kx
Two successive identical results indicate that we have the solution.
pH log H O log= = 0.0051 = 2.29
3+
bg. The quadratic equation gives the same result
(0.0051 M) as this method of successive approximations.
7B (M) First we find [C5H11N]. We then use this value as the starting base concentration in a
set-up based on the balanced chemical equation.
CH N mg C H N
mL soln
mmol C H N
mg C H N M
511 511 511
511
=114
315
1
85.15 = 0.00425
Equation:
Initial:
Changes:
Equil:
511 2
C H N(aq) + H O(l)
0.00425 M —
M
x
—
0.00425 Mx —
+
511
CH NH (aq) +
0 M
+ Mx
M
x
OH(aq)
0 M
+ M
x
M
x
+
511 3
b
511
C H NH OH
==1.610=
C H N 0.00425 0.00425
x
xxx
Kx
We assumed that 0.00425x
x0 0016 0 00425 0 0026.. .M The assumption is not valid. Let’s assume
x
0 0026.
x0 0016 0 00425 0 0026 0 0016.(. .). Let’s try again, with
x
0 0016.
x0 0016 0 00425 0 0016 0 0021.(. .). Yet another try, with
x
0 0021.
x0 0016 0 00425 0 0021 0 0019.(. .). The last time, with
x
0 0019.
0.0016(0.00425 0.0019) 0.0019M = [OH ]x
3
pOH= log[H O ] log(0.0019) 2.72
pH pOH= 14.00 = 14.00 2.72 = 11.28
We could have solved the problem with the quadratic formula roots equation rather than by
successive approximations. The same answer is obtained. In fact, if we substitute
x
= 0.0019 into the Kb expression, we obtain 0.0019 / 0.00425 0.0019 = 1.5 10
23
bgbg
compared to Kb=1.6 10 3
. The error is due to rounding, not to an incorrect value.
Using
x
= 0.0020 gives a value of 1.8 10 3
, while using
x
= 0.0018 gives 1.3 10 3
.

Chapter 16: Acids and Bases
725
8A (M) We organize the solution around the balanced chemical equation; aM is [HF]initial.
Equation:
Initial:
Changes:
Equil:
2
HF(aq) + H O(l)
Ma —
M
x
—
Max —
+
3
HO(aq)
0 M
+ M
x
M
x
+
F(aq)
0 M
+ Mx
M
x
+2
34
a
HO F
===6.610
HF
xx x
Kax a
xa=6610
4
.
For 0.20 M HF, a = 0.20 M 4
= 0.20 6.6 10 0.011 Mx
0.011 M
% dissoc= 100%=5.5%
0.20 M
For 0.020 M HF, a = 0.020 M x= 0 020 6 6 10 0 0036
4
.. .
M
We need another cycle of approximation: x= 0 020 0 0036 6 6 10 0 0033
4
(. . ) . .
M
Yet another cycle with
x
0.0033 M : x= 0 020 0 0033 6 6 10 0 0033
4
(. . ) . .
M
0.0033M
% dissoc = 100% = 17%
0.020M
As expected, the weak acid is more dissociated.
8B (E) Since both H O
3
+ and C H O
353
come from the same source in equimolar amounts,
their concentrations are equal. HO CHO M M
3
+
353
= = 0.067 0.0284 = 0.0019
Ka
HO CHO
HC H O
==
0.0019 0.0019
0.0284 0.0019 =1.4 10
3+353
353
4
L
N
MO
Q
P
bgbg
9A (M) For an aqueous solution of a diprotic acid, the concentration of the divalent anion is
very close to the second ionization constant: 2
6
2a
OOCCH COO = 2.0 10 MK
. We
organize around the chemical equation.
Equation:
Initial:
Change:
Equil:
22
2
CH COOH (aq) + H O(l)
1.0 M —
x M —
(1.0 –x) M —
+
3
HO(aq)
0M
+ M
x
M
x
+
22
HCH COO (aq)
0 M
+ M
x
M
x
2
32 3
2
22
[H O ][HCH (COO) ] ()() 1.4 10
[CH (COOH) ] 1.0 1.0
a
xx x
Kx
32+
32
1.4 10 3.7 10 M [H O ] [HOOCCH COO ]x
1.0Mx is a valid assumption.

Chapter 16: Acids and Bases
726
9B (M) We know
2
adoubly charged anionK for a polyprotic acid. Thus,
2
52
a24
=5.3 10 COK
. From the pH, +pH0.67
3
HO =10 =10 =0.21M
. We also
recognize that HC O H O
24 3+
=
, since the second ionization occurs to only a very small
extent. We note as well that HC O
24
is produced by the ionization of H C O
224
. Each
mole of HC O
24
present results from the ionization of 1 mole of HCO
224
. Now we have
sufficient information to determine the 1
a
K.
1
+
324 2
a
224
HO HCO 0.21 0.21
===5.310
H C O 1.05 0.21
K
10A (M) HSO
24
is a strong acid in its first ionization, and somewhat weak in its second, with
2
2
a=1.1 10 = 0.011K
. Because of the strong first ionization step, this problem involves
determining concentrations in a solution that initially is 0.20 M H O
3+ and 0.20 M HSO4
.
We base the set-up on the balanced chemical equation.
Equation: HSO aq H O
42
+
bg(l)
HO aq
3+bg
+ 2-
4
SO (aq)
Initial: 0.20 M — 0.20 M 0 M
Changes: M
x
— + M
x
+ M
x
Equil:
0.20 Mx —
0.20 + Mx M
x
2
2
+
34
a
4
HO SO 0.20 + 0.20
= = = 0.011 , assuming that 0.20M.
0.20 0.20
HSO
= 0.011M Try one cycle of approximation:
xx x
Kx
x
x
0.011 0.20 + 0.011
0.20 0.011 =0.21
0.19 =0.19 0.011
0.21 = 0.010
bg
bgxxxM
The next cycle of approximation produces the same answer 2
4
0.010M = SO ,
+
34
H O = 0.010 + 0.20 M = 0.21 M, HSO = 0.20 0.010 M = 0.19 M
10B (M) We know that H SO
24
is a strong acid in its first ionization, and a somewhat weak
acid in its second, with 2
2
a=1.1 10 = 0.011K
. Because of the strong first ionization step,
the problem essentially reduces to determining concentrations in a solution that initially is
0.020 M H O
3+ and 0.020 M HSO4
. We base the set-up on the balanced chemical
equation. The result is solved using the quadratic equation.

Chapter 16: Acids and Bases
727
Equation: HSO aq H O
42
+
bg(l)
HO aq
3+bg
+ SO aq
4
2bg
Initial: 0.020 M — 0.020 M 0 M
Changes: M
x
— + M
x
+ M
x
Equil:
0.020 Mx —
0.020 + Mx M
x
2
2
+
34 24
a
4
HO SO 0.020 +
= = = 0.011 0.020 + = 2.2 10 0.011
0.020
HSO
xx
Kxxx
x
+
43
HSO = 0.020 0.0060 = 0.014 M H O = 0.020 + 0.0060 = 0.026 M
(The method of successive approximations converges to = 0.006 Mx in 8 cycles.)
11A (E)
(a) CH NH NO
33
+
3
is the salt of the cation of a weak base. The cation, +
33
CH NH , will
hydrolyze to form an acidic solution
++
33 2 32 3
CH NH + H O CH NH + H O
, while
NO3–, by virtue of being the conjugate base of a strong acid will not hydrolyze to a
detectable extent. The aqueous solutions of this compound will thus be acidic.
(b) NaI is the salt composed of the cation of a strong base and the anion of a strong
acid, neither of which hydrolyzes in water. Solutions of this compound will be pH
neutral.
(c) NaNO2 is the salt composed of the cation of a strong base that will not hydrolyze in
water and the anion of a weak acid that will hydrolyze to form an alkaline solution
22 2
NO + H O HNO + OH
. Thus aqueous solutions of this compound will be
basic (alkaline).
11B (E) Even without referring to the K values for acids and bases, we can predict that the
reaction that produces H O
3+ occurs to the greater extent. This, of course, is because the pH
is less than 7, thus acid hydrolysis must predominate.
We write the two reactions of H PO
24
with water, along with the values of their equilibrium
constants.
2
+2 8
24 2 3 4 a
HPO aq+HO(l) HO aq+HPO aq =6.310K
1
14 12
w
24 2 34 b 3
a
1.0 10
H PO aq + H O(l) OH aq + H PO aq = = =1.4 10
7.1 10
K
KK
As predicted, the acid ionization occurs to the greater extent.
2
24
0.031 0.00096 + 0.00088
+ 0.031 0.00022 = 0 = = 0.0060 M = SO
2
xx x
Chapter 16: Acids and Bases
728
12A (M) From the value of p b
K we determine the value of Kb and then Ka for the cation.
cocaine bpaw
b
: = 10 = 10 = 3.9 10 = = 1.0 10
3.9 10 =2.6 10
8.41 9 14
9
6
KK
K
K
K
codeine bpaw
b
: = 10 = 10 = 1.1 10 = = 1.0 10
1.1 10 =9.1 10
7.95 8 14
8
7
KK
K
K
K
(This method may be a bit easier:
pp
ab a
KK K= 14.00 = 14.00 8.41= 5.59, = 10 = 2.6 10
5.59 6
) The acid with the larger
Ka will produce the higher H+, and that solution will have the lower pH. Thus, the
solution of codeine hydrochloride will have the higher pH (i.e., codeine hydrochloride is
the weaker acid).
12B (E) Both of the ions of NH CN aq
4bg react with water in hydrolysis reactions.
14
++10
w
42 33 a 5
b
1.0 10
NH aq + H O(l) NH aq + H O aq = = = 5.6 10
1.8 10
K
KK
14 5
w
2b
10
a
1.0 10
CN aq + H O(l) HCN aq + OH aq = = =1.6 10
6.2 10
K
KK
Since the value of the equilibrium constant for the hydrolysis reaction of cyanide ion is
larger than that for the hydrolysis of ammonium ion, the cyanide ion hydrolysis reaction
will proceed to a greater extent and thus the solution of NH CN aq
4bg will be basic
(alkaline).
13A (M) NaF dissociates completely into sodium ions and fluoride ions. The released fluoride
ion hydrolyzes in aqueous solution to form hydroxide ion. The determination of the
equilibrium pH is organized around the balanced equation.
Equation:
Initial:
Changes:
Equil:
-
2
F(aq) + HO(l)
0.10 M —
M
x
—
0.10 Mx —
HF(aq)
0 M
+ M
x
M
x
+
OH(aq)
0 M
+M
x
M
x
14 2
11
4-
1.0 10 [HF][OH ] ( )( )
1.5 10
6.6 10 [F ] (0.10 ) 0.10
w
b
a
K
x
xx
KKx
11 6 6
= 0.10 1.5 10 1.2 10 M=[OH ]; pOH= log(1.2 10 ) 5.92
pH = 14.00 pOH = 14.00 5.92 = 8.08 (As expected, pH > 7)
x
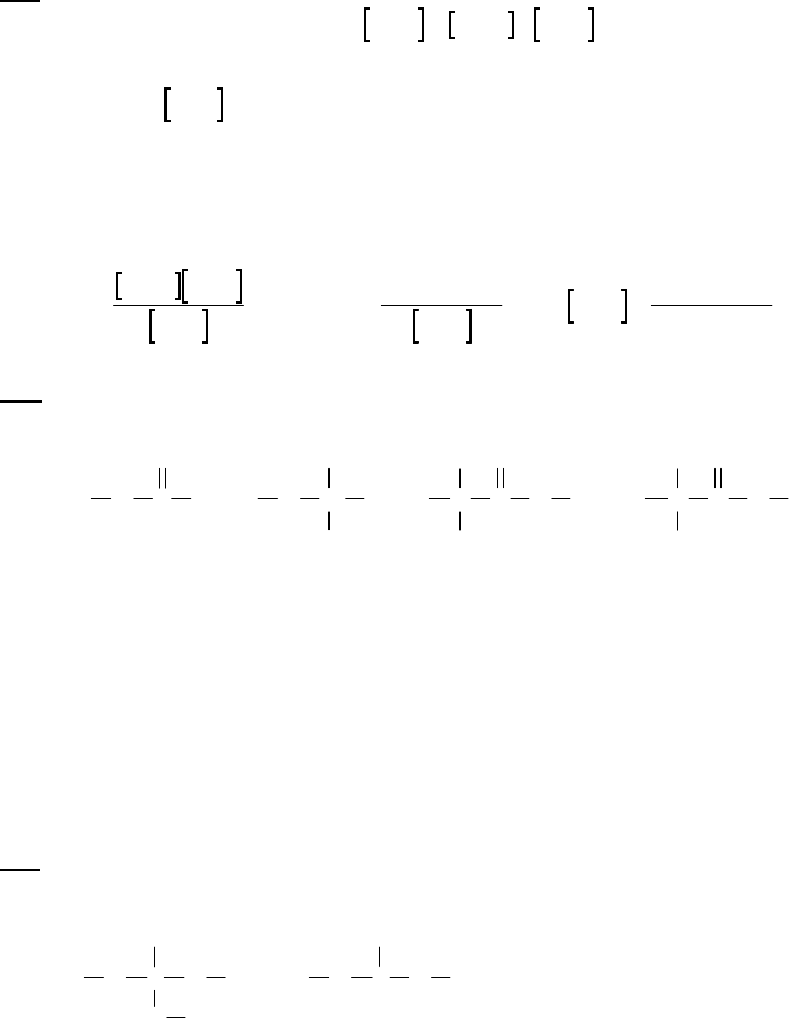
Chapter 16: Acids and Bases
729
13B (M) The cyanide ion hydrolyzes in solution, as indicated in Practice Example 16-12B. As a
consequence of the hydrolysis, OH HCN
=. OH can be found from the pH of the
solution, and then values are substituted into the Kb expression for CN, which is then
solved for CN.
pOH =14.00 pH =14.00 10.38 = 3.62
-pOH 3.62 4
OH = 10 = 10 = 2.4 10 M = HCN
Kb
HCN OH
CN CN CN M==1.610=
2.4 10 =2.4 10
1.6 10 =3.6 10
5
4242
5
3
ch ch
14A (M) First we draw the Lewis structures of the four acids. Lone pairs have been omitted
since we are interested only in the arrangements of atoms.
HClO4 should be stronger than HNO3. Although Cl and N have similar electronegativities,
there are more terminal oxygen atoms attached to the chlorine in perchloric acid than to the
nitrogen in nitric acid. By virtue of having more terminal oxygens, perchloric acid, when
ionized, affords a more stable conjugate base. The more stable the anion, the more easily it is
formed and hence the stronger is the conjugate acid from which it is derived.CH FCOOH
2
will be a stronger acid than CH BrCOOH
2 because F is a more electronegative atom than Br.
The F atom withdraws additional electron density from the O — H bond, making the bond
easier to break, which leads to increased acidity.
14B (M) First we draw the Lewis structures of the first two acids. Lone pairs are not depicted
since we are interested in the arrangements of atoms.
HPO
34
and H SO
23
both have one terminal oxygen atom, but S is more electronegative
than P. This suggests that
1
2
23 a
HSO =1.3 10K
should be a stronger acid than
1
3
34 a
HPO =7.1 10K
, and it is. The only difference between CCl CH COOH
32 and
CCl FCH COOH
22 is the replacement of Cl by F. Since F is more electronegative than Cl,
CCl CH COOH
32 should be a weaker acid than CCl FCH COOH
22 .
ONO
O
HOClO
O
H
O
OCC
O
FH
H
H
OCC
O
Br H
H
H
OPO
O
HH
OH
OSO
O
HH

Chapter 16: Acids and Bases
730
15A (M) We draw Lewis structures to help us decide.
(a) Clearly, BF3 is an electron pair acceptor, a Lewis acid, and NH3 is an electron pair
donor, a Lewis base.
(b) HO
2 certainly has electron pairs (lone pairs) to donate and thus it can be a Lewis
base. It is unlikely that the cation Cr3+ has any accessible valence electrons that can
be donated to another atom, thus, it is the Lewis acid. The product of the reaction,
[Cr(H2O)6]3+, is described as a water adduct of Cr3+.
Cr3+(aq) + H
H
O
6
OH2
OH2
OH2
OH2
H2O
H2OCr
3+
15B (M) The Lewis structures of the six species follow.
Both the hydroxide ion and the chloride ion have lone pairs of electrons that can be
donated to electron-poor centers. These two are the electron pair donors, or the Lewis
bases. Al OH
bg
3 and SnCl4 have additional spaces in their structures to accept pairs of
electrons, which is what occurs when they form the complex anions [Al(OH)4]- and
[SnCl6]2 -. Thus, Al OH
bg3 and SnCl4 are the Lewis acids in these reactions.
BF
F
F
N
H
H
H
BF
F
F
N
H
H
HO
H
H
Sn
Cl
Cl Cl
Cl
OH
+
AlOHOH
O
H
AlOHOH
O
H
O
H-
Cl
2Sn
Cl
Cl Cl
Cl
Cl
Cl 2-
2-

Chapter 16: Acids and Bases
731
INTEGRATIVE EXAMPLE
A. (D) To confirm the pH of rainwater, we have to calculate the concentration of CO2(aq) in
water and then use simple acid-base equilibrium to calculate pH.
Concentration of CO2 in water at 1 atm pressure and 298 K is 1.45 g/L, or
22 2
2
1.45 g CO 1mol CO 0.0329 M CO
L 44.0 g CO
Furthermore, if the atmosphere is 0.037% by volume CO2, then the mole fraction of CO2 is
0.00037, and the partial pressure of CO2 also becomes 0.00037 atm (because
22
CO CO atm
PP
)
From Henry’s law, we know that concentration of a gas in a liquid is proportional to its
partial pressure.
2
CO
11
C(mol / L) H P , which can rearrange to solve for H:
0.0329 M
H 0.0329 mol L atm
1atm
Therefore, concentration of CO2(aq) in water under atmospheric pressures at 298 K is:
2
11 5
CO
C (mol / L) 0.0329 mol L atm 0.00037 atm = 1.217 10 M
Using the equation for reaction of CO2 with water:
CO2 (aq) + 2 H2O (l) H3O+ (aq) + 3
HCO
(aq)
1.217×10-5 0 0
-x +x +x
1.217×10-5–x x X
27
a1 5
6
6
3
x
K 4.4 10
1.217 10 x
Using the quadratic formula, x = 2.104 10 M
pH log H O log 2.104 10 5.68 5.7
We can, of course, continue to refine the value of [H3O+] further by considering the
dissociation of HCO3–, but the change is too small to matter.
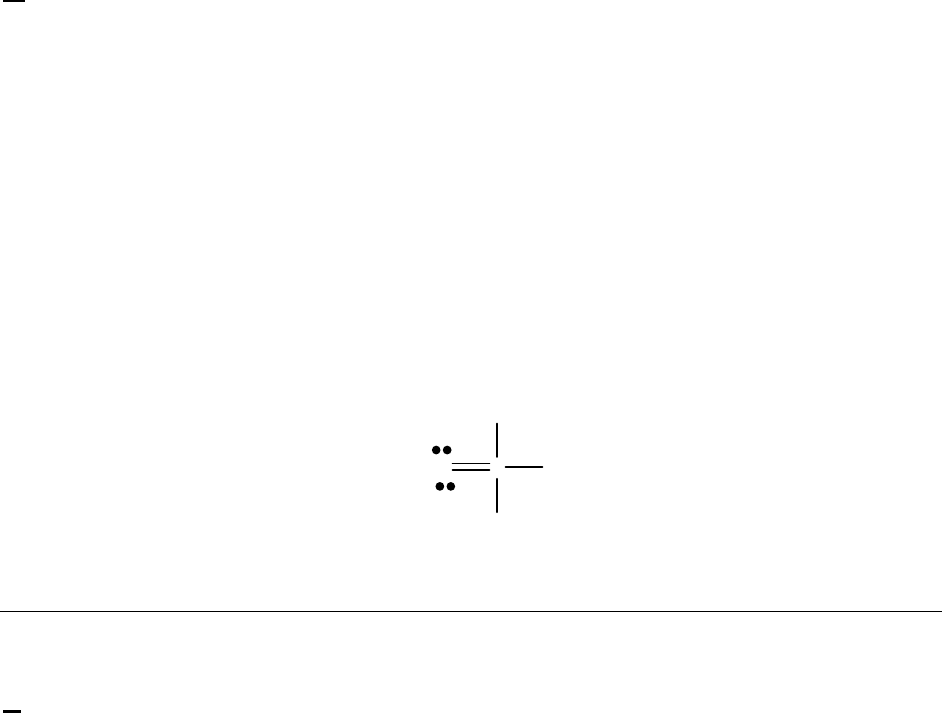
Chapter 16: Acids and Bases
732
B. (D)
(a) For the acids given, we determine values of m and n in the formula EOm(OH)n. HOCl or
Cl(OH) has m = 0 and n = 1. We expect Ka 10-7 or pKa 7, which is in good
agreement with the accepted pKa = 7.52. HOClO or ClO(OH) has m = 1 and n = 1. We
expect Ka 10-2 or pKa 2, in good agreement with the pKa = 1.92. HOClO2 or
ClO2(OH) has m = 2 and n = 1. We expect Ka to be large and in good agreement with
the accepted value of pKa = -3, Ka = 10-pKa = 103. HOClO3 or ClO3(OH) has m = 3 and
n = 1. We expect Ka to be very large and in good agreement with the accepted Ka = -8,
pKa = -8, Ka = 10-pKa = 108 which turns out to be the case.
(
b) The formula H3AsO4 can be rewritten as AsO(OH)3, which has m = 1 and n = 3. The
expected value is Ka = 10-2.
(
c) The value of pKa = 1.1 corresponds to Ka = 10-pKa = 10-1.1 = 0.08, which indicates that
m = 1. The following Lewis structure is consistent with this value of m.
OP
OH
H
OH
EXERCISES
Brønsted-Lowry Theory of Acids and Bases
1. (E)
(a) HNO2 is an acid, a proton donor. Its conjugate base is NO2
.
(b) OCl is a base, a proton acceptor. Its conjugate acid is HOCl.
(c) NH2
is a base, a proton acceptor. Its conjugate acid is NH3.
(d) NH4
+ is an acid, a proton donor. It’s conjugate base is NH3.
(e) CH NH
33
+ is an acid, a proton donor. It’s conjugate base is CH NH
32
.
2. (E) We write the conjugate base as the first product of the equilibrium for which the acid is
the first reactant.
(a)
+
32 3 3
HIO aq+HO(l) IO aq+HO aq
(b)
+
65 2 65 3
C H COOH aq + H O(l) C H COO aq + H O aq
(c)
23
+
42 43
HPO aq+HO(l) PO aq+HO aq
(d)
+
25 3 2 25 2 3
C H NH aq + H O(l) C H NH aq + H O aq
Chapter 16: Acids and Bases
733
3. (E) The acids (proton donors) and bases (proton acceptors) are labeled below their
formulas. Remember that a proton, in Brønsted-Lowry acid-base theory, is H+.
(a) +
23
HOBr(aq) + H O(l) H O (aq) + OBr (aq)
acid base acid base
(b)
2
+
42 3 4
HSO (aq) + H O(l) H O (aq) + SO (aq)
acid base acid base
(c) 22
HS (aq) + H O(l) H S(aq) + OH (aq)
base acid acid base
(d) 65 3 65 2 2
C H NH (aq) + OH (aq) C H NH (aq) + H O(l)
acid base base acid
4. (E) For each amphiprotic substance, we write both its acid and base hydrolysis reaction.
Even for the substances that are not usually considered amphiprotic, both reactions are
written, but one of them is labeled as unlikely. In some instances we have written an
oxygen as to keep track of it through the reaction.
2+
23 22
H +H O +H O unlikely H +H O H +OH
++
42 33 4
NH + H O NH + H O NH has no pairs that can be donatede
++
22 3 22 3
H +HO H +HO H +HO H +OH
2+
23 22
HS + H O S + H O HS + H O H S+ OH
2222
NO cannot act as an acid, (no protons) NO + H O HNO + OH
2+
32 3 3 32 23
HCO + H O CO + H O HCO + H O H CO + OH
++
23 22 unlikelyHBr+H O H O +Br HBr+H O H Br +OH
5. (E) Answer (b), NH3, is correct. HC H O
232
will react most completely with the strongest
base. 3
NO and Cl are very weak bases. HO
2 is a weak base, but it is amphiprotic,
acting as an acid (donating protons), as in the presence of NH3. Thus, NH3 must be the
strongest base and the most effective in deprotonating HC H O
232
.
6. (M) Lewis structures are given below each equation.
(a)
+
342
2NH l NH +NH
+
2 H N H
H
HNH
H
H
HNH

Chapter 16: Acids and Bases
734
(b)
+
2
2HF l H F + F
F
H
HF
FHFH ++
(c)
+
3323
2CHOH l CHOH +CHO
(d)
+
232 2232 232
2HCHO l HCHO +CHO
(e) 24 34 4
2 H SO ( ) 2 H SO HSOl
7. (E) The principle we will follow here is that, in terms of their concentrations, the weaker
acid and the weaker base will predominate at equilibrium. The reason for this is that a
strong acid will do a good job of donating its protons and, having done so, its conjugate
base will be left behind. The preferred direction is:
strong acid + strong base weak (conjugate) base + weak (conjugate) acid
(a) The reaction will favor the forward direction because OH (a strong base) NH3 (a
weak base) and 42
NH (relatively strong weak acid) H O (very weak acid)
.
(b) The reaction will favor the reverse direction because HNO HSO
34
(a weak acid
in the second ionization) (acting as acids), and SO NO
4
2
3
(acting as bases).
(c) The reaction will favor the reverse direction because HC H O CH OH
232 3
(not
usually thought of as an acid) (acting as acids), and CH O C H O
3232
(acting as
bases).
2 H C O
H
HCO
H
H
H
HH
H
HCO
H
H
2 H C C
H
HCC
H
H
H
OO
O
H
O
H
H
HCC
H
H
O
O
SO
O
OH
O
HSO
O
OH
O
H+ +
SO
O
OH
O
SO
O
OH
O
H
H
+
Chapter 16: Acids and Bases
735
8. (M) The principle we follow here is that, in terms of their concentrations, the weaker acid
and the weaker base predominate at equilibrium. This is because a strong acid will do a
good job of donating its protons and, having done so, its conjugate base will remain in
solution. The preferred direction is:
strong acid + strong base weak (conjugate) base + weak (conjugate) acid
(a) The reaction will favor the forward direction because HC H O
232
(a moderate acid)
HCO3 (a rather weak acid) (acting as acids) and CO C H O
3
2
232
(acting as
bases).
(b) The reaction will favor the reverse direction because HClO4 (a strong acid)
HNO2 (acting as acids), and NO ClO
24
(acting as bases).
(c) The reaction will favor the forward direction, because 23 3
HCO HCO
(acting as
acids) (because KK
12
) and CO HCO
3
2
3
(acting as bases).
Strong Acids, Strong Bases, and pH
9. (M) All of the solutes are strong acids or strong bases.
(a) +
+3
33
3
1mol HO
H O = 0.00165 M HNO 0.00165 M
1 mol HNO
14 12
w
+
3
1.0 10
OH = = = 6.1 10 M
0.00165M
HO
K
(b) 1mol OH
OH = 0.0087 M KOH 0.0087 M
1mol KOH
14
+12
w
3
1.0 10
H O = = = 1.1 10 M
0.0087M
OH
K
(c)
2
2
2mol OH
OH = 0.00213 M Sr OH 0.00426 M
1mol Sr OH
14
+12
w
3
1.0 10
H O = = = 2.3 10 M
0.00426 M
OH
K
(d) +
+4 4
3
3
1mol H O
H O = 5.8 10 M HI 5.8 10 M
1mol HI
14 11
w
4
+
3
1.0 10
OH = = 1.7 10 M
5.8 10 M
HO
K
Chapter 16: Acids and Bases
736
10. (M) Again, all of the solutes are strong acids or strong bases.
(a)
+
+3
3
1mol HO
H O = 0.0045 M HCl = 0.0045 M
1mol HCl
pH = log 0.0045 = 2.35
(b)
+
+4 4
3
33
3
4
1mol HO
H O = 6.14 10 M HNO = 6.14 10 M
1 mol HNO
pH = log 6.14 10 = 3.21
(c)
1mol OH
OH = 0.00683 M NaOH = 0.00683M
1mol NaOH
pOH = log 0.00683 = 2.166 and pH =14.000 pOH =14.000 2.166 = 11.83
(d)
33
2
2
3
2mol OH
OH = 4.8 10 M Ba OH = 9.6 10 M
1mol Ba OH
pOH = log 9.6 10 = 2.02 pH = 14.00 2.02 =11.98
11. (E)
22
22
22
22
3.9 g Ba OH 8H O 1 mol Ba OH 8H O
1000 mL 2 mol OH
OH = 100 mL soln 1 L 315.5 g Ba OH 8H O 1 mol Ba OH 8H O
=0.25M
14
+14
w
3
14
1.0 10
HO = = =4.0 10 M
0.25 M OH
OH pH = log 4.0 10 = 13.40
K
12. (M) The dissolved Ca OH
bg2 is completely dissociated into ions.
pOH pH= 14.00 = 14.00 12.35 = 1.65
pOH 1.65 2
OH =10 = 10 = 2.2 10 M OH = 0.022 M OH
22 2
22
2
2
1 mol Ca OH 74.09 g Ca OH 1000 mgCa OH
0.022 mol OH
solubility = 1 L soln 2 mol OH 1 mol Ca OH 1 g Ca OH
8.1 10 mg Ca OH
= 1L soln
In 100 mL the solubility is
2
2
2
8.1 10 mg Ca OH
1L
100 mL = 81 mg Ca OH
1000 mL 1 L soln
Chapter 16: Acids and Bases
737
13. (M) First we determine the moles of HCl, and then its concentration.
moles 3
11
1atm
751 mmHg 0.205 L
760 mmHg
HCl = 8.34 10 mol HCl
0.08206 L atm mol K 296 K
PV
RT
+3
+ 3
3
3
1mol HO
8.34 10 mol HCl
H O = =1.96 10 M
4.25 L soln 1 mol HCl
14. (E) First determine the concentration of NaOH, then of OH.
0.606 mol NaOH 1 mol OH
0.125 L 1L 1molNaOH
OH = = 0.00505 M
15.0 L final solution
pOH = log 0.00505 M = 2.297 pH =14.00 2.297 =11.703
15. (E) First determine the amount of HCl, and then the volume of the concentrated solution
required.
amount HCl L mol H O
L soln
mol HCl
mol H O mol HCl= 12.5 10
1
1
1= 0.099
2.10 3+
3+
solution
36.46 g HCl 100.0 g soln 1 mL soln
= 0.099 mol HCl = 8.5 mL soln
1 mol HCl 36.0 g HCl 1.18 g soln
V
16. (E) First we determine the amount of KOH, and then the volume of the concentrated solution
required.
pOH pH OH M
pOH
= 14.00 = 14.00 11.55 = 2.45 = 10 = 10 = 0.0035
2.45
amount KOH L M mol OH
L soln
mol KOH
mol OH mol KOH= 25.0 0.0035
1
1
1= 0.088
solution
56.11 g KOH 100.0 g soln 1 mL soln
= 0.088 mol KOH = 29 mL soln
1 mol KOH 15.0 g KOH 1.14 g soln
V
17. (E) The volume of HCl(aq) needed is determined by first finding the amount of NH aq
3bg
present, and then realizing that acid and base react in a 1:1 molar ratio.
+
33
HCl +
33
0.265 mol NH 1 mol H O 1mol HCl 1L acid
= 1.25 L base 1 L base 1 mol NH 6.15 mol HCl
1mol HO
= 0.0539 L acid or 53.9 mL acid.
V
Chapter 16: Acids and Bases
738
18. (M) NH3 and HCl react in a 1:1 molar ratio. According to Avogadro’s hypothesis, equal
volumes of gases at the same temperature and pressure contain equal numbers of moles.
Thus, the volume of H2(g) at 762 mmHg and 21.0C that is equivalent to 28.2 L of H2(g)
at 742 mmHg and 25.0C will be equal to the volume of NH3(g) needed for stoichiometric
neutralization.
3
3
3
NH g
273.2 + 21.0 K 1 L NH g
742 mmHg
= 28.2 L HCl g = 27.1 L NH g
762 mmHg 273.2 + 25.0 K 1 L HCl g
V
Alternatively, we can solve the ideal gas equation for the amount of each gas, and then, by
equating these two expressions, we can find the volume of NH3 needed.
nRK nV
RK
{HCl} = 742 mmHg 28.2 L {NH } mmHg NH }
33
298 2
762
294 2.
{
.
742 mmHg 28.2 L mmHg NH }
3
RK
V
RK298 2
762
294 2.
{
. This yields 33
{NH } 27.1 L NH (g)V
19. (M) Here we determine the amounts of H O
3+ and OH and then the amount of the one
that is in excess. We express molar concentration in millimoles/milliliter, equivalent to
mol/L.
50.00 0.0155
1
1
1= 0.775
3+
3+
mL mmol HI
mL soln
mmol H O
mmol HI mmol H O
75.00 0.0106
1
1
1= 0.795mL mmol KOH
mL soln
mmol OH
mmol KOH mmol OH
The net reaction is
+
32
HO aq +OH aq 2HO(l)
.
There is an excess of OH of (0.795 0.775=
) 0.020 mmol OH.
Thus, this is a basic solution. The total solution volume is (50.00 + 75.00 = ) 125.00 mL.
44
0.020 mmol OH
OH = = 1.6 10 M, pOH = log 1.6 10 = 3.80, pH = 10.20
125.00 mL
20. (M) In each case, we need to determine the HO
3+ or OH of each solution being
mixed, and then the amount of H O
3+ or OH, so that we can determine the amount in
excess. We express molar concentration in millimoles/milliliter, equivalent to mol/L.
+2.12 3 + 3 +
33 3
H O =10 = 7.6 10 M moles H O = 25.00 mL 7.6 10 M = 0.19 mmol H O
pOH OH M= 14.00 12.65 = 1.35 = 10 = 4.5 10
1.35 2
amount OH mL M mmol OH
= 25.00 4.5 10 = 1.13
2
Chapter 16: Acids and Bases
739
There is excess OH in the amount of 0.94 mmol (=1.13 mmol OH– – 0.19 mmol H3O+).
22
0.94 mmol OH
25.00 mL + 25.00 mL
OH = = 1.88 10 M pOH = log 1.88 10 = 1.73 pH=12.27
Weak Acids, Weak Bases, and pH
21. (M) We organize the solution around the balanced chemical equation.
Equation:
Initial:
Changes:
Equil:
22
HNO (aq) + H O(l)
0.143 M —
M
x
—
0.143 Mx —
+
32
H O (aq) + NO (aq)
0 M
0 M
+ M
x
+ M
x
M
x
M
x
+22
32 4
a
2
4
HO NO = 7.2×10 (if 0.143)
HNO 0.143 0.143
= 0.143 7.2 10 0.010 M
xx
Kx
x
x
We have assumed that 0.143 Mx, an almost acceptable assumption. Another cycle of
approximations yields:
4+
3
= (0.143 0.010) 7.2 10 0.0098 M [H O ] pH log(0.0098) 2.01x
This is the same result as is determined with the quadratic formula roots equation.
22. (M) We organize the solution around the balanced chemical equation, and solve first for
OH
+
25 2 2 25 3
Equation : C H NH (aq) + H O(l) OH (aq) + C H NH (aq)
Initial : 0.085 M 0 M 0 M
Changes : M + M + M
Equil : 0.085 M M M
xxx
xxx
+22
25 3 4
b
25 2
OH C H NH
= = = 4.3 10 assuming 0.085
C H NH 0.085 0.085
xx
Kx
x
x= 0 085 4 3 10 0 0060
4
.. .
M
We have assumed that 0.085x M, an almost acceptable assumption. Another cycle of
approximations yields:
x= 0 085 0 0060 4 3 10 0 0058
4
(. . ) . . ]
M =[OH Yet another cycle produces:
Chapter 16: Acids and Bases
740
4
(0.085 0.0058) 4.3 10 0.0058 M [OH ] pOH log(0.0058) 2.24x
pH H O M
pH
= 14.00 2.24 = 11.76 = 10 = 10 = 1.7 10
3+ 11.76 12
This is the same result as determined with the quadratic formula roots equation.
23. (M)
(a) The set-up is based on the balanced chemical equation.
Equation:
Initial:
Changes:
Equil:
872 2
HC H O (aq) + H O(l)
0.186 M —
M
x
—
0.186 Mx —
+
3
HO(aq)+
0 M
+ M
x
M
x
872
CHO (aq)
0 M
+ M
x
M
x
2
53 872
a
872
[H O ][C H O ]
4.9 10 [HC H O ] 0.186 0.186
x
xx
Kx
x= 0186 4 9 10 0 0030
5
.. . ][
M=[HO CH O ]
3+872
0.0030 M is less than 5 % OF 0.186 M, thus, the approximation is valid.
(b) The set-up is based on the balanced chemical equation.
+22
3872
5 +
a 3
872
HO CHO
= 4.9 10 = = = 0.0024 M = H O
HC H O 0.121 0.121
xx
Kx
x
Assumption 0.121,x is correct. pH log= 0.0024 = 2.62
bg
24. (E)
352
initial
352
equilibrium
0.275 mol 1000 mL
HC H O = = 0.440 M
625 mL 1 L
HC H O = 0.440 M 0.00239 M = 0.438 M
Ka
HO CHO
HC H O
==
0.00239
0.438 =1.30 10
3+352
352
2
5
L
N
MO
Q
P
bg
Equation: 872 2
HC H O (aq) + H O(l)
+
3
HO(aq) 872
CHO(aq)
Initial: 0.121 M —
0M 0 M
Changes: M
x
— + M
x
+ M
x
Equil:
0.121 Mx — M
x
M
x
Chapter 16: Acids and Bases
741
25. (M) We base our solution on the balanced chemical equation.
HO M
3+1.56 2
=10 =2.8 10
+
2223
Equation : CH FCOOH aq + H O(l) CH FCOO aq + H O aq
Initial : 0.318 M 0 M 0 M
Changes : 0.028 M + 0.028 M + 0.028 M
Equil : 0.290 M 0.028 M 0.028 M
Ka
HO CHFCOO
CH FCOOH
==
0.028 0.028
0.290 =2.7 10
3+2
2
3
bgbg
26. (M) HC H O g
L
mol HC H O
g HC H O MM
6112 6112
6112
2
=11
1
1
116.2 = 9.5 10 = 0.095
+2.94 3
3equil
H O = 10 = 1.1 10 M = 0.0011 M
The stoichiometry of the reaction, written below, indicates that HO CH O
3+6112
=
+
6112 2 6112 3
Equation : HC H O (aq) + H O(l) C H O (aq) + H O (aq)
Initial: 0.095 M 0 M 0 M
Changes : 0.0011 M +0.0011 M + 0.0011 M
Equil: 0.094 M 0.0011 M 0.0011 M
Ka
CH O HO
HC H O
==
0.0011
0.094 =1.3 10
6112 3+
6112
2
5
L
N
MO
Q
P
bg
27. (M) Here we need to find the molarity
S
of the acid needed that yields +2.85 3
3
HO =10 =1.4 10 M
Equation: 752 2
HC H O (aq) + H O(l)
+
3
HO(aq)
+ 752
CHO (aq)
Initial:
S
— 0 M 0 M
Changes: 0.0014 M — +0.0014M +0.0014M
Equil:
S
0.0014M — 0.0014 M 0.0014 M
KSS
a
HO CHO
HC H O
==
0.0014
0.0014 = 6.3 10 0.0014 = 0.0014
6.3 10 = 0.031
3+752
752
2
5
2
5
L
N
MO
Q
P
bgbg
752
= 0.031+ 0.0014 = 0.032 M = HC H OS
752 752 752
752
0.032 mol HC H O 122.1 g HC H O
1L
350.0 mL =1.4 g HC H O
1000 mL 1 L soln 1 mol HC H O
Chapter 16: Acids and Bases
742
28. (M) First we find OH and then use the Kb expression to find
33
(CH ) N
pOH 2.88
pOH =14.00 pH =14.00 11.12 = 2.88 OH =10 =10 = 0.0013 M
2
+
33
5
b33 33
equil
33 33
equil equil
(CH ) NH OH 0.0013
= 6.3 10 = = (CH ) N = 0.027 M (CH ) N
(CH ) N (CH ) N
K
33initial
33initial
CH N = 0.027 M(equil. concentration) + 0.0013 M(concentration ionized)
CH N = 0.028 M
29. (M) We use the balanced chemical equation, then solve using the quadratic formula.
+
22 3 2
Equation : HClO (aq) + H O(l) H O (aq) + ClO (aq)
Initial: 0.55 M 0M 0M
Changes : M + M + M
Equil: 0.55 M M M
xxx
xxx
+2
32 22
a
2
HO ClO
= = =1.1 10 = 0.011 = 0.0061 0.011
HClO 0.55
x
Kxx
x
x
x
2+ 0.011 0.0061= 0
2+
3
4 0.011 0.000121+ 0.0244 0.073 M H O
22
bb ac
xa
The method of successive approximations converges to the same answer in four cycles.
pH log H O log pOH pH= = 0.073 = 1.14 = 14.00 = 14.00 1.14 = 12.86
3+
bg
pOH 12.86 13
OH =10 = 10 =1.4 10 M
30. (M) Organize the solution around the balanced chemical equation, and solve first for
OH.
+
32 2 33
Equation : CH NH (aq) + H O(l) OH (aq) + CH NH (aq)
Initial: 0.386 M 0 M 0 M
Changes : M + M + M
Equil: 0.386 M M M
xxx
xxx
+22
33 4
b
32
OH CH NH
= = = 4.2 10 assuming 0.386
CH NH 0.386 0.386
xx
Kx
x
x= 0 386 4 2 10 0 013
4
.. . ]
M = [OH pOH = log(0.013) = 1.89
-
Chapter 16: Acids and Bases
743
+ pH 12.11 13
3
pH = 14.00 1.89 =12.11 H O = 10 =10 = 7.8 10 M
This is the same result as is determined with the quadratic equation roots formula.
31. (M)
10 7 2 10 7 2
2
10 7 2
21072
10 7 2
1g CHNH 1mol CHNH1.00 g H O 1000 mL
CHNH = 590 g H O 1 mL 1 L 143.2 g C H NH
= 0.012 M C H NH
p3.92 4
b=10 =10 =1.2 10
b
K
K
Equation: 10 7 2 2
CHNH(aq) + HO(l)
OH (aq) +
10 7 3
CHNH (aq)
Initial: 0.012 M — 0 M
0 M
Changes: M
x
— + M
x
+ M
x
Equil:
0.012 Mx — M
x
M
x
22
10 7 3 4
b
10 7 2
OH C H NH
===1.210
C H NH 0.012 0.012
x
x
Kx
assuming 0.012x
x= 0 012 12 10 0 0012
4
.. .
This is an almost acceptable assumption. Another
approximation cycle gives:
x= 0 012 0 0012 12 10 0 0011
4
(. . ) . .
Yet another cycle seems necessary.
4
= (0.012 0.0011) 1.2 10 0.0011M [OH ]x
The quadratic equation roots formula provides the same answer.
pOH log OH log pH pOH= = 0.0011 = 2.96 = 14.00 = 11.04
bg
pH 11.04 12
3
H O 10 10 9.1 10 M
32. (M) The stoichiometry of the ionization reaction indicates that
p
+7.238
3642a
H O = OC H NO , =10 = 10 = 5.9 10
b
K
K
and
HO M
3+4.53 5
=10 =3.0 10
. We let
S
= the molar solubility of o-nitrophenol.
Equation: 64 2 2
HOC H NO (aq) + H O(l)
64 2
OC H NO (aq) +
+
3
HO(aq)
Initial:
S
— 0 M 0 M
Changes: 5
3.0 10 M
— 5
+3.0 10 M
5
+3.0 10 M
Equil: ( 5
3.0 10 ) MS
— 5
3.0 10 M
5
3.0 10 M
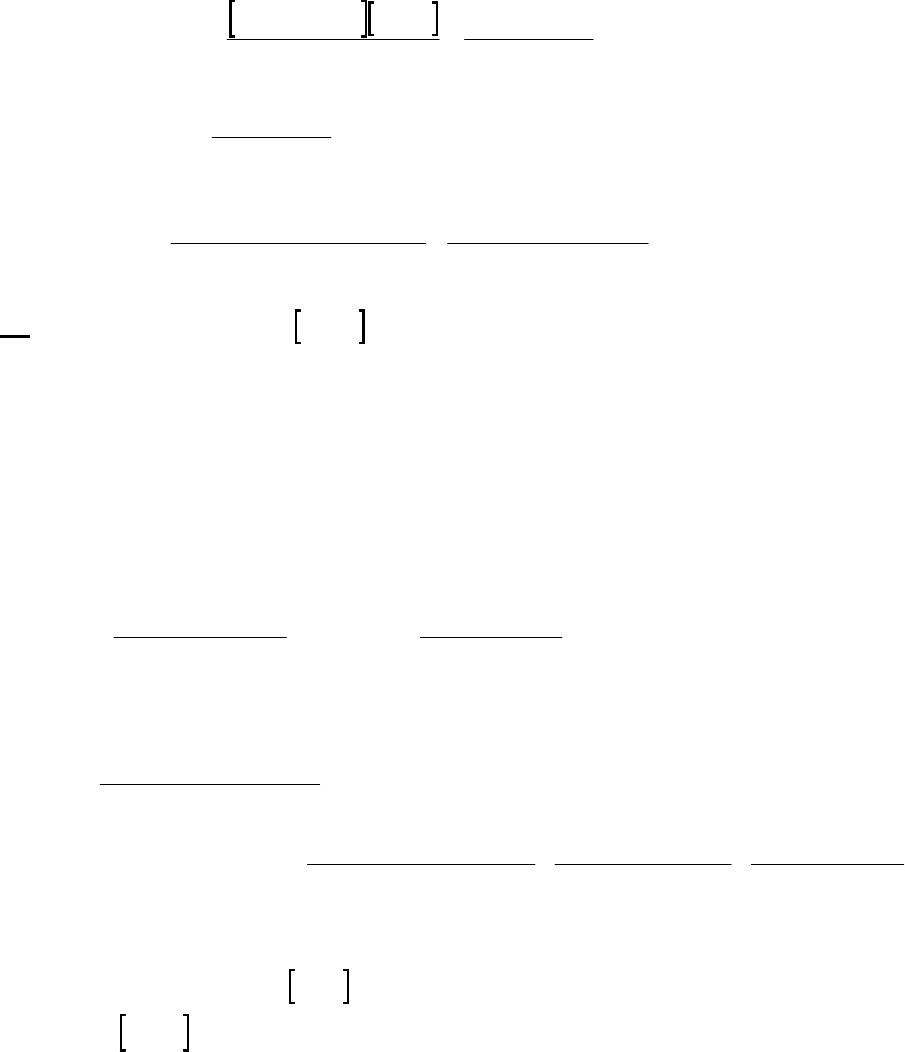
Chapter 16: Acids and Bases
744
KS
a
OC H NO H O
HOC H NO
=5.9 10 = = 3.0 10
3.0 10
864 2 3+
65 2
52
5
L
N
MO
Q
P
ch
SS
3.0 10 = 3.0 10
5.9 10 = 1.5 10 = 1.5 10 + 3.0 10 = 1.5 10
5
52
8
2252
ch MMMM
Hence,
solubility mol HOC H NO
L soln
g HOC H NO
mol HOC H NO g HOC H NO L soln=1.5 10
1
139.1
1=2.1 /
264 2 64 2
64 2
64 2
33. (M) Here we determine HO
3+ which, because of the stoichiometry of the reaction,
equals 232
CHO .
+pH4.52 5
3232
H O =10 =10 = 3.0 10 M = C H O
We solve for
S
, the concentration of HC H O
232
in the 0.750 L solution before it dissociates.
Equation: 232 2
HC H O (aq) + H O(l)
232
CHO (aq) +
+
3
HO(aq)
Initial:
S
M — 0 M 0M
Changes:
3.0 10 5M — +3.0 10 5
M +3.0 10 5
M
Equil:
5
3.0 10 MS
— 3.0 10 5
M 3.0 10 5
M
52
5
3232
5
232
[H O ][C H O ] (3.0 10 )
1.8 10
[HC H O ] ( 3.0 10 )
a
KS
3.0 10 = 1.8 10 3.0 10 = 9.0 10 = 1.8 10 5.4 10
525510510
ch c h
SS
S=9.0 10 +5.4 10
1.8 10 =8.0 10
10 10
5
5
M Now we determine the mass of vinegar needed.
5
232 232
232 232
8.0 10 mol HC H O 60.05 g HC H O 100.0 g vinegar
mass vinegar = 0.750 L 1L soln 1mol HCHO 5.7g HCHO
= 0.063 g vinegar
34. (M) First we determine OH which, because of the stoichiometry of the reaction,
equals NH4
.
pOH 2.45 3
4
pOH = 14.00 pH = 14.00 11.55 = 2.45 OH = 10 = 10 = 3.5 10 M = NH
We solve for
S
, the concentration of NH3 in the 0.625 L solution prior to dissociation.
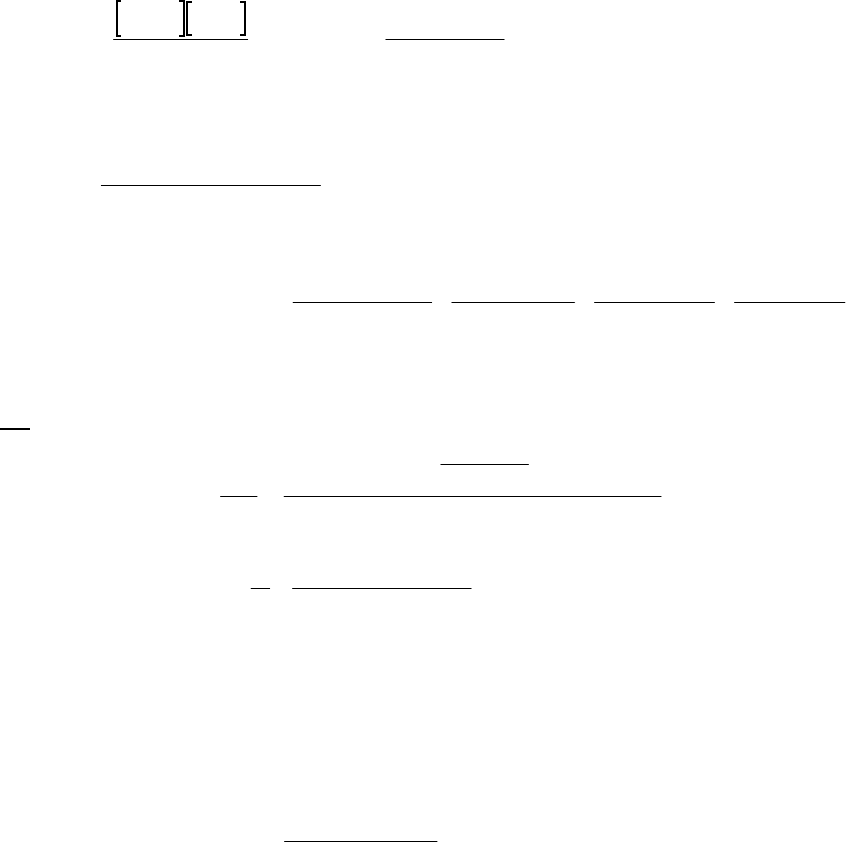
Chapter 16: Acids and Bases
745
Equation: 32
NH ( ) + H O(l)aq
4
NH (aq) +
OH (aq)
Initial:
S
M — 0 M 0 M
Changes: 0.0035 M — +0.0035 M +0.0035 M
Equil:
0.0035 MS — 0.0035 M 0.0035 M
KS
b
NH OH
NH
==1.810=
0.0035
0.0035
4
3
5
2
L
N
MO
Q
P
bg
bg
25558
0.0035 =1.8 10 0.0035 =1.225 10 =1.8 10 6.3 10SS
58
5
1.225 10 + 6.3 10
= = 0.68 M
1.8 10
S
Now we determine the volume of household ammonia needed
33
ammonia
33
0.68 mol NH 17.03 g NH 100.0 g soln 1 mL soln
= 0.625 L soln 1 L soln 1 mol NH 6.8 g NH 0.97 g soln
V
35. (D)
(a) nproplyamine = PV
R
T=
-1 -1
1 atm
316 Torr 0.275 L
760 Torr
0.08206 L atm K mol 298.15 K
= 4.67 103 mol propylamine
[propylamine] = n
V=-3
4.67 10 moles
0.500 L
= 9.35 103 M
Kb = 10pKb = 103.43 = 3.7 104
CH3CH2CH2NH2(aq) + H2O(l)
CH3CH2CH2NH3+(aq) + OH (aq)
Initial 9.35 103 M — 0 M
0 M
Change x M — +x M +x M
Equil. (9.35 103 x) M — x M x M
Kb = 3.7 104 = 2
-3
9.35 10
x
x
or 3.5 106 3. 7 104(x) = x2
x2 + 3.7 104x 3.5 106 = 0
2
= 1.1 10 mL household ammonia solution

Chapter 16: Acids and Bases
746
Find x with the roots formula:
-4 -4 2 -6
3.7 10 (3.7 10 ) 4(1)( 3.5 10 )
2(1)
x
Therefore x = 1.695 103 M = [OH ] pOH = 2.77 and pH = 11.23
(b) [OH] = 1.7 103 M = [NaOH] (MMNaOH = 39.997 g mol1)
nNaOH = (C)(V) = 1.7 103 M 0.500 L = 8.5 104 moles NaOH
mass of NaOH = (n)(MMNaOH) = 8.5 104 mol NaOH 39.997 g NaOH/mol NaOH
mass of NaOH = 0.034 g NaOH(34 mg of NaOH)
36. (M) Kb = 10pKb = 109.5 = 3.2 1010 MMquinoline = 129.16 g mol1
Solubility(25 C) = 0.6 g
100 mL
Molar solubility(25 C) = 0.6 g
100 mL 1 mol 1000 mL
129.16 g 1 L
= 0.046 M (note: only 1 sig fig)
C
9H7N(aq) + H2O(l) C9H7NH+(aq) + OH(aq)
Initial 0.046 M — 0 M
0 M
Change x M — +x M +x M
Equil. (0.046 x) M — x M x M
3.2 1010 = 2
0.046
x
x
2
0.046
x
, x = 3.8 106 M (x << 0.046, valid assumption)
Therefore, [OH ] = 4 106 M pOH = 5.4 and pH = 8.6
37. (M) If the molarity of acetic acid is doubled, we expect a lower initial pH (more H3O+(aq)
in solution) and a lower percent ionization as a result of the increase in concentration. The
ratio between [H3O+] of concentration “M” and concentration 2 M is 21.4. Therefore,
(b), containing 14 H3O+ symbols best represents the conditions (~(2)1/2 times greater).
38. (M) If NH3 is diluted to half its original molarity, we expect a lower pH (a lower [OH]) and a
higher percent ionization in the diluted sample. The ratio between [OH–] of concentration “M”
and concentration 0.5 M is 0.5 0.71. Since the diagram represent M has 24 OH– symbols,
then diagram (c), containing 17 OH– symbols would be the correct choice.
Chapter 16: Acids and Bases
747
Percent Ionization
39. (M) Let us first compute the HO
3+ in this solution.
Equation:
Initial:
Changes:
Equil:
352 2
HC H O (aq) + H O(l)
0.45 M —
M
x
—
0.45 Mx —
+
3 352
H O (aq) + C H O (aq)
0 M
0 M
+ M
x
+ M
x
M
x
M
x
+22
3352 4.89 5
a
352
HO CHO
===10=1.310
HC H O 0.45 0.45
x
x
Kx
x
=2.4 103
M ; We have assumed that 0.45 Mx, an assumption that clearly is correct.
(a)
+3
3equil
352
initial
HO 2.4 10 M
= = = 0.0053 = degree
HC H O 0.45 M
of ionization
(b) % = 100% 0.0053 100% 053% ionization =
.
40. (M) For C2H5NH2 (ethylamine), Kb = 4.3 104
C2H5NH2(aq) + H2O(l)
C2H5NH3+(aq) + OH(aq)
Initial 0.85 M — 0 M
0 M
Change x M — +x M +x M
Equil. (0.85 x) M — x M x M
4.3 104 = 2
(0.85 ) M
x
x
2
0.85 M
x x = 0.019 M (x << 0.85, thus a valid assumption)
Degree of ionization = 0.019M
0.85 M = 0.022 Percent ionization = 100% = 2.2 %
41. (M) Let x be the initial concentration of NH3, hence, the amount dissociated is 0.042 x
NH3(aq) + H2O(l) -5
a = 1.8 10K
NH4+(aq) + OH-(aq)
Initial x M — 0 M
0 M
Change 0.042x M — +0.042x M +0.042x M
Equil. (1x0.042x) M — 0.042x M 0.042x M
= 0.958 x

Chapter 16: Acids and Bases
748
2
4
5
b
3equil
NH OH 0.042
=1.8 10 = = = 0.00184
NH [0.958 ]
x
Kx
x
5
3initial
1.8 10
NH = 0.00978 0.0098
0.00184
x
MM
42. (M)
HC3H5O2(aq) + H2O(l) -5
a = 1.3 10K
C3H5O2(aq) + H3O+(aq)
Initial 0.100 M — 0 M
0 M
Change x M — +x M +x M
Equil. (0.100 x) M — x M x M
1.3 105 = 2
0.100 M
x
x
2
0.100
x
x = 1.1 103 (x << 0.100, thus a valid assumption)
Percent ionization = 0.0011
0.100 100% = 1.14 %
Next we need to find molarity of acetic acid that is 1.1% ionized
HC2H3O2(aq) + H2O(l) -5
a=1.8 10K
C2H3O2(aq) + H3O+(aq)
Initial X M — 0 M
0 M
Change 100
41.1 X M
— +100
41.1 X M + 100
41.1 X M
Equil. X 100
41.1 X
= 0.9886 X M
—
100
41.1 X M
= 0.0114 M
100
41.1 X M
= 0.0114 M
1.8 105 =
2
1.14
100
0.9886
X
X
= 1.3 104(X); X = 0.138 M
Consequently, approximately 0.14 moles of acetic acid must be dissolved in one liter of
water in order to have the same percent ionization as 0.100 M propionic acid.
43. (E) We would not expect these ionizations to be correct because the calculated degree of
ionization is based on the assumption that the [HC2H3O2]initial
[HC2H3O2]initial
[HC2H3O2]equil., which is invalid at the 13 and 42 percent levels of ionization seen here.
44. (M) HC2Cl3O2 (trichloroacetic acid) pKa = 0.52 Ka = 100.52 = 0.30
For a 0.035 M solution, the assumption will not work (the concentration is too small and
Ka is too large) Thus, we must solve the problem using the quadratic equation.
HC2Cl3O2(aq) + H2O(l)
C2Cl3O2(aq) +H
3O+(aq)
Initial 0.035 M — 0 M
0 M
Change x M — +x M +x M
Equil. (0.035 x) M — x M x M

Chapter 16: Acids and Bases
749
0.30 = 2
0.035
x
x
or 0.0105 0.30(x) = x2 or x2 + 0.30x 0.0105 = 0 ; solve quadratic:
2
-0.30 (0.30) 4(1)(0.0105)
2(1)
x
Therefore x = 0.032 M = [H3O+]
Degree of ionization = 0.032 M
0.035 M = 0.91 Percent ionization = 100% = 91. %
Polyprotic Acids
45. (E) Because H3PO4 is a weak acid, there is little HPO42- (produced in the 2nd ionization)
compared to the H3O+ (produced in the 1st ionization). In turn, there is little PO43- (produced
in the 3rd ionization) compared to the HPO42-, and very little compared to the H3O+.
46. (E) The main estimate involves assuming that the mass percents can be expressed as 0.057
g of 75% H PO
34
per 100. mL of solution and 0.084 g of 75% H PO
34
per 100. mL of
solution. That is, that the density of the aqueous solution is essentially 1.00 g/mL. Based
on this assumption, the initial minimum and maximum concentrations of H PO
34
is:
34 34
34
34 34
34
75g H PO 1molH PO
0.057gimpureH PO 100gimpureH PO 98.00 gH PO
[H PO ] 0.0044M
1L
100mLsoln 1000mL
34 34
34
34 34
34
75g H PO 1molH PO
0.084gimpureH PO 100gimpureH PO 98.00 g H PO
[H PO ] 0.0064M
1L
100mLsoln 1000mL
Equation: +
34 2 24 3
H PO (aq) + H O(l) H PO (aq) + H O (aq)
Initial: 0.0044 M — 0 M 0 M
Changes:
x
M — +
x
M +
x
M
Equil: (0.0044
x
) M —
x
M
x
M
1
+2
24 3 32 5
a
34
HPO HO
= = = 7.1 10 + 0.0071 3.1 10 = 0
H PO 0.0044
x
Kxx
x
254
3+
3
4 0.0071 5.0 10 +1.2 10
== =3.010M=HO
22
bb ac
xa
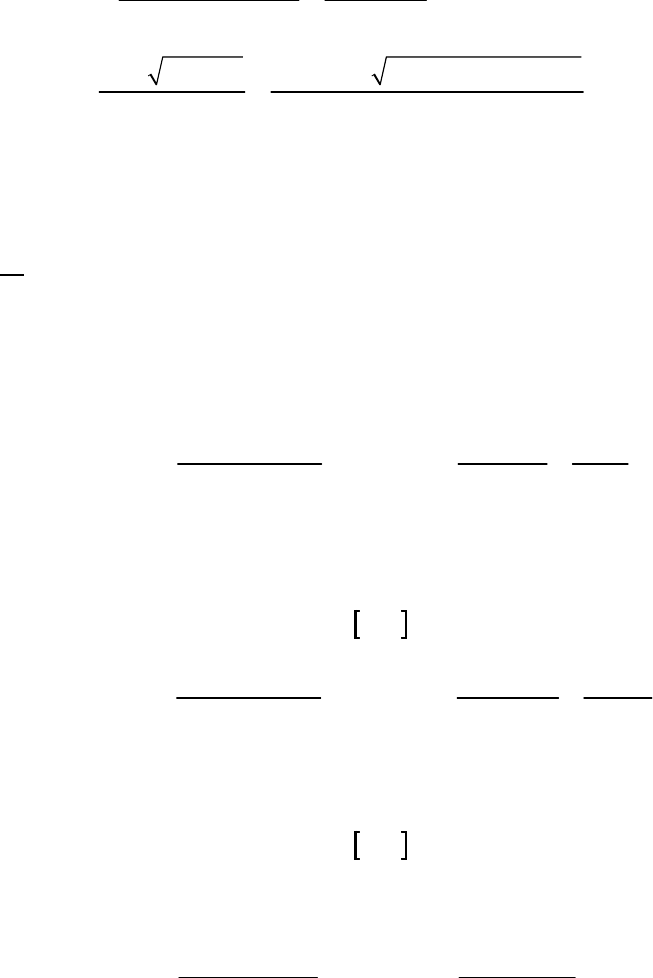
Chapter 16: Acids and Bases
750
The set-up for the second concentration is the same as for the first, with the exception that
0.0044 M is replaced by 0.0064 M.
1
+2
24 3 32 5
a
34
HPO HO
= = = 7.1 10 + 0.0071 4.5 10 = 0
H PO 0.0064
x
Kxx
x
254
3+
3
4 0.0071 5.0 10 +1.8 10
== =4.010M=HO
22
bb ac
xa
The two values of pH now are determined, representing the pH range in a cola drink.
3
pH = log 3.0 10 = 2.52
3
pH = log 4. 10 = 2.40
47. (D)
(a)
Equation: +
22 3
H S(aq) + H O(l) HS (aq) + H O (aq)
Initial: 0.075 M — 0 M 0 M
Changes:
x
M — +
x
M +
x
M
Equil: (0.075
x
) M —
x
M +
x
M
1
2
+22
375+
a 3
2
52 19
a
HS H O
= =1.0 10 = = 8.7 10 M = H O
H S 0.075 0.075
HS = 8.7 10 M and S = = 1 10 M
xx
Kx
x
K
(b) The set-up for this problem is the same as for part (a), with 0.0050 M replacing 0.075
M as the initial value of HS
2.
1
+22
375+
a 3
2
HS H O
= =1.0 10 = = 2.2 10 M = H O
H S 0.0050 0.0050
xx
Kx
x
2
52 19
a
HS = 2.2 10 M and S = = 1 10 MK
(c) The set-up for this part is the same as for part (a), with 1.0 10 5
M replacing 0.075
M as the initial value of HS
2. The solution differs in that we cannot
assume
x
1.0 10 5
. Solve the quadratic equation to find the desired equilibrium
concentrations.
1
+2
3
5
2
7
a
HS H O
HS 1.0 10
==1.010=
x
x
K
27 12
1.0 10 1.0 10 0xx
Chapter 16: Acids and Bases
751
714 12
1.0 10 1.0 10 4 1.0 10
= 2 1
x
2
7+ 72 19
3a
= 9.5 10 M = H O HS = 9.5 10 M S = =1 10 MxK
48. (M) For H CO
231 7
,=4.410K and K211
=4.7 10
(a) The first acid ionization proceeds to a far greater extent than does the second and
determines the value of HO
3+.
Equation: 23 2
H CO (aq) + H O(l) +
3
HO(aq)
+ 3
HCO (aq)
Initial: 0.045 M — 0 M
0 M
Changes:
x
M — +
x
M +
x
M
Equil: 0.045x
bg M —
x
M
x
M
Kx
x
x
1
3+3
23
272
==
0.045 =4.4 10 0.045
HO HCO
HCO
L
N
MO
Q
P
x=1.4 10 =
43+
MHO
(b) Since the second ionization occurs to only a limited extent,
4
3
HCO =1.4 10 M = 0.00014 M
(c) We use the second ionization to determine CO3
2.
Equation:
Initial:
Changes:
Equil:
32
HCO (aq) + H O(l)
0.00014 M —
M
x
—
0.00014 Mx —
+
3
HO(aq)
0.00014 M
+ M
x
0.00014 + Mx
2
3
CO (aq)
0 M
+ M
x
M
x
2
+
33 11
2
3
HO CO 0.00014 + 0.00014
===4.710
0.00014 0.00014
HCO
x
xx
Kx
x=4.7 10 =
11 3
2
MCO
Again we assumed that 0.00014x M, which clearly is the case. We also note that
our original assumption, that the second ionization is much less significant than the
first, also is a valid one. As an alternative to all of this, we could have recognized
that the concentration of the divalent anion equals the second ionization constant:
CO3
2
2
=
K.

Chapter 16: Acids and Bases
752
49. (D) In all cases, of course, the first ionization of H SO
24
is complete, and establishes the
initial values of HO
3+ and HSO4
. Thus, we need only deal with the second ionization
in each case.
(a) Equation:
2+
42 4 3
HSO (aq) + H O(l) SO (aq) + H O (aq)
Initial: 0.75 M — 0 M 0.75 M
Changes:
x
M — +
x
M +
x
M
Equil: (0.75
x
) M —
x
M (0.75+
x
) M
2
2+
43 2
a 4
4
SO H O 0.75+ 0.75
= = 0.011= = 0.011 M = SO
0.75 0.75
HSO
xx x
Kx
x
We have assumed that 0.75x M, an assumption that clearly is correct.
+
43
HSO = 0.75 0.011= 0.74M H O = 0.75+ 0.011 = 0.76M
(b) The set-up for this part is similar to part (a), with the exception that 0.75 M is
replaced by 0.075 M.
24
2
+ 0.086 8.3 10 = 0
4 0.086 0.0074 + 0.0033
= = = 0.0087M
22
xx
bb ac
xa
2
4
= 0.0087M = SOx
+
43
HSO = 0.075 0.0087 = 0.066M H O = 0.075 + 0.0088M = 0.084M
(c) Again, the set-up is the same as for part (a), with the exception that 0.75 M is
replaced by 0.00075 M
2
22
43
a26
4
0.011(0.00075 ) 0.00075
[SO ][H O ] (0.00075 )
0.011 0.00075 0.0118 8.3 10 0
[HSO ]
x
xx
xx
Kxxx
xbb ac
a
=4
2=0.0118 1.39 10 + 3.3 10
2=6.6 10
245
4
2
4 5
44
= 6.6 10 M = SO HSO = 0.00075 0.00066 = 9 10 Mx
+3+
3 3
H O = 0.00075 + 0.00066M = 1.41 10 M H O
is almost twice the initial
value of HSO
24
. Thus, the second ionization of H SO
24
is nearly complete in this
dilute solution.
2
2+
43 2
a
4
SO H O 0.075+
= = 0.011= 0.011 0.075 = 0.075 +
0.075
HSO
xx
Kxxx
x
Chapter 16: Acids and Bases
753
50. (D) First we determine HO
3+, with the calculation based on the balanced chemical
equation.
Equation:
+
22 23
44
HOOC CH COOH aq + H O(l) HOOC CH COO aq + H O aq
Initial: 0.10 M — 0 M 0 M
Changes:
x
M
— +
x
M +
x
M
Equil: 0.10x
bgM —
x
M
x
M
Kxx
x
x
a
H O HOOC CH COO
HOOC CH COOH
1==3.910=
0.10 0.10
3+24
24
52
bg
F
HI
K
x
010 39 10 20 10
53
.. . ]M=[HO
3+
We see that our simplifying assumption, that 0.10x M, is indeed valid. Now we
consider the second ionization. We shall see that very little H O
3+ is produced in this
ionization because of the small size of two numbers: Ka2and HOOC CH COO
24
bg.
Again we base our calculation on the balanced chemical equation.
Equation:
+
22 2 3
44
HOOC CH COO aq + H O(l) OOC CH COO aq + H O aq
Initial: 2.0 10 3
M — 0 M 2.0 10 3
M
Changes:
y
M — +
y
M +
y
M
Equil: 0.0020 y
bgM —
y
M 0.0020 + y
bg M
Kyy
y
y
a
H O OOC CH COO
HOOC CH COO
2==3.910=
0.0020 +
0.0020
0.0020
0.0020
3+24
24
6
F
HI
K
bgbg
6
24
3.9 10 M = [ OOC(CH ) COO ]y
Again, we see that our assumption, that 0.0020y M, is valid. In addition, we also note
that virtually no H O
3+ is created in this second ionization. The concentrations of all
species have been calculated above, with the exception of OH.
14 12
w2
34
+
3
1.0 10
OH = = = 5.0 10 M; HOOC CH COOH = 0.10M
2.0 10
HO
K
+3 6
32 2
44
H O = HOOC CH COO = 2.0 10 M; OOC CH COO = 3.9 10 M

Chapter 16: Acids and Bases
754
51. (M)
(a) Recall that a base is a proton acceptor, in this case, accepting H+ from H O
2.
1
2
+
20 24 2 2 2 20 24 2 2 b
2+
+
202422 2 2024222 b
First ionization : C H O N + H O C H O N H + OH p = 6.0
Second ionization : C H O N H + H O C H O N H + OH p = 9.8
K
K
(b)
1
3
20 24 2 2
6.0 6
b
1molquinine
1.00g quinine 324.4gquinine
[C H O N ] 1.62 10 M
1L
1900 mL 1000mL
10 1 10
K
Because the OH- produced in (a) suppresses the reaction in (b) and since Kb1 >> Kb2,
the solution’s pH is determined almost entirely by the first base hydrolysis of the
first reaction. Once again, we set-up the I.C.E. table and solve for the [OH ] in this
case:
Equation: +
20 24 2 2 2 20 24 2 2
C H ON(aq) + HO(l) C H ONH(aq) + OH(aq)
Initial: 0.00162 M — 0 M
0 M
Changes:
x
M — +
x
M +
x
M
Equil: 0.00162 x
bgM —
x
M
x
M
1
+22
20 24 2 2 65
b
20 24 2 2
CHONH OH
==110= 410M
C H O N 0.00162 0.00162
xx
Kx
x
The assumption 0.00162x, is valid.
5
pOH = log 4 10 = 4.4 pH = 9.6
52. (M) Hydrazine is made up of two NH2 units held together by a nitrogen–nitrogen single
bond:
H
N
HH
N
H
(a) N2H4(aq) + H2O(l)
N2H5+(aq) + OH-(aq) Kb1 = 10-6.07 = 8.5 ×10-7
(b) N2H5+(aq) + H2O(l)
N2H62+(aq) + OH-(aq) Kb2 = 10-15.05 = 8.9 ×10-16
Because the OH- produced in (a) suppresses the reaction in (b) and since Kb1 >> Kb2,
the solution’s pH is determined almost entirely by the first base hydrolysis reaction (a).
Thus we need only solve the I.C.E. table for the hydrolysis of N2H4 in order to find the
[OH-]equil, which will ultimately provide us with the pH via the relationship
[OH-]×[H3O+] = 1.00 × 10-14.

Chapter 16: Acids and Bases
755
Reaction: N2H4(aq) + H2O(l)
N2H5+(aq) + OH-(aq)
Initial: 0.245 M — 0 M
0 M
Changes:
x
M — +
x
M +
x
M
Equil: (0.245
x
) M —
x
M
x
M
1
+22
25 74-
b
equil
24
14
+11 11
34
NH OH
= = 8.5 10 = = = 4.56 10 M = [OH ]
N H 0.245 0.245
1.0 10
Thus, [H O ] = = 2.19 10 M pH = -log(2.19 10 ) = 10.66
4.56 10
xx
Kx
x
53. (E) Protonated codeine hydrolyzes water according to the following reaction:
18 21 3 2 18 21 3 3
a
ba
CHONH HO CHON HO
pK 6.05
pK 14 pK 7.95
54. (E) Protonated quinoline is, of course, an acid, which hydrolyzes water to give a
hydronium ion. The reaction is as follows:
97 2 97 3
14 5
W
b10
a
5
b
CHNH HO CHN HO
K110
K1.610
K6.310
pK log 1.6 10 4.8
55. (E) The species that hydrolyze are the cations of weak bases, namely, NH4
+ and
CHNH
65 3
+, and the anions of weak acids, namely, NO2
and CHO
752
.
(a)
++
432 333
NH aq+NO aq+HO(l) NH aq+NO aq+HO aq
(b)
++
22 2
Na aq+NO aq+HO(l) Na aq+HNO aq+OH aq
(c)
++
752 2 752
K aq +CHO aq +HO(l) K aq +HCHO aq +OH aq
(d)
++
2
K aq+Cl aq+Na aq+I aq+HO(l) no reaction
(e)
++
65 3 2 65 2 3
CHNH aq+Cl aq+HO(l) CHNH aq+Cl aq+HO aq

Chapter 16: Acids and Bases
756
56. (E) Recall that, for a conjugate weak acid–weak base pair, KK K
ab w
=
(a) 14 6+
w
a55
9
b
1.0 10
= = = 6.7 10 for C H NH
1.5 10
K
KK
(b) 14 11
w
b
2
4
a
1.0 10
= = 5.6 10 for CHO
1.8 10
K
KK
(c) 14 4
w
b65
10
a
1.0 10
= = 1.0 10 for C H O
1.0 10
K
KK
57. (E)
(a) Because it is composed of the cation of a strong base, and the anion of a strong acid,
KCl forms a neutral solution (i.e., no hydrolysis occurs).
(b) KF forms an alkaline (basic) solution. The fluoride ion, being the conjugate base of
a relatively strong weak acid, undergoes hydrolysis, while potassium ion, the weakly
polarizing cation of a strong base, does not react with water.
2
F (aq) + H O(l) HF(aq) +OH (aq)
(c) NaNO3 forms a neutral solution, being composed of a weakly polarizing cation and
anionic conjugate base of a strong acid. No hydrolysis occurs.
(d) Ca OCl
bg2 forms an alkaline (basic) solution, being composed of a weakly polarizing
cation and the anion of a weak acid Thus, only the hypochlorite ion hydrolyzes.
2
OCl (aq)+ H O(l) HOCl(aq) + OH (aq)
(e) NH NO
42
forms an acidic solution. The salt is composed of the cation of a weak base
and the anion of a weak acid. The ammonium ion hydrolyzes:
++10
42 33 a
NH (aq) + H O(l) NH aq + H O (aq) = 5.6 10K
as does the nitrite ion:
11
22 2 b
NO (aq) + H O(l) HNO (aq) + OH (aq) = 1.4 10K
Since NH4
+ is a stronger acid than NO2
is a base (as shown by the relative sizes of
the K values), the solution will be acidic. The ionization constants were computed
from data in Table 16-3 and with the relationship KKK
wab
=
.
For NH For NO
ab4
+14
5
10 2
14
4
11
,=
1.0 10
1.8 10 =5.6 10 , =1.0 10
7.2 10 =1.4 10
KK
54
b
3a2
Where 1.8 10 = of NH and 7.2 10 = of HNOKK
Chapter 16: Acids and Bases
757
58. (E) Our list in order of increasing pH is also in order of decreasing acidity. First we look
for the strong acids; there is just HNO3. Next we look for the weak acids; there is only
one, HC H O
232
. Next in order of decreasing acidity come salts with cations from weak
bases and anions from strong acids; NH ClO
44
is in this category. Then come salts in
which both ions hydrolyze to the same degree; NH C H O
42 32
is an example, forming a pH-
neutral solution. Next are salts that have the cation of a strong base and the anion of a
weak acid; NaNO2is in this category. Then come weak bases, of which NH aq
3bg is an
example. And finally, we terminate the list with strong bases: NaOH is the only one.
Thus, in order of increasing pH of their 0.010 M aqueous solutions, the solutes are:
HNO HC H O NH ClO NH C H O NaNO NH NaOH
3232 44 4232 2 3
59. (M) NaOCl dissociates completely in aqueous solution into Na aq
+bg
, which does not
hydrolyze, and OCl-(aq), which undergoes base hydrolysis. We determine [OH-] in a 0.089 M
solution ofOCl, finding the value of the hydrolysis constant from the ionization constant of
HOCl, Ka=2.9 108
.
2
Equation : OCl (aq) + H O(l) HOCl(aq) + OH (aq)
Initial: 0.089M 0M 0M
Changes : M + M + M
Equil: 0.089 M M M
xxx
xxx
KK
K
x
x
x
bw
a
HOCl OH
OCl
==
1.0 10
2.9 10 =3.4 10 = =0.089 0.089
14
8
722
4
1.7 10 M 0.089, the assumption is valid.
44
=1.7 10 M = OH ; pOH = log 1.7 10 = 3.77, pH = 14.00 3.77 =10.23x
60. (M) dissociates completely in aqueous solution intoNH aq
4
+bg, which hydrolyzes,
andCl aq
bg
, which does not. We determine HO
3+ in a 0.123 M solution of NH4
+, finding
the value of the hydrolysis constant from the ionization constant of 3
NH , 5
b=1.8 10K
.
+ +
42 33
Equation : NH (aq) + H O(l) NH (aq) H O (aq)
Initial: 0.123M 0 M 0M
Changes : M + M + M
Equil: 0.123 M M M
xxx
xxx
KK
K
x
x
x
bw
a
3
NH H O
NH
==
1.0 10
1.8 10 =5.6 10 = 0123 0123
14
5
10 3
4
22
[][ ]
[] ..

Chapter 16: Acids and Bases
758
6
8.3 10 M << 0.123, the assumption is valid
6+ 6
3
= 8.3 10 M = H O ; pH = log 8.3 10 = 5.08x
61. (M) KC H O
672
dissociates completely in aqueous solution into K aq),
+( which does not
hydrolyze, and the ion C H O (aq)
672
, which undergoes base hydrolysis. We determine
OH in 0.37 M KC H O
672
solution using an I.C.E. table.
Note:
p
4.77 5
a=10 =10 =1.7 10
K
K
672 2 672
Equation : C H O (aq) + H O(l) HC H O (aq) + OH (aq)
Initial: 0.37 M 0M 0M
Changes : M + M + M
Equil: 0.37 M M M
xxx
xxx
KK
K
x
x
x
bw
a
672
67
HC H O ][OH
CHO
10 10
17 10 59 10 037 037
14
5
10
2
22
.
..[]
[]
..
55
=1.5 10 M = OH , pOH = log 1.5 10 = 4.82, pH = 14.00 4.82 = 9.18x
62. (M)
+ +
55 2 55 3
Equation : C H NH (aq) + H O(l) C H N(aq) + H O (aq)
Initial: 0.0482M 0M 0M
Changes : M + M + M
Equil: 0.0482 M M M
xxx
xx x
+
14 2 2
55 3
6
w
a9+
b55
CHN HO
1.0 10
== =6.710= =
1.5 10 0.0482 0.0482
CHNH
K
x
x
KKx
4
5.7 10 M << 0.0482 M, the assumption is valid
4+ 4
3
= 5.7 10 M = H O , pH = log 5.7 10 = 3.24x
63. (M)
(a) 2
2
+8
3 2 3 3 a a ,Sulfurous
HSO + H O H O +SO = = 6.2 10KK
1
14 13
w
32 23b 2
a ,Sulfurous
1.0 10
HSO + H O OH + H SO = = = 7.7 10
1.3 10
K
KK
Since KK
ab
, solutions of HSO3
are acidic.

Chapter 16: Acids and Bases
759
(b) 2
+2 19
23 aa,Hydrosulfuric
HS + H O H O +S = = 1 10KK
1
14 7
w
22b 7
a ,Hydrosulfuric
1.0 10
HS + H O OH + H S = = =1.0 10
1.0 10
K
KK
Since KK
ab
, solutions of HS are alkaline, or basic.
(c) 3
23
+13
4 2 3 4 a a ,Phosphoric
HPO + H O H O + PO = = 4.2 10KK
2
14
27
w
42 24b 8
a ,Phosphoric
1.0 10
HPO + H O OH + H PO = = =1.6 10
6.3 10
K
KK
Since KK
ab
, solutions of HPO4
2 are alkaline, or basic.
64. (M) pH = 8.65 (basic). We need a salt made up of a weakly polarizing cation and an
anion of a weak acid, which will hydrolyze to produce a basic solution. The salt (c) KNO2
satisfies these requirements. (a) NH Cl
4is the salt of the cation of a weak base and the anion
of a strong acid, and should form an acidic solution. (b) KHSO4and (d) NaNO3 have
weakly polarizing cations and anions of strong acids; they form pH-neutral solutions.
pOH OH M= 14.00 8.65 = 5.35 = 10 = 4.5 10
5.35 6
22 2
666
666
Equation: NO (aq) + H O(l) HNO (aq) + OH (aq)
Initial: 0 M 0 M
Changes: 4.5 10 M +4.5 10 M +4.5 10 M
Equil: 4.5 10 M 4.5 10 M 4.5 10 M
S
S
KK
KS
bw
a
HNO OH
NO
==
1.0 10
7.2 10 =1.4 10 = = 4.5 10
4.5 10
14
4
11 2
2
62
6
ch
2
6
6 6
2
11
4.5 10
4.5 10 = = 1.4M = 1.4M +4.5 10 = 1.4M = KNO
1.4 10
SS
Molecular Structure and Acid-Base Behavior
65. (M)
(a) HClO3should be a stronger acid than is HClO2. In each acid there is an H – O – Cl
grouping. The remaining oxygen atoms are bonded directly to Cl as terminal O
atoms. Thus, there are two terminal O atoms in HClO3 and only one in HClO2.
For oxoacids of the same element, the one with the higher number of terminal
oxygen atoms is the stronger. With more oxygen atoms, the negative charge on the
conjugate base is more effectively spread out, which affords greater stability.
HClO3:1
2
a=5 10K and HClO2:Ka=1.1 10 2
.

Chapter 16: Acids and Bases
760
(b) HNO2and H CO
23
each have one terminal oxygen atom. The difference? N is more
electronegative than C, which makes
4
2a
HNO = 7.2 10K
, a stronger acid than
H2CO3
1
7
a=4.4 10K
.
(c) HPO
34
and HSiO
23
have the same number (one) of terminal oxygen atoms.
They differ in P being more electronegative than Si, which makes 34
HPO
1
3
a=7.1 10K
a stronger acid than
1
10
23a
HSiO =1.7 10K
.
66. (E) CCl COOH
3 is a stronger acid than CH COOH
3 because in CCl COOH
3 there are
electronegative (electro-withdrawing) Cl atoms bonded to the carbon atom adjacent to the
COOH group. The electron-withdrawing Cl atoms further polarize the OH bond and
enhance the stability of the conjugate base, resulting in a stronger acid.
67. (E)
(a) HI is the stronger acid because the H — I bond length is longer than the H — Br
bond length and, as a result, H — I is easier to cleave.
(b) HOClO is a stronger acid than HOBr because
(i) there is a terminal O in HOClO but not in HOBr
(ii) Cl is more electronegative than Br.
(c) H CCH CCl COOH
322 is a stronger acid than I CCH CH COOH
322 both because Cl is
more electronegative than is I and because the Cl atoms are closer to the acidic
hydrogen in the COOH group and thus can exert a stronger e withdrawing effect on
the OH bond than can the more distant I atoms.
68. (M) The weakest of the five acids isCH CH COOH
32 . The reasoning is as follows. HBr is a
strong acid, stronger than the carboxylic acids. A carboxylic acid—such as CH ClCOOH
2
and CH FCH COOH
22 —with a strongly electronegative atom attached to the hydrocarbon
chain will be stronger than one in which no such group is present. But the I atom is so
weakly electronegative that it barely influences the acid strength. Acid strengths of some
of these acids (as values of p a
K) follow. (Larger values of p a
K indicate weaker acids.)
Strength:
32 3 2 2 2
CH CH COOH 4.89 CI COOH CH FCH COOH CH ClCOOH HBr 8.72
69. (E) The largest Kb (most basic) belongs to (c) CH3CH2CH2NH2 (hydrocarbon chains have
the lowest electronegativity). The smallest Kb (least basic) is that of (a) o-chloroaniline
(the nitrogen lone pair is delocalized (spread out over the ring), hence, less available to
accept a proton (i.e., it is a poorer Brønsted base)).
70. (E) The most basic species is (c) CH3O (methoxide ion). Methanol is the weakest acid,
thus its anion is the strongest base. Most acidic: (b) ortho-chlorophenol. In fact, it is the
only acidic compound shown.
Chapter 16: Acids and Bases
761
Lewis Theory of Acids and Bases
71. (E)
(a) acid is CO2 and base is H2O
OCO+H
O
HO
C
O
OH
+O
HHH
(b) acid is BF3 and base is H2O
F
B
FF
+H
O
H
F
B
FF
H
O
H
(c) acid is H2O and base is O2–
OO
2-
+H
O
HOH
2
(d) acid is SO3 and base is S2–
SS
2-
+
O
S
OO
O
S
OO
S
2-
72. (E)
(a) SOI2 is the acid, and BaSO3 the base.
(b)
–
3
HgCl is the acid, Cl– the base.
73. (E) A Lewis base is an electron pair donor, while a Lewis acid is an electron pair acceptor.
We draw Lewis structures to assist our interpretation.
(a)
OH
The lone pairs on oxygen can readily be donated;
this is a Lewis base.
(b)
H C C B
H H
H H
C C H
H
H
H
H
C H
2
C H
3
The incomplete octet of B provides a site for
acceptance of an electron pair, this is a Lewis acid.
Chapter 16: Acids and Bases
762
(c)
HNCH
HH
H
The incomplete octet of B provides a site for
acceptance of an electron pair, this is a Lewis acid.
74. (M)
A Lewis base is an electron pair donor, while a Lewis acid is an electron pair acceptor.
We draw Lewis structures to assist our interpretation.
(a) According to the following Lewis structures, SO3 appears to be the electron pair
acceptor (the Lewis acid), and H O
2 is the electron pair donor (the Lewis base).
(Note that an additional sulfur-to-oxygen bond is formed upon successful attachment
of water to SO3.)
(b) The Zn metal center in Zn OH
bg
2accepts a pair of electrons. Thus, Zn OH
bg
2 is a
Lewis acid. OH donates the pair of electrons that form the covalent bond.
Therefore, OH is a Lewis base. We have assumed here that Zn has sufficient
covalent character to form coordinate covalent bonds with hydroxide ions.
OH OHZnOH ZnOO
O
O
HH
H
H
2+
2-
75. (M) (a)
OH +BOHOH
O
H
BOHOH
O
H
O
H
-
Acid: e
pair acceptor
Base: e pair donor
O S
O
H O H
O
O S
O
O
H O H
Base: e pair donor Acid: e
pair acceptor

Chapter 16: Acids and Bases
763
(b)
H HN
H
H
N
H
O
H
H
HO
H
H
H HN
H
H
N
The actual Lewis acid is H+, which is supplied by H3O+
(c)
H
CH
H
C
H
H
OC
H
H
C
H
H
H
Base: electron pair donor Acid: electron pair acceptor
F
FBF
F
FF
H
CH
H
C
H
H
C
H
H
C
H
H
H
B
O
76. (E) The C in a CO2 molecule can accept a pair of electrons. Thus, CO2 is the Lewis acid.
The hydroxide anion is the Lewis base as it has pairs of electrons it can donate.
OCO+OH OCO
OH
acid base
77. (E) 23
I (aq) I (aq) I (aq)
II I
Lewis acid
(e- pair acceptor)
Lewis base
(e- pair donor)
III
78. (E)
(a)
Lewis acid
(e- pair acceptor)
Lewis base
(e- pair donor)
HF Sb
F
F
FF
F
Sb
F
FF
FF
F
H
(b)
Lewis acid
(e- pair acceptor)
Lewis base
(e- pair donor)
HF BF
F
F
BF
F
F
F
H

Chapter 16: Acids and Bases
764
79. (E)
HOH OSO OS
O
O
H
H
OS
O
O
H
H
Lewis base
(
e
-
p
a
i
r
d
ono
r
)
Lewis acid
(
e
-
p
a
i
r
a
cce
p
to
r
)
80. (E)
H
N
H
H
2Ag+
H
NH
H
HN
H
H
Ag
+
electron pair donor electron pair acceptor ammonia aduct
INTEGRATIVE AND ADVANCED EXERCISES
81. (E) We use (ac) to represent the fact that a species is dissolved in acetic acid.
(a) 232 232 232 232
CHO (ac) HCHO(l) HCHO(l) CHO (ac)
C
2H3O2– is a base in acetic acid.
(b) 2 232 3 232
H O(ac) HC H O ( ) H O (ac) C H O (ac)l
Since H2O is a weaker acid than HC2H3O2 in aqueous solution, it will also be weaker in
acetic acid. Thus H2O will accept a proton from the solvent acetic acid, making H2O a
base in acetic acid.
(c) 232 232 2232 232
HCHO(l) HCHO() HCHO (ac) CHO (aq)l
Acetic acid can act as an acid or a base in acetic acid.
(d) 4232 42232
HClO (ac) HC H O (l) ClO (ac) H C H O (ac)
Since HClO4 is a stronger acid than HC2H3O2 in aqueous solution, it will also be
stronger in acetic acid. Thus, HClO4 will donate a proton to the solvent acetic acid,
making HClO4 an acid in acetic acid.
82. (E) Sr(OH)2 (sat'd)
Sr2+(aq) + 2 OH-(aq)
-0.88
pOH 14 pH=14-13.12 0.88
[OH ] 10 0.132 M
ammonia
adduct
Chapter 16: Acids and Bases
765
3
dilute
3
3
10.0 ml concentrate
[OH ] 0.132M ( ) 5.28 10 M
250.0 mL total
(10.0 ml ) (5.28 10 M)
[HCl] 2.10 10 M
25.1 mL
83. (M)
(a)
H2SO4 is a diprotic acid. A pH of 2 assumes no second ionization step and the second
ionization step alone would produce a pH of less than 2, so it is not matched.
(b) pH 4.6 matched; ammonium salts hydrolyze to form solutions with pH < 7.
(c) KI should be nearly neutral (pH 7.0) in solution since it is the salt of a strong acid (HI)
and a strong base (KOH). Thus it is not matched.
(d) pH of this solution is not matched as it's a weak base. A 0.002 M solution of KOH has a
pH of about 11.3. A 0.0020 M methylamine solution would be lower (~10.9).
(e) pH of this solution is matched, since a 1.0 M hypochlorite salt hydrolyzes to form a
solution of ~ pH 10.8.
(f) pH of this solution is not matched. Phenol is a very weak acid (pH >5).
(g) pH of this solution is 4.3. It is close, but not matched.
(h) pH of this solution is 2.1, matched as it's a strong organic acid.
(i) pH of this solution is 2.5, it is close, but not matched.
84. (M) We let [H3O+]a = 0.500 [H3O+]i pH = –log[H3O+]i
pHa = –log[H3O+]a = –log(0.500 [H3O+]i) = –log [H3O+]i – log (0.500) = pHi + 0.301
The truth of the statement has been demonstrated. Remember, however, that the extent of
ionization of weak acids and weak bases in water increases as these solutions become more
and more dilute. Finally, there are some solutions whose pH doesn’t change with dilution,
such as NaCl(aq), which has pH = 7.0 at all concentrations.
85. (M) Since a strong acid is completely ionized, increasing its concentration has the effect of
increasing [H3O+] by an equal degree. In the case of a weak acid, however, the solution of
the Ka expression gives the following equation (if we can assume that [H3O+] is negligible
compared to the original concentration of the undissociated acid, [HA]). x2 = Ka[HA] (where
x = [H3O+]), or ]HA[
a
Kx . Thus, if [HA] is doubled, [H3O+] increases by 2.
86. (E) H2O(l) + H2O(l) H3O+(aq) + OH-(aq) Ho = (-230.0 kJ mol) – (-285.8 kJ mol-1)
= 55.8 kJ
Since
Ho is positive, the value of Keq is larger at higher temperatures. Therefore, the ionic
products increase with increasing temperature. Le Ch âtelier’s principle or the Van’t Hoff
equation would show this to be true.
Chapter 16: Acids and Bases
766
87. (M) First we assume that molarity and molality are numerically equal in this dilute aqueous
solution. Then compute the molality that creates the observed freezing point, with Kf = 1.86
°C/m for water.
f0.096 C 0.052 concentration 0.052 M
1.86 C/
f
T
mm
Km
This is the total concentration of all species in solution, ions as well as molecules. We base
our remaining calculation on the balanced chemical equation.
452 2 452 3
Equation: HC H O (aq) H O C H O (aq) H O (aq)
Initial: 0.0500 M 0 M 0 M
Changes: M M M
Equil: (0.0500 )
xxx
x
M M Mxx
6 6
25
452 3 6
a
452 6
Total conc. 0.051 M (0.0500 ) M M M 0.0500 M M 0.001 M
[C H O ][H O ] (0.001 )
5 10
[HC H O ] 0.0500 0.0500 0.001
xxx x x
xx
Kx
88. (D) [H3O+] = 10–pH = 10–5.50 = 3.2 × 10–6 M
(a) To produce this acidic solution we could not use 15 M NH3(aq), because aqueous
solutions of NH3 have pH values greater than 7 owing to the fact that NH3 is a weak
base.
(b)
6
5
3
HCl
3
3.2 10 mol H O 1 mol HCl 1 L soln
V 100.0 mL 2.7 10 mL 12 M HCl soln
1 L 12 mol HCl
1 mol H O
(very unlikely, since this small a volume is hard to measure)
(c) Ka = 5.6 × 10–10 for NH4+(aq)
42 33
666
6
Equation: NH (aq) H O(l) NH (aq) H O (aq)
Initial: M 0 M 0 M
Changes: 3.2 10 M 3.2 10 M 3.2 10 M
Equil: ( 3.2 10 ) M
c
c
66
66
10 33
a6
4
3.2 10 M 3.2 10 M
[NH ][H O ] (3.2 10 )(3.2 10 )
5.6 10 [NH ] 3.2 10
Kc

Chapter 16: Acids and Bases
767
ClNH g 096.0
ClNH mol 1
ClNH g 49.53
NH mol 1
ClNH mol 1
mL 1000
NH mol 0.018
mL 100.0mass ClNH
M 018.0][NH M 108.1
106.5
)102.3(
102.3
4
4
4
4
44
4
4
2
10
26
6
c
This would be an easy mass to measure on a laboratory three decimal place balance.
(d) The set-up is similar to that for NH4Cl.
232 2 232 3
66
Equation: HC H O (aq) H O (l) C H O (aq) H O (aq)
Initial: M 0 M 0 M
Changes: 3.2 10 M 3.2 10 M
c
6
666
3.2 10 M
Equil: ( 3.2 10 ) M 3.2 10 M 3.2 10 M
c
66
5232 3
a6
232
62
67 6
232
5
6
232
232
[C H O ][H O ] (3.2 10 )(3.2 10 )
K 1.8 10 [HC H O ] 3.2 10
(3.2 10 )
3.2 10 5.7 10 [HC H O ] 3.8 10
1.8 10
3.8 10 mol HC H O 60.
HC H O mass 100.0 mL 1000 mL
c
cc
232
232
5
232
05 g HC H O
1 mol HC H O
2.3 10 g HC H O (an almost impossibly small mass to measure
using conventional laboratory scales)
89. (M)
(a) 1.0 × 10-5 M HCN:
HCN(aq) + H2O(l) 10
6.2 10
a
K
H3O+(aq) + CN-(aq)
Initial: 1.0 × 10-5 M – 1.0 × 10-7 M 0 M
Change: –x – +x +x
Equilibrium: (1.0
× 10-5-x) M – (1.0 × 10-7+x) M x
7
10 15 10 7 2
5
2715
772 15
7
(1.0 10 )
6.2 10 6.2 10 6.2 10 1.0 10
(1.0 10 )
1.006 10 6.2 10 0
1.006 10 (1.006 10 ) 4(1)( 6.2 10 ) 1.44 10
2(1)
xx
x
xx
x
x
x
Final pH = -log[H3O+] = -log(1.0 × 10-7+ 1.44 × 10-7) = 6.61

Chapter 16: Acids and Bases
768
(b) 1.0 × 10-5 M C6H5NH2:
C6H5NH2(aq) + H2O(l) 10
7.4 10
a
K
OH-(aq) + C6H5NH3+(aq)
Initial: 1.0 × 10-5 M – 1.0 × 10-7 M 0 M
Change: –x – +x +x
Equilibrium: (1.0 × 10-5–x) M – (1.0 × 10-7+x) M x
7
10 15 10 7 2
5
2715
772 15
8
(1.0 10 )
7.4 10 7.4 10 7.4 10 1.0 10
(1.0 10 )
1.0074 10 7.4 10 0
1.0074 10 (1.0074 10 ) 4(1)( 7.4 10 ) 4.93 10 M
2(1)
xx
x
xx
x
x
x
Final pOH = -log[OH-] = -log(1.0 × 10-8+ 4.93 × 10-7) = 6.83 Final pH = 7.17
90. (D)
(a) For a weak acid, we begin with the ionization constant expression for the weak acid, HA.
222
3
a
[H O ][A ] [H ] [H ] [H ]
[HA] [HA] M [H ] M
K
The first modification results from realizing that [H+] = [A–]. The second modification
is based on the fact that the equilibrium [HA] equals the initial [HA] minus the amount
that dissociates. And the third modification is an approximation, assuming that the
amount of dissociated weak acid is small compared to the original amount of HA in
solution. Now we take the logarithm of both sides of the equation.
MM
c
K log][H log 2 log][H log
]H[
log log 2
2
a
11
aa a
22
2 log [H ] log log 2 pH p log pH p log KM KM K M
For a weak base, we begin with the ionization constant expression for a weak base, B.
M
M
K222
b
]OH[
]OH[
]OH[
[B]
]OH[
[B]
]OH][BH[
The first modification results from realizing that [OH–] = [BH+]. The second
modification is based on the fact that the equilibrium [B] equals the initial [B] minus
the amount that dissociates. And the third modification is an approximation, assuming
that the amount of dissociated weak base is small compared to the original amount of B
in solution. Now we take the logarithm of both sides of the equation.
22
b
11
bbb
22
11
b
22
[OH ]
log K log log [OH ] log M 2 log [OH ] log M
M
2 log [OH ] log K log M 2 pOH pK log M pOH pK logM
pH 14.00 pOH 14.00 pK log M
The anion of a relatively strong weak acid is a weak base. Thus, the derivation is the
same as that for a weak base, immediately above, with the exception of the value for
Kb. We now obtain an expression for pKb.

Chapter 16: Acids and Bases
769
awbawb
aw
a
w
b
a
w
b
ppp log log log
log loglog log
KKKKKK
KK
K
K
K
K
K
K
Substitution of this expression for pKb into the expression above gives the following result.
MKK log p p14.00pH 2
1
a
2
1
w
2
1
(b) 0.10 M HC2H3O2 pH = 0.500 × 4.74 – 0.500 log 0.10 = 2.87
232 2 232 3
Equation: HC H O (aq) H O(l) C H O (aq) H O (aq)
Initial: 0.10 M 0 M 0 M
Changes: M M M
Equil: (0.1
xxx
0 ) M M Mxxx
2
5
3232
a
232
53 3
[H O ][C H O ]
1.8 10
[HC H O ] 0.10 0.10
0.10 1.8 10 1.3 10 M, pH log(1.3 10 ) 2.89
xx x
Kx
x
. pH 14.00 0.500 4.74 0.500 log 0.10 11.13
3
010 MNH
324
Equation: NH (aq) H O(l) NH (aq) OH (aq)
Initial: 0.10 M 0 M 0 M
Changes: M M M
Equil: (0.10 ) M
xxx
x
M Mxx
2
553
4
b
3
3
[NH ][OH ]
1.8 10 0.10 1.8 10 1.3 10 M
[NH ] 0.10 0.10
pOH log(1.3 10 ) 2.89 pH 14.00 2.89 11.11
xx x
Kx
x
3
. pH 14.00 0.500 14.00 0.500 4.74 0.500 log 0.10 8.87
22
010 M NaCHO
232 2 232
Equation: C H O (aq) H O(l) HC H O (aq) OH (aq)
Initial: 0.10 M 0 M 0 M
Changes: M M M
Equil: (0.10 )
xxx
x
14 2
232
a5
232
14 66
5
M M M
[OH ][HC H O ] 1.0 10
0.10 0.10
[C H O ] 1.8 10
0.10 1.0 10 7.5 10 M pOH log(7.5 10 ) 5.12
1.8 10
pH 14.00 5.12 8.88
xx
xx x
Kx
x
Chapter 16: Acids and Bases
770
91. (D)
(a) We know
eq
eqeq3
a[HA]
]A[]OH[
K,
i
[HA]
]A[ eq
and finally % ionized = × 100%.
Let us see how far we can get with no assumptions. Recall first what we mean by [HA]eq.
eqeqeqeq ][A HA][[HA]or ]A[HA][]HA[ ii
We substitute this expression into the expression for .
eqeq
eq
][[HA]
][
A
A
We solve both the and the Keq expressions for [HA]eq, equate the results, and solve for .
_
3
eq eq eq
a
_
3
a
[H O ][A ] [A ] α[A ]
[HA] [A ] [HA] [A ] [HA]
[H O ][A ] [A ](1 ) R
1
R 1 R 1 (1 R) 1R
K
K
Momentarily, for ease in writing, we have let pH)p(
pK
pH
a
310
10
10
O][H
R
K
K
Once we realize that 100 = % ionized, we note that we have proven the cited formula.
Notice that no approximations were made during the course of this derivation.
(b) Formic acid has pKa = 3.74. Thus 10(pK–pH) = 10(3.74–2.50) = 101.24 = 17.4
%43.5
17.41
100
ionization %
(c) [H3O+] = 10–2.85 = 1.4 × 10–3 M %93.0%100
M150.0
M 101.4
ionization % 3
588.4
a
pH)p(pH)p(
pH)p(
103.110 88.403.285.203.2pHp pHp03.2
10710 108
93.0
100
101
101
100
93.0
KKK
KK
K
92. (M) We note that, as the hydrocarbon chain between the two COOH groups increases in
length, the two values of pKa get closer together. The reason for this is that the ionized
COOH group, COO–, is negatively charged. When the two COOH groups are close together,
the negative charge on the molecule, arising from the first ionization, inhibits the second
ionization, producing a large difference between the two ionization constants. But as the
hydrocarbon chain lengthens, the effect of this negative COO- group on the second
ionization becomes less pronounced, due to the increasing separation between the two
carbonyl groups, and the values of the two ionization constants are more alike.

Chapter 16: Acids and Bases
771
93. (M) Consider only the 1st dissociation.
-5
6.2 10
24 44 2 3 4 4 4
Equation: H C H O (aq) H O(l) H O (aq) HC H O (aq)
Initial: 0.100 M 0 M 0 M
Changes: M x
M M
Equil: (0.100 ) M M M
xx
xxx
25
a 6.2 10 0.00246 M
0.100
Solve using the quadratic equation. Hence pH = log 0.00246 = 2.61
x
Kx
x
Consider only the 2nd dissociation.
-5
2.3 10 2
444 2 3 444
Equation: HC H O (aq) H O(l) H O (aq) C H O (aq)
Initial: 0.0975 M 0.00246 M
0 M
Changes: M M M
Equil: (0.0975 ) M 0.00246 + M M
xxx
xxx
6
a
(0.00246 ) (0.00246)
2.3 10
0.0975 0.0975
0.000091 M or 0.000088 M (solve quadratic) Hence pH 2.59
Thus, the pH is virually identical, hence, we need only consider the 1st ionization.
xx x
Kx
xx
94. (M) To have the same freezing point, the two solutions must have the same total
concentration of all particles of solute—ions and molecules. We first determine the
concentrations of all solute species in 0.150 M HC2H2ClO2, Ka = 1.4 × 10–3
22 2 2 3 22 2
Equation: HC H ClO (aq) H O(l) H O (aq) C H ClO (aq)
Initial: 0.150 M 0 M 0 M
Changes: M M xx
M
Equil: (0.150 ) M M M
x
xxx
3
3222
a
22 2
243 23 4
2364
[H O ][C H ClO ] 1.4 10
[HC H ClO ] 0.150
2.1 10 1.4 10 1.4 10 2.1 10 0
4 1.4 10 2.0 10 8.4 10 0.014 M
22
xx
Kx
xxxx
bb ac
xa
total concentration = (0.150 – x) + x + x = 0.150 + x = 0.150 + 0.014 = 0.164 M
Now we determine the [HC2H3O2] that has this total concentration.

Chapter 16: Acids and Bases
772
232 2 3 232
Equation: HC H O (aq) H O(l) H O (aq) C H O ( )
Initial: M 0 M 0 M
Changes: M
aq
z
y
5
3232
a
232
M M
Equil: ( ) M M M
[H O ][C H O ]
1.8 10
[HC H O ]
yy
z y y y
yy
Kzy
We also know that the total concentration of all solute species is 0.164 M.
5
2108.1
2 164.0
164.0 164.0
y
y
yzyzyyyz
We assume that 3652 107.1 100.3108.1164.0 0.164 2 yyy
The assumption is valid: 0.164 0034.02
y
Thus, [HC2H3O2] = z = 0.164 – y = 0.164 – 0.0017 = 0.162 M
232
232
232232
232 OHHC g 73.9
OHHC mol 1
OHHC g 05.60
soln L 1
OHHC mol 0.162
L 000.1OHHC mass
95. (M) The first ionization of H2SO4 makes the major contribution to the acidity of the
solution.
Then the following two ionizations, both of which are repressed because of the presence of
H3O+ in the solution, must be solved simultaneously.
-2
42 43
Equation: HSO (aq) H O(l) SO (aq) H O ( )
Initial: 0.68 M 0 M 0.68 M
Changes: M M
aq
xx
M
Equil: (0.68 ) M M (0.68 )M
x
x
xx
x
xx
K
68.0
) 68.0(
011.0
]HSO[
]][SOOH[
4
2
43
2
Let us solve this expression for x. 0.011 (0.68 – x) = 0.68x + x2 = 0.0075 – 0.011x
2
24 0.69 0.48 0.030
0.69 0.0075 0 0.01 M
22
bb ac
xx x a
Chapter 16: Acids and Bases
773
This gives [H3O+] = 0.68 + 0.01 = 0.69 M. Now we solve the second equilibrium.
22 2 3
Equation: HCHO (aq) H O( ) CHO (aq) H O ( )
Initial: 1.5 M 0 M 0.69 M
Changes: M
laq
x
4
32
a
2
M M
Equil: (1.5 ) M M (0.69 ) M
[H O ][CHO ] (0.69 ) 0.69
1.8 10
[HCHO ] 1.5 1.5
xx
xxx
xxx
Kx
4
3.9 10 Mx
We see that the second acid does not significantly affect the [H3O+], for which a final value is
now obtained. [H3O+] = 0.69 M, pH = –log(0.69) = 0.16
96. (D)
1
21
1111
1111
22
1
1
11
22
2
2
22
21/2
2
21
2
[][] [][]
Let [ ] [][][]
[][] [][]
Let [ ] 2 [][][]
[] [] []
[]
2 []2 [] 2 2
HA
HA HA
HA HA HA HA
HA HA HA HA
HA HH
HA M K HA H HA M
HA H H
HA M K K HA H HA M
H
KHKMHKMKM
M
H
KHKMHKMKM
M
/2
11
11
11 11
11
1/2 1/2
10
1/2 1/2
1/2 1/2
[ ] 2 (take the negative log of bothsides)
log([ ] ) log log 2
11
pH log log log log 2
22
11
pH log log 2 log
22
overall HA HA
overall HA HA
HA HA HA HA
HA HA
HKMKM
HKMKM
KM KM KM KM
KM KM K
11
11
2
11
pH 3 3
22
HA HA
HA HA
MK M
KM MK
Chapter 16: Acids and Bases
774
97. (M) HSbF6 H+ + SbF6-
Sb
F
F
F
F
F
F
H+
Sb has 6 sp3d2 hybrid orbitals
F has 2p orbital
The six bonds are all sigma bonds
(Sbsp3d2 - F2p)
HBF4 H+ + BF4-
B
F
FF
H+
B has 4 sp3 hybrid orbitals
F has 2p orbital
The four bonds are all sigma bonds
(Bsp3 - F2p)
F
98. (M) The structure of H3PO3 is shown on the right.
The two ionizable protons are bound to oxygen.
99. (M)
(a) H2SO3 > HF >N2H5+ > CH3NH3+ > H2O
(b) OH– > CH3NH2 > N2H4 > F–> HSO3–
(c) (i) to the right and (ii) to the left.
F uses one of its 2p orbitals
Sb uses all six of its sp3d2 hybrid orbitals
F uses one of its 2p orbitals
B uses all four of its sp3 hybrid orbitals
HH
H
OO P
O

Chapter 16: Acids and Bases
775
FEATURE PROBLEMS
100. (D)
(a) From the combustion analysis we can determine the empirical formula. Note that the
mass of oxygen is determined by difference.
2
2
22
1mol CO 1mol C
amount C = 1.599 g CO = 0.03633 mol C
44.01 g CO 1 mol CO
12.011 g C
mass of C = 0.03633 mol C = 0.4364 g C
1mol C
2
2
22
1 mol H O 2 mol H
amount H = 0.327 g H O = 0.03629 mol H
18.02 g H O 1 mol H O
1.008 g H
mass of H = 0.03629 mol H = 0.03658 g H
1 mol H
amount O g sample g C g H mol O
g O mol O= 1.054 0.4364 0.03568 1
16.00 = 0.0364
bg
There are equal moles of the three elements. The empirical formula is CHO.
The freezing-point depression data are used to determine the molar mass.
TKmmT
Km
m
ff f
f
C
C
===
0.82
3.90 / = 0.21
1 kg 0.21 mol solute
amount of solute = 25.10 g solvent = 0.0053 mol
1000 g 1 kg solvent
M=0.615
0.0053 = 1.2 102
g solute
mol solute g/mol
The formula mass of the empirical formula is: 12.0 +1.0 +16.0 = 29.0g C g H g O g / mol
Thus, there are four empirical units in a molecule, the molecular formula isC H O
444
,
and the molar mass is 116.1 g/mol.
(b) Here we determine the mass of maleic acid that reacts with one molOH,
mass 0.4250 g maleic acid 58.03g/molOH
1L 0.2152mol KOH
molOH 34.03mLbase 1000 mL 1Lbase
This means that one mole of maleic acid (116.1 g/mol) reacts with two moles of
hydroxide ion. Maleic acid is a diprotic acid: H C H O
24 24
.
(c) Maleic acid has two—COOH groups joined together by a bridging C2H2 group. A
plausible Lewis structure is shown below:
C
O
C
H
C
H
COHOH
O

Chapter 16: Acids and Bases
776
(d) We first determine +pH1.80
3
H O =10 = 10 = 0.016 M
and then the initial
concentration of acid.
2initial
0.215g 1000 mL 1 mol
CHCOOH = = 0.0370 M
50.00 mL 1L 116.1 g
We use the first ionization to determine the value of 1
a
K
+
23
22
Equation: CHCOOH (aq) + H O(l) H CHCOO (aq) + H O (aq)
Initial: 0.0370M 0M 0 M
Changes: 0.016M + 0.016M + 0.016M
Equil: 0.021M 0.016M 0.016M
+
3
22
a
2
H CHCOO H O 0.016 0.016
===1.210
0.021
CHCOOH
K
Ka2 could be determined if we had some way to measure the total concentration of all
ions in solution, or if we could determine
2
2
a
2
CHCOO K
(e) Practically all the HO
3+ arises from the first ionization.
+
23
22
Equation: CHCOOH (aq) + H O(l) H CHCOO (aq) + H O (aq)
Initial: 0.0500M 0 M 0 M
Changes: M + M + M
Equil: 0.0500 M M M
xxx
xxx
22
23
2
22
[H(CHCOO) ][H O ] 1.2 10
[(CHCOOH) ] 0.0500
0.00060 0.012 0.012 0.00060 0
a
x
Kx
xxxx
2+
3
4 0.012 0.00014 + 0.0024
= = = 0.019 M = H O
22
bb ac
xa
pH log= 0.019 = 1.72bg

Chapter 16: Acids and Bases
777
101. (D)
(a)
22 41
22
42
22
43
22
4.2 10 0.00102
0.00250 0.00250
4.2 10 0.000788
0.00250 0.00102 0.00148
4.2 10 0.000848
0.00250 0.000788 0.00171
4.
0.00250 0.000848 0.00165
xx x
x
xx x
xx x
xx
44
22
45
22
46
4
6
2 10 0.000833
4.2 10 0.000837
0.00250 0.000833 0.00167
4.2 10 0.000836
0.00250 0.000837 0.00166
0.000836 or 8.4 10 ,
x
xx x
xx x
x
which is the same as the value obtained using the quadratic equation.
(b) We organize the solution around the balanced chemical equation, as we have done before.
+
22 2 3
Equation: HClO (aq) + H O(l) ClO (aq) + H O (aq)
Initial: 0.500M 0M 0 M
Changes: M + M + M
Equil: M M M
xxx
xxx
+22
23 2
a
2
ClO H O
===1.110
HClO 0.500 0.500
x
x
Kx
Assuming 0.500 Mx,
22
= 0.500 1.1 10 0.074M Not significantly smaller than 0.500 M.xx
2
2
2
Assume 0.074 (0.500 0.0774) 1.1 10 0.068M Try once more.
Assume 0.068 (0.500 0.068) 1.1 10 0.069M One more time.
Assume 0.069 (0.500 0.069) 1.1 10 0.069M Final result!
xx
xx
xx
++
33
H O = 0.069 M, pH = log H O = log 0.069 =1.16

Chapter 16: Acids and Bases
778
102. (D)
(a) Here, two equilibria must be satisfied simultaneously. The common variable,
HO
3+=z.
+
232 2 232 3
+
3232 5
a
232
Equation: HC H O (aq) + H O(l) C H O (aq) + H O (aq)
Initial: 0.315M 0 M 0 M
Changes: + M + M + M
Equil: 0.315 M M M
HO CHO
= = = 1.8 10
HC H O 0.315
xxz
xxz
xz
Kx
+
22 23
+
32 4
a
2
Equation: HCHO (aq) + H O(l) CHO (aq) + H O (aq)
Initial: 0.250 M 0 M 0 M
Changes: M + M + M
Equil: (0.250 )M M M
HO CHO
===1.810
HCHO 0.250
yyz
yyz
yz
Ky
In this system, there are three variables, xy=,=
232 2
CHO CHO
, and z=3+
HO .
These three variables also represent the concentrations of the only charged species in
the reaction, and thus
x
y
z+ = . We solve the two Ka expressions for x and y. (Before
we do so, however, we take advantage of the fact that
x
and
y
are quite small:
x
0.315 and
y
0.250 .) Then we substitute these results into the expression for z,
and solve to obtain a value of that variable.
56 45
65
=1.8 10 0.315 = 5.7 10 =1.8 10 0.250 = 4.5 10
5.7 10 4.5 10
==
xz yz
xy
zz
65 5 53+
3
5.7 10 4.5 10 5.07 10
= + = + = = 5.07 10 = 7.1 10 M = [H O ]zxy z
zz z
pH log= 7.1 10 = 2.15
3
ch We see that our assumptions about the sizes of
x
and
y
must
be valid, since each of them is smaller than z. (Remember that
x
y
z+=.)
(b) We first determine the initial concentration of each solute.
5
3
2
3 b
3
1mol NH
12.5g NH
NH = =1.96M =1.8 10
0.375L soln 17.03g NH K
4
32 32
32 b
32
1.55 g CH NH 1 mol CH NH
CH NH = = 0.133M = 4.2 10
0.375L soln 31.06 g CH NH K
Now we solve simultaneously two equilibria, which have a common variable, OH=z.

Chapter 16: Acids and Bases
779
+
32 4
+
45
b
3
Equation: NH aq + H O NH aq + OH aq
Initial: 1.96 M 0 M 0M
Changes: M + M + M
Equil: 1.96 M M M
NH OH
==1.810=
NH 1.96 1.96
xxz
xxz
xz xz
Kx
+
32 2 33
+
33 4
b
32
Eqn: CH NH aq + H O(l) CH NH aq + OH aq
Initial: 0.133M 0M 0M
Changes: M M M
Equil: (0.133 )M M M
CH NH OH
==4.210==
CH NH 0.133 0.133
yyz
yyz
yz yz
Ky
In this system, there are three variables, xy=,=
4
+
33
+
NH CH NH , and z=OH
.
These three variables also represent the concentrations of the only charged species in
solution in substantial concentration, and thus
x
y
z+ = . We solve the two Kb expressions
for
x
and
y
. Then we substitute these results into the expression for z, and solve to obtain
the value of that variable.
55 55
55
=1.96 1.8 10 = 3.53 10 = 0.133 4.2 10 = 5.59 10
3.53 10 5.59 10
==
xz yz
xy
zz
55 5
25
3.53 10 5.59 10 9.12 10
= + = + = = 9.12 10zxy z
zz z
33
= 9.5 10 M = OH pOH = log 9.5 10 = 2.02 pH =14.00 2.02 =11.98z
We see that our assumptions about
x
and
y
(that x
1.96 M and y
0.133 M) must be
valid, since each of them is smaller than z. (Remember that
x
y
z+=.)
(c) In 1.0 M NH CN
4 there are the following species: NH aq NH aq CN aq
4
+
3
,,
bgbgbg
, HCN(aq),
HO aq
3+bg
, and OH aq
bg
. These species are related by the following six equations.
14
14 +
w3 +
3
1.0 10
1=1.010=HOOH OH=
HO
K
2=6.210=
10 3+
bgKa
HO CN
HCN
3=1.810=
54
+
3
bg Kb
NH OH
NH
L
N
MO
Q
P
Chapter 16: Acids and Bases
780
++
34 3 4
4NH+NH=1.0M NH=1.0NH
5 HCN + CN = 1.0 M HCN =1.0 CN
++ +
43 4
6 NH + H O = CN + OH or NH CN
Equation (6) is the result of charge balance, that there must be the same quantity of
positive and negative charge in the solution. The approximation is the result of
remembering that not much H O
3+ or OH will be formed as the result of hydrolysis of
ions. Substitute equation (4) into equation (3), and equation (5) into equation (2).
3’ = 1.8 10 = 1.0 2’ = 4.0 10 = 1.0
54
+
4
+
10 3+
bg bg
KK
ba
NH OH
NH
HO CN
CN
Now substitute equation (6) into equation 2’
bg, and equation (1) into equation 3’
bg.
2’’ = 6.2 10 = 1.0 3’’ 1.8 10
1.0 10 =1.0
10 3+4
+
4
+
5
14
4
+
3+4
+
bg bg ej
Ka
HO NH
NH
NH
HO NH
Now we solve both of these equations for NH4
+.
‘2 :6.2 10 6.2 10 = = 6.2 10
6.2 10 +
10 10 4
+
3+4
+
4
+10
10 3+
bg
NH H O NH NH HO
‘3 :1.8 10 1.8 10 = = 1.8 10
1.00 +1.8 10
93+9
3+4
+
4
+
4
+
93+
93+
bg
H O H O NH NH NH HO
HO
We equate the two results and solve for
HO
3+.6.2 10
6.2 10 + =1.8 10
1.00 +1.8 10
10
10 3+
93+
93+
HO
HO
HO
6.2 10 +1.1 = 1.1 +1.8 10 6.2 10 = 1.8 10
10 3+3+9
3+210 9 3+2
HO HO HO HO
HO M pH log
3+10
9
10 10
=62 10
18 10 59 10 = 5.9 10 = 9.23
.
..
ch
+aw
3awb
b
Note that H O = or pH=0.500 (p p p )
KK KK K
K
Chapter 16: Acids and Bases
781
SELF-ASSESSMENT EXERCISES
103. (E)
(a) KW: Dissociation constant of water, which is defined as [H3O+][OH¯]
(b) pH: A logarithmic scale of expressing acidity of a solution (H3O+); it is defined as
-log [H3O+]
(c) pKa: A logarithmic scale expressing the strength of an acid (which is how much an acid
dissociates in water at equilibrium); it is defined as –log Ka
(d) Hydrolysis: A reaction involving ionization of water
(e) Lewis acid: A compound or species that accepts electrons
104. (E)
(a) Conjugate base: A base that is derived by removing an abstractable proton from the acid
(b) Percent ionization of acid/base: The ratio between the conjugate of the acid or base
under study and the acid/base itself times 100
(c) Self-ionization: A reaction involving ionization of two molecules of water to give
[H3O+] and [OH¯]
(d) Amphiprotic behavior: A substance acting as either an acid or a base
105. (E)
(a) Brønstead–Lowry acid and base: A Brønsted–Lowry acid is a substance that when
placed in water will cause the formation of hydronium ion by donating a proton to
water. The base is one that abstracts a proton from water and results in a hydroxyl ion.
(b) [H3O+] and pH: [H3O+] is the molar concentration of hydronium ion in water, whereas
pH is the –log [H3O+]
(c) Ka for NH4+ and Kb for NH3: Kb of NH3 is the equilibrium constant for hydrolysis of
water with NH3 to generate NH4+ and OH¯. Ka of NH4+ is for deprotonation of NH4+
with water to give NH3 and OH¯.
(d) Leveling effect and electron-withdrawing effect: The leveling effect is the result of
reaction of water with any acid or base such that no acid or base can exist in water that
are more acidic than H3O+ or more basic than OH¯. The electron-withdrawing effect is
the tendency for a central atom with high electronegativity in an oxoacid to withdraw
electrons from the O–H bond.
106. (E) The answer is (a), HCO3–, because it can donate a proton to water to become CO32–, or
it can be protonated to give H2CO3 (i.e., CO2(aq)).
107. (E) The answer is (c). CH3CH2COOH is a weak acid, so the concentration of H3O+ ions it
will generate upon dissociation in water will be significantly less than 0.1 M. Therefore, its
pH will be higher the 0.10 M HBr, which dissociates completely in water to give 0.10 M
H3O+.
108. (E) The answer is (d). CH3NH2 is a weak base.
Chapter 16: Acids and Bases
782
109. (M) The answer is (e) because CO32- is the strongest base and it drives the dissociation of
acetic acid furthest.
110. (M) The answer is (c). H2SO4 dissociation is nearly complete for the first proton, giving a
[H3O+] = 0.10 M (pH = 1). The second dissociation is not complete. Therefore, (c) is the
only choice that makes sense.
111. (M) The answer is (b). You can write down the stepwise equations for dissociation of
H2SO3 and then the dissociation of HSO3¯ and calculate the equilibrium concentration of
each species. However, you can determine the answer without detailed calculations. The
two dissociation equations are given below:
Eq.1 23 2 3 3
HSO HO HSO HO
Ka1 = 1.3×10-2
Eq.2 2
32 3 3
HSO H O SO H O
Ka2 = 6.3×10-8
For the first equation, the equilibrium concentrations, of HSO3¯ and H3O+ are the same.
They become the initial concentration values for the second dissociation reaction. Since
Ka2 is 6.3×10-8 (which is small), the equilibrium concentrations of HSO3¯ and H3O+ won’t
change significantly. So, the equation simplifies as follows:
2- +
2- + 33
33
8
a2 -
3
SO H O
SO H O +
K 6.8 10 =
HSO -
x
x
-
3
HSO
82-
a2 3
K=6.810 SO
112. (E) Since both the acid and the base in this reaction are strong, they dissociate completely.
The pH is determined as follows:
mol H3O+: 0.248 M HNO3 × 0.02480 L = 0.00615 mol
mol OH¯: 0.394 M KOH × 0.01540 L = 0.00607 mol
Final: 0.00615 – 0.00607 = 8.00×10-5 mol H3O+
5
3
8.00 10 mol
H O 0.00200 M
0.02480 L + 0.01540 L
pH log 0.00200 2.70
113. (M) Since pH = 3.25, the [H3O+] = 10-3.25 = 5.62×10-4 M. Using the reaction below, we
can determine the equilibrium concentrations of other species
HC2H3O2 + H2O C2H3O2¯ + H3O+
Initial C 0 0
Change -x +x +x
Equil. C - x x x
Chapter 16: Acids and Bases
783
Since x = 5.62×10-4 M, the equilibrium expression becomes
44
3232 5
a4
232
5.62 10 M 5.62 10 M
HO CHO
K1.810
HC H O C5.6210M
Solving C gives a concentration of 0.0181 M.
Since concentrated acetic acid is 35% by weight and the density is 1.044 g/mL, the
concentration of acetic acid is:
35 g HAc 1.044 g Conc. HAc 1 mol HAc 6.084 M HAc
100 g Conc. HAc sol'n 0.001L sol'n 60.06 g HAc
Therefore, volume of concentrated solution required to make 12.5 L of 0.0181 M HAc
solution is:
dilute conc.
conc
MV MV
0.0181M 12500 mL
V 37.2 mL
6.084 M
114. (M) Table 16.3 has the Ka value for chloroacetic acid, HC2H2ClO2. Ka = 1.4×10-3. The
solution is made of the chloroacetate salt, which hydrolyzes water according to the
following reaction:
C
2H2ClO2¯ + H2O HC2H2ClO2+ OH¯
Initial 2.05 0 0
Change -x +x +x
Equil. 2.05 – x x x
14 12
W
b3
a
K1.0 10
K7.1410
K1.410
-
22 2
22 2
12
--6
-6
HC H ClO OH
CHClO
7.14 10 2.05
Solving the above simplified expression for x, we get x = OH =3.826×10
pH=14-pOH=14- -log 3.826×10 =8.58
b
K
xx
x

Chapter 16: Acids and Bases
784
115. (M) 0.10 M HI < 0.05 M H2SO4 < 0.05 M HC2H2ClO2 < 0.50 M HC2H3O2 < 0.50 M
NH4Cl < 1.0 M NaBr < 0.05 M KC2H3O2 < 0.05 M NH3 < 0.06 M NaOH < 0.05 M
Ba(OH)2
116. (M) Since pH = 5 pOH, pH must be significantly larger than pOH, which means that the
solution is basic. The pH can be determined by solving two simultaneous equations:
pH 5 pOH 0
pH + pOH = 14
pOH = 2.333
pH = 14 – 2.33 = 11.67.
Therefore, [H3O+] = 2.14×10-12 M (and [OH¯] = 4.67×10-3 M)
The solute must be NH3, because it is the only basic species (the other two are acidic and
neutral, respectively). Since the Kb of NH3 is 1.8×10-5, the concentration of NH3 can be
determined as follows:
33-+
45
b
3
4.67 10 4.67 10
OH NH
K= 1.8 10
NH
1.2 M
x
x
117. (M) The answer is (a). If HC3H5O2 is 0.42% ionized for a 0.80 M solution, then the
concentration of the acid at equilibrium is (0.80×0.0042) = 0.00336. The equilibrium
expression for the dissociation of HC3H5O2 is:
3352 5
a
352
HO CHO 0.00336 0.00336
K1.4210
HC H O 0.800 0.00336
118. (E) The answer is (b), because H2PO4¯ is a result of addition of one proton to the base
HPO42-.
119. (M) The answer is (d). This is because, in the second equation, HNO2 will give its proton
to ClO¯ (rather than HClO giving its proton to NO2¯), which means that HNO2 is a
stronger acid than HClO. Also, in the first equation, ClO¯ is not a strong enough base to
abstract a proton from water, which means that HClO is in turn a stronger acid than H2O.
120. (M) The dominant species in the solution is ClO2¯. Therefore, determine its concentration
and ionization constant first:
22
2
2
3.00 mol CaClO 2 mol ClO
ClO = 2.40 M
2.50 L 1 mol CaClO
14 13
W
b2
a
K1.0 10
K9.110
K1.110

Chapter 16: Acids and Bases
785
The reaction and the dissociation of ClO2¯ is as follows:
ClO2¯ + H2O HClO2 + OH¯
Initial 2.40 0 0
Change -x +x +x
Equil. 2.40 – x x x
-
2
-
2
13
--6
-6
HClO OH
ClO
9.1 10 2.40
Solving the above simplified expression for x, we get x = OH =1.478×10 .
pH=14-pOH=14- -log 1.478×10 =8.2
b
K
xx
x
121. (M) Section 16-8 discusses the effects of structure on acid/base behavior. The major
subtopics are effects of structure on binary acids, oxo acids, organic acids, and amine
bases. For binary acids, acidity can be discussed in terms of electronegativity of the main
atom, bond length, and heterolytic bond dissociation energy. For oxo acids, the main
things affecting acidity are the electronegativity of the central atom and number of oxygen
atoms surrounding the central atom. For organic acids, the main topic is the electron-
withdrawing capability of constituent groups attached to the carboxyl unit. For amines, the
basicity is discussed in terms of electron withdrawing or donating groups attached to the
nitrogen in the amine, and the number of resonance structures possible for the base
molecule.

786
CHAPTER 17
ADDITIONAL ASPECTS OF ACID–BASE EQUILIBRIA
PRACTICE EXAMPLES
1A (D) Organize the solution around the balanced chemical equation, as we have done before.
+
23
Equation: HF(aq) H O(l) H O (aq) F (aq)
Initial: 0.500M 0M 0M
Changes: M + M + M
Equil: (0.500 ) M M M
xxx
xxx
Kxx
x
x
a3+
HO F
HF]
[][]
[
()()
...0500 66 10 0500
42 assuming 0.500x
x
0500 6 6 10 0 018
4
. . . M One further cycle of approximations gives:
4+
3
(0.500 0.018) 6.6 10 0.018M [H O ]x
Thus, [HF] = 0.500M 0.018M 0.482M
Recognize that 0.100 M HCl means +
3initial
H O 0.100M
, since HCl is a strong acid.
+
23
Equation: HF(aq) + H O(l) H O (aq) + F (aq)
Initial: 0.500M 0.100M 0 M
Changes: M + M + M
Equil: (0.500 )M (0.100+ )M M
xxx
xxx
Kxx
x
x
a3+
HO F]
[HF]
+
[][ ()(. )
...
.
0100
0500 66 10 0100
0500
4 assuming x0.100
43
6.6 10 0.500
= = 3.3 10 M = F The assumption is valid.
0.100
x
HF = 0.500M 0.003M = 0.497M
[H3O+] = 0.100 M + x = 0.100 M + 0.003 M = 0.103 M
Chapter 17: Additional Aspects of Acid–Base Equilibria
787
1B (M) From Example 17-6 in the text, we know that [][ ].HO CHO M
3+232
13 10 3in
0.100 M HC H O
232
. We base our calculation, as usual, on the balanced chemical
equation. The concentration of H O
3+ from the added HCl is represented by x.
+
232 2 3 232
Equation: HC H O (aq) + H O(l) H O (aq) + C H O (aq)
Initial: 0.100M 0M 0M
Changes: 0.00010M +0.00010M +0.00010M
From HCl: + M
Equil: 0.100 M (0.00010 ) M 0.00010M
x
x
Kx
a3+232
232
HO CHO
HC H O ]
(0.00010 +
=0 00010
0100 18 10 5
[][ ]
[
).
..
5
1.8 10 0.100
0.00010 0.018M 0.018 M 0.00010M 0.018M
0.00010
xx
+
3
+
3
12 M HCl 0.018 mol H O 1molHCl 1 Lsoln 1000 mL 1 drop
1.00L 30.drops
1L 1molH O 12 mol HCl 1L 0.050 mL
=V
Since 30. drops corresponds to 1.5 mL of 12 M solution, we see that the volume of solution
does indeed remain approximately 1.00 L after addition of the 12 M HCl.
2A (M) We again organize the solution around the balanced chemical equation.
+
22 2 3
Equation: HCHO aq + H O(l) CHO aq + H O aq
Initial: 0.100M 0.150M 0M
Changes: M + M + M
Equil: (0.100 ) M (0.150 + ) M M
xxx
xxx
4
23
2
[CHO ][H O ] (0.150+ )( ) 0.150
1.8 10
[HCHO ] 0.100 0.100
a
x
xx
Kx
assuming 0.100x
44+
3
2
0.100 1.8 10
= = 1.2 10 M = H O , <<0.100, thus our assumptionis valid
0.150
CHO = 0.150 M + 0.00012 M = 0.150M
xx

Chapter 17: Additional Aspects of Acid–Base Equilibria
788
2B (M) This time, a solid sample of a weak base is being added to a solution of its
conjugate acid. We let
x
represent the concentration of acetate ion from the added
sodium acetate. Notice that sodium acetate is a strong electrolyte, thus, it completely
dissociates in aqueous solution. HO M M
pH
3+5.005
= 10 = 10 = 1.0 10 = 0.000010
+
232 2 232 3
Equation: HC H O aq + H O(l) C H O aq + H O aq
Initial: 0.100 M 0M 0M
Changes: 0.000010 M +0.000010M +0.000010M
From NaAc: + M
Equil: 0.100M (0.000010+ )M 0.000010M
x
x
+
3232 5
a
232
HO CHO 0.000010 0.000010 +
== =1.810
HC H O 0.100
x
K
5
1.8 10 0.100
0.000010+ 0.18 M 0.18 M 0.000010 M = 0.18 M
0.000010
xx
232 232 232
232
232
232
232
0.18 mol C H O 1mol NaC H O 82.03g NaC H O
mass of NaC H O = 1.00L 1L 1mol NaC H O
1mol C H O
=15gNaC H O
3A (M) A strong acid dissociates essentially completely, and effectively is a source of
+
3232
HO.NaCHO also dissociates completely in solution. The hydronium ion and the acetate
ion react to form acetic acid: 3232 2322
H O (aq) C H O (aq) HC H O (aq) H O(l)
All that is necessary to form a buffer is to have approximately equal amounts of a weak
acid and its conjugate base together in solution. This will be achieved if we add an
amount of HCl equal to approximately half the original amount of acetate ion.
3B (M) HCl dissociates essentially completely in water and serves as a source of hydronium
ion. This reacts with ammonia to form ammonium ion:
++
33 4 2
NH aq + H O aq NH aq + H O(l)
.
Because a buffer contains approximately equal amounts of a weak base (NH3) and its
conjugate acid (NH4+), to prepare a buffer we simply add an amount of HCl equal to
approximately half the amount of NH3(aq) initially present.
Chapter 17: Additional Aspects of Acid–Base Equilibria
789
4A (M) We first find the formate ion concentration, remembering that NaCHO2 is a strong
electrolyte, existing in solution as Na aq
+bg
and
2
CHO aq
.
222
2
22
23.1g NaCHO 1000 mL 1 mol NaCHO 1 mol CHO
[CHO ] 0.679M
500.0 mL soln 1L 68.01g NaCHO 1 mol NaCHO
As usual, the solution to the problem is organized around the balanced chemical equation.
+
22 2 3
Equation: HCHO aq + H O(l) CHO aq + H O aq
Initial: 0.432M 0.679M 0M
Changes: M + M + M
Equil: (0.432 ) M (0.679+ ) M M
xxx
xxx
+4
32 4
a
2
HO CHO 0.679 + 0.679 0.432 1.8 10
===1.810=
HCHO 0.432 0.432 0.679
xx x
Kx
x
This gives +4
3
HO =1.14 10 M
. The assumption that 0.432x is clearly correct.
4
3
pH log H O log 1.14 10 3.94 3.9
4B (M) The concentrations of the components in the 100.0 mL of buffer solution are found
via the dilution factor. Remember that NaC H O
232
is a strong electrolyte, existing in
solution as
Na aq
+bg
and CHO aq
232
bg.
232 232
63.0 mL 37.0 mL
[HC H O ] 0.200 M 0.126 M [C H O ] 0.200 M 0.0740M
100.0 mL 100.0mL
As usual, the solution to the problem is organized around the balanced chemical equation.
Equation:
+
232 2 232 3
HC H O aq + H O(l) C H O aq + H O aq
Initial: 0.126 M
0.0740 M 0 M
Changes:
x
M
x
M
x
M
Equil: ( . )0126
x
M
0.0740+ x
bgM x M
+5
3232
a
232
[H O ][C H O ] (0.0740 ) 0.0740
1.8 10
[HC H O ] 0.126 0.126
x
xx
Kx
x
18 10 0126
0 0740 31 10
55
..
..]M=[HO
3+; pH = H O
3+
log [ ] log . .31 10 451
5
Note that the assumption is valid: 0.0740 0.126.x
Thus,
x
is neglected when added or subtracted
Chapter 17: Additional Aspects of Acid–Base Equilibria
790
5A (M) We know the initial concentration of NH3 in the buffer solution and can use the pH
to find the equilibrium [OH-]. The rest of the solution is organized around the balanced
chemical equation. Our first goal is to determine the initial concentration of 4
NH .
pOH = 14.00 pH = 14.00 OH M
pOH
9 00 500 10 10 10 10
500 5
.. [] .
.
Equation:
+
32 4
NH aq + H O(l) NH aq + OH aq
Initial: 0.35 M
x M 0 M
Changes: 5
1.0 10 M
5
1.0 10 M
5
1.0 10 M
Equil: 5
(0.35 1.0 10 )M
( . )x
10 10 5M 10 10 5
.M
55 5
5
4
b5
3
[NH ][OH ] ( 1.0 10 )(1.0 10 ) 1.0 10
1.8 10
[NH ] 0.35 1.0 10 0.35
x
x
K
5
5+
4
5
0.35 1.8 10
Assume 1.0 10 = = 0.63 M = initial NH concentration
1.0 10
xx
+44 44
42 2
44
2+44
42
1 mol NH SO 132.1 g NH SO
0.63 mol NH
mass NH SO = 0.500L× × ×
1L soln 1mol NH SO
2mol NH
Mass of (NH4)2SO4 = 21 g
5B (M) The solution is composed of 33.05 g NaC2H3O2 3 H2O dissolved in 300.0 mL of 0.250 M
HCl. NaC2H3O2 3 H2O , a strong electrolyte, exists in solution as Na+(aq) and C2H3O2-(aq)
ions. First we calculate the number of moles of NaC2H3O2 3 H2O, which, based on the 1:1
stoichiometry, is also equal to the number of moles of C2HO- that are released into solution.
From this we can calculate the initial [C2H3O2-] assuming the solution's volume remains at
300. mL.
moles of 232
NaC H O 3 H2O (and moles of C2H3O2-)
= 232 2 232 2 232
232 2
232 2
33.05 g NaC H O 3H O 0.243moles NaC H O 3H O molesC H O
1 mole NaC H O 3H O
136.08 g NaC H O 3H O
232
232
0.243 mol C H O
[C H O ] 0.810
0.300 L soln
M
(Note: [HCl] is assumed to remain unchanged at 0.250 M)
We organize this information around the balanced chemical equation, as before. We
recognize that virtually all of the HCl has been hydrolyzed and that hydronium ion will
react to produce the much weaker acetic acid.
Chapter 17: Additional Aspects of Acid–Base Equilibria
791
Equation: 232 2
HC H O (aq) + H O(l)
232
CHO (aq)
+ H O (aq)
3+
Initial: 0 M
0.810 M 0.250 M
Form HAc: +0.250 M
–0.250 M –0.250 M
0.250 M
0.560 M 0 M
Changes: –x M
+x M +x M
Equil: (0.250 –
x) M
(0.560 + x) M +x M
+5
3232
a
232
[H O ][C H O ] (0.560 ) 0.560
1.8 10
[HC H O ] 0.250 0.250
x
xx
Kx
56+
3
1.8 10 0.250 8.0 10 M = [H O ]
0.560
x
(The approximation was valid since x << both 0.250 and 0.560 )
+6
3
pH = log [H O ] log 8.0 10 5.09 5.1
6A (D)
(a) For formic acid, p a
K
log( . ) . .18 10 374
4 The Henderson-Hasselbalch equation
provides the pH of the original buffer solution:
pH = p [CHO
HCHO
a2
2
K
log ]
[]
.log
.
..374 0 350
0550 354
(b) The added acid can be considered completely reacted with the formate ion to produce
formic acid. Each mole/L of added acid consumes 1 M of formate ion and forms 1 M of
formic acid: +
23 22
CHO + H O HCHO + H O(aq) (aq) (aq) (l).
Kneut = Kb/Kw ≈
5600. Thus, 2
CHO 0.350 M 0.0050 M = 0.345 M
and
2
HCHO = 0.550 M + 0.0050 M = 0.555 M . By using the Henderson-Hasselbalch
equation
2
a
2
[CHO ] 0.345
pH = p + log = 3.74 + log = 3.53
[HCHO ] 0.555
K
(c) Added base reacts completely with formic acid producing, an equivalent amount of
formate ion. This continues until all of the formic acid is consumed.
Each 1 mole of added base consumes 1 mol of formic acid and forms 1 mol of
formate ion: 222
HCHO + OH CHO + H O
. Kneut = Ka/Kw ≈ 1.8 × 1010. Thus,
2
CHO = 0.350M + 0.0050 M = 0.355 M
2
HCHO = 0.550 0.0050 M = 0.545 M. With the Henderson-Hasselbalch equation
we find 2
a
2
CHO 0.355
pH = p + log = 3.74 + log = 3.55
HCHO 0.545
K
Chapter 17: Additional Aspects of Acid–Base Equilibria
792
6B (D) The buffer cited has the same concentration as weak acid and its anion, as does the
buffer of Example 17-6. Our goal is to reach pH = 5.03 or
+pH5.03 6
3
H O =10 =10 = 9.3 10 M
. Adding strong acid H O
3+
ch, of course, produces
HC H O
232
at the expense of C H O
232
. Thus, adding H+ drives the reaction to the left.
Again, we use the data around the balanced chemical equation.
Equation:
232 2
HC H O aq + H O(l)
CHO aq
232
bg + H O aq
3+bg
Initial: 0.250 M
0.560 M 6
8.0 10
M
Add acid: +
y
M
Form HAc: +
y
M
y
M
y
M
0.250+ y
bg
M
0.560 y
bg
M 0 M
Changes:
x
M
x
M
x
M
Equil: 0.250 + yx
bg M
0.560 +
yx
bg M 9.3 10 6
M
+66
5
3232
a
232
[H O ][C H O ] 9.3 10 (0.560 ) 9.3 10 (0.560 )
1.8 10
[HC H O ] 0.250 0.250
(Assume that is negligible compared to )
yx y
Kyx y
xy
1.8 10 0.250 +
9.3 10 = 0.484 +1.94 = 0.560 = 0.560 0.484
1.94 +1.00 = 0.026
5
6
yyyy
bg M
Notice that our assumption is valid:
0.250 + = 0.276 0.560 = 0.534xy y.
3
+
3
3
+
3
HNO 3
1mL HNO aq
0.026 mmol H O
1 mL buffer 6.0 mmol H O
300.0 mL buffer =1.3 mL of 6.0 M HNOV
Instead of the algebraic solution, we could have used the Henderson-Hasselbalch
equation, since the final pH falls within one pH unit of the pa
K of acetic acid. We let z
indicate the increase in HC H O
232
, and also the decrease in CHO
232
pH p log CHO
HC H O log
a
=+ =4.74+
0.560
0.250+ = 5.03 0.560
0.250 + = 10 = 1.95
232
232
5.03 4.74
Kz
z
z
z
L
N
MO
Q
P
0.560 = 1.95 0.250 + = 0.488 +1.95 = 0.560 0.488
1.95+1.00 =0.024
zzzz
bg M
This is, and should be, almost exactly the same as the value of
y
we obtained by the
I.C.E. table method. The slight difference is due to imprecision arising from rounding
errors.
7A (D)
(a)
The initial pH is the pH of 0.150 M HCl, which we obtain from HO
3+ of that
strong acid solution.
[H O mol HCl
1Lsoln
mol H O
mol HCl M,
3+3+
]..
0150 1
10150
pH = [H O
3+
log ] log ( . ) .0150 0824
Chapter 17: Additional Aspects of Acid–Base Equilibria
793
(b) To determine HO
3+ and then pH at the 50.0% point, we need the volume of the
solution and the amount of H O
3+ left unreacted. First we calculate the amount of
hydronium ion present and then the volume of base solution needed for its
complete neutralization.
amount H O mL mmol HCl
mL soln
mmol H O
mmol HCl mmol H O
3+3+
3+
= 25.00 0.150
1
1
1=3.75
+
acid 3 +
3
1 mmol OH 1 mmol NaOH 1 mL titrant
= 3.75 mmol H O 1 mmol H O 1 mmol OH 0.250 mmol NaOH
15.0 mL titrant
V
At the 50.0% point, half of the H3O+ (1.88 mmol H O
3+) will remain unreacted and
only half (7.50 mL titrant) of the titrant solution will be added. From this information,
and the original 25.00-mL volume of the solution, we calculate HO
3+ and then pH.
+3
3
1.88 mmol H O left
H O = = 0.0578 M
25.00 mL original+ 7.50 mL titrant
pH = log 0.0578 =1.238
(c) Since this is the titration of a strong acid by a strong base, at the equivalence
point, the pH = 7.00 . This is because the only ions of appreciable concentration in
the equivalence point solution are Na+(aq) and Cl-(aq), and neither of these
species undergoes detectable hydrolysis reactions.
(d) Beyond the equivalence point, the solution pH is determined almost entirely by
the concentration of excess OH-(aq) ions. The volume of the solution is
40.00mL +1.00mL = 41.00 mL. The amount of hydroxide ion in the excess
titrant is calculated and used to determine OH, from which pH is computed.
0.250 mmol NaOH
amountof OH = 1.00 mL = 0.250 mmol OH
1mL
0.250 mmol OH
OH = = 0.006098M
41.00 mL
pOH = log 0.006098 = 2.215; pH = 14.00 2.215 = 11.785
7B (D)
(a) The initial pH is simply the pH of 0.00812 M Ba OH
bg
2, which we obtain from
OH for the solution.
OH mol Ba OH
L soln
mol OH
mol Ba OH
=0.00812
1
2
1= 0.01624
2
2
bgbgM
pOH = log OH = log 0.0162 =1.790; pH = 14.00 pOH =14.00 1.790 =12.21

Chapter 17: Additional Aspects of Acid–Base Equilibria
794
(b) To determine OH and then pH at the 50.0% point, we need the volume of the
solution and the amount of OH unreacted. First we calculate the amount of
hydroxide ion present and then the volume of acid solution needed for its complete
neutralization.
2
2
0.00812mmol Ba OH 2mmol OH
amount OH = 50.00mL = 0.812mmol OH
1mL soln 1mmol Ba OH
+
3
acid +
3
1mmol H O 1mmol HCl 1mL titrant
= 0.812mmol OH = 32.48mL titrant
0.0250mmol HCl
1mmol OH 1mmol H O
V
At the 50.0 % point, half (0.406 mmolOH) will remain unreacted and only half
(16.24 mL titrant) of the titrant solution will be added. From this information, and
the original 50.00-mL volume of the solution, we calculate OH and then pH.
OH mmol OH left
mL original mL titrant M
=0.406
50.00 +16.24 = 0.00613
pOH = log 0.00613 = 2.213; pH =14.00 pOH =11.79
(c) Since this is the titration of a strong base by a strong acid, at the equivalence
point,pH = 7.00. The solution at this point is neutral because the dominant ionic
species in solution, namely Ba2+(aq) and Cl-(aq), do not react with water to a
detectable extent.
8A (D)
(a) Initial pH is just that of 0.150 M HF ( p log
a
K= 6.6 10 = 3.18
4
ch).
[Initial solution contains 0.150mmol HF
20.00 mL 1mL
=3.00 mmol HF]
+
23
Equation : HF aq + H O(l) H O aq + F aq
Initial: 0.150M 0M 0M
Changes : M + M + M
Equil: (0.150 ) M M M
xxx
xxx
+- 2
34
a
HO F
== =6.610
HF 0.150 0.150
xx x
Kx
43
0.150 6.6 10 9.9 10 Mx
0.05 0.150x. The assumption is invalid. After a second cycle of
approximation, +3
3
H O = 9.6 10 M
;
3
pH = log 9.6 10 = 2.02

Chapter 17: Additional Aspects of Acid–Base Equilibria
795
(b) When the titration is 25.0% complete, there are (0.25×3.00=) 0.75 mmol F for every
3.00 mmol HF that were present initially. Therefore, (3.00-0.75=) 2.25 mmol HF
remain untitrated. We designate the solution volume (the volume holding these
3.00 mmol total) as V and use the Henderson-Hasselbalch equation to find the
pH.
pH p log F
HF log mmol
mmol
a
=+ =3.18+
0.75 /
2.25 / =2.70KV
V
(c) At the midpoint of the titration of a weak base, pH = pKa = 3.18.
(d) At the endpoint of the titration, the pH of the solution is determined by the
conjugate base hydrolysis reaction. We calculate the amount of anion and the
volume of solution in order to calculate its initial concentration.
0.150 mmol HF 1 mmol F
amount F = 20.00 mL = 3.00 mmol F
1 mL soln 1 mmol HF
1mmol OH 1 mL titrant
volume titrant = 3.00 mmol HF =12.0 mL titrant
1mmol HF 0.250 mmol OH
3.00mmol F
F = = 0.0938M
20.00mL original volume+12.0mL titrant
We organize the solution of the hydrolysis problem around its balanced equation.
2
Equation : F aq + H O(l) HF aq + OH aq
Initial: 0.0938M 0M 0M
Changes : M + M + M
Equil: 0.0938 M M M
xxx
xxx
14 2
11
w
b4
a
HF OH 1.0 10
====1.510 =
6.6 10 0.0938 0.0938
F
K
x
xx
KKx
11 6
0.0934 1.5 10 1.2 10 M = [OH ]x
The assumption is valid (x 0.0934).
6
pOH = log 1.2 10 = 5.92; pH = 14.00 pOH = 14.00 5.92 =8.08
8B (D)
(a) The initial pH is simply that of 0.106 M NH3.
Equation:
+
32 4
NH aq + H O(l) NH aq + OH aq
Initial: 0.106 M
0 M
0 M
Changes:
x
M
+
x
M +
x
M
Equil: 0.106 x
bgM
x M
x
M

Chapter 17: Additional Aspects of Acid–Base Equilibria
796
+2
4
b
3
NH OH
==
NH 0.106 0.106
x
xx
Kx
=1.8 10 5
43
0.106 1.8 10 1.4 10 Mx
= [OH-]
The assumption is valid (x << 0.106).
pOH = log 0.0014 = 2.85pH = 14.00 – pOH = 14.00 – 2.85 = 11.15
(b) When the titration is 25.0% complete, there are 25.0 mmol NH4
+ for every 100.0
mmol of NH3 that were present initially (i.e., there are 1.33 mmol of NH4+ in
solution), 3.98 mmol NH3 remain untitrated. We designate the solution volume
(the volume holding these 5.30 mmol total) as V and use the basic version of the
Henderson-Hasselbalch equation to find the pH.
+
4
b
3
1.33 mmol
NH
pOH = p + log = 4.74 + log = 4.26
3.98 mmol
NH
V
K
V
pH = 14.00 4.26 = 9.74
(c) At the midpoint of the titration of a weak base, b
pOH = p = 4.74 and pH = 9.26K
(d) At the endpoint of the titration, the pH is determined by the conjugate acid
hydrolysis reaction. We calculate the amount of that cation and the volume of the
solution in order to determine its initial concentration.
+
34
+
4
3
+
+
44
0.106 mmol NH 1mmolNH
amount NH = 50.00 mL 1 mL soln 1 mmol NH
amount NH = 5.30 mmol NH
+
3
titrant 3 +
33
1 mmol H O 1 mL titrant
=5.30mmol NH =23.6mL titrant
1 mmol NH 0.225 mmol H O
V
+
+4
4
5.30 mmol NH
NH = = 0.0720 M
50.00 mL original volume+ 23.6 mL titrant
We organize the solution of the hydrolysis problem around its balanced chemical
equation.
Equation:
++
42 33
NH aq + H O(l) NH aq + H O aq
Initial: 0.0720 M
0 M
0 M
Changes:
x
M
+
x
M +
x
M
Equil: 0.0720x
bgM
x M
x
M
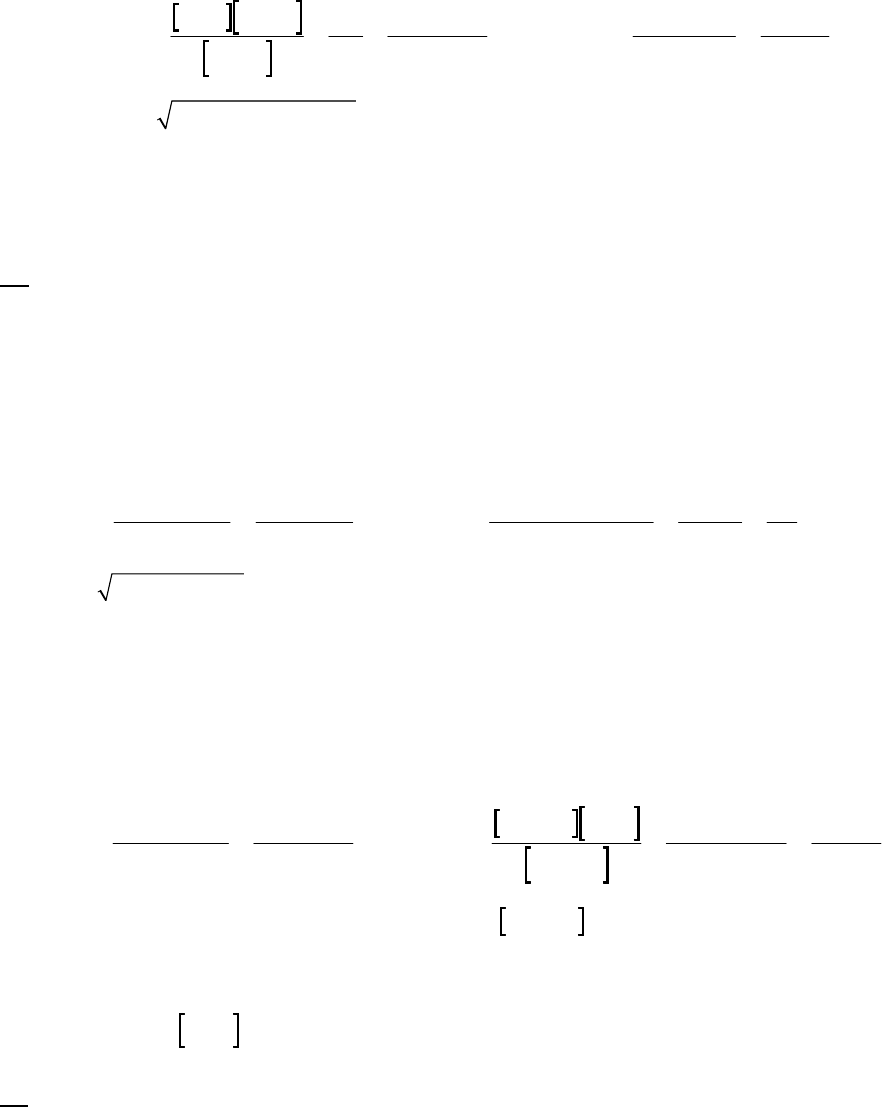
Chapter 17: Additional Aspects of Acid–Base Equilibria
797
KK
K
xx
x
x
bw
b
NH H O
NH
===
1.0 10
1.8 10 =5.6 10 =0.0720 0.0720
33
+
4
+
14
5
10 2
10 6 +
3
0.0720 5.6 10 6.3 10 M=[H O ]
The assumption is valid ( << 0.0720).
x
x
pH log= 6.3 10 = 5.20
6
ch
9A (M) The acidity of the solution is principally the result of the hydrolysis of the carbonate
ion, which is considered first.
Equation:
2
32 3
CO aq + H O(l) HCO aq + OH aq
Initial: 1.0 M
0 M
0 M
Changes:
x
M
+
x
M +
x
M
Equil: 1.0x
bgM
x
M
x
M
14 2
3
4
w
b11 2
a3 3
HCO OH
1.0 10
===2.110=
4.7 10 1.0 1.0
(HCO ) CO
K
x
xx
Kx
K
42
1.0 2.1 10 1.5 10 M 0.015 M [OH ] The assumption is valid ( 1.0 ).
x
xM
Now we consider the hydrolysis of the bicarbonate ion.
Equation:
32 23
HCO aq + HO(l) HCO aq + OH aq
Initial: 0.015 M
0 M 0.015 M
Changes:
y
M
+
y
M +
y
M
Equil: 0.015y
bgM
y
M 0.015+ y
bg M
KK
K
yy
x
yy
bw
aHCO
HCO OH
HCO
==
1.0 10
4.4 10 =2.3 10 = = 0.015+
0.015
0.015
0.015 =
23
14
7
823
3
F
HI
K
bg
The assumption is valid (y << 0.015) and y==2.310
23 8
HCO M. Clearly, the
second hydrolysis makes a negligible contribution to the acidity of the solution. For the
entire solution, then
pOH log OH log pH= = 0.015 = 1.82 = 14.00 1.82 = 12.18
bg
9B (M) The acidity of the solution is principally the result of hydrolysis of the sulfite ion.
Equation:
2
32 3
SO aq + H O(l) HSO aq + OH aq
Initial: 0.500 M
0 M
0 M
Changes:
x
M
+
x
M +
x
M
Equil: 0.500 x
bgM
x M
x
M

Chapter 17: Additional Aspects of Acid–Base Equilibria
798
14 2
3
7
b82
3
a3
HSO OH
1.0 10
===1.610
6.2 10 [SO ] 0.500 0.500
HSO
w
K
x
xx
Kx
K
74
0.500 1.6 10 2.8 10 M = 0.00028 M = [OH ]
The assumption is valid ( << 0.500).
x
x
Next we consider the hydrolysis of the bisulfite ion.
Equation:
32 23
HSO aq + HO(l) HSO aq + OH aq
Initial: 0.00028 M 0 M 0.00028 M
Changes:
y
M +
y
M +
y
M
Equil: 0.00028y
bgM
y
M 0.00028 + y
bgM
14 13
w
b2
a2 3
23
13
b
3
1.0 10
===7.710
HSO 1.3 10
HSO OH 0.00028+ 0.00028
=7.7 10 = = =
0.00028 0.00028
HSO
K
KK
yy y
Ky
y
The assumption is valid (y << 0.00028) and
13
23
=HSO =7.7 10y
M. Clearly, the
second hydrolysis makes a negligible contribution to the acidity of the solution. For the
entire solution, then
pOH log OH log pH= = 0.00028 = 3.55 = 14.00 3.55 = 10.45
bg
INTEGRATIVE EXAMPLE
A. (D)
From the given information, the following can be calculated:
pH of the solution = 2.716 therefore, [H+] = 1.92×10-3
pH at the halfway point = pKa
pH = 4.602 = pKa
pKa = -log Ka therefore Ka = 2.50×10-5
f
ff
f
FP = 0 C + T
T = -i K
T -1 1.86 C / molality
m
m
Chapter 17: Additional Aspects of Acid–Base Equilibria
799
molality =
# moles solute # moles solute
=
kg solvent 0.500 kg - 0.00750 kg
To determine the number of moles of solute, convert 7.50 g of unknown acid to moles by
using its molar mass. The molar mass can be calculated as follows:
pH = 2.716 [H+] = 1.92×10-3
+-
HA H + A
Initial
7.50 g
MM 0.500 L 0 0
Change –x x x
Equilibrium 3
7.50 g
MM 1.92 10
0.500 L
1.92×10-3 1.92×10-3
+-
-5
32
-5
3
[H ][A ]
2.50 10 = [HA]
(1.92 10 )
2.50 10 7.50MM 1.92 10
0.500
MM =100.4 g/mol
1 mol
#moles of solute = 7.50 g 0.0747 mol
100.4 g
Molality =
# moles solute 0.0747 mol
= 0.152
Kg solvent 0.500 Kg - 0.00750 Kg m
ff
f
f
f
T = -i K
T -1 1.86 C / 0.152
T -0.283 C
FP = 0 C + T = 0 C 0.283 C = 0.283 C
m
mm
Chapter 17: Additional Aspects of Acid–Base Equilibria
800
B. (M) By looking at the titration curve provided, one can deduce that the titrant was a strong acid.
The pH before titrant was added was basic, which means that the substance that was titrated was
a base. The pH at the end of the titration after excess titrant was added was acidic, which means
that the titrant was an acid.
Based on the titration curve provided, the equivalence point is at approximately 50 mL of
titrant added. At the halfway point, of approximately 25 mL, the pH = pKa. A pH ~8 is
obtained by extrapolation a the halfway point.
pH = 8 = pKa
K
a = 10-8 = 1 × 10-8
K
b = Kw/Ka = 1 × 10-6
~50 mL of 0.2 M strong acid (1×10-2 mol) was needed to reach the equivalence point. This
means that the unknown contained 1×10-2 mol of weak base. The molar mass of the unknown
can be determined as follows:
2
0.800 g 80 g/mol
110 mol
EXERCISES
The Common-Ion Effect
1. (M)
(a) Note that HI is a strong acid and thus the initial HO HI M
3+= = 0.0892
+
352 2 352 3
Equation : HC H O + H O C H O + H O
Initial: 0.275 M
0M 0.0892M
Changes : M
x
+ M + M
x
x
Equil : 0.275 Mx
M
x
0.0892 + Mx
+
2
35 3 55
a
352
CHO HO 0.0892 + 0.0892
= = 1.3 10 = 4.0 10 M
HC H O 0.275 0.275
xx x
Kx
x
The assumption that
0.0892x M is correct. HO M
3+= 0.0892
(b) OH HO M
w
==
1.0 10
0.0892 =1.1 10
3+
14 13
K
(c) 5
352
CHO = =4.0 10 Mx
Chapter 17: Additional Aspects of Acid–Base Equilibria
801
(d)
int
I = HI = 0.0892 M
2. (M)
(a) The NH Cl
4 dissociates completely, and thus, +
4int int
NH = Cl = 0.102 M
Equation:
32 4
NH (aq) + H O(l) NH (aq) + OH (aq)
Initial: 0.164 M
0.102 M
0 M
Changes:
x
M
+
x
M +
x
M
Equil: 0.164 x
bgM
0.102 + x
bgM
x
M
+
455
b
3
NH OH 0.102 + 0.102
= = = 1.8 10 ; = 2.9 10 M
NH 0.164 0.164
xx x
Kx
x
Assumed 0.102 Mx, a clearly valid assumption. OH M
==2.910
5
x
(b) 4
NH = 0.102 + = 0.102Mx
(c) Cl M
= 0.102
(d) HO M
3+14
5
10
=1.0 10
2.9 10 =3.4 10
3. (M)
(a) We first determine the pH of 0.100 M HNO2.
+
22 23
Equation HNO (aq) + H O(l) NO (aq) + H O (aq)
Initial : 0.100 M 0M 0M
Changes : M + M + M
Equil : 0.100 M M M
xxx
xxx
+2
23 4
a
2
NO H O
==7.210=
HNO 0.100
x
K
x
Via the quadratic equation roots formula or via successive approximations,
3+
3
= 8.1 10 M = H Ox
.
Thus
3
pH = log 8.1 10 = 2.09
When 0.100 mol NaNO2 is added to 1.00 L of a 0.100 M HNO2, a solution with
NO M HNO
22
= 0.100 =
is produced. The answer obtained with the Henderson-
Hasselbalch equation, is pH p log
a
= = 7.2 10 = 3.14
4
K
ch. Thus, the addition has
caused a pH change of 1.05 units.
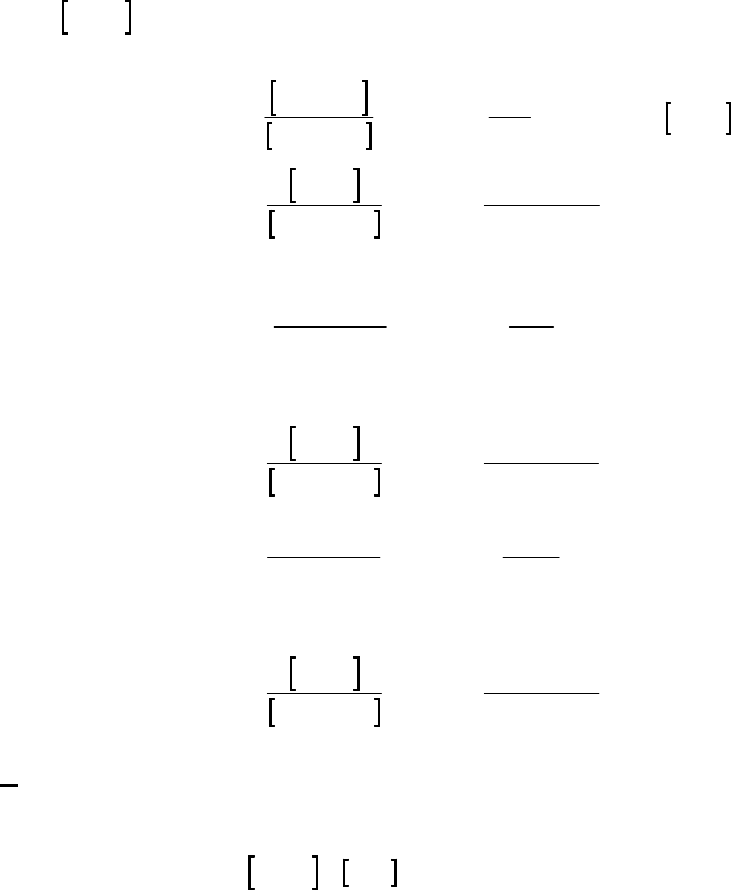
Chapter 17: Additional Aspects of Acid–Base Equilibria
802
(b) NaNO3 contributes nitrate ion, NO3
, to the solution. Since, however, there is no
molecular HNO aq
3bg in equilibrium with hydrogen and nitrate ions, there is no
equilibrium to be shifted by the addition of nitrate ions. The [H3O+] and the pH are thus
unaffected by the addition of NaNO3 to a solution of nitric acid. The pH changes are not
the same because there is an equilibrium system to be shifted in the first solution, whereas
there is no equilibrium, just a change in total ionic strength, for the second solution.
4. (M) The explanation for the different result is that each of these solutions has acetate
ion present, C H O
232
, which is produced in the ionization of acetic acid. The presence
of this ion suppresses the ionization of acetic acid, thus minimizing the increase in
HO
3+. All three solutions are buffer solutions and their pH can be found with the aid
of the Henderson-Hasselbalch equation.
(a) pH p log CHO
HC H O log H O M
a
=+ =4.74+
0.10
1.0 = 3.74 = 10 = 1.8 10
232
232
3+3.74 4
K
%. ionization HO
HC H O
M
M
= 100% 1.8 10
1.0 100% 0 018%
3
232
4
(b) 232
a
232
+4.74 5
3
CHO 0.10
pH = p + log = 4.74 + log = 4.74
HC H O 0.10
HO =10 =1.8 10 M
K
%. ionization HO
HC H O
M
M
= 100% 1.8 10
0.10 100% 0 018%
3
232
5
(c) 232
a
232
+5.74 6
3
CHO 0.10
pH = p + log = 4.74 + log = 5.74
HC H O 0.010
HO =10 =1.8 10 M
K
%. ionization HO
HC H O
M
M
= 100% 1.8 10
0.010 100% 0 018%
3
232
6
5. (M)
(a)
The strong acid HCl suppresses the ionization of the weak acid HOCl to such an
extent that a negligible concentration of H O
3+ is contributed to the solution by
HOCl. Thus, HO HCl M
3+= = 0.035

Chapter 17: Additional Aspects of Acid–Base Equilibria
803
(b) This is a buffer solution. Consequently, we can use the Henderson-Hasselbalch
equation to determine its pH.
4
a
p = log 7.2 10 = 3.14;K
2
a
2
NO 0.100M
pH = p + log = 3.14 + log = 3.40
HNO 0.0550M
K
HO M
3+3.40 4
=10 =4.0 10
(c) This also is a buffer solution, as we see by an analysis of the reaction between the
components.
Equation:
232
from HCl from NaC H O
+
3232 2322
HO aq, +CHO aq, HCHO aq +HO(l)
In soln: 0.0525 M 0.0768 M 0 M
Produce HAc:
0.0525 0.0525 +0.0525MMM
Initial: 0M 0.0243 M 0.0525 M
Now the Henderson-Hasselbalch equation can be used to find the pH.
plog
a
K= 1.8 10 = 4.74
5
ch
232
a
232
CHO 0.0243M
pH = p + log = 4.74 + log = 4.41
HC H O 0.0525M
K
+4.41 5
3
HO =10 =3.9 10 M
6. (M)
(a) Neither Ba aq
2+bg
nor Cl aq
bg
hydrolyzes to a measurable extent and hence they
have no effect on the solution pH. Consequently, OH is determined entirely
by the Ba OH
bg2 solute.
2
2
0.0062 mol Ba OH 2mol OH
OH = = 0.012 M
1 L soln 1mol Ba OH
(b) We use the Henderson-Hasselbalch equation to find the pH for this buffer
solution.
+
+ +
4
444 a4
244
2
2 mol NH
NH = 0.315 M NH SO = 0.630 M p = 9.26 for NH .
1 mol NH SO K
3
a+
4
NH 0.486 M
pH = p + log = 9.26 + log = 9.15 pOH = 14.00 9.15 = 4.85
0.630 M
NH
K
OH M
=10 =1.4 10
4.85 5
Chapter 17: Additional Aspects of Acid–Base Equilibria
804
(c) This solution also is a buffer, as analysis of the reaction between its components shows.
Equation:
4432
aq, from NH Cl aq, from NaOHNH + OH NH aq + H O(l)
In soln: 0.264 M 0.196 M 0 M
Form NH
3: 0.196 M 0.196 M +0.196 M
Initial: 0.068 M
0M 0.196 M
3
a+
4
NH 0.196M
pH = p + log = 9.26 + log = 9.72 pOH = 14.00 9.72 = 4.28
0.068M
NH
K
Buffer Solutions
7. (M) HO M
3+4.06 5
=10 =8.7 10
. We let 2int
= CHOS
+
22 2 3
555
55
Equation: HCHO aq + H O(l) CHO aq + H O aq
Initial : 0.366M M 0M
Changes : 8.7 10 M + 8.7 10 M +8.7 10 M
Equil : 0.366M + 8.7 10 M 8.7 10 M
S
S
KSS
a
HO CHO
HCHO
==1.810=
+8.7 10 8.7 10
0.366
8.7 10
0.366
3+2
2
4
55 5
L
N
MO
Q
P
ch; =0.76 MS
To determine
S
, we assumed 5
8.7 10 MS
, which is clearly a valid
assumption. Or, we could have used the Henderson-Hasselbalch equation (see
below). p log
a
K= 1.8 10 = 3.74
4
ch
22
2
22
CHO CHO
4.06 = 3.74+ log ; = 2.1; CHO = 2.1 0.366 = 0.77M
HCHO HCHO
The difference in the two answers is due simply to rounding.
8. (E) We use the Henderson-Hasselbalch equation to find the required [NH3].
plog
b
K= 1.8 10 = 4.74
5
ch
pp pH log
NH
NH
ab
KK= 14.00 = 14.00 4.74 = 9.26 = 9.12 = 9.26 + 3
4
+
+
30.14
34
+
4
NH =10 = 0.72 NH = 0.72 NH = 0.72 0.732M = 0.53M
NH

Chapter 17: Additional Aspects of Acid–Base Equilibria
805
9. (M)
(a) Equation:
+
752 2 752 3
HCHO aq + HO(l) CHO (aq) + HO(aq)
Initial: 0.012 M
0.033 M
0 M
Changes:
x
M
+
x
M +
x
M
Equil:
0.012 Mx
0.033+ x
bgM
x
M
+
3752 55
a
752
HO CHO 0.033+ 0.033
= = 6.3 10 = = 2.3 10 M
HC H O 0.012 0.012
xx x
Kx
x
To determine the value of
x
, we assumed 0.012x M, which is an assumption
that clearly is correct.
HO M pH log
3+5 5
= 2.3 10 = 2.3 10 = 4.64
ch
(b)
32 4
Equation: NH aq + H O(l) NH (aq) + OH (aq)
Initial : 0.408 M 0.153 M 0 M
Changes : M + M + M
Equil : 0.408 M 0.153 + M M
xxx
xxx
Kxx
x
xx
b
NH OH
NH M==1.810=
0.153+
0.408
0.153
0.408 =4.8 10
4
+
3
55
L
N
MO
Q
P
bg
To determine the value of
x
, we assumed 0.153x, which clearly is a valid
assumption.
55
OH = 4.8 10 M; pOH = log 4.8 10 = 4.32; pH =14.00 4.32 = 9.68
10. (M) Since the mixture is a buffer, we can use the Henderson-Hasselbalch equation to
determine Ka of lactic acid.
353 353 353
353
353 353
1.00 g NaC H O 1 mol NaC H O 1 mol C H O
1000 mL
CHO = =0.0892 M
100.0 mL soln 1 L soln 112.1 g NaC H O 1 mol NaC H O
353
aaa
353
CHO 0.0892 M
pH = 4.11= p + log = p + log = p +0.251
HC H O 0.0500 M
KKK
3.86 4
aa
p = 4.11 0.251= 3.86; =10 =1.4 10KK
11. (M)
(a)
0.100 M NaCl is not a buffer solution. Neither ion reacts with water to a
detectable extent.
(b) 0.100 M NaCl—0.100 M NH Cl
4 is not a buffer solution. Although a weak acid,
NH4
+, is present, its conjugate base, NH3, is not.
Chapter 17: Additional Aspects of Acid–Base Equilibria
806
(c) 0.100 M CH NH
32
and 0.150 M CH NH Cl
3
+
3
is a buffer solution. Both the weak
base, CH NH
32
, and its conjugate acid, CH NH3
+
3, are present in approximately
equal concentrations.
(d) 0.100 M HCl—0.050 M NaNO2 is not a buffer solution. All the NO2
has
converted to HNO2 and thus the solution is a mixture of a strong acid and a weak
acid.
(e) 0.100 M HCl—0.200 M NaC H O
232
is a buffer solution. All of the HCl reacts
with half of the C H O223
to form a solution with 0.100 M HC H O
232
, a weak acid,
and 0.100 M C H O223
, its conjugate base.
(f) 0.100 M HC H O
232
and 0.125 M NaC H O
352
is not a buffer in the strict sense
because it does not contain a weak acid and its conjugate base, but rather the
conjugate base of another weak acid. These two weak acids (acetic,
Ka=1.8 10 5
, and propionic, Ka=1.35 10 5
) have approximately the same
strength, however, this solution would resist changes in its pH on the addition of
strong acid or strong base, consequently, it could be argued that this system
should also be called a buffer.
12. (M)
(a) Reaction with added acid: 2+
43 242
HPO + H O H PO + H O
Reaction with added base: H PO OH HPO H O
24 4
2
2
++
(b) We assume initially that the buffer has equal concentrations of the two ions,
HPO HPO
24 4
2
=
2
2
4
a
24
HPO
pH = p + log = 7.20 + 0.00 = 7.20 (pH at which the
b
uffer is most effective).
HPO
K
(c)
2
4
24
HPO 0.150 M
pH = 7.20 + log = 7.20 + log = 7.20 + 0.48 = 7.68
0.050 M
HPO
13. (M) ++
65 3 65 3
+
65 3
6+
65 3
1mol C H NH Cl 1mol CH NH
1 g
moles of solute = 1.15 mg 1000 mg 129.6 g 1mol C H NH Cl
=8.87 10 mol C H NH
CHNH mol C H NH
L soln M
65 3
+665 3
+6
=8.87 10
3.18 =2.79 10
Equation:
+
65 2 2 65 3
C H NH aq + H O(l) C H NH aq + OH aq
Initial: 0.105 M
2.79 10 6
M 0 M
Changes:
x
M
+
x
M +
x
M
Equil: 0.105x
bgM
2.79 10 +
6
x
chM
x
M
Chapter 17: Additional Aspects of Acid–Base Equilibria
807
Kxx
x
b
C H NH OH
CHNH
==7.410=
2.79 10 +
0.105
65 3
+
65 2
10
6
L
N
MO
Q
P
ch
10 6 11 10 6 2
7.4 10 0.105 = 2.79 10 + ; 7.8 10 7.4 10 = 2.79 10 +
x
xx x x x
2 6 10 11 2 6 11
+ 2.79 10 + 7.4 10 7.8 10 = 0; + 2.79 10 7.8 10 0xxxx
xbb ac
a
=4
2=2.79 10 7.78 10 + 3.1 10
2=7.5 10 =
261210
6
MOH
pOH log pH= 7.5 10 = 5.12 = 14.00 5.12 = 8.88
6
ch
14. (M) We determine the concentration of the cation of the weak base.
++
65 3 65 3
+
+65 3
65 3
1 mmol C H NH Cl 1 mmol C H NH
8.50 g 129.6 g 1 mmol C H NH Cl
[C H NH ] 0.0874 M
1 L
750 mL 1000 mL
In order to be an effective buffer, each concentration must exceed the ionization
constant Kb=7.4 1010
ch by a factor of at least 100, which clearly is true. Also, the
ratio of the two concentrations must fall between 0.1 and 10:
CHNH
CHNH
M
M
65 3
+
65 2
=0.0874
0.215 = 0.407
L
N
MO
Q
P.
Since both criteria are met, this solution will be an effective buffer.
15. (M)
(a) First use the Henderson-Hasselbalch equation.
5
b
p = log 1.8 10 = 4.74,K
a
p = 14.00 4.74 = 9.26K to determine NH4
+ in the buffer solution.
333
+++
444
a
NH NH NH
NH NH NH
pH = 9.45 = p + log = 9.26 + log ; log = 9.45 9.26 = +0.19K
33
0.19 +
4
+
4
NH NH 0.258M
=10 =1.55 NH = = =0.17M
1.55 1.55
NH
We now assume that the volume of the solution does not change significantly when
the solid is added.
+44
42
44 +
2
4
1mol NH SO
1 L soln 0.17 molNH
mass NH SO = 425 mL 1000mL 1 L soln 2molNH
44
244
2
44
2
132.1 g NH SO =4.8g NH SO
1mol NH SO

Chapter 17: Additional Aspects of Acid–Base Equilibria
808
(b) We can use the Henderson-Hasselbalch equation to determine the ratio of
concentrations of cation and weak base in the altered solution.
333
a+++
444
NH NH NH
pH = 9.30 = p + log = 9.26 + log log = 9.30 9.26 = +0.04
NH NH NH
K
30.04
+
4
NH 0.258
=10 = 1.1= 0.19 1.1 0.258 0.062
0.17 M + M
NH
x
xM
x
The reason we decided to add
x
to the denominator follows. (Notice we cannot
remove a component.) A pH of 9.30 is more acidic than a pH of 9.45 and
therefore the conjugate acid’s NH4
+
di
concentration must increase. Additionally,
mathematics tells us that for the concentration ratio to decrease from 1.55 to 1.1,
its denominator must increase. We solve this expression for
x
to find a value of
0.062 M. We need to add NH4+ to increase its concentration by 0.062 M in 100
mL of solution.
+
44 44
42 2
44
2 +
44
42
44
2
1mol NH SO 132.1g NH SO
0.062mol NH
NH SO mass = 0.100 L 1 L 1mol NH SO
2mol NH
= 0.41g NH SO Hence,we need to add 0.4 g
16. (M)
(a) 752
752
HC H O 7 5 2 7 5 2
752
1mol HC H O
= 2.00 g HC H O = 0.0164mol HC H O
122.1g HC H O
n
752
752 752
752
CHO 752 752
752
1mol NaCHO 1mol CHO
=2.00 g NaCHO 144.1g NaC H O 1mol NaC H O
= 0.0139mol C H O
n
752 5752
a
752 752
CHO 0.0139mol C H O /0.7500L
pH = p + log = log 6.3 10 + log
HC H O 0.0164mol HC H O /0.7500 L
= 4.20 0.0718 = 4.13
K
(b) To lower the pH of this buffer solution, that is, to make it more acidic, benzoic acid
must be added. The quantity is determined as follows. We use moles rather than
concentrations because all components are present in the same volume of solution.
4.00 = 4.20 + 0.0139 0.0139 =0.20
752
752
752
752
log mol C H O
mol HC H O log mol C H O
mol HC H O
xx
0.20
752 752
752
0.0139mol C H O 0.0139
=10 = 0.63 = = 0.022mol HC H O (required)
mol HC H O 0.63
x
x
Chapter 17: Additional Aspects of Acid–Base Equilibria
809
752
752 752 752
752 752
HC H O that must beadded = amount required amount already in solution
HC H O that must beadded = 0.022mol HC H O 0.0164mol HC H O
HC H O that must beadded = 0.006mol HC H O
added mass
HCHO mol HCHO g HC H O
mol HC H O g HC H O
752 752 752
752
752
= 0.006 122.1
1=0.7
17. (M) The added HCl will react with the ammonia, and the pH of the buffer solution will
decrease. The original buffer solution has
3
NH = 0.258 M and 4
NH = 0.17 M
.
We first calculate the [HCl] in solution, reduced from 12 M because of dilution. [HCl]
added M mL
mL M=12 0.55
100.6 = 0.066 We then determine p a
K for ammonium ion:
plog p
ba
KK= 1.8 10 = 4.74 =14.00 4.74 = 9.26
5
ch
Equation:
+
+
33 42
NH aq + H O aq NH aq + H O l
Buffer: 0.258 M ≈ 0 M 0.17 M
Added: +0.066 M
Changes:
0.066 0.066 +0.066MMM
Final: 0.192 M 0 M 0.24 M
pH p log NH
NH log
a
4+
=+ =9.26+
0.192
0.24 =9.16
3
KL
N
MO
Q
P
18. (M) The added NH3 will react with the benzoic acid, and the pH of the buffer solution
will increase. Original buffer solution has [C7H5O2] = 0.0139 mol C7H5O2/0.750 L =
0.0185 M and
752 752
HC H O = 0.0164mol HC H O /0.7500L = 0.0219M . We first
calculate the NH3 in solution, reduced from 15 M because of dilution.
3
0.35 mL
NH added = 15 M = 0.0070 M
750.35 mL
For benzoic acid, p log
a
K= 6.3 10 = 4.20
5
ch
Equation:
+
3752 752
4
NH aq + HCHO aq NH aq + CHO aq
Buffer: 0 M 0.0219 M 0 M 0.0185 M
Added: 0.0070 M
Changes: 0.0070M 0.0070 M + 0.0070 M + 0.0070 M
Final: 0.000 M 0.0149 M 0.0070 M 0.0255 M
752
a
752
CHO 0.0255
pH = p + log = 4.20 + log = 4.43
HC H O 0.0149
K
Chapter 17: Additional Aspects of Acid–Base Equilibria
810
19. (M) The p ’s
a
K of the acids help us choose the one to be used in the buffer. It is the acid
with a p a
K within 1.00 pH unit of 3.50 that will do the trick. p a
K=3.74 for
HCHO p a2 , = 4.74K for HC H O
232
, and 1
p = 2.15
a
K for HPO
34
. Thus, we choose
HCHO2 and NaCHO2 to prepare a buffer with pH = 3.50 . The Henderson-Hasselbalch
equation is used to determine the relative amount of each component present in the buffer
solution.
22
22
20.24
2
CHO CHO
pH = 3.50 = 3.74 + log log = 3.50 3.74 = 0.24
HCHO HCHO
CHO =10 = 0.58
HCHO
This ratio of concentrations is also the ratio of the number of moles of each component
in the buffer solution, since both concentrations are a number of moles in a certain
volume, and the volumes are the same (the two solutes are in the same solution). This
ratio also is the ratio of the volumes of the two solutions, since both solutions being
mixed contain the same concentration of solute. If we assume 100. mL of acid solution,
acid = 100. mLV. Then the volume of salt solution is
salt 2
= 0.58 100. mL = 58 mL 0.100 M NaCHOV
20. (D) We can lower the pH of the 0.250 M HC H O M C H O
232 232
0.560— buffer
solution by increasing HC H O
232
or lowering CHO
232
. Small volumes of NaCl
solutions will have no effect, and the addition of NaOH(aq) or NaC H O aq
232
bg will
raise the pH. The addition of 0.150 M HCl will raise HC H O
232
and lower CHO
232
through the reaction +
3232 2322
HO(aq) + CHO (aq) HCHO(aq) + HO(l)
and bring
about the desired lowering of the pH. We first use the Henderson-Hasselbalch equation
to determine the ratio of the concentrations of acetate ion and acetic acid.
pH log CHO
HC H O
= 5.00 = 4.74 + 232
232
L
N
MO
Q
P
232 232 0.26
232 232
CHO CHO
log = 5.00 4.74 = 0.26; =10 =1.8
HC H O HC H O
Now we compute the amount of each component in the original buffer solution.
amount of C H O mL mmol C H O
mL soln mmol C H O
23
2
23
2
232
= 300. 0.560
1= 168
232
232 232
0.250mmol HC H O
amount of HC H O = 300. mL = 75.0mmol HC H O
1mL soln
Chapter 17: Additional Aspects of Acid–Base Equilibria
811
Now let
x
represent the amount of H O
3+ added in mmol.
168
1.8 = ; 168 = 1.8 75+ =135+1.8 168 135 = 2.8
75.0 +
x
x
xx x
x
+
3
168 135
x= =12mmol HO
2.7
+
3+
3
1mmol HCl 1mL soln
Volume of 0.150 M HCl = 12mmol H O 0.150mmol HCl
1mmol H O
= 80mL 0.150M HCl solution
21. (M)
(a)
The pH of the buffer is determined via the Henderson-Hasselbalch equation.
pH p log CHO
HC H O log M
M
a
=+ =4.89+
0.100
0.100 = 4.89
352
352
K
L
N
MO
Q
P
The effective pH range is the same for every propionate buffer: from pH = 3.89
to pH = 5.89 , one pH unit on either side of pa
K for propionic acid, which is 4.89.
(b) To each liter of 0.100 M HC H O M NaC H O
352 352
0.100— we can add 0.100
mol OH before all of the HC H O
352
is consumed, and we can add 0.100 mol
HO
3+ before all of the C H O
352
is consumed. The buffer capacity thus is 100.
millimoles (0.100 mol) of acid or base per liter of buffer solution.
22. (M)
(a) The solution will be an effective buffer one pH uniton either side of the p a
K of
methylammonium ion, 4
33 b
CH NH , = 4.2 10K
for methylamine,
p log
b
K= 4.2 10 = 3.38
4
ch. For methylammonium cation,
p a
K= 14.00 3.38 = 10.62. Thus, this buffer will be effective from a pH of 9.62 to
a pH of 11.62.
(b) The capacity of the buffer is reached when all of the weak base or all of the
conjugate acid has been neutralized by the added strong acid or strong base.
Because their concentrations are the same, the number of moles of base is equal to
the number of moles of conjugate acid in the same volume of solution.
32 33
0.0500 mmol
amount of weak base =125 mL = 6.25 mmol CH NH or CH NH
1mL
Thus, the buffer capacity is 6.25 millimoles of acid or base per 125 mL buffer solution.

Chapter 17: Additional Aspects of Acid–Base Equilibria
812
23. (M)
(a) The pH of this buffer solution is determined with the Henderson-Hasselbalch equation.
24
a
2
CHO 8.5mmol/75.0mL
pH = p + log = log 1.8 10 + log
HCHO 15.5mmol/75.0mL
= 3.74 0.26 = 3.48
K
[Note: the solution is not a good buffer, as CHO21
=1.1 10
, which is only ~
600 times Ka]
(b) Amount of added OH mmol Ba OH mmol OH
mmol Ba OH mmol OH
=0.25 2
1=0.50
2
2
bgbg
The OH
added reacts with the formic acid and produces formate ion.
222
Equation: HCHO (aq) + OH (aq) CHO (aq) + H O(l)
Buffer: 15.5mmol 0M 8.5mmol
Add base: +0.50mmol
React: 0.50mmol 0.50mmol +0.50mmol
Final: 15.0mmol 0mmol 9.0mmol
24
a
2
CHO 9.0mmol/75.0mL
pH = p + log = log 1.8 10 + log
HCHO 15.0mmol/75.0mL
= 3.74 0.22 = 3.52
K
(c) Amount of added
+
+ +
3
3 3
12 mmol HCl 1 mmol H O
H O = 1.05 mL acid = 13 mmol H O
1 mL acid 1 mmol HCl
The
3
HO
added reacts with the formate ion and produces formic acid.
+
23 22
Equation: CHO (aq) + H O (aq) HCHO (aq) + H O(l)
Buffer : 8.5mmol 0 mmol 15.5mmol
Add acid : 13mmol
React : 8.5mmol 8.5mmol +8.5mmol
Final : 0mmol 4.5mmol 24.0 mmol
The buffer's capacity has been exceeded. The pH of the solution is determined by
the excess strong acid present.
+
3
4.5mmol
H O = = 0.059M; pH = log 0.059 =1.23
75.0mL +1.05mL

Chapter 17: Additional Aspects of Acid–Base Equilibria
813
24. (D) For NH p log
b3 5
,= 1.810K
ch For NH p p
4a b
, = 14.00 = 14.00 4.74 = 9.26KK
(a)
33
3
3
1.68g NH 1 mol NH
NH = = 0.197 M
0.500 L 17.03 g NH
44 44 4
22
4
44 44
22
4.05 g NH SO 1 mol NH SO 2mol NH
NH = = 0.123 M
0.500L 132.1 g NH SO 1mol NH SO
pH p log NH
NH log M
M
a
=+ =9.26+
0.197
0.123 =9.46
3
4
K
L
N
MO
Q
P
(b) The OH aq
bg
reacts with the NH aq
4
bg to produce an equivalent amount of NH aq
3bg.
OH g NaOH
L
mol NaOH
g NaOH
mol OH
mol NaOH M
i=0.88
0.500
1
40.00
1
1= 0.044
432
Equation: NH aq + OH aq NH aq + H O(l)
Initial : 0.123M 0M 0.197M
Add NaOH : 0.044M
React : 0.044M 0.044M +0.044M
Final : 0.079M 0.0000M 0.241M
pH p log NH
NH log M
M
a
=+ =9.26+
0.241
0.079 =9.74
3
4
K
L
N
MO
Q
P
(c)
+
33 4 2
9
Equation: NH aq + H O aq NH aq + H O(l)
Initial: 0.197M 0M 0.123M
Add HCl: + M
React : M M + M
Final: 0.197 M 1 10 M 0 0.123+ M
x
xx x
xx
pH p log NH
NH log M
M
a
= 9.00 = + = 9.26 + 0.197
0.123+
3
4
Kx
x
L
N
MO
Q
P
bg
bg
log M
M
M
M
0.197
0.123+ = 9.00 9.26 = 0.26 0.197
0.123+ = 10 = 0.55
0.26
x
x
x
x
bg
bgbg
bg
0.197 = 0.55 0.123+ = 0.068 + 0.55 1.55 = 0.197 0.068 = 0.129
xxxx
bg
x=0.129
1.55 = 0.0832 M
+
3
+
3
0.0832 mol H O 1mol HCl 1000mL HCl
volume HCl = 0.500L = 3.5mL
1L soln 1mol H O 12 mol HCl
Chapter 17: Additional Aspects of Acid–Base Equilibria
814
25. (D)
(a) We use the Henderson-Hasselbalch equation to determine the pH of the solution.
The total solution volume is
5
ab
36.00mL + 64.00mL = 100.00mL. p = 14.00 p = 14.00 + log 1.8 10 = 9.26KK
NH mL M NH
mL
mmol NH
mL M
333
=36.00 0.200
100.00 =7.20
100.0 = 0.0720
NH mL M NH
mL
mmol NH
mL M
444
=64.00 0.200
100.00 =12.8
100.0 = 0.128
3
a
4
[NH ] 0.0720 M
pH = p log 9.26 log 9.01 9.00
0.128M
[NH ]
K
(b) The solution has OH M
=10 =1.0 10
4.99 5
The Henderson-Hasselbalch equation depends on the assumption that:
5
34
NH 1.8 10 M NH
If the solution is diluted to 1.00 L, NH M
33
=7.20 10, and
NH M
42
=1.28 10
. These concentrations are consistent with the assumption.
However, if the solution is diluted to 1000. L, NH M
36
=7.2 10, and
NH M
35
=1.28 10, and these two concentrations are not consistent with the
assumption. Thus, in 1000. L of solution, the given quantities of NH3 and NH4
will not produce a solution with pH = 9.00 . With sufficient dilution, the solution
will become indistinguishable from pure water (i.e.; its pH will equal 7.00).
(c) The 0.20 mL of added 1.00 M HCl does not significantly affect the volume of the
solution, but it does add 0.20 1.00 = 0.20 3+
mL M HCl mmol H O. This added
HO
3+ reacts with NH3, decreasing its amount from 7.20 mmol NH3 to 7.00
mmol NH3, and increasing the amount of NH4
from 12.8 mmol NH4
to 13.0
mmol NH4
, as the reaction: NH H O NH H O
33
+42
++
pH log mmol NH mL
mmol NH mL
=9.26+ 7.00 /100.20
13.0 /100.20 =8.99
3
4
(d) We see in the calculation of part (c) that the total volume of the solution does not
affect the pOH of the solution, at least as long as the Henderson-Hasselbalch
equation is obeyed. We let
x
represent the number of millimoles of H O
3+ added,

Chapter 17: Additional Aspects of Acid–Base Equilibria
815
through 1.00 M HCl. This increases the amount of NH4
and decreases the
amount of NH3, through the reaction NH H O NH H O
33
+42
++
7.20 7.20
pH = 8.90 = 9.26 + log ; log = 8.90 9.26 = 0.36
12.8+ 12.8 +
xx
xx
Inverting, we have:
0.36
12.8+ = 10 = 2.29; 12.8+ = 2.29 7.20 =16.5 2.29
7.20
x
x
xx
x
+
3
16.5 12.8
= =1.1 mmol H O
1.00 + 2.29
x
vol +
3+
3
1mmol HCl 1mL soln
1.00M HCl = 1.1mmol H O = 1.1mL 1.00 M HCl
1mmol H O 1.00 mmol HCl
26. (D)
(a) 232 232 232
232 232
232 232
12.0g NaCHO 1mol NaCHO 1mol CHO
CHO = =0.488M CHO
0.300L soln 82.03g NaC H O 1mol NaC H O
+
232 2 232 3
232
+
3
Equation: HCHO +HO CHO + HO
Initial : 0M 0M 0.200M
Add C H O 0M 0.488M 0M
Consume H O + 0.200M 0.200M 0.200M
Buffer : 0.200M 0.288M 0M
Then use the Henderson-Hasselbalch equation to find the pH.
pH p log CHO
HC H O log M
M
a
=+ =4.74+
0.288
0.200 = 4.74 + 0.16 = 4.90
232
232
K
L
N
MO
Q
P
(b) We first calculate the initial OH due to the added Ba OH
bg2.
OH g Ba OH
L
mol Ba OH
g Ba OH
mol OH
mol Ba OH M
=1.00
0.300
1
171.3
2
1= 0.0389
22
22
bg bg
bg bg
Then HCHO
232
is consumed in the neutralization reaction shown directly below.
Equation: 232 232 2
HC H O + OH C H O + H O
Initial: 0.200 M 0.0389 M 0.288 M —
Consume OH: -0.0389 M -0.0389 M +0.0389 M —
Buffer: 0.161 M ~ 0M 0.327 M —
Chapter 17: Additional Aspects of Acid–Base Equilibria
816
Then use the Henderson-Hasselbalch equation.
pH p log CHO
HC H O log M
M
a
=+ =4.74+
0.327
0.161 = 4.74 + 0.31= 5.05
232
232
K
L
N
MO
Q
P
(c) Ba OH
bg
2 can be added up until all of the HC H O
232
is consumed.
Ba OH HC H O Ba C H O H O
bg b g
2232 232
22
+2 +2
232 2
2 2
232
2
22 2
2
1mol Ba OH
0.200mol HC H O
moles of Ba OH = 0.300 L = 0.0300mol Ba OH
1L soln 2mol HC H O
171.3g Ba OH
mass of Ba OH = 0.0300 mol Ba OH = 5.14g Ba OH
1mol Ba OH
(d) 0.36 g Ba OH
bg2 is too much for the buffer to handle and it is the excess of OH-
originating from the Ba(OH)2 that determines the pOH of the solution.
OH g Ba OH
L soln
mol Ba OH
g Ba OH
mol OH
mol Ba OH M OH
=0.36
0.300
1
171.3
2
1=1.4 10
22
22
2
bgbg
bgbg
pOH log pH= 1.4 10 = 1.85 = 14.00 1.85 = 12.15
2
ch
Acid–Base Indicators
27. (E)
(a) The pH color change range is 1.00 pH unit on either side of p Hln
K. If the pH color
change range is below pH = 7.00, the indicator changes color in acidic solution. If
it is above pH = 7.00 , the indicator changes color in alkaline solution. If pH = 7.00
falls within the pH color change range, the indicator changes color near the neutral
point.
Indicator HIn
K HIn
pK pH Color Change Range Changes Color in?
Bromphenol blue 1.4 10 4
3.85 2.9 (yellow) to 4.9 (blue) acidic solution
Bromcresol green 2.1 10 5
4.68 3.7 (yellow) to 5.7 (blue) acidic solution
Bromthymol blue 7.9 10 8
7.10 6.1 (yellow) to 8.1 (blue) neutral solution
2,4-Dinitrophenol 1.3 10 4
3.89 2.9 (colorless) to 4.9 (yellow) acidic solution
Chlorophenol red 1.0 10 6
6.00 5.0 (yellow) to 7.0 (red) acidic solution
Thymolphthalein 1.0 10 10
10.00 9.0 (colorless) to 11.0 (blue) basic solution
(b) If bromcresol green is green, the pH is between 3.7 and 5.7, probably about pH = 4.7 .
If chlorophenol red is orange, the pH is between 5.0 and 7.0, probably about pH = 6.0 .
Chapter 17: Additional Aspects of Acid–Base Equilibria
817
28. (M) We first determine the pH of each solution, and then use the answer in Exercise
27 (a) to predict the color of the indicator. (The weakly acidic or basic character of the
indicator does not affect the pH of the solution, since very little indicator is added.)
(a)
+
+3
3
1 mol H O
H O = 0.100 M HCl = 0.100 M; pH = log 0.100 M = 1.000
1 mol HCl
2,4-dinitrophenol is colorless.
(b) Solutions of NaCl(aq) are pH neutral, with pH = 7.000. Chlorphenol red assumes
its neutral color in such a solution; the solution is red/orange.
(c) Equation: +
32 4
NH (aq) + H O(l) NH (aq) + OH (aq)
Initial: 1.00 M — 0 M
0 M
Changes:
x
M — +
x
M +
x
M
Equil:
1.00 Mx —
x
M
x
M
Kx
x
xx
b
NH OH
NH MOH==1.810=
1.00 1.00 =4.2 10 =
4
+
3
522 3
L
N
MO
Q
P
(
x << 1.00 M, thus the approximation was valid).
pOH log pH= 4.2 10 = 2.38 = 14.00 2.38 = 11.62
3
ch
Thus, thymolphthalein assumes its blue color in solutions with pH 11.62.
(d) From Figure 17-8, seawater has pH = 7.00 to 8.50. Bromcresol green solution is
blue.
29. (M)
(a) In an Acid–Base titration, the pH of the solution changes sharply at a definite pH
that is known prior to titration. (This pH change occurs during the addition of a
very small volume of titrant.) Determining the pH of a solution, on the other hand,
is more difficult because the pH of the solution is not known precisely in
advance. Since each indicator only serves to fix the pH over a quite small region,
often less than 2.0 pH units, several indicators—carefully chosen to span the
entire range of 14 pH units—must be employed to narrow the pH to 1 pH unit
or possibly lower.
(b) An indicator is, after all, a weak acid. Its addition to a solution will affect the
acidity of that solution. Thus, one adds only enough indicator to show a color
change and not enough to affect solution acidity.
Chapter 17: Additional Aspects of Acid–Base Equilibria
818
30. (E)
(a) We use an equation similar to the Henderson-Hasselbalch equation to determine the
relative concentrations of HIn, and its anion, I
n
, in this solution.
HIn
In In In
pH = p + log ; 4.55 = 4.95 + log ; log = 4.55 4.95 = 0.40
HIn HIn HIn
K
0.40
In 40
=10 = 0.40 = = 40 0.40 = = 29% In and 71% HIn
HIn 100 1.40
xxxx
x
(b) When the indicator is in a solution whose pH equals its p a
K (4.95), the ratio
In HIn
/ = 1.00 . And yet, at the midpoint of its color change range (about
pH = 5.3), the ratio In/[HIn] is greater than 1.00. Even though HIn In at
this midpoint, the contribution of HIn to establishing the color of the solution is
about the same as the contribution of I
n
. This must mean that HIn (red) is more
strongly colored than I
n
(yellow).
31. (E)
(a) 0.10 M KOH is an alkaline solution and phenol red will display its basic color in
such a solution; the solution will be red.
(b) 0.10 M HC H O
232
is an acidic solution, although that of a weak acid, and phenol
red will display its acidic color in such a solution; the solution will be yellow.
(c) 0.10 M NH NO
43
is an acidic solution due to the hydrolysis of the ammonium ion.
Phenol red will display its acidic color, that is, yellow, in this solution.
(d) 0.10 M HBr is an acidic solution, the aqueous solution of a strong acid. Phenol red
will display its acidic color in this solution; the solution will be yellow.
(e) 0.10 M NaCN is an alkaline solution because of the hydrolysis of the cyanide ion.
Phenol red will display its basic color, red, in this solution.
(f) An equimolar acetic acid–potassium acetate buffer has pH p a
= = 4.74K for acetic
acid. In this solution phenol red will display its acid color, namely, yellow.
32. (M)
(a) pH log= 0.205 = 0.688bg The indicator is red in this solution.
(b) The total volume of the solution is 600.0 mL. We compute the amount of each
solute.
amount H O mL M mmol H O
3+3+
= 350.0 0.205 = 71.8
amount NO mL M mmol NO
22
= 250.0 0.500 = 125
HO mmol
mL MNO mmol
mL M
3+2
=71.8
600.0 = 0.120 = 125
600.0 = 0.208
The HO
3+ and 2
NO react to produce a buffer solution in which
HNO M
2= 0.120 and NO M
2= 0.208 0.120 = 0.088
. We use the
Chapter 17: Additional Aspects of Acid–Base Equilibria
819
Henderson-Hasselbalch equation to determine the pH of this solution.
plog
a
K= 7.2 10 = 3.14
4
ch
2
a
2
NO 0.088M
pH = p + log = 3.14 + log = 3.01
HNO 0.120M
K
The indicator is yellow in this
solution.
(c) The total volume of the solution is 750. mL. We compute the amount and then the
concentration of each solute. Amount OH mL M mmol OH
= 150 0.100 = 15.0
This OH
reacts with HNO2 in the buffer solution to neutralize some of it and leave
56.8 mmol (= 71.8 15.0) unneutralized.
HNO mmol
mL MNO mmol
mL M
22
=56.8
750. = 0.0757 = 125+15
750. = 0.187
bg
We use the Henderson-Hasselbalch equation to determine the pH of this solution.
pH p log NO
HNO log M
M
a
=+ =3.14+0.187
0.0757 =3.53
2
2
K
L
N
MO
Q
P
The indicator is yellow in this solution.
(d) We determine the OH due to the added Ba OH
bg2.
OH g Ba OH
L
mol Ba OH
g Ba OH
mol OH
mol Ba OH M
=5.00
0.750
1
171.34
2
1= 0.0778
22
22
bgbg
bgbg
This is sufficient
OH to react with the existing HNO2 and leave an excess
OH = 0.0778M 0.0757M = 0.0021M. pOH = log 0.0021 = 2.68.
pH =14.00 2.68 = 11.32 The indicator is blue in this solution.
33. (M) Moles of HCl = C V = 0.04050 M 0.01000 L = 4.050 104 moles
Moles of Ba(OH)2 at endpoint = C V = 0.01120 M 0.01790 L = 2.005 104 moles.
Moles of HCl that react with Ba(OH)2 = 2 moles Ba(OH)2
Moles of HCl in excess 4.050 104 moles 4.010 104 moles = 4.05 106 moles
Total volume at the equivalence point = (10.00 mL + 17.90 mL) = 27.90 mL
[HCl]excess = 6
4.05 10 mole HCl
0.02790 L
= 1.45 104 M; pH = log(1.45 104) = 3.84
(a) The approximate pKHIn = 3.84 (generally + 1 pH unit)
(b) This is a relatively good indicator (with 1 % of the equivalence point volume),
however, pKHin is not very close to the theoretical pH at the equivalence point
(pH = 7.000) For very accurate work, a better indicator is needed (i.e.,
bromthymol blue (pKHin = 7.1). Note: 2,4-dinitrophenol works relatively well
here because the pH near the equivalence point of a strong acid/strong base
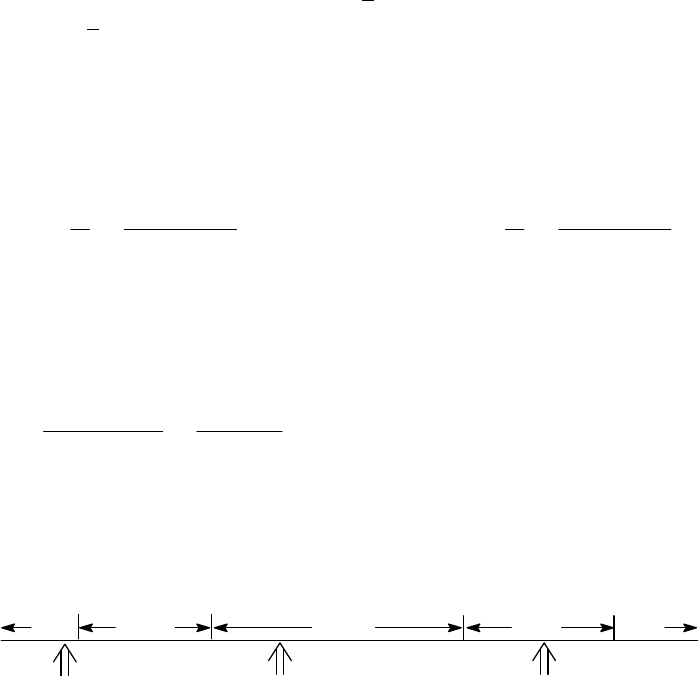
Chapter 17: Additional Aspects of Acid–Base Equilibria
820
titration rises very sharply ( 6 pH units for an addition of only 2 drops (0.10
mL)).
34. Solution (a): 100.0 mL of 0.100 M HCl, [H3O+] = 0.100 M and pH = 1.000 (yellow)
Solution (b): 150 mL of 0.100 M NaC2H3O2
Ka of HC2H3O3 = 1.8 105 Kb of C2H3O2 = 5.6 1010
C2H3O2(aq) + H2O(l) -10
b = 5.6 10K
HC2H3O2(aq) + OH(aq)
Initial 0.100 M — 0 M ~ 0 M
Change x — +x +x
Equil. 0.100 x — x x
Assume x is small: 5.6 1011 = x2; x = 7.48 106 M (assumption valid by inspection)
[OH] = x = 7.48 106 M, pOH = 5.13 and pH = 8.87 (green-blue)
Mixture of solution (a) and (b). Total volume = 250.0 mL
nHCl = C V = 0.1000 L 0.100 M = 0.0100 mol HCl
nC2H3O2 = C V = 0.1500 L 0.100 M = 0.0150 mol C2H3O2
HCl is the limiting reagent. Assume 100% reaction.
Therefore, 0.0050 mole C2H3O2 is left unreacted, and 0.0100 moles of HC2H3O2 form.
[C2H3O2] = n
V = 0.0050 mol
0.250 L = 0.020 M [HC2H3O2] = n
V = 0.0100 mol
0.250 L = 0.0400 M
HC2H3O2(aq) + H2O(l) -5
a = 1.8 10K
C2H3O2(aq) + H3O+(aq)
Initial 0.0400 M — 0.020 M ~ 0 M
Change x — +x +x
Equil. 0.0400 x — 0.020 +
x x
1.8 10-5 = (0.020 )
0.0400
x
x
x
(0.020)
0.0400
x x = 3.6 105
(proof 0.18 % < 5%, the assumption was valid)
[H3O+] = 3.6 105 pH = 4.44 Color of thymol blue at various pHs:
1.2 2.8 8.0 9.8
Red Orange Yellow Green Blue
pH pH pH
p
H
Solution (a)
RED Solution (b)
GREEN
Solution (c)
YELLOW

Chapter 17: Additional Aspects of Acid–Base Equilibria
821
Neutralization Reactions
35. (E) The reaction (to second equiv. pt.) is:
34 2 4 2
H PO aq +2KOH aq K HPO aq + 2H O(l).
The molarity of the H PO
34
solution is determined in the following manner.
34
34
34
1mmolH PO0.2420mmolKOH
31.15mL KOHsoln 1mLKOHsoln 2mmolKOH
H PO molarity = = 0.1508M
25.00mL H PO soln
36. (E) The reaction (first to second equiv. pt.) is:
24 2 4 2
NaH PO aq + NaOH aq Na HPO aq + H O(l) . The molarity of the H PO
34
solution is determined in the following manner.
H PO molarity
mL NaOH soln 0.1885mmol NaOH
1mLNaOHsoln
mmol H PO
mmol NaOH
mL H PO soln M
34
34
34
=
18 67 1
1
20.00 =0.1760
.
37. (M) Here we must determine the amount of H O
3+ or OH in each solution, and the
amount of excess reagent.
amount HO mL mmol H SO
mL soln
mmol H O
mmol H SO mmol H O
3+24 3
+
24
3+
= 50.00 0.0150
1
2
1=1.50
(assuming complete ionization of H2SO4 and HSO4 in the presence of OH)
amount 0.0385 mmol NaOH 1mmol OH
OH = 50.00mL =1.93 mmol OH
1mL soln 1mmol NaOH
Result:
+
32
Titration reaction : OH aq + H O aq 2H O(l)
Initial amounts : 1.93mmol 1.50mmol
After reaction : 0.43mmol 0mmol
3
3
0.43mmol OH
OH = = 4.3 10 M
100.0mL soln
pOH = log 4.3 10 = 2.37 pH = 14.00 2.37 = 11.63
Chapter 17: Additional Aspects of Acid–Base Equilibria
822
38. (M) Here we must determine the amount of solute in each solution, followed by the amount of
excess reagent.
HO M
3+2.50
= 10 = 0.0032
mmol HCl mL mmol H O
mL soln
mmol HCl
mmol H O mmol HCl= 100.0 0.0032
1
1
1=0.32
3+
3+
3.00 3
pOH = 14.00 11.00 = 3.00 OH =10 = 1.0 10 M
mmol NaOH mL mmol OH
mL soln
mmol NaOH
mmol OH mmol NaOH= 100.0 0.0010
1
1
1=0.10
Result:
2
Titration reaction : NaOH aq + HCl aq NaCl aq + H O(l)
Initial amounts : 0.10mmol 0.32mmol 0mmol
After reaction : 0.00mmol 0.22mmol 0.10mmol
+
+3
3
3
1mmol H O
0.22mmol HCl
HO = =1.1 10 M
200.0mL soln 1mmol HCl
3
pH = log 1.1 10 = 2.96
Titration Curves
39. (M) First we calculate the amount of HCl. The relevant titration reaction is
2
HCl aq + KOH aq KCl aq + H O(l)
+
3
0.160 mmol HCl
amount HCl = 25.00 mL = 4.00 mmol HCl = 4.00 mmol H O present
1 mL soln
Then, in each case, we calculate the amount of OH that has been added, determine
which ion, OH aq
bg
or H O aq
3+bg
, is in excess, compute the concentration of that ion,
and determine the pH.
(a) amount +
3
0.242 mmol OH
OH =10.00 mL = 2.42 mmol OH ; H O
1 mL soln
is in excess.
[H O ]
mmol H O mmol OH mmol H O
1 mmol OH
mL originally +10.00 mL titrant M
3+
33+
=
4.00 2 42 1
2500 = 0.0451
F
H
G
I
K
J
.
.
pH log= 0.0451 = 1.346bg
Chapter 17: Additional Aspects of Acid–Base Equilibria
823
(b) amount +
3
0.242 mmol OH
OH =15.00 mL = 3.63 mmol OH ; H O
1 mL soln
is in excess.
[H O ]
mmol H O mmol OH mmol H O
1 mmol OH
mL originally +15.00 mL titrant M
3+
33+
=
4.00 363 1
2500 = 0.00925
F
H
G
I
K
J
.
.
pH log= 0.00925 = 2.034bg
40. (M) The relevant titration reaction is
2
KOH aq + HCl aq KCl aq + H O(l)
mmol of 0.275 mmol KOH
KOH = 20.00 mL = 5.50 mmol KOH
1 mL soln
(a) The total volume of the solution is = 20.00 mL +15.00 mL = 35.00 mLV
0.350 mmol HCl
mmol HCl =15.00 mL = 5.25 mmol HCl
1 mL soln
-
- -
1 mmol OH
mmol excess OH = 5.50 mmol KOH-5.25 mmol HCl × = 0.25 mmol OH
1mmol KOH
0.25 mmol OH
OH = = 0.0071M pOH = log 0.0071 = 2.15
35.00 mL soln
pH = 14.00 2.15 = 11.85
(b) The total volume of solution is
V
= 20.00 + 20.00 = 40.00mL mL mL
0.350 mmol HCl
mmol HCl = 20.00 mL = 7.00 mmol HCl
1mL soln
+
+3
3
1 mmol H O
mmol excess H O = 7.00 mmol HCl 5.50 mmol KOH × 1 mmol HCl
= 1.50 3+
mmol H O
HO mmol H O
mL MpHlog
3+3+
=1.50
40.00 = 0.0375 = 0.0375 = 1.426bg
41. (M) The relevant titration reaction is
222
HNO aq + NaOH aq NaNO aq + H O(l)
2
2 2
0.132 mmol HNO
amount HNO = 25.00 mL = 3.30 mmol HNO
1 mL soln
Chapter 17: Additional Aspects of Acid–Base Equilibria
824
(a) The volume of the solution is 25.00 +10.00 = 35.00mL mL mL
amount NaOH mL mmol NaOH
mL soln mmol NaOH= 10.00 0.116
1=1.16
1.16 mmol NaNO2 are formed in this reaction and there is an excess of (3.30 mmol
22
HNO 1.16 mmol NaOH) = 2.14 mmol HNO. We can use the
Henderson-Hasselbalch equation to determine the pH of the solution.
plog
a
K= 7.2 10 = 3.14
4
ch
pH p log NO
HNO log mmol NO mL
mmol HNO mL
a
=+ =3.14+
1.16 / 35.00
2.14 / 35.00 = 2.87
2
2
2
2
K
L
N
MO
Q
P
(b) The volume of the solution is 25.00 +20.00 = 45.00mL mL mL
amount NaOH mL mmol NaOH
mL soln mmol NaOH= 20.00 0.116
1=2.32
2.32 mmol NaNO2 are formed in this reaction and there is an excess of
(3.30 mmol 2
HNO 2.32 mmol NaOH =) 0.98 mmol HNO2.
pH p log NO
HNO log mmol NO mL
mmol HNO mL
a
=+ =3.14+
2.32 / 45.00
0.98 / 45.00 = 3.51
2
2
2
2
K
L
N
MO
Q
P
42. (M) In this case the titration reaction is NH aq HCl aq NH Cl aq H O l
342
++
bgbgbgbg
amount NH mL mmol NH
mL soln mmol NH
333
= 20.00 0.318
1=6.36
(a) The volume of the solution is 20.00 +10.00 = 30.00mL mL mL
amount HCl mL mmol NaOH
mL soln mmol HCl= 10.00 0.475
1=4.75
4.75 mmol NH Cl
4 is formed in this reaction and there is an excess of (6.36 mmol
NH3 – 4.75 mmol HCl =) 1.61 mmol NH3. We can use the Henderson-
Hasselbalch equation to determine the pH of the solution.
5
bab
p = log 1.8 10 = 4.74; p =14.00 p = 14.00 4.74 = 9.26KKK
pH p log NH
NH log mmol NH mL
mmol NH mL
a
=+ =9.26+1.61 / 30.00
4.75 / 30.00 =8.79
3
4
+
3
4
+
K
(b) The volume of the solution is 20.00 +15.00 = 35.00mL mL mL
amount HCl mL mmol NaOH
mL soln mmol HCl= 15.00 0.475
1=7.13
Chapter 17: Additional Aspects of Acid–Base Equilibria
825
6.36 mmol NH Cl
4 is formed in this reaction and there is an excess of (7.13 mmol
HCl – 6.36 mmol NH3 =) 0.77 mmol HCl; this excess HCl determines the pH of
the solution.
+
+3
3
1mmol H O
0.77mmol HCl
H O = = 0.022M pH = log 0.022 =1.66
35.00mL soln 1mmol HCl
43. (E) In each case, the volume of acid and its molarity are the same. Thus, the amount of
acid is the same in each case. The volume of titrant needed to reach the equivalence point
will also be the same in both cases, since the titrant has the same concentration in each
case, and it is the same amount of base that reacts with a given amount (in moles) of acid.
Realize that, as the titration of a weak acid proceeds, the weak acid will ionize,
replenishing the H O
3+ in solution. This will occur until all of the weak acid has ionized
and all of the released H+ has subsequently reacted with the strong base. At the
equivalence point in the titration of a strong acid with a strong base, the solution contains
ions that do not hydrolyze. But the equivalence point solution of the titration of a weak
acid with a strong base contains the anion of a weak acid, which will hydrolyze to
produce a basic (alkaline) solution. (Don’t forget, however, that the inert cation of a
strong base is also present.)
44. (E)
(a) This equivalence point solution is the result of the titration of a weak acid with a
strong base. The CO3
2 in this solution, through its hydrolysis, will form an
alkaline, or basic solution. The other ionic species in solution, N
a
+, will not
hydrolyze. Thus, pH > 7.0.
(b) This is the titration of a strong acid with a weak base. The NH4
+present in the
equivalence point solution hydrolyzes to form an acidic solution. Cl does not
hydrolyze. Thus, pH < 7.0.
(c) This is the titration of a strong acid with a strong base. Two ions are present in the
solution at the equivalence point, namely,
K
+ and Cl, neither of which
hydrolyzes. Thus the solution will have a pH of 7.00.
45. (D)
(a)
Initial OH M OH pOH log pH
= 0.100 = 0.100 = 1.000 = 13.00
bg
Since this is the titration of a strong base with a strong acid, KI is the solute
present at the equivalence point, and since KI is a neutral salt, the pH = 7.00 . The
titration reaction is:
2
KOHaq+HIaq KIaq +HO(l)
HI
0.100mmol KOH soln 1mmol HI 1mL HI soln
= 25.0mL KOH soln 1mL soln 1mmol KOH 0.200mmol HI
=12.5mL HI soln
V

Chapter 17: Additional Aspects of Acid–Base Equilibria
826
Initial amount of KOH present mL KOH soln M mmol KOH= 25.0 0.100 = 2.50
At the 40% titration point: 5.00 0.200 = 1.00mL HI soln M HI mmol HI
excess KOH mmol KOH mmol HI mmol KOH= 2.50 1.00 = 1.50
1.50mmol KOH 1mmol OH
OH = = 0.0500M pOH = log 0.0500 =1.30
30.0mL total 1mmol KOH pH =14.00 1.30 =12.70
At the 80% titration point: 10.00 0.200 = 2.00mL HI soln M HI mmol HI
excess KOH mmol KOH mmol HI mmol KOH= 2.50 2.00 = 0.50
0.50 mmol KOH 1mmol OH
OH = = 0.0143M pOH = log 0.0143 =1.84
35.0mL total 1mmol KOH pH = 14.00 1.84 =12.16
At the 110% titration point:13.75 0.200 = 2.75mL HI soln M HI mmol HI
excess HI = 2.75 mmol HI 2.50mmol HI = 0.25mmol HI
+3
3
1mmolH O
0.25mmolHI
[H O ] 0.0064M; pH= log(0.0064) 2.19
38.8mL total 1mmolHI
Since the pH changes very rapidly at the equivalence point, from about pH = 10
to about pH = 4 , most of the indicators in Figure 17-8 can be used. The main
exceptions are alizarin yellow R, bromphenol blue, thymol blue (in its acid range),
and methyl violet.
(b) Initial pH:
Since this is the titration of a weak base with a strong acid, NH4Cl is the solute
present at the equivalence point, and since NH4+ is a slightly acidic cation, the pH
should be slightly lower than 7. The titration reaction is:
+
32 4
Equation: NH aq + H O(l) NH aq + OH aq
Initial : 1.00M 0M 0M
Changes : M + M + M
Equil : 1.00 M M M
xxx
xxx
+
45
b
3
NH OH
==1.810
NH
K
22
=1.00 1.00
x
x
x
(x << 1.0, thus the approximation is valid)
33
= 4.2 10 M = OH , pOH = log 4.2 10 = 2.38,
pH =14.00 2.38 = 11.62 = initial pH
x
342
:NH+HCl NHCl+HOVolume of titrant
Chapter 17: Additional Aspects of Acid–Base Equilibria
827
3
HCl
3
1.00mmol NH 1mmol HCl 1mL HCl soln
= 10.0mL = 40.0mL HCl soln
1mL soln 1mmol NH 0.250 mmol HCl
V
pH at equivalence point: The total solution volume at the equivalence point is
10.0 + 40.0 mL = 50.0mL
Also at the equivalence point, all of the NH3 has reacted to form NH4
+. It is this
NH4
+ that hydrolyzes to determine the pH of the solution.
NH
mL 1.00mmol NH
mLsoln
mmol NH
mmol NH
mL total solution M
34
+
3
4
+=
10 0 1
1
1
50.0 = 0.200
.
++
42 33
Equation : NH aq + H O(l) NH aq + H O aq
Initial : 0.200M 0M 0M
Changes : M + M + M
Equil : 0.200 M M M
xxx
xxx
+
14 2 2
33
w
a5
b3
NH H O
1.0 10
== = =
1.8 10 NH 0.200 0.200
K
x
x
KKx
(
x << 0.200, thus the approximation is valid)
5+5 5
3
=1.1 10 M; H O =1.1 10 M; pH = log 1.1 10 = 4.96x
Of the indicators in Figure 17-8, one that has the pH of the equivalence point
within its pH color change range is methyl red (yellow at pH = 6.2 and red at
pH = 4.5); Bromcresol green would be another choice. At the 50% titration point,
NH NH
34
+
= and pOH pK pH
b
= = 4.74 = 14.00 4.74 = 9.26
The titration curves for parts (a) and (b) follow.
Chapter 17: Additional Aspects of Acid–Base Equilibria
828
46. (M)
(a)
This part simply involves calculating the pH of a 0.275 M NH3 solution.
+
32 4
Equation: NH aq + H O(l) NH aq + OH aq
Initial: 0.275M 0M 0M
Changes: M + M + M
Equil: (0.275 )M M M
xxx
xxx
Kx
x
xx
b
NH OH
NH MOH==1.810=
0.275 0.275 =2.2 10 =
4
+
3
522 3
L
N
MO
Q
P
(
x << 0.275, thus the approximation is valid)
3
pOH = log 2.2 10 = 2.66 pH = 11.34
(b) This is the volume of titrant needed to reach the equivalence point.
The relevant titration reaction is NH aq HI aq NH I aq
34
+
bg bg bg
3
HI 3
33
HI
0.275mmol NH 1mmol HI 1mL HI soln
= 20.00 mL NH aq 1mL NH soln 1mmol NH 0.325mmol HI
=16.9mL HI soln
V
V
(c) The pOH at the half-equivalence point of the titration of a weak base with a strong
acid is equal to the pb
K of the weak base.
b
pOH = p = 4.74; pH =14.00 4.74 = 9.26K
(d) NH4
+is formed during the titration, and its hydrolysis determines the pH of the
solution. Total volume of solution = 20.00mL +16.9mL = 36.9mL
+
+ +
34
43 4
33
0.275mmol NH 1mmol NH
mmol NH = 20.00mL NH aq = 5.50mmol NH
1mL NH soln 1mmol NH
NH mmol NH
mL soln M
4
+4
+
=5.50
36.9 = 0.149
++
42 33
Equation: NH aq + H O(l) NH aq + H O aq
Initial: 0.149M 0M 0M
Changes: M + M + M
Equil: (0.149 )M M M
xxx
xxx
Chapter 17: Additional Aspects of Acid–Base Equilibria
829
+
14 2 2
33
w
a5+
b4
6+ 6
3
NH H O
1.0 10
== = =
0.149 0.149
1.8 10 NH
( << 0.149, thus the approximation is valid)
= 9.1 10 M = H O pH = log 9.1 10 = 5.04
K
x
x
KKx
x
x
47. (M) A pH greater than 7.00 in the titration of a strong base with a strong acid means that
the base is not completely titrated. A pH less than 7.00 means that excess acid has been
added.
(a) We can determine OH of the solution from the pH. OH is also the quotient
of the amount of hydroxide ion in excess divided by the volume of the solution:
20.00 mL base +
x
mL added acid.
pOH pH OH M
pOH
= 14.00 = 14.00 12.55 = 1.45 = 10 = 10 = 0.035
1.45
+
3
0.175 mmol OH 0.200 mmol H O
20.00 mL base mL acid
1mL base 1mL acid
[OH ] 0.035M
20.00 mL + mL
x
x
3.50 0.200 = 0.70+ 0.035 ; 3.50 0.70 = 0.035 + 0.200 ; 2.80 = 0.235
x
xxxx
x=2.80
0.235 = 11.9 .mL acid added
(b) The set-up here is the same as for part (a).
pOH pH OH M
pOH
=14.00 = 14.00 10.80 = 3.20 =10 =10 = 0.00063
3.20
+
3
0.200mmolH O
0.175mmolOH
20.00mLbase mLacid
1mL base 1mLacid
[OH ] 20.00mL+ mL
mmol
[OH ] 0.00063 =0.00063M
mL
x
x
3.50 0.200 = 0.0126 + 0.00063 ; 3.50 0.0126 = 0.00063 + 0.200 ; 3.49 = 0.201
x
xxxx
3.49
= =17.4mL acid added. This is close to the equivalence point at 17.5 mL.
0.201
x
Chapter 17: Additional Aspects of Acid–Base Equilibria
830
(c) Here the acid is in excess, so we reverse the set-up of part (a). We are just slightly
beyond the equivalence point. This is close to the “mirror image” of part (b).
HO M
pH
3+4.25
=10 = 10 = 0.000056
[]
.
HO =
mLacid 0.200 mmol H O
mLacid mL base 0.175 mmol OH
1mLbase
20.00 mL+ mL
M
3+
3+
x
x
F
H
GI
K
J
F
H
GI
K
J
120 00
=5.6 105
55
0.200 3.50 = 0.0011+5.6 10 ; 3.50 + 0.0011 = 5.6 10 + 0.200 ;
3.50 = 0.200
x
xxx
x
3.50
= = 17.5mL acid added, which is the equivalence point for this titration.
0.200
x
48. (D) In the titration of a weak acid with a strong base, the middle range of the titration,
with the pH within one unit of p a
K (= 4.74 for acetic acid), is known as the buffer
region. The Henderson-Hasselbalch equation can be used to determine the ratio of weak
acid and anion concentrations. The amount of weak acid then is used in these
calculations to determine the amount of base to be added.
(a)
232
232 232
a
232 232
232 232 0.89
232 232
232
HC H O
CHO CHO
pH = p + log = 3.85 = 4.74 + log
HC H O HC H O
CHO CHO
log = 3.85 4.74 = 10 = 0.13;
HC H O HC H O
0.100 mmol HC H O
= 25.00 mL = 2.50 mmol
1mL acid
K
n
Since acetate ion and acetic acid are in the same solution, we can use their
amounts in millimoles in place of their concentrations. The amount of acetate ion
is the amount created by the addition of strong base, one millimole of acetate ion
for each millimole of strong based added. The amount of acetic acid is reduced by
the same number of millimoles. HC H O OH C H O H O
232 232 2
++
013
1
10 200
2 50 0 200
3
..
..
F
H
GI
K
J
x
x
x
x
mLbase 0.200mmolOH
mLbase
mmolC H O
mmolOH
2.50mmolHC H O mL base 0.200 mmolOH
mLbase
232
22
0.200 = 0.13 2.50 0.200 = 0.33 0.026 0.33 = 0.200 + 0.026 = 0.226xxxxxx
bg
0.33
= = 1.5 mL of base
0.226
x
Chapter 17: Additional Aspects of Acid–Base Equilibria
831
(b) This is the same set-up as part (a), except for a different ratio of concentrations.
pH log CHO
HC H O log CHO
HC H O
= 5.25 = 4.74 + = 5.25 4.74 = 0.51
232
232
232
232
L
N
MO
Q
P
L
N
MO
Q
P
CHO
HC H O
232
232
0.51
=10 =3.2 3.2= 0.200
2.50 0.200
L
N
MO
Q
P
x
x
0.200 = 3.2 2.50 0.200 = 8.0 0.64 8.0 = 0.200 + 0.64 = 0.84xxxxxx
bg
8.0
= = 9.5mL base. This is close to the equivalence point, which is reached
0.84
by adding 12.5 mL of base.
x
(c) This is after the equivalence point, where the pH is determined by the excess added
base.
pOH pH OH M
pOH
= 14.00 =14.00 11.10 = 2.90 =10 = 10 = 0.0013
2.90
OH M
mL 0.200mmolOH
mLbase
mL mL mL
= 0.0013 = 1
+ 12.50 + 25.00 =0.200
37.50 +
x
x
x
x
bg
0.200 = 0.0013 37.50+ = 0.049 + 0.0013 = 0.049
0.200 0.0013 =0.25xxxx
bg mL excess
Total base added =12.5 mL to equivalence point + 0.25 mL excess = 12.8 mL
49. (D) For each of the titrations, the pH at the half-equivalence point equals the pKa of the acid.
The initial pH is that of 0.1000 M weak acid: 2
a3
[H O ]
0.1000
x
Kx
x
x must be found using the quadratic formula roots equation unless the approximation is
valid.
One method of determining if the approximation will be valid is to consider the ratio Ca/Ka. If
the value of Ca/Ka is greater than 1000, the assumption should be valid, however, if the value of
Ca/Ka is less than 1000, the quadratic should be solved exactly (i.e., the 5% rule will not be
satisfied).
The pH at the equivalence point is that of 0.05000 M anion of the weak acid, for which
the OH is determined as follows.
2
ww
b
aa
= = 0.05000 [OH ]
0.05000
KK
x
Kx
KK
We can determine the pH at the quarter and three quarter of the equivalence point by
using the Henderson-Hasselbalch equation (effectively + 0.48 pH unit added to the
pKa).
Chapter 17: Additional Aspects of Acid–Base Equilibria
832
And finally, when 0.100 mL of base has been added beyond the equivalence point, the
pH is determined by the excess added base, as follows (for all three titrations).
OH
mL 0.1000mmol NaOH
1mLNaOH soln
mmolOH
mmol NaOH
mL soln total M
=
0100 1
1
20.1 = 4.98 10 4
.
pOH log pH= 4.98 10 = 3.303 = 14.000 3.303 = 10.697
4
ch
(a) Ca/Ka = 14.3; thus, the approximation is not valid and the full quadratic equation
must be solved.
Initial: From the roots equation x = 3
[H O ] 0.023M
pH=1.63
Half equivalence point: pH = pKa = 2.15
pH at quarter equivalence point = 2.15 - 0.48 = 1.67
pH at three quarter equivalence point = 2.15 + 0.48 = 2.63
Equiv: x = 14 7
3
1.0 10
OH = 0.05000 2.7 10
7.0 10
pOH 6.57
pH 14.00 6.57 7.43
Indicator: bromthymol blue, yellow at pH = 6.2 and blue at pH = 7.8
(b) Ca/Ka = 333; thus, the approximation is not valid and the full quadratic equation
must be solved.
Initial: From the roots equation x = 3
[H O ] 0.0053M
pH=2.28
Half equivalence point: pH = pKa = 3.52
pH at quarter equivalence point = 3.52 - 0.48 = 3.04
pH at three quarter equivalence point = 3.52 + 0.48 = 4.00
Equiv: x = 14 6
4
1.0 10
OH = 0.05000 1.3 10
3.0 10
pOH
pH =14.00
589
589 811
.
..
Indicator: thymol blue, yellow at pH = 8.0 and blue at pH = 9.6
(c) C
a/Ka = 5×106; thus, the approximation is valid..
Initial: []. . .HO M
3
01000 2 0 10 0 000045
8pH = 4.35
pH at quarter equivalence point = 4.35 - 0.48 = 3.87
pH at three quarter equivalence point = 4.35 + 0.48 = 4.83
Half equivalence point: pH = pKa = 7.70
Equiv: x = OH
=10 10
2.0 10 0.0500 16 10
14
8
4
..
pOH
pH
380
14 00 380 10 20
.
.. .

Chapter 17: Additional Aspects of Acid–Base Equilibria
833
Indicator: alizarin yellow R, yellow at pH = 10.0 and violet at pH = 12.0
The three titration curves are drawn with respect to the same axes in the diagram below.
0
2
4
6
8
10
12
024681012
Volume of 0.10 M NaOH added (mL)
pH
50. (D) For each of the titrations, the pOH at the half-equivalence point equals the pb
K of
the base. The initial pOH is that of 0.1000 M weak base, determined as follows.
2
ba
; 0.1000 [OH ]
0.1000
x
KxK
x
if Cb/Kb > 1000. For those cases
where this is not the case, the approximation is invalid and the complete quadratic
equation must be solved. The pH at the equivalence point is that of 0.05000 M cation of
the weak base, for which the HO
3+ is determined as follows.
2+
ww
a 3
bb
0.05000 [H O ]
0.05000
KK
x
Kx
KK
And finally, when 0.100 mL of acid has been added beyond the equivalence point, the
pH for all three titrations is determined by the excess added acid, as follows.
+
3
+ 4
3
1 mmol H O
0.1000mmol HCl
0.100 mL HCl 1 mL HCl soln 1 mmol HCl
H O = = 4.98 10 M
20.1 mL soln total
pH log= 4.98 10 = 3.303
4
ch
(a) Cb/Kb = 100; thus, the approximation is not valid and the full quadratic equation must be solved.
Initial: From the roots equation x = 0.0095. Therefore,
[OH ] 0.0095 M pOH=2.02 pH=11.98
Half-equiv: pOH log pH= 1 10 = 3.0 = 11.0
3
ch
Equiv: x = 14
+7
33
1.0 10
[H O ] 0.05000 7 10 pH = 6.2
110
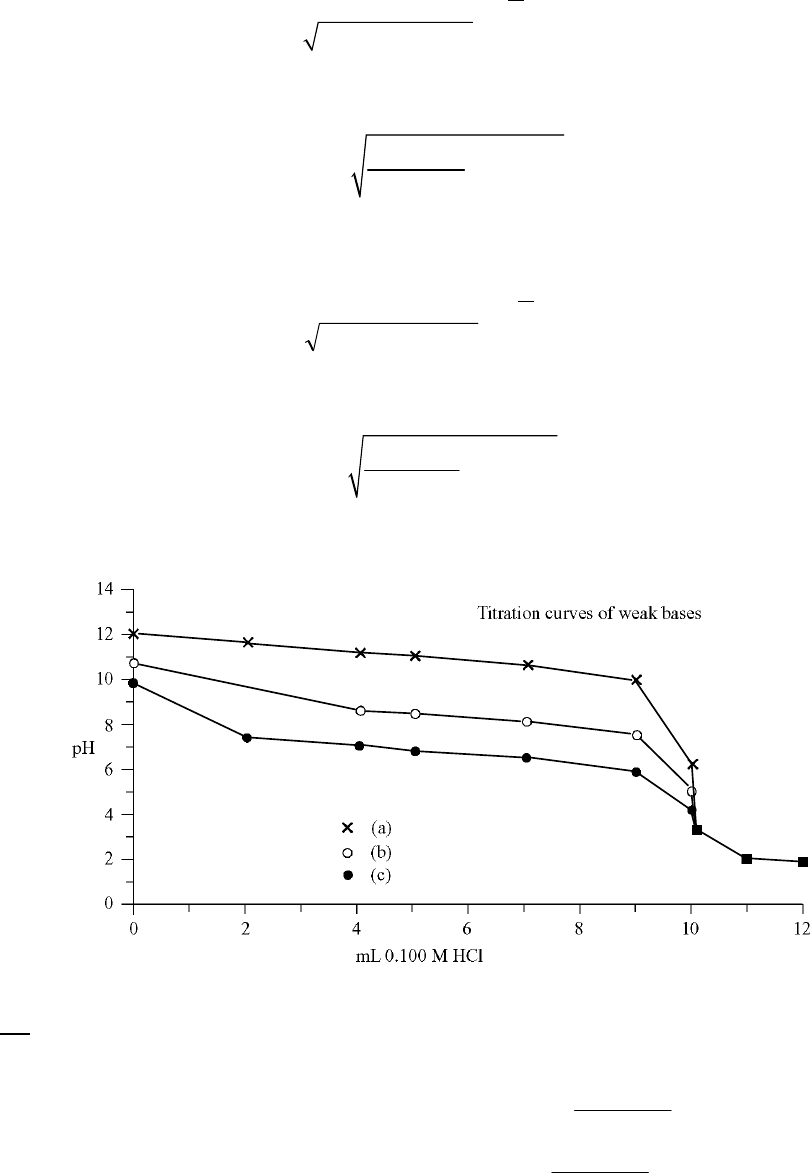
Chapter 17: Additional Aspects of Acid–Base Equilibria
834
Indicator: methyl red, yellow at pH = 6.3 and red at pH = 4.5
(b) Cb/Kb = 33,000; thus, the approximation is valid.
Initial: 64
[OH ] 0.1000 3 10 5.5 10 M pOH=3.3 pH=10.7
Half-equiv:
6
pOH = log 3 10 = 5.5 pH = 14 pOH pH = 8.5
Equiv: x = 14
+55
36
1.0 10
[H O ] 0.05000 1 10 pH -log(1 10 ) = 5.0
310
Indicator: methyl red, yellow at pH = 6.3 and red at pH = 4.5
(c) Cb/Kb = 1.4×106; thus, the approximation is valid.
Initial: [OH M pOH = 4.1 pH = 9.9
].01000 7 10 8 10
85
Half-equiv:
8
pOH = log 7 10 = 7.2 pH = 14 pOH pH = 6.8
Equiv: x = 14
+5
38
1.0 10
[H O ] 0.05000 8.5 10 pH=4.1
710
Indicator: bromcresol green, blue at pH = 5.5 and yellow at pH = 4.0
The titration curves are drawn with respect to the same axes in the diagram below.
51. (D) 25.00 mL of 0.100 M NaOH is titrated with 0.100 M HCl
(i) Initial pOH for 0.100 M NaOH: [OH] = 0.100 M, pOH = 1.000 or pH = 13.000
(ii) After addition of 24 mL: [NaOH] = 0.100 M 25.00 mL
49.00 mL = 0.0510 M
[HCl] = 0.100 M 24.00 mL
49.00 mL = 0.0490 M
Chapter 17: Additional Aspects of Acid–Base Equilibria
835
NaOH is in excess by 0.0020 M = [OH] pOH = 2.70
(iii) At the equivalence point (25.00 mL), the pOH should be 7.000 and pH = 7.000
(iv) After addition of 26 mL: [NaOH] = 0.100M 25.00
51.00 = 0.0490 M
[HCl] = 0.100 M 26.00 mL
51.00 mL = 0.0510 M
HCl is in excess by 0.0020 M = [H3O+] pH = 2.70 or pOH = 11.30
(v) After addition of 33.00 mL HCl( xs) [NaOH] = 0.100 M 25.00 mL
58.00 mL = 0.0431 M
[HCl] = 0.100 M 33.00 mL
58.00 mL = 0.0569 M [HCl]excess= 0.0138 M pH = 1.860, pOH = 12.140
The graphs look to be mirror images of one another. In reality, one must reflect about a
horizontal line centered at pH or pOH = 7 to obtain the other curve.
52. (D) 25.00 mL of 0.100 M NH3 is titrated with 0.100 M HCl Ka = w
b
K
K = 14
5
110
1.8 10
= 5.6 1010
(i) For initial pOH, use I.C.E.(initial, change, equilibrium) table.
NH3(aq) + H2O(l) -5
b
K = 1.8 10
NH4+(aq) + OH(aq)
Initial 0.100 M 0 M ≈ 0 M
Change x +x +x
Equil. 0.100 x x x
1.8 105 = 2
0.100
x
x
2
0.100
x
(Assume x ~0) x = 1.3 103
(x < 5% of 0.100, thus, the assumption is valid).
Hence, x = [OH] = 1.3 103 pOH = 2.89, pH = 11.11
(ii) After 2 mL of HCl is added: [HCl] = 0.100 M 2.00 mL
27.00 mL = 0.00741 M (after
dilution)
[NH3] = 0.100 M 25.00 mL
27.00 mL = 0.0926 M (after dilution)
0.100 M NaOH(25.00 mL) + 0.100 M HCl
0
2
4
6
8
10
12
14
0 102030405060
Volume of HCl (mL)
pOH
0.100 M NaOH(25.00 mL) + 0.100 M HCl
0
2
4
6
8
10
12
14
0 102030405060
Volume of HCl (mL)
pH

Chapter 17: Additional Aspects of Acid–Base Equilibria
836
The equilibrium constant for the neutralization reaction is large (Kneut = Kb/Kw =
1.9×105) and thus the reaction goes to nearly 100% completion. Assume that the
limiting reagent is used up (100% reaction in the reverse direction) and re-establish
the equilibrium by a shift in the forward direction. Here H3O+ (HCl) is the limiting
reagent.
NH4+(aq) + H2O(l) -10
a = 5.6 10K
NH3(aq) + H3O+(aq)
Initial 0 M
0.0926 M 0.00741 M
Change +x
x = 0.00741 x x
100% rxn 0.00741
0.0852 0
Change y
re-establish equilibrium +y +y
Equil 0.00741y
0.0852 + y y
5.6 1010 = (0.0852 )
(0.00741 )
yy
y
= (0.0852)
(0.00741)
y (set y ~ 0) y = 4.8 1011
(the approximation is clearly valid)
y = [H3O+] = 4.8 1011; pH = 10.32 and pOH = 3.68
(iii) pH at 1/2 equivalence point = pKa = log 5.6 1010 = 9.25 and pOH = 4.75
(iv) After addition of 24 mL of HCl:
[HCl] = 0.100 M 24.00 mL
49.00 mL = 0.0490 M; [NH3] = 0.100 M 25.00 mL
49.00 mL = 0.0510 M
The equilibrium constant for the neutralization reaction is large (see above), and thus
the reaction goes to nearly 100% completion. Assume that the limiting reagent is
used up (100% reaction in the reverse direction) and re-establish the equilibrium in
the reverse direction. Here H3O+ (HCl) is the limiting reagent.
NH4+(aq) + H2O(l) -10
a = 5.6 10K
NH3(aq) + H3O+(aq)
Initial 0 M
0.0541 M 0.0490 M
Change +x
x = 0.0490 x x
100% rxn 0.0490
0.0020 0
Change y
re-establish equilibrium +y +y
Equil 0.0490y
0.0020 + y y
5.6 1010 = (0.0020 )
(0.0490 )
y
y
y
= (0.0020)
(0.0490)
y (Assume y ~ 0) y = 1.3 108 (valid)
y = [H3O+] = 1.3 108 ; pH = 7.89 and pOH = 6.11
(v) Equiv. point: 100% reaction of NH3 NH4+: [NH4+] = 0.100 25.00 mL
50.00 mL =0.0500 M
NH4+(aq) + H2O(l) -10
a = 5.6 10K
NH3(aq) + H3O+(aq)
Initial 0.0500 M
0 M ~ 0 M
Change x
+x +x
Equil 0.0500x
x x

Chapter 17: Additional Aspects of Acid–Base Equilibria
837
5.6 1010=2
(0.0500 )
x
x
=2
0.0500
x
(Assume x ~ 0) x = 5.3 106
(the approximation is clearly valid)
x = [H3O+] = 5.3 106 ; pH = 5.28 and pOH = 8.72
(vi) After addition of 26 mL of HCl, HCl is in excess. The pH and pOH should be the
same as those in Exercise 51. pH = 2.70 and pOH = 11.30
(vii) After addition of 33 mL of HCl, HCl is in excess. The pH and pOH should be the
same as those in Exercise 51. pH = 1.860 and pOH = 12.140. This time the curves
are not mirror images of one another, but rather they are related through a
reflection in a horizontal line centered at pH or pOH = 7.
0.100 M NH3 (25mL) + 0.100 HCl
0
2
4
6
8
10
12
14
0 1020304050
Volume of HCl (mL)
pOH
0.100 M NH3 (25mL) + 0.100 HCl
0
2
4
6
8
10
12
14
0 1020304050
Volume of HCl (mL)
pH
Salts of Polyprotic Acids
53. (E) We expect a solution of Na S
2 to be alkaline, or basic. This alkalinity is created by the
hydrolysis of the sulfide ion, the anion of a very weak acid ( K219
=1 10for H S
2).
2
2
S aq+HO(l) HS aq+OH aq
54. (E) We expect the pH of a solution of sodium dihydrogen citrate, NaH Cit
2, to be acidic
because the p a
K values of first and second ionization constants of polyprotic acids are
reasonably large. The pH of a solution of the salt is the average of pK1 and pK2. For citric
acid, in fact, this average is
3.13+ 4.77 2 = 3.95. Thus, NaH2Cit affords acidic
solutions.
55. (M)
(a)
2
34 3 24 3
HPO aq+CO aq HPO aq+HCO aq
22
24 3 4 3
HPO aq+CO aq HPO aq+HCO aq
23
442
HPO aq + OH aq PO aq + H O(l)

Chapter 17: Additional Aspects of Acid–Base Equilibria
838
(b) The pH values of 1.00 M solutions of the three ions are;
1.0 M OH pH = 14.00 1.0 M CO3
2 pH =12.16 1.0 M PO4
3pH =13.15
Thus, we see that CO3
2 is not a strong enough base to remove the third proton
from HPO
34
. As an alternative method of solving this problem, we can compute
the equilibrium constants of the reactions of carbonate ion withHPO
34
, H2PO4-
and HPO42-.
3
28
34
1
34 3 24 3 11
23
2
{H PO } 7.1 10
HPO +CO HPO +HCO 1.5 10
{H CO } 4.7 10
a
a
K
KK
8
22 3
34
2
24 3 4 3 11
23
2
{H PO } 6.3 10
H PO + CO HPO + HCO 1.3 10
{H CO } 4.7 10
a
a
K
KK
13
22 3 3
34
3
43 4 3 11
23
2
{H PO } 4.2 10
HPO + CO PO + HCO 8.9 10
{H CO } 4.7 10
a
a
K
KK
Since the equilibrium constant for the third reaction is much smaller than 1.00, we
conclude that it proceeds to the right to only a negligible extent and thus is not a
practical method of producing PO4
3. The other two reactions have large
equilibrium constants, and products are expected to strongly predominate. They
have the advantage of involving an inexpensive base and, even if they do not go to
completion, they will be drawn to completion by reaction with OH in the last step
of the process.
56. (M) We expect CO32- to hydrolyze and the hydrolysis products to determine the pH of
the solution.
Equation: 32
HCO (aq) H O(l)
23
"H CO "(aq) + OH aq)
(
Initial 1.00 M
0 M
0 M
Changes: –x M
+x M +x M
Equil: (1.00 – x) M
x M x M
14 2
23
8
w
b7
13
HCO OH
1.00 10
== =2.310= =
4.4 10 1.00 1.00
HCO
xx
K
x
KKx
(Cb/Kb = a very large number; thus, the approximation is valid).
x
1002310 1510
84
.. . []MOH; pOH=
log( . ) .15 10 382
4 pH = 10.18
For
1.00M NaOH, OH = 1.00 pOH = log 1.00 = 0.00 pH =14.00
Both 1.00 3
M NaHCO and 1.00 M NaOH have an equal capacity to neutralize acids
since one mole of each neutralizes one mole of strong acid.
++
32
NaOH aq + H O aq Na aq + 2H O(l)

Chapter 17: Additional Aspects of Acid–Base Equilibria
839
++
33 2 2
NaHCO aq + H O aq Na aq + CO g + 2H O(l).
But on a per gram basis, the one with the smaller molar mass is the more effective.
Because the molar mass of NaOH is 40.0 g/mol, while that of NaHCO3 is 84.0 g/mol,
NaOH(s) is more than twice as effective as NaHCO3(s) on a per gram basis. NaHCO3 is
preferred in laboratories for safety and expense reasons. NaOH is not a good choice
because it can cause severe burns. NaHCO3, baking soda, by comparison, is relatively
non-hazardous. It also is much cheaper than NaOH.
57. (M) Malonic acid has the formula H2C3H2O4 MM = 104.06 g/mol
Moles of H2C3H2O4 = 19.5 g 1 mol
104.06 g = 0.187 mol
Concentration of H2C3H2O4 = moles
V = 0.187 moles
0.250 L = 0.748 M
The second proton that can dissociate has a negligible effect on pH ( 2
a
Kis very small).
Thus the pH is determined almost entirely by the first proton loss.
H
2A(aq) + H2O(l)
HA(aq) +H
3O+(aq)
Initial 0.748 M 0 M ≈ 0 M
Change x +x +x
Equil 0.748x x x
So, x = 2 = ;
0.748 a
xK
x pH = 1.47, therefore, [H3O+] = 0.034 M = x ,
1
a
K= 2
(0.034)
0.748 0.034= 1.6 103
(1.5 103 in tables, difference owing to ionization of the second proton)
HA-(aq) + H2O(l)
A2(aq) +H
3O+(aq)
Initial 0.300 M 0 M ≈ 0 M
Change x +x +x
Equil 0.300x x x
pH = 4.26, therefore, [H3O+] = 5.5 105 M = x, 2
a
K= 52
5
(5.5 10 )
0.300 5.5 10
= 1.0 108
58. (M) Ortho-phthalic acid. 1
a
K = 1.1 103, 2
a
K= 3.9 106
(a) We have a solution of HA.
HA(aq) + H2O(l)
A2(aq) +H
3O+(aq)
Initial 0.350 M
0 M ~ 0 M
Change x
+x +x
Equil 0.350x
x x

Chapter 17: Additional Aspects of Acid–Base Equilibria
840
3.9 106 = 22
0.350 0.350
x
x
x , x = 1.2 103
(x 0.350, thus, the approximation is valid)
x = [H3O+] = 1.2 103, pH = 2.92
(b) 36.35 g of potassium ortho-phthalate (MM = 242.314 g mol1)
moles of potassium ortho-phthalate = 36.35 g1 mol
242.314 g = 0.150 mol in 1 L
A2(aq) + H2O(l)
HA(aq) +OH(aq)
Initial 0.150 M
0 M ≈ 0 M
Change x
+x +x
Equil 0.150 x
x x
2
2
14 2 2
9
w
6
b,A a
1.0 10 2.6 10 0.150 0.150
3.9 10
K
x
x
KKx
5
2.0 10x
(x << 0.150, so the approximation is valid) = [OH]
pOH = log 2.0105 = 4.70; pH = 9.30
General Acid–Base Equilibria
59. (E)
(a) Ba OH
bg2 is a strong base.
2.12
p
OH = 14.00 11.88 = 2.12 OH = 10 = 0.0076 M
Ba OH mol OH
L
mol Ba OH
mol OH M
bgbg
2
2
=0.0076
1
1
2= 0.0038
(b) 232
a
232 232
CHO 0.294 M
pH = 4.52 = p + log = 4.74 + log
HC H O HC H O
K
232
0.294 M
log = 4.52 4.74
HC H O
0.22
232
0.294 M =10 = 0.60
HC H O
232
0.294 M
HC H O = = 0.49 M
0.60
Chapter 17: Additional Aspects of Acid–Base Equilibria
841
60. (M)
(a) pOH OH M= 14.00 8.95 = 5.05 = 10 = 8.9 10
5.05 6
Equation: 65 2 2
C H NH (aq) H O(l)
CHNH (aq)
65 3
OH aq)
(
Initial x M
0 M 0 M
Changes:
89 10 6
.M
89 10 6
.M
89 10 6
.M
Equil: (. )x
89 10 6M
89 10 6
.M 89 10 6
.M
Kx
b
C H NH OH
CHNH
= = 7.4 10 = 8.9 10
8.9 10
65 3
+
65 2
10
62
6
L
N
MO
Q
P
ch
xx
8.9 10 = 8.9 10
7.4 10 = 0.11 = 0.11 =
6
62
10
ch
M M molarity of aniline
(b) HO M
3+5.12 6
= 10 = 7.6 10
Equation: +
42
NH (aq) H O(l)
NH (aq)
3 HO aq)
3
(
Initial x M
0 M 0 M
Changes:
76 10 6
.M
76 10 6
.M
76 10 6
.M
Equil: (. )x
76 10 6M
76 10 6
.M 76 10 6
.M
KK
Kx
aw
b
NH H O
NH for NH
===
1.0 10
1.8 10 = 5.6 10 = 7.6 10
7.6 10
33
+
4
+3
14
5
10
62
6
ch
xx
7.6 10 = 7.6 10
5.6 10 = 0.10 = = = 0.10
6
62
10 4
+
4
ch
MNHNHClM
61. (M)
(a) A solution can be prepared with equal concentrations of weak acid and conjugate
base (it would be a buffer, with a buffer ratio of 1.00, where the pH = pKa = 9.26).
Clearly, this solution can be prepared, however, it would not have a pH of 6.07.
(b) These solutes can be added to the same solution, but the final solution will have an
appreciable HC H O
232
because of the reaction of H O aq
3+bg
with CHO aq
232
bg
Equation: HO(aq)
3+ + CHO (aq)
232
232 2
HC H O (aq) + H O(l)
Initial 0.058 M 0.10 M 0 M
Changes: –0.058 M –0.058 M +0.058 M
Equil: ≈0.000 M 0.04 M 0.058 M
Of course, some H O
3+ will exist in the final solution, but not equivalent to 0.058 M HI.
Chapter 17: Additional Aspects of Acid–Base Equilibria
842
(c) Both 0.10 M KNO2 and 0.25 M KNO3 can exist together. Some hydrolysis of the
NO aq
2
bg ion will occur, forming HNO aq
2bgand OH-(aq).
(d) Ba OH
bg2 is a strong base and will react as much as possible with the weak
conjugate acid NH4
, to form NH aq
3bg.We will end up with a solution
of BaCl aq NH aq
23
,
bgbg, and unreacted NH Cl aq
4bg.
(e) This will be a benzoic acid–benzoate ion buffer solution. Since the two
components have the same concentration, the buffer solution will have
pH p log
a
= = 6.3 10 = 4.20
5
K
ch. This solution can indeed exist.
(f) The first three components contain no ions that will hydrolyze. But C H O
232
is
the anion of a weak acid and will hydrolyze to form a slightly basic solution.
Since pH = 6.4 is an acidic solution, the solution described cannot exist.
62. (M)
(a) When HO
3+ and HC H O
232
are high and CHO
232
is very low, a common
+
3
ion H O has been added to a solution of acetic acid, suppressing its ionization.
(b) When CHO
232
is high and HO
3+ and HC H O
232
are very low, we are
dealing with a solution of acetate ion, which hydrolyzes to produce a small
concentration of HC H O
232
.
(c) When HC H O
232
is high and both HO
3+ and CHO
232
are low, the
solution is an acetic acid solution, in which the solute is partially ionized.
(d) When both HC H O
232
and CHO
232
are high while HO
3+ is low, the
solution is a buffer solution, in which the presence of acetate ion suppresses the
ionization of acetic acid.
INTEGRATIVE AND EXERCISES
63. (M)
(a) O(l)H(aq)SONaNaOH(aq)(aq)NaHSO 2424
O(l)Haq)(SO(aq)OHaq)(HSO 2
–2
4
–
4
(b) We first determine the mass of NaHSO4.
4
4
4
4
4
NaHSO g 988.0
NaHSO mol 1
NaHSO g 06.120
NaOH mol 1
NaHSO mol 1
L 1
NaOH mol 225.0
mL 1000
L 1
mL 56.36NaHSO mass
Chapter 17: Additional Aspects of Acid–Base Equilibria
843
4
1.016 g sample – 0.988 g NaHSO
% NaCl 100% 2.8% NaCl
1.016 g sample
(c) At the endpoint of this titration the solution is one of predominantly SO42–, from
which the pH is determined by hydrolysis. Since Ka for HSO4– is relatively large (1.1
× 10–2), base hydrolysis of SO42– should not occur to a very great extent. The pH of a
neutralized solution should be very nearly 7, and most of the indicators represented
in Figure 17-8 would be suitable. A more exact solution follows.
2
2- 444
4
44
1 mol SO
0.988 g NaHSO 1 mol NaHSO
[SO ] 0.225 M
0.03656 L 120.06 g NaHSO 1 mol NaHSO
2-–
42 4
Equation: SO (aq) H O(l) HSO (aq) OH (aq)
Initial: 0.225 M 0 M 0 M
Changes: M M M
Equil: (0.225 )M M M
xxx
xxx
225.0225.0
101.9
101.1
100.1
]SO[
]OH[][HSO 2
13
2
14
w
4
–
4
b
2
–2
–x
x
xx
K
K
K
a
–13 7
7
[OH ] 9.1 10 0.225 4.5 10 M
(the approximation was valid since << 0.225 M)
pOH –log(4.5 10 ) 6.35 pH 14.00 6.35 7.65
x
Thus, either bromthymol blue (pH color change range from pH = 6.1 to pH = 7.9) or
phenol red (pH color change range from pH = 6.4 to pH = 8.0) would be a suitable
indicator, since either changes color at pH = 7.65.
64. (D) The original solution contains 352 352
0.100 mmol HC H O
250.0 mL 25.0 mmol HC H O
1 mL soln
5
a
p log(1.35 10 ) 4.87K
We let V be the volume added to the solution, in mL.
(a) Since we add V mL of HCl solution (and each mL adds 1.00 mmol H3O+ to the
solution), we have added V mmol H3O+ to the solution. Now the final [H3O+] = 10–1.00
= 0.100 M.
3
3
mmol H O
[H O ] 0.100 M
(250.0 ) mL
25.0
25.0 0.100 , therefore, 27.8 mL added
0.900
V
V
VVV
Now, we check our assumptions. The total solution volume is 250.0 mL+ 27.8 mL =
277.8 mL There are 25.0 mmol HC2H3O2 present before equilibrium is established,
and 27.8 mmol H3O+ also.

Chapter 17: Additional Aspects of Acid–Base Equilibria
844
232 3
25.0 mmol 27.8 mmol
[HC H O ] 0.0900 M [H O ] 0.100 M
277.8 mL 277.8 mL
352 2 35 3
2
335 5
2
a
352
Equation: HC H O ( ) H O(l) C H O ( ) H O ( )
Initial: 0.0900 M 0 M 0.100 M
Changes: - M M M
Equil: (0.08999 M M (0.100 x)M
[H O ][C H O ] (0.100 ) 0.10
1.35 10
[HC H O ] 0.0900
aq aq aq
xxx
x) x
xx
Kx
5
0 1.22 10 M
0.0900
xx
The assumption used in solving this equilibrium situation, that x << 0.0900
clearly is correct. In addition, the tacit assumption that virtually all of the H3O+
comes from the HCl also is correct.
(b) The pH desired is within 1.00 pH unit of the pKa. We use the Henderson-
Hasselbalch equation to find the required buffer ratio.
-- -
-- -
-
–AA A
aa a
HA HA HA
0.87
AA A
A
HA HA
352
soln 3 5 2352
/V
[A ]
pH p p log P log 4.00 4.87 log
[HA] / V
log 0.87 10 0.13 3.3
25.00
1 mmol NaC H O 1 mL
V 3.3 mmol C H O 1 mmol C H O
nn n
KK K
nn n
nn n
n
nn
352
soln 3.3 mL added
1.00 mmol NaC H O
We have assumed that all of the C3H5O2– is obtained from the NaC3H5O2 solution,
since the addition of that ion in the solution should suppress the ionization of
HC3H5O2.
(c) We let V be the final volume of the solution.
352 2 35 3
2
Equation: HC H O ( ) H O(l) C H O ( ) H O ( )
Initial: 25.0/ 0 M 0 M
Changes: M M M
Equil: (25.0/ M M M
aq aq aq
V
x/V x/V x/V
V x/V) x/V x/V
0.25
/
//0.25
)/(
1035.1
]OHHC[
]OHC[]OH[ 22
5
253
2
533
a
Vx
VxV
Vx
K
When V = 250.0 mL, x = 0.29 mmol H3O+ M 102.1
mL 250.0
mmol 29.0
]OH[ 3
3
pH = –log(1.2 × 10–3) = 2.92
An increase of 0.15 pH unit gives pH = 2.92 + 0.15 = 3.07
Chapter 17: Additional Aspects of Acid–Base Equilibria
845
[H3O+] = 10–3.07 = 8.5 × 10–4 M This is the value of x/V. Now solve for V.
42 42
5 4
45
2
(8.5 10 ) (8.5 10 )
1.3 10 25.0 / 8.5 10 0.056
25.0 / 8.5 10 1.3 10
25.0
25.0 / 0.056 0.00085 0.057 4.4 10 mL
0.057
V
V
VV
On the other hand, if we had used [H3O+] = 1.16 × 10–3 M (rather than
1.2 × 10–3 M), we would obtain V = 4.8 × 102 mL. The answer to the problem thus
is sensitive to the last significant figure that is retained. We obtain V = 4.6 × 102
mL, requiring the addition of 2.1 × 102 mL of H2O.
Another possibility is to recognize that [H3O+] aa
KC for a weak acid with
ionization constant Ka and initial concentration Ca if the approximation is valid.
If Ca is changed to Ca/2, [H3O+] a22.
a
KC Since, pH = –log [H3O+], the
change in pH given by:
15.030103.05.02log5.02log2logpH 2/1 .
This corresponds to doubling the solution volume, that is, to adding 250 mL water.
Diluted by half with water, [H3O+] goes down and pH rises, then (pH1 – pH2) < 0.
65. (E) Carbonic acid is unstable in aqueous solution, decomposing to CO2(aq) and H2O.
The CO2(aq), in turn, escapes from the solution, to a degree determined in large part
by the partial pressure of CO2(g) in the atmosphere.
H2CO3(aq) H2O(l) + CO2(aq) CO2(g) + H2O(l)
Thus, a solution of carbonic acid in the laboratory soon will reach a low [H2CO3], since
the partial pressure of CO2(g) in the atmosphere is quite low. Thus, such a solution
would be unreliable as a buffer. In the body, however, the [H2CO3] is regulated in part
by the process of respiration. Respiration rates increase when it is necessary to decrease
[H2CO3] and respiration rates decrease when it is necessary to increase [H2CO3].
66. (E)
(a) At a pH = 2.00, in Figure 17-9 the pH is changing gradually with added NaOH. There
would be no sudden change in color with the addition of a small volume of NaOH.
(b) At pH = 2.0 in Figure 17-9, approximately 20.5 mL have been added. Since,
equivalence required the addition of 25.0 mL, there are 4.5 mL left to add.
Therefore,
4.5
% HCl unneutralized 100% 18%
25.0

Chapter 17: Additional Aspects of Acid–Base Equilibria
846
67. (D) Let us begin the derivation with the definition of [H3O+].
3
3
amount of excess H O
[H O ] volume of titrant volume of solution being titrated
Let volume of acid ( solution being titrated) volume of base (titrant)
molarity of a
a b
a
VV
M
3
cid molarity of base
[H O ]
b
aabb
ab
M
VMVM
VV
Now we solve this equation for Vb
b
aa
b
b
aa
b
aabbbabbaa
M
MV
V
M
MV
V
MVMVVVMVMV
pH
pH
3
3
333
10
)10(
]OH[
])OH[(
])OH[()]OH([)(]OH[
(a) pH 2.00 2 20.00 mL (0.1500 0.010)
10 10 1.0 10 M 25.45 mL
0.010 0.1000
b
V
(b) pH 3.50 4 20.00 mL (0.1500 0.0003)
10 10 3.2 10 M 29.85 mL
0.0003 0.1000
b
V
(c) pH 5.00 5 20.00 mL (0.1500 0.00001)
10 10 1.0 10 M 30.00 mL
0.00001 0.1000
b
V
Beyond the equivalence point, the situation is different.
ba
aabb
VV
MVMV
olumesolution v total
OH excess ofamount
]OH[ –
–
Solve this equation for Vb. [OH–](Va + Vb) = Vb × Mb – Va × Ma
]OH[
)]OH([
])OH[()]OH([ –
–
––
b
aa
bbbaa M
MV
VMVMV
(d) pOH 14.00 pH 3.50
[OH ] 10 10 10 0.00032 M;
0.00032 0.1500
20.00 mL 30.16 mL
0.1000 0.00032
b
V
(e)
pOH 14.00 pH 2.00
[OH ] 10 10 10 0.010 M;
0.010 0.1500
20.00 mL 35.56 mL
0.1000 0.010
b
V
The initial pH = –log(0.150) = 0.824. The titration curve is sketched below.
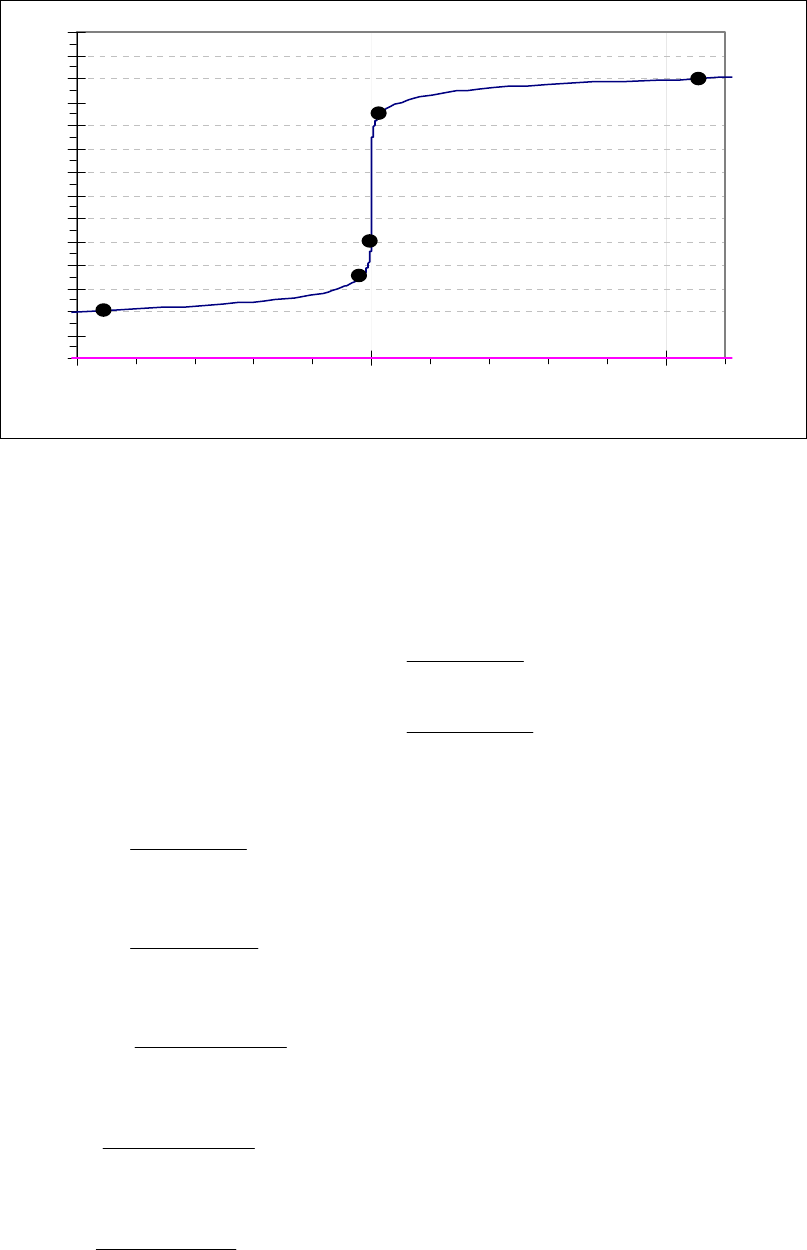
Chapter 17: Additional Aspects of Acid–Base Equilibria
847
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
25 30 35
Volume NaOH (ml)
pH
68. (D)
(a) The expressions that we obtained in Exercise 67 were for an acid being titrated by a
base. For this titration, we need to switch the a and b subscripts and exchange [OH–]
and [H3O+].
]OH[
]OH[
:point eequivalenc After the
]OH[
]OH[
:point eequivalenc theBefore
3
3
a
b
ba
a
b
ba
M
M
VV
M
M
VV
1.00 1
2.00 2
pH 13.00 pOH 14.00 13.00 1.00 [OH ] 10 1.0 10 0.10 M
0.250 0.10
25.00 mL 9.38 mL
0.10 0.300
pH 12.00 pOH 14.00 12.00 2.00 [OH ] 10 1.0 10 0.010 M
0.250 0.010
25.00 mL 0.0
a
a
V
V
19.4 mL
10 0.300
4.00 4
4.00 4
3
pH 10.00 pOH 14.00 10.00 4.00 [OH ] 10 1.0 10 0.00010 M
0.250 0.00010
25.00 mL 20.8 mL
0.00010 0.300
pH 4.00 [H O ] 10 1.0 10 0.00010 M
0.00010 0.250
25.00 20.
0.300 0.00010
a
a
V
V
3.00 3
3
8 mL
pH 3.00 [H O ] 10 1.0 10 0.0010 M
0.0010 0.250
25.00 21.0 mL
0.300 0.0010
a
V
Chapter 17: Additional Aspects of Acid–Base Equilibria
848
(b) Our expression does not include the equilibrium constant, Ka. But Ka is not needed
after the equivalence point. pOH = 14.00 – 11.50 = 2.50 [OH–] = 10–2.50 = 3.2 × 10–3
= 0.0032 M
mL 1.14
0032.00500.0
0.0032)(0.0100 mL 00.50
]O[
])O[(
HM
HMV
V
b
aa
b
Let us use the Henderson-Hasselbalch equation as a basis to derive an expression that
incorporates Ka. Note that because the numerator and denominator of that expression
are concentrations of substances present in the same volume of solution, those
concentrations can be replaced by numbers of moles.
Amount of anion = VbMb since the added OH– reacts 1:1 with the weak acid.
Amount of acid = VaMa – VbMb the acid left unreacted
bbaa
bb
MVMV
MV
KK
logp
HA][
][A
logppH aa
Rearrange and solve for Vb
bbaa
bb
MVMV
MV
pKpH
10
)101(
10
10 )( pKpH
pKpH
pKpH
b
aa
bbbbbaa M
MV
VMVMVMV
pH pK 4.50 4.20
pH pK 5.50 4.20
50.00 mL 0.0100 M 2.0
pH 4.50, 10 10 2.0 6.7 mL
0.0500(1 2.0)
50.00 mL 0.0100 M 20
pH 5.50, 10 10 20. 9.5 mL
0.0500(1 20.)
b
b
V
V
69. (M)
(a) We concentrate on the ratio of concentrations of which the logarithm is taken.
eq
eq
[conjugate base] equil. amount conj. base initial amt. weak acid
[weak acid] equil. amount weak acid (1 ) initial amt. weak acid 1
f
f
f
f
The first transformation is the result of realizing that the volume in which the weak acid
and its conjugate base are dissolved is the same volume, and therefore the ratio of
equilibrium amounts is the same as the ratio of concentrations. The second
transformation is the result of realizing, for instance, that if 0.40 of the weak acid has
been titrated, 0.40 of the original amount of weak acid now is in the form of its
conjugate base, and 0.60 of that amount remains as weak acid. Equation 17.2 then is:
pH = pKa + log (f /(1 – f ))
(b) We use the equation just derived.
0.27
pH 10.00 log 9.56
1 0.23
Chapter 17: Additional Aspects of Acid–Base Equilibria
849
70. (M)
(a) 0.20
2
222
2- 2- 2-
444
---
444
[HPO ] [HPO ] [HPO ]
pH p log 7.20 log 7.40 10 1.6
[H PO ] [H PO ] [H PO ]
a
K
(b) In order for the solution to be isotonic, it must have the same concentration of ions
as does the isotonic NaCl solution.
M 31.0
NaCl mol 1
ions mol 2
NaCl g 44.58
NaCl mol 1
soln L 1
NaCl g 9.2
ions][
Thus, 1.00 L of the buffer must contain 0.31 moles of ions. The two solutes that are
used to formulate the buffer both ionize: KH2PO4 produces 2 mol of ions (K+ and
H2PO4–) per mole of solute, while OH 12HPONa 242
produces 3 mol of ions (2 Na+
and HPO42– ) per mole of solute. We let x = amount of KH2PO4 and y = amount of
OH 12HPONa 242 .
24 2 4 2
1.6 or 1.6 2 3 0.31 2 3(1.6 ) 6.8
0.31 0.046 mol KH PO 1.6 0.046 0.074 mol Na HPO 12 H O
6.8
yyx xy x x x
x
xy
24
24 24 24
24
136.08 g KH PO
mass KH PO 0.046 mol KH PO 6.3 g KH PO
1 mol KH PO
24 2
24 2 24 2
24 2
24 2
358.1 g Na HPO 12H O
mass of Na HPO 12H O 0.074 mol Na HPO 12H O 1 mol Na HPO 12H O
26 g Na HPO 12H O
71. (M) A solution of NH4Cl should be acidic, hence, we should add an alkaline solution to
make it pH neutral. We base our calculation on the ionization equation for NH3(aq), and
assume that little NH4+(aq) is transformed to NH3(aq) because of the inhibition of that
reaction by the added NH3(aq), and because the added volume of NH3(aq) does not
significantly alter the Vtotal.
32 4
7
75
4
b
3
Equation: NH (aq) H O(l) NH (aq) OH (aq)
Initial: M 0.500 M 1.0 10 M
[NH ][OH ] (0.500 M)(1.0 10 M) 1.8 10
[NH ] M
(0.500 M)(1.0 10
M
x
Kx
x
73
3
5
3
3
3
M) 2.8 10 M [NH ]
1.8 10 M
2.8 10 mol NH 1 L conc. soln 1 drop
V 500 mL = 2.8 drops 3 drops
1 L final soln 10.0 mol NH 0.05 mL

Chapter 17: Additional Aspects of Acid–Base Equilibria
850
72. (D)
(a) In order to sketch the titration curve, we need the pH at the following points.
i ) Initial point. That is the pH of 0.0100 M p-nitrophenol, which we represent by
the general formula for an indicator that also is a weak acid, HIn.
–
23
Equation: HIn(aq) H O(l) H O (aq) In (aq)
Initial: 0.0100 M – 0 M 0 M
Changes: – M – M M
Equil: (0.0100– ) M – M M
xxx
xxx
–2
7.15 8 3
HIn
5
aa
85 –5
3
[H O ] [In ]
10 7.1 10 [HIn] 0.0100 0.0100
/ 1 10 ; thus, the approximation is valid
[H O ] 0.0100 7.1 10 2.7 10 M pH –log(2.7 10 ) 4.57
xx x
Kx
CK
ii) At the half-equivalence point, the pH = pKHIn = 7.15
iii) At the equiv point, pH is that of In–. nIn– = 25.00 mL × 0.0100 M = 0.250 mmol In–
titrant
3
1 mmol NaOH 1 mL titrant
V = 0.25 mmol HIn 12.5 mL titrant
1 mmol HIn 0.0200 mmol NaOH
0.25 mmol In
[In ] 6.67 10 M 0.00667 M
25.00 mL 12.5 mL
2
Equation: In (aq) H O(l) HIn(aq) OH (aq)
Initial: 0.00667 M 0 M 0 M
Changes: M M M
Equil: (0.00667 ) M M M
xxx
xxx
47
w
b8
a
[HIn][OH ] 1.0 10 1.4 10
[In ] 7.1 10 0.00667 0.00667
Kxx xx
KKx
(Ca/Ka = 1.4×105; thus, the approximation is valid)
75
5
[OH ] 0.00667 1.4 10 3.1 10
pOH log(3.1 10 ) 4.51; therefore, pH 14.00 pOH 9.49
iv) Beyond the equivalence point, the pH is determined by the amount of excess OH–
in solution. After 13.0 mL of 0.0200 M NaOH is added, 0.50 mL is in excess, and
the total volume is 38.0 mL.
10.42pH 3.58pOH M1063.2
mL 0.38
M 0.0200mL 50.0
]OH[ 4
After 14.0 mL of 0.0200 M NaOH is added, 1.50 mL is in excess, and Vtotal =
39.0 mL.
10.89pH 3.11pOH M 1069.7
mL 0.39
M 0.0200mL 50.1
]OH[ 4
v) In the buffer region, the pH is determined with the use of the Henderson-
Hasselbalch equation.
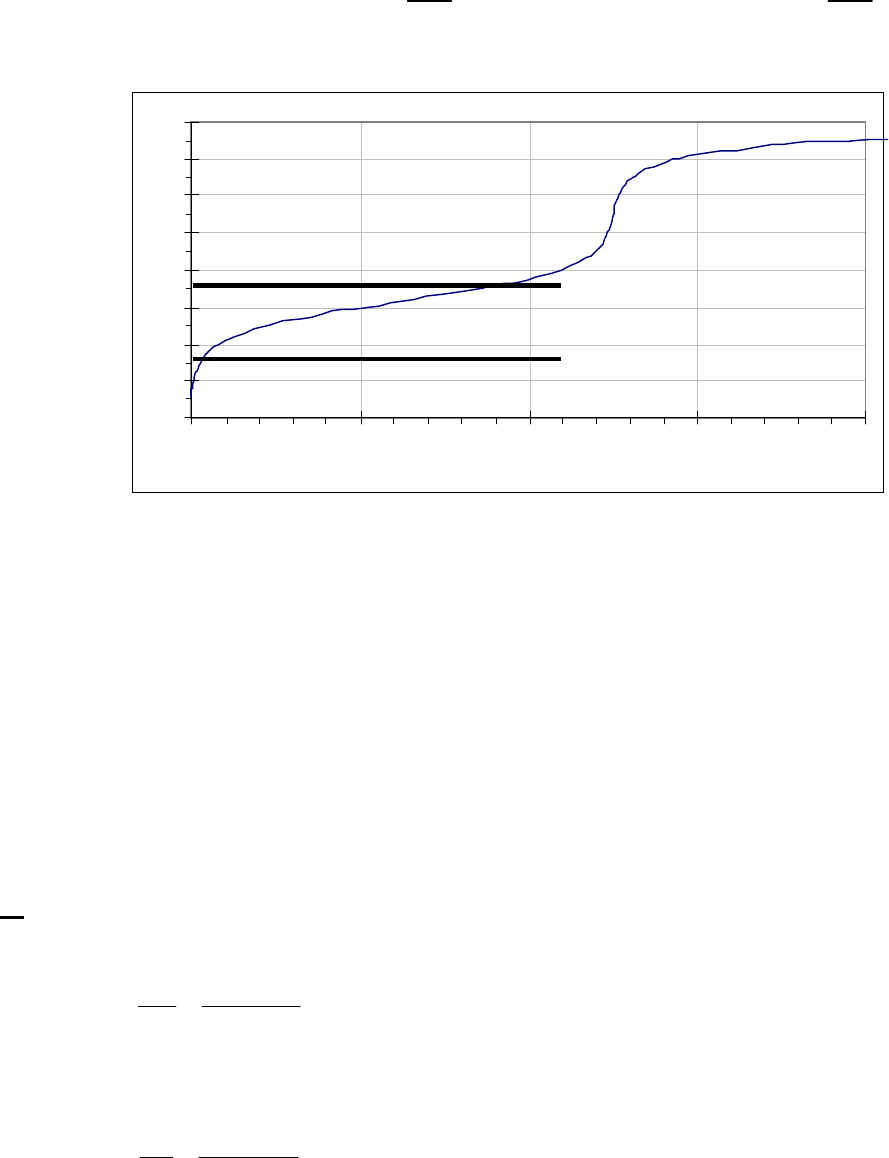
Chapter 17: Additional Aspects of Acid–Base Equilibria
851
0.10 0.90
At 0.10, pH 7.15 log 6.20 At 0.90, pH 7.15 log 8.10
0.90 0.10
ff
f = 0.10 occurs with 0.10 × 12.5 mL = 1.25 mL added titrant; f = 0.90 with 11.25
mL added. The titration curve plotted from these points follows.
4
5
6
7
8
9
10
11
12
0 5 10 15 20
Volume NaOH (ml)
pH
(b) The pH color change range of the indicator is shown on the titration curve.
(c) The equivalence point of the titration occurs at a pH of 9.49, far above the pH at which
p-nitrophenol has turned yellow. In fact, the color of the indicator changes gradually during the
course of the titration, making it unsuitable as an indicator for this titration.
Possible indicators are as follows.
Phenolphthalein: pH color change range from colorless at pH = 8.0 to red at pH = 10.0
Thymol blue: pH color change range from yellow at pH = 8.0 to blue at pH = 9.8
Thymolphthalein: pH color change range from colorless at 9pH
to blue at 11pH
The red tint of phenolphthalein will appear orange in the titrated p-nitrophenol
solution. The blue of thymol blue or thymolphthalein will appear green in the titrated
p-nitrophenol solution, producing a somewhat better yellow end point than the orange
phenolphthalein endpoint.
73. (M)
(a) Equation (1) is the reverse of the equation for the autoionization of water. Thus, its
equilibrium constant is simply the inverse of Kw.
14
14
w
1000.1
100.1
11
K
K
Equation (2) is the reverse of the hydrolysis reaction for NH4+. Thus, its equilibrium
constant is simply the inverse of the acid ionization constant for NH4+, Ka =
5.6 × 10-10
9
10
a
108.1
106.5
11
'
K
K

Chapter 17: Additional Aspects of Acid–Base Equilibria
852
(b) The extremely large size of each equilibrium constant indicates that each reaction goes
essentially to completion. In fact, a general rule of thumb suggests that a reaction is considered
essentially complete if Keq > 1000 for the reaction.
74. (D) The initial pH is that of 0.100 M HC2H3O2.
232 2 232 3
Equation: HC H O (aq) H O(l) C H O (aq) H O (aq)
Initial: 0.100 M 0 M 0 M
Changes: M M M
Equil:
xxx
2
5
3232
a
232
(0.100 ) M M M
[H O ][C H O ] 1.8 10
[HC H O ] 0.100 0.100
xxx
xx x
Kx
(Ca/Ka = 5.5×103; thus, the approximation is valid)
53 3
3
[H O ] 0.100 1.8 10 1.3 10 M pH log(1.3 10 ) 2.89
At the equivalence point, we have a solution of NH4C2H3O2 which has a pH = 7.00, because
both NH4+ and C2H3O2– hydrolyze to an equivalent extent, since
)(NH )OHHC( 3b232a KK and their hydrolysis constants also are virtually equal.
Total volume of titrant = 10.00 mL, since both acid and base have the same concentrations.
At the half equivalence point, which occurs when 5.00 mL of titrant have been added,
pH = pKa = 4.74. When the solution has been 90% titrated, 9.00 mL of 0.100 M NH3
has been added. We use the Henderson-Hasselbalch equation to find the pH after 90% of
the acid has been titrated
69.5
1
9
log74.4
]OHHC[
]OH[C
logppH
232
232
a
K
When the solution is 110% titrated, 11.00 mL of 0.100 M NH3 have been added.
amount NH3 added = 11.00 mL × 0.100 M = 1.10 mmol NH3
amount NH4+ produced = amount HC2H3O2 consumed = 1.00 mmol NH4+
amount NH3 unreacted = 1.10 mmol NH3 – 1.00 mmol NH4+ = 0.10 mmol NH3
We use the Henderson-Hasselbalch equation to determine the pH of the solution.
8.26pH 74.5
NH mmol 10.0
NH mmol 1.00
log74.4
]NH[
][NH
logppOH
3
4
3
4
b
K
When the solution is 150% titrated, 15.00 mL of 0.100 M NH3 have been added.
amount NH3 added = 15.00 mL × 0.100 M = 1.50 mmol NH3
amount NH4+ produced = amount HC2H3O2 consumed = 1.00 mmol NH4+
amount NH3 unreacted = 1.50 mmol NH3 – 1.00 mmol NH4+ = 0.50 mmol NH3
8.96pH 04.5
NH mmol 50.0
NH mmol 1.00
log74.4
]NH[
][NH
logppOH
3
4
3
4
b
K
The titration curve based on these points is sketched next. We note that the equivalence
point is not particularly sharp and thus, satisfactory results are not obtained from acetic
acid–ammonia titrations.
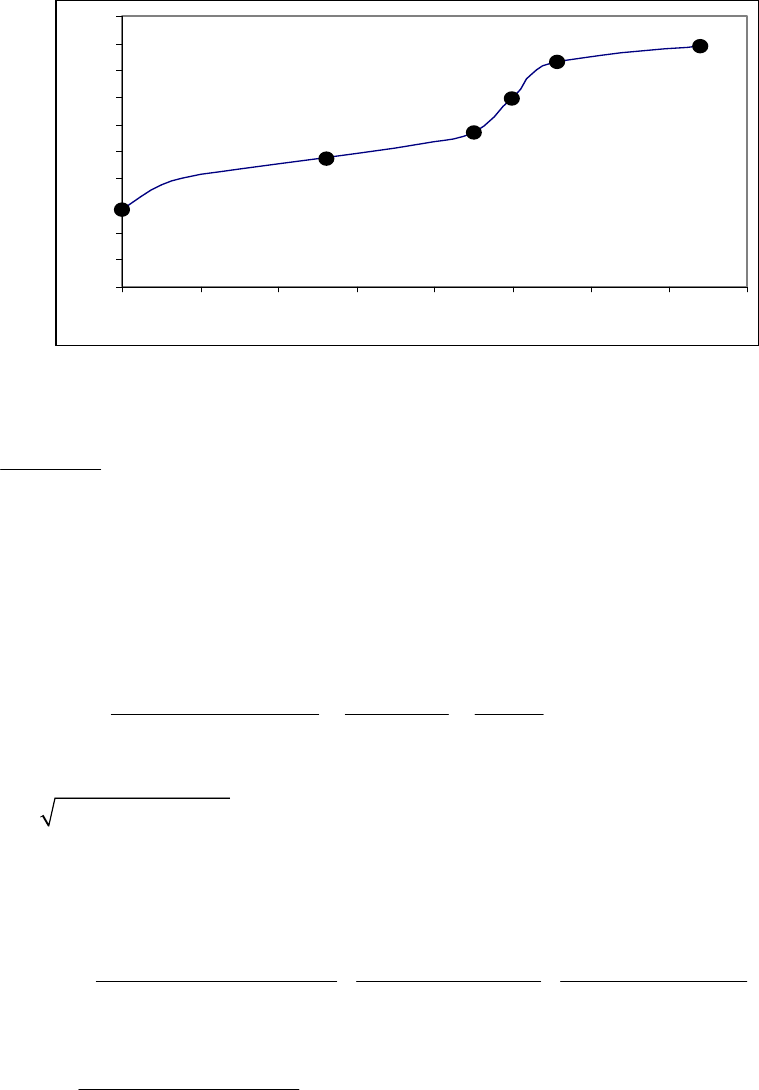
Chapter 17: Additional Aspects of Acid–Base Equilibria
853
75. (D)
C6H5NH3+ is a weak acid, whose acid ionization constant is determined from
Kb(C6H5NH2) = 7.4 × 10–10.
85.4pK and 104.1
104.7
100.1
a
5
10
14
a
K. We first determine the initial pH.
65 3 2 65 2 3
Equation: C H NH (aq) H O(l) C H NH (aq) H O (aq)
Initial: 0.0500 M 0 M 0 M
Changes: M M M
Equil: (0.0500 ) M M M
xxx
xxx
2
565 2 3
a
65 3
3
aa
54 –4
3
[C H NH ] [H O ]
1.4 10 0.0500 0.0500
[C H NH ]
(Since / = 3.6×10 ; thus, the approximation is valid)
[H O ] 0.0500 1.4 10 8.4 10 M pH log (8.4 10 ) 3.08
xx x
Kx
CK
At the equivalence point, we have a solution of C6H5NH2(aq). Now find the volume of
titrant.
65 3
65 3
65 2 65 2
65 2
65 2
0.0500 mmol C H NH 1 mmol NaOH 1 mL titrant
V 10.00 mL 5.00 mL
1 mL 1 mmol C H NH 0.100 mmol NaOH
amount C H NH 10.00 mL 0.0500 M 0.500 mmol C H NH
0.500 mmol C H NH
[C H NH ] 0.03
10.00 mL 5.00 mL
33 M
0
1
2
3
4
5
6
7
8
9
10
0246810121416
Volume of NH
3
(mL)
p
H

Chapter 17: Additional Aspects of Acid–Base Equilibria
854
65 2 2 65 3
Equation: C H NH (aq) H O(l) C H NH (aq) OH (aq)
Initial: 0.0333 M 0 M 0 M
Changes: M M M
Equil: (0.033
xxx
2
10 65 3
b
65 2
bb
10
3 ) M M M
[C H NH ][OH ]
7.4 10 [C H NH ] 0.0333 0.0333
( / = very large number; thus, the approximation is valid)
[OH ] 0.0333 7.4 10 5.
xxx
xx x
Kx
CK
6
0 10 pOH 5.30 pH 8.70
At the half equivalence point, when 5.00 mL of 0.1000 M NaOH has been added,
pH = pKa = 4.85. At points in the buffer region, we use the expression derived in Exercise
69.
After 4.50 mL of titrant has been added, f = 0.90, pH = 4.85 + 0.90
log 0.10 = 5.80
After 4.75 mL of titrant has been added, f = 0.95, pH = 4.85 + 0.95
log 0.05 = 6.13
After the equivalence point has been reached, with 5.00 mL of titrant added, the pH of the
solution is determined by the amount of excess OH– that has been added.
At 105% titrated, 0.25 mL 0.100 M
[OH ] 0.0016 M pOH 2.80 pH 11.20
15.25 mL
At 120% titrated, 1.00 mL 0.100 M
[OH ] 0.00625 M pOH 2.20 pH 11.80
16.00 mL
Of course, one could sketch a suitable titration curve by calculating fewer points. Below is
the titration curve.
2
4
6
8
10
12
05
Volume NaOH (ml)
pH

Chapter 17: Additional Aspects of Acid–Base Equilibria
855
76. In order for a diprotic acid to be titrated to two distinct equivalence points, the acid must
initially start out with two undissociated protons and the Ka values for the first and second
protons must differ by >1000. This certainly is not the case for H2SO4, which is a strong
acid (first proton is 100% dissociated). Effectively, this situation is very similar to the
titration of a monoprotic acid that has added strong acid (i.e., HCl or HNO3). With the
leveling effect of water, Ka1 = 1 and Ka2 = 0.011, there is a difference of only 100 between
Ka1 and Ka2 for H2SO4.
77. (D) For both titration curves, we assume 10.00 mL of solution is being titrated and the
concentration of the solute is 1.00 M, the same as the concentration of the titrant. Thus,
10.00 mL of titrant is required in each case. (You may be able to sketch titration curves
based on fewer calculated points. Your titration curve will look slightly different if you
make different initial assumptions.)
(a) The initial pH is that of a solution of HCO3–(aq). This is an anion that can ionize to
CO32 (aq) or be hydrolyzed to H2CO3(aq). Thus,
34.8)33.1035.6()pp(pH 2
1
2
1
21 aa KK
The final pH is that of 0.500 M H2CO3(aq). All of the NaOH(aq) has been
neutralized, as well as all of the HCO3–(aq), by the added HCl(aq).
23 2 3 3
Equation: H CO (aq) H O(l) HCO (aq) H O (aq)
Initial: 0.500 M 0 M 0 M
Changes: M M M
Equil
xxx
2
7
33
b
23
6
aa
: (0.500 ) M M M
[HCO ][H O ] 4.43 10
[H CO ] 0.500 0.500
( / = 1.1×10 ; thus, the approximation is valid)
[OH ] 0.500 4.4
xxx
xx x
Kx
CK
74
10 4.7 10 M pH 3.33
During the course of the titration, the pH is determined by the Henderson-
Hasselbalch equation, with the numerator being the percent of bicarbonate ion
remaining, and as the denominator being the percent of bicarbonate ion that has been
transformed to H2CO3.
90% titrated: pH = 6.35 + log 40.5
%90
%10 10% titrated: pH = 6.35 + log 30.7
%10
%90
95% titrated: pH = 6.35 + log 07.5
%95
%5 5% titrated: pH = 6.35 + log 63.7
%5
%95
After the equivalence point, the pH is determined by the excess H3O+.
1.61pH 024.0
mL5.20
M 1.00mL 50.0
]O[H titrated,105%At 3
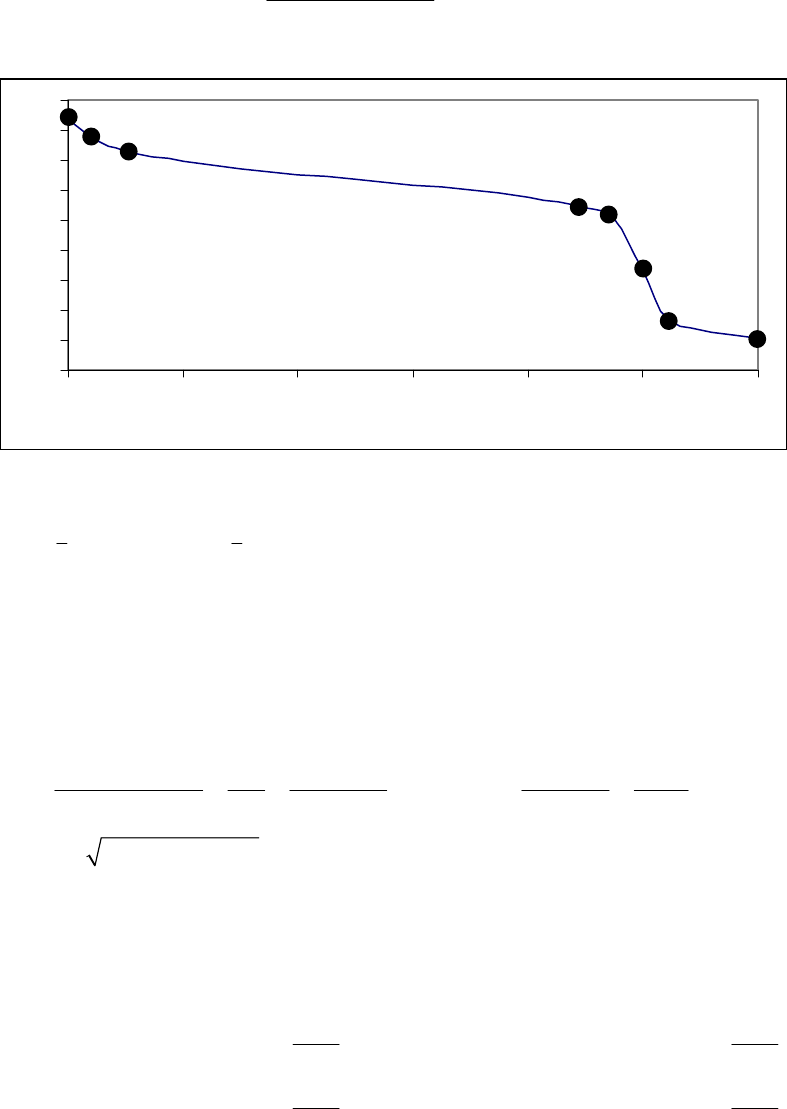
Chapter 17: Additional Aspects of Acid–Base Equilibria
856
1.04pH M 091.0
mL0.22
M 1.00mL 00.2
]O[H titrated,120%At 3
The titration curve derived from these data is sketched below.
0
1
2
3
4
5
6
7
8
9
024681012
Volume 1.00 M HCl
pH
(b) The final pH of the first step of the titration is that of a solution of HCO3–(aq). This
is an anion that can be ionized to CO32–(aq) or hydrolyzed to H2CO3(aq). Thus,
12
11
aa
22
pH (pK pK ) (6.35 10.33) 8.34. The initial pH is that of 1.000 M
CO32–(aq), which pH is the result of the hydrolysis of the anion.
2
32 3
3
b2
3
Equation: CO (aq) H O(l) HCO (aq) OH (aq)
Initial: 1.000 M 0 M 0 M
Changes: M M M
Equil: (1.000 ) M M M
[HCO ][OH ]
[CO
xxx
xxx
K
2
14 2
4
w
11
42
1.0 10 2.1 10
] 4.7 10 1.000 1.000
[OH ] 1.000 2.1 10 1.4 10 M pOH 1.85 pH 12.15
a
Kxx x
Kx
During the course of the first step of the titration, the pH is determined by the
Henderson-Hasselbalch equation, modified as in Exercise 69, but using as the
numerator the percent of carbonate ion remaining, and as the denominator the
percent of carbonate ion that has been transformed to HCO3–.
10% 90%
90% titrated: pH 10.33 log 9.38 10% titrated: pH 10.33 log 11.28
90% 10%
5% 95%
95% titrated: pH 10.33 log 9.05 5% titrated: pH 10.33 log 11.61
95% 5%
During the course of the second step of the titration, the values of pH are precisely as
they are for the titration of NaHCO3, except the titrant volume is 10.00 mL more (the
volume needed to reach the first equivalence point). The solution at the second
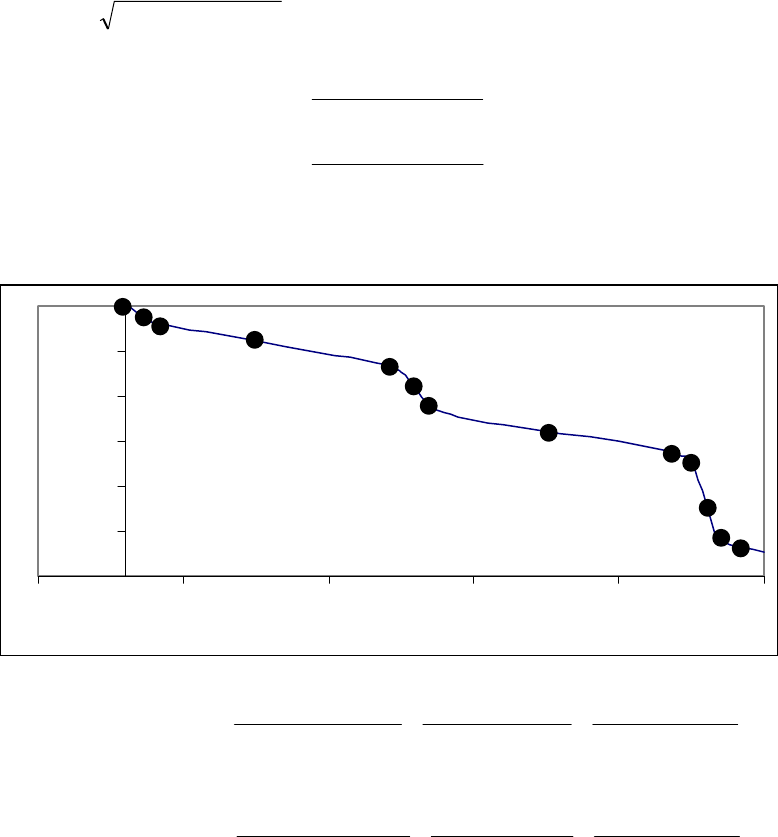
Chapter 17: Additional Aspects of Acid–Base Equilibria
857
equivalence point is 0.333 M H2CO3, for which the set-up is similar to that for 0.500 M
H2CO3.
3.42pH M 108.3104.4333.0]O[H 47
3
After the equivalence point, the pH is determined by the excess H3O+.
3
3
0.50 mL 1.00 M
At 105% titrated, [H O ] 0.0164 M pH 1.8
30.5 mL
2.00 mL 1.00 M
At 120% titrated, [H O ] 0.0625 M pH 1.20
32.0 mL
The titration curve from these data is sketched below.
0
2
4
6
8
10
12
-3 2 7 12 17 22
Volume 1.00 M HCl, mL
pH
(c) 3
HCl 3
33
1 mol NaHCO 1 mol HCl 1000 mL
V 1.00 g NaHCO 84.01 g NaHCO 1 mol NaHCO 0.100 mol HCl
HCl M 0.100 mL 119
(d) 23
HCl 2 3
23 23
1 mol Na CO 2 mol HCl 1000 mL
V 1.00 g Na CO 105.99 g Na CO 1 mol Na CO 0.100 mol HCl
HCl M 0.100 mL 189
(e) The phenolphthalein endpoint occurs at pH = 8.00 and signifies that the NaOH has
been neutralized, and that Na2CO3 has been half neutralized. The methyl orange
endpoint occurs at about pH = 3.3 and is the result of the second equivalence point
of Na2CO3. The mass of Na2CO3 can be determined as follows:

Chapter 17: Additional Aspects of Acid–Base Equilibria
858
323
23
3
23 23
23
23 23
1 mol HCO 1 mol Na CO
1 L 0.1000 mol HCl
mass Na CO 0.78 mL 1000 mL 1 L soln 1 mol HCl 1 mol HCO
105.99 g Na CO 0.0083 g Na CO
1 mol Na CO
0.0083g
% Na CO 100 8.3% Na CO by mass
0.1000g
78. (M) We shall represent piperazine as Pip in what follows. The cation resulting from the
first ionization is HPiP+, and that resulting from the second ionization is H2Pip2+.
(a) [Pip] = ••
410 2 2 410 2 2
•
410 2 2
1.00g C H N 6H O 1mol C H N 6H O 0.0515
0.100L 194.22g C H N 6H O
M
2
Equation: (aq) H O(l) H (aq) OH (aq)
Initial: 0.0515 M 0 M 0 M
Changes: M M M
Equil: (0.0515 ) M M
Pip Pip
xxx
xx
Mx
Ca/Ka = 858; thus, the approximation is not valid. The full quadratic equation must be
solved.
1
4.22 5
b
3
[H ][OH ]
10 6.0 10 [ ] 0.0515
From the roots of the equation, = [OH ] 1.7 10 M pOH 2.77 pH 11.23
Pip x x
KPip x
x
(b) At the half-equivalence point of the first step in the titration, pOH = pKb1 = 4.22
pH = 14.00 – pOH = 14.00 – 4.22 = 9.78
(c) Volume of HCl = 100. mL 0.0515mmolPip 1mmolHCl 1mL titrant
× × × = 10.3mL
1mL 1mmolPip 0.500 mmolHCl
(d) At the first equivalence point we have a solution of HPip+. This ion can react as a base
with H2O to form H2Pip2+ or it can react as an acid with water, forming Pip (i.e. HPip+
is amphoteric). The solution’s pH is determined as follows (base hydrolysis
predominates):
pOH = ½ (pKb1 + pKb2) = ½ (4.22 + 8.67) = 6.45, hence pH = 14.00 – 6.45 = 7.55
(e) The pOH at the half-equivalence point in the second step of the titration equals pKb2.
pOH = pKb2 = 8.67 pH = 14.00 – 8.67 = 5.33
(f) The volume needed to reach the second equivalence point is twice the volume
needed to reach the first equivalence point, that is 2 × 10.3 mL = 20.6 mL.
(g) The pH at the second equivalence point is determined by the hydrolysis of the
H2Pip2+ cation, of which there is 5.15 mmol in solution, resulting from the reaction

Chapter 17: Additional Aspects of Acid–Base Equilibria
859
of HPip+ with HCl. The total solution volume is 100. mL + 20.6 mL = 120.6 mL
[H2Pip2+] = 2
8.67 9
5.15 0.0427 10 2.1 10
120.6 b
mmol MK
mL
2+
22 3
Equation: H Pip (aq) H O(l) HPip (aq) H O (aq)
Initial: 0.0427 M 0 M 0 M
Changes: M M M
Equil: (0.0427 ) M
xxx
x
2
14 2
6
3
a92+
2
64
3
M M
[HPip ][H O ]
1.00 10 4.8 10
2.1 10 [H Pip ] 0.0427 0.0427
[H O ] 0.0427 4.8 10 4.5 10 M pH 3.347
w
b
xx
Kxx x
KKx
x
(
x << 0.0427; thus, the approximation is valid).
79. (M) Consider the two equilibria shown below.
H2PO4-(aq) + H2O(l)
HPO42-(aq) + H3O+(aq) Ka2 =
2- +
43
-
24
[HPO ][H O ]
[H PO ]
H2PO4-(aq) + H2O(l)
H3PO4(aq) + OH-(aq) Kb = Kw/Ka1 =
-
34
-
24
[H PO ][OH ]
[H PO ]
All of the phosphorus containing species must add up to the initial molarity M.
Hence, mass balance: [HPO42- ] + [H2PO4- ] + [H3PO4] = M
charge balance: [H3O+] + [Na+] = [H2PO4- ] + 2×[HPO42- ]
Note: [Na+] for a solution of NaH2PO4 = M
Thus, [H3O+ ] + [Na+ ] = [H2PO4- ] + 2×[HPO42- ] = [H3O+ ] + M (substitute mass balance equation)
[H3O+ ] + [HPO42- ] + [H2PO4- ] + [H3PO4] = [H2PO4- ] + 2×[HPO42- ] (cancel terms)
[H3O+ ] = [HPO42- ] - [H3PO4]
(Note: [HPO42- ] = initial [H3O+ ] and [H3PO4] = initial [OH- ])
Thus: [H3O+ ]equil = [H3O+ ]initial ]initial (excess H3O+ reacts with OH- to form H2O)
Rearrange the expression for Ka2 to solve for [HPO42-], and the expression for Kb to solve
for [H3PO4].
--
+2- a2 2 4 b 2 4
3434+-
3
K [HPO ] K[HPO ]
[H O ] = [HPO ] - [H PO ] = [H O ] [OH ]
-
w24
--+-
+a2 2 4 1 a2 2 4 3 2 4
3++
wa1
33
+
3
K[H PO ]
K [H PO ] K [H PO ] [H O ][H PO ]
[H O ] KK
[H O ] [H O ]
[H O ]
a
K
Multiply through by [H3O+] Ka1 and solve for [H3O+].

Chapter 17: Additional Aspects of Acid–Base Equilibria
860
++ - ++ -
a1 3 3 a1 a2 2 4 3 3 2 4
+2 - +2 -
a1 3 a1 a2 2 4 3 2 4
+2 +2 - - +2 -
a1 3 3 2 4 a1 a2 2 4 3 a1 2 4
+2 +2 - -
a1 3 3 2 4 a1 a2 2 4
K [H O ][H O ] K K [H PO ] [H O ][H O ][H PO ]
K [H O ] K K [H PO ] [H O ] [H PO ]
K [H O ] [H O ] [H PO ] K K [H PO ] = [H O ] (K [H PO ])
K [H O ] [H O ] [H PO ] K K [H PO ] =
+2 -
3a124
-
+2 --
a1 a2 2 4
324 a1 24
-
a1 2 4
[H O ] (K [H PO ])
KK[HPO]
[H O ] = For moderate concentrations of [H PO ], K << [H PO ]
(K [H PO ])
-
+2 a1 a2 2 4
3a1a2
-
24
+2 + 12
3 a1 a2 3 a1 a2 a1 a2
KK[HPO]
This simplifies our expression to: [H O ] = = K K
[H PO ]
Take the square root of both sides: [H O ] = K K [H O ] = K K (K K )
Take the -log of both sides and simplif
+12
3 a1a2 a1a2 a1 a2
++
3 a1 a2 3 a1 a1 a2 a2
+
3a1a2 a1
y:
-log[H O ] = log(K K ) 1 2 log(K K ) 1 2(log K +logK )
-log[H O ] 1 2( log K logK ) Use -log[H O ] = pH and log K pK logK pK
Hence, -log[H O ] = 1 2( logK logK ) becomes pH =1 2(pK
a2
+pK ) (Equation 17.5)
Equation 17.6 can be similarly answered.
80. (D) H2PO4– can react with H2O by both ionization and hydrolysis.
-2
24 2 4 3
H PO (aq) H O(l) HPO (aq) H O (aq)
2- 3
42 4 3
HPO (aq) H O(l) PO (aq) H O (aq)
The solution cannot have a large concentration of both H3O+ and OH– (cannot be
simultaneously an acidic and a basic solution). Since the solution is acidic, some of the
H3O+ produced in the first reaction reacts with virtually all of the OH– produced in the
second. In the first reaction [H3O+] = [HPO42–] and in the second reaction [OH–] =
[H3PO4]. Thus, following the neutralization of OH– by H3O+, we have the following.
221
2
1
-
w24
--
-
24 24
2- - b2 4
3424 w
33
3
--
24 324
3
31
3
Then multiply through by [H O ]
and solve for [H O ].
[H PO ]
[H PO ] [H PO ]
[H PO ]
[H O ] [HPO ] [H PO ] [H O ] [OH ] [H O ]
[H O ]
[H PO ] [H O ][H PO ]
[H O ]
aaa
a
a
a
K
K
KKK
K
K
K
K
12
112
1
-
24
2-2-
3243243 -
24
[H PO ]
[H O ] [H PO ] [H O ] [H PO ] [H O ] [[HPO]
aa
aaa
a
KK
KKK K
But, for a moderate [H2PO -
4], from Table 16-6, 1
a
K= 7.1 × 10–3 < [H2PO -
4] and thus
]POH[]POH[ 4242
1
a
K. Then we have the following expressions for [H3O+] and pH.
Chapter 17: Additional Aspects of Acid–Base Equilibria
861
12
12 12 1 2
12
3
1/2 11
322
1
2
[H O ]
pH log[H O ] log( ) [ log( )] ( log log )
pH (p p )
aa
aa aa a a
aa
KK
KK KK K K
KK
Notice that we assumed Ka < [H2PO4–]. This assumption is not valid in quite dilute
solutions because Ka = 0.0071.
81. (D)
(a) A buffer solution is able to react with small amounts of added acid or base. When strong acid is
added, it reacts with formate ion.
OH(aq)HCHO(aq)OHaq)(CHO 2232
Added strong base reacts with acetic acid.
(aq)OHCO(l)H(aq)OH(aq)OHHC 2322232
Therefore neither added strong acid nor added strong base alters the pH of the solution very much.
Mixtures of this type are referred to as buffer solutions.
(b) We begin with the two ionization reactions.
22 2 3
HCHO (aq) H O(l) CHO (aq) H O (aq)
232 2 232 3
HC H O (aq) H O(l) C H O (aq) H O (aq)
3232 2
[Na ] 0.250 [OH ] 0 [H O ] [C H O ] [CHO ]
x
yz
y 150.0]OHC[150.0]OH[HC ]OHC[]OHHC[150.0 232232232232
z 250.0]CHO[250.0][HCHO ]CHO[]HCHO[250.0 2222
]OH[]CHO[]OHC[]O[H]Na[ 22323
(electroneutrality)
zyx ]CHO[]OHC[250.0 2232 (1)
y
yx
K
150.0
108.1
]OH[HC
]OHC][OH[ 5
A
232
2323 (2)
z
zx
K
250.0
108.1
][HCHO
]][CHOO[H 4
F
2
23 (3)
There now are three equations—(1), (2), and (3)—in three unknowns—x, y, and z.
We solve equations (2) and (3), respectively, for y and z in terms of x.
Chapter 17: Additional Aspects of Acid–Base Equilibria
862
xK
K
zxzKzK
xK
K
yxyKyK
F
F
FF
A
A
AA
250.0
250.0
150.0
150.0
Then we substitute these expressions into equation (1) and solve for x.
4.40pH
]O[HM 100.4
2
106.7102.5102.7
109.1102.70 600.0 400.0
) 00.1 600.0( 60.1)(
)( 250.0)( 150.0)( )( 250.0
250.0 since 250.0
250.0 150.0
250.0
3
5
9116
962
FAA
2
FAFA
2
FAFA
AFFAAF
F
F
A
A
x
xxKKxKx
KKxKKxxKKKK
xKKxKKxKxK
x
xK
K
xK
K
x
(c) Adding 1.00 L of 0.100 M HCl to 1.00 L of buffer of course dilutes the
concentrations of all components by a factor of 2. Thus, [Na+] = 0.125 M; total
acetate concentration = 0.0750 M; total formate concentration = 0.125 M. Also, a
new ion is added to the solution, namely, [Cl–] = 0.0500 M.
zyx
][CHO ]OH[C M 0500.0][Cl ]O[H 0][OH 125.0]Na[ 22323
y 0750.0]OH[C– 0750.0]OH[HC ]OHC[]OH[HC0750.0 232232232232
z 125.0]CHO[125.0][HCHO ]CHO[]HCHO[125.0 2222
][Cl][CHO ]OH[]OHC[]O[H]Na[ 22323
(electroneutrality)
zyxzyx
0.0750500.00]Cl[]CHO[]OHC[125.0 2232
y
yx
K
0750.0
108.1
]OHHC[
]OHC][O[H 5
A
232
2323
4
32
F
2
[H O ][CHO ] 1.8 10
[HCHO ] 0.125
x
z
Kz
Again, we solve the last two equations for y and z in terms of x.
A
AA
A
F
FF
F
0.0750
0.0750
0.125
0.125
K
KyKxy y Kx
K
KzK xz z Kx
Chapter 17: Additional Aspects of Acid–Base Equilibria
863
Then we substitute these expressions into equation (1) and solve for x.
AF
AF
FA AF FA
2
AF A F AF F A
224
FAF
0.0750 K 0.125 K
0.0750 x 0.0750 since x 0.0750
Kx Kx
0.0750 (K x) (K x) 0.0750 K (K x) 0.125 K (K x)
K K (K K )x x 2.67 K K x(1.67 K 1.00 K )
x 0.67 K x 1.67 K K 0 x 1.2 10 x 5
9
488
4
3
.4 10
1.2 10 1.4 10 2.2 10
x1.5510 M[HO]
2
pH 3.81 3.8
As expected, the addition of HCl(aq), a strong acid, caused the pH to drop. The
decrease in pH was relatively small, nonetheless, because the H3O+(aq) was
converted to the much weaker acid HCHO2 via the neutralization reaction:
CHO2-(aq) + H3O+(aq) → HCHO2(aq) + H2O(l) (buffering action)
82. (M) First we find the pH at the equivalence point:
-
332
3
CH CH(OH)COOH(aq) OH ( ) CH CH(OH)COO (aq) H O(l)
1 mmol 1 mmol 1 mmol
The concentration of the salt is 1 10 mol/0.1 L = 0.01 M
The lactate anion undergoes hydrolysis
aq
-
323
thus:
CH CH(OH)COO ( ) H O(l) CH CH(OH)COOH(aq) OH ( )
Initial 0.01 M 0 M 0 M
Change + +
Equilibrium (0.01 ) M
Where
aq aq
xxx
xxx
x
-
is the [hydrolyzed lactate ion], as well as that of the [OH ] produced by hydrolysis
14 11
3w
-3.86
3a
22 11 - 7
[CH CH(OH)COOH][OH ] K 1.0 10
K for the above reaction 7.2 10
[CH CH(OH)COO ] K 10
so 7.2 10 and [OH ] 8.49 10 M
0.01 0.01
0.01, thus, the assumption is valid
log (8.49
xx x
x
x
pOH
7
10 ) 6.07 14 14.00 6.07 7.93MpHpOH
(a) Bromthymol blue or phenol red would be good indicators for this titration since they change
color over this pH range.
Chapter 17: Additional Aspects of Acid–Base Equilibria
864
(b) The H2PO4–/HPO42- system would be suitable because the pKa for the acid (namely, H2PO4–) is
close to the equivalence point pH of 7.93. An acetate buffer would be too acidic, an ammonia
buffer too basic.
(c) -28
44
22 3 a2
H PO H O H O HPO K 6.3 10
28
4a2
-7.93
4
23
K
[HPO ] 6.3 10
Solving for 5.4 (buffer ratio required)
[H PO ] [H O ] 10
83. (M)
2
3
2
22 2 3 a
22
[H O ][HO ]
HO(aq) HO(l) HO(aq) HO (aq) K [H O ]
Data taken from experiments 1 and 2:
22
22
222
()
3
(14.9
3
[H O ] [HO ] 0.259 M (6.78) (0.00357 M) [HO ] 0.259 M
[HO ] 0.235 M [H O ] (6.78)(0.00357 M) 0.0242 M
[H O ] 10
log 0.250 - 0.235) M NaOH log(0.015 M NaOH) = 1.824
[H O ] 10
pKw pOH
41.824) 14
14
213
3
a
22
a
7.7 10
[H O ][HO ] (7.7 10 M)(0.235 M)
K7.410
[H O ] (0.0242 M)
pK 12.14
From data taken from experiments 1 and 3:
2 2
22
2
[H O ] [HO ] 0.123 M (6.78)(0.00198 M) [HO ] 0.123 M
[HO ] 0.1096 M
22
()
3
[H O ] (6.78)(0.00198 M) 0.0134 M
[H O ] 10 , pOH = -log[(0.125- 0.1096 ) M NaOH] 1.81
pKw pOH
(14.94 1.81) 14
3
14
213
3
22
13
[H O ] 10 7.41 10
[H O ][HO ] (7.41 10 M)(0.1096 M) 6.06 10
[H O ] (0.0134 M)
p = -log (6.06 10 ) = 12.22
Average value for p = 12.17
a
a
a
K
K
K

Chapter 17: Additional Aspects of Acid–Base Equilibria
865
84. (D) Let's consider some of the important processes occurring in the solution.
2-13
4224 (1)a2
14
23 7
44
23 (2)b
8
423 3 (3)a
(1) HPO (aq) H O(l) H PO (aq) OH (aq) = 4.2 10
1.0 10
(2) HPO (aq) H O(l) H O (aq) PO (aq) = 1.6 10
6.3 10
1.0
(3) NH (aq) H O(l) H O (aq) NH (aq) =
KK
KK
KK 14 10
5
- 4
423 (4) 5
10 5.6 10
1.8 10
1
(4) NH (aq) OH (aq) H O(l) NH (aq) 5.6 10
1.8 10
K
-2
4 4
2-
44 4
23
May have interaction between NH and OH formed from the hydrolysis of HPO .
NH (aq) HPO (aq) H PO (aq) NH (aq)
Initial 0.10M 0.10M 0 M 0 M
Change
Equil
xx x x
4
. 0.100 0.100
(where is the molar concentration of NH that hydrolyzes)
xx x x
x
74 3
(2) (4)
(1.6 10 ) (5.6 10 ) 9.0 10KKK
-2
433
23
22
44
[H PO ] [NH ] [] 9.0 10 and 8.7 10 M
[NH ] [HPO ] [0.10- ]
x
Kx
x
23
48
a-3
4
2
4
3
Finding the pH of this buffer system:
[HPO ] 0.100-8.7 10 M
pH p log log(6.3 10 ) log 8.2
[H PO ] 8.7 10 M
As expected, we get the same result using the NH /NH buffer system.
K
85. Consider the two weak acids and the equilibrium for water (autodissociation)
+- +-
+- 33
23 HA
HA
+- +-
+- 33
23 HB
HB
+- +-
22 3 w3
[H O ][A ] [H O ][A ]
HA(aq) + H O(l) H O (aq) +A (aq) K = [HA]=
[HA] K
[H O ][B ] [H O ][B ]
HB(aq) + H O(l) H O (aq) + B (aq) K = [HB]=
[HB] K
H O(l) + H O(l) H O (aq) +OH (aq) K =[H O ][OH ] [O
-w
+
3
K
H] = [H O ]
Chapter 17: Additional Aspects of Acid–Base Equilibria
866
+- +
---
33
initial
HA HA
-initial
+
3
HA
[H O ][A ] [H O ]
Mass Balance: [HA] =[HA]+[A ] = +[A ] = [A ] +1
KK
[HA]
From which: [A ] = [H O ] +1
K
+- +
---
33
initial
HB HB
-initial
+
3
HB
[H O ][B ] [H O ]
[HB] = [HB] + [B ] = + [B ] = [B ] +1
KK
[HB]
From which: [B ] = [H O ] +1
K
+-- -
3
+initial initial w
3+
++
3
33
HA HB
Charge Balance: [H O ] = [A ] + [B ] + [OH ] (substitute above expressions)
[HA] [HB] K
[H O ] = [H O ]
[H O ] [H O ]
+1 +1
KK
86. (D) We are told that the solution is 0.050 M in acetic acid (Ka = 1.8 ×10-5) and 0.010 M in phenyl
acetic acid (Ka = 4.9 ×10-5). Because the Ka values are close, both equilibria must be satisfied
simultaneously. Note: [H3O+] is common to both equilibria (assume z is the concentration of
[H3O+]).
Reaction: HC2H3O2(aq) + H2O(l)
C2H3O2-(aq) + H3O+(aq)
Initial: 0.050 M — 0 M ≈ 0 M
Change: -x M — + x M + z M
Equilibrium (0.050 – x)M — x M z M
+- 5
5
3232
a
232
[H O ][C H O ] 1.8 10 (0.050 )
For acetic acid: K = 1.8 10 or
[HC H O ] (0.050 )
x
xz x
xz
Reaction: HC8H7O2(aq) + H2O(l)
C8H7O2-(aq) +
H3O+(aq)
Initial: 0.010 M — 0 M ≈ 0 M
Change: -y M — + y M + z M
Equilibrium (0.010 – y)M — y M z M
+- 5
3872
a
872
5
[H O ][C H O ]
For phenylacetic acid: K = 4.9 10
[HC H O ] (0.010 )
4.9 10 (0.010 )
or
yz
y
y
yz

Chapter 17: Additional Aspects of Acid–Base Equilibria
867
There are now three variables: x = [C2H3O2- ], y = [C8H7O2- ], and z = [H3O+ ]
These are the only charged species, hence, x + y = z.
(This equation neglects contribution from the [H3O+] from water.)
Next we substitute in the values of x and y from the rearranged Ka expressions above.
x + y = z =
5
1.8 10 (0.050 )
x
z
+
5
4.9 10 (0.010 )
y
z
Since these are weak acids, we can simplify this expression by assuming that x << 0.050 and y <<
0.010.
z =
5
1.8 10 (0.050)
z
+
5
4.9 10 (0.010)
z
Simplify even further by multiplying through by z.
z2 = 9.0×10-7 + 4.9×10-7 = 1.4 ×10-6
z = 1.18×10-3 = [H3O+] From which we find that x = 7.6 × 10-4 and y = 4.2×10-4
(as a quick check, we do see that x + y = z).
We finish up by checking to see if the approximation is valid (5% rule)..
44
7.6 10 4.2 10
For : 100% 1.5% For : 100% 4.2%
0.050 0.010
xy
Since both are less than 5%, we can be assured that the assumption is valid.
The pH of the solution = -log(1.18×10-3) = 2.93.
(If we simply plug the appropriate values into the equation developed in the previous question we
get the exact answer 2.933715 (via the method of successive approximations), but the final answers
can only be reported to 2 significant figures. Hence the best we can do is say that the pH is
expected to be 2.93 (which is the same level of precision as that for the result obtained following
the 5% rule).
87. (D)
(a) By using dilution, there are an infinite number of ways of preparing the pH = 7.79
buffer. We will consider a method that does not use dilution.
Let TRIS = weak base and TRISH+ be the conjugate acid.
pKb = 5.91, pKa = 14 – pKb = 8.09 Use the Henderson Hasselbalch equation.
pH = pKa + log (TRIS/TRISH+) = 7.79 = 8.09+ log (TRIS/TRISH+)
log (TRIS/TRISH+) = 7.79 – 8.09 = -0.30 Take antilog of both sides
(TRIS/TRISH+) = 10-0.30 = 0.50; Therefore, nTRIS = 0.50(nTRISH+)

Chapter 17: Additional Aspects of Acid–Base Equilibria
868
Since there is no guidance given on the capacity of the buffer, we will choose an arbitrary
starting point. We start with 1.00 L of 0.200 M TRIS (0.200 moles). We need to convert 2/3 of
this to the corresponding acid (TRISH+) using 10.0 M HCl, in order for the TRIS/TRISH+ ratio
to be 0.5. In all, we need (2/3)×0.200 mol of HCl, or a total of 0.133 moles of HCl.
Volume of HCl required = 0.133 mol 10.0 mol/L = 0.0133 L or 13.3 mL.
This would give a total volume of 1013.3 mL, which is almost a liter (within 1.3%).
If we wish to make up exactly one liter, we should only use 987 mL of 0.200 M TRIS.
This would require 13.2 mL of HCl, resulting in a final volume of 1.0002 L.
Let’s do a quick double check of our calculations.
nHCl = 0.0132 L×10.0 M = 0.132 mol = nTRISH+
nTRIS = ninitial – nreacted = 0.200 M×0.987 L – 0.132 mol = 0.0654 mol
pH = pKa + log (TRIS/TRISH+) = 8.09+ log (0.0654 mol/0.132 mol) = 7.785
We have prepared the desired buffer (realize that this is just one way of preparing the buffer).
(b) To 500 mL of the buffer prepared above, is added 0.030 mol H3O+.
In the 500 mL of solution we have 0.132 mol 2 mol TRISH+ = 0.0660 mol TRISH+
and 0.0654 mol 2 mol TRIS = 0.0327 mol TRIS (we will assume no change in
volume).
HCl will completely react (≈ 100%) with TRIS, converting it to TRISH+.
After complete reaction, there will be no excess HCl, 0.0327 mol – 0.0300 mol =
0.0027 mol TRIS and 0.0660 mol + 0.0300 mol = 0.0960 mol TRISH+.
By employing the Henderson Hasselbalch equation, we can estimate the pH of the
resulting solution:
pH = pKa + log (TRIS/TRISH+) = 8.09 + log (0.0027 mol/0.0960 mol) = 6.54
This represents a pH change of 1.25 units. The buffer is nearly exhausted owing to
the fact that almost all of the TRIS has been converted to TRISH+. Generally, a pH
change of 1 unit suggests that the capacity of the buffer has been pretty much
completely expended. This is the case here.
(Alternatively, you may solve this question using an I.C.E. table).
(c) Addition of 20.0 mL of 10.0 M HCl will complete exhaust the buffer (in part (b) we saw
that addition of 3 mL of HCl used up most of the TRIS in solution). The buffer may be
regenerated by adding 20.0 mL of 10.0 M NaOH. The buffer will be only slightly
diluted after the addition of HCl and NaOH (500 mL → 540 mL). Through the slow and
careful addition of NaOH, one can regenerate the pH = 7.79 buffer in this way (if a pH
meter is used to monitor the addition).
Chapter 17: Additional Aspects of Acid–Base Equilibria
869
88. (M)
(a) The formula given needs to be rearranged to isolate α, as shown below.
a
3
a
3
a
aa
pH
a
3a
1
pH pK log 1
HO 1
pH pKa log log 1
K
HO 11
K
KK
=10 K
HO K
Now, use the given Ka (6.3×10-8) and calculate α for a range of pH values.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
01234567891011121314
pH
(b) When pH = pKa, α = 0.5 or 50%.
(c) At a pH of 6.0, 8
a
pH 6.0 8
a
K6.3 10
= 0.059
10 K 10 6.3 10
or 5.9%.
(c)

Chapter 17: Additional Aspects of Acid–Base Equilibria
870
89. (D)
(a) We start by writing the equilibrium expression for all reactions:
2
1
2
CO aq
KCO g
22
23
KCaCO
3
32
33
HCO
KHO CO
2
4
33
CO aq
KHCO H O
First, we have to express [H3O+] using the available expressions:
3
32
33
2
3
43
2322
322
33 4 3 343
HCO
HO KCO
CO aq
HO KHCO
HCO CO aq CO aq
HO KCO KHCO KKCO
From the expression for K1, we know that [CO2(aq)] = K1[CO2(g)]. Therefore,
212
32
34 3
KCOg
HO KKCO
Now, the expression for K2 can be plugged into the above expression as follows:
2
212
12
32234
34 3
2
12
3
234
KCOg Ca
KCOg
HO KKK
KKCO
KCOg Ca
HO KKK
(b) The K values for the reactions are as follows:
K1 = 0.8317 (given in the problem)
K2 = Ksp (CaCO3) = 2.8×10-9
K3 = 1/Ka of HCO3– = 1/(4.7×10-11) = 2.13×1010
K4 = 1/Ka of H2CO3 = 1/(4.4×10-7) = 2.27×106
65
22 2
2
2
280 10 L CO 1mol CO mol CO
CO (g) 1.145 10
L air 24.45 L CO L air

Chapter 17: Additional Aspects of Acid–Base Equilibria
871
532
12
3910 6
234
8
0.8317 1.145 10 10.24 10
KCOg Ca
HO KKK 2.8 10 2.13 10 2.27 10
2.684 10 M
8
pH log 2.684 10 7.57
90. (M) To determine pH, we must first determine what is the final charge balance of the solution
without adding any H3O+ or OH¯ ions. As such, we have to calculate the number of moles of each
ion (assume 1 L):
Moles of Na+: 23.0 g Na+ × (1 mol/23.0 g) = 1.00 mol Na+
Moles of Ca2+: 10.0 g Ca2+ × (1 mol/40.0 g) = 0.250 mol Ca2+
Moles of CO32-: 40.02 g CO32- × (1 mol/60.01 g) = 0.670 mol CO32-
Moles of SO42-: 9.6 g SO42- × (1 mol/96.056 g) = 0.100 mol
Looking at the list of ions and consulting the solubility guide, we note that Ca2+ will precipitate
with both SO42- and CO32-. Since both of these anions have a 2– charge, it doesn’t matter with
which anion the precipitation occurs (in reality, it does a little, but the effects are small compared to
the effects of adding H3O+ or OH¯ ions).
Moles of anions left = (0.670 + 0.100) – 0.250 = 0.520 moles
Since we have 0.520 moles of 2– ions, we must have 1.04 moles of 1+ ions to balance. However,
we only have 1 mole of Na+. The difference in charge is:
1.04(-) – 1.0(+) = 0.04(-) moles of ions
To balance, we need 0.04 moles of H3O+. The pH = –log (0.04) = 1.40.
91. (M)
(a) We note that the pH is 5.0. Therefore, 5.0 5
3
H O 10 1.0 10 M
255
a3 3
22
55
a3
2.0 10 1.8 10 1.0 10
CK HO 4.6 10
1.8 10 1.0 10
KHO
(b)
AA
33
dC d pH d pH dC
d pH 1.0 10 4.6 10 0.22
pH 5 0.22 4.78
(c) At an acetic acid concentration of 0.1 M, C is also 0.1, because C is the total concentration of
the acetic acid and acetate. The maximum buffer index β (2.50×10-2) happens at a pH of 4.75,
Chapter 17: Additional Aspects of Acid–Base Equilibria
872
where [HAc] = [Ac–]. The minima are located at pH values of 8.87 (which correspond to pH of a
solution of 0.1 M acetic acid and 0.1 M acetate, respectively).
0.0E+00
5.0E-03
1. 0 E - 0 2
1. 5 E - 0 2
2.0E-02
2.5E-02
3.0E-02
0123456789
pH
β
FEATURE PROBLEMS
92. (D)
(a) The two curves cross the point at which half of the total acetate is present as
acetic acid and half is present as acetate ion. This is the half equivalence point in a
titration, where pH p a
= = 4.74K.
(b) For carbonic acid, there are three carbonate containing species: “ HCO
23
” which
predominates at low pH, 3
HCO
, and CO3
2, which predominates in alkaline
solution. The points of intersection should occur at the half-equivalence points in
each step-wise titration: at pH p log
a
= = 4.4 10 = 6.36
1
7
K
ch and at
pH p log
a
= = 4.7 10 = 10.33
2
11
K
ch. The following graph was computer-
calculated (and then drawn) from these equations. f in each instance represents
the fraction of the species whose formula is in parentheses.
112
2
++
2
+
2
+
1
2
++
2
12 2
1=1+ +
HA HH
H
1=+1+
HA H
HH
1=++1
A
KKK
f
K
K
f
KK K
f
Chapter 17: Additional Aspects of Acid–Base Equilibria
873
(c) For phosphoric acid, there are four phosphate containing species: H PO
34
under acidic
conditions, HPO HPO
424
2
,
, and PO4
3, which predominates in alkaline solution. The points
of intersection should occur at pH p log= = 7.1 10 = 2.15,
1
3
Ka
ch
pH p log= = 6.3 10 = 7.20
2
8
Ka
ch, and pH p log= = 4.2 10 = 12.38
3
13
Ka
ch, a quite alkaline
solution. The graph that follows was computer-calculated and drawn.
f (H3PO4)
f (H2PO4-)
f (HPO42-)
f (PO43-)
23
3
2
3
f
HCO
f
HCO
f
CO
34
24
2
4
3
4
f
HPO
f
HPO
f
HPO
f
PO
Chapter 17: Additional Aspects of Acid–Base Equilibria
874
93. (D)
(a) This is exactly the same titration curve we would obtain for the titration of 25.00 mL of
0.200 M HCl with 0.200 M NaOH, because the acid species being titrated is H O
3+. Both acids
are strong acids and have ionized completely before titration begins. The initial pH is that of
0.200 M H3O+ = [HCl] + [HNO3];
pH = log 0.200= 0.70. At the equivalence point,
pH = 7.000 . We treat this problem as we would for the titration of a single strong acid with a
strong base.
0
2
4
6
8
10
12
14
0 5 10 15 20 25
Volume of 0.200 M NaOH (ml)
pH
(b) In Figure 17-9, we note that the equivalence point of the titration of a strong acid occurs at
pH = 7.00 , but that the strong acid is essentially completely neutralized at pH = 4. In Figure 17-
13, we see that the first equivalence point of H PO
34
occurs at about pH = 4.6. Thus, the first
equivalence point represents the complete neutralization of HCl and the neutralization of
HPO
34
to H PO
24
. Then, the second equivalence point represents the neutralization of
HPO
24
to HPO4
2. To reach the first equivalence point requires about 20.0 mL of 0.216 M
NaOH, while to reach the second one requires a total of 30.0 mL of 0.216 M NaOH, or an
additional 10.0 mL of base beyond the first equivalence point. The equations for the two
titration reactions are as follows.
To the first equivalence point: 34 24 2
NaOH + H PO NaH PO + H O
2
NaOH + HCl NaCl + H O
To the second equivalence point: 24 2 4 2
NaOH + NaH PO Na HPO + H O
There is a third equivalence point, not shown in the figure, which would require an additional
10.0 mL of base to reach. Its titration reaction is represented by the following equation.
To the third equivalence point: 24 342
NaOH + Na HPO Na PO + H O

Chapter 17: Additional Aspects of Acid–Base Equilibria
875
We determine the molar concentration of HPO
34
and then of HCl. Notice that only 10.0 mL of
the NaOH needed to reach the first equivalence point reacts with the HCl(aq); the rest reacts
with HPO
34
.
34
34
0.216 mmol NaOH 1 mmol H PO
(30.0 20.0) mL NaOH(aq) 1 mL NaOH soln 1 mmol NaOH 0.216 M H PO
10.00 mL acid soln
0.216 mmol NaOH 1 mmol HCl
(20.0 10.0) mL NaOH(aq) 1 mL NaOH soln 1 mmol NaOH 0.216 M HCl
10.00 mL acid soln
(c) We start with a phosphoric acid-dihydrogen phosphate buffer solution and titrate until all of
the H PO
34
is consumed. We begin with
10.00 0.0400
1=0.400
34 34
mL mmol H PO
mL mmol H PO
and the diprotic anion,
2
24 24
0.0150 mmol H PO
10.00 mL = 0.150 mmol H PO
1mL
. The volume of 0.0200 M
NaOH needed is: 34
34
1 mmol NaOH 1 mL NaOH
0.400 mmol H PO = 20.00 mL
1 mmol H PO 0.0200 mmol NaOH
To reach the first equivalence point. The pH value of points during this titration are computed
with the Henderson-Hasselbalch equation.
24 3
1
34
HPO 0.0150
Initially : pH = p + log = log 7.1 10 + log = 2.15 0.43 = 1.72
H PO 0.0400
K
0.150 + 0.100
At 5.00 mL: pH = 2.15+ log = 2.15 0.08 2.07
0.400 0.100
0.150 0.200
At 10.0 mL, pH = 2.15 log 2.15 0.24 2.39
0.400 0.200
0.150 0.300
At 15.0 mL, pH = 2.15 log 2.15 0.65 2.80
0.400 0.300
This is the first equivalence point, a solution of 30.00 mL (= 10.00 mL originally + 20.00 mL
titrant), containing 0.400 mmol 24
HPO
from the titration and the 0.150 mmol 2
24
HPO
originally present.
This is a solution with

Chapter 17: Additional Aspects of Acid–Base Equilibria
876
24
24
(0.400 + 0.150) mmol H PO
H PO = = 0.0183 M
30.00 mL
, which has
8
12
1
pH = p + p = 0.50 2.15 log 6.3 10 = 0.50 2.15 + 7.20 = 4.68
2KK
To reach the second equivalence point means titrating 0.550 mmol H PO
24
, which
requires an additional volume of titrant given by
24
24
1 mmol NaOH 1 mL NaOH
0.550 mmol H PO = 27.5 mL
0.0200 mmol NaOH
1 mmol H PO
.
To determine pH during this titration, we divide the region into five equal portions
of 5.5 mL and use the Henderson-Hasselbalch equation.
22
44
2
24
24
At 20.0 +5.5 mL,
HPO 0.20 0.550 mmol HPO formed
pH = p + log = 7.20 + log 0.80 0.550 mmol H PO remaining
HPO
pH = 7.20 0.60 = 6.60
K
0.40 0.550
At 20.0 +11.0 mL = 31.0 mL, pH = 7.20 + log = 7.02
0.60 0.550
At 36.5 mL, pH = 7.38 At 42.0 mL, pH = 7.80
The pH at the second equivalence point is given by
pH p p log=1
2+ = 0.50 7.20 4.2 10 = 0.50 7.20 +12.38 = 9.79
23 13
KK
bg ch
ej
bg
.
Another 27.50 mL of 0.020 M NaOH would be required to reach the third
equivalence point. pH values at each of four equally spaced volumes of 5.50 mL
additional 0.0200 M NaOH are computed as before, assuming the Henderson-
Hasselbalch equation is valid.
3
4
32
4
PO 0.20 0.550
At 47.50 +5.50 mL = 53.00 mL, pH = p + log = 12.38+ log 0.80 0.550
HPO
=12.38 0.60 =11.78
K
Chapter 17: Additional Aspects of Acid–Base Equilibria
877
At 58.50 mL, pH =12.20 At 64.50 mL, pH =12.56 At 70.00 mL, pH =12.98
But at infinite dilution with 0.0200 M NaOH, the pH = 12.30, so this point can’t be
reached.
At the last equivalence point, the solution will contain 0.550 mmol PO4
3 in a total of
10.00 + 20.00 + 27.50 + 27.50 mL = 85.00 mL of solution, with
3
4
0.550 mmol
PO = = 0.00647
85.00 mL
M. But we can never reach this point, because the
pH of the 0.0200 M NaOH titrant is 12.30. Moreover, the titrant is diluted by its
addition to the solution. Thus, our titration will cease sometime shortly after the
second equivalence point. We never will see the third equivalence point, largely
because the titrant is too dilute. Our results are plotted below.
Chapter 17: Additional Aspects of Acid–Base Equilibria
878
94. (D) p 1
a
K= 2.34; 1
a
K = 4.6 103 and p 2
a
K= 9.69; 2
a
K= 2.0 1010
(a) Since the Ka values are so different, we can treat alanine (H2A+) as a monoprotic acid
with 1
a
K= 4.6 103. Hence:
H
2A+(aq) + H2O(l)
HA(aq) + H3O+(aq)
Initial 0.500 M — 0 M 0 M
Change x M — +x M +x M
Equilibrium (0.500 x) M — x M x M
1
a
K = +
3
+
2
[HA][H O ]
[H A ] = ()()
(0.500 )
x
x
x
= 4.6 103 2
0.500
x
x = 0.048 M = [H3O+] (x = 0.0457, solving the quadratic equation)
pH = log[H3O+] = log(0.046) = 1.34
(b) At the first half-neutralization point a buffer made up of H2A+/HA is formed, where
[H2A+] = [HA]. The Henderson-Hasselbalch equation gives pH = pKa = 2.34.
(c) At the first equivalence point, all of the H2A+(aq) is converted to HA(aq).
HA(aq) is involved in both 1
a
Kand 2
a
K, so both ionizations must be considered.
If we assume that the solution is converted to 100% HA, we must consider two
reactions. HA may act as a weak acid (HAA + H+ ) or HA may act as a base
(HA + H+ H2A+). See the following diagram.
Some HA
unreacted
+
A-H3O+
HA
reacts as
a base
Some HA
reacts as
an acid
H2A+
100 %
HA
amphoteric nature
(reactions occur)
HA as acid
HA as base
Using the diagram above, we see that the following relations must hold true.
[A] = [H3O+] + [H2A+]
2
a
K=+
3
[A ][H O ]
[HA]
or [A] = 2
a
+
3
[HA]
[H O ]
K & 1
a
K = +
3
+
2
[HA][H O ]
[H A ] or [H2A+] =
1
+
3
a
[H O ][HA]
K
Substitute for [A] and [H2A+] in [A] = [H3O+] + [H2A+]

Chapter 17: Additional Aspects of Acid–Base Equilibria
879
2
a
+
3
[HA]
[H O ]
K = [H3O+] +
1
+
3
a
[H O ][HA]
K (multiply both sides by 1
a
K[H3O+])
12
aa
[HA]KK = 1
a
K[H3O+][H3O+] + ++
33
[H O ][H O ][HA]
12
a[HA]
a
KK = [H3O+]2(1
a
K+ [HA])
[H3O+]2 = 12
1
aa
a
[HA]
( + [HA])
KK
K Usually, [HA] 1
a
K (Here, 0.500 4.6 103)
Make the assumption that 1
a
K+ [HA] [HA]
[H3O+]2 = 12
aa
[HA]
[HA]
KK = 12
aa
KK Take log of both sides
log[H3O+]2 = 2log [H3O+] = 2(pH) = log 12
aa
KK = log 1
a
Klog 2
a
K= p 1
a
K+ p 2
a
K
2(pH) = p 1
a
K+ p 2
a
K
pH = 12
aa
p + p
2
KK
= 2.34 + 9.69
2= 6.02
(d) Half-way between the first and second equivalence points, half of the HA(aq) is
converted to A(aq). We have a HA/A buffer solution where [HA] = [A]. The
Henderson-Hasselbalch equation yields pH = p 2
a
K= 9.69.
(e) At the second equivalence point, all of the H2A+(aq) is converted to A(aq). We can
treat this simply as a weak base in water having:
Kb =
2
w
a
K
K= 14
10
110
2.0 10
= 5.0 105
Note: There has been a 1:3 dilution, hence the [A] = 0.500 M 1 V
3 V = 0.167 M
A(aq) +H
2O(l)
HA(aq) + OH(aq)
Initial 0.167 M — 0 M 0 M
Change x M — +x M +x M
Equilibrium (0.167 x) M — x M x M
Kb = [HA][OH ]
[A ]
= ()()
(0.167 )
xx
x
= 5.0 105 2
0.167
x
x = 0.0029 M = [OH]; pOH = log[OH] = 2.54;
pH = 14.00 pOH = 14.00 2.54 = 11.46

Chapter 17: Additional Aspects of Acid–Base Equilibria
880
(f) All of the points required in (f) can be obtained using the Henderson-Hasselbalch
equation (the chart below shows that the buffer ratio for each point is within the
acceptable range (0.25 to 4.0))
0.0 10.0 20.0 30.0 40.0 50.0 60.0 70.0 80.0 90.0 100.0 110.0
mL NaOH
%H2A+
%HA
%A-
0000
0
0020406080100
0 2040608010080
60 40 20 0 0
1001008060
40
20000000
b
uffer
r
atio =base
acid 04.00.25 0.67 1.5 1.50.670.25 4.0
8
8
8
Ma
y
use Hende
r
son-Hassel
b
alch e
q
ua
t
ion May use Henderson-Hasselbalch equation
(i) After 10.0 mL
Here we will show how to obtain the answer using both the Henderson-Hasselbalch
equation and setting up the I. C. E. (Initial, Change, Equilibrium) table. The results
will differ within accepted experimental limitation of the experiment (+ 0.01 pH units)
nH2A+ = (CV) = (0.500 M)(0.0500 L) = 0.0250 moles H2A
nOH- = (CV) = (0.500 M)(0.0100 L) = 0.00500 moles OH
Vtotal = (50.0 + 10.0) mL = 60.0 mL or 0.0600 L
[H2A+] = +
2
HA
total
0.0250mol
= =0.417 M
0.0600L
n
V [OH] = OH
total
0.00500mol
= =0.0833M
0.0600L
n
V
Keq for titration reaction =
b
(HA)
1
K=
1
w
a
1
K
K
= 1
3
a11
14
w
4.6 10 4.6 10
1.00 10
K
K
H
2A+(aq) + OH(aq)
HA(aq) + H2O(l)
Initial: 0.417 M 0.0833 M 0 M —
100% rxn: -0.0833 -0.0833 M +0.0833 M —
New initial: 0.334 M 0 M 0.0833 M —
Change: +x M +x M x M —
Equilibrium: 0.334 M x M 0.0833 M —
4.6 1011 = (0.0833)
(0.334)( )
x
; x = 11
(0.0833)
(0.334)(4.6 10 )= 5.4 1013 (valid assumption)
x = 5.4 1013 = [OH]; pOH = log(5.4 1013) = 12.27;
pH = 14.00 – pOH = 14.00 – 12.27 = 1.73
Alternative method using the Henderson-Hasselbalch equation:

Chapter 17: Additional Aspects of Acid–Base Equilibria
881
(i) After 10.0 mL, 20% of H2A+ reacts, forming the conjugate base HA.
Hence the buffer solution is 80% H2A+ (acid) and 20% HA (base).
pH = 1
a
pK+ log
b
ase
acid = 2.34 + log
20.0
80.0 = 2.34 + (0.602) = 1.74 (within + 0.01)
For the remainder of the calculations we will employ the Henderson-Hasselbalch equation
with the understanding that using the method that employs the I.C.E. table gives the same
result within the limitation of the data.
(ii) After 20.0 mL, 40% of H2A+ reacts, forming the conjugate base HA.
Hence the buffer solution is 60% H2A+ (acid) and 40% HA (base).
pH = 1
a
pK+ log
b
ase
acid = 2.34 + log
40.0
60.0 = 2.34 + (0.176) = 2.16
(iii) After 30.0 mL, 60% of H2A+ reacts, forming the conjugate base HA.
Hence the buffer solution is 40% H2A+ (acid) and 60% HA (base).
pH = 1
a
pK+ log
b
ase
acid = 2.34 + log
60.0
40.0 = 2.34 + (+0.176) = 2.52
(iv) After 40.0 mL, 80% of H2A+ reacts, forming the conjugate base HA.
Hence the buffer solution is 20% H2A+ (acid) and 80% HA (base).
pH = 1
a
pK+ log
b
ase
acid = 2.34 + log 80.0
20.0 = 2.34 + (0.602) = 2.94
(v) After 50 mL, all of the H2A+(aq) has reacted, and we begin with essentially 100%
HA(aq), which is a weak acid. Addition of base results in the formation of the
conjugate base (buffer system) A(aq). We employ a similar solution, however,
now we must use p 2
a
K = 9.69.
(vi) After 60.0 mL, 20% of HA reacts, forming the conjugate base A.
Hence the buffer solution is 80% HA (acid) and 20% A (base)
pH = 2
a
pK+ log
b
ase
acid = 9.69 + log 20.0
80.0 = 9.69 + (0.602) = 9.09
(vii) After 70.0 mL, 40% of HA reacts, forming the conjugate base A.
Hence the buffer solution is 60% HA (acid) and 40% A (base).
pH = 2
a
pK+ log
b
ase
acid = 9.69 + log 40.0
60.0 = 9.69 + (0.176) = 9.51
Chapter 17: Additional Aspects of Acid–Base Equilibria
882
(viii) After 80.0 mL, 60% of HA reacts, forming the conjugate base A.
Hence the buffer solution is 40% HA (acid) and 60% A (base).
pH = 2
a
pK+ log
b
ase
acid = 9.69 + log 60.0
40.0 = 9.69 + (+0.176) = 9.87
(ix) After 90.0 mL, 80% of HA reacts, forming the conjugate base A.
Hence the buffer solution is 20% HA (acid) and 80% A (base).
pH = 2
a
pK+ log
b
ase
acid = 9.69 + log 80.0
20.0 = 9.69 + (0.602) = 10.29
(x) After the addition of 110.0 mL, NaOH is in excess. (10.0 mL of 0.500 M NaOH is in excess,
or, 0.00500 moles of NaOH remains unreacted). The pH of a solution that has NaOH in
excess is determined by the [OH] that is in excess.
(For a diprotic acid, this occurs after the second equivalence point.)
[OH]excess = OH
total
0.00500mol
= = 0.0312 M
0.1600L
n
V
; pOH = log(0.03125) = 1.51
pH = 14.00 – pOH = 14.00 –1.51 = 12.49
(g) A sketch of the titration curve for the 0.500 M solution of alanine hydrochloride,
with some significant points labeled on the plot, is shown below.
Plot of pH versus Volume of NaOH Added
0
2
4
6
8
10
12
14
0 20406080100120
NaOH volume (mL)
pH
isoelectric point
pH = pKa1
pH = pKa2
NaOH
in excess
H2A+/HA
buffer region
HA/A-
buffer region

Chapter 17: Additional Aspects of Acid–Base Equilibria
883
SELF-ASSESSMENT EXERCISES
95. (E)
(a) mmol: millimoles, or 1×10-3 mol
(b) HIn: An indicator, which is a weak acid
(c) Equivalence point of a titration: When the moles of titrant equals the moles of the substance
being titrated
(d) Titration curve: A curve of pH of the solution being titrated versus the pH of the titrating
solution
96. (E)
(a) The common-ion effect: A process by which ionization of a compound is suppressed by having
present one of the product ions (from another source) in the solution
(b) use of buffer to maintain constant pH: A buffer is a solution of a weak acid and its conjugate
base, and it resists large changes in pH when small amounts of an acid or base are added.
(c) determination of pKa from titration curve: At the half-way point (when half of the species being
titrated is consumed, the concentration of that species and its conjugate is the same, and the
equilibrium expression simplifies to pKa = pH
(d) measurement of pH with an indicator: An approximate method of measuring the pH, where the
color of an ionizable organic dye changes based on the pH
97. (E)
(a) Buffer capacity and buffer range: Buffer capacity is a measure of how much acid or base can be
added to the buffer without an appreciable change in the pH, and is determined by the
concentration of the weak acid and conjugate base in the buffer solution. The buffer range,
however, refers to the range over which a buffer effectively neutralizes added acids and bases
and maintains a fairly constant pH.
(b) Hydrolysis and neutralization: Hydrolysis is reaction of an acid or base with water molecules,
which causes water to split into hydronium and hydroxide ions. Neutralization is the reaction of
H3O+ and OH– together to make water.
(c) First and second equivalence points in the titration of a weak diprotic acid: First equivalence
point is when the first proton of a weak diprotic acid is completely abstracted and the resulting
acid salt and base have been consumed and neither is in excess. Second equivalence point is the
equivalence point at which all protons are abstracted from the acid and what remains is the (2-)
anion.
(d) Equivalence point of a titration and end point of an indicator: Equivalence point of a titration is
when the moles of titrant added are the same as the moles of acid or base in the solution being
titrated. The endpoint of an indicator is when the indicator changes color because of abstraction
or gain of a proton, and is ideally as close as possible to the pH of the equivalence point.
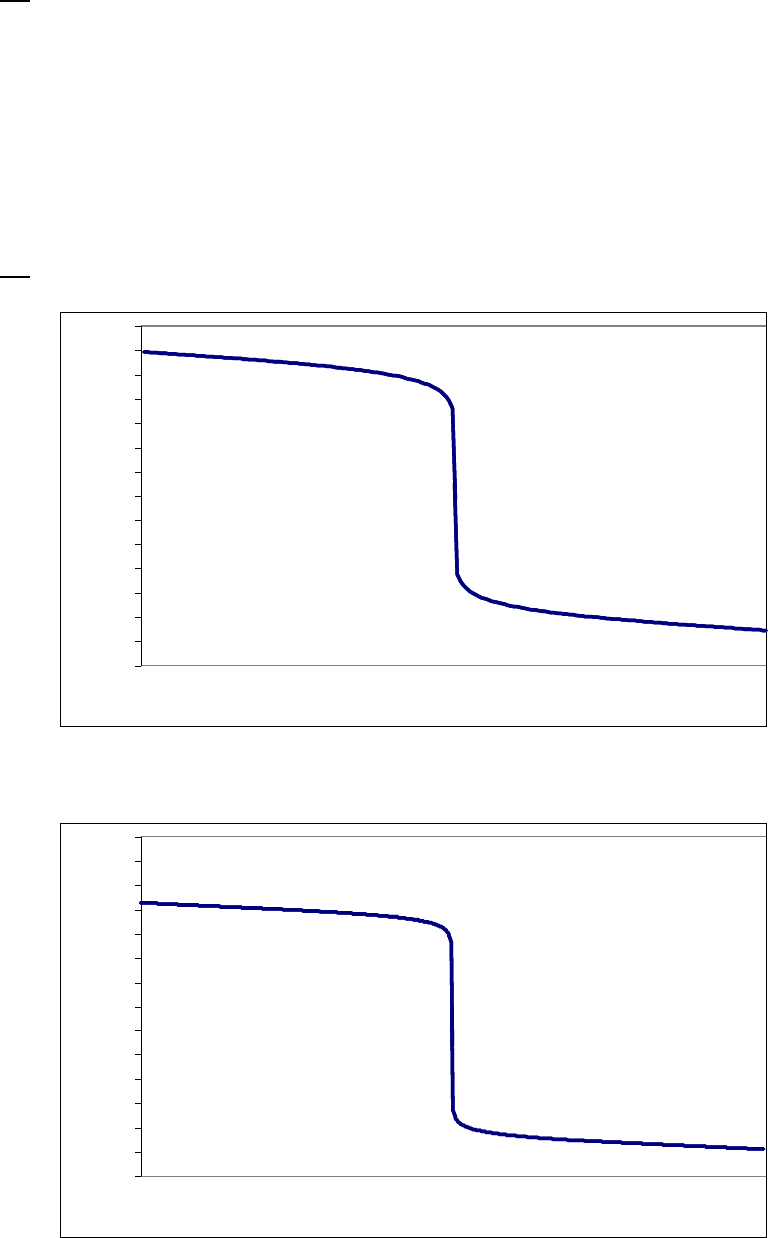
Chapter 17: Additional Aspects of Acid–Base Equilibria
884
98. (E)
(a) HCHO2 + OH¯ → CHO2¯ + H2O
CHO2¯ + H3O+ → HCHO2 + H2O
(b) C6H5NH3+ + OH¯ → C6H5NH2 + H2O
C6H5NH2 + H3O+ → C6H5NH3+ + H2O
(c) H2PO4¯ + OH¯ → HPO42- + H2O
HPO42- + H3O+ → H2PO4¯ + H2O
99. (M)
(a) The pH at theequivalence point is 7. Use bromthymol blue.
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Vol of Titrant (mL)
pH
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Vol of Titrant (mL)
pH
(b) The pH at the equivalence point is ~5.3 for a 0.1 M solution. Use methyl red.
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Vol of Titrant (mL)
pH
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Vol of Titrant (mL)
pH
Chapter 17: Additional Aspects of Acid–Base Equilibria
885
(c) The pH at the equivalence point is ~8.7 for a 0.1 M solution. Use phenolphthalein, because it
just begins to get from clear to pink around the equivalence point.
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Vol of Titrant (mL)
pH
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Vol of Titrant (mL)
pH
(d) The pH for the first equivalence point (NaH2PO4– to Na2HPO42–) for a 0.1 M solution is right
around ~7, so use bromthymol blue.
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Vol of Titrant (mL)
pH
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Vol of Titrant (mL)
pH
Chapter 17: Additional Aspects of Acid–Base Equilibria
886
100. (D)
(a) This is the initial equilibrium before any base has reacted with the acid. The reaction that
dominates, along with changes in concentration, is shown below:
HC7H5O2 + H2O C7H5O2¯ + H3O+
0.0100 0 0
- x + x +x
0.0100 − x x x
+-
3752
752
-5
4
+4
3
HO CHO
HC H O
6.3 10 0.0100 -
Solving for x using the quadratic formula, = 7.63 10 M.
pH = log H O log 7.63 10 3.12
a
K
xx
x
x
(b) In this case, we titrate the base with 0.00625 L of Ba(OH)2. Therefore, we have to calculate the
final moles of the base and the total volume to determine the concentration.
4
752 752
4
2
2
mol HC H O 0.02500 L 0.0100 M HC H O 2.5 10 mol
2mol OH
mol OH 0.00625 L 0.0100 M Ba OH = 1.25 10 mol
1mol Ba OH
Since the amount of OH¯ is half of the initial amount of HC7H5O2, the moles of HC7H5O2 and
C7H5O2¯ are equal. Therefore, Ka = [H3O+], and pH = −log(6.3×10-5) = 4.20.
(c) At the equivalence point, there is initially no HC7H5O2. The equilibrium is dominated by
C7H5O2¯ hydrolyzing water. The concentration of C7H5O2¯ is:
Total moles of HC7H5O2 = 2.5×10-4 mol as shown previously. At the equivalence point, the
moles of acid equal moles of OH¯.
44
2
2
1mol Ba OH
mol Ba OH 2.5 10 mol OH 1.25 10 mol
2 mol OH
Vol of Ba(OH)2 = 1.25×10-4 mol / 0.0100 M = 0.0125 L
Total volume of the solution at the equivalence point is the sum of the initial volume plus the
volume of Ba(OH)2 added. That is,
VTOT = 0.02500 L + 0.0125 L = 0.0375 L
Therefore, the concentration of C7H5O2¯ = 2.5×10-4/0.0375 L = 0.00667 M.

Chapter 17: Additional Aspects of Acid–Base Equilibria
887
C7H5O2¯ + H2O HC7H5O2 +OH¯
0.00667 0 0
-x +x +x
0.00667 − x x x
Since this is a base reaction,
45 10
bwa
K K K 1.00 10 6.3 10 1.587 10 .
-
752
b-
752
10
6
6
OH HC H O
K= CHO
1.59 10 0.00667
solving for (by simplifying the formula above) yields = 1.03 10 M.
pH = 14 pOH 14 log 1.03 10 14 6.00 8.00
xx
x
xx
(d) In this part, we have an excess of a strong base. As such, we have to determine how much
excess base there is and what is the final volume of the solution.
2
2
4
mol Ba OH 2mol OH
mol OH 0.01500 L 0.0100 L1mol BaOH
3.000 10 mol OH
44
752
5
Excess mol OH mol HC H O mol OH 3.000 10 2.500 10
5.000 10 mol
5
5.0 10 mol
OH 0.00125 M
0.02500 L+0.01500 L
pH = 14 pOH 14 log 0.00125 14 2.903 11.1
101. (E) The answer is (c); because of the common ion-effect, the presence of HCO2¯ will repress
ionization of formic acid.
102. (E) The answer is (d), because NaHCO3 is a weak base and will react with protons in water, shifting
the formic acid ionization equilibrium to the right.
103. (E) The answer is (b), raise the pH. NH4+ is an acid, and to be converted to its conjugate base, it
must react with a base to abstract its proton.
104. (E) The answer is (b), because at that point, the number of moles of weak base remaining is the
same as its conjugate acid, and the equilibrium expression simplifies to Ka = [H3O+].

Chapter 17: Additional Aspects of Acid–Base Equilibria
888
105. (M) The base, C2H5NH2, is reacted with HClO4. The reaction is:
25 2 4 25 3 4
C H NH HClO C H NH ClO
Assuming a volume of 1 L for each solution,
25 2
1.49 mol – 1.001 mol 0.489 mol
C H NH 0.2445 M
2L 2L
25 3
1.001 mol
C H NH 0.5005 M
2L
25 3
4
25 2
4
4
CHNH OH 0.5005 +
4.3 10 C H NH 0.2445
2.10 10
pOH log 2.10 10 3.68
pH 14 3.68 10.32
x
x
x
x
106. (D) We assume that all of Ca(HSe)2 dissociates in water. The concentration of HSe– is therefore:
2
2
2mol HSe
0.5 M Ca HSe 1.0 M HSe
1mol Ca HSe
We note that HSe– is amphoteric; that is, it can act either as an acid or a base. The acid reaction of
HSe– and the concentration of [H3O+] generated, are as follows:
HSe– + H2O Se2– + H3O+
2
3
11
11 6
Se H O
1.00 10 1.00
HSe
= 1.00 10 3.16 10
x
x
x
x
The basic reaction of HSe– and the concentration of [OH–] generated, are as follows:
HSe– + H2O H2Se + OH–
Kb = 1.00×10-14/1.3×10-4 = 7.69×10-11
2
11
11 6
HSe OH
7.69 10 1.00
HSe
= 7.69 10 8.77 10
x
x
x
x

Chapter 17: Additional Aspects of Acid–Base Equilibria
889
Therefore, we have [H3O+] = 3.16×10-6 and [OH–] = 8.77×10-6. Since these two react to give H2O,
the result is 8.77×10-6 – 3.16×10-6 = 5.61×10-6 M [OH–]. The pH of the solution is:
pH = 14 – pOH = 14 – 5.25 = 8.75
107. (E) The answer is (a). The solution system described is a buffer, and will resist large changes in
pH. Adding KOH should raise the pH slightly.
108. (E) The answer is (b), because HSO3¯ is a much stronger acid (Ka = 1.3×10-2) than H2PO4¯
(Ka = 6.3×10-8).
109. (E) The answer is (b). The pKa of the acid is 9, which puts it squarely in the middle of the 8–10 pH
range for the equivalence point.
110. (E)
(a) NaHCO3 titrated with NaOH: pH > 7, because HCO3¯ is itself slightly basic, and is being
titrated with NaOH to yield CO32- at the equivalence point, which is even more basic.
(b) HCl titrated with NH3: pH < 7, because the resulting NH4+ at the equivalence point is acidic.
(c) KOH titrated with HI: pH = 7, because a strong base is being titrated by a strong acid, and the
resulting anions and cations are all non-basic and non-acidic.
111. (M) The concepts that define Sections 17-2, 17-3, and 17-4 are buffers, indicators, and titrations.
For buffers, after definition, there are a number of concepts, such as composition, application, the
equilibrium expression (the Henderson-Hasselbalch equation is a subtopic of the equilibrium
expression). Under composition, there are other subtopics such as buffer range and capacity. For
indicators, after defining it, there are subtopics such as equilibrium expression and usage. With
titration, topics such as form (weak acid titrated by strong base, and weak base titrated by strong
acid), the titration curve, and the equivalence point. Look at these sections to find inter-related
terminology and other concepts.

890
CHAPTER 18
SOLUBILITY AND COMPLEX-ION EQUILIBRIA
PRACTICE EXAMPLES
1A (E) In each case, we first write the balanced equation for the solubility equilibrium and then
the equilibrium constant expression for that equilibrium, the Ksp expression:
(a)
2
2+
33
MgCO s Mg aq +CO aq
Ksp = [Mg2+][CO32]
(b)
3
+
34 4
Ag PO s 3Ag aq + PO aq
Ksp = [Ag+]3[PO43]
1B (E)
(a)
Provided the [OH] is not too high, the hydrogen phosphate ion is not expected to ionize
in aqueous solution to a significant extent because of the quite small values for the
second and third ionization constants of phosphoric acid.
2
2+
44
CaHPO s Ca aq + HPO aq
(b) The solubility product constant is written in the manner of a Kc expression:
Ksp = [Ca2+][HPO42] = 1. 107
2A (M) We calculate the solubility of silver cyanate, s, as a molarity. We then use the solubility
equation to (1) relate the concentrations of the ions and (2) write the Ksp expression.
4
7 mg AgOCN 1000 mL 1 g 1 mol AgOCN
==510 moles/L
100 mL 1 L 1000 mg 149.9 g AgOCN
s
+
Equation : AgOCN s Ag aq + OCN aq
Solubility Product : s s
2
+247
sp = Ag OCN = = = 5 10 = 3 10Ksss
2B (E) We calculate the solubility of lithium phosphate, s, as a molarity. We then use the
solubility equation to (1) relate the concentrations of the ions and (2) write the Ksp expression.
34 34
34
0.034 g Li PO 1 mol Li PO1000 mL
= = 0.0029 moles/L
100 mL soln 1 L 115.79 g Li PO
s
Equation:
3
+
34 4
Li PO s 3Li aq + PO aq
Solubility Product: (3 s)3 s
33
3
+
sp 4
=Li PO =3 =Kss
449
27 27(0.0029) 1.9 10s
Chapter 18: Solubility and Complex-Ion Equilibria
891
3A (E) We use the solubility equilibrium to write the Ksp expression, which we then solve to
obtain the molar solubility, s, of Cu3(AsO4)2.
2+
342 4
Cu (AsO ) . s 3 Cu aq + 2 AsO aq
32
32
2+ 5 36
sp 4
= AsO = 3 2 = 108 = 7.6 10KCu ss s
Solubility : 36 8
57.6 10 3.7 10 M
108
s
3B (E) First we determine the solubility of BaSO4, and then find the mass dissolved.
2
2+
44
BaSO aq Ba aq +SO aq
Ks
sp Ba SO==
2+ 4
22
The last relationship is true because Ba SO
2+ 4
2
= in a solution produced by dissolving
BaSO4 in pure water. Thus, 10 5
sp
s = K 1.1 10 1.05 10 M.
5
44
4 4
4
1.05 10 mmol BaSO 233.39mg BaSO
mass BaSO = 225 mL = 0.55mg BaSO
1 mL sat’d soln 1mmol BaSO
4A (M) For PbI Pb I
sp22+ 29
,= =7.110K
. The solubility equilibrium is the basis of the
calculation.
Equation: PbI s
2bg
Pb aq
2+bg
+ 2I aq
bg
Initial: — 0.10 M 0 M
Changes: — +s M +2s M
Equil: — (0.10 + s) M 2s M
Ksss
sp Pb I= = 7.1 10 = 0.10 + 2 0.40
2+ 2922
bgbg s
71 10
040 13 10
94
.
..M
(assumption 0.10 s is valid)
This value of s is the solubility of PbI2 in 0.10 M Pb NO aq
32
bgbg.
4B (E) We find pOH from the given pH:
pOH = 14.00 – 8.20 = 5.80; [OH–] = 10-pOH = 10-5.80 = 1.6×10-6 M.
We assume that pOH remains constant, and use the Ksp expression for Fe OH3
bg
.
38
33
3+ 38 3+ 6 3+ 21
sp 3
6
410
= Fe OH = 4 10 = Fe 1.6 10 Fe = = 9.8 10 M
1.6 10
K
Therefore, the molar solubility of Fe(OH)3 is 9.81021 M.
The dissolved Fe OH
bg
3 does not significantly affect OH.
Chapter 18: Solubility and Complex-Ion Equilibria
892
5A (M) First determine I as altered by dilution. We then compute Qsp and compare it with Ksp .
4
0.05mL 0.20mmolKI 1mmolI
3drops 1drop 1mL 1mmol KI
I= =310M
100.0mL soln
+46
sp =Ag I =0.010 310 =310Q
17
sp sp
8.5 10 = Thus, precipitation should occur.QK
5B (M) We first use the solubility product constant expression for PbI2 to determine the I
needed in solution to just form a precipitate when Pb2+ = 0.010 M. We assume that the
volume of solution added is small and that Pb2+ remains at 0.010 M throughout.
Ksp Pb I I I M= = 7.1 10 = 0.010 = 71 10
0 010 =8.4 10
2+ 29294
bg.
.
We determine the volume of 0.20 M KI needed.
volume of KI aq mL mmol I
mL
mmol KI
mmol I
mL KI aq
mmol KI
drop
mL
drops drops
bgbg
= 100.0 8.4 10
1
1
1
1
0.20
1
0.050
= 8.4 = 9
4
Since one additional drop is needed, 10 drops will be required. This is an insignificant volume
compared to the original solution, so Pb2+ remains constant.
6A (E) Here we must find the maximum Ca2+ that can coexist with OH = 0.040M.
6
22
62+ 2+ 2+ 3
sp 2
5.5 10
= 5.5 10 = Ca OH = Ca 0.040 ; Ca = = 3.4 10 M
0.040
K
For precipitation to be considered complete, Ca2+ should be less than 0.1% of its original
value. 3.4 10 3
M is 34% of 0.010 M and therefore precipitation of Ca OH
bg2 is not complete
under these conditions.
6B (E) We begin by finding Mg2+ that corresponds to1 /
2+
g Mg L.
2+ 2+
2+ 8
62+
1 g Mg 1 g 1 mol Mg
Mg = = 4 10 M
1 L soln 10 g 24.3 g Mg
Now we use the Ksp expression for Mg OH
bg
2 to determine OH.
Ksp Mg OH OH=1.8 10 = = 4 10
11 2+ 282
ch OH M
=18 10
410 0.02
11
8
.
Chapter 18: Solubility and Complex-Ion Equilibria
893
7A (M) Let us first determine Ag+ when AgCl(s) just begins to precipitate. At this point,
Qsp and Ksp are equal.
KQ
sp sp
Ag Cl Ag M= 1.8 10 = = = 0.115
10 + +
Ag M
+10 9
=1.8 10
0.115 =1.6 10
Now let us determine the maximum Br that can coexist with this Ag+.
Ksp Ag Br M Br= 5.0 10 = = 1.6 10
13 + 9
; Br M
=5.0 10
1.6 10 =3.1 10
13
9
4
The remaining bromide ion has precipitated as AgBr(s) with the addition ofAgNO aq
3bg.
Percent of 4
final
initial
[Br ] 3.1 10 M
Br remaining 100% 100% 0.12%
[Br ] 0.264M
7B (M) Since the ions have the same charge and the same concentrations, we look for two Ksp
values for the salt with the same anion that are as far apart as possible. The Ksp values for the
carbonates are very close, while those for the sulfates and fluorides are quite different.
However, the difference in the Ksp values is greatest for the chromates; Ksp for
10
4
BaCrO 1.2 10
is so much smaller than Ksp for
5
4
SrCrO 2.2 10 ,
4
BaCrO will
precipitate first and 4
SrCrO will begin to precipitate when 2
4
CrO
has the value:
5
2sp 4
42+
2.2 10
CrO = = = 2.2 10 M
0.10
Sr
K
.
At this point 2+
Ba
is found as follows.
10
sp
2+ 7
4
2
4
1.2 10
Ba = = = 5.5 10 M
2.2 10
CrO
K
;
[Ba2+] has dropped to 0.00055% of its initial value and therefore is considered to be
completely precipitated, before 4
SrCrO begins to precipitate. The two ions are thus effectively
separated as chromates. The best precipitating agent is a group 1 chromate salt.
8A (M) First determine OH resulting from the hydrolysis of acetate ion.
Equation:
-
232 2
CHO aq + HO(l)
HC H O aq
232
bg+OH aq
bg
Initial: 0.10 M — 0 M
0M
Changes:
x
M — +
x
M +
x
M
Equil: 0.10x
bgM —
x
M
x
M

Chapter 18: Solubility and Complex-Ion Equilibria
894
14 2
232
10
b5
232
HC H O OH
1.0 10 5.6 10 =
1.8 10 0.10 0.10
CHO
x
xx
Kx
x
[].. .OH M010 56 10 75 10
10 6 (the assumption 0.10x was valid)
Now compute the value of the ion product in this solution and compare it with the value of
Ksp for Mg OH
bg2.
QK
sp sp
Mg OH M M Mg OH= = 0.010 7.5 10 = 5.6 10 1.8 10 =
2+ 26213 11
2
bg
ch bg
Because Qsp is smaller than Ksp , this solution is unsaturated and precipitation of Mg OH s
bgbg
2
will not occur.
8B (M) Here we can use the Henderson–Hasselbalch equation to determine the pH of the buffer.
pH p log CHO
HC H O log log M
M
a
=+ = 1.810+
0.250
0.150 = 4.74 + 0.22 = 4.96
232
232
5
K
L
N
MO
Q
P
ch
pOH pH OH M
pOH 9
= 14.00 = 14.00 4.96 = 9.04 = 10 = 10 = 9.1 10
.04 10
Now we determine Qsp to see if precipitation will occur.
33
3+ 10 30
sp
38
sp sp 3
= Fe OH = 0.013M 9.1 10 = 9.8 10
4 10 = ; Thus, Fe(OH) precipitation should occur.
Q
QK
9A (M) Determine OH, and then the pH necessary to prevent the precipitation of Mn OH
bg2.
22
13 2+
sp =1.9 10 = Mn OH = 0.0050M OHK
13 6
1.9 10
OH = 6.2 10 M
0.0050
pOH log= 6.2 10 = 5.21
6
ch pH = 14.00 5.21= 8.79
We will use this pH in the Henderson–Hasselbalch equation to determine +
4
NH .
b
p = 4.74K for NH3.
3
a++
44
NH 0.025M
pH = p + log = 8.79 = 14.00 4.74 + log
NH NH
K
+
4
0.025M
log = 8.79 14.00 4.74 = 0.47
NH
0.47
+
4
0.025 =10 = 0.34
NH
+
4
0.025
NH = = 0.074M
0.34

Chapter 18: Solubility and Complex-Ion Equilibria
895
9B (M) First we must calculate the [H3O+] in the buffer solution that is being employed to
dissolve the magnesium hydroxide:
NH3(aq) + H2O(l)
NH4+(aq) + OH(aq) ; Kb = 1.8 105
5
4
b
3
14 2
510
32
5
[NH ][OH ] [0.100M][OH ] 1.8 10
[NH ] [0.250M]
1.00 10 M
[OH ] 4.5 10 M; [H O ] 2.2 10 M
4.5 10 M
K
Now we can employ Equation 18.4 to calculate the molar solubility of Mg(OH)2 in the buffer
solution; molar solubility Mg(OH)2 = [Mg2+]equil
Mg(OH)2(s) + 2 H3O+(aq) 17 K = 1.8 10
Mg2+(aq) + 4H2O(l) ;
Equilibrium 2.2 1010 x
217 3 2
equil
2102
3
-3
2
[Mg ]
K 1.8 10 8.7 10 M [Mg ]
[H O ] [2.2 10 M]
So, themolar solubility for Mg(OH) = 8.7 10 M.
xx
10A (M)
(a) In solution are Cu aq SO aq Na aq
2+ 4
2+
,,
bgbgbg
, and
OH aq .
2+
2
Cu aq + 2OH aq Cu OH s
(b) In the solution above, Cu OH s
bgbg
2 is Cu aq
2+bg
:
2+
2
Cu OH s Cu aq + 2OH aq
This Cu aq
2+bg
reacts with the added NH aq
3bg:
2+
2+
33
4
Cu aq + 4 NH aq Cu NH aq
The overall result is:
2+
33
24
Cu OH s + 4NH aq Cu NH aq + 2OH aq
(c) HNO aq
3bg (a strong acid), forms H O aq
3+bg
, which reacts with OH aq
bg
and NH aq
3bg.
+
32
OH aq + H O aq 2H O(l);
+
+
33 4 2
NH aq + H O aq NH aq + H O(l)
As NH aq
3bg is consumed, the reaction below shifts to the left.
2+
33
24
Cu OH s + 4 NH aq Cu NH aq + 2OH aq
But as OH aq
bg
is consumed, the dissociation reactions shift to the side with the
dissolved ions:
2+
2
Cu OH s Cu aq + 2OH aq
The species in solution at the end of all this are

Chapter 18: Solubility and Complex-Ion Equilibria
896
2+ + + + 2
34 3 4
Cu aq , NO aq , NH aq , excess H O aq , Na aq , and SO aq
(probably HSO4(aq) as well).
10B (M)
(a)
In solution are Zn (aq), SO aq),
2+ 4
2( and NH (aq),
3
2+
2+
33
4
Zn aq + 4 NH aq Zn NH aq
(b) HNO aq
3bg, a strong acid, produces HO aq
3+bg
, which reacts with NH aq
3bg.
+
+
33 4 2
NH aq + H O aq NH aq + H O(l) As NH aq
3bg is consumed, the tetrammine
complex ion is destroyed.
2+ 2+ +
+
33 2 4
44
Zn NH aq + 4H O aq Zn H O aq + 4NH aq
(c) NaOH(aq) is a strong base that produces OH aq
bg
, forming a hydroxide precipitate.
2+
2 2
42
Zn H O aq + 2OH aq Zn OH s + 4H O l
Another possibility is a reversal of the reaction of part (b).
2+ 2+
+
24 32
4 4
Zn H O aq + 4 NH aq + 4OH aq Zn NH aq +8H O l
(d) The precipitate dissolves in excess base.
2
24
Zn OH s + 2OH aq Zn OH aq
11A (M) We first determine Ag+ in a solution that is 0.100 M Ag+(aq) (from AgNO3) and
0.225 M NH aq
3bg. Because of the large value of Kf=1.6 107
, we start by having the
reagents form as much complex ion as possible, and approach equilibrium from this point.
Equation: Ag aq
+bg
+ 2 3
NH aq
bg
Ag NH aq
32
+
bgbg
In soln 0.100 M 0.225 M 0 M
Form complex –0.100 M –0.200 M +0.100 M
Initial 0 M 0.025 M 0.100 M
Changes +x M +2x M –x M
Equil x M (0.025 + x) M (0.100 – x) M
Kf
Ag NH
Ag NH
=1.6 10 =
732
+
+3
2
L
N
MO
Q
P
bg
22
0.100 0.100
=0.025+ 2 0.025
x
xxx
x=0.100
0.025 1.6 10 =1.0 10 = =
27
5+
bg
M Ag concentration of free silver ion
(x << 0.025 M, so the approximation was valid)
The Cl is diluted: initial
final initial final
1.00mL
Cl = Cl = 3.50M 1500 = 0.00233M
1,500mL

Chapter 18: Solubility and Complex-Ion Equilibria
897
Finally we compare Qsp with Ksp to determine if precipitation of AgCl(s) will occur.
QK
sp sp
Ag Cl M M= = 1.0 10 0.00233 = 2.3 10 1.8 10 =
+5 810
chbg
Because the value of the Qsp is larger than the value of the Ksp, precipitation of AgCl(s) should
occur.
11B (M) We organize the solution around the balanced equation of the formation reaction.
Equation: Pb aq
2+bg
+ EDTA aq
4bg
PbEDTA aq
2bg
Initial 0.100 M 0.250 M 0 M
Form Complex: –0.100 M (0.250 – 0.100) M 0.100 M
Equil
x
M 0.150 + x
bgM 0.100
x
bgM
2
18
f2+ 4
19
18
PbEDTA 0.100 0.100
==210=
0.150 + 0.150
Pb EDTA
0.100
= = 3 10 M ( << 0.100 M, thus the approximation was valid.)
0.150 2 10
x
Kxx x
xx
We calculate Qsp and compare it to Ksp to determine if precipitation will occur.
22
2+ 19 21
sp = Pb I = 3 10 M 0.10M = 3 10Q
.
9
sp sp
7.1 10 =QK
Thus precipitation will not occur.
12A (M) We first determine the maximum concentration of free +
Ag .
+10
sp =Ag Cl =1.810K
Ag+10 8
=1.8 10
0.0075 =2.4 10
M.
This is so small that we assume that all the Ag+ in solution is present as complex ion:
Ag NH32
+= 0.13
bg M. We use Kf to determine the concentration of free NH3.
Kf
Ag NH
Ag NH
M
NH
==1.610=
0.13
2.4 10
32
+
+3
2
7
83
2
bg
L
N
MO
Q
PL
N
MO
Q
P
NH M.
387
=013
2 4 10 16 10 = 0.58
.
..
If we combine this with the ammonia present in the complex ion, the total ammonia
concentration is 0.58 + 2 0.13 = 0.84MMM
bg. Thus, the minimum concentration of
ammonia necessary to keep AgCl(s) from forming is 0.84 M.

Chapter 18: Solubility and Complex-Ion Equilibria
898
12B (M) We use the solubility product constant expression to determine the maximum Ag+
that can be present in 0.010 M Cl without precipitation occurring.
10
10 + + + 8
sp
1.8 10
=1.8 10 = Ag Cl = Ag 0.010M Ag = =1.8 10 M
0.010
K
This is also the concentration of free silver ion in the Kf expression. Because of the large
value of Kf, practically all of the silver ion in solution is present as the complex ion,
[Ag(S2O3)2]3]. We solve the expression for [S2O32] and then add the [S2O32] “tied up” in
the complex ion.
3
23
2
13
f22
22
+8
23 23
Ag S O 0.10 M
1.7 10 Ag S O 1.8 10 M S O
K
2 2
4
23 23
813
0.10
S O = = 5.7 10 M = concentration of free S O
1.8 10 1.7 10
2
3
24 23
23 23 3
2
23
2
2mol S O
total S O = 5.7 10 M + 0.10M Ag S O 1mol Ag S O
= 0.20 M + 0.00057M = 0.20M
13A (M) We must combine the two equilibrium expressions, for Kf and for Ksp, to find Koverall.
3+
3
Fe OH s Fe aq + 3OH aq
Ksp =4 1038
3
2
3+
24 24
3
Fe aq +3C O aq Fe C O aq
Kf=2 10
20
3
2
24 24
33
Fe OH s +3C O aq Fe C O aq + 3OH aq
18
overall =8 10K
Initial 0.100 M 0 M
0M
Changes 3
x
M +
x
M +3
x
M
Equil 0.100 3
x
bgM M
x
3
x
M
3
overall
3
334
24
318
33
2
24
Fe C O 327
0.100 3 0.100
OH ==810
CO
=
xx x
x
K
(3x << 0.100 M, thus the approximation was valid.)
x
(. )0100 8 10
27 410
318
46M The assumption is valid.
Thus the solubility of Fe OH
bg3 in 0.100 M C O
24
2 is 4 10 6
M.

Chapter 18: Solubility and Complex-Ion Equilibria
899
13B (M) In Example 18-13 we saw that the expression for the solubility, s, of a silver halide in an
aqueous ammonia solution, where NH3 is the concentration of aqueous ammonia, is given
by:
2
sp f sp f
33
=NH 2 [NH ] 2
ss
KK or KK
ss
For all scenarios, the
3
NH stays fixed at 0.1000 M and 7
fis always 1.6 10K.
We see that s will decrease as does Ksp . The relevant values are:
10 13 17
sp sp sp
AgCl =1.8 10 , AgBr = 5.0 10 , AgI = 8.5 10KK K
.
Thus, the order of decreasing solubility must be: AgI > AgBr > AgCl.
14A (M) For FeS, we know that Kspa =6 10
2
; for Ag S spa230
,=610K.
We compute the value of Qspa in each case, with HS M
2= 0.10 and HO M
3
+=0.30 .
2
spa spa
2
0.020 0.10
For FeS, = = 0.022 6 10 =
0.30
QK
Thus, precipitation of FeS should not occur.
2
4
2spa 2
30
spa spa 2
0.010 0.10
For Ag S, = = 1.1 10
0.30
6 10 = ; thus, precipitation of Ag S should occur.
Q
QK
14B (M) The HO
3
+ needed to just form a precipitate can be obtained by direct substitution of the
provided concentrations into the Kspa expression. When that expression is satisfied, a
precipitate will just form.
2+ 2+
22
2+
spa 3
22 2
++
33
Fe H S 0.015M Fe 0.10M H S 0.015 0.10
= = 6 10 = , H O = = 0.002M
610
HO HO
K
pH log H O log= = 0.002 = 2.7
3
+
bg

Chapter 18: Solubility and Complex-Ion Equilibria
900
INTEGRATIVE EXAMPLES
A. (D) To determine the amount of Ca(NO3)2 needed, one has to calculate the amount of Ca2+ that
will result in only 1.00×10-12 M of PO43-
2+ 3-
34 4
2
32
sp
Ca PO 3 Ca +2 PO
32
Kss
Using the common–ion effect, we will try to determine what concentration of Ca2+ ions forces
the equilibrium in the lake to have only 1.00×10-12 M of phosphate, noting that (2s) is the
equilibrium concentration of phosphate.
2
3
32 2 12
1.30 10 Ca 1.00 10
Solving for [Ca2+] yields a concentration of 0.00235 M.
The volume of the lake: V = 300 m × 150 m × 5 m = 225000 m3 or 2.25×108 L.
Mass of Ca(NO3)2 is determined as follows:
233
822
32
232
6
32
1 mol Ca NO 164.1g Ca NO
0.00235 mol Ca
mass Ca NO 2.25 10 L L 1 mol Ca 1 mol Ca NO
87 10 g Ca NO
B. (M) The reaction of AgNO3 and Na2SO4 is as follows:
324 324
2
24
24 3
3
3
324
24
2AgNO Na SO 2NaNO Ag SO
1molAg SO
mol Ag SO 0.350 L 0.200 M AgNO 3.5 10 mol
2molAgNO
2 mol NaNO
mol NaNO 0.250 L 0.240 M Na SO 0.12mol
1molNa SO
Ag2SO4 is the precipitate. Since it is also the limiting reagent, there are 3.5×10-2 moles of
Ag2SO4 produced.
The reaction of Ag2SO4 with Na2S2O3 is as follows:
22 3 2 4 2 4 22 3
22 3 22 3
Na S O Ag SO Na SO Ag S O
mol Na S O 0.400 L 0.500 M Na S O = 0.200 mol
Ag2SO4 is the limiting reagent, so no Ag2SO4 precipitate is left.

Chapter 18: Solubility and Complex-Ion Equilibria
901
EXERCISES
Ksp and Solubility
1. (E)
(a)
2
+
24 4
Ag SO s 2 Ag aq + SO aq
22
+
sp 4
=Ag SOK
(b)
2+
33
2
Ra IO s Ra aq + 2IO aq
2
2+
sp 3
=Ra IOK
(c)
3
2+
34 4
2
Ni PO s 3Ni aq + 2PO aq
2
33
2+
sp 4
=Ni POK
(d)
2+ 2
23 2 3
PuO CO s PuO aq +CO aq
2+ 2
sp 2 3
=PuO COK
2. (E)
(a)
3
3+ 3+
sp 3
=Fe OH FeOH s Fe aq+3OH aqK
(b)
++
sp = BiO OH BiOOH s BiO aq + OH aqK
(c)
2
2+ 2+
sp 2 2 2 2
=Hg I HgI s Hg aq+2I aqK
(d)
2
33 3
2+ 2+
sp 4 3 4 4
2
=Pb AsO Pb AsO s 3Pb aq+2AsO aqK
3. (E)
(a)
3+
3
CrF s Cr aq +3F aq
3
3+ 11
sp =Cr F =6.610K
(b)
2
3+
224 24
3
Au C O s 2Au aq + 3C O aq
3
22
3+ 10
sp 2 4
=Au CO =110K
(c)
3
2+
34 4
2
Cd PO s 3Cd aq + 2PO aq
Ksp Cd PO==2.110
2+ 3
4
3233
(d)
2+
2
SrF s Sr aq + 2F aq
Ksp Sr F==2.510
2+ 29
4. (E) Let s= solubility of each compound in moles of compound per liter of solution.
(a) Ksss
sp Ba CrO====1.210
2+ 4
2210
bgbg s=1.1 10 5
M
(b) Ksss
sp Pb Br==2=4=4.010
2+ 2235
bgb g s=2.2 102
M
(c) Ksss
sp Ce F= = 3 = 27 = 8 10
3+ 33416
bgb g s=7 105
M
(d) Ksss
sp Mg AsO= = 3 2 = 108 = 2.1 10
2+ 3
4
3232 520
bgbg s=4.5 105
M
Chapter 18: Solubility and Complex-Ion Equilibria
902
5. (E) We use the value of Ksp for each compound in determining the molar solubility in a
saturated solution. In each case, s represents the molar solubility of the compound.
+2168
sp
AgCN = Ag CN = = = 1.2 10 = 1.1 10 MKssss
+284
3sp 3
AgIO = Ag IO = = = 3.0 10 = 1.7 10 MKssss
+2179
sp
AgI = Ag I = = = 8.5 10 = 9.2 10 MKssss
+242
2sp 2
AgNO = Ag NO = = = 6.0 10 = 2.4 10 MKssss
22
+2 3 5 2
24 sp 4
Ag SO = Ag SO = 2 = 4 =1.4 10 =1.5 10 MKssss
Thus, in order of increasing molar solubility, from smallest to largest:
AgI AgCN AgIO Ag SO AgNO
324 2
6. (E) We use the value of Ksp for each compound in determining Mg2+ in its saturated
solution. In each case, s represents the molar solubility of the compound.
(a) MgCO Mg CO
sp32+ 3
228
====3.510Ksss
bgbg
s=1.9 10 =1.9 10
42+4
MMg M
(b) MgF Mg F
sp22+ 2238
==2=4=3.710Ksss
bgb g
s=2.1 10 =2.1 10
32+3
MMg M
(c)
2
332
3
2+ 5 25
342 sp 4
Mg (PO ) = Mg PO = 3 2 =108 = 2.1 10Ksss
62+5
= 4.5 10 M Mg =1.4 10 Ms
Thus a saturated solution of MgF2 has the highest Mg2+ .
7. (M) We determine F in saturated CaF2, and from that value the concentration of F- in ppm.
For CaF Ca F M
sp22+ 2239 3
= = 2 = 4 = 5.3 10 = 1.1 10Ksss s
bgb g
The solubility in ppm is the number of grams of CaF2 in 106 g of solution. We assume a
solution density of 1.00g/mL.
3
62
2
1mL 1Lsoln 1.1 10 molCaF
mass of F 10 gsoln 1.00gsoln 1000mL 1Lsoln
2molF 19.0g F 42g F
1molCaF 1molF
This is 42 times more concentrated than the optimum concentration of fluoride ion for
fluoridation. CaF2 is, in fact, more soluble than is necessary. Its uncontrolled use might lead to
excessive F in solution.

Chapter 18: Solubility and Complex-Ion Equilibria
903
8. (E) We determine OH in a saturated solution. From this OH we determine the pH.
Kss
sp BiO OH M OH BiO==410==210==
+102 5 +
pOH log pH= 2 10 =4.7 =9.3
5
ch
9. (M) We first assume that the volume of the solution does not change appreciably when its
temperature is lowered. Then we determine the mass of Mg C H O
16 31 2 2
bg
dissolved in each
solution, recognizing that the molar solubility of Mg C H O
16 31 2 2
bg equals the cube root of one
fourth of its solubility product constant, since it is the only solute in the solution.
Ks sK
sp sp
44
33/
33
12 4 12 5
At50 C : = 4.8 10 / 4 1.1 10 M; At 25 C: = 3.3 10 / 4 9.4 10 Mss
amount of Mg C H O
16 31 2 2
bg(50C)
4
16 31 2 4
2
1.1 10 mol Mg C H O
= 0.965L = 1.1 10 mol
1L soln
amount of Mg C H O
16 31 2 2
bg(25C)
5
16 31 2 4
2
9.4 10 mol Mg C H O
= 0.965L = 0.91 10 mol
1L soln
16 31 2 2
16 31 2
42
16 31 2 2
mass of Mg C H O precipitated:
535.15g Mg C H O 1000mg
= 1.1 0.91 10 mol =11mg
1mol Mg C H O 1g
10. (M) We first assume that the volume of the solution does not change appreciably when its
temperature is lowered. Then we determine the mass of CaC O
24
dissolved in each solution,
recognizing that the molar solubility of CaC O
24
equals the square root of its solubility product
constant, since it is the only solute in the solution.
At 84 9 5
95 C = 1.2 10 1.1 10 M; At 13 C: 2.7 10 5.2 10 Mss
mass of 24
CaC O (95 C)
4
24 24
24
24
1.1 10 mol CaC O 128.1g CaC O
= 0.725 L = 0.010g CaC O
1L soln 1mol CaCO
mass of 24
CaC O (13 C)
5
424
24
24
5.2 10 mol PbSO 128.1g CaC O
= 0.725 L = 0.0048g CaC O
1L soln 1mol CaCO
mass of
24
1000 mg
CaC O precipitated = 0.010 g 0.0048 g = 5.2mg
1g

Chapter 18: Solubility and Complex-Ion Equilibria
904
11. (M) First we determine I in the saturated solution.
Kssss
sp Pb I M= = 7.1 10 = 2 = 4 = 1.2 10
2+ 29233
bgb g
The AgNO3 reacts with the I in this saturated solution in the titration.
Ag aq I aq AgI s
++
bg bg bg
We determine the amount of Ag+ needed for this titration, and
then AgNO3 in the titrant.
moles Ag L mol PbI
L soln
mol I
mol PbI
mol Ag
mol I mol Ag
+32
2
+5+
= 0.02500 1.2 10
1
2
1
1
1=6.0 10
AgNO molarity mol Ag
L soln
mol AgNO
mol Ag M
3
5+ 3
+
3
=6.0 10
0.0133
1
1=4.5 10
12. (M) We first determine CO
24
2=
s, the solubility of the saturated solution.
CO
mL 0.00134 mmol KMnO
mL soln
mmol C O
2mmolMnO
mL MCa
424
4
24
2
2
52+
=
48 1
5
250.0 =6.4 10 = =
.
s
Ksss
sp Ca C O= = = = 6.4 10 = 4.1 10
2+ 24
225
29
bgbgch
13. (M) We first use the ideal gas law to determine the moles of HS
2 gas used.
nPV
RT
F
H
G
I
K
J
F
H
G
I
K
J
748 30 4
0 08206 23 273 123 10
11
3
mmHg 1atm
760 mmHg mL 1L
1000 mL
Latmmol K K moles
.
.()
.
If we assume that all the H S
2 is consumed in forming Ag S
2, we can compute the Ag+ in
the AgBrO3 solution. This assumption is valid if the equilibrium constant for the cited reaction
is large, which is the case, as shown below:
+
22
2Ag aq + HS aq + OH aq Ag S s + H O(l)
2
19 31
asp 51
1.0 10
/= 3.810
2.6 10
KK
+
22 3
H S aq + H O(l) HS aq + H O aq
7
1=1.0 10K
+
23
2H O(l) H O aq +OH aq
14
w=1.0 10K
2
+ +
22 23
10
asp1w 31 7 14
overall
2Ag aq + H S aq + 2H O(l) Ag S s + 2H O aq
=3.8 10
=( / )( )( ) (3.8 10 )(1.0 10 )(1.0 10 )KKKKK
Ag mol H S
mL soln
mL
L soln
mol Ag
mol H S M
+32+
2
3
=1.23 10
338
1000
1
2
1=7.28 10
Then, for
2
+35
3sp 3
AgBrO , = Ag BrO = 7.28 10 = 5.30 10K
Chapter 18: Solubility and Complex-Ion Equilibria
905
14. (M) The titration reaction is
22
2
Ca OH aq + 2HCl aq CaCl aq + 2H O(l)
2
1 L 0.1032 mol HCl 1 mol OH
10.7 mL HCl 1000 mL 1 L 1 mol HCl
OH 0.0221 M
1L
50.00 mL Ca(OH) soln 1000 mL
In a saturated solution of
2+
2
Ca OH , Ca = OH 2
22
2+ 6
sp = Ca OH = 0.0221 2 0.0221 = 5.40 10K
(5.5 10 6
in Appendix D).
The Common-Ion Effect
15. (E) We let s=molar solubility of Mg OH
bg2 in moles solute per liter of solution.
(a) Ksss
sp Mg OH==2=4=1.810
2+ 22311
bgb g s=1.7 10 4
M
(b)
2+
2
Equation : Mg OH s Mg aq + 2OH aq
Initial : 0.0862M 0M
Changes : + M +2 Mss
Equil : 0.0862 + M 2 Mss
22
11 2 6
sp = 0.0862 + 2 = 1.8 10 0.0862 2 = 0.34 = 7.3 10 MKss sss
(s << 0.0802 M, thus, the approximation was valid.)
(c) OH KOH M
= = 0.0355
2+
2
Equation : Mg OH s Mg aq + 2OH aq
Initial : 0M 0.0355M
Changes : + M + 2 Mss
Equil : M 0.0355 + 2 Mss
22
11 8
sp = 0.0355+ 2 =1.8 10 0.0355 = 0.0013 =1.4 10 MKs s s s s
16. (E) The solubility equilibrium is
2
2+
33
CaCO s Ca aq + CO aq
(a) The addition of Na CO aq
23
bg produces CO aq
3
2bg in solution. This common ion
suppresses the dissolution ofCaCO s
3bg.
(b) HCl(aq) is a strong acid that reacts with carbonate ion:
2+
33 22
CO aq + 2H O aq CO g +3H O(l)
.
This decreases CO3
2 in the solution, allowing more CaCO s
3bg to dissolve.
Chapter 18: Solubility and Complex-Ion Equilibria
906
(c) HSO aq
4
bg is a moderately weak acid. It is strong enough to protonate appreciable
concentrations of carbonate ion, thereby decreasing CO3
2 and enhancing the solubility
of CaCO s
3bg, as the value of Kc indicates.
22
43 4 3
HSO aq + CO aq SO aq + HCO aq
8
a4
11
a3
(HSO ) 0.011 2.3 10
4.7 10
(HCO )
c
K
KK
17. (E) The presence of KI in a solution produces a significant I in the solution. Not as much AgI
can dissolve in such a solution as in pure water, since the ion product, Ag I
+, cannot exceed
the value of sp
K(i.e., the I- from the KI that dissolves represses the dissociation of AgI(s). In
similar fashion, AgNO3 produces a significant Ag+ in solution, again influencing the value of
the ion product; not as much AgI can dissolve as in pure water.
18. (E) If the solution contains KNO3, more AgI will end up dissolving than in pure water, because
the activity of each ion will be less than its molarity. On an ionic level, the reason is that ion
pairs, such as Ag+NO3– (aq) and K+I– (aq) form in the solution, preventing Ag+ and I– ions from
coming together and precipitating.
19. (E) Equation:
+2
24 4
Ag SO s 2Ag aq + SO aq
Original: — 0 M 0.150 M
Add solid: — +2
x
M +
x
M
Equil: — 2x M
0.150 + Mx
+3
2
22
2
+35
sp 4
2 = Ag = 9.7 10 M; =0.00485
= Ag SO = 2 0.150 + = 9.7 10 0.150 + 0.00485 = 1.5 10
xxM
Kxx
20. (M) Equation:
2
2+
44
CaSO s Ca aq + SO aq .
Soln: — 0 M 0.0025 M
4
Add CaSO s — +
x
M +
x
M
Equil: — x M
0.0025+ Mx
If we use the approximation that x << 0.0025, we find x = 0.0036. Clearly, x is larger than
0.0025 and thus the approximation is not valid. The quadratic equation must be solved.
2
2+
4
62
sp
26
Ca SO= = 9.1 10 = 0.0025+ = 0.0025 +
+ 0.0025 9.1 10 = 0
Kxxxx
xx

Chapter 18: Solubility and Complex-Ion Equilibria
907
xbb ac
a
=4
2=0.0025 6.3 10 + 3.6 10
2=2.0 10 =
265
34
MCaSO
3
44
4 4
4
2.0 10 mol CaSO 136.1 g CaSO
mass CaSO = 0.1000 L = 0.027 g CaSO
1L soln 1mol CaSO
21. (M) For PbI Pb I
sp292+
2
,=7.110=K
In a solution where 424
2
1.5 10 mol PbI is dissolved, Pb 1.5 10 M
, and
IPb
=2 =3.0 10
2+ 4 M
Equation:
2+
2
PbI s Pb aq + 2I aq
Initial: — 4
1.5 10 M
4
3.0 10 M
Add lead(II): — +
x
M
Equil: —
0.00015+ Mx 0.00030 M
2
9
sp = 7.1 10 = 0.00015 + 0.00030Kx
;
0.00015+ = 0.079x;2+
= 0.079 M = Pbx
22. (M) For PbI Pb I
sp292+
2
,=7.110=K
In a solution where 525
2
1.5 10 mol PbI /L is dissolved, Pb 1.5 10 M
, and
IPb
=2 =3.0 10
2+ 5 M
Equation:
2+
2
PbI s Pb aq + 2I aq
Initial: — 1.5 10 3.0 10
55
MM
Add KI: — +
x
M
Equil: — 55
1.5 10 M (3.0 10 ) Mx
Ksp = 7.1 × 10-9 = (1.5 × 10-5) × (3.0 × 10-5 + x)2
(3.0 × 10-5 + x) = (7.1 × 10-9 ÷ 1.5 × 10-5)1/2
x = (2.2 × 10-2) – (3.0 × 10-5) = 2.1 × 10-2 M = [I-]
23. (D) For 22
12 +
24sp 4
Ag CrO , = 1.1 10 = Ag CrOK
In a 828
24 4
5.0 10 M solution of Ag CrO , CrO = 5.0 10 M
and Ag+7
=1.0 10 M
Equation:
2
+
24 4
Ag CrO s 2Ag aq + CrO aq
Initial: — 1.0 10 5.0 10
78
MM
Add chromate: — +
x
M
Equil: — 1.0 10 5.0 10 +
78
MMx
ch
2
12 7 8
sp =1.1 10 = 1.0 10 5.0 10 + ;Kx
82
5.0 10 + =1.1 10x
2
4
=CrO
.

Chapter 18: Solubility and Complex-Ion Equilibria
908
This is an impossibly high concentration to reach. Thus, we cannot lower the solubility of
Ag CrO
24
to 8
5.0 10 M
with CrO4
2 as the common ion. Let’s consider using Ag+ as the
common ion.
Equation:
2
+
24 4
Ag CrO s 2Ag aq + CrO aq
Initial: — 7
1.0 10 M
8
5.0 10 M
Add silver(I) ion: — +
x
M
Equil: —
7
1.0 10 + Mx
8
5.0 10 M
-12
2
-12 -8 -7 -3
sp -8
1.1 10
= 1.1 10 = 1.0 + 5.0 10 1.0 10 + = = 4.7 10
5.0 10
Kx x
x= 4.7 10 1.0 10 = 4.7 10 =
37 3
M I ; this is an easy-to-reach concentration. Thus,
the solubility can be lowered to 5.0×10-8 M by carefully adding Ag+(aq).
24. (M) Even though BaCO3 is more soluble than 4
BaSO , it will still precipitate when 0.50 M
Na CO aq
23
bg is added to a saturated solution of 4
BaSO because there is a sufficient Ba2+
in such a solution for the ion product Ba CO
2+ 3
2 to exceed the value of Ksp for the compound.
An example will demonstrate this phenomenon. Let us assume that the two solutions being mixed
are of equal volume and, to make the situation even more unfavorable, that the saturated
BaSO4solution is not in contact with solid 4
BaSO , meaning that it does not maintain its
saturation when it is diluted. First we determine Ba2+ in saturated 4
BaSO (aq) .
Kss
sp Ba SO M= =1.110 = =1110 1010
2+ 4
210 2 10 5
..
Mixing solutions of equal volumes means that the concentrations of solutes not common to the
two solutions are halved by dilution.
52+
2+ 6
4
4
1 1.0 10 mol BaSO 1 mol Ba
Ba = = 5.0 10 M
21L1mol BaSO
2
223 3
3
23
0.50 mol Na CO 1 mol CO1
CO = = 0.25 M
21L1mol NaCO
2
2+ 6 6 9
sp 3 3 sp 3
{BaCO }= Ba CO = 5.0 10 0.25 =1.3 10 5.0 10 = {BaCO }QK
Thus, precipitation of BaCO3 indeed should occur under the conditions described.
25. (E) 2+ 2+
2+ 3
62+
115g Ca 1 mol Ca 1000 g soln
Ca = = 2.87 10 M
10 g soln 40.08 g Ca 1 L soln
22
2+ 9 3 3
sp
Ca F = = 5.3 10 = 2.87 10 F F =1.4 10 MK
36
1.4 10 mol F 19.00g F 1 L soln
ppm F = 10 g soln = 27 ppm
1 L soln 1 mol F 1000 g
Chapter 18: Solubility and Complex-Ion Equilibria
909
26. (M) We first calculate the Ag+ and the Cl in the saturated solution.
Kssss
sp Ag Cl M Ag Cl= = 1.8 10 = = = 1.3 10 = =
+102 5+
bgbg
Both of these concentrations are marginally diluted by the addition of 1 mL of NaCl(aq)
Ag Cl M mL
mL mL M
+5 5
==1.310 100.0
100.0 +1.0 =1.3 10
The Cl in the NaCl(aq) also is diluted. 3
1.0 mL
Cl =1.0 M = 9.9 10 M
100.0 mL +1.0 mL
Let us use this Cl to determine the Ag+ that can exist in this solution.
10
+10+3+ 8
3
1.8 10
Ag Cl =1.8 10 = Ag 9.9 10 M Ag = =1.8 10 M
9.9 10
We compute the amount of AgCl in this final solution, and in the initial solution.
mmol AgCl final mL mol Ag
L soln
mmol AgCl
mmol Ag mmol AgCl= 101.0 1.8 10
1
1
1=1.8 10
8+
+
6
mmol AgCl 5+ 3
+
1.3 10 mol Ag 1 mmol AgCl
initial = 100.0 mL =1.3 10 mmol AgCl
1 L soln 1 mmol Ag
The difference between these two amounts is the amount of AgCl that precipitates. Next we
compute its mass.
36 143.3 mg AgCl
mass AgCl = 1.3 10 1.8 10 mmol AgCl = 0.19 mg
1mmol AgCl
We conclude that the precipitate will not be visible to the unaided eye, since its mass is less
than 1 mg.
Criteria for Precipitation from Solution
27. (E) We first determine Mg2+ , and then the value of Qsp in order to compare it to the value of
sp.K We express molarity in millimoles per milliliter, entirely equivalent to moles per liter.
2+
2+ 4
222
22 2
22.5mg MgCl 1mmolMgCl 6H O 1mmolMg
[Mg ] 3.41 10 M
325mLsoln 203.3mg MgCl 6H O 1mmol MgCl
2+ 2 4 2 7 8
sp sp
[Mg ][F ] (3.41 10 )(0.035) 4.2 10 3.7 10QK
Thus, precipitation of MgF s
2bg should occur from this solution.
28. (E)
The solutions mutually dilute each other.
3
155 mL
Cl = 0.016 M = 6.2 10 M
155 mL + 245 mL
2+ 245 mL
Pb = 0.175 M = 0.107 M
245 mL +155 mL

Chapter 18: Solubility and Complex-Ion Equilibria
910
Then we compute the value of the ion product and compare it to the solubility product constant
value.
2
2
2+ 3 6 5
sp sp
= Pb Cl = 0.107 6.2 10 = 4.1 10 1.6 10 =QK
Thus, precipitation of PbCl s
2bg will not occur from these mixed solutions.
29. (E) We determine the OH needed to just initiate precipitation of Cd(OH)2.
Ksp Cd OH M OH OH M= = 2.5 10 = 0.0055 = 25 10
0.0055 =2.1 10
2+ 214 214 6
bg .
pOH log pH= 2.1 10 = 5.68 = 14.00 5.68 = 8.32
6
ch
Thus, Cd OH
bg
2 will precipitate from a solution with pH 8.32.
30. (E) We determine the OH needed to just initiate precipitation of Cr(OH)3.
3+ 3 31 3
sp [Cr ][OH ] 6.3 10 (0.086 M) [OH ]K
; 31 10
6.3 10
[OH ] 1.9 10 M
0.086
pOH log pH= 1.9 10 = 9.72 = 14.00 9.72 = 4.28
10
ch
Thus,Cr OH
bg
3 will precipitate from a solution with pH > 4.28.
31. (D)
(a) First we determine Cl due to the added NaCl.
6
0.10 mg NaCl 1 g 1 mol NaCl 1 mol Cl
Cl = =1.7 10 M
1.0 L soln 1000 mg 58.4 g NaCl 1 mol NaCl
Then we determine the value of the ion product and compare it to the solubility product
constant value.
+6710
sp sp
= Ag Cl = 0.10 1.7 10 =1.7 10 1.8 10 = for AgClQK
Thus, precipitation of AgCl(s) should occur.
(b) The KBr(aq) is diluted on mixing, but the Ag+ and Cl are barely affected by
dilution.
Br M mL
mL mL M
=0.10 0.05
0.05 + 250 =2 105
Now we determine Ag+ in a saturated AgCl solution.
Kssss
sp Ag Cl M= = = = 1.8 10 = 1.3 10
+2105
bgbg
Chapter 18: Solubility and Complex-Ion Equilibria
911
Then we determine the value of the ion product for AgBr and compare it to the solubility
product constant value.
+551013
sp sp
= Ag Br = 1.3 10 2 10 = 3 10 5.0 10 = for AgBrQK
Thus, precipitation of AgBr(s) should occur.
(c) The hydroxide ion is diluted by mixing the two solutions.
7
0.05 mL
OH = 0.0150 M = 2.5 10 M
0.05 mL +3000 mL
But the Mg2+ does not change significantly.
2+ 2+
2+ 5
2.0 mg Mg 1 g 1 mol Mg
Mg = = 8.2 10 M
1.0 L soln 1000 mg 24.3 g Mg
Then we determine the value of the ion product and compare it to the solubility product
constant value.
2
2
2+ 7 5 18
sp = Mg OH = 2.5 10 8.2 10 = 5.1 10Q
11
sp sp 2
1.8 10 = for Mg OHQK
Thus, no precipitate forms.
32. First we determine the moles of H2 produced during the electrolysis, then determine [OH–].
2 2
11
1atm
752 mmHg 0.652 L
760 mmHg
moles H = = = 0.0267 mol H
0.08206 L atm mol K 295 K
PV
RT
OH
0.0267 mol H mol OH
mol H
L sample M
2
2
=
2
1
0.315 = 0.170
22
2+ 3 11
sp sp
= Mg OH = 0.185 0.170 = 5.35 10 1.8 10 =QK
Thus, yes, precipitation of Mg OH s
bgbg
2 should occur during the electrolysis.
33. (D) First we must calculate the initial [H2C2O4] upon dissolution of the solid acid:
[H2C2O4]initial = 1.50 g H2C2O4224
224
1 mol H C O 1= 0.0833 M
90.036 g H C O 0.200 L
(We assume the volume of the solution stays at 0.200 L.)
Next we need to determine the [C2O42-] in solution after the hydrolysis reaction between oxalic
acid and water reaches equilibrium. To accomplish this we will need to solve two I.C.E. tables:
Chapter 18: Solubility and Complex-Ion Equilibria
912
Table 1: H2C2O4(aq) + H2O(l) 2
a1 5.2 10K
HC2O4-(aq) + H3O+(aq)
Initial: 0.0833 M — 0 M 0 M
Change: – x — +x M +x M
Equilibrium: 0.0833 – x M — x M x M
Since Ca/Ka = 1.6, the approximation cannot be used, and thus the full quadratic equation must
be solved: x2/(0.0833 – x) = 5.2×10-2; x2 + 5.2×10-2x – 4.33×10-3
-2 -3 -
24 3
-5.2×10 2.7×10 + 0.0173
= = 0.045 M = [HC O ] [H O ]
2
xx
Now we can solve the I.C.E. table for the second proton loss:
Table 2: HC2O4-(aq) + H2O(l) 5
a1 5.4 10K
C2O42-(aq) + H3O+(aq)
Initial: 0.045 M — 0 M ≈ 0.045 M
Change: – y — +y M + y M
Equilibrium: (0.045 – y) M — y M ≈ (0.045 +y) M
Since Ca/Ka = 833, the approximation may not be valid and we yet again should solve the full
quadratic equation:
-5
(0.045 ) = 5.4 10
(0.045 )
yy
y
; y2 + 0.045y = 2.43×10-6 – 5.4×10-5y
-3 -6 -5 2-
24
-0.045 2.03×10 + 9.72×10
= = 8.2 10 M = [C O ]
2
yy
Now we can calculate the Qsp for the calcium oxalate system:
Qsp = [Ca2+]initial×[ C2O42-]initial = (0.150)(8.2×10-5) = 1.2×10-5 > 1.3 ×10-9 (Ksp for CaC2O4)
Thus, CaC2O4 should precipitate from this solution.
34. (D) The solutions mutually dilute each other. We first determine the solubility of each
compound in its saturated solution and then its concentration after dilution.
5
3
22
2
+53 2
sp 4
1.4 10
= Ag SO =1.4 10 = 2 = 4 = 1.5 10 M
4
Kssss
2+
4
100.0 mL
SO = 0.015 M = 0.0043 M Ag = 0.0086 M
100.0 mL + 250.0 mL
Ksss
sp 2+ 4
2
Pb CrO
[][ ]. ()()28 10 13 2 s
2 8 10 5 3 10
13 7
..M
2
2+ 7 7
4
250.0 mL
Pb = CrO = 5.3 10 = 3.8 10 M
250.0 mL +100.0 mL
From the balanced chemical equation, we see that the two possible precipitates are PbSO4 and
24
Ag CrO . (Neither PbCrO4 nor Ag SO
24
can precipitate because they have been diluted
below their saturated concentrations.) 424 424
PbCrO + Ag SO PbSO + Ag CrO
Thus, we compute the value of sp
Q for each of these compounds and compare those values
with the solubility constant product value.

Chapter 18: Solubility and Complex-Ion Equilibria
913
2
2+ 7 9 8
sp 4 sp 4
= Pb SO = 3.8 10 0.0043 =1.6 10 1.6 10 = for PbSOQK
Thus, PbSO (s)
4 will not precipitate.
22
2
+ 7 11 12
sp 4 sp 2 4
= Ag CrO = 0.0086 3.8 10 = 2.8 10 1.1 10 = for Ag CrOQK
Thus, Ag CrO s
24
bg should precipitate.
Completeness of Precipitation
35. (M) First determine that a precipitate forms. The solutions mutually dilute each other.
CrO M mL
mL mL M
4
2= 0.350 200.0
200.0 + 200.0 = 0.175
Ag M mL
mL mL M
+= 0.0100 200.0
200.0 + 200.0 = 0.00500
We determine the value of the ion product and compare it to the solubility product constant
value.
22
2
+612
sp 4 sp 2 4
= Ag CrO = 0.00500 0.175 = 4.4 10 1.1 10 = for Ag CrOQK
Ag CrO
24
should precipitate.
Now, we assume that as much solid forms as possible, and then we approach equilibrium by
dissolving that solid in a solution that contains the ion in excess.
+2
24 4
12
1.1 10
Equation: Ag CrO s 2Ag aq + CrO aq
Orig. soln : 0.00500M 0.175 M
Form solid : 0.00500 M 0.00250 M
Not at equilibrium 0 M 0.173 M
Changes : +2 M
x
+ M
x
Equil : 2 M 0.173+ Mxx
2
212 2
4
Ag CrO 1.1 10 2 0.173 4 0.173
sp
Kxxx
12 6 + 6
= 1.1 10 4 0.173 =1.3 10 M Ag = 2 = 2.6 10 Mxx
%Ag
+unprecipitated
26 10 100% 0 052%
6
..
Mfinal
0.00500 M initial unprecipitated
36. (M) [Ag+]diluted = 0.0208 M 175 mL
425 mL = 0.008565 M
[CrO42]diluted = 0.0380 M 250 mL
425 mL = 0.02235 M
226
sp 4 sp
Ag CrO 1.6 10QK

Chapter 18: Solubility and Complex-Ion Equilibria
914
Because Qsp > Ksp, then more Ag2Cr2O4 precipitates out. Assume that the limiting reagent is
used up (100% reaction in the reverse direction) and re-establish the equilibrium in the reverse
direction. Here Ag+ is the limiting reagent.
Ag2CrO4(s) -12
sp(Ag CrO )
24
=1.1 10K
2 Ag+(aq) + CrO42(aq)
Initial 0.008565 M 0.02235 M
Change x = 0.00428 M 2x x
100% rxn 0 0.0181
Change re-establish equil +2y +y
Equil (assume y ~ 0) 2y 0.0181 + y
1.1 1012 = (2y)2(0.0181+ y) (2y)2(0.0181) y = 3.9 106 M
y << 0.0181, so this assumption is valid.
2y = [Ag+] = 7.8 106 M after precipitation is complete.
% [Ag+]unprecipitated = 6
7.8 10
0.00856
100% = 0.091% (precipitation is essentially quantitative)
37. (M) We first use the solubility product constant expression to determine Pb2+ in a solution
with 0.100 M Cl .
5
22
2+ 5 2+ 2+ 3
sp 2
1.6 10
= Pb Cl =1.6 10 = Pb 0.100 Pb = = 1.6 10 M
0.100
K
Thus, % unprecipitated 3
1.6 10 M 100% 2.5%
0.065 M
Now, we want to determine what [Cl-] must be maintained to keep 2+ final
[Pb ] 1%;
2+ 4
initial
[Pb ] 0.010 0.065M = 6.5 10 M
Ksp Pb Cl Cl Cl M==1.610=6.510 =
610
6.5 10 =0.16
2+ 254
25
4
ch
38. (M) Let’s start by assuming that the concentration of Pb2+ in the untreated wine is no higher
than 1.5 104M (this assumption is not unreasonable.) As long as the Pb2+ concentration is
less than 1.5 104 M, then the final sulfate ion concentration in the CaSO4 treated wine
should be virtually the same as the sulfate ion concentration in a saturated solution of CaSO4
formed by dissolving solid CaSO4 in pure water ( i.e., with [Pb2+] less than or equal to 1.5
104 M, the [SO42] will not drop significantly below that for a saturated solution, 3.0 103
M.) Thus, the addition of CaSO4 to the wine would result in the precipitation of solid PbSO4,
which would continue until the concentration of Pb2+ was equal to the Ksp for PbSO4 divided
by the concentration of dissolved sulfate ion, i.e.,
[Pb2+]max = 1.6 108M2/3.0 103 M = 5.3 106 M.
Chapter 18: Solubility and Complex-Ion Equilibria
915
Fractional Precipitation
39. (M) First, assemble all of the data. Ksp for Ca(OH)2 = 5.5×10-6, Ksp for Mg(OH)2 = 1.8×10-11
2+ 2+
2+
2+
440 g Ca 1 mol Ca 1 kg seawater 1.03 kg seawater
[Ca ] 0.0113 M
1000 kg seawater 1000 g seawater 1 L seawater
40.078 g Ca
[Mg2+] = 0.059 M, obtained from Example 18-6. [OH-] = 0.0020 M (maintained)
(a) Qsp = [Ca2+]×[OH-]2 = (0.0113)( 0.0020)2 = 4.5×10-8 Qsp < Ksp no precipitate forms.
(b) For the separation to be complete, >>99.9 % of the Mg2+ must be removed before Ca2+
begins to precipitate. We have already shown that Ca2+ will not precipitate if the [OH-] =
0.0020 M and is maintained at this level. Let us determine how much of the 0.059 M
Mg2+ will still be in solution when [OH-] = 0.0020 M.
Ksp = [Mg2+]×[OH-]2 = (x)( 0.0020)2 = 1.8×10-11 x = 4.5×10-6 M
The percent Mg2+ ion left in solution = 6
4.5 10 100% = 0.0076 %
0.059
This means that 100% - 0.0076 % Mg = 99.992 % has precipitated.
Clearly, the magnesium ion has been separated from the calcium ion (i.e., >> 99.9% of the
Mg2+ ions have precipitated and virtually all of the Ca2+ ions are still in solution.)
40. (D)
(a) 0.10 M NaCl will not work at all, since both BaCl2 and CaCl2 are soluble in water.
(b) Ksp =1.1 10 10
for BaSO4 and Ksp =9.1 10 6
for CaSO4. Since these values differ by
more than 1000, 0.05 M Na SO
24
would effectively separate B
a
2+ from Ca2+ .
We first compute SO4
2 when BaSO4 begins to precipitate.
10
22 2
2+ 10 9
44 4
1.1 10
Ba SO = 0.050 SO = 1.1 10 ; SO = = 2.2 10 M
0.050
And then we calculate SO4
2 when Ba2+ has decreased to 0.1% of its initial value,
that is, to 5.0 10 5
M.
10
222
2+ 5 10 6
444
5
1.1 10
Ba SO = 5.0 10 SO =1.1 10 ; SO = = 2.2 10 M
5.0 10
And finally, SO4
2 when CaSO4 begins to precipitate.
6
22 2
2+ 6 4
44 4
9.1 10
Ca SO = 0.050 SO = 9.1 10 ; SO = =1.8 10 M
0.050

Chapter 18: Solubility and Complex-Ion Equilibria
916
(c) Now, Ksp =5 10 3
for Ba OH
bg
2 and Ksp =5.5 10 6
for
2
Ca OH . The fact that these
two Ksp values differ by almost a factor of 1000 does not tell the entire story, because
OH is squared in both Ksp expressions. We compute OH when Ca OH
bg2 begins
to precipitate.
Ca OH OH OH M
2+ 26262
= 5.5 10 = 0.050 = 55 10
0 050 =1.0 10
bg.
.
Precipitation will not proceed, as we only have 0.001 M NaOH, which has
OH
=1 10 3 M.
(d) Ksp =5.1 10 9
for BaCO3 and Ksp =2.8 109
for 3
CaCO . Since these two values
differ by less than a factor of 2, 0.50 M Na CO
23
would not effectively separate Ba2+
from 2+
Ca .
41. (M)
(a) Here we need to determine I when AgI just begins to precipitate, and I when
PbI2 just begins to precipitate.
Ksp Ag I I I M= = 8.5 10 = 0.10 = 8.5 10
+17 16
bg
9
22
2+ 9 4
sp
7.1 10
= Pb I = 7.1 10 = 0.10 I I = 2.7 10 M
0.10
K
Since 8.5 10 16
M is less than 2.7 10 4
M, AgI will precipitate before PbI2.
(b) 4
I must be equal to 2.7 10 M
before the second cation, 2+
Pb , begins to precipitate.
(c) Ksp Ag I Ag Ag M= = 8.5 10 = 2.7 10 = 3.1 10
+17+4+13
ch
(d) Since Ag+ has decreased to much less than 0.1% of its initial value before any PbI2
begins to precipitate, we conclude that Ag+ and Pb2+ can be separated by precipitation
with iodide ion.
42. (D) Normally we would worry about the mutual dilution of the two solutions, but the values
of the solubility product constants are so small that only a very small volume of 0.50 M
Pb NO32
bg
solution needs to be added, as we shall see.
(a) Since the two anions are present at the same concentration and they have the same type
of formula (one anion per cation), the one forming the compound with the smallest Ksp
value will precipitate first. Thus, CrO4
2 is the first anion to precipitate.

Chapter 18: Solubility and Complex-Ion Equilibria
917
(b) At the point where SO4
2 begins to precipitate, we have
8
2
2+ 8 2+ 2+ 6
sp 4
1.6 10
= Pb SO =1.6 10 = Pb 0.010M ; Pb = =1.6 10 M
0.010
K
Now we can test our original assumption, that only a very small volume of 0.50 M
Pb NO32
bg
solution has been added. We assume that we have 1.00 L of the original
solution, the one with the two anions dissolved in it, and compute the volume of 0.50 M
Pb NO32
bg
that has to be added to achieve Pb2+ 6
=1.6 10 M.
62+ 2+
32
added 2+
32
52+ 2+
added
1mol Pb NO
1.6 10 mol Pb 1 L Pb soln
=1.00L 1 L soln 1 mol Pb 0.50 mol Pb NO
=3.2 10 L Pb soln = 0.0032mL Pb soln
V
V
This is less than one drop (0.05 mL) of the Pb2+ solution, clearly a very small volume.
(c) The two anions are effectively separated if Pb2+ has not reached 1.6 10 6
M when
CrO4
2 is reduced to 0.1% of its original value, that is, to
2
35
4
0.010 10 M = 1.0 10 M = CrO
Ksp Pb CrO Pb= = 2.8 10 = 1.0 10
2+ 4
213 2+ 5
ch
13
2+ 8
5
2.8 10
Pb = = 2.8 10 M
1.0 10
Thus, the two anions can be effectively separated by fractional precipitation.
43. (M) First, let’s assemble all of the data. Ksp for AgCl = 1.8×10-10 Ksp for AgI = 8.5×10-17
[Ag+] = 2.00 M [Cl-] = 0.0100 M [I-] = 0.250 M
(a) AgI(s) will be the first to precipitate by virtue of the fact that the Ksp value for AgI is
about 2 million times smaller than that for AgCl.
(b) AgCl(s) will begin to precipitate when the Qsp for AgCl(s) > Ksp for AgCl(s). The
concentration of Ag+ required is: Ksp = [Ag+][Cl-] = 1.8×10-10 = (0.0100)×(x) x =
1.8×10-8 M
Using this data, we can determine the remaining concentration of I- using the Ksp.
Ksp = [Ag+][I-] = 8.5×10-17 = (x)×( 1.8×10-8) x = 4.7×10-9 M
(c) In part (b) we saw that the [I-] drops from 0.250 M → 4.7×10-9 M. Only a small
percentage of the ion remains in solution. 9
4.7 10 100% = 0.0000019 %
0.250
This means that 99.999998% of the I- ion has been precipitated before any of the Cl- ion
has precipitated. Clearly, the fractional separation of Cl- from I- is feasible.
Chapter 18: Solubility and Complex-Ion Equilibria
918
44. (M)
(a) We first determine the Ag+ needed to initiate precipitation of each compound.
sp
10
+10++ 10
1.8 10
AgCl : = Ag Cl =1.8 10 = Ag 0.250 ; Ag = = 7.2 10 M
0.250
K
sp
13
+13++ 10
5.0 10
AgBr : = Ag Br = 5.0 10 = Ag 0.0022 ; Ag = = 2.3 10 M
0.0022
K
Thus, Br precipitates first, as AgBr, because it requires a lower Ag+.
(b) Ag+10
=7.2 10 M when chloride ion, the second anion, begins to precipitate.
(c) Cl and Br cannot be separated by this fractional precipitation. Ag+ will have to
rise to 1000 times its initial value, to 2.3 10 7
M, before AgBr is completely precipitated.
But as soon as Ag+ reaches 7.2 10 10
M, AgCl will begin to precipitate.
Solubility and pH
45. (E) In each case we indicate whether the compound is more soluble in water. We write the net
ionic equation for the reaction in which the solid dissolves in acid. Substances are more
soluble in acid if either (1) an acid-base reaction occurs or (2) a gas is produced, since escape
of the gas from the reaction mixture causes the reaction to shift to the right.
Same: KCl (K+ and Cl- do not react appreciably with H2O)
Acid:
+2+
322
MgCO s + 2H aq Mg aq + H O(l) + CO g
Acid:
+2+
2
FeS s + 2H aq Fe aq + H S g
Acid:
+2+
2
2
Ca OH s + 2H aq Ca aq + 2H O(l)
Water: C H COOH
65 is less soluble in acid, because of the H O
3+common ion.
46. (E) In each case we indicate whether the compound is more soluble in base than in water. We
write the net ionic equation for the reaction in which the solid dissolves in base. Substances are
soluble in base if either (1) acid-base reaction occurs [as in (b)] or (2) a gas is produced, since
escape of the gas from the reaction mixture causes the reaction to shift to the right.
Water: BaSO4 is less soluble in base, hydrolysis of SO4
2 will be repressed.
Base:
2
224 24 2
H C O s +2OH aq C O aq +2H O(l)
Water: Fe OH
bg
3 is less soluble in base because of the OH common ion.
Same: NaNO3(neither Na+ nor NO3- react with H2O to a measurable extent).
Water: MnS is less soluble in base because hydrolysis of S2 will be repressed.

Chapter 18: Solubility and Complex-Ion Equilibria
919
47. (E) We determine Mg2+ in the solution.
Mg g Mg OH
L soln
mol Mg OH
g Mg OH
mol Mg
mol Mg OH M
2+ 22
2
2+
2
=0.65
1
1
58.3
1
1= 0.011
bgbg
bgbg
Then we determine OH in the solution, and its pH.
22
211
sp Mg OH 1.8 10 0.011 OHK
; 11 5
1.8 10
OH 4.0 10 M
0.011
5
pOH = log 4.0 10 = 4.40 pH =14.00 4.40 = 9.60
48. (M) First we determine the [Mg2+] and [NH3] that result from dilution to a total volume of
0.500 L.
2+ initial initial
3
final final
0.150 L 0.350 L
Mg = 0.100M = 0.0300M; NH = 0.150 M = 0.105 M
0.500 L 0.500 L
Then determine the OH that will allow Mg2+ = 0.0300 M in this solution.
11
22
11 2+ 5
sp
1.8 10
1.8 10 = Mg OH = 0.0300 OH ; OH = = 2.4 10 M
0.0300
K
This OH is maintained by the +
34
NH / NH buffer; since it is a buffer, we can use the
Henderson–Hasselbalch equation to find the [NH4+].
33
5
a++
44
NH NH
pH = 14.00 pOH = 14.00 + log 2.4 10 = 9.38 = p + log = 9.26 + log
NH NH
K
33
+
+0.12 3
4
++
44
NH NH 0.105 M NH
log = 9.38 9.26 = +0.12; =10 =1.3; NH = = 0.081 M
1.3
NH NH
+
44 44
422
44 +
2
44
42
1 mol NH SO 132.1 g NH SO
0.081 mol NH
mass NH SO = 0.500 L = 2.7 g
L soln 1mol NH SO
2mol NH
49. (M)
(a)
Here we calculate OH needed for precipitation.
3+ 3 33 3
sp
333 11 11
[Al ][OH ] 1.3 10 (0.075 M)[OH ]
1.3 10
[OH ] 2.6 10 pOH = log 2.6 10 =10.59
0.075
pH = 14.00 10.59 = 3.41
K

Chapter 18: Solubility and Complex-Ion Equilibria
920
(b) We can use the Henderson–Hasselbalch equation to determine CHO
232
.
pH p log CHO
HC H O log CHO
M
a
= 3.41= + = 4.74 + 1.00
232
232
232
K
L
N
MO
Q
P
232 232 1.33 232
CHO CHO
log = 3.41 4.74 = 1.33; =10 = 0.047; C H O = 0.047 M
1.00 M 1.00 M
This situation does not quite obey the guideline that the ratio of concentrations must fall
in the range 0.10 to 10.0, but the resulting error is a small one in this circumstance.
232 232 232
232 232
232
232
0.047 mol C H O 1 mol NaC H O 82.03 g NaC H O
mass NaC H O = 0.2500 L 1L soln 1mol NaC H O
1mol C H O
0.96 g NaC H O
50. (D)
(a) Since HI is a strong acid, 33 3
I =1.05 10 M +1.05 10 M = 2.10 10 M.
We determine the value of the ion product and compare it to the solubility product
constant value.
2
2
2+ 3 3 9 9
sp sp 2
= Pb I = 1.1 10 2.10 10 = 4.9 10 7.1 10 = for PbIQK
Thus a precipitate of PbI2 will not form under these conditions.
(b) We compute the OH needed for precipitation.
22
211
sp Mg OH 1.8 10 0.0150 OHK
; 11 5
1.8 10
OH 3.5 10 M
0.0150
Then we compute OH in this solution, resulting from the ionization of NH3.
34
3
0.05 10 L
NH = 6.00 M = 1.2 10 M
2.50L
Even though NH3 is a weak base, the OH produced from the NH3 hydrolysis reaction
will approximate 4 10 5
M (3.85 if you solve the quadratic) in this very dilute solution.
(Recall that degree of ionization is high in dilute solution.) And since OH
=3.5 105
M is needed for precipitation to occur, we conclude that Mg OH
bg
2 will precipitate from
this solution (note: not much of a precipitate is expected).
(c) 0.010 M HC H O
232
and 0.010 M NaC H O
232
is a buffer solution with pH p a
=K of
acetic acid (the acid and its anion are present in equal concentrations.) From this, we
determine the OH.

Chapter 18: Solubility and Complex-Ion Equilibria
921
pH pOH OH= 4.74 = 14.00 4.74 = 9.26 = 10 = 5.5 10
9.26 10
3
3
3+ 10 30 33
sp 3
= Al OH = 0.010 5.5 10 = 1.7 10 1.3 10 = of Al OHQK
Thus, Al OH s
bgbg
3 should precipitate from this solution.
Complex-Ion Equilibria
51. (E) Lead(II) ion forms a complex ion with chloride ion. It forms no such complex ion with
nitrate ion. The formation of this complex ion decreases the concentrations of free Pb aq
2+bg
and free Cl aq
bg
. Thus, PbCl2 will dissolve in the HCl(aq) up until the value of the solubility
product is exceeded.
2+
3
Pb aq +3Cl aq PbCl aq
52. (E)
2+
2+ 8
33f
4
Zn aq + 4NH aq Zn NH aq = 4.1 10K
NH aq
3bg will be least effective in reducing the concentration of the complex ion. In fact, the
addition of NH aq
3bg will increase the concentration of the complex ion by favoring a shift of
the equilibrium to the right. NH aq
4
+bg will have a similar effect, but not as direct. NH aq
3bg is
formed by the hydrolysis of NH aq
4
+bg and, thus, increasing NH4
+ will eventually increase
NH aq
3bg:
++
42 33
NH aq + H O(l) NH aq + H O aq .
The addition of HCl(aq) will
cause the greatest decrease in the concentration of the complex ion. HCl(aq) will react with
NH aq
3bg to decrease its concentration (by forming NH4
+) and this will cause the complex ion
equilibrium reaction to shift left toward free aqueous ammonia and Zn2+(aq).
53. (E) We substitute the given concentrations directly into the Kf expression to calculate Kf.
330
4
f+4 324
[[Cu(CN) ] 0.0500 2.0 10
[Cu ][CN ] (6.1 10 )(0.80)
K
54. (M) The solution to this problem is organized around the balanced chemical equation. Free
NH3 is 6.0 M at equilibrium. The size of the equilibrium constant indicates that most
copper(II) is present as the complex ion at equilibrium.
Equation:
2+ 3
Cu aq + 4NH aq
Cu NH aq
34
2+
bgbg
Initial: 0.10 M 6.00 M 0 M
Change(100 % rxn): 0.10 M 0.40 M +0.10 M
Completion: 0 M 5.60 M 0.10 M
Changes: +
x
M +4x M x M
Equil:
x
M 5.60 + 4x M 0.10
x
bg M

Chapter 18: Solubility and Complex-Ion Equilibria
922
Let’s assume (5.60 + 4x) M ≈ 5.60 M and (0.10 –x) M ≈ 0.10 M
2+
3413
f444
2+
3
Cu NH 0.10 0.10 0.10
==1.110 983.4
(5.60)
5.60 4Cu NH
x
K
x
x
xx
18 2
13
0.10 9.2 10 M Cu ( << 0.10, thus the approximation was valid)
983.4 (1.1 10 )
xx
55. (M) We first find the concentration of free metal ion. Then we determine the value of Qsp for
the precipitation reaction, and compare its value with the value of Ksp to determine whether
precipitation should occur.
Equation: Ag aq
++
bg
2
23
2SO aq
Ag S O aq
23
2
3
bgbg
Initial: 0 M 0.76 M 0.048 M
Changes: +
x
M +2
x
M
x
M
Equil:
x
M
0.76 + 2 Mx
0.048 Mx
3
23
2
2
2
+
23
13
f22
Ag S O
Ag S O
0.048 0.048
==1.710=
(0.76)
0.76 + 2
x
K
x
xx
;15 +
=4.9 10 M= Agx
(x << 0.048 M, thus the approximation was valid.)
+151517
sp sp
= Ag I = 4.9 10 2.0 = 9.8 10 8.5 10 =QK
.
Because sp sp
QK, precipitation of AgI(s) should occur.
56. (M) We need to determine OH in this solution, and also the free Cu2+ .
3
a+
4
NH 0.10 M
pH = p + log = 9.26+ log = 9.26 pOH =14.00 9.26 = 4.74
0.10 M
NH
K
4.74 5
OH =10 =1.8 10 M
2+
2+
33
4
Cu aq + 4NH aq Cu NH aq
2+
34
413 4
2+ 4
2+
3
13 2+ 11
f
Cu NH 0.015 0.015
1.1 10 0.10
Cu 0.10
Cu NH
= =1.1 10 = ; Cu = = 1.4 10 MK
Now we determine the value of sp
Q and compare it with the value of Ksp for Cu OH
bg
2.
22
2+ 11 5 21 20
sp sp 2
Cu OH 1.4×10 1.8×10 )= = = 4.5×10 < 2.2×10 ( for Cu OH
QK
Precipitation of Cu OH s
bgbg
2 from this solution should not occur.
Chapter 18: Solubility and Complex-Ion Equilibria
923
57. (M) We first compute the free Ag+ in the original solution. The size of the complex ion
formation equilibrium constant indicates that the reaction lies far to the right, so we form as
much complex ion as possible stoichiometrically.
Equation: Ag aq
++
bg 23
NH aq
bg
Ag NH aq
32
+
bgbg
In soln: 0.10 M 1.00 M 0 M
Form complex: 0.10 M
0.20 M +0.10 M
0 M 0.80 M 0.10 M
Changes: +
x
M +2
x
M
x
M
Equil:
x
M 0.80 + 2x
bg M 0.10
x
bg M
+
32
7 9
f222 2
7
+3
Ag NH 0.10 0.10 0.10
=1.6 10 = = = = 9.8 10 M
0.80+ 2 0.80 1.6 10 0.80
Ag NH
x
Kx
xxx
.
(x << 0.80 M, thus the approximation was valid.)
Thus, +9
Ag = 9.8 10 M.
We next determine the I that can coexist in this solution
without precipitation.
17
+179 9
sp 9
8.5 10
= Ag I = 8.5 10 = 9.8 10 I ; I = = 8.7 10 M
9.8 10
K
Finally, we determine the mass of KI needed to produce this I
96
8.7 10 mol I 1mol KI 166.0 g KI
mass KI =1.00 L soln =1.4 10 g KI
1 L soln 1mol I 1mol KI
58. (M) First we determine Ag+ that can exist with this Cl. We know that Cl will be
unchanged because precipitation will not be allowed to occur.
10
+10+ + 9
sp
1.8 10
= Ag Cl = 1.8 10 = Ag 0.100 M; Ag = = 1.8 10 M
0.100
K
We now consider the complex ion equilibrium. If the complex ion’s final concentration is
x
,
then the decrease in NH3 is 2
x
, because 2 mol NH3 react to form each mole of complex
ion, as follows.
+
+
33
2
Ag aq + 2NH aq Ag NH aq
We can solve the Kf
expression for x.
Kx
x
f
Ag NH
Ag NH
=1.6 10 = =1.8 10 1.00 2
732
+
+3
292
L
N
MO
Q
P
bg
bg
xxxxxx= 1.6 10 1.8 10 1.00 2 = 0.029 1.00 4.00 + 4.00 = 0.029 0.12 + 0.12
79 222
chc h
bgch
2
0 = 0.029 1.12 + 0.12 We use the quadratic formula roots equation to solve for .
x
xx
2
21.12 (1.12) 4 0.029 0.12
4 1.12 1.114
= = = = 9.3, 0.025
2 2 0.12 0.24
bb ac
xa
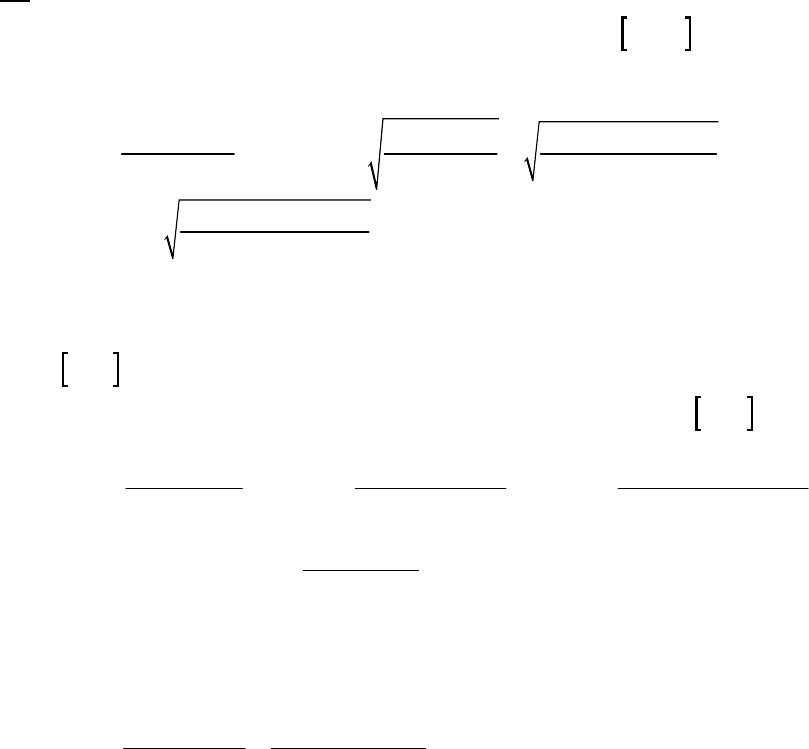
Chapter 18: Solubility and Complex-Ion Equilibria
924
Thus, we can add 0.025 mol AgNO3(~ 4.4 g AgNO3) to this solution before we see a
precipitate of AgCl(s) form.
Precipitation and Solubilities of Metal Sulfides
59. (M) We know that Kspa =3 10
7
for MnS and Kspa =6 10
2
for FeS. The metal sulfide will
begin to precipitate when QK
spa spa
=.
Let us determine the HO
3+ just necessary to form each
precipitate. We assume that the solution is saturated with
22
H S, H S = 0.10 M .
22
+ 5
22
spa 3
+2 7
3spa
[M ][H S] [M ][H S] (0.10 M)(0.10 M)
[H O ] 1.8 10 M for MnS
[H O ] 3 10
KK
+3
32
(0.10 M)(0.10 M)
H O = 4.1 10 M for FeS
610
Thus, if the [H3O+] is maintained just a bit higher than 5
1.8 10 M
, FeS will precipitate and
Mn aq
2+bg
will remain in solution. To determine if the separation is complete, we see whether
Fe2+ has decreased to 0.1% or less of its original value when the solution is held at the
aforementioned acidity. Let +5
3
H O = 2.0 10 M
and calculate Fe2+ .
2
2+ 2+ 25
2
22
5
+
3
22+ 6
spa
Fe H S Fe 0.10 M 6 10 2.0 10
0.10
2.0 10 MHO
==610= ; Fe= =2.410MK
6
2+ 2.4 10 M
%Fe aq remaining = 100% = 0.0024% Separation is complete.
0.10 M
60. (M) Since the cation concentrations are identical, the value of Qspa is the same for each one. It
is this value of Qspa that we compare with Kspa to determine if precipitation occurs.
2+
21
spa 22
+
3
MHS
0.05M 0.10M
== =510
0.010M
HO
Q
If QK
spa spa
, precipitation of the metal sulfide should occur. But, if QK
spa spa
, precipitation
will not occur.
For CuS, KQ
spa spa
= 6 10 = 5 10
16 1
Precipitation of CuS(s) should occur.
For HgS, KQ
spa spa
= 2 10 = 5 10
32 1
Precipitation of HgS(s) should occur.
For MnS, KQ
spa spa
= 3 10 = 5 10
71
Precipitation of MnS(s) will not occur.
Chapter 18: Solubility and Complex-Ion Equilibria
925
61. (M)
(a) We can calculate HO
3
+ in the buffer with the Henderson–Hasselbalch equation.
232 +4.52 5
a 3
232
CHO 0.15M
pH = p + log = 4.74 + log = 4.52 H O = 10 = 3.0 10 M
HC H O 0.25 M
K
We use this information to calculate a value of Qspa for MnS in this solution and then
comparison of Qspa with Kspa will allow us to decide if a precipitate will form.
2+
277
spa spa
22
+5
3
Mn H S 0.15 0.10
===1.710310=for MnS
HO 3.0 10
QK
Thus, precipitation of MnS(s) will not occur.
(b) We need to change HO
3+ so that
7+ +5
spa 3 3
27
+
3
0.15 0.10 (0.15) 0.10
= 3 10 = ; H O = [H O ] = 2.2 10 M pH = 4.66
310
HO
Q
This is a more basic solution, which we can produce by increasing the basic component
of the buffer solution, namely, the acetate ion. We can find out the necessary acetate ion
concentration with the Henderson–Hasselbalch equation.
232 232
a
232
232
[C H O ] [C H O ]
pH p log 4.66 4.74 log
[HC H O ] 0.25 M
[C H O ]
log 4.66 4.74 0.08
0.25 M
K
232 0.08 232
CHO =10 = 0.83 C H O = 0.83 0.25M = 0.21M
0.25 M
62. (M)
(a) CuS is in the hydrogen sulfide group of qualitative analysis. Its precipitation occurs
when 0.3 M HCl is saturated with 2
HS. It will certainly precipitate from a (non-acidic)
saturated solution of H2S which has a much higher S2.
2+ +
2
Cu aq + H S satd aq CuS s + 2H aq
This reaction proceeds to an essentially quantitative extent in the forward direction.
(b) MgS is soluble, according to the solubility rules listed in Chapter 5.
0.3 M HCl
2+ 2
Mg aq + H S satd aq no reaction
(c) As in part (a), PbS is in the qualitative analysis hydrogen sulfide group, which
precipitates from a 0.3 M HCl solution saturated with 2
HS. Therefore, PbS does not
dissolve appreciably in 0.3 M HCl.
PbS s + HCl 0.3M no reaction
Chapter 18: Solubility and Complex-Ion Equilibria
926
(d) Since ZnS(s) does not precipitate in the hydrogen sulfide group, we conclude that it is
soluble in acidic solution.
332
2
ZnS s + 2HNO aq Zn NO aq + H S g
Qualitative Cation Analysis
63. (E) The purpose of adding hot water is to separate Pb2+ from AgCl and 22
Hg Cl . Thus, the
most important consequence would be the absence of a valid test for the presence or absence
of 2+
Pb . In addition, if we add NH3 first, PbCl2 may form
2
Pb OH . If Pb OH
bg2 does
form, it will be present with Hg Cl
22
in the solid, although Pb OH
bg
2 will not darken with
added 3
NH . Thus, we might falsely conclude that Ag+ is present.
64. (M)
For
2+
2
PbCl aq , 2 Pb = Cl
where s= molar solubility of PbCl2.
Thus 2+
=Pbs
.
3
2+ 2 2 3 5 5 2 2+
sp [Pb ][Cl ] ( )(2 ) 4 1.6 10 ; 1.6 10 4 1.6 10 M = [Pb ]Kssss
Both Pb2+ and CrO4
2 are diluted by mixing the two solutions.
2
2+
4
1.00 mL 0.05 mL
Pb = 0.016 M = 0.015 M CrO =1.0 M = 0.048 M
1.05 mL 1.05 mL
2
2+ 4 13
sp 4 sp
= Pb CrO = 0.015 M 0.048 M = 7.2 10 2.8 10 =QK
Thus, precipitation should occur from the solution described.
65. (E)
(a) Ag+ and/or Hg2
2+ are probably present. Both of these cations form chloride precipitates
from acidic solutions of chloride ion.
(b) We cannot tell whether Mg2+ is present or not. Both MgS and MgCl2 are water soluble.
(c) Pb2+ possibly is absent; it is the only cation of those given which forms a precipitate in
an acidic solution that is treated with 2
HS,
and no sulfide precipitate was formed.
(d) We cannot tell whether Fe2+ is present. FeS will not precipitate from an acidic solution that
is treated with 2
HS;
the solution must be alkaline for a FeS precipitate to form.
(a) and (c) are the valid conclusions.
66. (E)
(a)
2+ 2
Pb aq + 2Cl aq PbCl s
(b)
2
24
Zn OH s + 2OH aq Zn OH aq
(c)
3+
+3+
322
3 6
Fe OH s + 3H O aq Fe aq + 6H O(l) or Fe H O aq

Chapter 18: Solubility and Complex-Ion Equilibria
927
(d)
2+ +
2
Cu aq + H S aq CuS s + 2H aq
INTEGRATIVE AND ADVANCED EXERCISES
67. (M) We determine s, the solubility of CaSO4 in a saturated solution, and then the concentration of
CaSO4 in ppm in this saturated solution, assuming that the solution’s density is 1.00 g/mL.
22 2 6 3
sp 4
6 2
44
4
4
[Ca ][SO ] ( )( ) 9.1 10 3.0 10 M
0.0030 mol CaSO 136.1 g CaSO
1 mL 1 L soln
ppm CaSO 10 g soln 4.1 10 ppm
1.00 g 1000 mL 1 L soln 1 mol CaSO
Kssss
Now we determine the volume of solution remaining after we evaporate the 131 ppm CaSO4
down to a saturated solution (assuming that both solutions have a density of 1.00 g/mL.)
mL 102.3
g 1.00
mL 1
CaSO g101.4
soln dsat' g 10
CaSO g 131 soln dsat' volume 5
4
2
6
4
Thus, we must evaporate 6.8 × 105 mL of the original 1.000 × 106 mL of solution, or 68% of the
water sample.
68. (M)
(a) First we compute the molar solubility, s, of CaHPO42H2O.
3
42 42
42
22 2 32 6
sp 4
0.32 g CaHPO 2H O 1 mol CaHPO 2H O 1.9 10 M
1 L soln 172.1 g CaHPO 2H O
[Ca ][HPO ] ( )( ) (1.9 10 ) 3.6 10
Thus the values are not quite consistent.
s
Ksss
(b) The value of Ksp given in the problem is consistent with a smaller value of the molar
solubility. The reason is that not all of the solute ends up in solution as HPO42– ions.
HPO42– can act as either an acid or a base in water (see below), but it is base hydrolysis that
predominates.
. 2313
42 3 4 3
HPO (aq) H O(l) H O (aq) PO (aq) 4.2 10
a
K
2 7
w
42 24b
2
HPO (aq) H O(l) OH (aq) H PO (aq) 1.6 10
K
KK
69. (M) The solutions mutually dilute each other and, because the volumes are equal, the
concentrations are halved in the final solution: [Ca2+] = 0.00625 M, [SO42–] = 0.00760 M. We
cannot assume that either concentration remains constant during the precipitation. Instead, we
assume that precipitation proceeds until all of one reagent is used up. Equilibrium is reached
from that point.
Chapter 18: Solubility and Complex-Ion Equilibria
928
226
44sp
22
sp 4
Equation: CaSO (s) Ca (aq) SO (aq) 9.1 10
In soln 0.00625 M 0.00760 M [Ca ][SO ]
Form ppt
K
K
sp
sp
0.00625 M 0.00625 M ( )(0.00135 )
Not at equil 0 M 0.00135 M 0.00135
Changes
Kx x
Kx
6
3
9.1 10
M M 6.7 10 M
0.00135
Equil: M (0.00135 ) M {not a reasonable assumption!}
xxx
xx
Solving the quadratic 0 = x2 + (1.35×10-2)x – 9.1×10-6 yields x = 2.4×10-3.
-3
2+ final
initial
2.4×10 M
% unprecipitated Ca = ×100% = 38% unprecipitated
0.00625 M
70. (M) If equal volumes are mixed, each concentration is reduced to one-half of its initial value.
We assume that all of the limiting ion forms a precipitate, and then equilibrium is achieved by
the reaction proceeding in the forward direction to a small extent.
22
33
Equation: BaCO (s) Ba (aq) CO (aq)
Orig. soln: 0.00050 M 0.0010 M
Form ppt: 0 M
0.0005 M
Changes: M M
Equil: M (0.0005 )M
xx
x
x
22 9
sp 3
95 2+ -4 -5
[Ba ][CO ] 5.1 10 ( )(0.0005 ) 0.0005
5.1 10 1 10 M The [Ba ] decreases from 5 × 10 M to 1 × 10 M.
0.0005
Kxxx
x
(x < 0.0005 M, thus the approximation was valid.)
%2%100
M105
M101
atedunprecipit % 4
5
Thus, 98% of the Ba2+ is precipitated as BaCO3(s).
71. (M) The pH of the buffer establishes [H3O+] = 10–pH = 10–3.00 = 1.0 × 10–3 M.
Now we combine the two equilibrium expressions, and solve the resulting expression for the
molar solubility of Pb(N3)2 in the buffer solution.

Chapter 18: Solubility and Complex-Ion Equilibria
929
2 9
32 3 sp
29
a
2
32 3 3
33 32 52
Pb(N ) (s) Pb (aq) 2 N (aq) 2.5 10
1/ 2.8 10
Pb(N ) (s) 2 H O (aq) Pb (aq) 2 HN (aq
1
2 H O (aq) 2 N (aq) 2 HN (aq) 2 H O(l) (1.9 10 )
K
K
2
2spa
2
32 3 3 2
) 2 H O (l) 7.0
Pb(N ) (s) 2 H O (aq) Pb (aq) 2 HN (aq) 2 H O (l)
Buffer: 0.0010 M 0 M 0 M
Dissolving: (buffer) M 2 M
(1 / )
KK K
xx
22 22
3
32
3
22
3
Equilibrium: 0.0010 M M 2 M
[Pb ][HN ] ( ) (2 ) 7.0(0.0010)
7.0 4 7.0 (0.0010) 0.012 M
[H O ] (0.0010) 4
xx
xx
Kxx
Thus, the molar solubility of Pb(N3)2 in a pH = 3.00 buffer is 0.012 M.
72. (M) We first determine the equilibrium constant of the suggested reaction.
2
24 32
Mg(OH) (s) 2 NH (aq) Mg (aq) 2 NH (aq) 2 H O(l)
Initial: 1.00 M 0 M 0 M
Changes: 2 M M 2 M
Equil: (1.00 2 ) M M 2
xxx
xx
22
11 2 3
sp 3
252 2 22
b4
3
M
[Mg ][NH ]
1.8 10 (2 ) 4
0.056
(1.8 10 ) [NH ] (1.00 2 ) 1.00
0.056
0.24 M
4
x
Kxx x
KKx
x
Take this as a first approximation and cycle through again. 2x = 0.48
M 16.0
4
)48.0 (1.00 056.0
056.0
)48.000.1(
432
2
3
x
x
K
Yet another cycle gives a somewhat more consistent value. 2x = 0.32
M 19.0
4
)38.0 (1.00 056.0
056.0
)32.000.1(
432
2
3
x
x
K
Another cycle gives more consistency. 2x = 0.38
211
2sp
252
432b
Mg(OH) (s) Mg (aq) 2 OH (aq) 1.8 10
2 NH (aq) 2 OH (aq) 2 NH (aq) 2 H O(l) 1/ 1/(1.8 10 )
K
K

Chapter 18: Solubility and Complex-Ion Equilibria
930
][MgM 18.0
4
)38.0 (1.00 056.0
056.0
)38.000.1(
42
32
2
3
x
x
K
The molar solubility of Mg(OH)2 in a 1.00 M NH4Cl solution is 0.18 M.
73. (D) First we determine the value of the equilibrium constant for the cited reaction.
22 9
33 sp
211
33 23 2
2
33 3 2 sp2
CaCO (s) Ca (aq) CO (aq) 2.8 10
H O (aq) CO (aq) H O(l) HCO (aq) 1/ 1/ 4.7 10
CaCO (aq) H O (aq) Ca (aq) HCO (aq) H O(l) 1/
2.8 10
a
overall a
overall
K
K
KKK
K
9
11 60
4.7 10
2
33 3 2
pH
Equation: CaCO (s) H O (aq) Ca (aq) HCO (aq) H O(l)
Initial: 10 0 M 0 M
Change: ( ) M M
Equil:
buffer x x
pH
10 M M
xx
In the above set-up, we have assumed that the pH of the solution did not change because of the
dissolving of the CaCO3(s). That is, we have treated the rainwater as if it were a buffer solution.
(a) ][CaM 10110360
103
.60
]OH[
]HCO][Ca[ 226
6
2
3
3
2
x
x
K
22522
3
5
3
[Ca ][HCO ] 60. 60 6.3 10 6.1 10 M [Ca ]
[H O ] 6.3 10
x
Kx
(b)
74. We use the Henderson-Hasselbalch equation to determine [H3O+] in this solution, and then use the
Ksp expression for MnS to determine [Mn2+] that can exist in this solution without precipitation
occurring.

Chapter 18: Solubility and Complex-Ion Equilibria
931
232
a
232
5.44 6
3
2 7
322spa
2
2
[C H O ] 0.500 M
pH p log 4.74 log 4.74 0.70 5.44
[HC H O ] 0.100 M
[H O ] 10 3.6 10 M
MnS(s) 2 H O (aq) Mn (aq) H S(aq) 2 H O(l) 3 10
Note that [H S] [Mn ] , the molar solubility of
K
K
s
22
7
2
spa 262
3
2
2
MnS.
[Mn ][H S] 3 10 0.02 M
[H O ] (3.6 10 M)
0.02 mol Mn 1 mol MnS 87 g MnS
mass MnS/L 2 g MnS/L
1 L soln 1 mol MnS
1 mol Mn
s
Ks
75. (M)
(a)
The precipitate is likely Ca3(PO4)2. Let us determine the %Ca of this compound (by mass)
aq)(H 2 s)()PO(Caaq)(HPO 2aq)(Ca 3
Ca %763.38%100
)PO(Ca g 18.310
Ca g 40.0783
Ca%
243
2
4
2
243
(b) aq)”(CO“HO(l)Hg)(CO:g)(CO are bubbles The 32222
2
23 3
2+ -
323 3
Ca (aq) H CO (aq) CaCO (s) 2 H (aq) precipitation
CaCO (s) + H CO (aq) Ca (aq) + 2 HCO (aq) redissolving
76. (D)
(a) A solution of CO2(aq) has [CO32- ] = Ka[H2CO3] = 5.6 × 10-11. Since Ksp = 2.8 × 10-9 for
CaCO3, the [Ca2+] needed to form a precipitate from this solution can be computed.
-9
sp
2+
2- -11
3
2.8×10
[Ca ] = = = 50.M
[CO ] 5.6×10
K
This is too high to reach by dissolving CaCl2 in solution. The reason why the technique works
is because the OH-(aq) produced by Ca(OH)2 neutralizes some of the HCO3-(aq) from the
ionization of CO2(aq), thereby increasing the [CO32-] above a value of 5.6 × 10-11.
(b) The equation for redissolving can be obtained by combining several equations.

Chapter 18: Solubility and Complex-Ion Equilibria
932
2+ 2- -9
33 sp
2- + -
33 32 -11
a2
-+ -7
22 33 a1
2+ -
322 3
CaCO (s) Ca (aq) + CO (aq) = 2.8×10
11
CO (aq) + H O (aq) HCO (aq) + H O(l) = 5.6×10
CO (aq)+ 2 H O(l) HCO (aq) +H O (aq) = 4.2×10
CaCO (s) + CO (aq)+ H O(l) Ca (aq) + 2HCO (aq)
K
K
K
Ksp a1
a2
×
= KK
K
2+ - 2
-9 -7 -5 3
-11
2
[Ca ][HCO ]
(2.8×10 )(4.2×10 )
= = 2.1×10 =
5.6×10 [CO ]
K
If CaCO3 is precipitated from 0.005 M Ca2+(aq) and then redissolved, [Ca2+] = 0.005 M and
[HCO32-] = 2×0.005 M = 0.010 M. We use these values in the above expression to compute
[CO2].
2+ - 2 2
3
2-5 -5
[Ca ][HCO ] (0.005)(0.010)
[CO ]= = = 0.02 M
2.1×10 2.1×10
We repeat the calculation for saturated Ca(OH)2, in which [OH-] = 2 [Ca2+], after first
determining [Ca2+] in this solution.
Ksp = [Ca2+][OH-]2 = 4 [Ca2+] = 5.5×10-6 [Ca2+] 6
35.5 10
4
= 0.011
M
2+ - 2 2
3
2-5 -5
[Ca ][HCO ] (0.011)(0.022)
[CO ]= = = 0.25 M
2.1×10 2.1×10
Thus, to redissolve the CaCO3 requires that [CO2] = 0.25 M if the solution initially is saturated
Ca(OH)2, but only 0.02 M CO2 if the solution initially is 0.005 M Ca(OH)2(aq).
A handbook lists the solubility of CO2 as 0.034 M. Clearly the CaCO3 produced cannot
redissolve if the solution was initially saturated with Ca(OH)2(aq).
77. (M)
(a)
22 -10
4
4sp
22-
33-9
2- 2
34
43
sp
BaSO (s) Ba (aq) SO (aq) 1.1 10
1
Ba (aq) CO (aq) BaCO (s) = 5.1 10
1.1
Sum BaSO (s) +CO (aq) BaCO (s) + SO (aq)
1
overall
K
K
K
-10
-9
10 0.0216
5.1 10
Initial 3 M 0
Equil. (3- )M
(where is the carbonate use
xx
xd up in the reaction)
2-
4
2-
3
[SO ] 0.0216 and 0.063 Since 0.063 M 0.050 M, the response is yes.
[CO ] 3
x
Kx
x

Chapter 18: Solubility and Complex-Ion Equilibria
933
-10 2
sp
2-
323 sp
-12
2-
323 overall
+-
2AgCl(s) 2Ag (aq) + 2 Cl (aq) = (1.8 10 )
1
+
2 Ag (aq) + CO (aq) Ag CO (s) 1/ = 8.5 10
-
Sum 2AgCl(s) +CO (aq) Ag CO (s) + 2 Cl (aq)
(b)
K
K
K-10 2 -9
-12
(1.8 10 )
= =3.8 10
8.5 10
Initial 3 M 0 M
Equil. (3- )M 2
(where is the carbona
xx
xte used up in the reaction)
22 -9 -5
overall 2-
3
-5
-
[Cl ] (2 )
= = = 3.8 10 and = 5.3 10 M
[CO ] 3-
Since 2 , (2(5.35 10 M)) , << 0.050 M, the response is no.
x
Kx
x
x
2+ -
2sp
2+ 2-
33 sp
-8
-8
MgF (s) Mg (aq) 2 F (aq) 3.7 10
1
Mg (aq) CO (aq) MgCO (s) 1/ 3.5 10
sum
(c)
K
K
-8
2- -
23 3 overall -8
3.7 10
MgF (s) CO (aq) MgCO (s) 2 F (aq) 1.1
3.5 10
initial 3 M 0 M
equil. (
K
22
overall 2-
3
3- )M 2
(where is the carbonate used up in the reaction)
[F ] (2 )
1.1 and 0.769M
[CO ] 3
Since 2 , (2(0.769M)) 0.
xx
x
x
Kx
x
x050 M, the response is yes.
78. (D) For ease of calculation, let us assume that 100 mL, that is, 0.100 L of solution, is to be
titrated. We also assume that [Ag+] = 0.10 M in the titrant. In order to precipitate 99.9% of the
Br– as AgBr, the following volume of titrant must be added.
0.010 mmol Br 1 mmol Ag 1 mL titrant
volume titrant 0.999 100 mL 9.99 mL
1 mL sample 1 mmol Br 0.10 mmol Ag
We compute [Ag+] when precipitation is complete.
M100.5
M 01.0001.0
100.5
][Br
]Ag[ 8
13
sp
f
K
Thus, during the course of the precipitation of AgBr, while 9.99 mL of titrant is added, [Ag+]
increases from zero to 5.0 × 10–8 M. [Ag+] increases from 5.0 × 10–8 M to 1.0 × 10–5 M from
the point where AgBr is completely precipitated to the point where Ag2CrO4 begins to
precipitate. Let us assume, for the purpose of making an initial estimate, that this increase in
[Ag+] occurs while the total volume of the solution is 110 mL (the original 100 mL plus 10 mL

Chapter 18: Solubility and Complex-Ion Equilibria
934
of titrant needed to precipitate all the AgBr.) The amount of Ag+ added during this increase is
the difference between the amount present just after AgBr is completely precipitated and the
amount present when Ag2CrO4 begins to precipitate.
titrantmL101.1
Ag mmol 10.0
titrantmL 1
Ag mmol 10 1.1 titrant added volume
Ag mmol 101.1
soln mL 1
Ag mmol105.0
mL 110
soln mL 1
Ag mmol101.0
mL 110added Agamount
23
3
85
We see that the total volume of solution remains essentially constant. Note that [Ag+] has
increased by more than two powers of ten while the volume of solution increased a very small
degree; this is indeed a very rapid rise in [Ag+], as stated.
79. (D) The chemistry of aluminum is complex, however, we can make the following assumptions.
Consider the following reactions at various pH:
pH > 7 Al(OH)3(s) + OH- overall = 1.43
sp
f
KKK
Al(OH)4-(aq)
pH < 7 Al(OH)3(s) 33
sp = 1.3 10K
Al3+(aq) + 3 OH-
For the solubilities in basic solutions, consider the following equilibrium at pH = 13.00 and 11.00.
At pH = 13.00: Al(OH)3(s) + OH- = 1.43
ov f sp
KKK
Al(OH)4-(aq)
Initial : – 0.10 0
Change: – –x +x
Equilibrium: – 0.10 – x x
K
f = 1.43 = (buffered at pH = 13.00)
0.10 0.10
xx
x
x = 0.143 M
At pH = 11.00: Kf = 1.43 = (buffered at pH = 11)
0.0010 0.0010
xx
x
x = 0.00143 M
Thus, in these two calculations we see that the formation of the aluminate ion [Al(OH)4] is
favored at high pH values. Note that the concentration of aluminum(III) increases by a factor of
one-hundred when the pH is increased from 11.00 to 13.00, and it will increase further still
above pH 13. Now consider the solubility equilibrium established at pH = 3.00, 4.00, and 5.00.
These correspond to [OH] = 1.0 1011 M, 1.0 1010 M, and 1.0 109 M, respectively.
Al(OH)3(s) 33
sp = 1.3 10K
Al3+(aq) + 3 OH(aq)
At these pH values, [Al3+] in saturated aqueous solutions of Al(OH)3 are
[Al3+] = 1.3 1033 /(1.0 1011)3 = 1.3 M at pH = 3.00

Chapter 18: Solubility and Complex-Ion Equilibria
935
[Al3+] = 1.3 1033 /(1.0 1010)3 = 1.3 103 M at pH = 4.00
[Al3+] = 1.3 1033 /(1.0 109)3 = 1.3 106 M at pH = 5.00
These three calculations show that in strongly acidic solutions the concentration of
aluminum(III) can be very high and is certainly not limited by the precipitation of Al(OH)3(s).
However, this solubility decreases rapidly as the pH increases beyond pH 4.
At neutral pH 7, a number of equilibria would need to be considered simultaneously, including
the self-ionization of water itself. However, the results of just these five calculations do
indicate that concentration of aluminum(III) increases at both low and high pH values, with a
very low concentration at intermediate pH values around pH 7, thus aluminum(III)
concentration as a function of pH is a U-shaped (or V-shaped) curve.
80. (M) We combine the solubility product expression for AgCN(s) with the formation expression
for [Ag(NH3)2]+(aq).
sp
7
332f
332overallspf
32
overall
Solubility: AgCN(s) Ag (aq) CN (aq) ?
Formation: Ag (aq) 2NH (aq) [Ag(NH ) ] (aq) 1.6 10
Net reaction: AgCN(s) 2 NH (aq) [Ag(NH ) ] CN (aq)
[[Ag(NH ) ] ][CN
K
K
KKK
K62 97
sp
22
3
916
sp 7
](8.8 10 ) 1.9 10 1.6 10
[NH ] (0.200)
1.9 10 1.2 10
1.6 10
K
K
Because of the extremely low solubility of AgCN in the solution, we assumed that [NH3] was
not altered by the formation of the complex ion.
81. We combine the solubility product constant expression for CdCO3(s) with the formation
expression for [CdI4]2–(aq).
22 12
33sp
22
4f
22
343
Solubility: CdCO (s) Cd (aq) CO (aq) 5.2 10
Formation: Cd (aq) 4 I (aq) [CdI ] (aq) ?
Net reaction: CdCO (s) 4 I (aq) [CdI ] (aq) CO
K
K
overall sp f
(aq) KKK
22 32 612
43
overall f
44
65
f12
[[CdI ] ][CO ] (1.2 10 ) 1.4 10 5.2 10
[I ] (1.00)
1.4 10 2.7 10
5.2 10
KK
K

Chapter 18: Solubility and Complex-Ion Equilibria
936
Because of the low solubility of CdCO3 in this solution, we assumed that [I–] was not
appreciably lowered by the formation of the complex ion.
82. (M) We first determine [Pb2+] in this solution, which has [Cl-] = 0.10 M.
M106.1
)10.0(
106.1
][Cl
]Pb[]Cl][Pb[106.1 3
2
5
2
sp
2225
sp
K
K
Then we use this value of [Pb2+] in the Kf expression to determine [[PbCl3]–].
M108.3106.124]]PbCl[[
106.1
]]PbCl[[
)10.0)(106.1(
]]PbCl[[
24
]Cl][Pb[
]]PbCl[[
56
3
6
3
33
3
32
3
f
K
The solubility of PbCl2 in 0.10 M HCl is the following sum.
solubility = [Pb2+] + [[PbCl3]–] = 1.6 × 10–3 M + 3.8 × 10–5 M = 1.6 × 10–3 M
83. (M) Two of the three relationships needed to answer this question are the two solubility product
expressions. 1.6 × 10–8 = [Pb2+][SO42–] 4.0 × 10–7 = [Pb2+][S2O32–]
The third expression required is the electroneutrality equation, which states that the total
positive charge concentration must equal the total negative charge concentration:
[Pb2+] = [SO42–] + [S2O32–], provided [H3O+] = [OH-].
Or, put another way, there is one Pb2+ ion in solution for each SO42– ion and for each S2O32– ion.
We solve each of the first two expressions for the concentration of each anion, substitute these
expressions into the electroneutrality expression, and then solve for [Pb2+].
8787
222
423
2222
22 8 7 7 2 7 4
1.6 10 4.0 10 1.6 10 4.0 10
[SO ] [S O ] [Pb ]
[Pb] [Pb] [Pb] [Pb]
[Pb ] 1.6 10 4.0 10 4.2 10 [Pb ] 4.2 10 6.5 10 M
84. (D)
The chemical equations are:
22
22
PbCl (s) Pb (aq) 2 Cl (aq) and PbBr (s) Pb (aq) 2 Br (aq)
The two solubility constant expressions, [Pb2+][Cl–]2 = 1.6 × 10–5, [Pb2+][Br–]2 = 4.0 × 10–5 and
the condition of electroneutrality, 2 [Pb2+] = [Cl–] + [Br–], must be solved simultaneously to
determine [Pb2+]. (Rearranging the electroneutrality relationship, one obtains:
]Br[]Cl[]Pb[ 2
1
2
1
2 .) First we solve each of the solubility constant expressions for the
concentration of the anion. Then we substitute these values into the electroneutrality expression
and solve the resulting equation for [Pb2+].
M100.3]Pb[107.2]Pb[102.5]Pb[
1003.1103.6100.4100.4106.1]Pb[2
]Pb[
100.4
]Pb[
106.1
]Pb[ 2
]Pb[
100.4
]Br[
]Pb[
106.1
]Cl[
22532332
2335532
2
5
2
5
2
2
5
2
5

Chapter 18: Solubility and Complex-Ion Equilibria
937
85. (D) (a) First let us determine if there is sufficient Ag2SO4 to produce a saturated solution, in
which [Ag+] = 2 [SO42–].
M 0535.0
SOAgmol 1
SO mol 1
SOAg g 8.311
SO Ag mol 1
L 150.0
SOAg g 50.2
][SO
M 015.0
4
104.1
]SO[]SO[ 4]SO[]Ag[104.1
42
2
4
42
4242
2
4
3
5
2
4
3
2
4
2
4
25
sp
K
Thus, there is more than enough Ag2SO4 present to form a saturated solution. Let us now see if
AgCl or BaSO4 will precipitate under these circumstances. [SO42–] = 0.015 M and [Ag+] = 0.030
M.
Q = [Ag+][Cl–] = 0.030 × 0.050 = 1.5 × 10–3 > 1.8 × 10–10 = Ksp, thus AgCl should precipitate.
Q = [Ba2+][SO42–] = 0.025 × 0.015 = 3.8 × 10–4 > 1.1 × 10–10 = Ksp, thus BaSO4 should precipitate.
Thus, the net ionic equation for the reaction that will occur is as follows.
AgCl(s) 2s)(BaSOaq)(Cl 2aq)(Bas)(SOAg 4
2
42
(b) Let us first determine if any Ag2SO4(s) remains or if it is all converted to BaSO4(s) and
AgCl(s). Thus, we have to solve a limiting reagent problem.
2
3
2
2
42
3
42
42
4242
aCl mol 1075.3
soln L 1
BaCl mol 0.025
L 150.0BaClamount
SOAg mol 1002.8
SOAg g 8.311
SOAg mol 1
SOAg g 50.2SOAg amount
Since the two reactants combine in a 1 mole to 1 mole stoichiometric ratio, BaCl2 is the limiting
reagent. Since there must be some Ag2SO4 present and because Ag2SO4 is so much more soluble
than either BaSO4 or AgCl, we assume that [Ag+] and [SO42–] are determined by the solubility of
Ag2SO4. They will have the same values as in a saturated solution of Ag2SO4.
[SO42–] = 0.015 M [Ag+] = 0.030 M
We use these values and the appropriate Ksp values to determine [Ba2+] and [Cl–].
M 100.6
030.0
108.1
][ClM 103.7
015.0
101.1
]Ba[ 9
10
9
10
2
Since BaCl2 is the limiting reagent, we can use its amount to determine the masses of
BaSO4 and AgCl.
AgCl g 07.1
AgCl mol 1
AgCl g 3.143
BaCl mol 1
AgCl mol 2
BaCl mol 0.00375AgCl mass
BaSO g 875.0
BaSO mol 1
BaSO g 4.233
BaCl mol 1
BaSO mol 1
BaCl mol 00375.0BaSO mass
2
2
4
4
4
2
4
24

Chapter 18: Solubility and Complex-Ion Equilibria
938
The mass of unreacted Ag2SO4 is determined from the initial amount and the amount that
reacts with BaCl2.
24 24
24 24 2
224
24 24
1 mol Ag SO 311.8 g Ag SO
mass Ag SO 0.00802 mol Ag SO 0.00375 mol BaCl 1 mol BaCl 1 mol Ag SO
mass Ag SO 1.33 g Ag SO unreacted
Of course, there is some Ag2SO4 dissolved in solution. We compute its mass.
24 24
24
24
24 24
0.0150 mol Ag SO 311.8 g Ag SO
mass dissolved Ag SO 0.150 L 0.702 g dissolved
1 L soln 1 mol Ag SO
mass Ag SO (s) 1.33 g 0.702 g 0.63 g Ag SO (s)
86. (M) To determine how much NaF must be added, determine what the solubility of BaF2 is
considering that the final concentration of F– must be 0.030 M.
Ksp = 1×10-6.
BaF2 (s) Ba2+ (aq) + 2F– (aq)
0 0
+
s +2s
s 2s → (0.030 M)
2
6. 4
sp 1 10 0.030 9.0 10 ; Therefore, 0.0011 MKss s
.
Since s is 0.0011 M, the F– contribution from BaF2 considering the common ion effect exerted
by NaF is 0.0022 M. Therefore, the total number of moles of NaF in a 1 L solution required is
therefore 0.0278 moles.
To determine how much BaF2 precipitates, we must first determine what the value of s is for a
saturated solution in absence of the common ion effect. That is,
2
6. 3
sp 1 10 2 4 ; Therefore, 0.0063 MKssss
.
Since in absence of the common ion effect from NaF the solubility of BaF2 is 0.0063 M, and
with NaF the solubility is 0.0011, the difference between the two (0.0063 – 0.0011 =
0.0052 M) has to be precipitated. The mass of the precipitate is therefore:
22
2
2
0.0052 mol BaF 175.3 g BaF
mass of BaF 0.91g
1L solution 1 mol BaF

Chapter 18: Solubility and Complex-Ion Equilibria
939
FEATURE PROBLEMS
87. (M) Ca SO
2+ 4
2
= in the saturated solution. Let us first determine the amount of H O
3+ in
the 100.0 mL diluted effluent.
++
32
H O aq + NaOH aq 2H O(l) + Na aq
+
+3
3
+
3
1 mmol H O8.25 mL base 0.0105 mmol NaOH
mmol H O =100.0 mL 10.00 mL sample 1 mL base 1 mmol NaOH
= 0.866 mmol H O aq
Now we determine Ca2+ in the original 25.00 mL sample, remembering that 2 3+
HO were
produced for each 2+
Ca .
2
+
3
2+ 3
1mmolCa
0.866mmol H O (aq) 2 mmolH O
Ca = = 0.0173 M
25.00 mL
2
2+ 2 4 6
sp 4 4
= Ca SO = 0.0173 = 3.0 10 ; the for CaSO is 9.1 10 in Appendix D.
sp
KK
88. (D)
(a) We assume that there is little of each ion present in solution at equilibrium (that this is a
simple stoichiometric calculation). This is true because the K value for the titration
reaction is very large. Ktitration = 1/Ksp(AgCl) = 5.6 ×109. We stop the titration when just
enough silver ion has been added.
+
Ag aq + Cl aq AgCl s
+
3
29.5 mg Cl 1 mmol Cl 1 mmol Ag 1mL
=100.0 mL 1000 mL 35.45 mg Cl 1 mmol Cl 0.01000 mmol AgNO
= 8.32 mL
V
(b) We first calculate the concentration of each ion as the consequence of dilution. Then we
determine the [Ag+] from the value of Ksp.
+ 4
8.32 mL added
initial Ag = 0.01000 M = 7.68 10 M
108.3mL final volume
4
1mmolCl
29.5 mg Cl 100.0 mL taken
35.45mgCl
initial Cl = = 7.68 10 M
1000 mL 108.3 mL final volume
The slight excess of each ion will precipitate until the solubility constant is satisfied.
Ag Cl M
sp
+105
= = 18 10 13 10
K..
(c) If we want Ag CrO
24
to appear just when AgCl has completed precipitation,
+5
Ag =1.3 10 M
. We determine CrO4
2 from the Ksp expression.

Chapter 18: Solubility and Complex-Ion Equilibria
940
12
2
5
2
2
+2 12 52 2
sp 444
1.1 10
1.3 10
= Ag CrO =1.1 10 = 1.3 10 CrO ; CrO = = 0.0065 MK
(d) If CrO4
2 were greater than the answer just computed for part (c), Ag CrO
24
would
appear before all Cl had precipitated, leading to a false early endpoint. We would
calculate a falsely low Cl for the original solution.
If CrO4
2 were less than computed in part 3, Ag CrO
24
would appear somewhat after
all Cl had precipitated, leading one to conclude there was more Cl in solution than
actually was the case.
(e) If it was Ag+that was being titrated, it would react immediately with the CrO4
2 in the
sample, forming a red-orange precipitate. This precipitate would not likely dissolve, and
thus, very little if any AgCl would form. There would be no visual indication of the
endpoint.
89. (D)
(a) We need to calculate the Mg2+ in a solution that is saturated with Mg(OH)2.
22
11 2+ 3
sp =1.8 10 = Mg OH = 2 = 4Ksss
11
342+
1.8 10
= 1.7 10 M = [Mg ]
4
s
(b) Even though water has been added to the original solution, it remains saturated (it is in
equilibrium with the undissolved solid
2
Mg OH ). 2+ 4
Mg =1.7 10 M.
(c) Although HCl(aq) reacts with OH ,
it will not react with 2+
Mg . The solution is simply
a more dilute solution of Mg2+.
2+ 4 5
100.0 mL initial volume
Mg =1.7 10 M = 2.8 10 M
100.0 +500. mL final volume
(d) In this instance, we have a dual dilution to a 275.0 mL total volume, followed by a
common-ion scenario.
42+ 2+
2+
1.7 10 mmol Mg 0.065 mmol Mg
25.00 mL 250.0 mL
1mL 1mL
initial Mg = 275.0 mL total volume
0.059M
42+
2+ 5
1.7 10 mmolMg 2 mmolOH
25.00 mL 1 mL 1 mmol Mg
initial OH = 3.1 10 M
275.0 mL total volume

Chapter 18: Solubility and Complex-Ion Equilibria
941
Let’s see if precipitation occurs.
QK
sp sp
Mg OH= = 0.059 3.1 10 = 5.7 10 1.8 10 =
2+ 25211 11
bg
ch
Thus, precipitation does occur, but very little precipitate forms. If OH goes down by
5
1.4 10 M
(which means that Mg2+ drops by 0.7 10 5
M), then
OH M
= 1.7 10 5 and
2+ 5
Mg = 0.059 M 0.7 10 M = 0.059 M
, then QK
sp sp
and precipitation will
stop. Thus, 2+
Mg = 0.059 M
.
(e) Again we have a dual dilution, now to a 200.0 mL final volume, followed by a common-
ion scenario.
42+
2+ 5
1.7 10 mmolMg
50.00 mL 1mL
initial Mg = 4.3 10 M
200.0 mL total volume
150.0 mLinitial volume
initial OH = 0.150 M 0.113 M
200.0 mL total volume
Now it is evident that precipitation will occur. Next we determine the Mg2+ that can
exist in solution with 0.113 M OH .
It is clear that Mg2+ will drop dramatically to
satisfy the Ksp expression but the larger value of OH will scarcely be affected.
22
2+ 11 2+
sp
11
2+ 9
2
= Mg OH =1.8 10 = Mg 0.0113 M
1.8 10
Mg = = 1.4 10 M
0.113
K

Chapter 18: Solubility and Complex-Ion Equilibria
942
SELF-ASSESSMENT EXERCISES
90. (E)
(a) Ksp: The solubility product constant, which is the constant for the equilibrium established
between a solid solute and its ions in a saturated solution
(b) Kf: The formation constant of a complex ion, which is the equilibrium constant describing
the formation of a complex ion from a central ion (typically a metal cation) and the ligands
that attach to it
(c) Qsp: The ion product, which is the product of concentrations of the constituent ions of a
compound, and is used to determine if they meet the precipitation criteria or not.
(d) Complex ion: A polyatomic cation or anion composed of a central metal ion to which other
groups (molecules or ions) called ligands are coordinated/attached to.
91. (E)
(a) Common-ion effect in solubility equilibrium: Where the solubility of a sparingly soluble
compound is suppressed by the presence of a quantity (often large) of one of the
compound’s ions from another source
(b) Fractional precipitation: A technique in which two or more ions in solution, each capable
of being precipitated by the same reagent, are separated by the proper use of that reagent:
One ion is precipitated, while the other(s) remains in solution.
(c) Ion-pair formation: Pair of ions held loosely together by electrostatic interactions in water
(d) Qualitative cation analysis: A qualitative method that is used to identify various the cations
present in a solution by stepwise addition of various anions in order to selectively
precipitate out various cations in steps.
92. (E)
(a) Solubility and solubility product constant: Solubility is the number of moles of a
precipitate dissolved in a certain mass of water (or some other solvent.) The solubility
product constant is the constant for the equilibrium established between a solid solute and
its ions in a saturated solution.
(b) Common–ion effect and salt effect: The common ion effect is a consequence of Le
Châtelier’s principle, where the equilibrium concentration of all ions resulting from the
dissolution of a sparingly soluble precipitate is reduced because a large amount of one (or
more) of the ions from another source is present. The salt effect is the presence of a large
quantity of ions from a very soluble salt which slightly increases the solubility of a
sparingly soluble precipitate.
(c) Ion pair and ion product: An ion pair comprises two oppositely charged ions held together
by electrostatic forces. The ion product (Qsp) is the product of concentrations of the
constituent ions of a compound, and is used to determine if they meet the precipitation
criteria or not.
Chapter 18: Solubility and Complex-Ion Equilibria
943
93. (E) The answer is (d). See the reasoning below.
(a) Wrong, because the stoichiometry is wrong
(b) Wrong, because Ksp = [Pb2+]·[I-]2
(c) Wrong, because [Pb2+] = Ksp/[ I-]2
(d) Correct because of the [Pb2+]:2[I-] stoichiometry
94. (E) The answer is (a).
22
44
BaSO s Ba SO
. If Na2SO4 is added, the common–ion effect
forces the equilibrium to the left and reduces [Ba2+].
95. (E) The answer is (c). Choices (b) and (d) reduce solubility because of the common–ion effect.
In the case of choice (c), the diverse non-common–ion effect or the “salt effect” causes more
Ag2CrO4 to dissolve.
96. (E) The answer is (b). The sulfate salt of Cu is soluble, whereas the Pb salt is insoluble.
97. (M) The answers are (c) and (d). Adding NH3 causes the solution to become basic (adding
OH–). Mg, Fe, Cu, and Al all have insoluble hydroxides. However, only Cu can form a
complex ion with NH3, which is soluble. In the case of (NH4)2SO4, it is slightly acidic and
dissolved readily in a base.
98. (M) The answer is (a). CaCO3 is slightly basic, so it is more soluble in an acid. The only
option for an acid given is NH4Cl.
99. (M) The answer is (c). Referring to Figure 18-7, it is seen that ammonia is added to an
aqueous H2S solution to precipitate more metal ions. Since ammonia is a base, increasing the
pH should cause more precipitation.
100. (M)
(a) H2C2O4 is a moderately strong acid, so it is more soluble in a basic solution.
(b) MgCO3 is slightly basic, so it is more soluble in an acidic solution.
(c) CdS is more soluble in acidic solutions, but the solubility is still so small that it is
essentially insoluble even in acidic solutions.
(d) KCl is a neutral salt, and therefore its solubility is independent of pH.
(e) NaNO3 is a neutral salt, and therefore its solubility is independent of pH.
(f) Ca(OH)2, a strong base, is more soluble in an acidic solution.
101. (E) The answer is NH3. NaOH(aq) precipitates both, and HCl(aq) precipitates neither.
Mg(OH)2 precipitates from an NH3(aq) solution but forms the soluble complex
Cu(NH3)4(OH)2.
102. (D) Al(OH)3 will precipitate. To demonstrate this, the pH of the acetate buffer needs to be
determined first, from which the OH– can be determined. The OH– concentration can be used
to calculate Qsp, which can then be compared to Ksp to see if any Al(OH)3 will precipitate. This
is shown below:
Chapter 18: Solubility and Complex-Ion Equilibria
944
5
a
14 pH 10
Ac 0.35 M
pH pK log log 1.8 10 log 4.65
HAc 0.45 M
[OH ] 10 4.467 10 M
3+
3
3
sp
3
10 29
sp
sp sp
Al OH Al +3OH
()(3)
0.275 4.467 10 2.45 10
, therefore there will be precipitation.
-
Qss
Q
QK
103. (E) The answer is (b). Based on solubility rules, Cu3(PO4)2 is the only species that is sparingly
soluble in water.
104. (M) The answer is (d). The abbreviated work shown for each part calculates the molar
solubility (s) for all the salts. They all follow the basic outlined below:
xy
xy
sp
M A xM + yA
Kxsys
and we solve for s.
(a) 2
2
MgF Mg 2F
823
3
3.7 10 s (2s) 4s
s2.110M
(c)
23
34 4
2
Mg PO 3Mg 2PO
32
25 5
6
1 10 3s 2s 108s
s3.910M
(b) 22
33
MgCO Mg CO
8
4
3.5 10 s s
s1.910M
(d) 3
34 4
Li PO 3Li PO
3
94
3
3.2 10 3s s 27s
s3.310M
105. (E) The answer is (b). This is due to the “salt effect.” The more moles of salt there are
available, the greater the solubility. For (b), there are 0.300 moles of ions (3×0.100 M Na2S2-
O3).
106. (E) It will decrease the amount of precipitate. Since all salts of NO3– are highly soluble and
Ag+ and Hg2+ salts of I– are not, anything that forms a soluble complex ion with Ag+ and Hg2+
will reduce the amount of those ions available for precipitation with I– and therefore will
reduce the amount of precipitate.
Chapter 18: Solubility and Complex-Ion Equilibria
945
107. (M) No precipitate will form. To demonstrate this, one has to calculate [Ag+], and then, using
[I–], determine the Qsp and compare it to Ksp of AgI.
Since Kf is for the formation of the complex ion Ag(CN)2¯, its inverse is for the dissociation of
Ag(CN)2¯ to Ag+ and CN¯.
18 19
dis f
1 1 5.6 10 1.786 10
KK
The dissociation of Ag(CN)2¯ is as follows:
+-
2
19
dis
Ag CN ¯(aq) Ag +2CN
(1.05 ) 1.786 10
(0.012 )
xx
Kx
We can simplify the calculations by noting that x is very small in relation to [Ag+] and [CN¯].
Therefore, x = 1.70×10-19 M.
Dissociation of AgI is as follows:
+-
19 19
sp
AgI Ag + I
1.7 10 2.0 3.4 10
Q
Since Qsp < Ksp, no precipitate will form.
108. (M) In both cases, the dissolution reaction is similar to reaction (18.5), for which K = Kf × Ksp.
This is an exceedingly small quantity for (a) but large for (b). CuCO3 is soluble in NH3(aq) and
CuS(s) is not.
109. (M) In this chapter, the concept of solubility of sparingly soluble precipitates is the overarching
concept. Deriving from this overall concept is the dissociation constant for the precipitate, Ksp
and molar solubility. Also emanating from the solubility concept are factors that affect
solubility: the common ion–effect, the salt effect, the effects of pH on solubility, and formation
of complex ions. Take a look at the subsection headings and problems for more refining of the
general and specific concepts.

946
CHAPTER 19
SPONTANEOUS CHANGE:
ENTROPY AND GIBBS ENERGY
PRACTICE EXAMPLES
1A (E) In general,
S
0 if ngas 0. This is because gases are very dispersed compared to
liquids or solids; (gases possess large entropies). Recall that
ngas is the difference
between the sum of the stoichiometric coefficients of the gaseous products and a similar
sum for the reactants.
(a) ngas =2+02+1
=1. One mole of gas is consumed here. We predict
S
0.
(b) ngas =1+ 0 0 = +1. Since one mole of gas is produced, we predict
S
0.
1B (E) (a) The outcome is uncertain in the reaction between ZnS(s) and Ag2Os
. We have
used ngas to estimate the sign of entropy change. There is no gas involved in this
reaction and thus our prediction is uncertain.
(b) In the chlor-alkali process the entropy increases because two moles of gas have
formed where none were originally present (
ngas
(1
1
0)(0 0) 2
2A (E) For a vaporization,
GHTS
vap vap vap
=0= . Thus,
SHT
vap vap vap
=/.
We substitute the given values. Svap
=Hvap
Tvap
=20.2 kJ mol1
29.79 + 273.15
K= 83.0 J mol1K1
2B (E) For a phase change,
GHTS
tr tr tr
= 0 = . Thus,
HTS
tr tr
= . We substitute in the
given values. Htr
=TStr
= 95.5 + 273.2
K1.09 J mol1K1= 402 J/mol
3A (M) The entropy change for the reaction is expressed in terms of the standard entropies of
the reagents.
32 2
11 11 11 11
=2 NH g N g 3 H g
= 2 192.5 J mol K 191.6 J mol K 3 130.7 J mol K = 198.7 J mol K
SS S S
Thus to form one mole of NH3g
, the standard entropy change is
99.4 11
J mol K
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
947
3B (M) The entropy change for the reaction is expressed in terms of the standard entropies of
the reagents.
So=SoNO g
+SoNO2g
SoN2O3g
11 11 11 23
11 23
138.5 J mol K = 210.8 J mol K + 240.1 J mol K N O g
= 450.9 J mol K N O g
S
S
11 11 1
23
N O g = 450.9 J mol K 138.5 J mol K = 312.4 J mol KS
4A (E) (a) Because ngas =21+3
=
2 for the synthesis of ammonia, we would predict
S
0 for the reaction. We already know that
H
0. Thus, the reaction falls into
case 2, namely, a reaction that is spontaneous at low temperatures and non-
spontaneous at high temperatures.
(b) For the formation of ethylene
ngas =1
2+0
=
1 and thus
S
0 . We are given
that
H
0 and, thus, this reaction corresponds to case 4, namely, a reaction that is
non-spontaneous at all temperatures.
4B (E) (a) Because ngas = +1 for the decomposition of calcium carbonate, we would predict
S
0 for the reaction, favoring the reaction at high temperatures. High
temperatures also favor this endothermic
Ho0
reaction.
(b) The “roasting” of ZnS(s) has
ngas = 2 3 = 1 and, thus,
S
0. We are given that
H
0 ; thus, this reaction corresponds to case 2, namely, a reaction that is
spontaneous at low temperatures, and non-spontaneous at high ones.
5A (E) The expression
G
H
T
S
= is used with
T
=298.15
K
.
Go=HoTSo=1648 kJ 298.15 K 549.3 J K1
1 kJ /1000 J
=1648 kJ +163.8 kJ = 1484 kJ
5B (M) We just need to substitute values from Appendix D into the supplied expression.
f2 f f2
1111
= 2 NO g 2 NO g O g
= 2 51.31 kJ mol 2 86.55 kJ mol 0.00 kJ mol = 70.48 kJ mol
GG G G
6A (M) Pressures of gases and molarities of solutes in aqueous solution appear in
thermodynamic equilibrium constant expressions. Pure solids and liquids (including
solvents) do not appear.
(a)
K=P
SiCl4
P
Cl2
2Kp (b) K=HOCl
H+
Cl
P
Cl2
p
=KK for (a) because all terms in the K expression are gas pressures.
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
948
6B (M) We need the balanced chemical equation in order to write the equilibrium constant
expression. We start by translating names into formulas.
PbS s
+HNO3aq
Pb NO3
2aq
+S s
+NO g
The equation then is balanced with the ion-electron method.
2+
+
32
oxidation : {PbS s Pb aq + S s + 2e } 3
reduction :{NO aq + 4H aq +3e NO g + 2H O(l) } 2
+2+
3 2
net ionic : 3 PbS s + 2NO aq +8H aq 3Pb aq + 3S s + 2NO g + 4H O(l)
In writing the thermodynamic equilibrium constant, recall that
neither pure solids (PbS(s) and S(s)) nor pure liquids
2
HO(l)
appear in the thermodynamic equilibrium constant expression. Note
also that we have written H+aq
here for brevity even though we
understand that H3O+aq
is the acidic species in aqueous solution.
K[Pb2]3pNO
2
[NO3
]2[H]8
7A (M) Since the reaction is taking place at 298.15 K, we can use standard free energies of
formation to calculate the standard free energy change for the reaction:
24 2
NO(g) 2NO(g)
f2 f24
= 2 NO g N O g 2 51.31 kJ/mol 97.89 kJ/mol 4.73kJGG G
Gorxn = +4.73 kJ . Thus, the forward reaction is non-spontaneous as written at 298.15 K.
7B (M) In order to answer this question we must calculate the reaction quotient and compare
it to the Kp value for the reaction:
2
24 2 p
(0.5)
N O (g) 2 NO (g) 0.5
0.5
0.5 bar 0.5 bar
Q
Gorxn = +4.73 kJ = RTlnKp; 4.73 kJ/mol = (8.3145 10 –3 kJ/Kmol)(298.15 K)lnKp
Therefore, Kp = 0.148. Since Qp is greater than Kp, we can conclude that the reverse
reaction will proceed spontaneously, i.e. NO2 will spontaneously convert into N2O4.
8A (D) We first determine the value of
G and then set =lnGRTK
to determine K.
+
fff
Ag aq + [I (aq)] AgI s
[(77.11 51.57) ( 66.19)] kJ/mol 91.73
GG G G
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
949
11
37.00 17
91.73 kJ / mol 1000 J
ln 37.00
1kJ
8.3145 J mol K 298.15 K
e8.510
G
KRT
K
This is precisely equal to the value for the Ksp of AgI listed in Appendix D.
8B (D) We begin by translating names into formulas.
MnO2s
+HCl aq
Mn2+ aq
+Cl2aq
Then we produce a balanced net ionic
equation with the ion-electron method.
2
+2+
22
oxidation : 2 Cl aq Cl g + 2e
reduction : MnO s + 4H aq + 2e Mn aq + 2H O(l)
+2+
222
net ionic: MnO s + 4H aq + 2Cl aq Mn aq + Cl g + 2H O(l)
Next we determine the value of
G for the reaction and then the value of K.
2+
ff2f2
+
f2 f f
=Mnaq+Clg+2HOl
MnO s 4 H aq 2 Cl aq
= 228.1 kJ + 0.0 kJ + 2 237.1 kJ
465.1 kJ 4 0.0 kJ 2 131.2 kJ = +25.2 kJ
GG G G
GGG
31 10.2 5
-1 1
( 25.2 10 J mol )
ln 10.17 e 4 10
8.3145 J mol K 298.15
G
KK
RT K
Because the value of K is so much smaller than unity, we do not expect an appreciable
forward reaction.
9A (M) We set equal the two expressions for
G and solve for the absolute temperature.
= = ln = ln = lnG H TS RT K H TS RT K T S R K
o3
o11
114.1 10 J/mol
= = = 607 K
ln 146.4 8.3145 ln 150 J mol K
H
TSRK
9B (D) We expect the value of the equilibrium constant to increase as the temperature
decreases since this is an exothermic reaction and exothermic reactions will have a larger
equilibrium constant (shift right to form more products), as the temperature decreases.
Thus, we expect K to be larger than 1000, which is its value at 4.3 102
K.
(a) The value of the equilibrium constant at 25C is obtained directly from the value of
G
o, since that value is also for 25C. Note:
oo o
= = 77.1 kJ/mol 298.15 K 0.1213 kJ/mol K = 40.9 kJ/molGHTS
31 +16.5 7
11
( 40.9 10 J mol )
ln 16.5 e 1.5 10
8.3145 J mol K 298.15 K
G
KK
RT
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
950
(b) First, we solve for
G
o at 75 = 348
C K
oo o
3
kJ 1000 J J
= = 77.1 348.15 K 121.3
mol 1 kJ mol K
= 34.87 10 J/mol
GHTS
Then we use this value to obtain the value of the equilibrium constant, as in part (a).
31 +12.05 5
-1 1
( 34.87 10 J mol )
ln 12.05 e 1.7 10
8.3145 J mol K 348.15 K
G
KK
RT
As expected, K for this exothermic reaction decreases with increasing temperature.
10A (M) We use the value of Kp=9.1 10
2
at 800 K and HoJ/mol=1.810
5, for the
appropriate terms, in the van't Hoff equation.
25
211 5
5.8 10 1.8 10 J/mol 1 1 1 1 9.66 8.3145
ln = = 9.66; =
9.1 10 8.3145 J mol K 800 K K 800 1.8 10TT
34 4
1/ =1.25 10 4.5 10 = 8.0 10 =1240 K 970 CTT
This temperature is an estimate because it is an extrapolated point beyond the range of the
data supplied.
10B (M) The temperature we are considering is 235 = 508
C K. We substitute the value of
Kp=9.1 10
2
at 800 K and
H
o=1.810
5 J/mol, for the appropriate terms, in the van't
Hoff equation.
6
5
p p +15. 6
.6
211 2
1.8 10 J/mol 1 1
ln = =+15 ; =e =6 10
9.1 10 8.3145 J mol K 800 K 508 K 9.1 10
KK
629
p= 6 10 9.1 10 = 5 10K
INTEGRATIVE EXAMPLE
11A (D) The value of
G
ocan be calculated by finding the value of the equilibrium constant Kp
at 25 oC. The equilibrium constant for the reaction is simply given by Kpp{N2O5(g)} .
The vapor pressure of N2O5(g) can be determined from the Clausius-Clapeyron eqution,
which is a specialized version of the van’t Hoff equation.
Stepwise approach:
We first determine the value of
Hsub .
ln p2
p1
Hsub
R
1
T1
1
T2
ln 760 mmHg
100 mmHg Hsub
8.314Jmol-1K-1
1
7.5 273.15 1
32.4 273.15
Hsub 2.028
3.49 1055.81104J/mol
Using the same formula, we can now calculate the vapor pressure of N2O5 at 25 oC.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
951
ln p3
100 mmHg 5.81104J/mol
8.314Jmol-1K-1
1
280.7 1
298.2
1.46 p3
100 mmHg e1.46 4.31
p34.31100mmHg 1 atm
760 mmHg 0.567atm Kp
GoRT ln Kp(8.314 103kJmol-1K-1 298.15K)ln(0.567) 1.42kJ/mol
Conversion pathway approach:
ln p2
p1
Hsub
R
1
T1
1
T2
Hsub
Rln p2
p1
1
T1
1
T2
Hsub
8.314Jmol-1K-1 ln 760mmHg
100mmHg
1
7.5 273.15 1
32.4 273.15
2.028
3.49 105Jmol-1 5.81104Jmol-1
ln p3
p1
Hsub
R
1
T1
1
T2
p3p1e
Hsub
R
1
T1
1
T2
p3100mmHg e
5.81104Jmol-1
8.314JK-1mol-1
1
280.7 1
298.2
K-1
431mmHg 1atm
760mmHg 0.567atm Kp
GoRT ln Kp(8.314 103kJmol-1K-1 298.15K)ln(0.567) 1.42kJ/mol
11B (D) The standard entropy change for the reaction (
S
o) can be calculated from the known
values of
H
oand Go.
Stepwise approach:
GoHoTSoSoHoGo
T454.8kJmol-1 (323.1kJmol-1 )
298.15K 441.7JK-1mol-1
Plausible chemical reaction for the production of ethylene glycol can also be written as:
2C(s)+3H2(g)+O2(g) CH2OHCH2OH(l)
Since So{Sproducts
o}{Sreac tan ts
o}
it follows that:
Srxn
oSo(CH2OHCH2OH(l)) [2 So(C(s)) 3So(H2(g)) So(O2(g))]
441.7JK-1mol-1 So(CH2OHCH2OH(l)) [2 5.74JK-1mol-1 3130.7JK-1mol-1 205.1JK-1mol-1 ]
So(CH2OHCH2OH(l)) 441.7JK-1mol-1 608.68JK-1mol-1 167JK-1mol-1

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
952
Conversion pathway approach:
GoHoTSoSoHoGo
T454.8kJmol-1 (323.1kJmol-1 )
298.15K 441.7JK-1mol-1
441.7JK-1mol-1 So(CH2OHCH2OH(l)) [2 5.74JK-1mol-1 3130.7JK-1mol-1 205.1JK-1mol-1 ]
So(CH2OHCH2OH(l)) 441.7JK-1mol-1 608.68JK-1mol-1 167JK-1mol-1
EXERCISES
Spontaneous Change and Entropy
1. (E) (a) The freezing of ethanol involves a decrease in the entropy of the system. There is
a reduction in mobility and in the number of forms in which their energy can be
stored when they leave the solution and arrange themselves into a crystalline state.
(b) The sublimation of dry ice involves converting a solid that has little mobility into a
highly dispersed vapor which has a number of ways in which energy can be stored
(rotational, translational). Thus, the entropy of the system increases substantially.
(c) The burning of rocket fuel involves converting a liquid fuel into the highly dispersed
mixture of the gaseous combustion products. The entropy of the system increases
substantially.
2. (E) Although there is a substantial change in entropy involved in (a) changing HO
2(1iq., 1
atm) to HO
2(g, 1 atm), it is not as large as (c) converting the liquid to a gas at 10 mmHg.
The gas is more dispersed, (less ordered), at lower pressures. In (b), if we start with a solid
and convert it to a gas at the lower pressure, the entropy change should be even larger,
since a solid is more ordered (concentrated) than a liquid. Thus, in order of increasing
S
,
the processes are: (a) (c) (b).
3. (E) The first law of thermodynamics states that energy is neither created nor destroyed (thus,
“The energy of the universe is constant”). A consequence of the second law of
thermodynamics is that entropy of the universe increases for all spontaneous, that is, naturally
occurring, processes (and therefore, “the entropy of the universe increases toward a
maximum”).
4. (E) When pollutants are produced they are usually dispersed throughout the environment.
These pollutants thus start in a relatively compact form and end up dispersed throughout a
large volume mixed with many other substances. The pollutants are highly dispersed, thus,
they have a high entropy. Returning them to their original compact form requires reducing
this entropy, which is a highly non-spontaneous process. If we have had enough foresight to
retain these pollutants in a reasonably compact form, such as disposing of them in a secure
landfill, rather than dispersing them in the atmosphere or in rivers and seas, the task of
permanently removing them from the environment, and perhaps even converting them to
useful forms, would be considerably easier.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
953
5. (E) (a) Increase in entropy because a gas has been created from a liquid, a condensed
phase.
(b) Decrease in entropy as a condensed phase, a solid, is created from a solid and a gas.
(c) For this reaction we cannot be certain of the entropy change. Even though the number
of moles of gas produced is the same as the number that reacted, we cannot conclude
that the entropy change is zero because not all gases have the same molar entropy.
(d) 2H2Sg
+3O
2g
2H2Og
+2SO2g
Decrease in entropy since five moles of
gas with high entropy become only four moles of gas, with about the same quantity
of entropy per mole.
6. (E) (a) At 75C , 1 mol HO
2 (g, 1 atm) has a greater entropy than 1 mol H O
2 (1iq., 1
atm) since a gas is much more dispersed than a liquid.
(b) 1mol Fe
50.0 g Fe = 0.896
55.8 g Fe
mol Fe has a higher entropy than 0.80 mol Fe, both (s)
at 1 atm and 5C, because entropy is an extensive property that depends on the
amount of substance present.
(c) 1 mol Br2(1iq., 1 atm, 8C ) has a higher entropy than 1 mol Br2(s, 1atm, 8C)
because solids are more ordered (concentrated) substances than are liquids, and
furthermore, the liquid is at a higher temperature.
(d) 0.312 mol SO2 (g, 0.110 atm, 32.5C ) has a higher entropy than 0.284 mol O2 (g,
15.0 atm, 22.3C ) for at least three reasons. First, entropy is an extensive property
that depends on the amount of substance present (more moles of SO2 than O2). Second,
entropy increases with temperature (temperature of SO2 is greater than that for O2.
Third, entropy is greater at lower pressures (the O2 has a much higher pressure).
Furthermore, entropy generally is higher per mole for more complicated molecules.
7. (E) (a) Negative; A liquid (moderate entropy) combines with a solid to form another
solid.
(b) Positive; One mole of high entropy gas forms where no gas was present before.
(c) Positive; One mole of high entropy gas forms where no gas was present before.
(d) Uncertain; The number of moles of gaseous products is the same as the number of
moles of gaseous reactants.
(e) Negative; Two moles of gas (and a solid) combine to form just one mole of gas.
8. (M)
The entropy of formation of a compound would be the difference between the absolute
entropy of one mole of the compound and the sum of the absolute entropies of the
appropriate amounts of the elements constituting the compound, with each species in its
most stable form.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
954
Stepwise approach:
It seems as though CS21
would have the highest molar entropy of formation of the
compounds listed, since it is the only substance whose formation does not involve the
consumption of high entropy gaseous reactants. This prediction can be checked by
determining Sf
ovalues from the data in Appendix D:
(a)
24
C graphite + 2H g CH g
Sf
oCH4g
=SoCH4g
SoC graphite
2SoH2g
= 186.3 J mol1K15.74 J mol1K12130.7 J mol1K1
=80.8 J mol1K1
(b)
1
22 32
2
2C graphite + 3H g + O g CH CH OH l
oo ooo
32 32 2 2
f
11 11 11 11
1
2
11
1
CH CH OH l = CH CH OH l 2 C graphite 3 H g O g
2
=160.7J mol K 2 5.74 J mol K 3 130.7 J mol K 205.1J mol K
= 345.4 J mol K
SS SSS
(c)
2
C graphite + 2S rhombic CS l
oo o
f2 2
11 11 11
11
CS l = CS l C graphite 2 S rhombic
= 151.3 J mol K 5.74 J mol K 2 31.80 J mol K
= 82.0 J mol K
SSS S
Conversion pathway approach:
CS2 would have the highest molar entropy of formation of the compounds listed, because
it is the only substance whose formation does not involve the consumption of high
entropy gaseous reactants.
(a)
24
C graphite + 2H g CH g
Sf
oCH4g
= 186.3 J mol1K15.74 J mol1K12130.7 J mol1K1
80.8 J mol1K1
(b)
1
22 32
2
2C graphite + 3H g + O g CH CH OH l
Sf
oCH3CH2OH l
= (160.725.74 3130.71
2205.1)J mol1K1
=345.4 J mol1K1
(c)
2
C graphite + 2S rhombic CS l
Sf
CS2l
= 151.3 J mol1 K15.74 J mol1K1231.80 J mol1K1
= 82.0 J mol1K1

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
955
Phase Transitions
9. (M) (a) vap f 2 f 2
[H O(g)] [H O(l)] 241.8 kJ/mol ( 285.8kJ/mol)
44.0 kJ/mol
HH H
oo 1111
vap 2 2
11
= H O g H O l = 188.8 J mol K 69.91 J mol K
=118.9 J mol K
SS S
There is an alternate, but incorrect, method of obtaining
Svap .
3
vap 11
vap
44.0 10 J/mol
= = =148 J mol K
298.15K
H
ST
This method is invalid because the temperature in the denominator of the equation
must be the temperature at which the liquid-vapor transition is at equilibrium. Liquid
water and water vapor at 1 atm pressure (standard state, indicated by) are in
equilibrium only at 100 = 373
C K.
(b) The reason why
Hvap is different at 25C from its value at 100 C has to do with
the heat required to bring the reactants and products down to 298 K from 373 K. The
specific heat of liquid water is higher than the heat capacity of steam. Thus, more
heat is given off by lowering the temperature of the liquid water from 100C to
25 C than is given off by lowering the temperature of the same amount of steam.
Another way to think of this is that hydrogen bonding is more disrupted in water at
100C than at 25C (because the molecules are in rapid—thermal—motion), and
hence, there is not as much energy needed to convert liquid to vapor (thus vap
H
has
a smaller value at 100 C. The reason why
Svap has a larger value at 25 C than at
100 C has to do with dispersion. A vapor at 1 atm pressure (the case at both
temperatures) has about the same entropy. On the other hand, liquid water is more
disordered (better able to disperse energy) at higher temperatures since more of the
hydrogen bonds are disrupted by thermal motion. (The hydrogen bonds are totally
disrupted in the two vapors).
10. (M) In this problem we are given standard enthalpies of the formation (Hf
o) of liquid
and gas pentane at 298.15 K and asked to estimate the normal boiling point of
pentane, Gvap
o and furthermore comment on the significance of the sign of Gvap
o.
The general strategy in solving this problem is to first determine Hvap
ofrom the
known enthalpies of formation. Trouton’s rule can then be used to determine the
normal boiling point of pentane. Lastly, Gvap,298K
o can be calculated using
GHTS
vap vap vap
=.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
956
Stepwise approach:
Calculate Hvap
o from the known values of Hf
o (part a):
C
5H12(l)
C5H12(g)
Hf
o -173.5 kJmol-1 -146.9 kJmol-1
Hvap
o146.9 (173.5)kJmol-1 26.6kJmol-1
Determine normal boiling point using Trouton’s rule (part a):
Svap
oHvap
o
Tnbp
87Jmol-1K-1
Tnbp Hvap
o
Svap
o26.6kJmol1
87kJK 1mol1
1000
306K
Tnbp 32.9oC
Use
GHTS
vap vap vap
=to calculate Gvap,298K
(part b):
GHTS
vap vap vap
=
Gvap,298K
26.6kJmol-1 298.15K87kJmol-1K-1
1000
Gvap,298K
0.66kJmol-1
Comment on the value of Gvap,298K
(part c):
The positive value of
Gvap indicates that normal boiling (having a vapor pressure
of 1.00 atm) for pentane should be non-spontaneous (will not occur) at 298. The
vapor pressure of pentane at 298 K should be less than 1.00 atm.
Conversion pathway approach:
C
5H12(l)
C5H12(g)
Hf
o -173.5 kJmol-1 -146.9 kJmol-1
Hvap
o146.9 (173.5)kJmol-1 26.6kJmol-1
Svap
oHvap
o
Tnbp
87Jmol-1K-1 Tnbp Hvap
o
Svap
o26.6kJmol-1
87kJK-1mol-1
1000
306K
Gvap
=Hvap
TSvap
26.6kJmol-1 298.15K87kJmol-1K-1
1000 0.66kJmol-1
11. (M) Trouton's rule is obeyed most closely by liquids that do not have a high degree of
order within the liquid. In both HF and CH OH
3, hydrogen bonds create considerable order
within the liquid. In C H CH
65 3
, the only attractive forces are non-directional London
forces, which have no preferred orientation as hydrogen bonds do. Thus, of the three
choices, liquid C H CH
65 3
would most closely follow Trouton’s rule.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
957
12. (E) vap f 2 f 2
[Br (g)] [Br (l)] 30.91 kJ/mol 0.00 kJ/mol = 30.91 kJ/molHH H
3
vap vap
11 2
vap vap 11
vap vap
30.91 10 J/mol
= 87 J mol K or = = 3.5 10 K
87J mol K
HH
ST
TS
The accepted value of the boiling point of bromine is 2
58.8 C = 332 K = 3.32 10 K
.
Thus, our estimate is in reasonable agreement with the measured value.
13. (M) The liquid water-gaseous water equilibrium 22
H O (l, 0.50 atm) H O (g, 0.50 atm)
can only be established at one temperature, namely the boiling point for water under 0.50
atm external pressure. We can estimate the boiling point for water under 0.50 atm external
pressure by using the Clausius-Clapeyron equation:
ln 2
1
P
P= vap
o
H
R
12
11
TT
We know that at 373 K, the pressure of water vapor is 1.00 atm. Let's make P1 = 1.00
atm, P2 = 0.50 atm and T1 = 373 K. Thus, the boiling point under 0.50 atm pressure is T2.
To find T2 we simply insert the appropriate information into the Clausius-Clapeyron
equation and solve for T2:
ln 0.50 atm
1.00 atm = 1
311
40.7 kJ mol
8.3145 10 kJ K mol
2
11
373 K T
-1.416 104 K =
2
11
373 K T
Solving for T2 we find a temperature of 354 K or 81C. Consequently, to achieve an
equilibrium between gaseous and liquid water under 0.50 atm pressure, the temperature
must be set at 354 K.
14. (M) Figure 12-19 (phase diagram for carbon dioxide) shows that at 60C and under 1
atm of external pressure, carbon dioxide exists as a gas. In other words, neither solid nor
liquid CO2 can exist at this temperature and pressure. Clearly, of the three phases,
gaseous CO2 must be the most stable and, hence, have the lowest free energy when T =
60 C and Pext = 1.00 atm.
Gibbs Energy and Spontaneous Change
15. (E) Answer (b) is correct. Br—Br bonds are broken in this reaction, meaning that it is
endothermic, with
H
0. Since the number of moles of gas increases during the
reaction,
S
0 . And, because
GHTS= , this reaction is non-spontaneous
(G0) at low temperatures where the
H
term predominates and spontaneous
(
G
0) at high temperatures where the TS
term predominates.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
958
16. (E) Answer (d) is correct. A reaction that proceeds only through electrolysis is a reaction
that is non-spontaneous. Such a reaction has
G
0.
17. (E) (a)
H
o0 and
S
o0 (since
ngas
0) for this reaction. Thus, this reaction is case
2 of Table 19-1. It is spontaneous at low temperatures and non-spontaneous at high
temperatures.
(b) We are unable to predict the sign of
S
o for this reaction, sincengas = 0 . Thus, no
strong prediction as to the temperature behavior of this reaction can be made. Since
Ho > 0, we can, however, conclude that the reaction will be non-spontaneous at low
temperatures.
(c)
H
o0 and
S
o0 (since gas 0n
) for this reaction. This is case 3 of Table 19-1.
It is non-spontaneous at low temperatures, but spontaneous at high temperatures.
18. (E) (a)
H
o0 and
S
o0 (since
ngas
0) for this reaction. This is case 4 of Table
19-1. It is non-spontaneous at all temperatures.
(b)
H
o0 and
S
o0 (since
ngas 0) for this reaction. This is case 1 of Table 19-1.
It is spontaneous at all temperatures.
(c)
H
o0 and
S
o0 (since
ngas
0) for this reaction. This is case 2 of Table 19-1.
It is spontaneous at low temperatures and non-spontaneous at high temperatures.
19. (E) First of all, the process is clearly spontaneous, and therefore
G
0. In addition, the
gases are more dispersed when they are at a lower pressure and therefore
S
0. We also
conclude that
H
= 0 because the gases are ideal and thus there are no forces of attraction
or repulsion between them.
20. (E) Because an ideal solution forms spontaneously,
G
0. Also, the molecules of solvent
and solute that are mixed together in the solution are in a more dispersed state than the
separated solvent and solute. Therefore,
S
0 . However, in an ideal solution, the
attractive forces between solvent and solute molecules equal those forces between solvent
molecules and those between solute molecules. Thus,
H
= 0 . There is no net energy of
interaction.
21. (M) (a) An exothermic reaction (one that gives off heat) may not occur spontaneously if,
at the same time, the system becomes more ordered (concentrated) that is,
S
o
0.
This is particularly true at a high temperature, where the
T
S
term dominates the
G
expression. An example of such a process is freezing water (clearly exothermic
because the reverse process, melting ice, is endothermic), which is not spontaneous
at temperatures above0 C.
(b) A reaction in which
S
0 need not be spontaneous if that process also is
endothermic. This is particularly true at low temperatures, where the
H
term
dominates the
G
expression. An example is the vaporization of water (clearly an
endothermic process, one that requires heat, and one that produces a gas, so
S
0),

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
959
which is not spontaneous at low temperatures, that is, below100 C (assuming Pext =
1.00 atm).
22. (M) In this problem we are asked to explain whether the reaction AB(g)A(g)+B(g) is
always going to be spontaneous at high rather than low temperatures. In order to answer
this question, we need to determine the signs of
H
,
S
and consequently
G
. Recall
that
G
H
T
S
.
Stepwise approach:
Determine the sign of
S:
We are generating two moles of gas from one mole. The randomness of the system
increases and
Smust be greater than zero.
Determine the sign of
H:
In this reaction, we are breaking A-B bond. Bond breaking requires energy, so the reaction
must be endothermic. Therefore, His also greater than zero.
Use
G
H
T
S
to determine the sign of
G
:
G
H
T
S
. Since His positive and Sis positive there will be a temperature at
which
T
S
will become greater than
H
. The reaction will be favored at high
temperatures and disfavored at low temperatures.
Conversion pathway approach:
Sfor the reaction is greater than zero because we are generating two moles of gas from
one mole. Hfor the reaction is also greater than zero because we are breaking A-B
(bond breaking requires energy). Because
G
H
T
S
, there will be a temperature at
which
T
S
will become greater than
H
. The reaction will be favored at high
temperatures and disfavored at low temperatures.
Standard Gibbs Energy Change
23.
(M) Ho=Hf
NH4Cl s
Hf
NH3g
Hf
HCl g
314.4kJ/mol (46.11 kJ/mol 92.31 kJ/mol) 176.0 kJ/mol
GoGf
NH4Cl s
Gf
NH3g
Gf
HCl g
202.9kJ/mol (16.48 kJ/mol 95.30 kJ/mol) 91.1 kJ/mol
GoHoTSo
SoHoGo
T176.0kJ/mol 91.1 kJ/mol
298 K 1000 J
1kJ 285 J mol1
24. (M) (a)
o
f26 f22 f 2
=CHg CHg2Hg
= 32.82 kJ/mol 209.2 kJ/mol 2 0.00 kJ/mol = 242.0 kJ/mol
GG G G
(b) Go=2Gf
SO2g
+Gf
O2g
2Gf
SO3g
=2 300.2 kJ/mol
+0.00kJ/mol2371.1 kJ/mol
= +141.8 kJ/mol

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
960
(c)
o
ff2f34f2
=3Fes+4HOg FeOs4Hg
= 3 0.00 kJ/mol + 4 228.6 kJ/mol 1015 kJ/mol 4 0.00 kJ/mol = 101 kJ/mol
GG G G G
(d)
o3+ +
ff2ff
=2 Al aq +3 H g 2 Al s 6 H aq
= 2 485 kJ/mol + 3 0.00 kJ/mol 2 0.00kJ/mol 6 0.00 kJ/mol = 970. kJ/mol
GG G G G
25. (M) (a)
oo o o
332
=2 POCl 1 2 PCl g O g
= 2 222.4 J/K 2 311.7 J/K 205.1 J/K = 383.7 J/K
SS S S
oo o 3 3
= = 620.2 10 J 298 K 383.7 J/K = 506 10 J = 506 kJGHTS
(b) The reaction proceeds spontaneously in the forward direction when reactants and
products are in their standard states, because the value of
G
o is less than zero.
26. (M) (a)
oo o o+ o o
22 2
= Brl+2 HNOaq 2 Haq 2 Braq 2 NOg
= 152.2 J/K + 2 135.6 J/K 2 0 J/K 2 82.4 J/K 2 240.1 J/K = 221.6 J/K
SS S S S S
oo o 3 3
= = 61.6 10 J 298K 221.6 J/K = +4.4 10 J = +4.4kJGHTS
(b) The reaction does not proceed spontaneously in the forward direction when reactants and
products are in their standard states, because the value of
G
o is greater than zero.
27. (M) We combine the reactions in the same way as for any Hess's law calculations.
(a) N2Og
N2g
+1
2O2g
Go=1
2+208.4kJ
=104.2kJ
N2g
+2O2g
2NO2g
Go= +102.6kJ
Net: N2Og
+3
2O2g
2NO2g
Go=104.2 +102.6 = 1.6 kJ
This reaction reaches an equilibrium condition, with significant amounts of all
species being present. This conclusion is based on the relatively small absolute
value of
G
o.
(b) 2N2g
+6H2g
4NH3g
Go=2 33.0 kJ
=66.0 kJ
4NH3g
+5O2g
4NO g
+6H2Ol
Go=1010.5 kJ
4NO g
2N2g
+2O2g
Go=2 +173.1 kJ
=346.2 kJ
Net: 6H2g
+3O2g
6H2Ol
Go=66.0kJ 1010.5kJ 346.2kJ = 1422.7kJ
This reaction is three times the desired reaction, which therefore has
o= 1422.7 kJ 3 = 474.3G kJ.
The large negative
G
o value indicates that this reaction will go to completion at 25C.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
961
(c) 4NH3g
+5O2g
4NO g
+6H2Ol
Go=1010.5 kJ
4NO g
2N2g
+2O2g
Go=2 +173.1 kJ
=346.2 kJ
o
22 2
2N g + O g 2N O g = +208.4 kJG
o
32 2 2
4NH g + 4O g 2N O g + 6H O l = 1010.5kJ 346.2kJ + 208.4kJ
= 1148.3kJ
G
This reaction is twice the desired reaction, which, therefore, has
G
o= -574.2 kJ.
The very large negative value of the
G
o for this reaction indicates that it will go to
completion.
28. (M) We combine the reactions in the same way as for any Hess's law calculations.
(a) COS g
+2CO2g
SO2g
+3CO g
Go=246.4 kJ
= +246.6 kJ
2CO g
+2H2Og
2CO2g
+2H2g
Go=2 28.6 kJ
=57.2 kJ
COS g
+2H2Og
SO2g
+CO g
+2H2g
Go= +246.6 57.2 = +189.4 kJ
This reaction is spontaneous in the reverse direction, because of the large positive
value of
G
o
(b) COS g
+2CO2g
SO2g
+3CO g
Go=246.4 kJ
= +246.6 kJ
3CO g
+3H2Og
3CO2g
+3H2g
Go=3 28.6 kJ
=85.8 kJ
COS g
+3H2Og
CO2g
+SO2g
+3H2g
Go= +246.6 85.8 = +160.8 kJ
This reaction is spontaneous in the reverse direction, because of the large positive value
of
G
o.
(c)
o
22
COS g +H g CO g +H S g = +1.4 kJG
o
222
CO g + H O g CO g + H g = 28.6 kJ = 28.6 kJG
COS g
+H2Og
CO2g
+H2Sg
Go=1.4 kJ 28.6 kJ = 30.0 kJ
The negative value of the
G
o for this reaction indicates that it is spontaneous in the
forward direction.
29. (D) The combustion reaction is :C6H6l
+15
2O2g
6CO2g
+3H2Og or l
(a)
o15
f2 f2 f66 f2
2
15
2
=6 CO g +3 HO l CH l O g
= 6 394.4 kJ +3 237.1 kJ +124.5 kJ 0.00 kJ = 3202 kJ
GG G G G
(b)
o15
f2 f2 f66 f2
2
15
2
=6 CO g +3 HO g CH l O g
= 6 394.4 kJ +3 228.6 kJ +124.5 kJ 0.00 kJ = 3177 kJ
GG G G G

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
962
We could determine the difference between the two values of
G
o by noting the
difference between the two products: 3H2Ol
3H2Og
and determining the
value of
G
o for this difference:
o
f2 f2
= 3 H O g 3 H O l = 3 228.6 237.1 kJ = 25.5 kJGG G
30. (M) We wish to find the value of the
H
o for the given reaction: F2g
2F(g)
oo o 1 1 1
2
= 2 F g F g = 2 158.8 J K 202.8 J K = +114.8 J KSS S
oo o 3
= + = 123.9 10 J + 298 K 114.8 J/K = 158.1 kJ/mole of bondsHGTS
The value in Table 10.3 is 159 kJ/mol, which is in quite good agreement with the value
found here.
31. (M) (a)
S
rxn = Sproducts - Sreactants
= [1 mol 301.2 J K1mol1 + 2 mol 188.8 J K1mol1] [2 mol 247.4 J K1mol1
+ 1 mol 238.5 J K1mol1] = 54.5 J K1
S
rxn = = 0.0545 kJ K1
(b)
H
rxn= bonds broken in reactants (kJ/mol)) –bonds broken in products(kJ/ mol))
= [4 mol (389 kJ mol1)N-H + 4 mol (222 kJ mol1)O-F]
[4 mol (301 kJ mol1)N-F + 4 mol (464 kJ mol1)O-H]
H
rxn= 616 kJ
(c)
G
rxn =
H
rxn T
S
rxn = 616 kJ 298 K(0.0545 kJ K1) = 600 kJ
Since the
G
rxn is negative, the reaction is spontaneous, and hence feasible
(at 25 C ). Because both the entropy and enthalpy changes are negative, this
reaction will be more highly favored at low temperatures (i.e., the reaction is
enthalpy driven)
32. (D) In this problem we are asked to find G at 298 K for the decomposition of
ammonium nitrate to yield dinitrogen oxide gas and liquid water. Furthermore, we are
asked to determine whether the decomposition will be favored at temperatures above or
below 298 K. In order to answer these questions, we first need the balanced chemical
equation for the process. From the data in Appendix D, we can determine Hrxn and
Srxn. Both quantities will be required to determine Grxn (Grxn=Hrxn-TSrxn).
Finally the magnitude of Grxn as a function of temperature can be judged depending on
the values of Hrxn and Srxn.
Stepwise approach:
First we need the balanced chemical equation for the process:
NH4NO3(s)
N2O(g) + 2H2O(l)
Now we can determine Hrxn by utilizing Hf
ovalues provided in Appendix D:
NH4NO3(s)
N2O(g) + 2H2O(l)
Hf
o -365.6 kJmol-1 82.05 kJmol-1 -285.6 kJmol-1
Hrxn=Hfproducts Hfreactants
Hrxn=[2 mol(285.8 kJ mol1) + 1 mol(82.05 kJ mol1)] [1 mol (365.6 kJ
mol
1)]
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
963
Hrxn= 124.0 kJ
Similarly, Srxn can be calculated utilizing S values provided in Appendix D
NH4NO3(s)
N2O(g) + 2H2O(l)
So 15.1 Jmol-1K-1 219.9 Jmol-1K-1 69.91 Jmol-1K-1
Srxn=Sproducts Sreactants
Srxn=[2 mol 69.91 J K1mol1 + 1 mol 219.9 J K1mol1 ] [1 mol 151.1 J
K1mol1]
Srxn=208.6 J K1 = 0.2086 kJ K1
To find Grxn we can either utilize Gf values provided in Appendix D or Grxn=Hrxn-
TSrxn:
Grxn=Hrxn-TSrxn=-124.0 kJ – 298.15 K0.2086 kJK-1
Grxn=-186.1 kJ
Magnitude of Grxn as a function of temperature can be judged depending on the values of
Hrxn and Srxn:
Since Hrxn is negative and Srxn is positive, the decomposition of ammonium nitrate is
spontaneous at all temperatures. However, as the temperature increases, the TS term gets
larger and as a result, the decomposition reaction shift towards producing more products.
Consequently, we can say that the reaction is more highly favored above 298 K (it will also
be faster at higher temperatures)
Conversion pathway approach:
From the balanced chemical equation for the process
NH4NO3(s)
N2O(g) + 2H2O(l)
we can determine Hrxn and Srxn by utilizing Hf
o and S values provided in Appendix
D:
Hrxn=[2 mol(285.8 kJ mol1) + 1 mol(82.05 kJ mol1)] [1 mol (365.6 kJ mol1)]
Hrxn= 124.0 kJ
Srxn=[2 mol 69.91 J K1mol1 + 1 mol 219.9 J K1mol1 ] [1 mol 151.1 J
K1mol1]
Srxn=208.6 J K1 = 0.2086 kJ K1
Grxn=Hrxn-TSrxn=-124.0 kJ – 298.15 K0.2086 kJK-1
Grxn=-186.1 kJ
Since Hrxn is negative and Srxn is positive, the decomposition of ammonium nitrate is
spontaneous at all temperatures. However, as the temperature increases, the TS term gets
larger and as a result, the decomposition reaction shift towards producing more products.
The reaction is highly favored above 298 K (it will also be faster).
The Thermodynamic Equilibrium Constant
33. (E) In all three cases, KK
eq p
= because only gases, pure solids, and pure liquids are present
in the chemical equations. There are no factors for solids and liquids in Keq expressions,
and gases appear as partial pressures in atmospheres. That makes Keq the same as Kp for
these three reactions.
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
964
We now recall thatKp=KcRT
n. Hence, in these three cases we have:
(a)
1
22 3 gas pc
2SO g + O g 2SO g ; = 2 2 +1 = 1; = =nKKKRT
(b)
11 11
22 gas pc
22 22
HI g H g + I g ; = 1 + = 0; = =nKKK
(c)
43 3 2 2
2
gas p c
NH HCO s NH g + CO g + H O l ;
=2 0 =+2 = =nKKKRT
34. (M) (a)
4
2
4
2
{H g }
={H O g }
P
KP
(b) Terms for both solids, Fe(s) and Fe3O4s
, are properly excluded from the
thermodynamic equilibrium constant expression. (Actually, each solid has an activity
of 1.00.) Thus, the equilibrium partial pressures of both H2g
and H2Og
do not
depend on the amounts of the two solids present, as long as some of each solid is
present. One way to understand this is that any chemical reaction occurs on the
surface of the solids, and thus is unaffected by the amount present.
(c) We can produce H2g
from H2Og
without regard to the proportions of Fe(s) and
Fe3O4s
with the qualification, that there must always be some Fe(s) present for the
production of H2g
to continue.
35. (M) In this problem we are asked to determine the equilibrium constant and the change in
Gibbs free energy for the reaction between carbon monoxide and hydrogen to yield
methanol. The equilibrium concentrations of each reagent at 483K were provided. We
proceed by first determining the equilibrium constant. Gibbs free energy can be
calculated using
G
o
R
T
ln
K
.
Stepwise approach:
First determine the equilibrium constant for the reaction at 483K:
23
CO(g)+2H (g) CH OH(g)
K[CH3OH(g)]
[CO(g)][H2(g)] 0.00892
0.09110.0822214.5
Now use
G
o
R
T
ln
K
to calculate the change in Gibbs free energy at 483 K:
G
o
R
T
ln
K
Go8.314 483ln(14.5)Jmol-1 1.1104Jmol-1
Go11kJ
m
ol-1
Conversion pathway approach:
K[CH3OH(g)]
[CO(g)][H2(g)] 0.00892
0.09110.0822214.5
GoRT ln K8.314 483ln(14.5)Jmol-1 1.1104Jmol-1
Go11kJ
m
ol-1
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
965
36. (M) Gibbs free energy for the reaction (
G
o
H
o
T
S
o) can be calculated using Hf
o
and
S
ovalues for CO(g), H2(g) and CH3OH(g) from Appendix D.
HoHf
o(CH3OH(g)) [Hf
o(CO(g)) 2Hf
o(H2(g)]
Ho200.7kJmol-1 (110.5kJmol-1 0kJmol-1 )90.2kJmol-1
SoSo(CH3OH(g)) [So(CO(g)) 2So(H2(g)]
So239.8JK1mol-1 (197.7JK1mol-1 2130.7JK1mol-1 )219.3JK-1mol-1
Go90.2kJmol-1 483K(219.3)kJK-1mol-1
1000 15.7kJmol-1
Equilibrium constant for the reaction can be calculated using
Go
R
T
ln
K
ln KGo
RT ln K15.7 1000Jmol1
8.314JK1mol1483K3.9 Ke3.9 2.0 102
The values are different because in this case, the calculated K is the thermodynamic
equilibrium constant that represents the reactants and products in their standard states. In
Exercise 35, the reactants and products were not in their standard states.
Relationships Involving G, G o, Q and K
37. (M)
off2f2
311
pp
=2 NO g NO g 0.5 O g
= 2 86.55 kJ/mol 104.2 kJ/mol 0.5 0.00 kJ/mol = 68.9 kJ/mol
= ln = 8.3145 10 kJ mol K 298 K ln
GG G G
RT K K
p311
68.9 kJ/mol
ln = = 27.8
8.3145 10 kJ mol K 298 K
K
27.8 13
p=e =8 10K
38. (M) (a)
o
f25 f24 f2
=2 NO g 2 NO g O g
= 2 115.1 kJ/mol 2 97.89 kJ/mol 0.00 kJ/mol = 34.4 kJ/mol
GG G G
(b)
o3
o
pp 11
13.9 7
p
34.4 10 J/mol
= ln ln = = = 13.9
8.3145 J mol K 298K
=e =9 10
G
GRTK K RT
K
39. (M) We first balance each chemical equation, then calculate the value of
G
o with data
from Appendix D, and finally calculate the value of Keq with the use of GRTK
oln=.
(a)
22 2
4HCl g + O g 2H O g + 2Cl s
o
f2 f 2 f f2
=2 HO g +2 Cl g 4 HCl g O g
kJ kJ kJ kJ kJ
= 2 228.6 + 2 0 4 95.30 0 = 76.0
mol mol mol mol mol
GG G G G
o3 +30.7 13
11
+76.0 10 J/mol
ln = = = +30.7 = e = 2 10
8.3145 J mol K 298 K
G
KK
RT
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
966
(b)
23 2 34 2
3FeO s+H g 2FeO s+HOg
of34 f2 f23 f2
=2 FeO s + HO g 3 FeO s H g
= 2 1015 kJ/mol 228.6 kJ/mol 3 742.2 kJ/mol 0.00 kJ/mol
=32kJ/mol
GG G G G
o3 +13 5
11
32 10 J/mol
ln = = = 13; = e = 4 10
8.3145 J mol K 298 K
G
KK
RT
(c)
+2
424
2Ag aq +SO aq Ag SO s
Go=Gf
Ag2SO4s
2Gf
Ag+aq
Gf
SO4
2aq
=618.4kJ/mol 277.11kJ/mol 744.5kJ/mol
=28.1kJ/mol
o3 +11.3 4
11
28.1 10 J/mol
ln = = = 11.3; = e = 8 10
8.3145 J mol K 298 K
G
KK
RT
40. (E)
oo o o o
22 2
11 11 11 11
11
= {CO g }+ {H g } {CO g } {H O g }
= 213.7 J mol K +130.7 J mol K 197.7 J mol K 188.8 J mol K
= 42.1 J mol K
SS S S S
41. (M) In this problem we need to determine in which direction the reaction
22 3
2SO g + O g 2SO g is spontaneous when the partial pressure of SO2, O2, and
SO3 are 1.010-4, 0.20 and 0.10 atm, respectively. We proceed by first determining the
standard free energy change for the reaction (
G
o) using tabulated data in Appendix D.
Change in Gibbs free energy for the reaction (
G) is then calculated by employing the
equation oln p
GGRTQ ,where Qp is the reaction quotient. Based on the sign of
G
, we can determine in which direction is the reaction spontaneous.
Stepwise approach:
First determine
G
o for the reaction using data in Appendix D:
22 3
2SO g + O g 2SO g
Go=2Gf
oSO3g
2Gf
oSO2g
Gf
oO2g
Go2(371.1 kJ/mol) 2(300.2 kJ/mol) 0.0 kJ/mol
G
o141.8
k
J
Calculate
G by employing the equation oln p
GGRTQ , where Qp is the reaction
quotient:
oln p
GGRTQ
2
3
p2
22
{SO g }
={O g } {SO g }
P
QPP

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
967
2
6
p2
4
0.10 atm
=5.010
0.20 atm 1.0 10 atm
Q
G = 141.8 kJ + (8.3145 103 kJ/Kmol )(298 K)ln(5.0 106)
G = 141.8 kJ + 38.2 kJ = 104 kJ.
Examine the sign of G to decide in which direction is the reaction spontaneous:
Since
Gis negative, the reaction is spontaneous in the forward direction.
Conversion pathway approach:
Go=2Gf
oSO3g
2Gf
oSO2g
Gf
oO2g
Go2(371.1 kJ/mol) 2(300.2 kJ/mol) 0.0 kJ/mol=-141.8kJ
oln p
GGRTQ
Qp=P{SO3g
}2
P{O2g
}P{SO2g
}20.10 atm
2
0.20 atm
1.0 104 atm
25.0 106
G = 141.8 kJ + (8.3145 103 kJ/Kmol )(298 K)ln(5.0 106)=-104 kJ.
Since
G is negative, the reaction is spontaneous in the forward direction.
42. (M) We begin by calculating the standard free energy change for the reaction:
22
Hg+Clg 2HClg
ff2f2
=2 HCl g Cl g H g
2 ( 95.30 kJ/mol) 0.0 kJ/mol 0.0 kJ/mol 190.6kJ
GG G G
Now we can calculate G by employing the equation oln p
GGRTQ , where
2
p
22
{HCl g }
={H g } {Cl g }
P
QPP ;
2
p
0.5 atm
=1
0.5 atm 0.5 atm
Q
G = 190.6 kJ + (8.3145 103 kJ/Kmol )(298 K)ln(1)
G = 190.6 kJ + 0 kJ = 190.6 kJ.
Since Gis negative, the reaction is spontaneous in the forward direction.
43. (M) In order to determine the direction in which the reaction is spontaneous, we need to
calculate the non-standard free energy change for the reaction. To accomplish this, we will
employ the equation oln c
GGRTQ , where
+
332
c
32
[H O aq ] [CH CO aq ]
=[CH CO H aq ]
Q
;
2
3
5
c
1.0 10 M
=1.010
(0.10 M)
Q
G = 27.07 kJ + (8.3145 103 kJ/Kmol )(298 K)ln(1.0 105)
G = 27.07 kJ + (28.53 kJ) = 1.46 kJ.
Since G is negative, the reaction is spontaneous in the forward direction.
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
968
44. (M) As was the case for exercise 39, we need to calculate the non-standard free energy
change for the reaction. Once again, we will employ the equation olnGGRTQ , but
this time
+
4
c
3
[NH aq ] [OH aq ]
=[NH aq ]
Q
;
2
3
5
c
1.0 10 M
=1.010
(0.10 M)
Q
G = 29.05 kJ + (8.3145 103 kJ/Kmol)(298 K)ln(1.0 105)
G = 29.05 kJ + (28.53 kJ) = 0.52 kJ.
Since
Gis positive, the reaction is spontaneous in the reverse direction.
45. (E) The relationship So = (Go Ho)/T (Equation (b)) is incorrect. Rearranging this
equation to put Go on one side by itself gives Go = Ho + TSo. This equation is not
valid. The TSo term should be subtracted from the Ho term, not added to it.
46. (E) The Go value is a powerful thermodynamic parameter because it can be used to
determine the equilibrium constant for the reaction at each and every chemically
reasonable temperature via the equation Go = RT ln K.
47. (M) (a) To determine Kp we need the equilibrium partial pressures. In the ideal gas law,
each partial pressure is defined by
P
nR
T
V=
/
. Because R, T, and V are the same for
each gas, and because there are the same number of partial pressure factors in the
numerator as in the denominator of the Kp expression, we can use the ratio of amounts
to determine Kp.
22 2
p
22 22 2 2
CO(g) H O(g) CO(g) H O(g) 0.224 mol CO 0.224 mol H O
= = = = 0.659
CO (g) H (g) CO (g) H (g) 0.276 mol CO 0.276 mol H
PP nn
KPP nn
(b)
o11
1000K p
3
= ln = 8.3145 J mol K 1000. K ln 0.659
= 3.467 10 J/mol = 3.467 kJ/mol
GRTK
(c)
2
p
p
22
0.0340 mol CO 0.0650mol H O
= = 0.31 0.659 =
0.0750 mol CO 0.095 mol H
QK
Since Qp is smaller than Kp, the reaction will proceed to the right, forming products,
to attain equilibrium, i.e., G = 0.
48. (M) (a)
We know that Kp=KcRT
n. For the reaction
22 3
2SO g + O g 2SO g ,
gas =2 2+1 = 1n , and therefore a value of Kp can be obtained.
Kp=KcRT
12.8 102
0.08206 L atm
mol K 1000 K
3.41K
We recognize that
p
=KK since all of the substances involved in the reaction are
gases. We can now evaluate
Go.
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
969
o 4
eq
8.3145 J
= ln = 1000 K ln 3.41 = 1.02 10 J/mol = 10.2 kJ/mol
mol K
GRTK
(b) We can evaluate Qc for this situation and compare the value with that of Kc=2.8 10
2
to
determine the direction of the reaction to reach equilibrium.
2
3
22
3
c c
2
2
22 22
0.72 mol SO
2.50 L
[SO ] 45 2.8 10
[SO ] [O ] 0.40 mol SO 0.18 mol O
2.50 L 2.50 L
QK
Since Qc is smaller than Kc the reaction will shift right, producing sulfur trioxide
and consuming sulfur dioxide and molecular oxygen, until the two values are equal.
49. (M) (a) c
=KK
o311
eq
= ln = 8.3145 10 kJ mol K 445 + 273 K ln 50.2 = 23.4 kJGRTK
(b)
g
n1/2
13 13
pc
= = = 1.7 10 0.0821 298 = 8.4 10KK KRT
o31113
p
o
= ln = 8.3145 10 kJ mol K 298 K ln 8.4 10
= +68.9 kJ/mol
GRTK
G
(c)
+1
3
pc
= = = 4.61 10 0.08206 298 = 0.113
n
KK KRT
Go=RT ln Kp=8.3145 103kJ mol1K1
298K
ln 0.113
= +5.40 kJ/mol
(d) 6
c
= = 9.14 10KK
o3116
c
o
= ln = 8.3145 10 kJ mol K 298 K ln 9.14 10
= +28.7 kJ/mol
GRTK
G
50. (M) (a) The first equation involves the formation of one mole of Mg2+ aq
from
Mg OH
2s
and
+
2H aq , while the second equation involves the formation of
only half-a-mole ofMg2+ aq
. We would expect a free energy change of half the
size if only half as much product is formed.
(b) The value of K for the first reaction is the square of the value of K for the second
reaction. The equilibrium constant expressions are related in the same fashion.
K1=Mg2+
H+
2=Mg2+
1/2
H+
2
=K2
2
(c) The equilibrium solubilities will be the same regardless which expression is used.
The equilibrium conditions (solubilities in this instance) are the same no matter how
we choose to express them in an equilibrium constant expression.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
970
51. (E)
o31111
p
= ln = 8.3145 10 kJ mol K 298K ln 6.5 10 = 67.4 kJ/molGRTK
22
CO g + Cl g COCl g o= 67.4kJ/molG
12
2
C graphite + O g CO g f= 137.2 kJ/molG
122 2
2
C graphite + O g + Cl g COCl g f= 204.6 kJ/molG
Gf of COCl2g
given in Appendix D is
204.6 kJ/mol, thus the agreement is excellent.
52. (M) In each case, we first determine the value of
Go for the solubility reaction. From
that, we calculate the value of the equilibrium constant, sp
K, for the solubility reaction.
(a)
+
AgBr s Ag aq + Br aq
o+
fff
=Agaq+Braq AgBrs
= 77.11 kJ/mol 104.0 kJ/mol 96.90 kJ/mol = +70.0 kJ/mol
GG G G
3
o28.2 13
sp
11
70.0 10 J/mol
ln = = = 28.2; = e = 6 10
8.3145 J mol K 298.15 K
G
KK
RT
(b)
2+ 2
44
CaSO s Ca aq +SO aq
oo2o
o2+
ff4f4
=Caaq+SOaq CaSOs
= 553.6 kJ/mol 744.5 kJ/mol 1332 kJ/mol = +34 kJ/mol
GG G G
3
o14 7
sp
11
34 10 J/mol
ln = = = 14; = e = 8 10
8.3145 J mol K 298.15 K
G
KK
RT
(c)
3+
3
Fe OH s Fe aq + 3OH aq
Go=Gf
Fe3+ aq
+3Gf
OHaq
Gf
Fe OH
3s
=4.7 kJ/mol + 3157.2 kJ/mol
696.5 kJ/mol
= +220.2 kJ/mol
3
o88.83 39
sp
11
220.2 10 J/mol
ln = = = 88.83 = e = 2.6 10
8.3145 J mol K 298.15 K
G
KK
RT
53. (M)(a) We can determine the equilibrium partial pressure from the value of the equilibrium
constant.
o3
o
pp 11
58.54 10 J/mol
= ln ln = = = 23.63
8.3145 J mol K 298.15 K
G
GRTK K RT
2
1/2 23.63 11 11 21
p2 2
= {O g } = e = 5.5 10 {O g } = 5.5 10 = 3.0 10 atmKP P
(b) Lavoisier did two things to increase the quantity of oxygen that he obtained. First, he ran
the reaction at a high temperature, which favors the products (i.e., the side with
molecular oxygen.) Second, the molecular oxygen was removed immediately after it was
formed, which causes the equilibrium to shift to the right continuously (the shift towards
products as result of the removal of the O2 is an example of Le Châtelier's principle).

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
971
54. (D) (a) We determine the values of
H
o and
S
o from the data in Appendix D, and then
the value of Go at 25 = 298
C K.
o
f 3 f2 f 2 f2
=CHOHg+HOg COg3Hg
= 200.7 kJ/mol + 241.8 kJ/mol 393.5 kJ/mol 3 0.00 kJ/mol = 49.0 kJ/mol
HH H H H
oo o o o
3222
11 11
=CHOHg+HOg COg3Hg
= (239.8+188.8 213.7 3 130.7)J mol K = 177.2 J mol K
SS S S S
oo o 11
= = 49.0 kJ/mol 298 K 0.1772 kJ mol K = +3.81 kJ/molGHTS
Because the value of Go is positive, this reaction does not proceed in the forward
direction at 25C.
(b) Because the value of
H
o is negative and that of
S
o is negative, the reaction is non-
spontaneous at high temperatures, if reactants and products are in their standard states.
The reaction will proceed slightly in the forward direction, however, to produce an
equilibrium mixture with small quantities of
3
CH OH g and H2Og
. Also, because
the forward reaction is exothermic, this reaction is favored by lowering the
temperature. That is, the value of K increases with decreasing temperature.
(c)
ooo 11
500K
3p
= = 49.0 kJ/mol 500.K 0.1772 kJ mol K = 39.6 kJ/mol
= 39.6 10 J/mol = ln
GHTS
RT K
39.53 5
p p
11
39.6 10 J/mol
ln 9.53; e 7.3 10
8.3145 J mol K 500. K
G
KK
RT
(d) Reaction: CO2g
+ 3H2g
CH3OH g
+H2Og
Initial: 1.00 atm 1.00 atm 0 atm 0 atm
Changes:
x
atm
3
x
atm +
x
atm +
x
atm
Equil: (1.00
x
) atm 1.00
3x
atm
x
atm
x
atm
32
5 2
p33
22
CH OH H O
=7.3 10 = =
CO H 1.00 1.00 3
PP xx
Kx
PP x x
53
3
7.3 10 8.5 10 atm P CH OHx
Our assumption, that 31.00x atm, is valid.
Go and K as Function of Temperature
55 (M)(a)
oo o o o
23 2 2 3
JJ J J J
K mol K mol K mol K mol K mol
=NaCOs+HOl+COg2NaHCOs
= 135.0 + 69.91 + 213.7 2 101.7 = 215.2
SS S S S

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
972
(b)
o
f23 f2 f 2 f 3
kJ kJ kJ kJ kJ
mol mol mol mol mol
=NaCOs+HOl+COg2NaHCOs
= 1131 285.8 393.5 2 950.8 = +91
HH H H H
(c)
oo o 3 11
= = 91 kJ/mol 298 K 215.2 10 kJ mol K
= 91 kJ/mol 64.13 kJ/mol = 27 kJ/mol
GHTS
(d) 3
o
o
11
27 10 J/mol
= ln ln = = = 10.9
8.3145J mol K 298K
G
GRTK KRT
K=e
10.9 =2105
56. (M) (a)
32 2 2 3
oo o o o o
o
o
CH CH OH g H O g CO g H g CH OH g
JJJ J J
K mol K mol K mol K mol K mol
J
K mol
=+ 2
= 282.7 +188.8 197.7 2 130.7 239.8
= 227.4
SS S S S S
S
S
32 232
offfff
o
o
CH CH OH g H g CH OH gHOg COg
kJ kJ kJ kJ kJ
mol mol mol mol mol
kJ
mol
=+ 2
= 235.1 241.8 110.5 2 0.00 200.7
= 165.7
HH H H H H
H
H
o3
kJ kJ kJ kJ kJ
mol K mol mol mol mol
= 165.7 298K 227.4 10 = 165.4 +67.8 = 97.9G
(b)
H
o0 for this reaction. Thus it is favored at low temperatures. Also, because
ngas = +2 4 = 2, which is less than zero, the reaction is favored at high pressures.
(c) First we assume that neither
S
o nor
H
o varies significantly with temperature. Then
we compute a value for
Go at 750 K. From this value of
Go, we compute a value
for Kp.
Go=HoTSo=165.7kJ/mol 750.K
227.4 103kJ mol1K1
=165.7kJ/mol + 170.6kJ/mol = +4.9kJ/mol = RT ln Kp
ln Kp=Go
RT =4.9103J/mol
8.3145 J mol1K1750.K =0.79 Kp=e
0.79 = 0.5
57. (E) In this problem we are asked to determine the temperature for the reaction between
iron(III) oxide and carbon monoxide to yield iron and carbon dioxide given Go,
H
o,
and
S
o. We proceed by rearranging
Go=
H
o
T
S
oin order to express the
temperature as a function of Go,
H
o, and
S
o.
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
973
Stepwise approach:
Rearrange Go=
H
o
T
So in order to express T as a function of
Go,
H
o, and
S
o:
Go=HoTSo
TSo=HoGo
T=HoGo
S
o
Calculate T:
T=24.8 103J45.510 3J
15.2 J/K =1.36103K
Conversion pathway approach:
Go=HoTSoTHoGo
So24.8 103J45.5 10 3J
15.2 J/K =1.36103K
58. (E) We use the van't Hoff equation with o5
1
= 1.8 10 J/mol, = 800HT . K,
T2= 100. = 373
CK, andK1
2
=9.1 10.
ln K2
K1
=Ho
R
1
T1
1
T2
=1.8 105J/mol
8.3145J mol1K1
1
800K 1
373K
=31
31 13 13 2 16
22
2
2
1
= e = 2.9 10 = = 2.9 10 9.1 10 = 3 10
9.1 10
KK
K
K
59. (M) We first determine the value of
Go at 400 C
, from the values of
H
o and
S
o,
which are calculated from information listed in Appendix D.
o
f3 f2 f2
2
=2 NH g N g 3 H g
= 2 46.11kJ/mol 0.00kJ/mol 3 0.00 kJ/mol = 92.22kJ/mol N
HH H H
oo o o
32 2
11 11 11 1 1
=2 NH g N g 3 H g
= 2 192.5 J mol K 191.6J mol K 3 130.7J mol K = 198.7 J mol K
SS S S
oo o 11
p
= = 92.22 kJ/mol 673 K 0.1987 kJ mol K
= +41.51kJ/mol = ln
GHTS
RT K
o3 7.42 4
p p
11
41.51 10 J/mol
ln = = = 7.42; = e = 6.0 10
8.3145J mol K 673K
G
KK
RT

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
974
60. (M) (a)
o
f2 f2 f f2
=COg+Hg COg HOg
= 393.5 kJ/mol 0.00 kJ/mol 110.5 kJ/mol 241.8 kJ/mol = 41.2 kJ/mol
HH H H H
oo o o o
22 2
11 11 11 11
11
=COg+Hg COg HOg
= 213.7 J mol K +130.7 J mol K 197.7 J mol K 188.8 J mol K
= 42.1J mol K
SS S S S
GoHoTSo41.2kJ/mol 298.15K (42.1103)kJ/molK
Go41.2
k
J
/
m
ol 12.6
k
J
/
m
ol
28.6
k
J
/
m
ol
(b) Go=HoTSo=41.2 kJ/mol 875 K
42.1103kJ mol1K1
=41.2 kJ/mol + 36.8 kJ/mol = 4.4 kJ/mol = RT ln Kp
o3 +0.60
p p
11
4.4 10 J/mol
ln = = = +0.60 = e =1.8
8.3145J mol K 875K
G
KK
RT
61. (M) We assume that both
H
o and
S
o are constant with temperature.
Ho=2Hf
SO3g
2Hf
SO2g
Hf
O2g
=2 395.7 kJ/mol
2296.8 kJ/mol
0.00 kJ/mol
=197.8 kJ/mol
oo o o
322
11 11 11
11
=2 SO g 2 SO g O g
= 2 256.8 J mol K 2 248.2 J mol K 205.1J mol K
= 187.9 J mol K
SS S S
o
oo o o o
o
==ln=ln=
ln
H
G H T S RT K H T S RT K T SRK
3
11 11 6
197.8 10 J/mol
= 650 K
187.9 J mol K 8.3145 J mol K ln 1.0 10
T
This value compares very favorably with the value of
T
=6.37 10
2
that was obtained in
Example 19-10.
62. (E) We use the van't Hoff equation to determine the value of o(448 C = 721 KH and
350 C = 623 K)
.
ln K1
K2
=Ho
R
1
T2
1
T1
=ln50.0
66.9 =0.291 = Ho
R
1
623 1
721
=Ho
R2.2 104
o3
4-1
o 3 -1 -1 3 -1 -1
0.291
==1.310 K;
2.2 10 K
= 1.3 10 K 8.3145 J K mol = 11 10 J mol = 11 kJ mol
H
R
H

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
975
63. (M) (a) o3
2
11
112
1 1 57.2 10 J/mol 1 1
ln = = = 2.11
8.3145 J mol K 298 K 273 K
KH
KRTT
2.11
22
1
= e = 0.121 = 0.121 0.113 = 0.014 at 273 K
KK
K
(b) ln K2
K1
=Ho
R
1
T1
1
T2
=57.2 103J/mol
8.3145 J mol1K1
1
T1
1
298 K
=ln0.113
1.00 =2.180
1
T1
1
298K
=2.180 8.3145
57.2 103K1=3.17 104K1
43431
1
1
11
= 3.17 10 = 3.36 10 3.17 10 = 3.04 10 K ; = 329 K
298 T
T
64. (D) First we calculate Go at 298 K to obtain a value for Keq at that temperature.
o
f2 f f2
=2 NO g 2 NO g O g
= 2 51.31kJ/mol 2 86.55 kJ/mol 0.00 kJ/mol = 70.48 kJ/mol
GG G G
328.43 12
70.48 10 J/mol K
ln 28.43 e 2.2 10
8.3145 J 298.15 K
mol K
G
KK
RT
Now we calculate
H
o for the reaction, which then will be inserted into the van't Hoff equation.
Ho=2Hf
NO2g
2Hf
NO g
Hf
O2g
= 2 33.18 kJ/mol
2 90.25 kJ/mol
0.00 kJ/mol = 114.14 kJ/mol
o3
2
11
112
1 1 114.14 10 J/mol 1 1
ln = = = 9.26
8.3145 J mol K 298 K 373 K
KH
KRTT
9.26 5 5 12 8
22
1
= e = 9.5 10 ; = 9.5 10 2.2 10 = 2.1 10
KK
K
Another way to find K at 100 ºC is to compute Ho114.14 kJ/mol
from Hf
o values
and
o11
146.5 J mol KS
from
S
o values. Then determine Go(59.5 kJ/mol), and
find Kp with the expression GRTK
op
ln=. Not surprisingly, we obtain the same
result, 8
p=2.2 10K.
65. (M) First, the van't Hoff equation is used to obtain a value of
H
o. 200 = 473
C
K
and
260 = 533
C
K
.
o11o
2
811
112
1 1 2.15 10 1 1
ln = = ln = 6.156 =
4.56 10 8.3145 J mol K 533K 473 K
KH H
KRTT
6.156 = 2.9 10 = 6.156
2.9 10 = 2.1 10 = 2.1 10
5
5
52
HH
oo J/mol kJ/mol
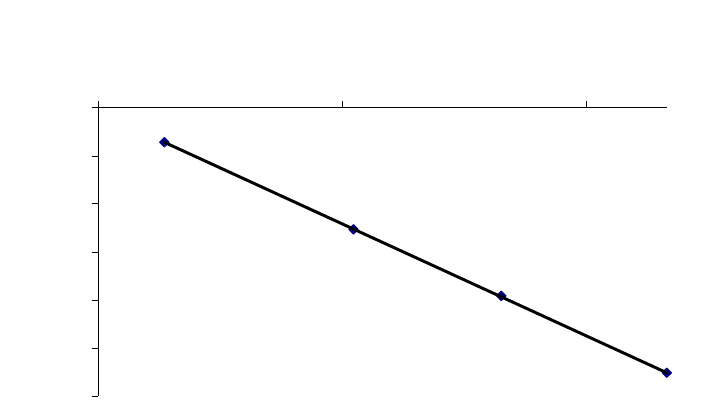
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
976
Another route to
H
o is the combination of standard enthalpies of formation.
242
CO g +3H g CH g + H O g
o
f4 f2 f f2
=CHg+HOg COg3Hg
= 74.81kJ/mol 241.8 kJ/mol 110.5 3 0.00 kJ/mol = 206.1kJ/mol
HH H H H
Within the precision of the data supplied, the results are in good agreement.
66. (D) (a)
t,C
T
, K 1/ , 1
TK Kp ln p
K
30. 303 3.30 10 3
1.66 10 5
11.006
50. 323 3.10 10 3
3.90 10 4
7.849
70. 343 2.92 10 3
6.27 10 3
5.072
100. 373 2.68 10 3
2.31 10 1
1.465
The slope of this graph is
H
R
o/ = 1.54 104 K
o1143
= 8.3145 J mol K 1.54 10 K =128 10 J/mol =128 kJ/molH
(b) When the total pressure is 2.00 atm, and both gases have been produced from NaHCO3s
,
22
{H O g }= {CO g }=1.00 atmPP
p2 2
= {H O g } {CO g } = 1.00 1.00 =1.00KP P
Thus, ln Kp=ln 1.00
= 0.000 . The corresponds to 31
1/ = 2.59 10 KT
;
= 386 KT.
We can compute the same temperature from the van't Hoff equation.
Plot of ln(Kp) versus 1/T
y = -15402.12x + 39.83
-12
-10
-8
-6
-4
-2
0
0.0026 0.0029 0.0032
1/T(K-1)
ln K
p
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
977
ln K2
K1
=Ho
R
1
T1
1
T2
=128 103J/mol
8.3145 J mol1K1
1
T1
1
303 K
=ln1.66 105
1.00 =11.006
1
T1
1
303 K
=11.006 8.3145
128 103K1=7.15 104K1
43431
1
1
11
= 7.15 10 = 3.30 10 7.15 10 = 2.59 10 K ; = 386 K
303 T
T
This temperature agrees well with the result obtained from the graph.
Coupled Reactions
67. (E) (a) We compute
G
o for the given reaction in the following manner
of4 f2 f2 f2
= TiCl l + O g TiO s 2 Cl g
= 804.2 kJ/mol+ 0.00 kJ/mol 944.7 kJ/mol 2 0.00 kJ/mol
= +140.5 kJ/mol
HH H H H
11 11 11
oo o o o
42 2 2
11
11
J mol K J mol K J mol K
= TiCl l + O g TiO s 2 Cl g
= 252.3 + 205.1J mol K 50.33 2 223.1
= 39.1J mol K
SS S S S
oo o 3 11
= = +140.5 kJ/mol 298 K 39.1 10 kJ mol K
= +140.5 kJ/mol +11.6 kJ/mol = +152.1 kJ/mol
GHTS
Thus the reaction is non-spontaneous at25C . (we also could have used values of Gf
o
to calculate
G
o).
(b) For the cited reaction, Go=2Gf
CO2g
2Gf
CO g
Gf
O2g
Go=2 394.4 kJ/mol
2137.2 kJ/mol
0.00 kJ/mol = 514.4 kJ/mol
Then we couple the two reactions.
22 42
TiO s + 2Cl g TiCl l + O g o= +152.1kJ/molG
22
2CO g + O g 2CO g o= 514.4 kJ/molG
_________________________________________________________________
o
22 4 2
TiO s + 2Cl g + 2CO g TiCl l + 2CO g ; = 362.3 kJ/molG
The coupled reaction has
G
o
0, and, therefore, is spontaneous.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
978
68. (E) If
G
o0 for the sum of coupled reactions, the reduction of the oxide with carbon is
spontaneous.
(a)
12
2
NiO s Ni s + O g o= +115 kJG
12
2
Cs+ O g COg o= 250 kJG
Net : NiO + C s Ni s +CO gs o= +115 kJ 250 kJ = 135 kJG
Therefore the coupled reaction is spontaneous
(b)
12
2
MnO s Mn s + O g o= +280 kJG
12
2
Cs+ O g COg o= 250 kJG
Net : MnO s +C s Mn s + CO g o= +280 kJ 250 kJ = +30 kJG
Therefore the coupled reaction is non-spontaneous
(c)
22
TiO s Ti s + O g o= +630 kJG
2
2C s + O g 2CO g
o= 2 250 kJ = 500 kJG
2
Net : TiO s + 2C s Ti s + 2CO g o= +630 kJ 500 kJ = +130 kJG
Therefore the coupled reaction is non-spontaneous
69. (E) In this problem we need to determine if the phosphorylation of arginine with ATP is a
spontaneous reaction. We proceed by coupling the two given reactions in order to
calculate Gt
ofor the overall reaction. The sign of Gt
o can then be used to determine
whether the reaction is spontaneous or not.
Stepwise approach:
First determine Gt
ofor the coupled reaction:
ATP+H2OADP+P Gt
o31.5kJmol-1
arginine+P phosphorarginine+H2O Gt
o33.2kJmol-1
___________________________________________
ATP+arginine phosphorarginine+ADP
Go(31.5 33.2)kJmol-1 1.7kJmol-1
Examine the sign of Gt
o:
Gt
o0 . Therefore, the reaction is not spontaneous.
Conversion pathway approach:
Gt
o for the coupled reaction is:
ATP+arginine phosphorarginine+ADP
Go(31.5 33.2)kJmol-1 1.7kJmol-1
Since Gt
o0,the reaction is not spontaneous.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
979
70. (E) By coupling the two reactions, we obtain:
Glu-+NH4
+Gln+H2O Gt
o14.8kJmol-1
ATP+H2OADP+P Gt
o31.5kJmol-1
_________________________________________
Glu-+NH4
++ATP Gln+ADP+P Go(14.8 31.5)kJmol-1 16.7kJmol-1
Therefore, the reaction is spontaneous.
INTEGRATIVE AND ADVANCED EXERCISES
71. (M) (a) The normal boiling point of mercury is that temperature at which the mercury
vapor pressure is 1.00 atm, or where the equilibrium constant for the vaporization
equilibrium reaction has a numerical value of 1.00. This is also the temperature where
0G, since eq
ln KRTG and 0)00.1(ln
.
Hg(l) Hg(g)
111111
ff
KmolJ0.99KmolJ02.76KmolJ0.175)]Hg(l[)]Hg(g[
kJ/mol32.61kJ/mol00.0kJ/mol32.61)]Hg(l[)]Hg(g[
SSS
HHH
113 KmolJ0.99J/mol1032.610
TSTH
K619
KmolJ0.99
J/mol1032.61
11
3
T
(b) The vapor pressure in atmospheres is the value of the equilibrium constant, which is
related to the value of the free energy change for formation of Hg vapor.
eqf lnkJ/mol82.31]Hg(g)[ KRTG
3
11
31.82 10 J/mol
ln 12.84
8.3145J mol K 298.15K
K
12.84 6
e2.6510atmK
Therefore, the vapor pressure of Hg at 25ºC is 2.65×10-6 atm.
72. (M) (a) TRUE; It is the change in free energy for a process in which
reactants and products are all in their standard states (regardless of
whatever states might be mentioned in the statement of the problem).
When liquid and gaseous water are each at 1 atm at 100 °C (the normal
boiling point), they are in equilibrium, so that
G =
G° = 0 is only true
when the difference of the standard free energies of products and reactants
is zero. A reaction with G = 0 would be at equilibrium when products
and reactants were all present under standard state conditions and the
pressure of H2O(g) = 2.0 atm is not the standard pressure for H2O(g).
(b) FALSE; .0G The system is not at equilibrium.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
980
(c) FALSE;
G° can have only one value at any given temperature, and that is the
value corresponding to all reactants and products in their standard states,
so at the normal boiling point
G° = 0 [as was also the case in answering
part (a)]. Water will not vaporize spontaneously under standard conditions
to produce water vapor with a pressure of 2 atmospheres.
(d) TRUE; .0G The process of transforming water to vapor at 2.0 atm pressure
at 100°C is not a spontaneous process; the condensation (reverse) process
is spontaneous. (i.e. for the system to reach equilibrium, some H2O(l)
must form)
73. (D) ]BrCl(g)[](g)Cl[](g)Br[ f2f
2
1
2f
2
1
GGGG
p
2
1
2
1lnkJ/mol54.2)kJ/mol98.0()kJ/mol00.0()kJ/mol11.3( KRT
02.1
K15.298KmolJ3145.8
J/mol1054.2
ln 11
3
p
TR
G
K 1.02
pe 0.361K
For ease of solving the problem, we double the reaction, which squares the value of the
equilibrium constant. 130.0)357.0( 2
eq K
22
Reaction: 2BrCl(g) Br (g) Cl (g)
Initial: 1.00mol 0mol 0mol
Changes: 2 mol mol mol
Equil: (1.00 2 )mol mol mol
xxx
xx x
xx
x
x
x
x
n
nn
VRTn
VRTnVRTn
P
PP
K
722.0361.0361.0
200.1
)361.0(
)200.1(
}BrCl(g){
}(g)Cl{}(g)Br{
]/}BrCl(g){[
]/}(g)Cl{[]/)}(gBr{[
}BrCl(g){
}(g)Cl{}(g)Br{
2
2
2
2
22
2
22
2
22
p
BrClmol580.0200.1Clmol210.0Brmol210.0
722.1
361.0
22 xx
74. (M)
First we determine the value of Kp for the dissociation reaction. If I2(g) is 50% dissociated,
then for every mole of undissociated I2(g), one mole of I2(g) has dissociated, producing two
moles of I(g). Thus, the partial pressure of I(g) is twice the partial pressure of I2(g)
(2
I(g) 2I(g)).
atm333.032atm00.1 )(gI(g)I(g)I(g)I)I(g(g)Itotal 22222
PPPPPPP
293.0ln34.1
333.0
)667.0(
p
2
)(gI
2
I(g)
p
2
K
P
P
K
111111
2
2ff
KmolJ9.100KmolJ7.260KmolJ8.1802](g)I[]I(g)[2S
kJ/mol2.151kJ/mol44.62kJ/mol8.1062](g)I[]I(g)[2
SS
HHH
Now we equate two expressions for
G and solve for T.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
981
GHTSRT ln Kp151.2 103100.9T8.3145 T0.293
151.2 103100.9T2.44T98.4TT151.2 103
98.5 1535K 1.5 103K
75. (M) (a) The oxide with the most positive (least negative) value of f
G is the one that
most readily decomposes to the free metal and O2(g), since the decomposition is the
reverse of the formation reaction. Thus the oxide that decomposes most readily is
Ag2O(s).
(b) The decomposition reaction is (g)OAg(s)4)O(sAg2 22 For this reaction
(g)Op 2
PK . Thus, we need to find the temperature where 00.1
pK.Since
p
ln KRTG and 0)00.1(ln
, we wish to know the temperature where 0
G.
Note also that the decomposition is the reverse of the formation reaction. Thus, the
following values are valid for the decomposition reaction at 298 K.
kJ/mol20.11GkJ/mol05.31
H
We use these values to determine the value of
S for the reaction.
11
33
KmolJ6.66
K298
J/mol1020.11J/mol1005.31
S
T
GH
SGHSTSTHG
Now we determine the value of T where 0
G.
C193K466
KmolJ6.66
J/mol0.0J/mol1005.31
11
3
S
GH
T
76. (M) At 127 °C = 400 K, the two phases are in equilibrium, meaning that
](red)(yellow)[](red)(yellow)[0 ff
SSTHHSTHG rxnrxnrxn
J/mol1020.7yellow)(K400J/mol105.2
]KmolJ180yellow)([K400J10)]4.105(9.102[
43
113
S
S
11
34 KmolJ186
K400
J/mol)105.21020.7(
)yellow(
S
Then we compute the value of the “entropy of formation” of the yellow form at 298 K.
11 11
f2 2
[HgI ] [Hg(l)] [I (s)] [186 76.02 116.1] Jmol K 6J mol KSS S S
Now we can determine the value of the free energy of formation for the yellow form.
ff f
kJ J 1kJ kJ
102.9 [298K ( 6 ) ] 101.1
mol K mol 1000J mol
GHTS
77. (M) First we need a value for the equilibrium constant. 1% conversion means that 0.99 mol
N2(g) are present at equilibrium for every 1.00 mole present initially.
22
222
NO(g)
p
N (g) O (g) 2 2 2 2
[ {NO(g)}RT/V] {NO(g)}
[ {N (g)}RT/V][ {O (g)}RT/V] {N (g)} {O (g)}
Pnn
KK PP n n n n
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
982
22
Reaction: N (g) O (g) 2 NO(g)
Initial: 1.00mol 1.00mol 0mol
Changes(1% rxn): 0.010mol 0.010mol 0.020mol
Equil: 0.99mol 0.99mol 0.020mol
24
(0.020) 4.1 10
(0.99)(0.99)
K
The cited reaction is twice the formation reaction of NO(g), and thus
f
22
-1 -1 -1 -1 -1 -1 -1
-1 -1 -
H = 2 H° [NO(g)] = 2 90.25kJ/mol = 180.50kJ/mol
S° = 2S°[NO(g)] - S°[N (g)] - S°[O (g)]
=2(210.7 J mol K)-191.5J mol K -205.0J mol K = 24.9J mol K
G° = -RTlnK = -8.31447JK mol (T)ln(4.1 10
4
-1 -1
-1 -1 3
) = 64.85(T)
G° = H°-T S° = 64.85(T) = 180.5kJ/mol -(T)24.9J mol K
180.5 10J/mol = 64.85(T) + (T)24.9J mol K = 89.75(T) T = 2.01 10 K
78. (E) Sr(IO3)2(s)
Sr2+(aq) + 2 IO3-(aq)
G = (2 mol×(-128.0 kJ/mol) + (1 mol ×-500.5 kJ/mol)) (1 mol × -855.1 kJ/mol) = -0.4 kJ
G = -RTlnK = -8.31447 JK-1mol-1(298.15 K)ln K = -0.4 kJ = -400 J
ln K = 0.16 and K = 1.175 = [Sr2+][IO3-]2 Let x = solubility of Sr(IO3)2
[Sr2+][IO3-]2 = 1.175 = x(2x)2 = 4x3 x = 0.665 M for a saturated solution of Sr(IO3)2.
79. (M) PH2O = 75 torr or 0.0987 atm. K = (PH2O)2 = (0.0987)2 = 9.74 × 10-3
G = (2 mol×(-228.6 kJ/mol) + (1 mol)×-918.1 kJ/mol) – (1 mol)×-1400.0 kJ/mol = 309.0 kJ
H = (2 mol×(-241.8 kJ/mol) + (1 mol)×-1085.8.1 kJ/mol) – (1 mol)×-1684.3 kJ/mol = 114.9 kJ
S = (2 mol×(188.J/K mol) + (1 mol×146.J/K mol) + (1 mol)×221.3.J/K mol = 302.3 J/K mol
-1 -1 -3
eq
-1 -1 -1
-1 o
G = -RTln K = -8.3145J mol K T ln (9.74 10 ) = 38.5(T)
G° = 38.5(T) = H°-T S° = 114,900J mol - (T) 302.3J K mol
114,900 = 340.8K (T) Hence: T = 337K = 64 C
80. (D) (a) 3
11
131 10 J/mol
ln ln 52.8
8.3145J mol K 298.15K
G
GRTK KRT
52.8 23 21
760mmHg
e 1.2 10 atm 8.9 10 mmHg
1atm
K
Since the system cannot produce a vacuum lower than 10–9 mmHg, this partial pressure
of CO2(g) won't be detected in the system.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
983
(b) Since we have the value of
G for the decomposition reaction at a specified
temperature (298.15 K), and we need
H
and
S for this same reaction to
determine (g)}P{CO2 as a function of temperature, obtaining either
H
or
S will
enable us to determine the other.
(c) ](s)[CaCO](g)CO[)]CaO(s[ 3f2ff
HHHH
kJ/mol178)kJ/mol1207(kJ/mol5.393kJ/mol1.635
HG
G H TS TS H G S T
211
178 kJ/mol 131 kJ/mol 1000 J 1.6 10 J mol K
298. K 1 kJ
S
912
1atm
1.0 10 mmHg 1.3 10
760 mmHg
K
eq
ln KRTSTHG lnHTSRTK
3
2
211 11 12
178 10 J/mol 4.6 10 K
1.6 10 J mol K 8.3145J mol K ln(1.3 10 )
ln
H
TSRK
81. (D) ](g)PCl[](g)Cl[)](gPCl[ 5f2f3f
HHHH
32 5
-1 -1 -1 -1 -1 -1 -1 -1
287.0 kJ/mol 0.00 kJ/mol ( 374.9 kJ/mol) 87.9 kJ/mol
[PCl (g)] [Cl (g)] [PCl (g)]
311.8 J mol K + 223.1 J mol K 364.6 J mol K = +170.3 J mol K
SS S S
113 KmolJ3.170K500J/mol109.87
STHG
Gº 3
p
2.8 10 J/mol ln
R
TK
0.67
p p
11
2.8 10 J/mol
ln 0.67 e 0.51
8.3145J mol K 500K
G
KK
RT
atm74.2
L50.1
K500KmolatmL08206.0mol100.0
]PCl[
11
5
V
nRT
Pi
532
Reaction: PCl (g) PCl (g) Cl (g)
Initial: 2.74atm 0 atm 0 atm
Changes: atm atm atm
Equil: (2.74 )atm atm atm
xxx
xxx

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
984
32
p
5
22
[PCl ] [Cl ]
0.51
[PCl ] 2.74
0.51(2.74 ) 1.4 0.51 0.51 1.4 0
PP xx
KPx
xxxxx
24 0.51 0.26 5.6 0.96atm, 1.47atm
22
bb ac
xa
atm70.396.074.274.2)74.2(
235 ClPClPCltotal
xxxxPPPP
82. (M) The value of
H
determined in Exercise 64 is kJ/mol128
H. We use any one of
the values of eqp KK to determine a value of
G. At 30 °C = 303 K,
J/mol1077.2)1066.1ln()K303)(KmolJ3145.8(ln 4511
eq
KRTG
Now we determine S.
STHG
11
43
KmolJ331
K303
J/mol1077.2J/mol10128
T
GH
S
By using the appropriate S° values in Appendix D, we calculate 11 KmolJ334
S.
83. (M) In this problem we are asked to estimate the temperature at which the vapor pressure of
cyclohexane is 100 mmHg. We begin by using Trouton’s rule to determine the value of
vap
H for cyclohexane. The temperature at which the vapor pressure is 100.00 mmHg can
then be determined using Clausius–Clapeyron equation.
Stepwise approach:
Use Trouton’s rule to find the value of vap
H
:
J/mol1031KmolJ87K9.353 311
vapnbpvap
STH
Next, use Clausius–Clapeyron equation to find the required temperature:
ln P2
P
1
Hvap
R
1
T1
1
T2
ln 100mmHg
760mmHg
31103J/mol
8.3145Jmol1K1
1
353.9K 1
T
2.028
1
353.9 1
T2.028 8.3145
311035.4 104
2.826 1031
T
1
T3.37 103K1
T297K 24C

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
985
Conversion pathway approach:
ln P2
P
1
Hvap
R
1
T1
1
T2
Tnbp Svap
R
1
T1
1
T2
1
T1
1
T2
R
Tnbp Svap
ln P2
P
1
1
T2
1
T1
R
Tnbp Svap
ln P2
P
1
1
T2
1
353.9K 8.314JK-1mol-1
353.9K87JK-1mol-1 ln 100mmHg
760mmHg 3.37 103
T2297K=24oC
92. (M)(a) 2Ag(s) 1
2O2(g) Ag 2O
Gf
oGf
o(Ag2O(s))-{2Gf
o(Ag(s)) 1
2Gf
o(O2)}
Gf
o -11.2 kJ-{2(0) 1
2(0)}11.2 kJ Ag 2O is thermodynamically stable at 25oC
(b) Assuming Ho, So are constant from 25-200oC (not so, but a reasonable assumption !)
SoSo(Ag2O)-{2 So(Ag(s)) 1
2 So(O2)} 121.3(2(42.6) 1
2(205.1)) 66.5 J/K
Go31.0 kJ (473 K)(-66.5 J/K)
1000 J/kJ HoTSo0.45 kJ
thermodynamically unstable at 200oC
85. (M) G = 0 since the system is at equilibrium. As well, G = 0 because this process is
under standard conditions. Since G = H - TS = 0. = H = TS =273.15 K×21.99 J
K-1 mol-1 = 6.007 kJ mol-1. Since we are dealing with 2 moles of ice melting, the
values of H and S are doubled. Hence, H = 12.01 kJ and S = 43.98 J K-1.
Note: The densities are not necessary for the calculations required for this question.
86. (D) First we determine the value of Kp that corresponds to 15% dissociation. We represent
the initial pressure of phosgene as x atm.
22
Reaction: COCl (g) CO(g) Cl (g)
Initial: atm 0 atm 0 atm
Changes: 0.15 atm 0.15 atm 0.15 atm
Equil: 0.85 atm 0.15 atm 0.15 atm
x
xxx
xxx
84.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
986
atm870.0
15.1
00.1
atm00.1atm15.1atm15.0atm15.0atm85.0 total xxxxxP
0230.0
870.085.0
)870.015.0( 2
COCl
ClCO
p
2
2
P
PP
K
Next we find the value of
H
for the decomposition reaction.
)1018.1(
0.373
1
668
1
71.15
1044.4
107.6
ln
11
ln 3
2
9
122
1
R
H
R
H
TTR
H
K
K
4
31033.1
1018.1
71.15
R
H,
kJ/mol111J/mol101113145.81033.1 34 H
And finally we find the temperature at which K = 0.0230.
C374K647
10546.1
11
10497.11093.4
10111
3145.8658.01
668
1
658.0
1
K668
1
KmolJ3145.8
J/mol10111
0444.0
0230.0
ln
11
ln
335
3
11
3
122
1
T
TTT
TTTR
H
K
K
87. (D) First we write the solubility reaction for AgBr. Then we calculate values of
H
and
S for the reaction: 2
eq sp
AgBr(s) Ag (aq) Br (aq) [Ag ][Br ]KK s
AgBr(s)][](aq)Br[)](aqAg[ fff HHHH
kJ/mol4.84)kJ/mol4.100(kJ/mol6.121kJ/mol6.105
]AgBr(s)[](aq)Br[](aq)Ag[ SSSS
11111111 KmolJ0.48KmolJ1.107KmolJ4.82KmolJ68.72
These values are then used to determine the value of
G for the solubility reaction, and the
standard free energy change, in turn, is used to obtain the value of K.
31 11 3
321.4 10 2
5sp
84.4 10 J mol (100 273)K 48.0J mol K 66.5 10 J/mol
66. 10
ln 21.4 e 5.0 10 s
8.3145J 373K
mol K
GHTS
G
KKK
RT
And now we compute the solubility of AgBr in mg/L.
AgBr/Lmg2.4
g1
mg1000
AgBrmol1
AgBrg187.77
100.5 10
s

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
987
88. (M) S298.15 = S274.68 + Sfusion + Sheating
S298.15 = 67.15 J K- mol-1 + -1
12,660 J mol
274.68 K +
298.15
2
274.68
JJ
97.78 + 0.0586 274.68
mol K mol K T
S298.15 = 67.15 J K-1 mol-1 + 46.09 J K-1 mol-1 + 8.07 J K-1 mol-1 = 121.3 J K-1 mol-1
89. (M) S = Ssolid + Sfusion + Sheating + Svaporization + Spressure change
S = 128.82 J K-1 mol-1 + -1
9866 J mol
278.68 K +298.15
278.68
J
134.0 mol K
T
dT
+ -1
33,850 J mol
298.15 K
+ 8.3145 J K-1 mol-1 × 95.13 torr
ln 760 torr
S
= 128.82 J K-1 mol-1 + 35.40 J K-1 mol-1 + 9.05 J K-1 mol-1 + 113.5 J K-1 mol-1 + (-17.28 J K-1 mol-1 )
S
= 269.53 J K-1 mol-1
90. (D) Start by labeling the particles A, B and C. Now arrange the particles among the states.
One possibility includes A, B, and C occupying one energy state (=0,1,2 or 3). This counts as
one microstate. Another possibility is two of the particles occupying one energy state with the
remaining one being in a different state. This possibility includes a total of three microstates.
The final set of combinations is one with each particle being in different energy state. This
combination includes a total of six microstates. Therefore, the total number of microstates in the
system is 10. See pictorial representation on the following page illustrating the three different
cases.
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
988
=0
=1
=2
=3
ABC
=0
=1
=2
=3
AB
C
1 microstate
=0
=1
=2
=3
A
B
C
1 microstate
=0
=1
=2
=3
B
A
C
1 microstate
1 microstate
3 microstates
=0
=1
=2
=3
A
B
C
1 microstate
=0
=1
=2
=3
1 microstate
=0
=1
=2
=3
1 microstate
=0
=1
=2
=3
1 microstate
=0
=1
=2
=3
1 microstate
=0
=1
=2
=3
1 microstate
6 microstates
B
A
C
C
A
B
A
C
B
B
C
A
C
B
A
All particles are in a single
energy level ( i.e. =0)
Two particles are in one energy level (i.e. =0) and the remaining
particle is in a different level (i.e. =2)
All particles are in different energy levels (i.e. =0, 1 and 2)
91. (M) (a) In the solid as the temperature increases, so do the translational, rotational, and
vibrational degrees of freedom. In the liquid, most of the vibrational degrees of freedom are
saturated and only translational and rotational degrees of freedom can increase. In the gas phase,
all degrees of freedom are saturated. (b) The increase in translation and rotation on going from
solid to liquid is much less than on going from liquid to gas. This is where most of the change in
entropy is derived.
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
989
92. (D) Because KNO3 is a strong electrolyte, its solution reaction will be:
32 3
() () ()KNO s H O K aq NO aq
This reaction can be considered to be at equilibrium when the solid is in contact with a
saturated solution, i.e. the conditions when crystallization begins. The solubility, s, of the
salt, in moles per liter, can be calculated from the amount of salt weighted out and the
volume of the solution. The equilibrium constant K for the reaction will be:
K=[K+(aq)][NO3
-(aq)]=(s)(s)=s2
In the case of 25.0 mL solution at 340 K, the equilibrium constant K is:
n(KNO3)m
M20.2g
101.103gmol10.200mol s= n
V0.200mol
0.0250L 8.0molL-1
Ks28264
The equilibrium constant K can be used to calculate G for the reaction using G=-RTlnK:
G8.314J
K
-1
m
ol-1 340
K
ln64
12
k
J
m
ol-1
The values for K and G at all other temperatures are summarized in the table below.
Volume (mL) T/(K) 1/T (K-1) s (molL-1) K lnK
G (kJmol-1)
25.0 340 0.00294 8.0 64 4.2 -12
29.2 329 0.00304 6.9 48 3.9 -11
33.4 320 0.00312 6.0 36 3.6 -9.6
37.6 313 0.00320 5.3 28 3.3 -8.6
41.8 310 0.00322 4.8 23 3.1 -8.0
46.0 306 0.00327 4.3 18.5 2.9 -7.4
51.0 303 0.00330 3.9 15 2.7 -6.8
The plot of lnK v.s. 1/T provides H (slope=-H/R) and S (y-intercept=S/R) for the
reaction:
2.5
3
3.5
4
4.5
0.0029 0.003 0.0031 0.0032 0.0033 0.0034
y = 16.468 - 4145.7x R= 0.99156
ln K
1/T (K-1)
Hslope R4145.7 8.314JK-1mol-1 34.5kJmol1
Syintercept R16.468 8.314JK-1mol-1 136.9JK-1mol-1

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
990
H for the crystallization process is -35.4 kJmol-1. It is negative as expected because
crystallization is an exothermic process. Furthermore, the positive value for S shows that
crystallization is a process that decreases the entropy of a system.
FEATURE PROBLEMS
93. (M) (a) The first method involves combining the values ofGf
o. The second uses
G
H
T
S
oo o
=
o
f2 f2
=HOg HOl
= 228.572 kJ/mol 237.129 kJ/mol = +8.557 kJ/mol
GG G
o
f2 f2
=HOg HOl
= 241.818 kJ/mol 285.830 kJ/mol = +44.012 kJ/mol
HH H
oo o
22
11 11 11
=HOg HOl
=188.825 J mol K 69.91 J mol K = +118.92 J mol K
SS S
oo o
311
=
= 44.012 kJ/mol 298.15 K 118.92 10 kJ mol K = +8.556 kJ/mol
GHTS
(b) We use the average value: o3
= +8.558 10 J/mol = lnGRTK
3.452
11
8558 J/mol
ln = = 3.452; = e = 0.0317 bar
8.3145 J mol K 298.15 K
KK
(c) 2
1atm 760mmHg
{H O} = 0.0317 bar = 23.8mmHg
1.01325bar 1atm
P
(d) 11
8590 J/mol
ln = = 3.465
8.3145 J mol K 298.15 K
K
;
3.465
7
= e = 0.0312 atmK;
2
760mmHg
{H O} = 0.0313atm = 23.8 mmHg
1atm
P
94. (D) (a) When we combine two reactions and obtain the overall value ofGo, we subtract
the value on the plot of the reaction that becomes a reduction from the value on the
plot of the reaction that is an oxidation. Thus, to reduce ZnO with elemental Mg, we
subtract the values on the line labeled “2+ 2
2
Zn O ZnO” from those on the line
labeled “2+ 2
2
Mg O MgO”. The result for the overall
Go will always be
negative because every point on the “zinc” line is above the corresponding point on
the “magnesium” line
(b) In contrast, the “carbon” line is only below the “zinc” line at temperatures above about
1000C . Thus, only at these elevated temperatures can ZnO be reduced by carbon.
Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
991
(c) The decomposition of zinc oxide to its elements is the reverse of the plotted reaction,
the value of Go for the decomposition becomes negative, and the reaction becomes
spontaneous, where the value of
Go for the plotted reaction becomes positive. This
occurs above about 1850C.
(d) The “carbon” line has a negative slope, indicating that carbon monoxide becomes
more stable as temperature rises. The point where CO(g) would become less stable
than 2C(s) and O2(g) looks to be below
1000C (by extrapolating the line to lower
temperatures). Based on this plot, it is not possible to decompose CO(g) to C(s) and
O2g
in a spontaneous reaction.
(e)
Reaction 1
2 CO(g) + O2(g) 2 CO2(g)
Reaction 2
C(s) + O2(g) CO2(g)
Reaction 3
2 C(s) + O2(g) 2 CO(g)
All three lines are straight-line plots of G vs. T following the equation G = H TS.
The general equation for a straight line is given below with the slightly modified
Gibbs Free-Energy equation as a reference: G = STH (here H assumed
constant)
y = mx + b (m = S = slope of the line)
Thus, the slope of each line multiplied by minus one is equal to the S for the oxide
formation reaction. It is hardly surprising, therefore, that the slopes for these lines
differ so markedly because these three reactions have quite different S values (S
for Reaction 1 = -173 J K1, S for Reaction 2 = 2.86 J K1, S for Reaction 3
= 178.8 J K1)
(f) Since other metal oxides apparently have positive slopes similar to Mg and Zn, we
can conclude that in general, the stability of metal oxides decreases as the
temperature increases. Put another way, the decomposition of metal oxides to their
elements becomes more spontaneous as the temperature is increased. By contrast,
the two reactions involving elemental carbon, namely Reaction 2 and Reaction 3,
have negative slopes, indicating that the formation of CO2(g) and CO(g) from
graphite becomes more favorable as the temperature rises. This means that the G
for the reduction of metal oxides by carbon becomes more and more negative with
-700
-600
-500
-400
-300
-200
-100
0
0 500 1000 1500 2000
Temperature (°C)
Standard Free Energy Change
(kJ)
3
1
2

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
992
increasing temperature. Moreover, there must exist a threshold temperature for each
metal oxide above which the reaction with carbon will occur spontaneously. Carbon
would appear to be an excellent reducing agent, therefore, because it will reduce
virtually any metal oxide to its corresponding metal as long as the temperature
chosen for the reaction is higher than the threshold temperature (the threshold
temperature is commonly referred to as the transition temperature).
Consider for instance the reaction of MgO(s) with graphite to give CO2(g) and Mg metal:
2 MgO(s) + C(s)
2 Mg(s) + CO2(g) Srxn = 219.4 J/K and
rxn = 809.9 kJ
T
transition = o
rxn
o
rxn
H
S
= 1
809.9 kJ
0.2194 kJ K
= 3691 K = Tthreshold
Consequently, above 3691 K, carbon will spontaneously reduce MgO to Mg metal.
95. (D) (a) With a 36% efficiency and a condenser temperature (Tl) of 41 °C = 314 K,
h1
h
efficiency 100% 36%
TT
T
h
h
314 0.36
T
T
;
Th = (0.36 T h) + 314 K; 0.64 Th = 314 K; Th = 4.9
102 K
(b) The overall efficiency of the power plant is affected by factors other than the
thermodynamic efficiency. For example, a portion of the heat of combustion of the
fuel is lost to parts of the surroundings other than the steam boiler; there are
frictional losses of energy in moving parts in the engine; and so on. To compensate
for these losses, the thermodynamic efficiency must be greater than 36%. To obtain
this higher thermodynamic efficiency, Th must be greater than 4.9 102 K.
(c) The steam pressure we are seeking is the vapor pressure of water at 4.9 102 K. We
also know that the vapor pressure of water at 373 K (100 °C) is 1 atm. The enthalpy of
vaporization of water at 298 K is H° = Hf°[H2O(g) Hf°[H2O(l)] = 241.8 kJ/mol
(285.8 kJ/mol) = 44.0 kJ/mol. Although the enthalpy of vaporization is somewhat
temperature dependent, we will assume that this value holds from 298 K to 4.9 102
K, and make appropriate substitutions into the Clausius-Clapeyron equation.
133 3
2
31
44.0 kJ mol 1 1
ln = = 5.29 10 2.68 10 2.04 10
1 atm 8.3145 10 kJ mol 373 K 490 K
P
2
ln = 3.39
1atm
P
;
P
2
1atm
= 29.7 ; P2 30 atm
The answer cannot be given with greater certainty because of the weakness of the
assumption of a constant H°vapn.
(d) It is not possible to devise a heat engine with 100% efficiency or greater. For 100%
efficiency, Tl = 0 K, which is unattainable. To have an efficiency greater than 100 %
would require a negative Tl, which is also unattainable.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
993
96. (D) (a) Under biological standard conditions:
ADP3– + HPO42– + H+ ATP4–+ H2O Go' = 32.4 kJ/mol
If all of the energy of combustion of 1 mole of glucose is employed in the
conversion of ADP to ATP, then the maximum number of moles ATP produced is
1
1
2870 kJ mol
Maximum number = 88.6 moles ATP
32.4 kJ mol
(b) In an actual cell the number of ATP moles produced is 38, so that the efficiency is:
number of ATP's actually produced 38
Efficiency = 0.43
Maximum number of ATP's that can be produced 88.6
Thus, the cell’s efficiency is about 43%.
(c) The previously calculated efficiency is based upon the biological standard state. We
now calculate the Gibbs energies involved under the actual conditions in the cell. To
do this we require the relationship between G and G' for the two coupled
reactions. For the combustion of glucose we have
GGo
RT ln aCO2
6aH2O
6
agluaO2
6
For the conversion of ADP to ATP we have
GGo
RT ln aATPaH2O
aADPaPiH+
/107
Using the concentrations and pressures provided we can calculate the Gibbs energy
for the combustion of glucose under biological conditions. First, we need to replace
the activities by the appropriate effective concentrations. That is,
GGo
RT ln p/po
CO2
6aH2O
6
glu
/glu
op/po
O2
6
using 2
HO 1a
for a dilute solution we obtain
66
6
0.050 bar /1 bar 1
ln glu /1 0.132 bar /1 bar
GGRT
The concentration of glucose is given in mg/mL and this has to be converted to
molarity as follows:
1
1
1.0 mg g 1000 mL 1
[glu] = 0.00555 mol L
mL 1000 mg L 180.16 g mol
,
where the molar mass of glucose is 180.16 g mol1.
Assuming a temperature of 37 oC for a biological system we have, for one mole of
glucose:

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
994
66
31
6
0.050 1
2870 10 J 8.314JK 310K ln 0.00555/1 0.132
G
G2870 103J8.314JK1310K ln 2.954 103
0.00555
31
2870 10 J 8.314JK 310K ln 0.5323G
31
2870 10 J 8.314JK 310K 0.6305G
G2870 103J1.625 103J
G2872 103J
In a similar manner we calculate the Gibbs free energy change for the conversion of
ADP to ATP:
GGo
RT ln ATP
/11
ADP
/1P
i
/1(H
/107)
31
77
0.0001
32.4 10 J 8.314JK 310K ln 0.0001 0.0001 (10 /10 )
G
31 4
32.4 10 J 8.314JK 310K ln 10G
31 3 33
32.4 10 J 8.314JK 310K 9.2103) 32.4 10 J 23.738 10 J 56.2 10 JG
(d) The efficiency under biological conditions is
number of ATP's actually produced 38
Efficiency = 0.744
Maximum number of ATP's that can be produced 2872/56.2
Thus, the cell’s efficiency is about 74%.
The theoretical efficiency of the diesel engine is:
h1
h
1923 873
Efficiency 100% 100% 55%
1923
TT
T
Thus, the diesel’s actual efficiency is 0.78 55 % = 43 %.
The cell’s efficiency is 74% whereas that of the diesel engine is only 43 %. Why is
there such a large discrepancy? The diesel engine supplies heat to the surroundings,
which is at a lower temperature than the engine. This dissipation of energy raises the
temperature of the surroundings and the entropy of the surroundings. A cell operates
under isothermal conditions and the energy not utilized goes only towards changing
the entropy of the cell’s surroundings. The cell is more efficient since it does not
heat the surroundings.

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
995
97. (E) (a) In this case CO can exist in two states, therefore, W=2. There are N of these
states in the crystal, and so we have
S
k
ln2N1.3811023J
K
-1
6.022
1023
m
ol-1 ln2
5.8J
K
-1
m
ol-1
(b) For water, W=3/2, which leads to
Skln( 3
2)N1.3811023JK-1 6.022 1023 mol-1 ln1.5 3.4JK-1mol-1
SELF-ASSESSMENT EXERCISES
98. (E) (a) Suniv or total entropy contains contributions from the entropy change of the
system ( Ssys ) and the surroundings (
Ssurr ). According to the second law of
thermodynamics, Suniv is always greater then zero.
(b) Gf
o or standard free energy of formation is the free energy change for a reaction in
which a substances in its standard state is formed from its elements in their reference
forms in their standard states.
(c) For a hypothetical chemical reaction
aA+bB cC+dD, the equilibrium constant K is
defined as K[C]c[D]d
[A]a[B]b.
99. (E) (a) Absolute molar entropy is the entropy at zero-point energy (lowest possible
energy state) and it is equal to zero.
(b) Coupled reactions are spontaneous reactions (G<0) that are obtained by pairing
reactions with positive G with the reactions with negative G.
(c) Trouton’s rule states that for many liquids at their normal boiling points, the standard
molar entropy of vaporization has a value of approximately 87 Jmol-1K-1.
(d) Equilibrium constant K for a certain chemical reaction can be evaluated using either
Gf
o or Hf
o in conjunction with
S
o (which are often tabulated). The relationship used
to calculate K is
G
o
R
T
ln
K
.
100. (E) (a) A spontaneous process is a process that occurs in a system left to itself; once
started, no external action form outsize the system is necessary to make the process
continue. A nonspontaneous process is a process that will not occur unless some external
action is continuously applied.
(b) Second law of thermodynamics states that the entropy of universe is always greater
than zero or in other words that all spontaneous processes produce an increase in the
entropy of the universe. The third law of thermodynamics states that the entropy of
perfect pure crystal at 0K is zero.
(c) G is the Gibbs free energy defined as G=H-TS. G0 is the standard free energy
change.
101. (E) Second law of thermodynamics states that all spontaneous processes produce an
increase in the entropy of the universe. In other words,
Suniv Ssys Ssurr 0.
Therefore, the correct answer is (d).

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
996
102. (E) The Gibbs free energy is a function of H, S and temperature T. It cannot be used
to determine how much heat is absorbed from the surroundings or how much work the
system does on the surroundings. Furthermore, it also cannot be used to determine the
proportion of the heat evolved in an exothermic reaction that can be converted to various
forms of work. Since Gibbs free energy is related to the equilibrium constant of a
chemical reaction (
G
R
T
ln
K
) its value can be used to access the net direction in
which the reaction occurs to reach equilibrium. Therefore, the correct answer is (c).
103. (M) In order to answer this question, we must first determine whether the entropy
change for the given reaction is positive or negative. The reaction produces three moles
of gas from two moles, therefore there is an increase in randomness of the system, i.e.
entropy change for the reaction is positive. Gibbs free energy is a function of enthalpy,
entropy and temperature (
G
H
T
S
). Since
H
0 and
S
0 , this reaction
will be spontaneous at any temperature. The correct answer is (a).
104. (M) Recall that
G
o
R
T
ln
K
. If
G
o
0 , then it follows that
G
o
R
T
ln
K
0.
Solving for K yields: lnK0Ke01. Therefore, the correct answer is (b).
105. (E) In this reaction, the number of moles of reactants equals the number of moles of
products. Therefore, K is equal to Kp and Kc. The correct answers are (a) and (d).
106. (M) (a) The two lines will intersect at the normal melting point of I2(s) which is 113.6
oC. (b)
G
o for this process must be equal to zero because solid and liquid are at
equilibrium and also in their standard states.
107. (M) (a) No reaction is expected because of the decrease in entropy and the expectation
that the reaction is endothermic. As a check with data from Appendix D,
G
o=326.4
kJmol-1 for the reaction as written-a very large value. (b) Based on the increase in
entropy, the forward reaction should occur, at least to some extent. For this reaction
G
o=75.21 kJmol-1. (c) Sis probably small, and
H
is probably also small (one Cl-Cl
bond and one Br-Br bonds are broken and two Br-Cl bonds are formed).
G
o should be
small and the forward reaction should occur to a significant extent. For this reaction
G
o=-5.07 kJmol-1.
108. (M) (a) Entropy change must be accessed for the system and its surroundings (
Suniv ),
not just for the system alone. (b) Equilibrium constant can be calculated from
G
o(
G
o
R
T
ln
K
), and K permits equilibrium calculations for nonstandard
conditions.
109. (D) (a) First we need to determine Hvap
o which is simply equal to:
Hvap
oHf
o[(C5H10 (g)] Hf
o[(C5H10 (l)] 77.2kJ/mol (105.9kJ/mol) 28.7kJ/mol . Now
we use Trouton’s rule to calculate the boiling point of cyclopentane:

Chapter 19: Spontaneous Change: Entropy and Gibbs Energy
997
Svap
oHvap
o
Tbp
87Jmol-1K-1 Tbp Hvap
o
87Jmol-1K-1 28.7 1000Jmol-1
87Jmol-1K-1 330K
Tbp 330K273.15K57oC
(b) If we assume that Hvap
o and Svap
oare independent of T we can calculate Gvap
o:
Gvap,298K
oHvap
oTSvap
o28.7kJmol-1 298.15K87
1000 kJK-1mol-1 2.8kJmol-1
(c) Because Gvap,298K
o>0, the vapor pressure is less than 1 atm at 298 K, consistent with
T
bp=57 oC.
110. (M) (a) We can use the data from Appendix D to determine the change in enthalpy and
entropy for the reaction:
HoHf
o(N2O(g)) 2Hf
o(H2O(l)) Hf
o(NH4NO3(s))
Ho82.05kJmol-1 2(285.8kJmol-1 )(365.6kJmol-1 )124kJmol-1
SoSo(N2O(g)) 2So(H2O(l)) So(NH4NO3(s))
So219.9JK-1mol-1 269.91JK-1mol-1 151.1JK-1mol-1 208.6JK-1mol-1
(b) From the values of
H
oand
S
odetermined in part (a) we can calculate
G
o at
298K:
GoHoTSo
Go124kJmol-1 298K208.6kJmol-1K-1
1000 186.1kJmol-1
Alternatively,
G
o can also be calculated directly using Gf
ovalues tabulated in
Appendix D.
(c) The equilibrium constant for the reaction is calculated using
G
o
R
T
ln
K
:
GoRT ln K186.11000Jmol-1 8.314JK-1mol-1 298Kln K
186100J
m
ol-1 2477.6ln
K
ln
K
75.1
K
e75.1
4.1
1032
(d) The reaction has
H
o0 and
S
o0 . Because
G
o
H
o
T
S
o, the reaction
will be spontaneous at all temperatures.
111. (M) Recall from exercise 104 that
G
o
0 when K=1. Therefore, we are looking for
the diagram with smallest change in Gibbs free energy between the products and the
reactants. The correct answer is diagram (a). Notice that diagrams (b) and (c) represent
chemical reactions with small and large values of equilibrium constants, respectively.
112. (M) Carbon dioxide is a gas at room temperature. The melting point of carbon dioxide is
expected to be very low. At room temperature and normal atmospheric pressure this
process is spontaneous. The entropy of the universe if positive.
998
CHAPTER 20
ELECTROCHEMISTRY
PRACTICE EXAMPLES
1A (E) The conventions state that the anode material is written first, and the cathode material is written
last.
Anode, oxidation: Sc s
Sc3+ aq
+3e
Cathode, reduction:
+
{Ag aq +e Ag s } 3
___________________________________
Net reaction Sc s
+3Ag+aq
Sc3+ aq
+3Ag s
1B (E) Oxidation of Al(s) at the anode: Al s
Al3+ aq
+3e
Reduction of Ag+aq
at the cathode: Ag+aq
+eAg s
________________
Overall reaction in cell: Al s
+3Ag+aq
Al3+ aq
+3Ag s
Diagram: 3+ +
Al(s)|Al (aq)||Ag (aq)|Ag(s)
2A (E) Anode, oxidation: Sn s
Sn2+ aq
+2e
Cathode, reduction: {Agaq
1eAg(s)} 2
___________________________________________
Overall reaction in cell: Sn(s)2Ag(aq)Sn2(aq)2Ag(s)
2B (E) Anode, oxidation: {In s
In3+ aq
+3e}2
Cathode, reduction: {Cd2aq
2eCd(s)} 3
___________________________________________
Overall reaction in cell: 2In(s)3Cd2(aq)2In3(aq)3Cd(s)
3A (M) We obtain the two balanced half-equations and the half-cell potentials from Table 20-1.
Oxidation:
2+ 3+
{Fe aq Fe aq + e } 2
o= 0.771VE
Reduction:
2
Cl g + 2e 2Cl aq
o= +1.358VE
Net:
2+ 3+
2
2Fe aq + Cl g 2Fe aq + 2Cl aq
; o
cell = +1.358V 0.771V = +0.587 VE
3B (M) Since we need to refer to Table 20-1, in any event, it is perhaps a bit easier to locate the
two balanced half-equations in the table. There is only one half-equation involving both
Fe2+ aq
and Fe3+ aq
ions. It is reversed and written as an oxidation below. The half-
equation involving MnO4
aq
is also written below. [Actually, we need to know that in
acidic solution Mn2+ aq
is the principal reduction product of MnO4
aq
.]
Oxidation:
2+ 3+
{Fe aq Fe aq + e } 5
o= 0.771VE
Reduction:
+2+
42
MnO aq +8 H aq +5e Mn aq + 4H O(l)
o= +1.51VE
Net:
2+ + 2+ 3+
4 2
MnO aq + 5 Fe aq +8H aq Mn aq +5Fe aq +4H O(l)
anode
cathode
e
-
salt bridge
NO
3-
Ag
+
K
+
Al
3+
Al Ag
Chapter 20: Electrochemistry
999
Ecell
oVV V= +1.51 0.771 = +0.74
4A (M) We write down the oxidation half-equation following the method of Chapter 5, and
obtain the reduction half-equation from Table 20-1, along with the reduction half-cell
potential.
Oxidation: +
224 2
{HCO(aq) 2CO(aq)2H(aq)2e}3
2224
{CO/HCO}E
Reduction:
2+3+
27 2
CrO aq+14H aq+6e 2Cr aq+7HO(l)
o= +1.33VE
Net:
2+3+
27 224 2 2
Cr O aq +8H aq +3H C O aq 2Cr aq +7H O(l) + 6CO g
oo
2224
cell =+1.81V=+1.33V {CO /H C O }; EE o2224
{CO /H C O }=1.33V 1.81V = 0.48VE
4B (M) The 2nd half-reaction must have O2g
as reactant and 2
HO(l) as product.
Oxidation: 2+ 3+
{Cr (aq) Cr (aq) e } 4
32
{Cr /Cr }E
Reduction:
+
22
Og+4Haq+4e 2HO(l)
o= +1.229VE
______________________________________
Net:
+2+ 3+
22
O g +4H aq 4Cr (aq) 2H O(l)+4Cr aq
oo3 2
cell 1.653V 1.229V E {Cr /Cr }E
; o3 2
{Cr /Cr } 1.229V 1.653V 0.424VE
5A (M) First we write down the two half-equations, obtain the half-cell potential for each, and
then calculate Ecell
o. From that value, we determine
G
o
Oxidation:
3+
{Al s Al aq +3e } 2
o= +1.676VE
Reduction:
2
{Br l +2e 2 Br aq } 3
o= +1.065VE
____________________________
Net:
3+ o
2cell
2Al s + 3Br l 2 Al aq + 6Br aq = 1.676V +1.065V = 2.741VE
oo 6
cell
96,485 C
= = 6mol e 2.741V = 1.587 10 J = 1587kJ
1mol e
GnFE
5B (M) First we write down the two half-equations, one of which is the reduction equation from
the previous example. The other is the oxidation that occurs in the standard hydrogen
electrode.
Oxidation:
+
2
2H g 4H aq + 4e
Reduction:
+
22
Og+4Haq+4e 2HO(l)
Net:
22 2
2H g +O g 2HO l =4 in this reaction.n
This net reaction is simply twice the formation reaction for 2
HO(l) and, therefore,
o
o3o
f2 cell
= 2 H O l = 2 237.1 kJ = 474.2 10 J =GG nFE
3
o
o o
cell
474.2 10 J
== 1.229V
96,485C
4mole mole
G
EE
nF
, as we might expect.
6A (M) Cu(s) will displace metal ions of a metal less active than copper. Silver ion is one
example.

Chapter 20: Electrochemistry
1000
Oxidation:
2+ o
Cu s Cu aq + 2e = 0.340VE
(from Table 20.1)
Reduction:
+o
{Ag aq + e Ag s } 2 = +0.800VE
Net:
+2+ o
cell
2Ag aq + Cu s Cu aq + 2Ag s = 0.340V + 0.800V = +0.460VE
6B (M) We determine the value for the hypothetical reaction's cell potential.
Oxidation:
+
{Na s Na aq + e } 2
o= +2.713VE
Reduction:
2+
Mg aq +2e Mg s
o= 2.356VE
Net:
2+ +
2 Na s +Mg aq 2 Na aq + Mg s o
cell = 2.713V 2.356 V = +0.357VE
The method is not feasible because another reaction occurs that has a more positive cell
potential, i.e., Na(s) reacts with water to form H2g
and NaOH(aq):
Oxidation:
+
{Na s Na aq + e } 2
o= +2.713VE
Reduction: 2H2O+2e-H2(g)+2OH-(aq) Eo=-0.828V
Ecell
oVV V= 2.713 0.828 = +1.885.
7A (M) The oxidation is that of SO42 to S2O82, the reduction is that of O2 to H2O.
Oxidation:
22 o
428
{2 SO aq S O aq + 2e } 2 = 2.01VE
Reduction:
+o
22
O g + 4H aq + 4e 2H O(l) = +1.229VE
________________
Net:
22
+
24282
O g+4H aq+2SO aq SO aq+2HO(l)
Ecell = -0.78 V
Because the standard cell potential is negative, we conclude that this cell reaction is
nonspontaneous under standard conditions. This would not be a feasible method of producing
peroxodisulfate ion.
7B (M) (1) The oxidation is that of Sn2+ aq
to Sn4+ aq
; the reduction is that of O2 to
H2O.
Oxidation: {Sn2+ aq
Sn4+ aq
+2e}2Eo=0.154 V
Reduction:
+o
22
O g + 4H aq + 4e 2H O(l) = +1.229VE
___________
Net:
+2+ 4+
2 2
O g +4H aq +2Sn aq 2Sn aq +2H O(l)o
cell = +1.075VE
Since the standard cell potential is positive, this cell reaction is spontaneous under
standard conditions.
(2) The oxidation is that of Sn(s) to Sn2+ aq
; the reduction is still that of O2 to H2O.
Oxidation: {Sn s
Sn2+ aq
+2e}2Eo= +0.137 V
Reduction:
+o
22
O g + 4H aq + 4e 2H O(l) = +1.229VE
_______________
Net:
+2+
22
O g +4H aq +2Sn s 2Sn aq +2H O(l)
o
cell = 0.137V +1.229V = +1.366VE
Chapter 20: Electrochemistry
1001
The standard cell potential for this reaction is more positive than that for situation (1).
Thus, reaction (2) should occur preferentially. Also, if Sn4+ aq
is formed, it should
react with Sn(s) to form Sn2+ aq
.
Oxidation: Sn s
Sn2+ aq
+2eEo= +0.137V
Reduction:
4+ 2+ o
Sn aq + 2e Sn aq = +0.154VE
___________________________________
Net: Sn4+ aq
+Sn s
2Sn2+ aq
Ecell
o= +0.137V + 0.154V = +0.291V
8A (M) For the reaction 2Al s
+3Cu2+ aq
2Al3+ aq
+3Cu s
we know n= 6 and
Ecell
oV= +2.013 . We calculate the value of Keq .
o
o470 204
cell
cell eq eq eq
0.0257 6 (+2.013)
= ln ; ln = = = 470; = e = 10
0.0257 0.0257
nE
EKK K
n
The huge size of the equilibrium constant indicates that this reaction indeed will go to
essentially 100% to completion.
8B (M) We first determine the value of Ecell
o from the half-cell potentials.
Oxidation:
2+
Sn s Sn aq +2e
o
–=+0.137VE
Reduction:
2+
Pb aq +2e Pb s
o= 0.125 VE
_________________________________
Net:
2+ 2+
Pb aq +Sn s Pb s +Sn aq o
cell = +0.137V 0.125V = +0.012VE
o
o0.93
cell
cell eq eq eq
0.0257 2 (+0.012)
= ln ln = = =0.93 = e = 2.5
0.0257 0.0257
nE
EKK K
n
The equilibrium constant's small size (0.001 < K <1000) indicates that this reaction will not
go to completion.
9A (M) We first need to determine the standard cell voltage and the cell reaction.
Oxidation:
3+
{Al s Al aq +3 e } 2
o= +1.676VE
Reduction:
4+ 2+
{Sn aq + 2 e Sn aq } 3
o= +0.154VE
_________________________
Net:
4+ 3+ 2+
2Al s +3Sn aq 2Al aq +3Sn aqo
cell = +1.676V + 0.154V = +1.830 VE
Note that n= 6. We now set up and substitute into the Nernst equation.
Ecell =Ecell
o0.0592
nlog Al3+
2Sn2+
3
Sn4+
3= +1.830 0.0592
6log 0.36M
20.54M
3
0.086M
3
= +1.830V 0.0149V = +1.815V
9B (M) We first need to determine the standard cell voltage and the cell reaction.
Oxidation:
2
2 Cl 1.0 M Cl 1 atm + 2e
o=1.358VE
Reduction:
+2+
22
PbO s + 4H aq + 2e Pb aq + 2H O(l)
o= +1.455 VE
__________________________________________
Chapter 20: Electrochemistry
1002
Net:
+2+
222
PbO s + 4H 0.10 M + 2Cl 1.0 M Cl 1 atm + Pb 0.050 M + 2H O(l)
Ecell
oVV V= 1.358 +1.455 = +0.097 Note that n= 2. Substitute values into the Nernst
equation.
2+
2
o
cell cell 42 4 2
+
P{Cl } Pb 1.0atm 0.050M
0.0592 0.0592
= log = +0.097 log
20.10M 1.0M
HCl
= +0.097 V 0.080 V = +0.017 V
EE n
10A (M) The cell reaction is
3+ 2+ 2+
2 Fe 0.35 M + Cu s 2 Fe 0.25 M +Cu 0.15 M with
n=2and Ecell
oVV V= 0.337 + 0.771 = 0.434 Next, substitute this voltage and the
concentrations into the Nernst equation.
22
2+ 2+
o
cell cell 22
3+
Fe Cu 0.25 0.15
0.0592 0.0592
= log = 0.434 log = 0.434 0.033
20.35
Fe
EE n
cell = +0.467VE Thus the reaction is spontaneous under standard conditions as written.
10B (M) The reaction is not spontaneous under standard conditions in either direction when
Ecell V= 0.000 . We use the standard cell potential from Example 20-10.
Ecell =Ecell
o0.0592
nlog Ag+
2
Hg2+
; 0.000 V = 0.054 V 0.0592
2log Ag+
2
Hg2+
log Ag+
2
Hg2+
=0.054 2
0.0592 =1.82; Ag+
2
Hg2+
=101.82 = 0.0150
11A (M) In this concentration cell Ecell
oV= 0.000 because the same reaction occurs at anode and
cathode, only the concentrations of the ions differ. +
Ag = 0.100 M
in the cathode
compartment. The anode compartment contains a saturated solution of AgCl(aq).
Ks
sp Ag Cl=1.8 10 = =
10 + 2
; 10 5
1.8 10 1.3 10 Ms
Now we apply the Nernst equation. The cell reaction is
Ag+0.100M
Ag+1.3 105M
Ecell log M
MV= 0.000 0.0592
1
1.3 10
0.100 = +0.23
5
11B (D) Because the electrodes in this cell are identical, the standard electrode potentials are
numerically equal and subtracting one from the other leads to the value o
cell = 0.000V.E
However, because the ion concentrations differ, there is a potential difference between the
Chapter 20: Electrochemistry
1003
two half cells (non-zero nonstandard voltage for the cell). 2+
Pb = 0.100 M
in the cathode
compartment, while the anode compartment contains a saturated solution of PbI2.
We use the Nernst equation (with n= 2 ) to determine Pb2+ in the saturated solution.
cell
0.0592 M M 2 0.0567
= +0.0567 V = 0.000 log ; log = = 1.92
2 0.100M 0.100M 0.0592
xx
E
1.92 2+
anode
M=10 = 0.012; Pb = M = 0.012 0.100 M = 0.0012 M;
0.100M
I = 2 0.0012 M 0.0024 M
xx
Ksp =Pb
2+
I
2= 0.0012
0.0024
2=6.9109 compared with 7.1 10 9
in Appendix
D
12A (M) From Table 20-1 we choose one oxidations and one reductions reaction so as to get the
least negative cell voltage. This will be the most likely pair of ½ -reactions to occur.
Oxidation:
2
2I aq I s + 2 e
o= 0.535 VE
+
22
2H O(l) O g +4H aq +4e
o= 1.229VE
Reduction:
+
Kaq+e Ks
o= 2.924 VE
22
2H O(l)+2e H g +2OH aq
o= 0.828 VE
The least negative standard cell potential 0.535V 0.828V = 1.363V
occurs when I2s
is
produced by oxidation at the anode, and H2g
is produced by reduction at the cathode.
12B (M) We obtain from Table 20-1 all the possible oxidations and reductions and choose one of each
to get the least negative cell voltage. That pair is the most likely pair of half-reactions to occur.
Oxidation:
+o
22
2H O(l) O g + 4H aq + 4e = 1.229VE
Ag s
Ag+aq
+eEo=0.800V
[We cannot further oxidize NO3
aq
or Ag+aq
.]
Reduction:
+o
Ag aq + e Ag s = +0.800VE
o
22
2H O(l) + 2e H g + 2OH aq = 0.828VE
Thus, we expect to form silver metal at the cathode and Ag+aq
at the anode.
13A (M) The half-cell equation is Cu2+ aq
+2eCu s
, indicating that two moles of
electrons are required for each mole of copper deposited. Current is measured in amperes, or
coulombs per second. We convert the mass of copper to coulombs of electrons needed for the
reduction and the time in hours to seconds.
Chapter 20: Electrochemistry
1004
Current
12.3 gCu 1molCu
63.55gCu 2mole
1molCu96,485 C
1mole
5.50h 60 min
1h 60 s
1min
3.735 104C
1.98 104s1.89 amperes
13B (D) We first determine the moles of O2g
produced with the ideal gas equation.
2 2
1atm
738 mmHg 2.62 L
760 mmHg
molesO (g) 0.104 molO
0.08206 Latm 26.2 273.2 K
mol K
Then we determine the time needed to produce this amount of O2.
elapsed time mol O mol e
mol O
C
mol e
s
C
h
sh= 0.104 4
1
96,485
1
1
2.13
1
3600 = 5.23
2
2
INTEGRATIVE EXAMPLE
14A (D) In this problem we are asked to determine
E
o for the reduction of CO2(g) to C3H8(g) in
an acidic solution. We proceed by first determining
Go for the reaction using tabulated
values for Gf
o in Appendix D. Next, Ecell
o for the reaction can be determined using
GozFEcell
o. Given reaction can be separated into reduction and oxidation. Since we are
in acidic medium, the reduction half-cell potential can be found in Table 20.1. Lastly, the
oxidation half-cell potential can be calculated using
Ecell
oEo(reduction half-cell) Eo(oxidation half-cell).
Stepwise approach
First determine Go for the reaction using tabulated values for Gf
o in Appendix D:
C3H8(g) + 5O2(g) 3CO2(g) + 4H2O(l)
Gf
o -23.3 kJ/mol 0 kJ/mol -394.4 kJ/mol -237.1 kJ/mol
Go3Gf
o(CO2(g)) 4Gf
o(H2O(l)) [Gf
o(C3H8(g)) 5Gf
o(O2(g))]
Go3(394.4) 4(237.1) [23.350]kJ/mol
Go2108
k
J
/
m
ol
In order to calculate Ecell
o for the reaction using GozFEcell
o, z must be first determined.
We proceed by separating the given reaction into oxidation and reduction:
Reduction: 5{O2(g)+4H+(aq)+4e- 2H2O(l)} Eo=+1.229 V
Oxidation: C3H8(g) + 6H2O(l) 3CO2(g) + 20H+ + 20e- Eo=xV
_____________________________________________________
Overall: C3H8(g) + 5O2(g) 3CO2(g) + 4H2O(l) Eo=+1.229 V-xV
Since z=20,
Ecell
o can now be calculated using GozFEcell
o:
Chapter 20: Electrochemistry
1005
GozFEcell
o
2108 1000J/mol 20mol e-96485C
1mol e-Ecell
o
Ecell
o2108 1000
20 96485 V1.092V
Finally, Eo(reduction half-cell) can be calculated using
Ecell
oEo(reduction half-cell) Eo(oxidation half-cell):
1.092 V = 1.229 V – Eo(oxidation half-cell) V
Eo(oxidation half-cell) =1.229 V – 1.092 V = 0.137 V
Therefore, Eo for the reduction of CO2(g) to C3H8(g) in an acidic medium is 0.137 V.
Conversion pathway approach:
Reduction: 5{O2(g)+4H+(aq)+4e- 2H2O(l)} Eo=+1.229 V
Oxidation: C3H8(g) + 6H2O(l) 3CO2(g) + 20H+ + 20e- Eo=x V
_____________________________________________________
Overall: C3H8(g) + 5O2(g) 3CO2(g) + 4H2O(l) Eo=+1.229 V-x V
Gf
o -23.3 kJ/mol 0 kJ/mol -394.4 kJ/mol -237.1 kJ/mol
Go3Gf
o(CO2(g)) 4Gf
o(H2O(l)) [Gf
o(C3H8(g)) 5Gf
o(O2(g))]
Go3(394.4) 4(237.1) [23.350]kJ/mol
Go2108
k
J
/
m
ol
GozFEcell
o
2108 1000J/mol 20mol e-96485C
1mol e-Ecell
o
Ecell
o2108 1000
20 96485 V1.092V
1.092 V = 1.229 V – Eo(oxidation half-cell) V
Eo(oxidation half-cell) =1.229 V – 1.092 V = 0.137 V
14B (D) This is a multi component problem dealing with a flow battery in which oxidation
occurs at an aluminum anode and reduction at a carbon-air cathode. Al3+ produced at the
anode is complexed with OH- anions from NaOH(aq) to form [Al(OH)4]-.
Stepwise approach:
Part (a): The flow battery consists of aluminum anode where oxidation occurs and the formed
Al3+ cations are complexes with OH- anions to form [Al(OH)4]-. The plausible half-reaction
for the oxidation is:
Oxidation: Al(s) + 4OH-(aq) [Al(OH)4]- + 3e-
The cathode, on the other hand consists of carbon and air. The plausible half-reaction for the
reduction involves the conversion of O2 and water to form OH- anions (basic medium):
Reduction: O2(g) + 2H2O(l) + 4e- 4OH-(aq)
Combining the oxidation and reduction half-reactions we obtain overall reaction for the
process:
Oxidation: {Al(s) + 4OH-(aq) [Al(OH)4]- + 3e-}4
Chapter 20: Electrochemistry
1006
Reduction: {O2(g) + 2H2O(l) + 4e- 4OH-(aq)} 3
____________________________________________
Overall: 4Al(s) + 4OH-(aq) +3O2(g) + 6H2O(l) 4[Al(OH)4]-(aq)
Part(b): In order to find Eo for the reduction, use the known value for Ecell
oas well as Eo for
the reduction half-reaction from Table 20.1:
Ecell
oEo(reduction half-cell) Eo(oxidation half-cell)
Ecell
o0.401VEo(oxidation half-cell) 2.73V
Eo(oxidation half-cell) 0.401V2.73V2.329V
Part (c): From the given value for Ecell
o (+2.73V) first calculate
Gousing GozFEcell
o
(notice that z=12 from part (a) above):
GozFEcell
o12mol e-96485C
1mol e-2.73V
Go3161kJ/mol
Given the overall reaction (part (a)) and Gf
o for OH-(aq) anions and H2O(l), we can
calculate the Gibbs energy of formation of the aluminate ion, [Al(OH)4]-:
Overall reaction: 4Al(s) + 4OH-(aq) + 3O2(g) + 6H2O(l) 4[Al(OH)4]-(aq)
Gf
o 0 kJ/mol -157 kJ/mol 0 kJ/mol -237.2 kJ/mol x
Go4x[4 04(157) 306(237.2)kJ/mol 3161kJ/mol
4x31612051.2 5212.2kJ/mol
x
1303
k
J
/
m
ol
Therefore,
Gf
o([Al(OH )4])1303kJ/mol
Part(d): First calculate the number of moles of electrons:
number of mol ecurrent(C/s)time(s) 1mol e-
96485C
number of mol e4.00h60min
1h60s
1min 10.0 C
s1mol e-
96485C
nu
m
b
e
r
of
m
ol e1.49
m
ol e-
Now, use the oxidation half-reaction to determine the mass of Al(s) consumed:
mass(Al)1.49mol e-1mol Al
3mol e-26.98g Al
1mol Al 13.4g
Conversion pathway approach:
Part (a):
Oxidation: {Al(s) + 4OH-(aq) [Al(OH)4]- + 3e-}4
Reduction: {O2(g) + 2H2O(l) + 4e- 4OH-(aq)} 3
____________________________________________
Overall: 4Al(s) + 4OH-(aq) +3O2(g) + 6H2O(l) 4[Al(OH)4]-(aq)
Part (b):

Chapter 20: Electrochemistry
1007
Ecell
oEo(reduction half-cell) Eo(oxidation half-cell)
Ecell
o0.401VEo(oxidation half-cell) 2.73V
Eo(oxidation half-cell) 0.401V2.73V2.329V
Part (c):
GozFEcell
o12mol e-96485C
1mol e-2.73V
Go3161kJ/mol
Overall reaction: 4Al(s) + 4OH-(aq) + 3O2(g) + 6H2O(l) 4[Al(OH)4]-(aq)
Gf
o 0 kJ/mol -157 kJ/mol 0 kJ/mol -237.2 kJ/mol x
Go4x[4 04(157) 306(237.2)kJ/mol 3161kJ/mol
4x31612051.2 5212.2kJ/mol
xGf
o([Al(OH )4])1303kJ/mol
Part (d):
number of mol ecurrent(C/s)time(s) 1mol e-
96485C
number of mol e4.00h60min
1h60s
1min 10.0 C
s1mol e-
96485C
nu
m
b
e
r
of
m
ol e1.49
m
ol e-
mass(Al)1.49mol e-1mol Al
3mol e-26.98g Al
1mol Al 13.4g
EXERCISES
Standard Electrode Potential
1. (E) (a) If the metal dissolves in HNO3, it has a reduction potential that is smaller than
o
3
NO aq /NO g = 0.956VE. If it also does not dissolve in HCl, it has a
reduction potential that is larger than
o+
2
H aq /H g = 0.000VE. If it displaces
Ag+aq
from solution, then it has a reduction potential that is smaller than
o+
Ag aq /Ag s = 0.800VE. But if it does not displace Cu2+ aq
from solution,
then its reduction potential is larger than
o2+ o
Cu aq /Cu s = 0.340V Thus, 0.340 V 0.800VEE
(b) If the metal dissolves in HCl, it has a reduction potential that is smaller than
o+
2
H aq /H g = 0.000 VE. If it does not displace Zn2+ aq
from solution, its
reduction potential is larger than
o2+
Zn aq /Zn s = 0.763 VE. If it also does not
displace Fe2+ aq
from solution, its reduction potential is larger than

Chapter 20: Electrochemistry
1008
o2+
Fe aq /Fe s = 0.440 VE. 0.440 0.000VV
o
E
2. (E) We would place a strip of solid indium metal into each of the metal ion solutions and see
if the dissolved metal plates out on the indium strip. Similarly, strips of all the other metals
would be immersed in a solution of In3+ to see if indium metal plates out. Eventually, we
will find one metal whose ions are displaced by indium and another metal that displaces
indium from solution, which are adjacent to each other in Table 20-1. The standard
electrode potential for the In/In3+(aq) pair will lie between the standard reduction potentials
for these two metals. This technique will work only if indium metal does not react with
water, that is, if the standard reduction potential of In3+ aq
/In s
is greater than about
1.8 V. The inaccuracy inherent in this technique is due to overpotentials, which can be as
much as 0.200 V. Its imprecision is limited by the closeness of the reduction potentials for
the two bracketing metals
3. (M) We separate the given equation into its two half-equations. One of them is the reduction
of nitrate ion in acidic solution, whose standard half-cell potential we retrieve from Table 20-1
and use to solve the problem.
Oxidation: 2
4
{Pt(s) 4Cl (aq) [PtCl ] (aq) 2 e } 3
; o2
4
{[PtCl ] (aq)/Pt(s)}E
Reduction:
+
32
{NO aq +4H aq +3e NO g +2H O(l)} 2
; o= +0.956VE
Net: 3Pt s
+2NO3
aq
+8H+aq
+12Claq
3PtCl
4
2aq
+2NO g
+6H2Ol
oo2
cell 4
0.201V 0.956 V {[PtCl ] (aq)/Pt(s)}EE
o2
4
{[PtCl ] (aq)/Pt(s)} 0.956V 0.201V 0.755VE
4. (M) In this problem, we are dealing with the electrochemical reaction involving the oxidation
of Na(in Hg) to Na+(aq) and the reduction of Cl2(s) to Cl-(aq). Given that Ecell
o3.20V, we
are asked to find
E
ofor the reduction of Na+ to Na(in Hg). We proceed by separating the
given equation into its two half-equations. One of them is the reduction of Cl (g)
2 to Cl (aq)
whose standard half-cell potential we obtain from Table 20-1 and use to solve the problem.
Stepwise approach:
Separate the given equation into two half-equations:
Oxidation:{Na(in Hg) Na (aq) e } 2
{Na (aq)/ Na(in Hg)}E
Reduction: 2
Cl (g) 2e 2Cl (aq)
1.358 VE
Net: 2
2Na(in Hg) Cl (g) 2 Na (aq) 2Cl (aq)
cell 3.20 VE
Use Ecell
oEo(reduction half-cell) Eo(oxidation half-cell) to solve for
Eo(oxidation half-cell) :
Ecell
o3.20 V=+1.385 V Eo
{Na(aq) / Na(in Hg)}
{Na (aq) / Na(in Hg)} 1.358 V 3.20 V 1.84 V
E
Conversion pathway approach:
Oxidation:{Na(in Hg) Na (aq) e } 2
{Na (aq)/ Na(in Hg)}E

Chapter 20: Electrochemistry
1009
Reduction: 2
Cl (g) 2e 2Cl (aq)
1.358 VE
Net: 2
2Na(in Hg) Cl (g) 2 Na (aq) 2Cl (aq)
cell 3.20 VE
3.20V1.358 Eo{Na(aq)/Na(in Hg)}
Eo{Na(aq)/Na(in Hg)} 1.358V3.20V1.84V
5. (M) We divide the net cell equation into two half-equations.
Oxidation:
4
{Al s + 4 OH aq [Al(OH) ] aq + 3 e } 4
; o
4
{[Al(OH) ] (aq)/Al(s)}E
Reduction:
22
{O g + 2 H O(l) + 4e 4 OH aq } 3
; o= +0.401VE
Net:
22 4
4Al s + 3O g + 6H O(l) + 4OH aq 4[Al(OH) ] aq
o
cell =2.71VE
oo
cell 4
=2.71V=+0.401V {[Al(OH) ] (aq)/Al(s)}EE
o
4
{[Al(OH) ] (aq)/Al(s)} = 0.401V 2.71V = 2.31VE
6. (M) We divide the net cell equation into two half-equations.
Oxidation:
+
42 2
CH g + 2H O(l) CO g +8H aq +8e
o24
CO g /CH gE
Reduction:
+
22
{O g + 4H aq + 4e 2H O(l)} 2
o= +1.229VE
Net:
42 22
CH g + 2 O g CO g + 2HO(l) o
cell =1.06VE
oo
cell 2 4
o24
1.06V 1.229V CO g /CH g
CO g /CH g 1.229V 1.06V 0.17 V
EE
E
7. (M) (a) We need standard reduction potentials for the given half-reactions from Table 10.1:
Ag+(aq)+e- Ag(s) Eo=+0.800 V
Zn2+(aq)+2e- Zn(s) Eo=-0.763 V
Cu2+(aq)+2e- Cu(s) Eo=+0.340 V
Al3+(aq)+3e- Al(s) Eo=-1.676 V
Therefore, the largest positive cell potential will be obtained for the reaction involving the
oxidation of Al(s) to Al3+(aq) and the reduction of Ag+(aq) to Ag(s):
Al(s) + 3Ag+(aq) 3Ag(s)+Al3+(aq) Ecell
o1.676V0.800V2.476V
Ag is the anode and Al is the cathode.
(b) Reverse to the above, the cell with the smallest positive cell potential will be obtained for
the reaction involving the oxidation of Zn(s) to Zn2+(aq) (anode) and the reduction of Cu+2(aq)
to Cu(s) (cathode):
Zn(s) + Cu2+(aq) Cu(s)+Zn2+(aq) Ecell
o0.763V0.340V1.103V
8. (M) (a) The largest positive cell potential will be obtained for the reaction:
Zn(s) + 4NH3(aq) + 2VO2+(aq) + 4H+(aq) [Zn(NH3)4]2+(aq)+2V3+(aq)+2H2O(l)
Ecell
oEo(reduction half-cell) Eo(oxidation half-cell) 0.340V(1.015V)1.355V
Zn is the anode and VO2+ is the cathode.
Chapter 20: Electrochemistry
1010
(b) Reverse to the above, the cell with the smallest positive cell potential will be obtained for the
reaction involving the oxidation of Ti2+(aq) to Ti3+(aq) (anode) and the reduction of Sn+2(aq) to
Sn(s) (cathode):
2Ti2+(aq) + Sn2+(aq) 2Ti3+(aq)+Sn(aq)
Ecell
oEo(reduction half-cell) Eo(oxidation half-cell) 0.14V(0.37V)0.23V
Predicting Oxidation-Reduction Reactions
9. (E) (a) Ni2+, (b) Cd.
10. (E) (a) potassium, (b) barium.
11. (M) (a) Oxidation:
2+
Sn s Sn aq + 2e
o= +0.137 VE
Reduction:
2+
Pb aq +2e Pb s
o=0.125VE
________________________________
Net:
2+ 2+
Sn s + Pb aq Sn aq + Pb s
o
cell = +0.012V SpontaneousE
(b) Oxidation:
2
2I aq I s + 2e
o= 0.535 VE
Reduction:
2+
Cu aq +2e Cu s
o= +0.340VE
________________________
Net:
2+
2
2I aq + Cu aq Cu s + I s
o
cell = 0.195 V NonspontaneousE
(c) Oxidation:
+
22
{2H O(l) O g + 4H aq + 4e } 3
o= 1.229 VE
Reduction:
+
32
{NO (aq) + 4H aq +3e NO g +2H O(l)} 4
o = +0.956 VE
_______________________ _
Net:
+
322
4NO aq + 4H aq 3O g + 4NOg + 2HO(l)
o
cell = 0.273 VE
Nonspontaneous
(d) Oxidation:
2
Cl aq + 2OH aq OCl aq + H O(l) + 2e
o= 0.890VE
Reduction:
32 2
O g + H O(l) + 2 e O g + 2OH aq
o = +1.246 VE
Net:
32
Cl aq + O g OCl aq + O g
(basic solution) o
cell = +0.356VE
Spontaneous
12. (M) It is more difficult to oxidize Hg(l) to Hg2
2+ 0.797V
than it is to reduce H+ to H2
(0.000 V); Hg(l) will not dissolve in 1 M HCl. The standard reduction of nitrate ion to NO(g)
in acidic solution is strongly spontaneous in acidic media ( +0.956V ). This can help overcome
the reluctance of Hg to be oxidized. Hg(l) will react with and dissolve in the HNO3aq
.
13. (M) (a) Oxidation:
2+
Mg s Mg aq + 2 e
o= +2.356VE
Reduction:
2+
Pb aq + 2 e Pb s
o= 0.125VE
_____________________________________
Net:
2+ 2+
Mg s + Pb aq Mg aq + Pb s o
cell = +2.231VE
Chapter 20: Electrochemistry
1011
This reaction occurs to a significant extent.
(b) Oxidation:
2+
Sn s Sn aq + 2e
o= +0.137 VE
Reduction:
+2
2H aq H g o= 0.000VE
________________________________________
Net:
+2+
2
Sn s + 2H aq Sn aq + H g o
cell = +0.137VE
This reaction will occur to a significant extent.
(c) Oxidation:
2+ 4+
Sn aq Sn aq + 2e
o= 0.154VE
Reduction:
2+
422
SO aq+4H aq+2e SO g+2HO(l)
o= + 0.17 VE
________________________
Net:
2
2+ + 4+
422
Sn aq +SO aq + 4H aq Sn aq +SO g + 2H O(l)
o
cell = + 0.02VE
This reaction will occur, but not to a large extent.
(d) Oxidation:
+
22 2
{H O aq O g + 2 H aq + 2e } 5
o= 0.695VE
Reduction:
-+-2+
42
{MnO aq +8H aq +5e Mn aq +4H O(l)} 2
o= +1.51VE
Net:
-+2+
22 4 2 2
5H O aq +2MnO aq +6H aq 5O g +2Mn aq +8H O(l)o
cell = +0.82VE
This reaction will occur to a significant extent.
(e) Oxidation:
o
2
2Br aq Br aq + 2e = 1.065VE
Reduction:
o
2
I s + 2e 2I aq = +0.535VE
__________________________________
Net:
o
22 cell
2Br aq + I s Br aq + 2I aq = 0.530VE
This reaction will not occur to a significant extent.
14. (M) In this problem we are asked to determine whether the electrochemical reaction between
Co(s) and Ni2+(aq) to yield Co2+(aq) + Ni(s) will proceed to completion based on the known
Ecell
ovalue. This question can be answered by simply determining the equilibrium constant.
Stepwise approach
First comment on the value of Ecell
o:
The relatively small positive value of Ecell
o for the reaction indicates that the reaction will
proceed in the forward direction, but will stop short of completion. A much larger positive
value of Ecell
o would be necessary before we would conclude that the reaction goes to
completion.
Calculate the equilibrium constant for the reaction using Ecell
o0.0257
nln Keq :
Ecell
o0.0257
nln Keq ln Keq nEcell
o
0.0257 20.02
0.0257 2
2
eq e7K
Comment on the value of Keq:
Chapter 20: Electrochemistry
1012
K
eq is small. A value of 1000 or more is needed before we can describe the reaction as one
that goes to completion.
Conversion pathway approach:
Ecell
o0.0257
nln Keq
ln Keq nEcell
o
0.0257
Keq e
nEcell
o
0.0257 e
20.02
0.0257 7
K
eq is too small. The reaction does not go to completion.
15. (M) If Ecell
o is positive, the reaction will occur. For the reduction of Cr2O72 to Cr3+ aq
:
2+3+ o
27 2
CrO aq+14H aq+6e 2Cr aq+7HO(l) =+1.33VE
If the oxidation has
E
o smaller (more negative) than
1.33V, the oxidation will not occur.
(a)
2+ 4+ o
Sn aq Sn aq +2e = 0.154VE
Hence, Sn2+ aq
can be oxidized to Sn4+ aq
by Cr2O7
2aq
.
(b)
+o
22 3
I s + 6H O(l) 2IO aq +12 H aq +10e = 1.20VE
I 2s
can be oxidized to IO3
aq
by Cr2O7
2aq
.
(c)
2+ + o
24
Mn aq + 4H O(l) MnO aq +8H aq +5e = 1.51VE
Mn2+ aq
cannot be oxidized to MnO4
aq
by Cr2O7
2aq
.
16. (M) In order to reduce Eu3+ to Eu2+, a stronger reducing agent than Eu2+ is required. From
the list given, Al(s) and H2C2O4(aq) are stronger reducing agents. This is determined by
looking at the reduction potentials (-1.676 V for Al3+/Al(s) and -0.49 V for CO2,
H+/H2C2O4(aq)), are more negative than -0.43 V). Co(s), H2O2 and Ag(s) are not strong
enough reducing agents for this process. A quick look at their reduction potentials shows
that they all have more positive reduction potentials than that for Eu3+ to Eu2+ (-0.277 V for
Co2+/Co(s), +0.695 V for O2, H+/H2O2(aq) and +0.800 V for Ag+/Ag(s).
17. (M) (a) Oxidation:
+
{Ag s Ag aq + e } 3
o= 0.800VE
Reduction:
+
32
NO aq + 4 H aq +3 e NO g + 2H O(l)
o= +0.956VE
______________ _____________
Net:
++
32
3Ags+NO aq+4H aq 3Ag aq+NOg+2HO(l)
o
cell = +0.156VE
Ag(s) reacts with HNO3aq
to form a solution of AgNO3aq
.
(b) Oxidation:
2+
Zn s Zn aq + 2e
o= +0.763VE
Reduction:
+2
2H aq +2e H g
o= 0.000VE
Net:
+2+
2
Zn s + 2H aq Zn aq + H g o
cell = +0.763VE
Zn(s) reacts with HI(aq) to form a solution of
2
ZnI aq .

Chapter 20: Electrochemistry
1013
(c) Oxidation:
3+
Au s Au aq + 3e
o=1.52VE
Reduction:
+
32
NO aq + 4H aq +3e NO g + 2H O(l)
o= +0.956VE
Net:
+3+
32
Au s + NO aq + 4H aq Au aq + NO g + 2 H O(l)
;o
cell =0.56VE
Au(s) does not react with 1.00 M HNO3aq
.
18. (M) In each case, we determine whether Ecell
is greater than zero; if so, the reaction will
occur.
(a) Oxidation:
2+
Fe s Fe aq + 2e
o0.440VE
Reduction:
2+
Zn aq + 2e Zn s
o= 0.763VE
Net:
2+ 2+
Fe s + Zn aq Fe aq + Zn s o
cell 0.323VE
The reaction is not spontaneous under standard conditions as written
(b) Oxidation:
2
{2Cl aq Cl g + 2e } 5
o= 1.358VE
Reduction:
+2+
42
{MnO aq +8H aq +5e Mn aq +4H O(l)}×2
;o=1.51VE
Net:
+2+
422
10Cl aq + 2MnO aq +16H aq 5Cl g + 2Mn aq +8H O(l)
o
cell = +0.15VE. The reaction is spontaneous under standard conditions as written.
(c) Oxidation:
+
{Ag s Ag aq + e } 2
o= 0.800VE
Reduction:
+2
2H aq +2e H g
o= +0.000VE
Net:
++
2
2Ag s +2H aq 2Ag aq +H g o
cell =0.800VE
The reaction is not spontaneous under standard conditions as written.
(d) Oxidation:
2
{2Cl aq Cl g + 2e } 2
o= 1.358VE
Reduction:
+
22
Og+4Haq+4e 2HO(l)
o= +1.229VE
_______________________________________
Net:
+222
4Cl aq+4H aq+O g 2Cl g+2HO(l)
o
cell =0.129VE
The reaction is not spontaneous under standard conditions as written.
Galvanic Cells
19. (M) (a) Oxidation:
3+
{Al s Al aq + 3e } 2
o= +1.676 VE
Reduction:
2+
{Sn aq + 2e Sn s } 3
o= 0.137 VE
____________________________
Net:
2+ 3+
2Al s +3Sn aq 2Al aq +3Sn s o
cell = +1.539 VE
(b) Oxidation:
2+ 3+
Fe aq Fe aq + e
o= 0.771 VE
Reduction:
+
Ag aq + e Ag s
o= +0.800 VE
____________________
Net:
2+ + 3+
Fe aq + Ag aq Fe aq +Ag s o
cell = +0.029 VE
(c) Oxidation: {Cr(s)Cr2+ (aq)+2e-}3 Eo=0.90V

Chapter 20: Electrochemistry
1014
Reduction: {Au3+ (aq)+3e-Au(s)} 2 Eo= 1.52V
____________________
Net: 3Cr(s)+2Au
3+(aq) 3Cr2+ (aq)+2Au(s) Ecell
o= 2.42V
(d) Oxidation: 2H2O(l) O2(g)+4H+(aq)+4e- Eo=1.229V
Reduction: O2(g)+2H2O(l)+4e-4OH-(aq) Eo=0.401V
____________________
Net: H2O(l) H+(aq)+OH-(aq) Ecell
o=0.828V
20. (M) In this problem we are asked to write the half-reactions, balanced chemical equation
and determine Ecell
o for a series of electrochemical cells.
(a) Stepwise approach
First write the oxidation and reduction half-reactions and find Eo values from
Appendix D:
Oxidation: Cu(s) Cu2+ (aq)+2e- Eo=0.340 V
Reduction:
Cu+(aq)+e-Cu(s) Eo= +0.520 V
In order to obtain balanced net equation, the reduction half-reaction needs to be
multiplied by 2:
2Cu+(aq)+2e-2Cu(s)
Add the two half-reactions to obtain the net reaction:
Cu(s) Cu2+ (aq)+2e-
2Cu+(aq)+2e-2Cu(s)
____________________
Net: 2Cu+(aq) Cu2+ (aq)+Cu(s)
Determine
Ecell
o:
Ecell
o =-0.340V+0.520V= +0.18 V
Conversion pathway approach:
Oxidation: Cu(s) Cu2+ (aq)+2e- Eo=0.340 V
Reduction:
{Cu+(aq)+e-Cu(s)}2 Eo= +0.520 V
___________
Net: 2Cu+(aq) Cu2+ (aq)+Cu(s) Ecell
o0.18V
Follow the same methodology for parts (b), (c), and (d).
(b) Oxidation: Ag(s)+I-(aq) AgI(s)+e- Eo=0.152 V
Reduction:
AgCl(s)+e-Ag(s)+Cl-(aq) Eo=0.2223 V
____________________
Net: AgCl(s)+I-(aq) AgI(s)+Cl-(aq) Ecell
o = +0.3743 V
(c) Oxidation:
{Ce3+ (aq) Ce4+ (aq)+e-}2
Eo=1.76V
Reduction:
I2(s)+2e-2I-(aq)
Eo= +0.535 V
____________________
Net: 2Ce3+ (aq)+I2(s) 2Ce4+ (aq)+2I-(aq)
Ecell
o = -1.225 V

Chapter 20: Electrochemistry
1015
(d) Oxidation:
{U(s) U3+ (aq)+3e-}2 Eo=1.66V
Reduction: {V2+ (aq)+2e-V(s)}3
Eo=1.13V
____________________
Net: 2U(s)+3V2+ (aq) 2U3+ (aq)+3V(s)
Ecell
o = +0.53 V
21. (M) In each case, we determine whether Ecell
is greater than zero; if so, the reaction will
occur.
(a) Oxidation:
2
H(g) 2H +2e aq
o0.000VE
Reduction:
2
F(g)+2e 2F aq
o=2.866VE
Net: +-
22
H (g) + F (g) 2 H (aq) + 2 F (aq) o
cell 2.866VE
The reaction is spontaneous under standard conditions as written
(b) Oxidation: 2+
Cu(s) Cu (aq) + 2e
o= 0.340VE
Reduction: 2+
Ba (aq) + 2e Ba(s)
; Eo=2.92V
Net: 2+ 2+
Cu(s) + Ba (aq) Cu (aq) + Ba(s)
o
cell =3.26 VE.
The reaction is not spontaneous under standard conditions as written.
(c) Oxidation:
2+ 3+
Fe (aq) Fe (aq) + e 2
o= 0.771 VE
Reduction: 2+
Fe (aq) + 2e Fe(s)
o= 0.440 VE
Net: 2+ 3+
3 Fe (aq) Fe(s) + 2 Fe (aq) o
cell = 1.211 VE
The reaction is not spontaneous as written.
(d) Oxidation: -
22
2 Hg(l) + 2 Cl Hg Cl (s) +2 e
o= (0.2676)VE
Reduction: -
222
2 HgCl (aq) +2 e Hg Cl (s) + 2 Cl (aq)
o= +0.63VE
Net: 222
2 Hg(l) + 2 HgCl (aq) 2 Hg Cl (s) o
cell =0.36VE
(divide by 2 to get 222
Hg(l) + HgCl (aq) Hg Cl (s))
The reaction is spontaneous under standard conditions as written.

Chapter 20: Electrochemistry
1016
22. (M) (a)
e-
salt bridge
a
n
o
d
e
c
a
t
h
o
d
e
Cu
Cu2+
Pt
Fe3+
Fe2+
Anode, oxidation:
2+
Cu s Cu aq + 2e
o= 0.340VE
Cathode, reduction:
3+ 2+
{Fe aq + e Fe aq } 2
;o= +0.771VE
Net:
3+ 2+ 2+
Cu s +2Fe aq Cu aq +2Fe aq o
cell = +0.431VE
(b)
e-
salt bridge
a
n
o
d
e
c
a
t
h
o
d
e
Al
Al3+
Pb
Pb2+
Anode, oxidation:
3+
{Al s Al aq + 3e } 2
o= +1.676VE
Cathode, reduction:
2+
{Pb aq + 2e Pb s } 3
; o= 0.125 VE
Net:
2+ 3+
2Al s +3Pb aq 2Al aq +3Pb s
o
cell = +1.551 VE
(c)
e-
salt bridge
a
n
o
d
e
c
a
t
h
o
d
e
Pt
H2O
Pt
Cl-Cl2(g)
H+
O2(g)
Anode, oxidation:
+
22
2H O(l) O g +4H aq +4e
o= 1.229VE
Cathode, reduction:
2
{Cl g + 2e 2Cl aq } 2
o= +1.358VE
Chapter 20: Electrochemistry
1017
Net:
+
222
2H O(l)+2Cl g O g +4H aq +4Cl aq
o
cell = +0.129VE
(d)
e-
salt bridge
a
n
o
d
e
c
a
t
h
o
d
e
Zn Pt
HNO3NO(g)
Zn+2
Anode, oxidation:
2+
{Zn s Zn aq + 2e } 3
o= +0.763VE
Cathode, reduction:
+
32
{NO aq +4H aq +3e NO g +2H O(l)} 2
; o= +0.956 VE
Net:
+2+ o
32cell
3Zn s + 2NO aq +8H aq 3Zn aq + 2NO g + 4H O(l) = +1.719VE
23. (M) In each case, we determine whether Ecell
is greater than zero; if so, the reaction will
occur.
(a) Oxidation: Ag(s) Ag+(aq)+e- Eo0.800V
Reduction: Fe3+ (aq)+e-Fe2+ (aq) Eo=0.771 V
Net: Ag(s)+Fe3+ (aq) Ag+(aq)+Fe2+ (aq) Ecell
o0.029V
The reaction is not spontaneous under standard conditions as written.
(b) Oxidation:
Sn(s) Sn2+ (aq)+2e- Eo0.137 V
Reduction: Sn4+ (aq)+2e-Sn+2 (aq) Eo=0.154 V
Net: Sn(s)+Sn4+ (aq) 2Sn2+ (aq) Ecell
o0.291V
The reaction is spontaneous under standard conditions as written.
(c) Oxidation:
2Br-(aq) Br2(l)+2e- Eo1.065V
Reduction: 2Hg2+ (aq)+2e-Hg2
+(aq) Eo=0.630 V
Net: 2Br-(aq)+2Hg2+ (aq) Br2(l)+Hg2
+ Ecell
o0.435V
The reaction is not spontaneous under standard conditions as written.
(d) Oxidation:
{NO3
-(aq)+2H+(aq)+e-NO2(g)+H2O(l)}2 Eo2.326V
Reduction: Zn(s) Zn2+ (aq)+2e- Eo=1.563V
Net: 2NO3
-(aq)+4H+(aq)+Zn(s) 2NO2(g)+2H2O(l)+Zn2(aq)
Ecell
o0.435V
The reaction is not spontaneous under standard conditions as written.
Chapter 20: Electrochemistry
1018
24. (M) (a) Fe s
Fe2+ aq
Claq
Cl2g
Pt s
Oxidation:
2+
Fe s Fe aq + 2e
o= +0.440VE
Reduction:
2
Cl g + 2e 2Cl aq
o= +1.358VE
Net:
2+
2
Fe s + Cl g Fe aq + 2Cl aq
o
cell = +1.798 VE
(b)
2+
Zn s Zn aq Ag aq Ag s
Oxidation:
2+
Zn s Zn aq + 2e
o= +0.763VE
Reduction:
+
{Ag aq + e Ag s } 2
o= +0.800VE
Net:
+2+
Zn s +2Ag aq Zn aq +2Ag s o
cell = +1.563VE
(c) Pt s
Cu+aq
,Cu2+ aq
Cu+aq
Cu s
Oxidation:
+2+
Cu aq Cu aq + e
o= 0.159VE
Reduction:
+
Cu aq + e Cu s
o= +0.520VE
Net:
+2+
2Cu aq Cu aq +Cu s
o
cell = +0.361VE
(d) Mg s
Mg2+ aq
Braq
Br2l
Pt s
Oxidation:
2+
Mg s Mg aq + 2e
o= +2.356VE
Reduction:
2
Br l + 2e 2Br aq
o= +1.065VE
Net:
2+
2
Mg s + Br l Mg aq + 2Br aq
o
cell = +3.421VE
Pt
Fe Cl-
salt bridge
e-
cathode
anode
Cl2(g)
34(a)
Fe2+
34(b)
anode
cathode
e-
salt bridge
Zn2+
Zn Ag
Ag+
34(c)
anode
cathode
e-
salt bridge
Cu+ Cu2+ Cu+
Cu
Pt
34(d)
anode
cathode
e-
salt bridge
Mg2+
Mg Pt
Br2Br-
24(a) 24(b)
24(c) 24(d)

Chapter 20: Electrochemistry
1019
o
G, o
cell
E
, and K
25. (M) (a) Oxidation:
3+
{Al s Al aq +3e } 2
o= +1.676VE
Reduction:
2+
{Cu aq +2 e Cu s } 3
o= +0.337 VE
______________________
Net:
2+ 3+
2Al s +3Cu aq 2Al aq +3Cu s o
cell = +2.013VE
oo
cell
o6 3
= = 6 mol e 96,485 C/mol e 2.013V
= 1.165 10 J = 1.165 10 kJ
GnFE
G
(b) Oxidation:
2
{2I aq I s +2e } 2
o= 0.535 VE
Reduction:
+
22
Og+4Haq+4e 2HO(l)
o= +1.229 VE
_________________________________________
Net:
+
222
4I aq +O g +4H aq 2I s +2H O(l)
o
cell = +0.694 VE
oo 5
cell
= = 4 mol e 96,485 C/mol e 0.694 V = 2.68 10 J = 268 kJGnFE
(c) Oxidation:
+
{Ag s Ag aq + e } 6
o= 0.800 VE
Reduction:
2+3+
27 2
CrO aq+14H aq+6e 2Cr aq+7HO(l)
o= +1.33VE
Net:
2++3+
27 2
6Ags+CrO aq+14H aq 6Ag aq+2Cr aq+7HO(l)
Ecell
o= 0.800V +1.33V = +0.53V
oo 52
cell
= = 6mol e 96,485C/mol e 0.53V = 3.1 10 J = 3.1 10 kJGnFE
26. (M) In this problem we need to write the equilibrium constant expression for a set of redox
reactions and determine the value of K at 25 oC. We proceed by calculating Ecell
o from
standard electrode reduction potentials (Table 20.1). Then we use the expression
Go=nFEcell
o=RTln Kto calculate K.
(a)
Stepwise approach:
Determine Ecell
ofrom standard electrode reduction potentials (Table 20.1):
Oxidation: Ni(s) Ni2+ (aq)+2e- Eo0.257 V
Reduction:
{V3+ (aq)+e-V2+ (aq)}2 Eo0.255 V
_________________________
Net: Ni(s)+2V3+ (aq) Ni2+ (aq)+2V2+ (aq) Ecell
o=0.003V
Use the expression
Go=nFEcell
o=RTln Kto calculate K:

Chapter 20: Electrochemistry
1020
Go=nFEcell
o=RTln K;
Go2mole96485 C
mol 0.003V578.9J
GoRT ln K578.9J8.314JK1mol1298.15Kln K
ln K0.233Ke0.233 1.26
K1.26 Ni2+
V2+
2
V3+
2
Conversion pathway approach:
Determine Ecell
ofrom standard electrode reduction potentials (Table 20.1):
Oxidation: Ni(s) Ni2+ (aq)+2e- Eo0.257 V
Reduction:
{V3+ (aq)+e-V2+ (aq)}2 Eo0.255 V
_________________________
Net: Ni(s)+2V3+ (aq) Ni2+ (aq)+2V2+ (aq) Ecell
o=0.003V
Go=nFEcell
o=RTln Kln Keq nFEcell
o
RT n96485Cmol1
8.314JK1mol1298.15KEcell
o
ln Keq n
0.0257 Ecell
o2 mol e0.003V
0.0257 0.233
Keq e0.233 1.26 Ni2+
V2+
2
V3+
2
Similar methodology can be used for parts (b) and (c)
(b) Oxidation: 2Claq
Cl2g
+2e EoV= 1.358
Reduction:
+2+
22
MnO s + 4H aq + 2e Mn aq + 2H O(l)
o= +1.23VE
Net:
+2+ o
222cell
2 Cl aq + MnO s + 4 H aq Mn aq + Cl g + 2 H O(l) = 0.13VE
2+
2
10.1 5
eq 1 eq 24
+
Mn {Cl g }
2 mol e 0.13 V
ln = = 10. ; = e = 4 10 =
0.0257 Cl H
P
KK
(c) Oxidation:
22
4OH aq O g +2HO(l)+4e
o= 0.401 VE
Reduction: 2
{OCl (aq)+H O(l)+2e Cl (aq)+2OH } 2
o0.890 VE
Net: 2
2OCI (aq) 2CI (aq) O (g)
o
cell 0.489 VE
ln
2
2
76.1 33
eq eq 2
Cl P O (g)
4 mol e (0.489 V) 76.1 e 1 10
0.0257 OCl
KK
27. (M) First calculate Ecell
ofrom standard electrode reduction potentials (Table 20.1). Then use
Go=nFEcell
o=RTln K to determine
Goand K.
Chapter 20: Electrochemistry
1021
(a)
Oxidation: {Ce3(aq)Ce4(aq)e}5 Eo=1.61 V
Reduction: MnO4
-(aq)+8H+(aq)+5e-Mn2+ (aq)+4H2O(l) Eo= +1.51V
Net:MnO4
-(aq)+8H+(aq)+5Ce3+(aq) Mn2+ (aq)+4H2O(l)+5Ce4+ (aq) Ecell
o0.100V
(b)
Go=nFEcell
o=RTln K;
Go596485 C
mol (0.100V)48.24kJmol-1
(c)
GoRT ln K48.24 1000Jmol-1 8.314JK-1mol-1 298.15K ln K
ln K19.46 Ke19.46 3.5 109
(d) Since K is very small the reaction will not go to completion.
28. (M) First calculate Ecell
ofrom standard electrode reduction potentials (Table 20.1). Then use
Go=nFEcell
o=RTln K to determine
Goand K.
(a) Oxidation:Pb2+ (aq) Pb4+ (aq)+2e- Eo0.180V
Reduction:Sn4+(aq)+2e-Sn2+(aq) Eo0.154V
Net: Pb2+(aq)+Sn4+(aq) Pb4+ (aq)+Sn2+ (aq) Ecell
o0.026V
(b) Go=nFEcell
o=RTln K Go296485 C
mol (0.026) 5017Jmol-1
(c)
GoRT ln K5017Jmol-1 8.314JK-1mol-1 298.15K ln K
ln K2.02 Ke2.02 0.132
(d)
The value of K is small and the reaction does not go to completion.
29. (M) (a) A negative value of Ecell
o (
0.0050V ) indicates that oo
cell
=GnFE is positive
which in turn indicates that Keq is less than one Keq 1.00
; GRTK
oeq
ln=.
Keq
Cu Sn
Cu Sn
=
2+ 22+
+24+
Thus, when all concentrations are the same, the ion product, Q, equals 1.00. From the
negative standard cell potential, it is clear that Keq must be (slightly) less than one.
Therefore, all the concentrations cannot be 0.500 M at the same time.
(b) In order to establish equilibrium, that is, to have the ion product become less than 1.00,
and equal the equilibrium constant, the concentrations of the products must decrease
and those of the reactants must increase. A net reaction to the left (towards the
reactants) will occur.
Chapter 20: Electrochemistry
1022
30. (D) (a) First we must calculate the value of the equilibrium constant from the standard
cell potential.
Ecell
o=0.0257
nln Keq ;lnKeq =nEcell
o
0.0257 =2mol e
(0.017)V
0.0257 =1.32
Keq =e
1.32 = 0.266
To determine if the described solution is possible, we compare
Keq with Q. Now
Keq =BrO3
-
Ce4+
2
H+
2BrO4
-
Ce3+
2. Thus, when
BrO4
-
=Ce
4+
0.675 M , BrO3
-
=Ce
3+
0.600 M and pH=1 ( H+
=0.1M
the ion product, Q=0.600 0.6752
0.120.675 0.6002= 112.5 0.266 = Keq . Therefore, the
described situation can occur
(b) In order to establish equilibrium, that is, to have the ion product (112.5) become equal
to 0.266, the equilibrium constant, the concentrations of the reactants must increase and
those of the products must decrease. Thus, a net reaction to the left (formation of
reactants) will occur.
31. (M) Cell reaction: Zn s
+Ag2Os
ZnO s
+2Ag s
. We assume that the cell operates at
298 K.
oo o o o
ffff2
o
cell
=ZnOs+2Ags Zns AgOs
= 318.3 kJ/mol + 2 0.00 kJ/mol 0.00 kJ/mol 11.20 kJ/mol
= 307.1 kJ/mol =
GG G G G
nFE
o3
o
cell
307.1 10 J/mol
= = =1.591V
2 mol e /mol rxn 96,485C/mol e
G
EnF
32. (M) From equation (20.15) we know n= 12 and the overall cell reaction. First we must
compute value of Go.
oo 63
cell
96485 C
= = 12 mol e 2.71 V = 3.14 10 J = 3.14 10 kJ
1mol e
GnFE
Then we will use this value, the balanced equation and values of Gf
o to calculate
o
f4
Al OHG
.
22 4
4Al s +3O g +6HO(l)+4OH aq 4 Al OH aq
oo o o o o
fff2f2f
4
= 4 Al OH 4 [Al s ] 3 [O g ] 6 [H O l ] 4 [OH aq ]GG G G G G
Chapter 20: Electrochemistry
1023
3o
f4
o
f4
3.14 10 kJ = 4 Al OH 4 0.00 kJ 3 0.00 kJ 6 237.1 kJ 4 157.2
= 4 Al OH + 2051.4 kJ
G
G
o
f4
33
Al OH = 3.14 10 kJ 2051.4 kJ 4 = 1.30 10 kJ/molG
33. (D) From the data provided we can construct the following Latimer diagram.
Latimer diagrams are used to calculate the standard potentials of non-adjacent half-cell
couples. Our objective in this question is to calculate the voltage differential between IrO2
and iridium metal (Ir), which are separated in the diagram by Ir3+. The process basically
involves adding two half-reactions to obtain a third half-reaction. The potentials for the two
half-reactions cannot, however, simply be added to get the target half-cell voltage because
the electrons are not cancelled in the process of adding the two half-reactions. Instead, to
find E1/2 cell for the target half-reaction, we must use free energy changes, which are additive.
To begin, we will balance the relevant half-reactions in acidic solution:
4 H+(aq) + IrO2(s) + e Ir3+(aq) + 2 H2O(l) E1/2red(a) = 0.223 V
Ir3+(aq)+ 3 e Ir(s) E1/2red(b) = 1.156V
4 H+(aq) + IrO2(s) + 4e 2 H2O(l) + Ir(s) E1/2red(c) = ?
E1/2red(c) E1/2red(a) + E1/2red(b) but G(a) + G(b) = G(c) and G = nFE
4F(E1/2red(c)) = 1F(E1/2red(a)) + 3F(E1/2red(b)
4F(E1/2red(c)) = 1F(0.223) + 3F(1.156
E1/2red(c) = 1 (0.223) 3 (1.156)
4
FF
F
= 1(0.223) 3(1.156)
4
= 0.923 V
In other words, E(c) is the weighted average of E(a) and E(b)
34. (D) This question will be answered in a manner similar to that used to solve 31.
Let's get underway by writing down the appropriate Latimer diagram:
This time we want to calculate the standard voltage change for the 1 e reduction of MoO2 to
Mo3+. Once again, we must balance the half-cell reactions in acidic solution:
H2MoO4(aq) + 2 e + 2 H+(aq) MoO2(s) + 2 H2O(l) E1/2red(a) = 0.646 V
MoO2(s) + 4 H+(aq) + 1 e Mo3+(aq) + 2 H2O(l) E1/2red(b) = ? V
H2MoO4(aq) + 3 e + 6 H+(aq) Mo3+(aq) + 4 H2O(l) E1/2red(c) = 0.428 V
So, 3F(E1/2red(c)) = 2F(E1/2red(a)) + 1F(E1/2red(b)
3F(0.428 V) = 2F(0.646) + 1F(E1/2red(b)
1FE1/2red(b) = 3F(0.428 V) + 2F(0.646)
IrO2
(IV)
Ir3+
(III) Ir
(0) (Acidic conditions)
0.223 V 1.156 V
H2MoO4
(VI)
MoO2
(IV)
Mo3+
(III) (Acidic conditions)
0.646 V ? V
0.428 V
Chapter 20: Electrochemistry
1024
E1/2red(c) = 3 (0.428 V) 2 (0.646)
1
FF
F
= 1.284 V 1.292 V = 0.008 V
Concentration Dependence of Ecell —the Nernst Equation
35. (M) In this problem we are asked to determine the concentration of [Ag+] ions in
electrochemical cell that is not under standard conditions. We proceed by first determining
Ecell
o. Using the Nerst equation and the known value of E, we can then calculate the
concentration of [Ag+].
Stepwise approach:
First, determine Ecell
o:
Oxidation:
2+
Zn s Zn aq + 2e
o= +0.763VE
Reduction:
+
{Ag aq + e Ag s } 2
o= +0.800VE
Net:
+2+ o
cell
Zn s + 2Ag aq Zn aq + 2Ag s = +1.563VE
Use the Nerst equation and the known value of E to solve for [Ag]+:
2+
o
cell 22
+
Zn 1.00
0.0592 0.0592
= log = +1.563V log = +1.250V
2
Ag
EE nx
2
1.00M 2 (1.250 1.563)
log 10.6
0.0592x
; 11 6
2.5 10 5 10 Mx
Therefore, [Ag+] = 5 × 10-6 M
Conversion pathway approach:
Oxidation:
2+
Zn s Zn aq + 2e
o= +0.763VE
Reduction:
+
{Ag aq + e Ag s } 2
o= +0.800VE
Net:
+2+ o
cell
Zn s + 2Ag aq Zn aq + 2Ag s = +1.563VE
E=Ecell
o0.0592
nlog Zn2+
Ag+
2log Zn2+
Ag+
2 n
0.0592 (EEcell
o)
Ag+
2Zn2+
10n
0.0592(EEcell
o)Ag+
Zn2+
10n
0.0592(EEcell
o)
Ag+
1.00
102
0.0592(1.2501.563) 5106
36. (M) In each case, we employ the equation cell = 0.0592 pHE.
(a) cell = 0.0592 pH = 0.0592 5.25 = 0.311 VE
(b) pH = log 0.0103
=1.987 Ecell = 0.0592 pH = 0.0592
1.987 = 0.118V

Chapter 20: Electrochemistry
1025
(c) Ka=H+
C2H3O2
HC2H3O2
=1.8105=x2
0.158 xx2
0.158
53
0.158 1.8 10 1.7 10 Mx
pH log(1.7 10 ) 2.77
3
cell = 0.0592 pH = 0.0592 2.77 = 0.164VE
37. (M) We first calculate Ecell
o for each reaction and then use the Nernst equation to calculate
Ecell .
(a) Oxidation:
3+
{Al s Al 0.18 M +3 e } 2
o= +1.676VE
Reduction:
2+
{Fe 0.85M + 2e Fe s } 3
o= 0.440VE
Net:
2+ 3+
2Al s +3Fe 0.85 M 2Al 0.18 M + 3Fe s o
cell = +1.236VE
22
3+
o
cell cell 33
2+
Al 0.18
0.0592 0.0592
= log = 1.236V log 1.249 V
60.85
Fe
EE n
(b) Oxidation:
+
{Ag s Ag 0.34M + e } 2
o= 0.800VE
Reduction:
2
Cl 0.55 atm + 2 e 2 Cl 0.098 M
o= +1.358VE
Net:
+
2
Cl 0.55atm + 2 Ag s 2 Cl 0.098M + 2Ag 0.34M
;o
cell = +0.558VE
22
+22
2
o
cell cell
Cl Ag 0.34 0.098
0.0592 0.0592
{Cl g } 2 0.55
= = log = +0.558 log = +0.638 V
nP
EE
38. (M) (a) Oxidation:
2+
Mn s Mn 0.40M + 2e
o= +1.18VE
Reduction:
3+ 2+
{Cr 0.35M +1e Cr 0.25 M } 2
o= 0.424 VE
Net:
3+ 2+ 2+
2Cr 0.35M +Mn s 2Cr 0.25M +Mn 0.40M o
cell = +0.76VE
22
2+ 2+
o
cell cell 22
3+
Cr Mn 0.25 0.40
0.0592 0.0592
= log = +0.76V log = +0.78V
20.35
Cr
EE n
(b) Oxidation:
2+
{Mg s Mg 0.016M + 2e } 3
o= +2.356VE
Reduction:{ Al OH
4
0.25M
+3 e4OH0.042 M
+Al s
}2;o= 2.310VE
___________
Net:
4
2
3 Mg s +2[Al OH ] 0.25M 3Mg 0.016 M +8OH 0.042M +2Al s
;
o
cell = +0.046VE

Chapter 20: Electrochemistry
1026
Ecell =Ecell
o0.0592
6log Mg2+
3OH
8
Al OH
4
2= +0.046 0.0592
6log 0.016
30.042
8
0.25
2
= 0.046 V + 0.150V = 0.196 V
39. (M) All these observations can be understood in terms of the procedure we use to balance
half-equations: the ion—electron method.
(a) The reactions for which E depends on pH are those that contain either H+aq
or
OHaq
in the balanced half-equation. These reactions involve oxoacids and
oxoanions whose central atom changes oxidation state.
(b) H+aq
will inevitably be on the left side of the reduction of an oxoanion because
reduction is accompanied by not only a decrease in oxidation state, but also by the loss
of oxygen atoms, as in 32
ClO CIO
, 2
42
SO SO
, and 3
NO NO
. These
oxygen atoms appear on the right-hand side as HO
2 molecules. The hydrogens that are
added to the right-hand side with the water molecules are then balanced with H+aq
on the left-hand side.
(c) If a half-reaction with H+aq
ions present is transferred to basic solution, it may be
re-balanced by adding to each side OHaq
ions equal in number to the H+aq
originally present. This results in 2
HO(l) on the side that had H+aq
ions (the left
side in this case) and OHaq
ions on the other side (the right side.)
40. (M) Oxidation:
2
2Cl aq Cl g +2e
o= 1.358VE
Reduction:
+2+
22
PbO s + 4H aq + 2e Pb aq + 2H O(l)
o= +1.455VE
Net:
+2+
222
PbO s+4H aq+2Cl aq Pb aq+2HO(l)+Cl g
; o
cell = +0.097 VE
We derive an expression for Ecell that depends on just the changing H+.
2
o2
cell cell 42 4 2
+
0.0592 P{Cl }[Pb ] (1.00 atm)(1.00 M)
= log = +0.097 0.0296log
2 [H ] [Cl ] [H ] (1.00)
0.097 4 0.0296log[H ] 0.097 0.118log[H ] 0.097 0.118 pH
EE
(a) Ecell = +0.097 + 0.118 log 6.0
= +0.189 V
Forward reaction is spontaneous under standard conditions
(b) Ecell = +0.097 + 0.118 log 1.2
= +0.106 V
Forward reaction is spontaneous under standard conditions
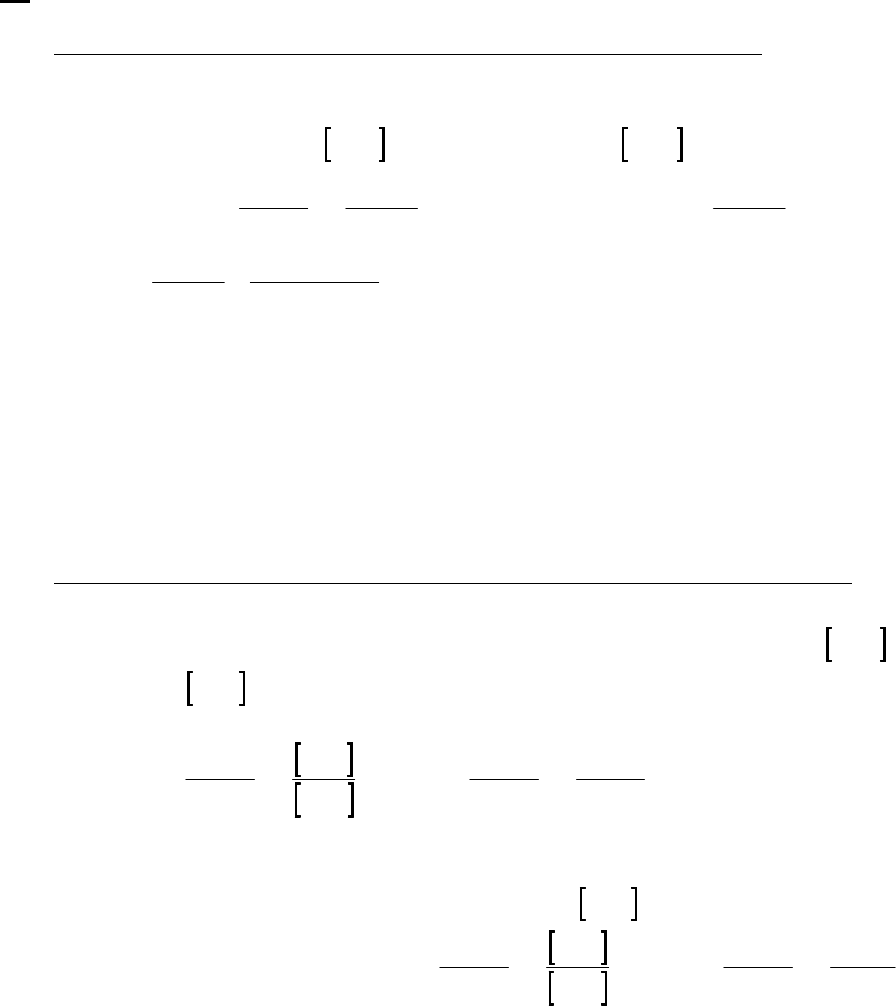
Chapter 20: Electrochemistry
1027
(c) Ecell V= +0.097 0.118 4.25 = 0.405
Forward reaction is nonspontaneous under standard conditions
The reaction is spontaneous in strongly acidic solutions (very low pH), but is
nonspontaneous under standard conditions in basic, neutral, and weakly acidic solutions.
41. (M) Oxidation:
2+
Zn s Zn aq 2e
o= +0.763VE
Reduction:
2+
Cu aq + 2e Cu s
o= +0.337 VE
Net:
2+ 2+
Zn s +Cu aq Cu s + Zn aq o
cell = +1.100VE
(a) We set
E
= 0.000V , Zn M
2+ = 1.00 , and solve for Cu2+ in the Nernst equation.
2+
o
cell cell 2+ 2+
Zn
0.0592 1.0M
= log ; 0.000 =1.100 0.0296 log
2Cu Cu
EE
2+ 37.2 38
2+
1.0M 0.000 1.100
log = = 37.2; Cu =10 = 6 10 M
0.0296
Cu
(b) If we work the problem the other way, by assuming initial concentrations of
2+
Cu =1.0M
initial
and 2+
Zn = 0.0 M
initial
, we obtain 2+ 38
Cu = 6 10 M
final
and
2+
Zn = 1.0 M
final
. Thus, we would conclude that this reaction goes to completion.
42. (M) Oxidation:
2+ o
Sn s Sn aq + 2e = +0.137 VE
Reduction: Pb2+ aq
+2ePb s
Eo=0.125 V
Net: Sn s
+Pb2+ aq
Sn2+ aq
+Pb s
Ecell
o= +0.012V
Now we wish to find out if Pb2+ aq
will be completely displaced, that is, will Pb2+ reach
0.0010 M, if Sn2+ is fixed at 1.00 M? We use the Nernst equation to determine if the cell
voltage still is positive under these conditions.
EE
cell cell
olog Sn
Pb log V=0.0592
2= +0.012 0.0592
2
1.00
0.0010 = +0.012 0.089 = 0.077
2+
2+
The negative cell potential tells us that this reaction will not go to completion under the conditions
stated. The reaction stops being spontaneous when Ecell =0. We can work this the another way as
well: assume that Pb2+
=1.0x
M and calculate Sn M
2+ =x at equilibrium, that is,
where Ecell =0. EE x
x
cell cell
olog Sn
Pb log=0.00= 0.0592
2= +0.012 0.0592
21.0
2+
2+

Chapter 20: Electrochemistry
1028
log x
1.0 x=20.012
0.0592 =0.41 x=100.41 1.0 x
=2.62.6xx=2.6
3.6 =0.72M
We would expect the final Sn2+ to equal 1.0 M (or at least 0.999 M) if the reaction went to
completion. Instead it equals 0.72 M and consequently, the reaction fails to go to completion.
43. (M) (a) The two half-equations and the cell equation are given below. Ecell
oV= 0.000
Oxidation: H2g
2H
+0.65 M KOH
+2e
Reduction: 2H+1.0 M
+2eH2g
Net: 2H+1.0 M
2H+0.65 M KOH
14 2
+14
w
base
1.00 10 M
H= = =1.510M
0.65 M
OH
K
Ecell =Ecell
o0.0592
2log H+
base
2
H+
acid
2=0.0000.0592
2log 1.5 1014
2
1.0
2=+0.818V
(b) For the reduction of 2
HO(l)
to H2g
in basic solution,
22
2H O(l)+2e 2 H g +2OH aq
, EoV= 0.828. This reduction is the
reverse of the reaction that occurs in the anode of the cell described, with one small
difference: in the standard half-cell, [OH] = 1.00 M, while in the anode half-cell in
the case at hand, [OH] = 0.65 M. Or, viewed in another way, in 1.00 M KOH, [H+]
is smaller still than in 0.65 M KOH. The forward reaction (dilution of H+) should be
even more spontaneous, (i.e. a more positive voltage will be created), with 1.00 M
KOH than with 0.65 M KOH. We expect that Ecell
o (1.000 M NaOH) should be a
little larger than Ecell (0.65 M NaOH), which, is in fact, the case.
44. (M) (a) Because NH3aq
is a weaker base than KOH(aq), [OH] will be smaller than in
the previous problem. Therefore the [H+] will be higher. Its logarithm will be less
negative, and the cell voltage will be less positive. Or, viewed as in Exercise 41(b), the
difference in [H+] between 1.0 M H+ and 0.65 M KOH is greater than the difference in
[H+] between 1.0 M H+ and 0.65 M NH3. The forward reaction is “less spontaneous”
and cell
E is less positive.
Reaction:
Initial:
Changes:
Equil:
32
NH aq + H O(l)
0.65M
x
M
0.65 x
M
+
4
NH aq +
0M
+
x
M
x
M
OHaq
0M
+
x
M
x
M
+2
45
3
NH OH
==1.810=
NH 0.65 0.65
b
x
xx
Kx
14
53 + 12
33
1.00 10
= OH = 0.65 1.8 10 3.4 10 M; [H O ] 2.9 10 M
3.4 10
x
(b
)
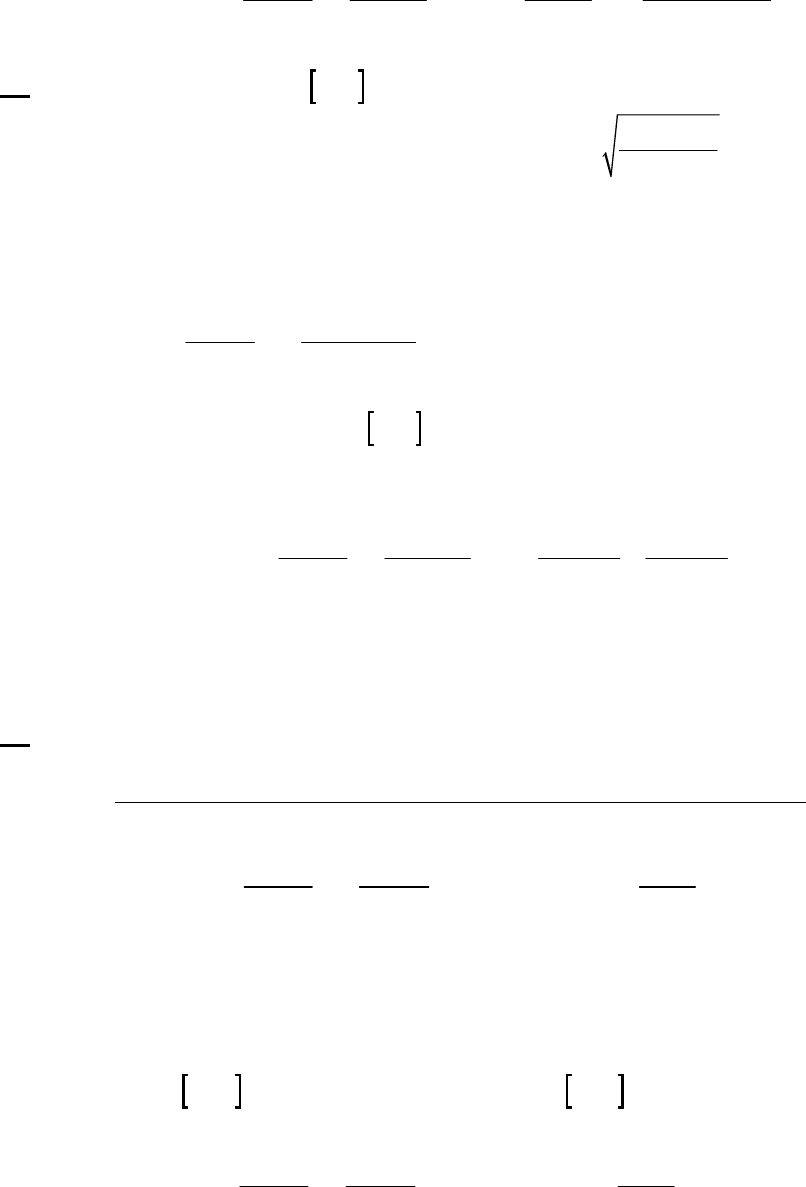
Chapter 20: Electrochemistry
1029
EE
cell cell
obase
2
acid
2
H]
H] V= 0.0592
20 000 0 0592
2
29 10
10 0 683
12 2
2
log[
[..log (. )
(.) .
45. (M) First we need to find Ag+ in a saturated solution of 24
Ag CrO .
Ksp =Ag
+
2CrO4
2
=2
s
2s
=4s3=1.11012 s1.11012
4
36.5 105M
The cell diagrammed is a concentration cell, for which Ecell
oV= 0.000 , n=1,
+4
anode
Ag = 2 = 1.3 10 Ms
Cell reaction: Ag s
+Ag+0.125 M
Ag s
+Ag+1.3104M
EE
cell cell
olog M
MVV=0.0592
1
1.3 10
0.125 = 0.000 + 0.177 = 0.177
4
46. (M) First we need to determine Ag+ in the saturated solution of Ag PO
34
.
The cell diagrammed is a concentration cell, for which o
cell = 0.000V, =1En.
Cell reaction: Ag s
+Ag+0.140 M
Ag s
+Ag+xM
o
cell cell
0.0592 M M 0.180
= 0.180V = log ; log = = 3.04
1 0.140 M 0.140M 0.0592
xx
EE
3.04 4 4 +
anode
M = 0.140 M 10 = 0.140 M 9.1 10 =1.3 10 M = Agx
3
33
+3 4 4 17
sp 4
= Ag PO = 3 = 1.3 10 1.3 10 3 = 9.5 10Kss
47. (D) (a) Oxidation:
2+ o
Sn s Sn 0.075 M + 2 e = +0.137 VE
Reduction: Pb2+ 0.600 M
+2ePb s
Eo=0.125 V
_____
Net:
2+ 2+ o
cell
Sn s + Pb 0.600M Pb s +Sn 0.075 M ; = +0.012VE
2+
o
cell cell 2+
Sn
0.0592 0.075
= log = 0.012 0.0296 log = 0.012 + 0.027 = 0.039 V
2 0.600
Pb
EE
(b) As the reaction proceeds, [Sn2+] increases while [Pb2+] decreases. These changes cause
the driving force behind the reaction to steadily decrease with the passage of time.
This decline in driving force is manifested as a decrease in Ecell with time.
(c) When Pb M M M
2+ = 0.500 = 0.600 0.100, Sn M M
2+ = 0.075 + 0.100 , because
the stoichiometry of the reaction is 1:1 for S
n
2+ and Pb2+ .
2+
o
cell cell 2+
Sn
0.0592 0.175
= log = 0.012 0.0296log = 0.012 + 0.013 = 0.025 V
2 0.500
Pb
EE
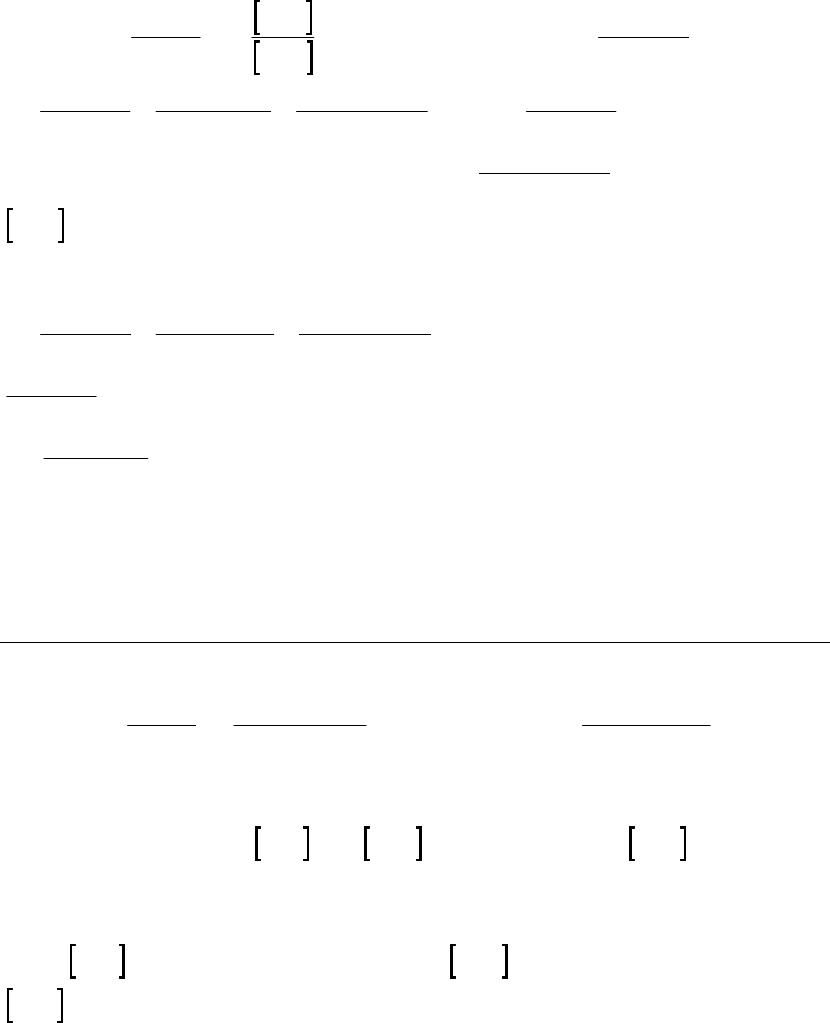
Chapter 20: Electrochemistry
1030
Reaction: Sn(s) +
2+
Pb aq
Pb s + Sn2+ aq
Initial: 0.600 M 0.075 M
Changes:
x
M +
x
M
Final:
0.600 Mx
0.075+ Mx
EE x
x
cell cell
olog Sn
Pb log=0.0592
2= 0.020 = 0.012 0.0296 0.075+
0.600
2+
2+
0.27
cell 0.012
0.075+ 0.020 0.012 0.075+
log = = = 0.27; =10 = 0.54
0.600 0.0296 0.0296 0.600
E
xx
xx
0.324 0.075
0.075+ = 0.54 0.600 = 0.324 0.54 ; = = 0.162 M
1.54
xxxx
Sn M
2+ = 0.075+ 0.162 = 0.237
(e) Here we use the expression developed in part (d).
log cell
0.075+
0.600 =0.012
0.0296 =0.000 0.012
0.0296 = +0.41
x
x
E
+0.41
0.075+ = 10 = 2.6; 0.075+ = 2.6 0.600 = 1.6 2.6
0.600
x
x
xx
x
1.6 0.075
= = 0.42 M
3.6
x
2+ 2+
Sn = 0.075+ 0.42 = 0.50 M; Pb = 0.600 0.42 = 0.18 M
48. (D) (a) Oxidation:
+
Ag s Ag 0.015 M + e
o= 0.800 VE
Reduction:
3+ 2+
Fe 0.055 M + e Fe 0.045 M
o= +0.771VE
Net:
3+ + 2+
Ag s + Fe 0.055 M Ag 0.015 M + Fe 0.045 M o
cell =0.029VE
+2+
o
cell cell 3+
Ag Fe
0.0592 0.015 0.045
= log = 0.029 0.0592log
1 0.055
Fe
= 0.029 V + 0.113 V = +0.084 V
EE
(b) As the reaction proceeds, Ag+ and Fe2+ will increase, while Fe3+ decrease. These
changes cause the driving force behind the reaction to steadily decrease with the passage
of time. This decline in driving force is manifested as a decrease in Ecell with time.
(c) When Ag M M M
+= 0.020 = 0.015 + 0.005 , Fe M M M
2+ = 0.045 + 0.005 = 0.050 and
Fe M M M
3+ = 0.055 0.005 = 0.500, because, by the stoichiometry of the reaction, a mole
of Fe2+ is produced and a mole of Fe3+ is consumed for every mole of Ag+ produced.
(d
)

Chapter 20: Electrochemistry
1031
EE
cell cell
olog Ag Fe
Fe log
VV V
=0.0592
1= 0.029 0.0592 0.020 0.050
0.050
= 0.029 + 0.101 = +0.072
+2+
3+
Reaction: Ag s
+
3+
Fe 0.055M
Ag+0.015 M
+ Fe2+ 0.045 M
Initial: 0.055 M 0.015 M 0.045 M
Changes: M
x
+M
x
+M
x
Final:
0.055 Mx
0.015+ Mx
0.045+ Mx
Ecell =Ecell
o0.0592
1log Ag+
Fe2+
Fe3+
=0.029 0.0592 log 0.015 + x
0.045 + x
0.055 x
log 0.015 + x
0.045 + x
0.055 x
=Ecell + 0.029
0.0592 =0.010 + 0.029
0.0592 =0.66
0.015 + x
0.045 + x
0.055 x
=100.66 = 0.22
0.00068 + 0.060x+x2= 0.22 0.055 x
= 0.012 0.22xx
2+0.28x0.011 = 0
xbb ac
a
=4
2=0.28 (0.28) + 4 0.011
2= 0.035
22
M
Ag M M M
+= 0.015 + 0.035 = 0.050
Fe M M M
2+ = 0.045 + 0.035 = 0.080
Fe M M M
3+ = 0.055 0.035 = 0.020
(e) We use the expression that was developed in part (d).
log 0.015 + x
0.045 + x
0.055 x
=Ecell + 0.029
0.0592 =0.000 + 0.029
0.0592 =0.49
0.015 + x
0.045 + x
0.055 x
=100.49 = 0.32
0.00068 + 0.060x+x2= 0.32 0.055 x
= 0.018 0.32xx
2+0.38x0.017 = 0
xbb ac
a
=4
2=0.38 (0.38) + 4 0.017
2= 0.040
22
M
Ag M M M
+= 0.015 + 0.040 = 0.055
Fe M M M
2+ = 0.045 + 0.040 = 0.085
Fe M M M
3+ = 0.055 0.040 = 0.015
(d
)

Chapter 20: Electrochemistry
1032
49. (M) First we will need to come up with a balanced equation for the overall redox reaction.
Clearly, the reaction must involve the oxidation of Cl(aq) and the reduction of Cr2O72(aq):
14 H+(aq) + Cr2O72(aq) + 6 e 2 Cr3+(aq) + 7 H2O(l) E1/2red = 1.33 V
{Cl(aq) 1/2 Cl2(g) + 1 e} 6 E1/2ox = 1.358 V
_____________________________________________
14 H+(aq) + Cr2O72(aq) + 6 Cl(aq) 2 Cr3+(aq) + 7 H2O(l) + 3 Cl2(g) Ecell = 0.03 V
A negative cell potential means, the oxidation of Cl(aq) to Cl2(g) by Cr2O72(aq) at standard
conditions will not occur spontaneously. We could obtain some Cl2(g) from this reaction by
driving it to the product side with an external voltage. In other words, the reverse reaction is
the spontaneous reaction at standard conditions and if we want to produce some Cl2(g) from
the system, we must push the non-spontaneous reaction in its forward direction with an
external voltage, (i.e., a DC power source). Since Ecell is only slightly negative, we could
also drive the reaction by removing products as they are formed and replenishing reactants as
they are consumed.
50. (D) We proceed by first deriving a balanced equation for the reaction occurring in the cell:
Oxidation: Fe(s)Fe2+ (aq)+2e-
Reduction: {Fe3+ (aq)+e-Fe2+ (aq)} 2
Net: Fe(s)+2Fe3+ (aq) 3Fe2+ (aq)
(a)
G
oand the equilibrium constant Keq can be calculated using
Go=nFEcell
oRT ln Keq :
Go=nFEcell
o=296485Cmol-1 1.21V 233.5kJmol-1
GoRT ln K8.314JK-1mol-1 298.15K ln K233.5 1000Jmol-1
ln K94.2 Ke94.2 8.11040
(b) Before calculating voltage using the Nernst equation, we need to re-write the net reaction
to take into account concentration gradient for Fe2+(aq):
Oxidation: Fe(s) Fe2+(aq,1.0 103M)+2e-
Reduction: {Fe3+ (aq,1.0 103M)+e-Fe2+ (aq,0.10M)} 2
Net: Fe(s)+2Fe3+ (aq,1.0 10-3 )Fe2+ (aq,1.0 10-3M)+2Fe2+(aq,0.10M)
Therefore,
Q1.0 103(0.10)2
(1.0 103)210
Now, we can apply the Nerst equation to calculate the voltage:
Ecell Ecell
o0.0592
nlog Q
=1.21 V 0.0592
2log10 1.18 V
(c) From parts (a) and (b) we can conclude that the reaction between Fe(s) and Fe3+(aq) is
spontaneous. The reverse reaction (i.e. disproportionation of Fe2+(aq)) must therefore be
nonspontaneous.
50.

Chapter 20: Electrochemistry
1033
Batteries and Fuel Cells
51. (M) Stepwise approach:
(a) The cell diagram begins with the anode and ends with the cathode.
Cell diagram: Cr s
|Cr2+ aq
,Cr3+ aq
||Fe2+ aq
,Fe3+ aq
|Fe s
(b) Oxidation:
2+ 3+
Cr aq Cr aq + e
o= +0.424VE
Reduction:
3+ 2+
Fe aq + e Fe aq
o= +0.771VE
Net:
2+ 3+ 3+ 2+
Cr aq + Fe aq Cr aq + Fe aq o
cell = +1.195VE
Conversion pathway approach:
Cr s
|Cr2+ aq
,Cr3+ aq
||Fe2+ aq
,Fe3+ aq
|Fe s
o= +0.424VE o= +0.771VE
Ecell
o=0.424V0.771V1.195V
52. (M) (a) Oxidation:
2+ o
Zn s Zn aq + 2e = +0.763VE
Reduction:
22 23
2MnO s + H O(l) + 2e Mn O s + 2OH aq
Acid-base:
+
432
{NH aq+OH aq NH g+HOl} 2
Complex: Zn2+ aq
+2NH3aq
+2Claq
Zn NH3
2
Cl2s
___________________________________________________
Net:
+
24 232 32
2
Zns+2MnO s+2NH aq+2Cl aq MnO s+HOl+[ZnNH ]Cl s
(b)
oo 5
cell
= = 2 mol e 96485 C/mol e 1.55 V = 2.99 10 J/molGnFE
This is the standard free energy change for the entire reaction, which is composed of
the four reactions in part (a). We can determine the values of
G
o for the acid-base
and complex formation reactions by employing the appropriate data from Appendix D
and pKf=4.81(the negative log of the Kf for [Zn(NH3)2]2+).
2
2
o1154
ab b
= ln = 8.3145 J mol K 298.15 K ln 1.8 10 = 5.417 10 J/molGRTK
o 1 4.81 4
cmplx = ln = 8.3145J mol K 298.15 K ln 10 = 2.746 10 J/mol
f
GRTK
oo oo
total redox a b cmplx redox total a b cmplx
544 5
Then = + + =
= 2.99 10 J/mol 5.417 10 + 2.746 10 J/mol = 3.26 10 J/mol
oo o o
GG GG G GGG
Thus, the voltage of the redox reactions alone is
EoJ
mol e C mol e V= 3.26 10
2 96485 / =1.69
5
o223
1.69V = +0.763V + MnO /Mn OE
o223
MnO /Mn O =1.69V 0.763V = +0.93VE
The electrode potentials were calculated by using equilibrium constants from Appendix D.
These calculations do not take into account the cell’s own internal resistance to the flow of
electrons, which makes the actual voltage developed by the electrodes less than the
theoretical values derived from equilibrium constants. Also because the solid species

Chapter 20: Electrochemistry
1034
(other than Zn) do not appear as compact rods, but rather are dispersed in a paste, and
since very little water is present in the cell, the activities for the various species involved
in the electrochemical reactions will deviate markedly from unity. As a result, the
equilibrium constants for the reactions taking place in the cell will be substantially
different from those provided in Appendix D, which apply only to dilute solutions and
reactions involving solid reactants and products that posses small surface areas. The
actual electrode voltages, therefore, will end up being different from those calculated here.
53. (M) (a) Cell reaction: 2H2g
+O2g
2H2Ol
oo
f2
= 2 H O l = 2 237.1 kJ/mol = 474.2 kJ/mol
rxn
GG
o3
o
cell
474.2 10 J/mol
= = = 1.229 V
4 mol e 96485 C/mol e
G
EnF
(b) Anode, oxidation:
2+
{Zn s Zn aq + 2e } 2
o= +0.763VE
Cathode, reduction:
+
22
Og+4Haq+4e 2HO(l)
o= +1.229 VE
Net:
+2+
22
2Zn s +O g +4H aq 2Zn aq +2H O(l) o
cell = +1.992VE
(c) Anode, oxidation:
2+
Mg s Mg aq + 2e
o= +2.356VE
Cathode, reduction:
2
Is+2e 2Iaq
o= +0.535VE
Net:
2+
2
Mg s + I s Mg aq + 2 I aq
o
cell = +2.891VE
54. (M) (a) Oxidation: Zn(s)
Zn2+(aq) + 2 e
Precipitation: Zn2+(aq) + 2 OH(aq)
Zn(OH)2(s)
Reduction: 2 MnO2(s) + H2)(l) + 2 e
Mn2O3(s) + 2 OH(aq)
__
Net : Zn(s) + 2 MnO2(s) + H2O(l) + 2 OH(aq)
Mn2O3(s) + Zn(OH)2(s)
(b) In 50, we determined that the standard voltage for the reduction reaction is +0.93 V (n
= 2 e). To convert this voltage to an equilibrium constant (at 25 C) use:
o
red
2(0.93)
log 31.4
0.0592 0.0592
nE
K
; 31.42 31
red 10 3 10K
and for Zn(s)
Zn2+(aq) + 2 e (E = 0.763 V and n = 2 e)
o
ox
2(0.763)
log 25.8
0.0592 0.0592
nE
K ; 25.78 25
ox 10 6 10K
Gtotal = Gprecipitation + Goxidation + Greduction
Gtotal = RT ln
2
sp, Zn(OH)
1
K + (RT lnKox) + (RT lnKred)
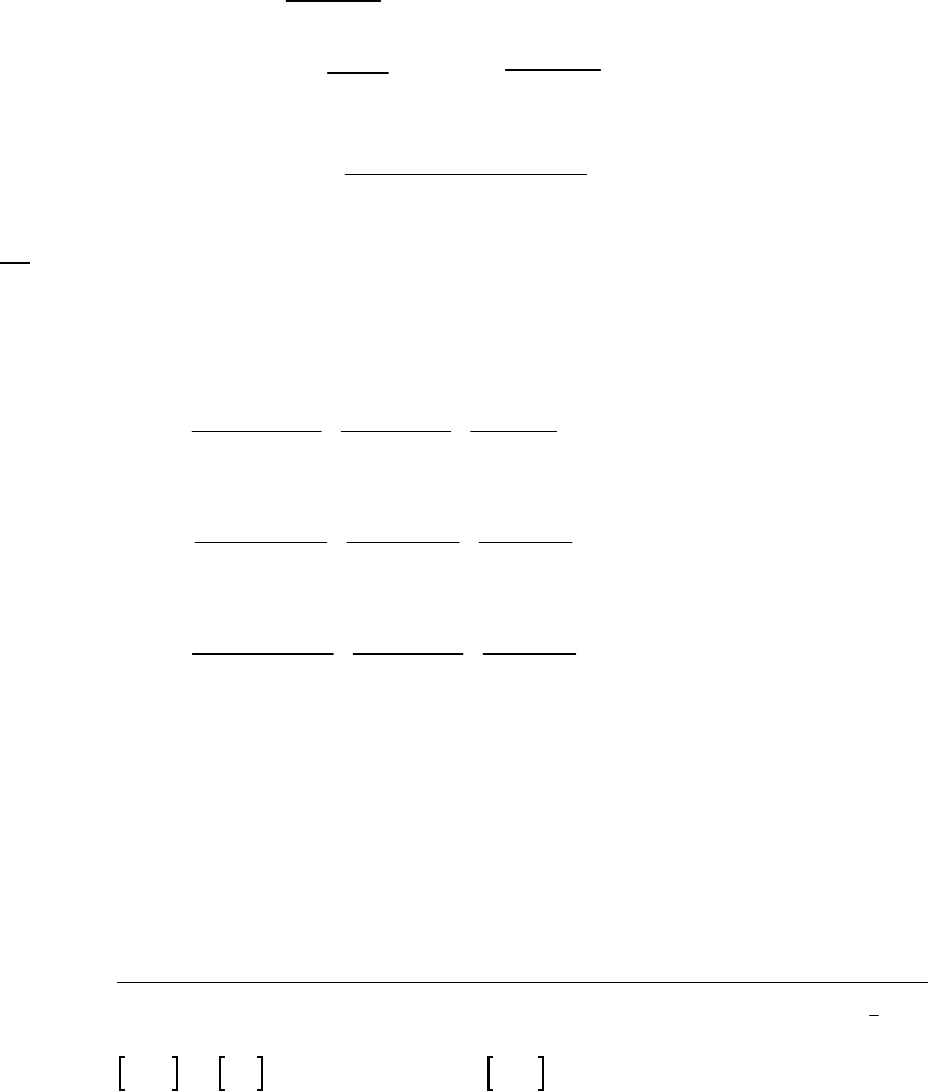
Chapter 20: Electrochemistry
1035
Gtotal = RT (ln
2
sp, Zn(OH)
1
K + lnKox + lnKred)
Gtotal = 0.0083145 kJ
Kmol(298 K) (ln 17
1
1.2 10
+ ln(6.0 1025) + ln(2.6 1031))
Gtotal = 423 kJ = nFEtotal
Hence, Etotal = Ecell = 3
1
423 10 J
(2mol)(96485 C mol )
= 2.19 V
55. (M) Aluminum-Air Battery: 2 Al(s) + 3/2 O2(g) Al2O3(s)
Zinc-Air Battery: Zn(s) + ½ O2(g) ZnO(s)
Iron-Air Battery Fe(s) + ½ O2(g) FeO(s)
Calculate the quantity of charge transferred when 1.00 g of metal is consumed in each cell.
Aluminum-Air Cell:
4
1 mol Al(s) 3 mol e 96,485C
1.00 g Al(s) 1.07 10 C
26.98 g Al(s) 1 mol Al(s) 1 mol e
Zinc-Air Cell:
3
1 mol Zn(s) 2 mol e 96,485 C
1.00 g Zn(s) 2.95 10 C
65.39 g Zn(s) 1 mol Zn(s) 1 mol e
Iron-Air Cell:
3
1 mol Fe(s) 2 mol e 96,485 C
1.00 g Fe(s) 3.46 10 C
55.847 g Fe(s) 1 mol Fe(s) 1 mol e
As expected, aluminum has the greatest quantity of charge transferred per unit mass
(1.00 g) of metal oxidized. This is because aluminum has the smallest molar mass and forms
the most highly charged cation (3+ for aluminum vs 2+ for Zn and Fe).
56. (M) (a) A voltaic cell with a voltage of 0.1000 V would be possible by using two half-
cells whose standard reduction potentials differ by approximately 0.10 V, such as the
following pair.
Oxidation:
2
3+ +
7
22
2Cr aq+7HO(l) CrO aq+14H aq+6e
o=1.33VE
Reduction:
+2+
22
{PbO s + 4 H aq + 2e Pb aq + 2 H O(l)} 3
o= +1.455 VE
______________________________
Net:
2-
3+ 2+ +
22 27
2Cr aq +3PbO s +H O(l) Cr O aq +3Pb aq +2H aqo
cell =0.125VE
The voltage can be adjusted to 0.1000 V by a suitable alteration of the concentrations.
Pb2+ or H+ could be increased or Cr3+ could be decreased, or any combination
of the three of these.
(b) To produce a cell with a voltage of 2.500 V requires that one start with two half-cells
whose reduction potentials differ by about that much. An interesting pair follows.
Oxidation:
3+
Al s Al aq + 3e
o= +1.676VE
Chapter 20: Electrochemistry
1036
Reduction:
+
{Ag aq + e Ag s } 3
o= +0.800VE
___________________________
Net:
+3+
Al s + 3Ag aq Al aq + 3Ag s o
cell = +2.476 VE
Again, the desired voltage can be obtained by adjusting the concentrations. In this case
increasing Ag+ and/or decreasing Al3+ would do the trick.
(c) Since no known pair of half-cells has a potential difference larger than about 6 volts,
we conclude that producing a single cell with a potential of 10.00 V is currently
impossible. It is possible, however, to join several cells together into a battery that
delivers a voltage of 10.00 V. For instance, four of the cells from part (b) would deliver
~10.0 V at the instant of hook-up.
57. (M) Oxidation (anode): Li(s) Li+(aq)+e-
E
o3.040V
Reduction (cathode): MnO2(s)+2H2O(l)+e-Mn(OH)3(s)+OH-(aq)
E
o
0.20V
________________________________________________________________________________________________________
Net:MnO
2(s)+2H2O(l)+Li(s) Mn(OH)3(s)+OH-(aq)+Li(aq) Ecell
o2.84V
Cell diagram:
Li(s), Li(aq)KOH(satd)MnO2(s), Mn(OH )3(s)
58. (M) (a) Oxidation (anode): Zn(s)Zn+2 (aq)+2e-
E
o0.763V
Reduction (cathode):
Br2(l)+2e-2Br-(aq)
E
o1.065V
________________________________________________________________________________________________________
Net: Zn(s)+Br
2(l) Zn2+(aq)+2Br-(aq) Ecell
o1.828V
(b) Oxidation (anode): {Li(s) Li+(aq)+e-}2
E
o3.040V
Reduction (cathode):
F2(g)+2e-2F-(aq)
E
o2.866V
________________________________________________________________________________________________________
Net: 2Li(s)+F
2(g) 2Li+(aq)+2F-(aq) Ecell
o4.868V
Electrochemical Mechanism of Corrosion
59. (M) (a) Because copper is a less active metal than is iron (i.e. a weaker reducing agent),
this situation would be similar to that of an iron or steel can plated with a tin coating
that has been scratched. Oxidation of iron metal to Fe2+(aq) should be enhanced in the
body of the nail (blue precipitate), and hydroxide ion should be produced in the vicinity
of the copper wire (pink color), which serves as the cathode.
(b) Because a scratch tears the iron and exposes “fresh” metal, it is more susceptible to
corrosion. We expect blue precipitate in the vicinity of the scratch.
(c) Zinc should protect the iron nail from corrosion. There should be almost no blue
precipitate; the zinc corrodes instead. The pink color of OH should continue to form.
60. (M) The oxidation process involved at the anode reaction, is the formation of Fe2+(aq). This
occurs far below the water line. The reduction process involved at the cathode, is the formation
of OHaq
from O2(g). It is logical that this reaction would occur at or near the water line
close to the atmosphere (which contains O2). This reduction reaction requires O2(g) from the
atmosphere and H2O(l) from the water. The oxidation reaction, on the other hand simply

Chapter 20: Electrochemistry
1037
requires iron from the pipe together with an aqueous solution into which the Fe2+ aq
can
disperse and not build up to such a high concentration that corrosion is inhibited.
Anode, oxidation: Fe s
Fe2+ aq
+2e
Cathode, reduction:
22
O g + 2H O(l) + 4e 4OH aq
61. (M)During the process of corrosion, the metal that corrodes loses electrons. Thus, the metal
in these instances behaves as an anode and, hence, can be viewed as bearing a latent negative
polarity. One way in which we could retard oxidation of the metal would be to convert it
into a cathode. Once transformed into a cathode, the metal would develop a positive charge
and no longer release electrons (or oxidize). This change in polarity can be accomplished by
hooking up the metal to an inert electrode in the ground and then applying a voltage across
the two metals in such a way that the inert electrode becomes the anode and the metal that
needs protecting becomes the cathode. This way, any oxidation that occurs will take place at
the negatively charged inert electrode rather than the positively charged metal electrode.
62. (M) As soon as the iron and copper came into direct contact, an electrochemical cell was
created, in which the more powerfully reducing metal (Fe) was oxidized. In this way, the
iron behaved as a sacrificial anode, protecting the copper from corrosion. The two half-
reactions and the net cell reaction are shown below:
Anode (oxidation) Fe(s) Fe2+(aq) + 2 e E = 0.440 V
Cathode (reduction)
Cu2+(aq) + 2 e Cu(s) E = 0.337 V
Net: Fe(s) + Cu2+(aq) Fe2+(aq) + Cu(s) Ecell = 0.777 V
Note that because of the presence of iron and its electrical contact with the copper, any
copper that does corrode is reduced back to the metal.
Electrolysis Reactions
63. (M) Here we start by calculating the total amount of charge passed and the number of moles
of electrons transferred.
60 s 2.15 C 1 mol e
mol e = 75 min = 0.10 mol e
1 min 1 s 96485 C
(a) mass Zn mol e mol Zn
mol e
mol Zn
mol Zn
g Zn
mol Zn g Zn=0.10 1
2
1
1
65.39
1=3.3
2+
2+
(b) 3+
3+
1 mol Al 1 mol Al 26.98 g Al
mass Al = 0.10 mol e = 0.90 g Al
3 mol e 1 mol Al 1 mol Al
(c) mass Ag mol e mol Ag
mol e
mol Ag
mol Ag
g Ag
mol Ag g Ag=0.10 1
1
1
1
107.9
1=11
+
+
Chapter 20: Electrochemistry
1038
(d) 2+
2+
1 mol Ni 1 mol Ni 58.69 g Ni
mass Ni = 0.10 mol e = 2.9 g Ni
2 mol e 1 mol Ni 1 mol Ni
64. (M) We proceed by first writing down the net electrochemical reaction. The number of
moles of hydrogen produced in the reaction can be calculated from the reaction
stoichiometry. Lastly, the volume of hydrogen can be determined using ideal gas law.
Stepwise approach:
The two half reactions follow: Cu2+ aq
+2eCu s
and 2 H+aq
+2eH2g
Thus, two moles of electrons are needed to produce each mole of Cu(s) and two moles of
electrons are needed to produce each mole of H2g
. With this information, we can
compute the moles of H2g
that will be produced.
2
2 2
1mol H g
1 mol Cu 2mol e
mol H g = 3.28 g Cu = 0.0516mol H g
63.55g Cu 1 mol Cu 2mol e
Then we use the ideal gas equation to find the volume of H2g
.
Volume of H(g)
0.0516mol H 0.08206 Latm
mol K (273.2 28.2) K
763 mmHg 1atm
760 mmHg
1.27 L
2
2
This answer assumes the H2g
is not collected over water, and that the H2(g) formed is the
only gas present in the container (i.e. no water vapor present)
Conversion pathway approach:
Cu2+ aq
+2eCu s
and 2 H+aq
+2eH2g
2
2 2
1mol H g
1 mol Cu 2mol e
mol H g = 3.28 g Cu = 0.0516mol H g
63.55g Cu 1 mol Cu 2mol e
V(H2(g))
0.0516molH20.08206 L atm
molK (273.2 28.2)K
763 mmHg 1atm
760 mmHg
1.27 L
65. (M) Here we must determine the standard cell voltage of each chemical reaction. Those
chemical reactions that have a negative voltage are the ones that require electrolysis.
(a) Oxidation:
+
22
2H O(l) 4H aq +O g +4e
o= 1.229 VE
Reduction:
+2
{2H aq + 2e H g } 2
o= 0.000VE
Net:
222
2H O(l) 2H g +O g o
cell =1.229VE
This reaction requires electrolysis, with an applied voltage greater than +1.229V .
(b) Oxidation:
2+
Zn s Zn aq + 2e
o= +0.763 VE
Reduction:
2+
Fe aq + 2e Fe s
o= 0.440VE

Chapter 20: Electrochemistry
1039
Net:
2+ 2+
Zn s + Fe aq Fe s + Zn aq o
cell = +0.323VE
This is a spontaneous reaction under standard conditions.
(c) Oxidation: {Fe2+ aq
Fe3+ aq
+e}2Eo=0.771 V
Reduction:
o
2
I s + 2e 2I aq = +0.535VE
Net: 2Fe2+ aq
+I
2s
2Fe3+ aq
+2I
aq
Ecell
o=0.236V
This reaction requires electrolysis, with an applied voltage greater than +0.236V .
(d) Oxidation:
2+ o
Cu s Cu aq + 2e = 0.337VE
Reduction:
4+ 2+ o
{Sn aq + 2e Sn aq } 2 = +0.154VE
Net: Cu s
+Sn4+ aq
Cu2+ aq
+Sn2+ aq
Ecell
o=0.183V
This reaction requires electrolysis, with an applied voltage greater than +0.183V.
66. (M) (a) Because oxidation occurs at the anode, we know that the product cannot be H2
(H2 is produced from the reduction of HO
2), SO2, (which is a reduction product of
SO4
2), or SO3 (which is produced from SO4
2 without a change of oxidation state;
it is the dehydration product of H SO
24
). It is, in fact O2 that forms at the anode.
The oxidation of water at the anode produces the O2(g).
(b) Reduction should occur at the cathode. The possible species that can be reduced are
HO
2 to H2g
, K+aq
to K s
, and SO4
2aq
to perhaps SO2g
. Because
potassium is a highly active metal, it will not be produced in aqueous solution. In order
for SO4
2aq
to be reduced, it would have to migrate to the negatively charged
cathode, which is not very probable since like charges repel each other. Thus, H2g
is produced at the cathode.
(c) At the anode:
+
22
2H O(l) 4H aq +O g +4e
o= 1.229VE
At the cathode:
+2
{2H aq + 2e H g } 2
o= 0.000VE
Net cell reaction:
222
2H O(l) 2H g +O g
o
cell =1.229VE
A voltage greater than 1.229 V is required. Because of the high overpotential required
for the formation of gases, we expect that a higher voltage will be necessary.
67. (M) (a) The two gases that are produced are H2g
and O2g
.
(b) At the anode:
+
22
2HO(l) 4H aq +O g +4e
o= 1.229VE
At the cathode:
+2
{2H aq + 2e H g } 2
o= 0.000VE
Net cell reaction:
222
2H O(l) 2H g +O g o
cell =1.229VE
68. (M) The electrolysis of Na2SO4aq
produces molecular oxygen at the anode.
o22
O g /H O = 1.229 VE
. The other possible product is S2O8
2aq
. It is however,
Chapter 20: Electrochemistry
1040
unlikely to form because it has a considerably less favorable half-cell potential.
22
o
28 4
S O aq /SO aq = 2.01 VE
.
H2g
is formed at the cathode.
mol O h s
h
C
s
mol e
C
mol O
mol e mol O
222
=3.75 3600
1
2.83
1
1
96485
1
4= 0.0990
The vapor pressure of water at 25C, from Table 12-2, is 23.8 mmHg.
11
2
0.0990 mol 0.08206 Latm mol K 298 K 2.56 L O (g)
1atm
(742 23.8) mmHg 760 mmHg
nRT
VP
69. (M) (a) Zn2+ aq
+2eZn s
65.39g Zn
60 s 1.87 C 1 mol e 1 mol Zn
mass of Zn = 42.5 min =1.62 g Zn
1 min 1 s 96,485 C 1 mol Zn
2mol e
(b) 2Iaq
I2s
+2e
2
222
1molI 2mole 1s 1min
96,485 C
time needed = 2.79g I = 20.2 min
253.8g I 1molI 1.75C 60 s
1mol e
70. (M) (a) Cu2+ aq
+2eCu s
2+
2+
2+
2.68 C 1 mol e 1 mol Cu 1000mmol
mmol Cu consumed = 282 s 1 s 96,485 C 1mol
2mol e
= 3.92 mmol Cu
decrease in Cu mmol Cu
mL M
2+ 2+
=3.92
425 = 0.00922
final Cu M M M
2+ = 0.366 0.00922 = 0.357
(b)
+ +
mmol Ag consumed = 255 mL 0.196 M 0.175 M = 5.36 mmol Ag
time needed = 5.36 mmol Ag+1mol Ag+
1000 mmol Ag+1mol e
1mol Ag+96485C
1mol e1s
1.84 C
=281 s 2.8 102 s
71. (M) (a) charge g Ag mol Ag
g Ag
mol e
mol Ag
C
mol e C= 1.206 1
107.87
1
1
96,485
1= 1079
(b) current C
sA= 1079
1412 = 0.7642

Chapter 20: Electrochemistry
1041
72. (D) (a) Anode, oxidation:
+
22
2H O(l) 4H aq + 4e + O g
o= 1.229VE
Cathode, reduction:
+
{Ag aq + e Ag s } 4
o= +0.800VE
Net:
++
22
2H O(l) + 4Ag aq 4H aq + O g + 4Ag s o
cell =0.429VE
(b)
1 mol Ag 1 mol e 96,485 C
charge = 25.8639 25.0782 g Ag = 702.8C
107.87g Ag 1 mol Ag 1mol e
current C
h
h
sA= 702.8
2.00
1
3600 = 0.0976
(c) The gas is molecular oxygen.
2
22
1mol O
1mole Latm
702.8 C 0.08206 (23+273) K
96485 C molK
4mole
1atm
755 mmHg 760 mmHg
1000 mL
0.0445 L O 44.5 mL of O
1L
nRT
VP
73. (D) (a) The electrochemical reaction is:
Anode (oxidation): {Ag(s)Ag+(aq)+e-(aq)} 2
E
o0.800V
Cathode (reduction): Cu2+(aq)+2e-Cu(s) Eo0.340V
___________________________________________________________________________________________________
Net: 2Ag(s)+Cu2+ (aq) Cu(s)+2Ag+(aq) Ecell
o0.46V
Therefore, copper should plate out first.
(b) current = charge
2.50hmin 1h
3600 s =0.75Acharge 6750C
mass=6750 C 1 mole-
96485 C 1mol Cu
2 mol e-63.546 g Cu
1 mol Cu =2.22 g Cu
(c) The total mass of the metal is 3.50 g out of which 2.22g is copper. Therefore, the mass
of silver in the sample is 3.50g-2.22g=1.28g or (1.28/3.50)x100=37%.
74. (D) First, calculate the number of moles of electrons involved in the electrolysis:
1.20C/s32.0min60sec
1min 1mole e-
96485C0.0239mol e-
From the known mass of platinum, determine the number of moles:
2.12gPt 1mol Pt
195.078gPt 0.0109molPt
Determine the number of electrons transferred:
0.0239 mol e-
0.0109 mol Pt 2.19
Chapter 20: Electrochemistry
1042
Therefore, 2.19 is shared between Pt2+ and Ptx+. Since we know the mole ratio between
Pt2+ and Ptx+, we can calculate x:
2.19=0.90(+2) + 0.10 (x).
2.19 1.80 0.10
x
x
4
(a) The oxidation state of the contaminant is +4.
INTEGRATIVE AND ADVANCED EXERCISES
75. (M) 32
2
Oxidation: V H O VO 2 H e a
E
o
32o
2cell
o
a
Reduction: Ag e Ag(s) 0.800 V
Net: V H O Ag VO 2 H Ag(s) 0.439 V
0.439 V 0.800 V 0
a
E
E
EE
.800 V 0.439 V 0.361 V
2 3 o
23 o
2
22 3
2
Oxidation: V V e
Reduction: VO 2 H e V H O 0.361 V
Net: V VO 2 H 2 V H O
b
E
E
o
cell
oo
32 o
0.616 V
0.616 V 0.361 V 0.361 V 0.616 V 0.255 V
Thus, for the cited reaction: V V = 0.255 V
bb
E
EE
eE
76. (M)The cell reaction for discharging a lead storage battery is equation (20.24).
O(l)H 2(s)PbSO(aq)HSO 2 aq)(H 2s)(PbOPb(s) 2442
The half-reactions with which this equation was derived indicates that two moles of electrons
are transferred for every two moles of sulfate ion consumed. We first compute the amount of
H2SO4 initially present and then the amount of H2SO4 consumed.
M 63.4
L 50.1
mol 56.0 mol 50.7
]SO[H final
SOH mol 0.56
SO mol 1
SOH mol 1
e mol 2
SO mol 2
C 96485
e mol 1
s 1
C 50.2
h 1
s 3600
h 6.0 consumedSOHamount
SOH mol 50.7
soln L 1
SOH mol 5.00
L 50.1SOHamount initial
42
42
2
4
42
2
4
42
42
42
42
77. (M) The cell reaction is (g)Cl(g)H(aq)OH 2O(l)H 2 (aq)Cl 2 222
We first determine the charge transferred per 1000 kg Cl2.
9
2
2
22
1 mol Cl
1000 g 2 mol e 96,485 C
charge 1000 kg Cl 2.72 10 C
1 kg 70.90 g Cl 1 mol Cl 1 mol e

Chapter 20: Electrochemistry
1043
(a) kJ 1038.9
J1000
kJ 1
CV1
J 1
C 10 2.72 V 3.45 energy 69
(b) kWh 1061.2
h
W
1000
kWh 1
s3600
h 1
J 1
s W1
J 10 9.38 energy 39
78. (D) We determine the equilibrium constant for the reaction.
3+ 2+ 2+ °
cell
Net: Fe(s) + 2 Cr (aq) Fe (aq) + 2 Cr (aq) E = +0.016 V
GonFEcell
oRT ln Kln KnFEcell
o
RT
3.3e2.1
K298Kmol J 8.3145
V016.0eCoul/mol96485emol2
ln 1..2
1-1-
__
KK
32 2
Reaction: Fe(s) 2 Cr (aq) Fe (aq) 2Cr (aq)
Initial : 1.00 M 0 M 0 M
Changes : –2 M M 2 M
Equil: (
xxx
222 2
32 2
1.00 – 2 )M M 2 M
[Fe ][Cr ] (2 )
3.3
[Cr ] (1.00 2 )
xx x
xx
Kx
Let us simply substitute values of x into this cubic equation to find a solution. Notice that x
cannot be larger than 0.50, (values > 0.5 will result in a negative value for the denominator.
3.38.3
)76.000.1(
(0.76) 38.0
38.03.30.3
)74.000.1(
(0.74) 37.0
37.0
3.3 9.1
)70.000.1(
(0.70) 35.0
35.03.3 4.6
)80.000.1(
(0.80) 40.0
40.0
2
2
2
2
2
2
2
2
KxKx
KxKx
Thus, we conclude that x = 0.37 M = [Fe2+].
79. (D) First we calculate the standard cell potential.
23 o
o
23o
cell
Oxidation: Fe (aq) Fe (aq) e 0.771 V
Reduction: Ag (aq) e Ag(s) 0.800 V
Net: Fe (aq) Ag (aq) Fe (aq) Ag(s) 0.029 V
E
E
E
Next, we use the given concentrations to calculate the cell voltage with the Nernst equation.
3
o
cell cell 2
0.0592 [Fe ] 0.0050
log 0.029 0.0592 log 0.029 0.018 0.047 V
1 0.0050 2.0
[Fe ][Ag ]
EE
The reaction will continue to move in the forward direction until concentrations of reactants
decrease and those of products increase a bit more. At equilibrium, Ecell = 0, and we have the
following.
V424.02 (aq)}Creaq)(Cr{:Reduction
V440.02e(aq)FeFe(s):Oxidation
2_3
_
E
E

Chapter 20: Electrochemistry
1044
33
o
cell 22
2 3
0.0592 [Fe ] [Fe ] 0.029
log 0.029 log 0.49
1 [Fe ][Ag ] [Fe ][Ag ] 0.0592
Reaction: Fe (aq) Ag (aq) Fe (aq) Ag(s)
Initial: 0.0050 M 2.0 M
E
30.49
2
0.0050 M
Changes: M M M
Equil: (0.0050 ) M (2.0 - ) M (0.0050 ) M
[Fe ] 0.0050
10 3.1
[Fe ][Ag ] (0.0050 )(2.0 )
xx x
xx x
x
xx
0.0050
2.0(0.0050 )
0.026
6.2(0.0050 ) 0.0050 0.031 6.2 7.2 0.026 0.0036 M
7.2
x
x
xx xxx
Note that the assumption that 2.0 x is valid. [Fe2+] = 0.0050 M – 0.0036 M = 0.0014 M
80. (D) We first note that we are dealing with a concentration cell, one in which the standard
oxidation reaction is the reverse of the standard reduction reaction, and consequently its
standard cell potential is precisely zero volts. For this cell, the Nernst equation permits us to
determine the ratio of the two silver ion concentrations.
cell
1.45
0.0592 [Ag (satd AgI)]
0.000 V log 0.0860 V
1[Ag (satd AgCl, M Cl )]
[Ag (satd AgI)] 0.0860 [Ag (satd AgI)]
log 1.45 10
0.0592
[Ag (satd AgCl, M Cl )] [Ag (satd AgCl, M Cl )]
Ex
xx
0.035
We can determine the numerator concentration from the solubility product expression for AgI(s)
917217
sp 102.9105.8105.8]I][Ag[ ssK M
This permits the determination of the concentration in the denominator.
M 106.2
035.0
102.9
)]Cl M AgCl, (satdAg[ 7
9
x
We now can determine the value of x. Note: Cl– arises from two sources, one being the dissolved
AgCl.
][ClM109.6
106.2
108.6108.1
106.2108.6)106.2)(106.2(108.1]Cl][Ag[
4
7
1410
7147710
sp
x
xxK
81. (M) The Faraday constant can be evaluated by measuring the electric charge needed to
produce a certain quantity of chemical change. For instance, let’s imagine that an electric
circuit contains the half-reaction 2
Cu (aq) 2 e Cu(s)
. The electrode on which the
solid copper plates out is weighed before and after the passage of electric current. The mass
gain is the mass of copper reduced, which then is converted into the moles of copper
reduced. The number of moles of electrons involved in the reduction then is computed from
the stoichiometry for the reduction half-reaction. In addition, the amperage is measured
during the reduction, and the time is recorded. For simplicity, we assume the amperage is
constant. Then the total charge (in coulombs) equals the current (in amperes, that is,

Chapter 20: Electrochemistry
1045
coulombs per second) multiplied by the time (in seconds). The ratio of the total charge (in
coulombs) required by the reduction divided by the amount (in moles) of electrons is the
Faraday constant. To determine the Avogadro constant, one uses the charge of the electron,
1.602 × 10–19 C and the Faraday constant in the following calculation.
mole
electrons
10023.6
C 10602.1
electron 1
electrons mol 1
C 485,96 23
19
A
N
82. (M) In this problem we are asked to determine Gf
o for N2H4(aq) using the electrochemical
data for hydrazine fuel cell. We first determine the value of o
G for the cell reaction, a
reaction in which n = 4. Gf
o can then be determined using data in Appendix D.
Stewise approach:
Calculate o
G for the cell reaction (n=4):
Gon FEcell
o4 mol e- 96,485 C
1 mol e1.559 V 6.017 105 J 601.7 kJ
Using the data in Appendix D, determine Gf
ofor hydrazine (N2H4):
-601.7 kJ Go
f[N2(g)] 2 Go
f[H2O(l)] Go
f[N2H4(aq)]Go
f[O2(g)]
0.00 kJ 2 ( 237.2 kJ) Go
f[N2H4(aq)] 0.00 kJ
Go
f[N2H4(aq)] 2(237.2 kJ) 601.7 kJ 127.3 kJ
Conversion pathway approach:
Gon FEcell
o4 mol e- 96,485 C
1 mol e1.559 V 6.017 105 J 601.7 kJ
-601.7 kJ Go
f[N2(g)] 2 Go
f[H2O(l)] Go
f[N2H4(aq)]Go
f[O2(g)]
0.00 kJ 2 ( 237.2 kJ) Go
f[N2H4(aq)] 0.00 kJ
Go
f[N2H4(aq)] 2(237.2 kJ) 601.7 kJ 127.3 kJ
83. (M) In general, we shall assume that both ions are present initially at concentrations of 1.00 M.
Then we shall compute the concentration of the more easily reduced ion when its reduction
potential has reached the point at which the other cation starts being reduced by electrolysis. In
performing this calculation we use the Nernst equation, but modified for use with a half-
reaction. We find that, in general, the greater the difference in E° values for two reduction
half-reactions, the more effective the separation.
(a) In this case, no calculation is necessary. If the electrolysis takes place in aqueous solution,
H2(g) rather than K(s) will be produced at the cathode. Cu2+ can be separated from K+ by
electrolysis.
(b) 2o o
Cu (aq) 2 e Cu(s) 0.340 V Ag (aq) e Ag(s) 0.800 VEE
Ag+ will be reduced first. Now we ask what [Ag+] will be when E = +0.337 V.
77.7
0592.0
340.0800.0
]Ag[
1
log
]Ag[
1
log
1
0592.0
V 0.800V 337.0
Chapter 20: Electrochemistry
1046
[Ag+] = 1.7 × 10–8 M. Separation of the two cations is essentially complete.
(c) 2o2 o
Pb (aq) 2 e Pb(s) 0.125 V Sn (aq) 2 e Sn(s) 0.137 VEE
Pb2+ will be reduced first. We now ask what [Pb2+] will be when E° = –0.137 V.
22
0.0592 1 1 2(0.137 0.125)
0.137 V 0.125 V log log 0.41
2 0.0592
[Pb ] [Pb ]
[Pb2+] = 10–0.41 = 0.39 M Separation of Pb2+ from Sn2+ is not complete.
84. (D) The efficiency value for a fuel cell will be greater than 1.00 for any exothermic reaction
(0
oH) that has G that is more negative than its o
H
value. Since ooo STHG , this
means that the value of o
S must be positive. Moreover, for this to be the case, ngas is usually
greater than zero. Let us consider the situation that might lead to this type of reaction. The
combustion of carbon-hydrogen-oxygen compounds leads to the formation of H2O(l) and
CO2(g). Since most of the oxygen in these compounds comes from O2(g) (some is present in
the C-H-O compound), there is a balance in the number of moles of gas produced—CO2(g)—
and those consumed—O2(g)—which is offset in a negative direction by the H2O(l) produced.
Thus, the combustion of these types of compounds will only have a positive value of gas
n
if
the number of oxygens in the formula of the compound is more than twice the number of
hydrogens. By comparison, the decomposition of NOCl(g), an oxychloride of nitrogen, does
produce more moles of gas than it consumes. Let us investigate this decomposition reaction.
278.1
kJ/mol 71.51
kJ/mol 08.66
kJ/mol 08.66kJ/mol 08.66kJ/mol) 0.00 kJ/mol 0.00 kJ/mol (0.00 0.500
NOCl(g)][(g)]Cl[(g)]O[(g)]N[G
kJ/mol 71.51kJ/mol 71.51kJ/mol) 0.00kJ/mol 0.00 kJ/mol (0.00 0.500
NOCl(g)][(g)]Cl[(g)]O[(g)]N[
(g)Cl g)(O (g)NNOCl(g)
o
o
f
o
2
f
o
2
1
2
f
o
2
1
2
f
o
2
1
o
f
o
2
f
o
2
1
2
f
o
2
1
2
f
o
2
1
o
2
2
1
2
2
1
2
2
1
H
G
GGGG
HHHHH
Yet another simple reaction that meets the requirement that oo HG is the combustion of
graphite: g)(COg)(O)C(graphite 22 We see from Appendix D that
kJ/mol 4.394g)](CO[ 2
o
fG is more negative than kJ/mol 5.393g)](CO[ 2
o
fH. (This
reaction is accompanied by an increase in entropy; S =213.7-5.74-205.1 =2.86 J/K, = 1.002.)
oo HG is true of the reaction in which CO(g) is formed from the elements. From
Appendix D, kJ/mol 5.110CO(g)}{
o
fH, and kJ/mol 2.137g)}(CO{
o
fG, producing
= (–137.2/–110.5) = 1.242.
Note that any reaction that has > 1.00 will be spontaneous under standard conditions at all
temperatures. (There, of course, is another category, namely, an endothermic reaction that has
0
oS. This type of reaction is nonspontaneous under standard conditions at all temperatures. As
such it consumes energy while it is running, which is clearly not a desirable result for a fuel cell.)
Chapter 20: Electrochemistry
1047
85. (M) We first write the two half-equations and then calculate a value of o
G from
thermochemical data. This value then is used to determine the standard cell potential.
_
32 2 2
_
22
32 2 2 2
Oxidation: CH CH OH(g) 3 H O(l) 2 CO ( ) 12 H (aq) 12 e
Reduction: {O (g ) 4 H (aq) 4e 2 H O(l)} 3
Overall: CH CH OH(g) 3 O (g) 3 H O(l) 2 CO ( )
g
g
Thus, 12n
(a) g)](O[3OH(g)]CHCH[O(l)]H[G3g)](CO[2 2
o
f23
o
f2
o
f2
o
f
oGGGG
2( 394.4 kJ/mol) 3( 237.1 kJ/mol) ( 168.5 kJ/mol) 3(0.00 kJ/mol) 1331.6 kJ/mol
3
cell
1331.6 10 J/mol 1.1501 V
12 mol e 96,485 C/mol e
G
EnF
(b) V1501.1)]OH(gCH/CH)g(CO[O](g)/HO[ 23222cell
EEE
V079.01501.11.229OH(g)]CHCH/)g([CO
OH(g)]CHCH/)g(CO[V1.229
232
232
E
E
86. (M) First we determine the change in the amount of H+ in each compartment.
22 2
Oxidation: 2 H O(l) O ( ) 4 H (aq) 4 e Reduction: 2 H (aq) 2 e H (g)
60 s 1.25 C 1 mol e 1 mol H
amount H 212 min 0.165 mol H
1 min 1 s 96,485 C 1mole
g
Before electrolysis, there is 0.500 mol H2PO4– and 0.500 mol HPO42– in each compartment. The
electrolysis adds 0.165 mol H+ to the anode compartment, which has the effect of transforming
0.165 mol HPO42– into 0.165 mol H2PO4–, giving a total of 0.335 mol HPO42– (0.500 mol – 0.165
mol) and 0.665 mol H2PO4– (0.500 mol + 0.165 mol). We can use the Henderson-Hasselbalch
equation to determine the pH of the solution in the anode compartment.
90.6
L500.0/POHmol665.0
L500.0/HPOmol335.0
log20.7
]POH[
]HPO[
logp pH
42
2
4
42
2
4
2
a
K
Again we use the Henderson-Hasselbalch equation in the cathode compartment. After electrolysis
there is 0.665 mol HPO42– and 0.335 mol H2PO4–. Again we use the Henderson-Hasselbalch
equation.
50.7
L500.0/POH mol335.0
L500.0/HPOmol665.0
log20.7
]POH[
]HPO[
logppH
42
2
4
42
2
4
2
a
K
87. (M) We first determine the change in the amount of M2+ ion in each compartment.
M2+ =10.00h 3600 s
1 h 0.500 C
1 s 1mol e-
96485 C 1mol M2+
2mol e-=0.0933 mol M2+
This change in amount is the increase in the amount of Cu2+ and the decrease in the amount of
Zn2+. We can also calculate the change in each of the concentrations.

Chapter 20: Electrochemistry
1048
22
22
0.0933 mol Cu 0.0933 mol Zn
[Cu ] 0.933 M [Zn ] 0.933 M
0.1000 L 0.1000 L
Then the concentrations of the two ions are determined.
22
[Cu ] 1.000 M 0.933 M 1.933 M [Zn ] 1.000 M 0.933 M 0.067 M
Now we run the cell as a voltaic cell, first determining the value of Ecell°.
2
2
2
cell
Oxidation : Zn(s) Zn (aq) 2 e 0.763 V
Reduction : Cu (aq) 2 e Cu(s) 0.340 V
Net: Zn(s) Cu (aq) Cu(s) 1.103 V
E
E
E
Then we use the Nernst equation to determine the voltage of this cell.
2
cell cell 2
0.067 M
0.0592 [Zn ] 0.0592
log 1.103 log 1.103 0.043 1.146 V
2 2 1.933 M
[Cu ]
EE
88. (M)(a)
2
Anode: Zn(s) Zn (aq) 2e 0.763 VE
--
2+ - cell
Cathode: {AgCl(s) + e (aq) Ag(s) + Cl (1 M)} × 2 E°=+0.2223 V
Net: Zn(s) + 2AgCl(s) Zn (aq) + 2Ag(s) + 2Cl (1 M) E° = +0.985 V
(b) The major reason why this electrode is easier to use than the standard hydrogen
electrode is that it does not involve a gas. Thus there are not the practical difficulties
involved in handling gases. Another reason is that it yields a higher value of cell
E,
thus, this is a more spontaneous system.
(c) o
Oxidation: Ag(s) Ag (aq) e 0.800 VE
o
cell
Reduction: AgCl(s) e Ag(s) Cl (aq) 0.2223 V
Net: AgCl(s) Ag (aq) Cl (aq) 0.578 V
E
E
The net reaction is the solubility reaction, for which the equilibrium constant is Ksp.
sp
ln KRTnFEG
sp 11
22.5 10
sp
-10
96485 C 1 J
1 mol e ( 0.578 V) 1V.C
1mole
ln 22.5
8.3145 J mol K 298.15 K
e 1.7 10
This value is in good agreement with the value of 1.8 × 10 given in Table 18-1.
nFE
KRT
K
89. (D) (a) Ag(s) Ag+(aq) + e- -E = -0.800 V
AgCl(s) + e- Ag(s) + Cl-(aq) E = 0.2223 V
AgCl(s) Ag+(aq) + Cl-(aq) Ecell = -0.5777 V
Ecell =E
cell -0.0592
1log [Ag+][Cl-]
1
= -0.5777 V 0.0592
1log [1.00][1.00 10-3]
1
= -0.400 V
(b) 10.00 mL of 0.0100 M CrO42- + 100.0 mL of 1.00 × 10-3 M Ag+ (Vtotal = 110.0 mL)

Chapter 20: Electrochemistry
1049
Concentration of CrO42-after dilution: 0.0100 M×10.00 mL /110.00 mL = 0.000909 M
Concentration of Ag+ after dilution: 0.00100 M×100.0 mL /110.00 mL = 0.000909 M
Ag2CrO4(s) 12
1.1 10
sp
K
2Ag+(aq) + CrO42-(aq)
Initial 0.000909 M 0.000909 M
Change(100% rxn) -0.000909 M -0.000455 M
New initial 0 M 0.000455 M
Change +2x +x
Equilibrium 2x 0.000455 M+x
0.000455 M
1.1 × 10-12 = (2x)2(0.000454)
x = 0.0000246 M Note: 5.4% of 0.000455 M (assumption may be considered valid)
(Answer would be x = 0.0000253 using method of successive approx.)
[Ag+] = 2x = 0.0000492 M (0.0000506 M using method of successive approx.)
-4
cell cell
0.0592 0.0592
log [ ][Cl ] 0.5777 log [1.00 ][4.92 10 ]
11
0.323 V (-0.306 V for method of successive approximations)
E
EA
g
MM
(c) 10.00 mL 0.0100 M NH3 + 10.00 mL 0.0100 M CrO42- + 100.0 mL 1.00×10-3 M Ag+
(Vtotal = 120.0 mL)
Concentration of NH3 after dilution: 10.0 M×10.00 mL /120.00 mL = 0.833 M
Concentration of CrO42-after dilution: 0.0100 M×10.00 mL /110.00 mL = 0.000833 M
Concentration of Ag+ after dilution: 0.00100 M×100.0 mL /110.00 mL = 0.000833 M
In order to determine the equilibrium concentration of free Ag+(aq), we first consider
complexation of Ag+(aq) by NH3(aq) and then check to see if precipitation occurs.
Ag+(aq) + 2NH3(aq) 7
1.6 10
f
K
Ag(NH3)2+(aq)
Initial 0.000833 M 0.833 M 0 M
Change(100% rxn) -0.000833 M -0.00167 M +0.000833 M
New initial 0 M 0.831 M 0.000833 M
Change +x +2x -x
Equilibrium x (0.831+2x) M (0.000833 –x) M
Equilibrium (x 0) x 0.831 M 0.000833 M
1.6 × 107 = 0.000833 /x(0.831)2 x = 7.54×10-11 M = [Ag+]
Note: The assumption is valid
Now we look to see if a precipitate forms: Qsp = (7.54×10-11)2(0.000833) = 4.7 ×10-24
Since Qsp < Ksp (1.1 × 10-12), no precipitate forms and [Ag+] = 7.54 × 10-11 M
+- -11
cell cell
cell
0.0592 0.0592
E = E° - log [Ag ][Cl ]= -0.5777 V - log [1.00M][7.54 × 10 M]
11
E = 0.0215V
90. (M) We assume that the Pb2+(aq) is “ignored” by the silver electrode, that is, the silver
electrode detects only silver ion in solution.

Chapter 20: Electrochemistry
1050
V800.0Ag(s)2(aq)H2Ag2(g)H:Net
V800.02Ag(s)}e(aq){Ag:Reduction
V000.0e2aq)(H2(g)H:Oxidation
cell2
2
E
E
E
2 2
cell cell 2 2
0.0592 [H ] 0.0592 1.00
log 0.503 V 0.800 V log
22
[Ag] [Ag]
EE
100.10
2
2
2
2100.110
]Ag[
00.1
0.10
0592.0
)503.0800.0(2
]Ag[
00.1
log
[Ag+]2=1.0 10-10 M2[Ag+]=1.0 10-5
Agg104.5
Agmol1
Agg87.107
Agmol1
Agmol1
solnL1
Agmol100.1
L0.500Ag mass 4
5
Ag%051.0%100
sampleg050.1
Agg105.4
Ag%
4
(by mass)
91. (M) 250.0 mL of 0.1000 M CuSO4 = 0.02500 moles Cu2+ initially.
moles of Cu2+ plated out =3.512C
s1368 s 1 mol e-
96,485 C 1 mol Cu2+
2 mole-0.02490mol Cu2+
moles of Cu2+ in solution = 0.02500 mol – 0.02490 mol = 0.00010 mol Cu2+
[Cu2+] = 0.00010 mol Cu2+/0.250 L = 4.0 × 10-4 M
Cu2+(aq) + 4NH3(aq) 13
1.1 10
f
K
Cu(NH3)42+(aq)
Initial 0.00040 M 0.10 M 0 M
Change(100% rxn) -0.00040M maintained +0.00040 M
New initial 0 M 0.10 M 0.00040 M
Change +x maintained -x
Equilibrium x 0.10 M (0.00040 –x) M 0.00040 M
2+ 13 2+ 13
34
f2+ 4 2+ 4
3
[Cu(NH ) ] 0.00040
K = = 1.1 10 [Cu ] = 3.6 10
[Cu ][NH ] [Cu ](0.10)
M
Hence, the assumption is valid. The concentration of Cu(NH3)42+(aq) = 0.00040 M which is
40 times greater than the 1 × 10-5 detection limit. Thus, the blue color should appear.
92. (M) First we determine the molar solubility of AgBr in 1 M NH3 .
26
33 spf
um AgBr(s) 2NH (aq) Ag(NH ) (aq) Br (aq) K K K 8.0 10
Initial 1.00 M 0 M 0 M
quil. 1.00-2s
S
E
2
263
3
2
3
13
sp 10
3
s s {s AgBr molar solubility}
[Ag(NH ) ][Br ]
K 8.0 10 s 2.81 10 M (also [Br ])
[NH (aq)] (1 2 )
K5.0 10
So [Ag ] 1.8 10
[Br ] 2.81 10
s
s
M
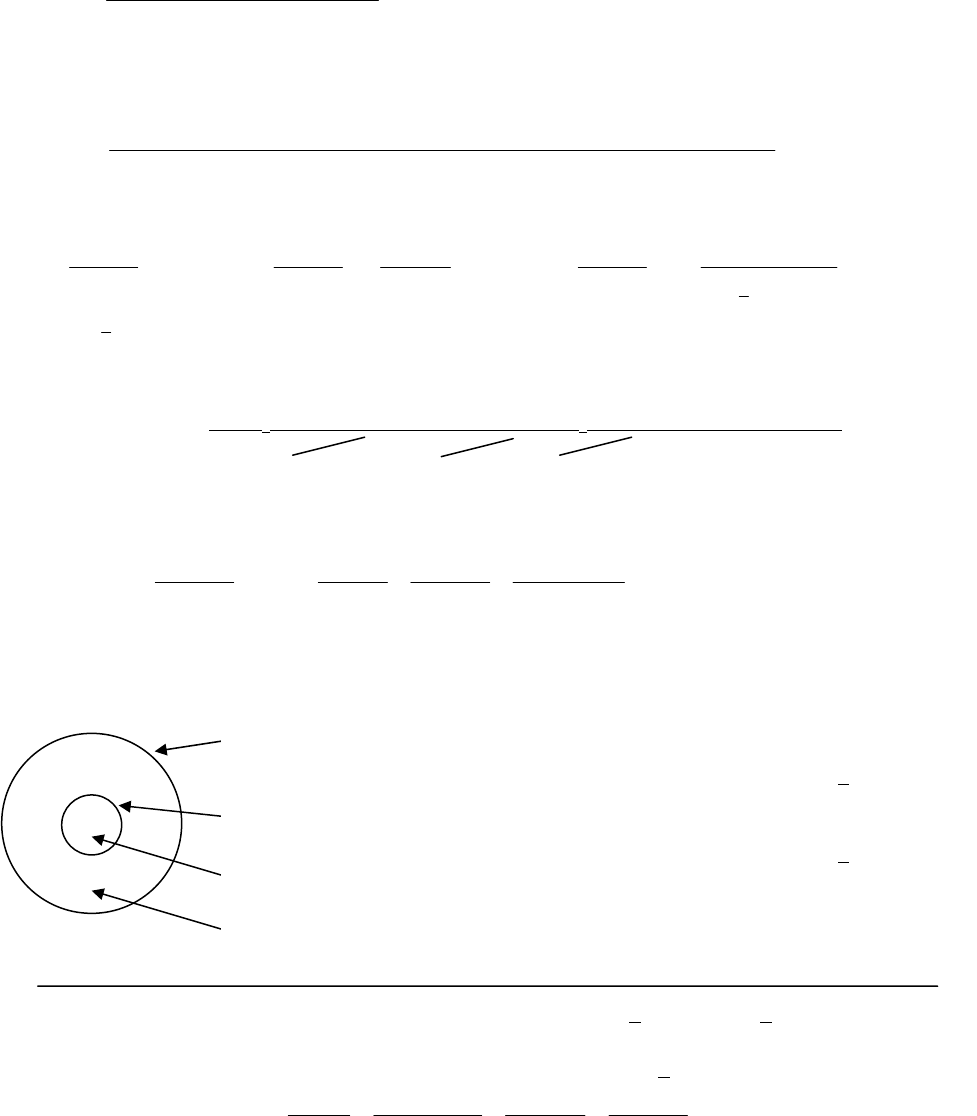
Chapter 20: Electrochemistry
1051
13
sp
7
2
33 f
6
2
33 spf
AgBr(s) Ag Br K 5.0 10
Ag 2NH Ag(NH ) K 1.6 10
(sum) AgBr(s) 2NH (aq) Ag(NH ) Br K K K 8.0 10
Now, let's construct the cell, guessing that the standard hydrogen electrode is the anode.
o
2
Oxidation: (g) 2 H 2 e 0.000 VHE
Reduction: {Ag(aq) eAg(s) } 2 Eo0.800 V
Net: 2 Ag(aq) H2(g) 2 Ag(s) 2 H(aq) Ecell
o0.800V
22
oo
10 10
2102
From the Nernst equation:
0.0592 0.0592 [ ] 0.0592 1
E E - log E - log 0.800 V log
nn 2
[] (1.7810)
and E 0.223 V. Since the voltage is positive, our guess is correct and the standard
hydrogen
H
QAg
electrode is the anode (oxidizing ele ).ctrode
93. (M) (a) Anode: 2H2O(l) 4 e- + 4 H+(aq) + O2(g)
Cathode: 2 H2O(l) + 2 e- 2 OH-(aq) + H2(g)
Overall: 2 H2O(l) + 4 H2O(l) 4 H+(aq) + 4 OH-(aq) + 2 H2(g) + O2(g)
2 H2O(l) 2 H2(g) + O2(g)
(b) 21.5 mA = 0.0215 A or 0.0215 C s-1 for 683 s
mol H2SO4 = 0.0215 C
s683s 1 mol e-
96485C 1 mol H+
1 mol e-1 mol H2SO4
2 mol H+=7.6110-5 mol H2SO4
7.6110-5 mol H2SO4 in 10.00 mL. Hence [H2SO4] = 7.61 10-5 mol / 0.01000 L = 7.6110-3M
94. (D) First we need to find the total surface area
Volume of metal needed = surface area × thickness of plating = 43.91 cm2 0.0050 cm = 0.22 cm3
Charge required =
0.22 cm38.90 g
cm31 mol Ni
58.693 g Ni 2 mol e-
1 mol Ni 96485 C
1 mol e-6437.5 C
Time = charge/time = 6437.5 C / 1.50 C/s = 4291.7 s or 71.5 min
Outer circumference = 2
r = 2
(2.50 cm) = 15.7 cm
Surface area = circumference × thickness = 15.7 cm × 0.50 cm = 7.85 cm2
Inner circumference = 2r = 2(1.00 cm) = 6.28 cm
Surface area = circumference × thickness = 6.28 cm × 0.50 cm = 3.14 cm2
Area of small circle = r2 = (1.00 cm)2 = 3.14 cm2
Area of large circle = r2 = (2.50 cm)2 = 19.6 cm2
Total area = 7.85 cm2 + 3.14 cm2 + 2×(19.6 cm2) – 2×(3.14 cm2) = 43.91 cm2
Chapter 20: Electrochemistry
1052
95. (M) The overall reaction for the electrolytic cell is:
Cu(s)+Zn2+ (aq) Cu2+ (aq)+Zn(s) Ecell
o1.103V
Next, we calculate the number of moles of Zn2+(aq) plated out and number of moles of
Cu2+(aq) formed:
n(Cu2+ )=0.500C
s10 h 60min
1h 60s
1min 1 mol e-
96,485 C 1 mol Cu2+
2 mol e-0.0935mol Cu2+
n(Zn2+ )n(Cu2+ )=0.0935mol
Initially, solution contained
1.00molL-1 0.100L=0.100 molZn2+(aq). Therefore, at the end
of electrolysis we are left with:
n(Zn2+ )LEFT =(0.100-0.0935)mol=6.510-3mol [Zn2+ ]= 6.510-3mol
0.1L =6.510-2M
n(Cu2+ )FORMED =0.0935mol [Cu2+ ]= 0.0935mol
0.1L =0.936M
The new potential after the cell was switched to a voltaic one can be calculated using Nernst
equation:
Ecell E
cell 0.0592
2log [Zn2]
[Cu2]1.103 0.0592
2log 6.5103M
0.935 M 1.103 0.0641.167 V
96. (M) (a) The metal has to have a reduction potential more negative than -0.691 V, so that
its oxidation can reverse the tarnishing reaction’s -0.691 V reduction potential.
Aluminum is a good candidate, because it is inexpensive, readily available, will not react
with water and has an Eo of -1.676 V. Zinc is also a possibility with an Eo of -0.763 V,
but we don't choose it because there may be an overpotential associated with the
tarnishing reaction.
3
-2
2
Oxidation: {Al(s) Al (aq) 3 e } 2
Reduction: {Ag S(s) 2 e Ag(s) S (aq) } 3
Net:
(b)
32
2
2 Al(s) 3 Ag S(s) 6Ag(s) 2 Al (aq) 3 S (aq)
(c) The dissolved NaHCO3(s) serves as an electrolyte. It would also enhance the electrical
contact between the two objects.
(d) There are several chemicals involved: Al, H2O, and NaHCO3. Although the aluminum
plate will be consumed very slowly because silver tarnish is very thin, it will,
nonetheless, eventually erode away. We should be able to detect loss of mass after
many uses.
97. (M) (a) Overall: C3H8(g) + 5 O2(g) 3 CO2(g) + 4 H2O(l)
Anode: 6 H2O(l) + C3H8(g) 3 CO2(g) + 20 H+(g) + 20 e-
Cathode: 20 e- + 20 H+(g) + 5 O2(g) 10 H2O(l)
Grxn = 3(-394.4 kJ/mol) + 4(-237.1 kJ/mol) – 1(-23.3 kJ/mol) = -2108.3 kJ/mol

Chapter 20: Electrochemistry
1053
Grxn = -2108.3 kJ/mol = -2,108,300 J/mol
Grxn = -nFEcell = -20 mol e- × (96485 C/mol e-) × Ecell
Ecell = +1.0926 V
20 e- + 20 H+(g) + 5 O2(g) 10 H2O(l) Ecathode = +1.229 V
Hence Ecell = Ecathode Eanode +1.0926 V = +1.229 V Eanode
Eanode = +0.136 V (reduction potential for 3 CO2(g) + 20 H+(g) + 20 e- 6 H2O(l) + C3H8(g))
(b) Use thermodynamic tables for 3 CO2(g) + 20 H+(g) + 20 e- 6 H2O(l) + C3H8(g)
Grxn = 6(-237.1 kJ/mol) + 1(-23.3 kJ/mol) [(-394.4 kJ/mol) + 20( 0kJ/mol)]= -262.7 kJ/mol
Gred = -262.7 kJ/mol = -262,700 J/mol = -nFEred = -20 mol e-×(96,485 C/mol e-)×Ered
Ered = 0.136 V (Same value, as found in (a))
98. (D) (a) Equation 20.15 ( GozFEcell
o) gives the relationship between the standard Gibbs
energy of a reaction and the standard cell potential. Gibbs free energy also varies with
temperature (
G
o
H
o
T
S
o). If we assume that
H
o and
S
odo not vary
significantly over a small temperature range, we can derive an equation for the temperature
variation of Ecell
o:
GoHoTSozFEcell
oEcell
oHoTSo
zF
Considering two different temperatures one can write:
Ecell
o(T1)HoT1So
zF and Ecell
o(T2)HoT2So
zF
Ecell
o(T1)Ecell
o(T2)HoT1So
zF HoT2So
zF
Ecell
o(T1)Ecell
o(T2)T1SoT2So
zF So
zF T2T1
(b) Using this equation, we can now calculate the cell potential of a Daniel cell at 50 oC:
Ecell
o(25oC)Ecell
o(50oC)10.4JK 1mol1
296485Cmol150 25
K0.00135
Ecell
o(50oC)1.103V0.00135 1.104V
99. (D) Recall that under non-standard conditions
G
Go
R
T
ln
K
. Substituting
Go
H
o
T
S
o and G
zFEcell one obtains:
zFEcell HoTSoRT lnQ
For two different temperatures (T1 and T2) we can write:

Chapter 20: Electrochemistry
1054
zFEcell (T1)HoT1SoRT1lnQ
zFEcell (T2)HoT2SoRT2lnQ
Ecell (T1)Ecell (T2)HoT1SoRT1lnQHoT2SoRT2lnQ
zF
Ecell (T1)Ecell (T2)T1SoRT1lnQT2SoRT2lnQ
zF
Ecell (T1)Ecell (T2)T1SoRT1lnQ
zF T2SoRT2lnQ
zF
Ecell (T1)Ecell (T2)T1
SoRlnQ
zF
T2
SoRlnQ
zF
Ecell (T1)Ecell (T2)(T1T2)SoRlnQ
zF
The value of Q at 25 oC can be calculated from Ecell
o and Ecell . First calculate Ecell
o:
Oxidation: Cu(s) Cu2+ (aq)+2e-
Eo0.340V
Reduction: 2Fe3+ (aq)+2e-2Fe2+(aq)
Eo0.771V
_____________________________________________________________________________________________________________
Overall: Cu(s)+2Fe3Cu2+ (aq)+2Fe2 Ecell
o0.431V
0.370 0.4310.0592
2logQ0.296logQ0.4310.370 0.061
logQ0.206 Q100.206 1.61
Now, use the above derived equation and solve for
S
o:
0.394 0.370 (50 25) So8.314 ln1.61
296485
0.024 25 (So3.96
192970 )So3.96 185.3 So189.2JK-1
Since GoHoTSozFEcell
owe can calculate
Go, K (at 25 oC) and
H
o:
GozFEcell
o296485 0.431 83.2kJ
GoRT ln K83.2 1000 8.314 298.15 ln K
ln K33.56 Ke33.56 3.77 1014
-83.2kJ=Ho298.15 189.2
1000 kJ Ho83.2 56.4 26.8kJ
Since we have
H
oand
S
owe can calculate the value of the equilibrium constant at 50
oC:
GoHoTSo26.8kJ (273.15 50)K 189.2
1000 kJK-1 87.9kJ
87.9 1000J 8.314JK-1mol-1 (273.15 50)K ln K
ln
K
32.7
K
e32.7 1.59
1014
Chapter 20: Electrochemistry
1055
Choose the values for the concentrations of Fe2+, Cu2+ and Fe3+ that will give the value of
the above calculated Q. For example:
Q= Fe2+
2Cu2+
Fe3+
2=1.61
0.121.61
0.121.61
Determine the equilibrium concentrations at 50 oC. Notice that since Q<K, a net change
occurs from left to right (the direction of the forward reaction):
Cu(s)+2Fe
3Cu2+ (aq)+2Fe2
Initial: 0.1 1.61 0.1
Change: 0.1-x 1.61+x 0.1+x
K=Fe2+
eq
2Cu2+
eq
Fe3+
eq
2=1.59 1014 (0.1x)2(1.61 x)
(0.1x)2
Obviously, the reaction is almost completely shifted towards products. First assume that
the reaction goes to completion, and then let the equilibrium be shifted towards reactants:
Cu(s)+2Fe
3Cu2+ (aq)+2Fe2
Initial: 0.1 1.61 0.1
Fina l 0 1.71 0.2
Equilibrium 0+x 1.71-x 0.2-x
K=Fe2+
eq
2Cu2+
eq
Fe3+
eq
2=1.59 1014 (0.2 x)2(1.71 x)
(x)20.221.71
x2
x20.221.71
1.59 1014 4.31016
x
2.1108
M
Therefore, [Cu2+]1.7M, [Fe2+]0.2M and [Fe3+]2.1x10-8M
100. (D) This problem can be solved by utilizing the relationship between
G
oand Ecell
o(
G
o=-
zF Ecell
o):
Consider a hypothetical set of the following reactions:
AneAn E1
o and G1
o
BmeBm E2
o and G2
o
Overall: ABnemeAnBm Erxn
o? and Grxn
oG1
oG2
o
Grxn
oG1
oG2
onFE1
omFE2
o
(nm)FErxn
onFE1
omFE2
o
(nm)FErxn
onFE1
omFE2
oErxn
onFE1
omFE2
o
n
m
Therefore, for n-sets of half-reactions:

Chapter 20: Electrochemistry
1056
Eo
niEi
o
ni
The Eo for the given half-reaction can be determined by combining four half-reactions:
H6IO6+H++2e-IO3
-+3H2O Eo1.60V
IO3
-+6H++5e-1
2I2+3H2O Eo1.19V
I2+2H2O2HIO+2H++2e-Eo1.45V
2II22eEo0.535V
Overall :
H6IO6+H++2e-IO3
-+6H++5e-I2+2H2O+2IIO3
-+3H2O+ 1
2I2+3H2O+2HIO+2H++2e-I22e
H6IO6+5H++2I-+3e-1
2I2+4H2O+2HIO
Eo1.60 31.19 51.45 20.535 2
25222.26V
FEATURE PROBLEMS
101. (D) (a) Anode:
+
2
Hg,1atm 2H1M+2e
o= 0.0000VE
Cathode:
+
{Ag M + e Ag s } 2x o= 0.800VE
_________________________________________
Net:
++
2
H g,1atm + 2Ag aq 2H 1M + 2Ag s o
cell =0.800E
(b) Since the voltage in the anode half-cell remains constant, we use the Nernst equation to
calculate the half-cell voltage in the cathode half-cell, with two moles of electrons.
This is then added to
E
for the anode half-cell. Because
E
o= 0.000 for the anode
half cell, EE
cell cathode
=
o +
2
+
0.0592 1
= log 0.800 + 0.0592 log Ag 0.800 0.0592log
2Ag
EE x
(c) (i) Initially +
Ag = 0.0100
; cell
= 0.800+0.0592 log 0.0100 = 0.682 V =EE
Note that 50.0 mL of titrant is required for the titration, since both AgNO3 and
KI have the same concentrations and they react in equimolar ratios.
(ii) After 20.0 mL of titrant is added, the total volume of solution is 70.0 mL and the
unreacted Ag+ is that in the untitrated 30.0 mL of 0.0100 M AgNO3aq
.
Chapter 20: Electrochemistry
1057
+
+
cell
30.0 mL 0.0100 M Ag
Ag = = 0.00429M
70.0 mL
= 0.800 + 0.0592log 0.00429 = 0.660 V =EE
(iii) After 49.0 mL of titrant is added, the total volume of solution is 99.0 mL and the
unreacted Ag+ is that in the untitrated 1.0 mL of 0.0100 M AgNO3aq
.
+
+
cell
1.0 mL 0.0100 M Ag
Ag = = 0.00010 M
99.0 mL
= 0.800 + 0.0592log 0.00010 = 0.563 V =EE
(iv) At the equivalence point, we have a saturated solution of AgI, for which
+179
sp
Ag = (AgI) 8.5 10 9.2 10K
9
cell
= 0.800 + 0.0592log 9.2 10 = 0.324 V =EE
.
After the equivalence point, the Ag+ is determined by the I resulting from
the excess KI(aq).
(v) When 51.0 mL of titrant is added, the total volume of solution is 101.0 mL and
the excess I is that in 1.0 mL of 0.0100 M KI(aq).
I-
=1.0 mL 0.0100 M I-
101.0 mL =9.9 10-5 M Ag+
=Ksp
I-
=8.510-17
0.000099 =8.6 10-13 M
13 cell
= 0.800 + 0.0592 log 8.6 10 = 0.086 V =
E
E
(vi) When 60.0 mL of titrant is added, the total volume of solution is 110.0 mL and
the excess I is that in 10.0 mL of 0.0100 M KI(aq).
-
-
-17
sp
+-14
-
10.0 mL×0.0100 M I
I = =0.00091 M
110.0 mL
K8.5×10
Ag = = = 9.3×10 M
0.00091
I
E= 0.800 + 0.0592 log 9.3 1014
= 0.029 V = Ecell

Chapter 20: Electrochemistry
1058
(d) The titration curve is presented below.
102. (D) (a) (1) anode: Na s
Na+in ethylamine
+e
cathode: Na (in ethylamine) Na(amalgam, 0.206 %)
Net:
Na s Na amalgam, 0.206%
(2) anode:
+
2Na amalgam, 0.206% 2Na 1 M + 2e
cathode:
+2
2H (aq,1M) +2e H g,1 atm
Net: ++
2
2Na (amalgam, 0.206 %) +2H (aq,1M) 2 Na (1 M) + H (g,1 atm)
(b) (1) 4
96,485 C
= 1 mol e 0.8453V = 8.156 10 J
1mol e
G
or 81.56 kJ
(2) 4
96,485C
= 2 mol e 1.8673V = 36.033 10 J
1 mol e
G
or –360.33 kJ
(c) (1) 4
1
2Na(s) 2Na(amalgam, 0.206%) 2 8.156 10 JG
(2) +
2
2Na (amalg, 0.206%) + 2H (aq,1M) 2 Na (1M) + H (g, 1 atm)
4
236.033 10 JG
Overall: 2 2Na(s)+2H aq) Na (1M)+H g,1atm)
+2
((
44 4
12
= + = 16.312 10 J 36.033 10 J = 52.345 10 JGGG or –523.45 kJ
Since standard conditions are implied in the overall reaction, o
GG .
(d)
4
oo+o+
2
52.345 10 J
= = H 1 M/H 1atm Na 1M/Nas
96,485 C 1 J
2 mol e 1V C
1 mol e
cell
EEE
o+
Na 1 M /Na s = 2.713VE. This is precisely the same as the value in
Appendix D.
Plot of Voltage versus volume of I
-
(aq)
0
0.2
0.4
0.6
0.8
0204060
Volume of I
-
(mL)
Voltage (V)

Chapter 20: Electrochemistry
1059
103. (D) The question marks in the original Latimer diagram have been replaced with letters in the
diagram below to make the solution easier to follow:
By referring to Appendix D and by employing the correct procedure for adding together half-
reactions of the same type we obtain:
(c) 2
Br (l) 2e 2Br (aq)
o
c1.065VE (Appendix D)
(d) 2
BrO (aq) H O(l) 2e Br (aq) 2OH (aq)
o
d0.766VE (Appendix D)
(b) 22
2BrO (aq) 2H O(l) 2e Br (l) 4OH (aq)
o
b0.455VE (Appendix D)
(a) 32
{BrO (aq) 2H O(l) 4e BrO (aq) 4OH (aq)} 2
o
a?E
(b) 22
2BrO (aq) 2H O(l) 2e Br (l) 4OH (aq)
o
b0.455VE
(c) 2
Br (l) 2e 2Br (aq)
o
c1.065VE
__________________________________
(e) 32
2BrO (aq) 6H O(l) 12e 12OH (aq) 2Br (aq)
o
e0.584VE
oooo
(a) (b) (c)Total
GGGG
oooo
eabc
12 8 -2 -2FE FE FE FE
o
a
12 0.584V 8 -2 0.455V -2 1.065VFFEFF
o
a
12 0.584V 2 0.455V 2 1.065V =0.496 V
8
FFF
EF
104. (D) (a) The capacitance of the cell membrane is given by the following equation,
0A
Cl
where 0 = 3 8.854 1012 C2 N1 m2;
A = 1 106 cm2; and l = 1 106 cm.
Together with the factors necessary to convert
from cm to m and from cm2 to m2, these data yield
2
2
12 6 2
12
6
C1 m
3 8.854 10 (1 10 cm )
N m 100 cm
1 m
(1 10 cm) 100 cm
C
= 2.66 1013 2
C
Nm
2
13 13
2
C1F
2.66 10 = 2.66 10 F
C
Nm 1Nm
C
BrO4-BrO3-BrO-Br2Br-
(a) (b) (c)
(d)
1.025 V
0.584 V
(e)
Chapter 20: Electrochemistry
1060
(b) Since the capacitance C is the charge in coulombs per volt, the charge on the membrane,
Q, is given by the product of the capacitance and the potential across the cell membrane.
Q = 2.66 1013 C
V 0.085 V = 2.26 1014 C
(c) The number of K+ ions required to produce this charge is
14 5+
19
2.26 10 C
= 1.41 10 K ions
e 1.602 10 C/ion
Q
(d) The number of K+ ions in a typical cell is
23 3 8 3 11
3
ions mol 1L
6.022 10 155 10 (1 10 cm )= 9.3 10 ions
mol L 1000 cm
(e) The fraction of the ions involved in establishing the charge on the cell membrane is
57
11
1.4 10 ions =1.5 10 (~ 0.000015 %)
9.3 10 ions
Thus, the concentration of K+ ions in the cell remains constant at 155 mM.
105. (M) Reactions with a positive cell potential are reactions for which
G
o0 , or reactions
for which K>1.
S
o,
H
oand
U
ocannot be used alone to determine whether a
particular electrochemical reaction will have a positive or negative value.
106. (M) The half-reactions for the first cell are:
Anode (oxidation): X(s) X+(aq)+e- EX/X
o
Cathode (reduction): 2H+(aq)+2e-H2(g)
E
o
0V
Since the electrons are flowing from metal X to the standard hydrogen electrode,
EX/X
o0V.
The half-reactions for the second cell are:
Anode (oxidation): X(s) X+(aq)+e- EX/X
o
Cathode (reduction): Y2+ +2e-Y(s) EY2/Y
o
Since the electrons are flowing from metal X to metal Y, EX/X
o+EY2/Y
o>0.
From the first cell we know that EX/X
o0V. Therefore, EX/X
o>EY2/Y
o.
107. (M) The standard reduction potential of the Fe2+(aq)/Fe(s) couple can be determined from:
Fe2+(aq) Fe3+ (aq)+e-Eo0.771V
Fe3+ (aq)+3e-Fe(s) Eo0.04V
Overall:
Fe2+(aq)+2e-Fe(s)
We proceed similarly to the solution for 100:

Chapter 20: Electrochemistry
1061
Eo
niEi
o
ni
0.771(1) 0.04 3
310.445V
SELF-ASSESSMENT EXERCISES
108. (E) (a) A standard electrode potential
E
omeasures the tendency for a reduction process to
occur at an electrode.
(b) F is the Faraday constant, or the electric charge per mole of electrons (96485 C/mol).
(c) The anode is the electrode at which oxidation occurs.
(d) The cathode is the electrode at which reduction occurs.
109. (E) (a) A salt bridge is a devise used to connect the oxidation and reduction half-cells of a
galvanic (voltaic) cell.
(b) The standard hydrogen electrode (abbreviated SHE), also called normal hydrogen
electrode (NHE), is a redox electrode which forms the basis of the thermodynamic scale of
oxidation-reduction potentials. By definition electrode potential for SHE is 0.
(c) Cathodic protection is a technique commonly used to control the corrosion of a metal
surface by making it work as a cathode of an electrochemical cell. This is achieved by
placing in contact with the metal to be protected another more easily corroded metal to act as
the anode of the electrochemical cell.
(d) A fuel cell is an electrochemical cell that produces electricity from fuels. The essential
process in a fuel cell is fuel+oxygenoxidation products.
110. (E) (a) An overall cell reaction is a combination of oxidation and reduction half-
reactions.
(b) In a galvanic (voltaic) cell, chemical change is used to produce electricity. In an
electrolytic cell, electricity is used to produce a nonspontaneous rection.
(c) In a primary cell, the cell reaction is not reversible. In a secondary cell, the cell
reaction can be reversed by passing electricity through the cell (charging).
(d) Ecell
orefers to the standard cell potential (the ionic species are present in aqueous
solution at unit activity (approximately 1M), and gases are at 1 bar pressure (approximately 1
atm).
111. (M) (a) False. The cathode is the positive electrode in a voltaic cell and negative in
electrolytic cell.
(b) False. The function of the salt bridge is to permit the migration of the ions not
electrons.
(c) True. The anode is the negative electrode in a voltaic cell.
(d) True.
(e) True. Reduction always occurs at the cathode of an electrochemical cell. Because of
the removal of electrons by the reduction half-reaction, the cathode of a voltaic cell is
positive. Because of the electrons forced onto it, the cathode of an electrolytic cell is
negative. For both types, the cathode is the electrode at which electrons enter the cell.
Chapter 20: Electrochemistry
1062
(f) False. Reversing the direction of the electron flow changes the voltaic cell into an
electrolytic cell.
(g) True. The cell reaction is an oxidation-reduction reaction.
112. (M) The correct answer is (b), Hg2(aq) is more readily reduced than H(aq).
113. (M) Under non-standard conditions, apply the Nernst equation to calculate Ecell :
Ecell Ecell
o0.0592
zlogQ
Ecell 0.66 0.0592
2log 0.10
0.01 0.63V
The correct answer is (d).
114. (E) (c) The displacement of Ni(s) from the solution will proceed to a considerable extent,
but the reaction will not go to completion.
115. (E) The gas evolved at the anode when K2SO4(aq) is electrolyzed between Pt electrodes is
most likely oxygen.
116. (M) The electrochemical reaction in the cell is:
Anode (oxidation): {Al(s) Al3+ (aq)+3e-}2
Cathode (reduction): {H2(g)+2e-2H+(aq)} 3
Overall: 2Al(s)+3H2(g) 2Al3+ (aq)+6H+(aq)
4.5g Al 1mol Al
26.98g Al 3 mol H2
2 mol Al 0.250mol H2
0.250 mol H222.4L H2
1mol H2
=5.6L H2
117. (E) The correct answer is (a)
G.
118. (M) Anode (oxidation):{Zn(s) Zn2+ (aq)+2e-}3
E
o
0.763V
Cathode (reduction):{NO3
-(aq)+4H+(aq)+3e-NO(g)+2H2O(l)} 2
E
o
0.956V
_________________________________________________________________________________________________________
Overall: 3Zn(s)+2NO3
-(aq)+8H+(aq) 3Zn2+(aq)+2NO(g)+4H2O(l) Ecell
o1.719V
Cell diagram: Zn(s) Zn2+ (1M) H+(1M),NO3
-(1M) NO(g,1atm) Pt(s)
119. (M) Apply the Nernst equation:
Chapter 20: Electrochemistry
1063
Ecell Ecell
o0.0592
zlogQ
0.108 00.0592
2log x2log x23.65
x2103.65 x0.0150M
pH log(0.0150) 1.82
120. (M) (a) Since we are given Ecell
o, we can calculate K for the given reaction:
Ecell
oRT
nF ln K
0.0050V8.314JK1mol1298K
296485Cmol1ln Kln K0.389
K
e0.389 0.68
Since for the given conditions Q=1, the system is not at equilibrium.
(b) Because Q>K, a net reaction occurs to the left.
121. (M) (a) Fe(s)+Cu2+(1M) Fe2+ (1M)+Cu(s) , Ecell
o0.780V, electron flow from B to A
(b) Sn2+ (1M)+2Ag+(1M) Sn4+(aq)+2Ag(s) , Ecell
o0.646V, electron flow from A to B.
(c) Zn(s)+Fe2+ (0.0010M) Zn2+ (0.10M)+Fe(s) , Ecell
o0.264V,electron flow from A to
B.
122. (M) (a) Cl2(g) at anode and Cu(s) at cathode.
(b) O
2(g) at anode and H2(g) and OH-(aq) at cathode.
(c) Cl2(g) at anode and Ba(l) at cathode.
(d) O
2(g) at anode and H2(g) and OH-(aq) at cathode.

1163
CHAPTER 24
COMPLEX IONS AND COORDINATION COMPOUNDS
PRACTICE EXAMPLES
1A (E) There are two different kinds of ligands in this complex ion, I and CN. Both are
monodentate ligands, that is, they each form only one bond to the central atom. Since there
are five ligands in total for the complex ion, the coordination number is 5: C.N. = 5 . Each
CN ligand has a charge of 1, as does the I ligand. Thus, the O.S. must be such that:
O.S. + 4 +1
1
=3= O.S.5. Therefore, O.S. = +2 .
1B (E) The ligands are all CN. Fe3+ is the central metal ion. The complex ion is
Fe CN
6
3.
2A (E) There are six “Cl” ligands (chloride), each with a charge of 1. The platinum metal
center has an oxidation state of +4 . Thus, the complex ion is PtCl6
2, and we need two
K
+ to balance charge: K2PtCl6
.
2B (E) The “SCN” ligand is the thiocyanato group, with a charge of 1bonding to the
central metal ion through the sulfur atom. The “NH3” ligand is ammonia, a neutral ligand.
There are five (penta) ammine ligands bonded to the metal. The oxidation state of the
cobalt atom is +3. The complex ion is not negatively charged, so its name does not end
with “-ate”. The name of the compound is pentaamminethiocyanato-S-cobalt(III) chloride.
3A (M) The oxalato ligand must occupy two cis- positions. Either the two NH3 or the two Cl
ligands can be coplanar with the oxalate ligand, leaving the other two ligands axial. The
other isomer has one NH3 and one Cl ligand coplanar with the oxalate ligand. The
structures are sketched below.
3B (M) We start out with the two pyridines, C5H5N, located cis to each other. With this
assignment imposed, we can have the two Clligands trans and the two CO ligands cis, the
two CO ligands trans and the two Cl ligands cis, or both the Clligands and the two CO
ligands cis. If we now place the two pyridines trans, we can have either both other pairs
trans, or both other pairs cis. There are five geometric isomers. They follow, in the order
described.
Co NH3
NH3
Cl
Cl
o
x
Co Cl
Cl
H3N
NH3
ox
Co NH3
Cl
H3N
Cl
ox
Chapter 24: Complex Ions and Coordination Compounds
1164
4A (M) The F ligand is a weak field ligand. MnF6
2 is an octahedral complex. Mn4+ has
three 3d electrons. The ligand field splitting diagram for MnF6
2is sketched below. There
are three unpaired electrons.
eg
t2g
4B (M) Co2+ has seven 3d electrons. Cl is a weak field ligand. H2O is a moderate field
ligand. There are three unpaired electrons in each case. The number of unpaired electrons
has no dependence on geometry for either metal ion complex.
CoCl4
2 Co H2O
6
2+
5A (M) CN is a strong field ligand. Co2+ has seven 3d electrons. In the absence of a crystal
field, all five d orbitals have the same energy. Three of the seven d electrons in this case
will be unpaired. We need an orbital splitting diagram in which there are three orbitals of
the same energy at higher energy. This is the case with a tetrahedral orbital diagram.
t2g
eg
In absence of a
crystal field eg
t2g
Tetrahedral geometry Octahedralgeometry
Thus, Co CN
4
2 must be tetrahedral (3 unpaired electrons) and not octahedral (1
unpaired electron) because the magnetic behavior of a tetrahedral arrangement would
agree with the experimental observations (3 unpaired electrons).
5B (M) NH3 is a strong field ligand. C
u
2+ has nine 3d electrons. There is only one way to
arrange nine electrons in five d-orbitals and that is to have four fully occupied orbitals (two
electrons in each orbital), and one half-filled orbital. Thus, the complex ion must be
paramagnetic to the extent of one unpaired electron, regardless of the geometry the ligands
adopt around the central metal ion.
6A (M) We are certain that Co H2O
6
2 is octahedral with a moderate field ligand.
Tetrahedral CoCl4
2 has a weak field ligand. The relative values of ligand field splitting
for the same ligand are t=0.44
o. Thus, Co H2O
6
2+ absorbs light of higher energy,
E
E
E
Chapter 24: Complex Ions and Coordination Compounds
1165
blue or green light, leaving a light pink as the complementary color we observe. CoCl4
2
absorbs lower energy red light, leaving blue light to pass through and be seen.
Cl Mo Cl
NC5H5
CO
OC
NC5H5OC Mo CO
NC5H5
Cl
Cl
NC5H5Cl Mo CO
NC5H5
Cl
OC
NC5H5Cl Mo Cl
NC5H5
NC5H5
OC
CO Cl Mo CO
NC5H5
NC5H5
Cl
CO
6B (M) In order, the two complex ions are Fe H2O
6
2+ and Fe CN
6
4. We know that
CN is a strong field ligand; it should give rise to a large value of o and absorb light of
the shorter wavelength. We would expect the cyano complex to absorb blue or violet light
and thus K4Fe CN
6
3 H2O should appear yellow. The compound
Fe H2O
6
NO3
2, contains the weak field ligand H2O and thus should be green. (The
weak field would result in the absorption of light of long wavelength (namely, red light),
which would leave green as the color we observe.)
INTEGRATIVE EXAMPLE
A (M) (a) There is no reaction with AgNO3 or en, so the compound must be trans-
chlorobis(ethylenediamine)nitrito-N-cobalt(III) nitrite
Co
H2N
H2
NH2
N
N
H2
Cl
NO2
+
NO2-
(b) If the compound reacts with AgNO3, but not with en, it must be trans-
bis(ethylenediamine)dinitrito-N-cobalt(III) chloride.
Co
HN
H
NH
N
N
H
NO2
NO2
+
Cl-
(c) If it reacts with AgNO3 and en and is optically active, it must be cis-
bis(ethylenediamine)dinitrito-N-cobalt(III) chloride.
Co
H2N
H2
NH2
N
N
H2
NO2
NO2
+
Cl-

Chapter 24: Complex Ions and Coordination Compounds
1166
B (D) We first need to compute the empirical formula of the complex compound:
46.2 g Pt 1 mol Pt
195.1 g Pt =0.236 mol Pt 0.236
0.236 =1 mol Pt
33.6 g Cl 1 mol Cl
35.5 g Cl =0.946 mol Cl 0.946
0.236 =4 mol Pt
16.6 g N 1 mol N
14.01 g N =1.18 mol N 1.18
0.236 =5 mol N
3.6 g Pt 1 mol H
1 g H =3.6 mol H 3.6
0.236 =15 mol H
The nitrogen ligand is NH3, apparently, so the empirical formula is Pt(NH3)5Cl4.
The effective molality of the solution is mT
Kfp
0.74oC
1.86oC/m0.4m. The effective
molality is 4 times the stated molality, so we have 4 particles produced per mole of Pt
complex, and therefore 3 ionizable chloride ions. We can write this in the following way:
[Pt(NH3)5Cl][Cl]3. Only one form of the cation (with charge 3+) shown below will exist.
Pt
H3N
H3NNH3
NH3
NH3
Cl
+3
EXERCISES
Nomenclature
1. (E) (a) CrCl4NH3
2
diamminetetrachlorochromate(III) ion
(b) Fe CN
6
3 hexacyanoferrate(III) ion
(c)
34
3
2
Cr en Ni CN
. tris(ethylenediamine)chromium(III) tetracyanonickelate(II)
ion
2. (E) (a) Co NH3
6
2+ The coordination number of Co is 6; there are six
monodentate NH3 ligands attached to Co. Since the NH3 ligand is neutral, the
oxidation state of cobalt is +2 , the same as the charge for the complex ion;
hexaamminecobalt(II) ion.

Chapter 24: Complex Ions and Coordination Compounds
1167
(b) AlF6
3 The coordination number of Al is 6; F is monodentate. Each F has a 1
charge; thus the oxidation state of Al is +3; hexafluoroaluminate(III) ion.
(c)
2
4
Cu CN
The coordination number of Cu is 4; CN
is monodentate. CN
has a
1 charge; thus the oxidation state of Cu is +2 ; tetracyanocuprate(II) ion
(d)
+
23
4
CrBr NH
The coordination number of Cr is 6; NH3 and B
r
are
monodentate. NH3 has no charge; B
r
has a 1
charge. The oxidation state of
chromium is +3; tetraamminedibromochromium(III) ion
(e) Co ox
3
4 The coordination number of Co is 6; oxalate is bidentate. C2O4
2ox
has a 2 charge; thus the oxidation state of cobalt is +2 ; trioxalatocobaltate(II) ion.
(f) Ag S2O3
2
3 The coordination number of Ag is 2; SO
23
2
is monodentate. SO
23
2
has a 2 charge; thus the oxidation state of silver is +1; dithiosulfatoargentate(I)
ion. ( Although +1 is by far the most common oxidation state for silver in its
compounds, stable silver(III) complexes are known. Thus, strictly speaking, silver is
not a non-variable metal, and hence when naming silver compounds, the oxidation
state(s) for the silver atom(s) should be specified).
3. (M) (a) Co OH
H2O
4NH3
2+ amminetetraaquahydroxocobalt(III) ion
(b) Co ONO
3NH3
3
triamminetrinitrito-O-cobalt(III)
(c) Pt H2O
4
PtCl6
tetraaquaplatinum(II) hexachloroplatinate(IV)
(d) Fe ox
2H2O
2
diaquadioxalatoferrate(III) ion
(e) Ag HgI
24
silver(I) tetraiodomercurate(II)
4. (M) (a) K3Fe CN
6
potassium hexacyanoferrate(III)
(b) Cu en
2
2+ bis(ethylenediamine)copper(II) ion
(c) Al OH
H2O
5
Cl2 pentaaquahydroxoaluminum(III) chloride
(d) CrCl en
2NH3
SO4 amminechlorobis(ethylenediammine)chromium(III) sulfate
(e) Fe en
3
4Fe CN
6
3 tris(ethylenediamine)iron(III) hexacyanoferrate(II)

Chapter 24: Complex Ions and Coordination Compounds
1168
Bonding and Structure in Complex Ions
5. (E) The Lewis structures are grouped together at the end.
(a) H
2O has 1×2 + 6 = 8 valence electrons, or 4 pairs.
(b) CH NH
32
has 4 +3 1+5+2 1= 14
valence electrons, or 7 pairs.
(c) ONO has 2 6 +5+1= 18 valence electrons, or 9 pairs. The structure has a 1
formal charge on the oxygen that is singly bonded to N.
(d) SCN has 6+4 +5+1= 16 valence electrons, or 8 pairs. This structure,
appropriately, gives a 1 formal charge to N.
SCN
(c) (d)(a)
NC
H
H
H
H
H
(b)
ONO
OH
H
6. (M) The Lewis structures are grouped together at the end.
(a) OH- has 6+1 + 1=8 valence electrons, or 4 pairs.
(b) SO42- has 6+6 4+2=32 valence electrons, or 16 pairs.
(c) C
2O42- has 24+64+2=34 valence electrons, or 17 pairs.
(d) SCN has 6+4 +5+1= 16 valence electrons, or 8 pairs. This structure,
appropriately, gives a 1 formal charge to N.
SO
O
O
O
2+
OH OO
O
OO
O
monodentate
or bidentate
CNS
(a) (b) (c) (d)
7. (M) We assume that PtCl4
2 is square planar by analogy with PtCl2NH3
2
in Figure
24-5. The other two complex ions are octahedral.
PtCl
Cl
Cl
Cl
CrH2O
Cl
OH2
OH2
OH2
H2O
CoH2O
NH3
NH3
OH2
NH3
H2O
2- 2+ 2+
(a) (b) (c)
Chapter 24: Complex Ions and Coordination Compounds
1169
8. (M) The structures for Pt ox
2
2 and Cr ox
3
3 are drawn below. The structure of
Fe EDTA
2 is the same as the generic structure for
2
MEDTA
drawn in Figure 24-23,
with Mn+= Fe2+ .
(a) (b)
(c) See Figure 24-23.
9. (M) (a) (b)
pentaamminesulfateochromium(III) trioxalatocobaltate(III)
(c)
Co
NH3
ClCl
NH3
ONO
NH3
Co
NH3
NH3
Cl
Cl
ONO
NH3
Co
NH3
ONOCl
NH3
Cl
NH3
f
ac-triamminedichloronitro-O-cobalt(III) mer-triammine-cis-dichloronitro-O-cobalt(III)
mer-triammine-trans-dichloronitro-O-cobalt(III)
10. (M) (a) pentaamminenitroto-N-cobalt(III) ion (b) ethylenediaminedithiocyanato-S-
copper(II)
Pt
O
O
O
C
C
CC
CO
O
O
O
O
O
Cr O
O
O
OC
CO
O
C
CO
O
C
CO
O
O
O
Co O
O
O
OC
CO
O
C
CO
O
C
CO
O
2-
3-
3-
Cr
NH3
OSO3
H3N
NH3
H3N
NH3
+
Co
NH
3
NH
3
O
2
N
NH
3
H
3
N
NH
3
2+
Cu
N
CS
H
2
N
NH
2
SCN
CH
2
CH
2
Chapter 24: Complex Ions and Coordination Compounds
1170
(c) hexaaquanickel(II) ion
Isomerism
11. (E) (a) cis-trans isomerism cannot occur with tetrahedral structures because all of the
ligands are separated by the same angular distance from each other. One ligand
cannot be on the other side of the central atom from another.
(b) Square planar structures can show cis-trans isomerism. Examples are drawn following,
with the cis-isomer drawn on the left, and the trans-isomer drawn on the right.
(c) Linear structures do not display cis-trans isomerism; there is only one way to bond
the two ligands to the central atom.
12. (M) (a) CrOH NH3
5
2+ has one isomer.
(b) CrCl2H2O
NH3
3
+ has three isomers.
(c) CrCl2en
2
+ has two geometric isomers, cis- and trans-.
M
B
A
A
B
cis-iso
m
e
r
M
B
B
A
A
t
r
ans-iso
m
e
r
Ni
H
2
O
OH
2
H
2
O
H
2
O
H
2
O
OH
2
2+
Cr
NH
3
NH
3
HO
NH
3
H
3
N
NH
3
2+
Cr
Cl
ClH
2
O
NH
3
H
3
N
NH
3
+
Cr
Cl
NH
3
H
2
O
NH
3
H
3
N
Cl
+
Cr
Cl
NH
3
H
2
O
Cl
H
3
N
NH
3
+
Cr
N
NN
N
Cl
Cl
C
C
CC
Cr
Cl
NN
N
N
Cl
C
CC
C
++
Chapter 24: Complex Ions and Coordination Compounds
1171
(d) CrCl4en
has only one isomer since the ethylenediamine (en) ligand cannot
bond trans to the central metal atom.
(e) Cr en
3
3+ has only one geometric isomer; it has two optical isomers.
13. (M) (a) There are three different square planar isomers, with D, C, and B, respectively,
trans to the A ligand. They are drawn below.
(b) Tetrahedral ZnABCD 2+ does display optical isomerism. The two optical isomers
are drawn above.
14. (M) There are a total of four coordination isomers. They are listed below. We assume that
the oxidation state of each central metal ion is +3.
Co en
3
Cr ox
3
tris(ethylenediamine)cobalt(III) trioxalatochromate(III)
Co ox
en
2
Cr ox
2en
bis(ethylenediamine)oxalatocobalt(III)
(ethylenediamine)dioxalatochromate(III)
Cr ox
en
2
Co ox
2en
bis(ethylenediamine)oxalatochromium(III)
(ethylenediamine)dioxalatocobaltate(III)
Cr en
3
Co ox
3
tris(ethylenediamine)chromium(III) trioxalatocobaltate(III)
Pt
A
D
B
C
Pt
A
C
B
D
Pt
A
B
C
D
Zn
A
D
B
C
Zn
B
D
A
C
Cr
Cl
NCl
N
Cl
Cl
CC
-
Cr
N
NN
N
N
N
C
CC
C
CC3+

Chapter 24: Complex Ions and Coordination Compounds
1172
15. (M) The cis-dichlorobis(ethylenediamine)cobalt(III) ion is optically active. The two optical
isomers are drawn below. The trans-isomer is not optically active: the ion and its mirror
image are superimposable.
16. (M) Complex ions (a) and (b) are identical; complex ions (a) and (d) are geometric
isomers; complex ions (b) and (d) are geometric isomers; complex ion (c) is distinctly
different from the other three complex ions (it has a different chemical formula).
Crystal Field Theory
17. (E) In crystal field theory, the five d orbitals of a central transition metal ion are split into
two (or more) groups of different energies. The energy spacing between these groups often
corresponds to the energy of a photon of visible light. Thus, the transition-metal complex
will absorb light with energy corresponding to this spacing. If white light is incident on the
complex ion, the light remaining after absorption will be missing some of its components.
Thus, light of certain wavelengths (corresponding to the energies absorbed) will no longer
be present in the formerly white light. The resulting light is colored. For example, if blue
light is absorbed from white light, the remaining light will be yellow in color.
18. (E) The difference in color is due to the difference in the value of
, which is the ligand field
splitting energy. When the value of
is large, short wavelength light, which has a blue color,
is absorbed, and the substance or its solution appears yellow. On the other hand, when the
value of is small, light of long wavelength, which has a red or yellow color, is absorbed,
and the substance or its solution appears blue. The cyano ligand is a strong field ligand,
producing a large value of , and thus yellow complexes. On the other hand, the aqua ligands
are weak field ligands, which produce a small value of
, and hence blue complexes.
19. (M) We begin with the 7 electron d-orbital diagram for Co2+ [Ar]
The strong field and weak field diagrams for octahedral complexes follow, along with the
number of unpaired electrons in each case.
Strong Field Weak Field
(1 unpaired (3 unpaired
electron) electrons)
N
Cl
Co N
N
Cl
N
C
CC
C
N
N
Co N
N
Cl
Cl C
C
C
C
N
Cl
Co
N
N
Cl
NC
C
CC
cis-iso
m
e
r
st
r
ans-iso
m
e
r
eg eg
t2g
t2g
Chapter 24: Complex Ions and Coordination Compounds
1173
20. (M) We begin with the 8 electron d-orbital diagram for
2+
Ni Ar
The strong field and weak field diagrams for octahedral complexes follow, along with the
number of unpaired electrons in each case.
Strong Field Weak Field
(2 unpaired
electrons)
(2 unpaired
electrons)
The number of unpaired electrons is the same in both cases.
21. (M) (a) Both of the central atoms have the same oxidation state, +3. We give the electron
configuration of the central atom to the left, then the completed crystal field diagram
in the center, and finally the number of unpaired electrons. The chloro ligand is a
weak field ligand in the spectrochemical series.
Mo3+ Kr 4 3
d weak field
Kr 4d
3 unpaired electrons; paramagnetic
The ethylenediamine ligand is a strong field ligand in the spectrochemical series.
Co3+ Ar 3 6
d strong field
Ar
no unpaired electrons; diamagnetic
(b) In CoCl4
2 the oxidation state of cobalt is 2+. Chloro is a weak field ligand. The
electron configuration of Co2+ is
7
Ar 3d or
Ar
The tetrahedral ligand field diagram is weak field
shown on the right. 3 unpaired electrons
22. (M) (a) In
2+
4
Cu py
the oxidation state of copper is +2. Pyridine is a strong field
ligand. The electron configuration of 2+
Cu is
9
Ar 3d or
Ar
There is no possible way that an odd number of electrons can be paired up, without
at least one electron being unpaired.
2+
4
Cu py
is paramagnetic.
eg
t2g
eg
t2g
eg
t2g
eg
t2g
t2g
eg
Chapter 24: Complex Ions and Coordination Compounds
1174
eg
(b) In Mn CN
6
3 the oxidation state of manganese is +3. Cyano is a strong field
ligand. The electron configuration of Mn3+ is
4
Ar 3d or
Ar
The ligand field diagram follows, on the left-hand side. In
4
FeCl the oxidation
state of iron is +3. Chloro is a weak field ligand. The electron configuration of Fe3+
is
5
Ar 3d or [Ar]
The ligand field diagram follows, below.
strong field weak field
2 unpaired electrons 5 unpaired electrons
There are more unpaired electrons in FeCl4
than in
3
6
Mn CN .
23. (M) The electron configuration of Ni2+ is
8
Ar 3d or
Ar
Ammonia is a strong field ligand. The ligand field diagrams follow, octahedral at left,
tetrahedral in the center and square planar at right.
Octahedral Tetrahedral Square Planar
Since the octahedral and tetrahedral configurations have the same number of unpaired
electrons (that is, 2 unpaired electrons), we cannot use magnetic behavior to determine
whether the ammine complex of nickel(II) is octahedral or tetrahedral. But we can
determine if the complex is square planar, since the square planar complex is diamagnetic
with zero unpaired electrons.
24. (M) The difference is due to the fact that Fe CN6
4 is a strong field complex ion, while
Fe H2O
6
2+ is a weak field complex ion. The electron configurations for an iron atom
and an iron(II) ion, and the ligand field diagrams for the two complex ions follow.
Fe CN
6
4
26
[Fe H O ]2+
iron atom Ar
iron(II) ion [Ar] 3d 4s
eg
3d4s
t2g
eg
t2g
eg
t2g
t2g
eg
t2g
eg
t2g
dx2-y2
dxy
dz2
dxz, d
y
z

Chapter 24: Complex Ions and Coordination Compounds
1175
Complex-Ion Equilibria
25. (E) (a)
2+
33
24
Zn OH s + 4 NH aq Zn NH aq + 2 OH aq
(b)
2+
2
Cu aq + 2 OH aq Cu OH s
The blue color is most likely due to the presence of some unreacted [Cu(H2O)4]2+ (pale blue)
2+
33
24
Cu OH s + 4 NH aq Cu NH aq, dark blue + 2 OH aq
2+ 2+
++
33 2 4
44
Cu NH aq + 4 H O aq Cu H O aq + 4 NH aq
26. (M) (a)
2
24
CuCl s + 2 Cl aq CuCl aq, yellow
2
42
2CuCl aq +4HO(l)
2+
2
42
4
22
2
CuCl aq, yellow Cu H O aq, pale blue + 4 Cl aq
or
2CuHO Cl aq, green+4 Cl aq
Either
2+
2
42 2
4
CuCl aq + 4 H O(l) Cu H O aq + 4 Cl aq
Or
2+
22 2 2
24
Cu HO Cl aq +2HO(l) Cu HO aq +2 Cl aq
(b) The blue solution is that of [Cr(H2O)6]2+. This is quickly oxidized to C
r
3+ by O2g
from the atmosphere. The green color is due to CrCl2H2O
4
3+ .
2+
26 2
224 2
4 [Cr(H O) ] (aq, blue)+4 H (aq)+8 Cl (aq)+O (g)
4 [CrCl (H O) ] (aq, green)+10 H O(l)
Over a period of time, we might expect volatile HCl(g) to escape, leading to the
formation of complex ions with more HO
2 and less Cl.
+
Haq+ Claq HClg
2+
+
22 2 2
45
CrCl H O aq, green + H O(l) CrCl H O aq, blue-green + Cl aq

Chapter 24: Complex Ions and Coordination Compounds
1176
2+ 3+
222
56
CrCl H O aq, blue-green + H O(l) Cr H O aq, blue + Cl aq
Actually, to ensure that these final two reactions actually do occur in a timely
fashion, it would be helpful to dilute the solution with water after the chromium
metal has dissolved.
27. (M) Co en
3
3+ should have the largest overall Kf value. We expect a complex ion with
polydentate ligands to have a larger value for its formation constant than complexes that
contain only monodentate ligands. This phenomenon is known as the chelate effect. Once
one end of a polydentate ligand becomes attached to the central metal, the attachment of
the remaining electron pairs is relatively easy because they already are close to the central
metal (and do not have to migrate in from a distant point in the solution).
28. (M) (a) Zn NH3
4
2+
41234 222 8
= = 3.9 10 2.1 10 1.0 10 50.= 4.1 10KKKK
.
(b) Ni H2O
2NH3
4
2+
41234 22 7
= = 6.3 10 1.7 10 54 15 = 8.7 10KKKK
29. (M) First:
3+ 3+
222
64
Fe H O aq + en aq Fe H O en aq + 2H O(l)
K1=104.34
Second:
3+ 3+
222
422
Fe H O en aq + en aq Fe H O en aq + 2H O(l)
K2=103.31
Third:
3+
3+
2 2
22 3
Fe H O en aq + en aq Fe en aq + 2H O(l)
K32.05
=10
Net:
3+ 3+
2 2
63
Fe H O aq +3 en aq Fe en aq + 6H O(l)
K
K
K
K
f=123
log f
K
= 4.34 + 3.31+ 2.05 = 9.70 Kf=10 =5.0 10 =
9.70 9 3
30. (E) Since the overall formation constant is the product of the individual stepwise formation
constants, the logarithm of the overall formation constant is the sum of the logarithms of
the stepwise formation constants.
log log log log log
f
K
K
K
K
K
= + + + = 2.80 +1.60 + 0.49 + 0.73 = 5.62
1234
Kf=10 =4.2 10
5.62 5

Chapter 24: Complex Ions and Coordination Compounds
1177
31. (M) (a) Aluminum(III) forms a stable (and soluble) hydroxo complex but not a stable
ammine complex.
222
33 24
Al HO OH s +OH aq Al HO OH aq +HO(l)
(b) Although zinc(II) forms a soluble stable ammine complex ion, its formation constant
is not sufficiently large to dissolve highly insoluble ZnS. However, it is sufficiently
large to dissolve the moderately insoluble ZnCO3. Said another way, ZnS does not
produce sufficient Zn2+ to permit the complex ion to form.
2+ 2
33 3 3
4
ZnCO s + 4 NH aq Zn NH aq + CO aq
(c) Chloride ion forms a stable complex ion with silver(I) ion, that dissolves the AgCl(s)
that formed when Cl is low.
++
2
AgCl s Ag aq + Cl aq and Ag aq + 2 Cl aq AgCl aq
Overall:
2
AgCl s + Cl aq AgCl aq
32. (M) (a) Because of the large value of the formation constant for the complex ion,
Co NH3
6
3+ aq
, the concentration of free Co3+ aq
is too small to enable it to
oxidize water to O2g
. Since there is not a complex ion present, except, of course,
Co H2O
6
3+ aq
, when CoCl3 is dissolved in water, the Co3+ is sufficiently
high for the oxidation-reduction reaction to be spontaneous.
3+ 2+ +
22
4 Co aq +2 H O(l) 4 Co aq +4 H aq +O g
(b) Although AgI(s) is often described as insoluble, there is actually a small
concentration of Ag+aq
present because of the solubility equilibrium:
2 AgI(s) Ag(aq) +I-(aq)
These silver ions react with thiosulfate ion to form the stable dithiosulfatoargentate(I)
complex ion:
+2
23 23
2
Ag aq + 2S O aq Ag S O aq

Chapter 24: Complex Ions and Coordination Compounds
1178
Acid-Base Properties
33. (E) Al H2O
6
3+ aq
is capable of releasing H+:
3+ 2+ +
22 23
65
Al H O aq + H O(l) AlOH H O aq + H O aq
The value of its ionization constant (
pK
a= 5.01) approximates that of acetic acid.
34. (M) (a)
2+ +
222
524
CrOH HO aq +OH aq Cr OH HO aq + HO(l)
(b)
2+ 3+
+
23 22
56
CrOH HO aq + HO aq Cr HO aq + HO(l)
Applications
35. (M) (a) Solubility:
13
sp =5.0 10 +
AgBr s Ag aq + Br aq
K
Cplx. Ion Formation:
13
f3
=1.7 10
+2
23 23
2
Ag aq + 2S O aq Ag S O aq
K
Net:
3
2-
23 23 overall sp f
2
AgBr s + 2S O aq Ag S O aq + Br (aq) =KKK
13 13
overall = 5.0 10 1.7 10 = 8.5K
With a reasonably high SO
23
2, this reaction will go essentially to completion.
(b) NH3aq
cannot be used in the fixing of photographic film because of the relatively
small value of Kf for Ag NH3
2
+aq
,Kf=1.6 107
. This would produce a
value of
K
=8.0 10 6
in the expression above, which is nowhere large enough to
drive the reaction to completion.
36. (M) Oxidation: Co NH3
6
2+ aq
Co NH3
6
3+ aq
e
2 0.10V.E
Reduction: H2O2aq
2e2OHaq
0.88VE
Net:
2+ 3+
22 3 3
66
HO aq+2CoNH aq 2CoNH aq+2OH(aq)
cell = +0.88 V+ 0.10 V = +0.78 V.E
The positive value of the standard cell potential indicates that this is a spontaneous reaction.
37. (M) To make the cis isomer, we must use ligands that show a strong tendency for
directing incoming ligands to positions that are trans to themselves. I− has a stronger
tendency than does Cl− or NH3 for directing incoming ligands to the trans positions, and
so it is beneficial to convert K2[PtCl4] to K2[PtI4] before replacing ligands around Pt with
NH3 molecules.
Chapter 24: Complex Ions and Coordination Compounds
1179
38. (M) Transplatin is more reactive and is involved in more side reactions before it reaches
its target inside of cancer cells. Thus, although it is more reactive, it is less effective at
killing cancer cells.
Pt
H3N
Cl NH3
Cl
trans-Pt(NH3)2Cl2
Pt
Cl
Cl NH3
NH3
cis-Pt(NH3)2Cl2
INTEGRATIVE AND ADVANCED EXERCISES
39. (M)
(a) cupric tetraammine ion tetraamminecopper(II) ion [Cu(NH3)4]2+
(b) dichlorotetraamminecobaltic chloride tetraamminedichlorocobalt(III) chloride [CoCl2(NH3)4]Cl
(c) platinic(IV) hexachloride ion hexachloroplatinate(IV) ion [PtCl6]2–
(d) disodium copper tetrachloride sodium tetrachlorocuprate(II) Na2[CuCl4]
(e) dipotassium antimony(III) pentachloride potassium pentachloroantimonate(III) K2[SbCl5]
40. (E)[Pt(NH3)4][PtCl4] tetraammineplatinum(II) tetrachloroplatinate(II)
41. (M) The four possible isomers for [CoCl2(en)(NH3)2]+ are sketched below:
Co
Cl
Cl NH2
H2N
NH3
NH3
Co
H3N
H3NNH2
H2N
Cl
Cl
Co
H3N
Cl NH2
H2N
Cl
NH3
Co
Cl
H3NNH2
H2N
Cl
NH3
42. (M)The color of the green solid, as well as that of the green solution, is produced by the complex
ion [CrCl2(H2O)4]+. Over time in solution, the chloro ligands are replaced by aqua ligands,
producing violet [Cr(H2O)6]3+(aq). When the water is evaporated, the original complex is re-
formed as the concentration of chloro ligand, [Cl–], gets higher and the chloro ligands replace the
aqua ligands.
Cr
H2O
H2OOH2
OH2
Cl
Cl
+2H20Cr
H2O
H2OOH2
OH2
OH2
OH2
2Cl
3
+2H20Cr
H2O
H2OOH2
OH2
Cl
Cl
43. (M)The chloro ligand, being lower in the spectrochemical series than the ethylenediamine ligand,
is less strongly bonded to the central atom than is the ethylenediamine ligand. Therefore, of the
two types of ligands, we expect the chloro ligand to be replaced more readily. In the cis isomer,
the two chloro ligands are 90° from each other. This is the angular spacing that can be readily
spanned by the oxalato ligand, thus we expect reaction with the cis isomer to occur rapidly. On
the other hand, in the trans isomer, the two chloro ligands are located 180° from each other. After
Chapter 24: Complex Ions and Coordination Compounds
1180
the chloro ligands are removed, at least one end of one ethylenediamine ligand would have to be
relocated to allow the oxalato ligand to bond as a bidentate ligand. Consequently, replacement of
the two chloro ligands by the oxalato ligand should be much slower for the trans isomer than for
the cis isomer.
44. (M) Cl2 + 2 e- 2 Cl-
[Pt(NH3)4]2+ [Pt(NH3)4]4+ + 2 e-
Cl2 + [Pt(NH3)4]2+ [Pt(Cl2NH3)4]2+
45. (M) The successive acid ionizations of a complex ion such as [Fe(OH)6]3+ are more nearly
equal in magnitude than those of an uncharged polyprotic acid such as H3PO4 principally
because the complex ion has a positive charge. The second proton is leaving a species which
has one fewer positive charge but which is nonetheless positively charged. Since positive
charges repel each other, successive ionizations should not show a great decrease in the
magnitude of their ionization constants. In the case of polyprotic acids, on the other hand,
successive protons are leaving a species whose negative charge is increasingly greater with
each step. Since unlike charges attract each other, it becomes increasingly difficult to
remove successive protons.
46. (M)
QuickTime™ and a
TIFF (LZW) decompressor
are needed to see this picture.
Pt
NH3
Cl
Cl Cl
K+
-1
(a)
Pt
NH3
Cl
Cl NH3
(b)
Pt
NH3
Cl
H3NNH3
Cl-
+1
Pt
NH3
H3N
H3NNH3
2Cl-
+2
(c)
(d)
Pt
Cl
Cl
Cl Cl
2K+
-2
C
o
n
d
u
c
t
i
v
i
t
y
Number of
Cl ligands
(e)
47. (M) (a)
2+ + 2-4
25 3
3+
26
3+
3
3
[[Fe(H O) OH] ] [H O ]
K = 9.0 10
0.100-
[[Fe(H O) ] ]
Solving, we find 9.5 10 M, which is the [H O ] so:
pH log(9.5 10 ) 2.02
x
x
x
-4
K 9.0 10
3+ 2
26 2 25 3
Fe(H O) (aq) H O(l) Fe(H O) OH (aq) H O
Initial 0.100 M 0 M 0 M
Equil. (0.100 ) M
xxx
3+
26
{where is the molar quantity of Fe(H O) (aq) hydrolyzed}x
Pt
H3N
H3NNH3
NH3
+ Cl-Cl Pt
H3N
H3NNH3
NH3
Cl
Cl

Chapter 24: Complex Ions and Coordination Compounds
1181
(b) -4
K 9.0 10
3+ 2
26 2 25 3
[Fe(H O) ] (aq) H O(l) [Fe(H O) OH] (aq) H O
initial 0.100 M 0 M 0.100 M
equil. (0.100 )x
3+
26
2+ -4
25 3
3+
26
-4
25
M M (0.100 ) M
{where is [[Fe(H O) ] ] reacting}
[[Fe(H O) OH] ] [H O ] (0.100 )
K9.0 10
[[Fe(H O) ] ] (0.100- )
Solving, we find 9.0 10 M, which is the [[Fe(H O) OH]
xx
x
xx
x
x
2]
(c) 2-6
25 a
3+ +
26 3
3+ -4
+a26
32
25
We simply substitute [[Fe(H O) OH] ] = 1.0 10 M into the K expression
with [Fe(H O) ] 0.100 M and determine the concentration of H O
K [[Fe(H O) ] ] 9.0 10 (0.100 M)
[H O ] [[Fe(H O) OH] ]
-6
+
3
90. M
[1.0 10 M]
To maintain the concentration at this level requires an impossibly high concentration of H O
48. (D) Let us first determine the concentration of the uncomplexed (free) Pb2+(aq). Because of
the large value of the formation constant, we assume that most of the lead(II) ion is present as
the EDTA complex ion ([Pb(EDTA)]2-). Once equilibrium is established, we can see if there
is sufficient lead(II) ion present in solution to precipitate with the sulfide ion. Note: the
concentration of EDTA remains constant at 0.20 M)
Reaction: Pb2+(aq) + EDTA4-(aq)
18
210
[Pb(EDTA)]2-(aq)
Initial: 0 M 0.20 M 0.010 M
Change: +x M constant -x M
Equilibrium: x M 0.20 M (0.010-x) M 0.010 M
Kf = [Pb(EDTA)2- ]
[Pb2+ ][EDTA4- ]=21018 =0.010
0.20(x)x = 2.5 10-20 M = [Pb2+ ]
Now determine the [S2- ] required to precipitate PbS from this solution. Ksp = [Pb2][S2]81028
[S2- ]= 810-28
(5 10-20 )=2.510-8 M Recall (i) that a saturated H2S solution is ~0.10 M H2S
and (ii) That the [S2- ] = Ka2 = 110-14
Qsp = [Pb2][S2] 2.510-20 110-14 2.5 10-34 Ksp 81028
Qsp << Ksp Hence, PbS(s) will not precipitate from this solution.
49. (M) The formation of [Cu(NH3)4]2+(aq) from [Cu(H2O)4]2+(aq) has K1 = 1.9 × 104, K2 = 3.9 ×
103, K3 = 1.0 × 103, and K4 = 1.5 × 102. Since these equilibrium constants are all considerably
larger than 1.00, one expects that the reactions they represent, yielding ultimately the ion
[Cu(NH3)4]2+(aq), will go essentially to completion. However, if the concentration of NH3
were limited to less than the stoichiometric amount, that is, to less than 4 mol NH3 per mol of

Chapter 24: Complex Ions and Coordination Compounds
1182
Cu2+(aq), one would expect that the ammine-aqua complex ions would be present in
significantly higher concentrations than the [Cu(NH3)4]2+(aq) ions.
50. (D) For [Ca(EDTA)]2–, Kf = 4 × 1010 and for [Mg(EDTA)]2–, Kf = 4 × 108. In Table 18-1, the
least soluble calcium compound is CaCO3, Ksp = 2.8 × 10–9, and the least soluble magnesium
compound is Mg3(PO4)2, Ksp = 1 × 10–25. We can determine the equilibrium constants for
adding carbonate ion to [Ca(EDTA)]2–(aq) and for adding phosphate ion to [Mg(EDTA)]2–(aq)
as follows:
224 10
22 -9
3 3 ppt
Instability: [Ca(EDTA)] (aq) Ca (aq) EDTA (aq) 1/4 10
Precipitation: Ca (aq) CO (aq) CaCO (s) 1/2.8 10
Net: [Ca(EDTA)
i
K
K
22 4
33 ppt
-3
10 -9
] + CO (aq) CaCO (s) + EDTA (aq)
1
9 10
(4 10 )( 2.8 10 )
i
KK K
K
The small value of the equilibrium constant indicates that this reaction does not proceed
very far toward products.
224 383
23 25
4 3 4 2 ppt
2- 3-
4
Instability: {[Mg(EDTA)] (aq) Mg (aq) EDTA (aq)} 3 1/(4 10 )
Precipitation: 3 Mg (aq) 2 PO (aq) Mg (PO ) (s) 1/1 10
Net : 3 [Mg(EDTA)] +2 PO (aq)
i
K
K
4- 3
3 4 2 ppt
6
83 25
Mg (PO ) (s) +3 EDTA (aq)
1 0.1
(4 10 ) (1 10 )
i
KK K
K
This is not such a small value, but again we do not expect the formation of much product,
particularly if the [EDTA4– ] is kept high. We can approximate what the concentration of
precipitating anion must be in each case, assuming that the concentration of complex ion is
0.10 M and that of [EDTA4– ] also is 0.10 M.
22 4
33
4-3 2 2
3
22 2
33
Reaction: [Ca(EDTA)] CO (aq) CaCO (s) EDTA (aq)
[EDTA ] 0.10 M
9 10 [CO ] 1 10 M
[[Ca(EDTA)] ][CO ] 0.10 M [CO ]
K
This is an impossibly high [CO32–].
23 4
4342
43 3 3
645
23 32 3 32
44
Reaction: 3[Mg(EDTA)] 2 PO (aq) Mg (PO ) (s) 3 EDTA (aq)
[EDTA ] (0.10 M)
0.1 [PO ] 2. M
[[Mg(EDTA)] ] [PO ] (0.10 M) [PO ]
K
Although this [PO43–] is not impossibly high, it is unlikely that it will occur without
the deliberate addition of phosphate ion to the water. Alternatively, we can substitute
[[M(EDTA)]2– ] = 0.10 M and [EDTA4– ] = 0.10 M into the formation constant
expression: ]EDTA][M[
][[M(EDTA)]
42
2
f
K

Chapter 24: Complex Ions and Coordination Compounds
1183
This substitution gives 2
f
1
[M ] K
, hence, [Ca2+] = 2.5 × 10–11 M and [Mg2+] = 2.5 × 10–9 M,
which are concentrations that do not normally lead to the formation of precipitates unless the
concentrations of anions are substantial. Specifically, the required anion concentrations are [CO32–] =
1.1 × 102 M for CaCO3, and [PO43–] = 2.5 M, just as computed above.
51. (M) If a 99% conversion to the chloro complex is achieved, which is the percent conversion
necessary to produce a yellow color, [[CuCl4]2–] = 0.99 × 0.10 M = 0.099 M, and
[[Cu(H2O)4]2+] = 0.01 × 0.10 M = 0.0010 M. We substitute these values into the formation
constant expression and solve for [Cl–].
M 0.12
10 4.2 0.0010
0.099
]Cl[
][Cl M 0.0010
M 0.099
10 4.2
][Cl ]]O)Cu(H[[
]][[CuCl
5
4
4
5
42
42
2
4
f
K
This is the final concentration of free chloride ion in the solution. If we wish to account for all
chloride ion that has been added, we must include the chloride ion present in the complex ion.
total [Cl–] = 0.12 M free Cl– + (4 × 0.099 M) bound Cl– = 0.52 M
52. (M)(a) -
22
Oxidation: 2H O(l) O (g) 4 H (aq) 4 e -1.229 VE
3-2
32
22cell
Reduction: {Co ((aq) e Co (aq)} 1.82 V
Net: 4 Co (aq) 2 H O(l) 4 Co (aq) 4 H (aq) O (g) 0.59 V
E
E
(b) 33
336
Reaction: Co (aq) 6 NH (aq) [Co(NH ) ] (aq)
3
36
f 36
3
Initial: 1.0 M 0.10 M 0 M
Changes: M constant M
Equil: (1.0 )M 0.10 M M
[[Co(NH ) ] ]
4.5 1
[Co ][NH ]
xx
xx
K
33 27
6
0 4.5 10
1.0
(1.0 )(0.10)
xx
x
x
Thus [[Co(NH3)6]3+] = 1.0 M because K is so large, and
M 10 2.2
10 4.5
1
]Co[ 28-
27
3

Chapter 24: Complex Ions and Coordination Compounds
1184
(c) The equilibrium and equilibrium constant for the reaction of NH3 with water follows.
32 4
-2
5 5
4
3
NH (aq) H O(l) NH (aq) OH (aq)
[NH ][OH ] [OH ]
1.8 10 [OH ] 0.10(1.8 10 ) 0.0013 M
[NH ] 0.10
b
K
In determining the [OH– ], we have noted that [NH4+] = [OH– ] by stoichiometry, and also that
[NH3] = 0.10 M, as we assumed above. M 10 7.7
0013.0
10 1.0
]OH[
]OH[ 12
14
3
w
K
We use the Nernst equation to determine the potential of reaction (24.12) at the conditions
described.
24 4
2
cell 34
44 124
28 4
[Co ] [H ] [O ]
0.0592
log
4[Co ]
0.0592 (1 10 ) (7.7 10 ) 0.2
0.59 log 0.59 V 0.732 V 0.142 V
4(2.2 10 )
P
EE
E
The negative cell potential indicates that the reaction indeed does not occur.
53. (M) We use the Nernst equation to determine the value of [Cu2+]. The cell reaction follows.
M 10 8 ]Cu[1.14
0592.0
)08.0 337.0( 2
][Cu log
)00.1(
][Cu
log
2
0592.0
337.0 V 0.08
]H[
][Cu
log
2
0.0592
V 337.0 g)(H aq)(Cu aq)(H 2 Cu(s)
1522
2
2
2
2
cell2
2
EE
E
Now we determine the value of Kf.
14
4154
3
2
2
43
f 10 1
)00.1(10 8
1.00
][NH ]Cu[
]])[[Cu(NH
K
This compares favorably with the value of Kf = 1.1 × 1013 given in Table 18-2, especially
considering the imprecision with which the data are known. (Ecell = 0.08 V is known to but
one significant figure.)

Chapter 24: Complex Ions and Coordination Compounds
1185
54. (M) We first determine [Ag+] in the cyanide solution.
18
218
2
18
2
2
f
10 1.8
(0.10) 10 5.6
0.10
]Ag[
(0.10.) ][Ag
0.10
10 5.6
]CN][Ag[
]][[Ag(CN)
K
The cell reaction is as follows. It has
V 0.000
cell E; the same reaction occurs at both anode and cathode and thus the Nernstian
voltage is influenced only by the Ag+ concentration.
KCN) M 0.10 ,][Ag(CN) M (0.10 Ag M) 10.0(Ag 2
V 0.99
10.0
10 1.8
log 0.0592 0.000
]Ag[
][Ag
log
1
0592.0
18
CN
EE
55. (M)
Co
H3N
H3NNH3
NH3
OH2
Cl
+
Cl-Co
H3N
H3NNH3
NH3
OH2
OH2
+2
2Cl-
A 0.10 mol/L solution of these compounds would result in ion concentration of
0.20 mol/L for [Co Cl (H2O(NH3)4)]Cl•H2O or 0.30 mol/L for [Co(H2O)2 (NH3)4]Cl2.
Observed freezing point depression = -0.56 C.
T = -Kf×m×i = -0.56 deg = -1.86 mol kg-1 deg(0.10 mol/L)×i
Hence, i = 3.0 mol/kg or 3.0 mol/L. This suggests that the compound is [Co(H2O)2 (NH3)4]Cl2.
56. (M) Sc(H2O)63+ and Zn(H2O)42+ have outer energy shells with 18 electrons, and thus they do not
have any electronic transitions in the energy range corresponding to visible light. Fe(H2O)63+ has 17
electrons (not 18) in its outer shell; thus, it does have electronic transitions in the energy range
corresponding to visible light.
57. (M) The Cr3+ ion would have 3 unpaired electrons, each residing in a 3d orbital and would be sp3d2
hybridized. The hybrid orbitals would be hybrids of 4s, 4p, and 3d (or 4d) orbitals. Each Cr–NH3
coordinate covalent bond is a σ bond formed when a lone pair in an sp3 orbital on N is directed
toward an empty sp3d2 orbital on Cr3+. The number of unpaired electrons predicted by valence bond
theory would be the same as the number of unpaired electrons predicted by crystal field theory.
58. (M) Since these reactions involve Ni2+ binding to six identical nitrogen donor atoms, we can
assume the H for each reaction is approximately the same. A large formation constant indicates
a more negative free energy. This indicates that the entropy term for these reactions is different.
The large increase in entropy for each step, can be explained by the chelate effect. The same
number of water molecules are displaced by fewer ligands, which is directly related to entropy
change.
Chapter 24: Complex Ions and Coordination Compounds
1186
59. (M)
Co(acac)3
Co O
OO
O
O
O
H3C
CH3
H3C
CH3
CH3
CH3
Co
O
O O
O
O
O
CH3
H3C
CH3
H3C
H3C
H3C
This compound has a non-
superimposable mirror image
(therefore it is optically active). These
are enantiomers. One enantiomer
rotates plane polarized light clockwise,
while the other rotates plane polarized
light counter-clockwise. Polarimetry
can be used to determine which isomer
rotates plane polarized light in a
particular direction.
trans-[Co(acac)2(H2O)2]Cl2
Co O
OO
O
OH2
OH2
CH3
CH3
H3C
H3C
Co
O
O O
O
OH2
OH2
H3C
H3C
CH3
CH3
This compound has a
superimposable mirror image
(therefore it is optically inactive).
These are the same compound.
This compound will not rotate
plane polarized light (net rotation
= 0).
cis-[Co(acac)2(H2O)2]Cl2
Co OH
OH2
O
O
O
O
H3C
CH3
H3C
OH2
Co
HO
H2O O
O
O
O
CH3
H3C
CH3
H2O
This compound has a non-
superimposable mirror image
(therefore it is optically active).
These are enantiomers. One
enantiomer rotates plane
polarized light clockwise, while
the other rotates plane polarized
light counter-clockwise. By
using a polarimeter, we can
determine which isomer rotates
plane polarized light in a
particular direction.
60. (D)[Co(H2O)6]3+(aq) + e- [Co(H2O)6]2+(aq)
log K = nE/0.0592 = (1)(1.82)/0.0592 = 30.74 K = 1030.74
[Co(en)3]3+(aq) + 6 H2O(l) [Co(H2O)6]3+(aq) + 3 en K = 1/1047.30
[Co(H2O)6]2+(aq) + 3 en [Co(en)3]2+(aq) + 6 H2O(l) K = 1012.18
[Co(H2O)6]3+(aq) + e- [Co(H2O)6]2+(aq) K = 1030.74
[Co(en)3]3+(aq) + e- [Co(en)3]2+(aq) Koverall = ?
Chapter 24: Complex Ions and Coordination Compounds
1187
K
overall = 1/1047.30×1012.18×1030.74 = 10-4.38 = 0.0000417
E = (0.0592/n)log K = (0.0592/1)log(0.0000417) = -0.26 V
4 Co3+(aq) + 4 e- 4 Co2+(aq) Ecathode = 1.82 V
2 H2O(l) 4 H+(aq) + O2(g) + 4 e- Eanode = 1.23 V
4 Co3+(aq) +2 H2O(l) 4 H+(aq) + O2(g) + 4 Co2+(aq)
Ecell = Ecathode– Eanode = 1.82V – 1.23 V = +0.59 V (Spontaneous)
4 [Co(en)3]3+(aq) + 4 e- 4 [Co(en)3]2+(aq) Ecathode = -0.26 V
2 H2O(l) 4 H+(aq) + O2(g) + 4 e- Eanode = 1.23 V
4 [Co(en)3]3+(aq) +2 H2O(l) 4 H+(aq) + O2(g) + 4 [Co(en)3]2+(aq)
Ecell = Ecathode– E = -0.26 V – 1.23 V = -1.49 V (non-spontaneous)
61. (M) There are two sets of isomers for Co(gly)3. Each set comprises two enantiomers (non-
superimposable mirror images). One rotates plane polarized light clockwise (+), the other counter-
clockwise (). Experiments are needed to determine which enantiomer is (+) and which is ().
Co
H2N
O O
NH2
H2N
O
O
O
O
Co
NH2
OO
H2N
NH2
O
O
O
O
Co
H2N
ONH2
NH2
O
O
O
O
O
Co
NH2
OH2N
H2N
O
O
O
O
O
(+)-fac-tris(glycinato)cobalt(III) (+)-mer-tris(glycinato)cobalt(III)
()-fac-tris(glycinato)cobalt(III) ()-mer-tris(glycinato)cobalt(III)
[Co(gly)2Cl(NH3)] has 10 possible isomer, four pairs of enantiomers and two achiral isomers.
Co
H2N
OH2
N
O
Cl
O
NH3
O
Co
H2N
OO
NH2
Cl
O
NH3
O
Co
H3N
Cl NH2
NH2
O
O
O
O
Co
NH3
Cl
H2N
H2N
O
O
O
O
Chapter 24: Complex Ions and Coordination Compounds
1188
Co
H3N
Cl O
O
H2N
H2N
O
O
Co
NH3
Cl
O
O
NH2
NH2
O
O
Co
H3N
Cl O
NH2
H2N
O
O
O
Co
NH3
Cl
O
H2N
NH2
O
O
O
Co
Cl
H3N O
NH2
H2N
O
O
O
Co Cl
NH3
O
H2N
NH2
O
O
O
62. (M) The coordination compound is face-centered cubic, K+ occupies tetrahedral holes, while
PtCl62- occupies octahedral holes.
63. (M)
# NH3 0 1 2 3
Formula: K2[PtCl6] K[PtCl5(NH3)] PtCl4(NH3)2 [PtCl3(NH3)3]Cl
Total # ions 3 2 0 2
(per formula
unit)
# NH3 4 5 6
Formula: [PtCl2(NH3)4]Cl2 [PtCl(NH3)5]Cl3 [Pt(NH3)6]Cl4
Total # ions 3 4 5
(per formula
unit)
Chapter 24: Complex Ions and Coordination Compounds
1189
FEATURE PROBLEMS
64. (M)(a) A trigonal prismatic structure predicts three geometric isomers for [CoCl2(NH3)4]+,
which is one more than the actual number of geometric isomers found for this complex ion.
All three geometric isomers arising from a trigonal prism are shown below.
Cl
Cl Cl
Cl Cl
Cl
(i) (ii) (iii)
The fact that the trigonal prismatic structure does not afford the correct number of isomers is a
clear indication that the ion actually adopts some other structural form (i.e., the theoretical model
is contradicted by the experimental result). We know now of course, that this ion has an
octahedral structure and as a result, it can exist only in cis and trans configurations.
(b) All attempts to produce optical isomers of [Co(en)3]3+ based upon a trigonal prismatic structure are
shown below. The ethylenediamine ligand appears as an arc in diagrams below:
(i) (ii) (iii)
Only structure (iii), which has an ethylenediamine ligand connecting the diagonal corners of a
face can give rise to optical isomers. Structure (iii) is highly unlikely, however, because the
ethylenediamine ligand is simply too short to effectively span the diagonal distance across the
face of the prism. Thus, barring any unusual stretching of the ethylenediamine ligand, a trigonal
prismatic structure cannot account for the optical isomerism that was observed for [Co(en)3]3+.
65. (D) Assuming that each hydroxide ligand bears its normal 1– charge, and that each ammonia
ligand is neutral, the total contribution of negative charge from the ligands is 6 –. Since the
net charge on the complex ions is 6+, the average oxidation state for each Co atom must be
+3 (i.e., each Co in the complex can be viewed as a Co3+ 3d 6 ion surrounded by six
ligands.) The five 3d orbitals on each Co are split by the octahedrally arranged ligands into
three lower energy orbitals, called t2g orbitals, and two higher energy orbitals, called eg
orbitals. We are told in the question that the complex is low spin. This is simply another
way of saying that all six 3d electrons on each Co are paired up in the t2g set as a result of the
eg and t2g orbitals being separated by a relatively large energy gap (see below). Hence, there
should be no unpaired electrons in the hexacation (i.e., the cation is expected to be
diamagnetic).
Chapter 24: Complex Ions and Coordination Compounds
1190
Low Spin Co3+
(Octahedral Environment):
Relatively Large Crystal Field Splitting
The Lewis structures for the two optical isomers (enantiomers) are depicted below:
66. (D) The data used to construct a plot of hydration energy as a function of metal ion atomic
number is collected in the table below. The graph of hydration energy (kJ/mol) versus
metal ion atomic number is located beneath the table.
Metal ion Atomic number Hydration energy
Ca2+ 20 2468 kJ/mol
Sc2+ 21
2673 kJ/mol
Ti2+ 22
2750 kJ/mol
V2+ 23
2814 kJ/mol
Cr2+ 24
2799 kJ/mol
Mn2+ 25 2743 kJ/mol
Fe2+ 26
2843 kJ/mol
Co2+ 27 2904 kJ/mol
Ni2+ 28
2986 kJ/mol
Cu2+ 29 2989 kJ/mol
Zn2+ 30 2936 kJ/mol
Hydration Enthalpy of M
2+
ions (Z = 20-30)
-3000
-2800
-2600
20 22 24 26 28 30
Atomic Number (Z)
Hydration Energy (kJ/mol)
Co
NH
3
NH
3
NH
3
NH
3
Co
O
O
OO
OO
Co
NH
3
H
3
N
H
3
N
H
3
N
Co
NH
3
H
3
N
H
3
N
NH
3
HH
H
H
H
H
Co
H
3
N
H
3
N
H
3
N
H
3
NCo
O
O
OO
OO
Co
H
3
N
NH
3
NH
3
NH
3
Co
H
3
N
NH
3
NH
3
NH
3
H
H
HH
H
H
Non-superimposable mirror images of one another
eg
t
2g
(a)
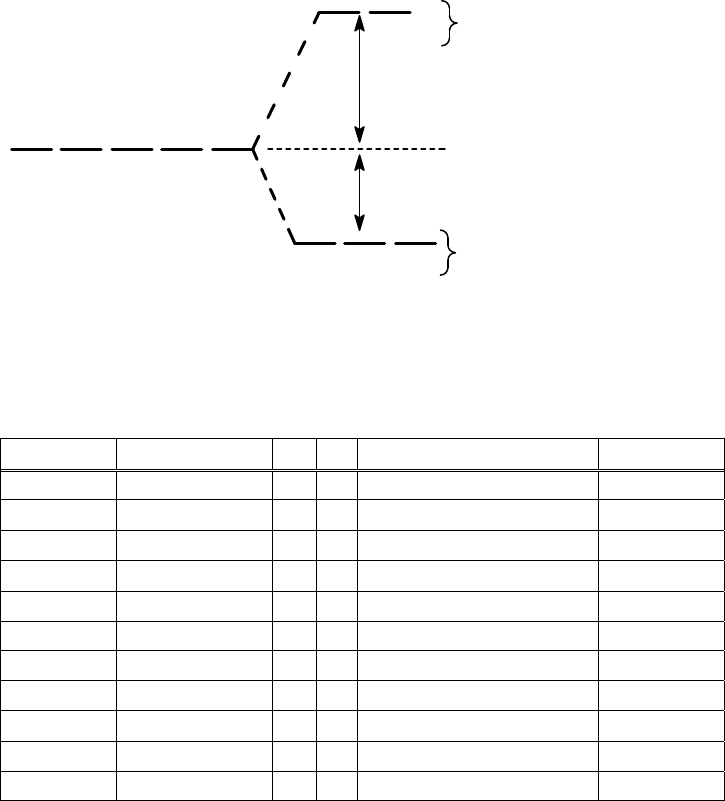
Chapter 24: Complex Ions and Coordination Compounds
1191
(b) When a metal ion is placed in an octahedral field of ligands, the five d-
orbitals are split into eg and t2g subsets, as shown in the diagram below:
3/5o
2/5o
d-orbitals
(symmerical field)
(octahedral field)
dxy dyz dxz
dz2dx - y
22
t2g
eg
Since water is a weak field ligand, the magnitude of the splitting is relatively small. As a
consequence, high-spin configurations result for all of the hexaaqua complexes. The
electron configurations for the metal ions in the high-spin hexaaqua complexes and their
associated crystal field stabilization energies (CFSE) are provided in the table below
Metal Ion Configuration t2g egnumber of unpaired e CFSE(o)
Ca2+ 3d 0 0 0 0 0
Sc2+ 3d 1 1 0 1 2/5
Ti2+ 3d 2 2 0 2 4/5
V2+ 3d 3 3 0 3 6/5
Cr2+ 3d 4 3 1 4 3/5
Mn2+ 3d 5 3 2 5 0
Fe2+ 3d 6 4 2 4 2/5
Co2+ 3d 7 5 2 3 4/5
Ni2+ 3d 8 6 2 2 6/5
Cu2+ 3d 9 6 3 1 3/5
Zn2+ 3d 10 6 4 0 0
Thus, the crystal field stabilization energy is zero for Ca2+. Mn2+ and Zn2+.
(c) The lines drawn between those ions that have a CFSE = 0 show the trend for the enthalpy of
hydration after the contribution from the crystal field stabilization energy has been subtracted
from the experimental values. The Ca to Mn and Mn to Zn lines are quite similar. Both line
have slopes that are negative and are of comparable magnitude. This trend shows that as one
proceeds from left to right across the periodic table, the energy of hydration for dications
becomes increasingly more negative. The hexaaqua complexes become progressively more
stable because the Zeff experienced by the bonding electrons in the valence shell of the metal
ion steadily increases as we move further and further to the right. Put another way, the Zeff
climbs steadily as we move from left to right and this leads to the positive charge density on
the metal becoming larger and larger, which results in the water ligands steadily being pulled
closer and closer to the nucleus. Of course, the closer the approach of the water ligands to the
metal, the greater is the energy released upon successful coordination of the ligand.

Chapter 24: Complex Ions and Coordination Compounds
1192
(d) Those ions that exhibit crystal field stabilization energies greater than zero have heats of
hydration that are more negative (i.e. more energy released) than the hypothetical heat of
hydration for the ion with CFSE subtracted out. The heat of hydration without CFSE for
a given ion falls on the line drawn between the two flanking ions with CFSE = 0 at a
position directly above the point for the experimental hydration energy. The energy
difference between the observed heat of hydration for the ion and the heat of hydration
without CFSE is, of course, approximately equal to the CFSE for the ion.
(e) As was mentioned in the answer to part (c), the straight line drawn between manganese
and zinc (both ions with CFSE = 0) on the previous plot, describes the enthalpy trend
after the ligand field stabilization energy has been subtracted from the experimental
values for the hydration enthalpy. Thus, o for Fe2+ in [Fe(H2O)6]2+ is approximately
equal to 5/2 of the energy difference (in kJ/mol) between the observed hydration energy
for Fe2+(g) and the point for Fe2+ on the line connecting Mn2+ and Zn2+, which is the
expected enthalpy of hydration after the CFSE has been subtracted out. Remember that
the crystal field stabilization energy for Fe2+ that is obtained from the graph is not o, but
rather 2/5o, since the CFSE for a 3d6 ion in an octahedral field is just 2/5 of o.
Consequently, to obtain o , we must multiply the enthalpy difference by 5/2. According
to the graph, the high-spin CFSE for Fe2+ is 2843 kJ/mol (2782 kJ/mol) or 61
kJ/mol. Consequently, o = 5/2(61 kJ/mol) = 153 kJ/mol, or 1.5 102 kJ/mol is the
energy difference between the eg and t2g orbital sets.
(f) The color of an octahedral complex is the result of the promotion of an electron on the
metal from a t2g orbital eg orbital. The energy difference between the eg and t2g orbital
sets is o. As the metal-ligand bonding becomes stronger, the separation between the t2g
and eg orbitals becomes larger. If the eg set is not full, then the metal complex will exhibit
an absorption band corresponding to a t2g eg transition. Thus, the [Fe(H2O)6]2+complex
ion should absorb electromagnetic radiation that has Ephoton = o. Since o 150 kJ/mol
(calculated in part (e) of this question) for a mole of [Fe(H2O)6]2+(aq),
Ephoton = 2+226
2+ 23 2+
26 26
1mol [Fe(H O) ]
1.5 10 kJ 1000J
1mol[Fe(H O) ] 6.022 10 [Fe(H O) ] 1kJ
= 2.5 1019 J per ion
= 19
34
2.5 10 J
=6.626 10 Js
E
h
= 3.8 1014 s1
-
= 8-1
14 -1
2.998 10 ms
=3.8 10 s
c
h
= 7.8
107 m (780 nm)
So, the [Fe(H2O)6]2+ ion will absorb radiation with a wavelength of 780 nm, which is
red light in the visible part of the electromagnetic spectrum.
Chapter 24: Complex Ions and Coordination Compounds
1193
SELF-ASSESSMENT EXERCISES
67. (E) (a) Coordination number is the number of ligands coordinated to a transition metal
complex.
(b) 0 is the crystal field splitting parameter which depends on the coordination geometry
of a transition metal complex.
(c) Ammine complex is the complex that contains NH3 ligands.
(d) An enantiomer is one of two stereoisomers that are mirror images of each other that
are "non-superposable" (not identical).
68. (E) (a) A spectrochemical series is a list of ligands ordered on ligand strength and a list
of metal ions based on oxidation number, group and identity.
(b) Crystal field theory (CFT) is a model that describes the electronic structure of
transition metal compounds, all of which can be considered coordination complexes.
(c) Optical isomers are two compounds which contain the same number and kinds of
atoms, and bonds (i.e., the connectivity between atoms is the same), and different spatial
arrangements of the atoms, but which have non-superimposable mirror images.
(d) Structural isomerism in accordance with IUPAC, is a form of isomerism in which
molecules with the same molecular formula have atoms bonded together in different
orders.
69. (E) (a) Coordination number is the number of ligands coordinated to a transition metal
complex. Oxidation number of a central atom in a coordination compound is the charge
that it would have if all the ligands were removed along with the electron pairs that were
shared with the central atom.
(b) A monodentate ligand has one point at which it can attach to the central atom.
Polydentate ligand has many points at which it can coordinate to a transition metal.
(c) Cis isomer has identical groups on the same side. In trans isomer, on the other hand,
identical groups are on the opposite side.
(d) Dextrorotation and levorotation refer, respectively, to the properties of rotating plane
polarized light clockwise (for dextrorotation) or counterclockwise (for levorotation). A
compound with dextrorotation is called dextrorotary, while a compound with levorotation
is called levorotary.
(e) When metal is coordinated to ligands to form a complex, its "d" orbital splits into high
and low energy groups of suborbitals. Depending on the nature of the ligands, the energy
difference separating these groups can be large or small. In the first case, electrons of the
d orbital tend to pair in the low energy suborbitals, a configuration known as "low spin".
If the energy difference is low, electrons tend to distribute unpaired, giving rise to a "high
spin" configuration. High spin is associated with paramagnetism (the property of being
attracted to magnetic fields), while low spin is associated to diamagnetism (inert or
repelled by magnets).
70. (E) (d)
71. (E) (e)
Chapter 24: Complex Ions and Coordination Compounds
1194
72. (E) (b)
73. (E) (a)
74. (E) (d)
75. (E) (c)
76. (E) (b)
77. (M) (a) pentaamminebromocobalt(III)sulfate, no isomerism.
(b) hexaamminechromium(III)hexacyanocobaltate(III), no isomerism.
(c) sodiumhexanitrito-N-cobaltate(III), no isomerism
(d) tris(ethylenediamine)cobalt(III)chloride, two optical isomers.
78. (M) (a) [Ag(CN)2]-; (b) [Pt(NO2)(NH3)3]+; (c) [CoCl(en)2(H2O)]2+; (d) K4[Cr(CN)6]
79. (M)
Pt
Cl
Cl Cl
Cl
2-
Fe
H2N
H2
NCl
Cl
Cl
Cl
Fe
O
OCl
NH2
Cl
H2N
O
O
Cr
H3N
H3NNH3
NH3
Cl
OH
-
-+
(a) (b) (c) (d)
80. (M) (a) one structure only (all positions are equivalent for the H2O ligand; NH3 ligands
attach at the remaining five sites).
Co
H3N
H2ONH3
NH3
NH3
NH3
+3
(b) two structures, cis and trans, based on the placement of H2O.
Co
H3N
H2ONH3
OH2
NH3
NH3
+3
trans
Co
H2O
H2ONH3
NH3
NH3
NH3
+3
cis

Chapter 24: Complex Ions and Coordination Compounds
1195
(c) two structures, fac and mer.
Co
H2O
H3NNH3
OH2
NH3
OH2
+3
fac
Co
H2O
H2O OH2
NH3
NH3
NH3
+3
mer
(d) two structures, cis and trans, based on the placement of NH3.
Co
H2O
H2OOH2
OH2
NH3
NH3
+3
trans
Co
H3N
H3NOH2
OH2
OH2
OH2
+3
cis
81. (M) (a) coordination isomerism, based on the interchange of ligands between the
complex cation and complex anion.
(b) linkage isomerism, based on the mode of attachment of the SCN- ligand (either –
SCN- or –NCS-).
(c) no isomerism
(d) geometric isomerism, based on whether Cl- ligands are cis or trans.
(e) geometric isomerism, based on whether the NH3 or OH- ligands are fac or mer.
82. (M) (a) geometric isomerism (cis and trans) and optical isomerism in the cis isomer.
(b) geometric isomerism (cis and trans), optical isomerism in the cis isomer, and linkage
isomerism in the thiocyanate ligand.
(c) no isomers.
(d) no isomers for this square-planar complex.
(e) two geometric isomers, one with the tridentate ligand occupying meridional positions
and the other with the tridentate ligand occupying facial positions.
83. (M) Because ethylenediamine (en) is a stronger field ligand than H2O, more energy must
be absorbed by [Co(en)3]3+ than by [Co(H2O)6]3+ to simulate an electronic transition.
This means that [Co(en)3]3+(aq) absorbs shorter wavelength light and transmits longer
wavelength light than does [Co(H2O)6]3+(aq). Thus [Co(en)3]3+(aq) is yellow and
[Co(H2O)6]3+(aq) is blue.