Analysis Guide
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 194 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- I Drawing Statistical Conclusions
- II Inferences Using the t-distribution
- III A Closer look at Assumptions
- IV Alternatives to the t tools
- Problem 2: Logging problem
- Problem 3: Welch's Two Sample T-Test with Education Data
- Problem 4: Trauma and Metabolic Expenditure rank sum
- Problem 5: Autism and Yoga signed rank
- sexy ranked permutation test
- Unit 4 lecture slides
- V ANOVA
- VI Multiple comparisons and post hoc tests
- VII Workflow for testing hypotheses
MSDS 6371-405 Analysis Guide
David Josephs
October 13, 2018
Contents
I Drawing Statistical Conclusions 3
1 Problem 1: Randomized Experiment vs Random Sample 4
2 Problem 2: Identifying Confounding Variables 5
3 Problem 3: Identifying a Scope of Inference 6
4 Problem 4: Visual comparison of population means and a permutation test 8
5 Unit 1 Lecture Slides 12
II Inferences Using the t-distribution 19
6 Problem 1: A one sample t test 20
6.1 Complete Analysis 20
Hypothesis definition 20
Identification of a critical value and drawing a shaded t distribution 20
Value of Test Statistic 21
P value 21
Assessment of the Hypothesis test 21
Conclusion and scope of inference 21
Some R code 22
7 Problem 2: Two sample one sided t test 23
7.1 Permutation test 23
7.2 Two sample T test, full analysis 24
Hypothesis definition 24
critval and distribution 24
Calculation of the T statistic 25
P value 25
hypothesis assement 25
conclusion 26
Incorrect calculations 26
7.3 Rcode 26
8 Problem 3: two sample two sided t test 28
8.1 Full Analysis 28
Hypothesis Definition 28
Critical value and shaded distribution 28
T statistic 29
P value 29
Hypothesis Assessment 29
Conclusion and Scope of inference 29
9 Problem 4: power 31
9.1 Single power curve 31
9.2 Multiple power curves 32
9.3 Calculating change in N 32
10 Unit 2 Lecture Slides 34
III A Closer look at Assumptions 44
11 Problem 1: Two Sample T test with assumptions 45
11.1 Complete Analysis 45
Assmuption checking in SAS 45
Assumption Checking in R 47
Complete Analysis: 48
1

Analysis Guide Midterm
12 Outliers and Logarithmic Transformations 51
13 Log Transformed data 65
13.1 Full Analysis 65
Problem Statement: 65
Assumptions 65
3.3 Hypothesis testing 67
Statement of Hypotheses: 67
Critical Value 67
Calculation of the t statistic: 68
Calculation of the p-value: 68
3.3.5 Discussion of the Null hypothesis 68
Conclusion 68
14 Unit 3 Lecture slides 70
IV Alternatives to the t tools 89
15 Problem 2: Logging problem 90
15.1 Complete Rank-Sum Analysis Using SAS 90
Problem Statement 90
Assumptions 90
Statement of the Hypothesis 90
Calculation of the P-value 90
Results of the Hypothesis Test 91
Statistical Conclusion 91
Scope of Inference 91
Confirmation Using R 92
16 Problem 3: Welch’s Two Sample T-Test with Education Data 93
16.1 Problem Statement and Assumptions 93
Problem Statement 93
Assumptions 93
16.2 Complete Analysis Using SAS 94
Statement of Hypotheses 94
Critical t Value 94
Calculation of the t Statistic 95
Calculation of the p Value 95
Results of Hypothesis Test 95
Conclusion 95
Scope of Inference 96
Verification using R 96
Preferences 96
17 Problem 4: Trauma and Metabolic Expenditure rank sum 97
17.1 Hand-Written Calculations 97
17.2 SAS verification 100
17.3 Full Statistical Analysis 100
Problem Statement 100
Assumptions 100
Hypothesis definitions 100
Critical Value 101
Calculation of the z statistic 101
Calculation of the p value 101
Discussion of the hypothesis 101
Conclusion 102
18 Problem 5: Autism and Yoga signed rank 103
18.1 Hand-Written Calculations 103
18.2 Verification in SAS and R 105
Verification in SAS 105
Verification in R 105
18.3 6 step Sign Rank test using SAS 105
Statement of Hypothesis 105
Critical Values 105
Calculation of a Z statistic 106
Calculation of a p value 106
Assessment of hypothesis 106
Conclusion 106
18.4 Paired t test in SAS 107
Statement of Hypothesis 107
Critical Values 107
2

Analysis Guide Midterm
Calculation of a t statistic 107
Calculation of a P value 108
Assessment of Hypothesis 108
Conclusion 108
18.5 Confirmation with R 108
18.6 Complete Statistical Analysis 108
Assumptions 108
Statement of Hypothesis 109
Critical Values 109
Calculation of a t statistic 110
Calculation of a P value 110
Assessment of Hypothesis 110
Conclusion 110
19 sexy ranked permutation test 112
20 Unit 4 lecture slides 114
V ANOVA 125
21 Problem 1: Plots and Logged Data 126
21.1 Plots and Transformations 126
Raw Data Analysis 126
Transformed Data Analysis 130
21.2 Complete Analysis 132
Problem Statement 132
Assumptions 132
Hypothesis Definition 132
F Statistic 133
P-value 133
Hypothesis Assessment 133
Conclusion 133
Scope of Inference 134
21.3 Extra Values 134
Value of R2134
Mean Square Error and Degrees of Freedom 134
ANOVA in R! 134
22 Extra Sum of Squares 136
22.1 Building the Extra Sum of Squares Anova Table 136
22.2 Complete Analysis 137
Problem Statement 137
Assumptions 137
Hypothesis Definition 137
F Statistic 137
P-value 137
Hypothesis Assessment 137
Conclusion 137
Scope of Inference 137
22.3 Degrees of Freedom and Comparison to T-Test 138
23 Welch’s ANOVA 139
23.1 Complete Analysis 139
Problem Statement 139
Assumptions 139
Hypothesis Definition 139
F Statistic 139
P-value 140
Hypothesis Assessment 140
Conclusion 140
Scope of Inference 140
24 unit 5 lecture slides 141
VI Multiple comparisons and post hoc tests 156
25 Bonferroni CIs 157
26 Multiple Comparison 159
3

Analysis Guide Midterm
27 Tukey’s test and Dunnett’s test 162
27.1 Assumptions 162
Raw Data Analysis 162
Transformed Data Analysis 164
28 Multiple samples 168
28.1 ANOVA 168
Problem Statement 168
Assumptions 168
Hypothesis Definition 168
F Statistic 168
P-value 169
Hypothesis Assessment 169
Conclusion 169
28.2 Tukey’s test 169
Dunnett’s Test 170
29 Unit 6 lecture slides 172
VII Workflow for testing hypotheses 187
4
List of Codes
4.1 Creating Paneled histograms in SAS 8
4.2 Producing histograms in R 9
4.3 Two Tailed permutation test in SAS, using manually input groups 10
4.4 Two Tailed permutation test in R, using manually input groups 11
6.1 One sample t test in R with manual data input 20
6.2 Critical value and two sided shaded t distribution using SAS 21
6.3 One sample t test in SAS 21
6.4 one sample t test in r 22
7.1 A one sided permutation test in SAS 23
7.2 One sided shaded t distribution in SAS and Critval 25
7.3 Two sample t test using SAS 25
7.4 two sample t test in R 27
8.1 Two sided two sample t test in SAS 29
9.1 Proc power single with pooled variance 31
9.2 Producing several curves with proc power 32
11.1 Checking the assumptions of a t test in SAS 45
11.2 t test Assumption checking in R, Q-Q plot 47
11.3 t test Assumption checking in R, Histogram 48
12.1 Automatically input permutation test in SAS 64
12.2 Outlier removal in SAS 64
13.1 log transform in SAS 66
15.1 Exact rank sum test using SAS 90
15.2 wilcoxon rank sum test using R 92
16.1 welch’s t test 93
18.1 Signed Rank test in SAS 105
18.2 Paired T test in SAS 108
19.1 handcrafted rank sum test 112
21.1 Scatterplot of Raw Data Using SAS 126
21.2 Boxplot of Raw Data Using SAS 127
21.3 Histogram of Raw Data Using SAS 127
21.4 Q-Q of Raw Data Using SAS 128
21.5 Logging of Raw Data Using SAS 130
21.6 Scatterplot of Logged Data Using SAS 130
21.7 Boxplot of Logged Data Using SAS 130
21.8 Histogram of Logged Data Using SAS 131
21.9 Q-Q of Logged Data Using SAS 132
21.10ANOVA Test Using SAS 133
21.11Comparison of distributions using SAS 133
21.12ANOVA in R 135
22.1 Regrouping data using SAS 136
22.2 Secondary ANOVA using SAS 136
23.1 Welch’s ANOVA in SAS 139
25.1 Bonferroni in SAS 157
26.1 all the multiple comparisons in SAS 159
26.2 Multiple comparisons with R 161
28.1 Tukeys test in SAS and R 169
5
Part I
Drawing Statistical Conclusions
7
Chapter 1
Problem 1: Randomized Experiment vs
Random Sample
Question 1
What is the difference between a randomized experiment and a random sample? Under what type of
study/sample can a causal inference be made?
Answer to Question 1
A randomized experiment is when the the application of the experimental variable (“treatment”) is applied
to subjects chosen randomly. So for example, in a study with 400 subjects, and treatments A, B, and a
control group, each subject would randomly be assigned into either the control group, group A, or group
B. This is done to eliminate confounding variables, as well as possible bias. In a random sample, subjects
are randomly chosen from the population. This is done so that the subjects of the study can be assumed
to be representative of the population as a whole. [1]. We can make causal inferences from a randomized
experiment, but not from a random sample.
Score: 20/20. Explanation: This answer gets full marks because it covers all of the points made in the
key, it defines both random sampling and randomization in the same manner as the key. However in the
future it should be less wordy.
8
Chapter 2
Problem 2: Identifying Confounding
Variables
Question 2
In 1936, the Literary Digest polled 1 out of every 4 Americans and concluded that Alfred Landon would
win the presidential election in a landon-slide. Of course, history turned out dramatically different (see
http://historymatters.gmu.edu/d/5168/ for further details). The magazine combined three sampling sources:
subscribers to its magazine, phone number records, and automobile registration records. Comment on the
desired population of interest of the survey and what population the magazine actually drew from.
Answer To Question 2
The magazine had hoped to get a random sample, or a dichotomy of the voting population, which would
be representative of the entire voting population of the country as a whole. Instead, they only polled
subscribers to the magazine, phone number records, and automobile registration records. 1936 was in
the height of the great depression, which means that the average American was struggling to survive.
Therefore, while in the past this sampling techique had worked, this time around they ended up only
sampling the wealthiest people, those who could afford phones, cars, and magazine subscriptions, and the
results were not representative of the population. Without truly random sampling, “the statistical results
only apply to [those] sampled”, and cannot be representative of the entire population. [2]. Therefore, itis
just chance that in the previous years, the polls worked.
Score: 10/10. Explanation: This answer gets full marks because it states that the poll wanted to cover
all of the voters (5 points), and it identifies the actual group polled with some explanation (affluent people)
(5 points).
9
Chapter 3
Problem 3: Identifying a Scope of
Inference
Question 3
3. Suppose we have developed a new fertilizer that is supposed to help corn yields. This fertilizer is so
potent that a small vial of it sprayed over an entire field is a sufficient dose. We find that the new fertilizer
results in an average yield of 60 more bushels over the old fertilizer with a p-value of 0.0001. Write up a
scope of inference under the following study designs that generated this data.
1. We offer the new fertilizer at a discount to customers who have purchased the old fertilizer along with
a survey for them to fill out. Some farmers send in the survey after the growing season, reporting their
crop yield. From our records, we know which of these farmers used the new fertilizer and which used
the old one.
2. When a customer makes an order, we randomly send them either the old or new fertilizer. At the end
of the season, some of the farmers send us a report of their yield. Again, from our records, we know
which of these farmers used the new fertilizer and which used the old.
3. When a customer makes an order, we randomly send them either the old or new fertilizer. At the end
of the season, we sub-select from the fertilizer orders and send a team out to count those farmers’
crop yields.
4. We offer the new fertilizer at a discount to customers who have purchased the old fertilizer. At the
end of the season, we sub-select from the fertilizer orders and send a team out to count those farmers’
crop yields. From our records, we know which of these farmers used the new fertilizer and which
used the old one.
Answer
1. We cannot make causal inferences or inferences about the population, as it was not randomized or
a random sample. Available units from distinct groups were selected, however the treatment was
not assigned randomly, which may mean only farmers who needed a change in fertilizer or were
struggling and could not afford the old fertilizer decided to go for the discount, and then the study is
also only representative of those who submitted reports, as no random sampling was done
Score: 8/8. Explanation: This answer gets full credit because it states that causal inferences cannot
be made and that population inferences cannot be made, which agrees with the key
2. We can make causal inferences but not inferences about the population. The treatment was applied
at random to the subjects, but no random sampling was done. Therefore this study only speaks to the
effect of the treatment on farmers who submitted reports, which may mean that they had noteably
different yields.
Score: 8/8. Explanation: This answer receives full credit because it states that causal inferences can
be made, and that population statements cannot be made, with explanations, all agreeing with the
key
3. We can make causal inferences and inferences about the population. The farmers were randomly
assigned different treatments, which allows us to make causal inferences, and then the farmers were
randomly selected for the yield to be counted, which means that the selected farmers should be rep-
resentative of the entire population. With these experimental parameters, we can decide whether the
new fertilizer worked better, worse, or the same.
Score: 7/8. Explanation: This answer loses a point because the problem does not explicitly state
that the sub sample was random. I assumed it was a random sample, and with that assumption, the
answer is entirely correct, however the randomness is not explicitly stated. Therefore a point is taken
away. The rest of the answer agrees entirely with the key, therefore no more points will be lost
4. We can make inferences about the population but not causal inferences. The treatment was not sup-
plied randomly, so maybe only farmers who needed a discount or the old fertilizer wasnt working for
10

Analysis Guide Midterm
chose the new fertilizer. However, they were randomly sampled, which means we can make infer-
ences about the population to some degree but we definitely cannot make causaul inferences.
Score: 7/8. Explanation: This answer loses a point because the problem does not explicitly state
that the sub sample was random. I assumed it was a random sample, and with that assumption, the
answer is entirely correct, however the randomness is not explicitly stated. Therefore a point is taken
away. The rest of the answer agrees entirely with the key, therefore no more points will be lost.
11
Chapter 4
Problem 4: Visual comparison of
population means and a permutation test
Question 4
4. A Business Stats class here at SMU was polled, and students were asked how much money (cash) they
had in their pockets at that very moment. The idea was to see if there was evidence that those in charge of
the vending machines should include the expensive bill / coin acceptor or if the machines should just have
the credit card reader. Also, a professor from Seattle University polled her class last year with the same
question. Below are the results of the polls. SMU 34, 1200, 23, 50, 60, 50, 0, 0, 30, 89, 0, 300, 400, 20, 10, 0
Seattle U 20, 10, 5, 0, 30, 50, 0, 100, 110, 0, 40, 10, 3, 0
1. Use SAS to make a histogram of the amount of money in a student’s pocket from each school. Does
it appear there is any difference in population means? What evidence do you have? Discuss your
thoughts.
2. Use the following R code to reproduce your histograms. Simply cut and paste the histograms into
your HW. SMU = c(34, 1200, 23, 50, 60, 50, 0, 0, 30, 89, 0, 300, 400, 20, 10, 0) Seattle = c(20, 10, 5, 0,
30, 50, 0, 100, 110, 0, 40, 10, 3, 0) hist(SMU) hist(Seattle)
3. Run a permutation test to test if the mean amount of pocket cash from students at SMU is different
than that of students from Seattle University. Write up a statistical conclusion and scope of inference
(similar to the one from the PowerPoint). (This should include identifying the Ho and Ha as well as
the p-value.)
Answer
1. Code (see Appendix 1) for the SAS histogram (Figure 1) was inspired by [3]. The code used to
produce this histogram is as follows:
Code 4.1. Creating Paneled histograms in SAS
proc sgpanel data=CashMoney;
panelby School / rows=2 layout=rowlattice;
histogram cash / binwidth = 25;
run;
12

Analysis Guide Midterm
Figure 4.0.1. Distribution of Cash by School, produced in SAS
It appears that for the sample means, the SMU sample has a slighly higher mean, however I do not
believe that means that the population of SMU has a higher mean than Seattle U, as this was not a
random sample, it was just of business students. It appears that the SMU cash distribution is wider,
with higher values, but again it is hard to tell if it is indicative of the entire population, I believe,
based offof where the majority of the distributions lie, both populations would have similar means,
with SMU having a slightly higher mean. SMU is a private school and Seattle U is one of the best
value schools in the country, so it is possible that SMU students might have in general, more money
than students at Seattle U, and therefore more cash.
Score: 5/5. Explanation: This receives full marks, the histograms are correct and the conclusions are
similar to the key, and are very logical. The code is included in the appendix.
2. The code used to generate the R histograms (Figure 2) was given in the homework and is presented
below
Code 4.2. Producing histograms in R
1SMU = c(34, 1200, 23, 50, 60, 50, 0, 0, 30, 89, 0, 300, 400, 20, 10, 0)
2Seattle = c(20, 10, 5, 0, 30, 50, 0, 100, 110, 0, 40, 10, 3, 0)
3par(mfrow=c(1,2))
4hist(SMU)
5hist(Seattle)
Figure 4.0.2. Cash Distributions at SMU and Seattle U, Produced using R
he code used to generate the permutation test (Appendix 2), using SAS, is given in [4]. The results of
the permutation test, with 999999 permutations can be seen in Figure 3 Below is SAS and R code for
permutation tests:
13

Analysis Guide Midterm
Code 4.3. Two Tailed permutation test in SAS, using manually input groups
proc iml;
G1 = {/*SMU student data*/};
G2 = {/*Seattle U student data*/};
obsdiff = mean(G1) - mean(G2); /*difference in the means of the two data sets*/
print obsdiff;
call randseed(12345); /*set random number seed */
alldata = G1 // G2; /*stack data in a single vector */
N1 = nrow(G1); N = N1 + nrow(G2);
NRepl = 999999; /*number of permutations, I did ~1 million just because I thought the shape of the distribution was very interesting */
nulldist = j(NRepl,1); /*allocate vector to hold results */
do k=1to NRepl;
x = sample(alldata, N, "WOR"); /*permute the data */
nulldist[k] = mean(x[1:N1]) - mean(x[(N1+1):N]); /*difference of means */
end;
title "Histogram of Null Distribution";
refline = "refline " + char(obsdiff) + " / axis=x lineattrs=(color=red);";/*build a nice little red line to show where the data lies */
call Histogram(nulldist) other=refline;
pval = (1 + sum(abs(nulldist) >=abs(obsdiff))) / (NRepl+1); print pval;/*calculate the p value
/*https://blogs.sas.com/content/iml/2014/11/21/resampling-in-sas.html*/
Figure 4.0.3. Results of Permutation Tests
And some R code: In this test, the null hypothesis is that there is no difference between the mean
amount of cash in a student’s pocket in the two groups, while the alternative hypothesis is that there
is a meaningful difference between the two[4]. The permutations were used to generate the null
distribution of differences, and the red line shows where the experimental difference lies. Further
calculation shows that the p value of the experimental mean was 0.149, meaning about 15% of the
null distribution is greater than our mean[5]. With a 5 or 10 % confidence interval, we cannot reject
the null hypothesis, and therefore we cannot say there is any difference between the two means. The
SMU students and Seattle U students have more or less the same amount of cash in their pockets,
the result of the study does not bear statistical inference. As for scope of inference, this was not
a randomized experiment or random sample, and therefore we cannot make any causal inferences
(there was no treatment applied, and we definitely cannot say going to SMU makes you have more
or less money in your pocket than going to Seattle U), and we cannot make any inferences about the
student bodies as a whole (population inferences). The sample is only representative of the students
sampled, so we have very little scope of inference.
Score: 15/15. Explanation: This receives full marks, 5 points for running the test, 5 points for the p value,
and 5 points for mentioning the null and alternative hypotheses and getting the correct conclusion. The code
is included in the Appendix.
14

Analysis Guide Midterm
Code 4.4. Two Tailed permutation test in R, using manually input groups
1school1 <- rep(’SMU’, 16)
2school2 <- rep(’Seattle’, 14)
3school <- as.factor(c(school1 , school2))
4all.money <- data.frame( name=school , money=c(SMU , Seattle))
5
6t.test(money ~name , data=all.money)
7number_of_permutations <- 1000
8xbarholder <- numeric(0)
9counter <- 0
10 observed_diff <- mean(subset(all.money , name == "SMU")\$money)-mean(subset(all
.money , name == "Seattle")\$money)
11
12 set.seed(123)
13 for(i in 1:number_of_permutations)
14 {
15 scramble <- sample(all.money\$money , 30)
16 smu <- scramble [1:16]
17 seattle <- scramble [17:30]
18 diff <- mean(smu)-mean(seattle)
19 xbarholder[i] <- diff
20 if(abs(diff) > abs(observed_diff))
21 counter <- counter + 1
22 }
23 hist(xbarholder , xlab=’Permuted SMU - Seattle’, main=’Histogram of Permuted
Mean Differences’)
24 box()
25 pvalue <- counter /number_of_permutations
26 pvalue
27 observed_diff
15
Chapter 5
Unit 1 Lecture Slides
16

10/12/2018
1
MSDS 6371:
Lecture 1
DRAWING STATISTICAL CONCLUSIONS
RA NDOMIZED EXPERIMENTS V. OBS ERVATIONAL STUDIES
RA NDOM SAMP LES V. SELF- SELECTION
Symbols!
Sample
Population
Mean
Standard
Deviation Variance
Creativity Scores:
Intrinsic vs. Extrinsic Motivation
Subjects volunteered for the study.
Then, treatments were randomly assigned.
Starting Salaries:
Female vs. Male
Subjects were NOT randomly
chosen by the researcher (all
employees at a bank were
included), and the group
assignments were not random
either.
If a random sample of the
employees had been used…

10/12/2018
2
Creativity Study
Salary Study
Randomized
Experiment
Observational
Study
Types of Studies Causal Inference:
Randomized vs. Observational Study
•Causal inferences can be drawn from randomized experiments
•Causal inferences cannot be drawn from observational studies due to C
ONFOUNDING
C
ONFOUNDING
V
ARIABLE
:Related to both group membership and to the outcome
Example: Since 2000, the U.S. median wage…
•has overall increased about 1%
•has decreased for high school (or below) dropouts and high school graduates (no college)
•Is this a paradox?
No, more people are going to college.
Causal Inference:
Randomized vs. Observational Study
•Causal inferences can be drawn from randomized experiments
•Causal inferences cannot be drawn from observational studies due to C
ONFOUNDING
What are some possible confounding variables in the gender/salary study?
In the starting
salaries study,
maybe males have
•more education
•more seniority
•more age (older)
•more willingness
to negotiate
starting salary
o
y
y
o
y
y
y
o
y
o
o
o
o
o
y
y
y
o
y
o
y
y
o
y
y
o
y
y
y
o
y
o
o
y
o
o
o
y
y
y
o
y
o
y
y
In a randomized experiment, variables like age are also randomly distributed to each group,
removing the confounding effect.
Older Younger
Why do an observational
study?
•Establishing causation not always the goal
•Randomization may not be ethical
•May be arguable scientifically that a confounder is “unlikely”
•Might have an incidentally observed dataset
•Predict whether or not an email is spam
•Assign subjects of a clinical trial of a cancer drug to treatment or placebo
•6 month smoking ban in Helena, MT coinciding with 40%
reduction in heart attacks
•Walmart collects petabytes of data/day. Should this data
be discarded because it is observational?

10/12/2018
3
Inference to Populations:
Random Sample vs. Self-Selection
•Inference to populations can be drawn from a R
ANDOM SAMPLE FROM THAT POPULATION
.
•Inference to populations cannot be drawn if units are self-selected. In this creativity
example, inference can only be drawn to the subjects in the sample that was taken.
R
ANDOM SAMPLE
:Experimental units selected via a “chance mechanism” from a well
defined population
Example: call randomly selected phone numbers for a survey.
•What is the population from which the sample is taken? If drawing from a physical
phone book, is it the people who live in the city?
•Would this sampling method result in inferences to different populations if it were
used in 1950? 1990? Present day?
S
IMPLE RANDOM SAMPLE
:Every subset of size nis equally likely
Example: I’ll assign everyone in this class a random integer 17, 200, -3, 472, … and
survey the npeople (units) with smallest numbers
Inference to Populations:
Random Sample vs. Self-Selection
•Inference to populations can be drawn from a R
ANDOM SAMPLE
•Inference to populations cannot be drawn if units are self-selected
•W
HICH OF THE STUDIES USES RANDOM SAMPLING
?
•Neither study uses random
sampling
•Creativity study: units
are volunteers
•Bank study: units are
the entire staff
•No inference about a larger
population is possible
•Does not mean the results
are not interesting or
compelling!
Statistical Inferences
Permitted by Study Design Practice with Scope: Q1
A particular study focused on high school freshman and seniors and their GPAs in a
required economics class. The study consisted of enumerating every freshman and
senior in the school and randomly selecting them from that sampling frame. Their
scores in the economics class were then recorded, and a hypothesis test for the
difference of means was conducted. The seniors were found to have a significantly
greater mean score in the class than the freshman. What sort of conclusions can be
made from this study? In other words, what is the scope of this study? In this class,
scope typically constitutes both the causal inferences and populations inferences.
Since the subjects cannot be randomly assigned to be freshman or seniors, this is an observational
study, and thus the difference in mean scores is only associated with the freshman / senior status.
We can’t tell if the class (freshman or senior) caused the difference or not.
The sample was a random sample from the school; therefore, these findings can be generalized to
all freshman and seniors in the school. In conclusion, it can be inferred that the mean economics
score of the seniors in the school is greater than that of the freshman although the cause of this
difference cannot be determined from this study.
x

10/12/2018
4
Practice with Scope: Q2
Since the subjects were randomly assigned to the control and treatment groups, this is a
randomized experiment; thus, the difference in mean scores can be concluded to be
caused by the sleep deprivation. Since the subjects were volunteers who responded to a
radio advertisement, it is easy to see that every member of the population did not have
the same chance of being selected, and thus the sample is NOT a random sample.
Therefore these findings cannot be generalized to all U.S. nonsmokers between the age
of 18 and 35. In conclusion, it can be inferred that sleep deprivation caused the decrease
in cognitive ability (as measured by the timed math test) for these 57 individuals only.
The Navy is very interested in the effects of sleep deprivation on cognitive ability. In order
to test the effect, the Navy put out a radio advertisement asking for 18 to 35 year old
nonsmokers to participate in the study. The volunteers were then placed in either the
control group (no sleep deprivation) or the treatment group (36 hours of sleep deprivation)
based on the flip of a fair coin (Heads = Control, Tails = Treatment). After the data was
collected, the sleep deprived group was found to have a significantly lower mean math score
than the group not deprived of sleep. What sort of conclusions can be made from this
study? In other words, what is the scope of this study (causal inferences and population
inferences)?
x
Drawing Statistical
Conclusions
MEASURING UNCERTAINTY IN RANDOMIZED AND
OBSERVATIONAL STUDIES
Creativity Study
(
NULL HYPOTHESIS
)
(
TEST STATISTIC
)
(
ALTERNATE HYPOTHESIS
)
I
E
I
Creativity Study
For the sake of the example, supposed there are only 4 subjects.
Int (Grp 1) Ext (Grp 2)
12 Bob 5 Dan
17 Sue 15 Sal
Avg. 14.5 Avg. 10
Diff 14.5 – 10 = 4.5
All other possible groupings:
(Grp 1) (Grp 2)
12 Bob 5 Dan
15 Sal 17 Sue
Avg. 13.5 Avg. 11
Diff 13.5 – 11 = 2.5
(Grp 1) (Grp 2)
5 Dan 12 Bob
17 Sue 15 Sal
Avg. 11 Avg. 13.5
Diff 11 – 13.5 = -2.5
(Grp 1) (Grp 2)
5 Dan 12 Bob
15 Sal 17 Sue
Avg. 10 Avg. 14.5
Diff 10 – 14.5 = -4.5
(Grp 1) (Grp 2)
12 Bob 17 Sue
5 Dan 15 Sal
Avg. 8.5 Avg. 16
Diff 8.5 – 16 = -7.5
(Grp 1) (Grp 2)
15 Sal 5 Dan
17 Sue 12 Bob
Avg. 16 Avg. 8.5
Diff 16 – 8.5 = 7.5
4 out of 6 groupings have test statistics as extreme or more extreme than the
original grouping.
As extreme or more extreme means the absolute value of the test statistic is at
least 4.5.
So the p-value is 4/6 = 0.667. This answers the question of how unusual our
test statistic would be if the treatments had the same effect.
To quantify “large,” we can randomly reallocate units to two groups and recompute
the difference in sample means many times.
*Everyone has the same score with each grouping. The group each person is
artificially put in changes with each regrouping. If the treatments had the same
effect, then each participant would have the same score regardless of grouping.

10/12/2018
5
Creativity Study: all 47 subjects
(
P
-
VALUE
)
E
I
Creativity Study:
Testing the Hypothesis
1000
different
groupings
(relabelings)*
Number of
random
regroupings:
1.6 x 10
13
Half a year with a
computer that can
perform a million
calculations per
second!
-4.14 4.14
*Everyone has the same score with each grouping. What group each person is artificially put in changes with each regrouping. If the
treatments had the same effect, then each participant would have the same score regardless of grouping.
Creativity Study
(go to SAS code)
treatment Method Mean 95% CL Mean Std Dev 95% CL Std Dev
019.8833 18.0087 21.7580 4.4395 3.4504 6.2276
115.7391 13.4677 18.0105 5.2526 4.0623 7.4343
Diff (1-2) Pooled 4.1442 1.2914 6.9970 4.8541 4.0261 6.1138
Diff (1-2) Satterthwaite 4.1442 1.2776 7.0108
The TTEST Procedure
Variable: score
Creativity Study
1000 different
groupings
(relabelings)
There is strong evidence to suggest that the mean score of those who receive intrinsic motivation is not equal to those who receive the
extrinsic motivation (p-value = .008). The burden to reject the null hypothesis is lower under a one-sided test, so we can say that the
evidence supports the claim that the intrinsic mean is higher than the extrinsic mean.
Since this was a randomized experiment, we can conclude that the intrinsic motivation caused this increase. In addition, since these were
volunteers, this inference can only be assumed to apply to these 47 subjects, although the findings are very intriguing.
-4.14 4.14
Obs Variable Class Meth od V ariance s Mean Lo w erCLMe an UpperCLM ean StdDev Lowe rCLStdDev UpperCLStd Dev UMPULower CLSt
dDev
UMPUUppe rCLSt
dDev
1COL139 Diff (1-2) Pooled Equal 4.4678 1.6594 7.2762 4.7786 3.9635 6.0187 3.9360 5.9708
2COL170 Diff (1-2) Pooled Equal -4.3192 -7.1485 -1.4899 4.8141 3.9930 6.0634 3.9653 6.0152
3COL279 Diff (1-2) Pooled Equal -4.5576 -7.3530 -1.7623 4.7564 3.9451 5.9908 3.9178 5.9430
4COL360 Diff (1-2) Pooled Equal -4.8897 -7.6340 -2.1454 4.6695 3.8731 5.8814 3.8462 5.8345
5COL537 Diff (1-2) Pooled Equal 4.3826 1.5621 7.2031 4.7991 3.9806 6.0446 3.9530 5.9964
6COL551 Diff (1-2) Pooled Equal -5.0514 -7.7692 -2.3337 4.6243 3.8356 5.8245 3.8090 5.7781
7COL604 Diff (1-2) Pooled Equal -4.7109 -7.4832 -1.9385 4.7172 3.9127 5.9415 3.8855 5.8942
8COL664 Diff (1-2) Pooled Equal 4.6636 1.8840 7.4431 4.7295 3.9228 5.9569 3.8956 5.9095

10/12/2018
6
From Randomized to
Observational Studies
•In the Creativity study, the Intrinsic/Extrinsic groups were randomly
assigned to subjects
•This motivated comparing the observed difference to re-randomized
difference to test a hypothesis about the questionnaire having no effect
•This is known as a
RANDOMIZATION TEST
•In observational studies, the groups are not randomly assigned
•Though not technically the same test, we can still apply exactly the
same re-randomization idea to observational data
•However, now it is called a
PERMUTATION TEST
Appendix
Age Discrimination
In the United States, it is illegal to discriminate against people based on various
attributes. One such attribute is age. An active lawsuit, filed August 30, 2011, in the
Los Angeles District Office is a case against the American Samoa Government for
systematic age discrimination by preferentially firing older workers.
Is there evidence for age discrimination in this study?
Data sampled at random from all American Samoa government workers:
Fired
34 37 37 38 41 42 43 44 44 45 45 45 46 48 49 53 53 54 54 55 56
Not fired
27 33 36 37 38 38 39 42 42 43 43 44 44 44 45 45 45 45 46 46 47 47 48 48 49 49 51 51
52 54
Age Discrimination (Two Sided)
Fired
34 37 37 38 41 42 43 44 44 45 45
45 46 48 49 53 53 54 54 55 56
Not fired
27 33 36 37 38 38 39 42 42 43 43 44
44 44 45 45 45 45 46 46 47 47 48 48
49 49 51 51 52 54
There is not sufficient evidence to suggest that the mean age of those who were fired is different from the mean age of those who were not fired (p-value =
0.204). The p-value is so high that even the null hypothesis of a one-sided test cannot be rejected. (There is insufficient evid
ent to claim that the mean age of
fired employees is greater than that of not fired employees.)
Since this was a random sample of government employees in Samoa, we can generalize this inference to all government-employed people in Samoa.
Note: since we FTR (fail to reject) Ho, there is no need to discuss causation or association.
1000 different
groupings
(relabelings)
1.9238
-1.9238
Part II
Inferences Using the t-distribution
23

Chapter 6
Problem 1: A one sample t test
Question 1
The world’s smallest mammal is the bumblebee bat, also known as the Kitti’s hog nosed bat. Such bats are
roughly the size of a large bumblebee! Listed below are weights (in grams) from a sample of these bats. Test
the claim that these bats come from the same population having a mean weight equal to 1.8 g. (Beware:
This data is NOT the same as in the lecture slides!) Sample: 1.7 1.6 1.5 2.0 2.3 1.6 1.6 1.8 1.5 1.7 1.2 1.4 1.6
1.6 1.6
1. Perform a complete analysis using SAS. Use the six step hypothesis test with a conclusion that includes
a statistical conclusion, a confidence interval and a scope of inference (as best as can be done with the
information above . . . there are many correct answers given the vagueness of the description of the
sampling mechanism.)
2. Inspect and run this R Code and compare the results (t statistic, p-value and confidence interval) to
those you found in SAS. To run the code, simply copy and paste the below code into R.
Code 6.1. One sample t test in R with manual data input
1sample =c(1.7, 1.6, 1.5, 2.0, 2.3, 1.6, 1.6, 1.8, 1.5, 1.7, 1.2, 1.4, 1.6,
1.6, 1.6)
2t.test(x=sample , mu = 1.8, conf.int = "TRUE", alternative = "two.sided")
Answer
6.1 Complete Analysis
Hypothesis definition
H0:µ= 1.8 (6.1.1)
H1:µ,1.8 (6.1.2)
Identification of a critical value and drawing a shaded t distribution
We have that n= 15 →df =n−1 = 14, α = 0.05. We input this into SAS and get our lovely shaded
distribution and critical value with the following code: This gives us a critical t value of ±2.14479, as seen
in the following figures:
Figure 6.1.1. Critical t value
24

Analysis Guide Midterm
Code 6.2. Critical value and two sided shaded t distribution using SAS
data critval;
p = quantile("T",.975,14); /*two sided test*/;
proc print data=critval;
run;
data pdf;
do x=-4to 4by .001;
pdf = pdf("T", x, 14);
if x<= quantile("T",.025,14) then lower = pdf;
else lower = 0;
if x>= quantile("T",.975,14) then upper = pdf;
else upper = 0;
output;
end;
run;
title ’Shaded t distribution’;
proc sgplot data=pdf noautolegend noborder;
yaxis display=none;
band x = x lower = lower upper = upper / fillattrs=(color=gray8a);
series x = x y = pdf / lineattrs = (color = black);
series x = x y = lower / lineattrs = (color = black);
run;
Value of Test Statistic
The t statistic was calculated using the following SAS code
Code 6.3. One sample t test in SAS
proc ttest data=bats h0=1.8
sides=2 alpha=0.05;
run;
t=¯
x−µ
s
√n≈1.65 −1.8
0.25
15
=−2.35
P value
This gives us a p-value of p= 0.0342
Assessment of the Hypothesis test
From here we can see that p=.0342<α=.05, indicating that we REJECT the null hypothesis, which claims
that µ= 1.8
Conclusion and scope of inference
We cannot say that this sample of bats comes from a population with a mean weight of 1.8 grams (p value
= 0.0242 from a two sided t test). Below is a graph produced with the code from step 4 which shoes a 95%
confidence interval on the distribution of the data (green) vs the null hypothesis(gray bar)
25

Analysis Guide Midterm
The mean of 1.8 lies outside the reasonable range of the data from the sample, and as our hypothesis
test showed, vice versa is also true. We cannot say that our sample of bats has a mean weight of 1.8, and it
is difficult to say that it came from a population of mean 1.8. However, we cannot make any conclusions
about the population this sample came from, because it is not a random sample (we also clearly cant make
any causal inferences), We only know, with 95% confidence, that our sample does not have a mean of 1.8
grams, and that is about all we can say.
Some R code
Code 6.4. one sample t test in r
1sample <- c(1.7, 1.6, 1.5, 2.0, 2.3, 1.6, 1.6,
21.8, 1.5, 1.7, 1.2, 1.4, 1.6, 1.6, 1.6)
3t.test(x=sample , mu = 1.8,
4conf.int = "TRUE", alternative = "two.sided")
26
Chapter 7
Problem 2: Two sample one sided t test
Question
2. In the United States, it is illegal to discriminate against people based on various attributes. One ex-
ample is age. An active lawsuit, filed August 30, 2011, in the Los Angeles District Office is a case against
the American Samoa Government for systematic age discrimination by preferentially firing older workers.
Though the data and details are currently sealed, suppose that a random sample of the ages of fired and
not fired people in the American Samoa Government are listed below: Fired 34 37 37 38 41 42 43 44 44 45
45 45 46 48 49 53 53 54 54 55 56 Not fired 27 33 36 37 38 38 39 42 42 43 43 44 44 44 45 45 45 45 46 46 47
47 48 48 49 49 51 51 52 54
a. Perform a permutation test to test the claim that there is age discrimination. Provide the Ho and
Ha, the p-value, and full statistical conclusion, including the scope (inference on population and causal
inference). Note: this was an example in Live Session 1. You may start from scratch or use the sample code
and PowerPoints from Live Session 1.
b. Now run a two sample t-test appropriate for this scientific problem. (Use SAS.) (Note: we may not
have talked much about a two-sided versus a one-sided test. If you would like to read the discussion on pg.
44 (Statistical Sleuth), you can run a one-sided test if it seems appropriate. Otherwise, just run a two-sided
test as in class. There are also examples in the Statistics Bridge Course.) Be sure to include all six steps, a
statistical conclusion, and scope of inference.
c. Compare this p-value to the randomized p-value found in the previous sub-question.
d. The jury wants to see a range of plausible values for the difference in means between the fired and
not fired groups. Provide them with a confidence interval for the difference of means and an interpretation.
f. Inspect and run this R Code and compare the results (t statistic, p-value, and confidence interval) to
those you found in SAS. To run the code, simply copy and paste the code below into R.
Answers
7.1 Permutation test
First, a permutation test is ran using n= 9999, using the code I wrote in homework one, inspired by [2].
The code used to run the permutation test is shown below: In this scenario, we have that:
Code 7.1. A one sided permutation test in SAS
obsdiff = mean(G1) - mean(G2); /*G1 and G2 represent the two groups*/
print obsdiff;
call randseed(12345); /*set random number seed */
alldata = G1 // G2; /*stack data in a single vector */
N1 = nrow(G1);
N = N1 + nrow(G2);
NRepl = 9999; /*number of permutations */
nulldist = j(NRepl,1); /*allocate vector to hold results */
do k=1to NRepl;
x = sample(alldata, N, "WOR"); /*permute the data */
nulldist[k] = mean(x[1:N1]) - mean(x[(N1+1):N]);
/*difference of means */
end;
title "Histogram of Null Distribution";
refline = "refline " + char(obsdiff) + " / axis=x lineattrs=(color=red);";
call Histogram(nulldist) other=refline;
pval = (1 + sum(abs(nulldist) >= (obsdiff))) / (NRepl+1);
print pval;
H0:µf−µuf ≤0
H1:µf−µuf >0
27

Analysis Guide Midterm
where the null hypothesis is that the average age of the unfired individuals is the same as the average age of
the fired individuals, and the alternative is that the average age of the individuals who were fired is higher.
The results of the permutation test are as follows:
In the above figure, the red line represents the mean of the difference between the two samples, and
the rest of the bars represent our null distribution. SAS tells us that the P-value is 0.2812, meaning 28.12
percent of the null distribution is greater than our sample mean. Therefore, with a 5%, or even a 10%
confidence interval, we cannot reject the null hypothesis. We cannot say whether or not there was age
discrimination in the firing of workers with the given sample. With this procedure, we can make general-
izations about the population, and generalize about all of the government-employed people in Samoa, as
we did a random sample, however, we cannot make causal inferences, as there may be confounding vari-
ables in the system, and we did not run a randomized experiment. There is also no need to discuss causal
problems, because we failed to reject the null hypothesis.
7.2 Two sample T test, full analysis
This time we will conduct a t test on the two data sets to determine whether age discrimination occured or
not. Because we believe the older workers may have been fired, we are going to perform a one sided t-test.
Hypothesis definition
First we construct our hypotheses:
H0:µf−µuf ≤0
H1:µf−µuf >0
critval and distribution
Next we draw and shade our distribution:
In a two sample t-test, we have that:
df =nf+nnf −2
where in our case, df = 21 + 30 −2 = 49, α = 0.05
Now we input this information into SAS to draw our distribution[1]:
Giving us this lovely graph:
Next we find a number for the critical value, using the same code as problem 1:
28

Analysis Guide Midterm
Code 7.2. One sided shaded t distribution in SAS and Critval
data pdf;
do x=-4to 4by .01;
pdf = pdf("T", x, 49);
lower = 0;
if x>= quantile("T",0.95,49) then upper = pdf;/*one sided*/else upper = 0;
output;
end;
run;
title ’Shaded t distribution’;
proc sgplot data=pdf noautolegend noborder;
yaxis display=none;
band x = x
lower = lower
upper = upper / fillattrs=(color=gray8a);
series x = x y = pdf / lineattrs = (color = black);
series x = x y = lower / lineattrs = (color = black);
run;
data critval;
p = quantile("T",.95,49); /*one sided test*/;
proc print data=critval;
run;
This gives us a critical t value of 1.67655.
Calculation of the T statistic
Next we calculate our two sample t statistic using SAS:
Code 7.3. Two sample t test using SAS
proc ttest data=samoa
alpha=.05 test=diff
sides=U;
class fired;
var age;
run;
Which tells us that our t statistic is 1.10
P value
With the code from the previous step, we also see the p value:
p= 0.1385
hypothesis assement
p= 0.1385 > α = 0.05 for the one tailed hypothesis test, indicating that we CANNOT REJECT the null
hypothesis
29

Analysis Guide Midterm
conclusion
The p value for the t test was about half of the p value for the random test, I believe this is because I ran a
one-sided t test. It is interesting to note that if you do a two sided t-test in SAS, you get roughly the same
value for p as in the permutation test:
This means that maybe a permutation test is a good estimator of the two-sided t-test.
We cannot reject the null hypothesis, meaning we cannot say that older workers were fired from the
samoan government. Note that we used a one tailed hypothesis test in this scenario, as we wanted to
deternine if the fired group was OLDER than the nonfired group. As a result of this test, we cannot say
that the fired group was older than the unfired group, and since this sample was random, we can say the
same thing about the entire samoan government. However, we cannot make causal inferences and there is
no need to because we did not reject the null hypothesis
We can provide a lot of confidence intervals for the jury. I think the most telling is the one sided
confidence interval, which would tell us what difference in the means constitutes age discrimination. This
was produced using the following SAS code:
proc ttest data=samoa
alpha=.05 test=diff
sides=U; /*an upper tailed test*/
class fired;
var age;
run;
which gives us a confidence interval of [−1.0107,∞). This confidence interval represents the upper differ-
ence of means at a 95% confidence level. We can interpret this as follows: if the confidence interval contains
the null hypothesis, then we cannot reject it. However if it does not contain the null hypothesis, we must
reject it. As we can see in this beautifully drawn figure, the null hypothesis, µf−µnf ≤0 is contained within
our CI:
. This means we cannot reject the null hypothesis, we cannot say there was age discrimination. It is
plausible that the mean differnence of the entire population of samoan government employees is less than
or equal to zero, as it is within the 95% confidence interval, which means we cannot, as objective jurors,
claim there was age discrimination.
Incorrect calculations
The pooled sample standard deviation, sp,is defined as
s2
p=Pk
i=1(ni−1)s2
i
Pk
i=1(ni−1)
which for us is:
sp=r(21 −1)(6.5214)2+ (30 −1)(5.8835)2
20 + 29 = 6.152
The equation for standard error in the difference of means is given as
σ¯
x1−¯
x2=ss2
1
n1
+s2
2
n2
Which gives us that
σ¯
x1−¯
x2=r6.52142
21 +5.88352
30 = 1.811
7.3 Rcode
The following code (supplied in the homework) was put into R: returning this:
30

Analysis Guide Midterm
Code 7.4. two sample t test in R
1Fired = c(34, 37, 37, 38, 41, 42, 43,
244, 44, 45, 45, 45, 46, 48, 49, 53,
353, 54, 54, 55, 56)
4Not_fired = c(27, 33, 36, 37, 38, 38,
539, 42, 42, 43, 43, 44, 44, 44, 45,
645, 45, 45, 46, 46, 47, 47, 48, 48,
749, 49, 51, 51, 52, 54)
8t.test(x = Fired , y = Not_fired , conf .int = .95 , var.equal = TRUE , alternative =
"greater")
1Two Sample t-test
2data: Fired and Not_fired
3t= 1.0991,
4df = 49,
5p-value = 0.1385 alternative hypothesis: true difference in means is greater than 0
695 percent confidence interval : -1.010728 Inf sample estimates: mean of x mean of y 45.85714 43.93333
The results are near identical, I cannot tell which one is better but I imagine R is more accurate as well,
but just a very small difference between the results in all regards . The var.Equal statement is important
because it uses the pooled test.
31
Chapter 8
Problem 3: two sample two sided t test
Question
3. In the last homework, it was mentioned that a Business Stats professor here at SMU polled his class and
asked students them how much money (cash) they had in their pockets at that very moment. The idea was
that we wanted to see if there was evidence that those in charge of the vending machines should include the
expensive bill / coin acceptor or if it should just have the credit card reader. However, another professor
from Seattle University was asked to poll her class with the same question. Below are the results of our
polls.
SMU 34, 1200, 23, 50, 60, 50, 0, 0, 30, 89, 0, 300, 400, 20, 10, 0 Seattle U 20, 10, 5, 0, 30, 50, 0, 100,
110, 0, 40, 10, 3, 0 a. Run a two sample t-test to test if the mean amount of pocket cash from students at
SMU is different than that of students from Seattle University. Write up a complete analysis: all 6 steps
including a statistical conclusion and scope of inference (similar to the one from the PowerPoint). (This
should include identifying the Ho and Ha as well as the p-value.) Also include the appropriate confidence
interval. FUTURE DATA SCIENTIST’S CHOICE!: YOU MAY USE SAS OR R TO DO THIS PROBLEM!
b. Compare the p-value from this test with the one you found from the permutation test from last week.
Provide a short 2 to 3 sentence discussion on your thoughts as to why they are the same or different.
Answer
8.1 Full Analysis
Hypothesis Definition
Hypothesis set up:
H0:µ1−µ2= 0
H1:µ1−µ2,0
Critical value and shaded distribution
Next we draw and shade our distribution: In a two sample t-test, we have that:
df =n1+n2−2
where in our case, df = 16 + 14 −2 = 28, α = 0.05. In this case we are performing a two tailed test. Now we
input this information into SAS to draw our distribution[1]:
data pdf;
do x=-4to 4by .001;
pdf = pdf("T", x, 14);
/*here it is important to set up a two sided test*/
if x<= quantile("T",.025,28) then lower = pdf;
else lower = 0;
if x>= quantile("T",.975,28) then upper = pdf;
else upper = 0;
output;end;run;
title ’Shaded t distribution’;
proc sgplot data=pdf noautolegend noborder;
yaxis display=none;
band x = x lower = lower upper = upper / fillattrs=(color=gray8a);
series x = x y = pdf / lineattrs = (color = black);
series x = x y = lower / lineattrs = (color = black);
run;
With this bit of code, we have produced our shaded two tailed PDF:
32

Analysis Guide Midterm
This critical value, where the bands start, is calculated using the following SAS code:
data critval;
p = quantile("T",.975,28); /*two sided test*/;
proc print data=critval;
run;
This gives us a critical t value of ±2.04841
T statistic
the t stat is calculated using the following code:
Code 8.1. Two sided two sample t test in SAS
proc ttest data=wallet
alpha=.05 test=diff
sides=2; /*an upper tailed test*/
class school;
var cash;
run;
which tells us that our t statistic is −1.37
P value
With the code from the previous step, we also see the p value, p= 0.1812:
Hypothesis Assessment
p= 0.1812 > α = 0.05 for the one tailed hypothesis test, indicating that we CANNOT REJECT the null
hypothesis
Conclusion and Scope of inference
We cannot reject the null hypothesis, meaning we cannot say that the mean amount of cash in an SMU
student’s wallet is any different than the mean amount of cash in a Seattle U student’s wallet. The following
figure is a good reference for the results of this test:
33

Analysis Guide Midterm
The circled area tells us the difference between the mean amount of cash in a Seattle student’s wallet and
an SMU student’s wallet. We can see that the average student from the seattle sample had about 112 dollars
less in his wallet than the average SMU student. This may sound like a lot, however it is not significant.
For this result to be statistically significant, and the mean amount of cash in a Seattle U student’s wallet to
be considered different than the mean amount of cash in an SMU student’s wallet, the difference of the two
means would have to fall outside of the 95% confidence interval. The confidence interval is highlighted,
and is (−281.2,55.6817), which tells us that for the means to be considered truly different, the seattle
student should have either 281 dollars less than the SMU student, or 55 dollars more. Our p value of
0.1812 tells us a similar story. It tells us that there is an 18% chance that a greater difference in the means
would occur, which, at a 5 or 10 percent confidence interval, is not statistically significant at all. As for
scope of inference, we cannot make inferences about the greater population of either university, because
these were not random samples. We also cannot make causal inferences (eg going to SMU makes you have
money in your wallet!), as this is not a randomized experiment either. Something about outliers!
34
Chapter 9
Problem 4: power
Question
4. A. Calculate the estimate of the pooled standard deviation from the Samoan discrimination problem.
Use this estimate to build a power curve. Assume we would like to be able to detect effect sizes between 0.5
and 2 and we would like to calculate the sample size required to have a test that has a power of .8. Simply
cut and paste your power curve and SAS code. HINT: USE THE CODE FROM DR. McGEE’s lecture. Instead
of using groupstddevs, use stddev since we are using the pooled estimate. B. Now suppose we decided that
we may be able to live with slightly less power if it means savings in sample size. Provide the same plot as
above but this time calculate curves of sample size (y-axis) vs. effect size (.5 to 2) (x axis) for power = 0.8,
0.7, and 0.6. There should be three plots on your final plot. Simply cut and paste your power curve and
SAS code. HINT: USE THE CODE FROM DR. McGEE’s lecture. Instead of using groupstddevs, use stddev
since we are using the pooled estimate. The effect size here refers to a difference in means, though there are
many effect size metrics, such a Cohen’s D. C. Using similar code, estimate the savings in sample size from
a test aimed at detecting an effect size of 0.8 with a power of 80% versus a power of 60%. Note: You will
learn how to do this in R in a future HW!
Answers
9.1 Single power curve
he pooled standard deviation, calculated in Problem 2, part e, part 1, is sp= 6.5215. The difference of
the means of the two groups, meandiffin the code, is just set to the difference between the means of our
two populations, calculated using the R-generated means in Problem 2, Part f, µf−µuf = 1.924. The value
of meandiffis not important, because by plotting the effect size, we are cycling through mean differences
between 0.5 and 6, so the meandiffparameter only really matters if you want to know a sample size for a
specific difference of means. When building a power curve it is not important at all, but you need it to get
proc power to work. The SAS code used to build the power curve is shown below:
Code 9.1. Proc power single with pooled variance
proc power;
twosamplemeans
/*test=diff not diffsatt bc pooled variance*/
test=diff
stddev=6.5215
/*meandiff is a dummy variable in this case*/
meandiff=1.924
power=.8
ntotal = .;
plot x=effect min=.5 max=6;
run;
And the power curve:
35

Analysis Guide Midterm
9.2 Multiple power curves
The same notes as above apply here, this time we used the SAS code to generate multiple power curves:
Code 9.2. Producing several curves with proc power
proc power;
twosamplemeans
/*test=diff not diffsatt bc pooled variance*/
test=diff
stddev=6.5215
/*meandiff is a dummy variable in this case*/
meandiff=1.924
power=.8 .7 .6
ntotal = .;
plot x=effect min=.5 max=6;
run;
And the curves:
9.3 Calculating change in N
It is important to remember that the “effect size” calculated in this SAS code is the exact same thing as the
“mean difference”. Therefore we can write our SAS code as follows:
proc power;
twosamplemeans
test=diff /*diff not diffsatt bc pooled variance*/
stddev=6.5215
meandiff= 0.8 /*this represents the effect size*/
power=.8 .6
ntotal = .;
run;
Which gives us our sample size savings:
36

Analysis Guide Midterm
As we see from the figure above, by raising the power from 0.6 to 0.8, we actually have to nearly double
the sample size to meet the test parameters. By using a power of 0.6, we save 784 N’s (or sample size units)
37
Chapter 10
Unit 2 Lecture Slides
38

10/13/2018
1
Inference Using
t-Distributions
ME ASU RIN G U NCE RTAINT Y IN RAN DOM IZE D AND O BSE RVAT IONA L
ST UDI ES
-D IST RI B UTI ON OF THE SAM PLE AV ERA GE
-U SIN G T -DI STR IBU TIO N FOR ON E S AMPL E I NFE REN CE
-S TA RTI NG T O E X PLOR E T-D IST RIB UTI ON FOR TW O SAM PLE PRO BLE MS
1
Central Limit Theorem
2
Distribution of Sample Average
3
is a point estimate for µ
The sample mean is an unbiased estimator for the population mean.
Distribution of Sample Average
4
is unbiased.
µ
The more data you pick for each sample, the more normal (and tighter) the distribution of
the sample mean is.
Note that the
distribution of the
original data is the
distribution of a
sample mean of size
1.
http://onlinestatbook.com/stat_sim/sampling_dist/
The more data you pick for each sample, the more normal (and tighter) the distribution of the sample
mean is.
If original data is approx. normal, then the distribution of the sample mean will be approx. normal,
regardless of sample size.

10/13/2018
2
Trial Value (x)
X
1
X
2
X
3
X
5
…
X
6000
4
3
3
1
6
…
4
5
0
200
400
600
800
1000
123456
Frequency
Roll of the Die
Dice: Individual Rolls (n = 1)
Trial
…
3.5
2
3
5.5
…
3.5
4
3.5
0
500
1000
1500
2000
11.5 22.5 33.5 44.5 55.5 6
Frequency
Average of 2 Dice
Dice: Sample Means of Size n = 2
Trial
…
3
2
3
5.5
…
4.2
3.4
3.6
… …
1
0
200
400
600
800
1000
1200
1400
1600
1800
11.5 22.5 33.5 44.5 55.5 6
Frequency
Average of 5 Dice
Dice: Sample Means of Size n = 5
Trial
…
3.1
2.9
4.3
3.1
…
4.2
3.7
3.3
0
200
400
600
800
1000
1200
1400
1600
1800
2000
11.5 22.5 33.5 44.5 55.5 6
Frequency
Average of 10 Dice
Dice: Sample Means of Size n = 10
0
123456
Frequency
Roll of the Die
Dice: Individual Rolls (n = 1)
0
500
1000
1500
2000
11.5 22.5 33.5 44.5 55.5 6
Frequency
Average of 2 Dice
Dice: Sample Means of Size n = 2
0
1000
2000
11.5 22.5 33.5 44.5 55.5 6
Frequency
Average of 10 Dice
Dice: Sample Means of Size n = 10
THE CENTRAL LIMIT
THEOREM!!!
CENTRAL LIMIT THEOREM Cont.

10/13/2018
3
13
Example: If we have data 79, 83, 84, 89, 90 mm for digitus tertius (the
human middle finger). What is an estimate of the standard deviation?
T-ratio
14
*This ratio HAS a t – distribution if Y is normally distributed.
is unbiased est. for
Student tDistributions for
n= 3 and n= 12
William Sealy Gosset (Student)
Student t
distributions have
the same general
shape and
symmetry as the
standard normal
distribution but
reflect a greater
variability (heavier
tails), which is
expected with
small samples.
Example: 1 Sample Confidence Interval
The following are ages of 7 randomly selected patrons at the
Beach Comber in South Mission Beach at 7pm. We assume that
the data come from a normal distribution and would like to
build a 95% confidence interval for the actual mean age of
patrons at the Comber.
25, 19, 37, 29, 40, 28, 31
n = 7
= 29.86
σ= 7.08
= 0.05
/2= 0.025
z
/2= 1.96
E=z
2
σ=
(1.96)(7.08) = 5.24
n7
29.86 – 5.24 < µ< 29.86 + 5.24
24.62 <
< 35.10
We are 95% confident that the mean age of Beach Comber patrons at
7pm is contained in any 95% confidence interval, such as
(24.62 years, 35.10 years).
x–E< µ< x+ E, where
IMPORTANT:
These are the
plausible values
of the mean
given the data!
n = 7
= 29.86
s= 7.08
= 0.05
/2= 0.025
t
/2, n-1
= 2.447
E=t
2, n-1
s=
(2.447)(7.08) = 6.55
n7
29.86 – 6.55 < µ< 29.86 + 6.55
23.31 <
< 36.41
We are 95% confident that the mean age of Beach Comber patrons at 7pm
is contained any 95% confidence interval, such as (23.31 yrs., 36.41 yrs.).
x–E< µ< x+ E, where
IMPORTANT:
These are the
plausible values
of the mean
given the data!

10/13/2018
4
Comparison of
z
to
t
n = 7
= 29.86
σ= 7.08
= 0.05
/2= 0.025
z
/2
= 1.96
E=z
2 σ=(1.96)(7.08) = 5.24
n7
29.86 – 5.24 <
µ
< 29.86 + 5.24
24.62 <
< 35.10
We are 95% confident that
the mean age of Beach
Comber patrons at 7pm is
contained in the interval
(24.62 years, 35.10 years).
x–E< µ< x+ E
n = 7
= 29.86
s= 7.08
= 0.05
/2= 0.025
t
/2, n-1
= 2.447
E=t
2, n-1
s=
(2.447)(7.08) = 6.55
n7
29.86 – 6.55 <
µ
< 29.86 + 6.55
23.31 <
< 36.41
We are 95% confident that the
mean age of Beach Comber
patrons at 7pm is contained in
the interval (23.31 years, 36.41
years).
23.31 36.41
24.62 35.10
1 Sample Hypothesis Testing:
The 6 Steps
1. Identify Ho and Ha.
2. Find the Critical Value(s) and Draw and Shade.
3. Calculate the Test – Statistic. (The evidence!)
4. Calculate the P-value.
5. Make a decision… Reject Ho or FTR Ho.
6. Write a clear conclusion in the context of the problem…. Use mostly
non statistical terms but always report the p-value! Add a
confidence interval if appropriate. End this conclusion with a
statement about the scope.
20
Example: 1 Sample t-test
The following are ages of 7 randomly chosen patrons seen leaving
the Beach Comber in South Mission Beach at 7pm. We assume that
the data come from a normal distribution and would like to test the
claim that the mean age of the distribution of Comber patrons is
different than 21.
25, 19, 37, 29, 40, 28, 31
Let’s Formalize This Test Into 6 Steps!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Let’s Formalize This Test Into 6 Steps!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Step 2: Draw and Shade and Find the Critical Value.
21
df = 7 – 1 = 6
t
Let’s Formalize This Test Into 6 Steps!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Step 2: Draw and Shade and Find the Critical Value.
Step 3: Find the test statistic. (The t value for the data.)
21
df = 7 – 1 = 6
t

10/13/2018
5
Let’s Formalize This Test Into 6 Steps!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Step 2: Draw and Shade and Find the Critical Value.
Step 3: Find the test statistic. (The t value for the data.)
Step 4: Find the p-value: The probability of observing by random
chance something as extreme or more extreme than what was
observed under the assumption that the null hypothesis is true.
(Usually found with software.) The red shaded region above is 0.0162
(sum of both red areas)
Let’s Formalize This Test Into 6 Steps!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Step 2: Draw and Shade and Find the Critical Value.
Step 3: Find the test statistic. (The t value for the data.)
Step 4: Find the p-value: P-value 0.0162< .05
Step 5: Key! The sample mean we found is very unusual under the
assumption that the true mean age is 21. So we Reject the
assumption that the true mean age is 21. That is, we REJECT Ho.
Let’s Formalize This Test Into 6 Steps!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Step 2: Draw and Shade and Find the Critical Value.
Step 3: Find the test statistic. (The t value for the data.)
Step 4: Find the p-value: P-value 0.0162 < .05
Step 5: REJECT Ho
Step 6: There is sufficient evidence to conclude that the true mean age of patrons at the
Comber at 7pm is not equal to 21 (p-value =0.0162 from a t-test). We could also say that
there is sufficient evidence to conclude that the true mean is greater than 21. (Consider the
red area in the right most tail.) This was not a random sample of all times, only at 7pm; thus,
the result cannot be applied to the bar at all times. The results are nevertheless intriguing.
Finding the P-value – more detail
28
Step 4: Find the p-value: p-value < .05
You could use Stat Trek / or the t-table.
OR
Software like SAS:
Confidence interval
One-Sided Test + Two-Sided CI Demonstration
29
One-Sided Test + Two-Sided CI Demonstration
30

10/13/2018
6
One-Sided Test + Two-Sided CI Demonstration
31
Suppose we
would like to test the claim that the mean age of patrons is
greater than 24.
One Sided-Test at alpha = 0.05 Two Sided-Test at alpha = 0.05
One-Sided Test + Two-Sided CI Demonstration
32
Suppose we
would like to test the claim that the mean age of patrons is
greater than 24.
Two Sided-Test at alpha = 0.1 Two Sided-Test at alpha = 0.05
One-Sided Test + Two-Sided CI Demonstration
33 34
Perform a two sample t-test for the difference in the mean score between the
Intrinsic and Extrinsic groups from the chapter problem. Provide a complete
analysis, including a full conclusion, confidence interval, and scope of inference. Use
an alpha = .01 level of significance.
TWO SAMPLE T-TEST FOR THE
DIFFERENCE OF MEANS WITH
INDEPENDENT SAMPLES
Let’s Formalize This Test Into 6 Steps!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Which is equivalent to:
Let’s Formalize This Test Into 6 Steps!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Step 2: Draw and Shade and Find the Critical Value.
0
df = 24 +23 – 2 = 45
t

10/13/2018
7
Let’s Formalize This Test Into 6 Steps!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Step 2: Draw and Shade and Find the Critical Value.
Step 3: Find the test statistic. (The t value for the data.)
0
df = 24 +23 – 2 = 45
t
Let’s Formalize This Test Into 6 Steps!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Step 2: Draw and Shade and Find the Critical Value.
Step 3: Find the test statistic. (The t value for the data.)
Step 4: Find the p-value: The probability of observing by random
chance something as extreme or more extreme than what was
observed under the assumption that the null hypothesis is true.
(Usually found with software.) The red shaded regions above. 0.0054
Let’s Formalize This Test Into 6 Steps!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Step 2: Draw and Shade and Find the Critical Value.
Step 3: Find the test statistic. (The t value for the data.)
Step 4: Find the p-value: P-value 0.0054< 0.01
Let’s Formalize This Test Into 6 Steps!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Step 2: Draw and Shade and Find the Critical Value.
Step 3: Find the test statistic. (The t value for the data.)
Step 4: Find the p-value: P-value 0.0054< .01
Step 5: REJECT Ho
Step 6: There is sufficient evidence to suggest that those who receive the Intrinsic treatment have a
different mean score than those who receive the Extrinsic treatment (p-value = .0054 from a t-test). We can
also claim that the mean intrinsic score is greater than the extrinsic one. (The burden of rejecting the null
hypothesis for a one-tailed test is less than a two-tailed test, given the test is in the relevant direction.) A
99% confidence interval for this difference is (.3347, 7.95). Since this was a randomized experiment, we can
conclude that the Intrinsic treatment caused this difference. However, since the study was of volunteers
(sampling bias), this inference can only be generalized to the 47 participants.
Finding the P-value
41
Step 4: Find the p-value: P-value < .01
You could use Stat Trek / or the t-table.
OR
Software like SAS:
COMPARE WITH RANDOMIZATION
(PERMUTATION) TEST
1000 different
groupings
(relabelings)
There is strong evidence to suggest that the mean score of those who receive intrinsic motivation is not equal to those who receive the
extrinsic motivation (p-value = .008). The burden to reject the null hypothesis is lower under a one-sided test, so we can say that the
evidence supports the claim that the intrinsic mean is higher than the extrinsic mean.
Since this was a randomized experiment, we can conclude that the intrinsic motivation caused this increase. In addition, since these were
volunteers, this inference can only be assumed to apply to these 47 subjects, although the findings are very intriguing.
-4.14 4.14
Obs Varia ble Class Method Varia nces Mean Lower CLMea n UpperCLMean StdDev Low e rCLStdDev UpperCLStdDev UMPULow erCLSt
dDev
UMPUUpperCLSt
dDev
1COL139 Diff (1-2) Pooled Equal 4.4678 1.6594 7.2762 4.7786 3.9635 6.0187 3.9360 5.9708
2COL170 Diff (1-2) Pooled Equal -4.3192 -7.1485 -1.4899 4.8141 3.9930 6.0634 3.9653 6.0152
3COL279 Diff (1-2) Pooled Equal -4.5576 -7.3530 -1.7623 4.7564 3.9451 5.9908 3.9178 5.9430
4COL360 Diff (1-2) Pooled Equal -4.8897 -7.6340 -2.1454 4.6695 3.8731 5.8814 3.8462 5.8345
5COL537 Diff (1-2) Pooled Equal 4.3826 1.5621 7.2031 4.7991 3.9806 6.0446 3.9530 5.9964
6COL551 Diff (1-2) Pooled Equal -5.0514 -7.7692 -2.3337 4.6243 3.8356 5.8245 3.8090 5.7781
7COL604 Diff (1-2) Pooled Equal -4.7109 -7.4832 -1.9385 4.7172 3.9127 5.9415 3.8855 5.8942
8COL664 Diff (1-2) Pooled Equal 4.6636 1.8840 7.4431 4.7295 3.9228 5.9569 3.8956 5.9095

10/13/2018
8
Let’s Talk Power!!!
43
Effect size basically
measures the
difference between
the population mean
(106) and the null
mean(100). (It’s not
exactly this, though.)
Explore power!
Here is an applet that will show you what happens to the power/beta
when you change the sample size, alpha, standard deviation, or effect
size (measure of the difference between null mean and actual
(alternative) mean).
http://shiny.stat.tamu.edu:3838/eykolo/power/
44
(Go to break out)
Consider the following options.
A. The probability of rejecting Ho when the null is true.
B. The probability of accepting Ho when the null is true.
C. The probability of rejecting Ho when the null is false.
D. The probability of FTR Ho when the null is true.
E. The probability of FTR Ho when the null is false.
WHICH IS POWER? ___
WHICH IS ALPHA? ___
WHICH IS BETA? ___
45
C
A
E
Pick all that are true.
The power increases when:
A. The sample size decreases.
B. The sample size increases.
C. The standard deviation / standard error decreases.
D. The effect size increases.
E. The effect size decreases.
46
Pick all that are true.
The power increases when:
A. The sample size decreases.
B. The sample size increases.
C. The standard deviation / standard error decreases.
D. The effect size increases.
E. The effect size decreases.
47
Appendix
48

10/13/2018
9
Distribution of Sample
Average
49
ANOTHER EXAMPLE
FOR PRACTICE
50
H0:
= 1.8
H1:
≠ 1.8
= 0.05
x= 1.713
s = .2588
Critical Values t = ±2.145
H0:
= 1.8
H1:
≠ 1.8
= 0.05
x= 1.713
s = .2588
On the basis of this test, there is not enough evidence to reject the claim that the mean weight of
bumblebee bats is equal to 1.8g (p-value = .2155 from a t-test). A 95% confidence interval is (1.57 g,
1.8566 g). The problem was ambiguous on the randomness of the sample; thus, we will assume that it
was not a random sample, which makes inference to all bats strictly speculative.
Part III
A Closer look at Assumptions
48
Chapter 11
Problem 1: Two Sample T test with
assumptions
Question
1. In the United States, it is illegal to discriminate against people based on various attributes. One ex-
ample is age. An active lawsuit, filed August 30, 2011, in the Los Angeles District Office is a case against
the American Samoa Government for systematic age discrimination by preferentially firing older workers.
Though the data and details are currently sealed, suppose that a random sample of the ages of fired and
not fired people in the American Samoa Government are listed below: Fired 34 37 37 38 41 42 43 44 44 45
45 45 46 48 49 53 53 54 54 55 56 Not fired 27 33 36 37 38 38 39 42 42 43 43 44 44 44 45 45 45 45 46 46
47 47 48 48 49 49 51 51 52 54 a. Check the assumptions (with SAS) of the two-sample t-test with respect
to this data. Address each assumption individually as we did in the videos and live session and make sure
and copy and paste the histograms, q-q plots or any other graphic you use (boxplots, etc.) to defend your
written explanation. Do you feel that the t-test is appropriate? b. Check the assumptions with R and com-
pare them with the plots from SAS. c. Now perform a complete analysis of the data. You may use either the
permutation test from HW 1 or the t-test from HW 2 (copy and paste) depending on your answer to part
a. In your analysis, be sure and cover all the steps of a complete analysis: 1. State the problem. 2. Address
the assumptions of t-test (from part a). 3. Perform the t-test if it is appropriate and a permutation test if it
is not (judging from your analysis of the assumptions). 4. Provide a conclusion including the p-value and
a confidence interval. 5. Provide the scope of inference.
Answer
11.1 Complete Analysis
Assmuption checking in SAS
The assumptions were tested using proc ttest, which outputs histograms, box plots, QQ-plots, and performs
an F-test on the variances. The code used to produce all information in this section is presented below:
Code 11.1. Checking the assumptions of a t test in SAS
proc ttest data=samoa
alpha=.05 test=diff
sides=U; /*an upper tailed test*/
class fired;
var age;
run;
Normality
The normality of the data is checked using a QQ plot, a boxplot, and a histogram. First we will examine
the QQ plot:
49

Analysis Guide Midterm
Figure 11.1.1. Q-Q Plot for Normality
In Figure 1.1, the y axis represents the data set, and the x axis the theoretical normal quantile. The line
represents what a normal data set should look like, a 1-1 ratio between the data variable and the theoretical
normal quantile. The data set follows the normal line pretty well, so in this case on a visual inspection, we
can say both samples are normal. We can double check this using Figure 1.2, a histogram and boxplot:
Figure 11.1.2. Histogram and Boxplot for Normality
It is a bit harder to assess the normality using the histogram and boxplot, but SAS gives us useful kernel
lines which show the distribution of the data in the histogram (the red line is the data and the blue line is
normal). As we can see, the data loosely follows the normal distribution, it is a bit different but it is pretty
close. The box plot tells the same story, as in both cases the mean is very near the medium (in a normal
distribution the mean and median are the same), with slight left and right skewing, but overall we can
assume the data is normal.
Equal Variances
In order to assess the equality of the variances visually, we can again use the histogram and boxplot, this
time displayed in Figure 1.3 (for ease of grading):
Figure 11.1.3. Histogram and Boxplot for Variance Equality
As we can see from the bounds of the histogram, the range of each data set is more or less the same
size, with their means more or less in the center. This hints that the two data sets would have near equal
variances. This is confirmed when looking at the box plot, the distance from the mean to the far left whisker
and far right whisker is more or less the same for both data sets, which indicates again the variances are
50

Analysis Guide Midterm
equal. This is confirmed by examining the F test for equal variances, the results of which are displayed
below:
Figure 11.1.4. F Test for Equal Variances
The F test is valid here, because the data is normal and the sample size is large (n∼30), and we see that
the probability the variance difference is greater than what it is in our case is 60%, or a p value of 0.6 At a
5, 10, 15 or 20 percent confidence interval, the f test will tell us the variances are equal. Therefore, we can
assume equal variances.
Independence
In this case, we can assume independence, the two data sets do not relate to each other. Any dependence
that exists we will assume away, for the sake of the problem
Conclusion
In my opinion, we can use a t-test for this data set, based on the fact that all the assumptions are true.
Assumption Checking in R
Normality test
To test for normality, we are going to again use the Q-Q plot and the histogram. To produce the Q-Q plots,
the following code was used: The plots produced are shown below:
Code 11.2. t test Assumption checking in R, Q-Q plot
1#producing adjacent Q-Q plots
2par(mfrow=c(1,2))
3qqnorm(Fired ,main="Normal Q-Q Plot for Fired data",
4xlab = "Normal Quantiles",
5ylab = "Fired Quantiles ")
6qqnorm(Not_fired ,main="Normal Q-Q Plot for Not Fired data",
7xlab = "Normal Quantiles",
8ylab = "Not Fired Quantiles")
Figure 11.1.5. Q-Q plots for Normality in R
From the linearity of the data points in this figure, we can see that the data follows a more or less normal
ditribution. The Q-Q plot produced in R is almost exactly the same as the Q-Q plot produced using SAS,
however it is different in that it does not have a lovely line representing perfect normality, and the size of
the boxes changes with window size, as does the aspect ratio, which is a bit of a pain. The following code is
used to produce a histogram, further examining normality: This produces the following figure:
51

Analysis Guide Midterm
Code 11.3. t test Assumption checking in R, Histogram
1#producing the adjacent histograms
2par(mfrow=c(1,2))
3hist(Fired)
4hist(Not_fired)
Figure 11.1.6. Histogram for Normality in R
As can be seen in the figure, the distribution of these two data sets is again more or less normal, with
what appears to be the mean and median lying in the center, however there is a bit of a bump in the fired
data set, but again it is loosely normal in appearance. The graphs again look the same as in SAS more or
less, other than formatting differences. We can identify numbers better in R. In this case, we can ASSUME
NORMAL
Equality of Variances
Looking at the histogram in Figure 1.6, we can see that the fired data has a mean of about 45 years old,
spanning from 30 to 60, and the not fired data has a mean of about 40 years old, spanning from 25 to
55. The spread of the two means is more or less the same in this case, therefore we can ASSUME EQUAL
VARIANCEs
Independence
We can again assume independence.
Conclusion:
The t-test is appropriate
Complete Analysis:
Problem statement:
We would like to test the claim that the mean age of the individuals who were fired is greater than the mean
age of the individuals who were not fired.
Assumptions:
We can assume normality, independence, and equal variances and therefore we can use the student t test,
as proven in sections 1.a and 1.b.
t-test
Statement of the Hypotheses:
H0:µf−µuf ≤0
H1:µf−µuf >0
Shaded Distribution and Critical Values: In a two sample t-test, we have that:
df =nf+nnf −2
where in our case, df = 21 + 30 −2 = 49, α = 0.05 Now we input this information into SAS to draw our
distribution[1]:
data pdf;
do x=-4to 4by .01;
pdf = pdf("T", x, 49);
lower = 0;
52

Analysis Guide Midterm
if x>= quantile("T",0.9,49) then upper = pdf;/*one sided*/
else upper = 0;
output;
end;
run;
title ’Shaded t distribution’;
proc sgplot data=pdf noautolegend noborder;
yaxis display=none;
band x = x
lower = lower
upper = upper / fillattrs=(color=gray8a);
series x = x y = pdf / lineattrs = (color = black);
series x = x y = lower / lineattrs = (color = black);
run;
Giving us this lovely graph:
Next we find a number for the critical value, using the same code as problem 1:
data critval;
p = quantile("T",.95,49); /*one sided test*/;
proc print data=critval;
run;
This gives us a critical t value of 1.67655.
Calculation of t statistic: Next we calculate our two sample t statistic using SAS:
proc ttest data=samoa
alpha=.05 test=diff
sides=U;
class fired;
var age;
run;
Which tells us that our t statistic is 1.10
Calculation of P-value With the code from the previous step, we also see the p value:
53

Analysis Guide Midterm
p= 0.1385
Discussion of the Null Hypothesis p= 0.1385 > α = 0.05 for the one tailed hypothesis test, indicating
that we CANNOT REJECT the null hypothesis
Conclusion:
We cannot reject the null hypothesis, meaning we cannot say that older workers were fired from the Samoan
government. Note that we used a one tailed hypothesis test in this scenario, as we wanted to deternine if
the fired group was OLDER than the nonfired group. With a one-sided p-value of 0.1385, there is a nearly
14% chance that there be a greater difference in mean ages given the distribution. At a critical p-value of
.05 (5%), we can say that this data fails to reject the null hypothesis. Using the code that calculated the t
statisitic, we produce the following one sided confidence interval:
The confidence interval is: [−1.0107,∞). This confidence interval represents the upper difference of
means at a 95% confidence level. We can interpret this as follows: if the confidence interval contains the
null hypothesis, then we cannot reject it. However if it does not contain the null hypothesis, we must reject
it. As we can see in this beautifully drawn figure, the null hypothesis, µf−µnf ≤0 is contained within our
CI:
. This means we cannot reject the null hypothesis, we cannot say there was age discrimination. It is
plausible that the mean differnence of the entire population of samoan government employees is less than
or equal to zero, as it is within the 95% confidence interval, which means we cannot, as objective jurors,
claim there was age discrimination.
Scope of Inference:
Since this sample was random, we can make generalizations about the Samoan Government as a whole,
however, we cannot make causal inferences, as this was not a randomized experiment.
54
Chapter 12
Outliers and Logarithmic
Transformations
55












Analysis Guide Midterm
The permutation test was performed using the following code: We will now perform the same procedure
on the assumptions without an outlier, as well as some other comparisons. Unless otherwise noted, the
following code was used to produce the results and to remove outliers:
67

Analysis Guide Midterm
Code 12.1. Automatically input permutation test in SAS
/*Permutation test*/
data Wallet;
INFILE ’file location’;
INPUT school $ cash;
run;
proc iml;
use Wallet var {school cash};
/*making two groups in IML*/
read all var {cash} where(school=’SMU’) into g1;
read all var {cash} where(school=’SEU’) into g2;
obsdiff = mean(g1) - mean(g2);
print obsdiff;
call randseed(12345); /*set random number seed */
alldata = g1 // g2; /*stack data in a single vector */
N1 = nrow(g1);
N = N1 + nrow(g2);
NRepl = 9999; /*number of permutations */
nulldist = j(NRepl,1); /*allocate vector to hold results */
do k=1to NRepl;
x = sample(alldata, N, "WOR"); /*permute the data */
nulldist[k] = mean(x[1:N1]) - mean(x[(N1+1):N]); /*difference of means */
end;
title "Histogram of Null Distribution";
refline = "refline " + char(obsdiff) + " / axis=x lineattrs=(color=red);";
call Histogram(nulldist) other=refline;
pval = (1 + sum(abs(nulldist) >=abs(obsdiff))) / (NRepl+1);
/*this means two sided test*/
print pval;
run;
Code 12.2. Outlier removal in SAS
data Wallet;
INFILE ’file location’;
INPUT school \$ cash;
run;
data CleanCash;
set Wallet;
/*we are going to remove all the really high values*/
if cash >150 then delete;
run;
proc ttest data=CleanCash
alpha=.05 test=diff
sides=2; /*a 2 tailed test*/
class school;
var cash;
run;
68

Chapter 13
Log Transformed data
13.1 Full Analysis
Problem Statement:
We would like to test the claim that the distribution of incomes for those who have 16 years of education is
greater than those who have 12 years of education.
Assumptions
We first produce the plots for our assumption analysis using the following bit of code:
proc import
/*to use proc import first we specify the file*/
datafile=’genericfilepath/genericname.csv’
/*then we specify the name of the output dataset*/
out=edudata /*then we specify the data type*/
dbms=CSV;
run;
proc sort data=edudata;
by descending educ;
run;
proc ttest data=edudata
order=DATA /*This changes theorder of the groups you are using to the one you set*/
sides=U; /*an Upper tailed test*/
class Educ;
var Income2005;
run;
Producing the following figures:
Figure 13.1.1. Q-Q plot of sample
69

Analysis Guide Midterm
Figure 13.1.2. Histogram and Boxplot of the sample
Normality assumption:
Looking at the Q-Q plot(Figure 3.1), it is clear to see that the data is not normal at all. To investigate further,
we will look at the histograms and box plots in Figure 3.2. These paint a more complete picture, we see that
the data is skewed to the right, and that the higher values are much greater than the lower values (hundreds
of thousands of times). To combat this, lets perform a natural log transformation with this bit of code and
see whatthe data looks like:
Code 13.1. log transform in SAS
data edudata2;
set edudata;
lincome=log(Income2005);
run;
proc ttest data=edudata2
order=DATA sides=U; /*an Upper tailed test*/
class Educ;
var lincome;
run;
Producing the following figures:
Figure 13.1.3. Q-Q plot of logs
Figure 13.1.4. Histogram and Boxplot of Logs
70

Analysis Guide Midterm
With this transformation, we first look at the Q-Q plot (Figure 3.3), and we see that the data is mostly
normal! Looking at the histograms (Figure 3.4) this is confirmed, just in their shape and the shape of the
kernel density plots. The nearness of the median to the mean is also a telltale sign the data is normal.
Therefore, we can assume the log-transformed data is normal.
Equality of Variances
Since we cannot assume normality with the untransformed data, it makes little sense to analyze the equality
of variances of that data set. We will look at the log transformed data for the equality of variances. Looking
at figure 3.4, we see that the spread of the two data sets is pretty similar, just in the histograms, they are
of similar length, where the 12 year data set is a bit narrowerthan the 16 year set. The Boxplot confirms
this, the distance from the means to the end of the whiskers is roughly the same for both plots, as well as
within the IQRS. The one with the larger mean also has a larger variance, Therefore, we can assume the
log transformed data has equal variances.
Independence
We can assume the data is independent in this scenario.
3.3 Hypothesis testing
We will be using a one tailed pooled t test of the log transformation of the data in this scenario, so that we
can do a t test
Statement of Hypotheses:
Note that since we are dealing with a pooled t-test of a log transformation, we are dealing in medians
rather than means, the medians should tell us whether or not the distribution of the people with 16 years
of education exceeds that of those with 12 years of education
H0:Median16 =Median12
H1:Median16 > Median12
H0:distribution16 =distribution12
H1:distribution16 >distribution12
Critical Value
In this scenario, α= 0.1 and df = 1424, and from that we can shade a one sided distribution and find a
critical value, using the code below:
data pdf;
do x=-4to 4by .01;
pdf = pdf("T", x, 1424);
lower = 0;
if x>= quantile("T",0.9,1424) then upper = pdf;/*one sided*/
else upper = 0;
output;
end;run;
title ’Shaded t distribution’;
proc sgplot data=pdf noautolegend noborder;
yaxis display=none;
band x = x
lower = lower
upper = upper / fillattrs=(color=gray8a);
series x = x y = pdf / lineattrs = (color = black);
series x = x y = lower / lineattrs = (color = black);
run;
data critval;
p = quantile("T",.9,1424); /*one sided test*/;
proc print data=critval; run;
This produces the shaded distribution:
71

Analysis Guide Midterm
Figure 13.1.5. Shaded t distribution
and a critical value of t= 1.28215
Calculation of the t statistic:
Now we calculate our t statististic using the code from Section 3.2.1, which tells us that t= 10.98, which is
an astounding value!
Calculation of the p-value:
p < 0.0001, see the figure above!
3.3.5 Discussion of the Null hypothesis
We REJECT the null hypothesis, p≈0<0.1 = α
Conclusion
We Reject the null hypothesis which states that the two distributions are equal. We have convincing evi-
dence that the income distribution of the people with 16 years of education is greater than those with 12.
With a one-sided p value of ~0, the distributions are very different, the median income of the people with
a 16 year education is evidently greater than the median income of people with a 12 year education. The
figure below shows the difference between the natural logarithm of the two medians:
This tells us that the median income of people with 16 years education is e0.5699 = 1.77 times greater
than those with 12 years of education. A 90% confidence interval for this multiplicative effect is 1.62 to
1.93 times.
72

Analysis Guide Midterm
We cannot make causal inferences in this scenario, as there was no random experimentation, and we
cannot make population inferences either, as there was no random sampling
73
Chapter 14
Unit 3 Lecture slides
74

10/13/2018
1
Chapter 3
A Closer Look at Assumptions!
1
Confidence
Intervals
and
Hypothesis
Tests
95% CI
Vs.
α = .05 Hyp Test
α = .05
2
For the corresponding
alpha, a (1-alpha)% CI will
contain mu_0 when the
test of Ho: mu = mu_0
fails to reject Ho and will
not contain mu_0 when
the test rejects Ho.
99% CI
Vs.
α = .01 Hyp Test
α = .01
3
Confidence
Intervals
and
Hypothesis
Tests
The Take Away
Two-Sided 100(1-α)% Confidence Intervals are Equivalent to Two-
Tailed Hypothesis Tests that have an α level of significance.
“Equivalent” here means that if we test any specific value in the
interval, the test will FTR Ho. And if we test any specific value outside
the interval, the test will Reject Ho.
Example:
95% confidence interval for the mean is equivalent to an α = .05
hypothesis test.
Example:
99% confidence interval for the mean is equivalent to an α = .01 level
hypothesis test.
So we can evaluate hypothesis tests through the
evaluation of confidence intervals! 4
Assumptions of one sample T-Tests
1. Samples are drawn from a normally
distributed population.
2. The observations in the sample are
independent of one another.
5
Robustness of One Sample T-test / CI
When the original (population) distribution is not
normal, the one sample t-test is still valid with a
large enough sample size. (Central Limit Theorem)
That is, the one sample t-test is robust to the
normality assumption when the sample size is large
enough.
6

10/13/2018
2
Assume the population distribution is Exponential.
With 𝜆= 1.
7
1000 CIs for the Mean of an
Exponential(1) Distribution: n = 10
Note the
Right Skew!
Note the
Right Skew!
8
1000 CIs for the Mean of an
Exponential(1) Distribution: n = 100
Note the greater
symmetry and
smaller standard
deviation.
Note the
Right Skew!
9
Given Data, How Do We Check the
Normality Assumption? Visually!
Histogram q-q Plot
n = 100 n = 100
10
Normal q-q Plot
DATA
41.2
76.6
109.3
134.5
148.6
11
Q-Q plots are constructed differently depending
on the software or textbook, but usually include
some combination of the above columns. If the
graph plots green vs. green or orange vs. orange,
if the data is normal, then points should fall close
to the line y=x. If one green and one orange are
used, if the data is normal, the points should fall
along a straight line, but not necessarily one with
slope=1. Different software will calculate this line
differently.
data rank
middle = (rank +
previous rank)/2n
standard normal
hypothetical value
based on middle
hypothetical data if data
were perfectly normal
z-score of data
= (data -xbar)/s
41.2 1 0.1 -1.28 46.09 -1.39
76.6 2 0.3 -0.52 79.15 -0.58
109.3 3 0.5 0.00 102.04 0.17
134.5 4 0.7 0.52 124.93 0.74
148.6 5 0.9 1.28 157.99 1.07
102.04 =xbar
43.65459 =s
5 =n
Normal q-q Plot
12

10/13/2018
3
Given Data, How Do We Check the
Normality Assumption? Visually!
Histogram q-q Plot
n = 100 n = 100
13
Not normal! Data is skewed to the right and does not fall along a straight line in this q-q
plot.
Given Data, How Do We Check the
Normality Assumption? Visually!
Histogram q-q Plot
n = 15 n = 15
14
Data comes from a normal distribution, but it is hard to tell given the small sample size.
Given Data, How Do We Check the
Normality Assumption? Visually!
Histogram q-q Plot
n = 15 n = 15
15
It looks like the data might not be normal (skew, curvature of q-q plot), but it is
hard to tell with this small sample size.
Beware of small sample sizes!
Histogram q-q Plot
n = 15
n = 15
16
The histogram shows an almost bimodal distribution (definitely not normal), but again it is
hard to tell with small sample sizes. The q-q plot does not look too far away from normality.
A Way to Decide:
Small Sample Size Large Sample Size
Little to no Evidence
Against Normality
No Problem if you feel
Normality is a safe
assumption … run the T-
Test. (You may want to
be “conservative” here
and run a test with
fewer assumptions.)
No Problem!
Run the T-Test
Significant Evidence
Against Normality
Assumptions are not
met and test is not
robust here … Try a
transformation and, if
appropriate, run a t-test.
If not appropriate, do
NOT run the T-Test and
proceed to a test with
fewer / different
assumptions.
No Problem .. You have
the Central Limit
Theorem. Run the T-
Test.
17
A Complete Analysis:
•Statement of the Problem
•Address the Assumptions
•Perform the Appropriate Test (5 Steps)
•Step 6: Provide a conclusion that a non
statistician can understand, include a p-value
and confidence interval.
•Scope of Inference
18

10/13/2018
4
Example: Beach Comber
The following are ages of 7 randomly chosen patrons seen leaving
the Beach Comber in South Mission Beach at 7pm! We assume
that the data come from a normal distribution and would like to
test the claim that the mean age of the distribution of Comber
patrons is different than 21.
25, 19, 37, 29, 40, 28, 31
19
Example: Comber
ASSUMPTIONS:
Normal Population Distribution: Judging from the histogram and q-q plots,
there is little to no evidence that the population distribution of patron ages at
the Comber at 7pm is not normal. We will assume that this distribution is
normal and proceed.
Independence: These subjects were randomly selected from the population;
thus, we will assume that the observations are independent.
20
PROBLEM STATEMENT:
Test the claim that the mean age of Beach Comber patrons at 7pm is different from
21.
Revised Write Up!
We would like to test the claim that the population mean is different from 21. To do this,
we take a sample of size n = 7 and find that 𝑥̅ = 29.86 years and s = 7.09 years.
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis. Ho: µ = 21
Ha: µ ≠ 21
Step 2: Draw and Shade and Find the Critical Value.
Step 3: Find the test statistic. (The t value for the data.)
=29.86 − 21
7.09
7
= 𝟑. 𝟑𝟏
𝑡 = 𝑥̅ − 𝜇
𝑠
𝑛
Step 4: Find the p-value: P-value = .0162 < .05
Step 5: REJECT Ho
Step 6: There is sufficient evidence to conclude that the true mean age of patrons at the
Comber at 7pm is different from 21 (p-value =.0162 from a t-test). A 95% confidence
interval for the mean age is (23.3, 36.4) years. Scope: Since this was a random sample, we
can generalize these findings to the entire population of Comber patrons at 7pm. Note that
we have evidence to support the claim that the mean age is greater than 21 as well.
Example: Bats
22
Example: Bats
ASSUMPTIONS:
Normal Population Distribution: Judging from the histogram and q-q plots, there
is some visual evidence of a departure from normality. With a sample size of 15
and no extreme outliers, we will assume the distribution of sample means is
decently approximated by a normal distribution via the CLT and proceed with
caution.
Independence: Not much is known about the sampling scheme used to obtain this
sample. We will
assume
the observations are independent.
23
PROBLEM STATEMENT:
Test the claim that the mean weight of the bumble bee bat is different from 1.8 g.
H0: 𝝁= 1.8
H1: 𝝁≠ 1.8
𝜶= 0.05
𝒙
= 1.713
s = .2588
t = -1.297
Test Statistic
Critical Values t = ± 2.145
Fail to Reject H0
On the basis of this test, there is not enough evidence to reject the claim that the mean weight of
bumblebee bats is equal to 1.8 g (p-value = .2155 from a t-test). A 95% confidence interval is (1.57, 1.8566)
grams. The problem was ambiguous on the randomness of the sample; thus, we will assume that it was
not a random sample, which makes inference to all bats strictly speculative.
P-value: .2155 > .05
24

10/13/2018
5
Assumptions of one and two
sample T-Tests
1. Samples are drawn from a normally
distributed population.
2. If it is a two sample test, both populations
are assumed to have the same standard
deviation (same shape).
3. The observations in the sample are
independent of one another.
25
What happens if the normality
assumption is broken?
Many times ….
NO PROBLEM!!!
𝐶𝑒𝑛𝑡𝑎𝑙 𝐿𝑖𝑚𝑖𝑡 𝑇ℎ𝑒𝑜𝑟𝑒𝑚
xx
𝜇
𝑥̅
𝜇
𝑥̅
26
27
When data is not normal
2. In a two sample test, both populations are
assumed to have the same standard deviation
(same shape).
𝜇𝜇
𝐴𝑠𝑠𝑢𝑚𝑒: 𝜎= 𝜎
𝑊𝑒 𝑤𝑎𝑛𝑡 𝑖𝑛𝑓𝑒𝑟𝑒𝑛𝑐𝑒 𝑜𝑛 ∶ 𝜇− 𝜇
28
Evidence of Inequality of Variance:
VISUAL
Little visual evidence against equal standard deviations (variances).
29
Evidence of Inequality of Variance:
F-Test for Equal Variance
There is not sufficient evidence to conclude the variances are different (p-value =
.4289 from a F-Test.)
Ho: population variances are equal
Ha: population variances are not equal
30

10/13/2018
6
Evidence of Inequality of Variance:
VISUAL
Strong visual evidence against equal standard deviations (variances).
31
Evidence of Inequality of Variance:
F-Test for Equal Variance
Ho: population variances are equal
Ha: population variances are not equal
There is not sufficient evidence to conclude the variances are different (p-value =
.1043 from a F-Test.)
32
Evidence of Inequality of Variance:
F-Test / VISUAL
The F-test has a strong assumption that the two
populations that it is testing the variances of must
be normal. It is not robust to this assumption.
Since the second distribution has strong evidence of
right skew, the F-test for Equal Variance is not
appropriate here.
For this example, the visual evidence is so strong
that we would not need to consult a hypothesis
test to test this assumption of equal variances.
However, later in the semester we will study a test of spread/dispersion that does not
have this assumption and can be used in a wider range of statistical environments.
33
What happens if the assumption of
equal variances (standard deviations)
is broken?
In some circumstances ….
This could be serious …. In others…..
No Problem!
34
When variances are not equal
35
The Take Away
What you will find in practice will most likely not fit exactly into the scenarios
identified here. There will be some judgment involved … this is the “art” of
statistics.
Here are some general rules of thumb that we will assume this semester.
1. If sample sizes are the same and sufficiently large, the t tools (tests and
confidence intervals) are valid … since they are robust to the violation of
normality.
2. If the two populations have the same standard deviation, then the t tests
are valid … given sufficient sample sizes.
3. If the standard deviations are different and the sample sizes are different
then the t tools are not valid and another procedure should be used.
(Ch. 4)
36

10/13/2018
7
A Complete Analysis:
•Statement of the Problem
•Address the Assumptions
•Perform the Appropriate Test (5 Steps)
•Step 6: Provide a conclusion that a non
statistician can understand. Include a p-value
and confidence interval
•Scope of Inference
37
FULL EXAMPLE: CREATIVITY STUDY!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Ho: µ
𝐼
= µ
𝐸
Ha: µ
𝐼
≠µ
𝐸
Which is equivalent to:
Ho: µ
𝐼
− µ
𝐸
= 0
Ha:
µ
𝐼
−
µ
𝐸
≠
0
We would like to test the claim that the mean score of the Intrinsic group is different than that
of the Extrinsic group.To do this we take a sample of size n
I
= 24 and n
E
= 23 and find that 𝑥̅
I
=
19.88 points, 𝑥̅
E
= 15.74, s
I
= 4.44, and s
E
= 5.25 points.
Full Example: Creativity Data
State the Problem: We would like to test the claim
that the mean score of the Intrinsic group is
different than that of the Extrinsic group.
Check Assumptions:
1. Normally Distributed Populations
39
First Check …. q-q Plot
The q-q plots for both populations look sufficiently
normal. We look at the histograms as well … but there is
not sufficient evidence here to suggest that they are not
normal.
40
Histograms
•Keeping in mind the relative small sample size from each
population, we do not observe any extreme outliers and
observe a pretty strong bell shape which lends evidence to
support normality of the populations.
41
Normality Assumption
Visual inspection of the histograms and q-q plots of each
population are consistent with the normality of each
population. We assume normality and move on to the second
assumption.
42

10/13/2018
8
Full Example: Creativity Data
State the Problem: We would like to test the claim that
the mean score of those with intrinsic motivation is the
same for those with extrinsic motivation.
Check Assumptions:
1. Normally Distributed Populations
2. Equal Standard Deviations
43
Equality of Variances
A visual check was done by looking at the histograms, which reveal similar shapes and
support the equal variances assumption. You can assume equal variances here.
Since we are able to assume normal population distributions, we can use the F-Test to provide
secondary evidence if the visual is inconclusive. Since the p-value is greater than our
significance level of alpha = 0.05, we fail to reject the null hypothesis of equality (p-value =
0.1043) and conclude that there is not enough evidence to suggest the variances are different.
44
Full Example: Creativity Data
State the Problem: We would like to test the claim
that the mean score of those with intrinsic
motivation is the same for those with extrinsic
motivation.
Check Assumptions:
1. Normally Distributed Populations
2. Equal Standard Deviations
3. Independent Observations
45
Independent Observations
The sample consisted of volunteers and thus
subjects may not be independent of one
another. However, we will assume
independence and proceed with caution.
46
Full Example: Creativity Data
State the Problem: We would like to test the claim that
the mean intrinsic score is the same as the extrinsic score.
Check Assumptions:
1. Normally Distributed Populations
2. Equal Standard Deviations
3. Independent Observations
Run the Test:
1. First 5 steps.
47
Let’s Formalize This Test Into 6 Steps!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Step 2: Draw and Shade and Find the Critical Value.
Step 3: Find the test statistic. (The t value for the data.)
Step 4: Find the p-value: P-value 0.0054< .01
Step 5: Key! The sample mean we found is very unusual under the
assumption that the group means are equal (µ𝐼− µ𝐸). So we Reject
this assumption. That is, we REJECT Ho.
Ho:
µ
𝐼
− µ
𝐸= 0
Ha:
µ
𝐼
− µ
𝐸≠0
𝑡 = (𝑥𝐼
− 𝑥𝐸)
𝑠𝑝1
𝑛𝐼+1
𝑛𝐸
= 2.93
We would like to test the claim that the mean score of the Intrinsic group is different than that
of the Extrinsic group.To do this we take a sample of size n
I
= 24 and n
E
= 23 and find that 𝑥̅
I
=
19.88 points, 𝑥̅
E
= 15.74, s
I
= 4.44, and s
E
= 5.25 points.

10/13/2018
9
Full Example: Creativity Data
State the Problem: We would like to test the claim that
the mean intrinsic score is the same as the extrinsic score.
Check Assumptions:
1. Normally Distributed Populations
2. Equal Standard Deviations
3. Independent Observations
Run the Test:
1. First 5 steps.
State the Scope and Conclusion.
49
Let’s Fill in the P-value (and add a CI)!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Step 2: Draw and Shade and Find the Critical Value.
Step 3: Find the test statistic. (The t value for the data.)
Step 4: Find the p-value: P-value = .0054
Step 5: REJECT Ho
Step 6:
Conclusion: There is sufficient evidence to suggest that those who receive the Intrinsic
treatment have a higher mean score than those who receive the Extrinsic treatment (p-value =
.0054 from a two sided t-test). A 99% confidence interval for this difference is (1.29, 7.00).
SCOPE: Since this was a randomized experiment, we can conclude that the Intrinsic treatment
caused this difference. However, since the study was of volunteers, this inference can only be
generalized to the 47 participants.
Ho:
µ
𝐼
− µ
𝐸= 0
Ha:
µ
𝐼
− µ
𝐸≠0
𝑡 = (𝑥𝐼
− 𝑥𝐸)
𝑠𝑝1
𝑛𝐼+1
𝑛𝐸
=2.93
We would like to test the claim that the mean score of the Intrinsic group is different than that
of the Extrinsic group.To do this we take a sample of size n
I
= 24 and n
E
= 23 and find that 𝑥̅
I
=
19.88 points, 𝑥̅
E
= 15.74, s
I
= 4.44, and s
E
= 5.25 points.
LET’S TRY SOME!
For each of these data sets, write up the assumption statement with
respect to checking the assumptions for a one or two sample t-test.
You may assume the data to be independent.
51
Mice Experiment Data Set
Happiness Data Set
All data sets can be found in one file in this week’s materials.
You will need to add the proc ttest statement for each.
However, you will not need the data for this exercise.
Happiness Study
52
Address each assumption of the two sample t-test and then decide if the two-sample t-
test is appropriate to answer this QOI with this data.
5 randomly selected people were asked to rate their happiness on a scale from 1 – 100
on a cloudy day and 8 randomly selected people were asked the same question on a
sunny day.
QOI: Is the mean happiness of individuals different on a cloudy day than a sunny day?
If possible, can we test if cloudy weather causes a change in happiness?
Happiness Study
53
Normality of Distributions: Judging from the histograms and q-q plots, there is
evidence of outliers in both the Cloudy and Sunny sets. The most pronounced
outlier seems to be in the Sunny data set; thus, there is significant visual evidence
against these data being normally distributed. In addition, we are not satisfied that
the t-test will be robust to this assumption since the sample sized are so small.
Equal Standard Deviations: Judging from the histograms, q-q plots and box plots,
there is significant visual evidence that the standard deviations are different. In
addition, since the sample sizes are different we know that the t-test is not robust to
this assumption.
Independence: We will assume that these data are independent.
The two sample t-test is not appropriate here. We should look for a different test.
Mice Study
54
A large sample of mice were randomly assigned to receive a drug or a placebo (sample
size n
D
= 32 and n
P
= 32). The mice’s tcell counts were then taken and histograms and
q-q plots are displayed above.
QOI: Is the mean tcell count of mice that receive the drug greater than that of the
mice that receive the placebo?
Can we draw draw evidence of causality from this study?
Address each assumption of the two sample t-test and then decide if the two-sample t-
test is appropriate to answer this QOI with this data.

10/13/2018
10
Mice Study
55
Normality of Distributions: Judging from the histograms and q-q plots, there is
significant visual evidence to suggest the data come from right skewed distributions.
However, since the sample size is large n
D
= 32 and n
P
= 32 the t-test is robust to this
assumption violation.
Equal Standard Deviations: There is strong visual evidence to suggest that the data
come from distributions with different standard deviations. However, since we have
the same sample size in each group, the t-test is robust to this assumption violation,
by a previous “rule of thumb”.
Independence: We will assume that these data are independent.
The two sample t-test is appropriate here.
Transformations
56
Log Transformation
Appropriate Interpretations After a Log
Transformation –
Example Write Ups….
Observational Study:
“It is estimated that the median for population X is
exp(mean(log(x)) – mean(log(y))) times as large as
the median for population Y.”
Randomized Experiment:
“It is estimated that the median response of an
experimental unit to treatment x will be
exp(mean(log(x)) – mean(log(y))) times as large as
its response to treatment y.”
Cloud Seeding!
Does Cloud Seeding Work?
On days that were deemed suitable for cloud seeding, a
random mechanism was used to decide whether to seed
the target cloud on that day or to leave it unseeded as a
control. Precipitation was measured as the total rain
volume falling from the cloud base following the airplane
seeding run, as measured by radar. We would like to test at
the alpha = .05 level of significance whether cloud seeding
is effective in increasing precipitation.

10/13/2018
11
Cloud Seeding: Original Data After Log Transformation
T Test and Confidence!!!
H0: Cloud Seeding does not work.
H1: Cloud Seeding does work.
It is estimated that the median volume of rainfall on days when clouds were seeded was e1.1438=3.1 times as large as
when not seeded (p-value = .007). A 90% confidence interval for this multiplicative effect on the median is 1.5 to 6.7
times. Since randomization was used to determine whether any particular suitable day was seeded or not, it is safe to
interpret this as evidence that the seeding caused the larger median rainfall.
H0: Medianseeded = Medianunseeded
H1: Medianseeded > Medianunseeded
For the one sided test. For confidence interval.
e
0.3904
= 1.5,
e
1.8972
= 6.7 Cloud Seeding Book Example
0 500 1000 1500 2000 2500
Unseeded Seeded
Rainfall (acre-feet)
Figure 1. Box Plots of Cloud Seeding Data.
0 2 4 6 8
Unseeded Seeded
Log(Rainfall)
Figure 2. Box Plots of Log-Transformed Cloud Seeding Data.
Original
Logged
Recap: The Take Away
What you will find in practice will most likely not fit exactly into the scenarios
we identified here. There will be some judgment involved … this is the “art”
of statistics.
Here are some general rules of thumb that we will assume this semester.
1. If sample sizes are the same and sufficiently large, the t tools (tests and
confidence intervals) are valid … since they are robust to the violation of
normality.
2. If the two populations have the same standard deviation then the t tests
are valid … given sufficient sample sizes.
3. If the standard deviations are different and the sample sizes are different
then the t tools are not valid and another procedure should be used.
(Ch. 4)
65
Appendix
66

10/13/2018
12
Log Transformations: Theory
67
Prop 1:
xy
Log(x) Log(y)
Mean[log(x)] = Median[log(x)]
Mean[log(y)] = Median[log(y)]
Prop 2:
X Log(X)
X1 log(X1)
X2 log(X2)
X3 log(X3)
X4 log(X4)
X5 log(X5)
The logarithm is a
monotonically increasing
function. If X1 > X2 then
log(X1) > log(X2).
Therefore consider X1 through
X5 in ascending order so that
X1 < X2 < X3 < X4 < X5.
Then log(X1) < log(X2) <
log(X3) < log(X4) < log(X5).
log(Median(X)) = log(X3) = Median(log(X))
log(Median(X)) = Median(log(X))
Because data is
now symmetric
(median =mean)
Log Transformations: Theory
68
Prop 3: Prop 4a:
log 𝑋 − log 𝑌 = log (𝑋
𝑌)𝑒 () = 𝑋
e is a pretty remarkable number!:
Prop 4b:
10
() = 𝑋
Log (base e) Transformations: Theory
Prop 3:
Prop 4a:
Derivation:
𝑀𝑒𝑎𝑛(log 𝑋 ) − 𝑀𝑒𝑎𝑛(𝑙𝑜𝑔 𝑌 ) = 𝛿 Diff of means on log scale
𝑀𝑒𝑑𝑖𝑎𝑛(log 𝑋 ) − 𝑀𝑒𝑑𝑖𝑎𝑛(𝑙𝑜𝑔 𝑌) = 𝛿 Prop 1
log 𝑀𝑒𝑑𝑖𝑎𝑛 𝑋 − log (𝑀𝑒𝑑𝑖𝑎𝑛 𝑌) = 𝛿 Prop 2
log
()
()
= 𝛿 Prop 3
Therefore:
𝑒
= 𝑒log
()
()
=
()
()
Prop 4a
𝑒
=
()
(
)
log 𝑋 − log 𝑌 = log (𝑋
𝑌)
𝑒 () = 𝑋
Prop 1:
Mean[log(x)] = Median[log(x)]
Prop 2:
log(Median(X)) = Median(log(X))
Log (base 10) Transformations: Theory
Prop 3:
Prop 4b:
Derivation:
𝑀𝑒𝑎𝑛(log 𝑋 ) − 𝑀𝑒𝑎𝑛(𝑙𝑜𝑔 𝑌 ) = 𝛿 Diff of means on log scale
𝑀𝑒𝑑𝑖𝑎𝑛(log 𝑋 ) − 𝑀𝑒𝑑𝑖𝑎𝑛(𝑙𝑜𝑔 𝑌) = 𝛿 Prop 1
log 𝑀𝑒𝑑𝑖𝑎𝑛 𝑋 − log (𝑀𝑒𝑑𝑖𝑎𝑛 𝑌) = 𝛿 Prop 2
log
()
()
= 𝛿 Prop 3
Therefore:
10
= 10log10
()
()
=
()
()
Prop 4b
10
=
(
)
(
)
log 𝑋 − log 𝑌 = log (𝑋
𝑌)
10
() = 𝑋
Prop 1:
Mean[log(x)] = Median[log(x)]
Prop 2:
log(Median(X) = Median(log(X))
FULL EXAMPLE: SSHA Data
The Survey of Study Habits and Attitudes (SSHA) is a psychological test designed
to measure the motivation, study habits, and attitudes toward learning of college
students. These factors, along with ability, are important to explain success in
school. Scores on the SSHA range from 0 to 200. A selective private college gives
the SSGA to an SRS of both male and female first-year students.
The data for the women are as follows:
156 109 137 115 152 140 154 178 111 123 126 126 137 165 129 200 150
140 116 120 130 131 130 140 142 117 118 145 130 145
The data for men are as follows:
118 140 114 180 115 126 92 169 139 121 132 75 88 113 151 70 115 187
114 116 117 145 149 150 120 121 117 129 92 110
Most studies have found that the mean SSHA score for men is lower than the mean
score in a comparable group of women. Test this claim at the alpha = .05 level of
significance. (Show all 6 steps.)
H
0
:
w
=
m
H
1
:
w
>
m
71
Full Example: SSHA Data
State the Problem: We would like to test the claim
that the mean SSHA score of men is less than that
of women.
Check Assumptions:
1. Normally Distributed Populations
72

10/13/2018
13
First Check …. q-q Plot
The q-q plots for both populations look sufficiently
normal. We look at the histograms as well … but there is
not sufficient evidence here to suggest that they are not
normal.
73
Histograms
•Keeping in mind the relative small sample size from each
population, we do not observe any extreme outliers and
observe a pretty strong bell shape which lends evidence to
support normality of the populations.
74
Normality Assumption
Visual inspection of the histograms and q-q plots of each
population is consistent with the normality of each
population. We assume normality and move on to the second
assumption.
75
Full Example: SSHA Data
State the Problem: We would like to test the claim that
the mean SSHA score of men is less than that of women.
Check Assumptions:
1. Normally Distributed Populations
2. Equal Standard Deviations
76
Equality of Variances
A visual check was done by looking at the histograms which reveal similar shapes and
support the equal variances assumption. You can assume equal variances here.
Since we are able to assume normal population distributions, we can use the F-Test to provide
secondary evidence if the visual is inconclusive. Since the p-value is greater than our
significance level of alpha = 0.05, we fail to reject the null hypothesis of equality (p-value =
0.1043) of variances and conclude that there is not enough evidence to suggest the variances
are different.
77
Full Example: SSHA Data
State the Problem: We would like to test the claim
that the mean SSHA score of men is less than that
of women.
Check Assumptions:
1. Normally Distributed Populations
2. Equal Standard Deviations
3. Independent Observations
78

10/13/2018
14
Independent Observations
The sample was indeed a SRS (simple random
sample) from the population of the selective
private college, therefore we assume the
observations are independent of one another.
79
Full Example: SSHA Data
State the Problem: We would like to test the claim that
the mean SSHA score of men is less than that of women.
Check Assumptions:
1. Normally Distributed Populations
2. Equal Standard Deviations
3. Independent Observations
Run the Test:
1. First 5 steps.
80
Run The Two Sample T-Test!!!
•There is no reason to pair these observations and
we have two samples …. Therefore we should use
the two sample t-test with pooled standard
deviation since we are assuming the population
standard deviations are equal. We are testing
here:
H
0
: 𝜇
= 𝜇
H
1
:
𝜇
>
𝜇
81
Critical Value
82
0
𝑡., = 1.67
𝛼= .05 = significance level.
.05 df = 60 – 2 = 58
𝑥̅
W
-𝑥̅
M
Two Sample T-Test … SAS Output
83
Let’s Formalize This Test Into 6 Steps!
Step 1: Identify the null (Ho) and alternative (Ha) hypothesis.
Step 2: Draw and Shade and Find the Critical Value.
Step 3: Find the test statistic. (The t value for the data.)
Step 4: Find the p-value: P-value = .0211
Step 5: REJECT Ho.
Ho:
µ
𝑊
− µ
𝑀= 0
Ha:
µ
𝑊
− µ
𝑀> 0
𝑡 = (𝑥̅𝑊− 𝑥̅ 𝑀)
𝑠𝑝1
𝑛𝐼+1
𝑛𝐸
= 2.08
We would like to test the claim that the mean SSHA score of the men is less than the mean
score of women.To do this we take a sample of size n
M
= 30 and n
W
= 30 and find that 𝑥̅
M
=
124.2 points, 𝑥̅
W
= 137.1 and s
M
= 27.2 s
W
= 20.2 points.

10/13/2018
15
Full Example: SSHA Data
State the Problem: We would like to test the claim that
the mean SSHA score of men is less than that of women.
Check Assumptions:
1. Normally Distributed Populations
2. Equal Standard Deviations
3. Independent Observations
Run the Test:
1. First 5 steps.
State the Scope and Conclusion.
85
Scope
Since the study is between women and men, the
subjects cannot be randomly assigned to the
two groups, and we have an observational
study. For this reason, we cannot make any
causal inference and must limit our conclusions
to differences of group means.
However, the sample was an SRS and thus any
results can be inferred back to the population of
students at this particular private college.
86
Two Sample T-Test … SAS Output
87
Conclusion
There is sufficient evidence to support the claim at the α=.05 level of significance (p-
value = .0211) that the mean SSHA score is lower for men than for women at this
college. A 95% one side confidence interval for this difference is (2.5238 points, ∞.)
Scope of Inference: Since the study is between women and men, the subjects
cannot be randomly assigned to the two groups, and we have an observational
study. For this reason, we cannot make any causal inference and must limit our
conclusions to differences of group means.
However, the sample was an SRS, and thus any results can be inferred back to
the population of students at this particular private college.
88
ANOTHER FULL EXAMPLE
89
FULL EXAMPLE: Promotion Data
H
0
:
U
=
S
H
1
:
S
<
U
The Revenue Commissioners in Ireland conducted a contest for promotion.
The ages of the unsuccessful and successful applicants are given below.
Some of the applicants who were unsuccessful in getting the promotion
charged that the competition involved discrimination based on age. Treat
the data as samples from larger populations and use a .05 significance level
to test the claim that the unsuccessful applicants are from a population with
a greater mean age than the mean age of successful applicants. Based on
the result, does there appear to be discrimination based on age? (Show all
6 steps.) Assume all data comes from a normally distributed population.
Unsuccessful Applicants:
34 37 37 38 41 42 43 44 44 45
45 60 46 65 49 65 53 54
62 55 56 70 64
Successful Applicants
27 33 36 37 38 38 39 42 42 43
43 44 44 44 45 70 71 72
80 46 47 75 48 72 49 49
51 51 52 54
90

10/13/2018
16
Full Example: Promotion Data
State the Problem: We would like to test the
claim that the mean of the successful group is
less than the mean of the unsuccessful group.
Check Assumptions:
1. Normally Distributed Populations
91
First Check …. q-q Plot
The q-q plot for the successful data provides some
evidence of non normality, while the q-q plot for the
unsuccessful data looks consistent with normally
distributed data.
92
Successful Unsuccessful
Histograms
•The successful group (top) has a clear right skew to the data, while the unsuccessful group shows a
possible mild right skew. This suggests that both sets of data may be from right skewed
populations. We know that the t-tools are robust to non normality for these types of distributions
so we proceed with the t test…. We will readdress these concerns when we talk about the standard
deviation.
93
Normality Assumption
Visual Inspection of the histograms and q-q plots indicates the
both data sets may be from a right skewed distribution. We
know that the t-tests are robust to violations of the normality
assumption when the data are from a right skewed
distribution (when the sample size is sufficient), so we proceed
with the t-test.
94
Full Example: Promotion Data
State the Problem: We would like to test the
claim that the mean of the successful group is
less than the mean of the unsuccessful group.
Check Assumptions:
1. Normally Distributed Populations
2. Equal Standard Deviations
95
Equality of Variances
A visual check was done by looking at the histograms, which reveal similar shapes and
support the equal variances assumption. We will assume equal variances here.
As secondary evidence of the visual is inconclusive, given that the p-value is greater than
our significance level of alpha = 0.05, we fail to reject the null hypothesis of equality of
variances (p-value = 0.2286) and conclude that there is not enough evidence to suggest the
variances are different.
96

10/13/2018
17
Full Example: Promotion Data
State the Problem: We would like to test the
claim that the mean of the successful group is
less than the mean of the unsuccessful group.
Check Assumptions:
1. Normally Distributed Populations
2. Equal Standard Deviations
3. Independent Observations
97
Independent Observations
The sample was indeed a SRS (simple random
sample) from the population of the selective
private college, therefore we assume the
observations are independent of one another.
98
Full Example: Promotion Data
State the Problem: We would like to test the claim that
the mean of the successful group is less than the mean of
the unsuccessful group.
Check Assumptions:
1. Normally Distributed Populations
2. Equal Standard Deviations
3. Independent Observations
Run the Test:
1. First 5 steps.
99
Run The Two Sample T-Test!!!
•There is no reason to pair these observations,
and we have two samples. Therefore, we should
use the two sample t-test with a pooled standard
deviation, since we are assuming the population
standard deviations are equal. We are testing
here:
H
0
:
s
=
u
H
1
:
s
<
u
100
Two Sample T-Test … SAS Output
101
H
0
:
s
=
u
H
1
:
s
<
u
Fail to reject the null
hypothesis at 0.05 level.
Full Example: Promotion Data
State the Problem: We would like to test the claim that
the mean of the successful group is less than the mean of
the unsuccessful group.
Check Assumptions:
1. Normally Distributed Populations
2. Equal Standard Deviations
3. Independent Observations
Run the Test:
1. First 5 steps.
State the Scope and Conclusion.
102

10/13/2018
18
Since the study is between successful and
unsuccessful candidates for a promotion, subjects
cannot be randomly assigned to the two groups,
and we have an observational study. For this
reason we cannot make any causal inference and
must limit our conclusions to differences of group
means.
However, the sample was an SRS and thus any
results can be inferred back to candidates for
promotion from the population that the Revenue
Commissioners of Ireland sampled.
SCOPE
103
Conclusion
There is not sufficient evidence to support the
claim at the α=.05 level of significance (p-value
= .4357) that the mean age of those who were
given a promotion is lower than those who
were not given the promotion in this . A 90%
confidence interval for this difference is (-6.3
points, 5.2 points.)
104
Part IV
Alternatives to the t tools
93
Chapter 15
Problem 2: Logging problem
We are doing rank sum analysis
15.1 Complete Rank-Sum Analysis Using SAS
Problem Statement
We would like to test the claim that logging burned trees increased the percentage of seedlings lost in the
Biscuit Fire region from 2004 to 2005.
Assumptions
Independence
The two-sample Wilcoxon Rank-Sum test assumes that the samples are independent. In this case, the two
sets of tree plots are independent of each other, the amount of tree seedlings in one plot is not directly
related to the amount of tree seedlings in another, if it is, it is not a tangible amount of dependence.
Therefore, we can assume independence. We can also assume ordinality with numericla data
Statement of the Hypothesis
Our null hypothesis, H0, is that the distribution of percent of saplings lost in the logged plots is less than
or equal to the distribution of percent of saplings lost in the unlogged plots. Our alternative hypothesis,
H1, is that the distribution of percent of saplings lost in the logged plots is greater than the distribution of
percent of saplings lost in the unlogged plots. Mathematically speaking, we have:
H0:meanRanklogged −meanRankunlogged ≤0 (15.1.1)
H1:meanRanklogged −meanRankunlogged >0 (15.1.2)
The significance level, α,is:
α= 0.05 (15.1.3)
Calculation of the P-value
To find the p value, I performed a Wilcoxon Rank-Sum test. Because the sample size is small, an exact test
was used, as there is no need for a normal approximation. The code used to perform the test is as follows:
Code 15.1. Exact rank sum test using SAS
/*We want the wilcoxon test and the Hodges-Lehman Confidence Interval*/
proc NPAR1WAY data=loggingData Wilcoxon HL;
class Action;
Var PercentLost;
/*Because our sample size is small, we want to do an Exact test*/
Exact;
run;
The output of this code is displayed in Figure 2.1:
94

Analysis Guide Midterm
Figure 15.1.1. Results of the Rank-Sum Test on the Logging Data
The calculated p value is
p=0.0058 (15.1.4)
Results of the Hypothesis Test
We have that:
p= 0.0058 < α =.05 (15.1.5)
Therefore, we Reject the Null Hypothesis There is sufficient evidence at the α= 0.5 significance level
(p−value = 0.0058 for the exact test) to suggest that the distribution of percentages of saplings lost in the
logged plots was greater than the distribution of percentages of saplings lost.
Statistical Conclusion
MEDIANS FOR NONPAR The data provides convincing evidence that forest recovery is decreased in areas
where burned trees were logged. At a significance level of .05 (or even .01), the distribution/MEDIAN of
the percentage of saplings lost in the logged plots was greater than that of the unlogged areas. This was
done with a one sided, exact p-value of 0.0058. A range of plausible values (95 % confidence interval) for
how much greater the median loss of saplings was for the logged trees is [10.8,65.1], as displayed in Figure
2.2
Figure 15.1.2. 95% Confidence Interval
Note that the negative of these values was taken, because this figure shows Unlogged −Logged.
Scope of Inference
This study was a random sample of trees in the plots, therefore we can make generalizations about all of the
trees in the 16 plots, and say that the areas which were logged had a greater loss of saplings and therefore
recovered more poorly than the unlogged areas. However, this was not a randomized experiment, and
therefore we cannot make causal inferences. That is, we cannot say that the logging of burnt trees caused
the greater percent loss of saplings.
Since the plots were not randomized to receive either the logging or not logging treatment, no causation
can be implied here. Since the transect patterns were randomly selected, this inference can be generalized
to the 16 larger plots.
95

Analysis Guide Midterm
Confirmation Using R
In this section we confirm our findings using R. The R code input is shown below:
Code 15.2. wilcoxon rank sum test using R
1loggingData <- read.csv("Data/Logging.csv",header =TRUE , sep=",")
2wilcox.test( PercentLost ~Action ,
3data = loggingData,
4exact = TRUE ,
5alternative = "greater")
And the output:
1Wilcoxon rank sum test
2
3data: PercentLost by Action
4W = 55, p-value = 0.005769
5alternative hypothesis : true location shift is greater than 0
The results of the two programs are identical!
96

Chapter 16
Problem 3: Welch’s Two Sample T-Test
with Education Data
16.1 Problem Statement and Assumptions
Problem Statement
We would like to examine the claim that the mean income of college educated people (16 years of education)
is greater than the mean income of people with only a high school education (12 years of education)
Assumptions
The code used to produce everything in this section is shown below:
Code 16.1. welch’s t test
proc ttest data=edudata order=DATA
sides=U; /*an Upper tailed test*/
class Educ;
var Income2005;
run;
Normality
Figure 3.1 shows histograms and Box plots relating to the data:
Figure 16.1.1. Histograms and Box plots
As we can see from the figure, the data is not normal, it is heavily right skewed in both cases. Both the
histograms and the Box plots show this, as the histograms are way taller on the left side than on the right,
while the box plots show that there is a bunch of data on the left with a ton of outliers, clearly not normal.
We examine this further with the Q-Q plot in Figure 3.2
97

Analysis Guide Midterm
Figure 16.1.2. Q-Q Plot
The Q-Q plot conifrims our findings that the data is not very normal. However, the sample sizes are
400 and 1000, which means that we can definitely apply the central limit theorem. This means that we can
treat the data as normal, we will assume normality.
Independence
We will assume independence in this case.
16.2 Complete Analysis Using SAS
Statement of Hypotheses
H0:µ16yeareduc −µ12yeareduc ≤0 (16.2.1)
H1:µ16yeareduc −µ12yeareduc >0 (16.2.2)
Critical t Value
With α=.05 and a one sided test, the critical t value (with the appropriate degrees of freedom) is calculated
using the code shown below.
data critval;
p = quantile("T",.95,473.85); /*one sided test*/;
proc print data=critval;
run;
The critical t value is shown in Figure 3.3:
Figure 16.2.1. Critical t-value
The critical t value is t= 1.64. This is illustrated using the following bit of SAS code:
data pdf;
do x=-4to 4by .01;
pdf = pdf("T", x, 473.85);
lower = 0;
if x>= quantile("T",0.95,473.85) then upper = pdf;/*one sided*/
else upper = 0;
output;
end;
run;
title ’Shaded t distribution’;
proc sgplot data=pdf noautolegend noborder;
yaxis display=none;
band x = x
lower = lower
upper = upper / fillattrs=(color=gray8a);
series x = x y = pdf / lineattrs = (color = black);
series x = x y = lower / lineattrs = (color = black);
run;
98

Analysis Guide Midterm
This produces Figure 3.4
Figure 16.2.2. Shaded t Distribution
Calculation of the t Statistic
To calculate Welch’s t Statistic, we use the code seen in Section 3.a.2, giving us a t value of t= 9.98, as seen
in Figure 3.5
Figure 16.2.3. Results of Welch’s t-test
We see that in this case, we have a t-value of 9.98
Calculation of the p Value
We also see from Figure 3.5 that p= 0
Results of Hypothesis Test
We have that p= 0 < α =.05 and therefore we reject the null hypothesis
Conclusion
We have convincing evidence that the mean income of people with an education of 16 years is greater than
the mean income of people with an education of 12 years. A one sided p-value of zero shows us that the
means are truly different. The figure below shows a one sided 95% confidence interval on our data:
Figure 16.2.4. Confidence Interval on the Difference of Means
The confidence interval on the difference of means is [27662.2,∞). This estimates what is a plausible
difference between the means of the two samples. As we can see, the distribution of income of the sample
with a 16-year education is at least $27,000 greater than the distribution of income of the sample with a
12-year education.
99

Analysis Guide Midterm
Scope of Inference
This was an observational study; therefore, we cannot conclude that the extra education caused the change
(increase) in mean incomes. Households were selected from a random sample of a previously selected “area
of the United States” and the subjects in this study are the members of those households. Therefore, since
every member of the “area” had the same chance of being selected, it is a random sample of the “areas.”
However, no indication is given on how the “areas” were selected. In conclusion, the association between
education and income above can be generalized to all the members of the “areas” that were selected for this
study, but not generalized to the U.S. as a who
Verification using R
The following R code was used to verify the analysis
1eduData <- read.csv("Data/EducationData.csv",header =TRUE , sep =",")
2t.test(Income2005 ~Educ ,
3data = eduData ,
4# we use less because R is doing 12 - 16 #
5alternative = "less")
This gives the following output:
1Welch Two Sample t-test
2
3data: Income2005 by Educ
4t= -9.9827, df = 473.85 , p- value < 2.2e-16
5alternative hypothesis : true difference in means is less than 0
695 percent confidence interval:
7-Inf -27662.19
8sample estimates:
9mean in group 12 mean in group 16
10 36864.90 69996.97
Note that R is telling us that the distribution of income of the sample with a 12 year education is at least
27,000 less than those with a 16 year education
Preferences
I prefer the log transformed analysis, they both assume normality, however the log transformed analysis
has the more actually normal data to start with, and the variances are roughly equal. It also speaks more
to the medians, instead of the means, which is much more robust to the huge number of outliers. I think
because of the outliers, I definitely prefer the log method, as the mean is not such a good measurement
with these crazy outliers.
100

Chapter 17
Problem 4: Trauma and Metabolic
Expenditure rank sum
17.1 Hand-Written Calculations
To summarize, T= 82, µ(T) = 56, sd(T)=8.632 The handwritten work was done before the author under-
stood continuity correction, the continuity corrected Z and P values were calculated as follows:
Z=(T−0.5) −mean(T)
SD(T)= 2.95 (17.1.1)
→p=.001568 (17.1.2)
With a continuity correction of 0.5
101



Analysis Guide Midterm
17.2 SAS verification
To verify the Z and p values calculated in Section 4.a, the following SAS code was run:
proc NPAR1WAY data=TraumaStudy Wilcoxon HL;
class PatientType;
Var MetabolicEx;
run;
The results of this code are shown in Figure 4.1
Figure 17.2.1. Continuity Corrected Wilcoxon Test Using SAS
The Results of the two tests are the same! Note that if you add the phrase "correct=no" to the proc
NPAR1WAY statement, you get the same values as the non corrected ones in the handwritten work
17.3 Full Statistical Analysis
Problem Statement
We would like to test the claim that the Trauma patients had higher metabolic expenditures/
Assumptions
The Wilcoxon Rank-Sum test only assumes the data are independent, which in this case we will assume
independence because the patients were not related to each other in any way, or at least their metabolic
expenditures aren’t dependent on the other people’s metabolic expenditures. ALSO obviously normal
Hypothesis definitions
H0:meanRankT rauma −meanRankN onT rauma ≤0 (17.3.1)
H1:meanRankT rauma −meanRankN onT rauma >0 (17.3.2)
In other words, the null hypothesis is that the nontrauma and trauma patients have equal distributions of
metabolic expenditures, while the alternative hypothesis claims that the distribution of the trauma patients’
metabolic expenditures is higher. We are using a one sided hypothesis test because that is what the book
calls for. In this scenario, we will say α= 0.05
104

Analysis Guide Midterm
Critical Value
The critical value was calculated using the following chink of SAS code:
data critval;
p = quantile("Normal",.95); /*one sided test*/;
proc print data=critval;
run;
Producing a critical t value of t= 1.64485
Figure 17.3.1. Critical Value
The critical value is shown on a normal distribution using the following bit of SAS code
data pdf;
do x=-4to 4by .01;
pdf = pdf("Normal", x);
lower = 0;
if x>= quantile("Normal",0.95) then upper = pdf;/*one sided*/
else upper = 0;
output;
end;
run;
title ’Shaded Normal distribution’;
proc sgplot data=pdf noautolegend noborder;
yaxis display=none;
band x = x
lower = lower
upper = upper / fillattrs=(color=gray8a);
series x = x y = pdf / lineattrs = (color = black);
series x = x y = lower / lineattrs = (color = black);
run;
The shaded distribution is displayed in Figure 4.3
Figure 17.3.2. Shaded Normal Distribution
Calculation of the z statistic
Our z statistic, calculated in Sections 4.a and 4.b is 2.95.
Calculation of the p value
Our p-value, calculated in Sections 4.a and 4.b is 0.0016
Discussion of the hypothesis
We Reject the null hypothesis,p=.0016 <0.5 = α
105

Analysis Guide Midterm
Conclusion
We have convincing evidence that the distribution of metabolic expenditure of trauma patients is than the
nontrauma patients (p=0.0016 on a one sided Wilcoxon rank-sum test). The figure below shows a 95%
Hodges-Lehmann confidence interval on the difference of the two distributions:
Figure 17.3.3. 95% Confidence Interval
This tells us that a plausible difference between the two distributions is between 1.9 and 16.7. As we
can see this does not include the null hypothesis which says their difference is less than or equal to zero.
This cannot give us causal or population inferences because it was neither a randomized experiment nor a
random sample ALSO MEDIANS DUH
106

Chapter 18
Problem 5: Autism and Yoga signed rank
18.1 Hand-Written Calculations
The results of the calculations are as follows: S= 41, µS= 22.5, SDS= 8.4409, The Z value on the paper is
incorrect, as it does not correct for continuity. So, here we will aplply the continuity correction:
z=S−0.5−¯
S
SDS
(18.1.1)
z=40.5−22.5
8.4409 = 2.13 →poneT ail =.0166ptwoT ail =.033 (18.1.2)
107


Analysis Guide Midterm
18.2 Verification in SAS and R
Verification in SAS
To verify this, the following bit of SAS code was employed: Producing:
Code 18.1. Signed Rank test in SAS
data Autismdiff;
set Autism;
diff= Before-After;
run;
proc univariate data=Autismdiff;
var diff;
run;
Figure 18.2.1. Signed Rank Test In SAS
This two sided p value of 0.0313 is the same as a one sided p value of .01565, and a z value of 2.15. It is
slightly different with my calculations and SAS’s because they didnt use a normal approximation, I did.
Verification in R
This R code was employed for the same purposes:
1AutismData <- read.csv("Data/Autism.csv",header=TRUE , sep=",")
2wilcox.test( AutismData \$Before , AutismData \$After,
3paired = TRUE ,
4alternative = "greater",
5conf.int=TRUE)
Yielding:
1Wilcoxon signed rank test with continuity correction
2
3data: AutismData\$Before and AutismData\$After
4V = 41, p-value = 0.01618
5alternative hypothesis : true location shift is greater than 0
695 percent confidence interval:
74.999993 Inf
8sample estimates:
9(pseudo)median
10 17.49993
The R code applied a continuity correction, instead of doing the exact permutation like SAS. Their P value
corresponds with a Z score of 2.139
18.3 6 step Sign Rank test using SAS
Statement of Hypothesis
H0:MedianBef ore −MedianAf ter ≤0 (18.3.1)
H1:MedianBef ore −MedianAf ter >0 (18.3.2)
We will say that α=.05 and we are doing a one sided test
Critical Values
The critical value was calculated using the following chunk of SAS code:
data critval;
p = quantile("Normal",.95); /*one sided test*/;
proc print data=critval;
run;
Producing a critical t value of t= 1.64485
109

Analysis Guide Midterm
Figure 18.3.1. Critical Value
The critical value is shown on a normal distribution using the following bit of SAS code
data pdf;
do x=-4to 4by .01;
pdf = pdf("Normal", x);
lower = 0;
if x>= quantile("Normal",0.95) then upper = pdf;/*one sided*/
else upper = 0;
output;
end;
run;
title ’Shaded Normal distribution’;
proc sgplot data=pdf noautolegend noborder;
yaxis display=none;
band x = x
lower = lower
upper = upper / fillattrs=(color=gray8a);
series x = x y = pdf / lineattrs = (color = black);
series x = x y = lower / lineattrs = (color = black);
run;
The shaded distribution is displayed in Figure 5.3
Figure 18.3.2. Shaded Normal Distribution
Calculation of a Z statistic
We will use the Z statistic calculated using R/by hand,Z = 2.13, however it will not have a huge effect on
the outcome of the test
Calculation of a p value
For our z value, a one sided p value is p= 0.016.
Assessment of hypothesis
p=.016 < α =.05 →We reject the null hypothesis.
Conclusion
We have conclusive evidence that the median time to complete the puzzle for Autistic children is greater
before 20 minutes of Yoga than after 20 minutes of Yoga. We cannot infer causality becuase this was not a
randomized experiment, and we cannot infer anything about the population because this was not a random
sample. The median time for the children was at least 5 seconds longer before Yoga as compared to after
Yoga, as seen by the confidence interval displayed in the R output.
110

Analysis Guide Midterm
18.4 Paired t test in SAS
Statement of Hypothesis
H0:µbef ore−af ter ≤0 (18.4.1)
H1:µbef ore −af ter > 0 (18.4.2)
We will say that α=.05 and we are doing a one sided test.
Critical Values
The critical value was calculated using the following chunk of SAS code:
data critval;
p = quantile("T",.95,8); /*one sided test*/;
proc print data=critval;
run;
With the following output:
Figure 18.4.1. Critical Value
With a critical t value of t=1.86. This is demonstrated in a shaded t distribution with the following
chunk of code:
data pdf;
do x=-4to 4by .01;
pdf = pdf("T", x,8);
lower = 0;
if x>= quantile("T",0.95,8) then upper = pdf;/*one sided*/
else upper = 0;
output;
end;
run;
title ’Shaded Normal distribution’;
proc sgplot data=pdf noautolegend noborder;
yaxis display=none;
band x = x
lower = lower
upper = upper / fillattrs=(color=gray8a);
series x = x y = pdf / lineattrs = (color = black);
series x = x y = lower / lineattrs = (color = black);
run;
The shaded distribution is displayed in Figure 5.5
Figure 18.4.2. Shaded T Distribution
Calculation of a t statistic
The T statistic was calculated using the following SAS code: The t value is shown in Figure 5.6
Figure 18.4.3. Paired t statistic
We have a t value of 2.54.
111
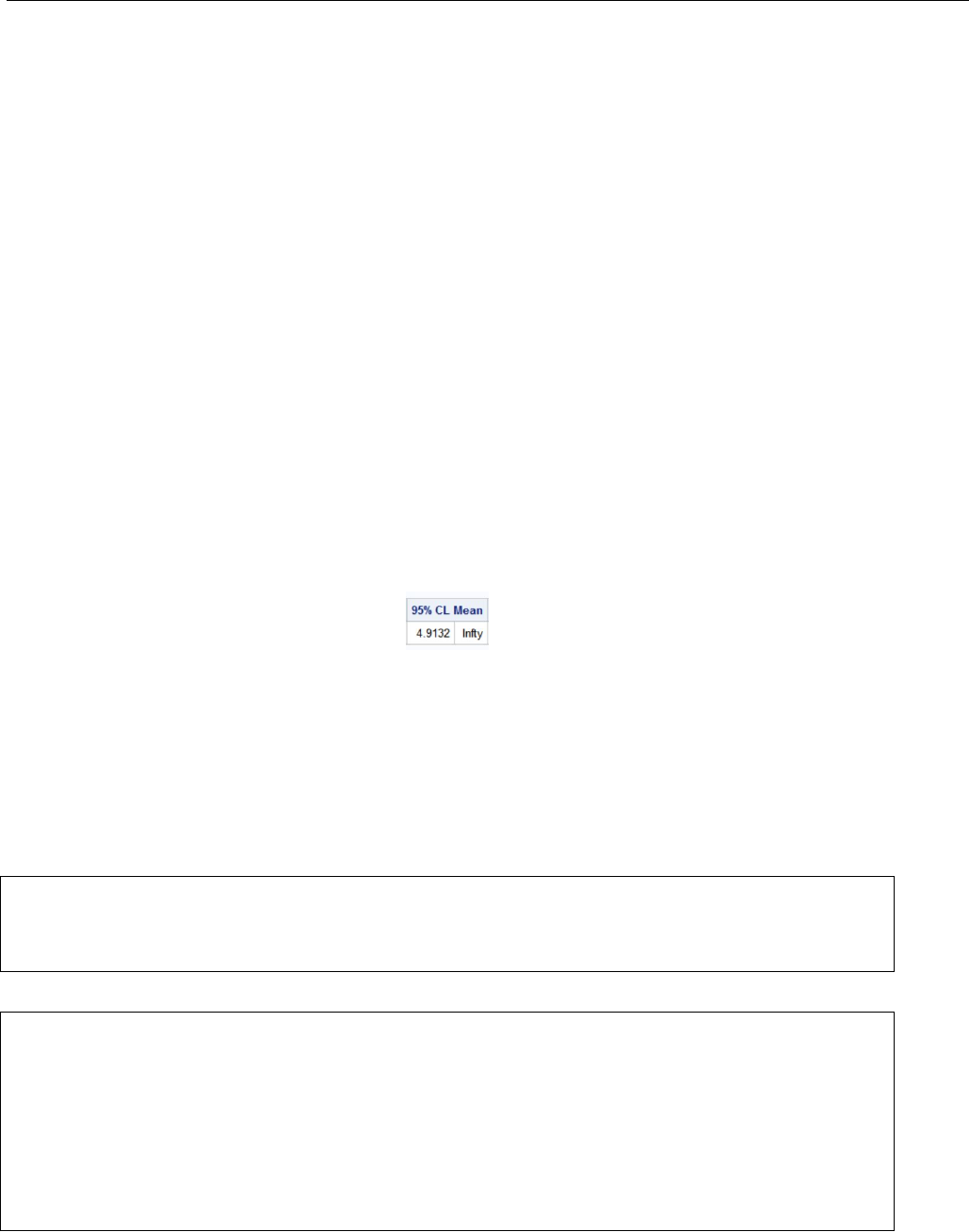
Analysis Guide Midterm
Code 18.2. Paired T test in SAS
proc ttest data=Autism alpha = .05 sides=U;
paired Before*After;
run;
Calculation of a P value
The p value can be seen in Figure 5.6:p=.0173
Assessment of Hypothesis
p=.0173 > α =.05 →we reject the null hypothesis.
Conclusion
We have conclusive evidence that the mean of the differences of times before and after the yoga is greater
than zero (p=.0173 on a one sided paired t test). A confidence interval for the mean of the difference of
time for the children to finish the puzzle before and after yoga is shown in Figure 5.7:
Figure 18.4.4. 95% Confidence interval
This means that the mean of the differences was at least 4.9 seconds. We cannot infer causality because
this was not a randomized experiment, and we cannot make inferences about the population because this
was not a random sample. We also cannot make causal inferences with a paired t test
18.5 Confirmation with R
The R code below was used to verify the results of the previous section:
1t.test(AutismData\$Before , AutismData\$After,
2paired = TRUE ,
3alternative = "greater",
4conf.int=TRUE)
The output is presented below:
1Paired t-test
2
3data: AutismData\$Before and AutismData\$After
4t= 2.5403 , df = 8, p-value = 0.01735
5alternative hypothesis : true difference in means is greater than 0
695 percent confidence interval:
74.913201 Inf
8sample estimates:
9mean of the differences
10 18.33333
18.6 Complete Statistical Analysis
In this section, I will be using a paired t-test, because the data is pretty normal, as we will see in the
following section. When both are possible, I believe the paired t test is better because it doesnt mess with
the data in any way, we can see the magnitudes etc.
Assumptions
We can assume the differences are independent because the children did not affect the other children.
To check for normality we examine the following figure:
112

Analysis Guide Midterm
Figure 18.6.1. Histogram and Box Plot
As we see from Figure 5.8, the data is fairly normally distributed. The histogram is heavier in the center
than on the edges, and the mean is near the median on the Box plot. We will examine this further in Figure
5.9
Figure 18.6.2. Q-Q Plot
As we can see, the data follows the line of normality closely, and therefore we can assume normality.
This means that a paired t test is appropriate.
Statement of Hypothesis
H0:µbef ore−af ter ≤0 (18.6.1)
H1:µbef ore −af ter > 0 (18.6.2)
We will say that α=.05 and we are doing a one sided test.
Critical Values
The critical value was calculated using the following chunk of SAS code:
data critval;
p = quantile("T",.95,8); /*one sided test*/;
proc print data=critval;
run;
With the following output:
Figure 18.6.3. Critical Value
With a critical t value of t=1.86. This is demonstrated in a shaded t distribution with the following
chunk of code:
113

Analysis Guide Midterm
data pdf;
do x=-4to 4by .01;
pdf = pdf("T", x,8);
lower = 0;
if x>= quantile("T",0.95,8) then upper = pdf;/*one sided*/
else upper = 0;
output;
end;
run;
title ’Shaded Normal distribution’;
proc sgplot data=pdf noautolegend noborder;
yaxis display=none;
band x = x
lower = lower
upper = upper / fillattrs=(color=gray8a);
series x = x y = pdf / lineattrs = (color = black);
series x = x y = lower / lineattrs = (color = black);
run;
The shaded distribution is displayed in Figure 5.11
Figure 18.6.4. Shaded T Distribution
Calculation of a t statistic
The T statistic was calculated using the following SAS code:
proc ttest data=Autism alpha = .05 sides=U;
paired Before*After;
run;
The t value is shown in Figure 5.12
Figure 18.6.5. Paired t statistic
We have a t value of 2.54.
Calculation of a P value
The p value can be seen in Figure 5.6:p=.0173
Assessment of Hypothesis
p=.0173 > α =.05 →we reject the null hypothesis.
Conclusion
We have conclusive evidence that the mean of the differences of times before and after the yoga is greater
than zero (p=.0173 on a one sided paired t test). A confidence interval for the mean of the difference of
time for the children to finish the puzzle before and after yoga is shown in Figure 5.13:
Figure 18.6.6. 95% Confidence interval
114

Analysis Guide Midterm
This means that the mean of the differences was at least 4.9 seconds. We cannot infer causality because
this was not a randomized experiment, and we cannot make inferences about the population because this
was not a random sample. We also cannot make causal inferences with a paired t test
115
Chapter 19
sexy ranked permutation test
Here is the SAS code I designed to conduct a Ranked permutation test I did not have time to add a normal
Code 19.1. handcrafted rank sum test
proc import
datafile=’c:\Users\david\Desktop\MSDS\MSDS6371\Homework\Week4\Data\Trauma.csv’
out=TraumaStudy
DBMS=CSV;
run;
proc rank data=TraumaStudy out=Ranked ties=mean;
var MetabolicEx;
ranks rank;
run;
proc print data=Ranked;
run;
proc iml;
use Ranked var {PatientType rank};
/*making two groups in IML*/
read all var {rank} where(PatientType=’Nontrauma’) into g2;
read all var {rank} where(PatientType=’Trauma’) into g1;
obsdiff = sum(g1) - sum(g2);
print obsdiff;
call randseed(12345); /*set random number seed */
alldata = g1 // g2; /*stack data in a single vector */
N1 = nrow(g1); N = N1 + nrow(g2);
NRepl = 5000; /*number of permutations */
nulldist = j(NRepl,1); /*allocate vector to hold results */
do k=1to NRepl;
x = sample(alldata, N, "WOR"); /*permute the data */
nulldist[k] = sum(x[1:N1]) - sum(x[(N1+1):N]); /*difference of sums */
end;
title "Histogram of Null Distribution";
refline = "refline " + char(obsdiff) + " / axis=x lineattrs=(color=red);";
call Histogram(nulldist) other=refline ;
pval = (1 + sum((nulldist) >= (obsdiff))) / (NRepl+1); /*this means one sided test, no absolute values*/
print pval;
quit;
curve to my figure, however, the p value is more or less the same as the wilcoxon test however it is a more
reasonable number.
116

Analysis Guide Midterm
Figure 19.0.1. Permutation Test
117
Chapter 20
Unit 4 lecture slides
Here it is
118

10/13/2018
1
Alternatives to (Student)
t-Tools
RANK SUM TEST
WELCH’S TE ST
SIGN TEST / SIGNED RANK TEST
Let’s Start With an Example
New Method Traditional Method
37 23
49 31
55 46
77
•IBM gives each employee in the marketing department technical training
•Based on further testing, it appears the traditional training method isn’t effective
•Hence, a new training method is developed
•Below are the test scores of 4 individuals who just finished the “New Method” and the last 3 test
scores from employees trained via the “Traditional Method” course
•Is there evidence to suggest that the “New Method” increases test scores?
Since the standard deviations appear (visual check) to be different and the sample sizes are both different and
exceptionally small, the t-test was not deemed appropriate and the nonparametric rank sum test was performed.
Examining the t-Tools Assumptions
1
22
1
4
Which situation does it appear we are in?
Using a t-test could have low power.
1
2
Nonparametric Methods:
The Rank Sum Test
5
Nonparametric Methods
•A
NONPARAMETRIC
or
DISTRIBUTION
-
FREE
test doesn’t depend on underlying assumptions
•This makes them ideal for use when the assumptions of non-nonparametric (that is,
PARAMETRIC
)
tests aren’t met
•The trade-off is that nonparametric methods perform somewhat worse than parametric
methods if the assumptions are approximately correct
•The first nonparametric method we will consider is the ”rank sum test”

10/13/2018
2
Rank Sum Test: Advantages
•No distributional assumptions
•Resistant to outliers
•Performs nearly as well as the t-test when the two populations are normal and considerably
better when there are extreme outliers
•Works well with
ORDINAL
(as opposed to interval data)
•Works with censored values
•It still requires some assumptions:
1. All observations are independent
2. The Y values are ordinal
59 patients with arthritis who participated in a clinical
trial were assigned to two groups, active and placebo.
The response status:
(excellent=5, good=4, moderate=3, fair=2, poor=1)
of each patient was recorded.
The Hypothesis Test
(T
WO SIDED
)
(
ONE SIDED
)
The Rank Sum test
•We can compute the rank sum test statistic using the following steps:
1. List all observations from both groups in increasing order
2. Assign each observation a rank, from 1 to n
3. If there are any ties, assign each tied observation’s rank to be the average of their ranks.
4. Identify each observation by its group
•The test statistic, T, is the sum of the ranks in one of the groups.
•We can find a p-value in two ways:
•Normal approximation
•Re-randomization (exact or approximate)
Note: nis the total # of observations
The Sampling Distribution of …
The Rank Sum Statistic!
Rank Sum test statistic (sum
of ranks of one group) is
approximately normally
distributed!
Rank-Sum Test: Normal Approximation Rank Sum Test: randomly assign ranks
Record sum of ranks of one group (e.g. “Trad.”) for all 7! permutations of ranks. (7!=7*6*5*4*3*2*1=5040)
P-value is the number of permutations with a sum equal to or more extreme than the one in the original data
set divided by the total number of permutations.
*Could also do an approximate p-value by randomly choosing, say, 1000 orderings of the data.
Name Order # Group Rank
Bob 1 New 5
Sue 2 New 7
Fred 3 New 2
Jim 4 New 1
Pam 5 Trad 3
Tim 6 Trad 4
Zac 7 Trad 6
Name Order # Group Rank
Sue 1 New 7
Bob 2 New 5
Fred 3 New 2
Jim 4 New 1
Pam 5 Trad 3
Tim 6 Trad 4
Zac 7 Trad 6
Name Order # Group Rank
Pam 1 New 3
Tim 2 New 4
Sue 3 New 7
Zac 4 New 6
Fred 5 Trad 2
Bob 6 Trad 5
Jim 7 Trad 1
…

10/13/2018
3
There is mild evidence (alpha = 0.1) to suggest that the distribution of scores
from the “New” method is greater than the distribution of the “Traditional”
method (normal approximation to rank-sum test p-value = 0.0558).
Rank-Sum Test:
Normal Approximation
Common interpretation:
H
0
: The distribution of New Method Scores = The distribution of the Traditional Method Scores
H
1
:The distribution of New Method Scores > The distribution of the Traditional Method Scores
Technical mathematical interpretation:
H
0
: Average rank of New Method Scores = Average rank of all Scores (constant)
H
1
:Average rank of New Method Scores > Average rank of all Scores (constant)
Common interpretation:
H
0
: The distribution of New Method Scores = The distribution of the Traditional Method Scores
H
1
:The distribution of New Method Scores > The distribution of the Traditional Method Scores
There is mild evidence (alpha = 0.1) to suggest that the distribution of scores
from the “New” method is greater than the distribution of the “Traditional”
method (normal approximation to rank-sum test p-value = 0.0558).
Rank-Sum Test:
Normal Approximation
Permutation Test
(Exact P-value)
Normal approximation p-values
Exact p-values
Rank Sum Test (Wilcoxon)
H
0
:
The distribution of New Method Scores = The distribution of the Traditional Method Scores
H
1
:
The distribution of New Method Scores > The distribution of the Traditional Method Scores
There is sufficient evidence at the alpha = 0.1 level of significance (p-value = .0571
for the exact test) to suggest that the distribution of scores from four IBM
employees that were given the New Method is greater than the distribution of the
3 employees that took the test having had the Traditional Method of instruction.
•Researchers compared the effectiveness of conventional textbook examples to modified ones
•They selected 28 ninth-year students who had no previous exposure to coordinate geometry
•The students were randomly assigned to one of two self study instructional groups, using conventional
and modified instructional materials
•After instruction, they were given a test and the time to complete one of the problems was recorded.
Cognitive Load Experiment
Is there sufficient evidence to suggest that the
cognitive load theory (modified instruction)
shortened response times?
(
CENSORED DATA
)
Cognitive Load Experiment

10/13/2018
4
Cognitive Load Experiment
With ties, the ranks are averaged.
Statistical Conclusion: The data provide convincing evidence that a student could solve the problem more quickly after
the “modified” rather than the the “conventional” method (one-sided, normal approximation w/ C.C. p-value = 0.0013,
from the rank-sum test).
Cognitive Load Experiment:
Normal Approximation
(
CONTINUITY CORRECTION
)
Cognitive Load Experiment:
Using SAS Confidence Interval for the Location Parameter (Median):
Hodges Lehman Confidence Interval
https://en.wikipedia.org/wiki/Hodges%E2%80%93Lehmann_estimator
*We will look at an example later
Statistical Conclusion (continued): A range of plausible values for how much smaller the “modified” distribution is than
the “traditional” (treatment effect) is [-158, -59] s. (95% confidence interval based on a rank-sum test) with a point-
estimate of 108.5 s.
Cognitive Load Experiment
Ho: Distribution of Modified and Conventional Scores are equal
Ha: Distribution of Modified Scores is less than that of
Conventional
Critical Value (left sided): -1.645 (alpha = .05)
Test Statistic: z-stat = -3.0183
P-value (left sided)= .0013
Reject Ho
Statistical Conclusion (continued): The data provide convincing evidence that a student could
solve the problem more quickly after the “modified” rather than the “conventional” method
(one-sided, normal approximation w/ C.C. p-value = 0.0013, from the rank-sum test). A range of
plausible values for how much smaller the “modified” distribution is than the “traditional”
(treatment effect) is [-158, -59] sec. (95% confidence interval based on a rank-sum test) with a
point-estimate of 108.5 sec.
Cognitive Load Experiment (All Together)

10/13/2018
5
Welch’s t-Test
25
Creativity Study: Reminder
E
I
What if this assumption
isn’t true?
Welch’s t-Test Testing Hypothesis:
Welch’s t-Tools
28
Gender Income Discrimination Gender Income Discrimination
Strong evidence against normality, but CTL applies.
Strong evidence against equal standard deviations and
different sample sizes. (They are close but the standard
deviations appear to be so different that this may make
a real difference.)
We will assume independence.
Student’s t-test not a good idea here.

10/13/2018
6
Gender Income Discrimination!
Test Statistic: t
stat
= -3.88
P-value = .0006
Reject H
0
Conclusion: There is strong evidence to suggest that
the mean income of the female group is different
from the mean income of the male group (p-value =
.0006). A 95% confidence interval for this difference
is ($29,124, $94,176) in favor of the males.
That is quite a difference!
Rank Sum versus Welch’s … the Take Away
If you wish to make inference on the difference of means and you have the sample size to invoke the CLT, Welch’s
t-test is preferred by most statisticians, and it is robust to different standard deviations even when the sample
size is not equal.
Often, especially in skewed distributions, the median is a better measure of center. For this reason, one may
prefer the rank sum test even when Welch’s t-test is available.
If you have small sample sizes, you may not be very confident about the normality assumption even if the
histograms and q-q plots look okay. For this reason, one may wish to be “conservative” and run the rank sum
test and obtain inference on the median.
If there are outliers or censored values, the rank sum test is often the most appropriate as the t-test is not
resistant to outliers and has no way of using censored data.
Performance of Welch’s t-test
Paired T-Test
Paired T-Test
Known alternatively as Matched Pairs or Dependent t-Test
Assumptions
•Data are either:
•From one sample that has been tested twice (example pre- and post-test or
repeated measures)
•From a group of subjects that are thought to be similar and can thus be
matched or paired (example from same family, or twins)
•Differences are normally distributed, independent between observations (but
dependent from one group to the next).
35
A Look at the Variance
36
•If data can be paired, the variance can be reduced.

10/13/2018
7
Example:
Medical Reasoning Test
•The AMA has a diagnostic test for medical reasoning
•On average, people score about 500 points on this test
•We have data from 10 subjects who took the medical
reasoning test. These subjects were randomly selected
from St. Paul Hospital in Dallas
•Not fatigued: is the baseline, taking the test before a shift
•Fatigued: is after the treatment; working for 12
operational hours prior to re-taking the test.
37
Subject # Not Fatigued Fatigued
1 567 530
2 512 492
3 509 510
4 593 580
5 588 600
6 491 483
7 520 512
8 588 575
9 529 530
10 508 490
(Lower numbers = worse score)
Example:
Keith’s Medical Reasoning Test
We can try to test whether the
DIFFERENCE OF THE MEANS
between the fatigued scores and the not
fatigued scores is less than zero.
38
Example:
Medical Reasoning Test
39
If we did this, we would be wrong! Why?
A fundamental assumption is violated:
independence
Assumption Check Failure
40
We need to account for the dependence between the two groups
Example:
Keith’s Medical Reasoning Test
Instead of testing the
DIFFERENCE OF THE MEANS
:
41
Subject Fatigued Not Fatigued Difference
1 530 567 -37
2 492 512 -20
3 510 509 1
4 580 593 -13
5 600 588 12
6 483 491 -8
7 512 520 -8
8 575 588 -13
9 530 529 1
10 490 508 -18
We should test the
MEAN OF THE DIFFERENCES
:
Paired t-test reduces to a one-sample t-test
42
Subject Fatigued Not Fatigued Difference
1 530 567 -37
2 492 512 -20
3 510 509 1
4 580 593 -13
5 600 588 12
6 483 491 -8
7 512 520 -8
8 575 588 -13
9 530 529 1
10 490 508 -18
(d
i
)H
0
: d = 0
H
a
: d < 0

10/13/2018
8
A SAS Code Comparison
43
Two (independent) sample T-Test Paired T-test
A SAS Code Comparison
44
Two (independent) sample T-Test
Paired T-test
Using paired data (when appropriate) instead of
unpaired data allows us to tighten the
confidence interval for the difference in means
(yeah!) AND increase the power (the likelihood
that our data properly detects a shift in score).
Checking the Assumptions
45
There is little to no evidence that the differences do
not come from a normal distribution.
We will assume that the differences are independent.
Is this a reasonable assumption?
Additional Information
46
•We can look at a
PROFILE PLOT
•The lines connect the scores on the MRT in
the “fatigued” versus “not fatigued” states
•This plot is standard for SAS proc ttest with
paired data.
Conclusion (alpha = 0.01)
Fail to Reject Ho
47
Critical Value: t
0.01,9
= -2.821
Test Statistic: t
stat
= -2.41
P-value = 0.0196 > 0.01
Statistical Conclusion: There is not enough evidence to suggest that, on average, the fatigued subjects score lower than the non-fatigued
subjects (p-value = .0196). A 99% one sided confidence interval for the mean difference in scores is (-infinity, 1.76). Perhaps, a more
meaningful confidence interval would be a two-sided 98% confidence interval of (-22.36, 1.76).
Scope of Inference: Since this was a random sample from St. Paul Hospital in Dallas, we can infer that this result would be repeated for
any group selected from this hospital. There is no way to guarantee a causal inference from a paired t-test.
Note: The elusiveness of the causal inference comes from the fact that the treatment that induces fatigue may itself be a confounder.
Some may work for 12 hours as a surgeon and others may work 12 hours writing reports. There is reason to believe that if a difference is
detected, this difference may not be due to fatigue rather may be due to the type of work.
Appendix

10/13/2018
9
Alternatives to the t-Test for Paired Data
For each of the 9 horses, a veterinary anatomist measured the density
of nerve cells at specified sites in the intestine.
horse site1 site2
6 14.2 16.4
4 17 19
8 37.4 37.6
5 11.2 6.6
7 24.2 14.4
9 35.2 24.4
3 35.2 23.2
1 50.6 38
2 39.2 18.6
Example: Nerve Data
Using the paired t-Test
The sample size is rather small, hence the normality assumption is somewhat suspect.
The Hypothesis Test
(T
WO SIDED
)
(
ONE SIDED
)
52
horse site1 site2 diff Sign
8 37.4 37.6 -0.2 -
4 17 19 -2 -
6 14.2 16.4 -2.2 -
5 11.2 6.6 4.6 +
7 24.2 14.4 9.8 +
9 35.2 24.4 10.8 +
3 35.2 23.2 12 +
1 50.6 38 12.6 +
2 39.2 18.6 20.6 +
K = 6
Sign Test: Horse Data
(
ONE SIDED
, CC
P
-
VALUE
)
Test and Conclusion
Statistical Conclusion: There is not enough evidence that the median nerve density at site 1 is
greater than the median nerve density at site 2 (Wilcoxon sign test one-sided p-value of 0.2527).
54
Critical Value (right sided): z
0.05
=1.645
t statistic: t
stat
= 0.666
P-value (one sided) = .2527
Fail to Reject H
0
.

10/13/2018
10
horse site1 site2 abs(diff) Sign rank
8 37.4 37.6 0.2 - 1
4 17 19 2 - 2
6 14.2 16.4 2.2 - 3
5 11.2 6.6 4.6 + 4
7 24.2 14.4 9.8 + 5
9 35.2 24.4 10.8 + 6
3 35.2 23.2 12 + 7
1 50.6 38 12.6 + 8
2 39.2 18.6 20.6 + 9
S = 39
Signed Rank Test: Horse Data
(
ONE SIDED
, CC
P
-
VALUE
)
Test, Conclusion and Some Notes
Statistical Conclusion: There is strong evidence that the median nerve density at site 1 is greater
than the median nerve density at site 2 (Wilcoxon signed rank test one-sided p-value of 0.0294).
Note:
•The signed-rank test has more power than the sign test
(Compare the p-values 0.254 vs. 0.0294)
•Both tests make very few assumptions about the distributions
56
Critical Value (right sided): z
0.05
=1.645
t statistic: t
stat
= 1.89
P-value (one sided) = .0294
Reject Ho.
Horse Data
Note: For n < 20 SAS uses the probabilities from the binomial
distribution rather than the normal approximation. These are more
accurate (exact) and we should use these when SAS is available.
Note: These are two sided…. Half of this is close
to our calculated one sided p-values from
earlier.
Part V
ANOVA
129

Chapter 21
Problem 1: Plots and Logged Data
We begin our work looking at raw and transformed data.
21.1 Plots and Transformations
Raw Data Analysis
First, we will look at the raw data. To check if the raw data fits the assumptions, we will first look at a
scatter plot. The scatter plot of the raw data was produced by the following bit of SAS code:
Code 21.1. Scatterplot of Raw Data Using SAS
proc sgplot data=EduData;
scatter x=educ y=Income2005;
run;
This results in the following plot21.1:
Figure 21.1.1. Scatter Plot of the Raw Data
Looking at Figure 21.1.1, we see that the raw data is very heavy in between 0 and 20,000 for all cat-
egories, but some groups spread further and wider than others, which suggests the variances may not be
equal. The heaviness of the lower end of each group may also suggest a lack of normality. We will examine
this further with some Box plots. These were produced using the following chunk of SAS code: This results
in the following plot:
130

Analysis Guide Midterm
Code 21.2. Boxplot of Raw Data Using SAS
proc sgplot data=EduData;
vbox Income2005 / category=educ
dataskin=matte
;
xaxis display=(noline noticks);
yaxis display=(noline noticks) grid;
run;
Figure 21.1.2. Box Plot of the Raw Data
Figure 21.1.2 tells us a lot about our data. We see from the size and shape of the boxes that the variances
of our data are by no means homogeneous. Note that there are a lot of outliers while the distribution is
heavily weighted towards the bottom, this suggests our data may have departed from normality. We will
examine this phenomenaa further using histograms.
To produce histograms of the raw data, the following SAS code was used: This results in the following
Code 21.3. Histogram of Raw Data Using SAS
proc sgpanel data=EduData;
panelby educ / rows=5 layout=rowlattice;
histogram Income2005;
run;
plot:
131

Analysis Guide Midterm
Figure 21.1.3. Histogram of the Raw Data
Figure 21.1.3 confirms our suspicions, the variances of the data are likely unequal, but more impor-
tantly, the data is clearly skewed to the right. We will confirm this using Q-Q plots.
To produce Q-Q plots of the raw data, the following SAS code was used:
Code 21.4. Q-Q of Raw Data Using SAS
/*Normal = blom produces normal quantiles from the data */
/*To find out more, look at the SAS documentation!*/
proc rank data=EduData normal=blom out=EduQuant;
var Income2005;
/*Here we produce the normal quantiles!*/
ranks Edu_Quant;
run;
proc sgpanel data=EduQuant;
panelby educ;
scatter x=Edu_Quant y=Income2005 ;
colaxis label="Normal Quantiles";
run;
This results in the following plot:
132

Analysis Guide Midterm
Figure 21.1.4. Q-Q Plot of the Raw Data
The Q-Q plots in Figure 21.1.4 tell us what we already know: The raw data is not normal, and does
not have equal variances. The ANOVA test is not super robust to highly skewed, long tailed data, and it
relies entirely on equal variances, so we absolutely cannot use the raw data
133

Analysis Guide Midterm
Transformed Data Analysis
Now we will perform a log transformation on the data and see if that helps it meet our assumptions better.
To do a log transformation, we will employ the following SAS code: We will begin our analysis of the
Code 21.5. Logging of Raw Data Using SAS
data LogEduData;
set EduData;
LogIncome=log(Income2005);
run;
transformed data with a scatter plot, produced with the following SAS code: This results in the following
Code 21.6. Scatterplot of Logged Data Using SAS
proc sgplot data=LogEduData;
scatter x=educ y=LogIncome;
run;
plot:
Figure 21.1.5. Scatter Plot of the Log-Transformed Data
As we can see in Figure 21.1.5, the groups have a much more similar size, suggesting similar variances,
and the heavy part of the scatter plot is closer to the center, in between the outliers, which tells us the log
transformation may have done a good deal towards normalizing our data. We can examine this further
using Box plots.
To produce Box plots of the transformed data, the following SAS code was used: This gives us the
Code 21.7. Boxplot of Logged Data Using SAS
proc sgplot data=LogEduData;
vbox LogIncome / category=educ
dataskin=matte
;
xaxis display=(noline noticks);
yaxis display=(noline noticks ) grid;
run;
following plot:
134

Analysis Guide Midterm
Figure 21.1.6. Box Plot of the Log-Transformed Data
Figure 21.1.6 gives us some useful information about our data. We see the boxes and whiskers are of
similar size, which tells us the variances are likely homogeneous. Furthermore, the medians and means
are near each other, and the boxes are near the center of the distribution, which suggests that the data may
be normal. We will examine these two phenomena further with histograms. To produce histograms of the
log-transformed data, the following SAS code was used: This results in the following plot:
Code 21.8. Histogram of Logged Data Using SAS
proc sgpanel data=LogEduData;
panelby educ / rows=5 layout=rowlattice;
histogram LogIncome;
run;
Figure 21.1.7. Histogram of the Log-Transformed Data
135

Analysis Guide Midterm
From the spread of the histograms in Figure 21.1.7, we see two things. First, the similar width of
the histograms confirms that variances are roughly equal. Second, the shape of the histograms, and their
location near the center suggests that the data is very nearly normal. We will further examine the normality
of the data using Q-Q plots.
To produce the Q-Q plots of the transformed data, the following SAS code was used: This results in the
Code 21.9. Q-Q of Logged Data Using SAS
proc rank data=LogEduData normal=blom out= LogEduQuant;
var LogIncome;
ranks LogEduQuant;
run;
proc sgpanel data=LogEduQuant;
panelby educ;
scatter x=LogEduQuant y=LogIncome ;
colaxis label="Normal Quantiles";
run;
following plot:
Figure 21.1.8. Q-Q Plot of the Log-Transformed Data
Examining Figure 21.1.8, we see a confirmation of our beliefs: The log-transformed data, when plotted
against normal quantiles, is fairly normal. This means, with the log transformed data, we can reasonably
assume normality and homogeneity of variances.
21.2 Complete Analysis
We will now perform a complete analysis of our data, using Pure ANOVA.
Problem Statement
We would like to determine whether or not at least one of the five population distributions (corresponding
to different years of education) is different from the rest.
Assumptions
As seen in Section 21.1, the raw data does not meet the assumption of normality nor of homogeneity of
variance. However, in Section 21.1, we proved that after a log transformation, the data does meet both of
these assumptions. The ANOVA test is fairly robust to the slight departure from normality presented by
the log transformed data, and the variances are equal. The data is clearly independent, so that assumption
is met. Therefore, all assumptions of ANOVA are met by the log transformed data.
Hypothesis Definition
In this problem, our Null (Reduced Model) Hypothesis, H0, is that all the groups have the same distribu-
tion and our Alternative (Full Model) Hypothesis, H1is that the distributions are different. Mathemati-
136

Analysis Guide Midterm
cally, that is written as:
H0:mediangrand mediangrand mediangrand mediangrand mediangrand (21.2.1)
H1:median<12 median12 median13−15 median16 median>16 (21.2.2)
We will consider our confidence level, αto be 0.05
F Statistic
To conduct this hypothesis test, the following SAS code was used: This results in the following ANOVA
Code 21.10. ANOVA Test Using SAS
proc glm data = LogEduData;
class educ;
model LogIncome = educ;
run;
Output:
Figure 21.2.1. ANOVA Table
Figure 21.2.1 tells us what our F statistic is. We see that
F= 62.87 (21.2.3)
P-value
Figure 21.2.1 also tells us our p-value. In this case,
p < .0001 (21.2.4)
Hypothesis Assessment
In this scenario, we have that p < .0001 < α =.05 and therefore we reject the null hypothesis.
Conclusion
There is substantial evidence (p < 0.0001) that at least one of the distributions is different from the others.
To further examine this, we will see if the distribution varies within similar levels of schooling. We will
compare <12 and 12 years of school, 12 and 13-15 years of school, 13-15 and 16 years of school, and 16
and >16 years of school. To do this, we will compare medians, using the following SAS code: This results
Code 21.11. Comparison of distributions using SAS
proc sort data=LogEduData;
by educ;
run;
proc means data = LogEduData median order=data;
by educ;
var LogIncome;
run;
in the following Table:
137

Analysis Guide Midterm
Table 21.1. Comparison of Logged Means
Education µ
<12 9.9
12 10.22
13-15 10.39
16 10.79
>16 10.89
From Table 21.1, we can calculate the differences of the means for our log transformed groups, and see
how much the distributions differ, shown in the following table:
Table 21.2. Comparison of Distributions
Pair Difference Multiplicative Effect (eµ1−µ2) % Increase
<12 and 12 0.32 1.38 38
12 and 13-15 0.17 1.19 19
13-15 and 16 .4 1.49 49
16 and >16 .1 1.11 11
Table 21.2 shows us how many times greater the distribution of the income of the larger education in
each pair is than the lower education level.
Scope of Inference
As this was a random sample, we can make inferences about the population, however, we cannot make
causal inferences, as this was not a randomized experiment. That means, we can say that in general, people
with X years of education make Y many times as people with Z years of education, but we cannot say it is
due to the education itself.
21.3 Extra Values
The extra values were produced with the same code as in Section 28.1. They can be found in Figure 21.2.1,
and in the figure below:
Figure 21.3.1. Extra Values
Value of R2
Figure 21.3.1 tells us R2is 0.0888
Mean Square Error and Degrees of Freedom
The Mean Square Error, shown in Figure 21.2.1, is 2232.12, with 2579 degrees of freedom
ANOVA in R!
Here is the R code and output to do ANOVA in R on the log transformed data:
138

Analysis Guide Midterm
Code 21.12. ANOVA in R
1##################### Anova in R ######################
2edudata <- read.csv(file=’data/ex0525.csv’, header=TRUE , sep = ",")
3edudata$logincome <- log( edudata $Income2005 )
4
5# http://www.sthda.com/english/wiki/one -way -anova -test -in -r
6anovatest <- aov(logincome~Educ ,data =edudata)
7summary(anovatest)
8
9######################### Results #####################
10
11 Df Sum Sq Mean Sq F value Pr(>F)
12 Educ 4 217.7 54.41 62.87 <2e -16 ***
13 Residuals 2579 2232.1 0.87
139

Chapter 22
Problem 2: Build Your Own Anova!
In this section we will be building an ANOVA table to determine whether or not the distribution of income
of people with > 16 years is different than the distribution of income of people with exactly 16 years of
education. To build this ANOVA table, we need two preliminary ANOVA analyses. First, is the ANOVA
analysis seen in Section 21.2. This has the null hypothesis that all the distributions are the same, and
the alternative hypothesis that the distributions differ. Next, we build a second ANOVA table, which will
have a null hypothesis that all the distributions are the same, and an alternative hypothesis that all the
distributions are different, except the group with 16 years and the group with >16 years are still the same.
This is done by grouping the two into one group, with the following SAS code: Next, to compute important
Code 22.1. Regrouping data using SAS
data EduGroupData;
set LogEduData;
Others = educ;
if educ eq "16" educ = ">16" then Others="a";run;
parameters, an ANOVA test is conducted on the grouped, logged, data, with the following bit of code: This
Code 22.2. Secondary ANOVA using SAS
proc glm data = EduGroupData;
class Others;
model LogIncome = Others;
run;
results in the following intermediate ANOVA table:
Figure 22.0.1. Grouped ANOVA Table
22.1 Building the Extra Sum of Squares Anova Table
Using the data from 22.0.1 and the data from 21.2.1, we can make our own ANOVA table, which has
a null hypothesis that all the distributions different and (except 16 and >16, which are the same), and
an alternative hypothesis that all the distributions are different. Since both hypotheses have the same
prediction about the data for <12, 12, and 13-15, the null hypothesis of our custom-made ANOVA table
is that 16 and >16 have the same distribution, and the alternative is that they have different distributions.
We will now construct our new, extra sum of squares ANOVA table.
First, for our full model (the "Error" row in the ANOVA table), we will use the full model (alternative
hypothesis, or the "Error" row), from Figure 21.2.1. This represents our alternative hypothesis, where the
distribution of 16 and >16 are different. Next, we will construct our reduced model (The "Total" row in
the ANOVA table) using the full model (alternative hypothesis, or the "Error") from 22.0.1. This represents
our null hypothesis, where 16 and >16 have the same distribution. To generate our Model, or Extra Sum
of Squares, which will allow us to find our F statistic and p value, we need to take a couple of steps. To
determine the number of degrees of freedom of our model, we subtract the number of degrees of freedom
from the Error row from the number of degrees of freedom of the Total row. To calculate the extra sum of
squares, we subtract the residual sum of squares of the full model (error) from the residual sum of squares
of the reduced model (total). Then, to find the mean square, we divide the extra sum of squares by the
number of degrees of freedom in our model. Our F statistic is then produced by normalizing the Extra Sum
of Squares, dividing it by the Mean Square Error (in the Error row). To get a p value from the F statistic,
140

Analysis Guide Midterm
we examine an F distribution with degrees of freedom = dfmodel
dff ull . The results of these computations are
displayed in the following table:
Table 22.1. Homemade ANOVA Table
Source DF Sum of Squares Mean Square F Value Pr>F
Model (Extra SS) 1 1.98 1.98 2.3 0.129
Error (Full) 2579 2232.12 .86
Total (Reduced) 2580 2234.1
22.2 Complete Analysis
Problem Statement
We would like to determine whether or not people with a college degree or a graduate degree have different
distributions of incomes.
Assumptions
There are three assumptions of ANOVA: normality,homogeneity of variance, and independence. We have
shown, in Section 21.1 that while the raw data does not meet the first two assumptions, the log transformed
data does. Both the transformed and raw data meet the assumption of independence. We will proceed with
our ANOVA test.
Hypothesis Definition
Our null hypothesis states that the distribution of the >16 and 16 groups is the same, and our alternative
hypothesis states that the distribution of the >16 and 16 groups is different. We proved this in Section
22.1, and this is written mathematically as:
H0:median<12 median12 median13−15 median16,>16 median16,>16 (22.2.1)
H1:median<12 median12 median13−15 median16 median>16 (22.2.2)
OR:
H0:median16 =median>16 (22.2.3)
H1:median16 ,median>16 (22.2.4)
We will consider our confidence level, αto be 0.05
F Statistic
The F statistic is calculated with the following equation:
F=SSextra
DFextra
ˆ
σ2
f ull
=SSextra
DFextra
MSE (22.2.5)
The results of this calculation can be seen in Table 22.1, we have that F=2.3This is a small F statistic,
which is likely indicative of weak evidence.
P-value
The P value is calculated using F, the Extra degrees of freedom, and the Full (Error) degrees of freedom.
Using the values calculated in Table 22.1, we have that p=0.129
Hypothesis Assessment
At a confidence level α= 0.05, we have that p=.0129 > α =.05. Therefore, we cannot reject the null
hypothesis.
Conclusion
There is not enough evidence to suggest that the distribution of income of people with a college only (16
years) is different from the distribution of income of people with a postgraduate education (>16 years).
Scope of Inference
It is not necessary to write a scope of inference as we did not reject the null hypothesis, however this is a
random sample, so we can make inferences about the population as whole, but we cannot infer causality,
as this was not a random experiment.
141

Analysis Guide Midterm
22.3 Degrees of Freedom and Comparison to T-Test
This test had 2579 degrees of freedom (as seen in Table 22.1). This is a lot more than than the t test, which
is a lot more than the number of degrees of freedom in the t test. Therefore, this ANOVA test has more
power than the t test!.
142

Chapter 23
Problem 3: Nonhomogeneous Standard
Deviations
23.1 Complete Analysis
Problem Statement
We would like to determine whether or not at least one of the five population distributions (corresponding
to different years of education) is different from the rest.
Assumptions
As seen in Section 21.1, the raw data does not meet the assumption of normality nor of homogeneity of vari-
ance. However, in Section 21.1, we proved that after a log transformation, the data is at least normal. The
ANOVA test is fairly robust to the slight departure from normality presented by the log transformed data,
so we can safely assume normality. However, we cannot assume homogeneity variances. Therefore, pure
ANOVA is not appropriate. Since the data is to some extent normal, we should try and use a parametric
test, as they have more power in general than their nonparametric analogs. Therefore, the Kruskal-Wallis
test is not the most appropriate test. We will instad use Welch’s ANOVA Test, which assumes normality
but does not assume homogeneity of variance, on the log transformed data. We can assume the data is
independent.
Hypothesis Definition
In this problem, our Null (Reduced Model) Hypothesis, H0, is that all the groups have the same distribu-
tion and our Alternative (Full Model) Hypothesis, H1is that the distributions are different. Mathemati-
cally, that is written as:
H0:mediangrand mediangrand mediangrand mediangrand mediangrand (23.1.1)
H1:median<12 median12 median13−15 median16 median>16 (23.1.2)
We will consider our confidence level, αto be 0.05
F Statistic
To conduct this hypothesis test, the following SAS code was used: This results in the following table:
Code 23.1. Welch’s ANOVA in SAS
proc glm data = LogEduData;
class educ;
model LogIncome = educ;
means educ / welch;
run;
Figure 23.1.1. Welch’s ANOVA Table
From Figure 23.1.1, we have that F=56.59. This is a pretty large F statistic, which means that we
probably have some good evidence in favor of the alternative hypothesis.
143

Analysis Guide Midterm
P-value
Figure 23.1.1 Also tells us that the p-value associated with the F statistic, which is given as p<0.0001.
Hypothesis Assessment
We have that p<0.0001 < α =.05 and therefore we Reject the null hypothesis
Conclusion
There is convincing evidence (p < 0.0001) that at least one of the distributions is different from the others.
Scope of Inference
As this was a random sample, we can make inferences about the population, however, we cannot make
causal inferences, as this was not a randomized experiment. That means, we can say that in general, people
with X years of education make Y many times as people with Z years of education, but we cannot say it is
due to the education itself.
144
Chapter 24
unit 5 lecture slides
More slides
145

10/13/2018
1
UNIT 5: Chapter 5
ANOVA
ANOVA
Level i=1 Level i=2 Level i=3
Y
1
|X=i 3 10 20
Y
2
|X=i 5 12 22
Y
3
|X=i 7 14 24
1. Make a Scatterplot of the data in the table below. “Level” is
the Explanatory Variable (X=1, 2, or 3).
2. Find the Grand Mean … this is the mean of
all the Ys together … regardless of Level.
ANOVA
Level i=1 Level i=2 Level i=3
Y
1
|X=i 3 10 20
Y
2
|X=i 5 12 22
Y
3
|X=i 7 14 24
5 12 22
1. Make a Scatterplot of the data in the table below. “Level” is
the Explanatory Variable (X=1, 2, or 3).
2. Find the Grand Mean … this is the mean of
the sample means. If the sample size is the
same in each group, then this is the mean of
all the Ys together … regardless of Level.
Pure ANOVA
Level i=1 Level i=2 Level i=3
Level i=1 Level i=2 Level i=3
4. Now we need to find the Sum of the Squared
Residuals for the Equal Means Model.
6. Compare the Total Sum of Squares for each model. Which do you think “fits” better?
Level i=1 Level i=2 Level i=3
Y
1
|X=i 3 10 20
Y
2
|X=i 5 12 22
Y
3
|X=i 7 14 24
5 12 22
Pure ANOVA
Level i=1 Level i=2 Level i=3
Level i=1 Level i=2 Level i=3
(3-13)
2
= 100 (10-13)
2
= 9 49
(5-13)
2
= 64 1 81
36 1 121
4. Now we need to find the Sum of the Squared
Residuals for the Equal Means Model.
6. Compare the Total Sum of Squares for each model. Which do you think “fits” better?
Level i=1 Level i=2 Level i=3
Y
1
|X=i 3 10 20
Y
2
|X=i 5 12 22
Y
3
|X=i 7 14 24
5 12 22
Pure ANOVA
Level i=1 Level i=2 Level i=3
(3-5)
2
= 4 (10-12)
2
= 4 (20-22)
2
= 4
0 0 0
4 4 4
Level i=1 Level i=2 Level i=3
(3-13)
2
= 100 9 49
64 1 81
36 1 121
4. Now we need to find the Sum of the Squared
Residuals for the Equal Means Model.
6. Compare the Total Sum of Squares for each model. Which do you think “fits” better?
Level i=1 Level i=2 Level i=3
Y
1
|X=i 3 10 20
Y
2
|X=i 5 12 22
Y
3
|X=i 7 14 24
5 12 22

10/13/2018
2
Sum of Squares in ANOVA
*To compute the sum of squares column
for the ANOVA table, square each
distance (lines in black) and then add.
The sum of squared* distances (black
lines) for left two graphs = the sum of
squared distances (black lines) for the
right graph.
*Each distance squared for the top left graph is multiplied by
the number in each group.
Within group variation (middle row)
Between group variation (top row) Total variation (bottom row)
Pure ANOVA
df SS MS F Pr > F
Model / Extra SS
Error / Residual/Full Model
Total (Reduced)
7. Now we would like to make an ANOVA table to test the alternative hypothesis!
Extra Sum of Squares = Residual Sum of Squares Reduced – Residual Sum of Squares Full
Formally write the H
o
and H
a
and fill in the table.
Level
i=1 Level
i=2 Level
i=3
Y
1
|X=i 3 10 20
Y
2
|X=i 5 12 22
Y
3
|X=i 7 14 24
Pure ANOVA
df SS MS F Pr > F
Model / Extra SS
Error / Residual/Full Model 6 24 4
Total (Reduced) 8 462
7. Now we would like to make an ANOVA table to test the alternative hypothesis!
Extra Sum of Squares = Residual Sum of Squares Reduced – Residual Sum of Squares Full
Formally write the Ho and Ha and fill in the table.
H
o
: µ
1
= µ
2
= µ
3
(Equal Means Model µ µ µ)
H
a
: At least 1 pair are different (Separate Means Model µ
1
µ
2
µ
3
)
Pure ANOVA
df SS MS F Pr > F
Model / Extra SS 8-6=2 462-24=438
Error / Residual/Full Model 6 24 4
Total (Reduced) 8 462
7. Now we would like to make an ANOVA table to test the alternative hypothesis!
Extra Sum of Squares = Residual Sum of Squares Reduced – Residual Sum of Squares Full
Formally write the Ho and Ha and fill in the table.
H
o
: µ
1
= µ
2
= µ
3
(Equal Means Model µ µ µ)
H
a
: At least 1 pair are different (Separate Means Model µ
1
µ
2
µ
3
)
Pure ANOVA
df SS MS F Pr > F
Model / Extra SS 2 438 438/2=219
Error / Residual/Full Model 6 24 4
Total (Reduced) 8 462
7. Now we would like to make an ANOVA table to test the alternative hypothesis!
Extra Sum of Squares = Residual Sum of Squares Reduced – Residual Sum of Squares Full
Formally write the Ho and Ha and fill in the table.
H
o
: µ
1
= µ
2
= µ
3
(Equal Means Model µ µ µ)
H
a
: At least 1 pair are different (Separate Means Model µ
1
µ
2
µ
3
)
Pure ANOVA
df SS MS F Pr > F
Model / Extra SS 2 438 219 219/4=54.75
Error / Residual/Full Model 6 24 4
Total (Reduced) 8 462
7. Now we would like to make an ANOVA table to test the alternative hypothesis!
Extra Sum of Squares = Residual Sum of Squares Reduced – Residual Sum of Squares Full
Formally write the Ho and Ha and fill in the table.
H
o
: µ
1
= µ
2
= µ
3
(Equal Means Model µ µ µ)
H
a
: At least 1 pair are different (Separate Means Model µ
1
µ
2
µ
3
)

10/13/2018
3
Pure ANOVA
df SS MS F Pr > F
Model / Extra SS 2 438 219 54.75 .0001
Error / Residual/Full Model 6 24 4
Total (Reduced) 8 462
7. Now we would like to make an ANOVA table to test the alternative hypothesis!
Extra Sum of Squares = Residual Sum of Squares Reduced – Residual Sum of Squares Full
Formally write the H
o
and H
a
and fill in the table.
H
o
: µ
1
= µ
2
= µ
3
(Equal Means Model µ µ µ)
H
a
: At least 1 pair are different (Separate Means Model µ
1
µ
2
µ
3
)
F -Test of Different Means …
H
o
: µ
1
= µ
2
= µ
3
(Equal Means Model)
H
a
: At least 1 pair are different (Separate Means Model)
6 Steps for ANOVA F Test (diff means)!
H
o
: µ
1
= µ
2
= µ
3
(Equal Means Model)
H
a
: At least 1 pair are different (Separate Means Model)
1.
2.
3.
4.
5.
6.
Critical value: You can skip this step for ANOVA.
F statistic = 54.75
P-value = .0001
Reject Ho.
The evidence suggests that at least 1 pair
of the group means are different. (P-value
< .0001 from an ANOVA.)
F-Distribution
R-Squared!
R =correlation coefficient
R
2
= coefficient of determination
Coefficient of Variation

10/13/2018
4
ANOVA: Assumptions and Robustness
1. Normality: Similar to t-tools hypothesis testing,
ANOVA is robust to this assumption. Extremely long-
tailed distributions (outliers) or skewed distributions,
coupled with different sample sizes (especially when
the sample sizes are small) present the only serious
distributional problems.
2. Equal Standard Deviations: This assumption is crucial,
paramount, and VERY important.
3. The assumptions of independence within and across
groups are critical. If lacking, different analysis should
be attempted.
Samples drawn from
Normal Distributions
•Same visual checks as with t-tools, just for
more groups.
–Histograms
–Q-Q plots
More on Constant SD
95% confidence interval accuracy with different sample
sizes and standard deviations for three groups.
Levene’s Test (Median)
But … proc ttest does not have Levene’s Test!!!
Ho: σ1= σ2
Ha: σ1≠ σ2
Proc GLM Has Levene’s Test Check of Assumptions: Constant SD
There is some visual evidence against
equal standard deviations. The Brown-
Forsythe test was used as secondary
evidence and does not provide
significant evidence against equal
standard deviations. (p-value = .2558)

10/13/2018
5
Archeology in New Mexico
An archeological dig in New Mexico yielded four
sites with lots of artifacts. The depth (cm) that each
artifact was found was recorded along with which
site it was found in.
The researcher has reason to believe that sites 1
and 4 and sites 2 and 3 may be similar in age. In
theory, the deeper the find, the older the village.
Is there any evidence that sites 1 and 4 have a
mean depth that is different than the mean depth
of artifacts from sites 2 and 3?
Archaeology Example
Depth Site Depth Site Depth Site Depth Site
93 1 85 2 100 3 96 4
120 1 45 2 75 3 58 4
65 1 80 2 65 3 95 4
105 1 28 2 40 3 90 4
115 1 75 2 73 3 65 4
82 1 70 2 65 3 80 4
99 1 65 2 50 3 85 4
87 1 55 2 30 3 95 4
100 1 50 2 45 3 82 4
90 1 40 2 50 3
78 1 45 3
95 1 55 3
93 1
88 1
110 1
Archeology Example
Assumptions: Normality
Histograms will be helpful as well!
Archeology Example
Assumptions: Homogeneity (Equal SD)
Archeology Example
Assumption: Independence
The discovered artifacts associated with the
depths were randomly selected from the log
(book of recordings … not logarithms!) of
discoveries.
Since the artifacts and, thus, the depths are
associated with completely different sites, it is
assumed that the data are independent
between sites.
Question of Interest:
1. Are any of the means different?
2. Are the means of sites 1 and 4 different?
3. Are the means of sites 2 and 3 different?
4. Satisfactory results of questions 1 and 2 will allow us to ask
the third question: are sites 1 and 4 different than 2 and 3?

10/13/2018
6
Are sites 1 and 4 different from 2 and 3?
*Assumes ANOVA assumptions are met
Perform regular ANOVA to
test if any of the means are
different from the rest.
Reduced Model Ho: µ µ µ µ
Full Model Ha: µ1µ2 µ3µ4
BYO ANOVA to test if the
means of 1 and 4 are different,
given at least one pair is
different.
Reduced Model Ho: µ0µ2 µ3µ0
Full Model Ha: µ1µ2 µ3µ4
Reject Hoin
favor of Ha:
µ1µ2 µ3µ4?
Reject Hoin
favor of Ha:
µ1µ2 µ3µ4?
Stop:
Insufficient
evidence
that any
means are
different
Stop:
Groups 1
and 4 are
different
and should
not be
treated as
having the
same
means, as
the QoI
suggests.
BYO ANOVA to test if the
means of 2 and 3 are different,
given at least one pair is
different.
Reduced Model Ho: µ1µ0 µ0µ4
Full Model Ha: µ1µ2 µ3µ4
Reject Hoin
favor of Ha:
µ1µ2 µ3µ4?
Stop:
Groups 2
and 3 are
different
and should
not be
treated as
having the
same
means, as
the QoI
suggests.
Perform ANOVA to test if the means of 1 and 4,
when taken together are different than means
2 and 3, when also taken together.
Reduced Model Ho: µ µ µ µ
Full Model Ha: µaµb µbµa
Reject Hoin
favor of Ha:
µaµb µbµa?
Stop:
Evidence
does NOT
support the
claim in QoI
Stop:
Evidence
does
support the
claim in QoI
yes
yes
yes
yes
no
no
no
no
First Ask: Is there reason to believe any
of them are different?
(H
a
) Full Model: µ
1
µ
2
µ
3
µ
4
(H
o
) Reduced Model: µ µµ µ
There is evidence to suggest that at the alpha = .05 level of significance (p-
value < .0001) that at least 2 of the sites have different mean depths.
The reduced and
full models are
associated with
H
o
and H
a
,
respectively,
although they
are not exactly
equal to the
hypotheses.
Question of Interest:
2. Are the means of sites 1 and 4 different?
(H
a
) Full Model: µ
1
µ
2
µ
3
µ
4
(H
o
) Reduced Model: µ
o
µ
2
µ
3
µ
o
(H
o
) Reduced: µ µµ µ
(H
a
) Full: µ
1
µ
2
µ
3
µ
4
(H
a
) Full*: µ
o
µ
2
µ
3
µ
o
(H
o
) Reduced: µ µµ µ
Source DF SS MS F Pr>F
Model (Full) 1 780.3 780.3 2.86 .098
Error (From Full) 42 11464.6 273.0
Total (From Reduced*) 43 12244.9
There is not enough
evidence to suggest
(alpha = .05, p-value =
.098) that site 1 and
site 4 have different
mean depths.
*Recode the
variables into
three groups: 2,
3, and 1/4
combined and
perform ANOVA
to get the first
table.
Compare this model
against equal means
model (µ µ µ µ)
Compare this model
against equal means
model (µ µ µ µ)
Question of Interest: (try it!)
3. Are the means of sites 2 and 3 different?
µ
1
µ
o
µ
o
µ
4
µ
1
µ
2
µ
3
µ
4
µ µ µ µ
µ
1
µ
o
µ
o
µ
4
Source DF SS MS F Pr>F
Model (Full)
Error (From Full)
Total (From Reduced*)
*Recode the
variables into
three groups: 1,
4, and 2/3
combined and
perform ANOVA
to get the first
table.
(H
o
) Reduced Model:
(H
a
) Full Model:
(H
o
) Reduced:
(H
a
) Full*:
(H
o
) Reduced:
(H
a
) Full:
µ µ µ µ
µ
1
µ
2
µ
3
µ
4
Question of Interest: (try it!)
3. Are the means of sites 2 and 3 different?
µ
1
µ
o
µ
o
µ
4
µ
1
µ
2
µ
3
µ
4
µ µ µ µ
µ
1
µ
o
µ
o
µ
4
Source DF SS MS F Pr>F
Model (Full)
Error (From Full) 42 11464.6 273
Total (From Reduced) 43 11477.7
*Recode the
variables into
three groups:
1, 4, and 2/3
combined and
perform
ANOVA to get
the first table.
(H
o
) Reduced Model:
(H
a
)Full Model:
(H
o
) Reduced:
(H
a
) Full*:
(H
o
) Reduced:
(H
a
) Full:
µ µ µ µ
µ
1
µ
2
µ
3
µ
4
Question of Interest: (try it!)
3. Are the means of sites 2 and 3 different?
µ
1
µ
o
µ
o
µ
4
µ
1
µ
2
µ
3
µ
4
µ µ µ µ
µ
1
µ
o
µ
o
µ
4
Source DF SS MS F Pr>F
Model (Full) 1 13.1 13.1 .048 .828
Error (From Full) 42 11464.6 273
Total (From Reduced) 43 11477.7
There is not enough
evidence to suggest
(alpha = .05, p-value =
.828) that site 2 and site
3 have different mean
depths.
*Recode the
variables into
three groups:
1, 4, and 2/3
combined and
perform
ANOVA to get
the first table.
(H
o
) Reduced Model:
(H
a
) Full Model:
(H
o
) Reduced:
(H
a
) Full*:
(H
o
) Reduced:
(H
a
) Full:
µ µ µ µ
µ
1
µ
2
µ
3
µ
4

10/13/2018
7
Question of Interest:
4. Are sites 1 and 4 different than 2 and 3?
(H
o
) Reduced: µ µ µ µ
(H
a
) Full: µ
b
µ
a
µ
a
µ
b
There is sufficient evidence to suggest (alpha = .05,
p-value < .0001) that sites 1 and 4 have different
mean depths than sites 2 and 3.
*Recode the
variables into two
groups 1/4 and 2/3
and perform ANOVA
to get the table.
A Small Example
Normality Assumption
There is strong evidence against these data
coming from a normal distribution and the
sample size is small. ANOVA? WELCH’S ANOVA?
Homogeneity of Variance Assumption
There is some (weak) evidence in
support of these data coming from
distributions with different standard
deviations. If the standard deviation
assumption and normality
assumption are both violated, what
should we do?
So …. NONPARAMETRIC!!!! Kruskal-Wallis Test
There is not sufficient evidence at the alpha = .05 level of significance (p-value =
.3766 from Kruskal-Wallis Test) to suggest that at least two of the medians are
different.
Notice that each test failed to reject their respective H
o
. The point isn’t so much
that one test will reject when the other will fail to reject. We must remember
that as statisticians, we don’t personally favor one outcome over the other. We
just want the appropriate test: the one with the most power. Kruskal-Wallis Test is
the appropriate test here.

10/13/2018
8
Another Analysis!!!!
…
Normality Assumption
There is strong evidence in
favor of these data coming
from a normal distribution.
We will proceed under this
assumption.
Assumptions and Analysis:
There is sufficient evidence at the alpha = .05 level of
significance (p-value = .0201 from Welch’s ANOVA) to
suggest that at least two of the means are different.
However, remember caveat to any different SD’s
approach.
There is strong evidence in support of these data
coming from distributions with different standard
deviations. We will proceed under this
assumption and run the Welch’s ANOVA.
Regular ANOVA:
Fixed Effects vs. Random Effects
Quick answer:
•Do your groupings exhaust the data (e.g., data on
four different machines and there are only four
machines)? Fixed Effects! Use Proc GLM in SAS.
•Are your groupings a random sample of a larger
population that could have been chosen to be a
group (e.g., data on four different machines that
were chosen from a random sample of 100
machines)? Random Effects! Use Proc Mixed in
SAS.
Fixed or random effects
Fixed Effects
Scenario 1: There is only one machine of each type.
Scenario 2: There are several of each type of machine.
The Coke samples all came from the same Coke
bottling machine, and the Diet Coke samples all came
from the same Diet Coke machine.
Random effects
Measured the amount of liquid in twenty randomly selected cans of
Coke and twenty randomly selected cans of Diet Coke at a regional
bottling company. Coke and Diet Coke are bottled using different types
of machines.
APPENDIX

10/13/2018
9
MSE vs. Variance in each group
Examples
Another example!
5 different sports were analyzed to see if the average height of basketball
players was greater than the average of all the other sports. We could, of
course, compare each pairwise grouping of sports, but that would result in
4 tests. This would take a lot of time, and those tests would each have less
power since they don’t use all the data. Let’s use ANOVA similarly to how
we did in prior problems.
1. Make a side by side box plot of the data.
2. Run a basic ANOVA to test for any pairwise difference of means.
Check the assumptions here, but no need to address them after this.
3. Test the model that keeps basketball by itself but groups the other
sports as “others.”
4. Use the previous two models to conduct an extra sum of squares F-
Test:
5. Depending on the results of this test, test to see if there is evidence
that basketball has a different mean than each of the sports.
(Equivalent to testing basketball versus the others.)
6. Make sure and provide written conclusions for questions 2,3,4 and 5.
H
o
: Reduced Model: µ
B
µ
O
µ
O
µ
O
µ
O
H
a
: Full Model: µ
B
µ
F
µ
Soc
µ
Swim
µ
T
H
o
: Reduced Model: µ
O
µ
O
µ
O
µ
O
µ
O
H
a
: Full Model: µ
B
µ
O
µ
O
µ
O
µ
O

10/13/2018
10
First … Plot the Data! Plot the Data cont.
Normality: We have very small sample sizes here. There is not a lot of evidence against
normality for each group, although there is not a lot of evidence to begin with. We will
proceed with caution under the assumption of normal distributions for each sport.
Homogeneity of Variance: Judging from the box plots, there is some visual evidence
against equal standard deviations, although the sample size is still small. A secondary
test would be nice to lean on here.
We will assume the observations are independent both between and within groups.
Brown and Forsythe Test for Equality
of Variance.
There is some visual evidence against equal standard deviations between
sports. The Brown and Forsythe test was used as secondary evidence and
does not provide significant evidence against equal standard deviations. (p-
value = .9672)
1 Way ANOVA
H
o
: µ
Basketball
= µ
Football
= µ
Soccer
= µ
Swim
= µ
Tennis
H
a
: At least one pair of means is different.
There is strong evidence to suggest that the at least one of the sports has a mean height
that is different than the others (p-value < .0001 from an ANOVA).
F-TEST
Fail to Reject Ho
There is not sufficient evidence at
the alpha = .05 level of significance
(p-value = 0.5375) to suggest that
the mean heights of non-basketball
sports are not equal. Therefore we
will proceed as if they are equal.
H
o
: µ
Basketball
= µ
Football
= µ
Soccer
= µ
Swim
= µ
Tennis
H
a
: At least one pair of means are different.
H
o
: µ
Basketball
= µ
Football
= µ
Soccer
= µ
Swim
= µ
Tennis
H
a
: µ
Basketball
is different than the Others.
H
o
: The Others are equal. (Including Basketball)
H
a
: The Others are different (Including Basketball)
F-TEST
Fail to Reject Ho
There is not sufficient evidence at
the alpha = .05 level of significance
(p-value = 0.5375) to suggest that
the mean heights of non-basketball
sports are not equal. Therefore we
will proceed as if they are equal.
H
o
: Reduced Model: µ µ µ µ µ
H
a
: Full Model: µ
B
µ
F
µ
Soc
µ
Swim
µ
T
H
o
: Reduced Model: µ µ µ µ µ
H
a
: Full Model: µ
B
µ
O
µ
O
µ
O
µ
O
H
o
: Reduced Model: µ
B
µ
O
µ
O
µ
O
µ
O
H
a
: Full Model: µ
B
µ
F
µ
Soc
µ
Swim
µ
T
Same Test as last slide ….
Different Notation

10/13/2018
11
F-TEST: Another Look
Source DF SS MS F Pr > F
Model 3 11.63 3.87 .74 0.5375
Error 27 141.56 5.24
Corrected Total 30 153.19
µ
B
µ
O
µ
O
µ
O
µ
O
H
o
: Reduced Model: µ
B
µ
O
µ
O
µ
O
µ
O
H
a
: Full Model: µ
B
µ
F
µ
Soc
µ
Swim
µ
T
µ
B
µ
F
µ
Soc
µ
Swim
µ
TSince we are proceeding under the assumption
that the mean heights of the other sports
(besides basketball) are equal, we can test
whether basketball has a mean height different
than the other sports by testing:
There is strong evidence at the
alpha = .05 level of significance (p-
value < .0001) that supports the
claim that the mean height of
basketball players is different than
that of the other 4 sports.
H
o
: µ
Basketball
= µ
Others
H
a
: µ
Basketball
≠ µ
Others
Resources
www.itl.nist.gov/div898/handbook/prc/section4/prc433.htm
Spock Example
Spock Trial
•1968: Dr. Ben Spock was accused of conspiracy to violate the
Selective Service Act by encouraging young men to resist being
drafted into military service for Vietnam.
•Jury Selection: A “venire” of 30 potential jurors is selected at
random from a list of 300 names that were previously selected at
random from citizens of Boston.
•A jury is then selected NOT at random by the attorneys trying the
case.
•For this case, the venire consisted of only one woman, who was let
go by the prosecution, thus resulting in an all male jury.
•There was reason to believe that women were more sympathetic to
Dr. Spock’s actions due to his popular child rearing books.
•The defense argued that the judge in this case had a history of
venires that underrepresented women, which is contrary to the law.
•Let’s see if there is any evidence for this claim!
The Raw Data

10/13/2018
12
Comparing Two Means
From Many Groups.
Judge N Xbar Sd
Spock 9 14.6 5.04
A 5 34.1 11.94
B 6 33.6 6.58
C 9 29.1 4.59
D 2 27.0 3.81
E 6 27.0 9.01
F 9 26.8 5.97
H
o
: µ
S
= µ
F
H
a
: µ
S
≠ µ
F
s
p
= 6.91
With 2 groups estimating the
pooled SD.
With all 7 groups estimating the pooled SD, bigger ‘n’ greater df! More POWER!!!
P-value = .0006
Spock Data Steps
Question: Suppose we wish to test
if the “S” judge’s venires are
different from the “F” judge’s.
Two Judge Analysis w/
t-Tools
Statistical Conclusion: We find
that there is substantial
evidence that the difference in
the mean percentage of
females on judge S and judge
F venires is not equal to zero.
Estimated Diff = -12.1778
S
p
= 5.5234
Pooled Std. Error = 2.6038
t-Statistic = -4.68
Deg. of freedom = 16
Two Judge Analysis w/
Several-Groups
From PROC TTEST:
Estimated Diff = -12.1778
S
p
= 5.5234
Pooled Std. Error = 2.6038
t-Statistic = -4.68
Deg. of freedom = 16
Deg. of freedom = 46 – 7 = 39
Two Judge Analysis:
Conclusion
Question: Suppose we wish to test
if the “S” judge’s venires are
different from the “F” judge’s.
Answer: There is evidence that
the mean of the two groups is
different.
Spock Trial QOI 2
•QOI2: Is the percent of women on recent venires of Spock’s judge
(which we will call S) significantly lower than those of 6 other judges
(which we notate A to F)?
•There are two key questions:
1. Is there evidence that women are underrepresented on S’s venires relative to
A to F’s?
2. Is there evidence of a difference in women’s representation on A to F’s
venires?
•The question of interest is addressed by 1
•The strength of the result in 1 would be substantially diminished if 2 is true
The defense argued that the judge in this case had a history of venires that
underrepresented women, which is contrary to the law.

10/13/2018
13
Spock: The Strategy Step 1: Compare Judges A - F
H
o
: All “other” means are equal (A, B, C, D, E, F)
H
a
: At least 2 “other” means are different (A, B, C, D, E, F)
Full Model: µ
s
µ
A
µ
B
µ
C
µ
D
µ
E
µ
F
Reduced Model: µ
s
µ
o
µ
o
µ
o
µ
o
µ
o
µ
o
But … Let’s use all the data to estimate the pooled standard deviation!
Different Models in SAS
At Least 2 are different (S, A, B, … F)
Spock is different than the Others
µsµo µoµoµoµoµo
µsµA µBµCµDµEµF
Different Models in SAS
At Least 2 are different (S, A, B, … F)
Spock is different than the Others
µsµo µoµoµoµoµo
µsµA µBµCµDµEµF
Comparing Two Models:
Both are not Equal Means Model
Source DF SS MS F Pr > F
Model
Error
Corrected Total
Equal Means
Model
SAS (proc glm) compares models to the equal means model. When you run proc glm,
it always makes the “Corrected Total Row” the equal means model. However, we can
build our own ANOVA table (BYOA) to compare two models, both of which are not
the equal means model.
To do this we will need to identify the “full” model and the “reduced” model. The
“full” model will be the model with the most parameters (means) in it while the
“reduced model” will have fewer parameters. (Note that the equal means model
(with one parameter) is the most reduced model you can have.)
Separate
Means Model
(Reduced Model)
(Full Model)
Extra Sum of Squares
Test / BYOA
F-TEST: Another Look
H
a
: At least 2 are different (A,B,C …F)
H
o
: µ
A
, µ
B
, µ
C
…. µ
F
are Equal
Source DF SS MS F Pr > F
Model 5 326.5 65.29 1.37 0.26
Error 39 1864.4 47.81
Corrected Total 44 2190.9
Spock is different than othersAt least 2 are different (Spock, A, B, C … F)
µ
s
µ
A
µ
B
µ
C
µ
D
µ
E
µ
F
µ
s
µ
o
µ
o
µ
o
µ
o
µ
o
µ
o
Reduced : µ
s
µ
o
µ
o
µ
o
µ
o
µ
o
µ
o
Full: µ
s
µ
A
µ
B
µ
C
µ
D
µ
E
µ
F
Reduced
Full

10/13/2018
14
F-TEST
H
a
: At least 2 are different (A,B, .. F)
H
o
: µ
A
– µ
F
are Equal
Fail to Reject Ho
There is not sufficient evidence
at the alpha = .05 level of
significance (p-value = 0.26) to
suggest that the means are not
equal. Therefore, we will
proceed as if they are equal.
H
o
: All means are equal (Spock,A,B,C…,F)
H
a
: At least 2 are different (Spock,A,B,….F)
Ho: Spock is equal to Others
Ha: Spock is diff from Others
EXTRA SUMS OF SQUARES F TEST
Step 1 Complete!
F-TEST: Another Look
H
a
: At least 2 are different (A,B,C …F)
H
o
: µ
A
, µ
B
, µ
C
…. µ
F
are Equal
Source DF SS MS F Pr > F
Model 5 326.5 65.29 1.37 0.26
Error 39 1864.4 47.81
Corrected Total 44 2190.9
There is not sufficient evidence to suggest that the mean percent of women on judge’s A-F
venires are different from one another (p-value = .26 from an ANOVA). Therefore, we will
now move on to Step 2 and compare Spock’s judge’s mean to the single mean that will
represent the other judges.
Since we are proceeding under the assumption that the mean percentage of women
in venires of the non-Spock judges are equal, we can test whether the Spock judge has
a mean percentage different than the other judges by testing:
Ha: Mean of Spock is different than the mean others.
Ho: Mean of Spock is equal to the mean of the others.
Step 2!
There is strong evidence at the alpha = .05 level
of significance (p-value < .0001 from an ANOVA)
to support the claim that the mean percentage of
women in the Spock judge’s venires is less than
that of the other 6 judges and that there is no
evidence that the other 6 judges have different
mean percentages of women on their venires (p-
value = .26 from an Extra Sum of Squares F Test).
Spock’s lawyer has evidence for a mistrial.
Part VI
Multiple comparisons and post hoc tests
160

Chapter 25
Problem 1: Bonferroni and the Handicap
Study
The Bonferroni method was used to construct some simultaneous confidence intervals for µ1−µ2,µ2−µ5
and µ3−µ5, to see whether there are differences in attitude toward the mobility type of handicaps. The
Bonferroni CIs were calculated using the following SAS code: Note that lsmeans and means have the same
Code 25.1. Bonferroni in SAS
proc glm data = handicap;
class handicap;
model score = handicap;
means handicap / hovtest = bf bon cldiff;
lsmeans handicap / pdiff adjust = bon cl;
run;
results, because we are dealing with balanced data The result of this code is shown below:
Figure 25.0.1. Bonferroni Confidence Intervals
Another nice way to visualize these confidence intervals is like this:
161

Analysis Guide Midterm
Figure 25.0.2. Diffogram of the Bonferroni Confidence Intervals
As we see from these two figures, the only statistically significant mean difference was the crutches vs
the hearing, which means that the attitude towards the different mobility handicaps is the same (µ1−µ2,
µ2−µ5and µ3−µ5are not different)
162

Chapter 26
Multiple Comparison and the Handicap
Study
To generate all the multiple comparisons, and the half widths, the follwoing SAS code was used: Here we
Code 26.1. all the multiple comparisons in SAS
proc glm data = handicap;
class handicap;
model score = handicap;
means handicap / tukey bon scheffe LSD Dunnett(’None’);
run;
see the results of this
(a) Bonferroni
(b) Tukey (c) Dunnet
(d) Scheffe(e) LSD
Figure 26.0.1. Half widths of different post hoc analyses in SAS
163

Analysis Guide Midterm
We did the same thing in R, with code and output shown below:
164

Analysis Guide Midterm
Code 26.2. Multiple comparisons with R
1prob2 <- case0601
2# we make none the first group so that dunnetts test behaves
3prob2$Handicap<-factor(prob2$Handicap,levels=c(’None’,’Amputee ’,’Crutches’,
’Hearing’,’Wheelchair ’))
4aovmodel <- aov(Score ~Handicap, data=Handi)
5# Now we can begin our tests
6# Tukey ’s test
7tukey <- glht(aovmodel ,linfct=mcp(Handicap="Tukey"))
8confint(tukey) #Tukey
9
10
11
12 Simultaneous Confidence Intervals
13
14 Multiple Comparisons of Means: Tukey Contrasts
15
16
17 Fit: aov(formula = Score ~Handicap, data = Handi)
18
19 Quantile = 2.8066
20 95% family -wise confidence level
21
22
23 Linear Hypotheses:
24 Estimate lwr upr
25 Amputee - None == 0 -0.4714 -2.2037 1.2608
26 Crutches - None == 0 1.0214 -0.7108 2.7537
27 Hearing - None == 0 -0.8500 -2.5822 0.8822
28 Wheelchair - None == 0 0.4429 -1.2894 2.1751
29 Crutches - Amputee == 0 1.4929 -0.2394 3.2251
30 Hearing - Amputee == 0 -0.3786 -2.1108 1.3537
31 Wheelchair - Amputee == 0 0.9143 -0.8179 2.6465
32 Hearing - Crutches == 0 -1.8714 -3.6037 -0.1392
33 Wheelchair - Crutches == 0 -0.5786 -2.3108 1.1537
34 Wheelchair - Hearing == 0 1.2929 -0.4394 3.0251
35
36 # Calculated by hand
37 half width = 1.73225
38
39 # bonferroni ##
40 confint(tukey , test=adjusted(type="bonferroni")) # bonferroni , we can just
apply the bonferroni to whatever
41 # according to the documentation
42
43 Simultaneous Confidence Intervals
44
45 Multiple Comparisons of Means: Tukey Contrasts
46
47
48 Fit: aov(formula = Score ~Handicap, data = Handi)
49
50 Quantile = 2.8057
51 95% family -wise confidence level
52
53
54 Linear Hypotheses:
55 Estimate lwr upr
56 Amputee - None == 0 -0.4714 -2.2031 1.2602
57 Crutches - None == 0 1.0214 -0.7102 2.7531
58 Hearing - None == 0 -0.8500 -2.5817 0.8817
59 Wheelchair - None == 0 0.4429 -1.2888 2.1745
60 Crutches - Amputee == 0 1.4929 -0.2388 3.2245
61 Hearing - Amputee == 0 -0.3786 -2.1102 1.3531
62 Wheelchair - Amputee == 0 0.9143 -0.8174 2.6459
63 Hearing - Crutches == 0 -1.8714 -3.6031 -0.1398
64 Wheelchair - Crutches == 0 -0.5786 -2.3102 1.1531
65 Wheelchair - Hearing == 0 1.2929 -0.4388 3.0245
66
67 # Calculated by hand
68 half width = 1.73165
69
70 ## LSD #
71 LSD <- LSD.test(aov(lm(Score ~Handicap, data=ppp)), "Handicap")# LSD
72 LSD$statistics$LSD # LSD Half int
73
74
75 [1] 1.232618
76
77 # Dunnett
78 dunnett <- glht(aovmodel ,linfct=mcp(Handicap="Dunnett"))
79 confint(dunnett) #Dunnett
80
81
82
83 Simultaneous Confidence Intervals
84
85 Multiple Comparisons of Means: Dunnett Contrasts
86
87
88 Fit: aov(formula = Score ~Handicap, data = Handi)
89
90 Quantile = 2.5037
91 95% family -wise confidence level
92
93
94 Linear Hypotheses:
95 Estimate lwr upr
96 Amputee - None == 0 -0.4714 -2.0167 1.0738
97 Crutches - None == 0 1.0214 -0.5238 2.5667
98 Hearing - None == 0 -0.8500 -2.3953 0.6953
99 Wheelchair - None == 0 0.4429 -1.1024 1.9881
100
101 # Calculated by hand
102 half width = 1.54525
103
104 # Scheffe
105 scheffe <- scheffe.test(aov(lm(Score ~Handicap, data=ppp)), "Handicap")
106 scheffe$statistics$CriticalDifference # scheffe
107
108
109 [1] 1.956817
165

Chapter 27
Comparing groups: Education study
27.1 Assumptions
Raw Data Analysis
First, we will look at the raw data. To check if the raw data fits the assumptions, we will first look at a
scatter plot. The scatter plot of the raw data was produced by the following bit of SAS code:
proc sgplot data=EduData;
scatter x=educ y=Income2005;
run;
This results in the following plot:
Figure 27.1.1. Scatter Plot of the Raw Data
Looking at Figure 27.1.1, we see that the raw data is very heavy in between 0 and 20,000 for all cat-
egories, but some groups spread further and wider than others, which suggests the variances may not be
equal. The heaviness of the lower end of each group may also suggest a lack of normality. We will examine
this further with some Box plots. These were produced using the following chunk of SAS code:
proc sgplot data=EduData;
vbox Income2005 / category=educ
dataskin=matte
;
xaxis display=(noline noticks);
yaxis display=(noline noticks) grid;
run;
This results in the following plot:
166

Analysis Guide Midterm
Figure 27.1.2. Box Plot of the Raw Data
Figure 27.1.2 tells us a lot about our data. We see from the size and shape of the boxes that the variances
of our data are by no means homogeneous. Note that there are a lot of outliers while the distribution is
heavily weighted towards the bottom, this suggests our data may have departed from normality. We will
examine this phenomenaa further using histograms. To produce histograms of the raw data, the following
SAS code was used:
proc sgpanel data=EduData;
panelby educ / rows=5 layout=rowlattice;
histogram Income2005;
run;
This results in the following plot:
Figure 27.1.3. Histogram of the Raw Data
Figure 27.1.3 confirms our suspicions, the variances of the data are likely unequal, but more impor-
tantly, the data is clearly skewed to the right. We will confirm this using Q-Q plots. To produce Q-Q plots
of the raw data, the following SAS code was used:
/*Normal = blom produces normal quantiles from the data */
/*To find out more, look at the SAS documentation!*/
167

Analysis Guide Midterm
proc rank data=EduData normal=blom out=EduQuant;
var Income2005;
/*Here we produce the normal quantiles!*/
ranks Edu_Quant;
run;
proc sgpanel data=EduQuant;
panelby educ;
scatter x=Edu_Quant y=Income2005 ;
colaxis label="Normal Quantiles";
run;
This results in the following plot:
Figure 27.1.4. Q-Q Plot of the Raw Data
The Q-Q plots in Figure 27.1.4 tell us what we already know: The raw data is not normal, and does
not have equal variances. The ANOVA test is not super robust to highly skewed, long tailed data, and it
relies entirely on equal variances, so we absolutely cannot use the raw data
Transformed Data Analysis
Now we will perform a log transformation on the data and see if that helps it meet our assumptions better.
To do a log transformation, we will employ the following SAS code:
data LogEduData;
set EduData;
LogIncome=log(Income2005);
run;
We will begin our analysis of the transformed data with a scatter plot, produced with the following SAS
code:
proc sgplot data=LogEduData;
scatter x=educ y=LogIncome;
run;
This results in the following plot:
168

Analysis Guide Midterm
Figure 27.1.5. Scatter Plot of the Log-Transformed Data
As we can see in Figure 27.1.5, the groups have a much more similar size, suggesting similar variances,
and the heavy part of the scatter plot is closer to the center, in between the outliers, which tells us the log
transformation may have done a good deal towards normalizing our data. We can examine this further
using Box plots. To produce Box plots of the transformed data, the following SAS code was used:
proc sgplot data=LogEduData;
vbox LogIncome / category=educ
dataskin=matte
;
xaxis display=(noline noticks);
yaxis display=(noline noticks ) grid;
run;
This gives us the following plot:
Figure 27.1.6. Box Plot of the Log-Transformed Data
Figure 27.1.6 gives us some useful information about our data. We see the boxes and whiskers are of
similar size, which tells us the variances are likely homogeneous. Furthermore, the medians and means
are near each other, and the boxes are near the center of the distribution, which suggests that the data may
be normal. We will examine these two phenomena further with histograms. To produce histograms of the
log-transformed data, the following SAS code was used:
proc sgpanel data=LogEduData;
169

Analysis Guide Midterm
panelby educ / rows=5 layout=rowlattice;
histogram LogIncome;
run;
This results in the following plot:
Figure 27.1.7. Histogram of the Log-Transformed Data
From the spread of the histograms in Figure 27.1.7, we see two things. First, the similar width of
the histograms confirms that variances are roughly equal. Second, the shape of the histograms, and their
location near the center suggests that the data is very nearly normal. We will further examine the normality
of the data using Q-Q plots. To produce the Q-Q plots of the transformed data, the following SAS code was
used:
proc rank data=LogEduData normal=blom out= LogEduQuant;
var LogIncome;
ranks LogEduQuant;
run;
proc sgpanel data=LogEduQuant;
panelby educ;
scatter x=LogEduQuant y=LogIncome ;
colaxis label="Normal Quantiles";
run;
This results in the following plot:
170

Analysis Guide Midterm
Figure 27.1.8. Q-Q Plot of the Log-Transformed Data
Examining the previous figure, we see a confirmation of our beliefs: The log-transformed data, when
plotted against normal quantiles, is fairly normal. This means, with the log transformed data, we can
reasonably assume normality and homogeneity of variances. We have fulfilled the assumptions of the
ANOVA test and now we are ready to go!
171

Chapter 28
selection and execution
First, we run an f test to see if any of the means are different!
28.1 ANOVA
We will now perform a complete analysis of our data, using Pure ANOVA.
Problem Statement
We would like to determine whether or not at least one of the five population distributions (corresponding
to different years of education) is different from the rest.
Assumptions
As seen in Section ??, the raw data does not meet the assumption of normality nor of homogeneity of
variance. However, in Section 27.1, we proved that after a log transformation, the data does meet both of
these assumptions. The ANOVA test is fairly robust to the slight departure from normality presented by
the log transformed data, and the variances are equal. The data is clearly independent, so that assumption
is met. Therefore, all assumptions of ANOVA are met by the log transformed data.
Hypothesis Definition
In this problem, our Null (Reduced Model) Hypothesis, H0, is that all the groups have the same distribu-
tion and our Alternative (Full Model) Hypothesis, H1is that the distributions are different. Mathemati-
cally, that is written as:
H0:mediangrand mediangrand mediangrand mediangrand mediangrand (28.1.1)
H1:median<12 median12 median13−15 median16 median>16 (28.1.2)
We will consider our confidence level, αto be 0.05
F Statistic
To conduct this hypothesis test, the following SAS code was used:
proc glm data = LogEduData;
class educ;
model LogIncome = educ;
run;
This results in the following ANOVA Output:
Figure 28.1.1. ANOVA Table
Figure 28.1.1 tells us what our F statistic is. We see that
F= 62.87 (28.1.3)
172

Analysis Guide Midterm
P-value
Figure 28.1.1 also tells us our p-value. In this case,
p < .0001 (28.1.4)
Hypothesis Assessment
In this scenario, we have that p < .0001 < α =.05 and therefore we reject the null hypothesis.
Conclusion
There is substantial evidence (p < 0.0001) that at least one of the distributions is different from the others.
28.2 Tukey’s test
We want to compare all of the group means to see if they are different, so we do tukey’s test! we do this
with the following SAS code: With this we see that aside from the college and graduate school educations,
Code 28.1. Tukeys test in SAS and R
proc glm data = LogEduData;
class educ;
model LogIncome = educ;
lsmeans LogIncome / pdiff = ALL adjust=tukey cl;
run;
and the following R code (and output)
1edudata <- read.csv(file=’c:/Users/david/Desktop/MSDS/MSDS6371/Homework/Week6/
Data/ex0525.csv’, header =TRUE , sep = ",")
2edudata$logincome <- log( edudata $Income2005 )
3prob3 <- edudata
4aovmodel2 <- aov(logincome~Educ ,data =prob3)
5tukkey <- glht(aovmodel2 ,linfct=mcp(Educ="Tukey"))
6summary(tukkey)
7
8Simultaneous Tests for General Linear Hypotheses
9
10 Multiple Comparisons of Means: Tukey Contrasts
11
12
13 Fit: aov(formula = logincome ~Educ , data = prob3)
14
15 Linear Hypotheses:
16 Estimate Std. Error tvalue Pr(>|t|)
17 <12 - <<12 == 0 -0.32787 0.08493 -3.861 0.00101 **
18 >16 - <<12 == 0 0.67069 0.05624 11.926 < 0.001 ***
19 13-15 - <<12 == 0 0.16400 0.04674 3.509 0.00389 **
20 16 - <<12 == 0 0.56987 0.05459 10.439 < 0.001 ***
21 >16 - <12 == 0 0.99856 0.09316 10.719 < 0.001 ***
22 13-15 - <12 == 0 0.49187 0.08775 5.606 < 0.001 ***
23 16 - <12 == 0 0.89775 0.09217 9.740 < 0.001 ***
24 13-15 - >16 == 0 -0.50669 0.06041 -8.387 < 0.001 ***
25 16 - >16 == 0 -0.10082 0.06668 -1.512 0.54057
26 16 - 13-15 == 0 0.40588 0.05888 6.893 < 0.001 ***
27 ---
they are all different. A confidence interval for these differences, the % change of the medians, is calculated
by raising e to the confidence interval, and subtracting one from that and multiplying by 100. These are
shown in the following figure:
173

Analysis Guide Midterm
Figure 28.2.1. Tukey CIs on percent increase in the median
Dunnett’s Test
To compare to a control, dunnets test is the best! We do this with the following SAS code: lets look at the
Code 28.2. DUnnett’s test
proc glm data = LogEduData;
class educ;
model LogIncome = educ;
lsmeans LogIncome / pdiff = ALL adjust=dunnett cl;
run;
and the following R code (and output!).
1summary(dunnbett) #Dunnett
2
3Simultaneous Tests for General Linear Hypotheses
4
5Multiple Comparisons of Means: Dunnett Contrasts
6
7
8Fit: aov(formula = logincome ~Educ , data = prob3)
9
10 Linear Hypotheses:
11 Estimate Std. Error tvalue Pr(>|t|)
12 <12 - <<12 == 0 -0.32787 0.08493 -3.861 0.000461 ***
13 >16 - <<12 == 0 0.67069 0.05624 11.926 < 1e-04 ***
14 13-15 - <<12 == 0 0.16400 0.04674 3.509 0.001818 **
15 16 - <<12 == 0 0.56987 0.05459 10.439 < 1e-04 ***
16 ---
SAS output too!
Figure 28.2.2. SAS p values
We see that all of the groups are different from the control. We can calculate confidence intervals on
174

Analysis Guide Midterm
how much percent different by raising e to the power of the CI, and then subtracting one and multiplying
by 100, as seen in the next figure
Figure 28.2.3. Dunnett CIs on percent increase in the median
175
Chapter 29
Unit 6 lecture slides
lol
176

10/13/2018
1
UNIT 6 Live Session
Contrasts
Multiple Comparison
Overview
•ANOVA provides an F-test for equality of
several means
•The main weaknesses are
•It doesn’t tell us which means are different
•It doesn’t account for any structure in the groups
•The downside to this more refined analysis is
that we need to control for the number of
comparisons we end up making
(Example: Is the average treatment effect across 3
levels of treatments different from the placebo?)
Example:
Handicap & Capability Study
•Goal: How do physical handicaps affect perception of
employment qualification?
•(Cesare, Tannenbaum, and Dalessio “Interviewers’ decisions related to applicant handicap type and rater empathy” (1990) Human
Performance)
•The researchers prepared 5 video taped job interviews
with same actors
•The tapes differed only in the handicap of the applicant:
•No handicap (This is the control group)
•One leg amputated
•Crutches
•Hearing Impaired
•Wheelchair
•14 students were randomly assigned to each tape to rate
applicants: 0-10 pts (70 students total.)
Example:
Handicap & Capability Study
•Do subjects systematically evaluate qualifications
differently according to handicap?
•If so, which handicaps are evaluated differently?

10/13/2018
2
Is There Any Difference at All?
•We should begin any analysis involving several
groups by using the ANOVA framework
•If there isn’t any (statistically) significant
difference in the population means, then there is
no reason to address more refined questions
•The tapes differed only in the handicap of the
applicant:
•No handicap (This is the control group.)
•One leg amputated
•Crutches
•Hearing Impaired
•Wheelchair
There is NO visual evidence to suggest that the data are
not normally distributed. We will proceed with the
assumption of normally distributed groups.
Handicap & Capability Study:
Normality Assumption
Handicap & Capability Study:
Equal Variances Assumption
There is NO evidence to suggest variances are unequal.
Handicap & Capability Study:
ANOVA results
There is evidence to support the claim that at least two population means
are different from each other (p-value of 0.0301 from a 1-way ANOVA).
Notice that since there is
virtually no evidence of a
difference in standard
deviations, Welch’s test is
almost identical to the pure F
ANOVA.

10/13/2018
3
Handicap & Capability Study:
More Specific Questions
(
CONTRAST
)
Linear Combinations & Contrasts
(this requires independence)
Handicap & Capability Study:
A Contrast
Calculate mean difference and standard error.
There is evidence that the sum of points assigned to
Amp & Hear handicaps is smaller than the sum of
points assigned to Crutch & Wheel handicaps at level
alpha equal to 0.05 because the CI does not contain 0.
Handicap & Capability Study:
A Contrast
CI: Point estimate ±multiplier* standard error

10/13/2018
4
Chapter 6: Compare with book!
Note the sign switch
and division by 2 of
the coefficients.
Handicap & Capability Study:
In SAS
Order = data keeps
the data in the order
it came in, so that
“none” group is first
and can be assigned
a coefficient of 0.
Comes in handy when doing division by hand would result in the need to input a
rounded number (example 0.33)
Handicap & Capability Study:
In SAS
Three different ways (contrast, estimate, estimate with divisor =2) to test for the same
idea. (There are many more than three!)
Handicap & Capability Study:
In SAS
There is evidence that the average points assigned to Amp & Hear
handicaps is smaller than the average points assigned to Crutch & Wheel
handicaps (t-tools linear contrast p-value of 0.0022). We estimate that this
difference is -1.39 pts with an associated 99% confidence interval of….
-1.39±2.65*0.436
-1.39±1.155
(-2.55, -0.23), which of course does not include 0
99% CI for the difference in averages of
Amp and Hear vs. Crutch and Wheel:
Point estimate ±multiplier* standard error
Confidence Intervals

10/13/2018
5
Chapter 6
With no Order = data in the code, the contrasts are assigned in alphabetical
order, so that “none” group is fourth.
Let’s Try Some from Spock Example!!
Answer on Next Slide ->
Contrast vector (assume alphabetical order):
Groups: A, B, C, D, E, F, S
Let’s Try Some from Spock Example!!
Contrast vector (assume alphabetical order): -1 -1 -1 -1 -1 -1 6
Groups: A, B, C, D, E, F, S
Let’s Try ANOTHER (from Spock)!!
Contrast vector (assume alphabetical order):
Groups: A, B, C, D, E, F, S

10/13/2018
6
Let’s Try ANOTHER (from Spock)!!
ADDITIONAL QUESTION:
Why is it better to include the Spock data in the calculation of the pooled SD
(and thus the MSE) even though the hypothesis does not include it?
Contrast vector (assume alphabetical order): 1 1 1 -1 -1 -1 0
Groups: A, B, C, D, E, F, S
Let’s Try ONE MORE (from Spock)!!
Answer on Next Slide ->
Contrast vector (assume alphabetical order):
Groups: A, B, C, D, E, F, S
Let’s Try ONE MORE (from Spock)!!
Contrast vector (assume alphabetical order): 3 0 3 -2 -2 -2 0
Groups: A, B, C, D, E, F, S
Multiple Comparison: Motivation
K tests

10/13/2018
7
Multiple Comparison: Example k = 100
Gene 1
Gene 2
Gene 3
Gene 4
Gene 5
Gene 6
Gene 7
Gene 8
Gene 9
Gene 10
Gene 11
Gene 12
Gene 97
Gene 98
Gene 99
Gene 100
…
Confidence Intervals
When we make a correction for multiple comparisons, it is the critical value in the
hypothesis test and thus the multiplier in the confidence interval that is adjusted.
*The multiplier is usually the same as the critical value for a hypothesis test.
Planned & Post-hoc Tests
A planned test is one in which you know the comparisons (tests) you
want to make before you look at the data.
If you have k planned comparisons then you need to correct for just
those k comparisons.
Post-Hoc / Unplanned Tests
Post Hoc tests are appropriate when:
1. The researcher wants to examine all
possible comparisons among pairs of group
means (or a large number of comparisons).
2. Predictions about which groups will differ
are not made prior to setting up the
analysis.

10/13/2018
8
Multiple Comparison: Bonferroni
This approach is very conservative,
meaning that the intervals are much
wider than the nominal level,
particularly if the tests are not really
independent.
For a set of Bonferroni adjusted t-tests, (α/k) we
must have normal distributions, equal spreads, and
independence (same as typical t-tests).
However, the Bonferroni correction can be extended
to tests that have no assumptions about distributions
(e.g. rank sum test). For any set of independent
parametric or non-parametric tests, the Bonferroni
correction works the same.
Multiple Comparison: Tukey-Kramer
Multiplier =
Assumes normal distributions, equal spreads, independence (same as typical t-tests), and
equal group sample sizes.
More consistent than Bonferroni with respect to Type I Error but not robust to its
assumptions…. Bonferroni is a good alternative when the assumptions are violated.
Studentized Range Statistic Table
The Tukey-Kramer adjustment is a
modification to this test to
account for different sample sizes
in the groups.
Multiple Comparison: Dunnett
Many Groups to one Control
Replaces t-distribution with a multivariate t-
distribution (n=# of groups versus control),
where the tests are not independent.
…
Assumes normal
distributions, equal
spreads, and
independence (same as
typical t-tests).
Handicap / Capability Study: Data

10/13/2018
9
Handicap Data Analysis
Questions of Interest:
1. Is there any evidence that at least one pair of mean
qualification scores are different from each other?
2. Let’s say we are only interested in Amputee versus None.
Test the claim the Amputee has a different mean score than
the None group.
3. Now let’s assume that we are interested in identifying
specific differences between any two of the group means.
Find evidence of any differences in the means between the
groups.
4. Next, assume that we were interested in testing the means
of the handicapped groups to the non-handicap group. Test
this claim and identify any significant differences.
First Test!!!
Normality: Handicap Data
There is no visual evidence to suggest that the data are not
normally distributed. We will proceed with the assumption of
normally distributed groups.
Homogeneity of SD Assumption
There is no evidence to suggest variances are unequal.
Independence may be violated here. We are going to proceed anyway for
the sake of the example.

10/13/2018
10
First QOI!!!
There is sufficient evidence to suggest at the alpha = .05 level of
significance (p-value = .0301) that at least 2 of the means are different
from each other in this standard ANOVA.
1. Is there any evidence that at least one pair of mean qualification scores are
different from each other?
Second QOI!!!
The results of these tests are equivalent! There is not sufficient evidence to suggest
that the mean qualification rating of the amputee group is different than the group
without handicap. (P-value = .4678 from a t-test and an ANOVA using only these two
groups.)
2. Let’s say we are only interested in Amputee versus None. Test the claim the
Amputee has a different mean score than the None group.
Second QOI: Better approach!!!
There is not sufficient evidence to suggest that the mean qualification rating of the amputee group is
different than the group with no handicap (p-value = .4477 from a contrast using all available data). Even
though the p-values for the two tests are only slightly different, it is better to use all available data (the
procedure on the right).
Comparing a pair of means can be just a simple contrast.
2. Let’s say we are only interested in Amputee versus None. Test the claim the Amputee has a
different mean score than the None group.
Third QOI!!!
There are 10 different two sided tests conducted
here; thus, we need to adjust alpha per test to be
.05/10 = .005. With this adjustment, only one of the
tests has a statistically significant result. Therefore,
there is evidence (p-value = .0035 from a t-test) that
the crutches and hearing groups have different mean
qualification rating scores. We will provide a
confidence interval in a few slides.
Now let’s assume that we are interested
in identifying specific differences
between any two group means. Find
evidence of any differences in the means
between the groups.

10/13/2018
11
Bonferroni Adjusted P-Values
x 10, up to 1
Compare to alpha = 0.005 Compare to alpha = 0.05
P-values not adjusted- compare to
individual alpha P-values adjusted- compare to family-
wise alpha
Third QOI!!!
A 95% confidence interval for the
difference in means of the
crutches and hearing groups is
(.0779, 3.66499).
Now let’s assume that we are interested
in identifying specific differences
between any two group means. Find
evidence of any differences in the means
between the groups.
Third QOI!!!
A 95% confidence interval for the
difference in means of crutches and
hearing groups is (.0779, 3.66499).
Now let’s assume that we are interested
in identifying specific differences
between any two group means. Find
evidence of any differences in the means
between the groups.
*Slightly different code from the last slide, producing slightly
different output. Note the cl versus cldiff.
4
th
QOI: Next, assume that we are interested in testing the means of
the handicapped groups with the non-handicapped group. Test this
claim and identify any significant differences. (Using CIs)
There is NOT sufficient evidence
in this study to suggest that there
are any differences between the
average of the means of each
handicap group and the mean of
the group without handicap.
The 95% family-wise confidence
intervals are constructed using
Dunnett’s procedure. All CIs
contain zero, thus not providing
sufficient evidence to conclude
that the difference is not zero.
(The study results do not
constitute sufficient evidence to
support the claim that any means
tested are individually different
than the control.)
Specify the
control group

10/13/2018
12
4
th
QOI: Next, assume that we were interested in testing the means of
the handicapped groups with the non-handicap group. Test this claim
and identify any significant differences. (Using HTs)
Hypothesis tests also conclude that there is not sufficient evidence to suggest that there
are any differences between the means of each handicapped group and the mean of the
of the group without handicap. The above Dunnett adjusted p-values are all greater
than alpha = .05, as is visible from the table above.
R Code for Handicap Example Question 1
Question 1: Reading in Data and ANOVA
R Code for Handicap Example Question 2
Note: Must Load
pairwiseCI package
Note: Must
Load
multcomp
package
R Code for Handicap Example Question 3
Note: Must Load multcomp package

10/13/2018
13
R Code for Handicap Example Question 4
Note: Must Load multcomp package
Appendix
Bonferroni’s Correction Bonferroni’s Correction

10/13/2018
14
Bonferroni’s Correction Multivariate distribution
•A multivariate
distribution is
distribution of a
vector of conditional
random variables.
•Bivariate normal
distribution can
easily be shown
graphically.
Part VII
Workflow for testing hypotheses
191

DATA TRANSFORMATION MULTIPLE HYPOTHESIS TESTRESEARCH STRUCTURE
POST HOC TESTS
NORMAL DISTRIBUTION VARIANCESAMPLE SIZE
UNPAIRED TESTING (TWO SAMPLES)
Difference between independent groups
(between-groups)
Single measure or observation
MATCHED PAIRS
Difference between same group before and
after treatment (within-groups)
Repeated measures or observations
nonparametric
WILCOXON RANK SUM
(aka Mann-Whitney U Test)
Inference on medians
NO
nonparametric
KRUSKAL-WALLIS
Inference on medians
CHOOSING A HYPOTHESIS TEST
ONE SAMPLE
Difference between mean of independent
samples and a hypothesized mean
Single measure or observation
YES
parametric
ONE-SAMPLE T-TEST
Inference on means
(medians if log-transform)
NO
YES (CLT)
NO
noonparametric
SIGN TEST or
WILCOXON SINGED RANK TEST
Inference on medians
UNPAIRED TESTING (MORE THAN TWO
SAMPLES)
Difference between independent groups
(between-groups)
Single measure or observation
YES (CLT)
parametric
WELCH’S T
Inference on means
YES
parametric
POOLED TWO-SAMPLE T
Inference on means
NO
NO
YES
EVIDENCE AGAINST
NORMALITY? SUFFICIENT SAMPLE
SIZE?
SUFFICIENT SAMPLE
SIZE?
EVIDENCE AGAINST
NORMALITY?
SAME SAMPLE
SIZES?
* TESTS USING LOG-TRANSFORMED
DATA (INFERENCE ON MEDIANS)
YES
EVIDENCE AGAINST SAME
STANDARD DEVIATION?
NO
EVIDENCE AGAINST
NORMALITY?
NO
parametric
ONE-WAY ANOVA
Inference on means
(medians if log-transform)
YES (w/LOG TRANSFORMATION)*
EVIDENCE AGAINST SAME
STANDARD DEVIATION?
NO
NO
YES (w/LOG-TRANSFORMATION)*
parametric
WELCH’S ANOVA
Inference on means
TUKEY-KRAMER
(aka TUKEY’S HSD)
DUNNETT
for comparison to a control group
REGWQ
Lower Type II error rate than either
Bonferroni or Tukey-Kramer
BONFERRONI CORRECTION
distribution-free, more conservative,
wider interval
Rev. 5 (6/25/2015)
Michael Burkhardt • mburkhardt@smu.edu
HYPOTHESIS TESTING STEP-BY-STEP
1 Read the problem carefully. Is it a
randomized experiment or an
observational study?
2 Plot the data using histograms, box
plots, or QQ plots.
3 Determine which test to use. Do the
data satisfy the test’s assumptions?
4 State the null and alternative
hypotheses. Is this a one-sided or
two-sided test?
5 Select a test statistic and confidence
level (1-α). Find the critical value.
6 Sketch the distribution, including
the critical value and the
acceptance and/or rejection
region(s).
7 Compute the test statistic and the
probability (p-value) of obtaining
the observed results if the null
hypothesis is true.
8Reject or fail to reject the null
hypothesis. (Never accept the null
hypothesis.)
9 Perform post hoc testing, if
applicable, to determine which
groups are different.
10 State the statistical conclusion in
the context of the original problem.
YES
NO (w/LOG TRANSFORMATION)*
SUFFICIENT SAMPLE
SIZE?
YES
YES (CLT)

Analysis Guide Midterm
note that the nonparamteric ones do medians, kruskal is nonparametric for ANOVA
193
