Anany Levitin Introduction To The Design And Analysis Of Algorithms Solution Manual (2012)
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 389 [warning: Documents this large are best viewed by clicking the View PDF Link!]

This file contains the exercises, hints, and solutions for Chapter 1 of the
book ”Introduction to the Design and Analysis of Algorithms,” 2nd edition, by
A. Levitin. The problems that might be challenging for at least some students
are marked by ;those that might be difficult for a majority of students are
marked by .
Exercises 1.1
1. Do some research on al-Khorezmi (also al-Khwarizmi), the man from
whose name the word “algorithm” is derived. In particular, you should
learn what the origins of the words “algorithm” and “algebra” have in
common.
2. Given that the official purpose of the U.S. patent system is the promo-
tion of the “useful arts,” do you think algorithms are patentable in this
country? Should they be?
3. a. Write down driving directions for going from your school to your home
with the precision required by an algorithm.
b. Write down a recipe for cooking your favorite dish with the precision
required by an algorithm.
4. Design an algorithm for computing √nfor any positive integer n.Be-
sides assignment and comparison, your algorithm may only use the four
basic arithmetical operations.
5. a. Find gcd(31415, 14142) by applying Euclid’s algorithm.
b. Estimate how many times faster it will be to find gcd(31415, 14142)
by Euclid’s algorithm compared with the algorithm based on checking
consecutive integers from min{m, n}down to gcd(m, n).
6. Prove the equality gcd(m, n)=gcd(n, m mod n)for every pair of positive
integers mand n.
7. What does Euclid’s algorithm do for a pair of numbers in which the first
number is smaller than the second one? What is the largest number of
times this can happen during the algorithm’s execution on such an input?
8. a. What is the smallest number of divisions made by Euclid’s algorithm
among all inputs 1≤m, n ≤10?
b. What is the largest number of divisions made by Euclid’s algorithm
among all inputs 1≤m, n ≤10?
9. a. Euclid’s algorithm, as presented in Euclid’s treatise, uses subtractions
rather than integer divisions. Write a pseudocode for this version of
Euclid’s algorithm.
1
b.Euclid’s game (see [Bog]) starts with two unequal positive numbers
on the board. Two players move in turn. On each move, a player has
to write on the board a positive number equal to the difference of two
numbers already on the board; this number must be new, i.e., different
from all the numbers already on the board. The player who cannot move
loses the game. Should you choose to move first or second in this game?
10. The extended Euclid’s algorithm determines not only the greatest
common divisor dof two positive integers mand nbut also integers (not
necessarily positive) xand y, such that mx +ny =d.
a. Look up a description of the extended Euclid’s algorithm (see, e.g.,
[KnuI], p. 13) and implement it in the language of your choice.
b. Modify your program for finding integer solutions to the Diophan-
tine equation ax +by =cwith any set of integer coefficients a,b,and
c.
11. Locker doors There are nlockers in a hallway numbered sequentially
from 1 to n. Initially, all the locker doors are closed. You make npasses
by the lockers, each time starting with locker #1. On the ith pass, i=
1,2,...,n, you toggle the door of every ith locker: if the door is closed,
you open it, if it is open, you close it. For example, after the first pass
every door is open; on the second pass you only toggle the even-numbered
lockers (#2, #4, ...) so that after the second pass the even doors are
closed and the odd ones are opened; the third time through you close the
door of locker #3 (opened from the first pass), open the door of locker
#6 (closed from the second pass), and so on. After the last pass, which
locker doors are open and which are closed? How many of them are open?
2

Hints to Exercises 1.1
1. It is probably faster to do this by searching the Web, but your library
should be able to help too.
2. One can find arguments supporting either view. There is a well established
principle pertinent to the matter though: scientific facts or mathematical
expressions of them are not patentable. (Why do you think it is the case?)
But should this preclude granting patents for all algorithms?
3. You may assume that you are writing your algorithms for a human rather
than a machine. Still, make sure that your descriptions do not contain ob-
vious ambiguities. Knuth [KnuI], p.6 provides an interesting comparison
between cooking recipes and algorithms.
4. There is a quite straightforward algorithm for this problem based on the
definition of √n.
5. a. Just follow Euclid’s algorithm as described in the text.
b. Compare the number of divisions made by the two algorithms.
6. Prove that if ddivides both mand n(i.e., m=sd and n=td for some
positive integers sand t), then it also divides both nand r=mmod n
and vice versa.Use the formula m=qn+r(0 ≤r<n)and the fact that
if ddivides two integers uand v, it also divides u+vand u−v. (Why?)
7. Perform one iteration of the algorithm for two arbitrarily chosen integers
m<n.
8. The answer to part (a) can be given immediately; the answer to part
(b) can be given by checking the algorithm’s performance on all pairs
1<m<n≤10.
9. a. Use the equality
gcd(m, n)=gcd(m−n, n)for m≥n>0.
b. The key is to figure out the total number of distinct integers that can be
written on the board, starting with an initial pair m, n where m>n≥1.
You should exploit a connection of this question to the question of part
(a). Considering small examples, especially those with n=1and n=2,
should help, too.
10. Of course, for some coefficients, the equation will have no solutions.
11. Tracing the algorithm by hand for, say, n=10and studying its outcome
should help answering both questions.
3

Solutions to Exercises 1.1
1. Al-Khwarizmi (9th century C.E.) was a great Arabic scholar, most fa-
mous for his algebra textbook. In fact, the word “algebra” is derived
from the Arabic title of this book while the word “algorithm” is derived
from a translation of Al-Khwarizmi’s last name (see, e.g., [KnuI], pp. 1-2,
[Knu96], pp. 88-92, 114).
2. This legal issue has yet to be settled. The current legal state of affairs
distinguishes mathematical algorithms, which are not patentable, from
other algorithms, which may be patentable if implemented as computer
programs (e.g., [Cha00]).
3. n/a
4. A straightforward algorithm that does not rely on the availability of an
approximate value of √ncan check the squares of consecutive positive
integers until the first square exceeding nis encountered. The answer will
be the number’s immediate predecessor. Note: A much faster algorithm
for solving this problem can be obtained by using Newton’s method (see
Sections 11.4 and 12.4).
5. a. gcd(31415,14142) = gcd(14142,3131) = gcd(3131,1618) =
gcd(1618,1513) = gcd(1513,105) = gcd(1513,105) = gcd(105,43) =
gcd(43,19) = gcd(19,5) = gcd(5,4) = gcd(4,1) = gcd(1,0) = 1.
b. To answer the question, we need to compare the number of divisions
the algorithms make on the input given. The number of divisions made
by Euclid’s algorithm is 11 (see part a). The number of divisions made
by the consecutive integer checking algorithm on each of its 14142 itera-
tions is either 1 and 2; hence the total number of multiplications is be-
tween 1·14142 and 2·14142. Therefore, Euclid’s algorithm will be between
1·14142/11 ≈1300 and 2·14142/11 ≈2600 times faster.
6. Let us first prove that if ddivides two integers uand v, it also divides
both u+vand u−v. By definition of division, there exist integers sand
tsuch that u=sd and v=td. Therefore
u±v=sd ±td =(s±t)d,
i.e., ddivides both u+vand u−v.
4

Also note that if ddivides u, it also divides any integer multiple ku of
u. Indeed, since ddivides u, u =sd. Hence
ku =k(sd)=(ks)d,
i.e., ddivides ku.
Now we can prove the assertion in question. For any pair of positive
integers mand n, if ddivides both mand n, it also divides both nand
r=mmod n=m−qn. Similarly, if ddivides both nand r=mmod n=
m−qn, it also divides both m=r+qn and n. Thus, the two pairs
(m, n)and (n, r)have the same finite nonempty set of common divisors,
including the largest element in the set, i.e., gcd(m, n)=gcd(n, r).
7. For any input pair m, n such that 0≤m<n,Euclid’s algorithm simply
swaps the numbers on the first iteration:
gcd(m, n)=gcd(n, m)
because mmod n=mif m<n. Such a swap can happen only once since
gcd(m, n)=gcd(n, m mod n)implies that the first number of the new pair
(n)will be greater than its second number (mmod n)after every iteration
of the algorithm.
8. a. For any input pair m≥n≥1,in which mis a multiple of n, Euclid’s
algorithm makes exactly one division; it is the smallest number possible
for two positive numbers.
b. The answer is 5 divisions, which is made by Euclid’s algorithm in
computing gcd(5,8).It is not too time consuming to get this answer by
examining the number of divisions made by the algorithm on all input
pairs 1<m<n≤10.
Note: A pertinent general result (see [KnuII], p. 360) is that for any
input pair m, n where 0≤n<N,the number of divisions required by
Euclid’s algorithm to compute gcd(m, n)is at most logφ(3−φ)N)where
φ=(1+√5)/2.
9. a. Here is a nonrecursive version:
Algorithm Euclid2 (m, n)
//Computes gcd(m, n)by Euclid’s algorithm based on subtractions
//Input: Two nonnegative integers mand nnot both equal to 0
//Output: The greatest common divisor of mand n
while n=0do
if m<n swap(m, n)
m←m−n
return m
5

b. It is not too difficult to prove that the integers that can be written on
the board are the integers generated by the subtraction version of Euclid’s
algorithm and only them. Although the order in which they appear on
the board may vary, their total number always stays the same: It is equal
to m/ gcd(m, n),where mis the maximum of the initial numbers,which
includes two integers of the initial pair. Hence, the total number of
possible moves is m/ gcd(m, n)−2.Consequently, if m/ gcd(m, n)is odd,
one should choose to go first; if it is even, one should choose to go second.
10. n/a
11. Since all the doors are initially closed, a door will be open after the last
pass if and only if it is toggled an odd number of times. Door i(1 ≤i≤n)
is toggled on pass j(1 ≤j≤n)if and only if jdivides i. Hence, the total
number of times door iis toggled is equal to the number of its divisors.
Note that if jdivides i, i.e. i=jk, then kdivides itoo. Hence all the
divisors of icanbepaired(e.g.,fori=12,such pairs are 1 and 12, 2
and 6, 3 and 4) unless iis a perfect square (e.g., for i=16,4doesnot
have another divisor to be matched with). This implies that ihas an
odd number of divisors if and only if it is a perfect square, i.e., i=j2.
Hence doors that are in the positions that are perfect squares and only
such doors will be open after the last pass. The total number of such
positions not exceeding nis equal to √n: these numbers are the squares
of the positive integers between 1 and √ninclusively.
6

Exercises 1.2
1. Old World puzzle A peasant finds himself on a riverbank with a wolf,
a goat, and a head of cabbage. He needs to transport all three to the
other side of the river in his boat. However, the boat has room for only
the peasant himself and one other item (either the wolf, the goat, or the
cabbage). In his absence, the wolf would eat the goat, and the goat would
eat the cabbage. Solve this problem for the peasant or prove it has no
solution. (Note: The peasant is a vegetarian but does not like cabbage
and hence can eat neither the goat nor the cabbage to help him solve the
problem. And it goes without saying that the wolf is a protected species.)
2. New World puzzle There are four people who want to cross a bridge; they
all begin on the same side. You have 17 minutes to get them all across to
the other side. It is night, and they have one flashlight. A maximum of two
people can cross the bridge at one time. Any party that crosses, either one
or two people, must have the flashlight with them. The flashlight must be
walked back and forth; it cannot be thrown, for example. Person 1 takes
1 minute to cross the bridge, person 2 takes 2 minutes, person 3 takes 5
minutes, and person 4 takes 10 minutes. A pair must walk together at the
rate of the slower person’s pace. For example, if person 1 and person 4
walk across first, 10 minutes have elapsed when they get to the other side
of the bridge. If person 4 returns the flashlight, a total of 20 minutes have
passed and you have failed the mission. (Note: According to a rumor on
the Internet, interviewers at a well-known software company located near
Seattle have given this problem to interviewees.)
3. Which of the following formulas can be considered an algorithm for com-
puting the area of a triangle whose side lengths are given positive numbers
a,b,andc?
a. S=p(p−a)(p−b)(p−c),where p=(a+b+c)/2
b. S=1
2bc sin A, where Ais the angle between sides band c
c. S=1
2aha,where hais the height to base a
4. Write a pseudocode for an algorithm for finding real roots of equation
ax2+bx +c=0for arbitrary real coefficients a, b, and c. (You may
assume the availability of the square root function sqrt(x).)
5. Describe the standard algorithm for finding the binary representation of
a positive decimal integer
a. in English.
b. in a pseudocode.
7
6. Describe the algorithm used by your favorite ATM machine in dispensing
cash. (You may give your description in either English or a pseudocode,
whichever you find more convenient.)
7. a. Can the problem of computing the number πbe solved exactly?
b. How many instances does this problem have?
c. Look up an algorithm for this problem on the World Wide Web.
8. Give an example of a problem other than computing the greatest common
divisor for which you know more than one algorithm. Which of them is
simpler? Which is more efficient?
9. Consider the following algorithm for finding the distance between the two
closestelementsinanarrayofnumbers.
Algorithm MinDistance(A[0..n−1])
//Input: Array A[0..n−1]ofnumbers
//Output: Minimum distance between two of its elements
dmin ←∞
for i←0to n−1do
for j←0to n−1do
if i=jand |A[i]−A[j]|<dmin
dmin ←|A[i]−A[j]|
return dmin
Make as many improvements as you can in this algorithmic solution to
the problem. (If you need to, you may change the algorithm altogether; if
not, improve the implementation given.)
10. One of the most influential books on problem solving, titled How To Solve
It [Pol57], was written by the Hungarian-American mathematician George
Polya (1887—1985). Polya summarized his ideas in a four-point summary.
Find this summary on the Web or, better yet, in his book, and compare
it with the plan outlined in Section 1.2. What do they have in common?
How are they different?
8
Hints to Exercises 1.2
1. The peasant would have to make several trips across the river, starting
with the only one possible.
2. Unlike the Old World puzzle of Problem 1, the first move solving this
puzzleisnotobvious.
3. The principal issue here is a possible ambiguity.
4. Your algorithm should work correctly for all possible values of the coeffi-
cients, including zeros.
5. You almost certainly learned this algorithm in one of your introductory
programming courses. If this assumption is not true, you have a choice
between designing such an algorithm on your own or looking it up.
6. You may need to make a field trip to refresh your memory.
7. Question (a) is difficult though the answer to it–discovered in 1760s by
the German mathematician Johann Lambert –is well-known. By com-
parison, question (b) is incomparably simpler.
8. You probably know two or more different algorithms for sorting an array
of numbers.
9. You can: decrease the number of times the innermost loop is executed,
make that loop run faster (at least for some inputs), or, more significantly,
design a faster algorithm from scratch.
10. n/a
9

Solutions to Exercises 1.2
1. Let P,w,g,andcstand for the peasant, wolf, goat, and cabbage head,
respectively. The following is one of the two principal sequences that
solve the problem:
Pwgc
Pg
wc
g
Pw c
Pwg
c
w
Pgc
Pw c
g
wc
Pg
Pwgc
Note: This problem is revisited later in the book (see Section 6.6).
2. Let1,2,5,10belabelsrepresentingthemenoftheproblem,frepresent
the flashlight’s location, and the number in the parenthesis be the total
amount of time elapsed. The following sequence of moves solves the
problem:
(0)
f,1,2,5,10
f,1,2
(2)
5,10
2
(3)
f,1,5,10
f,2,5,10
(13)
1
5,10
(15)
f,1,2
f,1,2,5,10
(17)
3. a. The formula can be considered an algorithm if we assume that we know
how to compute the square root of an arbitrary positive number.
b. The difficulty here lies in computing sin A. Since the formula says
nothing about how it has to be computed, it should not be considered an
algorithm. This is true even if we assume, as we did for the square root
function, that we know how to compute the sine of a given angle. (There
are several algorithms for doing this but only approximately, of course.)
The problem is that the formula says nothing about how to compute angle
Aeither.
c. The formula says nothing about how to compute ha.
4. Algorithm Quadratic(a, b, c)
//The algorithm finds real roots of equation ax2+bx +c=0
//Input: Real coefficients a, b, c
//Output: The real roots of the equation or a message about their absence
if a=0
D←b∗b−4∗a∗c
if D>0
temp ←2∗a
x1←(−b+sqrt(D))/temp
x2←(−b−sqrt(D))/temp
10
return x1,x2
else if D=0return −b/(2 ∗a)
else return ‘no real roots’
else //a=0
if b=0return −c/b
else //a=b=0
if c=0return ‘allrealnumbers’
else return ‘no real roots ’
Note: See a more realistic algorithm for this problem in Section 11.4.
5. a. Divide the given number nby 2: the remainder rn(0 or 1) will be
the next (from right to left) digit of the binary representation in question.
Replace nby the quotient of the last division and repeat this operation
until nbecomes 0.
b. Algorithm Binary(n)
//The algorithm implements the standard method for finding
//the binary expansion of a positive decimal integer
//Input: A positive decimal integer n
//Output: The list bkbk−1...b1b0of n’s binary digits
k←0
while n=0
bk←nmod 2
n←n/2
k←k+1
6. n/a
7. a. π, as an irrational number, can be computed only approximately.
b. It is natural to consider, as an instance of this problem, computing
π’s value with a given level of accuracy, say, with ncorrect decimal digits.
With this interpretation, the problem has infinitely many instances.
8. n/a
9. The following improved version considers the same pair of elements only
once and avoids recomputing the same expression in the innermost loop:
Algorithm MinDistance2 (A[0..n −1])
//Input: An array A[0..n−1]ofnumbers
//Output: The minimum distance dbetween two of its elements
11
dmin ←∞
for i←0to n−2do
for j←i+1to n−1do
temp ←|A[i]−A[j]|
if temp < dmin
dmin ←temp
return dmin
A faster algorithm is based on the idea of presorting (see Section 6.1).
10. Polya’s general four-point approach is:
1. Understand the problem
2. Devise a plan
3. Implement the plan
4. Look back/check
12
Exercises 1.3
1. Consider the algorithm for the sorting problem that sorts an array by
counting, for each of its elements, the number of smaller elements and
then uses this information to put the element in its appropriate position
in the sorted array:
Algorithm ComparisonCountingSort(A[0..n −1],S[0..n −1])
//Sorts an array by comparison counting
//Input: Array A[0..n −1] of orderable values
//Output: Array S[0..n −1] of A’s elements sorted in nondecreasing order
for i←0to n−1do
Count[i]←0
for i←0to n−2do
for j←i+1to n−1do
if A[i]<A[j]
Count[j]←Count[j]+1
else Count[i]←Count[i]+1
for i←0to n−1do
S[Count[i]] ←A[i]
a. Apply this algorithm to sorting the list 60, 35, 81, 98, 14, 47.
b. Is this algorithm stable?
c. Is it in place?
2. Name the algorithms for the searching problem that you already know.
Give a good succinct description of each algorithm in English. (If you
know no such algorithms, use this opportunity to design one.)
3. Design a simple algorithm for the string-matching problem.
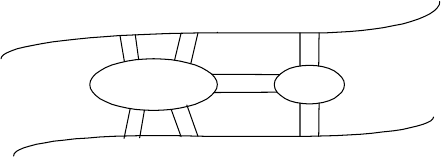
4. Königsberg bridges The Königsberg bridge puzzle is universally accepted
as the problem that gave birth to graph theory. It was solved by the great
Swiss-born mathematician Leonhard Euler (1707—1783). The problem
asked whether one could, in a single stroll, cross all seven bridges of the
city of Königsberg exactly once and return to a starting point. Following
is a sketch of the river with its two islands and seven bridges:
a. State the problem as a graph problem.
13
b. Does this problem have a solution? If you believe it does, draw such
a stroll; if you believe it does not, explain why and indicate the small-
est number of new bridges that would be required to make such a stroll
possible.
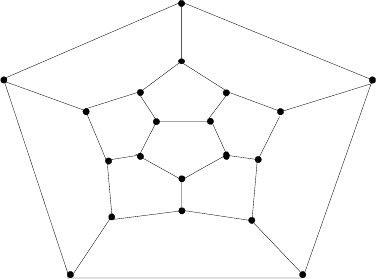
5. Icosian Game A century after Euler’s discovery (see Problem 4), an-
other famous puzzle–this one invented by the renown Irish mathemati-
cian Sir William Hamilton (1805-1865)–was presented to the world under
thenameoftheIcosianGame. Thegamewasplayedonacircularwooden
board on which the following graph was carved:
Find a Hamiltonian circuit–a path that visits all the graph’s vertices
exactly once before returning to the starting vertex–for this graph.
6. Consider the following problem: Design an algorithm to determine the
best route for a subway passenger to take from one designated station to
another in a well-developed subway system similar to those in such cities
as Washington, D.C., and London, UK.
a. The problem’s statement is somewhat vague, which is typical of real-
life problems. In particular, what reasonable criterion can be used for
defining the “best” route?
b. How would you model this problem by a graph?
7. a. Rephrase the traveling salesman problem in combinatorial object terms.
b. Rephrase the graph-coloring problem in combinatorial object terms.
8. Consider the following map:
14

a
b
cd
ef
a. Explain how we can use the graph-coloring problem to color the map
so that no two neighboring regions are colored the same.
b. Use your answer to part (a) to color the map with the smallest number
of colors.
9. Design an algorithm for the following problem: Given a set of npoints
in the Cartesian plane, determine whether all of them lie on the same
circumference.
10. Write a program that reads as its inputs the (x, y)coordinates of the
endpoints of two line segments P1Q1and P2Q2and determines whether
thesegmentshaveacommonpoint.
15
Hints to Exercises 1.3
1. Trace the algorithm on the input given. Use the definitions of stability
and being in place that were introduced in the section.
2. If you do not recall any searching algorithms, you should design a simple
searching algorithm (without succumbing to the temptation to find one in
the latter chapters of the book).
3. This algorithm is introduced later in the book but you should have no
trouble to design it on your own.
4. If you have not encountered this problem in your previous courses, you
may look up the answers on the Web or in a discrete structures textbook.
The answers are, in fact, surprisingly simple.
5. No efficient algorithm for solving this problem for an arbitrary graph is
known. This particular graph does have Hamiltonian circuits which are
not difficult to find. (You need to find just one of them.)
6. a. Put yourself (mentally) in a passenger’s place and ask yourself what
criterion for the “best” route you would use. Then think of people that
may have different needs.
b. The representation of the problem by a graph is straightforward. Give
some thoughts though to stations where trains can be changed.
7. a. What are tours in the traveling salesman problem?
b. It would be natural to consider vertices colored the same color as
elements of the same subset.
8. Create a graph whose vertices represent the map’s regions. You will have
to decide on the edges on your own.
9. Assume that the circumference in question exists and find its center first.
Also, do not forget to give a special answer for n≤2.
10. Be careful not to miss some special cases of the problem.
16
Solutions to Exercises 1.3
1. a. Sorting 60, 35, 81, 98, 14, 47 by comparison counting will work as
follows:
Array A[0..5] 60 35 81 98 14 47
Initially Count[] 0 0 0 0 0 0
After pass i=0 Count[] 3 0 1 1 0 0
After pass i=1 Count[] 1 2 2 0 1
After pass i=2 Count[] 4 3 0 1
After pass i=3 Count[] 5 0 1
After pass i=4 Count[] 0 2
Final state Count[] 3 1 4 5 0 2
Array S[0..5] 14 35 47 60 81 98
b. The algorithm is not stable. Consider, as a counterexample, the
result of its application to 1,1 .
c. The algorithm is not in place because it uses two extra arrays of size
n:Count and S.
2. Answers may vary but most students should be familiar with sequential
search, binary search, binary tree search and, possibly, hashing from their
introductory programming courses.
3. Align the pattern with the beginning of the text. Compare the corre-
sponding characters of the pattern and the text left-to right until either
all the pattern characters are matched (then stop–the search is success-
ful) or the algorithm runs out of the text’s characters (then stop–the
search is unsuccessful) or a mismatching pair of characters is encountered.
In the latter case, shift the pattern one position to the right and resume
the comparisons.
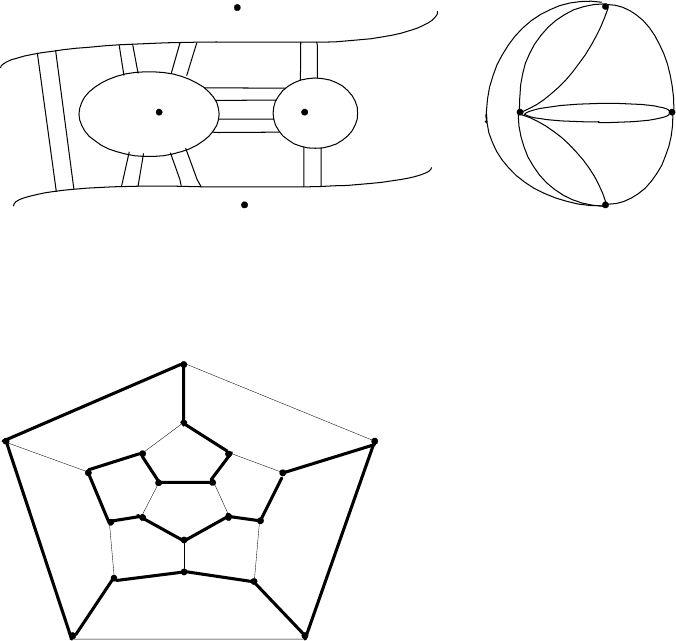
4. a. If we represent each of the river’s banks and each of the two islands by
vertices and the bridges by edges, we will get the following graph:
17

b
a
c
d
b
a
c
d
(This is, in fact, a multigraph, not a graph, because it has more than one
edge between the same pair of vertices. But this doesn’t matter for the is-
sue at hand.) The question is whether there exists a path (i.e., a sequence
of adjacent vertices) in this multigraph that traverses all the edges exactly
once and returns to a starting vertex. Such paths are called Eulerian cir-
cuits; if a path traverses all the edges exactly once but does not return to
itsstartingvertex,itiscalledanEulerian path.
b. Euler proved that an Eulerian circuit exists in a connected (multi)graph
if and only if all its vertices have even degrees, where the degree of a ver-
tex is defined as the number of edges for which it is an endpoint. Also,
an Eulerian path exists in a connected (multi)graph if and only if it has
exactly two vertices of odd degrees; such a path must start at one of those
two vertices and end at the other. Hence, for the multigraph of the puz-
zle, there exists neither an Eulerian circuit nor an Eulerian path because
all its four vertices have odd degrees.
If we are to be satisfied with an Eulerian path, two of the multigraph’s
vertices must be made even. This can be accomplished by adding one new
bridge connecting the same places as the existing bridges. For example,
a new bridge between the two islands would make possible, among others,
the walk a−b−c−a−b−d−c−b−d
b
a
c
d
b
a
c
d
If we want a walk that returns to its starting point, all the vertices in the
18
corresponding multigraph must be even. Since a new bridge/edge changes
the parity of two vertices, at least two new bridges/edges will be needed.
For example, here is one such “enhancement”:
b
a
c
d
b
a
c
d
This would make possible a−b−c−a−b−d−c−b−d−a, among
several other such walks.
5. A Hamiltonian circuit is marked on the graph below:
6. a. At least three “reasonable”criteria come to mind: the fastest trip, a
trip with the smallest number of train stops, and a trip that requires the
smallest number of train changes. Note that the first criterion requires
the information about the expected traveling time between stations and
the time needed for train changes whereas the other two criteria do not
require such information.
b. A natural approach is to mimic subway plans by representing sta-
tions by vertices of a graph, with two vertices connected by an edge if
there is a train line between the corresponding stations. If the time spent
on changing a train is to be taken into account (e.g., because the station
in question is on more than one line), the station should be represented
by more then one vertex.
19
7. a. Find a permutation of ngiven cities for which the sum of the distances
between consecutive cities in the permutation plus the distance between
its last and first city is as small as possible.
b. Partition all the graph’s vertices into the smallest number of disjoint
subsets so that there is no edge connecting vertices from the same subset.
8. a. Create a graph whose vertices represent the map’s regions and the
edges connect two vertices if and only if the corresponding regions have a
common border (and therefore cannot be colored the same color). Here
is the graph for the map given:
b
c
b
ad
c
e f
Solving the graph coloring problem for this graph yields the map’s color-
ing with the smallest number of colors possible.
b. Without loss of generality, we can assign colors 1 and 2 to vertices
cand a, respectively. This forces the following color assignment to the
remaining vertices: 3 to b, 2tod, 3tof, 4toe. Thus, the smallest number
of colors needed for this map is four.
Note: It’s a well-known fact that any map can be colored in four colors
or less. This problem–known as the Four-Color Problem–has remained
unresolved for more than a century until 1976 when it was finally solved by
theAmericanmathematiciansK.AppelandW.Hakenbyacombination
of mathematical arguments and extensive computer use.
9. If n=2, the answer is always “yes”; so, we may assume that n≥3.
Select three points P1,P
2,and P3from the set given. Write an equation
of the perpendicular bisector l1ofthelinesegmentwiththeendpointsat
P1and P2, which is the locus of points equidistant from P1and P2.Write
an equation of the perpendicular bisector l2of the line segment with the
endpoints at P2and P3, which is the locus of points equidistant from P2
and P3. Find the coordinates (x, y)of the intersection point Pof the lines
l1and l2by solving the system of two equations in two unknowns xand
y. (If the system has no solutions, return “no”: such a circumference
does not exist.) Compute the distances (or much better yet the distance
squares!) from Pto each of the points Pi,i=3,4, ..., n and check whether
all of them are the same: if they are, return “yes,” otherwise, return “no”.
20
Exercises 1.4
1. Describe how one can implement each of the following operations on an
array so that the time it takes does not depend on the array’s size n.
a. Delete the ith element of an array (1≤i≤n).
b. Delete the ith element of a sorted array (the remaining array has
to stay sorted, of course).
2. If you have to solve the searching problem for a list of nnumbers, how
can you take advantage of the fact that the list is known to be sorted?
Give separate answers for
a. lists represented as arrays.
b. lists represented as linked lists.
3. a. Show the stack after each operation of the following sequence that
starts with the empty stack:
push(a), push(b), pop, push(c), push(d), pop
b. Show the queue after each operation of the following sequence that
starts with the empty queue:
enqueue(a), enqueue(b), dequeue, enqueue(c), enqueue(d), dequeue
4. a. Let Abe the adjacency matrix of an undirected graph. Explain what
property of the matrix indicates that
i. the graph is complete.
ii. the graph has a loop, i.e., an edge connecting a vertex to itself.
iii. the graph has an isolated vertex, i.e., a vertex with no edges incident
to it.
b. Answer the same questions for the adjacency list representation.
5. Give a detailed description of an algorithm for transforming a free tree
into a tree rooted at a given vertex of the free tree.
6. Prove the inequalities that bracket the height of a binary tree with n
vertices:
log2n≤h≤n−1.
7. Indicate how the ADT priority queue can be implemented as
a. an (unsorted) array.
21
b.asortedarray.
c. a binary search tree.
8. How would you implement a dictionary of a reasonably small size nif
you knew that all its elements are distinct (e.g., names of 50 states of the
United States)? Specify an implementation of each dictionary operation.
9. For each of the following applications, indicate the most appropriate data
structure:
a. answering telephone calls in the order of their known priorities.
b. sending backlog orders to customers in the order they have been re-
ceived.
c. implementing a calculator for computing simple arithmetical expres-
sions.
10. Anagram checking Design an algorithm for checking whether two given
words are anagrams, i.e., whether one word can be obtained by permut-
ing the letters of the other. (For example, the words tea and eat are
anagrams.)
22
Hints to Exercises 1.4
1. a. Take advantage of the fact that the array is not sorted.
b. We used this trick in implementing one of the algorithms in Section
1.1.
2. a. For a sorted array, there is a spectacularly efficient algorithm you al-
most certainly have heard about.
b. Unsuccessful searches can be made faster.
3. a. Push(x) puts xon the top of the stack, pop deletes the item from the
topofthestack.
b. Enqueue(x) adds xto the rear of the queue, dequeue deletes the item
from the front of the queue.
4. Just use the definitions of the graph properties in question and data struc-
tures involved.
5. There are two well-known algorithms that can solve this problem. The
first uses a stack, the second uses a queue. Although these algorithms
are discussed later in the book, do not miss this chance to discover them
by yourself!
6. The inequality h≤n−1follows immediately from the height’s definition.
The lower bound inequality follows from inequality 2h+1 −1≥n, which
can be proved by considering the largest number of vertices a binary tree
of height hcan have.
7. You need to indicate how each of the three operations of the priority queue
will be implemented.
8. Because of insertions and deletions, using an array of the dictionary’s
elements (sorted or unsorted) is not the best implementation possible.
9. You need to know about the postfix notation in order to answer one of
these questions. (If you are not familiar with it, find the information on
the Internet.)
10. There are several algorithms for this problem. Keep in mind that the
words may contain multiple occurrences of the same letter.
23
Solutions to Exercises 1.4
1. a. Replace the ith element with the last element and decrease the array
size by 1.
b. Replace the ith element with a special symbol that cannot be a value
of the array’s element (e.g., 0 for an array of positive numbers) to mark
the ith position as empty. (This method is sometimes called the “lazy
deletion”.)
2. a. Use binary search (see Section 4.3 if you are not familiar with this
algorithm).
b. When searching in a sorted linked list, stop as soon as an element
greater than or equal to the search key is encountered.
3. a.
d
push(a)push(b)bpop push(c)cpush(d)cpopc
aaaaaa
b.
enqueue(a)enqueue(b)dequeue enqueue(c)enqueue(d)dequeue
aabbbcbcdcd
4. a. For the adjacency matrix representation:
i. A graph is complete if and only if all the elements of its adjacency
matrix except those on the main diagonal are equal to 1, i.e., A[i, j]=1
for every 1≤i, j ≤n, i =j.
ii. A graph has a loop if and only if its adjacency matrix has an ele-
ment equal to 1 on its main diagonal, i.e., A[i, i]=1for some 1≤i≤n.
iii. An (undirected, without loops) graph has an isolated vertex if and
only if its adjacency matrix has an all-zero row.
b. For the adjacency list representation:
i. A graph is complete if and only if each of its linked lists contains
all the other vertices of the graph.
ii. A graph has a loop if and only if one of its adjacency lists contains the
24
vertex defining the list.
iii. An (undirected, without loops) graph has an isolated vertex if and
only if one of its adjacency lists is empty.
5. The first algorithm works as follows. Mark a vertex to serve as the root
of the tree, make it the root of the tree to be constructed, and initialize
a stack with this vertex. Repeat the following operation until the stack
becomes empty: If there is an unmarked vertex adjacent to the vertex on
the top to the stack, mark the former vertex, attach it as a child of the
top’s vertex in the tree, and push it onto the stack; otherwise, pop the
vertex off the top of the stack.
The second algorithm works as follows. Mark a vertex to serve as the
root of the tree, make it the root of the tree to be constructed, and ini-
tialize a queue with this vertex. Repeat the following operations until
the queue becomes empty: If there are unmarked vertices adjacent to the
vertex at the front of the queue, mark all of them, attach them as children
to the front vertex in the tree, and add them to the queue; then dequeue
the queue.
6. Since the height is defined as the length of the longest simple path from
the tree’s root to its leaf, such a pass will include no more than nvertices,
which is the total number of vertices in the tree. Hence, h≤n−1.
The binary tree of height hwith the largest number of vertices is the full
tree that has all its h+1levels filled with the largest number of vertices
possible. The total number of vertices in such a tree is h
l=0 2l=2
h+1 −1.
Hence, for any binary tree with nvertices and height h
2h+1 −1≥n.
This implies that
2h+1 ≥n+1
or, after taking binary logarithms of both hand sides and taking into
account that h+1is an integer,
h+1≥log2(n+1).
Since log2(n+1)=log2n+1(see Appendix A), we finally obtain
h+1≥log2n+1or h≥log2n.
7. a. Insertion can be implemented by adding the new item after the ar-
ray’s last element. Finding the largest element requires a standard scan
25
through the array to find its largest element. Deleting the largest ele-
ment A[i]can be implemented by exchanging it with the last element and
decreasing the array’s size by 1.
b. We will assume that the array A[0..n −1] representing the priority
queue is sorted in ascending order. Inserting a new item of value vcan be
done by scanning the sorted array, say, left to right until an element A[j]
≥vor the end of the array is reached. (A faster algorithm for finding
a place for inserting a new element is binary search discussed in Section
4.3.) In the former case, the new item is inserted before A[j]by first mov-
ing A[n−1], ..., A[j]one position to the right; in the latter case, the new
item is simply appended after the last element of the array. Finding the
largest element is done by simply returning the value of the last element
of the sorted array. Deletion of the largest element is done by decreasing
thearray’ssizebyone.
c. Insertion of a new element is done by using the standard algorithm
for inserting a new element in a binary search tree: recursively, the new
key is inserted in the left or right subtree depending on whether it is
smaller or larger than the root’s key. Finding the largest element will
require finding the rightmost element in the binary tree by starting at
the root and following the chain of the right children until a vertex with
no right subtree is reached. The key of that vertex will be the largest
element in question. Deleting it can be done by making the right pointer
of its parent to point to the left child of the vertex being deleted;. if the
rightmost vertex has no left child, this pointer is made “null”. Finally, if
the rightmost vertex has no parent, i.e., if it happens to be the root of the
tree, its left child becomes the new root; if there is no left child, the tree
becomes empty.
8. Use a bit vector, i.e., an array on nbits in which the ith bit is 1 if
the ith element of the underlying set is currently in the dictionary and
0 otherwise. The search, insertion, and deletion operations will require
checking or changing a single bit of this array.
9. Use: (a) a priority queue; (b) a queue; (c) a stack (and reverse Polish
notation–a clever way of representing arithmetical expressions without
parentheses, which is usually studied in a data structures course).
10. The most straightforward solution is to search for each successive letter
of the first word in the second one. If the search is successful, delete the
first occurrence of the letter in the second word, stop otherwise.
Another solution is to sort the letters of each word and then compare
26
them in a simple parallel scan.
We can also generate and compare “letter vectors” of the given words:
Vw[i]=the number of occurrences of the alphabet’s ith letter in the word
w. Such a vector can be generated by initializing all its components to
0 and then scanning the word and incrementing appropriate letter counts
in the vector.
27
This file contains the exercises, hints, and solutions for Chapter 2 of the
book ”Introduction to the Design and Analysis of Algorithms,” 2nd edition, by
A. Levitin. The problems that might be challenging for at least some students
are marked by ;those that might be difficult for a majority of students are
marked by .
Exercises 2.1
1. For each of the following algorithms, indicate (i) a natural size metric for
its inputs; (ii) its basic operation; (iii) whether the basic operation count
can be different for inputs of the same size:
a. computing the sum of nnumbers
b. computing n!
c. finding the largest element in a list of nnumbers
d. Euclid’s algorithm
e. sieve of Eratosthenes
f. pen-and-pencil algorithm for multiplying two n-digit decimal integers
2. a. Consider the definition-based algorithm for adding two n-by-nmatri-
ces. What is its basic operation? How many times is it performed as
a function of the matrix order n? As a function of the total number of
elements in the input matrices?
b. Answer the same questions for the definition-based algorithm for matrix
multiplication.
3. Consider a variation of sequential search that scans a list to return the
number of occurrences of a given search key in the list. Will its efficiency
differ from the efficiency of classic sequential search?
4. a. Glove selection There are 22 gloves in a drawer: 5 pairs of red gloves,
4 pairs of yellow, and 2 pairs of green. You select the gloves in the dark
and can check them only after a selection has been made. What is the
smallest number of gloves you need to select to have at least one matching
pair in the best case? in the worst case? (after [Mos01], #18)
b. Missing socks Imagine that after washing 5 distinct pairs of socks,
you discover that two socks are missing. Of course, you would like to have
the largest number of complete pairs remaining. Thus, you are left with
4 complete pairs in the best-case scenario and with 3 complete pairs in
the worst case. Assuming that the probability of disappearance for each
1

of the 10 socks is the same, find the probability of the best-case scenario;
the probability of the worst-case scenario; the number of pairs you should
expect in the average case. (after [Mos01], #48)
5. a.Prove formula (2.1) for the number of bits in the binary representation
of a positive integer.
b. What would be the analogous formula for the number of decimal digits?
c. Explain why, within the accepted analysis framework, it does not mat-
ter whether we use binary or decimal digits in measuring n’s size.
6. Suggest how any sorting algorithm can be augmented in a way to make
the best-case count of its key comparisons equal to just n−1(nis a list’s
size, of course). Do you think it would be a worthwhile addition to any
sorting algorithm?
7. Gaussian elimination, the classic algorithm for solving systems of nlinear
equations in nunknowns, requires about 1
3n3multiplications, which is the
algorithm’s basic operation.
a. How much longer should you expect Gaussian elimination to work
on a system of 1000 equations versus a system of 500 equations?
b. You are considering buying a computer that is 1000 times faster than
the one you currently have. By what factor will the faster computer in-
crease the sizes of systems solvable in the same amount of time as on the
old computer?
8. For each of the following functions, indicate how much the function’s value
will change if its argument is increased fourfold.
a. log2nb. √nc. nd. n2e. n3f. 2n
9. Indicate whether the first function of each of the following pairs has a
smaller, same, or larger order of growth (to within a constant multiple)
than the second function.
a. n(n+1) and 2000n2b. 100n2and 0.01n3
c. log2nand ln nd. log2
2nand log2n2
e. 2n−1and 2nf. (n−1)! and n!
10. Invention of chess According to a well-known legend, the game of chess
was invented many centuries ago in northwestern India by a sage named
Shashi. When he took his invention to his king, the king liked the game
2
so much that he offered the inventor any reward he wanted. Sashi asked
for some grain to be obtained as follows: just a single grain of wheat was
to be placed on the first square of the chess board, two on the second, four
on the third, eight on the fourth, and so on, until all 64 squares had been
filled. What would the ultimate result of this algorithm have been?
3
Hints to Exercises 2.1
1. The questions are indeed as straightforward as they appear, though some
of them may have alternative answers. Also, keep in mind the caveat
about measuring an integer’s size.
2. a. The sum of two matrices is defined as the matrix whose elements are
the sums of the corresponding elements of the matrices given.
b. Matrix multiplication requires two operations: multiplication and ad-
dition. Which of the two would you consider basic and why?
3. Will the algorithm’s efficiency vary on different inputs of the same size?
4. a. Gloves are not socks: they can be right-handed and left-handed.
b. You have only two qualitatively different outcomes possible. Count
the number of ways to get each of the two.
5. a. Prove first that if a positive decimal integer nhas bdigits in its binary
representation then
2b−1≤n<2b.
Then take logarithms to base 2 of the terms in this inequality.
b. The formula will be the same, with just one small adjustment to ac-
count for the different radix.
c. How can we switch from one logarithm base to another?
6. Insert a verification of whether the problem is already solved.
7. A similar question was investigated in the section.
8. Use either the difference between or the ratio of f(4n)and f(n),whichever
is more convenient for getting a compact answer. If it is possible, try to
get an answer that does not depend on n.
9. If necessary, simplify the functions in question to single out terms defining
their orders of growth to within a constant multiple. (We will discuss
formal methods for answering such questions in the next section; however,
these questions can be answered without knowledge of such methods.)
10. Use the formula n
i=0 2i=2
n+1 −1.
4
Solutions to Exercises 2.1
1. The answers are as follows.
a. (i) n;(ii) addition of two numbers; (iii) no
b. (i) the magnitude of n, i.e., the number of bits in its binary repre-
sentation; (ii) multiplication of two integers; (iii) no
c. (i) n;(ii) comparison of two numbers; (iii) no (for the standard
list scanning algorithm)
d. (i) either the magnitude of the larger of two input numbers, or the
magnitude of the smaller of two input numbers, or the sum of the magni-
tudes of two input numbers; (ii) modulo division; (iii) yes
e. (i) the magnitude of n, i.e., the number of bits in its binary represen-
tation; (ii) elimination of a number from the list of remaining candidates
to be prime; (iii) no
f. (i) n; (ii) multiplication of two digits; (iii) no
2. a. Addition of two numbers. It’s performed n2times (once for each of
n2elements in the matrix being computed). .Since the total number of
elements in two given matrices is N=2n2,the total number of additions
can also be expressed as n2=N/2.
b. Since on most computers multiplication takes longer than addition,
multiplication is a better choice for being considered the basic operation
of the standard algorithm for matrix multiplication. Each of n2elements
of the product of two n-by-nmatrices is computed as the scalar (dot)
product of two vectors of size n, which requires nmultiplications. The
total number of multiplications is n·n2=n3=(N/2)3/2.
3. This algorithm will always make nkey comparisons on every input of size
n, whereas this number may vary between nand 1 for the classic version
of sequential search.
4. a. The best-case number is, obviously, two. The worst-case number is
twelve: one more than the number of gloves of one handedness.
b. There are just two possible outcomes here: the two missing socks
make a pair (the best case) and the two missing stocks do not make a
pair (the worst case). The total number of different outcomes (the ways
5

to choose the missing socks) is 10
2=45.The number of best-case ones
is 5; hence its probability is 5
45 =1
9.The number of worst-case ones is
45 −5 = 40; hence its probability is 40
45 =8
9.On average, you should
expect 4·1
9+3·8
9=28
9=3
1
9matching pairs.
5. a. The smallest positive integer that has bbinary digits in its binary
expansion is 10...0
b−1
,which is 2b−1;the largest positive integer that has b
binary digits in its binary expansion is 11...1
b−1
,which is 2b−1+2b−2+...+1 =
2b−1.Thus,
2b−1≤n<2b.
Hence
log22b−1≤log2n<log22b
or
b−1≤log2n<b.
These inequalities imply that b−1is the largest integer not exceeding
log2n. In other words, using the definition of the floor function, we con-
clude that
b−1=log2nor b=log2n+1.
b. B=log10 n+1.
c. b=log2n+1 ≈log2n=log
210 log10 n≈(log210)B,whereB=
log10 n+1.That is, the two size metrics are about equal to within a
constant multiple for large values of n.
6. Before applying a sorting algorithm, compare the adjacent elements of
its input: if ai≤ai+1 for every i=0, .., n −2,stop. Generally, it
is not a worthwhile addition because it slows down the algorithm on all
but very special inputs. Note that some sorting algorithms (notably
bubble sort and insertion sort, which are discussed in Sections 3.1 and
5.1, respectively) intrinsically incorporate this test in the body of the
algorithm.
7. a. T(2n)
T(n)≈c(2n)
c n =8,wherecMis the time of one multiplication.
b. We can estimate the running time for solving systems of order non
the old computer and that of order Non the new computer as Told(n)≈
cM1
3n3and Tnew (N)≈10−3cM1
3N3,respectively, where cMis the time of
one multiplication on the old computer. Replacing Told(n)and Tnew(N)
6
by these estimates in the equation Told(n)=Tnew(N)yields cM1
3n3≈
10−3cM1
3N3or N
n≈10.
8. a. log24n−log2n= (log24+log
2n)−log2n=2.
b. √4n
√n=2.
c. 4n
n=4.
d. (4n)
n=4
2.
e. (4n)
n=4
3.
f. 2
2=2
3n=(2
n)3.
9. a. n(n+1)≈n2has the same order of growth (quadratic) as 2000n2to
within a constant multiple.
b. 100n2(quadratic) has a lower order of growth than 0.01n3(cubic).
c. Since changing a logarithm’s base can be done by the formula
logan=log
ablogbn,
all logarithmic functions have the same order of growth to within a con-
stant multiple.
d. log2
2n=log
2nlog2nand log2n2= 2 log n. Hence log2
2nhas a higher
order of growth than log2n2.
e. 2n−1=1
22nhas the same order of growth as 2nto within a con-
stant multiple.
f. (n−1)! has a lower order of growth than n!=(n−1)!n.
10. An unimaginable ruin: 64
i=1 2i−1=63
j=0 2j=2
64 −1≈1.8·1019.
(You may want to estimate the amount of space all this grain would have
occupied.)
7

Exercises 2.2
1. Use the most appropriate notation among O, Θ,and Ωto indicate the
time efficiency class of sequential search (see Section 2.1)
a. in the worst case.
b. in the best case.
c. in the average case.
2. Use the informal definitions of O, Θ,and Ωto determine whether the fol-
lowing assertions are true or false.
a. n(n+1)/2∈O(n3)b. n(n+1)/2∈O(n2)
c. n(n+1)/2∈Θ(n3)d. n(n+1)/2∈Ω(n)
3. For each of the following functions, indicate the class Θ(g(n)) the function
belongs to. (Use the simplest g(n)possible in your answers.) Prove your
assertions.
a. (n2+1)
10 b. √10n2+7n+3
c. 2nlg(n+2)
2+(n+2)
2lg n
2d. 2n+1 +3
n−1
e. log2n
4. a. Table 2.1 contains values of several functions that often arise in analysis
of algorithms. These values certainly suggest that the functions
log n, n, n log n, n2,n
3,2n,n!
are listed in increasing order of their order of growth. Do these values
prove this fact with mathematical certainty?
b. Prove that the functions are indeed listed in increasing order of their
order of growth.
5. Order the following functions according to their order of growth (from the
lowest to the highest):
(n−2)!,5lg(n+ 100)10,22n,0.001n4+3n3+1,ln2n,√n, 3n.
6. a. Prove that every polynomial of degree k, p(n)=aknk+ak−1nk−1+
... +a0,with ak>0belongs to Θ(nk).
b. Prove that exponential functions anhave different orders of growth
for different values of base a>0.
8
7. Prove (by using the definitions of the notations involved) or disprove (by
giving a specific counterexample) the following assertions.
a. If t(n)∈O(g(n)),then g(n)∈Ω(t(n)).
b. Θ(αg(n)) = Θ(g(n)),where α>0.
c. Θ(g(n)) = O(g(n)) ∩Ω(g(n)).
d.For any two nonnegative functions t(n)and g(n)defined on the set of
nonnegative integers, either t(n)∈O(g(n)),or t(n)∈Ω(g(n)),or both.
8. Prove the section’s theorem for
a. Ωnotation.
b. Θnotation.
9. We mentioned in this section that one can check whether all elements of an
array are distinct by a two-part algorithm based on the array’s presorting.
a. If the presorting is done by an algorithm with the time efficiency in
Θ(nlog n),what will be the time efficiency class of the entire algorithm?
b. If the sorting algorithm used for presorting needs an extra array of
size n, what will be the space efficiency class of the entire algorithm?
10. Door in a wall You are facing a wall that stretches infinitely in both
directions. There is a door in the wall, but you know neither how far
away nor in which direction. You can see the door only when you are
right next to it. Design an algorithm that enables you to reach the door
by walking at most O(n)steps where nis the (unknown to you) number
of steps between your initial position and the door. [Par95], #652
9
Hints to Exercises 2.2
1. Use the corresponding counts of the algorithm’s basic operation (see Sec-
tion 2.1) and the definitions of O, Θ,and Ω.
2. Establishtheorderofgrowthofn(n+1)/2first and then use the informal
definitions of O, Θ,and Ω. (Similar examples were given in the section.)
3. Simplify the functions given to single out the terms defining their orders
of growth.
4. a. Check carefully the pertinent definitions.
b. Compute the ratio limits of every pair of consecutive functions on
the list.
5. First simplify some of the functions. Then use the list of functions in Table
2.2 to “anchor” each of the functions given. Prove their final placement
by computing appropriate limits.
6. a. You can prove this assertion either by computing an appropriate limit
or by applying mathematical induction.
b. Compute lim
n→∞
an
1/an
2.
7. Prove the correctness of (a), (b), and (c) by using the appropriate de-
finitions; construct a counterexample for (d) (e.g., by constructing two
functions behaving differently for odd and even values of their arguments).
8. The proof of part (a) is similar to the one given for the theorem’s assertion
in Section 2.2. Of course, different inequalities need to be used to bound
the sum from below.
9. Follow the analysis plan used in the text when the algorithm was men-
tioned for the first time.
10. You should walk intermittently left and right from your initial position
until the door is reached.
10
Solutions to Exercises 2.2
1. a. Since Cworst(n)=n, Cworst(n)∈Θ(n).
b. Since Cbest(n)=1,C
best(1) ∈Θ(1).
c. Since Cavg(n)=p(n+1)
2+n(1 −p)=(1−p
2)n+p
2where 0≤p≤1,
Cavg(n)∈Θ(n).
2. n(n+1)/2≈n2/2is quadratic. Therefore
a. n(n+1)/2∈O(n3)is true. b. n(n+1)/2∈O(n2)is true.
c. n(n+1)/2∈Θ(n3)is false. d. n(n+1)/2∈Ω(n)is true.
3. a. Informally, (n2+1)
10 ≈(n2)10 =n20 ∈Θ(n20)Formally,
lim
n→∞
(n+1)
n= lim
n→∞
(n+1)
(n)=lim
n→∞ n+1
n10 == lim
n→∞ 1+ 1
n10 =1.
Hence (n2+1)
10 ∈Θ(n20).
Note: An alternative proof can be based on the binomial formula and
the assertion of Exercise 6a.
b. Informally, √10n2+7n+3≈√10n2=√10n∈Θ(n).Formally,
lim
n→∞
√10n+7n+3
n=lim
n→∞10n+7n+3
n= lim
n→∞10 + 7
n+3
n=√10.
Hence √10n2+7n+3∈Θ(n).
c. 2nlg(n+2)
2+(n+2)
2lg n
2=2n2lg(n+2)+(n+2)
2(lg n−1) ∈
Θ(nlg n)+Θ(n2lg n)=Θ(n2lg n).
d. 2n+1 +3
n−1=2
n2+3
n1
3∈Θ(2n)+Θ(3
n)=Θ(3
n).
e. Informally, log2n≈log2n∈Θ(log n).Formally, by using the in-
equalities x−1<x≤x(see Appendix A), we obtain an upper bound
log2n≤log2n
andalowerbound
log2n>log2n−1≥log2n−1
2log2n(for every n≥4) = 1
2log2n.
Hence log2n∈Θ(log2n) = Θ(log n).
11
4. a. The order of growth and the related notations O, Ω,andΘdeal with
the asymptotic behavior of functions as ngoes to infinity. Therefore no
specific values of functions within a finite range of n’s values, suggestive
as they might be, can establish their orders of growth with mathematical
certainty.
b. lim
n→∞
log n
n=lim
n→∞
(log n)
(n)=lim
n→∞
log e
1=log
2elim
n→∞
1
n=0.
lim
n→∞
n
nlog n= lim
n→∞
1
log n=0.
lim
n→∞
nlog n
n= lim
n→∞
log n
n=(see the first limit of this exercise) =0.
lim
n→∞
n
n= lim
n→∞
1
n=0.
lim
n→∞
n
2= lim
n→∞
(n)
(2 )= lim
n→∞
3n
2ln 2 =3
ln 2 lim
n→∞
n
2=3
ln 2 lim
n→∞
(n)
(2 )
=3
ln 2 lim
n→∞
2n
2ln 2 =6
ln 2lim
n→∞
n
2=6
ln 2lim
n→∞
(n)
(2 )
=6
ln 2lim
n→∞
1
2ln 2 =6
ln 2lim
n→∞
1
2=0.
lim
n→∞
2
n!=(see Example 3 in the section) 0.
5. (n−2)! ∈Θ((n−2)!),5lg(n+100)10 =50lg(n+100) ∈Θ(log n),22n=
(22)n∈Θ(4n),0.001n4+3n3+1∈Θ(n4),ln2n∈Θ(log2n),√n∈
Θ(n),3n∈Θ(3n).The list of these functions ordered in increasing
order of growth looks as follows:
5lg(n+ 100)10,ln2n, √n, 0.001n4+3n3+1,3n,22n,(n−2)!
6. a. lim
n→∞
p(n)
n= lim
n→∞
an+a n +...+a
n= lim
n→∞
(ak+a
n+... +a
n)
=ak>0.
Hence p(n)∈Θ(nk).
b.
lim
n→∞
an
1
an
2
=lim
n→∞ a1
a2n
=
0if a1<a
2⇔an
1∈o(an
2)
1if a1=a2⇔an
1∈Θ(an
2)
∞if a1>a
2⇔an
2∈o(an
1)
7. a. The assertion should be correct because it states that if the order of
growth of t(n)is smaller than or equal to the order of growth of g(n),then
12

the order of growth of g(n)is larger than or equal to the order of growth
of t(n).The formal proof is immediate, too:
t(n)≤cg(n)for all n≥n0,where c>0,
implies
(1
c)t(n)≤g(n)for all n≥n0.
b. The assertion that Θ(αg(n)) = Θ(g(n)) should be true because αg(n)
and g(n)differ just by a positive constant multiple and, hence, by the
definition of Θ,must have the same order of growth. The formal proof
has to show that Θ(αg(n)) ⊆Θ(g(n)) and Θ(g(n)) ⊆Θ(αg(n)).Let
f(n)∈Θ(αg(n)); we’ll show that f(n)∈Θ(g(n)).Indeed,
f(n)≤cαg(n)for all n≥n0(where c>0)
can be rewritten as
f(n)≤c1g(n)for all n≥n0(where c1=cα > 0),
i.e., f(n)∈Θ(g(n)).
Let now f(n)∈Θ(g(n)); we’ll show that f(n)∈Θ(αg(n)) for α>0.
Indeed, if f(n)∈Θ(g(n)),
f(n)≤cg(n)for all n≥n0(where c>0)
and therefore
f(n)≤c
αag(n)=c1αg(n)for all n≥n0(where c1=c
α>0),
i.e., f(n)∈Θ(αg(n)).
c. The assertion is obviously correct (similar to the assertion that a=b
if and only if a≤band a≥b). The formal proof should show that
Θ(g(n)) ⊆O(g(n)) ∩Ω(g(n)) and that O(g(n)) ∩Ω(g(n)) ⊆Θ(g(n)),
which immediately follow from the definitions of O, Ω,andΘ.
d. The assertion is false. The following pair of functions can serve as
a counterexample
t(n)=
nif nis even
n2if nis odd
and g(n)=
n2if nis even
nif nis odd
13
8. a. We need to prove that if t1(n)∈Ω(g1(n)) and t2(n)∈Ω(g2(n)), then
t1(n)+t2(n)∈Ω(max{g1(n),g
2(n)}).
Proof Since t1(n)∈Ω(g1(n)),there exist some positive constant c1
and some nonnegative integer n1such that
t1(n)≥c1g1(n)for all n≥n1.
Since t2(n)∈Ω(g2(n)),there exist some positive constant c2and some
nonnegative integer n2such that
t2(n)≥c2g2(n)for all n≥n2.
Let us denote c=min{c1,c
2}and consider n≥max{n1,n
2}so that we
can use both inequalities. Adding the two inequalities above yields the
following:
t1(n)+t2(n)≥c1g1(n)+c2g2(n)
≥cg1(n)+cg2(n)=c[g1(n)+g2(n)]
≥cmax{g1(n),g
2(n)}.
Hence t1(n)+t2(n)∈Ω(max{g1(n),g
2(n)}), with the constants cand
n0required by the Odefinition being min{c1,c
2}and max{n1,n
2},re-
spectively.
b. The proof follows immediately from the theorem proved in the text
(the Opart), the assertion proved in part (a) of this exercise (the Ωpart),
and the definition of Θ(see Exercise 7c).
9. a. Since the running time of the sorting part of the algorithm will still
dominate the running time of the second, it’s the former that will deter-
mine the time efficiency of the entire algorithm. Formally, it follows from
equality
Θ(nlog n)+O(n)=Θ(nlog n),
whose validity is easy to prove in the same manner as that of the section’s
theorem.
b. Since the second part of the algorithm will use no extra space, the
space efficiency class will be determined by that of the first (sorting) part.
Therefore, it will be in Θ(n).
10. The key idea here is to walk intermittently right and left going each time
exponentially farther from the initial position. A simple implementation
of this idea is to do the following until the door is reached: For i=0,1, ...,
make 2isteps to the right, return to the initial position, make 2isteps to
14
the left, and return to the initial position again. Let 2k−1<n≤2k.The
number of steps this algorithm will need to find the door can be estimated
aboveasfollows:
k−1
i=0
4·2i+3·2k=4(2
k−1) + 3 ·2k<7·2k=14·2k−1<14n.
Hence the number of steps made by the algorithm is in O(n).(Note:
It is not difficult to improve the multiplicative constant with a better
algorithm.)
15

Exercises 2.3
1. Compute the following sums.
a. 1+3+5+7+... + 999
b. 2+4+8+16+... + 1024
c. n+1
i=3 1d. n+1
i=3 ie. n−1
i=0 i(i+1)
f. n
j=1 3j+1 g. n
i=1 n
j=1 ij h. n−1
i=0 1/i(i+1)
2. Find the order of growth of the following sums.
a. n−1
i=0 (i2+1)2b. n−1
i=2 lg i2
c. n
i=1(i+1)2
i−1d. n−1
i=0 i−1
j=0(i+j)
Use the Θ(g(n)) notation with the simplest function g(n)possible.
3. The sample variance of nmeasurements x1,x
2, ..., xncan be computed as
n
i=1(xi−¯x)2
n−1where ¯x=n
i=1 xi
n
or n
i=1 x2
i−(n
i=1 xi)2/n
n−1.
Find and compare the number of divisions, multiplications, and addi-
tions/subtractions (additions and subtractions are usually bunched to-
gether) that are required for computing the variance according to each of
these formulas.
4. Consider the following algorithm.
Algorithm Mystery( n)
//Input: A nonnegative integer n
S←0
for i←1to ndo
S←S+i∗i
return S
a. What does this algorithm compute?
b. What is its basic operation?
c. How many times is the basic operation executed?
16

d. What is the efficiency class of this algorithm?
e. Suggest an improvement or a better algorithm altogether and indi-
cate its efficiency class. If you cannot do it, try to prove that, in fact, it
cannot be done.
5. Consider the following algorithm.
Algorithm Secret(A[0..n −1])
//Input: An array A[0..n −1] of nreal numbers
minval ←A[0]; maxval ←A[0]
for i←1to n−1do
if A[i]<minval
minval ←A[i]
if A[i]>maxval
maxval ←A[i]
return maxval −minval
Answer questions a—e of Problem 4 about this algorithm.
6. Consider the following algorithm.
Algorithm Enigma(A[0..n −1,0..n −1])
//Input: A matrix A[0..n −1,0..n −1] of real numbers
for i←0to n−2do
for j←i+1to n−1do
if A[i, j]=A[j, i]
return false
return true
Answer the questions a—e of Problem 4 about this algorithm.
7. Improve the implementation of the matrix multiplication algorithm (see
Example 3) by reducing the number of additions made by the algorithm.
What effect will this change have on the algorithm’s efficiency?
8. Determine the asymptotic order of growth for the total number of times all
the doors are toggled in the Locker Doors puzzle (Problem 11 in Exercises
1.1).
9. Prove the formula
n
i=1
i=1+2+... +n=n(n+1)
2
either by mathematical induction or by following the insight of a 10-year
old schoolboy named Karl Friedrich Gauss (1777—1855) who grew up to
become one of the greatest mathematicians of all times.
17

10. Consider the following version of an important algorithm that we will
study later in the book.
Algorithm GE (A[0..n−1,0..n])
//Input: An n-by-n+1 matrix A[0..n −1,0..n]of real numbers
for i←0to n−2do
for j←i+1to n−1do
for k←ito ndo
A[j, k]←A[j, k]−A[i, k]∗A[j, i]/A[i, i]
a.Find the time efficiency class of this algorithm.
b.What glaring inefficiency does this pseudocode contain and how can
it be eliminated to speed the algorithm up?
11. von Neumann’s neighborhood How many one-by-one squares are gener-
ated by the algorithm that starts with a single square square and on each
of its niterations adds new squares all round the outside. How many
one-by-one squares are generated on the nth iteration? [Gar99, p.88] (In
the parlance of cellular automata theory, the answer is the number of cells
in the von Neumann neighborhood of range n.) The results for n=0,1,
and 2 are illustrated below:
n=0 n=1 n=2
18
Hints to Exercises 2.3
1. Use the common summation formulas and rules listed in Appendix A. You
may need to perform some simple algebraic operations before applying
them.
2. Find a sum among those in Appendix A that looks similar to the sum in
question and try to transform the latter to the former. Note that you
do not have to get a closed-end formula for a sum before establishing its
order of growth.
3. Just follow the formulas in question.
4. a. Tracing the algorithm to get its output for a few small values of n(e.g.,
n=1,2,and 3) should help if you need it.
b. We faced the same question for the examples discussed in the text.
One of them is particularly pertinent here.
c. Follow the plan outlined in this section.
d. As a function of n, the answer should follow immediately from your
answer to part c. You may also want to give an answer as a function of
the number of bits in the n’s representation (why?).
e. Have you not encountered this sum somewhere?
5. a. Tracing the algorithm to get its output for a few small values of n(e.g.,
n=1,2,and 3) should help if you need it.
b. We faced the same question for the examples discussed in the text.
One of them is particularly pertinent here.
c. You can either follow the section’s plan by setting up and comput-
ing a sum or answer the question directly. (Try to do both.)
d. Your answer will immediately follow from the answer to part c).
e. Does the algorithm always have to make two comparisons on each
iteration? This idea can be developed further to get a more significant
improvement than the obvious one–try to do it for a two-element array
and then generalize the insight. But can we hope to find an algorithm
with a better than linear efficiency?
6. a. Elements A[i, j]and A[j, i]are symmetric with respect to the main
diagonal of the matrix.
b. There is just one candidate here.
19
c. You may investigate the worst case only.
d. Your answer will immediately follow from the answer to part c.
e. Compare the problem the algorithm solves with the way it does this.
7. Computing a sum of nnumbers can be done with n−1additions. How
many does the algorithm make in computing each element of the product
matrix?
8. Set up a sum for the number of times all the doors and toggled and find
its asymptotic order of growth by using some properties from Appendix
A.
9. For the general step of the proof by induction, use the formula
n
i=1
i=
n−1
i=1
i+n.
The young Gauss computed the sum 1+2+... + 99 + 100 by noticing that
it can be computed as the sum of 50 pairs, each with the same sum.
10. a. Setting up a sum should pose no difficulties. Using the standard sum-
mation formulas and rules will require more effort than in the previous
examples, however.
b. Optimize the algorithm’s innermost loop.
11. Set up a sum for the number of squares after niterations of the algorithm
and then simplify it to get a closed-form answer.
20

Solutions to Exercises 2.3
1. a. 1+3+5+7+...+999 =
500
i=1
(2i-1) =
500
i=1
2i-
500
i=1
1=2
500∗501
2-500 = 250,000.
(Or by using the formula for the sum of odd integers:
500
i=1
(2i-1) = 5002=
250,000.
Or by using the formula for the sum of the arithmetic progression with
a1=1,a
n= 999,and n= 500:(a+a)n
2=(1+999)500
2=250,000.)
b. 2+4+8+16+... +1,024 =
10
i=1
2i=
10
i=0
2i−1=(2
11 −1) −1=2,046.
(Or by using the formula for the sum of the geometric series with a=2,
q=2,andn=9:aq−1
q−1=2
2−1
2−1=2,046.)
c.
n+1
i=3
1=(n+1)−3+1=n−1.
d.
n+1
i=3
i=
n+1
i=0
i−
2
i=0
i=(n+1)(n+2)
2−3=n+3n−4
2.
e.
n−1
i=0
i(i+1)=
n−1
i=0
(i2+i)=
n−1
i=0
i2+
n−1
i=0
i=(n−1)n(2n−1)
6+(n−1)n
2
=(n−1)n
3.
f.
n
j=1
3j+1 =3
n
j=1
3j=3[
n
j=0
3j−1] = 3[3−1
3−1−1] = 3−9
2.
g.
n
i=1
n
j=1
ij =
n
i=1
i
n
j=1
j=
n
i=1
in(n+1)
2=n(n+1)
2
n
i=1
i=n(n+1)
2
n(n+1)
2
=n(n+1)
4.
h. n
i=1 1/i(i+1)=n
i=1(1
i−1
i+1 )
=(
1
1−1
2)+(1
2−1
3)+... +( 1
n−1−1
n)+(1
n−1
n+1 )=1−1
n+1 =n
n+1 .
(This is a special case of the so-called telescoping series–see Appendix
A–u
i=l(ai−ai−1)=au−al−1.)
2. a.
n−1
i=0
(i2+1)
2=
n−1
i=0
(i4+2i2+1)=
n−1
i=0
i4+2
n−1
i=0
i2+
n−1
i=0
1
∈Θ(n5)+Θ(n3)+Θ(n)=Θ(n5)(or just
n−1
i=0
(i2+1)
2≈
n−1
i=0
i4∈Θ(n5)).
b.
n−1
i=2
log2i2=
n−1
i=2
2log
2i=2
n−1
i=2
log2i=2
n
i=1
log2i−2log
2n
∈2Θ(nlog n)−Θ(log n)=Θ(nlog n).
21
c.
n
i=1
(i+1)2
i−1=
n
i=1
i2i−1+
n
i=1
2i−1=1
2
n
i=1
i2i+
n−1
j=0
2j
∈Θ(n2n)+Θ(2
n)=Θ(n2n)(or
n
i=1
(i+1)2
i−1≈1
2
n
i=1
i2i∈Θ(n2n)).
d.
n−1
i=0
i−1
j=0
(i+j)=
n−1
i=0
[
i−1
j=0
i+
i−1
j=0
j]=
n−1
i=0
[i2+(i−1)i)
2]=
n−1
i=0
[3
2i2−1
2i]
=3
2
n−1
i=0
i2−1
2
n−1
i=0
i∈Θ(n3)−Θ(n2)=Θ(n3).
3. For the first formula: D(n)=2,M(n)=n, A(n)+S(n)=[(n−1) +
(n−1)] + (n+1)=3n−1.
For the second formula: D(n)=2,M(n)=n+1,A(n)+S(n)=
[(n−1) + (n−1)] + 2 = 2n.
4. a. Computes S(n)=
n
i=1
i2.
b. Multiplication (or, if multiplication and addition are assumed to take
the same amount of time, either of the two).
c. C(n)=
n
i=1
1=n.
d. C(n)=n∈Θ(n).Since the number of bits b=log2n+1≈log2n
and hence n≈2b,C(n)≈2b∈Θ(2b).
e. Use the formula
n
i=1
i2=n(n+1)(2n+1)
6to compute the sum in Θ(1)
time (which assumes that the time of arithmetic operations stay constant
irrespective of the size of the operations’ operands).
5. a. Computes the range, i.e., the difference between the array’s largest and
smallest elements.
b. An element comparison.
c. C(n)=
n−1
i=1
2=2(n−1).
d. Θ(n).
e. An obvious improvement for some inputs (but not for the worst case)
is to replace the two if-statements by the following one:
if A[i]<minval minval ←A[i]
22

else if A[i]>maxval maxval ←A[i].
Another improvement, both more subtle and substantial, is based on the
observation that it is more efficient to update the minimum and maximum
values seen so far not for each element but for a pair of two consecutive
elements. If two such elements are compared with each other first, the
updates will require only two more comparisons for the total of three com-
parisons per pair. Note that the same improvement can be obtained by
a divide-and-conquer algorithm (see Chapter 4).
6. a. The algorithm returns “true” if its input matrix is symmetric and
“false” if it is not.
b. Comparison of two matrix elements.
c. Cworst(n)=
n−2
i=0
n−1
j=i+1
1=
n−2
i=0
[(n−1) −(i+1)+1)
=
n−2
i=0
(n−1−i)=(n−1) + (n−2) + ... +1= (n−1)n
2.
d. Quadratic: Cworst(n)∈Θ(n2)(or C(n)∈O(n2)).
e. The algorithm is optimal because any algorithm that solves this prob-
lem must, in the worst case, compare (n−1)n/2elements in the upper-
triangular part of the matrix with their symmetric counterparts in the
lower-triangular part, which is all this algorithm does.
7. Replace the body of the jloop by the following fragment:
C[i, j]←A[i, 0] ∗B[0,j]
for k←1to n−1do
C[i, j]←C[i, j]+A[i, k]∗B[k, j]
This will decrease the number of additions from n3to n3−n2,butthe
number of multiplications will still be n3.The algorithm’s efficiency class
will remain cubic.
8. Let T(n)be the total number of times all the doors are toggled. The
problem statement implies that
T(n)=
n
i=1n/i.
Since x−1<x≤xand n
i=1 1/i ≈ln n+γ,whereγ=0.5772...(see
23
Appendix A),
T(n)≤
n
i=1
n/i =n
n
i=1
1/i ≈n(ln n+γ)∈Θ(nlog n).
Similarly,
T(n)>
n
i=1
(n/i −1) = n
n
i=1
1/i −
n
i=1
1≈n(ln n+γ)−n∈Θ(nlog n).
This implies that T(n)∈Θ(nlog n).
Note: Alternatively, we could use the formula for approximating sums
by definite integrals (see Appendix A):
T(n)≤
n
i=1
n/i =n(1+
n
i=2
1/i)≤n(1+n
1
1
xdx)=n(1+ln n)∈Θ(nlog n)
and
T(n)>
n
i=1
(n/i−1) = n
n
i=1
1/i−
n
i=1
1≥nn+1
1
1
xdx−n=nln(n+1)−n∈Θ(nlog n).
9. Here is a proof by mathematical induction that
n
i=1
i=n(n+1)
2for every
positive integer n.
(i) Basis step: For n=1,
n
i=1
i=
1
i=1
i=1and n(n+1)
2n=1 =1(1+1)
2=1.
(ii) Inductive step: Assume that
n
i=1
i=n(n+1)
2for a positive integer n.
We need to show that then
n+1
i=1
i=(n+1)(n+2)
2.This is obtained as follows:
n+1
i=1
i=
n
i=1
i+(n+1)= n(n+1)
2+(n+1)= n(n+1)+2(n+1)
2=(n+1)(n+2)
2.
The young Gauss computed the sum
1+2+... +99+100
bynoticingthatitcanbecomputedasthesumof50pairs,eachwiththe
sum 101:
1+100=2+99=... =50+51=101.
Hence the entire sum is equal to 50·101 = 5,050.(The well-known historic
anecdote claims that his teacher gave this assignment to a class to keep
24
the class busy.) The Gauss idea can be easily generalized to an arbitrary
nby adding
S(n)=1+2+... +(n−1) + n
and
S(n)=n+(n−1) + ... +2+1
to obtain
2S(n)=(n+1)nand hence S(n)=n(n+1)
2.
10. a. The number of multiplications M(n)and the number of divisions D(n)
made by the algorithm are given by the same sum:
M(n)=D(n)=
n−2
i=0
n−1
j=i+1
n
k=i
1=
n−2
i=0
n−1
j=i+1
(n−i+1)=
=
n−2
i=0
(n−i+1)(n−1−(i+1)+1)=
n−2
i=0
(n−i+1)(n−i−1)
=(n+1)(n−1) + n(n−2) + ... +3∗1
=
n−1
j=1
(j+2)j=
n−1
j=1
j2+
n−1
j=1
2j=(n−1)n(2n−1)
6+2(n−1)n
2
=n(n−1)(2n+5)
6≈1
3n3∈Θ(n3).
b. The inefficiency is the repeated evaluation of the ratio A[j, i]/A[i, i]
in the algorithm’s innermost loop, which, in fact, does not change with
the loop variable k. Hence, this loop invariant can be computed just once
before entering this loop: temp ←A[j, i]/A[i, i]; the innermost loop is
then changed to
A[j, k]←A[j, k]−A[i, k]∗temp.
This change eliminates the most expensive operation of the algorithm, the
division, from its innermost loop. The running time gain obtained by this
change can be estimated as follows:
Told(n)
Tnew(n)≈cM1
3n3+cD1
3n3
cM1
3n3=cM+cD
cM
=cD
cM
+1,
where cDand cMare the time for one division and one multiplication,
respectively.
25
11. The answer can be obtained by a straightforward evaluation of the sum
2
n
i=1
(2i−1) + (2n+1)=2n2+2n+1.
(One can also get the closed-form answer by noting that the cells on the al-
ternating diagonals of the von Neumann neighborhood of range ncompose
two squares of sizes n+1 and n, respectively.)
26
Exercises 2.4
1. Solve the following recurrence relations.
a. x(n)=x(n−1) + 5 for n>1,x(1) = 0
b. x(n)=3x(n−1) for n>1,x(1) = 4
c. x(n)=x(n−1) + nfor n>0,x(0) = 0
d. x(n)=x(n/2) + nfor n>1,x(1) = 1 (solve for n=2
k)
e. x(n)=x(n/3) + 1 for n>1,x(1) = 1 (solve for n=3
k)
2. Set up and solve a recurrence relation for the number of calls made by
F(n),the recursive algorithm for computing n!.
3. Consider the following recursive algorithm for computing the sum of the
first ncubes: S(n)=1
3+2
3+... +n3.
Algorithm S(n)
//Input: A positive integer n
//Output: The sum of the first ncubes
if n=1return 1
else return S(n−1) + n∗n∗n
a. Set up and solve a recurrence relation for the number of times the
algorithm’s basic operation is executed.
b. How does this algorithm compare with the straightforward nonrecursive
algorithm for computing this function?
4. Consider the following recursive algorithm.
Algorithm Q(n)
//Input: A positive integer n
if n=1return 1
else return Q(n−1) + 2 ∗n−1
a. Set up a recurrence relation for this function’s values and solve it
to determine what this algorithm computes.
b. Set up a recurrence relation for the number of multiplications made by
this algorithm and solve it.
c. Set up a recurrence relation for the number of additions/subtractions
made by this algorithm and solve it.
27
5. a. In the original version of the Tower of Hanoi puzzle, as it was published
by Edouard Lucas, a French mathematician, in the 1890s, the world will
end after 64 disks have been moved from a mystical Tower of Brahma.
Estimate the number of years it will take if monks could move one disk
per minute. (Assume that monks do not eat, sleep, or die.)
b. Howmanymovesaremadebytheith largest disk (1 ≤i≤n)in
this algorithm?
c.Design a nonrecursive algorithm for the Tower of Hanoi puzzle.
6. a. Prove that the exact number of additions made by the recursive algo-
rithm BinRec( n)for an arbitrary positive integer nis log2n.
b. Set up a recurrence relation for the number of additions made by
the nonrecursive version of this algorithm (see Section 2.3, Example 4)
and solve it.
7. a. Design a recursive algorithm for computing 2nfor any nonnegative
integer nthat is based on the formula: 2n=2
n−1+2
n−1.
b. Set up a recurrence relation for the number of additions made by
the algorithm and solve it.
c. Draw a tree of recursive calls for this algorithm and count the number
of calls made by the algorithm.
d. Is it a good algorithm for solving this problem?
8. Consider the following recursive algorithm.
Algorithm Min1 (A[0..n −1])
//Input: An array A[0..n −1] of real numbers
if n=1return A[0]
else temp ←Min1 (A[0..n −2])
if temp ≤A[n−1] return temp
else return A[n−1]
a. What does this algorithm compute?
b. Set up a recurrence relation for the algorithm’s basic operation count
and solve it.
9. Consider another algorithm for solving the same problem as the one in
Problem 8 which recursively divides an array into two halves:
28
call Min2 (A[0..n −1]) where
Algorithm Min2 (A[l..r])
if l=rreturn A[l]
else temp1←Min2 (A[l..(l+r)/2])
temp2←Min2 (A[(l+r)/2+1..r])
if temp1≤temp2return temp1
else return temp2
a. Set up a recurrence relation for the algorithm’s basic operation and
solve it.
b. Which of the algorithms Min1 or Min2 is faster? Can you sug-
gest an algorithm for the problem they solve that would be more efficient
than either of them?
10. The determinant of an n-by-nmatrix
A=
a11 a1n
a21 a2n
an1ann
,
denoted det A, can be defined as a11 for n=1and, for n>1,by the
recursive formula
det A=
n
j=1
sja1jdet Aj,
where sjis +1 if jis odd and -1 if jis even, a1jis the element in row
1 and column j,andAjis the (n−1)-by-(n−1) matrix obtained from
matrix Aby deleting its row 1 and column j.
a.Set up a recurrence relation for the number of multiplications made
by the algorithm implementing this recursive definition.
b.Without solving the recurrence, what can you say about the solu-
tion’s order of growth as compared to n!?
9. von Neumann neighborhood revisited Find the number of cells in the von
Neumannneighborhoodofrangen(see Problem 11 in Exercises 2.3) by
setting up and solving a recurrence relation.
29
Hints to Exercises 2.4
1. Each of these recurrences can be solved by the method of backward sub-
stitutions.
2. The recurrence relation in question is almost identical to the recurrence
relation for the number of multiplications, which was set up and solved in
the section.
3. a. The question is similar to that about the efficiency of the recursive
algorithm for computing n!.
b. Write a pseudocode for the nonrecursive algorithm and determine its
efficiency.
4. a. Note that you are asked here about a recurrence for the function’s
values, not about a recurrence for the number of times its operation is
executed. Just follow the pseudocode to set it up. It is easier to solve this
recurrence by forward substitutions (see Appendix B).
b. This question is very similar to one we have already discussed.
c. You may want to include the substraction needed to decrease n.
5. a. Use the formula for the number of disk moves derived in the section.
b. Solve the problem for 3 disks to investigate the number of moves made
by each of the disks. Then generalize the observations and prove their
validity for the general case of ndisks.
c. If you fail, do not feel discouraged: though a nonrecursive algorithm
for this problems is not complicated, it is not easy to discover. As a
consolation, find a solution on the Web.
6. a. Consider separately the cases of even and odd values of nand show that
for both of them log2nsatisfies the recurrence relation and its initial
condition.
b. Just follow the algorithm’s pseudocode.
7. a. Use the formula 2n=2
n−1+2
n−1without simplifying it; do not forget
to provide a condition for stopping your recursive calls.
b. A similar algorithm was investigated in Section 2.4.
c. A similar question was investigated in Section 2.4.
d. A bad efficiency class of an algorithm by itself does not mean that
30
the algorithm is bad. For example, the classic algorithm for the Tower of
Hanoi puzzle is optimal despite its exponential-time efficiency. Therefore
a claim that a particular algorithm is not good requires a reference to a
better one.
8. a. Tracing the algorithm for n=1and n=2should help.
b. It is very similar to one of the examples discussed in this section.
9. Tracing the algorithm for n=1and n=4should help.
10. a. Use the definition’s formula to get the recurrence relation for the num-
ber of multiplications made by the algorithm.
b. Investigate the right-hand side of the recurrence relation. Computing
the first few values of M(n)may be helpful, too.
11. You might want to use the neighborhood’s symmetry to obtain a simple
formula for the number of squares added to the neighborhood on the nth
iteration of the algorithm.
31

Solutions to Exercises 2.4
1. a. x(n)=x(n−1) + 5 for n>1,x(1) = 0
x(n)=x(n−1) + 5
=[x(n−2) + 5] + 5 = x(n−2) + 5 ·2
=[x(n−3) + 5] + 5 ·2=x(n−3) + 5 ·3
=...
=x(n−i)+5·i
=...
=x(1) + 5 ·(n−1) = 5(n−1).
Note: The solution can also be obtained by using the formula for the n
term of the arithmetical progression:
x(n)=x(1) + d(n−1) = 0 + 5(n−1) = 5(n−1).
b. x(n)=3x(n−1) for n>1,x(1) = 4
x(n)=3x(n−1)
=3[3x(n−2)] = 32x(n−2)
=3
2[3x(n−3)] = 33x(n−3)
=...
=3
ix(n−i)
=...
=3
n−1x(1) = 4 ·3n−1.
Note: The solution can also be obtained by using the formula for the n
term of the geometric progression:
x(n)=x(1)qn−1=4·3n−1.
c. x(n)=x(n−1) + nfor n>0,x(0) = 0
x(n)=x(n−1) + n
=[x(n−2) + (n−1)] + n=x(n−2) + (n−1) + n
=[x(n−3) + (n−2)] + (n−1) + n=x(n−3) + (n−2) + (n−1) + n
=...
=x(n−i)+(n−i+1)+(n−i+2)+... +n
=...
=x(0)+1+2+... +n=n(n+1)
2.
32
d. x(n)=x(n/2) + nfor n>1,x(1) = 1 (solve for n=2
k)
x(2k)=x(2k−1)+2
k
=[x(2k−2)+2
k−1]+2
k=x(2k−2)+2
k−1+2
k
=[x(2k−3)+2
k−2]+2
k−1+2
k=x(2k−3)+2
k−2+2
k−1+2
k
=...
=x(2k−i)+2
k−i+1 +2
k−i+2 +... +2
k
=...
=x(2k−k)+2
1+2
2+... +2
k=1+2
1+2
2+... +2
k
=2
k+1 −1=2·2k−1=2n−1.
e. x(n)=x(n/3) + 1 for n>1,x(1) = 1 (solve for n=3
k)
x(3k)=x(3k−1)+1
=[x(3k−2)+1]+1=x(3k−2)+2
=[x(3k−3)+1]+2=x(3k−3)+3
=...
=x(3k−i)+i
=...
=x(3k−k)+k=x(1) + k=1+log
3n.
2. C(n)=C(n−1) + 1,C(0) = 1 (there is a call but no multiplications
when n=0).
C(n)=C(n−1) + 1 = [C(n−2) + 1] + 1 = C(n−2) + 2 = ...
=C(n−i)+i=... =C(0) + n=1+n.
3. a. Let M(n)be the number of multiplications made by the algorithm.
We have the following recurrence relation for it:
M(n)=M(n−1) + 2,M(1) = 0.
33
We can solve it by backward substitutions:
M(n)=M(n−1) + 2
=[M(n−2) + 2] + 2 = M(n−2)+2+2
=[M(n−3)+2]+2+2=M(n−3)+2+2+2
=...
=M(n−i)+2i
=...
=M(1) + 2(n−1) = 2(n−1).
b. Here is a pseudocode for the nonrecursive option:
Algorithm NonrecS (n)
//Computes the sum of the first ncubes nonrecursively
//Input: A positive integer n
//Output: The sum of the first ncubes.
S←1
for i←2to ndo
S←S+i∗i∗i
return S
The number of multiplications made by this algorithm will be
n
i=2
2=2
n
i=2
1=2(n−1).
This is exactly the same number as in the recursive version, but the nonre-
cursive version doesn’t carry the time and space overhead associated with
the recursion’s stack.
4. a. Q(n)=Q(n−1) + 2n−1for n>1,Q(1) = 1.
Computing the first few terms of the sequence yields the following:
Q(2) = Q(1) + 2 ·2−1=1+2·2−1=4;
Q(3) = Q(2) + 2 ·3−1=4+2·3−1=9;
Q(4) = Q(3) + 2 ·4−1=9+2·4−1=16.
Thus, it appears that Q(n)=n2.We’ll check this hypothesis by substi-
tuting this formula into the recurrence equation and the initial condition.
The left hand side yields Q(n)=n2.The right hand side yields
Q(n−1) + 2n−1=(n−1)2+2n−1=n2.
34

The initial condition is verified immediately: Q(1) = 12=1.
b. M(n)=M(n−1) + 1 for n>1,M(1) = 0.Solving it by backward
substitutions (it’s almost identical to the factorial example–see Example
1 in the section) or by applying the formula for the nth term of an arith-
metical progression yields M(n)=n−1.
c. Let C(n)bethenumberofadditionsandsubtractionsmadebythe
algorithm. The recurrence for C(n)is C(n)=C(n−1) + 3 for n>1,
C(1) = 0.Solving it by backward substitutions or by applying the formula
for the nth term of an arithmetical progression yields C(n)=3(n−1).
Note: If we don’t include in the count the subtractions needed to de-
crease n, the recurrence will be C(n)=C(n−1) + 2 for n>1,C(1) = 0.
Its solution is C(n)=2(n−1).
5. a. The number of moves is given by the formula: M(n)=2
n−1.Hence
264 −1
60 ·24 ·365 ≈3.5·1013 years
vs. the age of the Universe estimated to be about 13 ·109years.
b. Observe that for every move of the ith disk, the algorithm first moves
the tower of all the disks smaller than it to another peg (this requires one
move of the (i+1)st disk) and then, after the move of the ith disk, this
smaller tower is moved on the top of it (this again requires one move of
the (i+1)st disk). Thus, for each move of the ith disk, the algorithm
moves the (i+1)st disk exactly twice. Since for i=1, the number of
moves is equal to 1, we have the following recurrence for the number of
movesmadebytheith disk:
m(i+1)=2m(i)for 1≤i<n, m(1) = 1.
Its solution is m(i)=2
i−1for i=1,2, ..., n. (The easiest way to obtain
this formula is to use the formula for the generic term of a geometric
progression.) Note that the answer agrees nicely with the formula for the
total number of moves:
M(n)=
n
i=1
m(i)=
n
i=1
2i−1=1+2+... +2
n−1=2
n−1.
c. Here is a description of the well-known nonrecursive algorithm by P.
Buneman and L. Levy as presented in [Har92], p.115. Arrange the three
pegs in a circle and do the following repeatedly until, prior to Step 2, all
disks are correctly piled on some other peg:
35
Step 1: Move the smallest disk from its current peg to the next peg in
clockwise direction.
Step 2: Make the only move possible that does not involve the smallest
disk.
Note: There are other iterative algorithms for the Tower of Hanoi puzzle
(see, in particular, http://hanoitower.mkolar.org/algo.html for examples
of such algorithms and http://www.cs.wm.edu/~pkstoc/h_papers.html
for an extensive bibliography on this problem).
6. a. We’ll verify by substitution that A(n)=log2nsatisfies the recurrence
for the number of additions
A(n)=A(n/2)+1 for every n>1.
Let nbe even, i.e., n=2k.
The left-hand side is:
A(n)=log2n=log22k=log22+log
2k=(1+log2k)=
log2k+1.
Theright-handsideis:
A(n/2)+1=A(2k/2)+1=A(k)+1=log2k+1.
Let nbe odd, i.e., n=2k+1.
The left-hand side is:
A(n)=log2n=log2(2k+1)=using log2x=log2(x+1)−1
log2(2k+2)−1=log22(k+1)−1
=log22 + log2(k+1)−1=1+log2(k+1)−1=log2k+1.
Theright-handsideis:
A(n/2)+1=A((2k+1)/2)+1= A(k+1/2)+1= A(k)+1 =
log2k+1.
The initial condition is verified immediately: A(1) = log21=0.
b. The recurrence relation for the number of additions is identical to
the one for the recursive version:
A(n)=A(n/2)+1 for n>1,A(1) = 0,
with the solution A(n)=log2n+1.
7. a. Algorithm Power(n)
//Computes 2nrecursively by the formula 2n=2
n−1+2
n−1
//Input: A nonnegative integer n
//Output: Returns 2n
if n=0 return 1
else return Power(n−1) + Power(n−1)
36
b. A(n)=2A(n−1) + 1,A(0) = 0.
A(n)=2A(n−1) + 1
=2[2A(n−2) + 1] + 1 = 22A(n−2)+2+1
=2
2[2A(n−3)+1]+2+1=2
3A(n−3) + 22+2+1
=...
=2
iA(n−i)+2
i−1+2
i−2+... +1
=...
=2
nA(0) + 2n−1+2
n−2+... +1=2
n−1+2
n−2+... +1=2
n−1.
c. The tree of recursive calls for this algorithm looks as follows:
n
n-1 n-1
n-2 n-2 n-2 n-2
00
... ... ...
1
00
1
00
1
00
1
Note that it has one extra level compared to the similar tree for the Tower
of Hanoi puzzle.
d. It’s a very bad algorithm because it is vastly inferior to the algo-
rithm that simply multiplies an accumulator by 2 ntimes, not to mention
much more efficient algorithms discussed later in the book. Even if only
additions are allowed, adding two 2n−1times is better than this algorithm.
8. a. The algorithm computes the value of the smallest element in a given
array.
b. The recurrence for the number of key comparisons is
C(n)=C(n−1) + 1 for n>1,C(1) = 0.
Solving it by backward substitutions yields C(n)=n−1.
9. a. The recurrence for the number of key comparisons is
C(n)=C(n/2)+C(n/2)+1 for n>1,C(1) = 0.
37
Solving it for n=2
kby backward substitutions yields the following:
C(2k)=2C(2k−1)+1
=2[2C(2k−2)+1]+1=2
2C(2k−2)+2+1
=2
2[2C(2k−3)+1]+2+1=2
3C(2k−3)+2
2+2+1
=...
=2
iC(2k−i)+2
i−1+2
i−2+... +1
=...
=2
kC(2k−k)+2
k−1+2
k−2+... +1=2
k−1=n−1.
One can verify that this solution is, in fact, valid for every (positive inte-
ger) value of nby checking it separately for the even (n=2k)and odd
(n=2k+1) cases.
b. A simple standard scan through the array in question requires the
same number of key comparisons while avoiding the overhead associated
with recursive calls. (It is clear, however, that any algorithm for this
problem must be in Ω(n).)
10. a. Let M(n)be the number of multiplications made by the algorithm
based on the formula det A=n
j=1 sja1jdet Aj.If we don’t include
multiplications by sj, which are just ±1,then
M(n)=
n
j=1
(M(n−1) + 1),
i.e.,
M(n)=n(M(n−1) + 1) for n>1and M(1) = 0.
b. Since M(n)=nM(n−1) + n, the sequence M(n)grows to infinity at
least as fast as the factorial function defined by F(n)=nF (n−1).
8. The number of squares added on the nth iteration to each of the four
symmertic sides of the von Neumann neighborhood is equal to n. Hence
we obtain the following recurrence for S(n),the total number of squares
in the neighborhood after the nth iteration:
S(n)=S(n−1) + 4nfor n>0and S(0) = 1.
38
Solving the recurrence by backward substitutions yields the following:
S(n)=S(n−1) + 4n
=[S(n−2) + 4(n−1)] + 4n=S(n−2) + 4(n−1) + 4n
=[S(n−3) + 4(n−2)] + 4(n−1) + 4n=S(n−3) + 4(n−2) + 4(n−1) + 4n
=...
=S(n−i)+4(n−i+1)+4(n−i+2)+... +4n
=...
=S(0) + 4 ·1+4·2+... +4n=1+4(1+2+... +n)=1+4n(n+1)/2=2n2+2n+1.
39

Exercises 2.5
1. Find a Web site dedicated to applications of the Fibonacci numbers and
study it.
2. Check by direct substitutions that the function 1
√5(φn−ˆ
φn)indeed satisfies
recurrence (2.6) and initial conditions (2.7).
3. The maximum values of the Java primitive types int and long are 231 −1
and 263 −1, respectively. Find the smallest nfor which the nth Fibonacci
number is not going to fit in a memory allocated for
a. the type int.b.thetypelong.
4. Climbing stairs Find the number of different ways to climb an n-stair
staircase if each step is either or two stairs. (For example, a 3-stair
staircase can be climbed three ways: 1-1-1, 1-2, and 2-1.) [TUC80]
5. Consider the recursive definition-based algorithm for computing the nth
Fibonacci number F(n).LetC(n)and Z(n)be the number of times F(1)
and F(0),respectively, are computed. Prove that
a. C(n)=F(n).b. Z(n)=F(n−1).
6. Improve algorithm Fib ofthetextsothatitrequiresonlyΘ(1) space.
7. Prove the equality
F(n−1) F(n)
F(n)F(n+1) =01
11
n
for n≥1.
8. How many modulo divisions are made by Euclid’s algorithm on two
consecutive Fibonacci numbers F(n)and F(n−1) as the algorithm’s in-
put?
9. a. Prove Cassini’s identity :
F(n+1)F(n−1) −[F(n)]2=(−1)nfor n≥1.
b. Disappearing square Consider the following paradox, which is based
on Cassini’s identity. Take an 8-by-8 chessboard (more generally, any
F(n)-by-F(n)board divided into [F(n)]2squares). Cut it into two trape-
zoids and two triangles as shown in the left portion of the figure. Then
reassemble it as shown in the right portion of the figure. The area of the
left rectangle is 8×8=64squares, while the area of the right triangle is
40
13 ×5=65squares. Explain the paradox.
‘
10. In the language of your choice, implement two algorithms for computing
the last five digits of the nth Fibonacci number that are based on (a)
the recursive definition-based algorithm F(n); (b) the iterative definition-
based algorithm Fib(n). Perform an experiment to find the largest value
of nfor which your programs run under 1 minute on your computer.
41
Hints to Exercises 2.5
1. Use a search engine.
2. It is easier to substitute φnand ˆ
φninto the recurrence equation separately.
Why will this suffice?
3. Use an approximate formula for F(n)to find the smallest values of nto
exceed the numbers given.
4. There are several ways to solve this problem. The most elegant of them
makes it possible to put the problem in this section.
5. Set up the recurrence relations for C(n)and Z(n),with appropriate initial
conditions, of course.
6. All the information needed on each iteration of the algorithm is the values
of the last two consecutive Fibonacci numbers. Modify the algorithm to
takeadvantageofthisfact.
7. Prove it by mathematical induction.
8. Consider first a small example such as computing gcd(13,8).
9. a. Prove it by mathematical induction.
b. The renowned authors of “Concrete Mathematics”–R. Graham, D.
Knuth, and O. Patashnik–note in their well-known book on discrete
mathematics [Gra94] that this was one of Lewis Carroll’s favorite puz-
zles. Unfortunately, they also note that “The paradox is explained be-
cause...well, magic tricks aren’t supposed to be explained.” Given the
prominence of these scientists, I have no choice but to obey and refrain
from giving you a hint.
10. The last kdigits of an integer Ncan be obtained by computing Nmod 10k.
Performing all operations of your algorithms modulo 10k(see Appendix
A) will enable you to circumvent the exponential growth of the Fibonacci
numbers. Also note that Section 2.6 is devoted to a general discussion of
the empirical analysis of algorithms.
42
Solutions to Exercises 2.5
1. n/a
2. On substituting φninto the left-hand side of the equation, we obtain
F(n)−F(n−1) −F(n−2) = φn−φn−1−φn−2=φn−2(φ2−φ−1) = 0
because φis one of the roots of the characteristic equation r2−r−1=0.
The verification of ˆ
φnworks out for the same reason. Since the equation
F(n)−F(n−1) −F(n−2) = 0 is homogeneous and linear, any linear
combination of its solutions φnand ˆ
φn, i.e., any sequence of the form
αφn+βˆ
φnwill also be a solution to F(n)−F(n−1) −F(n−2) = 0.In
particular, it will be the case for the Fibonacci sequence 1
√5φn−1
√5ˆ
φn.
Both initial conditions are checked out in a quite straightforward manner
(but, of course, not individually for φnand ˆ
φn).
3. a. The question is to find the smallest value of nsuch that F(n)>231 −1.
Using the formula F(n)= 1
√5φnrounded to the nearest integer, we get
(approximately) the following inequality:
1
√5φn>231 −1or φn>√5(231 −1).
After taking natural logarithms of both hand sides, we obtain
n>ln(√5(231 −1))
ln φ≈46.3.
Thus, the answer is n=47.
b. Similarly, we have to find the smallest value of nsuch that F(n)>
263 −1.Thus,
1
√5φn>263 −1,or φn>√5(263 −1)
or, after taking natural logarithms of both hand sides,
n>ln(√5(263 −1))
ln φ≈92.4.
Thus, the answer is n=93.
4. Let W(n)be the number of different ways to climb an n-stair staircase.
W(n−1) of them start with a one-stair climb and W(n−2) of them start
with a two-stair climb. Thus,
W(n)=W(n−1) + W(n−2) for n≥3,W(1) = 1,W(2) = 2.
43
Solving this recurrence either “from scratch” or better yet noticing that
the solution runs one step ahead of the canonical Fibonacci sequence F(n),
we obtain W(n)=F(n+1)for n≥1.
5. Since F(n)is computed recursively by the formula F(n)=F(n−1) +
F(n−2),the recurrence equations for C(n)and Z(n)willbethesameas
the recurrence for F(n). The initial conditions will be:
C(0) = 0,C(1) = 1 and Z(0) = 1,Z(1) = 0
for C(n)and Z(n),respectively. Therefore, since both the recurrence
equation and the initial conditions for C(n)and F(n)are the same, C(n)=
F(n).As to the assertion that Z(n)=F(n−1),it is easy to see that it
should be the case since the sequence Z(n)looks as follows:
1,0, 1, 1, 2, 3, 5, 8, 13, 21, ...,
i.e., it is the same as the Fibonacci numbers shifted one position to the
right. This can be formally proved by checking that the sequence F(n−1)
(in which F(−1) is defined as 1) satisfies the recurrence relation
Z(n)=Z(n−1) + Z(n−2) for n>1and Z(0) = 1,Z(1) = 0.
It can also be proved either by mathematical induction or by deriving an
explicit formula for Z(n)and showing that this formula is the same as the
value of the explicit formula for F(n)with nreplaced by n−1.
6. Algorithm Fib2( n)
//Computes the n-th Fibonacci number using just two variables
//Input: A nonnegative integer n
//Output: The n-th Fibonacci number
u←0; v←1
for i←2to ndo
v←v+u
u←v−u
if n=0return 0
else return v
7. (i) The validity of the equality for n=1follows immediately from the
definition of the Fibonacci sequence.
(ii) Assume that
F(n−1) F(n)
F(n)F(n+1) =01
11
n
for a positive integer n.
44
We need to show that then
F(n)F(n+1)
F(n+1) F(n+2) =01
11
n+1
.
Indeed,
01
11
n+1
=01
11
01
11
n
=01
11
F(n−1) F(n)
F(n)F(n+1) =F(n)F(n+1)
F(n+1) F(n+2) .
8. The principal observation here is the fact that Euclid’s algorithm replaces
two consecutive Fibonacci numbers as its input by another pair of consec-
utive Fibonacci numbers, namely:
gcd(F(n),F(n−1)) = gcd(F(n−1),F(n−2)) for every n≥4.
Indeed, since F(n−2) <F(n−1) for every n≥4,
F(n)=F(n−1) + F(n−2) <2F(n−1).
Therefore for every n≥4,the quotient and remainder of division of F(n)
by F(n−1) are 1 and F(n)−F(n−1) = F(n−2),respectively. This
is exactly what we asserted at the beginning of the solution. In turn, this
leads to the following recurrence for the number of of divisions D(n):
D(n)=D(n−1) + 1 for n≥4,D(3) = 1,
whose initial condition D(3) = 1 is obtained by tracing the algorithm on
the input pair F(3),F(2),i.e., 2,1. The solution to this recurrence is:
D(n)=n−2for every n≥3.
(One can also easily find directly that D(2) = 1 and D(1) = 0.)
9. a. (i) For n=1:F(2)F(0) −[F(1)]2=1·0−12=(−1)1.
(ii) Let F(n+1)F(n−1) −[F(n)]2=(−1)nfor some positive integer n.
We’ll show that
F(n+2)F(n)−[F(n+1)]
2=(−1)n+1.
Indeed,
F(n+2)F(n)−[F(n+1)]
2
=[F(n+1)+F(n)]F(n)−[F(n+1)]
2
=F(n+1)F(n)+[F(n)]2−[F(n+1)]
2
=F(n+1)F(n)+[F(n+1)F(n−1) −(−1)n]−[F(n+1)]
2
=F(n+1)[F(n)+F(n−1) −F(n+1)]+(−1)n+1 =(−1)n+1.
45
b. The paradox is based on a bit of visual mischief: the four pieces
don’t actually form the rectangle because the sides of the triangle and
trapezoid don’t form a straight line. If they did, the smaller and larger
right triangles would be similar, and hence the ratios of their sides, which
are 3:8 and 5:13, respectively, would have to be the same.
10. n/a
46

Exercises 2.6
1. Consider the following well-known sorting algorithm (we shall study it
more closely later in the book) with a counter inserted to count the num-
ber of key comparisons.
Algorithm SortAnalysis(A[0..n −1])
//Input: An array A[0..n −1] of norderable elements
//Output: The total number of key comparisons made
count ←0
for i←1to n−1do
v←A[i]
j←i−1
while j≥0and A[j]>vdo
count ←count +1
A[j+1]←A[j]
j←j−1
A[j+1] ←v
Is the comparison counter inserted in the right place? If you believe it is,
prove it; if you believe it is not, make an appropriate correction.
2. a. Run the program of Problem 1, with a properly inserted counter (or
counters) for the number of key comparisons, on 20 random arrays of sizes
1000, 1500, 2000, 2500,...,9000, 9500.
b. Analyze the data obtained to form a hypothesis about the algorithm’s
average-case efficiency.
c. Estimate the number of key comparisons one should expect for a ran-
domly generated array of size 10,000 sorted by the same algorithm.
3. Repeat Problem 2 by measuring the program’s running time in millisec-
onds.
4. Hypothesize a likely efficiency class of an algorithm based on the following
empirical observations of its basic operation’s count:
size 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
count 11,966 24,303 39,992 53,010 67,272 78,692 91,274 113,063 129,799 140,538
5. What scale transformation will make a logarithmic scatterplot look like a
linear one?
6. How can we distinguish a scatterplot for an algorithm in Θ(lg lg n)from
a scatterplot for an algorithm in Θ(lg n)?
47

7. a. Find empirically the largest number of divisions made by Euclid’s al-
gorithm for computing gcd(m, n)for 1≤n≤m≤100.
b. For each positive integer k, find empirically the smallest pair of in-
tegers 1≤n≤m≤100 for which Euclid’s algorithm needs to make k
divisions in order to find gcd(m, n).
8. The average-case efficiency of Euclid’s algorithm on inputs of size ncan
be measured by the average number of divisions Davg(n)made by the
algorithm in computing gcd(n, 1),gcd(n, 2),..., gcd(n, n).For example,
Davg (5) = 1
5(1+2+3+2+1)=1.8.
Produce a scatterplot of Davg(n)and indicate a likely average-case effi-
ciency class of the algorithm.
9. Run an experiment to ascertain the efficiency class of the sieve of Eratos-
thenes (see Section 1.1).
10. Run a timing experiment for the three algorithms for computing gcd(m, n)
presented in Section 1.1.
48
Hints to Exercises 2.6
1. Does it return a correct comparison count for every array of size 2?
2. Debug your comparison counting and random input generating for small
array sizes first.
3. On a reasonably fast desktop, you may well get zero time at least for
smaller sizes in your sample. Section 2.6 mentions a trick for overcoming
this difficulty.
4. Check how fast the count values grow with doubling the size.
5. A similar question was discussed in the section.
6. Compare the values of the functions lg lg nand lg nfor n=2
k.
7. Insert the division counter into a program implementing the algorithm
and run it for the input pairs in the range indicated.
8. Get the empirical data for random values of nin a range of between, say,
102and 104or 105and plot the data obtained. (You may want to use
different scales for the axes of your coordinate system.)
9. n/a
10. n/a
49
Solutions to Exercises 2.6
1. It doesn’t count the comparison A[j]>vwhen the comparison fails (and,
hence, the body of the while loop is not executed). If the language
implies that the second comparison will always be executed even if the
first clause of the conjunction fails, the count should be simply incremented
by one either right before the while statement or right after the while
statement’s end. If the second clause of the conjunction is not executed
after the first clause fails, we should add the line
if j≥0count ←count +1
right after the while statement’s end.
2. a. One should expect numbers very close to n2/4(the approximate the-
oretical number of key comparisons made by insertion sort on random
arrays).
b. The closeness of the ratios C(n)/n2to a constant suggests the Θ(n2)
average-case efficiency. The same conclusion can also be drawn by observ-
ing the four-fold increase in the number of key comparisons in response to
doubling the array’s size.
c. C(10,000) can be estimated either as 10,0002/4or as 4C(5,000).
3. See answers to Exercise 2. Note, however, that the timing data is inher-
ently much less accurate and volatile than the counting data.
4. The data exhibits a behavior indicative of an nlg nalgorithm.
5. If M(n)≈clog n, then the transformation n=ak(a>1) will yield
M(ak)≈(clog a)k.
6. The function lg lg ngrows much more slowly than the slow-growing func-
tion lg n. Also, if we transform the plots by substitution n=2
k,the plot
of the former would look logarithmic while the plot of the latter would
appear linear.
7. a. 9 (for m=89and n= 55)
b. Two consecutive Fibonacci numbers–m=Fk+2,n=Fk+1–are the
smallest pair of integers m≥n>0that requires kcomparisons for every
k≥2.(This is a well-known theoretical fact established by G. Lamé (e.g.,
[KnuII].) For k=1,the answer is Fk+1 and Fk,whicharebothequalto
1.
50

8. The experiment should confirm the known theoretical result: the average-
case efficiency of Euclid’s algorithm is in Θ(lg n).For a slightly different
metric T(n)investigated by D. Knuth, T(n)≈12 ln 2
πln n≈0.843 ln n(see
[KnuII], Section 4.5.3).
9. n/a
10. n/a
51
This file contains the exercises, hints, and solutions for Chapter 3 of the
book ”Introduction to the Design and Analysis of Algorithms,” 2nd edition, by
A. Levitin. The problems that might be challenging for at least some students
are marked by ;those that might be difficult for a majority of students are
marked by .
Exercises 3.1
1. a. Give an example of an algorithm that should not be considered an
application of the brute-force approach.
b. Give an example of a problem that cannot be solved by a brute-force
algorithm.
2. a. What is the efficiency of the brute-force algorithm for computing an
as a function of n? As a function of the number of bits in the binary
representation of n?
b. If you are to compute anmod mwhere a>1and nis a large positive
integer, how would you circumvent the problem of a very large magnitude
of an?
3. For each of the algorithms in Problems 4, 5, and 6 of Exercises 2.3, tell
whether or not the algorithm is based on the brute-force approach.
4. a. Design a brute-force algorithm for computing the value of a polynomial
p(x)=anxn+an−1xn−1+... +a1x+a0
at a given point x0and determine its worst-case efficiency class.
b. If the algorithm you designed is in Θ(n2),design a linear algorithm
for this problem.
c. Is it possible to design an algorithm with a better than linear efficiency
for this problem?
5. Sort the list E, X, A, M, P, L, E in alphabetical order by selection sort.
6. Is selection sort stable? (The definition of a stable sorting algorithm was
giveninSection1.3.)
7. Is it possible to implement selection sort for linked lists with the same
Θ(n2)efficiency as the array version?
8. Sort the list E, X, A, M, P, L, E in alphabetical order by bubble sort.
9. a. Prove that if bubble sort makes no exchanges on its pass through a list,
the list is sorted and the algorithm can be stopped.
1

b. Write a pseudocode of the method that incorporates this improve-
ment.
c. Prove that the worst-case efficiency of the improved version is quadratic.
10. Is bubble sort stable?
11. Alternating disks You have a row of 2ndisks of two colors, ndark and
nlight. They alternate: dark, light, dark, light, and so on. You want to
get all the dark disks to the right-hand end, and all the light disks to the
left-hand end. The only moves you are allowed to make are those which
interchange the positions of two neighboring disks.
Design an algorithm for solving this puzzle and determine the number of
moves it makes. [Gar99], p.75
2
Hints to Exercises 3.1
1. a. Think of algorithms that have impressed you with their efficiency
and/or sophistication. Neither characteristic is indicative of a brute-
force algorithm.
b. Surprisingly, it is not a very easy question to answer. Mathemati-
cal problems (including those you have studied in your secondary school
and college courses) are a good source of such examples.
2. a. The first question was all but answered in the section. Expressing
the answer as a function of the number of bits can be done by using the
formula relating the two metrics.
b. How can we compute (ab)modm?
3. It helps to have done the exercises in question.
4. a. The most straightforward algorithm, which is based on substituting x0
into the formula, is quadratic.
b. Analyzing what unnecessary computations the quadratic algorithm
does should lead you to a better (linear) algorithm.
c. How many coefficients does a polynomial of degree nhave? Can one
compute its value at an arbitrary point without processing all of them?
5. Just trace the algorithm on the input given. (It was done for another
input in the section.)
6. Although the majority of elementary sorting algorithms are stable, do not
rush with your answer. A general remark about stability made in Section
1.3, where the notion of stability is introduced, could be helpful, too.
7. Generally speaking, implementing an algorithm for a linked list poses prob-
lems if the algorithm requires accessing the list’s elements not in a sequen-
tial order.
8. Just trace the algorithm on the input given. (See an example in the
section.)
9. a. A list is sorted if and only if all its adjacent elements are in a correct
order. Why?
b. Add a boolean flag to register the presence or absence of switches.
c. Identify worst-case inputs first.
10. Can bubble sort change the order of two equal elements in its input?
3
11. Thinking about the puzzle as a sorting-like problem may and may not
lead you to the most simple and efficient solution.
4
Solutions to Exercises 3.1
1. a. Euclid’s algorithm and the standard algorithm for finding the binary
representation of an integer are examples from the algorithms previously
mentioned in this book. There are, of course, many more examples in its
other chapters.
b. Solving nonlinear equations or computing definite integrals are ex-
amples of problems that cannot be solved exactly (except for special in-
stances) by any algorithm.
2. a. M(n)=n≈2bwhere M(n)is the number of multiplications made by
the brute-force algorithm in computing anand bis the number of bits in
the n’s binary representation. Hence, the efficiency is linear as a function
of nand exponential as a function of b.
b. Perform all the multiplications modulo m, i.e.,
aimod m=(ai−1mod m·amod m)modmfor i=1, ..., n.
3. Problem 4 (computes n
1i2):yes
Problem 5 (computes the range of an array’s values): yes
Problem 6 (checks whether a matrix is symmetric): yes
4. a. Here is a pseudocode of the most straightforward version:
Algorithm BruteForcePolynomialEvaluation(P[0..n],x)
//The algorithm computes the value of polynomial Pat a given point x
//by the “highest-to-lowest term” brute-force algorithm
//Input: Array P[0..n]of the coefficients of a polynomial of degree n,
// stored from the lowest to the highest and a number x
//Output: The value of the polynomial at the point x
p←0.0
for i←ndownto 0do
power ←1
for j←1to ido
power ←power ∗x
p←p+P[i]∗power
return p
We will measure the input’s size by the polynomial’s degree n. The ba-
sic operation of this algorithm is a multiplication of two numbers; the
number of multiplications M(n)depends on the polynomial’s degree only.
5

Although it is not difficult to find the total number of multiplications in
this algorithm, we can count just the number of multiplications in the
algorithm’s inner-most loop to find the algorithm’s efficiency class:
M(n)=
n
i=0
i
j=1
1=
n
i=0
i== n(n+1)
2∈Θ(n2).
b. The above algorithm is very inefficient: we recompute powers of xagain
and again as if there were no relationship among them. Thus, the obvious
improvement is based on computing consecutive powers more efficiently.
If we proceed from the highest term to the lowest, we could compute
xi−1by using xibut this would require a division and hence a special
treatment for x=0. Alternatively, we can move from the lowest term to
the highest and compute xiby using xi−1. Since the second alternative
uses multiplications instead of divisions and does not require any special
treatment for x=0,it is both more efficient and cleaner. It leads to the
following algorithm:
Algorithm BetterBruteForcePolynomialEvaluation(P[0..n],x)
//The algorithm computes the value of polynomial Pat a given point x
//by the “lowest-to-highest term” algorithm
//Input: Array P[0..n]of the coefficients of a polynomial of degree n,
// from the lowest to the highest, and a number x
//Output: The value of the polynomial at the point x
p←P[0]; power ←1
for i←1to ndo
power ←power ∗x
p←p+P[i]∗power
return p
The number of multiplications here is
M(n)=
n
i=1
2=2n
(while the number of additions is n), i.e., we have a linear algorithm.
Note: Horner’s Rule discussed in Section 6.5 needs only nmultiplications
(and nadditions) to solve this problem.
c. No, because any algorithm for evaluating an arbitrary polynomial of
degree nat an arbitrary point xmust process all its n+1 coefficients.
(Note that even when x=1,p(x)=an+an−1+... +a1+a0,which needs
at least nadditions to be computed correctly for arbitrary an,a
n−1,...,a
0.)
6
5. EXAMP LE
AXEMP LE
AEXM P L E
AEEMP LX
AEE L PMX
AEE LM PX
AEE LM P X
6. Selection sort is not stable: In the process of exchanging elements that are
not adjacent to each other, the algorithm can reverse an ordering of equal
elements. The list 2,2
, 1 is such an example.
7. Yes. Both operations–finding the smallest element and swapping it–can
be done as efficiently with a linked list as with an array.
8. E, X, A,M, P,L,E
E?
↔X?
↔AMP LE
EAX
?
↔MP L E
EAMX
?
↔PLE
EAMPX
?
↔LE
EAMPLX
?
↔E
EAMPLE|X
E?
↔AMPLE
AE
?
↔M?
↔P?
↔LE
AEMLP
?
↔E
AEMLE|P
A?
↔E?
↔M?
↔LE
AELM
?
↔E
AELE|M
A?
↔E?
↔L?
↔E
AEE|L
A?
↔E?
↔E?
↔L
The algorithm can be stopped here (see the next question).
9. a. Pass i(0 ≤i≤n−2) of bubble sort can be represented by the following
diagram:
A0, ..., Aj
?
↔Aj+1,...,A
n−i−1≤| An−i≤... ≤An−1
in their final positions
7

If there are no swaps during this pass, then
A0≤A1≤... ≤Aj≤Aj+1 ≤... ≤An−i−1,
with the larger (more accurately, not smaller) elements in positions n−i
through n−1being sorted during the previous iterations.
b. Here is a pseudocode for the improved version of bubble sort:
Algorithm BetterBubbleSort(A[0..n −1])
//The algorithm sorts array A[0..n−1] by improved bubble sort
//Input: An array A[0..n−1] of orderable elements
//Output: Array A[0..n−1] sorted in ascending order
count ←n−1//number of adjacent pairs to be compared
sflag ←true //swap flag
while sflag do
sflag ←false
for j←0to count −1do
if A[j+1]<A[j]
swap A[j]and A[j+1]
sflag ←true
count ←count −1
c. The worst-case inputs will be strictly decreasing arrays. For them, the
improved version will make the same comparisons as the original version,
which was shown in the text to be quadratic.
10. Bubble sort is stable. It follows from the fact that it swaps adjacent
elements only, provided A[j+1]<A[j].
5. Here is a simple and efficient (in fact, optimal) algorithm for this problem:
Starting with the first and ending with the last light disk, swap it with
each of the i(1 ≤i≤n)dark disks to the left of it. The ith iteration
of the algorithm can be illustrated by the following diagram, in which 1s
and 0s correspond to the dark and light disks, respectively.
00..0
i−1
11..1
i−1
1010..10 ⇒00..00
i
11..11
i
10..10
Thetotalnumberofswapsmadeisequalton
i=1 i=n(n+1)/2.
8

Exercises 3.2
1. Find the number of comparisons made by the sentinel version of sequential
search
a. in the worst case.
b. in the average case if the probability of a successful search is p(0 ≤
p≤1).
2. As shown in Section 2.1, the average number of key comparisons made by
sequential search (without a sentinel, under standard assumptions about
its inputs) is given by the formula
Cavg (n)= p(n+1)
2+n(1 −p),
where pis the probability of a successful search. Determine, for a fixed n,
thevaluesofp(0≤p≤1) for which this formula yields the largest value
of Cavg (n)and the smallest value of Cavg (n).
3. Gadgets testing A firm wants to determine the highest floor of its n-
story headquarters from which a gadget can fall with no impact on the
gadget’s functionality. The firm has two identical gadgets to experiment
with. Design an algorithm in the best efficiency class you can to solve
this problem.
4. Determine the number of character comparisons made by the brute-force
algorithm in searching for the pattern GANDHI in the text
THERE_IS_MORE_TO_LIFE_THAN_INCREASING_ITS_SPEED
(Assume that the length of the text–it is 47 characters long–is known
before the search starts.)
5. How many comparisons (both successful and unsuccessful) are made by the
brute-force string-matching algorithm in searching for each of the following
patterns in the binary text of 1000 zeros?
a. 00001 b. 10000 c. 01010
6. Give an example of a text of length nand a pattern of length mthat
constitutes the worst-case input for the brute-force string-matching al-
gorithm. Exactly how many character comparisons are made for such
input?
7. Write a visualization program for the brute-force string-matching algo-
rithm.
9
8. In solving the string-matching problem, would there be any advantage in
comparing pattern and text characters right-to-left instead of left-to-right?
9. Consider the problem of counting, in a given text, the number of substrings
that start with an A and end with a B. (For example, there are four such
substrings in CABAAXBYA.)
(a) Design a brute-force algorithm for this problem and determine its
efficiency class.
(b) Design a more efficient algorithm for this problem [Gin04].
10. Word Find A popular diversion in the United States, Word Find, asks
the player to find each of a given set of words in a square table filled with
single letters. A word can read horizontally (left or right), vertically (up
or down), or along a 45 degree diagonal (in any of the four directions),
formed by consecutively adjacent cells of the table; it may wrap around
the table’s boundaries but it must read in the same direction with no
zigzagging. The same cell of the table may be used in different words,
but, in a given word, the same cell may be used no more than once. Write
a computer program for solving this puzzle.
11. Battleship game Write a program for playing Battleship (a classic strat-
egy game) on the computer which is based on a version of brute-force
pattern matching. The rules of the game are as follows. There are two
opponents in the game (in this case, a human player and the computer).
The game is played on two identical boards (10-by-10 tables of squares)
on which each opponent places his or her ships, not seen by the opponent.
Each player has five ships, each of which occupies a certain number of
squares on the board: a destroyer (2 squares), a submarine (3 squares),
a cruiser (3 squares), a battleship (4 squares), and an aircraft carrier (5
squares). Each ship is placed either horizontally or vertically, with no two
ships touching each other. The game is played by the opponents taking
turns “shooting” at each other’s ships. A result of every shot is displayed
as either a hit or a miss. In case of a hit, the player gets to go again and
keeps playing until this player misses. The goal is to sink all the oppo-
nent’s ships before the opponent succeeds in doing it first. (To sink a ship,
all squares occupied by the ship must be hit.)
10
Hints to Exercises 3.2
1. Modify the analysis of the algorithm’s version in Section 2.1.
2. As a function of p, what kind of function is Cavg?
3. Solve a simpler problem with a single gadget first. Then design a better
than linear algorithm for the problem with two gadgets.
4. The content of this quote from Mahatma Gandhi is more thought provok-
ing than this drill.
5. For each input, one iteration of the algorithm yields all the information
you need to answer the question.
6. It will suffice to limit your search for an example to binary texts and
patterns.
7. You may use either bit strings or a natural language text for the visual-
ization program. It would be a good idea to implement, as an option, a
search for all occurrences of a given pattern in a given text.
8. The answer, surprisingly, is yes.
9. a. For a given occurrence of A in the text, what are the substrings you
need to count?
b. For a given occurrence of B in the text, what are the substrings you
need to count?
10. Test your program thoroughly. Be especially careful about a possibility
of words read diagonally with wrapping around the table’s border.
11. A (very) brute-force algorithm can simply shoot at adjacent feasible cells
starting at, say, one of the corners of the board. Can you suggest a better
strategy? (You can investigate relative efficiencies of different strategies
by making two programs implementing them play each other.) Is your
strategy better than the one that shoots at randomly generated cells of
the opponent’s board?
11
Solutions to Exercises 3.2
1. a. Cworst(n)=n+1.
b. Cavg (n)= (2−p)(n+1)
2.In the manner almost identical to the analysis
in Section 2.1, we obtain
Cavg(n)=[1·p
n+2·p
n+... +i·p
n+... +n·p
n]+(n+1)·(1 −p)
=p
n[1+2+... +i+... +n]+(n+ 1)(1 −p)
=p
n
n(n+1)
2+(n+1)(1−p)=(2 −p)(n+1)
2.
2. The expression
p(n+1)
2+n(1 −p)=pn+1
2+n−np =n−p(n−n+1
2)=n−n−1
2p
is a linear function of p. Since the p’s coefficient is negative for n>1,
the function is strictly decreasing on the interval 0≤p≤1from nto
(n+1)/2.Hence p=0and p=1are its maximum and minimum points,
respectively, on this interval. (Of course, this is the answer we should
expect: The average number of comparisons should be the largest when
the probability of a successful search is 0, and it should be the smallest
when the probability of a successful search is 1.)
3. Drop the first gadget from floors √n,2√n,and so on until either the
floor i√na drop from which makes the gadget malfunction is reached
or no such floor in this sequence is encountered before the top of the
building is reached. In the former case, the floor to be found is higher
than (i−1)√nand lower than i√n.So, drop the second gadget from
floors (i−1)√n+1,(i−1)√n+2,andsoonuntilthefirstfloor
a drop from which makes the gadget malfunction is reached. The floor
immediately preceeding that floor is the floor in question. If no drop in the
first-pass sequence resulted in the gadget’s failure, the floor in question is
higher than i√n,the last tried floor of that sequence. Hence, continue
the successive examination of floors i√n+1,i√n+2,and so on until
either a failure is registered or the last floor is reached. The number of
times the two gadgets are dropped doesn’t exceed √n+√n,which
puts it in O(√n).
4. 43 comparisons.
The algorithm will make 47 −6+1 =42trials: In the first one, the G
of the pattern will be aligned against the first T of the text; in the last
one, it will be aligned against the last space. On each but one trial, the
algorithm will make one unsuccessful comparison; on one trial–when the
G of the pattern is aligned against the G of the text –it will make two
12

comparisons. Thus, the total number of character comparisons will be
41 ·1+1·2=43.
5. a. For the pattern 00001, the algorithm will make four successful and one
unsuccessful comparison on each of its trials and then shift the pattern
one position to the right:
000000 00000
00001
00001
etc.
00001
The total number of character comparisons will be C=5·996 = 4980.
b. For the pattern 10000, the algorithm will make one unsuccessful com-
parisononeachofitstrialsandthenshiftthepatternonepositiontothe
right:
000000 00000
10000
10000
etc.
10000
The total number of character comparisons will be C=1·996 = 996.
c. For the pattern 01010, the algorithm will make one successful and
one unsuccessful comparison on each of its trials and then shift the pat-
tern one position to the right:
000000 00000
01010
01010
etc.
01010
The total number of character comparisons will be C=2·996 = 1,992.
6. The text composed of nzeros and the pattern 0... 0
m−1
1isanexampleof
the worst-case input. The algorithm will make m(n−m+1) character
comparisons on such input.
7. n/a
8. Comparing pairs of the pattern and text characters righ-to-left can allow
farther pattern shifts after a mismatch. This is the main insight the two
string matching algoirthms discussed in Section 7.2 are based on. (As a
specific example, consider searching for the pattern 11111 in the text of
one thousand zeros.)
13
9. a. Note that the number of desired substrings that starts with an A at a
given position i(0 ≤i<n−1) in the text is equal to the number of B’s
to the right of that position. This leads to the follwing simple algorithm:
Initialize the count of the desired substrings to 0. Scan the text left to
right doing the following for every character except the last one: If an A
is encountered, count the number of all the B’s following it and add this
number to the count of desired substrings. After the scan ends, return
the last value of the count.
For the worst case of the text composed of nA’s, the total number of
character comparisons is
n+(n−1) + ... +2=n(n+1)/2−1∈Θ(n2).
b. Note that the number of desired substrings that ends with a B at
agivenpositioni(0 <i≤n−1) in the text is equal to the number of A’s
to the left of that position. This leads to the follwing algorithm:
Initialize the count of the desired substrings and the count of A’s en-
countered to 0. Scan the text left to right until the text is exhausted and
do the following. If an A is encountered, increment the A’s count; if a
B is encountered, add the current value of the A’s count to the desired
substring count. After the text is exhausted, return the last value of the
desired substring count.
Since the algorithm makes a single pass through a given text spending
constant time on each of its characters, the algorihtm is linear.
10. n/a
11. n/a
14
Exercises 3.3
1. Can you design a more efficient algorithm than the one based on the brute-
force strategy to solve the closest-pair problem for npoints x1, ..., xnon
the real line?
2. Let x1<x
2<...<x
nbe real numbers representing coordinates of n
villages located along a straight road. A post office needs to be built in
one of these villages.
a. Design an efficient algorithm to find the post-office location minimizing
the average distance between the villages and the post office.
b. Design an efficient algorithm to find the post-office location minimizing
the maximum distance from a village to the post office.
3. a.There are several alternative ways to define a distance between two
points P1=(x1,y
1)and P2=(x2,y
2). In particular, the Manhattan
distance is defined as
dM(P1,P
2)=|x1−x2|+|y1−y2|.
Prove that dMsatisfies the following axioms that every distance function
must satisfy:
(i) dM(P1,P
2)≥0for any two points P1and P2and dM(P1,P
2)=0
if and only if P1=P2;
(ii) dM(P1,P
2)=dM(P2,P
1);
(iii) dM(P1,P
2)≤dM(P1,P
3)+dM(P3,P
2)for any P1,P
2,and P3.
b. Sketch all the points in the x, y coordinate plane whose Manhattan
distance to the origin (0,0) is equal to 1. Do the same for the Euclidean
distance.
c.True or false: A solution to the closest-pair problem does not depend
on which of the two metrics–dE(Euclidean) or dM(Manhattan)–is used.
4. Odd pie fight There are n≥3people positioned in a field (Euclidean
plane) so that each has a unique nearest neighbor. Each person has a
cream pie. At a signal, everybody hurles his or her pie at the nearest
neighbor. Assuming that nis odd and that nobody can miss his or her
target, true or false: There always remains at least one person not hit by
a pie? [Car79].
5. The closest-pair problem can be posed in k-dimensional space in which
the Euclidean distance between two points P=(x
1, ..., x
k)and P =
15

(x
1, ..., x
k)is defined as
d(P,P)=
k
s=1
(x
s−x
s)2.
What is the time-efficiency class of the brute-force algorithm for the k-
dimensional closest-pair problem?
6. Find the convex hulls of the following sets and identify their extreme points
(if they have any).
a. a line segment
b. a square
c. the boundary of a square
d. a straight line
7. Design a linear-time algorithm to determine two extreme points of the
convex hull of a given set of n>1points in the plane.
8. What modification needs to be made in the brute-force algorithm for the
convex-hull problem to handle more than two points on the same straight
line?
9. Write a program implementing the brute-force algorithm for the convex-
hull problem.
10. Consider the following small instance of the linear programming problem:
maximize 3x+5y
subject to x+y≤4
x+3y≤6
x≥0,y≥0
a. Sketch, in the Cartesian plane, the problem’s feasible region de-
fined as the set of points satisfying all the problem’s constraints.
b. Identify the region’s extreme points.
c. Solve the optimization problem given by using the following theorem:
A linear programming problem with a nonempty bounded feasible region
always has a solution, which can be found at one of the extreme points of
its feasible region.
16
Hints to Exercises 3.3
1. Sorting nreal numbers can be done in O(nlog n)time.
2. a. Solving the problem for n=2and n=3should lead you to the critical
insight.
b. Where would you put the post office if it would not have to be at
one of the village locations?
3. a. Check requirements (i)—(iii) by using basic properties of absolute values.
b. For the Manhattan distance, the points in question are defined by
equation |x−0|+|y−0|=1.You can start by sketching the points in
the positive quadrant of the coordinate system (i.e., the points for which
x, y ≥0) and then sketch the rest by using the symmetries.
c. The assertion is false. You can choose, say, P1(0,0),P
2(1,0) and
find P3to complete a counterexample.
4. True; prove it by mathematical induction.
5. Your answer should be a function of two parameters: nand k. A special
case of this problem (for k=2)was solved in the text.
6. Review the examples given in the section.
7. Some of the extreme points of a convex hull are easier to find than others.
8. If there are other points of a given set on the straight line through Piand
Pj, which of all these points need to be preserved for further processing?
9. Your program should work for any set of ndistinct points, including sets
with many colinear points.
10. a. The set of points satisfying inequality ax +by ≤cis the half-plane of
the points on one side of the straight line ax +by =c, including all the
points on the line itself. Sketch such a half-plane for each of the inequal-
ities and find their intersection.
b. The extreme points are the vertices of the polygon obtained in part a.
c. Compute and compare the values of the objective function at the ex-
treme points.
17

Solutions to Exercises 3.3
1. Sort the numbers in ascending order, compute the differences between ad-
jacent numbers in the sorted list, and find the smallest such difference. If
sorting is done in O(nlog n)time, the running time of the entire algorithm
will be in
O(nlog n)+Θ(n)+Θ(n)=O(nlog n).
2. a. If we put the post office at location xi,the average distance between it
and all the points x1<x
2<...<x
nis given by the formula 1
nn
j=1 |xj−
xi|.Since the number of points nstays the same, we can ignore the multiple
1
nand minimize n
j=1 |xj−xi|.We’ll have to consider the cases of even
and odd nseparately.
Let nbe even. Consider first the case of n=2.The sum |x1−x|+|x2−x|
is equal to x2−x1,the length of the interval with the endpoints at x1and x2,
for any point xof this interval (including the endpoints), and it is larger than
x2−x1for any point xoutside of this interval. This implies that for any even
n, the sum
n
j=1 |xj−x|=[|x1−x|+|xn−x|]+[|x2−x|+|xn−1−x|]+...+[|xn/2−x|+|xn/2+1−x|]
is minimized when xbelongs to each of the intervals [x1,x
n]⊃[x2,x
n−1]⊃... ⊃
[xn/2,x
n/2+1].If xmust be one of the points given, either xn/2or xn/2+1 solves
the problem.
Let n>1be odd. Then, the sum n
j=1 |xj−x|is minimized when x=
xn/2,the point for which the number of the given points to the left of it is
equal to the number of the given points to the right of it.
Note that the point xn/2–the n/2th smallest called the median–solves
the problem for even n’s as well. For a sorted list implemented as an array,
themediancanbefoundinΘ(1) time by simply returning the n/2th.element
of the array. (Section 5.6 provides a more general discussion of algorithms for
computing the median.)
b. Assuming that the points x1,x
2, ..., xnare given in increasing order, the
answer is the point xithat is the closest to m=(x1+xn)/2,the middle point
between x1and xn.(The middle point would be the obvious solution if the
post-post office didn’t have to be at one of the given locations.) Indeed, if we
put the post office at any location xito the left of m, the longest distance from
a village to the post office would be xn−xi;this distance is minimal for the
rightmost among such points. If we put the post office at any location xito
the right of m, the longest distance from a village to the post office would be
xi−x1;this distance is minimal for the leftmost among such points.
Algorithm PostOffice1 (P)
//Input: List Pof n(n≥2) points x1,x
2, ..., xnin increasing order
18
//Output: Point xithat minimizes max
1≤j≤n|xj−xi|among all x1,x
2,...,x
n
m←(x1+xn)/2
i←1
while xi<mdo
i←i+1
if xi−x1<x
n−xi−1
return xi
else return xi−1
The time efficiency of this algorithm is O(n).
3. a. For dM(P1,P
2)=|x1−x2|+|y1−y2|,we have the following:
(i) dM(P1,P
2)=|x1−x2|+|y1−y2|≥0and dM(P1,P
2)=0if and
only if both x1=x2and y1=y2,i.e., P1and P2coincide.
(ii) dM(P1,P
2)=|x1−x2|+|y1−y2|=|x2−x1|+|y2−y1|
=dM(P2,P
1).
(iii) dM(P1,P
2)=|x1−x2|+|y1−y2|
=|(x1−x3)+(x3−x2)|+|(y1−y3)+(y3−y2)|
≤|x1−x3|+|x3−x2|+|y1−y3|+|y3−y2|=d(P1,P
3)+d(P3,P
2).
b. For the Manhattan distance, the points in question are defined by
the equation
|x−0|+|y−0|=1,i.e., |x|+|y|=1.
The graph of this equation is the boundary of the square with its vertices
at (1,0),(0,1),(−1,0),and(−1,−1).
For the Euclidean distance, the points in question are defined by the equa-
tion (x−0)2+(y−0)2=1, i.e., x2+y2=1.
The graph of this equation is the circumference of radius 1 and the center
at (0,0).
c. False. Consider points P1(0,0),P
2(1,0),and, say, P3(1
2,3
4).Then
dE(P1,P
2)=1and dE(P3,P
1)=dE(P3,P
2)=1
22
+3
42
<1.
Therefore, for the Euclidean distance, the two closest points are either P1
and P3or P2and P3.For the Manhattan distance, we have
dM(P1,P
2)=1and dM(P3,P
1)=dM(P3,P
2)=1
2+3
4=5
4>1.
19

Therefore, for the Manhattan distance, the two closest points are P1and
P2.
4. We’ll prove by induction that there will always remain at least one person
not hit by a pie. The basis step is easy: If n=3,the two persons with
the smallest pairwise distance between them throw at each other, while
the third person throws at one of them (whoever is closer). Therefore,
this third person remains “unharmed”.
For the inductive step, assume that the assertion is true for odd n≥3,
and consider n+2 persons. Again, the two persons with the smallest
pairwise distance between them (the closest pair) throw at each other.
Consider two possible cases as follows. If the remaining npersons all
throw at one another, at least one of them remains “unharmed” by the
inductive assumption. If at least one of the remaining npersons throws
at one of the closest pair, among the remaining n−1persons, at most
n−1pies are thrown at one another, and hence at least one person must
remain “unharmed” because there is not enough pies to hit everybody in
that group. This completes the proof.
5. The number of squarings will be
C(n, k)=
n−1
i=1
n
j=i+1
k
s=1
1=
n−1
i=1
n
j=i+1
k=k
n−1
i=1
(n−i)
=k[(n−1) + (n−2) + .... +1]= k(n−1)n
2∈Θ(kn2).
6. a. The convex hull of a line segment is the line segment itself; its extreme
points are the endpoints of the segment.
b. The convex hull of a square is the square itself; its extreme points
are the four vertices of the square.
c. The convex hull of the boundary of a square is the region comprised of
the points within that boundary and on the boundary itself; its extreme
points are the four vertices of the square.
d. The convex hull of a straight line is the straight line itself. It doesn’t
have any extreme points.
7. Find the point with the smallest xcoordinate; if there are several such
points, find the one with the smallest ycoordinate among them. Similarly,
find the point with the largest xcoordinate; if there are several such points,
find the one with the largest ycoordinate among them.
20
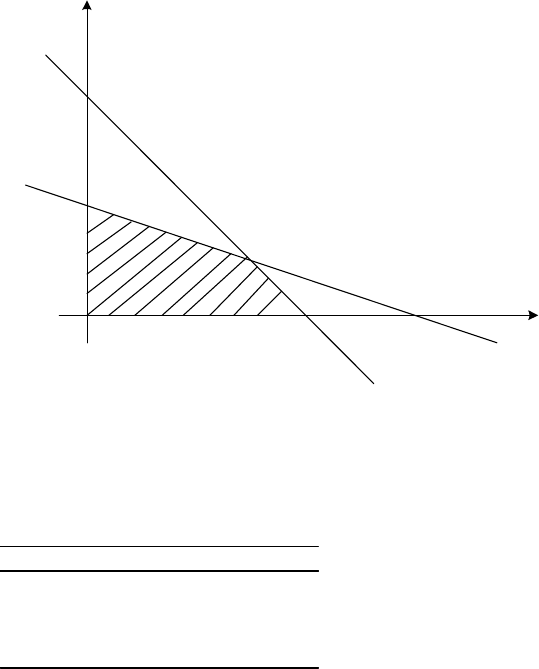
8. If there are other points of a given set on the straight line through Piand
Pj(while all the other points of the set lie on the same side of the line), a
line segment of the convex hull’s boundary will have its end points at the
two farthest set points on the line. All the other points on the line can
be eliminated from further processing.
9. n/a
10. a. Here is a sketch of the feasible region in question:
.
..
.
.
x + y = 4
x
y
x + 3y = 6
( 0, 2 )
( 0, 0 ) ( 4, 0 )
( 3, 1 )
.
.
b. The extreme points are: (0,0),(4,0), (3,1), and (0,2).
c.
Extreme point Value of 3x+5y
(0,0) 0
(4,0) 12
(3,1) 14
(0,2) 10
So, the optimal solution is (3, 1), with the maximal value of 3x+5yequal to 14.
(Note: This instance of the linear programming problem is discussed further in
Section 10.1.)
21
Exercises 3.4
1. a. Assuming that each tour can be generated in constant time, what will
be the efficiency class of the exhaustive-search algorithm outlined in the
text for the traveling salesman problem?
b. If this algorithm is programmed on a computer that makes one billion
additions per second, estimate the maximum number of cities for which
the problem can be solved in (i) one hour;(ii) 24-hours; (iii) one year; (iv)
one century.
2. Outline an exhaustive-search algorithm for the Hamiltonian circuit prob-
lem.
3. Outline an algorithm to determine whether a connected graph represented
by its adjacency matrix has an Eulerian circuit. What is the efficiency
class of your algorithm?
4. Complete the application of exhaustive search to the instance of the as-
signment problem started in the text.
5. Give an example of the assignment problem whose optimal solution does
not include the smallest element of its cost matrix.
6. Consider the partition problem:givennpositive integers, partition
them into two disjoint subsets with the same sum of their elements. (Of
course, the problem does not always have a solution.) Design an exhaus-
tive search algorithm for this problem. Try to minimize the number of
subsets the algorithm needs to generate.
7. Consider the clique problem:given a graph Gand a positive integer k,
determine whether the graph contains a clique of size k, i.e., a complete
subgraph of kvertices. Design an exhaustive-search algorithm for this
problem.
8. Explain how exhaustive search can be applied to the sorting problem and
determine the efficiency class of such an algorithm.
9. A magic square of order nis an arrangement of the numbers from 1 to
n2in an n-by-nmatrix, with each number occurring exactly once, so that
each row, each column, and each main diagonal has the same sum.
a. Prove that if a magic square of order nexists, the sum in question
must be equal to n(n2+1)/2.
b. Design an exhaustive search algorithm for generating all magic squares
of order n.
c. Go to the Internet or your library and find a better algorithm for
22
generating magic squares.
d. Implement the two algorithms–the exhaustive search and the one
you have found–and run an experiment to determine the largest value of
nfor which each of the algorithms is able to find a magic square of order
nin less than one minute of your computer’s time.
10. Famous alphametic A puzzle in which the digits in a correct mathemati-
cal expression, such as a sum, are replaced by letters is called cryptarithm;
if, in addition, the puzzle’s words make sense, it is said to be an al-
phametic. The most well-known alphametic was published by the renowned
British puzzlist H. E. Dudeney (1857-1930):
SEND
+MORE
–––––—
MONEY
Two conditions are assumed: First, the correspondence between letters
and digits is one-to-one, that is each letter represents one digit only and
different letters represent different digits. Second, the digit zero does
not appear as the left-most digit in any of the numbers. To solve an
alphametic means to find which digit each letter represents. Note that
a solution’s uniqueness cannot be assumed and has to be verified by the
solver.
a. Write a program for solving cryptarithms by exhaustive search. As-
sume that a given cryptarithm is a sum of two words.
b. Solve Dudeney’e puzzle the way it was expected to be solved when
it was first published in 1924.
23
Hints to Exercises 3.4
1. a. Identify the algorithm’s basic operation and count the number of times
it will be executed.
b. For each of the time amounts given, find the largest value of nfor
which this limit will not be exceeded.
2. How different is the traveling salesman problem from the problem of find-
ing a Hamiltonian circuit?
3. Your algorithm should check the well-known conditions that are both nec-
essary and sufficient for the existence of a Eulerian circuit in a connected
graph.
4. Generate the remaining 4! −6=18possible assignments, compute their
costs, and find the one with the smallest cost.
5. Make the size of your counterexample as small as possible.
6. Rephrase the problem so that the sum of elements in one subset, rather
than two, needs to be checked on each try of a possible partition.
7. Follow the definitions of a clique and of an exhaustive search algorithm.
8. Try all possible orderings of the elements given.
9. a. Add all the elements in the magic square in two different ways.
b. What combinatorial objects do you have to generate here?
10. a. For testing, you may use alphametic collections available on the Inter-
net.
b. Given the absence of electronic computers in 1924, you must refrain
here from using the Internet.
24
Solutions to Exercises 3.4
1. a. Θ(n!)
For each tour (a sequence of n+1 cities), one needs nadditions to compute
the tour’s length. Hence, the total number of additions A(n)will be n
times the total number of tours considered, i.e., n∗1
2(n−1)! = 1
2n!∈Θ(n!).
b. (i) nmax = 15; (ii) nmax = 16; (iii) nmax = 18; (iv) nmax =20.
Given the answer to part a, we have to find the largest value of nsuch
that 1
2n!10−9≤t
where tis the time available (in seconds). Thus, for t=1hr =3.6∗103sec,
we get the inequality
n!≤2∗109t=7.2∗1012.
Thelargestvalueofnfor which this inequality holds is 15 (since 15!
≈1.3∗1012 and 16! ≈2.1∗1013).
For the other given values of t, the answers can be obtained in the same
manner.
2. The problem of finding a Hamiltonian circuit is very similar to the travel-
ing salesman problem. Generate permutations of nvertices that start and
end with, say, the first vertex, and check whether every pair of successive
vertices in a current permutation are connected by an edge. If it’s the
case, the current permutation represents a Hamiltonian circuit, otherwise,
a next permutation needs to be generated.
3. A connected graph has a Eulerian circuit if and only if all its vertices
have even degrees. An algorithm should check this condition until either
an odd vertex is encountered (then a Eulerian circuit doesn’t exist) or
all the vertices turn out to be even (then a Eulerian circuit must exist).
For a graph (with no loops) represented by its n-by-nadjacency matrix,
the degree of a vertex is the number of ones in the vertex’s row. Thus,
computing its degree will take the Θ(n)time, checking whether it’s even
will take Θ(1) time, and it will be done between 1 and ntimes. Hence,
the algorithm’s efficiency will be in O(n2).
4. The following assignments were generated in the chapter’s text:
C=
9278
6437
5818
7694
1, 2, 3, 4 cost = 9+4+1+4 = 18
1, 2, 4, 3 cost = 9+4+8+9 = 30
1, 3, 2, 4 cost = 9+3+8+4 = 24
1, 3, 4, 2 cost = 9+3+8+6 = 26
1, 4, 2, 3 cost = 9+7+8+9 = 33
1, 4, 3, 2 cost = 9+7+1+6 = 23
etc.
25
The remaining ones are
2, 1, 3, 4 cost = 2+6+1+4 = 13
2, 1, 4, 3 cost = 2+6+8+9 = 25
2, 3, 1, 4 cost = 2+3+5+4 = 14
2, 3, 4, 1 cost = 2+3+8+7 = 20
2, 4, 1, 3 cost = 2+7+5+9 = 23
2, 4, 3, 1 cost = 2+7+1+7 = 17
3, 1, 2, 4 cost = 7+6+8+4 = 25
3, 1, 4, 2 cost = 7+6+8+6 = 27
3, 2, 1, 4 cost = 7+4+5+4 = 20
3, 2, 4, 1 cost = 7+4+8+7 = 26
3, 4, 1, 2 cost = 7+7+5+6 = 25
3, 4, 2, 1 cost = 7+7+8+7 = 29
4, 1, 2, 3 cost = 8+6+8+9 = 31
4, 1, 3, 2 cost = 8+6+1+6 = 21
4, 2, 1, 3 cost = 8+4+5+9 = 26
4, 2, 3, 1 cost = 8+4+1+7 = 20
4, 3, 1, 2 cost = 8+3+5+6 = 22
4, 3, 2, 1 cost = 8+3+8+7 = 26
The optimal solution is: Person 1 to Job 2, Person 2 to Job 1, Person
3toJob3,andPerson4toJob4,withthetotal(minimal)costofthe
assignment being 13.
5. Here is a very simple example:
12
29
6. Start by computing the sum Sof the numbers given. If Sis odd, stop
because the problem doesn’t have a solution. If Sis even, generate the
subsets until either a subset whose elements’ sum is S/2is encountered or
no more subsets are left. Note that it will suffice to generate only subsets
with no more than n/2elements.
7. Generate a subset of kvertices and check whether every pair of vertices
in the subset is connected by an edge. If it’s true, stop (the subset is a
clique); otherwise, generate the next subset.
8. Generate a permutation of the elements given and check whether they
are ordered as required by comparing values of its consecutive elements.
If they are, stop; otherwise, generate the next permutation. Since the
26

number of permutations of nitems is equal to n!and checking a permu-
tation requires up to n−1comparisons, the algorithm’s efficiency class is
in O(n!(n−1)) = O((n+1)!).
9. a. Let sbe the sum of the numbers in each row of an n-by-nmagic square.
Letusaddallthenumbersinrows1throughn. We will get the following
equality:
sn = 1+2+...+n2, i.e., sn =n2(n2+1)
2,which implies that s=n(n2+1)
2.
b. Number positions in an n-by-nmatrix from 1 through n2.Generate a
permutation of the numbers 1 through n2, put them in the corresponding
positions of the matrix, and check the magic-square equality (proved in
part (a)) for every row, every column, and each of the two main diagonals
of the matrix.
c. n/a
d. n/a
10. a. Since the letter-digit correspondence must be one-to-one and there
are only ten distinct decimal digits, the exhaustive search needs to check
P(10,k) = 10!/(10 −k)! possible substitutions, where kis the number
of distinct letters in the input. (The requirement that the first letter of
a word cannot represent 0 can be used to reduce this number further.)
Thus a program should run in a quite reasonable amount of time on to-
day’s computers. Note that rather than checking two cases–with and
without a “1-carry”–for each of the decimal positions, the program can
check just one equality, which stems from the definition of the decimal
number system. For Dudeney’s alphametic, for example, this equality is
1000(S+M) + 100(E+O) + 10(N+R) + (D+E) = 10000M + 1000O +
100N + 10E + Y
b. Here is a “computerless” solution to this classic problem. First, no-
tice that M must be 1. (Since both S and M are not larger than 9, their
sum, even if increased by 1 because of the carry from the hundred column,
must be less than 20.) We will have to rely on some further insigts into
specifics of the problem. The leftmost digits of the addends imply one of
the two possibilities: either S + M = 10 + O (if there was no carry from
thehundredcolumn)or1+S+M=10+O(iftherewassuchacarry).
First, let us pursue the former of the two possibilities. Since M = 1, S ≤
9 and O ≥0,theequationS+1=10+Ohasonlyonesolution:S=9
and O = 0. This leaves us with
27
END
+ORE
–––—
NEY
Since we deal here with the case of no carry from the hundreds and E and
N must be distinct, the only possibility is a carry from the tens: 1 + E = N
and either N + R = 10 + E (if there was no carry from the rightmost column)
or1+N+R=10+E(iftherewassuchacarry). Thefirstcombination
leadstoacontradiction: Substituting1+EforNintoN+R=10+E,we
obtain R = 9, which is incompatible with the same digit already represented by
S. Thesecondcombinationof1+E=Nand1+N+R=10+Eimplies,
after substituting the first of these equations into the second one, R = 8. Note
that the only remaining digit values still unassigned are 2, 3, 4, 5, 6, and 7.
Finally, for the righmost column, we have the equation D + E = 10 + Y. But
10+Y≥12, because the smallest unassigned digit value is 2 while D + E ≤12
because the two largest unassigned digit values are 6 and 7 and E <N. Thus,
D+E=10+Y=12. HenceY=2andD+E=12. Theonlypairofstill
unassigned digit values that add up to 12, 5 and 7, must be assigned to E and
D, respectively, since doing this the other way (E = 7, D = 5) would imply N
= E + 1 = 8, which is already represented by R. Thus, we found the following
solution to the puzzle:
9567
+1085
––––—
10652
Is this the only solution? To answer this question, we should pursue the
carry possibility from the hundred column to the thousand column (see above).
Then1+S+M=10+Oor,sinceM=1,S=8+O. ButS≤9, while 8 +
O≥10 since O ≥2. Hence the last equation has no solutions in our domain.
This proves that the puzzle has no other solutions.
28
This file contains the exercises, hints, and solutions for Chapter 4 of the
book ”Introduction to the Design and Analysis of Algorithms,” 2nd edition, by
A. Levitin. The problems that might be challenging for at least some students
are marked by ;those that might be difficult for a majority of students are
marked by .
Exercises 4.1
1. a. Write a pseudocode for a divide-and-conquer algorithm for finding the
position of the largest element in an array of nnumbers.
b. What will be your algorithm’s output for arrays with several elements
of the largest value?
c. Set up and solve a recurrence relation for the number of key com-
parisons made by your algorithm.
d. How does this algorithm compare with the brute-force algorithm for
this problem?
2. a. Write a pseudocode for a divide-and-conquer algorithm for finding val-
ues of both the largest and smallest elements in an array of nnumbers.
b. Set up and solve (for n=2
k) a recurrence relation for the number
of key comparisons made by your algorithm.
c. How does this algorithm compare with the brute-force algorithm for
this problem?
3. a. Write a pseudocode for a divide-and-conquer algorithm for the ex-
ponentiation problem of computing anwhere a>0and nis a positive
integer.
b. Set up and solve a recurrence relation for the number of multipli-
cationsmadebythisalgorithm.
c. How does this algorithm compare with the brute-force algorithm for
this problem?
4. As mentioned in Chapter 2, logarithm bases are irrelevant in most contexts
arising in analyzing an algorithm’s efficiency class. Is it true for both
assertions of the Master Theorem that include logarithms?
5. Find the order of growth for solutions of the following recurrences.
a. T(n)=4T(n/2) + n, T (1) = 1
1
b. T(n)=4T(n/2) + n2,T(1) = 1
c. T(n)=4T(n/2) + n3,T(1) = 1
6. Apply mergesort to sort the list E, X, A, M, P, L, E in alphabetical
order.
7. Is mergesort a stable sorting algorithm?
8. a. Solve the recurrence relation for the number of key comparisons made
by mergesort in the worst case. (You may assume that n=2
k.)
b. Set up a recurrence relation for the number of key comparisons made
by mergesort on best-case inputs and solve it for n=2
k.
c. Set up a recurrence relation for the number of key moves made by
the version of mergesort given in Section 4.1.Does taking the number of
key moves into account change the algorithm’s efficiency class?
9. Let A[0..n −1] be an array of ndistinct real numbers. A pair (A[i],A[j])
is said to be an inversion if these numbers are out of order, i.e., i<j
but A[i]>A[j].Design an O(nlog n)algorithm for counting the number
of inversions.
10. One can implement mergesort without a recursion by starting with merg-
ing adjacent elements of a given array, then merging sorted pairs, and so
on. Implement this bottom-up version of mergesort in the language of
your choice.
11. Tromino puzzle A tromino is an L-shaped tile formed by adjacent 1-
by-1 squares. The problem is to cover any 2n-by-2nchessboard with
one missing square (anywhere on the board) with trominoes. Trominoes
should cover all the squares of the board except the missing one with no
overlaps.
Design a divide-and-conquer algorithm for this problem.
2
Hints to Exercises 4.1
1. In more than one respect, this question is similar to the divide-and-conquer
computation of the sum of nnumbers. Also, you were asked to analyze
an almost identical algorithm in Exercises 2.4.
2. Unlike Problem 1, a divide-and-conquer algorithm for this problem can be
more efficient by a constant factor than the brute-force algorithm.
3. How would you compute a8by solving two exponentiation problems of
size 4? How about a9?
4. Look at the notations used in the theorem’s statement.
5. Apply the Master Theorem.
6. Trace the algorithm as it was done for another input in the section.
7. How can mergesort reverse a relative ordering of two elements?
8. a. Use backward substitutions, as usual.
b. What inputs minimize the number of key comparisons made by merge-
sort? How many comparisons are made by mergesort on such inputs
during the merging stage?
c. Do not forget to include key moves made both before the split and
during the merging.
9. Modify mergesort to solve the problem.
10. n/a
11. A divide-and-conquer algorithm works by reducing a problem’s instance
to several smaller instances of the same problem.
3
Solutions to Exercises 4.1
1. a. Call Algorithm MaxIndex (A[0..n −1]) where
Algorithm MaxIndex (A[l..r])
//Input: A portion of array A[0..n −1] between indices land r(l≤r)
//Output: The index of the largest element in A[l..r]
if l=rreturn l
else temp1←MaxIndex (A[l..(l+r)/2])
temp2←MaxIndex (A[(l+r)/2+1..r])
if A[temp1] ≥A[temp2]
return temp1
else return temp2
b. This algorithm returns the index of the leftmost largest element.
c. The recurrence for the number of element comparisons is
C(n)=C(n/2)+C(n/2)+1 for n>1,C(1) = 0.
Solving it by backward substitutions for n=2
kyields the following:
C(2k)=2C(2k−1)+1
=2[2C(2k−2)+1]+1=2
2C(2k−2)+2+1
=2
2[2C(2k−3)+1]+2+1=2
3C(2k−3)+2
2+2+1
=...
=2
iC(2k−i)+2
i−1+2
i−2+... +1
=...
=2
kC(2k−k)+2
k−1+2
k−2+... +1=2
k−1=n−1.
We can verify that C(n)=n−1satisfies, in fact, the recurrence for
every value of n>1by substituting it into the recurrence equation and
considering separately the even (n=2i)and odd (n=2i+1) cases. Let
n=2i, where i>0.Then the left-hand side of the recurrence equation
is n−1=2i−1.The right-hand side is
C(n/2)+C(n/2)+1 = C(2i/2)+C(2i/2)+1
=2C(i)+1=2(i−1) + 1 = 2i−1,
which is the same as the left-hand side.
Let n=2i+1,where i>0.Then the left-hand side of the recurrence
equation is n−1=2i. The right-hand side is
C(n/2)+C(n/2)+1 = C((2i+1)/2)+C((2i+1)/2)+1
=C(i+1)+C(i)+1=(i+1−1) + (i−1) + 1 = 2i,
4

which is the same as the left-hand side in this case, too.
d. A simple standard scan through the array in question requires the
same number of key comparisons but avoids the overhead associated with
recursive calls.
2. a. Call Algorithm MinMax (A[0..n −1],minval, maxval)where
Algorithm MinMax (A[l..r],minval, maxval)
//Finds the values of the smallest and largest elements in a given subarray
//Input: A portion of array A[0..n −1] between indices land r(l≤r)
//Output: The values of the smallest and largest elements in A[l..r]
//assigned to minval and maxval, respectively
if r=l
minval ←A[l]; maxval ←A[l]
else if r−l=1
if A[l]≤A[r]
minval ←A[l]; maxval ←A[r]
else minval ←A[r]; maxval ←A[l]
else //r−l>1
MinMax (A[l..(l+r)/2],minval, maxval)
MinMax (A[(l+r)/2+1..r],minval2, maxval2 )
if minval2 <minval
minval ←minval2
if maxval2 >maxval
maxval ←maxval2
b. Assuming for simplicity that n=2
k,we obtain the following recurrence
for the number of element comparisons C(n):
C(n)=2C(n/2) + 2 for n>2,C(2) = 1,C(1) = 0.
Solving it by backward substitutions for n=2
k,k≥1,yields the following:
C(2k)=2C(2k−1)+2
=2[2C(2k−2)+2]+2=2
2C(2k−2)+2
2+2
=2
2[2C(2k−3)+2]+2
2+2=2
3C(2k−3)+2
3+2
2+2
=...
=2
iC(2k−i)+2
i+2
i−1+... +2
=...
=2
k−1C(2) + 2k−1+... +2=2
k−1+2
k−2=3
2n−2.
c. This algorithm makes about 25% fewer comparisons–1.5ncompared to
2n–than the brute-force algorithm. (Note that if we didn’t stop recursive
calls when n=2,we would’ve lost this gain.) In fact, the algorithm is
5

optimal in terms of the number of comparisons made. As a practical
matter, however, it might not be faster than the brute-force algorithm
because of the recursion-related overhead. (As noted in the solution to
Problem 5 of Exercises 2.3, a nonrecursive scan of a given array that
maintains the minimum and maximum values seen so far and updates
them not for each element but for a pair of two consecutive elements makes
the same number of comparisons as the divide-and-conquer algorithm but
doesn’t have the recursion’s overhead.)
3. a. The following divide-and-conquer algorithm for computing anis based
on the formula an=an/2an/2]:
Algorithm DivConqPower(a, n)
//Computes anby a divide-and-conquer algorithm
//Input: A positive number aand a positive integer n
//Output: The value of an
if n=1return a
else return DivConqPower(a, n/2)∗DivConqPower(a, n/2)
b. The recurrence for the number of multiplications is
M(n)=M(n/2)+M(n/2)+1 for n>1,M(1) = 0.
The solution to this recurrence (solved above for Problem 1) is n−1.
c. Though the algorithm makes the same number of multiplications as the
brute-force method, it has to be considered inferior to the latter because
of the recursion overhead.
4. For the second case, where the solution’s class is indicated as Θ(ndlog n),
the logarithm’s base could change the function by a constant multiple only
and, hence, is irrelevant. For the third case, where the solution’s class is
Θ(nlog a),the logarithm is in the function’s exponent and, hence, must be
indicated since functions nαhave different orders of growth for different
values of α.
5. The applications of the Master Theorem yield the following.
a. T(n)=4T(n/2) + n. Here, a=4,b=2,and d=1.Since a>b
d,
T(n)∈Θ(nlog 4)=Θ(n2).
b. T(n)=4T(n/2) + n2.Here, a=4,b=2,and d=2.Since a=bd,
T(n)∈Θ(n2log n).
6
c. T(n)=4T(n/2) + n3.Here, a=4,b=2,and d=3.Since a<b
d,
T(n)∈Θ(n3).
6. Here is a trace of mergesort applied to the input given:
E X A M P L E
E X A M P L E
X A M P L E
E X A M P L E
A X M P E L
A E X E L M P
A E E L M P X
E
E
7. Mergesort is stable, provided its implementation employs the comparison
≤in merging. Indeed, assume that we have two elements of the same
value in positions iand j,i<j,in a subarray before its two (sorted) halves
are merged. If these two elements are in the same half of the subarray,
their relative ordering will stay the same after the merging because the
elements of the same half are processed by the merging operation in the
FIFO fashion. Consider now the case when A[i]is in the first half while
A[j]is in the second half. A[j]is placed into the new array either after the
first half becomes empty (and, hence, A[i]has been already copied into
the new array) or after being compared with some key k>A[j]of the first
half. In the latter case, since the first half is sorted before the merging
begins, A[i]=A[j]<kcannot be among the unprocessed elements of the
first half. Hence, by the time of this comparison, A[i]has been already
copied into the new array and therefore will precede A[j]after the merging
operation is completed.
7

8. a. The recurrence for the number of comparisons in the worst case, which
was given in Section 4.1, is
Cw(n)=2Cw(n/2) + n−1for n>1(and n=2
k),C
w(1) = 0.
Solving it by backward substitutions yields the following:
Cw(2k)=2Cw(2k−1)+2
k−1
=2[2Cw(2k−2)+2
k−1−1] + 2k−1=2
2Cw(2k−2)+2·2k−2−1
=2
2[2Cw(2k−3)+2k−2−1]+2·2k-2-1=23Cw(2k−3)+3·2k−22−2−1
=...
=2
iCw(2k−i)+i2k−2i−1−2i−2−... −1
=...
=2
kCw(2k−k)+k2k−2k−1−2k−2−... −1=k2k−(2k−1)=nlog n−n+1.
b. The recurrence for the number of comparisons on best-case inputs (lists
sorted in ascending or descending order) is
Cb(n)=2Cb(n/2) + n/2for n>1(and n=2
k),C
b(1) = 0.
Thus,
Cb(2k)=2Cb(2k−1)+2
k−1
=2[2Cb(2k−2)+2
k−2]+2
k−1=2
2Cb(2k−2)+2
k−1+2
k−1
=2
2[2Cb(2k−3)+2
k−3]+2
k−1+2
k−1=2
3Cb(2k−3)+2
k−1+2
k−1+2
k−1
=...
=2
iCb(2k−i)+i2k−1
=...
=2
kCb(2k−k)+k2k−1=k2k−1=1
2nlog n.
c. If n>1,the algorithm copies n/2+n/2=nelements first and
then makes nmore moves during the merging stage. This leads to the
following recurrence for the number of moves M(n):
M(n)=2M(n/2) + 2nfor n>1,M(1) = 0.
According to the Master Theorem, its solution is in Θ(nlog n)–the same
class established by the analysis of the number of key comparisons only.
5. Let ModifiedMergesort be a mergesort modified to return the number of
inversions in its input array A[0..n −1] in addition to sorting it. Obvi-
ously, for an array of size 1, ModifiedMergesort(A[0]) should return 0. Let
8

ileft and iright be the number of inversions returned by ModifiedMerge-
sort(A[0..mid −1]) and ModifiedMergesort(A[mid..n −1]),respectively,
where mid is the index of the middle element in the input array A[0..n−1].
The total number of inversions in A[0..n −1] canthenbecomputedas
ileft+iright +imerge,where imerge,the number of inversions involving
elements from both halves of A[0..n −1],is computed during the merging
as follows. Let A[i]and A[j]be two elements from the left and right half
of A[0..n −1],respectively, that are compared during the merging. If
A[i]<A[j],we output A[i]to the sorted list without incrementing imerge
because A[i]cannot be a part of an inversion with any of the remaining
elements in the second half, which are greater than A[j].If, on the other
hand, A[i]>A[j],we output A[j]and increment imerge by mid −i, the
number of remaining elements in the first half, because all those elements
(and only they) form an inversion with A[j].
10. n/a
11. For n>1,we can always place one L-tromino at the center of the 2n×
2nchessboard with one missing square to reduce the problem to four
subproblems of tiling 2n−1×2n−1boards, each with one missing square
too. The orientation of this centrally placed piece is determined by the
board’s quarter with the missing square as shown by the example below.
Then each of the four smaller problems can be solved recursively until a
trivial case of a 2×2board with a missing square is reached.
9
Exercises 4.2
1. Apply quicksort to sort the list
E, X, A, M, P, L, E
in alphabetical order. Draw the tree of the recursive calls made.
2. For the partitioning procedure outlined in Section 4.2:
a. Prove that if the scanning indices stop while pointing to the same
element, i.e., i=j, the value they are pointing to must be equal to p.
b. Prove that when the scanning indices stop, jcannot point to an ele-
ment more than one position to the left of the one pointed to by i.
c. Why is it worth stopping the scans after encountering an element equal
to the pivot?
3. Is quicksort a stable sorting algorithm?
4. Give an example of an array of nelements for which the sentinel mentioned
in the text is actually needed. What should be its value? Also explain
why a single sentinel suffices for any input.
5. For the version of quicksort given in the text:
a. Are arrays made up of all equal elements the worst-case input, the
best-case input, or neither?
b. Are strictly decreasing arrays the worst-case input, the best-case input,
or neither?
6. a. For quicksort with the median-of-three pivot selection, are increasing
arrays the worst-case input, the best-case input, or neither?
b. Answer the same question for decreasing arrays.
7. Solve the average-case recurrence for quicksort.
8. Design an algorithm to rearrange elements of a given array of nreal num-
bers so that all its negative elements precede all its positive elements.
Your algorithm should be both time- and space-efficient.
9. The Dutch flag problem is to rearrange an array of characters R,W,
and B(red, white, and blue are the colors of the Dutch national flag) so
that all the R’s come first, the W’s come next, and the B’s come last.
Design a linear in-place algorithm for this problem.
10
10. Implement quicksort in the language of your choice. Run your program on
a sample of inputs to verify the theoretical assertions about the algorithm’s
efficiency.
11. Nuts and bolts Youaregivenacollectionofnbolts of different widths
and ncorresponding nuts. You are allowed to try a nut and bolt together,
from which you can determine whether the nut is larger than the bolt,
smaller than the bolt, or matches the bolt exactly. However, there is no
way to compare two nuts together or two bolts together. The problem is
to match each bolt to its nut. Design an algorithm for this problem with
average-case efficiency in Θ(nlog n).[Raw91]
11
Hints to Exercises 4.2
1. We traced the algorithm on an another instance in the section.
2. a. Use the rules for stopping the scans.
b. Use the rules for stopping the scans.
c. Consider an array whose all elements are the same.
3. The definition of stability of a sorting algorithm was given in Section 1.3.
Generally speaking, algorithms that can exchange elements far apart are
not stable.
4. Trace the algorithm to see on which inputs index igets out of bounds.
5. Study what the text’s version of quicksort does on such arrays. You
should base your answers on the number of key comparisons, of course.
6. Where will splits occur on the inputs in question?
7. This requires several standard tricks for solving more sophisticated recur-
rence relations. A solution can be found in most books on the design and
analysis of algorithms.
8. Use the partition idea.
9. You may want to solve first the two-color flag problem, i.e., rearrange
efficiently an array of R’s and B’s. (A similar problem is Problem 8 in
these exercises.)
10. n/a
11. Use the partition idea.
12
Solutions to Exercises 4.2
1. Applying the version of quicksort given in Section 4.2, we get the follow-
ing:
0123 456
Ei
XAM P L j
E
EEj
Ai
MPLX
AE EMP LX
Aij
E
j
Ai
E
AE
E
Mi
PLj
X
Mi
P
j
LX
Mi
Lj
PX
Mj
Li
PX
LMPX
L
P
ij
X
j
Pi
X
PX
X
l = 6, r = 6
l = 3, r = 6
s = 4
l = 5, r = 4
l =1, r = 1l = 0, r = -1
l = 0, r = 1
s = 0
l = 0, r = 6
s = 2
l = 5, r = 6
s = 5
l = 3, r = 3
13

2. a. Let i=jbe the coinciding values of the scanning indices. Accord-
ing to the rules for stopping the i(left-to-right) and j(right-to-left) scans,
A[i]≥pand A[j]≤pwhere pis the pivot’s value. Hence, A[i]=A[j]=p.
b. Let ibe the value of the left-to-right scanning index after it stopped.
Since A[i−1] ≤p, the right-to-left scanning index will have to stop no
later than reaching i−1.
c. Stopping the scans after encountering an element equal to the pivot
tends to yield better (i.e., more equal) splits. For example, if we did
otherwise for an array of nequal elements, we would have gotten a split
into subarrays of sizes n−1and 0.
3. Quicksort is not stable. As a counterexample, consider its performance
on a two-element array of equal values.
4. With the pivot being the leftmost element, the left-to-right scan will get
out of bounds if and only if the pivot is larger than all the other elements.
Appending a sentinel of value equal A[0] (or larger than A[0]) after the
array’s last element will stop the index of the left-to-right scan of A[0..n−1]
from going beyond position n. A single sentinel will suffice by the following
reason. In quicksort, when Partition(A[l..r]) is called for r<n−1,all
the elements to the right of position rare greater than or equal to all the
elements in A[l..r].Hence, A[r+1] will automatically play the role of a
sentinel to stop index igoing beyond position r+1.
5. a. Arrays composed of all equal elements constitute the best case because
all the splits will happen in the middle of corresponding subarrays.
b. Strictly decreasing arrays constitute the worst case because all the
splits will yield one empty subarray. (Note that we need to show this
to be the case on two consecutive iterations of the algorithm because the
first iteration does not yield a decreasing array of size n−1.)
6. The best case for both questions. For either an increasing or decreasing
subarray, the median of the first, last, and middle values will be the median
of the entire subarray. Using it as a pivot will split the subarray in the
middle. This will cause the total number of key comparisons be the
smallest.
7. Here is a solution that follows [Sed88], p. 121:
C(n)= 1
n
n−1
s=0
[(n+1)+C(s)+C(n−1−s)]
14
can be rewritten as
C(n)=(n+1)+ 1
n
n−1
s=0
[C(s)+C(n−1−s)].
Since n−1
s=0 C(s)=n−1
s=0 C(n−1−s),the equation can be reduced to
C(n)=(n+1)+ 2
n
n−1
s=0
C(s)
or
nC(n)=n(n+1)+2
n−1
s=0
C(s).
Substituting n−1for nin the last equation yields
(n−1)C(n−1) = (n−1)n+2
n−2
s=0
C(s).
Subtracting the last equation from the one before yields, after obvious
simplifications, the recurrence
nC(n)=(n+1)C(n−1) + 2n,
which, after dividing both hand sides by n(n+1),becomes
C(n)
n+1 =C(n−1)
n+2
n+1.
Substituting B(n)= C(n)
n+1 ,we obtain the following recurrence relation:
B(n)=B(n−1) + 2
n+1 for n≥2,B(1) = B(0) = 0.
The latter can be solved either by backward substitutions (or by “tele-
scoping”) to obtain
B(n)=2
n+1
k=3
1
k.
Hence
B(n)=2Hn+1 −3,where Hn+1 =
n+1
k=1
1
k≈ln(n+1) (see Appendix A).
Thus,
C(n)=(n+1)B(n)≈2(n+ 1) ln(n+1)≈2nln n.
15

8. The following algorithm uses the partition idea similar to that of quicksort,
although it’s implemented somewhat differently. Namely, on each iter-
ation the algorithm maintains three sections (possibly empty) in a given
array: all the elements in A[0..i−1] are negative, all the elements in A[i..j]
are unknown, and all the elements in A[j+1..n]are nonnegative:
A[0] ... A[i−1] A[i]... A[j]A[j+1] ... A[n−1]
all are <0unknown all are ≥0
On each iteration, the algorithm shrinks the size of the unknown section
by one element either from the left or from the right.
Algorithm NegBeforePos(A[0..n −1])
//Puts negative elements before positive (and zeros, if any) in an array
//Input: Array A[0.n−1] of real numbers
//Output: Array A[0.n−1] in which all its negative elements precede
nonnegative
i←0; j←n−1
while i≤jdo //i<jwould suffice
if A[i]<0//shrink the unknown section from the left
i←i+1
else //shrink the unknown section from the right
swap(A[i],A[j])
j←j−1
Note: If we want all the zero elements placed after all the negative el-
ements but before all the positive ones, the problem becomes the Dutch
flag problem (see Problem 9 in these exercises).
9. The following algorithm uses the partition idea similar to that of quick-
sort. (See also a simpler 2-color version of this problem in Problem 8 in
these exercises.) On each iteration, the algorithm maintains four sections
(possibly empty) in a given array: all the elements in A[0..r −1] are filled
with R’s, all the elements in A[r..w−1] are filled with W’s, all the elements
in A[w..b]are unknown, and all the elements in A[b+1..n −1] are filled
with B’s.
A[0] ... A[r−1] A[r]... A[w−1] A[w]... A[b]A[b+1] ... A[n−1]
all are filled with R’s all are filled with W’s unknown all are filled with B’s
On each iteration, the algorithm shrinks the size of the unknown section
by one element either from the left or from the right.
Algorithm DutchFlag(A[0..n −1])
//Sorts an array with values in a three-element set
//Input: An array A[0..n −1] of characters from {’R’, ’W’, ’B’}
16

//Output: Array A[0..n−1] in which all its Relements precede
// all its Welements that precede all its Belements
r←0; w←0; b←n−1
while w≤bdo
if A[w]=’R’
swap(A[r],A[w]); r←r+1; w←w+1
else if A[w]=’W’
w←w+1
else //A[w]=’B’
swap(A[w],A[b]); b←b−1
10. n/a
11. Randomly select a nut and try each of the bolts for it to find the matching
bolt and separate the bolts that are smaller and larger than the selected
nut into two disjoint sets. Then try each of the unmatched nuts against
the matched bolt to separate those that are larger from those that are
smaller than the bolt. As a result, we’ve identified a matching pair and
partitioned the remaining nuts and bolts into two smaller independent
instances of the same problem. The average number of nut-bolt compar-
isons C(n)is defined by the recurrence very similar to the one for quicksort
in Section 4.2:
C(n)= 1
n
n−1
s=0
[(2n−1) + C(s)+C(n−1−s)],C(1) = 0,C(0) = 0.
The solution to this recurrence can be shown to be in Θ(nlog n)by re-
peating the steps outlined in the solution to Problem 7.
Note: See a O(nlog n)deterministic algorithm for this problem in the
paper by Janos Komlos, Yuan Ma and Endre Szemeredi "Matching Nuts
and Bolts in O(nlogn) Time," SIAM J. Discrete Math. 11, No.3, 347-372
(1998).
17

Exercises 4.3
1. a. What is the largest number of key comparisons made by binary search
in searching for a key in the following array?
314 27 31 39 42 55 70 74 81 85 93 98
b. List all the keys of this array that will require the largest number of
key comparisons when searched for by binary search.
c. Find the average number of key comparisons made by binary search in
a successful search in this array. (Assume that each key is searched for
with the same probability.)
d. Find the average number of key comparisons made by binary search in
an unsuccessful search in this array. (Assume that searches for keys in
each of the 14 intervals formed by the array’s elements are equally likely.)
2. Solve the recurrence Cworst(n)=Cworst(n/2)+1 for n>1,C
worst(1) =
1,for n=2
kby backward substitutions.
3. a.Prove the equality
log2n+1=log2(n+1)for n≥1.
b.Prove that Cworst(n)=log2n+1satisfies equation (4.2) for every
positive integer n.
4. Estimate how many times faster an average successful search will be in
a sorted array of 100,000 elements if it is done by binary search versus
sequential search.
5. Sequential search can be used with about the same efficiency whether a
list is implemented as an array or as a linked list. Is it also true for binary
search? (Of course, we assume that a list is sorted for binary search.)
6. How can one use binary search for range searching, i.e., for finding all the
elements in a sorted array whose values fall between two given values L
and U(inclusively), L≤U? What is the worst-case efficiency of this
algorithm?
7. Write a pseudocode for a recursive version of binary search.
8. Design a version of binary search that uses only two-way comparisons such
as ≤and =. Implement your algorithm in the language of your choice
and carefully debug it (such programs are notorious for being prone to
bugs).
9. Analyze the time efficiency of the two-way comparison version designed in
Problem 8.
18
10. A version of the popular problem-solving task involves presenting people
with an array of 42 pictures–seven rows of six pictures each–and asking
them to identify the target picture by asking questions that can be an-
swered yes or no. Further, people are then required to identify the picture
with as few questions as possible. Suggest the most efficient algorithm for
this problem and indicate the largest number of questions that may be
necessary.
19

Hints to Exercises 4.3
1. a. Take advantage of the formula that gives the immediate answer.
(b)—(d) The most efficient prop for answering such questions is a binary
tree that mirrors the algorithm’s operations in searching for an arbitrary
search key. The first three nodes of such a tree for the instance in question
will look as follows:
6(55)
2(27) 9(81)
(The first number inside a node is the index mof the array’s element being
compared with a search key; the number in the parentheses is the value
of the element itself, i.e., A[m].)
2. If you need to refresh your memory, look up Section 2.4, where we solved
an almost identical recurrence relation, and Appendix B.
3. a. Use the fact that nis bounded below and above by some consecutive
powers of 2, i.e., 2k≤n<2k+1.
b. Thecaseofanevenn(n=2i)was considered in the section. For
an odd n(n=2i+1),substitute the function into both hand sides of
the equation and show their equality.The formula of part (a) might be
useful. Do not forget to verify the initial condition, too.
4. Estimate the ratio of the average number of key comparisons made in a
successful search by sequential search to that for binary search.
5. How would you reach the middle element in a linked list?
6. Find separately the elements that are greater than or equal to Land those
that are smaller than or equal to U. DonotforgetthatneitherLnor U
have to be among the array values.
7. You may find the diagram of binary search in the text helpful.
8. Use the comparison K≤A[m]where m←(l+r)/2until l=r. Then
check whether the search is successful or not.
9. The analysis is almost identical to that of the text’s version of binary
search.
10. Number the pictures and use this numbering in your questions.
20
Solutions to Exercises 4.3
1. a. According to formula (4.4), Cworst(13) = log2(13+1)=4.
b. In the comparison tree below, the first number indicates the element’s
index, the second one is its value:
6(55)
2(27) 9(81)
0(3) 4(39) 7(70) 11(93)
no 1(14) 3(31) 5(42) no 8(74) 10(85) 12(98)
The searches for each of the elements on the last level of the tree, i.e.,
the elements in positions 1(14), 3(31), 5(42), 8(74), 10(85), and 12(98)
will require the largest number of key comparisons.
c. Cyes
avg =1
13 ·1·1+ 1
13 ·2·2+ 1
13 ·3·4+ 1
13 ·4·6=41
13 ≈3.2.
d. Cno
avg =1
14 ·3·2+ 1
14 ·4·12 = 54
14 ≈3.9.
2. For n=2
k(and omitting the subscript to simplify the notation),we get
the recurrence relation
C(2k)=C(2k−1)+1 for k>0,C(1) = 1.
By making backward substitutions, we obtain the following:
C(2k)=C(2k−1)+1 substitute C(2k−1)=C(2k−2)+1
=[C(2k−2)+1]+1=C(2k−2)+2 substitute C(2k−2)=C(2k−3)+1
=[C(2k−3)+1]+2=C(2k−3)+3 ...
... ...
=C(2k−i)+i
...
=C(2k−k)+k.
Thus, we end up with
C(2k)=C(1) + k=1+k
21

or, after returning to the original variable n=2
kand hence k=log
2n,
C(n) = log2n+1.
3. a. Every positive integer nis bounded below and above by some consec-
utive powers of 2, i.e.,
2k≤n<2k+1,
where kis a nonnegative integer (uniquely defined by the value of n).
Taking the base-2 logarithms, we obtain
k≤log2n<k+1.
Hence k≤log2nand, since log2n≤log2n<k+1,we have the
inequality
k≤log2n<k+1,
which implies that log2n=k. Similarly, 2k<n+1≤2k+1,and an
argument analogous to the one just used to show that log2n=k, we
obtain that log2(n+1)=k+1.Hence, log2(n+1)=log2n+1.
b. ThecaseofevennwasconsideredinthetextofChapter4.3. Let
n>1be odd, i.e., n=2i+1,where i>0.The left-hand side is:
Cw(n)=log2n+1 = log2(2i+1)+1 = log2(2i+2)=log22(i+1)
=log22+log2(i+1)=1+log2(i+1)=1+(log2i+1) = log2i+2.
Theright-handsideis:
Cw(n/2)+1=Cw((2i+1)/2)+1=Cw(i+1/2)+1=Cw(i)+1=
(log2i+1)+1=log2i+2,
which is the same as the left-hand side.
The initial condition is verified immediately: Cw(1) = log21+1=1.
4. The ratio in question can be estimated as follows:
Cseq.
avg (n)
Cbin.
avg (n)≈n/2
log2n=(for n=10
5)105/2
log2105=1
2∗5
105
log210 =104
log210 ≈3000.
5. Unlike an array, where any element can be accessed in constant time,
reaching the middle element in a linked list is a Θ(n)operation. Hence,
though implementable in principle, binary search would be a horribly in-
efficient algorithm for searching in a (sorted) linked list.
22
6. Step 1: Check whether A[0] ≤Uand A[n−1] ≤L. If this is not true,
stop: there are no such elements.
Step 2: Search for Lusing the text’s version of binary search. If the
search was successful, record the value mof the index returned by the
algorithm; if the search was unsuccessful, record the value of lon the exit
from the algorithm.
Step 3: Search for Uusing the text’s version of binary search. If the
search was successful, record the value mof the index returned by the
algorithm; if the search was unsuccessful, record the value of ron the exit
from the algorithm.
The final answer (if the problem has a solution) is the range of the array
indices between land r(inclusively), where land rare the values recorded
in Steps 2 and 3, respectively.
7. Call BSR(A[0..n −1],K)where
Algorithm BSR( A[l..r],K)
//Implements binary search recursively.
//Input: A sorted (sub)array A[l..r]and a search key K
//Output: An index of the array’s element equal to K
// or -1 if there is no such element.
if l>rreturn -1
else m←(l+r)/2
if K=A[m]return m
else if K<A[m]return BSR(A[l..m −1],K)
else return BSR(A[m+1..r],K)
8. Algorithm TwoWayBinary Search(A[0..n −1],K)
//Implements binary search with two-way comparisons
//Input: A sorted array A[0..n −1] and a search key K
//Output: An index of the array’s element equal to K
// or -1 if there is no such element.
l←0; r←n−1
while l<rdo
m←(l+r)/2
if K≤A[m]
r←m
else l←m+1
if K=A[l]return l
else return -1
9. Algorithm TwoWayBinarySearch makes log2n+1 two-way comparisons
in the worst case, which is obtained by solving the recurrence Cw(n)=
Cw(n/2)+1 for n>1,C
w(1) = 1. Also note that the best-case
efficiency of this algorithm is not in Θ(1) but in Θ(log n).
23
10. Apply a two-way comparison version of binary search using the picture
numbering. That is, assuming that pictures are numbered from 1 to 42,
start with a question such as “Is the picture’s number >21?”.The largest
number of questions that may be required is 6. (Because the search
can be assumed successful, one less comparison needs to be made than in
TwoWayBinarySearch, yielding here log242=6.)
24
Exercises 4.4
1. Design a divide-and-conquer algorithm for computing the number of levels
in a binary tree. What is the efficiency class of your algorithm?
2. The following algorithm seeks to compute the number of leaves in a binary
tree.
Algorithm LeafCounter( T)
//Computes recursively the number of leaves in a binary tree
//Input: A binary tree T
//Output: The number of leaves in T
if T=∅return 0
else return LeafCounter(TL)+ LeafCounter (TR)
Is this algorithm correct? If it is, prove it; if it is not, make an ap-
propriate correction.
3. Prove equality (4.5) by mathematical induction.
4. Traverse the following binary tree
a.. in preorder. b. in inorder. c. in postorder.
a
b
d e f
c.
5. Write a pseudocode for one of the classic traversal algorithms (preorder,
inorder, and postorder) for binary trees. Assuming that your algorithm
is recursive, find the number of recursive calls made.
6. Which of the three classic traversal algorithms yields a sorted list if applied
to a binary search tree? Prove this property.
7. a. Draw a binary tree with ten nodes labeled.0, 1, 2, ..., 9 in such a way
that the inorder and postorder traversals of the tree yield the following
lists: 9, 3, 1, 0, 4, 2, 7, 6, 8, 5 (inorder) and 9, 1, 4, 0, 3, 6, 7, 5, 8, 2
(postorder).
b. Give an example of two permutations of the same nlabels 0,1,2, .., n−1
that cannot be inorder and postorder traversal lists of the same binary tree.
c. Design an algorithm that constructs a binary tree for which two given
lists of nlabels 0,1,2, .., n −1are generated by the inorder and postorder
traversals of the tree. Your algorithm should also identify inputs for which
the problem has no solution.
25
8. The internal path length Iof an extended binary tree is defined as
the sum of the lengths of the paths–taken over all internal nodes–from
the root to each internal node. Similarly, the external path length Eof
an extended binary tree is defined as the sum of the lengths of the paths–
taken over all external nodes–from the root to each external node. Prove
that E=I+2nwhere nis the number of internal nodes in the tree.
9. Write a program for computing the internal path length of a binary search
tree. Use it to investigate empirically the average number of key compar-
isons for searching in a randomly generated binary search tree.
10. Chocolate bar puzzle Given an n-by-mchocolate bar, you need to break
it into nm 1-by-1 pieces. You can break a bar only in a straight line, and
only one bar can be broken at a time. Design an algorithm that solves the
problem with the minimum number of bar breaks. What is this minimum
number? Justify your answer by using properties of a binary tree.
26
Hints to Exercises 4.4
1. The problem is almost identical to the one discussed in this section.
2. Trace the algorithm on a small input.
3. Use strong induction on the number of internal nodes.
4. This is a standard exercise that you have probably done in your data
structures course. With the traversal definitions given at the end of this
section, you should be able to trace them even if you have never seen them
before.
5. The pseudocodes can simply mirror the traversals’ descriptions.
6. If you do not know the answer to this important question, you may want
to check the results of the traversals on a small binary search tree. For a
proof, answer the question: what can be said about two nodes with keys
k1and k2if k1<k
2?
7. Find the root’s label of the binary tree first and then identify the labels
of the nodes in its left and right subtrees.
8. Use strong induction on the number of internal nodes.
9. n/a
10. Breaking the chocolate bar can be represented by a binary tree.
27
Solutions to Exercises 4.4
1. Algorithm Levels(T)
//Computes recursively the number of levels in a binary tree
//Input: Binary tree T
//Output: Number of levels in T
if T=∅return 0
else return max{Levels(TL),Levels (TR)}+1
This is a Θ(n)algorithm, by the same reason Height(T)discussed in the
section is.
2. The algorithm is incorrect because it returns 0 instead of 1 for the one-
node binary tree. Here is a corrected version:
Algorithm LeafCounter (T)
//Computes recursively the number of leaves in a binary tree
//Input: A binary tree T
//Output: The number of leaves in T
if T=∅return 0 //empty tree
else if TL=∅and TR=∅return 1 //one-node tree
else return LeafCounter(TL)+ LeafCounter(TR)//general case
3. Here is a proof of equality (4.5) by strong induction on the number of
internal nodes n≥0. Thebasisstepistruebecauseforn=0we have
the empty tree whose extended tree has 1 external node by definition. For
the inductive step, let us assume that
x=k+1
for any extended binary tree with 0≤k<ninternal nodes. Let Tbe
a binary tree with ninternal nodes and let nLand xLbe the numbers
of internal and external nodes in the left subtree of T, respectively, and
let nRand xRbe the numbers of internal and external nodes in the right
subtree of T, respectively. Since n>0,T has a root, which is its internal
node, and hence
n=nL+nR+1.
Since both nL<nand nR<n,we can use equality (4.5), assumed to be
correct for the left and right subtree of T, to obtain the following:
x=xL+xR=(nL+1)+(nR+1)=(nL+nR+1)+1=n+1,
which completes the proof.
28
4. a. Preorder: abdecf
b. Inorder: dbeacf
c. Postorder: debfca
5. Here is a pseudocode of the preorder traversal:
Algorithm Preorder(T)
//Implements the preorder traversal of a binary tree
//Input: Binary tree T(with labeled vertices)
//Output: Node labels listed in preorder
if T=∅
print label of T’s root
Preorder (TL)//TLis the root’s left subtree
Preorder (TR)//TRis the root’s right subtree
The number of calls, C(n),made by the algorithm is equal to the number of
nodes, both internal and external, in the extended tree. Hence, according
to the formula in the section,
C(n)=2n+1.
6. The inorder traversal yields a sorted list of keys of a binary search tree.
In order to prove it, we need to show that if k1<k
2are two keys in a
binary search tree then the inorder traversal visits the node containing k1
before the node containing k2.Let k3be the key at their nearest common
ancestor. (Such a node is uniquely defined for any pair of nodes in a
binary tree. If one of the two nodes at hand is an ancestor of the other,
their nearest common ancestor coincides with the ancestor.) If the k3’s
node differ from both k1’s node and k2’s node, the definition of a binary
search tree implies that k1and k2are in the left and right subtrees of k3,
respectively. If k3’s node coincides with k2’s node (k1’s node), k1’s node
(k2’s node) is in the left (right) subtree rooted at k2’s node (k1’s node).
In each of these cases, the inorder traversal visits k1’s node before k2’s
node.
7. a. The root’s label is listed last in the postorder tree: hence, it is 2. The
labels preceding 2 in the order list–9,3,1,0,4–form the inorder traversal
list of the left subtree; the corresponding postorder list for the left subtree
traversal is given by the first four labels of the postorder list: 9,1,4,0,3.
Similarly, for the right subtree, the inorder and postorder lists are, respec-
tively, 7,6,8,5 and 6,7,5,8. Applying the same logic recursively to each of
29
the subtrees yields the following binary tree:
2
3
90
8
5
7
6
14
b. There is no such example for n=2.For n=3,lists 0,1,2 (inorder)
and 2,0,1 (postorder) provide one.
c. The problem can be solved by a recursive algorithm based on the
following observation: There exists a binary tree with inorder traversal
list i0,i
1, ..., in−1and postorder traversal list p0,p
1, ..., pn−1if and only
if pn−1=ik(the root’s label), the sets formed by the first klabels
in both lists are the same: {i0,i
1,...,i
k−1}={p0,p
1,...,p
k−1}(the la-
bels of the nodes in the left subtree) and the sets formed by the other
n−k−1labels excluding the root are the same: {ik+1,i
k+2, ..., in−1}=
{pk,p
k+1, ..., pn−2}(the labels of the nodes in the right subtree).
Algorithm Tree (i0,i
1, ..., in−1,p
0,p
1, ..., pn−1)
//Construct recursively the binary tree based on the inorder and postorder
traversal lists
//Input: Lists i0,i
1, ..., in−1and p0,p
1,...,p
n−1of inorder and postorder
traversals, respectively
//Output: Binary tree T, specified in preorder, whose inorder and pos-
torder traversals yield the lists given or
// -1 if such a tree doesn’t exist
Find element ikin the inorder list that is equal to the last element pn−1
of the postorder list.
if the previous search was unsuccessful return −1
else print(ik)
Tree (i0,i
1, ..., ik−1,p
0,p
1,...,p
k−1)
Tree (ik+1,i
k+2, ..., in−1,p
k,p
k+1, ..., pn−2)
8. We can prove equality E=I+2n,whereEand Iare, respectively,.
the external and internal path lengths in an extended binary tree with n
internal nodes by induction on n. The basis case, for n=0, holds because
both Eand Iare equal to 0 in the extended tree of the empty binary tree.
30
For the general case of induction, we assume that
E=I+2k
for any extended binary tree with 0≤k<ninternal nodes. To prove
the equality for an extended binary tree Twith ninternal nodes, we are
going to use this equality for TLand TR, the left and right subtrees of
T. (Since n>0,the root of the tree is an internal node, and hence the
number of internal nodes in both the left and right subtree is less than n.)
Thus,
EL=IL+2nL,
where ELand ILare external and internal paths, respectively, in the left
subtree TL,which has nLinternal and xLexternal nodes, respectively.
Similarly,
ER=IR+2nR,
where ERand IRare external and internal paths, respectively, in the right
subtree TR,which has nRinternal and xRexternal nodes, respectively.
Since the length of the simple path from the root of TL(TR)to a node in
TL(TR)is one less than the length of the simple path from the root of T
to that node, we have
E=(EL+xL)+(ER+xR)
=(IL+2nL+xL)+(IR+2nR+xR)
=[(IL+nL)+(IR+nR)] + (nL+nR)+(xL+xR)
=I+(n−1) + x,
where xis the number of external nodes in T. Since x=n+1 (see Section
4.4), we finally obtain the desired equality:
E=I+(n−1) + x=I+2n.
9. n/a
10. We can represent operations of any algorithm solving the problem by a full
binary tree in which parental nodes represent breakable pieces and leaves
represent 1-by-1 pieces of the original bar. The number of the latter is
nm;and the number of the former, which is equal to the number of the
bar breaks, is one less, i.e., nm −1,according to equation (4.5) in Section
4.4. (Note: This elegant solution was suggested to the author by Simon
Berkovich, one of the book’s reviewers.)
Alternatively, we can reason as follows: Since only one bar can be broken
at a time, any break increases the number of pieces by 1. Hence, nm −1
31
breaks are needed to get from a single n-by-mpiece to nm one-by-one
pieces, which is obtained by any sequence of nm −1allowed breaks. (The
same argument can be made more formally by mathematical induction.)
32
Exercises 4.5
1. What are the smallest and largest numbers of digits the product of two
decimal n-digit integers can have?
2. Compute 2101 ∗1130 by applying the divide-and-conquer algorithm out-
lined in the text.
3. a. Prove the equality alog c=clog a, which was used twice in Section 4.5.
b. Why is nlog 3better than 3log nas a closed-form formula for M(n)?
4. a. Why did we not include multiplications by 10nin the multiplication
count M(n)of the large-integer multiplication algorithm?
b. In addition to assuming that nis a power of 2, we made, for the
sake of simplicity, another, more subtle, assumption in setting up a recur-
rence relation for M(n)which is not always true (it does not change the
final answer, however.) What is this assumption?
5. How many one-digit additions are made by the pen-and-pencil algorithm
in multiplying two n-digit integers? (You may disregard potential carries.)
6. Verify the formulas underlying Strassen’s algorithm for multiplying 2-by-2
matrices.
7. Apply Strassen’s algorithm to compute
1021
4110
0130
5021
∗
0101
2104
2011
1350
exiting the recursion when n=2,i.e., computing the products of 2-by-2
matrices by the brute-force algorithm.
8. Solve the recurrence for the number of additions required by Strassen’s
algorithm. (Assume that nis a power of 2.)
9. V. Pan [Pan78] has discovered a divide-and-conquer matrix multiplication
algorithm that is based on multiplying two 70-by-70 matrices using 143,640
multiplications. Find the asymptotic efficiency of Pan’s algorithm (you
can ignore additions) and compare it with that of Strassen’s algorithm.
10. Practical implementations of Strassen’s algorithm usually switch to the
brute-force method after matrix sizes become smaller than some “crossover
point”. Run an experiment to determine such crossover point on your
computer system.
33
Hints to Exercises 4.5
1. You might want to answer the question for n=2first and then generalize
it.
2. Trace the algorithm on the input given. You will have to use it again in
order to compute products of two-digit numbers as well.
3. a. Take logarithms of both sides of the equality.
b What did we use the closed-form formula for?
4. a. How do we multiply by powers of 10?
b. Try to repeat the argument for, say, 98 ∗76.
5. Counting the number of one-digit additions made by the pen-and-pencil
algorithm in multiplying, say, two four-digit numbers, should help answer-
ing the general question.
6. Check the formulas by simple algebraic manipulations.
7. Trace Strassen’s algorithm on the input given. (It takes some work, but
it would have been much more of it if you were asked to stop the recursion
when n=1.) It is a good idea to check your answer by multiplying the
matrices by the brute-force (i.e., definition-based) algorithm, too.
8. Use the method of backward substitutions to solve the recurrence given
in the text.
9. The recurrence for the number of multiplications in Pan’s algorithm is
similar to that for Strassen’s algorithm. Use the Master Theorem to find
the order of growth of its solution.
10. n/a
34

Solutions to Exercises 4.5
1. The smallest decimal n-digit positive integer is 10...0
n−1
,i. e.,10
n−1.The
product of two such numbers is 10n−1·10n−1=10
2n−2, which has 2n−1
digits (1 followed by 2n−2zeros).
The largest decimal n-digit integer is 9...9
n
, i.e., 10n−1.The product
of two such numbers is (10n−1)(10n−1) = 102n−2·10n+1, which has 2n
digits (because 102n−1and 102n−1are the smallest and largest numbers
with 2ndigits, respectively, and 102n−1<102n−2·10n+1<102n−1).
2. For 2101 ∗1130:
c2=21∗11
c0=01∗30
c1= (21+01)∗(11 + 30) −(c2+c0)=22∗41 −21 ∗11 −01 ∗30.
For 21 ∗11:
c2=2∗1=2
c0=1∗1=1
c1= (2+1)∗(1+1)−(2+1)=3∗2−3=3.
So, 21 ∗11 = 2 ·102+3·101+ 1 = 231.
For 01 ∗30:
c2=0∗3=0
c0=1∗0=0
c1= (0+1)∗(3+0)−(0+0)=1∗3−0=3.
So, 01 ∗30 = 0 ·102+3·101+0=30.
For 22 ∗41:
c2=2∗4=8
c0=2∗1=2
c1= (2+2)∗(4+1)−(8+2)=4∗5−10 = 10.
So, 22 ∗41 = 8 ·102+10·101+ 2 = 902.
Hence
2101 ∗1130 = 231 ·104+(902−231 −30) ·102+30=2,374,130.
35

3. a. Taking the base-blogarithms of both hand sides of the equality alog c=
clog ayields logbclogba=log
balogbc. Since two numbers are equal if
and only if their logarithms to the same base are equal, the equality in
question is proved.
b. It is easier to compare nlog 3with n2(the number of digit multipli-
cations made by the classic algorithm) than 3log nwith n2.
4. a. When working with decimal integers, multiplication by a power of 10
canbedonebyashift.
b. In the formula for c1,the sum of two n/2-digit integers can have
not n/2digits, as it was assumed, but n/2+1.
5. Let aand bbe two n-digit integers such that the product of each pair of
their digits is a one-digit number. Then the result of the pen-and-pencil
algorithm will look as follows:
a:an−1... a1a0
b:bn−1... b1b0
dn−1,0... d1,0d0,0
dn−1,1dn−2,1d0,1
dn−2,n−1...
dn−1,n−1dn−2,n−1... d1,n−1d0,n−1
# additions 0 1 ... n −2n−1... 10
Hence, the total number of additions without carries will be
1+2+... +(n−1) + (n−2) + ... +1
= [1+2+... +(n−1)] + [(n−2) + ... +1]
=(n−1)n
2+(n−2)(n−1)
2=(n−1)2.
6. m1+m4−m5+m7=
(a00 +a11)(b00 +b11)+a11(b10 −b00)−(a00+a01)b11+(a01 −a11)(b10 +b11)=
a00b00 +a11b00 +a00b11 +a11b11 +a11b10 −a11b00 −a00b11 −a01b11 +a01b10 −
a11b10 +a01b11 −a11b11
=a00b00 +a01b10
m3+m5=a00(b01−b11)+(a00+a01)b11 =a00b01−a00b11+a00b11+a01b11 =
a00b01 +a01b11
m2+m4=(a10+a11)b00+a11(b10−b00)=a10b00+a11b00+a11b10−a11b00 =
36

a10b00 +a11b10
m1+m3−m2+m6=(a00 +a11)(b00 +b11)+a00(b01 −b11)−(a10 +
a11)b00 +(a10 −a00)(b00 +b01)=
a00b00 +a11b00 +a00b11 +a11b11 +a00b01 −a00b11 −a10b00 −a11b00 +a10b00 −
a00b00 +a10b01 −a00b01
=a10b01 +a11b11.
7. For the matrices given, Strassen’s algorithm yields the following:
C=C00 C01
C10 C11 =A00 A01
A10 A11 B00 B01
B10 B11
where
A00 =10
41
,A
01 =21
10
,A
10 =01
50
,A
11 =30
21
,
B00 =01
21
,B
01 =01
04
,B
10 =20
13
,B
11 =11
50
.
Therefore,
M1=(A00 +A11)(B00 +B11)=40
62
12
71
=48
20 14 ,
M2=(A10 +A11)B00 =31
71
01
21
=24
28
,
M3=A00(B01 −B11)=10
41
−10
−54
=−10
−94
,
M4=A11(B10 −B00)=30
21
2−1
−12
=6−3
30
,
M5=(A00 +A01)B11 =31
51
11
50
=83
10 5 ,
M6=(A10 −A00)(B00 +B01)=−11
1−102
25
=23
−2−3,
M7=(A01 −A11)(B10 +B11)=−11
−1−131
63
=32
−9−4.
37
Accordingly,
C00 =M1+M4−M5+M7
=48
20 14 +6−3
30
−83
10 5 +32
−9−4=54
45
,
C01 =M3+M5
=−10
−94
+83
10 5 =73
19
,
C10 =M2+M4
=24
28
+6−3
30
=81
58
,
C11 =M1+M3−M2+M6
=48
20 14 +−10
−94
−24
28
+23
−2−3=37
77
.
That is,
C=
5473
4519
8137
5877
.
8. For n=2
k,the recurrence A(n)=7A(n/2)+18(n/2)2for n>1,A(1) = 0,
becomes
A(2k)=7A(2k−1)+9
24kfor k>1,A(1) = 0.
Solving it by backward substitutions yields the following:
A(2k)=7A(2k−1)+9
24k
=7[7A(2k−2)+9
24k−1]+9
24k=7
2A(2k−2)+7·9
24k−1+9
24k
=7
2[7A(2k−3)+9
24k−2]+7·9
24k−1+9
24k
=7
3A(2k−3)+7
2·9
24k−2+7·9
24k−1+9
24k
=...
=7
kA(2k−k)+9
2
k−1
i=0
7i4k−i=7
k·0+9
24k
k−1
i=0 7
4i
=9
24k(7/4)k−1
(7/4) −1=6(7
k−4k).
38

Returning back to the variable n=2
k,we obtain
A(n)=6(7
log n−4log n)=6(nlog 7−n2).
(Note that the number of additions in Strassen’s algorithm has the same
order of growth as the number of multiplications: Θ(ns)where s=
nlog 7≈n2.807.)
9. The recurrence for the number of multiplications in Pan’s algorithm is
M(n) = 143640M(n/70) for n>1,M(1) = 1.
Solving it for n=70
kor applying the Master Theorem yields M(n)∈
Θ(np)where
p=log
70 143640 = ln 143640
ln 70 ≈2.795.
This number is slightly smaller than the exponent of Strassen’s algorithm
s=log
27=ln 7
ln 2 ≈2.807.
10. n/a
39
Exercises 4.6
1. a. For the one-dimensional version of the closest-pair problem, i.e., for the
problem of finding two closest numbers among a given set of nreal num-
bers, design an algorithm that is directly based on the divide-and-conquer
technique and determine its efficiency class.
b. Is it a good algorithm for this problem?
2. Consider the version of the divide-and-conquer two-dimensional closest-
pair algorithm in which we simply sort each of the two sets C1and C2in
ascending order of their ycoordinates on each recursive call. Assuming
that sorting is done by mergesort, set up a recurrence relation for the
running time in the worst case and solve it for n=2
k.
3. Implement the divide-and-conquer closest-pair algorithm, outlined in this
section, in the language of your choice.
4. Find a visualization of an algorithm for the closest-pair problem on the
Web. What algorithm does this visualization represent?
5. The Voronoi polygon for a point Pof a set Sof points in the plane is
defined to be the perimeter of the set of all points in the plane closer to
Pthan to any other point in S. The union of all the Voronoi polygons of
the points in Sis called the Voronoi diagram of S.
a. What is the Voronoi diagram for a set of three points?
b. Find a visualization of an algorithm for generating the Voronoi dia-
gram on the Web and study a few examples of such diagrams. Based on
your observations, can you tell how the solution to the previous question
is generalized to the general case?
6. Explain how one can find point Pmax in the quickhull algorithm analyti-
cally.
7. What is the best-case efficiency of quickhull?
8. Give a specific example of inputs that make the quickhull algorithm run
in quadratic time.
9. Implement the quickhull algorithm in the language of your choice.
10. Shortest path around There is a fenced area in the two-dimensional Euclid-
ean plane in the shape of a convex polygon with vertices at points P1(x1,y
1),
P2(x2,y
2), ..., Pn(xn,y
n)(not necessarily in this order). There are two
more points, A(xA,y
A)and B(xB,y
B),such that xA<min{x1,x
2,...,x
n}
and xB>max{x1,x
2, ..., xn}.Design a reasonably efficient algorithm for
computing the length of the shortest path between Aand B. [ORo98],
p.68
40
Hints to Exercises 4.6
1. a. How many points need to be considered in the combining-solutions
stage of the algorithm?
b. Design a simpler algorithm in the same efficiency class.
2. Recall (see Section 4.1) that the number of comparisons made by mergesort
in the worst case is Cworst(n)=nlog2n−n+1(for n=2
k).You may
use just the highest-order term of this formula in the recurrence you need
to set up.
3. n/a
4. n/a
5. The answer to part (a) comes directly from a textbook on plane geometry.
6. Use the formula relating the value of a determinant with the area of a
triangle.
7. It must be in Ω(n),ofcourse. (Why?)
8. Design a sequence of npoints for which the algorithm decreases the prob-
lem’s size just by one on each of its recursive calls.
9. n/a
10. The path cannot cross inside the fenced area but it can go along the fence.
41

Solutions to Exercises 4.6
1. a. Assuming that the points are sorted in increasing order, we can find the
closest pair (or, for simplicity, just the distance between two closest points)
by comparing three distances: the distance between the two closest points
in the first half of the sorted list, the distance between the two closest
points in its second half, and the distance between the rightmost point in
the first half and the leftmost point in the second half. Therefore, after
sorting the numbers of a given array P[0..n −1] in increasing order, we
can call ClosestNumbers(P[0..n −1]),where
Algorithm ClosestNumbers(P[l..r])
//A divide-and-conquer alg. for the one-dimensional closest-pair problem
//Input: A subarray P[l..r](l≤r)ofagivenarrayP[0..n −1]
// of real numbers sorted in nondecreasing order
//Output: The distance between the closest pair of numbers
if r=lreturn ∞
else if r−l=1return P[r]−P[l]
else return min{ClosestNumbers(P[l..(l+r)/2]),
ClosestNumbers(P[((l+r)/2+1..r]),
P[(l+r)/2+1]−P[(l+r)/2]}
For n=2
k,the recurrence for the running time T(n)of this algorithm is
T(n)=2T(n/2) + c.
Its solution, according to the Master Theorem, is in Θ(nlog 2)=Θ(n).If
sorting of the input’s numbers is done with a Θ(nlog n)algorithm such
as mergesort, the overall running time will be in Θ(nlog n)+Θ(n)=
Θ(nlog n).
b. A simpler algorithm can sort the numbers given (e.g., by mergesort) and
then compare the distances between the adjacent elements in the sorted
list. The resulting algorithm has the same Θ(nlog n)efficiency but it is
arguably simpler than the divide-and-conquer algorithms above.
Note: In fact, any algorithm that solves this problem must be in Ω(nlog n)
(see Problem 11 in Exercises 11.1).
2. T(n)=2T(n/2) + 2n
2log2n
2for n>2(and n=2
k),T(2) = 1.
Thus, T(2k)=2T(2k−1)+2
k(k−1).Solving it by backward substi-
tutions yields the following:
42
T(2k)=2T(2k−1)+2
k(k−1)
=2[2T(2k−2)+2
k−1(k−2)] + 2k(k−1) = 22T(2k−2)+2
k(k−2) + 2k(k−1)
=2
2[2T(2k−3)+2k−2(k-3)]+2k(k-2)+2k(k-1)=23T(2k−3)+2k(k-3)+2k(k-2)+2k(k-1)
...
=2
iT(2k−i)+2
k(k−i)+2
k(k−i+1)+... +2
k(k−1)
...
=2
k−1T(21)+2
k+2
k2+... +2
k(k−1)
=2
k−1+2
k(1 + 2 + ... +(k−1)) = 2k−1+2
k(k−1)k
2
=2
k−1(1 + (k−1)k)=n
2(1+(log
2n−1) log2n)∈Θ(nlog2n).
3. n/a
4. n/a
5. a. The Voronoi diagram of three points not on the same line is formed by
the perpendicular bisectors of the sides of the triangle with vertices at P1,
P2,and P3:
1
P
2
P
3
P
(If P1,P
2,and P3lie on the same line, with P2between P1and P3,the
Voronoi diagram is formed by the perpendicular bisectors of the segments
with the endpoints at P1and P2and at P2and P3.)
b. The Voronoi polygon of a set of points is made up of perpendicu-
lar bisectors; a point of their intersection has at least three of the set’s
points nearest to it.
43
6. Since all the points in question serve as the third vertex for triangles with
thesamebaseP1Pn,the farthest point is the one that maximizes the area
of such a triangle. The area of a triangle, in turn, can be computed as
one half of the magnitude of the determinant
x1y11
x2y21
x3y31
=x1y2+x3y1+x2y3−x3y2−x2y1−x1y3.
In other words, Pmax is a point whose coordinates (x3,y
3)maximize the
absolute value of the above expression in which (x1,y
1)and (x2,y
2)are
the coordinates of P1and Pn, respectively.
7. If all npoints lie on the same line, both S1and S2will be empty and the
convex hull (a line segment) will be found in linear time, assuming that
the input points have been already sorted before the algorithm begins.
Note: Any algorithm that finds the convex hull for a set of npoints must
be in Ω(n)because all npoints must be processed before the convex hull
is found.
8. Among many possible answers, one can take two endpoints of the hori-
zontal diameter of some circumference as points P1and Pnand obtain
the other points Pi,i=2, ..., n −1,of the set in question by placing them
successively in the middle of the circumference’s upper arc between Pi−1
and Pn.
9. n/a
10. Find the upper and lower hulls of the set {A, B, P1, ..., Pn}(e.g., by
quickhull), compute their lengths (by summing up the lengths of the line
segments making up the polygonal chains) and return the smaller of the
two.
44
This file contains the exercises, hints, and solutions for Chapter 5 of the
book ”Introduction to the Design and Analysis of Algorithms,” 2nd edition, by
A. Levitin. The problems that might be challenging for at least some students
are marked by ;those that might be difficult for a majority of students are
marked by .
Exercises 5.1
1. Ferrying soldiers A detachment of nsoldiers must cross a wide and deep
river with no bridge in sight. They notice two 12-year-old boys playing
in a rowboat by the shore. The boat is so tiny, however, that it can only
hold two boys or one soldier. How can the soldiers get across the river
andleavetheboysinjointpossessionoftheboat? Howmanytimesneed
the boat pass from shore to shore?
2. Alternating glasses There are 2nglassesstandingnexttoeachother
in a row, the first nof them filled with a soda drink while the remaining n
glasses are empty. Make the glasses alternate in a filled-empty-filled-empty
pattern in the minimum number of glass moves. [Gar78], p.7.
3. Design a decrease-by-one algorithm for generating the power set of a set
of nelements. (The power set of a set Sis the set of all the subsets of S,
including the empty set and Sitself.)
4. Apply insertion sort to sort the list E, X, A,M,P,L,Ein alphabetical
order.
5. a. What sentinel should be put before the first element of an array being
sorted in order to avoid checking the in-bound condition j≥0on each
iteration of the inner loop of insertion sort?
b. Will the version with the sentinel be in the same efficiency class as
the original version?
6. Is it possible to implement insertion sort for sorting linked lists? Will it
have the same O(n2)efficiency as the array version?
7. Consider the following version of insertion sort.
Algorithm InsertSort2 (A[0..n −1])
for i←1to n−1do
j←i−1
while j≥0and A[j]>A[j+1] do
swap(A[j],A[j+1])
j←j−1
What is its time efficiency? How is it compared to that of the version
giveninthetext?
1

8. Let A[0..n −1] be an array of nsortable elements. (For simplicity, you
can assume that all the elements are distinct.) Recall that a pair of its
elements (A[i],A[j]) is called an inversion if i<j and A[i]>A[j].
a. What arrays of size nhave the largest number of inversions and what
is this number? Answer the same questions for the smallest number of
inversions.
b.Show that the average-case number of key comparisons in insertion
sort is given by the formula
Cavg (n)≈n2
4.
9. Binary insertion sort uses binary search to find an appropriate position
to insert A[i]among the previously sorted A[0] ≤... ≤A[i−1].Determine
the worst-case efficiency class of this algorithm.
10. Shellsort (more accurately Shell’s sort) is an important sorting algorithm
which works by applying insertion sort to each of several interleaving sub-
lists of a given list. On each pass through the list, the sublists in question
are formed by stepping through the list with an increment hitaken from
some predefined decreasing sequence of step sizes, h1>...>h
i>...>1,
which must end with 1. (The algorithm works for any such sequence,
though some sequences are known to yield a better efficiency than others.
For example, the sequence 1, 4, 13, 40, 121, ... , used, of course, in reverse,
is known to be among the best for this purpose.)
a. Apply shellsort to the list
S, H, E, L, L, S, O, R, T, I, S, U, S, E, F, U, L
b. Is shellsort a stable sorting algorithm?
c. Implement shellsort, straight insertion sort, binary insertion sort, merge-
sort, and quicksort in the language of your choice and compare their per-
formance on random arrays of sizes 102,10
3,10
4,and 105as well as on
increasing and decreasing arrays of these sizes.
2
Hints to Exercises 5.1
1. Solve the problem for n=1.
2. You may consider pouring soda from a filled glass into an empty glass as
one move.
3. Use the fact that all the subsets of an n-element set S={a1, ..., an}can
be divided into two groups: those that contain anand those that do not.
4. Trace the algorithm as we did in the text for another input (see Fig. 5.4).
5. a. The sentinel should stop the smallest element from moving beyond the
first position in the array.
b. Repeat the analysis performed in the text for the sentinel version.
6. Recall that we can access elements of a singly linked list only sequentially.
7. Since the only difference between the two versions of the algorithm is in the
inner loop’s operations, you should estimate the difference in the running
times of one repetition of this loop.
8. a. Answering the questions for an array of three elements should lead to
the general answers.
b. Assume for simplicity that all elements are distinct and that insert-
ing A[i]in each of the i+1 possible positions among its predecessors is
equally likely. Analyze the sentinel version of the algorithm first.
9. The order of growth of the worst-case number of key comparisons made
by binary insertion sort can be obtained from formulas in Section 4.3
and Appendix A. For this algorithm, however, a key comparison is not
the operation that determines the algorithm’s efficiency class. Which
operation does?
10. a. Note that it is more convenient to sort sublists in parallel, i.e., compare
A[0] with A[hi],then A[1] with A[1 + hi],and so on.
b. Recall that, generally speaking, sorting algorithms that can exchange
elements far apart are not stable.
3
Solutions to Exercises 5.1
1. First, the two boys take the boat to the other side, after which one of
them returns with the boat. Then a soldier takes the boat to the other
side and stays there while the other boy returns the boat. These four
trips reduce the problem’s instance of size n(measured by the number of
soldiers to be ferried) to the instance of size n−1.Thus, if this four-trip
procedure repeated ntimes, the problem will be solved after the total of
4ntrips.
2. Assuming that the glasses are numbered left to right from 1 to 2n, pour
soda from glass 2 into glass 2n−1.This makes the first and last pair of
glasses alternate in the required pattern and hence reduces the problem to
the same problem with 2(n−2) middle glasses. If nis even, the number
of times this operation needs to be repeated is equal to n/2; if nis odd, it
is equal to (n−1)/2.The formula n/2provides a closed-form answer for
both cases. Note that this can also be obtained by solving the recurrence
M(n)=M(n−2) + 1 for n>2,M(2) = 1,M(1) = 0,where M(n)is the
number of moves made by the decrease-by-two algorithm described above.
Since any algorithm for this problem must move at least one filled glass
for each of the n/2nonoverlapping pairs of the filled glasses, n/2is
the least number of moves needed to solve the problem.
3. Here is a general outline of a recursive algorithm that create list L(n)of
all the subsets of {a1, ..., an}(seeamoredetaileddiscussioninSection5.4):
if n=0return list L(0) containing the empty set as its only element
else create recursively list L(n−1) of all the subsets of {a1, ..., an−1}
append anto each element of L(n−1) to get list T
return L(n)obtained by concatenation of L(n−1) and T
4. Sorting the list E,X,A,M,P,L,Ein alphabetical order with insertion
sort: EXA MP L E
EX
EXA
AEX M
AEMX P
AEMP X L
AEL MP XE
AEE L MP X
4
5. a. -∞or, more generally, any value less than or equal to every element in
the array.
b. Yes, the efficiency class will stay the same. The number of key com-
parisons for strictly decreasing arrays (the worst-case input) will be
Cworst(n)=
n−1
i=1
i−1
j=−1
1=
n−1
i=1
(i+1) =
n−1
i=1
i+
n−1
i=1
1=(n−1)n
2+(n−1) ∈Θ(n2).
6. Yes, but we will have to scan the sorted part left to right while inserting
A[i]to get the same O(n2)efficiency as the array version.
7. The efficiency classes of both versions will be the same. The inner loop
of InsertionSort consists of one key assignment and one index decrement;
the inner loop of InsertionSort2 consists of one key swap (i.e., three key
assignments) and one index decrement. If we disregard the time spent on
the index decrements, the ratio of the running times should be estimated as
3ca/ca=3;if we take into account the time spent on the index decrements,
the ratio’s estimate becomes (3ca+cd)/(ca+cd),where caand cdare the
times of one key assignment and one index decrement, respectively.
8. a. The largest number of inversions for A[i](0≤i≤n−1) is n−1−i;
this happens if A[i]is greater than all the elements to the right of it.
Therefore, the largest number of inversions for an entire array happens for
a strictly decreasing array. This largest number is given by the sum:
n−1
i=0
(n−1−i)=(n−1) + (n−2) + ... +1+0= (n−1)n
2.
The smallest number of inversions for A[i](0≤i≤n−1) is 0; this hap-
pens if A[i]is smaller than or equal to all the elements to the right of it.
Therefore, the smallest number of inversions for an entire array will be 0
for nondecreasing arrays.
b. Assuming that all elements are distinct and that inserting A[i]in each
of the i+1possible positions among its predecessors is equally likely, we
obtain the following for the expected number of key comparisons on the
ith iteration of the algorithm’s sentinel version:
1
i+1
i+1
j=1
j=1
i+1
(i+1)(i+2)
2=i+2
2.
Hence for the average number of key comparisons, Cavg (n),we have
Cavg (n)=
n−1
i=1
i+2
2=1
2
n−1
i=1
i+
n−1
i=1
1=1
2
(n−1)n
2+n−1≈n2
4.
5
For the no-sentinel version, the number of key comparisons to insert A[i]
before and after A[0] will be the same. Therefore the expected number
of key comparisons on the ith iteration of the no-sentinel version is:
1
i+1
i
j=1
j+i
i+1 =1
i+1
i(i+1)
2+i
i+1 =i
2+i
i+1.
Hence, for the average number of key comparisons, Cavg (n),we have
Cavg(n)=
n−1
i=1
(i
2+i
i+1)=1
2
n−1
i=1
i+
n−1
i=1
i
i+1.
We have a closed-form formula for the first sum:
1
2
n−1
i=1
i=1
2
(n−1)n
2=n2−n
4.
The second sum can be estimated as follows:
n−1
i=1
i
i+1 =
n−1
i=1
(1 −1
i+1)=
n−1
i=1
1−
n−1
i=1
1
i+1 =n−1−
n
j=2
j=n−Hn,
where Hn=n
j=1 1/j ≈ln naccording to a well-known formula quoted
in Appendix A. Hence, for the no-sentinel version of insertion sort too,
we have
Cavg (n)≈n2−n
4+n−Hn≈n2
4.
9. The largest number of key comparisons will be, in particular, for strictly
increasing or decreasing arrays:
Cmax(n)=
n−1
i=1
(log2i+1) =
n−1
i=1
log2i+
n−1
i=1
1∈Θ(nlog n)+Θ(n)=Θ(nlog n).
It is the number of key moves, however, that will dominate the number
of key comparisons in the worst case of strictly decreasing arrays. The
number of key moves will be exactly the same as for the classic insertion
sort, putting the algorithm’s worst-case efficiency in Θ(n2).
6
10. a. Applying shellsort to the list S1,H,E1,L1,L2,S2,O,R,T,I,S3,U1,S4,E2,F,U2,L3
with the step-sizes 13, 4, and 1 yields the following:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
S1HE
1L1L2S2OR T I S
3U1S4E2FU
2L3
S1E2
E2S1
HF
FH
E1U2
L1L3
E2L2
FS
2
E1O
L1R
L2T
S2I
IS
2
OS
3
RU
1
TS
4
S4T
S2S1
S3H
HS
3
U1U2
TL
3
L3T
E2FE
1L1L2IORS
4S2HU
1L3S1S3U2T
The final pass–sorting the last array by insertion sort–is omitted from
the solution because of its simplicity. Note that since relatively few ele-
ments in the last array are out of order as a result of the work done on the
preceding passes of shellsort, insertion sort will need significantly fewer
comparisons to finish the job than it would have needed if it were applied
to the initial array.
b. Shellsort is not stable. As a counterexample for shellsort with the
sequence of step-sizes 4 and 1, consider, say, the array 5, 1, 2, 3, 1. The
first pass with the step-size of 4 will exchange 5 with the last 1, changing
the relative ordering of the two 1’s in the array. The second pass with the
step-size of 1, which is insertion sort, will not make any exchanges because
the array is already sorted.
7
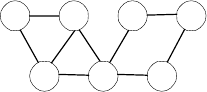
Exercises 5.2
1. Consider the graph
f b
d a e
gc
a. Write down the adjacency matrix and adjacency lists specifying this
graph. (Assume that the matrix rows and columns and vertices in the
adjacency lists follow in the alphabetical order of the vertex labels.)
b. Starting at vertex aand resolving ties by the vertex alphabetical order,
traverse the graph by depth-first search and construct the corresponding
depth-first search tree. Give the order in which the vertices were reached
for the first time (pushed onto the traversal stack) and the order in which
the vertices became dead ends (popped off the stack).
2. If we define sparse graphs as graphs for which |E|∈O(|V|), which im-
plementation of DFS will have a better time efficiency for such graphs,
the one that uses the adjacency matrix or the one that uses the adjacency
lists?
3. Let Gbe a graph with nvertices and medges.
a. True or false: All its DFS forests (for traversals starting at differ-
ent vertices) will have the same number of trees?
b. True or false: All its DFS forests will have the same number of tree
edgesandthesamenumberofbackedges?
4. Traverse the graph of Problem 1 by breadth-first search and construct the
corresponding breadth-first search tree. Start the traversal at vertex a
and resolve ties by the vertex alphabetical order.
5. Prove that a cross edge in a BFS tree of an undirected graph can connect
vertices only on either the same level or on two adjacent levels of a BFS
tree.
6. a. Explain how one can check a graph’s acyclicity by using breadth-first
search.
b. Does either of the two traversals–DFS or BFS–always find a cy-
cle faster than the other? If you answer yes, indicate which of them is
better and explain why it is the case; if you answer no, give two examples
supporting your answer.
8

7. Explain how one can identify connected components of a graph by using
a. a depth-first search.
b. a breadth-first search.
8. A graph is said to be bipartite if all its vertices can be partitioned into
two disjoint subsets Xand Yso that every edge connects a vertex in X
with a vertex in Y. (We can also say that a graph is bipartite if its vertices
can be colored in two colors so that every edge has its vertices colored in
different colors; such graphs are also called 2-colorable). For example,
graph (i) is bipartite while graph (ii) is not.
x y x
y x y
11 3
22
3
a
c
b
d
(i) (ii)
a. Design a DFS-based algorithm for checking whether a graph is bipartite.
b. Design a BFS-based algorithm for checking whether a graph is bi-
partite.
9. Write a program that, for a given graph, outputs
a. vertices of each connected component;
b. its cycle or a message that the graph is acyclic.
10. One can model a maze by having a vertex for a starting point, a finishing
point, dead ends, and all the points in the maze where more than one path
can be taken, and then connecting the vertices according to the paths in
the maze.
a. Construct such a graph for the following maze.
b. Which traversal–DFS or BFS–would you use if you found yourself in
a maze and why?
9
Hints to Exercises 5.2
1. a. Use the definitions of the adjacency matrix and adjacency lists given
in Section 1.4.
b. Perform the DFS traversal the same way it is done for another graph
in the text (see Fig. 5.5).
2. Compare the efficiency classes of the two versions of DFS for sparse graphs.
3. a. What is the number of such trees equal to?
b. Answer this question for connected graphs first.
4. Perform the BFS traversal the same way it is done in the text (see Fig.
5.6).
5. You may use the fact that the level of a vertex in a BFS tree indicates
the number of edges in the shortest (minimum-edge) path from the root
to that vertex.
6. a. What property of a BFS forest indicates a cycle’s presence? (The
answer is similar to the one for a DFS forest.)
b. The answer is no. Find two examples supporting this answer.
7. Given the fact that both traversals can reach a new vertex if and only if it
is adjacent to one of the previously visited vertices, which vertices will be
visited by the time either traversal halts (i.e., its stack or queue becomes
empty)?
8. Use a DFS forest and a BFS forest for parts (a) and (b), respectively.
9. Use either DFS or BFS.
10. a. Follow the instructions of the problem’s statement.
b. Trying both traversals should lead you to a correct answer very fast.
10
Solutions to Exercises 5.2
1. a. Here are the adjacency matrix and adjacency lists for the graph in
question:
abcdefg
a
b
c
d
e
f
g
0111100
1001010
1000001
1100010
1000001
0101000
0010100
a→b→c→d→e
b→a→d→f
c→a→g
d→a→b→f
e→a→g
f→b→d
g→c→e
b. See below: (i) the graph; (ii) the traversal’s stack (the first subscript
number indicates the order in which the vertex was visited, i.e., pushed
onto the stack, the second one indicates the order in which it became a
dead-end, i.e., popped off the stack); (iii) the DFS tree (with the tree
edges shown with solid lines and the back edges shown with dashed lines).
f b
d a e
gc f4,1e7,4
d3,2g6,5
b2,3c5,6
a1,7
b
d
c
g
e
a
f
(i) (ii) (iii)
2. The time efficiency of DFS is Θ(|V|2)for the adjacency matrix representa-
tion and Θ(|V|+|E|)for the adjacency lists representation, respectively.
If |E|∈O(|V|),the former remains Θ(|V|2)while the latter becomes
Θ(|V|).Hence, for sparse graphs, the adjacency lists version of DFS is
more efficient than the adjacency matrix version.
3. a. The number of DFS trees is equal to the number of connected compo-
nents of the graph. Hence, it will be the same for all DFS traversals of
the graph.
b. For a connected (undirected) graph with |V|vertices, the number of
tree edges |E(tree)|in a DFS tree will be |V|−1and, hence, the number of
11

back edges |E(back)|will be the total number of edges minus the number
of tree edges: |E|−(|V|−1) = |E|−|V|+1.Therefore, it will be indepen-
dent from a particular DFS traversal of the same graph. This observation
canbeextendedtoanarbitrarygraphwith|C|connected components by
applying this reasoning to each of its connected components:
|E(tree)|=
|C|
c=1
|E(tree)
c|=
|C|
c=1
(|Vc|−1) =
|C|
c=1
|Vc|−
|C|
c=1
1=|V|−|C|
and
|E(back)|=|E|−|E(tree)|=|E|−(|V|−|C|)=|E|−|V|+|C|,
where |E(tree)
c|and |Vc|are the numbers of tree edges and vertices in the
cth connected component, respectively.
4. Here is the result of the BFS traversal of the graph of Problem 1:
f b
d a e
gc
abcdefg
a
c
g
b
f
d e
(i) (ii) (iii)
(i) the graph; (ii) the traversal’s queue; (iii) the tree (the tree and
cross edges are shown with solid and dotted lines, respectively).
5. We’ll prove the assertion in question by contradiction. Assume that
a BFS tree of some undirected graph has a cross edge connecting two
vertices uand vsuch that level[u]≥level[v]+2.But level[u]=d[u]and
level[v]=d[v],where d[u]and d[v]are the lengths of the minimum-edge
paths from the root to vertices uand v, respectively. Hence, we have
d[u]≥d[v]+2.The last inequality contradicts the fact that d[u]is the
length of the minimum-edge path from the root to vertex ubecause the
minimum-edge path of length d[v]from the root to vertex vfollowed by
edge (v, u)has fewer edges than d[u].
6. a. A graph has a cycle if and only if its BFS forest has a cross edge.
b. Both traversals, DFS and BFS, can be used for checking a graph’s
12

acyclicity. For some graphs, a DFS traversal discovers a back edge in its
DFS forest sooner than a BFS traversal discovers a cross edge (see exam-
ple (i) below); for others the exactly opposite is the case (see example (ii)
below).
a
a
aa
a a
. . .
23
1
45na
aa . . .
12
a3an-1
n
(i) (ii)
7. Start a DFS (or BFS) traversal at an arbitrary vertex and mark the visited
vertices with 1. By the time the traversal’s stack (queue) becomes empty,
all the vertices in the same connected component as the starting vertex,
and only they, will have been marked with 1. If there are unvisited vertices
left, restart the traversal at one of them and mark all the vertices being
visited with 2, and so on until no unvisited vertices are left.
8. a. Let Fbe a DFS forest of a graph. It is not difficult to see that F
is 2-colorable if and only if there is no back edge connecting two vertices
both on odd levels or both on even levels. It is this property that a DFS
traversal needs to verify. Note that a DFS traversal can mark vertices as
even or odd when it reaches them for the first time.
b. Similarly to part (a), a graph is 2-colorable if and only if its BFS
forest has no cross edge connecting vertices on the same level. Use a BFS
traversal to check whether or not such a cross edge exists.
9. n/a
10. a. Here is the maze and a graph representing it:
13
b. DFS is much more convenient for going through a maze than BFS.
When DFS moves to a next vertex, it is connected to a current vertex by
an edge (i.e., “close nearby” in the physical maze), which is not generally
the case for BFS. In fact, DFS can be considered a generalization of an
ancient right-hand rule for maze traversal: go through the maze in such a
way so that your right hand is always touching a wall.
14

Exercises 5.3
1. Apply the DFS-based algorithm to solve the topological sorting problem
for the following digraphs:
d
g
a
c
f
b
e
(a)
b
a
f
c d
e g
(b)
.
2. a. Prove that the topological sorting problem has a solution for a digraph
if and only if it is a dag.
b. For a digraph with nvertices, what is the largest number of distinct
solutions the topological sorting problem can have?
3. a. What is the time efficiency of the DFS-based algorithm for topological
sorting?
b. How can one modify the DFS-based algorithm to avoid reversing the
vertex ordering generated by DFS?
4. Can one use the order in which vertices are pushed onto the DFS stack
(instead of the order they are popped off it) to solve the topological sorting
problem?
5. Apply the source-removal algorithm to the digraphs of Problem 1.
6. a. Prove that a dag must have at least one source.
b. How would you find a source (or determine that such a vertex does
not exist) in a digraph represented by its adjacency matrix? What is the
time efficiency of this operation?
c. How would you find a source (or determine that such a vertex does
not exist) in a digraph represented by its adjacency lists? What is the
time efficiency of this operation?
7. Can you implement the source-removal algorithm for a digraph repre-
sented by its adjacency lists so that its running time is in O(|V|+|E|)?
8. Implement the two topological sorting algorithms in the language of your
choice. Run an experiment to compare their running times.
9. A digraph is called strongly connected if for any pair of two distinct ver-
tices uand v, there exists a directed path from uto vand a directed path
15
from vto u. In general, a digraph’s vertices can be partitioned into dis-
joint maximal subsets of vertices that are mutually accessible via directed
paths of the digraph; these subsets are called strongly connected com-
ponents. There are two DFS-based algorithms for identifying strongly
connected components. Here is the simpler (but somewhat less efficient)
one of the two:
Step 1. Do a DFS traversal of the digraph given and number its vertices
in the order that they become dead ends.
Step 2. Reverse the directions of all the edges of the digraph.
Step 3. Do a DFS traversal of the new digraph by starting (and, if neces-
sary, restarting) the traversal at the highest numbered vertex among still
unvisited vertices.
The strongly connected components are exactly the subsets of vertices in
each DFS tree obtained during the last traversal.
a. Apply this algorithm to the following digraph to determine its strongly
connected components.
e
b
e
a
d
c
g
f h
b. What is the time efficiency class of this algorithm? Give separate
answers for the adjacency matrix representation and adjacency list repre-
sentation of an input graph.
c. How many strongly connected components does a dag have?
10. Celebrity problem A celebrity among a group of npeople is a person
who knows nobody but is known by everybody else. The task is to
identify a celebrity by only asking questions to people of the form: "Do
you know him/her?" Design an efficient algorithm to identify a celebrity
or determine that the group has no such person. How many questions
does your algorithm need in the worst case?
16
Hints to Exercises 5.3
1. Trace the algorithm as it is done in the text for another digraph (see Fig.
5.10).
2. a. You need to prove two assertions: (i) if a digraph has a directed cycle,
then the topological sorting problem does not have a solution; (ii) if a
digraph has no directed cycles, the problem has a solution.
b. Consider an extreme type of a digraph.
3. a. How does it relate to the time efficiency of DFS?
b. Do you know the length of the list to be generated by the algorithm?
Where should you put, say, the first vertex being popped off a DFS tra-
versal stack for the vertex to be in its final position?
4. Try to do this for a small example or two.
5. Trace the algorithm on the instances given as it is done in the section (see
Fig. 5.11).
6. a. Use a proof by contradiction.
b. If you have difficulty answering the question, consider an example
of a digraph with a vertex with no incoming edges and write down its
adjacency matrix.
c. The answer follows from the definitions of the source and adjacency
lists.
7. For each vertex, store the number of edges entering the vertex in the
remaining subgraph. Maintain a queue of the source vertices.
8. n/a
9. a. Trace the algorithm on the input given by following the steps of the
algorithm as indicated.
b. Determine the efficiency for each of the three principal steps of the
algorithm and then determine the overall efficiency. Of course, the an-
swers will depend on whether a graph is represented by its adjacency
matrix or by its adjacency lists.
10. Solve first a simpler version in which a celebrity must be present.
17
Solutions to Exercises 5.3
1. a. The digraph and the stack of its DFS traversal that starts at vertex a
are given below:
d
g
a
c
f
b
e
f
eg
bc
ad
The vertices are popped off the stack in the following order:
efgbcad.
The topological sorting order obtained by reversing the list above is
dacbgfe.
b. Thedigraphbelowisnotadag. ItsDFStraversalthatstartsata
encounters a back edge from eto a:
b
a
f
c d
e g
e
g
d
c
b
a
2. a. Let us prove by contradiction that if a digraph has a directed cycle,
then the topological sorting problem does not have a solution. Assume
that vi, ..., viis a solution to the topological sorting problem for a di-
graph with a directed cycle. Let vibe the leftmost vertex of this cycle
on the list vi, ..., vi.Since the cycle’s edge entering vigoes right to left,
we have a contradiction that proves the assertion.
If a digraph has no directed cycles, a solution to the topological sorting
problem is fetched by either of the two algorithms discussed in the sec-
tion. (The correctness of the DFS-based algorithm was explained there;
the correctness of the source removal algorithm stems from the assertion
of Problem 6a.)
b. For a digraph with nvertices and no edges, any permutation of its
vertices solves the topological sorting problem. Hence, the answer to the
question is n!.
18
3. a. Since reversing the order in which vertices have been popped off the
DFS traversal stack is in Θ(|V|),the running time of the algorithm will
bethesameasthatofDFS(exceptforthefactthatitcanstopbefore
processing the entire digraph if a back edge is encountered). Hence, the
running time of the DFS-based algorithm is in O(|V|2)for the adjacency
matrix representation and in O(|V|+|E|)for the adjacency lists represen-
tation.
b. Fill the array of length |V|with vertices being popped off the DFS
traversal stack right to left.
4. The answer is no. Here is a simple counterexample:
b
a c
TheDFStraversalthatstartsatapushes the vertices on the stack in the
order a, b, c, and neither this ordering nor its reversal solves the topological
sorting problem correctly.
5. a.
g
c
f
b
e
delete b
f
e
d
g
a
c
f
b
edelete d
g
a
c
f
b
e
delete a
g
c
f
e
delete c
delete g
f
delete e
g
e
f
delete f
The topological ordering obtained is dabcgef.
19
b.
b
a
f
c d
e g
delete f
b
a c d
e g
stop
(no source)
The topological sorting is impossible.
6. a. Assume that, on the contrary, there exists a dag with every vertex
having an incoming edge. Reversing all its edges would yield a dag with
every vertex having an outgoing edge. Then, starting at an arbitrary ver-
tex and following a chain of such outgoing edges, we would get a directed
cycle no later than after |V|steps. This contradiction proves the assertion.
b. A vertex of a dag is a source if and only if its column in the adja-
cency matrix contains only 0’s. Looking for such a column is a O(|V|2)
operation.
c. A vertex of a dag is a source if and only if this vertex appears in none
of the dag’s adjacency lists. Looking for such a vertex is a O(|V|+|E|)
operation.
7. The answer to this well-known problem is yes (see, e.g., [KnuI], pp. 264-
265).
8. n/a
9. a. The digraph given is
e
b
e
a
d
c
g
f h
The stack of the first DFS traversal, with aas its starting vertex, will
look as follows:
f1
g2h6
b3d5e7
a4c8
(The numbers indicate the order in which the vertices are popped off the
stack.)
20
The digraph with the reversed edges is
b
4
a43
1
f2
g
8
c
5
d
6
h
7
e
The stack and the DFS trees (with only tree edges shown) of the DFS
traversal of the second digraph will be as follows:
b
eg
hf
cda
c
h
e
d a
f
g
b
The strongly connected components of the given digraph are:
{c, h, e},{d},{a, f, g, b}.
b. If a graph is represented by its adjacency matrix, then the efficiency
of the first DFS traversal will be in Θ(|V|2).The efficiency of the edge-
reversal step (set B[j, i]to 1 in the adjacency matrix of the new digraph
if A[i, j]=1in the adjacency matrix of the given digraph and to 0 other-
wise) will also be in Θ(|V|2).The time efficiency of the last DFS traversal
of the new graph will be in Θ(|V|2),too. Hence, the efficiency of the
entire algorithm will be in Θ(|V|2)+Θ(|V|2)+Θ(|V|2)=Θ(|V|2).
The answer for a graph represented by its adjacency lists will be, by
similar reasoning (with a necessary adjustment for the middle step), in
Θ(|V|+|E|).
10. The problem can be solved by a recursive algorithm based on the decrease-
by-one strategy. Indeed, by asking just one question, we can eliminate the
number of people who can be a celebrity by 1, solve the problem for the
remaining group of n−1people recursively, and then verify the returned
solution by asking no more than two questions. Here is a more detailed
description of this algorithm:
If n=1,return that one person as a celebrity. If n>1,proceed as
follows:
21
Step 1 Select two people from the group given, say, A and B, and ask A whether
A knows B. If A knows B, remove A from the remaining people who can
be a celebrity; if A doesn’t know B, remove B from this group.
Step 2 Solve the problem recursively for the remaining group of n−1people
who can be a celebrity.
Step 3 If the solution returned in Step 2 indicates that there is no celebrity
among the group of n−1people, the larger group of npeople cannot
contain a celebrity either. If Step 2 identified as a celebrity a person
other than either A or B, say, C, ask whether C knows the person removed
in Step 1 and, if the answer is no, whether the person removed in Step
1 knows C. If the answer to the second question is yes," return C as a
celebrity and "no celebrity" otherwise. If Step 2 identified B as a celebrity,
just ask whether B knows A: return B as a celebrity if the answer is no
and "no celebrity" otherwise. If Step 2 identified A as a celebrity, ask
whether B knows A: return A as a celebrity if the answer is yes and "no
celebrity" otherwise.
The recurrence for Q(n), the number of questions needed in the worst case,
is as follows:
Q(n)=Q(n−1) + 3 for n>2,Q(2) = 2,Q(1) = 0.
Its solution is Q(n)=2+3(n−2) for n>1and Q(1) = 0.
Note: A computer implementation of this algorithm can be found, e.g., in
Manber’s Introduction to Algorithms: A Creative Approach. Addison-Wesley,
1989.
22
Exercises 5.4
1. Is it realistic to implement an algorithm that requires generating all per-
mutations of a 25-element set on your computer? What about all the
subsetsofsuchaset?
2. Generate all permutations of {1,2,3,4}by
a. the bottom-up minimal-change algorithm.
b. the Johnson-Trotter algorithm.
c. the lexicographic—order algorithm.
3. Write a program for generating permutations in lexicographic order.
4. Consider a simple implementation of the following algorithm for gener-
ating permutations discovered by B. Heap [Hea63].
Algorithm HeapPermute(n)
//Implements Heap’s algorithm for generating permutations
//Input: A positive integer nandaglobalarrayA[1..n]
//Output: All permutations of elements of A
if n=1
write A
else
for i←1to ndo
HeapPermute(n−1)
if nis odd
swap A[1] and A[n]
else swap A[i]and A[n]
a. Trace the algorithm by hand for n=2,3,and 4.
b. Prove correctness of Heap’s algorithm.
c. What is the time efficiency of this algorithm?
5. Generate all the subsets of a four-element set A={a1,a
2,a
3,a
4}by each
of the two algorithms outlined in this section.
6. What simple trick would make the bit string—based algorithm generate
subsets in squashed order?
7. Write a pseudocode for a recursive algorithm for generating all 2nbit
strings of length n.
8. Write a nonrecursive algorithm for generating 2nbit strings of length n
that implements bit strings as arrays and does not use binary additions.
23
9. a. Use the decrease-by-one technique to generate the binary reflected Gray
code for n=4.
b.Design a general decrease-by-one algorithm for generating the binary
reflected Gray code of order n.
10. Design a decrease-and-conquer algorithm for generating all combina-
tions of kitems chosen from n, i.e., all k-element subsets of a given n-
element set.Is your algorithm a minimal-change algorithm?
11. Gray code and the Tower of Hanoi
(a) Show that the disk moves made in the classic recursive algorithm
for the Tower-of-Hanoi puzzle can be used for generating the binary
reflected Gray code.
(b) Show how the binary reflected Gray code can be used for solving
the Tower-of-Hanoi puzzle.
24

Hints to Exercises 5.4
1. Use standard formulas for the numbers of these combinatorial objects. For
the sake of simplicity, you may assume that generating one combinatorial
object takes the same time as, say, one assignment.
2. We traced the algorithms on smaller instances in the section.
3. See an outline of this algorithm in the section.
4. a. Trace the algorithm for n=2;take advantage of this trace in tracing
the algorithm for n=3and then use the latter for n=4.
b. Show that the algorithm generates n!permutations and that all of
them are distinct. Use mathematical induction.
c. Set up a recurrence relation for the number of swaps made by the
algorithm. Find its solution and the solution’s order of growth. You
may need the formula: e≈n
i=0 1
i!.
5. We traced both algorithms on smaller instances in the section.
6. Tricks become boring after they have been given away.
7. This is not a difficult exercise because of the obvious way of getting bit
strings of length nfrom bit strings of length n−1.
8. You may still mimic the binary addition without using it explicitly.
9. AGraycodeforn=3is given at the end of the section. It is not difficult
to see how to use it to generate a Gray code for n=4.Gray codes
have a useful geometric interpretation based on mapping its bit strings to
vertices of the n-dimensional cube. Find such a mapping for n=1,2,
and 3. This geometric interpretation might help you with designing a
general algorithm for generating a Gray code of order n.
10. There are several decrease-and—conquer algorithms for this problem. They
are more subtle than one might expect. Generating combinations in a pre-
defined order (increasing, decreasing, lexicographic) helps with both a de-
sign and a correctness proof. The following simple property is very helpful.
Assuming with no loss of generality that the underlying set is {1,2, ..., n},
there are n−i
k−1k-subsets whose smallest element is i, i =1,2,...,n−k+1.
11. Represent the disk movements by flipping bits in a binary n-tuple.
25

Solutions to Exercises 5.4
1. Since 25! ≈1.5·1025,it would take an unrealistically long time to generate
this number of permutations even on a supercomputer. On the other
hand, 225 ≈3.3·107, which would take about 0.3seconds to generate on
a computer making one hundred million operations per second.
2. a. The permutations of {1,2,3,4}generated by the bottom-up minimal-
change algorithm:
start 1
insert 2into 1 right to left 12 21
insert 3into 12 right to left 123 132 312
insert 3into 21 left to right 321 231 213
insert 4 into 123 right to left 1234 1243 1423 4123
insert 4 into 132 left to right 4132 1432 1342 1324
insert 4 into 312 right to left 3124 3142 3412 4312
insert 4 into 321 left to right 4321 3421 3241 3214
insert 4 into 231 right to left 2314 2341 2431 4231
insert 4 into 213 left to right 4213 2413 2143 2134
b. The permutations of {1,2,3,4}generated by the Johnson-Trotter al-
gorithm. (Read horizontally; the largest mobile element is shown in bold.)
←
1
←
2
←
3
←
4
←
1
←
2
←
4
←
3
←
1
←
4
←
2
←
3
←
4
←
1
←
2
←
3
→
4
←
1
←
3
←
2
←
1
→
4
←
3
←
2
←
1
←
3
→
4
←
2
←
1
←
3
←
2
→
4
←
3
←
1
←
2
←
4
←
3
←
1
←
4
←
2
←
3
←
4
←
1
←
2
←
4
←
3
←
1
←
2
→
4
→
3
←
2
←
1
→
3
→
4
←
2
←
1
→
3
←
2
→
4
←
1
→
3
←
2
←
1
→
4
←
2
→
3
←
1
←
4
←
2
→
3
←
4
←
1
←
2
←
4
→
3
←
1
←
4
←
2
→
3
←
1
→
4
←
2
←
1
→
3
←
2
→
4
←
1
→
3
←
2
←
1
→
4
→
3
←
2
←
1
→
3
→
4
c. The permutations of {1,2,3,4}generated in lexicographic order. (Read
horizontally.)
1234 1243 1324 1342 1423 1432
2134 2143 2314 2341 2413 2431
3124 3142 3214 3241 3412 3421
4123 4132 4213 4231 4312 4321
3. n/a
26
4. a. For n=2:
12 21
For n=3(read along the rows):
123 213
312 132
231 321
For n=4(read along the rows):
1234 2134 3124 1324 2314 3214
4231 2431 3421 4321 2341 3241
4132 1432 3412 4312 1342 3142
4123 1423 2413 4213 1243 2143
b. Let C(n)be the number of times the algorithm writes a new per-
mutation (on completion of the recursive call when n=1). We have the
following recurrence for C(n):
C(n)=
n
i=1
C(n−1) or C(n)=nC(n−1) for n>1,C(1) = 1.
Its solution (see Section 2.4) is C(n)=n!.The fact that all the permu-
tations generated by the algorithm are distinct, can be proved by mathe-
matical induction.
c. We have the following recurrence for the number of swaps S(n):
S(n)=
n
i=1
(S(n−1)+1) or S(n)=nS(n−1)+nfor n>1,S(1) = 0.
Although it can be solved by backward substitution, this is easier to do
after dividing both hand sides by n!
S(n)
n!=S(n−1)
(n−1)! +1
(n−1)! for n>1,S(1) = 0
and substituting T(n)=S(n)
n!to obtain the following recurrence:
T(n)=T(n−1) + 1
(n−1)! for n>1,T(1) = 0.
Solving the last recurrence by backward substitutions yields
T(n)=T(1) +
n−1
i=1
1
i!=
n−1
i=1
1
i!.
27

On returning to variable S(n)=n!T(n),weobtain
S(n)=n!
n−1
i=1
1
i!≈n!(e−1−1
n!)∈Θ(n!).
5. Generate all the subsets of a four-element set A={a1,a
2,a
3,a
4}bottom
up:
nsubsets
0∅
1∅{a1}
2∅{a1}{a2}{a1,a
2}
3∅{a1}{a2}{a1,a
2}{a3}{a1,a
3}{a2,a
3}{a1,a
2,a
3}
4∅{a1}{a2}{a1,a
2}{a3}{a1,a
3}{a2,a
3}{a1,a
2,a
3}
{a4}{a1,a
4}{a2,a
4}{a1,a
2,a
4}{a3,a
4}{a1,a
3,a
4}{a2,a
3,a
4}{a1,a
2,a
3,a
4}
Generate all the subsets of a four-element set A={a1,a
2,a
3,a
4}with
bit vectors:
bit strings 0000 0001 0010 0011 0100 0101 0110 0111
subsets ∅{a4}{a3}{a3,a
4}{a2}{a2,a
4}{a2,a
3}{a2,a
3,a
4}
bit strings 1000 1001 1010 1011 1100 1101 1110 1111
subsets {a1}{a1,a
4}{a1,a
3}{a1,a
3,a
4}{a1,a
2}{a1,a
2,a
4}{a1,a
2,a
3}{a1,a
2,a
3,a4
}
6. Establish the correspondence between subsets of A={a1, ..., an}and bit
strings b1...bnof length nby associating bit iwith the presence or absence
of element an−i+1 for i=1, ..., n.
7. Algorithm BitstringsRec(n)
//Generates recursively all the bit strings of a given length
//Input: A positive integer n
//Output: All bit strings of length nas contents of global array B[0..n−1]
if n=0
print(B)
else
B[n−1] ←0; BitstringsRec(n−1)
B[n−1] ←1; BitstringsRec(n−1)
8. Algorithm BitstringsNonrec(n)
//Generates nonrecursively all the bit strings of a given length
//Input: A positive integer n
28
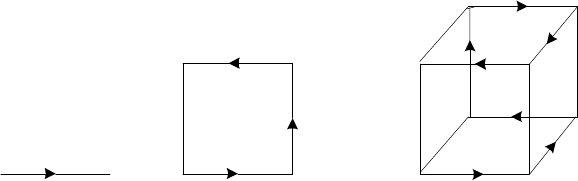
//Output: All bit strings of length nas contents of global array B[0..n−1]
for i←0to n−1do
B[i]=0
repeat
print(B)
k←n−1
while k≥0and B[k]=1
k←k−1
if k≥0
B[k]←1
for i←k+1to n−1do
B[i]←0
until k=−1
9. a. As mentioned in the hint to this problem, binary Gray codes have
a useful geometric interpretation based on mapping their bit strings to
vertices of the n-dimensional cube. Such a mapping is shown below for
n=1,2,and 3.
01
00 01
10 11
000 001
100 101
010 011
110 111
n = 1 n = 2 n = 3
The list of bit strings in the binary reflexive Gray code for n=3given in
the section is obtained by traversing the vertices of the three-dimensional
cube by starting at 000 and following the arrows shown:
000 001 011 010 110 111 101 100.
We can obtain the binary reflexive Gray code for n=4as follows. Make
two copies of the list of bit strings for n=3;add 0 in front of each bit
string in the first copy and 1 in front of each bit sting in the second copy
and then append the second list to the first in reversed order to obtain:
0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000
(Note that the last bit string differs from the first one by a single bit, too.)
b. The mechanism employed in part (a) can be used for constructing
29
the binary reflexive Gray code for an arbitrary n≥1:Ifn=1,returnthe
list 0,1. If n>1,generate recursively the list of bit strings of size n−1
and make a copy of this list; add 0 in front of each bit string in the first
list and add 1 in front of each bit string in the second list; then append
the second list in reversed order to the first list.
Note: The correctness of the algorithm stems from the fact that it gen-
erates 2nbit strings and all of them are distinct. (Both these assertions
are very easy to check by mathematical induction.)
10. Here is a recursive algorithm from “Problems on Algorithms” by Ian Par-
berry [Par95], p.120:
call Choose(1,k)where
Algorithm Choose(i, k)
//Generates all k-subsets of {i, i +1, ..., n}stored in global array A[1..k]
//in descending order of their components
if k=0
print(A)
else
for j←ito n−k+1do
A[k]←j
Choose(j+1,k−1)
11. a. Number the disks from 1 to nin increasing order of their size. The
disk movements will be represented by a tuple of nbits, in which the bits
will be counted right to left so that the rightmost bit will represent the
movements of the smallest disk and the leftmost bit will represent the
movements of the largest disk. Initialize the tuple with all 0’s. For each
move in the puzzle’s solution, flip the ith bit if the move involves the ith
disk.
b. Use the correspondence described in part a between bit strings of
the binary reflected Gray code and the disk moves in the Tower of Hanoi
puzzle with the following additional rule for situations when there is a
choice of where to place a disk: When faced with a choice in placing a
disk, always place an odd numbered disk on top of an even numbered disk;
if an even numbered disk is not available, place the odd numbered disk on
an empty peg. Similarly, place an even numbered disk on an odd disk, if
available, or else on an empty peg.
30
Exercises 5.5
1. Design a decrease-by-half algorithm for computing log2nand determine
its time efficiency.
2. Consider ternary search–the following algorithm for searching in a
sorted array A[0..n −1]:ifn=1,simply compare the search key K
with the single element of the array; otherwise, search recursively by com-
paring Kwith A[n/3],and if Kis larger, compare it with A[2n/3]to
determine in which third of the array to continue the search.
a. What design technique is this algorithm based on?
b. Set up a recurrence relation for the number of key comparisons in
the worst case. (You may assume that n=3
k.)
c. Solve the recurrence for n=3
k.
d. Compare this algorithm’s efficiency with that of binary search.
3. a. Write a pseudocode for the divide-into-three algorithm for the fake-coin
problem. (Make sure that your algorithm handles properly all values of
n, not only those that are multiples of 3.)
b. Set up a recurrence relation for the number of weighings in the divide-
into-three algorithm for the fake-coin problem and solve it for n=3
k.
c. For large values of n, about how many times faster is this algorithm
than the one based on dividing coins into two piles? (Your answer should
not depend on n.)
4. Apply multiplication à la russe to compute 26 ·47.
5. a. From the standpoint of time efficiency, does it matter whether we mul-
tiply nby mor mby nby the multiplication à la russe algorithm?
b. What is the efficiency class of multiplication à la russe?
6. Write a pseudocode for the multiplication à-la-russe algorithm.
7. Find J(40)–the solution to the Josephus problem for n=40.
8. Prove that the solution to the Josephus problem is 1 for every nthat is a
power of 2.
9. For the Josephus problem,
a. compute J(n)for n=1,2, ...., 15.
31
b. discern a pattern in the solutions for the first fifteen values of nand
prove its general validity.
c. prove the validity of getting J(n)by a one-bit cyclic shift left of the
binary representation of n.
32
Hints to Exercises 5.5
1. If the instance of size nis to compute log2n,what is the instance of size
n/2? What is the relationship between the two?
2. The algorithm is quite similar to binary search, of course. In the worst
case, how many key comparisons does it make on each iteration and what
fraction of the array remains to be processed?
3. While it is obvious how one needs to proceed if nmod 3 = 0 or nmod3=1,
it is somewhat less so if nmod 3 = 2.
4. Trace the algorithm for the numbers given as it is done in the text for
another input (see Figure 5.14b).
5. How many iterations does the algorithm do?
6. You can implement the algorithm either recursively or nonrecursively.
7. The fastest way to the answer is to use the formula that exploits the binary
representation of n, which is mentioned at the end of Section 5.5.
8. Use the binary representation of n.
9. a. Use forward substitutions (see Appendix B) into the recurrence equa-
tions given in the text.
b. On observing the pattern in the first fifteen values of nobtained in
part (a), express it analytically. Then prove its validity by mathematical
induction.
c. Start with the binary representation of nand translate into binary
the formula for J(n)obtained in part (b).
33

Solutions to Exercises 5.5
1. Algorithm LogFloor (n)
//Input: A positive integer n
//Output: Returns log2n
if n=1return 0
else return LogFloor (n
2)+1
The algorithm is almost identical to the algorithm for computing the num-
ber of binary digits, which was investigated in Section 2.4. The recurrence
relation for the number of additions is
A(n)=A(n/2)+1 for n>1,A(1) = 0.
Its solution is A(n)=log2n∈Θ(log n).
2. a. The algorithm is based on the decrease-by-a constant factor (equal to
3) strategy.
b. C(n)=2+C(n/3) for n=3
k(k>0),C(1) = 1.
c. C(3k)=2+C(3k−1)[sub. C(3k−1)=2+C(3k−2)]
=2+[2+C(3k−2)] = 2 ·2+C(3k−2)= [sub. C(3k−2)=2+C(3k−3)]
=2·2+[2+C(3k−3)] = 2 ·3+C(3k−3)=... =2i+C(3k−i)=... =
2k+C(3k−k)=2log
3n+1.
d. We have to compare this formula with the worst-case number of key
comparisons in the binary search, which is about log2n+1. Since
2log
3n+1=2log2n
log23+1= 2
log23log2n+1
and 2/log23>1,binary search has a smaller multiplicative constant and
henceismoreefficient(byaboutthefactorof2/log23) in the worst case,
although both algorithms belong to the same logarithmic class.
3. a. If nis a multiple of 3 (i.e., nmod 3 = 0),we can divide the coins into
three piles of n/3coins each and weigh two of the piles. If n=3k+1
(i.e., nmod 3 = 1),we can divide the coins into the piles of sizes k,k,and
k+1 or k+1,k+1,and k−1.(We will use the second option.) Finally,
if n=3k+2(i.e., nmod3=2),we will divide the coins into the piles of
sizes k+1,k+1,andk. The following pseudocode assumes that there
is exactly one fake coin among the coins given and that the fake coin is
lighter than the other coins.
if n=1the coin is fake
34
else divide the coins into three piles of n/3,n/3,and n−2n/3coins
weigh the first two piles
if they weigh the same
discard all of them and continue with the coins of the third pile
else continue with the lighter of the first two piles
b. The recurrence relation for the number of weighing W(n)needed in
the worst case is as follows:
W(n)=W(n/3)+1 for n>1,W(1) = 0.
For n=3
k,the recurrence becomes W(3k)=W(3k−1)+1.Solving it by
backward substitutions yields W(3k)=k=log
3n.
c. The ratio of the numbers of weighings in the worst case can be ap-
proximated for large values of nby
log2n
log3n=log2n
log32log
2n=log
23≈1.6.
4. Compute 26 ·47 by the multiplication à la russe algorithm:
nm
26 47
13 94 94
6188
3376 376
1752 752
1,222
5. a. The number of divisions multiplication à la russe needs for computing
n·mand m·nis log2nand log2m, respectively.
b. Its time efficiency is in Θ(log n)where nis the first factor of the
product. As a function of b, the number of binary digits of n, the time
efficiency is in Θ(b).
6. Algorithm Russe(n, m)
//Implements multiplication à la russe nonrecursively
//Input: Two positive integers nand m
//Output: The product of nand m
p←0
35

while n=1do
if nmod2=1 p←p+m
n←n/2
m←2∗m
return p+m
Algorithm RusseRec(n, m)
//Implements multiplication à la russe recursively
//Input: Two positive integers nand m
//Output: The product of nand m
if nmod 2 = 0 return RusseRec(n/2,2m)
else if n=1 return m
else return RusseRec((n−1)/2,2m)+m
7. Using the fact that J(n)can be obtained by a one-bit left cyclic shift of
n, we get the following for n=40:
J(40) = J(1010002) = 100012=17.
8. We can use the fact that J(n)can be obtained by a one-bit left cyclic shift
of n.Ifn=2
k,where kis a nonnegative integer, then J(2k)=J(10...0
2
)
kzeros
=1.
9. a. Using the initial condition J(1) = 1 and the recurrences J(2k)=
2J(k)−1and J(2k+1)=2J(k)+1 forevenandoddvaluesofn, respec-
tively, we obtain the following values of J(n)for n=1,2, ..., 15:
n123456789101112131415
J(n)113135713 5 7 9 111315
b. On inspecting the values obtained in part (a), it is not difficult to
observe that for the n’s values between consecutive powers of 2, i.e., for
2k≤n<2k+1 (k=0,1,2,3) or n=2
k+iwhere i=0,1,...,2k−1,
the corresponding values of J(n)run the range of odd numbers from 1 to
2k+1 −1.This observation can be expressed by the formula
J(2k+i)=2i+1 for i=0,1,...,2k−1.
We’ll prove that this formula solves the recurrences of the Josephus prob-
lem for any nonnegative integer kby induction on k. For the basis value
36
k=0,wehaveJ(20+0)=2·0+1=1as it should for the initial con-
dition. Assuming that for a given nonnegative integer kand for every
i=0,1, ..., 2k−1,J(2k+i)=2i+1,we need to show that
J(2k+1 +i)=2i+1 for i=0,1,...,2k+1 −1.
If iis even, it can be represented as 2jwhere j=0,1, ..., 2k−1.Then we
obtain
J(2k+1 +i)=J(2(2k+j)) = 2J(2k+j)−1
and, using the induction’s assumption, we can continue as follows
2J(2k+j)−1=2[2j+1]−1=2i+1.
If iis odd, it can be expressed as 2j+1 where 0≤j<2k.Then we
obtain
J(2k+1 +i)=J(2k+1 +2j+1)=J(2(2k+j)+1)=2J(2k+j)+1
and, using the induction’s assumption, we can continue as follows
2J(2k+j)+1=2[2j+1]+1=2i+1.
c. Let n=(bkbk−1...b0)2where the first binary digit bkis 1.In the
n’s representation used in part (b), n=2
k+i, i =(bk−1...b0)2.Further,
as proved in part (b),
J(n)=2i+1=(bk−1...b00)2+1=(bk−1...b01)2=(bk−1...b0bk)2,
which is a one-bit left cyclic shift of n=(bkbk−1...b0)2.
Note: The solutions to Problem 9 are from [Gra94].
37
Exercises 5.6
1. a. If we measure the size of an instance of the problem of computing the
greatest common divisor of mand nby the size of the second parameter
n, by how much can the size decrease after one iteration of Euclid’s algo-
rithm?
b. Prove that an instance size will always decrease at least by a factor of
2 after two successive iterations of Euclid’s algorithm.
2. a. Apply the partition-based algorithm to find the median of the list of
numbers 9, 12, 5, 17, 20.
b. Show that the worst-case efficiency of the partition-based algorithm
for the selection problem is quadratic.
3. a. Write a pseudocode for a nonrecursive implementation of the partition-
based algorithm for the selection problem.
b. Write a pseudocode for a recursive implementation of this algorithm.
4. Derive the formula underlying interpolation search.
5. Give an example of the worst-case input for interpolation search and
show that the algorithm is linear in the worst case.
6. a. Find the smallest value of nfor which log2log2n+1 is greater than 6.
b. Determine which, if any, of the following assertions are true:
i. log log n∈o(log n)ii. log log n∈Θ(log n)iii. log log n∈Ω(log n).
7. a. Outline an algorithm for finding the largest key in a binary search tree.
Would you classify your algorithm as a variable-size-decrease algorithm?
b. What is the time efficiency class of your algorithm in the worst case?
8. a. Outline an algorithm for deleting a key from a binary search tree.
Would you classify this algorithm as a variable-size-decrease algorithm?
b. What is the time efficiency class of your algorithm?
9. Misere one-pile Nim Consider the so-called misere version of the one-
pile Nim, in which the player taking the last chip looses the game. All
the other conditions of the game remain the same, i.e., the pile contains
nchips and on each move a player takes at least one but no more than m
chips. Identify the winning and loosing positions (for the player to move)
in this game.
38
10. a. Moldy chocolate Two payers take turns by breaking an m-by-n
chocolate bar, which has one spoiled 1-by-1square. Each break must be a
single straight line cutting all the way across the bar along the boundaries
between the squares. After each break, the player who broke the bar last
eats the piece that does not contain the spoiled corner. The player left
with the spoiled square loses the game. Is it better to go first or second
in this game?
b. Write an interactive program to play this game with the computer.
Your program should make a winning move in a winning position and a
random legitimate move in a loosing position.
11. Flipping pancakes There are npancakes all of different sizes that are
stacked on top of each other. You are allowed to slip a flipper under
one of the pancakes and flip over the whole sack above the flipper. The
purpose is to arrange pancakes according to their size with the biggest at
the bottom. (You can see a visualization of this puzzle on the Interactive
Mathematics Miscellany and Puzzles site [Bog].) Design an algorithm for
solving this puzzle.
39

Hints to Exercises 5.6
1. a. The answer follows immediately from the formula underlying Euclid’s
algorithm.
b. Let r=mmod n. Investigate two cases of r’s value relative to n’s
value.
2. a. Trace the algorithm on the input given, as was done in the section for
another input.
b. Since the algorithm in question is based on the same partitioning idea
as quicksort is, it is natural to expect the worst-case inputs to be similar
for these algorithms.
3. You should have difficulties with neither implementation of the algorithm
outlined in the text.
4. Write an equation of the straight line through the points (l, A[l]) and
(r, A[r]) and find the xcoordinate of the point on this line whose ycoor-
dinate is v.
5. Construct an array for which interpolation search decreases the remaining
subarray by one element on each iteration.
6. a. Solve the inequality log2log2n+1>6.
b. Compute lim
n→∞
log log n
log n.Note that to within a constant multiple, you
can consider the logarithms to be natural, i.e., base e.
7. a. The definition of the binary search tree suggests such an algorithm.
b. What will be the worst-case input for your algorithm? How many
key comparisons will it make on such an input?
8. a. Consider separately three cases: (1) the key’s node is a leaf; (2) the
key’s node has one child; (3) the key’s node has two children.
b. Assume that you know a location of the key to be deleted.
9. Follow the plan used in Section 5.6 for analyzing the standard version of
the game.
10. Play several rounds of the game on the graphed paper to become comfort-
able with the problem. Considering special cases of the spoiled square’s
location should help you to solve it.
11. Do yourself a favor: try to design an algorithm on your own. It does not
have to be optimal, but it should be reasonably efficient.
40
Solutions to Exercises 5.6
1. a. Since the algorithm uses the formula gcd(m, n)=gcd(n, m mod n),the
size of the new pair will be mmod n. Hence it can be any integer between
0andn−1.Thus, the size ncan decrease by any number between 1 and n.
b. Two consecutive iterations of Euclid’s algorithm are performed ac-
cording to the following formulas:
gcd(m, n)=gcd(n, r)=gcd(r, n mod r)where r=mmod n.
We need to show that nmod r≤n/2.Consider two cases: r≤n/2and
n/2<r<n. If r≤n/2,then
nmod r<r≤n/2.
If n/2<r<n,then
nmod r=n−r<n/2,
too.
2. a. Since n=5,k=5/2=3.For the given list 9, 12, 5, 17, 20, with
the first element as the pivot, we obtain the following partition
912 5 17 20
5912 17 20
Since s=2<k=3,we proceed with the right part of the list:
12 17 20
12 17 20
Since s=k=3,12 is the median of the list given.
b. Consider an instance of the selection problem with k=nand a strictly
increasing array. The situation is identical to the worst-case analysis of
quicksort (see Section 4.2).
3. a. Algorithm Selection(A[0..n −1],k)
//Solves the selection problem by partition-based algorithm
//Input: An array A[0..n −1] of orderable elements and integer k(1 ≤
k≤n)
//Output: The value of the kth smallest element in A[0..n −1]
l←0; r←n−1
A[n]←∞ //append sentinel
while l≤rdo
p←A[l]//the pivot
41

i←l;j←r+1
repeat
repeat i←i+1until A[i]≥p
repeat j←j−1until A[j]≤pdo
swap(A[i],A[j])
until i≥j
swap(A[i],A[j]) //undo last swap
swap(A[l],A[j]) //partition
if j>k−1r←j−1
else if j<k−1l←j+1
else return A[k−1]
b. call SelectionRec(A[0..n −1],k)where
Algorithm SelectionRec(A[l..r],k)
//Solves the selection problem by recursive partition-based algorithm
//Input: A subarray A[l..r]of orderable elements and
// integer k(1 ≤k≤r−l+1)
//Output: The value of the kth smallest element in A[l..r]
s←Partition(A[l..r]) //see Section 4.2; must return lif l=r
if s>l+k−1SelectionRec(A[l..s −1],k)
else if s<l+k−1SelectionRec(A[s+1..r],k−1−s)
else return A[s]
4. Using the standard form of an equation of the straight line through two
given points, we obtain
y−A[l]=A[r]−A[l]
r−l(x−l).
Substituting a given value vfor yand solving the resulting equation for x
yields
x=l+(v−A[l])(r−l)
A[r]−A[l]
after the necessary round-off of the second term to guarantee index lto
be an integer.
5. If v=A[l]or v=A[r],formula (5.4) will yield x=land x=r, respec-
tively, and the search for vwill stop successfully after comparing vwith
A[x].If A[l]<v<A[r],
0<(v−A[l])(r−l)
A[r]−A[l]<r−l;
therefore
0≤
(v−A[l])(r−l)
A[r]−A[l]≤r−l−1
42
and
l≤l+(v−A[l])(r−l)
A[r]−A[l]≤r−1.
Hence, if interpolation search does not stop on its current iteration, it
reduces the size of the array that remains to be investigated at least by
one. Therefore, its worst-case efficiency is in O(n).We want to show that
it is, in fact, in Θ(n).Consider, for example, array A[0..n −1] in which
A[0] = 0 and A[i]=n−1for i=1,2, ..., n−1.If we search for v=n−1.5
in this array by interpolation search, its kth iteration (k=1,2,...,n)will
have l=0and r=n−k. We will prove this assertion by mathematical
induction on k. Indeed, for k=1we have l=0and r=n−1.For
the general case, assume that the assertion is correct for some iteration k
(1 ≤k<n)so that l=0and r=n−k. On this iteration, we will obtain
the following by applying the algorithm’s formula
x=0+((n−1.5) −0)(n−k)
(n−1) −0.
Since
(n−1.5)(n−k)
(n−1) =(n−1)(n−k)−0.5(n−k)
(n−1) =(n−k)−0.5(n−k)
(n−1) <(n−k)
and
(n−1.5)(n−k)
(n−1) =(n−k)−0.5(n−k)
(n−1) >(n−k)−(n−k)
(n−1) ≥(n−k)−1,
x=(n−1.5)(n−k)
(n−1) −0=(n−k)−1=n−(k+1).
Therefore A[x]=A[n−(k+1)] =n−1(unless k=n−1),implying that
l=0and r=n−(k+1) on the next (k+1) iteration.(If k=n−1,the
assertion holds true for the next and last iteration, too: A[x]=A[0] = 0,
implying that l=0and r=0.)
6. a. We can solve the inequality log2log2n+1>6as follows:
log2log2n+1 >6
log2log2n>5
log2n>25
n>232 (>4·109).
43

b. Using the formula logan=log
aeln n, we can compute the limit as
follows:
lim
n→∞
logalogan
logan=lim
n→∞
logaeln(logaeln n)
logaeln n= lim
n→∞
ln logae+lnlnn
ln n
=lim
n→∞
ln logae
ln n+ lim
n→∞
ln ln n
ln n= 0 + lim
n→∞
ln ln n
ln n.
The second limit can be computed by using L’Hôpital’s rule:
lim
n→∞
ln ln n
ln n= lim
n→∞
[ln ln n]
[ln n]= lim
n→∞
(1/ln n)(1/n)
1/n =lim
n→∞(1/ln n)=0.
Hence, log log n∈o(log n).
7. a. Recursively, go to the right subtree until a node with the empty right
subtree is reached; return the key of that node. We can consider this al-
gorithm as a variable-size-decrease algorithm: after each step to the right,
we obtain a smaller instance of the same problem (whether we measure a
tree’s size by its height or by the number of nodes).
b. The worst-case efficiency of the algorithm is linear; we should expect
its average-case efficiency to be logarithmic (see the discussion in Section
5.6).
8. a. This is an important and well-known algorithm. Case 1: If a key to
be deleted is in a leaf, make the pointer from its parent to the key’s node
null. (If it doesn’t have a parent, i.e., it is the root of a single-node tree,
make the tree empty.) Case 2: If a key to be deleted is in a node with a
single child, make the pointer from its parent to the key’s node to point to
that child. (If the node to be deleted is the root with a single child, make
its child the new root.) Case 3: If a key Kto be deleted is in a node
with two children, its deletion can be done by the following three-stage
procedure. First, find the smallest key Kin the right subtree of the K’s
node. (Kis the immediate successor of Kin the inorder traversal of the
given binary tree; it can be also found by making one step to the right
from the K’s node and then all the way to the left until a node with no
left subtree is reached). Second, exchange Kand K.Third, delete Kin
its new node by using either Case 1 or Case 2, depending on whether that
node is a leaf or has a single child.
This algorithm is not a variable-size-decrease algorithm because it does
not work by reducing the problem to that of deleting a key from a smaller
binary tree.
44
b. Consider, as an example of the worst case input, the task of delet-
ing the root from the binary tree obtained by successive insertions of keys
2, 1, n, n −1,...,3.Since finding the smallest key in the right subtree
requires following a chain of n−2pointers, the worst-case efficiency of
the deletion algorithm is in Θ(n).Since the average height of a binary
tree constructed from nrandom keys is a logarithmic function (see Section
5.6), we should expect the average-case efficiency of the deletion algorithm
be logarithmic as well.
9. If n=1,Player 1 (the player to move first) loses by definition of the
misere game because s/he has no choice but to take the last chip. If
2≤n≤m+1,Player 1 wins by taking n−1chips to leave Player 2 with
one chip. If n=m+2=1+(m+1),Player 1 loses because any legal
move puts Player 2 in a winning position. If m+3≤n≤2m+2(i.e.,
2+(m+1) ≤n≤2(m+1)), Player 1 can win by taking (n−1) mod(m+1)
chips to leave Player 2 with m+2 chips, which is a losing position for the
player to move next. Thus, an instance is a losing position for Player
1 if and only if nmod(m+1) = 1.Otherwise, Player 1 wins by taking
(n−1) mod(m+1) chips; any deviation from this winning strategy puts
the opponent in a winning position. The formal proof of the solution’s
correctness is by strong induction.
10. The problem is equivalent to the game of Nim, with the piles represented
by the rows and columns of the bar between the spoiled square and the
bar’s edges. Thus, the Nim’s theory outlined in the section identifies
both winning positions and winning moves in this game. According to
this theory, an instance of Nim is a winning one (for the player to move
next) if and only if its binary digital sum contains at least one 1. In
such a position, a wining move can be found as follows. Scan left to
right the binary digital sum of the bit strings representing the number of
chips in the piles until the first 1 is encountered. Let jbe the position
of this 1. Select a bit string with a 1 in position j–this is the pile from
which some chips will be taken in a winning move. To determine the
number of chips to be left in that pile, scan its bit string starting at posi-
tion jand flip its bits to make the new binary digital sum contain only 0’s.
Note: Under the name of Yucky Chocolate, the special case of this problem–
with the spoiled square in the bar’s corner–is discussed, for example, by
Yan Stuart in "Math Hysteria: Fun and Games with Mathematics," Ox-
ford University Press, 2004. For such instances, the player going first loses
if m=n, i.e., the bar has the square shape, and wins if m=n. Here is a
proof by strong induction, which doesn’t involve binary representations of
the pile sizes. If m=n=1,the player moving first looses by the game’s
definition. Assuming that the assertion is true for every k-by-ksquare
bar for all k≤n, consider the n+1-by-n+1 bar.Any move (i.e., a break
45
of the bar) creates a rectangular bar with one side of size k≤nand the
other side’s size remaining n+1.The second player can always follow
with a break creating a k-by-ksquare bar with a spoiled corner, which is
a loosing instance by the inductive assumption. And if m=n, the first
player can always "even" the bar by creating the square with the side’s
size min{m, n],putting the second player in a losing position.
11. Here is a decrease-and-conquer algorithm for this problem. Repeat the
following until the problem is solved: Find the largest pancake that is out
of order. (If there is none, the problem is solved.) If it is not on the top of
the stack, slide the flipper under it and flip to put the largest pancake on
the top. Slide the flipper under the first-from-the-bottom pancake that
is not in its proper place and flip to increase the number of pancakes in
their proper place at least by one.
The number of flips needed by this algorithm in the worst case is W(n)=
2n−3,where n≥2is the number of pancakes. Here is a proof of this
assertion by mathematical induction. For n=2,the assertion is cor-
rect: the algorithm makes one flip for a two-pancake stack with a larger
pancake on the top, and it makes no flips for a two-pancake stack with a
larger pancake at the bottom. Assume now that the worst-case number
of flips for some value of n≥2is given by the formula W(n)=2n−3.
Consider an arbitrary stack of n+1 pancakes. With two flips or less, the
algorithm puts the largest pancake at the bottom of the stack, where it
doesn’t participate in any further flips. Hence, the total number of flips
needed for any stack of n+1pancakes is bounded above by
2+W(n)=2+(2n−3) = 2(n+1)−3.
Infact,thisupperboundisattainedonthestackofn+1pancakes con-
structed as follows: flip a worst-case stack of npancakes upside down
and insert a pancake larger than all the others between the top and the
next-to-the-top pancakes. (On the new stack, the algorithm will make two
flips to reduce the problem to flipping the worst-case stack of npancakes.)
This completes the proof of the fact that
W(n+1)=2(n+1)−3,
which, in turn, completes our mathematical induction proof.
Note: The Web site mentioned in the problem’s statement contains, in ad-
dition to a visualization applet, an interesting discussion of the problem.
(Among other facts, it mentions that the only research paper published
by Bill Gates was devoted to this problem.)
46
This file contains the exercises, hints, and solutions for Chapter 6 of the
book ”Introduction to the Design and Analysis of Algorithms,” 2nd edition, by
A. Levitin. The problems that might be challenging for at least some students
are marked by ;those that might be difficult for a majority of students are
marked by .
Exercises 6.1
1. Recall that the median of a list of nnumbers is defined as its n/2
smallest element. (The median is larger than one half the elements and
is smaller than the other half.) Design a presorting-based algorithm for
finding the median and determine its efficiency class.
2. Consider the problem of finding the distance between the two closest num-
bers in an array of nnumbers. (The distance between two numbers xand
yis computed as |x−y|.)
a. Design a presorting-based algorithm for solving this problem and de-
termine its efficiency class.
b. Compare the efficiency of this algorithm with that of the brute-force
algorithm (see Problem 9 in Exercises 1.2).
3. Let A={a1,...,a
n}and B={b1, ..., bm}be two sets of numbers. Consider
the problem of finding their intersection, i.e., the set Cof all the numbers
that are in both Aand B.
a. Design a brute-force algorithm for solving this problem and deter-
mine its efficiency class.
b. Design a presorting-based algorithm for solving this problem and de-
termine its efficiency class.
4. Consider the problem of finding the smallest and largest elements in an
array of nnumbers.
a. Design a presorting-based algorithm for solving this problem and de-
termine its efficiency class.
b. Compare the efficiency of the three algorithms: (i) the brute-force
algorithm, (ii) this presorting-based algorithm, and (iii) the divide-and-
conquer algorithm (see Problem 2 in Exercises 4.1).
5. Show that the average-case efficiency of one-time searching by the algo-
rithm that consists of the most efficient comparison-based sorting algo-
rithm followed by binary search is inferior to the average-case efficiency of
sequential search.
1

6. Estimate how many searches will be needed to justify time spend on pre-
sorting an array of 103elements if sorting is done by mergesort and search-
ing is done by binary search. (You may assume that all searches are for
elements known to be in the array.) What about an array of 106elements?
7. To sort or not to sort? Design a reasonably efficient algorithm for solving
each of the following problems and determine its efficiency class.
a. You are given ntelephone bills and mchecks sent to pay the bills
(n≥m).Assuming that telephone numbers are written on the checks,
find out who failed to pay. (For simplicity, you may also assume that
only one check is written for a particular bill and that it covers the bill in
full.)
b. You have a file of nstudent records indicating each student’s num-
ber, name, home address, and date of birth. Find out the number of
students from each of the 50 U.S. states.
8. Given a set of n≥3points in the Cartesian plane, connect them in a
simple polygon, i.e., a closed path through all the points so that its line
segments (the polygon’s edges) do not intersect (except for neighboring
edges at their common vertex). For example,
P
5
P
3
P
6
P
1
P
2
P
4
=⇒
P5
P
3
P
6
P
1
P
4
P
2
a. Does the problem always have a solution? Does it always have a unique
solution?
b. Design a reasonably efficient algorithm for solving this problem and
indicate its efficiency class.
9. Youhaveanarrayofnnumbersandanumbers. Find out whether
the array contains two elements whose sum is s. (For example, for the
array5,9,1,3ands=6,the answer is yes, but for the same array and
s=7,the answer is no.) Design an algorithm for this problem with a
better than quadratic time efficiency.
10. You have a list of nopen intervals (a1,b
1),(a2,b
2),..., (an,b
n)on the
2
real line. (An open interval (a, b)comprisesallthepointsstrictlybetween
its endpoints aand b, i.e., (a, b)={x|a<x<b}.) Find the maximal
number of these intervals that have a common point. For example, for
the intervals (1, 4), (0, 3), (-1.5, 2), (3.6, 5), this maximal number is 3.
Design an algorithm for this problem with a better than quadratic time
efficiency.
11. a. Design an efficient algorithm for finding all sets of anagrams in a large
file such as a dictionary of English words [Ben00]. For example, eat, ate,
and tea belong to one such a set.
b. Write a program implementing the algorithm.
3
Hints to Exercises 6.1
1. The algorithm is suggested by the problem’s statement. Its analysis is
similar to the examples discussed in this section.
2. This problem is similar to one of the examples in this section.
3. a. Compare every element in one set with all the elements in the other.
b. In fact, you can use presorting in three different ways: sort elements of
just one of the sets, sort elements of each of the sets separately, and sort
elements of the two sets together.
4. a. How do we find the smallest and largest elements in a sorted list?
b. The brute-force algorithm and the divide-and-conquer algorithm are
both linear.
5. Use the known results about the average-case efficiencies of the algorithms
in this question.
6. Assume that sorting requires about nlog2ncomparisons. Use the known
results about the number of comparisons made, on the average, in a suc-
cessful search by binary search and by sequential search.
7. a. The problem is similar to one of the preceding problems in these exer-
cises.
b. How would you solve this problem if the student information were
written on index cards? Better yet, think how somebody else, who has
never taken a course on algorithms but possesses a good dose of common
sense, would solve this problem.
8. a. Many problems of this kind have exceptions for one particular config-
uration of points. As to the question about a solution’s uniqueness, you
can get the answer by considering a few small “random” instances of the
problem.
b. Construct a polygon for a few small “random” instances of the problem.
Try to construct polygons in some systematic fashion.
9. It helps to think about real numbers as ordered points on the real line.
Considering the special case of s=0,with a given array containing both
negative and positive numbers, might be helpful, too.
10. After sorting the ai’s and bi’s, the problem can be solved in linear time.
11. Use the presorting idea twice.
4
Solutions to Exercises 6.1
1. Sort the list and then simply return the n/2th element of the sorted list.
Assuming the efficiency of the sorting algorithm is in O(nlog n),the time
efficiency of the entire algorithm will be in
O(nlog n)+Θ(1)=O(nlog n).
2. a. Sort the array first and then scan it to find the smallest difference
between two successive elements A[i]and A[i+1] (0≤i≤n−2).
b. The time efficiency of the brute-force algorithm is in Θ(n2)because
the algorithm considers n(n−1)/2pairs of the array’s elements. (In the
crude version given in Problem 9 of Exercises 1.2, the same pair is con-
sidered twice but this doesn’t change the efficiency’s order, of course.) If
the presorting is done with a O(nlog n)algorithm, the running time of
the entire algorithm will be in
O(nlog n)+Θ(n)=O(nlog n).
3. a. Initialize a list to contain elements of C=A∩Bto empty. Compare
every element aiin Awith successive elements of B:ifai=bj, add this
value to the list Cand proceed to the next element in A. (In fact, if
ai=bj,b
jneed not be compared with the remaining elements in Aand
may be deleted from B.) In the worst case of input sets with no common
elements, the total number of element comparisons will be equal to nm,
putting the algorithm’s efficiency in O(nm).
b. First solution: Sort elements of one of the sets, say, A,storedin
an array. Then use binary search to search for each element of Bin the
sorted array A: if a match is found, add this value to the list C.Ifsorting
is done with a O(nlog n)algorithm, the total running time will be in
O(nlog n)+mO(log n)=O((m+n)logn).
Note that the efficiency formula implies that it is more efficient to sort the
smaller one of the two input sets.
Second solution: Sort the lists representing sets Aand B, respectively.
Scan the lists in the mergesort-like manner but output only the values
common to the two lists. If sorting is done with a O(nlog n)algorithm,
the total running time will be in
O(nlog n)+O(mlog m)+O(n+m)=O(slog s)where s=max{n, m}.
5

Third solution: Combine the elements of both Aand Bin a single list
and sort it. Then scan this sorted list by comparing pairs of its consec-
utive elements: if Li=Li+1,add this common value to the list Cand
increment iby two. If sorting is done with an nlog nalgorithm, the total
running time will be in
O((n+m)log(n+m)) + Θ(n+m)=O(slog s)where s=max{n, m}.
4. a. Sort the list and return its first and last elements as the values of
the smallest and largest elements, respectively. Assuming the efficiency
of the sorting algorithm used is in O(nlog n),the time efficiency of the
entire algorithm will be in
O(nlog n)+Θ(1)+Θ(1)=O(nlog n).
b. The brute-force algorithm and the divide-and-conquer algorithm are
both linear, and, hence, superior to the presorting-based algorithm.
5. Since the average-case efficiency of any comparison-based sorting algo-
rithm is known to be in Ω(nlog n)while the average-case efficiency of
binary search is in Θ(log n),the average-case efficiency of the searching
algorithm combining the two will be in
Ω(nlog n) + Θ(log n)=Ω(nlog n).
This is inferior to the average-case efficiency of sequential search, which is
linear (see Section 2.1).
6. Let kbe the smallest number of searches needed for the sort—binary search
algorithm to make fewer comparisons than ksearches by sequential search
(for average successful searches). Assuming that a sorting algorithm
makes about nlog ncomparisons on the average and using the formulas
for the average number of key comparisons for binary search (about log2n)
and sequential search (about n/2), we get the following inequality
nlog2n+klog2n≤kn/2.
Thus, we need to find the smallest value of kso that
k≥nlog2n
n/2−log2n.
Substituting n=10
3into the right-hand side yields kmin = 21; substitut-
ing n=10
6yields kmin =40.
6

Note: For large values of n, we can simplify the last inequality by elimi-
nating the relatively insignificant term log2nfrom the denominator of the
right-hand side to obtain
k≥nlog2n
n/2or k≥2log
2n.
This inequality would yield the answers of 20 and 40 for n=10
3and
n=10
6,respectively.
7. a. The following algorithm will beat the brute-force comparisons of the
telephone numbers on the bills and the checks: Using an efficient sorting
algorithm, sort the bills and sort the checks. (In both cases, sorting has
to be done with respect to their telephone numbers, say, in increasing or-
der.) Then do a merging-like scan of the two sorted lists by comparing the
telephone numbers biand cjon the current bill and check, respectively:
if bi<c
j,addbito the list of unpaid telephone numbers and increment
i;if bi>c
j, increment j;if bi=cj,increment both iand j. Stop as
soon as one of the two lists becomes empty and append all the remain-
ing telephone numbers on the bill list, if any, to the list of the unpaid ones.
The time efficiency of this algorithm will be in
O(nlog n)+O(mlog m)+O(n+m)=
n≥mO(nlog n).
This is superior to the O(nm)efficiency of the brute-force algorithm (but
inferior, for the average case, to solving this problem with hashing dis-
cussedinSection7.3).
b. Initialize 50 state counters to zero. Scan the list of student records and,
for a current student record, increment the corresponding state counter.
The algorithm’s time efficiency will be in Θ(n), which is superior to any
algorithm that uses presorting of student records by a comparison-based
algorithm.
8. a. The problem has a solution if and only if all the points don’t lie on the
same line. And, if a solution exists, it may not be unique.
b. Find the lowest point P∗,i.e., the one with the smallest ycoordi-
nate. in the set. (If there is a tie, take, say, the leftmost among them,
i.e., the one with the smallest xcoordinate.) For each of the other n−1
points, compute its angle in the polar coordinate system with the origin
at P∗and sort the points in increasing order of these angles, breaking ties
in favor of a point closer to P∗.(Instead of the angles, you can use the
7
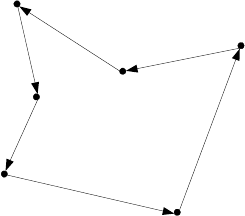
line slopes with respect to the horizontal line through P∗.) Connect the
points in the order generated, adding the last segment to return to P∗.
P*
Finding the lowest point P∗is in Θ(n),computing the angles (slopes)
is in Θ(n),sorting the points according to their angles can be done with a
O(nlog n)algorithm. The efficiency of the entire algorithm is in O(nlog n).
9. Assume first that s=0.Then A[i]+A[j]=0if and only if A[i]=−A[j],
i.e., these two elements have the same absolute value but opposite signs.
Wecancheckforpresenceofsuchelementsinagivenarrayinseveraldif-
ferent ways. If all the elements are known to be distinct, we can simply
replace each element A[i]by its absolute value |A[i]|and solve the element
uniqueness problem for the array of the absolute values in O(nlog n)time
with the presorting based algorithm. If a given array can have equal ele-
ments, we can modify our approach as follows: We can sort the array in
nondecreasing order of their absolute values (e.g., -6, 3, -3, 1, 3 becomes
1, 3, -3, 3, -6), and then scan the array sorted in this fashion to check
whether it contains a consecutive pair of elements with the same absolute
value and opposite signs (e.g., 1, 3, -3, 3, -6 does). If such a pair of
elements exists, the algorithm returns yes, otherwise, it returns no.
The case of an arbitrary value of sis reduced to the case of s=0by the fol-
lowing substitution: A[i]+A[j]=sif and only if (A[i]−s/2)+(A[j]−s/2) =
0.In other words, we can start the algorithm by subtracting s/2from
each element and then proceed as described above.
(Note that we took advantage of the instance simplification idea twice:
by reducing the problem’s instance to one with s=0and by presorting
the array.)
10. Sort all the ai’s and bj’s by a O(nlog n)algorithm in a single nondecreas-
ing list, treating bjas if it were smaller than aiin case of the tie ai=bj.
Scan the list left to right computing the running difference Dbetween
the number of ai’s and bj’s seen so far. In other words, initialize Dto 0
8
and then increment or decrement it by 1 depending on whether the next
element on the list is a left endpoint aior a right endpoint bj,respectively.
The maximum value of Dis the number in question.
Note 1: One can also implement this algorithm by sorting ai’s and bj’s
separately and then computing the running difference Dby merging-like
processing of the two sorted lists.
Note 2: This solution is suggested by D. Ginat in his paper "Algorith-
mic Pattern and the Case of the Sliding Delta," SIGCSE Bulletin,vol36,
no. 2, June 2004, pp. 29-33.
11. First, attach to every word in the file–as another field of the word’s
record, for example–its signature defined as the string of the word’s let-
ters in alphabetical order. (Obviously, words belong to the same anagram
set if and only if they have the same signature.) Sort the records in al-
phabetical order of their signatures. Scan the list to identify contiguous
subsequences, of length greater than one, of records with the same signa-
ture.
Note: Jon Bentley describes a real system where a similar problem oc-
curred in [Ben00], p.17, Problem 6.
9
Exercises 6.2
1. Solve the following system by Gaussian elimination.
x1+x2+x3=2
2x1+x2+x3=3
x1−x2+3x3=8.
2. a. Solve the system of the previous question by the LU decomposition
method.
b. From the standpoint of general algorithm design techniques, how would
you classify the LU-decomposition method?
3. Solve the system of Problem 1 by computing the inverse of its coefficient
matrix and then multiplying it by the right-hand side vector.
4. Would it be correct to get the efficiency class of the elimination stage of
Gaussian elimination as follows?
C(n)=
n−1
i=1
n
j=i+1
n+1
k=i
1=
n−1
i=1
(n+2−i)(n−i)
=
n−1
i=1
[(n+2)n−i(2n+2)+i2]
=
n−1
i=1
(n+2)n−
n−1
i=1
(2n+2)i+
n−1
i=1
i2.
Since s1(n)=n−1
i=1 (n+2)n∈Θ(n3),s
2(n)=n−1
i=1 (2n+2)i∈Θ(n3),
and s3(n)=n−1
i=1 i2∈Θ(n3),s
1(n)−s2(n)+s3(n)∈Θ(n3).
5. Write a pseudocode for the back-substitution stage of Gaussian elimination
and show that its running time is in Θ(n2).
6. Assuming that division of two real numbers takes three times longer than
their multiplication, estimate how much faster BetterGaussElimination
is than GaussElimination. (Of course, you should also assume that a
compiler is not going to eliminate the inefficiency in GaussElimination.)
7. a. Give an example of a system of two linear equations in two unknowns
that has a unique solution and solve it by Gaussian elimination.
b. Give an example of a system of two linear equations in two unknowns
that has no solution and apply Gaussian elimination to it.
c. Give an example of a system of two linear equations in two unknowns
that has infinitely many solutions and apply Gaussian elimination to it.
10
8. The Gauss-Jordan elimination method differs from Gaussian elimina-
tion in that the elements above the main diagonal of the coefficient matrix
are made zero at the same time and by the same use of a pivot row as the
elements below the main diagonal.
a. Apply the Gauss-Jordan method to the system of Problem 1 of these
exercises.
b. What general design technique is this algorithm based on?
c.In general, how many multiplications are made by this method while
solving a system of nequations in nunknowns? How does this compare
with the number of multiplications made by the Gaussian elimination
method in both its elimination and its back-substitution stages?
9. A system Ax =bof nlinear equations in nunknowns has a unique solution
if and only if det A=0.Is it a good idea to check this condition before
applying Gaussian elimination to a system?
10. a. Apply Cramer’s rule to solve the system of Problem 1 of these exercises.
b. Estimate how many times longer it will take to solve a system of n
linear equations in nunknowns by Cramer’s rule than by Gaussian elimi-
nation. (Assume that all the determinants in Cramer’s rule formulas are
computed independently by Gaussian elimination.)
11. Lights out This one-person game is played on an n-by-nboard com-
posed of 1-by-1 light panels. Each panel has a switch that can be turned
on and off, thereby toggling the on/off state of this and four vertically and
horizontally adjacent panels. (Of course, toggling a corner square affects
the total of three panels, and toggling a noncorner panel on the board’s
border affects the total of four squares.) Given an initial subset of lighted
squares, the goal is to turn all the lights off.
(a) Show that an answer can be found by solving a system of linear
equations with 0/1 coefficients and right-hand sides using modulo 2
arithmetic.
(b) Use Gaussian elimination to solve the 2-by-2 “all-ones” instance of
this problem, where all the panels of the 2-by-2 board are initially
lit.
(c) Use Gaussian elimination to solve the 3-by-3 “all-ones” instance of
this problem, where all the panels of the 3-by-3 board are initially
lit.
11
Hints to Exercises 6.2
1. Trace the algorithm as we did in solving another system in the section.
2. a. Use the Gaussian elimination results as explained in the text.
b. It is one of the varieties of the transform-and-conquer technique. Which
one?
3. To find the inverse, you can either solve the system with three simul-
taneous right-hand side vectors representing the columns of the 3-by-3
identity matrix or use the LU decomposition of the system’s coefficient
matrixfoundinProblem2.
4. Though the final answer is correct, its derivation contains an error you
have to find.
5. The pseudocode of this algorithm is quite straightforward. If you are
in doubt, see the section’s example tracing the algorithm. The order of
growth of the algorithm’s running time can be estimated by following the
standard plan for the analysis of nonrecursive algorithms.
6. Estimate the ratio of the algorithm running times, by using the approxi-
mate formulas for the number of divisions and the number of multiplica-
tions in both algorithms.
7. a. This is a “normal” case: one of the two equations should not be pro-
portional to the other.
b. The coefficients of one equation should be the same or proportional
to the corresponding coefficients of the other equation while the right-
hand sides should not.
c. The two equations should be either the same or proportional to each
other (including the right-hand sides).
8. a. Manipulate the matrix rows above a pivot row the same way the rows
below the pivot row are changed.
b. Are the Gauss-Jordan method and Gaussian elimination based on the
same algorithm design technique or on different ones?
c. Derive the formula for the number of multiplications in the Gauss-
Jordan method the same way it was done for Gaussian elimination in
Section 6.2.
9. How long will it take to compute the determinant compared to the time
needed to apply Gaussian elimination to the system?
12
10. a. Apply Cramer’s rule to the system given.
b. How many distinct determinants are there in the Cramer’s rule for-
mulas?
11. a. If xij is the number of times the panel in the ith row and jth column
needs to be toggled in a solution, what can be said about xij ? After you
answer this question, show that the binary matrix representing an initial
state of the board can be represented as a linear combination (in modulo
2 arithmetic) of n2binary matrices each representing the affect of toggling
an individual panel.
b. Set up a system of four equations in four unknowns (see part a) and
solve it by Gaussian elimination performing all operations in modulo-2
arithmetic.
c. If you believe that a system of nine equations in nine unknowns is too
large to solve by hand, write a program to solve the problem.
13

Solutions to Exercises 6.2
1. a. Solve the following system by Gaussian elimination
x1+x2+x3=2
2x1+x2+x3=3
x1−x2+3x3=8
111 2
211 3
1−13 8
row 2 - 2
1row 1
row 3 - 1
1row 1
1112
0−1−1−1
0−226
row 3 - −2
−1row 2
1112
0−1−1−1
0048
Then, by backward substitutions, we obtain the solution as follows:
x3=8/4= 2,x
2=(−1+x3)/(−1) = −1,and x1=(2−x3−x2)/1=1.
2. a. Repeating the elimination stage (or using its results obtained in Prob-
lem 1), we get the following matrices Land U:
L=
100
210
121
,U=
111
0−1−1
004
.
On substituting y=Ux into LUx =b, the system Ly =bneeds to be
solved first. Here, the augmented coefficient matrix is:
1002
2103
1218
Its solution is
y1=2,y
2=3−2y1=−1,y
3=8−y1−2y2=8.
Solving now the system Ux =y, whose augmented coefficient matrix is
1112
0−1−1−1
0048
,
14

yields the following solution to the system given:
x3=2,x
2=(−1+x3)/(−1) = −1,x
1=2−x3−x2=1.
b. The most fitting answer is the representation change technique.
3. Solving simultaneously the system with the three right-hand side vectors:
111100
211010
1−13001
row 2 - 2
1row 1
row 3 - 1
1row 1
111100
0−1−1−210
0−22−101
row 3 - −2
−1row 1
111100
0−1−1−210
0043−21
Solving the system with the first right-hand side column
1
−2
3
yields the following values of the first column of the inverse matrix:
−1
5
4
3
4
.
Solving the system with the second right-hand side column
0
1
−2
yields the following values of the second column of the inverse matrix:
1
−1
2
−1
2
.
Solving the system with the third right-hand side column
0
0
1
15

yields the following values of the third column of the inverse matrix:
0
−1
4
1
4
.
Thus, the inverse of the coefficient matrix is
−110
5
4−1
2−1
4
3
4−1
2
1
4
,
which leads to the following solution to the original system
x=A−1b=
−110
5
4−1
2−1
4
3
4−1
2
1
4
2
3
8
=
1
−1
2
.
4. In general, the fact that f1(n)∈Θ(n3),f
2(n)∈Θ(n3),and f3(n)∈Θ(n3)
does not necessarily imply that f1(n)−f2(n)+f3(n)∈Θ(n3),because the
coefficients of the highest third-degree terms can cancel each other. As a
specific example, consider f1(n)=n3+n, f2(n)=2n3,and f3(n)=n3.
Each of this functions is in Θ(n3),but f1(n)−f2(n)+f3(n)=n∈Θ(n).
5. Algorithm GaussBackSub(A[1..n, 1..n +1])
//Implements the backward substitution stage of Gaussian elimination
//by solving a given system with an upper-triangular coefficient matrix
//Input: Matrix A[1..n, 1,..n+1], with the first ncolumns in the upper-
//triangular form
//Output: A solution of the system of nlinear equations in nunknowns
//whose coefficient matrix and right-hand side are the first ncolumns
//of Aand its (n+1)st column, respectively
for i←ndownto 1do
temp ←0.0
for j←ndownto i+1
temp ←temp +A[i, j]∗x[j]
x[i]←(A[i, n +1]−temp)/A[i, i]
return x
The basic operation is multiplication of two numbers. The number of
times it will be executed is given by the sum
M(n)=
n
i=1
n
j=i+1
1=
n
i=1
(n−(i+1)+1)=
n
i=1
(n−i)
=(n−1) + (n−2) + ... +1= (n−1)n
2∈Θ(n2).
16
6. Let D(G)(n)and M(G)(n)be the numbers of divisions and multiplications
made by GaussElimination, respectively. Using the count formula derived
in Section 6.2, we obtain the following approximate counts:
D(G)(n)=M(G)(n)≈
n−1
i=1
n
j=i+1
n+1
k=i
1≈1
3n3.
Let D(BG)(n)and M(BG)(n)be the numbers of divisions and multiplica-
tions made by BetterGaussElimination, respectively. We have the follow-
ing approximations:
D(BG)(n)≈
n−1
i=1
n
j=i+1
1≈1
2n2and M(BG)(n)=M(G)(n)≈1
3n3.
Let cdand cmbe the times of one division and of one multiplication,
respectively. We can estimate the ratio of the running times of the two
algorithms as follows:
T(G)(n)
T(BG)(n)≈cdD(G)(n)+cmM(G)(n)
cdD(BG)(n)+cmM(BG)(n)≈cd1
3n3+cm1
3n3
cd1
2n2+cm1
3n3
≈cd1
3n3+cm1
3n3
cm1
3n3=cd+cm
cm
=cd
cm
+1=4.
7. a. The elimination stage should yield a 2-by-2 upper-triangular matrix
with nonzero coefficients on its main diagonal.
b. The elimination stage should yield a 2-by-2 matrix whose second row
is 0 0 αwhere α=0.
c. The elimination stage should yield a 2-by-2 matrix whose second row
is 0 0 0.
8. a. Solve the following system by the Gauss-Jordan method
x1+x2+x3=2
2x1+x2+x3=3
x1−x2+3x3=8
1112
2113
1−138
row 2 −2
1row 1
row 3 −1
1row 1
1112
0−1−1−1
0−226
row 1 −1
−1row 2
row 3 −−2
−1row 2
1001
0−1−1−1
0048
row 1 −0
4row 3
row 2 −−1
4row 3
1001
0−101
0048
17

We obtain the solution by dividing the right hand side values by the cor-
responding elements of the diagonal matrix:
x1=1/1=1,x
2=1/−1=−1,x
3=8/4=2.
b. The Gauss-Jordan method is also an example of an algorithm based
on the instance simplification idea. The two algorithms differ in the kind
of a simpler instance to which they transfer a given system: Gaussian
elimination transforms a system to an equivalent system with an upper-
triangular coefficient matrix whereas the Gauss-Jordan method transforms
it to a system with a diagonal matrix.
c. Here is a basic pseudocode for the Gauss-Jordan elimination:
Algorithm GaussJordan(A[1..n, 1..n],b[1..n])
//Applies Gaussian-Jordan elimination to matrix Aofasystem’s
//coefficients, augmented with vector bof the system’s right-hand sides
//Input: Matrix A[1..n, 1,..n]and column-vector b[1..n]
//Output: An equivalent diagonal matrix in place of Awith the
//corresponding right-hand side values in its (n+1)st column
for i←1to ndo A[i, n +1]←b[i]//augment the matrix
for i←1to ndo
for j←1to ndo
if j=i
temp ←A[j, i]/A[i, i]//assumes A[i, i]=0
for k←ito n+1do
A[j, k]←A[j, k]−A[i, k]∗temp
The number of multiplications made by the above algorithm can be com-
puted as follows:
M(n)=
n
i=1
n
j=1
n+1
k=i
1=
n
i=1
n
j=1
(n+1−i+1)=
n
i=1
n
j=1
(n+2−i)
=
n
i=1
(n+2−i)(n−1) = (n−1)
n
i=1
(n+2−i)
=(n−1)[(n+1)+n+... +2]=(n−1)[(n+1)+n+... +1−1]
=(n−1)[(n+1)(n+2)
2−1] = (n−1)n(n+3)
2≈1
2n3.
The total number of multiplications made in both elimination and back-
ward substitution stages of the Gaussian elimination method is equal to
n(n−1)(2n+5)
6+(n−1)n
2=(n−1)n(n+4)
3≈1
3n3,
which is about 1.5 smaller than in the Gauss-Jordan method.
18

Note: The Gauss-Jordan method has an important advantage over Gaussian
elimination: being more uniform, it is more suitable for efficient implemen-
tation on a parallel computer.
9. Since the time needed for computing the determinant of the system’s coef-
ficient matrix is about the same as the time needed for solving the system
(or detecting that the system does not have a unique solution) by Gaussian
elimination, computing the determinant of the coefficient matrix to check
whether it is equal to zero is not a good idea from the algorithmic point
of view.
10. a. Solve the following system by Cramer’s rule:
x1+x2+x3=2
2x1+x2+x3=3
x1−x2+3x3=8
|A|=
111
211
1−13
=1·1·3+1·1·1+2·(−1) ·1−1·1·1−2·1·3−(−1) ·1·1=−4,
|A1|=
211
311
8−13
=2·1·3+1·1·8+3·(−1) ·1−8·1·1−3·1·3−(−1) ·1·2=−4,
|A2|=
121
231
183
=1·3·3+2·1·1+2·8·1−1·3·1−2·2·3−8·1·1=4,
|A3|=
112
213
1−18
=1·1·8+1·3·1+2·(−1) ·2−1·1·2−2·1·8−(−1) ·3·1=−8.
Hence,
x1=|A1|
|A|=−4
−4=1,x
2=|A2|
|A|=4
−4=−1,x
3=|A3|
|A|=−8
−4=2.
b. Cramer’s rule requires computing n+1distinct determinants. If each
of them is computed by applying Gaussian elimination, it will take about
n+1 times longer than solving the system by Gaussian elimination. (The
time for the backward substitution stage was not accounted for in the
preceding argument because of its quadratic efficiency vs. cubic efficiency
of the elimination stage.)
19
11. a. Any feasible state of the board can be described by an n-by-nbinary
matrix, in which the element in the ith row and jth column is equal to
1 if and only if the corresponding panel is lit. Let Sand Fbe such
matrices representing the initial and final (all-zeros) boards, respectively.
The impact of toggling the panel at (i, j)on a board represented by a
binary matrix Mcan be interpreted as the modulo-2 matrix addition
M+Aij ,whereAij is the matrix in which the only entries equal to 1 are
those that are in the (i, j)and adjacent to it positions. For example, if
Mis a 3-by-3 all-ones matrix representing a 3-by-3 board of all-lit panels,
then the impact of turning off the (2,2) panel can be represented as
M+A22 =
111
111
111
+
010
111
010
=
101
000
101
.
Let xij is the number of times the (i, j)panel is toggled in a solution that
transforms the board from a starting state Sto a final state F. Since the
ultimate impact of toggling this panel depends only on whether xij is even
or odd, we can assume with no loss in generality that xij is either 0 or 1.
Then a solution to the puzzle can be expressed by the matrix equation
S+
n
i,j=1
xij Aij =F,
where all the operations are assumed to be performed modulo 2. Taking
into account that F=0,the all-zeros n-by-nmatrix, the last equation is
equivalent to n
i,j=1
xij Aij =S.
(The last equation can also be interpreted as transforming the final all-
zero board to the initial board S.)
Note: This solution follows Eric W. Weisstein et al. "Lights Out Puzzle"
from MathWorld—A Wolfram Web Resource at http://mathworld.wolfram.com/LightsOutPuzzle.html
b. The system of linear equations for the instance in question (see part a)
is
x11 11
10
+x12 11
01
+x21 10
11
+x22 01
11
=11
11
or
1·x11 +1·x12 +1·x21 +0·x22 =1
1·x11 +1·x12 +0·x21 +1·x22 =1
1·x11 +0·x12 +1·x21 +1·x22 =1
0·x11 +1·x12 +1·x21 +1·x22 =1.
20
Solving this system in modulo-2 arithmetic by Gaussian elimination pro-
ceeds as follows:
11101
11011
10111
01111
11101
00110
01010
01111
11101
01010
00110
01111
11101
01010
00110
00101
11101
01010
00110
00011
.
The backward substitutions yield the solution: x11 =1,x
12 =1,x
21 =1,
x22 =1,i.e., each of the four panel switches should be toggled once (in
any order).
c. The solution to this instance of the puzzle is x11 =x13 =x22 =
x31 =x33 =1(with all the other components being 0).
21
Exercises 6.3
1. Which of the following binary trees are AVL trees?
5
3
2
6
8
5
4
2
6
8
5
3
12
6
9
7
( a )
1379
( b ) ( c )
2. a. For n=1,2,3,4,and 5, draw all the binary trees with nnodes that
satisfy the balance requirement of AVL trees.
b. Draw a binary tree of height 4 that can be an AVL tree and has
the smallest number of nodes among all such trees.
3. Draw diagrams of the single L-rotation and of the double RL-rotation in
their general form.
4. For each of the following lists, construct an AVL tree by inserting their
elements successively, starting with the empty tree.
a. 1, 2, 3, 4, 5, 6
b. 6, 5, 4, 3, 2, 1
c. 3, 6, 5, 1, 2, 4
5. a. For an AVL tree containing real numbers, design an algorithm for
computing the range (i.e., the difference between the largest and smallest
numbers in the tree) and determine its worst-case efficiency.
b.True or false: The smallest and the largest keys in an AVL tree
can always be found on either the last level or the next-to-last level?
6. Write a program for constructing an AVL tree for a given list of ndistinct
integers.
7. a. Constructa2-3treeforthelistC,O,M,P,U,T,I,N,G.(Usethe
alphabetical order of the letters and insert them successively starting with
the empty tree.)
b. Assuming that the probabilities of searching for each of the keys (i.e.,
the letters) are the same, find the largest number and the average number
of key comparisons for successful searches in this tree.
22
8. Let TBand T2-3be, respectively, a classical binary search tree and a 2-3
tree constructed for the same list of keys inserted in the corresponding
trees in the same order. True or false: Searching for the same key in T2-3
always takes fewer or the same number of key comparisons as searching
in TB?
9. For a 2-3 tree containing real numbers, design an algorithm for computing
the range (i.e., the difference between the largest and smallest numbers in
the tree) and determine its worst-case efficiency.
10. Write a program for constructing a 2-3 tree for a given list of nintegers.
23
Hints to Exercises 6.3
1. Use the definition of AVL trees. Do not forget that an AVL tree is a
special case of a binary search tree.
2. For both questions, it is easier to construct the required trees bottom up,
i.e., for smaller values of nfirst.
3. The single L-rotation and the double RL-rotation are the mirror images
of the single R-rotation and the double LR-rotation, whose diagrams can
be found in this section.
4. Insert the keys one after another doing appropriate rotations the way it
was done in the section’s example.
5. a. An efficient algorithm immediately follows from the definition of the
binary search tree of which the AVL tree is a special case.
b. The correct answer is opposite to the one that immediately comes
to mind.
6. n/a
7. a. Trace the algorithm for the input given (see Figure 6.8) for an example.
b. Keep in mind that the number of key comparisons made in search-
ing for a key in a 2-3 tree depends not only on its node’s depth but also
whether the key is the first or second one in the node.
8. False; find a simple counterexample.
9. Where will the smallest and largest keys be located?
10. n/a
24

Solutions to Exercises 6.3
1. Only (a) is an AVL tree; (b) has a node (in fact, there are two of them:
4 and 6) that violates the balance requirement; (c) is not a binary search
tree because 2 is in the right subtree of 3 (and 7 is in the left subtree of
6).
2. a . Here are all the binary trees with nnodes (for n=1,2,3,4,and 5)
that satisfy the balance requirement of AVL trees.
n = 1 n = 2 n = 3
n = 4
n =5
25
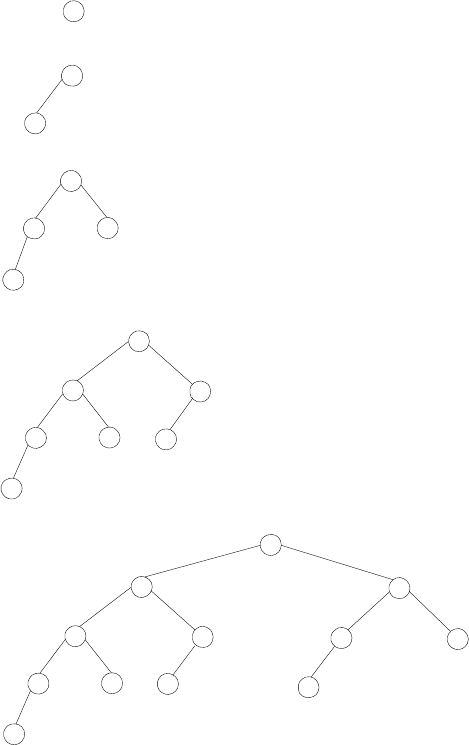
b. A minimal AVL tree (i.e., a tree with the smallest number of nodes) of
height 4 must have its left and right subtrees being minimal AVL trees of
heights 3 and 2. Following the same recursive logic further, we will find,
as one of the possible examples, the following tree with 12 nodes built
bottom up:
h = 0
h =1
h =2
h =3
h =4
26
3. a. Here is a diagram of the single L-rotation in its general form:
r
v
>
single L-rotation
T2
v
T3
r
T3
T1
T1T2
b. Here is a diagram of the double RL-rotation in its general form:
T
r
w
T
23
>
double RL-rotation
T
v
1
or
T
v
r
2
T1
w
T3
or
T4
T4
27
4. a. Construct an AVL tree for the list 1, 2, 3, 4, 5, 6.
1
2
0
1 1
-2
2
-1
3
0
>2
0
3
0
1
0
L(1)
-10
2
-1
3
-1
1
0
2
-2
3
-2
1
4
-1
5
0
>
L(3)
2
-1
4
0
1
0
5
0
3
0
4
0
2
-2
4
-1
1
5
-1
3
0
6
0
0
>
L(2)
4
0
5
-1
2
0
6
0
1
0
3
0
0
b. Construct an AVL tree for the list 6, 5, 4, 3, 2, 1.
6
5
0
6
1
0
6
5
1
2
4
0
R(6)>
5
4
0
0
6
0
5
4
1
0
6
0
3
0
5
4
2
2
6
0
3
1
2
0
R(4)>
5
3
1
6
0
2
0
4
0
0
5
3
1
2
6
0
2
1
R(5)>
3
2
1
5
1
0
6
0
1
4
01
0
4
0
0
28
c.ConstructanAVLtreeforthelist3,6,5,1,2,4.
3
6
0
3 3
-2
6
1
5
0
>5
0
6
0
3
0
RL(3)
-1
5
1
6
3
1
1
0
0
5
6
2
13
1
>
LR(3)
5
6
3
1
2
2
20
-1
0
0
0
0
0
3
5
2
1 6
>
LR(5)
5
6
2
13
2
01
0
0
4
2
-1
0-1
0
4
0
0
0
5. a. The simple and efficient algorithm is based on the fact that the smallest
and largest keys in a binary search tree are in the leftmost and rightmost
nodes of the tree, respectively. Therefore, the smallest key can be found
by starting at the root and following the chain of left pointers until a node
with the null left pointer is reached: its key is the smallest one in the tree.
Similarly, the largest key can be obtained by following the chain of the
right pointers. Finally, the range is computed as the difference between
the largest and smallest keys found.
In the worst case, the leftmost and rightmost nodes will be on the last
level of the tree. Hence, the worst-case efficiency will be in Θ(log n)+
Θ(log n) + Θ(1) = Θ(log n).
b. False. Here is a counterexample in which neither the smallest nor
the largest keys are on the last, or the next-to-last, level of an AVL tree:
29
3
5
1
6
4
7
8
13
15
11
12
210 14
9
6. n/a
7. a.Constructa2-3treeforthelistC,O,M,P,U,T,I,N,G.
C>M
O
C
C, O C, M, O
M
CO, P
M
CO, P, U >
M, P
U
CO
M, P
COT, U
M, P
OT, UC, I
M, P
T, UC, I N, O
M, P
T, UN, O
M
P
G
IT, U
G, M, P
T, U
N, O
C, G, I
>>
C I N, O
C
b. The largest number of key comparisons in a successful search will be
in the searches for O and U; it will be equal to 4. The average number
of key comparisons will be given by the following expression:
1
9C(C)+1
9C(O)+1
9C(M)+1
9C(P)+1
9C(U)+1
9C(T)+1
9C(I)+1
9C(N)+1
9C(G)
=1
9·3+1
9·4+1
9·1+1
9·2+1
9·4+1
9·3+1
9·3+1
9·3+1
9·2=25
9≈2.8.
8. False. Consider the list B, A. Searching for B in the binary search tree
requires 1 comparison while searching for B in the 2-3 tree requires 2
comparisons.
30
9. The smallest and largest keys in a 2-3 tree are the first key in the leftmost
leaf and the second key in the rightmost leaf, respectively. So searching
for them requires following the chain of the leftmost pointers from the
root to the leaf and of the rightmost pointers from the root to the leaf.
Since the height of a 2-3 tree is always in Θ(log n),the time efficiency of
the algorithm for all cases is in Θ(log n) + Θ(log n)+Θ(1)=Θ(logn).
10. n/a
31
Exercises 6.4
1. a. Construct a heap for the list 1, 8, 6, 5, 3, 7, 4 by the bottom-up algo-
rithm.
b. Construct a heap for the list 1, 8, 6, 5, 3, 7, 4 by successive key
insertions (top-down algorithm).
c. Is it always true that the bottom-up and top-down algorithms yield
the same heap for the same input?
2. Outline an algorithm for checking whether an array H[1..n]isaheapand
determine its time efficiency.
3. a. Find the minimum and the maximum number of keys that a heap of
height hcan contain.
b.Prove that the height of a heap with nnodes is equal to log2n.
4. Prove the following equation used in Section 6.4
h−1
i=0
2(h−i)2i=2(n−log2(n+1)) where n=2
h+1 −1.
5. a. Design an efficient algorithm for finding and deleting an element of the
smallest value in a heap and determine its time efficiency.
b. Design an efficient algorithm for finding and deleting an element of
a given value vin a given heap Hand determine its time efficiency
6. Sort the following lists by heapsort by using the array representation of
heaps.
a. 1, 2, 3, 4, 5 (in increasing order)
b. 5, 4, 3, 2, 1 (in increasing order)
c. S, O, R, T, I, N, G (in alphabetical order)
7. Is heapsort a stable sorting algorithm?
8. What variety of the transform-and-conquer technique does heapsort rep-
resent?
9. Which sorting algorithm other than heapsort uses a priority queue?
32
10. Implement three advanced sorting algorithms–mergesort, quicksort, and
heapsort–in the language of your choice and investigate their performance
on arrays of sizes n=10
2,103,104,105,and 106.For each of these sizes
consider:
a. randomly generated files of integers in the range [1..n].
b. increasing files of integers 1,2, ..., n.
c. decreasing files of integers n,n−1, ..., 1.
11. Spaghetti sort Imagine a handful of uncooked spaghetti, individual rods
whose lengths represent numbers that need to be sorted.
a. Outline a “spaghetti sort”–a sorting algorithm that takes advantage
of this unorthodox representation.
b. What does this example of computer science folklore (see [Dew93])
have to do with the topic of this chapter in general and heapsort in par-
ticular?
33
Hints to Exercises 6.4
1. a. Trace the two algorithms outlined in the text on the inputs given.
b. Trace the two algorithms outlined in the text on the inputs given.
c. A mathematical fact may not be established by checking its validity for
a few examples.
2. For a heap represented by an array, only the parental dominance require-
ment needs to be checked.
3. a. What structure does a complete tree of height hwith the maximum
number of nodes have? What about a complete tree with the minimum
number of nodes?
b. Use the results established in part (a).
4. First, express the right-hand side as a function of h. Then prove the
obtained equality by either using the formula for the sum i2igiven in
Appendix A or by mathematical induction on h.
5. a. Where in a heap should we look for its smallest element?
b. Deleting an arbitrary element of a heap can be done by generalizing
the algorithm for deleting its root.
6. Trace the algorithm on the inputs given (see Figure 6.14 for an example).
7. As a rule, sorting algorithms that can exchange far apart elements are not
stable.
8. One can claim that the answers are different for the two principal repre-
sentations of heaps.
9. This algorithm is less efficient than heapsort because it uses the array
rather than the heap to implement the priority queue.
10. n/a
11. Pick the spaghetti rods up in a bundle and place them end-down (i.e.,
vertically) onto a tabletop.
34
Solutions to Exercises 6.4
1.a. Constructingaheapforthelist1,8,6,5,3,7,4bythebottom-up
algorithm (a root of a subtree being heapified is shown in bold):
1865374 ⇒1875364
1875364
1875364 ⇒8571364
b. Constructing a heap for the list 1, 8, 6, 5, 3, 7, 4 by the top-down
algorithm (a new element being inserted into a heap is shown in bold):
1
18⇒81
816
8165⇒8561
85613
856137⇒857136
8571364
c. False. Although for the input to questions (a) and (b) the constructed
heaps are the same, in general, it may not be the case. For example,
for the input 1, 2, 3, the bottom-up algorithm yields 3, 2, 1 while the
top-down algorithm yields 3, 1, 2.
2. For i=1,2, ..., n/2,check whether
H[i]≥max{H[2i],H[2i+1]}.
(Of course, if 2i+1 >n, just H[i]≥H[2i]needs to be satisfied.) If
the inequality doesn’t hold for some i, stop–the array is not a heap; if it
holds for every i=1,2, ..., n/2,thearrayisaheap.
Since the algorithm makes up to 2n/2key comparisons, its time effi-
ciency is in O(n).
3. a. A complete binary tree of height hwith the minimum number of nodes
has the maximum number of nodes on levels 0 through h−1and one node
on the last level. The total number of nodes in such a tree is
nmin(h)=
h−1
i=0
2i+1=(2
h−1) + 1 = 2h.
A complete binary tree of height hwith the maximum number of nodes
has the maximum number of nodes on levels 0 through h. The total
35
number of nodes in such a tree is
nmax(h)=
h
i=0
2i=2
h+1 −1.
b. The results established in part (a) imply that for any heap with n
nodes and height h
2h≤n<2h+1 .
Taking logarithms to base 2 yields
h≤log2n<h+1.
This means that his the largest integer not exceeding log2n, i.e., h=
log2n.
4. We are asked to prove that h−1
i=0 2(h−i)2i=2(n−log2(n+1)) where
n=2
h+1 −1.
For n=2
h+1 −1,the right-hand side of the equality in question becomes
2(2h+1 −1−log2(2h+1 −1 + 1)) = 2(2h+1 −1−(h+ 1)) = 2(2h+1 −h−2).
Using the formula h−1
i=1 i2i=(h−2)2h+2 (see Appendix A), the left-hand
side can be simplified as follows:
h−1
i=0
2(h−i)2i=2
h−1
i=0
(h−i)2i=2[
h−1
i=0
h2i−
h−1
i=0
i2i]
=2[h(2h−1) −(h−2)2h−2]
=2(h2h−h−h2h+2
h+1 −2) = 2(2h+1 −h−2).
5. a. The parental dominance requirement implies that we can always find
the smallest element of a heap H[1..n]among its leaf positions, i.e., among
H[n/2+1],..H[n].(One can easily prove this assertion by contradic-
tion.) Therefore, we can find the smallest element by simply scanning
sequentially the second half of the array H. Deleting this element can
be done by exchanging the found element with the last element H[n],
decreasing the heap’s size by one, and then, if necessary, sifting up the
former H[n]from its new position until it is not larger than its parent.
The time efficiency of searching for the smallest element in the second
halfofthearrayisinΘ(n); the time efficiency of deleting it after it has
36

been found is in Θ(1) + Θ(1) + O(log n)=O(log n).
b. Searching for vby sequential search in H[1..n]takes care of the search-
ing part of the question. Assuming that the first matching element is
found in position i, the deletion of H[i]can be done with the following
three-part procedure (which is similar to the ones used for deleting the
root and the smallest element): First, exchange H[i]with H[n]; second,
decrease nby 1; third, heapify the structure by sifting the former H[n]
either up or down depending on whether it is larger than its new parent
or smaller than the larger of its new children, respectively.
The time efficiency of searching for an element of a given value is in O(n);
the time efficiency of deleting it after it has been found is in Θ(1) +Θ(1) +
O(log n)=O(log n).
6. a. Sort 1, 2, 3, 4, 5 by heapsort
Heap Construction
12345
15342
15342
54312
Maximum Deletions
54312
24315
4231
1234
321
123
21
12
1
b. Sort 5, 4, 3, 2, 1 (in increasing order) by heapsort
Heap Construction
54321
54321
Maximum Deletions
54321
14325
4231
1234
321
123
21
12
1
37
c. Sort S, O, R, T, I, N, G (in alphabetic order) by heapsort
Heap Construction
1234567
SORTING
SORTING
STROING
STROING
TSROING
Maximum Deletions
1234567
TSROING
GSRO IN
T
SORG I N
NORG I S
RONG I
IONG
R
OING
GIN
O
NIG
GIN
IG
GI
G
7. Heapsort is not stable. For example, it sorts 1,1
into 1 ,1
.
8. If the heap is thought of as a tree, heapsort should be considered a
representation-change algorithm; if the heap is thought of as an array with
a special property, heapsort should be considered an instance-simplification
algorithm.
9. The answer is selection sort. Note that selection sort is less efficient
than heapsort because it uses the array, which is an inferior (to the heap)
structure for implementing the priority queue.
10. n/a
11. a. After the bunch of spaghetti rods is put in a vertical position on a
tabletop, repeatedly take the tallest rod among the remaining ones out
until no more rods are left. This will sort the rods in decreasing order of
their lengths.
b. The method shares with heapsort its principal idea: represent the items
to be sorted in a way that makes finding and deleting the largest item a
simple task. From a more general perspective, the spaghetti sort is an
example, albeit a rather exotic one, of a representation-change algorithm.
38
Exercises 6.5
1. Consider the following brute-force algorithm for evaluating a polynomial.
Algorithm BruteForcePolynomialEvaluation(P[0..n],x)
//The algorithm computes the value of polynomial Pat a given point x
//by the “highest to lowest term” brute-force algorithm
//Input: An array P[0..n]of the coefficients of a polynomial of degree n,
// stored from the lowest to the highest and a number x
//Output: The value of the polynomial at the point x
p←0.0
for i←ndownto 0do
power ←1
for j←1to ido
power ←power ∗x
p←p+P[i]∗power
return p
Find the total number of multiplications and the total number of additions
made by this algorithm.
2. Write a pseudocode for the brute-force polynomial evaluation that stems
form substituting a given value of the variable into the polynomial’s for-
mula and evaluating it from the lowest term to the highest one. Determine
the number of multiplications and the number of additions made by this
algorithm.
3. a. Estimate how much faster Horner’s rule is compared to the “lowest-
to-highest term” brute-force algorithm of Problem 2 if (i) the time of one
multiplication is significantly larger than the time of one addition; (ii) the
time of one multiplication is about the same as the time of one addition.
b. Is Horner’s rule more time efficient at the expense of being less space
efficient than the brute-force algorithm?
4. a. Apply Horner’s rule to evaluate the polynomial
p(x)=3x4−x3+2x+5 at x=−2.
b. Use the results of the above application of Horner’s rule to find the
quotient and remainder of the division of p(x)by x+2.
5. Compare the number of multiplications and additions/subtractions needed
by the “long division” of a polynomial p(x)=anxn+an−1xn−1+... +a0
by x−c, where cis some constant, with the number of these operations
in the “synthetic division.”
39
6. a. Apply the left-to-right binary exponentiation algorithm to compute a17.
b. Is it possible to extend the left-to-right binary exponentiation algo-
rithm to work for every nonnegative integer exponent?
7. Apply the right-to-left binary exponentiation algorithm to compute a17 .
8. Design a nonrecursive algorithm for computing anthat mimics the right-
to-left binary exponentiation but does not explicitly use the binary repre-
sentation of n.
9. Is it a good idea to use a general-purpose polynomial evaluation algorithm
such as Horner’s rule to evaluate the polynomial p(x)=xn+xn−1+... +
x+1?
10. According to the corollary of the Fundamental Theorem of Algebra, every
polynomial
p(x)=anxn+an−1xn−1+... +a0
can be represented in the form
p(x)=an(x−x1)(x−x2)...(x−xn)
where x1, ..., xnare the roots of the polynomial (generally, complex and
not necessarily distinct). Discuss which of the two representations is more
convenient for each of the following operations:
a. Polynomial evaluation at a given point
b. Addition of two polynomials
c. Multiplication of two polynomials
11. Polynomial puzzle Given that a polynomial p(x)of degree eight is such
that p(i)=1/i for i=1,2, ..., 9,findp(10).
40
Hints to Exercises 6.5
1. Set up a sum and simplify it by using the standard formulas and rules for
sum manipulation. Do not forget to include the multiplications outside
the inner loop.
2. Take advantage of the fact that the value of xican be easily computed
from the previously computed xi−1.
3. a. Use the formulas for the number of multiplications (and additions) for
both algorithms.
b. Does Horner’s rule use any extra memory?
4. Apply Horner’s rule to the instance given the same way it is applied to
another one in the section.
5. If you implement the algorithm for long division by x−cefficiently, the
answer might surprise you.
6. a. Trace the left-to-right binary exponentiation algorithm on the instance
given the same way it is done for another instance in the section.
b. The answer is yes: the algorithm can be extended to work for the
zero exponent as well. How?
7. Trace the right-to-left binary exponentiation algorithm on the instance
given the same way it is done for another instance in the section.
8. Compute and use the binary digits of n“on the fly”.
9. Use a formula for the sum of the terms of this special kind of a polynomial.
10. Compare the number of operations needed to implement the task in ques-
tion.
11. Transform p(x)to a polynomial with roots at xi=ifor i=1,2, ..., 9and
represent it in the form mentioned in Problem 10.
41

Solutions to Exercises 6.5
1. The total number of multiplications made by the algorithm can be com-
puted as follows:
M(n)=
n
i=0
(
i
j=1
1+1)=
n
i=0
(i+1)=
n
i=0
i+
n
i=0
1
=n(n+1)
2+(n+1)= (n+1)(n+2)
2∈Θ(n2).
The number of additions is obtained as
A(n)=
n
i=0
1=n+1.
2. Algorithm BetterBruteForcePolynomialEvaluation(P[0..n],x)
//Computes the value of polynomial Pat a given point x
//by the “lowest-to-highest term” algorithm
//Input: Array P[0..n]of the coefficients of a polynomial of degree n,
// from the lowest to the highest and a number x
//Output: The value of the polynomial at the point x
p←P[0]; power ←1
for i←1to ndo
power ←power ∗x
p←p+P[i]∗power
return p
The number of multiplications made by this algorithm is
M(n)=
n
i=1
2=2n.
The number of additions is
A(n)=
n
i=1
1=n.
3. a. If only multiplications need to be taken into account, Horner’s rule
will be about twice as fast because it makes just nmultiplications vs. 2n
multiplications required by the other algorithm. If one addition takes
about the same amount of time as one multiplication, then Horner’s rule
will be about (2n+n)/(n+n)=1.5times faster.
b. The answer is no, because Horner’s rule doesn’t use any extra memory.
42

4. a. Evaluate p(x)=3x4−x3+2x+5 at x=−2.
coefficients 3 -1 0 2 5
x=−23(-2)·3+(-1)= -7 (-2)·(-7)+0=14 (-2)·14+2= -26 (-2)·(-26)+5=57
b. The quotient and the remainder of the division of 3x4−x3+2x+5 by
x+2are 3x3−7x2+14x−26 and 57, respectively.
5. The long division by x−cis done as illustrated below
anxn−1+...
x−c anxn+an−1xn−1+... +a1x+a0
−anxn−canxn−1
(can+an−1)xn−1+... +a1x+a0
This clearly demonstrates that the first iteration–the one needed to get
rid of the leading term anxn–requires one multiplication (to get can)
and one addition (to add an−1). After this iteration is repeated n−1
more times, the total number of multiplications and the total number of
additions will be neach–exactly the same number of operations needed
by Horner’s rule. (In fact, it does exactly the same computations as
Horner’s algorithm would do in computing the value of the polynomial at
x=c.)Thus, the long division, though much more cumbersome than the
synthetic division for hand-and-pencil computations, is actually not less
time efficient from the algorithmic point of view.
6. a. Compute a17 by the left-to-right binary exponentiation algorithm.
Here, n= 17 = 100012.So, we have the following table filled left-to-right:
binary digits of n10 0 0 1
product accumulator aa
2(a2)2=a4(a4)2=a8(a8)2·a=a17
b. Algorithm LeftRightBinaryExponentiation will work correctly for n=0
if the variable product is initialized to 1 (instead of a)and the loop starts
with I(instead of I−1).
7. Compute a17 by the right-to-left binary exponentiation algorithm.
Here, n= 17 = 100012.So, we have the following table filled right-to-left:
1 0 0 0 1 binary digits of n
a16 a8a4a2aterms a2
a·a16 =a17 aproduct accumulator
43
8. Algorithm ImplicitBinaryExponentiation(a,n)
//Computes anby the implicit right-to-left binary exponentiation
//Input: A number aand a nonnegative integer n
//Output: The value of an
product ←1; term ←a
while n=0do
b←nmod 2; n←n/2
if b=1
product ←product ∗term
term ←term ∗term
return product
9. Since the polynomial’s terms form a geometric series,
p(x)=xn+xn−1+... +x+1=
x−1
x−1if x=1
n+1 if x=1
Its value can be computed faster than with Horner’s rule by computing
the right-hand side formula with an efficient exponentiation algorithm for
evaluating xn+1.
10. a. With Horner’s rule, we can evaluate a polynomial in its coefficient form
with nmultiplications and nadditions. The direct substitution of the
xvalue in the factorized form requires the same number of operations,
although these may be operations on complex numbers even for a polyno-
mial with real coefficients.
b. Addition of two polynomials is incomparably simpler for polynomi-
als in their coefficient forms, because, in general, knowing the roots of
polynomials p(x)and q(x)helps little in deducing the root values of their
sum p(x)+q(x).
c. Multiplication of two polynomials is trivial when they are represented
in their factorized form. Indeed, if
p(x)=a
n(x−x
1)...(x−x
n)and q(x)=a
m(x−x
1)...(x−x
m),
then
p(x)q(x)=a
na
n(x−x
1)...(x−x
n)(x−x
1)...(x−x
m).
To multiply two polynomials in their coefficient form, we need to multiply
out
p(x)q(x)=(a
nxn+... +a
0)(a
mxm+... +a
0)
and collect similar terms to get the product represented in the coefficient
form as well.
44
11. Consider q(x)=xp(x)−1.For every xi=i(i=1,2, ..., 9),we have
q(xi)=xip(xi)−1=ip(i)−1=i(1/i)−1=0.
Using the factorized form mentioned in Problem 10,
q(x)=c(x−1)(x−2)...(x−9).
Since, on the one hand, q(0) = 0p(0) −1=−1,and, on the other, q(0) =
c(0−1)(0−2)...(0−9) = −c9!,we have the following equation to determine
the value of constant c:
−c9! = −1.
Hence c=1/9! and q(10) = (1/9!)(10 −1)(10 −2)...(10 −9) = 1.Since
q(10) = 10p(10) −1=1,
p(10) = 2/10.
Note: The problem of finding a polynomial of degree not higher than n
from its values at n+1points is one of the fundamental problems in numerical
analysis, called interpolation. Although there exists exactly one such polyno-
mial, there are several different ways to represent it. For example, you may
look up Lagrange’s interpolation formula and apply it to the polynomial in
question.
45

Exercises 6.6
1. a. Prove the equality
lcm(m, n)= m·n
gcd(m, n)
that underlies the algorithm for computing lcm(m, n).
b. Euclid’s algorithm is known to be in O(log n).If it is the algorithm that
is used for computing gcd(m, n),what is the efficiency of the algorithm
for computing lcm(m, n)?
2. You are given a list of numbers for which you need to construct a min-heap.
(A min-heap is a complete binary tree in which every key is less than or
equal to the keys in its children.) How would you use an algorithm for
constructingamax-heap(aheapasdefinedinSection6.4)toconstructa
min-heap?
3. Prove that the number of different paths of length k>0from the ith
vertex to the jth vertex in a graph (undirected or directed) equals the
(i, j)th element of Akwhere Ais the adjacency matrix of the graph.
4. a.Design an algorithm with a time efficiency better than cubic for check-
ingwhetheragraphwithnvertices contains a cycle of length 3 [Man89].
b. Consider the following algorithm for the same problem. Starting
at an arbitrary vertex, traverse the graph by depth-first search and check
whether its depth-first search forest has a vertex with a back edge leading
to its grandparent. If it does, the graph contains a triangle; if it does not,
the graph does not contain a triangle as its subgraph. Is this algorithm
correct?
5. Given n>3points P1=(x1,y
1), ..., Pn=(xn,y
n)in the coordinate
plane, design an algorithm to check whether all the points lie within a
triangle with its vertices at three of the points given. (You can either
design an algorithm from scratch or reduce the problem to another one
with a known algorithm.)
6. Consider the problem of finding, for a given positive integer n, the pair of
integers whose sum is nand whose product is as large as possible. Design
an efficient algorithm for this problem and indicate its efficiency class.
7. The assignment problem introduced in Section 3.4 can be stated as follows.
There are npeople who need to be assigned to execute njobs, one person
per job. (That is, each person is assigned to exactly one job and each job
is assigned to exactly one person.) The cost that would accrue if the ith
person is assigned to the jthjobisaknownquantityC[i, j]for each pair
i, j =1, ..., n. The problem is to assign the people to the jobs to minimize
46

the total cost of the assignment. Express the assignment problem as a
0—1 linear programming problem.
8. Solve the instance of the linear programming problem given in Section 6.6
maximize 0.10x+0.07y+0.03z
subject to x+y+z=100
x≤1
3y
z≥0.25(x+y)
x≥0,y≥0,z≥0.
9. The graph-coloring problem is usually stated as the vertex-coloring prob-
lem: assign the smallest number of colors to vertices of a given graph so
that no two adjacent vertices are the same color. Consider the edge-
coloring problem: assign the smallest number of colors possible to edges
of a given graph so that no two edges with the same endpoint are the
same color. Explain how the edge-coloring problem can be reduced to a
vertex-coloring problem.
10. Consider the two-dimensional post-office location problem:Givenn
points (x1,y
1),(x2,y
2), ..., (xn,y
n)in the Cartesian plane, find a location
(x, y)for a post office that minimizes 1
nn
i=1(|xi−x|+|yi−y|),the average
Manhattan distance from the post office to these points. Explain how
the problem can be efficiently solved by the problem reduction technique,
provided the post office does not have to be located at one of the input
points.
11. Jealous husbands There are n≥2married couples who need to cross
a river. They have a boat that can hold no more than two people at a
time. To complicate matters, all the husbands are jealous and will not
agree on any crossing procedure that would put a wife on the same bank
of the river with another woman’s husband without the wife’s husband
being there too, even if there are other people on the same bank. Can
they cross the river under such constraints?
a. Solve the problem for n=2.
b.Solve the problem for n=3, which is the classical version of this
problem.
c.Does the problem have a solution for every n≥4? If it does, explain
how and indicate how many river crossings it will take; if it does not,
explain why.
47
Hints to Exercises 6.6
1. a. Use the rules for computing lcm(m, n)and gcd(m, n)from the prime
factors of mand n.
b. The answer immediately follows from the formula for computing lcm(m, n).
2. Use a relationship between minimization and maximization problems.
3. Prove the assertion by induction on k.
4. a. Base your algorithm on the following observation: a graph contains a
cycle of length 3 if and only if it has two adjacent vertices iand jthat are
also connected by a path of length 2.
b. Do not jump to a conclusion in answering this question.
5. An easier solution is to reduce the problem to another one with a known
algorithm. Since we did not discuss many geometric algorithms in the
book, it should not be difficult to figure out to which one this problem
needs to be reduced.
6. Express this problem as a maximization problem of a function in one
variable.
7. Introduce double-indexed variables xij to indicate an assignment of the
ith person to the jth job.
8. Take advantage of the specific features of this instance to reduce the prob-
lem to one with fewer variables.
9. Create a new graph.
10. Solve first the one-dimensional version of this problem (Problem 2(a) in
Exercises 3.3).
11. a, b. Create a state-space graph for the problem as it is done for the
river-crossing puzzle in the section.
c. Look at the state obtained after the first six river crossings in the
solution to part (b).
48

Solutions to Exercises 6.6
1. a. Since
lcm(m, n)=the product of the common prime factors of mand n
·the product of the prime factors of mthat are not in n
·the product of the prime factors of nthat are not in m
and
gcd(m, n)=the product of the common prime factors of mand n,
the product of lcm(m, n)and gcd(m, n)is equal to
the product of the common prime factors of mand n
·theproductoftheprimefactorsofmthat are not in n
·theproductoftheprimefactorsofnthat are not in m
·the product of the common prime factors of mand n.
Since the product of the first two terms is equal to mand the product of the
last two terms is equal to n, we showed that lcm(m, n)·gcd(m, n)=m·n,
and, hence,
lcm(m, n)= m·n
gcd(m, n).
b. If gcd(m, n)is computed in O(log n)time, lcm(m, n)will also be com-
puted in O(log n)time, because one extra multiplication and one extra
division take only constant time.
2. Replace every key Kiof a given list by −Kiand apply a max-heap con-
struction algorithm to the new list. Then change the signs of all the keys
again.
3. The induction basis: For k=1,A
1[i, j]is equal to 1 or 0 depending on
whether there is an edge from vertex ito vertex j. In either case, it is
also equal to the number of paths of length 1 from ito j. For the general
step, assume that for a positive integer k,Ak[i, j]is equal to the number of
different paths of length kfrom vertex ito vertex j.SinceAk+1 =AkA,
we have the following equality for the (i, j)element of Ak+1:
Ak+1[i, j]=Ak[i, 1]A[1,j]+... +Ak[i, t]A[t, j]+... +Ak[i, n]A[n, j],
where Ak[i, t]is equal to the number of different paths of length kfrom
vertex ito vertex taccording to the induction hypothesis and A[t, j]is
equal to 1 or 0 depending on whether there is an edge from vertex tto
49
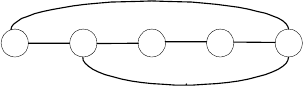
vertex jfor t=1, ..., n. Further, any path of length k+1 from vertex
ito vertex jmust be made up of a path of length kfrom vertex ito
some intermediate vertex tand an edge from that tto vertex j. Since for
different intermediate vertices twe get different paths, the formula above
yields the total number of different paths of length k+1 from ito j.
4. a. For the adjacency matrix Aof a given graph, compute A2with an al-
gorithm whose time efficiency is better than cubic (e.g., Strassen’s matrix
multiplication discussed in Section 4.5). Check whether there exists a
nonzero element A[i, j]in the adjacency matrix such that A2[i, j]>0:if
there is, the graph contains a triangle subgraph, if there is not, the graph
does not contain a triangle subgraph.
b. The algorithm is incorrect because the condition is sufficient but not
necessary for a graph to contain a cycle of length 3. Consider, as a coun-
terexample, the DFS tree of the traversal that starts at vertex aof the
following graph and resolves ties according to alphabetical order of ver-
tices:
a b c d e
It does not contain a back edge to a grandparent of a vertex, but the graph
does have a cycle of length 3: a−b−e−a.
5. The problem can be reduced to the question about the convex hull of a
given set of points: if the convex hull is a triangle, the answer is yes,
otherwise, the answer is no. There are several algorithms for finding the
convex hull for a set of points; quickhull, which was discussed in section
4.6, is particularly appropriate for this application.
6. Let xbe one of the numbers in question; hence, the other number is n−x.
The problem can be posed as the problem of maximizing f(x)=x(n−x)
on the set of all integer values of x. Since the graph of f(x)=x(n−x)
is a parabola with the apex at x=n/2,the solution is n/2if nis even
and n/2(or n/2)if nis odd. Hence, the numbers in question can
be computed as n/2and n−n/2,which works both for even and
odd values of n. Assuming that one division by 2 takes a constant time
irrespective of n’s size, the algorithm’s time efficiency is clearly in Θ(1).
7. Let xij be a 0-1 variable indicating an assignment of the ith person to
the jth job (or, in terms of the cost matrix C, a selection of the matrix
50

element from the ith row and the jth column). The assignment problem
can then be posed as the following 0—1 linear programming problem:
minimize n
i=1 n
j=1 cij xij (the total assignment cost)
subject to n
j=1 xij =1for i=1,...n (person iis assigned to one job)
n
i=1 xij =1for j=1, ...n (job jis assigned to one person)
xij ∈{0,1}for i=1, ..., n and j=1, ..., n
8. We can exploit the specific features of the instance in question to solve it
by the following reasoning. Since the expected return from cash is the
smallest, the value of cash investment needs to be minimized. Hence,
z=0.25(x+y)in an optimal solution. Substituting z=0.25(x+y)into
x+y+z=100,yields x+y=80and hence z=20.Similarly, since
the expected return on stocks is larger than that of bonds, the amount
invested in stocks needs to be maximized. Hence, in an optimal allocation
x=y/3.Substituting this into x+y=80yields y=60and x=20.Thus,
the optimal allocation is to put 20 million in stocks, 60 millions in bonds,
and 20 million in cash.
Note: This method should not be construed as having a power beyond
this particular instance. Generally speaking, we need to use general
algorithms such as the simplex method for solving linear programming
problems with three or more unknowns. A special technique applicable
to instances with only two variables is discussed in Section 10.1 (see also
the solution to Problem 10 in Exercises 3.3).
9. Create a new graph whose vertices represent the edges of the given graph
and connect two vertices in the new graph by an edge if and only if these
vertices represent two edges with a common endpoint in the original graph.
A solution of the vertex-coloring problem for the new graph solves the
edge-coloring problem for the original graph.
10. The problem is obviously equivalent to minimizing independently 1
nn
i=1 |xi−
x|and 1
nn
i=1 |yi−y|.Thus we have two instances of the same problem,
whose solution is the median of the numbers defining the instance (see the
solution to Problem 2a in Exercises 3.3). Thus, xand ycan be found by
computing the medians of x1,x
2, ..., xnand y1,y
2, ..., yn, respectively.
11. a. Here is a state-space graph for the two jealous husbands puzzle: Hi,W
i
denote the husband and wife of couple i(i=1,2),respectively; the two
bars ||denote the river; the arrow indicates the direction of the next trip,
which is defined by the boat’s location. (For the sake of simplicity, the
graph doesn’t include crossings that differ by obvious index substitutions
such as starting with the first couple H1W1crossing the river instead of
51
thesecondoneH
2W2.) The vertices corresponding to the initial and final
states are shown in bold.
H H
W W
12
12
H H
W W
12
12
H H
W W
12
12
H
W
2
1
H H
W
12
2
H1
W2W1
H H
W
12
2
H H
W
12
2
H
W
1
2
H H
W W
12
12
H H
W W
12
12
W1
W1
W1
H2
W W
12 H W
22 W2
H2
W1
W2
H1
H H
12
W W
12
H W
11
H H
12
There are four simple paths from the initial-state vertex to the final-state
vertex, each five edges long, in this graph. If specified by their edges,
they are:
W1W2W1H1H2H1H1W1
W1W2W1H1H2W2W1W2
H2W2H2H1H2H1H1W1
H2W2H2H1H2W2W1W2
Hence, there are four (to within obvious symmetric substitutions) optimal
solutions to this problem, each requiring five river crossings.
52
b. Here is a state-space graph for the three jealous husbands puzzle:
Hi,W
idenote the husband and wife of couple i(i=1,2,3),respectively;
bstands for the boat; the two bars ||denote the river; the arrow indi-
cates the possible direction of the next trip, which is defined by the boat’s
location. (For the sake of simplicity, the graph doesn’t include cross-
ings that differ by obvious index substitutions such as starting with the
first or second couple crossing the river instead of the third one H3W3.)
The vertices corresponding to the initial and final states are shown in bold.
1
H H H
W W
12
12
W W W
12 W
3H H H
W W
12
12
3
3W1
H H H
123
W3
H H H
123
W3
H H H
123
W3W
H H
12 HH H H
123
W1W2W3
W
3
3W1
H1
H H H
123
H H H
123
W1W3
H1H3
W1W3
H H
23 H H
12
W W W
12 3
W W
12
W W
23
W W
23
W W
12 W W
12
W W W
12 3 W W W
12 3
W W
23
W W
23 W W
12
W W
12
H H H
123
H H H
123
H H H
123
H H H
123
H H
23
W3
There are four simple paths from the initial-state vertex to the final-state
vertex, each eleven edges long, in this graph. If specified by their edges,
53
they are:
W2W3W2W1W2W1H2H3H2W2H1H2W3W2W3W2W1W2
W2W3W2W1W2W1H2H3H2W2H1H2W3W2W3H1H1W1
H3W3H3W1W2W1H2H3H2W2H1H2W3W2W3W2W1W2
H3W3H3W1W2W1H2H3H2W2H1H2W3W2W3H1H1W1
Hence, there are four (to within obvious symmetric substitutions) optimal
solutions to this problem, each requiring eleven river crossings.
c. The problem doesn’t have a solution for the number of couples n≥
4.If we start with one or more extra (i.e., beyond 3) couples, no new
qualitatively different states will result and after the first six river crossings
(see the solution to part (b)), we will arrive at the state with n−1couples
and the boat on the original bank and one couple on the other bank. The
only allowed transition from that state will be going back to its predecessor
by ferrying a married couple to the other side.
54
This file contains the exercises, hints, and solutions for Chapter 7 of the
book ”Introduction to the Design and Analysis of Algorithms,” 2nd edition, by
A. Levitin. The problems that might be challenging for at least some students
are marked by ;those that might be difficult for a majority of students are
marked by .
Exercises 7.1
1. Is it possible to exchange numeric values of two variables, say, uand v,
without using any extra storage?
2. Will the comparison counting algorithm work correctly for arrays with
equal values?
3. Assuming that the set of possible list values is {a, b, c, d }, sort the
following list in alphabetical order by the distribution counting algorithm:
b, c, d, c, b, a, a, b.
4. Is the distribution counting algorithm stable?
5. Design a one-line algorithm for sorting any array of size nwhose values
are ndistinct integers from 1 to n.
6. The ancestry problem asks to determine whether a vertex uis an
ancestor of vertex vin a given binary (or, more generally, rooted ordered)
tree of nvertices. Design a O(n)input enhancement algorithm that
provides sufficient information to solve this problem for any pair of the
tree’s vertices in constant time.
7. The following technique, known as virtual initialization, provides a
time-efficient way to initialize just some elements of a given array A[0..n−
1] so that for each of its elements, we can say in constant time whether it
has been initialized and, if it has been, with which value. This is done
by utilizing a variable counter for the number of initialized elements in A
and two auxiliary arrays of the same size, say B[0..n −1] and C[0..n −1],
defined as follows. B[0],...,B[counter −1] contain the indices of the el-
ements of Athat were initialized: B[0] contains the index of the element
initialized first, B[1] contains the index of the element initialized second,
and so on. Furthermore, if A[i]was the kth element (0 ≤k≤counter−1)
to be initialized, C[i]contains k.
a. Sketch the state of arrays A[0..7],B[0..7],and C[0..7] after the three
assignments
A[3] ←x;A[7] ←z;A[1] ←y.
b. In general, how can we check with this scheme whether A[i]has been
initialized and, if it has been, with which value?
1
8. a. Write a program for multiplying two sparse matrices, a p-by-qmatrix
Aand a q-by-rmatrix B.
b. Write a program for multiplying two sparse polynomials p(x)and q(x)
of degrees mand n, respectively.
9. Write a program that plays the game of tic-tac-toe with the human user
by storing all possible positions on the game’s 3-by-3 board along with the
best move for each of them.
2
Hints to Exercises 7.1
1. Yes, it is possible. How?
2. Check the algorithm’s pseudocode to see what it does upon encountering
equal values.
3. Trace the algorithm on the input given (see Figure 7.2 for an example).
4. Check whether the algorithm can reverse a relative ordering of equal ele-
ments.
5. Where will A[i]be in the sorted array?
6. Take advantage of the standard traversals of such trees.
7. a. Follow the definitions of the arrays Band Cin the description of the
method.
b. Find, say, B[C[3]] for the example in part (a).
8. a. Use linked lists to hold nonzero elements of the matrices.
b. Represent each of the given polynomials by a linked list with nodes
containing exponent iand coefficient aifor each nonzero term aixi.
9. You may want to take advantage of the board’s symmetry to decrease the
number of the positions that need to be stored.
3
Solutions to Exercises 7.1
1. The following operations will exchange values of variables uand v:
u←u+v//uholds u+v, v holds v
v←u−v//uholds u+v, v holds u
u←u−v//uholds v, v holds u
Note: The same trick is applicable, in fact, to any binary data by em-
ploying the “exclusive or” (XOR) operation:
u←uXORv
v←uXORv
u←uXORv
2. Yes, it will work correctly for arrays with equal elements.
3. Input: A: b, c, d, c, b, a, a, b
abcd abcd
Frequencies 2 3 2 1 Distribution values 2 5 7 8
D[a..d]S[0..7]
A[7] = b257 8 b
A[6] = a24 7 8 a
A[5] = a14 7 8 a
A[4] = b047 8 b
A[3] = c0 3 78c
A[2] = d0368d
A[1] = c0 3 67c
A[0] = b035 7 b
4. Yes, it is stable because the algorithm scans its input right-to-left and puts
equal elements into their section of the sorted array right-to-left as well.
5. for i←0to n−1do S[A[i]−1] ←A[i]
6. Vertex uis an ancestor of vertex vin a rooted ordered tree Tif and only
if the following two inequalities hold
preorder(u)≤preorder(v)and postorder(u)≥postorder(v),
where preorder and postorder are the numbers assigned to the vertices by
the preorder and postorder traversals of T, respectively. Indeed, preorder
traversal visits recursively the root and then the subtrees numbered from
left to right. Therefore,
preorder(u)≤preorder(v)
4

if and only if either uis an ancestor of v(i.e., uis on the simple path from
the root’s tree to v)oruis to the left of v(i.e., uand vare not on the
same simple path from the root to a leaf and T(u)is to the left of T(v)
where T(u)and T(v)are the subtrees of the nearest common ancestor of
uand v, respectively). Similarly, postorder traversal visits recursively the
subtrees numbered from left to right and then the root. Therefore,
postorder(u)≥postorder(v)
if and only if either uis an ancestor of vor vis to the left of u. Hence,
preorder(u)≤preorder(v)and postorder(u)≥postorder(v)
is necessary and sufficient for uto be an ancestor of v.
The time efficiencies of both traversals are in O(n)(Section 4.4); once
the preorder and postorder numbers are precomputed, checking the two
inequalities takes constant time for any given pair of the vertices.
7. a. The following diagram depicts the results of these assignments (the
values of the unspecified elements in the arrays are undefined):
B
01234567
371
20 1
A
C
yx z
counter = 3
b. A[i]is initialized if and only if 0≤C[i]≤counter −1and B[C[i]] =
i. (It is useful to note that the elements of array Cdefine the inverse
to the mapping defined by the elements of array B.) Hence, if these
two conditions hold, A[i]contains the value it has been initialized with;
otherwise, it has not been initialized.
8. n/a
9. n/a
5
Exercises 7.2
1. Apply Horspool’s algorithm to search for the pattern BAOBAB in the text
BESS_KNEW_ABOUT_BAOBABS
2. Consider the problem of searching for genes in DNA sequences using Hor-
spool’s algorithm. A DNA sequence consists of a text on the alphabet
{A,C,G,T} and the gene or gene segment is the pattern.
a. Construct the shift table for the following gene segment of your chro-
mosome 10:
TCCTATTCTT
b. Apply Horspool’s algorithm to locate the above pattern in the following
DNA sequence:
TTATAGATCTCGTATTCTTTTATAGATCTCCTATTCTT
3. How many character comparisons will be made by Horspool’s algorithm
in searching for each of the following patterns in the binary text of 1000
zeros?
a. 00001
b. 10000
c. 01010
4. For searching in a text of length nfor a pattern of length m(n≥m)with
Horspool’s algorithm, give an example of
a. worst-case input.
b. best-case input.
5. Is it possible for Horspool’s algorithm to make more character comparisons
than the brute-force algorithm would make in searching for the same pat-
tern in the same text?
6. If Horspool’s algorithm discovers a matching substring, how large a shift
should it make to search for a next possible match?
7. How many character comparisons will the Boyer-Moore algorithm make
in searching for each of the following patterns in the binary text of 1000
zeros?
6
a. 00001
b. 10000
c. 01010
8. a. Would the Boyer-Moore algorithm work correctly with just the bad-
symbol table to guide pattern shifts?
b. Would the Boyer-Moore algorithm work correctly with just the good-
suffix table to guide pattern shifts?
9. a. If the last characters of a pattern and its counterpart in the text do
match, does Horspool’s algorithm have to check other characters right to
left, or can it check them left to right too?
b. Answer the same question for the Boyer-Moore algorithm.
10. Implement Horspool’s algorithm, the Boyer-Moore algorithm, and the
brute-force algorithm of Section 3.2 in the language of your choice and
run an experiment to compare their efficiencies for matching
a. random binary patterns in random binary texts.
b. random natural language patterns in natural language texts.
7
Hints to Exercises 7.2
1. Trace the algorithm in the same way it is done in the section for another
instance of the string-matching problem.
2. A special alphabet notwithstanding, this application is not different than
applications to natural language strings.
3. For each pattern, fill in its shift table and then determine the number
of character comparisons (both successful and unsuccessful) on each trial
and the total number of trials.
4. Find an example of a binary string of length mand a binary string of
length n(n≥m)so that Horspool’s algorithm makes
a. the largest possible number of character comparisons before making
the smallest possible shift.
b. the smallest possible number of character comparisons.
5. It is logical to try a worst-case input for Horspool’s algorithm.
6. Can the algorithm shift the pattern by more than one position without
the possibility of missing another matching substring?
7. For each pattern, fill in the two shift tables and then determine the number
of character comparisons (both successful and unsuccessful) on each trial
and the total number of trials.
8. Check the description of the Boyer-Moore algorithm.
9. Check the descriptions of the algorithms.
10. n/a
8

Solutions to Exercises 7.2
1. The shift table for the pattern BAOBAB in a text comprised of English
letters, the period, and a space will be
cA B C D ... O... Z . _
t(c)1 2 6 6 6 3 6 6 6 6
The actual search will proceed as shown below:
BESS_KNEW_ABOUT_BAOBABS
BAOBAB BAOBAB
BAOBAB BAOBAB
BAOBAB
2. a. For the pattern TCCTATTCTT and the alphabet {A,C,G,T}, the shift
table looks as follows:
cA C G T
t(c)5 2 10 1
b. Below the text and the pattern, we list the characters of the text that
are aligned with the last Tof the pattern, along with the corresponding
number of character comparisons (both successful and unsuccessful) and
the shift size:
the text: TTATAGATCTCGTATTCTTTTATAGATCTCCTATTCTT
the pattern: TCCTATTCTT
T: 2 comparisons, shift 1
C: 1 comparison, shift 2
T: 2 comparisons, shift 1
A: 1 comparison, shift 5
T: 8 comparisons, shift 1
T: 3 comparisons, shift 1
T: 3 comparisons, shift 1
A: 1 comparison, shift 5
T: 2 comparisons, shift 1
C: 1 comparison, shift 2
C: 1 comparison, shift 2
T: 2 comparisons, shift 1
A: 1 comparison, shift 5
T: 10 comparisons to stop the successful search
3. a. For the pattern 00001, the shift table is
c0 1
t(c)1 5
9

The algorithm will make one unsuccessful comparison and then shift the
pattern one position to the right on each of its trials:
000000 00000
00001
00001
etc.
00001
The total number of character comparisons will be C=1·996 = 996.
b. For the pattern 10000, the shift table is
c0 1
t(c)1 4
The algorithm will make four successful and one unsuccessful comparison
and then shift the pattern one position to the right on each of its trials:
000000 00000
10000
10000
etc.
10000
The total number of character comparisons will be C=5·996 = 4980.
c. For the pattern 01010, the shift table is
c0 1
t(c)2 1
The algorithm will make one successful and one unsuccessful comparison
and then shift the pattern two positions to the right on each of its trials:
000000 000000
01010
01010
etc.
01010
The left end of the pattern in the trials will be aligned against the text’s
characters in positions 0, 2, 4, ..., 994, which is 498 trials. (We can also
get this number by looking at the positions of the right end of the pattern.
This leads to finding the largest integer ksuch that 4+2(k−1) ≤999,
which is k= 498.) Thus, the total number of character comparisons will
be C=2·498 = 996.
10
4. a. The worst case: e.g., searching for the pattern 10...0
m−1
in the text of n
0’s. Cw=m(n−m+1).
b. The best case: e.g., searching for the pattern 0...0
m
in the text of n
0’s. Cb=m.
5. Yes: e.g., for the pattern 10...0
m−1
and the text 0...0
n
,C
bf =n−m+1while
CHorspool =m(n−m+1).
6. We can shift the pattern exactly in the same manner as we would in the
case of a mismatch, i.e., by the entry t(c)in the shift table for the text’s
character caligned against the last character of the pattern.
7. a. For the pattern 00001, the shift tables will be filled as follows:
the bad-symbol table the good-suffix table
c0 1
t1(c)1 5 .
kthe pattern d2
1000015
200001 5
300001 5
4 00001 5
On each of its trials, the algorithm will make one unsuccessful comparison
and then shift the pattern by d1=max{t1(0) −0,1}=1position to the
right without consulting the good-suffix table:
000000 00000
00001
00001
etc.
00001
The total number of character comparisons will be C=1·996 = 996.
b. For the pattern 10000, the shift tables will be filled as follows:
the bad-symbol table the good-suffix table
c.0 1
t1(c)1 4 .
kthe pattern d2
1 100003
2 10000 2
3 10000 1
4 10000 5
.
On each of its trials, the algorithm will make four successful and one
11

unsuccessful comparison and then shift the pattern by the maximum of
d1=max{t1(0) −4,1}=1and d2=t2(4) = 5,i.e., by 5 characters to
the right:
0000000000 00000
10000
10000
etc.
10000
The total number of character comparisons will be C=5·200 = 1000.
c. For the pattern 01010, the shift tables will be filled as follows:
the bad-symbol table the good-suffix table
c0 1
t1(c)2 1 .
kthe pattern d2
1010104
201010 4
301010 2
401010 2
.
On each trial, the algorithm will make one successful and one unsuccessful
comparison. The shift’s size will be computed as the maximum of d1=
max{t1(0) −1,1}=1and d2=t2(1) = 4 , which is 4. If we count
character positions starting with 0, the right end of the pattern in the
trials will be aligned against the text’s characters in positions 4, 8, 12, ...,
with the last term in this arithmetic progression less than or equal to 999.
This leads to finding the largest integer ksuch that 4+4(k−1) ≤999,
which is k= 249.
000000 000000
01010
01010
etc.
01010
Thus, the total number of character comparisons will be C=2·249 = 498.
8. a. Yes, the Boyer-Moore algorithm can get by with just the bad-symbol
shift table.
b. No: The bad-symbol table is necessary because it’s the only one used
by the algorithm if the first pair of characters does not match.
9. a. Horspool’s algorithm can also compare the remaining m−1characters
of the pattern from left to right because it shifts the pattern based only
on the text’s character aligned with the last character of the pattern.
12
b. The Boyer-Moore algorithm must compare the remaining m−1char-
acters of the pattern from right to left because of the good-suffix shift
table.
10. n/a
13
Exercises 7.3
1. For the input 30, 20, 56, 75, 31, 19 and hash function h(K)=Kmod 11
a. construct the open hash table.
b. find the largest number of key comparisons in a successful search in
this table.
c. find the average number of key comparisons in a successful search
in this table.
2. For the input 30, 20, 56, 75, 31, 19 and hash function h(K)=Kmod 11
a. construct the closed hash table.
b. find the largest number of key comparisons in a successful search in
this table.
c. find the average number of key comparisons in a successful search
in this table.
3. Why is it not a good idea for a hash function to depend on just one letter
(say, the first one) of a natural language word?
4. Find the probability of all nkeys being hashed to the same cell of a hash
table of size mif the hash function distributes keys evenly among all the
cells of the table.
5. The birthday paradox asks how many people should be in a room so
that the chances are better than even that two of them will have the same
birthday (month and day). Find the quite unexpected answer to this
problem. What implication for hashing does this result have?
6. Answer the following questions for the separate-chaining version of hash-
ing.
a. Wherewouldyouinsertkeysifyouknewthatallthekeysinthe
dictionary are distinct? Which dictionary operations, if any, would ben-
efit from this modification?
b. We could keep keys of the same linked list sorted. Which of the
dictionary operations would benefit from this modification? How could
we take advantage of this if all the keys stored in the entire table need to
be sorted?
7. Explain how hashing can be applied to check whether all elements of a list
are distinct. What is the time efficiency of this application?
14

8. Fill in the following table with the average-case efficiency classes for the
five implementations of the ADT dictionary:
unordered
array
ordered
array
binary
search
tree
separate
chaining
linear
probing
search
insertion
deletion
9. We have discussed hashing in the context of techniques based on space-
time tradeoffs. But it also takes advantage of another general strategy.
Which one?
10. Write a computer program that uses hashing for the following problem.
Given a natural language text, generate a list of distinct words with the
number of occurrences of each word in the text. Insert appropriate coun-
ters in the program to compare the empirical efficiency of hashing with
the corresponding theoretical results.
15
Hints to Exercises 7.3
1. Apply the open hashing (separate chaining) scheme to the input given as
it is done in the chapter’s text for another input (see Figure 7.5). Then
compute the largest number and average number of comparisons for suc-
cessful searches in the constructed table.
2. Apply the closed hashing (open addressing) scheme to the input given as
it is done in the chapter’s text for another input (see Figure 7.6). Then
compute the largest number and average number of comparisons for suc-
cessful searches in the constructed table.
3. How many different addresses can such a hash function produce? Would
it distribute keys evenly?
4. The question is quite similar to computing the probability of having the
same result in nthrows of a fair die.
5. Find the probability that npeople have different birthdays. As to the
hashing connection, what hashing phenomenon deals with coincidences?
6. a. There is no need to insert a new key at the end of the linked list it is
hashed to.
b. Which operations are faster in a sorted linked list and why? For
sorting, do we have to copy all elements in the nonempty lists in an array
and then apply a general purpose sorting algorithm or is there a way to
take advantage of the sorted order in each of the nonempty linked lists?
7. After you answer these questions, compare the efficiency of this algorithm
with that of the brute-force algorithm (Section 2.3) and of the presorting-
based algorithm (Section 6.1).
8. Consider this question as a mini-review: the answers are in Section 7.3 for
the last two columns and in the appropriate sections of the book for the
others. (Of course, you should use the best algorithms available.)
9. If you need to refresh you memory, check the book’s table of contents.
10. n/a
16
Solutions to Exercises 7.3
1. a.
The list of keys: 30, 20, 56, 75, 31, 19
The hash function: h(K)=Kmod 11
The hash addresses: K30 20 56 75 31 19
h(K)8 9 1 9 9 8
Theopenhashtable:
0 1 234567 8 9 10
↓↓↓
56 30 20
↓↓
19 75
↓
31
b. The largest number of key comparisons in a successful search in this
table is 3 (in searching for K=31).
c. The average number of key comparisons in a successful search in this
table, assuming that a search for each of the six keys is equally likely, is
1
6·1+1
6·1+1
6·1+1
6·2+1
6·3+1
6·2=10
6≈1.7.
2. a.
The list of keys: 30, 20, 56, 75, 31, 19
The hash function: h(K)=Kmod 11
The hash addresses: K30 20 56 75 31 19
h(K)8 9 1 9 9 8
0 1 2 34567 8 9 10
30
30 20
56 30 20
56 30 20 75
31 56 30 20 75
31 56 19 30 20 75
b. The largest number of key comparisons in a successful search is 6
(when searching for K=19).
c. The average number of key comparisons in a successful search in this
table, assuming that a search for each of the six keys is equally likely, is
1
6·1+1
6·1+1
6·1+1
6·2+1
6·3+1
6·6=14
6≈2.3.
17
3. The number of different values of such a function would be obviously
limited by the size of the alphabet. Besides, it is usually not the case
that the probability of a word to start with a particular letter is the same
for all the letters.
4. The probability of all nkeys to be hashed to a particular address is equal
to 1
mn.Since there are mdifferent addresses, the answer is 1
mnm=
1
m.
5. The probability of npeople having different birthdays is 364
365
363
365 ... 365−(n−1)
365 .
The smallest value of nfor which this expression becomes less than 0.5 is
23. Sedgewick and Flajolet [SF96] give the following analytical solution
to the problem:
(1 −1
M)(1 −2
M)...(1 −n−1
M)≈1
2where M= 365.
Taking the natural logarithms of both sides yields
ln(1 −1
M)(1 −2
M)...(1 −n−1
M)≈−ln 2 or
n−1
k=1
ln(1 −k
M)≈−ln 2.
Using ln(1 −x)≈−x, we obtain
n−1
k=1
k
M≈ln 2 or (n−1)n
2M≈ln 2.Hence, n≈√2Mln 2 ≈22.5.
The implication for hashing is that we should expect collisions even if the
size of a hash table is much larger (by more than a factor of 10) than the
number of keys.
6. a. If all the keys are known to be distinct, a new key can always be inserted
at the beginning of its linked list; this will make the insertion operation
Θ(1).This will not change the efficiencies of search and deletion, however.
b. Searching in a sorted list can be stopped as soon as a key larger than
the search key is encountered. Both deletion (that must follow a search)
and insertion will benefit for the same reason. To sort a dictionary stored
in linked lists of a hash table, we can merge the knonempty lists to get
the entire dictionary sorted. (This operation is called the k-way merge.)
To do this efficiently, it’s convenient to arrange the current first elements
of the lists in a min-heap.
18

7. Insert successive elements of the list in a hash table until a matching
element is encountered or the list is exhausted. The worst-case efficiency
will be in Θ(n2):allndistinct keys are hashed to the same address so that
the number of key comparisons will be n
i=1(i−1) ∈Θ(n2).The average-
case efficiency, with keys distributed about evenly so that searching for
each of them takes Θ(1) time,willbeinΘ(n).
8.
unordered
array
ordered
array
binary
search
tree
separate
chaining
linear
probing
search Θ(n) Θ(log n) Θ(log n)Θ(1) Θ(1)
insertion Θ(1) Θ(n) Θ(log n)Θ(1) Θ(1)
deletion Θ(1) Θ(n) Θ(log n)Θ(1) Θ(1)
9. Representation change–one of the three varieties of transform-and-conquer.
10. n/a
19
Exercises 7.4
1. Give examples of using an index in real-life applications that do not involve
computers.
2. a. Prove the equality
1+
h−1
i=1
2m/2i−1(m/2−1) + 2m/2h−1=4m/2h−1−1
that was used in the derivation of upper bound (7.7) for the height of a
B-tree.
b. Complete the derivation of inequality (7.7).
3. Find the minimum order of the B-tree that guarantees that the number of
disk accesses in searching in a file of 100 million records does not exceed
3. Assume that the root’s page is stored in main memory.
4. Draw the B-tree obtained after inserting 30 and then 31 in the B-tree in
Figure 7.8. Assume that a leaf cannot contain more than three items.
5. Outline an algorithm for finding the largest key in a B-tree.
6. a. A top-down 2-3-4 tree is a B-tree of order 4 with the following
modification of the insert operation. Whenever a search for a leaf for a
new key encounters a full node (i.e., a node with three keys), the node is
split into two nodes by sending its middle key to the node’s parent (or, if
the full node happens to be the root, the new root for the middle key is
created). Construct a top-down 2-3-4 tree by inserting the following list
of keys in the initially empty tree:
10, 6, 15, 31, 20, 27, 50, 44, 18.
b. What is the principal advantage of this insertion procedure compared
with the one described for 2-3 trees in Section 6.3? What is its disadvan-
tage?
7. a. Write a program implementing a key insertion algorithm in a B-tree.
b. Write a program for visualization of a key insertion algorithm in
aB-tree.
20
Hints to Exercises 7.4
1. Thinking about searching for information should lead to a variety of ex-
amples.
2. a. Use the standard rules of sum manipulation and, in particular, the
geometric series formula.
b. You will need to take the logarithms base m/2in your derivation.
3. Find this value from the inequality in the text that provides the upper-
bound of the B-tree’s height.
4. Follow the insertion algorithm outlined in this section.
5. The algorithm is suggested by the definition of the B-tree.
6. a. Just follow the description of the algorithm given in the statement of
the problem. Note that a new key is always inserted in a leaf and that
full nodes are always split on the way down, even though the leaf for the
newkeymayhavearoomforit.
b. Can a split of a full node cause a cascade of splits through the chain of
its ancestors? Can we get a taller search tree than necessary?
7. n/a
21
Solutions to Exercises 7.4
1. Here are a few common examples of using an index: labeling drawers of a
file cabinet with, say, a range of letters; an index of a book’s terms indicat-
ing the page or pages on which the term is defined or mentioned; marking
a range of pages in an address book, a dictionary; or an encyclopedia;
marking a page of a telephone book or a dictionary with the first and last
entry on the page; indexing areas of a geographic map by dividing the
map into square regions.
2. a.
1+
h−1
i=1
2m/2i−1(m/2−1) + 2m/2h−1
=1+2(m/2−1)
h−1
i=1 m/2i−1+2m/2h−1
=1+2(m/2−1)
h−2
j=0m/2j+2m/2h−1
=1+2(m/2−1) m/2h−1−1
(m/2−1) +2m/2h−1
=1+2m/2h−1−2+2m/2h−1
=4m/2h−1−1.
b. The inequality
n≥4m/2h−1−1
is equivalent to n+1
4≥m/2h−1.
Taking the logarithms base m/2of both hand sides yields
logm/2
n+1
4≥logm/2m/2h−1
or
logm/2
n+1
4≥h−1.
Hence,
h≤logm/2
n+1
4+1
or, since his an integer,
h≤logm/2
n+1
4+1.
22
3. If the tree’s root is stored in main memory, the number of disk accesses
will be equal to the number of the levels minus 1, which is exactly the
height of the tree. So, we need to find the smallest value of the order
mso that the height of the B-tree with n=10
8keys does not exceed
3. Using the upper bound of the B-tree’s height, we obtain the following
inequality
logm/2
n+1
4+1≤3or logm/2
n+1
4≤2.
By “trial and error,” we can find that the smallest value of mthat satisfies
this inequality is 585.
4. Since there is enough room for 30 in the leaf for it, the resulting B-tree
will look as follows
11 15
4, 7,10 11, 14 15, 16, 19
40.25 34
20, 24 25, 28, 30 34, 38
60
51, 55 60, 68, 8040, 43, 46
20 51
Inserting 31 will require the leaf’s split and then its parent’s split:
11 15
4, 7,10 11, 14 15, 16, 19
25 30
20, 24 25, 28 34, 38
60
51, 55 60, 68, 8040, 43, 46
5120 34
30, 31
34 40
5. Starting at the root, follow the chain of the rightmost pointers to the
(rightmost) leaf. The largest key is the last key in that leaf.
6. a. Constructing a top-down 2-3-4 tree by inserting the following list of
keys in the initially empty tree:
10, 6, 15, 31, 20, 27, 50, 44, 18.
23
10
10
6
6, 10 6, 10, 15
10, 20
615
20
10
6
31
27
15, 31
10
615, 20, 31
27, 31
10, 20
615 27, 31, 50
10,20,31
615 27 44, 50
15, 18 44, 50
b. The principal advantage of splitting full nodes (4-nodes with 3 keys)
on a way down during insertion of a new key lies in the fact that if the
appropriate leaf turns out to be full, its split will never cause a chain re-
action of splits because the leaf’s parent will always have a room for an
extra key. (If the parent is full before the insertion, it is split before the
leaf is reached.) This is not the case for the insertion algorithm employed
for 2-3 trees (see Section 6.3).
The disadvantage of splitting full nodes on the way down lies in the fact
that it can lead to a taller tree than necessary. For the list of part (a),
for example, the tree before the last one had a room for key 18 in the
leaf containing key 15 and therefore didn’t require a split executed by the
top-down insertion.
7. n/a
24

This file contains the exercises, hints, and solutions for Chapter 8 of the
book ”Introduction to the Design and Analysis of Algorithms,” 2nd edition, by
A. Levitin. The problems that might be challenging for at least some students
are marked by ;those that might be difficult for a majority of students are
marked by .
Exercises 8.1
1. a. What does dynamic programming have in common with divide-and-
conquer?
b. What is a principal difference between the two techniques?
2. a. Compute C(6,3) by applying the dynamic programming algorithm.
b. Is it also possible to compute C(n, k)by filling the algorithm’s dy-
namic programming table column by column rather than row by row?
3. Prove the following assertion made in the text while investigating the time
efficiency of the dynamic programming algorithm for computing C(n, k):
(k−1)k
2+k(n−k)∈Θ(nk).
4. a. What is the space efficiency of Binomial, the dynamic programming
algorithm for computing C(n, k)?
b. Explain how the space efficiency of this algorithm can be improved.
(Try to make as much of an improvement as you can.)
5. a. Find the order of growth of the following functions:
i. C(n, 1) ii. C(n, 2) iii. C(n, n/2) for even n’s.
b. What major implication for computing C(n, k)do the answers to the
questions in part (a) have?
6. Find the exact number of additions made by the following recursive algo-
rithm based directly on formulas (8.3) and (8.4).
Algorithm BinomCoeff (n, k)
if k=0or k=nreturn 1
else return BinomCoeff (n−1,k−1)+BinomCoeff (n−1,k)
7. Which of the following algorithms for computing a binomial coefficient is
most efficient?
1

a. Use the formula
C(n, k)= n!
k!(n−k)!.
b. Use the formula
C(n, k)=n(n−1)...(n−k+1)
k!.
c. Apply recursively the formula
C(n, k)=C(n−1,k−1) + C(n−1,k)for n>k>0,
C(n, 0) = C(n, n)=1.
d. Apply the dynamic programming algorithm.
8. Prove that
C(n, k)=C(n, n −k)for n≥k≥0
and explain how this formula can be utilized in computing C(n, k).
9. Shortest path counting A chess rook can move horizontally or vertically
to any square in the same row or in the same column of a chessboard.
Find the number of shortest paths by which a rook can move from one
corner of a chessboard to the diagonally opposite corner [Gar78], p.10
(a) by a dynamic programming algorithm.
(b) by using elementary combinatorics.
10. World Series odds Consider two teams, Aand B, playing a series of
games until one of the teams wins ngames. Assume that the probabil-
ity of Awinning a game is the same for each game and equal to pand
the probability of Alosing a game is q=1−p. (Hence, there are no
ties.) Let P(i, j)be the probability of Awinning the series if Aneeds
imoregamestowintheseriesandBneeds jmore games to win the series.
a. Set up a recurrence relation for P(i, j)that can be used by a dy-
namic programming algorithm.
b. Find the probability of team Awinning a seven-game series if the
probability of it winning a game is 0.4.
c. Write a pseudocode of the dynamic programming algorithm for solving
this problem and determine its time and space efficiencies.
2

Hints to Exercises 8.1
1. Compare the definitions of the two techniques.
2. a. Trace the algorithm Binomial for n=6and k=3by filling the table
similar to that in Figure 8.1.
b. Check the algorithm’s formula to see which values need to be known
to compute C(n, k).
3. Show that there exist positive constants c1,c
2,and a positive integer n0
such that
c2nk ≤(k−1)k
2+k(n−k)≤c1nk
for all pairs of integers n, k such that n≥n0and 0≤k≤n.
4. a. The space efficiency can be investigated in almost the same way the
time efficiency is investigated in Section 8.1.
b. With some care, one can write a new row of the table over its im-
mediate predecessor.
5. Use an explicit formula for C(n, k)and Stirling’s formula if necessary.
6. Set up a recurrence relation for the number of additions A(n, k);solveit
by substituting A(n, k)=B(n, k)−1.
7. Find and compare the efficiency classes of these algorithms.
8. The formula can be proved by using either one of the explicit formulas for
C(n, k)or by its combinatorial interpretation.
9. a. Relate the number of the rook’s shortest paths to the square in the ith
row and the jth column of the chessboard to the numbers of the shortest
paths to the adjacent squares.
b. Consider one shortest path as 14 consecutive moves to adjacent squares.
10. a. In the situation where teams Aand Bneed iand jgames, respectively,
to win the series, consider the result of team Awinning the game and the
result of team Alosing the game.
b. Set up a table with five rows (0 ≤i≤4) and five columns (0 ≤j≤4)
and fill it by using the recurrence derived in part (a).
c. A pseudocode should be guided by the recurrence set up in part (a).
The efficiency answers follow immediately from the table’s size and the
time spent on computing each of its entries.
3
Solutions to Exercises 8.1
1. a. Both techniques are based on dividing a problem’s instance into smaller
instances of the same problem.
b. Typically, divide-and-conquer divides an instance into smaller instances
with no intersection whereas dynamic programming deals with problems
in which smaller instances overlap. Consequently, divide-and-conquer al-
gorithms do not explicitly store solutions to smaller instances and dynamic
programming algorithms do.
2. a. 01 2 3
0 1
111
212 1
313 3 1
414 6 4
51 5 10 10
6161520
b. Yes, the table can also be filled column-by-column, with each column
filled top-to-bottom starting with 1on the main diagonal of the table.
3. First, the simple algebra yields
(k−1)k
2+k(n−k)=nk −1
2k2−1
2k.
So, we can obtain an upper bound by eliminating the negative terms:
nk −1
2k2−1
2k≤nk for all n, k ≥0.
We can get a lower bound by considering n≥2and 0≤k≤n:
nk −1
2k2−1
2k≥nk −1
2nk −1
2k1
2n=1
4nk.
4. a. The total size of the algorithm’s table is (n+1)(k+1) ∈Θ(nk).
Considering only the memory cells actually used by the algorithm still
yields the same asymptotic class:
S(n, k)=
k
i=0
(i+1)+
n
i=k+1
(k+1) = (k+1)(k+2)
2+(k+1)(n−k)∈Θ(nk).
4

b. The following algorithm uses just a one-dimensional array by writing
a new row over its immediate predecessor; each row is filled from right to
left.
Algorithm Binomial2 (n, k)
//Computes C(n, k)by the dynamic programming algorithm
//with a one-dimensional table
//Input: A pair of nonnegative integers n≥k≥0
//Output: The value of C(n, k)
for i←0to ndo
if i≤k//in the triangular part
T[i]←1//the diagonal element
u←i−1//the rightmost element to be computed
else u←k//in the rectangular part
//overwrite the preceding row moving right to left
for j←udownto 1do
T[j]←T[j−1] + T[j]
return T[k]
5. a.
i. C(n, 1) = n∈Θ(n)
ii. C(n, 2) = n(n−1)
2∈Θ(n2)
iii. C(n, n
2)= n!
(n/2)!(n−n/2)! =n!
[(n/2)!]2
≈√2πn(n/e)n
[2πn/2(n/2e)n/2]2=2
√2πn2n∈Θ(2nn−0.5)
b. A major implication is a very fast growth of C(n, k)if kis close to
n/2.
6. The recurrence relation for the number of additions made by the algorithm
is
A(n, k)=A(n−1,k−1) + A(n−1,k)+1 for n>k>0,
A(n, 0) = A(n, n)=0 for n≥0.
Substituting A(n, k)=B(n, k)−1yields
B(n, k)=B(n−1,k−1) + B(n−1,k)for n>k>0,
B(n, 0) = B(n, n)=1 for n≥0.
5

Since the last recurrence relation is identical to the recurrence relation for
the binomial coefficient, B(n, k)=C(n, k)and hence
A(n, k)=B(n, k)−1=C(n, k)−1.
7. a. Assuming that 1! is computed as 0! ·1and, hence, requires one multi-
plication, the use of the formula
C(n, k)= n!
k!(n−k)!
requires n+k+n−k=2nmultiplications and one division.
b. The use of the formula
C(n, k)= n(n−1)...(n−k+1)
k!
requires only k+k=2kmultiplications and one division. (We assumed
that the product in the numerator is initialized to 1.) Hence, (b) is more
efficient than (a). Also note that the overflow problem is less severe for
formula (b) than for formula (a). It can be further alleviated by using
the formula
n(n−1)...(n−k+1)
k!=n
k
n−1
k−1...n−(k−1)
1.
c. Applying recursively the formula
C(n, k)=C(n−1,k−1)+C(n−1,k)for n>k>0,C(n, 0) = C(n, n)=1
requires C(n, k)−1additions (see Problem 6), which is much worse than
the dynamic programming algorithm that requires nk −1
2k2−1
2k.addi-
tions(seeSection8.1).
d. The efficiency of the dynamic programming algorithm, as explained
in the section, is in Θ(nk).
Thus, the choice comes to be between algorithms (b) and (d). Making a
choice between two algorithms with different basic operations should be
conditioned on their relative speeds. Still, since the time efficiency of
algorithm (b) is in Θ(k)while the time efficiency of algorithm (d) is in
Θ(nk),we have to conclude that the former is more time efficient, at least
asymptotically, than the latter. Algorithm (b) is obviously more space
efficient than algorithm (d), too.
6
8. Using the formula C(n, k)= n!
k!(n−k)! ,we obtain the following equality:
C(n, n−k)= n!
(n−k)!(n−(n−k))! =n!
(n−k)!k!=n!
k!(n−k)! =C(n, k).
Alternatively, C(n, k)is the number of ways to choose a k-element subset
from a set of nelements, which is the same as selecting n−kelements
not to be included in a k-element subset.
The formula can be used for speeding up algorithms (b), (c), and (d) of
Problem 7: compute C(n, k)if k≤n−k(i.e., if k≤n/2)andC(n, n −k)
otherwise.
9. a. With no loss of generality, we can assume that the rook is initially
located in the lower left corner of a chessboard, whose rows and columns
are numbered from 1 to 8. Let P(i, j)be the number of the rook’s
shortest paths from square (1,1) to square (i, j)in the ith row and the jth
column, where 1≤i, j ≤8.Any such path will be composed of vertical
and horizontal moves directed toward the goal. Obviously, P(i, 1) =
P(1,j)=1for any 1≤i, j ≤8.In general, any shortest path to square
(i, j)will be reached either from square (i, j −1) or from square (i−1,j)
square. Hence, we have the following recurrence
P(i, j)=P(i, j −1) + P(i−1,j)for 1<i,j≤8,
P(i, 1) = P(1,j)=1 for 1≤i, j ≤8.
Using this recurrence, we can compute the values of P(i, j)for each square
(i.j)of the board. This can be done either row by row, or column by
column, or diagonal by diagonal. (One can also take advantage of the
board’s symmetry to make the computations only for the squares either
on and above or on and below the board’s main diagonal.) The results
7

are given in the diagram below:
1 8 36 120 330 792 1716 3432
17161 7 28 84 210 462 924
1 6 21 56 126 252 462 792
3301 5 15 35 70 126 210
1 4 10 20 35 56 84 120
361 3 6 10 15 21 28
1 2 3 4 5 6 7 8
11 1 1 1 1 1 1
b. Any shortest path from square (1,1) to square (8,8) can be thought
of as 14 consecutive moves to adjacent squares, seven of which being up
while the other seven being to the right. For example, the shortest path
composed of the vertical move from (1,1) to (8,1) followed by the horizon-
tal move from (8,1) to (8,8) corresponds to the following sequence of 14
one-square moves:
(u,u,u,u,u,u,u,r,r,r,r,r,r,r),
where uand rstand for a move up and to the right, respectively. Hence,
the total number of distinct shortest paths is equal to the number of
different ways to choose seven u-positions among the total of 14 possible
positions, which is equal to C(14,7).
10. a. Let P(i, j)be the probability of Awinning the series if Aneeds imore
games to win the series and Bneeds jmore games to win the series. If
team Awins the game, which happens with probability p,Awill need
i−1more wins to win the series while Bwill still need jwins. If team
Alooses the game, which happens with probability q=1−p,Awill still
need iwins while Bwill need j−1wins to win the series. This leads to
the recurrence
P(i, j)=pP (i−1,j)+qP(i, j −1) for i, j > 0.
8

The initial conditions follow immediately from the definition of P(i, j):
P(0,j)=1 for j>0,P(i, 0) = 0 for i>0.
b. Here is the dynamic programming table in question, with its entries
rounded-off to two decimal places. (It can be filled either row-by-row, or
column-by-column, or diagonal-by-diagonal.)
i\j01 2 3 4
01111
10 0.40 0.64 0.78 0.87
20 0.16 0.35 0.52 0.66
30 0.06 0.18 0.32 0.46
40 0.03 0.09 0.18 0.29
Thus, P[4,4] ≈0.29.
c. Algorithm WorldSeries(n, p)
//Computes the odds of winning a series of ngames
//Input: A number of wins nneeded to win the series
// and probability pof one particular team winning a game
//Output: The probability of this team winning the series
q←1−p
for j←1to ndo
P[0,j]←1.0
for i←1to ndo
P[i, 0] ←0.0
for j←1to ndo
P[i, j]←p∗P[i−1,j]+q∗P[i, j −1]
return P[n, n]
Both the time efficiency and the space efficiency are in Θ(n2)because each
entry of the n+1-by-n+1table (except P[0,0],which is not computed)
is computed in Θ(1) time.
9
Exercises 8.2
1. Apply Warshall’s algorithm to find the transitive closure of the digraph
defined by the following adjacency matrix
0100
0010
0001
0000
2. a. Prove that the time efficiency of Warshall’s algorithm is cubic.
b. Explain why the time efficiency of Warshall’s algorithm is inferior
to that of the traversal-based algorithm for sparse graphs represented by
their adjacency lists.
3. Explain how to implement Warshall’s algorithm without using extra mem-
ory for storing elements of the algorithm’s intermediate matrices.
4. Explain how to restructure the innermost loop of the algorithm Warshall
to make it run faster at least on some inputs.
5. Rewrite the pseudocode of Warshall’s algorithm assuming that the matrix
rows are represented by bit strings on which the bitwise or operation can
be performed.
6. a. Explain how Warshall’s algorithm can be used to determine whether a
given digraph is a dag (directed acyclic graph). Is it a good algorithm for
this problem?
b. Is it a good idea to apply Warshall’s algorithm to find the transitive
closureofanundirectedgraph?
7. Solve the all-pairs shortest path problem for the digraph with the following
weight matrix
02∞18
6032∞
∞∞ 04∞
∞∞ 203
3∞∞∞ 0
8. Prove that the next matrix in sequence (8.8) of Floyd’s algorithm can be
written over its predecessor.
9. Give an example of a graph or a digraph with negative weights for which
Floyd’s algorithm does not yield the correct result.
10. Enhance Floyd’s algorithm so that shortest paths themselves, not just
their lengths, can be found.
10
11. Jack Straws InthegameofJackStraws,anumberofplasticorwooden
"straws" are dumped on the table and players try to remove them one-by-
one without disturbing the other straws. Here, we are only concerned with
if various pairs of straws are connected by a path of touching straws. Given
a list of the endpoints for n>1straws (as if they were dumped on a large
piece of graph paper), determine all the pairs of straws that are connected.
Note that touching is connecting, but also two straws can be connected
indirectly via other connected straws [1994 East-Central Regionals of the
ACM International Collegiate Programming Contest].
11
Hints to Exercises 8.2
1. Apply the algorithm to the adjacency matrix given as it is done in the
section for another matrix.
2. a. The answer can be obtained either by considering how many values the
algorithm computes or by following the standard plan for analyzing the
efficiency of a nonrecursive algorithm (i.e., by setting up a sum to count
its basic operation).
b. What is the efficiency class of the traversal-based algorithm for sparse
graphs represented by their adjacency lists?
3. Show that we can simply overwrite elements of R(k−1) with elements of
R(k)without any other changes in the algorithm.
4. What happens if R(k−1)[i, k]=0?
5. Show first that formula (8.7) (from which the superscripts can be elimi-
nated according to the solution to Problem 3)
rij =rij or rik and rkj.
is equivalent to
if rik rij ←rij or rkj.
6. a. What property of the transitive closure indicates a presence of a di-
rected cycle? Is there a better algorithm for checking this?
b. Which elements of the transitive closure of an undirected graph are
equal to 1? Can you find such elements with a faster algorithm?
7. See an example of applying the algorithm to another instance in the sec-
tion.
8. What elements of matrix D(k−1) does d(k)
ij , the element in the ith row and
the jth column of matrix D(k),depend on? Can these values be changed
by the overwriting?
9. Your counterexample must contain a cycle of a negative length.
10. It will suffice to store, in a single matrix P, indices of intermediate vertices
kused in updates of the distance matrices. This matrix can be initialized
with all zero elements.
11. The problem can be solved by utilizing two well-known algorithms: one
from computational geometry, the other dealing with graphs.
12
Solutions to Exercises 8.2
1. Applying Warshall’s algorithm yields the following sequence of matrices
(in which newly updated elements are shown in bold):
R(0) =
0100
0010
0001
0000
R(1) =
0100
0010
0001
0000
R(2) =
0110
0010
0001
0000
R(3) =
0111
0011
0001
0000
R(4) =
0111
0011
0001
0000
=T
2. a. For a graph with nvertices, the algorithm computes nmatrices R(k)
(k=1,2,...,n),eachofwhichhasn2elements. Hence, the total number
of elements to be computed is n3.Since computing each element takes
constant time, the time efficiency of the algorithm is in Θ(n3).
b. Since one DFS or BFS traversal of a graph with nvertices and m
edges, which is represented by its adjacency lists, takes Θ(n+m)time,
doing this ntimes takes nΘ(n+m)=Θ(n2+nm)time.For sparse graphs
(i.e., if m∈O(n)), Θ(n2+nm)=Θ(n2), which is more efficient than the
Θ(n3)time efficiency of Warshall’s algorithm.
3. The algorithm computes the new value to be put in the ith row and the
jth column by the formula
R(k)[i, j]=R(k−1)[i, j]or (R(k−1)[i, k]and R(k−1)[k, j]).
The formula implies that all the elements in the kth row and all the
elements in the kth column never change on the kth iteration, i.e., while
computing elements of R(k)from elements of R(k−1).(Substitute kfor
iand kfor j, respectively, into the formula to verify these assertions.)
Hence, the new value of the element in the ith row and the jth column,
R(k)[i, j],can be written over its old value R(k−1)[i, j]for every i, j.
13
4. If R(k−1)[i, k]=0,
R(k)[i, j]=R(k−1)[i, j]or (R(k−1)[i, k]and R(k−1)[k, j]) = R(k−1)[i, j],
and hence the innermost loop need not be executed. And, since R(k−1)[i, k]
doesn’t depend on j, its comparison with 0 can be done outside the jloop.
This leads to the following implementation of Warshall’s algorithm:
Algorithm Warshall2(A[1..n, 1..n])
//Implements Warshall’s algorithm with a more efficient innermost loop
//Input: The adjacency matrix Aof a digraph with nvertices
//Output: The transitive closure of the digraph in place of A
for k←1to ndo
for i←1to ndo
if A[i, k]
for j←1to ndo
if A[k, j]
A[i, j]←1
return A
5. First, it is easy to check that
rij ←rij or (rik and rkj).
is equivalent to
if rik rij ←rij or rkj
Indeed, if rik =1(i.e., true),
rij or (rik and rkj)=rij or rkj,
which is exactly the value assigned to rij by the if statement as well. If
rik =0(i.e., false),
rij or (rik and rkj)=rij,
i.e., the new value of rij will be the same as its previous value–exactly,
the result we obtain by executing the if statement.
Here is the algorithm that exploits this observation and the bitwise or
operation applied to matrix rows:
Algorithm Warshall3(A[1..n, 1..n])
//Implements Warshall’s algorithm for computing the transitive closure
//with the bitwise or operation on matrix rows
//Input: The adjacency matrix Aof a digraph
//Output: The transitive closure of the digraph in place of A
for k←1to ndo
14
for i←1to ndo
if A[i, k]
row[i]←row[i]bitwiseor row[k]//rows of matrix A
return A
6. a. With the book’s definition of the transitive closure (which considers
only nontrivial paths of a digraph), a digraph has a directed cycle if and
only if its transitive closure has a 1 on its main diagonal. The algorithm
that finds the transitive closure by applying Warshall’s algorithm and then
checks the elements of its main diagonal is cubic. This is inferior to the
quadratic algorithms for checking whether a digraph represented by its
adjacency matrix is a dag, which were discussed in Section 5.3.
b. No. If Tis the transitive closure of an undirected graph, T[i, j]=1if
and only if there is a nontrivial path from the ith vertex to the jth vertex.
If i=j, this is the case if and only if the ith vertex and the jth vertex
belong to the same connected component of the graph. Thus, one can
find the elements outside the main diagonal of the transitive closure that
are equal to 1 by a depth-first search or a breadth-first search traversal,
which is faster than applying Warshall’s algorithm. If i=j, T [i, i]=1
ifandonlyiftheith vertex is not isolated, i.e., if it has an edge to at
least one other vertex of the graph. Isolated vertices, if any, can be easily
identified by the graph’s traversal as one-node connected components of
the graph.
7. Applying Floyd’s algorithm to the given weight matrix generates the fol-
lowing sequence of matrices:
D(0) =
02∞18
6032∞
∞∞ 04∞
∞∞ 203
3∞∞∞ 0
D(1) =
02∞18
603214
∞∞ 04∞
∞∞ 203
35∞40
D(2) =
02518
603214
∞∞04∞
∞∞20 3
35840
D(3) =
02518
603214
∞∞04∞
∞∞20 3
35840
D(4) =
02314
60325
∞∞047
∞∞203
35640
D(5) =
02314
60325
10 12 047
68203
35640
=D
15

8. The formula
d(k)
ij =min{d(k−1)
ij ,d
(k−1)
ik +d(k−1)
kj }
implies that the value of the element in the ith row and the jth column of
matrix D(k)is computed from its own value and the values of the elements
in the ith row and the kth column and in the kth row and the jth column
in the preceding matrix D(k−1).The latter two cannot change their values
when the elements of D(k)are computed because of the formulas
d(k)
ik =min{d(k−1)
ik ,d
(k−1)
ik +d(k−1)
kk }=min{d(k−1)
ik ,d
(k−1)
ik +0}=d(k−1)
ik
and
d(k)
kj =min{d(k−1)
kj ,d
(k−1)
kk +d(k−1)
kj }=min{d(k−1)
kj ,0+d(k−1)
kj }=d(k−1)
kj .
(Note that we took advantage of the fact that the elements dkk on the main
diagonal remain 0’s. This can be guaranteed only if the graph doesn’t
contain a cycle of a negative length.)
9. As a simple counterexample, one can suggest the following digraph:
ab
- 2
1
Floyd’s algorithm will yield:
D(0) =01
−20
D(1) =01
−2−1D(2) =−10
−3−2
None of the four elements of the last matrix gives the correct value of the
shortest path, which is, in fact, −∞ because repeating the cycle enough
times makes the length of a path arbitrarily small.
Note: Floyd’s algorithm can be used for detecting negative-length cy-
cles, but the algorithm should be stopped as soon as it generates a matrix
with a negative element on its main diagonal.
10. As pointed out in the hint to this problem, Floyd’s algorithm should be
enhanced by recording in an n-by-nmatrix index kof an intermediate
vertex causing an update of the distance matrix. This is implemented in
the pseudocode below:
Algorithm FloydEnhanced (W[1..n, 1..n])
//Input: The weight matrix Wof a graph or a digraph
//Output: The distance matrix D[1..n, 1..n]and
16
// the matrix of intermediate updates P[1..n, 1..n]
D←W
for i←1to ndo
for j←1to ndo
P[i, j]←0//initial mark
for k←1to ndo
for i←1to ndo
for j←1to ndo
if D[i, k]+D[k, j]<D[i, j]
D[i, j]←D[i, k]+D[k, j]}
P[i, j]←k
For example, for the digraph in Fig. 8.7 whose vertices are numbered from
1to4,matrixPwill be as follows:
P=
0303
0013
4000
0310
.
The list of intermediate vertices on the shortest path from vertex ito
vertex jcan be then generated by the call to the following recursive algo-
rithm, provided D[i, j]<∞:
Algorithm ShortestPath(i, j, P [1..n, 1..n])
//The algorithm prints out the list of intermediate vertices of
//a shortest path from the ith vertex to the jth vertex
//Input: Endpoints iand jof the shortest path desired;
// matrix Pof updates generated by Floyd’s algorithm
//Output: The list of intermediate vertices of the shortest path
// from the ith vertex to the jth vertex
k←P[i, j]
if k=0
ShortestPath(i, k)
print(k)
ShortestPath(k, j)
11. First, for each pair of the straws, determine whether the straws intersect.
(Although this can be done in nlog ntime by a sophisticated algorithm,
the quadratic brute-force algorithm would do because of the quadratic ef-
ficiency of the subsequent step; both geometric algorithms can be found,
e.g., in R. Sedgewick’s “Algorithms,” Addison-Wesley, 1988.) Record the
obtained information in a boolean n-by-nmatrix, which must be symmet-
ric. Then find the transitive closure of this matrix in n2time by DFS or
BFS (see the solution to Problem 6b).
17
Exercises 8.3
1. Finish the computations started in the section’s example of constructing
an optimal binary search tree.
2. a. Why is the time efficiency of algorithm OptimalBST cubic?
b. Why is the space efficiency of algorithm OptimalBST quadratic?
3. Write a pseudocode for a linear-time algorithm that generates the optimal
binary search tree from the root table.
4. Devise a way to compute the sums j
s=ips,which are used in the dynamic
programming algorithm for constructing an optimal binary search tree, in
constant time (per sum).
5. True or false: The root of an optimal binary search tree always contains
the key with the highest search probability?
6. How would you construct an optimal binary search tree for a set of n
keys if all the keys are equally likely to be searched for? What will be
the average number of comparisons in a successful search in such a tree if
n=2
k?
7. a. Show that the number of distinct binary search trees b(n)that can be
constructed for a set of norderable keys satisfies the recurrence relation
b(n)=
n−1
k=0
b(k)b(n−1−k)for n>0,b(0) = 1.
b. It is known that the solution to this recurrence is given by the Catalan
numbers. Verify this assertion for n=1,2, ..., 5.
c. Find the order of growth of b(n).What implication does the answer
to this question have for the exhaustive search algorithm for constructing
an optimal binary search tree?
8. Design a Θ(n2)algorithm for finding an optimal binary search tree.
9. Generalize the optimal binary search algorithm by taking into account
unsuccessful searches.
10. Matrix chain multiplication Consider the problem of minimizing the
total number of multiplications made in computing the product of nma-
trices
A1·A2·... ·An
whose dimensions are d0by d1,d
1by d2, ..., dn−1by dn, respectively. (As-
sume that all intermediate products of two matrices are computed by the
18
brute-force (definition-based) algorithm.
a. Give an example of three matrices for which the number of multi-
plications in (A1·A2)·A3and A1·(A2·A3)differ at least by a factor 1000.
b.How many different ways are there to compute the chained prod-
uct of nmatrices?
c.Design a dynamic programming algorithm for finding an optimal order
of multiplying nmatrices.
19
Hints to Exercises 8.3
1. Continue applying formula (8.11) as prescribed by the algorithm.
2. a. The algorithm’s time efficiency can be investigated by following the
standard plan of analyzing the time efficiency of a nonrecursive algorithm.
b. How much space do the two tables generated by the algorithm use?
3. k=R[1,n]indicates that the root of an optimal tree is the kth key in the
list of ordered keys a1,...,a
n.The roots of its left and right subtrees are
specified by R[1,k−1] and R[k+1,n], respectively.
4. Use a space-for-time tradeoff.
5. If the assertion were true, would we not have a simpler algorithm for
constructing an optimal binary search tree?
6. The structure of the tree should simply minimize the average depth of its
nodes. Do not forget to indicate a way to distribute the keys among the
nodes of the tree.
7. a. Since there is a one-to-one correspondence between binary search trees
for a given set of norderable keys and the total number of binary trees
with nnodes (why?), you can count the latter. Consider all the possibil-
ities of partitioning the nodes between the left and right subtrees.
b. Compute the values in question using the two formulas.
c. Use the formula for the nth Catalan number and Stirling’s formula
for n!.
8. Change the bounds of the innermost loop of algorithm OptimalBST by
exploiting the monotonicity of the root table mentioned at the end of
Section 8.3.
9. Assume that a1, ..., anare distinct keys ordered from the smallest to the
largest, p1, ..., pnare the probabilities of searching for them, and q0,q
1,...,q
n
are probabilities of unsuccessful searches for keys in intervals (−∞,a
1),
(a1,a
2), ..., (an,∞),respectively; (p1+... +pn)+(q0+... +qn)=1.
Set up a recurrence relation similar to recurrence (8.11) for the expected
number of key comparisons that takes into account both successful and
unsuccessful searches.
10. a. It is easier to find a general formula for the number of multiplications
needed for computing (A1·A2)·A3and A1·(A2·A3)for matrices A1with
dimensions d0-by-d1,A
2with dimensions d1-by-d2,and A3with dimen-
sions d2-by-d3and then choose some specific values for the dimensions to
get a required example.
20
b. You can get the answer by following the approach used for count-
ing binary trees.
c. The recurrence relation for the optimal number of multiplications in
computing Ai·... ·Ajis very similar to the recurrence relation for the
optimal number of comparisons in searching in a binary tree composed of
keys ai,...,a
j.
21

Solutions to Exercises 8.3
1. The instance of the problem in question is defined by the data
key ABCD
probability 0.1 0.2 0.4 0.3
The table entries for the dynamic programming algorithm are computed
as follows:
C[1,2] = min k=1:C[1,0] + C[2,2] + 2
s=1 ps=0+0.2+0.3=0.5
k=2:C[1,1] + C[3,2] + 2
s=1 ps=0.1+0+0.3=0.4=0.4
C[2,3] = min k=2:C[2,1] + C[3,3] + 3
s=2 ps=0+0.4+0.6=1.0
k=3:C[2,2] + C[4,3] + 3
s=2 ps=0.2+0+0.6=0.8=0.8
C[3,4] = min k=3:C[3,2] + C[4,4] + 4
s=3 ps=0+0.3+0.7=1.0
k=4:C[3,3] + C[5,4] + 4
s=3 ps=0.4+0+0.7=1.1=1.0
C[1,3] = min
k=1:C[1,0] + C[2,3] + 3
s=1 ps=0+0.8+0.7=1.5
k=2:C[1,1] + C[3,3] + 3
s=1 ps=0.1+0.4+0.7=1.2
k=3:C[1,2] + C[4,3] + 3
s=1 ps=0.4+0+0.7=1.1
=1.1
C[2,4] = min
k=2:C[2,1] + C[3,4] + 4
s=2 ps=0+1.0+0.9=1.9
k=3:C[2,2] + C[4,4] + 4
s=2 ps=0.2+0.3+0.9=1.4
k=4:C[2,3] + C[5,4] + 4
s=2 ps=0.8+0+0.9=1.7
=1.1
C[1,4] = min
k=1:C[1,0] + C[2,4] + s=4
s=1 ps=0+1.4+1.0=2.4
k=2:C[1,1] + C[3,4] + 4
s=1 ps=0.1+1.0+1.0=2.1
k=3:C[1,2] + C[4,4] + 4
s=1 ps=0.4+0.3+1.0=1.7
k=4:C[1,3] + C[5,4] + 4
s=1 ps=1.1+0+1.0=2.1
=1.7
the main table
01234
10 0.1 0.4 1.1 1.7
20 0.2 0.8 1.4
30 0.4 1.0
400.3
50
the root table
01234
11233
2233
333
44
5
the optimal tree
C
B D
A
22

2. a. The number of times the innermost loop is executed is given by the
sum
n−1
d=1
n−d
i=1
i+d
k=i
1=
n−1
d=1
n−d
i=1
(i+d−i+1)=
n−1
d=1
n−d
i=1
(d+1)
=
n−1
d=1
(d+1)(n−d)=
n−1
d=1
(dn +n−d2−d)
=
n−1
d=1
nd +
n−1
d=1
n−
n−1
d=1
d2−
n−1
d=1
d
=n(n−1)n
2+n(n−1) −(n−1)n(2n−1)
6−(n−1)n
2
=1
2n3−2
6n3+O(n2)∈Θ(n3).
b. The algorithm generates the (n+1)-by-(n+1) table Cand the n-by-n
table Rand fills about one half of each. Hence, the algorithm’s space
efficiency is in Θ(n2).
3. Call OptimalTree(1,n)below:
Algorithm OptimalTree(i, j)
//Input: Indices iand jof the first and last keys of a sorted list of keys
//composing the tree and table R[1..n, 1..n]obtained by dynamic
//programming
//Output: Indices of nodes of an optimal binary search tree in preorder
if i≤j
k←R[i, j]
print(k)
OptimalTree(i, k −1)
OptimalTree(k+1,j)
4. Precompute Sk=k
s=1 psfor k=1,2,...,nand set S0=0.Then j
s=ips
can be found as Sj−Si−1for any 1≤i≤j≤n.
5. False. Here is a simple counterexample: A(0.3),B(0.3),C(0.4).(The
numbers in the parentheses indicate the search probabilities.) The average
number of comparisons in a binary search tree with Cin its root is 0.3·2
+0.3·3+0.4·1=1.9,while the average number of comparisons in the
binary search tree with Bin its root is 0.3·1+0.3·2+0.4·2=1.7.
23

6. The binary search tree in question should have a maximal number of nodes
on each of its levels except the last one. (For simplicity, we can put all
the nodes of the last level in their leftmost positions possible to make it
complete.) The keys of a given sorted list can be distributed among the
nodes of the binary tree by performing its in-order traversal.
Let p/n be the probability of searching for each key, where 0≤p≤1.
The complete binary tree with 2knodes will have 2inodes on level ifor
i=0, ..., k −1and one node on level k. Hence, the average number of
comparisons in a successful search will be given by the following formula:
C(2k)=
k−1
i=0
(p/2k)(i+1)2
i+(p/2k)(k+1)
=(p/2k)1
2
k−1
i=0
(i+1)2
i+1 +(p/2k)(k+1)
=(p/2k)1
2
k
j=1
j2j+(p/2k)(k+1)
=(p/2k)1
2[(k−1)2k+1 +2]+(p/2k)(k+1)
=(p/2k)[(k−1)2k+k+2].
7. a. Let b(n)be the number of distinct binary trees with nnodes. If the
left subtree of a binary tree with nnodes has knodes (0 ≤k≤n−1),
the right subtree must have n−1−knodes. The number of such trees
is therefore b(k)b(n−1−k).Hence,
b(n)=
n−1
k=0
b(k)b(n−1−k)for n>0,b(0) = 1.
b. Substituting the first five values of ninto the formula above and into
the formula for the nth Catalan number yields the following values:
n0123 4 5
b(n)=c(n)11251442
24

c.
b(n)=c(n)=2n
n1
n+1 =(2n)!
(n!)2
1
n+1
≈√2π2n(2n/e)2n
[√2πn(n/e)n]2
1
n+1 =√4πn(2n/e)2n
2πn(n/e)2n
1
n+1
≈1
√πn 2n/e
n/e 2n1
n+1 =1
√πn22n1
n+1 ∈Θ(4nn−3/2).
This implies that finding an optimal binary search tree by exhaustive
search is feasible only for very small values of nand is, in general, vastly
inferior to the dynamic programming algorithm.
8. The dynamic programming algorithm finds the root akmin of an optimal
binary search tree for keys ai,...,a
jby minimizing {C[i, k−1]+C[k+1,j]}
for i≤k≤j. As pointed out at the end of Section 8.3 (see also [KnuIII],
p. 456, Exercise 27), R[i, j −1] ≤kmin ≤R[i+1,j].This observation
allows us to change the bounds of the algorithm’s innermost loop to the
lower bound of R[i, j −1] and the upper bound of R[i+1,j],respectively.
The number of times the innermost loop of the modified algorithm will
be executed can be estimated as suggested by Knuth (see [KnuIII], p.439):
n−1
d=1
n−d
i=1
R[i+1,j]
k=R[i,j−1]
1=
n−1
d=1
n−d
i=1
R[i+1,i+d]
k=R[i,i+d−1]
1
=
n−1
d=1
n−d
i=1
(R[i+1,i+d]−R[i, i +d−1] + 1)
=
n−1
d=1
(
n−d
i=1
(R[i+1,i+d]−R[i, i +d−1]) +
n−d
i=1
1).
By ”telescoping” the first sum, we can see that all its terms except the
two get cancelled to yield
n−d
i=1 (R[i+1,i+d]−R[i, i +d−1]) =
=(R[2,1+d]−R[1,1+d−1])
+(R[3,2+d]−R[2,2+d−1])
+...
+(R[n−d+1,n−d+d]−R[n−d, n −d+d−1])
=R[n−d+1,n]−R[1,d].
Since the second sum n−d
i=1 1is equal to n−d,weobtain
n−d
i=1
(R[i+1,i+d]−R[i, i+d−1])+
n−d
i=1
1=R[n−d+1,n]−R[1,d]+n−d<2n.
25

Hence,
n−1
d=1
n−d
i=1
R[i+1,j]
k=R[i,j−1]
1=
n−1
d=1
(R[n−d+1,n]−R[1,d]+n−d)<
n−1
d=1
2n<2n2.
On the other hand, since R[i+1,i+d]−R[i, i +d−1] ≥0,
n−1
d=1
n−d
i=1
R[i+1,j]
k=R[i,j−1]
1=
n−1
d=1
n−d
i=1
(R[i+1,i+d]−R[i, i +d−1] + 1)
≥
n−1
d=1
n−d
i=1
1=
n−1
d=1
(n−d)=(n−1)n
2≥1
4n2for n≥2.
Therefore, the time efficiency of the modified algorithm is in Θ(n2).
9. Let a1, ...anbe a sorted list of ndistinct keys, pibe a known probability
of searching for key aifor i=1,2, ..., n, and qibe a known probability of
searching (unsuccessfully) for a key between aiand ai+1 for i=0,1, ..., n
(with q0being a probability of searching for a key smaller than a1and qn
being a probability of searching for a key greater than an). It’s convenient
to associate unsuccessful searches with external nodes of a binary search
tree (see Section 5.4). Repeating the derivation of equation (8.11) for
such a tree yields the following recurrence for the expected number of key
comparisons
C[i, j]= min
i≤k≤j{C[i, k−1]+C[k+1,j]}+
j
s=i
ps+
j
s=i−1
qsfor 1≤i<j≤n
with the initial condition
C[i, i]=pi+qi−1+qifor i=1, ..., n.
In all other respects, the algorithm remains the same.
10. a. Multiplying two matrices of dimensions α-by-βand β-by-γby the
definition-based algorithm requires αβγ multiplications. (There are αγ
elements in the product, each requiring βmultiplications to be computed.)
If the dimensions of A1,A
2,and A3are d0-by-d1,d
1-by-d2,and d2-by-d3,
respectively, then (A1·A2)·A3will require
d0d1d2+d0d2d3=d0d2(d1+d3)
multiplications, while A1·(A2·A3)will need
d1d2d3+d0d1d3=d1d3(d0+d2)
26
multiplications. Here is a simple choice of specific values to make, say,
the first of them be 1,000 times larger than the second:
d0=d2=10
3,d
1=d3=1.
b. Let m(n)be the number of different ways to compute a chain product
of nmatrices A1·... ·An.Any parenthesization of the chain will lead to
multiplying, as the last operation, some product of the first kmatrices
(A1·... ·Ak)and the last n−kmatrices (Ak+1 ·... ·An).There are m(k)
ways to do the former, and there are m(n−k)ways to do the latter.
Hence, we have the following recurrence for the total number of ways to
parenthesize the matrix chain of nmatrices:
m(n)=
n−1
k=1
m(k)m(n−k)for n>1,m(1) = 1.
Since parenthesizing a chain of nmatrices for multiplication is very similar
to constructing a binary tree of nnodes, it should come as no surprise that
the above recurrence is very similar to the recurrence
b(n)=
n−1
k=0
b(k)b(n−1−k)for n>1,b(0) = 1,
for the number of binary trees mentioned in Section 8.3. Nor is it sur-
prising that their solutions are very similar, too: namely,
m(n)=b(n−1) for n≥1,
where b(n)is the number of binary trees with nnodes. Let us prove
this assertion by mathematical induction. The basis checks immediately:
m(1) = b(0) = 1.For the general case, let us assume that m(k)=b(k−1)
for all positive integers not exceeding some positive integer n(we’re using
the strong version of mathematical induction); we’ll show that the equality
holds for n+1as well. Indeed,
m(n+1) =
n
k=1
m(k)m(n+1−k)
=[using the induction’s assumption]
n
k=1
b(k−1)b(n−k)
=[substituting l=k−1]
n−1
l=0
b(l)b(n−1−l)
=[see the recurrence for b(n)]b(n).
27
c. Let M[i, j]be the optimal (smallest) number of multiplications needed
for computing Ai·... ·Aj.If kis an index of the last matrix in the first
factor of the last matrix product, then
M[i, j]= max
1≤k≤j−1{M[i, k]+M[k+1,j]+di−1dkdj}for 1≤i<j≤n,
M[i, i]=0.
This recurrence, which is quite similar to the one for the optimal binary
search tree problem, suggests filling the n+1-by-n+1table diagonal by
diagonal as in the following algorithm:
Algorithm MatrixChainMultiplication(D[0..n])
//Solves matrix chain multiplication problem by dynamic programming
//Input: An array D[0..n]of dimensions of nmatrices
//Output: The minimum number of multiplications needed to multiply
//a chain of nmatrices of the given dimensions and table T[1..n, 1..n]
//for obtaining an optimal order of the multiplications
for i←1to ndo M[i, i]←0
for d←1to n−1do //diagonal count
for i←1to n−ddo
j←i+d
minval ←∞
for k←ito j−1do
temp ←M[i, k]+M[k+1,j]+D[i−1] ∗D[k]∗D[j]
if temp <minval
minval ←temp
kmin ←k
T[i, j]←kmin
return M[1,n],T
To find an optimal order to multiply the matrix chain, call OptimalMulti-
plicationOrder(1,n)below:
Algorithm OptimalOrder (i, j)
//Outputs an optimal order to multiply nmatrices
//Input: Indices iand jof the first and last matrices in Ai...Ajand
// table T[1..n, 1..n]generated by MatrixChainMultiplication
//Output: Ai...Ajparenthesized for optimal multiplication
if i=j
print(“Ai”)
else
k←T[i, j]
print(“(”)
OptimalOrder(i, k)
OptimalOrder(k+1,j)
print(“)”)
28

Exercises 8.4
1. a. Apply the bottom-up dynamic programming algorithm to the following
instance of the knapsack problem:
item weight value
13 $25
22 $20
31 $15
44 $40
55 $50
,capacity W=6.
b. How many different optimal subsets does the instance of part (a) have?
c. In general, how can we use the table generated by the dynamic pro-
grammingalgorithmtotellwhetherthereismorethanoneoptimalsubset
for the knapsack problem’s instance?
2. a. Write a pseudocode of the bottom-up dynamic programming algorithm
for the knapsack problem.
b. Write a pseudocode of the algorithm that finds the composition of
an optimal subset from the table generated by the bottom-up dynamic
programming algorithm for the knapsack problem.
3. For the bottom-up dynamic programming algorithm for the knapsack
problem, prove that
a.itstimeefficiencyisinΘ(nW ).
b. its space efficiency is in Θ(nW ).
c. the time needed to find the composition of an optimal subset from
a filled dynamic programming table is in O(n+W).
4. a. True or false: A sequence of values in a row of the dynamic program-
ming table for an instance of the knapsack problem is always nondecreas-
ing.
b. True or false: A sequence of values in a column of the dynamic pro-
gramming table for an instance of the knapsack problem is always nonde-
creasing?
5. Apply the memory function method to the instance of the knapsack prob-
lem given in Problem 1. Indicate the entries of the dynamic programming
table that are: (i) never computed by the memory function method on
this instance; (ii) retrieved without a recomputation.
29
6. Prove that the efficiency class of the memory function algorithm for the
knapsack problem is the same as that of the bottom-up algorithm (see
Problem 3).
7. Write a pseudocode of a memory function for the optimal binary search
tree problem. (You may limit your function to finding the smallest number
of key comparisons in a successful search.)
8. Give two reasons why the memory function approach is unattractive for
the problem of computing a binomial coefficient.
9. Design a dynamic programming algorithm for the change-making
problem : given an amount nand unlimited quantities of coins of each of
the denominations d1,d
2, ..., dm,find the smallest number of coins that
adduptonor indicate that the problem does not have a solution.
10. Write a research report on one of the following well-known applications
of dynamic programming:
a. finding the longest common subsequence in two sequences
b. optimal string editing
c. minimal triangulation of a polygon
30
Hints to Exercises 8.4
1. a. Use formulas (8.12) and (8.13) to fill in the appropriate table as it is
done for another instance of the problem in this section.
b.—c. What would the equality of the two terms in
max{V[i−1,j],v
i+V[i−1,j−wi]}
mean?
2. a. Write a pseudocode to fill the table in Fig. 8.11 (say, row by row) by
using formulas (8.12) and (8.13).
b. An algorithm for identifying an optimal subset is outlined in the section
via an example.
3. Howmanyvaluesdoesthealgorithmcompute? Howlongdoesittaketo
compute one value? How many table cells need to be traversed to identify
the composition of an optimal subset?
4. Use the definition of V[i, j]to check whether it is always true that
a. V[i, j −1] ≤V[i, j]for 1≤j≤W.
b. V[i−1,j]≤V[i, j]for 1≤i≤n.
5. Trace the calls of the function MemoryKnapsack(i, j)on the instance in
question. (An application to another instance can be found in the section.)
6. The algorithm applies formula (8.12) to fill some of the table’s cells. Why
can we still assert that its efficiencies are in Θ(nW )?
7. Modify the bottom-up algorithm of Section 8.3 in the same manner the
bottom-up algorithm of Section 8.4 was modified there.
8. Oneofthereasonsdealswiththetimeefficiency,theotherdealswiththe
space efficiency.
9. Set up a recurrence for C[i, j],the smallest number of coins in the prob-
lem’s instance with coins of the first idenominations (1 ≤i≤m)and
amount j(0 ≤j≤n).Use +∞as C[i, j]’s value for instances without a
solution.
10. n/a
31

Solutions to Exercises 8.4
1. a. capacity j
i0123456
00000000
w1=3,v
1=25 10 0 0 25252525
w2=2,v
2=20 20 0 20 25 25 45 45
w3=1,v
3=15 30152035404560
w4=4,v
4=40 40152035405560
w5=5,v
5=50 50152035405565
The maximal value of a feasible subset is V[5,6] = 65.The optimal subset
is {item 3, item 5}.
b.-c. The instance has a unique optimal subset in view of the follow-
ing general property: An instance of the knapsack problem has a unique
optimal solution if and only if the algorithm for obtaining an optimal sub-
set, which retraces backward the computation of V[n, W ],encounters no
equality between V[i−1,j]and vi+V[i−1,j−wi]during its operation.
2. a. Algorithm DPKnapsack(w[1..n],v[1..n],W)
//Solves the knapsack problem by dynamic programming (bottom up)
//Input: Arrays w[1..n]and v[1..n]of weights and values of nitems,
// knapsack capacity W
//Output: Table V[0..n, 0..W ]that contains the value of an optimal
// subset in V[n, W ]and from which the items of an optimal
// subset can be found
for i←0to ndo V[i, 0] ←0
for j←1to Wdo V[0,j]←0
for i←1to ndo
for j←1to Wdo
if j−w[i]≥0
V[i, j]←max{V[i−1,j],v[i]+V[i−1,j−w[i]]}
else V[i, j]←V[i−1,j]
return V[n, W ],V
b. Algorithm OptimalKnapsack (w[1..n],v[1..n],W)
//Finds the items composing an optimal solution to the knapsack problem
//Input: Arrays w[1..n]and v[1..n]of weights and values of nitems,
// knapsack capacity W, and table V[0..n, 0..W ]generated by
// the dynamic programming algorithm
//Output: List L[1..k]of the items composing an optimal solution
k←0//size of the list of items in an optimal solution
j←W//unused capacity
32
for i←ndownto 1do
if V[i, j]>V[i−1,j]
k←k+1; L[k]←i//include item i
j←j−w[i]
return L
Note: In fact, we can also stop the algorithm as soon as j, the unused
capacity of the knapsack, becomes 0.
3. The algorithm fills a table with n+1rows and W+1 columns, spending
Θ(1) time to fill one cell (either by applying (8.12) or (8.13). Hence, its
time efficiency and its space efficiency are in Θ(nW ).
In order to identify the composition of an optimal subset, the algorithm
repeatedly compares values at no more than two cells in a previous row.
Hence, its time efficiency class is in O(n).
4. Both assertions are true:
a. V[i, j −1] ≤V[i, j]for 1≤j≤Wis true because it simply means that
the maximal value of a subset that fits into a knapsack of capacity j−1
cannot exceed the maximal value of a subset that fits into a knapsack of
capacity j.
b. V[i−1,j]≤V[i, j]for 1≤i≤nis true because it simply means
that the maximal value of a subset of the first i−1items that fits into
a knapsack of capacity jcannot exceed the maximal value of a subset of
the first iitems that fits into a knapsack of the same capacity j.
5. In the table below, the cells marked by a minus indicate the ones for which
no entry is computed for the instance in question; the only nontrivial entry
that is retrieved without recomputation is (2,1).
capacity j
i0123456
0 0 000000
w1=3,v
1=25 100 025252525
w2=2,v
2=20 20020--45 45
w3=1,v
3=15 3 0 15 20 ---60
w4=4,v
4=40 4 0 15 ----60
w5=5,v
5=50 5 0 -----65
6. Since some of the cells of a table with n+1 rows and W+1 columns
are filled in constant time, both the time and space efficiencies are in
33
O(nW ).But all the entries of the table need to be initialized (unless
virtual initialization is used); this puts them in Ω(nW ).Hence, both
efficiencies are in Θ(nW ).
7. Algorithm MFOptimalBST (i, j)
//Returns the number of comparisons in a successful search in a BST
//Input: Indices i, j indicating the range of keys in a sorted list of nkeys
//and an array P[1..n]of search probabilities used as a global variable
//Uses a global table C[1..n +1,0..n]initialized with a negative number
//Output: The average number of comparisons in the optimal BST
if j=i−1return 0
if j=ireturn P[i]
if C[i, j]<0
minval ←∞
for k←ito jdo
temp ←MFOptimalBST (i, k −1)+MFOptimalBST (k+1,j)
if temp < minval
minval ←temp
sum ←0; for s←ito jdo sum ←sum +P[s]
C[i, j]←minval +sum
return C[i, j]
Note: The first two lines of this pseudocode can be eliminated by an
appropriate initialization of table C.
8. For the problem of computing a binomial coefficient, we know in advance
what cells of the table need to be computed. Therefore unnecessary
computations can be avoided by the bottom-up dynamic programming
algorithm as well. Also, using the memory function method requires
Θ(nk)space, whereas the bottom-up algorithm needs only Θ(n)because
the next row of the table can be written over its immediate predecessor.
9. Let C[i, j]be the smallest number of coins in the problem’s instance with
coins of the first idenominations (1 ≤i≤m)and amount j(0 ≤j≤n).
We will use +∞as C[i, j]’s value for instances without a solution. We
have the following recurrence relation for C[i, j]:
C[i, j]=min{[C[i−1,j],1+C[i, j −di]}for 1≤i≤m, 1≤j≤n
C[i, 0] = 0 for 1≤i≤m.
(In the recurrence above, we assume that C[i−1,j]=+∞if i=1and
C[i, j −di]=+∞if j−di<0.)The following pseudocode fills the m-by-
(n+1) dynamic programing table, which will contain the smallest number
of coins in C[m, n].
34
Algorithm MinimumChange(D[1..m],n)
//Solves the change-making problem by dynamic programming
//Input: Array D[1..m]of positive numbers (coin denominations) and
// positive integer n(amount)
//Output: The smallest number of coins adding up to n
//Note: Assumes that ∞+1=∞
for i←1to mdo C[i, 0] = 0
for i←1to mdo
for j←1to ndo
if i=1
if j<D[1] C[1,j]=∞
else C[1,j]=1+C[1,j−D[1]]
else // i>1
if j<D[i]C[i, j]=C[i−1,j]
else C[i, j]=min{[C[i−1,j],1+C[i, j −D[i]]}
return C[m, n]//C[m, n]=∞signifies solution absence
The composition of an optimal solution can be easily obtained from the dy-
namic programming table by calling OptimalCoins(D[1..m],C[1..m, 0..n],m,n)
below:
Algorithm OptimalCoins(D[1..m],C[1..m, 0..n],i,j)
//Finds the coins composing an optimal change
//Input: Arrays D[1..m]of coin denominations, table C[1..m, 0..n]
//generated by the dynamic programming algorithm for amount n,
// integers i(1 ≤i≤m)and j(1 ≤j≤n)
//Output: List L[1..i]of coins composing an optimal solution to
//the change problem for the first idenominations and amount j
for k←1to ido L[k]←0
if C[i, j]<∞
while i>0and j>0do
if C[i, j]=C[i−1,j]
i←i−1
else
L[i]←L[i]+1 //add one coin of denomination D[i]
j←j−D[i]
return L
10. n/a
35
This file contains the exercises, hints, and solutions for Chapter 9 of the
book ”Introduction to the Design and Analysis of Algorithms,” 2nd edition, by
A. Levitin. The problems that might be challenging for at least some students
are marked by ;those that might be difficult for a majority of students are
marked by .
Exercises 9.1
1. Give an instance of the change-making problem for which the greedy al-
gorithm does not yield an optimal solution.
2. Write a pseudocode of the greedy algorithm for the change-making prob-
lem, with an amount nand coin denominations d1>d
2>...>d
mas its
input. What is the time efficiency class of your algorithm?
3. Consider the problem of scheduling njobs of known durations t1, ..., tnfor
execution by a single processor. The jobs can be executed in any order,
one job at a time. You want to find a schedule that minimizes the total
time spent by all the jobs in the system. (The time spent by one job in
the system is the sum of the time spent by this job in waiting plus the
time spent on its execution.)
Design a greedy algorithm for this problem. Does the greedy algo-
rithm always yield an optimal solution?
4. Design a greedy algorithm for the assignment problem (see Section 3.4).
Does your greedy algorithm always yield an optimal solution?
5. Bridge crossing revisited Consider the generalization of the bridge cross-
ing puzzle (Problem 2 in Exercises 1.2) in which we have n>1people
whose bridge crossing times are t1,t
2, ..., tn.All the other conditions of
the problem remain the same: at most two people at the time can cross
thebridge(andtheymovewiththespeedoftheslowerofthetwo)and
they must carry with them the only flashlight the group has.
Design a greedy algorithm for this problem and find how long it will
take to cross the bridge by using this algorithm. Does your algorithm
yields a minimum crossing time for every instance of the problem? If it
does–prove it, if it does not–find an instance with the smallest number
of people for which this happens.
6. Bachet-Fibonacci weighing problem Find an optimal set of nweights
{w1,w
2, ..., wn}so that it would be possible to weigh on a balance scale
any integer load in the largest possible range from 1 to W, provided
a.weights can be put only on the free cup of the scale.
b.weights can be put on both cups of the scale.
1
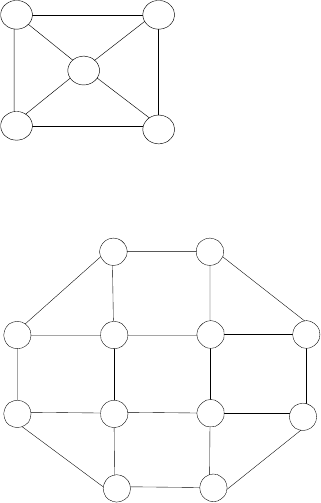
7. a. Apply Prim’s algorithm to the following graph. Include in the priority
queue all the vertices not already in the tree.
c
a b
d
5
4
76
e
23
45
b. Apply Prim’s algorithm to the following graph. Include in the priority
queue only the fringe vertices (the vertices not in the current tree which
are adjacent to at least one tree vertex).
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
8. The notion of a minimum spanning tree is applicable to a connected
weighted graph. Do we have to check a graph’s connectivity before ap-
plying Prim’s algorithm or can the algorithm do it by itself?
9. a. How can we use Prim’s algorithm to find a spanning tree of a connected
graph with no weights on its edges?
b. Is it a good algorithm for this problem?
10. Prove that any weighted connected graph with distinct weights has
exactly one minimum spanning tree.
11. Outline an efficient algorithm for changing an element’s value in a min-
heap. What is the time efficiency of your algorithm?
2
Hints to Exercises 9.1
1. As coin denominations for your counterexample, you may use, among a
multitude of other possibilities, the ones mentioned in the text: d1=7,
d2=5,d
3=1.
2. You may use integer divisions in your algorithm.
3. Considering the case of two jobs might help. Of course, after forming a
hypothesis, you will have to either prove the algorithm’s optimality for an
arbitrary input or find a specific counterexample showing that it is not
the case.
4. You can apply the greedy approach either to the entire cost matrix or to
each of its rows (or columns).
5. Simply apply the greedy approach to the situation at hand. You may
assume that t1≤t2≤... ≤tn.
6. For both versions of the problem, it is not difficult to get to a hypothesis
about the solution’s form after considering the cases of n=1,2,and 3.
It is proving the solutions’ optimality that is at the heart of this problem.
7. a. Trace the algorithm for the graph given. An example can be found in
the text of the section.
b. After the next fringe vertex is added to the tree, add all the unseen
vertices adjacent to it to the priority queue of fringe vertices.
8. Applying Prim’s algorithm to a weighted graph that is not connected
should help in answering this question.
9. a. Since Prim’s algorithm needs weights on a graph’s edges, some weights
have to be assigned.
b. Do you know other algorithms that can solve this problem?
10. Strictly speaking, the wording of the question asks you to prove two things:
the fact that at least one minimum spanning tree exists for any weighted
connected graph and the fact that a minimum spanning tree is unique
if all the weights are distinct numbers. The proof of the former stems
from the obvious observation about finiteness of the number of spanning
trees for a weighted connected graph. The proof of the latter can be
obtained by repeating the correctness proof of Prim’s algorithm with a
minor adjustment at the end.
11. Consider two cases: the key’s value was decreased (this is the case needed
for Prim’s algorithm) and the key’s value was increased.
3

Solutions to Exercises 9.1
1. Here is one of many such instances: For the coin denominations d1=7,
d2=5,d
3=1and the amount n=10,the greedy algorithm yields one
coin of denomination 7and three coins of denomination 1.Theactual
optimal solution is two coins of denomination 5.
2. Algorithm Change(n, D[1..m])
//Implements the greedy algorithm for the change-making problem
//Input: A nonnegative integer amount nand
// a decreasing array of coin denominations D
//Output: Array C[1..m]of the number of coins of each denomination
// in the change or the ”no solution” message
for i←1to mdo
C[i]←n/D[i]
n←nmod D[i]
if n=0 return C
else return ”no solution”
The algorithm’s time efficiency is in Θ(m).(We assume that integer di-
visions take a constant time no matter how big dividends are.) Note also
that if we stop the algorithm as soon as the remaining amount becomes
0, the time efficiency will be in O(m).
3. a. Sort the jobs in nondecreasing order of their execution times and exe-
cute them in that order.
b. Yes, this greedy algorithm always yields an optimal solution.
Indeed, for any ordering (i.e., permutation) of the jobs i1,i
2, ..., in,the
total time in the system is given by the formula
ti+(ti+ti)+... +(ti+ti+... +ti)=nti+(n−1)ti+... +ti.
Thus, we have a sum of numbers n, n −1,...,1 multiplied by “weights” t1,
t2,...tnassigned to the numbers in some order. To minimize such a sum,
we have to assign smaller t’s to larger numbers. In other words, the jobs
should be executed in nondecreasing order of their execution times.
Here is a more formal proof of this fact. We will show that if jobs are ex-
ecuted in some order i1,i
2, ..., in,inwhichti>t
ifor some k, then the
total time in the system for such an ordering can be decreased. (Hence,
no such ordering can be an optimal solution.) Let us consider the other
job ordering, which is obtained by swapping the jobs kand k+1.Obvi-
ously, the time in the systems will remain the same for all but these two
4
jobs. Therefore, the difference between the total time in the system for
the new ordering and the one before the swap will be
[(
k−1
j=1
ti+ti)+(
k−1
j=1
ti+ti+ti)] −[(
k−1
j=1
ti+ti)+(
k−1
j=1
ti+ti+ti)]
=ti−ti<0.
4. a. The all-matrix version: Repeat the following operation ntimes. Select
the smallest element in the unmarked rows and columns of the cost matrix
and then mark its row and column.
The row-by-row version: Starting with the first row and ending with the
last row of the cost matrix, select the smallest element in that row which
is not in a previously marked column. After such an element is selected,
mark its column to prevent selecting another element from the same col-
umn.
b. Neither of the versions always yields an optimal solution. Here is
a simple counterexample:
C=12
2100
5. Repeat the following step n−2times: Send to the other side the pair of two
fastest remaining persons and then return the flashlight with the fastest
person. Finally, send the remaining two people together. Assuming that
t1≤t2≤... ≤tn,the total crossing time will be equal to
(t2+t1)+(t3+t1)+...+(tn−1+t1)+tn=
n
i=2
ti+(n−2)t1=
n
i=1
ti+(n−3)t1.
Note: For an algorithm that always yields a minimal crossing time, see
Günter Rote, “Crossing the Bridge at Night,” EATCS Bulletin, vol. 78
(October 2002), 241—246.
The solution to the instance of Problem 2 in Exercises 1.2 shows that the
greedy algorithm doesn’t always yield the minimal crossing time for n>3.
No smaller counterexample can be given as a simple exhaustive check for
n=3demonstrates. (The obvious solution for n=2is the one generated
by the greedy algorithm as well.)
5

6. a. Let’s apply the greedy approach to the first few instances of the problem
in question. For n=1,we have to use w1=1to balance weight 1.For
n=2,we simply add w2=2to balance the first previously unattainable
weight of 2.The weights {1,2}can balance every integral weights up to
their sum 3. For n=3,in the spirit of greedy thinking, we take the next
previously unattainable weight: w3=4.The three weights {1,2,4}allow
to weigh any integral load lbetween 1 and their sum 7, with l’s binary
expansion indicating the weights needed for load l:
load l1 2 3 4 5 6 7
l’s binary expansion 1 10 11 100 101 110 111
weights for load l1 2 2+1 44+1 4+2 4+2+1
Generalizing these observations, we should hypothesize that for any posi-
tive integer nthe set of consecutive powers of 2 {wi=2
i−1,i=1,2, ...n}
makes it possible to balance every integral load in the largest possible
range, which is up to and including n
i=1 2i−1=2
n−1.The fact that
every integral weight lin the range1≤l≤2n−1can be balanced with this
set of weights follows immediately from the binary expansion of l, which
yields the weights needed for weighing l. (Notethatwecanobtainthe
weights needed for a given load lby applying to it the greedy algorithm for
the change-making problem with denominations di=2
i−1,i=1,2,...n.)
In order to prove that no set of nweights can cover a larger range of
consecutive integral loads, it will suffice to note that there are just 2n−1
nonempty selections of nweights and, hence, no more than 2n−1sums
they yield. Therefore, the largest range of consecutive integral loads they
can cover cannot exceed 2n−1.
[Alternatively, to prove that no set of nweights can cover a larger range of
consecutive integral loads, we can prove by induction on ithat if any mul-
tiset of nweights {wi,i=1, ..., n}–which we can assume without loss of
generality to be sorted in nondecreasing order–can balance every integral
load starting with 1, then wi≤2i−1for i=1,2, ..., n. The basis checks
out immediately: w1must be 1, which is equal to 21−1.For the general
case, assume that wk≤2k−1for every 1≤k<i. The largest weight the
first i−1weights can balance is i−1
k=1 wk≤i−1
k=1 2k−1=2
i−1−1.If
wiwere larger than 2i,then this load could have been balanced neither
with the first i−1weights (which are too light even taken together) nor
with the weights wi≤... ≤wn(which are heavier than 2ieven individ-
ually). Hence, wi≤2i−1,which completes the proof by induction. This
immediately implies that no nweights can balance every integral load up
to the upper limit larger than n
i=1 wi≤n
i=1 2i−1=2
n−1,the limit
attainable with the consecutive powers of 2 weights.]
b. If weights can be put on both cups of the scale, then a larger range can
6
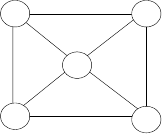
be reached with nweights for n>1.(For n=1,the single weight still
needs to be 1, of course.) The weights {1,3}enable weighing of every
integral load up to 4; the weights {1,3,9}enable weighing of every inte-
gral load up to 13, and, in general, the weights {wi=3
i−1,i=1,2, ..., n}
enable weighing of every integral load up to and including their sum of
n
i=1 3i−1=(3
n−1)/2.A load’s expansion in the ternary system indicates
the weights needed. If the ternary expansion contains only 0’s and 1’s, the
load requires putting the weights corresponding to the 1’s on the opposite
cup of the balance. If the ternary expansion of load l, l ≤(3n−1)/2,
contains one or more 2’s, we can replace each 2 by (3-1) to represent it in
the form
l=
n
i=1
βi3i−1,where βi∈{0,1,−1},n=log3(l+1).
In fact, every positive integer can be uniquely represented in this form,
obtained from its ternary expansion as described above. For example,
5=12
3=1·31+2·30=1·31+(3−1) ·30=2·31−1·30
=(3−1) ·31−1·30=1·32−1·31−1·30.
(Note that if we start with the rightmost 2, after a simplification, the new
rightmost 2, if any, will be at some position to the left of the starting one.
This proves that after a finite number of such replacements, we will be
able to eliminate all the 2’s.) Using the representation l=n
i=1 βi3i−1,
we can weigh load lby placing all the weights wi=3
i−1for negative βi’s
along with the load on one cup of the scale and all the weights wi=3
i−1
for positive βi’s on the opposite cup.
Now we’ll prove that no set of nweights can cover a larger range of con-
secutive integral loads than (3n−1)/2.Each of the nweights can be either
put on the left cup of the scale, or put on the right cup, or not to be used
at all. Hence, there are 3n−1possible arrangements of the weights on the
scale, with each of them having its mirror image (where all the weights are
switched to the opposite pan of the scale). Eliminating this symmetry,
leaves us with
just (3n−1)/2arrangements, which can weight at most (3n−1)/2different
integral loads. Therefore, the largest range of consecutive integral loads
they can cover cannot exceed (3n−1)/2.
7. a. Apply Prim’s algorithm to the following graph:
c
a b
d
5
4
76
e
23
45
7
Tree vertices Priority queue of remaining vertices
a(-,-) b(a,5) c(a,7) d(a,∞)e(a,2)
e(a,2) b(e,3) c(e,4) d(e,5)
b(e,3) c(e,4) d(e,5)
c(e,4) d(c,4)
d(c,4)
The minimum spanning tree found by the algorithm comprises the edges
ae, eb, ec, and cd.
b. Apply Prim’s algorithm to the following graph:
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
Tree vertices Priority queue of fringe vertices
a(-,-) b(a,3) c(a,5) d(a,4)
b(a,3) c(a,5) d(a,4) e(b,3) f(b,6)
e(b,3) c(a,5) d(e,1) f(e,2) i(e,4)
d(e,1) c(d,2) f(e,2) i(e,4) h(d,5)
c(d,2) f(e,2) i(e,4) h(d,5) g(c,4)
f(e,2) i(e,4) h(d,5) g(c,4) j(f,5)
i(e,4) h(d,5) g(c,4) j(i,3) l(i,5)
j(i,3) h(d,5) g(c,4) l(i,5)
g(c,4) h(g,3) l(i,5) k(g,6)
h(g,3) l(i,5) k(g,6)
l(i,5) k(g,6)
k(g,6)
The minimum spanning tree found by the algorithm comprises the edges
ab, be, ed, dc, ef, ei, ij, cg, gh, il, gk.
8. There is no need to check the graph’s connectivity because Prim’s algo-
rithm can do it itself. If the algorithm reaches all the graph’s vertices
(via edges of finite lengths), the graph is connected, otherwise, it is not.
9. a. The simplest and most logical solution is to assign all the edge weights
to 1.
8
b. Applying a depth-first search (or breadth-first search) traversal to get
a depth-first search tree (or a breadth-first search tree), is conceptually
simpler and for sparse graphs represented by their adjacency lists faster.
10. The number of spanning trees for any weighted connected graph is a pos-
itive finite number. (At least one spanning tree exists, e.g., the one
obtained by a depth-first search traversal of the graph. And the number
of spanning trees must be finite because any such tree comprises a subset
of edges of the finite set of edges of the given graph.) Hence, one can
always find a spanning tree with the smallest total weight among the finite
number of the candidates.
Let’s prove now that the minimum spanning tree is unique if all the weights
are distinct. We’ll do this by contradiction, i.e., by assuming that there
exists a graph G=(V,E)with all distinct weights but with more than
one minimum spanning tree. Let e1, ..., e|V|−1be the list of edges com-
posing the minimum spanning tree TPobtained by Prim’s algorithm with
some specific vertex as the algorithm’s starting point and let Tbe an-
other minimum spanning tree. Let ei=(v, u)be the first edge in the list
e1, ..., e|V|−1of the edges of TPwhichisnotinT(if TP=T,such edge
must exist) and let (v, u)be an edge of Tconnecting vwith a vertex
not in the subtree Ti−1formed by {e1, ..., ei−1}(if i=1,T
i−1consists of
vertex vonly). Similarly to the proof of Prim’s algorithms correctness,
let us replace (v, u)by ei=(v, u)in T.It will create another spanning
tree, whose weight is smaller than the weight of Tbecause the weight
of ei=(v, u)is smaller than the weight of (v, u).(Since eiwas chosen
by Prim’s algorithm, its weight is the smallest among all the weights on
the edges connecting the tree vertices of the subtree Ti−1and the vertices
adjacent to it. And since all the weights are distinct, the weight of (v, u)
must be strictly greater than the weight of ei=(v, u).)This contradicts
the assumption that Twas a minimum spanning tree.
11. If a key’s value in a min-heap was decreased, it may need to be pushed
up (via swaps) along the chain of its ancestors until it is smaller than or
equal to its parent or reaches the root. If a key’s value in a min-heap was
increased, it may need to be pushed down by swaps with the smaller of its
current children until it is smaller than or equal to its children or reaches a
leaf. Since the height of a min-heap with nnodes is equal to log2n(by
the same reason the height of a max-heap is given by this formula–see
Section 6.4), the operation’s efficiency is in O(log n).(Note: The old value
of the key in question need not be known, of course. Comparing the new
value with that of the parent and, if the min-heap condition holds, with
the smaller of the two children, will suffice.)
9
Exercises 9.2
1. Apply Kruskal’s algorithm to find a minimum spanning tree of the follow-
ing graphs.
a.
a
b
d
1c
e
5
62
6
34
b.
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
2. Indicate whether the following statements are true or false:
a. If eis a minimum-weight edge in a connected weighted graph, it must
be among edges of at least one minimum spanning tree of the graph.
b. If eis a minimum-weight edge in a connected weighted graph, it must
be among edges of each minimum spanning tree of the graph.
c. If edge weights of a connected weighted graph are all distinct, the
graph must have exactly one minimum spanning tree.
d. If edge weights of a connected weighted graph are not all distinct,
the graph must have more than one minimum spanning tree.
3. What changes, if any, need to be made in algorithm Kruskal to make it
find a minimum spanning forest for an arbitrary graph? (A minimum
spanning forest is a forest whose trees are minimum spanning trees of the
graph’s connected components.)
10
4. Will either Kruskal’s or Prim’s algorithm work correctly on graphs that
have negative edge weights?
5. Design an algorithm for finding a maximum spanning tree–a spanning
tree with the largest possible edge weight–of a weighted connected graph.
6. Rewrite the pseudocode of Kruskal’s algorithm in terms of the operations
of the disjoint subsets’ ADT.
7. Prove the correctness of Kruskal’s algorithm.
8. Prove that the time efficiency of find(x)is in O(log n)for the union-by-size
version of quick union.
9. Find at least two Web sites with animations of Kruskal’s and Prim’s al-
gorithms. Discuss their merits and demerits..
10. Design and conduct an experiment to empirically compare the efficiencies
of Prim’s and Kruskal’s algorithms on random graphs of different sizes
and densities.
11. Steiner tree Four villages are located at the vertices of a unit square
in the Euclidean plane. You are asked to connect them by the shortest
network of roads so that there is a path between every pair of the villages
along those roads. Find such a network.
11
Hints to Exercises 9.2
1. Trace the algorithm for the given graphs the same way it is done for
another input in the section.
2. Two of the four assertions are true, the other two are false.
3. Applying Kruskal’s algorithm to a disconnected graph should help to an-
swer the question.
4. The answer is the same for both algorithms. If you believe that the
algorithms work correctly on graphs with negative weights, prove this
assertion; it you believe this is not to be the case, give a counterexample
for each algorithm.
5. Is the general trick of transforming maximization problems to their mini-
mization counterparts (see Section 6.6) applicable here?
6. Substitute the three operations of the disjoint subsets’ ADT–makeset(x),
find(x),and union(x, y)–in the appropriate places of the pseudocode
given in the section.
7. Follow the plan used in Section 9.1 to prove the correctness of Prim’s
algorithm.
8. The argument is very similar to the one made in the section for the union-
by-size version of quick find.
9. You may want to take advantage of the list of desirable characteristics in
algorithm visualizations, which is given in Section 2.7.
10. n/a
11. The question is not trivial because introducing extra points (called Steiner
points ) may make the total length of the network smaller than that of a
minimum spanning tree of the square. Solving first the problem for three
equidistant points might give you an indication how a solution to the
problem in question could look like.
12
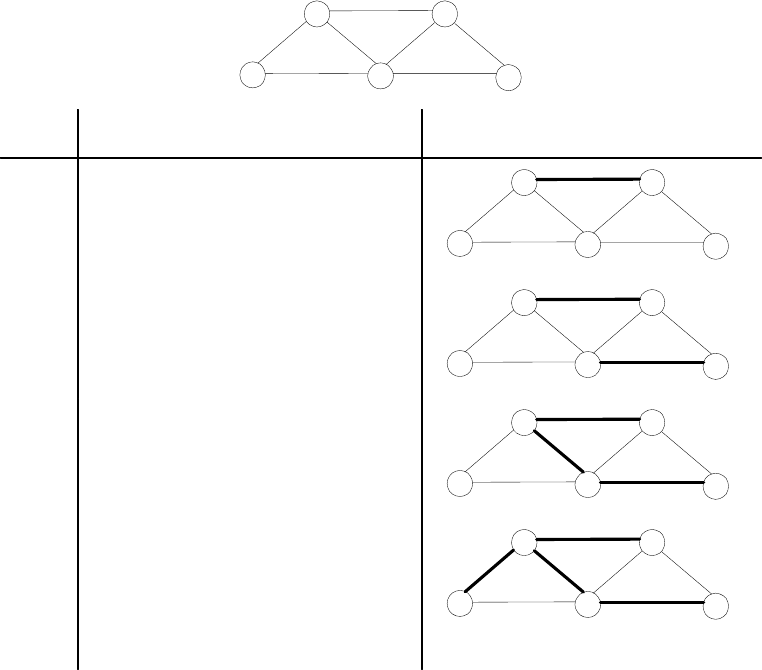
Solutions to Exercises 9.2
1. a.
a
b
d
1c
e
5
62
6
34
Tree Sorted list of edges Illustration
edges (selected edges are shown in bold)
bc
1de
2bd
3cd
4ab
5ad
6ce
6a
b
d
1c
e
5
62
6
34
bc
1bc
1de
2bd
3cd
4ab
5ad
6ce
6a
b
d
1c
e
5
62
6
34
de
2bc
1de
2bd
3cd
4ab
5ad
6ce
6a
b
d
1c
e
5
62
6
34
bd
3bc
1de
2bd
3cd
4ab
5ad
6ce
6a
b
d
1c
e
5
62
6
34
ab
5
13
b.
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
⇒
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
⇒
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
⇒
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
⇒
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
⇒
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
⇒
14
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
⇒
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
⇒
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
⇒
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
⇒
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
⇒
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
2. a. True. (Otherwise, Kruskal’s algorithm would be invalid.)
b. False. As a simple counterexample, consider a complete graph with
three vertices and the same weight on its three edges
c. True (Problem 10 in Exercises 9.1).
15

d. False (see, for example, the graph of Problem 1a).
3. Since the number of edges in a minimum spanning forest of a graph with
|V|vertices and |C|connected components is equal to |V|−|C|(this for-
mula is a simple generalization of |E|=|V|−1for connected graphs),
Kruskal(G) will never get to |V|−1tree edges unless the graph is con-
nected. A simple remedy is to replace the loop while ecounter < |V|−1
with while k<|E|to make the algorithm stop after exhausting the sorted
list of its edges.
4. Both algorithms work correctly for graphs with negative edge weights.
One way of showing this is to add to all the weights of a graph with
negative weights some large positive number. This makes all the new
weights positive, and one can “translate” the algorithms’ actions on the
new graph to the corresponding actions on the old one. Alternatively,
you can check that the proofs justifying the algorithms’ correctness do
not depend on the edge weights being nonnegative.
5. Replace each weight w(u, v)by −w(u, v)and apply any minimum spanning
tree algorithm that works on graphs with arbitrary weights (e.g., Prim’s
or Kruskal’s algorithm) to the graph with the new weights.
6. Algorithm Kruskal(G)
//Kruskal’s algorithm with explicit disjoint-subsets operations
//Input: A weighted connected graph G=V,E
//Output: ET, the set of edges composing a minimum spanning tree of G
sort Ein nondecreasing order of the edge weights w(ei)≤... ≤w(ei)
for each vertex v∈Vmake(v)
ET←∅;ecounter ←0//initialize the set of tree edges and its size
k←0//the number of processed edges
while ecounter < |V|−1
k←k+1
if find(u)=find (v)//u, v are the endpoints of edge ei
ET←ET∪{ei};ecounter ←ecounter +1
union(u, v)
return ET
7. Let us prove by induction that each of the forests Fi,i=0, ..., |V|−1,of
Kruskal’s algorithm is a part (i.e., a subgraph) of some minimum span-
ning tree. (This immediately implies, of course, that the last forest in the
sequence, F|V|−1,is a minimum spanning tree itself. Indeed, it contains
all vertices of the graph, and it is connected because it is both acyclic
and has |V|−1edges.) The basis of the induction is trivial, since F0is
16
made up of |V|single-vertex trees and therefore must be a subgraph of
any spanning tree of the graph. For the inductive step, let us assume that
Fi−1is a subgraph of some minimum spanning tree T. We need to prove
that Fi,generated from Fi−1by Kruskal’s algorithm, is also a part of a
minimum spanning tree. We prove this by contradiction by assuming that
no minimum spanning tree of the graph can contain Fi.Letei=(v, u)
be the minimum weight edge added by Kruskal’s algorithm to forest Fi−1
to obtain forest Fi.(Note that vertices vand umust belong to different
trees of Fi−1–otherwise, edge (v, u)would’ve created a cycle.) By our
assumption, eicannot belong to T. Therefore, if we add eito T, a cycle
must be formed (see the figure below). In addition to edge ei=(v, u),
this cycle must contain another edge (v,u
)connecting a vertex vin the
same tree of Fi−1as vto a vertex unot in that tree. (It is possible
that vcoincides with vor ucoincides with ubut not both.) If we now
delete the edge (v,u
)from this cycle, we will obtain another spanning
tree of the entire graph whose weight is less than or equal to the weight
of Tsince the weight of eiis less than or equal to the weight of (v,u
).
Hence, this spanning tree is a minimum spanning tree, which contradicts
the assumption that no minimum spanning tree contains Fi.This com-
pletes the correctness proof of Kruskal’s algorithm.
ei
v'
v
u'
u
8. In the union-by-size version of quick-union, each vertex starts at depth
0 of its own tree. The depth of a vertex increases by 1 when the tree
it is in is attached to a tree with at least as many nodes during a union
operation. Since the total number of nodes in the new tree containing
the node is at least twice as much as in the old one, the number of such
increases cannot exceed log2n. Therefore the height of any tree (which is
the largest depth of the tree’s nodes) generated by a legitimate sequence
of unions will not exceed log2n. Hence, the efficiency of find(x)is in
O(log n)because find(x)traverses the pointer chain from the x’s node to
the tree’s root.
9. n/a
10. n/a
17
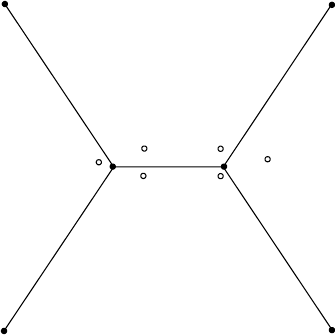
11. The minimum Steiner tree that solves the problem is shown below. (The
other solution can be obtained by rotating the figure 90◦.)
120 120
120 120
120 120
ab
dc
A popular discussion of Steiner trees can be found in “Last Recreations:
Hydras, Eggs, and Other Mathematical Mystifications” by Martin Gard-
ner. In general, no polynomial time algorithm is known for finding a
minimum Steiner tree; moreover, the problem is known to be NP-hard
(see Section 11.3). For the state-of-the-art information, see, e.g., The
Steiner Tree Page at http://ganley.org/steiner/.
18
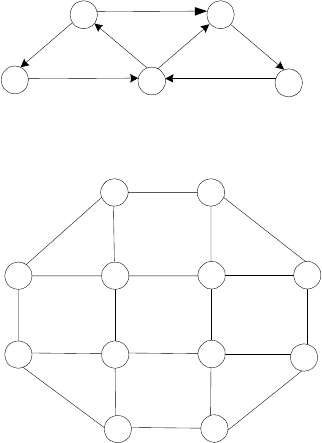
Exercises 9.3
1. Explain what adjustments if any need to be made in Dijkstra’s algorithm
and/or in an underlying graph to solve the following problems.
a. Solve the single-source shortest-paths problem for directed weighted
graphs.
b. Find a shortest path between two given vertices of a weighted graph or
digraph. (This variation is called the single-pair shortest-path prob-
lem.)
c. Find the shortest paths to a given vertex from each other vertex
of a weighted graph or digraph. (This variation is called the single-
destination shortest-paths problem.)
d. Solve the single-source shortest-path problem in a graph with nonneg-
ative numbers assigned to its vertices (and the length of a path defined as
the sum of the vertex numbers on the path).
2. Solve the following instances of the single-source shortest-paths problem
with vertex aas the source:
a.
a
b
d
4c
e
3
74
6
25
b.
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
3. Give a counterexample that shows that Dijkstra’s algorithm may not work
for a weighted connected graph with negative weights.
19
4. Let Tbe a tree constructed by Dijkstra’s algorithm in the process of
solving the single-source shortest-path problem for a weighted connected
graph G.
a. True or false: Tis a spanning tree of G?
b. True or false: Tis a minimum spanning tree of G?
5. Write a pseudocode of a simpler version of Dijkstra’s algorithm that finds
only the distances (i.e., the lengths of shortest paths but not shortest paths
themselves) from a given vertex to all other vertices of a graph represented
by its weight matrix.
6. Prove the correctness of Dijkstra’s algorithm for graphs with positive
weights.
7. Design a linear-time algorithm for solving the single-source shortest-paths
problem for dags (directed acyclic graphs) represented by their adjacency
lists.
8. Design an efficient algorithm for finding the length of a longest path in a
dag. (This problem is important because it determines a lower bound on
the total time needed for completing a project composed of precedence-
constrained tasks.)
9. Shortest-path modeling Assume you have a model of a weighted con-
nected graph made of balls (representing the vertices) connected by strings
of appropriate lengths (representing the edges).
a. Describe how you can solve the single-pair shortest-path problem with
this model.
b. Describe how you can solve the single-source shortest-paths problem
with this model.
10. Revisit Problem 6 in Exercises 1.3 about determining the best route for
a subway passenger to take from one designated station to another in a
well-developed subway system like those in Washington, DC and London,
UK. Write a program for this task.
20
Hints to Exercises 9.3
1. One of the questions requires no changes in either the algorithm or the
graph; the others require simple adjustments.
2. Just trace the algorithm on the given graphs the same way it is done for
an example in the section.
3. The nearest vertex does not have to be adjacent to the source in such a
graph.
4. Only one of the assertions is correct. Find a small counterexample for
the other.
5. Simplify the pseudocode given in the section by implementing the priority
queue as an unordered array and ignoring the parental labeling of vertices.
6. Prove it by induction on the number of vertices included in the tree con-
structed by the algorithm.
7. Topologically sort the dag’s vertices first.
8. Topologically sort the dag’s vertices first.
9. Take advantage of the ways of thinking used in geometry and physics.
10. Before you embark on implementing a shortest-path algorithm, you have
to decide what criterion determines the “best route”. Of course, it would
be highly desirable to have a program asking the user which of several
possible criteria he or she wants applied.
21
Solutions to Exercises 9.3
1. a. It will suffice to take into account edge directions in processing adjacent
vertices.
b. Start the algorithm at one of the given vertices and stop it as soon
as the other vertex is added to the tree.
c. If the given graph is undirected, solve the single-source problem with
the destination vertex as the source and reverse all the paths obtained in
the solution. If the given graph is directed, reverse all its edges first, solve
the single-source problem for the new digraph with the destination vertex
as the source, and reverse the direction of all the paths obtained in the
solution.
d. Create a new graph by replacing every vertex vwith two vertices
vand v connected by an edge whose weight is equal to the given weight
of vertex v. All the edges entering and leaving vin the original graph will
enter vand leave v in the new graph, respectively.Assign the weight of
0 to each original edge. Applying Dijkstra’s algorithm to the new graph
will solve the problem.
2. a.
a
b
d
4c
e
3
74
6
25
Tree vertices Remaining vertices
a(-,0) b(-,∞)c(—,∞)d(a,7) e(-,∞)
d(a,7) b(d,7+2) c(d,7+5) e(-,∞)
b(d,9) c(d,12) e(-,∞)
c(d,12) e(c,12+6)
e(c,18)
The shortest paths (identified by following nonnumeric labels backwards
from a destination vertex to the source) and their lengths are:
from ato d:a−dof length 7
from ato b:a−d−bof length 9
from ato c:a−d−cof length 12
from ato e:a−d−c−eof length 18
22
b.
i
e f
j
9
5
h
d
g
c
ba
l
k
3
6
8
6
5
4
363
212
54
75
43
Tree vertices Fringe vertices Shortest paths from a
a(-,0) b(a,3) c(a,5) d(a,4) to b:a−bof length 3
b(a,3) c(a,5) d(a,4) e(b,3+3) f(b,3+6) to d:a−dof length 4
d(a,4) c(a,5) e(d,4+1) f(a,9) h(d,4+5) to c:a−cof length 5
c(a,5) e(d,5) f(a,9) h(d,9) g(c,5+4)) to e:a−d−eof length 5
e(d,5) f(e,5+2) h(d,9) g(c,9) i(e,5+4) to f:a−d−e−fof length 7
f(e,7) h(d,9) g(c,9) i(e,9) j(f,7+5) to h:a−d−hof length 9
h(d,9) g(c,9) i(e,9) j(f,12) k(h,9+7)) to g:a−c−gof length 9
g(c,9) i(e,9) j(f,12) k(g,9+6) to i:a−d−e−iof length 9
i(e,9) j(f,12) k(g,15) l(i,9+5) to j:a−d−e−f−jof length 12
j(f,12) k(g,15) l(i,14) to l:a−d−e−i−lof length 14
l(i,14) k(g,15) to k:a−c−g−kof length 15
k(g,15)
3. Consider, for example, the graph
a
c
b
3
2
- 2
As the shortest path from ato b, Dijkstra’s algorithm yields a−bof length
2, which is longer than a−c−bof length 1.
4. a. True: On each iteration, we add to a previously constructed tree an
edge connecting a vertex in the tree to a vertex that is not in the tree.
So, the resulting structure must be a tree. And, after the last operation,
it includes all the vertices of the graph. Hence, it’s a spanning tree.
b. False. Here is a simple counterexample:
23
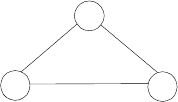
a
c
b
3
2
2
With vertex aas the source, Dijkstra’s algorithm yields, as the short-
est path tree, the tree composed of edges (a, b)and (a, c).The graph’s
minimum spanning tree is composed of (a, b)and (b, c).
5. Algorithm SimpleDijkstra(W[0..n −1,0..n −1],s)
//Input: A matrix of nonnegative edge weights Wand
// integer sbetween 0 and n−1indicating the source
//Output: An array D[0..n −1] of the shortest path lengths
// from sto all vertices
for i←0to n−1do
D[i]←∞;treeflag[i]←false
D[s]←0
for i←0to n−1do
dmin ←∞
for j←0to n−1do
if not treeflag[j]and D[j]<dmin
jmin ←j;dmin ←D[jmin]
treeflag[jmin]←true
for j←0to n−1do
if not treeflag[j]and dmin +W[jmin,j]<∞
D[j]←dmin +W[jmin,j]
return D
6. We will prove by induction on the number of vertices iin tree Ticon-
structed by Dijkstra’s algorithm that this tree contains iclosest vertices
to source s(including the source itself), for each of which the tree path
from sto visashortestpathoflengthdv.For i=1,the assertion is
obviously true for the trivial path from the source to itself. For the gen-
eral step, assume that it is true for the algorithm’s tree Tiwith ivertices.
Let vi+1 be the vertex added next to the tree by the algorithm. All the
vertices on a shortest path from sto vi+1 preceding vi+1 must be in Ti
because they are closer to sthan vi+1.(Otherwise, the first vertex on the
path from sto vi+1 that is not in Tiwould’ve been added to Tiinstead of
vi+1.) Hence, the (i+1)st closest vertex can be selected as the algorithm
does: by minimizing the sum of dv(the shortest distance from sto v∈Ti
by the assumption of the induction) and the length of the edge from vto
an adjacent vertex not in the tree.
24
7. Algorithm DagShortestPaths(G, s)
//Solves the single-source shortest paths problem for a dag
//Input: A weighted dag G=V,Eand its vertex s
//Output: The length dvof a shortest path from sto vand
// its penultimate vertex pvfor every vertex vin V
topologically sort the vertices of G
for every vertex vdo
dv←∞;pv←null
ds←0
for every vertex vtaken in topological order do
for every vertex uadjacent to vdo
if dv+w(v, u)<d
u
du←dv+w(v, u); pu←v
Topological sorting can be done in Θ(|V|+|E|)time (see Section 5.3). The
distance initialization takes Θ(|V|)time. The innermost loop is executed
for every edge of the dag. Hence, the total running time is in Θ(|V|+|E|).
8. Algorithm DagLongestPath(G)
//Finds the length of a longest path in a dag
//Input: A weighted dag G=V,E
//Output: The length of its longest path dmax
topologically sort the vertices of G
for every vertex vdo
dv←0//the length of the longest path to vseen so far
for every vertex vtaken in topological order do
for every vertex uadjacent to vdo
if dv+w(v, u)>d
u
du←dv+w(v, u)
dmax ←0
for every vertex vdo
if dv>dmax
dmax ←dv
return dmax
9. a. Take the two balls representing the two singled out vertices in two
hands and stretch the model to get the shortest path in question as a
straight line between the two ball-vertices.
b. Hold the ball representing the source in one hand and let the rest
of the model hang down: The force of gravity will make the shortest path
to each of the other balls be on a straight line down.
10. n/a
25
Exercises 9.4
1. a. Construct a Huffman code for the following data:
character ABC D _
probability 0.4 0.1 0.2 0.15 0.15
b. Encode the text ABACABADusing the code of question a.
c. Decode the text whose encoding is 100010111001010 in the code of
question a.
2. For data transmission purposes, it is often desirable to have a code with
a minimum variance of the codeword lengths (among codes of the same
average length). Compute the average and variance of the codeword
length in two Huffman codes that result from a different tie breaking
during a Huffman code construction for the following data:
character ABCDE
probability 0.1 0.1 0.2 0.2 0.4
3. Indicate whether each of the following properties are true for every Huff-
man code.
a. The codewords of the two least frequent characters have the same
length.
b. The codeword’s length of a more frequent character is always smaller
than or equal to the codeword’s length of a less frequent one.
4. What is the maximal length of a codeword possible in a Huffman encoding
of an alphabet of ncharacters?
5. a. Write a pseudocode for the Huffman tree construction algorithm.
b. What is the time efficiency class of the algorithm for constructing
a Huffman tree as a function of the alphabet’s size?
6. Show that a Huffman tree can be constructed in linear time if the alpha-
bet’s characters are given in a sorted order of their frequencies.
7. Given a Huffman coding tree, which algorithm would you use to get the
codewords for all the characters? What is its time-efficiency class as a
function of the alphabet’s size?
8. Explain how one can generate a Huffman code without an explicit gener-
ationofaHuffmancodingtree.
9. a. Write a program that constructs a Huffman code for a given English
text and encode it.
26
b. Write a program for decoding an English text which has been en-
coded with a Huffman code.
c. Experiment with your encoding program to find a range of typical
compression ratios for Huffman’s encoding of English texts of, say, 1000
words.
d. Experiment with your encoding program to find out how sensitive the
compression ratios are to using standard estimates of frequencies instead
of actual frequencies of character occurrences in English texts.
10. Card guessing Design a strategy that minimizes the expected number of
questions asked in the following game [Gar94], #52. You have a deck of
cards that consists of one ace of spades, two deuces of spades, three threes,
and on up to nine nines, making 45 cards in all. Someone draws a card
from the shuffled deck, which you have to identify by asking questions
answerable with yes or no.
27
Hints to Exercises 9.4
1. See the example given in the section.
2. After combining the two nodes with the lowest probabilities, resolve the
tie arising on the next iteration in two different ways. For each of the two
Huffman codes obtained, compute the mean and variance of the codeword
length.
3. You may base your answers on the way Huffman’s algorithm works or on
the fact that Huffman codes are known to be optimal prefix codes.
4. The maximal length of a codeword relates to the height of Huffman’s
coding tree in an obvious fashion. Try to find a set of nspecific frequencies
for an alphabet of size nfor which the tree has the shape yielding the
longest codeword possible.
5. a. What is the most appropriate data structure for an algorithm whose
principal operation is finding the two smallest elements in a given set,
deleting them, and then adding a new item to the remaining ones?
b. Identify the principal operations of the algorithm, the number of times
they are executed, and their efficiencies for the data structure used.
6. Maintain two queues: one for given frequencies, the other for weights of
new trees.
7. It would be natural to use one of the standard traversal algorithms.
8. Generate the codewords right to left.
9. n/a
10. A similar example was discussed at the end of Section 9.4. Construct
Huffman’s tree and then come up with specific questions that would yield
that tree. (You are allowed to ask questions such as: Is this card the ace,
or a seven, or an eight?)
28
Solutions to Exercises 9.4
1. a.
0.25
0.1
B
0.15
D
0.15
_
0.2
C
0.4
A
0.15
_
0.2
C
0.4
A
0.1
B
0.15
D
0.25
0.1
B
0.15
D
0.35
0.15
_
0.2
C
0.4
A
0.4
A0.6
0.25
0.1
B
0.15
D
0.35
0.15
_
0.2
C
0.4
A0.6
0.25
0.1
B
0.15
D
0.35
0.15
_
0.2
C
1.0
01
1
0
0101
29

character ABC D _
probability 0.4 0.1 0.2 0.15 0.15
codeword 0 100 111 101 110
b. The text ABACABAD will be encoded as 0100011101000101.
c. With the code of part a, 100010111001010 will be decoded as
100
B|0
A|101
D|110
_
|0
A|101
D|0
A
30
2. Here is one way:
0.1
A
0.1
B
0.2
C
0.2
D
0.4
E
0.4
0.6
0.2
0.1
A
0.1
B
0.2
D
0.2
C
0.2
0.1
A
0.1
B
0.2
C
0.2
D
0.4
E
0.4
0.2
0.1
A
0.1
B
0.2
C
0.4
E
0.2
D
0.4
E
0.4
E
1.0
01
0.4
0.6
0.2
0.1
A
0.1
B
0.2
C
0.2
D
01
01
1
0
31

character ABCDE
probability 0.1 0.1 0.2 0.2 0.4
codeword 1100 1101 111 10 0
length 44321
Thus, the mean and variance of the codeword’s length are, respectively,
¯
l=
5
i=1
lipi=4·0.1+4·0.1+3·0.2+2·0.2+1·0.4=2.2and
Var=
5
i=1
(li−¯
l)2pi=(4-2.2)20.1+(4-2.2)20.1+(3-2.2)20.2+(2-2.2)20.2+(1-2.2)20.4 =1.36.
32
Here is another way:
0.1
A
0.1
B
0.2
C
0.2
D
0.4
E
0.6
0.2
0.1
A
0.1
B
0.2
C
0.2
D
0.4
E
0.4
E
0.4
E
0.2
0.1
A
0.1
B
0.4
0.2
C
0.2
D
0.2
0.1
A
0.1
B
0.4
0.2
C
0.2
D
1.0
01
0.4
E0.6
0.2
0.1
A
0.1
B
0.4
0.2
C
0.2
D
0
011
1
0
33

character ABCDE
probability 0.10.10.20.20.4
codeword 100 101 110 111 0
length 33331
Thus, the mean and variance of the codeword’s length are, respectively,
¯
l=
5
i=1
lipi=2.2and Var=
5
i=1
(li−¯
l)2pi=0.96.
3. a. Yes. This follows immediately from the way Huffman’s algorithm oper-
ates: after each of its iterations, the two least frequent characters that are
combined on the first iteration are always on the same level of their tree in
the algorithm’s forest. An easy formal proof of this obvious observation
is by induction.
(Note that if there are more than two least frequent characters, the asser-
tion may be false for some pair of them, e.g., A(1
3),B(1
3),C(1
3).)
b. Yes. Let’s use the optimality of Huffman codes to prove this property
by contradiction. Assume that there exists a Huffman code containing
two characters ciand cjsuch that p(ci)>p(cj)and l(w(ci)) >l(w(cj)),
where p(ci)and l(w(ci)) are the probability and codeword’s length of ci,
respectively, and p(cj)and l(w(cj)) are the probability and codeword’s
length of cj,respectively.Let’s create a new code by simply swapping
the codewords of c1and c2and leaving the codewords for all the other
characters the same. The new code will obviously remain prefix-free and
its expected length n
k=1 l(w(ck))p(ck)) will be smaller than that of the
initial code. This contradicts the optimality of the initial Huffman code
and, hence, proves the property in question.
4. The answer is n−1.Since two leaves corresponding to the two least fre-
quent characters must be on the same level of the tree, the tallest Huffman
coding tree has to have the remaining leaves each on its own level. The
height of such a tree is n−1.An easy and natural way to get a Huffman
tree of this shape is by assuming that p1≤p2< ... < pnand having the
weight Wiof a tree created on the ith iteration of Huffman’s algorithm,
i=1,2, ..., n−2,be less than or equal to pi+2.(Note that for such inputs,
Wi=i+1
k=1 pkfor every i=1,2, ..., n −1.)
As a specific example, it’s convenient to consider consecutive powers of
2:
p1=p2and pi=2
i−n−1for i=2, ..., n.
(For, say, n=4,we have p1=p2=1/8,p
3=1/4and p4=1/2.)
34
Indeed, pi=2
i/2n+1 is an increasing sequence as a function of i. Further,
Wi=pi+2 for every i=1,2,...,n−2, since
Wi=
i+1
k=1
pk=p1+
i+1
k=2
pk=2
2/2n+1 +
i+1
k=2
2k/2n+1 =1
2n+1 (22+
i+1
k=2
2k)
=1
2n+1 (22+(2
i+2 −4)) = 2i+2
2n+1 =pi+2.
5. a. The following pseudocode is based on maintaining a priority queue of
trees, with the priorities equal the trees’ weights.
Algorithm Huffman(W[0..n −1])
//Constructs Huffman’s tree
//Input: An array W[0..n −1] of weights
//Output: A Huffman tree with the given weights assigned to its leaves
initialize priority queue Qof size nwith one-node trees and priorities equal
to the elements of W[0..n −1]
while Qhas more than one element do
Tl←the minimum-weight tree in Q
delete the minimum-weight tree in Q
Tr←the minimum-weight tree in Q
delete the minimum-weight tree in Q
create a new tree Twith Tland Tras its left and right subtrees
and the weight equal to the sum of Tland Trweights
insert Tinto Q
return T
Note: See also Problem 6 for an alternative algorithm.
b. The algorithm requires the following operations: initializing a pri-
ority queue, deleting its smallest element 2(n−1) times, computing the
weight of a combined tree and inserting it into the priority queue n−1
times. The overall running time will be dominated by the time spent on
deletions, even taking into account that the size of the priority queue will
be decreasing from nto 2.For the min-heap implementation, the time
efficiency will be in O(nlog n); for the array or linked list representations,
it will be in O(n2). (Note: For the coding application of Huffman trees,
the size of the underlying alphabet is typically not large; hence, a simpler
data structure for the priority queue might well suffice.)
6. The critical insight here is that the weights of the trees generated by Huff-
man’s algorithm for nonnegative weights (frequencies) form a nondecreas-
ing sequence. As the hint to this problem suggests, we can then maintain
35
two queues: one for given frequencies in nondecreasing order, the other
for weights of new trees. On each iteration, we do the following: find
the two smallest elements among the first two (ordered) elements in the
queues (the second queue is empty on the first iteration and can contain
just one element thereafter); add their sum to the second queue; and then
delete these two elements from their queues. The algorithm stops after
n−1iterations (where nis the alphabet’s size), each of which requiring a
constant time.
7. Use one of the standard traversals of the binary tree and generate a bit
string for each node of the tree as follows:. Starting with the empty bit
string for the root, append 0 to the node’s string when visiting the node’s
left subtree begins and append 1 to the node’s string when visiting the
node’s right subtree begins. At a leaf, print out the current bit string as
the leaf’s codeword. Since Huffman’s tree with nleaves has a total of
2n−1nodes (see Sec. 4.4), the efficiency will be in Θ(n).
8. We can generate the codewords right to left by the following method that
stems immediately from Huffman’s algorithm: when two trees are com-
bined, append 0 in front of the current bit strings for each leaf in the left
subtree and append 1 in front of the current bit strings for each leaf in the
right subtree. (The substrings associated with the initial one-node trees
are assumed to be empty.)
9. n/a
10. See the next page
36
10. The probabilities of a selected card be of a particular type is given in the
following table:
card ace deuce three four five six seven eight nine
probability 1/45 2/45 3/45 4/45 5/45 6/45 7/45 8/45 9/45
Huffman’s tree for this data looks as follows:
1/45 2/45 3/45 4/45 5/45 6/45 7/45 8/45 9/45
3/45 9/45 15/45
6/45
12/45
18/45
27/45
45/45
The first question this tree implies can be phrased as follows: ”Is the se-
lected card a four, a five, or a nine?” . (The other questions can be
phrased in a similar fashion.)
The expected number of questions needed to identify a card is equal to
theweightedpathlengthfromtheroottotheleavesinthetree:
¯
l=
9
i=1
lipi=5·1
45 +5·2
45 +4·3
45 +3·5
45 +3·6
45 +3·7
45 +3·8
45 +2·9
45 =135
45 =3.
37
This file contains the exercises, hints, and solutions for Chapter 10 of the
book ”Introduction to the Design and Analysis of Algorithms,” 2nd edition, by
A. Levitin. The problems that might be challenging for at least some students
are marked by ;those that might be difficult for a majority of students are
marked by .
Exercises 10.1
1. Solve the following linear programming problems geometrically.
(a)
maximize 3x+y
subject to −x+y≤1
2x+y≤4
x≥0,y≥0
(b)
maximize x+2y
subject to 4x≥y
y≤3+x
x≥0,y≥0
2. Consider the linear programming problem
minimize c1x+c2y
subject to x+y≥4
x+3y≥6
x≥0,y≥0
where c1and c2aresomerealnumbersnotbothequaltozero.
(a) Give an example of the coefficient values c1and c2for which the
problem has a unique optimal solution.
(b) Give an example of the coefficient values c1and c2for which the
problem has infinitely many optimal solutions.
(c) Give an example of the coefficient values c1and c2for which the
problem does not have an optimal solution.
3. Would the solution to problem (10.2) be different if its inequality con-
straints were strict, i.e., x+y<4and x+3y<6,respectively?
4. Trace the simplex method on
(a) the problem of Exercise 1a.
(b) the problem of Exercise 1b.
5. Trace the simplex method on the problem of Example 1 in Section 6.6
1
(a) by hand.
(b) by using one of the implementations available on the Internet.
6. Determine how many iterations the simplex method needs to solve the
problem
maximize n
j=1 xj
subject to 0≤xj≤bj,where bj>0for j=1,2, ..., n.
7. Can we apply the simplex method to solve the knapsack problem (see
Example 2 in Section 6.6)? If you answer yes, indicate whether it is a
good algorithm for the problem in question; if you answer no, explain why
not.
8. Prove that no linear programming problem can have exactly k≥1
optimal solutions unless k=1.
9. If a linear programming problem
maximize n
j=1 cjxj
subject to n
j=1 aij xj≤bifor i=1,2, ..., m
x1,x
2, ..., xn≥0
is considered as primal,thenitsdual is defined as the linear program-
ming problem
minimize m
i=1 biyi
subject to m
i=1 aij yi≥cjfor j=1,2, ..., n
y1,y
2, ..., ym≥0.
(a) Express the primal and dual problems in matrix notations.
(b) Find the dual of the following linear programming problem
maximize x1+4x2−x3
subject to x1+x2+x3≤6
x1−x2−2x3≤2
x1,x
2,x
3≥0.
(c) Solve the primal and dual problems and compare the optimal values
of their objective functions.
10. Parliament pacification In a parliament, each parliamentarian has at
most three enemies. Design an algorithm that divides the parliament into
two chambers in such a way that no parliamentarian has more than one
enemy in his or her chamber (after [Sav03], p.1, #4).
2
Hints to Exercises 10.1
1. Sketch the feasible region of the problem in question. Follow this up by
either applying the Extreme-Point Theorem or by inspecting level lines,
whichever is more appropriate. Both methods were illustrated in the text.
2. Sketch the feasible region of the problem. Then choose values of the pa-
rameters c1and c2to obtain a desired behavior of the objective function’s
level lines.
3. What is the principal difference between maximizing a linear function,
say f(x)=2x, on a closed vs. semi-open interval, e.g., 0≤x≤1vs.
0≤x<1?
4. Trace the simplex method on the instances given, as it was done for an
example in the text.
5. When solving the problem by hand, you might want to start by getting rid
of fractional coefficients in the problem’s statement. Also note that the
problem’s specifics make it possible to replace its equality constraint by
one inequality constraint. You were asked to solve this problem directly
in Exercises 6.6 (see Problem 8).
6. The specifics of the problem make it possible to see the optimal solution
at once. Sketching its feasible region for n=2or n=3,thoughnot
necessary, may help to see both this solution and the number of iterations
needed by the simplex method to solve it.
7. Consider separately two versions of the problem: continuous and 0-1 (see
Example 2 in Section 6.6).
8. If x=(x
1,x
2, ..., x
n)and x =(x
1,x
2, ..., x
n)are two distinct optimal
solutions to the same linear programming problem, what can we say about
any point of the line segment with the endpoints at xand x ?Note that
any such point xcan be expressed as x=tx+(1−t)x =(tx
1+(1−
t)x
1,tx
2+(1−t)x
2, ..., tx+(1−t)x
n),where 0≤t≤1.
9. a. You will need to use the notion of a matrix transpose, defined as the
matrix whose rows are the columns of the given matrix.
b. Apply the general definition to the specific problem given. Note the
change from maximization to minimization, the change of the roles played
by objective function’s coefficients and constraints’ right-hand sides, the
transposition of the constraints and the reversal of their signs.
c. You may use either the simplex method or the geometric approach.
10. The problem can be solved by an iterative improvement algorithm that
decreases the number of enemy pairs who are members of the same cham-
ber.
3
Solutions to Exercises 10.1
1. a. The feasible region of the linear programming problem
maximize 3x+y
subject to −x+y≤1
2x+y≤4
x≥0,y≥0
is given in the following figure:
x
y
( 0,1 )
( 0, 0 ) ( 2, 0 )
( 1, 2 )
-x+y=1
2x+y=4
Since the feasible region of the problem is nonempty and bounded, an
optimal solution exists and can be found at one of the extreme points of
the feasible region. The extreme points and the corresponding values of
the objective function are given in the following table:
Extremepoint Valueof3x+y
(0,0) 0
(2,0) 6
(1,2) 5
(0,1) 1
Hence, the optimal solution is x=2,y=0,with the corresponding
value of the objective function equal to 6.
4
b. The feasible region of the linear programming problem
maximize x+2y
subject to 4x≥y
x+3≥y
x≥0,y≥0
is given in the following figure:
x
y
( 0, 0 )
( 1,4 )
y=4x
y=x+3
The feasible region is unbounded. On considering a few level lines x+2y=
z, it is easy to see that level lines can be moved in the north-east direc-
tion, which corresponds to increasing values of z, as far as we wish without
losing common points with the feasible region. (Alternatively, we can con-
sider a simple sequence of points, such as (n, 0), which are feasible for any
nonnegative integer value of nand make the objective function z=x+2y
aslargeaswewishasngoes to infinity.) Hence, the problem is unbounded
and therefore does not have a finite optimal solution.
5
2. The feasible region of the problem with the constraints x+y≥4,
x+3y≥6,x≥0,y≥0is given in Figure 10.3 of Section 10.1:
x
y
( 0, 4 )
( 0, 0 ) ( 6, 0 )
( 3, 1 )
3x + 5y = 24
3x + 5y = 14
3x + 5y = 20
a. Minimization of z=c1x+c2yon this feasible region, with c1,c
2>0,
pushes level lines c1x+c2y=zin the south-west direction. Any family of such
lines with a slope strictly between the slopes of the boundary lines x+y=4
and x+3y=6will hit the extreme point (3,1) as the only minimum solution
to the problem. For example, as mentioned in Section 10.1, we can minimize
3x+5yamong infinitely many other possible answers.
b. For a linear programming problem to have infinitely many solutions, the
optimal level line of its objective function must contain a line segment that is
a part of the feasible region’s boundary. Hence, there are four qualitatively
distinct answers:
i. minimize 1·x+0·y(or, more generally, any objective function of the
form c·x+0·y,wherec>0);
ii. minimize x+y(or, more generally, any objective function of the form
cx +cy,wherec>0);
iii. minimize x+3y(or, more generally, any objective function of the form
cx +3cy,wherec>0);
iv. minimize 0·x+1·y(or, more generally, any objective function of the
form 0·x+c·y,wherec>0).
6
3. The problem with the strict inequalities does not have an optimal solution:
The objective function values of any sequence of feasible points approaching
x1=3,x
2=1(the optimal solution to Problem (10.2)) will approach z=14as
its limit, but this value will not be attained at any feasible point of the problem
with the strict inequalities.
4. a. The standard form of the problem given is
maximize 3x+y
subject to −x+y+u=1
2x+y++v=4
x, y, u, v ≥0.
Here are the tableaux generated by the simplex method in solving this problem:
11101
21014
31000
xyuv
u
v~v=4
2
0
13
02
06
xyuv
u
x
3
2
1
2
1
2
0
1
2
1
2
3
2
1
0
~v=4
2
0
The optimal solution found is x=2,y=0,with the maximal value of the
objective function equal to 6.
7
b. The standard form of the problem given is
maximize x+2y
subject to −4x+y+u=0
−x+y++v=3
x, y, u, v ≥0.
Here are the tableaux generated by the simplex method in solving this problem:
41100
11013
12000
xyuv
u
v
~
0u = 0
1
~v=3
1
0
41100
3013
92
000
xyuv
y
v1~v=3
3
0
014
34
01
31
019
xyuv
y
x
1
3
1
3
1
03
~v=3
3
0
Since there are no positive elements in the pivot column of the last tableau, the
problem is unbounded.
8
5. To simplify the task of getting an initial basic feasible solution here, we can
replace the equality constraint x+y+z=100by the inequality x+y+z≤100,
because an optimal solution (x∗,y
∗,z∗)to the problem with the latter constraint
must satisfy the former one.. (Otherwise, we would’ve been able to increase the
maximal value of the objective function by increasing the value of z∗.)then,
after an optional replacement of the objective function and the constraints by
the equivalent ones without fractional coefficients, the problem can be presented
in the standard form as follows
maximize 10x+7y+3z
subject to x+y+z+u= 100
3x−y++v=0
x+y−4z++w=0
x, y, z, u, v, w ≥0.
Here are the tableaux generated by the simplex method in solving this problem:
00100
40010
30000
zuvw
u
w~
w=0
1
31
11
110010011
xy
v
10 7
~u=100
1
0
~v=0
3
0
0
00 00
40 10
30 00
zuvw
u
w
1
0
1 1 0 1000
xy
x
0
~u=100
4/3
0
~w=0
4/3
0
4
3
4
3
1
3
31
3
1
3
1
3
1
3
10
3
9
00
30 0
00
zuvw
u
y
1
0
5 1 0 1000
xy
x
0
~u=100
5
0
1
4
1
4
3
4
01
01 1
4
13
4
31
4
340
20
060
680
zuvw
z
y
1
0
10200
xy
x
0
~u=100
5
0
1
4
3
4
0
00
13
20
19
20
0
1
51
5
1
5
3
5
034
5
1
20
1
4
The optimal solution found is x=20,y=60,z=20, with the maximal value
of the objective function equal to 680.
6. The optimal solution to the problem is x1=b1, ..., xn=bn.After
introducing a slack variable siin the ith inequality xi=bito get to the standard
form and starting with x1=0, ..., xn=0,s
1=b1, ..., sn=bn, the simplex
method will need niterations to get to an optimal solution x1=b1, ..., xn=
bn,s
1=0, ..., sn=0.It follows from the fact that on each iteration the simplex
method replaces only one basic variable. Here, on each of its niterations, it
will replace some slack variable siby the corresponding xi
7. The continuous version of the knapsack problem can be solved by the
simplex method, because it is a special case of the general linear programming
problem (see Example 2 in Section 6.6). However, it is hardly a good method
for solving this problem because it can be solved more efficiently by a much
simpler algorithm based on the greedy approach. You may want to design such
an algorithm by yourself before looking it up in the book.
The 0-1 version of the knapsack problem cannot be solved by the simplex
method because of the integrality (0-1) constraints imposed on the problem’s
variables.
10
8. The assertion follows immediately from the fact that if x=(x
1, ..., x
n)
and x =(x
1, ..., x
n)are two distinct optimal solutions to the same linear
programming problem, then any of the infinite number of points of the line
segment with endpoints at xand x will be an optimal solution to this problem
as well. Indeed, let xtbesuchapoint:
xt=tx+(1−t)x =(tx
1+(1−t)x
1, ..., tx
n+(1−t)x
n),where 0≤t≤1.
First, xtwill satisfy all the constraints of the problem, whether they are
linear inequalities or linear equations, because both xand x do. Indeed, let
the ith constraint be inequality n
j=1 aij xj≤bi.Then n
j=1 aij x
j≤biand
n
j=1 aij x
j≤bi.Multiplying these inequalities by tand 1−t, respectively, and
adding the results, we obtain
t
n
j=1
aij x
j+(1−t)
n
j=1
aij x
j≤tbi+(1−t)bi
or
n
j=1
(taij x
j+(1−t)aij x
j)=
n
j=1
aij (tx
j+(1−t)x
j)=
n
j=1
aij xt
j≤bi,
i.e., xsatisfies the inequality. The same argument holds for inequalities n
j=1 aij xj≥
biand equations n
j=1 aij xj=bi.
Second, xt=tx+(1−t)x will maximize the value of the objective function.
Indeed, if the maximal value of the objective function is z∗,then
n
j=1
cjx
j=z∗and
n
j=1
cjx
j=z∗.
Multiplying these equalities by tand 1−t, respectively, and adding the results,
we will obtain
t
n
j=1
cjx
j+(1−t)
n
j=1
cjx
j=tz∗+(1−t)z∗
or
n
j=1
(tcjx
j+(1−t)cjx
j)=
n
j=1
cj(tx
j+(1−t)x
j)=
n
j=1
cjxt
j=z∗.
I.e.,weprovedthatxtdoes maximize the objective function and hence will be
an optimal solution to the problem in question for any 0≤t≤1.
Note: What we actually proved is the fact that the set of optimal solutions
to a linear programming problem is convex. And any nonempty convex set can
contain either a single point or infinitely many points.
11
9. a. A linear programming problem
maximize n
j=1 cjxj
subject to n
j=1 aij xj≤bifor i=1,2, ..., m
x1,x
2,...,x
n≥0
can be compactly written using the matrix notations as follows:
maximize cx
subject to Ax ≤b
x≥0,
where
c=c1... cn,x=
x1
.
.
.
xn
,A=
a11 ... a1n
.
.
..
.
.
am1... amn
,b=
b1
.
.
.
bm
,
Ax ≤bholds if and only if each coordinate of the product Ax is less than or
equal to the corresponding coordinate of vector b,andx≥0is shorthand for
the nonnegativity requirement for all the variables. The dual can be written
as follows: minimize bTy
subject to ATy≥cT
y≥0,
where bTis the transpose of b(i.e., bT=[b1, ..., bm]), cTis the transpose of c
(i.e., cTis the column-vector made up of the coordinates of the row-vector c), AT
is the transpose of A(i.e., the n-by-mmatrix whose jth row is the jth column
of matrix A,j=1,2, ..., n), and yis the vector-column of mnew unknowns
y1, ..., ym.
b. The dual of the linear programming problem
maximize x1+4x2−x3
subject to x1+x2+x3≤6
x1−x2−2x3≤2
x1,x
2,x
3≥0
is minimize 6y1+2y2
subject to y1+y2≥1
y1−y2≥4
y1−2y2≥−1
y1,y
2≥0.
c. The standard form of the primal problem is
maximize x1+4x2−x3
subject to x1+x2+x3+x4=6
x1−x2−2x3+x5=2
x1,x
2,x
3,x
4,x
5≥0.
12
The simplex method yields the following tableaux:
10
2
1
x
1
1
1234
xxx
116
x4
x51012
00014
0~x=6
1
4
5
x
10
1
5
x
1
2
1234
xxx
116
x2
x50118
402430
0~x=
6
2
4
5
x
The found optimal solution is x1=0,x
2=6,x
3=0.
Since the dual problem has just two variables, it is easier to solve it geo-
metrically. Its feasible region is presented in the following figure:
13
y
y
( 1, 0 ) ( 4, 0 )
( 9, 5 )
y - 2y = -1
( 1/3, 2/3 )
2
1
12
y + y = 1
12
y - y = 4
12
Although it is unbounded, the minimization problem in question does have
a finite optimal solution y1=4,y
2=0.Note that the optimal values of the
objective functions in the primal and dual problems are equal to each other:
0+4·6−0=6·4+2·0.
This is the principal assertion of the Duality Theorem, one of the most important
facts in linear programming theory.
10. Partition the parliamentarians into two chambers in an arbitrary way.
Let pbe the total number of enemy pairs who are members of the same
chamber. While there is a parliamentarian who has at least two enemies in
his or her chamber, transform this parliamentarian into the other chamber.
(Since the transformed parliamentarian will have no more than one enemy
in his or her new chamber and the number of enemy pairs in his or her
old chamber will decrease by two, the total number of enemy pairs will
decrease at least by one. Hence, the algorithm will terminate after no
more than piterations, with the final partition of the parliamentarians in
which every parliamentarian has no more than one enemy in his or her
chamber.)
14
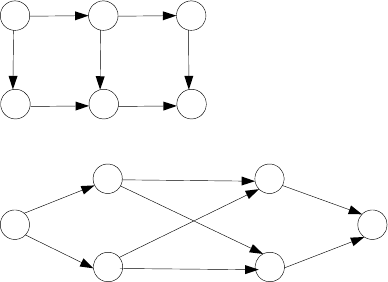
Exercises 10.2
1. Since maximum-flow algorithms require processing edges in both direc-
tions, it is convenient to modify the adjacency matrix representation of a
network as follows: If there is a directed edge from vertex ito vertex jof
capacity uij ,then the element in the ith row and the jth column is set to
uij ,while the element in the jth row and the ith column is set to −uij ;if
there is no edge between vertices iand j, both these elements are set to
zero. Outline a simple algorithm for identifying a source and a sink in a
network presented by such a matrix and indicate its time efficiency.
2. Apply the shortest-augmenting path algorithm to find a maximum flow
and a minimum cut in the following networks:
a.
1 2 5
36
4
52
4
8
7
64
b.
2 4
3 5
3
2
1 6
1
2
75
44
3. a. Does the maximum-flow problem always have a unique solution? Would
your answer be different for networks with different capacities on all their
edges?
b. Answer the same questions for the minimum-cut problem of finding
a cut of the smallest capacity in a given network.
4. a. Explain how the maximum-flow problem for a network with several
sources and sinks can be transformed to the same problem for a network
with a single source and a single sink.
b. Some networks have capacity constraints on flow amounts that can
flow through their intermediate vertices. Explain how the maximum-flow
problem for such a network can be transformed to the maximum-flow
problem for a network with edge capacity constraints only.
5. Consider a network that is a rooted tree, with the root as its source,
theleavesasitssinks,andalltheedgesdirectedalongthepathsfromthe
root to the leaves. Design an efficient algorithm for finding of a maximum
flow in such a network What is the time efficiency of your algorithm?
15
6. a. Prove equality (10.9).
b. Prove that for any flow in a network and any cut in it, the value of
the flow is equal to the flow across the cut (see equality (10.12)). Explain
the relationship between this property and equality (10.9).
7. a. Express the maximum-flow problem for the network of Figure 10.4 as
a linear programming problem.
b. Solve this linear programming problem by the simplex method.
8. As an alternative to the shortest-augmenting-path algorithm, Edmonds
and Karp [Edm72] suggested the maximal-augmenting-path algorithm in
which a flow is augmented along the path that increases the flow by the
largest amount. Implement both these algorithms in the language of your
choice and perform an empirical investigation of their relative efficiency.
9. Write a report on a more advanced maximum-flow algorithm such as
(i) Dinitz’s algorithm; (ii) Karzanov’s algorithm; (iii) Malhotra-Kamar-
Maheshwari algorithm; (iv) Goldberg-Tarjan algorithm.
10. Dining problem Several families go out to dinner together. To increase
their social interaction, they would like to sit at tables so that no two
members of the same family are at the same table. Show how to find
a seating arrangement that meets this objective (or prove that no such
arrangement exists) by using a maximum flow problem. Assume that the
dinner contingent has pfamilies and that the ith family has aimembers.
Also assume that qtables are available and the jth table has a seating
capacity of bj[Ahu93].
16
Hints to Exercises 10.2
1. What properties of the adjacency matrix elements stem from the source
and sink definitions, respectively?
2. See the algorithm and an example illustrating it in the text.
3. Of course, the value (capacity) of an optimal flow (cut) is the same for
any optimal solution. The question is whether distinct flows (cuts) can
yield the same optimal value.
4. a. Add extra vertices and edges to the network given.
b. If an intermediate vertex has a constraint on a flow amount that can
flow through it, split the vertex into two.
5. Take advantage of the recursive structure of a rooted tree.
6. a. Sum the equations expressing the flow-conservation requirement.
b. Sum the equations defining the flow value and flow-conservation re-
quirements for the vertices in set Xinducing the cut.
7. a. Use template (10.11) given in the text.
b. Use either an add-on tool of your spreadsheet or some software available
on the Internet.
10. Use edge capacities to impose the problem’s constraints. Also, take ad-
vantage of the solution to Problem 4a.
17
Solutions to Exercises 10.2
1. The definition of a source implies that a vertex is a source if and only if
there are no negative elements in its row in the adjacency matrix. Simi-
larly, the definition of a sink implies that a vertex is a sink if and only if
there are no positive elements in its row of the adjacency matrix. Thus
a simple scan of the adjacency matrix rows solves the problem in O(n2)
time, where nis the number of vertices in the network.
2. a. Here is an application of the shortest-augmenting path algorithm to
the network of Problem 2a:
1 2 5
36
4
0 / 5 0 / 2
0 / 4
0 / 8
0 / 7
0 / 6 0 / 4
, - 2, 2+
4, 4+
4, 2+
5, 1+
6, 1+
1 2 5
36
4
4 / 5 0 / 2
0 / 4
4 / 8
0 / 7
0 / 6 4 / 4
, - 1, 2+
1, 5+
6, 3+
1, 1+
6, 1+
1 2 5
36
4
5 / 5 1 / 2
1 / 4
4 / 8
0 / 7
0 / 6 4 / 4
, -
4, 4+
6, 3+
4, 4 -
6, 1+
1 2 5
36
4
5 / 5 1 / 2
1 / 4
8 / 8
4 / 7
4 / 6 4 / 4
, - 1, 2+
1, 5+
2, 3+
2, 4 -
2, 1+
1 2 5
36
4
5 / 5 2 / 2
2 / 4
8 / 8
5 / 7
5 / 6 3 / 4
, -
1, 3+
1, 4 -
1, 1+
18
The maximum flow is shown on the last diagram above. The minimum
cut found is {(2,5},(4,6)}.
b. Here is an application of the shortest-augmenting path algorithm to
the network of Problem 10.2b:
2 4
3 5
0 / 3
0 / 2
1 6
0 / 1
0 / 2
0 / 7 0 / 5
2, 1+2, 2 +
0 / 4 0 / 4 1, 4 +
2, 2 +
7, 1 +
_
,
2 4
3 5
1 / 3
0 / 2
1 6
1 / 1
1 / 2
0 / 7 0 / 5
1, 1+1, 2 +
0 / 4 0 / 4 1, 5 +
1, 2 +
7, 1 +
_
,
2 4
3 5
1 / 3
0 / 2
1 6
1 / 1
2 / 2
0 / 7 1 / 5
1, 4 -4, 3 +
0 / 4 1 / 4 2, 5 +
2, 3 +
7, 1 +
_
,
2 4
3 5
1 / 3
2 / 2
1 6
1 / 1
2 / 2
2 / 7 3 / 5
1, 4 -4, 3 +
0 / 4 1 / 4 1, 5 +
1, 2 +
5 ,1 +
_
,
2 4
3 5
0 / 3
2 / 2
1 6
1 / 1
2 / 2
3 / 7 4 / 5
3, 3 +
1 / 4 2 / 4
4 ,1 +
_
,
The maximum flow of value 5 is shown on the last diagram above. The
minimum cut found is {(1,2),(3,5),(4,6)}.
19
3. a. The maximum-flow problem may have more than one optimal solution.
In fact, there may be infinitely many of them if we allow (as the definition
does) non-integer edge flows. For example, for any 0≤t≤1, the flow
depicted in the diagram below is a maximum flow of value 1. Exactly two
of them–for t=0and t=1–are integer flows.
3
4
2 5
t / 1 t / 1
1 - t / 1
1 - t / 1
11 / 1
The answer does not change for networks with distinct capacities: e.g.,
consider the previous example with the capacities of edges (2,3),(3,5),
(2,4),and (4,5) changed to, say, 2,3,4,and 5,respectively.
b. The answer for the number of distinct minimum cuts is analogous
to that for maximum flows: there can be more than one of them in the
same network (though, of course, their number must always be finite be-
cause the number of all edge subsets is finite to begin with). For example,
the network
2
3
1 4
11
11
has four minimum cuts: {(1,2),(1,3)},{(1,2),(3,4)},{(1,3),(2,4)},and
{(2,4),(3,4)}.The answer does not change for networks with distinct edge
capacities. For example, the network
2
3
1 4
14
52
5
3
has two minimum cuts: {(1,2),(1,3)}and {(4,5)}.
20
4. a. Add two vertices to the network given to serve as the source and sink
of the new network, respectively. Connect the new source to each of the
original sources and each of the original sinks to the new sink with edges
of some large capacity M. (It suffices to take Mgreater than or equal to
the sum of the capacities of the edges leaving each source of the original
network.)
b. Replace each intermediate vertex iwith an upper bound bion a flow
amount that can flow through it with two vertices iand i connected by
an edge of capacity bias shown below:
i i
bi
i
bi
‘‘‘
Note that all the edges entering and leaving iin the original network
should enter iand leave i,respectively, in the new one.
5. The problem can be solved by calling TreeFlow (T(r),∞),where
Algorithm TreeFlow (T(r),v)
//Finds a maximum flow for tree T(r)rooted at r,
//whose value doesn’t exceed v(available at the root),
//and returns its value
if ris a leaf maxflowval ←v
else
maxflowval ←0
for every child cof rdo
xrc ←TreeFlow (T(c),min{urc,v})
v←v−xrc
maxflowval ←maxflowval + xrc
return maxflowval
The efficiency of the algorithm is clearly linear because a Θ(1) call is
made for each of the nodes of the tree.
6. a. Adding the i−2equalities expressing the flow conservation require-
ments yields
n−1
i=2
j
xji =
n−1
i=2
j
xij .
For any edge from an intermediate vertex pto an intermediate vertex q
(2 ≤p, q ≤n−1),theedgeflowxpq occurs once in both the left- and
21
right-hand sides of the last equality and hence will cancel out. The re-
maining terms yield:
n−1
i=2
x1i=
n−1
i=2
xin.
Adding x1nto both sides of the last equation, if there is an edge from
source 1 to sink n, results in the desired equality:
i
x1i=
i
xin.
b. Summing up the flow-value definition v=
j
x1jand the flow-conservation
requirement
j
xji =
j
xij for every i∈X(i>1),we obtain
v+
i:i∈X, i>1
j
xji =
j
x1j+
i:i∈X, i>1
j
xij ,
or, since there are no edges entering the source,
v+
i∈X
j
xji =
i∈X
j
xij .
Moving the summation from the left-hand side to the right-hand side and
splitting the sum into the sum over the vertices in Xand the sum over
the vertices in ¯
X,weobtain:
v=
i∈X
j
xij −
i∈X
j
xji
=
i∈X
j∈X
xij +
i∈X
j∈¯
X
xij −
i∈X
j∈X
xji −
i∈X
j∈¯
X
xji
=
i∈X
j∈¯
X
xij −
i∈X
j∈¯
X
xji,Q.E.D.
Note that equation (10.9) expresses this general property for two special
cuts: C1(X1,¯
X1)induced by X1={1}and C2(X2,¯
X2)induced by X2=
V−{n}.
22
7. a. maximize v=x12 +x14
subject to x12 −x23 −x25 =0
x23 +x43 −x36 =0
x14 −x43 =0
x25 −x56 =0
0≤x12 ≤2
0≤x14 ≤3
0≤x23 ≤5
0≤x25 ≤3
0≤x36 ≤2
0≤x43 ≤1
0≤x56 ≤4.
b. The optimal solution is x12 =2,x
14 =1,x
23 =1,x
25 =1,x
36 =2,
x43 =1,x
56 =1.
8. n/a
9. n/a
10. Solve the maximum flow problem for the following network:
1
1
1
1
a1
ap
b1
bq
If the maximum flow value is equal to p
i=1 ai,then the problem has
a solution indicated by the full edges of capacity 1 in the maximum flow;
otherwise, the problem does not have a solution.
23
Exercises 10.3
1. For each matching shown below in bold, find an augmentation or explain
why no augmentation exists.
a.
1 2 3 4
567
b.
1 2 3 4
5678
2. Apply the maximum-matching algorithm to the following bipartite graph:
1 2 3
456
3. a. What is the largest and what is the smallest possible cardinality of a
matching in a bipartite graph G=V,U, Ewith nvertices in each vertex
set Vand Uand at least nedges?
b. What is the largest and what is the smallest number of distinct solu-
tions the maximum-cardinality matching problem can have for a bipartite
graph G=V,U,Ewith nvertices in each vertex set Vand Uand at
least nedges?
4. a. Hall’s Marriage Theorem asserts that a bipartite graph G=
V,U,Ehas a matching that matches all vertices of the set Vif and
only if for each subset S⊆V, |R(S)|≥|S|where R(S) is the set of all
vertices adjacent to a vertex in S. Check this property for the following
graphwith(i)V={1,2,3,4}and (ii) V={5,6,7}.
1 2 3 4
567
b. You have to devise an algorithm that returns “yes” if there is a match-
ing in a bipartite graph G=V,U,Ethat matches all vertices in Vand
returns “no” otherwise. Would you base your algorithm on checking the
condition of Hall’s Marriage Theorem?
24

5. Suppose there are five committees A, B, C, D, and Ecomposed of six
persons a, b, c, d, e, f as follows: committee A’s members are band e;
committee B’s members are b,dand e;committeeC’s members are a,
c, d, e, f;committeeD’s members are b,d,e; committee E’s members
are band e. Is there a system of distinct representatives, i.e., is
it possible to select a representative from each committee so that all the
selected persons are distinct?
6. Show how the maximum-cardinality matching problem in a bipartite graph
can be reduced to the maximum-flow problem discussed in Section 10.2.
7. Consider the following greedy algorithm for finding a maximum matching
in a bipartite graph G=V,U,E: Sort all the vertices in nondecreasing
order of their degrees. Scan this sorted list to add to the current matching
(initially empty) the edge from the list’s free vertex to an adjacent free
vertex of the lowest degree. If the list’s vertex is matched or if there are
no adjacent free vertices for it, the vertex is simply skipped. Does this
algorithm always produce a maximum matching in a bipartite graph?
8. Design a linear algorithm for finding a maximum matching in a tree.
9. Implement the maximum-matching algorithm of this section in the lan-
guage of your choice. Experiment with its performance on bipartite
graphs with nvertices in each of the vertex sets and randomly gener-
ated edges (in both dense and sparse modes) to compare the observed
running time with the algorithm’s theoretical efficiency.
10. Domino puzzle Adominoisa2-by-1tilethatcanbeorientedeither
horizontally or vertically. A tiling of a given board composed of 1-by-1
squares is covering it with dominoes exactly without overlap. Which of
the following boards can be tiled with dominoes? If you answer yes, in-
dicate a tiling; if you answer no, explain why.
a. b. c.
25
Hints to Exercises 10.3
1. You may but do not have to use the algorithm described in the section.
2. See an application of this algorithm to another bipartite graph in the
section.
3. The definition of a matching and its cardinality should lead you to the
answers to these questions with no difficulty.
4. a. You do not have to check the inequality for each subset Sof Vif you
can point out a subset for which the inequality does not hold. Otherwise,
fill in a table for all the subsets Sof the indicated set Vwith columns for
S, R(S),and |R(S)|≥|S|.
b. Think time efficiency.
5. Reduce the problem to finding a maximum matching in a bipartite graph.
6. Transform a given bipartite graph into a network by making vertices of
the former be intermediate vertices of the latter.
7. Since this greedy algorithm is arguably simpler than the augmenting path
algorithm given in the section, should we expect a positive or negative
answer? Of course, this point cannot be substituted for a more specific
argument or a counterexample.
8. Start by presenting a tree given as a BFS tree.
9. For pointers regarding an efficient implementation of the algorithm, see
[Pap82], Section 10.2.
10. Although it is possible to answer the questions without referring to the
matching problem explicitly, you should ultimately coach your answers
using the notions discussed in the section.
26
Solutions to Exercises 10.3
1. a. The matching given in the exercise is reproduced below:
1 2 3 4
567
Its possible augmentations are:
1 2 3 4
567
1 2 3 4
567
b. No augmentation of the matching given in part b (reproduced below)
is possible.
1 2 3 4
5678
This conclusion can be arrived at either by applying the maximum-matching
algorithm or by simply noting that only one of vertices 5 and 8 can be
matched (and, hence, no more than three of vertices 5, 6, 7, and 8 can be
matched in any matching).
27
2. Here is a trace of the maximum-matching algorithm applied to the bipar-
tite graph in question:
1 2 3
456
3
V
U
1 2 3
456
1
Queue: 1 2 3 Queue: 1
↑23
Augment from 5
1 2 3
456
3
3
2
1 2 3
456
32
Queue: 2 3 Queue: 2
↑3
↑5
Augment from 4
1 2 3
456
3
3
1 2 3
456
2
5
Queue: 2 Queue: 2
↑5
↑1
↑
Augment from 6
1 2 3
456
No free vertices ⇒maximum (here perfect) matching
3. a. The largest cardinalilty of a matching is nwhen all the vertices of a
graph are matched (perfect matching). For example, if V={v1,v
2, ..., vn},
U={u1,u
2, ..., un}and E={(v1,u
1),(v2,u
2), ..., (vn,u
n)},then M=E
28

is a perfect matching of size n.
The smallest cardinality of a matching is 1.(It cannot be zero because
the number of edges is assumed to be at least n≥1.) For example,
in the bipartite graph with V={v1,v
2,...,v
n},U={u1,u
2, ..., un},and
E={(v1,u
1),(v1,u
2),...,(v1,u
n)},the size of any matching is 1.
b. Consider Kn,n,the bipartite graph in which each of the nvertices
in Vis connected to each of the nvertices in U. To obtain a perfect
matching, there are npossible mates for vertex v1,n−1possible remain-
ing mates for v2,and so on until there is just one possible remaining mate
for vn.Therefore the total number of distinct perfect matchings for Kn,n
is n(n−1)...1=n!.
The smallest number of distinct maximum matchings is 1. For ex-
ample, if V={v1,v
2, ..., vn},U={u1,u
2, ..., un},and E={(v1,u
1),
(v2,u
2), ..., (vn,u
n)},M=Eis the only perfect (and hence maximum)
matching.
4. a. (i) For V={1,2,3,4},the inequality obviously fails for S=Vsince
|R(S)|=|U|=3while |S|=4.
Hence, according to Hall’s Marriage Theorem, there is no matching that
matches all the vertices of the set {1,2,3,4}.
(ii) For subsets Sof V={5,6,7},we have the following table:
SR(S)|R(S)|≥|S|
{5} {1,2,3} 3≥1
{6} {1} 1≥1
{7} {2,3,4} 3≥1
{5,6} {1,2,3} 3≥2
{5,7} {1,2,3,4} 4≥2
{6,7} {1,2,3,4} 4≥2
{5,6,7} {1,2,3,4} 4≥3
Hence, according to Hall’s Marriage Theorem, there is a matching that
matches all the vertices of the set {5,6,7}.(Obviously, such a matching
must be maximal.)
b. Since Hall’s theorem requires checking an inequality for each subset
S⊆V, the worst-case time efficiency of an algorithm based on it would
be in Ω(2|V|).A much better solution is to find a maximum matching M∗
(e.g., by the section’s algorithm) and return “yes” if |M∗|=|V|and “no”
otherwise.
5. It is convenient to model the situation by a bipartite graph G=V,U, E
where Vrepresents the committees, Urepresents the committee members,
and (v, u)∈Eif and only if ubelongs to committee v:
29

A
a
B C D E
b c d e f
There exists no matching that would match all the vertices of the set
V. One way to prove it is based on Hall’s Marriage Theorem (see Prob-
lem 4) whose necessary condition is violated for set S={A, B, D, E}
with R(S)={b, d, e}. Another way is to select a matching such as
M={(B,b),(C, c),(D, d),(E,e)}(shown in bold) and check that the
maximum-matching algorithm fails to find an augmenting path for it.
6. Add one source vertex sand connect it to each of the vertices in the set V
by directed edges leaving s. Add one sink vertex tand connect each of the
vertices in the set Uto tby a directed edge entering t. Direct all the edges
of the original graph to point from Vto U. Assign 1 as the capacity of
every edge in the network. A solution to the maximum-flow problem for
the network yields a maximum matching for the original bipartite graph:
it consists of the full edges (edges with the unit flow on them) between
vertices of the original graph.
7. The greedy algorithm does not always find a maximum matching. As a
counterexample, consider the bipartite graph shown below:
1 2 3
456
Since all its vertices have the same degree of 2, we can order them in
numerical order of their labels: 1, 2, 3, 4, 5, 6. Using the same rule to
break ties for selecting mates for vertices on the list, the greedy algorithm
yields the matching M={(1,4),(2,5)},which is smaller than, say, M∗=
{(1,4),(2,6),(3,5)}.
8. A crucial observation is that for any edge between a leaf and its parent
there is a maximum matching containing this edge. Indeed, consider a
leaf vand its parent p.LetMbe a maximum matching in the tree. If
(v, p)is in M, we have a maximum matching desired. If Mdoes not
include (v, p),itmustcontainanedge(u, p)from some vertex u=vto p
30
because otherwise we could have added (v, p)to Mto get a larger match-
ing. But then simply replacing (u, p)by (v, p)in the matching Myields
a maximum marching containing (v, p).This operation is to be repeated
recursively for the smaller forest obtained.
Based on this observation, Manber ([Man89], p. 431) suggested the fol-
lowing recursive algorithm. Take an arbitrary leaf vand match it to its
parent.p. Remove from the tree both vand palong with all the edges
incident to p. Also remove all the former sibling leaves of v, if any. This
operation is to be repeated recursively for the smaller forest obtained.
Thieling Chen [Thieling Chen, "Maximum Matching and Minimum Vertex
Covers of Trees," The Western Journal of Graduate Research, vol. 10, no.
1, 2001, pp. 10-14] suggested to implement the same idea by processing
vertices of the tree in the reverse BFS order (i.e., bottom up and right to
left across each level) as in the following pseudocode:
Algorithm Tree-Max-Matching
//Constructs a maximum matching in a free tree
//Input: A tree T
//Output: A maximum cardinality matching Min T
initialize matching Mto the empty set
starting at an arbitrary vertex, traverse Tby BFS, numbering the visited
vertices sequentially from 0 to n−1and saving pointers to a visited
vertex and its parent
for i←n−1downto 0do
if vertex numbered iand its parent are both not marked
add the edge between them to M
mark the parent
return M
The time efficiency of this algorithm is obviously in Θ(n),where nis the
number of vertices in an input tree.
10. a. No domino tiling of the 7-by-7 board exists because the total number
of the board’s squares is odd. For a domino tiling of a board to exist, the
total number of squares on the board must be a multiple of two squares of
a single domino. This is necessary (but not sufficient) condition for tiling
with dominoes.
b. Note that any n-by-1 or 1-by-nboard where nis even can be tiled
with dominoes in an obvious way. Hence any board that is composed of
such strips, where n’s need not be the same, can be tiled as well. Here is
a tiling of the board given in part b:
31
c. No domino tiling of the board given in part c is possible. Think of
the board as being an 8-by-8 chessboard (with two missing squares at the
diagonally opposite corners) whose squares of the board colored alternat-
ingly black and white. Since a single domino would cover exactly one
black and one white square, no tiling of the board is possible because it
has 32 squares of one color and 30 squares of the other color.
Note: Obviously, a domino tiling can be considered a matching of the
board’s adjacent squares. The board in question can be represented by a
bipartite graph, with the sets Vand Urepresenting diagonally adjacent
squares (i.e., colored the same color as on the chessboard). Such graphs
for the boards given are shown below:
abc
The domino tiling question then becomes the perfect matching problem
for the graph representing the board. For the graph of part a no perfect
matching exists because the total number of vertices in the sets Vand
Uis odd. A perfect matching for part b was outlined above. Finally,
no perfect matching exists for the graph of part c because the number of
vertices in the sets Vand Uis not the same. Note that while we could
answer the domino tiling question for the three boards given without in-
troducing the boards’ graphs, this might be necessary for a more complex
configuration of the board.
32
Exercises 10.4
1. Consider an instance of the stable marriage problem given by the ranking
matrix ABC
α1,32,23,1
β3,11,32,2
γ2,23,11,3
For each of its marriage matchings, indicate whether it is stable or not.
For the unstable matchings, specify a blocking pair. For the stable match-
ings, indicate whether they are man-optimal, woman-optimal, or neither.
(Assume that the Greek and Roman letters denote the men and women,
respectively.)
2. Design a simple algorithm for checking whether a given marriage matching
is stable and determine its time efficiency class.
3. Find a stable-marriage matching for the instance given in Problem 1 by
applying the stable-marriage algorithm
(a) in its men-proposing version.
(b) in its women-proposing version.
4. Find a stable-marriage matching for the instance defined by the following
ranking matrix:
ABCD
α1,32,33,24,3
β1,44,13,42,2
γ2,21,43,34,1
δ4,12,23,11,4
5. Determine the time-efficiency class of the stable-marriage algorithm
(a) in the worst case.
(b) in the best case.
6. Prove that a man-optimal stable marriage set is always unique. Is it also
true for a woman-optimal stable marriage matching?
7. Prove that in the man-optimal stable matching, each woman has the worst
partner that she can have in any stable marriage matching.
8. Implement the stable-marriage algorithm given in Section 10.4 so that its
running time is in O(n2).Run an experiment to ascertain its average-case
efficiency.
9. Write a report on the college admission problem (residents-hospitals as-
signment) that generalizes the stable marriage problem.
33
10. Consider the problem of the roommates, which is related to but more
difficult than the stable marriage problem: “An even number of boys wish
to divide up into pairs of roommates. A set of pairings is called stable
if under it there are no two boys who are not roommates and who prefer
each other to their actual roommates.” [Gal62] Give an instance of this
problem that does not have a stable pairing.
34
Hints to Exercises 10.4
1. A marriage matching is obtained by selecting three matrix cells, one cell
from each row and column. To determine the stability of a given mar-
riage matching, check each of the remaining matrix cells for containing a
blocking pair.
2. It suffices to consider each member of one sex (say, the men) as a potential
member of a blocking pair.
3. An application of the men-proposing version to another instance is given
in the section. For the women-proposing version, reverse the roles of the
sexes.
4. You may use either the men-proposing or women-proposing version of the
algorithm.
5. The time efficiency is clearly defined by the number of proposals made.
You may but are not required to provide the exact number of proposals in
the worst and best cases, respectively; an appropriate Θclass will suffice.
6. Prove it by contradiction.
7. Prove it by contradiction.
8. Choose data structures so that the innermost loop of the algorithm can
runinconstanttime.
9. The principal references are [Gal62] and [Gus89].
10. Consider four boys, three of whom rate the fourth boy as the least desired
roommate. Complete these rankings to obtain an instance with no stable
pairing.
35

Solutions to Exercises 10.4
1. There are the total of 3! = 6 one-one matchings of two disjoint 3-element
sets: ABC
α1,3 2,23,1
β3,11,3 2,2
γ2,23,11,3
{(α, A),(β, B),(γ,C)}is stable: no other cell can be blocking since each
man has his best choice. This is obviously the man-optimal matching.
ABC
α1,3 2,23,1
β3,11,32,2
γ2,23,1 1,3
{(α, A),(β, C),(γ,B)}is unstable: (γ,A)is a blocking pair.
ABC
α1,32,2 3,1
β3,1 1,32,2
γ2,23,11,3
{(α, B),(β,A),(γ,C)}is unstable: (β,C)is a blocking pair.
ABC
α1,32,2 3,1
β3,11,32,2
γ2,2 3,11,3
{(α, B),(β,C),(γ, A)}is stable: all the other cells contain a 3 (the lowest
rank) and hence cannot be a blocking pair. This is neither a man-optimal
nor a woman-optimal matching since it’s inferior to {(α, A),(β,B),(γ,C)}
for the men and inferior to {(α, C),(β,A),(γ, B)}for the women.
ABC
α1,32,23,1
β3,1 1,32,2
γ2,23,1 1,3
36

{(α, C),(β,A),(γ,B)}is stable: no other cell can be blocking since each
woman has her best choice. This is obviously the woman-optimal match-
ing.
ABC
α1,32,23,1
β3,11,3 2,2
γ2,2 3,11,3
{(α, C),(β,B),(γ,A)}is unstable: (α, B)is a blocking pair.
2. Stability-checking algorithm
Input: A marriage matching Mof n(m, w)pairs along with rankings of the
women by each man and rankings of the men by each woman
Output: “yes” if the input is stable and a blocking pair otherwise
for m←1to ndo
for each wsuch that mprefers wto his mate in Mdo
if wprefers mto her mate in M
return (m, w)
return “yes”
With appropriate data structures, it is not difficult to implement this algo-
rithm to run in O(n2)time. For example, the mates of the men and the mates
of the women in a current matching can be stored in two arrays of size nand
all the preferences can be stored in the n-by-nranking matrix containing two
rankings in each cell.
37
3. a.
Free men:
α, β, γ
ABC
α1,3 2,23,1
β3,11,32,2
γ2,23,11,3
αproposed to A
Aaccepted
Free men:
β, γ
ABC
α1,3 2,23,1
β3,11,3 2,2
γ2,23,11,3
βproposed to B
Baccepted
Free men:
γ
ABC
α1,3 2,23,1
β3,11,3 2,2
γ2,23,11,3
γproposed to C
Caccepted
The (man-optimal) stable marriage matching is M={(α, A),(β,B),(γ,C)}.
38

b.
Free women:
A, B, C
ABC
α1,32,23,1
β3,1 1,32,2
γ2,23,11,3
Aproposed to β
βaccepted
Free women:
B, C
ABC
α1,32,23,1
β3,1 1,32,2
γ2,23,1 1,3
Bproposed to γ
γaccepted
Free women:
C
ABC
α1,32,23,1
β3,1 1,32,2
γ2,23,1 1,3
Cproposed to α
αaccepted
The (woman-optimal) stable marriage matching is M={(β, A),(γ,B),(α, C)}.
39
4. The solution is given on the next page.
40
iteration 1
Free men: α, β, γ, δ
ABCD
α1,3 2,33,24,3
β1,44,13,42,2
γ2,21,43,34,1
δ4,12,23,11,4
αproposed to A;Aaccepted
iteration 2
Free men: β,γ,δ
ABCD
α1,3 2,33,24,3
β1,44,13,42,2
γ2,21,43,34,1
δ4,12,23,11,4
βproposed to A;Arejected
iteration 3
Free men: β,γ,δ
ABCD
α1,3 2,33,24,3
β1,44,13,42,2
γ2,21,43,34,1
δ4,12,23,11,4
βproposed to D;Daccepted
iteration 4
Free men: γ,δ
ABCD
α1,3 2,33,24,3
β1,44,13,42,2
γ2,21,4 3,34,1
δ4,12,23,11,4
γproposed to B;Baccepted
iteration 5
Free men: δ
ABCD
α1,3 2,33,24,3
β1,44,13,42,2
γ2,21,4 3,34,1
δ4,12,23,11,4
δproposed to D;Drejected
iteration 6
Free men: δ
ABCD
α1,3 2,33,24,3
β1,44,13,42,2
γ2,21,43,34,1
δ4,12,2 3,11,4
δproposed to B;Breplaced γwith δ
iteration 7
Free men: γ
ABCD
α1,32,33,24,3
β1,44,13,42,2
γ2,2 1,43,34,1
δ4,12,2 3,11,4
γproposed to A;Areplaced αwith γ
iteration 8
Free men: α
ABCD
α1,32,33,24,3
β1,44,13,42,2
γ2,2 1,43,34,1
δ4,12,2 3,11,4
αproposed to B;Brejected
iteration 9
Free men: α
ABCD
α1,32,33,2 4,3
β1,44,13,42,2
γ2,2 1,43,34,1
δ4,12,2 3,11,4
αproposed to C;Caccepted
Free men: none
M={(α, C),(β,D),(γ,A),(δ, B)}
41
5. a. The worst-case time efficiency of the algorithm is in Θ(n2).On the one
hand, the total number of the proposals, P(n),cannot exceed n2,the total
number of possible partners for nmen, because a man does not propose
to the same woman more than once. On the other hand, for the instance
of size nwhere all the men and women have the identical preference list
1, 2, ..., n, P (n)=n
i=1 i=n(n+1)/2.Thus, if Pw(n)is the number of
proposals made by the algorithm in the worst case,
n(n+1)/2≤Pw(n)≤n2,
i.e., Pw(n)∈Θ(n2).
b. The best-case time efficiency of the algorithm is in Θ(n): the algo-
rithm makes the minimum of nproposals, one by each man, on the input
that ranks first a different woman for each of the nmen.
6. Assume that there are two distinct man-optimal solutions to an instance
of the stable marriage problem. Then there must exist at least one man
mmatched to two different women w1and w2in these solutions. Since
no ties are allowed in the rankings, mmust prefer one of these two women
to the other, say, w1to w2.But then the marriage matching in which m
is matched with w2is not man-optimal in contradiction to the assumption.
Of course, a woman-optimal solution is unique too due to the complete
symmetry of these notions.
7. Assume that on the contrary there exists a man-optimal stable matching
Min which some woman wdoesn’t have the worst possible partner in a
stable matching, i.e., wprefers her partner min Mto her partner ¯min
another stable matching ¯
M. Since (m, w)/∈¯
M, m must prefer his partner
¯win ¯
Mto wbecause otherwise (m, w)would be a blocking pair for ¯
M. But
this contradicts the assumption that Mis a man-optimal stable matching
in which every man, including m, has the best possible partner in a stable
matching.
8. n/a
9. n/a
10. Consider an instance of the problem of the roommates with four boys α,
β, γ, and δand the following preference lists (∗stands for any legitimate
42
rating):
boy rank 1 rank 2 rank 3
αβ γ δ
βγ α δ
γα β δ
δ∗∗∗
Any pairing would have to pair one of the boys α, β, γ with δ. But any
such pairing would be unstable since whoever is paired with δwill want to
move out and one of the other two boys, having him rated first, will prefer
him to his current roommate. For example, if αis paired with δthen β
and γare paired too while γprefers αto β(in addition to αpreferring γ
to δ).
Note: This example is from the seminal paper by D. Gale and L. S. Shapley
"College Admissions and the Stability of Marriage", American Mathemat-
ical Monthly, vol. 69 (Jan. 1962), 9-15. For an in-depth discussion of the
problem of the roommates see the monograph by D. Gusfield and R.W.
Irwing TheStableMarriageProblem:Structure and Algorithms,.MIT
Press, 1989.
43