Contents BS 5950 90 Example 001

User Manual: BS-5950-90 Example 001

Open the PDF directly: View PDF .
Page Count: 7

Software Verification

PROGRAM NAME:

ETABS

REVISION NO.:

3

BS-5950-90 Example-001

STEEL DESIGNERS MANUAL SIXTH EDITION - DESIGN OF SIMPLY SUPPORTED COMPOSITE

BEAM

EXAMPLE DESCRIPTION

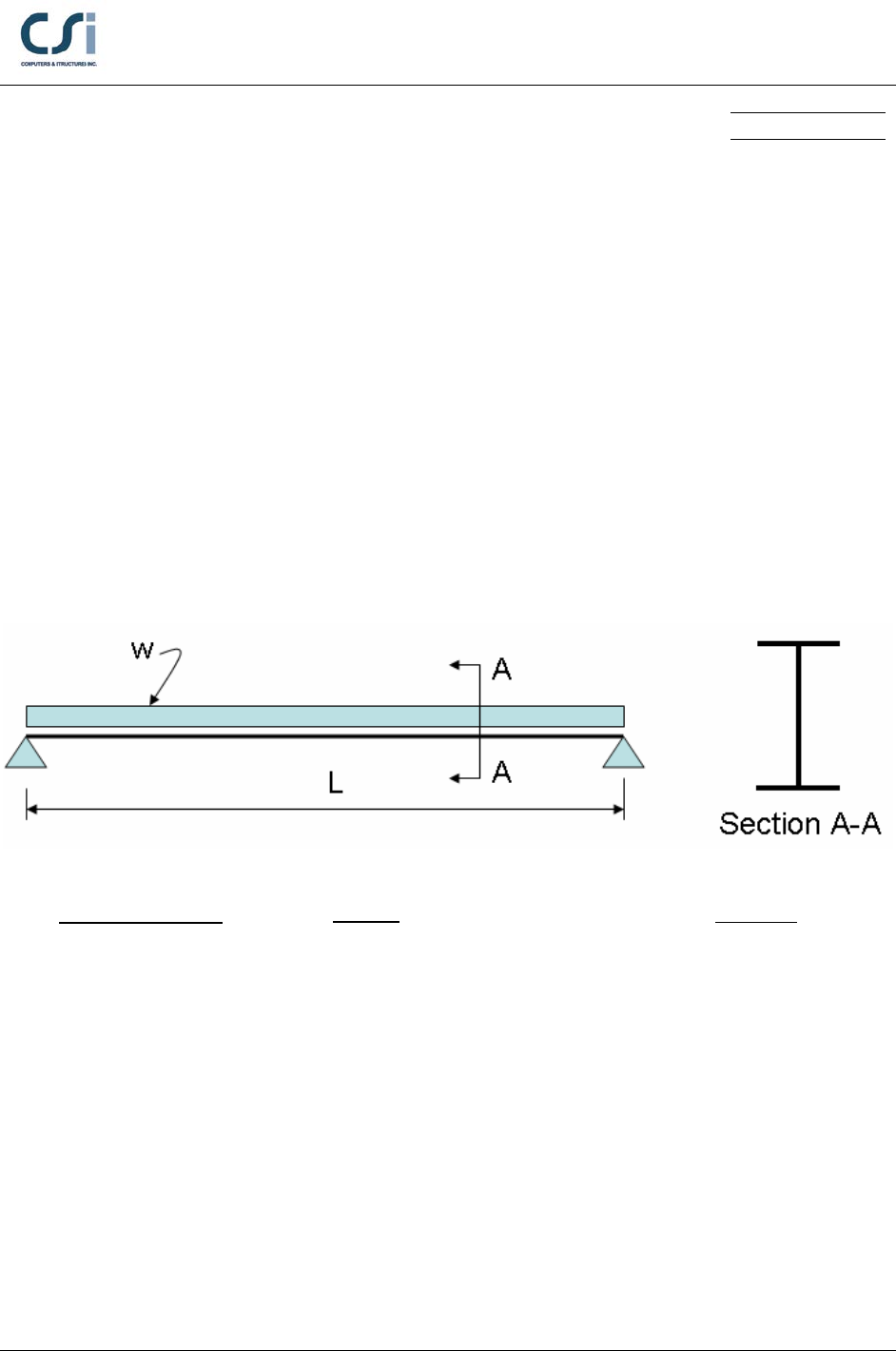
Design a composite floor with beams at 3-m centers spanning 12 m. The

composite slab is 130 mm deep. The floor is to resist an imposed load of 5.0

kN/m2, partition loading of 1.0 kN/m2 and a ceiling load of 0.5 kN/m2. The floor

is to be un-propped during construction.

GEOMETRY, PROPERTIES AND LOADING

TECHNICAL FEATURES OF ETABS TESTED

Composite beam design, including:

 Selection of steel section, camber and shear stud distribution

 Member bending capacities, at construction and in service

 Member deflections, at construction and in service

Member Properties

UKB457x191x67

E = 205,000 MPa

F

y

= 355 MPa

Loading

w = 6.67kN/m (Dead Load)

w = 1.5kN/m (Construction)

w = 1.5kN/m (Superimposed Load)

w = 18.00kN/m (Live Load)

Geometry

Span, L = 12 m

BS-5950-90 Example-001 - 1

Software Verification

PROGRAM NAME:

ETABS

REVISION NO.:

3

RESULTS COMPARISON

Independent results are referenced from the first example, Design of Simply

Supported Composite Beam, in Chapter 21 of the Steel Construction Institute

Steel Designer’s Manual, Sixth Edition.

Output Parameter ETABS Independent Percent

Difference

Construction Design

Moment (kN-m)

211.2 211.3 0.05%

Construction Ms (kN-m) 522.2 522.2 0.00%

Construction Deflection (mm) 29.9 29.9 0.00%

Design Moment (kN-m) 724.2 724.3 0.01%

Full Composite Mpc (kN-m) 968.9 968.9 0.00%

Partial Composite Mc (kN-m) 910.8 910.9 0.01%

Shear Stud Capacity Qn (kN) 57.6 57.6 0.00%

Live Load Deflection (mm) 33.2 33.2 0.00%

Applied Shear Force Fv (kN) 241.4 241.4 0.00%

Shear Resistance Pv (kN) 820.9 821.2 0.00%

COMPUTER FILE: BS-5950-90 EXAMPLE 001.EDB

CONCLUSION

The ETABS results show an excellent comparison with the independent results.

BS-5950-90 Example-001 - 2

Software Verification

PROGRAM NAME:

ETABS

REVISION NO.:

3

HAND CALCULATION

Properties:

Materials:

S355 Steel:

E = 205,000 MPa, py = 355 MPa, γs = 7850 kg/m3

Light-weight concrete:

E = 24,855 MPa, fcu = 30 MPa, γc = 1800 kg/m3

Section:

UKB457x191x67

D = 453.6 mm, bf = 189.9 mm, tf = 12.7 mm, tw = 8.5 mm

Asteel = 8,550 mm2, Isteel = 29,380 cm4

Deck:

Ds =130 mm, Dp = 50 mm, sr = 300 mm, br = 150 mm

Shear Connectors:

d = 19 mm, h = 95 mm, Fu = 450 MPa

Loadings:

Self weight slab = 2.0 kN/m2

Self weight beam = 0.67 kN/m

Construction load = 0.5 kN/m2

Ceiling = 0.5 kN/m2

Partitions (live load) = 1.0 kN/m2

Occupancy (live load) = 5.0 kN/m2

Design for Pre-Composite Condition:

Construction Required Flexural Strength:

( )

construction

1.4 0.67 1.4 2.0 1.6 0.5 3.0 11.74 kN/m=• + •+• •=

ult

w

BS-5950-90 Example-001 - 3

Software Verification

PROGRAM NAME:

ETABS

REVISION NO.:

3

22

construction

construction

11.74 12 211.3kN-m

88

••

= = =

ult

ult

wL

M

36

1,471 10 355 10 522.2 kN-m

s zy

M SP −

=•= • • • =

Pre-Composite Deflection:

construction 2.0 3.0 0.67 6.67 kN/m=•+ =w

44

construction 4

55 6.67 12,000 29.9 mm

384 384 205,000 29,380 10

•• ••

δ= = =

•• • • •

wL

EI

Camber 0.8 24 mm, which is rounded down to 20 mm= •δ=

Design for Composite Flexural Strength:

Required Flexural Strength:

()

1.4 0.67 1.4 2.0 1.6 1 1.6 5 3.0 40.24 kN/m=• + •+•+••=

ult

w

22

40.24 12 724.3kN-m

88

ult

ult

wL

M••

= = =

Full Composite Action Available Flexural Strength:

Effective width of slab:

L 12,000 3,000 mm 3,000 mmm

44

e

B= = = ≤

Resistance of slab in compression:

( )

3

0.45 ( ) 0.45 30 3,000 130 50 10 3,240 kN

−

= • •• − = •• • − • =

c cu e s p

R f B DD

Resistance of steel in tension:

3

8,550 355 10 3,035 kN

s y sy

R P Ap

−

==•= • • =

controls

Moment resistance of composite beam for full composite action:

( )

sp

3

DD for

22

453.6 3,035 80

3,035 130 10 968.9 kN-m

2 3,240 2

s

pc s s s c

c

DR

M R D RR

R

−



−

= +− ≤









= +− •• =





BS-5950-90 Example-001 - 4

Software Verification

PROGRAM NAME:

ETABS

REVISION NO.:

3

Partial Composite Action Available Flexural Strength:

Assume 72% composite action – the 75% assumed in the example requires more

shear studs than can fit on the beam given its actual clear length.

0.72 2,189 kN

qs

RR= •=

Tensile Resistance of web:

( )

( )

3

y

2 p 8.5 453.6 2 12.7 355 10 1,292 kN

−

= • −• • = • −• • • =

ww f

Rt D t

As Rq > Rw, the plastic axis is in the steel flange, and

( )

( )

( )

2

2

3 33

()

2 24

3,035 2,189

453.6 2,189 80 12.7

3,035 10 2,1899 130 10 10

2 3,240 2 3,035 1,292 4

910.9 kN-m

sp

q s qf

c s qs

cf

DD

R RRt

D

M R RD RR

− −−



−−

=+− −







−



= •+ − ••− •



−



=

Shear Stud Strength:

Characteristic resistance of 19 mm-diameter studs in normal weight 30 MPa

concrete:

Qk = 100 kN from BS 5950: Part 3 Table 5

Adjusting for light-weight concrete:

90 kN

k

Q=

Reduction factor for profile shape with ribs perpendicular to the beam and two studs

per rib:

( )

( )

95 50

150

0.6 0.6 1.62 but 0.8

50 50

−−

=•• =• • = ≤

p

r

pp

hD

b

kk

DD

Design strength:

0.8 0.8 0.8 90 57.6 kN

pk

Qk Q=••=••=

Shear Stud Distribution:

The example places two rows of shear studs and computes the numbers of deck ribs

available for placing shear studs based on the beam center to center span and the

deck rib spacing: 12 m / 300 mm = 40

BS-5950-90 Example-001 - 5

Software Verification

PROGRAM NAME:

ETABS

REVISION NO.:

3

However, the number of deck ribs available for placing shear studs must be based on

the beam clear span, and since the clear beam span is somewhat less than the 12 m

center to center span there are only 39 deck ribs available.

ETABS selects 72% composite action, which is the highest achievable and sufficient

to meet the live load deflection criteria. ETABS satisfies this 72% composite action

by placing one stud per deck rib along the entire length of the beam, plus a second

stud per rib in all the deck ribs except the mid-span rib since this is the location of

the beam zero moment and a stud in that rib would not contribute anything to the

total resistance of the shear connectors. The total resistance of the shear connectors

is:

2 19 38 57.6 2,189 kN

qp

RQ=•• =• =

Live Load Deflection:

The second moment of area of the composite section, based on elastic properties, Ic

is given by:

()

()

( )

23

steel eff

steel

D

4 1 12

•+ + • −

= ++

• +α • •α

sp sp

c

ee

A DD b DD

II

r

( )

steel

eff

8,550 0.0356

( ) 3,000 130 50

sp

A

rb DD

= = =

•− • −

For light-weight concrete:

10α=

s

25α=

l

Proportion of total loading which is long term:

live

live

0.33 6.67 1.5 0.33 18 0.541

6.67 1.5 18

++ • ++ •

ρ= = =

+ + ++

dl sdl

l

dl sdl

ww w

ww w

( ) ( )

10 0.541 25 10 18.1α =α +ρ • α −α = + • − =

e sl l s

( )

( )

( )

236

6 64

8,550 453.4 130 50 3,000 80 294 10

4 1 18.1 0.0356 12 18.1

521 7 294 10 822 10 mm

c

I• ++ •

= + +•

•+ • •

= ++ • = •

Live load deflection assuming full composite action:

BS-5950-90 Example-001 - 6

Software Verification

PROGRAM NAME:

ETABS

REVISION NO.:

3

( )

4

4

live 6

5 18 12,000

528.8 mm

384 384 205,000 822 10

c

c

wL

EI

••

••

δ= = =

•• • • •

Adjust for partial composite action:

( )

4

4

live 6

5 18 12,000

5

384 384 205,000 294 10

80.7 mm non-composite reference deflection

••

••

δ= =

•• • • •

=

s

c

wL

EI

( ) ( )

( ) ( )

partial

0.3 1

28.9 0.3 1 0.72 80.7 28.9 33.2 mm

c sc

Kδ =δ + • − • δ −δ

= + •− • − =

Design for Shear Strength:

Required Shear Strength:

40.24 12 241.4 kN

22

ult

v

wL

F••

= = =

Shear Resistance of Steel Section:

3

0.6 0.6 355 453.4 8.5 10 820.9 kN

y sw

P p Dt

V−

= ••• = • • •• =

BS-5950-90 Example-001 - 7