Barrier Approach Visual Guide
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 11

D.H.J. Polymath
June 2018
Overview of the “Barrier Approach”
to lower the upper bound of the
de Bruijn-Newman constant.

The basic De Bruijn idea leading to the function Ht(x+iy).
How to effectively bound a good estimate for Ht?
Some observations on the zeros of Ht.
How could zeros of Htbe 'blocked' to lower the Λupper bound.
The key ideas behind the “Barrier approach”.
How to ensure no zeros have passed the Barrier?
How to show that Htdoesn’t vanish from the Barrier to Nb?
Numerical results showing Λ< 0.22 (and lower, but conditionally on RH).
Software used and detailed results available.
High level storyline
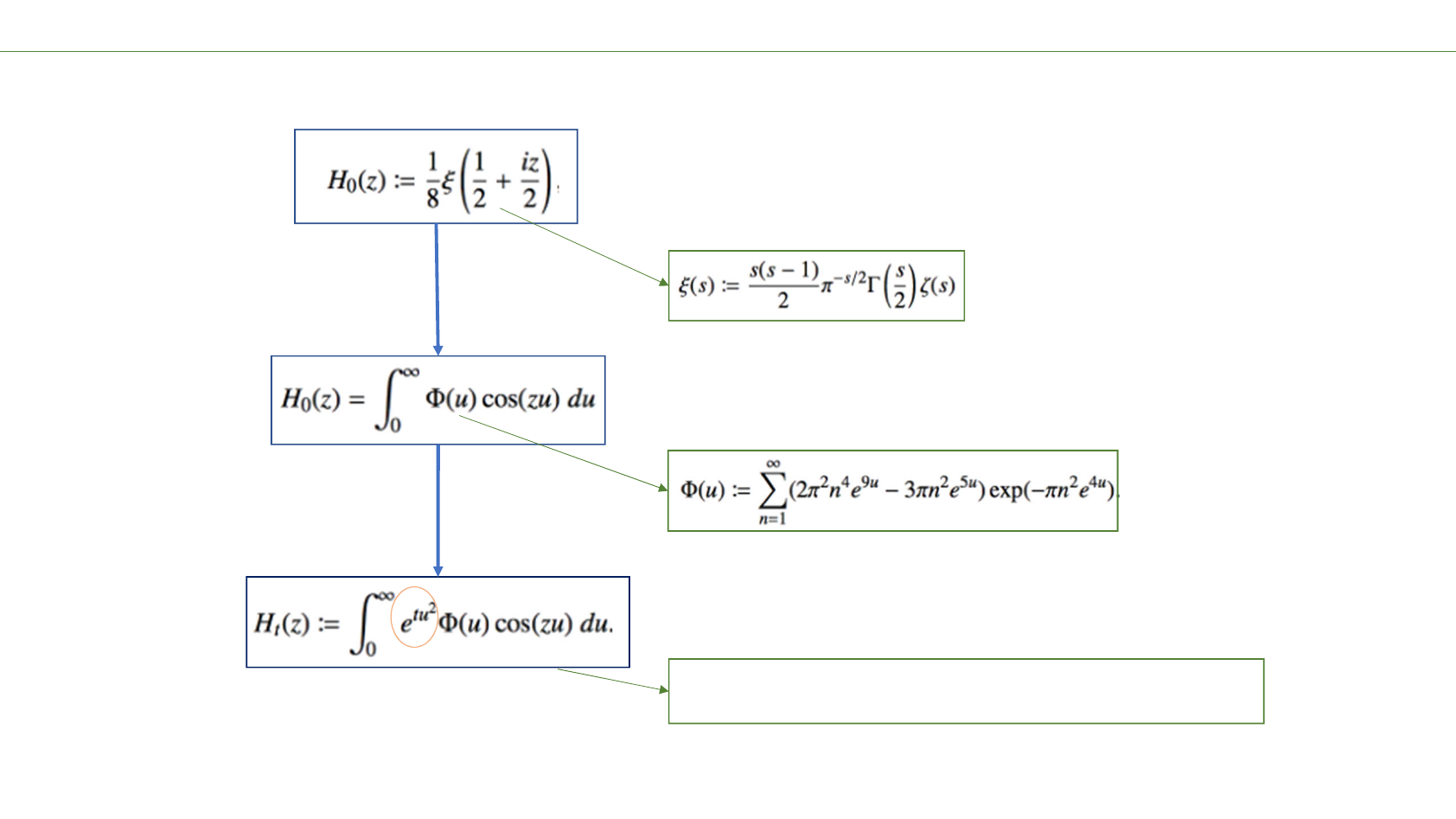
Fourier
transform
New family
introduced
by De Bruijn
Basic idea by De Bruijn
First step: develop an effectively bounded estimate.
Optionally: a more effective C-term is available
Choice of ‘Euler mollifiers’
Error terms
Error upper bounds
If Lower bound ≥Upper bound then
Hence,
Main estimate
Main estimate lower bound
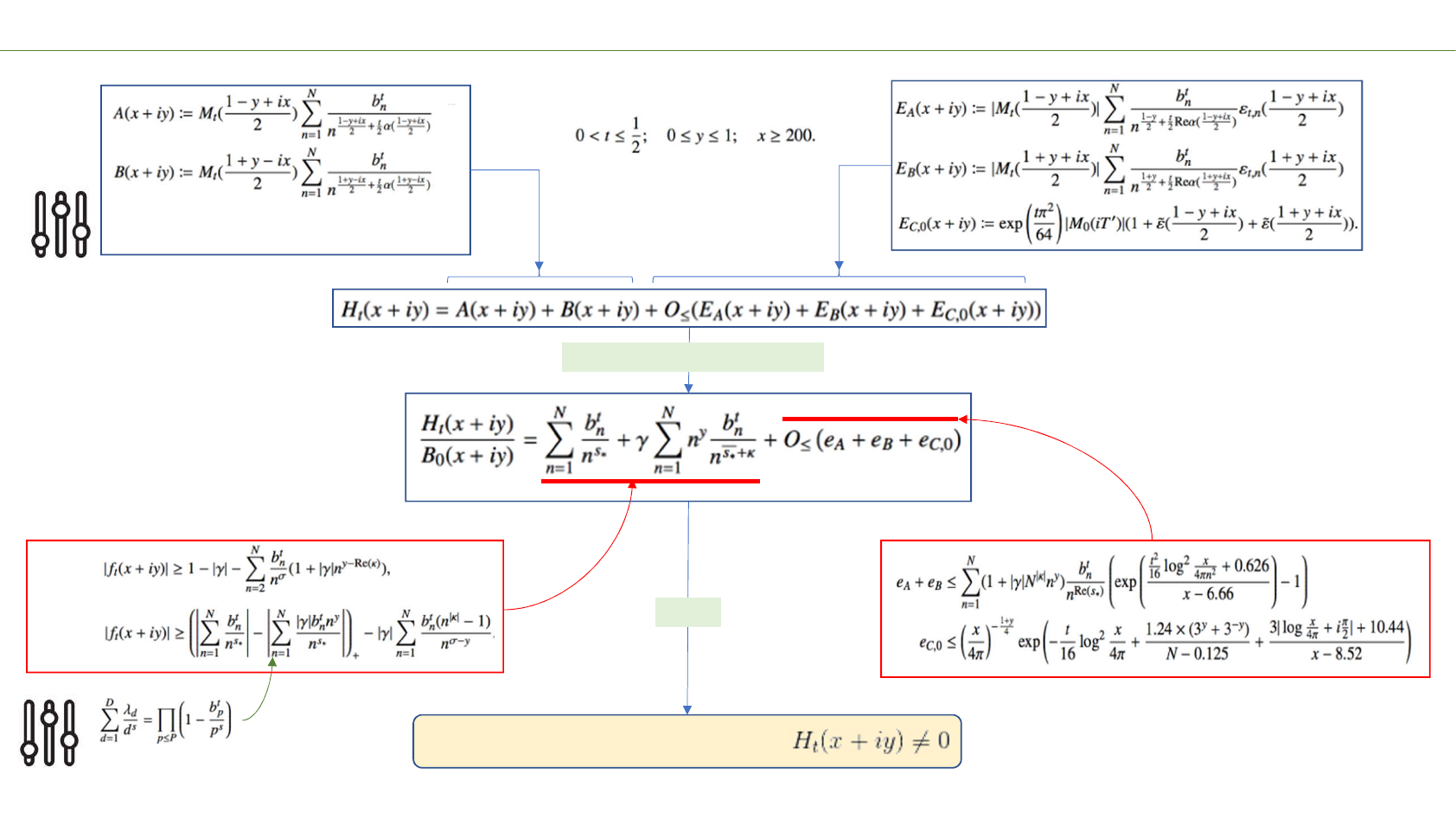
Estimating and effectively bounding Ht(x+iy)
Designed for:
Normalize by B0and bound effectively
(triangle)
(lemma)
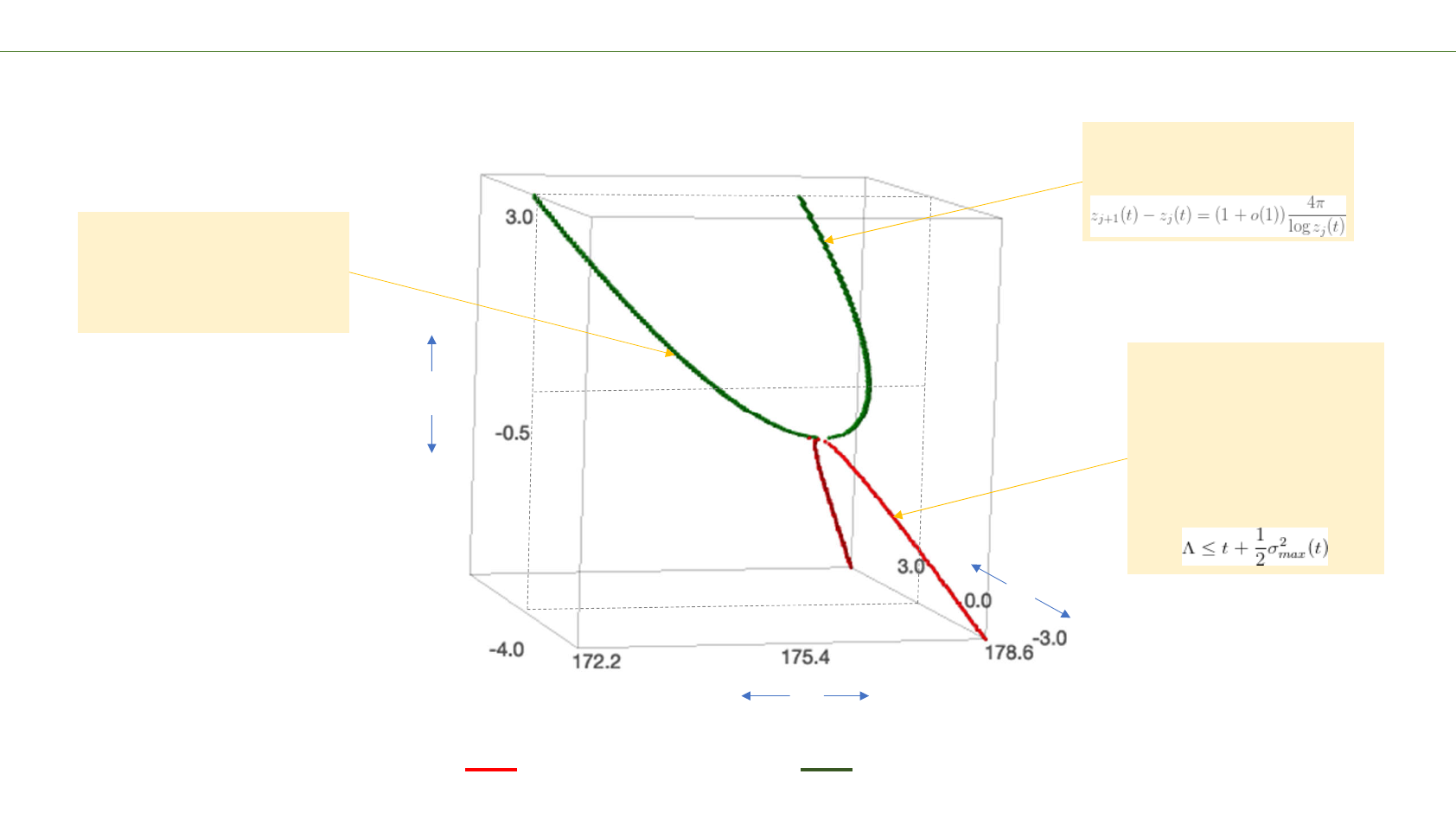
Real example of trajectories of real and complex zeros of Ht(x+iy)
x
t
y
0
trajectory of a complex zero trajectory of a real zero
Zeroes get denser as one moves
away from the origin, so there
are more zeros to the right of xn
then to the left, hence their
trajectories “lean” leftwards.
Once a zero becomes real, it stays
real forever and ends up roughly
equally spaced with:
The complex parts of zeros
attract each other and the real
parts repel each other. From
isolating the imaginary “force”,
it can be derived that all
complex zeroes will be forced
into the real axis in a finite time
leading to the bound:
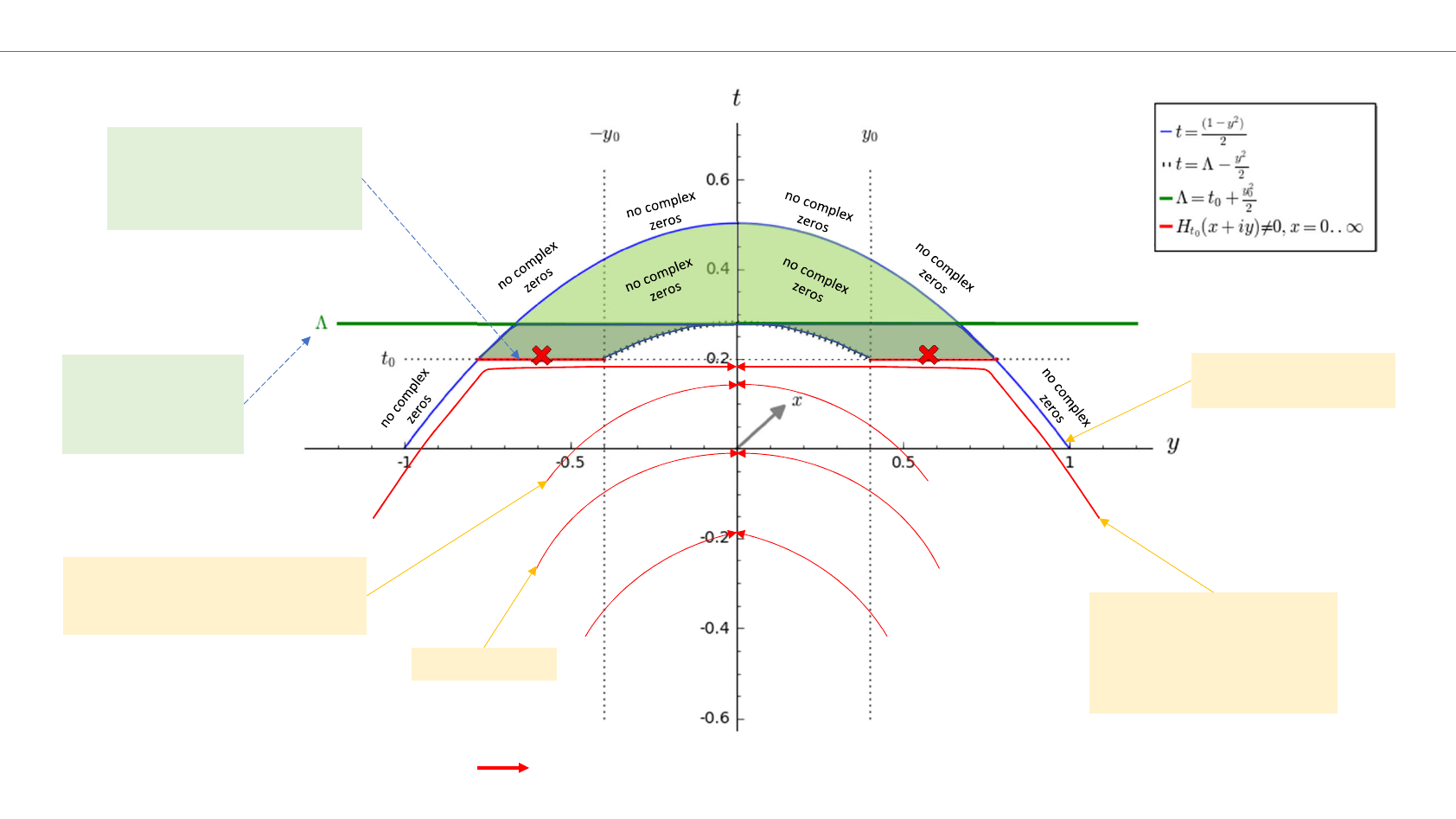
The De Bruijn – Newman
Λ
and a ‘ceiling’ the complex zeroes can’t cross
Possible trajectory of a complex zero (Ht(x+||>0)
=
0)
x1
x2
x3
x4
1. Introduce a ‘ceiling’ and
verify that Ht0 (x+iy) ≠0
for = 0 . . ∞, = 0..1 (or
the blue hyperbola).
Even this extreme trajectory is
theoretically possible since
there is no upper bound on
the speed by which zeros fall
to the real line.
A “Lehmer pair”.
Complex zeros are “attracted” to their
conjugates and “fall” to the real line
with a lower bounded speed.
The blue DbN hyperbola
is only valid for t ≥ 0.
2. If so, then the new
upper bound:
Λ ≤ t0+ 0.5 y02
has been established.
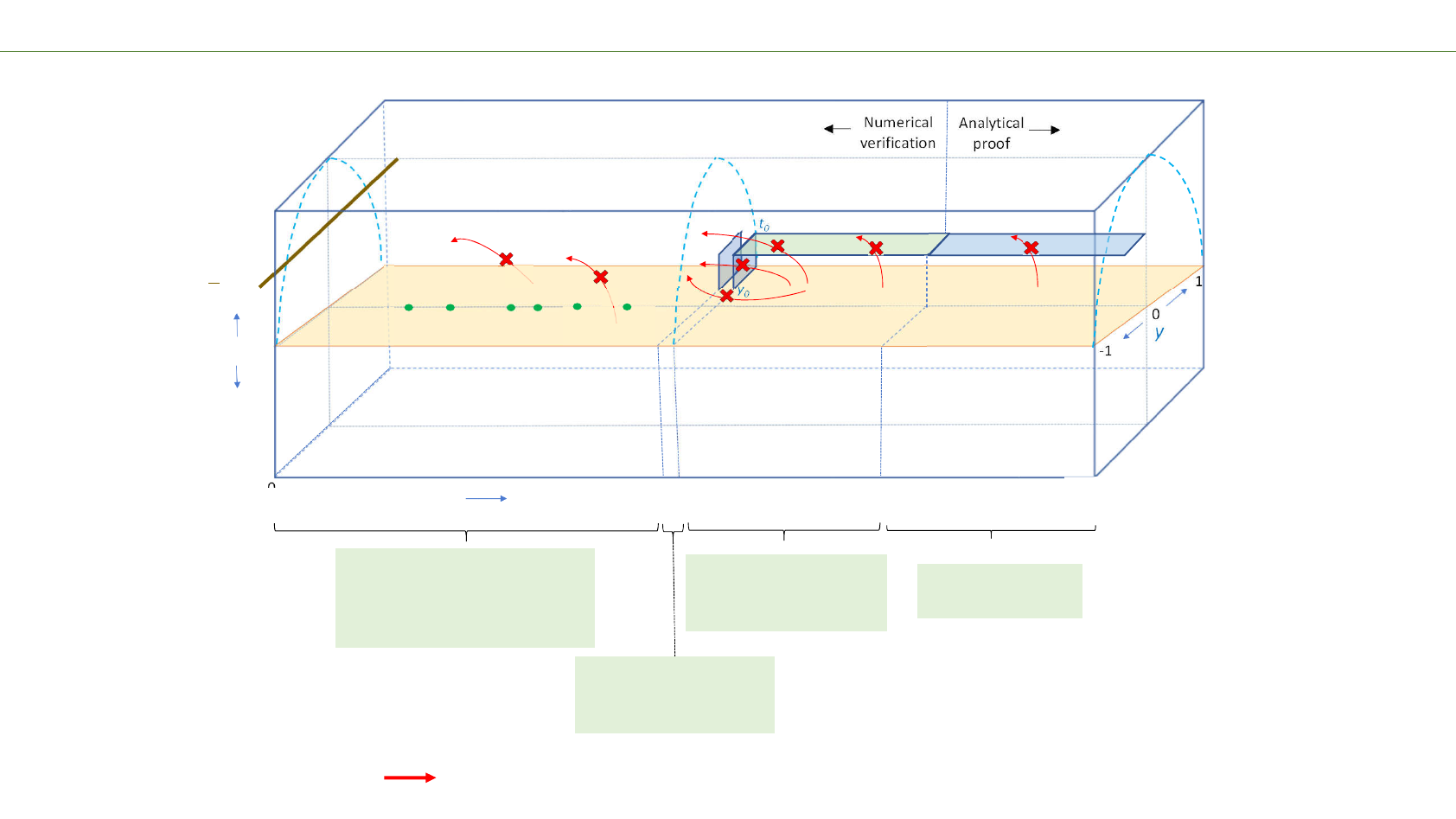
“ Barrier” approach to assure Ht(x+iy)
≠
0 for a certain y>y0, t0.
Numerical
verification
Analytical
proof
0
-1
1
0x
t
-t
0.5
0
y0
t0
y
X+1
X∞
Nb
Na
1. Area where the RH has been
verified e.g. 6x1010 certain, 1013
to be confirmed. Or assume
that it has been verified up to X.
3. Verify Ht0 (x+iy0) ≠0
i.e. Lemma lower bound
> Error upper bound.
2. Verify Ht(x+iy) ≠0
in the Barrier area
x=X..X+1, y=y0..1, t=0..t0
4. Analytical proof
that Ht0 (x+iy0) ≠0
≤ +
Possible trajectories of a complex zeros that should be “blocked”.
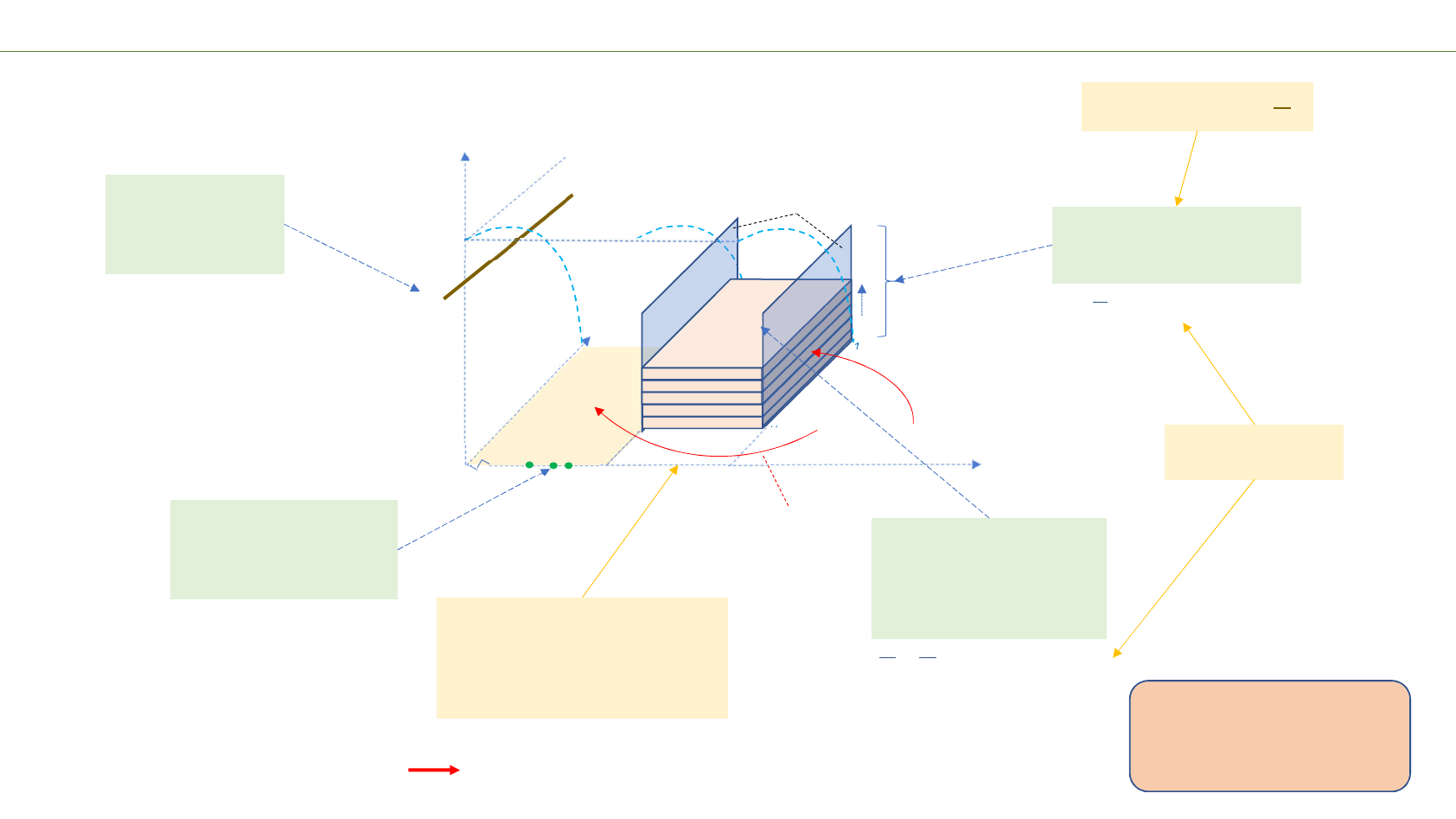
“Barrier” approach: how to clear the barrier?
1. Area cleared since all -
zeros have been, or are
assumed to be, verified to
be on the critical line.
2. For a given t, clear
rectangle X..X+1, y=y0..1 (or
a point on the hyperbola)
using the argument principle
and Rouché's theorem.
3. Use an adaptive mesh to
establish the optimal next t
and continue with 2. until t=t0.
0. Pick a promising
combination of t0,y0
and an X to lower
Λ ≤ t0+ 0.5 y02
Possible trajectories of a complex zeros that should be “blocked”.
Y0
1
x
t
y
t0
0
X X+1
Λ
0.5
1
0
upper bound required
=
upper bound required
Can’t happen due
to double barrier.
Will be detected
by barrier.
Known areas where
Ht(x+iy) ≠0
Fast integral based
approach developed.
Location of Barrier can be optimized
by selecting an X and X+1 with a
relatively high value of ABBeff (and
where the ‘mollified’ lower lemma
bound is sufficiently positive).
t=t + (minABBeff - 0.5) /|
|
Available software tools:
Barrier_Location_Optimizer
Stored_Sums_Generator
WindingNumber_Calculator
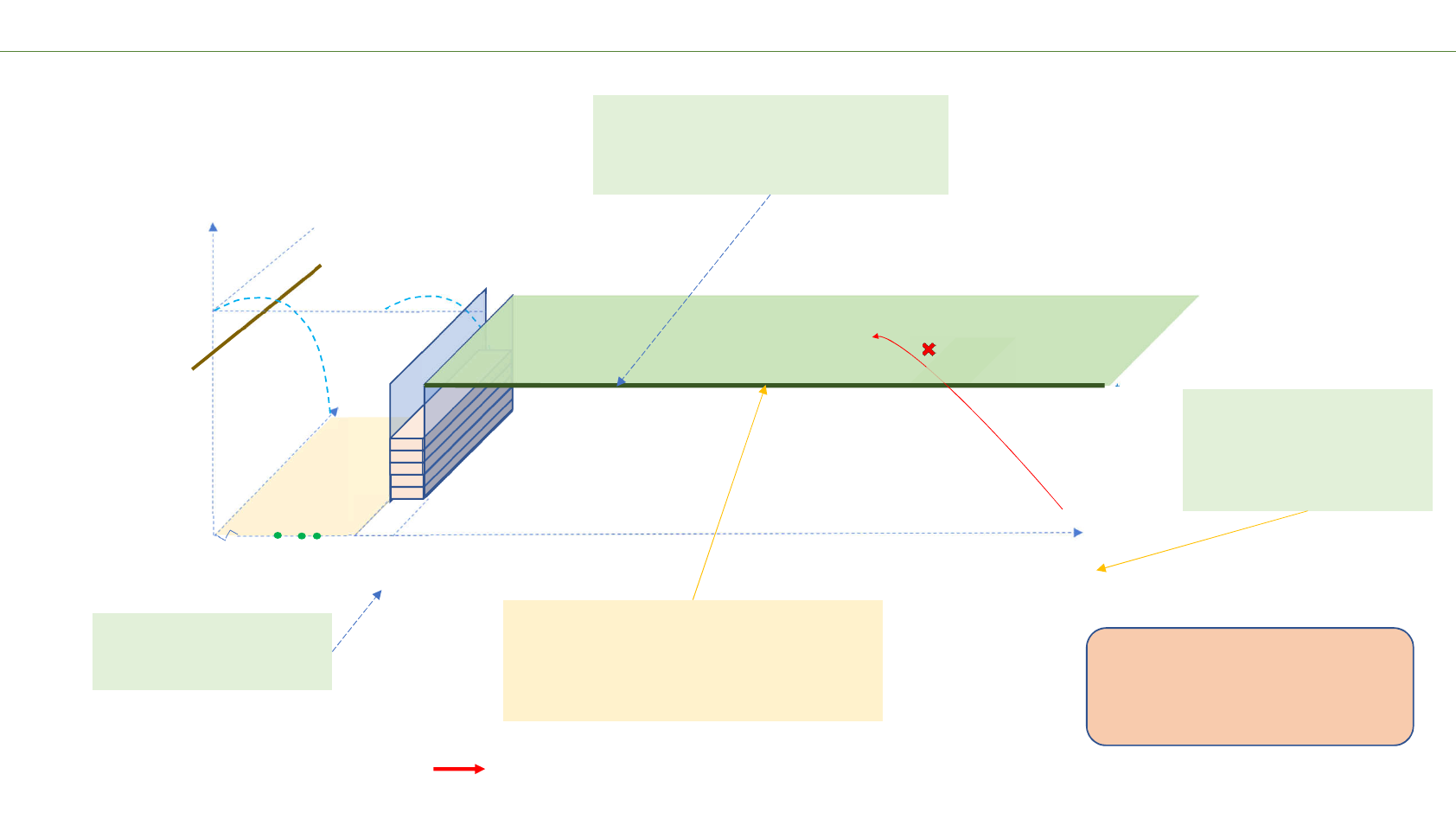
“Barrier” approach: how to verify the area from the barrier up to Nb?
y0
x
t
yt0
X X+1
Λ
0.5
1
0
2. A fast Approximate Triangle
bound is used to establish the
Nb point after which analytical
proof takes over (currently
‘unmollified’ bound only).
NaNb
3. Only the lower Lemma bound for the line
y0, t0needs to be verified to stay above the
error bounds, since the Lemma bound
monotonically increases for y going to 1.
A fast “Sawtooth” mechanism has been
developed, that only calculates the required
incremental Lemma Bound terms and only
requires a full calculation when the incremental
bound passes a user defined threshold.
1. Select a ‘mollifier’ that
makes the Lemma bound
sufficiently positive.
Possible trajectory of a complex zeros that should be “blocked”.
Available software tools:
Na_Lemmabound_calculator
Nb_Location_Finder
LemmaBound_Sawtooth_calculator

The Barrier model in action: some real numbers (wip)
Selected with Barrier
Location optimizer
Selected with
NbLocation finder
Selected with
LemmaBound utility
1) Gourdon-Demichel 2004
x
Barrier
offset
RH
verified?
t
0
y
0
Λ
Winding
number
mollifier
# primes
Lemma
bound value Na Triangle
bound value Nb
6.00E+10 155019
yes
0.20 0.20 0.22 04 0.067 69098 0.077 1.7E+06
1.00E+11 78031
yes
0.19 0.20 0.21 04 0.067 89206 0.081 6.0E+06
1.00E+12 46880
yes
0.18 0.20 0.20 03 0.135 282094 0.089 1.3E+07
5.00E+12 194858
yes
0.17 0.20 0.19 03 0.180 630783 0.116 1.5E+07
1.00E+13 9995
not yet
0.16 0.20 0.18 03 0.109 892062 0.091 3.0E+07
1.00E+14 2659
not yet
0.15 0.20 0.17 03 0.195 2820947 0.076 7.0E+07
1.00E+15 21104
not yet
0.14 0.20 0.16 03 0.251 8920620 0.073 2.0E+08
1.00E+16 172302
not yet
0.13 0.20 0.15 03 0.278 28209479 0.077 7.0E+08
1.00E+17 31656
not yet
0.12 0.20 0.14 03 0.279 89206205 0.080 3.0E+09
1.00E+18 44592
not yet
0.11 0.20 0.13 tbd 2 0.207 282094791 0.103 2.0E+10
1.00E+19 12010
not yet
0.10 0.20 0.12 tbd 2 0.128 892062059 0.097 1.5E+11
1.00E+20 37221
not yet
0.09 0.20 0.11 tbd 3 0.037 2820947918 0.075 1.5E+12
1)

Software used and useful links
All software was developed in two languages and all results were reconciled:
Symbolic math programming language - pari/gp (https://pari.math.u-bordeaux.fr )
Short development time
Relatively fast
Arithmetic Balls C-based library - Arb (http://arblib.org)
Longer development time
Very fast (up to 20 x pari/gp)
All software and results are free to use (under the LGPL-terms) and can be found here:
https://github.com/km-git-acc/dbn_upper_bound