Binary Guide Part 1
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 2

Introduction
The numbering system we use on a daily basis is base 10 or the decimal system. It turns out that
while the numbering system we use is a natural choice for humans, when computers are concerned,
abinary numbering system is more suitable.
Base 10 or Decimal Numbers
Let’s revisit how we were taught to read and write decimal numbers. This will help us understand
the structure of binary numbers.
Digits: There are 10 digits 0 1 2 3 4 5 6 7 8 9
Place Value: The position of each digit determines what that value is. Recall that from right
to left the first 5 place values are: ones, tens, hundreds, thousands, ten thousands.
ten thousands thousands hundreds tens ones
10,000 1,000 100 10 1
Base 10: Each place value can be represented in terms of 10 by using exponents. 10 is the base
and each place value is a power of 10 The table below shows the place values represented in
terms of 10.
104103102101100
10,000 1,000 100 10 1
Expanded Form: Consider the decimal number 123. Recall that the digit and place value
determine what that number is. We can add the quantities in each place value to get the number
123.
100s place 10s place 1s place
1 2 3
(1 ×100) (2 ×10) (3 ×1)
100 20 3
123 = (1 ×100) + (2 ×10) + (3 ×1)
123 = 100 + 20 + 3
Quick Practice: Write the following numbers in their expanded form like the example above.
432 = 76 = 8632 =
154 = 90 = 5120 =
801 = 43 = 2922 =
Base 2 or Binary Numbers
Abinary number system follows the same structure, but instead of powers of 10, place values are
powers of 2 as shown below:
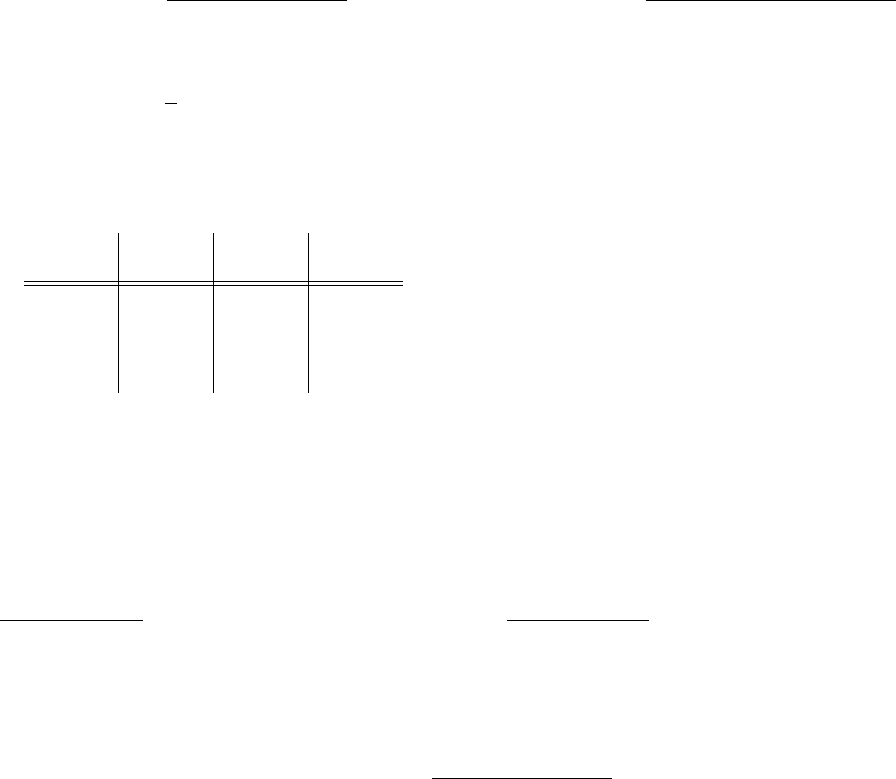
Binary 23222120
8 4 2 1 Decimal 103102101100
1,000 100 10 1
Digits: There are 2 digits 0 and 1
Expanded Form: Consider the binary number 1110. Recall that the digit and place value
determine what that number is. We can add the quantities in each place value to rewrite 1110.
8 4 2 1
1 1 1 0
(1 ×8) (1 ×4) (1 ×2) (0 ×1)
8 4 2 0
1110 = (1 ×8) + (1 ×4) + (1 ×2) + (0 ×1)
1110 =8+4+2+0
1110 = 14
Shortcut: Since there are only two digits, 0 and 1, you can simply add every place value with a
digit of 1.
8421
1111 8 + 4 + 2 + 1 = 15 8421
1001 8+1=9
Quick Practice: Convert the following binary numbers to decimal numbers as shown above. You
may use a table with binary place values.23222120
8 4 2 1
0 0 1 0 = 0 1 1 0 = 0 0 1 1 = 1 0 0 1 =
1 1 1 1 = 0 1 0 0 = 0 0 0 1 = 0 0 1 1 =
0 1 1 0 = 1 0 0 0 = 0 1 1 1 = 1 1 0 1 =