Contents CSA A23.3 14 RC BM 001
User Manual: CSA A23.3-14 RC-BM-001
Open the PDF directly: View PDF ![]() .
.
Page Count: 7

Software Verification
PROGRAM NAME:
SAFE
REVISION NO.:
0
EXAMPLE CSA A23.3-14 RC-BM-001 - 1
EXAMPLE CSA A23.3-14 RC-BM-001
Flexural and Shear Beam Design
PROBLEM DESCRIPTION
The purpose of this example is to verify slab flexural design in SAFE. The load
level is adjusted for the case corresponding to the following conditions:
The stress-block extends below the flange but remains within the balanced
condition permitted by CSA A23.3-14.
The average shear stress in the beam is below the maximum shear stress
allowed by CSA A23.3-14, requiring design shear reinforcement.
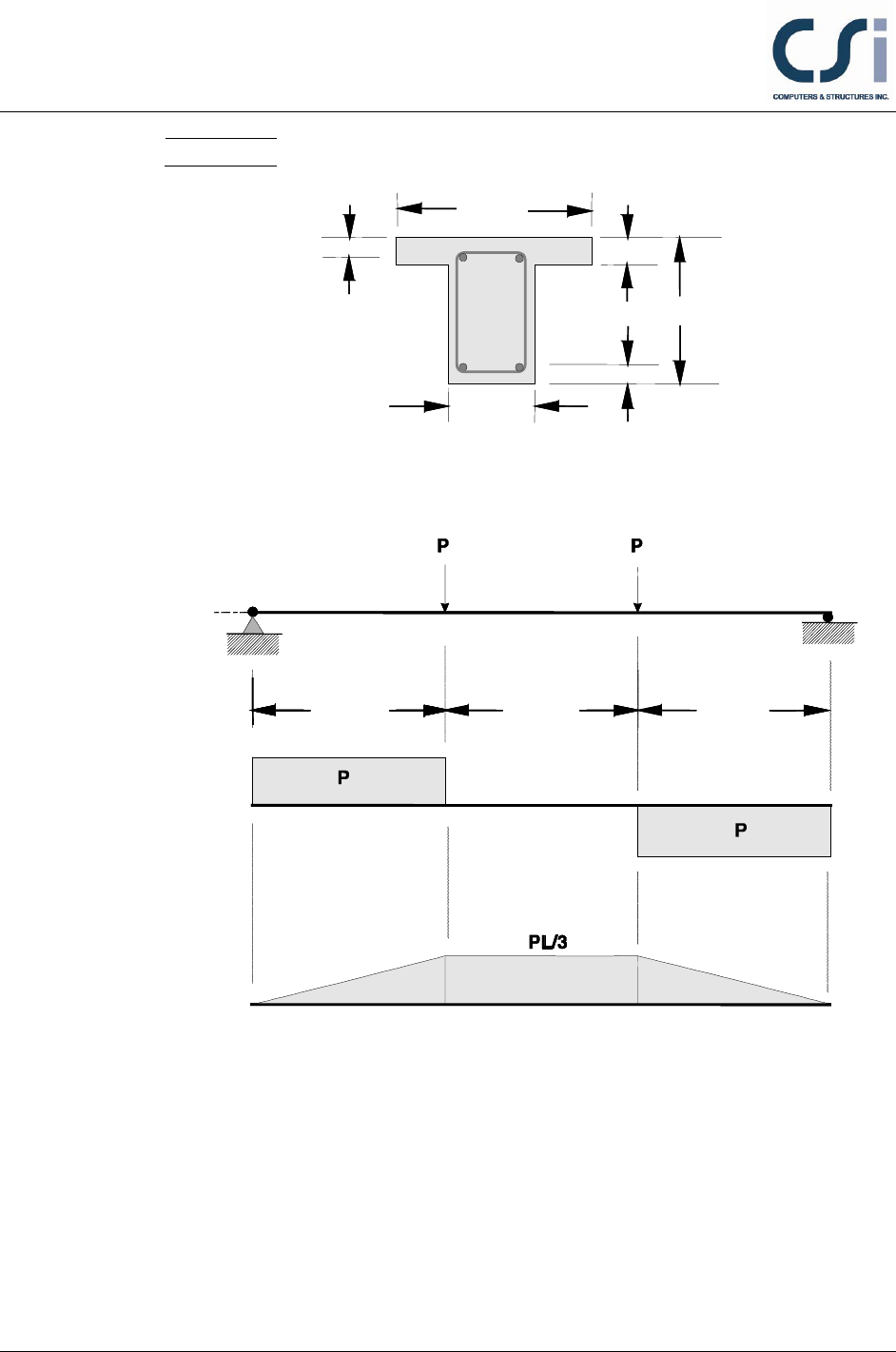
A simple-span, 6-m-long, 300-mm-wide, and 500-mm-deep T-beam with a
flange 100 mm thick and 600 mm wide is modeled using SAFE. The beam is
shown in Figure 1. The computational model uses a finite element mesh of frame
elements, automatically generated by SAFE. The maximum element size has
been specified to be 200 mm. The beam is supported by columns without
rotational stiffnesses and with very large vertical stiffness (1 × 1020 kN/m).
The beam is loaded with symmetric third-point loading. One dead load case
(DL30) and one live load case (LL100) with only symmetric third-point loads of
magnitudes 30, and 100 kN, respectively, are defined in the model. One load
combinations (COMB100) is defined using the CSA A23.3-14 load combination
factors of 1.25 for dead loads and 1.5 for live loads. The model is analyzed for
both of these load cases and the load combinations.
The beam moment and shear force are computed analytically. The total factored
moment and shear force are compared with the SAFE results. These moment and
shear force are identical. After completing the analysis, design is performed
using the CSA A23.3-14 code in SAFE and also by hand computation. Table 1
shows the comparison of the design longitudinal reinforcements. Table 2 shows
the comparison of the design shear reinforcements.
Software Verification
PROGRAM NAME:
SAFE
REVISION NO.:
0
EXAMPLE CSA A23.3-14 RC-BM-001 - 2
Beam Section
75 mm 100 mm
300 mm
600 mm
75 mm
500 mm
Shear Force
Bending Moment
2000 mm 2000 mm 2000 mm
Beam Section
75 mm 100 mm
300 mm
600 mm
75 mm
500 mm
Shear Force
Bending Moment
2000 mm 2000 mm 2000 mm
Figure 1 The Model Beam for Flexural and Shear Design
Software Verification
PROGRAM NAME:
SAFE
REVISION NO.:
0
EXAMPLE CSA A23.3-14 RC-BM-001 - 3
GEOMETRY, PROPERTIES AND LOADING
Clear span, l = 6000 mm
Overall depth, h = 500 mm
Flange thickness, ds = 100 mm
Width of web, bw = 300 mm
Width of flange, bf = 600 mm
Depth of tensile reinf., dc = 75 mm
Effective depth, d = 425 mm
Depth of comp. reinf., d' = 75 mm
Concrete strength, f'c = 30 MPa
Yield strength of steel, fy = 460 MPa
Concrete unit weight, wc = 0 kN/m3
Modulus of elasticity, Ec = 25x105 MPa
Modulus of elasticity, Es = 2x108 MPa
Poisson’s ratio, v = 0.2
Dead load, Pd = 30 kN
Live load, Pl = 100 kN
TECHNICAL FEATURES OF SAFE TESTED
Calculation of flexural and shear reinforcement
Application of minimum flexural and shear reinforcement
RESULTS COMPARISON
Table 1 shows the comparison of the SAFE total factored moments in the design
strip with the moments obtained by the analytical method. They match exactly
for this problem. Table 1 also shows the design reinforcement comparison.
Table 1 Comparison of Moments and Flexural Reinforcements
Method Moment (kN-m)
Reinforcement Area (sq-cm)
As+
SAFE 375 25.844
Calculated 375 25.844
,mins
+
A
= 535.82 sq-m

Software Verification
PROGRAM NAME:
SAFE
REVISION NO.:
0
EXAMPLE CSA A23.3-14 RC-BM-001 - 4
Table 2 Comparison of Shear Reinforcements
Shear Force (kN)
Reinforcement Area,
s
A
v
(sq-cm/m)
SAFE Calculated
187.5 12.573 12.573
COMPUTER FILE: CSA A23.3-14 RC-BM-001.FDB
CONCLUSION
The SAFE results show an exact comparison with the independent results.

Software Verification
PROGRAM NAME:
SAFE
REVISION NO.:
0
EXAMPLE CSA A23.3-14 RC-BM-001 - 5
HAND CALCULATION
Flexural Design
The following quantities are computed for all the load combinations:
φ
c = 0.65 for concrete
φ
s = 0.85 for reinforcement
As,min =
0.2 c
y
f
f
′
bw h = 357.2 sq-mm
α1 = 0.85 – 0.0015f'c ≥ 0.67 = 0.805
β1 = 0.97 – 0.0025f'c ≥ 0.67 = 0.895
cb =
y
f+700
700
d = 256.46 mm
ab =
β
1cb = 229.5366 mm
As = min[As,min, (4/3) As,required] = min[357.2, (4/3)2445] = 357.2 sq-mm
COMB100
P = (1.25Pd + 1.5Pt) =187.5kN
*
3
Pl
M=
= 375 kN-m
Mf = 375 kN-m
The depth of the compression block is given by:
( )
( )
1min ,
f c f w sb
C f b b ha
α
′
= −
= 724.5 kN
Therefore,
sy
cf
s
f
C
A
φ
φ
=
1
and the portion of Mf that is resisted by the flange is given
by:

Software Verification
PROGRAM NAME:
SAFE
REVISION NO.:
0
EXAMPLE CSA A23.3-14 RC-BM-001 - 6
s
y
cf
s
f
C
A
φ
φ
=
1
= 1204.411 sq-mm
( )
c
b
s
f
ff
a
h
dC
M
φ
−= 2
,
min
= 176.596 kN-m
Therefore, the balance of the moment, Mf to be carried by the web is:
Mfw = Mf − Mff = 198.403 kN-m
The web is a rectangular section with dimensions bw and d, for which the design
depth of the compression block is recalculated as:
wcc
fw
bf
M
dda
φα
'
2
1
2
1
−−=
= 114.5745 mm
If a1 ≤ ab, the area of tension reinforcement is then given by:
−
=
2
1
2
a
df
M
A
ys
fw
s
φ
= 1379.94 sq-mm
As = As1 + As2 = 2584.351 sq-mm
Shear Design
The basic shear strength for rectangular section is computed as,
φ
c = 0.65 for shear
{
. , for normal density concrete1 00
λ
=
v
d
is the effective shear depth. It is taken as the greater of 0.9d or 0.72h =
382.5 mm (governing) or 360 mm.
300 if minimum transverse reinforcement=
ze
S
( )
ss
ffvf
xAE
N
VdM
2
5.0++
=
ε
and
003.0≤
x
ε

Software Verification
PROGRAM NAME:
SAFE
REVISION NO.:
0
EXAMPLE CSA A23.3-14 RC-BM-001 - 7
()()
0.40 1300
1 1500 1000
βε
= •
++
x ze
S
= 0.07272
c c cwv
V f bd
φ λβ
′
=
= 29.708 kN
dbfV wccr '25.0
max,
φ
=
= 621.56 kN
θ = 50
( )
vyt
s
cf
v
df
VV
s
A
φ
θ
tan−
=
= 1.2573 mm2/mm = 12.573 cm2/m.