Solutions COA8e Computer Organization And Architecture Designing For Performance, 8th Edition Solution Manual

Solution%20Manual%20Computer%20Organization%20And%20Architecture%208th%20Edition

Solution_Manual_Computer_Organization_And_Architecture_8th_Edition

Solution%20Manual%20Computer%20Organization%20And%20Architecture%208th%20Edition

User Manual:

Open the PDF directly: View PDF .
Page Count: 134 [warning: Documents this large are best viewed by clicking the View PDF Link!]

SOLUTIONS MANUAL

COMPUTER ORGANIZATION AND

ARCHITECTURE

DESIGNING FOR PERFORMANCE

EIGHTH EDITION

WILLIAM STALLINGS

Originally Shared for

http://www.mashhoood.webs.com

Mashhood's Web Family

-4-

Chapter 1 Introduction...........................................................................................5

Chapter 2 Computer Evolution and Performance .............................................6

Chapter 3 Computer Function and Interconnection........................................14

Chapter 4 Cache Memory....................................................................................19

Chapter 5 Internal Memory.................................................................................32

Chapter 6 External Memory................................................................................38

Chapter 7 Input/Output......................................................................................43

Chapter 8 Operating System Support................................................................50

Chapter 9 Computer Arithmetic.........................................................................57

Chapter 10 Instruction Sets: Characteristics and Functions ...........................69

Chapter 11 Instruction Sets: Addressing Modes and Formats.......................80

Chapter 12 Processor Structure and Function ..................................................85

Chapter 13 Reduced Instruction Set Computers..............................................92

Chapter 14 Instruction-Level Parallelism and Superscalar Processors.........97

Chapter 15 Control Unit Operation..................................................................103

Chapter 16 Microprogrammed Control...........................................................106

Chapter 17 Parallel Processing..........................................................................109

Chapter 18 Multicore Computers.....................................................................118

Chapter 19 Number Systems.............................................................................121

Chapter 20 Digital Logic ....................................................................................122

Chapter 21 The IA-64 Architecture ..................................................................126

Appendix B Assembly Language and Related Topics ..................................130

TABLE OF CONTENTS

Originally Shared for

http://www.mashhoood.webs.com

Mashhood's Web Family

-5-

CHAPTER 1 INTRODUCTION

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

1.1 Computer architecture refers to those attributes of a system visible to a

programmer or, put another way, those attributes that have a direct impact on the

logical execution of a program. Computer organization refers to the operational

units and their interconnections that realize the architectural specifications.

Examples of architectural attributes include the instruction set, the number of bits

used to represent various data types (e.g., numbers, characters), I/O mechanisms,

and techniques for addressing memory. Organizational attributes include those

hardware details transparent to the programmer, such as control signals;

interfaces between the computer and peripherals; and the memory technology

used.

1.2 Computer structure refers to the way in which the components of a computer are

interrelated. Computer function refers to the operation of each individual

component as part of the structure.

1.3 Data processing; data storage; data movement; and control.

1.4 Central processing unit (CPU): Controls the operation of the computer and

performs its data processing functions; often simply referred to as processor.

Main memory: Stores data.

I/O: Moves data between the computer and its external environment.

System interconnection: Some mechanism that provides for communication

among CPU, main memory, and I/O. A common example of system

interconnection is by means of a system bus, consisting of a number of conducting

wires to which all the other components attach.

1.5 Control unit: Controls the operation of the CPU and hence the computer

Arithmetic and logic unit (ALU): Performs the computer’s data processing

functions

Registers: Provides storage internal to the CPU

CPU interconnection: Some mechanism that provides for communication among

the control unit, ALU, and registers

-6-

CHAPTER 2 COMPUTER EVOLUTION AND

PERFORMANCE

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

2.1 In a stored program computer, programs are represented in a form suitable for

storing in memory alongside the data. The computer gets its instructions by reading

them from memory, and a program can be set or altered by setting the values of a

portion of memory.

2.2 A main memory, which stores both data and instructions: an arithmetic and logic

unit (ALU) capable of operating on binary data; a control unit, which interprets

the instructions in memory and causes them to be executed; and input and output

(I/O) equipment operated by the control unit.

2.3 Gates, memory cells, and interconnections among gates and memory cells.

2.4 Moore observed that the number of transistors that could be put on a single chip

was doubling every year and correctly predicted that this pace would continue

into the near future.

2.5 Similar or identical instruction set: In many cases, the same set of machine

instructions is supported on all members of the family. Thus, a program that

executes on one machine will also execute on any other. Similar or identical

operating system: The same basic operating system is available for all family

members. Increasing speed: The rate of instruction execution increases in going

from lower to higher family members. Increasing Number of I/O ports: In going

from lower to higher family members. Increasing memory size: In going from

lower to higher family members. Increasing cost: In going from lower to higher

family members.

2.6 In a microprocessor, all of the components of the CPU are on a single chip.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

2.1 This program is developed in [HAYE98]. The vectors A, B, and C are each stored

in 1,000 contiguous locations in memory, beginning at locations 1001, 2001, and

3001, respectively. The program begins with the left half of location 3. A counting

variable N is set to 999 and decremented after each step until it reaches –1. Thus,

the vectors are processed from high location to low location.

-7-

Location

Instruction

Comments

999

Constant (count N)

Constant

1000

Constant

LOAD M(2000)

Transfer A(I) to AC

ADD M(3000)

Compute A(I) + B(I)

STOR M(4000)

Transfer sum to C(I)

LOAD M(0)

Load count N

SUB M(1)

Decrement N by 1

JUMP+ M(6, 20:39)

Test N and branch to 6R if nonnegative

JUMP M(6, 0:19)

Halt

STOR M(0)

Update N

ADD M(1)

Increment AC by 1

ADD M(2)

STOR M(3, 8:19)

Modify address in 3L

ADD M(2)

STOR M(3, 28:39)

Modify address in 3R

ADD M(2)

10L

STOR M(4, 8:19)

Modify address in 4L

10R

JUMP M(3, 0:19)

Branch to 3L

2.2 a.

Opcode

Operand

00000001

000000000010

b. First, the CPU must make access memory to fetch the instruction. The

instruction contains the address of the data we want to load. During the execute

phase accesses memory to load the data value located at that address for a total

of two trips to memory.

2.3 To read a value from memory, the CPU puts the address of the value it wants into

the MAR. The CPU then asserts the Read control line to memory and places the

address on the address bus. Memory places the contents of the memory location

passed on the data bus. This data is then transferred to the MBR. To write a value

to memory, the CPU puts the address of the value it wants to write into the MAR.

The CPU also places the data it wants to write into the MBR. The CPU then asserts

the Write control line to memory and places the address on the address bus and

the data on the data bus. Memory transfers the data on the data bus into the

corresponding memory location.

-8-

2.4

Address

Contents

08A

08B

08C

08D

LOAD M(0FA)

STOR M(0FB)

LOAD M(0FA)

JUMP +M(08D)

LOAD –M(0FA)

STOR M(0FB)

This program will store the absolute value of content at memory location 0FA into

memory location 0FB.

2.5 All data paths to/from MBR are 40 bits. All data paths to/from MAR are 12 bits.

Paths to/from AC are 40 bits. Paths to/from MQ are 40 bits.

2.6 The purpose is to increase performance. When an address is presented to a memory

module, there is some time delay before the read or write operation can be

performed. While this is happening, an address can be presented to the other

module. For a series of requests for successive words, the maximum rate is

doubled.

2.7 The discrepancy can be explained by noting that other system components aside from clock

speed make a big difference in overall system speed. In particular, memory systems and

advances in I/O processing contribute to the performance ratio. A system is only as fast as

its slowest link. In recent years, the bottlenecks have been the performance of memory

modules and bus speed.

2.8 As noted in the answer to Problem 2.7, even though the Intel machine may have a

faster clock speed (2.4 GHz vs. 1.2 GHz), that does not necessarily mean the system

will perform faster. Different systems are not comparable on clock speed. Other

factors such as the system components (memory, buses, architecture) and the

instruction sets must also be taken into account. A more accurate measure is to run

both systems on a benchmark. Benchmark programs exist for certain tasks, such as

running office applications, performing floating-point operations, graphics

operations, and so on. The systems can be compared to each other on how long

they take to complete these tasks. According to Apple Computer, the G4 is

comparable or better than a higher-clock speed Pentium on many benchmarks.

2.9 This representation is wasteful because to represent a single decimal digit from 0

through 9 we need to have ten tubes. If we could have an arbitrary number of

these tubes ON at the same time, then those same tubes could be treated as binary

bits. With ten bits, we can represent 210 patterns, or 1024 patterns. For integers,

these patterns could be used to represent the numbers from 0 through 1023.

2.10 CPI = 1.55; MIPS rate = 25.8; Execution time = 3.87 ns. Source: [HWAN93]

-9-

2.11 a.

€

CPIA=CPIi×Ii

∑

=8×1+4×3+2×4+4×3

( )

×106

8+4+2+4

( )

×106≈2.22

MIPSA=f

CPIA×106=200 ×106

2.22 ×106=90

CPUA=Ic×CPIA

f=18 ×106×2.2

200 ×106=0.2 s

CPIB=CPIi×Ii

∑

=10 ×1+8×2+2×4+4×3

( )

×106

10 +8+2+4

( )

×106≈1.92

MIPSB=f

CPIB×106=200 ×106

1.92 ×106=104

CPUB=Ic×CPIB

f=24 ×106×1.92

200 ×106=0.23 s

b. Although machine B has a higher MIPS than machine A, it requires a longer

CPU time to execute the same set of benchmark programs.

2.12 a. We can express the MIPs rate as: [(MIPS rate)/106] = Ic/T. So that:

Ic = T × [(MIPS rate)/106]. The ratio of the instruction count of the RS/6000 to

the VAX is [x × 18]/[12x × 1] = 1.5.

b. For the Vax, CPI = (5 MHz)/(1 MIPS) = 5.

For the RS/6000, CPI = 25/18 = 1.39.

2.13 From Equation (2.2), MIPS = Ic/(T × 106) = 100/T. The MIPS values are:

Computer A

Computer B

Computer C

Program 1

100

Program 2

0.1

Program 3

0.2

0.1

Program 4

0.125

Arithmetic

mean

Rank

Harmonic

mean

Rank

Computer A

25.325

0.25

Computer B

2.8

0.21

Computer C

3.26

2.1

-10-

2.14 a. Normalized to R:

Processor

Benchmark

1.00

1.71

3.11

1.00

1.19

1.00

0.43

0.49

1.00

1.11

0.60

1.00

2.10

2.09

Arithmetic

mean

1.00

1.31

1.50

b. Normalized to M:

Processor

Benchmark

0.59

1.00

1.82

0.84

1.00

2.32

1.00

1.13

0.90

1.00

0.54

0.48

1.00

Arithmetic

mean

1.01

1.00

1.10

c. Recall that the larger the ratio, the higher the speed. Based on (a) R is the

slowest machine, by a significant amount. Based on (b), M is the slowest

machine, by a modest amount.

d. Normalized to R:

Processor

Benchmark

1.00

1.71

3.11

1.00

1.19

1.00

0.43

0.49

1.00

1.11

0.60

1.00

2.10

2.09

Geometric

mean

1.00

1.15

1.18

-11-

Normalized to M:

Processor

Benchmark

0.59

1.00

1.82

0.84

1.00

2.32

1.00

1.13

0.90

1.00

0.54

0.48

1.00

Geometric

mean

0.87

1.00

1.02

Using the geometric mean, R is the slowest no matter which machine is used

for normalization.

2.15 a. Normalized to X:

Processor

Benchmark

2.0

0.5

2.0

Arithmetic

mean

1.25

Geometric

mean

Normalized to Y:

Processor

Benchmark

0.5

0.25

2.0

4.0

Arithmetic

mean

1.25

2.125

Geometric

mean

Machine Y is twice as fast as machine X for benchmark 1, but half as fast for

benchmark 2. Similarly machine Z is half as fast as X for benchmark 1, but

twice as fast for benchmark 2. Intuitively, these three machines have equivalent

performance. However, if we normalize to X and compute the arithmetic mean

-12-

of the speed metric, we find that Y and Z are 25% faster than X. Now, if we

normalize to Y and compute the arithmetic mean of the speed metric, we find

that X is 25% faster than Y and Z is more than twice as fast as Y. Clearly, the

arithmetic mean is worthless in this context.

b. When the geometric mean is used, the three machines are shown to have equal

performance when normalized to X, and also equal performance when

normalized to Y. These results are much more in line with our intuition.

2.16 a. Assuming the same instruction mix means that the additional instructions for

each task should be allocated proportionally among the instruction types. So

we have the following table:

Instruction Type

CPI

Instruction Mix

Arithmetic and logic

60%

Load/store with cache hit

18%

Branch

12%

Memory reference with cache

miss

10%

CPI = 0.6 + (2 × 0.18) + (4 × 0.12) + (12 × 0.1) = 2.64. The CPI has increased due

to the increased time for memory access.

b. MIPS = 400/2.64 = 152. There is a corresponding drop in the MIPS rate.

c. The speedup factor is the ratio of the execution times. Using Equation 2.2, we

calculate the execution time as T = Ic/(MIPS × 106). For the single-processor

case, T1 = (2 × 106)/(178 × 106) = 11 ms. With 8 processors, each processor

executes 1/8 of the 2 million instructions plus the 25,000 overhead instructions.

For this case, the execution time for each of the 8 processors is

€

T8=

2×106

8+0.025 ×106

152 ×106=

1.8 ms

Therefore we have

€

Speedup =time to execute program on a single processor

time to execute program on N parallel processors =11

1.8 =6.11

d. The answer to this question depends on how we interpret Amdahl's' law. There

are two inefficiencies in the parallel system. First, there are additional

instructions added to coordinate between threads. Second, there is contention

for memory access. The way that the problem is stated, none of the code is

inherently serial. All of it is parallelizable, but with scheduling overhead. One

could argue that the memory access conflict means that to some extent memory

reference instructions are not parallelizable. But based on the information

given, it is not clear how to quantify this effect in Amdahl's equation. If we

assume that the fraction of code that is parallelizable is f = 1, then Amdahl's law

reduces to Speedup = N =8 for this case. Thus the actual speedup is only about

75% of the theoretical speedup.

-13-

2.17 a. Speedup = (time to access in main memory)/(time to access in cache) = T2/T1.

b. The average access time can be computed as T = H × T1 + (1 – H) × T2

Using Equation (2.8):

€

Speedup = Execution time before enhancement

Execution time after enhancement =T2

T=T2

H×T

1+1−H

( )

1−H

( )

+HT

c. T = H × T1 + (1 – H) × (T1 + T2) = T1 + (1 – H) × T2)

This is Equation (4.2) in Chapter 4. Now,

€

Speedup = Execution time before enhancement

Execution time after enhancement =T2

T=T2

1+1−H

( )

1−H

( )

In this case, the denominator is larger, so that the speedup is less.

-14-

CHAPTER 3 COMPUTER FUNCTION AND

INTERCONNECTION

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

3.1 Processor-memory: Data may be transferred from processor to memory or from

memory to processor. Processor-I/O: Data may be transferred to or from a

peripheral device by transferring between the processor and an I/O module. Data

processing: The processor may perform some arithmetic or logic operation on

data. Control: An instruction may specify that the sequence of execution be

altered.

3.2 Instruction address calculation (iac): Determine the address of the next instruction

to be executed. Instruction fetch (if): Read instruction from its memory location

into the processor. Instruction operation decoding (iod): Analyze instruction to

determine type of operation to be performed and operand(s) to be used. Operand

address calculation (oac): If the operation involves reference to an operand in

memory or available via I/O, then determine the address of the operand. Operand

fetch (of): Fetch the operand from memory or read it in from I/O. Data operation

(do): Perform the operation indicated in the instruction. Operand store (os): Write

the result into memory or out to I/O.

3.3 (1) Disable all interrupts while an interrupt is being processed. (2) Define priorities

for interrupts and to allow an interrupt of higher priority to cause a lower-priority

interrupt handler to be interrupted.

3.4 Memory to processor: The processor reads an instruction or a unit of data from

memory. Processor to memory: The processor writes a unit of data to memory. I/O

to processor: The processor reads data from an I/O device via an I/O module.

Processor to I/O: The processor sends data to the I/O device. I/O to or from

memory: For these two cases, an I/O module is allowed to exchange data directly

with memory, without going through the processor, using direct memory access

(DMA).

3.5 With multiple buses, there are fewer devices per bus. This (1) reduces propagation

delay, because each bus can be shorter, and (2) reduces bottleneck effects.

3.6 System pins: Include the clock and reset pins. Address and data pins: Include 32

lines that are time multiplexed for addresses and data. Interface control pins:

Control the timing of transactions and provide coordination among initiators and

targets. Arbitration pins: Unlike the other PCI signal lines, these are not shared

lines. Rather, each PCI master has its own pair of arbitration lines that connect it

directly to the PCI bus arbiter. Error Reporting pins: Used to report parity and

-15-

other errors. Interrupt Pins: These are provided for PCI devices that must generate

requests for service. Cache support pins: These pins are needed to support a

memory on PCI that can be cached in the processor or another device. 64-bit Bus

extension pins: Include 32 lines that are time multiplexed for addresses and data

and that are combined with the mandatory address/data lines to form a 64-bit

address/data bus. JTAG/Boundary Scan Pins: These signal lines support testing

procedures defined in IEEE Standard 1149.1.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

3.1 Memory (contents in hex): 300: 3005; 301: 5940; 302: 7006

Step 1: 3005 → IR; Step 2: 3 → AC

Step 3: 5940 → IR; Step 4: 3 + 2 = 5 → AC

Step 5: 7006 → IR; Step 6: AC → Device 6

3.2 1. a. The PC contains 300, the address of the first instruction. This value is loaded

in to the MAR.

b. The value in location 300 (which is the instruction with the value 1940 in

hexadecimal) is loaded into the MBR, and the PC is incremented. These two

steps can be done in parallel.

c. The value in the MBR is loaded into the IR.

2. a. The address portion of the IR (940) is loaded into the MAR.

b. The value in location 940 is loaded into the MBR.

c. The value in the MBR is loaded into the AC.

3. a. The value in the PC (301) is loaded in to the MAR.

b. The value in location 301 (which is the instruction with the value 5941) is

loaded into the MBR, and the PC is incremented.

c. The value in the MBR is loaded into the IR.

4. a. The address portion of the IR (941) is loaded into the MAR.

b. The value in location 941 is loaded into the MBR.

c. The old value of the AC and the value of location MBR are added and the

result is stored in the AC.

5. a. The value in the PC (302) is loaded in to the MAR.

b. The value in location 302 (which is the instruction with the value 2941) is

loaded into the MBR, and the PC is incremented.

c. The value in the MBR is loaded into the IR.

6. a. The address portion of the IR (941) is loaded into the MAR.

b. The value in the AC is loaded into the MBR.

c. The value in the MBR is stored in location 941.

3.3 a. 224 = 16 MBytes

b. (1) If the local address bus is 32 bits, the whole address can be transferred at

once and decoded in memory. However, because the data bus is only 16 bits, it

will require 2 cycles to fetch a 32-bit instruction or operand.

(2) The 16 bits of the address placed on the address bus can't access the whole

memory. Thus a more complex memory interface control is needed to latch the

first part of the address and then the second part (because the microprocessor

will end in two steps). For a 32-bit address, one may assume the first half will

decode to access a "row" in memory, while the second half is sent later to access

-16-

a "column" in memory. In addition to the two-step address operation, the

microprocessor will need 2 cycles to fetch the 32 bit instruction/operand.

c. The program counter must be at least 24 bits. Typically, a 32-bit microprocessor

will have a 32-bit external address bus and a 32-bit program counter, unless on-

chip segment registers are used that may work with a smaller program counter.

If the instruction register is to contain the whole instruction, it will have to be

32-bits long; if it will contain only the op code (called the op code register) then

it will have to be 8 bits long.

3.4 In cases (a) and (b), the microprocessor will be able to access 216 = 64K bytes; the

only difference is that with an 8-bit memory each access will transfer a byte, while

with a 16-bit memory an access may transfer a byte or a 16-byte word. For case (c),

separate input and output instructions are needed, whose execution will generate

separate "I/O signals" (different from the "memory signals" generated with the

execution of memory-type instructions); at a minimum, one additional output pin

will be required to carry this new signal. For case (d), it can support 28 = 256 input

and 28 = 256 output byte ports and the same number of input and output 16-bit

ports; in either case, the distinction between an input and an output port is defined

by the different signal that the executed input or output instruction generated.

3.5 Clock cycle =

8MHz =125 ns

Bus cycle = 4 × 125 ns = 500 ns

2 bytes transferred every 500 ns; thus transfer rate = 4 MBytes/sec

Doubling the frequency may mean adopting a new chip manufacturing technology

(assuming each instructions will have the same number of clock cycles); doubling

the external data bus means wider (maybe newer) on-chip data bus

drivers/latches and modifications to the bus control logic. In the first case, the

speed of the memory chips will also need to double (roughly) not to slow down

the microprocessor; in the second case, the "wordlength" of the memory will have

to double to be able to send/receive 32-bit quantities.

3.6 a. Input from the Teletype is stored in INPR. The INPR will only accept data from

the Teletype when FGI=0. When data arrives, it is stored in INPR, and FGI is

set to 1. The CPU periodically checks FGI. If FGI =1, the CPU transfers the

contents of INPR to the AC and sets FGI to 0.

When the CPU has data to send to the Teletype, it checks FGO. If FGO = 0,

the CPU must wait. If FGO = 1, the CPU transfers the contents of the AC to

OUTR and sets FGO to 0. The Teletype sets FGI to 1 after the word is printed.

b. The process described in (a) is very wasteful. The CPU, which is much faster

than the Teletype, must repeatedly check FGI and FGO. If interrupts are used,

the Teletype can issue an interrupt to the CPU whenever it is ready to accept or

send data. The IEN register can be set by the CPU (under programmer control)

3.7 a. During a single bus cycle, the 8-bit microprocessor transfers one byte while the

16-bit microprocessor transfers two bytes. The 16-bit microprocessor has twice

the data transfer rate.

b. Suppose we do 100 transfers of operands and instructions, of which 50 are one

byte long and 50 are two bytes long. The 8-bit microprocessor takes 50 + (2 x

-17-

50) = 150 bus cycles for the transfer. The 16-bit microprocessor requires 50 + 50

= 100 bus cycles. Thus, the data transfer rates differ by a factor of 1.5.

3.8 The whole point of the clock is to define event times on the bus; therefore, we wish

for a bus arbitration operation to be made each clock cycle. This requires that the

priority signal propagate the length of the daisy chain (Figure 3.26) in one clock

period. Thus, the maximum number of masters is determined by dividing the

amount of time it takes a bus master to pass through the bus priority by the clock

period.

3.9 The lowest-priority device is assigned priority 16. This device must defer to all the

others. However, it may transmit in any slot not reserved by the other SBI devices.

3.10 At the beginning of any slot, if none of the TR lines is asserted, only the priority 16

device may transmit. This gives it the lowest average wait time under most

circumstances. Only when there is heavy demand on the bus, which means that

most of the time there is at least one pending request, will the priority 16 device

not have the lowest average wait time.

3.11 a. With a clocking frequency of 10 MHz, the clock period is 10–9 s = 100 ns. The

length of the memory read cycle is 300 ns.

b. The Read signal begins to fall at 75 ns from the beginning of the third clock

cycle (middle of the second half of T3). Thus, memory must place the data on

the bus no later than 55 ns from the beginning of T3.

3.12 a. The clock period is 125 ns. Therefore, two clock cycles need to be inserted.

b. From Figure 3.19, the Read signal begins to rise early in T2. To insert two clock

cycles, the Ready line can be put in low at the beginning of T2 and kept low for

250 ns.

3.13 a. A 5 MHz clock corresponds to a clock period of 200 ns. Therefore, the Write

signal has a duration of 150 ns.

b. The data remain valid for 150 + 20 = 170 ns.

c. One wait state.

3.14 a. Without the wait states, the instruction takes 16 bus clock cycles. The

instruction requires four memory accesses, resulting in 8 wait states. The

instruction, with wait states, takes 24 clock cycles, for an increase of 50%.

b. In this case, the instruction takes 26 bus cycles without wait states and 34 bus

cycles with wait states, for an increase of 33%.

3.15 a. The clock period is 125 ns. One bus read cycle takes 500 ns = 0.5 µs. If the bus

cycles repeat one after another, we can achieve a data transfer rate of 2 MB/s.

b. The wait state extends the bus read cycle by 125 ns, for a total duration of 0.625

µs. The corresponding data transfer rate is 1/0.625 = 1.6 MB/s.

3.16 A bus cycle takes 0.25 µs, so a memory cycle takes 1 µs. If both operands are even-

aligned, it takes 2 µs to fetch the two operands. If one is odd-aligned, the time

required is 3 µs. If both are odd-aligned, the time required is 4 µs.

-18-

3.17 Consider a mix of 100 instructions and operands. On average, they consist of 20 32-

bit items, 40 16-bit items, and 40 bytes. The number of bus cycles required for the

16-bit microprocessor is (2 × 20) + 40 + 40 = 120. For the 32-bit microprocessor, the

number required is 100. This amounts to an improvement of 20/120 or about 17%.

3.18 The processor needs another nine clock cycles to complete the instruction. Thus,

the Interrupt Acknowledge will start after 900 ns.

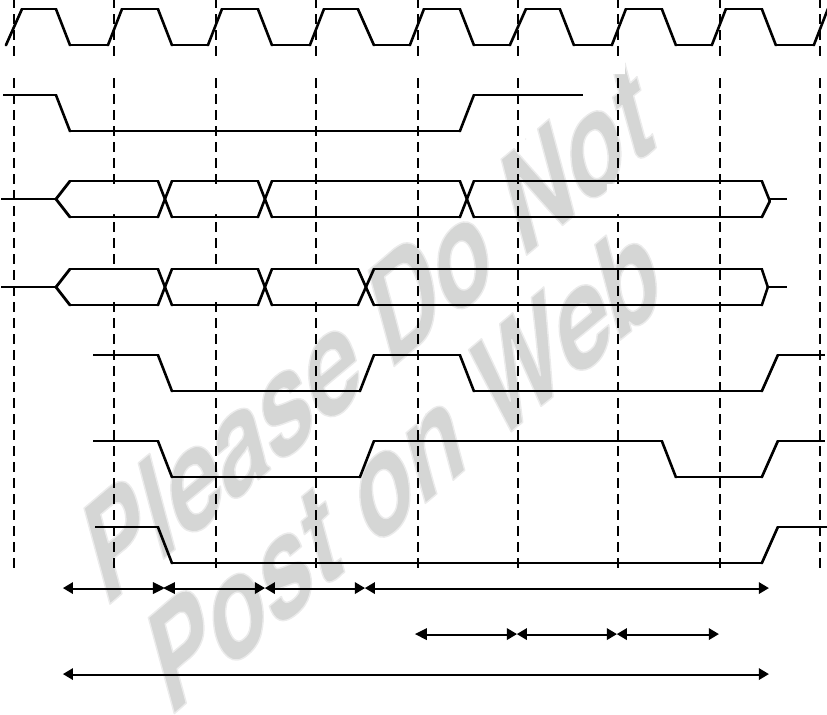
3.19

Address

Bus Cmd

Address PhaseAddress Phase Address Phase Address Phase

Byte Enable Byte Enable Byte Enable

Data-1 Data-2 Data-3

CLK

123456789

FRAME#

C/BE#

IRDY#

TRDY#

DEVSEL#

Wait State Wait State Wait State

Bus Transaction

-19-

CHAPTER 4 CACHE MEMORY

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

4.1 Sequential access: Memory is organized into units of data, called records. Access

must be made in a specific linear sequence. Direct access: Individual blocks or

records have a unique address based on physical location. Access is accomplished

by direct access to reach a general vicinity plus sequential searching, counting, or

waiting to reach the final location. Random access: Each addressable location in

memory has a unique, physically wired-in addressing mechanism. The time to

access a given location is independent of the sequence of prior accesses and is

constant.

4.2 Faster access time, greater cost per bit; greater capacity, smaller cost per bit; greater

capacity, slower access time.

4.3 It is possible to organize data across a memory hierarchy such that the percentage

of accesses to each successively lower level is substantially less than that of the

level above. Because memory references tend to cluster, the data in the higher-

level memory need not change very often to satisfy memory access requests.

4.4 In a cache system, direct mapping maps each block of main memory into only one

possible cache line. Associative mapping permits each main memory block to be

loaded into any line of the cache. In set-associative mapping, the cache is divided

into a number of sets of cache lines; each main memory block can be mapped into

any line in a particular set.

4.5 One field identifies a unique word or byte within a block of main memory. The

remaining two fields specify one of the blocks of main memory. These two fields

are a line field, which identifies one of the lines of the cache, and a tag field, which

identifies one of the blocks that can fit into that line.

4.6 A tag field uniquely identifies a block of main memory. A word field identifies a

unique word or byte within a block of main memory.

4.7 One field identifies a unique word or byte within a block of main memory. The

remaining two fields specify one of the blocks of main memory. These two fields

are a set field, which identifies one of the sets of the cache, and a tag field, which

identifies one of the blocks that can fit into that set.

4.8 Spatial locality refers to the tendency of execution to involve a number of memory

locations that are clustered. Temporal locality refers to the tendency for a

processor to access memory locations that have been used recently.

-20-

4.9 Spatial locality is generally exploited by using larger cache blocks and by

incorporating prefetching mechanisms (fetching items of anticipated use) into the

cache control logic. Temporal locality is exploited by keeping recently used

instruction and data values in cache memory and by exploiting a cache hierarchy.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

4.1 The cache is divided into 16 sets of 4 lines each. Therefore, 4 bits are needed to

identify the set number. Main memory consists of 4K = 212 blocks. Therefore, the

set plus tag lengths must be 12 bits and therefore the tag length is 8 bits. Each

block contains 128 words. Therefore, 7 bits are needed to specify the word.

TAG

SET

WORD

Main memory address =

4.2 There are a total of 8 kbytes/16 bytes = 512 lines in the cache. Thus the cache

consists of 256 sets of 2 lines each. Therefore 8 bits are needed to identify the set

number. For the 64-Mbyte main memory, a 26-bit address is needed. Main memory

consists of 64-Mbyte/16 bytes = 222 blocks. Therefore, the set plus tag lengths must

be 22 bits, so the tag length is 14 bits and the word field length is 4 bits.

TAG

SET

WORD

Main memory address =

4.3

Address

111111

666666

BBBBBB

a. Tag/Line/Word

11/444/1

66/1999/2

BB/2EEE/3

b. Tag /Word

44444/1

199999/2

2EEEEE/3

c. Tag/Set/Word

22/444/1

CC/1999/2

177/EEE/3

4.4 a. Address length: 24; number of addressable units: 224; block size: 4; number of

blocks in main memory: 222; number of lines in cache: 214; size of tag: 8.

b. Address length: 24; number of addressable units: 224; block size: 4; number of

blocks in main memory: 222; number of lines in cache: 4000 hex; size of tag: 22.

c. Address length: 24; number of addressable units: 224; block size: 4; number of

blocks in main memory: 222; number of lines in set: 2; number of sets: 213;

number of lines in cache: 214; size of tag: 9.

4.5 Block frame size = 16 bytes = 4 doublewords

Number of block frames in cache =

16 KBytes

16 Bytes =1024

Number of sets =

Number of block frames

Associativity =1024

4=256 sets

-21-

Offset

SetTag

20 bits 8 4

Decoder

Comp1

Comp2

Comp3

Comp4

820

Set 0

Set 1

Set 255

•

Set

255

Tag (20) 4 DWs

Hit

Example: doubleword from location ABCDE8F8 is mapped onto: set 143, any

line, doubleword 2:

(1000)A B C D E (1111) (1000)

8 F 8

Set = 143

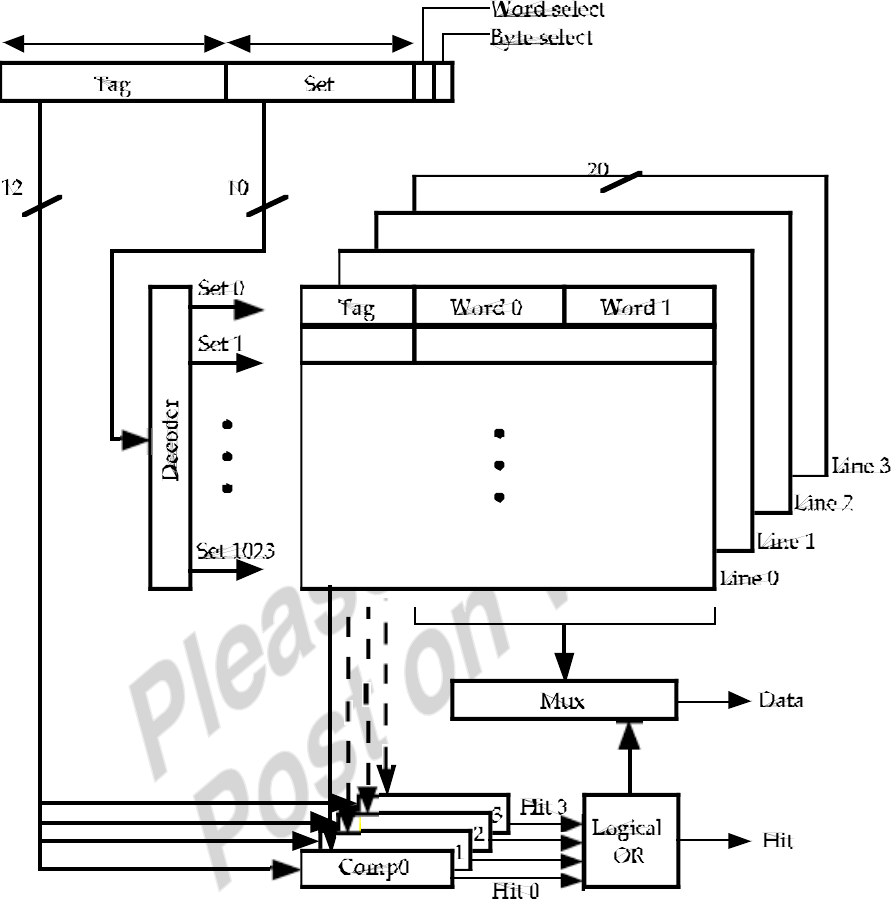
-22-

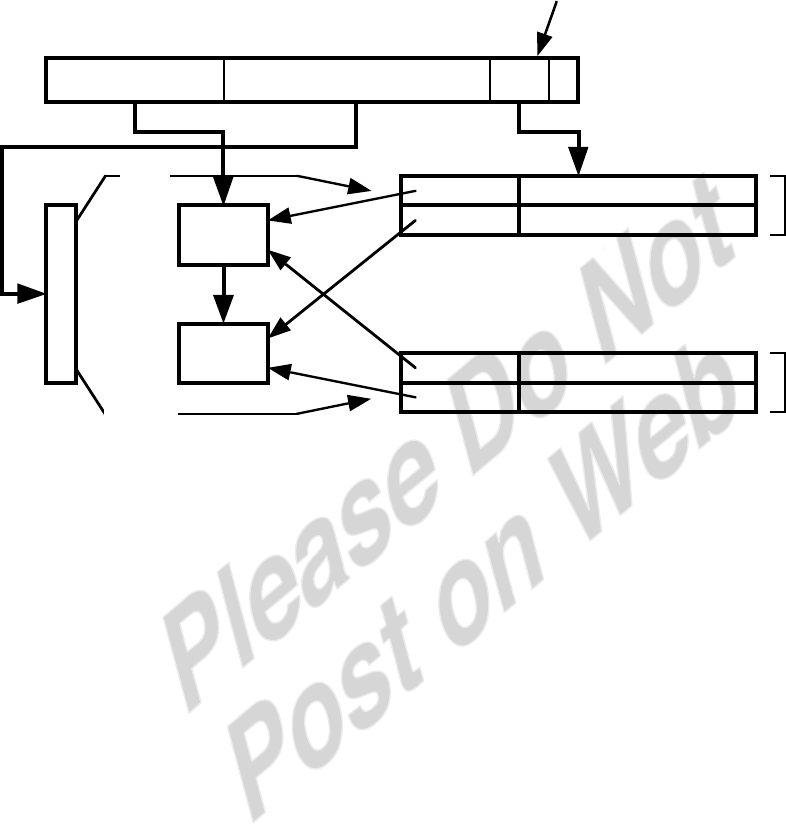
4.6

12 bits 10 bits

4.7 A 32-bit address consists of a 21-bit tag field, a 7-bit set field, and a 4-bit word

field. Each set in the cache includes 3 LRU bits and four lines. Each line consists of

4 32-bit words, a valid bit, and a 21-bit tag.

4.8 a. 8 leftmost bits = tag; 5 middle bits = line number; 3 rightmost bits = byte

number

b. slot 3; slot 6; slot 3; slot 21

c. Bytes with addresses 0001 1010 0001 1000 through 0001 1010 0001 1111 are

stored in the cache

d. 256 bytes

e. Because two items with two different memory addresses can be stored in the

same place in the cache. The tag is used to distinguish between them.

-23-

4.9 a. The bits are set according to the following rules with each access to the set:

1. If the access is to L0 or L1, B0 ← 1.

2. If the access is to L0, B1 ← 1.

3. If the access is to L1, B1 ← 0.

4. If the access is to L2 or L3, B0 ← 0.

5. If the access is to L2, B2 ← 1.

6. If the access is to L3, B2 ← 0.

The replacement algorithm works as follows (Figure 4.15): When a line must be

replaced, the cache will first determine whether the most recent use was from

L0 and L1 or L2 and L3. Then the cache will determine which of the pair of

blocks was least recently used and mark it for replacement. When the cache is

initialized or flushed all 128 sets of three LRU bits are set to zero.

b. The 80486 divides the four lines in a set into two pairs (L0, L1 and L2, L3). Bit

B0 is used to select the pair that has been least-recently used. Within each pair,

one bit is used to determine which member of the pair was least-recently used.

However, the ultimate selection only approximates LRU. Consider the case in

which the order of use was: L0, L2, L3, L1. The least-recently used pair is (L2,

L3) and the least-recently used member of that pair is L2, which is selected for

replacement. However, the least-recently used line of all is L0. Depending on

the access history, the algorithm will always pick the least-recently used entry

or the second least-recently used entry.

c. The most straightforward way to implement true LRU for a four-line set is to

associate a two bit counter with each line. When an access occurs, the counter

for that block is set to 0; all counters with values lower than the original value

for the accessed block are incremented by 1. When a miss occurs and the set is

not full, a new block is brought in, its counter is set to 0 and all other counters

are incremented by 1. When a miss occurs and the set is full, the block with

counter value 3 is replaced; its counter is set to 0 and all other counters are

incremented by 1. This approach requires a total of 8 bits.

In general, for a set of N blocks, the above approach requires 2N bits. A

more efficient scheme can be designed which requires only N(N–1)/2 bits. The

scheme operates as follows. Consider a matrix R with N rows and N columns,

and take the upper-right triangular portion of the matrix, not counting the

diagonal. For N = 4, we have the following layout:

R(1,2)

R(1,3)

R(1,4)

R(2,3)

R(2,4)

R(3,4)

When line I is referenced, row I of R(I,J) is set to 1, and column I of R(J,I) is set

to 0. The LRU block is the one for which the row is entirely equal to 0 (for those

bits in the row; the row may be empty) and for which the column is entirely 1

(for all the bits in the column; the column may be empty). As can be seen for N

= 4, a total of 6 bits are required.

-24-

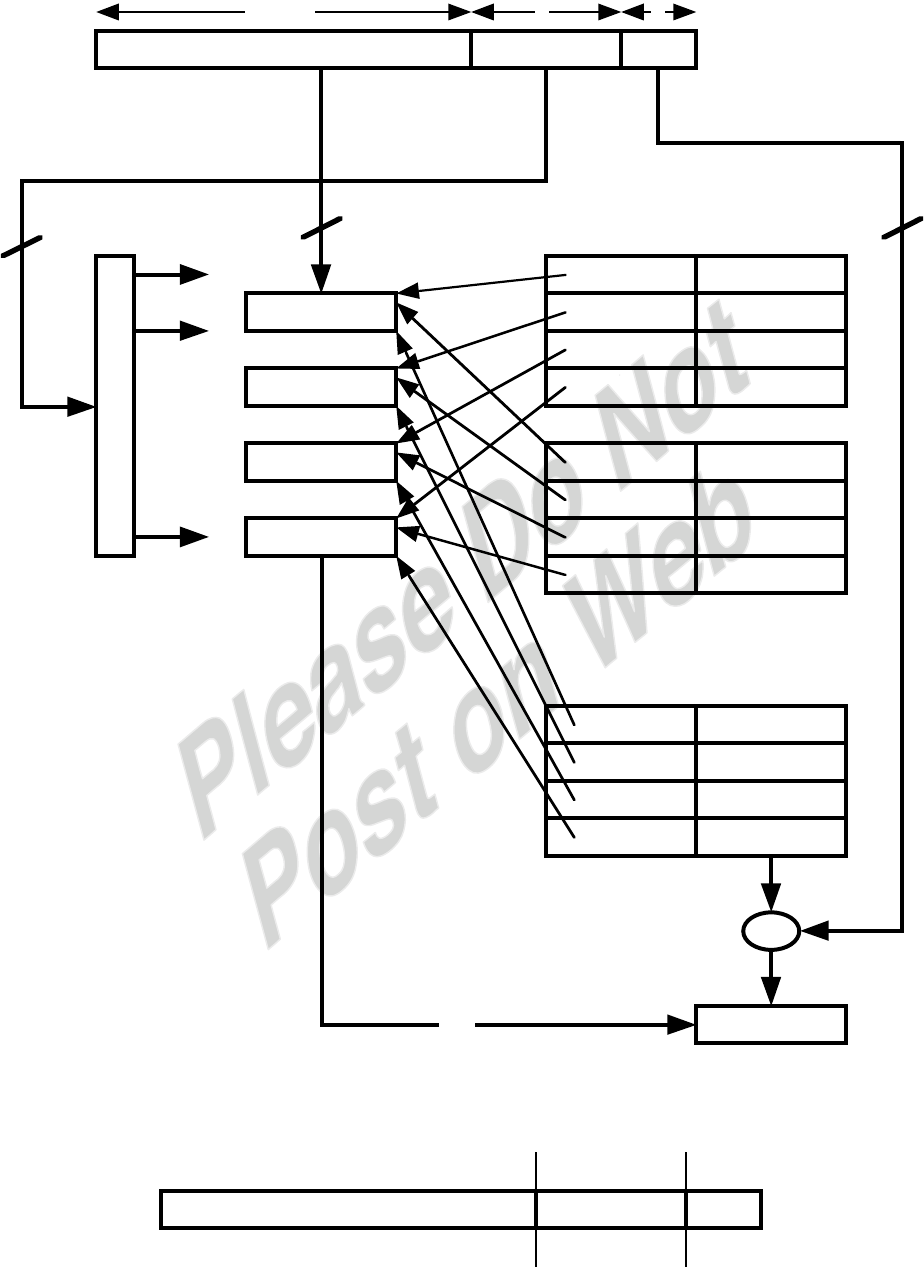
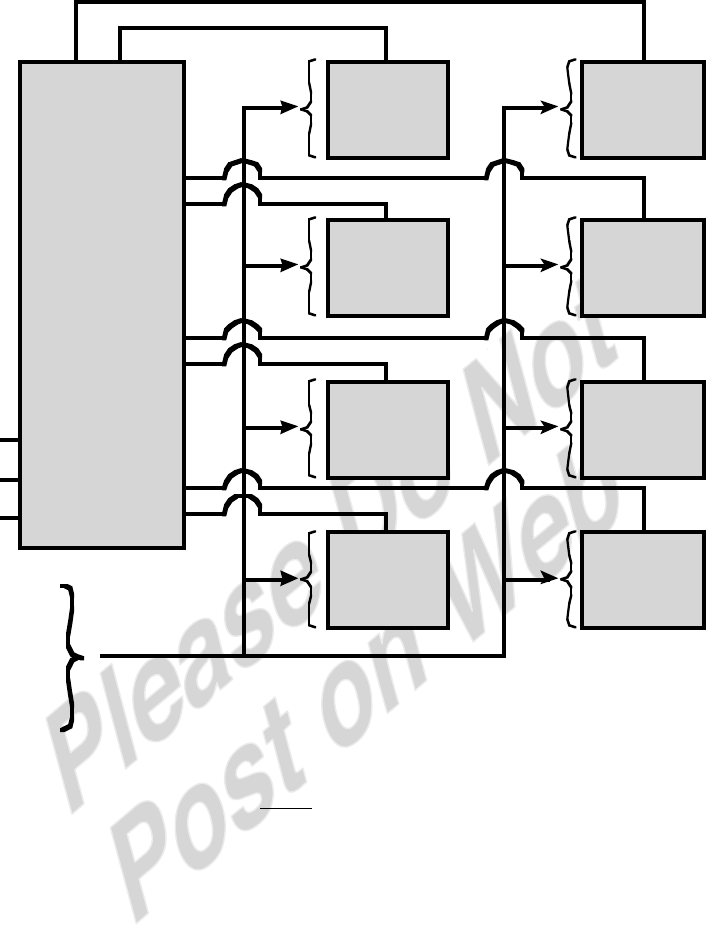
4.10 Block size = 4 words = 2 doublewords; associativity K = 2; cache size = 4048

words; C = 1024 block frames; number of sets S = C/K = 512; main memory = 64K

× 32 bits = 256 Kbytes = 218 bytes; address = 18 bits.

Tag Set

Word bits

(6 bits) (9) (2) (1)

Compare

Decoder

Set 0

Set 511

•

Tag (6) 4 words

Set 0

(8 words)

Set 511

(8 words)

•

word select

4.11 a. Address format: Tag = 20 bits; Line = 6 bits; Word = 6 bits

Number of addressable units = 2s+w = 232 bytes; number of blocks in main

memory = 2s = 226; number of lines in cache 2r = 26 = 64; size of tag = 20 bits.

b. Address format: Tag = 26 bits; Word = 6 bits

Number of addressable units = 2s+w = 232 bytes; number of blocks in main

memory = 2s = 226; number of lines in cache = undetermined; size of tag = 26

bits.

c. Address format: Tag = 9 bits; Set = 17 bits; Word = 6 bits

Number of addressable units = 2s+w = 232 bytes; Number of blocks in main

memory = 2s = 226; Number of lines in set = k = 4; Number of sets in cache = 2d

= 217; Number of lines in cache = k × 2d =219; Size of tag = 9 bits.

4.12 a. Because the block size is 16 bytes and the word size is 1 byte, this means there

are 16 words per block. We will need 4 bits to indicate which word we want

out of a block. Each cache line/slot matches a memory block. That means each

cache slot contains 16 bytes. If the cache is 64Kbytes then 64Kbytes/16 = 4096

cache slots. To address these 4096 cache slots, we need 12 bits (212 = 4096).

Consequently, given a 20 bit (1 MByte) main memory address:

Bits 0-3 indicate the word offset (4 bits)

Bits 4-15 indicate the cache slot (12 bits)

Bits 16-19 indicate the tag (remaining bits)

F0010 = 1111 0000 0000 0001 0000

Word offset = 0000 = 0

Slot = 0000 0000 0001 = 001

Tag = 1111 = F

01234 = 0000 0001 0010 0011 0100

Word offset = 0100 = 4

Slot = 0001 0010 0011 = 123

-25-

Tag = 0000 = 0

CABBE = 1100 1010 1011 1011 1110

Word offset = 1110 = E

Slot = 1010 1011 1011 = ABB

Tag = 1100 = C

b. We need to pick any address where the slot is the same, but the tag (and

optionally, the word offset) is different. Here are two examples where the slot

is 1111 1111 1111

Address 1:

Word offset = 1111

Slot = 1111 1111 1111

Tag = 0000

Address = 0FFFF

Address 2:

Word offset = 0001

Slot = 1111 1111 1111

Tag = 0011

Address = 3FFF1

c. With a fully associative cache, the cache is split up into a TAG and a

WORDOFFSET field. We no longer need to identify which slot a memory block

might map to, because a block can be in any slot and we will search each cache

slot in parallel. The word-offset must be 4 bits to address each individual word

in the 16-word block. This leaves 16 bits leftover for the tag.

F0010

Word offset = 0h

Tag = F001h

CABBE

Word offset = Eh

Tag = CABBh

d. As computed in part a, we have 4096 cache slots. If we implement a two -way

set associative cache, then it means that we put two cache slots into one set.

Our cache now holds 4096/2 = 2048 sets, where each set has two slots. To

address these 2048 sets we need 11 bits (211 = 2048). Once we address a set, we

will simultaneously search both cache slots to see if one has a tag that matches

the target. Our 20-bit address is now broken up as follows:

Bits 0-3 indicate the word offset

Bits 4-14 indicate the cache set

Bits 15-20 indicate the tag

F0010 = 1111 0000 0000 0001 0000

Word offset = 0000 = 0

Cache Set = 000 0000 0001 = 001

Tag = 11110 = 1 1110 = 1E

CABBE = 1100 1010 1011 1011 1110

Word offset = 1110 = E

Cache Set = 010 1011 1011 = 2BB

Tag = 11001 = 1 1001 = 19

4.13 Associate a 2-bit counter with each of the four blocks in a set. Initially, arbitrarily

set the four values to 0, 1, 2, and 3 respectively. When a hit occurs, the counter of

the block that is referenced is set to 0. The other counters in the set with values

-26-

originally lower than the referenced counter are incremented by 1; the remaining

counters are unchanged. When a miss occurs, the block in the set whose counter

value is 3 is replaced and its counter set to 0. All other counters in the set are

incremented by 1.

4.14 Writing back a line takes 30 + (7 × 5) = 65 ns, enough time for 2.17 single-word

memory operations. If the average line that is written at least once is written more

than 2.17 times, the write-back cache will be more efficient.

4.15 a. A reference to the first instruction is immediately followed by a reference to the

second.

b. The ten accesses to a[i] within the inner for loop which occur within a short

interval of time.

4.16 Define

Ci = Average cost per bit, memory level i

Si = Size of memory level i

Ti = Time to access a word in memory level i

Hi = Probability that a word is in memory i and in no higher-level memory

Bi = Time to transfer a block of data from memory level (i + 1) to memory level i

Let cache be memory level 1; main memory, memory level 2; and so on, for a total

of N levels of memory. Then

Cs=

CiSi

i=1

∑

i=1

∑

The derivation of Ts is more complicated. We begin with the result from

probability theory that:

Expected Value of x = iPr x=1

[ ]

i=1

∑

We can write:

Ts = TiHi

i=1

∑

We need to realize that if a word is in M1 (cache), it is read immediately. If it is in

M2 but not M1, then a block of data is transferred from M2 to M1 and then read.

Thus:

T2 = B1 + T1

-27-

Further

T3 = B2 + T2 = B1 + B2 + T1

Generalizing:

Ti= Bj+T1

j=1

i−1

∑

Ts= BjHi

( )

j=1

i−1

∑

i=2

∑+T1Hi

i=1

∑

But

i=1

∑=1

Finally

Ts= BjHi

( )

j=1

i−1

∑

i=2

∑+T1

4.17 Main memory consists of 512 blocks of 64 words. Cache consists of 16 sets; each set

consists of 4 slots; each slot consists of 64 words. Locations 0 through 4351 in main

memory occupy blocks 0 through 67. On the first fetch sequence, block 0 through

15 are read into sets 0 through 15; blocks 16 through 31 are read into sets 0 through

15; blocks 32-47 are read into sets 0 through 15; blocks 48-63 are read into sets 0

through 15; and blocks 64-67 are read into sets 0 through 3. Because each set has 4

slots, there is no replacement needed through block 63. The last 4 groups of blocks

involve a replacement. On each successive pass, replacements will be required in

sets 0 through 3, but all of the blocks in sets 4 through 15 remain undisturbed.

Thus, on each successive pass, 48 blocks are undisturbed, and the remaining 20

must read in.

Let T be the time to read 64 words from cache. Then 10T is the time to read 64

words from main memory. If a word is not in the cache, then it can only be ready

by first transferring the word from main memory to the cache and then reading the

cache. Thus the time to read a 64-word block from cache if it is missing is 11T.

We can now express the improvement factor as follows. With no cache

Fetch time = (10 passes) (68 blocks/pass) (10T/block) = 6800T

With cache

Fetch time = (68) (11T) first pass

+ (9) (48) (T) + (9) (20) (11T) other passes

= 3160T

Improvement = 6800T

3160T = 2.15

-28-

4.18 a. Access 63 1 Miss Block 3 → Slot 3

Access 64 1 Miss Block 4 → Slot 0

Access 65-70 6 Hits

Access 15 1 Miss Block 0 → Slot 0 First Loop

Access 16 1 Miss Block 1 → Slot 1

Access 17-31 15 Hits

Access 32 1 Miss Block 2 → Slot 2

Access 80 1 Miss Block 5 → Slot 1

Access 81-95 15 Hits

Access 15 1 Hit Second Loop

Access 16 1 Miss Block 1 → Slot 1

Access 17-31 15 hits

Access 32 1 Hit

Access 80 1 Miss Block 5 → Slot 1

Access 81-95 15 hits

Access 15 1 Hit Third Loop

Access 16 1 Miss Block 1 → Slot 1

Access 17-31 15 hits

Access 32 1 Hit

Access 80 1 Miss Block 5 → Slot 1

Access 81-95 15 hits

Access 15 1 Hit Fourth Loop

… Pattern continues to the Tenth Loop

For lines 63-70 2 Misses 6 Hits

First loop 15-32, 80-95 4 Misses 30 Hits

Second loop 15-32, 80-95 2 Misses 32 Hits

Third loop 15-32, 80-95 2 Misses 32 Hits

Fourth loop 15-32, 80-95 2 Misses 32 Hits

Fifth loop 15-32, 80-95 2 Misses 32 Hits

Sixth loop 15-32, 80-95 2 Misses 32 Hits

Seventh loop 15-32, 80-95 2 Misses 32 Hits

Eighth loop 15-32, 80-95 2 Misses 32 Hits

Ninth loop 15-32, 80-95 2 Misses 32 Hits

Tenth loop 15-32, 80-95 2 Misses 32 Hits

Total: 24 Misses 324 Hits

Hit Ratio = 324/348 = 0.931

b. Access 63 1 Miss Block 3 → Set 1 Slot 2

Access 64 1 Miss Block 4 → Set 0 Slot 0

Access 65-70 6 Hits

Access 15 1 Miss Block 0 → Set 0 Slot 1 First Loop

Access 16 1 Miss Block 1 → Set 1 Slot 3

Access 17-31 15 Hits

Access 32 1 Miss Block 2 → Set 0 Slot 0

Access 80 1 Miss Block 5 → Set 1 Slot 2

Access 81-95 15 Hits

Access 15 1 Hit Second Loop

Access 16-31 16 Hits

Access 32 1 Hit

Access 80-95 16 Hits

… All hits for the next eight iterations

-29-

For lines 63-70 2 Misses 6 Hits

First loop 15-32, 80-95 4 Misses 30 Hits

Second loop 15-32, 80-95 0 Misses 34 Hits

Third loop 15-32, 80-95 0 Misses 34 Hits

Fourth loop 15-32, 80-95 0 Misses 34 Hits

Fifth loop 15-32, 80-95 0 Misses 34 Hits

Sixth loop 15-32, 80-95 0 Misses 34 Hits

Seventh loop 15-32, 80-95 0 Misses 34 Hits

Eighth loop 15-32, 80-95 0 Misses 34 Hits

Ninth loop 15-32, 80-95 0 Misses 34 Hits

Tenth loop 15-32, 80-95 0 Misses 34 Hits

Total = 6 Misses 342 Hits

Hit Ratio = 342/348 = 0.983

4.19 a. Cost = Cm × 8 × 106 = 8 × 103 ¢ = $80

b. Cost = Cc × 8 × 106 = 8 × 104 ¢ = $800

c. From Equation (4.1) : 1.1 × T1 = T1 + (1 – H)T2

(0.1)(100) = (1 – H)(1200)

H = 1190/1200

4.20 a. Under the initial conditions, using Equation (4.1), the average access time is

T1 + (1 - H) T2 = 1 + (0.05) T2

Under the changed conditions, the average access time is

1.5 + (0.03) T2

For improved performance, we must have

1 + (0.05) T2 > 1.5 + (0.03) T2

Solving for T2, the condition is T2 > 50

b. As the time for access when there is a cache miss become larger, it becomes

more important to increase the hit ratio.

4.21 a. First, 2.5 ns are needed to determine that a cache miss occurs. Then, the

required line is read into the cache. Then an additional 2.5 ns are needed to

read the requested word.

Tmiss = 2.5 + 50 + (15)(5) + 2.5 = 130 ns

b. The value Tmiss from part (a) is equivalent to the quantity (T1 + T2) in Equation

(4.1). Under the initial conditions, using Equation (4.1), the average access time

Ts = H × T1 + (1 – H) × (T1 + T2) = (0.95)(2.5) + (0.05)(130) = 8.875 ns

Under the revised scheme, we have:

-30-

Tmiss = 2.5 + 50 + (31)(5) + 2.5 = 210 ns

and

Ts = H × T1 + (1 – H) × (T1 + T2) = (0.97)(2.5) + (0.03)(210) = 8.725 ns

4.22 There are three cases to consider:

Location of referenced word

Probability

Total time for access in ns

In cache

0.9

Not in cache, but in main

memory

(0.1)(0.6) = 0.06

60 + 20 = 80

Not in cache or main memory

(0.1)(0.4) = 0.04

12ms + 60 + 20 = 12,000,080

So the average access time would be:

Avg = (0.9)(20) + (0.06)(80) + (0.04)(12000080) = 480026 ns

4.23 a. Consider the execution of 100 instructions. Under write-through, this creates

200 cache references (168 read references and 32 write references). On average,

the read references result in (0.03) × 168 = 5.04 read misses. For each read miss,

a line of memory must be read in, generating 5.04 × 8 = 40.32 physical words of

traffic. For write misses, a single word is written back, generating 32 words of

traffic. Total traffic: 72.32 words. For write back, 100 instructions create 200

cache references and thus 6 cache misses. Assuming 30% of lines are dirty, on

average 1.8 of these misses require a line write before a line read. Thus, total

traffic is (6 + 1.8) × 8 = 62.4 words. The traffic rate:

Write through = 0.7232 byte/instruction

Write back = 0.624 bytes/instruction

b. For write-through: [(0.05) × 168 × 8] + 32 = 99.2 → 0.992 bytes/instruction

For write-back: (10 + 3) × 8 = 104 → 0.104 bytes/instruction

c. For write-through: [(0.07) × 168 × 8] + 32 = 126.08 → 0.12608 bytes/instruction

For write-back: (14 + 4.2) × 8 = 145.6 → 0.1456 bytes/instruction

d. A 5% miss rate is roughly a crossover point. At that rate, the memory traffic is

about equal for the two strategies. For a lower miss rate, write-back is superior.

For a higher miss rate, write-through is superior.

4.24 a. One clock cycle equals 60 ns, so a cache access takes 120 ns and a main memory

access takes 180 ns. The effective length of a memory cycle is (0.9 × 120) + (0.1 ×

180) = 126 ns.

b. The calculation is now (0.9 × 120) + (0.1 × 300) = 138 ns. Clearly the

performance degrades. However, note that although the memory access time

increases by 120 ns, the average access time increases by only 12 ns.

4.25 a. For a 1 MIPS processor, the average instruction takes 1000 ns to fetch and

execute. On average, an instruction uses two bus cycles for a total of 600 ns, so

the bus utilization is 0.6

b. For only half of the instructions must the bus be used for instruction fetch. Bus

utilization is now (150 + 300)/1000 = 0.45. This reduces the waiting time for

other bus requestors, such as DMA devices and other microprocessors.

-31-

4.26 a. Ta = Tc + (1 – H)Tb + W(Tm – Tc)

b. Ta = Tc + (1 – H)Tb + Wb(1 – H)Tb = Tc + (1 – H)(1 + Wb)Tb

4.27 Ta = [Tc1 + (1 – H1)Tc2] + (1 – H2)Tm

4.28 a. miss penalty = 1 + 4 = 5 clock cycles

b. miss penalty = 4 × (1 + 4 ) = 20 clock cycles

c. miss penalty = miss penalty for one word + 3 = 8 clock cycles.

4.29 The average miss penalty equals the miss penalty times the miss rate. For a line

size of one word, average miss penalty = 0.032 x 5 = 0.16 clock cycles. For a line

size of 4 words and the nonburst transfer, average miss penalty = 0.011 x 20 = 0.22

clock cycles. For a line size of 4 words and the burst transfer, average miss penalty

= 0.011 x 8 = 0.132 clock cycles.

-32-

CHAPTER 5 INTERNAL MEMORY

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

5.1 They exhibit two stable (or semistable) states, which can be used to represent

binary 1 and 0; they are capable of being written into (at least once), to set the state;

they are capable of being read to sense the state.

5.2 (1) A memory in which individual words of memory are directly accessed through

wired-in addressing logic. (2) Semiconductor main memory in which it is possible

both to read data from the memory and to write new data into the memory easily

and rapidly.

5.3 SRAM is used for cache memory (both on and off chip), and DRAM is used for

main memory.

5.4 SRAMs generally have faster access times than DRAMs. DRAMS are less

expensive and smaller than SRAMs.

5.5 A DRAM cell is essentially an analog device using a capacitor; the capacitor can

store any charge value within a range; a threshold value determines whether the

charge is interpreted as 1 or 0. A SRAM cell is a digital device, in which binary

values are stored using traditional flip-flop logic-gate configurations.

5.6 Microprogrammed control unit memory; library subroutines for frequently

wanted functions; system programs; function tables.

5.7 EPROM is read and written electrically; before a write operation, all the storage

cells must be erased to the same initial state by exposure of the packaged chip to

ultraviolet radiation. Erasure is performed by shining an intense ultraviolet light

through a window that is designed into the memory chip. EEPROM is a read-

mostly memory that can be written into at any time without erasing prior contents;

only the byte or bytes addressed are updated. Flash memory is intermediate

between EPROM and EEPROM in both cost and functionality. Like EEPROM,

flash memory uses an electrical erasing technology. An entire flash memory can be

erased in one or a few seconds, which is much faster than EPROM. In addition, it is

possible to erase just blocks of memory rather than an entire chip. However, flash

memory does not provide byte-level erasure. Like EPROM, flash memory uses

only one transistor per bit, and so achieves the high density (compared with

EEPROM) of EPROM.

5.8 A0 - A1 = address lines:. CAS = column address select:. D1 - D4 = data lines. NC: =

no connect. OE: output enable. RAS = row address select:. Vcc: = voltage source.

Vss: = ground. WE: write enable.

-33-

5.9 A bit appended to an array of binary digits to make the sum of all the binary

digits, including the parity bit, always odd (odd parity) or always even (even

parity).

5.10 A syndrome is created by the XOR of the code in a word with a calculated version

of that code. Each bit of the syndrome is 0 or 1 according to if there is or is not a

match in that bit position for the two inputs. If the syndrome contains all 0s, no

error has been detected. If the syndrome contains one and only one bit set to 1,

then an error has occurred in one of the 4 check bits. No correction is needed. If the

syndrome contains more than one bit set to 1, then the numerical value of the

syndrome indicates the position of the data bit in error. This data bit is inverted for

correction.

5.11 Unlike the traditional DRAM, which is asynchronous, the SDRAM exchanges data

with the processor synchronized to an external clock signal and running at the full

speed of the processor/memory bus without imposing wait states.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

5.1 The 1-bit-per-chip organization has several advantages. It requires fewer pins on

the package (only one data out line); therefore, a higher density of bits can be

achieved for a given size package. Also, it is somewhat more reliable because it has

only one output driver. These benefits have led to the traditional use of 1-bit-per-

chip for RAM. In most cases, ROMs are much smaller than RAMs and it is often

possible to get an entire ROM on one or two chips if a multiple-bits-per-chip

organization is used. This saves on cost and is sufficient reason to adopt that

organization.

5.2 In 1 ms, the time devoted to refresh is 64 × 150 ns = 9600 ns. The fraction of time

devoted to memory refresh is (9.6 × 10–6 s)/10–3 s = 0.0096, which is approximately

1%.

5.3 a. Memory cycle time = 60 + 40 = 100 ns. The maximum data rate is 1 bit every 100

ns, which is 10 Mbps.

b. 320 Mbps = 40 MB/s.

-34-

5.4

S0 S1

A19

A20

A21

A22

Decoder

Chip select

1 Mb

Chip select

1 Mb

Chip select

1 Mb

Chip select

1 Mb

Chip select

1 Mb

Chip select

1 Mb

Chip select

1 Mb

Chip select

1 Mb

•

5.5 a. The length of a clock cycle is 100 ns. Mark the beginning of T1 as time 0.Address

Enable returns to a low at 75.

€

RAS

goes active 50 ns later, or time 125. Data

must become available by the DRAMs at time 300 – 60 = 240. Hence, access time

must be no more than 240 – 125 = 115 ns.

b. A single wait state will increase the access time requirement to 115 + 100 = 215

ns. This can easily be met by DRAMs with access times of 150 ns.

5.6 a. The refresh period from row to row must be no greater than

4000/256 = 15.625 µs.

b. An 8-bit counter is needed to count 256 rows (28 = 256).

5.7 a.

pulse a = write

pulse b = write

pulse c = write

pulse d = write

pulse e= write

pulse f = write

pulse g = store-disable outputs

pulse h = read

pulse i = read

pulse j = read

pulse k = read

pulse l = read

pulse m = read

pulse n = store-disable outputs

-35-

b. Data is read in via pins (D3, D2, D1, D0)

word 0 = 1111 (written into location 0 during pulse a)

word 1 = 1110 (written into location 0 during pulse b)

word 2 = 1101 (written into location 0 during pulse c)

word 3 = 1100 (written into location 0 during pulse d)

word 4 = 1011 (written into location 0 during pulse e)

word 5 = 1010 (written into location 0 during pulse f)

word 6 = random (did not write into this location 0)

c. Output leads are (O3, O2, O1, O0)

pulse h: 1111 (read location 0)

pulse i: 1110 (read location 1)

pulse j: 1101 (read location 2)

pulse k: 1100 (read location 3)

pulse l: 1011 (read location 4)

pulse m: 1010 (read location 5)

5.8 8192/64 = 128 chips; arranged in 8 rows by 64 columns:

• • •

•

01 7

112 113 119

Section 0 (even)

• • •

•

89 15

120 121 127

Section 1 (odd)

A0 = L A0 = H

Decoder

Row 0

Row 1

Row 7

•

Rows

All zeros

Ak-A10 A9-A7

A6-A1

Depends on

type of

processor

5.9 Total memory is 1 megabyte = 8 megabits. It will take 32 DRAMs to construct the

memory (32 × 256 Kb = 8 Mb). The composite failure rate is 2000 × 32 = 64,000

FITS. From this, we get a MTBF = 109/64,000 = 15625 hours = 22 months.

5.10 The stored word is 001101001111, as shown in Figure 5.10. Now suppose that the

only error is in C8, so that the fetched word is 001111001111. Then the received

block results in the following table:

Position

Bits

Block

Codes

1010

1001

0111

0011

-36-

The check bit calculation after reception:

Position

Code

Hamming

1111

1010

1001

0111

0011

XOR = syndrome

1000

The nonzero result detects and error and indicates that the error is in bit position 8,

which is check bit C8.

5.11 Data bits with value 1 are in bit positions 12, 11, 5, 4, 2, and 1:

Position

Bits

Block

Codes

1100

1011

0101

The check bits are in bit numbers 8, 4, 2, and 1.

Check bit 8 calculated by values in bit numbers: 12, 11, 10 and 9

Check bit 4 calculated by values in bit numbers: 12, 7, 6, and 5

Check bit 2 calculated by values in bit numbers: 11, 10, 7, 6 and 3

Check bit 1 calculated by values in bit numbers: 11, 9, 7, 5 and 3

Thus, the check bits are: 0 0 1 0

5.12 The Hamming Word initially calculated was:

bit number:

Doing an exclusive-OR of 0111 and 1101 yields 1010 indicating an error in bit 10 of

the Hamming Word. Thus, the data word read from memory was 00011001.

5.13 Need K check bits such that 1024 + K ≤ 2K – 1.

The minimum value of K that satisfies this condition is 11.

-37-

5.14 As Table 5.2 indicates, 5 check bits are needed for an SEC code for 16-bit data

words. The layout of data bits and check bits:

Bit Position

Position Number

Check Bits

Data Bits

10101

M16

10100

M15

10011

M14

10010

M13

10001

M12

10000

C16

01111

M11

01110

M10

01101

01100

01011

01010

01001

01000

00111

00110

00101

00100

00011

00010

00001

The equations are calculated as before, for example,

C1= M1 ⊕ M2 ⊕ M4 ⊕ M5 ⊕ M7 ⊕ M9 ⊕ M11 ⊕ M12 ⊕ M14 ⊕ M16.

For the word 0101000000111001, the code is

C16 = 1; C8 = 1; C 4 = 1; C2 = 1; C1 = 0.

If an error occurs in data bit 4:

C16 = 1 ; C8 =1; C4 = 0; C2 = 0; C1 = 1.

Comparing the two:

C16

The result is an error identified in bit position 7, which is data bit 4.

-38-

CHAPTER 6 EXTERNAL MEMORY

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

6.1 Improvement in the uniformity of the magnetic film surface to increase disk

reliability. A significant reduction in overall surface defects to help reduce

read/write errors. Ability to support lower fly heights (described subsequently).

Better stiffness to reduce disk dynamics. Greater ability to withstand shock and

damage

6.2 The write mechanism is based on the fact that electricity flowing through a coil

produces a magnetic field. Pulses are sent to the write head, and magnetic patterns

are recorded on the surface below, with different patterns for positive and negative

currents. An electric current in the wire induces a magnetic field across the gap,

which in turn magnetizes a small area of the recording medium. Reversing the

direction of the current reverses the direction of the magnetization on the

recording medium.

6.3 The read head consists of a partially shielded magnetoresistive (MR) sensor. The

MR material has an electrical resistance that depends on the direction of the

magnetization of the medium moving under it. By passing a current through the

MR sensor, resistance changes are detected as voltage signals.

6.4 For the constant angular velocity (CAV) system, the number of bits per track is

constant. An increase in density is achieved with multiple zoned recording, in

which the surface is divided into a number of zones, with zones farther from the

center containing more bits than zones closer to the center.

6.5 On a magnetic disk. data is organized on the platter in a concentric set of rings,

called tracks. Data are transferred to and from the disk in sectors. For a disk with

multiple platters, the set of all the tracks in the same relative position on the platter

is referred to as a cylinder.

6.6 512 bytes.

6.7 On a movable-head system, the time it takes to position the head at the track is

known as seek time. Once the track is selected, the disk controller waits until the

appropriate sector rotates to line up with the head. The time it takes for the

beginning of the sector to reach the head is known as rotational delay. The sum of

the seek time, if any, and the rotational delay equals the access time, which is the

time it takes to get into position to read or write. Once the head is in position, the

read or write operation is then performed as the sector moves under the head; this

is the data transfer portion of the operation and the time for the transfer is the

transfer time.

-39-

6.8 1. RAID is a set of physical disk drives viewed by the operating system as a single

logical drive. 2. Data are distributed across the physical drives of an array. 3.

Redundant disk capacity is used to store parity information, which guarantees

data recoverability in case of a disk failure.

6.9 0: Non-redundant 1: Mirrored; every disk has a mirror disk containing the same

data. 2: Redundant via Hamming code; an error-correcting code is calculated

across corresponding bits on each data disk, and the bits of the code are stored in

the corresponding bit positions on multiple parity disks. 3: Bit-interleaved parity;

similar to level 2 but instead of an error-correcting code, a simple parity bit is

computed for the set of individual bits in the same position on all of the data disks.

4: Block-interleaved parity; a bit-by-bit parity strip is calculated across

corresponding strips on each data disk, and the parity bits are stored in the

corresponding strip on the parity disk. 5: Block-interleaved distributed parity;

similar to level 4 but distributes the parity strips across all disks. 6: Block-

interleaved dual distributed parity; two different parity calculations are carried out

and stored in separate blocks on different disks.

6.10 The disk is divided into strips; these strips may be physical blocks, sectors, or some

other unit. The strips are mapped round robin to consecutive array members. A set

of logically consecutive strips that maps exactly one strip to each array member is

referred to as a stripe.

6.11 For RAID level 1, redundancy is achieved by having two identical copies of all

data. For higher levels, redundancy is achieved by the use of error-correcting

codes.

6.12 In a parallel access array, all member disks participate in the execution of every

I/O request. Typically, the spindles of the individual drives are synchronized so

that each disk head is in the same position on each disk at any given time. In an

independent access array, each member disk operates independently, so that

separate I/O requests can be satisfied in parallel.

6.13 For the constant angular velocity (CAV) system, the number of bits per track is

constant. At a constant linear velocity (CLV), the disk rotates more slowly for

accesses near the outer edge than for those near the center. Thus, the capacity of a

track and the rotational delay both increase for positions nearer the outer edge of

the disk.

6.14 1. Bits are packed more closely on a DVD. The spacing between loops of a spiral on

a CD is 1.6 µm and the minimum distance between pits along the spiral is 0.834

µm. The DVD uses a laser with shorter wavelength and achieves a loop spacing of

0.74 µm and a minimum distance between pits of 0.4 µm. The result of these two

improvements is about a seven-fold increase in capacity, to about 4.7 GB. 2. The

DVD employs a second layer of pits and lands on top of the first layer A dual-layer

DVD has a semireflective layer on top of the reflective layer, and by adjusting

focus, the lasers in DVD drives can read each layer separately. This technique

almost doubles the capacity of the disk, to about 8.5 GB. The lower reflectivity of

the second layer limits its storage capacity so that a full doubling is not achieved.

-40-

3. The DVD-ROM can be two sided whereas data is recorded on only one side of a

CD. This brings total capacity up to 17 GB.

6.15 The typical recording technique used in serial tapes is referred to as serpentine

recording. In this technique, when data are being recorded, the first set of bits is

recorded along the whole length of the tape. When the end of the tape is reached,

the heads are repositioned to record a new track, and the tape is again recorded on

its whole length, this time in the opposite direction. That process continues, back

and forth, until the tape is full.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

6.1 It will be useful to keep the following representation of the N tracks of a disk in

mind:

• • •

j – 1

• • •

N – j

• • •

N – 2

N – 1

a. Let us use the notation Ps [j/t] = Pr [seek of length j when head is currently

positioned over track t]. Recognize that each of the N tracks is equally likely to

be requested. Therefore the unconditional probability of selecting any

particular track is 1/N. We can then state:

Ps[j/t]=1

if t ≤ j – 1 OR t ≥ N – j

Ps[j/t]=2

if j – 1 < t < N – j

In the former case, the current track is so close to one end of the disk (track 0 or

track N – 1) that only one track is exactly j tracks away. In the second case,

there are two tracks that are exactly j tracks away from track t, and therefore

the probability of a seek of length j is the probability that either of these two

tracks is selected, which is just 2/N.

b. Let Ps [K] = Pr [seek of length K, independent of current track position]. Then:

Ps K

[ ]

=Ps K/t

[ ]

t=0

N−1

∑×Pr current track is track t

[ ]

Ps K/t

[ ]

t=0

N−1

∑

From part (a), we know that Ps[K/t] takes on the value 1/N for 2K of the

tracks, and the value 2/N for (N – 2K) of the tracks. So

Ps K

[ ]

N+2N−2K

( )





 



 = 2K+2N−2K

( )

N2=2

N−2K

-41-

[ ]

=K×Ps K

[ ]

K=0

N−1

∑=2K

N−2K2

K=0

N−1

∑=2

K=0

N−1

∑−2

N2K2

K=0

N−1

∑

N−1

( )

2−2

N−1

( )

N2N−1

( )

6=N−1

( )

−N−1

( )

2N−1

( )

=3N N −1

( )

−N−1

( )

2N−1

( )

3N=N2−1

d. This follows directly from the last equation.

6.2

tA=tS+1

2r+n

tA=tS+1

2r+n

6.3 a. Capacity = 8 × 512 × 64 × 1 KB = 256 MB

b. Rotational latency = rotation_time/2 = 60/(3600 × 2) = 8.3 ms.

Average access time = seek time + rotational latency = 16.3 ms

c. Each cylinder consists of 8 tracks × 64 sectors/track × 1 KB/sector = 512 KB, so

5 MB requires exactly 10 cylinders. The disk will need the seek time of 8 ms to

find cylinder i, 8.3 ms on average to find sector 0, and 8 × (60/3.6) = 133.3 ms to

read all 8 tracks on one cylinder. Then, the time needed to move to the next

adjoining cylinder is 1.5 ms, which is the track-to-track access time. Assume a

rotational latency before each track.

Access Time = 8 + 9 × (8.3 + 133.3 + 1.5) + (8.3 + 133.3) = 1425.5 ms

€

Burst rate = revolutions

second ×sectors

revolution ×bytes

secter =3600

60 ×64 ×1 KB = 3.84 MB/s

6.4 a. If we assume that the head starts at track 0, then the calculations are simplified.

If the request track is track 0, then the seek time is 0; if the requested track is

track 29,999, then the seek time is the time to traverse 29,999 tracks. For a

random request, on average the number of tracks traversed is 29,999/2 =

14999.5 tracks. At one ms per 100 tracks, the average seek time is therefore

149.995 ms.

b. At 7200 rpm, there is one revolution every 8.333 ms. Therefore, the average

rotational delay is 4.167 ms.

c. With 600 sectors per track and the time for one complete revolution of 8.333 ms,

the transfer time for one sector is 8.333 ms/600 = 0.01389 ms.

d. The result is the sum of the preceding quantities, or approximately 154 ms.

6.5 Each sector can hold 4 logical records. The required number of sectors is 300,000/4

= 75,000 sectors. This requires 75,000/96 = 782 tracks, which in turn requires

782/110 = 8 surfaces.

6.6 a. The time consists of the following components: sector read time; track access

time; rotational delay; and sector write time. The time to read or write 1 sector

is calculated as follows: A single revolution to read or write an entire track

takes 60,000/360 = 16.7 ms. Time to read or write a single sector = 16.7/32 =

-42-

0.52 ms. Track access time = 2 ms, because the head moves between adjacent

tracks. The rotational delay is the time required for the head to line up with

sector 1 again. This is 16.7 × (31/32) = 16.2 ms. The head movement time of 2

ms overlaps the with the 16.2 ms of rotational delay, and so only the rotational

delay time is counted. Total transfer time = 0.52 + 16.2 + 0.52 = 17.24 ms.

b. The time to read or write an entire track is simply the time for a single

revolution, which is 16.7 ms. Between the read and the write there is a head

movement time of 2 ms to move from track 8 to track 9. During this time the

head moves past 3 sectors and most of a fourth sector. However, because the

entire track is buffered, sectors can be written back in a different sequence from

the read sequence. Thus, the write can start with sector 5 of track 9. This sector

is reached 0.52 × 4 = 2.08 ms after the completion of the read operation. Thus

the total transfer time = 16.7 + 2.08 + 16.7 = 35.48 ms.

6.8

RAID 0: 800 GB

RAID 1: 400 GB

RAID 3: 600 GB

RAID 4: 600 GB

RAID 5: 600 GB

RAID 6: 400 GB

6.9 With the CD scheme, bit density improves by a factor of 3, but there is an increase

in the number of bits by a factor of 14/8. Net improvement factor is 3 × (8/14) ≈

1.7. That is, the CD scheme has a data storage density 1.7 times greater than the

direct recording scheme.

6.10 a. 2 × 3 × $150 = $900

b. $2500 + (3 × 3 × $50) = $2950

c. Let Z = the number of GB at which the two approaches yield approximately the

same cost. For the disk, the cost is Cd = (Z/500) × 3 × $150. For tape, the cost is

Ct = 2500 + ((Z/400) × 3 × $50). If we set Cd = Ct and solve for Z, we get Z =

4762. So the size of the backup would have to be about 5 TB for tape to be less

expensive.

d. One where you keep a lot of backup sets.

6.7 It depends on the nature of the I/O request pattern. On one extreme, if only a

single process is doing I/O and is only doing one large I/O at a time, then disk

striping improves performance. If there are many processes making many small

I/O requests, then a nonstriped array of disks should give comparable

performance to RAID 0.

-43-

CHAPTER 7 INPUT/OUTPUT

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

7.1 Human readable: Suitable for communicating with the computer user. Machine

readable: Suitable for communicating with equipment. Communication: Suitable

for communicating with remote devices

7.2 The most commonly used text code is the International Reference Alphabet (IRA),

in which each character is represented by a unique 7-bit binary code; thus, 128

different characters can be represented.

7.3 Control and timing. Processor communication. Device communication. Data

buffering. Error detection.

7.4 Programmed I/O: The processor issues an I/O command, on behalf of a process, to

an I/O module; that process then busy-waits for the operation to be completed

before proceeding. Interrupt-driven I/O: The processor issues an I/O command on

behalf of a process, continues to execute subsequent instructions, and is

interrupted by the I/O module when the latter has completed its work. The

subsequent instructions may be in the same process, if it is not necessary for that

process to wait for the completion of the I/O. Otherwise, the process is suspended

pending the interrupt and other work is performed. Direct memory access

(DMA): A DMA module controls the exchange of data between main memory and

an I/O module. The processor sends a request for the transfer of a block of data to

the DMA module and is interrupted only after the entire block has been

transferred.

7.5 With memory-mapped I/O, there is a single address space for memory locations

and I/O devices. The processor treats the status and data registers of I/O modules

as memory locations and uses the same machine instructions to access both

memory and I/O devices. With isolated I/O, a command specifies whether the

address refers to a memory location or an I/O device. The full range of addresses

may be available for both.

7.6 Four general categories of techniques are in common use: multiple interrupt lines;

software poll; daisy chain (hardware poll, vectored); bus arbitration (vectored).

7.7 The processor pauses for each bus cycle stolen by the DMA module.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

-44-

7.1 In the first addressing mode, 28 = 256 ports can be addressed. Typically, this would

allow 128 devices to be addressed. However, an opcode specifies either an input or

output operation, so it is possible to reuse the addresses, so that there are 256 input

port addresses and 256 output port addresses. In the second addressing mode, 216

= 64K port addresses are possible.

7.2 In direct addressing mode, an instruction can address up to 216 = 64K ports. In

indirect addressing mode, the port address resides in a 16-bit registers, so again,

the instruction can address up to 216 = 64K ports.

7.3 64 KB

7.4 Using non-block I/O instructions, the transfer takes 20 × 128 = 2560 clock cycles.

With block I/O, the transfer takes 5 × 128 = 640 clock cycles (ignoring the one-time

fetching of the iterative instruction and its operands). The speedup is

(2560 – 640)/2560 = 0.75, or 75%.

7.5 a. Each I/O device requires one output (from the point of view of the processor)

port for commands and one input port for status.

b. The first device requires only one port for data, while the second devices

requires and input data port and an output data port. Because each device

requires one command and one status port, the total number of ports is seven.

c. seven.

7.6 a. The printing rate is slowed to 5 cps.

b. The situation must be treated differently with input devices such as the

keyboard. It is necessary to scan the buffer at a rate of at least once per 60 ms.

Otherwise, there is the risk of overwriting characters in the buffer.

7.7 At 8 MHz, the processor has a clock period of 0.125 µs, so that an instruction cycle

takes 12 × 0.125 = 1.5 µs. To check status requires one input-type instruction to

read the device status register, plus at least one other instruction to examine the

present data to the device handler. The total is 3 instructions, requiring 4.5 µs.

7.8 Advantages of memory mapped I/O:

1. No additional control lines are needed on the bus to distinguish memory

commands from I/O commands.

2. Addressing is more flexible. Examples: The various addressing modes of

the instruction set can be used, and various registers can be used to

exchange data with I/O modules.

Disadvantages of memory-mapped I/O:

1. Memory-mapped I/O uses memory-reference instructions, which in most

machines are longer than I/O instructions. The length of the program

therefore is longer.

2. The hardware addressing logic to the I/O module is more complex, because

the device address is longer.

7.9 a. The processor scans the keyboard 10 times per second. In 8 hours, the number

of times the keyboard is scanned is 10 × 60 × 60 × 8 = 288,000.

-45-

b. Only 60 visits would be required. The reduction is 1 – (60/288000) = 0.999, or

99.9%

7.10 a. The device generates 8000 interrupts per second or a rate of one every 125 µs. If

each interrupt consumes 100 µs, then the fraction of processor time consumed

is 100/125 = 0.8

b. In this case, the time interval between interrupts is 16 × 125 = 2000 µs. Each

interrupt now requires 100 µs for the first character plus the time for

transferring each remaining character, which adds up to 8 × 15 = 120 µs, for a

total of 220 µs. The fraction of processor time consumed is 220/2000 = 0.11

c. The time per byte has been reduced by 6 µs, so the total time reduction is 16 × 6

= 96 µs. The fraction of processor time consumed is therefore (220 – 96)/2000 =

0.062. This is an improvement of almost a factor of 2 over the result from part

(b).

7.11 If a processor is held up in attempting to read or write memory, usually no

damage occurs except a slight loss of time. However, a DMA transfer may be to or

from a device that is receiving or sending data in a stream (e.g., disk or tape), and

cannot be stopped. Thus, if the DMA module is held up (denied continuing access

to main memory), data will be lost.

7.12 Let us ignore data read/write operations and assume the processor only fetches

instructions. Then the processor needs access to main memory once every

microsecond. The DMA module is transferring characters at a rate of 1200

characters per second, or one every 833 µs. The DMA therefore "steals" every 833rd

cycle. This slows down the processor approximately

833 ×100% =0.12%

7.13 a. For the actual transfer, the time needed is (128 bytes)/(50 KBps) = 2.56 ms.

Added to this is the time to transfer bus control at the beginning and end of the

transfer, which is 250 + 250 = 500 ns. This additional time is negligible, so that

the transfer time can be considered as 2.56 ms.

b. The time to transfer one byte in cycle stealing mode is 250 + 500 + 250 = 1000 ns

= 1 µs. Total amount of time the bus is occupied for the transfer is 128 µs. This

is less than the result from part (a) by a factor of 20.

7.14 a. At 5 MHz, on clock cycle takes 0.2 µs. A transfer of one byte therefore takes 0.6

µs.

b. The data rate is 1/(0.6 × 10–6) = 1.67 MB/s

c. Two wait states add an addition 0.4 µs, so that a transfer of one byte takes 1 µs.

The resulting data rate is 1 MB/s.

7.15 A DMA cycle could take as long as 0.75 µs without the need for wait states. This

corresponds to a clock period of 0.75/3 = 0.25 µs, which in turn corresponds to a

clock rate of 4 MHz. This approach would eliminate the circuitry associated with

wait state insertion and also reduce power dissipation.

7.16 a. Telecommunications links can operate continuously, so burst mode cannot be

used, as this would tie up the bus continuously. Cycle-stealing is needed.

b. Because all 4 links have the same data rate, they should be given the same

priority.

-46-

7.17 Only one device at a time can be serviced on a selector channel. Thus,

Maximum rate = 800 + 800 + 2 × 6.6 + 2 × 1.2 + 10 × 1 = 1625.6 KBytes/sec

7.18 a. The processor can only devote 5% of its time to I/O. Thus the maximum I/O

instruction execution rate is 106 × 0.05 = 50,000 instructions per second. The I/O

transfer rate is therefore 25,000 words/second.

b. The number of machine cycles available for DMA control is

106(0.05 × 5 + 0.95 × 2) = 2.15 × 106

If we assume that the DMA module can use all of these cycles, and ignore any

setup or status-checking time, then this value is the maximum I/O transfer

rate.

7.19 For each case, compute the fraction g of transmitted bits that are data bits. Then the

maximum effective data rate ER is

ER = gR

a. There are 7 data bits, 1 start bit, 1.5 stop bits, and 1 parity bit.

g = 7

1 + 7 + 1 + 1.5 = 7/10.5

ER = 0.67 × R

b. Each frame contains 48 + 128 = 176 bits. The number of characters is 128/8 = 16,

and the number of data bits is 16 × 7 = 112.

ER= 112

176 × R = 0.64 × R

c. Each frame contains 48 = 1024 bits. The number of characters is 1024/8 = 128,

and the number of data bits is 128 × 7 = 896.

ER= 896

1072 × R = 0.84 × R

d. With 9 control characters and 16 information characters, each frame contains

(9 + 16) × 8 = 200 bits. The number of data bits is 16 × 7 = 112 bits.

ER= 112

200 × R = 0.56 × R

e. With 9 control characters and 128 information characters, each frame contains

(9 + 128) × 8 = 1096 bits. The number of data bits is 128 × 7 = 896 bits.

ER= 896

1096 × R = 0.82 × R

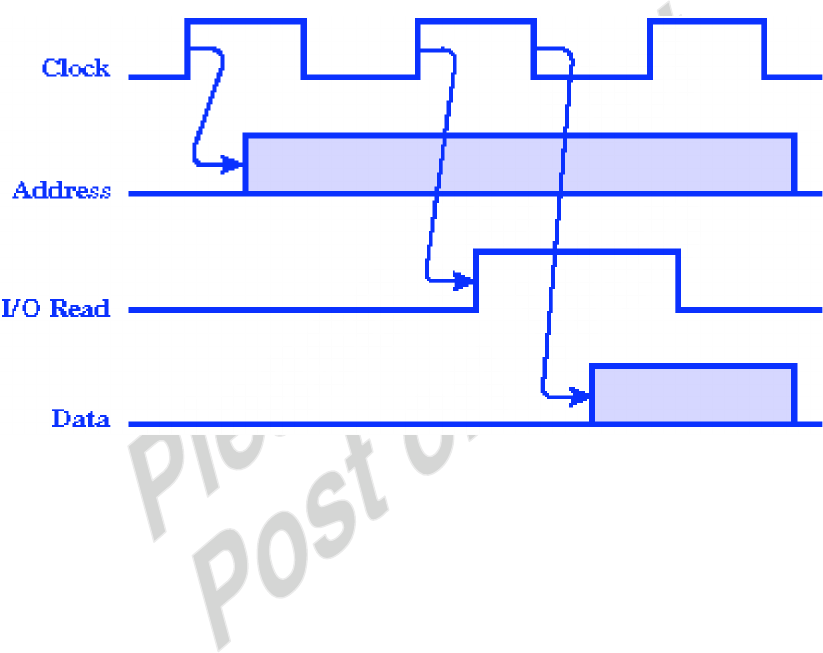
-47-

7.20 a. Assume that the women are working, or sleeping, or otherwise engaged. The

first time the alarm goes off, it alerts both that it is time to work on apples. The

next alarm signal causes apple-server to pick up an apple an throw it over the

fence. The third alarm is a signal to Apple-eater that he can pick up and eat the

apple. The transfer of apples is in strict synchronization with the alarm clock,

which should be set to exactly match Apple-eater's needs. This procedure is

analogous to standard synchronous transfer of data between a device and a

computer. It can be compared to an I/O read operation on a typical bus-based

system. The timing diagram is as follows:

On the first clock signal, the port address is output to the address bus. On the

second signal, the I/O Read line is activated, causing the selected port to place its

data on the data bus. On the third clock signal, the CPU reads the data.

A potential problem with synchronous I/O will occur if Apple-eater's

needs change. If he must eat at a slower or faster rate than the clock rate, he will

either have too many apples or too few.

b. The women agree that Apple-server will pick and throw over an apple

whenever he sees Apple-eater's flag waving. One problem with this approach

is that if Apple-eater leaves his flag up, Apple-server will see it all the time and

will inundate her friend with apples. This problem can be avoided by giving

Apple-server a flag and providing for the following sequence:

1. Apple-eater raises her "hungry" flag when ready for an apple.

2. Apple-server sees the flag and tosses over an apple.

3. Apple-server briefly waves her "apple-sent" flag

4. Apple-eater sees the "apple-sent" flag, takes down her "hungry" flag, and

grabs the apple.

5. Apple-eater keeps her "hungry" flag stays down until she needs another

apple.

This procedure is analogous to asynchronous I/O. Unfortunately, Apple-

-48-

server may be doing something other than watching for her friend's flag (like

sleeping!). In that case, she will not see the flag, and Apple-eater will go

hungry. One solution is to not permit apple-server to do anything but look for

her friend's flag. This is a polling, or wait-loop, approach, which is clearly

inefficient.

c. Assume that the string that goes over the fence and is tied to Apple-server's

wrist. Apple-eater can pull the string when she needs an apple. When Apple-

server feels a tug on the string, she stops what she is doing and throws over an

apple. The string corresponds to an interrupt signal and allows Apple-server to

use her time more efficiently. Moreover, if Apple-server is doing something

really important, she can temporarily untie the string, disabling the interrupt.

-49-

7.21

-50-

CHAPTER 8 OPERATING SYSTEM SUPPORT

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

8.1 The operating system (OS) is the software that controls the execution of programs

on a processor and that manages the processor's resources.

8.2 Program creation: The operating system provides a variety of facilities and

services, such as editors and debuggers, to assist the programmer in creating

programs. Program execution: A number of tasks need to be performed to execute

a program. Instructions and data must be loaded into main memory, I/O devices

and files must be initialized, and other resources must be prepared. Access to I/O

devices: Each I/O device requires its own peculiar set of instructions or control

signals for operation. Controlled access to files: In the case of files, control must

include an understanding of not only the nature of the I/O device (disk drive, tape

drive) but also the file format on the storage medium. System access: In the case of

a shared or public system, the operating system controls access to the system as a

whole and to specific system resources. Error detection and response: A variety of

errors can occur while a computer system is running. Accounting: A good

operating system will collect usage statistics for various resources and monitor

performance parameters such as response time.

8.3 Long-term scheduling: The decision to add to the pool of processes to be executed.

Medium-term scheduling: The decision to add to the number of processes that are

partially or fully in main memory. Short-term scheduling: The decision as to

which available process will be executed by the processor

8.4 A process is a program in execution, together with all the state information

required for execution.

8.5 The purpose of swapping is to provide for efficient use of main memory for

process execution.

8.6 Addresses must be dynamic in the sense that absolute addresses are only resolved

during loading or execution.

8.7 No, if virtual memory is used.

8.8 No.

8.9 No.

-51-

8.10 The TLB is a cache that contains those page table entries that have been most

recently used. Its purpose is to avoid, most of the time, having to go to disk to

retrieve a page table entry.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

8.1 The answers are the same for (a) and (b). Assume that although processor

operations cannot overlap, I/O operations can.

1 Job: TAT = NT Processor utilization = 50%

2 Jobs: TAT = NT Processor utilization = 100%

4 Jobs: TAT = (2N – 1)NT Processor utilization = 100%

8.2 I/O-bound programs use relatively little processor time and are therefore favored

by the algorithm. However, if a processor-bound process is denied processor time

for a sufficiently long period of time, the same algorithm will grant the processor

to that process because it has not used the processor at all in the recent past.

Therefore, a processor-bound process will not be permanently denied access.

8.3 Main memory can hold 5 pages. The size of the array is 10 pages. If the array is

stored by rows, then each of the 10 pages will need to be brought into main

memory once. If it is stored by columns, then each row is scattered across all ten

pages, and each page will have to be brought in 100 times (once for each row

calculation).

8.4 The number of partitions equals the number of bytes of main memory divided by

the number of bytes in each partition: 224/216 = 28. Eight bits are needed to identify

one of the 28 partitions.

8.5 Let s and h denote the average number of segments and holes, respectively. The

probability that a given segment is followed by a hole in memory (and not by

another segment) is 0.5, because deletions and creations are equally probable in

equilibrium. so with s segments in memory, the average number of holes must be

s/2. It is intuitively reasonable that the number of holes must be less than the

number of segments because neighboring segments can be combined into a single

hole on deletion.

8.6 a. Split binary address into virtual page number and offset; use VPN as index into

page table; extract page frame number; concatenate offset to get physical

memory address

b. (i) 1052 = 1024 + 28 maps to VPN 1 in PFN 7, (7 × 1024+28 = 7196)

(ii) 2221 = 2 × 1024 + 173 maps to VPN 2, page fault

(iii) 5499 = 5 × 1024 + 379 maps to VPN 5 in PFN 0, (0 × 1024+379 = 379)

8.7 With very small page size, there are two problems: (1) Because very little data is

brought in with each page, there will need to be a lot of I/O to bring in the many

small pages. (2) The overhead (page table size, length of field for page number)

will be disproportionately high.

If pages are very large, main memory will be wasted because the principle of

locality suggests that only a small part of the large page will be used.

-52-

8.8 9 and 10 page transfers, respectively. This is referred to as "Belady's anomaly," and

was reported in "An Anomaly in Space-Time Characteristics of Certain Programs

Running in a Paging Machine," by Belady et al, Communications of the ACM, June

1969.

8.9 A total of fifteen pages are referenced, the hit ratios are:

Ratio

0/15

2/15

3/15

5/15

8/15

8.10 The principal advantage is a savings in physical memory space. This occurs for

two reasons: (1) a user page table can be paged in to memory only when it is

needed. (2) The operating system can allocate user page tables dynamically,

creating one only when the process is created.

Of course, there is a disadvantage: address translation requires extra work.

8.11 The machine language version of this program, loaded in main memory starting at

address 4000, might appear as:

4000 (R1) ← ONE Establish index register for i

4001 (R1) ← n Establish n in R2

4002 compare R1, R2 Test i > n

4003 branch greater 4009

4004 (R3) ← B(R1) Access B[i] using index register R1

4005 (R3) ← (R3) + C(R1) Add C[i] using index register R1

4006 A(R1) ← (R3) Store sum in A[i] using index register R1

4007 (R1) ← (R1) + ONE Increment i

4008 branch 4002

6000-6999 storage for A

7000-7999 storage for B

8000-8999 storage for C

9000 storage for ONE

9001 storage for n

The reference string generated by this loop is

494944(47484649444)1000

consisting of over 11,000 references, but involving only five distinct pages.

8.12 The S/370 segments are fixed in size and not visible to the programmer. Thus,

none of the benefits listed for segmentation are realized on the S/370, with the

exception of protection. The P bit in each segment table entry provides protection

for the entire segment.

8.13 On average, p/2 words are wasted on the last page. Thus the total overhead or

waste is w = p/2 + s/p. To find the minimum, set the first derivative to 0.

-53-

dp =1

2−s

p2=0

p=2s

8.14 There are three cases to consider:

Location of referenced

word

Probability

Total time for access in ns

In cache

0.9

Not in cache, but in main

memory

(0.1)(0.6) = 0.06

60 + 20 = 80

Not in cache or main

memory

(0.1)(0.4) = 0.04

12ms + 60 + 20 = 12000080

So the average access time would be:

Avg = (0.9)(20) + (0.06)(80) + (0.04)(12000080) = 480026 ns

8.15

232 memory

211 page size =221 page frames

Segment: 0

Page descriptor

table

00021ABC

Main memory

(232 bytes)

232 memory

211 page size =221 page frames

a. 8 × 2K = 16K

b. 16K × 4 = 64K

c. 232 = 4 GBytes

8.16 •The starting physical address of a segment is always evenly divisible by 1048, i.e.,

its rightmost 11 bits are always 0.

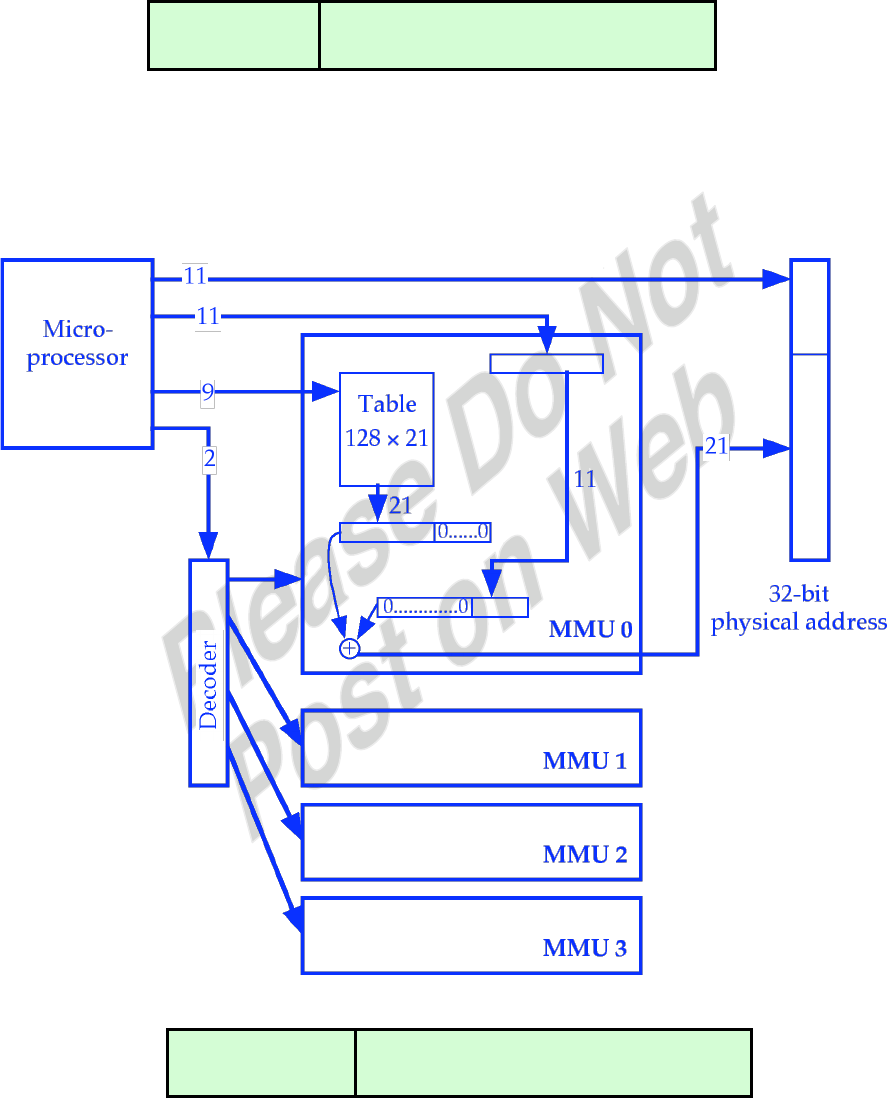
-54-

•Maximum logical address space = 29 = 512 segments (× 222 bytes/segment) = 231

bytes.

•Format of logical address:

segment

number (9)

offset (22)

•Entries in the mapping table: 29 = 512.

•Number of memory management units needed = 4.

•Each 9-bit segment number goes to an MMU; 7 bits are needed for the 128-entry

table, the other 2 most significant bits are decoded to select the MMU.

•Each entry in the table is 22 bits.

8.17 a.

page number

(5)

offset (11)

b. 32 entries, each entry is 9 bits wide.

c. If total number of entries stays at 32 and the page size does not change, then

each entry becomes 8 bits wide.

-55-

8.18 The system operator can review this quantity to determine the degree of "stress" on

the system. By reducing the number of active jobs allowed on the system, this

average can be kept high. A typical guideline is that this average should be kept

above 2 minutes. This may seem like a lot, but it isn't.

8.19

0192031

Section base address Section of fsetSection

0111231

Page base address Page of fset

Small

page

0151631

Large page base address Page offset

La rge

page

0232431

Supersection base address Supersection offset

Super

section

-56-

8.20

Main Memory

Virtual address

Level 1 (L1) section table

L1 index

section base addr

section index

4095

192031

-57-

CHAPTER 9 COMPUTER ARITHMETIC

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

9.1 Sign–Magnitude Representation: In an N-bit word, the left-most bit is the sign (0

= positive, 1 = negative) and the remaining N – 1 bits comprise the magnitude of

the number. Twos Complement Representation: A positive integer is represented

as in sign magnitude. A negative number is represented by taking the Boolean

complement of each bit of the corresponding positive number, then adding 1 to the

resulting bit pattern viewed as an unsigned integer. Biased representation: A

fixed value, called the bias, is added to the integer.

9.2 In sign-magnitude and twos complement, the left-most bit is a sign bit. In biased

representation, a number is negative if the value of the representation is less than

the bias.

9.3 Add additional bit positions to the left and fill in with the value of the original sign

bit.

9.4 Take the Boolean complement of each bit of the positive number, then adding 1 to

the resulting bit pattern viewed as an unsigned integer.

9.5 When the operation is performed on the n-bit integer –2n–1 (one followed by n – 1

zeros).

9.6 The twos complement representation of a number is the bit pattern used to

represent an integer. The twos complement of a number is the operation that

computes the negation of a number in twos complement representation.

9.7 The algorithm for performing twos complement addition involves simply adding

the two numbers in the same way as for ordinary addition for unsigned numbers,

with a test for overflow. For multiplication, if we treat the bit patterns as unsigned

numbers, their magnitude is different from the twos complement versions and so

the magnitude of the result will be different.

9.8 Sign, significand, exponent, base.

9.9 An advantage of biased representation is that nonnegative floating-point numbers

can be treated as integers for comparison purposes.

9.10 Positive overflow refers to integer representations and refers to a number that is

larger than can be represented in a given number of bits. Exponent overflow refers

to floating point representations and refers to a positive exponent that exceeds the

maximum possible exponent value. Significand overflow occurs when the

-58-

addition of two significands of the same sign result in a carry out of the most

significant bit.

9.11 1. Check for zeros. 2. Align the significands. 3. Add or subtract the significands.

4. Normalize the result.

9.12 To avoid unnecessary loss of the least significant bit.

9.13 Round to nearest: The result is rounded to the nearest representable number.

Round toward +∞: The result is rounded up toward plus infinity. Round toward –

∞: The result is rounded down toward negative infinity. Round toward 0: The

result is rounded toward zero.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

9.1 Sign Magnitude: 512 = 0000 0010 0000 0000

–29 = 1000 0000 0001 1101

Two’s Complement: 512 = 0000 0010 0000 0000

–29 = 1111 1111 1110 0011

9.2 1101011: Because this starts with a leftmost 1, it is a negative number. The

magnitude of the negative number is determined by flipping the bits and adding 1:

0010100 + 1 = 0010101

This is 21, so the original value was –21.

0101101

Because this starts with a leftmost 0, it is a positive number and we just compute

the magnitude as an unsigned binary number, which is 45.

9.3 a.

A=−2n−1−1

( )

an−1+2iai

i=0

n−2

∑

b. From –(2n–1 – 1) through (2n–1 – 1)

c. (1) Add the two numbers as if they were unsigned integers. (2) If there is a carry

out of the sign position, then add that bit to the first bit position of the result and

propagate carries as necessary. This is known as the end-around carry rule. (3)

An overflow occurs if two positive numbers are added and the result is negative

of if two negative numbers are added and the result is positive.

-59-

9.4

sign-magnitude

ones complement

Range

–(2n–1 – 1) to (2 n–1 – 1)

–(2n–1 – 1) to (2n–1 – 1)

Number of

representations of 0

Negation

Complement the sign bit

Complement each bit

Expansion of bit

length

Move the sign bit to the new

leftmost bit; fill in with zeros

Fill all new bit

positions to the left

with the sign bit

Subtract B from A

Complement the sign bit of B and

add B to A using rules for addition

of sign-magnitude numbers

Take the ones

complement of B and

add it to A

Rules for adding two sign-magnitude numbers:

1. If A and B have the same sign, then add the two magnitudes. If there is a carry

out of the last magnitude bit, there is an overflow. If there is no carry the result

is the sum of the magnitudes with the same sign bit as A and B.

2. (a) If the magnitude of A equals the magnitude of B, the result is zero; (b) if the

magnitude of A is greater than the magnitude of B, then the sign bit of the

result is the sign of A, and the magnitude of the result is the magnitude of A

minus the magnitude of B. (b) Otherwise, the sign bit of the result is the sign of

B, and the magnitude of the result is the magnitude of B minus the magnitude

of A.

9.5 The twos complement of the original number.

9.6 a. We can express 2n as (1 + Z), where Z is an n-bit quantity of all 1 bits. Then,

treating all quantities as unsigned integers, we have (2n – X) = 1 + Z – X. But (Z

– X) results in the Boolean complement of each bit of X. Example:

11111111

–01110100

10001011

Therefore, (2n – X) adds one to the quantity formed by taking the Boolean

complement of each bit of X, which is how we defined the twos complement of

b. In Figure 9.5a, notice that we can subtract X or (add –X) by moving 16 – X

positions clockwise. Similarly, in Figure 9.5b, we can subtract X or (add –X) by

moving 2n – X positions clockwise. But the quantity (2n – X) is what we just

defined as the twos complement of X, which is the twos complement

representation of –X. So we can subtract X by adding –X.

9.7 The tens complement is calculated as 105 – 13250 = 100000 -13250 = 86750.

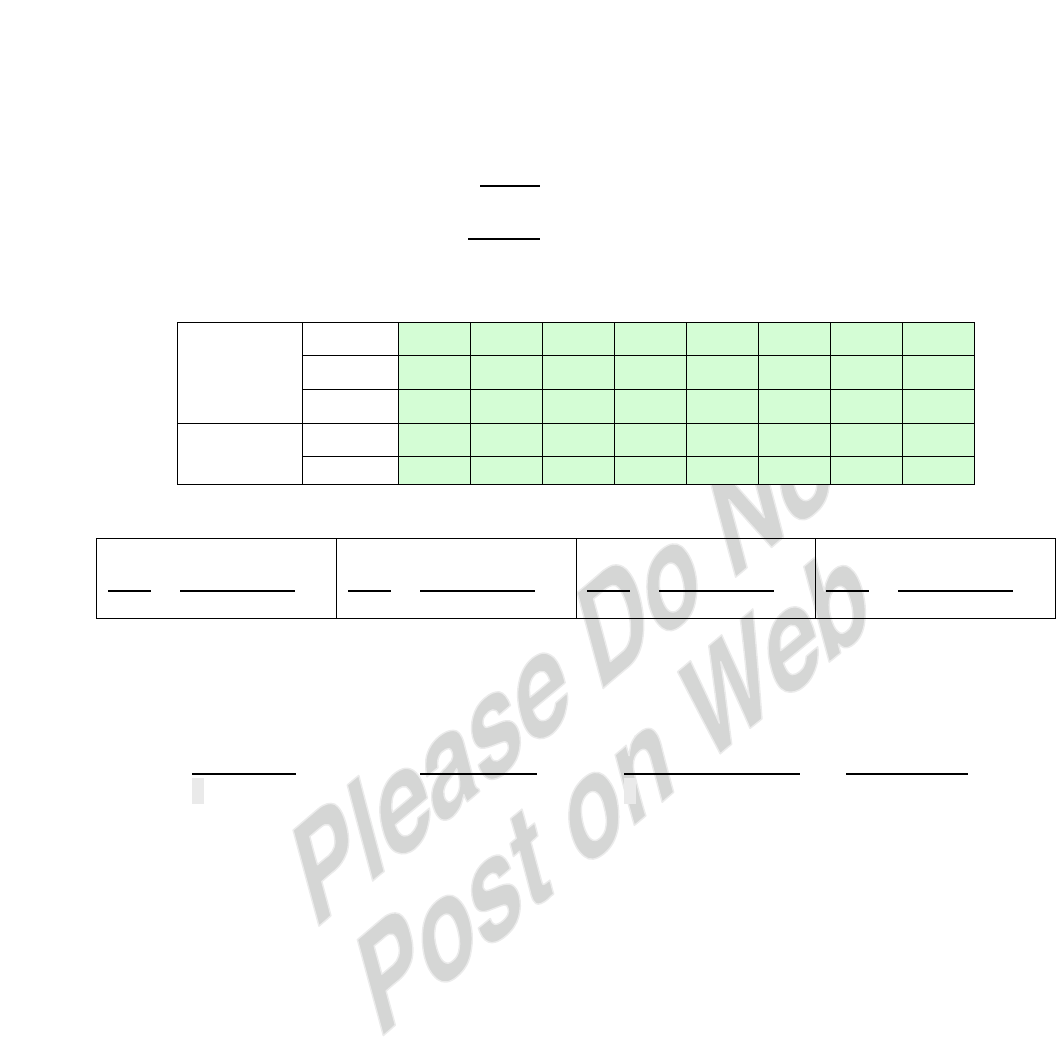
-60-

9.8 We subtract M – N, where M = 72532 and N = 13250:

M = 72532

tens complement of N = +86750

sum = 159282

discard carry digit = –100000

result = 59282

9.9

xn–1

yn–1

Input

cn–2

zn–1

Output

9.10

+6 00000110

+13 00001101

+19 00010011

–6 11111010

+13 00001101

+7 00000111

+6 00000110

–13 11110011

–7 11111001

–6 11111010

–13 11110011

–19 11101101

9.11 Add the twos complement, and check for overflow. For b, we must first sign-

extend the second term.

a. 111000 b. 11001100 c. 111100001111 d. 11000011

+ 001101 + 00010010 + 001100001101 + 00011000

1 000101 11011110 1 001000011100 11011000

In all cases, the signs of the two numbers to be added are different, so there is no

overflow.

9.12 The overflow rule was stated as follows: If two numbers are added, and they are

both positive or both negative, then overflow occurs if and only if the result has

the opposite sign. There are four cases:

•Both numbers positive (sign bit = 0) and no carry into the leftmost bit position:

There is no carry out of the leftmost bit position, so the XOR is 0. The result has a

sign bit = 0, so there is no overflow.

•Both numbers positive and a carry into the leftmost bit position: There is no carry

out of the leftmost position, so the XOR is 1. The result has a sign bit = 1, so there

is overflow.

•Both numbers negative and no carry into the leftmost position: There is a carry

out of the leftmost position, so the XOR is 1. The result has a sign bit of 0, so there

is overflow.

•Both numbers negative and a carry into the leftmost position. There is a carry out

of the leftmost position, so the XOR is 0. The result has a sign bit of 1, so there is

no overflow.

Therefore, the XOR result always agrees with the presence or absence of overflow.

9.13 An overflow cannot occur because addition and subtraction alternate. As a

consequence, the two numbers that are added always have opposite signs, a

condition that excludes overflow.

-61-

9.14

Q–1

0000

1010

0101

Initial

0000

0101

Shift

1011

0101

A ← A – M

1101

1010

0101

Shift

0010

1010

0101

A ← A + M

0001

0101

Shift

1100

0101

A ← A – M

1110

0010

0101

Shift

9.15 Using M=010111 (23) and Q = 010011 (19) we should get 437 as the result.

Q–1

000000

010111

010011

Initial

101101

010111

010011

A ← A – M

110110

101011

010011

Shift

111011

010101

010011

Shift

111101

101010

010011

Shift

010000

101010

010011

A ← A + M

001000

010101

010011

Shift

110101

010101

010011

A ← A – M

111010

101010

010011

Shift

001101

101010

010011

A ← A + M

000110

110101

010011

Shift

Answer = 0001 1011 0101 (which is 437)

9.16 An n-digit number in base B has a maximum value of Bn – 1. We need to show that

the maximum product is less than B2n – 1.

(Bn – 1) (Bn – 1) = B2n – 2Bn + 1 ≤ B2n – 1.

The inequality is true if

–2Bn + 1 ≤ –1 or 1 ≤ Bn

This is always true for B ≥ 2 and n ≥ 1.

-62-

9.17

00000000

10010011

1011

Initial

00000001

00100110

1011

Shift

11110110

1011

A ← A – M

00000001

00100110

1011

Restore

00000010

01001100

1011

Shift

11110111

1011

A ← A – M

00000010

01001100

1011

Restore

00000100

10011000

1011

Shift

11111001

1011

A ← A – M

00000100

10011000

1011

Restore

00001001

00110000

1011

Shift

11111100

1011

A ← A – M

00001001

00110000

1011

Restore

00010010

01100000

1011

Shift

00000111

1011

A ← A – M

00000111

01100001

1011

Q0 ← 1

00001110

11000010

1011

Shift

00000011

1011

A ← A – M

00000011

11000011

1011

Q0 ← 1

00000111

10000110

1011

Shift

11111100

1011

A ← A – M

00000111

10000110

1011

Restore

00001111

00001100

1011

Shift

00000100

1011

A ← A – M

00000100

00001101

1011

Q0 ← 1

9.18 The nonrestoring division algorithm is based on the observation that a restoration

in iteration I of the form A(I) ← A(I) + M is followed in iteration (I + 1) by the

subtraction A(I+1) ← 2A(I) – M. These two operations can be combined into a

single operation: A(I+1) ← 2A(I) + M.

9.19 False. For a negative quotient, truncation yields a larger number.

-63-

9.20 Divisor = 13 = (001101)2 is placed in M register.

Dividend = –145 = (111101101111)2 is placed in A and Q registers

111101

101111

001101

Initial

111011

011110

Shift

001101

Add

001000

111011

011110

Restore

110110

111100

Shift

001101

Add

000011

110110

111100

Restore

101101

111000

Shift

001101

Add

111010

111001

Q0 ← 1

110101

110010

Shift

001101

Add

000110

110101

110010

Restore

101011

100100

Shift

001101

Add

111000

100101

Q0 ← 1

110001

001010

Shift

001101

Add

111110

001011

Q0 ← 1

Remainder = (111110)2 = –2

Quotient = twos complement of 001011 = (110101)2 = –11

9.21 a. Planck's constant:

6.63 × 10–27 → 0.00000000000000000000000000663

b. Avogadro's number:

6.02 × 1023 → 602000000000000000000000.0

-64-

To represent the approximation of Planck's constant 29 radix-10 fractional

digits are needed, while representing the approximation of Avogadro's number

requires 24 integer decimal digits. To represent the approximations of both

Planck's constant and Avogadro's number in a fixed-point number format, 29 +

54 = 53 radix-10 digits are needed.

b. In the considered radix-10 base-10 biased representation for the exponent (such

that Ebiased = E + 50), the exponent of both Planck's constant and Avogadro's

number can be represented using 2 digits, because 27+50 = 23 and 23+50 = 73.

To represent the significands, 3 radix-10 digits are needed. Therefore, to

represent the approximations of both Planck's constant and Avogadro's

number in a floating-point radix- 10 base-10 number format, 3 + 2 = 5 decimal

digits are needed. Source: [ERCE04]

9.22 a. bX–q(1 – b–p), b–q–p

b. bX–q(1 - b–p), b–q–1

9.23 a. 1 10000001 01000000000000000000000

b. 1 10000001 10000000000000000000000

c. 1 01111111 10000000000000000000000

d. 384 = 110000000 = 1.1 × 21000

Change binary exponent to biased exponent:

127 + 8 = 135 = 10000111

Format: 0 10000111 00000000000000000000000

e. 1/16 = 0.0001 = 1.0 × 2–100

127 – 4 = 123 = 01111011

Format: 0 01111011 00000000000000000000000

f. –1/32 = –0.00001 = –1.0 × 2–101

127 – 5 = 122 = 01111010

Format: 0 01111010 00000000000000000000000

9.24 a. –28 (don't forget the hidden bit)

b. 13/16 = 0.8125

c. 2

9.25 In this case, the exponent has a bias of 3. Special cases are shaded in the table. The

first shaded column contains the denormalized numbers. It is worthwhile to study

this table to get a feel for the distribution and spacing of numbers represented in

this format.

-65-

Exponent

sign bit

and

significand

000

001

010

011

100

101

110

111

0 000

0.25

0.5

+∞

0 001

0.03125

0.28125

0.5625

1.125

2.25

4.5

NaN

0 010

0.0625

0.3125

0.625

1.25

2.5

NaN

0 011

0.09375

0.34375

0.6875

1.375

2.75

5.5

NaN

0 100

0.125

0.375

0.75

1.5

NaN

0 101

0.15625

0.40625

0.8125

1.625

3.25

6.5

NaN

0 110

0.1875

0.4375

0.875

1.75

3.5

NaN

0 111

0.21875

0.46875

0.9375

1.875

3.75

7.5

NaN

1 000

–0

–0.25

–0.5

–1

–2

–4

–8

–∞

1 001

–

0.03125

–

0.28125

–

0.5625

–1.125

–2.25

–2.5

–9

NaN

1 010

–0.0625

–0.3125

–0.625

–1.25

–2.5

–5

–10

NaN

1 011

–

0.09375

–

0.34375

–

0.6875

–1.375

–2.75

–5.5

–11

NaN

1 100

–0.125

–0.375

–0.75

–1.5

–3

–6

–12

NaN

1 101

–

0.15625

–

0.40625

–

0.8125

–1.625

–3.25

–6.5

–13

NaN

1 110

–0.1875

–0.4375

–0.875

–1.75

–3.5

–7

–14

NaN

1 111

–

0.21875

–

0.46875

–

0.9375

–1.875

–3.75

–7.5

–15

NaN

9.26 a. 1.0 = +1/16 × 161 = 0 100 0001 0001 0000 0000 0000 0000 0000

b. 0.5 = +8/16 × 160 = 0 100 0000 1000 0000 0000 0000 0000 0000

c. 1/64 = +4/16 × 16–1 = 0 011 1111 0100 0000 0000 0000 0000 0000

d. 0.0 = +0 × 16–64 = 0 000 0000 0000 0000 0000 0000 0000 0000

e. –15.0 = –15/16 × 161 = 1 100 0001 1111 0000 0000 0000 0000 0000

f. 5.4 × 10–79 ≈ +1/16 × 16–64 = 0 000 0000 0000 0000 0000 0000 0000 0000

g. 7.2 × 1075 ≈ 1 × 1663 = 0 111 1111 1111 1111 1111 1111 1111 1111

h. 65535 = 164 –1 = 0 100 0100 1111 1111 1111 1111 0000 0000

9.27 Step 1: Sign positive

Step 2: Extract the exponent (5B)16 and subtract the bias (40)16, yielding

(1B)16 = 27

Step 3: The significand (CA 0000)16 = 12/16 + 10/256 = 0.7890625.

The decimal result is 0.7890625 × 1627.

9.28 The base is irrelevant

a. Bias = 26–1 = 25 = 32

b. Bias = 27–1 = 26 = 64

-66-

9.29

Expressible Negative

Numbers

Negative

Overflow

Positive

Overflow

Negative

Underflow

Zero

Positive

Underflow

Expressible Positive

Numbers

00.5 × 2–1022

– 0.5 × 2–1022

– (1 – 2–53

) × 21023 (1 – 2–53) × 21023

9.30 a. 1. Express the number in binary form: 1011010000 (normalize to 1.1bbbb)

2. Normalize the number into the form 0.1bbbbbbbbbbbbb

0.1011010000 × 2k where k = 10(base10) or 1010(base2)

0.1011010000 × 2(1010)

Once in normalized form every number will have a 1 after the decimal

point. We do not need to store this number; it is implicit. Therefore in the

Significand field we will store 01101000000000000000000.

3. For the 8-bit exponent field, a bias of 128 is used. Add the bias to the

exponent and store the answer: 1010 + 10000000 = 1001010

4. Sign bit = 1

5. Result = 1 1001010 01101000000000000000000

b. We have 0.645 = 0.101001...; therefore the significand is 01001 (the first 1 is

implicit). The sign = 0, and the exponent = 0.

Result: 0 0000000 01001000000000000000000

9.31 There are 232 different bit patterns available. However, because of special cases,

not all of these bit patterns represent unique numbers. In particular, an exponent

of all ones together with a nonzero fraction is given the value NaN, which means

Not a Number, and is used to signal various exception conditions. Because the

fraction field is 23 bits, the number of nonzero fractions is 223 – 1. The sign bit may

be 0 or 1 for this case, so the total number of NaN values is 224 – 2. Therefore, the

number of different numbers that can be represented is 232 – 224 + 2. This number

includes both plus and minus zero and plus and minus infinity. If we exclude

minus zero and plus and minus infinity, then the total is 232 – 224 –1.

9.32 We have 0.4 × 20. Because 0.4 is less than 0.5, this is not normalized. Thus, we

rewrite as

0.4 = 0.8 × 2–1

Next, convert 0.8 to binary, we have repeating binary number: 0.110011001100...

The closest we can get (7 bits) is 0.1100110. Converting this back to decimal, we

have

(1/2 + 1/4 + 1/32 + 1/64) × 2-1 = 0.3984375

The relative error is 0.4 - 0.3984375

0.4 = 0.0039

-67-

9.33 EA = A - A'

Truncation: EA = 1.427 - 1.42

1.427 = 0.0049

Rounding: EA = 1.427 -1.43

1.427 = –0.0021

9.34 Cancellation reveals previous errors in the computation of X and Y. For example, if

ε is small, we often get poor accuracy when computing f(x + ε) - f(x), because the

rounded calculation of f(x + ε) destroys much of the information about ε. It is

desirable to rewrite such formulas as ε × g(x,ε), where g(x,ε) =

f(x+

)−f(x)

first computed symbolically. Thus, if f(x) = x2, then g(x,ε) = 2x + ε; if f(x) = x ,

then g(x,ε) = 1

x + ε + x .

9.35 We have

EA = A - A'

A = 1 – A'

A' = A(1 – EA)

B' = B (1 – EB)

A'B' = AB (1 – EA)(1 -EB) = AB [1– (EA +EB) + EAEB ]

≈ AB [1– (EA + EB)]

The product term EAEB should be negligible in comparison to the sum.

Consequently

EAB = EA +EB.

9.36 a. EA = 0.22288 - 0.2228

0.2228 = 0.00036

EB = 0.22211 - 0.2221

0.22211 = 0.00045

b. C = A – B = 0.00077

C'= A' – B' = 0.0007

EC = 0.00077 - 0.0007

0.00077 = 0.09

-68-

9.37 a. (2.50000 × 10–60) × (3.50000 × 10–43) = 8.75000 × 10–103 → 0.00088 × 10–99

The otherwise exact product underflows and must be denormalized by

four digits. The number then requires rounding.

b. (2.50000 × 10–60) × (3.50000 × 10–60) = 8.75000 × 10–120 → 0.0

The intermediate result falls below the underflow threshold and must be

set to zero.

c. (5.67834 × 10–97) – (5.67812 × 10–97) = 2.20000 × 10–101 → 0.02200 × 10–99

This example illustrates how underflowed sums and differences of

numbers in the same format are always free from rounding errors.

9.38 a. The exponents are equal. Therefore the mantissas are added, keeping the

common exponent, and the sum is renormalized if necessary.

5.566 × 103 + 7.777 × 103 = 1.3343 × 103 ≈ 1.334 × 103

b. The exponents must be equalized first.

3.344 × 101 + 8.877 × 10–2 = 3.344 × 101 + 0.008877 × 101 =

3.352877 × 101 ≈ 3.352 × 101

9.39 a. 7.744 × 10–3 – 6.666 × 10–3 = 1.078 × 10–3

b. 8.844 × 10–3 – 2.233 × 10–1 = 0.08844 × 10–1 – 2.233 × 10–1 =

–2.14456 × 10–1 ≈ –2.144 × 10–1

9.40 a. 2.255 × 101 × 1.234 × 100 = 2.58267 × 101 ≈ 2.582 × 101

b. 8.833 × 102 ÷ 5.555 × 104 = 1.590 × 10–2

-69-

CHAPTER 10 INSTRUCTION SETS:

CHARACTERISTICS AND FUNCTIONS

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

10.1 The essential elements of a computer instruction are the opcode, which specifies

the operation to be performed, the source and destination operand references,

which specify the input and output locations for the operation, and a next

instruction reference, which is usually implicit.

10.2 Registers and memory.

10.3 Two operands, one result, and the address of the next instruction.

10.4 Operation repertoire: How many and which operations to provide, and how

complex operations should be. Data types: The various types of data upon which

operations are performed. Instruction format: Instruction length (in bits), number

of addresses, size of various fields, and so on. Registers: Number of CPU registers

that can be referenced by instructions, and their use. Addressing: The mode or

modes by which the address of an operand is specified.

10.5 Addresses, numbers, characters, logical data.

10.6 For the IRA bit pattern 011XXXX, the digits 0 through 9 are represented by their

binary equivalents, 0000 through 1001, in the right-most 4 bits. This is the same

code as packed decimal.

10.7 With a logical shift, the bits of a word are shifted left or right. On one end, the bit

shifted out is lost. On the other end, a 0 is shifted in. The arithmetic shift operation

treats the data as a signed integer and does not shift the sign bit. On a right

arithmetic shift, the sign bit is replicated into the bit position to its right. On a left

arithmetic shift, a logical left shift is performed on all bits but the sign bit, which is

retained.

10.8 1. In the practical use of computers, it is essential to be able to execute each

instruction more than once and perhaps many thousands of times. It may require

thousands or perhaps millions of instructions to implement an application. This

would be unthinkable if each instruction had to be written out separately. If a table

or a list of items is to be processed, a program loop is needed. One sequence of

instructions is executed repeatedly to process all the data. 2. Virtually all programs

involve some decision making. We would like the computer to do one thing if one

condition holds, and another thing if another condition holds. 3. To compose

-70-

correctly a large or even medium-size computer program is an exceedingly

difficult task. It helps if there are mechanisms for breaking the task up into smaller

pieces that can be worked on one at a time.

10.9 First, most machines provide a 1-bit or multiple-bit condition code that is set as the

result of some operations. Another approach that can be used with a three-address

instruction format is to perform a comparison and specify a branch in the same

instruction.

10.10 The term refers to the occurrence of a procedure call inside a procedure.

10.11 Register, start of procedure, top of stack.

10.12 A reentrant procedure is one in which it is possible to have several calls open to it

at the same time.

10.13 In this notation, the operator follows its two operands.

10.14 A multibyte numerical value stored with the most significant byte in the lowest

numerical address is stored in big-endian fashion. A multibyte numerical value

stored with the most significant byte in the highest numerical address is stored in

little-endian fashion.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

10.1 a. 23

b. 32 33

10.2 a. 7309

b. 582

c. 1010 is not a valid packed decimal number, so there is an error

10.3 a. 0; 255

b. –127; 127

c. –127; 127

d. –128; 127

e. 0; 99

f. –9; +9

-71-

10.4 Perform the addition four bits at a time. If the 4-bit digit of the result of binary

addition is greater then 9 (binary 1001), then add 6 to get the correct result.

1698 0001 0110 1001 1000

+ 1798 0001 0111 1000 0110

0010 1100 1 0001 1110

1 1 1 0110

0011 1110 0110 1 0100

0110 1000

1 0100

3484 0011 0100 1000 0100

10.5 The tens complement of a number is formed by subtracting each digit from 9, and

adding 1 to the result, in a manner similar to twos complement. To subtract,

simply take the tens complement and add:

0736

9674

1 0410

10.6

PUSH A

PUSH B

PUSH C

MUL

ADD

PUSH D

PUSH E

PUSH F

MUL

SUB

DIV

POP X

LOAD E

MUL F

STORE T

LOAD D

SUB T

STORE T

LOAD B

MUL C

ADD A

DIV T

STO X

MOV R0, E

MUL RO, F

MOV R1, D

SUB R1, R0

MOV R0, B

MOV R0, C

ADD R0, A

DIV R0, R1

MOV X, R0

MUL R0, E, F

SUB R0, D, R0

MUL R1, B, C

ADD R1, A, R1

DIV X, R0, R1

Source: [TANE90]

10.7 a. A memory location whose initial contents are zero is needed for both X → AC

and AC → X. The program for X → AC, and its effects are shown below.

Assume AC initially contains the value a.

Instruction

Effect on

M(0)

M(X)

SUBS 0

SUBS X

–x

SUBS 0

–x

SUBS 0

–x

SUBS X

-72-

b. For addition, we again need a location, M(0), whose initial value is 0. We also

need destination location, M(1). Assume the initial value in M(1) is y.

Instruction

M(0)

M(1)

M(X)

SUBS 0

SUBS 1

a – y

SUBS 1

SUBS X

–x

SUBS 0

–x – a

–x

SUBS 1

–x – a

–x

SUBS 0

–x – a

–x

SUBS X

–x – a

SUBS 0

–x – a

SUBS 0

–x – a

SUBS 1

a + x

10.8 1. A NOOP can be useful for debugging. When it is desired to interrupt a program

at a particular point, the NOOP is replaced with a jump to a debug routine. When

temporarily patching or altering a program, instructions may be replaced with

NOOPs. 2. A NOOP introduces known delay into a program, equal to the

instruction cycle time for the NOOP. This can be used for measuring time or

introducing time delays. 3. NOOPs can be used to pad out portions of a program

to align instructions on word boundaries or subroutines on page boundaries. 4.

NOOPs are useful in RISC pipelining, examined in Chapter 13.

-73-

10.9

Bit pattern

Value

Arithmetic

left shift

Value

Logical left

shift

Value

00000

00001

00010

00100

00011

00110

00100

01000

00101

01010

00110

01100

00111

01110

01000

00000

overflow

10000

overflow

01001

00010

overflow

10010

overflow

01010

00100

overflow

10100

overflow

01011

00110

overflow

10110

overflow

01100

01000

overflow

11000

overflow

01101

01010

overflow

11010

overflow

01110

01100

overflow

11100

overflow

01111

01110

overflow

11110

overflow

10000

–16

10000

overflow

00000

overflow

10001

–15

00010

overflow

00010

overflow

10010

–14

10100

overflow

00100

overflow

10011

–13

10110

overflow

00110

overflow

10100

–12

11000

overflow

01000

overflow

10101

–11

11010

overflow

01010

overflow

10110

–10

11100

overflow

01100

overflow

10111

–9

11110

overflow

01110

overflow

11000

–8

10000

–16

10000

–16

11001

–7

10010

–14

10010

–14

11010

–6

10100

–12

10100

–12

11011

–5

10110

–10

10110

–10

11100

–4

11000

–8

11000

–8

11101

–3

11010

–6

11010

–6

11110

–2

11100

–4

11100

–4

11111

–1

11110

–2

11110

–2

10.10 Round toward –∞.

10.11 Yes, if the stack is only used to hold the return address. If the stack is also used to

pass parameters, then the scheme will work only if it is the control unit that

removes parameters, rather than machine instructions. In the latter case, the CPU

would need both a parameter and the PC on top of the stack at the same time.

10.12 The DAA instruction can be used following an ADD instruction to enable using

the add instruction on two 8-bit words that hold packed decimal digits. If there is

a decimal carry (i.e., result greater than 9) in the rightmost digit, then it shows up

either as the result digit being greater than 9, or by setting AF. If there is such a

carry, then adding 6 corrects the result. For example:

2 7

-74-

+ 4 6

6 D

+ 0 6

7 3

The second test similarly corrects a carry from the left digit of an 8-bit byte. A

multiple-digit packed decimal addition can thus be programmed using the

normal add-with-carry (ADC) instruction in a loop, with the insertion of a single

DAA instruction after each addition.

10.13 a.

CMP result

destination < source

destination > source

destination = source

CMP result

Flags

destination < source

S ≠ O

destination > source

S = O

destination = source

ZF = 1

c. •Equal: The two operands are equal, so subtraction produces a zero result (Z

= 1).

•Greater than: If A is greater than B, and A and B are both positive or both

negative, then the twos complement operation (A – B) will produce a

positive result (S = 0) with no overflow (O = 0). If A is greater than B with A

positive and B negative, then the result is either positive with no overflow

or negative (S = 1) with overflow (O = 1). In all these cases, the result is

nonzero (Z = 0)

•Greater than or equal: The same reasoning as for "Greater than" applies,

except that the result may be zero or nonzero.

•Less than: This condition is the opposite of "Greater than or equal" and so

the opposite set of conditions apply.

•Less than or equal: This condition is the opposite of "Greater than" and so

the opposite set of conditions apply.

•Not equal: The two operands are unequal, so subtraction produces a

nonzero result (Z = 0).

10.14 a. sign bit in the most significant position, then exponent, then significand

b. sign, exponent, and significand are all zero; that is, all 32 bits are zero

c. biased representation of the exponent

d. yes. However, note that the IEEE has a representation for minus zero, which

would yield results indicating that –0 < 0.

10.15 a. It might be convenient to have a word-length result for passing as a

parameter via a stack, to make it consistent with typical parameter passing.

This is an advantage of Scond. There doesn't seem to be any particular

advantage to the result value for true being integer one versus all binary ones.

b. The case for setting the flags: In general, instructions that operate on data

values will, as a side effect, set the condition codes according to the result of

the operation. Thus, the condition code should reflect the state of the machine

after the execution of each instruction that has altered a data value in some

-75-

way. These instructions violate this principle and are therefore inconsistent

with the remainder of the architecture.

The case against: These instructions are similar to branch on condition

instructions in that they operate on the result of another operation, which is

reflected in the condition codes. Because a branch on condition code

instruction does not itself set the condition codes, the fact that these other

instructions do not is not inconsistent.

For a further discussion, see "Should Scc Set Condition Codes?" by F.

Williams, Computer Architecture News, September 1988.

c. SUB CX, CX ;set register CX to 0

MOV AX, B ;move contents of location B to register AX

CMP AX, A ;compare contents of register AX and location A

SETGT CX ;CX = (a GT b)

TEST JCXZ OUT ;jump if contents of CX equal 0

THEN

OUT

d. MOV EAX, B ; move from location B to register EAX

CMP EAX, C

SETG BL ; BL = 0/1 depending on result

MOV EAX, D

CMP EAX, F

MOV BH, 0

SETE BH

OR BL, BH

10.16 a. Add one byte at a time: AB 08 90 C2

+ 45 98 EE 50

F0 A0 7E 12

b. Add 16 bits at a time: AB08 90C2

+ 4598 EE50

F0A0 7F12

10.17 If the processor makes use of a stack for subroutine handling, it only uses the

stack while executing CALL and RETURN instructions. No explicit stack-

oriented instructions are needed.

10.18 a. (A + B + C) * D

b. (A/B) + (C/D)

c. A/(B * C * (D + E))

d. A + (B * ((C + (D – E)/F) – G)/H)

10.19 a. AB + C + D + E +

b. AB + CD + * E +

c. AB * CD * + E +

d. AB - CDE * – F/G/ * H *

10.20 Postfix Notation: AB + C –

Equivalent to (A + B) – C

-76-

It matters because of rounding and truncation effects.

10.21

Input

Output

Stack (top on

right)

(A – B) / (C + D × E)

empty

A – B) / (C + D × E)

empty

(

– B) / (C + D × E)

(

B) / (C + D × E)

( –

) / (C + D × E)

A B

( –

/ (C + D × E)

A B –

empty

(C + D × E)

A B –

C + D × E)

A B –

/ (

+ D × E)

A B – C

/ (

D × E)

A B – C

/ ( +

× E)

A B – C D

/ ( +

A B – C D

/ ( + ×

)

A B – C D E

/ ( + ×

empty

A B – C D E × +

empty

A B – C D E × + /

empty

10.22

The final step combines the top two stack elements using the + operator.

10.23

-77-

10.24 a.

12 13 14

01 02 03 04 05 06 07

15 16 17 1811

06 05 04 03 02 01 0007

LE 15 16 17 18 12 13 1411

-78-

The purpose of this question is to compare halfword, word, and doubleword

integers as members of a data structure in Big- and Little-Endian form.

10.25 Figure 10.12 is not a "true" Little-Endian organization as usually defined. Rather,

it is designed to minimize the data manipulation required to convert from one

Endian to another. Note that 64-byte scalars are stored the same in both formats

on the PowerPC. To accommodate smaller scalars, a technique known as address

munging is used.

When the PowerPC is in Little-Endian mode, it transforms the three low-

order bits of an effective address for a memory access. These three bits are

XORed with a value that depends on the transfer size: 100b for 4-byte transfers;

110 for 2-byte transfers; and 111 for 1-byte transfers. The following are the

possible combinations:

4-Byte Transfers

(XOR with 100)

2-Byte Transfers

(XOR with 110)

1-Byte Transfers

(XOR with 111)

Original

Address

Munged

Address

Original

Address

Munged

Address

Original

Address

Munged

Address

000

100

000

110

000

111

001

101

001

111

001

110

010

110

010

100

010

101

011

111

011

101

011

100

000

100

010

100

011

101

001

101

011

101

010

110

010

110

000

110

001

111

011

111

001

111

000

For example, the two-byte value 5152h is stored at location 1C in Big-

Endian mode. In Little-Endian mode, it is viewed by the processor as still being

stored in location 1C but in Little-Endian mode. In fact, the value is still stored in

Big-Endian mode, but at location 1A. When a transfer occurs, the system must do

an address unmunging and a byte transfer to convert data to the form expected

by the processor. The processor generates effective addresses of 1C and 1D for

the two bytes. These addresses are munged (XOR with 110) to 1A and 1B. The

data bytes are retrieved, swapped, and presented as if found in the unmunged

addresses 1D and 1C.

-79-

10.26 There are a number of ways to do this. Here is one way that will work:

#include <stdio.h>

main()

{

int integer;

char *p;

integer = 0x30313233; /* ASCII for chars '0', '1', '2', '3' */

p = (char *)&integer

if (*p=='0' && *(p+1)=='1' && *(p+2)=='2' && *(p+3)=='3')

printf("This is a big endian machine.\n");

else if (*p=='3' && *(p+1)=='2' && *(p+2)=='1' && *(p+3)=='0')

printf("This is a little endian machine.\n");

else

printf("Error in logic to determine machine endian-ness.\n");

}

10.27 BigEndian

10.28 The documentation uses little-endian bit ordering, stating that the most

significant bit of a byte (leftmost bit) is bit 7. However, the instructions that

operate on bit fields operate in a big-endian manner. Thus, the leftmost bit of a

byte is bit 7 but has a bit offset of 0, and the rightmost bit of a byte is bit 0 but has

a bit offset of 7.

-80-

CHAPTER 11 INSTRUCTION SETS: ADDRESSING

MODES AND FORMATS

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

11.1 Immediate addressing: The value of the operand is in the instruction.

11.2 Direct addressing: The address field contents the effective address of the operand.

11.3 Indirect addressing: The address field refers to the address of a word in memory,

which in turn contains the effective address of the operand.

11.4 Register addressing: The address field refers to a register that contains the

operand.

11.5 Register indirect addressing: The address field refers to a register, which in turn

contains the effective address of the operand.

11.6 Displacement addressing: The instruction has two address fields, at least one of

which is explicit. The value contained in one address field (value = A) is used

directly. The other address field refers to a register whose contents are added to A

to produce the effective address.

11.7 Relative addressing: The implicitly referenced register is the program counter

(PC). That is, the current instruction address is added to the address field to

produce the EA.

11.8 It is typical that there is a need to increment or decrement the index register after

each reference to it. Because this is such a common operation, some systems will

automatically do this as part of the same instruction cycle, using autoindexing.

11.9 These are two forms of addressing, both of which involve indirect addressing and

indexing. With preindexing, the indexing is performed before the indirection.

With postindexing, the indexing is performed after the indirection.

11.10 Number of addressing modes: Sometimes an addressing mode can be indicated

implicitly. In other cases, the addressing modes must be explicit, and one or

more mode bits will be needed. Number of operands: Typical instructions on

today’s machines provide for two operands. Each operand address in the

instruction might require its own mode indicator, or the use of a mode indicator

could be limited to just one of the address fields. Register versus memory: The

more that registers can be used for operand references, the fewer bits are needed.

-81-

Number of register sets: One advantage of using multiple register sets is that, for

a fixed number of registers, a functional split requires fewer bits to be used in the

instruction. Address range: For addresses that reference memory, the range of

addresses that can be referenced is related to the number of address bits. Because

this imposes a severe limitation, direct addressing is rarely used. With

displacement addressing, the range is opened up to the length of the address

can reference a word or a byte at the designer’s choice. Byte addressing is

convenient for character manipulation but requires, for a fixed-size memory,

more address bits.

11.11 Advantages: It easy to provide a large repertoire of opcodes, with different

opcode lengths. Addressing can be more flexible, with various combinations of

increase in the complexity of the CPU.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

11.1 a. 20 b. 40 c, 60 d. 30 e. 50 f.70

11.2 a. X3 = X2

b. X3 = (X2)

c. X3 = X1 + X2 + 1

d. X3 = X2 + X4

11.3 a. the address field

b. memory location 14

c. the memory location whose address is in memory location 14

d. register 14

e. the memory location whose address is in register 14

11.4

Operand

500

1100

600

1200

201

500

400

1100

1700

400

1000

702

1302

400

1000

The autoindexing with increment is the same as the register indirect mode except

that R1 is incremented to 401 after the execution of the instruction.

11.5 Recall that relative addressing uses the contents of the program counter, which

points to the next instruction after the current instruction. In this case, the current

instruction is at decimal address 256028 and is 3 bytes long, so the PC contains

256031. With the displacement of –31, the effective address is 256000.

11.6 (PC + 1) + Relative Address = Effective Address

Relative Address = –621 + 530 = –91

Converting to twos-complement representation, we have: 1110100101.

11.7 a. 3 times: fetch instruction; fetch operand reference; fetch operand.

-82-

b. 2 times: fetch instruction; fetch operand reference and load into PC.

11.8 Load the address into a register. Then use displacement addressing with a

displacement of 0.

11.9 The PC-relative mode is attractive because it allows for the use of a relatively

small address field in the instruction format. For most instruction references, and

many data references, the desired address will be within a reasonably short

distance from the current PC address.

11.10 This is an example) of a special-purpose CISC instruction, designed to simplify

the compiler. Consider the case of indexing an array, where the elements of the

array are 32 bytes long. The following instruction is just what is needed:

IMUL EBX, I, 32

EBX is a 32-bit register that now contains the byte offset into the array whose

subscript is 1.

11.11 The three values are added together: 1970 + 48022 + 8 = 50000.

11.12 a. No, because the source operand is the contents of X, rather than the top of the

stack, which is in the location pointed to by X.

b. No, because address of the top of the stack is not changed until after the

fetching of the destination operand.

c. Yes. The stack grows away from memory location 0.

d. No, because the second element of the stack is fetched twice.

e. No, because the second element of the stack is fetched twice.

f. No, because the stack pointer is incremented twice, so that the result is

thrown away.

g. Yes. The stack grows toward memory location 0.

11.13

Instruction

Stack (top on left)

PUSH 4

PUSH 7

7, 4

PUSH 8

8, 7, 4

ADD

15, 4

PUSH 10

10, 15, 4

SUB

5, 4

MUL

11.14 The 32-bit instruction length yields incremental improvements. The 16-bit length

can already include the most useful operations and addressing modes. Thus,

relatively speaking, we don't have twice as much "utility".

11.15 With a different word length, programs written for older IBM models would not

execute on the newer models. Thus the huge investment in existing software was

lost by converting to the newer model. Bad for existing IBM customers, and

therefore bad for IBM.

-83-

11.16 Let X be the number of one-address instructions. The feasibility of having K two-

address, X one-address, and L zero-address instructions, all in a 16-bit instruction

word, requires that:

(K × 26 × 26) + (X × 26) + L = 216

Solving for X:

X = (216 – (K × 26 × 26) – L)/26

To verify this result, consider the case of no zero-address and no two-address

instructions; that is, L = K = 0. In this case, we have

X = 216/26 = 210

This is what it should be when 10 bits are used for opcodes and 6 bits for

addresses.

11.17 The scheme is similar to that for problem 11.16. Divide the 36-bit instruction into

4 fields: A, B, C, D. Field A is the first 3 bits; field B is the next 15 bits; field C is

the next 15 bits, and field D is the last 3 bits. The 7 instructions with three

operands use B, C, and D for operands and A for opcode. Let 000 through 110 be

opcodes and 111 be a code indicating that there are less than three operands. The

500 instructions with two operands are specified with 111 in field A and an

opcode in field B, with operands in D and C. The opcodes for the 50 instructions

with no operands can also be accommodated in B.

Source: [TANE90]

11.18 a. The zero-address instruction format consists of an 8-bit opcode and an

optional 16-bit address. The program has 12 instructions, 7 of which have an

address. Thus:

N0 = 12 × 8 + 7 × 16 = 208 bits

b. The one-address instruction format consists of an 8-bit opcode and a 16-bit

address. The program has 11 instructions.

N1 = 24 × 11 = 264 bits

c. For two-address instructions, there is an 8-bit opcode and two operands, each

of which is 4 bits (register) or 16 bits (memory).

N2 = 9 × 8 + 7 × 16 + 11 × 4 = 228 bits

d. For three-address instructions

N3 = 5 × 8 + 7 × 16 + 8 × 4 = 184 bits

11.19 No. If the two opcodes conflict, the instruction is meaningless. If one opcode

modifies the other or adds additional information, this can be viewed as a single

-84-

opcode with a bit length equal to that of the two opcode fields. However,

instruction bundles, such as seen on the IA-64 Itanium architecture, have

multiple opcodes.

11.20 a. The opcode field can take on one of 25 = 32 different values. Each value can be

interpreted to ways, depending on whether the Operand 2 field is all zeros,

for a total of 64 different opcodes.

b. We could gain an additional 32 opcodes by assigning another Operand 2

pattern to that purpose. For example, the pattern 0001 could be used to

specify more opcodes. The tradeoff is to limit programming flexibility,

because now Operand 2 cannot specify register R1. Source: [PROT88].

-85-

CHAPTER 12 PROCESSOR STRUCTURE AND

FUNCTION

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

12.1 User-visible registers: These enable the machine- or assembly language

programmer to minimize main-memory references by optimizing use of registers.

Control and status registers: These are used by the control unit to control the

operation of the CPU and by privileged, operating system programs to control the

execution of programs.

12.2 General purpose; Data; Address; Condition codes

12.3 Condition codes are bits set by the CPU hardware as the result of operations. For

example, an arithmetic operation may produce a positive, negative, zero, or

overflow result. In addition to the result itself being stored in a register or memory,

a condition code is also set. The code may subsequently be tested as part of a

conditional branch operation.

12.4 All CPU designs include a register or set of registers, often known as the program

status word (PSW), that contain status information. The PSW typically contains

condition codes plus other status information.

12.5 (1)The execution time will generally be longer than the fetch time. Execution will

involve reading and storing operands and the performance of some operation.

Thus, the fetch stage may have to wait for some time before it can empty its buffer.

(2) A conditional branch instruction makes the address of the next instruction to be

fetched unknown. Thus, the fetch stage must wait until it receives the next

instruction address from the execute stage. The execute stage may then have to

wait while the next instruction is fetched.

12.6 Multiple streams: A brute-force approach is to replicate the initial portions of the

pipeline and allow the pipeline to fetch both instructions, making use of two

streams. Prefetch branch target: When a conditional branch is recognized, the

target of the branch is prefetched, in addition to the instruction following the

branch. This target is then saved until the branch instruction is executed. If the

branch is taken, the target has already been prefetched. Loop buffer: A loop buffer

is a small, very-high-speed memory maintained by the instruction fetch stage of

the pipeline and containing the n most recently fetched instructions, in sequence. If

a branch is to be taken, the hardware first checks whether the branch target is

within the buffer. If so, the next instruction is fetched from the buffer. Branch

prediction: A prediction is made whether a conditional branch will be taken when

-86-

executed, and subsequent instructions are fetched accordingly. Delayed branch: It

is possible to improve pipeline performance by automatically rearranging

instructions within a program, so that branch instructions occur later than actually

desired.

12.7 One or more bits that reflect the recent history of the instruction can be associated

with each conditional branch instruction. These bits are referred to as a taken/not

taken switch that directs the processor to make a particular decision the next time

the instruction is encountered.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

12.1 a. 00000010

00000011

00000101

Carry = 0; Zero = 0; Overflow = 0; Sign = 0; Even parity = 1; Half-carry= 0.

Even parity indicates that there is an even number of 1s in the result. The Half-

Carry flag is used in the addition of packed decimal numbers. When a carry

takes place out of the lower-order digit ( lower-order 4 bits), this flag is set. See

problem 10.1.

b. 11111111

00000001

100000000

Carry = 1; Zero = 1; Overflow = 1; Sign = 0; Even Parity = 1; Half-Carry = 1.

12.2 To perform A – B, the ALU takes the twos complement of B and adds it to A:

A: 11110000

€

+ 1: +11101100

A – B: 11011100

Carry = 1; Zero = 0; Overflow = 0; Sign = 1; Even parity = 0; Half-carry= 0.

12.3 a. 0.2 ns

b. 0.6 ns

12.4 a. The length of a clock cycle is 0.1 ns. The length of the instruction cycle for this

case is [10 + (15 × 64)] × 0.1 = 960 ns.

b. The worst-case delay is when the interrupt occurs just after the start of the

instruction, which is 960 ns.

c. In this case, the instruction can be interrupted after the instruction fetch,

which takes 10 clock cycles, so the delay is 1 ns. The instruction can be

interrupted between byte transfers, which results in a delay of no more than

15 clock cycles = 1.5 ns. Therefore, the worst-case delay is 1.5 ns.

12.5 a. A factor of 2.

b. A factor of 1.5. Source: [PROT88].

-87-

12.6 a. The occurrence of a program jump wastes up to 4 bus cycles (corresponding

to the 4 bytes in the instruction queue when the jump is encountered). For 100

instructions, the number of nonwasted bus cycles is, on average, 90 × 2 = 180.

The number wasted is as high as 10 × 4 = 40. Therefore the fraction of wasted

cycles is 40/(180 + 40) = 0.18.

b. If the capacity of the instruction queue is 8, then the fraction of wasted cycles

is 80/(180 + 80) = 0.3. Source: [PROT88].

12.7

Instruction 1

Time

Instruction 2

Instruction 3

Instruction 4

2345

F E

This diagram distorts the true picture. The execute stage will be much longer than

the fetch stage.

-88-

12.8

I1 FI

I15

2345678910

DA FO EX

FI DA FO EX

DA FO

FI DA FO EX

12.9 a. We can ignore the initial filling up of the pipeline and the final emptying of

the pipeline, because this involves only a few instructions out of 1.5 million

instructions. Therefore the speedup is a factor of five.

b. One instruction is completed per clock cycle, for an throughput of 2500 MIPS.

12.10 a. Using Equation (12.2), we can calculate the speedup of the pipelined 2-GHz

processor versus a comparable 2-GHz processor without pipelining:

S = (nk)/[k + (n – 1) = 500/104 = 4.8

However, the unpipelined 2-GHz processor will have a reduced speed of a

factor of 0.8 compared to the 2.5-GHz processor. So the overall speedup is

4.8 × 0.8 = 3.8.

b. For the first processor, each instruction takes 4 clock cycle, so the MIPS rate is

2500 MHz/4 = 625 MIPS. For the second processor, instructions are

completed at the rate of one per clock cycle, so that the MIPS rate is 2000

MIPs.

-89-

12.11 The number of instructions causing branches to take place is pqn, and the

number that do not cause a branch is (1 – pq)n. As a good approximation, we can

replace Equation (12.1) with:

Tk = pqnkτ + (1 – pq)[k + (n - 1)]τ

Equation (12.2) then becomes

Sk=T1

=nk

( )

+1−pq

( )

k+n−1

( )

[ ]

=nk

( )

nk +1−pq

( )

k+n−1

( )

[ ]

12.12 (1) The branch target cannot be fetched until its address is determined, which

may require an address computation, depending on the addressing mode. This

causes a delay in loading one of the streams. The delay may be increased if a

component of the address calculation is a value that is not yet available, such as a

displacement value in a register that has not yet been stored in the register. Other

delays relate to contention for the register file and main memory. (2) The cost of

replicating significant parts of the pipeline is substantial, making this mechanism

of questionable cost-effectiveness.

12.13 a. Call the first state diagram Strategy A. Strategy A corresponds to the

following behavior. If both of the last two branches of the given instruction

have not taken the branch, then predict that the branch will not be taken;

otherwise, predict that the branch will be taken.

Call the second state diagram Strategy B. Strategy B corresponds to the

following behavior. Two errors are required to change a prediction. That is,

when the current prediction is Not Taken, and the last two branches were not

taken, then two taken branches are required to change the prediction to

Taken. Similarly, if the current prediction is Taken, and the last two branches

were taken, then two not-taken branches are required to change the

prediction to Not Taken. However, if there is a change in prediction followed

by an error, the previous prediction is restored.

b. Strategy A works best when it is usually the case that branches are taken. In

both Figure 12.17 and Strategy B, two wrong guesses are required to change

the prediction. Thus, for both a loop exit will not serve to change the

prediction. When most branches are part of a loop, these two strategies are

superior to Strategy A. The difference between Figure 12.17 and Strategy B is

that in the case of Figure 12.17, two wrong are also required to return to the

previous prediction, whereas in Strategy B, only one wrong guess is required

to return to the previous prediction. It is unlikely that either strategy is

superior to the other for most programs.

12.14 a. The comparison of memory addressed by A0 and A1 renders the BNE

condition false, because the data strings are the same. The program loops

between the first two lines until the contents of D1 are decremented below 0

(to -1). At that point, the DBNE loop is terminated. D1 is decremented from

255 ($FF) to -1; thus the loop runs a total of 256 times. Due to the longword

access and the postincrement addressing, the A0 and A1 registers are

incremented by 4 × $100 = $400, to $4400 and $5400, respectively.

-90-

b. The first comparison renders the BNE condition true, because the compared

data patterns are different. Therefore the DBNE loop is terminated at the first

comparison. However, the A0 and A1 registers are incremented to $4004 and

$5004, respectively. D1 still contains $FF.

12.15

Fetch D1 D2 EX WB

Fetch D1 D2 EX

Fetch D1 D2 EX Target

Jcc Target

CMP Reg1, Imm

12.16 We need to add the results for the three types of branches, weighted by the

fraction of each type that go to the target. For the scientific environment, the

result is:

[0.725 × (0.2 + 0.432)] + [0.098 × 0.91] + 0.177 = 0.724

For the commercial environment, the result is:

[0.725 × (0.4 + 0.243)] + [0.098 × 0.91] + 0.177 = 0.732

For the systems environment, the result is:

[0.725 × (0.35 + 0.325)] + [0.098 × 0.91] + 0.177 = 0.756

-91-

12.17

compare

exponents

by subtraction

choose exponentstage 2

stage 3

stage 4

stage 1

align significands

a b

exponents

normalize

result

adjust

exponents

add or subtract

mantissas

A B

significands

-92-

CHAPTER 13 REDUCED INSTRUCTION SET

COMPUTERS

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

13.1 (1) a limited instruction set with a fixed format, (2) a large number of registers or

the use of a compiler that optimizes register usage, and (3) an emphasis on

optimizing the instruction pipeline.

13.2 Two basic approaches are possible, one based on software and the other on

hardware. The software approach is to rely on the compiler to maximize register

usage. The compiler will attempt to allocate registers to those variables that will

be used the most in a given time period. This approach requires the use of

sophisticated program-analysis algorithms. The hardware approach is simply to

use more registers so that more variables can be held in registers for longer

periods of time.

13.3 (1) Variables declared as global in an HLL can be assigned memory locations by

the compiler, and all machine instructions that reference these variables will use

memory-reference operands. (2) Incorporate a set of global registers in the

processor. These registers would be fixed in number and available to all

procedures

13.4 One instruction per cycle. Register-to-register operations. Simple addressing

modes. Simple instruction formats.

13.5 Delayed branch, a way of increasing the efficiency of the pipeline, makes use of a

branch that does not take effect until after execution of the following instruction.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

13.1 a. Figure 4.16 shows the movement of the window for a size of five. Each

movement is an underflow or an overflow. Total = 18.

b. The results for W = 8 can easily be read from Figure 4.16. Each movement of a

window in the figure is by an increment of 1. Initially, the window covers 1

through 5, then 2 through 6, and so on. Only when the window reaches 5

through 9 have we reached a point at which a window of size 8 would have to

move. Total = 8.

c. The greatest call depth in the figure is 15, hence for W = 16, Total = 0.

-93-

13.2 The temporary registers of level J are the parameter registers of level J + 1. Hence,

those registers are saved and restored as part of the window for J + 1.

13.3 Two-way pipeline: The I and E phases can overlap; thus we use N rather than

2N. Each D phase adds delay, so that term still must be included. Finally, each

jump wastes the next instruction fetch opportunity. Hence

2-Way: N + D + J

Three-way pipeline: Because the D phase can overlap with the subsequent E

phase, it would appear that we can eliminate the D term. However, as can be

seen in Figure 13.6, the data fetch is not completed prior to the execution of the

following instruction. If this following instruction utilizes the fetched data as

one of its operands, it must wait one phase. If this data dependency occurs a

fraction α of the time, then:

3-Way: N + α D + J

Four-way pipeline: In this case, each jump causes a loss of two phases, and a data-

dependent D causes a delay of one phase. However, the phases may be

shorter.

4-Way: N + α D + 2J

13.4

Load!rA ← M I E1 E2 D

I E1 E2

I E1 E2 D

Load!rB ← M

NOOP

Branch!X

Add!rC ← rA + rB

Store!M ← rC

13.5 If we replace I by 32 × I, we can generate the following code:

MOV ECX, 32 ; use register ECX to hold 32 × I

LP: MOV EBX, Q[ECX] ; load VAL field

ADD S, EBX ; add to S

ADD ECX, 32 ; add 32 to 32 × I

CMP ECX, 3200 ; test against adjusted limit

JNE LP ; loop until I × 32 = 100 × 32

-94-

13.6 LD R1, 0 ; keep value of S in R1

LD R2,1 ; keep value of K in R2

LP SUB R1, R1, R2 ; S := S – 1

LP1 BEQ R2, 100, EXIT ; done if K = 100

NOP

ADD R2, R2, 1 ; else increment K

JMP LP1 ; back to start of loop

SUB R1, R1, R2 ; execute SUB in JMP delay slot

13.7 a. LD MR1, A ;load A into machine register 1

LD MR2, B ;load B into machine register 2

ADD MR1, MR1, MR2 ;add contents of MR1 and MR2 and store in MR3

LD MR2, C

LD MR3, D

ADD MR2, MR2, MR3

A total of 3 machine registers are used, but now that the two additions use

the same register, we no longer have the opportunity to interleave the

calculations for scheduling purposes.

b. First we do instruction reordering from the original program:

LD SR1, A

LD SR2, B

LD SR4, C

LD SR5, D

ADD SR3, SR1, SR2

ADD SR6, SR4, SR5

This avoids the pipeline conflicts caused by immediately referencing loaded

data. Now we do the register assignment:

LD MR1, A

LD MR2, B

LD MR3, C

LD MR4, D

ADD MR5, MR1, MR2

ADD MR1, MR3, MR4

Five machine registers are used instead of three, but the scheduling is

improved.

-95-

13.8

Number of

instruction

sizes

Max

instruction

size in bytes

Number of

addressing

modes

Indirect

addressing

Load/store

combined with

arithmetic

Pentium II

yes

PowerPC

Max

number

memory

operands

Unaligned

addressing

allowed

Max

Number of

MMU uses

Number of bits

for integer

specifier

Number of bits for

FP register specifier

Pentium II

yes

PowerPC

13.9 Register-to-Register Move Rd ← Rs + R0

Increment, Decrement Use ADD with immediate constant of 1, –1

Complement Rs XOR (–1)

Negate R0 - Rs

Clear Rd ← R0 + R0

13.10 N = 8 + (16 × K)

13.11 a. OR src with Go and store the result in dst

b. SUBCC src2 from src1 and store the result in G0

c. ORCC src1 with G0 and store the result in G0

d. XNOR dst with G0

e. SUB dst from G0 and store in dst

f. ADD 1 to dst (immediate operand)

g. SUB 1 from dst (immediate operand)

h. OR G0 with G0 and store in dst

i. SETHI G0 with 0

j. JMPL %I7+8m %G0

Source: [TANE99]

-96-

13.12 a.

sethi %hi(K), %r8 ;load high-order 22 bits of address of location

;K into register r8

ld [%r8 + %lo(K)], %r8 ;load contents of location K into r8

cmp %r8, 10 ;compare contents of r8 with 10

ble L1 ;branch if (r8) ≤ 10

nop

inc %r8 ;add 1 to (r8)

b L2

nop

L1: dec %r8 ;subtract 1 from (r8)

L2: sethi %hi(L), %r10

st %r8, [%r10 + %lo(L)] ;store (r8) into location L

sethi %hi(K), %r8 ;load high-order 22 bits of address of location

;K into register r8

ld [%r8 + %lo(K)], %r8 ;load contents of location K into r8

cmp %r8, 10 ;compare contents of r8 with 10

ble.a L1 ;branch if (r8) ≤ 10

dec %r8 ;subtract 1 from (r8)

inc %r8 ;add 1 to (r8)

b L2

nop

L1:

L2: sethi %hi(L), %r10

st %r8, [%r10 + %lo(L)] ;store (r8) into location L

sethi %hi(K), %r8 ;load high-order 22 bits of address of location

;K into register r8

ld [%r8 + %lo(K)], %r8 ;load contents of location K into r8

cmp %r8, 10 ;compare contents of r8 with 10

ble.a L1 ;branch if (r8) ≤ 10

dec %r8 ;subtract 1 from (r8)

inc %r8 ;add 1 to (r8)

L2: sethi %hi(L), %r10

st %r8, [%r10 + %lo(L)] ;store (r8) into location L

-97-

CHAPTER 14 INSTRUCTION-LEVEL PARALLELISM

AND SUPERSCALAR PROCESSORS

ANSWERS TO

NSWERS TO Q

QUESTIO

UESTIONS

14.1 A superscalar processor is one in which multiple independent instruction

pipelines are used. Each pipeline consists of multiple stages, so that each pipeline

can handle multiple instructions at a time. Multiple pipelines introduce a new

level of parallelism, enabling multiple streams of instructions to be processed at a

time.

14.2 Superpipelining exploits the fact that many pipeline stages perform tasks that

require less than half a clock cycle. Thus, a doubled internal clock speed allows the

performance of two tasks in one external clock cycle

14.3 Instruction-level parallelism refers to the degree to which the instructions of a

program can be executed in parallel.

14.4 True data dependency: A second instruction needs data produced by the first

instruction. Procedural dependency: The instructions following a branch (taken or

not taken) have a procedural dependency on the branch and cannot be executed

until the branch is executed. Resource conflicts: A resource conflict is a

competition of two or more instructions for the same resource at the same time.

Output dependency: Two instructions update the same register, so the later

instruction must update later. Antidependency: A second instruction destroys a

value that the first instruction uses.

14.5 Instruction-level parallelism exists when instructions in a sequence are

independent and thus can be executed in parallel by overlapping. Machine

parallelism is a measure of the ability of the processor to take advantage of

instruction-level parallelism. Machine parallelism is determined by the number of

instructions that can be fetched and executed at the same time (the number of

parallel pipelines) and by the speed and sophistication of the mechanisms that the

processor uses to find independent instructions.

14.6 In-order issue with in-order completion: Issue instructions in the exact order that

would be achieved by sequential execution and to write results in that same order.

In-order issue with out-of-order completion: Issue instructions in the exact order

that would be achieved by sequential execution but allow instructions to run to

completion out of order. Out-of-order issue with out-of-order completion: The

processor has a lookahead capability, allowing it to identify independent

instructions that can be brought into the execute stage. Instructions are issued with

-98-

little regard for their original program order. Instructions may also run to

completion out of order.

14.7 For an out-of-order issue policy, the instruction window is a buffer that holds

decoded instructions. These may be issued from the instruction window in the

most convenient order.

14.8 Registers are allocated dynamically by the processor hardware, and they are

associated with the values needed by instructions at various points in time. When

a new register value is created (i.e., when an instruction executes that has a register

as a destination operand), a new register is allocated for that value.

14.9 (1) Instruction fetch strategies that simultaneously fetch multiple instructions,

often by predicting the outcomes of, and fetching beyond, conditional branch

instructions. These functions require the use of multiple pipeline fetch and decode

stages, and branch prediction logic. (2) Logic for determining true dependencies

involving register values, and mechanisms for communicating these values to

where they are needed during execution. (3) Mechanisms for initiating, or issuing,

multiple instructions in parallel. (4) Resources for parallel execution of multiple

instructions, including multiple pipelined functional units and memory hierarchies

capable of simultaneously servicing multiple memory references. (5) Mechanisms

for committing the process state in correct order.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

14.1 This problem is discussed in [JOHN91]. One approach to restarting after an

interrupt relies on processor hardware to maintain a simple, well-defined restart

state that is identical to the state of a processor having in-order completion. A

processor providing this form of restart state is said to support precise interrupts.

With precise interrupts, the interrupt return address indicates both the location of

the instruction that caused the interrupt and the location where the program

should be restarted. Without precise interrupts, the processor needs a mechanism

to indicate the exceptional instruction and another to indicate where the program

should be restarted. With out-of-order completion, providing precise interrupts is

harder than not providing them, because of the hardware required to give the

appearance of in-order completion.

-99-

14.2 a.

Instruction

Fetch

Decode

Execute

Writeback

0 ADD r3, r1, r2

1 LOAD r6, [r3]

2 AND r7, r5, 3

3 ADD r1, r6, r0

4 SRL r7, r0, 8

5 OR r2, r4, r7

6 SUB r5, r3, r4

7 ADD r0, r1, 10

8 LOAD r6, [r5]

9 SUB r2, r1, r6

10 AND r3, r7, 15

Instruction

Fetch

Decode

Execute

Writeback

0 ADD r3, r1, r2

1 LOAD r6, [r3]

2 AND r7, r5, 3

3 ADD r1, r6, r0

4 SRL r7, r0, 8

5 OR r2, r4, r7

6 SUB r5, r3, r4

7 ADD r0, r1, 10

8 LOAD r6, [r5]

9 SUB r2, r1, r6

10 AND r3, r7, 15

Instruction

Fetch

Decode

Execute

Writeback

0 ADD r3, r1, r2

1 LOAD r6, [r3]

2 AND r7, r5, 3

3 ADD r1, r6, r0

4 SRL r7, r0, 8

5 OR r2, r4, r7

6 SUB r5, r3, r4

7 ADD r0, r1, 10

8 LOAD r6, [r5]

9 SUB r2, r1, r6

10 AND r3, r7, 15

-100-

14.3 •write-write: I1, I3

•read-write: I2, I3

•write-read: I1. I2

14.4 a.

write-read

write-write

read-write

L2 – L4

L2 – L5

L1 – L4

L1 – L5

L1 – L2

L2 – L5

L1 – L5

L2 – L3

L2 – L4

L3 – L4

L4 – L5

b. L1: R1b = 100

L2: R1c = R2a + R4a

L3: R2b = R4a - 25

L4: R4b = R1c + R3a

L5: R1d = R1c + 30

14.5 a. Since I2 and I1 are in different columns of the execution unit, it is unlikely that

there is a resource conflict, i.e., I2 is not waiting for I1 to finish using one of the

CPU's resources. What is far more likely is that there is a true data dependency

here. In other words, the result of I1 is needed to execute I2. True data

dependencies cannot be fixed using out-of-order issue or out-of-order

completion. Therefore, there will be no speed up of I2 with respect to I1 by

changing the issue sequence or output sequence.

b. The in-order completion requirements of the system require I5 to be completed

before I6 can be written. The pair went into the pipe together and they must

come out together. This is not the case for out-of-order completion, so either

"in-order-issue/out-of-order completion" or "out-of-order-issue/out-of-order

completion" will fix this. As a side note, let's look at what happens to the

execution of these instructions if we do pass this through an "out-of-order

issue/out-of-order completion" machine. Assume that the only true data

dependency we have is between I1 and I2. and therefore, I2 must stay in the

instruction window until I1 is finished. The first benefit of going to "out-of-

order issue/out-of-order completion" is the ability to get instructions into the

execution stage as soon as the resource becomes available. The decode unit

takes one cycle to pull in a pair of instructions then pass them to the window.

As long as the window has room for the instruction, nothing should hold up

the decode stage. The instructions must stay in the window until either the

dependency is resolved (e.g., I1 – I2) or until the execute resource frees up

allowing the stage to execute.

• I2 waits in the window until I1 is completed to satisfy the dependency

• I3 comes out of the window as soon as I1 is finished with the resource that I3

needs

• I4 comes out of the window as soon as I2 is finished with the resource that I4

needs

• I5 doesn't need to stay in the window because its resource is free as soon as

it's done with decoding

• I6 has to wait until I4 is finished with the resource that I6 needs

The out-of-order completion allows instructions to enter the write cycle as

soon as they are completed. The only hiccup in this process is that I5, I4, and I3

-101-

are all completed at the same time, but since there are only two write pipes, I5

must wait until cycle 7 to be written. In the end, "out-of-order issue/out-of-

order completion" saves two cycles. This reduces the execution time by 2

cycles/9 cycles = 22%.

14.6 a. True data dependency: I1, I2; I5, I6

Antidependency: I3, I4

Output dependency: I5, I6

lookahead

window I5

14.7 The figure is from [SMIT95]. w = instruction dispatch; x = load/store units; y =

integer units; z = floating-point units. Part a is the single-queue method, with no

out of order issuing. Part b is a multiple-queue method; instructions issue from

each queue in order, but the queues may issue out of order with respect to one

another. Part c is a reservation station scheme; instructions may issue out of order.

14.8 a. Figure 14.16d is equivalent to Figure 12.19

Figure 14.16b is equivalent to Figure 12.28a

Figure 14.16c is equivalent to Figure 12.28b

Figure 14.16a: If the last branch was taken, predict that this branch will be

taken; if the last branch was not taken, predict that this branch will not be

taken.

Figure 14.7e: This is very close to Figure 14.7c. The difference is as follows. For

Figure 14.7c, if there is a change in prediction followed by an error, the previous

prediction is restored; this is true for either type of error. For Figure 14.7c, if there is a

change in prediction from taken to not taken followed by an error, the prediction of

taken is restored. However if there is a change in prediction from not taken to taken

followed by an error, the taken prediction is retained.

-102-

b. The rationale is summarized in [OMON99, page 114]: "Whereas in loop-closing

branches, the past history of an individual branch instruction is usually a good

guide to future behavior, with more complex control-flow structures, such as

sequences of IF-ELSE constructs or nestings of similar constructs, the direction

of a branch is frequently affected by the directions taken by related branches. If

we consider each of the possible paths that lead to a given nested branch, then

it is clear that prediction in such a case should be based on the subhistories

determined by such paths, i.e., how a particular branch is arrived at, rather

than just on the individual history of a branch instruction. And in sequences of

conditionals, there will be instances when the outcome of one condition-test

depends on that of a preceding condition if the conditions are related in some

way — for example, if part of the conditions are common."

-103-

CHAPTER 15 CONTROL UNIT OPERATION

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

15.1 The operation of a computer, in executing a program, consists of a sequence of

instruction cycles, with one machine instruction per cycle. This sequence of

instruction cycles is not necessarily the same as the written sequence of

instructions that make up the program, because of the existence of branching

instructions. The actual execution of instructions follows a time sequence of

instructions.

15.2 A micro-operation is an elementary CPU operation, performed during one clock

pulse. An instruction consists of a sequence of micro-operations.

15.3 The control unit of a processor performs two tasks: (1) It causes the processor to

execute micro-operations in the proper sequence, determined by the program

being executed, and (2) it generates the control signals that cause each micro-

operation to be executed.

15.4 1. Define the basic elements of the processor. 2. Describe the micro-operations that

the processor performs. 3. Determine the functions that the control unit must

perform to cause the micro-operations to be performed.

15.5 Sequencing: The control unit causes the processor to step through a series of

micro-operations in the proper sequence, based on the program being executed.

Execution: The control unit causes each micro-operation to be performed.

15.6 The inputs are: Clock: This is how the control unit “keeps time.” The control unit

causes one micro-operation (or a set of simultaneous micro-operations) to be

performed for each clock pulse. This is sometimes referred to as the processor

cycle time, or the clock cycle time. Instruction register: The opcode of the current

instruction is used to determine which micro-operations to perform during the

execute cycle. Flags: These are needed by the control unit to determine the status

of the processor and the outcome of previous ALU operations. Control signals

from control bus: The control bus portion of the system bus provides signals to the

control unit, such as interrupt signals and acknowledgments. The outputs are:

Control signals within the processor: These are two types: those that cause data to

be moved from one register to another, and those that activate specific ALU

functions. Control signals to control bus: These are also of two types: control

signals to memory, and control signals to the I/O modules.

15.7 (1) Those that activate an ALU function. (2) those that activate a data path. (3)

Those that are signals on the external system bus or other external interface

-104-

15.8 In a hardwired implementation, the control unit is essentially a combinatorial

circuit. Its input logic signals are transformed into a set of output logic signals,

which are the control signals.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

15.1 Consider the instruction SUB R1, X, which subtracts the contents of location X

from the contents of register R1, and places the result in R1.

t1: MAR ← (IR(address))

t2: MBR ← Memory

t3: MBR ← Complement(MBR)

t4: MBR ← Increment(MBR)

t5: R1 ← (R1) + (MBR)

15.2 LOAD AC: t1: MAR ← (IR(address)) C8

t2: MBR ← Memory C5, CR

t3: AC ← (MBR) C10

STORE AC t1: MAR ← (IR(address)) C8

t2: MBR ← (AC) C11

t3: Memory ← (MBR) C12, CW

ADD AC t1: MAR ← (IR(address)) C8

t2: MBR ← Memory C5,CR

t3: AC ← (AC) + (MBR) CALU, C6, C7, C9

Note: There must be a delay between the activation of C8 and C9, and one or

more control signals must be sent to the ALU. All of this would be done during

one or more clock pulses, depending on control unit design.

AND AC t1: MAR ← (IR(address)) C8

t2: MBR ← Memory C5, CR

t3: AC ← (AC) AND (MBR) CALU, C6, C7, C9

JUMP t1: PC ← IR(address) C3

JUMP if AC= 0 Test AC and activate C3 if AC = 0

Complement AC t1: AC ← ( AC ) CALU, C6, C7, C9

-105-

15.3 a. Time required = propagation time + copy time

= 30 ns

b. Incrementing the program counter involves two steps:

(1) Z ← (PC) + 1

(2) PC ← (Z)

The first step requires 20 + 100 + 10 = 130 ns.

The second step requires 30 ns.

Total time = 160 ns.

15.4 a. t1: Y ← (IR(address))

t2: Z ← (AC) + (Y)

t3: AC ← (Z)

b. t1: MAR ← (IR(address))

t2: MBR ← Memory

t3: Y ← (MBR)

t4: Z ← (AC) + (Y)

t5: AC ← (Z)

c. t1: MAR ← (IR(address))

t2: MBR ← Memory

t3: MAR ← (MBR)

t4: MBR ← Memory

t5: Y ← (MBR)

t6: Z ← (AC) + (Y)

t7: AC ← (Z)

15.5 Assume configuration of Figure 10.14a. For the push operation, assume value to be

pushed is in register R1.

POP: t1: SP ← (SP) + 1

PUSH: t1: SP ← (SP) – 1

MBR ← (R1)

t2: MAR ← (SP)

t3: Memory ← (MBR)

-106-

CHAPTER 16 MICROPROGRAMMED CONTROL

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

16.1 A hardwired control unit is a combinatorial circuit, in which input logic signals

are transformed into a set of output logic signals that function as the control

signals. In a microprogrammed control unit, the logic is specified by a

microprogram. A microprogram consists of a sequence of instructions in a

microprogramming language. These are very simple instructions that specify

micro-operations.

16.2 1. To execute a microinstruction, turn on all the control lines indicated by a 1 bit;

leave off all control lines indicated by a 0 bit. The resulting control signals will

cause one or more micro-operations to be performed. 2. If the condition indicated

by the condition bits is false, execute the next microinstruction in sequence. 3. If

the condition indicated by the condition bits is true, the next microinstruction to be

executed is indicated in the address field.

16.3 The control memory contains the set of microinstructions that define the

functionality of the control unit.

16.4 The microinstructions in each routine are to be executed sequentially. Each routine

ends with a branch or jump instruction indicating where to go next.

16.5 In a horizontal microinstruction every bit in the control field attaches to a control

line. In a vertical microinstruction, a code is used for each action to be performed

and the decoder translates this code into individual control signals.

16.6 Microinstruction sequencing: Get the next microinstruction from the control

memory. Microinstruction execution: Generate the control signals needed to

execute the microinstruction.

16.7 The degree of packing relates to the degree of identification between a given

control task and specific microinstruction bits. As the bits become more packed, a

given number of bits contains more information. An unpacked microinstruction

has no coding beyond assignment of individual functions to individual bits.

16.8 Hard microprograms are generally fixed and committed to read-only memory.

Soft microprograms are more changeable and are suggestive of user

microprogramming.

16.9 Two approaches can be taken to organizing the encoded microinstruction into

fields: functional and resource. The functional encoding method identifies

-107-

functions within the machine and designates fields by function type. For example,

if various sources can be used for transferring data to the accumulator, one field

can be designated for this purpose, with each code specifying a different source.

Resource encoding views the machine as consisting of a set of independent

resources and devotes one field to each (e.g., I/O, memory, ALU).

16.10 Realization of computers. Emulation. Operating system support. Realization of

special-purpose devices. High-level language support. Microdiagnostics. User

Tailoring.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

16.1 The multiply instruction is implemented by locations 27 through 37 of the

microprogram in Table 16.2. It involves repeated additions.

16.2 Assume that the microprogram includes a fetch routine that starts at location 0 and

a BRM macroinstruction that starts at location 40.

40: IF (AC0 = 1) THEN CAR ← 42; ELSE CAR ← (CAR) + 1

41: CAR ← 43; PC ← (PC) + 1

42: PC ← (IR(address))

43: CAR ← 0

16.3 a. These flags represent Boolean variables that are input to the control unit logic.

Together with the time input and other flags, they determine control unit

output.

b. The phase of the instruction cycle is implicit in the organization of the

microprogram. Certain locations in the microprogram memory correspond to

each of the four phases.

16.4 a. Three bits are needed to specify one of 8 flags.

b. 24 – 13 – 3 = 8

c. 28 = 256 words × 24 bits/word = 6144 bits.

16.5 Two of the codes in the address selection field must be dedicated to that purpose.

For example, a value of 000 could correspond to no branch, a value of 111 could

correspond to unconditional branch.

16.6 An address for control memory requires 10 bits (210 = 1024). A very simple

mapping would be this:

opcode XXXXX

control address 00XXXXX000

This allows 8 words between successive addresses.

16.7 A field of 5 bits yields 25 – 1 = 31 different combinations of control signals. A field

of 4 bits yields 24 – 1 = 15 different combinations, for a total of 46.

-108-

16.8 A 20-bit format consisting of the following fields:

A1 (4 bits): specify register to act as one of the inputs to ALU

A2 (4 bits): specifies other ALU input

A3 (4 bits): specifies register to store ALU result

AF (5 bits): specifies ALU function

SH (3 bits): specifies shift function

In addition, an address field for sequencing is needed.

-109-

CHAPTER 17 PARALLEL PROCESSING

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

17.1 Single instruction, single data (SISD) stream: A single processor executes a single

instruction stream to operate on data stored in a single memory. Single

instruction, multiple data (SIMD) stream: A single machine instruction controls

the simultaneous execution of a number of processing elements on a lockstep

basis. Each processing element has an associated data memory, so that each

instruction is executed on a different set of data by the different processors.

Multiple instruction, multiple data (MIMD) stream: A set of processors

simultaneously execute different instruction sequences on different data sets.

17.2 1. There are two or more similar processors of comparable capability. 2.These

processors share the same main memory and I/O facilities and are interconnected

by a bus or other internal connection scheme, such that memory access time is

approximately the same for each processor. 3. All processors share access to I/O

devices, either through the same channels or through different channels that

provide paths to the same device. 4. All processors can perform the same functions

(hence the term symmetric). 5. The system is controlled by an integrated operating

system that provides interaction between processors and their programs at the job,

task, file, and data element levels.

17.3 Performance: If the work to be done by a computer can be organized so that some

portions of the work can be done in parallel, then a system with multiple

processors will yield greater performance than one with a single processor of the

same type. Availability: In a symmetric multiprocessor, because all processors can

perform the same functions, the failure of a single processor does not halt the

machine. Instead, the system can continue to function at reduced performance.

Incremental growth: A user can enhance the performance of a system by adding

an additional processor. Scaling: Vendors can offer a range of products with

different price and performance characteristics based on the number of processors

configured in the system.

17.4 Simultaneous concurrent processes: OS routines need to be reentrant to allow

several processors to execute the same IS code simultaneously. With multiple

processors executing the same or different parts of the OS, OS tables and

management structures must be managed properly to avoid deadlock or invalid

operations. Scheduling: Any processor may perform scheduling, so conflicts must

be avoided. The scheduler must assign ready processes to available processors.

Synchronization: With multiple active processes having potential access to shared

address spaces or shared I/O resources, care must be taken to provide effective

synchronization. Synchronization is a facility that enforces mutual exclusion and

-110-

event ordering. Memory management: Memory management on a multiprocessor

must deal with all of the issues found on uniprocessor machines, as is discussed in

Chapter 8. In addition, the operating system needs to exploit the available

hardware parallelism, such as multiported memories, to achieve the best

performance. The paging mechanisms on different processors must be coordinated

to enforce consistency when several processors share a page or segment and to

decide on page replacement. Reliability and fault tolerance: The operating system

should provide graceful degradation in the face of processor failure. The scheduler

and other portions of the operating system must recognize the loss of a processor

and restructure management tables accordingly.

17.5 Software cache coherence schemes attempt to avoid the need for additional

hardware circuitry and logic by relying on the compiler and operating system to

deal with the problem. In hardware schemes, the cache coherence logic is

implemented in hardware.

17.6 Modified: The line in the cache has been modified (different from main memory)

and is available only in this cache. Exclusive: The line in the cache is the same as

that in main memory and is not present in any other cache. Shared: The line in the

cache is the same as that in main memory and may be present in another cache.

Invalid: The line in the cache does not contain valid data.

17.7 Absolute scalability: It is possible to create large clusters that far surpass the

power of even the largest standalone machines. Incremental scalability: A cluster

is configured in such a way that it is possible to add new systems to the cluster in

small increments. Thus, a user can start out with a modest system and expand it as

needs grow, without having to go through a major upgrade in which an existing

small system is replaced with a larger system. High availability: Because each

node in a cluster is a standalone computer, the failure of one node does not mean

loss of service. Superior price/performance: By using commodity building blocks,

it is possible to put together a cluster with equal or greater computing power than

a single large machine, at much lower cost.

17.8 The function of switching an applications and data resources over from a failed

system to an alternative system in the cluster is referred to as failover. A related

function is the restoration of applications and data resources to the original system

once it has been fixed; this is referred to as failback.

17.9 Uniform memory access (UMA): All processors have access to all parts of main

memory using loads and stores. The memory access time of a processor to all

regions of memory is the same. The access times experienced by different

processors are the same. Nonuniform memory access (NUMA): All processors

have access to all parts of main memory using loads and stores. The memory

access time of a processor differs depending on which region of main memory is

accessed. The last statement is true for all processors; however, for different

processors, which memory regions are slower and which are faster differ. Cache-

coherent NUMA (CC-NUMA): A NUMA system in which cache coherence is

maintained among the caches of the various processors.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

-111-

17.1 a. MIPS rate = [nα + (1 – α)] x = (nα – α + 1)x

b. α = 0.6

17.2 a. If this conservative policy is used, at most 20/4 = 5 processes can be active

simultaneously. Because one of the drives allocated to each process can be idle

most of the time, at most 5 drives will be idle at a time. In the best case, none of

the drives will be idle.

b. To improve drive utilization, each process can be initially allocated with three

tape drives, with the fourth drive allocated on demand. With this policy, at

most

20/3

 

processes can be active simultaneously. The minimum

number of idle drives is 0 and the maximum number is 2.

Source: [HWAN93]

17.3 Processor A has a block of memory in its cache. When A writes to the block the

first time, it updates main memory. This is a signal to other processors to

invalidate their own copy (if they have one) of that block of main memory.

Subsequent writes by A to that block only affect A's cache. If another processor

attempts to read the block from main memory, the block is invalid. Solution: If A

makes a second update, it must somehow tag that block in main memory as being

invalid. If another processor wants the block, it must request that A write the latest

version from its cache to main memory. All of this requires complex circuitry.

17.4

-112-

-113-

17.5 a. This is the simplest possible cache coherence protocol. It requires that all

processors use a write-through policy. If a write is made to a location cached in

remote caches, then the copies of the line in remote caches are invalidated. This

approach is easy to implement but requires more bus and memory traffic

because of the write-through policy.

b. This protocol makes a distinction between shared and exclusive states. When a

cache first loads a line, it puts it in the shared state. If the line is already in the

modified state in another cache, that cache must block the read until the line is

updated back to main memory, similar to the MESI protocol. The difference

between the two is that the shared state is split into the shared and exclusive

states for MESI. This reduces the number of write-invalidate operations on the

bus.

17.6 If the L1 cache uses a write-through policy, as is done on the S/390 described in

Section 17.2, then the L1 cache does not need to know the M state. If the L1 cache

uses a write-back policy, then a full MESI protocol is needed between L1 and L2.

-114-

17.7 If only the L1 cache is used, then 89% of the accesses are to L1 and the remaining

11% of the accesses are to main memory. Therefore, the average penalty is (1 ×

0.89) + (32 × 0.11) = 4.41. If both L1 and L2 are present, the average penalty is (1 ×

0.89) + (5 × 0.05) + (32 × 0.06) = 3.06. This normalizes to 3.06/4.41 = 0.69. Thus, with

the addition of the L2 cache, the average penalty is reduced to 69% of that with

only one cache. If all three caches are present, the average penalty is (1 × 0.89) + (5

× 0.05) + (14 × 0.03) + (32 × 0.03) = 2.52, and normalized average penalty is

2.52/4.41 = 0.57. The reduction of the average penalty from 0.69 to 0.57 would

seem to justify the inclusion of the L3 cache.

17.8 a. ta = fi[Hic + (1 – Hi)(b + c) + (1 – fi)(Hdc) + (1 – Hd)((b + c)(1 – fd) + (2b + c)fd)]

€

′

= ta + (1 – fi)finvi Source: [HWAN93]

17.9 a. chip multiprocessor

b. interleaved multithreading superscalar

c. blocked multithreading superscalar

d. simultaneous multithreading

17.10 [UNGE03] refers to these as horizontal losses and vertical losses, respectively.

With a horizontal loss, full parallelism is not achieved; that is, fewer instructions

are dispatched than the hardware would allow. With a vertical loss, the

dispatching mechanism is stalled because no new instructions can be

accommodated due to latency issues.

17.11 a.

A15

A16

b. The two pipelines are operating independently on two separate processors on

the same chip. Therefore, the diagrams of Figure 17.25 and part (a) of this

solution apply.

c. We assume that the A thread requires a latency of two clock cycles before it is

able to execute instruction A15, and we assume that the interleaving

mechanism is able to use the same thread on two successive clock cycles if

necessary.

-115-

A15

instruction

issue

diagram

pipeline execution diagram

B5 B6

A16

CO F0

B5 B6

B1A3

EI WO

CO F0

B2A4

EI WO

A5B5 B6

B5 B6

A15 A16

B1 B2

A15

instruction

issue

diagram

pipeline execution diagram

B3 B4

A16

B5 B6

CO F0

B3 B4

A3A5

EI WO

CO F0

A4 A2

EI WO

B2B3 B4

B3 B4

A15 A16

B5 B6

A15 A16

-116-

B5 B6

instruction

issue

diagram

A15 A16

pipeline execution diagram

CO F0

A15 A16

A3A5

EI WO

CO F0

A4 A2

EI WO

B6A15 A16

A15 A16

CO F0

B3 B1

EI WO

CO F0

B4 B2

EI WO

17.12 a. Sequential execution time = 1664 processor cycles.

b. SIMD execution time = 26 cycles.

c. Speedup factor = 64. Source: [HWAN93]

17.13 To begin, we can distribute the outer loop without affecting the computation.

DO 20A I = 1, N

B (I,1) = 0

20A CONTINUE

DO 20B I = 1, N

DO 10 J = 1, M

A(I) = A(I) + B (I, J) * C (I, J)

10 CONTINUE

20B CONTINUE

DO 20C I = 1, N

D (I) = E (I) + A (I)

20C CONTINUE

Using vectorized instructions:

B (I,1) = 0 (I = 1, N)

DO 20B I= 1, N

A(I) = A(I) + B(I, J) * C(I, J) (J = 1, M)

20B CONTINUE

D(I) = E(I0 + A(I) (I = 1, N)

17.14 a. One computer executes for a time T. Eight computers execute for a time T/4,

which would take a time 2T on a single computer. Thus the total required time

on a single computer is 3T. Effective speedup = 3. α = 0.75.

b. New speedup = 3.43

-117-

17.15 a. Sequential execution time = 1,051,628 cycles

b. Speedup = 16.28

c. Each computer is assigned 32 iterations balanced between the beginning and

end of the I-loop.

d. The ideal speedup of 32 is achieved.

Source: [HWAN93]

17.16 a. The I loop requires N cycles, as does the J loop. With the L4 statement, the

total is 2N + 1.

b. The sectioned I loop can be done in L cycles. The sectioned J loop produces M

partial sums in L cycles. Total = 2L + l(k + 1).

c. Sequential execution of the original program takes 2N = 221 cycles. Parallel

execution requires 213 + 1608 = 9800 cycles. This is a speedup factor of

approximately 214 (221/9800). Therefore, an efficiency of 214/256 = 83.6% is

achieved.

-118-

CHAPTER 18 MULTICORE COMPUTERS

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

18.1 •Pipelining: Individual instructions are executed through a pipeline of stages so

that while one instruction is executing in one stage of the pipeline, another

instruction is executing in another stage of the pipeline.

•Superscalar: Multiple pipelines are constructed by replicating execution

resources. This enables parallel execution of instructions in parallel pipelines, so

long as hazards are avoided.

•Simultaneous multithreading (SMT): Register banks are replicated so that

multiple threads can share the use of pipeline resources.

18.2 In the case of pipelining, simple 3-stage pipelines were replaced by pipelines with

5 stages, and then many more stages, with some implementations having over a

dozen stages. There is a practical limit to how far this trend can be taken, because

with more stages, there is the need for more logic, more interconnections, and

more control signals. With superscalar organization, performance increases can be

achieved by increasing the number of parallel pipelines. Again, there are

diminishing returns as the number of pipelines increases. More logic is required to

manage hazards and to stage instruction resources. Eventually, a single thread of

execution reaches the point where hazards and resource dependencies prevent the

full use of the multiple pipelines available. This same point of diminishing returns

is reached with SMT, as the complexity of managing multiple threads over a set of

pipelines limits the number of threads and number of pipelines that can be

effectively utilized.

18.3 Cache memory uses less power than logic .

18.4 • Multi-threaded native applications: Multi-threaded applications are

characterized by having a small number of highly threaded processes. Examples of

threaded applications include Lotus Domino or Siebel CRM (Customer

Relationship Manager).

• Multi-process applications: Multi-process applications are characterized by the

presence of many single-threaded processes. Examples of multi-process

applications include the Oracle database, SAP, and PeopleSoft.

• Java applications: Java applications embrace threading in a fundamental way.

Not only does the Java language greatly facilitate multithreaded applications, but

the Java Virtual Machine is a multi-threaded process that provides scheduling and

memory management for Java applications. Java applications that can benefit

directly from multicore resources include application servers such as Sun’s Java

Application Server, BEA’s Weblogic, IBM’s Websphere, and the open-source

Tomcat application server. All applications that use a Java 2 Platform, Enterprise

-119-

Edition (J2EE platform) application server can immediately benefit from multicore

technology.

• Multi-instance applications: Even if an individual application does not scale to

take advantage of a large number of threads, it is still possible to gain from

multicore architecture by running multiple instances of the application in parallel.

If multiple application instances require some degree of isolation, virtualization

technology (for the hardware of the operating system) can be used to provide each

of them with its own separate and secure environment.

18.5 • The number of core processors on the chip

• The number of levels of cache memory

• The amount of cache memory that is shared

18.6 1. Constructive interference can reduce overall miss rates. That is, if a thread on

one core accesses a main memory location, this brings the frame containing the

referenced location into the shared cache. If a thread on another core soon

thereafter accesses the same memory block, the memory locations will already be

available in the shared on-chip cache.

2. A related advantage is that data shared by multiple cores is not replicated at the

shared cache level.

3. With proper frame replacement algorithms, the amount of shared cache

allocated to each core is dynamic, so that threads that have a less locality can

employ more cache.

4. Interprocessor communication is easy to implement, via shared memory

locations.

5. The use of a shared L2 cache confines the cache coherency problem to the L1

cache level, which may provide some additional performance advantage.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

18.1 a. The speedup is due to two factors: the performance gain perf(r) in each core

and the Amdahl performance gain from using multiple cores. Thus:

€

Speedup =perf r

( )

×1

1−f

( )

=perf r

( )

×1

1−f

( )

+f×r

1−f

( )

perf r

( )

+f×r

perf r

( )

×n

b, c. The conclusions are the same for both figures. The figures are from

"Amdahl's Law in the Multicore Era," by Hill and Marty, Computer, July 2008.

The article draws the following conclusions:

A value r = 1 says the chip has 16 base cores, while a value of r = 16 uses

all resources for a single core. Lines assume different values for the parallel

fraction (f = 0.5, 0.9, …, 0.999). The y-axis gives the symmetric multicore chip’s

speedup relative to its running on one core. The maximum speedup for f = 0.9,

for example, is 6.7 using eight cores.

Similarly, the second figure illustrates how tradeoffs change when

Moore’s law allows n = 256 cores per chip. With f = 0.975, for example, the

maximum speedup of 51.2 occurs with 36 cores of 7.1 core equivalents each.

-120-

Result 1. Amdahl’s law applies to multicore chips because achieving the best

speedups requires fs that are near 1. Thus, finding parallelism is still critical.

Implication 1. Researchers should target increasing f through architectural

support, compiler techniques, programming model improvements, and so on.

This implication is the most obvious and important. Recall, however, that a

system is cost-effective if speedup exceeds its costup.4 Multicore costup is the

multicore system cost divided by the single-core system cost. Because this

costup is often much less than n, speedups less than n can be cost-effective.

Result 2. Using more core equivalents per core, r > 1, can be optimal, even

when performance grows by only r . For a given f, the maximum speedup can

occur at one big core, n base cores, or with an intermediate number of

middlesized cores. Recall that for n = 256 and f = 0.975, the maximum speedup

occurs using 7.1 core equivalents per core.

Implication 2. Researchers should seek methods of increasing core

performance even at a high cost.

Result 3. Moving to denser chips increases the likelihood that cores will be

nonminimal. Even at f = 0.99, minimal base cores are optimal at chip size n =

16, but more powerful cores help at n = 256.

Implication 3. As Moore’s law leads to larger multicore chips, researchers

should look for ways to design more powerful cores.

-121-

CHAPTER 19 NUMBER SYSTEMS

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

19.1 a. 12 b. 3 c. 28 d. 60 e. 42

19.2 a. 28.375 b. 51.59375 c. 682.5

19.3 a. 1000000 b. 1100100 c. 1101111 d. 10010001 e. 11111111

19.4 a. 100010.11 b. 11001.01 c. 11011.0011

19.5 A BAD ADOBE FACADE FADED (Source: [KNUT98])

19.6 a. 12 b. 159 c. 3410 d. 1662 e. 43981

19.7 a. 15.25 b. 211.875 c. 4369.0625 d. 2184.5 e. 3770.75

19.8 a. 10 b. 50 c. A00 d. BB8 e. F424

19.9 a. CC.2 b. FF.E c. 277.4 d. 2710.01

19.10 a. 1110 b. 11100 c. 101001100100 d. 11111.11 e. 1000111001.01

19.11 a. 9.F b. 35.64 c. A7.EC

19.12 1/2k = 5k/10k

19.13 a. 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20, 21, 22, 23, 24

b. 1, 2, 3, 4, 5, 10, 11, 12, 13, 14, 15, 20, 21, 22, 23, 24, 25, 30, 31, 32

c. 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30, 31, 32, 33, 34, 40

d. 1, 2, 10, 11, 12, 20, 21, 22, 100, 101, 102, 110, 111, 112, 120, 121, 122, 200, 201, 202

19.14 a. 134 b. 105 c. 363 d. 185

19.15 Given the representation of a number x in base n and base np, every p digits in

the base n representation can be converted to a single base np digit. For example,

the base 3 representation of 7710 is 2212 and the base 9 representation is 85. Thus

it is easy to convert between a base n representation and a base np representation

without the intermediate step of converting to base 10. In other cases, the

intermediate step facilitates conversion.

-122-

CHAPTER 20 DIGITAL LOGIC

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

20.1

20.2 Recall the commutative law: AB = BA; A + B = B + A

a. A B + CDE + C DE

b. AB + AC

c. (LMN) (AB) (CDE)

d. F (K + R) + SV + W X

20.3 a.

F=V •A •L

. This is just a generalization of DeMorgan's Theorem, and is easily

proved.

F=ABCD

. Again, a generalization of DeMorgan's Theorem.

20.4 a. A = ST + VW

b. A = TUV + Y

c. A = F

d. A = ST

e. A = D + E

f. A = YZ (W + X +YZ) = YZ

g. A = C

20.5 A XOR B = A B + A B

20.6 ABC = NOR ( A , B , C )

20.7 Y = NAND (A, B, C, D) = ABCD

-123-

20.8 a.

b. All of the terms have the form illustrated as follows:

Z5 = X1X2X3X4 + X1X2 X3X4 + X1 X2X3X4 + X1 X2X3X4

c. Whereas the SOP form lists all combinations that produce an output of 1, the

POS lists all combinations that produce an output of 0.

For example,

Z3 = ( X1X2X3X4) ( X1X2X3X4)

= (X1X2 X3X4 ) (X1X2X3 X4)

20.9 Label the 8 inputs I0, ... , I7 and the select lines S0, S1, S2.

F = I0 + I1

S0S1S2

+ I2

S1 S2 + I3

S1 S2

+ I4 S0

S1S2

+ I5 S0

S2 + I6 S0

S2 + I7 S0 S1 S2

20.10 Add a data input line and connect it to the input side of each AND gate.

-124-

20.11 Define the input leads as B2, B1, B0 and the output leads as G2, G1, G0. Then

G2 = B2

G1=B2B1+B2B1

G0=B1B0+B1

20.12 The Input is A4A3A2A1A0. Use A2A1A0 as the input to each of the 3 × 8 decoders.

There are a total of 32 outputs from these four 3 × 8 decoders. Use A4A3 as input

to a 2 × 4 decoder and have the four outputs go to the enable leads of the four 3 ×

8 decoders. The result is that one and only one of the 32 outputs will have a value

of 1.

20.13 SUM = A ⊕ B ⊕ C

CARRY = AB ⊕ AC ⊕ BC

20.14 a. The carry to the second stage is available after 20 ns; the carry to the third

stage is available 20 ns after that, and so on. When the carry reaches the 32nd

stage, another 30 ns are needed to produce the final sum. Thus

T = 31 × 20 + 30 = 650 ns

b. Each 8-bit adder produces a sum in 30 ns and a carry in 20 ns. Therefore,

T = 3 × 20 + 30 = 90 ns

20.15 a.

Characteristic table

Simplified characteristic table

Current

input

Current

state

Next state

Qn+1

—

-125-

20.16

Data

Clock Ck

20.17

B A

O1O0

20.18 a. Use a PLA with 12-bit addresses and 96 8-bit locations. Each of the 96

locations is set to an ASCII code, and a character is converted by simply using

its original, 12-bit code as an address to the PLA. The content of that address

is the required ASCII code.

b. Yes. This would require a 4K×8 ROM where only 96 of the 4096 locations are

actually used.

-126-

CHAPTER 21 THE IA-64 ARCHITECTURE

ANSWERS TO

NSWERS TO Q

QUESTIONS

UESTIONS

21.1 I-unit: For integer arithmetic, shift-and-add, logical, compare, and integer

multimedia instructions. M-unit: Load and store between register and memory

plus some integer ALU operations. B-unit: Branch instructions. F-unit: Floating-

point instructions.

21.2 The template field contains information that indicates which instructions can be

executed in parallel.

21.3 A stop indicates to the hardware that one or more instructions before the stop may

have certain kinds of resource dependencies with one or more instructions after

the stop.

21.4 Predication is a technique whereby the compiler determines which instructions

may execute in parallel. With predicated execution, every IA-64 instruction

includes a reference to a 1-bit predicate register, and only executes if the predicate

value is 1 (true).

21.5 Predicates enable the processor to speculatively execute both branches of an if

statement and only commit after the condition is determined.

21.6 With control speculation, a load instruction is moved earlier in the program and its

original position replaced by a check instruction. The early load saves cycle time; if

the load produces an exception, the exception is not activated until the check

instruction determines if the load should have been taken.

21.7 Associated with each register is a NaT bit used to track deferred speculative

exceptions. If a ld.s detects an exception, it sets the NaT bit associated with the

target register. If the corresponding chk.s instruction is executed, and if the NaT bit

is set, the chk.s instruction branches to an exception-handling routine.

21.8 With data speculation, a load is moved before a store instruction that might alter

the memory location that is the source of the load. A subsequent check is made to

assure that the load receives the proper memory value.

21.9 Software pipelining is a technique in which instructions from multiple iterations

of a loop are enabled to execute in parallel. Parallelism is achieved by grouping

together instructions from different iterations. Hardware pipelining refers to the

use of a physical pipeline as part of the hardware

-127-

21.10 Rotating registers are used for software pipelining. During each iteration of a

software-pipeline loop, register references within these ranges are automatically

incremented. Stacked registers implement a stack.

ANSWERS TO

NSWERS TO P

PROBLEMS

ROBLEMS

21.1 Eight. The operands and result require 7 bits each, and the controlling predicate 6.

A major opcode is specified by 4 bits; 38 bits of the 41-bit syllable are committed,

leaving 3 bits to specify a suboperation. Source: [MARK00]

21.2 Table 21.3 reveals that any opcode can be interpreted as referring to on of 6

different execution units (M, B, I, L, F, X). So, the potential maximum number of

different major opcodes is 24 × 6 = 96.

21.3 16

21.4 a. Six cycles. The single floating-point unit is the limiting factor.

b. Three cycles.

21.5 The pairing must not exceed a sum of two M or two I slots with the two bundles.

For example, two bundles, both with template 00, or two bundles with templates

00 and 01 could not be paired because they require 4 I-units. Source: [EVAN03]

21.6 Yes. On IA-64s with fewer floating-point units, more cycles are needed to dispatch

each group. On an IA-64 with two FPUs, each group requires two cycles to

dispatch. A machine with three FPUs will dispatch the first three floating-point

instructions within a group in one cycle, and the remaining instruction in the next.

Source: [MARK00]

21.7

comparison

not present

21.8 a. (3) and (4); (5) and (6)

b. The IA-64 template field gives a great deal of flexibility, so that many

combinations are possible. One obvious combination would be (1), (2), and (3)

in the first instruction; (4), (5), and (6) in the second instruction; and (7) in the

third instruction.

21.9 Branching to label error should occur if and only if at least one of the 8 bytes in

but are not as helpful as they could be. Source: [EVAN03]

-128-

21.10 a.

mov r1, 0

mov r2, 0

ld r3, addr(A)

L1: ld r4, mem(r3+r2)

bge r4, 50, L2

add r5, r5, 1

jump L3

L2: add r6, r6, 1

L3: add r1, r1, 1

add r2, r2, 4

blt r1, 100, L1

mov r1, 0

mov r2, 0

ld r3, addr(A)

L1: ld r4, mem(r3+r2)

cmp.ge p1, p2 = r4. 50

(p2) add r5 = 1, r5

(p1) add r6 = 1, r6

add r1 = 1, r1

add r2 = 4, r2

blt r1, 100, L1

21.11 a.

fmpy t = p, q //floating-point multiply

ldf.a c = [rj];; //advanced floating point load

//load value stored in location specified by address

//in register rj; place value in floating-point register c

//assume rj points to a[j]

stf [ri] = t;; //store value in floating-point register t in location

//specified by address in register ri

//assume ri points to a[i]

ldf.c c = [rj];; //executes only if ri = rj

If the advanced load succeeded, the ldf.c will complete in one cycle, and c can be

used in the following instruction. The effective latency of the ldf.a instruction has

been reduced by the latency of the floating-point multiplication. The stf and ldf.c

cannot be in the same instruction group, because there may be a read-after -write

dependency.

fmpy t = p, q

cmp.ne p8, p9 = ri, rj;;

(p8) ldf c = [rj];; //p8 ⇒ no conflict

stf [ri] = t;; //if ri = rj, then c = t

(p9) mov c = t;;

c. In the predicated version, the load begins one cycle later than with the

advanced load. Also, two predicated registers are required. Source: [MARK00]

-129-

21.12 a. The number of output registers is

SOO = SOF – SOL = 48 – 16 = 32

b. Because the stacked register group starts at r32, the local register and output

Local register group: r32 through r47

Output register group: r48 through r63

Source: [TRIE01]

-130-

APPENDIX B ASSEMBLY LANGUAGE AND

Solutions COA8e Computer Organization And Architecture Designing For Performance, 8th Edition Solution Manual

Solution%20Manual%20Computer%20Organization%20And%20Architecture%208th%20Edition

Solution_Manual_Computer_Organization_And_Architecture_8th_Edition

Solution%20Manual%20Computer%20Organization%20And%20Architecture%208th%20Edition

Navigation menu

Versions of this User Manual:

Views

Navigation