Analysis Of Epidemiological Data Using R And Epicalc Epicalc_Book Book
User Manual: Epicalc_Book
Open the PDF directly: View PDF ![]() .
.
Page Count: 328 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Chapter 1: Starting to use R
- Chapter 2: Vectors
- Chapter 3: Arrays, Matrices and Tables
- Chapter 4: Data Frames
- Chapter 5: Simple Data Exploration
- Chapter 6: Date and Time
- Chapter 7: An Outbreak Investigation: Describing Time
- Chapter 8: An Outbreak Investigation: Risk Assessment
- Chapter 9: Odds Ratios, Confounding and Interaction
- Chapter 10: Basic Data Management
- Chapter 11: Scatter Plots and Linear Regression
- Chapter 12: Stratified Linear Regression
- Chapter 13: Curvilinear Relationship
- Chapter 14: Generalized Linear Models
- Chapter 15: Logistic Regression
- Chapter 16: Matched Case Control Study
- Chapter 17: Polytomous Logistic Regression
- Chapter 18: Ordinal Logistic Regression
- Chapter 19: Poisson ad Negative Binomial Regression
- Chapter 20: Introduction to Multi-level Modelling
- Chapter 21: Survival Analysis
- Chapter 22: Cox Regression
- Chapter 23: Analysing Attitudes Data
- Chapter 24: Sample Size Calculation
- Chapter 25: Documentation
- Chapter 26: Strategies for Handling Large Datasets
- Chapter 27: Table Stacking for a Manuscript
- Solutions to Exercises
- Index
- Epicalc Functions
- Epicalc Datasets

Analysis of epidemiological
data using R and Epicalc
Epidemiology Unit
Prince of Songkla University
THAILAND
> help.start()
> exp(-5)
[1] 0.006738
9
> log(3.8
+ )
[1] 1.335001
> help.start()
> exp(-5)
[1] 0.006738
9
> log(3.8
+ )
[1] 1.335001
0
10
20
30
40
50
Virasakdi Chongsuvivatwong
0
10
20
30
40
50
EPICALC–OK.indd 1 20.2.2008 15:24:54
Analysis of Epidemiological Data Using
R and Epicalc
Author: Virasakdi Chongsuvivatwong
cvirasak@medicine.psu.ac.th
Epidemiology Unit
Prince of Songkla University
THAILAND
i
Preface
Data analysis is very important in epidemiological research. The capacity of
computing facilities has been steadily increasing, moving state of the art
epidemiological studies along the same direction of computer advancement.
Currently, there are many commercial statistical software packages widely used by
epidemiologists around the world. For developed countries, the cost of software is
not a major problem. For developing countries however, the real cost is often too
high. Several researchers in developing countries thus eventually rely on a pirated
copy of the software.
Freely available software packages are limited in number and readiness of use.
EpiInfo, for example, is free and useful for data entry and simple data analysis.
Advanced data analysts however find it too limited in many aspects. For example, it
is not suitable for data manipulation for longitudinal studies. Its regression analysis
facilities cannot cope with repeated measures and multi-level modelling. The
graphing facilities are also limited.
A relatively new and freely available software called R is promising. Supported by
leading statistical experts worldwide, it has almost everything that an
epidemiological data analyst needs. However, it is difficult to learn and to use
compared with similar statistical packages for epidemiological data analysis such as
Stata. The purpose of this book is therefore to bridge this gap by making R easy to
learn for researchers from developing countries and also to promote its use.
My experience in epidemiological studies spans over twenty years with a special
fondness of teaching data analysis. Inspired by the spirit of the open-source
software philosophy, I have spent a tremendous effort exploring the potential and
use of R. For four years, I have been developing an add-on package for R that
allows new researchers to use the software with enjoyment. More than twenty
chapters of lecture notes and exercises have been prepared with datasets ready for
self-study.
Supported by WHO, TDR and the Thailand Research Fund, I have also run a
number of workshops for this software in developing countries including Thailand,
Myanmar, North Korea, Maldives and Bhutan, where R and Epicalc was very much
welcomed. With this experience, I hereby propose that the use of this software
should be encouraged among epidemiological researchers, especially for those who
cannot afford to buy expensive commercial software packages.
ii
R is an environment that can handle several datasets simultaneously. Users get
access to variables within each dataset either by copying it to the search path or by
including the dataset name as a prefix. The power of R in this aspect is a drawback
in data manipulation. When creating a variable or modifying an existing one,
without prefixing the dataset name, the new variable is isolated from its parental
dataset. If prefixing is the choice, the original data is changed but not the copy in
the search path. Careful users need to remove the copy in the search path and
recopy the new dataset into it. The procedure in this aspect is clumsy. Not being
tidy will eventually end up with too many copies in the search path overloading the
system or confusing the analyst on where the variable is actually located.
Epicalc presents a concept solution for common types of work where the data
analyst works on one dataset at a time using only a few commands. In Epicalc the
user can virtually eliminate the necessity of specifying the dataset and can avoid
overloading of the search path very effectively and efficiently. In addition to make
tidying of memory easy to accomplished, Epicalc makes it easy to recognize the
variables by adopting variable labels or descriptions which have been prepared
from other software such as SPSS or Stata or locally prepared by Epicalc itself.
R has very powerful graphing functions that the user has to spend time learning.
Epicalc exploits this power by producing a nice plot of the distribution
automatically whenever a single variable is summarised. A breakdown of the first
variable by a second categorical variable is also simple and graphical results are
automatically displayed. This automatic graphing strategy is also applied to one-
way tabulation and two-way tabulation. Description of the variables and the value
or category labels are fully exploited with these descriptive graphs.
Additional epidemiological functions added in by Epicalc include calculation of
sample size, matched 1:n (n can vary) tabulation, kappa statistics, drawing of ROC
curve from a table or from a logistic regression results, population pyramid plots
from age and sex and follow-up plots.
R has several advanced regression modelling functions such as multinomial logistic
regression, ordinal logistic regression, survival analysis and multi-level modelling.
By using Epicalc nice tables of odds ratios and 95% CI are produced, ready for
simple transferal into a manuscript document with minimal further modification
required.
Although use of Epicalc implies a different way of working with R from
conventional use, installation of Epicalc has no effect on any existing or new
functions of R. Epicalc functions only increase efficiency of data analysis and
makes R easier to use.
iii
This book is essentially about learning R with an emphasis on Epicalc. Readers
should have some background in basic computer usage. With R, Epicalc and the
supplied datasets, the users should be able to go through each lesson learning the
concepts of data management, related statistical theories and the practice of data
analysis and powerful graphing.
The first four chapters introduce R concepts and simple handling of important basic
elements such as scalars, vectors, matrices, arrays and data frames. Chapter 5 deals
with simple data exploration. Date and time variables are defined and dealt with in
Chapter 6 and fully exploited in a real dataset in Chapter 7. Descriptive statistics
and one-way tabulations are automatically accompanied by corresponding graphs
making it rather unlikely that important information is overlooked. Finally, time
plots of exposure and disease onsets are plotted with a series of demonstrating
commands. Chapter 8 continues to investigate the outbreak by two-way tabulation.
Various kinds of risk assessment, such as the risk ratio and protective efficacy, are
analysed with numeric and graphic results.
Chapter 9 extends the analysis of the dataset to deal with levels of association or
odds ratios. Stratified tabulation, the Mantel-Haenzsel odds ratio, and test of
homogeneity of odds ratios are explained in detail. All results are complemented by
simultaneous plots. With these graphs, the concept of confounding is made more
understandable.
Before proceeding further, the reader has a thorough exercise of data cleaning and
standard data manipulation in Chapter 10. Simple looping commands are
introduced to increase the efficiency of data management. Subsequently, and from
time to time in the book, readers will learn how to develop these loops to create
powerful graphs.
Scatter plots, simple linear regression and analysis of variance are presented in
Chapter 11. Stratified scatter plots to enhance the concept of confounding and
interaction for continuous outcome variables are given in Chapter 12. Curvilinear
models are discussed in Chapter 13. Linear modelling is extended to generalized
linear modelling in Chapter 14.
For binary outcome variables, Chapter 15 introduces logistic regression with
additional comparison with stratified cross-tabulation learned in Chapter 9. The
concept of a matched case control study is discussed in Chapter 16 with matched
tabulation for 1:1 and 1:n matching. Finally, conditional logistic regression is
applied. Chapter 17 introduces polytomous logistic regression using a case-control
study in which one type of case series is compared with two types of control
groups. Ordinal logistic regression is applied for ordered outcomes in Chapter 18.
iv
For a cohort study, with grouped exposure datasets, Poisson regression is used in
Chapter 19. Extra-Poisson regression for overdispersion is also discussed. This
includes modeling the outcome using the negative binomial error distribution.
Multi-level modelling and longitudinal data analysis are discussed in Chapter 20.
For cohort studies with individual follow-up times, survival analysis is discussed in
Chapter 21 and the Cox proportional hazard model is introduced in Chapter 22. In
chapter 23 the focus is on analyzing datasets involving attitudes, such as those
encountered in the social sciences. Chapter 24 deals with day-to-day work in
calculation of sample sizes and the technique of documentation that all professional
data analysts must master is explained in Chapter 25.
Some suggested strategies for handling large datasets are given in chapter 26. The
book ends with a demonstration of the tableStack command, which dramatically
shortens the preparation of a tidy stack of tables with a special technique of copy
and paste into a manuscript.
At the end of each chapter some references are given for further reading. Most
chapters also end with some exercises to practice on. Solutions to these are given at
the end of the book.
Colour
It is assumed that the readers of this book will simultaneously practice the
commands and see the results on the screen. The explanations in the text sometimes
describe the colour of graphs that appear in black and white in this book (the reason
for this is purely for reducing the printing costs). The electronic copy of the book,
however, does include colour.
Explanations of fonts used in this book
MASS An R package or library
Attitudes An R dataset
plot An R function
summ An Epicalc function (italic)
'abc' An R object
'pch' An argument to a function
'saltegg' A variable within a data frame
"data.txt" A data file on disk

v
Table of Contents
Chapter 1: Starting to use R __________________________________________ 1
Installation _____________________________________________________ 1
Text Editors ____________________________________________________ 3
Starting R Program_______________________________________________ 3
R libraries & packages ____________________________________________ 4
On-line help ____________________________________________________ 7
Using R _______________________________________________________ 8
Exercises _____________________________________________________ 14
Chapter 2: Vectors ________________________________________________ 15
Concatenation__________________________________________________ 16
Subsetting a vector with an index vector _____________________________ 17
Missing values _________________________________________________ 22
Exercises _____________________________________________________ 24
Chapter 3: Arrays, Matrices and Tables________________________________ 25
Arrays________________________________________________________ 25
Matrices ______________________________________________________ 29
Tables________________________________________________________ 29
Lists _________________________________________________________ 31
Exercises _____________________________________________________ 33
Chapter 4: Data Frames____________________________________________ 35
Data entry and analysis __________________________________________ 37
Datasets included in Epicalc ______________________________________ 38
Reading in data_________________________________________________ 38
Attaching the data frame to the search path ___________________________ 43
The 'use' command in Epicalc _____________________________________ 45
Exercises______________________________________________________ 48
vi
Chapter 5: Simple Data Exploration __________________________________ 49
Data exploration using Epicalc ____________________________________ 49
Exercise_______________________________________________________ 62
Chapter 6: Date and Time __________________________________________ 63
Computation functions related to date _______________________________ 63
Reading in a date variable ________________________________________ 66
Dealing with time variables _______________________________________ 67
Exercises______________________________________________________ 76
Chapter 7: An Outbreak Investigation: Describing Time ___________________ 77
Case definition _________________________________________________ 78
Paired plot ____________________________________________________ 83
Exercise_______________________________________________________ 86
Chapter 8: An Outbreak Investigation: Risk Assessment ___________________ 87
Recoding missing values _________________________________________ 87
Exploration of age and sex________________________________________ 90
Comparison of risk: Risk ratio and attributable risk ____________________ 92
Dose-response relationship _______________________________________ 94
Exercise_______________________________________________________ 96
Chapter 9: Odds Ratios, Confounding and Interaction ____________________ 97
Odds and odds ratio _____________________________________________ 97
Confounding and its mechanism ___________________________________ 99
Interaction and effect modification ________________________________ 103
Exercise______________________________________________________ 104
Chapter 10: Basic Data Management ________________________________ 105
Data cleaning _________________________________________________ 105
Identifying duplication ID _______________________________________ 105
Missing values ________________________________________________ 107
Recoding values using Epicalc____________________________________ 110
vii
Labelling variables with 'label.var'_________________________________ 112
Adding a variable to a data frame _________________________________ 115
Collapsing categories ___________________________________________ 118
Exercises_____________________________________________________ 120
Chapter 11: Scatter Plots & Linear Regression _________________________ 121
Scatter plots __________________________________________________ 122
Components of a linear model ____________________________________ 124
Regression line, fitted values and residuals __________________________ 127
Checking normality of residuals __________________________________ 128
Exercise______________________________________________________ 130
Chapter 12: Stratified linear regression_______________________________ 131
Exercise______________________________________________________ 138
Chapter 13: Curvilinear Relationship ________________________________ 139
Stratified curvilinear model ______________________________________ 144
Modelling with a categorical independent variable ____________________ 146
References ___________________________________________________ 148
Exercise______________________________________________________ 148
Chapter 14: Generalized Linear Models ______________________________ 149
Model attributes _______________________________________________ 150
Attributes of model summary_____________________________________ 151
Covariance matrix _____________________________________________ 152
References ___________________________________________________ 155
Exercise______________________________________________________ 156
Chapter 15: Logistic Regression_____________________________________ 157
Distribution of binary outcome ___________________________________ 157
Logistic regression with a binary independent variable_________________ 161
Interaction ___________________________________________________ 166
Interpreting the odds ratio _______________________________________ 168
viii
References ___________________________________________________ 175
Exercises_____________________________________________________ 176
Chapter 16: Matched Case Control Study _____________________________ 177
1:n matching__________________________________________________ 179
Logistic regression for 1:1 matching _______________________________ 180
Conditional logistic regression____________________________________ 183
References ___________________________________________________ 184
Exercises_____________________________________________________ 184
Chapter 17: Polytomous Logistic Regression___________________________ 185
Polytomous logistic regression using R _____________________________ 187
Exercises_____________________________________________________ 192
Chapter 18: Ordinal Logistic Regression ______________________________ 193
Modelling ordinal outcomes______________________________________ 195
References ___________________________________________________ 196
Exercise______________________________________________________ 196
Chapter 19: Poisson and Negative Binomial Regression __________________ 197
Modelling with Poisson regression ________________________________ 201
Goodness of fit test_____________________________________________ 201
Incidence density ______________________________________________ 204
Negative binomial regression_____________________________________ 206
References ___________________________________________________ 209
Exercise______________________________________________________ 210
Chapter 20: Introduction to Multi-level Modelling ______________________ 211
Random intercepts model________________________________________ 215
Model with random slopes_______________________________________ 219
Exercises_____________________________________________________ 224
Chapter 21: Survival Analysis ______________________________________ 225
Survival object in R ____________________________________________ 228
ix
Life table ____________________________________________________ 229
Kaplan-Meier curve ____________________________________________ 231
Cumulative hazard rate _________________________________________ 232
References ___________________________________________________ 235
Exercises_____________________________________________________ 236
Chapter 22: Cox Regression________________________________________ 237
Testing the proportional hazards assumption_________________________ 238
Stratified Cox regression ________________________________________ 241
References ___________________________________________________ 243
Exercises_____________________________________________________ 244
Chapter 23 Analysing Attitudes Data _________________________________ 245
tableStack for logical variables and factors __________________________ 247
Cronbach's alpha ______________________________________________ 249
Summary ____________________________________________________ 253
References ___________________________________________________ 253
Exercise______________________________________________________ 254
Chapter 24: Sample size calculation__________________________________ 255
Field survey __________________________________________________ 255
Comparison of two proportions ___________________________________ 258
Comparison of two means _______________________________________ 263
Lot quality assurance sampling ___________________________________ 264
Power determination for comparison of two proportions________________ 266
Power for comparison of two means _______________________________ 267
Exercises_____________________________________________________ 268
Chapter 25: Documentation ________________________________________ 269
Crimson Editor________________________________________________ 270
Tinn-R ______________________________________________________ 271
Saving the output text___________________________________________ 274
x
Saving a graph ________________________________________________ 275
Chapter 26: Strategies of Handling Large Datasets _____________________ 277
Simulating a large dataset _______________________________________ 277
Chapter 27 Table Stacking for a Manuscript ___________________________ 281
Concept of 'tableStack'__________________________________________ 281
Colum of total ________________________________________________ 286
Exporting 'tableStack' and other tables into a manuscript _______________ 287
Solutions to Exercises _____________________________________________ 289
Index __________________________________________________________ 310
Epicalc Functions ________________________________________________ 312
Epicalc Datasets _________________________________________________ 313

Chapter 1: Starting to use R
This chapter concerns first use of R, covering installation, how to obtain help,
syntax of R commands and additional documentation. Note that this book was
written for Windows users, however R also works on other operating systems.
Installation
R is distributed under the terms of the GNU General Public License. It is freely
available for use and distribution under the terms of this license. The latest version
of R and Epicalc and their documentation can be downloaded from CRAN (the
Comprehensive R Archive Network).
The main web site is http://cran.r-project.org/ but there are mirrors all around the
world. Users should download the software from the nearest site. R runs on the
three common contemporary operating systems, Linux, MacOS X and Windows.
To install R, first go to the CRAN website and select your operating system from
the top of the screen. For Windows users click the Windows link and follow the
link to the base subdirectory. In this page you can download the setup file for
Windows, which at the time of publication of this book was R-2.6.1-win32.exe.
Click this link and click the "Save" button.
The set-up file for R is around 28Mb. To run the installation simply double-click
this file and follow the instructions. After installation, a shortcut icon of R should
appear on the desktop. Right-click this R icon to change its start-up properties.
Replace the default 'Start in' folder with your own working folder. This is the folder
where you want R to work. Otherwise, the input and output of files will be done in
the program folder, which is not a good practice. You can create multiple shortcut
icons with different start-in folders for each project you are working on.
Suppose the work related to this book will be stored in a folder called
'C:\RWorkplace'. The 'Properties' of the icon should have the 'Start in:' text box
filled with 'C:\RWorkplace' (do not type the single quote signs ' and '. They are used
in this book to indicate objects or technical names).
R detects the main language of the operating system in the computer and tries to
use menus and dialog boxes in that language. For example, if you are running R on
a Windows XP in the Chinese language, the menus and dialog boxes will appear in
Chinese. Since this book is written in English, it is advised to set the language to be

2
English so that the responses on your computer will be the same as those in this
book. In the 'Shortcut' tab of the R icon properties, add Language=en at the end
of the 'Target'. Include a space before the word 'Language'.
So, the Target text box for R-2.6.1 version icon would be:
"C:\Program Files\R\R-2.6.1\bin\Rgui.exe" Language=en
To use this book efficiently, a specialised text editor such as Crimson Editor or
Tinn-R must be installed on your computer. In addition, the Epicalc package needs
to be installed and loaded.

3
Text Editors
Crimson Editor
This software can be installed in the conventional fashion as all other software, i.e.
by executing the setup.exe file and following the instructions.
Crimson Editor has some nice features that can assist the user when working with
R. It is very powerful for editing script or command files used by various software
programs, such as C++, PHP and HTML files. Line numbers can be shown and
open and closed brackets can be matched. These features are important because
they are commonly used in the R command language.
Installation and set-up of Crimson Editor is explained in Chapter 25.
Tinn-R
Tinn-R is probably the best text file editor to use in conjunction with the R
program. It is specifically designed for working with R script files. In addition to
syntax highlighting of R code, Tinn-R can interact with R using specific menus and
tool bars. This means that sections of commands can be highlighted and sent to the
R console (sourced) with a single button click. Tinn-R can be downloaded from the
Internet at: www.sciviews.org/Tinn-R.
Starting R Program
After modifying the start-up properties of the R icon, double-click the R icon on the
desktop. The program should then start and the following output is displayed on the
R console.
R version 2.6.1 (2007-11-26)
Copyright (C) 2007 The R Foundation for Statistical Computing
ISBN 3-900051-07-0
R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under certain conditions.
Type 'license()' or 'licence()' for distribution details.
Natural language support but running in an English locale
R is a collaborative project with many contributors.
Type 'contributors()' for more information and
'citation()' on how to cite R or R packages in publications.
Type 'demo()' for some demos, 'help()' for on-line help, or
'help.start()' for an HTML browser interface to help.
Type 'q()' to quit R.
>

4
The output shown above was produced from R version 2.6.1, released on
November 26, 2007. The second paragraph declares and briefly explains the
warranty and license. The third paragraph gives information about contributors and
how to cite R in publications. The fourth paragraph suggests a few commands for
first-time users to try.
In this book, R commands begin with the ">" sign, similar to what is shown at the
R console window. You should not type the ">". Just type the commands. Within
this document both the R commands and output lines will be in Courier New
font whereas the explanatory text are in Times New Roman. Epicalc commands are
shown in italic, whereas standard R commands are shown in normal font style.
The first thing to practice is to quit the program. Click the cross sign at the far right
upper corner of the program window or type the following at the R console:
> q()
A dialog box will appear asking "Save workspace image?" with three choices:
"Yes", "No" and "Cancel". Choose "Cancel" to continue working with R. If you
choose "Yes", two new files will be created in your working folder. Any previous
commands that have been typed at the R console will be saved into a file called
'.Rhistory' while the current workspace will be saved into a file called ".Rdata".
Notice that these two files have no prefix. In the next session of computing, when R
is started in this folder, the image of the working environment of the last saved R
session will be retrieved automatically, together with the command history.
Continued use of R in this fashion (quitting and saving the unnamed workspace
image) will result in these two files becoming larger and larger. Usually one would
like to start R afresh every time so it is advised to always choose "No" when
prompted to save the workspace. Alternatively you may type:
> q("no")
to quit without saving the workspace image and prevent the dialog box message
appearing.
Note that before quitting R you can save your workspace image by typing
> save.image("C:/RWorkplace/myFile.RData")
where 'myFile' is the name of your file. Then when you quit R you should answer
"No" to the question.
R libraries & packages
R can be defined as an environment within which many classical and modern
statistical techniques, called functions, are implemented. A few of these techniques
are built into the base R environment, but many are supplied as packages. A
package is simply a collection of these functions together with datasets and
documentation. A library is a collection of packages typically contained in a single
directory on the computer.

5
There are about 25 packages supplied with R (called “standard” or “recommended”
packages) and many more are available through the CRAN web site. Only 7 of
these packages are loaded into memory when R is executed. To see which packages
are currently loaded into memory you can type:
> search()
[1] ".GlobalEnv" "package:methods" "package:stats"
[4] "package:graphics" "package:grDevices" "package:utils"
[7] "package:datasets" "Autoloads" "package:base"
The list shown above is in the search path of R. When R is told to do any work, it
will look for a particular object for it to work with from the search path. First, it will
look inside '.GlobalEnv', which is the global environment. This will always be the
first search position. If R cannot find what it wants here, it then looks in the second
search position, in this case "package:methods", and so forth. Any function that
belongs to one of the loaded packages is always available during an R session.
Epicalc package
The Epicalc package can be downloaded from the web site http://cran.r-project.org.
On the left pane of this web page, click 'Packages'. Move down along the
alphabetical order of various packages to find 'epicalc'. The short and humble
description is 'Epidmiological calculator'. Click 'epicalc' to hyperlink to the
download page. On this page you can download the Epicalc source code(.tar.gz),
and the two binary versions for MacIntosh (.tgz) and Windows (.zip) versions,
along with the documentation (.pdf).
The Epicalc package is updated from time to time. The version number is in the
suffix. For example, epicalc_2.6.1.6.zip is the binary file for use on the Windows
operating system and the version of Epicalc is 2.6.1.6. A newer version is created to
have bugs (errors in the programme) fixed, to improve the features of existing
functions (commands) and to include new functions.
The file epicalc_version.zip ('version' increases with time) is a
compressed file containing the fully compiled Epicalc package. Installation of this
package must be done within R itself. Usually there is only one session of
installation needed unless you want to overwrite the old package with a newer one
of the same name. You will also need to reinstall this package if you install a new
version of R. To install Epicalc, click 'Packages' on the menu bar at the top of the
window. Choose 'Install packages from local zip files...". When the navigating
window appears, browse to find the file and open it.

6
Successful installation will result in:
> utils:::menuInstallLocal()
package 'epicalc' successfully unpacked and MD5 sums checked
updating HTML package descriptions
Installation is now complete; however functions within Epicalc are still not
available until the following command has been executed:
> library(epicalc)
Note the use of lowercase letters. When the console accepts the command quietly,
we can be reasonably confident that the command has been accepted. Otherwise,
errors or warnings will be reported.
A common warning is a report of a conflict. This warning is, most of the time, not
very serious. This just means that an object (usually a function) with the same name
already exists in the working environment. In this case, R will give priority to the
object that was loaded more recently. The command library(epicalc) must
be typed everytime a new session of R is run.
Updating packages
Whenever a new version of a package is released it is advised to keep up to date by
removing (unloading) the old one and loading the new one. To unload the Epicalc
package, you may type the following at the R console:
> detach(package:epicalc)
After typing the above command, you may then install the new version of the
package as mentioned in the previous section. If there are any problems, you may
need to quit R and start afresh.
RProfile.site
Whenever R is run it will execute the commands in the "RProfile.site" file, which
is located in the C:\Program Files\R\R-2.6.1\etc folder. Remember to replace the R
version with the one you have installed. By including the command
library(epicalc) in the RProfile.site file, every time R is run, the Epicalc
package will be automatically loaded and ready for use. You may edit this file and
insert the command above.
Your Rprofile.site file should look something like this:
library(epicalc)
# Things you might want to change
# options(papersize="a4")
# options(editor="notepad")
# options(pager="internal")

7
# to prefer Compiled HTML help
# options(chmhelp=TRUE)
# to prefer HTML help
# options(htmlhelp=TRUE)
On-line help
On-line help is very useful when using software, especially for first time users.
Self-studying is also possible from the on-line help of R, although with some
difficulty. This is particularly true for non-native speakers of English, where
manuals can often be too technical or wordy. It is advised to combine the use of this
book as a tutorial and on-line help as a reference manual.
On-line help documentation comes in three different versions in R. The default
version is to show help information in a separate window within R. This format is
written in a simple markup language that can be read by R and can be converted to
LaTeX, which is used to produce the printed manuals. The other versions, which
can be set in the "Rprofile.site" file mentioned previously, are HTML
(htmlhelp=TRUE) and compiled HTML (chmhelp=TRUE). The later version is
Windows specific and if chosen, help documentation will appear in a Windows help
viewer. Each help format has its own advantages and you are free to choose the
format you want.
For self study, type
> help.start()
The system will open your web browser from the main menu of R. 'An Introduction
to R' is the section that all R users should try to read first. Another interesting
section is 'Packages'. Click this to see what packages you have available. If the
Epicalc package has been loaded properly, then this name should also appear in the
list. Click 'Epicalc' to see the list of the functions available. Click each of the
functions one by one and you will see the help for that individual function. This
information can also be obtained by typing 'help(myFun)' at the R console, where
'myFun' is the name of the function. To get help on the 'help' function you can type
> help(help)
or perhaps more conveniently
> ?help
For fuzzy searching you can try
> help.search("...")
Replace the dots with the keyword you want to search for. This function also allows
you to search on multiple keywords. You can use this to refine a query when you
get too many responses.

8
Very often the user would want to know how to get other statistical analysis
functions that are not available in a currently installed package. A better option
would be to search from the CRAN website using the 'search' feature located on the
left side of the web page and Google will do a search within CRAN. The results
would be quite extensive and useful. The user then can choose the website to go to
for further learning.
Now type
> search()
You should see "package:epicalc" in the list. If the Epicalc package has not been
loaded, then the functions contained inside will not be available for use.
Having the Epicalc package in the search path means we can use all commands or
functions in that package. Other packages can be called when appropriate. For
example, the package survival is necessary for survival analysis. We will encounter
this in the corresponding section.
The order of the search path is sometimes important. For Epicalc users, it is
recommended that any additional library should be called early in the session of R,
i.e. before reading in and attaching to a data frame. This is to make sure that the
active dataset will be in the second search position. More details on this will be
discussed in Chapter 4.
Using R
A basic but useful purpose of R is to perform simple calculations.
> 1+1
[1] 2
When you type '1+1' and hit the <Enter> key, R will show the result of the
calculation, which is equal to 2.
For the square root of 25:
> sqrt(25)
[1] 5
The wording in front of the left round bracket is called a 'function'. The entity inside
the bracket is referred to as the function's 'argument'. Thus in the last example,
'sqrt()' is a function, and when imposed on 25, the result is 5.
To find the value of e:
> exp(1)
[1] 2.718282

9
Exponentiation of 1 results in the value of e, which is about 2.7. Similarly, the
exponential value of -5 or e-5 would be
> exp(-5)
[1] 0.006738
Syntax of R commands
R will compute only when the commands are syntactically correct. For example, if
the number of closed brackets is fewer than the number of opened ones and the
<Enter> key is pressed, the new line will start with a '+' sign, indicating that R is
waiting for completion of the command. After the number of closed brackets equals
the number of opened ones, computation is carried out and the result appears.
> log(3.8
+ )
[1] 1.335001
However, if the number of closed brackets exceeds the number of opened ones, the
result is a syntax error, or computer grammatical.
> log(3.2))
Error: syntax error
R objects
In the above simple calculation, the results are immediately shown on the screen
and are not stored. To perform a calculation and store the result in an object type:
> a = 3 + 5
We can check whether the assignment was successful by typing the name of the
newly created object:
> a
[1] 8
More commonly, the assignment is written in the following way.
> a <- 3 + 5
> a
[1] 8
For ordinary users, there is no obvious difference between the use of = and <-. The
difference applies at the R programming level and will not be discussed here.
Although <- is slightly more awkward to type than =, the former technique is
recommended to avoid any confusion with the comparison operator (==). Notice
that there is no space between the two components of the assignment operator <-.
Now create a second object called 'b' equal to the square root of 36.
> b <- sqrt(36)

10
Then, add the two objects together.
> a + b
[1] 14
We can also compute the value on the left and assign the result to a new object
called 'c' on the right, using the right assign operator, ->.
> a + 3*b -> c
> c
[1] 26
However, the following command does not work.
> a + 3b -> c
Error: syntax error
R does not recognise '3b'. The * symbol is needed, which indicates multiplication.
The name of an object can consist of more than one letter.
> xyx <- 1
> xyx
[1] 1
A nonsense thing can be typed into the R console such as:
> qwert
Error: Object "qwert" not found
What is typed in is syntactically correct. The problem is that 'qwert' is not a
recognizable function nor a defined object.
A dot can also be used as a delimiter for an object name.
> baht.per.dollar <- 40
> baht.per.dollar
[1] 40
In conclusion, when one types in anything at the R console, the program will try to
show the value of that object. If the signs = or <- or -> are encountered, the value
will be stored to the object on the left of = and <- or the right hand side of ->.
Character or string objects
Character or string means alphanumeric or letter. Examples include the name of a
person or an address. Objects of this type cannot be used for calculation. Telephone
numbers and post-codes are also strings.

11
> A <- "Prince of Songkla University"
> A
[1] "Prince of Songkla University"
R is case sensitive, so 'A' is not the same as 'a'.
> a
[1] 8
> A
[1] "Prince of Songkla University"
Putting comments in a command line
In this book, as with most other programming documents, the author usually inserts
some comments as a part of documentation to remind him/herself or to show some
specific issue to the readers.
R ignores any words following the # symbol. Thus, such a sentence can be used for
comments. Examples:
> 3*3 = 3^2 # This gives a syntax error
> 3*3 == 3^2 # This is correct syntax-wise.
> 3*2 == 3^2 # Correct syntax but the result is FALSE
Logical: TRUE and FALSE
In the last few commands:
> 3*3 == 3^2
[1] TRUE
But
> 3*2 == 3^2
[1] FALSE
Note that we need two equals signs to check equality but only one for assignment.
> 3*2 < 3^2
[1] TRUE
Logical connection using & (logical 'and')
Both TRUE and FALSE are logical objects. They are both in upper case.
Connection of more than one such object results in either TRUE or FALSE. If all
are TRUE, the final result is TRUE. For example:
> TRUE & TRUE
[1] TRUE

12
A combination of FALSE with any other logical is always FALSE.
> TRUE & FALSE
[1] FALSE
> FALSE & FALSE
[1] FALSE
Note that
> (FALSE & TRUE) == (TRUE & FALSE)
[1] TRUE
Without brackets, computation is carried out from left to right.
> FALSE & TRUE == TRUE & FALSE
[1] FALSE
Logical connection with | (logical 'or')
This kind of connection looks for anything which is TRUE.
> TRUE | TRUE
[1] TRUE
> TRUE | FALSE
[1] TRUE
> 3*3 == 3^2 | 3*2 == 3^2
[1] TRUE
Value of TRUE and FALSE
Numerically, TRUE is equal to 1 and FALSE is equal to 0.
> TRUE == 1
[1] TRUE
> FALSE == 0
[1] TRUE
> (3*3 == 3^2) + (9 > 8)
[1] 2
Each of the values in the brackets is TRUE, which is equal to 1. The addition of two
TRUE objects results in a value of 2. However,
> 3*3 == 3^2 + 9 > 8
Error: syntax error in "3*3 == 3^2 + 9 >"
This is due to the complicated sequence of the operation. Therefore, it is always
better to use brackets in order to specify the exact sequence of computation.
Let's leave R for the time being. Answer "Yes" to the question: "Save work space
image?".

13
Please remember that answering "No" is the preferred response in this book as we
recommend typing
> q("no")
to end each R session. Responding "Yes" here is just an exercise in understanding
the concept of workspace images, which follows in chapter 2.
References
An Introduction to R. ISBN 3-900051-12-7.
R Language Definition. ISBN 3-900051-13-5.
Both references above can be downloaded from the CRAN web site.

14
Exercises
Problem 1.
The formula for sample size of a descriptive survey is
()
π=n −1
1.96
2
2
π
δ
where n is the sample size,
π is the prevalence in the population (not to be confused with the constant pi), and
δ is half the width of the 95% confidence interval (precision).
Compute the required sample size if the prevalence is estimated to be 30% of the
population and the 95% confidence interval is not farther from the estimated
prevalence by more than 5%.
Problem 2.
Change the above prevalence to 5% and suppose each side of the 95% confidence
interval is not farther from the estimated prevalence by more than 2%.
Problem 3.
The term 'logit' denotes 'log{P/(1-P)}' where P is the risk or prevalence of a disease.
Compute the logits from the following prevalences: 1%, 10%, 50%, 90% and
100%.

15
Chapter 2: Vectors
In the previous chapter, we introduced simple calculations and storage of the results
of the calculations. In this chapter, we will learn slightly more complicated issues.
History and saved objects
Outside R, examine the working folder; you should see two new files: ".Rdata",
which is the working environment saved from the latest R session, and
".Rhistory", which recorded all the commands in the preceding R session.
".Rdata" is a binary file and only recognised by the R program, while ".Rhistory"
is a text file and can be edited using any text editor such as Notepad, Crimson
Editor or Tinn-R.
Open R from the desktop icon. You may see this in the last line:
[Previously saved workspace restored]
This means that R has restored commands from the previous R session (or history)
and the objects stored form this session. Press the up arrow key and you will see the
previous commands (both correct and incorrect ones). Press <Enter> following the
command; the results will come up as if you continued to work in the previous
session.
> a
[1] 8
> A
[1] "Prince of Songkla University"
Both 'a' and 'A' are retained from the previous session.
Note: ______________________________________________________________________
The image saved from the previous session contains only objects in the '.GlobalEnv', which is
the first position in the search path. The whole search path is not saved. For example, any
libraries manually loaded in the previous session need to be reloaded. However, the Epicalc
library is automatically loaded every time we start R (from the setting of the "Rprofile.site"
file that we modified in the previous chapter). Therefore, under this setting, regardless of
whether the workspace image has been saved in the previous session or not, Epicalc will
always be in the search path.

16
If you want to remove the objects in the environment and the history, quit R
without saving. Go to the 'start in' folder and delete the two files ".Rhistory" and
".Rdata". Then restart R. There should be no message indicating restoration of
previously saved workspace and no history of previous commands.
Concatenation
Objects of the same type, i.e. numeric with numeric, string with string, can be
concatenated. In fact, a vector is an object containing concatenated, atomised (no
more divisible) objects of the same type.
To concatenate, the function 'c()' is used with at least one atomised object as its
argument. Create a simple vector having the integers 1, 2 and 3 as its elements.
> c(1,2,3)
[1] 1 2 3
This vector has three elements: 1, 2 and 3. Press the up arrow key to reshow this
command and type a right arrow to assign the result to a new object called 'd'. Then
have a look at this object.
> c(1,2,3) -> d
> d
Do some calculation with 'd' and observe the results.
> d + 4
> d - 3
> d * 7
> d / 10
> d * d
> d ^ 2
> d / d
> d == d
In addition to numbers, words can be used to create string vectors.
> B <- c("Faculty of Medicine","Prince of Songkla University")
> B
[1] "Faculty of Medicine" "Prince of Songkla University"
Vectors of systematic numbers
Sometimes a user may want to create a vector of numbers with a certain pattern.
The following command will create a vector of integers from 1 to 10.
> x <- 1:10; x
[1] 1 2 3 4 5 6 7 8 9 10

17
For 5 repetitions of 13:
> rep(13, times=5)
[1] 13 13 13 13 13
The function 'rep' is used to replicate values of the argument. For sequential
numbers from -1 to 11 with an incremental step of 3 type:
> seq(from = -1, to = 11, by = 3)
[1] -1 2 5 8 11
In this case 'seq' is a function with three arguments 'from', 'to' and 'by'. The
function can be executed with at least two parameters, 'from' and 'to', since the 'by'
parameter has a default value of 1 (or -1 if 'to' is less than 'from').
> seq(10, 23)
[1] 10 11 12 13 14 15 16 17 18 19 20 21 22 23
> seq(10, -3)
[1] 10 9 8 7 6 5 4 3 2 1 0 -1 -2 -3
The order of the arguments 'from', 'to' and 'by' is assumed if the words are omitted.
When explicitly given, the order can be changed.
> seq(by=-1, to=-3, from=10)
This rule of argument order and omission applies to all functions. For more details
on 'seq' use the help feature.
Subsetting a vector with an index vector
In many instances, only a certain part of a vector needs to be used. Let's assume we
have a vector of running numbers from 3 to 100 in steps of 7. What would be the
value of the 5th number?
> seq(from=3, to=100, by=7) -> x
> x
[1] 3 10 17 24 31 38 45 52 59 66 73 80 87 94
In fact, the vector does not end with 100, but rather 94, since a further step would
result in a number that exceeds 100.
> x[5]
[1] 31
The number inside the square brackets '[]' is called a subscript. It denotes the
position or selection of the main vector. In this case, the value in the 5th position of
the vector 'x' is 31. If the 4th, 6th and 7th positions are required, then type:
> x[c(4,6,7)]
[1] 24 38 45

18
Note that in this example, the object within the subscript can be a vector, thus the
concatenate function c is needed, to comply with the R syntax. The following
would not be acceptable:
> x[4,6,7]
Error in x[4, 6, 7] : incorrect number of dimensions
To select 'x' with the first four elements omitted, type:
> x[-(1:4)]
[1] 31 38 45 52 59 66 73 80 87 94
A minus sign in front of the subscript vector denotes removal of the elements of 'x'
that correspond to those positions specified by the subscript vector.
Similarly, a string vector can be subscripted.
> B[2]
[1] "Prince of Songkla University"
Using a subscript vector to select a subset
A vector is a set of numbers or strings. Application of a condition within the
subscript results in a subset of the main vector. For example, to choose only even
numbers of the vector 'x' type:
> x[x/2 == trunc(x/2)]
[1] 10 24 38 52 66 80 94
The function trunc means to truncate or remove the decimals. The condition that
'x' divided by 2 is equal to its truncated value is true iff (if and only if) 'x' is an even
number. The same result can be obtained by using the 'subset' function.
> subset(x, x/2==trunc(x/2))
If only odd numbers are to be chosen, then the comparison operator can simply be
changed to !=, which means 'not equal'.
> subset(x, x/2!=trunc(x/2))
[1] 3 17 31 45 59 73 87
The operator ! prefixing an equals sign means 'not equal', thus all the chosen
numbers are odd. Similarly, to choose the elements of 'x' which are greater than 30
type:
> x[x>30]
[1] 31 38 45 52 59 66 73 80 87 94

19
Functions related to manipulation of vectors
R can compute statistics of vectors very easily.
> fruits <- c(5, 10, 1, 20)
> summary(fruits)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.0 4.0 7.5 9.0 12.5 20.0
> sum(fruits)
[1] 36
There are 36 fruits in total.
> length(fruits) # number of different types of fruits
[1] 4
> mean(fruits) # mean of number of fruits
[1] 9
> sd(fruits) # standard deviation
[1] 8.205689
> var(fruits) # variance
[1] 67.33333
Non-numeric vectors
Let's create a string vector called 'person' containing 11 elements.
> person <- c("A","B","C","D","E","F","G","H","I","J","K")
Alternatively, and more economically:
> person <- LETTERS[1:11]
Now check the class of the 'person' and 'fruits' objects.
> class(person)
[1] "character"
> class(fruits)
[1] "numeric"
Character types are used for storing names of individuals. To store the sex of the
person, initially numeric codes are given: 1 for male, 2 for female, say.
> sex <- c(1,2,1,1,1,1,1,1,1,1,2)
> class(sex)
[1] "numeric"
> sex1 <- as.factor(sex) # Creating sex1 from sex
The function as.factor coerces the object 'sex' into a factor, which is a
categorical data type in R.
> sex1
[1] 1 2 1 1 1 1 1 1 1 1 2
Levels: 1 2

20
There are two levels of sex.
> class(sex1)
[1] "factor"
> is.factor(sex)
[1] FALSE
> is.factor(sex1)
[1] TRUE
Now try to label 'sex1'.
> levels(sex1) <- c("male", "female")
The levels of 'sex' is a string vector used for labeling it.
> sex1
[1] male female male male male male male
[8] male male male female
Levels: male female
Ordering elements of a vector
Create an 11-element vector of ages.
> age <- c(10,23,48,56,15,25,40,21,60,59,80)
To sort the ages:
> sort(age)
[1] 10 15 21 23 25 40 48 56 59 60 80
The function sort creates a vector with the elements in ascending order. However,
the original vector is not changed.
> median(age)
[1] 40
The median of the ages is 40. To get other quantiles, the function quantile can
be used.
> quantile(age)
0% 25% 50% 75% 100%
10.0 22.0 40.0 57.5 80.0
By default (if other arguments omitted), the 0th, 25th, 50th, 75th and 100th percentiles
are displayed. To obtain the 30th percentile of age, type:
> quantile(age, prob = .3)
30%
23

21
Creating a factor from an existing vector
An age group vector can be created from age using the cut function.
> agegr <- cut(age, breaks=c(0,15,60,100))
This creates 3 distinct groups, which we can call 'children', 'adults' and 'elderly'.
Note that the minimum and maximum of the arguments in cut are the outer most
boundaries.
> is.factor(agegr)
[1] TRUE
> attributes(agegr)
$levels
[1] "(0,15]" "(15,60]" "(60,100]"
$class
[1] "factor"
The object 'agegr' is a factor, with levels shown above. We can check the
correspondence of 'age' and 'agegr' using the data.frame function, which
combines (but not saves) the 2 variables in a data frame and displays the result.
More details on this function is given the chapter 4.
> data.frame(age, agegr)
age agegr
1 10 (0,15]
2 23 (15,60]
3 48 (15,60]
4 56 (15,60]
5 15 (0,15]
6 25 (15,60]
7 40 (15,60]
8 21 (15,60]
9 60 (15,60]
10 59 (15,60]
11 80 (60,100]
Note that the 5th person, who is 15 years old, is classified into the first group and the
9th person, who is 60 years old, is in the second group. The label of each group uses
a square bracket to end the bin indicating that the last number is included in the
group (inclusive cutting). A round bracket in front of the group is exclusive or not
including that value. To obtain a frequency table of the age groups, type:
> table(agegr)
agegr
(0,15] (15,60] (60,100]
2 8 1
There are two children, eight adults and one elderly person.
> summary(agegr) # same result as the preceding command
> class(agegr)
[1] "factor"

22
The age group vector is a factor or categorical vector. It can be transformed into a
simple numeric vector using the 'unclass' function, which is explained in more
detail in chapter 3.
> agegr1 <- unclass(agegr)
> summary(agegr1)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.000 2.000 2.000 1.909 2.000 3.000
> class(agegr1)
[1] "integer"
Categorical variables, for example sex, race and religion should always be factored.
Age group in this example is a factor although it has an ordered pattern. Declaring a
vector as a factor is very important, particularly when performing regression
analysis, which will be discussed in future chapters.
The unclassed value of a factor is used when the numeric (or integer) values of the
factor are required. For example, if we are have a dataset containing a 'sex' variable,
classed as a factor, and we want to draw a scatter plot in which the colours of the
dots are to be classified by the different levels of 'sex', the colour argument to the
plot function would be 'col = unclass(sex)'. This will be demonstrated in future
chapters.
Missing values
Missing values usually arise from data not being collected. For example, missing
age may be due to a person not giving his or her age. In R, missing values are
denoted by 'NA', abbreviated from 'Not Available'. Any calculation involving NA
will result in NA.
> b <- NA
> b * 3
[1] NA
> c <- 3 + b
> c
[1] NA
As an example of a missing value of a person in a vector series, type the following
commands:
> height <- c(100,150,NA,160)
> height
[1] 100 150 NA 160
> weight <- c(33, 45, 60,55)
> weight
[1] 33 45 60 55

23
Among four subjects in this sample, all weights are available but one height is
missing.
> mean(weight)
[1] 48.25
> mean(height)
[1] NA
We can get the mean weight but not the mean height, although the length of this
vector is available.
> length(height)
[1] 4
In order to get the mean of all available elements, the NA elements should be
removed.
> mean(height, na.rm=TRUE)
[1] 136.6667
The term 'na.rm' means 'not available (value) removed', and is the same as when it
is omitted by using the function na.omit().
> length(na.omit(height))
[1] 3
> mean(na.omit(height))
[1] 136.6667
Thus na.omit() is an independent function that omits missing values from the
argument object. 'na.rm = TRUE' is an internal argument of descriptive statistics
for a vector.

24
Exercises
Problem 1.
Compute the value of 12 + 22 + 32 ... + 1002
Problem 2.
Let 'y' be a series of integers running from 1 to 1,000. Compute the sum of the
elements of 'y' which are multiples of 7.
Problem 3.
The heights (in cm) and weights (in kg) of 10 family members are shown below:
ht wt
Niece 120 22
Son 172 52
GrandPa 163 71
Daughter 158 51
Yai 153 51
GrandMa 148 60
Aunty 160 50
Uncle 170 67
Mom 155 53
Dad 167 64
Create a vector called 'ht' corresponding to the heights of the 11 family members.
Assign the names of the family members to the 'names' attribute of this vector.
Create a vector called 'wt' corresponding to the family member's weights.
Compute the body mass index (BMI) of each person where BMI = weight / height2.
Identify the persons who have the lowest and highest BMI and calculate the
standard deviation of the BMI.

25
Chapter 3: Arrays, Matrices and Tables
Real data for analysis rarely comes as a vector. In most cases, they come as a
dataset containing many rows or records and many columns or variables. In R,
these datasets are called data frames. Before delving into data frames, let us go
through something simpler such as arrays, matrices and tables. Gaining concepts
and skills in handing these types of objects will empower the user to manipulate the
data very effectively and efficiently in the future.
Arrays
An array may generally mean something finely arranged. In mathematics and
computing, an array consists of values arranged in rows and columns. A dataset is
basically an array. Most statistical packages can handle only one dataset or array at
a time. R has a special ability to handle several arrays and datasets simultaneously.
This is because R is an object-oriented program. Moreover, R interprets rows and
columns in a very similar manner.
Folding a vector into an array
Usually a vector has no dimension.
> a <- (1:10)
> a
[1] 1 2 3 4 5 6 7 8 9 10
> dim(a)
NULL
Folding a vector to make an array is simple. Just declare or re-dimension the
number of rows and columns as follows:
> dim(a) <- c(2,5)
> a
[,1] [,2] [,3] [,4] [,5]
[1,] 1 3 5 7 9
[2,] 2 4 6 8 10

26
The numbers in the square brackets are the row and column subscripts. The
command 'dim(a) <- c(2,5)' folds the vector into an array consisting of 2 rows
and 5 columns.
Extracting cells, columns, rows and subarrays using subscripts
While extracting a subset of a vector requires only one component number (or
vector), an array requires two components. Individual elements of an array may be
referenced by giving the name of the array followed by two subscripts separated by
commas inside the square brackets. The first subscript defines row selection; the
second subscript defines column selection. Specific rows and columns may be
extracted by omitting one of the components, but keeping the comma.
> a[1,] # for the first row and all columns of array 'a'
> a[,3] # for all rows of the third column
> a[2,4] # extract 1 cell from the 2nd row and 4th column
> a[2,2:4] # 2nd row, from 2nd to 4th columns
The command a[,] and a[] both choose all rows and all columns of 'a' and thus
are the same as typing 'a'. An array may also have 3 dimensions.
> b <- 1:24
> dim(b) <- c(3,4,2) # or b <- array(1:24, c(3,4,2))
> b
, , 1
[,1] [,2] [,3] [,4]
[1,] 1 4 7 10
[2,] 2 5 8 11
[3,] 3 6 9 12
, , 2
[,1] [,2] [,3] [,4]
[1,] 13 16 19 22
[2,] 14 17 20 23
[3,] 15 18 21 24
The first value of the dimension refers to the number of rows, followed by number
of columns and finally the number of strata.
Elements of this three-dimensional array can be extracted in a similar way.
> b[1:3,1:2,2]
[,1] [,2]
[1,] 13 16
[2,] 14 17
[3,] 15 18
In fact, an array can have much higher dimensions, but for most epidemiological
analysis are rarely used or needed.

27
Vector binding
Apart from folding a vector, an array can be created from vector binding, either by
column (using the function cbind) or by row (using the function rbind). Let's
return to our fruits vector.
> fruit <- c(5, 10, 1, 20)
Suppose a second person buys fruit but in different amounts to the first person.
> fruit2 <- c(1, 5, 3, 4)
To bind 'fruits' with 'fruits2', which are vectors of the same length, type:
> Col.fruit <- cbind(fruits, fruits2)
We can give names to the rows of this array:
> rownames(Col.fruit) <- c("orange","banana","durian","mango")
> Col.fruit
fruits fruits2
orange 5 1
banana 10 5
durian 1 3
mango 20 4
Alternatively, the binding can be done by row.
> Row.fruit <- rbind(fruits, fruits2)
> colnames(Col.fruit) <- c("orange","banana","durian","mango")
> Row.fruit
orange banana durian mango
fruits 5 10 1 20
fruits2 1 5 3 4
Transposition of an array
Array transposition means exchanging rows and columns of the array. In the above
example, 'Row.fruits' is a transposition of 'Col.fruits' and vice versa.
Array transposition is achieved using the t function.
> t(Col.fruit)
> t(Row.fruit)
Basic statistics of an array
The total number of fruits bought by both persons is obtained by:
> sum(Col.fruit)
The total number of bananas is obtained by:
> sum(Col.fruit[2,])
To obtain descriptive statistics of each buyer:

28
> summary(Col.fruit)
To obtain descriptive statistics of each kind of fruit:
> summary(Row.fruit)
Suppose fruits3 is created but with one more kind of fruit added:
> fruits3 <- c(20, 15, 3, 5, 8)
> cbind(Col.fruit, fruits3)
fruits fruits2 fruits3
orange 5 1 20
banana 10 5 15
durian 1 3 3
mango 20 4 5
Warning message:
number of rows of result is not a multiple of vector length
(arg 2) in: cbind(Col.fruit, fruits3)
Note that the last element of 'fruits3' is removed before being added.
> fruits4 <- c(1,2,3)
> cbind(Col.fruit, fruits4)
fruits fruits2 fruits4
orange 5 1 1
banana 10 5 2
durian 1 3 3
mango 20 4 1
Warning message:
number of rows of result is not a multiple of vector length
(arg 2) in: cbind(Col.fruit, fruits4)
Note that 'fruits4' is shorter than the length of the first vector argument. In this
situation R will automatically recycle the element of the shorter vector, inserting
the first element of 'fruits4' into the fourth row, with a warning.
String arrays
Similar to a vector, an array can consist of character string objects.
> Thais <- c("Somsri", "Daeng", "Somchai", "Veena")
> dim(Thais) <- c(2,2); Thais
[,1] [,2]
[1,] "Somsri" "Somchai"
[2,] "Daeng" "Veena"
Note that the elements are folded in colum-wise, not row-wise, sequence.
Implicit array of two vectors of equal length
Two vectors, especially with the same length, may refer to each other without
formal binding.

29
> cities <- c("Bangkok","Hat Yai","Chiang Mai")
> postcode <- c(10000, 90110, 50000)
> postcode[cities=="Bangkok"]
[1] 10000
This gives the same result as
> subset(postcode, cities=="Bangkok")
[1] 10000
For a single vector, thre are many ways to identify the order of a specific element.
For example, to find the index of "Hat Yai" in the city vector, the following four
commands all give the same result.
> (1:length(cities))[cities=="Hat Yai"]
> (1:3)[cities=="Hat Yai"]
> subset(1:3, cities=="Hat Yai")
> which(cities=="Hat Yai")
Note that when a character vector is binded with a numeric vector, the numeric
vector is coerced into a character vector, since all elements of an array must be of
the same type.
> cbind(cities,postcode)
cities postcode
[1,] "Bangkok" "10000"
[2,] "Hat Yai" "90110"
[3,] "Chiang Mai" "50000"
Matrices
A matrix is a two-dimensional array. It has several mathematical properties and
operations that are used behind statistical computations such as factor analysis,
generalized linear modelling and so on.
Users of statistical packages do not need to deal with matrices directly but some of
the results of the analyses are in matrix form, both displayed on the screen that can
readily be seen and hidden as a returned object that can be used later. For exercise
purposes, we will examine the covariance matrix, which is an object returned from
a regression analysis in a future chapter.
Tables
A table is an array emphasizing the relationship between values among cells.
Usually, a table is a result of an analysis, e.g. a cross-tabulation between to
categorical variables (using function table).

30
Suppose six patients who are male, female, female, male, female and female attend
a clinic. If the code is 1 for male and 2 for female, then to create this in R type:
> sex <- c(1,2,2,1,2,2)
Similarly, if we characterize the ages of the patients as being either young or old
and the first three patients are young, the next two are old and the last one is young,
and the codes for this age classification are 1 for young and 2 for old, then we can
create this in R by typing.
> age <- c(1,1,1,2,2,1)
Suppose also that these patients had one to six visits to the clinic, respectively.
> visits <- c(1,2,3,4,5,6)
> table1 <- table(sex, age); table1
age
sex 1 2
1 1 1
2 3 1
Note that table1 gives counts of each combination of the vectors sex and age
while 'table2' (below) gives the sum of the number of visits based on the four
different combinations of sex and age.
> table2 <- tapply(visits, list(Sex=sex, Age=age), FUN=sum)
> table2
Age
Sex 1 2
1 1 4
2 11 5
To obtain the mean of each combination type:
> tapply(visits, list(Sex=sex, Age=age), FUN=mean)
Age
Sex 1 2
1 1.000 4
2 3.667 5
Although 'table1' has class table, the class of 'table2' is still a matrix. One can
convert it simply using the function as.table.
> table2 <- as.table(table2)
Summary of table vs summary of array
In R, applying the function summary to a table performs a chi squared test of
independence.

31
> summary(table1)
Number of cases in table: 6
Number of factors: 2
Test for independence of all factors:
Chisq = 0.375, df = 1, p-value = 0.5403
Chi-squared approximation may be incorrect
In contrast, applying summary to a non-table array produces descriptive statistics
of each column.
> is.table(Col.fruits)
[1] FALSE
> summary(Col.fruits)
fruits fruits2
Min. : 1.0 Min. :1.00
1st Qu.: 4.0 1st Qu.:2.50
Median : 7.5 Median :3.50
Mean : 9.0 Mean :3.25
3rd Qu.:12.5 3rd Qu.:4.25
Max. :20.0 Max. :5.00
> fruits.table <- as.table(Col.fruits)
> summary(fruits.table)
Number of cases in table: 49
Number of factors: 2
Test for independence of all factors:
Chisq = 6.675, df = 3, p-value = 0.08302
Chi-squared approximation may be incorrect
> fisher.test(fruits.table)
Fisher's Exact Test for Count Data
data: fruits.table
p-value = 0.07728
alternative hypothesis: two.sided
Lists
An array forces all cells from different columns and rows to be the same type. If
any cell is a character then all cells will be coerced into a character. A list is
different. It can be a mixture of different types of objects compounded into one
entity. It can be a mixture of vectors, arrays, tables or any object type.
> list1 <- list(a=1, b=fruits, c=cities)
> list1
$a
[1] 1
$b
[1] 5 10 1 20
$c
[1] "Bangkok" "Hat Yai" "Chiang Mai"

32
Note that the arguments of the function list consist of a series of new objects
being assigned a value from existing objects or values. When properly displayed,
each new name is prefixed with a dollar sign, $.
The creation of a list is not a common task in ordinary data analysis. However, a list
is sometimes required in the arguments to some functions.
Removing objects from the computer memory also requires a list as the argument to
the function rm.
> rm(list=c("list1", "fruits"))
This is equivalent to
> rm(list1); rm(fruits)
A list may also be returned from the results of an analysis, but appears under a
special class.
> sample1 <- rnorm(10)
This generates a sample of 10 numbers from a normal distribution.
> qqnorm(sample1)
The qqnorm function plots the sample quantiles, or the sorted observed values,
against the theoretical quantiles, or the corresponding expected values if the data
were perfectly normally distributed. It is used here for the sake of demonstration of
the list function only.
> list2 <- qqnorm(sample1)
This stores the results into an object called list2.
> list2
$x
[1] 0.123 -1.547 -0.375 0.655 1.000 0.375 -0.123
[8] -1.000 -0.655 1.547
$y
[1] -0.4772 -0.9984 -0.7763 0.0645 0.9595 -0.1103
[7] -0.5110 -0.9112 -0.8372 2.4158
The command qqnorm(sample1) is used as a graphical method for checking
normality. While it produces a graph on the screen, it also gives a list of the x and y
coordinates, which can be saved and used for further calculation.
Similarly, boxplot(sample1) returns another list of objects to facilitate
plotting of a boxplot.

33
Exercises
Problem 1.
Demonstrate a few simple ways to create the array below
[,1][,2][,3][,4][,5][,6][,7][,8][,9][,10]
[1,] 1 2 3 4 5 6 7 8 9 10
[2,] 11 12 13 14 15 16 7 18 19 20
Problem 2.
Extract from the above array the odd numbered columns.
Problem 3.
Cross-tabulation between status of a disease and a putative exposure have the
following results:
Diseased Non-diseased
Exposed 15 20
Non-exposed 30 22
Create the table in R and perform chi-squared and Fisher's exact tests.
34
35
Chapter 4: Data Frames
In the preceding chapter, examples were given on arrays and lists. In this chapter,
data frames will be the main focus. For most researchers, these are sometimes
called datasets. However, a complete dataset can contain more than one data frame.
These contain the real data that most researchers have to work with.
Comparison of arrays and data frames
Many rules used for arrays are also applicable to data frames. For example, the
main structure of a data frame consists of columns (or variables) and rows (or
records). Rules for subscripting, column or row binding and selection of a subset in
arrays are directly applicable to data frames.
Data frames are however slightly more complicated than arrays. All columns in an
array are forced to be character if just one cell is a character. A data frame, on the
other hand, can have different classes of columns. For example, a data frame can
consist of a column of 'idnumber', which is numeric and a column of 'name', which
is character.
A data frame can also have extra attributes. For example, each variable can have
lengthy variable descriptions. A factor in a data frame often has 'levels' or value
labels. These attributes can be transferred from the original dataset in other formats
such as Stata or SPSS. They can also be created in R during the analysis.
Obtaining a data frame from a text file
Data from various sources can be entered using many different software programs.
They can be transferred from one format to another through the ASCII file format.
In Windows, a text file is the most common ASCII file, usually having a ".txt"
extension. There are several other files in ASCII format, including the ".R"
command file discussed in chapter 25.
Data from most software programs can be exported or saved as an ASCII file. From
Excel, a very commonly used spreadsheet program, the data can be saved as ".csv"
(comma separated values) format. This is an easy way to interface between Excel
spreadsheet files and R. Simply open the Excel file and 'save as' the csv format. As
an example suppose the file "csv1.xls" is originally an Excel spreadsheet. After

36
'save as' into csv format, the output file is called "csv1.csv", the contents of which
is:
"name","sex","age"
"A","F",20
"B","M",30
"C","F",40
Note that the characters are enclosed in quotes and the delimiters (variable
separators) are commas. Sometimes the file may not contain quotes, as in the file
"csv2.csv".
name,sex,age
A,F,20
B,M,30
C,F,40
For both files, the R command to read in the dataset is the same.
> a <- read.csv("csv1.csv", as.is=TRUE)
> a
name sex age
1 A F 20
2 B M 30
3 C F 40
The argument 'as.is=TRUE' keeps all characters as they are. Had this not been
specified, the characters would have been coerced into factors. The variable 'name'
should not be factored but 'sex' should. The following command should therefore be
typed:
> a$sex <- factor(a$sex)
Note firstly that the object 'a' has class data frame and secondly that the names of
the variables within the data frame 'a' must be referenced using the dollar sign
notation. If not, R will inform you that the object 'sex' cannot be found.
For files with white space (spaces and tabs) as the separator, such as in the file
"data1.txt", the command to use is read.table.
> a <- read.table("data1.txt", header=TRUE, as.is=TRUE)
The file "data2.txt" is in fixed field format without field separators.
namesexage
1AF20
2BM30
3CF40

37
To read in such a file, the function read.fwf is preferred. The first line, which is
the header, must be skipped. The width of each variable and the column names
must be specified by the user.
> a <- read.fwf("data2.txt", skip=1, width=c(1,1,2), col.names
= c("name", "sex", "age"), as.is=TRUE)
Data entry and analysis
The above section deals with creating data frames by reading in data created from
programs outside R, such as Excel. It is also possible to enter data directly into R
by using the function data.entry. However, if the data size is large (say more
than 10 columns and/or more than 30 rows), the chance of human error is high with
the spreadsheet or text mode data entry. A software program specially designed for
data entry, such as Epidata, is more appropriate. Their web site is:
http://www.epidata.dk. Epidata has facilities for setting up useful constraints such
as range checks, automatic jumps and labelling of variables and values (codes) for
each variable. There is a direct transfer between Epidata and R (using 'read.epiinfo')
but it is recommended to export data from Epidata (using the export procedure
inside that software) to Stata format and use the function read.dta to read the
dataset into R. Exporting data into Stata format maintains many of the attributes of
the variables, such as the variable labels and descriptions.
Clearing memory and reading in data
At the R console type:
> rm(list=ls())
The function rm stands for "remove". The command above removes all objects in
the workspace. To see what objects are currently in the workspace type:
> ls()
character(0)
The command ls() shows a list of objects in the current workspace. The name(s)
of objects have class character. The result "character(0)" means that there are
no ordinary objects in the environment.
If you do not see "character(0)" in the output but something else, it means
those objects were left over from the previous R session. This will happen if you
agreed to save the workspace image before quitting R. To avoid this, quit R and
delete the file ".Rdata", which is located in your working folder, or rename it if you
would like to keep the workspace from the previous R session.
Alternatively, to remove all objects in the current workspace without quitting R,
type:
> zap()

38
This command will delete all ordinary objects from R memory. Ordinary objects
include data frames, vectors, arrays, etc. Function objects are spared deletion.
Datasets included in Epicalc
Most add-on packages for R contain datasets used for demonstration and teaching.
To check what datasets are available in all loaded packages in R type:
> data()
You will see names and descriptions of several datasets in various packages, such
as datasets and epicalc. In this book, most of the examples use datasets from the
Epicalc package.
Reading in data
Let's try to load an Epicalc dataset.
> data(Familydata)
The command data loads the Familydata dataset into the R workspace. If there
is no error you should be able to see this object in the workspace.
> ls()
[1] "Familydata"
Viewing contents of a data frame
If the data frame is small such as this one (11 records, 6 variables), just type its
name to view the entire dataset.
> Familydata
code age ht wt money sex
1 K 6 120 22 5 F
2 J 16 172 52 50 M
3 A 80 163 71 100 M
4 I 18 158 51 200 F
5 C 69 153 51 300 F
6 B 72 148 60 500 F
7 G 46 160 50 500 F
8 H 42 163 55 600 F
9 D 58 170 67 2000 M
10 F 47 155 53 2000 F
11 E 49 167 64 5000 M
To get the names of the variables (in order) of the data frame, you can type:
> names(Familydata)
[1] "code" "age" "ht" "wt" "money" "sex"
Another convenient function that can be used to explore the data structure is str.

39
> str(Familydata)
'data.frame': 11 obs. of 6 variables:
$ code : chr "K" "J" "A" "I" ...
$ age : int 6 16 80 18 69 72 46 42 58 47 ...
$ ht : int 120 172 163 158 153 148 160 163 170 155 ...
$ wt : int 22 52 71 51 51 60 50 55 67 53 ...
$ money: int 5 50 100 200 300 500 500 600 2000 2000 ...
$ sex : Factor w/ 2 levels "F","M": 1 2 2 1 1 1 1 1 2 ...
=============+=== remaining output omitted =====+===========
Summary statistics of a data frame
A quick exploration of a dataset should be to obtain the summary statistics of all
variables. This can be achieved in a single command.
> summary(Familydata)
code age ht
Length:11 Min. : 6.0 Min. :120
Class :character 1st Qu.:30.0 1st Qu.:154
Mode :character Median :47.0 Median :160
Mean :45.7 Mean :157
3rd Qu.:63.5 3rd Qu.:165
Max. :80.0 Max. :172
wt money sex
Min. :22.0 Min. : 5 F:7
1st Qu.:51.0 1st Qu.: 150 M:4
Median :53.0 Median : 500
Mean :54.2 Mean :1023
3rd Qu.:62.0 3rd Qu.:1300
Max. :71.0 Max. :5000
The function summary is from the base library. It gives summary statistics of each
variable. For a continuous variable such as 'age', 'wt', 'ht' and 'money', non-
parametric descriptive statistics such as minimum, first quartile, median, third
quartile and maximum, as well as the mean (parametric) are shown. There is no
information on the standard deviation or the number of observations. For
categorical variables, such as sex, a frequency tabulation is displayed. The first
variable code is a character variable. There is therefore no summary for it.
Compare this result with the version of summary statistics using the function summ
from the Epicalc package.
> summ(Familydata)
Anthropometric and financial data of a hypothetical family
No. of observations = 11
Var. name Obs. mean median s.d. min. max.
1 code
2 age 11 45.73 47 24.11 6 80
3 ht 11 157.18 160 14.3 120 172
4 wt 11 54.18 53 12.87 22 71
5 money 11 1023.18 500 1499.55 5 5000
6 sex 11 1.364 1 0.505 1 2

40
The function summ gives a more concise output, showing one variable per line. The
number of observations and standard deviations are included in the report replacing
the first and third quartile values in the original summary function from the R base
library. Descriptive statistics for factor variables use their unclassed values. The
values 'F' and 'M' for the variable 'sex' have been replaced by the codes 1 and 2,
respectively. This is because R interprets factor variables in terms of levels, where
each level is stored as an integer starting from 1 for the first level of the factor.
Unclassing a factor variable converts the categories or levels into integers. More
discussion about factors will appear later.
From the output above the same statistic from different variables are lined up into
the same column. Information on each variable is completed without any missing as
the number of observations are all 11. The minimum and maximum are shown close
to each other enabling the range of the variable to be easily determined.
In addition, summary statistics for each variable is possible with both choices of
functions. The results are similar to summary statistics of the whole dataset. Try the
following commands:
> summary(Familydata$age)
> summ(Familydata$age)
> summary(Familydata$sex)
> summ(Familydata$sex)
Note that summ, when applied to a variable, automatically gives a graphical output.
This will be examined in more detail in subsequent chapters.
Extracting subsets from a data frame
A data frame has a subscripting system similar to that of an array. To choose only
the third column of Familydata type:
> Familydata[,3]
[1] 120 172 163 158 153 148 160 163 170 155 167
This is the same as
> Familydata$ht
Note that subscripting the data frame Familydata with a dollar sign $ and the
variable name will extract only that variable. This is because a data frame is also a
kind of list (see the previous chapter).
> typeof(Familydata)
[1] "list"

41
To extract more than one variable, we can use either the index number of the
variable or the name. For example, if we want to display only the first 3 records of
'ht', 'wt' and 'sex', then we can type:
> Familydata[1:3,c(3,4,6)]
ht wt sex
1 120 22 F
2 172 52 M
3 163 71 M
We could also type:
> Familydata[1:3,c("ht","wt","sex")]
ht wt sex
1 120 22 F
2 172 52 M
3 163 71 M
The condition in the subscript can be a selection criteria, such as selecting the
females.
> Familydata[Familydata$sex=="F",]
code age ht wt money sex
1 K 6 120 22 5 F
4 I 18 158 51 200 F
5 C 69 153 51 300 F
6 B 72 148 60 500 F
7 G 46 160 50 500 F
8 H 42 163 55 600 F
10 F 47 155 53 2000 F
Note that the conditional expression must be followed by a comma to indicate
selection of all columns. In addition, two equals signs are needed in the conditional
expression. Recall that one equals sign represents assignment.
Another method of selection is to use the subset function.
> subset(Familydata, sex=="F")
To select only the 'ht' and 'wt' variables among the females:
> subset(Familydata, sex=="F", select = c(ht,wt))
Note that the commands to select a subset do not have any permanent effect on the
data frame. The user must save this into a new object if further use is needed.
Adding a variable to a data frame
Often it is necessary to create a new variable and append it to the existing data
frame. For example, we may want to create a new variable called 'log10money'
which is equal to log base 10 of the pocket money.

42
> Familydata$log10money <- log10(Familydata$money)
Alternatively we can use the transform function.
> Familydata <- transform(Familydata, log10money=log10(money))
The data frame is now changed with a new variable 'log10money' added. This can
be checked by the following commands.
> names(Familydata)
> summ(Familydata)
Anthropometric and financial data of a hypothetic family
No. of observations = 11
Var. name Obs. mean median s.d. min. max.
1 code
2 age 11 45.73 47 24.11 6 80
3 ht 11 157.18 160 14.3 120 172
4 wt 11 54.18 53 12.87 22 71
5 money 11 1023.18 500 1499.55 5 5000
6 sex 11 1.364 1 0.505 1 2
7 log10money 11 2.51 2.7 0.84 0.7 3.7
Removing a variable from a data frame
Conversely, if we want to remove a variable from a data frame, just specify a minus
sign in front of the column subscript:
> Familydata[,-7]
code age ht wt money sex
1 K 6 120 22 5 F
2 J 16 172 52 50 M
3 A 80 163 71 100 M
4 I 18 158 51 200 F
5 C 69 153 51 300 F
6 B 72 148 60 500 F
7 G 46 160 50 500 F
8 H 42 163 55 600 F
9 D 58 170 67 2000 M
10 F 47 155 53 2000 F
11 E 49 167 64 5000 M
Note again that this only displays the desired subset and has no permanent effect on
the data frame. The following command permanently removes the variable and
returns the data frame back to its original state.
> Familydata$log10money <- NULL
Assigning a NULL value to a variable in the data frame is equivalent to removing
that variable.

43
At this stage, it is possible that you may have made some typing mistakes. Some of
them may be serious enough to make the data frame Familydata distorted or
even not available from the environment. You can always refresh the R
environment by removing all objects and then read in the dataset afresh.
> zap()
> data(Familydata)
Attaching the data frame to the search path
Accessing a variable in the data frame by prefixing the variable with the name of
the data frame is tidy but often clumsy, especially if the data frame and variable
names are lengthy. Placing or attaching the data frame into the search path
eliminates the tedious requirement of prefixing the name of the variable with the
data frame. To check the search path type:
> search()
[1] ".GlobalEnv" "package:epicalc"
[3] "package:methods" "package:stats"
[5] "package:graphics" "package:grDevices"
[7] "package:utils" "package:datasets"
[9] "package:foreign" "Autoloads"
[11] "package:base"
The general explanation of search() is given in Chapter 1. Our data frame is not
in the search path. If we try to use a variable in a data frame that is not in the search
path, an error will occur.
> summary(age)
Error in summary(age) : Object "age" not found
Try the following command:
> attach(Familydata)
The search path now contains the data frame in the second position.
> search()
[1] ".GlobalEnv" "Familydata" "package:methods"
[4] "package:datasets" "package:epicalc" "package:survival"
[7] "package:splines" "package:graphics" "package:grDevices"
[10] "package:utils" "package:foreign" "package:stats"
[13] "Autoloads" "package:base"
Since 'age' is inside Familydata, which is now in the search path, computation of
statistics on 'age' is now possible.
> summary(age)
Min. 1st Qu. Median Mean 3rd Qu. Max.
6.00 30.00 47.00 45.73 63.50 80.00
Attaching a data frame to the search path is similar to loading a package using the
library function. The attached data frame, as well as the loaded packages, are
actually read into R's memory and are resident in memory until they are detached.

44
This is true even if the original data frame has been removed from the memory.
> rm(Familydata)
> search()
The data frame Familydata is still in the search path allowing any variable
within the data frame to be used.
> age
[1] 6 16 80 18 69 72 46 42 58 47 49
Loading the same library over and over again has no effect on the search path but
re-attaching the same data frame is possible and may eventually overload the
system resources.
> data(Familydata)
> attach(Familydata)
The following object (s) are masked from Familydata
( position 3 ) :
age code ht money sex wt
These variables are already in the second position of the search path. Attaching
again creates conflicts in variable names.
> search()
[1] ".GlobalEnv" "Familydata" "Familydata"
[4] "package:methods" "package:datasets" "package:epicalc"
[7] "package:survival" "package:splines" "package:graphics"
[10] "package:grDevices" "package:utils" "package:foreign"
[13] "package:stats" "Autoloads" "package:base"
The search path now contains two objects named Familydata in positions 2 and
3. Both have more or less the same set of variables with the same names. Recall that
every time a command is typed in and the <Enter> key is pressed, the system will
first check whether it is an object in the global environment. If not, R checks
whether it is a component of the remaining search path, that is, a variable in an
attached data frame or a function in any of the loaded packages.
Repeatedly loading the same library does not add to the search path because R
knows that the contents in the library do not change during the same session.
However, a data frame can change at any time during a single session, as seen in the
previous section where the variable 'log10money' was added and later removed.
The data frame attached at position 2 may well be different to the object of the same
name in another search position. Confusion arises if an independent object (e.g.
vector) is created outside the data frame (in the global environment) with the same
name as the data frame or if two different data frames in the search path each
contain a variable with the same name. The consequences can be disastrous.
In addition, all elements in the search path occupy system memory. The data frame
Familydata in the search path occupies the same amount of memory as the one
in the current workspace. Doubling of memory is not a serious problem if the data
frame is small. However, repeatedly attaching to a large data frame may cause R to

45
not execute due to insufficient memory.
With these reasons, it is a good practice firstly, to remove a data frame from the
search path once it is not needed anymore. Secondly, remove any objects from the
environment using rm(list=ls()) when they are not wanted anymore. Thirdly,
do not define a new object (say vector or matrix) that may have the same name as
the data frame in the search path. For example, we should not create a new vector
called Familydata as we already have the data frame Familydata in the
search path.
Detach both versions of Familydata from the search path.
> detach(Familydata)
> detach(Familydata)
Note that the command detachAllData() in Epicalc removes all attachments
to data frames. The command zap() does the same, but in addition removes all
non-function objects. In other words, the command zap() is equivalent to
rm(list=lsNoFunction()) followed by detachAllData().
The 'use' command in Epicalc
Attaching to and detaching from a data frame is often tedious and cumbersome and
if there is more than one data frame in the workspace then users must be careful that
they are attached to the correct data frame when working with their data. Most data
analysis deals only with a single data frame. In order to reduce these steps of
attaching and detaching, Epicalc contains a command called use which eases the
process. At the R console type:
> zap()
> data(Familydata)
> use(Familydata)
The command use()reads in a data file from Dbase (.dbf), Stata (.dta), SPSS
(.sav), EpiInfo (.rec) and comma separated value (.csv) formats, as well as those
that come pre-supplied with R packages. The Familydata data frame comes with
Epicalc. If you want to read a dataset from a Stata file format, such as
"family.dta", simply type use("family.dta") without typing the data
command above. The dataset is copied into memory in a default data frame called
.data. If .data already exists, it will be overwritten by the new data frame. The
original Familydata, however, remains.
In fact, all the datasets in Epicalc were originally in one of the file formats of .dta,
.rec, .csv or .txt. These datasets in their original format can be downloaded from
http://medipe.psu.ac.th/Epicalc/. If you download the files and set the working
directory for R to the default folder "C:\RWorkplace", you do not need to type
data(Familydata) and use(Familydata), but instead simply type:
> use("family.dta")

46
The original Stata file will be read into R and saved as .data. If successful, it will
make no difference whether you type data(Familydata) followed by
use(Familydata) or simply use("family.dta").
In most parts of the book, we chose to tell you to type data(Familydata) and
use(Familydata) instead of use("family.dta") because the dataset is
already in the Epicalc package, which is readily available when you practice
Epicalc to this point. However, putting "filename.extension" as the argument such
as use("family.dta") in this chapter or use("timing.dta") in the next
chapter, and so forth, may give you a real sense of reading actual files instead of the
approach that is used in this book.
The command use also automatically places the data frame, .data, into the
search path. Type:
> search()
You will see that .data is in the second position of the search path. Type:
> ls()
You will see only the Familydata object, and not .data because the name of
this object starts with a dot and is classified as a hidden object. In order to show that
.data is really in the memory, Type
> ls(all=TRUE)
You will see .data in the first position of the list.
.data is resistant to zap()
Type the following at the R console:
> zap()
> ls(all=TRUE)
The object Familydata is gone but .data is still there. However, the
attachment to the search path is now lost
> search()
In order to put it back to the search path, we have to attach to it manually.
> attach(.data)
The advantage of use() is not only that it saves time by making attach and
detach unnecessary, but .data is placed in the search path as well as being
made the default data frame. Thus des() is the same as des(.data), summ()
is equivalent to summ(.data).
> des()
> summ()
47
The sequence of commands zap, data(datafile), use(datafile),
des() and summ() is recommended for starting an analysis of almost all datasets
in this book. A number of other commands from the Epicalc package work based
on this strategy of making .data the default data frame and exclusively attached
to the search path (all other data frames will be detached, unless the argument
'clear=FALSE' is specified in the use function). For straightforward data
analysis, the command use() is sufficient to create this setting. In many cases
where the data that is read in needs to be modified, it is advised to rename or copy
the final data frame to .data. Then detach from the old .data and re-attach to
the most updated one in the search path.
This strategy does not have any effect on the standard functions of R. The users of
Epicalc can still use the other commands of R while still enjoying the benefit of
Epicalc.
48
Exercises________________________________________________
With several datasets provided with Epicalc, use the last commands (zap, data,
use, des, summ) to have a quick look at them.

49
Chapter 5: Simple Data Exploration
Data exploration using Epicalc
In the preceding chapter, we learnt the commands zap for clearing the workspace
and memory, use for reading in a data file and codebook, des and summ for
initially exploring the data frame, keeping in mind that these are all Epicalc
commands. The use function places the data frame into a hidden object called
.data, which is automatically attached to the search path. In this chapter, we will
work with more examples of data frames as well as ways to explore individual
variables.
> zap()
> data(Familydata)
> use(Familydata)
> des()
Anthropometric and financial data of a hypothetical family
No. of observations = 11
Variable Class Description
1 code character
2 age integer Age(yr)
3 ht integer Ht(cm.)
4 wt integer Wt(kg.)
5 money integer Pocket money(B.)
6 sex factor
The first line after the des() command shows the data label, which is the
descriptive text for the data frame. This is usually created by the software that was
used to enter the data, such as Epidata or Stata. Subsequent lines show variable
names and individual variable descriptions. The variable 'code' is a character string
while 'sex' is a factor. The other variables have class integer. A character variable is
not used for statistical calculations but simply for labelling purposes or for record
identification. Recall that a factor is what R calls a categorical or group variable.
The remaining integer variables ('age', 'ht', 'wt' and 'money') are intuitively
continuous variables. The variables 'code' and 'sex' have no variable descriptions
due to omission during the preparation of the data prior to data entry.

50
> summ()
Anthropometric and financial data of a hypothetical family
No. of observations = 11
Var. name Obs. mean median s.d. min. max.
1 code
2 age 11 45.73 47 24.11 6 80
3 ht 11 157.18 160 14.3 120 172
4 wt 11 54.18 53 12.87 22 71
5 money 11 1023.18 500 1499.55 5 5000
6 sex 11 1.364 1 0.505 1 2
As mentioned in the previous chapter, the command summ gives summary statistics
of all variables in the default data frame, in this case .data. Each of the six
variables has 11 observations, which means that there are no missing values in the
dataset. Since the variable 'code' is class 'character' (as shown from the 'des()'
command above), information about this variable is not shown. The ages of the
subjects in this dataset range from 6 to 80 (years). Their heights range from 120 to
172 (cm), and their weights range from 22 to 71 (kg). The variable 'money' ranges
from 5 to 5,000 (baht). The mean and median age, height and weight are quite close
together indicating relatively non-skewed distributions. The variable 'money' has a
mean much larger than the median signifying that the distribution is right skewed.
The last variable, 'sex', is a factor. However, the statistics are based on the
unclassed values of this variable. We can see that there are two levels, since the
minimum is 1 and the maximum is 2. For factors, all values are stored internally as
integers, i.e. only 1 or 2 in this case. The mean of 'sex' is 1.364 indicating that 36.4
percent of the subjects have the second level of the factor (in this case it is male). If
a factor has more than two levels, the mean will have no useful interpretation.
Codebook
The function summ gives summary statistics of each variable, line by line. This is
very useful for numeric variables but less so for factors, especially those with more
than two levels. Epicalc has another function that gives summary statistics for a
numeric variable and a frequency table with level labels and codes for factors.
> codebook()
Anthropometric and financial data of a hypothetical family
code :
A character vector
==================
age : Age(yr)
obs. mean median s.d. min. max.
11 45.727 47 24.11 6 80
==================

51
ht : Ht(cm.)
obs. mean median s.d. min. max.
11 157.182 160 14.3 120 172
==================
wt : Wt(kg.)
obs. mean median s.d. min. max.
11 54.182 53 12.87 22 71
==================
money : Pocket money(B.)
obs. mean median s.d. min. max.
11 1023.182 500 1499.55 5 5000
==================
sex :
Label table: sex1
code Frequency Percent
F 1 7 63.6
M 2 4 36.4
==================
Unlike results from the summ function, codebook deals with each variable in the
data frame with more details. If a variable label exists, it is given in the output. For
factors, the name of the table for the label of the levels is shown and the codes for
the levels are displayed in the column, followed by frequency and percentage of the
distribution. The function is therefore very useful. The output can be used to write a
table of baseline data of the manuscript coming out from the data frame.
The output combines variable description with summary statistics for all numeric
variables. For 'sex', which is a factor, the original label table is named 'sex1' where
1 = F and 2 = M. There are 7 females and 4 males in this family.
Note that the label table for codes of a factor could easily be done in the phase of
preparing data entry using Epidata with setting of the ".chk" file. If the data is
exported in Stata format, then the label table of each variable will be exported along
with the dataset. The label tables are passed as attributes in the corresponding data
frame. The Epicalc codebook command fully utilizes this attribute allowing users
to see and document the coding scheme for future referencing.
We can also explore individual variables in more detail with the same commands
des and summ by placing the variable name inside the brackets.
> des(code)
'code' is a variable found in the following source(s):
Var. source Var. order Class # records Description
.data 1 character 11

52
The output tells us that 'code' is in .data. Suppose we create an object, also called
'code', but positioned freely outside the hidden data frame.
> code <- 1
> des(code)
'code' is a variable found in the following source(s):
Var. source Var. order Class # records Description
.GlobalEnv numeric 1
.data 1 character 11
The output tells us that there are two 'codes'. The first is the recently created object
in the global environment. The second is the variable inside the data frame, .data.
To avoid confusion, we will delete the recently created object 'code'.
> rm(code)
After removal of 'code' from the global environment, the latest des() command
will describe the old 'code' variable, which is the part of .data, and remains
usable. Using des() with other variables shows similar results.
Now try the following command:
> summ(code)
This gives an error because 'code' is a character vector. Next type:
> summ(age)
Obs. mean median s.d. min. max.
11 45.727 47 24.11 6 80
20 40 60 80
Distribution of Age(yr)
Subject sorted by X−axis values

53
The results are similar to what we saw from summ. However, since the argument to
the summ command is a single variable a graph is also produced showing the
distribution of age.
The main title of the graph contains a description of the variable after the words
"Distribution of". If the variable has no description, the variable name will be
presented instead. Now try the following commands:
> abc <- 1:20
> summ(abc)
Obs. mean median s.d. min. max.
20 10.5 10.5 5.916 1 20
5 101520
Distribution of abc
Subject sorted by X−axis values
The object 'abc' has a perfectly uniform distribution since the dots form a straight
line.
The graph produced by the command summ is called a sorted dot chart. A dot chart
has one axis (in this case the X-axis) representing the range of the variable. The
other axis, the Y-axis, labelled 'Subject sorted by X-axis values', represents each
subject or observation sorted by the values of the variable. For the object 'abc', the
smallest number is 1, which is plotted at the bottom left, then 2, 3, 4 etc. The final
observation is 20, which is plotted at the top right. The values increase from one
observation to the next higher value. Since this increase is steady, the line is
perfectly straight.

54
To look at a graph of age again type:
> summ(age)
> axis(side=2, 1:length(age))
The 'axis' command adds tick marks and value labels on the specified axis (in this
case, 'side=2' denotes the Y-axis). The ticks are placed at values of 1, 2, 3, up to 11
(which is the length of the vector age). The ticks are omitted by default since if the
vector is too long, the ticks would be too congested. In this session, the ticks will
facilitate discussion.
20 40 60 80
Distribution of Age(yr)
Subject sorted by X−axis values
1234567891011
To facilitate further detailed consideration, the sorted age vector is shown with the
graph.
> sort(age)
[1] 6 16 18 42 46 47 49 58 69 72 80
The relative increment on the X-axis from the first observation (6 years) to the
second one (16 years) is larger than from the second to the third (18 years). Thus
we observe a steep increase in the Y-axis for the second pair. From the 3rd
observation to the 4th (42 years), the increment is even larger than the 1st one; the
slope is relatively flat. In other words, there is no dot between 20 and 40 years. The
4th, 5th, 6th and 7th values are relatively close together, thus these give a relatively
steep increment on the Y-axis.
> summ(ht)
Obs. mean median s.d. min. max.
11 157.182 160 14.303 120 172
> axis(side=2, 1:length(ht))
> sort(ht)
[1] 120 148 153 155 158 160 163 163 167 170 172

55
The distribution of height as displayed in the graph is interesting. The shortest
subject (120cm) is much shorter than the remaining subjects. In fact, she is a child
whereas all the others are adults. There are two persons (7th and 8th records) with the
same height (163cm). The increment on the Y-axis is hence vertical.
120 130 140 150 160 170
Distribution of Ht(cm.)
Subject sorted by X−axis values
1234567891011
> summ(wt)
> axis(side=2, 1:length(wt))
30 40 50 60 70
Distribution of Wt(kg.)
Subject sorted by X−axis values
1234567891011

56
There is a higher level of clustering of weight than height from the 2nd to 7th
observations; these six persons have very similar weights. From the 8th to 11th
observations, the distribution is quite uniform.
For the distribution of the money variable, type:
> summ(money)
Money has the most skewed distribution. The first seven persons carry less than
1,000 baht. The next two persons carry around 2,000 baht whereas the last carries
5,000 baht, far away (in the X-axis) from the others. This is somewhat consistent
with a theoretical exponential distribution.
0 1000 2000 3000 4000 5000
Distribution of Pocket money(B.)
Subject sorted by X−axis values
1234567891011
Next have a look at the distribution of the sex variable.
> summ(sex)
Obs. mean median s.d. min. max.
11 1.364 1 0.5 1 2
The graph shows that four out of eleven (36.4%, as shown in the textual statistics)
are male. When the variable is factor and has been labelled, the values will show
the name of the group.

57
246810
Distribution of sex
Subject sorted by X−axis values
FM
1234567891011
In fact, a better result can be obtained by typing
> tab1(sex)
sex :
Frequency Percent Cum. percent
F 7 63.6 63.6
M 4 36.4 100.0
Total 11 100.0 100.0
FM
Distribution of sex
Frequency
01234567
7
4

58
Since there are two sexes, we may simply compare the distributions of height by
sex.
> summ(ht, by=sex)
For sex = F
Obs. mean median s.d. min. max.
7 151 155 14.514 120 163
For sex = M
Obs. mean median s.d. min. max.
4 168 168.5 3.916 163 172
120 130 140 150 160 170
Distribution of Ht(cm.) by sex
F
M
Clearly, males are taller than females.
Dotplot
In addition to summ and tab1, Epicalc has another exploration tool called
dotplot.
> dotplot(money)
While the graph created from the summ command plots individual values against its
rank, dotplot divides the scale into several small equally sized bins (default =
40) and stacks each record into its corresponding bin. In the figure above, there are
three observations at the leftmost bin and one on the rightmost bin. The plot is very
similar to a histogram except that the original values appear on the X-axis. Most
people are more acquainted with a dot plot than the sorted dot chart produced by
summ. However, the latter plot gives more detailed information with better
accuracy. When the sample size is small, plots by summ are more informative.

59
When the sample size is large (say above 200), dotplot is more understandable
by most people.
0 5 10 15 20
Distribution of Pocket money(B.)
Frequency
0 1000 2000 3000 4000 5000
> dotplot(money, by=sex)
Distribution of Pocket money(B.) by sex
F
M
0 1000 2000 3000 4000 5000
The command summ easily produces a powerful graph. One may want to show
even more information. R can serve most purposes, but the user must spend some
time learning it.

60
Let's draw a sorted dot chart for the heights. The command below should be
followed step by step to see the change in the graphic window resulting from typing
in each line. If you make a serious mistake simply start again from the first line.
Using the up arrow key, the previous commands can be edited before executing
again.
> zap()
> data(Familydata)
> use(Familydata)
> sortBy(ht)
> .data
The command sortBy, unlike its R base equivalent sort, has a permanent effect
on .data. The whole data frame has been sorted in ascending order by the value
of height.
> dotchart(ht)
Had the data not been sorted, the incremental pattern would not be seen.
> dotchart(ht, col=unclass(sex), pch=18)
Showing separate colours for each sex is done using the 'unclass' function. Since
'sex' is a factor, uclassing it gives a numeric vector with 1 for the first level (female)
and 2 for the second level (male). Colours can be specified in several different ways
in R. One simple way is to utilise a small table of colours known as the palette. The
default palette has 9 colours, where the number 1 represents black, the number 2
represents the red, up to 9, which represents gray. Thus the black dots represent
females and the red dots represent males. More details on how to view or
manipulate the palette can be found in the help pages.
To add the y-axis, type the following command:
> axis(side=2,at=1:length(ht), labels=code, las=1)
The argument 'las' is a graphical parameter, which specifies the orientation of tick
labelling on the axes. When 'las=1', all the labels of the ticks will be horizontal to
the axis. A legend is added using the 'legend' command:
> legend(x=130, y=10, legend=c("female","male"), pch=18,
col=1:2, text.col=1:2)
The argument 'pch' stands for point or plotting character. Code 18 means the
symbol is a solid diamond shape which is more prominent than pch=1 (a hollow
round dot). Note that 'col' is for plot symbol colours and 'text.col' is for text colour
in the legend.
To add the titles type:
> title(main="Distribution of height")
> title(xlab="cms")

61
120 130 140 150 160 170
K
B
C
F
I
G
A
H
E
D
J
female
male
Distribution of height
cms
To summarise, after use(datafile), des and summ, individual variables can
be explored simply by summ(var.name) and summ(var.name,
by=group.var). In addition to summary statistics, the sorted dot chart can be
very informative. The dotplot command trades in accuracy of the individual
values with frequency dot plots, which is similar to a histogram. Further use of this
command will be demonstrated when the number of observations is larger.

62
Exercise_________________________________________________
Try the following simulations for varying sample sizes and number of groups.
Compare the graph of different types from using three commands, summ, dotplot
and boxplot. For each condition, which type of graph is the best?
## Small sample size, two groups.
> grouping1 <- rep(1:2, times=5)
> random1 <- rnorm(10, mean=grouping1, sd=1)
> summ(random1, by=grouping1)
> dotplot(random1, by=grouping1)
> boxplot(random1 ~ grouping1)
## Moderate sample size, three groups.
> grouping2 <- c(rep(1, 10),rep(2, 20), rep(3, 45))
> random2 <- rnorm(75, mean=grouping2, sd=1)
> summ(random2, by=grouping2)
> dotplot(random2, by=grouping2)
> boxplot(random2 ~ grouping2, varwidth=TRUE, col=1:3,
horizontal=TRUE, las=1)
## Large sample size, four groups.
> grouping3 <- c(rep(1, 100), rep(2, 200), rep(3,450), rep(4,
1000))
> random3 <- rnorm(1750, mean=grouping3, sd=1)
> summ(random3, by=grouping3)
> dotplot(random3, by=grouping3)
> boxplot(random3 ~ grouping3, varwidth=TRUE, col=1:4,
horizontal=TRUE, las=1)
Which kind of graph is the best for the different conditions?
63
Chapter 6: Date and Time
One of the purposes of an epidemiological study is to describe the distribution of a
population's health status in terms of time, place and person. Most data analyses,
however deal more with a person than time and place. In this chapter, the emphasis
will be on time.
The time unit includes century, year, month, day, hour, minute and second. The
most common unit that is directly involved in epidemiological research is day. The
chronological location of day is date, which is a serial function of year, month and
day.
There are several common examples of the use of dates in epidemiological studies.
Birth date is necessary for computation of accurate age. In an outbreak
investigation, description of date of exposure and onset is crucial for computation
of incubation period. In follow up studies, the follow-up time is usually marked by
date of visit. In survival analysis, date starting treatment and assessing outcome are
elements needed to compute survival time.
Computation functions related to date
Working with dates can be computationally complicated. There are leap years,
months with different lengths, days of the week and even leap seconds. Dates can
even be stored in different eras depending on the calendar. The basic task in
working with dates is to link the time from a fixed date to the display of various
date formats that people are familiar with.
Different software use different starting dates for calculating dates. This is called an
epoch. R uses the first day of 1970 as its epoch (day 0). In other words, dates are
stored as the number of days since 1st January 1970, with negative values for earlier
dates. Try the following at the R console:

64
> a <- as.Date("1970-01-01")
> a
[1] "1970-01-01"
> class(a)
[1] "Date"
> as.numeric(a)
[1] 0
The first command above creates an object 'a' with class Date. When converted to
numeric, the value is 0. Day 100 would be
> a + 100
[1] "1970-04-11"
The default display format in R for a Date object is ISO format. The American
format of 'month, day, year' can be achieved by
> format(a, "%b %d, %Y")
[1] "Jan 01, 1970"
The function 'format' displays the object 'a' in a fashion chosen by the user. '%b'
denotes the month in the three-character abbreviated form. '%d' denotes the day
value and '%Y' denotes the value of the year, including the century.
Under some operating system conditions, such as the Thai Windows operating
system, '%b' and '%a' may not work or may present some problems with fonts. Try
the following command:
> Sys.setlocale("LC_ALL", "C")
Now try the above format command again. This time, it should work. R has the
'locale' or working location set by the operating system, which varies from country
to country. "C" is the motherland of R and the language "C" is American English.
'%A' and '%a' are formats representing full and abbreviated weekdays, respectively,
while '%B' and '%b' represent the months. These are language and operating system
dependent.
Try these:
> b <- a + (0:3)
> b
Then change the language and see the effect on the R console and graphics device.
> setTitle("German"); summ(b)
> setTitle("French"); summ(b)
> setTitle("Italian"); summ(b)

65
The command setTitle changes the locale as well as the fixed wording of the
locale to match it. To see what languages are currently available in Epicalc try:
> titleString()
> titleString(return.look.up.table=TRUE)
Note that these languages all use standard ASCII text characters. The displayed
results from these commands will depend on the operating system. Thai and
Chinese versions of Windows may give different results.
You may try setTitle with different locales. To reset the system to your original
default values, type
> setTitle("")
For languages with non-standard ASCII characters, the three phrases often used in
Epicalc ("Distribution of", "by", and "Frequency") can be changed to your own
language. For more details see the help for the 'titleString' function.
Manipulation of title strings, variable labels and levels of factors using your own
language means you can have the automatic graphs tailored to your own needs. This
is however a bit too complicated to demonstrate in this book. Interested readers can
contact the author for more information.
Epicalc displays the results of the summ function in ISO format to avoid country
biases. The graphic results in only a few range of days, like the vector 'b', has the X-
axis tick mark labels in '%a%d%b' format. Note that '%a' denotes weekday in the
three-character abbreviated form.
In case the dates are not properly displayed, just solve the problem by typing:
> Sys.setlocale("LC_ALL", "C")
Then, check whether the date format containing '%a' and '%b' works.
> format(b, "%a %d%b%y")
[1] "Thu 01Jan70" "Fri 02Jan70" "Sat 03Jan70" "Sun 04Jan70"
> summ(b)
obs. mean median s.d. min. max.
4 1970-01-02 1970-01-02 <NA> 1970-01-01 1970-01-04

66
Distribution of b
Subject sorted by X−axis values
Thu01Jan Fri02Jan Sat03Jan Sun04Jan
Reading in a date variable
Each software has its own way of reading in dates. Transferring date variables from
one software to another sometimes results in 'characters' which are not directly
computable by the destination software.
R can read in date variables from Stata files directly but not older version of
EpiInfo with <dd/mm/yy> format. This will be read in as 'character' or 'AsIs'.
When reading in data from a comma separated variable (.csv) file format, it is a
good habit to put an argument 'as.is = TRUE' in the read.csv command to avoid
date variables being converted to factors.
It is necessary to know how to create date variables from character format. Create a
vector of three dates stored as character:
> date1 <- c("07/13/2004","08/01/2004","03/13/2005")
> class(date1)
[1] "character"
> date2 <- as.Date(date1, "%m/%d/%Y")
The format or sequence of the original characters must be reviewed. In the first
element of 'date1', '13', which can only be day (since there are only 12 months), is
in the middle position, thus '%d' must also be in the middle position. Slashes '/'
separate month, day and year. This must be correspondingly specified in the format
of the as.Date command.

67
> date2
[1] "2004-07-13" "2004-08-01" "2005-03-13"
> class(date2)
[1] "Date"
The default date format is "%Y-%m-%d". Changing into the format commonly
used in Epicalc is achieved by:
> format(date2, "%d%b%y")
[1] "13Jul04" "01Aug04" "13Mar05"
Other formats can be further explored by the following commands:
> help(format.Date)
> help(format.POSIXct)
It is not necessary to have all day, month and year presented. For example, if only
month is to be displayed, you can type:
> format(date2, "%B")
[1] "July" "August" "March"
To include day of the week:
> format(date2, "%a-%d%b")
[1] "Tue-13Jul" "Sun-01Aug" "Sun-13Mar"
> weekdays(date2)
[1] "Tuesday" "Sunday" "Sunday"
This is the same as
> format(date2, "%A")
Conversely, if there are two or more variables that are parts of date:
> day1 <- c("12","13","14");
> month1 <- c("07","08","12")
> paste(day1, month1)
[1] "12 07" "13 08" "14 12"
> as.Date(paste(day1,month1), "%d %m")
[1] "2007-07-12" "2007-08-13" "2007-12-14"
The function paste joins two character variables together. When the year value is
omitted, R automatically adds the current year of the system in the computer.
Dealing with time variables
A Date object contains year, month and day values. For time, values of hour,
minute and second must be available.

68
A sample dataset involving a number of timing variables was collected from
participants of a workshop on 14th December 2004, asking about personal
characteristics, times they went to bed, woke up, and arrived at the workshop. The
workshop commenced at 8.30 am.
> zap()
> data(Timing)
> use(Timing)
Note: ______________________________________________________________________
The original file for this dataset is in Stata format and is called "timing.dta". If you have
downloaded this file into the working directory (as explained in the previous chapter), you
may simply type use("timing.dta").
> des()
Timing questionnaire
No. of observations =18
Variable Class Description
1 id integer
2 gender factor
3 age integer
4 marital factor
5 child integer No. of children
6 bedhr integer Hour to bed
7 bedmin integer Min. to bed
8 wokhr integer Hour woke up
9 wokmin integer Min. woke up
10 arrhr integer Hour arrived at wkshp
11 arrmin integer Min. arrived at wkshp
> summ()
Timing questionnaire
No. of observations = 18
Var. name Obs. mean median s.d. min. max.
1 id 18 9.5 9.5 5.34 1 18
2 gender 18 1.611 2 0.502 1 2
3 age 18 31.33 27.5 12.13 19 58
4 marital 18 1.611 2 0.502 1 2
5 child 18 0.33 0 0.59 0 2
6 bedhr 18 7.83 1.5 10.34 0 23
7 bedmin 18 19.83 17.5 17.22 0 45
8 wokhr 18 5.61 6 1.61 1 8
9 wokmin 18 23.83 30 17.2 0 49
10 arrhr 18 8.06 8 0.24 8 9
11 arrmin 18 27.56 29.5 12.72 0 50

69
To create a variable equal to the time the participants went to bed, the function
ISOdatetime is used.
> bed.time <- ISOdatetime(year=2004, month=12, day=14,
hour=bedhr, min=bedmin, sec=0, tz="")
> summ(bed.time)
Min. Median Mean Max.
2004-12-14 00:00 2004-12-14 01:30 2004-12-14 08:09 2004-12-14 23:45
51015
Distribution of bed.time
Subject sorted by X−axis values
00:00 03:00 06:00 09:00 12:00 15:00 18:00 21:00
The graph shows interrupted time. In fact, the day should be calculated based on the
time that the participants went to bed. If the participant went to bed between 12pm
(midday) and 12am (midnight), then the day should be December 13th, otherwise
the day should be the 14th, the day of the workshop. To recalculate the day type:
> bed.day <- ifelse(bedhr > 12, 13, 14)
The ifelse function chooses the second argument if the first argument is TRUE,
the third otherwise.
> bed.time <- ISOdatetime(year=2004, month=12, day=bed.day,
hour=bedhr, min=bedmin, sec=0, tz="")
> summ(bed.time)
Min. Median Mean Max.
2004-12-13 21:30 2004-12-14 00:22 2004-12-14 00:09 2004-12-14 02:30

70
51015
Distribution of bed.time
Subject sorted by X−axis values
21:30 22:30 23:30 00:30 01:30 02:30
After this, woke up time and arrival time can be created and checked.
> woke.up.time <- ISOdatetime(year=2004, month=12, day=14,
hour=wokhr, min=wokmin, sec=0, tz="")
> summ(woke.up.time)
Min. Median Mean Max.
2004-12-14 01:30 2004-12-14 06:10 2004-12-14 06:00 2004-12-14 08:20
The object 'woke.up.time' looks normal, although one or two participants woke
up quite early in the morning. To compute sleeping duration type:
> sleep.duration <- difftime(woke.up.time, bed.time)
> summ(sleep.duration)
Obs. mean median s.d. min. max.
18 5.844 6.25 1.7 1 8

71
12345678
Distribution of sleep.duration
Subject sorted by X−axis values
hours
A suitable choice of units for 'sleep.duration' are chosen, but can be changed
by the user if desired. Somebody slept very little.
Displaying two variables in the same graph
The command summ of Epicalc is not appropriate for displaying two variables
simultaneously. The original dotchart of R is the preferred graphical method.
> sortBy(bed.time)
> plot(bed.time, 1:length(bed.time),
xlim=c(min(bed.time),max(woke.up.time)), pch=18, col="blue",
ylab=" ", yaxt="n")
The argument 'xlim' (x-axis limits) is set to be the minimum of 'bed.time' and the
maximum of 'woke.up.time'. The argument yaxt="n" suppresses the tick labels
on the Y-axis.
> n <- length(bed.time)
> segments(bed.time, 1:n, woke.up.time, 1:n)
> points(woke.up.time, 1:n, pch=18, col="red")
> title(main="Distribution of Bed time and Woke up time")

72
23:00 01:00 03:00 05:00 07:00
Distribution of Bed time and woke up time
Subject sorted by bed time
Finally, arrival time at the workshop is created:
> arrival.time <- ISOdatetime(year=2004, month=12, day=14,
hour=arrhr, min=arrmin, sec=0, tz="")
> summ(arrival.time)
Min. Median Mean Max.
2004-12-14 08:00 2004-12-14 08:30 2004-12-14 08:30 2004-12-14 09:20
> summ(arrival.time, by=gender)
For gender = male
Min. Median Mean Max.
2004-12-14 08:25 2004-12-14 08:30 2004-12-14 08:37 2004-12-14 09:20
For gender = female
Min. Median Mean Max.
2004-12-14 08:00 2004-12-14 08:30 2004-12-14 08:26 2004-12-14 08:50

73
Distribution of arrival.time by gender
08:00 08:20 08:40 09:00 09:20
male
female
The command summ works relatively well with time variables. In this case, it
demonstrates that there were more females than males. Females varied their arrival
time considerably. Quite a few of them arrived early because they had to prepare
the workshop room. Most males who had no responsibility arrived just in time.
There was one male who was slightly late and one male who was late by almost one
hour.
Age and difftime
Computing age from birth date usually gives more accurate results than obtaining
age from direct interview. The following dataset contains subject's birth dates that
we can use to try computing age.
> zap()
> data(Sleep3)
> use(Sleep3)
> des()
Sleepiness among the participants in a workshop
No. of observations =15
Variable Class Description
1 id integer code
2 gender factor gender
3 dbirth Date Date of birth
4 sleepy integer Ever felt sleepy in workshop
5 lecture integer Sometimes sleepy in lecture
6 grwork integer Sometimes sleepy in group work
7 kg integer Weight in Kg
8 cm integer Height in cm

74
The date of analysis was 13th December 2004.
> age <- as.Date("2005-12-13") - dbirth
The variable 'age' has class difftime as can be seen by typing:
> class(age)
[1] "difftime"
The unit of age is 'days'.
> attr(age, "unit")
[1] "days"
To display age:
> age
Time differences of 7488, 10557, 8934, 9405, 11518, 11982,
10741, 11122, 12845, 9266, 11508, 12732, 11912, 7315,
NA days
> summ(age)
Obs. mean median s.d. min. max.
15 10520 10930 1787.88 7315 12850
8000 9000 10000 11000 12000 13000
Distribution of age
Subject sorted by X−axis values
days
Note the one missing value. To convert age into years:
> age.in.year <- age/365.25
> attr(age.in.year, "units") <- "years"
> summ(age.in.year)
Obs. mean median s.d. min. max.
14 28.81 29.93 4.89 20.03 35.17

75
> summ(age.in.year, by=gender)
For gender = male
Obs. mean median s.d. min. max.
4 29.83 32.06 6.712 20.03 35.17
For gender = female
Obs. mean median s.d. min. max.
10 28.4 29.16 4.353 20.5 34.86
20 25 30 35
Distribution of age.in.year by gender
years
male
female
Note that there is a blank dotted line at the top of the female group. This a missing
value. Males have an obviously smaller sample size with the same range as women
but most observations have relatively high values.
76
Exercises________________________________________________
In the Timing dataset:
Compute time since woke up to arrival at the workshop.
Plot time to bed, time woke up and arrival time on the same axis.

77
Chapter 7: An Outbreak Investigation:
Describing Time
An outbreak investigation is a commonly assigned task to an epidemiologist. This
chapter illustrates how the data can be described effectively. Time and date data
types are not well prepared and must be further modified to suit the need of the
descriptive analysis.
On 25 August 1990, the local health officer in Supan Buri Province of Thailand
reported the occurrence of an outbreak of acute gastrointestinal illness on a national
handicapped sports day. Dr Lakkana Thaikruea and her colleagues went to
investigate. The dataset is called Outbreak.. Most variable names are self-
explanatory. Variables are coded as 0 = no, 1 = yes and 9 = missing/unknown for
three food items consumed by participants: 'beefcurry' (beef curry), 'saltegg' (salted
eggs) and 'water'. Also on the menu were eclairs, a finger-shaped iced cake of
choux pastry filled with cream. This variable records the number of pieces eaten by
each participant. Missing values were coded as follows: 88 = "ate but do not
remember how much", while code 90 represents totally missing information. Some
participants experienced gastrointestinal symptoms, such as: nausea, vomiting,
abdominal pain and diarrhea. The ages of each participant are recorded in years
with 99 representing a missing value. The variables 'exptime' and 'onset' are the
exposure and onset times, which are in character format, or 'AsIs' in R terminology.
Quick exploration
Let's look at the data. Type the following at the R console:
> zap()
> data(Outbreak)
> use(Outbreak)
> des()
No. of observations =1094

78
Variable Class Description
1 id numeric
2 sex numeric
3 age numeric
4 exptime AsIs
5 beefcurry numeric
6 saltegg numeric
7 eclair numeric
8 water numeric
9 onset AsIs
10 nausea numeric
11 vomiting numeric
12 abdpain numeric
13 diarrhea numeric
> summ()
No. of observations = 1094
Var. name valid obs. mean median s.d. min. max.
1 id 1094 547.5 547.5 315.95 1 1094
2 sex 1094 0.66 1 0.47 0 1
3 age 1094 23.69 18 19.67 1 99
4 exptime
5 beefcurry 1094 0.95 1 0.61 0 9
6 saltegg 1094 0.96 1 0.61 0 9
7 eclair 1094 11.48 2 27.75 0 90
8 water 1094 1.02 1 0.61 0 9
9 onset
10 nausea 1094 0.4 0 0.49 0 1
11 vomiting 1094 0.38 0 0.49 0 1
12 abdpain 1094 0.35 0 0.48 0 1
13 diarrhea 1094 0.21 0 0.41 0 1
We will first define the cases, examine the timing in this chapter and investigate the
cause in the next section.
Case definition
It was agreed among the investigators that a case should be defined as a person who
had any of the four symptoms: 'nausea', 'vomiting', 'abdpain' or 'diarrhea'. A case
can then by computed as follows:
> case <- (nausea==1)|(vomiting==1)|(abdpain==1)|(diarrhea==1)
To incorporate this new variable into .data, we use the function label.var.
> label.var(case, "diseased")
The variable 'case' is now incorporated into .data as the 14th variable together
with a variable description.
> des()

79
Timing of exposure
For the exposure time, first look at the structure of this variable.
> str(exptime)
Class 'AsIs' chr [1:1094] "25330825180000" "25330825180000"...
The values of this variable contain fourteen digits. The first four digits represent the
year in the Buddhist Era (B.E.) calendar, which is equal to A.D. + 543. The 5th and
6th digits contain the two digits representing the month, the 7th and 8th represent the
day, 9th and 10th hour, 11th and 12th minute and 13th and 14th second.
> day.exptime <- substr(exptime, 7, 8)
The R command susbtr (from substring), extracts parts of character vectors.
First, let's look at the day of exposure.
> tab1(day.exptime)
day.exptime :
Frequency %(NA+) cum.%(NA+) %(NA-) cum.%(NA-)
25 1055 96.4 96.4 100 100
<NA> 39 3.6 100.0 0 100
Total 1094 100.0 100.0 100 100
The day of exposure was 25th of August for all records (ignoring the 39 missing
values). We can extract the exposure time in a similar fashion.
> hr.exptime <- substr(exptime, 9, 10)
> tab1(hr.exptime)
All values seem acceptable, with the mode at 18 hours.
> min.exptime <- substr(exptime, 11, 12)
> tab1(min.exptime)
These are also acceptable, although note that most minutes have been rounded to
the nearest hour or half hour. The time of exposure can now be calculated.
> time.expose <- ISOdatetime(year=1990, month=8, day=
day.exptime, hour=hr.exptime, min=min.exptime, sec=0)
Then, the variable is labelled in order to integrate it into the default data frame.
> label.var(time.expose, "time of exposure")
> summ(time.expose)
Min. Median Mean Max.
1990-08-25 11:00 1990-08-25 18:00 1990-08-25 18:06 1990-08-25 21:00

80
0 200 400 600 800 1000
Distribution of time of exposure
Subject sorted by X−axis values
11:00 13:00 15:00 17:00 19:00 21:00
A dotplot can also be produced.
> dotplot(time.expose)
0 100 200 300 400 500 600 700
Distribution of time of exposure
Frequency
11:00 13:00 15:00 17:00 19:00 21:00
HH:MM
Almost all the exposure times were during dinner; between 6 and 7 o'clock, while
only a few were during the lunchtime.

81
Timing the onset
Exploration of the data reveals that three non-cases have non-blank onset times.
> sum(!is.na(onset[!case])) # 3
For simplicitiy we will make sure that the 'onset' variable is exclusively used for
cases only.
> onset[!case] <- NA
The extraction of symptom onset times is similar to that for time of exposure.
> day.onset <- substr(onset, 7, 8)
> tab1(day.onset)
day.onset :
Frequency %(NA+) cum.%(NA+) %(NA-) cum.%(NA-)
25 429 39.2 39.2 92.9 92.9
26 33 3.0 42.2 7.1 100.0
<NA> 632 57.8 100.0 0.0 100.0
Total 1094 100.0 100.0 100.0 100.0
Of the subjects interviewed, 57.8% had a missing 'onset' and subsequently on the
derived variable 'day.onset'. This was due to either having no symptoms or the
subject could not remember. Among those who reported the time, 429 had the onset
on the 25th August. The remaining 33 had it on the day after.
> hr.onset <- substr(onset, 9, 10)
> tab1(hr.onset)
> min.onset <- substr(onset, 11, 12)
> tab1(min.onset)
> time.onset <- ISOdatetime(year = 1990, month = 8, day =
day.onset, hour = hr.onset, min = min.onset, sec=0, tz="")
> label.var(time.onset, "time of onset")
> summ(time.onset)
0 200 400 600 800 1000
Distribution of time of onset
Subject sorted by X−axis values
15:00 18:00 21:00 00:00 03:00 06:00 09:00

82
Min. Median Mean Max.
1990-08-25 15:00 1990-08-25 21:30 1990-08-25 21:40 1990-08-26 09:00
The upper part of the graph is empty due to the many missing values.
Perhaps a better visual display can be obtained wth a dotplot.
> dotplot(time.onset)
0 50 100 150 200 250
Distribution of time of onset
Frequency
15:00 18:00 21:00 00:00 03:00 06:00 09:00
HH:MM
Both graphs show the classic single-peak epidemic curve, suggesting a single point
source. The earliest case had the onset at 3pm in the afternoon of August 25. The
majority of cases had the onset in the late evening. By the next morning, only a few
cases were seen. The last reported case occurred at 9am on August 26.
Incubation period
The analysis for incubation period is straightforward.
> incubation.period <- time.onset - time.expose
> label.var(incubation.period, "incubation period")
> summ(incubation.period)
Valid obs. mean median s.d. min. max.
462 3.631 3.5 1.28 1 14.5
> dotplot(incubation.period, las=1)
Incubation period has a median of 3.5 hours with right skewness.

83
0 20 40 60 80 100 120 140
Distribution of incubation period
Frequency
2 4 6 8 10 12 14
hours
Paired plot
We now try putting the exposure and onset times in the same graph. A sorted graph
usually gives more information, so the whole data frame is now sorted.
> sortBy(time.expose)
With this large sample size, it is better to confine the graph to plot only complete
values for both 'time.exposure' and 'time.onset'. This subset is kept as another data
frame called 'data.for.graph'.
> data.for.graph <- subset(.data, (!is.na(time.onset) &
!is.na(time.expose)), select = c(time.onset, time.expose))
> des(data.for.graph)
No. of observations =462
Variable Class Description
1 time.onset POSIXt
2 time.expose POSIXt
There are only two variables in this data frame. All the missing values have been
removed leaving 462 records for plotting.
> n <- nrow(data.for.graph)
> with(data.for.graph, {
plot(time.expose, 1:n, col="red", pch=20,
xlim = c(min(time.expose), max(time.onset)),
main = "Exposure time & onset of food poisoning outbreak",
xlab = "Time (HH:MM)", ylab = "Subject ID" )
} )

84
The plot pattern looks similar to that produced by 'summ(time.expose)'. The point
character, 'pch', is 20, which plots small solid circles, thus avoiding too much
overlapping of the dots. The limits on the horizontal axis are from the minimum of
time of exposure to the maximum of the time of onset, allowing the points of onset
to be put on the same graph. These points are added in the following command:
> with(data.for.graph, {
points(time.onset, 1:n, col="blue", pch=20)
} )
The two sets of points are paired by subjects. A line joining each pair is now drawn
by the segments command.
> with(data.for.graph, {
segments(time.expose, 1:n, time.onset, 1:n, col = "grey45")
} )
The complete list of built in colour names used by R can be found from
colours().
A legend is inserted to make the graph self-explanatory.
> legend(x = ISOdatetime(1990,8,26,2,0,0), y = 150,
legend=c("Exposure time","Onset time","Incubation period"),
pch=c(20,20,-1), lty=c(0,0,1),col=c("red","blue","grey45"),
bg="lavender")
The left upper corner of the legend is located at the right lower quadrant of the
graph with the x coordinate being 2am and y coordinate being 150. The legend
consists of three items as indicated by the character vector. The point characters and
colours of the legend are specified in accordance with those inside the graph. The
last argument, incubation period, has 'pch' equal to -1 indicating no point is to be
drawn. The line type, 'lty', of exposure time and onset are 0 (no line) whereas that
for incubation period is 1 (solid line). The colours of the points and the lines are
corresponding to that in the graph. The background of the legend was given
lavender colour to supersede any lines or points behind the legend.
Finally, some text describing the key statistic of this variable is placed inside the
plot area at 5pm and centred at 200.
> text(x = ISOdatetime(1990, 8, 25, 17, 0, 0), y = 200, labels
= "median incubation period = 3.5 hours", srt = 90)

85
The middle of the text is located at x = 19:00 and y = 200 in the graph. The
parameter 'srt' comes from 'string rotation'. In this case a rotation of 90 degrees
gives the best picture. Since the background colour is already grey, white text
would be suitable.
0 100 200 300 400
Exposure time & onset of food poisoning outbreak
Time (HH:MM)
Subject ID sorted by Exposure Time
11:00 15:00 19:00 23:00 03:00 07:00
Exposure time
Onset
incubation period
Median incubation period = 3.5 hours
Analysis of timing data has finished. The main data frame .data is saved for
further use in the next chapter.
> save(.data, file = "Chapter7.Rdata")
Reference
Thaikruea, L., Pataraarechachai, J., Savanpunyalert, P., Naluponjiragul, U. 1995
An unusual outbreak of food poisoning. Southeast Asian J Trop Med Public Health
26(1):78-85.

86
Exercise_________________________________________________
We recode the original time variable 'onset' right from the beginning using the
command:
> onset[!case] <- NA
For the data frame that we are passing to the next chapter, has the variable 'onset'
been changed? If not, why and how can we get a permanent change to the data
frame that we are using? Note: the built-in Outbreak dataset cannot be modified.

87
Chapter 8: An Outbreak Investigation:
Risk Assessment
The next step in analysing the outbreak is to deal with the level of risk. However,
let's first load the data saved from the preceding chapter.
> zap()
> load("Chapter7.Rdata")
> ls(all=TRUE) # .data is there
> search() # No dataset in the search path
> use(.data)
> search() # .data is ready for use
> des()
Recoding missing values
There are a number of variables that need to be recoded. The first variable to recode
is 'age'. The Epicalc command recode is used here. More details on this function
are given in chapter 10.
> recode(var = age, old.value = 99, new.value = NA)
The variables with the same recoding scheme, 9 to missing value, are 'beefcurry',
'saltegg' and 'water'. They can be recoded together in one step as follows:
> recode(vars = c(beefcurry, saltegg, water), 9, NA)
The three variables can also be changed to factors with value labels attached.
> beefcurry <- factor(beefcurry, labels=c("No","Yes"))
> saltegg <- factor(saltegg, labels=c("No","Yes"))
> water <- factor(water, labels=c("No","Yes"))
> label.var(beefcurry, "Beefcurry")
> label.var(saltegg, "Salted egg")
> label.var(water, "Water")
For 'eclair', the absolute missing value is 90. This should be recoded first, then re-
check the data frame for the missing values.
> recode(eclair, 90, NA)
> summ()

88
All variables look fine except 'eclair' which still contains the value 80 representing
"ate but not remember how much". We will analyse its relationship with 'case' by
considering it as an ordered categorical variable.
At this stage, cross tabulation can be performed by using the Epicalc command
tabpct.
> tabpct(eclair, case)
Distribution of diseased by eclair
eclair
diseased
0 0.5 12
3456810
12
192080
FALSE
TRUE
The width of the columns of the mosaic graph denotes the relative frequency of that
category. The highest frequency is 2 pieces followed by 0 and 1 piece. The other
numbers have relatively low frequencies; particularly the 5 records where 'eclair'
was coded as 80.
There is a tendency of increasing red area or attack rate from left to right indicating
that the risk was increased when more pieces of eclair were consumed. We will use
the distribution of these proportions to guide our grouping of eclair consumption.
The first column of zero consumption has a very low attack rate, therefore it should
be a separate category. Only a few took half a piece and this could be combined
with those who took only one piece. Persons consuming 2 pieces should be kept as
one category as their frequency is very high. Others who ate more than two pieces
should be grouped into another category. Finally, those coded as '80' will be
dropped due to the unknown amount of consumption as well as its low frequency.
> eclairgr <- cut(eclair, breaks = c(0, 0.4, 1, 2, 79),
include.lowest = TRUE, labels=c("0","1","2",">2"))
The argument 'include.lowest=TRUE' indicates that 0 eclair must be included
in the lowest category.

89
It is a good practice to label the new variable in order to describe it as well as put it
into .data.
> label.var(eclairgr, "pieces of eclair eaten")
> tabpct(eclairgr, case)
======== lines omitted =========
Row percent
diseased
pieces of eclai FALSE TRUE Total
0 279 15 294
(94.9) (5.1) (100)
1 54 51 105
(51.4) (48.6) (100)
2 203 243 446
(45.5) (54.5) (100)
>2 38 89 127
(29.9) (70.1) (100)
======== lines omitted =========
Distribution of diseased
by pieces of eclair eaten
pieces of eclair eaten
diseased
012>2
FALSE
TRUE
The attack rate or percentage of diseased in each category of exposure, as shown in
the bracket of the column TRUE, increases from 5.1% among those who did not eat
any eclairs to 70.1% among those heavy eaters of eclair. The graph output is similar
to the preceding one except that the groups are more concise.
We now have a continuous variable of 'eclair' and a categorical variable of 'eclairgr'.
The next step is to create a binary exposure for eclair.
> eclair.eat <- eclair > 0
> label.var(eclair.eat, "eating eclair")
This binary exposure variable is now similar to the others, i.e. 'beefcurry', 'saltegg'
and 'water'

90
Exploration of age and sex
Simple exploration can be done by using the summ and dotplot commands on
'age', such as:
> summ(age); dotplot(age)
0 50 100 150 200
Distribution of age
Frequency
0 102030405060
The age distribution classified by sex can easily be done via:
> sex <- factor(sex, labels=c("Female","Male"))
> summ(age, by = sex)
> dotplot(age, by = sex)
Distribution of age by Sex
Female
Male
0 102030405060

91
An alternative is to draw a population pyramid of age and sex, using the Epicalc
function pyramid, as follows:
> pyramid(age, sex)
Female
200 150 100 50 0
[0,5]
(5,10]
(10,15]
(15,20]
(20,25]
(25,30]
(30,35]
(35,40]
(40,45]
(45,50]
(50,55]
(55,60]
Male
0 50 100 150 200
From the resulting graph, young adult males (aged 10-20 years) predominated. The
binwidth can also be changed to have fewer age groups.
> pyramid(age, sex, binwidth = 15)
The table generated by the pyramid function can also be shown, as follows:
> pyramid(age, sex, printTable=TRUE)
Tabulation of age by sex (frequency).
sex
age Female Male
[0,5] 1 1
(5,10] 12 7
(10,15] 170 217
(15,20] 81 223
(20,25] 25 112
(25,30] 41 54
(30,35] 23 20
(35,40] 7 10
(40,45] 5 8
(45,50] 3 12
(50,55] 0 1
(55,60] 0 1
The percentage (for each sex) can also be shown.
> pyramid(age, sex, printTable=TRUE, percent="each")

92
Tabulation of age by sex (percentage of each sex).
Female Male
[0,5] 0.272 0.150
(5,10] 3.261 1.051
(10,15] 46.196 32.583
(15,20] 22.011 33.483
(20,25] 6.793 16.817
(25,30] 11.141 8.108
(30,35] 6.250 3.003
(35,40] 1.902 1.502
(40,45] 1.359 1.201
(45,50] 0.815 1.802
(50,55] 0.000 0.150
(55,60] 0.000 0.150
Finally, both the table and age group can be saved as R objects for future use.
> (age.tab <- pyramid(age, sex))
> ageGrp <- age.tab$ageGroup
> label.var(ageGrp, "Age Group")
> des()
> des("age*")
No. of observations =1094
Variable Class Description
3 age numeric
20 ageGrp factor Age Group
The des function can also display variables using wild card matching.
> des("????????")
No. of observations =1094
Variable Class Description
11 vomiting numeric
13 diarrhea numeric
18 eclairgr factor pieces of eclair eaten
We have spent some time learning these features of Epicalc for data exploration (a
topic of the next chapter). Let's return to the analysis of risk, which is another main
feature of Epicalc.
Comparison of risk: Risk ratio and attributable risk
There are basically two methods for comparing the risk of disease in different
exposure groups.
Risk ratio – RR (also called relative risk) is the ratio of the risk of getting disease
among the exposed compared with that among the non-exposed. It indicates how
many times the risk would increase had the subject changed their status from non-
exposed to exposed. The increment is considered in fold, thus has a mathematical
notation of being a 'multiplicative model'.

93
Risk difference on the other hand, suggests the amount of risk gained or lost had the
subject changed from non-exposed to exposed. The increase is absolute, and has the
mathematical notation of an additive model.
The Epicalc command cs is used to analyse such relationships.
> cs(case, eclair.eat)
eating eclair
case FALSE TRUE Total
FALSE 279 300 579
TRUE 15 383 398
Total 294 683 977
Rne Re Rt
Risk 0.05 0.56 0.41
Estimate Lower95 Upper95
Risk difference (attributable risk) 0.51 0.44 0.58
Risk ratio 10.99 8 15.1
Attr. frac. exp. -- (Re-Rne)/Re 0.91
Attr. frac. pop. -- (Rt-Rne)/Rt*100 % 87.48
'Rne', 'Re' and 'Rt' are the risks in the non-exposed, exposed and the total
population, respectively. 'Rne' in this instance is 15/294 = 0.05. Similarly 'Re' is
383/683 = 0.56 and 'Rt' is 398/977 = 0.41. The risk difference is 'Re' - 'Rne', an
absolute increase of 51% whereas the risk ratio is 'Re' / 'Rne', a increase of 11 fold.
The risk of getting the disease among those eating eclairs could have been reduced
by 91% and the risk among all participants in the sports carnival could have been
reduced by 87.5% had they not eaten any eclairs.
The risk ratio is an important indicator for causation. A risk ratio above 10 would
strongly suggest a causal relationship.
The risk difference has more public health implications than the risk ratio. A high
risk ratio may not be of public health importance if the disease is very rare. The risk
difference, on the other hand, measures direct health burden and the need for health
services. Those who ate eclairs had a high chance (55%) of getting symptoms. A
reduction of 51% substantially reduces the burden of the sport game attendants and
the hospital services.
Attributable fraction population indicates that the number of cases could have been
reduced by 87% had the eclairs not been contaminated. This outbreak was transient
if we consider a chronic overwhelming problem such as cardio-vascular disease or
cancer. Even a relatively low level of fraction of risk attributable to tobacco in the
population, say 20%, could lead to a huge amount of resources spent in health
services.

94
Attributable fraction exposure has little to do with level of disease burden in the
population. It is equal to 1 - RR-1, and is therefore just another way to express the
risk ratio.
We have eclair as a cause of disease. There are some interventions that can prevent
the diseases such as vaccination, education, law enforcement and improvement of
environment. In our example, let's assume that not eating eclairs is a prevention
process.
> eclair.no <- !eclair.eat # The ! sign means "NOT"
> cs(case, eclair.no)
eclair.no
case FALSE TRUE Total
FALSE 300 279 579
TRUE 383 15 398
Total 683 294 977
Rne Re Rt
Risk 0.56 0.05 0.41
Estimate Lower95 Upper95
Risk difference (absolute change) -0.51 -0.44 -0.58
Risk ratio 0.09 0.12 0.07
protective efficacy (%) 90.9
Number needed to treat (NNT) 1.96
The risk among the exposed (not eating eclair) is lower than that among the non-
exposed (eating eclair). The risk difference changes sign to negative. The risk ratio
reciprocates to a small value of 0.09. Instead of displaying the attributable fraction
exposure and attributable fraction population, the command shows protective
efficacy and number needed to treat (NNT).
From the protective efficacy value, the exposure to the prevention program would
have reduced the risk of the eclair eater (unexposed under this hypothetical
condition) by 90.9%. NNT is just the reciprocal of the negative of risk difference. A
reduction of risk of 0.51 comes from an intervention on one individual. A reduction
of 1 would need to come from an intervention on 1/0.51 or 1.96 individuals. An
intervention of high NNT would need to be given to many individuals just to avert
one unwanted event. The lowest possible level of NNT is 1 or perfect prevention
which also has 100% protective efficacy. NNT is a part of measurement of
worthiness of intervention (either prevention or treatment) technology. To avert the
same type of unwanted event, an intervention with low NNT is preferred to another
with high NNT, although the cost must also be taken into account.
Dose-response relationship
One of the criteria for causation is the evidence of a dose-response relationship. If a
higher dose of exposure is associated with a higher level of risk in a linear fashion,
then the exposure is likely to be the cause.

95
We now explore the relationship between the risk of getting the disease and the
number of eclairs consumed.
> cs(case, eclairgr)
eclairgr
case 0 1 2 >2
FALSE 279 54 203 38
TRUE 15 51 243 89
Absolute risk 0.05 0.49 0.54 0.7
Risk ratio 1 9.52 10.68 13.74
lower 95% CI 6.6 8.04 10.11
upper 95% CI 13.72 14.19 18.66
Chi-squared = 237.12 , 3 d.f., P value = 0
Fisher's exact test (2-sided) P value = 0
12 51020
Risk ratio from a cohort study
eclairgr
Risk ratio
012>2
1
9.52 10.68
13.74
( 6.6 , 13.72 ) ( 8.04 , 14.19 )
( 10.11 , 18
.66
The risk ratio increases as the dose of exposure to eclairs increases. The step from
not eating to the first group (up to one piece) is wide whereas further increases are
shown at a flatter slope. The p values in the output are both zero. In fact, they are
not really zero, but have been rounded to three decimal places. The default
rounding of decimals of odds ratios and relative risks is two and for the p-values is
three. See 'help(cs)' for more details on the arguments.
Before finishing this chapter, the current data is saved for further use.
> save(.data, file = "Chapter8.Rdata")
96
Exercise_________________________________________________
Compute the attributable risk and risk ratio of 'beefcurry', 'saltegg' and 'water'. Are
these statistically significant? If so, what are the possible reasons?

97
Chapter 9: Odds Ratios, Confounding and
Interaction
Having assessed various parameters of risk of participants in the outbreak in the last
chapter, we now focus on confounding among various types of foods.
The assessment of risk in this chapter is changed from the possible cause. The next
step in analysing the outbreak is to deal with the level of risk. Let's first load the
data saved from the preceding chapter.
> zap()
> load("Chapter8.Rdata")
> use(.data)
Odds and odds ratio
Odds has a meaning related with probability. If 'p' is the probability, p/(1-p) is
known as the odds. Conversely, the probability would be equal to odds/(odds+1).
> tab1(case)
Frequency Percent
FALSE 625 57.1
TRUE 469 42.9
Total 1094 100.0
The probability of being a case is 469/1094 or 42.9%. In this situation where non-
cases are coded as 0 and cases as 1, the probability is
> mean(case)
On the other hand the odds of being a case is 469/625 = 0.7504, or
> mean(case)/(1 - mean(case))
Note that when there are missing values in the variable, the 'mean' must have 'na.rm
=TRUE' in the argument. For example the odds of eating eclairs is:
> m.eclair <- mean(eclair.eat, na.rm = TRUE)
> m.eclair /(1 - m.eclair)
[1] 2.323129

98
While a probability always ranges from 0 to 1, an odds ranges from 0 to infinity.
For a cohort study we may compute the ratios of the odds of being a case among the
exposed vs the odds among the non-exposed.
> table(case, eclair.eat)
eclair.eat
case FALSE TRUE
FALSE 279 300
TRUE 15 383
The conventional method for computing the odds ratio is therefore:
> (383/300)/(15/279)
[1] 23.746
This is the same value as the ratio of the odds of being exposed among cases and
among non-cases.
> (383/15)/(300/279)
It is also equal to the ratio between the cross-product.
> (383 * 279)/(300 * 15)
Epicalc has a function cc producing odds ratio, its 95% confidence interval,
performing the chi-squared and Fisher's exact tests and drawing a graph for the
explanation.
> cc(case, eclair.eat)
eating eclair
case FALSE TRUE Total
FALSE 279 300 579
TRUE 15 383 398
Total 294 683 977
OR = 23.68
95% CI = 13.74 43.86
Chi-squared = 221.21 , 1 d.f. , P value = 0
Fisher's exact test (2-sided) P value = 0
The value of odds ratio from the cc function is slightly different from the
calculations that we have done. This is because the 'cc' function uses the exact
method to calculate the odds ratio.
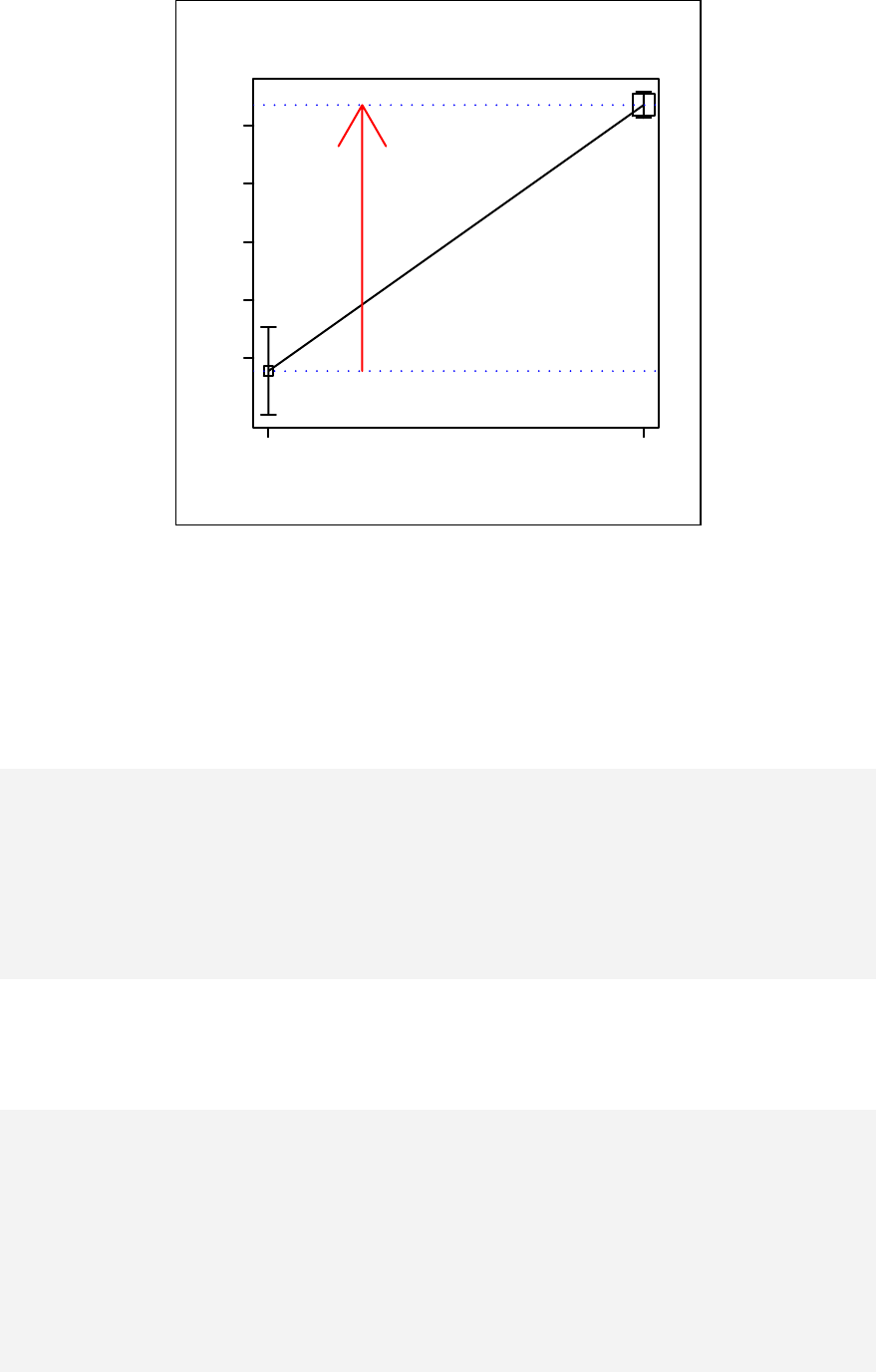
99
Odds ratio from prospective/X−sectional study
Exposure category
Odds of outcome
non−exposed exposed
1
1/16
1/8
1/4
1/2
OR = 23.68
95% CI = 13.74 , 43.86
The vertical lines of the resulting graph show the estimate and 95% confidence
intervals of the two odds of being diseased, non-exposed on the left and exposed on
the right, computed by the conventional method. The size of the box at the estimate
reflects the relative sample size of each subgroup. There were more exposed than
non-exposed. The non-exposed group has the estimate value slightly below 1/16
since it real value is 15/279. The exposed group estimate is 383/300 or slightly
higher than 1. The latter value is over 23 times of the former.
> fisher.test(table(case, eclair.eat))$estimate
odds ratio
23.681
> fisher.test(table(case, eclair.eat))$conf.int
[1] 13.736 43.862
attr(,"conf.level")
[1] 0.95
Confounding and its mechanism
For 'saltegg', the odds ratio can be similarly computed.
> cc(case, saltegg)
saltegg
case 0 1 Total
FALSE 66 554 620
TRUE 21 448 469
Total 87 1002 1089
OR = 2.54
95% CI = 1.51 4.44
Chi-squared = 13.82 , 1 d.f. , P value = 0
Fisher's exact test (2-sided) P value = 0

100
The total valid records for computation is 1,089, which is higher than 977 of the
cross-tabulation results between 'case' and 'eclair.eat'. The value of the odds ratio is
not as high but is of statistical significance. Similar to the analysis of the odds ratio
for 'eclair', the size of the box on the right is much larger than that on the left
indicating a large proportion of exposure.
Both eclairs and salted eggs have significant odds ratios and were consumed by a
large proportion of participants. Let's check the association between these two
variables.
> cc(saltegg, eclair.eat, graph = FALSE)
eating eclair
saltegg FALSE TRUE Total
0 53 31 84
1 241 647 888
Total 294 678 972
OR = 4.58
95% CI = 2.81 7.58
Chi-squared = 47.02 , 1 d.f. , P value = 0
Fisher's exact test (2-sided) P value = 0
There might be only one real cause and the other was just confounded. In other
words, those participants who ate salted eggs also tended to eat eclairs. Stratified
analysis gives the details of confounding as follows.
> mhor(case, saltegg, eclair.eat)
Stratified prospective/X−sectional analysis
Outcome= case , Exposure= saltegg
Odds of outcome
eclair.eatTRUE: OR = 1.07 (0.48, 2.36)
eclair.eatFALSE: OR = 0.87 (0.22, 5)
MH−OR = 1.02 (0.54, 1.93)
homogeneity test P value = 0.787
Non−exposed Exposed
1
2
1/32
1/16
1/8
1/4
1/2

101
Stratified analysis by eclair.eat
OR lower lim. upper lim. P value
eclair.eat FALSE 0.874 0.224 5.00 0.739
eclair.eat TRUE 1.073 0.481 2.36 0.855
M-H combined 1.023 0.541 1.93 0.944
M-H Chi2(1) = 0 , P value = 0.944
Homogeneity test, chi-squared 1 d.f.=0.07, P value = 0.787
The above analysis of association between the disease and salted egg is stratified by
level of eclair consumption based on records that have valid values of 'case',
'eclair.eat' and 'saltegg'. There are two main parts of the results. The first part
concerns the odds ratio of the exposure of interest in each stratum defined by the
third variable, in this case 'eclair.eat' as well as the odds ratio and chi-squared
statistics computed by Mantel-Haenszel's technique. The second part suggests
whether the odds ratio of these strata can be combined. We will focus on the first
part at this stage and come back to the second part later.
In both strata, the odds ratios are close to 1 and are not statistically significant. The
slopes of the two lines are rather flat. The Mantel-Haenszel (MH) odds ratio, also
called the adjusted odds ratio, is the weighted average of the two odds ratios, which
is also close to 1. Both the stratum-specific odds ratios and the MH odds ratio are
not significantly different from 1 but the crude odds ratio is significantly different.
The distortion of the crude result from the adjusted result is called confounding.
The mechanism of this confounding can be explained with the above graph. The
upper line of the graph denotes the subset or stratum of subjects who had eaten
eclairs whereas the lower line represents those who had not. The upper line lies far
above the lower line meaning that the subset of eclair eaters had a much higher risk
than the non-eaters. The distance between the two lines is between 16 to 32 fold of
odds. It is important to note that the distribution of subjects in this study is
imbalanced in relation to eclair and salted eggs consumption. On the right-hand side
(salted egg consumers), there are alot more eclair eaters (upper box) than non-eaters
(lower box). The centre of this right-hand side then tends to be closer to the location
of the upper box. In contrast, on the left-hand side, or those not consuming salted
eggs, the number of eclair non-consumers (as represented by the size of the lower
box) is higher than that of the consumers. The centre of the left-hand side therefore
tends to lie closer to the lower box. In other words, when the two strata are
combined, the (weighted average) odds of diseased among the salted egg consumers
is therefore closer to the upper box. The opposite is true for the left-hand side where
the weighted average odds of getting the disease should be closer to the lower box.
A higher average odds on the right-hand side leads to the crude odds ratio being
higher than one. This crude odds ratio misleads us into thinking that salted egg is
another cause of the disease where in fact it was just confounded by eclairs. The
level of confounding is noteworthy only if both of the following two conditions are
met.

102
Firstly, the stratification factor must be an independent risk factor. Secondly, there
must be a significant association between the stratification factor and the exposure
of interest.
Now we check whether the relationship between the disease and eclair is
confounded by salted egg.
> mhor(case, eclair.eat, saltegg)
Stratified analysis by saltegg
OR lower lim. upper lim. P value
saltegg 0 19.3 4.68 117.9 6.06e-07
saltegg 1 24.8 13.56 49.7 2.42e-51
M-H combined 24.3 13.96 42.4 8.12e-49
M-H Chi2(1) = 215.63 , P value = 0
Homogeneity test, chi-squared 1 d.f. = 0.11 , P value = 0.736
Stratified prospective/X−sectional analysis
Outcome= case , Exposure= eclair.eat
Odds of outcome
saltegg1: OR = 24.78 (13.56, 49.71)
saltegg0: OR = 19.31 (4.68, 117.88)
MH−OR = 24.32 (13.96, 42.36)
homogeneity test P value = 0.736
Non−exposed Exposed
1
2
1/32
1/16
1/8
1/4
1/2
Stratified by 'saltegg', the odds ratio of eclair.eat in both strata (19.3 and 24.8) and
the MH odds ratio (24.3) are strong and close to the crude odds ratio (23.68).
Graphically, the two lines of strata are very close together indicating that 'saltegg' is
not an independent risk factor. In each of the exposed and non-exposed groups, the
odds for disease are close and the weighted average odds is therefore not influenced
by the number of subjects. Thus not being an independent risk factor, a variable
cannot confound another exposure variable.

103
Interaction and effect modification
Let's analyse the association between eating eclairs and the developing acute
gastrointestinal illness again but now using 'beefcurry' as the stratification factor.
> mhor(case, eclair.eat, beefcurry)
Stratified analysis by beefcurry
OR lower lim. upper lim. P value
beefcurry 0 5.33 1.53 21.7 3.12e-03
beefcurry 1 31.63 16.49 68.1 4.79e-56
M-H combined 24.08 13.85 41.9 1.39e-48
M-H Chi2(1) = 214.56 , P value = 0
Homogeneity test, chi-squared 1 d.f. = 7.23 , P value = 0.007
Stratified prospective/X−sectional analysis
Outcome= case , Exposure= eclair.eat
Odds of outcome
beefcurry1: OR = 31.63 (16.49, 68.11)
beefcurry0: OR = 5.33 (1.53, 21.71)
MH−OR = 24.08 (13.85, 41.89)
homogeneity test P value = 0.007
Non−exposed Exposed
1
1/32
1/16
1/8
1/4
1/2
The slopes of the odds ratios of the two strata cross each other. Among those who
had not eaten beef curry, the odds of getting the disease among those not eating
eclair was slightly below 1 in 6. The odds increases to over 1 in 2 for those who ate
eclairs only. This increase is 5.33 fold or an odds ratio of 5.33. In contrast, the
baseline odds among those eating beef curry only (left point of the green line) is
somewhere between 1 in 32 and 1 in 16, which is the lowest risk group in the graph.
The odds however steps up very sharply to over 1 among the subjects who had
eaten both eclairs and beef curry. The homogeneity test in the last line concludes
that the odds ratios are not homogeneous. In statistics, this is called significant
interaction. In epidemiology, the effect of 'eclair' was modified by 'beefcurry'.
Eating beef curry increased the harmful effect of eclair or increased the
susceptibility of the person to get ill by eating eclairs.
We now check the effect of 'beefcurry' stratified by 'eclair.eat'.

104
> mhor(case, beefcurry, eclair.eat)
Stratified analysis by eclair.eat
OR lower lim. upper lim. P value
eclair.eat FALSE 0.376 0.111 1.47 0.1446
eclair.eat TRUE 2.179 1.021 4.83 0.0329
M-H combined 1.401 0.769 2.55 0.2396
M-H Chi2(1) = 1.38 , P value = 0.24
Homogeneity test, chi-squared 1 d.f. = 6.78 , P value = 0.009
Stratified prospective/X−sectional analysis
Outcome= case , Exposure= beefcurry
Odds of outcome
eclair.eatTRUE: OR = 2.18 (1.02, 4.83)
eclair.eatFALSE: OR = 0.38 (0.11, 1.47)
MH−OR = 1.4 (0.77, 2.55)
homogeneity test P value = 0.009
Non−exposed Exposed
1
2
1/32
1/16
1/8
1/4
1/2
The effect of beef curry among those not eating eclairs tends to be protective but
without statistical significance. The odds ratio among those eating eclairs is 2.18
with statistical significance. The homogeneity test also concludes that the two odds
ratios are not homogeneous. The stratification factor eclair has modified the effect
of beef curry from a non-significant protective factor to a significant risk factor.
Tabulation and stratified graphs are very useful in explaining confounding and
interaction. However, they are limited to only two or three variables. For a dataset
with a larger number of variables, logistic regression is needed. We put the new
variable 'eclair.eat' into .data by using label.var and save the whole data
frame for future use with logistic regression.
> label.var(eclair.eat, "ate at least some eclair")
> save(.data, file="chapter9.Rdata")
Exercise_________________________________________________
Analyse the effect of drinking water on the odds of the disease. Check whether it is
confounded with eating eclairs or other foods. Check for interaction.

105
Chapter 10: Basic Data Management
Data cleaning
The previous datasets were relatively clean. Let's look at an uncleaned dataset that
came from a family planning clinic in the mid 1980's. The coding scheme can be
seen from
> help(Planning)
Cleaning will enable you to learn Epicalc functions for data management.
> zap()
> data(Planning)
> des(Planning)
Note that all of the variable names are in upper case. To convert them to lower case
simply type the following command.
> names(Planning) <- tolower(names(Planning))
> use(Planning)
> summ()
No. of observations = 251
Var. name Obs. mean median s.d. min. max.
1 id 251 126 126 72.6 1 251
2 age 251 27.41 27 4.77 18 41
3 relig 251 1.14 1 0.59 1 9
4 ped 251 3.83 3 2.32 0 9
5 income 251 2.84 2 2.38 1 9
6 am 251 20.66 20 5.83 15 99
7 reason 251 1.55 1 0.86 1 9
8 bps 251 137.74 110 146.84 0 999
9 bpd 251 97.58 70 153.36 0 999
10 wt 251 52.85 51.9 11.09 0 99.9
11 ht 251 171.49 154 121.82 0 999
Identifying duplication ID
Let's look more closely at the 'id' object. This variable represents the unique
identification number for the subject.

106
> summ(id)
Valid obs. mean median s.d. min. max.
251 125.996 126 72.597 1 251
0 50 100 150 200 250
Distribution of id
Subject sorted by X−axis values
The graph looks quite uniformly distributed. However, the mean of id (125.996) is
not equal to what it should be.
> mean(1:251)
[1] 126
There must be some duplication and/or some gaps within these id numbers.
Looking carefully at the graph, there is no noticeable irregularity.
To check for duplication, we can type the following:
> any(duplicated(id))
[1] TRUE
The result tells us that there is in fact at least one duplicated id. To specify the id of
the duplicates type:
> id[duplicated(id)]
[1] 215
We see that id = 215 has one duplicate. Further inspection of the data reveals that
the record numbers are 215 and 216. These two records should be investigated as to
which one is incorrect. One of them should be changed to 'id' = 216.

107
Missing values
This file is not ready for analysis yet. As is often the case, the data were coded
using outlier numbers to represent missing codes.
We first explore the data with boxplots.
> boxplot(.data, horizontal=T, las=1, main="Family Planning
Clinic")
id
age
relig
ped
income
am
reason
bps
bpd
wt
ht
0 200 400 600 800 1000
Family Planning Clinic
The outlier values of 'bps', 'bpd' and 'ht' are rather obvious. These are confirmed
with the numerical statistics from the summ command seen earlier in this chapter.
In this dataset, the value '9' represents a missing code for religion (3rd variable),
patient education (4th variable), income group (5th variable) and reason for family
planning (7th variable).
There are four methods of changing values to missing (NA). The first method is
based on the function replace, which handles one vector or variable at a time.
The second uses extraction and indexing with subscript '[]'. This method can
handle either a vector or array (several variables at the same time). The third
method is based on the transform command. These three methods use
commands that are native to R. The fourth method uses the recode command
from Epicalc, which is by far the simplest method.

108
We will use the replace function for the 3rd variable, 'relig', extraction and
indexing for the 4th to 7th variables, 'ped', 'am', 'income' and 'reason', transform
for the 'wt' variable, and finally recode for the remaining necessary variables.
Replacing values in a data frame
We wish to replace all occurrences of 9 with the missing value 'NA'. The replace
function handles only one variable at a time.
> summ(relig)
We wish to replace all occurrences of 9 with the missing value 'NA'. The replace
function handles only one variable at a time.
> replace(relig, relig==9, NA) -> .data$relig
There are three essential arguments to the replace function; the target vector, the
index vector and the value. See the online help for more detailed information on its
usage.
The first argument, 'relig', is the target vector containing values to be replaced.
The second argument, 'relig==9', is the index vector specifying the condition, in
this case, whenever 'relig' is equal to 9. The final argument, 'NA', is the new
value that will replace the old value of 9. Thus, whenever 'relig' is equal to 9, it
will be replaced with 'NA'.
Note that the index vector, or condition for change, need not be the same vector as
the target vector. For example, one may want to coerce the value of diastolic blood
pressure to be missing if the systolic blood pressure is missing.
Secondly, replace is a function, not a command. It has no effect on the original
values. The values obtained from this function must be assigned to the original
values using the assignment operators, '->' or '<-'.
Right now, the variable has changed.
> summ(.data$relig)
Obs. mean median s.d. min. max.
250 1.108 1 0.31 1 2
There was one subject with a missing value leaving 250 records for statistical
calculations. The remaining subjects have values of one and two only for 'religion'.
Changing values with extraction and indexing
The first variable to be replaced with this method is the 6th one, 'am', which denotes
age at first marriage.

109
> summ(.data$am)
Valid obs. mean median s.d. min. max.
251 20.657 20 5.83 15 99
The value 99 represents a missing value code during data entry. Note that the mean,
median and standard deviation are not correct due to this coding of missing values.
Instead of using the previous method, the alternative is:
> .data$am[.data$am==99] <- NA
With the same three components of the target vector, conditions and replacing
value, this latter command is slightly more straightforward than the above one using
the replace function.
This method can also be used for many variables with the same missing code. For
example, the 4th, 5th and 7th variables all use the value 9 as the code for a missing
value.
> .data[,c(4,5,7)][.data[,c(4,5,7)]==9] <- NA
All the 4th, 5th, and 7th variables of .data that have a value of 9 are replaced with
'NA'. The above command can be explained as follows. There are two layers of
subsets of .data marked by '[ ]'.
.data[,c(4,5,7)] means extract all rows of columns 4, 5 and 7, ('ped',
'income' and 'reason').
'[.data[,c(4,5,7)]==9]'means the subset of each particular column where
the row is equal to 9.
' <- NA' means the epression on the left is to be assigned a missing value (NA).
Thus, for these four variables, any element in which the value equals 9 will be
replaced by 'NA'.
Transforming variables in a data frame
The function transform does a similar job as the previous methods described
above. For example, to transform 'wt'
> transform(.data, wt=ifelse(wt>99, NA, wt)) -> .data
The expression inside the function tells R to replace values of 'wt' that are greater
than 99 with the NA value. The resulting object is saved into the data frame.
Now check the 'wt' variable inside the data frame.
> summ(.data$wt)
Valid obs. mean median s.d. min. max.
246 51.895 51.45 8.91 0 73.8

110
Note the two outliers on the left-hand side of the graph. Similar to the results of
previous methods, transform did not change the 'wt' variable inside the data
frame in the search path.
> summ(wt)
Valid obs. mean median s.d. min. max.
251 52.851 51.9 11.09 0 99.9
Note that the transformed data frame does not keep the variable labels or
descriptions with it. The new .data will have all variable descriptions removed.
So this method reduces the power of Epicalc.
Recoding values using Epicalc
The function recode in Epicalc was created to make data transformation easier.
Similar to other commands in Epicalc, for example use, des, summ, tab1 and
label.var, the command recode is restricted to the setting of having .data
as the default data frame.
We require replacing the values '999' to a missing value for variables 'bps', 'bpd' and
'ht'. The command is simple. Let's start with 'bps'.
> recode(var=bps, old.value=999, new.value=NA)
> summ(.data)
Notice that the variable 'bps' has been changed. In fact, recode has automatically
detached the old data frame and attached to the new one, as shown below.
> summ(bps)
Valid obs. mean median s.d. min. max.
244 113.033 110 14.22 0 170
Variable 'bps' in .data and that in the search path have been synchronised. The
number of valid records is reduced to 244 and the maximum is now 170 not 999.
This automatic updating has also affected other variables in the search path that we
changed before.
> summ(am)
Valid obs. mean median s.d. min. max.
250 20.344 20 3.06 15 31
When the variable 'am' is used as the argument of summ, the program looks for an
independent object called 'am', which does not exist. It then looks in the search
path. Since the data frame in the search path ('search()[2]') has been updated with
the new .data, the variable 'am' that is used now is the updated one which has
been changed from the command in the preceding section. The command recode
makes variable manipulation simpler than the above three standard R methods.

111
The command recode can be further simplified:
> recode(bpd, 999, NA)
> recode(ht, 999, NA)
> summ()
All the maxima have been corrected but the minima of 0 are also missing values for
the last four variables plus 'ped'. We can use recode to turn all the zeros into
missing values in one step.
> recode(c(ped, bps, bpd, wt, ht), 0, NA)
> summ()
No. of observations = 251
Var. name Obs. mean median s.d. min. max.
============ variables #1, #2, #3 omitted =========
4 ped 226 3.3 2 1.66 2 7
============ variables #5, #6, #7 omitted =========
8 bps 243 113.5 110 12.25 90 170
9 bpd 243 72.02 70 9.9 60 110
10 wt 245 52.11 51.5 8.28 16 73.8
11 ht 245 155.3 153 28.08 141 585
The minimum weight of 16kg and the maximum height of 585cm are dubious and
in fact should not be accepted. Any weight below 30kg and any height above
200cm should also be treated as missing (unless there are very good reasons to
leave them as is). A scatter plot is also useful here.
> plot(wt, ht, pch=19)
20 30 40 50 60 70
200 300 400 500 600
wt
ht

112
The outlier is clearly seen (top left corner). To correct these errors type:
> recode(wt, wt < 30, NA)
> recode(ht, ht > 200, NA)
> summ()
It should be noted that after cleaning, the effective sample size is somewhat less
than the original value of 251. The box plot of all variables now has a different
appearance.
> boxplot(.data, horizontal=T, main="Family Planning Clinic",
las=1)
id
age
relig
ped
income
am
reason
bps
bpd
wt
ht
0 50 100 150 200 250
Family Planning Clinic
Labelling variables with 'label.var'
When there are only a few variables in the dataset, all of which are for common
purposes, such as 'age', 'sex', or 'education', naming is not a problem. However,
when there are a large number of variables, it is difficult to have intuitively
understandable names for each variable. A system separating variable labels from
variable names is a better way of documentation.
R does not come with a built-in variable labelling facility. Epicalc however, adds in
this useful facility in a simple way.
Firstly, the variable names of the data are displayed.
> names(.data)
[1] "id" "age" "relig" "ped" "income" "am"
[7] "reason" "bps" "bpd" "wt" "ht"

113
Then, an appropriate label or description for each variable can be created one at a
time.
> label.var(id, "Id code")
At this stage, checking description of the dataset will reveal the description of the
first variable.
> des()
No. of observations =251
Variable Class Description
1 id numeric Id code
2 age numeric
3 relig numeric
========= subsequent lines omitted ==========
A description of the variable alone can also be displayed.
> des(id)
'id' is a variable found in the following source(s):
Var. source Var. order Class # records Description
.data 1 numeric 251
Now let's complete all other variable labels.
> label.var(age, "age")
> label.var(relig, "religion")
> label.var(ped, "eduction")
> label.var(income, "monthly income")
> label.var(am, "age(yr) 1st marriage")
> label.var(reason, "reason for fam. plan.")
> label.var(bps, "systolic BP")
> label.var(bpd, "diastolic BP")
> label.var(wt, "weight (kg)")
> label.var(ht, "height (cm)")
> des()
No. of observations =251
Variable Class Description
1 id numeric ID code
2 age numeric age
3 relig numeric religion
4 ped numeric eduction
5 income numeric monthly income
6 am numeric age(yr) 1st marriage
7 reason numeric reason for fam. plan.
8 bps numeric systolic BP
9 bpd numeric diastolic BP
10 wt numeric weight (kg)
11 ht numeric height (cm)

114
It is advised to keep each label short since it will be frequently used in the process
of automatic graphical display and tabulation.
Labelling a categorical variable
Labelling values of a categorical variable is a good practice. It is a part of important
documentation. During the analysis, a labelled variable is much easier to understand
and interpret than an unlabelled one.
As mentioned previously, the best way to label variables is during the preparation
of data entry using the data entry software. However, occasionally one may
encounter an unlabelled dataset, such as those directly imported from EpiInfo, 'txt’
or 'csv' formats. It is therefore important to know how to label variables in R.
In our example of the family planning data the variable 'ped' (patient's education
level) is an unlabelled categorical variable. In fact, at this stage, it is not really a
categorical variable. When we summarise the statistics, either by the
summary(.data) command or by summ, both outputs show means, medians
and standard deviations, indicating a continuous, numeric variable.
> summary(ped)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
2.000 2.000 2.000 3.296 5.000 7.000 25.000
> summ(ped)
Obs. mean median s.d. min. max.
226 3.296 2 1.66 2 7
Note that there is no count for category 1 of 'ped'. According to the coding scheme:
1 = no education, 2 = primary school, 3 = secondary school, 4 = high school,
5 = vocational school, 6 = bachelor degree, 7 = other.
The data are numeric and therefore need to be converted into a factor. The labels
can be put into a list of 7 elements.
> label.ped <- list(None="1", Primary="2", "Secondary
school"="3", "High school"="4", Vocational="5", "Bachelor
degree"="6", Others="7")
Each label needs to be enclosed in double quotes if it contains a space, otherwise it
is optional. For example, one can have: None="1" or "None"="1".
To convert a numeric vector to a categorical one use the 'factor' function.
> educ <- factor(ped, exclude = NULL)
The new variable is a result of factoring the values of 'ped' in .data. The
argument 'exclude' is set to 'NULL' indicating no category (even missing or 'NA')
will be excluded in the factoring process.

115
> summary(educ)
2 3 4 5 6 7 <NA>
117 31 20 26 16 16 25
We can check the labels of a factor object using the levels command.
> levels(educ)
[1] "2" "3" "4" "5" "6" "7" NA
There are seven known levels, ranging from "2" to "7" and one missing level (NA).
Note that these numbers are actually characters or group names. There was no "1"
in the data and correspondingly is omitted in the levels.
The levels for the codes should be changed to meaningful words as defined
previouisly.
> levels(educ) <- label.ped
> levels(educ)
[1] "None" "Primary" "Secondary school"
[4] "High school" "Vocational" "Bachelor degree"
[7] "Others"
Adding a variable to a data frame
Note that the variable 'educ' is not inside the data frame .data. Remember that R
has the capacity to handle more than one object simultaneously. However, although
it is possible to go on analysing data with this variable outside the data frame,
incorporating all the important variables into the main data frame .data is
advised, especially if any sorting is done. In addition, the variable can have a
descriptive label. More importantly, when necessary, the whole data frame
including the old and new variables can be written into another data format easily
(see the function 'write.foreign' in the foreign package).
> des() # same as before
To incorporate a new variable derived from the data frame .data, simply label the
variable name as follows.
> label.var(educ, "education")
Then recheck.
> des()
No. of observations =251
Variable Class Description
1 id numeric ID code
============ Variables # 2 to 11 omitted =======
12 educ factor education

116
For a variable outside .data, the command label.var actually accomplishes
five tasks.
y The new variable is incorporated into the data frame .data,
y The new variable is labelled with a description,
y The old data frame is detached,
y The old 'free' variable outside the data frame is removed, unless the
argument 'pack=FALSE' is specified,
y The new data frame is attached to the search path.
Order of one-way tabulation
The new education variable can be tabulated.
> tab1(educ)
educ: education
Frequency %(NA+) %(NA-)
None 0 0.0 0.0
Primary 117 46.6 51.8
Secondary school 31 12.4 13.7
High school 20 8.0 8.8
Vocational 26 10.4 11.5
Bachelor degree 16 6.4 7.1
Others 16 6.4 7.1
NA's 25 10.0 0.0
Total 251 100.0 100.0
None
Primary
Secondary school
High school
Vocational
Bachelor degree
Others
Missing
Distribution of education
Frequency
0 20 40 60 80 100 120 140
0
117
31
20
26
16
16
25
The table and the graph show that most subjects had only primary education. A
horizontal bar chart is produced when the number of groups exceeds 6 and the
longest label of the group has more than 8 characters. The tabulation can also be
sorted.

117
> tab1(educ, sort.group = "decreasing")
educ : education
Frequency %(NA+) %(NA-)
Primary 117 46.6 51.8
Secondary school 31 12.4 13.7
Vocational 26 10.4 11.5
NA's 25 10.0 0.0
High school 20 8.0 8.8
Bachelor degree 16 6.4 7.1
Others 16 6.4 7.1
None 0 0.0 0.0
Total 251 100.0 100.0
None
Bachelor degree
Others
High school
Missing
Vocational
Secondary school
Primary
Distribution of education
Frequency
0 20 40 60 80 100 120 140
0
16
16
20
25
26
31
117
Alternatively the sorting can be increasing.
> tab1(educ, sort.group = "increasing")
educ : education
Frequency %(NA+) %(NA-)
None 0 0.0 0.0
Bachelor degree 16 6.4 7.1
Others 16 6.4 7.1
High school 20 8.0 8.8
NA's 25 10.0 0.0
Vocational 26 10.4 11.5
Secondary school 31 12.4 13.7
Primary 117 46.6 51.8
Total 251 100.0 100.0
A sorted table and bar chart are easier to read and viewed when there is no order of
category. However, education level is partially ordered in nature, so the non-sorted
chart may be better.

118
Collapsing categories
Sometimes a categorical variable may have too many levels. The analyst may want
to combine two or more categories together into one. For example, vocational and
bachelor degree, which are the 5th and the 6th levels, could be combined into one
level called 'tertiary'. We can do this by creating a new variable, which is then
incorporated into .data at the end.
> ped2 <- educ
> levels(ped2)[5:6] <- "Tertiary"
> label.var(ped2, "level of education")
> des()
> tab1(ped2)
ped2 : level of education
Frequency %(NA+) %(NA-)
None 0 0.0 0.0
Primary 117 46.6 51.8
Secondary school 31 12.4 13.7
High school 20 8.0 8.8
Tertiary 42 16.7 18.6
Others 16 6.4 7.1
NA's 25 10.0 0.0
Total 251 100.0 100.0
The two categories have been combined into one giving 42 subjects having a
tertiary level of education.
Conclusion
In this chapter, we have looked at a dataset with a lot of data cleaning required. In
real practice, it is very important to have preventive measures to minimise any
errors during data collection and data entry. For example, a constraint of range
check is necessary in data entry. Missing values would better be entered with
missing codes specific for the software. In EpiInfo, Stata and SPSS these are period
marks '.' or simply left blank.
One of the best ways of entering data is to use the EpiData software, which can set
legal ranges and several other logical checks as well as label the variables and
values in an easy way. If this had been properly done, then the difficult commands
used in this chapter would not have been necessary. In the remaining chapters, we
will use datasets which have been properly entered, treated for missing values and
properly labelled.
Whenever a variable is modified it is a good practice to update the variable inside
the attached data frame with the one outside.
119
The best way to modify data is to use recode, which is a powerful command of
Epicalc. It can work with one variable or a number of variables with the same
recoding scheme or recoding a variable or variables under a condition. Finally, the
best way to update the data frame with new or modified variable(s) is to use
label.var. This command not only labels the variable for further use but also
updates and incorporates the data frame with the variable outside. Attachment to the
new data frame is automatic, making data manipulation in R more smooth and
simple.
There are many other more advanced data management functions in R that are not
covered in this chapter. These include aggregate, reshape and merge, and
readers are encouraged to explore these very useful and powerful commands on
their own.
120
Exercises________________________________________________
The VCT dataset contains data from a questionnaire involving female sex workers
from Phuket, Thailand in 2004.
Read the file into R and use the commands in this chapter to clean the data.

121
Chapter 11: Scatter Plots & Linear
Regression
Linear regression involves modelling a continuous outcome variable with one or
more explanatory variables. With all data analysis the first step is always to explore
the data. In this case, scatter plots are very useful in determining whether or not the
relationships between the variables are linear.
Example: Hookworm & blood loss
The dataset in this chapter concerns the relationship between hookworm and blood
loss from a study conducted in 1970.
> zap()
> data(Suwit); use(Suwit)
> des()
HW and Blood loss SEAJTMH 1970;
No. of observations = 15
Variable Class Description
1 id numeric
2 worm numeric No. of worms
3 bloss numeric Blood loss/day
> summ()
HW and Blood loss SEAJTMH 1970;
No. of observations =15
Var. name Obs. mean median s.d. min. max.
1 id 15 8 8 4.47 1 15
2 worm 15 552.4 525 513.9 32 1929
3 bloss 15 33.45 33.8 24.85 5.03 86.65
There are 3 variables and 15 records.
> .data

122
The file is clean and ready for analysis. With this small sample size it is somewhat
straightforward to verify that there is no repetition of 'id' and no missing values. The
records have been sorted in ascending order of 'worm' (number of worms) ranging
from 32 in the first subject to 1,929 in the last one. Blood loss ('bloss') is however,
not sorted. The 13th record has the highest blood loss of 86 ml per day, which is
very high. The objective of this analysis is to examine the relationship between
these two variables.
Scatter plots
When there are two continuous variables cross plotting is the first necessary step.
> plot(worm, bloss)
The above command gives a simple scatter plot with the first variable on the
horizontal axis and the second on the vertical axis.
0 500 1000 1500 2000
20 40 60 80
worm
bloss
The names of the variables are used for the axis labels, and there is no title. The
axis labels can be modified and a title added by supplying extra arguments to the
plot function, as follows:
> plot(worm, bloss, xlab="No. of worms", ylab="ml. per day",
main = "Blood loss by number of hookworms in the bowel")

123
For a small sample size, putting the identification of each dot can improve the
information conveyed in the graph.
0 500 1000 1500 2000
20 40 60 80
Blood loss by number of hookworms in the bowel
No. of worms
ml. per day
> plot(worm, bloss, xlab="No. of worms", ylab="ml. per day",
main="Blood loss by number of hookworms in the bowel",
type="n")
The above command produces an empty plot. The argument 'type' specifies the type
of plot to be drawn. A value of "n" tells R not to plot anything. This is to set a
proper frame for further points and lines.
The variable 'id' can be used as the text to write at the coordinates using the 'text'
command.
> text(worm, bloss, labels=id)

124
0 500 1000 1500 2000
20 40 60 80
Blood loss by number of hookworms in the bowel
No. of worms
ml. per day
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1
5
In order to draw a regression line, a linear model using the above two variables
should be fit to the data.
Components of a linear model
The function lm is used to perform linear modelling in R.
> lm1 <- lm(bloss ~ worm)
> lm1
Call:
lm(formula = bloss ~ worm)
Coefficients:
(Intercept) worm
10.84733 0.04092
The model 'lm1' is created. Be careful not to confuse the letter "l" with the
number "1", which look very similar. Displaying the model by typing 'lm1' gives
limited information. To get more information, one can look at the attributes of this
model, its summary and attributes of its summary.
> attr(lm1, "names")
[1] "coefficients" "residuals" "effects"
[4] "rank" "fitted.values" "assign"
[7] "qr" "df.residual" "xlevels"
[10] "call" "terms" "model"
There are 12 attributes. Most of them can be displayed with the summary function.
> summary(lm1)

125
Call:
lm(formula = bloss ~ worm)
Residuals:
Min 1Q Median 3Q Max
-15.8461 -10.8118 0.7502 4.3562 34.3896
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 10.84733 5.30857 2.04 0.062
worm 0.04092 0.00715 5.73 7e-05
Residual standard error: 13.7 on 13 degrees of freedom
Multiple R-Squared: 0.716, Adjusted R-squared: 0.694
F-statistic: 32.8 on 1 and 13 DF, p-value: 6.99e-05
The first section of summary shows the formula that was 'called'. The second
section gives the distribution of residuals. The pattern is clearly not symmetric. The
maximum is too far on the right (34.38) compared to the minimum (-15.84) and the
first quartile is further left (-10.81) of the median (0.75) than the third quartile
(4.35) is. Otherwise, the median is close to zero. The third section gives coefficients
of the intercept and the effect of 'worm' on blood loss. The intercept is 10.8
meaning that when there are no worms, the blood loss is estimated to be 10.8 ml per
day. This is however, not significantly different from zero as the P value is 0.0618.
The coefficient of 'worm' is 0.04 indicating that each worm will cause an average of
0.04 ml of blood loss per day. Although the value is small, it is highly significantly
different from zero. When there are many worms, the level of blood loss can be
very substantial.
The multiple R-squared value of 0.716 indicates that 71.6% of the variation in the
data is explained by the model. The adjusted value is 0.6942. (The calculation of R-
squared is discussed in the analysis of variance section below). The last section
describes more details of the residuals and hypothesis testing on the effect of 'worm'
using the F-statistic. The P value from this section (6.99 × 10-5) is equal to that
tested by the t-distribution in the coefficient section. This F-test more commonly
appears in the analysis of variance table.
Analysis of variance table, R-squared and adjusted R-squared
> summary(aov(lm1))
Df Sum Sq Mean Sq F value Pr(>F)
worm 1 6192 6 192 32.8 7e-05
Residuals 13 2455 189
The above analysis of variance (aov) table breaks down the degrees of freedom,
sum of squares and mean square of the outcome (blood loss) by sources (in this
case there only two: worm + residuals).

126
The so-called 'square' is actually the square of difference between the value and the
mean. The total sum of squares of blood loss is therefore:
> SST <- sum((bloss-mean(bloss))^2); SST
[1] 8647
The sum of squares from residuals is:
> SSR <- sum(residuals(lm1)^2); SSR
[1] 2455.5 # See also the analysis of variance table
The sum of squares of worm or sum of squares of difference between the fitted
values and the grand mean is:
> SSW <- sum((fitted(lm1)-mean(bloss))^2); SSW
[1] 6191.6
The latter two sums add up to the first one. The R-squared is the proportion of sum
of squares of the fitted values to the total sum of squares.
> SSW/SST
[1] 0.71603
This value of R-squared can also be said to be the percent of reduction of total sum
of squares when the explanatory variable is fitted. Thus the number of worms can
reduce or explain the variation by about 72%.
Instead of sum of squares, one may consider the mean square as the level of
variation. In such a case, the number of worms can reduce the total mean square (or
variance) by: (total mean square - residual mean square) / total mean square, or
(variance - residual mean square) / variance.
> resid.msq <- sum(residuals(lm1)^2)/lm1$df.residual
> Radj <- (var(bloss)- resid.msq)/var(bloss); Radj
[1] 0.69419
This is the adjusted R-squared shown in 'summary(lm1)' in the above section.
F-test
When the mean square of 'worm' is divided by the mean square of residuals, the
result is:
> F <- SSW/resid.msq; F
[1] 32.78
Using this F value with the two corresponding degrees of freedom (from 'worm' and
residuals) the P value for testing the effect of 'worm' can be computed.
> pf(F, df1=1, df2=13, lower.tail=FALSE)
[1] 6.9904e-05

127
The function pf is used to compute a P value from a given F value together with
the two values of the degrees of freedom. The last argument 'lower.tail' is set to
FALSE to obtain the right margin of the area under the curve of the F distribution.
In summary, both the regression and analysis of variance give the same conclusion;
that number of worms has a significant linear relationship with blood loss. Now the
regression line can be drawn.
Regression line, fitted values and residuals
A regression line can be added to the scatter plot with the following command:
> abline(lm1)
The regression line has an intercept of 10.8 and a slope of 0.04. The expected value
is the value of blood loss estimated from the regression line with a specific value of
'worm'.
> points(worm, fitted(lm1), pch=18, col="blue")
A residual is the difference between the observed and expected value. The residuals
can be drawn by the following command.
> segments(worm, bloss, worm, fitted(lm1), col="pink")
0 500 1000 1500 2000
20 40 60 80
Blood loss by number of hookworms in the bowel
No. of worms
ml. per day
1
2
3
4
5
6
7
8
910
11
12
13
14
15
The actual values of the residuals can be checked from the specific attribute of the
defined linear model.
> residuals(lm1) -> lm1.res; lm1.res
Note that some residuals are positive and some are negative. The 13th residual has

128
the largest value (furthest from the fitted line). The sum of the residuals and the sum
of their squares can be checked.
> sum(lm1.res); sum(lm1.res ^2)
[1] 3.9968e-15
[1] 2455.5
The sum of residuals is close to zero whereas the sum of their squares is the value
previously displayed in the summary of the model. The distribution of residuals, if
the model fits well, should be normal. A common sense approach is to look at the
histogram.
> hist(lm1.res)
Checking normality of residuals
Plots from the above two commands do not suggest that residuals are normally
distributed. However, with such a small sample size, it is difficult to draw any
conclusion. A better way to check normality is to plot the residuals against the
expected normal score or (residual-mean) / standard deviation. A reasonably
straight line would indicate normality.
> qqnorm(lm1.res)
Numerically, Shapiro-Wilk test can also be applied.
> shapiro.test(lm1.res)
Shapiro-Wilk normality test
data: residuals (lm1)
W = 0.8978, p-value = 0.0882
> qqline(lm1.res)
Epicalc combines the three commands and adds the p-value of the test to the graph.
> qqnorm(lm1.res) -> a
This puts the coordinates of the residuals into an object.
> shapiro.qqnorm(lm1.res, type="n")
> text(a$x, a$y, labels=as.character(id))
The X and Y coordinates are 'a$x' and 'a$y', respectively.
If the residuals were perfectly normally distributed, the text symbols would have
formed along the straight dotted line. The graph suggests that the largest residual
(13th) is too high (positive) whereas the smallest value (7th) is not large enough
(negative). However, the P value from the Shapiro-Wilk test is 0.08 suggesting that
the possibility of residuals being normally distributed cannot be rejected.

129
−1 0 1
−100 102030
Normal Q−Q plot of lm1.res
Theoretical Quantiles
Sample Quantiles
Shapiro−Wilk test P value = 0.0882
1
23
4
5
6
7
8
9
10
11 12
13
14 15
Finally, the residuals are plotted against the fitted values to see if there is a pattern.
> plot(fitted(lm1), lm1.res, xlab="Fitted values")
> plot(fitted(lm1), lm1.res, xlab="Fitted values", type="n")
> text(fitted(lm1), lm1.res, labels=as.character(id))
> abline(h=0, col="blue")
20 40 60 80
−100 102030
Fitted values
residuals(lm1)
1
2
3
4
5
6
7
8
910
11 12
13
14 15
There is no obvious pattern. The residuals are quite independent of the expected
values. With this and the above findings from the 'qqnorm' command we may
conclude that the residuals are randomly and normally distributed.

130
The above two diagnostic plots for the model 'lm1' can also be obtained from:
> windows(7, 4)
> par(mfrow=c(1,2))
> plot.lm(lm1, which=1:2)
Final conclusion
From the analysis, it is clear that blood loss is associated with number of
hookworms. On average, each worm may cause 0.04 ml of blood loss. The
remaining uncertainty of blood loss, apart from hookworm, is explained by random
variation or other factors that were not measured.
Exercise_________________________________________________
Load the SO2 dataset and label the variables using the following commands.
> label.var(smoke, "Smoke (mg/cu.m.)")
> label.var(SO2, "SO2 (ppm.)")
Using scatter plots and linear regression check whether smoke or SO2 has more
influence on logarithm of deaths.
Interpret the results the best simple linear regression.

131
Chapter 12: Stratified linear regression
Datasets usually contain many variables collected during a study. It is often useful
to see the relationship between two variables within the different levels of another
third, categorical variable.
Example: Systolic blood pressure
A small survey on blood pressure was carried out. The objective is to see the
hypertensive effect of subjects putting additional table salt on their meal.
> zap()
> data(BP); use(BP)
> des()
cross-sectional survey on BP & risk factors
No. of observations =100
Variable Class Description
1 id integer id
2 sex factor sex
3 sbp integer Systolic BP
4 dbp integer Diastolic BP
5 saltadd factor Salt added on table
6 birthdate Date
> summ()
cross-sectional survey on BP & risk factors
No. of observations = 100
Var. name Obs. mean median s.d. min. max.
id 100 50.5 50.5 29.01 1 100
sex 100 1.55 2 0.5 1 2
sbp 100 154.34 148 39.3 80 238
dbp 100 98.51 96 22.74 55 158
saltadd 80 1.538 2 0.502 1 2
birthdate 100 1952-10-11 1951-11-17 <NA> 1930-11-14 1975-
12-08
Note that the maximum systolic and diastolic blood pressures are quite high. There
are 20 missing values in 'saltadd'. The frequencies of the categorical variables 'sex'
and 'saltadd' are now inspected.

132
> summary(data.frame(sex, saltadd))
sex saltadd
male :45 no :37
female:55 yes :43
NA's:20
The next step is to create a new age variable from birthdate. The calculation is
based on 12th March 2001, the date of the survey.
> age.in.days <- as.Date("2001-03-12") - birthdate
There is a leap year in every four years. Therefore, an average year will have
365.25 days.
> class(age.in.days)
[1] "difftime"
> age <- as.numeric(age.in.days)/365.25
The function as.numeric is needed to transform the units of age (difftime);
otherwise modelling would not be possible.
> summ(sbp, by = saltadd)
For saltadd = no
Obs. mean median s.d. min. max.
37 137.5 132 29.624 80 201
For saltadd = yes
Obs. mean median s.d. min. max.
43 163 171 39.39 80 224
For saltadd = missing
Obs. mean median s.d. min. max.
20 166.9 180 45.428 106 238
100 150 200
Distribution of Systolic BP
by Salt added on table
no
yes
missing

133
Recoding missing values into another category
The missing value group has the highest median and average systolic blood
pressure. In order to create a new variable with three levels type:
> saltadd1 <- saltadd
> levels(saltadd1) <- c("no", "yes", "missing")
> saltadd1[is.na(saltadd)] <- "missing"
> summary(saltadd1)
no yes missing
37 43 20
> summary(aov(age ~ saltadd1))
Df Sum Sq Mean Sq F value Pr(>F)
saltadd1 2 114.8 57.4 0.4484 0.64
Residuals 97 12421.8 128.1
Since there is not enough evidence that the missing group is important and for
additional reasons of simplicity, we will ignore this group and continue the analysis
with the original 'saltadd' variable consisting of only two levels. Before doing this
however, a simple regression model and regression line are first fitted.
> lm1 <- lm(sbp ~ age)
> summary(lm1)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 65.1465 14.8942 4.374 3.05e-05
age 1.8422 0.2997 6.147 1.71e-08
Residual standard error: 33.56 on 98 degrees of freedom
Multiple R-Squared: 0.2782, Adjusted R-squared: 0.2709
F-statistic: 37.78 on 1 and 98 DF, p-value: 1.712e-08
Although the R-squared is not very high, the P value is small indicating important
influence of age on systolic blood pressure.
A scatterplot of age against systolic blood pressure is now shown with the
regression line added using the 'abline' function, previously mentioned in chapter
11. This function can accept many different argument forms, including a regression
object. If this object has a 'coef' method, and it returns a vector of length 1, then the
value is taken to be the slope of a line through the origin, otherwise the first two
values are taken to be the intercept and slope, as is the case for 'lm1'.
> plot(age, sbp, main = "Systolic BP by age", xlab = "Years",
ylab = "mm.Hg")
> coef(lm1)
(Intercept) age
65.1465 1.8422
> abline(lm1)

134
30 40 50 60 70
100 150 200
Systolic BP by age
Years
mm.Hg
Subsequent exploration of residuals suggests a non-significant deviation from
normality and no pattern. Details of this can be adopted from the techniques
discussed in the previous chapter and are omitted here. The next step is to provide
different plot patterns for different groups of salt habits.
> lm2 <- lm(sbp ~ age + saltadd)
> summary(lm2)
====================
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 63.1291 15.7645 4.005 0.000142
age 1.5526 0.3118 4.979 3.81e-06
saltaddyes 22.9094 6.9340 3.304 0.001448
---
Residual standard error: 30.83 on 77 degrees of freedom
Multiple R-Squared: 0.3331, Adjusted R-squared: 0.3158
F-statistic: 19.23 on 2 and 77 DF, p-value: 1.68e-07
On the average, a one year increment of age increases systolic blood pressure by 1.5
mmHg. Adding table salt increases systolic blood pressure significantly by
approximately 23 mmHg.
Similar to the method used in the previous chapter, the following step creates an
empty frame for the plots:
> plot(age, sbp, main="Systolic BP by age", xlab="Years",
ylab="mm.Hg", type="n")

135
Add blue hollow circles for subjects who did not add table salt.
> points(age[saltadd=="no"], sbp[saltadd=="no"], col="blue")
Then add red solid points for those who did add table salt.
> points(age[saltadd=="yes"], sbp[saltadd=="yes"], col="red",
pch = 18)
Note that the red dots corresponding to those who added table salt are higher than
the blue circles. The final task is to draw two separate regression lines for each
group.
Since model 'lm2' contains 3 coefficients, the command abline now requires the
argument 'a' as the intercept and 'b' as the slope.
> coef(lm2)
(Intercept) age saltaddyes
63.129112 1.552615 22.909449
We now have two regression lines to draw, one for each group. The intercept for
non-salt users will be the first coefficient and for salt users will be the first plus the
third. The slope for both groups is the same. Thus the intercept for the non-salt
users is:
> a0 <- coef(lm2)[1]
For the salt users, the intercept is the first plus the third coefficient:
> a1 <- coef(lm2)[1] + coef(lm2)[3]
For both groups, the slope is fixed at:
> b <- coef(lm2)[2]
Now the first (lower) regression line is drawn in blue, then the other in red.
> abline(a = a0, b, col = "blue")
> abline(a = a1, b, col = "red")
Note that X-axis does not start at zero. Thus the intercepts are out of the plot frame.
The red line is for the red points of salt adders and the blue line is for the blue
points of non-adders. In this model, age has a constant independent effect on
systolic blood pressure.
Look at the distributions of the points of the two colours; the red points are higher
than the blue ones but mainly on the right half of the graph. To fit lines with
different slopes, a new model with interaction term is created.

136
30 40 50 60 70
100 150 200
Systolic BP by age
Years
mm.Hg
The next step is to prepare a model with different slopes (or different 'b' for the
abline arguments) for different lines. The model needs an interaction term
between 'addsalt' and 'age'.
> lm3 <- lm(sbp ~ age * saltadd)
> summary(lm3)
Call:
lm(formula = sbp ~ age * saltadd)
===============
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 78.0066 20.3981 3.824 0.000267 ***
age 1.2419 0.4128 3.009 0.003558 **
saltaddyes -12.2540 31.4574 -0.390 0.697965
age:saltaddyes 0.7199 0.6282 1.146 0.255441
---
Multiple R-Squared: 0.3445, Adjusted R-squared: 0.3186
F-statistic: 13.31 on 3 and 76 DF, p-value: 4.528e-07
In the formula part of the model, 'age * saltadd' is the same as 'age + saltadd +
age:saltadd'. The four coefficients are displayed in the summary of the model. They
can also be checked as follows.
> coef(lm3)
(Intercept) age saltaddyes age:saltaddyes
78.0065572 1.2418547 -12.2539696 0.7198851
The first coefficient is the intercept of the fitted line among non-salt users.

137
For the intercept of the salt users, the second term and the fourth are all zero (since
age is zero) but the third should be kept as such. This term is negative. The intercept
of salt users is therefore lower than that of the non-users.
> a0 <- coef(lm3)[1]
> a1 <- coef(lm3)[1] + coef(lm3)[3]
For the slope of the non-salt users, the second coefficient alone is enough since the
first and the third are not involved with each unit of increment of age and the fourth
term has 'saltadd' being 0. The slope for the salt users group includes the second and
the fourth coefficients since 'saltaddyes' is 1.
> b0 <- coef(lm3)[2]
> b1 <- coef(lm3)[2] + coef(lm3)[4]
These terms are used to draw the two regression lines.
Redraw the graph but this time with black representing the non-salt adders.
> plot(age, sbp, main="Systolic BP by age", xlab="Years",
ylab="mm.Hg", pch=18, col=as.numeric(saltadd))
> abline(a = a0, b = b0, col = 1)
> abline(a = a1, b = b1, col = 2)
> legend("topleft", legend = c("Salt added", "No salt added"),
lty=1, col=c("red","black"))
30 40 50 60 70
100 150 200
Systolic BP by age
Years
mm.Hg
Salt added
No salt added
Note that 'as.numeric(saltadd)' converts the factor levels into the integers 1
(black) and 2 (red), representing the non-salt adders and the salt adders,
respectively. These colour codes come from the R colour palette.

138
This model suggests that at the young age, the systolic blood pressure of two groups
are not much different as the two lines are close together on the left of the plot. For
example, at the age of 25, the difference is 5.7mmHg. Increasing age increases the
difference between the two groups. At 70 years of age, the difference is as great as
38mmHg. (For simplicity, the procedures for computation of these two levels of
difference are skipped in these notes). In this aspect, age modifies the effect of
adding table salt.
On the other hand the slope of age is 1.24mmHg per year among those who did not
add salt but becomes 1.24+0.72 = 1.96mmHg among the salt adders. Thus, salt
adding modifies the effect of age. Interaction is a statistical term whereas effect
modification is the equivalent epidemiological term.
The coefficient of the interaction term 'age:saltaddyes' is not statistically significant.
The two slopes just differ by chance.
Exercise_________________________________________________
Plot systolic and diastolic blood pressures of the subjects, use red colour of males
and blue for females as shown in the following figure. [Hint: segments]
0 20406080100
0
50
100
150
200
Index
blood pressure
Systolic and diastolic blood pressure of the subjects
Check whether there is any significant difference of diastolic blood pressure among
males and females after adjustment for age.

139
Chapter 13: Curvilinear Relationship
Example: Money carrying and age
This chapter returns to the family data and explores the relationship between money
carried and age.
> zap()
> data(Familydata)
> use(Familydata)
> des()
> plot(age, money, pch=" ")
The above command is equivalent to:
> plot(age, money, type="n")
20 40 60 80
0 1000 2000 3000 4000 5000
Relationship between age and money carried
age
money
KJA
ICBG
H
DF
E
To put the 'code' as text at the points, add a title and a regression line, type the
following:
140
> text(age, money, labels = code)
> title("Relationship between age and money carried")
> lm1 <- lm(money ~ age)
> abline(lm1)
The 'lm1' object can be inspected by using the summary function.
> summary(lm1)
============
Residual standard error: 1560 on 9 degrees of freedom
Multiple R-Squared: 0.0254, Adjusted R-squared: -0.08285
F-statistic: 0.2349 on 1 and 9 DF, p-value: 0.6395
The R-squared is very small indicating a poor fit. This is confirmed by the poor fit
of the regression line in the previous graph. People around 40-60 years old tend to
carry more money than those in other age groups.
Checking residuals reveals the following results.
> Residuals <- resid(lm1)
> Fitted.values <- fitted(lm1)
> windows(9,5)
> opar <- par(mfrow=c(1,2))
> shapiro.qqnorm(Residuals)
> plot(Fitted.values, Residuals, main="Residuals vs Fitted")
> abline(h=0, lty=3, col="blue")
−1.5 −1.0 −0.5 0.0 0.5 1.0 1.5
−1000 0 1000 2000 3000 4000
Normal Q−Q plot of Residuals
Theoretical Quantiles
Sample Quantiles
Shapiro−Wilk test P value <.001
600 800 1000 1200
−1000 0 1000 2000 3000 4000
Residuals vs Fitted Values
Fitted.values
Residuals
From the above plots the residuals are not normally distributed.
141
To reset the graphics device back to the orignal settings type:
> par(opar)
Variation in money usually has an exponential distribution. Taking logarithms may
help improve the model fit.
> plot(age, money, type="n", log = "y",
main = "Relationship between age and money carried")
> text(age, money, labels = code)
> lm2 <- lm(log10(money) ~ age)
> abline(lm2)
20 40 60 80
5 10 20 50 200 500 2000
Relationship between age and money carried
age
money
K
J
A
IC
BG
H
DF
E
With the log scale of the y-axis, the distribution of the relationship tends to be
curvilinear. Drawing a straight regression line through these points is thus not
appropriate. Residuals can be checked as follows:
> Residuals <- resid(lm2)
> Fitted.values <- fitted(lm2)
> windows(9,5)
> opar <- par(mfrow=c(1,2))
> shapiro.qqnorm(Residuals)
> plot(Fitted.values, Residuals, main="Residuals vs Fitted")
> abline(h=0, lty=3, col="blue")
142
−1.5 −1.0 −0.5 0.0 0.5 1.0 1.5
−1.0 −0.5 0.0 0.5 1.0
Normal Q−Q plot of Residuals
Theoretical Quantiles
Sample Quantiles
Shapiro−Wilk test P value = 0.6866
1.8 2.0 2.2 2.4 2.6 2.8 3.0
−1.0 −0.5 0.0 0.5 1.0
Residuals vs Fitted Values
Fitted.values
Residuals
The residuals now look normally distributed. However, the values of the high
residuals are in the middle of the range of the fitted values, indicating that perhaps
we need to include a quadratic term of age in the model.
To fit a regression line under the log scale but with a linear (non-log scale) value
would be too complicated. A better way would be to transform 'money' into a new
variable on a log base 10 scale and fit a new model with a quadratic term of age.
> lm3 <- lm(log10(money) ~ age + I(age^2))
> summary(lm3)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.102650 0.338502 0.30 0.76944
age 0.125355 0.017641 7.11 0.00010
I(age^2) -0.001268 0.000201 -6.30 0.00023
Residual standard error: 0.332 on 8 degrees of freedom
Multiple R-Squared: 0.875, Adjusted R-squared: 0.844
F-statistic: 28 on 2 and 8 DF, p-value: 0.000243
Both the adjusted and non-adjusted R-squared values are high. Adding the quadratic
age term improves the model substantially and is statistically significant. The next
step is to fit a regression line, a task that is not straightforward.
A regression line is a line joining fitted values. There are too few points of fitted
values in the model. A new data frame is now created to include a new 'age'
variable ranging from 6 to 80 (which is the age range of our subjects) and the
corresponding age-squared term.
> new <- data.frame(age = 6:80, age2 = (6:80)^2)
143
Then the predicted values of this data frame are computed based on the last model.
> predict1 <- predict.lm(lm3, new)
> plot(age, log10(money), type="n", ylab = "log10(money)",
main="Relationship between age and money carried",)
> text(age, log10(money), labels = code)
> lines(new$age, predict1, col = "blue")
20 40 60 80
1.0 1.5 2.0 2.5 3.0 3.5
Relationship between age and money carried
age
log10(money)
K
J
A
IC
BG
H
DF
E
Maximum value in the quadratic model
The quadratic model explains that, a young person such as "K" who is 5 years old
carries very little money. The money carried increases with age and peaks between
40-50 years of age. Then the value drops when age increases.
The maximum value of 'predict1' is
> max(predict1)
[1] 3.2012
The corresponding money value is
> 10^max(predict1)
[1] 1589.4
The corresponding age is
> new$age[which.max(predict1)]
[1] 49
However, more precise mathematical calculation from the coefficients can be
obtained as follows:
144
> coef(lm4)
(Intercept) age I(age^2)
0.1026501 0.1253546 -0.0012677
> a <- coef(lm3)[3]
> b <- coef(lm3)[2]
> c <- coef(lm3)[1]
> x <- -b/(2*a); x # 49.441
The corresponding value in the Y-axis is
> y <- a * x^2 + b * x + c
> y # 3.20148
Finally, the corresponding money is therefore:
> 10^y # 1590.3
The conclusion from the model is that at the age of 49 years, an average person will
carry approximately 1,590 baht. This amount is lower than the actual value of
money carried by "E", which is 5,000 baht or more than three times higher.
> 10^(log10(money)[code=="E"]-y) # 3.1441
Stratified curvilinear model
There are both males and females in the family. As an exercise, two parallel curves
will be used to fit the data.
> lm4 <- lm(log10(money) ~ sex + age + I(age^2))
> summary(lm4)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.027252 0.338084 0.08 0.93801
sexM 0.239320 0.207432 1.15 0.28648
age 0.126284 0.017305 7.30 0.00016
I(age^2) -0.001288 0.000198 -6.51 0.00033
Residual standard error: 0.325 on 7 degrees of freedom
Multiple R-Squared: 0.895, Adjusted R-squared: 0.85
F-statistic: 19.9 on 3 and 7 DF, p-value: 0.000834
The model 'lm4' gives a slightly higher R-squared than that from 'lm3'. Sex ("M"
compared with "F") is not significant. We use this model for a plotting exercise.
> plot(age, log10(money), type="n", ylab = "log10(money)"
main = "Relationship between age and money carried")
> text(age, log10(money), labels=code, col=unclass(sex))
145
Note that the first line is the same as previous plots. The second line however,
differentiates sex with colour. When 'sex', which is a factor, is unclassed, the values
become the numerical order of the levels. "F" is coded 1 and "M" is coded 2. as
given in the default colour palette of R.
> age.frame2.male <- data.frame(age = 6:80, age2 = (6:80)^2,
sex = factor ("M"))
> predict2.male <- predict.lm(lm4, age.frame2.male)
The first command creates a data frame containing variables used in 'lm4'. Note
that the 'sex' here is confined to males. The second command creates a new vector
based on 'lm4' and the new data frame. First we draw the line for males.
> lines(age.frame2.male$age, predict2.male, col = 2)
Finally the line for females.
> age.frame2.female <- data.frame(age = 6:80, age2 = (6:80)^2,
sex = factor ("F"))
> predict2.female <- predict.lm(lm4, age.frame2.female)
> lines(age.frame2.female$age, predict2.female, col=1)
20 40 60 80
1.0 1.5 2.0 2.5 3.0 3.5
Relationship between age and money carried
age
log10(money)
K
J
A
IC
BG
H
DF
E
The red line is located consistently above the black line, since our model did not
include an interaction term. For every value of age, males tend to carry 102.4 or
1.738 times more money than females. The difference is however, not significant.
From age to age group
So far, we have analysed the effect of age as a continuous variable. In most of the
epidemiological data analysis, age is often transformed to a categorical variable by
cutting it into age groups. For this small dataset, we divide the subjects into
children, adults and elderly subjects with cut points of 20 and 40 years with the two
146
extremes of 0 and 85 years.
> agegr <- cut(age, breaks = c(0, 20, 60, 85),
labels = c("Child", "Adult", "Elder"))
This method of cutting has already been explained in Chapter 2. Here, we put the
specific labels to replace the default bin names of "(0,20]","(20,60]" and "(60,80]".
To illustrate the change of log(money) by age, a series of box plots are drawn with
the statistical parameters stored in a new object 'a'.
> a <- boxplot(logmoney ~ agegr, varwidth = TRUE)
Then lines are drawn to join the median of log(money) of the age groups, which are
in the third row of 'a'.
> lines(x = 1:3, y = a$stats[3, ], col = "red")
> title(main = "Distribution of log(money) by age group",
ylab = "log(money)")
Child Adult Elder
1.0 1.5 2.0 2.5 3.0 3.5
Distribution of log(money) by age group
log(money)
Modelling with a categorical independent variable
A new model is now fit adding the categorical variable 'agegr'.
> lm5 <- lm(log10(money) ~ sex + agegr)
> summary(lm5)
=================== Lines omitted ===============
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.510 0.343 4.40 0.0031
sexM 0.169 0.351 0.48 0.6436
agegrAdult 1.578 0.408 3.87 0.0062
agegrElder 0.826 0.456 1.81 0.1129
=================== Lines omitted ===============

147
There are two age group parameters in the model; "Adult" and "Elder". The first
level, "Child", is omitted since it is the referent level. This means the other levels
will be compared to this level. Adults carried 101.578 or approximately 38 times
more money than children, which is statistically significant. Elders carried 100.8257 =
6.7 times more money than children, but is not statistically significant.
We could check the pattern of contrasts as follows:
> contrasts(agegr)
Adult Elder
Child 0 0
Adult 1 0
Elder 0 1
The columns of the matrix are the variables appearing in the model. The rows show
all the levels. The column 'Adult' in the model is equal to 1 when agegr is equal to
"Adult" and zero otherwise. The column 'Elder' is 1 when 'agegr' is "Elder" and zero
otherwise. There is no column of 'Child'. When both 'Adult' and 'Elder' are equal to
zero, the model then predicts the value of 'agegr' being "Child". If "Adult" is
required to be the referent level, the contrasts can be changed.
> contrasts(agegr) <- contr.treatment(levels(agegr), base=2)
The above command changes the referent group to level 2.
> contrasts(agegr)
Child Elder
Child 1 0
Adult 0 0
Elder 0 1
The 'Adult' column is now missing. Other tpes of contrast can also be specified. See
the references for more details.
> summary(lm(log10(money) ~ sex + agegr))
================== Lines omitted =================
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.088 0.286 10.78 1.3e-05
sexM 0.169 0.351 0.48 0.6436
agegrChild -1.578 0.408 -3.87 0.0062
agegrElder -0.752 0.408 -1.84 0.1079
================== Lines omitted =================
Note that he coefficient of 'Child' is the negative of that of 'Adult' from model
'lm5'. Moreover, elderly persons did not carry significantly more money than
adults.
148
References
Venables, W. N. and Ripley, B. D. (2002) Modern Applied Statistics with S. Fourth
edition. Springer.
Exercise_________________________________________________
What will happen in 'lm3' if log base 2 is used instead of log base 10? Would the
conclusion be the same?
149
Chapter 14: Generalized Linear Models
From lm to glm
Linear modelling using the lm function is based on the least squares method. The
concept is to minimise the sum of squares of residuals. Modelling from lm is
equivalent to that of analysis of variance or 'aov'. The only difference is that the
former focuses on coefficients of the independent variables whereas the latter
focuses on their sum of squares.
Generalized linear modelling (GLM) is, as it is called, more general that just linear
modelling. The method is based on the likelihood function. When the likelihood is
maximised, the coefficients and variances (and subsequently standard errors) of
independent variables are achieved. While classical linear modelling assumes the
outcome variable is defined on a continuous scale, such as blood loss in the
previous examples, (as well as assuming normality of errors and constant variance),
GLM can handle outcomes that are expressed as proportions, Poisson distributed
(counts) and others such as those from the gamma and negative binomial
distributions.
We will first start with the outcome on a continuous scale as in the previous
example of blood loss and hookworm infection.
> zap()
> data(Suwit)
> use(Suwit)
> bloodloss.lm <- lm(bloss ~ worm)
> summary(bloodloss.lm)
The results are already shown in the previous chapter.
Now we perform a generalised linear regression model using the function glm. For
the glm function the default family is the Gaussian distribution, and so this
argument can be omitted.
> bloodloss.glm <- glm(bloss ~ worm)

150
> summary(bloodloss.glm)
Call:
glm(formula = bloss ~ worm)
Deviance Residuals:
Min 1Q Median 3Q Max
-15.8461 -10.8118 0.7502 4.3562 34.3896
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 10.847327 5.308569 2.043 0.0618
worm 0.040922 0.007147 5.725 6.99e-05
(Dispersion parameter for gaussian family taken to be 188.882)
Null deviance: 8647.0 on 14 degrees of freedom
Residual deviance: 2455.5 on 13 degrees of freedom
AIC: 125.04
Number of Fisher Scoring iterations: 2
Using the same data frame and the same formula, i.e. 'bloss ~ worm', the results
from 'lm' and 'glm' for residuals (called deviance residuals in 'glm'), coefficients and
standard errors are the same. However, there are more attributes of the latter than
the former.
Model attributes
> attributes(bloodloss.lm)
$names
[1] "coefficients" "residuals" "effects" "rank"
[5] "fitted.values" "assign" "qr" "df.residual"
[9] "xlevels" "call" "terms" "model"
$class
[1] "lm"
> attributes(bloodloss.glm)
$names
[1] "coefficients" "residuals" "fitted.values"
[4] "effects" "R" "rank"
[7] "qr" "family" "linear.predictors"
[10] "deviance" "aic" "null.deviance"
[13] "iter" "weights" "prior.weights"
[16] "df.residual" "df.null" "y"
[19] "converged" "boundary" "model"
[22] "call" "formula" "terms"
[25] "data" "offset" "control"
[28] "method" "contrasts" "xlevels"
$class
[1] "glm" "lm"

151
Note that 'bloodloss.glm' also has class as lm in addition to its own glm. The
two sets of attributes are similar with more sub-elements for the
'bloodloss.glm '. Sub-elements of the same names are essentially the same. In
this setting, the 'deviance' from the glm is equal to the sum of squares of the
residuals.
> sum(bloodloss.glm$residuals^2)
[1] 2455.468
> bloodloss.glm$deviance
[1] 2455.468
Similarly, the 'null.deviance' is equal to the total sum of squares of the difference of
individual amount of blood loss from the mean blood loss.
> sum((bloss-mean(bloss))^2)
[1] 8647.044
> bloodloss.glm$null.deviance
[1] 8647.044
Some of the attributes in of the 'glm' are rarely used but some, such as 'aic', are very
helpful. There will be further discussion on this in future chapters.
Attributes of model summary
> attributes(summary(bloodloss.lm))
$names
[1] "call" "terms" "residuals" "coefficients"
[5] "aliased" "sigma" "df" "r.squared"
[9] "adj.r.squared" "fstatistic" "cov.unscaled"
$class
[1] "summary.lm"
> attributes(summary(bloodloss.glm))
$names
$names
[1] "call" "terms" "family"
[4] "deviance" "aic" "contrasts"
[7] "df.residual" "null.deviance" "df.null"
[10] "iter" "deviance.resid" "coefficients"
[13] "aliased" "dispersion" "df"
[16] "cov.unscaled" "cov.scaled"
$class
[1] "summary.glm"
A large proportion of the elements of both sets of attributes repeat those of the
models. The additional attributes include the R squared in the 'lm' model and the
covariance matrix ('cov.unscaled') in both models. This covariance matrix is used
for calculation of the standard errors and 95% confidence intervals of the
coefficients.
152
Covariance matrix
When there are two or more explanatory variables, and they are not independent,
the collective variation is denoted as covariance (compared to variance for a single
variable). It is stored as a symmetrical matrix since one variable can covary with
each of the others. A covariance matrix can be 'scaled' or 'unscaled'. The one from
the 'lm' model gives 'cov.unscaled' while 'glm' gives both.
> vcov(bloodloss.glm) # or summary(bloodloss.glm)$cov.scaled
(Intercept) worm
(Intercept) 28.18090491 -2.822006e-02
worm -0.02822006 5.108629e-05
> summary(bloodloss.glm)$cov.unscaled
(Intercept) worm
(Intercept) 0.1491983716 -1.494057e-04
worm -0.0001494057 2.704665e-07
The latter covariance matrix can also be obtained from the summary of the ordinary
linear model.
> summary(bloodloss.lm)$cov.unscaled
The scaling factor is, in fact, the dispersion, or sigma squared, which is the sum of
squares of residuals divided by degrees of freedom of the residual. Thus the first
matrix can be obtained from
> summary(bloodloss.glm)$cov.unscaled *
summary(bloodloss.glm)$dispersion
or
> summary(bloodloss.lm)$cov.unscaled *
summary(bloodloss.lm)$sigma^2
or
> summary(bloodloss.lm)$cov.unscaled *
sum(summary(bloodloss.lm)$residuals^2)/13
The scaled covariance matrix is used for computing standard errors of the
coefficients. The diagonal term of this matrix where the row name is the same as
the column name is the value of variance of the coefficient under the same name.
Taking the square root of this term will result in the standard error of the
coefficient.
Computation of standard errors, t values and 95% confidence
intervals
The standard error of 'worm' is
> vcov(bloodloss.glm)[2,2]^.5 -> se2
> se2
[1] 0.0071475

153
This can be checked against the summary of the coefficients.
> coef(summary(bloodloss.glm))
Estimate Std. Error t value Pr(>|t|)
(Intercept) 10.847327 5.3085690 2.043362 0.06183205
worm 0.040922 0.0071475 5.725392 0.00006990
Subsequently, the 't value' can be computed from division of the coefficient by the
standard error:
> coef(summary(bloodloss.glm))[2,1] /
summary(bloodloss.glm)$cov.scaled[2,2]^.5 -> t2
> t2
or
> 0.04092205 / 0.007147467 # 5.7254
The P value is the probability that 't' can be at this or a more extreme value. The
more extreme can be on both sides or signs of the t value. Therefore, the P value is
computed from
> pt(q=t2, df=13, lower.tail=FALSE) * 2
[1] 6.9904e-05
This value is equal to that in the summary of the coefficients. More details on the
computation of a probability from the t distribution can be search from 'help(TDist)'
or 'help(pt)'.
Finally to compute the 95% confidence interval:
> beta2 <- coef(summary(bloodloss.glm))[2,1]; beta2
[1] 0.04092205
> ci2 <- beta2 + qt(c(0.025, 0.975), 13)*se2; ci2
[1] 0.02548089 0.05636321
In fact, R has a command to compute the 95% confidence interval of the model as
follows:
> confint(bloodloss.lm)
2.5 % 97.5 %
(Intercept) -0.621139 22.315793
worm 0.025481 0.056363
The results are the same but faster. Note that the command
confint(bloodloss.glm) gives a slightly different confidence interval. This
is because the function uses the normal distribution instead of t distribution and
therefore it is not as appropriate.

154
Other parts of 'glm'
As mentioned before, the linear modelling or 'lm', after being generalized to
become 'glm', can accommodate more choices of outcome variables. The model is
said to have a 'family'. To check the family:
> family(bloodloss.glm) # or bloodloss$family
Family: gaussian
Link function: identity
Modelling by lm is equivalent to glm with family being 'gaussian'. The link
function is 'identity', which means that the outcome variable is not transformed.
Other types of 'family' and 'link' will be demonstrated in subsequent chapters.
Since the link function is 'identity', the 15 values of the linear predictors for this
family of 'glm' are the same as the fitted values (of both the 'lm' and 'glm' models).
> all(fitted(bloodloss.glm) == predict(bloodloss.glm))
[1] TRUE
The 'glm' summarises the error using the 'deviance'. For the linear model, this value
is equal to the sum of squares of the residuals.
> bloodloss.glm$deviance
[1] 2455.468
> sum(summary(bloodloss.lm)$res^2)
[1] 2455.468
The interpretation of the error is the same as from the linear model; a larger
deviance indicates a poorer fit.
Generalized linear modelling employs numerical iterations to achieve maximum
likelihood. The value of the maximum likelihood is small because it is the product
of probabilities. Its logarithmic form is therefore better to handle. The maximum
log likelihood can be obtained from the following function:
> logLik(bloodloss.glm)
'log Lik.' -59.51925 (df=3).

155
The higher (less negative) the log likelihood is, the better the model fits. However,
each model has its own explanatory parameters. Having too many parameters can
be inefficient. When fitting models one always strives for parsimony. An attribute
of a model that balances the log-likelihood and the number of parameters is the AIC
value. It is abbreviated from "Akaike Information Criterion" and is equal to -2×log-
likelihood + k×npar, where k is the penalty factor (usually 2) and npar represents
the number of parameters in the fitted model. A high likelihood or good fit will
result in a low AIC value. However, a large number of parameters also results in a
high AIC. The number of parameters of this model is 3. The AIC is therefore:
> -2*as.numeric(logLik(bloodloss.glm))+2*3
[1] 125.0385
> AIC(bloodloss.glm)
[1] 125.0385
The AIC is very useful when choosing between models from the same dataset. This
and other important attributes will be discussed in more details in subsequent
chapters.
References
Dobson, A. J. (1990). An Introduction to Generalized Linear Models. London:
Chapman and Hall.
McCullagh P. and Nelder, J. A. (1989). Generalized Linear Models. London:
Chapman and Hall.
156
Exercise_________________________________________________
In the dataset BP, use the glm command with "family=Gaussian" to analyse models
predicting systolic blood pressure from age and adding table salt with and without
the interaction term. Use the AIC to choose the most efficient model.

157
Chapter 15: Logistic Regression
Distribution of binary outcome
In epidemiological data, most of the outcomes are often binary or dichotomous. For
example, in the investigation of the cause of a disease, the status of the outcome, the
disease, is diseased vs non-diseased. For a mortality study, the outcome is usually
died or survived.
For a continuous variable such as weight or height, the single representative number
for the population or sample is the mean or median. For dichotomous data, the
representative number is the proportion or percentage of one type of the outcome.
For example, 'prevalence' is the proportion of the population with the disease of
interest. Case-fatality is the proportion of deaths among the people with the disease.
The other related term is 'probability'. Proportion is a simple straightforward term.
Probability denotes the likeliness, which is more theoretical. In the case of a
dichotomous variable, the proportion is used as the estimated probability.
For computation, having the outcome is often represented with 1 and 0 otherwise.
The prevalence is then the mean of diseased values among the study sample. For
example, if there are 50 subjects, 7 with disease (coded 1), 43 without disease
(coded 0), then the mean is 7/50 = 0.14, which is the prevalence.
Probability is useful due its simplicity. For complex calculations such as logistic
regression, log(odds) or logit is more feasible. If P is the probability of having a
disease, 1-P is probability of not having the disease. The odds is thus P/(1-P). The
relationship between probability and odds, mainly log(odds) can be plotted as
follows.
158
> p <- seq(from=0, to=1, by=.01)
> odds <- p/(1-p)
> plot(log(odds), p, type="l", col="blue", ylab="Probability",
main="Relationship between odds and probability", las=1)
> abline(h=.5)
> abline(v=0)
−4 −2 0 2 4
0.0
0.2
0.4
0.6
0.8
1.0
Relationship between odds and probability
log(odds)
Probability
The probability has a minimum of 0, maximum of 1 and mid value of 0.5. The odds
has its corresponding values at 0, infinity and 1. Log(odds), or often called 'logit',
has a linear increment with corresponding extremes of -infinity and +infinity and 0
for the mid-point. The curve is called a logistic curve. Being on a linear and well-
balanced scale, the logit is a more appropriate scale for a binary outcome than the
probability itself. Modelling logit(Y|X) ~ βX is the general form of logistic
regression. It means that the logit of Y given X (or under the condition of X), where
X denotes one or more independent variables, can be determined by the sum of
products between each specific coefficient with its value of X.
Suppose there are independent or exposure variables: X1 and X2. βX would be β0
+ β1X1 + β2X2, where β0 is the intercept.
In the medical field, the binary (also called dichotomous) outcome Y is often
disease vs non-disease, dead vs alive, etc. The X can be age, sex, and other
prognostic variables. Among these X variables, one or a few are under testing of the
specific hypothesis. Others are potential confounders, sometimes called co-variates.
159
Mathematically, it turns out that Pr(Y|X) is equal to exp(βX)/(1 + exp(βX)). Hence,
logistic regression is often used to compute the probability of an outcome under a
given set of exposures. For example, prediction of probability of getting a disease
under a given set of age, sex, and behaviour groups, etc.
Example: Tooth decay
The dataset Decay is a simple dataset containing two variables: 'decay', which is
binary and 'strep', which is a continuous variable.
> zap()
> data(Decay)
> use(Decay)
> des()
No. of observations =436
Variable Class Description
1 decay numeric Any decayed tooth
2 strep numeric CFU of mutan strep.
> summ()
No. of observations =436
Var. name Obs. mean median s.d. min. max.
1 decay 436 0.63 1 0.48 0 1
2 strep 436 95.25 105 53.5 0.5 152.5
The outcome variable is 'decay', which indicates whether a person has at least one
decayed tooth (1) or not (0). The exposure variable is 'strep', the number of colony
forming units (CFU) of streptococci, a group of bacteria suspected to cause tooth
decay.
The prevalence of having decayed teeth is equal to the mean of the 'decay' variable,
i.e. 0.63. To look at the 'strep' variable type:
> summ(strep)
The plot shows that the vast majority have the value at about 150. Since the natural
distribution of bacteria is logarithmic, a transformed variable is created and used as
the independent variable.
> log10.strep <- log10(strep)
> label.var(log10.strep, "Log strep base 10")
> glm0 <- glm(decay~log10.strep, family=binomial, data=.data)
> summary(glm0)
===============
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.554 0.518 -4.93 8.4e-07
log10.strep 1.681 0.276 6.08 1.2e-09
===============
AIC: 535.83
160
Both the coefficients of the intercept and 'log10.strep' are statistically significant.
Pr(>|z|) for 'log10.strep' is the P value from Wald's test. This tests whether the
co-efficient, 1.681, is significantly different from 0. In this case it is.
The estimated intercept is -2.554. This means that when log10.strep is 0 (or strep
equals 1 CFU), the logit of having at least a decayed tooth is -2.55. We can then
calculate the baseline odds and probability.
> exp(-2.554) -> baseline.odds
> baseline.odds
[1] 0.07777
> baseline.odds/(1+baseline.odds) -> baseline.prob
> baseline.prob
[1] 0.072158
There is an odds of 0.077 or a probability of 7.2% of having at least one decayed
tooth if the number of CFU of the mutan strep is at 1 CFU.
The coefficient of log10.strep is 1.681. For every unit increment of log10(strep), or
an increment of 10 CFU, the logit will increase by 1.681. This increment of logit is
constant but not the increment of probability because the latter is not on a linear
scale. The probability at each point of CFU is computed by replacing both
coefficients obtained from the model. For example, at 100 CFU, the probability is:
> coef(glm0)[1] + log10(100)*coef(glm0)[2]
(Intercept)
0.8078
To see the relationship for the whole dataset:
> plot(log10.strep, fitted(glm0))
A logistic nature of the curve is partly demonstrated. To make it clearer, the ranges
of X and Y axes are both expanded to allow a more extensive curve fitting.
> plot(log10.strep, fitted(glm0), xlim = c(-2,4),
ylim=c(0,1), xlab=" ", ylab=" ", xaxt="n", las=1)
Another vector of the same name 'log10.strep' is created in the form of a data frame
for plotting a fitted line on the same graph.
> newdata <- data.frame(log10.strep=seq(from=-2, to=4, by=.01))
> predicted.line <- predict.glm(glm0,newdata,type="response")
The values for predicted line on the above command must be on the same scale as
the 'response' variable. Since the response is either 0 or 1, the predicted line would
be in between, ie. the predicted probability for each value of log10(strep).
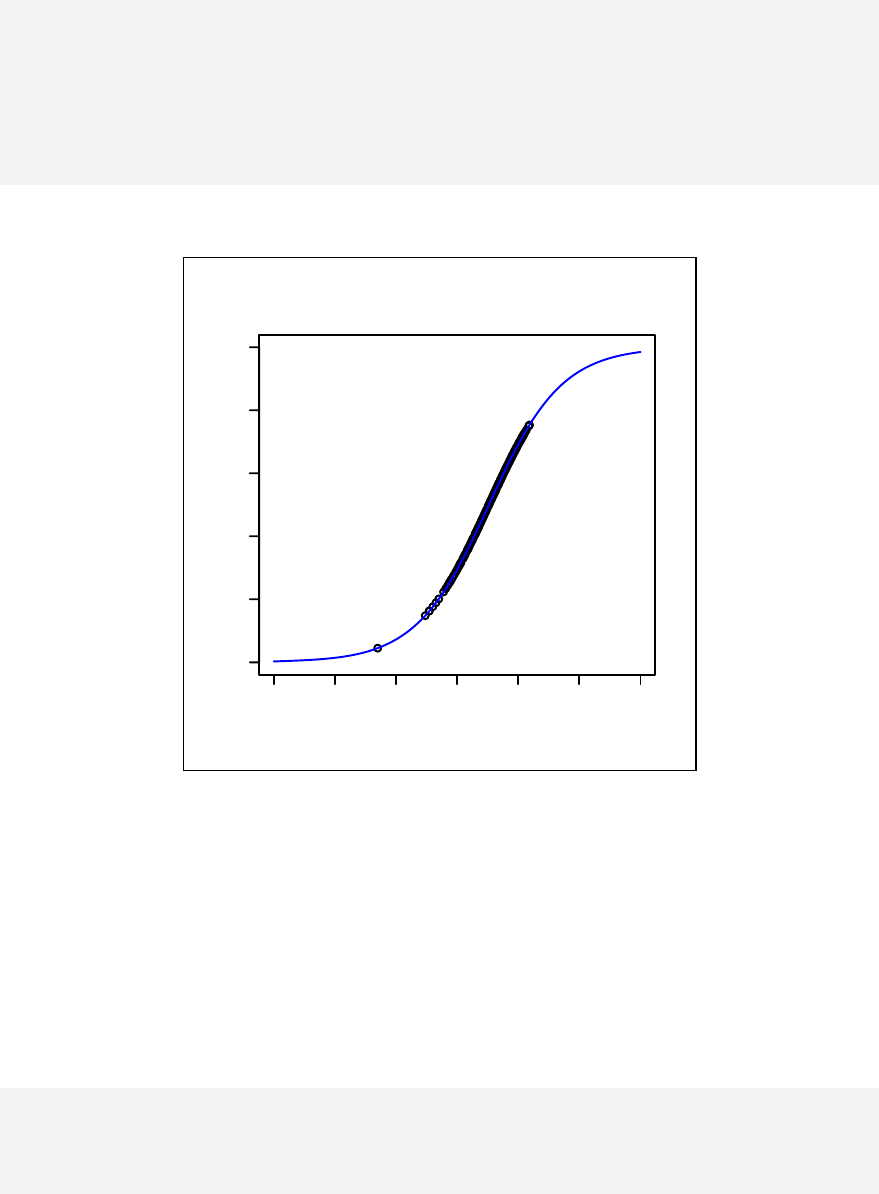
161
> lines(newdata$log10.strep, predicted.line, col="blue")
> axis(side=1, at=-2:4, labels=as.character(10^(-2:4)))
> title(main="Relationship between mutan streptococci \n
and probability of tooth decay", xlab="CFU",
ylab="Probability of having decayed teeth")
Note the use of the '\n' in the command above to separate a long title into two lines.
0.0
0.2
0.4
0.6
0.8
1.0
0.01 0.1 1 10 100 1000 10000
Relationship between mutan streptococci
and probability of tooth decay
CFU
Probability of having decayed teeth
Logistic regression with a binary independent variable
The above example of caries data has a continuous variable 'log10.strep' as the key
independent variable. In most epidemiological datasets, the independent variables
are often categorical. Remember that we have a dataset on outbreak of food
poisoning in Thailand analysed in Chapters 7-9. In this chapter, we will use logistic
regression to fit a model when the suspected causes are categorical variables.
Readers are advised to compare the results of logistic regression in this chapter with
those from the stratified analysis in previous chapters.
> zap()
> load("chapter9.Rdata")
> use(.data)
> des()
We model 'case' as the binary outcome variable and take 'eclair.eat' as the only
explanatory variable.
162
> glm0 <- glm(case ~ eclair.eat, family=binomial, data=.data)
> summary(glm0)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.923 0.265 -11.03 <2e-16
eclair.eatTRUE 3.167 0.276 11.48 <2e-16
=================== Lines omitted =================
The above part of the display is actually a matrix from the object
'coef(summary(glm0))'. Epicalc manipulates this matrix and gives rise to a
display more understandable by most epidemiologists.
> logistic.display(glm0)
Logistic regression predicting diseased
OR (95% CI) P(Wald's test) P(LR-test)
eating eclair 23.75 (13.82,40.79) < 0.001 < 0.001
Log-likelihood = -527.6075
No. of observations = 977
AIC value = 1059.2
The odds ratio from the logistic regression is derived from exponentiation of the
estimate, i.e. 23.75 is obtained from:
> exp(coef(summary(glm0))[2,1])
The 95% confidence interval of the odds ratio is obtained from
> exp(coef(summary(glm0))[2,1] + c(-1,1) * 1.96 *
coef(summary(glm0))[2,2])
These values are close to simple calculation of the 2-by-2 table discussed earlier in
Chapter 9. The log-likelihood and the AIC value will be discussed later.
The default values in logistic.display are 95% for the confidence intervals
and the digits are shown to two decimal places. See the online help for details.
> args(logistic.display)
> help(logistic.display)
You can change the default values by adding the extra argument(s) in the command.
> logistic.display(glm0, alpha=0.01, decimal=2)
If the data frame has been specified in the glm command, the output will show the
variable description instead of the variable names. The P value from Wald's test is
the same as that seen from the coefficient matrix of 'summary(glm0)'.

163
The output from logistic.display also contains the 'LR-test' result, which checks
whether the likelihood of the given model, 'glm0', would be significantly different
from the model without 'eclair.eat', which in this case would be the "null" model.
For an independent variable with two levels, the LR-test does not add further
important information because Wald's test has already tested the hypothesis. When
the independent variable has more than two levels, the LR-test is more important
than Wald's test as the following example demonstrates.
> glm1 <- glm(case ~ eclairgr, family=binomial, data=.data)
> logistic.display(glm1)
Logistic regression predicting diseased
OR(95%CI) P(Wald's test) P(LR-test)
pieces of eclair eaten: < 0.001
ref.=0
1 17.57 (9.21,33.49) < 0.001
2 22.27 (12.82,38.66) < 0.001
>2 43.56 (22.89,82.91) < 0.001
Log-likelihood = -516.8236
No. of observations = 972
AIC value = 1041.6
Interpreting Wald's test alone, one would conclude that all levels of eclair eaten
would be significant. However, this depends on the reference level. By default, R
assumes that the first level of an independent factor is the referent level. If we
relevel the reference level to be 2 pieces of eclair, Wald's test gives a different
impression.
> eclairgr <- relevel(eclairgr, ref="2")
> pack()
> glm2 <- glm(case ~ eclairgr, family=binomial, data=.data)
> logistic.display(glm2)
Logistic regression predicting diseased
OR(95%CI) P(Wald's test) P(LR-test)
pieces of eclair eaten: ref.=2 < 0.001
0 0.04 (0.03,0.08) < 0.001
1 0.79 (0.52,1.21) 0.275
>2 1.96 (1.28,2.99) 0.002
==============================================================
The results show that eating only one piece of eclair does not reduce the risk
significantly compared to eating two pieces.
While results from Wald's test depend on the reference level of the explanatory
variable, the LR-test is concerned only with the contribution of the variable as a
whole and ignores the reference level. We will return to this discussion in a later
chapter.

164
Next, try 'saltegg' as the explanatory variable.
> glm3 <- glm(case ~ saltegg, family = binomial, data=.data)
> logistic.display(glm3)
Logistic regression predicting case
OR (95% CI) P(Wald's test) P(LR-test)
saltegg: 2.54 (1.53,4.22) < 0.001 < 0.001
Yes vs No
Log-likelihood = -736.998
No. of observations = 1089
AIC value = 1478
The odds ratio for 'saltegg' is statistically significant and similar to that seen from
the cross-tabulation in Chapter 9. The number of valid records is also higher than
the model containing 'eclairgr'.
Note: ______________________________________________________________
One should always be careful when analysing data that contain missing values.
Methods to handle missing values are beyond the scope of this book and for reasons
of simplicity are ignored here. Readers are advised to deal with missing values
properly prior to conducting their analysis.
To check whether the odds ratio is confounded by 'eclairgr', the two explanatory
variables are put together in the next model.
> glm4 <- glm(case ~ eclairgr + saltegg, family=binomial)
> logistic.display(glm4, crude.p.value=TRUE)
Logistic regression predicting case
crude OR(95%CI) P value adj. OR(95%CI) P(Wald) P(LR-test)
eclairgr: ref.=2 < 0.001
0 0.04 (0.03,0.08) < 0.001 0.04 (0.03,0.08) < 0.001
1 0.79 (0.52,1.21) 0.275 0.79 (0.51,1.21) 0.279
>2 1.96 (1.28,2.99) 0.002 1.96 (1.28,2.99) 0.002
saltegg: 2.37 (1.4,3.99) 0.001 1.01 (0.53,1.93) 0.975
0.975
Yes vs No
Log-likelihood = -516.823
No. of observations = 972
AIC value = 1043.6
The odds ratios of the explanatory variables in glm4 are adjusted for each other.
The crude odds ratios are exactly the same as from the previous models with only
single variable. The P value of 'saltegg' is shown as 0 due to rounding. In fact, it is
0.00112, which is not less than 0.001. Epicalc, for aesthetic reasons, displays P
values as '< 0.001' whenever the original value is less than 0.001.

165
The adjusted odds ratios of 'eclairgr' do not change suggesting that it is not
confounded by 'saltegg', whereas the odds ratio of 'saltegg' is celarly changed
towards unity, and now has a very large P value. The difference between the
adjusted odds ratio and the crude odds ratio is an indication that 'saltegg' is
confounded by 'eclairgr', which is an independent risk factor. These adjusted odds
ratios are close to those obtained from the Mantel-Haenszel method shown in
chapter 9.
Now that we have a model containing two explanatory variables, we can compare
models 'glm4' and 'glm2' using the lrtest command.
> lrtest(glm4, glm2)
Likelihood ratio test for MLE method
Chi-squared 1 d.f. = 0.0009809 , P value = 0.975
The P value of 0.975 is the same as that from 'P(LR-test)' of 'saltegg' obtained from
the preceding command. The test determines whether removal of 'saltegg' in a
model would make a significant difference than if it were kept. When there is more
than one explanatory variable, 'P(LR-test)' from logistic.display is actually
obtained from the lrtest command, which compares the current model against
one in which the particular variable is removed, while keeping all remaining
variables.
Logistic regression gives both the adjusted odds ratios simultaneously. The Mantel-
Haenszel method only gives the odds ratio of the variable of main interest. An
additional advantage is that logistic regression can handle multiple covariates
simultaneously.
> glm5 <- glm(case~eclairgr+saltegg+sex, family=binomial)
> logistic.display(glm5)
Logistic regression predicting case
crude OR(95%CI) adj. OR(95%CI) P(Wald's test) P(LR-test)
eclairgr: ref.=2 < 0.001
0 0.04 (0.03,0.08) 0.04 (0.02,0.07) < 0.001
1 0.79 (0.52,1.21) 0.75 (0.49,1.16) 0.2
>2 1.96 (1.28,2.99) 1.82 (1.19,2.8) 0.006
saltegg: 2.37 (1.41,3.99) 0.92 (0.48,1.76) 0.807 0.808
Yes vs No
sex: 1.58 (1.19,2.08) 1.85 (1.35,2.53) < 0.001 < 0.001
Male vs Female
Log-likelihood = -509.5181
No. of observations = 972
AIC value = 1031.0

166
The third explanatory variable 'sex' is another independent risk factor. Since
females are the reference level, males have an increased odds of 90% compared to
females. This variable is not a confounder to either of the preceding variables
because it has not substantially changed the odds ratios of any of them (from
'glm4'). The reason for not being able to confound is its lack of association with
either of the preceding explanatory variables. In other words, males and females
were not different in terms of eating eclairs and salted eggs.
Interaction
An interaction term consists of at least two variables, at least one of which must be
categorical. If an interaction is present, the effect of one variable will depend on the
status of the other and thus they are not independent. In R the interaction term can
be specified in two ways: 'x1*x2' or 'x1:x2'. The former is equivalent to 'x1+
x2+x1:x2'.
Examine the following model where the variables 'eclairgr' and 'beefcurry' are
specified as an interaction term.
> glm6 <- glm(case ~ eclairgr*beefcurry, family=binomial)
> logistic.display(glm6, decimal=1)
Logistic regression predicting diseased
crude OR(95%CI) adj. OR(95%CI) P(Wald's test) P(LR-test)
eclairgr: ref.=2 < 0.001
0 0 (0,0.1) 0.1 (0,0.5) 0
1 0.8 (0.5,1.2) 0.5 (0.1,2.5) 0.39
>2 2 (1.3,3) 0.5 (0.1,3) 0.41
beefcurry: 2.7 (1.6,4.6) 1.4 (0.5,3.6) 0.53 < 0.001
(Yes vs No)
eclairgr:beefcurry: ref.=2:No 0.03
0:Yes - 0.3 (0.1,1.2) 0.09
1:Yes - 1.7 (0.3,9.7) 0.52
>2:Yes - 4.8 (0.7,33.9) 0.11
Log-likelihood = -511.8
No. of observations = 972
AIC value = 1039.6
The last term, 'eclairgr:beefcurry', is the interaction term. Interpretation of the P
values from Wald's test suggests that the interaction may not be significant.
However, the P value from the LR-test is more important, in fact it is decisive. The
value of 0.03 indicates that both 'eclairgr' and 'beefcurry' are not acting
independently from each other. Computation of the LR-test P values for the main
effects, 'eclairgr' and 'beefcurry', is not possible since models without main effects
(but with interaction terms) have the same Log-likelihood as ones with the main
effects included. The crude odds ratios for the interaction terms are also not
applicable.

167
Readers may like to relevel the 'eclairgr' variable back to the original reference level
(ref=0) and compare the output.
> eclairgr <- relevel(eclairgr, ref="0")
> pack()
> glm7 <- glm(case~eclairgr*beefcurry, family=binomial,
data=.data)
> logistic.display(glm7)
Stepwise selection of independent variables
The following section demonstrates stepwise selection of models in R.
First, a subset of the dataset is created to make sure that all the variables have valid
(non missing) records. Note that the glm command also allows a subset of the
dataset to be specified. Subsequent models use the 'eclair.eat' variable instead of
'eclairgr' in order to simplify the output.
> complete.data <- subset(.data, subset=!is.na(eclair.eat)
& !is.na(beefcurry) & !is.na(saltegg) & !is.na(sex))
> glm8 <- glm(case ~ eclair.eat * beefcurry + saltegg + sex,
family = binomial, data=complete.data)
The model may be too excessive. We let R select the model with lowest AIC.
> modelstep <- step(glm8, direction = "both")
Start: AIC= 1038.5
case ~ eclair.eat * beefcurry + saltegg + sex
Df Deviance AIC
- saltegg 1 1026 1036
<none> 1026 1038
- eclair.eat:beefcurry 1 1030 1040
- sex 1 1039 1049
Step: AIC= 1036.5
case ~ eclair.eat + beefcurry + sex + eclair.eat:beefcurry
Df Deviance AIC
<none> 1026 1036
- eclair.eat:beefcurry 1 1030 1038
+ saltegg 1 1026 1038
- sex 1 1039 1047
Initially, the AIC is 1038.5. The command step removes each independent
variable and compares the degrees of freedom reduced, the new deviance and the
new AIC. The results are increasingly sorted by AIC. The top one having the lowest
AIC is the best one. At the first step, removal of 'saltegg' would give the lowest AIC
and is therefore chosen and used for the next step.

168
In the second selection phase, not removing any remaining independent variable
gives the lowest AIC. Thus the selection process stops with the remaining variables
kept. Now, we check the results.
> summary(modelstep)
=================== Lines omitted ==================
Coefficients:
Estimate St. Error z value Pr(>|z|)
(Intercept) -2.672 0.494 -5.41 6.3e-08
eclair.eatTRUE 2.067 0.601 3.44 0.00059
beefcurry -0.903 0.573 -1.58 0.11484
sexMale 0.586 0.163 3.59 0.00033
eclair.eatTRUE:beefcurry 1.412 0.685 2.06 0.03923
=================== Lines omitted ==================
The final model has 'saltegg' excluded. Sex is an independent risk factor. Eating
eclairs is a risk factor, the effect of which was enhanced by eating beef curry.
Eating beef curry by itself is a protective factor. However, when eaten with eclairs,
the odds is increased and becomes positive.
It should be noted that stepwise regression is limited to exploration and often not
suitable for specific hypothesis testing, the way most epidemiological studies are
designed for. It tends to remove all non-significant independent variables from the
model. In hypothesis testing one or a few independent variables are set for testing.
The odds ratios and their confidence intervals must still be calculated regardless of
the statistical significance.
Interpreting the odds ratio
Let's look more carefully at the final model.
> logistic.display(modelstep, crude=FALSE)
Logistic regression predicting case
adj. OR(95%CI) P(Wald's) LR-test
eclair.eat 7.9 (2.43,25.66) < 0.001 < 0.001
beefcurry: Yes vs No 0.4 (0.13,1.25) 0.115 < 0.001
sex: Male vs Female 1.8 (1.31,2.47) < 0.001 < 0.001
eclair.eatTRUE:beefcurryYes 4.1 (1.07,15.71) 0.039 0.048
Log-likelihood = -513.2296
No. of observations = 972
AIC value = 1036.5
All the three variables 'eclair.eat', 'beefcurry' and 'sex' are dichotomous. The odds
ratio for 'sex' is that of males compared to females. For 'eclair.eat' it is TRUE vs
FALSE and for 'beefcurry', "Yes" is compared to "No".

169
The independent variable 'sex' has an odds ratio of approximately 1.8, which means
that males have approximately a 1.8 times higher risk than females. The other two
variables, 'eclair.eat' and beefcurry, are interacting. The odds ratio of 'eclair.eat'
depends on the value of 'beefcurry' and vice versa. Three terms 'eclair.eat',
'beefcurry' and their interaction term 'eclair.eat:beefcurry' need to be considered
simultaneously.
If 'beefcurry' is "No" (did not eat beef curry), the 'eclair.eat:beefcurry' term is 0. The
odds ratio for eclair.eat for this subgroup is therefore only 7.9. Among the beef
curry eaters, the interaction term should be multiplied by 1 (since 'eclair.eat' and
'beefcurry' are both 1), the odds ratio is then 7.9 × 4.1 or approximately 32.4.
The required odds ratio can be obtained from computing the product of the
appropriate odds ratio of the individual variables. However, the standard errors and
95% confidence interval cannot be easily computed from the above result.
A better way to get the odds ratio and 95% confidence interval for 'eclair.eat' among
'beefcurry' eaters is to relevel the variable and run the model again.
> complete.data$beefcurry <- relevel(complete.data$beefcurry,
ref="Yes")
> glm9 <- glm(case ~ eclair.eat * beefcurry + sex,
family = binomial, data = complete.data)
> logistic.display(glm9, crude=FALSE)
Logistic regression predicting case
adj. OR (95%CI) P(Wald's test) P(LR-test)
eclair.eat 32.4 (16.9,62.3) < 0.001 < 0.001
beefcurry: No vs Yes 2.47 (0.8,7.59) 0.115 < 0.001
sex: Male vs Female 1.8 (1.31,2.47) < 0.001 < 0.001
eclair.eatTRUE: 0.24 (0.06,0.93) 0.039 0.048
beefcurryNo
Log-likelihood = -513.2296
No. of observations = 972
AIC value = 1036.5
The odds ratio and 95% confidence interval of 'eclair.eat' among those who ate beef
curry are in the first row because the 'beefcurry' term in the second row and the
interaction term in the last row are all 0.

170
Other data formats
The above datasets are based on individual records. Sometimes, the regression is
required to be performed based on an existing, aggregated table.
> zap()
> data(ANCtable)
> ANCtable
> use(ANCtable)
> death <- factor(death)
> levels(death) <- c("no","yes")
> anc <- factor(anc)
> levels(anc) <- c("old","new")
> clinic <- factor(clinic)
> levels(clinic) <- c("A","B")
> pack()
The Epicalc function pack identifies all free vectors with the same length as the
number of records in .data and adds them into the data.frame. These free vectors
are then removed from the global environment.
> .data
death anc clinic Freq
1 no old A 176
2 yes old A 12
3 no new A 293
4 yes new A 16
5 no old B 197
6 yes old B 34
7 no new B 23
8 yes new B 4
This is a format with 'Freq' being a variable denoting numbers of subjects in each
category. This variable is put as the 'weight' in the model.
> glm(death ~ anc+clinic, binomial, weight=Freq, data=.data)
The coefficients are the same as those from using the original dataset, ANCdata.
However, the degrees of freedom is different.
Another data format for logistic regression is possible where the number of cases
and number of controls of the same exposure are in the same row, but separate
columns.
> .data$condition <- c(1,1,2,2,3,3,4,4)
> data2 <- reshape(.data, timevar="death", v.name="Freq",
idvar="condition", direction="wide")
The variable 'condition' is created to facilitate reshaping. The reshaped data, data2
has only four rows of data compared to .data, which has 8 rows.
171
> data2
anc clinic condition Freq.no Freq.yes
1 old A 1 176 12
3 new A 2 293 16
5 old B 3 197 34
7 new B 4 23 4
The first column in each row is the 'row.names' of the data frame. This data frame
can be written to a text file with 'row.names' and the variable 'condition' (the third
variable) omitted.
Logistic regression for 'data2' can be carried out as follows:
> glm(cbind(Freq.yes, Freq.no) ~ anc + clinic, data=data2,
family=binomial)
The left-hand side of the formula is a result of column binding the two outcome
frequency columns. The remaining parts of the commands remain the same as for
the case-by-case format. The coefficients and standard errors from this command
are the same as those above. However, the residual deviance and AIC are much
smaller due to the smaller number of degrees of freedom.
Case-by-case format of data is most commonly dealt with in the actual data
analysis. The formats in ANCtable and 'data2', which are occasionally found,
are mainly of theoretical interest.
More than 2 strata
The dataset Ectopic comes from a case-control study testing a hypothesis
whether previous induced abortion is a risk factor for current ectopic pregnancy.
There were three groups of patients studied: ectopic pregnancy patients ('EP'),
current clients who came for an induced abortion ('IA') and those who came for
delivery ('deli'). For simplicity, at this stage, the latter two groups are combined and
classed as the controls whereas the first group is classed as the cases. The exposure
of interest is 'hia' or history of previous induced abortion and a potential confounder
is 'gravi' or level of gravidity. Try the following commands in R:
> zap()
> data(Ectopic)
> use(Ectopic)
> des()
No. of observations = 723
Variable Class Description
1 id integer
2 outc factor Outcome
3 hia factor Previous induced abortion
4 gravi factor Gravidity
> summ()
172
No. of observations = 723
Var. name Obs. mean median s.d. min. max.
1 id 723 362 362 208.86 1 723
2 outc 723 2 2 0.817 1 3
3 hia 723 1.545 2 0.498 1 2
4 gravi 723 1.537 1 0.696 1 3
> tab1(outc, graph=F)
> tab1(hia, graph=F)
> tab1(gravi, graph=F)
> case <- outc == "EP"
> case <- factor(case)
> levels(case) <- c("control","case")
> tabpct(case, gravi)
Distribution of Gravidity by case
case
Gravidity
control case
1−2
3−4
>4
The cases had a higher level of gravidity.
> tabpct(case, hia) -> case.hia
The above command will show only the graph, since we have saved the output to an
object. Inspection of this object can be done by simply typing the object's name.
The cases also had a higher experience of induced abortion.
173
Distribution of Previous induced abortion
by case
case
Previous induced abortion
control case
never IAever IA
> cc(case, hia, design = "case-control")
hia
case no yes Total
control 268 214 482
case 61 180 241
Total 329 394 723
OR = 3.689
95% CI = 2.595 5.291
Chi-squared = 59.446 , 1 d.f. , P value = 0
Fisher's exact test (2-sided) P value = 0
II
II
Odds ratio from case control study
Odds of exposure
Outcome category
control
case
0.67 0.95 1.36 1.94 2.76 3.95
OR = 3.69
95% CI = 2.59 , 5.29
174
This odds ratio graph is specified with 'design' = "case-control", therefore the
orientation of it is adjusted toward the outcome variable. The odds of exposure
among the cases are on the right (higher value).
Next we adjust for gravidity.
> mhor(case, hia, gravi, design="case-control")
Stratified analysis by gravi
OR lower lim. upper lim. P value
gravi 1-2 3.72 2.328 5.98 6.26e-09
gravi 3-4 4.01 1.714 10.55 3.52e-04
gravi >4 2.02 0.307 22.42 4.62e-01
M-H combined 3.68 2.509 5.41 6.12e-12
M-H Chi2(1) = 47.29 , P value = 0
Homogeneity test, chi-squared 2 d.f. = 0.52 , P value = 0.769
The stratified analysis shows output tables for the three strata of gravi and
corresponding three exposure lines in the graph. The odds of exposure to induced
abortion increases (moving towards the right-hand side) with gravidity. The odds
among the control group is lower (more on the left) in each stratum of the gravidity
group. The slopes of the three lines are somewhat similar indicating minimal
interaction, and this is confirmed by the P value from the homogeneity test. The
MH combined odds ratio is similar to the crude odds ratio indicating rather little
effect of confounding by gravidity.
Stratified case control analysis
Odds of exposure
Outcome= case , Exposure= hia
II
II
gravi>4: OR= 2.02 (0.31, 22.42)
II
II
gravi3−4: OR= 4.01 (1.71, 10.55)
II
II
gravi1−2: OR= 3.72 (2.33, 5.98)
12481632641/2
MH−OR = 3.68 (2.51, 5.41)
homogeneity test P value = 0.769
Control
Case
For logistic regression we can use the glm function, as before:
> glm1 <- glm(case ~ hia, family = binomial)
> summary(glm1)

175
===========================
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.4801 0.1419 -10.433 < 2e-16
hiayes 1.3071 0.1742 7.502 6.26e-14
===========================
AIC: 862.77
Similar to the preceding section, logistic.display can be used in order to
obtain the odds ratio and 95% confidence interval of the exposure to induced
abortion. The intercept term here has no meaning and should be ignored.
> logistic.display(glm1)
Logistic regression predicting case : case vs control
OR(95%CI) P(Wald's test) P(LR-test)
hia: 3.7 (2.63,5.2) < 0.001 < 0.001
ever IA vs never IA
Log-likelihood = -429.3863
No. of observations = 723
AIC value = 862.77
> glm2 <- glm(case ~ hia + gravi, binomial)
> logistic.display(glm2)
Logistic regression predicting case : case vs control
crude OR(95%CI) adj. OR(95%CI) P(Wald's test) P(LR-test)
hia: 3.7 (2.6,5.2) 3.7 (2.5,5.4) < 0.001 < 0.001
ever IA vs never IA
gravi: ref.=1-2 1
3-4 1.7 (1.2,2.4) 1.0 (0.7,1.5) 0.989
>4 2.0 (1.2,3.2) 1.0 (0.6,1.7) 0.992
Log-likelihood = -429.3861
No. of observations = 723
AIC value = 866.77
The AIC from 'glm1' is lower than the one from 'glm2' indicating a better fit.
Cases of ectopic pregnancies had approximately 3.7 times the odds of previous
exposure to induced abortion compared to the control group. Gravidity has no effect
on the outcome and is not a confounder.
References
Hosmer Jr DW & Lemeshow S (2004). Applied Logistic Regression, 2nd Edition.
Kleinbaum DG & Klein M. Logistic Regression. A self-learning Text (2nd Edition).
Springer-Verlag New York, Inc. August 2002.

176
Exercises________________________________________________
Problem 1.
With the data frame 'complete.data', compute the odds ratio and 95%
confidence interval for combined exposure to 'eclair.eat' and 'beefcurry' using the
group who were exposed to neither eclair nor beef curry as the referent group.
Problem 2.
Use the ANCtable dataset and the function xtabs to create a stratified 2x2 table.
Then use the mhor function to analyse the adjusted odds ratio.
Hint: 'help(xtabs)', 'help(mhor)'.
Problem 3.
Use the Hakimi dataset to do a similar analysis.
Problem 4.
In the Ectopic dataset, unclass 'gravi' and use logistic regression to investigate a
dose response relationship (linear trend) between gravidity and risk of ectopic
pregnancy, after adjustment for the effect of previous induced abortion ('hia').

177
Chapter 16: Matched Case Control Study
Examples in previous chapters have cases and control independently recruited. For
a matched case control study, when a case is recruited, a control, or a set of controls
(more than one person), can be selected to match with the case in some parameters
such as age and sex and other conditions such as being siblings or neighbours. If
control series are chosen based on matching on only age and sex and the purpose of
such selection is only to avoid imbalances, then the dataset should probably be
analysed in a non-matched setting. There are many good books on how to analyse
case-control studies, particularly in the matched setting, and readers should consult
the references at the end of this chapter.
The examples in this chapter are for demonstration purposes only. The sample size
is rather small for making solid conclusions. However, the methods can still be
applied to other matched case-control studies.
In the analysis of matched sets, comparison is made within each matched set rather
than one series against the other. In this chapter, the datasets VC1to1 and VC1to6
consist of data from a matched case-control study testing whether smoking,
drinking alcohol and working in the rubber industry are risk factors for oesophageal
cancer. Each case was matched with his/her neighbours of the same sex and age
group. The matching ratio varied from 1:1 to 1:6. The file VC1to6 is the full
dataset whereas VC1to1 has the number of controls per case reduced to 1 for all
matched sets. This latter file is first used for matched pair analysis.
> zap()
> data(VC1to1)
> use(VC1to1)
> des()
No. of observations = 52
Variable Class Description
1 matset numeric
2 case numeric
3 smoking numeric
4 rubber numeric
5 alcohol numeric

178
> summ()
No. of observations = 52
Var. name obs. mean median s.d. min. max.
1 matset 52 13.5 13.5 7.57 1 26
2 case 52 0.5 0.5 0.5 0 1
3 smoking 52 0.81 1 0.4 0 1
4 rubber 52 0.33 0 0.47 0 1
5 alcohol 52 0.52 1 0.5 0 1
> head(.data)
matset case smoking rubber alcohol
1 1 1 1 0 0
2 1 0 1 0 0
3 2 1 1 0 1
4 2 0 1 1 0
5 3 1 1 1 0
6 3 0 1 1 0
There are 26 matched pairs as shown in the sorted 'matset' variable. The codes of
the variable 'case' are 1 for diseased and 0 for non-diseased. We now reshape the
data to facilitate data exploration.
> wide <- reshape(.data, timevar="case", v.names=c("smoking",
"rubber", "alcohol"), idvar="matset", direction="wide")
> head(wide,3)
matset smoke.1 rubber.1 alcohol.1 smoking.0 rubber.0 alcohol.0
1 1 1 0 0 1 0
3 2 1 0 1 1 1
5 3 1 1 0 1 1
The original data frame .data has the variables arranged in long form. Each
record represents one subject. The new data frame 'wide' is in wide form. Each
record represents one matched pair. Cross-tabulating the smoking habit of cases and
controls in each matched pair can now be done easily.
> attach(wide)
> table(smoking.1, smoking.0, dnn=c("smoking in case",
"smoking in control"))
smoking in control
smoking in case 0 1
0 0 5
1 5 16
The optional argument 'dnn' in the above table command allows the dimension
names to be specified, facilitating interpretation. From this cross tabulation, there
was no matched pair where both the case and control were non-smokers. There
were sixteen matched pairs where both were smokers. In five pairs, the cases
smoked but the controls did not (left lower corner). In the remaining five pairs
(right upper corner), the controls smoked while the cases did not.

179
The level of contrast of history of smoking between the two based on matched pairs
is called a conditional odds ratio. It is the value of the left lower corner cell divided
by the right upper corner cell. In this case the conditional odds ratio (sometimes
called McNemar's odds ratio) is 5/5 = 1. In fact, this means that the ratio of
discordant counts between cases having the exposure against controls having
exposure is 1.
Epicalc has a function matchTab that can be used to analyse the matched set (not
necessary 1 case per 1 control) from the original dataset as follows:
> detach(wide)
> rm(wide) # not required anymore
> matchTab(case, smoking, strata=matset)
Number of controls = 1
No. of controls exposed
No. of cases exposed 0 1
0 0 5
1 5 16
Odds ratio by Mantel-Haenszel method = 1
Odds ratio by maximum likelihood estimate (MLE) method = 1
95%CI= 0.29 , 3.454
The two methods give the same values for the odds ratio. The MLE method also
gives a 95% confidence interval of the estimate.
1:n matching
If there is no serious problem on scarcity of diseased cases, the best ratio of
matching is one case per control. Resources spent on collecting data from each
individual will be most efficient regardless of whether the subject is a case or a
control. However, when the disease of interest is rare, it is often cost-effective to
increase the number of controls per case. The efficiency (especially resources spent
on collecting data from extra controls) is decreased but it means that the study may
end sooner.
We now analyse the full dataset, where each case may have between 1 and 6
matched controls.
> zap()
> data(VC1to6); use(VC1to6)
> des()
> summ()
No. of observations = 119
================= lines omitted ============
> .data

180
matset case smoking rubber alcohol
1 1 1 1 0 0
2 1 0 1 0 0
3 2 1 1 0 1
4 2 0 1 1 0
================= lines omitted ============
116 26 0 0 0 0
117 26 0 1 1 0
118 26 0 0 0 0
119 26 0 1 1 1
It would be very cumbersome to reshape this data into a wide form. Let's use the
Epicalc function matchTab instead.
> matchTab(case, smoking, strata=matset)
Number of controls = 1
No. of controls exposed
No. of cases exposed 0 1
0 0 0
1 0 3
Number of controls = 2
No. of controls exposed
No. of cases exposed 0 1 2
0 0 0 1
1 1 1 0
================= lines omitted ============
Number of controls = 6
No. of controls exposed
No. of cases exposed 0 1 2 3 4 5 6
0 0 0 0 1 0 0 0
1 0 0 0 0 0 1 2
Odds ratio by Mantel-Haenszel method = 1.988
Odds ratio by maximum likelihood estimate (MLE) method = 2.066
95%CI= 0.678 , 6.299
The command gives six tables based on the matched sets of the same size (cases per
controls). The last table, for example, shows that there are four matched sets with
six controls per case. One of them has case non-exposed and three out of the
controls exposed. One has case exposed and five of the six controls non-exposed.
The remaining two sets have the case and all of the six controls exposed. The odds
ratios from the two different datasets are slightly different. However, the effect of
smoking on the outcome is still not statistically significant as the 95% confidence
interval of the odds ratio contains the value 1.
Logistic regression for 1:1 matching
As discussed above, the conditional odds ratio for the 1:1 matched case-control
study is based on the ratio of discordant exposures between cases and controls of

181
the same matched pair. From the modelling point of view, the difference of
outcome within the matched set is determined by the difference of exposure
between the case and the control. The former difference is fixed at one because the
outcome of a case is equal to 1 and the outcome of a control is equal to 0. The
exposure difference is computed within the matched set.
> zap()
> data(VC1to1); use(VC1to1)
> wide <- reshape(.data, timevar="case", idvar="matset",
v.names=c("smoking","rubber","alcohol"), direction="wide")
> use(wide)
> smoke.diff <- smoking.1 - smoking.0
> alcohol.diff <- alcohol.1 - alcohol.0
> rubber.diff <- rubber.1 - rubber.0
> outcome.1 <- rep(1, 26) # 26 cases with outcome being 1
> outcome.0 <- rep(0, 26) # 26 control with outcome being 0
> outcome.diff <- outcome.1 - outcome.0
> cbind(outcome.diff, smoke.diff, alcohol.diff)
> pack()
> summ()
No. of observations = 26
Var. name obs. mean median s.d. min. max.
1 matset 26 13.5 13.5 7.65 1 26
2 smoking.1 26 0.81 1 0.4 0 1
3 rubber.1 26 0.31 0 0.47 0 1
4 alcohol.1 26 0.65 1 0.49 0 1
5 smoking.0 26 0.81 1 0.4 0 1
6 rubber.0 26 0.35 0 0.49 0 1
7 alcohol.0 26 0.38 0 0.5 0 1
8 alcohol.diff 26 0.27 0 0.6 -1 1
9 outcome.0 26 0 0 0 0 0
10 outcome.1 26 1 1 0 1 1
11 outcome.diff 26 1 1 0 1 1
12 rubber.diff 26 -0.04 0 0.6 -1 1
13 smoking.diff 26 0 0 0.63 -1 1
Note that the variable 'outcome.diff' is 1 throughout all records because the outcome
for case is 1 and for control is 0 whereas difference in exposure to alchohol, rubber
and smoking can be 1 (case exposed control not exposed), 0 (either both case and
control exposed or none of them exposed) and -1 (case not exposed but control
exposed).
Now we perform logistic regression predicting difference of outcome from
difference in smoking history.
> co.lr1 <- glm(outcome.diff ~ smoke.diff-1, binomial)
> summary(co.lr1)
Call:
glm(formula = outcome.diff ~ smoke.diff-1, family=binomial)
Coefficients:

182
Estimate Std. Error z value Pr(>|z|)
smoke.diff 0.000 0.632 0 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 36.044 on 26 degrees of freedom
Residual deviance: 36.044 on 25 degrees of freedom
AIC: 38.04
In the above glm model, the difference of the outcome (which is always 1 for the
above reason) is predicted by the difference in smoking habit. There is an additional
term '-1' in the right-hand side of the formula, which indicates that the intercept
should be removed from the model. Usually, the intercept is the expected value of
the dependent variable (the variable on the left-hand side of the formula) when all
the independent variables are equal to 0. In conditional logistic regression, there is
no such intercept because the difference of the outcome is fixed to 1, the logit of
which is 0.
With the coefficient of 0, the odds ratio is exp(0) = 1, which is the same as the
result from the matched tabulation. The 95% confidence interval of the odds ratio
can be obtained from:
> exp(confint.default(co.lr1))
2.5 % 97.5 %
smoke.diff 0.2895 3.4542
These values are exactly the same as those obtained from the matched tabulation.
Epicalc can display the results in a more convenient format.
> logistic.display(co.lr1)
Logistic regression predicting outcome.diff
OR(95%CI) P(Wald's test) P(LR-test)
smoke.diff 1 (0.29,3.45) 1 -
Log-likelihood = -18.0218
No. of observations = 26
AIC value = 38.0437
Recall that the advantage of logistic regression is in its ability to handle more than
one exposure variable.
Run a logistic model again, adding the alcohol term.
> co.lr2 <- glm(outcome.diff ~ smoke.diff + alcohol.diff-1, binomial)
> logistic.display(co.lr2, decimal=1)
Logistic regression predicting outcome.diff
crude OR(95%CI) adj.OR(95%CI) P(Wald's) P(LR-test)
smoke.diff 1 (0.3,3.5) 0.7 (0.2,2.9) 0.66 0.66
alcohol.diff 4.5 (1,20.8) 4.8 (1,23.2) 0.05 0.03
Log-likelihood = -15.513
183
No. of observations = 26
AIC value = 35.026
The introduction of 'alcohol.diff' has changed the coefficient of 'smoke.diff'
substantially indicating that smoking is confounded by drinking alcohol.
Conditional logistic regression
The above logistic regression analysis, which is based on manipulating the data, is
still rather cumbersome. The statistical analyst needs to reshape the dataset, and
create the values of difference in the outcome and exposure variables. Moreover,
the method is applicable only for 1:1 matching.
A simpler method of multivariate analysis of the VC1to1 dataset is to use the
command clogit (short for 'conditional logit') from the survival package. The
original dataset in long format can be used.
> zap()
> library(survival)
> use(.data)
> clogit1 <- clogit(case ~ smoking+alcohol+strata(matset))
> summary(clogit1)
n= 52
coef exp(coef) se(coef) z p
smoking -0.314 0.73 0.708 -0.444 0.66
alcohol 1.572 4.81 0.803 1.957 0.05
exp(coef) exp(-coef) lower .95 upper .95
smoking 0.73 1.369 0.182 2.92
alcohol 4.81 0.208 0.998 23.23
Rsquare= 0.092 (max possible= 0.5 )
Likelihood ratio test= 5.02 on 2 df, p=0.0814
Wald test = 3.83 on 2 df, p=0.147
Score (logrank) test = 4.62 on 2 df, p=0.0991
The top section of the results reports that the clogit command actually calls another
generic command coxph. If the called command is used, the result will be the
same.
> coxph(formula = Surv(rep(1, 52), case) ~ smoking + alcohol +
strata(matset), method = "exact")
The odds ratios and their 95% confidence intervals from clogit are the same as
those obtained by modelling the difference. The last section contains several test
results, each of which indicates that the model is not significantly different from the
null model (the model that does not include any predictor variables).
184
The Epicalc function clogistic.display can be used to obtain a nicer output.
> clogistic.display(clogit1)
Conditional logistic regression predicting case : 1 vs 0
crude OR(95%CI) adj. OR(95%CI) P(Wald) P(LR)
smoking: 1 vs 0 1.0 (0.29, 3.45) 0.73 (0.18,2.92) 0.66 0.655
alcohol: 1 vs 0 4.5 (0.97,20.83) 4.81 (1,23.23) 0.05 0.025
No. of observations = 52
References
Breslow NE, Day NE (1980). The Analysis of Case-Control Studies (Statistical
Methods in Cancer Research, Vol. 1). Int Agency for Research on Cancer.
Exercises________________________________________________
Problem 1.
Carry out a matched tabulation for alcohol exposure in VC1to6. Compare the
results with those obtained from the conditional logistic regression analysis.
Problem 2.
Refer to the log likelihood and AIC values in the preceding chapter on generalized
linear model.
The conditional logistic regression model gives neither the log likelihood nor AIC
value but it does give the conditional log likelihood, which also indicates the level
of fit. This conditional log likelihood can be used for comparison of nested models
from the same dataset.
> clogit3 <- clogit(case ~ smoking + alcohol +rubber + strata(matset))
> attributes(clogit3)
> clogit3$loglik
[1] -37.89489 -31.89398
The element 'loglik' from each clogit command (analogous to 'logLik' of glm)
contains two sub-elements. The first sub-element, which is the conditional
likelihood of the null model, is the same for all the conditional logistic regression
models. The second sub-element is specific to the particular model. Twice the
absolute difference of the two sub-elements is equal to the likelihood ratio test for
the model. This test result can be seen from the display of the model.
Try different models and compare their conditional log likelihoods. Choose the best
fitting model.

185
Chapter 17: Polytomous Logistic
Regression
Logistic regression is well known for the modelling of binary outcomes. In some
occasions, the outcome can have more than two non-ordered categories.
In chapter 15 we looked at the Ectopic dataset, which came from a study testing
a hypothesis whether previous induced abortion is a risk factor for current ectopic
pregnancy (EP). The outcome has two groups of controls: subjects coming for
induced abortion services (IA) and women who delivered babies (Deli). Both
groups were used to represent intra-uterine pregnancy. The outcome in this study
has therefore three nominal categories.
Tabulation
> zap()
> data(Ectopic); use(Ectopic)
> des()
No. of observations =723
Variable Class Description
1 id integer
2 outc factor Outcome
3 hia factor Previous induced abortion
4 gravi factor Gravidity
> tabpct(outc, hia, graph=FALSE)
Original table
Previous induced abortion
Outcome never IA ever IA Total
EP 61 180 241
IA 110 131 241
Deli 158 83 241
Total 329 394 723
Row percent
Previous induced abortion
Outcome never IA ever IA Total
EP 61 180 241
(25.3) (74.7) (100)
IA 110 131 241
(45.6) (54.4) (100)
Deli 158 83 241
(65.6) (34.4) (100)
186
Column percent
Previous induced abortion
Outcome never IA % ever IA %
EP 61 (18.5) 180 (45.7)
IA 110 (33.4) 131 (33.2)
Deli 158 (48.0) 83 (21.1)
Total 329 (100) 394 (100)
Two-way tabulation reveals the highest proportion (74.7%) of ever IA in the EP
group compared to 54.4% and 34.4% in the IA and Deli groups, respectively.
> table1 <- table(outc, gravi, hia)
> plot(table1, col=c("white", "blue"), las=4, main="Previous
induced abortion by outcome & gravidity", xlab="Outcome",
ylab= "Gravidity")
Previous induced abortion by outcome & gravidity
Outcome
Gravidity
EP
IA
De
li
1−2
3−4
>4
never IA
ever IA
never IA
ever IA
never IA
ever IA
The mosaic plot gives complicated information. The column of the plot is outcome,
which is divided into EP, IA and Deli, as previously described. The sizes of the 3
“columns” are the same (241 subjects). Each row represents the three levels of
gravidity (number of pregnancies): 1-2, 3-4 and > 4, respectively. The distribution
of gravidity among the EP and IA groups are more or less the same, i.e. around a
half having 1-2 pregancies, whereas among the women coming to deliver a baby,
the percentage in this group is much higher (about 75%). Finally, information can
be obtained from the different colours. Blue areas represent women who
experienced previous induced abortion while white represents those who did not. In
each column, such a percentage appears to increase with gravidity, i.e. women who
have high gravidity will have a higher level of exposure to induced abortion in the
past. Comparison among the three columns, which is the main hypothesis of this
study, shows that the proportion of blue colour is highest among the EP group.

187
Polytomous logistic regression using R
Polytomous logistic regression, sometimes called multinomial logistic regression, is
used when the outcome contains more than two categories. In this case, the codes
for the outcome are: 1 = EP, 2=IA and 3=Deli. The command for such regression is
contained in the 'nnet' package, the package based on neural network concepts.
> library(nnet)
> multi1 <- multinom(outc ~ hia); multi1
# weights: 9 (4 variable)
initial value 794.296685
final value 753.732244
converged
Call:
multinom(formula = outc ~ hia)
Coefficients:
(Intercept) hiaever IA
IA 0.58958 -0.90735
Deli 0.95170 -1.72585
Residual Deviance: 1507.5
AIC: 1515.5
The upper part of the output concerns the iteration process of the neural network.
The important part for epidemiology is in the 'Coefficients:' section. Interpretation
of the coefficients of polytomous logistic regression is rather complicated,
especially when the design has one group of cases and more than one group of
controls.
There are three outcome categories. The first one, 'EP', is the reference against
which the two comparisons are made. The risk for being EP in this case is reverted
to the chance of not being EP within the dataset. Since this study was a case control
study, the intercept values should be ignored. The most important part is the
coefficients of 'hia'.
For those who had a history of induced abortion, the logit of being IA in this
pregnancy changes by -0.90735 unit. This is equivalent to an odds ratio of exp(-
0.90735) or 0.403.
"The odds of having intra-uterine pregnancy (and eventually came for induced
abortion) is reduced by a factor of 0.403 if the subject had a history of induced
abortion" can be rephrased as "The odds of having ectopic pregnancy (and therefore
not in the IA group) is increased by 1/0.403, or a factor of 2.48".
Similarly, the odds ratio for EP using Deli as the control is 1 / e-1.7258539 = 5.617.
It is worth remembering that in the chapter on logistic regression, the odds ratio for
history of previous induced abortion using two groups combined was obtained as
follows:

188
> logistic.display(glm(outc=="EP" ~ hia, binomial))
Logistic regression predicting outc == "EP"
OR(95%CI) P(Wald's test) P(LR-test)
hia: ever IA vs never IA 3.7 (2.63,5.2) < 0.001 < 0.001
Log-likelihood = -429.3863
No. of observations = 723
AIC value = 862.772
The odds ratio from the logistic regression in chapter 15 of 3.695 is between the
two odds ratios computed from polytomous logistic regression in this chapter.
Standard errors can be obtained by the following command:
> summary(multi1) -> s1; s1
========== coefficient section omitted =============
Std. Errors:
(Intercept) hiaever IA
IA 0.15964 0.19666
Deli 0.15074 0.20081
========== correlation section omitted ============
Only the standard errors section is displayed because the coefficients section is
shown above with the previous command and the correlation section is not directly
related here.
To obtain the z value for each cell, type:
> coef(s1) / s1$st -> z; z
(Intercept) hiaever IA
IA 3.6932 -4.6139
Deli 6.3136 -8.5943
High levels of 'z' indicate the coefficient is several times the value of the standard
error. In other words, the coefficient is far away from 0, which the null hypothesis
(of no association) is based on. P values can be further obtained by:
> pnorm(abs(z), lower.tail=FALSE)*2 -> p.values
> p.values
(Intercept) hiaever IA
IA 2.2143e-04 3.9513e-06
Deli 2.7264e-10 8.3774e-18
Note that the absolute values of 'z' were used before computing the P values.
The 95% confidence interval of the coefficients can be computed based on the
coefficients and the standard errors.
189
> coeff.lower.95ci <- coef(s1) - qnorm(.975) * s1$st
> coeff.lower.95ci
> coeff.upper.95ci <- coef(s1) + qnorm(.975) * s1$st
> coeff.upper.95ci
The odds ratios and their 95% confidence intervals can be achieved from
exponentiation of the coefficients and their upper and lower 95% CI.
Display of polytomous regression results
The above computing process is quite cumbersome. To simplify the amount of
typing and to obtain a tidy output of results, mlogit.display from Epicalc can be
used on the model summary.
> mlogit.display(multi1)
Outcome =outc; Referent group = EP
IA
Coeff./SE RRR(95%CI)
(Intercept) 0.59/0.16*** -
hiaever IA -0.91/0.197*** 0.404(0.275,0.593)
Deli
Coeff./SE RRR(95%CI)
(Intercept) 0.95/0.151*** -
hiaever IA -1.73/0.201*** 0.178(0.12,0.264)
Residual Deviance: 1507.464
AIC = 1515.464
The formatting of the output has been modified to fit on the page. The P values are
coded with the number of asterisks conforming to those used in the summary of the
'glm' and 'lm' models. Odds ratios for the intercepts are irrelevant and are therefore
omitted. As discussed previously, the odds ratios here are not for risk of ectopic
pregnancy but for their reciprocals.
To include the variable 'gravi' in the model, type:
> multi2 <- multinom(outc ~ hia + gravi)
> mlogit.display(multi2)
Optionally, the upper three commands can be combined and replaced with the one
below, which gives the same results.
> mlogit.display(multinom(outc ~ hia + gravi))
# weights: 15 (8 variable)
initial value 794.296685
iter 10 value 744.763718
final value 744.587307
converged
Outcome =outc; Referent group = EP

190
IA
Coeff./SE RRR(95%CI)
(Intercept) 0.51/0.165** -
hiaever IA -1.11/0.223*** 0.33(0.213,0.511)
gravi3-4 0.39/0.224 1.472(0.95,2.283)
gravi>4 0.47/0.295 1.599(0.897,2.85)
Deli
Coeff./SE RRR(95%CI)
(Intercept) 1.02/0.154*** -
hiaever IA -1.49/0.222*** 0.225(0.146,0.348)
gravi3-4 -0.47/0.24 0.628(0.392,1.004)
gravi>4 -0.7/0.366 0.499(0.243,1.022)
Residual Deviance: 1489.175
AIC = 1505.175
Again, the formatting of the output has been modified to fit on the page. None of
the coefficients and odds ratios of gravidity in this model are significant. However,
this model has a much lower residual deviance compared to model 'multi1'. A
reduction from 1507.464 to 1489.175 or 18.289 units at a cost of introducing four
more parameters (two gravi levels for two outcomes) can be considered worthwhile
since the P value from the chi-squared of 18.289 with 4 degrees of freedom is
0.001. Moreover, the AIC value from model 'multi2' of 1505.175 is obviously
smaller than that from 'multi1' of 1515.464.
For the final conclusion, after adjustment for gravidity, history of previous induced
abortion significantly increases the risk for ectopic pregnancy. The odds ratio is
1/.33 or 3.03 if the client currently requesting for induced abortion is used as the
referent group and 1/.225 or 4.4 if women who delivered a baby is the referent
group. It is well known that induced abortion is often repeated. Current clients for
this service usually experience more induced abortions than the general population.
Ectopic pregnancy patients have even more experience of induced abortion than
this group. Therefore, history of induced abortion is very likely a true risk factor for
ectopic pregnancy.
Selection of referent outcome group
The outcome variable in a polytomous logistic regression is usually a factor
containing more than two levels. The first level is usually taken as the referent
level. The same results of the analysis could be obtained by creating three dummy
outcome variables and using them in a matrix format with the cbind function.
> ep <- outc == "EP"
> ia <- outc == "IA"
> deli <- outc == "Deli"
> multi3 <- multinom(cbind(ep,ia,deli) ~ hia+gravi)
> summary(multi3)
> mlogit.display(multi3)

191
The above commands should give the same results as those from 'multi2' except
that the names of outcome groups are in lower case.
Since the first column is always used as the referent group, one can exploit this
method to shuffle the order of outcome variables in order to change the referent
group. For example, to use 'deli' as the referent level, 'deli' is put as the first column
of the outcome matrix:
> multi4 <- multinom(cbind(deli,ep,ia) ~ hia+gravi)
> mlogit.display(multi4)
Outcome =cbind(deli, ep, ia); Referent group = deli
ep
Coeff./SE RRR(95%CI)
(Intercept) -1.02/0.154*** -
hiaever IA 1.49/0.222*** 4.443(2.877,6.861)
gravi3-4 0.47/0.24 1.593(0.996,2.55)
gravi>4 0.7/0.366 2.005(0.979,4.107)
ia
Coeff./SE RRR(95%CI)
(Intercept) -0.51/0.131*** -
hiaever IA 0.38/0.215 1.466(0.963,2.233)
gravi3-4 0.85/0.237*** 2.346(1.475,3.732)
gravi>4 1.16/0.369** 3.205(1.554,6.607)
The output is relatively easy to interpret. Using delivery as the referent outcome, for
a woman with a history of induced abortion, the odds of being 'EP' or having an
ectopic pregnancy in this admission increased by 4.443 fold (which is highly
significant) and that for being a (repeating) induced abortion patient increased by
only 47 percent (OR = 1.466, which is non-significant). On the other hand,
increasing gravidity does not independently increase the risk for ectopic pregnancy
but significantly, and in a dose-response relationship fashion, increases the chance
for being a client for induced abortion service in the current visit.

192
Exercises________________________________________________
In a fictitious trial of a vaccine on 120 mice, 75 were given the vaccine ('vac' = 1)
while 45 were given a placebo ('vac' = 0). Among these were 35 young mice
('agegr' = 0) and 85 old mice ('agegr' = 1).
There were three levels of outcomes: 1 = no change, 2 = became immune, 3 = died.
Outcome vac agegr total
1 0 0 25
1 0 1 15
1 1 0 4
1 1 1 8
2 0 0 1
2 0 1 0
2 1 0 25
2 1 1 35
3 0 0 3
3 0 1 1
3 1 0 2
3 1 1 1
Problem 1.
Is there any difference in age group among the two groups of these vaccine
recipients?
Problem 2.
Is there any association between age group and outcome?
Problem 3.
Is there any difference in outcomes between the vaccine and placebo treatment
groups?
193
Chapter 18: Ordinal Logistic Regression
In the previous chapters, all variables that were factors were treated as non-ordered
categorical variables. Polytomous logistic regression deals with predicting
outcomes that are categorical but not ordered. In many situations, the outcome has
some kind of ordering. Using polytomous logistic regression for such situations
would lose power to detect the association as well as misinterpret the way the
outcome variable is related to the exposure variables.
Ordered factors
This chapter uses a dataset from a survey on hookworm infections in southern
Thailand conducted in 1993. The objective is to document the effect of age and
shoe wearing ('shoes') on the intensity of the infection.
> library(nnet) # For polytomous logistic regression
> library(MASS) # For ordinal logistic regression
> zap()
> data(HW93)
> use(HW93)
> des()
No. of observations = 637
Variable Class Description
1 id integer
2 epg numeric eggs per g of faeces
3 age integer
4 shoes factor Shoe wearing
5 intense factor Intensity (EPG)
6 agegr factor Age group
> summ()
No. of observations = 637
Var. name Obs. mean median s.d. min. max.
1 id 637 325.38 325 185.79 1 646
2 epg 637 1141.85 207 2961.82 0 39123
3 age 637 25.94 23 19.47 2 78
4 shoes 637 1.396 1 0.489 1 2
5 intense 637 1.834 2 0.652 1 3
6 agegr 637 1.667 2 0.608 1 3
The variable 'intense' is a categorical form of the variable 'epg'.
> summ(epg, by=intense)
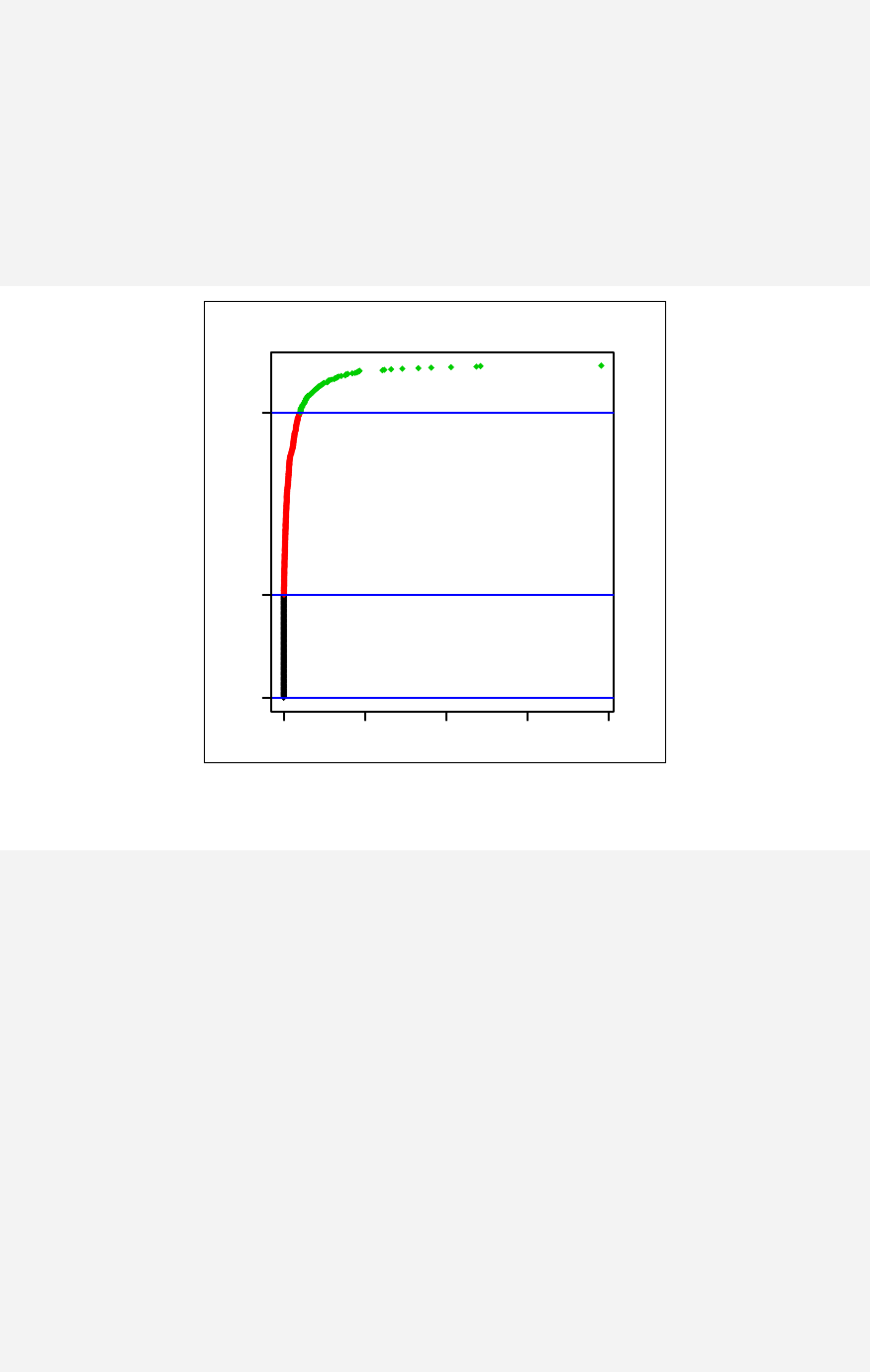
194
For intense = 0
obs. mean median s.d. min. max.
197 0 0 0 0 0
For intense = 1-1,999
obs. mean median s.d. min. max.
349 539 345 512.368 23 1910
For intense = 2,000+
obs. mean median s.d. min. max.
91 5930 3960 5792.453 2020 39100
0 10000 20000 30000 40000
Distribution of eggs per g of feces
by Intensity (EPG)
0
1
−1,999
2,000+
Using polytomous logistic regression
> poly.hw <- multinom(intense ~ agegr + shoes)
> mlogit.display(poly.hw)
Outcome =intense; Referent group = 0
1-1,999
Coeff./SE RRR(95%CI)
(Intercept) 0.29/0.138* -
agegr15-59 yrs 0.87/0.216*** 2.39(1.56,3.65)
agegr60+ yrs 0.77/0.41 2.16(0.97,4.82)
shoesyes -0.48/0.212* 0.62(0.41,0.94)
2,000+
Coeff./SE RRR(95%CI)
(Intercept) -0.97/0.204*** -
agegr15-59 yrs 1.03/0.306*** 2.8(1.54,5.1)
agegr60+ yrs 1.8/0.478*** 6.05(2.37,15.44)
shoesyes -1.34/0.317*** 0.26(0.14,0.49)
Residual Deviance: 1196.8
AIC = 1212.8

195
For light infection (1-1,999 epg), only young adults had a higher risk than the
children. For heavy infection (2,000+ epg), the young adults and the elder subjects
had a 2.8 and 6.1 times higher risk than the children, respectively. Shoe wearing has
a protective effect on both light and heavy infection with odds ratios of 0.62 and
0.262, respectively.
Modelling ordinal outcomes
Alternatively, since intensity is an ordered outcome variable, it is worth trying
ordinal logistic regression. The command polr from the MASS package will do
this. But first we have to tell R that the outcome is ordered.
> class(intense) # "factor"
> intense.ord <- ordered(intense)
> class(intense.ord) # "ordered" "factor"
> ord.hw <- polr(intense.ord ~ agegr + shoes)
> summary(ord.hw)
Coefficients:
Value Std. Error t value
agegr15-59 yrs 0.7744521 0.1834157 4.222388
agegr60+ yrs 1.2797213 0.3226504 3.966278
shoesyes -0.7234746 0.1780106 -4.064223
Intercepts:
Value Std. Error t value
0|1-1,999 -0.6301 0.1293 -4.8726
1-1,999|2,000+ 2.0745 0.1579 13.1363
Residual Deviance: 1204.920
AIC: 1214.920
This ordinal logistic regression model has two intercepts, one for each cut point of
the outcome. The values of these intercepts are not so meaningful and can be
ignored at this stage. The coefficients of all independent variables are shared by two
cut points of the dependent variable. At the first cut point, the logit of getting any
infection (intense= 1- 1,999 and 2,000 + epg vs no infection) is reduced by 72% if
the subject wore shoes, so is the logit at the second cut point (intensity of 2,000 +
epg vs any lower levels of intensity). Both coefficients are positive indicating that
the risk of infection increases with age. Shoe wearing has a negative coefficient
indicating that it protects both levels of infection.
> summary(ord.hw) -> s1
> attributes(s1)
$names
[1] "coefficients" "zeta" "deviance" "fitted.values"
[5] "lev" "terms" "df.residual" "edf"
[9] "n" "nobs" "call" "method"
[13] "convergence" "niter" "model" "contrasts"
[17] "xlevels" "pc" "digits"
$class
[1] "summary.polr"
196
To compute the P value for 'shoes', type:
> coef(s1)
> t <- coef(s1)[,3]
> df <- s1$df.residual
> pt(abs(t), df, lower.tail=F)
agegr15-59 yrs agegr60+ yrs shoesyes
1.386181e-05 4.067838e-05 2.713385e-05
0|1-1,999 1-1,999|2,000+
6.969506e-07 2.521906e-35
The above commands define 't' and 'df' from the summary of the regression. The
last command uses the absolute value of 't' for computation of the two-sided P
values. All P values are significant.
'ordinal.or.display'
Epicalc has a function to display ordinal odds ratios and 95% confidence intervals.
> ordinal.or.display(ord.hw)
Ordinal OR lower95ci upper95ci P.value
agegr15-59 yrs 2.169 1.517 3.116 1.39e-05
agegr60+ yrs 3.596 1.913 6.788 4.07e-05
shoesyes 0.485 0.341 0.686 2.71e-05
The conclusion from this ordinal logistic regression model is that intensity of
infection significantly increases with age group and is significantly reduced by
wearing shoes. At each cut point of the intensity of infection, on the average,
wearing shoes is associated with a reduction of 0.48 or a half of the odds of those
not wearing shoes.
References
Venables, W. N. and Ripley, B. D. (2002) Modern Applied Statistics with S. Fourth
edition. Springer.
Exercise_________________________________________________
The level of pain after treatment (1 = no pain, 2 = some pain, 3 = severe pain) was
measured after treatment of one group of subjects with a pain killer (Drug = 1 )
against placebo (Drug = 0 ) in males (1) and females (0) with the following data:
Male 0 0 0 0 0 0 1 1 1 1 1 1
Drug 0 1 0 1 0 1 0 1 0 1 0 1
Pain 1 2 3 1 2 3 1 2 3 1 2 3
Total 3 5 15 10 5 7 8 5 10 10 10 2
Analyse the effect of this drug with adjustment for sex using polytomous and
ordinal logistic regression.
197
Chapter 19: Poisson and Negative
Binomial Regression
The Poisson distribution
In nature, an event usually takes place in a very small amount of time. At any given
point of time, the probability of encountering such an event is very small. Instead of
probability, measurement is focused on density, which means incidence or 'count'
over a period of time. While time is one dimension, the same concept applies to the
density of counts of small objects in a two-dimensional area or three-dimensional
space.
When one event is independent from another, the occurrence is at random.
Mathematically, it can be proved that under this condition, the densities in different
units of time vary with a variance equal to the average density. When the
probability of having an event is affected by some factors, a model is needed to
explain and predict the density. Variation among different strata is explained by the
factors. Within each stratum, the distribution is random.
Poisson regression
Poisson regression deals with outcome variables that are counts in nature (whole
numbers or integers). Independent covariates are similar to those encountered in
linear and logistic regression.
In epidemiology, Poisson regression is used for analysing grouped cohort data,
looking at incidence density among person-time contributed by subjects of similar
characteristics of interest.
Poisson regression is one of three common generalized linear models (GLM) used
in epidemiological studies. The other two that are more commonly used are linear
regression and logistic regression, which have been covered in previous chapters.
There are two main assumptions for Poisson regression. Firstly, risk is
homogeneous among person-times contributed by different subjects who have the
same characteristics of interest (e.g. sex, age-group) and the same period. Secondly,
asymptotically, or as the sample size becomes larger and larger, the mean of the
counts is equal to the variance.

198
Benefits of Poisson regression models
Straightforward linear regression methods (assuming constant variance, normal
errors) are not appropriate for count data for four main reasons:
1. the model might lead to the prediction of negative counts,
2. the variance of the response may increase with the mean,
3. the errors will not be normally distributed,
4. zero counts are difficult to handle in transformations.
Poisson regression eliminates some of the problems faced by other regression
techniques. For example, in logistic regression, different subjects may have
different person-times of exposure. Analysing risk factors while ignoring
differences in person-times is therefore wrong. In survival analysis using Cox
regression (discussed in chapter 22), only the hazard ratio and not incidence density
of each subgroup is computed. The analysts and the readers may not have a clear
idea on the descriptive statistics of these baseline risks. In other words, Poisson
regression produces both 'baseline incidence density' as well as 'incidence density
ratio' among strata.
Example: Montana smelter study
The dataset Montana was extracted from an occupational cohort study conducted
to test the association between respiratory deaths and exposure to arsenic in the
industry, after adjusting for various other risk factors. The main outcome variable is
'respdeath'. This is the count of the number of deaths among 'personyrs' or person-
years of subjects in each category. The other variables are independent covariates
including age group 'agegr', period of employment 'period', starting time of
employment 'start' and the level of exposure to arsenic during the study period
'arsenic'. Read in the data first and examine the variables.
> zap()
> data(Montana)
> use(Montana)
> summ()
No. of observations = 114
Var. name Obs. mean median s.d. min. max.
1 respdeath 114 2.42 1 3.3 0 19
2 personyrs 114 1096.41 335.15 2123.1 4.2 12451
3 agegr 114 2.61 3 1.1 1 4
4 period 114 2.4 2 1.09 1 4
5 start 114 1.46 1 0.5 1 2
6 arsenic 114 2.47 2 1.11 1 4
199
> des()
No. of observations = 114
Variable Class Description
1 respdeath integer
2 personyrs numeric
3 agegr integer
4 period integer
5 start integer
6 arsenic integer
The last four variables are classed as integers. We need to tell R to interpret them as
categorical variables, or factors, and attach labels to each of the levels. This can be
done using the factor command with a 'labels' argument included.
> agegr <- factor(agegr, labels=c("40-49","50-59","60-69","70-
79"))
> period <- factor(period, labels=c("1938-1949", "1950-1959",
"1960-1969", "1970-1977"))
> start <- factor(start, labels=c("pre-1925", "1925 & after"))
> arsenic1 <- factor(arsenic, labels=c("<1 year", "1-4
years","5-14 years", "15+ years"))
> label.var(agegr, "Age group")
> label.var(period, "Period of employment")
> label.var(start, "Era of starting employment")
> label.var(arsenic1, "Amount of exposure to arsenic")
> des()
No. of observations =114
Variable Class Description
1 respdeath integer
2 personyrs numeric
3 agegr factor Age group
4 period factor Period of employment
5 start factor Era of starting employment
6 arsenic integer
7 arsenic1 factor Amount of exposure to arsenic
We keep the original 'arsenic' variable unchanged for use later on.
Breakdown of incidence by age and period
Let us explore the person-years breakdown by age and period. Firstly, create a table
for total person-years:
> tapply(personyrs, list(period, agegr), sum) -> table.pyears
Carry out the same procedure for number of deaths, and compute the table of
incidence per 10,000 person years for each cell.
> tapply(respdeath, list(period, agegr), sum) -> table.deaths
> table.inc10000 <- table.deaths/table.pyears*10000
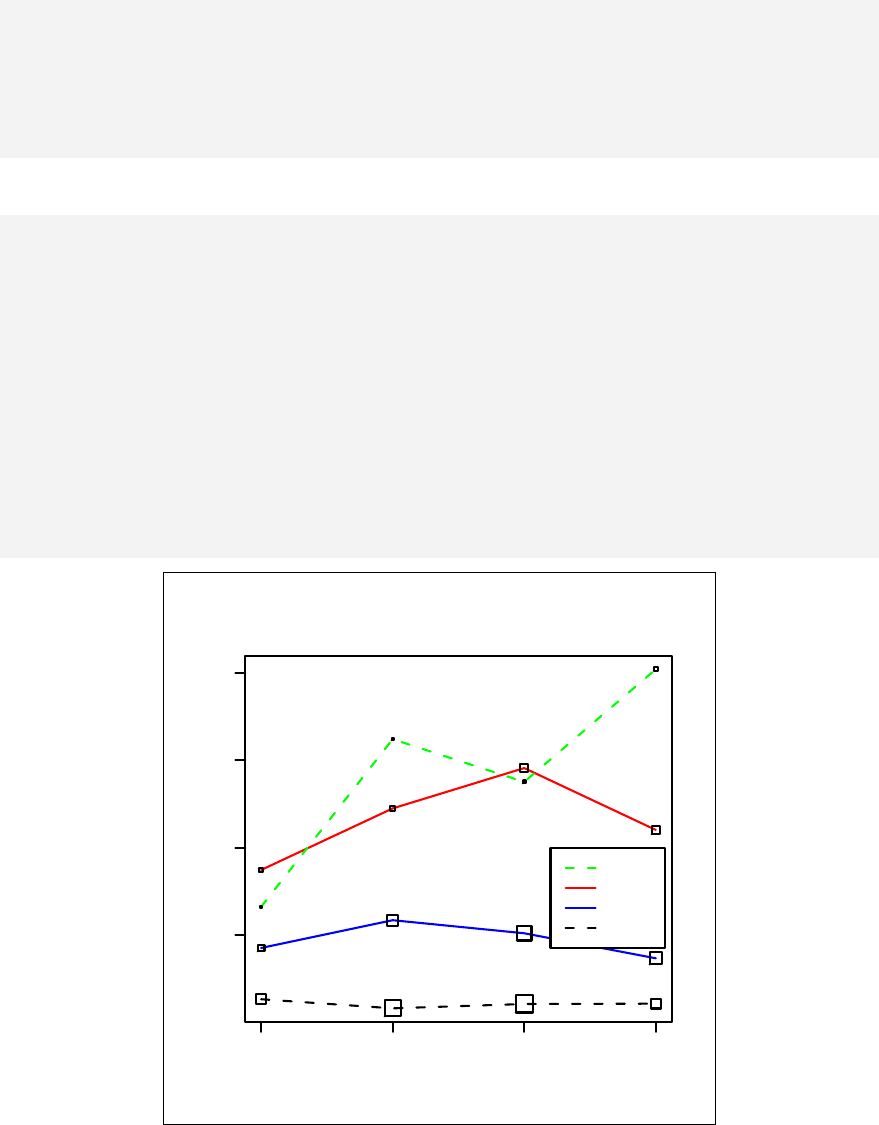
200
> table.inc10000
40-49 50-59 60-69 70-79
1938-1949 5.424700 17.13102 34.95107 26.53928
1950-1959 3.344638 23.47556 49.01961 64.82632
1960-1969 4.341516 20.49375 58.23803 55.06608
1970-1977 4.408685 14.77747 44.09949 80.81413
Now, create a time-series plot of the incidence:
> plot.ts(table.inc10000, plot.type="single", xlab=" ",
ylab="#/10,000 person-years", xaxt="n", col=c("black",
"blue","red","green"), lty=c(2,1,1,2), las=1)
> points(rep(1:4,4), table.inc10000, pch=22, cex=table.pyears
/ sum(table.pyears) * 20)
> title(main = "Incidence by age and period")
> axis(side = 1, at = 1:4, labels = levels(period))
> legend(3.2,40, legend=levels(agegr)[4:1], col=c("green",
"red", "blue", "black"), bg = "white", lty=c(2, 1, 1, 2))
#/10,000 person−years
20
40
60
80
Incidence by age and period
1938−1949 1950−1959 1960−1969 1970−1977
70−79
60−69
50−59
40−49
The above graph shows that the older age group is generally associated with a
higher risk. On the other hand, the sample size (reflected by the size of the squares
at each point) decreases with age.
The possibility of a confounding effect of age can better be examined by using
Poisson regression.
201
Modelling with Poisson regression
> mode11 <- glm(respdeath ~ period, offset = log(personyrs),
family = poisson)
> summary(mode11)
==============================
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -6.4331 0.1715 -37.511 <2e-16
period1950-1959 0.2365 0.2117 1.117 0.2638
period1960-1969 0.3781 0.2001 1.889 0.0588
period1970-1977 0.4830 0.2036 2.372 0.0177
AIC: 596
==============================
The option 'offset = log(personyrs)' allows the variable 'personyrs' to be the
denominator for the counts of 'respdeath'. A logarithmic transformation is needed
since, for a Poisson generalized linear model, the link function is the natural log,
and the default link for the Poisson family is the log link.
An important criterion in the choice of a link function for various families of
distributions is to ensure that the fitted values from the modelling stay within
reasonable bounds. Specifying a log link (default for Poisson) ensures that the fitted
counts are all greater than or equal to zero.
Note: ______________________________________________________________________
For more details on default links for various families of distributions related to generalized
linear modelling, see the help in R under 'help(family)'.
The first model above of Poisson regression with 'period' as the only independent
variable suggests that the death rate increased with time. The model can be tested
for goodness of fit and the checked whether the Poisson assumptions mentioned
earlier in the chapter have been violated.
Goodness of fit test
To test the goodness of fit of the Poisson model, type:
> poisgof(mode11)
$results
[1] "Goodness-of-fit test for Poisson assumption"
$chisq
[1] 369.27
$df
[1] 110
$p.value
[1] 9.5784e-30

202
The component '$chisq' is actually computed from the model deviance, a parameter
reflecting the level of errors. A large chi-squared value with small degrees of
freedom results in a significant violation of the Poisson assumption (p < 0.05). If
only the P value is wanted, the command can be shortened.
> poisgof(mode11)$p.value
The P value is very small indicating a poor fit.
Note: ______________________________________________________________________
It should be noted that this method is under assumption of a large sample size. An alternative
method is to a fit negative binomial regression model and check if the parameters are different
from 1, which is demonstrated in the latter section of this chapter.
We now add the second independent variable 'agegr' to the model.
> mode12 <- glm(respdeath~agegr+period, offset=log(personyrs),
family = poisson)
> AIC(mode12) # 396.64
The AIC has decreased remarkably from 'model1' to 'model2' indicating a poor
fit of the first model.
> poisgof(mode12)$p.value # 0.00032951
Model 'model2' still violates the Poisson assumption.
> mode13 <- glm(respdeath ~ agegr, offset = log(personyrs),
family = poisson)
> AIC(mode13) # 394.47
> poisgof(mode13)$p.value # 0.0003295
Removal of 'period' further reduces the AIC but still violates the Poisson
assumption to the same extent as the previous model. The next step is to add the
main independent variable 'arsenic1'.
> mode14 <- glm(respdeath ~ agegr + arsenic1,
offset=log(personyrs), family = poisson)
> summary(mode14)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -7.995 0.224 -35.74 < 2e-16
agegr50-59 1.462 0.245 5.96 2.5e-09
agegr60-69 2.350 0.238 9.87 < 2e-16
agegr70-79 2.599 0.256 10.14 < 2e-16
arsenic11-4 years 0.804 0.158 5.10 3.4e-07
arsenic15-14 years 0.596 0.206 2.89 0.0038
arsenic115+ years 0.998 0.176 5.67 1.4e-08
Null deviance: 376.02 on 113 degrees of freedom
Residual deviance: 122.25 on 107 degrees of freedom
AIC: 355.0
> poisgof(mode14)$p.value # 0.14869
'model4' has a much lower AIC than model3 and it now does not violate the
assumption.

203
Linear dose response relationship
Alternatively, instead of having arsenic as a categorical variable, it can be included
in the model as a continuous variable. If the P vaue is significant then this would
imply that there is a linear dose-response relationship between exposure to arsenic
and the risk for the disease. The original variable 'arsenic' is included in the next
model.
>model5 <- glm(respdeath~agegr+arsenic, offset=log(personyrs),
family=poisson)
>summary(model5)
=============================
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -8.2416 0.2327 -35.42 < 2e-16
agegr50-59 1.4572 0.2454 5.94 2.9e-09
agegr60-69 2.3236 0.2379 9.77 < 2e-16
agegr70-79 2.5572 0.2558 10.00 < 2e-16
arsenic 0.3358 0.0524 6.40 1.5e-10
AIC: 360.31
> poisgof(model5)$p.value # 0.069942
Although the linear term is significant, the AIC value in 'model5' is higher than
that of 'model4'. It would therefore be better keeping arsenic as factor. However,
from 'model4' there does not appear to be any increase in the risk of death from
more than 4 years of exposure to arsenic so it may be worth combining it into just
two levels.
> arsenic2 <- arsenic1
> levels(arsenic2) <- c("<1 year", rep("1+ years", 3))
> label.var(arsenic2, "Exposure to arsenic")
> model6 <- glm(respdeath ~ agegr + arsenic2,
offset=log(personyrs), family=poisson)
> summary(model6)
============================
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -8.009 0.223 -35.86 < 2e-16
agegr50-59 1.470 0.245 5.99 2.0e-09
agegr60-69 2.366 0.237 9.98 < 2e-16
agegr70-79 2.624 0.255 10.30 < 2e-16
arsenic21+ years 0.811 0.121 6.70 2.1e-11
============================
AIC: 353.8
> poisgof(model6)$p.value # 0.13999
At this stage, we would accept 'model6' as the model of choice as it has the
smallest AIC among all the models that we have tried. We conclude that exposure
to arsenic for at least one year would increase the risk for the disease by
exp(0.8109) or 2.25 times with statistical significance.

204
Incidence density
In the Poisson model, the outcome is a count. In the general linear model, the
relationship between the values of the outcome (as measured in the data and
predicted by the model in the fitted values) and the linear predictor is determined by
the link function. This link function relates the mean value of the outcome to its
linear predictor. By default, the link function for the Poisson distribution is the
natural logarithm. With the offset being log(person-time), the value of the outcome
becomes log(incidence density).
The matrix 'table.inc10000' (created previously) gives the crude incidence density
by age group and period. Each of the Poisson regression models above can be used
to compute the predicted incidence density when the variables in the model are
given. For example, to compute the incidence density from a population of 100,000
people aged between 40-49 years who were exposed to arsenic for less than one
year using 'model6', type:
> newdata <- as.data.frame(list(agegr="40-49",
arsenic2="<1 year", personyrs=100000))
> predict(model6, newdata, type="response")
[1] 33.257
This population would have an estimated incidence density of 33.26 per 100,000
person-years.
Incidence density ratio
In a case control study, the odds ratio is used to compare the prevalence of exposure
among cases and controls. In a cohort study, this value is equal to the ratio between
the odds of getting a disease among the exposed and the unexposed group. If the
disease is rare, the odds is close to the probability or risk. The ratio of the risks for
the two groups is then called the 'risk ratio' or the 'relative risk'.
In a real cohort study, subjects do not always have the same follow-up duration.
The relative risk ignores the duration of follow up. Therefore it is not a good
measure of comparison of risk between the two groups. In this chapter, all subjects
pool their follow-up times and this number is called 'person time', which is then
used as the denominator for the event, resulting in 'incidence density'. Comparing
the incidence density among two groups of subjects by their exposure status is
fairer than comparing the crude risks. The ratio between the incidence densities of
two groups is called the incidence density ratio (IDR), which is an improved form
of'relative risk.
In 'model6', to compute the incidence density ratio between the subjects exposed
to arsenic for one or more years against those exposed for less than one year, we
can divide the incidence among the former by that among the latter group.
205
> levels(newdata$arsenic2) <- c("<1 year", "1+ years")
> newdata <- rbind(newdata, list(agegr="40-49",
arsenic2="1+ years", personyrs=100000))
> newdata
agegr arsenic2 personyrs
1 40-49 <1 year 1e+05
2 40-49 1+ years 1e+05
> id <- predict(model6, newdata, type="response")
> idr.arsenic <- id[2]/id[1]
> idr.arsenic
[1] 2.2499
The above procedure starts by appending a new row to the data frame 'newdata'
having everything the same as the first row except that the variable 'arsenic2' is "1+
years". The responses or incidence densities of the two conditions are then
computed. The IDR is then obtained from division of the incidence densities for
arsenic2="<1 year" with arsenic2="1+ years".
A shorter way to obtain this IDR is to exponentiate the coefficient of the specific
variable 'arsenic', which is the fifth coefficient in the model.
> coef(model6)
(Intercept) agegr50-59 agegr60-69 agegr70-79 arsenic21+
-8.00865 1.47015 2.36611 2.62375 0.81087
> exp(coef(model6)[5])
arsenic21+ years
2.2499
'idr.display' to get 95% CI of IDR
The following steps explain how the 95% confidence interval of IDR for all
variables can be obtained.
> coeff <- coef(model6)
> coeff.95ci <- cbind(coeff, confint(model6))
Note that confint(glm6) provides a 95% confidence interval for the model
coefficients.
> IDR.95ci <- round(exp(coeff.95ci), 1)[-1,]
The required values are obtained from exponentiating the last matrix with the first
row or intercept removed. The display is rounded to 1 decimal place for better
viewing. Then the matrix column is labelled and the 95% CI is displayed.
> colnames(IDR.95ci) <- c("IDR", "lower95ci", "upper95ci")
> IDR.95ci
A simpler way is to use the command idr.display in Epicalc.
206
> idr.display(model6, decimal=1)
Poisson regression predicting respdeath with offset =
log(personyrs)
crude IDR(95%CI) adj. IDR(95%CI) P(Wald's) P(LR-test)
agegr: ref.=40-49 < 0.001
50-59 4.5 (2.8,7.3) 4.4 (2.7,7.0) < 0.001
60-69 11.3 (7.1,17.9) 10.7 (6.7,17.0) < 0.001
70-79 14.5 (8.8,23.8) 13.8 (8.4,22.7) < 0.001
arsenic2 2.5 (2.0,3.1) 2.3 (1.8,2.9) < 0.001 < 0.001
Log-likelihood = -171.8998
No. of observations = 114
AIC value = 353.8
The command idr.display gives results to 3 decimal places by default. This
can easily be changed by the user.
Negative binomial regression
Recall that for Poisson regression, one of the assumptions for a valid model is that
the mean and variance of the count variable are equal. The negative binomial
distribution is a more generalized form of distribution used for 'count' response
data, allowing for greater dispersion or variance of counts. In practice, it is quite
common for the variance of the outcome to be larger than the mean. This is called
overdispersion. If a count variable is overdispersed, Poisson regression
underestimates the standard errors of the predictor variables. When overdispersion
is evident, one solution is to specify that the errors have a negative binomial
distribution.
Negative binomial regression gives the same coefficients as those from Poisson
regression but give larger standard errors. The interpretation of the results is the
same as that from Poisson regression.
Take an example of counts of water containers infested with mosquito larvae in a
field survey. The data is contained in the dataset DHF99.
> library(MASS)
> data(DHF99); use(DHF99)
> des()
No. of observations = 300
Variable Class Description
1 houseid integer no
2 village integer Village
3 education factor Educational level
4 containers integer # infested vessels
5 viltype factor Village type
207
> summ()
No. of observations = 300
Var. name obs. mean median s.d. min. max.
1 houseid 300 174.27 154.5 112.44 1 385
2 village 300 48.56 51 32.25 1 105
3 education 300 2.09 1 1.455 1 5
4 containers 299 0.35 0 1.01 0 11
5 viltype 300 1.56 1 0.754 1 3
> summ(containers, by=viltype)
For viltype = rural
obs. mean median s.d. min. max.
179 0.492 0 1.251 0 11
For viltype = urban
obs. mean median s.d. min. max.
72 0.069 0 0.256 0 1
For viltype = slum
obs. mean median s.d. min. max.
48 0.25 0 0.526 0 2
0246810
Distribution of # infested vessels
by Village type
rural
urban
slum
The function for performing a negative binomial glm is glm.nb. This function is
located in the MASS library. In addition, a very helpful function for selecting the
best model based on the AIC value is the step function, which is located in the
stats library (a default library loaded on start-up).
> model.poisson <- step(glm(containers ~ education + viltype,
family=poisson, data=.data))

208
> model.nb <- step(glm.nb(containers ~ education + viltype,
data=.data))
> coef(model.poisson)
(Intercept) viltypeurban viltypeslum
-0.7100490 -1.9571792 -0.6762454
> coef(model.nb)
(Intercept) viltypeurban viltypeslum
-0.7100490 -1.9571792 -0.6762454
Both models end up with only 'viltype' being selected. The coefficients are very
similar. The Poisson model has significant overdispersion but not the negative
binomial model.
> poisgof(model.poisson)$p.value
[1] 0.0043878
> poisgof(model.nb)$p.value
[1] 1
The AIC of the negative binomial model is also better (smaller) than that of the
Poisson model.
> model.poisson$aic
[1] 505.92
> model.nb$aic
[1] 426.23
Finally, the main differences to be examined are their standard errors, the 95%
confidence intervals and P values.
> summary(model.poisson)$coefficients
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.7100490 0.1066000 -6.660873 2.722059e-11
viltypeurban -1.9571792 0.4597429 -4.257117 2.070800e-05
viltypeslum -0.6762454 0.3077286 -2.197538 2.798202e-02
> summary(model.nb)$coefficients
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.7100490 0.1731160 -4.101578 4.103414e-05
viltypeurban -1.9571792 0.5255707 -3.723912 1.961591e-04
viltypeslum -0.6762454 0.4274174 -1.582166 1.136116e-01
> idr.display(model.poisson)
IDR lower95ci upper95ci P value
viltypeurban 0.141 0.057 0.348 0.000
viltypeslum 0.509 0.278 0.930 0.028
> idr.display(model.nb)
IDR lower95ci upper95ci P value
viltypeurban 0.141 0.05 0.396 0.000
viltypeslum 0.509 0.22 1.175 0.114
209
The standard errors from the negative binomial model are slightly larger than those
from the Poisson model resulting in wider 95% confidence intervals and larger P
values. From the Poisson regression, both urban community and slum area had a
significantly lower risk (around 14% and a half reduction, respectively) for
infestation. However, from the negative binomial regression, only the urban
community had a significantly lower risk.
References
Agresti, A. (1996). An Introduction to Categorical Data Analysis. New York: John
Wiley and Sons.
Agresti, A. (2002). Categorical Data Analysis. Hoboken, NJ: John Wiley and Sons.
Powers, D.A., Xie, Y. (2000). Statistical Methods for Categorical Data Analysis.
San Diego: Academic Press.
Long, J.S. (1997). Regression Models for Categorical and Limited Dependent
Variables. Thousand Oakes, CA: Sage Publications.
Vermunt, J.K. (1997). Log-linear Models for Event Histories. Thousand Oakes,
CA: Sage Publications.
210
Exercise_________________________________________________
Use step to select the best model predicting incidence densities of the Montana
dataset. Check the Poisson goodness of fit. Compute the incidence density ratio for
significant independent variables. Fit a negative binomial regression model to check
the theta and its standard error term before conclusion whether there is any
evidence of dispersion.
211
Chapter 20: Introduction to Multi-level
Modelling
There are many other names for multi-level modelling, e.g. hierarchical modelling,
mixed effects modelling, modelling with random effects. They are all the same.
Each name has its own implication.
In epidemiological studies, variables often have a hierarchy. For example,
measurement of blood pressure belongs to an individual subject who can have more
than one measurement. In this case, the individual person is at higher hierarchy than
each measurement. An individual, however, belongs to a family, all members of
which may share several independent variables, such as ethnicity, housing, etc. In
turn a family is usually a member of a village, and so forth. Thus the hierarchy can
be country, province, district, village, family, individual and measurement. Certain
independent variables will be at the individual measurement level, such as time of
measurement. Some variables may belong to a higher hierarchical order, such as
sex and age (individual), ethnicity (family), and distance from the capital city
(village). Independent variables at different levels of the hierarchy should not be
treated in the same way. For this reason multi-level modelling is also called
hierarchical modelling.
In another aspect, modelling is usually meant for explanation of the relationship of
variables in an informative and efficient manner. In simple modelling, where the
number of groups are not high, say m ethnic groups under study, the number of
parameters used to explain the effect of 'ethnic' is m-1 because the omitted one is
used as the referent group. If the sample size is large and m is small the number of
parameters used would not be too high. On the other hand, if the sample size is
small but the number of groups is high, for example, 50 subjects with multiple
blood pressure measurements, the grouping variables would have too many levels
too put into the model. To do this, an average value for the group is computed and
the individual members are treated as random effects without a parameter. In this
situation, multi-level modelling is also called modelling with random effects.
However, the random effects must always have an average, which is used to
estimate the overall effect. This average or overall effect is called the fixed effects.
With the mixture of fixed and random effects in the same model, multi-level
modelling is also called 'mixed effects modelling'.
212
Multi-level modelling is relatively new compared to other common types of
modeling, such as linear and Poisson regression. There are variations in the
methods of numerical iteration for computation of coefficients and standard errors.
They generally give very close estimates but different standard errors, variances and
covariances. The examples in this chapter are confined to the 'glmmPQL' function
or Generalized Linear Mixed Models using Penalized Quasi-Likelihood. It can
handle all families used in GLMs with similar arguments in the command except
the additional terms defining the fixed and random effects. Readers are advised to
explore other functions such as lme (linear mixed effects) and nlme (non-linear
mixed effects).
From stratified analysis to random effects modelling
Analysis of the effect of putting additional table salt into the meal in chapter 12 was
carried out having two strata, each with a relatively high number of subjects. The
stratification factor (salt adding) has two levels 'yes/no' but only one parameter in
the model.
In a setting with a high number of strata, each with a relatively small number of
records, including individual strata would add too many parameters to the model,
thus reducing the efficiency of explanation (too many variables used for explaining
a small dataset). To solve this problem, each stratum is represented by the strata
mean and each sample stratum is taken as a random member of the sets of strata in
the population. Therefore, regardless of how large the number of strata is, there
would be only two parameters from the stratification factor: the mean and variance
(or standard deviation).
Example: Orthodontic Measurements
An example for such a situation, and the commands for computation, are available
from the nlme library. The growth of 27 children (16 boys and 11 girls) was
assessed by measuring the distance from the pituitary to pterygomaxillary fissure.
Measurements were made on each child every 4 years (ages 8, 10, 12 and 14 years).
The data is in hierarchical order. A child has more than one measurement recorded
over time. The individual records or measurements are at level 1 whereas the
individual children are at level 2. Age is also in level 1 since it can vary within
individual subjects, although the variation is constant for all children. On the other
hand, sex is at level 2, which is fixed for each child.
Each child can be initially interpreted as a stratum. The 27 strata are taken as a
random sample of infinite population of strata.

213
For the simplest multi-level modelling, the coefficient of 'age', or the slope of the
regression lines, is estimated as a single parameter, i.e. all subjects are assumed to
have the same growth rate. For the intercept, the model estimates the population
'mean intercept' and population standard deviation of the intercepts. The intercept
has 'random effects' (for individual children) whereas the slope has a 'fixed effect'
for the whole group. Combining these two types of random and fixed effects, the
model is often called a 'mixed model'.
Once the library nlme has been loaded, the dataset Orthodont can be used. Be
careful as some of the variable names in this data frame start with upper case.
> zap()
> library(MASS) # For the glmmPQL command
> library(nlme) # For the example dataset
> data(Orthodont)
> .data <- as.data.frame(Orthodont)
> use(.data); des()
No. of observations =108
Variable Class Description
1 distance numeric distance
2 age numeric age
3 Subject factor Subject
4 Sex factor Sex
> summ()
Var. name Obs. mean median s.d. min. max.
1 distance 108 24.02 23.75 2.93 16.5 31.5
2 age 108 11 11 2.25 8 14
3 Subject 108 14 14 7.825 1 27
4 Sex 108 1.407 1 0.494 1 2
A follow-up plot is useful to visualize the data. Epicalc has a function called
followup.plot, which plots the outcome for each subject over time.
> followup.plot(id=Subject, time=age, outcome=distance,
line.col="multicolor")
> title(main="PPMF distance by age", ylab="mm", xlab="years")
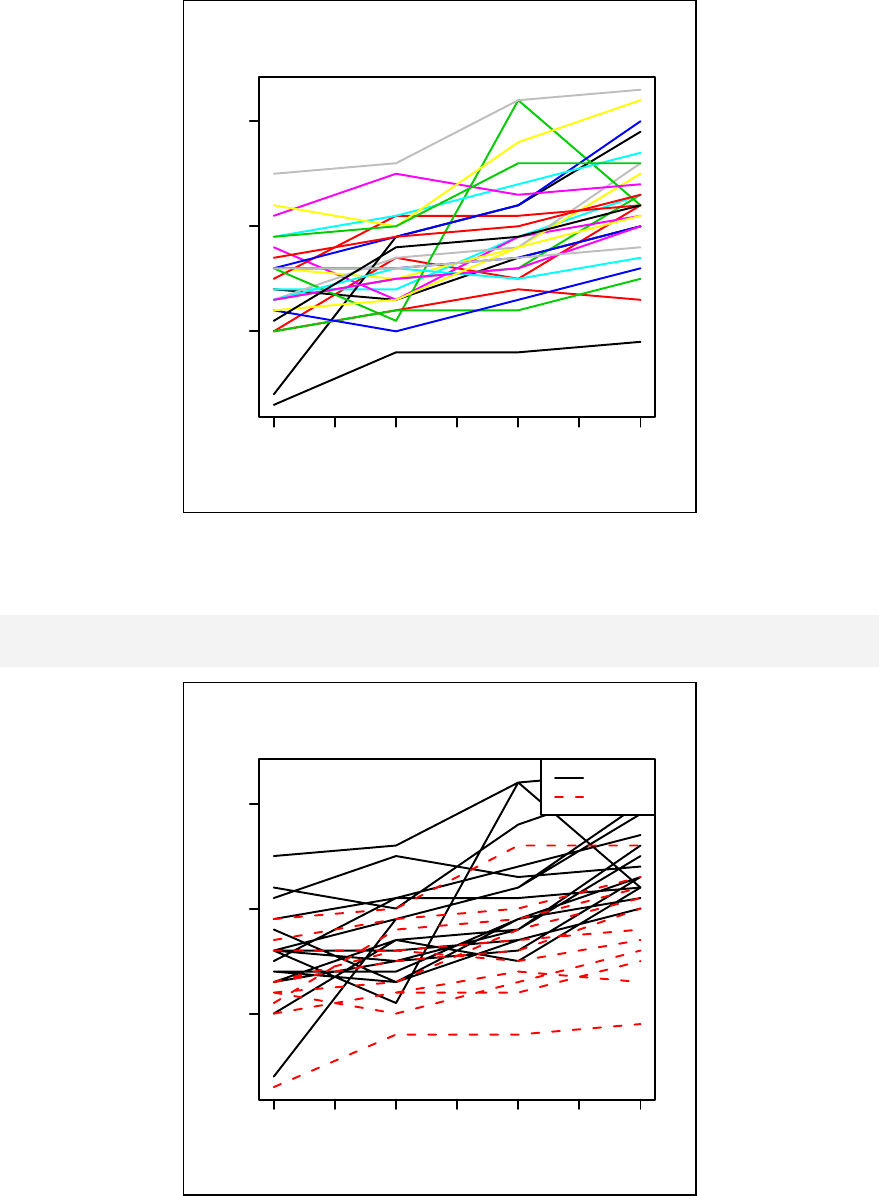
214
8 9 10 11 12 13 14
20 25 30
PPMF distance by age
years
mm
To see whether there is a gender difference, we replace the 'lines' argument with the
'by' argument in the command.
> followup.plot(id=Subject,time=age,outcome=distance,by=Sex)
> title(main="PPMF distance by age", ylab="mm", xlab="years")
8 9 10 11 12 13 14
20 25 30
Male
Femal
e
PPMF distance by age
years
mm
In both plots, it is evident that as age increases so does distance. The rates of
individuals are however criss-crossing to a certain extent. Otherwise, the highest
and the lowest lines are quite consistent. Males generally had larger pituitary to
pterygomaxillary fissure distances.

215
Random intercepts model
For multi-level modelling, each subject is taken as a stratum. For this first model,
the slopes are forced to be the same. There are 27 intercepts; too many to have each
of them as a parameter. Instead, a mean intercept is computed and the remaining are
taken as random effects.
> model0 <- glmmPQL(distance ~ age, random = ~1 | Subject,
data = .data, family = gaussian)
The above command creates a generalized linear multi-level model (glmm) using
the Penalized Quasi-Likelihood (PQL) method of iteration. The dependent variable
is 'distance'. The independent variable is 'age', which has fixed effects (for all
subjects). The random effects (as indicated by the word 'random') is a constant of 1.
The upper level of the model (following the '|' sign) is 'Subject' because the same
subject has 4 repeated measurements. In other words, 'Subject' is at a higher level.
The glmmPQL command handles the 'family' argument of the model in the same
way as the glm command. Since the errors are assumed to be normally distributed,
the family is specified as 'gaussian'.
> summary(model0)
Linear mixed-effects model fit by maximum likelihood
Data: .data
AIC BIC logLik
NA NA NA
Random effects:
Formula: ~1 | Subject
(Intercept) Residual
StdDev: 2.072142 1.422728
Variance function:
Structure: fixed weights
Formula: ~invwt
Fixed effects: distance ~ age
Value Std.Error DF t-value p-value
(Intercept) 16.761111 0.8020244 80 20.89851 0
age 0.660185 0.0617993 80 10.68272 0
Correlation:
(Intr)
age -0.848
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-3.68695131 -0.53862941 -0.01232442 0.49100161 3.74701484
Number of Observations: 108
Number of Groups: 27

216
The 'AIC' and 'BIC' values are derived from 'logLik', the log likelihood. They will
be used to compare the level of fit with other models using the same dataset and the
same method of iteration. Note that AIC is equal to -2×logLik + 2×npar and BIC is
equal to -2×logLik + log(n)×npar, where npar is the number of parameters in the
model (in this model, four; namely, the standard deviations of intercepts and
residuals, which are the random effects, and the coefficient of the fixed intercept
and the fixed effect of age) and n is the number of observations (108).
Random effects express themselves as standard deviations of errors. There are two
parts of errors. The first part is the standard deviations of difference between the
fixed intercept and the intercepts of individual subjects. The second part is the
standard deviation of the residuals or the difference between the final predicted
values and the observed values for each subject. There is no coefficient for these
random effects terms because the means should be close to zero. This is because
they are assumed to come from the standard normal distribution.
The fixed part of the summary, similar to a conventional regression model, contains
the coefficients and their standard errors. The coefficient of the intercept is 16.76.
This means that on the average, at the age of 0, the PPMF distance for a child is
expected to be 16.76 mm. The coefficient of age is 0.66. This means that for each
birthday reached, an average child is expected to gain 0.66 mm length of PPMF
distance. This coefficient is statistically significant as the standard error is relatively
small, resulting in a large t-value and a small P value. The standardised residuals
within groups (or within the child) are distributed with a certain degree of
symmetry since the median is close to 0, and the lower and upper quartiles are
relatively equidistant from the median, as are the minimum and the maximum.
Finally, the model confirms that there were 27 children giving 108 records.
Model attributes and graphing
The model has many attributes inside. We will examine only some of these.
> attributes(model0)
$names
[1] "modelStruct" "dims" "contrasts" "coefficients"
[5] "varFix" "sigma" "apVar" "logLik"
[9] "numIter" "groups" "call" "terms"
[13] "method" "fitted" "residuals" "fixDF"
[17] "na.action" "data" "family"
$class
[1] "glmmPQL" "lme"

217
The most important attributes are the coefficients.
> coef(model0)
$fixed
(Intercept) age
16.7611111 0.6601852
$random
$random$Subject
(Intercept)
M16 -0.9152788
M05 -0.9152788
M02 -0.5798146
===============
===============
F04 0.7620421
F11 2.1038989
There are two parts of the coefficients: the fixed part and the random part. The fixed
part, shown in the summary, is the average for all of the 27 strata (children). The
fixed intercept is 16.761111, which means that the (average) estimated distance at
birth (when age is 0) is 16.76 mm. For each increasing year of age, the PPMF
distance increases by approximately two-thirds of a millimetre (0.66). The second
or random part shows 'random intercepts only' since there is no variable in this part
as specified by 'random ~ 1'. There are 27 (additional coefficients for) intercepts,
one for each child. For the first child (M16) who has a negative random intercept,
or starting distance, the mean intercept from the fixed part (16.76) must be
subtracted by 0.9152788. The second person (M05) shares the same intercept.
Altogether, the random intercepts range from -4.940849 (F10) to +4.899434 (M10).
There are many other attributes worth exploring. The next interesting one is
'fitted(model0)', which contains the fitted or predicted values of each point of
observation.
> model0$fitted
fixed Subject
1 22.043 25.377
2 23.363 26.697
3 24.683 28.017
4 26.004 29.338
5 22.043 21.463
6 23.363 22.783
7 24.683 24.104
8 26.004 25.424
==== Up to 108th person ==========
There are two columns of fitted values: fixed (average of each point of time) and
random (by Subject). In fact, the fixed part has only four values predicting the
average value for each value of age.

218
> tab1(model0$fitted[, 1])
[model0$fitted 1 :
Frequency Percent
22.0425925925926 27 25
23.3629629629630 27 25
24.6833333333333 27 25
26.0037037037037 27 25
Total 108 100
Each value has 27 repeated records. In other words, there are only four terms of
fixed effects, each shared by all 27 subjects. The second component is predicting
the intercept value for each subject, which varies from one child to another.
> followup.plot(id=Subject, time=age, outcome=fitted(model0),
line.col="multicolor")
> title(main="Model 0: random intercepts", ylab="mm",
xlab="years")
The X-coordinates for each line are the ages for that child. The corresponding Y-
coordinates are the fitted values for the PPMF distance. Recall that there are two
columns for the fitted values (for the fixed and random effects). The plot uses the
second column, which is the predicted value for each child (random effects). The
colour varies according to the (order of) 'Subject'.
8 9 10 11 12 13 14
18 20 22 24 26 28 30
Model 0: Random intercepts
years
mm
The model fixes the coefficient of the slope, allowing only the intercepts to be a
random variable. The next model releases the effects of age to become random with
a mean value.
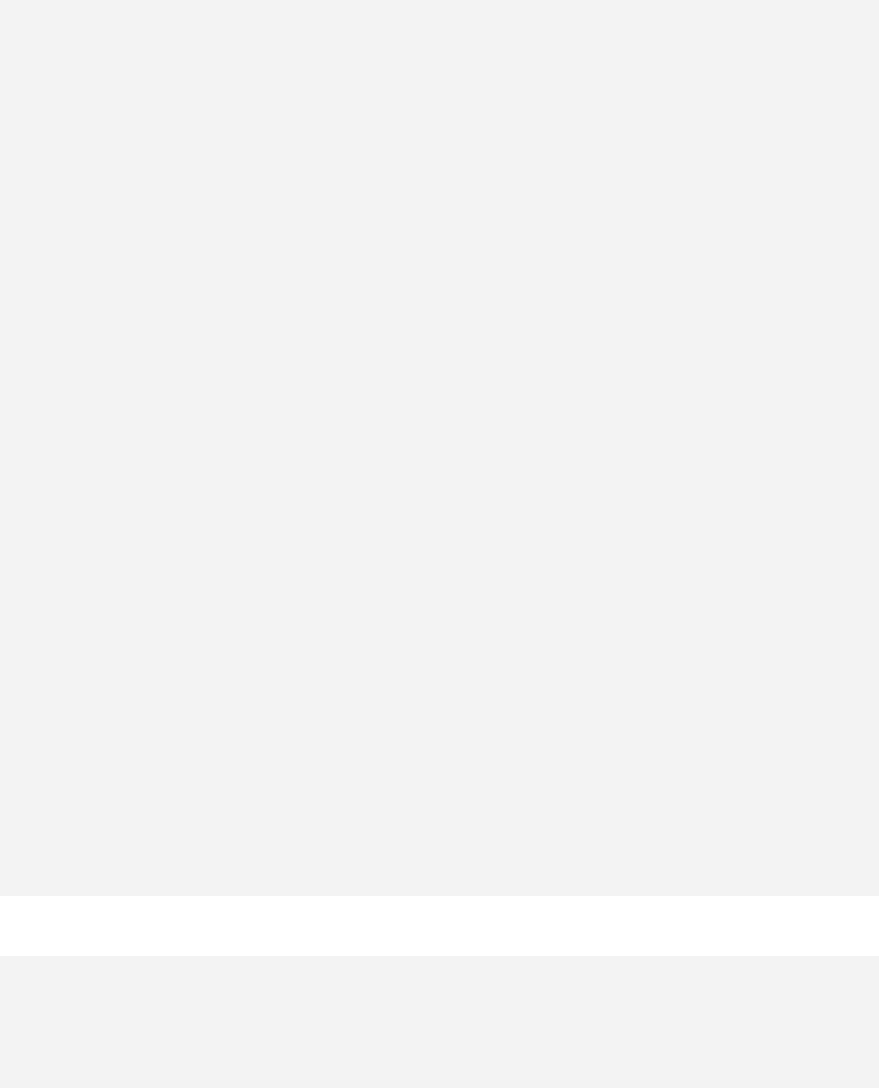
219
Model with random slopes
> model1 <- glmmPQL(distance ~ age, random = ~age | Subject,
data = .data, family = gaussian)
> summary(model1)
Linear mixed-effects model fit by maximum likelihood
Data: .data
AIC BIC logLik
NA NA NA
Random effects:
Formula: ~age | Subject
Structure: General positive-definite, Log-Cholesky
parametrization
StdDev Corr
(Intercept) 2.2023778 (Intr)
age 0.2152392 -0.585
Residual 1.3103646
Variance function:
Structure: fixed weights
Formula: ~invwt
Fixed effects: distance ~ age
Value Std.Error DF t-value p-value
(Intercept) 16.761111 0.7689227 80 21.798174 0
age 0.660185 0.0706254 80 9.347699 0
Correlation:
(Intr)
age -0.849
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-3.30002923 -0.48692999 0.00739127 0.48148182 3.92211226
Number of Observations: 108
Number of Groups: 27
Similar to 'model0', a graph can be plotted with the following commands.
> followup.plot(id=Subject, time=age, outcome=fitted(glmm1),
line.col="multicolor")
> title(main="Model1: random intercepts and slopes",
ylab="mm", xlab="years")
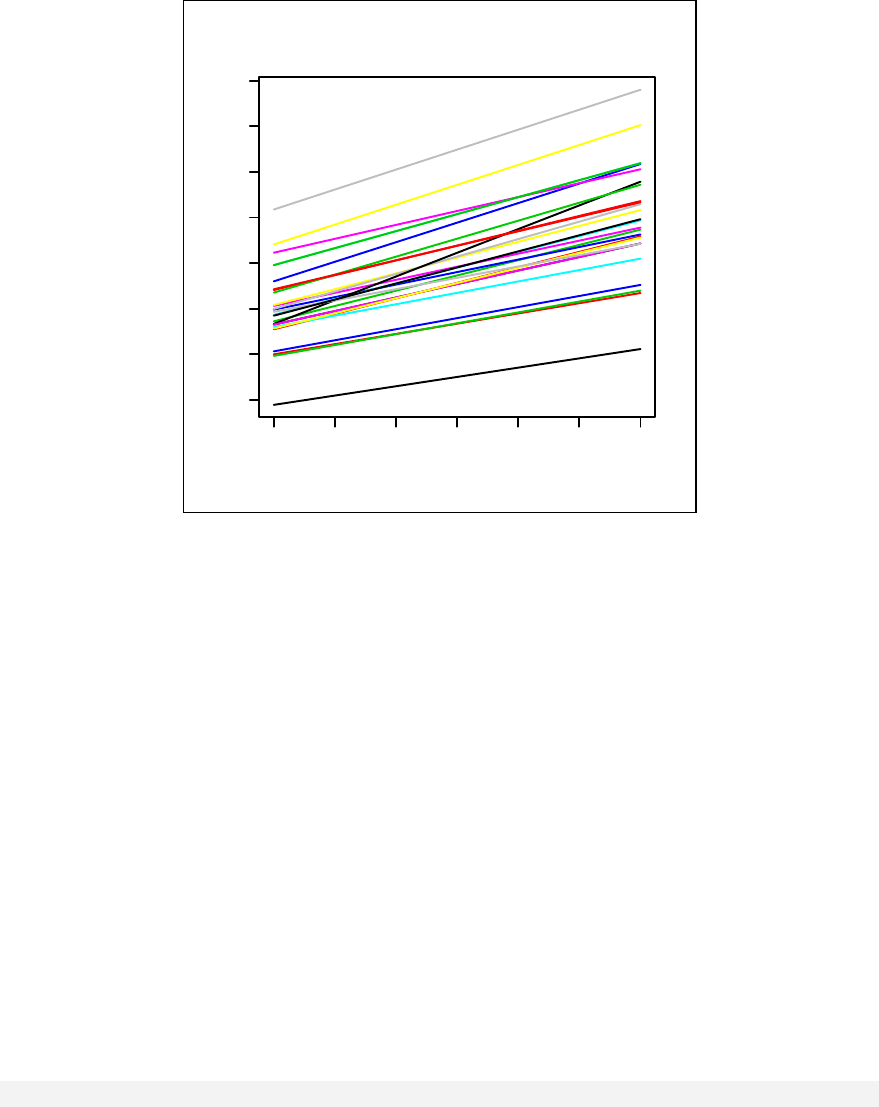
220
8 9 10 11 12 13 14
18 20 22 24 26 28 30 32
Model1: random intercepts and slopes
years
mm
Model 'model0' is equivalent to a stratified analysis without interaction whereas
'model1' is equivalent to keeping an interaction term. The latter model suggests
that each child has their own baseline distance (intercept) as well as their own
growth rate.
The graph shows different slopes for different subjects. The slopes are now a
random effect as well as a fixed effect.
In the random effects part, age has a standard deviation of 0.215 mm, which is
relatively small compared to the randomness of the intercept (2.2 mm) and the
residuals (1.3 mm). The variation due to differences in growth rate of the PPMF
distance among subjects is small compared to the variation in baselines and the
average growth rate. The correlation between age and intercept is negative (-0.585)
in the random effects suggesting that the slope of the subjects tends to be flatter as
the level of the Y-intercepts increases.
The coefficients of the fixed effects for the intercept and age are not different from
'model0'. In fact the coefficients are the same as those from ordinary glm.
> summary(glm(distance ~ age, family=gaussian))
The standard errors from the generalised linear model are much higher than those of
the multi-level models. These advanced models improve the precision of the
estimates. In this example 'model1' has wider standard errors than 'model0'.
When the age effect is partially individualised, the overall age effect reduces its
precision.
We have another independent variable 'Sex'. It would be interesting to examine
whether the boys have larger distance than girls and whether the growth rates are
different between the sexes.
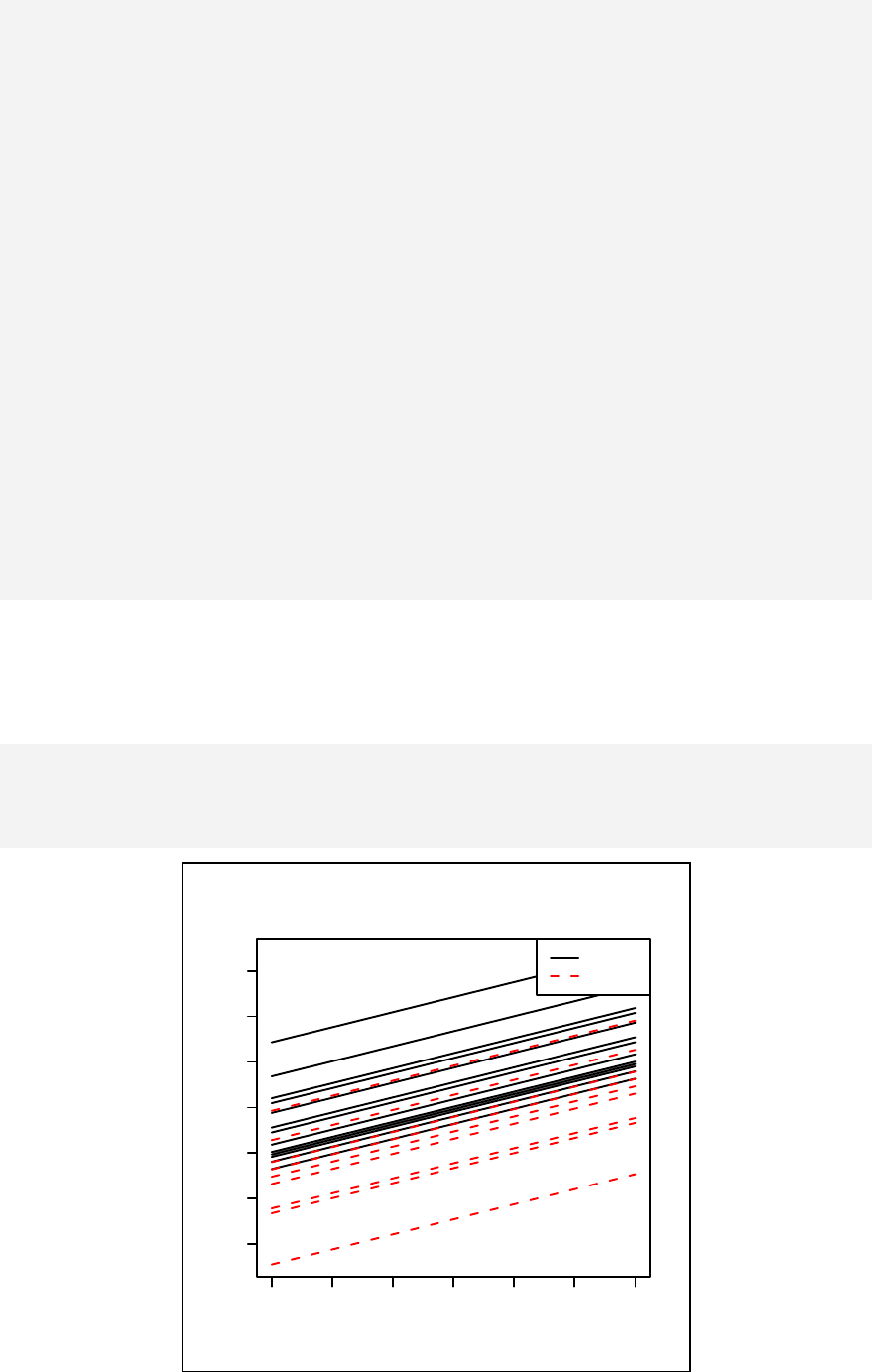
221
> model2 <- glmmPQL(distance ~ age + Sex, random = ~1 |
Subject, data = .data, family = gaussian)
> summary(model2)
Linear mixed-effects model fit by maximum likelihood
Data: .data
AIC BIC logLik
NA NA NA
Random effects:
Formula: ~1 | Subject
(Intercept) Residual
StdDev: 1.730079 1.422728
Variance function:
Structure: fixed weights
Formula: ~invwt
Fixed effects: distance ~ age + Sex
Value Std.Error DF t-value p-value
(Intercept) 17.706713 0.8315459 80 21.293729 0.0000
age 0.660185 0.0620929 80 10.632212 0.0000
SexFemale -2.321023 0.7430668 25 -3.123572 0.0045
========= Remaining parts of output omitted ========
'Sex' is introduced as a pure fixed effect. In fact, it cannot be a random effect
because there is no variation of sex in an individual subject.
The growth lines are now separated by 'Sex'.
> followup.plot(id=Subject, time=age, outcome=fitted(model2),
by=Sex)
> title(main="Model2: random intercepts", ylab="mm", xlab="years")
8 9 10 11 12 13 14
18 20 22 24 26 28 30
Male
Femal
e
Model2: random intercepts
years
mm
222
It is clear that the lines for males tend to be in the upper half of the plot whereas
those for females tend to be in the lower part.
To test whether the rates are different between the two sexes, and interaction term
between age and sex is introduced.
> model3 <- glmmPQL(distance ~ age*Sex, random = ~1 | Subject,
data = .data, family = gaussian)
> summary(model3)
Linear mixed-effects model fit by maximum likelihood
Data: .data
AIC BIC logLik
NA NA NA
Random effects:
Formula: ~1 | Subject
(Intercept) Residual
StdDev: 1.740851 1.369159
Variance function:
Structure: fixed weights
Formula: ~invwt
Fixed effects: distance ~ age * Sex
Value Std.Error DF t-value p-value
(Intercept) 16.340625 0.9814310 79 16.649795 0.0000
age 0.784375 0.0779963 79 10.056564 0.0000
SexFemale 1.032102 1.5376069 25 0.671239 0.5082
age:SexFemale -0.304830 0.1221968 79 -2.494580 0.0147
========= Remaining parts of output omitted ========
The interaction term between age and sex is significant. The coefficient of the main
effect of 'Female' is 1.03, indicating that under a linear growth assumption, at birth
(where age is 0), girls have a longer average PPMF distance of 1.03mm compared
to boys.
The coefficient of the interaction term is -0.30483 indicating that for each
increment of one year, girls will have a shorter average PPMF distance of 0.3mm
compared to boys. In other words, females have a shorter PPMF distance and a
smaller growth rate.
> followup.plot(id=Subject, time=age, outcome=fitted(model3),
by=Sex)
> title(main="Model3: random intercepts, fixed effects of
age:sex", ylab="mm", xlab="years")
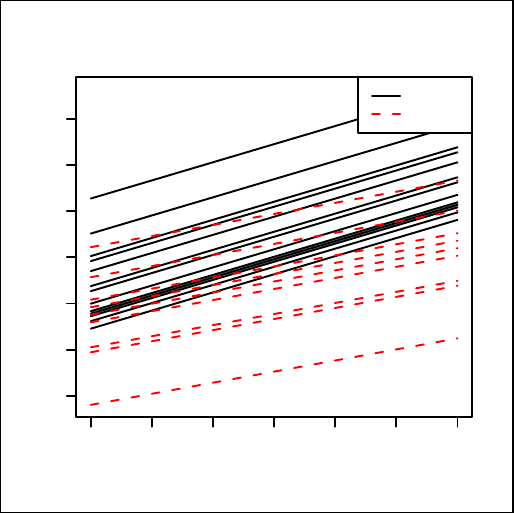
223
8 9 10 11 12 13 14
18 20 22 24 26 28 30
Male
Femal
e
Model3: random intercepts, fixed effects of
age:sex
years
mm
In conclusion, individual children have different baseline PPMF distances. Girls
tended to have a higher PPMF distance at birth. However, boys have a faster growth
rate than girls.
Note on lme4 package
Mixed effects modeling is a fast moving subject. A new package in R version 2.4.1,
called lme4, was introduced. The package contains a function called lmer, which
is more efficient than the glmmPQL function in the MASS package and can
accommodate more complicated types of nesting. For example, analysis of clinical
visits could be simultanesouly nested both by patient and by physician. While this
feature is more advanced than what has been demonstrated in this chapter, this new
package gives similar results for simple nesting. However, it is still in the
experimental stage. For example, fitted values cannot be easily obtained. When this
package is fully developed, it may replace the contents of this chapter.

224
Exercises________________________________________________
The dataset Bang consists of a subset of data from the '1988 Bangladesh Fertility
Survey'.
> zap()
> data(Bang)
> use(Bang)
> label.var(woman, "woman ID")
# Response variable
> label.var(user, "current contraceptive use")
> label.var(age_mean, "age(yr) centred around mean")
> living.children <- factor(living.children)
> label.var(living.children, "No. of children living")
Problem 1.
Use glmmPQL to compute the effects of the number of living children, age and
living in urban area on the probability of contraceptive use among the women.
Compute the 95% confidence interval of their odds ratios.
Problem 2.
Does number of living children have a linear dose response relationship with
contraceptive use?
Problem 3.
Should age be a random effect?
Problem 4.
Does age have the same effect among urban and rural women on contraceptive use?

225
Chapter 21: Survival Analysis
In a cohort study, a person is followed up from a starting time to the end of the
study or to the time the follow-up has been terminated by the outcome event,
whichever comes first. The event-free duration is an important outcome. For an
unwanted event, the desired outcome is a longer event-free duration.
For subjects whose events take place before the end of the study, the total duration
of time is known. For the subjects whose follow up times end without the event, the
end status is called 'censored' because the actual duration of time to the event is not
known or 'censored' by the study. The outcome variable for each subject is therefore
composed of 'time' and the 'status' at the end. Mathematically, the status is 1 if the
event takes place and 0 otherwise.
Example: Age at marriage
A data management workshop was carried out in 1997. Each of the 27 participants
was asked to provide personal information on their sex, birth year, education level,
marital status and year of marriage (for those who were married). The objective of
this analysis is to use survival analysis methods to examine this dataset.
> library(survival)
> data(Marryage)
> use(Marryage)
> des()
No. of observations =27
Variable Class Description
1 id integer
2 sex factor
3 birthyr integer year of birth
4 educ factor level of eduction
5 marital factor marital status
6 maryr integer year of marriage
7 endyr integer year of analysis
> summ()
No. of observations = 27
226
Var. name Obs. mean median s.d. min. max.
1 id 27 14 14 7.94 1 27
2 sex 27 1.667 2 0.48 1 2
3 birthyr 27 1962.15 1963 6.11 1952 1972
4 educ 27 1.519 2 0.509 1 2
5 marital 27 1.593 2 0.501 1 2
6 maryr 16 1987.56 1988 5.18 1979 1995
7 endyr 27 1997 1997 0 1997 1997
To see the codes for the factor variables type the following command:
> codebook()
id :
obs. mean median s.d. min. max.
27 14 14 7.94 1 27
==================
sex :
Label table: sexlab
code Frequency Percent
male 1 9 33.3
female 2 18 66.7
==================
birthyr : year of birth
obs. mean median s.d. min. max.
27 1962.148 1963 6.11 1952 1972
==================
educ : level of education
Label table: educlab
code Frequency Percent
bach- 2 13 48.1
>bachelor 3 14 51.9
==================
marital : marital status
Label table: marlab
code Frequency Percent
Single 1 11 40.7
Married 2 16 59.3
==================
maryr : year of marriage
obs. mean median s.d. min. max.
16 1987.562 1988 5.18 1979 1995
==================
endyr : year of analysis
obs. mean median s.d. min. max.
27 1997 1997 0 1997 1997
==================
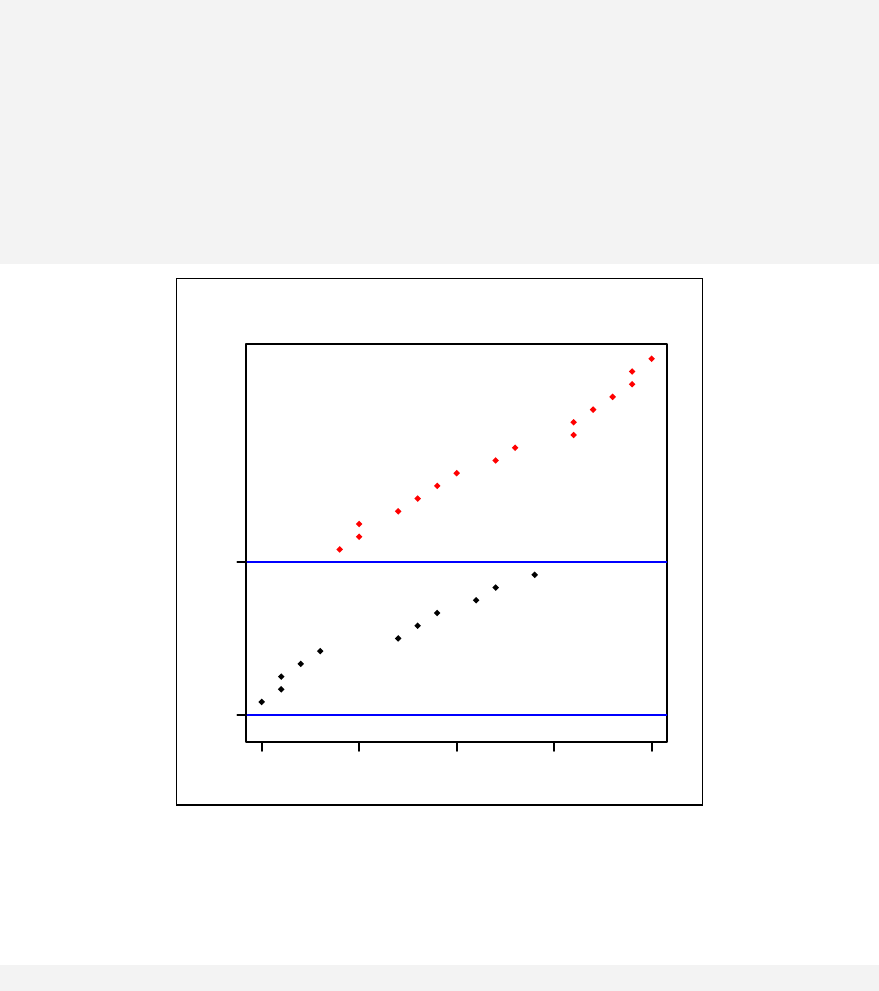
227
Note that the original codes for the variable 'educ' were 2 = bach-, 3 = >bachelor, as
shown in the output of the codebook command. This was how the codes were
defined in the original data entry program, and the label table associated with each
categorical variable were kept with the data. In the output from the summ function
however, the numeric codes for 'educ' are displayed as 1 (bach-) and 2 (>bachelor).
This anomaly is simply due to unclassing the levels of the factor variable in the
output from the summ command. When R converts something to a factor the first
level will always have an underlying code of 1. These numeric codes should not be
confused with the original coding scheme. In fact, the codes were only used during
the original entry of the data, and are never used during data analysis.
The variable 'endyr', fixed at 1997, is used for computation of age and age at
marriage.
> age <- endyr - birthyr
> label.var(age, "Age")
> summ(age, by = marital)
For marital = Single
Obs. mean median s.d. min. max.
11 31.18 32 4.996 25 39
For marital = Married
Obs. mean median s.d. min. max.
16 37.38 37.5 5.596 29 45
25 30 35 40 45
Distribution of Age by marital status
Single
Married
There were 16 (59%) married participants. Clearly the married participants were
older than the single ones.
228
> age.marr <- maryr - birthyr
> label.var(age.marr, "Age at marriage")
> summ(.data[,8:9])
No. of observations = 27
Var. name obs. mean median s.d. min. max.
1 age 27 34.85 34 6.11 25 45
2 age.marr 16 27.94 27.5 2.77 25 36
Among the 16 married participants the mean age at marriage was 27.94 years.
The whole essence of survival analysis is related to “time-to-event”. In this dataset
we are using age as the time variable and marriage as the event. In most
epidemiological studies 'time' is usually considered to be duration of follow up and
the event is usually occurrence of an unwanted event, such as death or disease
recurrence. Our data comes from a cross-sectional survey, whereas most data for
survival analysis come from follow up studies. However, the procedures used on
this simple dataset can be applied to other survival type data.
Survival object in R
The survival library contains all the functions necessary to analyse survival type
data. In order to analyse this data, we need to create an object of class Surv, which
combines the information of time and status in a single object. The status variable
must be either numeric or logical. If numeric, there are two options. Values must be
either 0=censored and 1=event, or 1=censored and 2=event. If logical,
FALSE=censored and TRUE=event. In the Marryage dataset, 'marital' is a factor
and so must be converted to one of the formats specified above. We will choose the
logical format, but this is arbitrary.
> married <- marital == "Married"
> time <- ifelse(married, age.marr, age)
Note that time for married and unmarried subjects are generated differently. For a
married person, we know exactly that the duration of time is their age at marriage.
Their survival time stops at the year of marriage. For an unmarried person, we do
not know this length of time. So their current age is used instead.
The survival object for marriage can now be created and compared against other
variables.
> (surv.marr <- Surv(time, married))
[1] 26 26 29 25+ 26 26+ 28 28 28 36+ 36 39+ 29 33+
[15] 25 31 27 34+ 37+ 26 27+ 25 27 26+ 28+ 30 32+
> head(data.frame(age, age.marr, married, surv.marr))

229
age age.marr married surv
1 44 26 TRUE 26
2 43 26 TRUE 26
3 45 29 TRUE 29
4 25 NA FALSE 25+
5 37 26 TRUE 26
6 26 NA FALSE 26+
For the first three subjects, and the 5th, who were all married, the values of
'surv.marr' are equal to their age at marriage. For the 4th and the 6th subjects, the
values are equal to their current age. The plus sign indicates that the actual 'time' is
beyond those values but were censored. Those participants had not married at the
time of the workshop.
For further exploration, subsets of variables sorted by 'time' are displayed by the
following command.
> cbind(age, sex, age.marr, married, surv.marr)[order(time),]
age sex age.marr married time status
[1,] 25 1 NA 0 25 0
[2,] 32 2 25 1 25 1
[3,] 29 1 25 1 25 1
[4,] 44 1 26 1 26 1
[5,] 43 2 26 1 26 1
[6,] 37 2 26 1 26 1
[7,] 26 2 NA 0 26 0
[8,] 34 1 26 1 26 1
======== subsequent lines omitted ========
The 'Surv' object consists of both 'time' and 'status'. The first person, a 25 year old
male, was single. His time is 25 and his status is 0, i.e. his event is censored. The
second person was a 32 year old woman who had married at age 25, so this is her
time. The event (marriage) had already occurred, thus her status = 1, etc.
Life table
A life table is a tabulation of the survival, event and survival probability over time.
The classical method for this analysis in the general population has been well
developed for centuries. In general, the method involves calculating the cumulative
survival probability, which is the product of the survival probabilities at each step.
For our simple dataset, the overall life table can be achieved by:

230
> fit <- survfit(surv.marr)
> summary(fit, censor=TRUE)
Call: survfit(formula = surv.marr)
time n.risk n.event survival std.err lower95CI upper95CI
25 27 2 0.926 0.0504 0.832 1.000
26 24 4 0.772 0.0820 0.627 0.950
27 18 2 0.686 0.0926 0.526 0.894
28 15 3 0.549 0.1025 0.380 0.791
29 11 2 0.449 0.1054 0.283 0.711
30 9 1 0.399 0.1048 0.238 0.668
31 8 1 0.349 0.1029 0.196 0.622
32 7 0 0.349 0.1029 0.196 0.622
33 6 0 0.349 0.1029 0.196 0.622
34 5 0 0.349 0.1029 0.196 0.622
36 4 1 0.262 0.1080 0.117 0.588
37 2 0 0.262 0.1080 0.117 0.588
39 1 0 0.262 0.1080 0.117 0.588
The first row of the output says that at time 25 (when all participants were aged 25 -
which is everyone), there were 27 subjects, two of whom were married at that time.
The survival probability (probability of getting married at this age) is calculated as
(27-2)/27 = 0.926. In fact, there is one person aged 25 years who is not shown. This
person is censored (not married) so is included in this row but not in subsequent
rows.
On the second row, there were 24 persons remaining who had reached or passed
their 26th birthday (27 started, 2 events and 1 censored at the end of the 25th year).
At this time, 4 events took place, and since the third row says that only 18 persons
remained at the next time point, 2 subjects must have been censored. The survival
probability for time 26 is therefore (24 - 4)/24 = 0.833. When multiplying this value
with the previous probability in the first row, the cumulative probability is (25/27) x
(20/24) = 0.772. This computation of cumulative survival probability continues in a
similar way until the end of the dataset. Note that at the time points of 32, 33, 34, 37
and 39 years, there were no events (n.event = 0). The probabilities are therefore
unchanged.
The above Kaplan-Meier life table is a slight modification from the classical
demographical method where the time interval is fixed (usually at every 5 years of
age) and adjustment for incomplete information of exact time of event is taken into
account.
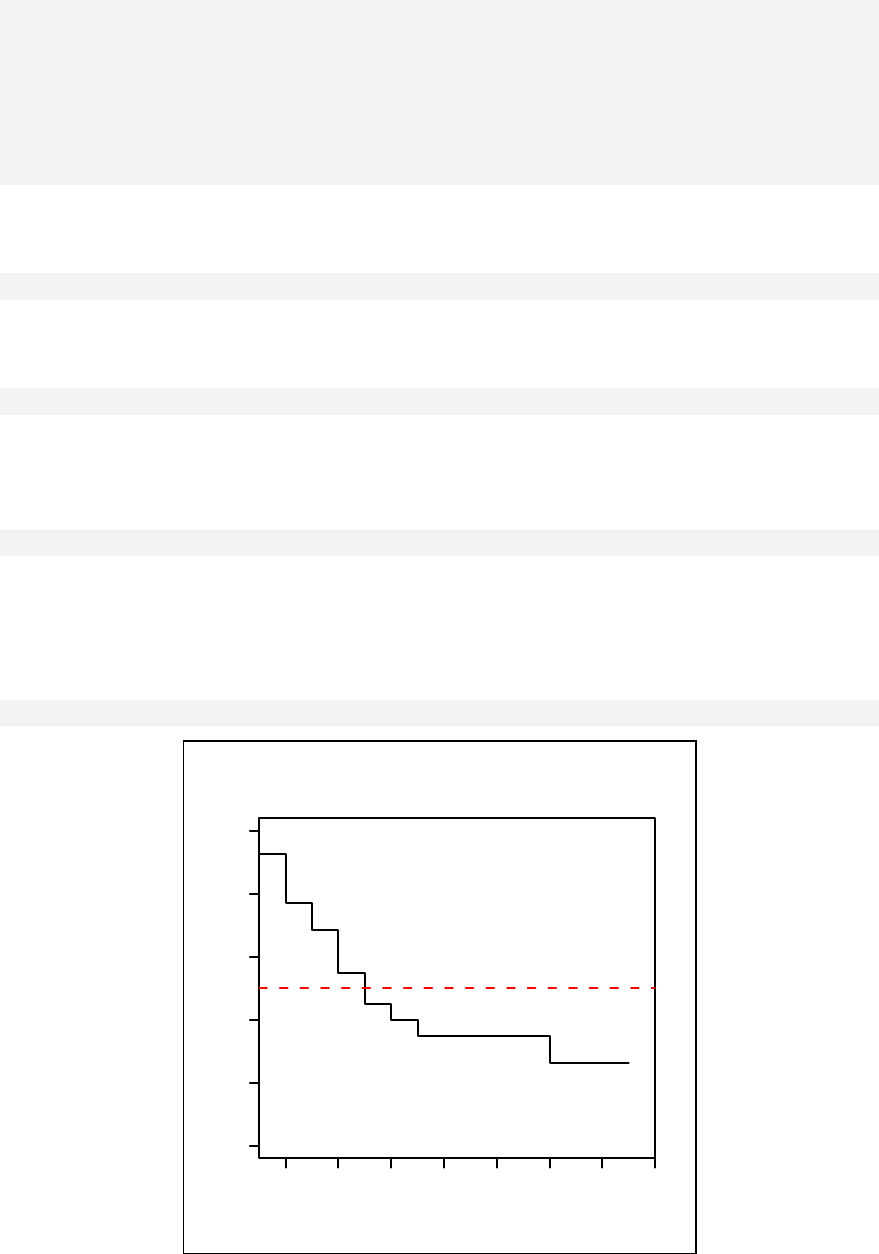
231
Kaplan-Meier curve
The summary of a survival object reveals many sub-objects.
> km1 <- summary(fit, censor=T)
> attributes(km1)
$names
[1] "surv" "time" "n.risk" "n.event" "conf.int"
"std.err" "lower" "upper" "call"
$class
[1] "summary.survfit"
We can use this 'km1' object to plot 'time' vs 'surv', to produce a stepped line plot,
which is called a survival curve or 'Kaplan-Meier curve'.
> plot(km1$time, km1$surv, type="s")
If 'xlim=c(25, 40)' is added to the command, the curve will be very similar to
that produced by the standard command.
> plot(fit, xlim=c(25, 40))
When there is only one curve plotted, the two 95% confidence interval lines and the
time marks for censored subjects are included in the plot. To suppress them, they
can be set be FALSE.
> plot(fit, conf.int=F, mark.time=F, xlim=c(25, 38), las=1)
The vertical axis is survival probability and the horizontal axis is time. If a
horizontal line were drawn at probability 50%, it would cross the survival curve at
the point of the median survival time. If less than half of the subjects have
experienced the event then the median survival time is undefined.
> abline(h=.5, lty=2, col="red")
26 28 30 32 34 36 38 40
0.0
0.2
0.4
0.6
0.8
1.0

232
In this dataset, the median survival time (age at marriage) is 29 years. This value is
actually displayed when the 'fit' object is typed.
> fit
Call: survfit(formula = surv.marr)
n events median 0.95LCL 0.95UCL
27 16 29 27 36
The numbers at risk at various time points can also be displayed on the plot.
> stimes <- seq(from=20, to=40, by=5)
> sfit <- summary(fit, times = stimes)
> sfit
Call: survfit(formula = surv.marr)
time n.risk n.event survival std.err lower95%CI upper95% CI
20 27 0 1.000 0.0000 1.000 1.000
25 27 2 0.926 0.0504 0.735 0.981
30 9 12 0.399 0.1048 0.200 0.592
35 4 1 0.349 0.1029 0.162 0.545
> n.risk <- sfit$n.risk
> n.time <- sfit$time
> mtext(n.risk, side=1, line=2, at=stimes, cex=0.8)
Cumulative hazard rate
The hazard rate is the proportion of failures per unit time. In epidemiological
studies, the rate can vary considerably over time. Graphically, it is better to draw
the cumulative rate since it is relatively easy to perceive the change of rate by the
slope of the cumulative curve.
> plot(fit, conf.int=FALSE, fun="cumhaz")
0 10203040
0.0 0.2 0.4 0.6 0.8 1.0 1.2

233
In the first 25 years, the slope is flat due to the absence of events. From 25-31 years,
the slope is relatively steep, indicating a high rate of marriage during these years.
The last steep rise occurs at 36 years. At the end of curve, the rate is not very
precise due to the smallness of the sample size in this time period.
Survival summaries can be obtained by different levels of a factor variable by
adding terms to the formula argument of the survfit function. Multiple survival
curves can also be shown in the same graph.
> fit <- survfit(surv.marr ~ sex)
> fit
Call: survfit(formula = surv.marr ~ sex)
n events median 0.95LCL 0.95UCL
sex=male 9 6 30 26 Inf
sex=female 18 10 28 28 Inf
> summary(fit)
Call: survfit(formula = surv.marr ~ sex)
sex=male
time n.risk n.event survival std.err lower 95%CI upper 95%CI
25 9 1 0.889 0.105 0.706 1.000
26 7 2 0.635 0.169 0.377 1.000
29 5 1 0.508 0.177 0.257 1.000
30 4 1 0.381 0.172 0.157 0.924
31 3 1 0.254 0.155 0.077 0.838
sex=female
time n.risk n.event survival std.err lower 95%CI upper 95%CI
25 18 1 0.944 0.0540 0.8443 1.000
26 17 2 0.833 0.0878 0.6778 1.000
27 13 2 0.705 0.1117 0.5169 0.962
28 10 3 0.494 0.1287 0.2961 0.823
29 6 1 0.411 0.1309 0.2204 0.768
36 3 1 0.274 0.1419 0.0994 0.756
> plot(fit, col=c("red", "blue"), lty=c(1,2), las=1)
> title(main="Age at Marriage", xlab="Time (years)")
> mtext(side=3, text="Proportion", at=-2)
> legend(10,.4, legend=c("male", "female"), lty=c(1,2),
col=c("red", "blue"))
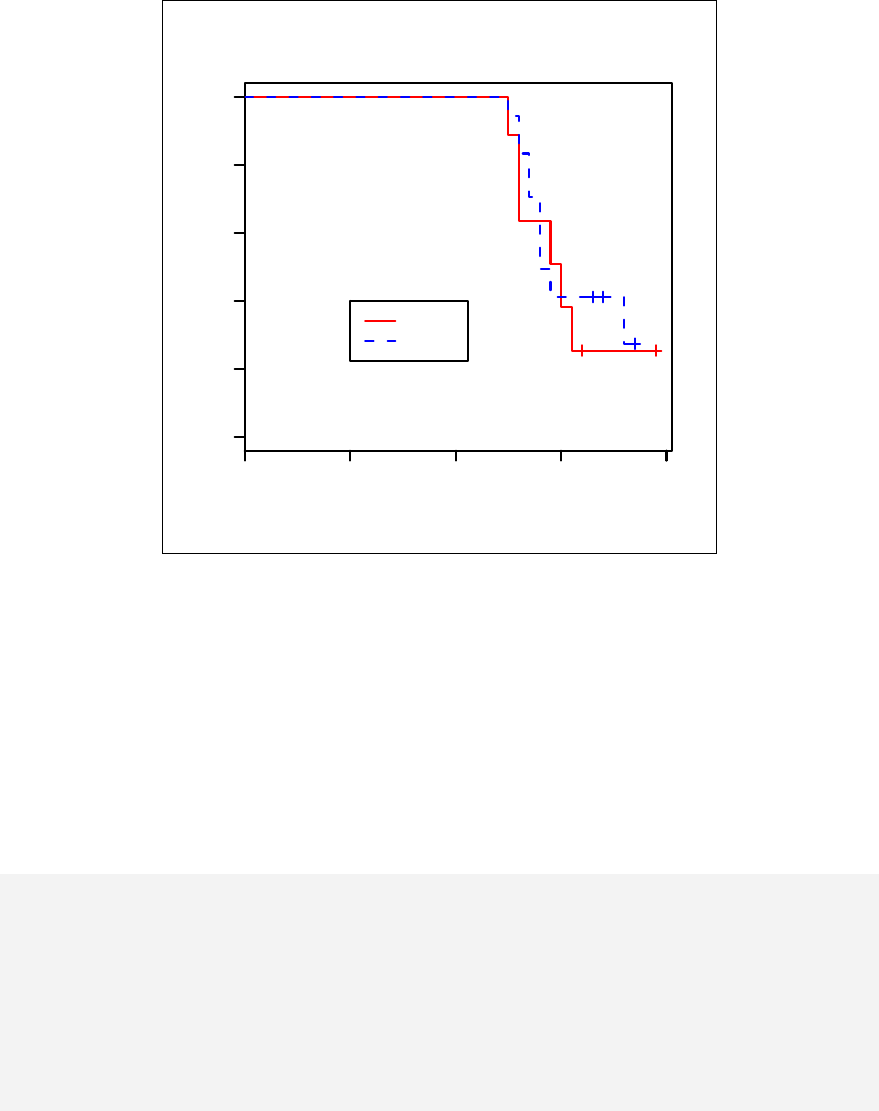
234
0 10203040
0.0
0.2
0.4
0.6
0.8
1.0
Age at Marriage
Time (years)
Proportion
male
female
When there are multiple survival curves, the 95% confidence interval lines are
omitted. The curves appear very similar, indicating that both the males and females
in the workshop married at similar rates. More formal comparison among groups is
explained in detail in the next section.
Statistical comparison among survival curves
Survival curves can be tested for statistical difference with the survdiff
command.
> survdiff(surv.marr ~ sex)
Call:
survdiff(formula = surv.marr ~ sex)
N Observed Expected (O-E)^2/E (O-E)^2/V
sex=male 9 6 5.37 0.0746 0.125
sex=female 18 10 10.63 0.0376 0.125
Chisq= 0.1 on 1 degrees of freedom, p= 0.724
With this small sample size, the difference can simply be explained by chance
alone. The survdiff command actually has 5 arguments, the last one being 'rho',
which specifies the type of test to use. When rho = 0 (by default) the log-rank or
Mantel-Haenszel chi-squared test is performed. This compares the expected number
of events in each group against the observed values. If the level of difference
between these two groups is too high, the chi-squared value will be high and the P
value will be small indicating that the curves are significantly different. If rho = 1
then the Peto modification of the Gehan-Wilcoxon test (sometimes called the Peto
test) is performed, which places more weight on earlier events.

235
Stratified comparison
There is a significant association between sex and education.
> cc(sex, educ)
educ
sex bach- >bachelor Total
male 1 8 9
female 12 6 18
Total 13 14 27
OR = 0.07
95% CI = 0.001 0.715
Chi-squared = 7.418 , 1 d.f. , P value = 0.006
Fisher's exact test (2-sided) P value = 0.013
Females are seen to have a higher level of education. The effect of sex on survival
with adjustment for education can be obtained as follows:
> survdiff(surv.marr ~ sex + strata(educ))
Call:
survdiff(formula=surv.marr ~ sex + strata(educ))
N Observed Expected (O-E)^2/E (O-E)^2/V
sex=male 9 6 5.61 0.0266 0.0784
sex=female 18 10 10.39 0.0144 0.0784
Chisq= 0.1 on 1 degrees of freedom, p= 0.779
The adjusted effect is not much different from the crude one. Lack of confounding
in this case is due to the lack of independent effect of education on age of marriage.
We will keep this working environment and return to work on it in the next chapter.
> save.image(file = "Marryage.Rdata")
References
Kleinbaum D, Klein M (2005). Survival Analysis: A Self-Learning Text.
Hosmer Jr D, Lemeshow S (1999). Applied Survival Analysis: Regression
Modeling of Time to Event Data.

236
Exercises________________________________________________
The dataset Compaq contains data from a follow up study on breast cancer in
Europe evaluating whether patients in private hospital ('hospital') had better
survival ('year').
Problem 1.
Check the distribution of year of deaths and censoring.
Problem 2.
Draw Kaplan-Meier curves for each hospital group with censoring marks shown on
the curves. Display the numbers at risk at reasonably spaced time intervals.
Problem 3.
Test the significance with and without adjustment for other potential confounders:
age ('agegr'), stage of disease ('stage') and socio-economic level ('ses').

237
Chapter 22: Cox Regression
Cox's proportional hazard model
Similar to other types of outcome variables, survival outcomes can be tested for
more than one predictor using regression modelling. There are many 'parametric
regression' choices for the survival object. Each of them has a specific assumption
about the distribution of the survival probability over time (so called hazard
function). In epidemiological studies, the most popular regression choice for
survival analysis is Cox regression, which has no assumption regarding the hazard
function.
While parametric regression models allow prediction of the probability of survival
at each point of time, Cox regression focuses on testing for differences of survival
probability among groups with adjustment for confounding factors. The only
important assumption it adheres to is 'proportional hazards'.
Mathematically, the hazard rate h=h(t) is a function of (or depends on) say, n
independent covariates X, where X denotes the vector X1, X2, X3 … , Xn each of
which is Xi, i = 1, 2, 3,…n, and t is time. The hazard function can also be written as
h(t, X). This denotes that the summation of influences of one group over the other is
a fixed proportion.
Under the proportional hazards assumption:
∑
ii
β
0
X
(t)eh=X)h(t,
The left-hand side of the equation says that the hazard is influenced by time and the
covariates. The right-hand side of the equation contains h0(t), which is the baseline
hazard function when all the Xi are zero. This baseline hazard function is multiplied
by e to the power of the summation of all the covariates weighted by the estimated
coefficients,
β
i.

238
Consequently,
∑
=ii
β
0
X
e
(t)h
X)h(t,
The left-hand side is the proportion, or ratio, between the hazard of the group with
exposure of X against the baseline hazard. The right-hand side is the exponentiation
of the sum of products of estimated coefficients and the covariate vector, Xi, which
is now independent of time, i.e. assumed constant over time. Thus eβiXi is the
increment of the hazard, or hazard ratio, due to the independent effect of the ith
variable.
Whenever there is an event, the conditional probability, or proportion of subjects
among different groups in getting the hazard, is assumed constant.
We will use the data from the preceding chapter to examine the independent effect
of sex on the age of marriage.
> zap()
> library(survival)
Loading required package: splines
> load("Marryage.Rdata")
> use(.data)
> cox1 <- coxph(surv.marr ~ sex)
> cox1
===============================
coef exp(coef) se(coef) z p
sexfemale -0.170 0.844 0.522 -0.325 0.74
The coefficient is negative and non-significant. The hazard ratio, exp(coef), is 0.844
suggesting an overall reduction of 16% hazard rate of females compared to males.
To obtain its 95% confidence interval, a summary of this 'coxph' object is
necessary.
> summary(cox1)
===============================
exp(coef) exp(-coef) lower .95 upper .95
sexfemale 0.844 1.19 0.304 2.35
===============================
Testing the proportional hazards assumption
Graphically, the curves of the two sexes can be compared after the vertical axis has
been transformed by -log(log(y)) and plotted against log(time). If the two curves are
parallel, the proportional hazards assumption is unlikely to be violated.

239
> fit <- survfit(surv.marr ~ sex)
> plot(fit, conf.int=FALSE, fun="cloglog", xlim=c(25,41),
col=c("red", "blue"))
25 30 35 40
−2.5 −2.0 −1.5 −1.0 −0.5 0.0
The two curves cross more than once. It is difficult to judge from the graph whether
the assumption has been violated. A formal test of the proportional hazards
assumption can be carried out as follows:
> cox.zph(model1) -> diag1; diag1
rho chisq p
sexfemale 0.00756 0.000883 0.976
The evidence against the proportional hazards assumption is very weak. This
diagnostic result can be further explored.
Time trend of the hazard ratio
These attributes can be summarised in a graph by plotting the change of beta, the
estimated coefficients, over time.
> diag1$x # x coordinates for plotting time
> diag1$y # y coordinates for plotting beta coefficients
> plot(cox.zph(model1))
This graph should be read along with the previous results earlier in the chapter
where the events and the information of sex of the subjects are sorted by time.
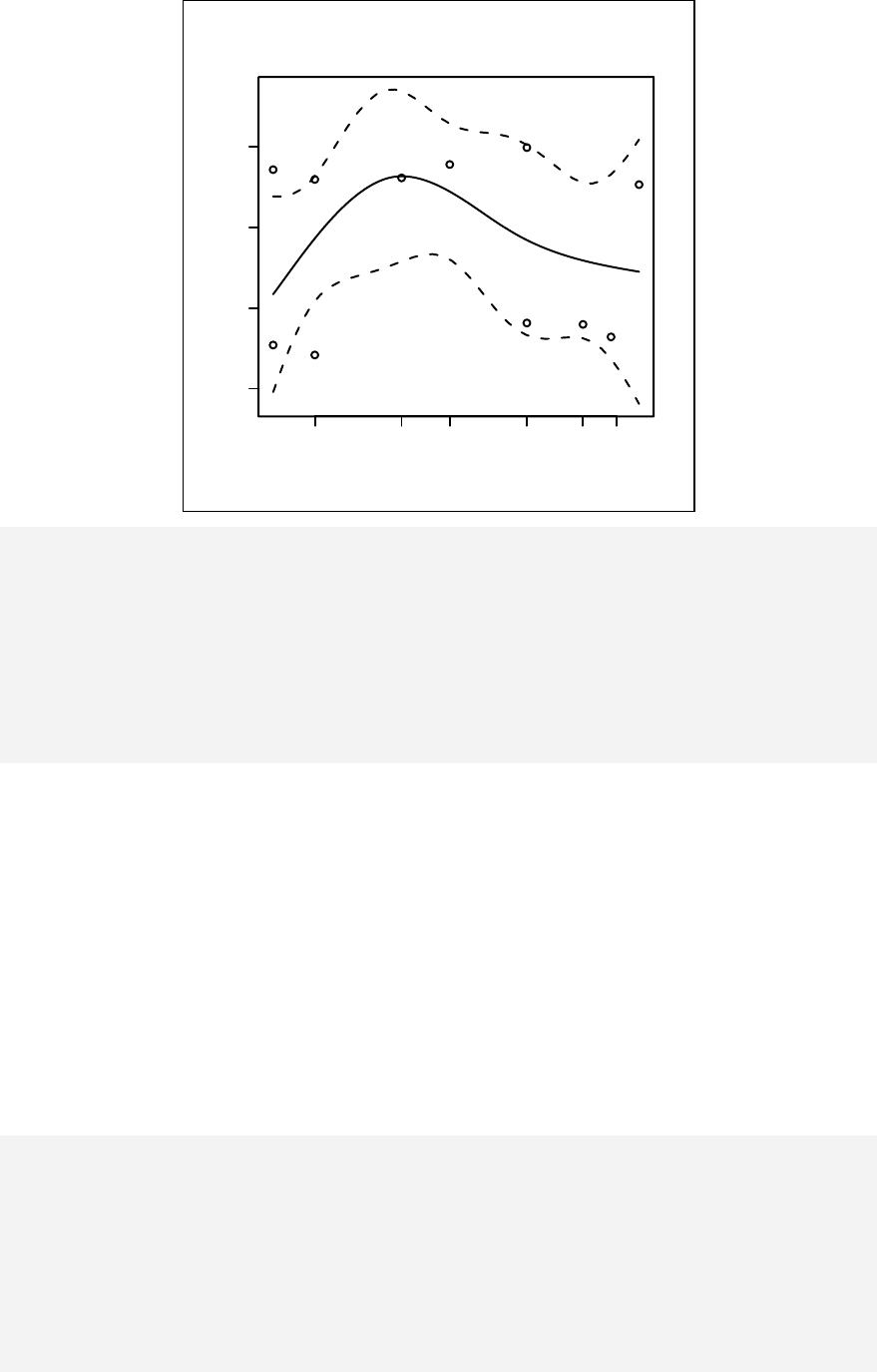
240
Time
Beta(t) for sexfemale
26 27 28 29 30 32
−4 −2 0 2
> data.frame(age, sex, age.marr, married,
surv.marr)[order(time),]
age sex age.marr married surv.marr
4 25 male NA FALSE 25+
15 32 female 25 TRUE 25
22 29 male 25 TRUE 25
1 44 male 26 TRUE 26
2 43 female 26 TRUE 26
========================================
The first two events occurred in the 25th year where one male and one female got
married. The hazard in 'diag1$y' is 1.43 and -2.92. In the 26th year, there were four
events of two males (beta = -3.16) and two females (beta = 1.19). The duplicate
values of beta result in a warning but this is not serious. Subsequent points are
plotted in the same fashion. A line is drawn to pass through these betas to illustrate
the level of stability of the coefficient over time. The probability of getting married
for females is lower than for males when they are younger than 26 years or older
than 29 years. In between, females have a higher probability of getting married.
However, the test suggests that this finding can be simply explained by chance
alone.
For multiple covariates the same principle applies.
> cox2 <- coxph(surv.marr ~ sex + educ)
> cox2
> summary(cox2)
===================================================
exp(coef) exp(-coef) lower.95 upper.95
sexfemale 0.831 1.20 0.230 2.99
educ>bachelor 0.975 1.03 0.278 3.42
===================================================
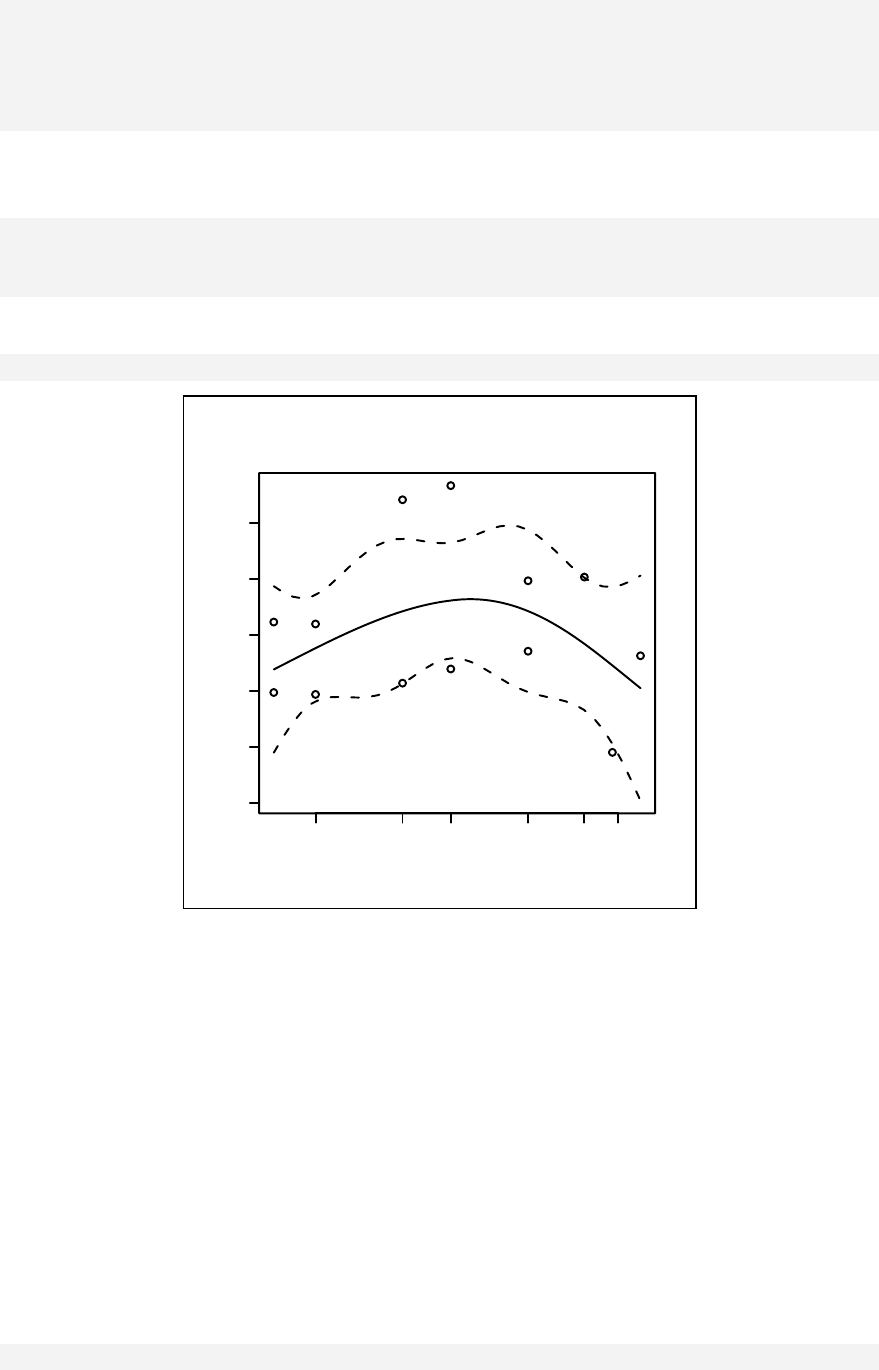
241
> cox.zph(cox2) -> diag2; diag2
rho chisq p
sexfemale 0.0246 0.00885 0.925
educ>bachelor 0.0321 0.01547 0.901
GLOBAL NA 0.01604 0.992
The test results are separated by each variable. Finally, a global test is performed
showing a non-significant result.
> diag2$x # x coordinates for plotting time: same as diag1
> diag2$y # two columns, one for each variable
> plot(cox.zph(cox2), var=1) # for the first variable of y
The coefficients of sex with adjustment for education were not much changed.
> plot(cox.zph(cox2), var=2)
Time
Beta(t) for educ>bachelor
26 27 28 29 30 32
−6 −4 −2 0 2 4
The hazard rate for marriage of persons who had a higher education rises at around
27-29 years. By the late twenties, they have a slightly higher chance of getting
married than those with a lower education. The reverse is true for the remaining
times. Again, these differences are not significant and can be explained by chance
alone.
Stratified Cox regression
The above example had very few subjects, and not surprisingly the results were not
significant. We now revisit the cancer dataset Compaq, which was used as the
exercise at the end of the preceding chapter. The main aim now is to test whether
breast cancer patients in private and public hospitals had different survival rates
after adjusting for stage, socio-economic status and age.
> zap()

242
> data(Compaq)
> use(Compaq)
> des(); summ(); codebook()
> surv.ca <- Surv(year, status)
> cox3 <- coxph(surv.ca ~ hospital + stage + ses + agegr)
> summary(cox3)
Call:
coxph(formula=surv.ca ~ hospital+stage+ses+agegr)
n= 1064
coef exp(coef) se(coef) z p
hospitalPrivate -0.4224 0.655 0.142 -2.971 3.0e-03
stageStage 2 0.7682 2.156 0.123 6.221 5.0e-10
stageStage 3 2.4215 11.263 0.156 15.493 0.0e+00
stageStage 4 1.3723 3.944 0.190 7.213 5.5e-13
sesHigh-middle -0.0944 0.910 0.133 -0.712 4.8e-01
sesPoor-middle 0.0341 1.035 0.178 0.192 8.5e-01
sesPoor -0.4497 0.638 0.144 -3.126 1.8e-03
agegr40-49 0.2574 1.294 0.164 1.569 1.2e-01
agegr50-59 0.4923 1.636 0.164 2.999 2.7e-03
agegr60+ 1.4813 4.399 0.159 9.343 0.0e+00
Patients in private hospitals have two-thirds the risk (hazard) compared to those in
public hospitals after adjustment for stage, socio-economic status and age. To check
whether all three categorical variables deserve to be included in the model, the
command step, meaning stepwise regression, can be used.
> step(cox3)
Start: AIC= 4854.56
surv.ca ~ hospital + stage + ses + agegr
Df AIC
<none> 4854.6
- ses 3 4860.2
- hospital 1 4862.0
- agegr 3 4951.6
- stage 3 5059.9
===== Further output omitted due to redundancy ====
The level of AIC is lowest when none of the variables is removed. Therefore, all
should be kept. Next the proportional hazards assumption is assessed.
> cox.zph(cox3)
rho chisq p
hospitalPrivate hospital 0.03946 0.6568 0.41768
stageStage 2 0.05406 1.1629 0.28086
stageStage 3 -0.09707 3.6786 0.05512
stageStage 4 -0.10222 4.2948 0.03823
sesHigh-middle 0.00968 0.0367 0.84818
sesPoor-middle -0.04391 0.7612 0.38297
sesPoor 0.10409 4.4568 0.03476
agegr40-49 -0.07835 2.3831 0.12266
agegr50-59 -0.09297 3.2339 0.07213
agegr60+ -0.09599 3.5242 0.06048
GLOBAL NA 23.3117 0.00965

243
The highest stage and the lowest socio-economic group contribute the most to the
chi-squared statistic. The global test gives a significant P value suggesting that the
assumption is violated. A possible solution is to do a stratified analysis on one of
the categorical variables, say 'stage'.
> cox4 <- coxph(surv.ca ~ hospital+strata(stage)+ses+agegr)
> cox.zph(cox4)
rho chisq p
hospitalPrivate hospital 0.04407 0.797 0.3720
sesHigh-middle 0.00801 0.025 0.8743
sesPoor-middle -0.04857 0.920 0.3376
sesPoor 0.09747 3.785 0.0517
agegr40-49 -0.07366 2.097 0.1476
agegr50-59 -0.08324 2.565 0.1093
agegr60+ -0.08521 2.761 0.0966
GLOBAL NA 10.297 0.1724
Using 'stage' as a stratification factor reduces all chi-squared values and the
proportional hazards assumption is now not violated.
> summary(cox4)
Call:
coxph(formula = surv.ca ~ hospital + strata(stage) + ses +
agegr)
n= 1064
coef exp(coef) se(coef) z p
hospitalPrivate -0.4049 0.667 0.141 -2.866 0.0042
sesHigh-middle -0.1078 0.898 0.133 -0.811 0.4200
sesPoor-middle 0.0374 1.038 0.179 0.209 0.8300
sesPoor -0.4201 0.657 0.144 -2.926 0.0034
agegr40-49 0.2532 1.288 0.164 1.542 0.1200
agegr50-59 0.4703 1.600 0.165 2.857 0.0043
agegr60+ 1.4514 4.269 0.159 9.141 0.0000
The coefficients of 'cox4' are quite similar to 'cox3'. Note the omission of the
'stage' terms. Stratified Cox regression ignores the coefficients of the stratification
factor. Since our objective is to document the difference between types of hospital,
the coefficients for other variables are not seriously required if the covariates are
well adjusted for.
References
Kleinbaum D, Klein M (2005). Survival Analysis: A Self-Learning Text.
Hosmer Jr D, Lemeshow S (1999). Applied Survival Analysis: Regression
Modeling of Time to Event Data.

244
Exercises________________________________________________
Problem 1.
Could the other 2 variables (socio-economic status and age) be used as a
stratification factor?
Problem 2.
Use the command plot(cox.zph) for 'cox3' and 'cox4' to check the change of
hazard ratio of private hospital over time. Discuss the pattern of residuals.

245
Chapter 23 Analysing Attitudes Data
The 'Attitudes' dataset
Although a study on attitudes is in the field of social sciences, an epidemiologist
should have some idea on the elementary methods of analysis of this kind of data. A
questionnaire on attitudes usually contains questions where the respondents specify
their level of agreement to a statement. These levels are often referred to as a Likert
scale. Traditionally a five-point scale is used; however seven and even nine-point
scales can also be used. Although mostly used in the field of psychometrics, this
kind of rating scale is sometimes used in epidemiological studies such as those
involving quality of life.
Epicalc offers the tableStack function to display the distribution of the score of
several variables that have the same rating scale. It also detects the items that need
to be reversed before the scores of the items are summed or averaged.
The Attitudes dataset comes from a survey on attitudes related to services
among hospital staff. Its details can be sought from the following commands.
> help(Attitudes)
> data(Attitudes)
> use(Attitudes)
> des()
> summ()
To obtain a compact summary of each questionnaire item simply type:
> tableStack(qa1:qa18)
1 2 3 4 5 count mean sd description
qa1 0 0 7 54 75 136 4.5 0.6 I have pride in my job
qa2 0 2 13 60 61 136 4.3 0.7 I'm happy to give service
qa3 30 52 25 20 9 136 2.5 1.2 I feel difficulty in giving service
qa4 0 0 10 90 36 136 4.2 0.6 I can improve my service
qa5 0 3 5 39 89 136 4.6 0.7 A service person must have patience
qa6 17 19 58 29 12 135 3 1.1 I would change my job if given ...
qa7 0 3 7 68 58 136 4.3 0.7 Devoting some personal time will...
qa8 0 5 20 59 52 136 4.2 0.8 Hard work will improve oneself
qa9 0 0 4 41 91 136 4.6 0.5 Smiling leads to trust
qa10 1 1 16 74 44 136 4.2 0.7 I feel bad if I cannot give service

246
qa11 6 20 35 52 23 136 3.5 1.1 A client is not always right
qa12 2 26 45 49 13 135 3.3 0.9 Experienced clients should not ...
qa13 13 54 37 22 10 136 2.7 1.1 A client violating the regulation..
qa14 0 13 45 62 16 136 3.6 0.8 Understanding colleagues will ...
qa15 0 2 18 82 33 135 4.1 0.7 Clients like this place due to ...
qa16 36 53 21 16 8 134 2.3 1.2 Clients who expect our smiling ...
qa17 4 41 32 44 14 135 3.2 1.1 Clients are often self-centred
qa18 2 1 13 87 33 136 4.1 0.7 Clients should be better served
Total score 130 67.1 4.9
Average score 130 3.7 0.3
All the items share the same response scale ranging from 1 to 5 although we can see
from the output that some items have a zero count for scales 1 and 2. The
tableStack function determines the minimum and maximum values of the all
the variables selected. These can easily be changed by modifying the 'minlevel' and
'maxlevel' arguments to the function, which are set to "auto" by default. Four
statistics are computed for each variable: counts, means and standard deviations are
presented by default, while medians are also available but must be set to TRUE if
wanted. Other arguments include 'var.labels', which controls the display of variable
descriptions, and 'total', which controls the appearance of the total and average
scores at the bottom.
The total and average scores are not appropriate if any of the items need to be
reversed. One can guess the items to reverse based on the wording of the question
and to a lesser extent by the reversed distribution compared to the other items. The
items to reverse can be specified with the argument 'vars.to.reverse'. For example, if
items 3, 6 and 16 are considered to be scaled in the reverse direction to the other
items, then these two items should be specified in the 'vars.to.reverse' argument as
follows:
> tableStack(qa1:qa18, vars.to.reverse=c(qa3,qa6,qa16))
Reversed 1 2 3 4 5 count mean sd
qa1 . 0 0 7 54 75 136 4.5 0.6
qa2 . 0 2 13 60 61 136 4.3 0.7
qa3 x 9 20 25 52 30 136 3.5 1.2
qa4 . 0 0 10 90 36 136 4.2 0.6
qa5 . 0 3 5 39 89 136 4.6 0.7
qa6 x 12 29 58 19 17 135 3 1.1
qa7 . 0 3 7 68 58 136 4.3 0.7
qa8 . 0 5 20 59 52 136 4.2 0.8
qa9 . 0 0 4 41 91 136 4.6 0.5
qa10 . 1 1 16 74 44 136 4.2 0.7
qa11 . 6 20 35 52 23 136 3.5 1.1
qa12 . 2 26 45 49 13 135 3.3 0.9
qa13 . 13 54 37 22 10 136 2.7 1.1
qa14 . 0 13 45 62 16 136 3.6 0.8
qa15 . 0 2 18 82 33 135 4.1 0.7
qa16 x 8 16 21 53 36 134 3.7 1.2
qa17 . 4 41 32 44 14 135 3.2 1.1
qa18 . 2 1 13 87 33 136 4.1 0.7
Total score 130 69.6 5.9
Average score 130 3.9 0.3
247
Reversed items are shown with a cross (x) in the column titled "Reversed",
indicating that the scale has been reversed for that item. The statistics for the total
and average scores will likely change due to the reversed direction of scale of those
items. An alternative way to select the items to reverse is to set the 'reverse'
argument to TRUE.
> tableStack(qa1:qa18, reverse=TRUE)
The function will compute the correlation between each score of an item against a
weighted average score of all the remaining ones. Items that are negatively
correlated with this average will be automatically reversed. In the Attitudes
dataset, these are items 3, 6, 12, 13, 16 and 17.
tableStack for logical variables and factors
All questions in the Attitudes dataset are integers, making it possible to obtain the
statistics for each item as well as those for the total score and grand mean. If the
classes of the variables are not numeric, only the frequency counts are shown. Let's
explore the Oswego dataset, which contains data on 75 persons under investigation
for the cause of acute food poisoning after a dinner party.
> data(Oswego)
> use(Oswego)
> des()
No. of observations = 75
Variable Class Description
1 age numeric
2 sex AsIs
3 timesupper numeric
4 ill logical
5 onsetdate AsIs
6 onsettime numeric
7 bakedham logical
8 spinach logical
9 mashedpota logical
10 cabbagesal logical
11 jello logical
12 rolls logical
13 brownbread logical
14 milk logical
15 coffee logical
16 water logical
17 cakes logical
18 vanilla logical
19 chocolate logical
20 fruitsalad logical

248
> tableStack(bakedham:fruitsalad)
No Yes count
bakedham 29 46 75
spinach 32 43 75
mashedpota 37 37 74
cabbagesal 47 28 75
jello 52 23 75
rolls 38 37 75
brownbread 48 27 75
milk 71 4 75
coffee 44 31 75
water 51 24 75
cakes 35 40 75
vanilla 21 54 75
chocolate 27 47 74
fruitsalad 69 6 75
To obtain the percentages, set the 'by' argument to "none".
> tableStack(bakedham:mashedpota, by="none")
Total
bakedham
No 29(38.7)
Yes 46(61.3)
spinach
No 32(42.7)
Yes 43(57.3)
mashedpota
No 37(50)
Yes 37(50)
Alternatively, the prevalence of eaters (Yes) could be displayed by setting the
'prevalence' argument to TRUE.
> tableStack(bakedham:mashedpota, by="none", prevalence=TRUE)
Total
bakedham = Yes
prevalence 46/75(61.3%)
spinach = Yes
prevalence 43/75(57.3%)
mashedpota = Yes
prevalence 37/74(50%)
249
Return to the Attitudes data and change all the variables to factors. This is often
the case when the choices are labelled during data entry.
> data(Attitudes)
> use(Attitudes)
> scales <- list("strongly agree"=1, "agree"=2, "neutral"=3,
"disagree"=4, "strongly disagree"=5)
> for(i in 4:21){
.data[,i] <- factor(.data[,i])
levels(.data[,i]) <- scales
}
The above sequence of commands simply converts the 4th to 21st columns of the
data (items 'qa1' : 'qa21') into factors and assigns the values of each item a label
corresponding to the elements in 'scales'. These are the levels of the items.
> des()
All the items should now be factors. Using the tableStack function with this
new data frame will result in statistics not being shown.
> tableStack(qa1:qa18)
Note that the columns are now labelled. If summary statistics are desired then one
would need to unclass all the variables in the data frame before using the function.
If the data frame contains many variables, this would be quite a laborious task.
Epicalc has a function to unclass all the variables inside a data frame resulting in
the variables being converted to integers, namely unclassDataframe.
> unclassDataframe(qa1:qa18)
> des()
> tableStack(qa1:qa18, reverse=TRUE)
Cronbach's alpha
For this attitude survey data, the next step in the analysis is to calculate the
reliability coefficient, namely Cronbach's alpha, which is a measure of the internal
consistency of the questionnaire survey. An analysis of attitude survey data would
never be accepted by most social science journals unless Cronbach's alpha has been
calculated.
In brief, this coefficient reflects the level of correlation among all items of the same
scale. Sometimes it is called the reliability coefficient since it reflects the
consistency among the items. If the value of this coefficient is too low (say less than
0.7), the scale is considered to have rather low internal consistency, and the total or
mean score calculated from these inconsistent items may not properly reflect the
domain that the questions are trying to measure.

250
The function alpha from Epicalc calculates Cronbach's alpha, and allows the user
to see the effect of removing each item on both the coefficient and the correlation
between each item and the remaining ones.
The arguments for the function are similar to the tableStack function. The first
argument is the vector of variable names (without quotes) or column index of the
variables in the data frame.
> alpha(qa1:qa18, var.labels=FALSE)
Number of items in the scale = 18
Sample size = 136
Average inter-item correlation = 0.1461
Cronbach's alpha: cov/cor computed with
'pairwise.complete.obs'
unstandardized value = 0.708
standardized value = 0.7549
Item(s) reversed and new alpha if the item omitted:
Reversed Alpha Std.Alpha r(item,rest) description
qa1 . 0.685817 0.732773 0.461288 I have pride in my job
qa2 . 0.674703 0.725548 0.556550 I'm happy to give
qa3 x 0.699929 0.749653 0.282889 I feel difficulty in
qa4 . 0.686278 0.730758 0.467432 I can improve my
qa5 . 0.691590 0.739174 0.329396 A service person must
qa6 x 0.682247 0.739252 0.392348 I would change my job
qa7 . 0.674438 0.722168 0.563173 Devoting some personal
qa8 . 0.677646 0.728148 0.484181 Hard work will improve
qa9 . 0.691061 0.736795 0.410533 Smiling leads to trust
qa10 . 0.708569 0.755929 0.153067 I feel bad if I cannot
qa11 . 0.729312 0.764704 0.007361 A client is not always
qa12 x 0.720390 0.765974 0.057229 Experienced clients
qa13 x 0.693353 0.748163 0.303587 A client violating the
qa14 . 0.710688 0.757130 0.128318 Understanding colleagues
qa15 . 0.685665 0.733966 0.415518 Clients like this place
qa16 x 0.692937 0.744674 0.311757 Clients who expect our
qa17 x 0.720186 0.764488 0.088212 Clients are often self…
qa18 . 0.695617 0.744489 0.296922 Clients should be...
The function first computes the covariance matrix among all selected variables.
This matrix is then used to compute the average of the inter-item correlation.
Secondly, the unstandardized and standardized alpha coefficients are computed
based on a formula, which can be found in most textbooks. The unstandardized
value is suitable when all items share the same value coding, such as the
Attitudes dataset where all items have a scale of 1 to 5. The standardized alpha
is appropriate when the variables are coded on a different scale, which is less
commonly found in a study on attitudes.

251
Finally, a table is shown, with items that have been automatically reversed marked
with an 'x', similar to the tableStack command with no 'by' argument given.
The columns 'alpha' and 'Std. alpha' are the unstandardized and standardized alpha
coefficients, respectively, obtained when each variable is omitted from the
computation.
The function also has a 'reverse' argument, the default value being TRUE. If set to
FALSE, then the scale of all items are assumed to be measured in the same
direction. In this dataset that would result in lower alpha values and most likely to
incorrect conclusions.
From the previous output, the unstandardized coefficient is 0.71 and the candidate
items that could be removed to improve (increase) the alpha coefficients are items
10, 11, 12, 14 and 17.
Further analysis could be pursued by successive omission of items. A successful
selection of items would be to have a questionnaire with not too many items yet
with an acceptably high alpha coefficient. Consider removing item 11, since it
results in the highest alpha coefficient if it is removed and also has the lowest
correlation with all other items.
> alpha(c(qa1:qa10, qa12:qa18))
Both the unstandardized and standardized alpha coefficients have increased. As
indicated by the third section of the results, the alpha coefficients can be further
increased by removing item 12.
> alpha(c(qa1:qa10, qa13:qa18))
and then item 17.
> alpha(c(qa1:qa10, qa13:qa16, qa18))
and then item 14.
> alpha(c(qa1:qa10, qa13, qa15:qa16, qa18))
and then item 10.
> alpha(c(qa1:qa9, qa13, qa15:qa16, qa18))
Further removal of items does not result in any improvement to the alpha
coefficients. Altogether, 5 items were removed from the original 18 items to arrive
at the best model. This somewhat tedious task can be automated by using another
Epicalc function called alphaBest.
252
> alphaBest(qa1:qa18)
$best.alpha
[1] 0.7620925
$removed
qa11 qa12 qa17 qa14 qa10
14 15 20 17 13
$remaining
qa1 qa2 qa3 qa4 qa5 qa6 qa7 qa8 qa9 qa13 qa15 qa16 qa18
4 5 6 7 8 9 10 11 12 16 18 19 21
The best Cronbach's alpha is achieved with the index of the items removed and the
ones remaining listed. The values of these two vectors are the index of the variables
in the data frame. For example, we first removed 'qa11', which is the 14th variable,
then 'qa12', which is the 15th, 'qa17', which is the 20th, and so on. Similarly, the
remaining variables are 'qa1', which the 4th variable, 'qa2', which is the 5th, 'qa3',
which is the 6th, etc.
By default, the function selects the best model based on the unstandardized alpha
coefficient. If best selection is to be based on the standardized alpha, then
'standardized' should be set to TRUE.
> alphaBest(qa1:qa18, standardized=TRUE)
The results are exactly the same in this case since all items have the same scale.
Saving the removed and the remaining items as an index has a very important
advantage as shown next. The vector of 'remaining' items can be saved and further
used in the tableStack command described previously.
> alphaBest(qa1:qa18)$remaining -> wanted
The tableStack function accepts an integer vector for the 'vars' argument. To
get the best final set of items, with necessary reversing, the next step is to use the
tableStack command on the wanted items saving the results to an R object.
> tableStack(vars=wanted, reverse=TRUE, var.labels=FALSE) -> b
Note that now the mean score has increased from 3.7 to 4.0 using the original
(perhaps naïve) method of keeping all items and without investigating the need to
reverse items. The saved object 'b' contains the mean and total scores, which can be
saved back to the default data frame for further hypothesis testing.
> mean.score <- b$mean.score
> total.score <- b$total.score
> pack()
> des()
> t.test(mean.score ~ sex) # p-value = 0.7348

253
An alternative way of displaying results from hypothesis testing for difference
between two genders in the items and mean score would be:
> tableStack(vars=c(wanted, mean.score), by=sex, var.=FALSE)
The function determines the appropriate statistical test to use for all variables. If the
distribution is not normal, then the Wilcoxon rank sum test is used instead of the t-
test. Details of the tableStack command using the 'by' argument are described
in Chapter 27 – "Table Stacking for a Manuscript".
Summary
In summary, when you have a dataset on attitudes, it is a good idea to explore the
variables with tableStack, initially without any of the items reversed. Have a
careful look at the comparative distribution of the items and read each question (or
variable description) to get an idea of the direction, either positive or negative, of
the item's scale. The items that should be reversed are usually the ones with the
distribution contrary to the remaining majority. If the variables are factors, use
unclassDataframe to convert them to integers. There is actually no need to
save the total or mean scores at this stage. Check Cronbach's alpha using the
functions alpha and subsequently alphaBest to get the best subsets of items
that maximize alpha. Save the results to an object and put the 'remaining' items as
the 'vars' argument to the final tableStack command with 'reverse=TRUE'. The
total and average scores of the best selected model with items correctly reversed
can be saved and ready for further analysis.
References
Cronbach, L. J. 1951. Coefficient alpha and internal structure of tests.
Psychometrika, 16: 297–334.

254
Exercise_________________________________________________
Download and install the psy library from the CRAN website. Load this library and
examine the expsy dataset.
> library(psy)
> data(expsy)
> des(expsy)
> head(expsy)
Determine which of the items (it1 to it10) need to be reversed. Find the best subset
of the items using Cronbach's alpha coefficient.
255
Chapter 24: Sample size calculation
Sample size calculation is very important for an epidemiological study. For most
surveys, the population size is large, consequently the costs involved in collecting
data from all subjects would be high. In clinical studies, recruiting too many
subjects into the study not only causes management and financial problems but also
raises ethical concerns. If a conclusion can be drawn from a small sample size,
recruiting more subjects than necessary may pose an unnecessary risk to the group
of subjects whose treatment is known to be inferior. On the other hand, a survey
with a sample size that is too small will not be able to detect a statistically
significant effect if there truly is one.
Functions to calculate sample size
Experimenting with functions to calculate sample sizes will enable new R users to
understand the principles of arguments more quickly and meaningfully.
Epicalc comes with four functions for sample size calculation. The first one is for a
prevalence survey. The second is for comparison of two proportions, which can be
for a case-control study, cross-sectional study, cohort study or randomised
controlled trial. The third function is used for the comparison of two means. The
last one is for lot quality assurance sampling.
In addition to these sample size calculations, there are two functions for computing
the power of a comparative study, one for comparing two means, and the other for
comparing two proportions.
Field survey
The aim of a field survey is usually to document the prevalence in the population on
a certain condition, such as helminthic infection, or coverage of a health service,
such as an immunization programme. The sample size required depends on the
estimated prevalence and the level of errors of prevalence that the researcher can
accept. For many circumstances, cluster sampling is employed. The advantage of
this sampling method is that it reduces the time and budget for travelling to collect
data.

256
For example, simple random sampling may require 96 persons from 96 different
villages to be surveyed. This can place a heavy burden on the travelling resources.
Instead, the number of villages can be reduced to, say, 30 and the sample size
compensated by sampling more subjects from each selected village. The slight
increase in sample size is more than offset by the large reduction in travelling costs.
The cluster sampling technique, however, encounters another problem. People in
the same villages often tend to be more similar to each other than from people from
other villages in terms of disease risk and coverage of service etc. In other words,
subjects selected from the same cluster are usually not 'independent'. Therefore the
sample size estimated from a simple random sampling technique must be inflated to
cover this 'alikeness among the same cluster' (or 'design effect') problem.
The function n.for.survey in Epicalc is used for the calculation of the sample
size for a survey. To have a look at the arguments of this function type:
> args(n.for.survey)
function(p, delta = 0.5 * min(c(p, 1 - p)), popsize = FALSE,
deff = 1, alpha = 0.05)
The arguments to this function are as follows:
p: The estimated prevalence as a proportion between 0 and 1.
delta: The difference between the estimated prevalence and the margin of the
confidence interval. For example, if p is estimated to be 30% but we still accept that
the maximum error can result in 50% prevalence, then delta is 0.5 - 0.3 = 0.2. If
delta is not given, the default value is set to be a half of either p or 1-p, whichever is
the smaller. In general, delta has more influence on the sample size than p. When p
is small, delta should be smaller than p. Otherwise, the lower limit of the
confidence interval will be negative or the upper limit will be higher than 100%,
both of which are invalid. The default value is therefore quite acceptable for a rather
low prevalence (say, below 15%) or a rather high prevalence (say, above 80%). If
the prevalence is in between these values, then half of p (or 1-p) would be too
imprecise. The user should then give a smaller delta.
popsize: Finite population size. This is the population size in which the survey is to
be conducted. A small population size will require a relatively smaller sample size.
If the value is FALSE, it will be ignored and assumed that the population is very
large. Usually when the size exceeds a certain value, say 5000, any further increase
in the population would have a rather little effect on the sample size.
deff: The design effect, which is the adjustment factor for cluster sampling as
explained above. By definition, for simple random sampling, deff is 1. In cluster
sampling with a large cluster size and the level of similarity among subjects in the
same cluster is high, deff can be large, and so would the required sample size.

257
alpha: Probability of a Type I error. In standard situations, alpha is set at 0.05 and
the confidence interval of p + delta is the 95% confidence limit of the prevalence.
With higher accuracy demands, for example, a 99% confidence limit, the required
sample size will be increased.
If a survey is to be conducted with a small (less than 15%) prevalence, in a large
population, all the default values of the arguments can be accepted. The command
then becomes:
> n.for.survey(p=.05)
Sample size for survey.
Assumptions:
Proportion = 0.05
Confidence limit = 95 %
Delta = 0.025 from the estimate.
Sample size = 292
The function sets the 'alpha' value at 0.05, since it was omitted. Thus the confidence
limit is 95%. The argument 'delta' is automatically set to half of 5% or 0.025. The
design effect, 'deff', is not given and so set at 1. The population size is assumed to
be very large and is thus not used in the calculation of the sample size.
In conclusion, the function suggests that if a 95% confidence limit of 5% + 2.5%
(from 2.5% to 7.5%) is desired for an estimated proportion of 0.05 in a large
population, then the sample size required is 292.
If the prevalence is low, 'deff' for cluster sampling is usually close to unity. The
sample size calculated is still relatively applicable even if cluster sampling is
employed because of the small prevalence.
If the estimated prevalence is close to 50%, a delta of 25% is too large. It would be
better to reduce this to +5% or +10% of the prevalence. If cluster sampling is
employed under such a condition, the value of 'deff' is usually greater than one.
For example, in standard 30-cluster sampling for assessment of immunization
coverage where the prevalence is estimated to be near 80%, 'deff' should be around
2. The population size in this case is usually large and a 99% confidence limit is
required instead of 95%. In this case, the suggested calculation would be:

258
> n.for.survey(p =.8, delta =.1, deff=2, alpha=.01)
Sample size for survey.
Assumptions:
Proportion = 0.8
Confidence limit = 99 %
Delta = 0.1 from the estimate.
Design effect = 2
Sample size = 212
With this total sample size of 212 and 30 clusters, the average size per cluster
would be 212/30 = 7 subjects. This sample size could be used for a standard survey
to assess immunization coverage in developing countries.
Comparison of two proportions
In epidemiological studies, comparison of two proportions is quite common.
As the name indicates the function 'n.for.2p' is written for this purpose. As before,
the necessary arguments to this function can be examined as follows:
> args(n.for.2p)
function(p1, p2, alpha = 0.05, power = 0.8, ratio=1)
In a case-control study, the proportion (p1) of subjects exposed to a risk factor
among the cases (diseased group) is compared against the proportion (p2) of
subjects exposed among the controls (non-diseased group).
In a cohort study, the probability (p1) of getting a disease among the exposed group
is compared to the probability (p2) among the non-exposed group.
In a randomised controlled trial, the probability (p1) of getting cured (or improving)
among subjects given a new treatment is compared with the probability (p2) of
getting cured (or improving) among subjects given the old treatment.
The argument alpha is the probability of committing a Type I error. If the two
groups actually have the same proportion at the population level (the null
hypothesis is true), with the sample size from this calculation, there will be a chance
of 'alpha' that the null hypothesis will be rejected. In other words, the difference in
the two samples would be erroneously decided as statistically significant. As
before, it is common practice to set the alpha value at 0.05.
The power of a study is the probability of rejecting the null hypothesis when it is
false. In this situation it is the probability of detecting a statistically significant
difference of proportions in the population, which is in fact as large as that in the
sample. It is quite acceptable to have the power level set at 80%. The type II error is
simply 1-power, and is the probability of not rejecting the null hypothesis when it is
false. Scientists usually allow a larger probability for a type II error than for a type I
error. Rejecting a new treatment that is actually better than the old one may
259
probably be considered less serious than replacing the old treatment with a new one
which is in fact not better.
The 'ratio' refers to the ratio of the number of subjects in sample 1 to the number of
subjects in sample 2. For these three types of studies, the most efficient sample size
(smallest size of total sample that can test the hypothesis) is achieved when the ratio
between the two stratified groups is 1:1. For example, if the collection of data per
subject is fixed, comparing two groups of treatment each of 50 subjects is much
better than comparing 5 subjects in one group against 95 subjects in the other. In
certain conditions, such as when a very rare disease is under investigation, it might
be quicker to finish the study with more than one control per case. In addition, in a
cross-sectional study, the status of a subject on exposure and outcome is not known
from the beginning; the sample is non-contrived. The ratio cannot be set at 1:1 but
will totally depend on the setting. Under these conditions where the ratios are not
1:1, the value of the ratio must be specified in the calculation.
For example, if a risk was determined to be as common as 50% among the diseased
group and 20% among the control group, the minimum sample size required to
detect this difference for a case control study can be calculated by:
> n.for.2p(p1=0.5, p2=0.2)
Estimation of sample size for testing Ho: p1==p2
Assumptions:
alpha = 0.05
power = 0.8
p1 = 0.5
p2 = 0.2
n2/n1 = 1
Estimated required sample size:
n1 = 45
n2 = 45
n1 + n2 = 90
The use of this function is not complicated, as only p1 and p2 are needed to be
input. The other arguments will be set to the default values automatically. In
conclusion, only 45 cases and 45 controls are needed to test the hypothesis of no
association. If the disease is rare, say only 10 cases per year, and the researcher
wanted to complete the study early, he/she may increase the case:control ratio to 1:4
260
> n.for.2p(p1=0.5, p2=0.2, ratio=4)
Estimation of sample size for testing Ho: p1==p2
Assumptions:
alpha = 0.05
power = 0.8
p1 = 0.5
p2 = 0.2
n2/n1 = 4
Estimated required sample size:
n1 = 27
n2 = 108
n1 + n2 = 135
Note that the ratio is n2/n1. This study can be finished in less than 3 years instead of
originally 4.5 years. Increasing the ratio above this has only a small effect on
reduction of number of cases but a remarkably high effect on increasing the number
of controls. For example, a ratio of 1 case per 9 controls will reduce the required
sample size to 23 cases (4 cases reduced) but increase the number of controls
required to 207 (an increase of nearly 100).
An increase in power from 0.8 to 0.9 also increases the requirement for the sample
size considerably. Fixing the ratio at 1:1
> n.for.2p(p1=0.5, p2=0.2, power=0.9)
The output is omitted, however 58 cases and 58 controls are required (an increase
of 29% of the sample size required on both arms).
Relationship between p1, p2 and odds ratio in a case control study
To be consistent with the above agreement, the odds ratio would be the ratio of the
two odds of exposure: p1/(1-p1) / {p2/(1-p2)}.
> .5/(1-.5)/(.2/(1-.2))
[1] 4
Setting up p1 and p2 for calculation of sample size for a case control study is
straightforward. However, in some instances, there may be a demand to compute
the sample size based on proportion of exposed in the general population (which is
equal to the proportion among the controls due to the rarity of the disease) and the
odds ratio. In other words, p2 and odds ratio are given. It remains necessary then to
find p1.
For example, if the proportion of exposures among the population (p2) is equal to
30%, and the odds ratio is 2, the proportion of exposures among the cases (p1) and
the required sample size can be calculated as follows:
261
> p2 <- 0.3
> or <- 2
> odds2 <- p2/(1-p2)
> odds1 <- or*odds2
> p1 <- odds1/(1+odds1); p1
[1] 0.4615385
> n.for.2p(p1,p2)
Estimation of sample size for testing Ho: p1==p2
Assumptions:
alpha = 0.05
power = 0.8
p1 = 0.4615385
p2 = 0.3
n2/n1 = 1
Estimated required sample size:
n1 = 153
n2 = 153
n1 + n2 = 306
The required sample size is larger than in the preceding example because the odds
ratio to be detected is closer to unity. In other words, the level of difference to be
detected is smaller.
Cohort study and randomised controlled trial
Given that p1 and p2 are the respective success rates among the two treatment or
exposure groups, the calculation is fairly straightforward.
In fact, whether the calculation is based on the success rate or the failure rate, the
answer is the same. For example, if treatment A gives a success rate of 90% and
treatment B gives a success rate of 80%, we may also say that treatment A and B
have failure rates of 10% and 20% respectively. The calculation of sample sizes in
both cases would yield the same result.
> n.for.2p(p1=0.9, p2=0.8)
===== details omitted =========
n1 = 219
n2 = 219
n1 + n2 = 438
> n.for.2p(p1=.1, p2=.2)
===== details omitted =========
n1 = 219
n2 = 219
n1 + n2 = 438

262
Cross-sectional study: testing a hypothesis
A cross-sectional survey serves two purposes, firstly to document the prevalence of
a condition (either a disease or an exposure condition or both), secondly to test the
association between the exposure and the outcome. This sample size for hypothesis
testing is different from that for the descriptive purpose (which has been fully
discussed above).
Calculation of the sample size for the second component (hypothesis testing) of the
cross-sectional study should be based on the n.for.2p function. Similar to the
cohort study and the randomised controlled trial, the proportions, p1 and p2, should
be orientated toward the outcome in each exposure group where p1 is equal to the
proportion of positive outcomes among the exposed group, and p2 is equal to the
proportion of positive outcomes among the non-exposed group.
On the other hand, the value of the 'ratio' is the ratio between the exposed and non-
exposed groups, which must be estimated from the prevalence of the exposure.
For example, in a survey, the prevalence of exposure might be estimated to be 20%,
the probabilities of getting a disease are 20% and 5% among the exposed and the
non-exposed population.
With the prevalence of exposure being 20% the ratio n2:n1 would be 0.8/0.2 = 4.
> n.for.2p(p1=0.2, p2=0.05, ratio=4)
Estimation of sample size for testing Ho: p1==p2
Assumptions:
alpha = 0.05
power = 0.8
p1 = 0.2
p2 = 0.05
n2/n1 = 4
Estimated required sample size:
n1 = 48
n2 = 192
n1 + n2 = 240
The total sample size for this cross-sectional survey to test the hypothesis is 240
subjects. This will include 48 exposed and 192 non-exposed persons.
This required sample size should be checked for adequacy of the other objective,
i.e. to describe the prevalence of exposure, which is estimated to be 20%.
263
> n.for.survey(p=0.2)
Sample size for survey.
Assumptions:
Proportion = 0.2
Confidence limit = 95 %
Delta = 0.1 from the estimate.
Sample size = 61
The required sample size of the descriptive study is smaller than that for hypothesis
testing. Thus, the latter (of 240 subjects) should be adopted.
Comparison of two means
In epidemiology, comparison of two means is not as common as that of two
proportions. This is mainly because a clinical or public health decision is mainly
based on a hard-evidenced dichotomous outcome and less on the level of difference
of the mean values. However, there are also a lot of important health outcomes that
are measured on a continuous scale, the difference of means of which can be of
important social concern. Examples of continuous outcomes include intelligence
quotient, pain scores and quality of life.
Two sample means usually have two different standard deviations. Thus the
function for this calculation requires a few more arguments.
> args(n.for.2means)
function(mu1, mu2, sd1, sd2, ratio=1, alpha=0.05, power=0.8)
Intuitively, the notation is straightforward. There are four compulsory arguments
that a user must supply to the function, namely the two means and their
corresponding standard deviations.
Note: ______________________________________________________________________
Readers may be aware now that function arguments that include an equals sign followed by a
value are optional. The value to the right of the sign is the default value used by the function
when the argument is omitted. Arguments that do not include an equals sign are, however,
compulsory. If omitted, an error is generated.
As an example, suppose a new therapeutic agent is expected to reduce the mean
pain score from 0.8 to 0.6 in a group of subjects and the expected corresponding
standard deviations are 0.2 and 0.25. To calculate the required sample size, type the
following command:

264
> n.for.2means(mu1=0.8, mu2=0.6, sd1=0.2, sd2=0.25)
Estimation of sample size for testing Ho: mu1==mu2
Assumptions:
alpha = 0.05
power = 0.8
mu1 = 0.8
mu2 = 0.6
sd1 = 0.2
sd2 = 0.25
Estimated required sample size:
n1 = 21
n2 = 21
n1 + n2 = 42
This anaesthesiological experiment would require 21 subjects in each group.
In fact, the mathematical formula for the calculation of the sample size does not
require the exact values of mu1 and mu2. If the difference in means and the
standard deviations are fixed, changing the two means will have no effect on the
calculated sample size. Thus the same results are obtained from the following
command (output omitted).
> n.for.2means(mu1=0.4, mu2=0.2, sd1=0.2, sd2=0.25)
Lot quality assurance sampling
Lot quality assurance sampling (LQAS) was initially applied to manufacturing
processes. A company takes a sample in order to check whether the lot of product is
ready to be shipped. If the percentage of defectives is estimated to be higher than a
certain level, the lot is rejected. Otherwise, the whole lot is shipped to the market.
The difference between LQAS and other sampling methods is that LQAS does not
estimate the exact percentage of defectives. It only checks whether the acceptable
level is exceeded. The required sample size for this process is smaller than that for
estimation of a prevalence or proportion. Thus, the costs of checking can be
decreased very considerably if the quality analysis of individual components is
high.
Health systems adopt LQAS mainly for surveillance of proportion of problems. For
example, in the process of quality assurance of anti-TB drugs in southern Thailand,
content assays and dissolution tests of the drug are rather expensive. The LQAS
method was employed to calculate the minimal sample size that is still sufficient to
test whether the quality is acceptable.

265
Suppose a highest acceptable proportion of defective specimens is set at 1 percent.
If the study suggests that the actual proportion is at this level or less, then the lot is
accepted. Otherwise, the whole lot will be rejected. The actual proportion (whether
it be higher or lower than this acceptable level) is not important. If the sample size
is too small, say 20, then even if all randomly selected specimens were accepted, it
would still not be certain that less than 1% of the whole lot was defective. If the
sample size is too big, say 1000, then even if the percent defective is within the
reasonable level, you have wasted all those specimens that were tested. This large
sample size is excessive.
With an optimal sample size, should any of the randomly selected specimens be
defective, the acceptable proportion of the whole lot would be expected to be
exceeded. One of the easiest ways to understand this is to look at the computation
results.
> n.for.lqas(p=0.01)
Lot quality assurance sampling
Method = Normal approximation
Population size = 10000
Maximum defective sample accepted = 0
Probability of defect accepted = 0.01
Alpha = 0.05
Sample size required = 262
From this computation, the threshold for the defective proportion (p) is set at 1%.
The final sample size is 262. The lot size is assumed to be 10,000 by default. The
maximum defective sample accepted is 0 (again the default). This means that if any
of the 262 specimens is defective, the proportion of 1% is considered to be
exceeded and the lot is rejected. With this sample size, the researcher would take a
random sample of 262 specimens and examine each one. If all of the specimens
pass the tests, the remaining lot of 10,000-262 = 9,738 specimens can be marketed.
Otherwise, all 10,000 will be rejected.
There are a few parameters controlling the sample size here. Alpha (the type I error
rate) is usually set at 5%. This means that if the null hypothesis (the defective
percentage is less than 1%) is true, there is a 5% chance that there would be at least
one defective specimen among the whole sample of 262. If alpha is set to a stricter
criterion, say 2.5%, the sample size will increase.
The threshold proportion for a sample being accepted varies inversely with the
sample size. If the threshold is increased, say to 3%, the required sample size would
be reduced (only 87 would be needed).

266
The maximum defective sample accepted is set at 0 by default in order to minimize
the sample size. In theory, this can be any number. However, the larger the number
is, the larger the required sample size.
Power determination for comparison of two proportions
Sometimes a reader may come across a study that reports no significant difference
between two groups. One may doubt whether the study had enough power to detect
the significant difference if a clinically significant difference existed at the
population level. Consider a trial with 105 subjects on one treatment arm consisting
of 35 failures versus 50 subjects on a placebo with 20 failures. To set up this
hypothetical data table, you may type the following commands:
> table1 <- c(35,70,20,30)
> dim(table1) <- c(2,2)
> table1 <- as.table(table1)
> cc(cctable=table1)
A B Total
A 35 20 55
B 70 30 100
Total 105 50 155
OR = 0.751
95% CI = 0.354 1.606
Chi-squared = 0.658 , 1 d.f. , P value = 0.417
Fisher's exact test (2-sided) P value = 0.474
The odds ratio of 0.75 has a rather wide confidence interval. It might be of interest
to know the power of the sample size for this particular study if the true odds ratio
is in fact 0.5 and the failure rate among the placebo group is the same.
> odds.placebo <- 20/30
> odds.treat <- .5 * odds.placebo
> p.placebo <- 20/50
> p.treat <- odds.treat/(1+odds.treat)
> power.for.2p(p1=p.treat, p2=p.placebo, n1=105, n2=50)
alpha = 0.05
p1 = 0.25
p2 = 0.4
n1 = 105
n2 = 50
power = 0.4082
The sample size used in this study only had a 40% chance of finding a significant
difference given that the treatment had an odds ratio of 0.5. The study was therefore
inconclusive.
Note that the power depends on the size of difference to be detected. To obtain
statistical significance for a large difference would require a smaller sample size
than that for detecting a small difference if the power was kept the same.
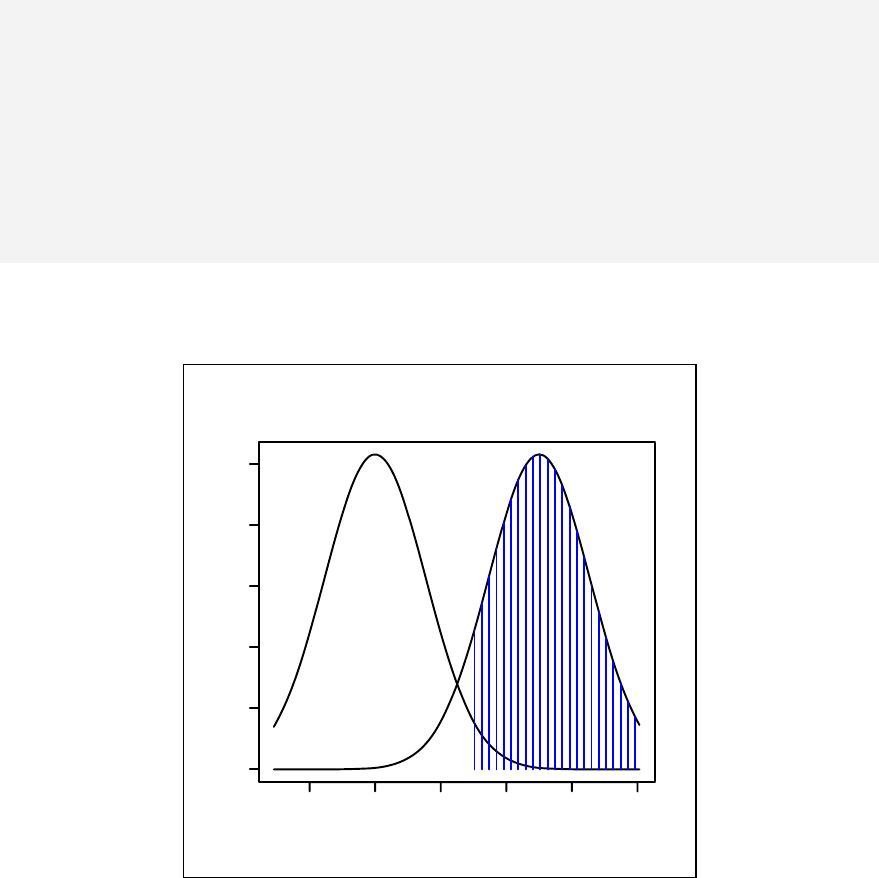
267
Power for comparison of two means
Suppose a study reports that in a randomised controlled trial a micro-nutrient is
given to 100 pupils and a placebo to another randomly selected 100. By the end of
the year, the mean ± standard deviation of the IQ scores in the two respective
groups is 98 ± 10.1 and 95 ± 11.7.
What is the power to determine an improvement of 5 units (new IQ = 100) if the
parameters in the placebo groups and the standard deviation of the treatment group
are not changed?
Let group 1 represent the pupils on the placebo and group 2 be the pupils receiving
the new treatment. The command to calculate the power is:
> power.for.2means(mu1=95, mu2=100, sd1=11.7, sd2=10.1,
n1=100, n2=100)
alpha = 0.05
mu1 = 95
mu2 = 100
n1 = 100
n2 = 100
sd1 = 11.7
sd2 = 10.1
power = 0.8988
With this relatively large sample size, the power to detect a difference of 5 points of
IQ under these assumptions is approximately 90%.
−202468
0.00 0.05 0.10 0.15 0.20 0.25
Power = 0.8988
mu2−mu1
mu1 = 95, mu2 = 100
sd1 = 11.7, sd2 = 10.1
n1 = 100, n2 = 100
Ho: mu2−mu1=0
Ha: mu2 − mu1 = 5

268
Exercises________________________________________________
Problem 1.
Calculate the maximum sample size required to estimate the prevalence of
respiratory tract infection, with a precision of 5%, in a target population consisting
of children aged 1-5 years in a particular region of a developing country.
Problem 2.
A case-control study is carried out to determine the efficacy of a vaccine for the
prevention of childhood tuberulosis with a placebo. Assume that 50% of the
controls are not vaccinated. If the number of cases and controls are equal, what
sample size is needed to detect, with 80% power and 5% type I error, an odds ratio
of at least 2 in the target population?
Problem 3.
A randomised trial is to be conducted comparing two new treatments aimed at
increasing the weights of malnourished children with a control group. The minimal
worthwhile benefit is an increase in mean weight of 2.5kg, and the standard
deviations of weight changes are beleived to be 3.5kg.
What are the required sample sizes, assuming that the control group is twice as
large as each of the two treatment groups and an 80% power is required for each
comparison?
269
Chapter 25: Documentation
Data can be analysed interactively as shown in the previous chapters or in a batch
mode as shown in this chapter.
Starting with interactive analysis
In the interactive mode, the analyst types commands directly into the console and, if
there are no errors, obtains the output specific to that command. This is very useful
when he/she starts to learn the software for the first time. Typing and reading
commands from the console is the most natural learning process. This learning
phase of typing commands one at a time often results in several mistakes, either
syntactically or otherwise. The most common type of mistake is syntax error or
violation of the rules imposed by the software. Examples include unbalanced
brackets, unbalanced quotes and omission of delimiters (such as commas). These
mistakes however are easy to correct. The user can simply press the up arrow key to
retrieve the previous command and make the appropriate corrections.
At the initial phase of the analysis, the analyst needs to get acquainted with the
dataset and the variables. This phase is often called 'Exploratory data analysis',
which is mainly carried out interactively. Under Epicalc, this can be done with the
following steps:
Starting with clearing the memory zap().
Loading the necessary libraries for a particular purpose of the analysis, such as
'library(survival)' for analyzing survival data, 'library(nlme)' and
'library(MASS)' for multi-level modelling.
Reading in data files
If the dataset is in EpiInfo format (file extension = '.rec'), Stata (".dta"), SPSS
(".sav"), or comma separated values (".csv") then it would be convenient to read in
the data file with the command use("myFile") from the Epicalc library.
270
If the data is in another format, check whether the first line is a header (variable
names) and check the type of the variable separator. The appropriate command to
read in the dataset is 'read.table' from the R base library.
For other data file formats, type help.start() . Choose 'packages' and then
'foreign'.
Explore the class and description of variables using des().
Quickly explore summary statistics of the variables using summ().
Explore each variable one at a time using the command summ(varname). Pay
attention to the minimum, maximum and look at the graph to see a detailed
distribution.
Explore categorical variables using codebook() and tab1(varname).
Save the commands that have been typed using 'savehistory("filename")'. The saved
file should have a ".r" or ".rhistory" extension. This file stores all the commands
that have been typed in. These commands will be used for further analysis.
Note that 'varname' and 'filename' in the above list should be replaced with the
appropriate variable name and file name. Commands typed in during the interactive
modes often contain mistakes. Since these commands will be reused in the future,
they should be 'cleaned up' using an appropriate text editor. The next step is to open
the saved file with a text editor. Crimson Editor and Tinn-R are recommended for
this purpose.
Crimson Editor
There are many good text editors available for editing a command file. A good one
should be able to show line numbers and matching brackets. The Notepad program
that comes with Windows does not have these features and is thus not suitable for
working with a long command file. The current recommended programs are
Crimson Editor and Tinn-R, which are both public domain software. Instructions
for installation are given in Chapter 1.
Use Windows Explorer to create a new text file. By default, Windows will offer to
name the file, say 'New Text Document.txt'. Do not accept this name. Instead
choose a name appropriate to the purpose of the file, such as 'Chapter1' or 'HIV' and
make sure you include the '.R' or '.r' extension. Double click this new file. If your
computer's file associations have been successfully set up, your computer should
open it with either Crimson Editor or Tinn-R. If not, right click and choose 'Open
with' then choose Crimson Editor (cedt.exe) or Tinn-R (Tinn-R.exe).

271
The following section is specific for Crimson Editor only. You may use this newly
created file to customise Crimson Editor menus and file preferences.
Choose 'View', 'Tool bars/Views'. Check 'Tool bar', 'MDI file tabs' and 'Status bar'.
If you want to know what work they do, just uncheck them one by one.
Note that Crimson Editor can have multiple files opened simultaneously. Any file
that has been changed but not yet saved will have a red dot in its MDI File tab. This
turns green once the file has been saved.
From the menu bar select 'Document', 'Syntax types'. See if R is in the list of known
file types. If not, select 'Customize...' at the very bottom of the list. The 'Preference'
dialog box will appear with 'Syntax Type' highlighted under the 'File' option. In the
list of Syntax Types, scroll down until you see the first '-Empty-' position and select
it with the mouse. Position the cursor in the 'Description' text box and type R. Next
to 'Lang Spec', type 'R.spc', and for 'Keywords' type 'R.key'. Finally Click 'OK'.
Language specification and key words for the R program will be available for any
file opened with Crimson Editor. But the R command file is still not automatically
associated with Crimson Editor yet. The user needs to activate this by clicking
'Document', 'Syntax types' and selecting 'R' from the list.
Finally, for the line number, Click 'Tool's from the menu bar, then 'Preferences...'.
In the Preferences box, highlight 'Visual'. Check 'Show line numbers', 'Highlight
active line' and 'Highlight matching pairs'.
Tinn-R
The advantage of using Tinn-R over Crimson Editor is it's ability to interface or
interact with R itself. Users can type the commands into the Tinn-R editor and send
them to the R console line by line, in blocks of lines, or even the whole command
file. Tinn-R has many other nice features similar to Crimson Editor that make
working with R easier and more convenient.
Viewing line numbers is strongly recommended. This can be set under the View
menu. Those who like to use the function keys instead of the mouse can set the
'hotkeys' of R, under the R menu. The authors preference is to set F2 for sending a
single line, F4 for sending the selected block, F5 for sending the current whole
command file without prior saving and F6 for saving the file and sending as
'source'. The function key F3 is preserved for Searching (and find again).
Editing a command file
A command file can be very simple or very complicated, depending on the nature
of the work. For a command file with only a few simple steps, the level of
complication is not high. Editing is not too difficult. The editing tasks include the
following steps:

272
Open the saved history file using either Crimson Editor or Tinn-R. Correct any lines
that have incorrect syntax. The last line 'savehistory("filename.r")' should be
removed because it is not needed in the batch mode.
Correct the typing mistakes by deleting lines of erroneous commands.
Remove any duplicate commands.
Check the structure of the commands. Make sure it includes proper order of key
commands as suggested above (with zap, use, etc) .
If you use Crimson Editor, you may copy blocks of commands and paste them into
the R console. If you use Tinn-R, you can simply highlight the commands that you
want to send to R and using the mouse, click on the “send” icon (or press the hot-
key) to perform the operation. Copying and pasting has the advantage of seeing
different colours of commands (red) and output (blue) on the R console. However,
any mistake or error in the middle of a large block of commands may escape notice.
If the block of commands contains an error, then saving and sending commands as
source will stop at the line containing the first error. For example,
Error in parse(file, n = -1, NULL, "?") : syntax error at
3: library(nlme
4: use("Orthodont.dta")
The report on syntax errors usually includes the line numbers of the (first) error. In
the above example, the error occurs at line 3 (missing closing bracket). Return to
the command file and make the appropriate correction, followed by saving the file.
Even when all syntax errors have been removed, there may remain other types of
command errors, such as typing mistakes in commands, objects not found or files
not being able to be opened. In these situations, the console will show the results in
the console up to the error line. However the line number will not be given. Switch
back to the command file and correct the error then return to the R console and re-
run the command 'source("filename.r", echo=TRUE)'.
The lines that need to be skipped by R, such as author's comments or commands
that the analyst want to skip for the time being can begin with '#'. It is highly
recommended that comments be included throughout the command file to enable
other readers to follow easily.
273
The amount of commands typed into the command file should be optimal. It is a
good practice to have the newly added command lines containing one set of related
actions. For example, commands to create a new categorical variable from a
continuous variable and to check the distribution of this new variable (using
'tab1(newvar)') should be kept together. Executing the command file at this stage
will allow the analyst to check this part of results instantly. Once the new variable is
assured, the line 'tab1(newvar)' may not be necessary and can be subsequently
deleted or skipped by placing a '#' before it.
One of R's advantages is in its graphing capabilities. Graphing however can involve
many steps and may require the addition of extra graphical parameters. It is a good
idea to start with a simple graph in a command. Other parameters such as 'pch'
(point character), 'lty' (line type), 'xlab' (X-axis label), 'col' (colour) etc, can be
added in the next round of command editing. Eventually, a good graph may need
several lines of commands to produce it.
Breaking in the middle of the command file
Since there can be several commands in the command file executed continuously,
the results coming out on the console can be too much to store in the console buffer
or too much to read. A graph created from a command line will also be overwritten
by a subsequent graph. It is often necessary to break or interrupt the command file
to see the details or graph at some point. To do so, insert a line where the break is
required. Type a single meaningless word such as 'xxx' on that line. Save and run
the file. When the command file is executed to this point, R does not know what to
do and thus stops with an error message. The output just before the 'xxx' can be
fully explored and any graph that is currently displayed can be saved.
The command at the R console 'source("filename.r")' to run the command file can
be easily repeated by pressing the up arrow key and then <Enter>. Changing the
breaking point of 'xxx' from one place to another in the command file followed by
saving it and rerunning 'source("filename.r")' at the R console is a standard method
of making good use of an existing command file.
Executing only a section of a command file
The above method, once established, ensures that the command file has no syntax
errors and the system works well up to the point of 'xxx'. The method however may
add too much time if some of the data file and/or command file are large or the
computation process is CPU intensive. Sometimes, the analyst may want to by-pass
these preceding sessions to get quick results from the section in the later part of the
command file. This can be done if and only if the preceding sections are not the
requirement of the section needed. For example, a section starting with 'zap()' or
'rm(list=ls())' will erase almost all objects and attachments. Any preceding sections
could possibly be bypassed without much a problem.

274
Bypassing several lines in the command file
If a few lines need to be bypassed but not erased, the easiest way is too put # in
front. However, if there are too many lines to do so and all the lines are contiguous,
one can bypass them using the 'if(){...}' control construct. If the expression in the
first (round) bracket is FALSE, all the commands inside the curly brackets {} will
be bypassed. Thus to bypass a large section, one simply inserts one line with the
command:
if(FALSE){
just before the to-be-bypassed section, and one line with a closing curly bracket at
the end of that section. The whole section contained by the curly brackets will be
skipped.
The main problem with this method is finding and removing the matching curly
brackets when the bypass is no longer required and the command file has been
unused for a long time. Crimson Editor and Tinn-R have a highlighting facility for
matching brackets but the opening and the closing ones sought may be very far
apart with several other curly brackets nested inside. To prevent this confusion,
several blank lines should be inserted before the command line 'if(FALSE){' and
after the matching closing bracket. These blank lines will make the skipped section
easily visualised.
Saving the output text
There are a number of methods to save the output text.
The simplest way is to highlight the area of text with the mouse and copy it to the
clipboard before pasting to a destination area such as a part of document text.
An alternative method is to use the sink(file = "myFile.txt") command
to divert all the subsequent output text to a file, named "myFile.txt". See 'help(sink)'
for more details about the usage of this function. To return to interactive mode, i.e.
to stop diverting output to the file, issue the command sink(). The use of sink
may be incorporated into the command file or carried out manually.
A complication of using sink arises when there is an error in subsequent
commands. Since the results are diverted to a file, not to the screen, the use will not
recognize the error and the process will stop in the middle of confusion. If this
happens, the solution is to type sink() at the console. This will return the route
back to the screen. The errors are can then be investigated in the output file. To
prevent this, 'sink' should used only when all the commands have been tested to
be error free, for example no 'xxx' or other garbage allowed. The command
sink(file="myFile.txt") can then be placed at the beginning of the
command file and 'sink()' placed at the end of the file. Then submit the
command file to R with the command source("command file").

275
Perhaps the simplest and best method to save the text output is to click 'File' at the
menu bar and choose 'Save to File...'. This will save all output currently in the
console to a text file. The default destination file is "lastsave.txt" but this can easily
be changed.
Note: ______________________________________________________________________
This last method will not save output if the 'clear console' command has been issued. In
addition, there is a limit to the number of lines that can be saved. R limits the console window
to the last 5,000 or so lines that can be saved. Therefore use this method only if your output is
not very long.
Saving a graph
Routing of a graph to a file is simpler than routing the output text. Copying a graph
to the clipboard and then pasting it to a program such as a word document or a
PowerPoint presentation slide is simple. Click at the graph window and choose
'File' from the menu bar and 'Copy to the clipboard. Choose as a Bitmap or Metafile
if the destination software can accept this format. A Metafile is slightly smaller in
size and has a sharper line. The Bitmap format may not have a sharp picture when
the size is enlarged. Alternatively, the graph can be saved in various other formats,
such as JPEG, postscript or PDF.
To save a graph when commands are run from a source file, simply type 'xxx' after
the graphing command to halt further execution of commands. Then copy or save
the graph as mentioned above.
Alternatively, instead of showing the graph on the screen, the graph can be routed
to a file by issuing one of the following graphics device commands:
bmp("filename.bmp")
jpeg("filename.jpg")
png("filename.jpg")
win.metafile("filename.wmf")
pdf("filename.pdf")
Each of these commands sets up the graphics device and must be followed by a
command that creates the actual graph. When the commands that create the graph
are executed, it is important that the device is turned off in order to write the graph
contents to the file and reroute future graphical output to the screen.
dev.off()
This rerouting method is useful because the whole process of the command file
need not be interrupted in the middle by the method mentioned in the preceding
paragraph.
The concept of turning the graphics device off after creating the graph is similar to
using the sink command, which requires a final sink() to save and close the
file. The commands below create a summary graph of the variable 'age' from the
Outbreak dataset in Epicalc. The graph is routed to a file called "graph1.jpg".

276
> zap()
> data(Outbreak)
> use(Outbreak)
> jpeg("graph1.jpg")
> summ(age)
> dev.off()
The re-routing process can be done either interactively or inside a command file if
there are no mistakes inside the graphics commands.

277
Chapter 26: Strategies of Handling
Large Datasets
The datasets given in the Epicalc package and used in this book are relatively small,
both in number of records and the number of variables. In real life, a data analyst
often faces over 50 variables and several thousand records. The requirements for
such analytical processing include a large amount of computing memory, fast CPU,
large hard disk space, and efficient data handling strategies. Without these
requirements, data analysis may take too long or may not even be possible.
Clearing R memory
R can handle many objects in one session. If the amount of memory is limited, it is
a good practice to clear all unnecessary objects from the working environment and
detach from all unnecessary data frames. Therefore, it is advisable to start any new
project with the zap() command.
> zap()
Simulating a large dataset
Instead of using an existing large dataset, let's create a data frame containing 30,000
records with 161 variables. The rnorm function is used to generate the random
numbers from a standard normal distribution.
> data1 <- rnorm(30000*160)
> dim(data1) <- c(30000, 160)
> data1 <- data.frame(id=1:30000, data1)
The first variable is called 'id'. The naming of the remaining 160 variables can be
achieved using two nested for loops and the built-in R constant 'letters', which
consists of the lower-case letters of the English alphabet. The outer loop generates
the first character of the variable names (a – h). The inner loop then pastes the
numbers 1 – 20 to these letters, separating the letters and numbers with a full stop.
278
> namesVar <- NULL
> for (i in letters[1:8])
{
for(j in 1:20){
namesVar <- c(namesVar, paste(i, j, sep="."))
}
}
> names(data1)[2:161] <- namesVar
Then give a variable description to each variable, using the attr function. This
process should only take a few seconds, depending on the speed of your computer.
> attr(data1, "var.labels")[1] <- "ID number"
> for(i in 2:161){
attr(data1, "var.labels")[i] <- paste("Variable No.", i)
}
> use(data1)
Describing a subset of variables
After entering commands at the R console, large output will usually scroll off the
screen, making viewing awkward. To show a subset of the variables in the data
frame, specify the select argument in the des function.
> des(select=1:20)
Only the first 10 variables, their class and description will be shown. Then we move
to see the next twenty.
> des(select=21:40)
... and so forth. Glancing at about 20 variables at a time will allow users to see the
variable descriptions more carefully, without having to scroll up and down the
screen.
If one wants to see only the variables names that start with "a", type:
> des(select="a*")
In these case, there are 20 of them.
To look at the variable descriptions of variables starting with "a." followed by only
one character, type:
> des(select="a.?")

279
Keeping only a subsample
Working with such a large data set can be time-consuming,. When testing R
commands it may be better to just keep a subset of records, thus reducing the time
involved. When you are satisfied that the commands work correctly, then you can
apply it to the whole dataset. The Epicalc function keepData can be used to select
a subset of records from the whole data frame.
> keepData(sample=300)
The data frame .data will be changed from having 30,000 to having only 300
records with the same number and description of variables, as can be seen from
> des(.data)
Note that the first few lines read:
(subset)
No. of observations =300
Variable Class Description
1 id integer ID number
2 a.1 numeric Variable No. 2
========= lines omitted=========================
which suggests that .data is just a subset of the original one.
If one wants to use the original data frame, simply type
> use(data1)
An alternative to specifying the number of records to randomly keep is to specify a
percentage of the original records. This is done by specifying a number between 0
and 1 for the 'sample' argument.
> keepData(sample=0.01)
The above command would again keep only 300 of the original number of records.
The criteria for keeping records can also be specified using the 'subset' argument:
> keepData(subset=a.1 < 0)
You will see a reduction of the total records, but not the variables.
> des()
The reduction is about a half since the variable 'a.1' was generated from a standard
normal distribution, which has a mean of 0 and is symmetric about this mean.
This method of selecting subsets of records can be applied to a real data frame, such
as keeping the records of only one sex or a certain age group.

280
Data exclusion
The keepData function can also be used to exclude variables. Return to the
original data frame and exclude the variables between 'a.1' and 'g.20'.
> use(data1)
> keepData(exclude = a.1:g.20)
> des()
Variables from 'a.1' to 'g .20' have been excluded but note that the number of
records remains the same.
To exclude the last 10 items of each section, the wildcard feature of Epicalc can be
exploited.
> use(data1)
> keepData(exclude = "????")
> des()
All the variables with a name of length four characters have been removed.
As mentioned before, if the size of the data frame is large, the analyst can choose
one or more of the above strategies to reduce the size. Further analysis can then be
carried out more quickly. If all the commands are documented in a file as suggested
by the previous chapter, and the commands are well organized, the first few lines of
the file can then be edited to use the full original data frame in the final analysis.
281
Chapter 27 Table Stacking for a
Manuscript
Readers of this book may wonder why simple statistical tests such as the t-test, chi-
squared test and non-parametric tests are rarely mentioned or explained in detail.
They are often used in the initial comparison of groups, which is commonly
presented as the first table in most epidemiological manuscripts. All these statistical
tests can be produced by one single Epicalc command, tableStack.
In chapter 23, this command is extensively used in parallel with the commands
alpha and alphaBest to display the distribution of each variable. An additional
(and also more important) goal is to compute the mean and total scores with the
items correctly reversed where necessary.
In this chapter, the same function is also extensively used but with the 'by' argument
included. The results of this can go directly into the manuscript.
Concept of 'tableStack'
Epidemiological and clinical manuscripts often have objectives of testing certain
hypothesis in human subjects. These subjects are usually grouped by type of
exposure (in a cohort or an interventional study) or outcome (in a case control
study) of interest. This grouping variable is initially analysed against baseline
characteristics in the first table of the manuscript and against the variables of
hypothesis testing in the second table. The orientation of the tables usually has the
group variable as the column and other variables as the rows.
In practice, if the row variable is a factor, then one can either use the table
function from standard R or tabpct from Epicalc, which will both show a cross-
tabulation of the variables. This is then subject to statistical testing using either a
chi-squared test or Fisher’s exact test.

282
If the row variable is on a continuous scale, the required table could be obtained by
the tapply or aggregate functions in the base and stats packages of R,
respectively, which give one statistic of each subgroup at a time or
aggregate.numeric from the Epicalc package, which gives multiple statistics
of the subgroups. If the data are normally distributed, means and standard
deviations are the two commonly displayed statistics. For data with skewed or non-
normal distributions, the median and inter-quartile range (25th and 75th percentiles)
are often used. For normally distributed data the t-test, for testing between two
groups, and one-way anova, for testing than two groups, are used. For non-normal
data, non-parametric tests are favoured, ie. the Wilcoxon rank sum test for 2 groups
and the Kruskal-Wallis test for more than 2 groups.
In doing so, the analyst has to go through various steps of exploring the
distributions, computing different statistics for the subgroups and then copying the
results into the manuscript, usually with some time-consuming formatting required.
This labourious work is easily accomplished by the Epicalc function
tableStack, which creates and stacks several tables with the appropriate
statistics together into one convenient table.
Example
All datasets with at least one factor variable can be used for trial. Let's start with the
dataset Familydata, a small dataset previously explored in chapter 4.
> zap
> data(Familydata)
> use(Familydata)
> des()
Anthropometric and financial data of a hypothetical family
No. of observations = 11
Variable Class Description
1 code character
2 age integer Age(yr)
3 ht integer Ht(cm.)
4 wt integer Wt(kg.)
5 money integer Pocket money(B.)
6 sex factor
The data contains only one factor variable, 'sex'. Now we create a summary table of
all variables by each level of sex, in a nice stacked format, with the appropriate
statistical test shown.
283
> tableStack(vars=2:5, by=sex)
F M Test stat. P value
Age(yr) t (9 df): t = 0.5 0.627
mean(SD) 42.9(24.3) 50.8(26.6)
Ht(cm.) Rank sum: W = 0.5 0.014
median(IQR) 155(150.5,159) 168.5(166,170.5)
Wt(kg.) Rank sum: W = 3 0.047
median(IQR) 51(50.5,54) 65.5(61,68)
Pocket money(B.) t (9 df): t = 1.33 0.218
mean(SD) 586.4(656.1) 1787.5(2326.1)
The numeric argument of 'vars' can also be replaced with the variable names.
> tableStack(age:money, by=sex)
The output table consists of four variables, which come from the second to the fifth
(vars=2:5) in the dataset. Age is determined to be normally distributed, thus a t-test
is conducted to test for a difference between the mean ages of males and females.
The test statistic is small (t=0.5), with 9 degrees of freedom and non-significant P
value.
Height and weight are significantly different among males and females. Both
variables are determined to have non-normal distributions, so the median is shown
instead of the mean. The inter-quartile range (IQR) is shown instead of the standard
deviation (SD) and the Wilcoxon rank sum test is conducted instead of the t-test.
Finally, pocket money was determined to be normally distributed and a t-test was
carried out with a non-significant result. Note that for such a small sample size our
conclusions are not so sound.
One can check the assumption for normality of residuals of 'money' by typing
> shapiro.test(lm(money ~ sex)$residuals)
Shapiro-Wilk normality test
data: lm(money ~ sex)$residuals
W = 0.8722, p-value = 0.08262
Moreover, the assumption of equal variance of residuals can be checked with
> bartlett.test(money ~ sex)
Bartlett test of homogeneity of variances
data: money by sex
Bartlett's K-squared = 5.8683, df = 1, p-value = 0.01542
284
Epicalc has preset the significance level for the Shapiro-Wilk and Bartlett tests to
switch the results from using the t-test to using the Wilcoxon rank sum test at
P>0.01, not P>0.05. The latest command has a P value of 0.015, not enough to
activate this switching.
One can try with other variables in this dataset to get familiar with the reasons for
choosing parametric and non-parametric tests. Users can also specify different
output features, such as not showing statistical test results, the name of the test, and
the variables to apply non-parametric statistical tests to. For example:
> tableStack(age:money, by=sex, test=FALSE)
> tableStack(age:money, by=sex, name.test=FALSE)
> tableStack(age:money, by=sex, iqr=c(age, money))
More examples
The 'by' argument in the tableStack function can also have more than 2 levels.
> data(Ectopic)
> use(Ectopic)
> des()
No. of observations = 723
Variable Class Description
1 id integer
2 outc factor Outcome
3 hia factor Previous induced abortion
4 gravi factor Gravidity
> table(outc)
outc
EP IA Deli
241 241 241
> tableStack(hia:gravi, by=outc, var.labels=FALSE)
EP IA Deli Test stat. P value
3 : hia Chi(2) = 78.72 < 0.001
never IA 61(25.3) 110(45.6) 158(65.6)
ever IA 180(74.7) 131(54.4) 83(34.4)
4 : gravi Chi(4) = 46.18 < 0.001
1-2 117(48.5) 121(50.2) 182(75.5)
3-4 87(36.1) 85(35.3) 46(19.1)
>4 37(15.4) 35(14.5) 13(5.4)
Note that when 'var.labels' is FALSE, the variable index and variable name is
displayed instead of the variable label. While this is not ready to 'copy & paste' to
the manuscript, it is useful for data exploration. An abnormal category for the row
variables, such as wrong levels of labeling, or rows with too small numbers, may
indicate a need to recode that variable before the final version can be used.

285
When the row variable is a factor, a cross-tabulation for that variable against the 'by'
variable is displayed. The table indicates that there are 241 records of EP (women
with an ectopic pregnancy). Out of these, 180 had a previous history of induced
abortion, thus the prevalence is 74.7%. This is much higher than the corresponding
IA group (54%) as well as in the delivery group (34%). The chi-squared test is
highly significant (P < 0.001). For 'gravi', the percentage of having 1-2 previous
pregnancies is highest in the 'Deli' group and the difference of gravidity is also
highly significant. Association of the outcome (column variable) and more than one
row variable suggests potential confounding problems that require further analysis.
These default settings of the arguments can always be overruled, such as setting the
output of hypothesis testing to FALSE or showing column percentages.
> tableStack(hia:gravi, by=outc, test=FALSE)
EP IA Deli
Previous induced abortion
never IA 61(25.3) 110(45.6) 158(65.6)
ever IA 180(74.7) 131(54.4) 83(34.4)
Gravidity
1-2 117(48.5) 121(50.2) 182(75.5)
3-4 87(36.1) 85(35.3) 46(19.1)
>4 37(15.4) 35(14.5) 13(5.4)
> tableStack(hia:gravi, by=outc, test=FALSE, percent="row")
Note that 'percent' should be set to "row" if we want to compare the percentage of
the outcome variable which has been designated to the column variable.
The above two data frames have row variables consisting of only one type, either
continuous variables or factors. Let's try with one with a mixture of both.
> data(Cars93, package="MASS")
> use(Cars93)
> des()
> tableStack(vars=4:25, by=Origin)
USA non-USA Test stat. P value
Min.Price Rank sum test 0.812
median(IQR) 14.5(11.4,19.4) 16.3(9.1,22.9)
Price Rank sum test 0.672
median(IQR) 16.3(13.5,20.7) 19.1(11.6,26.7)
Max.Price Rank sum test 0.489
median(IQR) 18.4(15,24.5) 21.7(12.9,28.5)
MPG.city Rank sum test 0.037
median(IQR) 20(18,23) 22(19,26)
MPG.highway Rank sum test 0.191
median(IQR) 28(26,30) 30(25,33)
AirBags Chi(2) = 0.48 0.786
Driver & Passenger 9(18.8) 7(15.6)
Driver only 23(47.9) 20(44.4)
None 16(33.3) 18(40)
286
DriveTrain Chi(2) = 0.17 0.919
4WD 5(10.4) 5(11.1)
Front 34(70.8) 33(73.3)
Rear 9(18.8) 7(15.6)
Cylinders Fisher's test 0.011
3 0(0) 3(6.7)
4 22(45.8) 27(60)
5 0(0) 2(4.4)
6 20(41.7) 11(24.4)
8 6(12.5) 1(2.2)
rotary 0(0) 1(2.2)
================== remaining lines omitted =================
Some of the variables, such as those related to price, rate of fuel consumption and
power, are either non-normally distributed or have a highly different variance
between the two origins of cars, thus were tested with the non-parametric rank sum
test. The other continuous variables are all tested with a t-test. There are four factor
variables. Location of airbags (AirBags), type of drive train (DriveTrain) and
availability of manual transmission (Man.trans.avail) were tested with a chi-squared
test. On the other hand, number of cylinders (Cylinders) violates the assumptions of
the chi-squared test, and so Fisher's exact test was used. The two-sided P-value is
very small indicating that pattern of cylinders between cars of US and non-US
origin is significantly different.
Colum of total
If required, an additional column of the total can be shown.
> tableStack(vars=4:25, by=Origin, total.column=TRUE)
In this case, omitting the test may look better.
> tableStack(vars=4:25, by=Origin, total.column=T, test=F)
USA non-USA Total
Min.Price
median(IQR) 14.5(11.4,19.4) 16.3(9.1,22.9) 4.7(10.8,20.3)
Price
median(IQR) 16.3(13.5,20.7) 19.1(11.6,26.7) 7.7(12.2,23.3)
Max.Price
median(IQR) 18.4(15,24.5) 21.7(12.9,28.5) 9.6(14.7,25.3)
MPG.city
median(IQR) 20(18,23) 22(19,26) 21(18,25)
MPG.highway
median(IQR) 28(26,30) 30(25,33) 28(26,31)
AirBags
Driver & Passenger 9(18.8) 7(15.6) 16(17.2)
Driver only 23(47.9) 20(44.4) 43(46.2)
None 16(33.3) 18(40) 34(36.6)
================== remaining lines omitted =================
287
In some occasions, only the total column is worth displaying. For example, in the
Compaq dataset, the first table may be a description of information of the subjects
on staging, age group, sex, etc.
> data(Compaq)
> use(Compaq)
> des()
> tableStack(vars=4:6, by="none")
Total
stage
Stage 1 530(49.8)
Stage 2 390(36.7)
Stage 3 81(7.6)
Stage 4 63(5.9)
Age group
<40 296(27.8)
40-49 285(26.8)
50-59 243(22.8)
60+ 240(22.6)
ses
Rich 279(26.2)
High-middle 383(36)
Poor-middle 154(14.5)
Poor 248(23.3)
In fact, the "none" string can be replaced with any quoted value with the same
results.
> tableStack(vars=4:6, by="junk")
Exporting 'tableStack' and other tables into a manuscript
R has a useful function to write a matrix, table or data frame into a comma
separated variable (csv) file that is readable by Excel. After being read into Excel,
the table can easily be copied into the manuscript.
> table1 <- tableStack(vars=4:25, by=Origin, data=Cars93)
> write.csv(table1, file="table1.csv")
> getwd()
The last command shows the current working directory, which should contain the
file "table1.csv". Go to that directory and open the file in Excel to see the results.
Then copy and paste the output table to your manuscript document.

288
This technique also works well with the display series of Epicalc, such as
regress.display, logistic.display, etc.
> glm1 <- glm(Origin ~ Price + AirBags + DriveTrain, binomial,
data=Cars93)
> logistic.display(glm1) -> glm1.display
> attributes(glm1.display)
$names
[1] "first.line" "table" "last.lines"
$class
[1] "display" "list"
> table2 <- glm1.display$table
> write.csv(table2, file="table2.csv")
Then see what you get.

289
Solutions to Exercises
Chapter 1
Problem 1
> p <- 0.3
> delta <- 0.05
> n <- 1.96^2*p*(1-p)/delta^2 ; n # 322.6944.
Thus 323 subjects are needed.
Problem 2
> p <- .05; delta <- .02
> n <- 1.96^2*p*(1-p)/delta^2 ; n # 456.19
Thus 457 subjects are needed.
Problem 3
> log(.01/(1-.01)) # -4.59512
> log(.1/(1-.1)) # -2.197225
> log(.5/(1-.5)) # 0
> log(.9/(1-.9)) # 2.197225
> log(1/(1-1)) # Inf
Alternatively, one can create a vector consisting of the probabilities.
> p <- c(.01, .1, .5, .9, 1)
> log(p/(1-p))
[1] -4.5951 -2.1972 0.0000 2.1972 Inf
Note that in R the function c is used to combine values into a vector. You will
discover that this function is very useful and is used throughout this book.
290
Chapter 2
Problem 1.
> sum(1:100*1:100) # or sum((1:100)^2)
[1] 338350
Problem 2.
> x <- 1:1000
> x7 <- x[x/7==trunc(x/7)] # or x7 <- x[x%%7==0]
> sum(x7)
[1] 71071
Problem 3.
> ht <- c(120,172,163,158,153,148,160,170,155,167)
> wt <- c(22,52,71,51,51,60,50,67,53,64)
> names <- c("Niece", "Son", "GrandPa", "Daughter", "Yai",
"GrandMa", "Aunty", "Uncle", "Mom", "Dad")
> names(ht) <- names
> names(wt) <- names
> cbind(ht,wt)
> bmi <- wt/(ht/100)^2
> sort(bmi)
Niece Son Aunty1 Daughter Yai
15.27778 17.57707 19.53125 20.42942 21.78649
Mom Dad Uncle GrandPa GrandMa
22.06035 22.94812 23.18339 26.72287 27.39226
> summary(bmi)
Min. 1st Qu. Median Mean 3rd Qu. Max.
15.28 19.76 21.92 21.69 23.12 27.39
> sd(bmi)
[1] 3.742951
In conclusion, 'Niece' has the lowest BMI at 15.27 kg/m2 and 'GrandMa' has the
highest BMI of 27.39 kg/m2. The average of the BMI is 21.7 kg/m2 and the standard
deviation is 3.7 kg/m2.

291
Chapter 3
Problem 1
There is more than one correct method.
First method
> a1 <- rbind(1:10, 11:20)
> a1
Second method
> a2 <- matrix(1:20, nr=2, byrow=TRUE)
> a2
Third method
> a2 <- cbind(1:20, nr=2)
> a2
Problem 2
> a1[,seq(from=1, to=10, by=2)]
Problem 3
> table1 <- cbind(c(15,30), c(20,22)); table1
> rownames(table1) <- c("Exposed","Non-exposed")
> colnames(table1) <- c("Diseased","Non-diseased")
> table1
> help(chisq.test)
> help(fisher.test)
> chisq.test(table1) # with Yates' continuity correction
> chisq.test(table1, correct=FALSE) # without
> fisher.test(table1) # default atlernative is "two.sided"
> fisher.test(table1, alternative="greater")
> fisher.test(table1, alternative="less")
Chapter 5
Values of individual elements on the scale
Dotchart The original values are all kept
Dotplot Each value is forced to fall into one of the bins.
Box plot Only the outlying values are displayed. Others are grouped into
parts of the box.

292
Power to discriminate different values
Dotchart Discrimination power is high. Even a small difference can be
noticed if the sample size is not large.
Dotplot Since adjacent values are often forced into the same bin, the power
of discrimination is lost.
Boxplot Poor discrimination power as most of the dots disappear in the box.
Perception for frequency distribution of the values
Dotchart Empty space in the graph promptly conveys the information that
there is no data in the area. Flat or slow rising indicates low
frequency whereas sharp or steep rising indicates high frequency.
Viewers must be educated to give proper interpretation.
Dotplot Information on relative frequency is best conveyed by this graph.
No need for education for interpretation.
Boxplot The length of the box is counter-intuitive. Since the box is divided
into two parts with more or less the same amount of data, a short
part means high density and a long part means low density. Many
people do not have this knowledge to interpret the result.
Information on sample size in each stratum
Dotchart Thickness of strata determined by the sample size.
Dotplot Thickness of strata determined by the height of the most frequent
bin, therefore, it can be visually distorted.
Boxplot When 'varwidth=TRUE', as indicated in the command, the width of
each box is determined by its sample size but not in linear
proportion.
Missing values
Dotchart Missing values are placed as empty space on the top of each
stratum
Dotplot Missing values are not shown.
Boxplot Missing values are not shown.
Suitability related to sample size and number of strata
Dotchart Most suitable when the sample size is not too large e.g. < 200.
Large number of strata can be a problem, especially when the
sample sizes among strata are grossly imbalanced.
Dotplot Similar problem with 'summ(var)' on the issue of stratification.
However, 'dotplot' is more friendly when the sample size is large
293
Boxplot Bearing only 5 values of a vector, this kind of graph is not
burdened by a large sample size. In stratification analysis, sample
sizes of strata are not proportional to the box width even if
'varwidth=TRUE' is imposed. Thus the graph can accommodate
these problems quite well. On the other hand, length of the box may
mislead the sample size as mentioned. Overall information on
sample size is generally lacking on box plots. Median knot is
introduced to indicate 95% confidence interval of the median. A
smaller knot indicates a larger sample size or lower level of
dispersion. However, the use of a knot is not popular.
Chapter 6
> zap()
> data(Timing)
> use(Timing)
> bed.day <- ifelse(bedhr > 20, 12, 13)
> bed.time <- ISOdatetime(year=2004, month=12, day=bed.day,
hour=bedhr, min=bedmin, sec=0, tz="")
> woke.up.time <- ISOdatetime(year=2004, month=12, day=13,
hour=wokhr, min=wokmin, sec=0, tz="")
> arrival.time <- ISOdatetime(year=2004, month=12, day=13,
hour=arrhr, min=arrmin, sec=0, tz="")
> from.woke.to.work <- arrival.time - woke.up.time
> summ(from.woke.to.work)
> sortBy(bed.time)
> par(bg="cornsilk")
> plot(bed.time, 1:length(bed.time), xlim=c(min(bed.time),
max(arrival.time)), pch=18, col="blue", ylab=" ", yaxt="n")
> points(woke.up.time, 1:length(woke.up.time), pch=18, col=2)
> points(arrival.time, 1:length(arrival.time), pch=18, col=1)
> abline(h=1:length(arrival.time), lty=3)
> title(main="Distribution of Bed time and woke up time")
23:00 01:00 03:00 05:00 07:00 09:00
Distribution of Bed time and woke up time
Subject sorted by bed time
Bed t ime
woke up time
arrival time
294
> title(ylab="Subject sorted by bed time")
> legend("topleft", legend=c("Bed time", "woke up time",
"arrival time"), pch=18, col=c("blue","red","black"),
bg="cornsilk")
Chapter 7
No. As seen from
> addmargins(table(.data$onset, .data$case))
Three non-cases had reported onset time. The 'onset' that had been changed was the
free vector created by the command
> onset[!case] <- NA
itself. In this command, both 'onset' and 'case' were those in the second position of
the search path 'search()', which was an attached copy of .data. From the
command
> onset[!case] <- NA
there would be three copies of 'onset'. The first and the second one in .data and in
'search()[2]' which is not changed. These two copies are then different from the free
vector which was created/modified by the command.
To get a permanent effect, the recode command in Epicalc should be used.
> recode(onset, !case, NA)
Then, check again:
> addmargins(table(.data$onset, .data$case))
By this method, the free vector 'onset' will be removed. The vectors in .data and
in 'search()[2]' would also be automatically synchronised to the new value.
However, the variable 'time.onset', a POSIXt object, does not have this problem.
Using this variable in the .data in the next chapter would give no problem.
Chapter 8
Both 'beefcurry' and 'saltegg' have significant attributable risk and risk ratio. One
might think that these foods would have been contaminated. In fact, the increase in
risk from consumption of these is due to confounding. This is discussed in the next
chapter.
Chapter 9
> cc(case, water) # OR =1.14, 95%CI = 0.47, 2.85
> table(case, eclair.eat, water)
295
Note one zero cell for a case who ate neither eclairs nor water. The following
subsequent commands give MH odds ratio but not stratum specific OR and the
homogeneity test results.
> mhor(case, eclair.eat, water)
# MH OR = 24.3, 95% CI = 14.11, 41.7
> mhor(case, water, eclair.eat)
# MH OR = 1.56, 95% CI = 0.60, 4.06
For stratification with beef curry, there is no problem with any cell with zero
counts. The homogeneity test could be done without any serious problems.
> table(case, beefcurry, water)
> mhor(case, beefcurry, water)
Graphs cross, homogeneity test P value = 0.018
> mhor(case, water, beefcurry)
Graphs cross, homogeneity test P value = 0.016
Note the strong interaction of beef curry with eclair and with water, which needs a
biological explanation.
Chapter 10
Solutions omitted.
Chapter 11
> des()
> plot(smoke, log(deaths))
> plot(SO2, log(deaths))
> plot(log(smoke), log(deaths))
> plot(log(SO2), log(deaths))
The last of the four plots looks the best.
> lm1 <- lm(log(deaths) ~ smoke)
> summary(lm1)$r.squared # 0.47
> lm2 <- lm(log(deaths) ~ SO2)
> summary(lm2)$r.squared # 0.59
> lm3 <- lm(log(deaths) ~ log(smoke))
> summary(lm3)$r.squared # 0.43
> lm4 <- lm(log(deaths) ~ log(SO2))
> summary(lm4)$r.squared # 0.66
The R-squared of lm4 is equal to the following model (using log base 2):
> lm5 <- lm(log2(deaths) ~ log2(SO2))
> summary(lm4)$r.squared # 0.66

296
The coefficients of log(SO2) from lm4 and of log2(SO2) from lm5 are the same:
0.45843.
For every unit increment of log2(SO2), the log2(deaths) increases by 0.458 units.
Similarly, for every unit increment of loge(SO2), the loge(SO2) also increases by
0.458 units. This coefficient is thus independent of the base of logarithm. This
means that the relationship between these two variables is on the power scale.
Given x is a positive number, for every increment of SO2 by x times, the number of
deaths will increase by x 0.45843 times.
> plot(log2(SO2), log2(deaths))
> abline(lm5)
From the regression coefficient and the graph. When the SO2 concentration in the
air is doubled, the number of deaths will increase by 2 0.45843 or 1.374 times. The
modelling for outcome variable that is discrete counting number can be more
appropriately dealt with Poisson regression in chapter 19.
Chapter 12
> zap()
> data(BP)
> use(BP)
> age.in.days <- as.Date("2001-03-12") - birthdate
> age <- as.numeric(age.in.days)/365.25
> sortBy(sbp)
> plot(sbp,ylim=c(0,max(sbp)),pch=" ",ylab="blood pressure")
> n <- length(sbp)
> segments(x=n, y=c(sbp, dbp), col=unclass(sex))
> title(main="Systolic and diastolic blood pressure of the
subjects")
> summary(lm(dbp ~ sex + age))
=======================
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 48.9647 9.4928 5.158 1.32e-06
sexfemale 7.2243 4.0798 1.771 0.0797
age 0.9412 0.1813 5.192 1.14e-06
=======================
After adjusting for age, the difference between sexes is not statistically significant.
Chapter 13
All the conclusions are independent of the base for logarithm and must be the same.
297
> log2money <- log2(money)
> summary(lm6 <- lm(log2money ~ age + age2))
==========================
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.340996 1.124481 0.303 0.769437
age 0.416419 0.058602 7.106 0.000101
age2 -0.004211 0.000668 -6.304 0.000232
---
> coef(lm6)
(Intercept) age age2
0.340996352 0.416418830 -0.004211267
> coef(lm4)
(Intercept) age age2
0.102650130 0.125354559 -0.001267718
> coef(lm4) / coef(lm6)
(Intercept) age age2
0.30103 0.30103 0.30103
The unit in horizontal axis in model lm4 is 30% that in lm6. The proportion is log
2 of base 10.
> log10(2) # 0.30103
or the proportion between the two logarithms.
> log(2)/log(10)
In computing the expected age where money is carried in the maximum amount:
> a1 <- coef(lm6)[3]
> b1 <- coef(lm6) [2]
> c1 <- coef(lm6) [1]
> x1 <- -b1/(2*a1); x1 # 49.44104
> y1 <- a1 * x1^2 + b1 * x1 + c1
> y1; 2^y1 # 1590.304
Money carried is a maximum at the age of 49.4 and the estimate is 1590.3 baht.
These results are the same as those from lm4, which uses logarithm base 10.
Chapter 14
The following commands are from a previous chapter.
> data(BP)
> use(BP)
> des()
> age.in.days <- as.Date("2001-03-12") - birthdate
> age <- as.numeric(age.in.days)/365.25
> saltadd1 <- saltadd
> levels(saltadd1) <- c("no", "yes", "missing")
> saltadd1[is.na(saltadd)] <- "missing"

298
These commands are specific for this chapter.
> glm1 <- glm(sbp ~ age * saltadd, family=gaussian)
> glm2 <- glm(sbp ~ age + saltadd, family=gaussian)
> glm3 <- glm(sbp ~ age, family=gaussian)
> glm1$aic
[1] 781.1646
> glm2$aic
[1] 780.535
> glm3$aic
[1] 990.425
Of the three models, glm2 has the lowest AIC. Of the three models it is therefore
the best.
> summary(glm2)
===============
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 63.1291 15.7645 4.005 0.000142 ***
age 1.5526 0.3118 4.979 3.81e-06 ***
saltaddyes 22.9094 6.9340 3.304 0.001448 **
---
Null deviance: 109757 on 79 degrees of freedom
Residual deviance: 73192 on 77 degrees of freedom
AIC: 780.53
Chapter 15
Problem 1
> use(complete.data)
> eclair.beefcurry <- eclair.eat + (beefcurry=="Yes")
> tab1(eclair.beefcurry)
> eclair.beefcurry <- factor(eclair.beefcurry)
> levels(eclair.beefcurry) <- c("none","either","both")
> pack()
> glm1 <- glm(case ~ eclair.beefcurry, binomial, data=.data)
> logistic.display(glm1)
Logistic regression predicting case
adj. OR(95%CI) P(Wald's test) P(LR-test)
eclair.beefcurry: ref.="none": < 0.001
either 0.79 (0.29,2.19) 0.651
both 11.88 (4.65,30.36) < 0.001
Log-likelihood = -534.7787
No. of observations = 972
AIC value = 1075.5574
The model has only two terms related to eclair and beef curry. The last term
contains the answer.

299
Problem 2
> zap()
> data(ANCtable); use(ANCtable)
> death <- factor(death, labels=c("no","yes"))
> anc <- factor(anc, labels=c("old","new"))
> clinic <- factor(clinic, labels=c("A","B"))
> data1 <- data.frame(death, anc, clinic, Freq)
> xtable <- xtabs(Freq~death+anc+clinic)
> mhor(mhtable=xtable)
Stratified analysis by clinic
OR lower lim. upper lim. P value
clinic A 0.801 0.346 1.90 0.556
clinic B 1.008 0.238 3.22 1.000
M-H combined 0.863 0.454 1.64 0.649
M-H Chi2(1) = 0.21 , P value = 0.649
Homogeneity test, chi-squared 1 d.f. = 0.11 , P value = 0.742
After stratifying by clinic, there is no difference in mortality between the two
methods of ante-natal care.
Problem 3
> zap()
> data(Hakimi)
> use(Hakimi)
> treatment <- 2 - treatment
> table(treatment)
> label.var(treatment, "Treatment")
> cc(dead, treatment)
treatment
dead 0 1 Total
0 196 204 400
1 28 37 65
Total 224 241 465
OR = 1.269
95% CI = 0.725 2.242
Chi-squared = 0.786 , 1 d.f. , P value = 0.375
Fisher's exact test (2-sided) P value = 0.423
> mhor(dead, treatment, malpres, graph=TRUE)
Stratified analysis by malpres
OR lower lim. upper lim. P value
malpres 0 0.672 0.335 1.32 0.2655
malpres 1 6.688 0.940 81.48 0.0386
M-H combined 0.911 0.514 1.62 0.7453
M-H Chi2(1) = 0.105 , P value = 0.745
Homogeneity test, chi-squared 1 d.f.=5.596, P value=0.018
300
The crude and adjusted odds ratios are different, however the homogeneity test is
significant indicating that the strata specific odds ratios can not be combined. When
'malpres'=1, the effect of treatment on death is significant.
> summary(glm(dead ~ treatment, binomial) -> cox1)
> summary(glm(dead ~ treatment + malpres, binomial) -> cox2)
> summary(glm(dead ~ treatment*malpres, binomial) -> cox3)
> summary(glm(dead ~ treatment*malpres+birthwt*treatment,
binomial) -> cox4)
> step(cox4)
We conclude that a significant interaction is evident between 'treatment' and
'malpres'. Birthweight is significant. The best model is found to be:
> m <- glm(dead ~ treatment*malpres+birthwt, family=binomial)
> logistic.display(m, decimal=1)
Logistic regression predicting dead
crude OR(95%CI) adj. OR(95%CI) P(Wald) P(LR-test)
treatment: 1.3 (0.7,2.2) 0.6 (0.3,1.1) 0.12 0.12
1 vs 0
malpres: 13.2 (6.2,27.7) 1.6 (0.3,8.6) 0.6 0.61
1 vs 0
birthwt 0.9985(0.998,0.999) 0.9986(0.998,0.999) < 0.001 < 0.001
treatment:malpres - 14.4 (2,103.3) 0.01 0
Log-likelihood = -154.5335
No. of observations = 465
AIC value = 319.07
Problem 4
> data(Ectopic)
> use(Ectopic)
> case <- outc == "EP"
> case <- factor(case)
> levels(case) <- c("control", "case")
> gravi1 <- unclass(gravi)
> m1 <- glm(case ~ hia + gravi1, family=binomial)
> logistic.display(m1, dec=1, crude=FALSE)
Logistic regression predicting case : case vs control
adj. OR(95%CI) P(Wald test) P(LR-test)
hia: ever IA vs never IA 3.7 (2.5,5.4) < 0.001 < 0.001
gravi1 (cont. var.) 1.0 (0.78,1.28) 1 1
Log-likelihood = -429.386
No. of observations = 723
AIC value = 864.773

301
There is no evidence of a linear dose-response relationship between gravidity and
risk of ectopic pregnancy, after adjusting for 'hia'.
Chapter 16
Problem 1
> zap()
> library(survival)
> use(VC1to6)
> matchTab(case, alcohol, strata = matset)
===============
Odds ratio by Mantel-Haenszel method = 5.386
Odds ratio by maximum likelihood estimate (MLE) method = 5.655
95%CI= 1.811 , 17.659
> clogit.display(clogit(case ~ alcohol + strata(matset)))
Call:
coxph(formula = Surv(rep(1, 119L), case) ~ alcohol +
strata(matset), method = "exact")
n= 119
coef exp(coef) se(coef) z p
alcohol 1.73 5.66 0.581 2.98 0.0029
exp(coef) exp(-coef) lower .95 upper .95
alcohol 5.66 0.177 1.81 17.7
Rsquare= 0.089 (max possible= 0.471 )
Likelihood ratio test= 11.1 on 1 df, p=0.000843
Wald test = 8.9 on 1 df, p=0.00286
Score (logrank) test = 10.7 on 1 df, p=0.00105
Problem 2
> clogit3 <- clogit(case ~ smoking + alcohol + rubber +
strata(matset))
> clogit2 <- clogit(case ~ alcohol + rubber + strata(matset))
> clogit1 <- clogit(case ~ alcohol + strata(matset))
> clogit3$loglik
> clogit2$loglik
> clogit1$loglik
> clogit3
===============
Likelihood ratio test=12 on 3 df, p=0.00738 n=119
> clogit2
===============
Likelihood ratio test=11.5 on 2 df, p=0.00314 n=119
> clogit1
===============
Likelihood ratio test=11.1 on 1 df, p=0.000843 n=119

302
The conditional log likelihood and the likelihood ratio test of 'clogit1', despite
being the smallest among the three, has the lowest degrees of freedom. This model
contains only 'alcohol', which is highly statistically significant whereas all other
two independent variables are not. All of these facts suggest that 'clogit1' should
be the model of choice.
We can confirm this by using the likelihood ratio test:
> lrtest(clogit3, clogit2)
Likelihood ratio test for Cox regression & conditional
logistic regression
Chi-squared 1 d.f. = 0.4743344 , P value = 0.491
Having one more degree of freedom with a small increase in likelihood is not
worthwhile. Therefore, 'clogit2' should be better than 'clogit3'. The
independent variable 'smoking' is now removed.
Similarity, we now test whether to keep 'rubber'.
> lrtest(clogit2, clogit1)
Likelihood ratio test for Cox regression & conditional
logistic regression
Chi-squared 1 d.f. = 0.383735 , P value = 0.5356
Again, the models 'clogit2' and 'clogit1' are not statistically significant. The
current choice should be 'clogit1'. Drinking alcohol is the only significant
predictor for oesophageal cancer.
Chapter 17
Set up the data:
> zap()
> outcome <- gl(n=3, k=4)
> levels(outcome) <- c("nochange","immuned","dead")
> vac <- gl(n=2, k=2, length= 12)
> levels(vac) <- c("placebo","vaccine")
> agegr <- gl(n=2, k=1, length=12)
> levels(agegr) <- c("young","old")
> total <- c(25,15,4,8,1,0,25,35,3,1,2,1)
> .data <- data.frame(outcome, vac, agegr, total)
> .data
Problem 1
> table1 <- xtabs(total ~ agegr+vac, data=.data)
> table1
> cc(cctable=table1) # OR = 2.552, P value = .023

303
Problem 2
> table2 <- xtabs(total~agegr+outcome, data=.data)
> table2
> fisher.test(table2) # p-value = 0.226
Problem 3
> table3 <- xtabs(total ~ outcome + vac, data=.data)
> table3
> fisher.test(table3) # p-value < 2.2e-16
> multi3 <- multinom(outcome ~ vac + agegr, weights=total,
data=.data)
> s3 <- summary(multi3)
> mlogit.display(multi3) # AIC = 137.13
Recreate a model with age group removed.
> multi4 <- multinom(outcome ~ vac, weights=total, data=.data)
> s4 <- summary(multi4)
> mlogit.display(multi4) # AIC = 134.471
The model 'multi4' has a lower AIC than that of 'multi3'. Age group is
therefore not appropriate to be in the model. From the last command, it is concluded
that the vaccine increases the chance of getting immune with a highly significant
odds ratio of 200. It should also be noted that the vaccine also (non-significantly)
increases the chances of death.
Chapter 18
> zap()
> library(nnet)
> library(MASS)
> male <- c(rep(0, times=6), rep(1, times=6))
> drug <- rep(c(0,1), times=6)
> pain <- rep(1:3, times=4)
> total <- c(3,5,15,10,5,7,8,5,10,10,10,2)
For polytomous logistic regression:
> pain.cat <- factor(pain)
> levels(pain.cat) <- c("nill","mild","severe")
> pain.ord <- ordered(pain.cat)
> model.polytom <- multinom(pain.cat ~ drug + male,
weights=total)
> summary(model.polytom)
> mlogit.display(model.polytom)
Shows a significant effect of drug in severe pain only. AIC = 191.623.
For ordinal logistic regression:
> model.ord <- polr(pain.ord ~ drug + male, weights=total)
> summary(model.ord)
304
The AIC = 189.037, which is better (lower) than the polytomous model.
> ordinal.or.display(model.ord)
In conclusion, both drugs and being male have significant reduction on pain.
Chapter 19
> data(Montana)
> use(Montana)
> arsenic1 <- arsenic != "<1 year"
> model.final <- step(glm(respdeath ~ agegr + period +
arsenic1 + start, offset=log(personyrs), family=poisson,
data = .data))
> summary(model.final)
> poisgof(model.final)
> idr.display(model.final)
Note that using 'arsenic1' in the model is better than using 'arsenic' suggesting no
evidence of a dose-response relationship. Moreover, workers who started to work
from 1925 had significantly lower risk than those who had started earlier.
Chapter 20
Problem 1
> model.bang1 <- glmmPQL(user ~ urban+ age_mean+
living.children, random=~1 | district, binomial, data=.data)
> summary(model.bang1)
To compute the 95% confidence interval of odds ratios
> exp(intervals(model.bang1)$fixed)
Note that urban women have two times the odds of using contraceptives compared
to rural women. A one year increment of age is associated with about a 3 percent
reduction of odds of use.
Problem 2
From the last output, increasing the number of living children does not have a linear
dose-response relationship with use. The odds almost doubles if the woman had two
children and almost triples for women with three living children. However, as the
number exceeds three, the odds of use does not further increase.
Problem 3
> model.bang2 <- glmmPQL(user ~ urban + age_mean +
living.children, random = ~ age_mean | district,
family=binomial, data=.data)
> logLik(model.bang1) # -4244.312 (df=8)
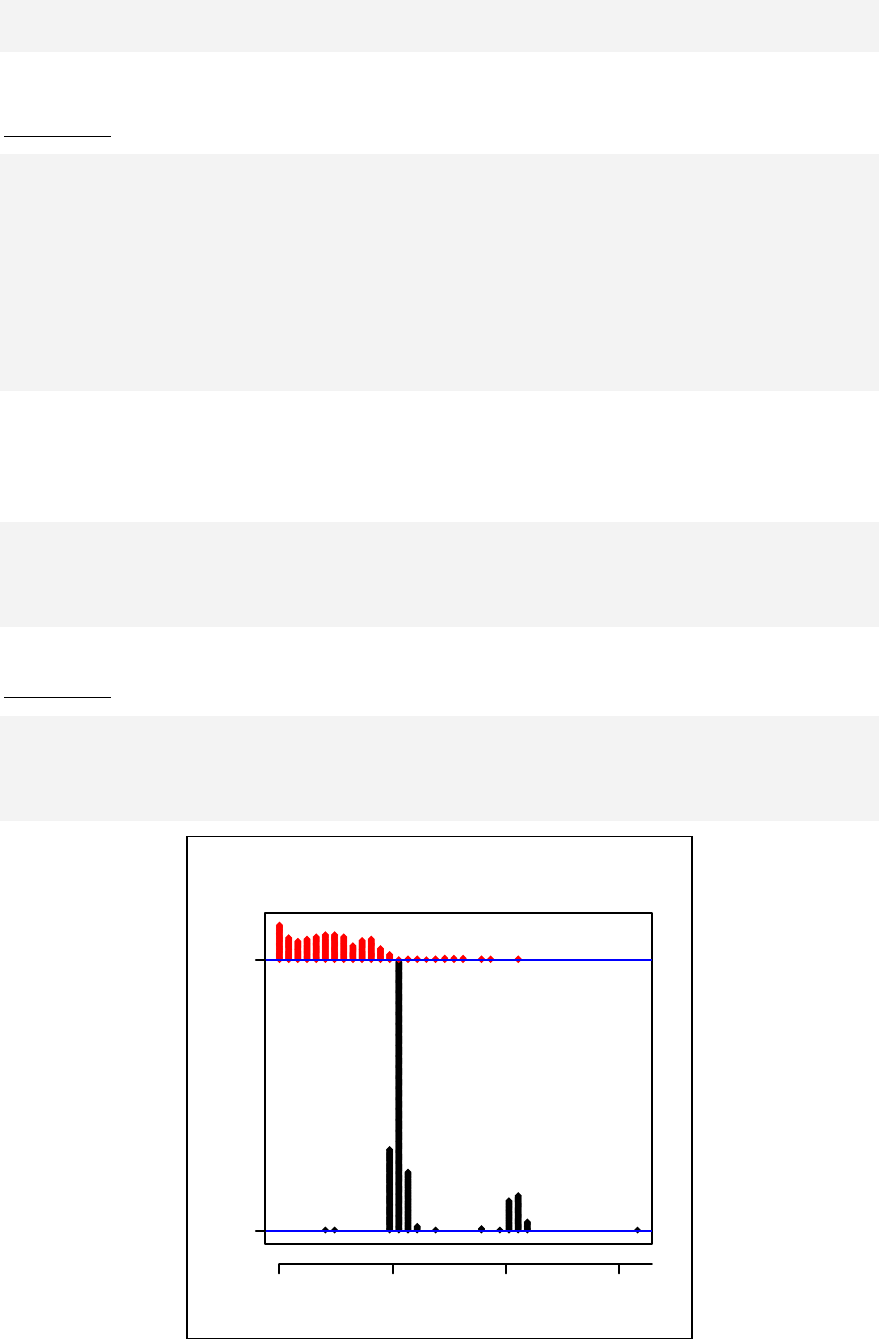
305
> logLik(model.bang2) # -4243.606 (df=10)
> lrtest(model.bang1, model.bang2) # P value=0.4933
Having age in the random effects is redundant.
Problem 4
> model.bang3 <- glmmPQL(user ~ urban * age_mean +
living.children, random=~1 | district, family=binomial,
data=.data)
> summary(model.bang3)
# P value for interaction terms = 0.3887
> lrtest(model.bang1, model.bang3)
# Error: Likelihood gets worse with more variables. Test not
executed
The evidence of age having a different effect in urban and rural areas is not found.
Chapter 21
> zap()
> data(Compaq)
> use(Compaq)
> des(); summ()
Problem 1
> summ(year)
> summ(year, by = status)
> abline(v=c(5,6))
> dotplot(year, by=status)
Distribution of year by status
0
1
0 5 10 15
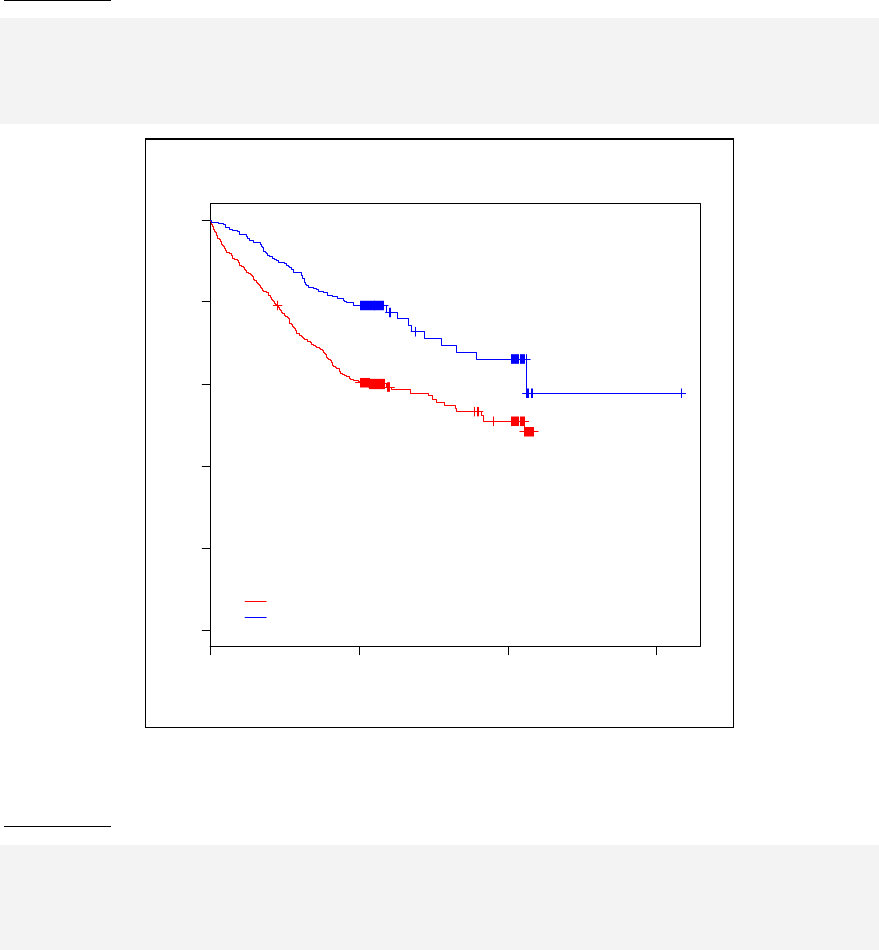
306
Note that deaths are uniformly distributed in the first five years where there were
only two censored observations. On the other hand, there was a lot censoring
between the 5th and the 6th years where there were very few deaths. The second
peak of censoring came after the 10th year. There is one patient who survived 15.8
years and was censored at the time the study ended. The alternating clustering of
deaths and censoring would not be detected if the exploratory analysis was not done
carefully.
Problem 2
> surv.ca <- Surv(year, status)
> plot(survfit(surv.ca ~ hospital), col = c("red", "blue"),
legend.text = levels(hospital), main="Breast Cancer
Survival")
0 5 10 15
0.0 0.2 0.4 0.6 0.8 1.0
Breast Cancer Survival
Public hospital
Private hospital
Note the very dense censoring immediately after the 5th and the 10th years.
Problem 3
> survdiff(surv.ca ~ hospital)
> survdiff(surv.ca ~ hospital + strata(stage))
> survdiff(surv.ca ~ hospital + strata(agegr))
> survdiff(surv.ca ~ hospital + strata(ses))
The difference of survival between patients from the two types of the hospitals is
highly significant despite the adjustments. Note that adjustment can only be done
one variable at a time using this approach. Multivariate adjustment using Cox
regression is presented in chapter 22.
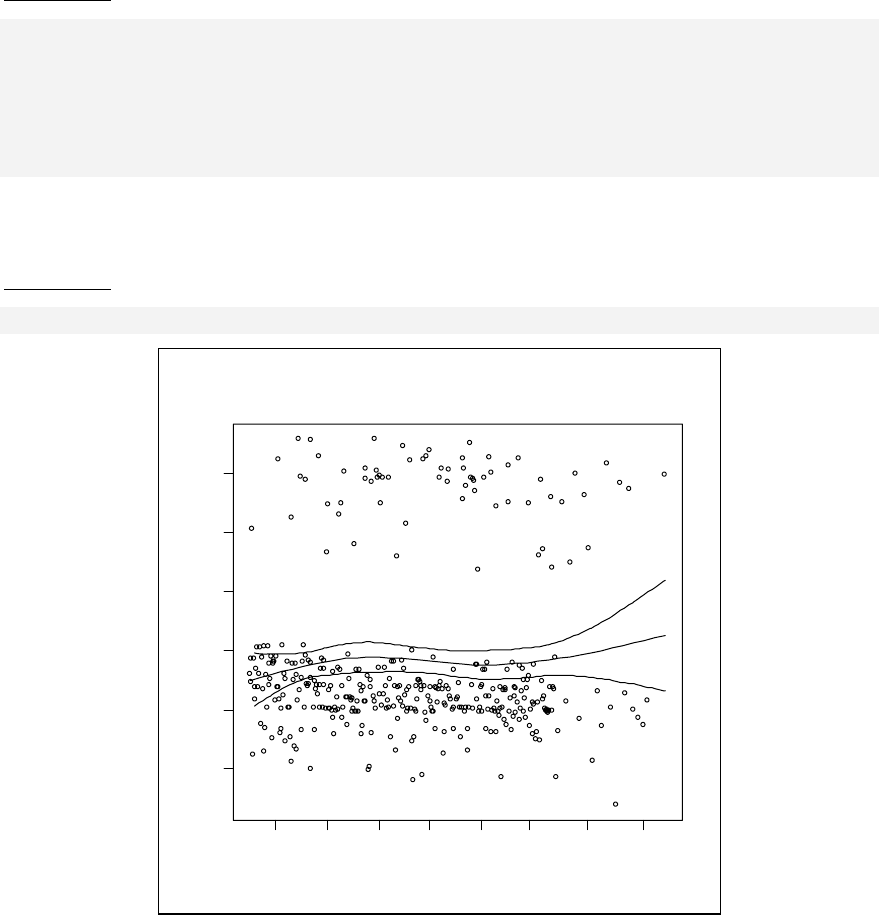
307
Chapter 22
Problem 1
> coxph(surv.ca ~ hospital + stage + strata(ses) + agegr) ->
model5
> cox.zph(model5) # Global test p value = 0.00802
> coxph(surv.ca ~ hospital + stage + ses + strata(agegr)) ->
model6
> cox.zph(model6) # Global test p value = 0.00494
Models based on stratification by socio-economic status and by age still violate the
proportional hazard assumption.
Problem 2
> plot(cox.zph(model4), var = 1)
Time
Beta(t) for hospitalPrivate hospital
0.24 0.99 1.8 2.6 3.4 4.3 7 9.2
-4-20246
The hazard ratio looks relative stable and slightly on the negative side for most of
the time period. A notable feature of the graph is that there are two clusters of
residuals. Some extreme positive values are sparsely found at the top of the plot
whereas the majority lie in another cluster within 0 to -3 units of beta. This may
suggest that the data actually came from more than one group of patients.
Unfortunately, we could not further investigate this finding.
308
Chapter 23
Problem 1
> help(expsy)
> summ(expsy)
The items 'it1' to 'it10' all share the same rating scale (1: low to 4: high). The dataset
is actually small enough to view on the screen
> expsy
Note the missing values.
> use(expsy)
> alpha(it1:it10) # 4 items reversed
> alphaBest(it1:it10)$remaining -> wanted
> tableStack(vars=wanted, reverse=TRUE) -> b
Chapter 24
Problem 1
An estimate of the population prevalence is not known. However, we can obtain a
range of sample sizes required corresponding to a range of values for p, say from
0.1 to 0.9.
> p <- seq(0.1,0.9,0.1)
> d <- 0.05
> n.for.survey(p, delta = d)
Sample size for survey.
Assumptions:
Confidence limit = 95 %
Delta = 0.05 from the estimate.
p delta n
1 0.1 0.05 138
2 0.2 0.05 246
3 0.3 0.05 323
4 0.4 0.05 369
5 0.5 0.05 384
6 0.6 0.05 369
7 0.7 0.05 323
8 0.8 0.05 246
9 0.9 0.05 138
We see from the output above that the maximum sample size required is found
when p is equal to 0.5. This is true for any survey where the estimated prevalence is
not known beforehand and the precision is fixed. For these situations, the safest
choice is to assume that p = 0.5.

309
Problem 2
> p2 <- 0.5; or <- 2
> odds2 <- p2/(1-p2)
> odds1 <- or*odds2
> p1 <- odds1/(1+odds1); p1
[1] 0.6666667
> n.for.2p(p1,p2)
Estimation of sample size for testing Ho: p1==p2
Assumptions:
alpha = 0.05
power = 0.8
p1 = 0.6666667
p2 = 0.5
n2/n1 = 1
Estimated required sample size:
n1 = 148
n2 = 148
n1 + n2 = 296
Nearly 300 subjects are needed.
Problem 3
The worthwhile benefit is 2.5kg and since we don't know the actual means in the
three groups, we can substitute any values for 'mu1' and 'mu2', so long as the
difference is 2.5. Also, given that we are performing two comparisons, a reasonable
type I error level (alpha) would be 0.02, instead of the conventional 0.05. The
required sample sizes can then be obtained as follows:
> n.for.2means(mu1=10, mu2=12.5, sd1=3.5, sd2=3.5, ratio=2,
alpha=0.02)
Estimation of sample size for testing Ho: mu1==mu2
====== assumptions omitted ======
Estimated required sample size:
n1 = 31
n2 = 61
n1 + n2 = 92
Thus 61 controls are required, whereas 31 are each required in the two treatment
groups, giving a total sample size required of 123. Note that if the standard
deviations in each group are increased to 4.5kg, the required sample size is
increased to 200.

310
Index
A
Arrays · 25, 26, 28, 29, 33, 35, 107
Attributable risk · 92, 96
Attributes · 35, 37, 51, 124, 150, 151,
155, 184, 216, 217, 231, 239
C
Calculator · 5
Chi-squared test · 33, 98, 101, 102, 103,
104, 174, 190, 202, 234, 243
Class · 19, 32, 36, 64, 66, 67, 74, 132,
151, 195, 228, 231, 270
Codebook · 50, 227, 242, 270
Colour · iv, 22, 84, 85, 138, 145, 273
Comments · 11
Concatenating · 16, 18
Confidence interval · 14, 98, 99, 151,
152, 153, 162, 168, 169, 175, 176,
179, 180, 182, 183, 188, 189, 196,
205, 208, 209, 224, 231, 234, 238,
256, 257, 266
Conflicts · 6
Confounding · 97, 99, 100, 101, 102,
104, 166, 171, 174, 175, 200, 235,
237, 294
Covariance matrix · 29, 151, 152
CRAN · 1, 5, 8, 13
Cronbach's alpha · 249, 252, 254
Cross-tabulation · 29, 33, 100, 164
Cumulative hazard rate · 232
D
Data entry · 37, 109, 114, 118, 227
Data frames · 35, 36, 40, 52, 83, 115,
145, 160
Design effect · 258
Dose-response relationship · 94, 191, 203
Dotplot · 58, 59, 61, 62, 80, 82, 90
Duplication · 105, 106
E
Effect modification · 103, 138
Extracting · 26, 40
F
Factor levels · 20, 22, 35, 40, 50, 115,
133, 145, 186, 188, 190, 192, 199,
200, 203, 211, 212, 227, 233
Factors · 21, 22, 35, 56, 60, 114, 115,
190, 203
Family, in glm · 60, 139, 154, 201, 211
Format · 7, 35, 64, 65, 66, 67, 77, 115,
170, 171, 190, 228, 269, 270, 275
F-test · 125, 126
Functions · 8
G
Generalized linear model · 184, 197, 201
Goodness of fit · 201, 210
H
Help · 7, 17, 60, 65, 108, 153, 162, 201,
270, 274
I
Incidence density · 204
Incubation period · 63, 82, 84
Index vector · 17, 108
Interaction · 97, 103, 104, 135, 136, 138,
145, 156, 166, 169, 174, 220, 222
ISOdatetime · 69, 84
K
Kaplan-Meier curve · 231, 236
L
Labelling · 37, 60, 112, 114
Language · 1, 2, 3, 7, 13, 64, 65, 271
Life table · 229, 230
Likelihood ratio test · 184, 301
Linear model · 29, 124, 127, 149, 152,
154, 184, 197, 201, 220
Locale · 64, 65
Logical · 11
Logit · 14, 157, 158, 160, 182, 183, 187
311
Lot quality assurance sampling · 264, 265
M
Mantel-Haenszel · 101, 165, 179, 180,
234
Matching · 92, 177, 179, 180, 183, 270,
271, 274
Matrix · 29, 30, 147, 151, 152, 162, 190,
191, 204, 205
Memory · 5, 32, 37, 43, 44, 269
Missing values · 22, 23, 50, 77, 79, 82,
83, 87, 97, 107, 109, 111, 118, 122,
131, 133, 292
Mixed effects modelling · 211
N
Negative binomial regression · 206
O
Offset · 201, 204, 256
One-way tabulation · 116
Overdispersion · 206, 208
P
Packages · 4
Population · 14, 63, 91, 93, 94, 157, 190,
204, 212, 213, 229, 255, 256, 257,
258, 260, 262, 266, 268
Power determination · 266
Prevalence · 14, 157, 159, 204, 255, 256,
257, 262, 264, 268, 308
Proportional hazards assumption · 237,
238, 242, 243
Protective efficacy · 94
Pyramid · 91, 92
R
R Objects · 1, 9, 11, 12, 15, 16, 19, 25,
32, 37, 45, 92, 197, 231, 272, 273
Random effects · 211, 212, 213, 215,
216, 218, 220, 304
Recoding · 87, 110, 119, 133
Referent level · 147, 163, 190, 191
Reshaping data · 119, 178, 180, 181, 183
Residuals · 125, 126, 127, 128, 129, 134,
140, 149, 150, 151, 152, 154, 216,
220, 244
Risk ratio · 92, 93, 94, 95, 96, 204
Rprofile.site file · 3, 6, 7, 15
R-squared · 125, 126, 133, 134, 136, 140,
142, 144, 295
S
Scatter plots · 121, 122, 130
Search · 5, 7, 8, 15, 43, 44, 45, 46, 87,
110, 153
Stratified analysis · 100, 161, 174, 212,
220, 243
Subscripts · 17, 18, 26, 41, 107
Survey · 14, 131, 132, 193, 206, 224,
228, 255, 256, 257, 258, 262, 263,
308
Syntax errors · 9
T
Transforming · 109
Transposition · 27
TRUE and FALSE · 11, 12
U
Update · 118, 119
V
Vectors · 15, 16, 19, 28, 79, 170, 294
W
Warnings · 6, 28, 240
312
Epicalc Functions
adjust Adjusted and standardize mean, proportion and rate
aggregate.numeric Compute summary statistics of a numeric variable
alpha, alphaBest Cronbach's alpha
be2ad Change year in B.E. to A.D.
cc Odds ratio calculation and graphing
ci Confidence interval of probability, mean and incidence
codebook Codebook of a data frame
des Desription of a data frame or a variable
detachAllData Detach all data frames
dotplot Dot plot
expand Expand an aggregated data frame
followup.plot Longitudinal followup plot
kap Kappa statistic
keepData Keep a subset of variables or records
label.var Variable manipulation
logistic.display Tables for multivariate odds ratio, incidence density etc
lookup Recode several values of a variable
lroc ROC curve
lrtest Likelihood ratio test
lsNoFunction List non-function objects
matchTab Matched tabulation
mhor Odds ratio calculation and graphing
n.for.2means Sample size calculation
n.for.2p Sample size calculation
n.for.survey Sample size calculation
pack Variable manipulation
poisgof Goodness of fit test for modeling of count data
power.for.2means Power calculation for two sample means and proportions
power.for.2p Power calculation for two sample means and proportions
pyramid Population pyramid
recode Recode variable(s)
rename Rename variable(s) in the default data frame
setTitle Setting language of Epicalc graph title
shapiro.qqnorm Normal Q-Q plots with Shapiro-Wilk's test
sortBy Variable manipulation
summ Summary with graph
tab1 One-way tabulation
tableStack Tabulation of variables in a stack form
tabpct Two-way tabulation
313
titleString Replace commonly used words in Epicalc graph title
unclassDataframe Unclass factor(s) in the default data frame
use Quick command to read in data and attach
zap Remove objects and detach all data frames
Epicalc Datasets
ANCdata Dataset on effect of new antenatal care method on mortality
ANCtable Dataset on effect of new ANC method on mortality (as a table)
Attitudes Dataset from an attitude survey among hospital staff
BP Dataset on blood pressure and determinants
Bang Dataset from a Bangladesh fertility survey, 1988
Compaq Dataset on cancer survival
DHF99 Dataset for exercise on predictors for mosquito larva infestation
Decay Dataset on tooth decay and mutan streptococci
Ectopic Dataset of a case-control study looking at history of abortion as a
risk factor for ectopic pregnancy
Familydata Dataset of a hypothetical family
HW93 Dataset from a study on hookworm prevalence and intensity
Hakimi Dataset on effect of training personnel on neonatal mortality
Marryage Dataset on age at marriage
Montana Dataset on arsenic exposure and respiratory deaths
Oswego Dataset from an outbreak of food poisoning in the US
Outbreak Dataset from an outbreak of food poisoning on a sportsday,
Thailand 1990.
Planning Dataset for practicing cleaning, labelling and recoding
SO2 Dataset on air pollution and deaths in UK
Sleep3 Dataset on sleepiness in a workshop
Suwit Hookworm infection and blood loss: SEAJTM 1970
Timing Dataset on bed time, waking up and arrival at a workshop
VC1to1, Datasets on a matched case-control study of esophageal cancer
VC1to6
314
About Epicalc
Open source and free software has been a mainstay for researchers, especially in the
developing countries, where the need for computer software and the cost of some
software applications has often been at odds. The increasing complexity of
research projects and associated analytical requirements led to the development of
R in the late 1990s. The current version of R, an open-source statistical software
initially written by Robert Gentleman and Ross Ihaka of the Statistics Department
of the University of Auckland, is the result of a collaborative effort involving
contributions from all over the world. R provides a wide variety of statistical and
graphical techniques, and is highly extensible.
The Special Programme for Research and Training in Tropical Diseases (TDR)
sponsored by UNICEF/UNDP/World Bank/WHO has supported the preparation of
an R add-on package, Epicalc, to enable R to more easily deal with
epidemiological data. Epicalc, written by Virasakdi Chongsuvivatwong of Prince
of Songkla University, Hat Yai, Thailand, has been well accepted by members of
the R core-team and the package is downloadable from CRAN (Comprehensive R
Archive Network) <http://www.cran.r-project.org> which is mirrored by 69
academic institutes in 29 countries. Equally, Epicalc has been welcomed by
students and users alike. On one hand, it assists data analysts in data exploration
and management. On the other hand, it helps young epidemiologists to learn the key
terms and concepts based on numerical and graphical results of the analysis.
Steven Wayling
Research Training Special Programme for Research and Training in Tropical
Diseases (TDR)
World Health Organization
October, 2007

Published with the support of:
Special Programme for Research & Training
in Tropical Diseases (TDR) sponsored by
UNICEF/UNDP/World Bank/WHO
Author:
Virasakdi Chongsuvivatwong
cvirasak@medicine.psu.ac.th
Editor:
Edward McNeil
edward.m@psu.ac.th
EPICALC–OK.indd 2 20.2.2008 15:24:54