Factoring Quadratic Trinomials TARSIA P310 2

User Manual: TARSIA P310

Open the PDF directly: View PDF .
Page Count: 7

FactoringQuadraticTrinomials





StudentProbe

Factor2310

x

x.



Answer:









52xx



LessonDescription

Thislessonusestheareamodelofmultiplicationto

factorquadratictrinomials.Part1ofthelesson

consistsof“circlepuzzles”asapreparationforthe

actualfactoringlesson inPart2. Whilethegoalof

thelessonisforstudentstobeabletofactor

quadratictrinomialswithoutdevicessuchascircle

puzzlesorrectangles,itmaytakesometimebefore

theydevelopfluencywhenfactoring.Part3ofthe

lessonusesthegraphingcalculatortohelpstudents

relatethefactorsofaquadratictrinomialtoitsx‐

intercepts.



Rationale

Factoringisavaluabletoolwhichhelpsstudents

becomeawareoftheconnectionsbetweenthe

rootsofaquadraticfunctionanditsintercepts.

Whilemany,infactmost,polynomialfunctionsare

primeovertherationalnumbers,studentscangain

valuableinsightintofunctionbehaviorbyanalyzing

functionsinthismanner.

Whenstudentsarerequiredtosolvequadratic

equations,factoringwillbeoneofthemethods

used.



Preparation

ForPart1ofthelesson,prepareseveralcirclepuzzlesforstudentstosolve.

ForPart2,prepareseveralrectanglesforstudentstousetowritetheareasasproducts.

Examplesofeachoftheseappearattheendofthelesson.

ForPart3,provideagraphingcalculatorforeachstudent.





AtaGlance

What:Factorquadratictrinomials

CommonCoreStateStandard:CC.9‐

12.A.SSE.3aFactoraquadraticexpressionto

revealthezerosofthefunctionitdefines.

MatchedArkansasStandard. CC.9‐12.A.SSE.3a.

Chooseandproduceanequivalentformofan

expressiontorevealandexplainpropertiesof

thequantityrepresentedbytheexpression.

(a)Factoraquadraticexpression to reveal the

zeros of the function it defines.

MathematicalPractices:

Lookforandmakeuseofstructure.

Lookforandexpressregularityinrepeated

reasoning.

Who:Studentswhocannotfactorquadratic

trinomials.

GradeLevel:Algebra1

PrerequisiteVocabulary:factor,quadratic,

trinomial

PrerequisiteSkills:polynomialarithmetic,

factoringwholenumbers,distributiveproperty

DeliveryFormat:individual,smallgroup,whole

group

LessonLength:30minutesperday,over

severaldays

Materials,Resources,Technology:graphing

calculator

StudentWorksheets:none

Lesson



Theteachersaysordoes…Expectstudentstosayordo…Ifstudentsdonot,thenthe

teachersaysordoes…

Part1

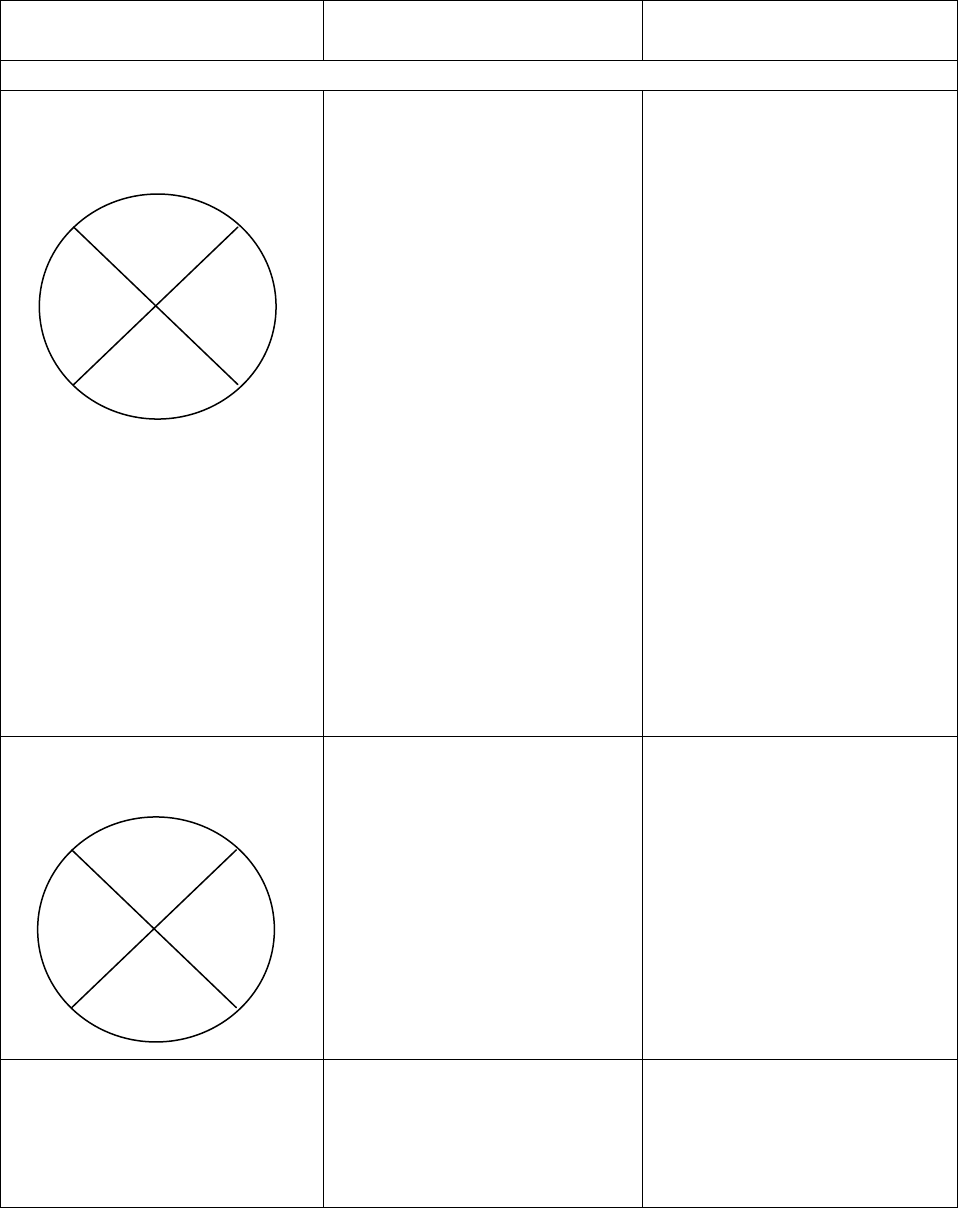
1. Wearegoingtosolvea

“circlepuzzle”.Circle

puzzleshavethisformat:



















Noticethattheproductof

twonumbers,aandb,isin

thetopsectionofthe

puzzleandthesumofthe

twonumbersisinthe

lowersection.Ifanytwo

sectionsofthepuzzleare

filledin,itispossibleto

determinetheremaining

twosections.

Whatdoesproductmean?

Whatdoessummean?

2. Completethiscirclepuzzle.





















a=2andb=1

or

a=1andb=2

Whattwonumbershavea

productof2?

Whichofthosenumberpairs

haveasumof3?

3. Repeatcirclepuzzleswith

avarietyofnumber

combinations.

(SeeCirclePuzzlesatthe

endofthelesson.)



ab

ba

a+b

2

ba

3

Theteachersaysordoes…Expectstudentstosayordo…Ifstudentsdonot,thenthe

teachersaysordoes…

Part2

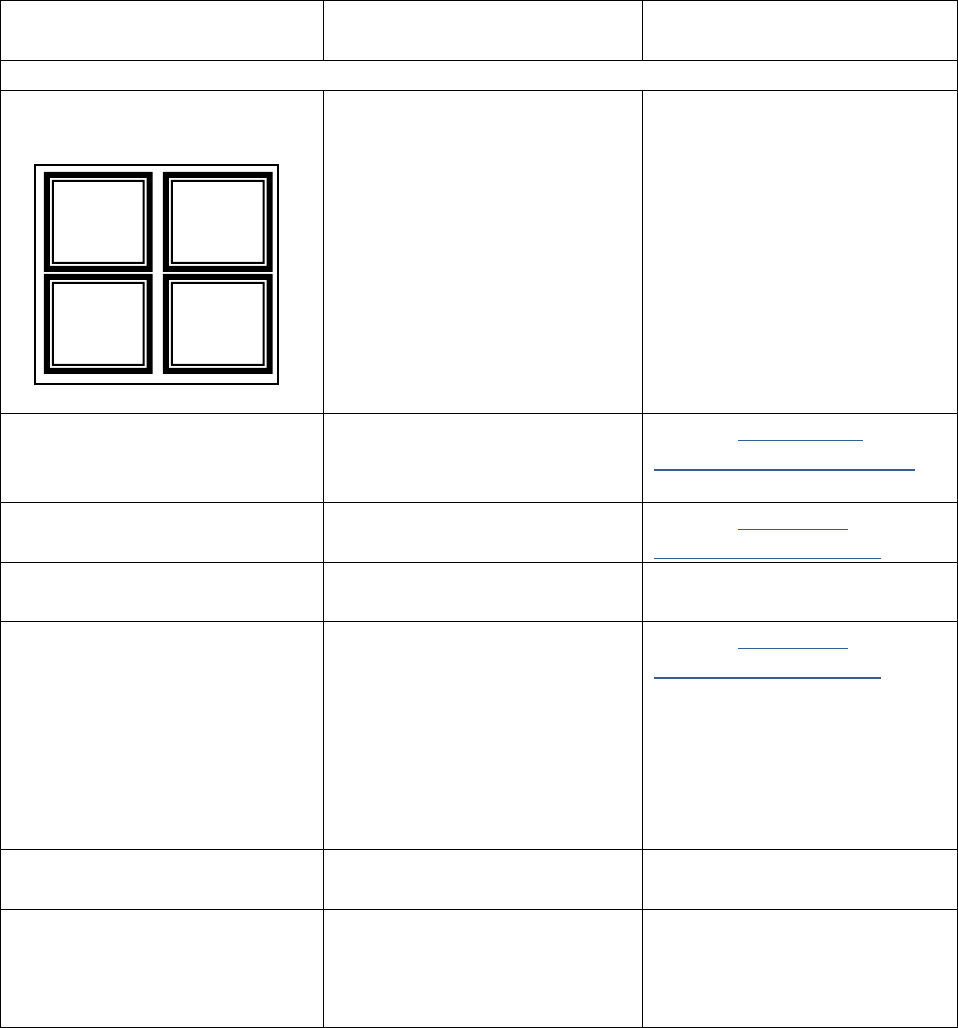
4. Writetheareaofthe

rectangleasasum.



















222

x

xx



Whatistheareaofeachpart

oftherectangle?

5. Canwecombineanylike

terms?

Whatdoweget?

232

x

x



RefertoAdditionand

SubtractionofPolynomials.

6. Whatarethedimensions

ofthelargerectangle?



1x



and





2x



RefertoMultiplying

PolynomialExpressions.

7. Whatisitsareaasa

product?







12xx



Howdowefindtheareaofa

rectangle?

8. Sincetheareaofthe

rectangleisthesame

regardlessofhowwewrite

it,wecansay



232 1 2xx x x .

Multiply



12xxto

verifyourresults.







2

2

12 22

32

x

xxxx

xx



 

 



RefertoMultiplying

PolynomialExpressions.

9. Writinganexpressionasa

productiscalledfactoring.



10. RepeatSteps4‐8witha

varietyofrectangles.

(SeeRectanglesattheend

ofthelesson.)



x2

2x

2x

Theteachersaysordoes…Expectstudentstosayor

do…

Ifstudentsdonot,thenthe

teachersaysordoes…

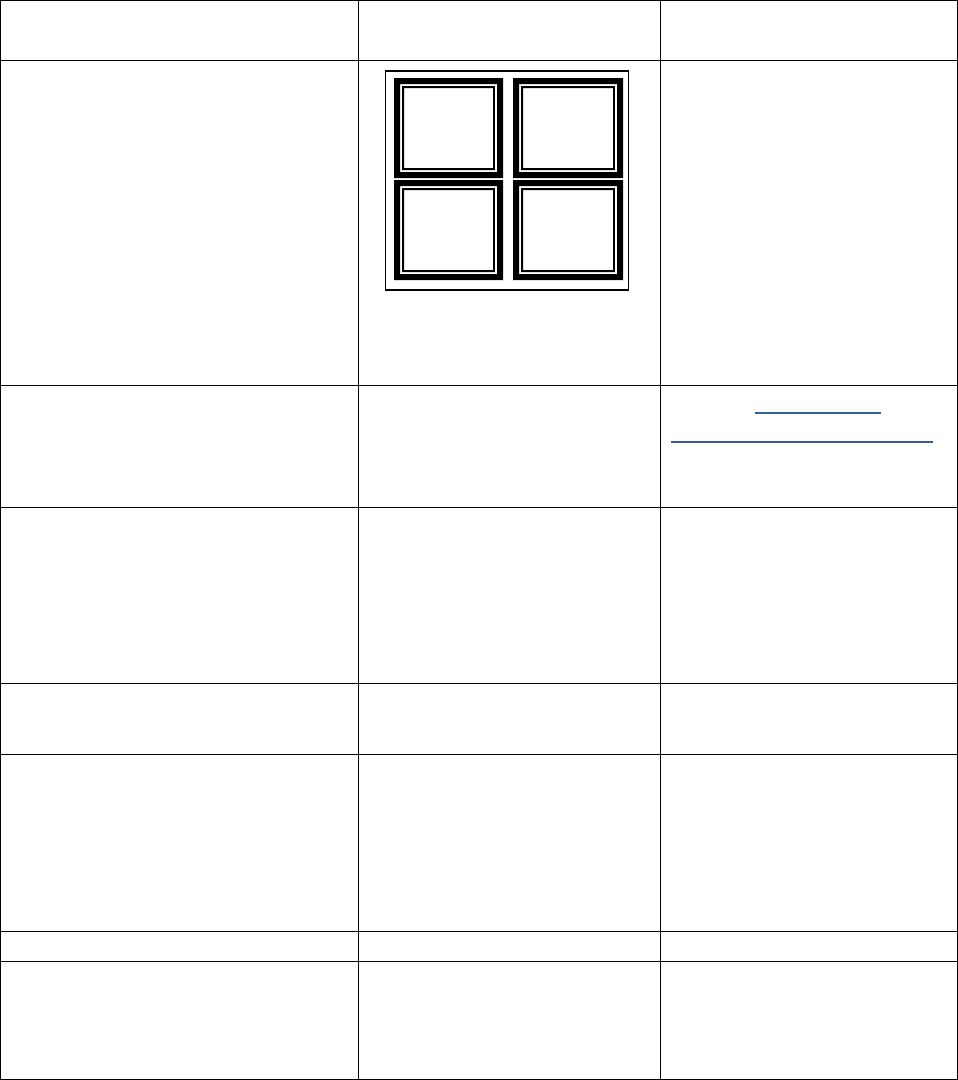
11. Factorthispolynomialby

writingthesumasaproduct:

2428

x

xx

Youmayusetherectangleto

helpyou.







































42xx





Modelforstudents.

12. Since4xand2xareliketerms,

thispolynomialcanbewritten

as268

x

x.

Howdoweknow?

426xxx



RefertoAdditionand

SubtractionofPolynomials.

13. WhenwedidtheCircle

Puzzles,welookedfor

numberswithacertain

productandacertainsum.

Whatnumbershaveaproduct

of8andasumof6?











4and2

Whatnumbershavea

productof8?(1and8or2

and4)

Whichofthesehaveasum

of6?

14. Sowecansay



268 4 2xx x x .



15. RepeatSteps11‐14witha

varietyofquadratic

trinomials,movingfrom

writingthetrinomialwith4

termstowritingitwith3

terms.



Part3

16. Nowthatweknowhowto

factoraquadratictrinomial,

let’sseewhatthegraphcan

tellus.



x24x

82x

Theteachersaysordoes…Expectstudentstosayor

do…

Ifstudentsdonot,thenthe

teachersaysordoes…

17. Usingyourgraphing

calculator,graph



268 4 2yx x x x 

.

Whatdoyounoticeaboutthe

graph?

(SeeTeacherNotes.)

Answerswillvary,butlisten

for“thex‐interceptsare‐4

and‐2andthey‐interceptis

8”.

Modelforstudents.Itmay

takeseveralexamples

beforestudentsseethe

relationship.

18. RepeatStep17withadditional

trinomialsuntilstudentsmake

theconnectionbetweenthe

factorsandthex‐intercepts.



19. Cansomeonesummarizewhat

wehavediscovered?

Thex‐interceptsarethe

oppositesofthenumbersin

thefactors.

They‐interceptisthe

constantterminthe

trinomial.



20. Useyourgraphingcalculator

tograph222yx x

.

Whatdoyounotice?

Answersmayvary,butlisten

for,“therearenox‐

intercepts”.

Wheredoesthegraphcross

thex‐axis?

21. Whatdoyouthinkthismeans

aboutitsfactors?



Therearenotanyfactors.





Notalltrinomialshavereal

factors.



TeacherNotes:

1. Itissuggestedthatthislessonbetaughtoveranumberofdays.Studentsseldomdevelop

fluencyinfactoringquickly.

2. Itisrecommendedthatteachersusethe“circlepuzzles”inpartoneaswarm‐upactivities

forseveraldayspriortotheactualfactoringlesson.Thesepuzzleswillhelpstudentsthink

aboutnumbersinwaysthatwillhelpthemintheactualfactoringlesson.

3. Useavarietyofcirclepuzzles,includingpositiveandnegativenumbers.

4. HelpstudentsremembertheformatofcirclepuzzlesbyplacingthediagraminStep1where

studentscanrefertoit.

5. Whensolvingcirclepuzzles,itmaybehelpfulforstudentstolistallofthefactorpairsfora

number.

6. Oncestudentscansolvecirclepuzzles,movetowritingareasassumsandasproductsin

Part2.

7. Remindstudentsthatthewordfactoringmeanstowriteanexpressionasaproduct.

8. Itmaytakeseveralexamplesofgraphingquadratictrinomialsbeforestudentsseethe

relationshipbetweenthefactorsandthex‐intercepts.Bepatientandletthestudents

“discover”thisrelationship.



Variations

Algebratilesmaybeusedinplaceof,orinadditionto,therectangles.



FormativeAssessment

Factor2536

x

x.



Answer:









94xx



References

RussellGersten,P.(n.d.).RTIandMathematicsIESPracticeGuide‐ResponsetoInterventionin

Mathematics.Retrieved225,2011,fromrti4sucess.





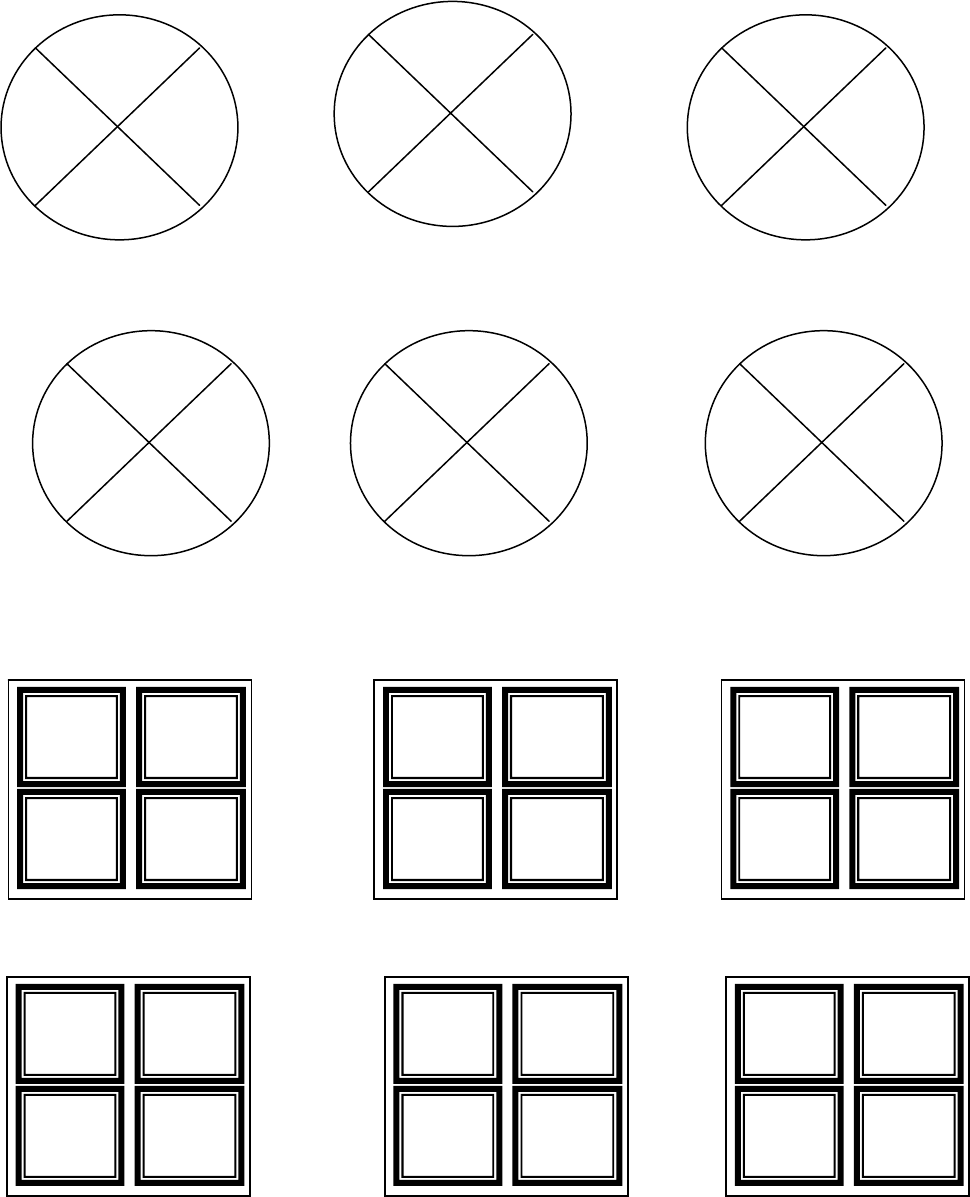
CirclePuzzles









































Rectangles

9

‐6

‐8

2

‐8

‐2

5

6

3

‐4

‐6

1

x2

4x

‐12‐3x

x2‐3x

3‐x

x2

5x

5x

x2

3x

93x

x2‐4x

‐205x

x2

‐5x

‐102x