Field Guide To Continuous Probability Distributions
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 206 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Preface: The search for GUD
- Acknowledgments & Version History
- Contents
- List of figures
- List of tables
- Distribution hierarchies
- Uniform Distribution
- Exponential Distribution
- Laplace Distribution
- Normal Distribution
- Power Function Distribution
- Log-Normal Distribution
- Gamma Distribution
- Gamma-Exponential Distribution
- Pearson VII Distribution
- Unit Gamma Distribution
- Amoroso Distribution
- Amoroso
- Special cases: Miscellaneous
- Stacy
- Pseudo-Weibull
- Half exponential power
- Hohlfeld
- Special cases: Positive integer beta
- Nakagami
- Half normal
- Chi
- Scaled chi
- Rayleigh
- Maxwell
- Wilson-Hilferty
- Special cases: Negative integer beta
- Inverse gamma
- Inverse exponential
- Lévy
- Scaled inverse chi-square
- Inverse chi-square
- Scaled inverse chi
- Inverse chi
- Inverse Rayleigh
- Special cases: Extreme order statistics
- Generalized Fisher-Tippett
- Fisher-Tippett
- Generalized Weibull
- Weibull
- Reversed Weibull
- Generalized Fréchet
- Fréchet
- Interrelations
- Beta Distribution
- Beta Prime Distribution
- Beta-Exponential Distribution
- Beta-Logistic Distribution
- Pearson IV Distribution
- Generalized Beta Distribution
- Gen. Beta Prime Distribution
- Pearson Distribution
- Grand Unified Distribution
- Miscellaneous Distributions
- Notation and Nomenclature
- Properties of Distributions
- Order statistics
- Limits
- Algebra of Random Variables
- Miscellaneous mathematics
- Bibliography
- Index of distributions
- Subject Index
SU
t3
α
α γ

Endorsements
https://twitter.com/dataandme/status/770732084872810496
https://twitter.com/groditi/status/772266190190194688
https://twitter.com/DHarrisPsyc/status/870614354529370112
https://xkcd.com/163/
Preface: The search for GUD 3
Acknowledgments & Version History 4
Contents 8
List of gures 17
List of tables 18
Distribution hierarchies 20
Zero shape parameters
1 Uniform Distribution 24
2 Exponential Distribution 28
3 Laplace Distribution 31
4 Normal Distribution 34
One shape parameter
5 Power Function Distribution 37
β
β
6 Log-Normal Distribution 45
7 Gamma Distribution 48
8 Gamma-Exponential Distribution 54
9 Pearson VII Distribution 60
t2
t3
Two shape parameters
10 Unit Gamma Distribution 67
11 Amoroso Distribution 72
β
β
12 Beta Distribution 88
13 Beta Prime Distribution 96
14 Beta-Exponential Distribution 101
15 Beta-Logistic Distribution 107
16 Pearson IV Distribution 113
Three (or more) shape parameters
17 Generalized Beta Distribution 116
18 Gen. Beta Prime Distribution 121
19 Pearson Distribution 128
20 Grand Unied Distribution 132
Miscellanea
21 Miscellaneous Distributions 139
Appendix
A Notation and Nomenclature 149
B Properties of Distributions 152
C Order statistics 157
D Limits 160
E Algebra of Random Variables 164
F Miscellaneous mathematics 171
Bibliography 177
Index of distributions 191
Subject Index 201

Uniform
Uniform(x;a,s) = 1
|s|
a,s R,
x∈[a,a+s],s > 0
x∈[a+s,a],s < 0
a b=a+s a s
Special cases
standard uniform x∈[0, 1]
StdUniform(x) = Uniform(x; 0, 1)
standardized uniform
Uniform(x;−√3, 2√3)
half-uniform
unbounded uni-
form
degenerate
Interrelations

0
1/s
a a+s
Uniform(x;a,s)
Uniform(x;a,s) = Beta(x;a,s, 1, 1)
=PearsonII(x;a+s
2,s)
OrderStatisticUniform(a,s)(x;α,γ) = Beta(x;a,s,α,γ)
X F−1
X(z)

X∼F−1
XStdUniform().
PowerFn(a,s,β)∼a+sStdUniform()
1
β
n
n
i=1
Uniformi(0, 1)∼IrwinHall(n)
n
i=1
Uniformi(0, 1)∼UniformProduct(n)
(x;a,s)
1
|s|
x−a
ss > 0s < 0
a,s R
a⩽x⩽a+s s > 0
a+s⩽x⩽a s < 0
a+1
2s
a+1
2s
1
12 s2
0
−6
5
ln |s|
eat(est −1)
|s|t
eiat(eist) − 1
i|s|t

Exponential
Exp(x;a,θ) = 1
|θ|exp−x−a
θ
a,θ, R
x > a,θ > 0
x < a,θ < 0
a=0, θ > 0
x > c c
Special cases
anchored exponential a=0 θ=1
standard exponential
Interrelations
Exp(x;a,θ) = Amoroso(x;a,θ, 1, 1)
=Gamma(x;a,θ, 1)
Exp(x; 0, θ) = Amoroso(x; 0, θ, 1, 1)
=Gamma(x; 0, θ, 1)
Exp(x;a,θ) = lim
β→∞
PowerFn(x;a−βθ,βθ,β)
Exp(x;a,θ)
1
|θ|exp−x−a
θ
1−exp−x−a
θθ > 0θ < 0
a,θ, R
[a,+∞]θ > 0
[−∞,a]θ < 0
a+θln 2
a
a+θ
θ2
sgn(θ)2
6
1+ln |θ|
exp(at)
(1−θt)
exp(iat)
(1−iθt)
n
i=1
Expi(0, θ)∼Gamma(0, θ,n)
θi>0
minExp1(0, θ1),Exp2(0, θ2), . . . , Expn(0, θn)∼Exp(0, θ′),
θ′= (n
i=1
1
θi)−1
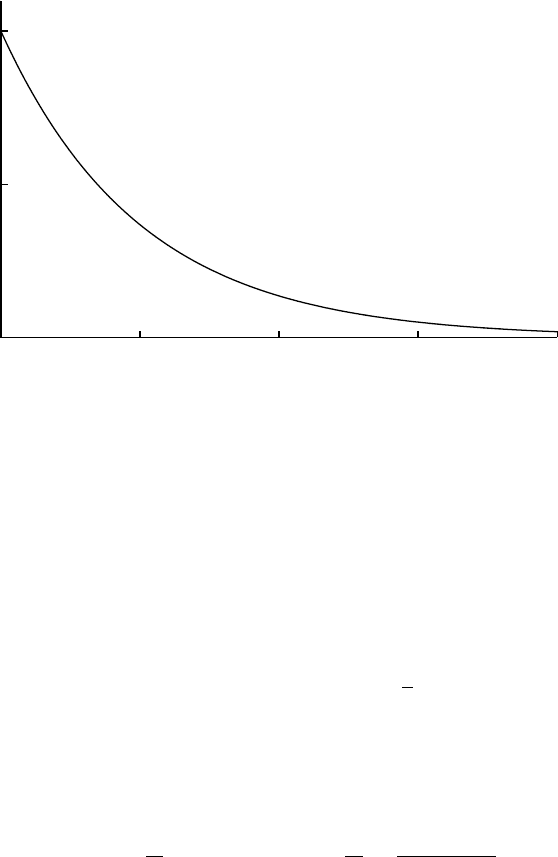
0
0.5
1
01234
Exp(x; 0, 1)
OrderStatisticExp(ζ,λ)(x;α,γ) = BetaExp(x;ζ,λ,α,γ)
Weibull(a,θ,β)∼a+θStdExp()
1
β
BetaPrime(0, θ1
θ2, 1, 1)∼ExpRatio(0, θ1
θ2)∼Exp1(0, θ1)
Exp2(0, θ2)

Laplace
Laplace(x;ζ,θ) = 1
2|θ|e−|x−ζ
θ|
x,ζ,θ R
ζ
θ
Special cases
standard Laplace
ζ=0 θ=1
Interrelations
θ
θ
Laplace(ζ,θ)∼Exp1(ζ,θ) − Exp2(ζ,θ)
Exp(ζ,|θ|)∼Laplace(ζ,θ) − ζ+ζ
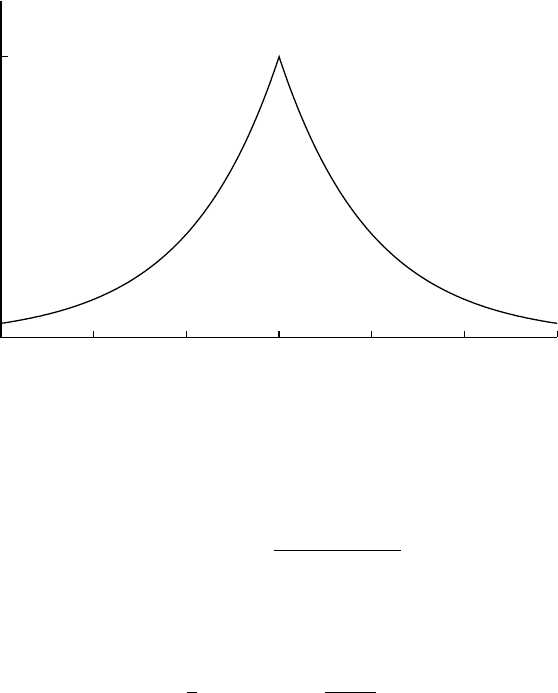
0
0.5
-3 -2 -1 0 1 2 3
Laplace(x; 0, 1)
Laplace(0, 1)∼ln StdUniform1()
StdUniform2()
+∞
−∞
1
2e−|x|eitxdx =1
1+t2

Laplace(x;ζ,θ)
1
2|θ|e−|x−ζ
θ|
1
2e−|x−ζ
θ|x⩽ζ
1−1
2e−|x−ζ
θ|x⩾ζ
ζ,θ R
x∈[−∞,+∞]
ζ
ζ
ζ
2θ2
0
3
1+ln(2|θ|)
exp(ζt)
1−θ2t2
exp(iζt)
1+θ2t2

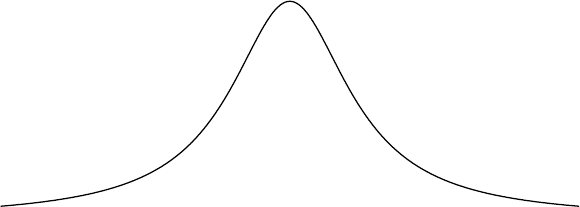
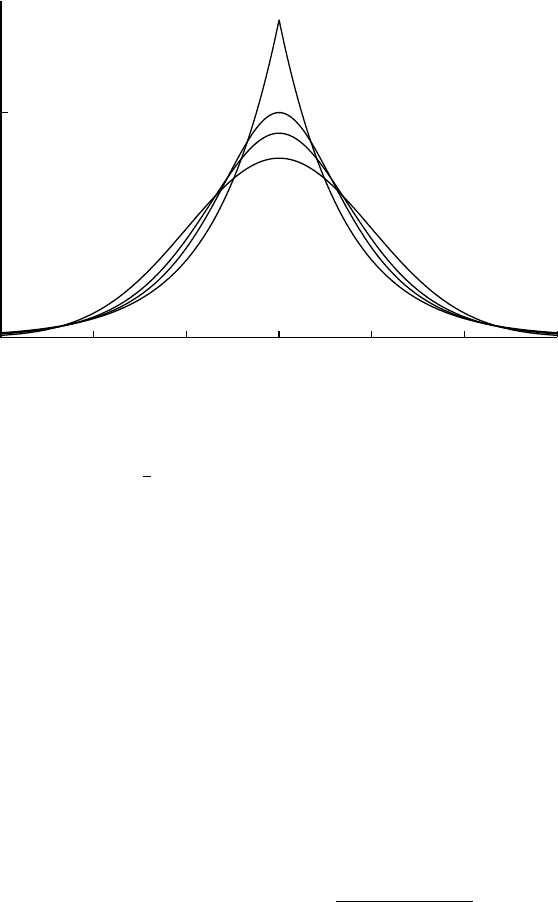
Normal
Normal(x;µ,σ) = 1
√2πσ2exp−(x−µ)2
2σ2
x,µ,σ R
µ σ
σ2
Special cases
µ=0 σ=1/√2h error function
µ=0 σ=1 standard normal Φz
Interrelations
σ→∞
σ→0
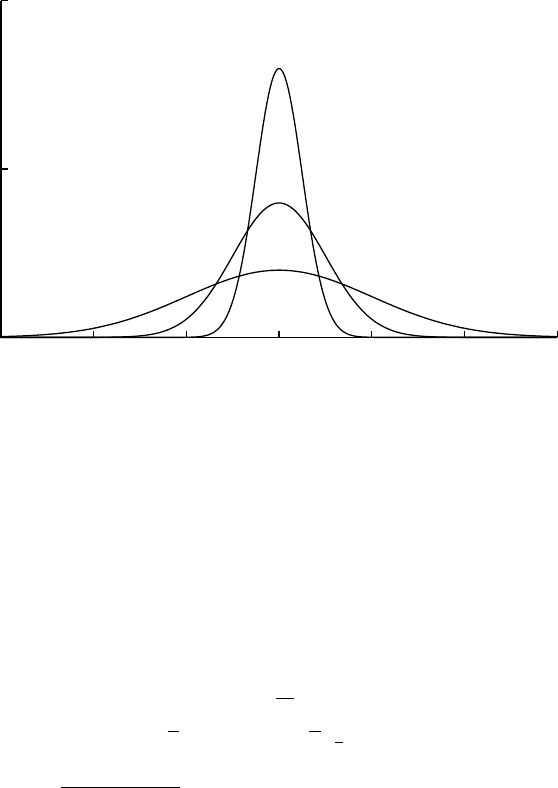
0
0.5
1
-4 -2 0 2 4 6
σ=2
σ=1
σ=0.5
Normal(x; 0, σ)
expNormal(µ,σ)∼LogNormal(0, eµ,σ)
Normal(0, σ)∼HalfNormal(σ)
StdNormal()2∼ChiSqr(1)
i=1,k
StdNormali()2∼ChiSqr(k)
Normal(0, σ)−2∼L´evy(0, 1
σ2)
Normal(0, σ)
2
β∼Stacy((2σ2)
1
β,1
2,β)
StdNormal1()
StdNormal2() ∼StdCauchy()
Normal1(µ1,σ1) + Normal2(µ2,σ2)∼Normal3(µ1+µ2,σ1+σ2)
Normal(x;µ,σ)
1
√2πσ2exp−(x−µ)2
2σ2
1
21+x−µ
√2σ2
µ,σ R
x∈[−∞,+∞]
µ
µ
µ
σ2
0
0
1
2ln(2πeσ2)
expµt +1
2σ2t2
expiµt −1
2σ2t2
StdNormal1() ∼ChiSqr(1)cos2πStdUniform2()
StdNormal2() ∼ChiSqr(1)sin2πStdUniform2()
ChiSqr(1)∼−2 ln StdUniform1()

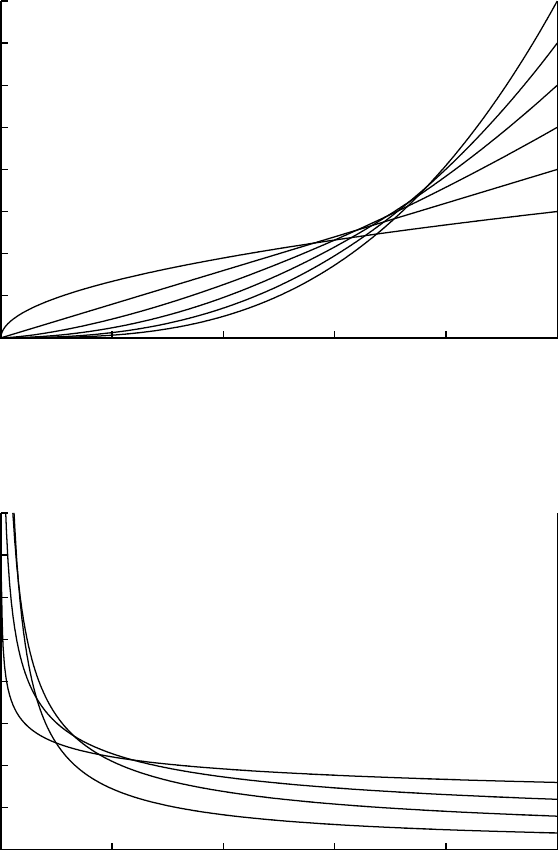
Power function
PowerFn(x;a,s,β) =
β
sx−a
sβ−1
x,a,s,β R
x∈[a,a+s],s > 0, β > 0
x∈[a+s,a],s < 0, β > 0
x∈[a+s,+∞],s > 0, β < 0
x∈[−∞,a+s],s < 0, β < 0
β
β
β→∞
Alternative parameterizations
Generalized Pareto
GenPareto(x;a′,s′,ξ)
=
1
|θ|1+ξx−ζ
θ−1
ξ−1ξ̸=0
1
|θ|exp−x−ζ
θξ=0
=PowerFn(x;ζ−θ
ξ,θ
ξ,−1
ξ)
q-exponential

expq(x)
QExp(x;ζ,θ,q)
=(2−q)
|θ|expq−x−ζ
θ
=
(2−q)
|θ|1− (1−q)x−ζ
θ
1
1−qq̸=1
1
|θ|exp−x−ζ
θq=1
=PowerFn(x;ζ+θ
1−q,−θ
1−q,2−q
1−q)
x,ζ,θ,q R
Special cases: Positive β
Pear-
son type VIII 0< β < 1 Pearson type IX
β > 1
Wedge
Wedge(x;a,s) = 2 sgn(s)x−a
s2
=PowerFn(x;a,s, 2)
ascending wedge
descending wedge
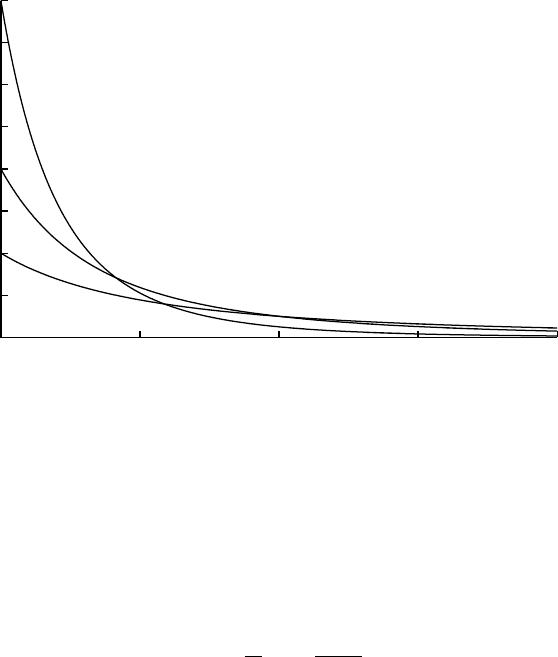
Special cases: Negative β
Pareto
Pareto(x;a,s,γ) =
¯
β
sx−a
s−¯
β−1
¯
β > 0
x > a +s,s > 0
x < a +s,s < 0
=PowerFn(x;a,s,−¯
β)
0
0.5
1
1.5
2
2.5
3
3.5
4
0 0.2 0.4 0.6 0.8 1
β
1.5
2.0
2.5
3.0
3.5
4.0
PowerFn(x; 0, 1, β)β > 1
0
0.5
1
1.5
2
2.5
3
3.5
4
0 0.2 0.4 0.6 0.8 1
β
0.2
0.4
0.6
0.8
PowerFn(x; 0, 1, β)0< β < 1
0
0.5
1
1.5
2
2.5
3
3.5
4
1 1.5 2 2.5 3
Pareto(x; 0, 1, ¯
β)¯
β
Lomax
Lomax(x;a,s,¯
β) = ¯
β
|s|1+x−a
s−¯
β−1
=Pareto(x;a−s,s,¯
β)
=PowerFn(x;a−s,s,−¯
β)

a s β
<0
(0, 1)
1
>1
∞
Exponential ratio
ExpRatio(x;s) = 1
|s|
1
1+x
s2
=Lomax(x; 0, s, 1)
=PowerFn(x;−s,s, 1)
Uniform-prime
UniPrime(x;a,s) = 1
|s|
1
1+x−a
s2
=Lomax(x;a,s, 1)
=PowerFn(x;a−s,s,−1)
Limits and subfamilies
β=1
PowerFn(a,s, 1)∼Uniform(a,s)

β
Exp(x;ν,λ) = lim
β→∞
PowerFn(x;ν−βλ,βλ,β)
=lim
β→∞
1
λ1+x−ν
βλ β−1
limc→∞1+x
cc=ex
Interrelations
β
PowerFn(x;a,s,β)
=GenBeta(x;a,s, 1, 1, β)
=GenBeta(x;a,s,β, 1, 1)β > 0
=Beta(x;a,s,β, 1)β > 0
=GenBeta(x;a+s,s, 1, −β,−1)β < 0
=BetaPrime(x;a+s,s, 1, −β)β < 0
=UnitGamma(x;a,s, 1, β)
OrderStatisticPowerFn(a,s,β)(x;α,γ) = GenBeta(x;a,s,α,γ,β)
GenBeta(x;a,s,α, 1, β) = PowerFn(x;a,s,αβ)
β
s>0 β
s<0

β
α
i=1
PowerFni(0, si,β)∼UnitGamma(0,
α
i=1
si,α,β)
β
α
α
i=1
PowerFni(0, si,β)∼UnitGamma(0,
α
i=1
si,α,αβ)
x→(x−a
s)β
PowerFn(a,s,β)∼a+sStdUniform()
1
β
Exp(x;a,θ) = lim
β→∞
PowerFn(x;a+βθ,−βθ,β)
(x;a,s,β)
β
sx−a
sβ−1
x−a
sβ
s
β>0s
β<0
a,s,β R
x∈[a,a+s]s > 0, β > 0
x∈[a+s,a]s < 0, β > 0
x∈[a+s,+∞]s > 0, β < 0
x∈[−∞,a+s]s < 0, β < 0
a β > 0
a+s β < 0
a+sβ
β+1β /∈[−1, 0]
s2β
(β+1)2(β+2)β /∈[−2, 0]
sgn(β
s)2(1−β)
(β+3)β+2
ββ /∈[−3, 0]
6(β3−β2−6β+2)
β(β+3)(β+4)β /∈[−4, 0]

Log-normal
Λ
LogNormal(x;a,ϑ,β)
=|β|
√2πϑ2x−a
ϑ−1
exp−1
2βln x−a
ϑ2
x,a,ϑ,β R,
x−a
ϑ>0
Special cases
anchored log-normal a=0
a=0ϑ=1σ=1
standard log-normal
Interrelations
LogNormal(a,ϑ,β)∼a+ϑStdLogNormal()1/β
LogNormal(a,ϑ,β)∼a+exp−Normal(− ln ϑ, 1/β)

0
0.5
1
1.5
0.5 1 1.5 2 2.5 3
β=1
β=2
β=4
LogNormal(x; 0, 1, β)
µ=ln ϑσ=1/β
Normal(x;µ,σ) = lim
β→∞
LogNormal(x;µ+βσ,−βσ,β)
n
i=1
LogNormali(0, ϑi,βi)∼LogNormali(0,
n
i=1
ϑi,(
n
i=0
β−2
i)−1
2)

LogNormal(x;a,ϑ,β)
|β|
√2πϑ2x−a
ϑ−1
exp−1
2βln x−a
ϑ2
1
2+1
21
√2βln x−a
ϑϑ > 0ϑ < 0
a,ϑ,β R
x∈[a,+∞]ϑ > 0
x∈[−∞,a]ϑ < 0
a+ϑ
a+ϑe−β−2
a+ϑe 1
2β−2
ϑ2(eβ−2−1)eβ−2
sgn(ϑ) (eβ−2+2)eβ−2−1
e4β−2+2e3β−2+3e2β−2−6
1
2+1
2ln(2πβ−2) + ln |ϑ|

Gamma Γ
Gamma(x;a,θ,α) = 1
Γ(α)|θ|x−a
θα−1
exp−x−a
θ
x,a,θ,α R,α > 0
=Amoroso(x;a,θ,α, 1)
Special cases
β=1
Wien Wien(x;T) = Gamma(x; 0, T, 4)
Erlang
α α
1/θ θ > 0 α=1
Standard gamma
StdGamma(x;α) = 1
Γ(α)xα−1e−x
=Gamma(x; 0, 1, α)
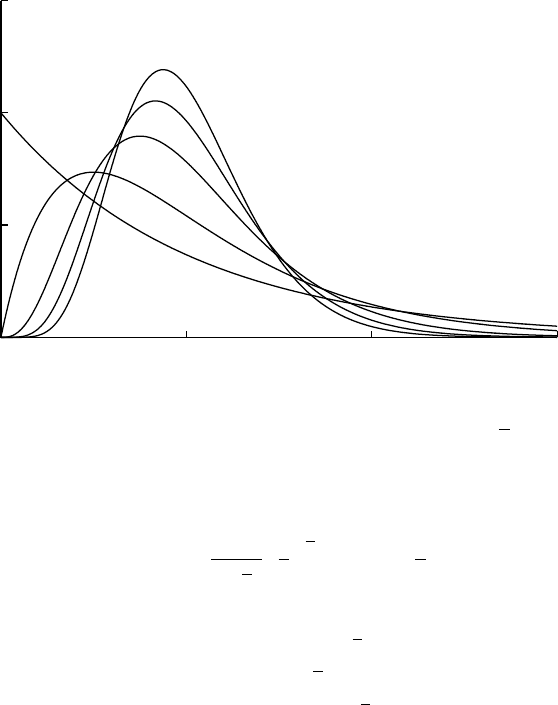
0
0.5
1
1.5
0 1 2 3
α=1
α=2
α=4
α=6
α=8
Gamma(x;1
α,α)
Chi-square χ2
ChiSqr(x;k) = 1
2Γ(k
2)x
2k
2−1
exp−x
2
k
=Gamma(x; 0, 2, k
2)
=Stacy(x; 2, k
2, 1)
=Amoroso(x; 0, 2, k
2, 1)
k
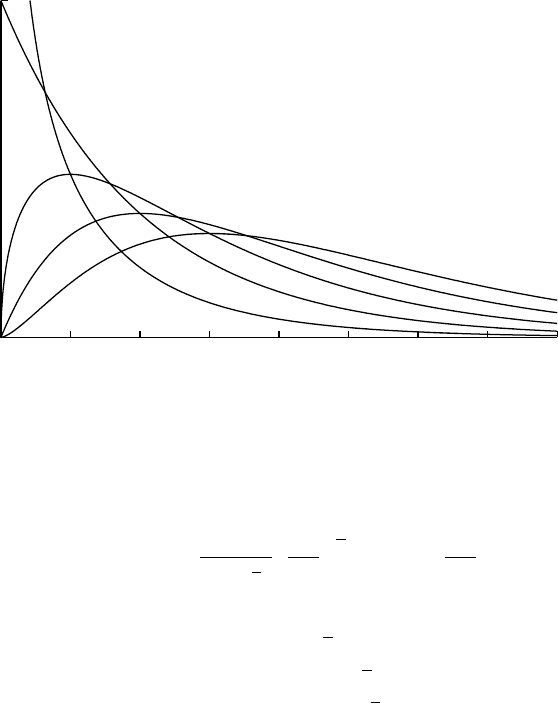
0
0.5
012345678
k=1
k=2
k=3
k=4
k=5
ChiSqr(x;k)
Scaled chi-square
ScaledChiSqr(x;σ,k) = 1
2σ2Γ(k
2)x
2σ2k
2−1
exp−x
2σ2
k
=Stacy(x; 2σ2,k
2, 1)
=Gamma(x; 0, 2σ2,k
2)
=Amoroso(x; 0, 2σ2,k
2, 1)
k
σ2
Gamma(x;a,θ,α)
1
Γ(α)|θ|x−a
θα−1
exp−x−a
θ
1−Qα,x−a
θθ > 0θ < 0
a,θ,α, R,α > 0
x⩾a θ > 0
x⩽a θ < 0
a+θ(α−1)α⩾1
a α ⩽1
a+θα
θ2α
sgn(θ)2
√α
6
α
ln|θ|Γ(α)+α+(1−α)ψ(α)
eat(1−θt)−α
eiat(1−iθt)−α
Porter-Thomas
PorterThomas(x;σ) = 1
2σ2Γ(1
2)x
2σ2−1
2exp−x
2σ2
=Stacy(x; 2σ2,1
2, 1)
=Gamma(x; 0, 2σ2,1
2)
=Amoroso(x; 0, 2σ2,1
2, 1)
Interrelations
Gamma1(0, θ,α1) + Gamma2(0, θ,α2)∼Gamma3(0, θ,α1+α2)
θ α
x7→ x−a
θβ
Amoroso(a,θ,α,β)∼a+θStdGamma(α)1/β
α
Normal(x;µ,σ) = lim
α→∞
Gamma(x;µ−σ√α,σ
√α,α)
i=1,k
StdNormali()2∼ChiSqr(k)∼Gamma(0, 2, k
2)

Normal(µ,σ)∼µ+σSgn() 2StdGamma(1
2)
GammaExp(a,s,α)∼a−slnStdGamma(α)
PearsonVII(a,s,m)∼a+sSgn()StdGamma1(1
2)
StdGamma2(m−1
2)
Cauchy(a,s)∼a+sSgn()StdGamma1(1
2)
StdGamma2(1
2)
UnitGamma(a,s,α,β)∼a+sexp−1
βStdGamma(α)
Beta(a,s,α,γ)∼a+s1+StdGamma2(γ)
StdGamma1(α)−1
BetaPrime(a,s,α,γ)∼a+sStdGamma1(α)
StdGamma2(γ)
Amoroso(a,θ,α,β)∼a+θStdGamma(α)
1
β
BetaExp(a,s,α,γ)∼a−sln1+StdGamma2(γ)
StdGamma1(α)−1
BetaLogistic(a,s,α,γ)∼a−slnStdGamma1(α)
StdGamma2(γ)
GenBeta(a,s,α,γ,β)∼a+s1+StdGamma2(γ)
StdGamma1(α)−1
β
GenBetaPrime(a,s,α,γ,β)∼a+sStdGamma1(α)
StdGamma2(γ)1
β
Sgn()
−1 +1

gamma-exponential
GammaExp(x;ν,λ,α)
=1
Γ(α)|λ|exp−αx−ν
λ−exp−x−ν
λ
x,ν,λ,α, R,α > 0,
−∞⩽x⩽∞
ν
λ α
λ
Special cases
Standard gamma-exponential
StdGammaExp(x;α) = 1
Γ(α)exp{−α x −exp(−x)}
=GammaExp(x; 0, 1, α)

ν λ α
0 1 α
ln 2 1 k
2
n
π
2
1
2
Chi-square-exponential
ChiSqrExp(x;k) = 1
2k
2Γ(k
2)exp−k
2x−1
2exp(−x)
k
=GammaExp(x; ln 2, 1, k
2)
Generalized Gumbel
GenGumbel(x;u,λ,n)
=nn
Γ(n)|λ|exp−nx−u
λ−nexp−x−u
λ
n
=GammaExp(x;u−λln n,λ,n)
n
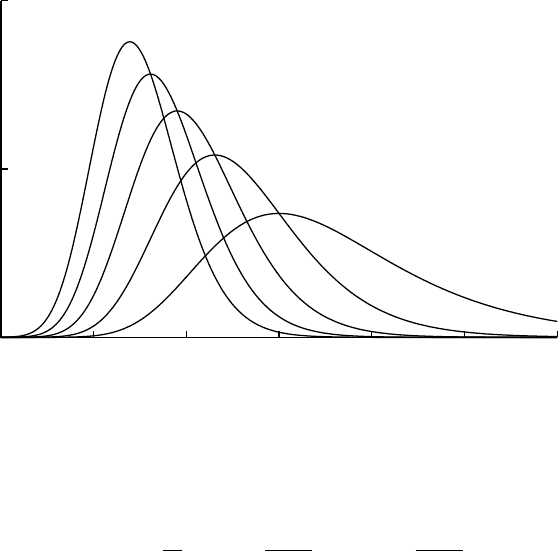
Gumbel
GammaExp(x;ν,λ,α)
1
Γ(α)|λ|exp−αx−ν
λ−exp−x−ν
λ
Qα,e−x−ν
λλ > 0λ < 0
ν,λ,α, R,α > 0,
x∈[−∞,+∞]
ν−λln α
ν−λψ(α)
λ2ψ1(α)
−(λ)ψ2(α)
ψ1(α)3/2
ψ3(α)
ψ1(α)2
eνt Γ(α−λt)
Γ(α)
eiνt Γ(α−iλt)
Γ(α)
0
0.5
1
-3 -2 -1 0 1 2 3
α=1
α=2
α=3
α=4
α=5
GammaExp(x; 0, 1, α)
Gumbel(x;u,λ) = 1
|λ|exp−x−u
λ−exp−x−u
λ
=GammaExp(x;u,λ, 1)
λ > 0
λ < 0
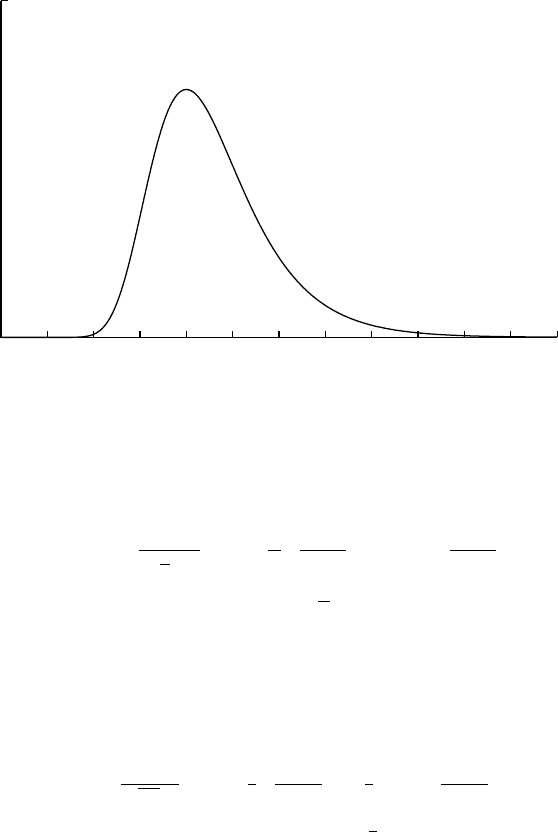
Standard Gumbel
StdGumbel(x) = exp−x−e−x
=GammaExp(x; 0, 1, 1)
0
0.5
-3 -2 -1 0 1 2 3 4 5 6 7 8
StdGumbel(x)
BHP
BHP(x;ν,λ) = 1
Γ(π
2)|λ|exp−π
2x−ν
λ−exp−x−ν
λ
=GammaExp(x;ν,λ,π
2)
Moyal
Moyal(x;µ,λ) = 1
√2π|λ|exp−1
2x−µ
λ−1
2exp−x−µ
λ
=GammaExp(x;µ+λln 2, λ,1
2)

Interrelations
StdGammaExp(α)∼−lnStdGamma(α)
GammaExp(ν,λ,α)∼−lnAmoroso(0, e−ν,α,1
λ)
BetaLogistic(x;ζ1−ζ2,λ,α,γ)∼GammaExp1(x;ζ1,λ,α)
−GammaExp2(x;ζ2,λ,γ)
lim
α→∞
GammaExp(x;µ+σ√αln α,σ√α,α) = Normal(x;µ,σ)
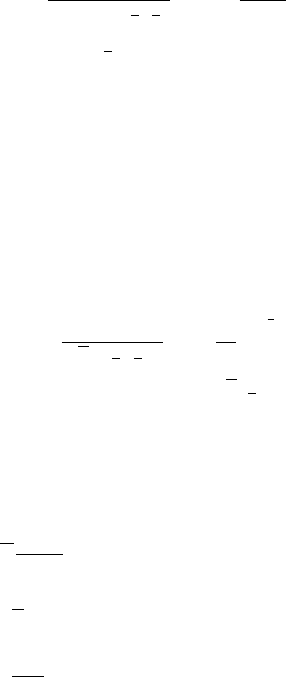
Pearson type VII
PearsonVII(x;a,s,m) = 1
|s|B(m−1
2,1
2)1+x−a
s2−m
m > 1
2
=PearsonIV(x;a,s,m, 0)
Special cases
Student’s t
StudentsT(x;k) = 1
√kB(1
2,1
2k)1+x2
k−1
2(k+1)
=PearsonVII(x; 0, √k,1
2(k+1))
k⩾0
t
t=√n¯
x−µ
¯
s
¯
x=1
n
n
i=1
Normali(µ,σ)
¯
s2=1
n−1
n
i=1Normali(µ,σ) − ¯
x2
¯
x n
µ σ2¯
s k=n−1
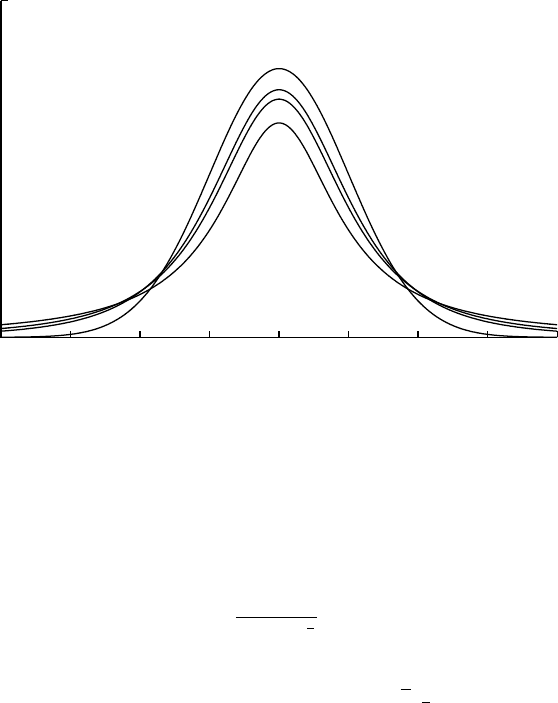
0
0.5
-3 -2 -1 0 1 2 3 4
k=1 t2k=2 t3
k=3 k→∞
Student’s t2t2
StudentsT2(x) = 1
(2+x2)
3
2
=StudentsT(x; 2)
=PearsonVII(x; 0, √2, 3
2)

a s m
t√kk+1
2
t2√23
2
t3√3 2
z
Student’s t3t3
StudentsT3(x) = 2
π1+x2
32
=StudentsT(x; 3)
=RelBreitWigner(x; 0, √3)
=PearsonVII(x; 0, √3, 2)
StudentsT3CDF(x) = 1
2+1
√3πarctan(x
√3) +
x
√3
1+x2
3
Student’s z
StudentsZ(z;n) = 1
B(n−1
2,1
2)1+z2−n
2
=PearsonVII(z; 0, 1, n
2)
z

z=¯
x−µ
s
¯
x=1
n
n
i=1
Normali(µ,σ),
s2=1
n
n
i=1Normali(µ,σ) − ¯
x2
¯
x n
µ σ2 s2
n n−1
t=z/√n−1
Cauchy
Cauchy(x;a,s) = 1
sπ1+x−a
s2−1
=PearsonVII(x;a,s, 1)
Cauchy1(a1,s1) + Cauchy2(a2,s2)∼Cauchy3(a1+a2,s1+s2)
Standard Cauchy
StdCauchy(x) = 1
π
1
1+x2
=1
π(x+i)−1(x−i)−1
=Cauchy(x; 0, 1)
=PearsonVII(x; 0, 1, 1)
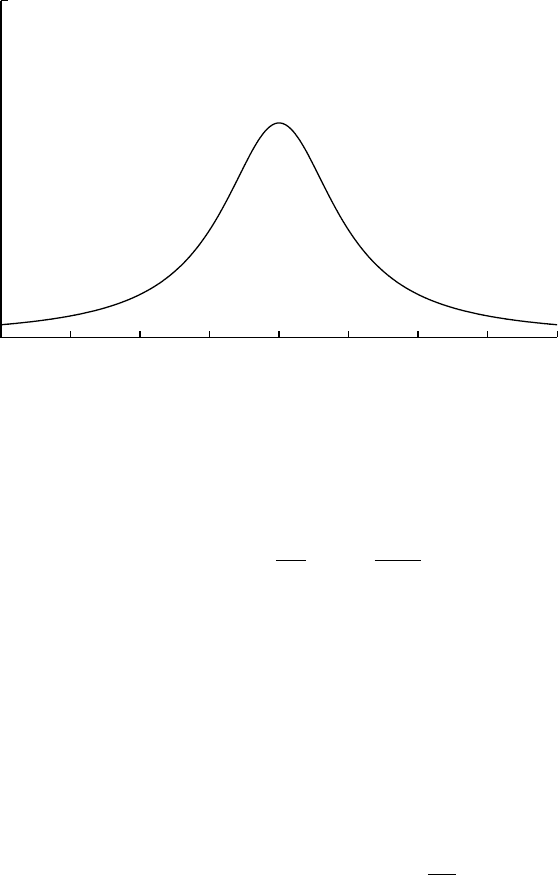
0
0.5
-3 -2 -1 0 1 2 3 4
StdCauchy(x)
Relativistic Breit-Wigner
RelBreitWigner(x;a,s) = 2
|s|π1+x−a
s2−2
=PearsonVII(x;a,s, 2)
Interrelations
m
Normal(x;µ,σ) = lim
m→∞
PearsonVII(x;µ,σ√2m,m)

PearsonVII(a,s,m)∼a+s√2m−1StdNormal()
StdGamma(m−1
2)
Cauchy(0, 1)∼Normal1(0, 1)
Normal2(0, 1)
Cauchy(0, 1)2
∼StdGamma1(1
2)
StdGamma2(1
2)
(x;a,s,m)
1
|s|B(m−1
2,1
2)1+x−a
s2−m
1
2+x−a
s1
B(m−1
2,1
2)2F11
2,m;3
2;−x−a
s2
a,s,m∈R
m > 1
2
−∞< x < +∞
a
a
a m > 1
s2
2m−3m > 3
2
0m > 2
eiat 2Km−1
2(s|t|)·1
2s|t|m−1
2
Γ(m−1
2)m > 1
2

Unit gamma
UnitGamma(x;a,s,α,β)
=1
Γ(α)
β
sx−a
sβ−1−βln x−a
sα−1
x,a,s,α,β R,α > 0
x∈[a,a+s],s > 0, β > 0
x∈[a+s,a],s < 0, β > 0
x∈[a+s,+∞],s > 0, β < 0
x∈[−∞,a+s],s < 0, β < 0
Special cases
Uniform product
UniformProduct(x;n) = 1
Γ(n)(−ln x)n−1
=UnitGamma(x; 0, 1, n, 1)
0> x > 1, n=1, 2, 3, . . .
n
Interrelations
α=1
UnitGamma(x;a,s, 1, β) = PowerFn(x;a,s,β)
UnitGamma(0, 1, α,β)∼exp−Gamma(0, 1
β,α)
UnitGamma(0, 1, α, 1)∼exp−StdGamma(α)
Gamma(x;a,s,α) = lim
β→∞
UnitGamma(x;a+βs,−βs,α,β)
lim
α→∞
UnitGamma(x;a,ϑeσ√α,α,√α
σ)
∝lim
α→∞x−a
ϑeσ√α
√α
σ−1−√α
σln x−a
ϑeσ√αα−1
∝x−a
ϑ−1
lim
α→∞
exp√α1
σln x−a
ϑ1−1
√α
1
σln x−a
ϑα−1
∝x−a
ϑ−1
lim
α→∞
e−z√α1+z
√αα,z= − 1
σln x−a
ϑ
∝x−a
ϑ−1
exp−1
2σ2ln x−a
ϑ2
=LogNormal(x;a,ϑ,σ)
limc→∞e−z√c1+z
√cc=
e−1
2z2
β
UnitGamma1(0, s1,α1,β)UnitGamma2(0, s2,α2,β)
∼UnitGamma3(0, s1s2,α1+α2,β)

0
0.5
1
1.5
2
2.5
3
0.5 1
α=1.5,β=1
α=2,β=2
α=5,β=8
UnitGamma(x; 0, 1, α,β)β > 0
UnitGamma1(0, s1,α1,β)UnitGamma2(0, s2,α2,β)
∼s1s2(UnitGamma1(0, 1, α1, 1)UnitGamma2(0, 1, α2, 1))
1
β
∼s1s2e−StdGamma1(α1)−StdGamma2(α2)1
β
∼s1s2e−StdGamma3(α1+α2)1
β
∼UnitGamma3(0, s1s2,α1+α2,β)
(x;a,s,α,β)
1
Γ(α)
β
sx−a
sβ−1−βln x−a
sα−1
1−Qα,−βln x−a
sβ
s>0β
s<0
a,s,α,β R,α,β > 0
[a,a+s],s > 0, β > 0
[a+s,a],s < 0, β > 0
[a+s,+∞]s > 0, β < 0
[−∞,a+s],s < 0, β < 0
a+sβ
β+1α
s2β
β+2α−s2β
β+12α
E(Xh)β
β+hαa=0

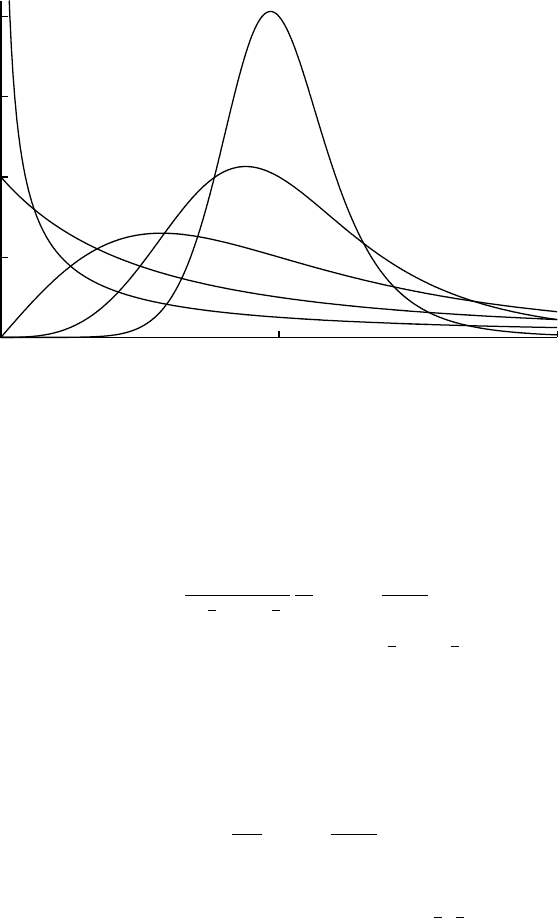
Amoroso
Amoroso(x;a,θ,α,β)
=1
Γ(α)
β
θx−a
θαβ−1
exp−x−a
θβ
x,a,θ,α,β R,α > 0,
x⩾a θ > 0, x⩽a θ < 0.
α
a θ α β
α α=n
α=k
2
¯
β= −β
σ θ= (2σ2)1/β
σ
Special cases: Miscellaneous
β=1
Stacy
a θ α β
0
1
β
n
<0
n <0
1
2k
1
√2
1
2k
01
1
2k
1
2
1
2k
1
2
1
0>0n1
1
2
1
2k
1
2k
1 1
2
3
3
2
2
1
2k
√21
2k
1
2
3
2
n >0
>0
11
β>0
(k,n )
Stacy(x;θ,α,β) = 1
Γ(α)
β
θx
θαβ−1
exp−x
θβ
=Amoroso(x; 0, θ,α,β)
Amoroso
β generalized inverse
gamma
Stacy(2σ2)
1
β,1
2,β∼Normal(0, σ)
2
β
k
Stacy(2σ2)
1
β,1
2k,β∼k
i=1Normal(0, σ)2
1
β
Pseudo-Weibull
PseudoWeibull(x;a,θ,β) = 1
Γ(1+1
β)
β
|θ|x−a
θβ
exp−x−a
θβ
β > 0
=Amoroso(x;a,θ, 1 +1
β,β)
Half exponential power
HalfExpPower(x;a,θ,β) = 1
Γ(1
β)
β
θ
exp−x−a
θβ
=Amoroso(x;a,θ,1
β,β)
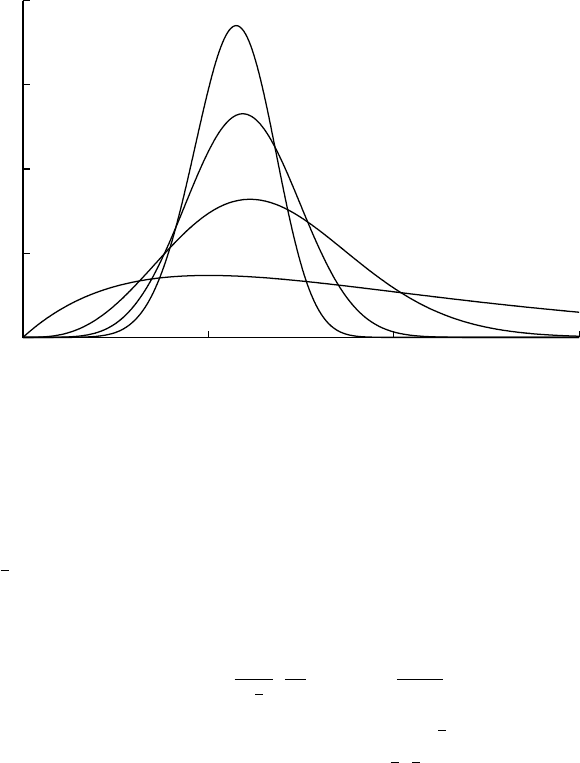
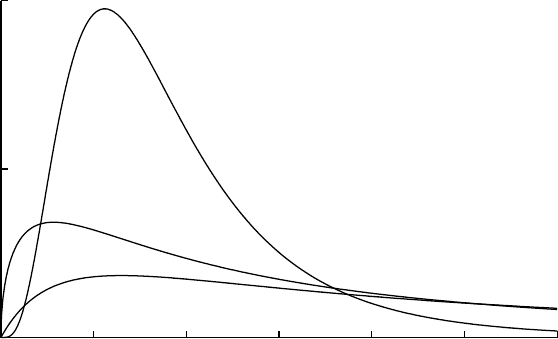
0
0.5
1
1.5
2
0 1 2 3
β=4
β=3,Wilson-Hilferty
β=2,scaledchi
β=1,gamma
Amoroso(x; 0, 1, 2, β)
β= −1 β=1
β=2
3 β=2
Hohlfeld
Hohlfeld(x;a,θ) = 1
Γ(2
3)
3
2θ
exp−x−a
θ3/2
=HalfExpPower(x;a,θ,3
2)
=Amoroso(x;a,θ,2
3,3
2)
Special cases: Positive integer β
β=1

Nakagami
Nakagami(x;a,θ,α)
=2
Γ(α)|θ|x−a
θ2α−1
exp−x−a
θ2
=Amoroso(x;a,θ,α, 2)
Half normal
HalfNormal(x;a,σ) = 2
√2πσ2exp−(x−a)2
2σ2
(x−a)/σ > 0
=Amoroso(x;a,√2σ2,1
2, 2)
Chi χ
Chi(x;k) = √2
Γ(k
2)x
√2k−1
exp−x2
2
k
=ScaledChi(x; 1, k)
=Stacy(x;√2, k
2, 2)
=Amoroso(x; 0, √2, k
2, 2)
k
Chi(k)∼ChiSqr(k)
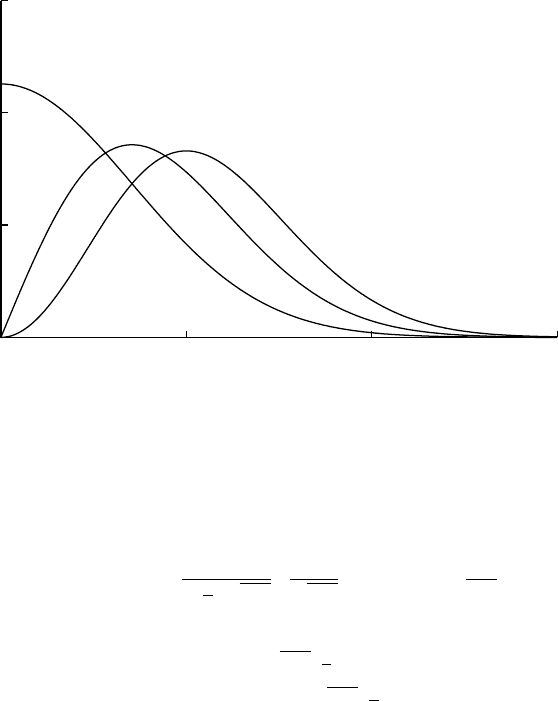
0
0.5
1
1.5
0 1 2 3
α=1/2,half-normal
α=1,Rayleigh
α=3/2,Maxwell
Amoroso(x;
0, 1, α, 2)
Scaled chi
ScaledChi(x;σ,k) = 2
Γ(k
2)√2σ2x
√2σ2k−1
exp−x2
2σ2
k
=Stacy(x;√2σ2,k
2, 2)
=Amoroso(x; 0, √2σ2,k
2, 2)
k
σ2

Rayleigh
Rayleigh(x;σ) = 1
σ2xexp−x2
2σ2
=ScaledChi(x;σ, 2)
=Stacy(x;√2σ2, 1, 2)
=Amoroso(x; 0, √2σ2, 1, 2)
σ2
Maxwell
Maxwell(x;σ) = √2
√πσ3x2exp−x2
2σ2
=ScaledChi(x;σ, 3)
=Stacy(x;√2σ2,3
2, 2)
=Amoroso(x; 0, √2σ2,3
2, 2)
σ2
Wilson-Hilferty
WilsonHilferty(x;θ,α) = 3
Γ(α)|θ|x
θ3α−1
exp−x
θ3
=Stacy(x;θ,α, 3)
=Amoroso(x; 0, θ,α, 3)
α
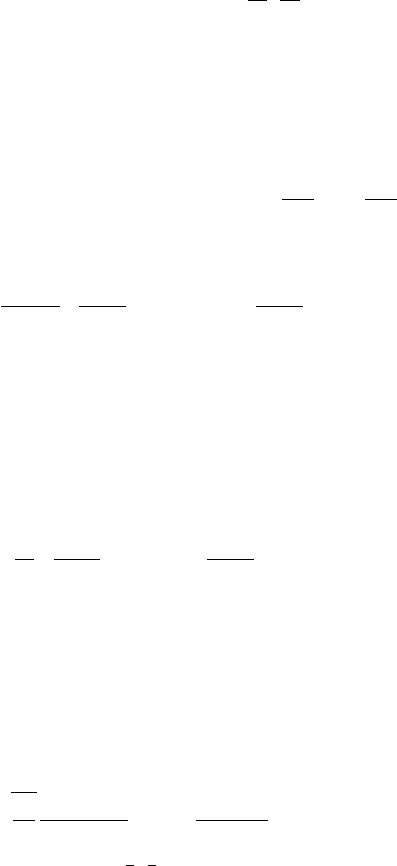
WilsonHilferty(x;θ,α)≈Normal(x; 1 −2
9α,2
9α)
Amoroso(x; 0, θ,α, 4)
Special cases: Negative integer β
β
β (x−a
θ)7→ (θ
x−a)
Inverse gamma
InvGamma(x;θ,α) = 1
Γ(α)|θ|θ
x−aα+1
exp−θ
x−a
=Amoroso(x;a,θ,α,−1)
Inverse exponential
InvExp(x;a,θ) = 1
|θ|θ
x−a2
exp−θ
x−a
=InvGamma(x;a,θ, 1)
=Amoroso(x;a,θ, 1, −1)
Lévy
L´evy(x;a,c) = |c|
2π
1
(x−a)3/2exp−c
2(x−a)
=Amoroso(x;a,c
2,1
2,−1)
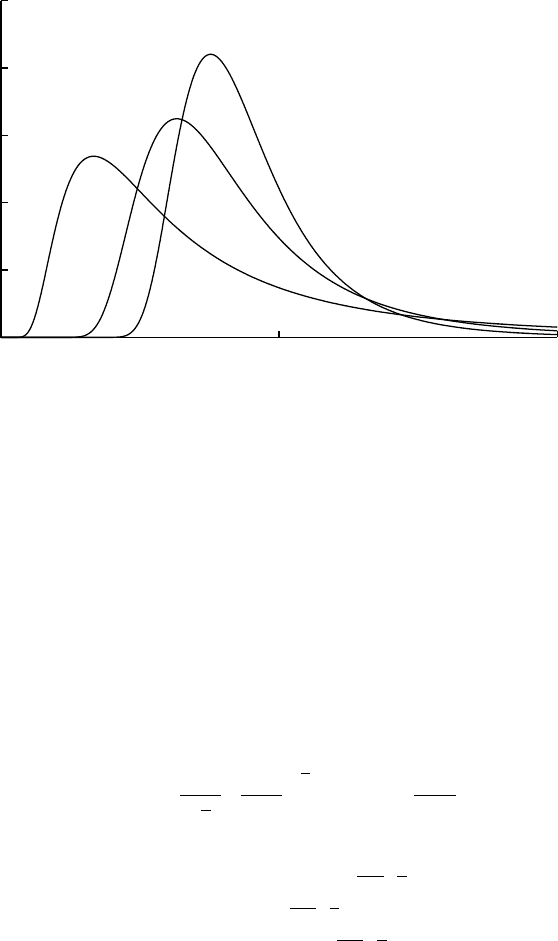
0
0.5
1
1.5
2
2.5
0 1 2
β=-1
inverse
gamma
β=-2
scaled
inverse-chi
β=-3
Amoroso(x;
0, 1, 2, β) β
Scaled inverse chi-square
ScaledInvChiSqr(x;σ,k)
=2σ2
Γ(k
2)1
2σ2xk
2+1
exp−1
2σ2x
k
=InvGamma(x; 0, 1
2σ2,k
2)
=Stacy(x;1
2σ2,k
2,−1)
=Amoroso(x; 0, 1
2σ2,k
2,−1)

α
Inverse chi-square
InvChiSqr(x;k) = 2
Γ(k
2)1
2xk
2+1
exp−1
2x
k
=ScaledInvChiSqr(x; 1, k)
=InvGamma(x; 0, 1
2,k
2)
=Stacy(x;1
2,k
2,−1)
=Amoroso(x; 0, 1
2,k
2,−1)
Scaled inverse chi
ScaledInvChi(x;σ,k)
=2√2σ2
Γ(k
2)1
√2σ2xk+1
exp−1
2σ2x2
=Stacy(x;1
√2σ2,k
2,−2)
=Amoroso(x; 0, 1
√2σ2,k
2,−2)
Inverse chi
InvChi(x;k) = 2√2
Γ(k
2)1
√2xk+1
exp−1
2x2
=Stacy(x;1
√2,k
2,−2)
=Amoroso(x; 0, 1
√2,k
2,−2)
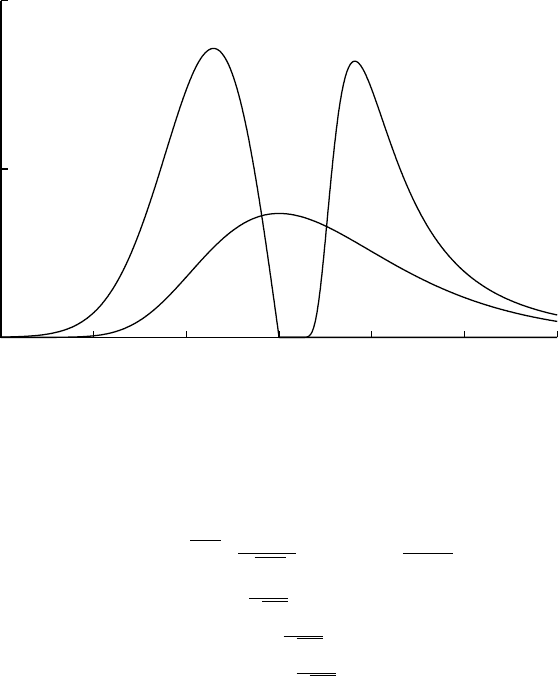
0
0.5
1
-3 -2 -1 0 1 2 3
standardGumbel
reversedWeibull,β=2 Frechet,β=-2
Inverse Rayleigh
InvRayleigh(x;σ) = 2√2σ21
√2σ2x3
exp−1
2σ2x2
=Stacy(x;1
√2σ2, 1, −2)
=Fr´echet(x; 0, 1
√2σ2, 2)
=Amoroso(x; 0, 1
√2σ2, 1, −2)

Special cases: Extreme order statistics
Generalized Fisher-Tippett
GenFisherTippett(x;a,ω,n,β)
=nn
Γ(n)
β
ωx−a
ωnβ−1
exp−nx−a
ωβ
n
=Amoroso(x;a,ω/n 1
β,n,β)
N
N n≪N n
β
β ∞
β < 0 β > 0
β/ω
n n
Fisher-Tippett
FisherTippett(x;a,ω,β)
=
β
ωx−a
ωβ−1
exp−x−a
ωβ
=GenFisherTippett(x;a,ω, 1, β)
=Amoroso(x;a,ω, 1, β)
max stable distribution
β/ω < 0 min stable distribution
β/ω > 0

β/ω > 0
max FisherTippett(a,ω1,β),FisherTippett(a,ω2,β)
∼FisherTippett(a,ω1ω2
(ωβ
1+ωβ
2)1/β ,β)
exp−x−a
ωβ
Generalized Weibull
GenWeibull(x;a,ω,n,β)
=nn
Γ(n)
β
|ω|x−a
ωnβ−1
exp−nx−a
ωβ
β > 0
=GenFisherTippett(x;a,ω,n,β)
=Amoroso(x;a,ω/n 1
β,n,β)
n
a ω
n
Weibull
Weibull(x;a,ω,β) = β
|ω|x−a
ωβ−1
exp−x−a
ωβ
β > 0
=FisherTippett(x;a,ω,β)
=Amoroso(x;a,ω, 1, β)
a ω

reversed Weibull
β=1 β=2
Generalized Fréchet
GenFr´echet(x;a,ω,n,¯
β)
=nn
Γ(n)
¯
β
|ω|x−a
ω−n¯
β−1
exp−nx−a
ω−¯
β
¯
β > 0
=GenFisherTippett(x;a,ω,n,−¯
β)
=Amoroso(x;a,ω/n 1
β,n,−¯
β),
n
ω
Fréchet
Fr´echet(x;a,ω,¯
β) = ¯
β
|ω|x−a
ω−¯
β−1
exp−x−a
ω−¯
β
¯
β > 0
=FisherTippett(x;a,ω,−¯
β)
=Amoroso(x;a,ω, 1, −¯
β)
ω
¯
β=1 ¯
β=2
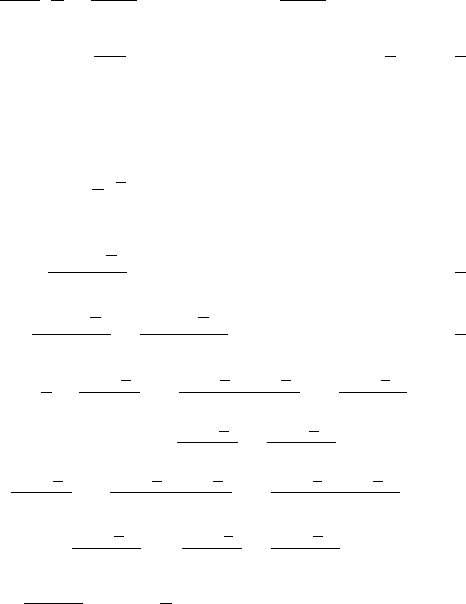
Amoroso(x;a,θ,α,β)
1
Γ(α)
β
θx−a
θαβ−1
exp−x−a
θβ
1−Qα,x−a
θβθ
β>0θ
β<0
a,θ,α,β R,α > 0
x⩾a θ > 0
x⩽a θ < 0
a+θ(α−1
β)1
βαβ ⩾1
a αβ ⩽1
a+θΓ(α+1
β)
Γ(α)α+1
β⩾0
θ2Γ(α+2
β)
Γ(α)−Γ(α+1
β)2
Γ(α)2α+2
β⩾0
sgn(β
θ)Γ(α+3
β)
Γ(α)−3Γ(α+2
β)Γ(α+1
β)
Γ(α)2+2Γ(α+1
β)3
Γ(α)3
Γ(α+2
β)
Γ(α)−Γ(α+1
β)2
Γ(α)23/2
Γ(α+4
β)
Γ(α)−4Γ(α+3
β)Γ(α+1
β)
Γ(α)2+6Γ(α+2
β)Γ(α+1
β)2
Γ(α)3
−3Γ(α+1
β)4
Γ(α)4Γ(α+2
β)
Γ(α)−Γ(α+1
β)2
Γ(α)22
−3
ln |θ|Γ(α)
|β|+α+1
β−αψ(α)
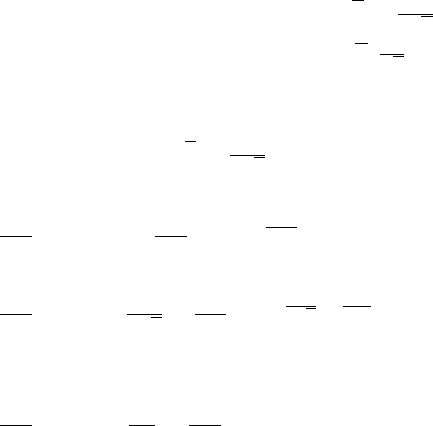
Interrelations
GammaExp(x;ν,λ,α) = lim
β→∞
Amoroso(x;ν+βλ,−βλ,α,β)
LogNormal(x;a,ϑ,σ) = lim
α→∞
Amoroso(x;a,ϑα−σ√α,α,1
σ√α)
Normal(x;µ,σ) = lim
α→∞
Amoroso(x; 0, µ−σ√α,σ
√α,α, 1)
lim
α→∞
Amoroso(x;a,ϑα−σ√α,α,1
σ√α)
∝x−a
θ−1expαln(x−a
θ)β−eln(x−a
θ)β
∝x−a
ϑ−1expα1
σ√αln(x−a
ϑ) − αe
1
σ√αln(x−a
ϑ)
∝x−a
ϑ−1exp−1
2σ2ln x−a
ϑ2
=LogNormal(x;a,ϑ,σ)

Beta β
Beta(x;a,s,α,γ)
=1
B(α,γ)
1
|s|x−a
sα−11−x−a
sγ−1
=GenBeta(x;a,s,α,γ, 1)
Special cases
β=1
α < 1 γ < 1
U-shaped beta (α−1)(γ−1)⩽0
J-shaped beta
Standard beta
StdBeta(x;α,γ) = 1
B(α,γ)xα−1(1−x)γ−1
=Beta(x; 0, 1, α,γ)
=GenBeta(x; 0, 1, α,γ, 1)
α > 0 γ > 0
x∈[0, 1]

0
0.5
1
1.5
2
2.5
3
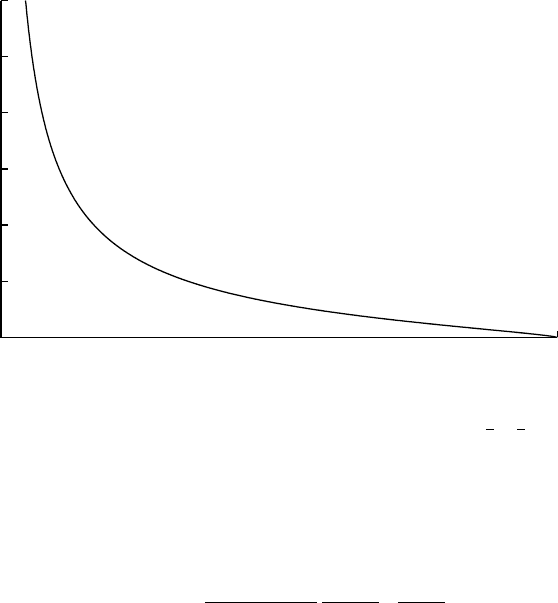
0 1
Beta(0, 1, 2, 4)
Pert
a b x
Pert(x;a,b,x)
=1
B(α,γ)(b−a)x−a
b−aα−1b−x
b−aγ−1
x =a+4x +b
6
α=(x −a)(2x −a−b)
(x −x)(b−a)
γ=α(b−x)
x −a
=Beta(x;a,b−a,α,γ)
=GenBeta(x;a,b−a,α,γ, 1)
modied
pert x =a+λx+b
2+λ
λ
0
0.5
1
1.5
2
2.5
3
0 1
Beta(0, 1, 1
4, 1 3
4)
Pearson XII
PearsonXII(x;a,b,α) = 1
B(α,−α+2)
1
|b−a|x−a
b−xα−1
=Beta(x;a,b−a,α, 2 −α)
=GenBeta(x;a,b−a,α, 2 −α, 1)
0<α<2

Beta(x;a,s,α,γ)
1
B(α,γ)
1
|s|x−a
sα−11−x−a
sγ−1
Bα,γ;x−a
s
B(α,γ)=I(α,γ;x−a
s)s > 0s < 0
a,s,α,γ, R,
α,γ⩾0
a⩾x⩾a+s,s > 0a+s⩾x⩾a,s < 0
a+sα−1
α+γ−2α,γ > 1
a+sα
α+γ
s2αγ
(α+γ)2(α+γ+1)
sgn(s)2(γ−α)√α+γ+1
(α+γ+2)√αγ
6(α−γ)2(α+γ+1) − αγ(α+γ+2)
αγ(α+γ+2)(α+γ+3)
ln(|s|) + lnB(α,γ)− (α−1)ψ(α)
− (γ−1)ψ(γ)+(α+γ−2)ψ(α+γ)
1F1(α;α+γ;it)
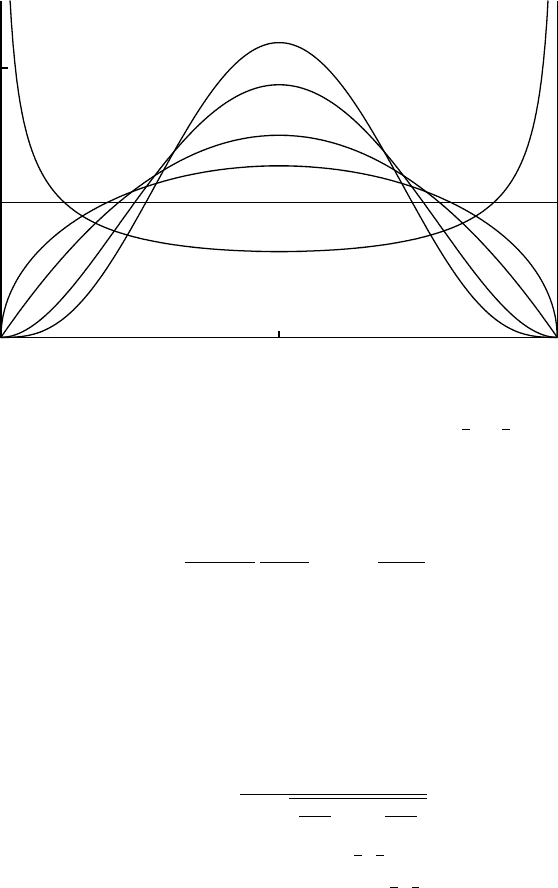
0
0.5
1
-1 0 1
Arcsine
Uniform
Semicircle
Epanechnikov
Biweight
Triweight
α=1
2, 1, 3
2, 2, 3, 4
Pearson II
PearsonII(x;µ,b,α) = 1
22α−1|b|
Γ(2α)
Γ(α)21−x−µ
b2α−1
=Beta(x;µ−b, 2b,α,α)
=GenBeta(x;µ−b, 2b,α,α, 1)
[µ−b,µ+b]
Arcsine
Arcsine(x;a,s) = 1
π|s|(x−a
s)(1−x−a
s)
=Beta(x;a,s,1
2,1
2)
=GenBeta(x;a,s,1
2,1
2, 1)
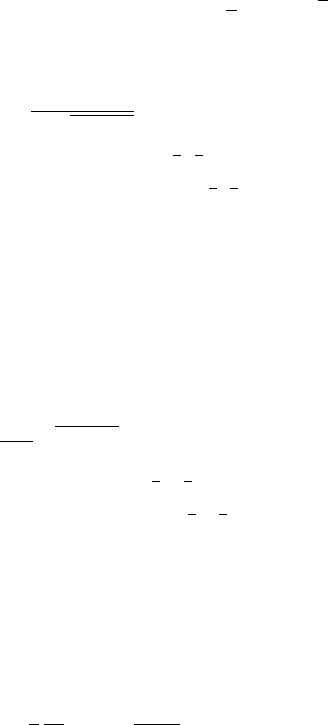
ArcsineCDF(x; 0, 1) = 2
πarcsin(√x)
Central arcsine
CentralArcsine(x;b) = 1
2π√b2−x2
=Beta(x;b,−2b,1
2,1
2)
=GenBeta(x;b,−2b,1
2,1
2, 1)
x∈[−b,b]
b b=1
Semicircle
Semicircle(x;b) = 2
πb2b2−x2
=Beta(x;−b, 2b, 1 1
2, 1 1
2)
=GenBeta(x;−b, 2b, 1 1
2, 1 1
2, 1)
Epanechnikov
Epanechnikov(x;µ,b) = 3
4
1
|b|1−x−µ
b2
=PearsonII(x;µ,b, 2)
=Beta(x;µ−b, 2b, 2, 2)
=GenBeta(x;µ−b, 2b, 2, 2, 1)

Biweight
Biweight(x;µ,b) = 15
16
1
|b|1−x−µ
b22
=PearsonII(x;µ,b, 3)
=Beta(x;µ−b, 2b, 3, 3)
=GenBeta(x;µ−b, 2b, 3, 3, 1)
Triweight
Triweight(x;µ,b) = 35
32
1
|b|1−x−µ
b23
=PearsonII(x;µ,b, 4)
=Beta(x;µ−b, 2b, 4, 4)
=GenBeta(x;µ−b, 2b, 4, 4, 1)
Interrelations
OrderStatisticUniform(a,s)(x;α,γ) = Beta(x;a,s,α,γ)
Beta(x;a,s, 1, 1) = Uniform(x;a,s)
StdBeta(α,γ)∼StdGamma1(α)
StdGamma1(α) + StdGamma2(γ)
Gamma(x;a,θ,α) = lim
γ→∞
Beta(x;a,θγ,α,γ)

Beta prime
β′
BetaPrime(x;a,s,α,γ)
=1
B(α,γ)
1
|s|x−a
sα−11+x−a
s−α−γ
=GenBetaPrime(x;a,s,α,γ, 1)
a,s,α,γ R,α > 0, γ > 0
x⩾a s > 0, x⩽a s < 0
Special cases
β=1
Standard beta prime
StdBetaPrime(x;α,γ) = 1
B(α,γ)xα−1(1+x)−α−γ
=BetaPrime(x; 0, 1, α,γ)
=GenBetaPrime(x; 0, 1, α,γ, 1)
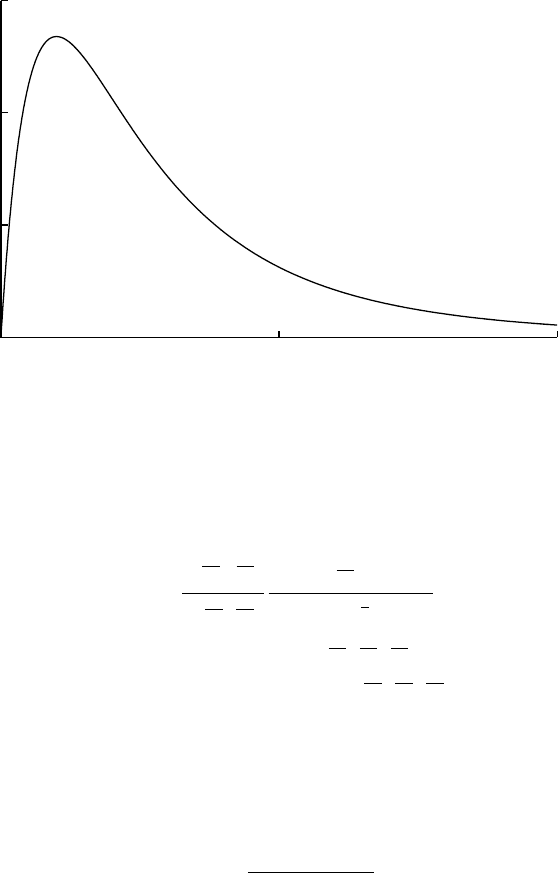
0
0.5
1
1.5
0 1 2
BetaPrime(0, 1, 2, 4)
F
F(x;k1,k2) = k
k1
2
1k
k2
2
2
B(k1
2,k2
2)
xk1
2−1
(k2+k1x)1
2(k1+k2)
=BetaPrime(x; 0, k2
k1,k1
2,k2
2)
=GenBetaPrime(x; 0, k2
k1,k1
2,k2
2, 1)
k1,k2
k1 k2
F(k1,k2)∼ChiSqr(k1)/k1
ChiSqr(k2)/k2
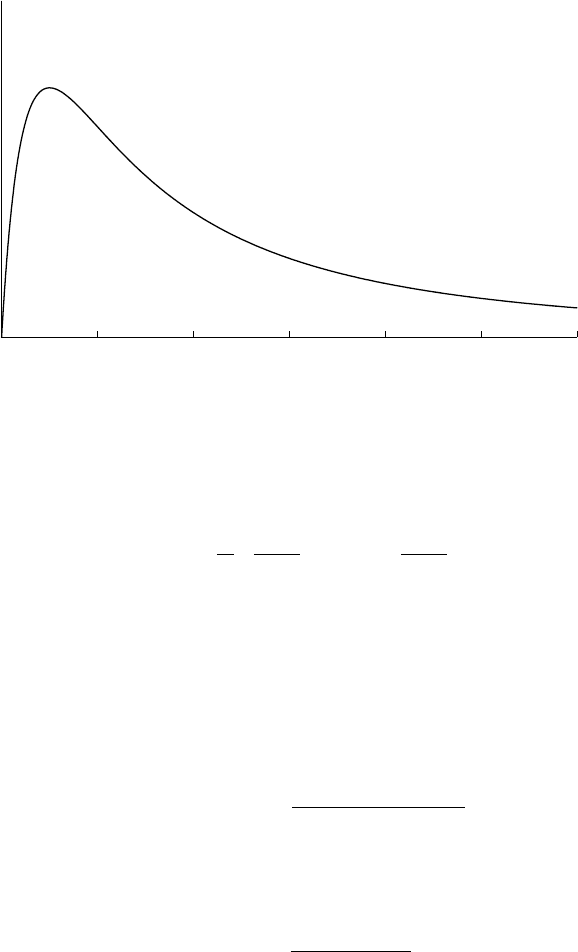
0
0123456
InvLomax(0, 1, 2)
Inverse Lomax
InvLomax(x;a,s,α) = α
|s|x−a
sα−11+x−a
s−α−1
=BetaPrime(x;a,s,α, 1)
=GenBetaPrime(x;a,s,α, 1, 1)
Interrelations
StdBetaPrime(α,γ)∼1
StdBetaPrime(γ,α)
StdBetaPrime(α,γ)∼1
StdBeta(α,γ)−1−1

BetaPrime(x;a,s,α,γ)
1
B(α,γ)
1
|s|x−a
sα−11+x−a
s−α−γ
Bα,γ;(1+ ( x−a
s)−1)−1
B(α,γ)s > 0s < 0
=Iα,γ;(1+ ( x−a
s)−1)−1
a,s,α,γ, R
α > 0, γ > 0
x⩾a s > 0
x⩽a s < 0
a+sα−1
γ+1α⩾1
a α < 1
a+sα
γ−1γ > 1
s2α(α+γ−1)
(γ−2)(γ−1)2γ > 2

GenBetaPrime(a,s,α,γ,β)∼a+sStdBeta(α,γ)−1−1−1
β
BetaPrime(0, s,α,γ)∼Gamma20, Gamma1(0, s,γ),α
compound gamma distribution
Gamma(x; 0, θ,α) = lim
γ→∞
BetaPrime(x; 0, θγ,α,γ)
InvGamma(x;θ,α) = lim
γ→∞
BetaPrime(x; 0, θ/γ,α,γ)

beta-exponential
BetaExp(x;ζ,λ,α,γ) = 1
B(α,γ)
1
|λ|e−αx−ζ
λ1−e−x−ζ
λγ−1
x,ζ,λ,α,γ R,
α,γ > 0, x−ζ
λ>0
ζ λ
α γ standard beta-exponential
ζ=0 λ=1
xγ−1
Special cases
Exponentiated exponential
ExpExp(x;ζ,λ,γ) = γ
|λ|e−x−ζ
λ1−e−x−ζ
λγ−1
=BetaExp(x;ζ,λ, 1, γ)
ExpExpCDF(x;ζ,λ,γ) = ExpCDF(x;ζ,λ)γ
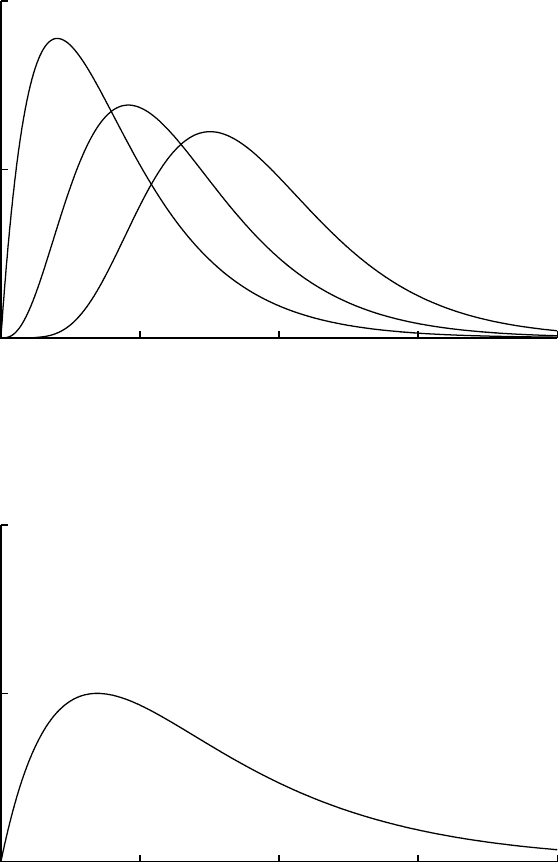
0
0.5
1
01234
BetaExp(x; 0, 1, 2, 2)
BetaExp(x; 0, 1, 2, 4) BetaExp(x; 0, 1, 2, 8)
0
0.5
1
01234
ExpExp(x; 0, 1, 2)
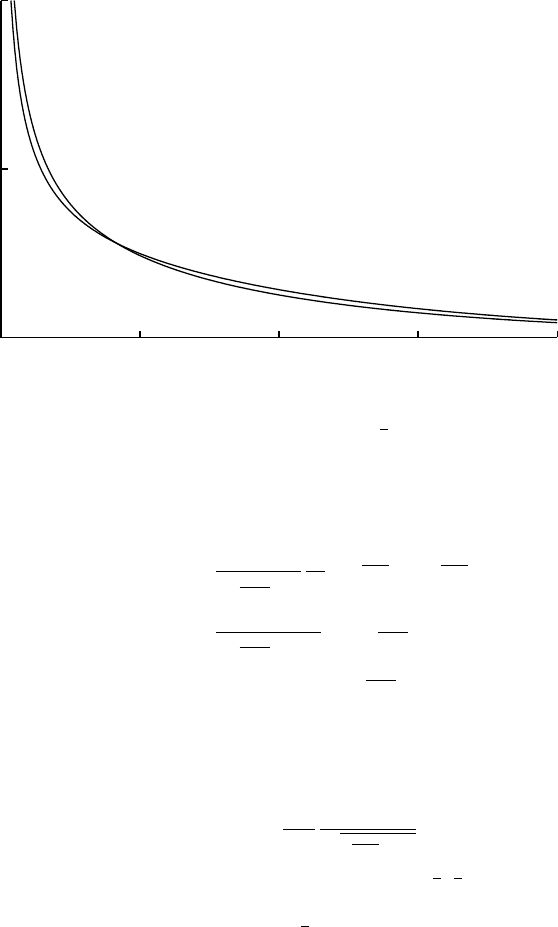
0
0.5
1
01234
HyperbolicSine(x;1
2)
NadarajahKotz(x)
Hyperbolic sine
HyperbolicSine(x;ζ,λ,γ) = 1
B(1−γ
2,γ)
1
|λ|e+x−ζ
2λ−e−x−ζ
2λγ−1
=2γ−1
B(1−γ
2,γ)|λ|sinh(x−ζ
2λ)γ−1
=BetaExp(x;ζ,λ,1−γ
2,γ), 0 <γ<1
Nadarajah-Kotz
NadarajahKotz(x;ζ,λ) = 1
π|λ|
1
ex−ζ
λ−1
=BetaExp(x;ζ,λ,1
2,1
2)
α=γ=1
2

ζ λ α γ
0 1
1
1
2(1γ)γ0<γ<1
1
2
1
2
1
NadarajahKotzCDF(x; 0, 1) = 2
πarctan exp(x) − 1 .
Interrelations
StdBetaExp(α,γ)∼−lnStdBeta(α,γ)
StdBetaExp(α,γ)∼−ln StdGamma1(α)
StdGamma1(α) + StdGamma2(γ)
OrderStatisticExp(ζ,λ)(x;γ,α) = BetaExp(x;ζ,λ,α,γ)
γ=1
BetaExp(x;ζ,λ,α, 1) = Exp(x;ζ,λ
α)
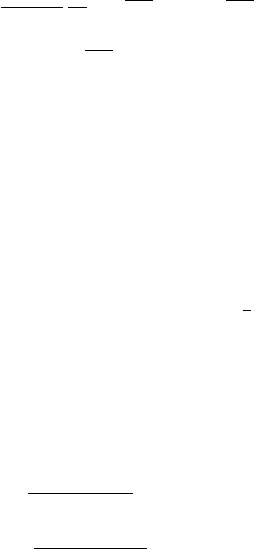
BetaExp(x;ζ,λ,α,γ)
1
B(α,γ)
1
|λ|e−αx−ζ
λ1−e−x−ζ
λγ−1
Iα,γ;e−x−ζ
λλ > 0λ < 0
ζ,λ,α,γ R
α,γ > 0
x⩾ζ λ > 0
x⩽ζ λ < 0
ζ+λ[ψ(α+γ) − ψ(α)]
λ2[ψ1(α) − ψ1(α+γ)]
−sgn(λ)ψ2(α) − ψ2(α+γ)
ψ1(α) − ψ1(α+γ)3
2
3ψ1(α)2−6ψ1(α)ψ1(α+γ) + 3ψ1(α+γ)2+ψ3(α)
−ψ3(α+γ)ψ1(α) − ψ1(α+γ)2
ln |λ|+ln B(α,γ)+(α+γ−1)ψ(α+γ)
− (γ−1)ψ(γ) − αψ(α)
eζt B(α−λt,γ)
B(α,γ)
eiζt B(α−iλt,γ)
B(α,γ)

beta-logistic
BetaLogistic(x;ζ,λ,α,γ) = 1
B(α,γ)|λ|
e−αx−ζ
λ
1+e−x−ζ
λα+γ
x,ζ,λ,α,γ R
α,γ > 0
ζ
λ α γ standard beta-logistic
ζ=0 λ=1
Special cases
Burr type II
BurrII(x;ζ,λ,γ) = γ
|λ|
e−x−ζ
λ
1+e−x−ζ
λγ+1
=BetaLogistic(x;ζ,λ, 1, γ)
0
0.5
-3 -2 -1 0 1 2 3 4 5 6
γ=2
γ=8
BurrII(x; 0, 1, γ)
Reversed Burr type II
RevBurrII(x;α) = γ
|λ|
e+x−ζ
λ
1+e+x−ζ
λγ+1
=BurrII(x;ζ,−λ,γ)
=BetaLogistic(x;ζ,−λ, 1, γ)
=BetaLogistic(x;ζ,+λ,γ, 1)
λ 1 α
Symmetric Beta-Logistic
ζ λ α γ
α α
1
2
1
2
BetaLogistic(x;ζ,λ,α,γ)
1
B(α,γ)|λ|
e−αx−ζ
λ
1+e−x−ζ
λα+γ
Bγ,α;(1+e−x−ζ
λ)−1
B(α,γ)λ > 0λ < 0
=Iγ,α;(1+e−x−ζ
λ)−1
ζ,λ,α,γ R
α,γ > 0
x∈[−∞,+∞]
ζ+λ[ψ(γ) − ψ(α)]
λ2[ψ1(α) + ψ1(γ)]
sgn(λ)ψ2(γ) − ψ2(α)
[ψ1(α) + ψ1(γ)]3/2
ψ3(α) + ψ3(γ)
[ψ1(α) + ψ1(γ)]2
eζt Γ(α−λt)Γ(γ+λt)
Γ(α)Γ(γ)
eiζt Γ(α+iλt)Γ(γ−iλt)
Γ(α)Γ(γ)
SymBetaLogistic(x;ζ,λ,α) = 1
B(α,α)|λ|
e−αx−ζ
λ
1+e−x−ζ
λ2α
=1
B(α,α)|λ|1
2sechx−ζ
2λ2α
=BetaLogistic(x;ζ,λ,α,α)
Logistic
Logistic(x;ζ,λ) = 1
|λ|
e−x−ζ
λ
1+e−x−ζ
λ2
=1
4|λ|sech2x−ζ
λ
=BetaLogistic(x;ζ,λ, 1, 1)
Hyperbolic secant
HyperbolicSecant(x;ζ,λ) = 1
π|λ|
1
e+x−ζ
2λ+e−x−ζ
2λ
=1
2π|λ|sech(x−ζ
2λ)
=BetaLogistic(x;ζ,λ,1
2,1
2)
gd(z)
HyperbolicSecantCDF(x;ζ,λ) = 1
πgd(x−ζ
2λ)
=2
πarctan(ex−ζ
2λ) − 1
2
0
0.5
-3 -2 -1 0 1 2 3
α→∞ α=1
α=1
2 α→0
HyperbolicSecant(x; 0, 1/π)
Interrelations
BetaLogistic(0, 1, α,γ)∼−ln BetaPrime(0, 1, α,γ)
BetaLogistic(ζ,λ,α,γ)∼ζ−λln StdGamma1(γ)
StdGamma2(α)
BetaLogistic(x;ζ,+λ,α,γ) = BetaLogistic(x;ζ,−λ,γ,α)
α γ
OrderStatisticLogistic(ζ,λ)(x;γ,α) = BetaLogistic(x;ζ,λ,α,γ)
GammaExp(x;ν,λ,α) = lim
γ→∞
BetaLogistic(x;ν+λ/ ln γ,λ,α,γ)
Laplace(x;η,θ) = lim
α→0BetaLogistic(x;η,θα α,α)

Pearson IV t
PearsonIV(x;a,s,m,v)
=2F1(−iv,iv;m; 1)
|s|B(m−1
2,1
2)1+x−a
s2−m
exp−2varctanx−a
s
=2F1(−iv,iv;m; 1)
|s|B(m−1
2,1
2)1+ix−a
s−m+iv1−ix−a
s−m−iv
x,a,s,m,v∈R
m > 1
2
arctan(z) = 1
2iln 1−iz
1+iz
Interrelations
PearsonIV(x;a,s,m,v) = PearsonIV(x;a,−s,m,−v).
v=0
PearsonIV(x;a,s,m, 0) = PearsonVII(x;a,s,m)

lim
v→∞
exp(−2varctan(−2vx) − πv) = e−1
x
v
lim
v→∞
PearsonIV(x; 0, −θ
2v,α+1
2,v) = InvGamma(x;θ,α)
α=1m=1

(x;a,s,m,v)
2F1(−iv,iv;m; 1)
|s|B(m−1
2,1
2)1+x−a
s2−m
×exp−2varctanx−a
s
(x;a,s,m,v)
×|s|
2m−1i−x−a
s2F11, m+iv; 2m;2
i−ix−a
s
a,s,m,v R
m > 1
2
x∈[−∞,+∞]
a−sv
m
a−sv
(m−1)(m > 1)
s2
2m−3(1+v2
(m−1)2) (m > 3
2)

Generalized beta
GenBeta(x;a,s,α,γ,β)
=1
B(α,γ)
β
sx−a
sαβ−11−x−a
sβγ−1
x,a,θ,α,γ,β R,
α > 0, γ > 0
x∈[a,a+s],s > 0, β > 0
x∈[a+s,a],s < 0, β > 0
x∈[a+s,+∞],s > 0, β < 0
x∈[−∞,a+s],s < 0, β < 0
x→(x−a
s)β
a s β
α γ
Special Cases
β
Kumaraswamy
Kumaraswamy(x;a,s,γ,β) = γ
β
sx−a
sβ−11−x−a
sβγ−1
=GenBeta(x;a,s, 1, γ,β)
a s α γ β
<1<1
(α1)(γ1)⩽0
α α
1
2
1
2
b2b1
2
1
2
b2b11
211
2
αα < 2
(x;a,s,α,γ,β)
1
B(α,γ)
β
sx−a
sαβ−11−x−a
sβγ−1
Bα,γ;(x−a
s)β
B(α,γ)
β
s>0β
s<0
=Iα,γ;(x−a
s)β
a,s,α,γ,β, R,
α,γ⩾0
x∈[a,a+s], 0 < s, 0 < β
x∈[a+s,a],s < 0, 0 < β
x∈[a+s,+∞], 0 < s,β < 0
x∈[−∞,a+s],s < 0, β < 0
a+sB(α+1
β,γ)
B(α,γ)α+1
β>0
s2B(α+2
β,γ)
B(α,γ)−s2B(α+1
β,γ)2
B(α,γ)2
E(Xh)shB(α+h
β,γ)
B(α,γ)a=0, α+h
β>0

0
0.5
1
1.5
2
2.5
3
0 1
Kumaraswamy(0, 1, 2, 4)
KumaraswamyCDF(x; 0, 1, γ,β) = 1− (1−xβ)γ.
Interrelations
OrderStatisticPowerFn(a,s,β)(x;α,γ) = GenBeta(x;a,s,α,γ,β)
GenBeta(x;a,s, 1, 1, β) = PowerFn(x;a,s,β)
β=1
GenBeta(x;a,s,α,γ, 1) = Beta(x;a,s,α,γ),

β= −1
GenBeta(x;a,s,α,γ,−1) = BetaPrime(x;a+s,s,γ,α).
limβ→0 αβ =
lim
β→0GenBeta(x;a,s,δ
β,γ,β) = UnitGamma(x;a,s,γ,δ).
γ→∞ α→∞
lim
γ→∞
GenBeta(x;a,θγ 1
β,α,γ,β) = Amoroso(x;a,θ,α,β).
limβ→+∞
lim
β→+∞
GenBeta(x;ζ+βλ,−βλ,α,γ,β) = BetaExp(x;ζ,λ,α,γ).

Generalized beta prime
GenBetaPrime(x;a,s,α,γ,β)
=1
B(α,γ)
β
sx−a
sαβ−11+x−a
sβ−α−γ
a,s,α,γ,β R,α,γ > 0
a s α γ
β α γ
Special cases
Transformed beta
TransformedBeta(x;s,α,γ,β)
=1
B(α,γ)
β
sx
sαβ−11+x
sβ−α−γ
=GenBetaPrime(x; 0, s,α,γ,β)
a=0
Burr
a s α γ β
β
β
1
βm1
β
k2
k1
k1
2
k2
2
1
2
1
2
1
2
Burr(x;a,s,γ,β) = βγ
|s|x−a
sβ−11+x−a
sβ−γ−1
=GenBetaPrime(x;a,s, 1, γ,β)
Dagum
(x;a,s,α,γ,β)
1
B(α,γ)
β
sx−a
sαβ−11+x−a
sβ−α−γ
Bα,γ;(1+ ( x−a
s)−β)−1
B(α,γ)
β
s>0β
s<0
=Iα,γ;(1+ ( x−a
s)−β)−1
a,s,α,γ,β R
α > 0, γ > 0
x⩾a s > 0
x⩽a s < 0
a+sB(α+1
β,γ−1
β)
B(α,γ)−α < 1
β< γ
s2
B(α+2
β,γ−2
β)
B(α,γ)−B(α+1
β,γ−1
β)
B(α,γ)2
−α < 2
β< γ
E[Xh]|s|hB(α+h
β,γ−h
β)
B(α,γ)a=0, −α < h
β< γ
Dagum(x;γ,β) = βγ
|s|x−a
sγβ−11+x−a
sβ−γ−1
=GenBetaPrime(x;a,s, 1, γ,−β)
=GenBetaPrime(x;a,s,γ, 1, +β)
Paralogistic
Paralogistic(x;a,s,β) = β2
|s|x−a
sβ−1
(1+x−a
sβ)β+1
=GenBetaPrime(x;a,s, 1, β,β)
Inverse paralogistic
InvParalogistic(x;a,s,β) = β2
|s|x−a
sβ2−1
(1+x−a
sβ)β+1
=GenBetaPrime(x;a,s,β, 1, β)
Log-logistic
LogLogistic(x;a,s,β) =
β
sx−a
sβ−1
1+x−a
sβ2
=Burr(x;a,s, 1, β)
=GenBetaPrime(x; 0, s, 1, 1, β)
LogLogistic(0, s,β)∼exp−Logistic(− ln s,1
β)
0
0.5
1
1.5
2
0 1 2
LogLogistic(x; 0, 1, β)
Half-Pearson VII
HalfPearsonVII(x;a,s,m)
=1
B(1
2,m−1
2)
2
|s|1+x−a
s2−m
=GenBetaPrime(x;a,s,1
2,m−1
2, 2)
Half-Cauchy
HalfCauchy(x;a,s) = 2
π|s|1+x−a
s2−1
=HalfPearsonVII(x;a,s, 1)
=GenBetaPrime(x;a,s,1
2,1
2, 2)
Half generalized Pearson VII
HalfGenPearsonVII(x;a,s,m,β)
=β
|s|B(m−1
β,1
β)1+x−a
sβ−m
=GenBetaPrime(x;a,s,1
β,m−1
β,β)
half Laha
HalfGenPearsonVII(x;a,s,m, 2) = HalfPearsonVII(x;a,s,m)
HalfGenPearsonVII(x;a,s, 1, 2) = HalfCauchy(x;a,s)
HalfGenPearsonVII(x;a,s, 1, 4) = HalfLaha(x;a,s)
HalfGenPearsonVII(x;a,s, 2, 1) = UniPrime(x;a,s)
m
lim
m→∞
HalfGenPearsonVII(x;a,θm 1
β,m,β) = HalfExpPower(x;a,θ,β)
Interrelations
α γ
GenBetaPrime(x;a,s,α,γ,β) = GenBetaPrime(x;a,s,γ,α,−β)
GenBetaPrime(a,s,α,γ,β)∼a+sStdGamma1(α)
StdGamma2(γ)1
β

lim
γ→∞
GenBetaPrime(x;a,θγ 1
β,α,γ,β) = Amoroso(x;a,θ,α,β)
lim
β→∞
GenBetaPrime(x;ζ+βλ,−βλ,α,γ,β) = BetaLogistic(x;ζ,λ,γ,α)
OrderStatisticLogLogistic(a,s,β)(x;γ,α) = GenBetaPrime(x;a,s,α,γ,β)

Pearson
Pearson(x;a,s;a1,a2;b0,b1,b2)
=1
N1−1
r0
x−a
se01−1
r1
x−a
se1
a,s,a1,a2,b0,b1,b2,x R
r0=−b1+√b2
1−4b2b0
2b2e0=−a1−a2r0
r1−r0
r1=−b1−√b2
1−4b2b0
2b2e1=a1+a2r1
r1−r0
N a2
a2
d
dx ln Pearson(x; 0, 1; a1,a2;b0,b1,b2) = − a1+a2x
b0+b1x+b2x2,
= − 1
x
a1x+a2x2
b0+b1x+b2x2,
=e0
x−r0
+e1
x−r1
.
a1,a2
a0
r0
r1
p(x)∝xα−1(1−x)γ−1, 0 < x < 1
p(x)∝xα−1(1+x)−α−γ, 0 < x < +∞
p(x)∝(i−x)m+iv(i+x)m−iv,−∞< x < +∞
Special cases
q-Gaussian
QGaussian(x;µ,σ,q) = 1
√2σ2Nexpq−1
2x−µ
σ2
=1
√2σ2N1−1
2(1−q)x−µ
σ21
1−q
−2< q < 3
x∈(−∞,+∞) 1⩽q < 3
x∈(µ−√2σ
√1−q,µ+√2σ
√1−q) q < 1
expq
N=
√π2Γ(1
1−q)
(3−q)√1−qΓ (3−q
2(1−q))−2< q < +1
√π q = +1
√πΓ(3−q
2(q−1))
√q−1Γ(1
q−1)+1< q < +3
QGaussian(x;µ,σ,q)
=
Beta(x;a−√2σ
√1−q,2√2σ
√1−q,2−q
1−q,2−q
1−q) −2< q < 1
PearsonII(x;a,√2σ
√1−q,2−q
1−q) −2< q < 1
Normal(x;µ,σ)q=1
PearsonVII(x;a,√2σ
√q−1,1
q−1)1< q < 3

a s a1a2b0b1b2
a s 0 0 0 1 −1
µb2b α −1 2α−2 0 1 −1
a s α −1α+γ−2 0 1 −1
a θ 0−10 1 0
a θ α −1−1 0 1 0
a s α −1−γ−1 0 1 1
a θ −1α+1 0 0 1
a θ −1 2 0 0 1
a s 2v2m1 0 1
a s 2m1 0 1
a s 2 1 0 1
µ σ 0 2 1 0 0

n
d
dx ln GUD(n)(x;a,s;a0,a1, . . . , an;b0,b1, . . . , bn;β)
= −
β
s
1
x−a
s
a0+a1x−a
sβ+··· +anx−a
snβ
b0+b1x−a
sβ+··· +bnx−a
snβ
a,s,a0,a1, . . . , an,b0,b1, . . . , bn,β,x R
β=1 a0=0
n=2
Special cases
Extended Pearson β=1
d
dx ln ExtPearson(x; 0, 1; a0,a1,a2;b0,b1,b2)
= − 1
x
a0+a1x+a2x2
b0+b1x+b2x2
a,s,a0,a1,a2,b0,b1,b2 R
Inverse Gaussian
InvGaussian(x;µ,λ) = λ
2πx3exp−λ(x−µ)2
2µ2x
=ExtPearson(x; 0, 1 ; −λ
2,2
3,λ
2µ2; 0, 1, 0)
=GUD(x; 0, 1 ; −λ
2,2
3,λ
2µ2; 0, 1, 0 ; 1)

a s a0a1a2b0b1b2β
1
1
2
3
−κ1α κ
−κ1α κ β
−κκ
1α−κ2
1α−κ−2
−λ1α κ

x > 0 µ > 0 λ > 0
Wald µ=1
x
t D
v Normal(vt,√2Dt)
y > 0
InvGaussian(y
v,y2
2D)
µ
lim
µ→∞
InvGaussian(x;µ,λ) = L´evy(x; 0, λ)
µ2/λ
i
InvGaussiani(x;µ′wi,λ′w2
i)
∼InvGaussianx;µ′
i
wi,λ′
i
wi2
µ λ
cInvGaussian(µ,λ)∼InvGaussian(cµ,cλ)
1
N
N
i=1
InvGaussiani(µ,λ)∼InvGaussian(µ,Nλ)
Halphen
Halphen(x;a,s,α,κ)
=1
2|s|Kα(2κ)x−a
sα−1
exp−κx−a
s−κx−a
s−1,
=GUD(x;a,s;−κ, 1 −α,κ; 0, 1, 0 ; 1)
0⩽x−a
s
Hyperbola
Hyperbola(x;a,s,κ)
=1
2|s|K0(2κ)x−a
s−1
exp−κx−a
s−κx−a
s−1,
=Halphen(x;a,s, 0, κ)
=GUD(x;a,s;−κ, 1, κ; 0, 1, 0 ; 1)
0⩽x−a
s
Halphen B
HalphenB(x;a,s,α,κ)
=2
|s|H2α(κ)x−a
sα−1
exp−x−a
s2
+κx−a
s,
=GUD(x;a,s; 1 −α,−κ, 2 ; 1, 0, 0 ; 1)
0⩽x−a
s
H2α(κ)
κ→∞
Inverse Halphen B
InvHalphenB(x;a,s,α,κ)
=2
|s|H2α(κ)x−a
s−α+1
exp−x−a
s−2
+κx−a
s−1,
=GUD(x;a,s; 1 −α,κ,−2; 0, 0, 1; 1)
0⩽x−a
s
κ→∞
Sichel
Sichel(x;a,s,α,κ,λ)
=(κ/λ)α/2
2|s|Kα(2√κλ)x−a
sα−1
exp−κx−a
s−λx−a
s−1,
=GUD(x;a,s;−λ, 1 −α,κ; 0, 1, 0 ; 1)
0⩽x−a
s
λ=κ
α=1
3
Libby-Novick
LibbyNovick(x;a,s,c,α,γ)
=1
|s|B(α,γ)x−a
sα−11−x−a
sγ−11− (1−c)x−a
s−α−γ
=GUD(x|a,s;α−1, 3 −α−c−cγ, 2c−2;
1, c−2, 1 −c; 1)
a,s,c,α,γ R,α,γ > 0
0⩽x−a
s⩽1
LibbyNovick(0, s1
s2,α,γ)∼Gamma1(0, s1,α)
Gamma1(0, s1,α) + Gamma2(0, s2,γ)

u=1 u→∞
Gauss hypergeometric
GaussHypergeometric(x;a,s,u,α,γ,δ)
=1
|s|N x−a
sα−11−x−a
sγ−11− (1−u)x−a
s−δ
N=B(α,γ)2F1(α,δ;α+γ, 1 −u)
a,s,u,α,γ,δ R,α,γ,δ > 0
=GUD(x;a,s;α−1, 2 −α−γ+ (1−u)(1+ρ+α),
u(α+γ−ρ−2); 1, −1−c,−u; 1)
0⩽x−a
s⩽1
Conuent hypergeometric
Confluent(x;α,γ,δ)
=1
Nx−a
sα−11−x−a
sγ−1
exp−κx−a
s
N=B(α,γ)1F1(α;α+γ;−κ)
=GUD(x; 0, 1; 1 −α,α+γ+κ−2; −κ; 1, −1, 0; 1)
0⩽x−a
s⩽1
Generalized Halphen
GenHalphen(x;a,s,α,κ,β)
=|β|
2|s|Kα(2κ)x−a
sβα−1
exp−κx−a
sβ
−κx−a
s−β
=GUD(x;a,s;−κ, 1 −α,κ; 0, 1, 0; β)
0⩽x−a
s⩽1

Greater Grand Unied Distributions
Appell Beta
AppellBeta(x;a,s,α,γ,ρ,δ)
=1
N |s|x−a
sα−11−x−a
sγ−1
1−ux−a
sρ1−vx−a
sδ
N=B(α,γ)F1(α,ρ,δ,α+γ;u,v)
=GUD(3)(x;a,s;a0,a1,a2,a3;b0,b1,b2,b3; 1)
b0= −1, b1=1+u+v,b2= −u−v−uv,b3=uv
F1
Laha
Laha(x;a,s) = √2
|s|π
1
1+ ( x−a
s)4
=GUD(4)(x;a,s; 0, −4, 0, 0, 0 ; 1, 0, 2, 0, 1 ; 1)

Bates
Bates(n)∼1
n
n
i=1
Uniformi(0, 1)
∼1
nIrwinHall(n)
n
Beta-Fisher-Tippett
BetaFisherTippett(x;ζ,λ,α,γ,β)
=1
B(α,γ)
β
λx−ζ
λβ−1
e−α(x−ζ
λ)β1−e−( x−ζ
λ)βγ−1
x,ζ,λ,α,γ,β R,
α,γ > 0, x−ζ
λ>0
OrderStatisticFisherTippett(a,s,β)(x;α,γ)
=BetaFisherTippett(x;a,s,α,γ,β)

β=1
inverse beta-exponentialβ= −1
expo-
nentiated Weibull α=1
Birnbaum-Saunders
BirnbaumSaunders(x;a,s,γ)
=1
2γ√2πs2
s
x−a(x−a
s+s
x−a)exp
(x−a
s−s
x−a)2
2γ2
Exponential power
ExpPower(x;ζ,θ,β) = β
2|θ|Γ(1
β)e−|x−ζ
θ|β
ExpPower(x;ζ,θ, 1) = Laplace(x;ζ,θ)
ExpPower(x;ζ,θ, 2) = Normal(x;ζ,θ/√2)
lim
β→∞
ExpPower(x;ζ,θ,β) = Uniform(x;ζ−θ, 2θ)
Generalized K
GenK(x;s,α1,α2,β) = 2|β|
|s|Γ(α1)Γ(α2)x
s1
2(α1+α2)β−1
Kα1−α22x
sβ
2
x⩾0, α1>0, α2>0
GenK(s1s2,α1,α2,β)∼Amoroso1(0, s1,α1,β)Amoroso2(0, s2,α2,β)
∼s1Gamma1(0, α1)1
βs2Gamma2(0, α2)1
β
∼s1s2Gamma1(1, α1)Gamma2(1, α2)1
β
∼s1s2K(1, α1,α2)1
β
Generalized Pearson VII
GenPearsonVII(x;a,s,m,β)
=β
2|s|B(m−1
β,1
β)1+
x−a
s
β−m
x,a,s,m,β R
β > 0, m > 0, βm > 1
GenPearsonVII(x;a,s,m, 2) = PearsonVII(x;a,s,m)
GenPearsonVII(x;a,s, 1, 2) = Cauchy(x;a,s)
GenPearsonVII(x;a,s, 1, 4) = Laha(x;a,s)
GenPearsonVII(x;a,s, 2, 1) = Meridian(x;a,s)
lim
m→∞
GenPearsonVII(x;a,m1/βθ,m,β) = ExpPower(x;a,θ,β)
half generalized Pearson VII
Holtsmark
Holtsmark(x;µ,c) = Stable(x;µ,c,3
2, 0)
Holtsmark(x;µ,c) = 1
πΓ(5
3)2F35
12 ,11
12 ;1
3,1
2,5
6;−4
729 (x−µ
c)6
−1
3π(x−µ
c)23F43
4, 1, 5
4;2
3,5
6,7
6,4
3;−4
729 (x−µ
c)6
+7
81πΓ(4
3)( x−µ
c)42F313
12 ,19
12 ;7
6,3
2,5
3;−4
729 (x−µ
c)6
K
K(x;s,α1,α2) = 2
|s|Γ(α1)Γ(α2)x
s1
2(α1+α2)−1
Kα1−α22x
s
x⩾0, α1>0, α2>0
Kv(+z) = Kv(−z)
K(x;s,α1,α2) =
K(x;s,α2,α1)
K(s1s2,α1,α2)∼Gamma1(0, s1,α1)Gamma2(0, s2,α2)
Irwin-Hall
IrwinHall(x;n) = 1
2(n−1)!
n
k=0
(−1)kn
k(x−k)n−1sgn(x−k)
n
IrwinHall(n)∼
n
i=1
Uniformi(0, 1)
n=1
n=2
Johnson SU
JohnsonSU(x;µ,σ,γ,δ) = δ
λ√2π
1
1+x−ξ
λ2e−1
2(γ+δsinh−1(x−ξ
λ))2
Johnsong(µ,σ,γ,δ)∼σg(StdNormal()−γ)
δ) + µ
SU g(x) = sinh(x) SB
g(x) = 1/(1+exp(x)) SLg(x) = exp(x))

SN
Landau
Landau(x;µ,c) = Stable(x;µ,c, 1, 1)
Log-Cauchy
LogCauchy(x;a,s,β) = |β|
|s|πx−a
s−11
1+lnx−a
sβ2
LogCauchy(0, s,β)∼exp−Cauchy(− ln s,1
β)
Meridian
Meridian(x;a,s) = 1
2|s|
1
1+|x−a
s|2
Meridian(x; 0, s1
s2)∼Laplace1(0, s1)
Laplace2(0, s2)

Noncentral chi-square χ2χ′2
NoncentralChiSqr(x;k,λ) = 1
2e−(x+λ)/2x
λk
4−1
2Ik
2−1(√λx)
k,λ,x R,>0
Iv(z)
k
µi
σi
NoncentralChiSqr(k,λ)∼
k
i=11
σi
Normali(µi,σi)2
λ=k
i=1(µi/σi)2
Non-central F
NoncentralF(k1,k2,λ1,λ2)∼NoncentralChiSqr1(k1,λ1)/k1
NoncentralChiSqr2(k2,λ2)/k2
k1,k2,λ1,λ2>0
x > 0
λ1,λ2 doubly non-central F
singly non-central F distribution
Pseudo Voigt
PseudoVoigt(x;a,σ,s,η) = (1−η)Normal(x;a,σ) + ηCauchy(x;a,s)
0⩽η⩽1

Rice
Rice(x;ν,σ) = x
σ2exp−x2+ν2
2σ2I0(x|ν|
σ2)
x > 0
I0(z)
Rice(ν,σ)∼Normal2
1(νcos θ,σ) + Normal2
2(νsin θ,σ)
Rice(ν, 1)2∼NoncentralChiSqr(2, ν2)
Slash
Slash(x) = StdNormal(x) − StdNormal(x)
x2
Slash() ∼StdNormal()
StdUniform()
limx→0Slash(x) = 1/√8π

Stable
StableCF(t;µ,c,α,β) = expitµ −|ct|α(1−iβ sgn(t)Φ(α)
Φ(α) = tan(πα/2) α̸=1 Φ(1) = −(2/π)log |t|
µ c
α∈(0, 2] β∈[−1, 1]
β=0
Lévy symmetric alpha-stable β=±1
0< α ⩽1 c α
α < 2 stable Paretian distributions
µ c α β
3
2
1
2
a1Stable1(µ,c,α,β) + a2Stable2(µ,c,α,β)∼a3Stable3(µ,c,α,β) + b
a1,a2,a3,b

Suzuki
Suzuki(ϑ,σ)∼Rayleigh(σ′)∧
σ′LogNormal(0, ϑ,σ)
Triangular
Triangular(x;a,b,c) = 2(x−a)
(b−a)(c−a)a⩽x⩽c
2(b−x)
(b−a)(b−c)c⩽x⩽b
x∈[a,b] c
Uniform difference
UniformDiff(x) = (1+x) −1⩾x⩾0
(1−x)0⩾x⩾1
=Triangular(x;−1, 1, 0)
Voigt
Voigt(a,σ,s) = Normal(0, σ) + Cauchy(a,s)

Notation
Amoroso(x;a,θ,α,β) AmorosoCDF(x;
a,θ,α,β) Amoroso(a,θ,α,β)
X∼Amoroso(a,θ,α,β)
a
b b=a+s
ζ
µ
ν
ζ
s
λ
σ
ϑ†
θ
ω
β
α >0
γ >0
n >0
k >0
m >1
2
v >0
†
β
abνµ sθσ αγmv
αγ m

β= −¯
β
Nomenclature
interesting
generalized-X
standard-X
shifted-X
anchored-X
scaled-X
inverse-X
x7→ 1
x
β7→ −β
log-X
exp −X() ∼log-X() −ln () ∼
log-X()
X-exponential ln () ∼
()
reversed-X
X of the Nth kind
folded-X X
beta-X

notation
probability density function (PDF) fX(x)
P[a⩽X⩽b] = b
a
fX(x)dx .
cumulative density function (CDF)
x FX(x)
FX(x) = x
−∞
fX(z)dz
fX(x) = d
dxFX(x)
=1−
complimentary cumulative density function (CCDF)
1−
FX(x) x
support
mode
⌢ ⌣
/ \
mean
E[X] = x fX(x)dx
µ
variance
var[X] = E(X−E[X])2=EX2−EX2
σ
central moment
µn[X] = EX−E[X]n
n
skew
3
2
skew[X] = EX−E[X]
σ[X]3=κ3
κ2
3
2

kurtosis
ExKurtosis[X] = κ4
κ22
µ4
κ4
κ22=µ4
κ22−3
entropy
entropy[X] = − f(x)ln f(x)dx
moment generating function (MGF)
MGFX(t) = E[etX].
n 0
n
dn
dtnMGFX(t)0=E[Xn]
cumulant generating function (CGF)
CGFX(t) = ln E[etX]

n 0
n
dn
dtnCGFX(t)0=κn(X)
n n
κ1=E[X]
κ2=E(X−E[X])2
κ3=E(X−E[X])3
κ4=E(X−E[X])4−3E(X−E[X])2
CGFX+Y(t) = CGFX(t) + CGFY(t)
characteristic function (CF)
ϕX(t) = E[eitX],
ϕX+Y(t) = ϕX(t)ϕY(t)
ϕZ(t) =
i
ϕXi(cit),Z=
i
ciXi.

quantile function
F−1(p) Q(p)
median[X] = F−1
X(1
2)
hazard function
hazardX(x) = fX(x)
1−FX(x)

Order statistics
m+n−1
m
n
OrderStatisticX(x;m,n) = (m+n−1)!
(m−1)!(n−1)!F(x)m−1f(x) (1−F(x))n−1
X f(x)
F(x)
m+n−1 m−1
n−1 m−1
m n−1
m=1
n=1 m=n
I(p,q;z)
OrderStatisticCDFX(x;m,n) = Im,n;F(x)
Im,n;F(x)
F(x)
Iα,γ;x
Iα,γ;FX(x)
α γ

OrderStatisticUniform(a,s)(x;α,γ) = Beta(x;a,s,α,γ)
OrderStatisticExp(ζ,λ)(x;γ,α) = BetaExp(x;ζ,λ,α,γ)
OrderStatisticPowerFn(a,s,β)(x;α,γ) = GenBeta(x;a,s,α,γ,β)
OrderStatisticUniPrime(a,s)(x;α,γ) = BetaPrime(x;a,s,α,γ)
OrderStatisticLogistic(ζ,λ)(x;γ,α) = BetaLogistic(x;ζ,λ,α,γ)
OrderStatisticLogLogistic(a,s,β)(x;α,γ) = GenBetaPrime(x;a,s,α,γ,β)
Extreme order statistics
n≫m m≫n
β
Median statistics
N N
MedianStatisticX(x;N) = OrderStatisticX(x;N−1
2,N−1
2)
MedianStatisticsUniform(a,s)(x; 2α+1) = PearsonII(x;a+s, 2s,α)
MedianStatisticsLogistic(a,s)(x; 2α+1) = SymBetaLogistic(x;a,s,α)

β=1
β→∞
β= −1
β→∞
β=±1
β=1
β→∞
β→∞
β±1
β= −1

Exponential function limit
lim
c→+∞1+x
cac =eax .
X
lim
β→∞
fx−a
sβ=lim
β→∞
f1−1
β
x−ζ
λβ=fe−x−ζ
λ
(a=ζ+βλ,s= −βλ)
Exp(x;a,θ) = lim
β→∞
PowerFn(x;a+βθ,−βθ,β)
GammaExp(x;ν,λ,α) = lim
β→∞
Amoroso(x;ν+βλ,−βλ,α,β)
Gamma(x;a,s,α) = lim
β→∞
UnitGamma(x;a+βs,−βs,α,β)
BetaExp(x;ζ,λ,α,γ) = lim
β→∞
GenBeta(x;ζ+βλ,−βλ,α,γ,β)
BetaLogistic(x;ζ,λ,α,γ) = lim
β→∞
GenBetaPrime(x;ζ+βλ,−βλ,α,γ,β)
Normal(x;µ,σ) = lim
β→∞
LogNormal(x;µ+βσ,−βσ,β)
γ
lim
γ→∞
f1−x−a
sβ
γ−1=lim
γ→∞
f1−1
γx−a
θβ
γ−1
=fe−( x−a
θ)βs=θγ 1
β
Amoroso(x;a,θ,α,β) = lim
γ→∞
GenBeta(x;a,θγ 1
β,α,γ,β)
Gamma(x;a,θ,α) = lim
γ→∞
Beta(x;a,θγ,α,γ)

lim
γ→∞
f1+x−a
sβ
−α−γ=lim
γ→∞
f1+1
γx−a
θβ
−α−γ
=fe−( x−a
θ)βs=θγ 1
β
Amoroso(x;a,θ,α,β) = lim
γ→∞
GenBetaPrime(x;a,θγ 1
β,α,γ,β)
Gamma(x; 0, θ,α) = lim
γ→∞
BetaPrime(x; 0, θγ,α,γ)
InvGamma(x;θ,α) = lim
γ→∞
BetaPrime(x; 0, θ/γ,α,γ)
GammaExp(x;ν,λ,α) = lim
γ→∞
BetaExp(x;ν+λ/ ln γ,λ,α,γ)
GammaExp(x;ν,λ,α) = lim
γ→∞
BetaLogistic(x;ν+λ/ ln γ,λ,α,γ)
Logarithmic function limit
lim
c→0
xc−1
c=ln x
UnitGamma(x;a,s,γ,β) = lim
α→∞
GenBeta(x;a,s,α,γ,β/α)
Gaussian function limit
lim
c→∞
e−z√c1+z
√cc=e−1
2z2
LogNormal(x;a,ϑ,σ) = lim
γ→∞
UnitGamma(x;a,ϑeσ√γ,α,√γ
σ)
Normal(x;µ,σ) = lim
α→∞
Gamma(x;µ−σ√α,σ
√α,α)
Normal(x;µ,σ) = lim
α→∞
InvGamma(x;µ−σ√α,σα 3
2,α)
lim
c→∞
ec+cz
√c−ce
z
√c=e−z2
2
LogNormal(x;a,ϑ,σ) = lim
α→∞
Amoroso(x;a,ϑα−σ√α,α,1
σ√α)
Normal(x;µ,σ) = lim
α→∞
GammaExp(x;µ+σ√αln α,σ√α,α)
Miscellaneous limits
InvGamma(x;θ,α) = lim
v→∞
PearsonIV(x; 0, −θ
2v,α+1
2,v)
Normal(x;µ,σ) = lim
m→∞
PearsonVII(x;µ,σ√2m,m)
Normal(x;µ,σ) = lim
α→∞
PearsonII(x;µ,σ√8α,α)
Laplace(x;η,θ) = lim
α→0BetaLogistic(x;η,θα,α,α)
β=1
β=1
β→∞
β= −1
∞←α
γ→∞
β→∞
β=±1
∞←γ
γ=α
γ→∞
γ→∞
∞←γ
∞←γ
γ→∞
∞←v
v=0
γ=1
β→∞
β=1
β→∞
β= −1
α=1
α→∞
β=1
β→∞
γ→∞
∞←α
α=1
α→∞
∞←α
α=1
∞←m
m=1
β→∞
α→∞

Transformations
X FX
fX h(x)
X
Y
Y∼h(X)
FY(y) = FXh−1(y)h(x)
1−FXh−1(y)h(x)
fY(y) =
d
dy h−1(y)fXh−1(y)
h h−1
FYy) = PY⩽y=Ph(X)⩽y=PX⩽h−1(y)=FXh−1(y)
FYy) = PY⩽y=Ph(X)⩽y=PX⩾h−1(y)=1−FXh−1(y).
Linear transformation
h(x) = a+sx
Weibull transformation
h(x) = a+sx
1
β
PowerFn(a,s,β)∼a+sStdUniform()
1
β
Weibull(a,θ,β)∼a+θStdExp() 1
β
LogNormal(a,ϑ,β)∼a+ϑStdLogNormal() 1
β
Amoroso(a,θ,α,β)∼a+θStdGamma(α)
1
β
GenBeta(a,s,α,γ,β)∼a+sStdBeta(α,γ)
1
β
GenBetaPrime(a,s,α,γ,β)∼a+sStdBetaPrime(α,γ)
1
β
s
β>0 s
β<0
Inverse (reciprocal) transformation
h(x) = x−1
a=0s=1 β= −1
Gamma(0, 1, α)∼InvGamma(0, 1, α)−1
Exp(0, 1)∼InvExp(0, 1)−1
Cauchy(0, 1)∼Cauchy(0, 1)−1
Log and anti-log transformations
h(x) = − ln(x)h(x) = exp(−x)
StdUniform() ∼exp−StdExp()
StdLogNormal() ∼exp−StdNormal()
StdGamma(α)∼exp−StdGammaExp(α)
StdBeta(α,γ)∼exp−StdBetaExp(α,γ)
StdBetaPrime(α,γ)∼exp−StdBetaLogistic(α,γ)
PowerFn(0, s,β)∼exp−Exp(− ln s,1
β)
LogLogistic(0, s,β)∼exp−Logistic(− ln s,1
β)
FisherTippett(0, s,β)∼exp−Gumbel(− ln s,1
β)
Amoroso(0, s,α,β)∼exp−GammaExp(− ln s,1
β,α)
LogNormal(0, ϑ,β)∼exp−Normal(− ln ϑ,1
β)
UnitGamma(0, s,α,β)∼exp−Gamma(− ln s,1
β,α)
GenBeta(0, s,α,γ,β)∼exp−BetaExp(− ln s,1
β,α,γ)
GenBetaPrime(0, s,α,γ,β)∼exp−BetaLogistic(− ln s,1
β,α,γ)
Prime transformation
prime(x) = 1
1
x−1, prime−1(y) = 1
1
y+1
StdUniPrime() ∼primeStdUniform()
StdBetaPrime(α,γ)∼primeStdBeta(α,γ)
Combinations
Sum
Z∼X+Y
fZ(z) = (fX∗fY)(z) = +∞
−∞
fX(x)fY(z−x)dx

ϕX+Y(t) = ϕX(t)ϕY(t)
Normal1(µ1,σ1) + Normal2(µ2,σ2)∼Normal3(µ1+µ2,σ2
1+σ2
2)
Exp1(a1,θ) + Exp(a2,θ)∼Gamma(a1,a2,θ, 2)
Gamma1(a1,θ,α1) + Gamma2(a2,θ,α2)∼Gamma3(a1+a2,θ,α1+α2)
Difference
Z∼X−Y
ϕX−Y(t) = ϕX(t)ϕY(−t)
UniformDiff(x)∼StdUniform1(x) − StdUniform2(x)
BetaLogistic(x;ζ1−ζ2,λ,α,γ)∼GammaExp1(x;ζ1,λ,α)
−GammaExp2(x;ζ2,λ,γ)
Product
Z∼XY
Z
fZ(z) = fX(x)fYz
x1
|x|dx
n
i=1
Uniformi(0, 1)∼UniformProduct(n)
n
i=1
PowerFni(0, si,β)∼UnitGamma(0,
n
i=1
si,n,β)
n
i=1
UnitGammai(0, si,αi,β)∼UnitGamma(0,
n
i=1
si,
n
i=1
αi,β)
n
i=1
LogNormali(0, ϑi,βi)∼LogNormali(0,
n
i=1
ϑi,(
n
i=0
β−2
i)−1
2)
Ratio
R∼X
Y
StdBetaPrime(α,γ)∼StdGamma1(α)
StdGamma2(γ)
StdCauchy() ∼StdNormal1()
StdNormal2()
Mixture
Z(x;α) = X(x;β)Y(β;α)dβ
Z(α)∼XY(α)
Z(α)∼X(β)∧
βY(α).
Transmutations
Fold
FoldedX(ζ)∼ |X−ζ|
folded normal
FoldedNormal(x;µ,σ)
=1
2Normal(x;+µ,σ) + 1
2Normal(x;−µ,σ)
x,µ,σ R,x⩾0
Truncate
TruncatedX(x;a,b) = f(x)
|F(a) − F(b)|
Gompertz
truncated nor-
mal distribution
Dual
Z(z;x) = X(x;z)
dz X(x;z)
z

Tilt
Tiltedθf(x)=f(x)eθx
f(x)eθxdx =f(x)eθx−κ(θ)
κ(θ) = ln f(x)eθxdx
Generation
Special functions
Gamma function
Γ(a) = ∞
0
ta−1e−tdt
= (a−1)!
= (a−1)Γ(a−1)
Γ(1
2) = √π
Γ(1) = 1
Γ(3
2) = √π
2
Γ(2) = 1
Incomplete gamma function
Γ(a,z) = ∞
z
ta−1e−tdt
Γ(a, 0) = Γ(a)
Γ(1, z) = exp(−x)
Γ(1
2,z) = √πerfc(√z)
Regularized gamma function
Q(a;z) = Γ(a;z)
Γ(a)
Q(1
2;z) = erfc(√z)
Q(1; z) = exp(−z)
d
dz Q(a;z) = − 1
Γ(a)za−1e−z
Beta function
B(a,b) = 1
0
ta−1(1−t)b−1dt
=Γ(a)Γ(b)
Γ(a+b)
B(a,b) = B(b,a)
B(1, b) = 1
b
B(1
2,1
2) = π
Incomplete beta function
B(a,b;z) = z
0
ta−1(1−t)b−1dt
d
dz B(a,b;z) = za−1(1−z)b−1
B(1, 1; z) = z
Regularized beta function
I(a,b;z) = B(a,b;z)
B(a,b)
I(a,b; 0) = 0
I(a,b; 1) = 1
I(a,b;z) = 1−I(b,a; 1 −z)
Error function
erf(z) = 2
√πz
0
e−t2dt

Complimentary error function
erfc(z) = 1−erf(z)
=2
√π∞
z
e−t2dt.
Gudermannian function
gd(z) = z
0
sech(t)dt
=2 arctan(ex) − π
2
Modied Bessel function of the rst kind
Iv(z) = 1
2zv∞
k=0
(1
4z2)k
k!Γ(v+k+1)
Modied Bessel function of the second kind
Kv(z) = π
2
I−v(z) − Iv(z)
sin(vπ)
Arcsine function
arcsin(z) = z
0
1
√1−x2dx
arcsin(sin(z)) = z
d
dz arcsin(z) = 1
√1−z2

Arctangent function
arctan(z) = 1
2iln 1−iz
1+iz
arctan(z) = z
0
1
1+x2dx
arctan(tan(z)) = z
d
dz arctan(z) = 1
1+z2
arctan(z) = − arctan(−z)
Hyperbolic sine function
sinh(z) = e+x−e−x
2
Hyperbolic cosine function
cosh(z) = e+x+e−x
2
Hyperbolic secant function
sech(z) = 2
e+x+e−x=1
cosh(z)
Hyperbolic cosecant function
csch(z) = 2
e+x−e−x=1
sinh(z)
Hypergeometric function
pFq(a1,a2, . . . , ap;b1,b2, . . . , bq;z) = ∞
n=0
a¯
n
1, . . . , a¯
n
p
b¯
n
1, . . . , b¯
n
q
zn
n!
x¯
n
x¯
n=x(x+1)···(x+n−1) = (x+n−1)!
(x−1)!.
2F1(a,b;c;z)
2F1(a,b;c;z) = 1
B(b,c−b)1
0
tb−1(1−t)c−b−1
(1−zt)adt |z|⩽1 .
1F1(a;c;z)
0F1(c;z)
B(a,b;z) = za
a2F1(a, 1 −b;a+1; z)
B(a,b) = 1
a2F1(a, 1 −b;a+1; 1)
Γ(a;z) = Γ(a) − za
a1F1(a;a+1; −z)
erfc(z) = 2z
√π1F1(1
2;3
2;−z2)
sinh(z) = z0F1(;3
2;z2
4)
cosh(z) = 0F1(;1
2;z2
4)
arctan(z) = z2F1(1
2, 1; 3
2;−z2)
arcsin(z) = z2F1(1
2,1
2;3
2;z2)
Iv(z) = (1
2v)v
Γ(v+1)0F1(;v+1; z2
4)
d
dz 2F1(a,b;c;z) = ab
c2F1(a+1, b+1; c+1; z)
Sign function
sgn(x) =
−1 x < 0
0 x=0
+1 x > 0
,
sgn(z) = z
|z| z̸=0
0 z=0.
Polygamma function (n+1)
digamma function
ψ(x)≡ψ0(x) trigamma function ψ1(x)
ψn(x) = dn+1
dzn+1ln Γ(x)
=dn
dznψ(x)
q-exponential and q-logarithmic functions
lim
c→0
xc−1
c=ln x
lim
c→+∞1+x
cac =eax .
expq(x) =
exp(x)q=1
1+ (1−q)x1
1−qq̸=1, 1 + (1−q)x > 0
0q < 1, 1 + (1−q)x⩽0
+∞q > 1, 1 + (1−q)x⩽0
lnq(x) = x1−q−1
1−qq̸=1
ln(x)q=1
http:
//threeplusone.com/fieldguide
http://www.math.wm.edu/~leemis/chart/UDR/UDR.html
http://www.jstor.org/stable/2983618
http://www.nrbook.com/devroye/
http://www.jstor.org/stable/2957731
ˇ
m
ˇ
ˇ
n
¯
http://www.jstor.org/stable/25049987
http://www.jstor.org/
stable/2235955
¯
http://www.jstor.org/
stable/25049460
http://www.jstor.org/stable/
41137425
q
http://www.jstor.org/stable/2984691
http://www.jstor.org/
stable/2348939
F1
t
http://www.jstor.
org/stable/3532334
n
L
http://www.jstor.org/stable/
2243119
q q
http://www.jstor.
org/stable/2334368
¯
http://www.jstor.org/stable/25664553

Distribution Synonym or Equation
β
β′
χ
χ2
Γ
Λ
Φ
SU
SBSU
SL SU
SNSU
SU
q
q
t
t
t
t2
t3
z
t
q
tt
t2t2
t3t3
z
B(a,b)
B(a,b;z)
F−1(p)
pFq
F(x)
I(a,b;z)
Iv(z)
Kv(z)
Q(a;z)
Γ(a)
Γ(a,z)
arcsin(z)
arctan(z)
csch(z)
E
cosh(z)
erfc(z)
erf(z)
gd(z)
sgn(x)
ϕ(t)
ψ(x)
ψ1(x)
ψn(x)
sech(z)
sinh(z)
∧