GDA2020Technical Manual V1.2

User Manual:

Open the PDF directly: View PDF .
Page Count: 77

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 1

Version 1.2

Geocentric Datum of Australia 2020

Technical Manual

Version 1.2

Intergovernmental Committee on Surveying and Mapping (ICSM)

Permanent Committee on Geodesy (PCG)

24 August 2018

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 2

Version 1.2

Foreword

Since the implementation of Geocentric Datum of Australia 1994 (GDA94), many advances

have occurred in the fields of space geodesy, which have resulted in the improvement of

the International Terrestrial Reference System (ITRS) to better define the shape of the

Earth. Furthermore, high performance computing allows for the rigorous adjustment of

jurisdictional archives of Global Navigation Satellite System (GNSS) data and terrestrial

data.

Recognising the need to align the Australian datum with the reference frame of GNSS in

which many current users and future users will access the datum, the Intergovernmental

Committee on Surveying and Mapping requested that the Permanent Committee on

Geodesy commence work on developing the Geocentric Datum of Australia 2020

(GDA2020) along with the required technical tools, services and documentation.

The Permanent Committee on Geodesy was assisted with contributions from a number of

Commonwealth, state and territory representatives and from institutions engaged in the

teaching of surveying and geodesy. Many useful suggestions received from these sources

have been incorporated into this manual.

The Intergovernmental Committee on Surveying and Mapping thanks those who have

contributed to this manual and hope it assists those seeking a definitive explanation of

GDA2020.

Permanent Committee on Geodesy

Intergovernmental Committee on Surveying and Mapping

25 July 2017

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 3

Version 1.2

Document history

DATE

VERSION

AMENDMENTS

24 August 2018

1.2

 Introduced Grid Reference information in Appendix D

 Corrections to remove duplicate Terms and Definitions

 Corrections to grammar

8 January 2018

1.1.1

 Fixed typographical error on Page 8. Changed “�′+

10,000,0000 metres” to “false origin �′+ 10,000,000” metres

13 December 2017

1.1

 Amendments to reflect the signing of the GDA2020

determination

 Minor changes to wording to improve clarity

 Inclusions to Table 3.4 for South Australian data

 Corrections to grammar, table numbers, equation numbers

 Added links to datum transformation tools

25 July 2017

1.0

 New document for the release of GDA2020

With the exception of the Commonwealth Coat of Arms, and where otherwise noted, this

product is provided under a Creative Commons Attribution 4.0 International Licence.

http://creativecommons.org/licenses/by/4.0/legalcode

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 4

Version 1.2

Table of contents

Foreword ....................................................................................................................... 2

Document history .......................................................................................................... 3

Table of contents ........................................................................................................... 4

Terms and definitions .................................................................................................... 7

1 Introduction ........................................................................................................... 11

1.1 Purpose of the Technical Manual ......................................................................... 11

1.2 The Geocentric Datum of Australia 2020 ............................................................. 11

1.2.1 Terminology .................................................................................................... 11

1.2.2 Definition ........................................................................................................ 11

1.2.3 Legal traceability of position and Australian Fiducial Network ...................... 11

1.2.4 GDA2020 extent ............................................................................................. 12

1.3 Geodetic Parameter Registries ............................................................................. 13

1.3.1 EPSG Registry .................................................................................................. 13

1.3.2 ISO Registry ..................................................................................................... 14

1.4 History of Australian datums ................................................................................ 14

1.4.1 Early history .................................................................................................... 14

1.4.2 Australian Geodetic Datum 1966 ................................................................... 14

1.4.3 Australian Geodetic Datum 1984 ................................................................... 15

1.4.4 Geocentric Datum of Australia 1994 .............................................................. 16

1.4.5 Geocentric Datum of Australia 2020 .............................................................. 17

1.4.6 Summary of Australian horizontal datums ..................................................... 18

1.5 Overview of the differences among GDA2020, ITRF2014 and GNSS reference

frames ................................................................................................................... 18

1.5.1 GDA2020 and ITRF2014 .................................................................................. 18

1.5.2 World Geodetic System 1984 ......................................................................... 19

1.6 Map Grid of Australia 2020 (MGA2020) ............................................................... 19

2 Reference frame and coordinate system fundamentals ........................................... 22

2.1 Coordinate systems .............................................................................................. 22

2.1.1 Cartesian ......................................................................................................... 22

2.1.2 Geographic ...................................................................................................... 22

2.1.3 Local ................................................................................................................ 24

2.2 Transformations between reference frames ....................................................... 25

2.2.1 Rotation matrix sign convention .................................................................... 25

3 Coordinate transformation ..................................................................................... 26

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 5

Version 1.2

3.1 GDA94 to GDA2020 transformation parameters ................................................. 26

3.1.1 Example: GDA94 to GDA2020 (7–parameter transformation) ...................... 26

3.2 Transformation Grids ........................................................................................... 27

3.2.1 Overview ......................................................................................................... 27

3.2.2 Types of transformation grids ........................................................................ 28

3.2.3 Development of transformation grids ............................................................ 30

3.3 Plate motion model (ITRF2014 to GDA2020) ....................................................... 30

3.3.1 Example: ITRF2014 to GDA2020 (3–parameter transformation) ................... 31

3.4 Transformation from / to AGD66 and AGD84 ...................................................... 31

3.5 Transformation from / to ITRF (historic) .............................................................. 32

3.6 Transformation from / to MGA2020 .................................................................... 32

3.7 Transformation tools and services ....................................................................... 32

3.7.1 Transformation grids ...................................................................................... 32

3.7.2 Similarity transformation................................................................................ 35

3.7.3 Online transformation .................................................................................... 35

3.7.4 QGIS Plug-ins .................................................................................................. 35

4 Coordinate conversion ........................................................................................... 36

4.1 Geographic from / to grid ..................................................................................... 36

4.1.1 Krueger n-series equations ............................................................................. 36

4.1.2 Krueger -series equations (Redfearn’s formulae) ........................................ 43

4.1.3 Zone-to-zone transformations ....................................................................... 43

4.1.4 Tools / services ............................................................................................... 44

5 Coordinate computations ....................................................................................... 45

5.1 Ellipsoid computations ......................................................................................... 45

5.1.1 Reduction of measured distances to the ellipsoid ......................................... 45

5.1.2 Reduction of measured directions to the ellipsoid ........................................ 47

5.1.3 Positions, azimuth and distances ................................................................... 49

6 Australian Height Datum and geoid models ............................................................ 52

6.1 Australian Height Datum background .................................................................. 52

6.1.1 Metropolitan and buffer zones ...................................................................... 53

6.2 Heighting fundamentals ....................................................................................... 53

6.2.1 AHD: Normal-Orthometric height system ...................................................... 55

6.3 AUSGeoid2020 ...................................................................................................... 55

6.3.1 Overview ......................................................................................................... 55

6.3.2 Format of AUSGeoid2020 ............................................................................... 55

6.3.3 Differences between AUSGeoid09 and AUSGeoid2020 ................................. 56

6.4 AUSGeoid2020 tools and services ........................................................................ 56

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 6

Version 1.2

6.5 Australian Gravimetric Quasigeoid 2017 .............................................................. 56

References ................................................................................................................... 58

Appendix A – Recognized-value standards of measurement in the Australian Fiducial

Network ................................................................................................................ 60

Appendix B .................................................................................................................. 66

B1. AGD66 / AGD84 to GDA94 transformations ............................................................ 66

B1.1 Transformation grid details ............................................................................ 66

B1.2 National transformation grid coverage .......................................................... 66

B2. National 7 parameter similarity transformations ................................................ 68

B3. Regional 7 parameter similarity transformations for AGD66 .............................. 68

Appendix C .................................................................................................................. 70

C1. Grid bearings and ellipsoidal distance ..................................................................... 70

C1.1 MGA2020 coordinates from grid bearing and ellipsoidal distance ................ 71

C1.2 Traverse computations using arc-to-chord corrections and scale factors ..... 72

Appendix D .................................................................................................................. 76

D1. Grid references ........................................................................................................ 76

D1.1 Grid zones ....................................................................................................... 76

D1.2 100 000 metre square identification .............................................................. 76

D1.3 The grid reference .......................................................................................... 77

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 7

Version 1.2

Terms and definitions

Symbol

Definition

Equation / Comment



Ellipsoid semi-major axis



Ellipsoid semi-minor axis





Flattening of the reference ellipsoid







Inverse flattening or reciprocal flattening





Third flattening







First eccentricity of the reference ellipsoid







Second eccentricity of the reference ellipsoid





The radius of curvature at a point on an ellipsoid with respect to

the meridian through that point.



The radius of curvature at a point on an ellipsoid with respect to

the prime vertical through that point.



Geodetic latitude; this is negative south of the equator.

The angle that the normal to the ellipsoid at a point makes with the

equatorial plane of the ellipsoid.

A geodetic latitude differs from the corresponding astronomic

latitude by the amount of the meridional component of the

local deflection of the vertical.



Geodetic longitude; positive measured eastwards from the

Greenwich meridian.

The angle between the plane of the local geodetic meridian and the

Greenwich meridian.

A geodetic longitude differs from the corresponding astronomic

longitude by the amount of the prime vertical component of the

local deflection of the vertical.



Geodetic longitude of the central meridian

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 8

Version 1.2



Geodetic longitude difference measured from the central meridian;

positive measured eastwards





Azimuth; the horizontal angle measured from the meridian

measured clockwise from true north.



Ellipsoidal distance; the distance on the ellipsoid. Spheroidal

distance is the same as an ellipsoidal distance.



Easting; positive measured eastwards from a central meridian



Easting measured from the false origin

 + 500,000 metres

for MGA2020



Northing; negative measured southwards from the equator



Northing measured from the false origin

+ 10,000,000

metres in the

southern hemisphere

for MGA2020



Grid convergence; the angular quantity to be added algebraically to

an azimuth to obtain a grid bearing. In the southern hemisphere,

grid convergence is positive for points east of the central meridian

(grid north is west of true north) and negative for points west of the

central meridian (grid north is east of true north)





Grid bearing; the angle between grid north and the tangent to the

arc at the point. It is measured from grid north clockwise through

360°



Arc-to-chord correction; the angular quantity to be added

algebraically to a grid bearing to obtain a plane bearing







Plane bearing; the angle measured clockwise through 360°,

between grid north and the straight line on the grid between the

ends of the arc formed by the projection of the ellipsoidal distance



Plane distance is the straight-line distance on the grid between the

ends of the arc of the projected ellipsoidal distance. The difference

in length between the plane distance () and the grid distance () is

nearly always negligible. Using plane bearings and plane distances,

the formulae of plane trigonometry hold rigorously:













Central scale factor; the scale factor on the central meridian

0.9996 for MGA2020

and UTM

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 9

Version 1.2



Point scale factor; the ratio of an infinitesimal distance at a point on

the grid to the corresponding distance on the ellipsoid









Line scale factor; the ratio of a plane distance  to the

corresponding ellipsoidal distance . The point scale factor will in

general vary from point to point along a line on the grid









Ellipsoidal height; the distance of a point measured along the

normal from the ellipsoid. Spheroidal height is the same as an

ellipsoidal height



Orthometric height; the height of a point above the geoid measured

along the plumbline



Height of a point above AHD



Ellipsoid to quasigeoid separation



Ellipsoid to AHD separation



A three dimensional coordinate system (Cartesian) which has its

origin at (or near) the centre of the Earth.



Meridian convergence; the change in the azimuth of a geodesic

between two points on the ellipsoid.

Reverse Azimuth =

Forward Azimuth +

Meridian

Convergence ± 180°



Line curvature; the change in grid bearing between two points on

the arc

Reverse grid bearing

= Forward grid

bearing + Line

curvature ± 180°



Meridian distance is the geodesic distance from the equator along

the meridian, negative southwards



Mean length of an arc of one degree of the meridian



Meridian distance expressed as units 





Grid distance; the length measured on the grid, along the arc of the

projected ellipsoid distance.



Geometric mean radius of curvature



Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 10

Version 1.2



Radius of curvature at a point in a given azimuth



 



 at the mean latitude 

 at 



Ratio of the ellipsoidal radii of curvature





Rectifying radius



Mean latitude







Foot point latitude; the latitude for which the meridian distance





Parametric latitude



Reduced latitude

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 11

Version 1.2

1 Introduction

1.1 Purpose of the Technical Manual

The purpose of the Geocentric Datum of Australia 2020 (GDA2020) Technical Manual is to:

 define GDA2020;

 provide descriptions, transformation parameters and examples to assist with

datum transformations between GDA2020, realisations of the International

Terrestrial Reference Frame (ITRF) and historic Australian datums;

 provide descriptions and examples to assist with coordinate conversions between

Earth-centred Cartesian, geodetic and map projected coordinates;

 provide descriptions and examples of coordinate computations; and

 define the Australian Height Datum (AHD) and AUSGeoid2020, and describe how to

convert between ellipsoidal heights and AHD heights.

1.2 The Geocentric Datum of Australia 2020

Prior to the release of the GDA2020, the Geocentric Datum of Australia 1994 (GDA94) was

the only Australian datum that used the acronym GDA. As a consequence, the acronym

GDA was often used interchangeably with GDA94. When referring to any documents or

software developed prior to the release of GDA2020, the reader can assume GDA refers to

GDA94.

1.2.1 Terminology

Table 1.1: GDA2020 terminology.

Datum

Geodetic Coordinate Set

Grid Coordinates

GDA2020

MGA2020

1.2.2 Definition

Table 1.2: GDA2020 definition.

Reference frame

Epoch

Ellipsoid

Semi-major axis (m)

Inverse flattening

ITRF2014

2020.0

GRS80

6378137

298.257222101

1.2.3 Legal traceability of position and Australian Fiducial Network

The National Measurement Institute (NMI) administers the National Measurement Act

1960 and has the authority to appoint legal metrology authorities to verify reference

standards of measurement. Geoscience Australia is appointed as a Verifying Authority for

Position. As a Verifying Authority for Position, Geoscience Australia can issue certificates of

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 12

Version 1.2

verification under Regulation 13 of the National Measurement Regulations 1999. These are

commonly referred to as Regulation 13 Certificates.

Regulation 13 Certificates provide coordinates and their uncertainty with respect to the

Recognized-value standard of measurement of position (RVS) in Australia, which is the

Australian Fiducial Network (AFN). The AFN was updated in October 2017 and includes 109

stations from the Australian Global Navigation Satellite System network which:

 are operated by Geoscience Australia or similar agency;

 are located on the Australian Tectonic Plate, within Australia’s jurisdiction and

on a high quality survey monument; and

 have residuals less than 1 mm/yr relative to the Australian plate motion model

(Section 3.3).

To define GDA2020, International Terrestrial Reference Frame 2014 (ITRF2014) coordinates

and velocities of the 109 AFN stations were mapped forward to the epoch of January 1,

2020 using the plate motion model (Section 3.3). GDA2020 is determined with respect to

the RVS with crustal velocities and their uncertainties. These velocities enable coordinates

to be mapped to any epoch. The list of 109 AFN stations including their coordinates and

velocities, and the equation for coordinate conversion is shown in Appendix A.

More information on Regulation 13 Certificates including the application process can be

found on the Geoscience Australia website (http://www.ga.gov.au/scientific-

topics/positioning-navigation/geodesy/regulation-13-certificates).

Table 1.3: Verifying Authority for Position scope of accreditation and least uncertainty.

Physical Quantity

Range of Measurement

Least Uncertainty (95%CI)

Position

(horizontal & vertical)

Australia and its Territories

7 mm horizontal

15 mm vertical

Note: “Least uncertainty” is synonymous with “best measurement capability”. It is the smallest

uncertainty of measurement that can realistically be expected under ideal conditions.

1.2.4 GDA2020 extent

The extent of the GDA2020 includes all the areas contained within Australia’s marine

jurisdiction (within 200 nautical miles of Australia) and its external territories, and the

areas of Australia’s continental shelf beyond 200 nautical miles as confirmed by the United

Nations Commission on the Limits of the Continental Shelf. The areas include Cocos

(Keeling) Islands, Christmas Island, Norfolk Island and Macquarie Island but excludes

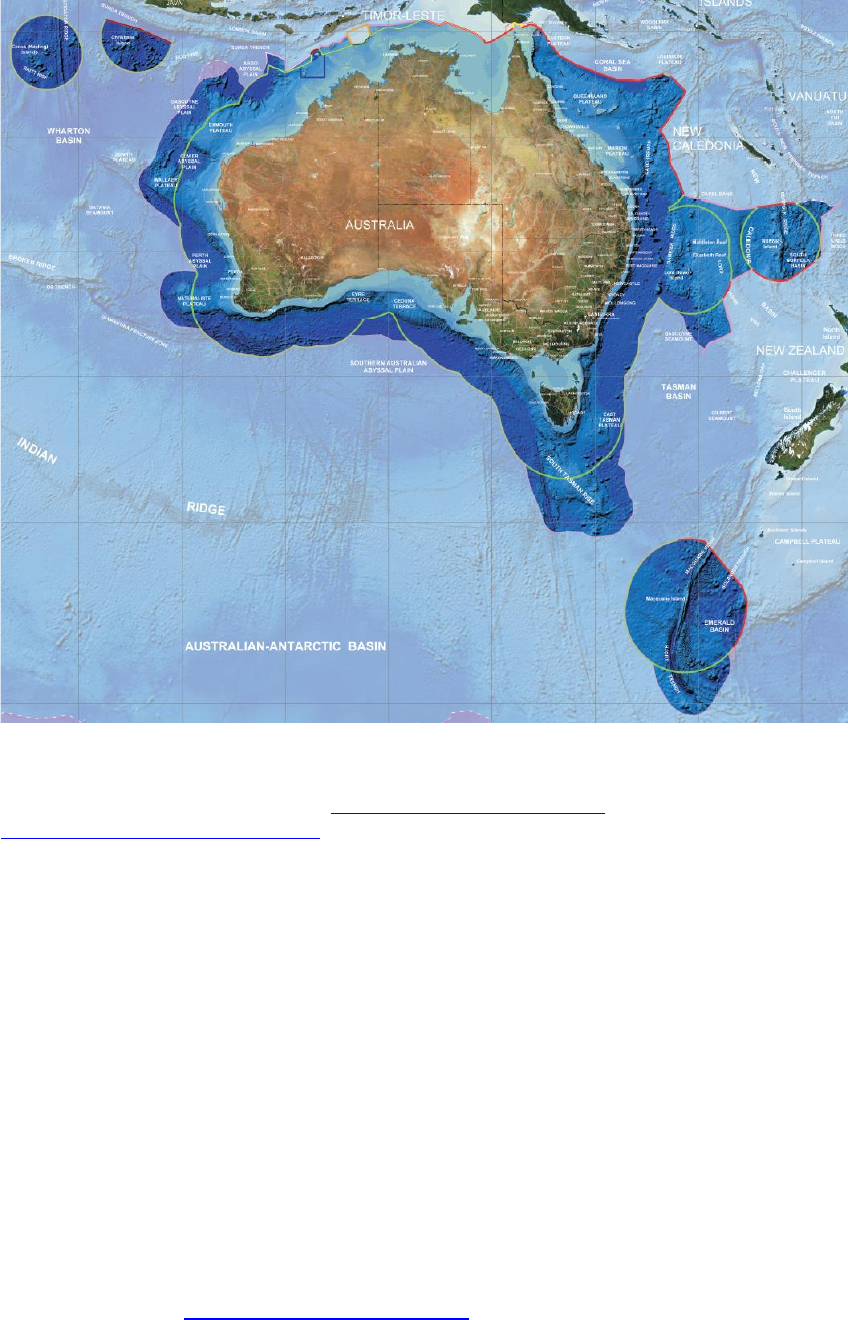
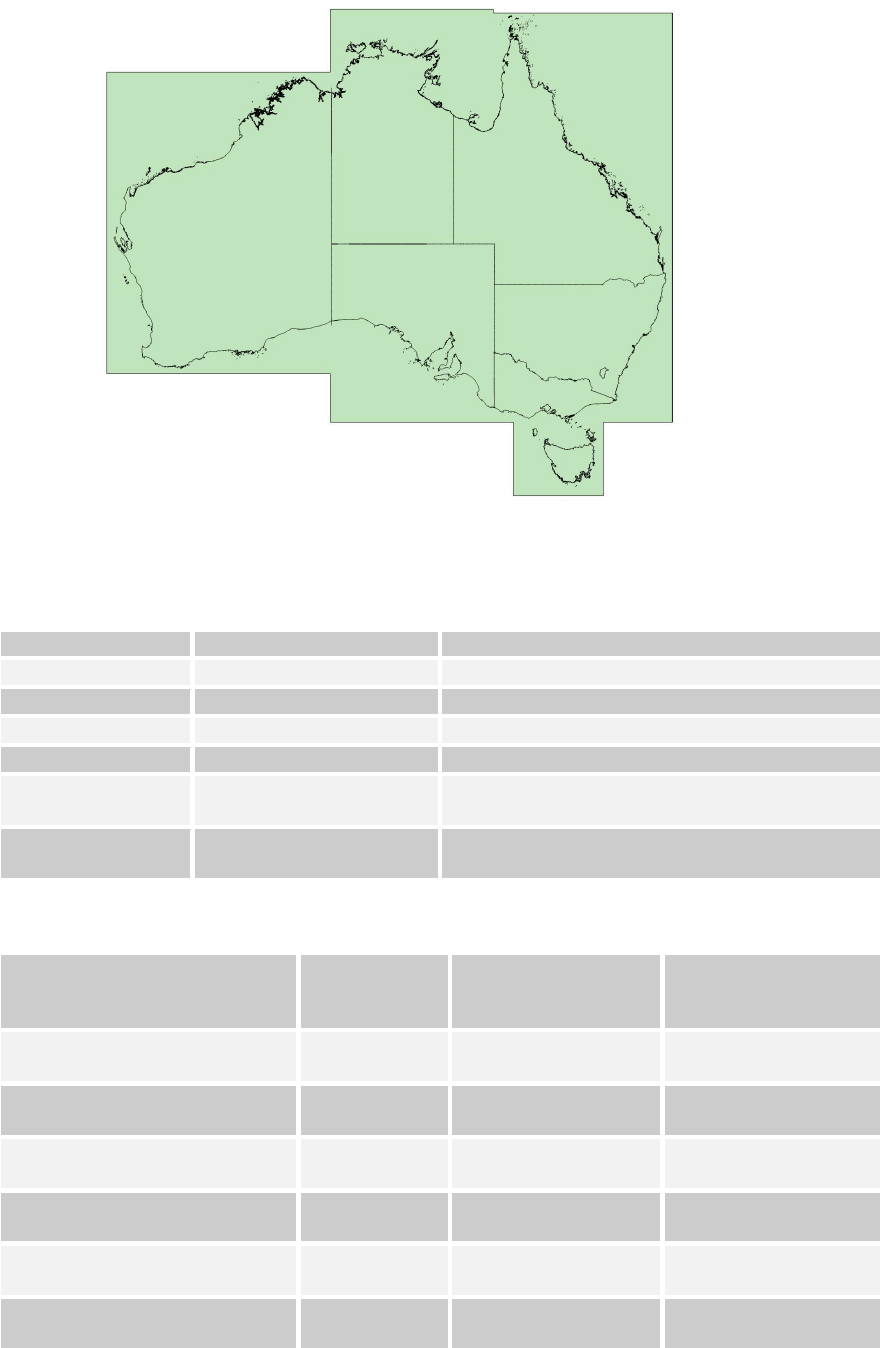
Heard-McDonald Islands and the Australian Antarctic Territory (AAT) as shown in Figure

1.1. The extent of GDA2020 is the same as the extent of GDA94.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 13

Version 1.2

Figure 1.1: The area shown in dark blue is the GDA2020 extent. The colours of the lines represent

different types of jurisdictional boundaries or proposed jurisdictional boundaries. For more information

on the type of boundary, please refer to http://www.ga.gov.au/metadata-

gateway/metadata/record/gcat_70362

1.3 Geodetic Parameter Registries

Internationally there are a number of geodetic registries that are relied upon as the source

of information for defining geodetic datums and the transformations between them. A

registry is a database of coordinate reference system information including ellipsoids,

units, datums, projections and transformations. Each database element is assigned a code

to identify it uniquely. The registry name, code number and type of registry element

provide a shorthand method for defining the relevant coordinate reference system

information.

For example, “EPSG::1168 Geodetic datum” refers to the defining elements of the

Geocentric Datum of Australia GDA2020 held in the EPSG registry.

1.3.1 EPSG Registry

The EPSG registry (http://www.epsg-registry.org/) is a reliable, freely available registry of

geodetic and transformation information. It is maintained on a “best effort” basis by the

Geomatics Committee of the International Association of Oil and Gas Producers (IOGP;

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 14

Version 1.2

previously known as the European Petroleum Survey Group or EPSG). It is updated on a

needs basis, which generally equates to two full release amendments per year.

Datum elements in this manual are identified by EPSG codes and registry element type

where they exist at the time of publication and the manual will be revised when additional

codes are available.

A number of organisations reproduce content from the EPSG registry but the IOGP site

http://www.epsg-registry.org/ is the only official EPSG dataset.

1.3.2 ISO Registry

The International Standards Organisation Technical Committee 211 Geographic

information / Geomatics (ISO/TC 211) is responsible for the ISO geographic information

series of standards. ISO/TC 211 is developing an ISO Geodetic Registry (ISO 19127) that will

ultimately replace the functions of the EPSG registry. Once ISO Registry codes are available

they will be referenced in future updates to this manual.

1.4 History of Australian datums

1.4.1 Early history

Between 1858 and 1966, geodetic surveys in Australia were computed on either a

jurisdiction (state or territory) or regional basis using more than four different spheroids

and as many as twenty coordinate origins.

The National Mapping Council (NMC), at its 23rd meeting in April 1965, adopted the

Geodetic Reference System 1967 (GRS 1967) ellipsoid, then recommended for general use

by the International Union of Geodesy and Geophysics, with the flattening term taken to

two decimal places. The NMC decided to call this spheroid the Australian National Spheroid

(ANS; see Table 1.6) (NMC, 1966).

1.4.2 Australian Geodetic Datum 1966

Re-computation and adjustment of all geodetic surveys in Australia on ANS were

commenced by the Division of National Mapping in June 1965. By 8 March 1966, all

geodetic surveys in Australia were re-computed and adjusted on the Australian Geodetic

Datum (AGD). This datum was subsequently adopted by the NMC on 21 April 1966, during

its 24th meeting in Melbourne, and was proclaimed in the Commonwealth Gazette No. 84

of 6 October 1966.

In 1966, the minor axis of the spheroid was defined as being parallel to the Earth's mean

axis of rotation at the start of 1962. In 1970 the NMC decided to adopt the Conventional

International Origin (CIO), previously known as the mean pole 1900.0-1906.0, for the

direction of the minor axis. The NMC decided that no change in the 1966 coordinates was

necessary. The AGD66 reference meridian plane of zero longitude was defined as being

parallel to the Bureau International de l'Heure (BIH) mean meridian plane near Greenwich.

This gave a value of 149° 00' 18.885” East for the plane contained by the vertical through

the Mount Stromlo photo zenith tube and the CIO. The position of the centre of the ANS is

defined by the following coordinates of Johnston Geodetic Station:

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 15

Version 1.2

Table 1.4: Johnston Geodetic Station coordinates.

Geodetic Latitude

25° 56' 54.5515” South

Geodetic Longitude

133° 12' 30.0771” East

Spheroidal Height

571.2 metres

The size, shape, position and orientation of ANS were thus completely defined, and

together with the coordinates of the Johnston Geodetic Station, defined AGD66. The

coordinates for Johnston Geodetic Station were derived from astronomical observations at

275 stations on the geodetic survey distributed all over Australia. The spheroidal height

was adopted to be 571.2 metres, which was equal to the height of the station above the

geoid as computed by trigonometrical levelling in 1965.

Due to the almost complete lack of geoidal profiles at the time of the 1966 national

adjustment, it was then assumed that the geoid-spheroid separation was zero not only at

Johnston Geodetic Station but also at all other geodetic stations listed in this adjustment.

This assumption implied that every distance used in the 1966 adjustment was a geoidal or

sea level distance (assumed spheroidal distance).

A Universal Transverse Mercator (UTM) projection was associated with AGD66 and was

referred to as the Australian Map Grid (AMG66). The AGD66 and UTM projection, AMG66,

were adopted by all the States and Territories in Australia, particularly in support of the

national mapping program.

1.4.3 Australian Geodetic Datum 1984

Since 1966, there were several readjustments of the national geodetic survey. Each

readjustment was referred to as a Geodetic Model of Australia (GMA) and was identified

by the year in which the data set used in the readjustment was compiled. The adjustment,

GMA82, included satellite Transit Doppler, Satellite Laser Ranging (SLR), Electronic Distance

Measurement (EDM) tellurometer and Very Long Baseline Interferometry (VLBI)

observations.

Recognising the need for Australia to eventually convert to a geocentric geodetic datum,

the NMC, at its 42nd meeting in October 1984, resolved that the GMA82 adjustment would

be adopted as the first step in the conversion process. However, the Council also resolved

that members could use their discretion in the timing of the conversion process.

The GMA82 adjustment maintained AGD as originally defined by the combination of the

1966 coordinate set for Johnston Geodetic Station and the defining parameters for the

ANS. This led to the development of the Australian Geodetic Datum 1984 (AGD84)

coordinate set and associated UTM projection, known as the Australian Map Grid 1984

(AMG84).

In order to prevent any confusion arising with regard to the terminology to be used in

conjunction with the 1966 and GMA82 adjustments, the NMC adopted the following

definitions for general usage:

Table 1.5: Terminology used to differentiate between AGD66 and AGD84.

Datum

Australian Geodetic Datum

Spheroid

Australian National Spheroid

1966 Coordinate Set

Australian Geodetic Datum 1966

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 16

Version 1.2

Australian Map Grid 1966

1982 Adjustment

GMA82

1984 Adopted Coordinate Set

Australian Geodetic Datum 1984

Australian Map Grid 1984

Unlike the 1966 adjustment, the GMA82 adjustment is a truly spheroidal adjustment.

Therefore, any observations used in conjunction with the AGD84 coordinate set should first

be reduced to the ANS using the appropriate geoid-spheroid separation values in terms of

N = +4.9 metres at Johnston Geodetic Station.

NOTE: Not all jurisdictions adopted AGD84. Northern Territory, New South Wales,

Australian Capital Territory, Victoria and Tasmania chose to stay on AGD66.

1.4.4 Geocentric Datum of Australia 1994

To align the Australian datum to a global reference frame, Australia adopted the

Geocentric Datum of Australia 1994 (GDA94) and UTM projection the Map Grid of Australia

1994 (MGA94). At this time the recommended reference ellipsoid was also changed from

ANS to the Geodetic Reference System 1980 (GRS80) ellipsoid after it was adopted at the

XVII General Assembly of the International Union of Geodesy and Geophysics (IUGG) in

Canberra, Australia, 1979 as the recommended best-fit ellipsoid for the Earth (Moritz,

2000). GRS80 has its geometric centre coincident with the centre of the mass of the Earth

whereas the centre of the ANS lay about 200 m from the centre. Hence, the GDA94

coordinates of a point differ by about 200 metres (north-east) compared to AGD

coordinates.

In 1992, as part of an International Global Navigation Satellite System Service (IGS)

campaign (previously known as the International GPS Service), continuous GPS

observations were undertaken on eight geologically stable marks at sites across Australia,

which formed the Australian Fiducial Network (AFN). During this campaign, GPS

observations were also carried out at a number of existing geodetic survey stations across

Australia. These were supplemented by further observations in 1993 and 1994, producing

a network of about 70 well-determined Global Navigation Satellite System (GNSS) sites,

with nominal 500 km spacing across Australia. These sites are collectively known as the

Australian National Network (ANN).

The GPS observations at both the AFN and ANN sites were combined in a single regional

GPS solution in terms of the International Terrestrial Reference Frame 1992 (ITRF92) and

the resulting coordinates were mapped to a common epoch of 1994.0.

The positions for the AFN sites were estimated to have an absolute accuracy of about 2 cm

at 95% confidence level in the horizontal component (Morgan et al., 1996), while the ANN

positions are estimated to have an absolute accuracy of about 5 cm in the horizontal

component. The positions of the AFN sites were used to determine GDA94 and were

published in the Commonwealth of Australia Government Gazette on 6 September 1995.

On 4 April 2012, the AFN was updated to include 21 sites. The purpose of the update was

to improve its consistency with the most recent realisation of International Terrestrial

Reference System (ITRS) at the time (ITRF2008). The updated AFN coordinates were

adopted from ITRF2008 and subsequently transformed to GDA94 (i.e. ITRF1992 at epoch

1994.0) using the Dawson and Woods (2010) transformation parameters. For those

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 17

Version 1.2

stations with multiple coordinate estimates in ITRF2008 the most recent coordinate

estimate was adopted.

1.4.5 Geocentric Datum of Australia 2020

Since the realisation of GDA94, there have been significant developments in technology

that provide ready access to accurate positioning systems. In the near future it is

anticipated that GNSS will be capable of providing positioning services with centimetre

accuracy in real-time to the mass market on mobile devices. Given that data from GNSS is

referenced to a global reference frame, it is appropriate that the Australian datum be

closely aligned to ITRF2014.

GDA2020 is based on a realisation of the ITRF2014 (ITRF2014; Altamimi et al., 2016) at

epoch 2020.0. The Geocentric Datum of Australia 1994 was based on the realisation of

ITRF1992 at epoch 1994.0. Since then:

 due to plate tectonic motion, GDA94 coordinates have continued to diverge from

ITRF92 coordinates. By 2020, the difference will be approximately 1.8 m;

 there have been many improvements and realisations of the ITRS which better

define the shape of the Earth. For example, differences between ITRF1992 and

ITRF2014 (on which GDA2020 is based) causes a ~9 cm change in ellipsoidal heights

in Australia (GDA2020 heights are ~9 cm less than GDA94 ellipsoidal heights); and

 parts of the Australian crust have deformed (e.g. subsidence).

These refinements to the reference frame and local scale distortions have not been

reflected in changes to the Australian datum; some of which will begin to be noticeable to

some users of positioning services.

1.4.5.1 Computation of GDA2020 coordinates

GDA2020 coordinates were computed using a rigorous, 3D network adjustment of all

available GNSS and terrestrial data from Commonwealth, state and territory jurisdictional

archives. This adjustment enables the determination of GDA2020 coordinates and supports

the computation of positional uncertainty and relative uncertainty between any survey

control marks in Australia. The national GDA2020 adjustment was undertaken by

Geoscience Australia with input from geodetic specialist representatives from all

jurisdictional survey organisations.

The national GDA2020 network adjustment involved a rigorous least squares adjustment of

all data. In the past, adjustments were undertaken with higher order data being held fixed

in lower order adjustments. This resulted in distortions in the datum that have become

more apparent when compared with high accuracy GNSS data observed in ITRF2008 or

ITRF2014 and transformed back to 1994 using a 7-parameter similarity transformation. By

performing a single national rigorous adjustment these distortions have been reduced and

relative uncertainty can be computed for any given points on the datum.

The national GDA2020 network adjustment includes all available GNSS and terrestrial data

from the jurisdictional archives, constrained using the Asia-Pacific Reference Frame

(APREF) time series combination solution. This solution is calculated weekly by Geoscience

Australia for approximately 450 APREF stations within Australia’s jurisdiction and it

provides a link between ITRF2014 and GDA2020. The development of GDA2020 has also

seen the creation of the National GNSS Campaign Archive stored at Geoscience Australia.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 18

Version 1.2

This archive contains all GNSS observations provided by state and territory jurisdictions

greater than six hours duration. The data was processed (and will continue to be as new

data is available) by Geoscience Australia to create a national high quality GNSS network.

1.4.6 Summary of Australian horizontal datums

A summary of the Australian datums is provided in Table 1.6. In some previous

documentation, GDA and AGD have been documented as the name of the datum and the

epoch has been appended to describe the coordinate set (e.g. AGD66). To avoid confusion,

it is recommended that the epoch be appended when describing the name of the datum so

users can differentiate between them (e.g. GDA94 and GDA2020). The EPSG codes for the

datums are shown in Table 1.7.

Table 1.6: Summary of the parameters of Australian datums.

Datum

Geographic

Coordinate

Set

Grid

Coordinates

Reference

Frame

Ellipsoid /

Spheroid

Semi-major

axis (m)

Inverse

Flattening

GDA2020

MGA2020

ITRF2014

GRS80

6378137.0

298.257222101

GDA94

MGA94

ITRF1992

GRS80

6378137.0

298.257222101

AGD84

AMG84

ANS

6378160.0

298.25

AGD66

AMG66

ANS

6378160.0

298.25

Table 1.7: EPSG codes of Australian datums.

Datum

Geographic

Coordinate

Set

EPSG Code

Geodetic

Datum

EPSG Code

Geodetic CRS

(Geocentric)

EPSG Code

Geodetic CRS

(Geographic 3D)

EPSG Code

Geodetic CRS

(Geographic 2D)

GDA2020

1168

7842

7843

7844

GDA94

6283

4938

4939

4283

AGD84

6203

4203

AGD66

6202

4202

1.5 Overview of the differences among GDA2020,

ITRF2014 and GNSS reference frames

1.5.1 GDA2020 and ITRF2014

GDA2020 is aligned with ITRF2014 (Altamimi et al., 2016) at epoch 2020.00. ITRF2014 is

the most recent realisation of a global network of accurate coordinates (and their

velocities) maintained by the International Earth Rotation and Reference Systems Service

(IERS) and derived from geodetic observations (VLBI, SLR, GPS and DORIS) (Seeber, 1993).

On January 1 2020, ITRF2014 at epoch 2020.0 will coincide with GDA2020. From January 1

2017 until January 1 2020, the difference between ITRF2014 coordinates (at the observed

epoch) and GDA2020 coordinates will continually converge as the Australian tectonic plate

moves 7 cm per year in a north-easterly direction. Until 2020, there will be an increasing

convergence in the coordinates of GDA2020 and ITRF2014. From January 1 2020, there will

be an increasing divergence in the coordinates of the GDA2020 and ITRF2014.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 19

Version 1.2

1.5.2 World Geodetic System 1984

The World Geodetic System, of which the latest revision is WGS84 (G1762), is the datum

used by the GPS operated by the U.S. Department of Defense. The datum is defined and

maintained by the United States National Geospatial-Intelligence Agency (NGA). WGS84

has been revised several times since its conception and is at present aligned at the

centimetre level to ITRF2014 (NGA, 2014a). The WGS84 coordinates of tracking stations

used to compute the GPS broadcast orbit are adjusted annually for plate tectonic motion

to an epoch at the half year mark, e.g. WGS84 as used in the GPS broadcast orbit during

calendar year 2014 was ITRF2008 at 2014.5. Consequently, differences between the

ITRF2014 and WGS84 are negligible for most users.

For information on the reference systems of GLObal NAvigation Satellite System

(GLONASS), Galileo, BeiDou, Indian Regional Navigation Satellite System (IRNSS) and Quasi

Zenith Satellite System (QZSS), please refer to the United Nations Office of Outer Space

Affairs (UNOOSA, 2016).

1.6 Map Grid of Australia 2020 (MGA2020)

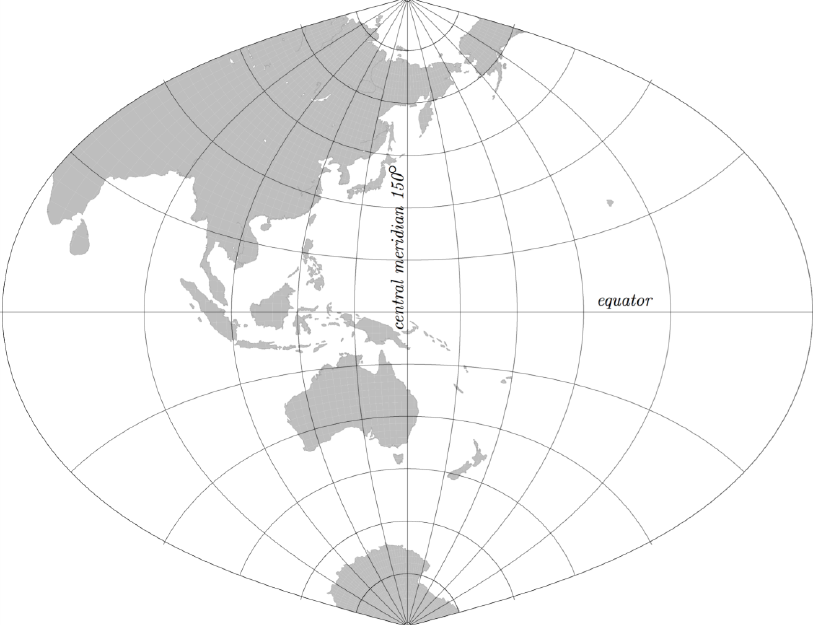
Geodetic coordinates (latitude and longitude) are represented on a map or chart, by

mathematically projecting them onto a two-dimensional plane. The Transverse Mercator

(TM) projection is a conformal mapping of geodetic coordinates from the ellipsoid onto a

plane where the equator and central meridian remain as straight lines and the scale along

the central meridian is constant while meridians and parallels are projected as complex

curves (Figure 1.2).

Figure 1.2: Transverse Mercator projection with central meridian of 150 degrees.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 20

Version 1.2

The TM projection is useful to map regions with large extents of latitude; however,

distortions increase rapidly away from the central meridian.

The UTM system (Table 1.8) uses the TM projection and attempts to overcome this

limitation by dividing the Earth into 60 zones, each with a width of 6° of longitude. A

central meridian is placed in the middle of each longitudinal zone. As a result, within a

zone nothing is more than 3° from the central meridian and therefore locations, shapes

and sizes and directions between all features are very accurate.

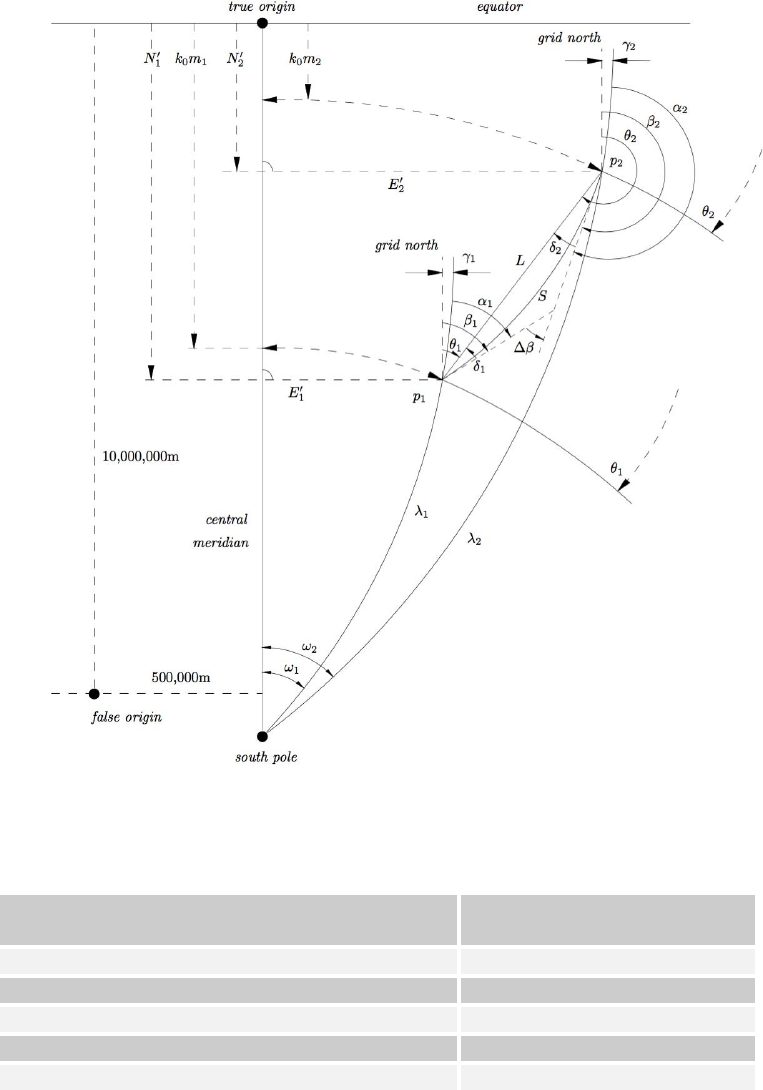
The true origin for each zone is the intersection of the equator and the central meridian,

but a false origin is often used to avoid negative coordinates (Figure 1.3).

Figure 1.3: Relationship between geographic coordinates and projected coordinates.

Table 1.8: UTM system parameters

Parameter

Value

Longitude of initial central meridian (Zone 1)

177 degrees west longitude

Zone width

6 degrees

Central scale factor

0.9996

False Easting

500,000 m

False Northing (in the southern hemisphere)

10,000,000 m

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 21

Version 1.2

The UTM system has been used with the GRS80 ellipsoid and GDA2020 latitudes and

longitudes to define Map Grid of Australia 2020 (MGA2020).

The Krueger n-series or Krueger -series formulae are used to convert between UTM (or

MGA2020) coordinates and geographic coordinates and vice versa (Section 4.1).

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 22

Version 1.2

2 Reference frame and coordinate system

fundamentals

2.1 Coordinate systems

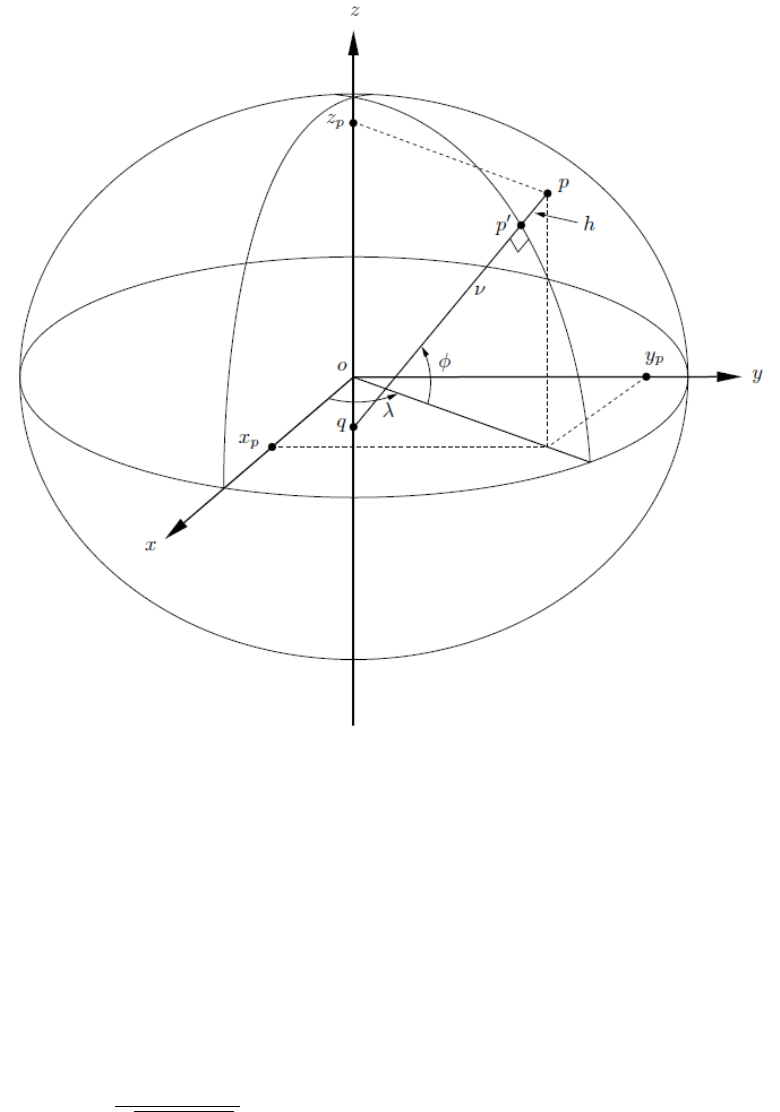
2.1.1 Cartesian

The Cartesian coordinate system is a three-dimensional system with positions  referenced

to orthogonal axes  with the origin at the centre of the reference ellipsoid (Figure

2.1). The -axis is in the direction of the rotational axis of the ellipsoid of revolution, the

 plane is, by convention, the Greenwich meridian plane (the origin of longitudes) and

the  plane is the equatorial plane of the ellipsoid (the origin of latitudes) (Gerdan and

Deakin, 1999).

2.1.2 Geographic

The geographic coordinate system is an ellipsoidal coordinate system. A specific type of

geographic coordinate system is a geodetic coordinate system; a three-dimensional system

with positions  referenced using geodetic latitude , geodetic longitude  and ellipsoidal

height (Figure 2.1). Geodetic latitude and longitude are, by convention, measured

relative to the equator and prime meridian plane respectively.

Equations 1-3 can be used to convert from Cartesian coordinates to geodetic coordinates.



 ( 1 )

 

 ( 2 )

 ( 3 )

where  ( 4 )





 ( 5 )

 ( 6 )

 ( 7 )

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 23

Version 1.2

Figure 2.1: Relationship between Cartesian and geographic coordinate systems.

The following formulae can be used to convert from geodetic coordinates to Cartesian

coordinates.

 ( 8 )

 ( 9 )

 ( 10 )

where  

 ( 11 )

 ( 12 )

 ( 13 )

Further reading on geographic to Cartesian conversion techniques including some well

suited for efficient use in software can be found in Gerdan and Deakin (1999).

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 24

Version 1.2

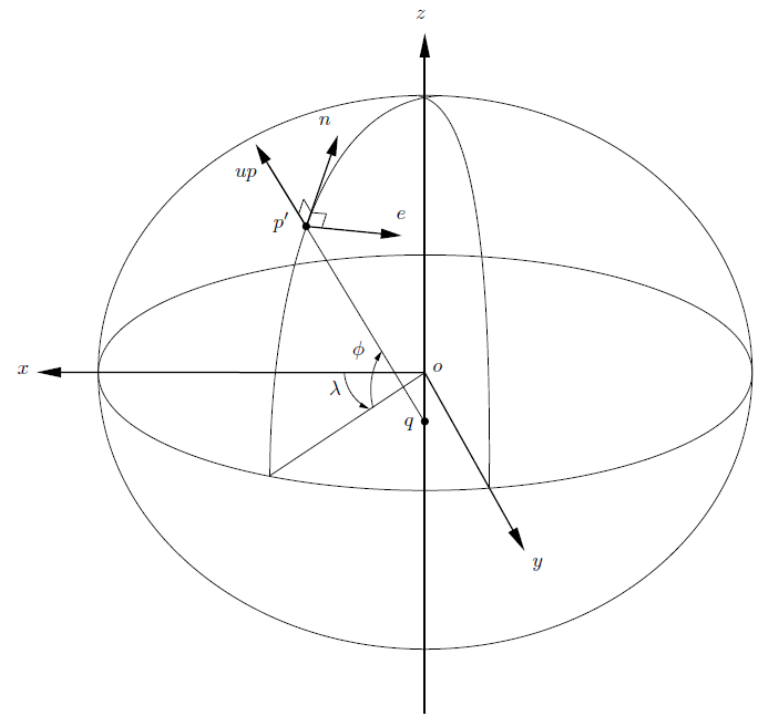
2.1.3 Local

The local reference system is a three-dimensional system with positions referenced using

orthogonal axes  with the origin on or above a point on the ellipsoid, and orientation

with respect to a local geodetic meridian (Fraser, Leahy and Collier, 2017; Figure 2.2).

Vectors in the Cartesian reference frame can be represented in the local reference frame

as 





 ( 14 )

A vector  in the local reference frame is related to the Cartesian reference frame by

 ( 15 )

where  is the rotation matrix with origin at latitude  and longitude 

  

  

    ( 16 )

Figure 2.2: The local coordinate reference system.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 25

Version 1.2

2.2 Transformations between reference frames

A similarity transformation (also known as a conformal transformation) can be used to

transform coordinates (or vectors) from one geodetic reference frame (A) to another (B).

At the computational level this transformation is performed on the Cartesian 

coordinates. The 14-parameter similarity transformation (Equation 17) is the 7-parameter

transformation (3 translations , 3 rotations  and scale ) with an additional

7 parameters used to describe the rates of change of the translation , rotation

 and scale  in time and eliminating the negligible terms (Altamimi et al., 2002). This

allows for transformation between datums with data sets at any given epoch  where  is

the reference epoch. The translations and their rates are expressed in m and m/yr,

respectively. The rotation and their rates are expressed in radians and radians/yr,

respectively. The scale is unit-less and the scale rate is expressed in yr-1. Parameters  

 are the transformed  coordinates.















 

 





 ( 17 )

2.2.1 Rotation matrix sign convention

There are two different ways of applying the sign conventions for the rotations. In both

cases a positive rotation is an anti-clockwise rotation, when viewed along the positive axis

towards the origin but:

1. The IERS assumes the rotations to be of the points around the Cartesian axes,

while;

2. The method historically used in Australia assumes the rotations to be of the

Cartesian axes around the points.

Although these two conventions exist, to enforce the property that all rotations describe

anticlockwise rotation as positive when viewed along the axis towards the origin, the

rotation of the coordinate axes around the points should be a skew-symmetric matrix with

the opposite sign to the rotation of the point/s around the coordinate axis.

The transformation parameters in the GDA2020 Technical Manual adhere to the Australian

convention. Due to the potential for confusion, it is advisable to ensure that the

conventions used in software are well understood and tested against the sample data

supplied in Section 3 of this manual.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 26

Version 1.2

3 Coordinate transformation

Coordinate transformation is the process of changing coordinates from one reference

frame to another. Options for the transformation of coordinates to, and from, GDA2020,

are transformation parameters and transformation grids.

Table 3.1: Quick reference guide for assistance with transformations.

From

Section

GDA94

GDA2020

3.1, 3.2

ITRF2014

GDA2020

3.3

AGD66/84

GDA2020

3.4

ITRF (historic)

GDA2020

3.5

MGA94

MGA2020

3.6

3.1 GDA94 to GDA2020 transformation parameters

The 7-parameter similarity transformation (Equation (18)) is also known as a conformal

transformation and accounts for the difference in scale, rotation and translation between

two reference frames. In this section, the parameters are shown to transform between

GDA94 and GDA2020. The official GDA94 to GDA2020 7 transformation parameters and

associated uncertainties (Table 3.2) were computed using 18 GNSS CORS common to both

the GDA94 RVS and the GDA2020 RVS. The GDA94 RVS (from 2011) had 21 AFN stations.

GNSS CORS located at Cocos Island (COCO), Christmas Island (XMIS) and Macquarie Island

(MAC1) were excluded from the computation due to earthquake deformation.















  

 





 ( 18 )

Table 3.2: Transformation parameters for GDA94 to GDA2020 along with the one-sigma uncertainties

(1σ). Units are in metres for the translation, parts-per-million for scale, and arcseconds for rotations.















0.06155

-0.01087

-0.04019

-0.009994

-0.0394924

-0.0327221

-0.0328979

uncertainty

0.0007

0.0006

0.0007

0.00010

0.000011

0.000010

0.000011

The parameters to transform from GDA2020 to GDA94 can be computed by multiplying the

values in Table 3.2 by -1.

3.1.1 Example: GDA94 to GDA2020 (7–parameter

transformation)

GDA94 coordinates of Alice Springs (ALIC)

Latitude (DMS)

Longitude (DMS)

Ellipsoidal Height (m)

-23 40’ 12.446019”

133 53’ 07.847844”

603.3466

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 27

Version 1.2

Latitude (DD)

Longitude (DD)

Ellipsoidal Height (m)

-23.6701239

133.8855133

603.3466

-4052051.7643

4212836.2017

-2545106.0245

GDA2020 coordinates of Alice Springs (ALIC)

-4052052.7379

4212835.9897

-2545104.5898

Latitude (DMS)

Longitude (DMS)

Ellipsoidal Height (m)

-23 40’ 12.39650”

133 53’ 07.87779”

603.2489

Latitude (DD)

Longitude (DD)

Ellipsoidal Height (m)

-23.6701101

133.8855216

603.2489

Difference (GDA2020 – GDA94)

Latitude

Longitude

Height (m)

Alice Springs (ALIC)

0.04952"

0.02995"

-0.0977

N (m)

E (m)

U (m)

Alice Springs (ALIC)

1.5236

0.8487

-0.0977

3.2 Transformation Grids

3.2.1 Overview

Transformation grids provide users of spatial data with a simple and nationally consistent

method to transform data between datums. The transformation grids are National

Transformation version 2 (NTv2) files of binary grid shift (.gsb) format and are the

preferred method for transforming between Australian datums. The transformation grids

Table 3.5 and 3.6) are available from the ICSM GitHub repository (https://github.com/icsm-

au/transformation_grids)

NOTE: The NTv2 format does not store ellipsoidal height information and therefore cannot

be used to transform the heights of data from one datum to the other. To transform

heights it is recommended that you convert your data from latitude, longitude, height 

to earth-centred Cartesian coordinates  using equations 8-10, apply the 7-parameter

transformation from GDA94 to GDA2020 (Table 3.2) and then convert back to  using

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 28

Version 1.2

equations 1-3. This step is shown in the similarity transformation spreadsheet (Section

3.7.2).

3.2.2 Types of transformation grids

Two types of GDA94 – GDA2020 transformation grids have been developed:

 Conformal: predominantly plate tectonic motion (~1.8 m NNE)

 Conformal + Distortion: includes regional distortion

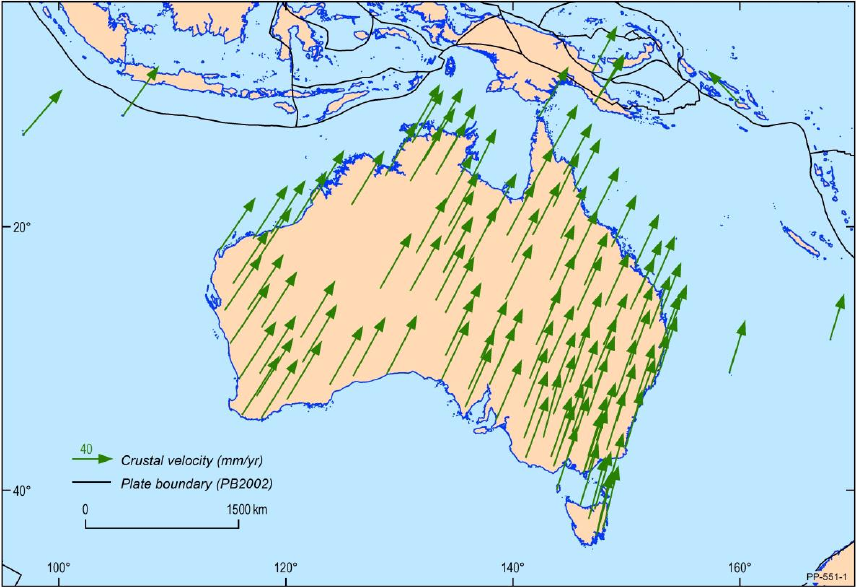
The difference between GDA94 and GDA2020 coordinates is comprised of a conformal

transformation component primarily due to plate tectonic motion (Figure 3.1), and an

irregular (non-conformal) distortion component. The distortion component is attributable

to several second-order effects, such as an improved realisation of the global reference

frame over time; irregular ground movement since GDA94 was established; and a lack of

rigour in the computation of GDA94. These effects vary in magnitude and direction around

the country and can be as large as ~0.5 m.

The combined conformal and distortion grids model both the conformal transformation

(i.e. translation, rotation and scale) and distortion components of the differences in the

datums. In the case of GDA94 to GDA2020, the distortion component is caused by the

different strategies used by state and territories to propagate GDA94 coordinates onto

ground survey control mark networks from the AFN and surface movement of parts of the

Australian crust. The magnitude of the distortion varies between jurisdictions and can be in

the order of decimetres.

The GDA94 - GDA2020 conformal only transformation grid delivers the same result as the

7-parameter similarity transformation (Section 3.1). It has been developed at the request

of some software providers who are moving towards the use of grids as the preferred

method of geodetic transformation in selected software platforms. A particular example of

its application would be for users who may be using GDA94 coordinates which were

observed in ITRF2008/2014 and transformed back to GDA94 (e.g. CORS network operators)

using a 7-parameter similarity transformation. These coordinates are not impacted by

distortion in the realisation of the GDA94 datum and the use of the conformal and

distortion transformation grid would actually introduce distortion, not remove it.

The appropriate NTv2 transformation grid to use differs between jurisdictions and the

Positional Uncertainty (or accuracy) of the dataset being transformed. Please refer to Table

3.4 for recommendations.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 29

Version 1.2

Figure 3.1: The difference between GDA94 and GDA2020 coordinates is primarily due to plate tectonic

motion.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 30

Version 1.2

3.2.3 Development of transformation grids

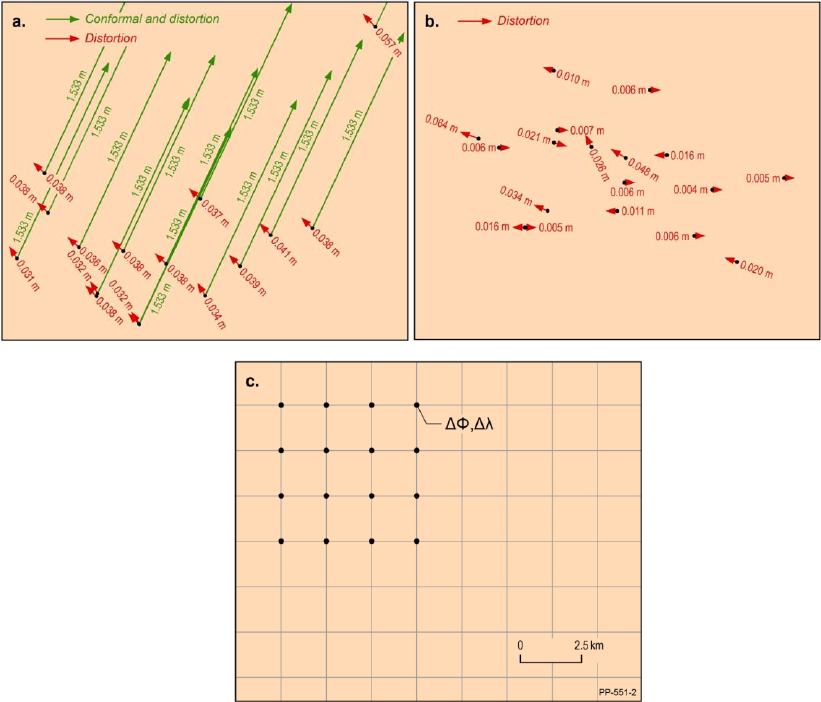
The GDA94 – GDA2020 grids were developed using over 170,000 points at which both GDA94

and GDA2020 coordinates were available. The differences that remain after the conformal

component is removed, is the distortion component. In some regions the distortion

component is regular (Figure 3.2a) with a similar magnitude and direction, while in other

cases it is irregular (Figure 3.2b) with a different magnitude and / or direction. In regions with

an irregular distortion component, the transformation grid will be less reliable.

Figure 3.2: a) conformal (green) and distortion (red; high reliability) components of the transformation

grids; b) low reliability; c) the grid has a latitude component and longitude component.

After removing the conformal component, a least squares prediction was used to compute

the distortion in latitude  and longitude  on a regular 1’ grid (Figure 3.2c). The

conformal component is then added back to each grid point to complete the conformal +

distortion grid. For further information on the development of transformation grids, refer

to Collier (2002).

3.3 Plate motion model (ITRF2014 to GDA2020)

The plate motion model enables the transformation of coordinates (or vectors) from

ITRF2014 to GDA2020 and vice versa. The model was derived using 109 ARGN and AuScope

GNSS CORS which were used to define the RVS.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 31

Version 1.2

The station coordinates and velocities were used to compute a conventional Euler plate

model. This 3-parameter model can be expressed as a 14-parameter transformation with

only rates of change rotation components (Table 3.3). Again, at the computational level

this transformation is performed on the Cartesian  coordinates.

Table 3.3: Transformation parameters for ITRF2014 to GDA2020 along with their one sigma

uncertainties (1σ). Units are in meters (m) and m/yr for the translation and their rates, respectively,

parts-per-million (ppm) and ppm/yr for scale and its rate, respectively, and arcseconds and

arcseconds/yr for rotations and their rates, respectively. The reference epoch  is 2020.0.















0.00

uncertainty

0.00

rates

0.00

0.00150379

0.00118346

0.00120716

uncertainty

0.00

0.00000417

0.00000401

0.00000370

3.3.1 Example: ITRF2014 to GDA2020 (3–parameter

transformation)

ITRF2014 at 2018.0 coordinates of Alice Springs (ALIC)

X (m)

Y (m)

Z (m)

-4052052.6588

4212835.9938

-2545104.6946

GDA2020 coordinates of Alice Springs (ALIC)

X (m)

Y (m)

Z (m)

-4052052.7373

4212835.9835

-2545104.5867

Difference (GDA2020 – ITRF2014 at 2018)

X (m)

Y (m)

Z (m)

Alice Springs (ALIC)

-0.0785

-0.0103

0.1079

3.4 Transformation from / to AGD66 and AGD84

ICSM has not defined a set of parameters that directly transform between historical

Australian geodetic datums (AGD66 and AGD84) and GDA2020. It is recommended to first

transform to GDA94 and then to GDA2020.

For transforming AGD66 or AGD84 coordinates to GDA94 the grid transformation process

using the appropriate ICSM transformation grids Appendix B is the most accurate and

preferred transformation method.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 32

Version 1.2

3.5 Transformation from / to ITRF (historic)

Transformations between older ITRF realisations (i.e. ITRF2008 and older) and GDA2020

should be performed by first transforming to GDA94 as described in Dawson and Woods

(2010) and then transforming to GDA2020 using the ICSM transformation grids (Section 3.2).

3.6 Transformation from / to MGA2020

To transform data from one map grid (AMG66, AMG84, MGA94, MGA2020) to a different

map grid, the projected coordinates need to first be converted into geographical

coordinates. In the case of transforming coordinates from MGA94 to MGA2020, the

suggested approach is:

 Grid to Geographic conversion (MGA94 to GDA94)

 Datum transformation (GDA94 to GDA2020)

 Geographic to Grid conversion (GDA2020 to MGA2020)

Options for converting coordinates are presented in Section 4.

3.7 Transformation tools and services

3.7.1 Transformation grids

If GDA94 coordinates were observed using Global Navigation Satellite System (GNSS)

technology, with corrections coming from a network of reference stations (e.g. GPSnet,

CORSnet-NSW), it is likely that the coordinates are unaffected by localised distortions and

the conformal only grid would be most suitable. However, if survey ground marks were

used for referencing / control, localised distortions will likely need to be accounted for and

the combined ‘conformal and distortion’ grid should be used. Some recommendations are

shown in Table 3.4, but if in doubt, contact your state / territory land survey authority.

Table 3.4: Advice on the use of NTv2 transformation grid files across jurisdictions

Jurisdiction

NTv2 transformation grid

Comments

ACT

GDA94_GDA2020_conformal

Recommended for users transforming

from GDA94 coordinates derived from

CORS

ACT

GDA94_GDA2020_conformal_and_distortion

Recommended for users transforming

from GDA94 coordinates derived from

survey control marks within ACTmapi

NSW

GDA94_GDA2020_conformal

Appropriate for users transforming

GDA94 coordinates derived from

unlocalised CORS or AUSPOS control.

NSW

GDA94_GDA2020_conformal_and_distortion

Appropriate for users transforming

GDA94 coordinates derived from SCIMS

(Survey Control Information

Management System) or SCIMS-localised

CORS control.

GDA94_GDA2020_conformal

Appropriate for users transforming from

GDA94 coordinates determined from

CORS.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 33

Version 1.2

GDA94_GDA2020_conformal_and_distortion

Recommended for users transforming

from GDA94 coordinates determined

from the survey ground control network.

Qld

GDA94_GDA2020_conformal

Recommended for transforming all

GDA94 data sets in Queensland.

Qld

GDA94_GDA2020_conformal_and_distortion

Not recommended for use on

Queensland data sets due to distortions

at the state borders.

GDA94_GDA2020_conformal

Appropriate for users transforming from

GDA94 coordinates determined from

CORS.

GDA94_GDA2020_conformal_and_distortion

Recommended for users transforming

from GDA94 coordinates determined

from the survey ground control network.

Tas

GDA94_GDA2020_conformal

Appropriate for users transforming from

GDA94 coordinates determined solely

from unlocalised CORS or AUSPOS

observations.

Tas

GDA94_GDA2020_conformal_and_distortion

Recommended for users transforming

from GDA94 coordinates determined

from the survey ground control network

and where the origin of survey control is

unknown or mixed (e.g. aggregated

datasets available from LISTdata.)

Vic

GDA94_GDA2020_conformal

Recommended for users transforming

from GDA94 coordinates derived directly

from GNSS CORS.

Vic

GDA94_GDA2020_conformal_and_distortion

Recommended for users transforming

from GDA94 coordinates derived from

survey control marks within the Survey

Marks Enquiry Service (SMES).

GDA94_GDA2020_conformal

Appropriate for users transforming from

GDA94 coordinates determined from

CORS.

GDA94_GDA2020_conformal_and_distortion

Recommended for users transforming

from GDA94 coordinates determined

from the local geodetic network (GOLA).

WA –

Christmas

and Cocos

Island

GDA94_GDA2020_conformal

Recommended for Christmas and Cocos

Island when they become available.

The transformation grids cover the regions shown in Figure 3.3. Note that this does not yet

include Christmas Island, Cocos Island which will be coming soon. In regions that are not

covered by the grids, but are within the GDA2020 extent (Section 1.2.4), the 7-parameter

similarity transformation is recommended to transform between GDA94 and GDA2020.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 34

Version 1.2

Figure 3.3: Extent of the GDA94-GDA2020 conformal, and conformal and distortion grids.

Table 3.5: NTv2 transformations grid files

Transformation

Grid File type

NTv2 Transformation file

AGD66 to GDA94

conformal and distortion

A66 National (13.09.01).gsb

AGD84 to GDA94

conformal and distortion

National 84(02.07.01).gsb

GDA94 to GDA2020

conformal

GDA94_GDA2020_conformal.gsb

GDA94 to GDA2020

conformal and distortion

GDA94_GDA2020_conformal_and_distortion.gsb

GDA94 to GDA2020

Christmas Island

conformal

GDA94_GDA2020_conformal_christmas_island.gsb

GDA94 to GDA2020

Cocos Island

conformal

GDA94_GDA2020_conformal_cocos_island.gsb

Table 3.6: EPSG codes for NTv2 transformation grid files

NTv2 Transformation file

EPSG

Transformation

Code

EPSG Transformation

Name

Comments

A66 National (13.09.01).gsb

1803

AGD66 to GDA94 (11)

See Appendix A for

coverage information

National 84(02.07.01).gsb

1804

AGD84 to GDA94 (5)

See Appendix A for

coverage information

GDA94_GDA2020_conformal.gsb

To be

confirmed

To be confirmed

GDA94_GDA2020_conformal_an

d_distortion.gsb

To be

confirmed

To be confirmed

GDA94_GDA2020_conformal_

christmas_island.gsb

To be

confirmed

To be confirmed

GDA94_GDA2020_conformal_

cocos_island.gsb

To be

confirmed

To be confirmed

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 35

Version 1.2

The transformation grids can be accessed under a BSD 3-Clause licence from the ICSM

GitHub repository (https://github.com/icsm-au) and by direct download from the Amazon

Simple Storage Service (S3):

GDA94-GDA2020 Conformal: https://s3-ap-southeast-2.amazonaws.com/transformation-

grids/GDA94_GDA2020_conformal.gsb

GDA94-GDA2020 Conformal and Distortion: https://s3-ap-southeast-

2.amazonaws.com/transformation-grids/GDA94_GDA2020_conformal_and_distortion.gsb

AGD66-GDA94: https://s3-ap-southeast-2.amazonaws.com/transformation-

grids/A66_National_13_09_01.gsb

AGD84-GDA94: https://s3-ap-southeast-2.amazonaws.com/transformation-

grids/National_84_02_07_01.gsb

3.7.2 Similarity transformation

An alternative to the transformation grid is the similarity transformation Spreadsheet

available from https://github.com/icsm-au/DatumSpreadsheets. This process performs the

7-parameter transformation (Table 3.2), i.e. only the conformal transformation and does

not include the distortion modelling.

3.7.3 Online transformation

ICSM has established a website (link available on http://positioning.fsdf.org.au) where you

can upload a file to be transformed. This transformation will use the transformation grids

and send you an email from where the transformed dataset can be downloaded.

3.7.4 QGIS Plug-ins

ICSM has arranged for an existing NTv2 transformation plugin for QGIS to be amended to

incorporate the NTv2 grids for transforming between AGD66 ⁄ 84 - GDA94 and GDA94 -

GDA2020. An ICSM branded plugin dealing only with the Australian datums has also been

developed.

Details of these plugins are available at http://www.icsm.gov.au/datum/gda-

transformation-products-and-tools/software-and-plugins.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 36

Version 1.2

4 Coordinate conversion

Coordinate conversion is a conversion of coordinates from one coordinate system to a

different coordinate system referenced to the same datum (e.g. Cartesian coordinates to

geographic coordinates).

4.1 Geographic from / to grid

Two methods are presented to convert geographic to / from grid coordinates; Krueger n-

series equations and Krueger -series equations (Krueger, 1912). The Krueger -series

equations are also known as Redfearn’s formulae (Redfearn, 1948) and were used in the

GDA94 Technical Manual. These equations are accurate to better than 1 mm within any

zone of the Map Grid of Australia 1994 and Map Grid of Australia 2020 and can still be used

for many purposes. However, for applications where users are working across multiple

UTM/MGA zones, Krueger n-series equations are recommended and are explained in this

Technical Manual. The Krueger n-series equations are particularly beneficial in software to

avoid error build up when conversions are done back and forth between geographic and

grid coordinates.

4.1.1 Krueger n-series equations

Krueger’s n-series equations (Karney, 2011) with coefficients that are functions of  (a

geometric constant of the reference ellipsoid known as the third flattening), give

micrometre accuracy anywhere within 30° of a central meridian (Deakin et al., 2012).

The National Geospatial-Intelligence Agency have adopted the Krueger n-series equations

(to the 6th power of n) for improved efficiency and expanded coverage of the ellipsoid.

Software that uses these formula are usually shorter and simpler to write, and, by

implication, less likely to have bugs than other methods (NGA, 2014b).

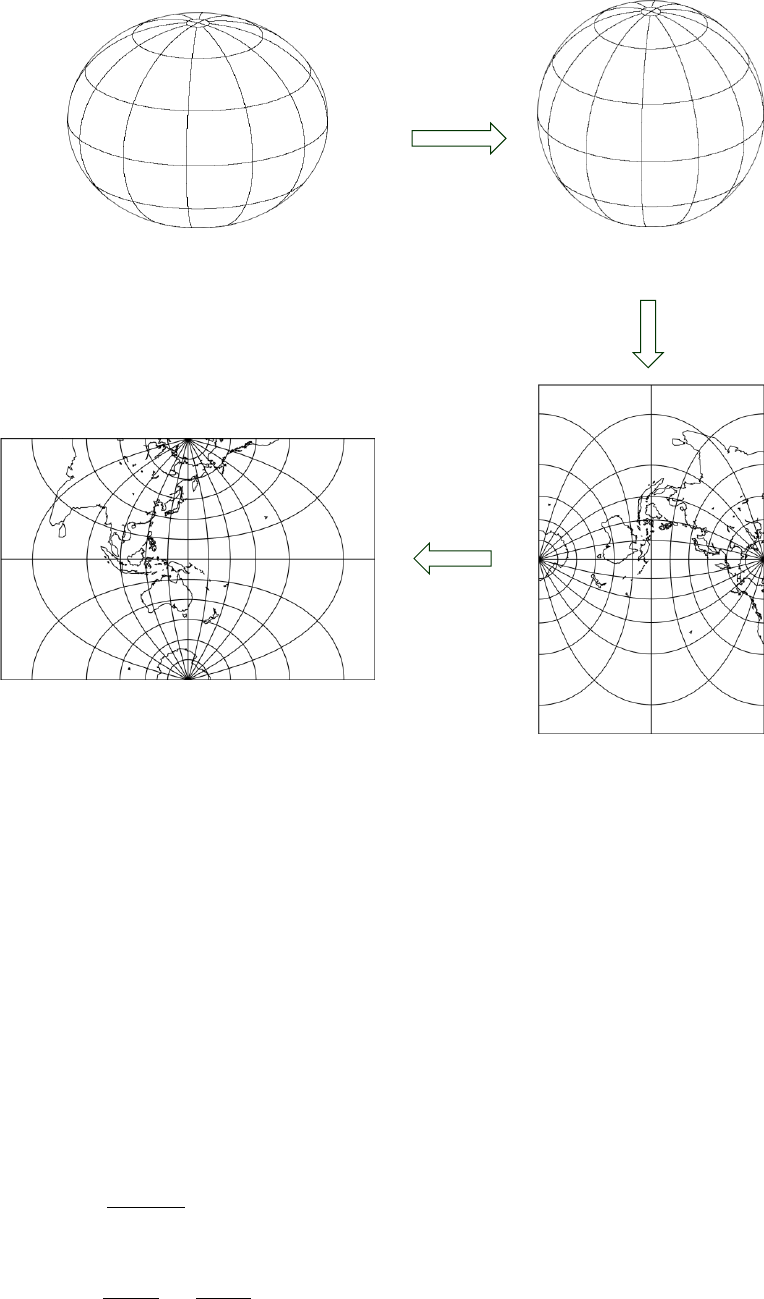
The development of the Krueger n-series equations for the transverse Mercator projection

involves three steps (Figure 4.1):

1. Mapping of the ellipsoid to a conformal sphere (a sphere of radius ).

2. Mapping of the conformal sphere to the plane using spherical transverse Mercator

projection equations with spherical latitude replaced by conformal latitude;

yielding Gauss-Schreiber coordinates with a scale factor on the central meridian,

which is not constant.

3. Mapping of Gauss-Schreiber coordinates (plane) to transverse Mercator

coordinates (plane) with a scale factor on the central meridian that is constant.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 37

Version 1.2

(a) Ellipsoid (b) Conformal sphere

(d) Transverse Mercator (c) Gauss-Schreiber

Figure 4.1: Sequence of conformal mapping used for geographic to grid conversion using Krueger n-

series (adapted from Deakin, 2014).

4.1.1.1 Forward transformation (geographic to grid)

The forward transformation (geographic to grid) converts the latitude and longitude to

eastings and northings using the ellipsoidal parameters, the longitude of the central

meridian, the central scale factor  and the offsets of the false origin.

The following are the steps required to perform the transformation. For more information

on the derivation of the equations or more efficient numerical evaluations, refer to Deakin

et al. (2012).

1. Compute ellipsoidal constants ()





( 18 )



 



( 19 )

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 38

Version 1.2

2. Compute the rectifying radius 

 











( 20 )

3. Compute the coefficients for 

2 3 4 5 6 7 8

3 4 5

1 2 5 41 127 7891 72161 18975107

2 3 16 180 288 37800 387072 50803200

13 3 557 281 1983433 13769 148003883

48 5 1440 630 1935360 28800 174182400

61 103 15061 1676

240 140 26880

n n n n n n n n

n n n n n n n

n n n



      

     

   





6 7 8

4 5 6 7 8

5 6 7 8

03 67102379 79682431

181440 29030400 79833600

49561 179 6601661 97445 40176129013

161280 168 7257600 49896 7664025600

34729 3418889 14644087 2605413599

80640 1995840 9123840 622702080

n n n

n n n n n

n n n n





   



6 7 8

212378941 30705481 175214326799

319334400 10378368 58118860800

1522256789 16759934899

1383782400 3113510400

1424729850961

743921418240

n n n









( 21 )

4. Compute conformal latitude 



( 22 )

where





( 23 )

5. Compute longitude difference



( 24 )

6. Compute the Gauss-Schreiber ratios from the 

 and 

 from the Gauss-

Schreiber coordinates 

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 39

Version 1.2





( 25 )





( 26 )

7. Compute the transverse Mercator ratios 

 and 









( 27 )







( 28 )

8. Compute the traverse Mercator coordinates 



( 29 )



( 30 )

9. Compute the MGA2020 coordinates 



( 31 )



( 32 )

where   are the false easting and northing respectively.

10. Compute  and  (to order  and )

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 40

Version 1.2







( 33 )







( 34 )

11. Compute the point scale factor 







( 35 )

12. Compute the grid convergence 





















( 36 )

4.1.1.2 Inverse transformation (grid to geographic)

The inverse transformation (grid to geographic) converts eastings and northings to latitude

and longitude.

1. Compute ellipsoidal constants (). See Equations (18, 19)

2. Compute the rectifying radius . See Equation (20)

3. Compute the coefficients  for . See Equation (21)

4. Compute the coefficients  for 

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 41

Version 1.2

2 3 4 5 6 7 8

3 4 5

1 2 37 1 81 96199 5406467 7944359

2 3 96 360 512 604800 38707200 67737600

1 1 437 46 1118711 51841 24749483

48 15 1440 105 3870720 1209600 348364800

17 37 209 5

480 840 4480

n n n n n n n n

n n n n n n n

n n n



    

   

  

   



6 7 8

4 5 6 7 8

5 6 7 8

569 9261899 6457463

90720 58060800 17740800

4397 11 830251 466511 324154477

161280 504 7257600 2494800 7664025600

4583 108847 8005831 22894433

161280 3991680 63866880 124540416

n n n

n n n n n

n n n n





  





  



6 7 8

20648693 16363163 2204645983

638668800 518918400 12915302400

219941297 497323811

5535129600 12454041600

191773887257

3719607091200

n n n









( 37 )

5. Compute the transverse Mercator coordinates 





( 38 )





( 39 )

6. Compute the transverse Mercator ratios and 





( 40 )





( 41 )

7. Compute the Gauss-Schreiber ratios 

 and 









( 42 )







( 43 )

8. Compute 

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 42

Version 1.2





( 44 )

9. Solve for  by Newton-Raphson iteration and then determine latitude 

The equations linking  and  are (22) and (23) given here in

modified form



( 45 )

where





( 46 )

 can be evaluated using the Newton-Raphson method for the real roots of the

equation  given in the form of an iterative equation





( 47 )

where  denotes the th iterate and  is given by



( 48 )

and  is a fixed value. The derivative is given by





( 49 )

An initial value for  can be taken as  and the functions  and

 evaluated from equations (46), (48) and (49).  is computed from equation (47)

and this process repeated to obtain . This iterative process can be concluded

when the difference between  and  reaches an acceptably small value, and then

the latitude is given by

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 43

Version 1.2



( 50 )

10. Compute longitude difference  and longitude  from





( 51 )



( 52 )

11. Compute  and . See Equations (33) and (34).

12. Compute the point scale factor . See Equation (35).

13. Compute the grid convergence . See Equation (36).

4.1.2 Krueger -series equations (Redfearn’s formulae)

The Krueger -series equations (also known as Redfearn's formulae) may be used to

convert between geographic coordinates (latitude, longitude) and grid coordinates

(easting, northing and zone) for a transverse Mercator projection, such as the Map Grid of

Australia (MGA). These formulae are accurate to better than 1 mm within any zone of the

Map Grid of Australia. Further information on the Krueger -series equations can be found

in the GDA94 Technical Manual.

If you require formulae to provide accurate geographic to / from grid conversion across

multiple zones, the Krueger n-series equations are recommended (Section 4.1.1).

4.1.3 Zone-to-zone transformations

If a point lies within 0.5° of a zone boundary, it is possible to compute the grid coordinate

of the point in terms of the adjacent zone. This can be done by:

1. converting the known grid coordinates to geographic coordinates using Krueger

n-series or Krueger -series equations (Redfearn's formulae), and then converting

back to grid coordinates in terms of the adjacent zone, or

2. using the formulae shown below (Jordan and Eggert 1941; Grossmann 1964).

These formulae have an accuracy of 10 mm anywhere within 0.5° of a zone

boundary.

Formulae



 ( 53 )

 ( 54 )

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 44

Version 1.2



( 55 )

 ( 56 )

where:

is a point on the zone boundary,

 are the known coordinates of the point to be transformed,

 are the coordinates of the point in terms of the adjacent zone,

 is the plane bearing from Z to the point to be transformed.

4.1.4 Tools / services

4.1.4.1 Krueger n-series

A spreadsheet is available on the ICSM GitHub repository (https://github.com/icsm-

au/DatumSpreadsheets) to perform geographic to grid conversions (and vice-versa) with

Krueger n-series equations (Karney, 2011; Deakin, 2014).

4.1.4.2 Krueger -series (Redfearn’s formulae)

A number of tools are available to perform conversions using Krueger -series equations

including:

 Geographic to Grid: (http://www.ga.gov.au/geodesy/datums/redfearn_geo_to_grid.jsp)

 Grid to Geographic: (http://www.ga.gov.au/geodesy/datums/redfearn_grid_to_geo.jsp)

 Spreadsheet (https://github.com/icsm-au/DatumSpreadsheets)

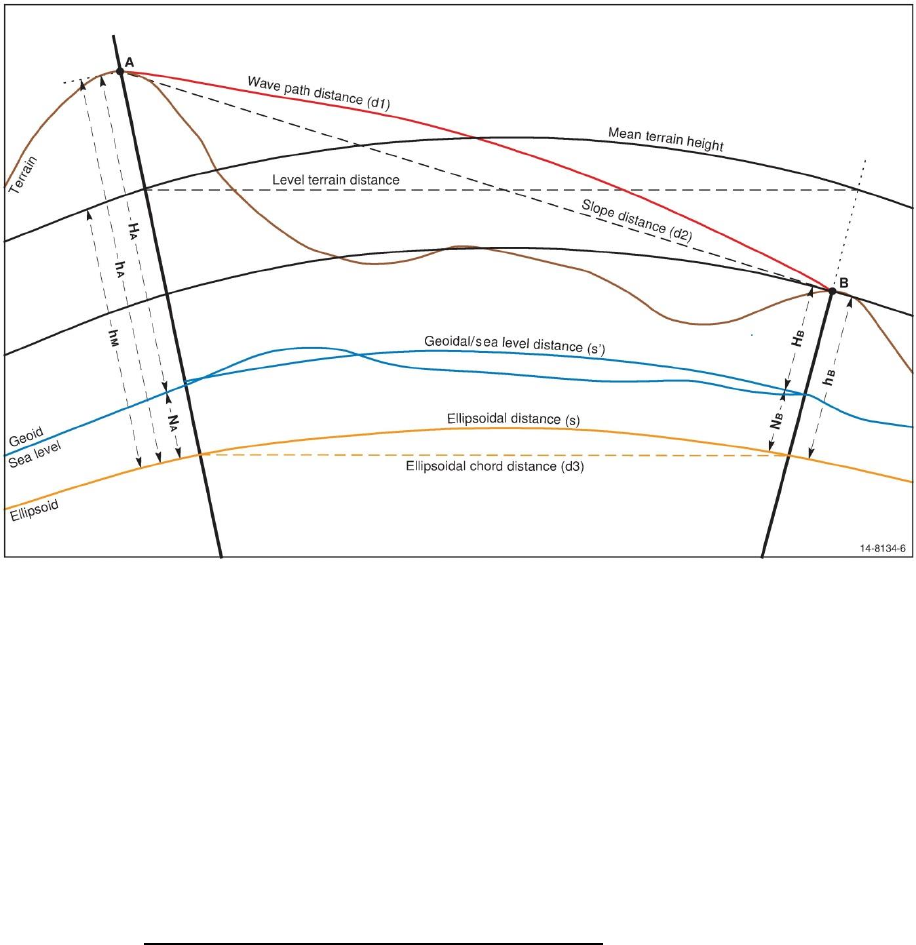
Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 45

Version 1.2

5 Coordinate computations

5.1 Ellipsoid computations

5.1.1 Reduction of measured distances to the ellipsoid

Due to the effects of atmospheric refraction, the light waves or microwaves used by

Electronic Distance Measurement (EDM) devices follow a curved path. Before this curved

wave path distance can be used for geodetic computations, it should be reduced to the

surface of the ellipsoid by the application of both physical and geometric corrections.

Figure 5.1 Reduction of distance to the ellipsoid.

The difference between the wave path length  and the wave path chord (slope distance)

 is a function of the EDM equipment used and also of the meteorological conditions

prevailing along the wave path at the time of measurement. This difference can often be

ignored for distance measurements of up to 15 kilometres, using either light waves or

microwaves. These physical corrections, which involve the application of certain velocity

corrections to the measured wave path distance, are not discussed in this manual.

5.1.1.1 Combined formula

The reduction of the wave path chord distance , to the ellipsoidal chord distance , can

be given as a single rigorous formula (Clark, 1966)



 

  ( 57 )

The ellipsoidal chord distance  is then easily reduced to the ellipsoidal arc distance 

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 46

Version 1.2



  ( 58 )

where  is the radius of curvature in the azimuth of the line.

For a distance of 30 kilometres in the Australian region the chord-to-arc correction is 0.028

m. For a distance of 50 km, the correction reaches about 0.13 m and it is more than 1 m at

100 km. The second term in the chord-to-arc correction is less than 1 mm for lines up to

100 km anywhere in Australia and can usually be ignored.

5.1.1.2 Separate formulae

The combined formula above includes the slope and ellipsoid level corrections. The slope

correction reduces the wave path chord  to a horizontal distance at the mean elevation

of the terminals of the line (terrain distance) and the ellipsoid level correction reduces the

horizontal distance to the ellipsoid chord distance . The chord-to-arc correction is then

applied to the ellipsoid chord distance, as with the combined formula, to give the

ellipsoidal arc distance s.

Slope correction  

 ( 59 )

Ellipsoidal correction 

  ( 60 )

Chord to arc correction 

  ( 61 )

Observations using total stations are often reduced to terrain distances, while GNSS

observations are reduced to the ellipsoid. These distances can be significantly different

depending on the height of the terrain. A change in height of 6.5 m causes approximately a

one part per million (1 ppm) effect on distances. For example, at 650 m above the ellipsoid,

the difference between terrain and ellipsoidal distances is approximately 100 ppm.

Similarly, variations in height across surveys covering a large area may also be significant

(DNRM, 2016).

5.1.1.3 Heights in distance reduction

The formulae given in this chapter use ellipsoidal heights . If the geoid-ellipsoid

separation  is ignored and only the height above the geoid  (orthometric or AHD height)

is used, an error of 1 ppm will be introduced for every 6.5 m of  (plus any error due to the

change in  value along the line). As the geoid-ellipsoid separation value varies from -35 m

in southwest Australia, to approximately 70 m in northeast Australia, errors from -5 to

approximately 11 ppm could be expected. In areas where the geoid-ellipsoid separation is

small and the corresponding error would also be small.

5.1.1.4 Radius of curvature

The radius of curvature of the ellipsoid is a function of latitude. For many applications the

geometric mean radius , can be used rather than the radius in the azimuth of the line

. However, there can be a large difference between the geometric mean radius and the

radius in the azimuth of the line.

For high accuracy applications the radius of curvature in the azimuth of the line should be

used.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 47

Version 1.2

 ( 62 )

  ( 63 )

where:

  



 ( 64 )

  



 ( 65 )

5.1.2 Reduction of measured directions to the ellipsoid

When a total station is levelled to make an angular observation (direction or azimuth) it is

levelled according to the plumbline at that point, i.e. the normal to the geoid. This is

generally different from the normal to the ellipsoid at the same point. This difference is

known as the deflection of the vertical. The correction for this deflection is generally small,

but should be applied for the highest quality results. Deflection of the vertical can be

computed from astronomic and geodetic coordinates at the same point, or they can be

produced from a geoid model such as AUSGeoid2020.

A further correction can be made to account for the fact that the normals at each end of

the line are not parallel (the skew normal correction). This too is a small correction and

except in mountainous country, it can reasonably be ignored (Bomford, 1980).

Because they are related to a particular ellipsoid, deflection of the vertical, like geoid

ellipsoid separations, will be different for different datums. Within Australia, the maximum

deflection in terms of GDA94 and GDA2020 is of the order of twenty seconds of arc, which

could result in a correction to an observed direction or azimuth approaching half a second

of arc.

The Laplace correction defines the relationship between an astronomically observed

azimuth and a geodetic azimuth. It can be a significant correction, of the order of several

seconds of arc, and should always be applied to an astronomic azimuth before computing

coordinates.

The formulae for these corrections are often given using the astronomic convention, with

east longitude negative. However, the formulae used here have been rearranged to use

the geodetic conventions, as used elsewhere in this manual (east longitude positive).

5.1.2.1 Formulae

Direction (reduced) = Direction (measured)

+ Deflection correction

+ Skew normal correction

+ Laplace correction (Laplace for azimuth only)

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 48

Version 1.2

Deflection correction =  ( 66 )

where  =  ( 67 )

If the elevation angle (e) is not known, an effective estimate can be obtained from:

 ( 68 )

Skew normal correction = 

 ( 69 )

Laplace correction =  ( 70 )

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 49

Version 1.2

5.1.3 Positions, azimuth and distances

There are a number of formulae available to calculate accurate geodetic positions,

azimuths and distances on the ellipsoid (Bomford, 1980). Vincenty's formulae (Vincenty,

1975) may be used for lines ranging from a few centimeters to nearly 20,000 km, with

millimetre accuracy. The formulae have been extensively tested for the Australian region

by comparison with results from other formulae (Rainsford 1955; Sodano 1965).

5.1.3.1 Vincenty’s inverse formula

Given the latitude and longitude of two points  and  Vincenty’s inverse formula

can be used to calculate the ellipsoidal arc distance and forward and reverse azimuths

between the points.

 ( 71 )

 ( 72 )

Starting with the approximation,

 ( 73 )

iterate the following equations, until there is no significant change in :

 ( 74 )

 ( 75 )

 

 ( 76 )

 

 ( 77 )



  ( 78 )



  ( 79 )



( 80 )

then:

 

 ( 81 )



  ( 82 )



  ( 83 )



 

 

 

 

( 84 )

 ( 85 )

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 50

Version 1.2

  ( 86 )

  ( 87 )

5.1.3.2 Vincenty’s direct formula

Given the latitude and longitude of a point , the geodetic azimuth  and

ellipsoidal distance to a second point , Vincenty’s direct formula can be used to calculate

the latitude and longitude of the second point () and the reverse azimuth ().

 ( 88 )



 ( 89 )

 ( 90 )



 ( 91 )



  ( 92 )



  ( 93 )

Starting with the approximation



  ( 94 )

iterate the following three equations until there is no significant change in 

 ( 95 )

 

  

 



( 96 )



  ( 97 )

then





 ( 98 )

  ( 99 )

 ( 100 )



( 101 )

 ( 102 )

  ( 103 )

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 51

Version 1.2

Note:

• "The inverse formulae may give no solution over a line between two nearly antipodal

points. This will occur when  is greater than  in absolute value." (Vincenty, 1975)

• In Vincenty (1975)  is used for the difference in longitude, however for consistency with

other formulae in this Manual,  is used here.

Sample Data

Table 5.1 Sample data to check Vincenty’s calculations

Flinders Peak

-37° 57’ 03.72030"

144° 25’ 29.52440"

Buninyong

-37° 39’ 10.15610"

143° 55’ 35.38390"

Ellipsoidal distance

54,972.271 m

Forward azimuth

306° 52’ 05.37"

Reverse azimuth

127° 10’ 25.07"

5.1.3.3 Ellipsoid computation tools

Tools available to perform ellipsoid computations are:

 Vincenty’s inverse: (http://www.ga.gov.au/geodesy/datums/vincenty_inverse.jsp)

 Vincenty’s direct: (http://www.ga.gov.au/geodesy/datums/vincenty_direct.jsp)

 Spreadsheet (https://github.com/icsm-au/DatumSpreadsheets)

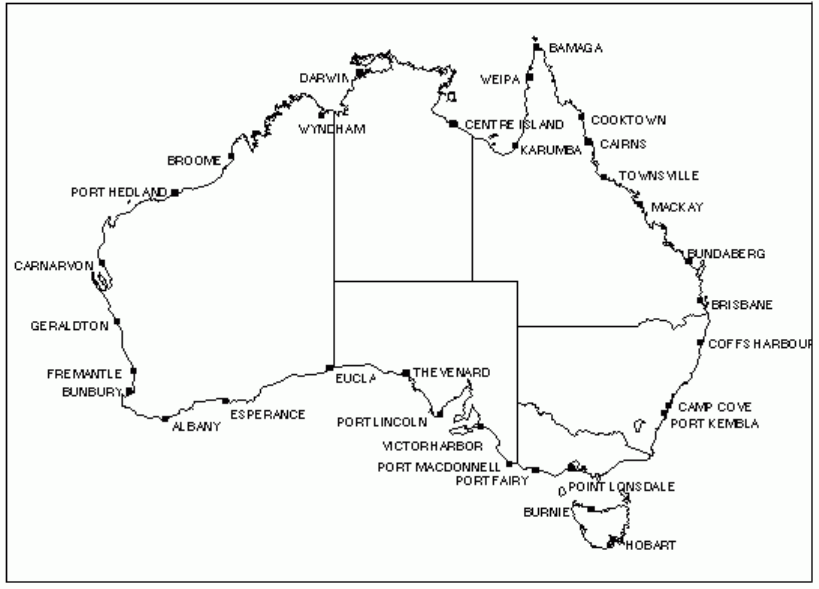
Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 52

Version 1.2

6 Australian Height Datum and geoid models

6.1 Australian Height Datum background

The Australian Height Datum (AHD) is the official national vertical datum for Australia and

refers to Australian Height Datum 1971 (AHD71; Australian mainland) and Australian

Height Datum (Tasmania) 1983 (AHD–TAS83). Prior to AHD, many local height datums were

used in the states and territories.

AHD was adopted by the NMC at its 29th meeting in May 1971 as the datum to which all

vertical control for mapping was to be referred. The datum surface passes through mean

sea level (MSL) realised between 1966 – 1968 at 30 tide gauges around the Australian

mainland (Figure 6.1).

Figure 6.1: The locations of the tide gauges used to define AHD.

AHD heights were derived across Australia via a least squares adjustment of 97,320 km of

‘primary’ levelling (used in the original adjustment) and 80,000 km of ‘supplementary’

levelling (applied in a subsequent adjustment) (Roelse et al., 1971). Levelling observations

ran between junction points in the network, and were known as level sections. These level

sections were created by combining levelling observations along level runs (usually

following major roads). The interconnected network of level sections and junction points

was constrained at the 30 tide gauge sites, which were assigned a value of zero AHD. The

least squares adjustment propagated mean sea level heights, or AHD, across the level

network. Despite the best efforts of surveyors, systematic, gross and random errors crept

into the level sections and were distributed across the network within the least squares

adjustment.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 53

Version 1.2

The Australian Height Datum (Tasmania) 1983 (AHD–TAS83) is based on mean sea level in

1972 at tides gauges in Hobart and Burnie. It was propagated throughout Tasmania using

third order differential levelling over 72 sections between 57 junction points and computed

via adjustment on 17 October 1983. Mean sea level at both Hobart and Burnie was

assigned the value of zero.

6.1.1 Metropolitan and buffer zones

Bench marks within the metropolitan areas of Perth and Adelaide were held fixed at

heights assigned by the Surveyors General of Western Australia and South Australia. The

areas in which these heights have been held fixed are termed "Metropolitan Zones". The

assigned heights within the Perth Metropolitan Zone are based on mean sea level at

Fremantle over a different epoch from that used in the adjustment of 5 May 1971. These

heights differed by not more than 40 mm from those computed in the adjustment.

The assigned heights within the Adelaide Metropolitan Zone are based on mean sea level

at Port Adelaide and these heights differ by not more than 18 mm from those determined

in the National Levelling Adjustment of 5 May 1971 (NMC, 1971)

The small differences between the heights determined by the adjustment of 5 May 1971

and those assigned by the Surveyors General to bench marks on the perimeter of the

Metropolitan Zones have been distributed through "Buffer Zones".

Details relating to the limits of the Metropolitan and Buffer Zones, and the levelling

sections within these zones may be obtained from the respective State Surveyors General.

The heights of bench marks in the Metropolitan Zones assigned by the Surveyors General

and the adjusted heights of bench marks in the Buffer Zones shall be regarded as being on

the Australian Height Datum.

6.2 Heighting fundamentals

Height determination in Australia requires a level of care due to the number and type of

reference and working surfaces to which heights can be referred, including: AHD, MSL,

Mean Sea Surface (MSS), ellipsoid and geoid (gravimetric or combined gravimetric and

geometric). These surfaces are shown in Figure 6.2.

The NMC 1971 reference to the Special Publication 8 is a WA annotated version in which the value of

40 mm is written and 4 mm is crossed out. PCG believe the value of 40 mm is correct. The notations

match the information in the document “Public Works Department Tidal Information – Western

Australian Coast”.

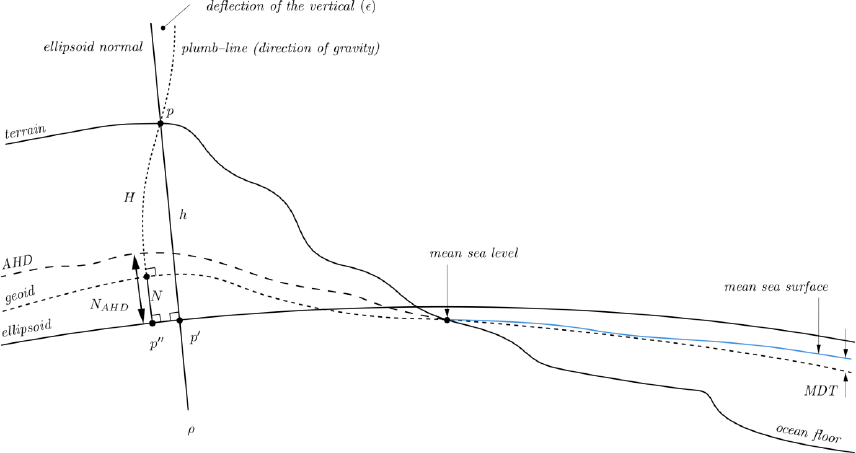
Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 54

Version 1.2

Figure 6.2: Reference and working surfaces for height in Australia.

Ellipsoid: Simplified mathematical representation of the Earth often used as a reference

surface for positioning, navigation, map projections and geodetic calculations.

Ellipsoidal height: Distance between the ellipsoid and point of interest measured along a

straight line perpendicular to the ellipsoid.

Geoid: Surface of equal gravitational potential (or equipotential) that closely approximates

mean sea level.

Deflection of the vertical (): Deviation of actual gravity (i.e. gravity observed by

gravimeter) from normal gravity (i.e. approximation of actual gravity using a model (e.g.

ellipsoid)). It is made up of two components: north–south component (deflection in the

prime meridian, ) and an east–west component (deflection in the prime vertical, ).

Mean Sea Level: Mean sea level (MSL) is an observed tidal datum and is used as the

conventional reference surface to which heights on the terrain (e.g. contours, heights of

mountains, flood plains, etc.) and other tidal datums are related (Fraser, Leahy and Collier,

2017).

Mean Sea Surface: Mean sea surface (MSS) is the sum of the geoid (closely approximated

by MSL) and Mean Dynamic Topography (MDT) which describes the thermodynamic

motion of the oceans.

Mean Dynamic Topography (MDT): Mean Dynamic Topography is the offset between the

geoid and MSS.

For a thorough description of heighting fundamentals, refer to Heiskanen and Moritz

(1967); Featherstone and Kuhn (2006); Filmer et al. (2010) and Fraser, Leahy and Collier

(2017).

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 55

Version 1.2

6.2.1 AHD: Normal-Orthometric height system

When the AHD was established, insufficient gravity observations were available to apply

gravimetric height corrections. Instead, a truncated version of the normal-orthometric

correction of Rapp (1961) was applied to the spirit levelling observations (Roelse et al.,

1975; Featherstone and Kuhn 2006) which has no requirement for observed gravity in the

correction. Instead it uses the normal gravity field only to derive all necessary gravity field

related quantities. As such, the AHD is considered a normal-orthometric height system

(Holloway 1988; Featherstone and Kuhn 2006; Filmer et al., 2010).

6.3 AUSGeoid2020

6.3.1 Overview

AUSGeoid2020 has been developed to support improved determination of AHD height

estimates  from GNSS observations. AUSGeoid2020 provides ellipsoid to AHD

separation values  onshore with uncertainty.

  ( 104 )

Given that AHD is only an onshore datum, the AUSGeoid2020 model should only be used

onshore and on islands near to the coast where connections to AHD are known to exist.

Christmas Island, Cocos Island and some islands off the coast of north Queensland are

exceptions to this rule where AUSGeoid2020 provides ellipsoid to local mean sea level as

determined by tidal observations. For converting geometric heights to physical heights in

areas not covered by AUSGeoid2020, you may consider using the Australian Gravimetric

Quasigeoid 2017 (see Section 6.5).

Onshore, AUSGeoid2020 is a combined gravimetric - geometric model. The gravimetric

component is a  by  grid of ellipsoid – quasigeoid separation values created using data

from gravity satellite missions (e.g. GRACE, GOCE), re-tracked satellite altimetry, localised

airborne gravity, land gravity data from the Australian national gravity database and a

Digital Elevation Model to apply terrain corrections.

The geometric component is a  by  grid of quasigeoid – AHD separation values and is

developed using a dataset of collocated GNSS ellipsoidal height and AHD heights. The

geometric component attempts to account for an offset between AHD and the quasigeoid

that ranges from about -0.5 m (AHD below quasigeoid) in the south-west of Australia to

about +0.5 m (AHD above quasigeoid) in the north-east of Australia. The offset between

AHD and the quasigeoid is primarily due to the method by which AHD was realised. Given

that the warmer, less dense water off the coast of northern Australia is approximately one

metre higher than the cooler, denser water off the coast of southern Australia, by

constraining each of the tide gauges to zero AHD, the effects of sea surface topography

were propagated into the adjustment.

6.3.2 Format of AUSGeoid2020

AUSGeoid2020 is provided in two formats; ASCII text file (.txt) and NTv2 binary grid (.gsb).

Separate ASCII files exist for the ellipsoid to AHD separation (Table 6.1) and the uncertainty

in the ellipsoid to AHD separation (Table 6.2)

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 56

Version 1.2

Table 6.1: ASCII format of AUSGeoid2020 ASCII file.

ellipsoid to AHD

separation (m)

Latitude

Longitude

deflection of the

vertical (seconds)

GEO







Table 6.2: ASCII format of AUSGeoid2020 uncertainty ASCII file. The deflection of the vertical are set to

zero in the uncertainty file.

uncertainty

(1 sigma)

Latitude

Longitude

deflection of the

vertical (seconds)

GEO







6.3.3 Differences between AUSGeoid09 and AUSGeoid2020

6.3.3.1 Aligned with GDA2020

The change in the reference frame used for the development of GDA2020 (i.e. ITRF2014

compared to ITRF92 used for GDA94) means the ellipsoidal height of a point in GDA94 is

approximately 9 cm higher than GDA2020. As a result, AUSGeoid2020 is incompatible with

GDA94. Data referenced to GDA94 is only compatible with AUSGeoid09.

6.3.3.2 Uncertainty provided

AUSGeoid09 provided an estimate of the root mean square error at the input data points

used in the construction of the model (Brown et al., 2011). AUSGeoid2020 provides a

rigorous uncertainty value associated with the offset between the ellipsoid and AHD,

varying as a function of location. This value includes the uncertainty from the gravimetric

component and geometric component of the model.

6.4 AUSGeoid2020 tools and services

A web application is available on the Geoscience Australia website to perform AUSGeoid

computations using AUSGeoid98, AUSGeoid09 and AUSGeoid2020

(http://www.ga.gov.au/ausgeoid/nvalcomp.jsp).

6.5 Australian Gravimetric Quasigeoid 2017

The Australian Gravimetric Quasigeoid 2017 (AGQG2017) is the gravimetric component of

the AUSGeoid2020 model. It differs from AUSGeoid2020 (and AHD/MSL) by about 0.5 m in

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 57

Version 1.2

the north and south of Australia because of the influence of sea surface topography. Given

that AGQG2017 is not biased by the influence of errors from GNSS heights or AHD, it is a

smoother working surface, which is useful for large surveys or LiDAR datasets.

To avoid confusion with AUSGeoid2020, AGQG2017 has restricted distribution, however, if

you are interested in using it, please contact geodesy@ga.gov.au.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 58

Version 1.2

References

Altamimi Z., Sillard P. and Boucher C., 2002, ITRF2000: A new release of the International

Terrestrial Reference Frame for earth science applications, Journal of Geophysical Research

107(B10).

Altamimi Z., Rebischung P., Métivier L. and Xavier C., 2016, ITRF2014: A new release of the

International Terrestrial Reference Frame modeling nonlinear station motions, Journal of

Geophysical Research Solid Earth, 121(8).

Bomford G., 1980, Geodesy (4th edn), Oxford, Clarendon Press.

Brown N. J, Featherstone W. E., Hu, G. and Johnston G. M., 2011, AUSGeoid09: a more

direct and more accurate model for converting ellipsoidal heights to AHD heights, Journal

of Spatial Science 56(1).

Clark D., 1966, Plane and Geodetic Surveying, London, England, Constable and Company,

Ltd.

Dawson J., and Woods A., 2010, ITRF to GDA94 coordination transformations, Journal of

Applied Geodesy, 4 (https://d28rz98at9flks.cloudfront.net/71433/71433.pdf).

Deakin R.E, 2014, Transverse Mercator Projection,

http://www.mygeodesy.id.au/documents/Karney-Krueger%20equations.pdf.

Deakin R.E., Hunter M.N., Karney C.F.F, 2012, A fresh look at the UTM projection: Karney-

Krueger equations, SSSI Conference, Melbourne, 18-21 April.

DNRM, Version 7.1, 2016, Cadastral Survey Requirements, Reprint 1,

(https://www.dnrm.qld.gov.au/?a=105601)

(https://www.dnrm.qld.gov.au/__data/assets/pdf_file/0011/223310/cadastral-survey-

requirements-consultation-changes-accepted.pdf)

Featherstone W.E. and Kuhn M., 2006, Height systems and vertical datums: a review in the

Australian context. Journal of Spatial Science 51(1).

Featherstone W.E. and Claessens S.J., 2008, Closed-form transformation between geodetic

and ellipsoidal coordinates, Geophysical Geodesy, 52(1).

Filmer M.S., Featherstone W.E. and Kuhn M, 2010, The effect of EGM2008-based normal,

normal-orthometric and Helmert orthometric height systems on the Australian levelling

network , Journal of Geodesy, 84(501).

Fraser R., Leahy F. and Collier P., (Eds.), 2017, DynaNet User's Guide, Geoscience Australia.

Gerdan G. P. and Deakin R. E., 1999, Transforming Cartesian coordinates X,Y,Z to

Geographical coordinates φ, λ, h, The Australian Surveyor, 44(1).

Grossmann, W., 1964, Geodetic calculations and illustrations in the National Survey

(Geodetische Rechnungen und Abbildungen). Wittwer-Verlag, Stuttgart.

Heiskanen and Moritz, 1967, Physical Geodesy, Freeman.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 59

Version 1.2

Holloway R., 1988, The integration of GPS heights into the Australian Height Datum,

UNISURV Report S-33, University of New South Wales, Sydney

Jordan W., and Eggert O., 1941, Handbuch der Vermessungskunde.

Karney C.F.F., 2011, Transverse Mercator projection with an accuracy of a few nanometers,

Journal of Geodesy, 85.

Krueger L., 1912, Konforme Abbildung des Erdellipsoids in der Ebene, New Series 52, Royal

Prussian Geodetic Institute, Potsdam.

Moritz, H. 2000, Geodetic Reference System 1980, Journal of Geodesy, 74(1).

Morgan P. J., Bock Y., et al., 1996, A Zero Order GPS Network for the Australian Region.

UNISURV, Report S-46, University of NSW, School of Geomatic Engineering.

National Mapping Council, 1966, Australian Map Grid Technical Manual, National Mapping

Council of Australia Special Publication #7.

National Mapping Council, 1971, The Australian Height Datum (WA annotated version),

National Mapping Council of Australia Special Publication #8.

NGA, 2014a, The Universal Grids and the Transverse Mercator and Polar Stereographic

Map Projections, National Geospatial-Intelligence Agency Standardization Document, Ver.

2.0.0.

NGA, 2014b, Department of Defense World Geodetic System 1984 - Its Definition and

Relationships with Local Geodetic Systems, NGA.STND.0036_1.0.0_WGS84, Version 1.0.0,

National Geospatial-Intelligence Agency, Arnold, MO.

Rainsford H. F., 1955, Long Geodesics on the Ellipsoid, Bulletin géodésique, 37.

Rapp R. H., 1961, The orthometric height. Dissertation, The Ohio State University,

Columbus.

Redfearn J.C.B., 1948, Transverse Mercator formulae, Empire Survey Review, 9(69).

Roelse A., Granger H. W., et al., 1971, The adjustment of the Australian levelling survey

1970-1971, National Mapping Technical Report No. 12, 2nd edition. Canberra, Department

of National Development.

Seeber G., 1993, Satellite Geodesy, New York, de Gruyter.

Sodano E. M., 1965, General non-iterative solution of the inverse and direct geodetic

problems, Bulletin géodésique, 75(1).

Soler T., 1998, A compendium of transformation formulas useful in GPS work, Journal of

Geodesy, 72.

UNOOSA, 2016, Regional Reference Systems,

http://www.unoosa.org/oosa/en/ourwork/icg/resources/Regl-ref.html

Vincenty T., 1975, Direct and inverse solutions of geodesics on the ellipsoid with

application of nested equations, Survey Review XXI, 176.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 60

Version 1.2

Appendix A – Recognized-value standards of measurement in the Australian

Fiducial Network

Global Cartesian coordinates of the Australian Fiducial Network can be expressed at any epoch t (years) through the application of the following

linear model using the coordinates and velocities 













 (A-1)

This model is valid for 15 years either side of 2020:

.

Coordinates (m) at 2020.0

Coordinate Uncertainty (m)

Velocity (m / year)

Velocity Uncertainty (m / year)

Site

95% CI

Ceduna (SA)

-3753473.1960

3912741.0310

-3347959.6998

0.0244

0.0249

0.0229

-0.0421

0.0024

0.0501

0.0002

Manton Dam (NT)

-4091359.6096

4684606.4258

-1408579.1371

0.0098

0.0105

0.0072

-0.0355

-0.0137

0.0576

0.0002

0.0001

0.0002

Mt Stromlo (ACT)

-4467103.2062

2683039.4818

-3666948.7613

0.0100

0.0080

0.0090

-0.0367

0.0006

0.0452

0.0002

Sydney (NSW)

-4648240.8666

2560636.4510

-3526317.7982

0.0107

0.0082

0.0093

-0.0352

-0.0015

0.0453

0.0002

Tidbinbilla (ACT)

-4460996.9609

2682557.0875

-3674442.6411

0.0104

0.0082

0.0093

-0.0368

0.0007

0.0452

0.0002

Hobart (TAS)

-3950072.2586

2522415.3710

-4311637.4095

0.0094

0.0079

0.0098

-0.0395

0.0083

0.0411

0.0002

Melbourne (VIC)

-4130636.7623

2894953.1442

-3890530.2534

0.0098

0.0083

0.0094

-0.0393

0.0042

0.0448

0.0002

Parkes (NSW)

-4554255.2088

2816652.4429

-3454059.6981

0.0107

0.0085

0.0093

-0.0363

-0.0015

0.0467

0.0002

Hillarys (WA)

-2355572.1203

4886093.2099

-3343993.6599

0.0081

0.0112

0.0091

-0.0478

0.0106

0.0491

0.0002

0.0001

0.0002

Bundaberg (QLD)

-5125977.5335

2688801.2479

-2669890.2146

0.0113

0.0082

-0.0311

-0.0105

0.0490

0.0002

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 61

Version 1.2

Coordinates (m) at 2020.0

Coordinate Uncertainty (m)

Velocity (m / year)

Velocity Uncertainty (m / year)

Site

95% CI

Kalgoorlie (WA)

-2862346.1852

4678388.0851

-3245553.1345

0.0091

0.0120

0.0096

-0.0460

0.0069

0.0505

0.0002

0.0001

0.0002

Norfolk Island (NSW)

-5457454.4185

1166108.4501

-3078178.9928

0.0120

0.0071

0.0088

-0.0245

-0.0095

0.0398

0.0001

0.0002

Albany (WA)

-2441715.0069

4629128.6333

-3633362.7930

0.0091

0.0125

0.0105

-0.0479

0.0122

0.0478

0.0002

Burnie (TAS)

-3989420.9187

2699532.9340

-4166619.7796

0.0100

0.0083

0.0101

-0.0397

0.0070

0.0426

0.0002

Liawenee (TAS)

-3973071.4774

2612492.7923

-4238233.8906

0.0099

0.0083

0.0103

-0.0396

0.0076

0.0418

0.0002

Burakin (WA)

-2511499.0840

4892172.2095

-3220858.0287

0.0088

0.0124

0.0096

-0.0471

0.0088

0.0501

0.0002

0.0001

0.0002

Kellerberrin (WA)

-2527265.3639

4813192.3590

-3324975.7001

0.0087

0.0124

0.0097

-0.0472

0.0095

0.0496

0.0002

0.0001

0.0002

Norseman (WA)

-2844072.6212

4589300.5857

-3385094.4352

0.0091

0.0117

0.0097

-0.0463

0.0080

0.0498

0.0002

0.0001

0.0002

Hyden (WA)

-2603131.0876

4717143.4739

-3402748.0718

0.0088

0.0122

0.0098

-0.0471

0.0096

0.0493

0.0002

0.0001

0.0002

Warakurna (WA)

-3583757.5864

4538446.7043

-2683056.6943

0.0090

0.0101

0.0081

-0.0420

-0.0014

0.0537

0.0002

0.0001

0.0002

Buckleboo (SA)

-3863896.2323

3723681.6406

-3436456.0075

0.0105

0.0102

0.0097

-0.0415

0.0024

0.0493

0.0002

Beechworth (VIC)

-4297030.4444

2827160.2393

-3759485.1907

0.0112

0.0091

0.0102

-0.0381

0.0023

0.0453

0.0002

Yeelana (SA)

-3787467.5311

3685160.4447

-3559786.1635

0.0093

0.0091

0.0090

-0.0420

0.0038

0.0486

0.0002

Saltia (SA)

-3998750.5658

3608798.4710

-3404651.9508

0.0098

0.0093

0.0090

-0.0407

0.0014

0.0493

0.0002

West Wylong (NSW)

-4471091.7769

2868001.2873

-3519326.3705

0.0103

0.0083

0.0091

-0.0370

-0.0005

0.0466

0.0002

Bairnsdale (VIC)

-4265638.5627

2701208.9154

-3884372.5851

0.0118

0.0094

0.0109

-0.0381

0.0034

0.0442

0.0002

Port Kembla (NSW)

-4599806.4397

2558778.9950

-3590075.1156

0.0116

0.0087

0.0100

-0.0356

-0.0007

0.0450

0.0002

Douglas Daly (NT)

-4079102.7002

4661682.9452

-1515238.0262

0.0113

0.0122

0.0079

-0.0360

-0.0128

0.0574

0.0002

0.0001

0.0002

Toowoomba (QLD)

-4994482.4972

2663618.0089

-2931171.1575

0.0121

0.0088

0.0091

-0.0324

-0.0079

0.0481

0.0002

Andamooka (SA)

-4035145.8277

3741808.3918

-3213842.4359

0.0098

0.0094

0.0088

-0.0403

-0.0002

0.0504

0.0002

Gabo Island (VIC)

-4379911.9542

2537393.8597

-3867574.2197

0.0112

0.0087

0.0103

-0.0370

0.0026

0.0436

0.0002

Coober Pedy (SA)

-3927330.9419

3965547.9511

-3077376.8165

0.0093

0.0083

-0.0409

-0.0005

0.0514

0.0002

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 62

Version 1.2

Coordinates (m) at 2020.0

Coordinate Uncertainty (m)

Velocity (m / year)

Velocity Uncertainty (m / year)

Site

95% CI

Katherine (NT)

-4147413.8177

4581462.5900

-1573359.0837

0.0098

0.0103

0.0072

-0.0358

-0.0128

0.0572

0.0002

0.0001

0.0002

Wagin (WA)

-2455774.3624

4735625.3849

-3485038.1973

0.0083

0.0112

0.0094

-0.0477

0.0110

0.0486

0.0002

0.0001

0.0002

Ravensthorpe (WA)

-2664852.2528

4602498.8360

-3509390.6909

0.0088

0.0116

0.0097

-0.0471

0.0100

0.0488

0.0002

0.0001

0.0002

Mt Cavanagh (NT)

-3929412.1216

4183417.4556

-2773890.6215

0.0096

0.0099

0.0083

-0.0404

-0.0028

0.0530

0.0002

Wiluna (WA)

-2871830.1215

4930661.0498

-2841419.6642

0.0083

0.0109

0.0083

-0.0452

0.0039

0.0524

0.0002

0.0001

0.0002

Tibooburra (NSW)

-4383698.9008

3417850.9363

-3117538.7823

0.0110

0.0096

0.0093

-0.0379

-0.0029

0.0501

0.0002

Ivanhoe (NSW)

-4310476.3634

3190508.6627

-3441393.5542

0.0098

0.0085

0.0088

-0.0384

-0.0001

0.0480

0.0002

Broome (WA)

-3234208.1569

5134028.8375

-1958815.1914

0.0088

0.0113

0.0075

-0.0413

-0.0046

0.0560

0.0002

0.0001

0.0002

Nhill (VIC)

-4035390.1167

3193137.6972

-3755906.1988

0.0100

0.0089

0.0095

-0.0402

0.0038

0.0464

0.0002

Warramunga (NT)

-4193700.6368

4289270.2773

-2160904.9454

0.0100

0.0102

0.0077

-0.0375

-0.0088

0.0553

0.0002

Mt Magnet (WA)

-2629526.8926

4978260.9506

-2987965.8480

0.0082

0.0112

0.0086

-0.0463

0.0064

0.0514

0.0002

0.0001

0.0002

Larrimah (NT)

-4208011.6662

4479077.7734

-1701337.7347

0.0111

0.0114

0.0078

-0.0360

-0.0122

0.0568

0.0002

0.0001

0.0002

Leonora (WA)

-2905528.2178

4775175.2276

-3062280.3715

0.0085

0.0109

0.0087

-0.0455

0.0053

0.0515

0.0002

0.0001

0.0002

Tuross Head (NSW)

-4477434.2788

2572331.0877

-3731376.5980

0.0101

0.0079

0.0092

-0.0365

0.0010

0.0444

0.0002

Bald Rock (VIC)

-4188591.0788

3020461.0294

-3731086.9242

0.0097

0.0083

0.0092

-0.0391

0.0027

0.0461

0.0002

Horn Island (QLD)

-4960946.6284

3834778.7885

-1164513.3408

0.0110

0.0094

0.0069

-0.0291

-0.0205

0.0564

0.0002

Mt Emu (VIC)

-4065544.7571

3013958.9753

-3869590.3370

0.0106

0.0090

0.0101

-0.0398

0.0044

0.0453

0.0002

Stony Point (VIC)

-4111952.8138

2856387.6375

-3938194.1385

0.0097

0.0082

0.0095

-0.0393

0.0046

0.0444

0.0002

Alice Springs (NT)

-4052052.7360

4212835.9841

-2545104.5883

0.0095

0.0098

0.0079

-0.0393

-0.0052

0.0540

0.0002

Roslyn Bay (QLD)

-5121089.4297

2863243.2415

-2493143.3274

0.0164

0.0118

0.0100

-0.0311

-0.0118

0.0503

0.0002

Larrakeyah (NT)

-4072230.1682

4713609.1735

-1366659.3497

0.0113

0.0122

0.0077

-0.0354

-0.0139

0.0577

0.0002

0.0001

0.0002

Broken Hill (NSW)

-4235701.4667

3372839.2104

-3360245.2676

0.0104

0.0092

-0.0390

-0.0003

0.0489

0.0002

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 63

Version 1.2

Coordinates (m) at 2020.0

Coordinate Uncertainty (m)

Velocity (m / year)

Velocity Uncertainty (m / year)

Site

95% CI

Cape Ferguson (QLD)

-5054583.3968

3275504.1131

-2091538.4726

0.0108

0.0086

0.0075

-0.0312

-0.0143

0.0529

0.0002

Wallal (WA)

-3060306.4338

5165740.4734

-2144656.6187

0.0086

0.0113

0.0077

-0.0425

-0.0023

0.0552

0.0002

0.0001

0.0002

Spring Bay (TAS)

-3988046.7045

2498705.5367

-4290516.8742

0.0113

0.0090

0.0113

-0.0392

0.0079

0.0411

0.0002

Eucla (WA)

-3410392.1827

4229088.8868

-3330284.3849

0.0093

0.0103

0.0091

-0.0439

0.0043

0.0504

0.0002

Coonabarabran (NSW)

-4687675.6162

2786705.8985

-3297865.3737

0.0110

0.0085

0.0092

-0.0352

-0.0034

0.0472

0.0002

Arubiddy (WA)

-3183133.6965

4393393.4410

-3342516.9213

0.0086

0.0100

0.0088

-0.0449

0.0057

0.0503

0.0002

Baladonia (WA)

-3002034.1354

4472882.6994

-3403723.4851

0.0087

0.0106

0.0091

-0.0457

0.0072

0.0498

0.0002

Mainoru (NT)

-4306320.1817

4444883.0498

-1537980.0653

0.0115

0.0116

0.0078

-0.0348

-0.0140

0.0571

0.0002

Bingleburra (NSW)

-4743762.8083

2559346.3040

-3399327.9127

0.0115

0.0085

0.0096

-0.0345

-0.0030

0.0459

0.0002

Portland (VIC)

-3926098.9113

3110284.5779

-3935497.1170

0.0110

0.0096

0.0108

-0.0408

0.0057

0.0452

0.0002

Rocklands (NT)

-4445289.3356

4025824.8715

-2164421.6420

0.0108

0.0103

0.0079

-0.0360

-0.0102

0.0549

0.0002

Thevanard (SA)

-3735034.6262

3908923.6990

-3372521.9630

0.0100

0.0102

0.0094

-0.0422

0.0027

0.0499

0.0002

Exmouth (WA)

-2417814.5397

5401707.5260

-2370380.3097

0.0080

0.0117

0.0079

-0.0452

0.0031

0.0533

0.0002

0.0001

0.0002

Fitzroy Crossing (WA)

-3547066.8913

4918047.3803

-1971686.4311

0.0095

0.0115

0.0077

-0.0401

-0.0064

0.0562

0.0002

0.0001

0.0002

Gnangara (WA)

-2368688.0424

4881316.7075

-3341794.9823

0.0081

0.0114

0.0092

-0.0477

0.0105

0.0492

0.0002

0.0001

0.0002

Flinders Island (TAS)

-4147112.4604

2567153.7563

-4096196.5874

0.0109

0.0087

0.0106

-0.0385

0.0056

0.0425

0.0002

New Norcia (WA)

-2414152.3781

4907778.6372

-3270644.2049

0.0088

0.0125

0.0096

-0.0475

0.0097

0.0496

0.0002

0.0001

0.0002

Tom Price (WA)

-2706524.4877

5221344.9511

-2461226.3825

0.0087

0.0124

0.0084

-0.0447

0.0021

0.0536

0.0002

0.0001

0.0002

North Star (NSW)

-4854589.1186

2752849.4480

-3078537.4439

0.0117

0.0088

0.0091

-0.0338

-0.0060

0.0479

0.0002

Cooladdi (QLD)

-4707740.5468

3213770.3725

-2852875.4128

0.0122

0.0098

0.0091

-0.0352

-0.0068

0.0504

0.0002

Birdsville (QLD)

-4355739.6469

3740194.4994

-2769171.5091

0.0113

0.0105

0.0090

-0.0378

-0.0053

0.0523

0.0002

Boulia (QLD)

-4496431.9209

3785936.3941

-2467980.3960

0.0111

0.0101

0.0083

-0.0363

-0.0083

0.0534

0.0002

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 64

Version 1.2

Coordinates (m) at 2020.0

Coordinate Uncertainty (m)

Velocity (m / year)

Velocity Uncertainty (m / year)

Site

95% CI

Hughenden (QLD)

-4833918.6817

3485758.7318

-2266147.6174

0.0125

0.0101

0.0084

-0.0334

-0.0118

0.0531

0.0002

Julia Creek (QLD)

-4687826.4385

3697044.2812

-2237232.1656

0.0118

0.0103

0.0083

-0.0345

-0.0111

0.0539

0.0002

Neutral Junction (NT)

-4123557.7648

4274539.2155

-2318810.9705

0.0122

0.0124

0.0089

-0.0383

-0.0072

0.0548

0.0002

Lambina (SA)

-3957272.6859

4088878.0706

-2872293.9157

0.0097

0.0098

0.0084

-0.0404

-0.0022

0.0525

0.0002

Mt Doreen (NT)

-3916571.9695

4428011.7783

-2388294.0779

0.0119

0.0126

0.0089

-0.0396

-0.0055

0.0548

0.0002

0.0001

0.0002

Jervois (NT)

-4237233.1317

4077484.9793

-2462642.0014

0.0117

0.0116

0.0087

-0.0380

-0.0068

0.0540

0.0002

Coen (QLD)

-4956013.1005

3710714.3539

-1528615.7435

0.0150

0.0117

0.0081

-0.0305

-0.0179

0.0555

0.0002

Laura (QLD)

-5000453.3825

3572456.4740

-1701780.3240

0.0132

0.0107

0.0079

-0.0307

-0.0169

0.0547

0.0002

Northcliffe (WA)

-2311144.1346

4712785.4091

-3611358.5979

0.0084

0.0119

0.0100

-0.0483

0.0128

0.0476

0.0002

0.0001

0.0002

Kilkivan (QLD)

-5073245.0941

2668929.5700

-2787555.0317

0.0127

0.0091

0.0090

-0.0316

-0.0094

0.0486

0.0002

Meadow (WA)

-2373305.7835

5181466.1948

-2854287.0682

0.0084

0.0126

0.0089

-0.0467

0.0069

0.0514

0.0002

0.0001

0.0002

Yarragadee (WA)

-2389026.6159

5043317.0600

-3078529.5586

0.0080

0.0114

0.0087

-0.0472

0.0085

0.0505

0.0002

0.0001

0.0002

North Bourke (NSW)

-4587935.3985

3116314.3026

-3139419.8358

0.0113

0.0092

0.0093

-0.0363

-0.0040

0.0490

0.0002

Harding River Dam (WA)

-2713833.2684

5303935.1133

-2269513.7542

0.0081

0.0113

0.0077

-0.0441

0.0007

0.0542

0.0002

0.0001

0.0002

Port Headland (WA)

-2867484.8313

5242158.9057

-2223764.3419

0.0085

0.0118

0.0079

-0.0434

-0.0006

0.0547

0.0002

0.0001

0.0002

Murchison (WA)

-2556630.0412

5097138.2863

-2848384.7843

0.0083

0.0117

0.0085

-0.0462

0.0058

0.0518

0.0002

0.0001

0.0002

Gascoyne (WA)

-2482748.2739

5243145.5489

-2642213.9892

0.0093

0.0143

0.0094

-0.0458

0.0047

0.0525

0.0002

0.0001

0.0002

Normanton (QLD)

-4728960.2818

3819993.0037

-1923811.0896

0.0140

0.0122

0.0085

-0.0334

-0.0137

0.0550

0.0002

King Island (TAS)

-3953946.8747

2888865.8595

-4073040.9386

0.0096

0.0083

0.0097

-0.0403

0.0066

0.0437

0.0002

Hernani (NSW)

-4887853.3609

2545879.9420

-3202305.1047

0.0124

0.0088

0.0097

-0.0333

-0.0053

0.0466

0.0002

Christmas Island (WA)

-1696344.7537

6039590.0096

-1149275.0866

0.0075

0.0132

0.0072

-0.0419

-0.0015

0.0538

0.0002

0.0001

0.0002

Lord Howe Island (NSW)

-5082756.5673

1944860.6793

-3315203.5926

0.0116

0.0076

0.0092

-0.0304

-0.0056

0.0433

0.0002

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 65

Version 1.2

Coordinates (m) at 2020.0

Coordinate Uncertainty (m)

Velocity (m / year)

Velocity Uncertainty (m / year)

Site

95% CI

Eidsvold (QLD)

-5049378.8605

2785132.1517

-2716869.1227

0.0147

0.0102

0.0100

-0.0319

-0.0097

0.0493

0.0002

Nebo (QLD)

-5068236.7291

3081711.6353

-2337561.3869

0.0163

0.0122

0.0101

-0.0314

-0.0126

0.0515

0.0002

Aramac (QLD)

-4827919.3114

3349814.0161

-2472422.8950

0.0114

0.0093

0.0082

-0.0338

-0.0102

0.0521

0.0002

Tambo (QLD)

-4820440.5593

3216767.7633

-2656380.4455

0.0154

0.0116

0.0104

-0.0341

-0.0088

0.0511

0.0002

Mulgathing (SA)

-3833528.0707

3961621.4057

-3197513.8708

0.0102

0.0103

0.0092

-0.0415

0.0009

0.0509

0.0002

Kidman Springs (NT)

-4017486.2068

4628837.9322

-1759281.7840

0.0171

0.0183

0.0106

-0.0372

-0.0107

0.0568

0.0002

0.0001

0.0002

Renner Springs (NT)

-4192073.9978

4368928.5517

-1999279.4623

0.0109

0.0112

0.0080

-0.0370

-0.0100

0.0559

0.0002

Esperance (WA)

-2800842.3479

4500734.2962

-3534898.1927

0.0171

0.0260

0.0185

-0.0466

0.0094

0.0489

0.0002

Jabiru (NT)

-4236472.9665

4559859.3702

-1388764.0422

0.0170

0.0175

0.0095

-0.0347

-0.0147

0.0576

0.0002

0.0001

0.0002

Yellowdine (WA)

-2698549.7646

4741476.9407

-3293657.2537

0.0147

0.0232

0.0163

-0.0466

0.0082

0.0501

0.0002

0.0001

0.0002

Walhallow (NT)

-4344184.0427

4247715.9745

-1934909.3899

0.0182

0.0186

0.0110

-0.0360

-0.0113

0.0559

0.0002

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 66

Version 1.2

Appendix B

B1. AGD66 / AGD84 to GDA94 transformations

B1.1 Transformation grid details

Initially State and Territories produced individual NTv2 transformation grids. These files

transformed from either AGD66 or AGD84 to GDA94, depending on which version of AGD

was previously adopted by that jurisdiction. Subsequently combined grids were produced

and ultimately two national transformation grid files (one each for AGD66 and AGD84)

were developed. It is these grids that are available under a BSD 3-Clause licence from the

ICSM GitHub repository (https://github.com/icsm-au) and recommended for use as the

preferred method to transform from AGD66 and AGD84 to GDA94. The uncertainty of each

of these transformations grids is estimated to be approximately 0.1 m.

See Tables B-1 and B-2 for details of various transformation files related to respective EPSG

transformation codes and names.

Table B-1 AGD66 to GDA94 NTv2 Transformation Grids

NTv2 Transformation file

name

EPSG

Transformation

Code

EPSG transformation

name

Comments

A66 National (13.09.01).gsb

1803

AGD66 to GDA94 (11)

Coverage - national. Replaces

Codes 1506, 1507, 1596

SEAust_21_06_00.gsb

1596

AGD66 to GDA94 (10)

Coverage - ACT, NSW, VIC.

Replaced code 1464

nt_0599.gsb

1507

AGD66 to GDA94 (7)

Coverage - NT.

tas_1098.gsb

1506

AGD66 to GDA94 (6)

Coverage – Tas

Vic_0799.gsb

1464

AGD66 to GDA94 (5)

Coverage – Vic

Table B-2 AGD84 to GDA94 NTv2 Transformation Grids

Transformation file name

EPSG

Transformation

Code

EPSG transformation

name

Comments

National 84(02.07.01).gsb

1804

AGD84 to GDA94 (5)

Coverage – Qld, SA, WA.

Replaces Code 1593

wa_0700.gsb

1593

AGD84 to GDA94 (4)

Coverage - WA. Replaced

code 1559

B1.2 National transformation grid coverage

Transformation file A66 National (13.09.01).gsb provides a complete national coverage

from AGD66 to GDA94. In NSW and Victoria the on-shore and close coastal areas of the

earlier combined State grid were included in the national grid, but elsewhere there may be

differences. These differences are generally small but may be larger near the state borders

and in areas where there was little or no common data (e.g. offshore). The AGD66 national

file also covers the offshore areas out to the Exclusive Economic Zone (EEZ). Although still

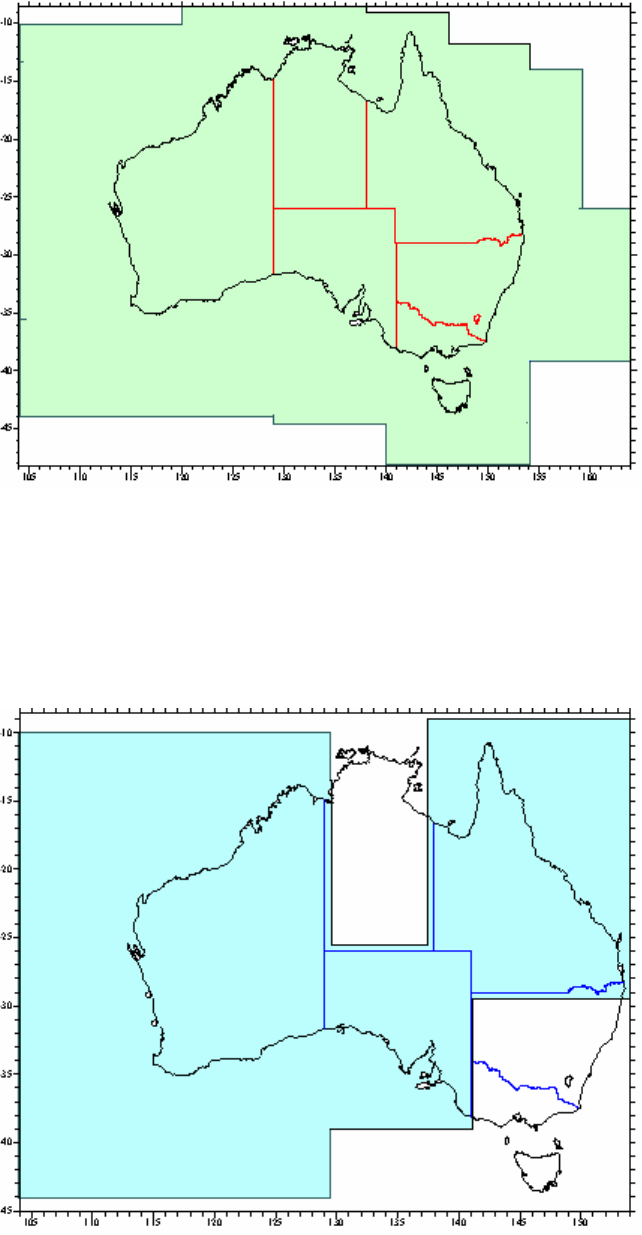
Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 67

Version 1.2

in NTv2 format, a simple conformal transformation was used to generate the shifts in these

offshore areas.

Figure B-1 AGD66 to GDA94 Transformation Grid Coverage

Transformation file National 84(02.07.01).gsb has coverage for the states that previously

adopted AGD84 (Queensland, South Australia and Western Australia). This coverage was

produced by merging individual Queensland, South Australian and West Australian

transformation files, and differs slightly from the previous state files only near the merged

borders.

Figure B-2 AGD84 to GDA94 Transformation Grid Coverage

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 68

Version 1.2

For mathematical convenience and to suit the rectangular convention of the NTv2 format,

the national grids extend outside the Australian EEZ in some places, but these extents do

not infer any rights, nor do they imply the use of AGD or GDA94 coordinates in these areas.

B2. National 7 parameter similarity transformations

National similarity transformation parameters to convert between AGD66 / AGD84 and

GDA94 were developed (Table B-3 and B-4). Due to the inconsistent nature of the AGD66

coordinate set, it is not possible to perform a highly accurate 7-parameter similarity

transformation. The estimated uncertainty of the national AGD66 parameters is 3 metres

and they are only recommended for use in offshore environments. The estimated

uncertainty of 7-parameter similarity transformation for AGD84 to GDA94 parameters is

about 1 metre.

The parameters to transform between AGD84 and GDA94 were computed from 327 points

across Australia, which had both AGD84 and GDA94 coordinates.

Table B-3 National transformation parameters for AGD84 and AGD66 to GDA94. Units are in m for the

translation, parts-per-million (ppm) for scale, and arc-seconds (as) for the rotations.

Datum

EPSG

Code















AGD84

1280

-117.763

-51.510

139.061

-0.191

-0.292

-0.443

-0.277

AGD66

15979

-117.808

-51.536

137.784

-0.290

-0.303

-0.446

-0.234

Refer to Section 2.2.1 Rotation Matrix Sign Convention for important information about

the rotation signs.

Table B-4 EPSG details of national transformations for AGD84 and AGD66 to GDA94.

EPSG

Transformation

Code

EPSG transformation

name

Comments

1280

AGD84 to GDA94 (2)

AGD84 officially adopted only

in QLD, SA and WA

15979

AGD66 to GDA94 (12)

Recommended for use in

offshore areas only.

B3. Regional 7 parameter similarity transformations for

AGD66

Although it is possible to compute national similarity transformation parameters between

AGD84 and GDA94 that provide an estimated accuracy of transformation of 1 metre

AGD66/GDA94 similarity transformation parameters can only be accurately computed for

smaller areas where AGD66 is more consistent.

The parameters shown in Table B-4 are only valid for transformation between AGD66 and

GDA94 for the jurisdiction indicated.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 69

Version 1.2

Table B-5 Regional transformation parameters for AGD66 to GDA94. Units are in m for the translation,

parts-per-million (ppm) for scale, and arc-seconds (as) for the rotations.

Region

EPSG

Code















ACT

5827

-129.164

-41.188

130.718

-2.955

-0.246

-0.374

-0.329

ACT

1458

-129.193

-41.212

130.730

-2.955

-0.246

-0.374

-0.329

TAS

1594

-120.271

-51.536

137.784

2.499

-0.217

0.067

0.129

VIC/NSW

1460

-119.353

-48.301

139.484

-0.613

-0.415

-0.260

-0.437

1595

-124.133

-42.003

137.400

-1.854

0.008

-0.557

-0.178

Table B-6 EPSG details of regional transformations for AGD66 to GDA94

EPSG

Transformation

Code

EPSG transformation

name

Comments

5827

AGD66 to GDA94 (19)

Coverage – ACT

1458

AGD66 to GDA94 (10)

Coverage – ACT. Parameters

replaced in Code 5827

1594

AGD66 to GDA94 (8)

Coverage - Tas

1460

AGD66 to GDA94 (4)

Coverage – VIC/NSW

1595

AGD66 to GDA94 (9)

Coverage – NT

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 70

Version 1.2

Appendix C

C1. Grid bearings and ellipsoidal distance

The following formulae provide the only direct method to obtain grid bearings and

ellipsoidal distance from MGA2020 coordinates.

 ( C-1 )

where  are the easting values measured positive eastwards from the central meridian

(i.e. does not include the false easting) of points 1 and 2 respectively

 ( C-1 )

 ( C-2 )

 ( C-3 )

 (radians) ( C-4 )

 (seconds) ( C-5 )

 (radians) ( C-6 )

 (seconds) ( C-7 )

 ( C-8 )

 ( C-9 )

The mean radius of curvature can be calculated as shown below, using an approximate

value for the mean latitude

. The approximate mean latitude can be calculated in two

steps, with an accuracy of about two minutes of arc, using the formulae shown below. This

approximation is derived from the formulae for meridian distance used with Krueger 

series equations (Redfearn's) and the constants shown are the values  and,

computed for GDA2020.

 (C-10)



 (C-11)





 (C-12)







 (C-13)



 (C-14)



 (C-15)

 (C-16)

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 71

Version 1.2

C1.1 MGA2020 coordinates from grid bearing and ellipsoidal

distance

This computation is commonly used when the coordinates of one station are known and

the grid bearing and ellipsoidal distance from this station to an adjacent station have been

determined. The bearing and distance are applied to the coordinates of the known station

to derive the coordinates of the unknown station and the reverse grid bearing. The

formulae shown are accurate to 0.02" and 0.1 ppm over any 100 kilometre line in an MGA

zone. For lower order surveys:

• the underlined terms are often omitted

• the latitude function 1/6r2 becomes a constant and

• the formulae for

and



are replaced by simplified versions

Formulae

First calculate approximate coordinates for the unknown station:

  (C-17)

  (C-18)

  (C-19)

If not already known the point scale factor  may be approximated by:

 (C-20)

 (C-21)

 (C-22)

 (C-23)

 (C-24)

 (C-25)

 (C-26)

 (C-27)

 (C-28)

 (C-29)

 (C-30)

The mean radius of curvature can be calculated as shown below, using an approximate

value for the mean latitude

. The approximate mean latitude can be calculated in two

steps, with an accuracy of about two minutes of arc, using the formulae shown below. This

approximation is derived from the formulae for meridian distance used with Krueger 

series equations (Redfearn's) and the constants shown are the values  and,

computed for GDA2020.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 72

Version 1.2

 (C-31)



 (C-32)





 (C-33)







 (C-34)



 (C-35)



 (C-36)

 (C-37)

C1.2 Traverse computations using arc-to-chord corrections and

scale factors

Traverses can be rigorously computed on the ellipsoid, using formulae such as those shown

in Section 5. The geographic results from these computations can then be rigorously

converted to grid coordinates using Krueger equations. However if necessary, the

computation can be varied to suit the requirements of the project. For example:

• the arc-to-chord corrections and line scale factors can be ignored and the

traverse computed using the formulae of plane trigonometry;

• if approximate MGA2020 coordinates of the traverse stations are available,

compute of the arc-to-chord corrections and line scale factors; or

• the arc-to-chord corrections and line scale factors can be computed precisely, and

the method becomes first order anywhere in a MGA2020 grid zone.

The precision obtained should be closely balanced against the labour involved, though with

modern computers and software, the difference between a rigorous and approximate

calculation is trivial. Prior to precise computation, approximate coordinates and bearings

may be carried through the traverse, using uncorrected field measurements, to ensure that

the observations are free of gross errors.

C1.2.1 Basic outline

There are many ways of arranging the computation. Essentially, the work is split into

stages:

1. approximate eastings and northings are computed from observed angles and

distances

2. arc-to-chord corrections and line scale factors are computed from the approximate

coordinates and applied to the observations to give plane angles and plane

distances

3. precise coordinates are computed by plane trigonometry

4. misclosure in grid bearing and position is analysed and the traverse is adjusted as

required.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 73

Version 1.2

For precise computation, each line is rigorously computed before the next line is

calculated, so that errors in the approximate coordinates do not accumulate. True eastings

 and differences in northing  are the quantities carried through the computation. Sign

conventions can be disregarded and signs determined by inspection of a traverse diagram.

C1.2.2 Formulae and symbols

Formulae for arc-to-chord corrections  and line scale factors  are given above. If the

underlined terms are omitted, the errors for a 100 km line running north and south on a

zone boundary do not exceed 0.08” in bearing and 0.25 ppm in distance. As the final

coordinates of a precise traverse will nearly always be computed and adjusted by least

squares. For short lines near a central meridian it may be possible to omit the arc-to-chord

corrections and line scale factors and compute the traverse with observed angles and

distances, using the formulae of plane trigonometry.

If the symbol  is used for the arc-to-chord correction at station 2 to station 1 and  for

the correction at station 2 to station 3 and the angles are measured clockwise from station

1 to station 3, then the plane angle  at station 2 is obtained from the observed angle 

by  (C-38)

where angles are measured clockwise only.

C1.2.3 Computations of arc-to-chord corrections and scale factors

Although there are several ways of arranging the computation, the following procedure, is

recommended:

1. compute the grid bearing to the "forward" station by applying the observed

horizontal angle at the "occupied" station to the known grid bearing of the "rear"

station

2. compute the point scale factor at the "occupied" station and multiply the

ellipsoidal distance to the "forward" station by this factor

3. using the distance obtained and the forward grid bearing, compute approximate

coordinates of the "forward" station by plane trigonometry

4. using the coordinates of the "occupied" station and the approximate coordinates of

the "forward" station, compute the arc-to-chord correction at the "occupied"

station and the line scale factor. If the line crosses the central meridian,   is

negative

5. add the arc-to-chord correction to the forward grid bearing to obtain the plane

bearing and multiply the ellipsoidal distance by the line scale factor to obtain the

plane distance

6. using the plane bearing and plane distance, compute the coordinates of the

"forward" station by plane trigonometry

7. compute the arc-to-chord correction from the new station to the previously

occupied station and add this to the plane bearing reversed by 180° to obtain the

reverse grid bearing from the new station.

The above process is repeated for each new line of a traverse with the reverse grid bearing

of the previous line becoming the known grid bearing to the rear station.

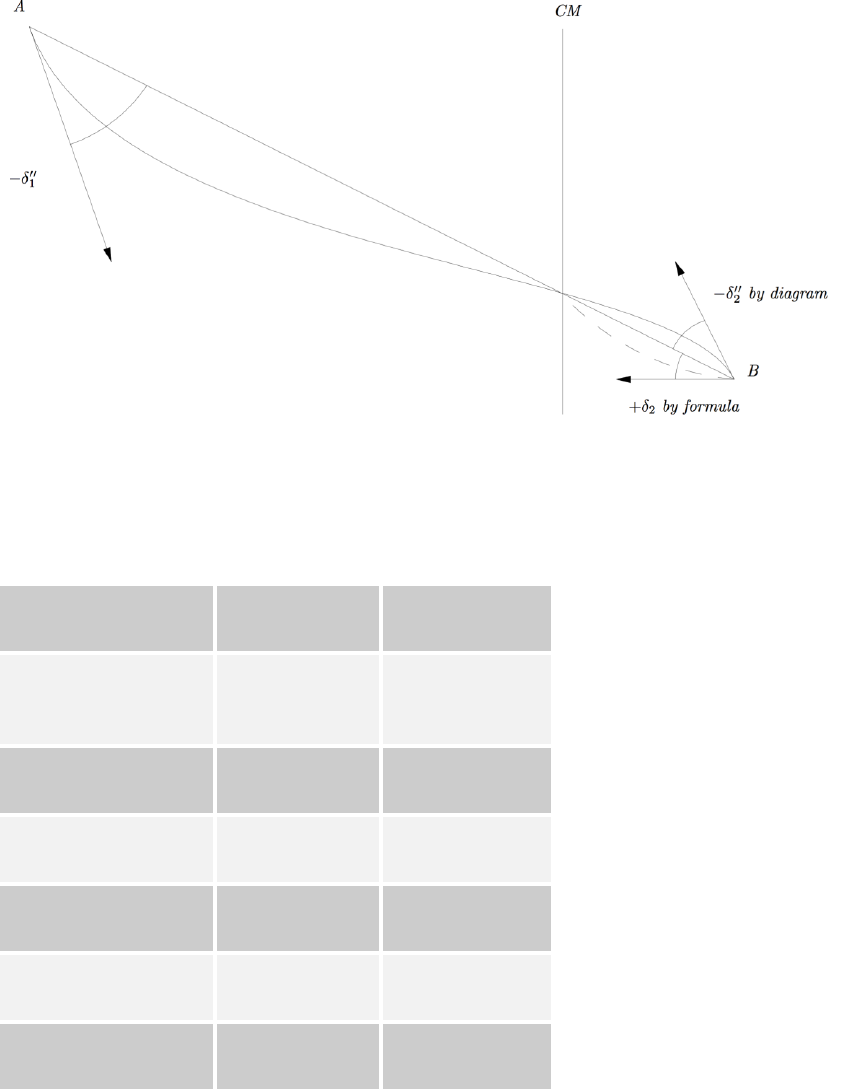
Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 74

Version 1.2

The traverse diagram shown in Figure C.2 should be referred to with the above text.

Figure C.1 Arc-to-chord correction

Sample Data

Table C.1 Sample data to check grid calculations

Flinders Peak

Buninyong

MGA2020 (zone 55)

E 273 741.297

N 5 796 489.777

E 228 854.051

N 5 828 259.038

Ellipsoidal Distance (m)

54972.271

Plane Distance (m)

54992.279

Grid Bearing

305° 17’ 01.72"

125° 17’ 41.86"

Arc to chord

+19.47"

-20.67”

Line scale factor

1.000 363 97

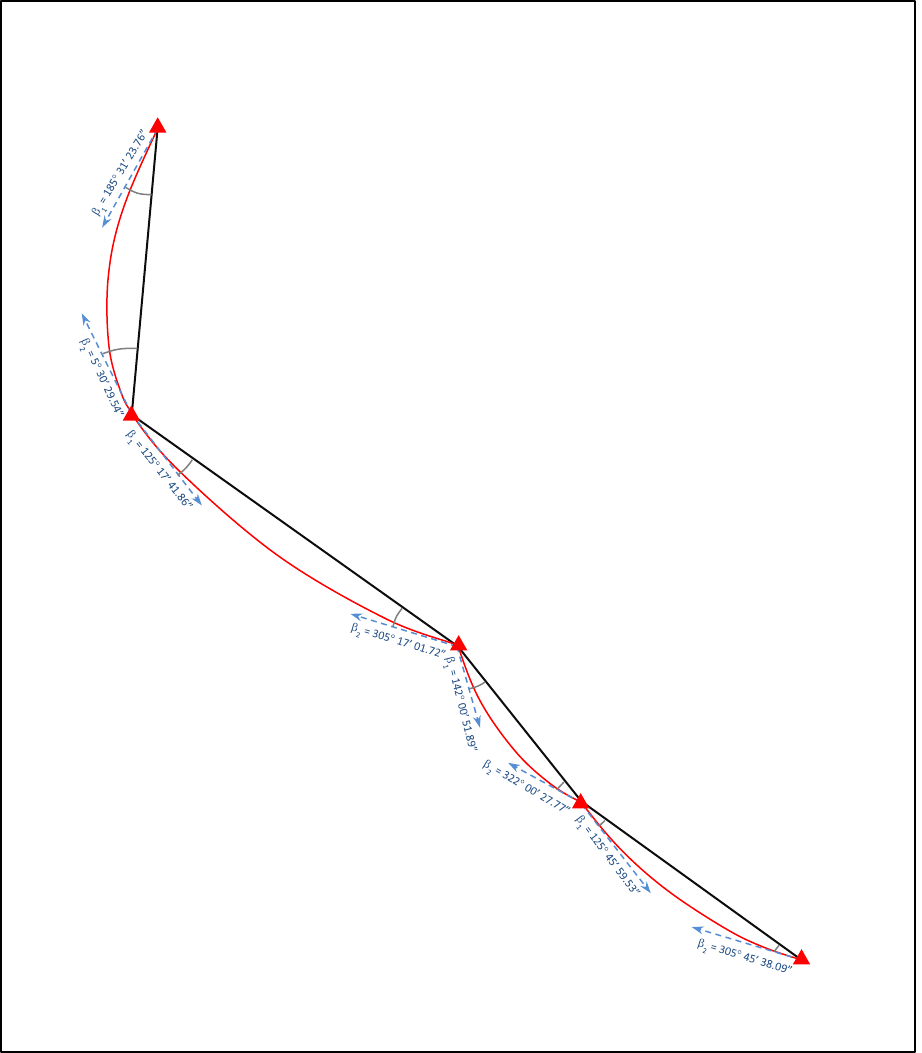
Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 75

Version 1.2

Traverse Diagram

Figure C.2 Traverse diagram.

E 273 741.297 S 37 57’ 03.72030” -1 35’ 03.647” 

N 5 796 489.777 E 144 25’ 29.52440” 1.000 230 558 6 k

FLINDERS

PEAK

E 228 854.051 S 37 39’ 10.15610” -1 52’ 43.219” 

N 5 828 259.038 E 143 55’ 35.38390” 1.000 505 669 1 k

BUNINYONG

E 232 681.853 S 37 17’ 49.73133” -1 49’ 42.581” 

N 5 867 898.032 E 143 59’ 03.16715” 1.000 480 346 2 k

SMEATON

E 290 769.028 S 38 09’ 05.22717” -1 28’ 32.238” 

N 5 774 686.632 E 144 36’ 43.67715” 1.000 139 188 5 k

BELLARINE

E 320 936.377 S 38 21’ 13.12685” -1 16’ 19.020” 

N 5 752 958.470 E 144 57’ 02.55485” 0.999 994 887 6 k

ARTHURS SEAT

1 = -27.05”

2 = +27.17”

1 = -20.67”

2 = +19.47”

1 = -12.22”

2 = +11.90”

1 = -11.00”

2 = +10.44”

s = 39 803.761 m

K = 1.000 492 99

L = 39 823.384 m

 = 185 30’ 56.71”

01 = 187 21’ 06.34”

10 = 7 23’ 12.76”

s = 54 972.271 m

K = 1.000 363 97

L = 54 992.279 m

 = 125 17’ 21.18”

12 = 127 10’ 25.07”

21 = 306 52’ 05.37”

s = 27 659.334 m

K = 1.000 184 28

L = 27 664.431 m

 = 142 00’ 39.67”

23 = 143 35’ 55.53”

32 = 323 29’ 00.01”

s = 37 175.286 m

K = 1.000 065 17

L = 37 177.709 m

 = 125 45’ 48.53”

34 = 127 14’ 31.76”

43 = 307 01’ 57.12”

All MGA2020 Eastings and Northings are in Zone 55

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 76

Version 1.2

Appendix D

D1. Grid references

The Universal Transverse Mercator (UTM) Grid, of which the Map Grid of Australia 2020

(MGA2020) is a part, provides the ability for the locations of features on the Earth to be

uniquely defined via a single grid reference. Grid references can be used with maps and

with online mapping systems, such as Google Maps.

Grid references are generalised forms of MGA2020 grid coordinates that consist of two

parts. The first part is an alphanumeric code that uniquely defines a rectangular region of

the Earth. The second part consists of the numerical location that defines the easting and

northing for the location within the region.

D1.1 Grid zones

A grid reference uses the UTM Grid Zones of 6 longitude bands together with the Military

Grid Reference System (MGRS) of 8 latitude bands (except for the most northerly band, X,

which covers 12 degrees of latitude from 72N to 84N). An extended MGRS can also be

used where the zones are further divided into 100 000 metre square regions identified by a

two letter code. This 100 000 metre square identification is presented in section D.1.2.

The Universal Polar Stereographic Grid is used north of the 84N latitude and south of the

80S latitude, but will not be discussed in this manual as it is outside the extents of

GDA2020 and thus beyond the limits of MGA2020.

The numbering of the longitude bands starts at the 180 meridian with zone 1 and

proceeds easterly with 6 intervals to define the 60 bands for the whole 360 around the

Earth.

The 8 bands of latitude are lettered from C to X (X is a 12 latitude band), omitting the

letters I and O, so as not to confuse them with the numbers one and zero. The southern

value of the first latitude band is 80S and with each band proceeding northwards to 84N.

There are 20 bands.

All the UTM longitude zones, MGRS latitude bands that lie within the extents of GDA2020

are depicted in figure D-1.

Each grid zone is thus one rectangle of the grid pattern established by these bands and is

designated by the figure of the longitude band followed by the letter of the latitude band.

Thus the zone hatched on figure D-1 lying between 132E and 138E and between 16S and

24S is designated 53K.

D1.2 100 000 metre square identification

To further subdivide the 6 x 8 grid zones, an extended MGRS has been defined where the

zones are divided into 100 000 metre square regions that are bounded by grid lines of

eastings and northings and identified by a two letter code.

Intergovernmental Committee on Surveying and Mapping

Geocentric Datum of Australia 2020 Technical Manual 77

Version 1.2

Each column and each row is identified by a letter which are combined to identify the

100 000 metre square. The letter pattern of 100 000 metre squares covers an area 18 east

to west by 2 000 000 metres north to south, and is not repeated within this area.

Starting at the 180 meridian and proceeding easterly along the equator for 18, the

100 000 metre columns, including partial columns along grid junctions, are consecutively

lettered A to Z, with I and O being omitted. This is repeated at 18 intervals.

The 100 000 metre rows are lettered A to V with I and O being omitted and reading from

south to north, with this partial alphabet being repeated every 2 000 000 metres. Every

odd-numbered UTM zone has the alphabet of the 100 000 metre row letters beginning at

the equator; the even-numbered UTM zones have the alphabet of the 100 000 metre row

letters beginning at the northing grid line 500 000 metres south of the equator. So for even

numbered easting zones the northing designators are offset by five characters, starting at

the equator with the letter F. This staggering lengthens the distance between 100 000

metre squares of the same identification.

For the extents of GDA2020, which lies wholly below the equator, the 100 000 metre row

letters also read from south to north, tying into the letters above in the same zone. These

principles are illustrated in figure D-2 for the south-eastern hemisphere of the Earth which

covers the extents of GDA2020.

D1.3 The grid reference

A grid reference will consist of a group of letters and numbers which indicate:

1. The Grid Zone Designation.

2. The 100 000 metre square identification.

3. The grid coordinates of the point expressed to the desired accuracy.

A reference will be written as a continuous number without spaces, parenthesis, dashes or

decimal points.

To assist in explaining how to define a grid reference, the GDA2020/MGA2020 location of

the Australian Fiducial Network site at Alice Springs (ALIC) is used as the example:

Latitude (DMS)

Longitude (DMS)

-23 40’ 12.39650”

133 53’ 07.87779”

Zone

Easting

Northing

386 353.2343

7,381,852.2986

This point would define the following grid references with increasing levels of accuracy:

1. 53KLP locating a point within a 100 000 metre square

2. 53KLP88 locating a point within a 10 000 metre square

3. 53KLP8681 locating a point within 1 000 metres

4. 53KLP863818 locating a point within 100 metres

5. 53KLP86358185 locating a point within 10 metres

6. 53KLP8635381852 locating a point within 1 metre

The Google Map reference for Alice Springs (ALIC) is 53KLP8635381852. Lower accuracy

grid references are not recognised by the web service, other than by adding zeros.

GDA2020Technical Manual V1.2

Navigation menu

Versions of this User Manual:

Views

Navigation