Mapping Virtual And Physical Reality Guide For

User Manual:

Open the PDF directly: View PDF .
Page Count: 10

Mapping Virtual and Physical Reality

Qi Sun Li-Yi Wei Arie Kaufman

Guide by Swanand Sawant

Introduction:

As the name suggests this paper aims at mapping the virtual environment to a real

world environment for a more immersive virtual reality experience. In the current

Virtual reality hardware like HMD(Head Mounted Displays) a user usually walks

at the same place and thus is not completely immersive. This paper implements a

mapping system such that a virtual environment is mapped on to a real world

environment like a small room in a office and the user is able to move around the

room without hitting any walls or interior obstacles while immersed in the virtual

environment through the wireless HMD. Thus it has the potential for realistic

interaction and immersive presence. The problem faced in doing so is that

generally a virtual environment is very different or unrelated to the real world

environment and hence a general method to bridge this gap is crucial for a real

immersive VR navigation. They propose a method to render a proper

representation of the virtual environment inside the HMD but change the camera

projections for navigating within the boundaries of real world environment as well

as avoid any interior obstacles within it.

Figure 1.)Mapping of a) to b) and c) is the actual room setup.

The Method proposed here as two key components: 1) a planar map between

virtual world and real world and 2) a camera projection from the planar map and

scene content. This planar map aims to preserve both angle and distance between

both the worlds for visual and locomotive consistency. The camera rendering

preserves both the virtual world appearance and real world geometry, while

guiding user navigation to avoid physical obstacles and maintain the balance of the

user at the same time and thus in the end aim to derive their camera projection

according to the planar map and scene content to balance between virtual realism,

geometric consistency, and perceptual discomfort.

Figure 2: Left side is virtual world view and the right side is user’s HMD view.

The main contributions of the paper include:

1. An HMD-VR system that allows real walking in a given physical

environment while perceiving a given virtual environment.

2. A custom planar map that minimizes the angular and distal distortions for

walkthroughs.

3. Optimization methods to compute this planar map as two maps:

a. Static forward map that minimizes angular and distal distortions

between the virtual and real world.

b. A dynamic reverse map that guides natural locomotion and resolves

local ambiguities

4. And finally a rendering method to preserve the virtual world appearance

while observing the physical world geometry to balance visual fidelity and

navigational comfort.

Proposed Method

With the given input world’s floor plan for Sv (virtual) and Sr (real) scenes, first

compute a static forward map f from Sv to Sr. This map is surjective and not

bijective in general when Sv > Sr, but should also minimize angular and distal

distortions for VR walkthroughs. It should reach every point in Sr and Sv, while

keeping inside Sr and away from interior obstacles. As the size of the both worlds

is different generally (Sv>Sr), folding is introduced tearing or breaking the virtual

world appart.

At runtime we compute the dynamic reverse map of f to place the user at proper

location in the virtual world (Sv) inside the HMD based on the user’s current

position in the real-world(Sr). This reverese mapping should be consistent with the

forward map f while maintaining motion and perception consistency for the user.

The last step is to render the virtual scene into the HMD which should have enough

quality and speed, and fit the appearance of the virtual scene into the geometry of

the real scene to balance between visual and motion fidelity.

Static Forward Mapping

This forward mapping proposed relies on conformality and isometry to minimize

angular and distal distortion during VR navigation. It does not require global

bijectivity (one to one correspondence) to allow proper folding of large virtual

scenes into small real scenes.

Figure 3. Static sampling example

The goal of this step is to surjectively map each virtual scene pixel

𝑥 = (𝑥,𝑦) ∈ 𝑆 to a real scene point 𝑢 = (𝑢,𝑣) ∈ 𝑆.

Their Method adopts a basis-function form to facilitate analytical computation of

the Jacobians and Hessians:

𝑢(𝑥,𝑦),𝑣(𝑥,𝑦)= 𝑢 = 𝑓 (𝑥)=𝑐𝑏(𝑥) + 𝑇𝑥



 , (1)

where {𝑏} are basis functions with weights {𝑐}, and T is an

affine transformation matrix. We use Gaussians for b, i.e.,

𝑏(𝑥)= 𝑒|_ |

 (2)

Where 𝑥 is is the i-th basis center (blue points in Figure below) and x is a sample

point in Sv (green points in Figure below).

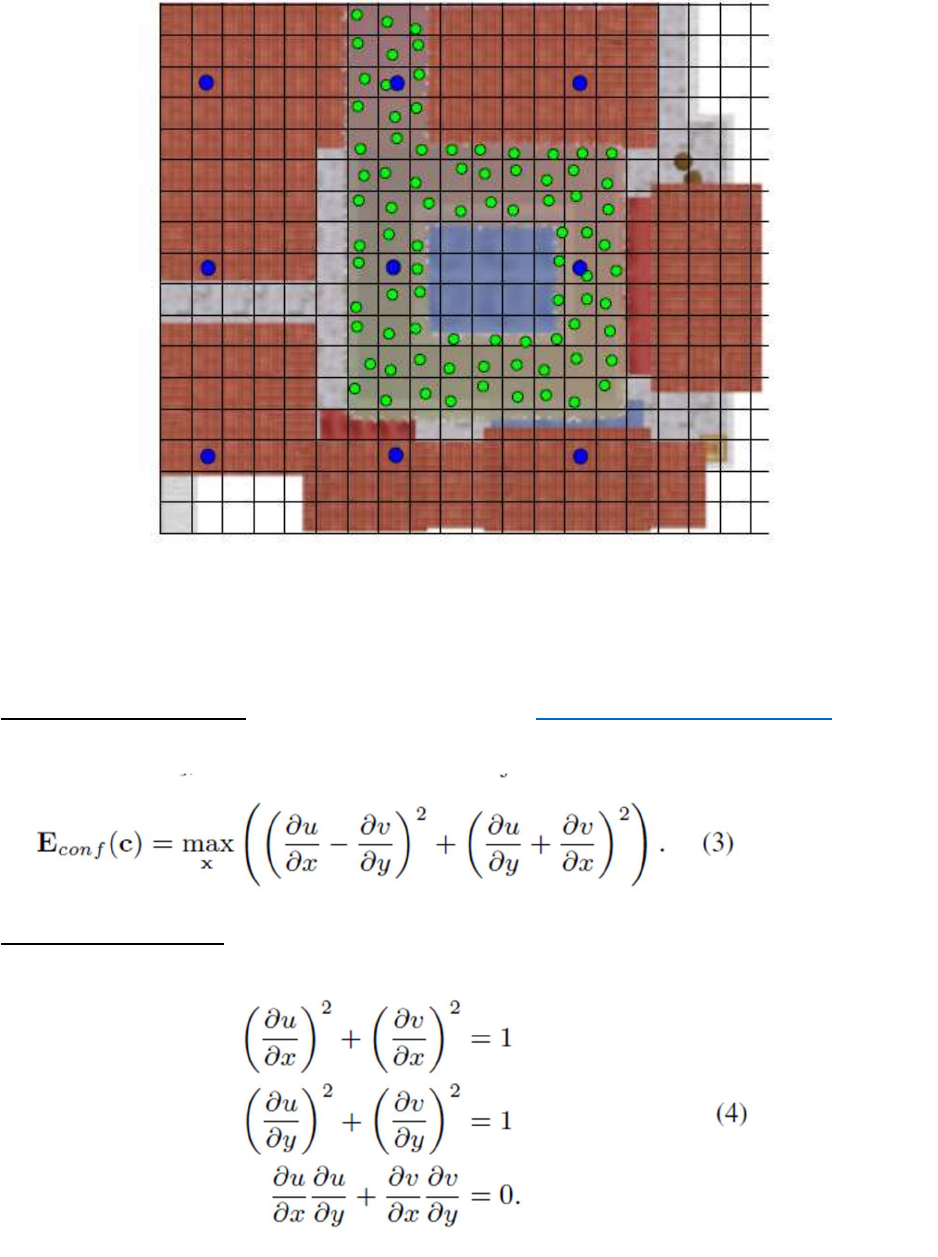
Figure : Stratified sampling of example for part of a game scene

The goal of this step is to find proper 𝑐 = {𝑐} and T so that mapping f as globally

conforming and locally isometric as possible via a collection of objectives and

constraints as follows:

Conformal Objective: 2d Mappings satisfy the Cauchy-Riemann function when it

preserves angles, define conformal objective as :

Distance constraint: This mapping only requires to be locally isometric and hence

requires Jacobian J to satisfy 𝐽𝐽 = 1 i.e

But to note an important fact here is that different virtual regions need different

amount of distance preservation in VR applications. Distances near the boundaries

should be more strictly preserved as the users can examine the virtual wall closely

than when the user is in the middle of a large room. To include this practical fact

the boundary conditions in Equation (4) are made more flexible

where ∈ [0, 1] and ∈ [1,+∞) are stretching ranges for each virtual scene point x.

When both and equal to 1, the mapping is strictly locally isometric. However, for

better conformality, we can relax the isometry into a range: the lower/higher the

𝛼/β value is, the more shrinking/stretching is allowed.

Exterior Boundary Constraint: To keep all u inside the real space Sr, construct a

polygon convex hull of Sr as a set of straight line functions {𝐵} and add a series

of linear constraints:

Where 𝐶 is the center of the physical space and the idea is to keep 𝐶 on the same

side of 𝐵 for test point inclusion.

Interior Obstacle Constraint: Preventing users from hitting interior obstacles can be

formulated as the opposite of the point inclusion test in Equation (6).

Relaxed Distance Constraint: To facilitate local bijectivity relax the distance

constraints in Equation (5) to encourage stretching over folding.

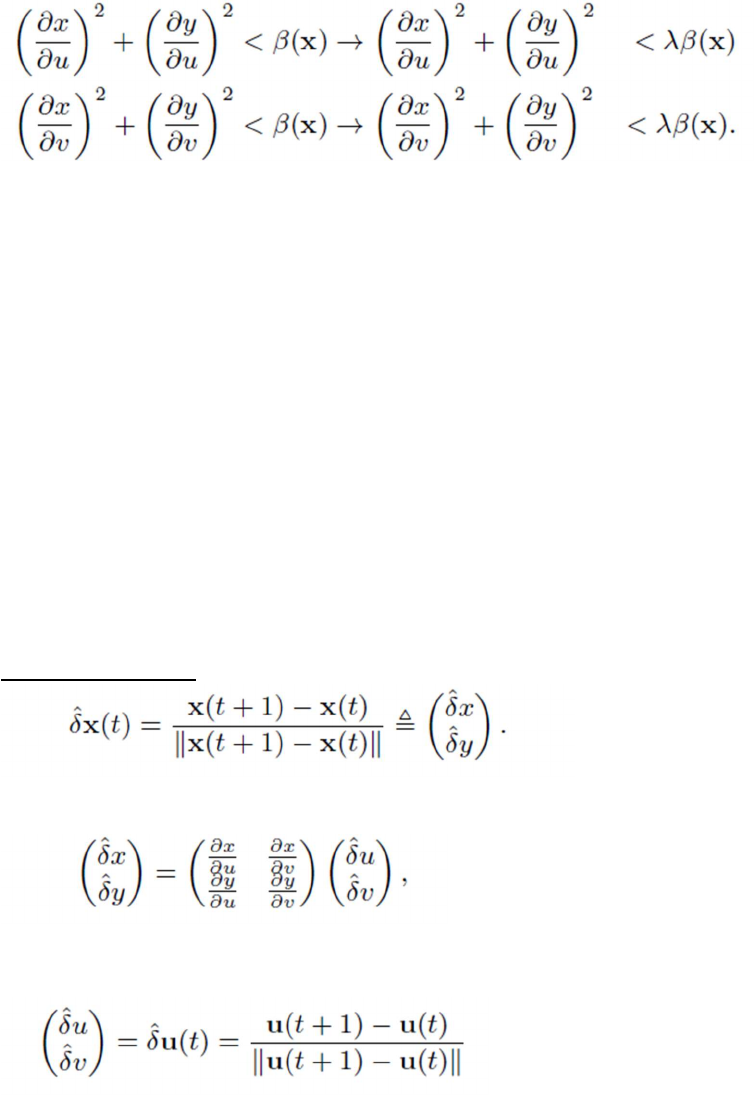
The authors imagine the virtual domain as a plastic floor plan sheet that can be

bent or fold but never cut. To encourage bending over folding we increase the

upper limit of Equation (5) as follows:

(7)

Dynamic Inverse Mapping

For VR walkthroughs we need the reverse map of users current position in Sr to

Sv. This revers map needs to deal with the fact that the forward map might not be

bijective and thus there can be multiple solutions. It also must minimize angular

and distal distortions during navigation.

Start by the given user positions u(t) and u(t + 1) as well as orientations U(t) and

U(t + 1) tracked in the real world Sr at time steps t and t + 1, and the corresponding

virtual position x(t) and orientation X(t) at time t, our goal is to compute the

corresponding virtual position x(t+1) and orientation X(t+1). Note that this is a

path dependent process as x(t + 1) and X(t + 1) are computed from x(t), X(t),

u(t+1), and U(t+1). We manually assign x(0) and X(0) for the initial virtual world

position and orientation.

Direction update: To compute x(t + 1), we first compute the moving direction:

(8)

The virtual and real world directions are related by the Jacobians of their mapping:

(9)

Where,

(10)

is the real world direction. Thus, the goal is to find the Jacoabian of the reverse

function of f in Equation (1):

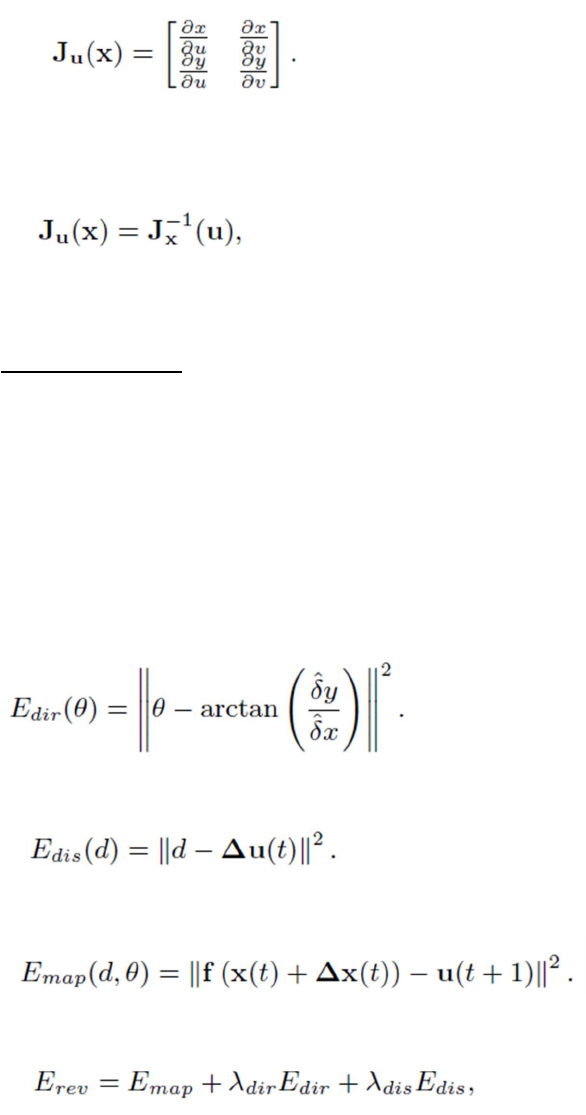
(11)

Even though f might not be globally bijective, the local bijectivity satisfies the

inverse function theorem and allows us to compute the inverse Jacobian via:

(12)

where Jx(u) can be computed from the analytic function f at position x(t).

Position update: We next compute the new virtual position x(t+1) based on the

estimated direction δx(t). We focus on the 2D x-y position, as the z/height value of

x can be directly assigned fromu after an initial correspondence. For computation

purposes, we define ∆x(t) = x(t+1)−x(t), and represent it in a polar coordinate

system, i.e., ∆x(t) = ∆xt(d, 𝜃) = (d cos(θ), d sin(θ)). The goal is to find optimized

(d, θ) to minimize an energy function as follows.

The first energy term measures how close the actual direction is to the estimated

direction δx(t):

(13)

The second term is to keep the virtual distance close to the real distance:

(14)

The last term is to match the mapping function f in Equation (1):

(15)

We find x(t + 1) = x(t) +∆x(t) to minimize

(16)

where 𝜆dir and λdis are relative weights.

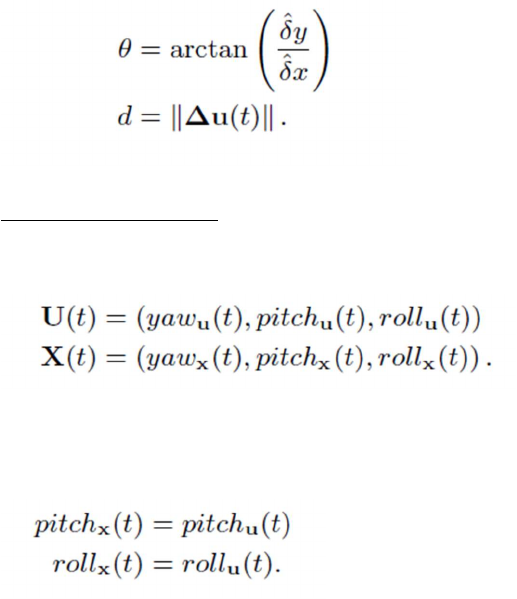
For fast convergence, we make the initial guess as:

(17)

Orientation update: For rendering, we also need to compute virtual camera

orientation X(t) from real camera orientation U(t), which is tracked by the HMD.

Represent both orientations by their Euler angles:

(18)

Since planar map f has only x-y positions, compute only 𝑦𝑎𝑤 and simply copy

𝑝𝑖𝑡𝑐ℎ and 𝑟𝑜𝑙𝑙 from 𝑝𝑖𝑡𝑐ℎ and 𝑟𝑜𝑙𝑙:

Rendering

Our goal is to render the appearance of the virtual world into the environment of

the real world, so that users can perceive the former while navigating in the latter.

The original virtual scene rendering, however, cannot be used for direct navigation

as it would cause motion sickness due to incompatibility with the real scene. We

thus fit the rendering of the virtual world into the geometry of the real world, as

discussed below.

Algorithm :

 We first render the virtual image Iv with virtual scene geometry Gv and

virtual camera Cv.

 We then initialize the real image Ir by mapping/warping Iv into Cr via f to

maintain visibility consistency with Iv.

 Parts of Ir might remain uncovered due to dis-occlusion, for which we

perform another rendering pass via the real scene geometry Gr and camera

Cr.

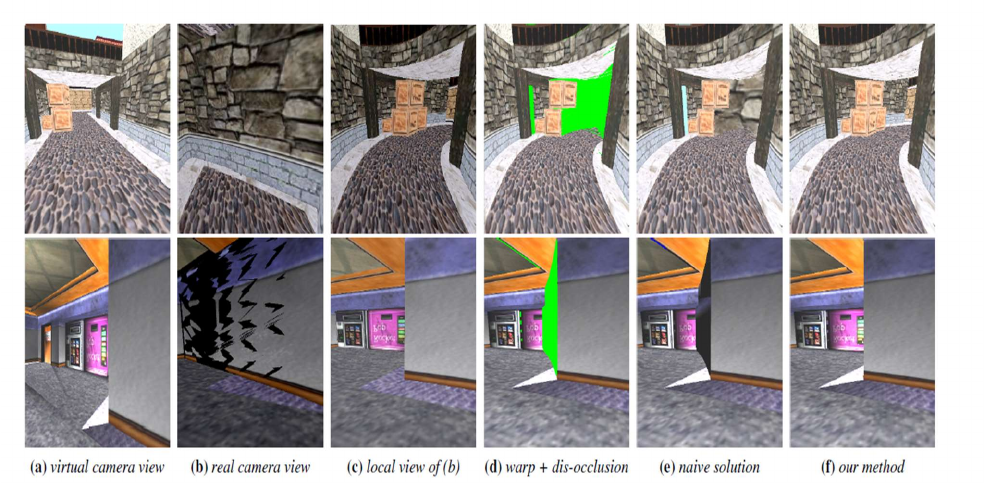
The figure below displays the effect of this rendering algorithm:

Similar to standard game level design, we surround the scene with an

environment-map box to ensure all pixels in Iv are initially covered. Thus,

all uncovered pixels in forward-warped Ir are caused by dis-occlusion. The

environment map is important to ensure robust dis-occlusion to prevent far-

away objects being mistakenly rendered into the background, as exemplified

in Figure below.