Hacking Secret Ciphers With Python ABeginners Guide To Cryptography And Computer Programming Al Sweigart
HackingSecretCiphersWithPythonABeginnersGuideToCryptographyAndComputerProgrammingWithPython-AlSweigart
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 442 [warning: Documents this large are best viewed by clicking the View PDF Link!]

Hacking Secret
Ciphers with Python
By Al Sweigart
Copyright © 2013 by Al Sweigart
Some Rights Reserved. “Hacking Secret Ciphers with Python” is licensed under a Creative
Commons Attribution-Noncommercial-Share Alike 3.0 United States License.
You are free:
To Share — to copy, distribute, display, and perform the work
To Remix — to make derivative works
Under the following conditions:
Attribution — You must attribute the work in the manner specified by the author or
licensor (but not in any way that suggests that they endorse you or your use of the work).
(Visibly include the title and author's name in any excerpts of this work.)
Noncommercial — You may not use this work for commercial purposes.
Share Alike — If you alter, transform, or build upon this work, you may distribute
the resulting work only under the same or similar license to this one.
This summary is located here: http://creativecommons.org/licenses/by-nc-sa/3.0/us/ Your fair use and other rights are
in no way affected by the above. There is a human-readable summary of the Legal Code (the full license), located here:
http://creativecommons.org/licenses/by-nc-sa/3.0/us/legalcode
Book Version 3
Special thanks to Ari Lacenski. I can’t thank her enough. Without her efforts there’d be typos literally on every page.
Thanks to Jason Kibbe. Cover lock photo by “walknboston” http://www.flickr.com/photos/walkn/3859852351/ Romeo
& Juliet and other public domain texts from Project Gutenberg. Various image resources from Wikipedia. Wrinkled
paper texture by Pink Sherbet Photography http://www.flickr.com/photos/pinksherbet/2978651767/ Computer User
icon by Katzenbaer.
If you've downloaded this book from a torrent, it’s probably out of date. Go
to http://inventwithpython.com/hacking to download the latest version.
ISBN 978-1482614374
1st Edition

Nedroid Picture Diary by Anthony Clark, http://nedroid.com
Movies and TV shows always make hacking look exciting with furious typing and meaningless
ones and zeros flying across the screen. They make hacking look like something that you have to
be super smart to learn. They make hacking look like magic.
It’s not magic. It’s based on computers, and everything computers do have logical
principles behind them which can be learned and understood. Even when you don’t
understand or when the computer does something frustrating or mysterious, there is always,
always, always a reason why.
And it’s not hard to learn. This book assumes you know nothing about cryptography or
programming, and helps you learn, step by step, how to write programs that can hack encrypted
messages. Good luck and have fun!
100% of the profits from this book are donated
to the Electronic Frontier Foundation, the Creative Commons, and the Tor Project.
Dedicated to Aaron Swartz, 1986 – 2013
“Aaron was part of an army of citizens that believes democracy
only works when the citizenry are informed, when we know about
our rights—and our obligations. An army that believes we must
make justice and knowledge available to all—not just the well born
or those that have grabbed the reins of power—so that we may
govern ourselves more wisely.
When I see our army, I see Aaron Swartz and my heart is broken.
We have truly lost one of our better angels.”
- C.M.

ABOUT THIS BOOK
There are many books that teach beginners how to write secret messages using ciphers. There are
a couple books that teach beginners how to hack ciphers. As far as I can tell, there are no books to
teach beginners how to write programs to hack ciphers. This book fills that gap.
This book is for complete beginners who do not know anything about encryption, hacking, or
cryptography. The ciphers in this book (except for the RSA cipher in the last chapter) are all
centuries old, and modern computers now have the computational power to hack their encrypted
messages. No modern organization or individuals use these ciphers anymore. As such, there’s no
reasonable context in which you could get into legal trouble for the information in this book.
This book is for complete beginners who have never programmed before. This book teaches basic
programming concepts with the Python programming language. Python is the best language for
beginners to learn programming: it is simple and readable yet also a powerful programming
language used by professional software developers. The Python software can be downloaded for
free from http://python.org and runs on Linux, Windows, OS X, and the Raspberry Pi.
There are two definitions of “hacker”. A hacker is a person who studies a system (such as the
rules of a cipher or a piece of software) to understand it so well that they are not limited by the
original rules of that system and can creatively modify it to work in new ways. “Hacker” is also
used to mean criminals who break into computer systems, violate people’s privacy, and cause
damage. This book uses “hacker” in the first sense. Hackers are cool. Criminals are just people
who think they’re being clever by breaking stuff. Personally, my day job as a software
developer pays me way more for less work than writing a virus or doing an Internet scam would.
On a side note, don’t use any of the encryption programs in this book for your actual files.
They’re fun to play with but they don’t provide true security. And in general, you shouldn’t trust
the ciphers that you yourself make. As legendary cryptographer Bruce Schneier put it, “Anyone,
from the most clueless amateur to the best cryptographer, can create an algorithm that he himself
can’t break. It’s not even hard. What is hard is creating an algorithm that no one else can break,
even after years of analysis. And the only way to prove that is to subject the algorithm to years of
analysis by the best cryptographers around.”
This book is released under a Creative Commons license and is free to copy and distribute (as
long as you don’t charge money for it). The book can be downloaded for free from its website at
http://inventwithpython.com/hacking. If you ever have questions about how these programs work,
feel free to email me at al@inventwithpython.com.

TABLE OF CONTENTS
About This Book ....................................................................................................................... 6
Table of Contents ..................................................................................................................... 7
Chapter 1 - Making Paper Cryptography Tools ...................................................................... 1
What is Cryptography? ................................................................................................................................................ 2
Codes vs. Ciphers ........................................................................................................................................................ 2
Making a Paper Cipher Wheel ..................................................................................................................................... 3
A Virtual Cipher Wheel ............................................................................................................................................... 7
How to Encrypt with the Cipher Wheel ....................................................................................................................... 8
How to Decrypt with the Cipher Wheel ....................................................................................................................... 9
A Different Cipher Tool: The St. Cyr Slide ............................................................................................................... 10
Practice Exercises, Chapter 1, Set A .......................................................................................................................... 11
Doing Cryptography without Paper Tools ................................................................................................................. 11
Practice Exercises, Chapter 1, Set B .......................................................................................................................... 13
Double-Strength Encryption?..................................................................................................................................... 13
Programming a Computer to do Encryption .............................................................................................................. 14
Chapter 2 - Installing Python ................................................................................................. 16
Downloading and Installing Python ........................................................................................................................... 17
Downloading pyperclip.py ......................................................................................................................................... 18
Starting IDLE ............................................................................................................................................................. 18
The Featured Programs .............................................................................................................................................. 19
Line Numbers and Spaces .......................................................................................................................................... 20
Text Wrapping in This Book ..................................................................................................................................... 20
Tracing the Program Online ....................................................................................................................................... 21
Checking Your Typed Code with the Online Diff Tool ............................................................................................. 21
Copying and Pasting Text .......................................................................................................................................... 21
More Info Links ......................................................................................................................................................... 22
Programming and Cryptography ................................................................................................................................ 22
Chapter 3 - The Interactive Shell .......................................................................................... 26
Some Simple Math Stuff ............................................................................................................................................ 26
Integers and Floating Point Values ............................................................................................................................ 27
Expressions ................................................................................................................................................................ 27
Order of Operations ................................................................................................................................................... 28
Evaluating Expressions .............................................................................................................................................. 29
Errors are Okay! ......................................................................................................................................................... 29
Practice Exercises, Chapter 3, Set A .......................................................................................................................... 30
Every Value has a Data Type ..................................................................................................................................... 30
Storing Values in Variables with Assignment Statements ......................................................................................... 30
Overwriting Variables ................................................................................................................................................ 32
Using More Than One Variable ................................................................................................................................. 33
Variable Names .......................................................................................................................................................... 34
Practice Exercises, Chapter 3, Set B .......................................................................................................................... 35
Summary - But When Are We Going to Start Hacking?............................................................................................ 35
Chapter 4 - Strings and Writing Programs ........................................................................... 36
Strings ........................................................................................................................................................................ 36
String Concatenation with the + Operator ................................................................................................................. 38
String Replication with the * Operator ...................................................................................................................... 39
Printing Values with the print() Function ............................................................................................................ 39
Escape Characters ...................................................................................................................................................... 40
Quotes and Double Quotes ........................................................................................................................................ 41
Practice Exercises, Chapter 4, Set A .......................................................................................................................... 42
Indexing ..................................................................................................................................................................... 42
Negative Indexes ........................................................................................................................................................ 44
Slicing ........................................................................................................................................................................ 44
Blank Slice Indexes.................................................................................................................................................... 45
Practice Exercises, Chapter 4, Set B .......................................................................................................................... 46
Writing Programs in IDLE’s File Editor .................................................................................................................... 46
Hello World! .............................................................................................................................................................. 47
Source Code of Hello World ...................................................................................................................................... 47
Saving Your Program ................................................................................................................................................ 48
Running Your Program .............................................................................................................................................. 49
Opening The Programs You’ve Saved ....................................................................................................................... 50
How the “Hello World” Program Works ................................................................................................................... 50
Comments .................................................................................................................................................................. 50
Functions.................................................................................................................................................................... 51
The print() function ............................................................................................................................................. 51
The input() function ............................................................................................................................................. 51
Ending the Program ................................................................................................................................................... 52
Practice Exercises, Chapter 4, Set C .......................................................................................................................... 52
Summary .................................................................................................................................................................... 53
Chapter 5 - The Reverse Cipher ............................................................................................ 54
The Reverse Cipher.................................................................................................................................................... 54
Source Code of the Reverse Cipher Program ............................................................................................................. 55
Sample Run of the Reverse Cipher Program .............................................................................................................. 55
Checking Your Source Code with the Online Diff Tool ............................................................................................ 56
How the Program Works............................................................................................................................................ 56
The len() Function ................................................................................................................................................. 57
Introducing the while Loop ..................................................................................................................................... 58
The Boolean Data Type ............................................................................................................................................. 59
Comparison Operators ............................................................................................................................................... 59
Conditions .................................................................................................................................................................. 62
Blocks ........................................................................................................................................................................ 62
The while Loop Statement ...................................................................................................................................... 63
“Growing” a String .................................................................................................................................................... 64
Tracing Through the Program, Step by Step .............................................................................................................. 67
Using input() In Our Programs ............................................................................................................................. 68
Practice Exercises, Chapter 5, Section A ................................................................................................................... 69
Summary .................................................................................................................................................................... 69
Chapter 6 - The Caesar Cipher .............................................................................................. 70
Implementing a Program ............................................................................................................................................ 70
Source Code of the Caesar Cipher Program ............................................................................................................... 71
Sample Run of the Caesar Cipher Program ................................................................................................................ 72
Checking Your Source Code with the Online Diff Tool ............................................................................................ 73
Practice Exercises, Chapter 6, Set A .......................................................................................................................... 73
How the Program Works............................................................................................................................................ 73
Importing Modules with the import Statement ....................................................................................................... 73
Constants.................................................................................................................................................................... 74
The upper() and lower() String Methods ........................................................................................................ 75
The for Loop Statement ........................................................................................................................................... 76
A while Loop Equivalent of a for Loop ................................................................................................................ 77
Practice Exercises, Chapter 6, Set B .......................................................................................................................... 78
The if Statement ...................................................................................................................................................... 78
The else Statement .................................................................................................................................................. 79
The elif Statement .................................................................................................................................................. 79
The in and not in Operators ................................................................................................................................. 80
The find() String Method ...................................................................................................................................... 81
Practice Exercises, Chapter 6, Set C .......................................................................................................................... 82
Back to the Code ........................................................................................................................................................ 82
Displaying and Copying the Encrypted/Decrypted String ......................................................................................... 85
Encrypt Non-Letter Characters .................................................................................................................................. 86
Summary .................................................................................................................................................................... 87
Chapter 7 - Hacking the Caesar Cipher with the Brute-Force Technique .......................... 88
Hacking Ciphers ........................................................................................................................................................ 88
The Brute-Force Attack ............................................................................................................................................. 89
Source Code of the Caesar Cipher Hacker Program .................................................................................................. 89
Sample Run of the Caesar Cipher Hacker Program ................................................................................................... 90
How the Program Works............................................................................................................................................ 91
The range() Function ............................................................................................................................................ 91
Back to the Code ........................................................................................................................................................ 93
String Formatting ....................................................................................................................................................... 94
Practice Exercises, Chapter 7, Set A .......................................................................................................................... 95
Summary .................................................................................................................................................................... 95
Chapter 8 - Encrypting with the Transposition Cipher ........................................................ 96
Encrypting with the Transposition Cipher ................................................................................................................. 96
Practice Exercises, Chapter 8, Set A .......................................................................................................................... 98
A Transposition Cipher Encryption Program ............................................................................................................. 98
Source Code of the Transposition Cipher Encryption Program ................................................................................. 98
Sample Run of the Transposition Cipher Encryption Program .................................................................................. 99
How the Program Works.......................................................................................................................................... 100
Creating Your Own Functions with def Statements ............................................................................................... 100
The Program’s main() Function ........................................................................................................................... 101
Parameters ................................................................................................................................................................ 102
Variables in the Global and Local Scope ................................................................................................................. 104
The global Statement ........................................................................................................................................... 104
Practice Exercises, Chapter 8, Set B ........................................................................................................................ 106
The List Data Type .................................................................................................................................................. 106
Using the list() Function to Convert Range Objects to Lists ............................................................................. 109
Reassigning the Items in Lists.................................................................................................................................. 110
Reassigning Characters in Strings ............................................................................................................................ 110
Lists of Lists ............................................................................................................................................................ 110
Practice Exercises, Chapter 8, Set C ........................................................................................................................ 111
Using len() and the in Operator with Lists ......................................................................................................... 111
List Concatenation and Replication with the + and * Operators.............................................................................. 112
Practice Exercises, Chapter 8, Set D ........................................................................................................................ 113
The Transposition Encryption Algorithm ................................................................................................................ 113
Augmented Assignment Operators .......................................................................................................................... 115
Back to the Code ...................................................................................................................................................... 116
The join() String Method .................................................................................................................................... 118
Return Values and return Statements .................................................................................................................. 119
Practice Exercises, Chapter 8, Set E ........................................................................................................................ 120
Back to the Code ...................................................................................................................................................... 120
The Special __name__ Variable ............................................................................................................................ 120
Key Size and Message Length ................................................................................................................................. 121
Summary .................................................................................................................................................................. 122
Chapter 9 - Decrypting with the Transposition Cipher ...................................................... 123
Decrypting with the Transposition Cipher on Paper ................................................................................................ 124
Practice Exercises, Chapter 9, Set A ........................................................................................................................ 125
A Transposition Cipher Decryption Program........................................................................................................... 126
Source Code of the Transposition Cipher Decryption Program ............................................................................... 126
How the Program Works.......................................................................................................................................... 127
The math.ceil(), math.floor() and round() Functions ......................................................................... 128
The and and or Boolean Operators ........................................................................................................................ 132
Practice Exercises, Chapter 9, Set B ........................................................................................................................ 133
Truth Tables ............................................................................................................................................................. 133
The and and or Operators are Shortcuts ................................................................................................................ 134
Order of Operations for Boolean Operators ............................................................................................................. 135
Back to the Code ...................................................................................................................................................... 135
Practice Exercises, Chapter 9, Set C ........................................................................................................................ 137
Summary .................................................................................................................................................................. 137
Chapter 10 - Programming a Program to Test Our Program ............................................ 138
Source Code of the Transposition Cipher Tester Program ....................................................................................... 139
Sample Run of the Transposition Cipher Tester Program ........................................................................................ 140
How the Program Works.......................................................................................................................................... 141
Pseudorandom Numbers and the random.seed() Function ............................................................................... 141
The random.randint() Function ..................................................................................................................... 143
References ................................................................................................................................................................ 143
The copy.deepcopy() Functions ...................................................................................................................... 147
Practice Exercises, Chapter 10, Set A ...................................................................................................................... 148
The random.shuffle() Function ..................................................................................................................... 148
Randomly Scrambling a String ................................................................................................................................ 149
Back to the Code ...................................................................................................................................................... 149
The sys.exit() Function ................................................................................................................................... 150
Testing Our Test Program ........................................................................................................................................ 151
Summary .................................................................................................................................................................. 152
Chapter 11 - Encrypting and Decrypting Files ................................................................... 153
Plain Text Files ........................................................................................................................................................ 154
Source Code of the Transposition File Cipher Program ........................................................................................... 154
Sample Run of the Transposition File Cipher Program ........................................................................................... 157
Reading From Files .................................................................................................................................................. 157
Writing To Files ....................................................................................................................................................... 158
How the Program Works.......................................................................................................................................... 159
The os.path.exists() Function ..................................................................................................................... 160
The startswith() and endswith() String Methods ..................................................................................... 161
The title() String Method ................................................................................................................................. 162
The time Module and time.time() Function .................................................................................................. 163
Back to the Code ...................................................................................................................................................... 164
Practice Exercises, Chapter 11, Set A ...................................................................................................................... 165
Summary .................................................................................................................................................................. 165
Chapter 12 - Detecting English Programmatically ............................................................ 166
How Can a Computer Understand English? ............................................................................................................. 167
Practice Exercises, Chapter 12, Section A ............................................................................................................... 169
The Detect English Module ..................................................................................................................................... 169
Source Code for the Detect English Module ............................................................................................................ 169
How the Program Works.......................................................................................................................................... 170
Dictionaries and the Dictionary Data Type .............................................................................................................. 171
Adding or Changing Items in a Dictionary .............................................................................................................. 172
Practice Exercises, Chapter 12, Set B ...................................................................................................................... 173
Using the len() Function with Dictionaries .......................................................................................................... 173
Using the in Operator with Dictionaries ................................................................................................................. 173
Using for Loops with Dictionaries ........................................................................................................................ 174
Practice Exercises, Chapter 12, Set C ...................................................................................................................... 174
The Difference Between Dictionaries and Lists ....................................................................................................... 174
Finding Items is Faster with Dictionaries Than Lists ............................................................................................... 175
The split() Method ............................................................................................................................................ 175
The None Value ...................................................................................................................................................... 176
Back to the Code ...................................................................................................................................................... 177
“Divide by Zero” Errors ........................................................................................................................................... 179
The float(), int(), and str() Functions and Integer Division ..................................................................... 179
Practice Exercises, Chapter 12, Set D ...................................................................................................................... 180
Back to the Code ...................................................................................................................................................... 180
The append() List Method ..................................................................................................................................... 182
Default Arguments ................................................................................................................................................... 183
Calculating Percentage ............................................................................................................................................. 184
Practice Exercises, Chapter 12, Set E ...................................................................................................................... 185
Summary .................................................................................................................................................................. 186
Chapter 13 - Hacking the Transposition Cipher ................................................................ 187
Source Code of the Transposition Cipher Hacker Program ..................................................................................... 187
Sample Run of the Transposition Breaker Program ................................................................................................. 189
How the Program Works.......................................................................................................................................... 190
Multi-line Strings with Triple Quotes ...................................................................................................................... 190
Back to the Code ...................................................................................................................................................... 191
The strip() String Method ................................................................................................................................. 193
Practice Exercises, Chapter 13, Set A ...................................................................................................................... 195
Summary .................................................................................................................................................................. 195
Chapter 14 - Modular Arithmetic with the Multiplicative and Affine Ciphers ................. 196
Oh No Math! ............................................................................................................................................................ 197
Math Oh Yeah! ........................................................................................................................................................ 197
Modular Arithmetic (aka Clock Arithmetic) ............................................................................................................ 197
The % Mod Operator ............................................................................................................................................... 199
Practice Exercises, Chapter 14, Set A ...................................................................................................................... 199
GCD: Greatest Common Divisor (aka Greatest Common Factor) ........................................................................... 199
Visualize Factors and GCD with Cuisenaire Rods ................................................................................................... 200
Practice Exercises, Chapter 14, Set B ...................................................................................................................... 202
Multiple Assignment ................................................................................................................................................ 202
Swapping Values with the Multiple Assignment Trick ............................................................................................ 203
Euclid’s Algorithm for Finding the GCD of Two Numbers..................................................................................... 203
“Relatively Prime” ................................................................................................................................................... 205
Practice Exercises, Chapter 14, Set C ...................................................................................................................... 205
The Multiplicative Cipher ........................................................................................................................................ 205
Practice Exercises, Chapter 14, Set D ...................................................................................................................... 207
Multiplicative Cipher + Caesar Cipher = The Affine Cipher ................................................................................... 207
The First Affine Key Problem.................................................................................................................................. 207
Decrypting with the Affine Cipher........................................................................................................................... 208
Finding Modular Inverses ........................................................................................................................................ 209
The // Integer Division Operator ........................................................................................................................... 210
Source Code of the cryptomath Module ............................................................................................................. 210
Practice Exercises, Chapter 14, Set E ...................................................................................................................... 211
Summary .................................................................................................................................................................. 211
Chapter 15 - The Affine Cipher ........................................................................................... 213
Source Code of the Affine Cipher Program ............................................................................................................. 214
Sample Run of the Affine Cipher Program .............................................................................................................. 216
Practice Exercises, Chapter 15, Set A ...................................................................................................................... 216
How the Program Works.......................................................................................................................................... 216
Splitting One Key into Two Keys ............................................................................................................................ 218
The Tuple Data Type ............................................................................................................................................... 218
Input Validation on the Keys ................................................................................................................................... 219
The Affine Cipher Encryption Function .................................................................................................................. 220
The Affine Cipher Decryption Function .................................................................................................................. 221
Generating Random Keys ........................................................................................................................................ 222
The Second Affine Key Problem: How Many Keys Can the Affine Cipher Have? ................................................. 223
Summary .................................................................................................................................................................. 225
Chapter 16 - Hacking the Affine Cipher ............................................................................. 226
Source Code of the Affine Cipher Hacker Program ................................................................................................. 226
Sample Run of the Affine Cipher Hacker Program .................................................................................................. 228
How the Program Works.......................................................................................................................................... 228
The Affine Cipher Hacking Function ....................................................................................................................... 230
The ** Exponent Operator ...................................................................................................................................... 230
The continue Statement ...................................................................................................................................... 231
Practice Exercises, Chapter 16, Set A ...................................................................................................................... 234
Summary .................................................................................................................................................................. 234
Chapter 17 - The Simple Substitution Cipher .................................................................... 235
The Simple Substitution Cipher with Paper and Pencil ........................................................................................... 236
Practice Exercises, Chapter 17, Set A ...................................................................................................................... 236
Source Code of the Simple Substitution Cipher ....................................................................................................... 237
Sample Run of the Simple Substitution Cipher Program ......................................................................................... 239
How the Program Works.......................................................................................................................................... 239
The Program’s main() Function ........................................................................................................................... 240
The sort() List Method ....................................................................................................................................... 241
Wrapper Functions ................................................................................................................................................... 242
The Program’s translateMessage() Function ............................................................................................... 243
The isupper() and islower() String Methods .............................................................................................. 245
Practice Exercises, Chapter 17, Set B ...................................................................................................................... 247
Generating a Random Key ....................................................................................................................................... 247
Encrypting Spaces and Punctuation ......................................................................................................................... 248
Practice Exercises, Chapter 17, Set C ...................................................................................................................... 249
Summary .................................................................................................................................................................. 249
Chapter 18 - Hacking the Simple Substitution Cipher ...................................................... 250
Computing Word Patterns ........................................................................................................................................ 251
Getting a List of Candidates for a Cipherword ........................................................................................................ 252
Practice Exercises, Chapter 18, Set A ...................................................................................................................... 253
Source Code of the Word Pattern Module ............................................................................................................... 253
Sample Run of the Word Pattern Module ................................................................................................................ 255
How the Program Works.......................................................................................................................................... 256
The pprint.pprint() and pprint.pformat() Functions ........................................................................ 256
Building Strings in Python with Lists ...................................................................................................................... 257
Calculating the Word Pattern ................................................................................................................................... 258
The Word Pattern Program’s main() Function ..................................................................................................... 259
Hacking the Simple Substitution Cipher .................................................................................................................. 262
Source Code of the Simple Substitution Hacking Program...................................................................................... 262
Hacking the Simple Substitution Cipher (in Theory) ............................................................................................... 266
Explore the Hacking Functions with the Interactive Shell ....................................................................................... 266
How the Program Works.......................................................................................................................................... 271
Import All the Things ............................................................................................................................................... 272
A Brief Intro to Regular Expressions and the sub() Regex Method ......................................................................... 272
The Hacking Program’s main() Function ............................................................................................................. 273
Partially Hacking the Cipher .................................................................................................................................... 274
Blank Cipherletter Mappings ................................................................................................................................... 275
Adding Letters to a Cipherletter Mapping ............................................................................................................... 276
Intersecting Two Letter Mappings ........................................................................................................................... 277
Removing Solved Letters from the Letter Mapping ................................................................................................. 278
Hacking the Simple Substitution Cipher .................................................................................................................. 281
Creating a Key from a Letter Mapping .................................................................................................................... 283
Couldn’t We Just Encrypt the Spaces Too? ............................................................................................................. 285
Summary .................................................................................................................................................................. 286
Chapter 19 - The Vigenère Cipher ...................................................................................... 287
Le Chiffre Indéchiffrable ......................................................................................................................................... 288
Multiple “Keys” in the Vigenère Key ...................................................................................................................... 288
Source Code of Vigenère Cipher Program ............................................................................................................... 291
Sample Run of the Vigenère Cipher Program .......................................................................................................... 294
How the Program Works.......................................................................................................................................... 294
Summary .................................................................................................................................................................. 298
Chapter 20 - Frequency Analysis ........................................................................................ 299
The Code for Matching Letter Frequencies ............................................................................................................. 304
How the Program Works.......................................................................................................................................... 306
The Most Common Letters, “ETAOIN” .................................................................................................................. 307
The Program’s getLettersCount() Function ................................................................................................. 307
The Program’s getItemAtIndexZero() Function .......................................................................................... 308
The Program’s getFrequencyOrder() Function ............................................................................................ 308
The sort() Method’s key and reverse Keyword Arguments ......................................................................... 310
Passing Functions as Values .................................................................................................................................... 311
Converting Dictionaries to Lists with the keys(), values(), items() Dictionary Methods ......................................... 313
Sorting the Items from a Dictionary ......................................................................................................................... 315
The Program’s englishFreqMatchScore() Function ................................................................................... 316
Summary .................................................................................................................................................................. 317
Chapter 21 - Hacking the Vigenère Cipher ........................................................................ 318
The Dictionary Attack .............................................................................................................................................. 319
Source Code for a Vigenère Dictionary Attack Program ......................................................................................... 319
Sample Run of the Vigenère Dictionary Hacker Program ....................................................................................... 320
The readlines() File Object Method ................................................................................................................ 321
The Babbage Attack & Kasiski Examination ........................................................................................................... 321
Kasiski Examination, Step 1 – Find Repeat Sequences’ Spacings ........................................................................... 321
Kasiski Examination, Step 2 – Get Factors of Spacings .......................................................................................... 322
Get Every Nth Letters from a String ........................................................................................................................ 323
Frequency Analysis .................................................................................................................................................. 323
Brute-Force through the Possible Keys .................................................................................................................... 325
Source Code for the Vigenère Hacking Program ..................................................................................................... 326
Sample Run of the Vigenère Hacking Program ....................................................................................................... 332
How the Program Works.......................................................................................................................................... 334
Finding Repeated Sequences ................................................................................................................................... 335
Calculating Factors .................................................................................................................................................. 337
Removing Duplicates with the set() Function .......................................................................................................... 338
The Kasiski Examination Algorithm........................................................................................................................ 341
The extend() List Method ................................................................................................................................... 342
The end Keyword Argument for print() ........................................................................................................... 347
The itertools.product() Function .............................................................................................................. 348
The break Statement ............................................................................................................................................. 352
Practice Exercises, Chapter 21, Set A ...................................................................................................................... 354
Modifying the Constants of the Hacking Program ................................................................................................... 354
Summary .................................................................................................................................................................. 355
Chapter 22 - The One-Time Pad Cipher .............................................................................. 356
The Unbreakable One-Time Pad Cipher .................................................................................................................. 357
Why the One-Time Pad is Unbreakable ................................................................................................................... 357
Beware Pseudorandomness ...................................................................................................................................... 358
Beware the Two-Time Pad ...................................................................................................................................... 358
The Two-Time Pad is the Vigenère Cipher .............................................................................................................. 359
Practice Exercises, Chapter 22, Set A ...................................................................................................................... 360
Summary .................................................................................................................................................................. 360
Chapter 23 - Finding Prime Numbers ................................................................................. 361
Prime Numbers ........................................................................................................................................................ 362
Composite Numbers................................................................................................................................................. 363
Source Code for The Prime Sieve Module ............................................................................................................... 363
How the Program Works.......................................................................................................................................... 364
How to Calculate if a Number is Prime ................................................................................................................... 365
The Sieve of Eratosthenes ........................................................................................................................................ 366
The primeSieve() Function............................................................................................................................... 368
Detecting Prime Numbers ........................................................................................................................................ 369
Source Code for the Rabin-Miller Module ............................................................................................................... 370
Sample Run of the Rabin Miller Module ................................................................................................................. 372
How the Program Works.......................................................................................................................................... 372
The Rabin-Miller Primality Algorithm .................................................................................................................... 372
The New and Improved isPrime() Function ...................................................................................................... 373
Summary .................................................................................................................................................................. 375
Chapter 24 - Public Key Cryptography and the RSA Cipher .............................................. 378
Public Key Cryptography......................................................................................................................................... 379
The Dangers of “Textbook” RSA ............................................................................................................................ 381
A Note About Authentication .................................................................................................................................. 381
The Man-In-The-Middle Attack .............................................................................................................................. 382
Generating Public and Private Keys......................................................................................................................... 383
Source Code for the RSA Key Generation Program ................................................................................................ 383
Sample Run of the RSA Key Generation Program .................................................................................................. 385
How the Key Generation Program Works ............................................................................................................... 386
The Program’s generateKey() Function ........................................................................................................... 387
RSA Key File Format .............................................................................................................................................. 390
Hybrid Cryptosystems ............................................................................................................................................. 391
Source Code for the RSA Cipher Program .............................................................................................................. 391
Sample Run of the RSA Cipher Program ................................................................................................................. 395
Practice Exercises, Chapter 24, Set A ...................................................................................................................... 397
Digital Signatures .................................................................................................................................................... 397
How the RSA Cipher Program Works ..................................................................................................................... 398
ASCII: Using Numbers to Represent Characters ..................................................................................................... 400
The chr() and ord() Functions .......................................................................................................................... 400
Practice Exercises, Chapter 24, Set B ...................................................................................................................... 401
Blocks ...................................................................................................................................................................... 401
Converting Strings to Blocks with getBlocksFromText() ............................................................................. 404
The encode() String Method and the Bytes Data Type ....................................................................................... 405
The bytes() Function and decode() Bytes Method ........................................................................................ 405
Practice Exercises, Chapter 24, Set C ...................................................................................................................... 406
Back to the Code ...................................................................................................................................................... 406
The min() and max() Functions .......................................................................................................................... 407
The insert() List Method ................................................................................................................................... 410
The Mathematics of RSA Encrypting and Decrypting ............................................................................................. 411
The pow() Function ............................................................................................................................................... 411
Reading in the Public & Private Keys from their Key Files ..................................................................................... 413
The Full RSA Encryption Process ........................................................................................................................... 413
The Full RSA Decryption Process ........................................................................................................................... 416
Practice Exercises, Chapter 24, Set D ...................................................................................................................... 418
Why Can’t We Hack the RSA Cipher ...................................................................................................................... 418
Summary .................................................................................................................................................................. 420
About the Author .................................................................................................................. 422

Chapter 1 – Making Paper Cryptography Tools 1
MAKING PAPER
CRYPTOGRAPHY TOOLS
Topics Covered In This Chapter:
What is cryptography?
Codes and ciphers
The Caesar cipher
Cipher wheels
St. Cyr slides
Doing cryptography with paper and pencil
“Double strength” encryption
“I couldn’t help but overhear, probably because I
was eavesdropping.”
Anonymous

2 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
What is Cryptography?
Look at the following two pieces of text:
“Zsijwxyfsi niqjsjxx gjyyjw. Ny nx jnymjw ktqqd tw
bnxitr; ny nx anwyzj ns bjfqym fsi anhj ns utajwyd.
Ns ymj bnsyjw tk tzw qnkj, bj hfs jsotd ns ujfhj ymj
kwznyx bmnhm ns nyx xuwnsl tzw nsizxywd uqfsyji.
Htzwynjwx tk lqtwd, bwnyjwx tw bfwwntwx, xqzrgjw
nx ujwrnyyji dtz, gzy tsqd zuts qfzwjqx.”
“Flwyt tsytbbnz jqtw yjxndwri iyn fqq knqrqt xj mh
ndyn jxwqswbj. Dyi jjkxxx sg ttwt gdhz js jwsn;
wnjyiyb aijnn snagdqt nnjwww, xstsxsu jdnxzz xkw
znfs uwwh xni xjzw jzwyjy jwnmns mnyfjx. Stjj wwzj
ti fnu, qt uyko qqsbay jmwskj. Sxitwru nwnqn
nxfzfbl yy hnwydsj mhnxytb myysyt.”
The text on the left side is a secret message. The message has been encrypted, or turned into a
secret code. It will be completely unreadable to anyone who doesn’t know how to decrypt it
(that is, turn it back into the plain English message.) This book will teach you how to encrypt and
decrypt messages.
The message on the right is just random gibberish with no hidden meaning whatsoever.
Encrypting your written messages is one way to keep them secret from other people, even if they
get their hands on the encrypted message itself. It will look exactly like random nonsense.
Cryptography is the science of using secret codes. A cryptographer is someone who uses and
studies secret codes. This book will teach you what you need to know to become a cryptographer.
Of course, these secret messages don’t always stay secret. A cryptanalyst is someone who can
hack secret codes and read other people’s encrypted messages. Cryptanalysts are also called code
breakers or hackers. This book will also teach you what you need to know to become a
cryptanalyst. Unfortunately the type of hacking you learn in this book isn’t dangerous enough to
get you in trouble with the law. (I mean, fortunately.)
Spies, soldiers, hackers, pirates, royalty, merchants, tyrants, political activists, Internet shoppers,
and anyone who has ever needed to share secrets with trusted friends have relied on cryptography
to make sure their secrets stay secret.
Codes vs. Ciphers
The development of the electric telegraph in the early 19th century allowed for near-instant
communication through wires across continents. This was much faster than sending a horseback
rider carrying a bag of letters. However, the telegraph couldn’t directly send written letters drawn
on paper. Instead it could send electric pulses. A short pulse is called a “dot” and a long pulse is
called a “dash”.

Chapter 1 – Making Paper Cryptography Tools 3
Figure 1-1. Samuel Morse
April 27, 1791 – April 2, 1872
Figure 1-2. Alfred Vail
September 25, 1807 – January 18, 1859
In order to convert these dots and dashes to
English letters of the alphabet, an encoding
system (or code) is needed to translate from
English to electric pulse code (called
encoding) and at the other end translate
electric pulses to English (called decoding).
The code to do this over telegraphs (and later,
radio) was called Morse Code, and was
developed by Samuel Morse and Alfred Vail.
By tapping out dots and dashes with a one-
button telegraph, a telegraph operator could
communicate an English message to someone
on the other side of the world almost instantly!
(If you’d like to learn Morse code, visit
http://invpy.com/morse.)
A
● ▬
T
▬
B
▬ ● ● ●
U
● ● ▬
C
▬ ● ▬ ●
V
● ● ● ▬
D
▬ ● ●
W
● ▬ ▬
E
●
X
▬ ● ● ▬
F
● ● ▬ ●
Y
▬ ● ▬ ▬
G
▬ ▬ ●
Z
▬ ▬ ● ●
H
● ● ● ●
I
● ●
J
● ▬ ▬ ▬
1
● ▬ ▬ ▬ ▬
K
▬ ● ▬
2
● ● ▬ ▬ ▬
L
● ▬ ● ●
3
● ● ● ▬ ▬
M
▬ ▬
4
● ● ● ● ▬
N
▬ ●
5
● ● ● ● ●
O
▬ ▬ ▬
6
▬ ● ● ● ●
P
● ▬ ▬ ●
7
▬ ▬ ● ● ●
Q
▬ ▬ ● ▬
8
▬ ▬ ▬ ● ●
R
● ▬ ●
9
▬ ▬ ▬ ▬ ●
S
● ● ●
0
▬ ▬ ▬ ▬ ▬
Figure 1-3. International Morse Code, with
characters represented as dots and dashes.
Codes are made to be understandable and publicly available. Anyone should be able to look
up what a code’s symbols mean to decode an encoded message.
Making a Paper Cipher Wheel
Before we learn how to program computers to do encryption and decryption for us, let’s learn
how to do it ourselves with simple paper tools. It is easy to turn the understandable English text
(which is called the plaintext) into the gibberish text that hides a secret code (called the

4 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
ciphertext). A cipher is a set of rules for converting between plaintext and ciphertext. These
rules often use a secret key. We will learn several different ciphers in this book.
Let’s learn a cipher called the Caesar cipher. This cipher was used by Julius Caesar two thousand
years ago. The good news is that it is simple and easy to learn. The bad news is that because it is
so simple, it is also easy for a cryptanalyst to break it. But we can use it as a simple learning
exercise. More information about the Caesar cipher is given on Wikipedia:
http://en.wikipedia.org/wiki/Caesar_cipher.
To convert plaintext to ciphertext using the Caesar cipher, we will create something called a
cipher wheel (also called a cipher disk). You can either photocopy the cipher wheel that
appears in this book, or print out the one from http://invpy.com/cipherwheel. Cut out the two
circles and lay them on top of each other like in Figure 1-8.
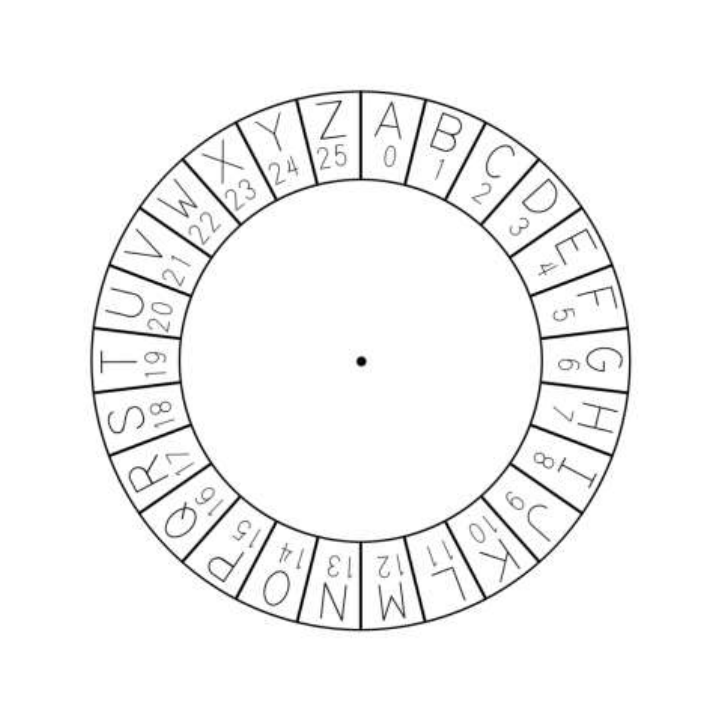
Chapter 1 – Making Paper Cryptography Tools 5
Figure 1-4. The inner circle of the cipher wheel cutout.
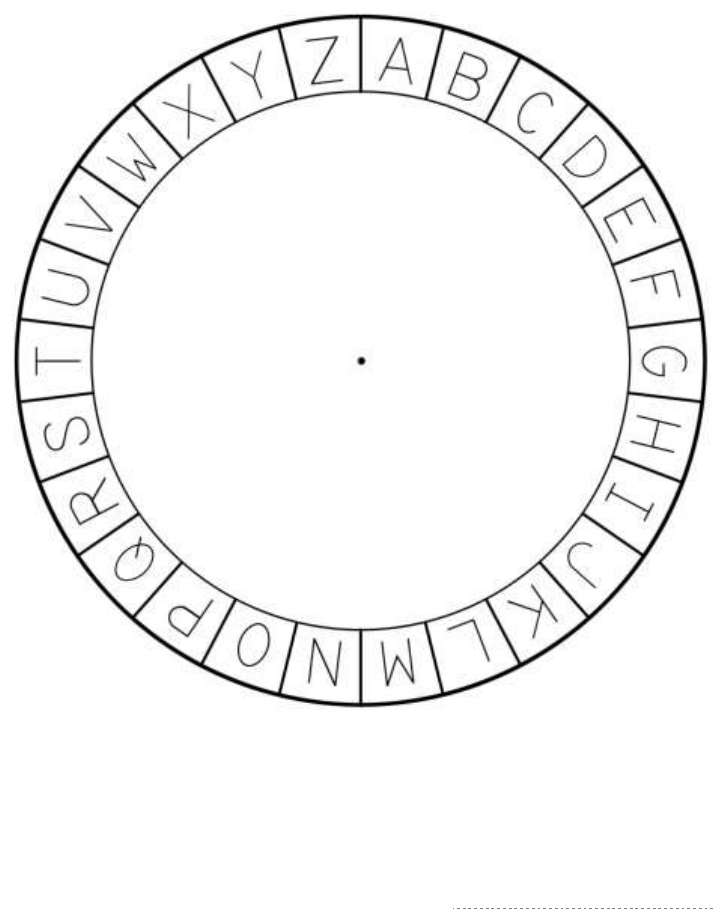
6 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Figure 1-5. The outer circle of the cipher wheel cutout.
Don’t cut out the page from this book!
Just make a photocopy of this page or print it from http://invpy.com/cipherwheel.

Chapter 1 – Making Paper Cryptography Tools 7
Figure 1-6. Cutting out
the cipher wheel
circles.
Figure 1-7. The cut-out circles.
Figure 1-8. The
completed cipher
wheel.
After you cut out the circles, place the smaller one in the middle of the larger one. Put a pin or
brad through the center of both circles so you can spin them around in place. You now have a tool
for creating secret messages with the Caesar cipher.
A Virtual Cipher Wheel
There is also a virtual cipher wheel online if you
don’t have scissors and a photocopier handy.
Open a web browser to
http://invpy.com/cipherwheel to use the software
version of the cipher wheel.
To spin the wheel around, click on it with the
mouse and then move the mouse cursor around
until the key you want is in place. Then click the
mouse again to stop the wheel from spinning.
Figure 1-9. The online cipher wheel.
8 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
How to Encrypt with the Cipher Wheel
First, write out your message in English on paper. For this example we will encrypt the message,
“The secret password is Rosebud.” Next, spin the inner wheel around until its letters match up
with letters in the outer wheel. Notice in the outer wheel there is a dot next to the letter A. Look at
the number in the inner wheel next to the dot in the outer wheel. This number is known the
encryption key.
The encryption key is the secret to encrypting or decrypting the message. Anyone who reads this
book can learn about the Caesar cipher, just like anyone who reads a book about locks can learn
how a door lock works. But like a regular lock and key, unless they have the encryption key, they
will not be able to unlock (that is, decrypt) the secret encrypted message. In Figure 1-9, the outer
circle’s A is over the inner circle’s number 8. That means we will be using the key 8 to encrypt
our message. The Caesar cipher uses the keys from 0 to 25. Let’s use the key 8 for our example.
Keep the encryption key a secret; the ciphertext can be read by anyone who knows that the
message was encrypted with key 8.
T
H
E
S
E
C
R
E
T
P
A
S
S
W
O
R
D
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
B
P
M
A
M
K
Z
M
B
X
I
A
A
E
W
Z
L
I
S
R
O
S
E
B
U
D
.
↓
↓
↓
↓
↓
↓
↓
↓
↓
Q
A
Z
W
A
M
J
C
L
.
For each letter in our message, we will find where it is in the outer circle and replace it with the
lined-up letter in the inner circle. The first letter in our message is T (the first “T” in “The
secret…”), so we find the letter T in the outer circle, and then find the lined-up letter in the inner
circle. This letter is B, so in our secret message we will always replace T’s with B’s. (If we were
using some other encryption key besides 8, then the T’s in our plaintext would be replaced with a
different letter.)
The next letter in our message is H, which turns into P. The letter E turns into M. When we have
encrypted the entire message, the message has transformed from “The secret password is
Rosebud.” to “Bpm amkzmb xiaaewzl qa Zwamjcl.” Now you can send this message to someone
(or keep it written down for yourself) and nobody will be able to read it unless you tell them the
secret encryption key (the number 8).

Chapter 1 – Making Paper Cryptography Tools 9
Figure 1-10. A message encrypted with the cipher wheel.
Each letter on the outer wheel will always be encrypted to the same letter on the inner wheel. To
save time, after you look up the first T in “The secret…” and see that it encrypts to B, you can
replace every T in the message with B. This way you only need to look up a letter once.
How to Decrypt with the Cipher Wheel
To decrypt a ciphertext, go from the inner circle to the outer circle. Let’s say you receive this
ciphertext from a friend, “Iwt ctl ephhldgs xh Hldgsuxhw.” You and everyone else won’t be able
to decrypt it unless you know the key (or unless you are a clever hacker). But your friend has
decided to use the key 15 for each message she sends you.
Line up the letter A on the outer circle (the one with the dot below it) over the letter on the inner
circle that has the number 15 (which is the letter P). The first letter in the secret message is I, so
we find I on the inner circle and look at the letter next to it on the outer circle, which is T. The W
in the ciphertext will decrypt to the letter H. One by one, we can decrypt each letter in the
ciphertext back to the plaintext, “The new password is Swordfish.”
I
W
T
C
T
L
E
P
H
H
L
D
G
S
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
T
H
E
N
E
W
P
A
S
S
W
O
R
D
X
H
H
L
D
G
S
U
X
H
W
.
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
I
S
S
W
O
R
D
F
I
S
H
.
If we use an incorrect key like 16 instead of the correct key 15, the decrypted message is “Sgd
mdv ozrrvnqc hr Rvnqcehrg.” This plaintext doesn’t look plain at all. Unless the correct key is
used, the decrypted message will never be understandable English.

10 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
A Different Cipher Tool: The St. Cyr Slide
Figure 1-11. Photocopy
these strips to make a St.
Cyr Slide.
There’s another paper tool that can be used to do encryption and
decryption, called the St. Cyr slide. It’s like the cipher wheel
except in a straight line.
Photocopy the image of the St. Cyr slide on the following page (or
print it out from http://invpy.com/stcyrslide) and cut out the three
strips.
Tape the two alphabet strips together, with the black box A next to
the white box Z on the other strip. Cut out the slits on either side of
the main slide box so that the taped-together strip can feed through
it. It should look like this:
Figure 1-12. The completed St. Cyr Slide
When the black box A is underneath the letter H (and the number
7), then to encrypt you must find where the plaintext letter is on
the long strip, and replace it with the letter above it. To decrypt,
find the ciphertext letter on the top row of letters and replace it
with the letter on the long strip below it.
The two slits on the larger box will hide any extra letters so that
you only see one of each letter on the slide for any key.
The benefit of the St. Cyr slide is that it might be easier to find the
letters you are looking for, since they are all in a straight line and
will never be upside down like they sometimes are on the cipher
wheel.
A virtual and printable St. Cyr slide can be found at
http://invpy.com/stcyrslide.

Chapter 1 – Making Paper Cryptography Tools 11
Practice Exercises, Chapter 1, Set A
Practice exercises can be found at http://invpy.com/hackingpractice1A.
Don’t ignore the practice exercises!
There isn’t enough room in this book to put in all the practice
exercises, but they’re still important.
You don’t become a hacker by just reading about hacking and
programming. You have to actually do it!
Doing Cryptography without Paper Tools
The cipher wheel and St. Cyr slide are nice tools to do encryption and decryption with the Caesar
cipher. But we can implement the Caesar cipher with just pencil and paper.
Write out the letters of the alphabet from A to Z with the numbers from 0 to 25 under each letter.
0 goes underneath the A, 1 goes under the B, and so on until 25 is under Z. (There are 26 letters
in the alphabet, but our numbers only go up to 25 because we started at 0, not 1.) It will end up
looking something like this:
A
B
C
D
E
F
G
H
I
J
K
L
M
0
1
2
3
4
5
6
7
8
9
10
11
12
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
13
14
15
16
17
18
19
20
21
22
23
24
25
With the above letters-to-numbers code, we can use numbers to represent letters. This is a very
powerful concept, because math uses numbers. Now we have a way to do math on letters.
Now to encrypt we find the number under the letter we wish to encrypt and add the key number
to it. This sum will be the number under the encrypted letter. For example, we encrypt, “Hello.
How are you?” with the key 13. First we find the number under the H, which is 7. Then we add
the key to this number. 7 + 13 = 20. The number 20 is under the letter U, which means the letter
H encrypts to the letter U. To encrypt the letter E, we add the 4 under E to 13 to get 17. The
number above 17 is R, so E gets encrypted to R. And so on.
This works fine until we get to the letter O. The number under O is 14. But when we add 14 + 13
we get 27. But our list of numbers only goes up to 25. If the sum of the letter’s number and the

12 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
key is 26 or more, we should subtract 26 from it. So 27 – 26 is 1. The letter above the number 1 is
B. So the letter O encrypts to the letter B when we are using the key 13. One by one, we can then
encrypt the letters in, “Hello. How are you?” to “Uryyb. Ubj ner lbh?”
So the steps to encrypt a letter are:
1. Decide on a key from 1 to 25. Keep this key secret!
2. Find the plaintext letter’s number.
3. Add the key to the plaintext letter’s number.
4. If this number is larger than 26, subtract 26.
5. Find the letter for the number you’ve calculated. This is the ciphertext letter.
6. Repeat steps 2 to 5 for every letter in the plaintext message.
Look at the following table to see how this is done with each letter in “Hello. How are you?” with
key 13. Each column shows the steps for turning the plaintext letter on the left to the ciphertext
letter on the right.
Table 1-1. The steps to encrypt “Hello. How are you?” with paper and pencil.
Plaintext
Letter
Plaintext
Number
+
Key
Result
Subtract
26?
Result
Ciphertext
Letter
H
7
+
13
= 20
= 20
20 = U
E
4
+
13
= 17
= 17
17 = R
L
11
+
13
= 24
= 24
24 = Y
L
11
+
13
= 24
= 24
24 = Y
O
14
+
13
= 27
- 26
= 1
1 = B
H
7
+
13
= 20
= 20
20 = U
O
14
+
13
= 27
- 26
= 1
1 = B
W
22
+
13
= 35
- 26
= 9
9 = J
A
0
+
13
= 13
= 13
13 = N
R
17
+
13
= 30
- 26
= 4
4 = E
E
4
+
13
= 17
= 17
17 = R
Y
24
+
13
= 37
- 26
= 11
11 = L
O
14
+
13
= 27
- 26
= 1
1 = B
U
20
+
13
= 33
- 26
= 7
7 = H

Chapter 1 – Making Paper Cryptography Tools 13
To decrypt, you will have to understand what negative numbers are. If you don’t know how to
add and subtract with negative numbers, there is a tutorial on it here: http://invpy.com/neg.
To decrypt, subtract the key instead of adding it. For the ciphertext letter B, the number is 1.
Subtract 1 – 13 to get -12. Like our “subtract 26” rule for encrypting, when we are decrypting and
the result is less than 0, we have an “add 26” rule. -12 + 26 is 14. So the ciphertext letter B
decrypts back to letter O.
Table 1-2. The steps to decrypt the ciphertext with paper and pencil.
Ciphertext
Letter
Ciphertext
Number
-
Key
Result
Add
26?
Result
Plaintext
Letter
U
20
-
13
= 7
= 7
7 = H
R
17
-
13
= 4
= 4
4 = E
Y
24
-
13
= 11
= 11
11 = L
Y
24
-
13
= 11
= 11
11 = L
B
1
-
13
= -12
+ 26
= 14
14 = O
U
20
-
13
= 7
= 7
7 = H
B
1
-
13
= -12
+ 26
= 14
14 = O
J
9
-
13
= -4
+ 26
= 22
22 = W
N
13
-
13
= 0
= 0
0 = A
E
4
-
13
= -9
+ 26
= 17
17 = R
R
17
-
13
= 4
= 4
4 = E
L
11
-
13
= -2
+ 26
= 24
24 = Y
B
1
-
13
= -12
+ 26
= 14
14 = O
H
7
-
13
= -6
+ 26
= 20
20 = U
As you can see, we don’t need an actual cipher wheel to do the Caesar cipher. If you memorize
the numbers and letters, then you don’t even need to write out the alphabet with the numbers
under them. You could just do some simple math in your head and write out secret messages.
Practice Exercises, Chapter 1, Set B
Practice exercises can be found at http://invpy.com/hackingpractice1B.
Double-Strength Encryption?
You might think that encrypting a message twice with two different keys would double the
strength of our encryption. But this turns out not to be the case with the Caesar cipher (and most
other ciphers). Let’s try double-encrypting a message to see why.

14 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
If we encrypt the word “KITTEN” with the key 3, the resulting cipher text would be
“NLWWHQ”. If we encrypt the word “NLWWHQ” with the key 4, the resulting cipher text of
that would be “RPAALU”. But this is exactly the same as if we had encrypted the word
“KITTEN” once with a key of 7. Our “double” encryption is the same as normal encryption, so it
isn’t any stronger.
The reason is that when we encrypt with the key 3, we are adding 3 to plaintext letter’s number.
Then when we encrypt with the key 4, we are adding 4 to the plaintext letter’s number. But
adding 3 and then adding 4 is the exact same thing as adding 7. Encrypting twice with keys 3 and
4 is the same as encrypting once with the key 7.
For most encryption ciphers, encrypting more than once does not provide additional
strength to the cipher. In fact, if you encrypt some plaintext with two keys that add up to 26, the
ciphertext you end up with will be the same as the original plaintext!
Programming a Computer to do Encryption
The Caesar cipher, or ciphers like it, were used to encrypt secret information for several centuries.
Here’s a cipher disk of a design invented by Albert Myer that was used in the American Civil
War in 1863.
Figure 1-13. American Civil War Union Cipher Disk at the National Cryptologic Museum.
If you had a very long message that you wanted to encrypt (say, an entire book) it would take you
days or weeks to encrypt it all by hand. This is how programming can help. A computer could do
Chapter 1 – Making Paper Cryptography Tools 15
the work for a large amount of text in less than a second! But we need to learn how to instruct
(that is, program) the computer to do the same steps we just did.
We will have to be able to speak a language the computer can understand. Fortunately, learning a
programming language isn’t nearly as hard as learning a foreign language like Japanese or
Spanish. You don’t even need to know much math besides addition, subtraction, and
multiplication. You just need to download some free software called Python, which we will cover
in the next chapter.

16 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
INSTALLING PYTHON
Topics Covered In This Chapter:
Downloading and installing Python
Downloading the Pyperclip module
How to start IDLE
Formatting used in this book
Copying and pasting text
“Privacy in an open society also requires
cryptography. If I say something, I want it
heard only by those for whom I intend it. If the
content of my speech is available to the world, I
have no privacy.”
Eric Hughes, “A Cypherpunk’s Manifesto”, 1993
http://invpy.com/cypherpunk
The content of this chapter is very similar to the first chapter of Invent Your Own Computer
Games with Python. If you have already read that book or have already installed Python, you only
need to read the “Downloading pyperclip.py” section in this chapter.

Chapter 2 – Downloading and Installing Python 17
Downloading and Installing Python
Before we can begin programming, you’ll need to install software called the Python interpreter.
(You may need to ask an adult for help here.) The interpreter is a program that understands the
instructions that you’ll write in the Python language. Without the interpreter, your computer won't
understand these instructions. (We'll refer to “the Python interpreter” as “Python” from now on.)
Because we’ll be writing our programs in the Python language we need to download Python from
the official website of the Python programming language, http://www.python.org. The installation
is a little different depending on if your computer’s operating system is Windows, OS X, or a
Linux distribution such as Ubuntu. You can also find videos of people installing the Python
software online at http://invpy.com/installing.
Important Note! Be sure to install Python 3, and not Python 2. The programs in this book use
Python 3, and you’ll get errors if you try to run them with Python 2. It is so important, I am
adding a cartoon penguin telling you to install Python 3 so that you do not miss this message:
Figure 2-1. “Be sure to install Python 3, not Python 2!”, says the incongruous penguin.
Windows Instructions
There is a list of links on the left side of the web page at http://www.python.org. Click on the
Download link to go to the download page, then look for the file called Python 3.3.0 Windows
Installer (“Windows binary — does not include source”) and click on its link to download Python
for Windows. (If there is a newer version than Python 3.3.0, you can download that one.)
Double-click on the python-3.3.0.msi file that you’ve just downloaded to start the Python
installer. (If it doesn’t start, try right-clicking the file and choosing Install.) Once the installer
starts up, click the Next button and accept the choices in the installer as you go. There’s no need
to make any changes. When the installer is finished, click Finish.

18 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
OS X Instructions
The installation for OS X is similar. Instead of downloading the .msi file from the Python
website, download the .dmg Mac Installer Disk Image file instead. The link to this file will look
something like “Python 3.3.0 Mac OS X” on the “Download Python Software” web page.
Ubuntu and Linux Instructions
If your operating system is Ubuntu, you can install Python by opening a terminal window (click
on Applications ► Accessories ► Terminal) and entering sudo apt-get install
python3.3 then pressing Enter. You will need to enter the root password to install Python, so
ask the person who owns the computer to type in this password.
You also need to install the IDLE software. From the terminal, type in sudo apt-get
install idle3. You will also need the root password to install IDLE.
Downloading pyperclip.py
Almost every program in this book uses a custom module I wrote called pyperclip.py. This
module provides functions for letting your program copy and paste text to the clipboard. This
module does not come with Python, but you can download it from: http://invpy.com/pyperclip.py
This file must be in the same folder as the Python program files that you type. (A folder is also
called a directory.) Otherwise you will see this error message when you try to run your program:
ImportError: No module named pyperclip
Starting IDLE
We will be using the IDLE software to type in our programs and run them. IDLE stands for
Interactive DeveLopment Environment. While Python is the software that interprets and runs
your Python programs, the IDLE software is what you type your programs in.
If your operating system is Windows XP, you should be able to run Python by clicking the Start
button, then selecting Programs ► Python 3.3 ► IDLE (Python GUI). For Windows Vista or
Windows 7, click the Windows button in the lower left corner, type “IDLE” and select “IDLE
(Python GUI)”.
If your operating system is Max OS X, start IDLE by opening the Finder window and clicking on
Applications, then click Python 3.3, then click the IDLE icon.
Chapter 2 – Downloading and Installing Python 19
If your operating system is Ubuntu or Linux, start IDLE by clicking Applications ► Accessories
► Terminal and then type idle3. You may also be able to click on Applications at the top of
the screen, and then select Programming and then IDLE 3.
Figure 2-2. IDLE running on Windows (left), OS X (center), and Ubuntu Linux (right).
The window that appears will be mostly blank except for text that looks something like this:
Python 3.3.0 (v3.3.0:bd8afb90ebf2, Sep 29 2012, 10:57:17) [MSC v.1600 64 bit
(AMD64)] on win32
Type "copyright", "credits" or "license()" for more information.
>>>
The window that appears when you first run IDLE is called the interactive shell. A shell is a
program that lets you type instructions into the computer. The Python shell lets you type Python
instructions in and then sends these instructions to the Python interpreter software to run. We can
type Python instructions into the shell and, because the shell is interactive, the computer will read
our instructions and perform them immediately.
The Featured Programs
“Hacking Secret Ciphers with Python” is different from other programming books because it
focuses on the source code for complete programs. Instead of teaching you programming
concepts and leaving it up to you to figure out how to make your own programs, this book shows
you complete programs and explains how they work.
As you read through this book, type the source code from this book into IDLE yourself. But you
can also download the source code files from this book’s website. Go to the web site
http://invpy.com/hackingsource and follow the instructions to download the source code files.
In general, you should read this book from front to back. The programming concepts build on
the previous chapters. However, Python is such a readable language that after the first few
chapters you can probably piece together what the code does. If you jump ahead and feel lost, try

20 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
going back to the previous chapters. Or email your programming questions to the author at
al@inventwithpython.com.
Line Numbers and Spaces
When entering the source code yourself, do not type the line numbers that appear at the beginning
of each line. For example, if you see this in the book:
1. number = random.randint(1, 20)
2. spam = 42
3. print('Hello world!')
…then you do not need to type the “1.” on the left side, or the space that immediately follows it.
Just type it like this:
number = random.randint(1, 20)
spam = 42
print('Hello world!')
Those numbers are only used so that this book can refer to specific lines in the code. They are not
a part of the actual program. Aside from the line numbers, be sure to enter the code exactly as it
appears. This includes the letter casing. In Python, HELLO and hello and Hello could refer to
three different things.
Notice that some of the lines don’t begin at the leftmost edge of the page, but are indented by four
or eight spaces. Be sure to put in the correct number of spaces at the start of each line. (Since each
character in IDLE is the same width, you can count the number of spaces by counting the number
of characters above or below the line you’re looking at.)
For example, you can see that the second line is indented by four spaces because the four
characters (“whil”) on the line above are over the indented space. The third line is indented by
another four spaces (the four characters “if n” are above the third line’s indented space):
while spam < 10:
if number == 42:
print('Hello')
Text Wrapping in This Book
Some lines of code are too long to fit on one line on the page, and the text of the code will wrap
around to the next line. When you type these lines into the file editor, enter the code all on one
line without pressing Enter.

Chapter 2 – Downloading and Installing Python 21
You can tell when a new line starts by looking at the line numbers on the left side of the code.
The example below has only two lines of code, even though the first line is too long to fit on the
page:
1. print('This is the first line! xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxx’)
2. print('This is the second line!')
Tracing the Program Online
Tracing a program means to step through the code one line at a time, in the same way that a
computer would execute it. You can visit http://invpy.com/hackingtraces to see a trace through of
each program in this book. The traces web page has notes and helpful reminders at each step of
the trace to explain what the program is doing, so it can help you better understand why these
programs work the way they do.
Checking Your Typed Code with the Online Diff Tool
Although it is very helpful to learn Python by typing out the source code for these programs, you
may accidentally make typos that cause your programs to crash. It may not be obvious where the
typo is.
You can copy and paste the text of your typed source code to the online diff tool on the book’s
website. The diff tool will show any differences between the source code in the book and the
source code you’ve typed. This is an easy way of finding any typos in your programs.
The online diff tool is at this web page: http://invpy.com/hackingdiff. A video tutorial of how to
use the diff tool is available from this book’s website at http://invpy.com/hackingvideos.
Copying and Pasting Text
Copying and pasting text is a very useful computer skill, especially for this book because many of
the texts that will be encrypted or decrypted are quite long. Instead of typing them out, you can
look at electronic versions of the text on this book’s website and copy the text from your browser
and paste it into IDLE.
To copy and paste text, you first need to drag the mouse over the text you want to copy. This will
highlight the text. Then you can either click on the Edit ► Copy menu item, or on Windows
press Ctrl-C. (That’s press and hold the Ctrl button, then press C once, then let go of the Ctrl
button.) On Macs, the keyboard shortcut is Command-C (the ⌘ button). This will copy the
highlighted text to the computer’s memory, or clipboard.

22 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
To paste the text that is on the clipboard, move the cursor to the place you want the text to be
inserted. Then either click on the Edit ► Paste menu item or press Ctrl-V or Command-V.
Pasting will have the same effect as if you typed out all the characters that were copied to the
clipboard. Copying and pasting can save you a lot of typing time, and unlike typing it will never
make a mistake in reproducing the text.
You should note that every time you copy text to the clipboard, the previous text that was on the
clipboard is forgotten.
There is a tutorial on copying and pasting at this book’s website at http://invpy.com/copypaste.
More Info Links
There is a lot that you can learn about programming and cryptography, but you don’t need to
learn all of it now. There are several times where you might like to learn these additional details
and explanations, but if I included them in this book then it would add many more pages.
Publication of this larger book would place so much combustible paper into a single space that
the book would be a fire hazard. Instead, I have included “more info” links in this book that you
can follow to this book’s website. You do not have to read this additional information to
understand anything in this book, but it will help you learn. These links begin with
http://invpy.com (which is the shortened URL for the “Invent with Python” book website.)
Even though this book is not a dangerous fire hazard, please do not set it on fire anyway.
Programming and Cryptography
Programming and cryptography are two separate skills, but learning both is useful because a
computer can do cryptography much faster than a human can. For example, here is the entire text
of William Shakespeare’s “Romeo and Juliet” encrypted with a simple substitution cipher:
WUMIU FOT LZNCIB JWUNURZI Dguwzh Bku guzhigunth, qubg fncei co tcrocbx, Co afcw Piwuof, kgiwi ki nfx uzw hdioi, Awum fodciob rwztri qwife bu oik mzbcox, Kgiwi dcpcn qnuut mfeih dcpcn gfoth zodnifo. Awum auwbg bgi afbfn nucoh ua bgihi bku auih F jfcw ua hbfw-dwuhh't nupiwh bfei bgicw ncai; Kguni mchftpiobzwit jcbiuzh
upiwbgwukh Tu kcbg bgicw tifbg qzwx bgicw jfwiobh' hbwcai. Bgi aifwazn jfhhfri ua bgicw tifbg-mfwe't nupi, Fot bgi duobcozfodi ua bgicw jfwiobh' wfri, Kgcdg, qzb bgicw dgcntwio'h iot, ouzrgb duznt wimupi, Ch ouk bgi bku guzwh' bwfaacd ua uzw hbfri; Bgi kgcdg ca xuz kcbg jfbciob ifwh fbbiot, Kgfb giwi hgfnn mchh, uzw bucn hgfnn hbwcpi bu
miot. WUMIU FOT LZNCIB FDB C HDIOI C Piwuof. F jzqncd jnfdi. [Iobiw HFMJHUO fot RWIRUWX, ua bgi guzhi ua Dfjznib, fwmit kcbg hkuwth fot qzdeniwh] HFMJHUO Rwiruwx, u' mx kuwt, ki'nn oub dfwwx dufnh. RWIRUWX Ou, auw bgio ki hguznt qi dunnciwh. HFMJHUO C mifo, fo ki qi co dguniw, ki'nn twfk. RWIRUWX Fx, kgcni xuz
ncpi, twfk xuzw oide uzb u' bgi dunnfw. HFMJHUO C hbwcei yzcdenx, qicor mupit. RWIRUWX Qzb bguz fwb oub yzcdenx mupit bu hbwcei. HFMJHUO F tur ua bgi guzhi ua Muobfrzi mupih mi. RWIRUWX Bu mupi ch bu hbcw; fot bu qi pfncfob ch bu hbfot: bgiwiauwi, ca bguz fwb mupit, bguz wzoo'hb fkfx. HFMJHUO F tur ua bgfb guzhi hgfnn
mupi mi bu hbfot: C kcnn bfei bgi kfnn ua fox mfo uw mfct ua Muobfrzi'h. RWIRUWX Bgfb hgukh bgii f kife hnfpi; auw bgi kifeihb ruih bu bgi kfnn. HFMJHUO Bwzi; fot bgiwiauwi kumio, qicor bgi kifeiw pihhinh, fwi ipiw bgwzhb bu bgi kfnn: bgiwiauwi C kcnn jzhg Muobfrzi'h mio awum bgi kfnn, fot bgwzhb gch mfcth bu bgi kfnn. RWIRUWX Bgi
yzfwwin ch qibkiio uzw mfhbiwh fot zh bgicw mio. HFMJHUO 'Bch fnn uoi, C kcnn hguk mxhina f bxwfob: kgio C gfpi auzrgb kcbg bgi mio, C kcnn qi dwzin kcbg bgi mfcth, fot dzb uaa bgicw gifth. RWIRUWX Bgi gifth ua bgi mfcth? HFMJHUO Fx, bgi gifth ua bgi mfcth, uw bgicw mfctiogifth; bfei cb co kgfb hiohi bguz kcnb. RWIRUWX Bgix mzhb
bfei cb co hiohi bgfb aiin cb. HFMJHUO Mi bgix hgfnn aiin kgcni C fm fqni bu hbfot: fot 'bch eouko C fm f jwibbx jcidi ua anihg. RWIRUWX 'Bch kinn bguz fwb oub achg; ca bguz gfthb, bguz gfthb qiio juuw Lugo. Twfk bgx buun! giwi dumih bku ua bgi guzhi ua bgi Muobfrzih. HFMJHUO Mx ofeit kifjuo ch uzb: yzfwwin, C kcnn qfde bgii.
RWIRUWX Guk! bzwo bgx qfde fot wzo? HFMJHUO Aifw mi oub. RWIRUWX Ou, mfwwx; C aifw bgii! HFMJHUO Nib zh bfei bgi nfk ua uzw hctih; nib bgim qirco. RWIRUWX C kcnn awuko fh C jfhh qx, fot nib bgim bfei cb fh bgix nchb. HFMJHUO Ofx, fh bgix tfwi. C kcnn qcbi mx bgzmq fb bgim; kgcdg ch f tchrwfdi bu bgim, ca bgix qifw cb.
[Iobiw FQWFGFM fot QFNBGFHFW] FQWFGFM Tu xuz qcbi xuzw bgzmq fb zh, hcw? HFMJHUO C tu qcbi mx bgzmq, hcw. FQWFGFM Tu xuz qcbi xuzw bgzmq fb zh, hcw? HFMJHUO [Fhcti bu RWIRUWX] Ch bgi nfk ua uzw hcti, ca C hfx fx? RWIRUWX Ou. HFMJHUO Ou, hcw, C tu oub qcbi mx bgzmq fb xuz, hcw, qzb C qcbi mx bgzmq,
hcw. RWIRUWX Tu xuz yzfwwin, hcw? FQWFGFM Yzfwwin hcw! ou, hcw. HFMJHUO Ca xuz tu, hcw, C fm auw xuz: C hiwpi fh ruut f mfo fh xuz. FQWFGFM Ou qibbiw. HFMJHUO Kinn, hcw. RWIRUWX Hfx 'qibbiw:' giwi dumih uoi ua mx mfhbiw'h ecohmio. HFMJHUO Xih, qibbiw, hcw. FQWFGFM Xuz nci. HFMJHUO Twfk, ca xuz qi mio.
Rwiruwx, wimimqiw bgx hkfhgcor qnuk. [Bgix acrgb] [Iobiw QIOPUNCU] QIOPUNCU Jfwb, auunh! Jzb zj xuzw hkuwth; xuz eouk oub kgfb xuz tu. [Qifbh tuko bgicw hkuwth] [Iobiw BXQFNB] BXQFNB Kgfb, fwb bguz twfko fmuor bgihi gifwbnihh gcoth? Bzwo bgii, Qiopuncu, nuue zjuo bgx tifbg. QIOPUNCU C tu qzb eiij bgi jifdi: jzb zj bgx
hkuwt, Uw mfofri cb bu jfwb bgihi mio kcbg mi. BXQFNB Kgfb, twfko, fot bfne ua jifdi! C gfbi bgi kuwt, Fh C gfbi ginn, fnn Muobfrzih, fot bgii: Gfpi fb bgii, dukfwt! [Bgix acrgb] [Iobiw, hipiwfn ua qubg guzhih, kgu luco bgi awfx; bgio iobiw Dcbcvioh, kcbg dnzqh] Acwhb Dcbcvio Dnzqh, qcnnh, fot jfwbchfoh! hbwcei! qifb bgim tuko! Tuko kcbg bgi
Dfjznibh! tuko kcbg bgi Muobfrzih! [Iobiw DFJZNIB co gch ruko, fot NFTX DFJZNIB] DFJZNIB Kgfb ouchi ch bgch? Rcpi mi mx nuor hkuwt, gu! NFTX DFJZNIB F dwzbdg, f dwzbdg! kgx dfnn xuz auw f hkuwt? DFJZNIB Mx hkuwt, C hfx! Unt Muobfrzi ch dumi, Fot anuzwchgih gch qnfti co hjcbi ua mi. [Iobiw MUOBFRZI fot NFTX MUOBFRZI]
MUOBFRZI Bguz pcnnfco Dfjznib,--Gunt mi oub, nib mi ru. NFTX MUOBFRZI Bguz hgfnb oub hbcw f auub bu hiie f aui. [Iobiw JWCODI, kcbg Fbbiotfobh] JWCODI Wiqinncuzh hzqlidbh, ioimcih bu jifdi, Jwuafoiwh ua bgch oicrgquzw-hbfcoit hbiin,-- Kcnn bgix oub gifw? Kgfb, gu! xuz mio, xuz qifhbh, Bgfb yziodg bgi acwi ua xuzw jiwocdcuzh
wfri Kcbg jzwjni auzobfcoh chhzcor awum xuzw picoh, Uo jfco ua buwbzwi, awum bguhi qnuutx gfoth Bgwuk xuzw mchbimjiw't kifjuoh bu bgi rwuzot, Fot gifw bgi hiobiodi ua xuzw mupit jwcodi. Bgwii dcpcn qwfknh, qwit ua fo fcwx kuwt, Qx bgii, unt Dfjznib, fot Muobfrzi, Gfpi bgwcdi tchbzwq't bgi yzcib ua uzw hbwiibh, Fot mfti Piwuof'h fodciob
dcbcvioh Dfhb qx bgicw rwfpi qihiimcor uwofmiobh, Bu kcint unt jfwbchfoh, co gfoth fh unt, Dfoeiw't kcbg jifdi, bu jfwb xuzw dfoeiw't gfbi: Ca ipiw xuz tchbzwq uzw hbwiibh frfco, Xuzw ncpih hgfnn jfx bgi auwaicb ua bgi jifdi. Auw bgch bcmi, fnn bgi wihb tijfwb fkfx: Xuz Dfjznib; hgfnn ru fnuor kcbg mi: Fot, Muobfrzi, dumi xuz bgch fabiwouuo, Bu
eouk uzw azwbgiw jnifhzwi co bgch dfhi, Bu unt Awii-buko, uzw dummuo lztrmiob-jnfdi. Uodi muwi, uo jfco ua tifbg, fnn mio tijfwb. [Isizob fnn qzb MUOBFRZI, NFTX MUOBFRZI, fot QIOPUNCU] MUOBFRZI Kgu hib bgch fodciob yzfwwin oik fqwufdg? Hjife, oijgik, kiwi xuz qx kgio cb qirfo? QIOPUNCU Giwi kiwi bgi hiwpfobh ua xuzw
ftpiwhfwx, Fot xuzwh, dnuhi acrgbcor iwi C tct fjjwufdg: C twik bu jfwb bgim: co bgi cohbfob dfmi Bgi aciwx Bxqfnb, kcbg gch hkuwt jwijfwit, Kgcdg, fh gi qwifbgit tiacfodi bu mx ifwh, Gi hkzor fquzb gch gift fot dzb bgi kcoth, Kgu oubgcor gzwb kcbgfn gchh't gcm co hduwo: Kgcni ki kiwi cobiwdgforcor bgwzhbh fot qnukh, Dfmi muwi fot muwi fot
auzrgb uo jfwb fot jfwb, Bcnn bgi jwcodi dfmi, kgu jfwbit icbgiw jfwb. NFTX MUOBFRZI U, kgiwi ch Wumiu? hfk xuz gcm bu-tfx? Wcrgb rnft C fm gi kfh oub fb bgch awfx. QIOPUNCU Mftfm, fo guzw qiauwi bgi kuwhgcjj't hzo Jiiw't auwbg bgi runtio kcotuk ua bgi ifhb, F bwuzqnit mcot twfpi mi bu kfne fqwuft; Kgiwi, zotiwoifbg bgi rwupi ua
hxdfmuwi Bgfb kihbkfwt wuubibg awum bgi dcbx'h hcti, Hu ifwnx kfnecor tct C hii xuzw huo: Bukfwth gcm C mfti, qzb gi kfh kfwi ua mi Fot hbuni cobu bgi dupiwb ua bgi kuut: C, mifhzwcor gch faaidbcuoh qx mx uko, Bgfb muhb fwi qzhcit kgio bgix'wi muhb fnuoi, Jzwhzit mx gzmuzw oub jzwhzcor gch, Fot rnftnx hgzoo't kgu rnftnx anit awum mi.
MUOBFRZI Mfox f muwocor gfbg gi bgiwi qiio hiio, Kcbg bifwh fzrmiobcor bgi awihg muwocor tik. Fttcor bu dnuzth muwi dnuzth kcbg gch tiij hcrgh; Qzb fnn hu huuo fh bgi fnn-dgiiwcor hzo Hguznt co bgi azwbgihb ifhb qirco bu twfk Bgi hgftx dzwbfcoh awum Fzwuwf'h qit, Fkfx awum bgi ncrgb hbifnh gumi mx gifpx huo, Fot jwcpfbi co gch
dgfmqiw jioh gcmhina, Hgzbh zj gch kcotukh, nudeh afw tfxncrgb uzb Fot mfeih gcmhina fo fwbcacdcfn ocrgb: Qnfde fot juwbiobuzh mzhb bgch gzmuzw jwupi, Zonihh ruut duzohin mfx bgi dfzhi wimupi. QIOPUNCU Mx ouqni zodni, tu xuz eouk bgi dfzhi? MUOBFRZI C oicbgiw eouk cb ouw dfo nifwo ua gcm. QIOPUNCU Gfpi xuz cmjuwbzoit gcm
qx fox mifoh? MUOBFRZI Qubg qx mxhina fot mfox ubgiw awcioth: Qzb gi, gch uko faaidbcuoh' duzohinnuw, Ch bu gcmhina--C kcnn oub hfx guk bwzi-- Qzb bu gcmhina hu hidwib fot hu dnuhi, Hu afw awum huzotcor fot tchdupiwx, Fh ch bgi qzt qcb kcbg fo iopcuzh kuwm, Iwi gi dfo hjwift gch hkiib nifpih bu bgi fcw, Uw titcdfbi gch qifzbx bu bgi
hzo. Duznt ki qzb nifwo awum kgiodi gch huwwukh rwuk. Ki kuznt fh kcnncornx rcpi dzwi fh eouk. [Iobiw WUMIU] QIOPUNCU Hii, kgiwi gi dumih: hu jnifhi xuz, hbij fhcti; C'nn eouk gch rwcipfodi, uw qi mzdg tiocit. MUOBFRZI C kuznt bguz kiwb hu gfjjx qx bgx hbfx, Bu gifw bwzi hgwcab. Dumi, mftfm, nib'h fkfx. [Isizob MUOBFRZI fot NFTX
MUOBFRZI] QIOPUNCU Ruut-muwwuk, duzhco. WUMIU Ch bgi tfx hu xuzor? QIOPUNCU Qzb oik hbwzde ocoi. WUMIU Fx mi! hft guzwh hiim nuor. Kfh bgfb mx afbgiw bgfb kiob giodi hu afhb? QIOPUNCU Cb kfh. Kgfb hftoihh niorbgioh Wumiu'h guzwh? WUMIU Oub gfpcor bgfb, kgcdg, gfpcor, mfeih bgim hguwb. QIOPUNCU Co nupi?
WUMIU Uzb-- QIOPUNCU Ua nupi? WUMIU Uzb ua giw afpuzw, kgiwi C fm co nupi. QIOPUNCU Fnfh, bgfb nupi, hu riobni co gch pcik, Hguznt qi hu bxwfoouzh fot wuzrg co jwuua! WUMIU Fnfh, bgfb nupi, kguhi pcik ch mzaanit hbcnn, Hguznt, kcbguzb ixih, hii jfbgkfxh bu gch kcnn! Kgiwi hgfnn ki tcoi? U mi! Kgfb awfx kfh giwi? Xib binn mi
oub, auw C gfpi gifwt cb fnn. Giwi'h mzdg bu tu kcbg gfbi, qzb muwi kcbg nupi. Kgx, bgio, U qwfkncor nupi! U nupcor gfbi! U fox bgcor, ua oubgcor acwhb dwifbi! U gifpx ncrgboihh! hiwcuzh pfocbx! Mch-hgfjio dgfuh ua kinn-hiimcor auwmh! Aifbgiw ua nift, qwcrgb hmuei, dunt acwi, hcde gifnbg! Hbcnn-kfecor hniij, bgfb ch oub kgfb cb ch! Bgch
nupi aiin C, bgfb aiin ou nupi co bgch. Tuhb bguz oub nfzrg? QIOPUNCU Ou, duv, C wfbgiw kiij. WUMIU Ruut gifwb, fb kgfb? QIOPUNCU Fb bgx ruut gifwb'h ujjwihhcuo. WUMIU Kgx, hzdg ch nupi'h bwfohrwihhcuo. Rwciah ua mcoi uko nci gifpx co mx qwifhb, Kgcdg bguz kcnb jwujfrfbi, bu gfpi cb jwihb Kcbg muwi ua bgcoi: bgch nupi bgfb bguz
gfhb hguko Tubg ftt muwi rwcia bu buu mzdg ua mcoi uko. Nupi ch f hmuei wfchit kcbg bgi azmi ua hcrgh; Qicor jzwrit, f acwi hjfwencor co nupiwh' ixih; Qicor pis't f hif ouzwchg't kcbg nupiwh' bifwh: Kgfb ch cb inhi? f mftoihh muhb tchdwiib, F dguecor rfnn fot f jwihiwpcor hkiib. Afwikinn, mx duv. QIOPUNCU Huab! C kcnn ru fnuor; Fo ca xuz nifpi
mi hu, xuz tu mi kwuor. WUMIU Bzb, C gfpi nuhb mxhina; C fm oub giwi; Bgch ch oub Wumiu, gi'h humi ubgiw kgiwi. QIOPUNCU Binn mi co hftoihh, kgu ch bgfb xuz nupi. WUMIU Kgfb, hgfnn C rwufo fot binn bgii? QIOPUNCU Rwufo! kgx, ou. Qzb hftnx binn mi kgu. WUMIU Qct f hcde mfo co hftoihh mfei gch kcnn: Fg, kuwt cnn zwrit bu uoi
bgfb ch hu cnn! Co hftoihh, duzhco, C tu nupi f kumfo. QIOPUNCU C fcm't hu oifw, kgio C hzjjuhit xuz nupit. WUMIU F wcrgb ruut mfwe-mfo! Fot hgi'h afcw C nupi. QIOPUNCU F wcrgb afcw mfwe, afcw duv, ch huuoihb gcb. WUMIU Kinn, co bgfb gcb xuz mchh: hgi'nn oub qi gcb Kcbg Dzjct'h fwwuk; hgi gfbg Tcfo'h kcb; Fot, co hbwuor jwuua ua
dgfhbcbx kinn fwm't, Awum nupi'h kife dgcntchg quk hgi ncpih zogfwm't. Hgi kcnn oub hbfx bgi hciri ua nupcor biwmh, Ouw qcti bgi ioduzobiw ua fhhfcncor ixih, Ouw uji giw nfj bu hfcob-hitzdcor runt: U, hgi ch wcdg co qifzbx, uonx juuw, Bgfb kgio hgi tcih kcbg qifzbx tcih giw hbuwi. QIOPUNCU Bgio hgi gfbg hkuwo bgfb hgi kcnn hbcnn ncpi
dgfhbi? WUMIU Hgi gfbg, fot co bgfb hjfwcor mfeih gzri kfhbi, Auw qifzbx hbfwpit kcbg giw hipiwcbx Dzbh qifzbx uaa awum fnn juhbiwcbx. Hgi ch buu afcw, buu kchi, kchinx buu afcw, Bu miwcb qnchh qx mfecor mi tihjfcw: Hgi gfbg auwhkuwo bu nupi, fot co bgfb puk Tu C ncpi tift bgfb ncpi bu binn cb ouk. QIOPUNCU Qi wznit qx mi, auwrib bu
bgcoe ua giw. WUMIU U, bifdg mi guk C hguznt auwrib bu bgcoe. QIOPUNCU Qx rcpcor ncqiwbx zobu bgcoi ixih; Isfmcoi ubgiw qifzbcih. WUMIU 'Bch bgi kfx Bu dfnn giwh isyzchcbi, co yzihbcuo muwi: Bgihi gfjjx mfheh bgfb echh afcw nftcih' qwukh Qicor qnfde jzb zh co mcot bgix gcti bgi afcw; Gi bgfb ch hbwzdeio qncot dfooub auwrib Bgi
jwidcuzh bwifhzwi ua gch ixihcrgb nuhb: Hguk mi f mchbwihh bgfb ch jfhhcor afcw, Kgfb tubg giw qifzbx hiwpi, qzb fh f oubi Kgiwi C mfx wift kgu jfhh't bgfb jfhhcor afcw? Afwikinn: bguz dfohb oub bifdg mi bu auwrib. QIOPUNCU C'nn jfx bgfb tudbwcoi, uw inhi tci co tiqb. [Isizob] WUMIU FOT LZNCIB FDB C HDIOI CC F hbwiib. [Iobiw
DFJZNIB, JFWCH, fot Hiwpfob] DFJZNIB Qzb Muobfrzi ch quzot fh kinn fh C, Co jiofnbx fncei; fot 'bch oub gfwt, C bgcoe, Auw mio hu unt fh ki bu eiij bgi jifdi. JFWCH Ua guouzwfqni wideuocor fwi xuz qubg; Fot jcbx 'bch xuz ncpit fb utth hu nuor. Qzb ouk, mx nuwt, kgfb hfx xuz bu mx hzcb? DFJZNIB Qzb hfxcor u'iw kgfb C gfpi hfct qiauwi: Mx
dgcnt ch xib f hbwforiw co bgi kuwnt; Hgi gfbg oub hiio bgi dgfori ua auzwbiio xifwh, Nib bku muwi hzmmiwh kcbgiw co bgicw jwcti, Iwi ki mfx bgcoe giw wcji bu qi f qwcti. JFWCH Xuzoriw bgfo hgi fwi gfjjx mubgiwh mfti. DFJZNIB Fot buu huuo mfww't fwi bguhi hu ifwnx mfti. Bgi ifwbg gfbg hkfnnuk't fnn mx gujih qzb hgi, Hgi ch bgi gujiazn
nftx ua mx ifwbg: Qzb kuu giw, riobni Jfwch, rib giw gifwb, Mx kcnn bu giw duohiob ch qzb f jfwb; Fo hgi frwii, kcbgco giw hduji ua dgucdi Ncih mx duohiob fot afcw fdduwtcor pucdi. Bgch ocrgb C gunt fo unt fddzhbum't aifhb, Kgiwibu C gfpi copcbit mfox f rzihb, Hzdg fh C nupi; fot xuz, fmuor bgi hbuwi, Uoi muwi, muhb kindumi, mfeih mx ozmqiw
muwi. Fb mx juuw guzhi nuue bu qigunt bgch ocrgb Ifwbg-bwiftcor hbfwh bgfb mfei tfwe gifpio ncrgb: Hzdg dumauwb fh tu nzhbx xuzor mio aiin Kgio kinn-fjjfwinn't Fjwcn uo bgi giin Ua ncmjcor kcobiw bwifth, ipio hzdg tincrgb Fmuor awihg aimfni qzth hgfnn xuz bgch ocrgb Cogiwcb fb mx guzhi; gifw fnn, fnn hii, Fot ncei giw muhb kguhi miwcb
muhb hgfnn qi: Kgcdg uo muwi pcik, ua mfox mcoi qicor uoi Mfx hbfot co ozmqiw, bguzrg co wideuocor ouoi, Dumi, ru kcbg mi. [Bu Hiwpfob, rcpcor f jfjiw] Ru, hcwwfg, bwztri fquzb Bgwuzrg afcw Piwuof; acot bguhi jiwhuoh uzb Kguhi ofmih fwi kwcbbio bgiwi, fot bu bgim hfx, Mx guzhi fot kindumi uo bgicw jnifhzwi hbfx. [Isizob DFJZNIB fot
JFWCH] Hiwpfob Acot bgim uzb kguhi ofmih fwi kwcbbio giwi! Cb ch kwcbbio, bgfb bgi hguimfeiw hguznt mittni kcbg gch xfwt, fot bgi bfcnuw kcbg gch nfhb, bgi achgiw kcbg gch jiodcn, fot bgi jfcobiw kcbg gch oibh; qzb C fm hiob bu acot bguhi jiwhuoh kguhi ofmih fwi giwi kwcb, fot dfo oipiw acot kgfb ofmih bgi kwcbcor jiwhuo gfbg giwi kwcb.
C mzhb bu bgi nifwoit.--Co ruut bcmi. [Iobiw QIOPUNCU fot WUMIU] QIOPUNCU Bzb, mfo, uoi acwi qzwoh uzb foubgiw'h qzwocor, Uoi jfco ch nihhio't qx foubgiw'h forzchg; Bzwo rcttx, fot qi gunj qx qfdekfwt bzwocor; Uoi tihjiwfbi rwcia dzwih kcbg foubgiw'h nforzchg: Bfei bguz humi oik coaidbcuo bu bgx ixi, Fot bgi wfoe juchuo ua bgi unt kcnn
tci. WUMIU Xuzw jnfcobfco-nifa ch isdinniob auw bgfb. QIOPUNCU Auw kgfb, C jwfx bgii? WUMIU Auw xuzw qwueio hgco. QIOPUNCU Kgx, Wumiu, fwb bguz mft? WUMIU Oub mft, qzb quzot muwi bgfo f mft-mfo ch; Hgzb zj co jwchuo, eijb kcbguzb mx auut, Kgcjj't fot buwmiobit fot--Rut-tio, ruut ainnuk. Hiwpfob Rut rc' rut-tio. C jwfx, hcw,
dfo xuz wift? WUMIU Fx, mcoi uko auwbzoi co mx mchiwx. Hiwpfob Jiwgfjh xuz gfpi nifwoit cb kcbguzb quue: qzb, C jwfx, dfo xuz wift fox bgcor xuz hii? WUMIU Fx, ca C eouk bgi nibbiwh fot bgi nforzfri. Hiwpfob Xi hfx guoihbnx: wihb xuz miwwx! WUMIU Hbfx, ainnuk; C dfo wift. [Wifth] 'Hcrocuw Mfwbcou fot gch kcai fot tfzrgbiwh; Duzobx
Fohinmi fot gch qifzbiuzh hchbiwh; bgi nftx kctuk ua Pcbwfpcu; Hcrocuw Jnfdiobcu fot gch nupinx ocidih; Miwdzbcu fot gch qwubgiw Pfniobcoi; mcoi zodni Dfjznib, gch kcai fot tfzrgbiwh; mx afcw ocidi Wuhfncoi; Ncpcf; Hcrocuw Pfniobcu fot gch duzhco Bxqfnb, Nzdcu fot bgi ncpinx Giniof.' F afcw fhhimqnx: kgcbgiw hguznt bgix dumi? Hiwpfob Zj.
Chapter 2 – Downloading and Installing Python 23
WUMIU Kgcbgiw? Hiwpfob Bu hzjjiw; bu uzw guzhi. WUMIU Kguhi guzhi? Hiwpfob Mx mfhbiw'h. WUMIU Cotiit, C hguznt gfpi fhe't xuz bgfb qiauwi. Hiwpfob Ouk C'nn binn xuz kcbguzb fhecor: mx mfhbiw ch bgi rwifb wcdg Dfjznib; fot ca xuz qi oub ua bgi guzhi ua Muobfrzih, C jwfx, dumi fot dwzhg f dzj ua kcoi. Wihb xuz miwwx! [Iscb]
QIOPUNCU Fb bgch hfmi fodciob aifhb ua Dfjznib'h Hzjh bgi afcw Wuhfncoi kgum bguz hu nupihb, Kcbg fnn bgi ftmcwit qifzbcih ua Piwuof: Ru bgcbgiw; fot, kcbg zofbbfcobit ixi, Dumjfwi giw afdi kcbg humi bgfb C hgfnn hguk, Fot C kcnn mfei bgii bgcoe bgx hkfo f dwuk. WUMIU Kgio bgi tipuzb wincrcuo ua mcoi ixi Mfcobfcoh hzdg afnhiguut,
bgio bzwo bifwh bu acwih; Fot bgihi, kgu uabio twuko't duznt oipiw tci, Bwfohjfwiob giwibcdh, qi qzwob auw ncfwh! Uoi afcwiw bgfo mx nupi! bgi fnn-hiicor hzo Oi'iw hfk giw mfbdg hcodi acwhb bgi kuwnt qirzo. QIOPUNCU Bzb, xuz hfk giw afcw, ouoi inhi qicor qx, Giwhina juchit kcbg giwhina co icbgiw ixi: Qzb co bgfb dwxhbfn hdfnih nib bgiwi
qi kicrg't Xuzw nftx'h nupi frfcohb humi ubgiw mfct Bgfb C kcnn hguk xuz hgcocor fb bgch aifhb, Fot hgi hgfnn hdfob hguk kinn bgfb ouk hgukh qihb. WUMIU C'nn ru fnuor, ou hzdg hcrgb bu qi hguko, Qzb bu wilucdi co hjniotuw ua mcoi uko. [Isizob] WUMIU FOT LZNCIB FDB C HDIOI CCC F wuum co Dfjznib'h guzhi. [Iobiw NFTX DFJZNIB fot
Ozwhi] NFTX DFJZNIB Ozwhi, kgiwi'h mx tfzrgbiw? dfnn giw auwbg bu mi. Ozwhi Ouk, qx mx mfctiogift, fb bkinpi xifw unt, C qfti giw dumi. Kgfb, nfmq! kgfb, nftxqcwt! Rut auwqct! Kgiwi'h bgch rcwn? Kgfb, Lzncib! [Iobiw LZNCIB] LZNCIB Guk ouk! kgu dfnnh? Ozwhi Xuzw mubgiw. LZNCIB Mftfm, C fm giwi. Kgfb ch xuzw kcnn? NFTX
DFJZNIB Bgch ch bgi mfbbiw:--Ozwhi, rcpi nifpi fkgcni, Ki mzhb bfne co hidwib:--ozwhi, dumi qfde frfco; C gfpi wimimqiw't mi, bguz'h gifw uzw duzohin. Bguz eouk'hb mx tfzrgbiw'h ua f jwibbx fri. Ozwhi Afcbg, C dfo binn giw fri zobu fo guzw. NFTX DFJZNIB Hgi'h oub auzwbiio. Ozwhi C'nn nfx auzwbiio ua mx biibg,-- Fot xib, bu mx biibg qi cb
hjueio, C gfpi qzb auzw-- Hgi ch oub auzwbiio. Guk nuor ch cb ouk Bu Nfmmfh-bcti? NFTX DFJZNIB F auwbocrgb fot utt tfxh. Ozwhi Ipio uw utt, ua fnn tfxh co bgi xifw, Dumi Nfmmfh-ipi fb ocrgb hgfnn hgi qi auzwbiio. Hzhfo fot hgi--Rut wihb fnn Dgwchbcfo huznh!-- Kiwi ua fo fri: kinn, Hzhfo ch kcbg Rut; Hgi kfh buu ruut auw mi: qzb, fh C hfct,
Uo Nfmmfh-ipi fb ocrgb hgfnn hgi qi auzwbiio; Bgfb hgfnn hgi, mfwwx; C wimimqiw cb kinn. 'Bch hcodi bgi ifwbgyzfei ouk inipio xifwh; Fot hgi kfh kifo't,--C oipiw hgfnn auwrib cb,-- Ua fnn bgi tfxh ua bgi xifw, zjuo bgfb tfx: Auw C gft bgio nfct kuwmkuut bu mx tzr, Hcbbcor co bgi hzo zotiw bgi tupi-guzhi kfnn; Mx nuwt fot xuz kiwi bgio fb
Mfobzf:-- Ofx, C tu qifw f qwfco:--qzb, fh C hfct, Kgio cb tct bfhbi bgi kuwmkuut uo bgi ocjjni Ua mx tzr fot ainb cb qcbbiw, jwibbx auun, Bu hii cb bibdgx fot afnn uzb kcbg bgi tzr! Hgfei yzubg bgi tupi-guzhi: 'bkfh ou oiit, C bwuk, Bu qct mi bwztri: Fot hcodi bgfb bcmi cb ch inipio xifwh; Auw bgio hgi duznt hbfot fnuoi; ofx, qx bgi wuut, Hgi duznt gfpi
wzo fot kfttnit fnn fquzb; Auw ipio bgi tfx qiauwi, hgi qwuei giw qwuk: Fot bgio mx gzhqfot--Rut qi kcbg gch huzn! F' kfh f miwwx mfo--buue zj bgi dgcnt: 'Xif,' yzubg gi, 'tuhb bguz afnn zjuo bgx afdi? Bguz kcnb afnn qfdekfwt kgio bguz gfhb muwi kcb; Kcnb bguz oub, Lzni?' fot, qx mx gunctfmi, Bgi jwibbx kwibdg niab dwxcor fot hfct 'Fx.' Bu hii, ouk,
guk f lihb hgfnn dumi fquzb! C kfwwfob, fo C hguznt ncpi f bguzhfot xifwh, C oipiw hguznt auwrib cb: 'Kcnb bguz oub, Lzni?' yzubg gi; Fot, jwibbx auun, cb hbcobit fot hfct 'Fx.' NFTX DFJZNIB Iouzrg ua bgch; C jwfx bgii, gunt bgx jifdi. Ozwhi Xih, mftfm: xib C dfooub dguuhi qzb nfzrg, Bu bgcoe cb hguznt nifpi dwxcor fot hfx 'Fx.' Fot xib, C
kfwwfob, cb gft zjuo cbh qwuk F qzmj fh qcr fh f xuzor dudeiwin'h hbuoi; F jfwnuzh eoude; fot cb dwcit qcbbiwnx: 'Xif,' yzubg mx gzhqfot,'afnn'hb zjuo bgx afdi? Bguz kcnb afnn qfdekfwt kgio bguz dumihb bu fri; Kcnb bguz oub, Lzni?' cb hbcobit fot hfct 'Fx.' LZNCIB Fot hbcob bguz buu, C jwfx bgii, ozwhi, hfx C. Ozwhi Jifdi, C gfpi tuoi. Rut mfwe
bgii bu gch rwfdi! Bguz kfhb bgi jwibbcihb qfqi bgfb i'iw C ozwhit: Fo C mcrgb ncpi bu hii bgii mfwwcit uodi, C gfpi mx kchg. NFTX DFJZNIB Mfwwx, bgfb 'mfwwx' ch bgi piwx bgimi C dfmi bu bfne ua. Binn mi, tfzrgbiw Lzncib, Guk hbfoth xuzw tchjuhcbcuo bu qi mfwwcit? LZNCIB Cb ch fo guouzw bgfb C twifm oub ua. Ozwhi Fo guouzw! kiwi
oub C bgcoi uonx ozwhi, C kuznt hfx bguz gfthb hzde't kchtum awum bgx bifb. NFTX DFJZNIB Kinn, bgcoe ua mfwwcfri ouk; xuzoriw bgfo xuz, Giwi co Piwuof, nftcih ua ihbiim, Fwi mfti fnwiftx mubgiwh: qx mx duzob, C kfh xuzw mubgiw mzdg zjuo bgihi xifwh Bgfb xuz fwi ouk f mfct. Bgzh bgio co qwcia: Bgi pfncfob Jfwch hiieh xuz auw gch nupi.
Ozwhi F mfo, xuzor nftx! nftx, hzdg f mfo Fh fnn bgi kuwnt--kgx, gi'h f mfo ua kfs. NFTX DFJZNIB Piwuof'h hzmmiw gfbg oub hzdg f anukiw. Ozwhi Ofx, gi'h f anukiw; co afcbg, f piwx anukiw. NFTX DFJZNIB Kgfb hfx xuz? dfo xuz nupi bgi riobnimfo? Bgch ocrgb xuz hgfnn qigunt gcm fb uzw aifhb; Wift u'iw bgi punzmi ua xuzor Jfwch' afdi, Fot
acot tincrgb kwcb bgiwi kcbg qifzbx'h jio; Isfmcoi ipiwx mfwwcit ncoifmiob, Fot hii guk uoi foubgiw nioth duobiob Fot kgfb uqhdzwit co bgch afcw punzmi ncih Acot kwcbbio co bgi mfwriob ua gch ixih. Bgch jwidcuzh quue ua nupi, bgch zoquzot nupiw, Bu qifzbcax gcm, uonx nfdeh f dupiw: Bgi achg ncpih co bgi hif, fot 'bch mzdg jwcti Auw afcw
kcbguzb bgi afcw kcbgco bu gcti: Bgfb quue co mfox'h ixih tubg hgfwi bgi rnuwx, Bgfb co runt dnfhjh nudeh co bgi runtio hbuwx; Hu hgfnn xuz hgfwi fnn bgfb gi tubg juhhihh, Qx gfpcor gcm, mfecor xuzwhina ou nihh. Ozwhi Ou nihh! ofx, qcrriw; kumio rwuk qx mio. NFTX DFJZNIB Hjife qwcianx, dfo xuz ncei ua Jfwch' nupi? LZNCIB C'nn nuue bu
ncei, ca nuuecor ncecor mupi: Qzb ou muwi tiij kcnn C iotfwb mcoi ixi Bgfo xuzw duohiob rcpih hbwiorbg bu mfei cb anx. [Iobiw f Hiwpfob] Hiwpfob Mftfm, bgi rzihbh fwi dumi, hzjjiw hiwpit zj, xuz dfnnit, mx xuzor nftx fheit auw, bgi ozwhi dzwhit co bgi jfobwx, fot ipiwx bgcor co isbwimcbx. C mzhb giodi bu kfcb; C qihiidg xuz, aunnuk hbwfcrgb.
NFTX DFJZNIB Ki aunnuk bgii. [Iscb Hiwpfob] Lzncib, bgi duzobx hbfxh. Ozwhi Ru, rcwn, hiie gfjjx ocrgbh bu gfjjx tfxh. [Isizob] WUMIU FOT LZNCIB FDB C HDIOI CP F hbwiib. [Iobiw WUMIU, MIWDZBCU, QIOPUNCU, kcbg acpi uw hcs Mfheiwh, Buwdg-qifwiwh, fot ubgiwh] WUMIU Kgfb, hgfnn bgch hjiidg qi hjuei auw uzw isdzhi? Uw
hgfnn ki uo kcbguzb f fjunurx? QIOPUNCU Bgi tfbi ch uzb ua hzdg jwuncscbx: Ki'nn gfpi ou Dzjct guutkcoe't kcbg f hdfwa, Qifwcor f Bfwbfw'h jfcobit quk ua nfbg, Hdfwcor bgi nftcih ncei f dwuk-eiijiw; Ouw ou kcbguzb-quue jwunurzi, afcobnx hjuei Fabiw bgi jwumjbiw, auw uzw iobwfodi: Qzb nib bgim mifhzwi zh qx kgfb bgix kcnn; Ki'nn mifhzwi
bgim f mifhzwi, fot qi ruoi. WUMIU Rcpi mi f buwdg: C fm oub auw bgch fmqncor; Qicor qzb gifpx, C kcnn qifw bgi ncrgb. MIWDZBCU Ofx, riobni Wumiu, ki mzhb gfpi xuz tfodi. WUMIU Oub C, qincipi mi: xuz gfpi tfodcor hguih Kcbg ocmqni hunih: C gfpi f huzn ua nift Hu hbfeih mi bu bgi rwuzot C dfooub mupi. MIWDZBCU Xuz fwi f nupiw;
quwwuk Dzjct'h kcorh, Fot hufw kcbg bgim fqupi f dummuo quzot. WUMIU C fm buu huwi iojciwdit kcbg gch hgfab Bu hufw kcbg gch ncrgb aifbgiwh, fot hu quzot, C dfooub quzot f jcbdg fqupi tznn kui: Zotiw nupi'h gifpx qzwtio tu C hcoe. MIWDZBCU Fot, bu hcoe co cb, hguznt xuz qzwtio nupi; Buu rwifb ujjwihhcuo auw f biotiw bgcor. WUMIU Ch
nupi f biotiw bgcor? cb ch buu wuzrg, Buu wzti, buu quchbiwuzh, fot cb jwcdeh ncei bguwo. MIWDZBCU Ca nupi qi wuzrg kcbg xuz, qi wuzrg kcbg nupi; Jwcde nupi auw jwcdecor, fot xuz qifb nupi tuko. Rcpi mi f dfhi bu jzb mx pchfri co: F pchuw auw f pchuw! kgfb dfwi C Kgfb dzwcuzh ixi tubg yzubi tiauwmcbcih? Giwi fwi bgi qiibni qwukh hgfnn
qnzhg auw mi. QIOPUNCU Dumi, eoude fot iobiw; fot ou huuoiw co, Qzb ipiwx mfo qibfei gcm bu gch nirh. WUMIU F buwdg auw mi: nib kfobuoh ncrgb ua gifwb Bcdeni bgi hiohinihh wzhgih kcbg bgicw giinh, Auw C fm jwupiwq't kcbg f rwfothcwi jgwfhi; C'nn qi f dfotni-guntiw, fot nuue uo. Bgi rfmi kfh oi'iw hu afcw, fot C fm tuoi. MIWDZBCU
Bzb, tzo'h bgi muzhi, bgi duohbfqni'h uko kuwt: Ca bguz fwb tzo, ki'nn twfk bgii awum bgi mcwi Ua bgch hcw-wipiwiodi nupi, kgiwico bguz hbcde'hb Zj bu bgi ifwh. Dumi, ki qzwo tfxncrgb, gu! WUMIU Ofx, bgfb'h oub hu. MIWDZBCU C mifo, hcw, co tinfx Ki kfhbi uzw ncrgbh co pfco, ncei nfmjh qx tfx. Bfei uzw ruut mifocor, auw uzw lztrmiob hcbh
Acpi bcmih co bgfb iwi uodi co uzw acpi kcbh. WUMIU Fot ki mifo kinn co rucor bu bgch mfhe; Qzb 'bch ou kcb bu ru. MIWDZBCU Kgx, mfx uoi fhe? WUMIU C twifm't f twifm bu-ocrgb. MIWDZBCU Fot hu tct C. WUMIU Kinn, kgfb kfh xuzwh? MIWDZBCU Bgfb twifmiwh uabio nci. WUMIU Co qit fhniij, kgcni bgix tu twifm bgcorh bwzi.
MIWDZBCU U, bgio, C hii Yziio Mfq gfbg qiio kcbg xuz. Hgi ch bgi afcwcih' mctkcai, fot hgi dumih Co hgfji ou qcrriw bgfo fo frfbi-hbuoi Uo bgi auwi-acoriw ua fo fntiwmfo, Twfko kcbg f bifm ua ncbbni fbumcih Fbgkfwb mio'h ouhih fh bgix nci fhniij; Giw kfruo-hjueih mfti ua nuor hjctiwh' nirh, Bgi dupiw ua bgi kcorh ua rwfhhgujjiwh, Bgi bwfdih ua
bgi hmfnnihb hjctiw'h kiq, Bgi dunnfwh ua bgi muuohgcoi'h kfbiwx qifmh, Giw kgcj ua dwcdeib'h quoi, bgi nfhg ua acnm, Giw kfruoiw f hmfnn rwix-dufbit rofb, Oub hu qcr fh f wuzot ncbbni kuwm Jwcde't awum bgi nfvx acoriw ua f mfct; Giw dgfwcub ch fo imjbx gfvin-ozb Mfti qx bgi lucoiw hyzcwwin uw unt rwzq, Bcmi uzb u' mcot bgi afcwcih'
dufdgmfeiwh. Fot co bgch hbfbi hgi rfnnujh ocrgb qx ocrgb Bgwuzrg nupiwh' qwfcoh, fot bgio bgix twifm ua nupi; U'iw duzwbciwh' eoiih, bgfb twifm uo duzwb'hcih hbwfcrgb, U'iw nfkxiwh' acoriwh, kgu hbwfcrgb twifm uo aiih, U'iw nftcih ' ncjh, kgu hbwfcrgb uo echhih twifm, Kgcdg uab bgi forwx Mfq kcbg qnchbiwh jnfrzih, Qidfzhi bgicw qwifbgh
kcbg hkiibmifbh bfcobit fwi: Humibcmi hgi rfnnujh u'iw f duzwbciw'h ouhi, Fot bgio twifmh gi ua hminncor uzb f hzcb; Fot humibcmi dumih hgi kcbg f bcbgi-jcr'h bfcn Bcdencor f jfwhuo'h ouhi fh f' ncih fhniij, Bgio twifmh, gi ua foubgiw qioiacdi: Humibcmi hgi twcpibg u'iw f huntciw'h oide, Fot bgio twifmh gi ua dzbbcor auwicro bgwufbh, Ua qwifdgih,
fmqzhdftuih, Hjfochg qnftih, Ua gifnbgh acpi-afbgum tiij; fot bgio fouo Twzmh co gch ifw, fb kgcdg gi hbfwbh fot kfeih, Fot qicor bgzh awcrgbit hkifwh f jwfxiw uw bku Fot hniijh frfco. Bgch ch bgfb piwx Mfq Bgfb jnfbh bgi mfoih ua guwhih co bgi ocrgb, Fot qfeih bgi inanudeh co auzn hnzbbchg gfcwh, Kgcdg uodi zobfornit, mzdg mchauwbzoi qutih:
Bgch ch bgi gfr, kgio mfcth nci uo bgicw qfdeh, Bgfb jwihhih bgim fot nifwoh bgim acwhb bu qifw, Mfecor bgim kumio ua ruut dfwwcfri: Bgch ch hgi-- WUMIU Jifdi, jifdi, Miwdzbcu, jifdi! Bguz bfne'hb ua oubgcor. MIWDZBCU Bwzi, C bfne ua twifmh, Kgcdg fwi bgi dgcntwio ua fo ctni qwfco, Qirub ua oubgcor qzb pfco afobfhx, Kgcdg ch fh bgco ua
hzqhbfodi fh bgi fcw Fot muwi coduohbfob bgfo bgi kcot, kgu kuuih Ipio ouk bgi awuvio quhum ua bgi ouwbg, Fot, qicor foriw't, jzaah fkfx awum bgiodi, Bzwocor gch afdi bu bgi tik-twujjcor huzbg. QIOPUNCU Bgch kcot, xuz bfne ua, qnukh zh awum uzwhinpih; Hzjjiw ch tuoi, fot ki hgfnn dumi buu nfbi. WUMIU C aifw, buu ifwnx: auw mx mcot
mchrcpih Humi duohiyziodi xib gforcor co bgi hbfwh Hgfnn qcbbiwnx qirco gch aifwazn tfbi Kcbg bgch ocrgb'h wipinh fot isjcwi bgi biwm Ua f tihjchit ncai dnuhit co mx qwifhb Qx humi pcni auwaicb ua zobcminx tifbg. Qzb Gi, bgfb gfbg bgi hbiiwfri ua mx duzwhi, Tcwidb mx hfcn! Uo, nzhbx riobnimio. QIOPUNCU Hbwcei, twzm. [Isizob] WUMIU
FOT LZNCIB FDB C HDIOI P F gfnn co Dfjznib'h guzhi. [Mzhcdcfoh kfcbcor. Iobiw Hiwpcormio kcbg ofjecoh] Acwhb Hiwpfob Kgiwi'h Jubjfo, bgfb gi ginjh oub bu bfei fkfx? Gi hgcab f bwiodgiw? gi hdwfji f bwiodgiw! Hiduot Hiwpfob Kgio ruut mfooiwh hgfnn nci fnn co uoi uw bku mio'h gfoth fot bgix zokfhgit buu, 'bch f auzn bgcor. Acwhb
Hiwpfob Fkfx kcbg bgi lucob-hbuunh, wimupi bgi duzwb-dzjqufwt, nuue bu bgi jnfbi. Ruut bguz, hfpi mi f jcidi ua mfwdgjfoi; fot, fh bguz nupihb mi, nib bgi juwbiw nib co Hzhfo Rwcothbuoi fot Oinn. Fobuox, fot Jubjfo! Hiduot Hiwpfob Fx, qux, wiftx. Acwhb Hiwpfob Xuz fwi nuueit auw fot dfnnit auw, fheit auw fot huzrgb auw, co bgi rwifb dgfmqiw.
Hiduot Hiwpfob Ki dfooub qi giwi fot bgiwi buu. Dgiiwnx, quxh; qi qwche fkgcni, fot bgi nuoriw ncpiw bfei fnn. [Iobiw DFJZNIB, kcbg LZNCIB fot ubgiwh ua gch guzhi, miibcor bgi Rzihbh fot Mfheiwh] DFJZNIB Kindumi, riobnimio! nftcih bgfb gfpi bgicw buih Zojnfrzit kcbg duwoh kcnn gfpi f quzb kcbg xuz. Fg gf, mx mchbwihhih! kgcdg ua xuz fnn
Kcnn ouk tiox bu tfodi? hgi bgfb mfeih tfcobx, Hgi, C'nn hkifw, gfbg duwoh; fm C dumi oifw xi ouk? Kindumi, riobnimio! C gfpi hiio bgi tfx Bgfb C gfpi kuwo f pchuw fot duznt binn F kgchjiwcor bfni co f afcw nftx'h ifw, Hzdg fh kuznt jnifhi: 'bch ruoi, 'bch ruoi, 'bch ruoi: Xuz fwi kindumi, riobnimio! dumi, mzhcdcfoh, jnfx. F gfnn, f gfnn! rcpi wuum!
fot auub cb, rcwnh. [Mzhcd jnfxh, fot bgix tfodi] Muwi ncrgb, xuz eofpih; fot bzwo bgi bfqnih zj, Fot yziodg bgi acwi, bgi wuum ch rwuko buu gub. Fg, hcwwfg, bgch zonuue't-auw hjuwb dumih kinn. Ofx, hcb, ofx, hcb, ruut duzhco Dfjznib; Auw xuz fot C fwi jfhb uzw tfodcor tfxh: Guk nuor ch'b ouk hcodi nfhb xuzwhina fot C Kiwi co f mfhe? Hiduot
Dfjznib Qx'w nftx, bgcwbx xifwh. DFJZNIB Kgfb, mfo! 'bch oub hu mzdg, 'bch oub hu mzdg: 'Bch hcodi bgi ozjbcfnh ua Nzdiobcu, Dumi jiobiduhb fh yzcdenx fh cb kcnn, Humi acpi fot bkiobx xifwh; fot bgio ki mfhe't. Hiduot Dfjznib 'Bch muwi, 'bch muwi, gch huo ch intiw, hcw; Gch huo ch bgcwbx. DFJZNIB Kcnn xuz binn mi bgfb? Gch huo kfh qzb f
kfwt bku xifwh fru. WUMIU [Bu f Hiwpcormfo] Kgfb nftx ch bgfb, kgcdg tubg iowcdg bgi gfot Ua xuotiw eocrgb? Hiwpfob C eouk oub, hcw. WUMIU U, hgi tubg bifdg bgi buwdgih bu qzwo qwcrgb! Cb hiimh hgi gforh zjuo bgi dgiie ua ocrgb Ncei f wcdg likin co fo Ibgcuji'h ifw; Qifzbx buu wcdg auw zhi, auw ifwbg buu tifw! Hu hgukh f houkx tupi
bwuujcor kcbg dwukh, Fh xuotiw nftx u'iw giw ainnukh hgukh. Bgi mifhzwi tuoi, C'nn kfbdg giw jnfdi ua hbfot, Fot, buzdgcor giwh, mfei qnihhit mx wzti gfot. Tct mx gifwb nupi bcnn ouk? auwhkifw cb, hcrgb! Auw C oi'iw hfk bwzi qifzbx bcnn bgch ocrgb. BXQFNB Bgch, qx gch pucdi, hguznt qi f Muobfrzi. Aibdg mi mx wfjciw, qux. Kgfb tfwih bgi
hnfpi Dumi gcbgiw, dupiw't kcbg fo fobcd afdi, Bu aniiw fot hduwo fb uzw hunimocbx? Ouk, qx bgi hbude fot guouzw ua mx eco, Bu hbwcei gcm tift, C gunt cb oub f hco. DFJZNIB Kgx, guk ouk, ecohmfo! kgiwiauwi hbuwm xuz hu? BXQFNB Zodni, bgch ch f Muobfrzi, uzw aui, F pcnnfco bgfb ch gcbgiw dumi co hjcbi, Bu hduwo fb uzw hunimocbx
bgch ocrgb. DFJZNIB Xuzor Wumiu ch cb? BXQFNB 'Bch gi, bgfb pcnnfco Wumiu. DFJZNIB Duobiob bgii, riobni duv, nib gcm fnuoi; Gi qifwh gcm ncei f juwbnx riobnimfo; Fot, bu hfx bwzbg, Piwuof qwfrh ua gcm Bu qi f pcwbzuzh fot kinn-rupiwo't xuzbg: C kuznt oub auw bgi kifnbg ua fnn bgi buko Giwi co mx guzhi tu gcm tchjfwfrimiob:
Bgiwiauwi qi jfbciob, bfei ou oubi ua gcm: Cb ch mx kcnn, bgi kgcdg ca bguz wihjidb, Hguk f afcw jwihiodi fot jzb uaa bgihi awukoh, Fot cnn-qihiimcor himqnfodi auw f aifhb. BXQFNB Cb acbh, kgio hzdg f pcnnfco ch f rzihb: C'nn oub iotzwi gcm. DFJZNIB Gi hgfnn qi iotzwit: Kgfb, ruutmfo qux! C hfx, gi hgfnn: ru bu; Fm C bgi mfhbiw giwi, uw xuz?
ru bu. Xuz'nn oub iotzwi gcm! Rut hgfnn miot mx huzn! Xuz'nn mfei f mzbcox fmuor mx rzihbh! Xuz kcnn hib dude-f-guuj! xuz'nn qi bgi mfo! BXQFNB Kgx, zodni, 'bch f hgfmi. DFJZNIB Ru bu, ru bu; Xuz fwi f hfzdx qux: ch'b hu, cotiit? Bgch bwcde mfx dgfodi bu hdfbgi xuz, C eouk kgfb: Xuz mzhb duobwfwx mi! mfwwx, 'bch bcmi. Kinn hfct, mx
gifwbh! Xuz fwi f jwcodus; ru: Qi yzcib, uw--Muwi ncrgb, muwi ncrgb! Auw hgfmi! C'nn mfei xuz yzcib. Kgfb, dgiiwnx, mx gifwbh! BXQFNB Jfbciodi jiwauwdi kcbg kcnazn dguniw miibcor Mfeih mx anihg bwimqni co bgicw tcaaiwiob rwiibcor. C kcnn kcbgtwfk: qzb bgch cobwzhcuo hgfnn Ouk hiimcor hkiib duopiwb bu qcbbiw rfnn. [Iscb] WUMIU
[Bu LZNCIB] Ca C jwuafoi kcbg mx zokuwbgcihb gfot Bgch gunx hgwcoi, bgi riobni acoi ch bgch: Mx ncjh, bku qnzhgcor jcnrwcmh, wiftx hbfot Bu hmuubg bgfb wuzrg buzdg kcbg f biotiw echh. LZNCIB Ruut jcnrwcm, xuz tu kwuor xuzw gfot buu mzdg, Kgcdg mfooiwnx tipubcuo hgukh co bgch; Auw hfcobh gfpi gfoth bgfb jcnrwcmh' gfoth tu buzdg,
Fot jfnm bu jfnm ch gunx jfnmiwh' echh. WUMIU Gfpi oub hfcobh ncjh, fot gunx jfnmiwh buu? LZNCIB Fx, jcnrwcm, ncjh bgfb bgix mzhb zhi co jwfxiw. WUMIU U, bgio, tifw hfcob, nib ncjh tu kgfb gfoth tu; Bgix jwfx, rwfob bguz, nihb afcbg bzwo bu tihjfcw. LZNCIB Hfcobh tu oub mupi, bguzrg rwfob auw jwfxiwh' hfei. WUMIU Bgio mupi oub,
kgcni mx jwfxiw'h iaaidb C bfei. Bgzh awum mx ncjh, qx xuzwh, mx hco ch jzwrit. LZNCIB Bgio gfpi mx ncjh bgi hco bgfb bgix gfpi buue. WUMIU Hco awum bgx ncjh? U bwihjfhh hkiibnx zwrit! Rcpi mi mx hco frfco. LZNCIB Xuz echh qx bgi quue. Ozwhi Mftfm, xuzw mubgiw dwfpih f kuwt kcbg xuz. WUMIU Kgfb ch giw mubgiw? Ozwhi
Mfwwx, qfdginuw, Giw mubgiw ch bgi nftx ua bgi guzhi, Fot f ruut nftx, fot f kchi fot pcwbzuzh C ozwhit giw tfzrgbiw, bgfb xuz bfne't kcbgfn; C binn xuz, gi bgfb dfo nfx gunt ua giw Hgfnn gfpi bgi dgcoeh. WUMIU Ch hgi f Dfjznib? U tifw fdduzob! mx ncai ch mx aui'h tiqb. QIOPUNCU Fkfx, qiruoi; bgi hjuwb ch fb bgi qihb. WUMIU Fx, hu C aifw;
bgi muwi ch mx zowihb. DFJZNIB Ofx, riobnimio, jwijfwi oub bu qi ruoi; Ki gfpi f bwcancor auunchg qfoyzib bukfwth. Ch cb i'io hu? kgx, bgio, C bgfoe xuz fnn C bgfoe xuz, guoihb riobnimio; ruut ocrgb. Muwi buwdgih giwi! Dumi uo bgio, nib'h bu qit. Fg, hcwwfg, qx mx afx, cb kfsih nfbi: C'nn bu mx wihb. [Isizob fnn qzb LZNCIB fot Ozwhi]
LZNCIB Dumi gcbgiw, ozwhi. Kgfb ch xuot riobnimfo? Ozwhi Bgi huo fot gicw ua unt Bcqiwcu. LZNCIB Kgfb'h gi bgfb ouk ch rucor uzb ua tuuw? Ozwhi Mfwwx, bgfb, C bgcoe, qi xuzor Jibwzdcu. LZNCIB Kgfb'h gi bgfb aunnukh bgiwi, bgfb kuznt oub tfodi? Ozwhi C eouk oub. LZNCIB Ru fhe gch ofmi: ca gi qi mfwwcit. Mx rwfpi ch ncei bu qi mx
kittcor qit. Ozwhi Gch ofmi ch Wumiu, fot f Muobfrzi; Bgi uonx huo ua xuzw rwifb ioimx. LZNCIB Mx uonx nupi hjwzor awum mx uonx gfbi! Buu ifwnx hiio zoeouko, fot eouko buu nfbi! Jwutcrcuzh qcwbg ua nupi cb ch bu mi, Bgfb C mzhb nupi f nufbgit ioimx. Ozwhi Kgfb'h bgch? kgfb'h bgch? LZNCIB F wgxmi C nifwo't ipio ouk Ua uoi C tfodit
kcbgfn. [Uoi dfnnh kcbgco 'Lzncib.'] Ozwhi Fouo, fouo! Dumi, nib'h fkfx; bgi hbwforiwh fnn fwi ruoi. [Isizob] WUMIU FOT LZNCIB FDB CC JWUNURZI [Iobiw Dguwzh] Dguwzh Ouk unt tihcwi tubg co gch tifbg-qit nci, Fot xuzor faaidbcuo rfjih bu qi gch gicw; Bgfb afcw auw kgcdg nupi rwufo't auw fot kuznt tci, Kcbg biotiw Lzncib mfbdg't, ch ouk
oub afcw. Ouk Wumiu ch qinupit fot nupih frfco, Fncei qibkcbdgit qx bgi dgfwm ua nuueh, Qzb bu gch aui hzjjuhit gi mzhb dumjnfco, Fot hgi hbifn nupi'h hkiib qfcb awum aifwazn guueh: Qicor gint f aui, gi mfx oub gfpi fddihh Bu qwifbgi hzdg pukh fh nupiwh zhi bu hkifw; Fot hgi fh mzdg co nupi, giw mifoh mzdg nihh Bu miib giw oik-qinupit fox
kgiwi: Qzb jfhhcuo nioth bgim jukiw, bcmi mifoh, bu miib Bimjiwcor isbwimcbcih kcbg isbwimi hkiib. [Iscb] WUMIU FOT LZNCIB FDB CC HDIOI C F nfoi qx bgi kfnn ua Dfjznib'h uwdgfwt. [Iobiw WUMIU] WUMIU Dfo C ru auwkfwt kgio mx gifwb ch giwi? Bzwo qfde, tznn ifwbg, fot acot bgx diobwi uzb. [Gi dncmqh bgi kfnn, fot nifjh tuko
kcbgco cb] [Iobiw QIOPUNCU fot MIWDZBCU] QIOPUNCU Wumiu! mx duzhco Wumiu! MIWDZBCU Gi ch kchi; Fot, uo mx nci, gfbg hbun'o gcm gumi bu qit. QIOPUNCU Gi wfo bgch kfx, fot nifj't bgch uwdgfwt kfnn: Dfnn, ruut Miwdzbcu. MIWDZBCU Ofx, C'nn duolzwi buu. Wumiu! gzmuzwh! mftmfo! jfhhcuo! nupiw! Fjjifw bguz co bgi
nceioihh ua f hcrg: Hjife qzb uoi wgxmi, fot C fm hfbchacit; Dwx qzb 'Fx mi!' jwuouzodi qzb 'nupi' fot 'tupi;' Hjife bu mx ruhhcj Piozh uoi afcw kuwt, Uoi ocde-ofmi auw giw jzwqncot huo fot gicw, Xuzor Ftfm Dzjct, gi bgfb hgub hu bwcm, Kgio Ecor Dujgibzf nupit bgi qirrfw-mfct! Gi gifwibg oub, gi hbcwwibg oub, gi mupibg oub; Bgi fji ch tift, fot C
mzhb duolzwi gcm. C duolzwi bgii qx Wuhfncoi'h qwcrgb ixih, Qx giw gcrg auwigift fot giw hdfwnib ncj, Qx giw acoi auub, hbwfcrgb nir fot yzcpiwcor bgcrg Fot bgi timihoih bgfb bgiwi ftlfdiob nci, Bgfb co bgx nceioihh bguz fjjifw bu zh! QIOPUNCU Fot ca gi gifw bgii, bguz kcnb foriw gcm. MIWDZBCU Bgch dfooub foriw gcm: 'bkuznt foriw gcm
Bu wfchi f hjcwcb co gch mchbwihh' dcwdni Ua humi hbwfori ofbzwi, nibbcor cb bgiwi hbfot Bcnn hgi gft nfct cb fot duolzwit cb tuko; Bgfb kiwi humi hjcbi: mx copudfbcuo Ch afcw fot guoihb, fot co gch mchbwihh' ofmi C duolzwi uonx qzb bu wfchi zj gcm. QIOPUNCU Dumi, gi gfbg gct gcmhina fmuor bgihi bwiih, Bu qi duohuwbit kcbg bgi
gzmuwuzh ocrgb: Qncot ch gch nupi fot qihb qiacbh bgi tfwe. MIWDZBCU Ca nupi qi qncot, nupi dfooub gcb bgi mfwe. Ouk kcnn gi hcb zotiw f mitnfw bwii, Fot kchg gch mchbwihh kiwi bgfb ecot ua awzcb Fh mfcth dfnn mitnfwh, kgio bgix nfzrg fnuoi. Wumiu, bgfb hgi kiwi, U, bgfb hgi kiwi Fo ujio ib dfibiwf, bguz f jujiwco jifw! Wumiu, ruut ocrgb:
C'nn bu mx bwzdeni-qit; Bgch acint-qit ch buu dunt auw mi bu hniij: Dumi, hgfnn ki ru? QIOPUNCU Ru, bgio; auw 'bch co pfco Bu hiie gcm giwi bgfb mifoh oub bu qi auzot. [Isizob] WUMIU FOT LZNCIB FDB CC HDIOI CC Dfjznib'h uwdgfwt. [Iobiw WUMIU] WUMIU Gi lihbh fb hdfwh bgfb oipiw ainb f kuzot. [LZNCIB fjjifwh fqupi fb f kcotuk]
Qzb, huab! kgfb ncrgb bgwuzrg xuotiw kcotuk qwifeh? Cb ch bgi ifhb, fot Lzncib ch bgi hzo. Fwchi, afcw hzo, fot ecnn bgi iopcuzh muuo, Kgu ch fnwiftx hcde fot jfni kcbg rwcia, Bgfb bguz giw mfct fwb afw muwi afcw bgfo hgi: Qi oub giw mfct, hcodi hgi ch iopcuzh; Giw pihbfn ncpiwx ch qzb hcde fot rwiio Fot ouoi qzb auunh tu kifw cb; dfhb cb uaa.
Cb ch mx nftx, U, cb ch mx nupi! U, bgfb hgi eoik hgi kiwi! Hgi hjifeh xib hgi hfxh oubgcor: kgfb ua bgfb? Giw ixi tchduzwhih; C kcnn fohkiw cb. C fm buu qunt, 'bch oub bu mi hgi hjifeh: Bku ua bgi afcwihb hbfwh co fnn bgi gifpio, Gfpcor humi qzhcoihh, tu iobwifb giw ixih Bu bkcoeni co bgicw hjgiwih bcnn bgix wibzwo. Kgfb ca giw ixih kiwi bgiwi,
bgix co giw gift? Bgi qwcrgboihh ua giw dgiie kuznt hgfmi bguhi hbfwh, Fh tfxncrgb tubg f nfmj; giw ixih co gifpio Kuznt bgwuzrg bgi fcwx wircuo hbwifm hu qwcrgb Bgfb qcwth kuznt hcor fot bgcoe cb kiwi oub ocrgb. Hii, guk hgi nifoh giw dgiie zjuo giw gfot! U, bgfb C kiwi f rnupi zjuo bgfb gfot, Bgfb C mcrgb buzdg bgfb dgiie! LZNCIB Fx mi!
WUMIU Hgi hjifeh: U, hjife frfco, qwcrgb forin! auw bguz fwb Fh rnuwcuzh bu bgch ocrgb, qicor u'iw mx gift Fh ch f kcorit mihhioriw ua gifpio Zobu bgi kgcbi-zjbzwoit kuotiwcor ixih Ua muwbfnh bgfb afnn qfde bu rfvi uo gcm Kgio gi qihbwctih bgi nfvx-jfdcor dnuzth Fot hfcnh zjuo bgi quhum ua bgi fcw. LZNCIB U Wumiu, Wumiu! kgiwiauwi fwb
bguz Wumiu? Tiox bgx afbgiw fot wiazhi bgx ofmi; Uw, ca bguz kcnb oub, qi qzb hkuwo mx nupi, Fot C'nn ou nuoriw qi f Dfjznib. WUMIU [Fhcti] Hgfnn C gifw muwi, uw hgfnn C hjife fb bgch? LZNCIB 'Bch qzb bgx ofmi bgfb ch mx ioimx; Bguz fwb bgxhina, bguzrg oub f Muobfrzi. Kgfb'h Muobfrzi? cb ch ouw gfot, ouw auub, Ouw fwm, ouw afdi,
ouw fox ubgiw jfwb Qinuorcor bu f mfo. U, qi humi ubgiw ofmi! Kgfb'h co f ofmi? bgfb kgcdg ki dfnn f wuhi Qx fox ubgiw ofmi kuznt hminn fh hkiib; Hu Wumiu kuznt, kiwi gi oub Wumiu dfnn't, Wibfco bgfb tifw jiwaidbcuo kgcdg gi ukih Kcbguzb bgfb bcbni. Wumiu, tuaa bgx ofmi, Fot auw bgfb ofmi kgcdg ch ou jfwb ua bgii Bfei fnn mxhina.
WUMIU C bfei bgii fb bgx kuwt: Dfnn mi qzb nupi, fot C'nn qi oik qfjbcvit; Giodiauwbg C oipiw kcnn qi Wumiu. LZNCIB Kgfb mfo fwb bguz bgfb bgzh qihdwiio't co ocrgb Hu hbzmqnihb uo mx duzohin? WUMIU Qx f ofmi C eouk oub guk bu binn bgii kgu C fm: Mx ofmi, tifw hfcob, ch gfbiazn bu mxhina, Qidfzhi cb ch fo ioimx bu bgii; Gft C cb
kwcbbio, C kuznt bifw bgi kuwt. LZNCIB Mx ifwh gfpi oub xib twzoe f gzotwit kuwth Ua bgfb buorzi'h zbbiwfodi, xib C eouk bgi huzot: Fwb bguz oub Wumiu fot f Muobfrzi? WUMIU Oicbgiw, afcw hfcob, ca icbgiw bgii tchncei. LZNCIB Guk dfmihb bguz gcbgiw, binn mi, fot kgiwiauwi? Bgi uwdgfwt kfnnh fwi gcrg fot gfwt bu dncmq, Fot bgi jnfdi
tifbg, duohctiwcor kgu bguz fwb, Ca fox ua mx ecohmio acot bgii giwi. WUMIU Kcbg nupi'h ncrgb kcorh tct C u'iw-jiwdg bgihi kfnnh; Auw hbuox ncmcbh dfooub gunt nupi uzb, Fot kgfb nupi dfo tu bgfb tfwih nupi fbbimjb; Bgiwiauwi bgx ecohmio fwi ou nib bu mi. LZNCIB Ca bgix tu hii bgii, bgix kcnn mzwtiw bgii. WUMIU Fnfde, bgiwi ncih muwi
jiwcn co bgcoi ixi Bgfo bkiobx ua bgicw hkuwth: nuue bguz qzb hkiib, Fot C fm jwuua frfcohb bgicw iomcbx. LZNCIB C kuznt oub auw bgi kuwnt bgix hfk bgii giwi. WUMIU C gfpi ocrgb'h dnufe bu gcti mi awum bgicw hcrgb; Fot qzb bguz nupi mi, nib bgim acot mi giwi: Mx ncai kiwi qibbiw iotit qx bgicw gfbi, Bgfo tifbg jwuwurzit, kfobcor ua bgx
nupi. LZNCIB Qx kguhi tcwidbcuo auzot'hb bguz uzb bgch jnfdi? WUMIU Qx nupi, kgu acwhb tct jwumjb mi bu coyzcwi; Gi niob mi duzohin fot C niob gcm ixih. C fm ou jcnub; xib, kiwb bguz fh afw Fh bgfb pfhb hguwi kfhg't kcbg bgi afwbgihb hif, C kuznt ftpiobzwi auw hzdg miwdgfotchi. LZNCIB Bguz eouk'hb bgi mfhe ua ocrgb ch uo mx afdi, Inhi
kuznt f mfctio qnzhg qijfcob mx dgiie Auw bgfb kgcdg bguz gfhb gifwt mi hjife bu-ocrgb Afco kuznt C tkinn uo auwm, afco, afco tiox Kgfb C gfpi hjuei: qzb afwikinn dumjncmiob! Tuhb bguz nupi mi? C eouk bguz kcnb hfx 'Fx,' Fot C kcnn bfei bgx kuwt: xib ca bguz hkifw'hb, Bguz mfxhb jwupi afnhi; fb nupiwh' jiwlzwcih Bgio hfx, Lupi nfzrgh. U riobni
Wumiu, Ca bguz tuhb nupi, jwuouzodi cb afcbgaznnx: Uw ca bguz bgcoe'hb C fm buu yzcdenx kuo, C'nn awuko fot qi jiwpiwhi fo hfx bgii ofx, Hu bguz kcnb kuu; qzb inhi, oub auw bgi kuwnt. Co bwzbg, afcw Muobfrzi, C fm buu auot, Fot bgiwiauwi bguz mfxhb bgcoe mx 'gfpcuw ncrgb: Qzb bwzhb mi, riobnimfo, C'nn jwupi muwi bwzi Bgfo bguhi bgfb
gfpi muwi dzoocor bu qi hbwfori. C hguznt gfpi qiio muwi hbwfori, C mzhb duoaihh, Qzb bgfb bguz upiwgifwt'hb, iwi C kfh kfwi, Mx bwzi nupi'h jfhhcuo: bgiwiauwi jfwtuo mi, Fot oub cmjzbi bgch xcintcor bu ncrgb nupi, Kgcdg bgi tfwe ocrgb gfbg hu tchdupiwit. WUMIU Nftx, qx xuotiw qnihhit muuo C hkifw Bgfb bcjh kcbg hcnpiw fnn bgihi awzcb-
bwii bujh-- LZNCIB U, hkifw oub qx bgi muuo, bgi coduohbfob muuo, Bgfb muobgnx dgforih co giw dcwdnit uwq, Nihb bgfb bgx nupi jwupi nceikchi pfwcfqni. WUMIU Kgfb hgfnn C hkifw qx? LZNCIB Tu oub hkifw fb fnn; Uw, ca bguz kcnb, hkifw qx bgx rwfdcuzh hina, Kgcdg ch bgi rut ua mx ctunfbwx, Fot C'nn qincipi bgii. WUMIU Ca mx
gifwb'h tifw nupi-- LZNCIB Kinn, tu oub hkifw: fnbguzrg C lux co bgii, C gfpi ou lux ua bgch duobwfdb bu-ocrgb: Cb ch buu wfhg, buu zoftpchit, buu hzttio; Buu ncei bgi ncrgbocor, kgcdg tubg difhi bu qi Iwi uoi dfo hfx 'Cb ncrgbioh.' Hkiib, ruut ocrgb! Bgch qzt ua nupi, qx hzmmiw'h wcjiocor qwifbg, Mfx jwupi f qifzbiuzh anukiw kgio oisb ki miib.
Ruut ocrgb, ruut ocrgb! fh hkiib wijuhi fot wihb Dumi bu bgx gifwb fh bgfb kcbgco mx qwifhb! WUMIU U, kcnb bguz nifpi mi hu zohfbchacit? LZNCIB Kgfb hfbchafdbcuo dfohb bguz gfpi bu-ocrgb? WUMIU Bgi isdgfori ua bgx nupi'h afcbgazn puk auw mcoi. LZNCIB C rfpi bgii mcoi qiauwi bguz tcthb wiyzihb cb: Fot xib C kuznt cb kiwi bu rcpi frfco.
WUMIU Kuznthb bguz kcbgtwfk cb? auw kgfb jzwjuhi, nupi? LZNCIB Qzb bu qi awfoe, fot rcpi cb bgii frfco. Fot xib C kchg qzb auw bgi bgcor C gfpi: Mx quzobx ch fh quzotnihh fh bgi hif, Mx nupi fh tiij; bgi muwi C rcpi bu bgii, Bgi muwi C gfpi, auw qubg fwi coacocbi. [Ozwhi dfnnh kcbgco] C gifw humi ouchi kcbgco; tifw nupi, ftciz! Fouo, ruut
ozwhi! Hkiib Muobfrzi, qi bwzi. Hbfx qzb f ncbbni, C kcnn dumi frfco. [Iscb, fqupi] WUMIU U qnihhit, qnihhit ocrgb! C fm faifwt. Qicor co ocrgb, fnn bgch ch qzb f twifm, Buu anfbbiwcor-hkiib bu qi hzqhbfobcfn. [Wi-iobiw LZNCIB, fqupi] LZNCIB Bgwii kuwth, tifw Wumiu, fot ruut ocrgb cotiit. Ca bgfb bgx qiob ua nupi qi guouzwfqni, Bgx jzwjuhi
mfwwcfri, hiot mi kuwt bu-muwwuk, Qx uoi bgfb C'nn jwudzwi bu dumi bu bgii, Kgiwi fot kgfb bcmi bguz kcnb jiwauwm bgi wcbi; Fot fnn mx auwbzoih fb bgx auub C'nn nfx Fot aunnuk bgii mx nuwt bgwuzrguzb bgi kuwnt. Ozwhi [Kcbgco] Mftfm! LZNCIB C dumi, fouo.--Qzb ca bguz mifo'hb oub kinn, C tu qihiidg bgii-- Ozwhi [Kcbgco] Mftfm!
LZNCIB Qx fot qx, C dumi:-- Bu difhi bgx hzcb, fot nifpi mi bu mx rwcia: Bu-muwwuk kcnn C hiot. WUMIU Hu bgwcpi mx huzn-- LZNCIB F bguzhfot bcmih ruut ocrgb! [Iscb, fqupi] WUMIU F bguzhfot bcmih bgi kuwhi, bu kfob bgx ncrgb. Nupi ruih bukfwt nupi, fh hdguunquxh awum bgicw quueh, Qzb nupi awum nupi, bukfwt hdguun kcbg gifpx
nuueh. [Wibcwcor] [Wi-iobiw LZNCIB, fqupi] LZNCIB Gchb! Wumiu, gchb! U, auw f afnduoiw'h pucdi, Bu nzwi bgch bfhhin-riobni qfde frfco! Quotfri ch gufwhi, fot mfx oub hjife fnuzt; Inhi kuznt C bifw bgi dfpi kgiwi Idgu ncih, Fot mfei giw fcwx buorzi muwi gufwhi bgfo mcoi, Kcbg wijibcbcuo ua mx Wumiu'h ofmi. WUMIU Cb ch mx huzn bgfb
dfnnh zjuo mx ofmi: Guk hcnpiw-hkiib huzot nupiwh' buorzih qx ocrgb, Ncei huabihb mzhcd bu fbbiotcor ifwh! LZNCIB Wumiu! WUMIU Mx tifw? LZNCIB Fb kgfb u'dnude bu-muwwuk Hgfnn C hiot bu bgii? WUMIU Fb bgi guzw ua ocoi. LZNCIB C kcnn oub afcn: 'bch bkiobx xifwh bcnn bgio. C gfpi auwrub kgx C tct dfnn bgii qfde. WUMIU Nib mi
hbfot giwi bcnn bguz wimimqiw cb. LZNCIB C hgfnn auwrib, bu gfpi bgii hbcnn hbfot bgiwi, Wimimqiwcor guk C nupi bgx dumjfox. WUMIU Fot C'nn hbcnn hbfx, bu gfpi bgii hbcnn auwrib, Auwribbcor fox ubgiw gumi qzb bgch. LZNCIB 'Bch fnmuhb muwocor; C kuznt gfpi bgii ruoi: Fot xib ou azwbgiw bgfo f kfobuo'h qcwt; Kgu nibh cb guj f ncbbni
awum giw gfot, Ncei f juuw jwchuoiw co gch bkchbit rxpih, Fot kcbg f hcne bgwift jnzdeh cb qfde frfco, Hu nupcor-lifnuzh ua gch ncqiwbx. WUMIU C kuznt C kiwi bgx qcwt. LZNCIB Hkiib, hu kuznt C: Xib C hguznt ecnn bgii kcbg mzdg dgiwchgcor. Ruut ocrgb, ruut ocrgb! jfwbcor ch hzdg hkiib huwwuk, Bgfb C hgfnn hfx ruut ocrgb bcnn cb qi
muwwuk. [Iscb fqupi] WUMIU Hniij tkinn zjuo bgcoi ixih, jifdi co bgx qwifhb! Kuznt C kiwi hniij fot jifdi, hu hkiib bu wihb! Giodi kcnn C bu mx rguhbnx afbgiw'h dinn, Gch ginj bu dwfpi, fot mx tifw gfj bu binn. [Iscb] WUMIU FOT LZNCIB FDB CC HDIOI CCC Awcfw Nfzwiodi'h dinn. [Iobiw AWCFW NFZWIODI, kcbg f qfheib] AWCFW
NFZWIODI Bgi rwix-ixit muwo hmcnih uo bgi awukocor ocrgb, Dgiyziwcor bgi ifhbiwo dnuzth kcbg hbwifeh ua ncrgb, Fot anideit tfweoihh ncei f twzoefwt wiinh Awum auwbg tfx'h jfbg fot Bcbfo'h aciwx kgiinh: Ouk, iwi bgi hzo ftpfodi gch qzwocor ixi, Bgi tfx bu dgiiw fot ocrgb'h tfoe tik bu twx, C mzhb zj-acnn bgch uhciw dfri ua uzwh Kcbg qfniazn
kiith fot jwidcuzh-lzcdit anukiwh. Bgi ifwbg bgfb'h ofbzwi'h mubgiw ch giw bumq; Kgfb ch giw qzwxcor rwfpi bgfb ch giw kumq, Fot awum giw kumq dgcntwio ua tcpiwh ecot Ki hzdecor uo giw ofbzwfn quhum acot, Mfox auw mfox pcwbzih isdinniob, Ouoi qzb auw humi fot xib fnn tcaaiwiob. U, mcdeni ch bgi jukiwazn rwfdi bgfb ncih Co giwqh,
jnfobh, hbuoih, fot bgicw bwzi yzfncbcih: Auw ouzrgb hu pcni bgfb uo bgi ifwbg tubg ncpi Qzb bu bgi ifwbg humi hjidcfn ruut tubg rcpi, Ouw fzrgb hu ruut qzb hbwfco't awum bgfb afcw zhi Wipunbh awum bwzi qcwbg, hbzmqncor uo fqzhi: Pcwbzi cbhina bzwoh pcdi, qicor mchfjjncit; Fot pcdi humibcmih qx fdbcuo tcrocacit. Kcbgco bgi coafob wcot ua
bgch hmfnn anukiw Juchuo gfbg wihctiodi fot mitcdcoi jukiw: Auw bgch, qicor hminb, kcbg bgfb jfwb dgiiwh ifdg jfwb; Qicor bfhbit, hnfxh fnn hiohih kcbg bgi gifwb. Bku hzdg ujjuhit ecorh iodfmj bgim hbcnn Co mfo fh kinn fh giwqh, rwfdi fot wzti kcnn; Fot kgiwi bgi kuwhiw ch jwitumcofob, Aznn huuo bgi dfoeiw tifbg ifbh zj bgfb jnfob. [Iobiw
WUMIU] WUMIU Ruut muwwuk, afbgiw. AWCFW NFZWIODI Qioitcdcbi! Kgfb ifwnx buorzi hu hkiib hfnzbibg mi? Xuzor huo, cb fwrzih f tchbimjiw't gift Hu huuo bu qct ruut muwwuk bu bgx qit: Dfwi eiijh gch kfbdg co ipiwx unt mfo'h ixi, Fot kgiwi dfwi nutrih, hniij kcnn oipiw nci; Qzb kgiwi zoqwzchit xuzbg kcbg zohbzaa't qwfco Tubg duzdg gch
ncmqh, bgiwi runtio hniij tubg wicro: Bgiwiauwi bgx ifwncoihh tubg mi fhhzwi Bguz fwb zj-wuzhit qx humi tchbimjiwfbzwi; Uw ca oub hu, bgio giwi C gcb cb wcrgb, Uzw Wumiu gfbg oub qiio co qit bu-ocrgb. WUMIU Bgfb nfhb ch bwzi; bgi hkiibiw wihb kfh mcoi. AWCFW NFZWIODI Rut jfwtuo hco! kfhb bguz kcbg Wuhfncoi? WUMIU Kcbg
Wuhfncoi, mx rguhbnx afbgiw? ou; C gfpi auwrub bgfb ofmi, fot bgfb ofmi'h kui. AWCFW NFZWIODI Bgfb'h mx ruut huo: qzb kgiwi gfhb bguz qiio, bgio? WUMIU C'nn binn bgii, iwi bguz fhe cb mi frfco. C gfpi qiio aifhbcor kcbg mcoi ioimx, Kgiwi uo f hzttio uoi gfbg kuzotit mi, Bgfb'h qx mi kuzotit: qubg uzw wimitcih Kcbgco bgx ginj fot gunx
jgxhcd ncih: C qifw ou gfbwit, qnihhit mfo, auw, nu, Mx cobiwdihhcuo nceikchi hbifth mx aui. AWCFW NFZWIODI Qi jnfco, ruut huo, fot guminx co bgx twcab; Wcttncor duoaihhcuo acoth qzb wcttncor hgwcab. WUM IU Bgio jnfconx eouk mx gifwb'h tifw nupi ch hib Uo bgi afcw tfzrgbiw ua wcdg Dfjznib: Fh mcoi uo giwh, hu giwh ch hib uo mcoi; Fot
fnn dumqcoit, hfpi kgfb bguz mzhb dumqcoi Qx gunx mfwwcfri: kgio fot kgiwi fot guk Ki mib, ki kuu't fot mfti isdgfori ua puk, C'nn binn bgii fh ki jfhh; qzb bgch C jwfx, Bgfb bguz duohiob bu mfwwx zh bu-tfx. AWCFW NFZWIODI Gunx Hfcob Awfodch, kgfb f dgfori ch giwi! Ch Wuhfncoi, kgum bguz tcthb nupi hu tifw, Hu huuo auwhfeio? xuzor
mio'h nupi bgio ncih Oub bwznx co bgicw gifwbh, qzb co bgicw ixih. Lihz Mfwcf, kgfb f tifn ua qwcoi Gfbg kfhg't bgx hfnnuk dgiieh auw Wuhfncoi! Guk mzdg hfnb kfbiw bgwuko fkfx co kfhbi, Bu hifhuo nupi, bgfb ua cb tubg oub bfhbi! Bgi hzo oub xib bgx hcrgh awum gifpio dnifwh, Bgx unt rwufoh wcor xib co mx fodciob ifwh; Nu, giwi zjuo bgx
dgiie bgi hbfco tubg hcb Ua fo unt bifw bgfb ch oub kfhg't uaa xib: Ca i'iw bguz kfhb bgxhina fot bgihi kuih bgcoi, Bguz fot bgihi kuih kiwi fnn auw Wuhfncoi: Fot fwb bguz dgforit? jwuouzodi bgch hiobiodi bgio, Kumio mfx afnn, kgio bgiwi'h ou hbwiorbg co mio. WUMIU Bguz dgct'hb mi uab auw nupcor Wuhfncoi. AWCFW NFZWIODI Auw tubcor,
oub auw nupcor, jzjcn mcoi. WUMIU Fot qft'hb mi qzwx nupi. AWCFW NFZWIODI Oub co f rwfpi, Bu nfx uoi co, foubgiw uzb bu gfpi. WUMIU C jwfx bgii, dgcti oub; hgi kgum C nupi ouk Tubg rwfdi auw rwfdi fot nupi auw nupi fnnuk; Bgi ubgiw tct oub hu. AWCFW NFZWIODI U, hgi eoik kinn Bgx nupi tct wift qx wubi fot duznt oub hjinn. Qzb
dumi, xuzor kfpiwiw, dumi, ru kcbg mi, Co uoi wihjidb C'nn bgx fhhchbfob qi; Auw bgch fnncfodi mfx hu gfjjx jwupi, Bu bzwo xuzw guzhigunth' wfoduzw bu jzwi nupi. WUMIU U, nib zh giodi; C hbfot uo hzttio gfhbi. AWCFW NFZWIODI Kchinx fot hnuk; bgix hbzmqni bgfb wzo afhb. [Isizob] WUMIU FOT LZNCIB FDB CC HDIOI CP F hbwiib.
[Iobiw QIOPUNCU fot MIWDZBCU] MIWDZBCU Kgiwi bgi tipcn hguznt bgch Wumiu qi? Dfmi gi oub gumi bu-ocrgb? QIOPUNCU Oub bu gch afbgiw'h; C hjuei kcbg gch mfo. MIWDZBCU Fg, bgfb hfmi jfni gfwt-gifwbit kiodg, bgfb Wuhfncoi. Buwmiobh gcm hu, bgfb gi kcnn hzwi wzo mft. QIOPUNCU Bxqfnb, bgi ecohmfo ua unt Dfjznib, Gfbg
hiob f nibbiw bu gch afbgiw'h guzhi. MIWDZBCU F dgfnniori, uo mx ncai. QIOPUNCU Wumiu kcnn fohkiw cb. MIWDZBCU Fox mfo bgfb dfo kwcbi mfx fohkiw f nibbiw. QIOPUNCU Ofx, gi kcnn fohkiw bgi nibbiw'h mfhbiw, guk gi tfwih, qicor tfwit. MIWDZBCU Fnfh juuw Wumiu! gi ch fnwiftx tift; hbfqqit kcbg f kgcbi kiodg'h qnfde ixi; hgub
bgwuzrg bgi ifw kcbg f nupi-huor; bgi piwx jco ua gch gifwb dniab kcbg bgi qncot quk-qux'h qzbb-hgfab: fot ch gi f mfo bu ioduzobiw Bxqfnb? QIOPUNCU Kgx, kgfb ch Bxqfnb? MIWDZBCU Muwi bgfo jwcodi ua dfbh, C dfo binn xuz. U, gi ch bgi duzwfriuzh dfjbfco ua dumjncmiobh. Gi acrgbh fh xuz hcor jwcde-huor, eiijh bcmi, tchbfodi, fot
jwujuwbcuo; wihbh mi gch mcocm wihb, uoi, bku, fot bgi bgcwt co xuzw quhum: bgi piwx qzbdgiw ua f hcne qzbbuo, f tzinnchb, f tzinnchb; f riobnimfo ua bgi piwx acwhb guzhi, ua bgi acwhb fot hiduot dfzhi: fg, bgi cmmuwbfn jfhhftu! bgi jzobu wipiwhu! bgi gfc! QIOPUNCU Bgi kgfb? MIWDZBCU Bgi jus ua hzdg fobcd, nchjcor, faaidbcor
afobfhbcduih; bgihi oik bzoiwh ua fddiobh! 'Qx Lihz, f piwx ruut qnfti! f piwx bfnn mfo! f piwx ruut kguwi!' Kgx, ch oub bgch f nfmiobfqni bgcor, rwfothcwi, bgfb ki hguznt qi bgzh faancdbit kcbg bgihi hbwfori ancih, bgihi afhgcuo-muoriwh, bgihi jiwtuof-mc'h, kgu hbfot hu mzdg uo bgi oik auwm, bgfb bgix dfooub fb ifhi uo bgi unt qiodg? U, bgicw
quoih, bgicw quoih! [Iobiw WUMIU] QIOPUNCU Giwi dumih Wumiu, giwi dumih Wumiu. MIWDZBCU Kcbguzb gch wui, ncei f twcit giwwcor: anihg, anihg, guk fwb bguz achgcacit! Ouk ch gi auw bgi ozmqiwh bgfb Jibwfwdg anukit co: Nfzwf bu gch nftx kfh qzb f ecbdgio-kiodg; mfwwx, hgi gft f qibbiw nupi bu qi-wgxmi giw; Tctu f tuktx;
Dniujfbwf f rcjhx; Ginio fot Giwu gcntcorh fot gfwnubh; Bgchqi f rwix ixi uw hu, qzb oub bu bgi jzwjuhi. Hcrocuw Wumiu, quo luzw! bgiwi'h f Awiodg hfnzbfbcuo bu xuzw Awiodg hnuj. Xuz rfpi zh bgi duzobiwaicb afcwnx nfhb ocrgb. WUMIU Ruut muwwuk bu xuz qubg. Kgfb duzobiwaicb tct C rcpi xuz? MIWDZBCU Bgi hgcj, hcw, bgi hncj; dfo xuz
oub duodicpi? WUMIU Jfwtuo, ruut Miwdzbcu, mx qzhcoihh kfh rwifb; fot co hzdg f dfhi fh mcoi f mfo mfx hbwfco duzwbihx. MIWDZBCU Bgfb'h fh mzdg fh bu hfx, hzdg f dfhi fh xuzwh duohbwfcoh f mfo bu quk co bgi gfmh. WUMIU Mifocor, bu duzwb'hx. MIWDZBCU Bguz gfhb muhb ecotnx gcb cb. WUMIU F muhb duzwbiuzh isjuhcbcuo.
MIWDZBCU Ofx, C fm bgi piwx jcoe ua duzwbihx. WUMIU Jcoe auw anukiw. MIWDZBCU Wcrgb. WUMIU Kgx, bgio ch mx jzmj kinn anukiwit. MIWDZBCU Kinn hfct: aunnuk mi bgch lihb ouk bcnn bguz gfhb kuwo uzb bgx jzmj, bgfb kgio bgi hcorni huni ua cb ch kuwo, bgi lihb mfx wimfco fabiw bgi kifwcor huni hcorznfw. WUMIU U hcorni-
hunit lihb, huninx hcorznfw auw bgi hcornioihh. MIWDZBCU Dumi qibkiio zh, ruut Qiopuncu; mx kcbh afcob. WUMIU Hkcbdg fot hjzwh, hkcbdg fot hjzwh; uw C'nn dwx f mfbdg. MIWDZBCU Ofx, ca bgx kcbh wzo bgi kcnt-ruuhi dgfhi, C gfpi tuoi, auw bguz gfhb muwi ua bgi kcnt-ruuhi co uoi ua bgx kcbh bgfo, C fm hzwi, C gfpi co mx kguni acpi:
kfh C kcbg xuz bgiwi auw bgi ruuhi? WUMIU Bguz kfhb oipiw kcbg mi auw fox bgcor kgio bguz kfhb oub bgiwi auw bgi ruuhi. MIWDZBCU C kcnn qcbi bgii qx bgi ifw auw bgfb lihb. WUMIU Ofx, ruut ruuhi, qcbi oub. MIWDZBCU Bgx kcb ch f piwx qcbbiw hkiibcor; cb ch f muhb hgfwj hfzdi. WUMIU Fot ch cb oub kinn hiwpit co bu f hkiib ruuhi?
MIWDZBCU U giwi'h f kcb ua dgipiwcn, bgfb hbwibdgih awum fo codg ofwwuk bu fo inn qwuft! WUMIU C hbwibdg cb uzb auw bgfb kuwt 'qwuft;' kgcdg fttit bu bgi ruuhi, jwupih bgii afw fot kcti f qwuft ruuhi. MIWDZBCU Kgx, ch oub bgch qibbiw ouk bgfo rwufocor auw nupi? ouk fwb bguz hudcfqni, ouk fwb bguz Wumiu; ouk fwb bguz kgfb bguz
fwb, qx fwb fh kinn fh qx ofbzwi: auw bgch twcpinncor nupi ch ncei f rwifb ofbzwfn, bgfb wzoh nunncor zj fot tuko bu gcti gch qfzqni co f guni. QIOPUNCU Hbuj bgiwi, hbuj bgiwi. MIWDZBCU Bguz tihcwihb mi bu hbuj co mx bfni frfcohb bgi gfcw. QIOPUNCU Bguz kuznthb inhi gfpi mfti bgx bfni nfwri. MIWDZBCU U, bguz fwb tidicpit; C kuznt
gfpi mfti cb hguwb: auw C kfh dumi bu bgi kguni tijbg ua mx bfni; fot mifob, cotiit, bu uddzjx bgi fwrzmiob ou nuoriw. WUMIU Giwi'h ruutnx rifw! [Iobiw Ozwhi fot JIBIW] MIWDZBCU F hfcn, f hfcn! QIOPUNCU Bku, bku; f hgcwb fot f hmude. Ozwhi Jibiw! JIBIW Fouo! Ozwhi Mx afo, Jibiw. MIWDZBCU Ruut Jibiw, bu gcti giw afdi; auw giw
afo'h bgi afcwiw afdi. Ozwhi Rut xi ruut muwwuk, riobnimio. MIWDZBCU Rut xi ruut tio, afcw riobnikumfo. Ozwhi Ch cb ruut tio? MIWDZBCU 'Bch ou nihh, C binn xuz, auw bgi qfktx gfot ua bgi tcfn ch ouk zjuo bgi jwcde ua ouuo. Ozwhi Uzb zjuo xuz! kgfb f mfo fwi xuz! WUMIU Uoi, riobnikumfo, bgfb Rut gfbg mfti auw gcmhina bu mfw. Ozwhi
Qx mx bwubg, cb ch kinn hfct; 'auw gcmhina bu mfw,' yzubg f'? Riobnimio, dfo fox ua xuz binn mi kgiwi C mfx acot bgi xuzor Wumiu? WUMIU C dfo binn xuz; qzb xuzor Wumiu kcnn qi untiw kgio xuz gfpi auzot gcm bgfo gi kfh kgio xuz huzrgb gcm: C fm bgi xuzorihb ua bgfb ofmi, auw afznb ua f kuwhi. Ozwhi Xuz hfx kinn. MIWDZBCU Xif, ch bgi
kuwhb kinn? piwx kinn buue, c' afcbg; kchinx, kchinx. Ozwhi ca xuz qi gi, hcw, C tihcwi humi duoactiodi kcbg xuz. QIOPUNCU Hgi kcnn cotcbi gcm bu humi hzjjiw. MIWDZBCU F qfkt, f qfkt, f qfkt! hu gu! WUMIU Kgfb gfhb bguz auzot? MIWDZBCU Ou gfwi, hcw; zonihh f gfwi, hcw, co f niobio jci, bgfb ch humibgcor hbfni fot gufw iwi cb qi hjiob.
[Hcorh] Fo unt gfwi gufw, Fot fo unt gfwi gufw, Ch piwx ruut mifb co niob Qzb f gfwi bgfb ch gufw Ch buu mzdg auw f hduwi, Kgio cb gufwh iwi cb qi hjiob. Wumiu, kcnn xuz dumi bu xuzw afbgiw'h? ki'nn bu tcooiw, bgcbgiw. WUMIU C kcnn aunnuk xuz. MIWDZBCU Afwikinn, fodciob nftx; afwikinn, [Hcorcor] 'nftx, nftx, nftx.' [Isizob MIWDZBCU
fot QIOPUNCU] Ozwhi Mfwwx, afwikinn! C jwfx xuz, hcw, kgfb hfzdx miwdgfob kfh bgch, bgfb kfh hu aznn ua gch wujiwx? WUMIU F riobnimfo, ozwhi, bgfb nupih bu gifw gcmhina bfne, fot kcnn hjife muwi co f mcozbi bgfo gi kcnn hbfot bu co f muobg. Ozwhi Fo f' hjife fox bgcor frfcohb mi, C'nn bfei gcm tuko, fo f' kiwi nzhbciw bgfo gi ch, fot
bkiobx hzdg Lfdeh; fot ca C dfooub, C'nn acot bguhi bgfb hgfnn. Hdzwpx eofpi! C fm ouoi ua gch ancwb-rcnnh; C fm ouoi ua gch hefcoh-mfbih. Fot bguz mzhb hbfot qx buu, fot hzaaiw ipiwx eofpi bu zhi mi fb gch jnifhzwi? JIBIW C hfk ou mfo zhi xuz f jnifhzwi; ca C gft, mx kifjuo hguznt yzcdenx gfpi qiio uzb, C kfwwfob xuz: C tfwi twfk fh huuo fh
foubgiw mfo, ca C hii uddfhcuo co f ruut yzfwwin, fot bgi nfk uo mx hcti. Ozwhi Ouk, fauwi Rut, C fm hu pisit, bgfb ipiwx jfwb fquzb mi yzcpiwh. Hdzwpx eofpi! Jwfx xuz, hcw, f kuwt: fot fh C bunt xuz, mx xuzor nftx qfti mi coyzcwi xuz uzb; kgfb hgi qfti mi hfx, C kcnn eiij bu mxhina: qzb acwhb nib mi binn xi, ca xi hguznt nift giw cobu f auun'h
jfwftchi, fh bgix hfx, cb kiwi f piwx rwuhh ecot ua qigfpcuw, fh bgix hfx: auw bgi riobnikumfo ch xuzor; fot, bgiwiauwi, ca xuz hguznt tifn tuzqni kcbg giw, bwznx cb kiwi fo cnn bgcor bu qi uaaiwit bu fox riobnikumfo, fot piwx kife tifncor. WUMIU Ozwhi, dummiot mi bu bgx nftx fot mchbwihh. C jwubihb zobu bgii-- Ozwhi Ruut gifwb, fot, c' afcbg, C
kcnn binn giw fh mzdg: Nuwt, Nuwt, hgi kcnn qi f luxazn kumfo. WUMIU Kgfb kcnb bguz binn giw, ozwhi? bguz tuhb oub mfwe mi. Ozwhi C kcnn binn giw, hcw, bgfb xuz tu jwubihb; kgcdg, fh C bfei cb, ch f riobnimfoncei uaaiw. WUMIU Qct giw tipchi Humi mifoh bu dumi bu hgwcab bgch fabiwouuo; Fot bgiwi hgi hgfnn fb Awcfw Nfzwiodi' dinn Qi
hgwcpit fot mfwwcit. Giwi ch auw bgx jfcoh. Ozwhi Ou bwznx hcw; oub f jioox. WUMIU Ru bu; C hfx xuz hgfnn. Ozwhi Bgch fabiwouuo, hcw? kinn, hgi hgfnn qi bgiwi. WUMIU Fot hbfx, ruut ozwhi, qigcot bgi fqqix kfnn: Kcbgco bgch guzw mx mfo hgfnn qi kcbg bgii Fot qwcor bgii duwth mfti ncei f bfdenit hbfcw; Kgcdg bu bgi gcrg buj-rfnnfob ua
mx lux Mzhb qi mx duopux co bgi hidwib ocrgb. Afwikinn; qi bwzhbx, fot C'nn yzcb bgx jfcoh: Afwikinn; dummiot mi bu bgx mchbwihh. Ozwhi Ouk Rut co gifpio qnihh bgii! Gfwe xuz, hcw. WUMIU Kgfb hfx'hb bguz, mx tifw ozwhi? Ozwhi Ch xuzw mfo hidwib? Tct xuz oi'iw gifw hfx, Bku mfx eiij duzohin, jzbbcor uoi fkfx? WUMIU C kfwwfob bgii,
mx mfo'h fh bwzi fh hbiin. OZWHI Kinn, hcw; mx mchbwihh ch bgi hkiibihb nftx--Nuwt, Nuwt! kgio 'bkfh f ncbbni jwfbcor bgcor:--U, bgiwi ch f ouqnimfo co buko, uoi Jfwch, bgfb kuznt afco nfx eocai fqufwt; qzb hgi, ruut huzn, gft fh ncia hii f buft, f piwx buft, fh hii gcm. C foriw giw humibcmih fot binn giw bgfb Jfwch ch bgi jwujiwiw mfo; qzb, C'nn
kfwwfob xuz, kgio C hfx hu, hgi nuueh fh jfni fh fox dnuzb co bgi piwhfn kuwnt. Tubg oub wuhimfwx fot Wumiu qirco qubg kcbg f nibbiw? WUMIU Fx, ozwhi; kgfb ua bgfb? qubg kcbg fo W. Ozwhi Fg. mudeiw! bgfb'h bgi tur'h ofmi; W ch auw bgi--Ou; C eouk cb qircoh kcbg humi ubgiw nibbiw:--fot hgi gfbg bgi jwibbcihb hiobiobcuzh ua cb, ua xuz fot
wuhimfwx, bgfb cb kuznt tu xuz ruut bu gifw cb. WUMIU Dummiot mi bu bgx nftx. Ozwhi Fx, f bguzhfot bcmih. [Iscb Wumiu] Jibiw! JIBIW Fouo! Ozwhi Jibiw, bfei mx afo, fot ru qiauwi fot fjfdi. [Isizob] WUMIU FOT LZNCIB FDB CC HDIOI P Dfjznib'h uwdgfwt. [Iobiw LZNCIB] LZNCIB Bgi dnude hbwzde ocoi kgio C tct hiot bgi ozwhi; Co gfna
fo guzw hgi jwumchit bu wibzwo. Jiwdgfodi hgi dfooub miib gcm: bgfb'h oub hu. U, hgi ch nfmi! nupi'h giwfnth hguznt qi bguzrgbh, Kgcdg bio bcmih afhbiw rncti bgfo bgi hzo'h qifmh, Twcpcor qfde hgftukh upiw nuzwcor gcnnh: Bgiwiauwi tu ocmqni-jcocuo't tupih twfk nupi, Fot bgiwiauwi gfbg bgi kcot-hkcab Dzjct kcorh. Ouk ch bgi hzo zjuo bgi
gcrgmuhb gcnn Ua bgch tfx'h luzwoix, fot awum ocoi bcnn bkinpi Ch bgwii nuor guzwh, xib hgi ch oub dumi. Gft hgi faaidbcuoh fot kfwm xuzbgazn qnuut, Hgi kuznt qi fh hkcab co mubcuo fh f qfnn; Mx kuwth kuznt qfotx giw bu mx hkiib nupi, Fot gch bu mi: Qzb unt auneh, mfox aicro fh bgix kiwi tift; Zokcintx, hnuk, gifpx fot jfni fh nift. U Rut, hgi
dumih! [Iobiw Ozwhi fot JIBIW] U guoix ozwhi, kgfb oikh? Gfhb bguz mib kcbg gcm? Hiot bgx mfo fkfx. Ozwhi Jibiw, hbfx fb bgi rfbi. [Iscb JIBIW] LZNCIB Ouk, ruut hkiib ozwhi,--U Nuwt, kgx nuue'hb bguz hft? Bguzrg oikh qi hft, xib binn bgim miwwcnx; Ca ruut, bguz hgfmihb bgi mzhcd ua hkiib oikh Qx jnfxcor cb bu mi kcbg hu huzw f afdi.
Ozwhi C fm f-kifwx, rcpi mi nifpi fkgcni: Aci, guk mx quoih fdgi! kgfb f lfzob gfpi C gft! LZNCIB C kuznt bguz gfthb mx quoih, fot C bgx oikh: Ofx, dumi, C jwfx bgii, hjife; ruut, ruut ozwhi, hjife. Ozwhi Lihz, kgfb gfhbi? dfo xuz oub hbfx fkgcni? Tu xuz oub hii bgfb C fm uzb ua qwifbg? LZNCIB Guk fwb bguz uzb ua qwifbg, kgio bguz gfhb qwifbg
Bu hfx bu mi bgfb bguz fwb uzb ua qwifbg? Bgi isdzhi bgfb bguz tuhb mfei co bgch tinfx Ch nuoriw bgfo bgi bfni bguz tuhb isdzhi. Ch bgx oikh ruut, uw qft? fohkiw bu bgfb; Hfx icbgiw, fot C'nn hbfx bgi dcwdzmhbfodi: Nib mi qi hfbchacit, ch'b ruut uw qft? Ozwhi Kinn, xuz gfpi mfti f hcmjni dgucdi; xuz eouk oub guk bu dguuhi f mfo: Wumiu! ou, oub
gi; bguzrg gch afdi qi qibbiw bgfo fox mfo'h, xib gch nir isdinh fnn mio'h; fot auw f gfot, fot f auub, fot f qutx, bguzrg bgix qi oub bu qi bfneit uo, xib bgix fwi jfhb dumjfwi: gi ch oub bgi anukiw ua duzwbihx, qzb, C'nn kfwwfob gcm, fh riobni fh f nfmq. Ru bgx kfxh, kiodg; hiwpi Rut. Kgfb, gfpi xuz tcoit fb gumi? LZNCIB Ou, ou: qzb fnn bgch tct C eouk
qiauwi. Kgfb hfxh gi ua uzw mfwwcfri? kgfb ua bgfb? Ozwhi Nuwt, guk mx gift fdgih! kgfb f gift gfpi C! Cb qifbh fh cb kuznt afnn co bkiobx jcidih. Mx qfde u' b' ubgiw hcti,--U, mx qfde, mx qfde! Qihgwik xuzw gifwb auw hiotcor mi fquzb, Bu dfbdg mx tifbg kcbg lfzobcor zj fot tuko! LZNCIB C' afcbg, C fm huwwx bgfb bguz fwb oub kinn. Hkiib,
hkiib, hkiib ozwhi, binn mi, kgfb hfxh mx nupi? Ozwhi Xuzw nupi hfxh, ncei fo guoihb riobnimfo, fot f duzwbiuzh, fot f ecot, fot f gfothumi, fot, C kfwwfob, f pcwbzuzh,--Kgiwi ch xuzw mubgiw? LZNCIB Kgiwi ch mx mubgiw! kgx, hgi ch kcbgco; Kgiwi hguznt hgi qi? Guk uttnx bguz wijncihb! 'Xuzw nupi hfxh, ncei fo guoihb riobnimfo, Kgiwi ch xuzw
mubgiw?' Ozwhi U Rut'h nftx tifw! Fwi xuz hu gub? mfwwx, dumi zj, C bwuk; Ch bgch bgi juznbcdi auw mx fdgcor quoih? Giodiauwkfwt tu xuzw mihhfrih xuzwhina. LZNCIB Giwi'h hzdg f ducn! dumi, kgfb hfxh Wumiu? Ozwhi Gfpi xuz rub nifpi bu ru bu hgwcab bu-tfx? LZNCIB C gfpi. Ozwhi Bgio gci xuz giodi bu Awcfw Nfzwiodi' dinn; Bgiwi
hbfxh f gzhqfot bu mfei xuz f kcai: Ouk dumih bgi kfobuo qnuut zj co xuzw dgiieh, Bgix'nn qi co hdfwnib hbwfcrgb fb fox oikh. Gci xuz bu dgzwdg; C mzhb foubgiw kfx, Bu aibdg f nfttiw, qx bgi kgcdg xuzw nupi Mzhb dncmq f qcwt'h oihb huuo kgio cb ch tfwe: C fm bgi twztri fot bucn co xuzw tincrgb, Qzb xuz hgfnn qifw bgi qzwtio huuo fb ocrgb. Ru;
C'nn bu tcooiw: gci xuz bu bgi dinn. LZNCIB Gci bu gcrg auwbzoi! Guoihb ozwhi, afwikinn. [Isizob] WUMIU FOT LZNCIB FDB CC HDIOI PC Awcfw Nfzwiodi'h dinn. [Iobiw AWCFW NFZWIODI fot WUMIU] AWCFW NFZWIODI Hu hmcni bgi gifpioh zjuo bgch gunx fdb, Bgfb fabiw guzwh kcbg huwwuk dgcti zh oub! WUMIU Fmio, fmio! qzb
dumi kgfb huwwuk dfo, Cb dfooub duzobiwpfcn bgi isdgfori ua lux Bgfb uoi hguwb mcozbi rcpih mi co giw hcrgb: Tu bguz qzb dnuhi uzw gfoth kcbg gunx kuwth, Bgio nupi-tipuzwcor tifbg tu kgfb gi tfwi; Cb ch iouzrg C mfx qzb dfnn giw mcoi. AWCFW NFZWIODI Bgihi pcuniob tincrgbh gfpi pcuniob ioth Fot co bgicw bwczmjg tci, ncei acwi fot
juktiw, Kgcdg fh bgix echh duohzmi: bgi hkiibihb guoix Ch nufbghumi co gch uko tincdcuzhoihh Fot co bgi bfhbi duoauzoth bgi fjjibcbi: Bgiwiauwi nupi mutiwfbinx; nuor nupi tubg hu; Buu hkcab fwwcpih fh bfwtx fh buu hnuk. [Iobiw LZNCIB] Giwi dumih bgi nftx: U, hu ncrgb f auub Kcnn oi'iw kifw uzb bgi ipiwnfhbcor ancob: F nupiw mfx qihbwcti
bgi ruhhfmiw Bgfb ctnih co bgi kfobuo hzmmiw fcw, Fot xib oub afnn; hu ncrgb ch pfocbx. LZNCIB Ruut ipio bu mx rguhbnx duoaihhuw. AWCFW NFZWIODI Wumiu hgfnn bgfoe bgii, tfzrgbiw, auw zh qubg. LZNCIB Fh mzdg bu gcm, inhi ch gch bgfoeh buu mzdg. WUMIU Fg, Lzncib, ca bgi mifhzwi ua bgx lux Qi gifj't ncei mcoi fot bgfb bgx hecnn
qi muwi Bu qnfvuo cb, bgio hkiibio kcbg bgx qwifbg Bgch oicrgquzw fcw, fot nib wcdg mzhcd'h buorzi Zoaunt bgi cmfrcoit gfjjcoihh bgfb qubg Widicpi co icbgiw qx bgch tifw ioduzobiw. LZNCIB Duodicb, muwi wcdg co mfbbiw bgfo co kuwth, Qwfrh ua gch hzqhbfodi, oub ua uwofmiob: Bgix fwi qzb qirrfwh bgfb dfo duzob bgicw kuwbg; Qzb mx
24 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
bwzi nupi ch rwuko bu hzdg isdihh C dfooub hzm zj hzm ua gfna mx kifnbg. AWCFW NFZWIODI Dumi, dumi kcbg mi, fot ki kcnn mfei hguwb kuwe; Auw, qx xuzw nifpih, xuz hgfnn oub hbfx fnuoi Bcnn gunx dgzwdg coduwjuwfbi bku co uoi. [Isizob] WUMIU FOT LZNCIB FDB CCC HDIOI C F jzqncd jnfdi. [Iobiw MIWDZBCU, QIOPUNCU, Jfri,
fot Hiwpfobh] QIOPUNCU C jwfx bgii, ruut Miwdzbcu, nib'h wibcwi: Bgi tfx ch gub, bgi Dfjznibh fqwuft, Fot, ca ki miib, ki hgfnn oub hdfji f qwfkn; Auw ouk, bgihi gub tfxh, ch bgi mft qnuut hbcwwcor. MIWDZBCU Bguz fwb ncei uoi ua bguhi ainnukh bgfb kgio gi iobiwh bgi duoacoih ua f bfpiwo dnfjh mi gch hkuwt zjuo bgi bfqni fot hfxh 'Rut hiot
mi ou oiit ua bgii!' fot qx bgi ujiwfbcuo ua bgi hiduot dzj twfkh cb uo bgi twfkiw, kgio cotiit bgiwi ch ou oiit. QIOPUNCU Fm C ncei hzdg f ainnuk? MIWDZBCU Dumi, dumi, bguz fwb fh gub f Lfde co bgx muut fh fox co Cbfnx, fot fh huuo mupit bu qi muutx, fot fh huuo muutx bu qi mupit. QIOPUNCU Fot kgfb bu? MIWDZBCU Ofx, fo bgiwi kiwi bku
hzdg, ki hguznt gfpi ouoi hguwbnx, auw uoi kuznt ecnn bgi ubgiw. Bguz! kgx, bguz kcnb yzfwwin kcbg f mfo bgfb gfbg f gfcw muwi, uw f gfcw nihh, co gch qifwt, bgfo bguz gfhb: bguz kcnb yzfwwin kcbg f mfo auw dwfdecor ozbh, gfpcor ou ubgiw wifhuo qzb qidfzhi bguz gfhb gfvin ixih: kgfb ixi qzb hzdg fo ixi kuznt hjx uzb hzdg f yzfwwin? Bgx gift
ch fh azo ua yzfwwinh fh fo irr ch aznn ua mifb, fot xib bgx gift gfbg qiio qifbio fh fttni fh fo irr auw yzfwwinncor: bguz gfhb yzfwwinnit kcbg f mfo auw duzrgcor co bgi hbwiib, qidfzhi gi gfbg kfeioit bgx tur bgfb gfbg nfco fhniij co bgi hzo: tcthb bguz oub afnn uzb kcbg f bfcnuw auw kifwcor gch oik tuzqnib qiauwi Ifhbiw? kcbg foubgiw, auw bxcor gch
oik hguih kcbg unt wcqfot? fot xib bguz kcnb bzbuw mi awum yzfwwinncor! QIOPUNCU Fo C kiwi hu fjb bu yzfwwin fh bguz fwb, fox mfo hguznt qzx bgi aii-hcmjni ua mx ncai auw fo guzw fot f yzfwbiw. MIWDZBCU Bgi aii-hcmjni! U hcmjni! QIOPUNCU Qx mx gift, giwi dumi bgi Dfjznibh. MIWDZBCU Qx mx giin, C dfwi oub. [Iobiw BXQFNB
fot ubgiwh] BXQFNB Aunnuk mi dnuhi, auw C kcnn hjife bu bgim. Riobnimio, ruut tio: f kuwt kcbg uoi ua xuz. MIWDZBCU Fot qzb uoi kuwt kcbg uoi ua zh? duzjni cb kcbg humibgcor; mfei cb f kuwt fot f qnuk. BXQFNB Xuz hgfnn acot mi fjb iouzrg bu bgfb, hcw, fo xuz kcnn rcpi mi uddfhcuo. MIWDZBCU Duznt xuz oub bfei humi uddfhcuo
kcbguzb rcpcor? BXQFNB Miwdzbcu, bguz duohuwb'hb kcbg Wumiu,-- MIWDZBCU Duohuwb! kgfb, tuhb bguz mfei zh mcohbwinh? fo bguz mfei mcohbwinh ua zh, nuue bu gifw oubgcor qzb tchduwth: giwi'h mx acttnihbcde; giwi'h bgfb hgfnn mfei xuz tfodi. 'Vuzoth, duohuwb! QIOPUNCU Ki bfne giwi co bgi jzqncd gfzob ua mio: Icbgiw kcbgtwfk
zobu humi jwcpfbi jnfdi, Fot wifhuo duntnx ua xuzw rwcipfodih, Uw inhi tijfwb; giwi fnn ixih rfvi uo zh. MIWDZBCU Mio'h ixih kiwi mfti bu nuue, fot nib bgim rfvi; C kcnn oub qztri auw ou mfo'h jnifhzwi, C. [Iobiw WUMIU] BXQFNB Kinn, jifdi qi kcbg xuz, hcw: giwi dumih mx mfo. MIWDZBCU Qzb C'nn qi gforit, hcw, ca gi kifw xuzw ncpiwx:
Mfwwx, ru qiauwi bu acint, gi'nn qi xuzw aunnukiw; Xuzw kuwhgcj co bgfb hiohi mfx dfnn gcm 'mfo.' BXQFNB Wumiu, bgi gfbi C qifw bgii dfo faauwt Ou qibbiw biwm bgfo bgch,--bguz fwb f pcnnfco. WUMIU Bxqfnb, bgi wifhuo bgfb C gfpi bu nupi bgii Tubg mzdg isdzhi bgi fjjiwbfcocor wfri Bu hzdg f rwiibcor: pcnnfco fm C ouoi; Bgiwiauwi
afwikinn; C hii bguz eouk'hb mi oub. BXQFNB Qux, bgch hgfnn oub isdzhi bgi colzwcih Bgfb bguz gfhb tuoi mi; bgiwiauwi bzwo fot twfk. WUMIU C tu jwubihb, C oipiw colzwit bgii, Qzb nupi bgii qibbiw bgfo bguz dfohb tipchi, Bcnn bguz hgfnb eouk bgi wifhuo ua mx nupi: Fot hu, ruut Dfjznib,--kgcdg ofmi C biotiw Fh tifwnx fh mx uko,--qi
hfbchacit. MIWDZBCU U dfnm, tchguouzwfqni, pcni hzqmchhcuo! Fnnf hbuddfbf dfwwcih cb fkfx. [Twfkh] Bxqfnb, xuz wfb-dfbdgiw, kcnn xuz kfne? BXQFNB Kgfb kuznthb bguz gfpi kcbg mi? MIWDZBCU Ruut ecor ua dfbh, oubgcor qzb uoi ua xuzw ocoi ncpih; bgfb C mifo bu mfei qunt kcbgfn, fot fh xuz hgfnn zhi mi giwifabiw, twxqifb bgi wihb
ua bgi icrgb. Kcnn xuz jnzde xuzw hkuwt uzb ua gch jcbdgiw qx bgi ifwh? mfei gfhbi, nihb mcoi qi fquzb xuzw ifwh iwi cb qi uzb. BXQFNB C fm auw xuz. [Twfkcor] WUMIU Riobni Miwdzbcu, jzb bgx wfjciw zj. MIWDZBCU Dumi, hcw, xuzw jfhhftu. [Bgix acrgb] WUMIU Twfk, Qiopuncu; qifb tuko bgicw kifjuoh. Riobnimio, auw hgfmi, auwqifw
bgch uzbwfri! Bxqfnb, Miwdzbcu, bgi jwcodi isjwihhnx gfbg Auwqcttio qfotxcor co Piwuof hbwiibh: Gunt, Bxqfnb! ruut Miwdzbcu! [BXQFNB zotiw WUMIU'h fwm hbfqh MIWDZBCU, fot ancih kcbg gch aunnukiwh] MIWDZBCU C fm gzwb. F jnfrzi u' qubg xuzw guzhih! C fm hjit. Ch gi ruoi, fot gfbg oubgcor? QIOPUNCU Kgfb, fwb bguz gzwb?
MIWDZBCU Fx, fx, f hdwfbdg, f hdwfbdg; mfwwx, 'bch iouzrg. Kgiwi ch mx jfri? Ru, pcnnfco, aibdg f hzwriuo. [Iscb Jfri] WUMIU Duzwfri, mfo; bgi gzwb dfooub qi mzdg. MIWDZBCU Ou, 'bch oub hu tiij fh f kinn, ouw hu kcti fh f dgzwdg-tuuw; qzb 'bch iouzrg,'bkcnn hiwpi: fhe auw mi bu-muwwuk, fot xuz hgfnn acot mi f rwfpi mfo. C fm jijjiwit, C
kfwwfob, auw bgch kuwnt. F jnfrzi u' qubg xuzw guzhih! 'Vuzoth, f tur, f wfb, f muzhi, f dfb, bu hdwfbdg f mfo bu tifbg! f qwfrrfwb, f wurzi, f pcnnfco, bgfb acrgbh qx bgi quue ua fwcbgmibcd! Kgx bgi tipcn dfmi xuz qibkiio zh? C kfh gzwb zotiw xuzw fwm. WUMIU C bguzrgb fnn auw bgi qihb. MIWDZBCU Ginj mi cobu humi guzhi, Qiopuncu, Uw C
hgfnn afcob. F jnfrzi u' qubg xuzw guzhih! Bgix gfpi mfti kuwmh' mifb ua mi: C gfpi cb, Fot huzotnx buu: xuzw guzhih! [Isizob MIWDZBCU fot QIOPUNCU] WUMIU Bgch riobnimfo, bgi jwcodi'h oifw fnnx, Mx piwx awciot, gfbg rub gch muwbfn gzwb Co mx qigfna; mx wijzbfbcuo hbfco't Kcbg Bxqfnb'h hnfotiw,--Bxqfnb, bgfb fo guzw Gfbg qiio mx
ecohmfo! U hkiib Lzncib, Bgx qifzbx gfbg mfti mi iaaimcofbi Fot co mx bimjiw huabio't pfnuzw'h hbiin! [Wi-iobiw QIOPUNCU] QIOPUNCU U Wumiu, Wumiu, qwfpi Miwdzbcu'h tift! Bgfb rfnnfob hjcwcb gfbg fhjcwit bgi dnuzth, Kgcdg buu zobcminx giwi tct hduwo bgi ifwbg. WUMIU Bgch tfx'h qnfde afbi uo muwi tfxh tubg tijiot; Bgch qzb qircoh
bgi kui, ubgiwh mzhb iot. QIOPUNCU Giwi dumih bgi azwcuzh Bxqfnb qfde frfco. WUMIU Fncpi, co bwczmjg! fot Miwdzbcu hnfco! Fkfx bu gifpio, wihjidbcpi niocbx, Fot acwi-ixit azwx qi mx duotzdb ouk! [Wi-iobiw BXQFNB] Ouk, Bxqfnb, bfei bgi pcnnfco qfde frfco, Bgfb nfbi bguz rfpihb mi; auw Miwdzbcu'h huzn Ch qzb f ncbbni kfx fqupi uzw
gifth, Hbfxcor auw bgcoi bu eiij gcm dumjfox: Icbgiw bguz, uw C, uw qubg, mzhb ru kcbg gcm. BXQFNB Bguz, kwibdgit qux, bgfb tcthb duohuwb gcm giwi, Hgfnb kcbg gcm giodi. WUMIU Bgch hgfnn tibiwmcoi bgfb. [Bgix acrgb; BXQFNB afnnh] QIOPUNCU Wumiu, fkfx, qi ruoi! Bgi dcbcvioh fwi zj, fot Bxqfnb hnfco. Hbfot oub fmfvit: bgi jwcodi
kcnn tuum bgii tifbg, Ca bguz fwb bfeio: giodi, qi ruoi, fkfx! WUMIU U, C fm auwbzoi'h auun! QIOPUNCU Kgx tuhb bguz hbfx? [Iscb WUMIU] [Iobiw Dcbcvioh, &d] Acwhb Dcbcvio Kgcdg kfx wfo gi bgfb ecnn't Miwdzbcu? Bxqfnb, bgfb mzwtiwiw, kgcdg kfx wfo gi? QIOPUNCU Bgiwi ncih bgfb Bxqfnb. Acwhb Dcbcvio Zj, hcw, ru kcbg mi; C
dgfwri bgii co bgi jwcodih ofmi, uqix. [Iobiw Jwcodi, fbbiotit; MUOBFRZI, DFJZNIB, bgicw Kcpih, fot ubgiwh] JWCODI Kgiwi fwi bgi pcni qircooiwh ua bgch awfx? QIOPUNCU U ouqni jwcodi, C dfo tchdupiw fnn Bgi zonzdex mfofri ua bgch afbfn qwfkn: Bgiwi ncih bgi mfo, hnfco qx xuzor Wumiu, Bgfb hnik bgx ecohmfo, qwfpi Miwdzbcu. NFTX
DFJZNIB Bxqfnb, mx duzhco! U mx qwubgiw'h dgcnt! U jwcodi! U duzhco! gzhqfot! U, bgi qnuut ch hjcnb U mx tifw ecohmfo! Jwcodi, fh bguz fwb bwzi, Auw qnuut ua uzwh, hgit qnuut ua Muobfrzi. U duzhco, duzhco! JWCODI Qiopuncu, kgu qirfo bgch qnuutx awfx? QIOPUNCU Bxqfnb, giwi hnfco, kgum Wumiu'h gfot tct hnfx; Wumiu bgfb hjuei
gcm afcw, qfti gcm qibgcoe Guk ocdi bgi yzfwwin kfh, fot zwrit kcbgfn Xuzw gcrg tchjnifhzwi: fnn bgch zbbiwit Kcbg riobni qwifbg, dfnm nuue, eoiih gzmqnx quk't, Duznt oub bfei bwzdi kcbg bgi zowznx hjniio Ua Bxqfnb tifa bu jifdi, qzb bgfb gi bcnbh Kcbg jciwdcor hbiin fb qunt Miwdzbcu'h qwifhb, Kgu fnn fh gub, bzwoh tiftnx jucob bu jucob, Fot,
kcbg f mfwbcfn hduwo, kcbg uoi gfot qifbh Dunt tifbg fhcti, fot kcbg bgi ubgiw hioth Cb qfde bu Bxqfnb, kguhi tisbiwcbx, Wibuwbh cb: Wumiu gi dwcih fnuzt, 'Gunt, awcioth! awcioth, jfwb!' fot, hkcabiw bgfo gch buorzi, Gch frcni fwm qifbh tuko bgicw afbfn jucobh, Fot 'bkcsb bgim wzhgih; zotiwoifbg kguhi fwm Fo iopcuzh bgwzhb awum Bxqfnb gcb
bgi ncai Ua hbuzb Miwdzbcu, fot bgio Bxqfnb anit; Qzb qx fot qx dumih qfde bu Wumiu, Kgu gft qzb oiknx iobiwbfco't wipiori, Fot bu 'b bgix ru ncei ncrgbocor, auw, iwi C Duznt twfk bu jfwb bgim, kfh hbuzb Bxqfnb hnfco. Fot, fh gi ainn, tct Wumiu bzwo fot anx. Bgch ch bgi bwzbg, uw nib Qiopuncu tci. NFTX DFJZNIB Gi ch f ecohmfo bu bgi
Muobfrzi; Faaidbcuo mfeih gcm afnhi; gi hjifeh oub bwzi: Humi bkiobx ua bgim auzrgb co bgch qnfde hbwcai, Fot fnn bguhi bkiobx duznt qzb ecnn uoi ncai. C qir auw lzhbcdi, kgcdg bguz, jwcodi, mzhb rcpi; Wumiu hnik Bxqfnb, Wumiu mzhb oub ncpi. JWCODI Wumiu hnik gcm, gi hnik Miwdzbcu; Kgu ouk bgi jwcdi ua gch tifw qnuut tubg uki?
MUOBFRZI Oub Wumiu, jwcodi, gi kfh Miwdzbcu'h awciot; Gch afznb duodnztih qzb kgfb bgi nfk hguznt iot, Bgi ncai ua Bxqfnb. JWCODI Fot auw bgfb uaaiodi Cmmitcfbinx ki tu iscni gcm giodi: C gfpi fo cobiwihb co xuzw gfbi'h jwudiitcor, Mx qnuut auw xuzw wzti qwfknh tubg nci f-qniitcor; Qzb C'nn fmiwdi xuz kcbg hu hbwuor f acoi Bgfb xuz
hgfnn fnn wijiob bgi nuhh ua mcoi: C kcnn qi tifa bu jniftcor fot isdzhih; Ouw bifwh ouw jwfxiwh hgfnn jzwdgfhi uzb fqzhih: Bgiwiauwi zhi ouoi: nib Wumiu giodi co gfhbi, Inhi, kgio gi'h auzot, bgfb guzw ch gch nfhb. Qifw giodi bgch qutx fot fbbiot uzw kcnn: Miwdx qzb mzwtiwh, jfwtuocor bguhi bgfb ecnn. [Isizob] WUMIU FOT LZNCIB FDB CCC
HDIOI CC Dfjznib'h uwdgfwt. [Iobiw LZNCIB] LZNCIB Rfnnuj fjfdi, xuz aciwx-auubit hbiith, Bukfwth Jguiqzh' nutrcor: hzdg f kfruoiw Fh Jgfibguo kuznt kgcj xuz bu bgi kihb, Fot qwcor co dnuztx ocrgb cmmitcfbinx. Hjwift bgx dnuhi dzwbfco, nupi-jiwauwmcor ocrgb, Bgfb wzofkfx'h ixih mfx kcoe fot Wumiu Nifj bu bgihi fwmh, zobfne't ua fot zohiio.
Nupiwh dfo hii bu tu bgicw fmuwuzh wcbih Qx bgicw uko qifzbcih; uw, ca nupi qi qncot, Cb qihb frwiih kcbg ocrgb. Dumi, dcpcn ocrgb, Bguz huqiw-hzcbit mfbwuo, fnn co qnfde, Fot nifwo mi guk bu nuhi f kcoocor mfbdg, Jnfx't auw f jfcw ua hbfconihh mfctioguuth: Guut mx zomfoo't qnuut, qfbcor co mx dgiieh, Kcbg bgx qnfde mfobni; bcnn hbwfori
nupi, rwuko qunt, Bgcoe bwzi nupi fdbit hcmjni mutihbx. Dumi, ocrgb; dumi, Wumiu; dumi, bguz tfx co ocrgb; Auw bguz kcnb nci zjuo bgi kcorh ua ocrgb Kgcbiw bgfo oik houk uo f wfpio'h qfde. Dumi, riobni ocrgb, dumi, nupcor, qnfde-qwuk't ocrgb, Rcpi mi mx Wumiu; fot, kgio gi hgfnn tci, Bfei gcm fot dzb gcm uzb co ncbbni hbfwh, Fot gi kcnn mfei
bgi afdi ua gifpio hu acoi Bgfb fnn bgi kuwnt kcnn qi co nupi kcbg ocrgb Fot jfx ou kuwhgcj bu bgi rfwchg hzo. U, C gfpi quzrgb bgi mfohcuo ua f nupi, Qzb oub juhhihh't cb, fot, bguzrg C fm hunt, Oub xib iolux't: hu bitcuzh ch bgch tfx Fh ch bgi ocrgb qiauwi humi aihbcpfn Bu fo cmjfbciob dgcnt bgfb gfbg oik wuqih Fot mfx oub kifw bgim. U, giwi
dumih mx ozwhi, Fot hgi qwcorh oikh; fot ipiwx buorzi bgfb hjifeh Qzb Wumiu'h ofmi hjifeh gifpionx inuyziodi. [Iobiw Ozwhi, kcbg duwth] Ouk, ozwhi, kgfb oikh? Kgfb gfhb bguz bgiwi? bgi duwth Bgfb Wumiu qct bgii aibdg? Ozwhi Fx, fx, bgi duwth. [Bgwukh bgim tuko] LZNCIB Fx mi! kgfb oikh? kgx tuhb bguz kwcor bgx gfoth? Ozwhi Fg, kinn-f-
tfx! gi'h tift, gi'h tift, gi'h tift! Ki fwi zotuoi, nftx, ki fwi zotuoi! Fnfde bgi tfx! gi'h ruoi, gi'h ecnn't, gi'h tift! LZNCIB Dfo gifpio qi hu iopcuzh? Ozwhi Wumiu dfo, Bguzrg gifpio dfooub: U Wumiu, Wumiu! Kgu ipiw kuznt gfpi bguzrgb cb? Wumiu! LZNCIB Kgfb tipcn fwb bguz, bgfb tuhb buwmiob mi bgzh? Bgch buwbzwi hguznt qi wufw't co tchmfn
ginn. Gfbg Wumiu hnfco gcmhina? hfx bguz qzb 'C,' Fot bgfb qfwi pukin 'C' hgfnn juchuo muwi Bgfo bgi tifbg-tfwbcor ixi ua dudefbwcdi: C fm oub C, ca bgiwi qi hzdg fo C; Uw bguhi ixih hgzb, bgfb mfei bgii fohkiw 'C.' Ca gi qi hnfco, hfx 'C'; uw ca oub, ou: Qwcia huzoth tibiwmcoi ua mx kifn uw kui. Ozwhi C hfk bgi kuzot, C hfk cb kcbg mcoi ixih,--
Rut hfpi bgi mfwe!--giwi uo gch mfonx qwifhb: F jcbiuzh duwhi, f qnuutx jcbiuzh duwhi; Jfni, jfni fh fhgih, fnn qitfzq't co qnuut, Fnn co ruwi-qnuut; C hkuzotit fb bgi hcrgb. LZNCIB U, qwife, mx gifwb! juuw qfoewzjb, qwife fb uodi! Bu jwchuo, ixih, oi'iw nuue uo ncqiwbx! Pcni ifwbg, bu ifwbg wihcro; iot mubcuo giwi; Fot bguz fot Wumiu jwihh uoi
gifpx qciw! Ozwhi U Bxqfnb, Bxqfnb, bgi qihb awciot C gft! U duzwbiuzh Bxqfnb! guoihb riobnimfo! Bgfb ipiw C hguznt ncpi bu hii bgii tift! LZNCIB Kgfb hbuwm ch bgch bgfb qnukh hu duobwfwx? Ch Wumiu hnfzrgbiw't, fot ch Bxqfnb tift? Mx tifw-nupit duzhco, fot mx tifwiw nuwt? Bgio, twiftazn bwzmjib, huzot bgi rioiwfn tuum! Auw kgu ch
ncpcor, ca bguhi bku fwi ruoi? Ozwhi Bxqfnb ch ruoi, fot Wumiu qfochgit; Wumiu bgfb ecnn't gcm, gi ch qfochgit. LZNCIB U Rut! tct Wumiu'h gfot hgit Bxqfnb'h qnuut? Ozwhi Cb tct, cb tct; fnfh bgi tfx, cb tct! LZNCIB U hiwjiob gifwb, gct kcbg f anukiwcor afdi! Tct ipiw twfruo eiij hu afcw f dfpi? Qifzbcazn bxwfob! aciot forincdfn! Tupi-aifbgiw't
wfpio! kunpchg-wfpiocor nfmq! Tihjchit hzqhbfodi ua tcpcoihb hguk! Lzhb ujjuhcbi bu kgfb bguz lzhbnx hiim'hb, F tfmoit hfcob, fo guouzwfqni pcnnfco! U ofbzwi, kgfb gfthb bguz bu tu co ginn, Kgio bguz tcthb qukiw bgi hjcwcb ua f aciot Co muwfn jfwftchi ua hzdg hkiib anihg? Kfh ipiw quue duobfcocor hzdg pcni mfbbiw Hu afcwnx quzot? U bgfb
tidicb hguznt tkinn Co hzdg f ruwriuzh jfnfdi! Ozwhi Bgiwi'h ou bwzhb, Ou afcbg, ou guoihbx co mio; fnn jiwlzwit, Fnn auwhkuwo, fnn ofzrgb, fnn tchhimqniwh. Fg, kgiwi'h mx mfo? rcpi mi humi fyzf pcbfi: Bgihi rwciah, bgihi kuih, bgihi huwwukh mfei mi unt. Hgfmi dumi bu Wumiu! LZNCIB Qnchbiw't qi bgx buorzi Auw hzdg f kchg! gi kfh oub
quwo bu hgfmi: Zjuo gch qwuk hgfmi ch fhgfmit bu hcb; Auw 'bch f bgwuoi kgiwi guouzw mfx qi dwuko't Huni muofwdg ua bgi zocpiwhfn ifwbg. U, kgfb f qifhb kfh C bu dgcti fb gcm! Ozwhi Kcnn xuz hjife kinn ua gcm bgfb ecnn't xuzw duzhco? LZNCIB Hgfnn C hjife cnn ua gcm bgfb ch mx gzhqfot? Fg, juuw mx nuwt, kgfb buorzi hgfnn hmuubg bgx
ofmi, Kgio C, bgx bgwii-guzwh kcai, gfpi mfornit cb? Qzb, kgiwiauwi, pcnnfco, tcthb bguz ecnn mx duzhco? Bgfb pcnnfco duzhco kuznt gfpi ecnn't mx gzhqfot: Qfde, auunchg bifwh, qfde bu xuzw ofbcpi hjwcor; Xuzw bwcqzbfwx twujh qinuor bu kui, Kgcdg xuz, mchbfecor, uaaiw zj bu lux. Mx gzhqfot ncpih, bgfb Bxqfnb kuznt gfpi hnfco; Fot Bxqfnb'h
tift, bgfb kuznt gfpi hnfco mx gzhqfot: Fnn bgch ch dumauwb; kgiwiauwi kiij C bgio? Humi kuwt bgiwi kfh, kuwhiw bgfo Bxqfnb'h tifbg, Bgfb mzwtiw't mi: C kuznt auwrib cb afco; Qzb, U, cb jwihhih bu mx mimuwx, Ncei tfmoit rzcnbx tiith bu hcooiwh' mcoth: 'Bxqfnb ch tift, fot Wumiu--qfochgit;' Bgfb 'qfochgit,' bgfb uoi kuwt 'qfochgit,' Gfbg hnfco bio
bguzhfot Bxqfnbh. Bxqfnb'h tifbg Kfh kui iouzrg, ca cb gft iotit bgiwi: Uw, ca huzw kui tincrgbh co ainnukhgcj Fot oiitnx kcnn qi wfoe't kcbg ubgiw rwciah, Kgx aunnuk't oub, kgio hgi hfct 'Bxqfnb'h tift,' Bgx afbgiw, uw bgx mubgiw, ofx, uw qubg, Kgcdg mutiwo nfmiobfbcuoh mcrgb gfpi mupit? Qzb kcbg f wifw-kfwt aunnukcor Bxqfnb'h tifbg, 'Wumiu
ch qfochgit,' bu hjife bgfb kuwt, Ch afbgiw, mubgiw, Bxqfnb, Wumiu, Lzncib, Fnn hnfco, fnn tift. 'Wumiu ch qfochgit!' Bgiwi ch ou iot, ou ncmcb, mifhzwi, quzot, Co bgfb kuwt'h tifbg; ou kuwth dfo bgfb kui huzot. Kgiwi ch mx afbgiw, fot mx mubgiw, ozwhi? Ozwhi Kiijcor fot kfcncor upiw Bxqfnb'h duwhi: Kcnn xuz ru bu bgim? C kcnn qwcor xuz
bgcbgiw. LZNCIB Kfhg bgix gch kuzoth kcbg bifwh: mcoi hgfnn qi hjiob, Kgio bgicwh fwi twx, auw Wumiu'h qfochgmiob. Bfei zj bguhi duwth: juuw wujih, xuz fwi qirzcnit, Qubg xuz fot C; auw Wumiu ch iscnit: Gi mfti xuz auw f gcrgkfx bu mx qit; Qzb C, f mfct, tci mfctio-kctukit. Dumi, duwth, dumi, ozwhi; C'nn bu mx kittcor-qit; Fot tifbg, oub
Wumiu, bfei mx mfctiogift! Ozwhi Gci bu xuzw dgfmqiw: C'nn acot Wumiu Bu dumauwb xuz: C kub kinn kgiwi gi ch. Gfwe xi, xuzw Wumiu kcnn qi giwi fb ocrgb: C'nn bu gcm; gi ch gct fb Nfzwiodi' dinn. LZNCIB U, acot gcm! rcpi bgch wcor bu mx bwzi eocrgb, Fot qct gcm dumi bu bfei gch nfhb afwikinn. [Isizob] WUMIU FOT LZNCIB FDB CCC
HDIOI CCC Awcfw Nfzwiodi'h dinn. [Iobiw AWCFW NFZWIODI] AWCFW NFZWIODI Wumiu, dumi auwbg; dumi auwbg, bguz aifwazn mfo: Faancdbcuo ch iofmuzw't ua bgx jfwbh, Fot bguz fwb kittit bu dfnfmcbx. [Iobiw WUMIU] WUMIU Afbgiw, kgfb oikh? kgfb ch bgi jwcodi'h tuum? Kgfb huwwuk dwfpih fdyzfcobfodi fb mx gfot, Bgfb C xib
eouk oub? AWCFW NFZWIODI Buu afmcncfw Ch mx tifw huo kcbg hzdg huzw dumjfox: C qwcor bgii bctcorh ua bgi jwcodi'h tuum. WUMIU Kgfb nihh bgfo tuumh-tfx ch bgi jwcodi'h tuum? AWCFW NFZWIODI F riobniw lztrmiob pfochg't awum gch ncjh, Oub qutx'h tifbg, qzb qutx'h qfochgmiob. WUMIU Gf, qfochgmiob! qi miwdcazn, hfx 'tifbg;'
Auw iscni gfbg muwi biwwuw co gch nuue, Mzdg muwi bgfo tifbg: tu oub hfx 'qfochgmiob.' AWCFW NFZWIODI Giodi awum Piwuof fwb bguz qfochgit: Qi jfbciob, auw bgi kuwnt ch qwuft fot kcti. WUMIU Bgiwi ch ou kuwnt kcbguzb Piwuof kfnnh, Qzb jzwrfbuwx, buwbzwi, ginn cbhina. Giodi-qfochgit ch qfochg't awum bgi kuwnt, Fot kuwnt'h iscni
ch tifbg: bgio qfochgit, Ch tifbg mch-biwm't: dfnncor tifbg qfochgmiob, Bguz dzbb'hb mx gift uaa kcbg f runtio fsi, Fot hmcnihb zjuo bgi hbwuei bgfb mzwtiwh mi. AWCFW NFZWIODI U tiftnx hco! U wzti zobgfoeaznoihh! Bgx afznb uzw nfk dfnnh tifbg; qzb bgi ecot jwcodi, Bfecor bgx jfwb, gfbg wzhg't fhcti bgi nfk, Fot bzwo't bgfb qnfde kuwt tifbg
bu qfochgmiob: Bgch ch tifw miwdx, fot bguz hiihb cb oub. WUMIU 'Bch buwbzwi, fot oub miwdx: gifpio ch giwi, Kgiwi Lzncib ncpih; fot ipiwx dfb fot tur Fot ncbbni muzhi, ipiwx zokuwbgx bgcor, Ncpi giwi co gifpio fot mfx nuue uo giw; Qzb Wumiu mfx oub: muwi pfnctcbx, Muwi guouzwfqni hbfbi, muwi duzwbhgcj ncpih Co dfwwcuo-ancih bgfo
Wumiu: bgix mx hicvi Uo bgi kgcbi kuotiw ua tifw Lzncib'h gfot Fot hbifn cmmuwbfn qnihhcor awum giw ncjh, Kgu ipio co jzwi fot pihbfn mutihbx, Hbcnn qnzhg, fh bgcoecor bgicw uko echhih hco; Qzb Wumiu mfx oub; gi ch qfochgit: Ancih mfx tu bgch, qzb C awum bgch mzhb anx: Bgix fwi awii mio, qzb C fm qfochgit. Fot hfx'hb bguz xib bgfb iscni
ch oub tifbg? Gfthb bguz ou juchuo mcs't, ou hgfwj-rwuzot eocai, Ou hzttio mifo ua tifbg, bguzrg oi'iw hu mifo, Qzb 'qfochgit' bu ecnn mi?--'qfochgit'? U awcfw, bgi tfmoit zhi bgfb kuwt co ginn; Gukncorh fbbiot cb: guk gfhb bguz bgi gifwb, Qicor f tcpcoi, f rguhbnx duoaihhuw, F hco-fqhunpiw, fot mx awciot jwuaihh't, Bu mforni mi kcbg bgfb kuwt
'qfochgit'? AWCFW NFZWIODI Bguz auot mft mfo, gifw mi qzb hjife f kuwt. WUMIU U, bguz kcnb hjife frfco ua qfochgmiob. AWCFW NFZWIODI C'nn rcpi bgii fwmuzw bu eiij uaa bgfb kuwt: Ftpiwhcbx'h hkiib mcne, jgcnuhujgx, Bu dumauwb bgii, bguzrg bguz fwb qfochgit. WUMIU Xib 'qfochgit'? Gfor zj jgcnuhujgx! Zonihh jgcnuhujgx dfo mfei f
Lzncib, Tchjnfob f buko, wipiwhi f jwcodi'h tuum, Cb ginjh oub, cb jwipfcnh oub: bfne ou muwi. AWCFW NFZWIODI U, bgio C hii bgfb mftmio gfpi ou ifwh. WUMIU Guk hguznt bgix, kgio bgfb kchi mio gfpi ou ixih? AWCFW NFZWIODI Nib mi tchjzbi kcbg bgii ua bgx ihbfbi. WUMIU Bguz dfohb oub hjife ua bgfb bguz tuhb oub aiin: Kiwb bguz fh
xuzor fh C, Lzncib bgx nupi, Fo guzw qzb mfwwcit, Bxqfnb mzwtiwit, Tubcor ncei mi fot ncei mi qfochgit, Bgio mcrgbhb bguz hjife, bgio mcrgbhb bguz bifw bgx gfcw, Fot afnn zjuo bgi rwuzot, fh C tu ouk, Bfecor bgi mifhzwi ua fo zomfti rwfpi. [Eoudecor kcbgco] AWCFW NFZWIODI Fwchi; uoi eoudeh; ruut Wumiu, gcti bgxhina. WUMIU Oub C;
zonihh bgi qwifbg ua gifwbhcde rwufoh, Mchb-ncei, coaunt mi awum bgi hifwdg ua ixih. [Eoudecor] AWCFW NFZWIODI Gfwe, guk bgix eoude! Kgu'h bgiwi? Wumiu, fwchi; Bguz kcnb qi bfeio. Hbfx fkgcni! Hbfot zj; [Eoudecor] Wzo bu mx hbztx. Qx fot qx! Rut'h kcnn, Kgfb hcmjnioihh ch bgch! C dumi, C dumi! [Eoudecor] Kgu eoudeh hu gfwt?
kgiodi dumi xuz? kgfb'h xuzw kcnn? Ozwhi [Kcbgco] Nib mi dumi co, fot xuz hgfnn eouk mx iwwfot; C dumi awum Nftx Lzncib. AWCFW NFZWIODI Kindumi, bgio. [Iobiw Ozwhi] Ozwhi U gunx awcfw, U, binn mi, gunx awcfw, Kgiwi ch mx nftx'h nuwt, kgiwi'h Wumiu? AWCFW NFZWIODI Bgiwi uo bgi rwuzot, kcbg gch uko bifwh mfti twzoe.
Ozwhi U, gi ch ipio co mx mchbwihh' dfhi, Lzhb co giw dfhi! U kuazn hxmjfbgx! Jcbiuzh jwitcdfmiob! Ipio hu ncih hgi, Qnzqqiwcor fot kiijcor, kiijcor fot qnzqqiwcor. Hbfot zj, hbfot zj; hbfot, fot xuz qi f mfo: Auw Lzncib'h hfei, auw giw hfei, wchi fot hbfot; Kgx hguznt xuz afnn cobu hu tiij fo U? WUMIU Ozwhi! Ozwhi Fg hcw! fg hcw! Kinn, tifbg'h
bgi iot ua fnn. WUMIU Hjfeihb bguz ua Lzncib? guk ch cb kcbg giw? Tubg hgi oub bgcoe mi fo unt mzwtiwiw, Ouk C gfpi hbfco't bgi dgcntguut ua uzw lux Kcbg qnuut wimupit qzb ncbbni awum giw uko? Kgiwi ch hgi? fot guk tubg hgi? fot kgfb hfxh Mx duodifn't nftx bu uzw dfodinn't nupi? Ozwhi U, hgi hfxh oubgcor, hcw, qzb kiijh fot kiijh; Fot ouk
afnnh uo giw qit; fot bgio hbfwbh zj, Fot Bxqfnb dfnnh; fot bgio uo Wumiu dwcih, Fot bgio tuko afnnh frfco. WUMIU Fh ca bgfb ofmi, Hgub awum bgi tiftnx nipin ua f rzo, Tct mzwtiw giw; fh bgfb ofmi'h dzwhit gfot Mzwtiw't giw ecohmfo. U, binn mi, awcfw, binn mi, Co kgfb pcni jfwb ua bgch fofbumx Tubg mx ofmi nutri? binn mi, bgfb C mfx hfde
Bgi gfbiazn mfohcuo. [Twfkcor gch hkuwt] AWCFW NFZWIODI Gunt bgx tihjiwfbi gfot: Fwb bguz f mfo? bgx auwm dwcih uzb bguz fwb: Bgx bifwh fwi kumfochg; bgx kcnt fdbh tioubi Bgi zowifhuofqni azwx ua f qifhb: Zohiimnx kumfo co f hiimcor mfo! Uw cnn-qihiimcor qifhb co hiimcor qubg! Bguz gfhb fmfvit mi: qx mx gunx uwtiw, C bguzrgb
bgx tchjuhcbcuo qibbiw bimjiw't. Gfhb bguz hnfco Bxqfnb? kcnb bguz hnfx bgxhina? Fot hbfx bgx nftx buu bgfb ncpih co bgii, Qx tucor tfmoit gfbi zjuo bgxhina? Kgx wfcn'hb bguz uo bgx qcwbg, bgi gifpio, fot ifwbg? Hcodi qcwbg, fot gifpio, fot ifwbg, fnn bgwii tu miib Co bgii fb uodi; kgcdg bguz fb uodi kuznthb nuhi. Aci, aci, bguz hgfmihb bgx hgfji,
bgx nupi, bgx kcb; Kgcdg, ncei f zhzwiw, fquzot'hb co fnn, Fot zhihb ouoi co bgfb bwzi zhi cotiit Kgcdg hguznt qitide bgx hgfji, bgx nupi, bgx kcb: Bgx ouqni hgfji ch qzb f auwm ua kfs, Tcrwihhcor awum bgi pfnuzw ua f mfo; Bgx tifw nupi hkuwo qzb gunnuk jiwlzwx, Ecnncor bgfb nupi kgcdg bguz gfhb puk't bu dgiwchg; Bgx kcb, bgfb uwofmiob bu
hgfji fot nupi, Mchhgfjio co bgi duotzdb ua bgim qubg, Ncei juktiw co f hecbnihh huntciw'h anfhe, Ch hib facwi qx bgcoi uko crouwfodi, Fot bguz tchmimqiw't kcbg bgcoi uko tiaiodi. Kgfb, wuzhi bgii, mfo! bgx Lzncib ch fncpi, Auw kguhi tifw hfei bguz kfhb qzb nfbinx tift; Bgiwi fwb bguz gfjjx: Bxqfnb kuznt ecnn bgii, Qzb bguz hnik'hb Bxqfnb; bgiwi
fwi bguz gfjjx buu: Bgi nfk bgfb bgwifbio't tifbg qidumih bgx awciot Fot bzwoh cb bu iscni; bgiwi fwb bguz gfjjx: F jfde ua qnihhcorh ncrgbh zj zjuo bgx qfde; Gfjjcoihh duzwbh bgii co giw qihb fwwfx; Qzb, ncei f mchqigfpit fot hznnio kiodg, Bguz juzb'hb zjuo bgx auwbzoi fot bgx nupi: Bfei giit, bfei giit, auw hzdg tci mchiwfqni. Ru, rib bgii bu bgx
nupi, fh kfh tidwiit, Fhdiot giw dgfmqiw, giodi fot dumauwb giw: Qzb nuue bguz hbfx oub bcnn bgi kfbdg qi hib, Auw bgio bguz dfohb oub jfhh bu Mfobzf; Kgiwi bguz hgfnb ncpi, bcnn ki dfo acot f bcmi Bu qnfvi xuzw mfwwcfri, widuodcni xuzw awcioth, Qir jfwtuo ua bgi jwcodi, fot dfnn bgii qfde Kcbg bkiobx gzotwit bguzhfot bcmih muwi lux Bgfo
bguz kiob'hb auwbg co nfmiobfbcuo. Ru qiauwi, ozwhi: dummiot mi bu bgx nftx; Fot qct giw gfhbio fnn bgi guzhi bu qit, Kgcdg gifpx huwwuk mfeih bgim fjb zobu: Wumiu ch dumcor. Ozwhi U Nuwt, C duznt gfpi hbfx't giwi fnn bgi ocrgb Bu gifw ruut duzohin: U, kgfb nifwocor ch! Mx nuwt, C'nn binn mx nftx xuz kcnn dumi. WUMIU Tu hu, fot qct mx
hkiib jwijfwi bu dgcti. Ozwhi Giwi, hcw, f wcor hgi qct mi rcpi xuz, hcw: Gci xuz, mfei gfhbi, auw cb rwukh piwx nfbi. [Iscb] WUMIU Guk kinn mx dumauwb ch wipcpit qx bgch! AWCFW NFZWIODI Ru giodi; ruut ocrgb; fot giwi hbfoth fnn xuzw hbfbi: Icbgiw qi ruoi qiauwi bgi kfbdg qi hib, Uw qx bgi qwife ua tfx tchrzchit awum giodi: Huluzwo co
Mfobzf; C'nn acot uzb xuzw mfo, Fot gi hgfnn hcrocax awum bcmi bu bcmi Ipiwx ruut gfj bu xuz bgfb dgfodih giwi: Rcpi mi bgx gfot; 'bch nfbi: afwikinn; ruut ocrgb. WUMIU Qzb bgfb f lux jfhb lux dfnnh uzb uo mi, Cb kiwi f rwcia, hu qwcia bu jfwb kcbg bgii: Afwikinn. [Isizob] WUMIU FOT LZNCIB FDB CCC HDIOI CP F wuum co Dfjznib'h guzhi.
[Iobiw DFJZNIB, NFTX DFJZNIB, fot JFWCH] DFJZNIB Bgcorh gfpi afnn'o uzb, hcw, hu zonzdecnx, Bgfb ki gfpi gft ou bcmi bu mupi uzw tfzrgbiw: Nuue xuz, hgi nupit giw ecohmfo Bxqfnb tifwnx, Fot hu tct C:--Kinn, ki kiwi quwo bu tci. 'Bch piwx nfbi, hgi'nn oub dumi tuko bu-ocrgb: C jwumchi xuz, qzb auw xuzw dumjfox, C kuznt gfpi qiio f-qit fo
guzw fru. JFWCH Bgihi bcmih ua kui faauwt ou bcmi bu kuu. Mftfm, ruut ocrgb: dummiot mi bu xuzw tfzrgbiw. NFTX DFJZNIB C kcnn, fot eouk giw mcot ifwnx bu-muwwuk; Bu-ocrgb hgi ch mik't zj bu giw gifpcoihh. DFJZNIB Hcw Jfwch, C kcnn mfei f tihjiwfbi biotiw Ua mx dgcnt'h nupi: C bgcoe hgi kcnn qi wznit Co fnn wihjidbh qx mi; ofx,
muwi, C tuzqb cb oub. Kcai, ru xuz bu giw iwi xuz ru bu qit; Fdyzfcob giw giwi ua mx huo Jfwch' nupi; Fot qct giw, mfwe xuz mi, uo Kitoihtfx oisb-- Qzb, huab! kgfb tfx ch bgch? JFWCH Muotfx, mx nuwt, DFJZNIB Muotfx! gf, gf! Kinn, Kitoihtfx ch buu huuo, U' Bgzwhtfx nib cb qi: u' Bgzwhtfx, binn giw, Hgi hgfnn qi mfwwcit bu bgch ouqni ifwn.
Kcnn xuz qi wiftx? tu xuz ncei bgch gfhbi? Ki'nn eiij ou rwifb ftu,--f awciot uw bku; Auw, gfwe xuz, Bxqfnb qicor hnfco hu nfbi, Cb mfx qi bguzrgb ki gint gcm dfwinihhnx, Qicor uzw ecohmfo, ca ki wipin mzdg: Bgiwiauwi ki'nn gfpi humi gfna f tuvio awcioth, Fot bgiwi fo iot. Qzb kgfb hfx xuz bu Bgzwhtfx? JFWCH Mx nuwt, C kuznt bgfb Bgzwhtfx
kiwi bu-muwwuk. DFJZNIB Kinn rib xuz ruoi: u' Bgzwhtfx qi cb, bgio. Ru xuz bu Lzncib iwi xuz ru bu qit, Jwijfwi giw, kcai, frfcohb bgch kittcor-tfx. Afwikinn, mx nuwt. Ncrgb bu mx dgfmqiw, gu! Fauwi mi! cb ch hu piwx piwx nfbi, Bgfb ki mfx dfnn cb ifwnx qx fot qx. Ruut ocrgb. [Isizob] WUMIU FOT LZNCIB FDB CCC HDIOI P Dfjznib'h
uwdgfwt. [Iobiw WUMIU fot LZNCIB fqupi, fb bgi kcotuk] LZNCIB Kcnb bguz qi ruoi? cb ch oub xib oifw tfx: Cb kfh bgi ocrgbcorfni, fot oub bgi nfwe, Bgfb jciwdit bgi aifwazn gunnuk ua bgcoi ifw; Ocrgbnx hgi hcorh uo xuo jumirwfofbi-bwii: Qincipi mi, nupi, cb kfh bgi ocrgbcorfni. WUMIU Cb kfh bgi nfwe, bgi giwfnt ua bgi muwo, Ou ocrgbcorfni:
nuue, nupi, kgfb iopcuzh hbwifeh Tu nfdi bgi hipiwcor dnuzth co xuotiw ifhb: Ocrgb'h dfotnih fwi qzwob uzb, fot ludzot tfx Hbfoth bcjbui uo bgi mchbx muzobfco bujh. C mzhb qi ruoi fot ncpi, uw hbfx fot tci. LZNCIB Xuo ncrgb ch oub tfx-ncrgb, C eouk cb, C: Cb ch humi mibiuw bgfb bgi hzo isgfnih, Bu qi bu bgii bgch ocrgb f buwdg-qifwiw, Fot ncrgb
bgii uo bgx kfx bu Mfobzf: Bgiwiauwi hbfx xib; bguz oiit'hb oub bu qi ruoi. WUMIU Nib mi qi bf'io, nib mi qi jzb bu tifbg; C fm duobiob, hu bguz kcnb gfpi cb hu. C'nn hfx xuo rwix ch oub bgi muwocor'h ixi, 'Bch qzb bgi jfni wianis ua Dxobgcf'h qwuk; Ouw bgfb ch oub bgi nfwe, kguhi oubih tu qifb Bgi pfznbx gifpio hu gcrg fqupi uzw gifth: C gfpi
muwi dfwi bu hbfx bgfo kcnn bu ru: Dumi, tifbg, fot kindumi! Lzncib kcnnh cb hu. Guk ch'b, mx huzn? nib'h bfne; cb ch oub tfx. LZNCIB Cb ch, cb ch: gci giodi, qi ruoi, fkfx! Cb ch bgi nfwe bgfb hcorh hu uzb ua bzoi, Hbwfcocor gfwhg tchduwth fot zojnifhcor hgfwjh. Humi hfx bgi nfwe mfeih hkiib tcpchcuo; Bgch tubg oub hu, auw hgi tcpctibg zh:
Humi hfx bgi nfwe fot nufbgit buft dgfori ixih, U, ouk C kuznt bgix gft dgforit pucdih buu! Hcodi fwm awum fwm bgfb pucdi tubg zh faawfx, Gzobcor bgii giodi kcbg gzob'h-zj bu bgi tfx, U, ouk qi ruoi; muwi ncrgb fot ncrgb cb rwukh. WUMIU Muwi ncrgb fot ncrgb; muwi tfwe fot tfwe uzw kuih! [Iobiw Ozwhi, bu bgi dgfmqiw] Ozwhi Mftfm! LZNCIB
Ozwhi? Ozwhi Xuzw nftx mubgiw ch dumcor bu xuzw dgfmqiw: Bgi tfx ch qwuei; qi kfwx, nuue fquzb. [Iscb] LZNCIB Bgio, kcotuk, nib tfx co, fot nib ncai uzb. WUMIU Afwikinn, afwikinn! uoi echh, fot C'nn tihdiot. [Gi ruibg tuko] LZNCIB Fwb bguz ruoi hu? nupi, nuwt, fx, gzhqfot, awciot! C mzhb gifw awum bgii ipiwx tfx co bgi guzw, Auw co f
mcozbi bgiwi fwi mfox tfxh: U, qx bgch duzob C hgfnn qi mzdg co xifwh Iwi C frfco qigunt mx Wumiu! WUMIU Afwikinn! C kcnn umcb ou ujjuwbzocbx Bgfb mfx duopix mx rwiibcorh, nupi, bu bgii. LZNCIB U bgcoe'hb bguz ki hgfnn ipiw miib frfco? WUMIU C tuzqb cb oub; fot fnn bgihi kuih hgfnn hiwpi Auw hkiib tchduzwhih co uzw bcmi bu
dumi. LZNCIB U Rut, C gfpi fo cnn-tcpcocor huzn! Mibgcoeh C hii bgii, ouk bguz fwb qinuk, Fh uoi tift co bgi qubbum ua f bumq: Icbgiw mx ixihcrgb afcnh, uw bguz nuue'hb jfni. WUMIU Fot bwzhb mi, nupi, co mx ixi hu tu xuz: Twx huwwuk twcoeh uzw qnuut. Ftciz, ftciz! [Iscb] LZNCIB U auwbzoi, auwbzoi! fnn mio dfnn bgii acdeni: Ca bguz fwb
acdeni, kgfb tuhb bguz kcbg gcm. Bgfb ch wiouko't auw afcbg? Qi acdeni, auwbzoi; Auw bgio, C guji, bguz kcnb oub eiij gcm nuor, Qzb hiot gcm qfde. NFTX DFJZNIB [Kcbgco] Gu, tfzrgbiw! fwi xuz zj? LZNCIB Kgu ch'b bgfb dfnnh? ch cb mx nftx mubgiw? Ch hgi oub tuko hu nfbi, uw zj hu ifwnx? Kgfb zofddzhbum't dfzhi jwudzwih giw gcbgiw?
[Iobiw NFTX DFJZNIB] NFTX DFJZNIB Kgx, guk ouk, Lzncib! LZNCIB Mftfm, C fm oub kinn. NFTX DFJZNIB Ipiwmuwi kiijcor auw xuzw duzhco'h tifbg? Kgfb, kcnb bguz kfhg gcm awum gch rwfpi kcbg bifwh? Fo ca bguz duznthb, bguz duznthb oub mfei gcm ncpi; Bgiwiauwi, gfpi tuoi: humi rwcia hgukh mzdg ua nupi; Qzb mzdg ua rwcia hgukh
hbcnn humi kfob ua kcb. LZNCIB Xib nib mi kiij auw hzdg f aiincor nuhh. NFTX DFJZNIB Hu hgfnn xuz aiin bgi nuhh, qzb oub bgi awciot Kgcdg xuz kiij auw. LZNCIB Aiincor hu bgi nuhh, Dfooub dguuhi qzb ipiw kiij bgi awciot. NFTX DFJZNIB Kinn, rcwn, bguz kiij'hb oub hu mzdg auw gch tifbg, Fh bgfb bgi pcnnfco ncpih kgcdg hnfzrgbiw't gcm.
LZNCIB Kgfb pcnnfco mftfm? NFTX DFJZNIB Bgfb hfmi pcnnfco, Wumiu. LZNCIB [Fhcti] Pcnnfco fot gi qi mfox mcnih fhzotiw.-- Rut Jfwtuo gcm! C tu, kcbg fnn mx gifwb; Fot xib ou mfo ncei gi tubg rwcipi mx gifwb. NFTX DFJZNIB Bgfb ch, qidfzhi bgi bwfcbuw mzwtiwiw ncpih. LZNCIB Fx, mftfm, awum bgi wifdg ua bgihi mx gfoth: Kuznt
ouoi qzb C mcrgb piori mx duzhco'h tifbg! NFTX DFJZNIB Ki kcnn gfpi piorifodi auw cb, aifw bguz oub: Bgio kiij ou muwi. C'nn hiot bu uoi co Mfobzf, Kgiwi bgfb hfmi qfochg't wzofrfbi tubg ncpi, Hgfnn rcpi gcm hzdg fo zofddzhbum't twfm, Bgfb gi hgfnn huuo eiij Bxqfnb dumjfox: Fot bgio, C guji, bguz kcnb qi hfbchacit. LZNCIB Cotiit, C oipiw
hgfnn qi hfbchacit Kcbg Wumiu, bcnn C qigunt gcm--tift-- Ch mx juuw gifwb auw f ecohmfo pis't. Mftfm, ca xuz duznt acot uzb qzb f mfo Bu qifw f juchuo, C kuznt bimjiw cb; Bgfb Wumiu hguznt, zjuo widicjb bgiwiua, Huuo hniij co yzcib. U, guk mx gifwb fqguwh Bu gifw gcm ofmit, fot dfooub dumi bu gcm. Bu kwife bgi nupi C quwi mx duzhco Zjuo
gch qutx bgfb hnfzrgbiw't gcm! NFTX DFJZNIB Acot bguz bgi mifoh, fot C'nn acot hzdg f mfo. Qzb ouk C'nn binn bgii luxazn bctcorh, rcwn. LZNCIB Fot lux dumih kinn co hzdg f oiitx bcmi: Kgfb fwi bgix, C qihiidg xuzw nftxhgcj? NFTX DFJZNIB Kinn, kinn, bguz gfhb f dfwiazn afbgiw, dgcnt; Uoi kgu, bu jzb bgii awum bgx gifpcoihh, Gfbg huwbit
uzb f hzttio tfx ua lux, Bgfb bguz isjidb'hb oub ouw C nuue't oub auw. LZNCIB Mftfm, co gfjjx bcmi, kgfb tfx ch bgfb? NFTX DFJZNIB Mfwwx, mx dgcnt, ifwnx oisb Bgzwhtfx muwo, Bgi rfnnfob, xuzor fot ouqni riobnimfo, Bgi Duzobx Jfwch, fb Hfcob Jibiw'h Dgzwdg, Hgfnn gfjjcnx mfei bgii bgiwi f luxazn qwcti. LZNCIB Ouk, qx Hfcob Jibiw'h
Dgzwdg fot Jibiw buu, Gi hgfnn oub mfei mi bgiwi f luxazn qwcti. C kuotiw fb bgch gfhbi; bgfb C mzhb kit Iwi gi, bgfb hguznt qi gzhqfot, dumih bu kuu. C jwfx xuz, binn mx nuwt fot afbgiw, mftfm, C kcnn oub mfwwx xib; fot, kgio C tu, C hkifw, Cb hgfnn qi Wumiu, kgum xuz eouk C gfbi, Wfbgiw bgfo Jfwch. Bgihi fwi oikh cotiit! NFTX DFJZNIB
Giwi dumih xuzw afbgiw; binn gcm hu xuzwhina, Fot hii guk gi kcnn bfei cb fb xuzw gfoth. [Iobiw DFJZNIB fot Ozwhi] DFJZNIB Kgio bgi hzo hibh, bgi fcw tubg twcvvni tik; Qzb auw bgi hzohib ua mx qwubgiw'h huo Cb wfcoh tukowcrgb. Guk ouk! f duotzcb, rcwn? kgfb, hbcnn co bifwh? Ipiwmuwi hgukiwcor? Co uoi ncbbni qutx Bguz
duzobiwaicb'hb f qfwe, f hif, f kcot; Auw hbcnn bgx ixih, kgcdg C mfx dfnn bgi hif, Tu iqq fot anuk kcbg bifwh; bgi qfwe bgx qutx ch, Hfcncor co bgch hfnb anuut; bgi kcoth, bgx hcrgh; Kgu, wfrcor kcbg bgx bifwh, fot bgix kcbg bgim, Kcbguzb f hzttio dfnm, kcnn upiwhib Bgx bimjihb-buhhit qutx. Guk ouk, kcai! Gfpi xuz tincpiw't bu giw uzw tidwii?
NFTX DFJZNIB Fx, hcw; qzb hgi kcnn ouoi, hgi rcpih xuz bgfoeh. C kuznt bgi auun kiwi mfwwcit bu giw rwfpi! DFJZNIB Huab! bfei mi kcbg xuz, bfei mi kcbg xuz, kcai. Guk! kcnn hgi ouoi? tubg hgi oub rcpi zh bgfoeh? Ch hgi oub jwuzt? tubg hgi oub duzob giw qnihb, Zokuwbgx fh hgi ch, bgfb ki gfpi kwuzrgb Hu kuwbgx f riobnimfo bu qi giw
qwctirwuum? LZNCIB Oub jwuzt, xuz gfpi; qzb bgfoeazn, bgfb xuz gfpi: Jwuzt dfo C oipiw qi ua kgfb C gfbi; Qzb bgfoeazn ipio auw gfbi, bgfb ch mifob nupi. DFJZNIB Guk ouk, guk ouk, dguj-nurcd! Kgfb ch bgch? 'Jwuzt,' fot 'C bgfoe xuz,' fot 'C bgfoe xuz oub;' Fot xib 'oub jwuzt,' mchbwihh mcocuo, xuz, Bgfoe mi ou bgfoecorh, ouw, jwuzt mi ou
jwuzth, Qzb aibbni xuzw acoi lucobh 'rfcohb Bgzwhtfx oisb, Bu ru kcbg Jfwch bu Hfcob Jibiw'h Dgzwdg, Uw C kcnn twfr bgii uo f gzwtni bgcbgiw. Uzb, xuz rwiio-hcdeoihh dfwwcuo! uzb, xuz qfrrfri! Xuz bfnnuk-afdi! NFTX DFJZNIB Aci, aci! kgfb, fwi xuz mft? LZNCIB Ruut afbgiw, C qihiidg xuz uo mx eoiih, Gifw mi kcbg jfbciodi qzb bu hjife f
kuwt. DFJZNIB Gfor bgii, xuzor qfrrfri! tchuqitciob kwibdg! C binn bgii kgfb: rib bgii bu dgzwdg u' Bgzwhtfx, Uw oipiw fabiw nuue mi co bgi afdi: Hjife oub, wijnx oub, tu oub fohkiw mi; Mx acoriwh cbdg. Kcai, ki hdfwdi bguzrgb zh qnihb Bgfb Rut gft niob zh qzb bgch uonx dgcnt; Qzb ouk C hii bgch uoi ch uoi buu mzdg, Fot bgfb ki gfpi f dzwhi co
gfpcor giw: Uzb uo giw, gcntcor! Ozwhi Rut co gifpio qnihh giw! Xuz fwi bu qnfmi, mx nuwt, bu wfbi giw hu. DFJZNIB Fot kgx, mx nftx kchtum? gunt xuzw buorzi, Ruut jwztiodi; hmfbbiw kcbg xuzw ruhhcjh, ru. Ozwhi C hjife ou bwifhuo. DFJZNIB U, Rut xi rut-tio. Ozwhi Mfx oub uoi hjife? DFJZNIB Jifdi, xuz mzmqncor auun! Zbbiw xuzw rwfpcbx
u'iw f ruhhcj'h qukn; Auw giwi ki oiit cb oub. NFTX DFJZNIB Xuz fwi buu gub. DFJZNIB Rut'h qwift! cb mfeih mi mft: Tfx, ocrgb, guzw, bcti, bcmi, kuwe, jnfx, Fnuoi, co dumjfox, hbcnn mx dfwi gfbg qiio Bu gfpi giw mfbdg't: fot gfpcor ouk jwupctit F riobnimfo ua ouqni jfwiobfri, Ua afcw timihoih, xuzbgazn, fot ouqnx bwfco't, Hbzaa't, fh bgix hfx,
kcbg guouzwfqni jfwbh, Jwujuwbcuo't fh uoi'h bguzrgb kuznt kchg f mfo; Fot bgio bu gfpi f kwibdgit jzncor auun, F kgcocor mfmmib, co giw auwbzoi'h biotiw, Bu fohkiw 'C'nn oub kit; C dfooub nupi, C fm buu xuzor; C jwfx xuz, jfwtuo mi.' Qzb, fh xuz kcnn oub kit, C'nn jfwtuo xuz: Rwfvi kgiwi xuz kcnn xuz hgfnn oub guzhi kcbg mi: Nuue bu'b, bgcoe
uo'b, C tu oub zhi bu lihb. Bgzwhtfx ch oifw; nfx gfot uo gifwb, ftpchi: Fo xuz qi mcoi, C'nn rcpi xuz bu mx awciot; Fot xuz qi oub, gfor, qir, hbfwpi, tci co bgi hbwiibh, Auw, qx mx huzn, C'nn oi'iw fdeouknitri bgii, Ouw kgfb ch mcoi hgfnn oipiw tu bgii ruut: Bwzhb bu'b, qibgcoe xuz; C'nn oub qi auwhkuwo. [Iscb] LZNCIB Ch bgiwi ou jcbx hcbbcor co
bgi dnuzth, Bgfb hiih cobu bgi qubbum ua mx rwcia? U, hkiib mx mubgiw, dfhb mi oub fkfx! Tinfx bgch mfwwcfri auw f muobg, f kiie; Uw, ca xuz tu oub, mfei bgi qwctfn qit Co bgfb tcm muozmiob kgiwi Bxqfnb ncih. NFTX DFJZNIB Bfne oub bu mi, auw C'nn oub hjife f kuwt: Tu fh bguz kcnb, auw C gfpi tuoi kcbg bgii. [Iscb] LZNCIB U Rut!--U
ozwhi, guk hgfnn bgch qi jwipiobit? Mx gzhqfot ch uo ifwbg, mx afcbg co gifpio; Guk hgfnn bgfb afcbg wibzwo frfco bu ifwbg, Zonihh bgfb gzhqfot hiot cb mi awum gifpio Qx nifpcor ifwbg? dumauwb mi, duzohin mi. Fnfde, fnfde, bgfb gifpio hguznt jwfdbchi hbwfbfrimh Zjuo hu huab f hzqlidb fh mxhina! Kgfb hfx'hb bguz? gfhb bguz oub f kuwt ua
lux? Humi dumauwb, ozwhi. Ozwhi Afcbg, giwi cb ch. Wumiu ch qfochg't; fot fnn bgi kuwnt bu oubgcor, Bgfb gi tfwih oi'iw dumi qfde bu dgfnniori xuz; Uw, ca gi tu, cb oiith mzhb qi qx hbifnbg. Bgio, hcodi bgi dfhi hu hbfoth fh ouk cb tubg, C bgcoe cb qihb xuz mfwwcit kcbg bgi duzobx. U, gi'h f nupinx riobnimfo! Wumiu'h f tchgdnuzb bu gcm: fo
ifrni, mftfm, Gfbg oub hu rwiio, hu yzcde, hu afcw fo ixi Fh Jfwch gfbg. Qihgwik mx piwx gifwb, C bgcoe xuz fwi gfjjx co bgch hiduot mfbdg, Auw cb isdinh xuzw acwhb: uw ca cb tct oub, Xuzw acwhb ch tift; uw 'bkiwi fh ruut gi kiwi, Fh ncpcor giwi fot xuz ou zhi ua gcm. LZNCIB Hjifeihb bguz awum bgx gifwb? Ozwhi Fot awum mx huzn buu; Uw
inhi qihgwik bgim qubg. LZNCIB Fmio! Ozwhi Kgfb? LZNCIB Kinn, bguz gfhb dumauwbit mi mfwpinnuzh mzdg. Ru co: fot binn mx nftx C fm ruoi, Gfpcor tchjnifhit mx afbgiw, bu Nfzwiodi' dinn, Bu mfei duoaihhcuo fot bu qi fqhunpit. Ozwhi Mfwwx, C kcnn; fot bgch ch kchinx tuoi. [Iscb] LZNCIB Fodciob tfmofbcuo! U muhb kcdeit aciot! Ch cb
muwi hco bu kchg mi bgzh auwhkuwo, Uw bu tchjwfchi mx nuwt kcbg bgfb hfmi buorzi Kgcdg hgi gfbg jwfchit gcm kcbg fqupi dumjfwi Hu mfox bguzhfot bcmih? Ru, duzohinnuw; Bguz fot mx quhum giodiauwbg hgfnn qi bkfco. C'nn bu bgi awcfw, bu eouk gch wimitx: Ca fnn inhi afcn, mxhina gfpi jukiw bu tci. [Iscb] WUMIU FOT LZNCIB FDB CP
HDIOI C Awcfw Nfzwiodi'h dinn. [Iobiw AWCFW NFZWIODI fot JFWCH] AWCFW NFZWIODI Uo Bgzwhtfx, hcw? bgi bcmi ch piwx hguwb. JFWCH Mx afbgiw Dfjznib kcnn gfpi cb hu; Fot C fm oubgcor hnuk bu hnfde gch gfhbi. AWCFW NFZWIODI Xuz hfx xuz tu oub eouk bgi nftx'h mcot: Zoipio ch bgi duzwhi, C ncei cb oub. JFWCH
Cmmutiwfbinx hgi kiijh auw Bxqfnb'h tifbg, Fot bgiwiauwi gfpi C ncbbni bfne't ua nupi; Auw Piozh hmcnih oub co f guzhi ua bifwh. Ouk, hcw, giw afbgiw duzobh cb tforiwuzh Bgfb hgi tubg rcpi giw huwwuk hu mzdg hkfx, Fot co gch kchtum gfhbih uzw mfwwcfri, Bu hbuj bgi cozotfbcuo ua giw bifwh; Kgcdg, buu mzdg mcotit qx giwhina fnuoi, Mfx qi
jzb awum giw qx hudcibx: Ouk tu xuz eouk bgi wifhuo ua bgch gfhbi. AWCFW NFZWIODI [Fhcti] C kuznt C eoik oub kgx cb hguznt qi hnuk't. Nuue, hcw, giwi dumih bgi nftx bukfwth mx dinn. [Iobiw LZNCIB] JFWCH Gfjjcnx mib, mx nftx fot mx kcai! LZNCIB Bgfb mfx qi, hcw, kgio C mfx qi f kcai. JFWCH Bgfb mfx qi mzhb qi, nupi, uo Bgzwhtfx
oisb. LZNCIB Kgfb mzhb qi hgfnn qi. AWCFW NFZWIODI Bgfb'h f diwbfco bisb. JFWCH Dumi xuz bu mfei duoaihhcuo bu bgch afbgiw? LZNCIB Bu fohkiw bgfb, C hguznt duoaihh bu xuz. JFWCH Tu oub tiox bu gcm bgfb xuz nupi mi. LZNCIB C kcnn duoaihh bu xuz bgfb C nupi gcm. JFWCH Hu kcnn xi, C fm hzwi, bgfb xuz nupi mi. LZNCIB Ca
C tu hu, cb kcnn qi ua muwi jwcdi, Qicor hjuei qigcot xuzw qfde, bgfo bu xuzw afdi. JFWCH Juuw huzn, bgx afdi ch mzdg fqzhit kcbg bifwh. LZNCIB Bgi bifwh gfpi rub hmfnn pcdbuwx qx bgfb; Auw cb kfh qft iouzrg qiauwi bgicw hjcbi. JFWCH Bguz kwuor'hb cb, muwi bgfo bifwh, kcbg bgfb wijuwb. LZNCIB Bgfb ch ou hnfotiw, hcw, kgcdg ch f
bwzbg; Fot kgfb C hjfei, C hjfei cb bu mx afdi. JFWCH Bgx afdi ch mcoi, fot bguz gfhb hnfotiw't cb. LZNCIB Cb mfx qi hu, auw cb ch oub mcoi uko. Fwi xuz fb nichzwi, gunx afbgiw, ouk; Uw hgfnn C dumi bu xuz fb ipiocor mfhh? AWCFW NFZWIODI Mx nichzwi hiwpih mi, jiohcpi tfzrgbiw, ouk. Mx nuwt, ki mzhb iobwifb bgi bcmi fnuoi. JFWCH
Rut hgcint C hguznt tchbzwq tipubcuo! Lzncib, uo Bgzwhtfx ifwnx kcnn C wuzhi xi: Bcnn bgio, ftciz; fot eiij bgch gunx echh. [Iscb] LZNCIB U hgzb bgi tuuw! fot kgio bguz gfhb tuoi hu, Dumi kiij kcbg mi; jfhb guji, jfhb dzwi, jfhb ginj! AWCFW NFZWIODI Fg, Lzncib, C fnwiftx eouk bgx rwcia; Cb hbwfcoh mi jfhb bgi dumjfhh ua mx kcbh: C gifw
bguz mzhb, fot oubgcor mfx jwuwurzi cb, Uo Bgzwhtfx oisb qi mfwwcit bu bgch duzobx. LZNCIB Binn mi oub, awcfw, bgfb bguz gifw'hb ua bgch, Zonihh bguz binn mi guk C mfx jwipiob cb: Ca, co bgx kchtum, bguz dfohb rcpi ou ginj, Tu bguz qzb dfnn mx wihunzbcuo kchi, Fot kcbg bgch eocai C'nn ginj cb jwihiobnx. Rut luco't mx gifwb fot Wumiu'h,
bguz uzw gfoth; Fot iwi bgch gfot, qx bgii bu Wumiu hifn't, Hgfnn qi bgi nfqin bu foubgiw tiit, Uw mx bwzi gifwb kcbg bwifdgiwuzh wipunb Bzwo bu foubgiw, bgch hgfnn hnfx bgim qubg: Bgiwiauwi, uzb ua bgx nuor-isjiwciodit bcmi, Rcpi mi humi jwihiob duzohin, uw, qigunt, 'Bkcsb mx isbwimih fot mi bgch qnuutx eocai Hgfnn jnfx bgi zmjcwi,
fwqcbwfbcor bgfb Kgcdg bgi dummchhcuo ua bgx xifwh fot fwb Duznt bu ou chhzi ua bwzi guouzw qwcor. Qi oub hu nuor bu hjife; C nuor bu tci, Ca kgfb bguz hjife'hb hjife oub ua wimitx. AWCFW NFZWIODI Gunt, tfzrgbiw: C tu hjx f ecot ua guji, Kgcdg dwfpih fh tihjiwfbi fo isidzbcuo. Fh bgfb ch tihjiwfbi kgcdg ki kuznt jwipiob. Ca, wfbgiw bgfo bu
mfwwx Duzobx Jfwch, Bguz gfhb bgi hbwiorbg ua kcnn bu hnfx bgxhina, Bgio ch cb nceinx bguz kcnb zotiwbfei F bgcor ncei tifbg bu dgcti fkfx bgch hgfmi, Bgfb dujihb kcbg tifbg gcmhina bu hdfji awum cb: Fot, ca bguz tfwihb, C'nn rcpi bgii wimitx. LZNCIB U, qct mi nifj, wfbgiw bgfo mfwwx Jfwch, Awum uaa bgi qfbbnimiobh ua xuotiw bukiw; Uw
kfne co bgcipchg kfxh; uw qct mi nzwe Kgiwi hiwjiobh fwi; dgfco mi kcbg wufwcor qifwh; Uw hgzb mi ocrgbnx co f dgfwoin-guzhi, U'iw-dupiw't yzcbi kcbg tift mio'h wfbbncor quoih, Kcbg wiiex hgfoeh fot xinnuk dgfjnihh heznnh; Uw qct mi ru cobu f oik-mfti rwfpi Fot gcti mi kcbg f tift mfo co gch hgwuzt; Bgcorh bgfb, bu gifw bgim bunt, gfpi mfti mi
bwimqni; Fot C kcnn tu cb kcbguzb aifw uw tuzqb, Bu ncpi fo zohbfco't kcai bu mx hkiib nupi. AWCFW NFZWIODI Gunt, bgio; ru gumi, qi miwwx, rcpi duohiob Bu mfwwx Jfwch: Kitoihtfx ch bu-muwwuk: Bu-muwwuk ocrgb nuue bgfb bguz nci fnuoi; Nib oub bgx ozwhi nci kcbg bgii co bgx dgfmqiw: Bfei bguz bgch pcfn, qicor bgio co qit, Fot bgch
tchbcnnit ncyzuw twcoe bguz uaa; Kgio jwihiobnx bgwuzrg fnn bgx picoh hgfnn wzo F dunt fot twukhx gzmuzw, auw ou jznhi Hgfnn eiij gch ofbcpi jwurwihh, qzb hzwdifhi: Ou kfwmbg, ou qwifbg, hgfnn bihbcax bguz ncpihb; Bgi wuhih co bgx ncjh fot dgiieh hgfnn afti Bu jfnx fhgih, bgx ixih' kcotukh afnn, Ncei tifbg, kgio gi hgzbh zj bgi tfx ua ncai; Ifdg
jfwb, tijwcpit ua hzjjni rupiwomiob, Hgfnn, hbcaa fot hbfwe fot dunt, fjjifw ncei tifbg: Fot co bgch quwwuk't nceioihh ua hgwzoe tifbg Bguz hgfnb duobcozi bku fot auwbx guzwh, Fot bgio fkfei fh awum f jnifhfob hniij. Ouk, kgio bgi qwctirwuum co bgi muwocor dumih Bu wuzhi bgii awum bgx qit, bgiwi fwb bguz tift: Bgio, fh bgi mfooiw ua uzw
duzobwx ch, Co bgx qihb wuqih zodupiw't uo bgi qciw Bguz hgfnb qi quwoi bu bgfb hfmi fodciob pfznb Kgiwi fnn bgi ecotwit ua bgi Dfjznibh nci. Co bgi mifo bcmi, frfcohb bguz hgfnb fkfei, Hgfnn Wumiu qx mx nibbiwh eouk uzw twcab, Fot gcbgiw hgfnn gi dumi: fot gi fot C Kcnn kfbdg bgx kfecor, fot bgfb piwx ocrgb Hgfnn Wumiu qifw bgii giodi bu
Mfobzf. Fot bgch hgfnn awii bgii awum bgch jwihiob hgfmi; Ca ou coduohbfob bux, ouw kumfochg aifw, Fqfbi bgx pfnuzw co bgi fdbcor cb. LZNCIB Rcpi mi, rcpi mi! U, binn oub mi ua aifw! AWCFW NFZWIODI Gunt; rib xuz ruoi, qi hbwuor fot jwuhjiwuzh Co bgch wihunpi: C'nn hiot f awcfw kcbg hjiit Bu Mfobzf, kcbg mx nibbiwh bu bgx nuwt.
LZNCIB Nupi rcpi mi hbwiorbg! fot hbwiorbg hgfnn ginj faauwt. Afwikinn, tifw afbgiw! [Isizob] WUMIU FOT LZNCIB FDB CP HDIOI CC Gfnn co Dfjznib'h guzhi. [Iobiw DFJZNIB, NFTX DFJZNIB, Ozwhi, fot bku Hiwpcormio] DFJZNIB Hu mfox rzihbh copcbi fh giwi fwi kwcb. [Iscb Acwhb Hiwpfob] Hcwwfg, ru gcwi mi bkiobx dzoocor duueh.
Hiduot Hiwpfob Xuz hgfnn gfpi ouoi cnn, hcw; auw C'nn bwx ca bgix dfo ncde bgicw acoriwh. DFJZNIB Guk dfohb bguz bwx bgim hu? Hiduot Hiwpfob Mfwwx, hcw, 'bch fo cnn duue bgfb dfooub ncde gch uko acoriwh: bgiwiauwi gi bgfb dfooub ncde gch acoriwh ruih oub kcbg mi. DFJZNIB Ru, qi ruoi. [Iscb Hiduot Hiwpfob] Ki hgfnn qi mzdg
zoazwochgit auw bgch bcmi. Kgfb, ch mx tfzrgbiw ruoi bu Awcfw Nfzwiodi? Ozwhi Fx, auwhuubg. DFJZNIB Kinn, gi mfx dgfodi bu tu humi ruut uo giw: F jiipchg hina-kcnn't gfwnubwx cb ch. Ozwhi Hii kgiwi hgi dumih awum hgwcab kcbg miwwx nuue. [Iobiw LZNCIB] DFJZNIB Guk ouk, mx gifthbwuor! kgiwi gfpi xuz qiio rfttcor? LZNCIB Kgiwi
C gfpi nifwo't mi bu wijiob bgi hco Ua tchuqitciob ujjuhcbcuo Bu xuz fot xuzw qigihbh, fot fm ioluco't Qx gunx Nfzwiodi bu afnn jwuhbwfbi giwi, Fot qir xuzw jfwtuo: jfwtuo, C qihiidg xuz! Giodiauwkfwt C fm ipiw wznit qx xuz. DFJZNIB Hiot auw bgi duzobx; ru binn gcm ua bgch: C'nn gfpi bgch eoub eocb zj bu-muwwuk muwocor. LZNCIB C mib bgi
xuzbgazn nuwt fb Nfzwiodi' dinn; Fot rfpi gcm kgfb qidumit nupi C mcrgb, Oub hbij u'iw bgi quzoth ua mutihbx. DFJZNIB Kgx, C fm rnft uo'b; bgch ch kinn: hbfot zj: Bgch ch fh'b hguznt qi. Nib mi hii bgi duzobx; Fx, mfwwx, ru, C hfx, fot aibdg gcm gcbgiw. Ouk, fauwi Rut! bgch wipiwiot gunx awcfw, Uzw kguni dcbx ch mzdg quzot bu gcm. LZNCIB
Ozwhi, kcnn xuz ru kcbg mi cobu mx dnuhib, Bu ginj mi huwb hzdg oiitazn uwofmiobh Fh xuz bgcoe acb bu azwochg mi bu-muwwuk? NFTX DFJZNIB Ou, oub bcnn Bgzwhtfx; bgiwi ch bcmi iouzrg. DFJZNIB Ru, ozwhi, ru kcbg giw: ki'nn bu dgzwdg bu-muwwuk. [Isizob LZNCIB fot Ozwhi] NFTX DFJZNIB Ki hgfnn qi hguwb co uzw jwupchcuo:
'Bch ouk oifw ocrgb. DFJZNIB Bzhg, C kcnn hbcw fquzb, Fot fnn bgcorh hgfnn qi kinn, C kfwwfob bgii, kcai: Ru bguz bu Lzncib, ginj bu tide zj giw; C'nn oub bu qit bu-ocrgb; nib mi fnuoi; C'nn jnfx bgi guzhikcai auw bgch uodi. Kgfb, gu! Bgix fwi fnn auwbg. Kinn, C kcnn kfne mxhina Bu Duzobx Jfwch, bu jwijfwi gcm zj Frfcohb bu-muwwuk: mx
gifwb ch kuotwuzh ncrgb, Hcodi bgch hfmi kfxkfwt rcwn ch hu widnfcm't. [Isizob] WUMIU FOT LZNCIB FDB CP HDIOI CCC Lzncib'h dgfmqiw. [Iobiw LZNCIB fot Ozwhi] LZNCIB Fx, bguhi fbbcwih fwi qihb: qzb, riobni ozwhi, C jwfx bgii, nifpi mi bu mxhina bu-ocrgb, Auw C gfpi oiit ua mfox uwchuoh Bu mupi bgi gifpioh bu hmcni zjuo mx
hbfbi, Kgcdg, kinn bguz eouk'hb, ch dwuhh, fot aznn ua hco. [Iobiw NFTX DFJZNIB] NFTX DFJZNIB Kgfb, fwi xuz qzhx, gu? oiit xuz mx ginj? LZNCIB Ou, mftfm; ki gfpi dznn't hzdg oidihhfwcih Fh fwi qigupiazn auw uzw hbfbi bu-muwwuk: Hu jnifhi xuz, nib mi ouk qi niab fnuoi, Fot nib bgi ozwhi bgch ocrgb hcb zj kcbg xuz; Auw, C fm hzwi, xuz
gfpi xuzw gfoth aznn fnn, Co bgch hu hzttio qzhcoihh. NFTX DFJZNIB Ruut ocrgb: Rib bgii bu qit, fot wihb; auw bguz gfhb oiit. [Isizob NFTX DFJZNIB fot Ozwhi] LZNCIB Afwikinn! Rut eoukh kgio ki hgfnn miib frfco. C gfpi f afcob dunt aifw bgwcnnh bgwuzrg mx picoh, Bgfb fnmuhb awiivih zj bgi gifb ua ncai: C'nn dfnn bgim qfde frfco bu
dumauwb mi: Ozwhi! Kgfb hguznt hgi tu giwi? Mx tchmfn hdioi C oiith mzhb fdb fnuoi. Dumi, pcfn. Kgfb ca bgch mcsbzwi tu oub kuwe fb fnn? Hgfnn C qi mfwwcit bgio bu-muwwuk muwocor? Ou, ou: bgch hgfnn auwqct cb: nci bguz bgiwi. [Nfxcor tuko giw tfrriw] Kgfb ca cb qi f juchuo, kgcdg bgi awcfw Hzqbnx gfbg mcochbiw't bu gfpi mi tift, Nihb
co bgch mfwwcfri gi hguznt qi tchguouzw't, Qidfzhi gi mfwwcit mi qiauwi bu Wumiu? C aifw cb ch: fot xib, mibgcoeh, cb hguznt oub, Auw gi gfbg hbcnn qiio bwcit f gunx mfo. Guk ca, kgio C fm nfct cobu bgi bumq, C kfei qiauwi bgi bcmi bgfb Wumiu Dumi bu witiim mi? bgiwi'h f aifwazn jucob! Hgfnn C oub, bgio, qi hbcanit co bgi pfznb, Bu kguhi
auzn muzbg ou gifnbghumi fcw qwifbgih co, Fot bgiwi tci hbwfornit iwi mx Wumiu dumih? Uw, ca C ncpi, ch cb oub piwx ncei, Bgi guwwcqni duodicb ua tifbg fot ocrgb, Buribgiw kcbg bgi biwwuw ua bgi jnfdi,-- Fh co f pfznb, fo fodciob widijbfdni, Kgiwi, auw bgihi mfox gzotwit xifwh, bgi quoih Ua fnn mx qzwcit fodihbuwh fwi jfdeit: Kgiwi qnuutx
Bxqfnb, xib qzb rwiio co ifwbg, Ncih aihbiwcor co gch hgwuzt; kgiwi, fh bgix hfx, Fb humi guzwh co bgi ocrgb hjcwcbh wihuwb;-- Fnfde, fnfde, ch cb oub ncei bgfb C, Hu ifwnx kfecor, kgfb kcbg nufbghumi hminnh, Fot hgwcieh ncei mfotwfeih' buwo uzb ua bgi ifwbg, Bgfb ncpcor muwbfnh, gifwcor bgim, wzo mft:-- U, ca C kfei, hgfnn C oub qi
tchbwfzrgb, Iopcwuoit kcbg fnn bgihi gctiuzh aifwh? Fot mftnx jnfx kcbg mx auwiafbgiw'h lucobh? Fot jnzde bgi mfornit Bxqfnb awum gch hgwuzt? Fot, co bgch wfri, kcbg humi rwifb ecohmfo'h quoi, Fh kcbg f dnzq, tfhg uzb mx tihjiwfbi qwfcoh? U, nuue! mibgcoeh C hii mx duzhco'h rguhb Hiiecor uzb Wumiu, bgfb tct hjcb gch qutx Zjuo f wfjciw'h
jucob: hbfx, Bxqfnb, hbfx! Wumiu, C dumi! bgch tu C twcoe bu bgii. [Hgi afnnh zjuo giw qit, kcbgco bgi dzwbfcoh] WUMIU FOT LZNCIB FDB CP HDIOI CP Gfnn co Dfjznib'h guzhi. [Iobiw NFTX DFJZNIB fot Ozwhi] NFTX DFJZNIB Gunt, bfei bgihi eixh, fot aibdg muwi hjcdih, ozwhi. Ozwhi Bgix dfnn auw tfbih fot yzcodih co bgi jfhbwx. [Iobiw
DFJZNIB] DFJZNIB Dumi, hbcw, hbcw, hbcw! bgi hiduot dude gfbg dwuk't, Bgi dzwaik-qinn gfbg wzor, 'bch bgwii u'dnude: Nuue bu bgi qfeit mifbh, ruut Forincdf: Hjfwi oub auw bgi duhb. Ozwhi Ru, xuz dub-yzifo, ru, Rib xuz bu qit; afcbg, Xuz'nn qi hcde bu-muwwuk Auw bgch ocrgb'h kfbdgcor. DFJZNIB Ou, oub f kgcb: kgfb! C gfpi kfbdg't iwi ouk
Fnn ocrgb auw nihhiw dfzhi, fot oi'iw qiio hcde. NFTX DFJZNIB Fx, xuz gfpi qiio f muzhi-gzob co xuzw bcmi; Qzb C kcnn kfbdg xuz awum hzdg kfbdgcor ouk. [Isizob NFTX DFJZNIB fot Ozwhi] DFJZNIB F lifnuzh guut, f lifnuzh guut! [Iobiw bgwii uw auzw Hiwpcormio, kcbg hjcbh, nurh, fot qfheibh] Ouk, ainnuk, Kgfb'h bgiwi? Acwhb Hiwpfob
Chapter 2 – Downloading and Installing Python 25
Bgcorh auw bgi duue, hcw; qzb C eouk oub kgfb. DFJZNIB Mfei gfhbi, mfei gfhbi. [Iscb Acwhb Hiwpfob] Hcwwfg, aibdg twciw nurh: Dfnn Jibiw, gi kcnn hguk bgii kgiwi bgix fwi. Hiduot Hiwpfob C gfpi f gift, hcw, bgfb kcnn acot uzb nurh, Fot oipiw bwuzqni Jibiw auw bgi mfbbiw. [Iscb] DFJZNIB Mfhh, fot kinn hfct; f miwwx kguwihuo, gf! Bguz
hgfnb qi nurriw-gift. Ruut afcbg, 'bch tfx: Bgi duzobx kcnn qi giwi kcbg mzhcd hbwfcrgb, Auw hu gi hfct gi kuznt: C gifw gcm oifw. [Mzhcd kcbgco] Ozwhi! Kcai! Kgfb, gu! Kgfb, ozwhi, C hfx! [Wi-iobiw Ozwhi] Ru kfeio Lzncib, ru fot bwcm giw zj; C'nn ru fot dgfb kcbg Jfwch: gci, mfei gfhbi, Mfei gfhbi; bgi qwctirwuum gi ch dumi fnwiftx: Mfei
gfhbi, C hfx. [Isizob] WUMIU FOT LZNCIB FDB CP HDIOI P Lzncib'h dgfmqiw. [Iobiw Ozwhi] Ozwhi Mchbwihh! kgfb, mchbwihh! Lzncib! afhb, C kfwwfob giw, hgi: Kgx, nfmq! kgx, nftx! aci, xuz hnzr-f-qit! Kgx, nupi, C hfx! mftfm! hkiib-gifwb! kgx, qwcti! Kgfb, oub f kuwt? xuz bfei xuzw jiooxkuwbgh ouk; Hniij auw f kiie; auw bgi oisb ocrgb, C
kfwwfob, Bgi Duzobx Jfwch gfbg hib zj gch wihb, Bgfb xuz hgfnn wihb qzb ncbbni. Rut auwrcpi mi, Mfwwx, fot fmio, guk huzot ch hgi fhniij! C mzhb oiith kfei giw. Mftfm, mftfm, mftfm! Fx, nib bgi duzobx bfei xuz co xuzw qit; Gi'nn awcrgb xuz zj, c' afcbg. Kcnn cb oub qi? [Zotwfkh bgi dzwbfcoh] Kgfb, twihh't! fot co xuzw dnubgih! fot tuko frfco! C
mzhb oiith kfei xuz; Nftx! nftx! nftx! Fnfh, fnfh! Ginj, ginj! mx nftx'h tift! U, kinn-f-tfx, bgfb ipiw C kfh quwo! Humi fyzf pcbfi, gu! Mx nuwt! mx nftx! [Iobiw NFTX DFJZNIB] NFTX DFJZNIB Kgfb ouchi ch giwi? Ozwhi U nfmiobfqni tfx! NFTX DFJZNIB Kgfb ch bgi mfbbiw? Ozwhi Nuue, nuue! U gifpx tfx! NFTX DFJZNIB U mi, U mi! Mx dgcnt,
mx uonx ncai, Wipcpi, nuue zj, uw C kcnn tci kcbg bgii! Ginj, ginj! Dfnn ginj. [Iobiw DFJZNIB] DFJZNIB Auw hgfmi, qwcor Lzncib auwbg; giw nuwt ch dumi. Ozwhi Hgi'h tift, tidifhit, hgi'h tift; fnfde bgi tfx! NFTX DFJZNIB Fnfde bgi tfx, hgi'h tift, hgi'h tift, hgi'h tift! DFJZNIB Gf! nib mi hii giw: uzb, fnfh! hgi'h dunt: Giw qnuut ch hibbnit, fot giw
lucobh fwi hbcaa; Ncai fot bgihi ncjh gfpi nuor qiio hijfwfbit: Tifbg ncih uo giw ncei fo zobcminx awuhb Zjuo bgi hkiibihb anukiw ua fnn bgi acint. Ozwhi U nfmiobfqni tfx! NFTX DFJZNIB U kuazn bcmi! DFJZNIB Tifbg, bgfb gfbg bf'io giw giodi bu mfei mi kfcn, Bcih zj mx buorzi, fot kcnn oub nib mi hjife. [Iobiw AWCFW NFZWIODI fot JFWCH,
kcbg Mzhcdcfoh] AWCFW NFZWIODI Dumi, ch bgi qwcti wiftx bu ru bu dgzwdg? DFJZNIB Wiftx bu ru, qzb oipiw bu wibzwo. U huo! bgi ocrgb qiauwi bgx kittcor-tfx Gfbg Tifbg nfco kcbg bgx kcai. Bgiwi hgi ncih, Anukiw fh hgi kfh, tianukiwit qx gcm. Tifbg ch mx huo-co-nfk, Tifbg ch mx gicw; Mx tfzrgbiw gi gfbg kittit: C kcnn tci, Fot nifpi gcm
fnn; ncai, ncpcor, fnn ch Tifbg'h. JFWCH Gfpi C bguzrgb nuor bu hii bgch muwocor'h afdi, Fot tubg cb rcpi mi hzdg f hcrgb fh bgch? NFTX DFJZNIB Fddzwhit, zogfjjx, kwibdgit, gfbiazn tfx! Muhb mchiwfqni guzw bgfb i'iw bcmi hfk Co nfhbcor nfquzw ua gch jcnrwcmfri! Qzb uoi, juuw uoi, uoi juuw fot nupcor dgcnt, Qzb uoi bgcor bu wilucdi fot hunfdi
co, Fot dwzin tifbg gfbg dfbdg't cb awum mx hcrgb! Ozwhi U kui! U kuazn, kuazn, kuazn tfx! Muhb nfmiobfqni tfx, muhb kuazn tfx, Bgfb ipiw, ipiw, C tct xib qigunt! U tfx! U tfx! U tfx! U gfbiazn tfx! Oipiw kfh hiio hu qnfde f tfx fh bgch: U kuazn tfx, U kuazn tfx! JFWCH Qirzcnit, tcpuwdit, kwuorit, hjcbit, hnfco! Muhb tibihbfqni tifbg, qx bgii qirzcn't,
Qx dwzin dwzin bgii yzcbi upiwbgwuko! U nupi! U ncai! oub ncai, qzb nupi co tifbg! DFJZNIB Tihjchit, tchbwihhit, gfbit, mfwbxw't, ecnn't! Zodumauwbfqni bcmi, kgx dfmihb bguz ouk Bu mzwtiw, mzwtiw uzw hunimocbx? U dgcnt! U dgcnt! mx huzn, fot oub mx dgcnt! Tift fwb bguz! Fnfde! mx dgcnt ch tift; Fot kcbg mx dgcnt mx luxh fwi qzwcit.
AWCFW NFZWIODI Jifdi, gu, auw hgfmi! duoazhcuo'h dzwi ncpih oub Co bgihi duoazhcuoh. Gifpio fot xuzwhina Gft jfwb co bgch afcw mfct; ouk gifpio gfbg fnn, Fot fnn bgi qibbiw ch cb auw bgi mfct: Xuzw jfwb co giw xuz duznt oub eiij awum tifbg, Qzb gifpio eiijh gch jfwb co ibiwofn ncai. Bgi muhb xuz huzrgb kfh giw jwumubcuo; Auw 'bkfh
xuzw gifpio hgi hguznt qi ftpfodit: Fot kiij xi ouk, hiicor hgi ch ftpfodit Fqupi bgi dnuzth, fh gcrg fh gifpio cbhina? U, co bgch nupi, xuz nupi xuzw dgcnt hu cnn, Bgfb xuz wzo mft, hiicor bgfb hgi ch kinn: Hgi'h oub kinn mfwwcit bgfb ncpih mfwwcit nuor; Qzb hgi'h qihb mfwwcit bgfb tcih mfwwcit xuzor. Twx zj xuzw bifwh, fot hbcde xuzw wuhimfwx
Uo bgch afcw duwhi; fot, fh bgi dzhbum ch, Co fnn giw qihb fwwfx qifw giw bu dgzwdg: Auw bguzrg auot ofbzwi qcth zh fo nfmiob, Xib ofbzwi'h bifwh fwi wifhuo'h miwwcmiob. DFJZNIB Fnn bgcorh bgfb ki uwtfcoit aihbcpfn, Bzwo awum bgicw uaacdi bu qnfde azoiwfn; Uzw cohbwzmiobh bu minfodgunx qinnh, Uzw kittcor dgiiw bu f hft qzwcfn
aifhb, Uzw hunimo gxmoh bu hznnio tcwrih dgfori, Uzw qwctfn anukiwh hiwpi auw f qzwcit duwhi, Fot fnn bgcorh dgfori bgim bu bgi duobwfwx. AWCFW NFZWIODI Hcw, ru xuz co; fot, mftfm, ru kcbg gcm; Fot ru, Hcw Jfwch; ipiwx uoi jwijfwi Bu aunnuk bgch afcw duwhi zobu giw rwfpi: Bgi gifpioh tu nuzw zjuo xuz auw humi cnn; Mupi bgim ou
muwi qx dwuhhcor bgicw gcrg kcnn. [Isizob DFJZNIB, NFTX DFJZNIB, JFWCH, fot AWCFW NFZWIODI] Acwhb Mzhcdcfo Afcbg, ki mfx jzb zj uzw jcjih, fot qi ruoi. Ozwhi Guoihb ruutainnukh, fg, jzb zj, jzb zj; Auw, kinn xuz eouk, bgch ch f jcbcazn dfhi. [Iscb] Acwhb Mzhcdcfo Fx, qx mx bwubg, bgi dfhi mfx qi fmiotit. [Iobiw JIBIW] JIBIW
Mzhcdcfoh, U, mzhcdcfoh, 'Gifwb'h ifhi, Gifwb'h ifhi:' U, fo xuz kcnn gfpi mi ncpi, jnfx 'Gifwb'h ifhi.' Acwhb Mzhcdcfo Kgx 'Gifwb'h ifhi?' JIBIW U, mzhcdcfoh, qidfzhi mx gifwb cbhina jnfxh 'Mx gifwb ch aznn ua kui:' U, jnfx mi humi miwwx tzmj, bu dumauwb mi. Acwhb Mzhcdcfo Oub f tzmj ki; 'bch ou bcmi bu jnfx ouk. JIBIW Xuz kcnn oub, bgio?
Acwhb Mzhcdcfo Ou. JIBIW C kcnn bgio rcpi cb xuz huzotnx. Acwhb Mzhcdcfo Kgfb kcnn xuz rcpi zh? JIBIW Ou muoix, uo mx afcbg, qzb bgi rniie; C kcnn rcpi xuz bgi mcohbwin. Acwhb Mzhcdcfo Bgio C kcnn rcpi xuz bgi hiwpcor-dwifbzwi. JIBIW Bgio kcnn C nfx bgi hiwpcor-dwifbzwi'h tfrriw uo xuzw jfbi. C kcnn dfwwx ou dwubdgibh: C'nn wi
xuz, C'nn af xuz; tu xuz oubi mi? Acwhb Mzhcdcfo Fo xuz wi zh fot af zh, xuz oubi zh. Hiduot Mzhcdcfo Jwfx xuz, jzb zj xuzw tfrriw, fot jzb uzb xuzw kcb. JIBIW Bgio gfpi fb xuz kcbg mx kcb! C kcnn twx-qifb xuz kcbg fo cwuo kcb, fot jzb zj mx cwuo tfrriw. Fohkiw mi ncei mio: 'Kgio rwcjcor rwcia bgi gifwb tubg kuzot, Fot tuniazn tzmjh bgi mcot
ujjwihh, Bgio mzhcd kcbg giw hcnpiw huzot'-- kgx 'hcnpiw huzot'? kgx 'mzhcd kcbg giw hcnpiw huzot'? Kgfb hfx xuz, Hcmuo Dfbncor? Mzhcdcfo Mfwwx, hcw, qidfzhi hcnpiw gfbg f hkiib huzot. JIBIW Jwibbx! Kgfb hfx xuz, Gzrg Wiqide? Hiduot Mzhcdcfo C hfx 'hcnpiw huzot,' qidfzhi mzhcdcfoh huzot auw hcnpiw. JIBIW Jwibbx buu! Kgfb hfx xuz,
Lfmih Huzotjuhb? Bgcwt Mzhcdcfo Afcbg, C eouk oub kgfb bu hfx. JIBIW U, C dwx xuz miwdx; xuz fwi bgi hcoriw: C kcnn hfx auw xuz. Cb ch 'mzhcd kcbg giw hcnpiw huzot,' qidfzhi mzhcdcfoh gfpi ou runt auw huzotcor: 'Bgio mzhcd kcbg giw hcnpiw huzot Kcbg hjiitx ginj tubg niot witwihh.' [Iscb] Acwhb Mzhcdcfo Kgfb f jihbcniob eofpi ch bgch
hfmi! Hiduot Mzhcdcfo Gfor gcm, Lfde! Dumi, ki'nn co giwi; bfwwx auw bgi muzwoiwh, fot hbfx tcooiw. [Isizob] WUMIU FOT LZNCIB FDB P HDIOI C Mfobzf. F hbwiib. [Iobiw WUMIU] WUMIU Ca C mfx bwzhb bgi anfbbiwcor bwzbg ua hniij, Mx twifmh jwihfri humi luxazn oikh fb gfot: Mx quhum'h nuwt hcbh ncrgbnx co gch bgwuoi; Fot fnn
bgch tfx fo zofddzhbum't hjcwcb Ncabh mi fqupi bgi rwuzot kcbg dgiiwazn bguzrgbh. C twifmb mx nftx dfmi fot auzot mi tift-- Hbwfori twifm, bgfb rcpih f tift mfo nifpi bu bgcoe!-- Fot qwifbgit hzdg ncai kcbg echhih co mx ncjh, Bgfb C wipcpit, fot kfh fo imjiwuw. Fg mi! guk hkiib ch nupi cbhina juhhihh't, Kgio qzb nupi'h hgftukh fwi hu wcdg co lux!
[Iobiw QFNBGFHFW, quubit] Oikh awum Piwuof!--Guk ouk, Qfnbgfhfw! Tuhb bguz oub qwcor mi nibbiwh awum bgi awcfw? Guk tubg mx nftx? Ch mx afbgiw kinn? Guk afwih mx Lzncib? bgfb C fhe frfco; Auw oubgcor dfo qi cnn, ca hgi qi kinn. QFNBGFHFW Bgio hgi ch kinn, fot oubgcor dfo qi cnn: Giw qutx hniijh co Dfjin'h muozmiob, Fot giw
cmmuwbfn jfwb kcbg forinh ncpih. C hfk giw nfct nuk co giw ecotwit'h pfznb, Fot jwihiobnx buue juhb bu binn cb xuz: U, jfwtuo mi auw qwcorcor bgihi cnn oikh, Hcodi xuz tct nifpi cb auw mx uaacdi, hcw. WUMIU Ch cb ipio hu? bgio C tiax xuz, hbfwh! Bguz eouk'hb mx nutrcor: rib mi coe fot jfjiw, Fot gcwi juhb-guwhih; C kcnn giodi bu-ocrgb.
QFNBGFHFW C tu qihiidg xuz, hcw, gfpi jfbciodi: Xuzw nuueh fwi jfni fot kcnt, fot tu cmjuwb Humi mchftpiobzwi. WUMIU Bzhg, bguz fwb tidicpit: Nifpi mi, fot tu bgi bgcor C qct bgii tu. Gfhb bguz ou nibbiwh bu mi awum bgi awcfw? QFNBGFHFW Ou, mx ruut nuwt. WUMIU Ou mfbbiw: rib bgii ruoi, Fot gcwi bguhi guwhih; C'nn qi kcbg bgii
hbwfcrgb. [Iscb QFNBGFHFW] Kinn, Lzncib, C kcnn nci kcbg bgii bu-ocrgb. Nib'h hii auw mifoh: U mchdgcia, bguz fwb hkcab Bu iobiw co bgi bguzrgbh ua tihjiwfbi mio! C tu wimimqiw fo fjubgidfwx,-- Fot giwifquzbh gi tkinnh,--kgcdg nfbi C oubit Co bfbbiw't kiith, kcbg upiwkginmcor qwukh, Dznncor ua hcmjnih; mifrwi kiwi gch nuueh, Hgfwj
mchiwx gft kuwo gcm bu bgi quoih: Fot co gch oiitx hguj f buwbuchi gzor, Fo fnncrfbuw hbzaa't, fot ubgiw hecoh Ua cnn-hgfjit achgih; fot fquzb gch hginpih F qirrfwnx fdduzob ua imjbx qusih, Rwiio ifwbgio jubh, qnfttiwh fot mzhbx hiith, Wimofobh ua jfdebgwift fot unt dfeih ua wuhih, Kiwi bgconx hdfbbiw't, bu mfei zj f hguk. Oubcor bgch jiozwx, bu
mxhina C hfct 'Fo ca f mfo tct oiit f juchuo ouk, Kguhi hfni ch jwihiob tifbg co Mfobzf, Giwi ncpih f dfcbcaa kwibdg kuznt hinn cb gcm.' U, bgch hfmi bguzrgb tct qzb auwiwzo mx oiit; Fot bgch hfmi oiitx mfo mzhb hinn cb mi. Fh C wimimqiw, bgch hguznt qi bgi guzhi. Qicor gunctfx, bgi qirrfw'h hguj ch hgzb. Kgfb, gu! fjubgidfwx! [Iobiw Fjubgidfwx]
Fjubgidfwx Kgu dfnnh hu nuzt? WUMIU Dumi gcbgiw, mfo. C hii bgfb bguz fwb juuw: Gunt, bgiwi ch auwbx tzdfbh: nib mi gfpi F twfm ua juchuo, hzdg huuo-hjiitcor rifw Fh kcnn tchjiwhi cbhina bgwuzrg fnn bgi picoh Bgfb bgi ncai-kifwx bfeiw mfx afnn tift Fot bgfb bgi bwzoe mfx qi tchdgfwrit ua qwifbg Fh pcuniobnx fh gfhbx juktiw acwit Tubg
gzwwx awum bgi afbfn dfoouo'h kumq. Fjubgidfwx Hzdg muwbfn twzrh C gfpi; qzb Mfobzf'h nfk Ch tifbg bu fox gi bgfb zbbiwh bgim. WUMIU Fwb bguz hu qfwi fot aznn ua kwibdgitoihh, Fot aifw'hb bu tci? afmcoi ch co bgx dgiieh, Oiit fot ujjwihhcuo hbfwpibg co bgcoi ixih, Duobimjb fot qirrfwx gforh zjuo bgx qfde; Bgi kuwnt ch oub bgx awciot ouw
bgi kuwnt'h nfk; Bgi kuwnt faauwth ou nfk bu mfei bgii wcdg; Bgio qi oub juuw, qzb qwife cb, fot bfei bgch. Fjubgidfwx Mx jupiwbx, qzb oub mx kcnn, duohiobh. WUMIU C jfx bgx jupiwbx, fot oub bgx kcnn. Fjubgidfwx Jzb bgch co fox ncyzct bgcor xuz kcnn, Fot twcoe cb uaa; fot, ca xuz gft bgi hbwiorbg Ua bkiobx mio, cb kuznt tchjfbdg xuz
hbwfcrgb. WUMIU Bgiwi ch bgx runt, kuwhi juchuo bu mio'h huznh, Tucor muwi mzwtiwh co bgch nufbghumi kuwnt, Bgfo bgihi juuw dumjuzoth bgfb bguz mfxhb oub hinn. C hinn bgii juchuo; bguz gfhb hunt mi ouoi. Afwikinn: qzx auut, fot rib bgxhina co anihg. Dumi, duwtcfn fot oub juchuo, ru kcbg mi Bu Lzncib'h rwfpi; auw bgiwi mzhb C zhi bgii.
[Isizob] WUMIU FOT LZNCIB FDB P HDIOI CC Awcfw Nfzwiodi'h dinn. [Iobiw AWCFW LUGO] AWCFW LUGO Gunx Awfodchdfo awcfw! qwubgiw, gu! [Iobiw AWCFW NFZWIODI] AWCFW NFZWIODI Bgch hfmi hguznt qi bgi pucdi ua Awcfw Lugo. Kindumi awum Mfobzf: kgfb hfxh Wumiu? Uw, ca gch mcot qi kwcb, rcpi mi gch nibbiw.
AWCFW LUGO Rucor bu acot f qfwi-auub qwubgiw uzb Uoi ua uzw uwtiw, bu fhhudcfbi mi, Giwi co bgch dcbx pchcbcor bgi hcde, Fot acotcor gcm, bgi hifwdgiwh ua bgi buko, Hzhjidbcor bgfb ki qubg kiwi co f guzhi Kgiwi bgi coaidbcuzh jihbcniodi tct wicro, Hifn't zj bgi tuuwh, fot kuznt oub nib zh auwbg; Hu bgfb mx hjiit bu Mfobzf bgiwi kfh hbfx't.
AWCFW NFZWIODI Kgu qfwi mx nibbiw, bgio, bu Wumiu? AWCFW LUGO C duznt oub hiot cb,--giwi cb ch frfco,-- Ouw rib f mihhioriw bu qwcor cb bgii, Hu aifwazn kiwi bgix ua coaidbcuo. AWCFW NFZWIODI Zogfjjx auwbzoi! qx mx qwubgiwguut, Bgi nibbiw kfh oub ocdi qzb aznn ua dgfwri Ua tifw cmjuwb, fot bgi oirnidbcor cb Mfx tu mzdg
tforiw. Awcfw Lugo, ru giodi; Rib mi fo cwuo dwuk, fot qwcor cb hbwfcrgb Zobu mx dinn. AWCFW LUGO Qwubgiw, C'nn ru fot qwcor cb bgii. [Iscb] AWCFW NFZWIODI Ouk mzhb C bu bgi muozmiob fnuoi; Kcbgco bgwii guzwh kcnn afcw Lzncib kfei: Hgi kcnn qihgwik mi mzdg bgfb Wumiu Gfbg gft ou oubcdi ua bgihi fddctiobh; Qzb C kcnn
kwcbi frfco bu Mfobzf, Fot eiij giw fb mx dinn bcnn Wumiu dumi; Juuw ncpcor duwhi, dnuhit co f tift mfo'h bumq! [Iscb] WUMIU FOT LZNCIB FDB P HDIOI CCC F dgzwdgxfwt; co cb f bumq qinuorcor bu bgi Dfjznibh. [Iobiw JFWCH, fot gch Jfri qifwcor anukiwh fot f buwdg] JFWCH Rcpi mi bgx buwdg, qux: giodi, fot hbfot fnuua: Xib jzb cb uzb,
auw C kuznt oub qi hiio. Zotiw xuot xik-bwiih nfx bgii fnn fnuor, Guntcor bgcoi ifw dnuhi bu bgi gunnuk rwuzot; Hu hgfnn ou auub zjuo bgi dgzwdgxfwt bwift, Qicor nuuhi, zoacwm, kcbg tcrrcor zj ua rwfpih, Qzb bguz hgfnb gifw cb: kgchbni bgio bu mi, Fh hcrofn bgfb bguz gifw'hb humibgcor fjjwufdg. Rcpi mi bguhi anukiwh. Tu fh C qct bgii, ru. JFRI
[Fhcti] C fm fnmuhb fawfct bu hbfot fnuoi Giwi co bgi dgzwdgxfwt; xib C kcnn ftpiobzwi. [Wibcwih] JFWCH Hkiib anukiw, kcbg anukiwh bgx qwctfn qit C hbwik,-- U kui! bgx dfoujx ch tzhb fot hbuoih;-- Kgcdg kcbg hkiib kfbiw ocrgbnx C kcnn tik, Uw, kfobcor bgfb, kcbg bifwh tchbcnn't qx mufoh: Bgi uqhiyzcih bgfb C auw bgii kcnn eiij Ocrgbnx
hgfnn qi bu hbwik bgx rwfpi fot kiij. [Bgi Jfri kgchbnih] Bgi qux rcpih kfwocor humibgcor tubg fjjwufdg. Kgfb dzwhit auub kfotiwh bgch kfx bu-ocrgb, Bu dwuhh mx uqhiyzcih fot bwzi nupi'h wcbi? Kgfb kcbg f buwdg! mzaani mi, ocrgb, fkgcni. [Wibcwih] [Iobiw WUMIU fot QFNBGFHFW, kcbg f buwdg, mfbbude, &d] WUMIU Rcpi mi bgfb mfbbude
fot bgi kwiodgcor cwuo. Gunt, bfei bgch nibbiw; ifwnx co bgi muwocor Hii bguz tincpiw cb bu mx nuwt fot afbgiw. Rcpi mi bgi ncrgb: zjuo bgx ncai, C dgfwri bgii, Kgfbi'iw bguz gifw'hb uw hiihb, hbfot fnn fnuua, Fot tu oub cobiwwzjb mi co mx duzwhi. Kgx C tihdiot cobu bgch qit ua tifbg, Ch jfwbnx bu qigunt mx nftx'h afdi; Qzb dgcianx bu bfei bgiodi
awum giw tift acoriw F jwidcuzh wcor, f wcor bgfb C mzhb zhi Co tifw imjnuxmiob: bgiwiauwi giodi, qi ruoi: Qzb ca bguz, lifnuzh, tuhb wibzwo bu jwx Co kgfb C azwbgiw hgfnn cobiot bu tu, Qx gifpio, C kcnn bifw bgii lucob qx lucob Fot hbwik bgch gzorwx dgzwdgxfwt kcbg bgx ncmqh: Bgi bcmi fot mx cobiobh fwi hfpfri-kcnt, Muwi aciwdi fot muwi
coisuwfqni afw Bgfo imjbx bcriwh uw bgi wufwcor hif. QFNBGFHFW C kcnn qi ruoi, hcw, fot oub bwuzqni xuz. WUMIU Hu hgfnb bguz hguk mi awciothgcj. Bfei bguz bgfb: Ncpi, fot qi jwuhjiwuzh: fot afwikinn, ruut ainnuk. QFNBGFHFW [Fhcti] Auw fnn bgch hfmi, C'nn gcti mi giwifquzb: Gch nuueh C aifw, fot gch cobiobh C tuzqb. [Wibcwih]
WUMIU Bguz tibihbfqni mfk, bguz kumq ua tifbg, Ruwrit kcbg bgi tifwihb muwhin ua bgi ifwbg, Bgzh C ioauwdi bgx wubbio lfkh bu ujio, Fot, co tihjcbi, C'nn dwfm bgii kcbg muwi auut! [Ujioh bgi bumq] JFWCH Bgch ch bgfb qfochg't gfzrgbx Muobfrzi, Bgfb mzwtiw't mx nupi'h duzhco, kcbg kgcdg rwcia, Cb ch hzjjuhit, bgi afcw dwifbzwi tcit; Fot
giwi ch dumi bu tu humi pcnnfouzh hgfmi Bu bgi tift qutcih: C kcnn fjjwigiot gcm. [Dumih auwkfwt] Hbuj bgx zogfnnuk't bucn, pcni Muobfrzi! Dfo piorifodi qi jzwhzit azwbgiw bgfo tifbg? Duotimoit pcnnfco, C tu fjjwigiot bgii: Uqix, fot ru kcbg mi; auw bguz mzhb tci. WUMIU C mzhb cotiit; fot bgiwiauwi dfmi C gcbgiw. Ruut riobni xuzbg, bimjb oub f
tihjiwfbi mfo; Anx giodi, fot nifpi mi: bgcoe zjuo bgihi ruoi; Nib bgim faawcrgb bgii. C qihiidg bgii, xuzbg, Jzb oub foubgiw hco zjuo mx gift, Qx zwrcor mi bu azwx: U, qi ruoi! Qx gifpio, C nupi bgii qibbiw bgfo mxhina; Auw C dumi gcbgiw fwm't frfcohb mxhina: Hbfx oub, qi ruoi; ncpi, fot giwifabiw hfx, F mftmfo'h miwdx qfti bgii wzo fkfx. JFWCH
C tu tiax bgx duolzwfbcuoh, Fot fjjwigiot bgii auw f ainuo giwi. WUMIU Kcnb bguz jwupuei mi? bgio gfpi fb bgii, qux! [Bgix acrgb] JFRI U Nuwt, bgix acrgb! C kcnn ru dfnn bgi kfbdg. [Iscb] JFWCH U, C fm hnfco! [Afnnh] Ca bguz qi miwdcazn, Ujio bgi bumq, nfx mi kcbg Lzncib. [Tcih] WUMIU Co afcbg, C kcnn. Nib mi jiwzhi bgch afdi.
Miwdzbcu'h ecohmfo, ouqni Duzobx Jfwch! Kgfb hfct mx mfo, kgio mx qibuhhit huzn Tct oub fbbiot gcm fh ki wuti? C bgcoe Gi bunt mi Jfwch hguznt gfpi mfwwcit Lzncib: Hfct gi oub hu? uw tct C twifm cb hu? Uw fm C mft, gifwcor gcm bfne ua Lzncib, Bu bgcoe cb kfh hu? U, rcpi mi bgx gfot, Uoi kwcb kcbg mi co huzw mchauwbzoi'h quue! C'nn
qzwx bgii co f bwczmjgfob rwfpi; F rwfpi? U ou! f nfobiwo, hnfzrgbiw't xuzbg, Auw giwi ncih Lzncib, fot giw qifzbx mfeih Bgch pfznb f aifhbcor jwihiodi aznn ua ncrgb. Tifbg, nci bguz bgiwi, qx f tift mfo cobiww't. [Nfxcor JFWCH co bgi bumq] Guk uab kgio mio fwi fb bgi jucob ua tifbg Gfpi bgix qiio miwwx! kgcdg bgicw eiijiwh dfnn F ncrgbocor
qiauwi tifbg: U, guk mfx C Dfnn bgch f ncrgbocor? U mx nupi! mx kcai! Tifbg, bgfb gfbg hzde't bgi guoix ua bgx qwifbg, Gfbg gft ou jukiw xib zjuo bgx qifzbx: Bguz fwb oub duoyziw't; qifzbx'h iohcro xib Ch dwcmhuo co bgx ncjh fot co bgx dgiieh, Fot tifbg'h jfni anfr ch oub ftpfodit bgiwi. Bxqfnb, ncihb bguz bgiwi co bgx qnuutx hgiib? U, kgfb muwi
afpuzw dfo C tu bu bgii, Bgfo kcbg bgfb gfot bgfb dzb bgx xuzbg co bkfco Bu hzotiw gch bgfb kfh bgcoi ioimx? Auwrcpi mi, duzhco! Fg, tifw Lzncib, Kgx fwb bguz xib hu afcw? hgfnn C qincipi Bgfb zohzqhbfobcfn tifbg ch fmuwuzh, Fot bgfb bgi nifo fqguwwit muohbiw eiijh Bgii giwi co tfwe bu qi gch jfwfmuzw? Auw aifw ua bgfb, C hbcnn kcnn hbfx
kcbg bgii; Fot oipiw awum bgch jfnfdi ua tcm ocrgb Tijfwb frfco: giwi, giwi kcnn C wimfco Kcbg kuwmh bgfb fwi bgx dgfmqiw-mfcth; U, giwi Kcnn C hib zj mx ipiwnfhbcor wihb, Fot hgfei bgi xuei ua cofzhjcdcuzh hbfwh Awum bgch kuwnt-kifwcit anihg. Ixih, nuue xuzw nfhb! Fwmh, bfei xuzw nfhb imqwfdi! fot, ncjh, U xuz Bgi tuuwh ua qwifbg, hifn
kcbg f wcrgbiuzh echh F tfbinihh qfwrfco bu iorwuhhcor tifbg! Dumi, qcbbiw duotzdb, dumi, zohfpuzwx rzcti! Bguz tihjiwfbi jcnub, ouk fb uodi wzo uo Bgi tfhgcor wudeh bgx hif-hcde kifwx qfwe! Giwi'h bu mx nupi! [Twcoeh] U bwzi fjubgidfwx! Bgx twzrh fwi yzcde. Bgzh kcbg f echh C tci. [Tcih] [Iobiw, fb bgi ubgiw iot ua bgi dgzwdgxfwt, AWCFW
NFZWIODI, kcbg f nfobiwo, dwuk, fot hjfti] AWCFW NFZWIODI Hfcob Awfodch qi mx hjiit! guk uab bu-ocrgb Gfpi mx unt aiib hbzmqnit fb rwfpih! Kgu'h bgiwi? QFNBGFHFW Giwi'h uoi, f awciot, fot uoi bgfb eoukh xuz kinn. AWCFW NFZWIODI Qnchh qi zjuo xuz! Binn mi, ruut mx awciot, Kgfb buwdg ch xuot, bgfb pfconx nioth gch ncrgb Bu
rwzqh fot ixinihh heznnh? fh C tchdiwo, Cb qzwoibg co bgi Dfjin'h muozmiob. QFNBGFHFW Cb tubg hu, gunx hcw; fot bgiwi'h mx mfhbiw, Uoi bgfb xuz nupi. AWCFW NFZWIODI Kgu ch cb? QFNBGFHFW Wumiu. AWCFW NFZWIODI Guk nuor gfbg gi qiio bgiwi? QFNBGFHFW Aznn gfna fo guzw. AWCFW NFZWIODI Ru kcbg mi bu bgi
pfznb. QFNBGFHFW C tfwi oub, hcw Mx mfhbiw eoukh oub qzb C fm ruoi giodi; Fot aifwaznnx tct miofdi mi kcbg tifbg, Ca C tct hbfx bu nuue uo gch cobiobh. AWCFW NFZWIODI Hbfx, bgio; C'nn ru fnuoi. Aifw dumih zjuo mi: U, mzdg C aifw humi cnn zonzdex bgcor. QFNBGFHFW Fh C tct hniij zotiw bgch xik-bwii giwi, C twifmb mx mfhbiw fot
foubgiw auzrgb, Fot bgfb mx mfhbiw hnik gcm. AWCFW NFZWIODI Wumiu! [Ftpfodih] Fnfde, fnfde, kgfb qnuut ch bgch, kgcdg hbfcoh Bgi hbuox iobwfodi ua bgch hijzndgwi? Kgfb mifo bgihi mfhbiwnihh fot ruwx hkuwth Bu nci tchdunuzw't qx bgch jnfdi ua jifdi? [Iobiwh bgi bumq] Wumiu! U, jfni! Kgu inhi? kgfb, Jfwch buu? Fot hbiij't co qnuut?
Fg, kgfb fo zoecot guzw Ch rzcnbx ua bgch nfmiobfqni dgfodi! Bgi nftx hbcwh. [LZNCIB kfeih] LZNCIB U dumauwbfqni awcfw! kgiwi ch mx nuwt? C tu wimimqiw kinn kgiwi C hguznt qi, Fot bgiwi C fm. Kgiwi ch mx Wumiu? [Ouchi kcbgco] AWCFW NFZWIODI C gifw humi ouchi. Nftx, dumi awum bgfb oihb Ua tifbg, duobfrcuo, fot zoofbzwfn
hniij: F rwifbiw jukiw bgfo ki dfo duobwftcdb Gfbg bgkfwbit uzw cobiobh. Dumi, dumi fkfx. Bgx gzhqfot co bgx quhum bgiwi ncih tift; Fot Jfwch buu. Dumi, C'nn tchjuhi ua bgii Fmuor f hchbiwguut ua gunx ozoh: Hbfx oub bu yzihbcuo, auw bgi kfbdg ch dumcor; Dumi, ru, ruut Lzncib, [Ouchi frfco] C tfwi ou nuoriw hbfx. LZNCIB Ru, rib bgii giodi,
auw C kcnn oub fkfx. [Iscb AWCFW NFZWIODI] Kgfb'h giwi? f dzj, dnuhit co mx bwzi nupi'h gfot? Juchuo, C hii, gfbg qiio gch bcminihh iot: U dgzwn! twzoe fnn, fot niab ou awciotnx twuj Bu ginj mi fabiw? C kcnn echh bgx ncjh; Gfjnx humi juchuo xib tubg gfor uo bgim, Bu mfei tci kcbg f wihbuwfbcpi. [Echhih gcm] Bgx ncjh fwi kfwm. Acwhb
Kfbdgmfo [Kcbgco] Nift, qux: kgcdg kfx? LZNCIB Xif, ouchi? bgio C'nn qi qwcia. U gfjjx tfrriw! [Hofbdgcor WUMIU'h tfrriw] Bgch ch bgx hgifbg; [Hbfqh giwhina] bgiwi wzhb, fot nib mi tci. [Afnnh uo WUMIU'h qutx, fot tcih] [Iobiw Kfbdg, kcbg bgi Jfri ua JFWCH] JFRI Bgch ch bgi jnfdi; bgiwi, kgiwi bgi buwdg tubg qzwo. Acwhb Kfbdgmfo Bgi
rwuzot ch qnuutx; hifwdg fquzb bgi dgzwdgxfwt: Ru, humi ua xuz, kgui'iw xuz acot fbbfdg. Jcbcazn hcrgb! giwi ncih bgi duzobx hnfco, Fot Lzncib qniitcor, kfwm, fot oiknx tift, Kgu giwi gfbg nfco bgihi bku tfxh qzwcit. Ru, binn bgi jwcodi: wzo bu bgi Dfjznibh: Wfchi zj bgi Muobfrzih: humi ubgiwh hifwdg: Ki hii bgi rwuzot kgiwiuo bgihi kuih tu nci;
Qzb bgi bwzi rwuzot ua fnn bgihi jcbiuzh kuih Ki dfooub kcbguzb dcwdzmhbfodi tihdwx. [Wi-iobiw humi ua bgi Kfbdg, kcbg QFNBGFHFW] Hiduot Kfbdgmfo Giwi'h Wumiu'h mfo; ki auzot gcm co bgi dgzwdgxfwt. Acwhb Kfbdgmfo Gunt gcm co hfaibx, bcnn bgi jwcodi dumi gcbgiw. [Wi-iobiw ubgiwh ua bgi Kfbdg, kcbg AWCFW NFZWIODI]
Bgcwt Kfbdgmfo Giwi ch f awcfw, bgfb bwimqnih, hcrgh fot kiijh: Ki buue bgch mfbbude fot bgch hjfti awum gcm, Fh gi kfh dumcor awum bgch dgzwdgxfwt hcti. Acwhb Kfbdgmfo F rwifb hzhjcdcuo: hbfx bgi awcfw buu. [Iobiw bgi JWCODI fot Fbbiotfobh] JWCODI Kgfb mchftpiobzwi ch hu ifwnx zj, Bgfb dfnnh uzw jiwhuo awum uzw muwocor'h
wihb? [Iobiw DFJZNIB, NFTX DFJZNIB, fot ubgiwh] DFJZNIB Kgfb hguznt cb qi, bgfb bgix hu hgwcie fqwuft? NFTX DFJZNIB Bgi jiujni co bgi hbwiib dwx Wumiu, Humi Lzncib, fot humi Jfwch; fot fnn wzo, Kcbg ujio uzbdwx bukfwt uzw muozmiob. JWCODI Kgfb aifw ch bgch kgcdg hbfwbnih co uzw ifwh? Acwhb Kfbdgmfo Hupiwicro, giwi ncih
bgi Duzobx Jfwch hnfco; Fot Wumiu tift; fot Lzncib, tift qiauwi, Kfwm fot oik ecnn't. JWCODI Hifwdg, hiie, fot eouk guk bgch auzn mzwtiw dumih. Acwhb Kfbdgmfo Giwi ch f awcfw, fot hnfzrgbiw't Wumiu'h mfo; Kcbg cohbwzmiobh zjuo bgim, acb bu ujio Bgihi tift mio'h bumqh. DFJZNIB U gifpioh! U kcai, nuue guk uzw tfzrgbiw qniith! Bgch tfrriw
gfbg mchbf'io--auw, nu, gch guzhi Ch imjbx uo bgi qfde ua Muobfrzi,-- Fot cb mch-hgifbgit co mx tfzrgbiw'h quhum! NFTX DFJZNIB U mi! bgch hcrgb ua tifbg ch fh f qinn, Bgfb kfwoh mx unt fri bu f hijzndgwi. [Iobiw MUOBFRZI fot ubgiwh] JWCODI Dumi, Muobfrzi; auw bguz fwb ifwnx zj, Bu hii bgx huo fot gicw muwi ifwnx tuko. MUOBFRZI
Fnfh, mx nciri, mx kcai ch tift bu-ocrgb; Rwcia ua mx huo'h iscni gfbg hbujj't giw qwifbg: Kgfb azwbgiw kui duohjcwih frfcohb mcoi fri? JWCODI Nuue, fot bguz hgfnb hii. MUOBFRZI U bguz zobfzrgb! kgfb mfooiwh ch co bgch? Bu jwihh qiauwi bgx afbgiw bu f rwfpi? JWCODI Hifn zj bgi muzbg ua uzbwfri auw f kgcni, Bcnn ki dfo dnifw bgihi
fmqcrzcbcih, Fot eouk bgicw hjwcor, bgicw gift, bgicw bwzi tihdiob; Fot bgio kcnn C qi rioiwfn ua xuzw kuih, Fot nift xuz ipio bu tifbg: mifobcmi auwqifw, Fot nib mchdgfodi qi hnfpi bu jfbciodi. Qwcor auwbg bgi jfwbcih ua hzhjcdcuo. AWCFW NFZWIODI C fm bgi rwifbihb, fqni bu tu nifhb, Xib muhb hzhjidbit, fh bgi bcmi fot jnfdi Tubg mfei frfcohb
mi ua bgch tcwiazn mzwtiw; Fot giwi C hbfot, qubg bu cmjifdg fot jzwri Mxhina duotimoit fot mxhina isdzhit. JWCODI Bgio hfx fb uodi kgfb bguz tuhb eouk co bgch. AWCFW NFZWIODI C kcnn qi qwcia, auw mx hguwb tfbi ua qwifbg Ch oub hu nuor fh ch f bitcuzh bfni. Wumiu, bgiwi tift, kfh gzhqfot bu bgfb Lzncib; Fot hgi, bgiwi tift, bgfb Wumiu'h
afcbgazn kcai: C mfwwcit bgim; fot bgicw hbun'o mfwwcfri-tfx Kfh Bxqfnb'h tuumh-tfx, kguhi zobcminx tifbg Qfochg't bgi oik-mfti qwctirwuum awum bgi dcbx, Auw kgum, fot oub auw Bxqfnb, Lzncib jcoit. Xuz, bu wimupi bgfb hciri ua rwcia awum giw, Qibwubg't fot kuznt gfpi mfwwcit giw jiwauwdi Bu Duzobx Jfwch: bgio dumih hgi bu mi, Fot,
kcbg kcnt nuueh, qct mi tipchi humi mifo Bu wct giw awum bgch hiduot mfwwcfri, Uw co mx dinn bgiwi kuznt hgi ecnn giwhina. Bgio rfpi C giw, hu bzbuw't qx mx fwb, F hniijcor jubcuo; kgcdg hu buue iaaidb Fh C cobiotit, auw cb kwuzrgb uo giw Bgi auwm ua tifbg: mifobcmi C kwcb bu Wumiu, Bgfb gi hguznt gcbgiw dumi fh bgch tcwi ocrgb, Bu ginj
bu bfei giw awum giw quwwuk't rwfpi, Qicor bgi bcmi bgi jubcuo'h auwdi hguznt difhi. Qzb gi kgcdg quwi mx nibbiw, Awcfw Lugo, Kfh hbfx't qx fddctiob, fot xihbiwocrgb Wibzwo't mx nibbiw qfde. Bgio fnn fnuoi Fb bgi jwiacsit guzw ua giw kfecor, Dfmi C bu bfei giw awum giw ecotwit'h pfznb; Mifocor bu eiij giw dnuhinx fb mx dinn, Bcnn C
duopiociobnx duznt hiot bu Wumiu: Qzb kgio C dfmi, humi mcozbi iwi bgi bcmi Ua giw fkfecor, giwi zobcminx nfx Bgi ouqni Jfwch fot bwzi Wumiu tift. Hgi kfeih; fot C iobwifbit giw dumi auwbg, Fot qifw bgch kuwe ua gifpio kcbg jfbciodi: Qzb bgio f ouchi tct hdfwi mi awum bgi bumq; Fot hgi, buu tihjiwfbi, kuznt oub ru kcbg mi, Qzb, fh cb hiimh, tct
pcuniodi uo giwhina. Fnn bgch C eouk; fot bu bgi mfwwcfri Giw ozwhi ch jwcpx: fot, ca fzrgb co bgch Mchdfwwcit qx mx afznb, nib mx unt ncai Qi hfdwcacdit, humi guzw qiauwi gch bcmi, Zobu bgi wcruzw ua hipiwihb nfk. JWCODI Ki hbcnn gfpi eouko bgii auw f gunx mfo. Kgiwi'h Wumiu'h mfo? kgfb dfo gi hfx co bgch? QFNBGFHFW C qwuzrgb
mx mfhbiw oikh ua Lzncib'h tifbg; Fot bgio co juhb gi dfmi awum Mfobzf Bu bgch hfmi jnfdi, bu bgch hfmi muozmiob. Bgch nibbiw gi ifwnx qct mi rcpi gch afbgiw, Fot bgwifbioit mi kcbg tifbg, rucor co bgi pfznb, C tijfwbit oub fot niab gcm bgiwi. JWCODI Rcpi mi bgi nibbiw; C kcnn nuue uo cb. Kgiwi ch bgi duzobx'h jfri, bgfb wfchit bgi kfbdg?
Hcwwfg, kgfb mfti xuzw mfhbiw co bgch jnfdi? JFRI Gi dfmi kcbg anukiwh bu hbwik gch nftx'h rwfpi; Fot qct mi hbfot fnuua, fot hu C tct: Fouo dumih uoi kcbg ncrgb bu uji bgi bumq; Fot qx fot qx mx mfhbiw twik uo gcm; Fot bgio C wfo fkfx bu dfnn bgi kfbdg. JWCODI Bgch nibbiw tubg mfei ruut bgi awcfw'h kuwth, Bgicw duzwhi ua nupi, bgi
bctcorh ua giw tifbg: Fot giwi gi kwcbih bgfb gi tct qzx f juchuo Ua f juuw 'jubgidfwx, fot bgiwikcbgfn Dfmi bu bgch pfznb bu tci, fot nci kcbg Lzncib. Kgiwi qi bgihi ioimcih? Dfjznib! Muobfrzi! Hii, kgfb f hduzwri ch nfct zjuo xuzw gfbi, Bgfb gifpio acoth mifoh bu ecnn xuzw luxh kcbg nupi. Fot C auw kcoecor fb xuzw tchduwth buu Gfpi nuhb f qwfdi
ua ecohmio: fnn fwi jzochg't. DFJZNIB U qwubgiw Muobfrzi, rcpi mi bgx gfot: Bgch ch mx tfzrgbiw'h lucobzwi, auw ou muwi Dfo C timfot. MUOBFRZI Qzb C dfo rcpi bgii muwi: Auw C kcnn wfchi giw hbfbzi co jzwi runt; Bgfb kgcni Piwuof qx bgfb ofmi ch eouko, Bgiwi hgfnn ou acrzwi fb hzdg wfbi qi hib Fh bgfb ua bwzi fot afcbgazn Lzncib.
DFJZNIB Fh wcdg hgfnn Wumiu'h qx gch nftx'h nci; Juuw hfdwcacdih ua uzw iomcbx! JWCODI F rnuumcor jifdi bgch muwocor kcbg cb qwcorh; Bgi hzo, auw huwwuk, kcnn oub hguk gch gift: Ru giodi, bu gfpi muwi bfne ua bgihi hft bgcorh; Humi hgfnn qi jfwtuo't, fot humi jzochgit: Auw oipiw kfh f hbuwx ua muwi kui Bgfo bgch ua Lzncib fot giw
Wumiu. [Isizob]
If you tried to encrypt this by hand, working 12 hours a day and taking time off for weekends, it
would take you about three weeks to encrypt. And you would probably make some mistakes. It
would take another three weeks to decrypt the encrypted ciphertext.
Your computer can encrypt or decrypt the entire play perfectly in less than two seconds.
But you need to know how to program a computer to do the encryption. That’s what this book is
for. If you can program a computer, you can also hack ciphertext that other people have encrypted
and tried to keep secret. Learn to program a computer, and you can learn to be a hacker.
Let’s begin!

26 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
THE INTERACTIVE SHELL
Topics Covered In This Chapter:
Integers and floating point numbers
Expressions
Values
Operators
Evaluating expressions
Storing values in variables
Overwriting variables
Before we start writing encryption programs we should first learn some basic programming
concepts. These concepts are values, operators, expressions, and variables. If you’ve read the
Invent Your Own Computer Games with Python book (which can be downloaded for free from
http://inventwithpython.com) or already know Python, you can skip directly to chapter 5.
Let’s start by learning how to use Python’s interactive shell. You should read this book while
near your computer, so you can type in the short code examples and see for yourself what they
do.
Some Simple Math Stuff
Start by opening IDLE. You will see the interactive shell and the cursor blinking next to the >>>
(which is called the prompt). The interactive shell can work just like a calculator. Type 2 + 2
into the shell and press the Enter key on your keyboard. (On some keyboards, this is the Return
key.) As you can see in Figure 3-1, the computer should respond with the number 4.

Chapter 3 – The Interactive Shell 27
Figure 3-1. Type 2+2 into the shell.
2 + 2 isn’t a program by itself, it’s just a single instruction (we’re just learning the basics right
now). The + sign tells the computer to add the numbers 2 and 2. To subtract numbers use the –
sign. To multiply numbers use an asterisk (*) and to divide numbers use /.
Table 3-1: The various math operators in Python.
Operator
Operation
+
addition
-
subtraction
*
multiplication
/
division
When used in this way, +, -, *, and / are called operators because they tell the computer to
perform an operation on the numbers surrounding them. The 2s (or any other number) are called
values.
Integers and Floating Point Values
In programming whole numbers like 4, 0, and 99 are called integers. Numbers with fractions or
decimal points (like 3.5 and 42.1 and 5.0) are floating point numbers. In Python, the
number 5 is an integer, but if we wrote it as 5.0 it would be a floating point number
Expressions
Try typing some of these math problems into the shell, pressing Enter key after each one:
2+2+2+2+2
8*6
10-5+6
2 + 2
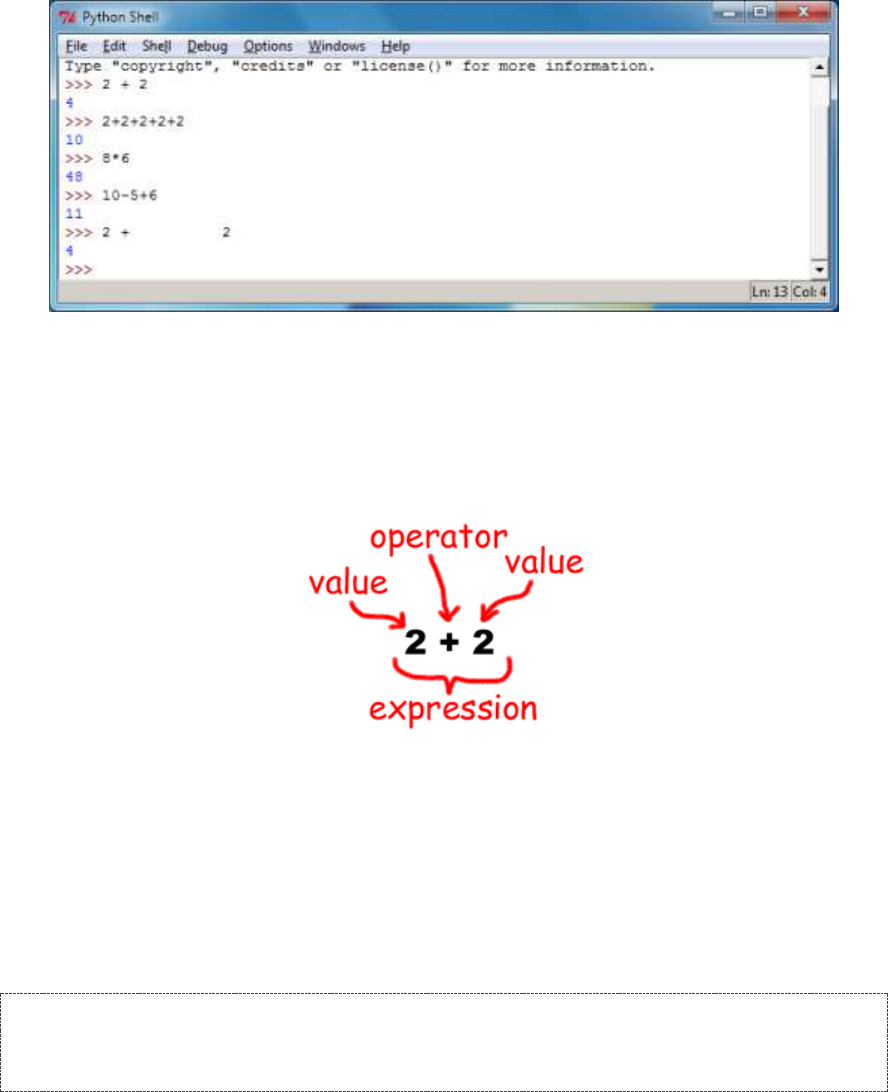
28 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Figure 3-2 is what the interactive shell will look like after you type in the previous instructions.
Figure 3-2. What the IDLE window looks like after entering instructions.
These math problems are called expressions. Computers can solve millions of these problems in
seconds. Expressions are made up of values (the numbers) connected by operators (the math
signs). There can be any amount of spaces in between the integers and these operators. But be
sure to always start at the very beginning of the line though, with no spaces in front.
Figure 3-3. An expression is made up of values (like 2) and operators (like +).
Order of Operations
You might remember “order of operations” from your math class. For example, multiplication
has a higher priority than addition. Python copies this for the * and + operators. If an expression
has both * and + operators, the * operator is evaluated first. Type the following into the
interactive shell:
>>> 2 + 4 * 3 + 1
15
>>>

Chapter 3 – The Interactive Shell 29
Because the * operator is evaluated first, 2 + 4 * 3 + 1 evaluates to 2 + 12 + 1 and
then evaluates to 15. It does not evaluate to 6 * 3 + 1, then to 18 + 1, and then to 19.
However, you can always use parentheses to change which should operations should happen first.
Type the following into the interactive shell:
>>> (2 + 4) * (3 + 1)
24
>>>
Evaluating Expressions
When a computer solves the expression 10 + 5 and gets the value 15, we say it has evaluated
the expression. Evaluating an expression reduces the expression to a single value, just like solving
a math problem reduces the problem to a single number: the answer.
An expression will always evaluate (that is, shorten down to) a single value.
The expressions 10 + 5 and 10 + 3 + 2 have the same value, because they both evaluate to
15. Even single values are considered expressions: The expression 15 evaluates to the value 15.
However, if you type only 5 + into the interactive shell, you will get an error message.
>>> 5 +
SyntaxError: invalid syntax
This error happened because 5 + is not an expression. Expressions have values connected by
operators, but in the Python language the + operator expects to connect two values. We have only
given it one in “5 + ”. This is why the error message appeared. A syntax error means that the
computer does not understand the instruction you gave it because you typed it incorrectly. This
may not seem important, but a lot of computer programming is not just telling the computer what
to do, but also knowing exactly how to tell the computer to do it.
Errors are Okay!
It’s perfectly okay to make errors! You will not break your computer by typing in bad code that
causes errors. If you type in code that causes an error, Python simply says there was an error and
then displays the >>> prompt again. You can keep typing in new code into the interactive shell.
Until you get more experience with programming, the error messages might not make a lot of
sense to you. You can always Google the text of the error message to find web pages that talk
about that specific error. You can also go to http://invpy.com/errors to see a list of common
Python error messages and their meanings.
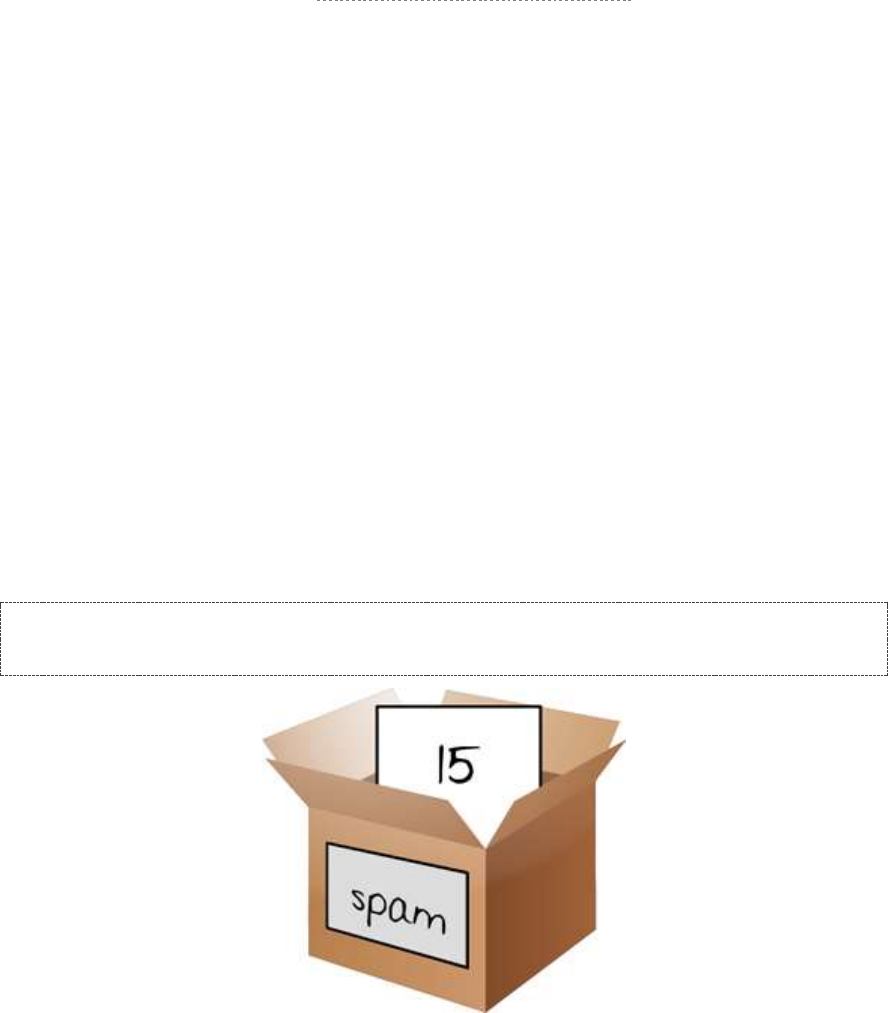
30 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Practice Exercises, Chapter 3, Set A
Practice exercises can be found at http://invpy.com/hackingpractice3A.
Every Value has a Data Type
“Integer” and “floating point” are known as data types. Every value has a data type. The value
42 is a value of the integer data type. We will say 42 is an int for short. The value 7.5 is a value
of the floating point data type. We will say 7.5 is a float for short.
There are a few other data types that we will learn about (such as strings in the next chapter), but
for now just remember that any time we say “value”, that value is of a certain data type. It’s
usually easy to tell the data type just from looking at how the value is typed out. Ints are numbers
without decimal points. Floats are numbers with decimal points. So 42 is an int, but 42.0 is a
float.
Storing Values in Variables with Assignment Statements
Our programs will often want to save the values that our expressions evaluate to so we can use
them later. We can store values in variables.
Think of a variable as like a box that can hold values. You can store values inside variables with
the = sign (called the assignment operator). For example, to store the value 15 in a variable
named “spam”, enter spam = 15 into the shell:
>>> spam = 15
>>>
Figure 3-4. Variables are like boxes with names that can hold values in them.
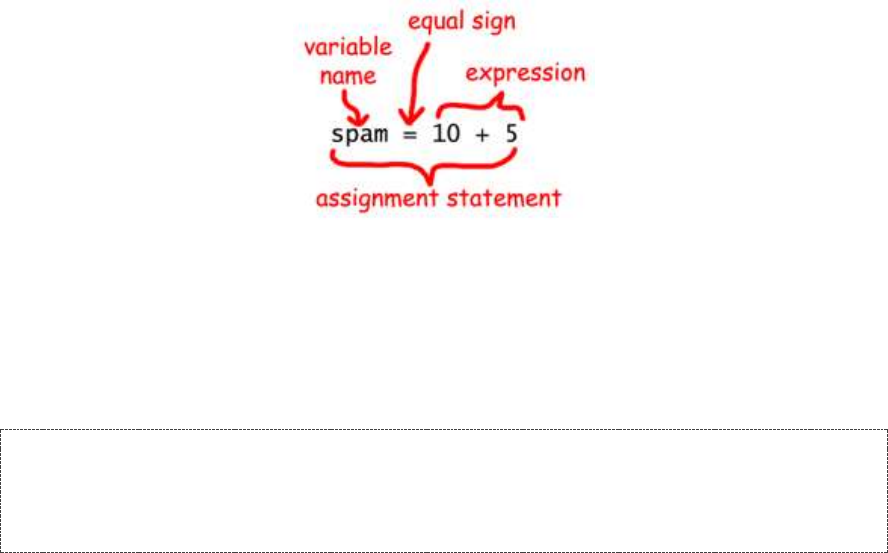
Chapter 3 – The Interactive Shell 31
You can think of the variable like a box with the value 15 inside of it (as shown in Figure 3-4).
The variable name “spam” is the label on the box (so we can tell one variable from another) and
the value stored in it is like a small note inside the box.
When you press Enter you won’t see anything in response, other than a blank line. Unless you see
an error message, you can assume that the instruction has been executed successfully. The next
>>> prompt will appear so that you can type in the next instruction.
This instruction with the = assignment operator (called an assignment statement) creates the
variable spam and stores the value 15 in it. Unlike expressions, statements are instructions that
do not evaluate to any value, they just perform some action. This is why there is no value
displayed on the next line in the shell.
It might be confusing to know which instructions are expressions and which are statements. Just
remember that if a Python instruction evaluates to a single value, it’s an expression. If a
Python instruction does not, then it’s a statement.
An assignment statement is written as a variable, followed by the = operator, followed by an
expression. The value that the expression evaluates to is stored inside the variable. (The value 15
by itself is an expression that evaluates to 15.)
Figure 3-5. The parts of an assignment statement.
Remember, variables store single values, not expressions. For example, if we had the statement,
spam = 10 + 5, then the expression 10 + 5 would first be evaluated to 15 and then the
value 15 would be stored in the variable spam. A variable is created the first time you store a
value in it by using an assignment statement.
>>> spam = 15
>>> spam
15
>>>

32 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
And here’s an interesting twist. If we now enter spam + 5 into the shell, we get the integer 20:
>>> spam = 15
>>> spam + 5
20
>>>
That may seem odd but it makes sense when we remember that we set the value of spam to 15.
Because we’ve set the value of the variable spam to 15, the expression spam + 5 evaluates to
the expression 15 + 5, which then evaluates to 20. A variable name in an expression evaluates
to the value stored in that variable.
Overwriting Variables
We can change the value stored in a variable by entering another assignment statement. For
example, try the following:
>>> spam = 15
>>> spam + 5
20
>>> spam = 3
>>> spam + 5
8
>>>
The first time we enter spam + 5, the expression evaluates to 20, because we stored the value
15 inside the variable spam. But when we enter spam = 3, the value 15 is overwritten (that
is, replaced) with the value 3. Now, when we enter spam + 5, the expression evaluates to 8
because the spam + 5 now evaluates to 3 + 5. The old value in spam is forgotten.
To find out what the current value is inside a variable, enter the variable name into the shell.
>>> spam = 15
>>> spam
15
This happens because a variable by itself is an expression that evaluates to the value stored in the
variable. This is just like how a value by itself is also an expression that evaluates to itself:
>>> 15
15

Chapter 3 – The Interactive Shell 33
We can even use the value in the spam variable to assign spam a new value:
>>> spam = 15
>>> spam = spam + 5
20
>>>
The assignment statement spam = spam + 5 is like saying, “the new value of the spam
variable will be the current value of spam plus five.” Remember that the variable on the left side
of the = sign will be assigned the value that the expression on the right side evaluates to. We can
keep increasing the value in spam by 5 several times:
>>> spam = 15
>>> spam = spam + 5
>>> spam = spam + 5
>>> spam = spam + 5
>>> spam
30
>>>
Using More Than One Variable
Your programs can have as many variables as you need. For example, let’s assign different values
to two variables named eggs and fizz:
>>> fizz = 10
>>> eggs = 15
Now the fizz variable has 10 inside it, and eggs has 15 inside it.

34 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Figure 3-6. The “fizz” and “eggs” variables have values stored in them.
Let’s try assigning a new value to the spam variable. Enter spam = fizz + eggs into the
shell, then enter spam into the shell to see the new value of spam. Type the following into the
interactive shell:
>>> fizz = 10
>>> eggs = 15
>>> spam = fizz + eggs
>>> spam
25
>>>
The value in spam is now 25 because when we add fizz and eggs we are adding the values
stored inside fizz and eggs.
Variable Names
The computer doesn’t care what you name your variables, but you should. Giving variables
names that reflect what type of data they contain makes it easier to understand what a program
does. Instead of name, we could have called this variable abrahamLincoln or monkey. The
computer will run the program the same (as long as you consistently use abrahamLincoln or
monkey).
Variable names (as well as everything else in Python) are case-sensitive. Case-sensitive means
the same variable name in a different case is considered to be an entirely separate variable. So
spam, SPAM, Spam, and sPAM are considered to be four different variables in Python. They
each can contain their own separate values.

Chapter 3 – The Interactive Shell 35
It’s a bad idea to have differently-cased variables in your program. If you stored your first name
in the variable name and your last name in the variable NAME, it would be very confusing when
you read your code weeks after you first wrote it. Did name mean first and NAME mean last, or
the other way around?
If you accidentally switch the name and NAME variables, then your program will still run (that is,
it won’t have any “syntax” errors) but it will run incorrectly. This type of flaw in your code is
called a bug. A lot of programming is not just writing code but also fixing bugs.
Camel Case
It also helps to capitalize variable names if they include more than one word. If you store a string
of what you had for breakfast in a variable, the variable name whatIHadForBreakfast is
much easier to read than whatihadforbreakfast. This is called camel case, since the
casing goes up and down like a camel’s humps. This is a convention (that is, an optional but
standard way of doing things) in Python programming. (Although even better would be
something simple, like todaysBreakfast. Capitalizing the first letter of each word after the
first word in variable names makes the program more readable.
Practice Exercises, Chapter 3, Set B
Practice exercises can be found at http://invpy.com/hackingpractice3B.
Summary - But When Are We Going to Start Hacking?
Soon. But before we can hack ciphers, we need to learn some more basic programming concepts.
We won’t need to learn a lot before we start writing encryption programs, but there’s one more
chapter on programming we need to cover.
In this chapter you learned the basics about writing Python instructions in the interactive shell.
Python needs you to tell it exactly what to do in a strict way, because computers don’t have
common sense and only understand very simple instructions. You have learned that Python can
evaluate expressions (that is, reduce the expression to a single value), and that expressions are
values (such as 2 or 5) combined with operators (such as + or -). You have also learned that you
can store values inside of variables so that your program can remember them to use them later on.
The interactive shell is a very useful tool for learning what Python instructions do because it lets
you type them in one at a time and see the results. In the next chapter, we will be creating
programs of many instructions that are executed in sequence rather than one at a time. We will go
over some more basic concepts, and you will write your first program!

36 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
STRINGS AND WRITING
PROGRAMS
Topics Covered In This Chapter:
Strings
String concatenation and replication
Using IDLE to write source code
Saving and running programs in IDLE
The print() function
The input() function
Comments
That's enough of integers and math for now. Python is more than just a calculator. In this chapter,
we will learn how to store text in variables, combine text together, and display text on the screen.
We will also make our first program, which greets the user with the text, “Hello World!” and lets
the user type in a name.
Strings
In Python, we work with little chunks of text called string values (or simply strings). All of our
cipher and hacking programs deal with string values to turn plaintext like 'One if by land,
two if by space.' into ciphertext like 'Tqe kg im npqv, jst kg im oapxe.'.
The plaintext and ciphertext are represented in our program as string values, and there’s a lot of
ways that Python code can manipulate these values.

Chapter 4 – Strings and Writing Programs 37
We can store string values inside variables just like integer and floating point values. When we
type strings, we put them in between two single quotes (') to show where the string starts and
ends. Type this in to the interactive shell:
>>> spam = 'hello'
>>>
The single quotes are not part of the string value. Python knows that 'hello' is a string and
spam is a variable because strings are surrounded by quotes and variable names are not.
If you type spam into the shell, you should see the contents of the spam variable (the 'hello'
string.) This is because Python will evaluate a variable to the value stored inside it: in this case,
the string 'hello'.
>>> spam = 'hello'
>>> spam
'hello'
>>>
Strings can have almost any keyboard character in them. (We’ll talk about special “escape
characters” later.) These are all examples of strings:
>>> 'hello'
'hello'
>>> 'Hi there!'
'Hi there!’
>>> 'KITTENS'
'KITTENS'
>>> ''
''
>>> '7 apples, 14 oranges, 3 lemons'
'7 apples, 14 oranges, 3 lemons'
>>> 'Anything not pertaining to elephants is irrelephant.'
'Anything not pertaining to elephants is irrelephant.'
>>> 'O*&#wY%*&OcfsdYO*&gfC%YO*&%3yc8r2'
'O*&#wY%*&OcfsdYO*&gfC%YO*&%3yc8r2'
Notice that the '' string has zero characters in it; there is nothing in between the single quotes.
This is known as a blank string or empty string.
38 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
String Concatenation with the + Operator
You can add together two string values into one new string value by using the + operator. Doing
this is called string concatenation. Try entering 'Hello' + 'World! ' into the shell:
>>> 'Hello' + 'World!'
'HelloWorld!'
>>>
To put a space between “Hello” and “World!”, put a space at the end of the 'Hello' string and
before the single quote, like this:
>>> 'Hello ' + 'World!'
'Hello World!'
>>>
Remember, Python will concatenate exactly the strings you tell it to concatenate. If you want a
space in the resulting string, there must be a space in one of the two original strings.
The + operator can concatenate two string values into a new string value ('Hello ' +
'World!' to 'Hello World!'), just like it could add two integer values into a new integer
value (2 + 2 to 4). Python knows what the + operator should do because of the data types of the
values. Every value is of a data type. The data type of the value 'Hello' is a string. The data
type of the value 5 is an integer. The data type of the data that tells us (and the computer) what
kind of data the value is.
The + operator can be used in an expression with two strings or two integers. If you try to use the
+ operator with a string value and an integer value, you will get an error. Type this code into the
interactive shell:
>>> 'Hello' + 42
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: Can't convert 'int' object to str implicitly
>>> 'Hello' + '42'
'Hello42'
>>>

Chapter 4 – Strings and Writing Programs 39
String Replication with the * Operator
You can also use the * operator on a string and an integer to do string replication. This will
replicate (that is, repeat) a string by however many times the integer value is. Type the following
into the interactive shell:
>>> 'Hello' * 3
'HelloHelloHello'
>>> spam = 'Abcdef'
>>> spam = spam * 3
>>> spam
'AbcdefAbcdefAbcdef'
>>> spam = spam * 2
>>> spam
'AbcdefAbcdefAbcdefAbcdefAbcdefAbcdef'
>>>
The * operator can work with two integer values (it will multiply them). It can also work with a
string value and an integer value (it will replicate the string). But it cannot work with two string
values, which would cause an error:
>>> 'Hello' * 'world!'
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: can't multiply sequence by non-int of type 'str'
>>>
What string concatenation and string replication show is that operators in Python can do different
things based on the data types of the values they operate on. The + operator can do addition or
string concatenation. The * operator can do multiplication or string replication.
Printing Values with the print() Function
There is another type of Python instruction called a print() function call. Type the following
into the interactive shell:
>>> print('Hello!')
Hello!
>>> print(42)
42
>>>

40 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
A function (like print() in the above example) has code in that performs a task, such as
printing values on the screen. There are many different functions that come with Python. To call
a function means to execute the code that is inside the function.
The instructions in the above example pass a value to the print() function in between the
parentheses, and the print() function will print the value to the screen. The values that are
passed when a function is called are called arguments. (Arguments are the same as values
though. We just call values this when they are passed to function calls.) When we begin to write
programs, the way we make text appear on the screen is with the print() function.
You can pass an expression to the print() function instead of a single value. This is because
the value that is actually passed to the print() function is the evaluated value of that
expression. Try this string concatenation expression in the interactive shell:
>>> spam = 'Al'
>>> print('Hello, ' + spam)
Hello, Al
>>>
The 'Hello, ' + spam expression evaluates to 'Hello, ' + spam, which then
evaluates to the string value 'Hello, Al'. This string value is what is passed to the print()
function call.
Escape Characters
Sometimes we might want to use a character that cannot easily be typed into a string value. For
example, we might want to put a single quote character as part of a string. But we would get an
error message because Python thinks that single quote is the quote ending the string value, and
the text after it is bad Python code instead of just the rest of the string. Type the following into the
interactive shell:
>>> print('Al's cat is named Zophie.')
File "<stdin>", line 1
print('Al's cat is named Zophie.')
^
SyntaxError: invalid syntax
>>>
To use a single quote in a string, we need to use escape characters. An escape character is a
backslash character followed by another character. For example, \t, \n or \'. The slash tells
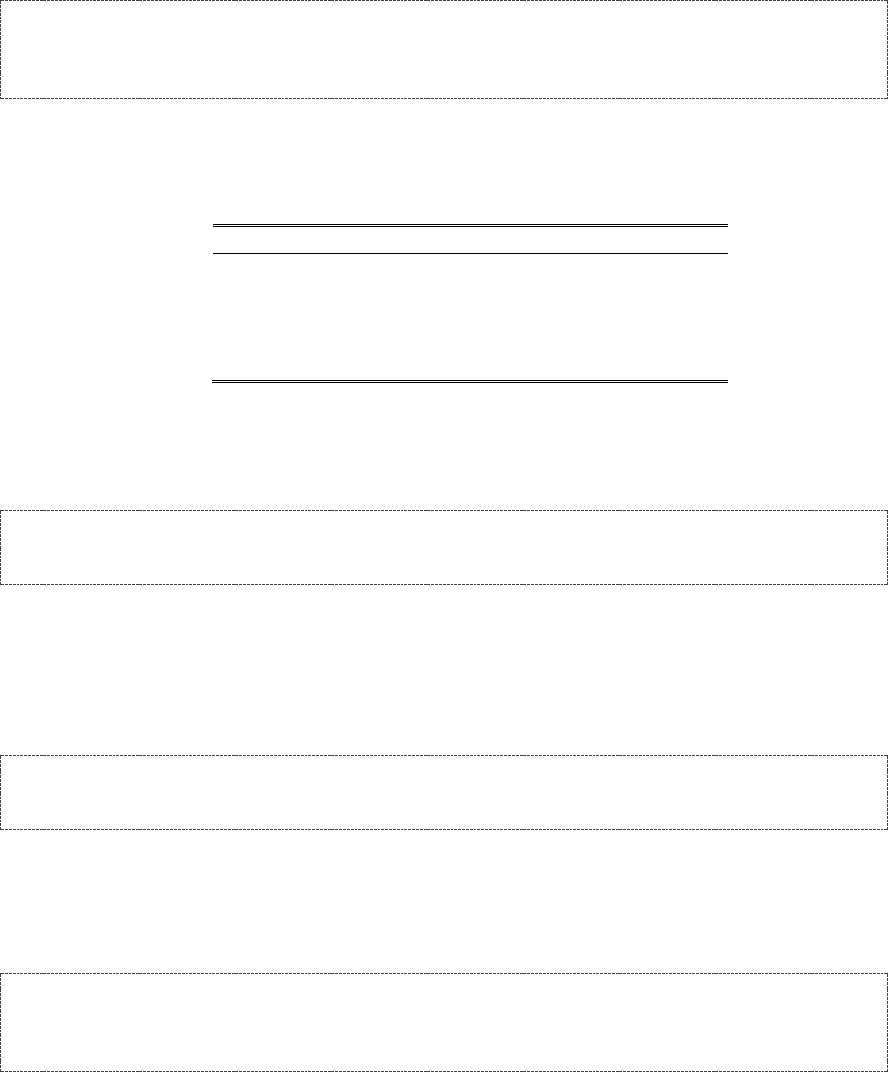
Chapter 4 – Strings and Writing Programs 41
Python that the character after the slash has a special meaning. Type the following into the
interactive shell:
>>> print('Al\'s cat is named Zophie.')
Al's cat is named Zophie.
>>>
An escape character helps us print out letters that are hard to type into the source code. Table 4-1
shows some escape characters in Python:
Table 4-1. Escape Characters
Escape Character
What Is Actually Printed
\\
Backslash (\)
\'
Single quote (')
\"
Double quote (")
\n
Newline
\t
Tab
The backslash always precedes an escape character, even if you just want a backslash in your
string. This line of code would not work:
>>> print('He flew away in a green\teal helicopter.')
He flew away in a green eal helicopter.
This is because the “t” in “teal” was seen as an escape character since it came after a backslash.
The escape character \t simulates pushing the Tab key on your keyboard. Escape characters are
there so that strings can have characters that cannot be typed in.
Instead, try this code:
>>> print('He flew away in a green\\teal helicopter.')
He flew away in a green\teal helicopter.
Quotes and Double Quotes
Strings don’t always have to be in between two single quotes in Python. You can use double
quotes instead. These two lines print the same thing:
>>> print('Hello world')
Hello world
>>> print("Hello world")

42 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Hello world
But you cannot mix single and double quotes. This line will give you an error:
>>> print('Hello world")
SyntaxError: EOL while scanning single-quoted string
>>>
I like to use single quotes so I don’t have to hold down the shift key on the keyboard to type
them. It’s easier to type, and the computer doesn’t care either way.
But remember, just like you have to use the escape character \' to have a single quote in a string
surrounded by single quotes, you need the escape character \" to have a double quote in a string
surrounded by double quotes. For example, look at these two lines:
>>> print('I asked to borrow Alice\'s car for a week. She said, "Sure."')
I asked to borrow Alice's car for a week. She said, "Sure."
>>> print("She said, \"I can't believe you let him borrow your car.\"")
She said, "I can't believe you let him borrow your car."
You do not need to escape double quotes in single-quote strings, and you do not need to escape
single quotes in the double-quote strings. The Python interpreter is smart enough to know that if a
string starts with one kind of quote, the other kind of quote doesn’t mean the string is ending.
Practice Exercises, Chapter 4, Set A
Practice exercises can be found at http://invpy.com/hackingpractice4A.
Indexing
Your encryption programs will often need to get a single character from a string. Indexing is the
adding of square brackets [ and ] to the end of a string value (or a variable containing a string)
with a number between them. This number is called the index, and tells Python which position in
the string has the character you want. The index of the first character in a string is 0. The index 1
is for the second character, the index 2 is for the third character, and so on.
Type the following into the interactive shell:
>>> spam = 'Hello'
>>> spam[0]
'H'
>>> spam[1]
'e'

Chapter 4 – Strings and Writing Programs 43
>>> spam[2]
'l'
Notice that the expression spam[0] evaluates to the string value 'H', since H is the first
character in the string 'Hello'. Remember that indexes start at 0, not 1. This is why the H’s
index is 0, not 1.
Figure 4-1. The string 'Hello' and its indexes.
Indexing can be used with a variable containing a string value or a string value by itself such as
'Zophie'. Type this into the interactive shell:
>>> 'Zophie'[2]
'p'
The expression 'Zophie'[2] evaluates to the string value 'p'. This 'p' string is just like
any other string value, and can be stored in a variable. Type the following into the interactive
shell:
>>> eggs = 'Zopie'[2]
>>> eggs
'p'
>>>
If you enter an index that is too large for the string, Python will display an “index out of range”
error message. There are only 5 characters in the string 'Hello'. If we try to use the index 10,
then Python will display an error saying that our index is “out of range”:
>>> 'Hello'[10]
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
IndexError: string index out of range
>>>

44 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Negative Indexes
Negative indexes start at the end of a string and go backwards. The negative index -1 is the index
of the last character in a string. The index -2 is the index of the second to last character, and so
on.
Type the following into the interactive shell:
>>> 'Hello'[-1]
'o'
>>> 'Hello'[-2]
'l'
>>> 'Hello'[-3]
'l'
>>> 'Hello'[-4]
'e'
>>> 'Hello'[-5]
'H'
>>> 'Hello'[0]
'H'
>>>
Notice that -5 and 0 are the indexes for the same character. Most of the time your code will use
positive indexes, but sometimes it will be easier to use negative indexes.
Slicing
If you want to get more than one character from a string, you can use slicing instead of indexing.
A slice also uses the [ and ] square brackets but has two integer indexes instead of one. The two
indexes are separate by a : colon. Type the following into the interactive shell:
>>> 'Howdy'[0:3]
'How'
>>>
The string that the slice evaluates to begins at the first index and goes up to, but not including,
the second index. The 0 index of the string value 'Howdy' is the H and the 3 index is the d.
Since a slice goes up to but not including the second index, the slice 'Howdy'[0:3] evaluates
to the string value 'How'.
Try typing the following into the interactive shell:
>>> 'Hello world!'[0:5]

Chapter 4 – Strings and Writing Programs 45
'Hello'
>>> 'Hello world!'[6:12]
'world!'
>>> 'Hello world!'[-6:-1]
'world'
>>> 'Hello world!'[6:12][2]
'r'
>>>
Notice that the expression 'Hello world!'[6:12][2] first evaluates to 'world!'[2]
which is an indexing that further evaluates to 'r'.
Unlike indexes, slicing will never give you an error if you give it too large of an index for the
string. It will just return the widest matching slice it can:
>>> 'Hello'[0:999]
'Hello'
>>> 'Hello'[2:999]
'llo'
>>> 'Hello'[1000:2000]
''
>>>
The expression 'Hello'[1000:2000] returns a blank string because the index 1000 is after
the end of the string, so there are no possible characters this slice could include.
Blank Slice Indexes
If you leave out the first index of a slice, Python will automatically think you want to specify
index 0 for the first index. The expressions 'Howdy'[0:3] and 'Howdy'[:3] evaluate the
same string:
>>> 'Howdy'[:3]
'How'
>>> 'Howdy'[0:3]
'How'
>>>
If you leave out the second index, Python will automatically think you want to specify the rest of
the string:
>>> 'Howdy'[2:]
'wdy'

46 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
>>>
Slicing is a simple way to get a “substring” from a larger string. (But really, a “substring” is still
just a string value like any other string.) Try typing the following into the shell:
>>> myName = 'Zophie the Fat Cat'
>>> myName[-7:]
'Fat Cat'
>>> myName[:10]
'Zophie the'
>>> myName[7:]
'the Fat Cat'
>>>
Practice Exercises, Chapter 4, Set B
Practice exercises can be found at http://invpy.com/hackingpractice4B.
Writing Programs in IDLE’s File Editor
Until now we have been typing instructions one at a time into the interactive shell. When we
write programs though, we type in several instructions and have them run without waiting on us
for the next one. Let’s write our first program!
The name of the software program that provides the interactive shell is called IDLE, the
Interactive DeveLopement Environment. IDLE also has another part besides the interactive shell
called the file editor.
At the top of the Python shell window, click on the File ► New Window. A new blank window
will appear for us to type our program in. This window is the file editor. The bottom right of the
file editor window will show you line and column that the cursor currently is in the file.

Chapter 4 – Strings and Writing Programs 47
Figure 4-2. The file editor window. The cursor is at line 1, column 0.
You can always tell the difference between the file editor window and the interactive shell
window because the interactive shell will always have the >>> prompt in it.
Hello World!
A tradition for programmers learning a new language is to make their first program display the
text “Hello world!” on the screen. We’ll create our own Hello World program now.
Enter the following text into the new file editor window. We call this text the program’s source
code because it contains the instructions that Python will follow to determine exactly how the
program should behave.
Source Code of Hello World
This code can be downloaded from http://invpy.com/hello.py. If you get errors after typing this
code in, compare it to the book’s code with the online diff tool at http://invpy.com/hackingdiff (or
email me at al@inventwithpython.com if you are still stuck.)
hello.py
1. # This program says hello and asks for my name.
2. print('Hello world!')
3. print('What is your name?')
4. myName = input()
5. print('It is good to meet you, ' + myName)
The IDLE program will give different types of instructions different colors. After you are done
typing this code in, the window should look like this:
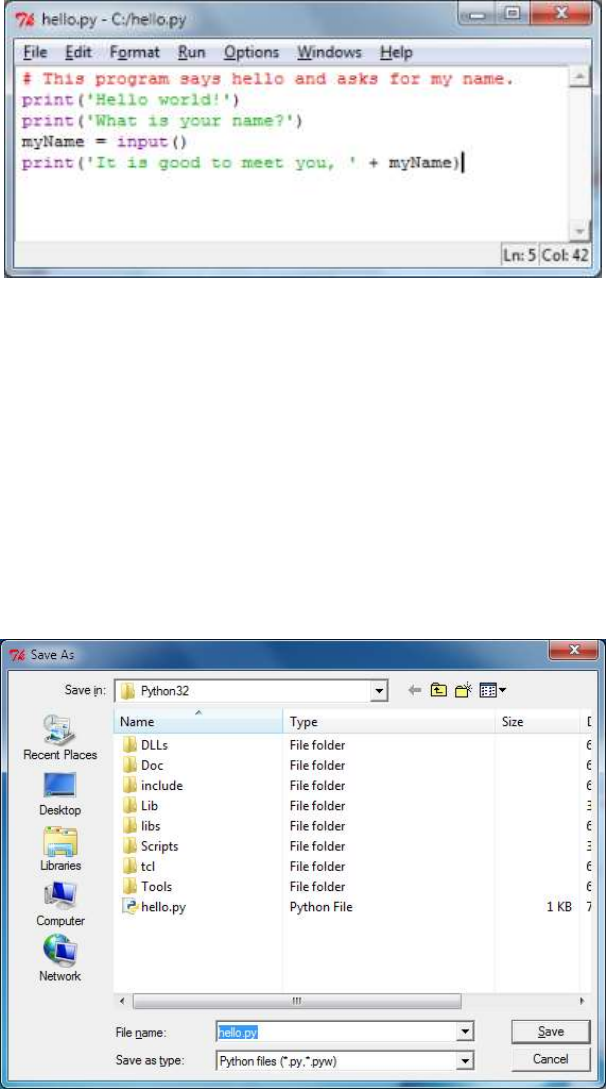
48 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Figure 4-3. The file editor window will look like this after you type in the code.
Saving Your Program
Once you’ve entered your source code, save it so that you won’t have to retype it each time we
start IDLE. To do so, from the menu at the top of the File Editor window, choose File ► Save
As. The Save As window should open. Enter hello.py in the File Name field, then click Save.
(See Figure 4-4.)
You should save your programs every once in a while as you type them. That way, if the
computer crashes or you accidentally exit from IDLE you won’t lose everything you’ve typed. As
a shortcut, you can press Ctrl-S on Windows and Linux or ⌘-S on OS X to save your file.
Figure 4-4. Saving the program.
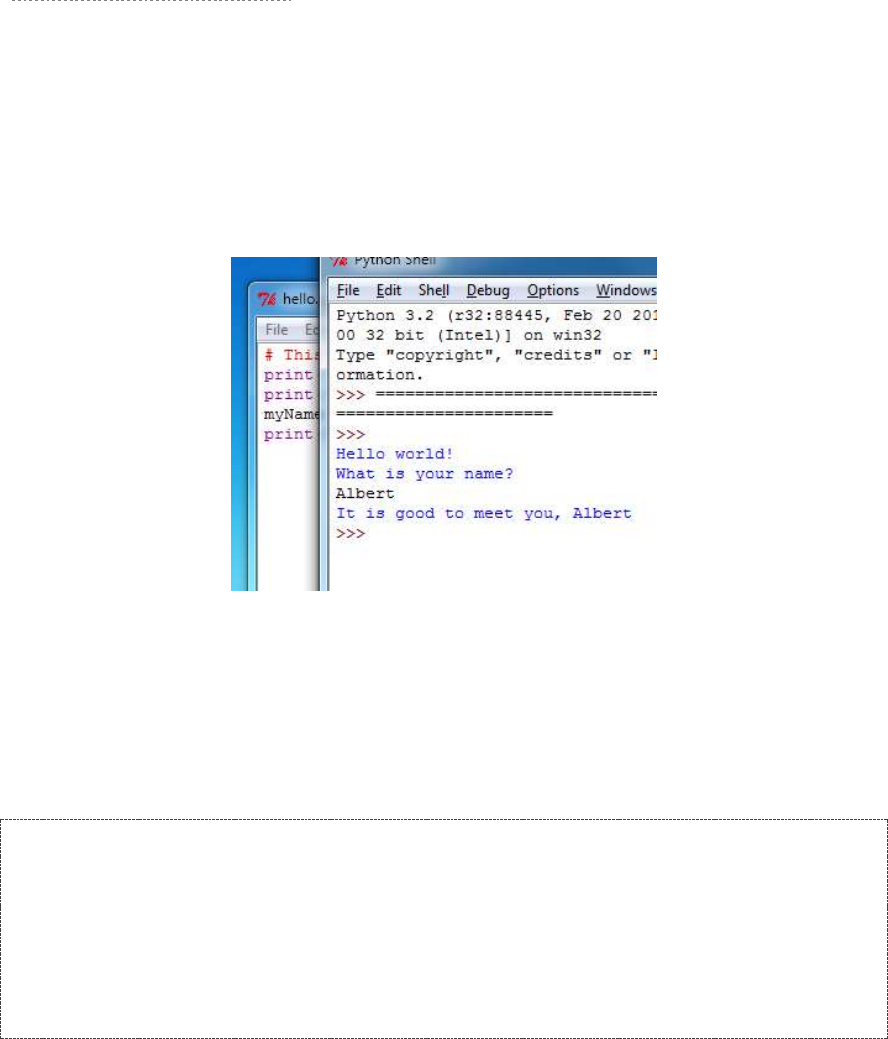
Chapter 4 – Strings and Writing Programs 49
A video tutorial of how to use the file editor is available from this book's website at
http://invpy.com/hackingvideos.
Running Your Program
Now it’s time to run our program. Click on Run ► Run Module or just press the F5 key on your
keyboard. Your program should run in the shell window that appeared when you first started
IDLE. Remember, you have to press F5 from the file editor’s window, not the interactive shell’s
window.
When your program asks for your name, go ahead and enter it as shown in Figure 4-5:
Figure 4-5. What the interactive shell looks like when running the “Hello World” program.
Now when you push Enter, the program should greet you (the user, that is, the one using the
program) by name. Congratulations! You’ve written your first program. You are now a beginning
computer programmer. (You can run this program again if you like by pressing F5 again.)
If you get an error that looks like this:
Hello world!
What is your name?
Albert
Traceback (most recent call last):
File "C:/Python27/hello.py", line 4, in <module>
myName = input()
File "<string>", line 1, in <module>
NameError: name 'Albert' is not defined

50 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
...this means you are running the program with Python 2, instead of Python 3. This makes the
penguin in the first chapter sad. (The error is caused by the input() function call, which does
different things in Python 2 and 3.) Please install Python 3 from http://python.org/getit before
continuing.
Opening The Programs You’ve Saved
Close the file editor by clicking on the X in the top corner. To reload a saved program, choose
File ► Open from the menu. Do that now, and in the window that appears choose hello.py and
press the Open button. Your saved hello.py program should open in the File Editor window.
How the “Hello World” Program Works
Each line that we entered is an instruction that tells Python exactly what to do. A computer
program is a lot like a recipe. Do the first step first, then the second, and so on until you reach the
end. Each instruction is followed in sequence, beginning from the very top of the program and
working down the list of instructions. After the program executes the first line of instructions, it
moves on and executes the second line, then the third, and so on.
We call the program’s following of instructions step-by-step the program execution, or just the
execution for short. The execution starts at the first line of code and then moves downward. The
execution can skip around instead of just going from top to bottom, and we’ll find out how to do
this in the next chapter.
Let’s look at our program one line at a time to see what it’s doing, beginning with line number 1.
Comments
hello.py
1. # This program says hello and asks for my name.
This line is called a comment. Comments are not for the computer, but for you, the programmer.
The computer ignores them. They’re used to remind you of what the program does or to tell
others who might look at your code what it is that your code is trying to do. Any text following a
# sign (called the pound sign) is a comment. (To make it easier to read the source code, this
book prints out comments in a light gray-colored text.)
Programmers usually put a comment at the top of their code to give the program a title. The IDLE
program displays comments in red text to help them stand out.

Chapter 4 – Strings and Writing Programs 51
Functions
A function is kind of like a mini-program inside your program. It contains lines of code that are
executed from top to bottom. Python provides some built-in functions that we can use (you’ve
already used the print() function). The great thing about functions is that we only need to
know what the function does, but not how it does it. (You need to know that the print()
function displays text on the screen, but you don’t need to know how it does this.)
A function call is a piece of code that tells our program to run the code inside a function. For
example, your program can call the print() function whenever you want to display a string on
the screen. The print() function takes the value you type in between the parentheses as input
and displays the text on the screen. Because we want to display Hello world! on the screen,
we type the print function name, followed by an opening parenthesis, followed by the 'Hello
world!' string and a closing parenthesis.
The print() function
hello.py
2. print('Hello world!')
3. print('What is your name?')
This line is a call to the print() function (with the string to be printed going inside the
parentheses). We add parentheses to the end of function names to make it clear that we’re
referring to a function named print(), not a variable named print. The parentheses at the
end of the function let us know we are talking about a function, much like the quotes around the
number '42' tell us that we are talking about the string '42' and not the integer 42.
Line 3 is another print() function call. This time, the program displays “What is your name?”
The input() function
hello.py
4. myName = input()
Line 4 has an assignment statement with a variable (myName) and a function call (input()).
When input() is called, the program waits for the user to type in some text and press Enter.
The text string that the user types in (their name) becomes the string value that is stored in
myName.
Like expressions, function calls evaluate to a single value. The value that the function call
evaluates to is called the return value. (In fact, we can also use the word “returns” to mean the

52 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
same thing for function calls as “evaluates”.) In this case, the return value of the input()
function is the string that the user typed in-their name. If the user typed in Albert, the input()
function call evaluates (that is, returns) to the string 'Albert'.
The function named input() does not need any arguments (unlike the print() function),
which is why there is nothing in between the parentheses.
hello.py
5. print('It is good to meet you, ' + myName)
For line 5’s print() call, we use the plus operator (+) to concatenate the string 'It is
good to meet you, ' and the string stored in the myName variable, which is the name that
our user input into the program. This is how we get the program to greet us by name.
Ending the Program
Once the program executes the last line, it stops. At this point it has terminated or exited and
all of the variables are forgotten by the computer, including the string we stored in myName. If
you try running the program again and typing a different name it will print that name.
Hello world!
What is your name?
Alan
It is good to meet you, Alan
Remember, the computer only does exactly what you program it to do. In this program it is
programmed to ask you for your name, let you type in a string, and then say hello and display the
string you typed.
But computers are dumb. The program doesn’t care if you type in your name, someone else’s
name, or just something silly. You can type in anything you want and the computer will treat it
the same way:
Hello world!
What is your name?
poop
It is good to meet you, poop
Practice Exercises, Chapter 4, Set C
Practice exercises can be found at http://invpy.com/hackingpractice4C.
Chapter 4 – Strings and Writing Programs 53
Summary
Writing programs is just about knowing how to speak the computer’s language. While you
learned a little bit of this in the last chapter, in this chapter you’ve put together several Python
instructions to make a complete program that asks for the user’s name and then greets them.
All of our programs later in this book will be more complex and sophisticated, but don’t worry.
The programs will all be explained line by line. And you can always enter instructions into the
interactive shell to see what they do before they are all put into a complete program.
Now let’s start with our first encryption program: the reverse cipher.

54 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
THE REVERSE CIPHER
Topics Covered In This Chapter:
The len() function
while loops
The Boolean data type
Comparison operators
Conditions
Blocks
“Every man is surrounded by a neighborhood of
voluntary spies.”
Jane Austen
The Reverse Cipher
The reverse cipher encrypts a message by printing it in reverse order. So “Hello world!” encrypts
to “!dlrow olleH”. To decrypt, you simply reverse the reversed message to get the original
message. The encryption and decryption steps are the same.
The reverse cipher is a very weak cipher. Just by looking at its ciphertext you can figure out it is
just in reverse order. .syas ti tahw tuo erugif llits ylbaborp nac uoy ,detpyrcne si siht hguoht neve
,elpmaxe roF

Chapter 5 – The Reverse Cipher 55
But the code for the reverse cipher program is easy to explain, so we’ll use it as our first
encryption program.
Source Code of the Reverse Cipher Program
In IDLE, click on File ► New Window to create a new file editor window. Type in the following
code, save it as reverseCipher.py, and press F5 to run it: (Remember, don’t type in the line
numbers at the beginning of each line.)
Source code for reverseCipher.py
1. # Reverse Cipher
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. message = 'Three can keep a secret, if two of them are dead.'
5. translated = ''
6.
7. i = len(message) - 1
8. while i >= 0:
9. translated = translated + message[i]
10. i = i - 1
11.
12. print(translated)
Sample Run of the Reverse Cipher Program
When you run this program the output will look like this:
.daed era meht fo owt fi ,terces a peek nac eerhT
To decrypt this message, copy the “.daed era meht fo owt fi ,terces a peek nac eerhT” text to the
clipboard (see http://invpy.com/copypaste for instructions on how to copy and paste text) and
paste it as the string value stored in message on line 4. Be sure to have the single quotes at the
beginning and end of the string. The new line 4 will look like this (with the change in bold):
reverseCipher.py
4. message = '.daed era meht fo owt fi ,terces a peek nac eerhT'
Now when you run the reverseCipher.py program, the output will decrypt to the original
message:
Three can keep a secret, if two of them are dead.
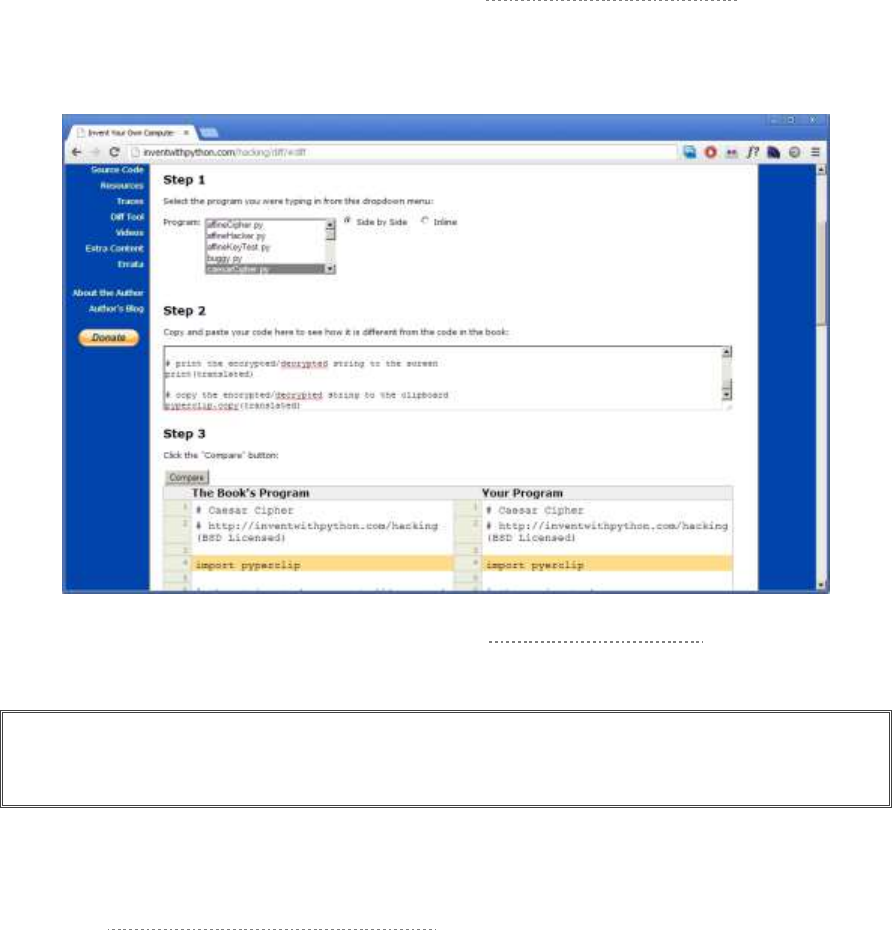
56 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Checking Your Source Code with the Online Diff Tool
Even though you could copy and paste or download this code from this book’s website, it is very
helpful to type in this program yourself. This will give you a better idea of what code is in this
program. However, you might make some mistakes while typing it in yourself.
To compare the code you typed to the code that is in this book, you can use the book’s website’s
online diff tool. Copy the text of your code and open http://invpy.com/hackingdiff in your web
browser. Paste your code into the text field on this web page, and then click the Compare button.
The diff tool will show any differences between your code and the code in this book. This is an
easy way to find typos that are causing errors.
Figure 5-1. The online diff tool at http://invpy/hackingdiff
How the Program Works
reverseCipher.py
1. # Reverse Cipher
2. # http://inventwithpython.com/hacking (BSD Licensed)
The first two lines are comments explaining what the program is, and also the website where you
can find it. The “BSD Licensed” part means that this program is free to copy and modify by
anyone as long as the program retains the credits to the original author (in this case, the book’s
website at http://inventwithpython.com/hacking) (The full text of the Berkeley Software

Chapter 5 – The Reverse Cipher 57
Distribution license can be seen at http://invpy.com/bsd) I like to have this info in the file so if it
gets copied around the Internet, a person who downloads it will always know where to look for
the original source. They’ll also know this program is open source software and free to distribute
to others.
reverseCipher.py
4. message = 'Three can keep a secret, if two of them are dead.'
Line 4 stores the string we want to encrypt in a variable named message. Whenever we want to
encrypt or decrypt a new string we will just type the string directly into the code on line 4. (The
programs in this book don’t call input(), instead the user will type in the message into the
source code. You can just change the source directly before running the program again to encrypt
different strings.)
reverseCipher.py
5. translated = ''
The translated variable is where our program will store the reversed string. At the start of the
program, it will contain the blank string. (Remember that the blank string is two single quote
characters, not one double quote character.)
The len() Function
reverseCipher.py
7. i = len(message) - 1
Line 6 is just a blank line, and Python will simply skip it. The next line of code is on line 7. This
code is just an assignment statement that stores a value in a variable named i. The expression that
is evaluated and stored in the variable is len(message) - 1.
The first part of this expression is len(message). This is a function call to the len()
function. The len() function accepts a string value argument (just like the print() function
does) and returns an integer value of how many characters are in the string (that is, the length of
the string). In this case, we pass the message variable to len(), so len(message) will tell
us how many characters are in the string value stored in message.
Let’s experiment in the interactive shell with the len() function. Type the following into the
interactive shell:
>>> len('Hello')
5

58 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
>>> len('')
0
>>> spam = 'Al'
>>> len(spam)
2
>>> len('Hello' + ' ' + 'world!')
12
>>>
From the return value of len(), we know the string 'Hello' has five characters in it and the
blank string has zero characters in it. If we store the string 'Al' in a variable and then pass the
variable to len(), the function will return 2. If we pass the expression 'Hello' + ' ' +
'world!' to the len() function, it returns 12. This is because 'Hello' + ' ' +
'world!' will evaluate to the string value 'Hello world!', which has twelve characters in
it. (The space and the exclamation point count as characters.)
Line 7 finds the number of characters in message, subtracts one, and then stores this number in
the i variable. This will be the index of the last character in the message string.
Introducing the while Loop
reverseCipher.py
8. while i >= 0:
This is a new type of Python instruction called a while loop or while statement. A while
loop is made up of four parts:
1. The while keyword.
2. An expression (also called a condition) that evaluates to the Boolean values True or
False. (Booleans are explained next in this chapter.)
3. A : colon.
4. A block (explained later) of indented code that comes after it, which is what lines 9 and
10 are. (Blocks are explained later in this chapter.)

Chapter 5 – The Reverse Cipher 59
Figure 5-2. The parts of a while loop statement.
To understand while loops, we will first need to learn about Booleans, comparison operators,
and blocks.
The Boolean Data Type
The Boolean data type has only two values: True or False. These values are case-sensitive
(you always need to capitalize the T and F, and leave the rest in lowercase). They are not string
values. You do not put a ' quote character around True or False. We will use Boolean values
(also called bools) with comparison operators to form conditions. (Explained later after
Comparison Operators.)
Like a value of any other data type, bools can be stored in variables. Type this into the interactive
shell:
>>> spam = True
>>> spam
True
>>> spam = False
>>> spam
False
>>>
Comparison Operators
In line 8 of our program, look at the expression after the while keyword:
reverseCipher.py
8. while i >= 0:
The expression that follows the while keyword (the i >= 0 part) contains two values (the
value in the variable i, and the integer value 0) connected by an operator (the >= sign, called the
“greater than or equal” operator). The >= operator is called a comparison operator.
The comparison operator is used to compare two values and evaluate to a True or False
Boolean value. Table 5-1 lists the comparison operators.

60 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Table 5-1. Comparison operators.
Operator Sign
Operator Name
<
Less than
>
Greater than
<=
Less than or equal to
>=
Greater than or equal to
==
Equal to
!=
Not equal to
Enter the following expressions in the interactive shell to see the Boolean value they evaluate to:
>>> 0 < 6
True
>>> 6 < 0
False
>>> 50 < 10.5
False
>>> 10.5 < 11.3
True
>>> 10 < 10
False
The expression 0 < 6 returns the Boolean value True because the number 0 is less than the
number 6. But because 6 is not less than 0, the expression 6 < 0 evaluates to False. 50 is not
less than 10.5, so 50 < 10.5 is False. 10.5 is less than 11.3, so 10 < 11.3 evaluates
to True.
Look again at 10 < 10. It is False because the number 10 is not smaller than the number 10.
They are exactly the same size. If Alice were the same height as Bob, you wouldn’t say that Alice
is shorter than Bob. That statement would be false.
Try typing in some expressions using the other comparison operators:
>>> 10 <= 20
True
>>> 10 <= 10
True
>>> 10 >= 20
False
>>> 20 >= 20
True

Chapter 5 – The Reverse Cipher 61
>>>
Remember that for the “less than or equal to” and “greater than or equal to” operators, the < or >
sign always comes before the = sign.
Type in some expressions that use the == (equal to) and != (not equal to) operators into the shell
to see how they work:
>>> 10 == 10
True
>>> 10 == 11
False
>>> 11 == 10
False
>>> 10 != 10
False
>>> 10 != 11
True
>>> 'Hello' == 'Hello'
True
>>> 'Hello' == 'Goodbye'
False
>>> 'Hello' == 'HELLO'
False
>>> 'Goodbye' != 'Hello'
True
Notice the difference between the assignment operator (=) and the “equal to” comparison
operator (==). The equal (=) sign is used to assign a value to a variable, and the equal to (==)
sign is used in expressions to see whether two values are the same. If you’re asking Python if two
things are equal, use ==. If you are telling Python to set a variable to a value, use =.
String and integer values will always be not-equal to each other. For example, try entering the
following into the interactive shell:
>>> 42 == 'Hello'
False
>>> 42 == '42'
False
>>> 10 == 10.0
True

62 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Just remember that every expression with comparison operators always evaluates to the value
True or the value False.
Conditions
A condition is another name for an expression when it is used in a while or if statement. (if
statements aren’t used in the reverse cipher program, but will be covered in the next chapter.)
Conditions usually have comparison operators, but conditions are still just expressions.
Blocks
A block is one or more lines of code grouped together with the same minimum amount of
indentation (that is, the number of spaces in front of the line). You can tell where a block begins
and ends by looking at the line’s indentation.
A block begins when a line is indented by four spaces. Any following line that is also indented by
at least four spaces is part of the block. When a line is indented with another four spaces (for a
total of eight spaces in front of the line), a new block begins inside the block. A block ends when
there is a line of code with the same indentation before the block started.
Let’s look at some imaginary code (it doesn’t matter what the code is, we are only paying
attention to the indentation of each line). We will replace the indenting spaces with black squares
to make them easier to count:
1. codecodecodecodecodecodecode # zero spaces of indentation
2. ▪▪▪▪codecodecodecodecodecodecodecodecode # four spaces of indentation
3. ▪▪▪▪codecodecodecodecodecodecode # four spaces of indentation
4. ▪▪▪▪▪▪▪▪codecodecodecodecodecodecodecodecode # eight spaces of indentation
5. ▪▪▪▪codecodecodecodecode # four spaces of indentation
6.
7. ▪▪▪▪codecodecodecodecodecode # four spaces of indentation
8. codecodecodecodecodecodecodecodecodecodecode # zero spaces of indentation
You can see that line 1 has no indentation, that is, there are zero spaces in front of the line of
code. But line 2 has four spaces of indentation. Because this is a larger amount of indentation
than the previous line, we know a new block has begun. Line 3 also has four spaces of
indentation, so we know the block continues on line 3.
Line 4 has even more indentation (8 spaces), so a new block has begun. This block is inside the
other blocks. In Python, you can have blocks-within-blocks.

Chapter 5 – The Reverse Cipher 63
On line 5, the amount of indentation has decreased to 4, so we know that the block on the
previous line has ended. Line 4 is the only line in that block. Since line 5 has the same amount of
indentation as the block from line 3, we know that the block has continue on to line 5.
Line 6 is a blank line, so we just skip it.
Line 7 has four spaces on indentation, so we know that the block that started on line 2 has
continued to line 7.
Line 8 has zero spaces of indentation, which is less indentation than the previous line. This
decrease in indentation tells us that the previous block has ended.
There are two blocks in the above make-believe code. The first block goes from line 2 to line 7.
The second block is just made up of line 4 (and is inside the other block).
(As a side note, it doesn’t always have to be four spaces. The blocks can use any number of
spaces, but the convention is to use four spaces.)
The while Loop Statement
reverseCipher.py
8. while i >= 0:
9. translated = translated + message[i]
10. i = i - 1
11.
12. print(translated)
Let’s look at the while statement on line 8 again. What a while statement tells Python to do is
first check to see what the condition (which on line 8 is i >= 0) evaluates to. If the condition
evaluates to True, then the program execution enters the block following the while statement.
From looking at the indentation, this block is made up of lines 9 and 10.
If the while statement’s condition evaluates to False, then the program execution will skip the
code inside the following block and jump down to the first line after the block (which is line 12).
If the condition was True, the program execution starts at the top of the block and executes each
line in turn going down. When it reaches the bottom of the block, the program execution jumps
back to the while statement on line 8 and checks the condition again. If it is still True, the
execution jumps into the block again. If it is False, the program execution will skip past it.
You can think of the while statement while i >= 0: as meaning, “while the variable i is
greater than or equal to zero, keep executing the code in the following block”.

64 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
“Growing” a String
Remember on line 7 that the i variable is first set to the length of the message minus one, and
the while loop on line 8 will keep executing the lines inside the following block until the
condition i >= 0 is False.
reverseCipher.py
7. i = len(message) - 1
8. while i >= 0:
9. translated = translated + message[i]
10. i = i – 1
11.
12. print(translated)
There are two lines inside the while statement’s block, line 9 and line 10.
Line 9 is an assignment statement that stores a value in the translated variable. The value
that is stored is the current value of translated concatenated with the character at the index i
in message. In this way, the string value stored in translated “grows” until it becomes the
fully encrypted string.
Line 10 is an assignment statement also. It takes the current integer value in i and subtracts one
from it (this is called decrementing the variable), and then stores this value as the new value of
i.
The next line is line 12, but since this line has less indentation, Python knows that the while
statement’s block has ended. So rather than go on to line 12, the program execution jumps back to
line 8 where the while loop’s condition is checked again. If the condition is True, then the
lines inside the block (lines 9 and 10) are executed again. This keeps happening until the
condition is False (that is, when i is less than 0), in which case the program execution goes to
the first line after the block (line 12).
Let’s think about the behavior of this loop. The variable i starts off with the value of the last
index of message and the translated variable starts off as the blank string. Then inside the
loop, the value of message[i] (which is the last character in the message string, since i will
have the value of the last index) is added to the end of the translated string.
Then the value in i is decremented (that is, reduced) by 1. This means that message[i] will
be the second to last character. So while i as an index keeps moving from the back of the string
in message to the front, the string message[i] is added to the end of translated. This is

Chapter 5 – The Reverse Cipher 65
what causes translated to hold the reverse of the string in the message. When i is finally
set to -1, then the while loop’s condition will be False and the execution jumps to line 12.
reverseCipher.py
12. print(translated)
At the end of our program on line 12, we print out the contents of the translated variable
(that is, the string '.daed era meht fo owt fi ,terces a peek nac eerhT') to
the screen. This will show the user what the reversed string looks like.
If you are still having trouble understanding how the code in the while loop reverses the string,
try adding this new line inside the while loop:
reverseCipher.py
8. while i >= 0:
9. translated = translated + message[i]
10. print(i, message[i], translated)
11. i = i - 1
12.
13. print(translated)
This will print out the three expressions i, message[i], and translated each time the
execution goes through the loop (that is, on each iteration of the loop). The commas tell the
print() function that we are printing three separate things, so the function will add a space in
between them. Now when you run the program, you can see how the translated variable
“grows”. The output will look like this:
48 . .
47 d .d
46 a .da
45 e .dae
44 d .daed
43 .daed
42 e .daed e
41 r .daed er
40 a .daed era
39 .daed era
38 m .daed era m
37 e .daed era me
36 h .daed era meh
35 t .daed era meht
34 .daed era meht
33 f .daed era meht f
32 o .daed era meht fo
31 .daed era meht fo

66 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
30 o .daed era meht fo o
29 w .daed era meht fo ow
28 t .daed era meht fo owt
27 .daed era meht fo owt
26 f .daed era meht fo owt f
25 i .daed era meht fo owt fi
24 .daed era meht fo owt fi
23 , .daed era meht fo owt fi ,
22 t .daed era meht fo owt fi ,t
21 e .daed era meht fo owt fi ,te
20 r .daed era meht fo owt fi ,ter
19 c .daed era meht fo owt fi ,terc
18 e .daed era meht fo owt fi ,terce
17 s .daed era meht fo owt fi ,terces
16 .daed era meht fo owt fi ,terces
15 a .daed era meht fo owt fi ,terces a
14 .daed era meht fo owt fi ,terces a
13 p .daed era meht fo owt fi ,terces a p
12 e .daed era meht fo owt fi ,terces a pe
11 e .daed era meht fo owt fi ,terces a pee
10 k .daed era meht fo owt fi ,terces a peek
9 .daed era meht fo owt fi ,terces a peek
8 n .daed era meht fo owt fi ,terces a peek n
7 a .daed era meht fo owt fi ,terces a peek na
6 c .daed era meht fo owt fi ,terces a peek nac
5 .daed era meht fo owt fi ,terces a peek nac
4 e .daed era meht fo owt fi ,terces a peek nac e
3 e .daed era meht fo owt fi ,terces a peek nac ee
2 r .daed era meht fo owt fi ,terces a peek nac eer
1 h .daed era meht fo owt fi ,terces a peek nac eerh
0 T .daed era meht fo owt fi ,terces a peek nac eerhT
.daed era meht fo owt fi ,terces a peek nac eerhT
The first line, which shows “48 . .”, is showing what the expressions i, message[i], and
translated evaluate to after the string message[i] has been added to the end of
translated but before i is decremented. You can see that the first time the program execution
goes through the loop, i is set to 48, and so message[i] (that is, message[48]) is the string
'.'. The translated variable started as a blank string, but when message[i] was added to
the end of it on line 9, it became the string value '.'.
On the next iteration of the loop, the print() call displays “47 . .d”. You can see that i has
been decremented from 48 to 47, and so now message[i] is message[47], which is the
'd' string. (That’s the second “d” in “dead”.) This 'd' gets added to the end of translated
so that translated is now set to '.d'.
Now you can see how the translated variable’s string is slowly “grown” from a blank string
to the reverse of the string stored in message.

Chapter 5 – The Reverse Cipher 67
Tracing Through the Program, Step by Step
The previous explanations have gone through what each line does, but let’s go step by step
through the program the same way the Python interpreter does. The interpreter starts at the very
top, executes the first line, then moves down a line to execute the next instruction. The blank lines
and comments are skipped. The while loop will cause the program execution will loop back to
the start of the loop after it finishes.
Here is a brief explanation of each line of code in the same order that the Python interpreter
executes it. Follow along with to see how the execution moves down the lines of the program, but
sometimes jumps back to a previous line.
reverseCipher.py
1. # Reverse Cipher
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. message = 'Three can keep a secret, if two of them are dead.'
5. translated = ''
6.
7. i = len(message) - 1
8. while i >= 0:
9. translated = translated + message[i]
10. i = i - 1
11.
12. print(translated)
Step 1
Line 1
This is a comment, so the Python interpreter skips it.
Step 2
Line 2
This is a comment, and skipped.
Step 3
Line 4
The string value 'Three can keep a secret, if two of
them are dead.' is stored in the message variable.
Step 4
Line 5
The blank string '' is stored in the translated variable.
Step 5
Line 7
len(message) - 1 evaluates to 48. The integer 48 is stored in the i
variable.
Step 6
Line 8
The while loop’s condition i >= 0 evaluates to True. Since the
condition is True, the program execution moves inside the following
block.
Step 7
Line 9
translated + message[i] to '.'. The string value '.' is stored
in the translated variable.
Step 8
Line 10
i - 1 evaluates to 47. The integer 47 is stored in the i variable.
Step 9
Line 8
When the program execution reaches the end of the block, the execution
moves back to the while statement and rechecks the condition. i >= 0

68 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
evaluates to True, the program execution moves inside the block again.
Step 10
Line 9
translated + message[i] evaluates '.d'. The string value '.d'
is stored in the translated variable.
Step 11
Line 10
i - 1 evaluates to 46. The integer 46 is stored in the i variable.
Step 12
Line 8
The while statement rechecks the condition. Since i >= 0 evaluates to
True, the program execution will move inside the block again.
Step 13
to
Step 149
...The lines of the code continue to loop. We fast-forward to when i is set to
0 and translated is set to ' .daed era meht fo owt fi
,terces a peek nac eerh'...
Step 150
Line 8
The while loop’s condition is checked, and 0 >= 0 evaluates to True.
Step 151
Line 9
translated + message[i] evaluates to '.daed era meht fo
owt fi ,terces a peek nac eerhT'. This string is stored in the
translated variable.
Step 152
Line 10
i - 1 evaluates to 0 - 1, which evaluates to -1. -1 is stored in the i
variable.
Step 153
Line 8
The while loop’s condition is i >= 0, which evaluates to -1 >= 0,
which evaluates to False. Because the condition is now False, the
program execution skips the following block of code and goes to line 12.
Step 154
Line 12
translated evaluates to the string value '.daed era meht fo
owt fi ,terces a peek nac eerhT'. The print() function is
called and this string is passed, making it appear on the screen.
There are no more lines after line 12, so the program terminates.
Using input() In Our Programs
The programs in this book are all designed so that the strings that are being encrypted or
decrypted are typed directly into the source code. You could also modify the assignment
statements so that they call the input() function. You can pass a string to the input()
function to appear as a prompt for the user to type in the string to encrypt. For example, if you
change line 4 in reverseCipher.py to this:
reverseCipher.py
4. message = input('Enter message: ')
Then when you run the program, it will print the prompt to the screen and wait for the user to
type in the message and press Enter. The message that the user types in will be the string value
that is stored in the message variable:
Enter message: Hello world!
!dlrow olleH

Chapter 5 – The Reverse Cipher 69
Practice Exercises, Chapter 5, Section A
Practice exercises can be found at http://invpy.com/hackingpractice5A.
Summary
Now that we have learned how to deal with text, we can start making programs that the user can
run and interact with. This is important because text is the main way the user and the computer
will communicate with each other.
Strings are just a different data type that we can use in our programs. We can use the + operator
to concatenate strings together. We can use indexing and slicing to create a new string from part
of a different string. The len() function takes a string argument and returns an integer of how
many characters are in the string.
The Boolean data type has only two values: True and False. Comparison operators ==, !=, <,
>, <=, and >= can compare two values and evaluate to a Boolean value.
Conditions are expression that are used in several different kinds of statements. A while loop
statement keeps executing the lines inside the block that follows it as long as its condition
evaluates to True. A block is made up of lines with the same level of indentation, including any
blocks inside of them.
A common practice in programs is to start a variable with a blank string, and then concatenate
characters to it until it “grows” into the final desired string.

70 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
THE CAESAR CIPHER
Topics Covered In This Chapter:
The import statement
Constants
The upper() string method
for loops
if, elif, and else statements
The in and not in operators
The find() string method
“BIG BROTHER IS WATCHING YOU.”
“1984” by George Orwell
Implementing a Program
In Chapter 1, we used a cipher wheel, a St. Cyr slide, and a chart of letters and numbers to
implement the Caesar cipher. In this chapter, we will use a computer program to implement the
Caesar cipher.
The reverse cipher always encrypts the same way. But the Caesar cipher uses keys, which encrypt
the message in a different way depending on which key is used. The keys for the Caesar cipher

Chapter 6 – The Caesar Cipher 71
are the integers from 0 to 25. Even if a cryptanalyst knows that the Caesar cipher was used, that
alone does not give her enough information to break the cipher. She must also know the key.
Source Code of the Caesar Cipher Program
Type in the following code into the file editor, and then save it as caesarCipher.py. Press F5 to
run the program. Note that first you will need to download the pyperclip.py module and place this
file in the same directory (that is, folder) as the caesarCipher.py file. You can download this file
from http://invpy.com/pyperclip.py
Source code for caesarCipher.py
1. # Caesar Cipher
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import pyperclip
5.
6. # the string to be encrypted/decrypted
7. message = 'This is my secret message.'
8.
9. # the encryption/decryption key
10. key = 13
11.
12. # tells the program to encrypt or decrypt
13. mode = 'encrypt' # set to 'encrypt' or 'decrypt'
14.
15. # every possible symbol that can be encrypted
16. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
17.
18. # stores the encrypted/decrypted form of the message
19. translated = ''
20.
21. # capitalize the string in message
22. message = message.upper()
23.
24. # run the encryption/decryption code on each symbol in the message string
25. for symbol in message:
26. if symbol in LETTERS:
27. # get the encrypted (or decrypted) number for this symbol
28. num = LETTERS.find(symbol) # get the number of the symbol
29. if mode == 'encrypt':
30. num = num + key
31. elif mode == 'decrypt':
32. num = num - key
33.
34. # handle the wrap-around if num is larger than the length of

72 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
35. # LETTERS or less than 0
36. if num >= len(LETTERS):
37. num = num - len(LETTERS)
38. elif num < 0:
39. num = num + len(LETTERS)
40.
41. # add encrypted/decrypted number's symbol at the end of translated
42. translated = translated + LETTERS[num]
43.
44. else:
45. # just add the symbol without encrypting/decrypting
46. translated = translated + symbol
47.
48. # print the encrypted/decrypted string to the screen
49. print(translated)
50.
51. # copy the encrypted/decrypted string to the clipboard
52. pyperclip.copy(translated)
Sample Run of the Caesar Cipher Program
When you run this program, the output will look like this:
GUVF VF ZL FRPERG ZRFFNTR.
The above text is the string 'This is my secret message.' encrypted with the Caesar
cipher with key 13. The Caesar cipher program you just ran will automatically copy this
encrypted string to the clipboard so you can paste it in an email or text file. This way you can
easily take the encrypted output from the program and send it to another person.
To decrypt, just paste this text as the new value stored in the message variable on line 7. Then
change the assignment statement on line 13 to store the string 'decrypt' in the variable mode:
caesarCipher.py
6. # the string to be encrypted/decrypted
7. message = 'GUVF VF ZL FRPERG ZRFFNTR.'
8.
9. # the encryption/decryption key
10. key = 13
11.
12. # tells the program to encrypt or decrypt
13. mode = 'decrypt' # set to 'encrypt' or 'decrypt'
When you run the program now, the output will look like this:

Chapter 6 – The Caesar Cipher 73
THIS IS MY SECRET MESSAGE.
If you see this error message when running the program:
Traceback (most recent call last):
File "C:\Python32\caesarCipher.py", line 4, in <module>
import pyperclip
ImportError: No module named pyperclip
…then you have not downloaded the pyperclip module into the right folder. If you still
cannot get the module working, just delete lines 4 and 52 (which have the text “pyperclip” in
them) from the program. This will get rid of the code that depends on the pyperclip module.
Checking Your Source Code with the Online Diff Tool
To compare the code you typed to the code that is in this book, you can use the online diff tool on
this book’s website. Open http://invpy.com/hackingdiff in your web browser. Copy and paste
your code into the text field on this web page, and then click the Compare button. The diff tool
will show any differences between your code and the code in this book. This can help you find
any typos you made when typing out the program.
Practice Exercises, Chapter 6, Set A
Practice exercises can be found at http://invpy.com/hackingpractice6A.
How the Program Works
Let’s go over exactly what each of the lines of code in this program does.
Importing Modules with the import Statement
caesarCipher.py
1. # Caesar Cipher
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import pyperclip
Line 4 is a new kind of statement called an import statement. While Python includes many
built-in functions, some functions exist in separate programs called modules. Modules are
Python programs that contain additional functions that can be used by your program. In this case,
we’re importing a module named pyperclip so that we can call the pyperclip.copy()
function later in this program.

74 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The import statement is made up of the import keyword followed by the module name. Line
4 is an import statement that imports the pyperclip module, which contains several
functions related to copying and pasting text to the clipboard.
caesarCipher.py
6. # the string to be encrypted/decrypted
7. message = 'This is my secret message.'
8.
9. # the encryption/decryption key
10. key = 13
11.
12. # tells the program to encrypt or decrypt
13. mode = 'encrypt' # set to 'encrypt' or 'decrypt'
The next few lines set three variables: message will store the string to be encrypted or
decrypted, key will store the integer of the encryption key, and mode will store either the string
'encrypt' (which will cause code later in the program to encrypt the string in message) or
'decrypt' (which will tell the program to decrypt rather than encrypting).
Constants
caesarCipher.py
15. # every possible symbol that can be encrypted
16. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
We also need a string that contains all the capital letters of the alphabet in order. It would be
tiring to type the full 'ABCDEFGHIJKLMNOPQRSTUVWXYZ' string value each time we use it in
the program (and we might make typos when typing it, which would cause errors in our
program). So instead we will type the code for the string value once and place it in a variable
named LETTERS. This string contains all the letters that our cipher program can possibly
encrypt. This set of letters (which don’t have to be just letters but can also be numbers,
punctuation, or any other symbol) is called the cipher’s symbol set. The end of this chapter will
tell you how to expand this program’s symbol set to include other characters besides letters.
The LETTERS variable name is in all capitals. This is the programming convention for constant
variables. Constants are variables whose values are not meant to be changed when the program
runs. Although we can change LETTERS just like any other variable, the all-caps reminds the
programmer to not write code that does so.

Chapter 6 – The Caesar Cipher 75
Like all conventions, we don’t have to follow it. But doing it this way makes it easier for other
programmers to understand how these variables are used. (It even can help you if you are looking
at code you wrote yourself a long time ago.)
The upper() and lower() String Methods
caesarCipher.py
18. # stores the encrypted/decrypted form of the message
19. translated = ''
20.
21. # capitalize the string in message
22. message = message.upper()
On line 19, the program stores a blank string in a variable named translated. Just like in the
reverse cipher from last chapter, by the end of the program the translated variable will
contain the completely encrypted (or decrypted) message. But for now it starts as a blank string.
Line 22 is an assignment statement that stores a value in a variable named message, but the
expression on the right side of the = operator is something we haven’t seen before:
message.upper().
This is a method call. Methods are just like functions, except they are attached to a non-module
value (or in the case of line 22, a variable containing a value) with a period. The name of this
method is upper(), and it is being called on the string value stored in the message variable.
A function is not a method just because it is in a module. You will see on line 52 that we call
pyperclip.copy(), but pyperclip is a module that was imported on line 4, so copy() is
not a method. It is just a function that is inside the pyperclip module. If this is confusing, then
you can always call methods and functions a “function” and people will know what you’re
talking about.
Most data types (such as strings) have methods. Strings have a method called upper() and
lower() which will evaluate to an uppercase or lowercase version of that string, respectively.
Try typing the following into the interactive shell:
>>> 'Hello world!'.upper()
'HELLO WORLD!'
>>> 'Hello world!'.lower()
'hello world!'
>>>
76 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Because the upper() method returns a string value, you can call a method on that string as
well. Try typing 'Hello world!'.upper().lower() into the shell:
>>> 'Hello world!'.upper().lower()
'hello world!'
>>>
'Hello world!'.upper() evaluates to the string 'HELLO WORLD!', and then we call
the lower() method on that string. This returns the string 'hello world!', which is the
final value in the evaluation. The order is important. 'Hello world!'.lower().upper()
is not the same as 'Hello world!'.upper().lower():
>>> 'Hello world'.lower().upper()
'HELLO WORLD!'
>>>
If a string is stored in a variable, you can call any string method (such as upper() or
lower()) on that variable. Look at this example:
>>> fizz = 'Hello world!'
>>> fizz.upper()
'HELLO WORLD!'
>>> fizz
'Hello world!'
Calling the upper() or lower() method on a string value in a variable does not change the
value inside a variable. Methods are just part of expressions that evaluate to a value. (Think about
it like this: the expression fizz + 'ABC' would not change the string stored in fizz to have
'ABC' concatenated to the end of it, unless we used it in an assignment statement like fizz =
fizz + 'ABC'.)
Different data types have different methods. You will learn about other methods as you read this
book. A list of common string methods is at http://invpy.com/stringmethods.
The for Loop Statement
caesarCipher.py
24. # run the encryption/decryption code on each symbol in the message string
25. for symbol in message:
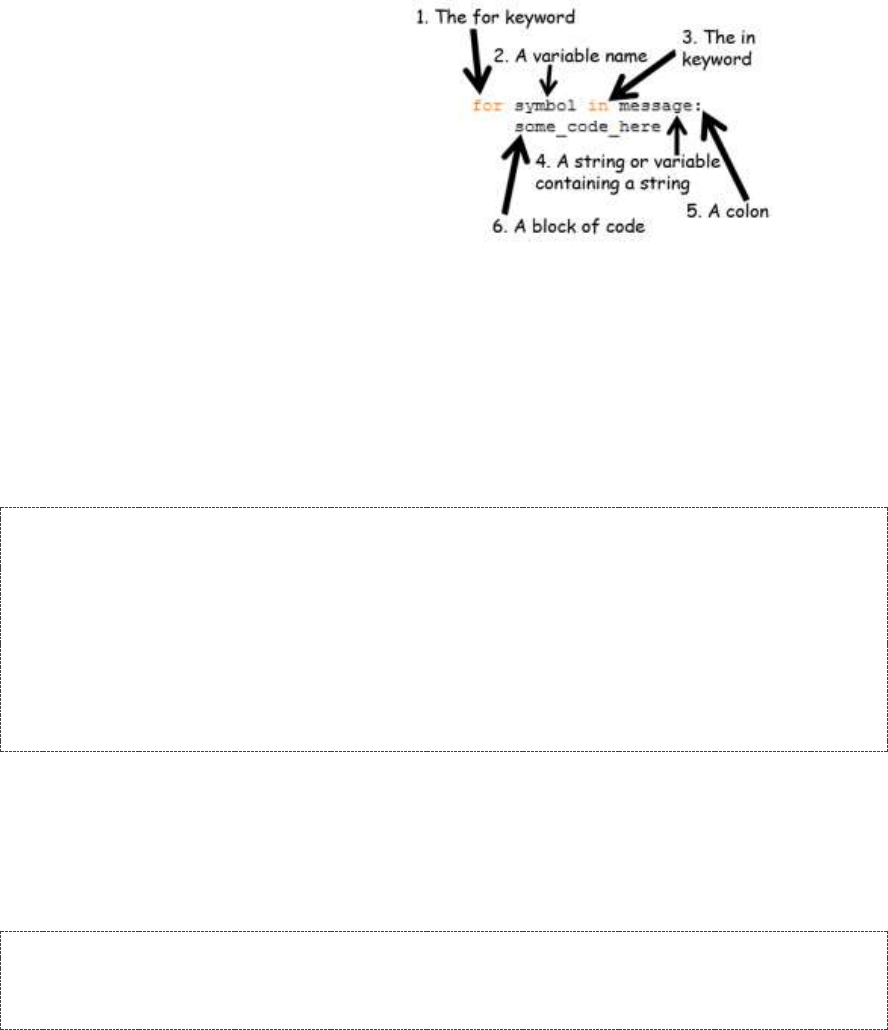
Chapter 6 – The Caesar Cipher 77
The for loop is very good at looping over a string or list of values (we will learn about lists
later). This is different from the while loop, which loops as long as a certain condition is True.
A for statement has six parts:
1. The for keyword.
2. A variable name.
3. The in keyword.
4. A string value (or a variable
containing a string value).
5. A colon.
6. A block of code.
Figure 6-1. The parts of a for loop statement.
Each time the program execution goes through the loop (that is, on each iteration through the
loop) the variable in the for statement takes on the value of the next character in the string.
For example, type the following into the interactive shell. Note that after you type the first line,
the >>> prompt will turn into ... (although in IDLE, it will just print three spaces) because the
shell is expecting a block of code after the for statement’s colon. In the interactive shell, the
block will end when you enter a blank line:
>>> for letter in 'Howdy':
... print('The letter is ' + letter)
...
The letter is H
The letter is o
The letter is w
The letter is d
The letter is y
>>>
A while Loop Equivalent of a for Loop
The for loop is very similar to the while loop, but when you only need to iterate over
characters in a string, using a for loop is much less code to type. You can make a while loop
that acts the same way as a for loop by adding a little extra code:
>>> i = 0
>>> while i < len('Howdy'):
... letter = 'Howdy'[i]
78 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
... print('The letter is ' + letter)
... i = i + 1
...
The letter is H
The letter is o
The letter is w
The letter is d
The letter is y
>>>
Notice that this while loop does the exact same thing that the for loop does, but is not as short
and simple as the for loop.
Before we can understand lines 26 to 32 of the Caesar cipher program, we need to first learn
about the if, elif, and else statements, the in and not in operators, and the find()
string method.
Practice Exercises, Chapter 6, Set B
Practice exercises can be found at http://invpy.com/hackingpractice6B.
The if Statement
An if statement can be read as “If this condition is True, execute the code in the following
block. Otherwise if it is False, skip the block.” Open the file editor and type in the following
small program. Then save the file as password.py and press F5 to run it.
Source code for password.py
1. print('What is the password?')
2. password = input()
3. if password == 'rosebud':
4. print('Access granted.')
5. if password != 'rosebud':
6. print('Access denied.')
7. print('Done.')
When the password = input() line is executed, the user can type in anything she wants and
it will be stored as a string in the variable password. If she typed in “rosebud” (in all lowercase
letters), then the expression password == 'rosebud' will evaluate to True and the
program execution will enter the following block to print the 'Access granted.' string.
If password == 'rosebud' is False, then this block of code is skipped. Next, the second
if statement will have its condition also evaluated. If this condition, password !=
Chapter 6 – The Caesar Cipher 79
'rosebud' is True, then the execution jumps inside of the following block to print out
'Access denied.'. If the condition is False, then this block of code is skipped.
The else Statement
Often we want to test a condition and execute one block of code if it is True and another block
of code if it is False. The previous password.py example is like this, but it used two if
statements.
An else statement can be used after an if statement’s block, and its block of code will be
executed if the if statement’s condition is False. You can read the code as “if this condition is
true, execute this block, or else execute this block.
Type in the following program and save it as password2.py. Notice that it does the same thing as
the previous password.py program, except it uses an if and else statement instead of two if
statements:
Source code for password2.py
1. print('What is the password?')
2. password = input()
3. if password == 'rosebud':
4. print('Access granted.')
5. else:
6. print('Access denied.')
7. print('Done.')
The elif Statement
There is also an “else if” statement called the elif statement. Like an if statement, it has a
condition. Like an else statement, it follows an if (or another elif) statement and executes if
the previous if (or elif) statement’s condition was False. You can read if, elif and else
statements as, “If this condition is true, run this block. Or else, check if this next condition is true.
Or else, just run this last block.” Type in this example program into the file editor and save it as
elifeggs.py:
Source code for elifeggs.py
1. numberOfEggs = 12
2. if numberOfEggs < 4:
3. print('That is not that many eggs.')
4. elif numberOfEggs < 20:
5. print('You have quite a few eggs.')
6. elif numberOfEggs == 144:

80 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
7. print('You have a lot of eggs. Gross!')
8. else:
9. print('Eat ALL the eggs!')
When you run this program, the integer 12 is stored in the variable numberOfEggs. Then the
condition numberOfEggs < 4 is checked to see if it is True. If it isn’t, the execution skips
the block and checks numberOfEggs < 20. If it isn’t True, execution skips that block and
checks if numberOfEggs == 144. If all of these conditions have been False, then the
else block is executed.
Notice that one and only one of these blocks will be executed. You can have zero or more
elif statements following an if statement. You can have zero or one else statements, and the
else statement always comes last.
The in and not in Operators
An expression of two strings connected by the in operator will evaluate to True if the first
string is inside the second string. Otherwise the expression evaluates to False. Notice that the
in and not in operators are case-sensitive. Try typing the following in the interactive shell:
>>> 'hello' in 'hello world!'
True
>>> 'ello' in 'hello world!'
True
>>> 'HELLO' in 'hello world!'
False
>>> 'HELLO' in 'HELLO world!'
True
>>> '' in 'Hello'
True
>>> '' in ''
True
>>> 'D' in 'ABCDEF'
True
>>>
The not in operator will evaluate to the opposite of in. Try typing the following into the
interactive shell:
>>> 'hello' not in 'hello world!'
False
>>> 'ello' not in 'hello world!'
False

Chapter 6 – The Caesar Cipher 81
>>> 'HELLO' not in 'hello world!'
True
>>> 'HELLO' not in 'HELLO world!'
False
>>> '' not in 'Hello'
False
>>> '' not in ''
False
>>> 'D' not in 'ABCDEF'
False
>>>
Expressions using the in and not in operators are handy for conditions of if statements so that
we can execute some code if a string exists inside of another string.
Also, the in keyword used in for statements is not the same as the in operator used here. They
are just typed the same.
The find() String Method
Just like the upper() method can be called on a string values, the find() method is a string
method. The find() method takes one string argument and returns the integer index of where
that string appears in the method’s string. Try typing the following into the interactive shell:
>>> 'hello'.find('e')
1
>>> 'hello'.find('o')
4
>>> fizz = 'hello'
>>> fizz.find('h')
0
>>>
If the string argument cannot be found, the find() method returns the integer -1. Notice that
the find() method is case-sensitive. Try typing the following into the interactive shell:
>>> 'hello'.find('x')
-1
>>> 'hello'.find('H')
-1
>>>

82 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The string you pass as an argument to find() can be more than one character. The integer that
find() returns will be the index of the first character where the argument is found. Try typing
the following into the interactive shell:
>>> 'hello'.find('ello')
1
>>> 'hello'.find('lo')
3
>>> 'hello hello'.find('e')
1
>>>
The find() string method is like a more specific version of using the in operator. It not only
tells you if a string exists in another string, but also tells you where.
Practice Exercises, Chapter 6, Set C
Practice exercises can be found at http://invpy.com/hackingpractice6C.
Back to the Code
Now that we understand how if, elif, else statements, the in operator, and the find()
string method works, it will be easier to understand how the rest of the Caesar cipher program
works.
caesarCipher.py
26. if symbol in LETTERS:
27. # get the encrypted (or decrypted) number for this symbol
28. num = LETTERS.find(symbol) # get the number of the symbol
If the string in symbol (which the for statement has set to be only a single character) is a
capital letter, then the condition symbol in LETTERS will be True. (Remember that on line
22 we converted message to an uppercase version with message = message.upper(), so
symbol cannot possibly be a lowercase letter.) The only time the condition is False is if
symbol is something like a punctuation mark or number string value, such as '?' or '4'.
We want to check if symbol is an uppercase letter because our program will only encrypt (or
decrypt) uppercase letters. Any other character will be added to the translated string without
being encrypted (or decrypted).

Chapter 6 – The Caesar Cipher 83
There is a new block that starts after the if statement on line 26. If you look down the program,
you will notice that this block stretches all the way to line 42. The else statement on line 44 is
paired to the if statement on line 26.
caesarCipher.py
29. if mode == 'encrypt':
30. num = num + key
31. elif mode == 'decrypt':
32. num = num - key
Now that we have the current symbol’s number stored in num, we can do the encryption or
decryption math on it. The Caesar cipher adds the key number to the letter’s number to encrypt it,
or subtracts the key number from the letter’s number to decrypt it.
The mode variable contains a string that tells the program whether or not it should be encrypting
or decrypting. If this string is 'encrypt', then the condition for line 29’s if statement will be
True and line 30 will be executed (and the block after the elif statement will be skipped). If
this string is any other value besides 'encrypt', then the condition for line 29’s if statement
is False and the program execution moves on to check the elif statement’s condition.
This is how our program knows when to encrypt (where it is adding the key) or decrypt (where it
is subtracting the key). If the programmer made an error and stored 'pineapples' in the
mode variable on line 13, then both of the conditions on lines 29 and 31 would be False and
nothing would happen to the value stored in num. (You can try this yourself by changing line 13
and re-running the program.)
caesarCipher.py
34. # handle the wrap-around if num is larger than the length of
35. # LETTERS or less than 0
36. if num >= len(LETTERS):
37. num = num - len(LETTERS)
38. elif num < 0:
39. num = num + len(LETTERS)
Remember that when we were implementing the Caesar cipher with paper and pencil, sometimes
the number after adding or subtracting the key would be greater than or equal to 26 or less than 0.
In those cases, we had to add or subtract 26 to the number to “wrap-around” the number. This
“wrap-around” is what lines 36 to 39 do for our program.

84 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
If num is greater than or equal to 26, then the condition on line 36 is True and line 37 is
executed (and the elif statement on line 38 is skipped). Otherwise, Python will check if num is
less than 0. If that condition is True, then line 39 is executed.
The Caesar cipher adds or subtracts 26 because that is the number of letters in the alphabet. If
English only had 25 letters, then the “wrap-around” would be done by adding or subtracting 25.
Notice that instead of using the integer value 26 directly, we use len(LETTERS). The function
call len(LETTERS) will return the integer value 26, so this code works just as well. But the
reason that we use len(LETTERS) instead of 26 is that the code will work no matter what
characters we have in LETTERS.
We can modify the value stored in LETTERS so that we encrypt and decrypt more than just the
uppercase letters. How this is done will be explained at the end of this chapter.
caesarCipher.py
41. # add encrypted/decrypted number's symbol at the end of translated
42. translated = translated + LETTERS[num]
Now that the integer in num has been modified, it will be the index of the encrypted (or
decrypted) letter in LETTERS. We want to add this encrypted/decrypted letter to the end of the
translated string, so line 42 uses string concatenation to add it to the end of the current value
of translated.
caesarCipher.py
44. else:
45. # just add the symbol without encrypting/decrypting
46. translated = translated + symbol
Line 44 has four spaces of indentation. If you look at the indentation of the lines above, you’ll see
that this means it comes after the if statement on line 26. There’s a lot of code in between this
if and else statement, but it all belongs in the block of code that follows the if statement on
line 26. If that if statement’s condition was False, then the block would have been skipped and
the program execution would enter the else statement’s block starting at line 46. (Line 45 is
skipped because it is a comment.)
This block has just one line in it. It adds the symbol string as it is to the end of translated.
This is how non-letter strings like ' ' or '.' are added to the translated string without being
encrypted or decrypted.

Chapter 6 – The Caesar Cipher 85
Displaying and Copying the Encrypted/Decrypted String
caesarCipher.py
48. # print the encrypted/decrypted string to the screen
49. print(translated)
50.
51. # copy the encrypted/decrypted string to the clipboard
52. pyperclip.copy(translated)
Line 49 has no indentation, which means it is the first line after the block that started on line 26
(the for loop’s block). By the time the program execution reaches line 49, it has looped through
each character in the message string, encrypted (or decrypted) the characters, and added them to
translated.
Line 49 will call the print() function to display the translated string on the screen. Notice
that this is the only print() call in the entire program. The computer does a lot of work
encrypting every letter in message, handling wrap-around, and handling non-letter characters.
But the user doesn’t need to see this. The user just needs to see the final string in translated.
Line 52 calls a function that is inside the pyperclip module. The function’s name is copy()
and it takes one string argument. Because copy() is a function in the pyperclip module, we
have to tell Python this by putting pyperclip. in front of the function name. If we type
copy(translated) instead of pyperclip.copy(translated), Python will give us an
error message.
You can see this error message for yourself by typing this code in the interactive shell:
>>> copy('Hello')
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
NameError: name 'copy' is not defined
>>>
Also, if you forget the import pyperclip line before trying to call pyperclip.copy(),
Python will give an error message. Try typing this into the interactive shell:
>>> pyperclip.copy('Hello')
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
NameError: name 'pyperclip' is not defined
>>>

86 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
That’s the entire Caesar cipher program. When you run it, notice how your computer can execute
the entire program and encrypt the string in less than a second. Even if you type in a very, very
long string for the value to store in the message variable, your computer can encrypt or decrypt
a message within a second or two. Compare this to the several minutes it would take to do this
with a cipher wheel or St. Cyr slide. The program even copies the encrypted text to the clipboard
so the user can simply paste it into an email to send to someone.
Encrypt Non-Letter Characters
One problem with the Caesar cipher that we’ve implemented is that it cannot encrypt non-letters.
For example, if you encrypt the string 'The password is 31337.' with the key 20, it will
encrypt to 'Dro zkccgybn sc 31337.' This encrypted message doesn’t keep the
password in the message very secret. However, we can modify the program to encrypt other
characters besides letters.
If you change the string that is stored in LETTERS to include more than just the uppercase letters,
then the program will encrypt them as well. This is because on line 26, the condition symbol
in LETTERS will be True. The value of num will be the index of symbol in this new, larger
LETTERS constant variable. The “wrap-around” will need to add or subtract the number of
characters in this new string, but that’s already handled because we use len(LETTERS) instead
of typing in 26 directly into the code. (This is why we programmed it this way.)
The only changes you have to make are to the LETTERS assignment statement on line 16 and
commenting out line 22 which capitalizes all the letters in message.
caesarCipher.py
15. # every possible symbol that can be encrypted
16. LETTERS = ' !"#$%&\'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\\]
^_`a bcdefghijklmnopqrstuvwxyz{|}~'
17.
18. # stores the encrypted/decrypted form of the message
19. translated = ''
20.
21. # capitalize the string in message
22. #message = message.upper()
Notice that this new string has the escape characters \' and \\ in it. You can download this new
version of the program from http://invpy.com/caesarCipher2.py.
This modification to our program is like if we had a cipher wheel or St. Cyr slide that had not
only uppercase letters but numbers, punctuation, and lowercase letters on it as well.
Chapter 6 – The Caesar Cipher 87
Even though the value for LETTERS has to be the same when running the program for decryption
as when it encrypted the message, this value doesn’t have to be secret. Only the key needs to be
kept secret, while the rest of program (including the code for the Caesar cipher program) can be
shared with the world.
Summary
You’ve had to learn several programming concepts and read through quite a few chapters to get
to this point, but now you have a program that implements a secret cipher. And more importantly,
you can understand how this code works.
Modules are Python programs that contain useful functions we can use. To use these functions,
you must first import them with an import statement. To call functions in an imported module,
put the module name and a period before the function name, like: module.function().
Constant variables are by convention written in UPPERCASE. These variables are not meant to
have their value changed (although nothing prevents the programmer from writing code that does
this). Constants are helpful because they give a “name” to specific values in your program.
Methods are functions that are attached to a value of a certain data type. The upper() and
lower() string methods return an uppercase or lowercase version of the string they are called
on. The find() string method returns an integer of where the string argument passed to it can
be found in the string it is called on.
A for loop will iterate over all the characters in string value, setting a variable to each character
on each iteration. The if, elif, and else statements can execute blocks of code based on
whether a condition is True or False.
The in and not in operators can check if one string is or isn’t in another string, and evaluates
to True or False accordingly.
Knowing how to program gives you the power to take a process like the Caesar cipher and put it
down in a language that a computer can understand. And once the computer understands how to
do it, it can do it much faster than any human can and with no mistakes (unless there are mistakes
in your programming.) This is an incredibly useful skill, but it turns out the Caesar cipher can
easily be broken by someone who knows computer programming. In the next chapter we will use
our skills to write a Caesar cipher “hacker” so we can read ciphertext that other people encrypted.
So let’s move on to the next chapter, and learn how to hack encryption.

88 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
HACKING THE CAESAR CIPHER
WITH THE BRUTE-FORCE
TECHNIQUE
Topics Covered In This Chapter:
Kerckhoffs’s Principle and Shannon’s Maxim
The brute-force technique
The range() function
String formatting (string interpolation)
Hacking Ciphers
We can hack the Caesar cipher by using a cryptanalytic technique called “brute-force”. Because
our code breaking program is so effective against the Caesar cipher, you shouldn’t use it to
encrypt your secret information.
Ideally, the ciphertext would never fall into anyone’s hands. But Kerckhoffs’s Principle (named
after the19th-century cryptographer Auguste Kerckhoffs) says that a cipher should still be secure
even if everyone else knows how the cipher works and has the ciphertext (that is, everything
except the key). This was restated by the 20th century mathematician Claude Shannon as
Shannon’s Maxim: “The enemy knows the system.”

Chapter 7 – Hacking the Caesar Cipher with the Brute Force Technique 89
Figure 7-1. Auguste Kerckhoffs
January 19, 1835 - August 9, 1903
Figure 7-2. Claude Shannon
April 30, 1916 - February 24, 2001
“A cryptosystem should be secure even if
everything about the system, except the key, is
public knowledge.”
“The enemy knows the system.”
The Brute-Force Attack
Nothing stops a cryptanalyst from guessing one key, decrypting the ciphertext with that key,
looking at the output, and if it was not the correct key then moving on to the next key. The
technique of trying every possible decryption key is called a brute-force attack. It isn’t a very
sophisticated hack, but through sheer effort (which the computer will do for us) the Caesar cipher
can be broken.
Source Code of the Caesar Cipher Hacker Program
Open a new file editor window by clicking on File ► New Window. Type in the following code
into the file editor, and then save it as caesarHacker.py. Press F5 to run the program. Note that
first you will need to download the pyperclip.py module and place this file in the same directory
as the caesarHacker.py file. You can download this file from http://invpy.com/pyperclip.py.
Source code for caesarHacker.py
1. # Caesar Cipher Hacker
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. message = 'GUVF VF ZL FRPERG ZRFFNTR.'

90 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
5. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
6.
7. # loop through every possible key
8. for key in range(len(LETTERS)):
9.
10. # It is important to set translated to the blank string so that the
11. # previous iteration's value for translated is cleared.
12. translated = ''
13.
14. # The rest of the program is the same as the original Caesar program:
15.
16. # run the encryption/decryption code on each symbol in the message
17. for symbol in message:
18. if symbol in LETTERS:
19. num = LETTERS.find(symbol) # get the number of the symbol
20. num = num - key
21.
22. # handle the wrap-around if num is 26 or larger or less than 0
23. if num < 0:
24. num = num + len(LETTERS)
25.
26. # add number's symbol at the end of translated
27. translated = translated + LETTERS[num]
28.
29. else:
30. # just add the symbol without encrypting/decrypting
31. translated = translated + symbol
32.
33. # display the current key being tested, along with its decryption
34. print('Key #%s: %s' % (key, translated))
You will see that much of this code is the same as the code in the original Caesar cipher program.
This is because the Caesar cipher hacker program does the same steps to decrypt the key.
Sample Run of the Caesar Cipher Hacker Program
Here is what the Caesar cipher program looks like when you run it. It is trying to break the
ciphertext, “GUVF VF ZL FRPERG ZRFFNTR.” Notice that the decrypted output for key 13 is
plain English, so the original encryption key must have been 13.
Key #0: GUVF VF ZL FRPERG ZRFFNTR.
Key #1: FTUE UE YK EQODQF YQEEMSQ.
Key #2: ESTD TD XJ DPNCPE XPDDLRP.
Key #3: DRSC SC WI COMBOD WOCCKQO.
Key #4: CQRB RB VH BNLANC VNBBJPN.

Chapter 7 – Hacking the Caesar Cipher with the Brute Force Technique 91
Key #5: BPQA QA UG AMKZMB UMAAIOM.
Key #6: AOPZ PZ TF ZLJYLA TLZZHNL.
Key #7: ZNOY OY SE YKIXKZ SKYYGMK.
Key #8: YMNX NX RD XJHWJY RJXXFLJ.
Key #9: XLMW MW QC WIGVIX QIWWEKI.
Key #10: WKLV LV PB VHFUHW PHVVDJH.
Key #11: VJKU KU OA UGETGV OGUUCIG.
Key #12: UIJT JT NZ TFDSFU NFTTBHF.
Key #13: THIS IS MY SECRET MESSAGE.
Key #14: SGHR HR LX RDBQDS LDRRZFD.
Key #15: RFGQ GQ KW QCAPCR KCQQYEC.
Key #16: QEFP FP JV PBZOBQ JBPPXDB.
Key #17: PDEO EO IU OAYNAP IAOOWCA.
Key #18: OCDN DN HT NZXMZO HZNNVBZ.
Key #19: NBCM CM GS MYWLYN GYMMUAY.
Key #20: MABL BL FR LXVKXM FXLLTZX.
Key #21: LZAK AK EQ KWUJWL EWKKSYW.
Key #22: KYZJ ZJ DP JVTIVK DVJJRXV.
Key #23: JXYI YI CO IUSHUJ CUIIQWU.
Key #24: IWXH XH BN HTRGTI BTHHPVT.
Key #25: HVWG WG AM GSQFSH ASGGOUS.
How the Program Works
caesarHacker.py
1. # Caesar Cipher Hacker
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. message = 'GUVF VF ZL FRPERG ZRFFNTR.'
5. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
The hacker program will create a message variable that stores the ciphertext string the program
tries to decrypt. The LETTERS constant variable contains every character that can be encrypted
with the cipher. The value for LETTERS needs to be exactly the same as the value for LETTERS
used in the Caesar cipher program that encrypted the ciphertext we are trying to hack, otherwise
the hacker program won’t work.
The range() Function
caesarHacker.py
7. # loop through every possible key
8. for key in range(len(LETTERS)):
92 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Line 8 is a for loop that does not iterate over a string value, but instead iterates over the return
value from a call to a function named range(). The range() function takes one integer
argument and returns a value of the range data type. These range values can be used in for loops
to loop a specific number of times. Try typing the following into the interactive shell:
>>> for i in range(4):
... print('Hello')
...
Hello
Hello
Hello
Hello
>>>
More specifically, the range value returned from the range() function call will set the for
loop’s variable to the integers 0 up to, but not including, the argument passed to range(). Try
typing the following into the interactive shell:
>>> for i in range(6):
... print(i)
...
0
1
2
3
4
5
>>>
Line 8 is a for loop that will set the key variable with the values 0 up to (but not including) 26.
Instead of hard-coding the value 26 directly into our program, we use the return value from
len(LETTERS) so that if we modify LETTERS the program will still work. See the “Encrypt
Non-Letter Characters” section in the last chapter to read why.
So the first time the program execution goes through this loop, key will be set to 0 and the
ciphertext in message will be decrypted with key 0. (The code inside the for loop does the
decrypting.) On the next iteration of line 8’s for loop, key will be set to 1 for the decryption.
You can also pass two integer arguments to the range() function instead of just one. The first
argument is where the range should start and the second argument is where the range should stop
(up to but not including the second argument). The arguments are separated by a comma:

Chapter 7 – Hacking the Caesar Cipher with the Brute Force Technique 93
>>> for i in range(2, 6):
... print(i)
...
2
3
4
5
>>>
The range() call evaluates to a value of the “range object” data type.
Back to the Code
caesarHacker.py
7. # loop through every possible key
8. for key in range(len(LETTERS)):
9.
10. # It is important to set translated to the blank string so that the
11. # previous iteration's value for translated is cleared.
12. translated = ''
On line 12, translated is set to the blank string. The decryption code on the next few lines
adds the decrypted text to the end of the string in translated. It is important that we reset
translated to the blank string at the beginning of this for loop, otherwise the decrypted text will
be added to the decrypted text in translated from the last iteration in the loop.
caesarHacker.py
14. # The rest of the program is the same as the original Caesar program:
15.
16. # run the encryption/decryption code on each symbol in the message
17. for symbol in message:
18. if symbol in LETTERS:
19. num = LETTERS.find(symbol) # get the number of the symbol
Lines 17 to 31 are almost exactly the same as the code in the Caesar cipher program from the last
chapter. It is slightly simpler, because this code only has to decrypt instead of decrypt or encrypt.
First we loop through every symbol in the ciphertext string stored in message on line 17. On
each iteration of this loop, line 18 checks if symbol is an uppercase letter (that is, it exists in the
LETTERS constant variable which only has uppercase letters) and, if so, decrypts it. Line 19

94 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
locates where symbol is in LETTERS with the find() method and stores it in a variable called
num.
caesarHacker.py
20. num = num - key
21.
22. # handle the wrap-around if num is 26 or larger or less than 0
23. if num < 0:
24. num = num + len(LETTERS)
Then we subtract the key from num on line 20. (Remember, in the Caesar cipher, subtracting the
key decrypts and adding the key encrypts.) This may cause num to be less than zero and require
“wrap-around”. Line 23 checks for this case and adds 26 (which is what len(LETTERS)
returns) if it was less than 0.
caesarHacker.py
26. # add number's symbol at the end of translated
27. translated = translated + LETTERS[num]
Now that num has been modified, LETTERS[num] will evaluate to the decrypted symbol. Line
27 adds this symbol to the end of the string stored in translated.
caesarHacker.py
29. else:
30. # just add the symbol without encrypting/decrypting
31. translated = translated + symbol
Of course, if the condition for line 18’s condition was False and symbol was not in
LETTERS, we don’t decrypt the symbol at all. If you look at the indentation of line 29’s else
statement, you can see that this else statement matches the if statement on line 18.
Line 31 just adds symbol to the end of translated unmodified.
String Formatting
caesarHacker.py
33. # display the current key being tested, along with its decryption
34. print('Key #%s: %s' % (key, translated))
Although line 34 is the only print() function call in our Caesar cipher hacker program, it will
print out several lines because it gets called once per iteration of line 8’s for loop.

Chapter 7 – Hacking the Caesar Cipher with the Brute Force Technique 95
The argument for the print() function call is something we haven’t used before. It is a string
value that makes use of string formatting (also called string interpolation). String formatting
with the %s text is a way of placing one string inside another one. The first %s text in the string
gets replaced by the first value in the parentheses after the % at the end of the string.
Type the following into the interactive shell:
>>> 'Hello %s!' % ('world')
'Hello world!'
>>> 'Hello ' + 'world' + '!'
'Hello world!'
>>> 'The %s ate the %s that ate the %s.' % ('dog', 'cat', 'rat')
'The dog ate the cat that ate the rat.'
>>>
String formatting is often easier to type than string concatenation with the + operator, especially
for larger strings. And one benefit of string formatting is that, unlike string concatenation, you
can insert non-string values such as integers into the string. Try typing the following into the
interactive shell:
>>> '%s had %s pies.' % ('Alice', 42)
'Alice had 42 pies.'
>>> 'Alice' + ' had ' + 42 + ' pies.'
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: Can't convert 'int' object to str implicitly
>>>
Line 34 uses string formatting to create a string that has the values in both the key and
translated variables. Because key stores an integer value, we’ll use string formatting to put
it in a string value that is passed to print().
Practice Exercises, Chapter 7, Set A
Practice exercises can be found at http://invpy.com/hackingpractice7A.
Summary
The critical failure of the Caesar cipher is that there aren’t that many different possible keys that
can be used to encrypt a message. Any computer can easily decrypt with all 26 possible keys, and
it only takes the cryptanalyst a few seconds to look through them to find the one that is in
English. To make our messages more secure, we will need a cipher that has more possible keys.
That transposition cipher in the next chapter can provide this for us.

96 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
ENCRYPTING WITH THE
TRANSPOSITION CIPHER
Topics Covered In This Chapter:
Creating functions with def statements.
main() functions
Parameters
The global and local scope, and global and local variables
The global statement
The list data type, and how lists and strings are similar
The list() function
Lists of lists
Augmented assignment operators (+=, -=, *=, /=)
The join() string method
Return values and the return statement
The special __name__ variable
The Caesar cipher isn’t secure. It doesn’t take much for a computer to brute-force through all
twenty-six possible keys. The transposition cipher has many more possible keys to make a brute-
force attack more difficult.
Encrypting with the Transposition Cipher
Instead of replacing characters with other characters, the transposition cipher jumbles up the
message’s symbols into an order that makes the original message unreadable. Before we start
writing code, let’s encrypt the message “Common sense is not so common.” with pencil and
Chapter 8 – The Transposition Cipher, Encrypting 97
paper. Including the spaces and punctuation, this message has 30 characters. We will use the
number 8 for the key.
The first step is to draw out a number of boxes equal to the key. We will draw 8 boxes since our
key for this example is 8:
The second step is to start writing the message you want to encrypt into the boxes, with one
character for each box. Remember that spaces are a character (this book marks the boxes with (s)
to indicate a space so it doesn’t look like an empty box).
C
o
m
m
o
n
(s)
s
We only have 8 boxes but there are 30 characters in the message. When you run out of boxes,
draw another row of 8 boxes under the first row. Keep creating new rows until you have written
out the full message:
1st
2nd
3rd
4th
5th
6th
7th
8th
C
o
m
m
o
n
(s)
s
e
n
s
e
(s)
i
s
(s)
n
o
t
(s)
s
o
(s)
c
o
m
m
o
n
.
We shade in the two boxes in the last row to remind us to ignore them. The ciphertext is the
letters read from the top left box going down the column. “C”, “e”, “n”, and “o” are from the 1st
column. When you get to the last row of a column, move to the top row of the next column to the
right. The next characters are “o”, “n”, “o”, “m”. Ignore the shaded boxes.
The ciphertext is “Cenoonommstmme oo snnio. s s c”, which is sufficiently scrambled to keep
someone from figuring out the original message by looking at it.
The steps for encrypting are:
1. Count the number of characters in the message and the key.
2. Draw a number of boxes equal to the key in a single row. (For example, 12 boxes for a
key of 12.)
3. Start filling in the boxes from left to right, with one character per box.
4. When you run out of boxes and still have characters left, add another row of boxes.
98 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
5. Shade in the unused boxes in the last row.
6. Starting from the top left and going down, write out the characters. When you get to the
bottom of the column, move to the next column to the right. Skip any shaded boxes. This
will be the ciphertext.
Practice Exercises, Chapter 8, Set A
Practice exercises can be found at http://invpy.com/hackingpractice8A.
A Transposition Cipher Encryption Program
Encrypting with paper and pencil involves a lot of work and it’s easy to make mistakes. Let’s
look at a program that can implement transposition cipher encryption (a decryption program will
be demonstrated later in this chapter).
Using the computer program has a slight problem, however. If the ciphertext has space characters
at the end, then it is impossible to see them since a space is just empty… well, space. To fix this,
the program adds a | character at the end of the ciphertext. (The | character is called the “pipe”
character and is above the Enter key on your keyboard.) For example:
Hello| # There are no spaces at the end of the message.
Hello | # There is one space at the end of the message.
Hello | # There are two spaces at the end of the message.
Source Code of the Transposition Cipher Encryption Program
Open a new file editor window by clicking on File ► New Window. Type in the following code
into the file editor, and then save it as transpositionEncrypt.py. Press F5 to run the program. Note
that first you will need to download the pyperclip.py module and place this file in the same
directory as the transpositionEncrypt.py file. You can download this file from
http://invpy.com/pyperclip.py.
Source code for transpositionEncrypt.py
1. # Transposition Cipher Encryption
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import pyperclip
5.
6. def main():
7. myMessage = 'Common sense is not so common.'
8. myKey = 8
9.
10. ciphertext = encryptMessage(myKey, myMessage)

Chapter 8 – The Transposition Cipher, Encrypting 99
11.
12. # Print the encrypted string in ciphertext to the screen, with
13. # a | (called "pipe" character) after it in case there are spaces at
14. # the end of the encrypted message.
15. print(ciphertext + '|')
16.
17. # Copy the encrypted string in ciphertext to the clipboard.
18. pyperclip.copy(ciphertext)
19.
20.
21. def encryptMessage(key, message):
22. # Each string in ciphertext represents a column in the grid.
23. ciphertext = [''] * key
24.
25. # Loop through each column in ciphertext.
26. for col in range(key):
27. pointer = col
28.
29. # Keep looping until pointer goes past the length of the message.
30. while pointer < len(message):
31. # Place the character at pointer in message at the end of the
32. # current column in the ciphertext list.
33. ciphertext[col] += message[pointer]
34.
35. # move pointer over
36. pointer += key
37.
38. # Convert the ciphertext list into a single string value and return it.
39. return ''.join(ciphertext)
40.
41.
42. # If transpositionEncrypt.py is run (instead of imported as a module) call
43. # the main() function.
44. if __name__ == '__main__':
45. main()
Sample Run of the Transposition Cipher Encryption Program
When you run the above program, it produces this output:
Cenoonommstmme oo snnio. s s c|
This ciphertext (without the pipe character at the end) is also copied to the clipboard, so you can
paste it into an email to someone. If you want to encrypt a different message or use a different

100 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
key, change the value assigned to the myMessage and myKey variables on lines 7 and 8. Then
run the program again.
How the Program Works
transpositionEncrypt.py
1. # Transposition Cipher Encryption
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import pyperclip
The transposition cipher program, like the Caesar cipher program, will copy the encrypted text to
the clipboard. So first we will import the pyperclip module so it can call
pyperclip.copy().
Creating Your Own Functions with def Statements
transpositionEncrypt.py
6. def main():
7. myMessage = 'Common sense is not so common.'
8. myKey = 8
A function (like print()) is a sort of mini-program in your program. When the function is
called, the execution moves to the code inside that function and then returns to the line after the
function call. You can create your own functions with a def statement like the one on line 6.
The def statement on line 6 isn't a call to a function named main(). Instead, the def statement
means we are creating, or defining, a new function named main() that we can call later in our
program. When the execution reaches the def statement Python will define this function. We can
then call it the same way we call other functions. When we call this function, the execution
moves inside of the block of code following the def statement.
Open a new file editor window and type the following code into it:
Source code for helloFunction.py
1. def hello():
2. print('Hello!')
3. total = 42 + 1
4. print('42 plus 1 is %s' % (total))
5. print('Start!')
6. hello()
7. print('Call it again.')
8. hello()

Chapter 8 – The Transposition Cipher, Encrypting 101
9. print('Done.')
Save this program with the name helloFunction.py and run it by pressing F5. The output looks
like this:
Start!
Hello!
42 plus 1 is 43
Call it again.
Hello!
42 plus 1 is 43
Done.
When the helloFunction.py program runs, the execution starts at the top. The first line is a def
statement that defines the hello() function. The execution skips the block after the def
statement and executes the print('Start!') line. This is why 'Start!' is the first string
printed when we run the program.
The next line after print('Start!') is a function call to our hello() function. The
program execution jumps to the first line in the hello() function’s block on line 2. This
function will cause the strings 'Hello!' and '42 plus 1 is 43' to be printed to the
screen.
When the program execution reaches the bottom of the def statement, the execution will jump
back to the line after the line that originally called the function (line 7). In helloFunction.py, this
is the print('Call it again.') line. Line 8 is another call to the hello() function. The
program execution will jump back into the hello() function and execute the code there again.
This is why 'Hello!' and '42 plus 1 is 43' are displayed on the screen two times.
After that function returns to line 9, the print('Done.') line executes. This is the last line in
our program, so the program exits.
The Program’s main() Function
transpositionEncrypt.py
6. def main():
7. myMessage = 'Common sense is not so common.'
8. myKey = 8

102 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The rest of the programs in this book have a function named main() which is called at the start
of program. The reason is explained at the end of this chapter, but for now just know that the
main() function in the programs in this book are always called soon after the programs are run.
On lines 7 and 8, the variables myMessage and myKey will store the plaintext message to
encrypt and the key used to do the encryption.
transpositionEncrypt.py
10. ciphertext = encryptMessage(myKey, myMessage)
The code that does the actual encrypting will be put into a function we define on line 21 named
encryptMessage(). This function will take two arguments: an integer value for the key and a
string value for the message to encrypt. When passing multiple arguments to a function call,
separate the arguments with a comma.
The return value of encryptMessage() will be a string value of the encrypted ciphertext.
(The code in this function is explained next.) This string will be stored in a variable named
ciphertext.
transpositionEncrypt.py
12. # Print the encrypted string in ciphertext to the screen, with
13. # a | (called "pipe" character) after it in case there are spaces at
14. # the end of the encrypted message.
15. print(ciphertext + '|')
16.
17. # Copy the encrypted string in ciphertext to the clipboard.
18. pyperclip.copy(ciphertext)
The ciphertext message is printed to the screen on line 15 and copied to the clipboard on line 18.
The program prints a | character (called the “pipe” character) at the end of the message so that the
user can see any empty space characters at the end of the ciphertext.
Line 18 is the last line of the main() function. After it executes, the program execution will
return to the line after the line that called it. The call to main() is on line 45 and is the last line
in the program, so after execution returns from main() the program will exit.
Parameters
transpositionEncrypt.py
21. def encryptMessage(key, message):
Chapter 8 – The Transposition Cipher, Encrypting 103
The code in the encryptMessage() function does the actual encryption. The key and
message text in between the parentheses next to encryptMessage()’s def statement
shows that the encryptMessage() function takes two parameters.
Parameters are the variables that contain the arguments passed when a function is called.
Parameters are automatically deleted when the function returns. (This is just like how variables
are forgotten when a program exits.)
When the encryptMessage() function gets called from line 10, two argument values are
passed (on line 10, they are the values in myKey and myMessage). These values get assigned to
the parameters key and message (which you can see on line 21) when the execution moves to
the top of the function.
A parameter is a variable name in between the parentheses in the def statement. An
argument is a value that is passed in between the parentheses for a function call.
Python will raise an error message if you try to call a function with too many or too few
arguments for the number of parameters the function has. Try typing the following into the
interactive shell:
>>> len('hello', 'world')
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: len() takes exactly one argument (2 given)
>>> len()
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: len() takes exactly one argument (0 given)
>>>
Changes to Parameters Only Exist Inside the Function
Look at the following program, which defines and then calls a function named func():
def func(param):
param = 42
spam = 'Hello'
func(spam)
print(spam)
When you run this program, the print() call on the last line will print out 'Hello', not 42.
When func() is called with spam as the argument, the spam variable is not being sent into the
104 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
func() function and having 42 assigned to it. Instead, the value inside spam is being copied
and assigned to param. Any changes made to param inside the function will not change the
value in the spam variable.
(There is an exception to this rule when you are passing something called a list or dictionary
value, but this will be explained in chapter 10 in the “List References” section.)
This is an important idea to understand. The argument value that is “passed” in a function call is
copied to the parameter. So if the parameter is changed, the variable that provided the argument
value is not changed.
Variables in the Global and Local Scope
You might wonder why we even have the key and message parameters to begin with, since we
already have the variables myKey and myMessage from the main() function. The reason is
because myKey and myMessage are in the main() function’s local scope and can’t be used
outside of the main() function.
Every time a function is called, a local scope is created. Variables created during a function call
exist in this local scope. Parameters always exist in a local scope. When the function returns, the
local scope is destroyed and the local variables are forgotten. A variable in the local scope is still
a separate variable from a global scope variable even if the two variables have the same name.
Variables created outside of every function exist in the global scope. When the program exits,
the global scope is destroyed and all the variables in the program are forgotten. (All the variables
in the reverse cipher and Caesar cipher programs were global.)
The global Statement
If you want a variable that is assigned inside a function to be a global variable instead of a local
variable, put a global statement with the variable’s name as the first line after the def
statement.
Here are the rules for whether a variable is a global variable (that is, a variable that exists in the
global scope) or local variable (that is, a variable that exists in a function call’s local scope):
1. Variables outside of all functions are always global variables.
2. If a variable in a function is never used in an assignment statement, it is a global variable.
3. If a variable in a function is not used in a global statement and but is used in an
assignment statement, it is a local variable.
4. If a variable in a function is used in a global statement, it is a global variable when
used in that function.

Chapter 8 – The Transposition Cipher, Encrypting 105
For example, type in the following short program, save it as scope.py, and press F5 to run it:
Source code for scope.py
1. spam = 42
2.
3. def eggs():
4. spam = 99 # spam in this function is local
5. print('In eggs():', spam)
6.
7. def ham():
8. print('In ham():', spam) # spam in this function is global
9.
10. def bacon():
11. global spam # spam in this function is global
12. print('In bacon():', spam)
13. spam = 0
14.
15. def CRASH():
16. print(spam) # spam in this function is local
17. spam = 0
18.
19. print(spam)
20. eggs()
21. print(spam)
22. ham()
23. print(spam)
24. bacon()
25. print(spam)
26. CRASH()
The program will crash when Python executes line 16, and the output will look like this:
42
In eggs(): 99
42
In ham(): 42
42
In bacon(): 42
0
Traceback (most recent call last):
File "C:\scope.py", line 27, in <module>
CRASH()
File "C:\scope.py", line 16, in CRASH

106 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
print(spam)
UnboundLocalError: local variable 'spam' referenced before assignment
When the spam variable is used on lines 1, 19, 21, 23, 25 it is outside of all functions, so this is
the global variable named spam. In the eggs() function, the spam variable is assigned the
integer 99 on line 4, so Python regards this spam variable as a local variable named spam.
Python considers this local variable to be completely different from the global variable that is also
named spam. Being assigned 99 on line 4 has no effect on the value stored in the global spam
variable since they are different variables (they just happen to have the same name).
The spam variable in the ham() function on line 8 is never used in an assignment statement in
that function, so it is the global variable spam.
The spam variable in the bacon() function is used in a global statement, so we know it is
the global variable named spam. The spam = 0 assignment statement on line 13 will change the
value of the global spam variable.
The spam variable in the CRASH() function is used in an assignment statement (and not in a
global statement) so the spam variable in that function is a local variable. However, notice that
it is used in the print() function call on line 16 before it is assigned a value on line 17. This is
why calling the CRASH() function causes our program to crash with the error,
UnboundLocalError: local variable 'spam' referenced before
assignment.
It can be confusing to have global and local variables with the same name, so even if you
remember the rules for how to tell global and local variables apart, you would be better off using
different names.
Practice Exercises, Chapter 8, Set B
Practice exercises can be found at http://invpy.com/hackingpractice8B.
The List Data Type
transpositionEncrypt.py
22. # Each string in ciphertext represents a column in the grid.
23. ciphertext = [''] * key
Line 23 uses a new data type called the list data type. A list value can contain other values. Just
like how strings begin and end with quotes, a list value begins with a [ open bracket and ends
Chapter 8 – The Transposition Cipher, Encrypting 107
with ] close bracket. The values stored inside the list are typed within the brackets. If there is
more than one value in the list, the values are separated by commas.

108 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Type the following into the interactive shell:
>>> animals = ['aardvark', 'anteater', 'antelope', 'albert']
>>> animals
['aardvark', 'anteater', 'antelope', 'albert']
>>>
The animals variable stores a list value, and in this list value are four string values. The
individual values inside of a list are also called items. Lists are very good when we have to store
lots and lots of values, but we don't want variables for each one. Otherwise we would have
something like this:
>>> animals1 = 'aardvark'
>>> animals2 = 'anteater'
>>> animals3 = 'antelope'
>>> animals4 = 'albert'
>>>
This makes working with all the strings as a group very hard, especially if you have hundreds,
thousands, or millions of different values that you want stored in a list.
Many of the things you can do with strings will also work with lists. For example, indexing
and slicing work on list values the same way they work on string values. Instead of individual
characters in a string, the index refers to an item in a list. Try typing the following into the
interactive shell:
>>> animals = ['aardvark', 'anteater', 'antelope', 'albert']
>>> animals[0]
'aardvark'
>>> animals[1]
'anteater'
>>> animals[2]
'antelope'
>>> animals[3]
'albert'
>>> animals[1:3]
['anteater', 'antelope']
>>>
Remember, the first index is 0 and not 1. While using slices with a string value will give you a
string value of part of the original string, using slices with a list value will give you a list value of
part of the original list.

Chapter 8 – The Transposition Cipher, Encrypting 109
A for loop can also iterate over the values in a list, just like it iterates over the characters in a
string. The value that is stored in the for loop’s variable is a single value from the list. Try
typing the following into the interactive shell:
>>> for spam in ['aardvark', 'anteater', 'antelope', 'albert']:
... print('For dinner we are cooking ' + spam)
...
For dinner we are cooking aardvark
For dinner we are cooking anteater
For dinner we are cooking antelope
For dinner we are cooking albert
>>>
Using the list() Function to Convert Range Objects to Lists
If you need a list value that has increasing integer amounts, you could have code like this to build
up a list value using a for loop:
>>> myList = []
>>> for i in range(10):
... myList = myList + [i]
...
>>> myList
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>>
However, it is simpler to directly make a list from a range object that the range() function
returned by using the list() function:
>>> myList = list(range(10))
>>> myList
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>>
The list() function can also convert strings into a list value. The list will have several single-
character strings that were in the original string:
>>> myList = list('Hello world!')
>>> myList
['H', 'e', 'l', 'l', 'o', ' ', 'w', 'o', 'r', 'l', 'd', '!']
>>>
110 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
We won’t be using the list() function on strings or range objects in this program, but it will
come up in later in this book.
Reassigning the Items in Lists
The items inside a list can also be modified. Use the index with a normal assignment statement.
Try typing the following into the interactive shell:
>>> animals = ['aardvark', 'anteater', 'antelope', 'albert']
>>> animals
['aardvark', 'anteater', 'antelope', 'albert']
>>> animals[2] = 9999
>>> animals
['aardvark', 'anteater', 9999, 'albert']
>>>
Reassigning Characters in Strings
While you can reassign items in a list, you cannot reassign a character in a string value. Try
typing the following code into the interactive shell to cause this error:
>>> 'Hello world!'[6] = 'x'
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: 'str' object does not support item assignment
>>>
To change a character in a string, use slicing instead. Try typing the following into the interactive
shell:
>>> spam = 'Hello world!'
>>> spam = spam[:6] + 'x' + spam[7:]
>>> spam
'Hello xorld!'
>>>
Lists of Lists
List values can even contain other list values. Try typing the following into the interactive shell:
>>> spam = [['dog', 'cat'], [1, 2, 3]]
>>> spam[0]
['dog', 'cat']
>>> spam[0][0]
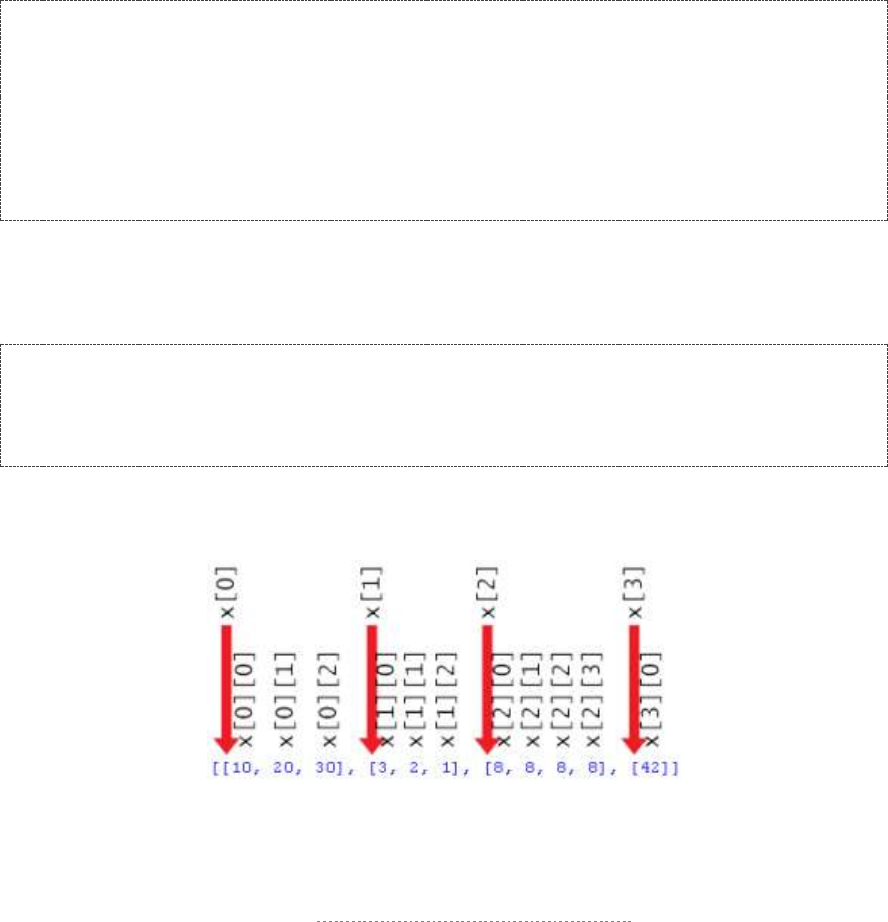
Chapter 8 – The Transposition Cipher, Encrypting 111
'dog'
>>> spam[0][1]
'cat'
>>> spam[1][0]
1
>>> spam[1][1]
2
>>>
The double index brackets used for spam[0][0] work because spam[0] evaluates to
['dog', 'cat'] and ['dog', 'cat'][0] evaluates to 'dog'. You could even use
another set of index brackets, since string values also use them:
>>> spam = [['dog', 'cat'], [1, 2, 3]]
>>> spam[0][1][1]
'a'
>>>
Say we had a list of lists stored in a variable named x. Here are the indexes for each of the items
in x. Notice that x[0], x[1], x[2], and x[3] refer to list values:
Figure 8-1. A list of lists with every item’s index labeled.
Practice Exercises, Chapter 8, Set C
Practice exercises can be found at http://invpy.com/hackingpractice8C.
Using len() and the in Operator with Lists
We’ve used the len() function to tell us how many characters are in a string (that is, the length
of the string). The len() function also works on list values and returns an integer of how many
items are in the list.

112 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Try typing the following into the interactive shell:
>>> animals = ['aardvark', 'anteater', 'antelope', 'albert']
>>> len(animals)
4
>>>
We’ve used the in operator to tell us if a string exists inside another string value. The in
operator also works for checking if a value exists in a list. Try typing the following into the
interactive shell:
>>> animals = ['aardvark', 'anteater', 'antelope', 'albert']
>>> 'anteater' in animals
True
>>> 'anteater' not in animals
False
>>> 'anteat' in animals
False
>>> 'delicious spam' in animals
False
>>>
Just like how a set of quotes next to each other represents the blank string value, a set of brackets
next to each other represents a blank list. Try typing the following into the interactive shell:
>>> animals = []
>>> len(animals)
0
>>>
List Concatenation and Replication with the + and * Operators
Just like how the + and * operators can concatenate and replicate strings, the same operators can
concatenate and replicate lists. Try typing the following into the interactive shell:
>>> ['hello'] + ['world']
['hello', 'world']
>>> ['hello'] * 5
['hello', 'hello', 'hello', 'hello', 'hello']
>>>
That’s enough about the similarities between strings and lists. Just remember that most things you
can do with string values will also work with list values.
Chapter 8 – The Transposition Cipher, Encrypting 113
Practice Exercises, Chapter 8, Set D
Practice exercises can be found at http://invpy.com/hackingpractice8D.
The Transposition Encryption Algorithm
We need to translate these paper-and-pencil steps into Python code. Let’s take a look at
encrypting the string 'Common sense is not so common.' with the key 8. If we wrote
out the boxes with pencil and paper, it would look like this:
C
o
m
m
o
n
(s)
s
e
n
s
e
(s)
i
s
(s)
n
o
t
(s)
s
o
(s)
c
o
m
m
o
n
.
Add the index of each letter in the string to the boxes. (Remember, indexes begin with 0, not 1.)
C
0
o
1
m
2
m
3
o
4
n
5
(s)
6
s
7
e
8
n
9
s
10
e
11
(s)
12
i
13
s
14
(s)
15
n
16
o
17
t
18
(s)
19
s
20
o
21
(s)
22
c
23
o
24
m
25
m
26
o
27
n
28
.
29
We can see from these boxes that the first column has the characters at indexes 0, 8, 16, and 24
(which are 'C', 'e', 'n', and 'o'). The next column has the characters at indexes 1, 9, 17,
and 25 (which are 'o', 'n', 'o' and 'm'). We can see a pattern emerging: The nth column
will have all the characters in the string at indexes 0 + n, 8 + n, 16 + n, and 24 + n:
C
0+0=0
o
1+0=1
m
2+0=2
m
3+0=3
o
4+0=4
n
5+0=5
(s)
6+0=6
s
7+0=7
e
0+8=8
n
1+8=9
s
2+8=10
e
3+8=11
(s)
4+8=12
i
5+8=13
s
6+8=14
(s)
7+8=15
n
0+16=16
o
1+16=17
t
2+16=18
(s)
3+16=19
s
4+16=20
o
5+16=21
(s)
6+16=22
c
7+16=23
o
0+24=24
m
1+24=25
m
2+24=26
o
3+24=27
n
4+24=28
.
5+24=29
There is an exception for the 6th and 7th columns, since 24 + 6 and 24 + 7 are greater than 29,
which is the largest index in our string. In those cases, we only use 0, 8, and 16 to add to n (and
skip 24).
114 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
What’s so special about the numbers 0, 8, 16, and 24? These are the numbers we get when,
starting from 0, we add the key (which in this example is 8). 0 + 8 is 8, 8 + 8 is 16, 16 + 8 is 24.
24 + 8 would be 32, but since 32 is larger than the length of the message, we stop at 24.
So, for the nth column’s string we start at index n, and then keep adding 8 (which is the key) to get
the next index. We keep adding 8 as long as the index is less than 30 (the message length), at
which point we move to the next column.
If we imagine a list of 8 strings where each string is made up of the characters in each column,
then the list value would look like this:
['Ceno', 'onom', 'mstm', 'me o', 'o sn', 'nio.', ' s ', 's c']
This is how we can simulate the boxes in Python code. First, we will make a list of blank strings.
This list will have a number of blank strings equal to the key because each string will represent a
column of our paper-and-pencil boxes. (Our list will have 8 blank strings since we are using the
key 8 in our example.) Let’s look at the code.
transpositionEncrypt.py
22. # Each string in ciphertext represents a column in the grid.
23. ciphertext = [''] * key
The ciphertext variable will be a list of string values. Each string in the ciphertext
variable will represent a column of the grid. So ciphertext[0] is the leftmost column,
ciphertext[1] is the column to the right of that, and so on.
The string values will have all the characters that go into one column of the grid. Let’s look again
at the grid from the “Common sense is not so common.” example earlier in this chapter (with
column numbers added to the top):
0
1
2
3
4
5
6
7
C
o
m
m
o
n
(s)
s
e
n
s
e
(s)
i
s
(s)
n
o
t
(s)
s
o
(s)
c
o
m
m
o
n
.
The ciphertext variable for this grid would look like this:
>>> ciphertext = ['Ceno', 'onom', 'mstm', 'me o', 'o sn', 'nio.', ' s ', 's c']
>>> ciphertext[0]
'Ceno'

Chapter 8 – The Transposition Cipher, Encrypting 115
The first step to making this list is to create as many blank strings in the ciphertext list as
there are columns. Since the number of columns is equal to the key, we can use list replication to
multiply a list with one blank string value in it by the value in key. This is how line 23 evaluates
to a list with the correct number of blank strings.
transpositionEncrypt.py
25. # Loop through each column in ciphertext.
26. for col in range(key):
27. pointer = col
The next step is to add text to each string in ciphertext. The for loop on line 26 will iterate
once for each column, and the col variable will have the correct integer value to use for the
index to ciphertext. The col variable will be set to 0 for the first iteration through the for
loop, then 1 on the second iteration, then 2 and so on. This way the expression
ciphertext[col] will be the string for the colth column of the grid.
Meanwhile, the pointer variable will be used as the index for the string value in the message
variable. On each iteration through the loop, pointer will start at the same value as col (which
is what line 27 does.)
Augmented Assignment Operators
Often when you are assigning a new value to a variable, you want it to be based off of the
variable’s current value. To do this you use the variable as the part of the expression that is
evaluated and assigned to the variable, like this example in the interactive shell:
>>> spam = 40
>>> spam = spam + 2
>>> print(spam)
42
>>>
But you can instead use the += augmented assignment operator as a shortcut. Try typing the
following into the interactive shell:
>>> spam = 40
>>> spam += 2
>>> print(spam)
42
>>> spam = 'Hello'
>>> spam += ' world!'
>>> print(spam)
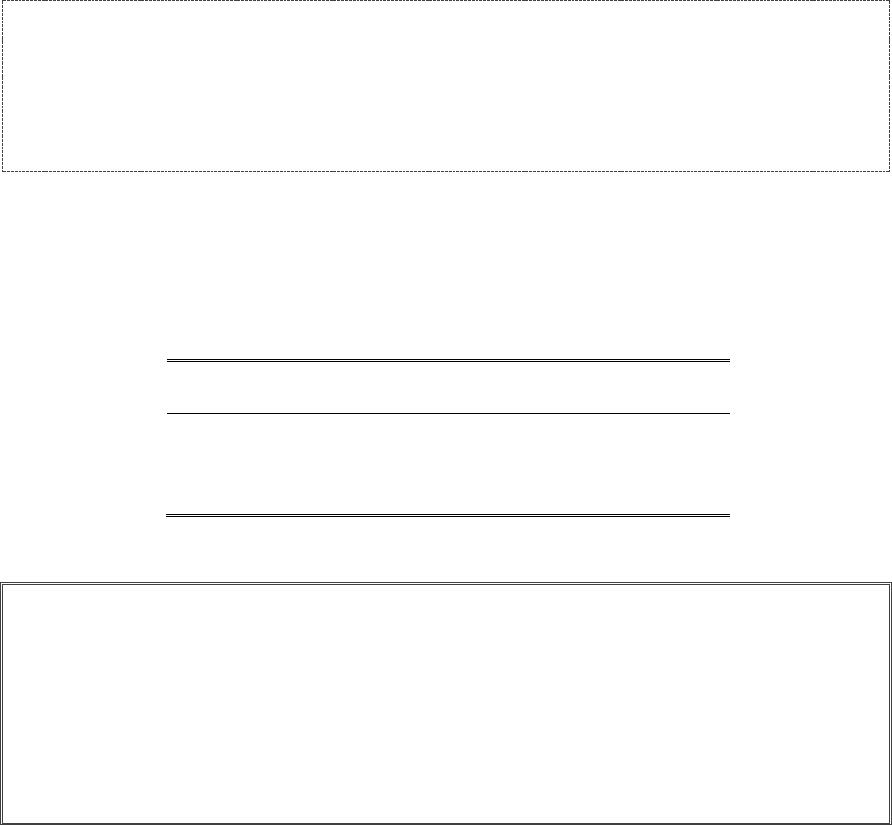
116 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Hello world!
>>> spam = ['dog']
>>> spam += ['cat']
>>> print(spam)
['dog', 'cat']
>>>
The statement spam += 2 does the exact same thing as spam = spam + 2. It’s just a little
shorter to type. The += operator works with integers to do addition, strings to do string
concatenation, and lists to do list concatenation. Table 8-1 shows the augmented assignment
operators and what they are equivalent to:
Table 8-1. Augmented Assignment Operators
Augmented Assignment
Equivalent Normal
Assignment
spam += 42
spam = spam + 42
spam -= 42
spam = spam - 42
spam *= 42
spam = spam * 42
spam /= 42
spam = spam / 42
Back to the Code
transpositionEncrypt.py
29. # Keep looping until pointer goes past the length of the message.
30. while pointer < len(message):
31. # Place the character at pointer in message at the end of the
32. # current column in the ciphertext list.
33. ciphertext[col] += message[pointer]
34.
35. # move pointer over
36. pointer += key
Inside the for loop that started on line 26 is a while loop that starts on line 30. For each
column, we want to loop through the original message variable and pick out every keyth
character. (In the example we’ve been using, we want every 8th character since we are using a key
of 8.) On line 27 for the first iteration of the for loop, pointer was set to 0.
While the value in pointer is less than the length of the message string, we want to add the
character at message[pointer] to the end of the colth string in ciphertext. We add 8
(that is, the value in key) to pointer each time through the loop on line 36. The first time it is
message[0], the second time message[8], the third time message[16], and the fourth
time message[24]. Each of these single character strings are concatenated to the end of
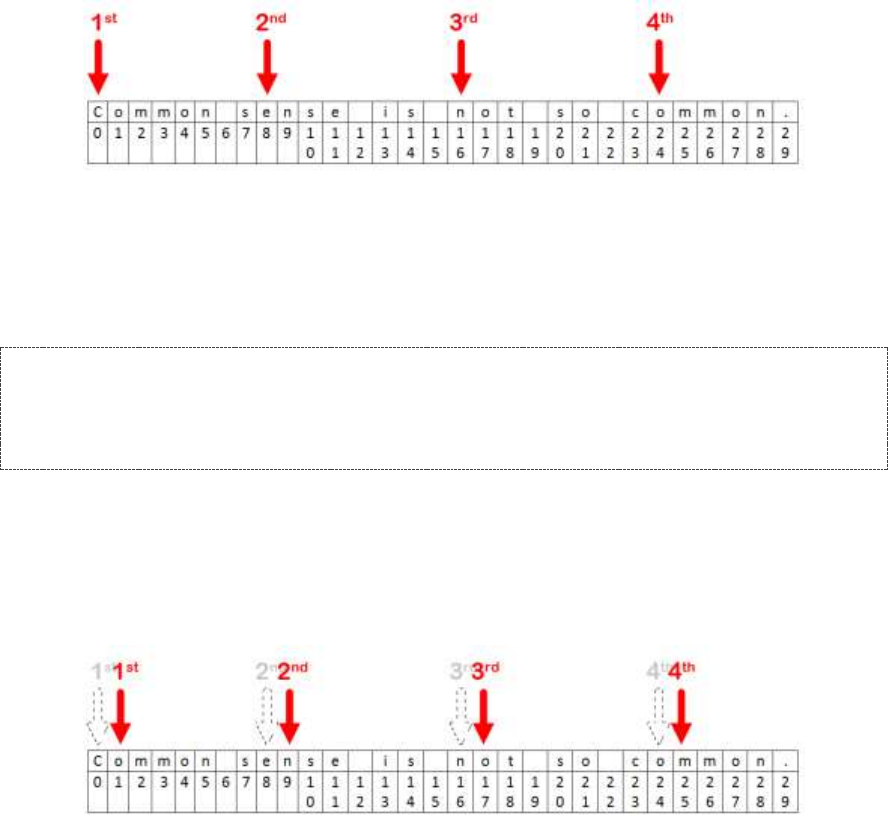
Chapter 8 – The Transposition Cipher, Encrypting 117
ciphertext[col] (and since col is 0 on the first time through the loop, this is
ciphertext[0]).
Figure 8-2. Arrows pointing to what message[pointer] refers to during the first iteration of
the for loop when col is set to 0.
Figure 8-2 shows the characters at these indexes, they will be concatenated together to form the
string 'Ceno'. Remember that we want the value in ciphertext to eventually look like this:
>>> ciphertext = ['Ceno', 'onom', 'mstm', 'me o', 'o sn', 'nio.', ' s ', 's c']
>>> ciphertext[0]
'Ceno'
>>>
Storing 'Ceno' as the first string in the ciphertext list is our first step.
On the next iteration of the for loop, col will be set to 1 (instead of 0) and pointer will start
at the same value as col. Now when we add 8 to pointer on each iteration of line 30’s
while loop, the indexes will be 1, 9, 17, and 25.
Figure 8-3. Arrows pointing to to what message[pointer] refers to during the second
iteration of the for loop when col is set to 1.
As message[1], message[9], message[17], and message[25] are concatenated to the
end of ciphertext[1], they form the string 'onom'. This is the second column of our grid.

118 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Once the for loop has finished looping for the rest of the columns, the value in ciphertext
will be ['Ceno', 'onom', 'mstm', 'me o', 'o sn', 'nio.', ' s ', 's c'].
We will use the join() string method to convert this list of strings into a single string.
The join() String Method
The join() method is used later on line 39. The join() method takes a list of strings and
returns a single string. This single string has all of the strings in the list concatenated (that is,
joined) together. The string that the join() method gets called on will be placed in between the
strings in the list. (Most of the time, we will just use a blank string for this.) Try typing the
following into the interactive shell:
>>> eggs = ['dogs', 'cats', 'moose']
>>> ''.join(eggs)
'dogscatsmoose'
>>> ' '.join(eggs)
'dogs cats moose'
>>> 'XYZ'.join(eggs)
'dogsXYZcatsXYZmoose'
>>> ''.join(eggs).upper().join(eggs)
'dogsDOGSCATSMOOSEcatsDOGSCATSMOOSEmoose'
>>>
That last expression, ''.join(eggs).upper().join(eggs), looks a little tricky, but if
you go through the evaluation one step at a time, it will look like this:
Figure 8-4. The steps of evaluation for ''.join(eggs).upper().join(eggs)

Chapter 8 – The Transposition Cipher, Encrypting 119
This is why ''.join(eggs).upper().join(eggs) returns the string,
'dogsDOGSCATSMOOSEcatsDOGSCATSMOOSEmoose'.
Whew!
Remember, no matter how complicated an expression looks, you can just evaluate it step by step
to get the single value the expression evaluates to.
Return Values and return Statements
transpositionEncrypt.py
38. # Convert the ciphertext list into a single string value and return it.
39. return ''.join(ciphertext)
Our use of the join() method isn’t nearly as complicated as the previous example. We just
want to call join() on the blank string and pass ciphertext as the argument so that the
strings in the ciphertext list are joined together (with nothing in between them).
Remember that a function (or method) call always evaluates to a value. We say that this is the
value returned by the function or method call, or that it is the return value of the function. When
we create our own functions with a def statement, we use a return statement to tell what the
return value for our function is.
A return statement is the return keyword followed by the value to be returned. We can also
use an expression instead of a value. In that case the return value will be whatever value that
expression evaluates to. Open a new file editor window and type the following program in and
save it as addNumbers.py, then press F5 to run it:
Source code for addNumbers.py
1. def addNumbers(a, b):
2. return a + b
3.
4. spam = addNumbers(2, 40)
5. print(spam)
When you run this program, the output will be:
42
That’s because the function call addNumbers(2, 40) will evaluate to 42. The return
statement in addNumbers() will evaluate the expression a + b and then return the evaluated

120 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
value. That is why addNumbers(2, 40) evaluates to 42, which is the value stored in spam
on line 4 and next printed to the screen on line 5.
Practice Exercises, Chapter 8, Set E
Practice exercises can be found at http://invpy.com/hackingpractice8E.
Back to the Code
transpositionEncrypt.py
38. # Convert the ciphertext list into a single string value and return it.
39. return ''.join(ciphertext)
The encryptMessage() function’s return statement returns a string value that is created
by joining all of the strings in the ciphertext list. This final string is the result of our
encryption code.
The great thing about functions is that a programmer only has to know what the function does,
but not how the function’s code does it. A programmer can understand that if she calls the
encryptMessage() function and pass it an integer and a string for the key and message
parameters, the function call will evaluate to an encrypted string. She doesn’t need to know
anything about how the code in encryptMessage() actually does this.
The Special __name__ Variable
transpositionEncrypt.py
42. # If transpositionEncrypt.py is run (instead of imported as a module) call
43. # the main() function.
44. if __name__ == '__main__':
45. main()
We can turn our transposition encryption program into a module with a special trick involving the
main() function and a variable named __name__.
When a Python program is run, there is a special variable with the name __name__ (that’s two
underscores before “name” and two underscores after) that is assigned the string value
'__main__' (again, two underscores before and after “main”) even before the first line of your
program is run.
At the end of our script file (and, more importantly, after all of our def statements), we want to
have some code that checks if the __name__ variable has the '__main__' string assigned to
it. If so, we want to call the main() function.

Chapter 8 – The Transposition Cipher, Encrypting 121
This if statement on line 44 ends up actually being one of the first lines of code executed when
we press F5 to run our transposition cipher encryption program (after the import statement on
line 4 and the def statements on lines 6 and 21).
The reason we set up our code this way is although Python sets __name__ to '__main__'
when the program is run, it sets it to the string 'transpositionEncrypt' if our program is
imported by a different Python program. This is how our program can know if it is being run as a
program or imported by a different program as a module.
Just like how our program imports the pyperclip module to call the functions in it, other
programs might want to import transpositionEncrypt.py to call its encryptMessage()
function. When an import statement is executed, Python will look for a file for the module by
adding “.py” to the end of the name. (This is why import pyperclip will import the
pyperclip.py file.)
When a Python program is imported, the __name__ variable is set to the filename part before
“.py” and then runs the program. When our transpositionEncrypt.py program is imported, we
want all the def statements to be run (to define the encryptMessage() function that the
importing program wants to use), but we don’t want it to call the main() function because that
will execute the encryption code for 'Common sense is not so common.' with key 8.
That is why we put that part of the code inside a function (which by convention is named
main()) and then add code at the end of the program to call main(). If we do this, then our
program can both be run as a program on its own and also imported as a module by
another program.
Key Size and Message Length
Notice what happens when the message length is less than twice the key size:
C
o
m
m
o
n
(s)
s
e
n
s
e
(s)
i
s
(s)
n
o
t
(s)
s
o
(s)
c
o
m
m
o
n
.
When using a key of 25, the “Common sense is not so common.” message encrypts to
“Cmommomno.n sense is not so co”. Part of the message isn’t encrypted! This happens whenever
key size becomes more than twice the message length, because that causes there to only be one
character per column and no characters get scrambled for that part of the message.
Because of this, the transposition cipher’s key is limited to half the length of the message it is
used to encrypt. The longer a message is, the more possible keys that can be used to encrypt it.
122 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Summary
Whew! There were a lot of new programming concepts introduced in this chapter. The
transposition cipher program is much more complicated (but much more secure) than the Caesar
cipher program in the last chapter. The new concepts, functions, data types, and operators we’ve
learned in this chapter let us manipulate data in much more sophisticated ways. Just remember
that much of understanding a line of code is just evaluating it step by step the way Python will.
We can organize our code into groups called functions, which we create with def statements.
Argument values can be passed to functions for the function’s parameters. Parameters are local
variables. Variables outside of all functions are global variables. Local variables are different
from global variables, even if they have the same name as the global variable.
List values can store multiple other values, including other list values. Many of the things you can
do with strings (such as indexing, slicing, and the len() function) can be used on lists. And
augmented assignment operators provide a nice shortcut to regular assignment operators. The
join() method can join a list that contains multiple strings to return a single string.
Feel free to go over this chapter again if you are not comfortable with these programming
concepts. In the next chapter, we will cover decrypting with the transposition cipher.

Chapter 9 – The Transposition Cipher, Decrypting 123
DECRYPTING WITH THE
TRANSPOSITION CIPHER
Topics Covered In This Chapter:
Decrypting with the transposition cipher
The math.ceil(), math.floor() and round() functions
The and and or boolean operators
Truth tables
“When stopping a terrorist attack or seeking to
recover a kidnapped child, encountering
encryption may mean the difference between
success and catastrophic failures.”
Attorney General Janet Reno, September 1999
“Even the Four Horsemen of Kid Porn, Dope
Dealers, Mafia and Terrorists don’t worry me
as much as totalitarian governments. It’s been a
long century, and we've had enough of them.”
Bruce Sterling, 1994 Computers, Freedom, and Privacy
conference

124 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Unlike the Caesar cipher, the decryption process for the transposition cipher is very different
from the encryption process. In this chapter we will create a separate program,
transpositionDecrypt.py, to handle decryption.
Decrypting with the Transposition Cipher on Paper
Let’s pretend we send the ciphertext “Cenoonommstmme oo snnio. s s c” to a friend (and she
already knows that the secret key is 8). The first step for her to decrypt the ciphertext is to
calculate how many boxes she needs to draw. To find this amount, divide the length of the
ciphertext message by the key and round up. The length of our ciphertext is 30 characters (exactly
the same as the plaintext) and the key is 8. So calculate 30 divided by 8 to get 3.75.
3.75 rounds up to 4. This means we want to draw a grid of boxes with 4 columns (the number we
just calculated) and 8 rows (the key). It will look like this:
(Note that if the length divided by the key was a whole number, like in 30 / 5 = 6.0, then 6.0
would not “round up” to 7.)
The second thing we need to calculate is how many boxes on the rightmost column to shade in.
Take the total number of boxes (32) and subtract the length of the ciphertext (30). 32 – 30 = 2, so
shade in the bottom 2 boxes on the rightmost column:

Chapter 9 – The Transposition Cipher, Decrypting 125
Then start filling in the boxes with one character of the ciphertext per box. Start at the top left and
go right, just like we did when we were encrypting. The ciphertext is “Cenoonommstmme oo
snnio. s s c”, and so “Ceno” goes in the first row, then “onom” in the second row, and so on.
After we are done, the boxes will look like this (where the (s) represents a space):
C
e
n
o
o
n
o
m
m
s
t
m
m
e
(s)
o
o
(s)
s
n
n
i
o
.
(s)
s
(s)
s
(s)
c
Our friend who received the ciphertext will see that if she reads the text going down the columns,
the original plaintext has been restored: “Common sense is not so common.”
The steps for decrypting are:
1. Calculate the number of columns you will have by taking the length of the message and
dividing by the key, then rounding up.
2. Draw out a number of boxes. The number of columns was calculated in step 1. The
number of rows is the same as the key.
3. Calculate the number of boxes to shade in by taking the number of boxes (this is the
number of rows and columns multiplied) and subtracting the length of the ciphertext
message.
4. Shade in the number of boxes you calculated in step 3 at the bottom of the rightmost
column.
5. Fill in the characters of the ciphertext starting at the top row and going from left to right.
Skip any of the shaded boxes.
6. Get the plaintext by reading from the leftmost column going from top to bottom, and
moving over to the top of the next column.
Note that if you use a different key, you will be drawing out the wrong number of rows. Even if
you follow the other steps in the decryption process correctly, the plaintext will come out looking
like random garbage (just like when you use the wrong key with the Caesar cipher).
Practice Exercises, Chapter 9, Set A
Practice exercises can be found at http://invpy.com/hackingpractice9A.

126 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
A Transposition Cipher Decryption Program
Open a new file editor window and type out the following code in it. Save this program as
transpositionDecrypt.py.
Source Code of the Transposition Cipher Decryption Program
Open a new file editor window by clicking on File ► New Window. Type in the following code
into the file editor, and then save it as transpositionDecrypt.py. Press F5 to run the program. Note
that first you will need to download the pyperclip.py module and place this file in the same
directory as the transpositionDecrypt.py file. You can download this file from
http://invpy.com/pyperclip.py.
Source code for transpositionDecrypt.py
1. # Transposition Cipher Decryption
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import math, pyperclip
5.
6. def main():
7. myMessage = 'Cenoonommstmme oo snnio. s s c'
8. myKey = 8
9.
10. plaintext = decryptMessage(myKey, myMessage)
11.
12. # Print with a | (called "pipe" character) after it in case
13. # there are spaces at the end of the decrypted message.
14. print(plaintext + '|')
15.
16. pyperclip.copy(plaintext)
17.
18.
19. def decryptMessage(key, message):
20. # The transposition decrypt function will simulate the "columns" and
21. # "rows" of the grid that the plaintext is written on by using a list
22. # of strings. First, we need to calculate a few values.
23.
24. # The number of "columns" in our transposition grid:
25. numOfColumns = math.ceil(len(message) / key)
26. # The number of "rows" in our grid will need:
27. numOfRows = key
28. # The number of "shaded boxes" in the last "column" of the grid:
29. numOfShadedBoxes = (numOfColumns * numOfRows) - len(message)
30.
31. # Each string in plaintext represents a column in the grid.

Chapter 9 – The Transposition Cipher, Decrypting 127
32. plaintext = [''] * numOfColumns
33.
34. # The col and row variables point to where in the grid the next
35. # character in the encrypted message will go.
36. col = 0
37. row = 0
38.
39. for symbol in message:
40. plaintext[col] += symbol
41. col += 1 # point to next column
42.
43. # If there are no more columns OR we're at a shaded box, go back to
44. # the first column and the next row.
45. if (col == numOfColumns) or (col == numOfColumns - 1 and row >=
numOfRows - numOfShadedBoxes):
46. col = 0
47. row += 1
48.
49. return ''.join(plaintext)
50.
51.
52. # If transpositionDecrypt.py is run (instead of imported as a module) call
53. # the main() function.
54. if __name__ == '__main__':
55. main()
When you run the above program, it produces this output:
Common sense is not so common.|
If you want to decrypt a different message, or use a different key, change the value assigned to
the myMessage and myKey variables on lines 5 and 6.
How the Program Works
transpositionDecrypt.py
1. # Transposition Cipher Decryption
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import math, pyperclip
5.
6. def main():
7. myMessage = 'Cenoonommstmme oo snnio. s s c'
8. myKey = 8
9.
128 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
10. plaintext = decryptMessage(myKey, myMessage)
11.
12. # Print with a | (called "pipe" character) after it in case
13. # there are spaces at the end of the decrypted message.
14. print(plaintext + '|')
15.
16. pyperclip.copy(plaintext)
The first part of the program is very similar to the first part of transpositionEncrypt.py. The
pyperclip module is imported along with a different module named math. If you separate the
module names with commas, you can import multiple modules with one import statement.
The main() function creates variables named myMessage and myKey, and then calls the
decryption function decryptMessage(). The return value of this function is the decrypted
plaintext of the ciphertext and key that we passed it. This is stored in a variable named
plaintext, which is then printed to the screen (with a pipe character at the end in case there
are spaces at the end of the message) and copied to the clipboard.
transpositionDecrypt.py
19. def decryptMessage(key, message):
Look at the six steps to decrypting from earlier in this chapter. For example, if we are decrypting
“Cenoonommstmme oo snnio. s s c” (which has 30 characters) with the key 8, then the final set of
boxes will look like this:
C
e
n
o
o
n
o
m
m
s
t
m
m
e
(s)
o
o
(s)
s
n
n
i
o
.
(s)
s
(s)
s
(s)
c
The decryptMessage() function implements each of the decryption steps as Python code.
The math.ceil(), math.floor() and round() Functions
When you divide numbers using the / operator, the expression returns a floating point number
(that is, a number with a decimal point). This happens even if the number divides evenly. For
example, 21 / 7 will evaluate to 3.0, not 3.

Chapter 9 – The Transposition Cipher, Decrypting 129
>>> 21 / 7
3.0
>>>
This is useful because if a number does not divide evenly, the numbers after the decimal point
will be needed. For example, 22 / 5 evaluates to 4.4:
>>> 22 / 5
4.4
>>>
(If the expression 22 / 5 evaluates to 4 instead of 4.4, then you are using version 2 of Python
instead of version 3. Please go to the http://python.org website and download and install Python
3.)
If you want to round this number to the nearest integer, you can use the round() function. Type
the following into the interactive shell:
>>> round(4.2)
4
>>> round(4.5)
4
>>> round(4.9)
5
>>> round(5.0)
5
>>> round(22 / 5)
4
>>>
If you only want to round up then use the math.ceil() function, which stands for “ceiling”. If
you only want to round down then use the math.floor() function. These functions exist in
the math module, so you will need to import the math module before calling them. Type the
following into the interactive shell:
>>> import math
>>> math.floor(4.0)
4
>>> math.floor(4.2)
4
>>> math.floor(4.9)
4
>>> math.ceil(4.0)

130 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
4
>>> math.ceil(4.2)
5
>>> math.ceil(4.9)
5
>>>
The math.ceil() function will implement step 1 of the transposition decryption.
transpositionDecrypt.py
19. def decryptMessage(key, message):
20. # The transposition decrypt function will simulate the "columns" and
21. # "rows" of the grid that the plaintext is written on by using a list
22. # of strings. First, we need to calculate a few values.
23.
24. # The number of "columns" in our transposition grid:
25. numOfColumns = math.ceil(len(message) / key)
26. # The number of "rows" in our grid will need:
27. numOfRows = key
28. # The number of "shaded boxes" in the last "column" of the grid:
29. numOfShadedBoxes = (numOfColumns * numOfRows) - len(message)
Line 25 calculates the number of columns (step 1 of decrypting) by dividing len(message) by
the integer in key. This value is passed to the math.ceil() function, and that return value is
stored in numOfColumns.
Line 27 calculates the number of rows (step 2 of decrypting), which is the integer stored in key.
This value gets stored in the variable numOfRows.
Line 29 calculates the number of shaded boxes in the grid (step 3 of decrypting), which will be
the number of columns times rows, minus the length of the message.
If we are decrypting “Cenoonommstmme oo snnio. s s c” with key 8, numOfColumns will be
set to 4, numOfRows will be set to 8, and numOfShadedBoxes will be set to 2.
transpositionDecrypt.py
31. # Each string in plaintext represents a column in the grid.
32. plaintext = [''] * numOfColumns
Just like the encryption program had a variable named ciphertext that was a list of strings to
represent the grid of ciphertext, the decryptMessage() function will have a variable named
plaintext that is a list of strings. These strings start off as blank strings, and we will need one
Chapter 9 – The Transposition Cipher, Decrypting 131
string for each column of the grid. Using list replication, we can multiply a list of one blank string
by numOfColumns to make a list of several blank strings.
(Remember that each function call has its own local scope. The plaintext in
decryptMessage() exists in a different local scope than the plaintext variable in
main(), so they are two different variables that just happen to have the same name.)
Remember that the grid for our 'Cenoonommstmme oo snnio. s s c' example looks
like this:
C
e
n
o
o
n
o
m
m
s
t
m
m
e
(s)
o
o
(s)
s
n
n
i
o
.
(s)
s
(s)
s
(s)
c
The plaintext variable will have a list of strings. Each string in the list is a single column of
this grid. For this decryption, we want plaintext to end up with this value:
>>> plaintext = ['Common s', 'ense is ', 'not so c', 'ommon.']
>>> plaintext[0]
'Common s'
That way, we can join all the list’s strings together to get the 'Common sense is not so
common.' string value to return.
transpositionDecrypt.py
34. # The col and row variables point to where in the grid the next
35. # character in the encrypted message will go.
36. col = 0
37. row = 0
38.
39. for symbol in message:
The col and row variables will track the column and row where the next character in message
should go. We will start these variables at 0. Line 39 will start a for loop that iterates over the
characters in the message string. Inside this loop the code will adjust the col and row
variables so that we concatenate symbol to the correct string in the plaintext list.
132 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
transpositionDecrypt.py
40. plaintext[col] += symbol
41. col += 1 # point to next column
As the first step in this loop we concatenate symbol to the string at index col in the
plaintext list. Then we add 1 to col (that is, we increment col) on line 41 so that on the
next iteration of the loop, symbol will be concatenated to the next string.
The and and or Boolean Operators
The Boolean operators and and or can help us form more complicated conditions for if and
while statements. The and operator connects two expressions and evaluates to True if both
expressions evaluate to True. The or operator connects two expressions and evaluates to True
if one or both expressions evaluate to True. Otherwise these expressions evaluate to False.
Type the following into the interactive shell:
>>> 10 > 5 and 2 < 4
True
>>> 10 > 5 and 4 != 4
False
>>>
The first expression above evaluates to True because the two expressions on the sides of the
and operator both evaluate to True. This means that the expression 10 > 5 and 2 < 4
evaluates to True and True, which in turn evaluates to True.
However, for the second above expression, although 10 > 5 evaluates to True the expression
4 != 4 evaluates to False. This means the whole expression evaluates to True and
False. Since both expressions have to be True for the and operator to evaluate to True,
instead they evaluate to False.
Type the following into the interactive shell:
>>> 10 > 5 or 4 != 4
True
>>> 10 < 5 or 4 != 4
False
>>>
For the or operator, only one of the sides must be True for the or operator to evaluate them
both to True. This is why 10 > 5 or 4 != 4 evaluates to True. However, because both
Chapter 9 – The Transposition Cipher, Decrypting 133
the expression 10 < 5 and the expression 4 != 4 are both False, this makes the second
above expression evaluate to False or False, which in turn evaluates to False.
The third Boolean operator is not. The not operator evaluates to the opposite Boolean value of
the value it operates on. So not True is False and not False is True. Type the following
into the interactive shell:
>>> not 10 > 5
False
>>> not 10 < 5
True
>>> not False
True
>>> not not False
False
>>> not not not not not False
True
>>>
Practice Exercises, Chapter 9, Set B
Practice exercises can be found at http://invpy.com/hackingpractice9B.
Truth Tables
If you ever forget how the Boolean operators work, you can look at these charts, which are called
truth tables:
Table 6-1: The and operator's truth table.
A
and
B
is
Entire statement
True
and
True
is
True
True
and
False
is
False
False
and
True
is
False
False
and
False
is
False
Table 6-2: The or operator's truth table.
A
or
B
is
Entire statement
True
or
True
is
True
True
or
False
is
True
False
or
True
is
True
False
or
False
is
False

134 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Table 6-3: The not operator's truth table.
not A
is
Entire statement
not True
is
False
not False
is
True
The and and or Operators are Shortcuts
Just like for loops let us do the same thing as while loops but with less code, the and and or
operators let us shorten our code also. Type in the following into the interactive shell. Both of
these bits of code do the same thing:
>>> if 10 > 5:
... if 2 < 4:
... print('Hello!')
...
Hello!
>>>
>>> if 10 > 5 and 2 < 4:
... print('Hello!')
...
Hello!
>>>
So you can see that the and operator basically takes the place of two if statements (where the
second if statement is inside the first if statement’s block.)
You can also replace the or operator with an if and elif statement, though you will have to
copy the code twice. Type the following into the interactive shell:
>>> if 4 != 4:
... print('Hello!')
... elif 10 > 5:
... print('Hello!')
...
Hello!
>>>
>>> if 4 != 4 or 10 > 5:
... print('Hello!')
...
Hello!
>>>

Chapter 9 – The Transposition Cipher, Decrypting 135
Order of Operations for Boolean Operators
Just like the math operators have an order of operations, the and, or, and not operators also
have an order of operations: first not, then and, and then or. Try typing the following into the
interactive shell:
>>> not False and False # not False evaluates first
False
>>> not (False and False) # (False and False) evaluates first
True
Back to the Code
transpositionDecrypt.py
43. # If there are no more columns OR we're at a shaded box, go back to
44. # the first column and the next row.
45. if (col == numOfColumns) or (col == numOfColumns - 1 and row >=
numOfRows - numOfShadedBoxes):
46. col = 0
47. row += 1
There are two cases where we want to reset col back to 0 (so that on the next iteration of the
loop, symbol is added to the first string in the list in plaintext). The first is if we have
incremented col past the last index in plaintext. In this case, the value in col will be equal
to numOfColumns. (Remember that the last index in plaintext will be numOfColumns
minus one. So when col is equal to numOfColumns, it is already past the last index.)
The second case is if both col is at the last index and the row variable is pointing to a row that
has a shaded box in the last column. Here’s the complete decryption grid with the column indexes
along the top and the row indexes down the side:
136 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
0
1
2
3
0
C
0
e
1
n
2
o
3
1
o
4
n
5
o
6
m
7
2
m
8
s
9
t
10
m
11
3
m
12
e
13
(s)
14
o
15
4
o
16
(s)
17
s
18
n
19
5
n
20
i
21
o
22
.
23
6
(s)
24
s
25
(s)
26
7
s
27
(s)
28
c
29
You can see that the shaded boxes are in the last column (whose index will be numOfColumns
- 1) and rows 6 and 7. To have our program calculate which row indexes are shaded, we use the
expression row >= numOfRows - numOfShadedBoxes. If this expression is True, and
col is equal to numOfColumns - 1, then we know that we want to reset col to 0 for the
next iteration.
These two cases are why the condition on line 45 is (col == numOfColumns) or (col
== numOfColumns - 1 and row >= numOfRows - numOfShadedBoxes). That
looks like a big, complicated expression but remember that you can break it down into smaller
parts. The block of code that executes will change col back to the first column by setting it to 0.
We will also increment the row variable.
transpositionDecrypt.py
49. return ''.join(plaintext)
By the time the for loop on line 39 has finished looping over every character in message, the
plaintext list’s strings have been modified so that they are now in the decrypted order (if the
correct key was used, that is). The strings in the plaintext list are joined together (with a
blank string in between each string) by the join() string method. The string that this call to
join() returns will be the value that our decryptMessage() function returns.

Chapter 9 – The Transposition Cipher, Decrypting 137
For our example decryption, plaintext will be ['Common s', 'ense is ', 'not so
c', 'ommon.'], so ''.join(plaintext) will evaluate to 'Common sense is not
so common.'.
transpositionDecrypt.py
52. # If transpositionDecrypt.py is run (instead of imported as a module) call
53. # the main() function.
54. if __name__ == '__main__':
55. main()
The first line that our program runs after importing modules and executing the def statements is
the if statement on line 54. Just like in the transposition encryption program, we check if this
program has been run (instead of imported by a different program) by checking if the special
__name__ variable is set to the string value '__main__'. If so, we execute the main()
function.
Practice Exercises, Chapter 9, Set C
Practice exercises can be found at http://invpy.com/hackingpractice9C.
Summary
That’s it for the decryption program. Most of the program is in the decryptMessage()
function. We can see that our programs can encrypt and decrypt the message “Common sense is
not so common.” with the key 8. But we should try several other messages and keys to see that a
message that is encrypted and then decrypted will result in the same thing as the original
message. Otherwise, we know that either the encryption code or the decryption code doesn’t
work.
We could start changing the key and message variables in our transpositionEncrypt.py and
transpositionDecrypt.py and then running them to see if it works. But instead, let’s automate this
by writing a program to test our program.

138 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
PROGRAMMING A PROGRAM TO
TEST OUR PROGRAM
Topics Covered In This Chapter:
The random.seed() function
The random.randint() function
List references
The copy.deepcopy() Functions
The random.shuffle() function
Randomly scrambling a string
The sys.exit() function
“It is poor civic hygiene to install technologies that
could someday facilitate a police state.”
Bruce Schneier, cryptographer
We can try out the transposition encryption and decryption programs from the previous chapter
by encrypting and decrypting a few messages with different keys. It seems to work pretty well.
But does it always work?

Chapter 10 – Programming a Program to Test Our Program 139
You won’t know unless you test the encryptMessage() and decryptMessage()
functions with different values for the message and key parameters. This would take a lot of
time. You’ll have to type out a message in the encryption program, set the key, run the encryption
program, paste the ciphertext into the decryption program, set the key, and then run the
decryption program. And you’ll want to repeat that with several different keys and messages!
That’s a lot of boring work. Instead we can write a program to test the cipher programs for us.
This new program can generate a random message and a random key. It will then encrypt the
message with the encryptMessage() function from transpositionEncrypt.py and then pass
the ciphertext from that to the decryptMessage() in transpositionDecrypt.py. If the plaintext
returned by decryptMessage() is the same as the original message, the program can know
that the encryption and decryption messages work. This is called automated testing.
There are several different message and key combinations to try, but it will only take the
computer a minute or so to test thousands different combinations. If all of those tests pass, then
we can be much more certain that our code works.
Source Code of the Transposition Cipher Tester Program
Open a new file editor window by clicking on File ► New Window. Type in the following code
into the file editor, and then save it as transpositionTest.py. Press F5 to run the program. Note
that first you will need to download the pyperclip.py module and place this file in the same
directory as the transpositionTest.py file. You can download this file from
http://invpy.com/pyperclip.py.
Source code for transpositionTest.py
1. # Transposition Cipher Test
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import random, sys, transpositionEncrypt, transpositionDecrypt
5.
6. def main():
7. random.seed(42) # set the random "seed" to a static value
8.
9. for i in range(20): # run 20 tests
10. # Generate random messages to test.
11.
12. # The message will have a random length:
13. message = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ' * random.randint(4, 40)
14.
15. # Convert the message string to a list to shuffle it.
16. message = list(message)
17. random.shuffle(message)

140 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
18. message = ''.join(message) # convert list to string
19.
20. print('Test #%s: "%s..."' % (i+1, message[:50]))
21.
22. # Check all possible keys for each message.
23. for key in range(1, len(message)):
24. encrypted = transpositionEncrypt.encryptMessage(key, message)
25. decrypted = transpositionDecrypt.decryptMessage(key, encrypted)
26.
27. # If the decryption doesn't match the original message, display
28. # an error message and quit.
29. if message != decrypted:
30. print('Mismatch with key %s and message %s.' % (key,
message))
31. print(decrypted)
32. sys.exit()
33.
34. print('Transposition cipher test passed.')
35.
36.
37. # If transpositionTest.py is run (instead of imported as a module) call
38. # the main() function.
39. if __name__ == '__main__':
40. main()
Sample Run of the Transposition Cipher Tester Program
When you run this program, the output will look like this:
Test #1: "KQDXSFQDBPMMRGXFKCGIQUGWFFLAJIJKFJGSYOSAWGYBGUNTQX..."
Test #2: "IDDXEEWUMWUJPJSZFJSGAOMFIOWWEYANRXISCJKXZRHMRNCFYW..."
Test #3: "DKAYRSAGSGCSIQWKGARQHAOZDLGKJISQVMDFGYXKCRMPCMQWJM..."
Test #4: "MZIBCOEXGRDTFXZKVNFQWQMWIROJAOKTWISTDWAHZRVIGXOLZA..."
Test #5: "TINIECNCBFKJBRDIUTNGDINHULYSVTGHBAWDQMZCNHZOTNYHSX..."
Test #6: "JZQIHCVNDWRDUFHZFXCIASYDSTGQATQOYLIHUFPKEXSOZXQGPP..."
Test #7: "BMKJUERFNGIDGWAPQMDZNHOQPLEOQDYCIIWRKPVEIPLAGZCJVN..."
Test #8: "IPASTGZSLPYCORCVEKWHOLOVUFPOMGQWZVJNYQIYVEOFLUWLMQ..."
Test #9: "AHRYJAPTACZQNNFOTONMIPYECOORDGEYESYFHROZDASFIPKSOP..."
Test #10: "FSXAAPLSQHSFUPQZGTIXXDLDMOIVMWFGHPBPJROOSEGPEVRXSX..."
Test #11: "IVBCXBIHLWPTDHGEGANBGXWQZMVXQPNJZQPKMRUMPLLXPAFITN..."
Test #12: "LLNSYMNRXZVYNPRTVNIBFRSUGIWUJREMPZVCMJATMLAMCEEHNW..."
Test #13: "IMWRUJJHRWAABHYIHGNPSJUOVKRRKBSJKDHOBDLOUJDGXIVDME..."
Test #14: "IZVXWHTIGKGHKJGGWMOBAKTWZWJPHGNEQPINYZIBERJPUNWJMX..."
Test #15: "BQGFNMGQCIBOTRHZZOBHZFJZVSRTVHIUJFOWRFBNWKRNHGOHEQ..."
Test #16: "LNKGKSYIPHMCDVKDLNDVFCIFGEWQGUJYJICUYIVXARMUCBNUWM..."

Chapter 10 – Programming a Program to Test Our Program 141
Test #17: "WGNRHKIQZMOPBQTCRYPSEPWHLRDXZMJOUTJCLECKEZZRRMQRNI..."
Test #18: "PPVTELDHJRZFPBNMJRLAZWRXRQVKHUUMRPNFKXJCUKFOXAGEHM..."
Test #19: "UXUIGAYKGLYUQTFBWQUTFNSOPEGMIWMQYEZAVCALGOHUXJZPTY..."
Test #20: "JSYTDGLVLBCVVSITPTQPHBCYIZHKFOFMBWOZNFKCADHDKPJSJA..."
Transposition cipher test passed.
Our testing program works by importing the transpositionEncrypt.py and transpositionDecrypt.py
programs as modules. This way, we can call the encryptMessage() and
decryptMessage() functions in these programs. Our testing program will create a random
message and choose a random key. It doesn’t matter that the message is just random letters, we
just need to check that encrypting and then decrypting the message will result in the original
message.
Our program will repeat this test twenty times by putting this code in a loop. If at any point the
returned string from transpositionDecrypt() is not the exact same as the original
message, our program will print an error message and exit.
How the Program Works
transpositionTest.py
1. # Transposition Cipher Test
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import random, sys, transpositionEncrypt, transpositionDecrypt
5.
6. def main():
First our program imports two modules that come with Python, random and sys. We also want
to import the transposition cipher programs we’ve written: transpositionEncrypt.py and
transpositionDecrypt.py. Note that we don’t put the .py extension in our import statement.
Pseudorandom Numbers and the random.seed() Function
transpositionTest.py
7. random.seed(42) # set the random "seed" to a static value
Technically, the numbers produced by Python’s random.randint() function are not really
random. They are produced from a pseudorandom number generator algorithm, and this
algorithm is well known and the numbers it produces are predictable. We call these random-
looking (but predictable) numbers pseudorandom numbers because they are not truly random.

142 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The pseudorandom number generator algorithm starts with an initial number called the seed. All
of the random numbers produced from a seed are predictable. You can reset Python’s random
seed by calling the random.seed() function. Type the following into the interactive shell:
>>> import random
>>> random.seed(42)
>>> for i in range(5):
... print(random.randint(1, 10))
...
7
1
3
3
8
>>> random.seed(42)
>>> for i in range(5):
... print(random.randint(1, 10))
...
7
1
3
3
8
>>>
When the seed for Python’s pseudorandom number generator is set to 42, the first “random”
number between 1 and 10 will always be 7. The second “random” number will always be 1, and
the third number will always be 3, and so on. When we reset the seed back to 42 again, the same
set of pseudorandom numbers will be returned from random.randint().
Setting the random seed by calling random.seed() will be useful for our testing program,
because we want predictable numbers so that the same pseudorandom messages and keys are
chosen each time we run the automated testing program. Our Python programs only seem to
generate “unpredictable” random numbers because the seed is set to the computer’s current clock
time (specifically, the number of seconds since January 1st, 1970) when the random module is
first imported.
It is important to note that not using truly random numbers is a common security flaw of
encryption software. If the “random” numbers in your programs can be predicted, then this can
provide a cryptanalyst with a useful hint to breaking your cipher. More information about
generating truly random numbers with Python using the os.urandom() function can be found
at http://invpy.com/random.

Chapter 10 – Programming a Program to Test Our Program 143
The random.randint() Function
transpositionTest.py
9. for i in range(20): # run 20 tests
10. # Generate random messages to test.
11.
12. # The message will have a random length:
13. message = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ' * random.randint(4, 40)
The code that does a single test will be in this for loop’s block. We want this program to run
multiple tests since the more tests we try, the more certain that we know our programs work.
Line 13 creates a random message from the uppercase letters and stores it in the message
variable. Line 13 uses string replication to create messages of different lengths. The
random.randint() function takes two integer arguments and returns a random integer
between those two integers (including the integers themselves). Type the following into the
interactive shell:
>>> import random
>>> random.randint(1, 20)
20
>>> random.randint(1, 20)
18
>>> random.randint(1, 20)
3
>>> random.randint(1, 20)
18
>>> random.randint(100, 200)
107
>>>
Of course, since these are pseudorandom numbers, the numbers you get will probably be different
than the ones above. Line 13 creates a random message from the uppercase letters and stores it in
the message variable. Line 13 uses string replication to create messages of different lengths.
References
Technically, variables do not store list values in them. Instead, they store reference values to list
values. Up until now the difference hasn’t been important. But storing list references instead of
lists becomes important if you copy a variable with a list reference to another variable. Try
entering the following into the shell:

144 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
>>> spam = 42
>>> cheese = spam
>>> spam = 100
>>> spam
100
>>> cheese
42
>>>
This makes sense from what we know so far. We assign 42 to the spam variable, and then we
copy the value in spam and assign it to the variable cheese. When we later change the value in
spam to 100, this doesn’t affect the value in cheese. This is because spam and cheese are
different variables that each store their own values.
But lists don’t work this way. When you assign a list to a variable with the = sign, you are
actually assigning a list reference to the variable. A reference is a value that points to some bit
of data, and a list reference is a value that points to a list. Here is some code that will make this
easier to understand. Type this into the shell:
>>> spam = [0, 1, 2, 3, 4, 5]
>>> cheese = spam
>>> cheese[1] = 'Hello!'
>>> spam
[0, 'Hello!', 2, 3, 4, 5]
>>> cheese
[0, 'Hello!', 2, 3, 4, 5]
This looks odd. The code only changed the cheese list, but it seems that both the cheese and
spam lists have changed.
Notice that the line cheese = spam copies the list reference in spam to cheese, instead of
copying the list value itself. This is because the value stored in the spam variable is a list
reference, and not the list value itself. This means that the values stored in both spam and
cheese refer to the same list. There is only one list because the list was not copied, the reference
to the list was copied. So when you modify cheese in the cheese[1] = 'Hello!' line,
you are modifying the same list that spam refers to. This is why spam seems to have the same
list value that cheese does.
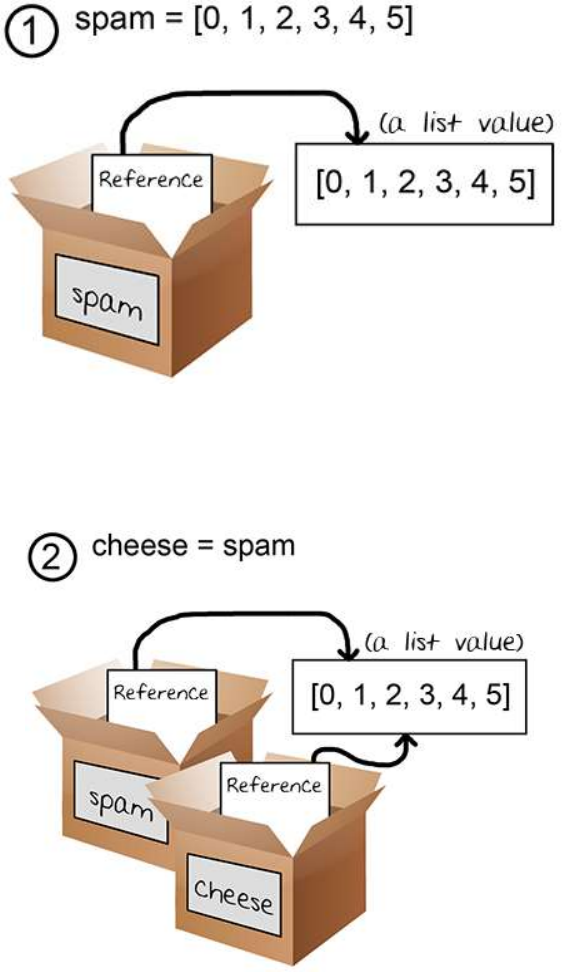
Chapter 10 – Programming a Program to Test Our Program 145
Remember that variables are like boxes that contain values. List variables don’t actually contain
lists at all, they contain references to lists. Here are some pictures that explain what happens in
the code you just typed in:
Figure 10-1. Variables do not store lists, but rather references to lists.
On the first line, the actual list is not contained in the spam variable but a reference to the list.
The list itself is not stored in any variable.
Figure 10-2. Two variables store two references to the same list.
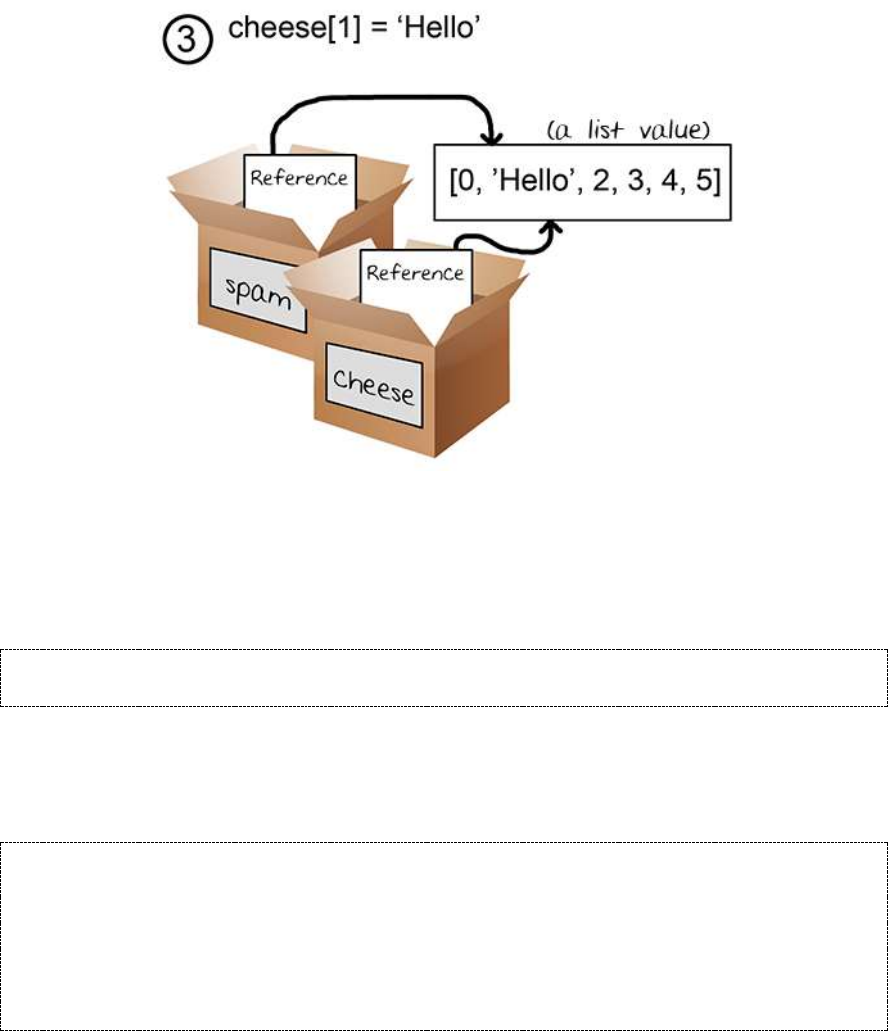
146 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
When you assign the reference in spam to cheese, the cheese variable contains a copy of the
reference in spam. Now both cheese and spam refer to the same list.
Figure 10-3. Changing the list changes all variables with references to that list.
When you alter the list that cheese refers to, the list that spam refers to is also changed because
they refer to the same list. If you want spam and cheese to store two different lists, you have to
create two different lists instead of copying a reference:
>>> spam = [0, 1, 2, 3, 4, 5]
>>> cheese = [0, 1, 2, 3, 4, 5]
In the above example, spam and cheese have two different lists stored in them (even though
these lists are identical in content). Now if you modify one of the lists, it will not affect the other
because spam and cheese have references to two different lists:
>>> spam = [0, 1, 2, 3, 4, 5]
>>> cheese = [0, 1, 2, 3, 4, 5]
>>> cheese[1] = 'Hello!'
>>> spam
[0, 1, 2, 3, 4, 5]
>>> cheese
[0, 'Hello!', 2, 3, 4, 5]
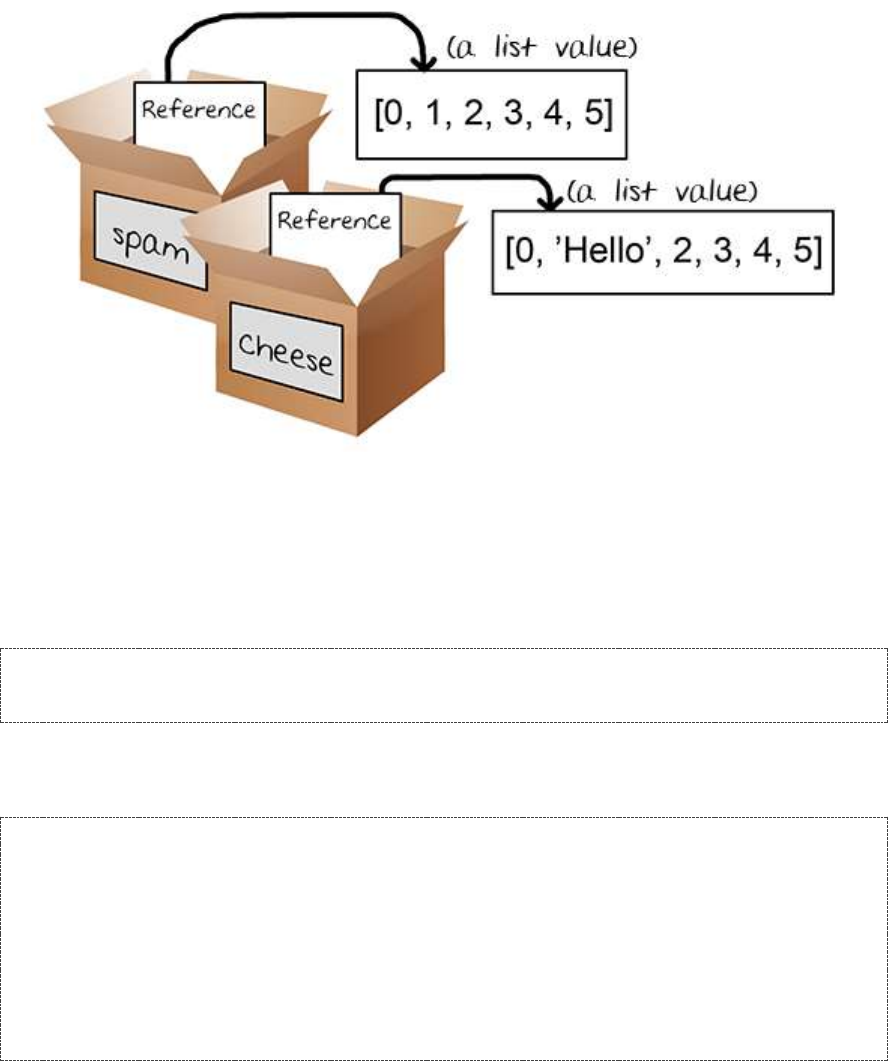
Chapter 10 – Programming a Program to Test Our Program 147
Figure 10-4 shows how the two references point to two different lists:
Figure 10-4. Two variables each storing references to two different lists.
The copy.deepcopy() Functions
As we saw in the previous example, the following code only copies the reference value, not the
list value itself:
>>> spam = [0, 1, 2, 3, 4, 5]
>>> cheese = spam # copies the reference, not the list
If we want to copy the list value itself, we can import the copy module to call the
copy.deepcopy() function, which will return a separate copy of the list it is passed:
>>> spam = [0, 1, 2, 3, 4, 5]
>>> import copy
>>> cheese = copy.deepcopy(spam)
>>> cheese[1] = 'Hello!'
>>> spam
[0, 1, 2, 3, 4, 5]
>>> cheese
[0, 'Hello!', 2, 3, 4, 5]
>>>

148 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The copy.deepcopy() function isn’t used in this chapter’s program, but it is helpful when
you need to make a duplicate list value to store in a different variable.
Practice Exercises, Chapter 10, Set A
Practice exercises can be found at http://invpy.com/hackingpractice10A.
The random.shuffle() Function
The random.shuffle() function is also in the random module. It accepts a list argument,
and then randomly rearranges items in the list. Type the following into the interactive shell:
>>> import random
>>> spam = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> spam
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> random.shuffle(spam)
>>> spam
[3, 0, 5, 9, 6, 8, 2, 4, 1, 7]
>>> random.shuffle(spam)
>>> spam
[1, 2, 5, 9, 4, 7, 0, 3, 6, 8]
>>>
An important thing to note is that shuffle() does not return a list value. Instead, it changes
the list value that is passed to it (because shuffle() modifies the list directly from the list
reference value it is passed.) We say that the shuffle() function modifies the list in-place.
This is why we only need to execute random.shuffle(spam) instead of spam =
random.shuffle(spam).
Remember that you can use the list() function to convert a string or range object to a list
value. Type the following into the interactive shell:
>>> import random
>>> eggs = list('Hello')
>>> eggs
['H', 'e', 'l', 'l', 'o']
>>> random.shuffle(eggs)
>>> eggs
['o', 'H', 'l', 'l', 'e']
>>>

Chapter 10 – Programming a Program to Test Our Program 149
And also remember you can use the join() string method to pass a list of strings and return a
single string:
>>> eggs
['o', 'H', 'l', 'l', 'e']
>>> eggs = ''.join(eggs)
>>> eggs
'oHlle'
>>>
Randomly Scrambling a String
transpositionTest.py
15. # Convert the message string to a list to shuffle it.
16. message = list(message)
17. random.shuffle(message)
18. message = ''.join(message) # convert list to string
In order to shuffle the characters in a string value, first we convert the string to a list with
list(), then shuffle the items in the list with shuffle(), and then convert back to string
value with the join() string method. Try typing the following into the interactive shell:
>>> import random
>>> spam = 'Hello world!'
>>> spam = list(spam)
>>> random.shuffle(spam)
>>> spam = ''.join(spam)
>>> spam
'wl delHo!orl'
>>>
We use this technique to scramble the letters in the message variable. This way we can test
many different messages just in case our transposition cipher can encrypt and decrypt some
messages but not others.
Back to the Code
transpositionTest.py
20. print('Test #%s: "%s..."' % (i+1, message[:50]))
Line 20 has a print() call that displays which test number we are on (we add one to i because
i starts at 0 and we want the test numbers to start at 1). Since the string in message can be very
long, we use string slicing to show only the first 50 characters of message.

150 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Line 20 uses string interpolation. The value that i+1 evaluates to will replace the first %s in the
string and the value that message[:50] evaluates to will replace the second %s. When using
string interpolation, be sure the number of %s in the string matches the number of values that are
in between the parentheses after it.
transpositionTest.py
22. # Check all possible keys for each message.
23. for key in range(1, len(message)):
While the key for the Caesar cipher could be an integer from 0 to 25, the key for the
transposition cipher can be between 1 and the length of the message. We want to test every
possible key for the test message, so the for loop on line 23 will run the test code with the keys
1 up to (but not including) the length of the message.
transpositionTest.py
24. encrypted = transpositionEncrypt.encryptMessage(key, message)
25. decrypted = transpositionDecrypt.decryptMessage(key, encrypted)
Line 24 encrypts the string in message using our encryptMessage() function. Since this
function is inside the transpositionEncrypt.py file, we need to add transpositionEncrypt.
(with the period at the end) to the front of the function name.
The encrypted string that is returned from encryptMessage() is then passed to
decryptMessage(). We use the same key for both function calls. The return value from
decryptMessage() is stored in a variable named decrypted. If the functions worked, then
the string in message should be the exact same as the string in decrypted.
The sys.exit() Function
transpositionTest.py
27. # If the decryption doesn't match the original message, display
28. # an error message and quit.
29. if message != decrypted:
30. print('Mismatch with key %s and message %s.' % (key,
message))
31. print(decrypted)
32. sys.exit()
33.
34. print('Transposition cipher test passed.')

Chapter 10 – Programming a Program to Test Our Program 151
Line 29 tests if message and decrypted are equal. If they aren’t, we want to display an error
message on the screen. We print the key, message, and decrypted values. This information
could help us figure out what happened. Then we will exit the program.
Normally our programs exit once the execution reaches the very bottom and there are no more
lines to execute. However, we can make the program exit sooner than that by calling the
sys.exit() function. When sys.exit() is called, the program will immediately end.
But if the values in message and decrypted are equal to each other, the program execution
skips the if statement’s block and the call to sys.exit(). The next line is on line 34, but you
can see from its indentation that it is the first line after line 9’s for loop.
This means that after line 29’s if statement’s block, the program execution will jump back to
line 23’s for loop for the next iteration of that loop. If it has finished looping, then instead the
execution jumps back to line 9’s for loop for the next iteration of that loop. And if it has
finished looping for that loop, then it continues on to line 34 to print out the string
'Transposition cipher test passed.'.
transpositionTest.py
37. # If transpositionTest.py is run (instead of imported as a module) call
38. # the main() function.
39. if __name__ == '__main__':
40. main()
Here we do the trick of checking if the special variable __name__ is set to '__main__' and if
so, calling the main() function. This way, if another program imports transpositionTest.py, the
code inside main() will not be executed but the def statements that create the main()
function will be.
Testing Our Test Program
We’ve written a test program that tests our encryption programs, but how do we know that the
test program works? What if there is a bug with our test program, and it is just saying that our
transposition cipher programs work when they really don’t?
We can test our test program by purposefully adding bugs to our encryption or decryption
functions. Then when we run the test program, if it does not detect a problem with our cipher
program, then we know that the test program is not correctly testing our cipher programs.
Change transpositionEncrypt.py’s line 36 from this:
transpositionEncrypt.py

152 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
35. # move pointer over
36. pointer += key
…to this:
transpositionEncrypt.py
35. # move pointer over
36. pointer += key + 1
Now that the encryption code is broken, when we run the test program it should give us an error:
Test #1: "JEQLDFKJZWALCOYACUPLTRRMLWHOBXQNEAWSLGWAGQQSRSIUIQ..."
Mismatch with key 1 and message
JEQLDFKJZWALCOYACUPLTRRMLWHOBXQNEAWSLGWAGQQSRSIUIQTRGJHDVCZECRESZJARAVIPFOBWZXX
TBFOFHVSIGBWIBBHGKUWHEUUDYONYTZVKNVVTYZPDDMIDKBHTYJAHBNDVJUZDCEMFMLUXEONCZXWAWG
XZSFTMJNLJOKKIJXLWAPCQNYCIQOFTEAUHRJODKLGRIZSJBXQPBMQPPFGMVUZHKFWPGNMRYXROMSCEE
XLUSCFHNELYPYKCNYTOUQGBFSRDDMVIGXNYPHVPQISTATKVKM.
JQDKZACYCPTRLHBQEWLWGQRIITGHVZCEZAAIFBZXBOHSGWBHKWEUYNTVNVYPDIKHYABDJZCMMUENZWW
XSTJLOKJLACNCQFEUROKGISBQBQPGVZKWGMYRMCELSFNLPKNTUGFRDVGNPVQSAKK
Summary
We can use our programming skills for more than just writing programs. We can also program
the computer to test those programs to make sure they work for different inputs. It is a common
practice to write code to test code.
This chapter covered a few new functions such as the random.randint() function for
producing pseudorandom numbers. Remember, pseudorandom numbers aren’t random enough
for cryptography programs, but they are good enough for this chapter’s testing program. The
random.shuffle() function is useful for scrambling the order of items in a list value.
The copy.deepcopy() function will create copies of list values instead of reference values.
The difference between a list and list reference is explained in this chapter as well.
All of our programs so far have only encrypted short messages. In the next chapter, we will learn
how to encrypt and decrypt entire files on your hard drive.

Chapter 11 – Encrypting and Decrypting Files 153
ENCRYPTING AND DECRYPTING
FILES
Topics Covered In This Chapter:
Reading and writing files
The open() function
The read() file object method
The close() file object method
The write() file object method
The os.path.exists() function
The startswith() string method
The title() string method
The time module and time.time() function
“Why do security police grab people and torture them? To get their
information. If you build an information management system that
concentrates information from dozens of people, you’ve made that
dozens of times more attractive. You’ve focused the repressive regime’s
attention on the hard disk. And hard disks put up no resistance to torture.
You need to give the hard disk a way to resist. That’s cryptography.”

154 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Patrick Ball
Up until now our programs have only worked on small messages that we type directly into the
source code as string values. The cipher program in this chapter will use the transposition cipher
to encrypt and decrypt entire files, which can be millions of characters in size.
Plain Text Files
This program will encrypt and decrypt plain text files. These are the kind of files that only have
text data and usually have the .txt file extension. Files from word processing programs that let
you change the font, color, or size of the text do not produce plain text files. You can write your
own text files using Notepad (on Windows), TextMate or TextEdit (on OS X), or gedit (on Linux)
or a similar plain text editor program. You can even use IDLE’s own file editor and save the files
with a .txt extension instead of the usual .py extension.
For some samples, you can download the following text files from this book’s website:
http://invpy.com/devilsdictionary.txt
http://invpy.com/frankenstein.txt
http://invpy.com/siddhartha.txt
http://invpy.com/thetimemachine.txt
These are text files of some books (that are now in the public domain, so it is perfectly legal to
download them.) For example, download Mary Shelley’s classic novel “Frankenstein” from
http://invpy.com/frankenstein.txt. Double-click the file to open it in a text editor program. There
are over 78,000 words in this text file! It would take some time to type this into our encryption
program. But if it is in a file, the program can read the file and do the encryption in a couple
seconds.
If you get an error that looks like “UnicodeDecodeError: 'charmap' codec can't
decode byte 0x90 in position 148: character maps to <undefined>”
then you are running the cipher program on a non-plain text file, also called a “binary file”.
To find other public domain texts to download, go to the Project Gutenberg website at
http://www.gutenberg.org/.
Source Code of the Transposition File Cipher Program
Like our transposition cipher testing program, the transposition cipher file program will import
our transpositionEncrypt.py and transpositionDecrypt.py files so we can use the

Chapter 11 – Encrypting and Decrypting Files 155
encryptMessage() and decryptMessage() functions in them. This way we don’t have
to re-type the code for these functions in our new program.
Open a new file editor window by clicking on File ► New Window. Type in the following code
into the file editor, and then save it as transpositionFileCipher.py. Press F5 to run the program.
Note that first you will need to download frankenstein.txt and place this file in the same directory
as the transpositionFileCipher.py file. You can download this file from
http://invpy.com/frankenstein.txt.
Source code for transpositionFileCipher.py
1. # Transposition Cipher Encrypt/Decrypt File
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import time, os, sys, transpositionEncrypt, transpositionDecrypt
5.
6. def main():
7. inputFilename = 'frankenstein.txt'
8. # BE CAREFUL! If a file with the outputFilename name already exists,
9. # this program will overwrite that file.
10. outputFilename = 'frankenstein.encrypted.txt'
11. myKey = 10
12. myMode = 'encrypt' # set to 'encrypt' or 'decrypt'
13.
14. # If the input file does not exist, then the program terminates early.
15. if not os.path.exists(inputFilename):
16. print('The file %s does not exist. Quitting...' % (inputFilename))
17. sys.exit()
18.
19. # If the output file already exists, give the user a chance to quit.
20. if os.path.exists(outputFilename):
21. print('This will overwrite the file %s. (C)ontinue or (Q)uit?' %
(outputFilename))
22. response = input('> ')
23. if not response.lower().startswith('c'):
24. sys.exit()
25.
26. # Read in the message from the input file
27. fileObj = open(inputFilename)
28. content = fileObj.read()
29. fileObj.close()
30.
31. print('%sing...' % (myMode.title()))
32.
33. # Measure how long the encryption/decryption takes.
34. startTime = time.time()
156 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
35. if myMode == 'encrypt':
36. translated = transpositionEncrypt.encryptMessage(myKey, content)
37. elif myMode == 'decrypt':
38. translated = transpositionDecrypt.decryptMessage(myKey, content)
39. totalTime = round(time.time() - startTime, 2)
40. print('%sion time: %s seconds' % (myMode.title(), totalTime))
41.
42. # Write out the translated message to the output file.
43. outputFileObj = open(outputFilename, 'w')
44. outputFileObj.write(translated)
45. outputFileObj.close()
46.
47. print('Done %sing %s (%s characters).' % (myMode, inputFilename,
len(content)))
48. print('%sed file is %s.' % (myMode.title(), outputFilename))
49.
50.
51. # If transpositionCipherFile.py is run (instead of imported as a module)
52. # call the main() function.
53. if __name__ == '__main__':
54. main()
In the directory that frankenstein.txt and transpositionFileCipher.py files are in, there will be a
new file named frankenstein.encrypted.txt that contains the content of frankenstein.txt in
encrypted form. If you double-click the file to open it, it should look something like this:
PtFiyedleo a arnvmt eneeGLchongnes Mmuyedlsu0#uiSHTGA r sy,n t ys
s nuaoGeL
sc7s,
(the rest has been cut out for brevity)
To decrypt, make the following changes to the source code (written in bold) and run the
transposition cipher program again:
transpositionFileCipher.py
7. inputFilename = 'frankenstein.encrypted.txt'
8. # BE CAREFUL! If a file with the outputFilename name already exists,
9. # this program will overwrite that file.
10. outputFilename = 'frankenstein.decrypted.txt'
11. myKey = 10
12. myMode = 'decrypt' # set to 'encrypt' or 'decrypt'
This time when you run the program a new file will appear in the folder named
frankenstein.decrypted.txt that is identical to the original frankenstein.txt file.

Chapter 11 – Encrypting and Decrypting Files 157
Sample Run of the Transposition File Cipher Program
When you run the above program, it produces this output:
Encrypting...
Encryption time: 1.21 seconds
Done encrypting frankenstein.txt (441034 characters).
Encrypted file is frankenstein.encrypted.txt.
A new frankenstein.encrypted.txt file will have been created in the same directory as
transpositionFileCipher.py. If you open this file with IDLE’s file editor, you will see the
encrypted contents of frankenstein.py. You can now email this encrypted file to someone for them
to decrypt.
Reading From Files
Up until now, any input we want to give our programs would have to be typed in by the user.
Python programs can open and read files directly off of the hard drive. There are three steps to
reading the contents of a file: opening the file, reading into a variable, and then closing the file.
The open() Function and File Objects
The open() function’s first parameter is a string for the name of the file to open. If the file is in
the same directory as the Python program then you can just type in the name, such as
'thetimemachine.txt'. You can always specify the absolute path of the file, which
includes the directory that it is in. For example, 'c:\\Python32\\frankenstein.txt'
(on Windows) and '/usr/foobar/frankenstein.txt' (on OS X and Linux) are
absolute filenames. (Remember that the \ backslash must be escaped with another backslash
before it.)
The open() function returns a value of the “file object” data type. This value has several
methods for reading from, writing to, and closing the file.
The read() File Object Method
The read() method will return a string containing all the text in the file. For example, say the
file spam.txt contained the text “Hello world!”. (You can create this file yourself using IDLE’s
file editor. Just save the file with a .txt extension.) Run the following from the interactive shell
(this codes assumes you are running Windows and the spam.txt file is in the c:\ directory):
>>> fo = open('c:\\spam.txt', 'r')
>>> content = fo.read()
>>> print(content)

158 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Hello world!
>>>
If your text file has multiple lines, the string returned by read() will have \n newline
characters in it at the end of each line. When you try to print a string with newline characters, the
string will print across several lines:
>>> print('Hello\nworld!')
Hello
world!
>>>
If you get an error message that says “IOError: [Errno 2] No such file or
directory” then double check that you typed the filename (and if it is an absolute path, the
directory name) correctly. Also make sure that the file actually is where you think it is.
The close() File Object Method
After you have read the file’s contents into a variable, you can tell Python that you are done with
the file by calling the close() method on the file object.
>>> fo.close()
>>>
Python will automatically close any open files when the program terminates. But when you want
to re-read the contents of a file, you must close the file object and then call the open() function
on the file again.
Here’s the code in our transposition cipher program that reads the file whose filename is stored in
the inputFilename variable:
transpositionFileCipher.py
26. # Read in the message from the input file
27. fileObj = open(inputFilename)
28. content = fileObj.read()
29. fileObj.close()
Writing To Files
We read the original file and now will write the encrypted (or decrypted) form to a different file.
The file object returned by open() has a write() function, although you can only use this

Chapter 11 – Encrypting and Decrypting Files 159
function if you open the file in “write” mode instead of “read” mode. You do this by passing the
string value 'w' as the second parameter. For example:
>>> fo = open('filename.txt', 'w')
>>>
Along with “read” and “write”, there is also an “append” mode. The “append” is like “write”
mode, except any strings written to the file will be appended to the end of any content that is
already in the file. “Append” mode will not overwrite the file if it already exists. To open a file in
append mode, pass the string 'a' as the second argument to open().
(Just in case you were curious, you could pass the string 'r' to open() to open the file in read
mode. But since passing no second argument at all also opens the file in read mode, there’s no
reason to pass 'r'.)
The write() File Object Method
You can write text to a file by calling the file object’s write() method. The file object must
have been opened in write mode, otherwise, you will get a “io.UnsupportedOperation:
not readable” error message. (And if you try to call read() on a file object that was
opened in write mode, you will get a “io.UnsupportedOperation: not readable”
error message.)
The write() method takes one argument: a string of text that is to be written to the file. Lines
43 to 45 open a file in write mode, write to the file, and then close the file object.
transpositionFileCipher.py
42. # Write out the translated message to the output file.
43. outputFileObj = open(outputFilename, 'w')
44. outputFileObj.write(translated)
45. outputFileObj.close()
Now that we have the basics of reading and writing files, let’s look at the source code to the
transposition file cipher program.
How the Program Works
transpositionFileCipher.py
1. # Transposition Cipher Encrypt/Decrypt File
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import time, os, sys, transpositionEncrypt, transpositionDecrypt
5.

160 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
6. def main():
7. inputFilename = 'frankenstein.txt'
8. # BE CAREFUL! If a file with the outputFilename name already exists,
9. # this program will overwrite that file.
10. outputFilename = 'frankenstein.encrypted.txt'
11. myKey = 10
12. myMode = 'encrypt' # set to 'encrypt' or 'decrypt'
The first part of the program should look familiar. Line 4 is an import statement for our
transpositionEncrypt.py and transpositionDecrypt.py programs. It also imports the Python’s
time, os, and sys modules.
The main() function will be called after the def statements have been executed to define all
the functions in the program. The inputFilename variable holds a string of the file to read,
and the encrypted (or decrypted) text is written to the file with the name in outputFilename.
The transposition cipher uses an integer for a key, stored in myKey. If 'encrypt' is stored in
myMode, the program will encrypt the contents of the inputFilename file. If 'decrypt' is
stored in myMode, the contents of inputFilename will be decrypted.
The os.path.exists() Function
Reading files is always harmless, but we need to be careful when writing files. If we call the
open() function in write mode with a filename that already exists, that file will first be deleted
to make way for the new file. This means we could accidentally erase an important file if we pass
the important file’s name to the open() function. Using the os.path.exists() function,
we can check if a file with a certain filename already exists.
The os.path.exists() file has a single string parameter for the filename, and returns True
if this file already exists and False if it doesn’t. The os.path.exists() function exists
inside the path module, which itself exists inside the os module. But if we import the os
module, the path module will be imported too.
Try typing the following into the interactive shell:
>>> import os
>>> os.path.exists('abcdef')
False
>>> os.path.exists('C:\\Windows\\System32\\calc.exe')
True
>>>

Chapter 11 – Encrypting and Decrypting Files 161
(Of course, you will only get the above results if you are running Python on Windows. The
calc.exe file does not exist on OS X or Linux.)
transpositionFileCipher.py
14. # If the input file does not exist, then the program terminates early.
15. if not os.path.exists(inputFilename):
16. print('The file %s does not exist. Quitting...' % (inputFilename))
17. sys.exit()
We use the os.path.exists() function to check that the filename in inputFilename
actually exists. Otherwise, we have no file to encrypt or decrypt. In that case, we display a
message to the user and then quit the program.
The startswith() and endswith() String Methods
transpositionFileCipher.py
19. # If the output file already exists, give the user a chance to quit.
20. if os.path.exists(outputFilename):
21. print('This will overwrite the file %s. (C)ontinue or (Q)uit?' %
(outputFilename))
22. response = input('> ')
23. if not response.lower().startswith('c'):
24. sys.exit()
If the file the program will write to already exists, the user is asked to type in “C” if they want to
continue running the program or “Q” to quit the program.
The string in the response variable will have lower() called on it, and the returned string from
lower() will have the string method startswith() called on it. The startswith()
method will return True if its string argument can be found at the beginning of the string. Try
typing the following into the interactive shell:
>>> 'hello'.startswith('h')
True
>>> 'hello world!'.startswith('hello wo')
True
>>> 'hello'.startswith('H')
False
>>> spam = 'Albert'
>>> spam.startswith('Al')
True

162 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
>>>
On line 23, if the user did not type in 'c', 'continue', 'C', or another string that begins
with C, then sys.exit() will be called to end the program. Technically, the user doesn’t have
to enter “Q” to quit; any string that does not begin with “C” will cause the sys.exit() function to
be called to quit the program.
There is also an endswith() string method that can be used to check if a string value ends with
another certain string value. Try typing the following into the interactive shell:
>>> 'Hello world!'.endswith('world!')
True
>>> 'Hello world!'.endswith('world')
False
>>>
The title() String Method
Just like the lower() and upper() string methods will return a string in lowercase or
uppercase, the title() string method returns a string in “title case”. Title case is where every
word is uppercase for the first character and lowercase for the rest of the characters. Try typing
the following into the interactive shell:
>>> 'hello'.title()
'Hello'
>>> 'HELLO'.title()
'Hello'
>>> 'hElLo'.title()
'Hello'
>>> 'hello world! HOW ARE YOU?'.title()
'Hello World! How Are You?'
>>> 'extra! extra! man bites shark!'.title()
'Extra! Extra! Man Bites Shark!'
>>>
transpositionFileCipher.py
26. # Read in the message from the input file
27. fileObj = open(inputFilename)
28. content = fileObj.read()
29. fileObj.close()
30.
31. print('%sing...' % (myMode.title()))

Chapter 11 – Encrypting and Decrypting Files 163
Lines 27 to 29 open the file with the name stored in inputFilename and read in its contents
into the content variable. On line 31, we display a message telling the user that the encryption
or decryption has begun. Since myMode should either contain the string 'encrypt' or
'decrypt', calling the title() string method will either display 'Encrypting...' or
'Decrypting...'.
The time Module and time.time() Function
All computers have a clock that keeps track of the current date and time. Your Python programs
can access this clock by calling the time.time() function. (This is a function named time()
that is in a module named time.)
The time.time() function will return a float value of the number of seconds since January 1st,
1970. This moment is called the Unix Epoch. Try typing the following into the interactive shell:
>>> import time
>>> time.time()
1349411356.892
>>> time.time()
1349411359.326
>>>
The float value shows that the time.time() function can be precise down to a millisecond
(that is, 1/1,000 of a second). Of course, the numbers that time.time() displays for you will
depend on the moment in time that you call this function. It might not be clear that
1349411356.892 is Thursday, October 4th, 2012 around 9:30 pm. However, the time.time()
function is useful for comparing the number of seconds between calls to time.time(). We can
use this function to determine how long our program has been running.
transpositionFileCipher.py
33. # Measure how long the encryption/decryption takes.
34. startTime = time.time()
35. if myMode == 'encrypt':
36. translated = transpositionEncrypt.encryptMessage(myKey, content)
37. elif myMode == 'decrypt':
38. translated = transpositionDecrypt.decryptMessage(myKey, content)
39. totalTime = round(time.time() - startTime, 2)
40. print('%sion time: %s seconds' % (myMode.title(), totalTime))
We want to measure how long the encryption or decryption process takes for the contents of the
file. Lines 35 to 38 call the encryptMessage() or decryptMessage() (depending on
whether 'encrypt' or 'decrypt' is stored in the myMode variable). Before this code

164 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
however, we will call time.time() and store the current time in a variable named
startTime.
On line 39 after the encryption or decryption function calls have returned, we will call
time.time() again and subtract startTime from it. This will give us the number of seconds
between the two calls to time.time().
For example, if you subtract the floating point values returned when I called time.time()
before in the interactive shell, you would get the amount of time in between those calls while I
was typing:
>>> 1349411359.326 - 1349411356.892
2.434000015258789
>>>
(The difference Python calculated between the two floating point values is not precise due to
rounding errors, which cause very slight inaccuracies when doing math with floats. For our
programs, it will not matter. But you can read more about rounding errors at
http://invpy.com/rounding.)
The time.time() - startTime expression evaluates to a value that is passed to the
round() function which rounds to the nearest two decimal points. This value is stored in
totalTime. On line 40, the amount of time is displayed to the user by calling print().
Back to the Code
transpositionFileCipher.py
42. # Write out the translated message to the output file.
43. outputFileObj = open(outputFilename, 'w')
44. outputFileObj.write(translated)
45. outputFileObj.close()
The encrypted (or decrypted) file contents are now stored in the translated variable. But this
string will be forgotten when the program terminates, so we want to write the string out to a file
to store it on the hard drive. The code on lines 43 to 45 do this by opening a new file (passing
'w' to open() to open the file in write mode) and then calling the write() file object
method.
transpositionFileCipher.py
47. print('Done %sing %s (%s characters).' % (myMode, inputFilename,
len(content)))
48. print('%sed file is %s.' % (myMode.title(), outputFilename))

Chapter 11 – Encrypting and Decrypting Files 165
49.
50.
51. # If transpositionCipherFile.py is run (instead of imported as a module)
52. # call the main() function.
53. if __name__ == '__main__':
54. main()
Afterwards, we print some more messages to the user telling them that the process is done and
what the name of the written file is. Line 48 is the last line of the main() function.
Lines 53 and 54 (which get executed after the def statement on line 6 is executed) will call the
main() function if this program is being run instead of being imported. (This is explained in
Chapter 8’s “The Special __name__ Variable” section.)
Practice Exercises, Chapter 11, Set A
Practice exercises can be found at http://invpy.com/hackingpractice11A.
Summary
Congratulations! There wasn’t much to this new program aside from the open(), write(),
read(), and close() functions, but this lets us encrypt text files on our hard drive that are
megabytes or gigabytes in size. It doesn’t take much new code because all of the implementation
for the cipher has already been written. We can extend our programs (such as adding file reading
and writing capabilities) by importing their functions for use in new programs. This greatly
increases our ability to use computers to encrypt information.
There are too many possible keys to simply brute-force and examine the output of a message
encrypted with the transposition cipher. But if we can write a program that recognizes English (as
opposed to strings of gibberish), we can have the computer examine the output of thousands of
decryption attempts and determine which key can successfully decrypt a message to English.

166 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
DETECTING ENGLISH
PROGRAMMATICALLY
Topics Covered In This Chapter:
Dictionaries
The split() Method
The None Value
"Divide by Zero" Errors
The float(), int(), and str() Functions and Python 2 Division
The append() List Method
Default Arguments
Calculating Percentage
The gaffer says something longer and more
complicated. After a while, Waterhouse (now
wearing his cryptoanalyst hat, searching for
meaning midst apparent randomness, his neural
circuits exploiting the redundancies in the signal)
realizes that the man is speaking heavily accented
English.
“Cryptonomicon” by Neal Stephenson

Chapter 12 – Detecting English Programmatically 167
A message encrypted with the transposition cipher can have thousands of possible keys. Your
computer can still easily brute-force this many keys, but you would then have to look through
thousands of decryptions to find the one correct plaintext. This is a big problem for the brute-
force method of cracking the transposition cipher.
When the computer decrypts a message with the wrong key, the resulting plaintext is garbage
text. We need to program the computer to be able to recognize if the plaintext is garbage text or
English text. That way, if the computer decrypts with the wrong key, it knows to go on and try the
next possible key. And when the computer tries a key that decrypts to English text, it can stop and
bring that key to the attention of the cryptanalyst. Now the cryptanalyst won’t have to look
through thousands of incorrect decryptions.
How Can a Computer Understand English?
It can’t. At least, not in the way that human beings like you or I understand English. Computers
don’t really understand math, chess, or lethal military androids either, any more than a clock
understands lunchtime. Computers just execute instructions one after another. But these
instructions can mimic very complicated behaviors that solve math problems, win at chess, or
hunt down the future leaders of the human resistance.
Ideally, what we need is a Python function (let’s call it isEnglish()) that has a string passed
to it and then returns True if the string is English text and False if it’s random gibberish. Let’s
take a look at some English text and some garbage text and try to see what patterns the two have:
Robots are your friends. Except for RX-686. She will try to eat you.
ai-pey e. xrx ne augur iirl6 Rtiyt fhubE6d hrSei t8..ow eo.telyoosEs t
One thing we can notice is that the English text is made up of words that you could find in a
dictionary, but the garbage text is made up of words that you won’t. Splitting up the string into
individual words is easy. There is already a Python string method named split() that will do
this for us (this method will be explained later). The split() method just sees when each word
begins or ends by looking for the space characters. Once we have the individual words, we can
test to see if each word is a word in the dictionary with code like this:
if word == 'aardvark' or word == 'abacus' or word == 'abandon' or word ==
'abandoned' or word == 'abbreviate' or word == 'abbreviation' or word ==
'abdomen' or …
We can write code like that, but we probably shouldn’t. The computer won’t mind running
through all this code, but you wouldn’t want to type it all out. Besides, somebody else has already

168 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
typed out a text file full of nearly all English words. These text files are called dictionary files.
So we just need to write a function that checks if the words in the string exist somewhere in that
file.
Remember, a dictionary file is a text file that contains a large list of English words. A dictionary
value is a Python value that has key-value pairs.
Not every word will exist in our “dictionary file”. Maybe the dictionary file is incomplete and
doesn’t have the word, say, “aardvark”. There are also perfectly good decryptions that might have
non-English words in them, such as “RX-686” in our above English sentence. (Or maybe the
plaintext is in a different language besides English. But we’ll just assume it is in English for
now.)
And garbage text might just happen to have an English word or two in it by coincidence. For
example, it turns out the word “augur” means a person who tries to predict the future by studying
the way birds are flying. Seriously.
So our function will not be foolproof. But if most of the words in the string argument are English
words, it is a good bet to say that the string is English text. It is a very low probability that a
ciphertext will decrypt to English if decrypted with the wrong key.
The dictionary text file will have one word per line in uppercase. It will look like this:
AARHUS
AARON
ABABA
ABACK
ABAFT
ABANDON
ABANDONED
ABANDONING
ABANDONMENT
ABANDONS
…and so on. You can download this entire file (which has over 45,000 words) from
http://invpy.com/dictionary.txt.
Our isEnglish() function will have to split up a decrypted string into words, check if each
word is in a file full of thousands of English words, and if a certain amount of the words are
English words, then we will say that the text is in English. And if the text is in English, then
there’s a good bet that we have decrypted the ciphertext with the correct key.
And that is how the computer can understand if a string is English or if it is gibberish.

Chapter 12 – Detecting English Programmatically 169
Practice Exercises, Chapter 12, Section A
Practice exercises can be found at http://invpy.com/hackingpractice12A.
The Detect English Module
The detectEnglish.py program that we write in this chapter isn’t a program that runs by itself.
Instead, it will be imported by our encryption programs so that they can call the
detectEnglish.isEnglish() function. This is why we don’t give detectEnglish.py a
main() function. The other functions in the program are all provided for isEnglish() to
call.
Source Code for the Detect English Module
Open a new file editor window by clicking on File ► New Window. Type in the following code
into the file editor, and then save it as detectEnglish.py. Press F5 to run the program.
Source code for detectEnglish.py
1. # Detect English module
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. # To use, type this code:
5. # import detectEnglish
6. # detectEnglish.isEnglish(someString) # returns True or False
7. # (There must be a "dictionary.txt" file in this directory with all English
8. # words in it, one word per line. You can download this from
9. # http://invpy.com/dictionary.txt)
10. UPPERLETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
11. LETTERS_AND_SPACE = UPPERLETTERS + UPPERLETTERS.lower() + ' \t\n'
12.
13. def loadDictionary():
14. dictionaryFile = open('dictionary.txt')
15. englishWords = {}
16. for word in dictionaryFile.read().split('\n'):
17. englishWords[word] = None
18. dictionaryFile.close()
19. return englishWords
20.
21. ENGLISH_WORDS = loadDictionary()
22.
23.
24. def getEnglishCount(message):
25. message = message.upper()
26. message = removeNonLetters(message)
27. possibleWords = message.split()

170 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
28.
29. if possibleWords == []:
30. return 0.0 # no words at all, so return 0.0
31.
32. matches = 0
33. for word in possibleWords:
34. if word in ENGLISH_WORDS:
35. matches += 1
36. return float(matches) / len(possibleWords)
37.
38.
39. def removeNonLetters(message):
40. lettersOnly = []
41. for symbol in message:
42. if symbol in LETTERS_AND_SPACE:
43. lettersOnly.append(symbol)
44. return ''.join(lettersOnly)
45.
46.
47. def isEnglish(message, wordPercentage=20, letterPercentage=85):
48. # By default, 20% of the words must exist in the dictionary file, and
49. # 85% of all the characters in the message must be letters or spaces
50. # (not punctuation or numbers).
51. wordsMatch = getEnglishCount(message) * 100 >= wordPercentage
52. numLetters = len(removeNonLetters(message))
53. messageLettersPercentage = float(numLetters) / len(message) * 100
54. lettersMatch = messageLettersPercentage >= letterPercentage
55. return wordsMatch and lettersMatch
How the Program Works
detectEnglish.py
1. # Detect English module
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. # To use, type this code:
5. # import detectEnglish
6. # detectEnglish.isEnglish(someString) # returns True or False
7. # (There must be a "dictionary.txt" file in this directory with all English
8. # words in it, one word per line. You can download this from
9. # http://invpy.com/dictionary.txt)
These comments at the top of the file give instructions to programmers on how to use this
module. They give the important reminder that if there is no file named dictionary.txt in the same

Chapter 12 – Detecting English Programmatically 171
directory as detectEnglish.py then this module will not work. If the user doesn’t have this file, the
comments tell them they can download it from http://invpy.com/dictionary.txt.
detectEnglish.py
10. UPPERLETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
11. LETTERS_AND_SPACE = UPPERLETTERS + UPPERLETTERS.lower() + ' \t\n'
Lines 10 and 11 set up a few variables that are constants, which is why they have uppercase
names. UPPERLETTERS is a variable containing the 26 uppercase letters, and
LETTERS_AND_SPACE contain these letters (and the lowercase letters returned from
UPPERLETTERS.lower()) but also the space character, the tab character, and the newline
character. The tab and newline characters are represented with escape characters \t and \n.
detectEnglish.py
13. def loadDictionary():
14. dictionaryFile = open('dictionary.txt')
The dictionary file sits on the user’s hard drive, but we need to load the text in this file as a string
value so our Python code can use it. First, we get a file object by calling open() and passing the
string of the filename 'dictionary.txt'. Before we continue with the
loadDictionary() code, let’s learn about the dictionary data type.
Dictionaries and the Dictionary Data Type
The dictionary data type has values which can contain multiple other values, just like lists do. In
list values, you use an integer index value to retrieve items in the list, like spam[42]. For each
item in the dictionary value, there is a key used to retrieve it. (Values stored inside lists and
dictionaries are also sometimes called items.) The key can be an integer or a string value, like
spam['hello'] or spam[42]. Dictionaries let us organize our program’s data with even
more flexibility than lists.
Instead of typing square brackets like list values, dictionary values (or simply, dictionaries) use
curly braces. Try typing the following into the interactive shell:
>>> emptyList = []
>>> emptyDictionary = {}
>>>
A dictionary’s values are typed out as key-value pairs, which are separated by colons. Multiple
key-value pairs are separated by commas. To retrieve values from a dictionary, just use square

172 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
brackets with the key in between them (just like indexing with lists). Try typing the following
into the interactive shell:
>>> spam = {'key1':'This is a value', 'key2':42}
>>> spam['key1']
'This is a value'
>>> spam['key2']
42
>>>
It is important to know that, just as with lists, variables do not store dictionary values themselves,
but references to dictionaries. The example code below has two variables with references to the
same dictionary:
>>> spam = {'hello': 42}
>>> eggs = spam
>>> eggs['hello'] = 99
>>> eggs
{'hello': 99}
>>> spam
{'hello': 99}
>>>
Adding or Changing Items in a Dictionary
You can add or change values in a dictionary with indexes as well. Try typing the following into
the interactive shell:
>>> spam = {42:'hello'}
>>> print(spam[42])
hello
>>> spam[42] = 'goodbye'
>>> print(spam[42])
goodbye
>>>
And just like lists can contain other lists, dictionaries can also contain other dictionaries (or lists).
Try typing the following into the interactive shell:
>>> foo = {'fizz': {'name': 'Al', 'age': 144}, 'moo':['a', 'brown', 'cow']}
>>> foo['fizz']
{'age': 144, 'name': 'Al'}
>>> foo['fizz']['name']
Chapter 12 – Detecting English Programmatically 173
'Al'
>>> foo['moo']
['a', 'brown', 'cow']
>>> foo['moo'][1]
'brown'
>>>
Practice Exercises, Chapter 12, Set B
Practice exercises can be found at http://invpy.com/hackingpractice12B.
Using the len() Function with Dictionaries
The len() function can tell you how many items are in a list or how many characters are in a
string, but it can also tell you how many items are in a dictionary as well. Try typing the
following into the interactive shell:
>>> spam = {}
>>> len(spam)
0
>>> spam['name'] = 'Al'
>>> spam['pet'] = 'Zophie the cat'
>>> spam['age'] = 89
>>> len(spam)
3
>>>
Using the in Operator with Dictionaries
The in operator can also be used to see if a certain key value exists in a dictionary. It is important
to remember that the in operator checks if a key exists in the dictionary, not a value. Try typing
the following into the interactive shell:
>>> eggs = {'foo': 'milk', 'bar': 'bread'}
>>> 'foo' in eggs
True
>>> 'blah blah blah' in eggs
False
>>> 'milk' in eggs
False
>>> 'bar' in eggs
True
>>> 'bread' in eggs
False

174 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
>>>
The not in operator works with dictionary values as well.
Using for Loops with Dictionaries
You can also iterate over the keys in a dictionary with for loops, just like you can iterate over
the items in a list. Try typing the following into the interactive shell:
>>> spam = {'name':'Al', 'age':99}
>>> for k in spam:
... print(k)
... print(spam[k])
... print('==========')
...
age
99
==========
name
Al
==========
>>>
Practice Exercises, Chapter 12, Set C
Practice exercises can be found at http://invpy.com/hackingpractice12C.
The Difference Between Dictionaries and Lists
Dictionaries are like lists in many ways, but there are a few important differences:
1. Dictionary items are not in any order. There is no “first” or “last” item in a dictionary like
there is in a list.
2. Dictionaries do not have concatenation with the + operator. If you want to add a new
item, you can just use indexing with a new key. For example, foo['a new key'] =
'a string'
3. Lists only have integer index values that range from 0 to the length of the list minus one.
But dictionaries can have any key. If you have a dictionary stored in a variable spam,
then you can store a value in spam[3] without needing values for spam[0],
spam[1], or spam[2] first.
Chapter 12 – Detecting English Programmatically 175
Finding Items is Faster with Dictionaries Than Lists
detectEnglish.py
15. englishWords = {}
In the loadDictionary() function, we will store all the words in the “dictionary file” (as in,
a file that has all the words in an English dictionary book) in a dictionary value (as in, the Python
data type.) The similar names are unfortunate, but they are two completely different things.
We could have also used a list to store the string values of each word from the dictionary file. The
reason we use a dictionary is because the in operator works faster on dictionaries than lists.
Imagine that we had the following list and dictionary values:
>>> listVal = ['spam', 'eggs', 'bacon']
>>> dictionaryVal = {'spam':0, 'eggs':0, 'bacon':0}
Python can evaluate the expression 'bacon' in dictionaryVal a little bit faster than
'bacon' in listVal. The reason is technical and you don’t need to know it for the
purposes of this book (but you can read more about it at http://invpy.com/listvsdict). This faster
speed doesn’t make that much of a difference for lists and dictionaries with only a few items in
them like in the above example. But our detectEnglish module will have tens of thousands
of items, and the expression word in ENGLISH_WORDS will be evaluated many times when
the isEnglish() function is called. The speed difference really adds up for the
detectEnglish module.
The split() Method
The split() string method returns a list of several strings. The “split” between each string
occurs wherever a space is. For an example of how the split() string method works, try typing
this into the shell:
>>> 'My very energetic mother just served us Nutella.'.split()
['My', 'very', 'energetic', 'mother', 'just', 'served', 'us', 'Nutella.']
>>>
The result is a list of eight strings, one string for each of the words in the original string. The
spaces are dropped from the items in the list (even if there is more than one space). You can pass
an optional argument to the split() method to tell it to split on a different string other than just
a space. Try typing the following into the interactive shell:
>>> 'helloXXXworldXXXhowXXXareXXyou?'.split('XXX')

176 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
['hello', 'world', 'how', 'areXXyou?']
>>>
detectEnglish.py
16. for word in dictionaryFile.read().split('\n'):
Line 16 is a for loop that will set the word variable to each value in the list
dictionaryFile.read().split('\n'). Let’s break this expression down.
dictionaryFile is the variable that stores the file object of the opened file. The
dictionaryFile.read() method call will read the entire file and return it as a very large
string value. On this string, we will call the split() method and split on newline characters.
This split() call will return a list value made up of each word in the dictionary file (because
the dictionary file has one word per line.)
This is why the expression dictionaryFile.read().split('\n') will evaluate to a
list of string values. Since the dictionary text file has one word on each line, the strings in the list
that split() returns will each have one word.
The None Value
None is a special value that you can assign to a variable. The None value represents the lack of
a value. None is the only value of the data type NoneType. (Just like how the Boolean data type
has only two values, the NoneType data type has only one value, None.) It can be very useful to
use the None value when you need a value that means “does not exist”. The None value is
always written without quotes and with a capital “N” and lowercase “one”.
For example, say you had a variable named quizAnswer which holds the user's answer to some
True-False pop quiz question. You could set quizAnswer to None if the user skipped the
question and did not answer it. Using None would be better because if you set it to True or
False before assigning the value of the user's answer, it may look like the user gave an answer
for the question even though they didn't.
Calls to functions that do not return anything (that is, they exit by reaching the end of the function
and not from a return statement) will evaluate to None.
detectEnglish.py

Chapter 12 – Detecting English Programmatically 177
17. englishWords[word] = None
In our program, we only use a dictionary for the englishWords variable so that the in
operator can find keys in it. We don’t care what is stored for each key, so we will just use the
None value. The for loop that starts on line 16 will iterate over each word in the dictionary file,
and line 17 will use that word as a key in englishWords with None stored for that key.
Back to the Code
detectEnglish.py
18. dictionaryFile.close()
19. return englishWords
After the for loop finishes, the englishWords dictionary will have tens of thousands of keys
in it. At this point, we close the file object since we are done reading from it and then return
englishWords.
detectEnglish.py
21. ENGLISH_WORDS = loadDictionary()
Line 21 calls loadDictionary() and stores the dictionary value it returns in a variable
named ENGLISH_WORDS. We want to call loadDictionary() before the rest of the code in
the detectEnglish module, but Python has to execute the def statement for
loadDictionary() before we can call the function. This is why the assignment for
ENGLISH_WORDS comes after the loadDictionary() function’s code.
detectEnglish.py
24. def getEnglishCount(message):
25. message = message.upper()
26. message = removeNonLetters(message)
27. possibleWords = message.split()
The getEnglishCount() function will take one string argument and return a float value
indicating the amount of recognized English words in it. The value 0.0 will mean none of the
words in message are English words and 1.0 will mean all of the words in message are
English words, but most likely getEnglishCount() will return something in between 0.0
and 1.0. The isEnglish() function will use this return value as part of whether it returns
True or False.

178 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
First we must create a list of individual word strings from the string in message. Line 25 will
convert it to uppercase letters. Then line 26 will remove the non-letter characters from the string,
such as numbers and punctuation, by calling removeNonLetters(). (We will see how this
function works later.) Finally, the split() method on line 27 will split up the string into
individual words that are stored in a variable named possibleWords.
So if the string 'Hello there. How are you?' was passed when
getEnglishCount() was called, the value stored in possibleWords after lines 25 to 27
execute would be ['HELLO', 'THERE', 'HOW', 'ARE', 'YOU'].
detectEnglish.py
29. if possibleWords == []:
30. return 0.0 # no words at all, so return 0.0
If the string in message was something like '12345', all of these non-letter characters would
have been taken out of the string returned from removeNonLetters(). The call to
removeNonLetters() would return the blank string, and when split() is called on the
blank string, it will return an empty list.
Line 29 does a special check for this case, and returns 0.0. This is done to avoid a “divide-by-
zero” error (which is explained later on).
detectEnglish.py
32. matches = 0
33. for word in possibleWords:
34. if word in ENGLISH_WORDS:
35. matches += 1
The float value that is returned from getEnglishCount() ranges between 0.0 and 1.0. To
produce this number, we will divide the number of the words in possibleWords that are
recognized as English by the total number of words in possibleWords.
The first part of this is to count the number of recognized English words in possibleWords,
which is done on lines 32 to 35. The matches variable starts off as 0. The for loop on line 33
will loop over each of the words in possibleWords, and checks if the word exists in the
ENGLISH_WORDS dictionary. If it does, the value in matches is incremented on line 35.
Once the for loop has completed, the number of English words is stored in the matches
variable. Note that technically this is only the number of words that are recognized as English
because they existed in our dictionary text file. As far as the program is concerned, if the word
exists in dictionary.txt, then it is a real English word. And if it doesn’t exist in the dictionary file,

Chapter 12 – Detecting English Programmatically 179
it is not an English word. We are relying on the dictionary file to be accurate and complete in
order for the detectEnglish module to work correctly.
“Divide by Zero” Errors
detectEnglish.py
36. return float(matches) / len(possibleWords)
Returning a float value between 0.0 and 1.0 is a simple matter of dividing the number of
recognized words by the total number of words.
However, whenever we divide numbers using the / operator in Python, we should be careful not
to cause a “divide-by-zero” error. In mathematics, dividing by zero has no meaning. If we try to
get Python to do it, it will result in an error. Try typing the following into the interactive shell:
>>> 42 / 0
Traceback (most recent call last):
File "<pyshell#0>", line 1, in <module>
42 / 0
ZeroDivisionError: int division or modulo by zero
>>>
But a divide by zero can’t possibly happen on line 36. The only way it could is if
len(possibleWords) evaluated to 0. And the only way that would be possible is if
possibleWords were the empty list. However, our code on lines 29 and 30 specifically checks
for this case and returns 0.0. So if possibleWords had been set to the empty list, the
program execution would have never gotten past line 30 and line 36 would not cause a “divide-
by-zero” error.
The float(), int(), and str() Functions and Integer
Division
detectEnglish.py
36. return float(matches) / len(possibleWords)
The value stored in matches is an integer. However, we pass this integer to the float()
function which returns a float version of that number. Try typing the following into the interactive
shell:
>>> float(42)
42.0
180 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
>>>
The int() function returns an integer version of its argument, and the str() function returns a
string. Try typing the following into the interactive shell:
>>> float(42)
42.0
>>> int(42.0)
42
>>> int(42.7)
42
>>> int("42")
42
>>> str(42)
'42'
>>> str(42.7)
'42.7'
>>>
The float(), int(), and str() functions are helpful if you need a value’s equivalent in a
different data type. But you might be wondering why we pass matches to float() on line 36
in the first place.
The reason is to make our detectEnglish module work with Python 2. Python 2 will do
integer division when both values in the division operation are integers. This means that the result
will be rounded down. So using Python 2, 22 / 7 will evaluate to 3. However, if one of the
values is a float, Python 2 will do regular division: 22.0 / 7 will evaluate to
3.142857142857143. This is why line 36 calls float(). This is called making the code
backwards compatible with previous versions.
Python 3 always does regular division no matter if the values are floats or ints.
Practice Exercises, Chapter 12, Set D
Practice exercises can be found at http://invpy.com/hackingpractice12D.
Back to the Code
detectEnglish.py
39. def removeNonLetters(message):
40. lettersOnly = []
41. for symbol in message:
Chapter 12 – Detecting English Programmatically 181
The previously explained getEnglishCount() function calls the removeNonLetters()
function to return a string that is the passed argument, except with all the numbers and
punctuation characters removed.
The code in removeNonLetters() starts with a blank list and loops over each character in
the message argument. If the character exists in the LETTERS_AND_SPACE string, then it is
added to the end of the list. If the character is a number or punctuation mark, then it won’t exist in
the LETTERS_AND_SPACE string and won’t be added to the list.
182 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The append() List Method
detectEnglish.py
42. if symbol in LETTERS_AND_SPACE:
43. lettersOnly.append(symbol)
Line 42 checks if symbol (which is set to a single character on each iteration of line 41’s for
loop) exists in the LETTERS_AND_SPACE string. If it does, then it is added to the end of the
lettersOnly list with the append() list method.
If you want to add a single value to the end of a list, you could put the value in its own list and
then use list concatenation to add it. Try typing the following into the interactive shell, where the
value 42 is added to the end of the list stored in spam:
>>> spam = [2, 3, 5, 7, 9, 11]
>>> spam
[2, 3, 5, 7, 9, 11]
>>> spam = spam + [42]
>>> spam
[2, 3, 5, 7, 9, 11, 42]
>>>
When we add a value to the end of a list, we say we are appending the value to the list. This is
done with lists so frequently in Python that there is an append() list method which takes a
single argument to append to the end of the list. Try typing the following into the shell:
>>> eggs = []
>>> eggs.append('hovercraft')
>>> eggs
['hovercraft']
>>> eggs.append('eels')
>>> eggs
['hovercraft', 'eels']
>>> eggs.append(42)
>>> eggs
['hovercraft', 'eels', 42]
>>>
For technical reasons, using the append() method is faster than putting a value in a list and
adding it with the + operator. The append() method modifies the list in-place to include the
new value. You should always prefer the append() method for adding values to the end of a
list.
Chapter 12 – Detecting English Programmatically 183
detectEnglish.py
44. return ''.join(lettersOnly)
After line 41’s for loop is done, only the letter and space characters are in the lettersOnly
list. To make a single string value from this list of strings, we call the join() string method on
a blank string. This will join the strings in lettersOnly together with a blank string (that is,
nothing) between them. This string value is then returned as removeNonLetters()’s return
value.
Default Arguments
detectEnglish.py
47. def isEnglish(message, wordPercentage=20, letterPercentage=85):
48. # By default, 20% of the words must exist in the dictionary file, and
49. # 85% of all the characters in the message must be letters or spaces
50. # (not punctuation or numbers).
The isEnglish() function will accept a string argument and return a Boolean value that
indicates whether or not it is English text. But when you look at line 47, you can see it has three
parameters. The second and third parameters (wordPercentage and letterPercentage)
have equal signs and values next to them. These are called default arguments. Parameters that
have default arguments are optional. If the function call does not pass an argument for these
parameters, the default argument is used by default.
If isEnglish() is called with only one argument, the default arguments are used for the
wordPercentage (the integer 20) and letterPercentage (the integer 85) parameters.
Table 12-1 shows function calls to isEnglish(), and what they are equivalent to:
Table 12-1. Function calls with and without default arguments.
Function Call
Equivalent To
isEnglish('Hello')
isEnglish('Hello', 20, 85)
isEnglish('Hello', 50)
isEnglish('Hello', 50, 85)
isEnglish('Hello', 50, 60)
isEnglish('Hello', 50, 60)
isEnglish('Hello',
letterPercentage=60)
isEnglish('Hello', 20, 60)

184 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
When isEnglish() is called with no second and third argument, the function will require that
20% of the words in message are English words that exist in the dictionary text file and 85% of
the characters in message are letters. These percentages work for detecting English in most
cases. But sometimes a program calling isEnglish() will want looser or more restrictive
thresholds. If so, a program can just pass arguments for wordPercentage and
letterPercentage instead of using the default arguments.
Calculating Percentage
A percentage is a number between 0 and 100 that shows how much of something there is
proportional to the total number of those things. In the string value 'Hello cat MOOSE
fsdkl ewpin' there are five “words” but only three of them are English words. To calculate
the percentage of English words, you divide the number of English words by the total
number of words and multiply by 100. The percentage of English words in 'Hello cat
MOOSE fsdkl ewpin' is 3 / 5 * 100, which is 60.
Table 12-2 shows some percentage calculations:
Table 12-2. Some percentage calculations.
Number of
English Words
Total Number
of Words
English
Words / Total
* 100
=
Percentage
3
5
0.6
* 100
=
60
6
10
0.6
*100
=
60
300
500
0.6
* 100
=
60
32
87
0.3678
* 100
=
36.78
87
87
1.0
* 100
=
100
0
10
0
* 100
=
0
The percentage will always be between 0% (meaning none of the words) and 100% (meaning all
of the words). Our isEnglish() function will consider a string to be English if at least 20% of
the words are English words that exist in the dictionary file and 85% of the characters in the
string are letters (or spaces).
detectEnglish.py
51. wordsMatch = getEnglishCount(message) * 100 >= wordPercentage
Line 51 calculates the percentage of recognized English words in message by passing
message to getEnglishCount(), which does the division for us and returns a float
between 0.0 and 1.0. To get a percentage from this float, we just have to multiply it by 100. If
this number is greater than or equal to the wordPercentage parameter, then True is stored in

Chapter 12 – Detecting English Programmatically 185
wordsMatch. (Remember, the >= comparison operator evaluates expressions to a Boolean
value.) Otherwise, False is stored in wordsMatch.
detectEnglish.py
52. numLetters = len(removeNonLetters(message))
53. messageLettersPercentage = float(numLetters) / len(message) * 100
54. lettersMatch = messageLettersPercentage >= letterPercentage
Lines 52 to 54 calculate the percentage of letter characters in the message string. To determine
the percentage of letter (and space) characters in message, our code must divide the number of
letter characters by the total number of characters in message. Line 52 calls
removeNonLetters(message). This call will return a string that has the number and
punctuation characters removed from the string. Passing this string to len() will return the
number of letter and space characters that were in message. This integer is stored in the
numLetters variable.
Line 53 determines the percentage of letters getting a float version of the integer in
numLetters and dividing this by len(message). The return value of len(message) will
be the total number of characters in message. (The call to float() was made so that if the
programmer who imports our detectEnglish module is running Python 2, the division done
on line 53 will always be regular division instead of integer division.)
Line 54 checks if the percentage in messageLettersPercentage is greater than or equal to
the letterPercentage parameter. This expression evaluates to a Boolean value that is stored
in lettersMatch.
detectEnglish.py
55. return wordsMatch and lettersMatch
We want isEnglish() to return True only if both the wordsMatch and lettersMatch
variables contain True, so we put them in an expression with the and operator. If both the
wordsMatch and lettersMatch variables are True, then isEnglish() will declare that
the message argument is English and return True. Otherwise, isEnglish() will return
False.
Practice Exercises, Chapter 12, Set E
Practice exercises can be found at http://invpy.com/hackingpractice12E.

186 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Summary
The dictionary data type is useful because like a list it can contain multiple values. However
unlike the list, we can index values in it with string values instead of only integers. Most of the
the things we can do with lists we can also do with dictionaries, such as pass it to len() or use
the in and not in operators on it. In fact, using the in operator on a very large dictionary
value executes much faster than using in on a very large list.
The NoneType data type is also a new data type introduced in this chapter. It only has one value:
None. This value is very useful for representing a lack of a value.
We can convert values to other data types by using the int(), float(), and str() functions.
This chapter brings up “divide-by-zero” errors, which we need to add code to check for and
avoid. The split() string method can convert a single string value into a list value of many
strings. The split() string method is sort of the reverse of the join() list method. The
append() list method adds a value to the end of the list.
When we define functions, we can give some of the parameters “default arguments”. If no
argument is passed for these parameters when the function is called, the default argument value is
used instead. This can be a useful shortcut in our programs.
The transposition cipher is an improvement over the Caesar cipher because it can have hundreds
or thousands of possible keys for messages instead of just 26 different keys. A computer has no
problem decrypting a message with thousands of different keys, but to hack this cipher, we need
to write code that can determine if a string value is valid English or not.
Since this code will probably be useful in our other hacking programs, we will put it in its own
module so it can be imported by any program that wants to call its isEnglish() function. All
of the work we’ve done in this chapter is so that any program can do the following:
>>> import detectEnglish
>>> detectEnglish.isEnglish('Is this sentence English text?')
True
>>>
Now armed with code that can detect English, let’s move on to the next chapter and hack the
transposition cipher!

Chapter 13 – Hacking the Transposition Cipher 187
HACKING THE TRANSPOSITION
CIPHER
Topics Covered In This Chapter:
Multi-line Strings with Triple Quotes
The strip() String Method
To hack the transposition cipher, we will use a brute-force approach. Of the thousands of keys,
the correct key is most likely that only one that will result in readable English. We developed
English-detection code in the last chapter so the program can realize when it has found the correct
key.
Source Code of the Transposition Cipher Hacker Program
Open a new file editor window by clicking on File ► New Window. Type in the following code
into the file editor, and then save it as transpositionHacker.py. Press F5 to run the program. Note
that first you will need to download the pyperclip.py module and place this file in the same
directory as the transpositionHacker.py file. You can download this file from
http://invpy.com/pyperclip.py.
Source code for transpositionHacker.py
1. # Transposition Cipher Hacker
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import pyperclip, detectEnglish, transpositionDecrypt
5.

188 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
6. def main():
7. # You might want to copy & paste this text from the source code at
8. # http://invpy.com/transpositionHacker.py
9. myMessage = """Cb b rssti aieih rooaopbrtnsceee er es no npfgcwu plri
ch nitaalr eiuengiteehb(e1 hilincegeoamn fubehgtarndcstudmd nM eu eacBoltaetee
oinebcdkyremdteghn.aa2r81a condari fmps" tad l t oisn sit u1rnd stara nvhn fs
edbh ee,n e necrg6 8nmisv l nc muiftegiitm tutmg cm shSs9fcie ebintcaets h a
ihda cctrhe ele 1O7 aaoem waoaatdahretnhechaopnooeapece9etfncdbgsoeb uuteitgna.
rteoh add e,D7c1Etnpneehtn beete" evecoal lsfmcrl iu1cifgo ai. sl1rchdnheev sh
meBd ies e9t)nh,htcnoecplrrh ,ide hmtlme. pheaLem,toeinfgn t e9yce da' eN eMp a
ffn Fc1o ge eohg dere.eec s nfap yox hla yon. lnrnsreaBoa t,e eitsw il ulpbdofg
BRe bwlmprraio po droB wtinue r Pieno nc ayieeto'lulcih sfnc ownaSserbereiaSm
-eaiah, nnrttgcC maciiritvledastinideI nn rms iehn tsigaBmuoetcetias rn"""
10.
11. hackedMessage = hackTransposition(myMessage)
12.
13. if hackedMessage == None:
14. print('Failed to hack encryption.')
15. else:
16. print('Copying hacked message to clipboard:')
17. print(hackedMessage)
18. pyperclip.copy(hackedMessage)
19.
20.
21. def hackTransposition(message):
22. print('Hacking...')
23.
24. # Python programs can be stopped at any time by pressing Ctrl-C (on
25. # Windows) or Ctrl-D (on Mac and Linux)
26. print('(Press Ctrl-C or Ctrl-D to quit at any time.)')
27.
28. # brute-force by looping through every possible key
29. for key in range(1, len(message)):
30. print('Trying key #%s...' % (key))
31.
32. decryptedText = transpositionDecrypt.decryptMessage(key, message)
33.
34. if detectEnglish.isEnglish(decryptedText):
35. # Check with user to see if the decrypted key has been found.
36. print()
37. print('Possible encryption hack:')
38. print('Key %s: %s' % (key, decryptedText[:100]))
39. print()
40. print('Enter D for done, or just press Enter to continue
hacking:')
41. response = input('> ')

Chapter 13 – Hacking the Transposition Cipher 189
42.
43. if response.strip().upper().startswith('D'):
44. return decryptedText
45.
46. return None
47.
48. if __name__ == '__main__':
49. main()
Sample Run of the Transposition Breaker Program
When you run this program, the output will look this:
Hacking...
(Press Ctrl-C or Ctrl-D to quit at any time.)
Trying key #1...
Trying key #2...
Trying key #3...
Trying key #4...
Trying key #5...
Trying key #6...
Trying key #7...
Trying key #8...
Trying key #9...
Trying key #10...
Possible encryption hack:
Key 10: Charles Babbage, FRS (26 December 1791 - 18 October 1871) was an
English mathematician, philosopher,
Enter D for done, or just press Enter to continue hacking:
> D
Copying hacked message to clipboard:
Charles Babbage, FRS (26 December 1791 - 18 October 1871) was an English
mathematician, philosopher, inventor and mechanical engineer who originated the
concept of a programmable computer. Considered a "father of the computer",
Babbage is credited with inventing the first mechanical computer that
eventually led to more complex designs. Parts of his uncompleted mechanisms are
on display in the London Science Museum. In 1991, a perfectly functioning
difference engine was constructed from Babbage's original plans. Built to
tolerances achievable in the 19th century, the success of the finished engine
indicated that Babbage's machine would have worked. Nine years later, the
Science Museum completed the printer Babbage had designed for the difference
engine.

190 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
When the hacker program has found a likely correct decryption, it will pause and wait for the user
to press “D” and then Enter. If the decryption is a false positive, the user can just press Enter and
the program will continue to try other keys.
Run the program again and skip the correct decryption by just pressing Enter. The program
assumes that it was not a correct decryption and continues brute-forcing through the other
possible keys. Eventually the program runs through all the possible keys and then gives up,
telling the user that it was unable to hack the ciphertext:
Trying key #757...
Trying key #758...
Trying key #759...
Trying key #760...
Trying key #761...
Failed to hack encryption.
How the Program Works
transpositionHacker.py
1. # Transposition Cipher Hacker
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import pyperclip, detectEnglish, transpositionDecrypt
The transposition hacker program is under 50 lines of code because much of it exists in other
programs. Several modules are imported on line 4.
Multi-line Strings with Triple Quotes
transpositionHacker.py
6. def main():
7. # You might want to copy & paste this text from the source code at
8. # http://invpy.com/transpositionHacker.py
9. myMessage = """Cb b rssti aieih rooaopbrtnsceee er es no npfgcwu plri
ch nitaalr eiuengiteehb(e1 hilincegeoamn fubehgtarndcstudmd nM eu eacBoltaetee
oinebcdkyremdteghn.aa2r81a condari fmps" tad l t oisn sit u1rnd stara nvhn fs
edbh ee,n e necrg6 8nmisv l nc muiftegiitm tutmg cm shSs9fcie ebintcaets h a
ihda cctrhe ele 1O7 aaoem waoaatdahretnhechaopnooeapece9etfncdbgsoeb uuteitgna.
rteoh add e,D7c1Etnpneehtn beete" evecoal lsfmcrl iu1cifgo ai. sl1rchdnheev sh
meBd ies e9t)nh,htcnoecplrrh ,ide hmtlme. pheaLem,toeinfgn t e9yce da' eN eMp a
ffn Fc1o ge eohg dere.eec s nfap yox hla yon. lnrnsreaBoa t,e eitsw il ulpbdofg
BRe bwlmprraio po droB wtinue r Pieno nc ayieeto'lulcih sfnc ownaSserbereiaSm
-eaiah, nnrttgcC maciiritvledastinideI nn rms iehn tsigaBmuoetcetias rn"""

Chapter 13 – Hacking the Transposition Cipher 191
The ciphertext to be hacked is stored in the myMessage variable. Line 9 has a string value that
begins and ends with triple quotes. These strings do not have to have literal single and double
quotes escaped inside of them. Triple quote strings are also called multi-line strings, because they
can also contain actual newlines within them. Try typing the following into the interactive shell:
>>> spam = """Dear Alice,
Why did you dress up my hamster in doll clothing?
I look at Mr. Fuzz and think, "I know this was Alice's doing."
Sincerely,
Bob"""
>>> print(spam)
Dear Alice,
Why did you dress up my hamster in doll clothing?
I look at Mr. Fuzz and think, "I know this was Alice's doing."
Sincerely,
Bob
>>>
Notice that this string value can span over multiple lines. Everything after the opening triple
quotes will be interpreted as part of the string until it reaches triple quotes ending it. Multi-line
strings can either use three double quote characters or three single quote characters.
Multi-line strings are useful for putting very large strings into the source code for a program,
which is why it is used on line 9 to store the ciphertext to be broken.
Back to the Code
transpositionHacker.py
11. hackedMessage = hackTransposition(myMessage)
The ciphertext hacking code exists inside the hackTransposition() function. This function
takes one string argument: the encrypted ciphertext message to be broken. If the function can
hack the ciphertext, it returns a string of the decrypted text. Otherwise, it returns the None value.
This value is stored in the hackedMessage variable.
transpositionHacker.py
13. if hackedMessage == None:
14. print('Failed to hack encryption.')
If None was stored in hackedMessage, the program prints that it was unable to break the
encryption on the message.

192 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
transpositionHacker.py
15. else:
16. print('Copying hacked message to clipboard:')
17. print(hackedMessage)
18. pyperclip.copy(hackedMessage)
Otherwise, the text of the decrypted message is printed to the screen on line 17 and also copied to
the clipboard on line 18.
transpositionHacker.py
21. def hackTransposition(message):
22. print('Hacking...')
23.
24. # Python programs can be stopped at any time by pressing Ctrl-C (on
25. # Windows) or Ctrl-D (on Mac and Linux)
26. print('(Press Ctrl-C or Ctrl-D to quit at any time.)')
Because there are many keys the program can go through, the program displays a message to the
user telling her that the hacking has started. The print() call on line 26 also tells her that she
can press Ctrl-C (on Windows) or Ctrl-D (on OS X and Linux) to exit the program at any point.
(Pressing these keys will always exit a running Python program.)
transpositionHacker.py
28. # brute-force by looping through every possible key
29. for key in range(1, len(message)):
30. print('Trying key #%s...' % (key))
The range of possible keys for the transposition cipher is the integers between 1 and the length of
the message. The for loop on line 29 will run the hacking part of the function with each of these
keys.
To provide feedback to the user, the key that is being tested is printed to the string on line 30,
using string interpolation to place the integer in key inside the 'Trying key #%s...' %
(key) string.
transpositionHacker.py
32. decryptedText = transpositionDecrypt.decryptMessage(key, message)
Using the decryptMessage() function in the transpositionDecrypt.py program that we’ve
already written, line 32 gets the decrypted output from the current key being tested and stores it in
the decryptedText variable.

Chapter 13 – Hacking the Transposition Cipher 193
transpositionHacker.py
34. if detectEnglish.isEnglish(decryptedText):
35. # Check with user to see if the decrypted key has been found.
36. print()
37. print('Possible encryption hack:')
38. print('Key %s: %s' % (key, decryptedText[:100]))
39. print()
40. print('Enter D for done, or just press Enter to continue
hacking:')
41. response = input('> ')
The decrypted output in decryptedText will most likely only be English if the correct key
was used (otherwise, it will appear to be random garbage). The string in decryptedText is
passed to the detectEnglish.isEnglish() function we wrote in the last chapter.
But just because detectEnglish.isEnglish() returns True (making the program
execution enter the block following the if statement on line 34) doesn’t mean the program has
found the correct key. It could be a “false positive”. To be sure, line 38 prints out the first 100
characters of the decryptedText string (by using the slice decryptedText[:100]) on
the screen for the user to look at.
The program pauses when line 41 executes, waiting for the user to type something in either D on
nothing before pressing Enter. This input is stored as a string in response.
The strip() String Method
The strip() string method returns a version of the string that has any
whitespace at the beginning and end of the string stripped out. Try typing in
the following into the interactive shell:
>>> ' Hello'.strip()
'Hello'
>>> 'Hello '.strip()
'Hello'
>>> ' Hello World '.strip()
'Hello World'
>>> 'Hello x'.strip()
'Hello x'
>>>
The strip() method can also have a string argument passed to it that tells the method which
characters should be removed from the start and end of the string instead of removing whitespace.

194 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The whitespace characters are the space character, the tab character, and the newline
character. Try typing the following into the interactive shell:
>>> 'Helloxxxxxx'.strip('x')
'Hello'
>>> 'aaaaaHELLOaa'.strip('a')
'HELLO'
>>> 'ababaHELLOab'.strip('ab')
'HELLO'
>>> 'abccabcbacbXYZabcXYZacccab'.strip('abc')
'XYZabcXYZ'
>>>
transpositionHacker.py
43. if response.strip().upper().startswith('D'):
44. return decryptedText
The expression on line 43 used for the if statement’s condition lets the user have some
flexibility with what has to be typed in. If the condition were response == 'D', then the user
would have to type in exactly “D” and nothing else in order to end the program.
If the user typed in 'd' or ' D' or 'Done' then the condition would be False and the
program would continue. To avoid this, the string in response has any whitespace removed
from the start or end with the call to strip(). Then the string that response.strip()
evaluates to has the upper() method called on it. If the user typed in either “d” or “D”, the
string returned from upper() will be 'D'. Little things like this make our programs easier for
the user to use.
If the user has indicated that the decrypted string is correct, the decrypted text is returned from
hackTransposition() on line 44.
transpositionHacker.py
46. return None
Line 46 is the first line after the for loop that began on line 29. If the program execution reaches
this point, it’s because the return statement on line 44 was never reached. That would only
happen if the correctly decrypted text was never found for any of the keys that were tried.
In that case, line 46 returns the None value to indicate that the hacking has failed.
transpositionHacker.py
48. if __name__ == '__main__':
Chapter 13 – Hacking the Transposition Cipher 195
49. main()
Lines 48 and 49 call the main() function if this program was run by itself, rather than imported
by another program that wants to use its hackTransposition() function.
Practice Exercises, Chapter 13, Set A
Practice exercises can be found at http://invpy.com/hackingpractice13A.
Summary
This chapter was short like the “Breaking the Caesar Cipher with the Brute-Force Technique”
chapter because (also like that chapter) most of the code was already written in other programs.
Our hacking program can import functions from these other programs by importing them as
modules.
The strip() string method is useful for removing whitespace (or other) characters from the
beginning or end of a string. If we use triple quotes, then a string value can span across multiple
lines in our source code.
The detectEnglish.py program removes a lot of the work of inspecting the decrypted output to see
if it’s English. This allows the brute-force technique to be applied to a cipher that can have
thousands of keys.
Our programs are becoming more sophisticated. Before we learn the next cipher, we should learn
how to use Python’s debugger tool to help us find bugs in our programs.

196 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
MODULAR ARITHMETIC WITH
THE MULTIPLICATIVE AND
AFFINE CIPHERS
Topics Covered In This Chapter:
Modular Arithmetic
“Mod” is “Remainder Of”(Sort Of)
GCD: Greatest Common Divisor (aka Greatest Common Factor)
Multiple Assignment Trick
Euclid’s Algorithm for Finding the GCD of Two Numbers
“Relatively Prime”
The Multiplicative Cipher
Finding Modular Inverses
The cryptomath Module
“People have been defending their own privacy for centuries
with whispers, darkness, envelopes, closed doors, secret
handshakes, and couriers. The technologies of the past did
not allow for strong privacy, but electronic technologies do.”
Eric Hughes, “A Cypherpunk's Manifesto”, 1993

Chapter 14 – Modular Arithmetic and the Multiplicative Cipher 197
The multiplicative and affine ciphers are similar to the Caesar cipher, except instead of adding a
key to a symbol’s index in a string, these ciphers use multiplication. But before we learn how to
encrypt and decrypt with these ciphers, we’re going to need to learn a little math. This knowledge
is also needed for the last cipher in this book, the RSA cipher.
Oh No Math!
Don’t let it scare you that you need to learn some math. The principles here are easy to learn from
pictures, and we’ll see that they are directly useful in cryptography.
Math Oh Yeah!
That’s more like it.
Modular Arithmetic (aka Clock Arithmetic)
This is a clock in which I’ve replaced the 12 with a 0. (I’m a programmer. I think it’s weird that
the day begins at 12 AM instead of 0 AM.) Ignore the hour, minute, and second hands. We just
need to pay attention to the numbers.
Figure 14-1. A clock with a zero o’clock.

198 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
3 O’Clock + 5 Hours = 8 O’Clock
If the current time is 3 o’clock, what time will it be in 5 hours? This is
easy enough to figure out. 3 + 5 = 8. It will be 8 o’clock. Think of the
hour hand on the clock in Figure 14-1 starting at 3, and then moving 5
hours clockwise. It will end up at 8. This is one way we can double-
check our math.
10 O’Clock + 5 Hours = 3 O’Clock
If the current time is 10 o’clock, what time will it be in 5 hours? If you
add 10 + 5, you get 15. But 15 o’clock doesn’t make sense for clocks
like the one to the right. It only goes up to 12. So to find out what time
it will be, we subtract 15 – 12 = 3. The answer is it will be 3 o’clock.
(Whether or not it is 3 AM or 3PM depends on if the current time is 10
AM or 10 PM. But it doesn’t matter for modular arithmetic.)
If you think of the hour hand as starting at 10 and then moving forward
5 hours, it will land on 3. So double-checking our math by moving the
hour hand clockwise shows us that we are correct.
10 O’Clock + 200 Hours = 6 O’Clock
If the current time is 10 o’clock, what time will it be in 200 hours? 200
+ 10 = 210, and 210 is larger than 12. So we subtract 210 – 12 = 198.
But 198 is still larger than 12, so we subtract 12 again. 198 – 12 = 186.
If we keep subtracting 12 until the difference is less than 12, we end up
with 6. If the current time is 10 o’clock, the time 200 hours later will be
6 o’clock.
If we wanted to double check our 10 o’clock + 200 hours math, we
would keep moving the hour hand around and around the clock face.
When we’ve moved the hour hand the 200th time, it will end up landing
on 6.

Chapter 14 – Modular Arithmetic and the Multiplicative Cipher 199
The % Mod Operator
This sort of “wrap-around” arithmetic is called modular arithmetic. We say “fifteen mod
twelve” is equal to 3. (Just like how “15 o’clock” mod twelve would be “3 o’clock.) In Python,
the mod operator is the % percent sign. Try typing the following into the interactive shell:
>>> 15 % 12
3
>>> 210 % 12
6
>>> 10 % 10
0
>>> 20 % 10
0
>>>
“Mod” is “Division Remainder”(Sort Of)
You can think of the mod operator as a “division remainder” operator. 21 ÷ 5 = 4 remainder 1.
And 21 % 5 = 1. This works pretty well for positive numbers, but not for negative numbers. -21 ÷
5 = -4 remainder -1. But the result of a mod operation will never be negative. Instead, think of
that -1 remainder as being the same as 5 – 1, which comes to 4. This is exactly what -21 % 5
evaluates to:
>>> -21 % 5
4
>>>
But for the purposes of cryptography in this book, we’ll only be modding positive numbers.
Practice Exercises, Chapter 14, Set A
Practice exercises can be found at http://invpy.com/hackingpractice14A.
GCD: Greatest Common Divisor (aka Greatest Common Factor)
Factors are the numbers that can be multiplied to produce a particular number. Look at this
simple multiplication:
4 × 6 = 24
In the above math problem, we say 4 and 6 are factors of 24. (Another name for factor is
divisor.) The number 24 also has some other factors:
200 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
8 × 3 = 24
12 × 2 = 24
24 × 1 = 24
From the above three math problems, we can see that 8 and 3 are also factors of 24, as are 12 and
2, and 24 and 1. So we can say the factors of 24 are: 1, 2, 3, 4, 6, 8, 12, and 24.
Let’s look at the factors of 30:
1 × 30 = 30
2 × 15 = 30
3 × 10 = 30
5 × 6 = 30
So the factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30. (Notice that any number will always have 1
and itself as factors.) If you look at the list of factors for 24 and 30, you can see that the factors
that they have in common are 1, 2, 3, and 6. The greatest number of these is 6, so we call 6 the
greatest common factor (or, more commonly, the greatest common divisor) of 24 and 30.
Visualize Factors and GCD with Cuisenaire Rods
Figure 14-2. Each Cuisenaire rod has a different color for each integer length.
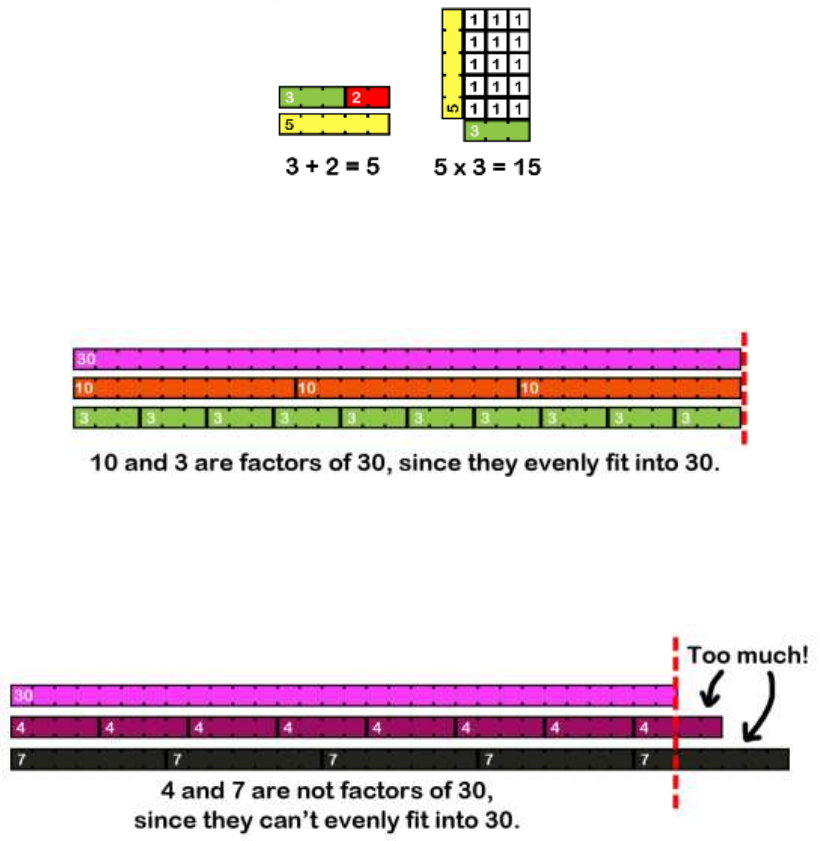
Chapter 14 – Modular Arithmetic and the Multiplicative Cipher 201
Above are some rectangular blocks with a width of 1 unit, 2 units, 3 units, and so on. The block’s
length can be used to represent a number. You can count the number of squares in each block to
determine the length and number. These blocks (sometimes called Cuisenaire rods) can be used to
visualize math operations, like 3 + 2 = 5 or 5 × 3 = 15:
Figure 14-3. Using Cuisenaire rods to demonstrate addition and multiplication.
If we represent the number 30 as a block that is 30 units long, a number is a factor of 30 if the
number’s blocks can evenly fit with the 30-block. You can see that 3 and 10 are factors of 30:
Figure 14-4. Cuisenaire rods demonstrating factors.
But 4 and 7 are not factors of 30, because the 4-blocks and 7-blocks won’t evenly fit into the 30-
block:
Figure 14-5. Cuisenaire rods demonstrating numbers that are not factors of 30.
The Greatest Common Divisor of two blocks (that is, two numbers represented by those blocks)
is the longest block that can evenly fit both blocks.
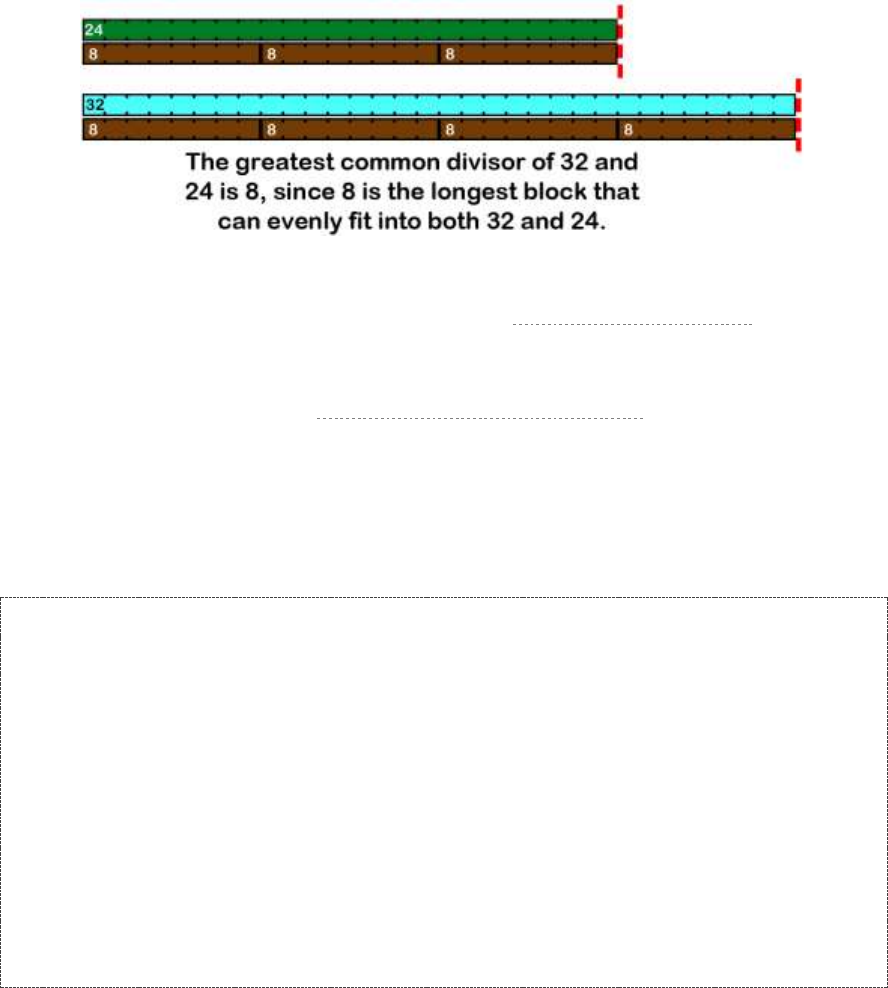
202 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Figure 14-6. Cuisenaire rods demonstrating Greatest Common Divisor.
More information about Cuisenaire rods can be found at http://invpy.com/cuisenaire.
Practice Exercises, Chapter 14, Set B
Practice exercises can be found at http://invpy.com/hackingpractice14B.
Multiple Assignment
Our GCD function will use Python’s multiple assignment trick. The multiple assignment trick lets
you assign more than one variable with a single assignment statement. Try typing the following
into the interactive shell:
>>> spam, eggs = 42, 'Hello'
>>> spam
42
>>> eggs
'Hello'
>>> a, b, c, d = ['Alice', 'Bob', 'Carol', 'David']
>>> a
'Alice'
>>> b
'Bob'
>>> c
'Carol'
>>> d
'David'
>>>
The variable names on the left side of the = operator and the values on the right side of the =
operator are separated by a comma. You can also assign each of the values in a list to its own
variable, if the number of items in the list is the same as the number of variables on the left side
of the = operator.

Chapter 14 – Modular Arithmetic and the Multiplicative Cipher 203
Be sure to have the same number of variables as you have values, otherwise Python will raise an
error that says the call needs more or has too many values:
>>> a, b, c = 1, 2
Traceback (most recent call last):
File "<pyshell#8>", line 1, in <module>
a, b, c = 1, 2
ValueError: need more than 2 values to unpack
>>> a, b, c = 1, 2, 3, 4, 5, 6
Traceback (most recent call last):
File "<pyshell#9>", line 1, in <module>
a, b, c = 1, 2, 3, 4, 5, 6
ValueError: too many values to unpack
>>>
Swapping Values with the Multiple Assignment Trick
One of the main uses of the multiple assignment trick is to swap the values in two variables. Try
typing the following into the interactive shell:
>>> spam = 'hello'
>>> eggs = 'goodbye'
>>> spam, eggs = eggs, spam
>>> spam
'goodbye'
>>> eggs
'hello'
We will use this swapping trick in our implementation of Euclid’s algorithm.
Euclid’s Algorithm for Finding the GCD of Two Numbers
Figuring out the GCD of two numbers will be important for doing the multiplicative and affine
ciphers. It seems simple enough: just look at the numbers and write down any factors you can
think of, then compare the lists and find the largest number that is in both of them.
But to program a computer to do it, we’ll need to be more precise. We need an algorithm (that is,
a specific series of steps we execute) to find the GCD of two numbers.
A mathematician who lived 2,000 years ago named Euclid came up with an algorithm for finding
the greatest common divisor of two numbers. Here’s a statue of Euclid at Oxford University:
204 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Figure 14-7. Euclid may or may not have looked like this.
Of course since no likeness or description of Euclid exists in any historical document, no one
knows what he actually looked like at all. (Artists and sculptors just make it up.) This statue could
also be called, “Statue of Some Guy with a Beard”.
Euclid’s GCD algorithm is short. Here’s a function that implements his algorithm as Python code,
which returns the GCD of integers a and b:
def gcd(a, b):
while a != 0:
a, b = b % a, a
return b
If you call this function from the interactive shell and pass it 24 and 30 for the a and b
parameters, the function will return 6. You could have done this yourself with pencil and paper.
But since you’ve programmed a computer to do this, it can easily handle very large numbers:
>>> gcd(24, 30)
6
>>> gcd(409119243, 87780243)
6837
>>>
How Euclid’s algorithm works is beyond the scope of this book, but you can rely on this function
to return the GCD of the two integers you pass it.

Chapter 14 – Modular Arithmetic and the Multiplicative Cipher 205
“Relatively Prime”
Relatively prime numbers are used for the multiplicative and affine ciphers. We say that two
numbers are relatively prime if their greatest common divisor is 1. That is, the numbers a and b
are relatively prime to each other if gcd(a, b) == 1.
Practice Exercises, Chapter 14, Set C
Practice exercises can be found at http://invpy.com/hackingpractice14C.
The Multiplicative Cipher
In the Caesar cipher, encrypting and decrypting symbols involved converting them to numbers,
adding or subtracting the key, and then converting the new number back to a symbol.
What if instead of adding the key to do the encryption, we use multiplication? There would be a
“wrap-around” issue, but the mod operator would solve that. For example, let’s use the symbol
set of just uppercase letters and the key 7. Here’s a list of the letters and their numbers:
0
1
2
3
4
5
6
7
8
9
10
11
12
A
B
C
D
E
F
G
H
I
J
K
L
M
13
14
15
16
17
18
19
20
21
22
23
24
25
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
To find what the symbol F encrypts to with key 7, multiply its number (5) by 7 and mod by 26 (to
handle the “wrap-around” with our 26-symbol set). Then use that number’s symbol. (5 × 7) mod
26 = 9, and 9 is the number for the symbol J. So F encrypts to J in the multiplicative cipher with
key 7. Do the same with all of the letters:

206 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Table 14-1. Encrypting each letter with the multiplicative cipher with key 7.
Plaintext
Symbol
Number
Encryption with
Key 7
Ciphertext
Symbol
A
0
(0 * 7) % 26 = 0
A
B
1
(1 * 7) % 26 = 7
H
C
2
(2 * 7) % 26 = 14
O
D
3
(3 * 7) % 26 = 21
V
E
4
(4 * 7) % 26 = 2
C
F
5
(5 * 7) % 26 = 9
J
G
6
(6 * 7) % 26 = 16
Q
H
7
(7 * 7) % 26 = 23
X
I
8
(8 * 7) % 26 = 4
E
J
9
(9 * 7) % 26 = 11
L
K
10
(10 * 7) % 26 = 18
S
L
11
(11 * 7) % 26 = 25
Y
M
12
(12 * 7) % 26 = 6
G
N
13
(13 * 7) % 26 = 13
N
O
14
(14 * 7) % 26 = 20
U
P
15
(15 * 7) % 26 = 1
B
Q
16
(16 * 7) % 26 = 8
I
R
17
(17 * 7) % 26 = 15
P
S
18
(18 * 7) % 26 = 22
W
T
19
(19 * 7) % 26 = 3
D
U
20
(20 * 7) % 26 = 10
K
V
21
(21 * 7) % 26 = 17
R
W
22
(22 * 7) % 26 = 24
Y
X
23
(23 * 7) % 26 = 5
F
Y
24
(24 * 7) % 26 = 12
M
Z
25
(25 * 7) % 26 = 19
T
You will end up with this mapping for the key 7: to encrypt you replace the top letter with the
letter under it, and vice versa to decrypt:
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
A
H
O
V
C
J
Q
X
E
L
S
Y
G
N
U
B
I
P
W
D
K
R
Y
F
M
T
It wouldn’t take long for an attacker to brute-force through the first 7 keys. But the good thing
about the multiplicative cipher is that it can work with very large keys, like 8,953,851 (which has
the letters of the alphabet map to the letters AXUROLIFCZWTQNKHEBYVSPMJGD). It would
take quite some time for a computer to brute-force through nearly nine million keys.
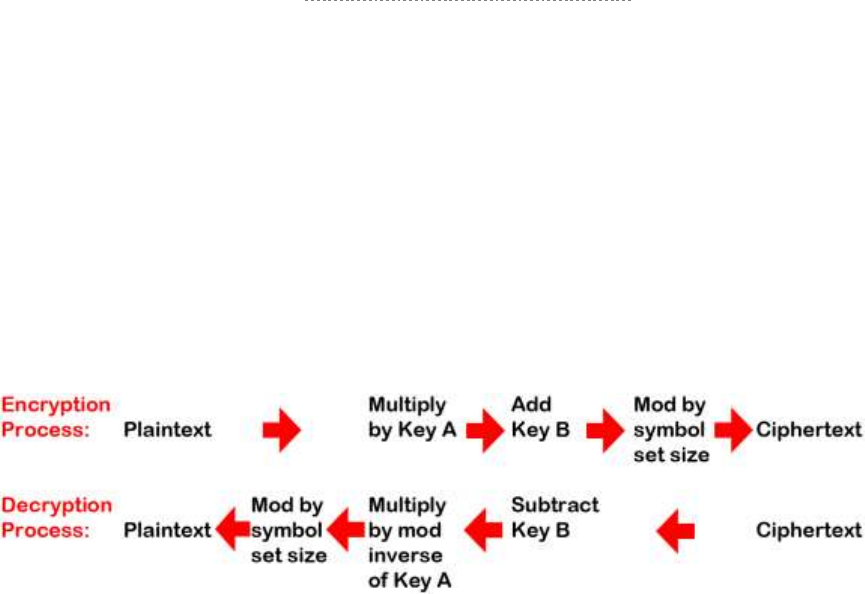
Chapter 14 – Modular Arithmetic and the Multiplicative Cipher 207
Practice Exercises, Chapter 14, Set D
Practice exercises can be found at http://invpy.com/hackingpractice14D.
Multiplicative Cipher + Caesar Cipher = The Affine Cipher
One downside to the multiplicative cipher is that the letter A always maps to the letter A. This is
because A’s number is 0, and 0 multiplied by anything will always be 0. We can fix this by
adding a second key that performs a Caesar cipher encryption after the multiplicative cipher’s
multiplication and modding is done.
This is called the affine cipher. The affine cipher has two keys. “Key A” is the integer that the
letter’s number is multiplied by. After modding this number by 26, “Key B” is the integer that is
added to the number. This sum is also modded by 26, just like in the original Caesar cipher.
This means that the affine cipher has 26 times as many possible keys as the multiplicative cipher.
It also ensures that the letter A does not always encrypt to the letter A.
Figure 14-8. The encryption and decryption are mirrors of each other.
The First Affine Key Problem
There are two problems with the multiplicative cipher’s key and affine cipher’s Key A. You
cannot just use any number for Key A. For example, if you chose the key 8, here is the mapping
you would end up with:
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
A
I
Q
Y
G
O
W
E
M
U
C
K
S
A
I
Q
Y
G
O
W
E
M
U
C
K
S
This mapping doesn’t work at all! Both the letters C and P encrypt to Q. When we encounter a Q
in the ciphertext, how do we know which it decrypts to?! The same problem exists for encrypting
A and N, F and S, and many others.
208 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
So some keys will work in the affine cipher while others will not. The secret to determining
which key numbers will work is this:
In the affine cipher, the Key A number and the size of the symbol set must be relatively
prime to each other. That is, gcd(key, size of symbol set) == 1.
We can use the gcd() function we wrote earlier to test this. The key 7 works as an affine cipher
key because gcd(7, 26) returns 1. The larger key 8,953,851 will also work because
gcd(8953851, 26) also returns 1. However, the key 8 did not work because gcd(8, 26)
is 2. If the GCD of the key and the symbol set size is not 1, then they are not relatively prime and
the key won’t work.
The math we learned earlier sure is coming in handy now. We need to know how mod works
because it is part of the GCD and affine cipher algorithms. And we need to know how GCD
works because that will tell us if a pair of numbers is relatively prime. And we need to know if a
pair of numbers is relatively prime or not in order to choose valid keys for the affine cipher.
The second problem with affine cipher’s key is discussed in the next chapter.
Decrypting with the Affine Cipher
In the Caesar cipher, we used addition to encrypt and subtraction to decrypt. In the affine cipher,
we use multiplication to encrypt. You might think that we need to divide to decrypt with the
affine cipher. But if you try this yourself, you’ll quickly see that it doesn’t work. To decrypt with
the affine cipher, we need to multiply by the key’s modular inverse.
A modular inverse (which we will call i) of two numbers (which we will call a and m) is such
that (a * i) % m == 1. For example, let’s find the modular inverse of “5 mod 7”. There is
some number i where (5 * i) % 7 will equal “1”. We will have to brute-force this
calculation:
1 isn’t the modular inverse of 5 mod 7, because (5 * 1) % 7 = 5.
2 isn’t the modular inverse of 5 mod 7, because (5 * 2) % 7 = 3.
3 is the modular inverse of 5 mod 7, because (5 * 3) % 7 = 1.
The encryption key and decryption keys for the affine cipher are two different numbers. The
encryption key can be anything we choose as long as it is relatively prime to 26 (which is the size
of our symbol set). If we have chosen the key 7 for encrypting with the affine cipher, the
decryption key will be the modular inverse of 7 mod 26:
1 is not the modular inverse of 7 mod 26, because (7 * 1) % 26 = 7.
2 is not the modular inverse of 7 mod 26, because (7 * 2) % 26 = 14.
Chapter 14 – Modular Arithmetic and the Multiplicative Cipher 209
3 is not the modular inverse of 7 mod 26, because (7 * 3) % 26 = 21.
4 is not the modular inverse of 7 mod 26, because (7 * 4) % 26 = 2.
5 is not the modular inverse of 7 mod 26, because (7 * 5) % 26 = 9.
6 is not the modular inverse of 7 mod 26, because (7 * 6) % 26 = 16.
7 is not the modular inverse of 7 mod 26, because (7 * 7) % 26 = 23.
8 is not the modular inverse of 7 mod 26, because (7 * 8) % 26 = 4.
9 is not the modular inverse of 7 mod 26, because (7 * 9) % 26 = 11.
10 is not the modular inverse of 7 mod 26, because (7 * 10) % 26 = 18.
11 is not the modular inverse of 7 mod 26, because (7 * 11) % 26 = 25.
12 is not the modular inverse of 7 mod 26, because (7 * 12) % 26 = 6.
13 is not the modular inverse of 7 mod 26, because (7 * 13) % 26 = 13.
14 is not the modular inverse of 7 mod 26, because (7 * 14) % 26 = 20.
15 is the modular inverse of 7 mod 26, because (7 * 15) % 26 = 1.
So the affine cipher decryption key is 15. To decrypt a ciphertext letter, we take that letter’s
number and multiply it by 15, and then mod 26. This will be the number of the original
plaintext’s letter.
Finding Modular Inverses
In order to calculate the modular inverse to get the decryption key, we could take a brute-force
approach and start testing the integer 1, and then 2, and then 3, and so on like we did above. But
this will be very time-consuming for large keys like 8,953,851.
There is an algorithm for finding the modular inverse just like there was for finding the Greatest
Common Divisor. Euclid’s Extended Algorithm can be used to find the modular inverse of a
number:
def findModInverse(a, m):
if gcd(a, m) != 1:
return None # no mod inverse exists if a & m aren't relatively prime
u1, u2, u3 = 1, 0, a
v1, v2, v3 = 0, 1, m
while v3 != 0:
q = u3 // v3 # // is the integer division operator
v1, v2, v3, u1, u2, u3 = (u1 - q * v1), (u2 - q * v2), (u3 - q * v3),
v1, v2, v3
return u1 % m
You don’t have to understand how Euclid’s Extended Algorithm works in order to make use of it.
We’re just going to have our programs call this function. If you’d like to learn more about how it
works, you can read http://invpy.com/euclid.

210 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The // Integer Division Operator
You may have noticed the // operator used in the findModInverse() function above. This
is the integer division operator. It divides two numbers and rounds down. Try typing the
following into the interactive shell:
>>> 41 // 7
5
>>> 41 / 7
5.857142857142857
>>> 10 // 5
2
>>> 10 / 5
2.0
>>>
Notice that an expression with the // integer division operator always evaluates to an int, not a
float.
Source Code of the cryptomath Module
The gcd() and findModInverse() functions will be used by more than one of our cipher
programs later in this book, so we should put this code into a separate module. In the file editor,
type in the following code and save it as cryptomath.py:
Source code for cryptomath.py
1. # Cryptomath Module
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. def gcd(a, b):
5. # Return the GCD of a and b using Euclid's Algorithm
6. while a != 0:
7. a, b = b % a, a
8. return b
9.
10.
11. def findModInverse(a, m):
12. # Returns the modular inverse of a % m, which is
13. # the number x such that a*x % m = 1
14.
15. if gcd(a, m) != 1:
16. return None # no mod inverse if a & m aren't relatively prime
17.
18. # Calculate using the Extended Euclidean Algorithm:
Chapter 14 – Modular Arithmetic and the Multiplicative Cipher 211
19. u1, u2, u3 = 1, 0, a
20. v1, v2, v3 = 0, 1, m
21. while v3 != 0:
22. q = u3 // v3 # // is the integer division operator
23. v1, v2, v3, u1, u2, u3 = (u1 - q * v1), (u2 - q * v2), (u3 - q *
v3), v1, v2, v3
24. return u1 % m
The GCD algorithm is described earlier in this chapter. The findModInverse() function
implements an algorithm called Euclid’s Extended Algorithm. How these functions work is
beyond the scope of this book, but you don’t have to know how the code works in order to make
use of it.
From the interactive shell, you can try out these functions after importing the module. Try typing
the following into the interactive shell:
>>> import cryptomath
>>> cryptomath.gcd(24, 32)
8
>>> cryptomath.gcd(37, 41)
1
>>> cryptomath.findModInverse(7, 26)
15
>>> cryptomath.findModInverse(8953851, 26)
17
>>>
Practice Exercises, Chapter 14, Set E
Practice exercises can be found at http://invpy.com/hackingpractice14E.
Summary
Since the multiplicative cipher is the same thing as the affine cipher except using Key B of 0, we
won’t have a separate program for the multiplicative cipher. And since it is just a less secure
version of the affine cipher, you shouldn’t use it anyway. The source code to our affine cipher
program will be presented in the next chapter.
The math presented in this chapter isn’t so hard to understand. Modding with the % operator finds
the “remainder” between two numbers. The Greatest Common Divisor function returns the
largest number that can divide two numbers. If the GCD of two numbers is 1, we say that those
numbers are “relatively prime” to each other. The most useful algorithm to find the GCD of two
numbers is Euclid’s Algorithm.
212 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The affine cipher is sort of like the Caesar cipher, except it uses multiplication instead of addition
to encrypt letters. Not all numbers will work as keys though. The key number and the size of the
symbol set must be relatively prime towards each other.
To decrypt with the affine cipher we also use multiplication. To decrypt, the modular inverse of
the key is the number that is multiplied. The modular inverse of “a mod m” is a number i such
that (a * i) % m == 1. To write a function that finds the modular inverse of a number, we
use Euclid’s Extended Algorithm.
Once we understand these math concepts, we can write a program for the affine cipher in the next
chapter.

Chapter 15 – The Affine Cipher 213
THE AFFINE CIPHER
Topics Covered In This Chapter:
The Affine Cipher
Generating random keys
How many different keys can the affine cipher have?
“I should be able to whisper something in your ear,
even if your ear is 1000 miles away, and the
government disagrees with that.”
Philip Zimmermann, creator of Pretty Good Privacy (PGP), the
most widely used email encryption software in the world.
This chapter’s programs implement the multiplicative and affine ciphers. The multiplicative
cipher is like the Caesar cipher from Chapter 6, except it uses multiplication instead of addition.
The affine cipher is the multiplicative cipher, which is then encrypted by the Caesar cipher on top
of that. The affine cipher needs two keys: one for the multiplicative cipher multiplication and the
other for the Caesar cipher addition.
For the affine cipher program, we will use a single integer for the key. We will use some simple
math to split this key into the two keys, which we will call Key A and Key B.

214 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Source Code of the Affine Cipher Program
How the affine cipher works was covered in the last chapter. Here is the source code for a Python
program that implements the affine cipher. Open a new file editor window by clicking on File ►
New Window. Type in the following code into the file editor, and then save it as affineCipher.py.
Press F5 to run the program. Note that first you will need to download the pyperclip.py module
and place this file in the same directory as the affineCipher.py file. You can download this file
from http://invpy.com/pyperclip.py.
Source code for affineCipher.py
1. # Affine Cipher
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import sys, pyperclip, cryptomath, random
5. SYMBOLS = """ !"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]
^_`abcdefghijklmnopqrstuvwxyz{|}~""" # note the space at the front
6.
7.
8. def main():
9. myMessage = """"A computer would deserve to be called intelligent if it
could deceive a human into believing that it was human." -Alan Turing"""
10. myKey = 2023
11. myMode = 'encrypt' # set to 'encrypt' or 'decrypt'
12.
13. if myMode == 'encrypt':
14. translated = encryptMessage(myKey, myMessage)
15. elif myMode == 'decrypt':
16. translated = decryptMessage(myKey, myMessage)
17. print('Key: %s' % (myKey))
18. print('%sed text:' % (myMode.title()))
19. print(translated)
20. pyperclip.copy(translated)
21. print('Full %sed text copied to clipboard.' % (myMode))
22.
23.
24. def getKeyParts(key):
25. keyA = key // len(SYMBOLS)
26. keyB = key % len(SYMBOLS)
27. return (keyA, keyB)
28.
29.
30. def checkKeys(keyA, keyB, mode):
31. if keyA == 1 and mode == 'encrypt':
32. sys.exit('The affine cipher becomes incredibly weak when key A is
set to 1. Choose a different key.')

Chapter 15 – The Affine Cipher 215
33. if keyB == 0 and mode == 'encrypt':
34. sys.exit('The affine cipher becomes incredibly weak when key B is
set to 0. Choose a different key.')
35. if keyA < 0 or keyB < 0 or keyB > len(SYMBOLS) - 1:
36. sys.exit('Key A must be greater than 0 and Key B must be between 0
and %s.' % (len(SYMBOLS) - 1))
37. if cryptomath.gcd(keyA, len(SYMBOLS)) != 1:
38. sys.exit('Key A (%s) and the symbol set size (%s) are not
relatively prime. Choose a different key.' % (keyA, len(SYMBOLS)))
39.
40.
41. def encryptMessage(key, message):
42. keyA, keyB = getKeyParts(key)
43. checkKeys(keyA, keyB, 'encrypt')
44. ciphertext = ''
45. for symbol in message:
46. if symbol in SYMBOLS:
47. # encrypt this symbol
48. symIndex = SYMBOLS.find(symbol)
49. ciphertext += SYMBOLS[(symIndex * keyA + keyB) % len(SYMBOLS)]
50. else:
51. ciphertext += symbol # just append this symbol unencrypted
52. return ciphertext
53.
54.
55. def decryptMessage(key, message):
56. keyA, keyB = getKeyParts(key)
57. checkKeys(keyA, keyB, 'decrypt')
58. plaintext = ''
59. modInverseOfKeyA = cryptomath.findModInverse(keyA, len(SYMBOLS))
60.
61. for symbol in message:
62. if symbol in SYMBOLS:
63. # decrypt this symbol
64. symIndex = SYMBOLS.find(symbol)
65. plaintext += SYMBOLS[(symIndex - keyB) * modInverseOfKeyA %
len(SYMBOLS)]
66. else:
67. plaintext += symbol # just append this symbol undecrypted
68. return plaintext
69.
70.
71. def getRandomKey():
72. while True:
73. keyA = random.randint(2, len(SYMBOLS))
74. keyB = random.randint(2, len(SYMBOLS))

216 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
75. if cryptomath.gcd(keyA, len(SYMBOLS)) == 1:
76. return keyA * len(SYMBOLS) + keyB
77.
78.
79. # If affineCipher.py is run (instead of imported as a module) call
80. # the main() function.
81. if __name__ == '__main__':
82. main()
Sample Run of the Affine Cipher Program
When you press F5 from the file editor to run this program, the output will look like this:
Key: 2023
Encrypted text:
fX<*h>}(rTH<Rh()?<?T]TH=T<rh<tT<*_))T?<ISrT))I~TSr<Ii<Ir<*h()?<?T*TI=T<_<4(>_S<
ISrh<tT)IT=IS~<r4_r<Ir<R_]<4(>_SEf<0X)_S<
k(HIS~
Full encrypted text copied to clipboard.
The message “"A computer would deserve to be called intelligent if it could deceive a human into
believing that it was human." -Alan Turing” gets encrypted with the key 2023 into the above
ciphertext.
To decrypt, paste this text as the new value to be stored in myMessage and change myMode to
the string 'decrypt'.
Practice Exercises, Chapter 15, Set A
Practice exercises can be found at http://invpy.com/hackingpractice15A.
How the Program Works
affineCipher.py
1. # Affine Cipher
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import sys, pyperclip, cryptomath, random
5. SYMBOLS = """ !"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]
^_`abcdefghijklmnopqrstuvwxyz{|}~""" # note the space at the front
Lines 1 and 2 are the usual comments describing what the program is. There is also an import
statement for the modules used in this program.

Chapter 15 – The Affine Cipher 217
The sys module is imported for the exit() function.
The pyperclip module is imported for the copy() clipboard function.
The cryptomath module that we created in the last chapter is imported for the gcd()
and findModInverse() function.
In our program, the string stored in the SYMBOLS variable is the symbol set. The symbol set is
the list of all characters that can be encrypted. Any characters in the message to be encrypted that
don’t appear in SYMBOLS will be added to the ciphertext unencrypted.
affineCipher.py
8. def main():
9. myMessage = """"A computer would deserve to be called intelligent if it
could deceive a human into believing that it was human." -Alan Turing"""
10. myKey = 2023
11. myMode = 'encrypt' # set to 'encrypt' or 'decrypt'
The main() function is almost exactly the same as the one from the transposition cipher
programs. The message, key, and mode are stored in variables on lines 9, 10, and 11.
affineCipher.py
13. if myMode == 'encrypt':
14. translated = encryptMessage(myKey, myMessage)
15. elif myMode == 'decrypt':
16. translated = decryptMessage(myKey, myMessage)
If myMode is set to 'encrypt', then line 14 will be executed and the return value of
encryptMessage() is stored in translated. Or else, if myMode is set to 'decrypt',
then decryptMessage() is called on line 16 and the return value is stored in translated.
Either way, after the execution has passed line 16, the translated variable will have the
encrypted or decrypted version of the message in myMessage.
affineCipher.py
17. print('Key: %s' % (myKey))
18. print('%sed text:' % (myMode.title()))
19. print(translated)
20. pyperclip.copy(translated)
21. print('Full %sed text copied to clipboard.' % (myMode))
The string in translated (which is the encrypted or decrypted version of the string in
myMessage) is displayed on the screen on line 19 and copied to the clipboard on line 20.

218 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Splitting One Key into Two Keys
affineCipher.py
24. def getKeyParts(key):
25. keyA = key // len(SYMBOLS)
26. keyB = key % len(SYMBOLS)
27. return (keyA, keyB)
The affine cipher is like the Caesar cipher, except that it uses multiplication and addition (with
two integer keys, which we called Key A and Key B) instead of just addition (with one key). It’s
easier to remember just one number, so we will use a mathematical trick to convert between two
keys and one key.
The getKeyParts() function splits a single integer key into two integers for Key A and Key
B. The single key (which is in the parameter key) is divided by the size of the symbol set, and
Key A is the quotient and Key B is the remainder. The quotient part (without any remainder) can
be calculated using the // integer division operator, which is what line 25 does. The remainder
part (without the quotient) can be calculated using the % mod operator, which is what line 26
does.
It is assumed that the symbol set, as well as the size of the symbol set, is publicly known along
with the rest of the source code.
For example, with 2023 as the key parameter and a SYMBOLS string of 95 characters, Key A
would be 2023 // 95 or 21 and Key B would be 2023 % 95 or 28.
To combine Key A and Key B back into the single key, multiply Key A by the size of the symbol
set and add Key B: (21 * 95) + 28 evaluates to 2023.
The Tuple Data Type
affineCipher.py
27. return (keyA, keyB)
A tuple value is similar to a list: it is a value that can store other values, which can be accessed
with indexes or slices. However, the values in a tuple cannot be modified. There is no
append() method for tuple values. A tuple is written using parentheses instead of square
brackets. The value returned on line 27 is a tuple.
For technical reasons beyond the scope of this book, the Python interpreter can execute code
faster if it uses tuples compared to code that uses lists.

Chapter 15 – The Affine Cipher 219
Input Validation on the Keys
affineCipher.py
30. def checkKeys(keyA, keyB, mode):
31. if keyA == 1 and mode == 'encrypt':
32. sys.exit('The affine cipher becomes incredibly weak when key A is
set to 1. Choose a different key.')
33. if keyB == 0 and mode == 'encrypt':
34. sys.exit('The affine cipher becomes incredibly weak when key B is
set to 0. Choose a different key.')
Encrypting with the affine cipher involves a character’s index in SYMBOLS being multiplied by
Key A and added to Key B. But if keyA is 1, the encrypted text will be very weak because
multiplying the index by 1 does not change it. Similarly, if keyB is 0, the encrypted text will be
weak because adding the index to 0 does not change it. And if both keyA was 1 and keyB was
0, the “encrypted” message would be the exact same as the original message. It wouldn’t be
encrypted at all!
The if statements on line 31 and 33 check for these “weak key” conditions, and exit the program
with a message telling the user what was wrong. Notice on lines 32 and 34, a string is being
passed to the sys.exit() call. The sys.exit() function has an optional parameter of a
string that will be printed to the screen before terminating the program. This can be used to
display an error message on the screen before the program quits.
Of course, these checks only apply to prevent you from encrypting with weak keys. If mode is set
to 'decrypt', then the checks on lines 31 and 33 don’t apply.
affineCipher.py
35. if keyA < 0 or keyB < 0 or keyB > len(SYMBOLS) - 1:
36. sys.exit('Key A must be greater than 0 and Key B must be between 0
and %s.' % (len(SYMBOLS) - 1))
The condition on line 35 checks if keyA is a negative number (that is, it is less than 0) or if
keyB is greater than 0 or less than the size of the symbol set minus one. (The reason the Key B
check has this range is described later in the “How Many Keys Does the Affine Cipher Have?”
section.) If any of these things are True, the keys are invalid and the program exits.
affineCipher.py
37. if cryptomath.gcd(keyA, len(SYMBOLS)) != 1:
38. sys.exit('Key A (%s) and the symbol set size (%s) are not
relatively prime. Choose a different key.' % (keyA, len(SYMBOLS)))

220 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Finally, Key A must be relatively prime with the symbol set size. This means that the greatest
common divisor of keyA and len(SYMBOLS) must be equal to 1. Line 37’s if statement
checks for this and exits the program if they are not relatively prime.
If all of the conditions in the checkKeys() function were False, there is nothing wrong with
the key and the program will not exit. Line 38 is the last line in the function, so the program
execution next returns to the line that originally called checkKeys().
The Affine Cipher Encryption Function
affineCipher.py
41. def encryptMessage(key, message):
42. keyA, keyB = getKeyParts(key)
43. checkKeys(keyA, keyB, 'encrypt')
First we get the integer values for Key A and Key B from the getKeyParts() function. These
values are checked if they are valid keys or not by passing them to the checkKeys() function.
If the checkKeys() function does not cause the program to exit, then the rest of the code in the
encryptMessage() function after line 43 can assume that the keys are valid.
affineCipher.py
44. ciphertext = ''
45. for symbol in message:
The ciphertext variable will eventually hold the encrypted string, but starts off as a blank
string. The for loop that begins on line 45 will iterate through each of the characters in
message, and then add the encrypted character to ciphertext. By the time the for loop is
done looping, the ciphertext variable will have the complete string of the encrypted message.
affineCipher.py
46. if symbol in SYMBOLS:
47. # encrypt this symbol
48. symIndex = SYMBOLS.find(symbol)
49. ciphertext += SYMBOLS[(symIndex * keyA + keyB) % len(SYMBOLS)]
50. else:
51. ciphertext += symbol # just append this symbol unencrypted
On each iteration of the loop, the symbol variable is assigned the single character from
message. If this character exists in SYMBOLS (that is, our symbol set), then the index in
SYMBOLS is found and assigned to symIndex. The value in symIndex is the “number”
version of the character.

Chapter 15 – The Affine Cipher 221
To encrypt it, we need to calculate the index of the encrypted letter. We multiply this symIndex
by keyA and add keyB, and mod the number by the size of the symbol set (that is, the
expression len(SYMBOLS)). We mod by len(SYMBOLS) because the affine cipher has a
similar “wrap-around” issue that the Caesar cipher had. Modding by len(SYMBOLS) handles
the “wrap-around” by ensuring the calculated index is always between 0 up to (but not including)
len(SYMBOLS). The number that we calculate will be the index in SYMBOLS of the encrypted
character, which is concatenated to the end of the string in ciphertext.
Everything that happens in the above paragraph was done on line 49.
If symbol was not in our symbol set, then symbol is concatenated to the end of the
ciphertext string on line 51.
affineCipher.py
52. return ciphertext
Once we have iterated through each character in the message string, the ciphertext variable
should contain the full encrypted string. This string is returned from encryptMessage().
The Affine Cipher Decryption Function
affineCipher.py
55. def decryptMessage(key, message):
56. keyA, keyB = getKeyParts(key)
57. checkKeys(keyA, keyB, 'decrypt')
58. plaintext = ''
59. modInverseOfKeyA = cryptomath.findModInverse(keyA, len(SYMBOLS))
The decryptMessage() function is almost the same as the encryptMessage(). Lines 56
to 58 are equivalent to lines 44 to 46.
However, instead of multiplying by Key A, the decryption process needs to multiply by the
modular inverse of Key A. The mod inverse can be calculated by calling
cryptomath.findModInverse(). This function was explained in the previous chapter.
affineCipher.py
61. for symbol in message:
62. if symbol in SYMBOLS:
63. # decrypt this symbol
64. symIndex = SYMBOLS.find(symbol)
65. plaintext += SYMBOLS[(symIndex - keyB) * modInverseOfKeyA %
len(SYMBOLS)]

222 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
66. else:
67. plaintext += symbol # just append this symbol undecrypted
68. return plaintext
Lines 61 to 68 are almost identical to the encryptMessage() function’s lines 45 to 52. The
only difference is on line 65. In the encryptMessage() function, the symbol index was
multiplied by Key A and then had Key B added to it. In decryptMessage()’s line 65, the
symbol index first has Key B subtracted from it, and then is multiplied by the modular inverse.
Then this number is modded by the size of the symbol set, len(SYMBOLS). This is how the
decryption process undoes the encryption.
Generating Random Keys
It can be difficult to come up with a valid key for the affine cipher, so we will create a
getRandomKey() function that generates a random (but valid) key for the user to use. To use
this, the user simply has to change line 10 to store the return value of getRandomKey() in the
myKey variable:
affineCipher.py
10. myKey = getRandomKey()
Now the key that is used to encrypt is randomly selected for us. It will be printed to the screen
when line 17 is executed.
affineCipher.py
71. def getRandomKey():
72. while True:
73. keyA = random.randint(2, len(SYMBOLS))
74. keyB = random.randint(2, len(SYMBOLS))
The code in getRandomKey()enters a while loop on line 72 where the condition is True.
This is called an infinite loop, because the loop’s condition is never False. If your program
gets stuck in an infinite loop, you can terminate it by pressing Ctrl-C or Ctrl-D.
The code on lines 73 and 74 determine random numbers between 2 and the size of the symbol set
for keyA and for keyB. This way there is no chance that Key A or Key B are equal to the invalid
values 0 or 1.
affineCipher.py
75. if cryptomath.gcd(keyA, len(SYMBOLS)) == 1:
76. return keyA * len(SYMBOLS) + keyB

Chapter 15 – The Affine Cipher 223
The if statement on line 75 checks to make sure that keyA is relatively prime with the size of
the symbol set by calling the gcd() function in the cryptomath module. If it is, then these
two keys are combined into a single key by multiplying keyA by the symbol set size and adding
keyB. (This is the opposite of what the getKeyParts() function does.) This value is returned
from the getRandomKey() function.
If the condition on line 75 was False, then the code loops back to the start of the while loop
on line 73 and picks random numbers for keyA and keyB again. The infinite loop ensures that
the program keeps looping again and again until it finds random numbers that are valid keys.
affineCipher.py
79. # If affineCipher.py is run (instead of imported as a module) call
80. # the main() function.
81. if __name__ == '__main__':
82. main()
Lines 81 and 82 call the main() function if this program was run by itself, rather than imported
by another program.
The Second Affine Key Problem: How Many Keys Can the Affine
Cipher Have?
Key B of the affine cipher is limited to the size of the symbol set (in the case of affineCipher.py,
len(SYMBOLS) is 95). But it seems like Key A could be as large as we want it to be (as long as
it is relatively prime to the symbol set size). Therefore the affine cipher should have an infinite
number of keys and therefore cannot be brute-forced.
As it turns out, no. Remember how large keys in the Caesar cipher ended up being the same as
smaller keys due to the “wrap-around” effect. With a symbol set size of 26, the key 27 in the
Caesar cipher would produce the same encrypted text as the key 1. The affine cipher also “wraps
around”.
Since the Key B part of the affine cipher is the same as the Caesar cipher, we know it is limited
from 1 to the size of the symbol set. But to find out if the affine cipher’s Key A is also limited, we
can write a small program to encrypt a message with several different integers for Key A and see
what the ciphertext looks like.
Open a new file editor window and type the following source code. Save this file as
affineKeyTest.py, and then press F5 to run it.

224 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Source code for affineKeyTest.py
1. # This program proves that the keyspace of the affine cipher is limited
2. # to len(SYMBOLS) ^ 2.
3.
4. import affineCipher, cryptomath
5.
6. message = 'Make things as simple as possible, but not simpler.'
7. for keyA in range(2, 100):
8. key = keyA * len(affineCipher.SYMBOLS) + 1
9.
10. if cryptomath.gcd(keyA, len(affineCipher.SYMBOLS)) == 1:
11. print(keyA, affineCipher.encryptMessage(key, message))
This is a fairly simple program. It imports the affineCipher module for its
encryptMessage() function and the cryptomath module for its gcd() function. We will
always encrypt the string stored in the message variable. The for loop will range between 2
(since 0 and 1 are not allowed as valid Key A integers) and 100.
On each iteration of the loop, we calculate the key from the current keyA value and always use 1
for Key B (this is why 1 is added on line 8). Remember that it is not valid to use a Key A that is
not relatively prime with the symbol set size. So if the greatest common divisor of the key and the
symbol set size is not equal to 1, the if statement on line 10 will skip the call to
encryptMessage() on line 11.
Basically, this program will print out the same message encrypted with several different integers
for Key A. The output of this program will look like this:
2 {DXL!jRT^Ph!Dh!hT\bZL!Dh!b`hhTFZL9!Flj!^`j!hT\bZLf=
3 I&D2!_;>M8\!&\!\>JSG2!&\!SP\\>)G2E!)b_!MP_!\>JSG2YK
4 vg0w!T$(< P!gP!P(8D4w!gP!D@PP(k4wQ!kXT!<@T!P(8D4wLY
6 q+gC!>U[yO8!+8!8[s&mC!+8!& 88[1mCi!1D>!y >!8[s&mC2u
...skipped for brevity...
92 X{]o!BfcTiE!{E!EcWNZo!{E!NQEEcxZo\!x?B!TQB!EcWNZoHV
93 &]IU!7OMCQ9!]9!9ME?GU!]9!?A99M[GUh
226 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
HACKING THE AFFINE CIPHER
Topics Covered In This Chapter:
The ** Exponent Operator
The continue Statement
We know that the affine cipher is limited to only a few thousand keys. This means it is trivial to
perform a brute-force attack against it. Open a new File Editor and type in the following code.
Save the file as affineHacker.py.
Source Code of the Affine Cipher Hacker Program
Open a new file editor window by clicking on File ► New Window. Type in the following code
into the file editor, and then save it as affineHacker.py. Press F5 to run the program. Note that
first you will need to download the pyperclip.py module and place this file in the same directory
as the affineHacker.py file. You can download this file from http://invpy.com/pyperclip.py.
Typing the string for the myMessage variable might be tricky, but you can copy and paste it
from http://invpy.com/affineHacker.py to save time.
Source Code for affineHacker.py
1. # Affine Cipher Hacker
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import pyperclip, affineCipher, detectEnglish, cryptomath
5.
6. SILENT_MODE = False
7.

Chapter 16 – Hacking the Affine Cipher 227
8. def main():
9. # You might want to copy & paste this text from the source code at
10. # http://invpy.com/affineHacker.py
11. myMessage = """U&'<3dJ^Gjx'-3^MS'Sj0jxuj'G3'%j'<mMMjS'g{GjMMg9j{G'g"'gG
'<3^MS'Sj<jguj'm'P^dm{'g{G3'%jMgjug{9'GPmG'gG'-m0'P^dm{LU'5&Mm{'_^xg{9"""
12.
13. hackedMessage = hackAffine(myMessage)
14.
15. if hackedMessage != None:
16. # The plaintext is displayed on the screen. For the convenience of
17. # the user, we copy the text of the code to the clipboard.
18. print('Copying hacked message to clipboard:')
19. print(hackedMessage)
20. pyperclip.copy(hackedMessage)
21. else:
22. print('Failed to hack encryption.')
23.
24.
25. def hackAffine(message):
26. print('Hacking...')
27.
28. # Python programs can be stopped at any time by pressing Ctrl-C (on
29. # Windows) or Ctrl-D (on Mac and Linux)
30. print('(Press Ctrl-C or Ctrl-D to quit at any time.)')
31.
32. # brute-force by looping through every possible key
33. for key in range(len(affineCipher.SYMBOLS) ** 2):
34. keyA = affineCipher.getKeyParts(key)[0]
35. if cryptomath.gcd(keyA, len(affineCipher.SYMBOLS)) != 1:
36. continue
37.
38. decryptedText = affineCipher.decryptMessage(key, message)
39. if not SILENT_MODE:
40. print('Tried Key %s... (%s)' % (key, decryptedText[:40]))
41.
42. if detectEnglish.isEnglish(decryptedText):
43. # Check with the user if the decrypted key has been found.
44. print()
45. print('Possible encryption hack:')
46. print('Key: %s' % (key))
47. print('Decrypted message: ' + decryptedText[:200])
48. print()
49. print('Enter D for done, or just press Enter to continue
hacking:')
50. response = input('> ')
51.

228 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
52. if response.strip().upper().startswith('D'):
53. return decryptedText
54. return None
55.
56.
57. # If affineHacker.py is run (instead of imported as a module) call
58. # the main() function.
59. if __name__ == '__main__':
60. main()
Sample Run of the Affine Cipher Hacker Program
When you press F5 from the file editor to run this program, the output will look like this:
Hacking...
(Press Ctrl-C or Ctrl-D to quit at any time.)
Tried Key 95... (U&'<3dJ^Gjx'-3^MS'Sj0jxuj'G3'%j'<mMMjS'g)
Tried Key 96... (T%&;2cI]Fiw&,2]LR&Ri/iwti&F2&$i&;lLLiR&f)
Tried Key 97... (S$%:1bH\Ehv%+1\KQ%Qh.hvsh%E1%#h%:kKKhQ%e)
...skipped for brevity...
Tried Key 2190... (?^=!-+.32#0=5-3*"="#1#04#=2-= #=!~**#"=')
Tried Key 2191... (` ^BNLOTSDQ^VNTKC^CDRDQUD^SN^AD^B@KKDC^H)
Tried Key 2192... ("A computer would deserve to be called i)
Possible encryption hack:
Key: 2192
Decrypted message: "A computer would deserve to be called intelligent if it
could deceive a human into believing that it was human." -Alan Turing
Enter D for done, or just press Enter to continue hacking:
> d
Copying hacked message to clipboard:
"A computer would deserve to be called intelligent if it could deceive a human
into believing that it was human." –Alan Turing
How the Program Works
affineHacker.py
1. # Affine Cipher Hacker
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import pyperclip, affineCipher, detectEnglish, cryptomath
5.

Chapter 16 – Hacking the Affine Cipher 229
6. SILENT_MODE = False
Our affine cipher hacking program fits in 60 lines of code because we’ve already written much of
the code it uses.
When you run the hacker program, you can see that this program produces a lot of output as it
works its way through all the possible decryptions. However, printing out this input does slow
down the program. If you change line 6 to set the SILENT_MODE variable to True, the program
will be silenced and not print out all these messages. This will speed up the program immensely.
But showing all that text while your hacking program runs makes it look cool. (And if you want
your programs to look cool by printing out text slowly one character at a time for a “typewriter”
effect, check out the typewriter.py module at http://invpy.com/typewriter.py.)
affineHacker.py
8. def main():
9. # You might want to copy & paste this text from the source code at
10. # http://invpy.com/affineHacker.py
11. myMessage = """U&'<3dJ^Gjx'-3^MS'Sj0jxuj'G3'%j'<mMMjS'g{GjMMg9j{G'g"'gG
'<3^MS'Sj<jguj'm'P^dm{'g{G3'%jMgjug{9'GPmG'gG'-m0'P^dm{LU'5&Mm{'_^xg{9"""
12.
13. hackedMessage = hackAffine(myMessage)
14.
15. if hackedMessage != None:
16. # The plaintext is displayed on the screen. For the convenience of
17. # the user, we copy the text of the code to the clipboard.
18. print('Copying hacked message to clipboard:')
19. print(hackedMessage)
20. pyperclip.copy(hackedMessage)
21. else:
22. print('Failed to hack encryption.')
The ciphertext to be hacked is stored as a string in myMessage, and this string is passed to the
hackAffine() function (described next). The return value from this call is either a string of
the original message (if the ciphertext was hacked) or the None value (if the hacking failed).
The code on lines 15 to 22 will check if hackedMessage was set to None or not. If
hackedMessage is not equal to None, then the message will be printed to the screen on line
19 and copied to the clipboard on line 20. Otherwise, the program will simply print that it was
unable to hack the message.

230 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The Affine Cipher Hacking Function
affineHacker.py
25. def hackAffine(message):
26. print('Hacking...')
27.
28. # Python programs can be stopped at any time by pressing Ctrl-C (on
29. # Windows) or Ctrl-D (on Mac and Linux)
30. print('(Press Ctrl-C or Ctrl-D to quit at any time.)')
The hackAffine() function has the code that does the decryption. This can take a while, so if
the user wants to exit the program early, she can press Ctrl-C (on Windows) or Ctrl-D (on OS X
and Linux).
The ** Exponent Operator
There is another math operator besides the basic +, -, *, /, and // operators. The ** operator is
Python’s exponent operator. This does “to the power of” math on two numbers. For example,
“two to the power of five” would be 2 ** 5 in Python code. This is equivalent to two
multiplied by itself five times: 2 * 2 * 2 * 2 * 2. Both the expressions 2 ** 5 and 2 *
2 * 2 * 2 * 2 evaluate to the integer 32.
Try typing the following into the interactive shell:
>>> 2 ** 6
64
>>> 4**2
16
>>> 2**4
16
>>> 123**10
792594609605189126649
>>>
affineHacker.py
32. # brute-force by looping through every possible key
33. for key in range(len(affineCipher.SYMBOLS) ** 2):
34. keyA = affineCipher.getKeyParts(key)[0]
The range of integers for the keys used to brute-force the ciphertext will range from 0 to the size
of the symbol set to the second power. The expression:
len(affineCipher.SYMBOLS) ** 2

Chapter 16 – Hacking the Affine Cipher 231
...is the same as:
len(affineCipher.SYMBOLS) * len(affineCipher.SYMBOLS)
We multiply this because there are at most len(affineCipher.SYMBOLS) possible integers
for Key A and len(affineCipher.SYMBOLS) possible integers for Key B. To get the
entire range of possible keys, we multiply these values together.
Line 34 calls the getKeyParts() function that we made in affineCipher.py to get the Key A
part of the key we are testing. Remember that the return value of this function call is a tuple of
two integers (one for Key A and one for Key B). Since hackAffine() only needs Key A, the
[0] after the function call works on the return value to evaluate to just the first integer in the
returned tuple.
That is, affineCipher.getKeyParts(key)[0] will evaluate to (for example), the tuple
(42, 22)[0], which will then evaluate to 42. This is how we can get just the Key A part of
the return value. The Key B part (that is, the second value in the returned tuple) is just ignored
because we don’t need Key B to calculate if Key A is valid.
The continue Statement
The continue statement is simply the continue keyword by itself. A continue statement
is found inside the block of a while or for loop. When a continue statement is executed, the
program execution immediately jumps to the start of the loop for the next iteration.
This is exactly the same thing that happens when the program execution reaches the end of the
loop’s block. But a continue statement makes the program execution jump back to the start of
the loop early.
Try typing the following into the interactive shell:
>>> for i in range(3):
... print(i)
... print('Hello!')
...
0
Hello!
1
Hello!
2
Hello!
>>>

232 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
This is pretty obvious. The for loop will loop through the range object, and the value in i
becomes each integer between 0 and 4. Also on each iteration, the print('Hello!')
function call will display “Hello!” on the screen.
Try typing in this code, which adds a continue statement before the print('Hello!')
line:
>>> for i in range(3):
... print(i)
... continue
... print('Hello!')
...
0
1
2
>>>
Notice that “Hello!” never appears, because the continue statement causes the program
execution to jump back to the start of the for loop for the next iteration. So the execution never
reaches the print('Hello!') line.
A continue statement is often put inside an if statement’s block so that execution will
continue at the beginning of the loop based on some condition.
affineHacker.py
35. if cryptomath.gcd(keyA, len(affineCipher.SYMBOLS)) != 1:
36. continue
With the Key A integer stored in the variable keyA, line 35 uses the gcd() function in our
cryptomath module to determine if Key A is not relatively prime with the symbol set size.
Remember, two numbers are relatively prime if their GCD (greatest common divisor) is one.
If Key A and the symbol set size are not relatively prime, then the condition on line 35 is True
and the continue statement on line 36 is executed. This will cause the program execution to
jump back to the start of the loop for the next iteration. This way, the program will skip line 38’s
call to decryptMessage() if the key is invalid, and continue to the next key.
affineHacker.py
38. decryptedText = affineCipher.decryptMessage(key, message)
39. if not SILENT_MODE:
40. print('Tried Key %s... (%s)' % (key, decryptedText[:40]))

Chapter 16 – Hacking the Affine Cipher 233
The message is then decrypted with the key by calling decryptMessage(). If
SILENT_MODE is False the “Tried Key” message will be printed on the screen. If
SILENT_MODE was set to True, the print() call on line 40 will be skipped.
affineHacker.py
42. if detectEnglish.isEnglish(decryptedText):
43. # Check with the user if the decrypted key has been found.
44. print()
45. print('Possible encryption hack:')
46. print('Key: %s' % (key))
47. print('Decrypted message: ' + decryptedText[:200])
48. print()
Next, we use the isEnglish() function from our detectEnglish module to check if the
decrypted message is recognized as English. If the wrong decryption key was used, then the
decrypted message will look like random characters and isEnglish() will return False.
But if the decrypted message is recognized as readable English (by the isEnglish() function
anyway), then we will display this to the user.
affineHacker.py
49. print('Enter D for done, or just press Enter to continue
hacking:')
50. response = input('> ')
51.
52. if response.strip().upper().startswith('D'):
53. return decryptedText
The program might not have found the correct key, but rather a key that produces gibberish that
the isEnglish() function mistakenly thinks is English. To prevent false positives, the
decrypted text is printed on the screen for the user to read. If the user decides that this is the
correct decryption, she can type in D and press Enter. Otherwise, she can just press Enter (which
returns a blank string from the input() call) and the hackAffine() function will continue
trying more keys.
affineHacker.py
54. return None
From the indentation of line 54, you can see that this is line is executed after the for loop on line
33 has completed. If this loop has finished, then it has gone through every possible decryption

234 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
key without finding the correct key. (If the program had found the correct key, then the execution
would have previously returned from the function on line 53.)
But at this point, the hackAffine() function returns the None value to signal that it was
unsuccessful at hacking the ciphertext.
affineHacker.py
57. # If affineHacker.py is run (instead of imported as a module) call
58. # the main() function.
59. if __name__ == '__main__':
60. main()
Just like the other programs, we want the affineHacker.py file to be run on its own or be imported
as a module. If affineHacker.py is run as a program, then the special __name__ variable will be
set to the string '__main__' (instead of 'affineHacker'). In this case, we want to call the
main() function.
Practice Exercises, Chapter 16, Set A
Practice exercises can be found at http://invpy.com/hackingpractice16A.
Summary
This chapter was fairly short because it hasn’t introduced any new hacking techniques. As long as
the number of possible keys is less than a million or so, it won’t take long for our computers to
brute-force through every possible key and use isEnglish() to check if it has found the right
key.
And a lot of the code we use for the affine cipher hacker has already been written in
affineCipher.py, detectEnglish.py, cryptomath.py, and pyperclip.py. The main() function trick
is really helpful in making the code in our programs reusable.
The ** exponent operator can be used to raise a number to the power of another number. The
continue statement sends the program execution back to the beginning of the loop (instead of
waiting until the execution reaches the end of the block).
In the next chapter, we will learn a new cipher that cannot be brute-forced by our computers. The
number of possible keys is more than a trillion trillion! A single laptop couldn’t possible go
through a fraction of those keys in our life time. This makes it immune to brute-forcing. Let’s
learn about the simple substitution cipher.

Chapter 17 – The Simple Substitution Cipher 235
THE SIMPLE SUBSTITUTION
CIPHER
Topics Covered In This Chapter:
The sort() list method
Getting rid of duplicate characters from a string
The isupper() and islower() string methods
Wrapper functions
“In my role as Wikileaks editor, I've been involved
in fighting off many legal attacks. To do that, and
keep our sources safe, we have had to spread
assets, encrypt everything, and move
telecommunications and people around the world
to activate protective laws in different national
jurisdictions.”
Julian Assange, editor-in-chief of Wikileaks

236 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The transposition and affine ciphers have thousands of possible keys, but a computer can still
brute-force through all of them easily. We’ll need a cipher that has so many possible keys, no
computer can possibly brute-force through them all.
The simple substitution cipher is effectively invulnerable to a brute-force attack. Even if your
computer could try out a trillion keys every second, it would still take twelve million years for it
to try out every key.
The Simple Substitution Cipher with Paper and Pencil
To implement the simple substitution cipher, choose a random letter to encrypt each letter of the
alphabet. Use each letter once and only once. The key will end up being a string of 26 letters of
the alphabet in random order. There are 403,291,461,126,605,635,584,000,000 possible orderings
for keys. (To see how this number was calculated, see http://invpy.com/factorial).
Let’s do the simple substitution cipher with paper and pencil first. For example, let’s encrypt the
message, “Attack at dawn.” with the key VJZBGNFEPLITMXDWKQUCRYAHSO. First write
out the letters of the alphabet and then write the key underneath it.
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
V
J
Z
B
G
N
F
E
P
L
I
T
M
X
D
W
K
Q
U
C
R
Y
A
H
S
O
To encrypt a message, find the letter from the plaintext in the top row and substitute it with the
letter in the bottom row. A encrypts to V, and T encrypts to C, C encrypts to Z, and so on. So the
message “Attack at dawn.” encrypts to “Vccvzi vc bvax.”
To decrypt, find the letter from the ciphertext in the bottom row and replace it with the letter from
the top row. V decrypts to A, C decrypts to T, Z decrypts to C, and so on.
This is very similar to how the Caesar cipher works with the St. Cyr slide, except the bottom row
is scrambled instead of in alphabetical order and just shifted over. The advantage of the simple
substitution cipher is that there are far more possible keys. The disadvantage is that the key is 26
characters long and harder to memorize. If you write down the key, make sure that this key is
never read by anyone else!
Practice Exercises, Chapter 17, Set A
Practice exercises can be found at http://invpy.com/hackingpractice17A.

Chapter 17 – The Simple Substitution Cipher 237
Source Code of the Simple Substitution Cipher
Open a new file editor window by clicking on File ► New Window. Type in the following code
into the file editor, and then save it as simpleSubCipher.py. Press F5 to run the program. Note that
first you will need to download the pyperclip.py module and place this file in the same directory
as the simpleSubCipher.py file. You can download this file from http://invpy.com/pyperclip.py.
Source code for simpleSubCipher.py
1. # Simple Substitution Cipher
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import pyperclip, sys, random
5.
6.
7. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
8.
9. def main():
10. myMessage = 'If a man is offered a fact which goes against his
instincts, he will scrutinize it closely, and unless the evidence is
overwhelming, he will refuse to believe it. If, on the other hand, he is
offered something which affords a reason for acting in accordance to his
instincts, he will accept it even on the slightest evidence. The origin of
myths is explained in this way. -Bertrand Russell'
11. myKey = 'LFWOAYUISVKMNXPBDCRJTQEGHZ'
12. myMode = 'encrypt' # set to 'encrypt' or 'decrypt'
13.
14. checkValidKey(myKey)
15.
16. if myMode == 'encrypt':
17. translated = encryptMessage(myKey, myMessage)
18. elif myMode == 'decrypt':
19. translated = decryptMessage(myKey, myMessage)
20. print('Using key %s' % (myKey))
21. print('The %sed message is:' % (myMode))
22. print(translated)
23. pyperclip.copy(translated)
24. print()
25. print('This message has been copied to the clipboard.')
26.
27.
28. def checkValidKey(key):
29. keyList = list(key)
30. lettersList = list(LETTERS)
31. keyList.sort()
32. lettersList.sort()

238 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
33. if keyList != lettersList:
34. sys.exit('There is an error in the key or symbol set.')
35.
36.
37. def encryptMessage(key, message):
38. return translateMessage(key, message, 'encrypt')
39.
40.
41. def decryptMessage(key, message):
42. return translateMessage(key, message, 'decrypt')
43.
44.
45. def translateMessage(key, message, mode):
46. translated = ''
47. charsA = LETTERS
48. charsB = key
49. if mode == 'decrypt':
50. # For decrypting, we can use the same code as encrypting. We
51. # just need to swap where the key and LETTERS strings are used.
52. charsA, charsB = charsB, charsA
53.
54. # loop through each symbol in the message
55. for symbol in message:
56. if symbol.upper() in charsA:
57. # encrypt/decrypt the symbol
58. symIndex = charsA.find(symbol.upper())
59. if symbol.isupper():
60. translated += charsB[symIndex].upper()
61. else:
62. translated += charsB[symIndex].lower()
63. else:
64. # symbol is not in LETTERS, just add it
65. translated += symbol
66.
67. return translated
68.
69.
70. def getRandomKey():
71. key = list(LETTERS)
72. random.shuffle(key)
73. return ''.join(key)
74.
75.
76. if __name__ == '__main__':
77. main()
Chapter 17 – The Simple Substitution Cipher 239
Sample Run of the Simple Substitution Cipher Program
When you run this program, the output will look like this:
Using key LFWOAYUISVKMNXPBDCRJTQEGHZ
The encrypted message is:
Sy l nlx sr pyyacao l ylwj eiswi upar lulsxrj isr sxrjsxwjr, ia esmm rwctjsxsza
sj wmpramh, lxo txmarr jia aqsoaxwa sr pqaceiamnsxu, ia esmm caytra jp famsaqa
sj. Sy, px jia pjiac ilxo, ia sr pyyacao rpnajisxu eiswi lyypcor l calrpx ypc
lwjsxu sx lwwpcolxwa jp isr sxrjsxwjr, ia esmm lwwabj sj aqax px jia rmsuijarj
aqsoaxwa. Jia pcsusx py nhjir sr agbmlsxao sx jisr elh. -Facjclxo Ctrramm
This message has been copied to the clipboard.
Notice that if the letter in the plaintext was lowercase, it will be lowercase in the ciphertext. If the
letter was uppercase in the plaintext, it will be uppercase in the ciphertext. The simple
substitution cipher does not encrypt spaces or punctuation marks. (Although the end of this
chapter explains how to modify the program to encrypt those characters too.)
To decrypt this ciphertext, paste it as the value for the myMessage variable on line 10 and
change myMode to the string 'decrypt'. Then run the program again. The output will look
like this:
Using key LFWOAYUISVKMNXPBDCRJTQEGHZ
The decrypted message is:
If a man is offered a fact which goes against his instincts, he will scrutinize
it closely, and unless the evidence is overwhelming, he will refuse to believe
it. If, on the other hand, he is offered something which affords a reason for
acting in accordance to his instincts, he will accept it even on the slightest
evidence. The origin of myths is explained in this way. -Bertrand Russell
This message has been copied to the clipboard.
How the Program Works
simpleSubCipher.py
1. # Simple Substitution Cipher
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import pyperclip, sys, random
5.
6.
7. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'

240 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The first few lines are comments describing the program. Then the pyperclip, sys, and
random modules are imported. Finally, the LETTERS constant variable is set to a string of all
the uppercase letters. The LETTERS string will be our symbol set for the simple substitution
cipher program.
The Program’s main() Function
simpleSubCipher.py
9. def main():
10. myMessage = 'If a man is offered a fact which goes against his
instincts, he will scrutinize it closely, and unless the evidence is
overwhelming, he will refuse to believe it. If, on the other hand, he is
offered something which affords a reason for acting in accordance to his
instincts, he will accept it even on the slightest evidence. The origin of
myths is explained in this way. -Bertrand Russell'
11. myKey = 'LFWOAYUISVKMNXPBDCRJTQEGHZ'
12. myMode = 'encrypt' # set to 'encrypt' or 'decrypt'
The main() function is similar to the main() function of cipher programs in the previous
chapters. It contains the variables that store the message, key, and mode that will be used for
the program.
simpleSubCipher.py
14. checkValidKey(myKey)
The keys for simple substitution ciphers are easy to get wrong. For example, the key might not
have every letter of the alphabet. Or the key may have the same letter twice. The
checkValidKey() function (which is explained later) makes sure the key is usable by the
encryption and decryption functions, and will exit the program with an error message if they are
not.
simpleSubCipher.py
16. if myMode == 'encrypt':
17. translated = encryptMessage(myKey, myMessage)
18. elif myMode == 'decrypt':
19. translated = decryptMessage(myKey, myMessage)
If the program execution returns from checkValidKey() instead of terminating, we can
assume the key is valid. Lines 16 through 19 check whether the myMode variable is set to
'encrypt' or 'decrypt' and calls either encryptMessage() or
decryptMessage(). The return value of encryptMessage() and decryptMessage()

Chapter 17 – The Simple Substitution Cipher 241
(which is explained later) will be a string of the encrypted (or decrypted) message. This string
will be stored in the translated variable.
simpleSubCipher.py
20. print('Using key %s' % (myKey))
21. print('The %sed message is:' % (myMode))
22. print(translated)
23. pyperclip.copy(translated)
24. print()
25. print('This message has been copied to the clipboard.')
The key that was used is printed to the screen on line 20. The encrypted (or decrypted) message is
printed on the screen and also copied to the clipboard. Line 25 is the last line of code in the
main() function, so the program execution returns after line 25. Since the main() call is done
at the last line of the program, the program will then exit.
The sort() List Method
simpleSubCipher.py
28. def checkValidKey(key):
29. keyList = list(key)
30. lettersList = list(LETTERS)
31. keyList.sort()
32. lettersList.sort()
A simple substitution key string value is only valid if it has each of the characters in the symbol
set with no duplicate or missing letters. We can check if a string value is a valid key by sorting it
and the symbol set into alphabetical order and checking if they are equal. (Although LETTERS is
already in alphabetical order, we still need to sort it since it could be expanded to contain other
characters.)
On line 29 the string in key is passed to list(). The list value returned is stored in a variable
named keyList. On line 30, the LETTERS constant variable (which, remember, is the string
'ABCDEFGHIJKLMNOPQRSTUVWXYZ') is passed to list() which returns the list ['A',
'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N',
'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z'].
The sort() list method will rearrange the order of items in the list into alphabetical order. The
lists in keyList and lettersList are then sorted in alphabetical order by calling the
sort() list method on them. Note that just like the append() list method, the sort() list
method modifies the list in place and does not have a return value. You want your code to look
like this:

242 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
keyList.sort()
...and not look like this:
keyList = keyList.sort()
simpleSubCipher.py
33. if keyList != lettersList:
34. sys.exit('There is an error in the key or symbol set.')
Once sorted, the keyList and lettersList values should be the same, since keyList was
just the characters in LETTERS with the order scrambled. If keyList and lettersList are
equal, we also know that keyList (and, therefore, the key parameter) does not have any
duplicates in it, since LETTERS does not have any duplicates in it.
However, if the condition on line 33 is True, then the value in myKey was set to an invalid
value and the program will exit by calling sys.exit().
Wrapper Functions
simpleSubCipher.py
37. def encryptMessage(key, message):
38. return translateMessage(key, message, 'encrypt')
39.
40.
41. def decryptMessage(key, message):
42. return translateMessage(key, message, 'decrypt')
43.
44.
45. def translateMessage(key, message, mode):
The code for encrypting and the code for decrypting are almost exactly the same. It’s always a
good idea to put code into a function and call it twice rather than type out the code twice. First,
this saves you some typing. But second, if there’s ever a bug in the duplicate code, you only have
to fix the bug in one place instead of multiple places. It is (usually) much more reasonable to
replace duplicate code with a single function that has the code.
Wrapper functions simply wrap the code of another function, and return the value the wrapped
function returns. Often the wrapper function might make a slight change to the arguments or
return value of wrapped function (otherwise you would just call the wrapped function directly.) In
this case, encryptMessage() and decryptMessage() (the wrapper functions) calls

Chapter 17 – The Simple Substitution Cipher 243
translateMessage() (the wrapped function) and returns the value
translateMessage() returns.
On line 45 notice that translateMessage() has the parameters key and message, but also
a third parameter named mode. When it calls translateMessage(), the call in
encryptMessage() function passes 'encrypt' for the mode parameter, and the call in
decryptMessage() function passes 'decrypt'. This is how the
translateMessage() function knows whether it should encrypt or decrypt the message it is
passed.
With these wrapper functions, someone who imports the simpleSubCipher.py program can call
functions named encryptMessage() and decryptMessage() like they do with all the
other cipher programs in this book. They might create a program that encrypts with various
ciphers, like below:
import affineCipher, simpleSubCipher, transpositionCipher
...some other code here...
ciphertext1 = affineCipher.encryptMessage(encKey1, 'Hello!')
ciphertext2 = transpositionCipher.encryptMessage(encKey2, 'Hello!')
ciphertext3 = simpleSubCipher.encryptMessage(encKey3, 'Hello!')
The wrapper functions give the simple substitution cipher program function names that are
consistent with the other cipher programs. Consistent names are very helpful, because it makes it
easier for someone familiar with one of the cipher programs in this book to already be familiar
with the other cipher programs. (You can even see that the first parameter was always made the
key and the second parameter is always the message.) This is the reason we have these wrapper
functions, because making the programmer call the translateMessage() function would be
inconsistent with the other programs.
The Program’s translateMessage() Function
simpleSubCipher.py
45. def translateMessage(key, message, mode):
46. translated = ''
47. charsA = LETTERS
48. charsB = key
49. if mode == 'decrypt':
50. # For decrypting, we can use the same code as encrypting. We
51. # just need to swap where the key and LETTERS strings are used.
52. charsA, charsB = charsB, charsA
244 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The translateMessage() function does the encryption (or decryption, if the mode
parameter is set to the string 'decrypt'). The encryption process is very simple: for each letter
in the message parameter, we look up its index in LETTERS and replace it with the letter at that
same index in the key parameter. To decrypt we do the opposite: we look up the index in key
and replace it with the letter at the same index in the LETTERS.
The table below shows why using the same index will encrypt or decrypt the letter. The top row
shows the characters in charsA (which is set to LETTERS on line 47), the middle row shows
the characters in charsB (which is set to key on line 48), and the bottom row are the integer
indexes (for our own reference in this example).
A
B
C
D
E
F
G
H
I
J
K
L
M
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
V
J
Z
B
G
N
F
E
P
L
I
T
M
0
1
2
3
4
5
6
7
8
9
10
11
12
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
X
D
W
K
Q
U
C
R
Y
A
H
S
O
13
14
15
16
17
18
19
20
21
22
23
24
25
The code in translateMessage() will always look up the message character’s index in
charsA and replace it with the character at that index in charsB.
So to encrypt, we can just leave charsA and charsB as they are. This will replace the character
in LETTERS with the character in key, because charsA is set to LETTERS and charsB is set
to key.
When decrypting, the values in charsA and charsB (that is, LETTERS and key) are swapped
on line 52, so the table would look like this:
V
J
Z
B
G
N
F
E
P
L
I
T
M
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
A
B
C
D
E
F
G
H
I
J
K
L
M
0
1
2
3
4
5
6
7
8
9
10
11
12
X
D
W
K
Q
U
C
R
Y
A
H
S
O
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
↕
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
13
14
15
16
17
18
19
20
21
22
23
24
25

Chapter 17 – The Simple Substitution Cipher 245
Remember, our code in translateMessage() always replaces the character in charsA (the
top row) with the character at that same index in charsB (the middle row). So when lines 47 and
48 will swap the values in charsA and charsB, the code in translateMessage() will be
doing the decryption process instead of the encryption process.
simpleSubCipher.py
54. # loop through each symbol in the message
55. for symbol in message:
56. if symbol.upper() in charsA:
57. # encrypt/decrypt the symbol
58. symIndex = charsA.find(symbol.upper())
The for loop on line 55 will set the symbol variable to a character in the message string on
each iteration through the loop. If the uppercase form of this symbol exists in charsA
(remember that both the key and LETTERS only have uppercase characters in them), then we
will find the index of the uppercase form of symbol in charsA. This index will be stored in a
variable named symIndex.
We already know that the find() method will never return -1 (remember, a -1 from the
find() method means the argument could not be found the string) because the if statement on
line 56 guarantees that symbol.upper() will exist in charsA. Otherwise line 58 wouldn’t
have been executed in the first place.
The isupper() and islower() String Methods
The isupper() string method returns True if:
1. The string has at least one uppercase letter.
2. The string does not have any lowercase letters in it.
The islower() string method returns True if:
1. The string has at least one lowercase letter.
2. The string does not have any uppercase letters in it.
Non-letter characters in the string do not affect whether these methods return True or False.
Try typing the following into the interactive shell:
>>> 'HELLO'.isupper()
True

246 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
>>> 'HELLO WORLD 123'.isupper()
True
>>> 'hELLO'.isupper()
False
>>> 'hELLO'.islower()
False
>>> 'hello'.islower()
True
>>> '123'.isupper()
False
>>> ''.islower()
False
>>>
simpleSubCipher.py
59. if symbol.isupper():
60. translated += charsB[symIndex].upper()
61. else:
62. translated += charsB[symIndex].lower()
If symbol is an uppercase letter, than we want to concatenate the uppercase version of the
character at charsB[symIndex] to translated. Otherwise we will concatenate the
lowercase version of the character at charsB[symIndex] to translated.
If symbol was a number or punctuation mark like '5' or '?', then the condition on line 59
would be False (since those strings don’t have at least one uppercase letter in them) and line 62
would have been executed. In this case, line 62’s lower() method call would have no effect on
the string since it has no letters in it. Try typing the following into the interactive shell:
>>> '5'.lower()
'5'
>>> '?'.lower()
'?'
>>>
So line 62 in the else block takes care of translating any lowercase characters and non-letter
characters.
simpleSubCipher.py
63. else:
64. # symbol is not in LETTERS, just add it
65. translated += symbol
Chapter 17 – The Simple Substitution Cipher 247
By looking at the indentation, you can tell that the else statement on line 63 is paired with the
if statement on line 56. The code in the block that follows (that is, line 65) is executed if
symbol is not in LETTERS. This means that we cannot encrypt (or decrypt) the character in
symbol, so we will just concatenate it to the end of translated as is.
simpleSubCipher.py
67. return translated
At the end of the translateMessage() function we return the value in the translated
variable, which will contain the encrypted or decrypted message.
Practice Exercises, Chapter 17, Set B
Practice exercises can be found at http://invpy.com/hackingpractice17B.
Generating a Random Key
simpleSubCipher.py
70. def getRandomKey():
71. key = list(LETTERS)
72. random.shuffle(key)
73. return ''.join(key)
Typing up a string that contains each letter of the alphabet once and only once can be difficult. To
aid the user, the getRandomKey() function will return a valid key to use. Lines 71 to 73 do
this by randomly scrambling the characters in the LETTERS constant. See the “Randomly
Scrambling a String” section in Chapter 10 for an explanation of how to scramble a string using
list(), random.shuffle(), and join().
To use the getRandomKey() function, line 11 can be changed to this:
11. myKey = getRandomKey()
Remember that our cipher program will print out the key being used on line 20. This is how the
user can find out what key the getRandomKey() function returned.
simpleSubCipher.py
76. if __name__ == '__main__':
77. main()

248 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Lines 76 and 77 are at the bottom of the program, and call main() if simpleSubCipher.py is
being run as a program instead of imported as a module by another program.
Encrypting Spaces and Punctuation
The simple substitution cipher in this chapter only encrypts the letters in the plaintext. This
artificial limitation is here because the hacking program in the next chapter only works if the
letters alone have been substituted.
If you want the simple substitution program to encrypt more than just the letter characters, make
the following changes:
simpleSubCipher.py
7. LETTERS = r""" !"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXY
Z[\]^_`abcdefghijklmnopqrstuvwxyz{|}~"""
Line 7’s value stored in the LETTERS constant is changed to a string of all the characters Using a
triple-quotes raw string so you do not have to escape the quotes and \ slash character makes
typing this easier.
The key used must also have all of these characters, so line 11 changes to something like this:
simpleSubCipher.py
11. myKey = r"""/{9@6hUf:q?_)^eTi|W1,NLD7xk(-
SF>Iz0E=d;Bu#c]w~'VvHKmpJ+}s8y& XtP43.b[OA!*\Q<M%$ZgG52YloaRCn"`rj"""
The code that differentiates between upper and lowercase letters on lines 58 to 62 can be replaced
with these two lines:
simpleSubCipher.py
58. symIndex = charsA.find(symbol.upper())
59. if symbol.isupper():
60. translated += charsB[symIndex].upper()
61. else:
62. translated += charsB[symIndex].lower()
58. symIndex = charsA.find(symbol)
59. translated += charsB[symIndex]
Now when you run the simple substitution cipher program, the ciphertext looks much more like
random gibberish:

Chapter 17 – The Simple Substitution Cipher 249
Using key /{9@6hUf:q?_)^eTi|W1,NLD7xk(-SF>Iz0E=d;Bu#c]w~'VvHKmpJ+}s8y&
XtP43.b[OA!*\Q<M%$ZgG52YloaRCn"`rj
The encrypted message is:
#A/3/%3$/\2/ZAAO5O[/3/A3bY/a*\b*/!ZO2/3!3\$2Y/*\2/\$2Y\$bY2)/*O/a\MM/2b5lY\$\nO
/\Y/bMZ2OMC)/3$[/l$MO22/Y*O/Oo\[O$bO/\2/ZoO5a*OM%\$!)/*O/a\MM/5OAl2O/YZ/.OM\OoO
/\Ye/#A)/Z$/Y*O/ZY*O5/*3$[)/*O/\2/ZAAO5O[/2Z%OY*\$!/a*\b*/3AAZ5[2/3/5O32Z$/AZ5/
3bY\$!/\$/3bbZ5[3$bO/YZ/*\2/\$2Y\$bY2)/*O/a\MM/3bbOgY/\Y/OoO$/Z$/Y*O/2M\!*YO2Y/
Oo\[O$bOe/p*O/Z5\!\$/ZA/%CY*2/\2/ORgM3\$O[/\$/Y*\2/a3Ce/^0O5Y53$[/Kl22OMM
This message has been copied to the clipboard.
Practice Exercises, Chapter 17, Set C
Practice exercises can be found at http://invpy.com/hackingpractice17C.
Summary
In this chapter, we have learned about the new “set” data type. In many of our programs, lists are
much easier to use than sets, but sets are a simple way to get rid of duplicate values from lists or
strings.
The isupper() and islower() string methods can tell us if a string value is made up of only
uppercase or lowercase letters. And the sort() list method is very useful at putting the items in
a list in order.
The simple substitution cipher has far too many possible keys to brute-force through. This makes
it impervious to the techniques that our previous cipher hacking programs have used. We are
going to have to make smarter programs in order to break this code.
In the next chapter, we will learn how to hack the simple substitution cipher. Instead of brute-
forcing through all the keys, we will use a much more intelligent and sophisticated algorithm.

250 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
HACKING THE SIMPLE
SUBSTITUTION CIPHER
Topics Covered In This Chapter:
Word patterns, candidates, potential decryption letters, and cipherletter mappings.
The pprint.pprint() and pprint.pformat() functions
Building strings using the list-append-join process
Regular expressions
The sub() regex method
“Cypherpunks deplore regulations on cryptography,
for encryption is fundamentally a private act. The
act of encryption, in fact, removes information from
the public realm. Even laws against cryptography
reach only so far as a nation’s border and the arm of
its violence.”
Eric Hughes, “A Cypherpunk’s Manifesto”, 1993
http://invpy.com/cypherpunk

Chapter 18 – Hacking the Simple Substitution Cipher 251
Computing Word Patterns
There are too many possible keys to brute-force a simple substitution cipher-encrypted message.
We need to employ a more intelligent attack if we want to crack a substitution ciphertext. Let’s
examine one possible word from an example ciphertext:
HGHHU
Think about what we can learn from this one word of ciphertext (which we will call a
cipherword in this book). We can tell that whatever the original plaintext word is, it must:
1. Be five letters long.
2. Have the first, third, and fourth letters be the same.
3. Have exactly three different letters in the word, where the first, second, and fifth letters in
the word are all different from each other.
What words in the English language fit this pattern? “Puppy” is one word that fits this pattern. It
is five letters long (P, U, P, P, Y) using three different letters (P, U, Y) in that same pattern (P for
the first, third, and fourth letter and U for the second letter and Y for the fifth letter). “Mommy”,
“Bobby”, “lulls”, “nanny”, and “lilly” fit the pattern too. (“Lilly” is a name, not to be confused
with “Lily” the flower. But since “Lilly” can appear in an Engish message it is a possible word
that fits the pattern.) If we had a lot of time on our hands, we could go through an entire
dictionary and find all the words that fit this pattern. Even better, we could have a computer go
through a dictionary file for us.
In this book a word pattern will be a set of numbers with periods in between the numbers that
tells us the pattern of letters for a word, in either ciphertext or plaintext.
Creating word patterns for cipherwords is easy: the first letter gets the number 0 and the first
occurrence of each different letter after that gets the next number. For example:
The word pattern for “cat” is 0.1.2.
The word pattern for “catty” is 0.1.2.2.3.
The word pattern for “roofer” is 0.1.1.2.3.0.
The word pattern for “blimp” is 0.1.2.3.4.
The word pattern for “classification” is 0.1.2.3.3.4.5.4.0.2.6.4.7.8.
A plaintext word and its cipherword will always have the same word pattern, no matter
which simple substitution key was used to do the encryption.

252 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Getting a List of Candidates for a Cipherword
To take a guess at what HGHHU could decrypt to, we can go through the dictionary file and find
all of the words that also have a word pattern of 0.1.0.0.2. In this book, we will call these
plaintext words (that have the same word pattern as the cipherword) the candidates for that
cipherword:
Ciphertext word:
H G H H U
Word pattern:
0.1.0.0.2
Candidates:
p u p p y
m o m m y
b o b b y
l u l l s
n a n n y
l i l l y
So if we look at the letters in the cipherword (which will be called cipherletters in this book),
we can guess which letters they may decrypt to (we will call these letters the cipherletter’s
potential decryption letters in this book):
Cipherletters:
H
G
U
Potential decryption letters:
p
u
y
m
o
y
b
o
y
l
u
s
n
a
y
l
i
y
From this table we can create a cipherletter mapping:
The cipher letter H has the potential decryption letters P, M, B, L, and N
The cipher letter G has the potential decryption letters U, O, A, and I
The cipher letter U has the potential decryption letters Y and S
All of the other cipher letters besides H, G, and U will have no potential decryption letters.
When we represent a cipherletter mapping in Python code, we will use a dictionary value:

Chapter 18 – Hacking the Simple Substitution Cipher 253
{'A': [], 'B': [], 'C': [], 'D': [], 'E': [], 'F': [], 'G': ['U', 'O', 'A',
'I'], 'H': ['P', 'B', 'L', 'N'], 'I': [], 'J': [], 'K': [], 'L': [], 'M': [],
'N': [], 'O': [], 'P': [], 'Q': [], 'R': [], 'S': [], 'T': [], 'U': ['Y', 'S'],
'V': [], 'W': [], 'X': [], 'Y': [], 'Z': []}
In our program, a cipherletter mapping dictionary will have 26 keys, one for each letter. The
mapping above has potential decryption letters for 'H', 'G', and 'U' above. The other keys
have no potential decryption letters, which is why they have empty lists for values.
If we reduce the number of potential decryption letters for a cipherletter to just one letter, then we
have solved what that cipherletter decrypts to. Even if we do not solve all 26 cipherletters, we
might be able to hack most of the ciphertext’s cipherletters.
But first we must find the pattern for every word in the dictionary file and sort them in a list so it
will be easy to get a list of all the candidates for a given cipherword’s word pattern. We can use
the same dictionary file from Chapter 12, which you can download from
http://invpy.com/dictionary.txt.
(Note that the terms “word pattern”, “candidate”, and “cipherletter mapping” are terms I came up
with to describe things in this particular hacking program. These are not general cryptography
terms.)
Practice Exercises, Chapter 18, Set A
Practice exercises can be found at http://invpy.com/hackingpractice18A.
Source Code of the Word Pattern Module
Since the word patterns for words never change, we can just calculate the word pattern for every
word in a dictionary file once and store them in another file. Our makeWordPatterns.py program
creates a file named wordPatterns.py that will contain a dictionary value with the word pattern for
every word in the dictionary file. Our hacking program can then just import wordPatterns to
look up the candidates for a certain word pattern.
Source code for makeWordPatterns.py
1. # Makes the wordPatterns.py File
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. # Creates wordPatterns.py based on the words in our dictionary
5. # text file, dictionary.txt. (Download this file from
6. # http://invpy.com/dictionary.txt)
7.
8. import pprint

254 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
9.
10.
11. def getWordPattern(word):
12. # Returns a string of the pattern form of the given word.
13. # e.g. '0.1.2.3.4.1.2.3.5.6' for 'DUSTBUSTER'
14. word = word.upper()
15. nextNum = 0
16. letterNums = {}
17. wordPattern = []
18.
19. for letter in word:
20. if letter not in letterNums:
21. letterNums[letter] = str(nextNum)
22. nextNum += 1
23. wordPattern.append(letterNums[letter])
24. return '.'.join(wordPattern)
25.
26.
27. def main():
28. allPatterns = {}
29.
30. fo = open('dictionary.txt')
31. wordList = fo.read().split('\n')
32. fo.close()
33.
34. for word in wordList:
35. # Get the pattern for each string in wordList.
36. pattern = getWordPattern(word)
37.
38. if pattern not in allPatterns:
39. allPatterns[pattern] = [word]
40. else:
41. allPatterns[pattern].append(word)
42.
43. # This is code that writes code. The wordPatterns.py file contains
44. # one very, very large assignment statement.
45. fo = open('wordPatterns.py', 'w')
46. fo.write('allPatterns = ')
47. fo.write(pprint.pformat(allPatterns))
48. fo.close()
49.
50.
51. if __name__ == '__main__':
52. main()

Chapter 18 – Hacking the Simple Substitution Cipher 255
Sample Run of the Word Pattern Module
Running this program doesn’t print anything out to the screen. Instead it silently creates a file
named wordPatterns.py in the same folder as makeWordPatterns.py. Open this file in IDLE’s file
editor, and you will see it looks like this:
allPatterns = {'0.0.1': ['EEL'],
'0.0.1.2': ['EELS', 'OOZE'],
'0.0.1.2.0': ['EERIE'],
'0.0.1.2.3': ['AARON', 'LLOYD', 'OOZED'],
...the rest has been cut for brevity...
The makeWordPatterns.py program creates wordPatterns.py. Our Python program creates a
Python program! The entire wordPatterns.py program is just one (very big) assignment statement
for a variable named allPatterns. Even though this assignment statement stretches over
many lines in the file, it is considered one “line of code” because Python knows that if a line ends
with a comma but it is currently in the middle of a dictionary value, it ignores the indentation of
the next line and just considers it part of the previous line. (This is a rare exception for Python’s
significant indentation rules.)
The allPatterns variable contains a dictionary value where the keys are all the word patterns
made from the English words in the dictionary file. The keys’ values are lists of strings of English
words with that pattern. When wordPatterns.py is imported as a module, our program will be able
to look up all the English words for any given word pattern.
After running the makeWordPatterns.py program to create the wordPatterns.py file, try typing the
following into the interactive shell:
>>> import wordPatterns
>>> wordPatterns.allPatterns['0.1.2.1.1.3.4']
['BAZAARS', 'BESEECH', 'REDEEMS', 'STUTTER']
>>>
>>> wordPatterns.allPatterns['0.1.2.2.3.2.4.1.5.5']
['CANNONBALL']
>>>
>>> wordPatterns.allPatterns['0.1.0.1.0.1']
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
KeyError: '0.1.0.1.0.1'
>>>
>>> '0.1.0.1.0.1' in wordPatterns.allPatterns
False
>>>
256 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The pattern '0.1.0.1.0.1' does not exist in the dictionary. This is why the expression
wordPatterns.allPatterns['0.1.0.1.0.1'] causes an error (because there is no
'0.1.0.1.0.1' key in allPatterns) and why '0.1.0.1.0.1' in
wordPatterns.allPatterns evaluates to False.
How the Program Works
makeWordPatterns.py
1. # Makes the wordPatterns.py File
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. # Creates wordPatterns.py based on the words in our dictionary
5. # text file, dictionary.txt. (Download this file from
6. # http://invpy.com/dictionary.txt)
The top part of this file has the usual comments describing what the program is.
The pprint.pprint() and pprint.pformat() Functions
makeWordPatterns.py
8. import pprint
The pprint module has functions for pretty printing values, which is useful for printing
dictionary and list values on the screen. The print() function simply prints these values going
left to right:
>>> print(someListOfListsVar))
[['ant'], ['baboon', 'badger', 'bat', 'bear', 'beaver'], ['camel', 'cat',
'clam', 'cobra', 'cougar', 'coyote', 'crow'], ['deer', 'dog', 'donkey',
'duck'], ['eagle'], ['ferret', 'fox', 'frog'], ['goat']]
The pprint module has a function named pprint(). The value passed to
pprint.pprint() will be “pretty printed” to the screen so that it is easier to read:
>>> import pprint
>>> pprint.pprint(someListOfListsVar))
[['ant'],
['baboon', 'badger', 'bat', 'bear', 'beaver'],
['camel', 'cat', 'clam', 'cobra', 'cougar', 'coyote', 'crow'],
['deer', 'dog', 'donkey', 'duck'],
['eagle'],
['ferret', 'fox', 'frog'],
['goat']]

Chapter 18 – Hacking the Simple Substitution Cipher 257
However, if you want to have this “prettified” text as a string value instead of displaying it on the
screen, you can use the pprint.pformat() function, which returns the prettified string:
>>> import pprint
>>> prettifiedString = pprint.pformat(someListOfListsVar)
>>> print(prettifiedString)
[['ant'],
['baboon', 'badger', 'bat', 'bear', 'beaver'],
['camel', 'cat', 'clam', 'cobra', 'cougar', 'coyote', 'crow'],
['deer', 'dog', 'donkey', 'duck'],
['eagle'],
['ferret', 'fox', 'frog'],
['goat']]
>>>
When we write the value of allPatterns to the wordPatterns.py file, we will use the
pprint module to prevent it from being printed crammed together all on one line.
Building Strings in Python with Lists
Almost all of our programs have done some form of “building a string” code. That is, a variable
will start as a blank string and then new characters are added with string concatenation. (We’ve
done this in many previous cipher programs with the translated variable.) This is usually
done with the + operator to do string concatenation, as in the following short program:
# The slow way to build a string using string concatenation.
building = ''
for c in 'Hello world!':
building += c
print(building)
The above program loops through each character in the string 'Hello world!' and
concatenates it to the end of the string stored in building. At the end of the loop, building
holds the complete string.
This seems like a straightforward way to do this. However, it is very inefficient for Python to
concatenate strings. The reasons are technical and beyond the scope of this book, but it is much
faster to start with a blank list instead of a blank string, and then use the append() list
method instead of string concatenation. After you are done building the list of strings, you can
convert the list of strings to a single string value with the join() method. The following short
program does exactly the same thing as the previous example, but faster:
258 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
# The fast way to build a string using a list, append(), and join().
building = []
for c in 'Hello world!':
building.append(c)
building = ''.join(building)
print(building)
Using this approach for building up strings in your code will result in much faster programs. We
will be using this list-append-join process to build strings in the remaining programs of this book.
Calculating the Word Pattern
makeWordPatterns.py
11. def getWordPattern(word):
12. # Returns a string of the pattern form of the given word.
13. # e.g. '0.1.2.3.4.1.2.3.5.6' for 'DUSTBUSTER'
14. word = word.upper()
15. nextNum = 0
16. letterNums = {}
17. wordPattern = []
The getWordPattern() function takes one string argument and returns a string of that
word’s pattern. For example, if getWordPattern() were passed the string 'Buffoon' as
an argument then getWordPattern() would return the string '0.1.2.2.3.3.4'.
First, in order to make sure all the letters have the same case, line 14 changes the word parameter
to an uppercase version of itself. We then need three variables:
nextNum stores the next number used when a new letter is found.
letterNums stores a dictionary with keys of single-letter strings of single letters, and
values of the integer number for that letter. As we find new letters in the word, the letter and
its number are stored in letterNums.
wordPattern will be the string that is returned from this function. But we will be building
this string one character at a time, so we will use the list-append-join process to do this. This
is why wordPattern starts as a blank list instead of a blank string.
makeWordPatterns.py
19. for letter in word:
20. if letter not in letterNums:
21. letterNums[letter] = str(nextNum)
22. nextNum += 1

Chapter 18 – Hacking the Simple Substitution Cipher 259
Line 19’s for loop will loop through each character in the word parameter, assigning each
character to a variable named letter.
Line 20 checks if letter has not been seen before by checking that letter does not exist as a
key in the letterNums dictionary. (On the first iteration of the loop, the condition on line 20
will always be True because letterNums will be a blank dictionary that doesn’t have
anything in it.)
If we have not seen this letter before, line 21 adds this letter as the key and the string form of
nextNum as the key’s value to the letterNums dictionary. For the next new letter we find we
want to use the next integer after the one currently in nextNum anymore, so line 22 increments
the integer in nextNum by 1.
makeWordPatterns.py
23. wordPattern.append(letterNums[letter])
On line 23, letterNums[letter] evaluates to the integer used for the letter in the letter
variable, so this is appended to the end of wordPattern. The letterNums dictionary is
guaranteed to have letter for a key, because if it hadn’t, then lines 20 to 22 would have
handled adding it to letterNums before line 23.
makeWordPatterns.py
24. return '.'.join(wordPattern)
After the for loop on line 19 is finished looping, the wordPattern list will contain all the
strings of the complete word pattern. Our word patterns have periods separating the integers, so
that we could tell the difference between “1.12” and “11.2”. To put these periods in between each
of the strings in the wordPattern list, line 24 calls the join() method on the string '.'.
This will evaluate to a string such as '0.1.2.2.3.3.4'. The completely-built string that
join() returns will be the return value of getWordPattern().
The Word Pattern Program’s main() Function
makeWordPatterns.py
27. def main():
28. allPatterns = {}
The value stored in allPatterns is what we will write to the wordPatterns.py file. It is a
dictionary whose keys are strings of word patterns (such as '0.1.2.3.0.4.5' or

260 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
'0.1.1.2') and the keys’ values are a list of strings of English words that match that pattern.
For example, here’s one of the key-value pairs that will end up in allPatterns:
'0.1.0.2.3.1.4': ['DEDUCER', 'DEDUCES', 'GIGABIT', 'RARITAN']
But at the beginning of the main() function on line 28, the allPatterns variable will start
off as a blank dictionary value.
makeWordPatterns.py
30. fo = open('dictionary.txt')
31. wordList = fo.read().split('\n')
32. fo.close()
Lines 30 to 32 read in the contents of the dictionary file into wordList. Chapter 11 covered
these file-related functions in more detail. Line 30 opens the dictionary.txt file in “reading” mode
and returns a file object. Line 31 calls the file object’s read() method which returns a string of
all text from this file. The rest of line 31 splits it up whenever there is a \n newline character, and
returns a list of strings: one string per line in the file. This list value returned from split() is
stored in the wordList variable. At this point we are done reading the file, so line 34 calls the
file object’s close() method.
The wordList variable will contain a list of tens of thousands of strings. Since the
dictionary.txt file has one English word per line of text, each string in the wordList variable
will be one English word.
makeWordPatterns.py
34. for word in wordList:
35. # Get the pattern for each string in wordList.
36. pattern = getWordPattern(word)
The for loop on line 34 will iterate over each string in the wordList list and store it in the
word variable. The word variable is passed to the getWordPattern() function, which
returns a word pattern string for the string in word. The word pattern string is stored in a variable
named pattern.
makeWordPatterns.py
38. if pattern not in allPatterns:
39. allPatterns[pattern] = [word]
40. else:
41. allPatterns[pattern].append(word)

Chapter 18 – Hacking the Simple Substitution Cipher 261
There must be a value for the pattern key first before we can append word to
allPatterns[pattern], otherwise this would cause an error. So, first line 38 will check if
the pattern is not already in allPatterns. If pattern is not a key in allPatterns yet,
line 39 creates a list with word in it to store in allPatterns[pattern].
If the pattern already is in allPatterns, we do not have to create the list. Line 41 will just
append the word to the list value that is already there.
By the time the for loop that started on line 34 finishes, the allPatterns dictionary will
contain the word pattern of each English word that was in wordList as its keys. Each of these
keys has a value that is a list of the words that produce the word pattern. With our data organized
this way, given a word pattern we can easily look up all the English words that produce that
particular pattern.
makeWordPatterns.py
43. # This is code that writes code. The wordPatterns.py file contains
44. # one very, very large assignment statement.
45. fo = open('wordPatterns.py', 'w')
46. fo.write('allPatterns = ')
47. fo.write(pprint.pformat(allPatterns))
48. fo.close()
Now that we have this very large dictionary in allPatterns, we want to save it to a file on the
hard drive. The last part of the main() function will create a file called wordPatterns.py which
will just have one huge assignment statement in it.
Line 45 creates a new file by passing the 'wordPatterns.py' string for the filename and
'w' to indicate that this file will be opened in “write” mode. If there is already a file with the
name 'wordPatterns.py', opening it in write mode will cause the file to be deleted to make
way for the new file we are creating.
Line 46 starts the file off with 'allPatterns = ', which is the first part of the assignment
statement. Line 47 finishes it by writing a prettified version of allPatterns to the file. Line
48 closes the file since we are done writing to it.
makeWordPatterns.py
51. if __name__ == '__main__':
52. main()

262 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Lines 51 and 52 call the main() function if this program was run by itself (to create the
wordPattern.py file) rather than imported by another program that wants to use its
getWordPattern() function.
Hacking the Simple Substitution Cipher
The hacking program uses the abstract concepts of “word patterns” and “cipherletter mappings”.
But don’t worry, in our Python program “word patterns” are represented by string values and
“cipherletter mappings” are represented with dictionary values. The previous sections explained
what word patterns are and how to generate them from a string. Cipherletter mappings are used in
the hacking program to keep track of the possible letters that each of the 26 cipherletters could
decrypt to. Go ahead and type in the source code for the simpleSubHacker.py program.
Source Code of the Simple Substitution Hacking Program
Source code for simpleSubHacker.py
1. # Simple Substitution Cipher Hacker
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import os, re, copy, pprint, pyperclip, simpleSubCipher, makeWordPatterns
5.
6. if not os.path.exists('wordPatterns.py'):
7. makeWordPatterns.main() # create the wordPatterns.py file
8. import wordPatterns
9.
10. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
11. nonLettersOrSpacePattern = re.compile('[^A-Z\s]')
12.
13. def main():
14. message = 'Sy l nlx sr pyyacao l ylwj eiswi upar lulsxrj isr
sxrjsxwjr, ia esmm rwctjsxsza sj wmpramh, lxo txmarr jia aqsoaxwa sr
pqaceiamnsxu, ia esmm caytra jp famsaqa sj. Sy, px jia pjiac ilxo, ia sr
pyyacao rpnajisxu eiswi lyypcor l calrpx ypc lwjsxu sx lwwpcolxwa jp isr
sxrjsxwjr, ia esmm lwwabj sj aqax px jia rmsuijarj aqsoaxwa. Jia pcsusx py
nhjir sr agbmlsxao sx jisr elh. -Facjclxo Ctrramm'
15.
16. # Determine the possible valid ciphertext translations.
17. print('Hacking...')
18. letterMapping = hackSimpleSub(message)
19.
20. # Display the results to the user.
21. print('Mapping:')
22. pprint.pprint(letterMapping)
23. print()
24. print('Original ciphertext:')

Chapter 18 – Hacking the Simple Substitution Cipher 263
25. print(message)
26. print()
27. print('Copying hacked message to clipboard:')
28. hackedMessage = decryptWithCipherletterMapping(message, letterMapping)
29. pyperclip.copy(hackedMessage)
30. print(hackedMessage)
31.
32.
33. def getBlankCipherletterMapping():
34. # Returns a dictionary value that is a blank cipherletter mapping.
35. return {'A': [], 'B': [], 'C': [], 'D': [], 'E': [], 'F': [], 'G': [],
'H': [], 'I': [], 'J': [], 'K': [], 'L': [], 'M': [], 'N': [], 'O': [], 'P':
[], 'Q': [], 'R': [], 'S': [], 'T': [], 'U': [], 'V': [], 'W': [], 'X': [],
'Y': [], 'Z': []}
36.
37.
38. def addLettersToMapping(letterMapping, cipherword, candidate):
39. # The letterMapping parameter is a "cipherletter mapping" dictionary
40. # value that the return value of this function starts as a copy of.
41. # The cipherword parameter is a string value of the ciphertext word.
42. # The candidate parameter is a possible English word that the
43. # cipherword could decrypt to.
44.
45. # This function adds the letters of the candidate as potential
46. # decryption letters for the cipherletters in the cipherletter
47. # mapping.
48.
49. letterMapping = copy.deepcopy(letterMapping)
50. for i in range(len(cipherword)):
51. if candidate[i] not in letterMapping[cipherword[i]]:
52. letterMapping[cipherword[i]].append(candidate[i])
53. return letterMapping
54.
55.
56. def intersectMappings(mapA, mapB):
57. # To intersect two maps, create a blank map, and then add only the
58. # potential decryption letters if they exist in BOTH maps.
59. intersectedMapping = getBlankCipherletterMapping()
60. for letter in LETTERS:
61.
62. # An empty list means "any letter is possible". In this case just
63. # copy the other map entirely.
64. if mapA[letter] == []:
65. intersectedMapping[letter] = copy.deepcopy(mapB[letter])
66. elif mapB[letter] == []:
67. intersectedMapping[letter] = copy.deepcopy(mapA[letter])

264 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
68. else:
69. # If a letter in mapA[letter] exists in mapB[letter], add
70. # that letter to intersectedMapping[letter].
71. for mappedLetter in mapA[letter]:
72. if mappedLetter in mapB[letter]:
73. intersectedMapping[letter].append(mappedLetter)
74.
75. return intersectedMapping
76.
77.
78. def removeSolvedLettersFromMapping(letterMapping):
79. # Cipher letters in the mapping that map to only one letter are
80. # "solved" and can be removed from the other letters.
81. # For example, if 'A' maps to potential letters ['M', 'N'], and 'B'
82. # maps to ['N'], then we know that 'B' must map to 'N', so we can
83. # remove 'N' from the list of what 'A' could map to. So 'A' then maps
84. # to ['M']. Note that now that 'A' maps to only one letter, we can
85. # remove 'M' from the list of letters for every other
86. # letter. (This is why there is a loop that keeps reducing the map.)
87. letterMapping = copy.deepcopy(letterMapping)
88. loopAgain = True
89. while loopAgain:
90. # First assume that we will not loop again:
91. loopAgain = False
92.
93. # solvedLetters will be a list of uppercase letters that have one
94. # and only one possible mapping in letterMapping
95. solvedLetters = []
96. for cipherletter in LETTERS:
97. if len(letterMapping[cipherletter]) == 1:
98. solvedLetters.append(letterMapping[cipherletter][0])
99.
100. # If a letter is solved, than it cannot possibly be a potential
101. # decryption letter for a different ciphertext letter, so we
102. # should remove it from those other lists.
103. for cipherletter in LETTERS:
104. for s in solvedLetters:
105. if len(letterMapping[cipherletter]) != 1 and s in
letterMapping[cipherletter]:
106. letterMapping[cipherletter].remove(s)
107. if len(letterMapping[cipherletter]) == 1:
108. # A new letter is now solved, so loop again.
109. loopAgain = True
110. return letterMapping
111.
112.

Chapter 18 – Hacking the Simple Substitution Cipher 265
113. def hackSimpleSub(message):
114. intersectedMap = getBlankCipherletterMapping()
115. cipherwordList = nonLettersOrSpacePattern.sub('',
message.upper()).split()
116. for cipherword in cipherwordList:
117. # Get a new cipherletter mapping for each ciphertext word.
118. newMap = getBlankCipherletterMapping()
119.
120. wordPattern = makeWordPatterns.getWordPattern(cipherword)
121. if wordPattern not in wordPatterns.allPatterns:
122. continue # This word was not in our dictionary, so continue.
123.
124. # Add the letters of each candidate to the mapping.
125. for candidate in wordPatterns.allPatterns[wordPattern]:
126. newMap = addLettersToMapping(newMap, cipherword, candidate)
127.
128. # Intersect the new mapping with the existing intersected mapping.
129. intersectedMap = intersectMappings(intersectedMap, newMap)
130.
131. # Remove any solved letters from the other lists.
132. return removeSolvedLettersFromMapping(intersectedMap)
133.
134.
135. def decryptWithCipherletterMapping(ciphertext, letterMapping):
136. # Return a string of the ciphertext decrypted with the letter mapping,
137. # with any ambiguous decrypted letters replaced with an _ underscore.
138.
139. # First create a simple sub key from the letterMapping mapping.
140. key = ['x'] * len(LETTERS)
141. for cipherletter in LETTERS:
142. if len(letterMapping[cipherletter]) == 1:
143. # If there's only one letter, add it to the key.
144. keyIndex = LETTERS.find(letterMapping[cipherletter][0])
145. key[keyIndex] = cipherletter
146. else:
147. ciphertext = ciphertext.replace(cipherletter.lower(), '_')
148. ciphertext = ciphertext.replace(cipherletter.upper(), '_')
149. key = ''.join(key)
150.
151. # With the key we've created, decrypt the ciphertext.
152. return simpleSubCipher.decryptMessage(key, ciphertext)
153.
154.
155. if __name__ == '__main__':
156. main()

266 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Hacking the Simple Substitution Cipher (in Theory)
Hacking the simple substitution cipher is pretty easy. The five steps are:
1. Find the word pattern for each cipherword in the ciphertext.
2. Find the list of English word candidates that each cipherword could decrypt to.
3. Create one cipherletter mapping for each cipherword using the cipherword’s list of
candidates. (A cipherletter mapping is just a dictionary value.)
4. Intersect each of the cipherletter mappings into a single intersected cipherletter mapping.
5. Remove any solved letters from the intersected cipherletter mapping.
The more cipher words that are in the ciphertext, the more cipherletter mappings we have that can
be intersected. The more cipherletter mappings we intersect together, the fewer the number of
potential decryption letters there will be for each cipher letter. This means that the longer the
ciphertext message, the more likely we are to hack and decrypt it.
Explore the Hacking Functions with the Interactive Shell
We’ve already described the steps used to hack a simple substitution encrypted message by using
word patterns. Before we learn how the code in these functions works, let’s use the interactive
shell to call them and see what values they return depending on what arguments we pass them.
Here is the example we will hack: OLQIHXIRCKGNZ PLQRZKBZB MPBKSSIPLC
The getBlankCipherletterMapping() function returns a cipherletter mapping. A
cipherletter mapping is just a dictionary with 26 keys of uppercase single-letter strings and
values of lists of single-letter uppercase strings like 'A' or 'Q'. We will store this blank
cipherletter mapping in a variable named letterMapping1. Try typing the following into the
interactive shell:
>>> letterMapping1 = simpleSubHacker.getBlankCipherletterMapping()
>>> letterMapping1
{'A': [], 'C': [], 'B': [], 'E': [], 'D': [], 'G': [], 'F': [], 'I': [], 'H':
[], 'K': [], 'J': [], 'M': [], 'L': [], 'O': [], 'N': [], 'Q': [], 'P': [],
'S': [], 'R': [], 'U': [], 'T': [], 'W': [], 'V': [], 'Y': [], 'X': [], 'Z':
[]}
>>>
Let’s start hacking the first cipherword, OLQIHXIRCKGNZ. First we will need to get the word
pattern for this cipherword by calling the makeWordPattern module’s
getWordPattern() function. Try typing the following into the interactive shell:
>>> import makeWordPatterns
Chapter 18 – Hacking the Simple Substitution Cipher 267
>>> wordPat = makeWordPatterns.getWordPattern('OLQIHXIRCKGNZ')
>>> wordPat
0.1.2.3.4.5.3.6.7.8.9.10.11
>>>
To figure out which English words in the dictionary have the word pattern
0.1.2.3.4.5.3.6.7.8.9.10.11 (that is, to figure out the candidates for the cipherword
OLQIHXIRCKGNZ) we will import the wordPatterns module and look up this pattern. Try
typing the following into the interactive shell:
>>> import wordPatterns
>>> candidates = wordPatterns.allPatterns['0.1.2.3.4.5.3.6.7.8.9.10.11']
>>> candidates
['UNCOMFORTABLE', 'UNCOMFORTABLY']
>>>
There are two English words that OLQIHXIRCKGNZ could decrypt to (that is, only two English
words that have the same word pattern that OLQIHXIRCKGNZ does): UNCOMFORTABLE and
UNCOMFORTABLY. (It’s also possible that the cipherword decrypts to a word that does not
exist in our dictionary, but we will just have to assume that’s not the case.) We need to create a
cipherletter mapping that has the cipherletters in OLQIHXIRCKGNZ map to letters in
UNCOMFORTABLE and UNCOMFORTABLY as potential decryption letters. That is, O maps
to U, L maps to N, Q maps to C, and so on. Z will map to two different letters: E and Y.
We can do this with the addLettersToMapping() function. We will need to pass it our
(currently blank) cipherletter mapping in letterMapping1, the string 'OLQIHXIRCKGNZ',
and the string 'UNCOMFORTABLE' (which is the first string in the candidates list). Try
typing the following into the interactive shell:
>>> letterMapping1 = simpleSubHacker.addLettersToMapping(letterMapping1,
'OLQIHXIRCKGNZ', candidates[0])
>>> letterMapping1
{'A': [], 'C': ['T'], 'B': [], 'E': [], 'D': [], 'G': ['B'], 'F': [], 'I':
['O'], 'H': ['M'], 'K': ['A'], 'J': [], 'M': [], 'L': ['N'], 'O': ['U'], 'N':
['L'], 'Q': ['C'], 'P': [], 'S': [], 'R': ['R'], 'U': [], 'T': [], 'W': [],
'V': [], 'Y': [], 'X': ['F'], 'Z': ['E']}
>>>
From the letterMapping1 value, you can see that the letters in OLQIHXIRCKGNZ map to
the letters in UNCOMFORTABLE: 'O' maps to ['U'], 'L' maps to ['N'], 'Q' maps to
['C'], and so on.
268 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
But since the letters in OLQIHXIRCKGNZ could also possibly decrypt to UNCOMFORTABLY,
we also need to add UNCOMFORTABLY to the cipherletter mapping. Try typing the following
into the interactive shell:
>>> letterMapping1 = simpleSubHacker.addLettersToMapping(letterMapping1,
'OLQIHXIRCKGNZ', candidates[1])
>>> letterMapping1
{'A': [], 'C': ['T'], 'B': [], 'E': [], 'D': [], 'G': ['B'], 'F': [], 'I':
['O'], 'H': ['M'], 'K': ['A'], 'J': [], 'M': [], 'L': ['N'], 'O': ['U'], 'N':
['L'], 'Q': ['C'], 'P': [], 'S': [], 'R': ['R'], 'U': [], 'T': [], 'W': [],
'V': [], 'Y': [], 'X': ['F'], 'Z': ['E', 'Y']}
>>>
You’ll notice that not much has changed in letterMapping1. The cipherletter mapping in
letterMapping1 now has 'Z' map to both 'E' and 'Y'. That’s because the candidates for
OLQIHXIRCKGNZ (that is, UNCOMFORTABLE and UNCOMFORTABLY) are very similar
to each other and addLettersToMapping() only adds the letter to the list if the letter is not
already there. This is why 'O' maps to ['U'] instead of ['U', 'U'].
We now have a cipherletter mapping for the first of the three cipherwords. We need to get a new
mapping for the second cipherword, PLQRZKBZB. Call
getBlankCipherletterMapping() and store the returned dictionary value in a variable
named letterMapping2. Get the word pattern for PLQRZKBZB and use it to look up all the
candidates in wordPatterns.allPatterns. This is done by typing the following into the
interactive shell:
>>> letterMapping2 = simpleSubHacker.getBlankCipherletterMapping()
>>> wordPat = makeWordPatterns.getWordPattern('PLQRZKBZB')
>>> candidates = wordPatterns.allPatterns[wordPat]
>>> candidates
['CONVERSES', 'INCREASES', 'PORTENDED', 'UNIVERSES']
>>>
Instead of typing out four calls to addLettersToMapping() for each of these four candidate
words, we can write a for loop that will go through the list in candidates and call
addLettersToMapping() each time.
>>> for candidate in candidates:
... letterMapping2 = simpleSubHacker.addLettersToMapping(letterMapping2,
'PLQRZKBZB', candidate)
...
>>> letterMapping2
Chapter 18 – Hacking the Simple Substitution Cipher 269
{'A': [], 'C': [], 'B': ['S', 'D'], 'E': [], 'D': [], 'G': [], 'F': [], 'I':
[], 'H': [], 'K': ['R', 'A', 'N'], 'J': [], 'M': [], 'L': ['O', 'N'], 'O': [],
'N': [], 'Q': ['N', 'C', 'R', 'I'], 'P': ['C', 'I', 'P', 'U'], 'S': [], 'R':
['V', 'R', 'T'], 'U': [], 'T': [], 'W': [], 'V': [], 'Y': [], 'X': [], 'Z':
['E']}
>>>
This finishes the cipherletter mapping for our second cipherword. Now we need to get the
intersection of the cipherletter mappings in letterMapping1 and letterMapping2 by
passing them to intersectMappings(). Try typing the following into the interactive shell:
>>> intersectedMapping = simpleSubHacker.intersectMappings(letterMapping1,
letterMapping2)
>>> intersectedMapping
{'A': [], 'C': ['T'], 'B': ['S', 'D'], 'E': [], 'D': [], 'G': ['B'], 'F': [],
'I': ['O'], 'H': ['M'], 'K': ['A'], 'J': [], 'M': [], 'L': ['N'], 'O': ['U'],
'N': ['L'], 'Q': ['C'], 'P': ['C', 'I', 'P', 'U'], 'S': [], 'R': ['R'], 'U':
[], 'T': [], 'W': [], 'V': [], 'Y': [], 'X': ['F'], 'Z': ['E']}
>>>
The intersected mapping is just a cipherletter mapping. The list of potential decryption letters for
any cipherletter in the intersected mapping will only be the potential decryption letters that were
in the cipherletter’s list in both letterMapping1 and letterMapping2.
For example, this is why intersectedMapping’s list for the 'Z' key is just ['E']:
because letterMapping1 had ['E', 'Y'] but letterMapping2 had ['E']. The
intersection of ['E', 'Y'] and ['E'] is just the potential decryption letters that exist in both
mappings: ['E']
There is an exception. If one of the mapping’s lists was blank, then all of the potential decryption
letters in the other mapping are put into the intersected mapping. This is because in our program a
blank map represents any possible letter can be used since nothing is known about the mapping.
Then we do all these steps for the third cipherword, MPBKSSIPLC. Try typing the following into
the interactive shell:
>>> letterMapping3 = simpleSubHacker.getBlankCipherletterMapping()
>>> wordPat = makeWordPatterns.getWordPattern('MPBKSSIPLC')
>>> candidates = wordPatterns.allPatterns[wordPat]
>>> candidates
['ADMITTEDLY', 'DISAPPOINT']
>>> for i in range(len(candidates)):
270 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
... letterMapping3 = simpleSubHacker.addLettersToMapping(letterMapping3,
'MPBKSSIPLC', candidates[i])
...
>>> letterMapping3
{'A': [], 'C': ['Y', 'T'], 'B': ['M', 'S'], 'E': [], 'D': [], 'G': [], 'F': [],
'I': ['E', 'O'], 'H': [], 'K': ['I', 'A'], 'J': [], 'M': ['A', 'D'], 'L': ['L',
'N'], 'O': [], 'N': [], 'Q': [], 'P': ['D', 'I'], 'S': ['T', 'P'], 'R': [],
'U': [], 'T': [], 'W': [], 'V': [], 'Y': [], 'X': [], 'Z': []}
We intersect letterMapping3 with intersectedMapping. This also ends up indirectly
intersecting letterMapping3 with letterMapping1 and letterMapping2, since
intersectedMapping is currently the intersection of letterMapping1 and
letterMapping2. Try typing the following into the interactive shell:
>>> intersectedMapping = simpleSubHacker.intersectMappings(intersectedMapping,
letterMapping3)
>>> intersectedMapping
{'A': [], 'C': ['T'], 'B': ['S'], 'E': [], 'D': [], 'G': ['B'], 'F': [], 'I':
['O'], 'H': ['M'], 'K': ['A'], 'J': [], 'M': ['A', 'D'], 'L': ['N'], 'O':
['U'], 'N': ['L'], 'Q': ['C'], 'P': ['I'], 'S': ['T', 'P'], 'R': ['R'], 'U':
[], 'T': [], 'W': [], 'V': [], 'Y': [], 'X': ['F'], 'Z': ['E']}
>>>
We can now pass the intersected cipherletter mapping to
decryptWithCipherletterMapping() to decrypt the ciphertext. Try typing the
following into the interactive shell:
>>> simpleSubHacker.decryptWithCipherletterMapping('OLQIHXIRCKGNZ PLQRZKBZB
MPBKSSIPLC', intersectedMapping)
UNCOMFORTABLE INCREASES _ISA__OINT
>>>
The intersected mapping is not yet complete. Notice how the intersected mapping has a solution
for the cipherletter K, because the key 'K'’s value to a list with just one string in it: ['A'].
Because we know that the K cipherletters will decrypt to A, no other cipherletter can possibly
decrypt to A.
In the intersected mapping, the cipherletter M maps to ['A', 'D']. This means that judging
from the candidates for the cipherwords in our encrypted message, the cipherletter M could
decrypt to A or D.
Chapter 18 – Hacking the Simple Substitution Cipher 271
But since we know K decrypts to A, we can remove A from the list of potential decryption letters
for cipherletter M. This shortens the list down to just ['D']. Because this new list only has one
string in it, we’ve also solved the cipherletter M!
The removeSolvedLettersFromMapping() function takes a cipherletter mapping and
removes these solved potential decryption letters from the other cipherletters’ lists. Try typing the
following into the interactive shell:
>>> letterMapping =
simpleSubHacker.removeSolvedLettersFromMapping(letterMapping)
>>> intersectedMapping
{'A': [], 'C': ['T'], 'B': ['S'], 'E': [], 'D': [], 'G': ['B'], 'F': [], 'I':
['O'], 'H': ['M'], 'K': ['A'], 'J': [], 'M
': ['D'], 'L': ['N'], 'O': ['U'], 'N': ['L'], 'Q': ['C'], 'P': ['I'], 'S':
['P'], 'R': ['R'], 'U': [], 'T': [], 'W': [],
'V': [], 'Y': [], 'X': ['F'], 'Z': ['E']}
>>>
Now when we pass the intersected mapping to decryptWithCipherletterMapping(), it
gives us the full solution. Try typing the following into the interactive shell:
>>> simpleSubHacker.decryptWithCipherletterMapping('OLQIHXIRCKGNZ PLQRZKBZB
MPBKSSIPLC', intersectedMapping)
UNCOMFORTABLE INCREASES DISAPPOINT
>>>
The ciphertext OLQIHXIRCKGNZ PLQRZKBZB MPBKSSIPLC decrypts to the message,
“Uncomfortable increases disappoint”.
This is a rather short ciphertext to hack. Normally the encrypted messages we hack will be much
longer. (Messages as short as our example usually cannot be hacked with our word pattern
method.) We’ll have to create a cipherletter mapping for each cipherword in these longer
messages and then intersect them all together, which is exactly what the hackSimpleSub()
function does.
Now that we know the basic steps and what each function does, let’s learn how the code in these
functions work.
How the Program Works
simpleSubHacker.py
1. # Simple Substitution Cipher Hacker

272 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
2. # http://inventwithpython.com/hacking (BSD Licensed)
The comments at the top of the source code explain what the program is.
Import All the Things
simpleSubHacker.py
4. import os, re, copy, pprint, pyperclip, simpleSubCipher, makeWordPatterns
Our simple substitution hacking program imports eight different modules, more than any other
program so far. By reusing the code in these modules, our hacking program becomes much
shorter and easier to write.
The re module is a module we haven’t seen before. This is the regular expression module which
lets our code do sophisticated string manipulation. Regular expressions are explained in the next
section.
simpleSubHacker.py
6. if not os.path.exists('wordPatterns.py'):
7. makeWordPatterns.main() # create the wordPatterns.py file
8. import wordPatterns
The simple substitution cipher also needs the wordPatterns module. The .py file for this
module is created when the makeWordPatterns.py program is run. But
makeWordPatterns.py might not have been run before our hacking program has. In this case, our
hacking program checks if this file exists on line 6 and if it doesn’t, the
makeWordPatterns.main() function is called.
Remember, the main() function is the function that is run in our programs when they are run as
programs (rather than just imported with an import statement.) When we imported the
makeWordPatterns module on line 4, the main() function in makeWordPatterns.py was
not run. Since main() is the function that creates the wordPatterns.py file, we will call
makeWordPatterns.main() if wordPatterns.py does not yet exist.
Either way, by the time the program execution reaches line 8, the wordPatterns module will
exist and can be imported.
A Brief Intro to Regular Expressions and the sub() Regex Method
simpleSubHacker.py
10. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'

Chapter 18 – Hacking the Simple Substitution Cipher 273
11. nonLettersOrSpacePattern = re.compile('[^A-Z\s]')
The simple substitution hacking program will have a LETTERS global variable like many of our
previous cipher programs.
The re.compile() function is new. This function compiles (that is, creates) a new regular
expression pattern object, or “regex object” or “pattern object” for short. Regular expressions are
strings that define a specific pattern that matches certain strings. Regular expressions can do
many special things with strings that are beyond the scope of this book, but you can learn about
them at http://invpy.com/regex.
The string '[^A-Za-z\s]' is a regular expression that matches any character that is not a
letter from A to Z or a “whitespace” character (e.g. a space, tab, or newline character). The
pattern object has a sub() method (short for “substitute”) that works very similar to the
replace() string method. The first argument to sub() is the string that replaces any instances
of the pattern in the second string argument. Try typing the following into the interactive shell:
>>> pat = re.compile('[^A-Z\s]')
>>> pat.sub('abc', 'ALL! NON!LETTERS? AND123 NONSPACES. REPLACED')
'ALLabc NONabcLETTERSabc ANDabcabcabc NONSPACESabc REPLACED'
>>> pat.sub('', 'ALL! NON!LETTERS? AND123 NONSPACES. REPLACED')
'ALL NONLETTERS AND NONSPACES REPLACED'
>>>
There are many sophisticated string manipulations you can perform if you learn more about
regular expressions, but we will only use them in this book to remove characters from a string
that are not uppercase letters or spaces.
The Hacking Program’s main() Function
simpleSubHacker.py
13. def main():
14. message = 'Sy l nlx sr pyyacao l ylwj eiswi upar lulsxrj isr
sxrjsxwjr, ia esmm rwctjsxsza sj wmpramh, lxo txmarr jia aqsoaxwa sr
pqaceiamnsxu, ia esmm caytra jp famsaqa sj. Sy, px jia pjiac ilxo, ia sr
pyyacao rpnajisxu eiswi lyypcor l calrpx ypc lwjsxu sx lwwpcolxwa jp isr
sxrjsxwjr, ia esmm lwwabj sj aqax px jia rmsuijarj aqsoaxwa. Jia pcsusx py
nhjir sr agbmlsxao sx jisr elh. -Facjclxo Ctrramm'
15.
16. # Determine the possible valid ciphertext translations.
17. print('Hacking...')
18. letterMapping = hackSimpleSub(message)

274 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Like all our previous hacking programs, the main() function will store the ciphertext to be
hacked in a variable named message. We will pass this variable to the hackSimpleSub()
function. However, unlike our previous hacking programs, the hacking function will not return a
string of the decrypted message (or None if it was unable to decrypt it).
Instead, hackSimpleSub() will return a cipherletter mapping (specifically, an intersected
cipherletter mapping that had the solved letters removed, like the kind we made in our interactive
shell exercise). This returned cipherletter mapping will be passed to
decryptWithCipherletterMapping() to decrypt the ciphertext in message.
Partially Hacking the Cipher
simpleSubHacker.py
20. # Display the results to the user.
21. print('Mapping:')
22. pprint.pprint(letterMapping)
23. print()
Since the cipherletter mapping stored in letterMapping is a dictionary, we can use the
pprint.pprint() “pretty print” function to display it on the screen. It will look something
like this:
{'A': ['E'],
'B': ['B', 'W', 'P'],
'C': ['R'],
'D': [],
'E': ['K', 'W'],
'F': ['B', 'P'],
'G': ['B', 'Q', 'X', 'Y', 'P', 'W'],
'H': ['B', 'K', 'P', 'W', 'X', 'Y'],
'I': ['H'],
'J': ['T'],
'K': [],
'L': ['A'],
'M': ['L'],
'N': ['M'],
'O': ['D'],
'P': ['O'],
'Q': ['V'],
'R': ['S'],
'S': ['I'],
'T': ['U'],
'U': ['G'],
'V': [],

Chapter 18 – Hacking the Simple Substitution Cipher 275
'W': ['C'],
'X': ['N'],
'Y': ['F'],
'Z': ['Z']}
In the above example, the cipherletters A, C, I, J, L, M, N, O, P, Q, R, S, T, U, X, Y, and Z all
have one and only one potential decryption letter. These cipher letters have been solved. The
decryptWithCipherletterMapping() function, explained later, will print underscores
for any cipherletters that have not been solved (that is, B, D, E, F, G, H, K, and V.)
simpleSubHacker.py
24. print('Original ciphertext:')
25. print(message)
26. print()
First the original encrypted message is displayed on the screen so the programmer can compare it
to the decryption.
simpleSubHacker.py
27. print('Copying hacked message to clipboard:')
28. hackedMessage = decryptWithCipherletterMapping(message, letterMapping)
29. pyperclip.copy(hackedMessage)
30. print(hackedMessage)
Next the decrypted message is returned from the decryptWithCipherletterMapping()
function on line 28. This hacked message is copied to the clipboard on line 29 and printed to the
screen on line 30.
Next, let’s look at all the functions that are called by main().
Blank Cipherletter Mappings
simpleSubHacker.py
33. def getBlankCipherletterMapping():
34. # Returns a dictionary value that is a blank cipherletter mapping.
35. return {'A': [], 'B': [], 'C': [], 'D': [], 'E': [], 'F': [], 'G': [],
'H': [], 'I': [], 'J': [], 'K': [], 'L': [], 'M': [], 'N': [], 'O': [], 'P':
[], 'Q': [], 'R': [], 'S': [], 'T': [], 'U': [], 'V': [], 'W': [], 'X': [],
'Y': [], 'Z': []}
Our program will need a cipherletter mapping for each cipherword in the ciphertext, so we will
create the getBlankCipherletterMapping() function which can return a new, blank
mapping when called.

276 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Adding Letters to a Cipherletter Mapping
simpleSubHacker.py
38. def addLettersToMapping(letterMapping, cipherword, candidate):
The addLettersToMapping() function attempts to make sure that every letter in the
candidate can be mapped to a letter in the cipherword. It checks over each letter in candidate
and adds its corresponding letter in cipherword to letterMapping if it wasn't already
there.
For example, if 'PUPPY' is our candidate word for the 'HGHHU' cipherword, the
addLettersToMapping() function will change letterMapping so that the key 'H' has
'P' added to its list of potential decryption letters. Then the function will change the key 'G' so
that its list has 'U' appended to it.
If the letter is already in the list of potential decryption letters, the addLettersToMapping()
will not add a letter to the list. We can skip adding 'P' to the 'H' key the next two times since
it’s already been done. Finally, the function will change the key 'U' so that it has 'Y' in its list
of potential decryption letters.
The code in this function assumes that len(cipherword) is the same as len(candidate).
simpleSubHacker.py
49. letterMapping = copy.deepcopy(letterMapping)
To avoid changing the original dictionary value passed for the letterMapping parameter, line
49 will copy the dictionary in letterMapping and make this copy the new value in
letterMapping. (We have to do this because letterMapping was passed a copy of a
dictionary reference value, instead of a copy of the dictionary value. See the “List Reference”
section in Chapter 10 for an explanation of references.)
simpleSubHacker.py
50. for i in range(len(cipherword)):
Line 50 will iterate over each index in the string in cipherword. We need the index (which is
stored in the variable i) because the potential decryption letter to be added will be
candidate[i] for the cipherletter cipherword[i].
simpleSubHacker.py
51. if candidate[i] not in letterMapping[cipherword[i]]:

Chapter 18 – Hacking the Simple Substitution Cipher 277
52. letterMapping[cipherword[i]].append(candidate[i])
The if statement on line 51 checks that the potential decryption letter is not already in the list of
potential decryption letters for the cipherletter. This prevents the list of potential decryption
letters in the cipherletter mapping from having duplicate letters in it. For example, we never want
the list to be a value like ['U', 'U'].
Line 52 adds the new potential decryption letter (that is, candidate[i]) to the list of potential
decryption letters in the cipherletter mapping (that is, letterMapping[cipherword[i]]).
simpleSubHacker.py
53. return letterMapping
After looping through all the indexes in cipherword, the additions to the cipherletter mapping
are complete and the dictionary in letterMapping is returned.
Intersecting Two Letter Mappings
simpleSubHacker.py
56. def intersectMappings(mapA, mapB):
57. # To intersect two maps, create a blank map, and then add only the
58. # potential decryption letters if they exist in BOTH maps.
59. intersectedMapping = getBlankCipherletterMapping()
60. for letter in LETTERS:
The intersectMappings() function will return a new cipherletter mapping that is an
intersection of the two cipherletter mappings passed for the mapA and mapB parameters. Line 59
creates a new cipherletter mapping by calling getBlankCipherletterMapping() and
storing the returned value in the intersectedMapping variable.
The for loop will loop through each of the uppercase letters in the LETTERS constant variable,
and the letter variable can be used for the keys of the mapA and mapB dictionaries.
simpleSubHacker.py
62. # An empty list means "any letter is possible". In this case just
63. # copy the other map entirely.
64. if mapA[letter] == []:
65. intersectedMapping[letter] = copy.deepcopy(mapB[letter])
66. elif mapB[letter] == []:
67. intersectedMapping[letter] = copy.deepcopy(mapA[letter])

278 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
If the list of potential decryption letters for a cipherletter in a cipherletter mapping is blank, this
means that this cipherletter could potentially decrypt to any letter. In this case, the intersected
cipherletter mapping will just be a copy of the other mapping’s list of potential decryption letters.
That is, if mapA’s list of potential decryption letters is blank, then set the intersected mapping’s
list to be a copy of mapB’s list. Or if mapB’s list is blank, then set the intersected mapping’s list
to be a copy of mapA’s list.
(If both mappings’ lists were blank, then line 65 will simply copy mapB’s blank list to the
intersected mapping. This is the behavior we want: if both lists are blank then the intersected
mapping will have a blank list.)
simpleSubHacker.py
68. else:
69. # If a letter in mapA[letter] exists in mapB[letter], add
70. # that letter to intersectedMapping[letter].
71. for mappedLetter in mapA[letter]:
72. if mappedLetter in mapB[letter]:
73. intersectedMapping[letter].append(mappedLetter)
The else block handles the case where neither mapA nor mapB are blank. In this case, line 71
loops through the uppercase letter strings in the list at mapA[letter]. Line 72 checks if this
uppercase letter in mapA[letter] also exists in the list of uppercase letter strings in
mapB[letter]. If it does, then line 73 will add this common letter to the list of potential
decryption letters at intersectedMapping[letter].
simpleSubHacker.py
75. return intersectedMapping
Once the for loop that started on line 60 has finished, the cipherletter mapping in
intersectedMapping will only have the potential decryption letters that exist in the lists of
potential decryption letters of both mapA and mapB. This completely intersected cipherletter
mapping is returned on line 75.
Removing Solved Letters from the Letter Mapping
simpleSubHacker.py
78. def removeSolvedLettersFromMapping(letterMapping):
79. # Cipher letters in the mapping that map to only one letter are
80. # "solved" and can be removed from the other letters.
81. # For example, if 'A' maps to potential letters ['M', 'N'], and 'B'
82. # maps to ['N'], then we know that 'B' must map to 'N', so we can

Chapter 18 – Hacking the Simple Substitution Cipher 279
83. # remove 'N' from the list of what 'A' could map to. So 'A' then maps
84. # to ['M']. Note that now that 'A' maps to only one letter, we can
85. # remove 'M' from the list of potential letters for every other
86. # key. (This is why there is a loop that keeps reducing the map.)
87. letterMapping = copy.deepcopy(letterMapping)
88. loopAgain = True
The removeSolvedLettersFromMapping() function searches for any cipherletters in the
letterMapping parameter which have one and only one potential decryption letter. These
cipherletters are considered solved: the cipherletter must decrypt to that one potential decryption
letter. This means that any other cipherletters that have this solved letter can have that letter
removed from their lists of potential decryption letters.
This could cause a chain reaction, because when the one potential decryption letter is removed
from other lists of potential decryption letters, it could result in a new solved cipherletter. In that
case, the program will loop and perform the solved letter removal over the whole cipherletter
mapping again.
The cipherletter mapping in letterMapping is copied on line 87 so that changes made to it in the
function do not affect the dictionary value outside the function. Line 88 creates loopAgain,
which is a variable that holds a Boolean value that tells us if the code found a new solved letter
and needs to loop again. In that case the loopAgain variable is set to True on line 88 so that
the program execution will enter the while loop on line 89.
simpleSubHacker.py
89. while loopAgain:
90. # First assume that we will not loop again:
91. loopAgain = False
At the very beginning of the loop, line 91 will set loopAgain to False. The code assumes that
this will be the last iteration through line 89’s while loop. The loopAgain variable is only set
to True if we find a new solved cipherletter during this iteration.
simpleSubHacker.py
93. # solvedLetters will be a list of uppercase letters that have one
94. # and only one possible mapping in letterMapping
95. solvedLetters = []
96. for cipherletter in LETTERS:
97. if len(letterMapping[cipherletter]) == 1:
98. solvedLetters.append(letterMapping[cipherletter][0])

280 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The next part of the code creates a list of cipherletters that have exactly one potential decryption
letter. We will put these cipherletter strings in a list that is in solvedLetters. The
solvedLetters variable starts off as a blank list on line 95.
The for loop on line 96 goes through all 26 possible cipherletters and looks at the cipherletter
mapping’s list of potential decryption letters for that cipherletter. (That is, the list is at
letterMapping[cipherletter].)
If the length of this list is 1 (which is checked on line 97), then we know that there is only one
letter that the cipherletter could decrypt to and the cipherletter is solved. We will add the letter
(the potential decryption letter, not the cipherletter) to the solvedLetters list on line 98. The
solved letter will always be at letterMapping[cipherletter][0] because
letterMapping[cipherletter] is a list of potential decryption letters that only has one
string value in it at index 0 of the list.
simpleSubHacker.py
100. # If a letter is solved, than it cannot possibly be a potential
101. # decryption letter for a different ciphertext letter, so we
102. # should remove it from those other lists.
103. for cipherletter in LETTERS:
104. for s in solvedLetters:
105. if len(letterMapping[cipherletter]) != 1 and s in
letterMapping[cipherletter]:
106. letterMapping[cipherletter].remove(s)
After the previous for loop that started on line 96 has finished, the solvedLetters variable
will be a list of all the letters that are solved decryptions of a cipherletter. The for loop on line
103 loops through all 26 possible cipherletters and looks at the cipherletter mapping’s list of
potential decryption letters.
For each cipherletter that is examined, the letters in solvedLetters are looped through on
line 104 to check if each of them exist in the list of potential decryption letters for
letterMapping[cipherletter]. Line 105 checks if a list of potential decryption letters is
not solved (that is, if len(letterMapping[cipherletter]) != 1) and the solved
letter exists in the list of potential decryption letters. If this condition is True, then the solved
letter in s is removed from the list of potential decryption letters on line 106.
simpleSubHacker.py
107. if len(letterMapping[cipherletter]) == 1:
108. # A new letter is now solved, so loop again.
109. loopAgain = True

Chapter 18 – Hacking the Simple Substitution Cipher 281
If by chance this removal caused the list of potential decryption letters to now only have one
letter in it, then the loopAgain variable is set to True on line 109 so that the code will check
for this new solved letter in the cipherletter mapping on the next iteration.
simpleSubHacker.py
110. return letterMapping
After the code in line 89’s while loop has gone through a full iteration without loopAgain
being set to True, the program execution goes past the loop and returns the cipherletter mapping
stored in letterMapping.
Hacking the Simple Substitution Cipher
simpleSubHacker.py
113. def hackSimpleSub(message):
114. intersectedMap = getBlankCipherletterMapping()
Now that we’ve created the getBlankCipherletterMapping(),
addLettersToMapping(), intersectMappings(), and
removeSolvedLettersFromMapping() functions that can manipulate the cipherletter
mappings we pass them, we can use them all together to hack a simple substitution message.
Remember the steps from our interactive shell exercise for hacking a simple substitution cipher
message: for each cipherword, get all the candidates based on the cipherword’s word pattern, then
add these candidates to a cipherletter mapping. Then take the cipherletter mapping for each
cipherword and intersect them together.
The intersectedMap variable will hold the intersected cipherletter mapping of each
cipherword’s cipherletter mapping. At the beginning of the hackSimpleSub() function, it
will start as a blank cipherletter mapping.
simpleSubHacker.py
115. cipherwordList = nonLettersOrSpacePattern.sub('',
message.upper()).split()
The sub() regex method will substitute (that is, replace) any occurrences of the string pattern in
the second argument (message.upper()) with the first argument (a blank string). Regular
expressions and the sub() method were explained earlier in this chapter.
On line 115, the regex object in nonLettersOrSpacePattern matches any string that is not
a letter or whitespace character. The sub() method will return a string that is the message

282 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
variable with all non-letter and non-space characters replaced by a blank string. This effectively
returns a string that has all punctuation and number characters removed from message.
This string then has the upper() method called on it to return an uppercase version of the
string, and that string has the split() method called on it to return the individual words in the
string in a list. To see what each part of line 115 does, type the following into the interactive
shell:
>>> import re
>>> nonLettersOrSpacePattern = re.compile('[^A-Z\s]')
>>> message = 'Hello, this is my 1st test message.'
>>> message = nonLettersOrSpacePattern.sub('', message.upper())
>>> message
'HELLO THIS IS MY ST TEST MESSAGE'
>>> cipherwordList = message.split()
>>> cipherwordList
['HELLO', 'THIS', 'IS', 'MY', 'ST', 'TEST', 'MESSAGE']
After line 115 executes, the cipherwordList variable will contain a list of uppercase strings
of the individual words that were previously in message.
simpleSubHacker.py
116. for cipherword in cipherwordList:
117. # Get a new cipherletter mapping for each ciphertext word.
118. newMap = getBlankCipherletterMapping()
The for loop on line 116 will assign each string in the message list to the cipherword
variable. Inside this loop we will get the cipherword’s candidates, add the candidates to a
cipherletter mapping, and then intersect this mapping with intersectedMap.
First, line 118 will get a new, blank cipherletter mapping from
getBlankCipherletterMapping() and store it in the newMap variable.
simpleSubHacker.py
120. wordPattern = makeWordPatterns.getWordPattern(cipherword)
121. if wordPattern not in wordPatterns.allPatterns:
122. continue # This word was not in our dictionary, so continue.
To find the candidates for the current cipherword, we call getWordPattern() in the
makeWordPatterns module on line 120. If the word pattern of the cipherword does not exist
in the keys of the wordPatterns.allPatterns dictionary, then whatever the cipherword

Chapter 18 – Hacking the Simple Substitution Cipher 283
decrypts to does not exist in our dictionary file. In that case the continue statement on line 122
will skip back to line 116, to the next cipherword in the list.
simpleSubHacker.py
124. # Add the letters of each candidate to the mapping.
125. for candidate in wordPatterns.allPatterns[wordPattern]:
126. newMap = addLettersToMapping(newMap, cipherword, candidate)
On line 125, we know the word pattern exists in wordPatterns.allPatterns. The values
in the allPatterns dictionary are lists of strings of the English words with the pattern in
wordPattern. Since it is a list, we can use a for loop to iterate over this list. The variable
candidate will be set to each of these English word strings on each iteration of the loop.
The only line inside line 125’s for loop is the call to addLettersToMapping() on line 126.
We will use this to update the cipherletter mapping in newMap with the letters in each of the
candidates.
simpleSubHacker.py
128. # Intersect the new mapping with the existing intersected mapping.
129. intersectedMap = intersectMappings(intersectedMap, newMap)
Once all of the letters in the candidates are added to the cipherletter mapping in newMap, line
129 will intersect newMap with intersectedMap, and make the return value the new value of
intersectedMap.
At this point the program execution jumps back to the beginning of the for loop on line 116 to
run the code on the next cipherword in the cipherwordList list.
simpleSubHacker.py
131. # Remove any solved letters from the other lists.
132. return removeSolvedLettersFromMapping(intersectedMap)
Once we have the final intersected cipherletter mapping, we can remove any solved letters from it
by passing it to removeSolvedLettersFromMapping(). The cipherletter mapping that is
returned from the function will be the return value for hackSimpleSubstitution().
Creating a Key from a Letter Mapping
simpleSubHacker.py
135. def decryptWithCipherletterMapping(ciphertext, letterMapping):
136. # Return a string of the ciphertext decrypted with the letter mapping,
137. # with any ambiguous decrypted letters replaced with an _ underscore.

284 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
138.
139. # First create a simple sub key from the letterMapping mapping.
140. key = ['x'] * len(LETTERS)
Since the simpleSubstitutionCipher.decryptMessage() function only decrypts
with keys instead of letter mappings, we need the decryptWithCipherletterMapping()
function to convert a letter mapping into a string key.
The simple substitution keys are strings of 26 characters. The character at index 0 in the key
string is the substitution for A, the character at index 1 is the substitution for B, and so on.
Since the letter mapping might only have solutions for some of the letters, we will start out with a
key of ['x', 'x', 'x', 'x', 'x', 'x', 'x', 'x', 'x', 'x', 'x', 'x',
'x', 'x', 'x', 'x', 'x', 'x', 'x', 'x', 'x', 'x', 'x', 'x', 'x',
'x']. This list is created on line 140 by using list replication to replicate the list ['x'] 26
times. Since LETTERS is a string of the letters of the alphabet, len(LETTERS) evaluates to
26. When the multiplication operator is used on a list and integer, it does list replication.
We don’t have to use 'x', we can use any lowercase letter. The reason we need to use a
lowercase letter is because it acts as a “placeholder” for the simple substitution key. The way
simpleSubCipher.py works, since LETTERS only contains uppercase letters, any lowercase letters
in the key will not be used to decrypt a message.
The 26-item list in key will be joined together into a 26-character string at the end of the
decryptWithCipherletterMapping() function.
simpleSubHacker.py
141. for cipherletter in LETTERS:
142. if len(letterMapping[cipherletter]) == 1:
143. # If there's only one letter, add it to the key.
144. keyIndex = LETTERS.find(letterMapping[cipherletter][0])
145. key[keyIndex] = cipherletter
The for loop on line 141 will let us go through each of the letters in LETTERS for the
cipherletter variable, and if the cipherletter is solved (that is,
letterMapping[cipherletter] has only one letter in it) then we can replace an 'x' in
the key with the letter.
So on line 144 letterMapping[cipherletter][0] is the decryption letter, and
keyIndex is the index of the decryption letter in LETTERS (which is returned from the
find() call). This index in the key list is set to the decryption letter on line 145.

Chapter 18 – Hacking the Simple Substitution Cipher 285
simpleSubHacker.py
146. else:
147. ciphertext = ciphertext.replace(cipherletter.lower(), '_')
148. ciphertext = ciphertext.replace(cipherletter.upper(), '_')
Or else, if the cipherletter does not have a solution, then we want to replace everywhere that
cipherletter appears in the ciphertext with an underscore so the user can tell which characters
were unsolved. Line 147 handles replacing the lowercase form of cipherletter with an
underscore and line 148 handles replacing the uppercase form of cipherletter with an
underscore.
simpleSubHacker.py
149. key = ''.join(key)
150.
151. # With the key we've created, decrypt the ciphertext.
152. return simpleSubCipher.decryptMessage(key, ciphertext)
When we have finally replaced all the parts in the list in key with the solved letters, we convert
the list of strings into a single string with the join() method to create a simple substitution key.
This string is passed to the decryptMessage() function in our simpleSubCipher.py program.
The decrypted message string returned from decryptMessage() is then returned from
decryptWithCipherletterMapping() on line 152.
simpleSubHacker.py
155. if __name__ == '__main__':
156. main()
That completes all the functions our hacking program needs. Lines 155 and 156 just call the
main() function to run the program if simpleSubHacker.py is being run directly, instead of
being imported as a module by another Python program.
Couldn’t We Just Encrypt the Spaces Too?
Yes. Our hacking approach only works if the spaces were not encrypted. You can modify the
simple substitution cipher from the previous chapter to encrypt spaces, numbers, and punctuation
characters as well as letters, and it would make your encrypted messages harder (but not
impossible) to hack. However, since the spaces will probably be the most common symbol in the
ciphertext, you can write a program to replace it back to spaces, and then hack the ciphertext as
normal. So encrypting the space characters would not offer much more protection.
286 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Summary
Whew! This hacking program was fairly complicated. The cipherletter mapping is the main tool
for modeling the possible letters that each ciphertext letter can decrypt to. By adding letters
(based on the candidates for each cipherword) to the mapping, and then intersecting mappings
and removing solved letters from other lists of potential decryption letters, we can narrow down
the number of possible keys. Instead of trying all 403,291,461,126,605,635,584,000,000 possible
keys we can use some sophisticated Python code to figure out exactly what most (if not all) of the
original simple substitution key was.
The main strength of the simple substitution cipher is the large number of possible keys. But the
downfall is that it is easy enough to compare the cipherwords to words in a dictionary file to
slowly figure out which cipherletters decrypt to which letters. The next chapter’s cipher is much
more powerful. For several hundred years, it was considered impossible to break. It is a
“polyalphabetic” substitution cipher called the Vigenère cipher.

Chapter 19 – The Vigenère Cipher 287
THE VIGENÈRE CIPHER
Topics Covered In This Chapter:
Subkeys
“I believed then, and continue to believe now, that
the benefits to our security and freedom of widely
available cryptography far, far outweigh the
inevitable damage that comes from its use by
criminals and terrorists... I believed, and continue
to believe, that the arguments against widely
available cryptography, while certainly advanced
by people of good will, did not hold up against the
cold light of reason and were inconsistent with the
most basic American values.”
Matt Blaze, AT&T Labs, September 2001

288 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Le Chiffre Indéchiffrable
The Vigenère cipher is a stronger cipher than the ones we’ve seen before. There are too many
possible keys to brute-force, even with English detection. It cannot be broken with the word
pattern attack that worked on the simple substitution cipher. It was possibly first described in
1553 by Italian cryptographer Giovan Battista Bellaso (though it has been reinvented many times,
including by Blaise de Vigenère). It is thought to have remained unbroken until Charles Babbage,
considered to be the father of computers, broke it in the 19th century. It was called “le chiffre
indéchiffrable”, French for “the indecipherable cipher”.
Figure 19-1. Blaise de Vigenère
April 5, 1523 - 1596
Figure 19-2. Charles Babbage
December 26, 1791 - October 18, 1871
Multiple “Keys” in the Vigenère Key
The Vigenère cipher is similar to the Caesar cipher, except with multiple keys. Because it uses
more than one set of substitutions, it is also called a polyalphabetic substitution cipher.
Remember that the Caesar cipher had a key from 0 to 25. For the Vigenère cipher, instead of
using a numeric key, we will use a letter key. The letter A will be used for key 0. The letter B will
be used for key 1, and so on up to Z for the key 25.
0
1
2
3
4
5
6
7
8
9
10
11
12
A
B
C
D
E
F
G
H
I
J
K
L
M
13
14
15
16
17
18
19
20
21
22
23
24
25
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
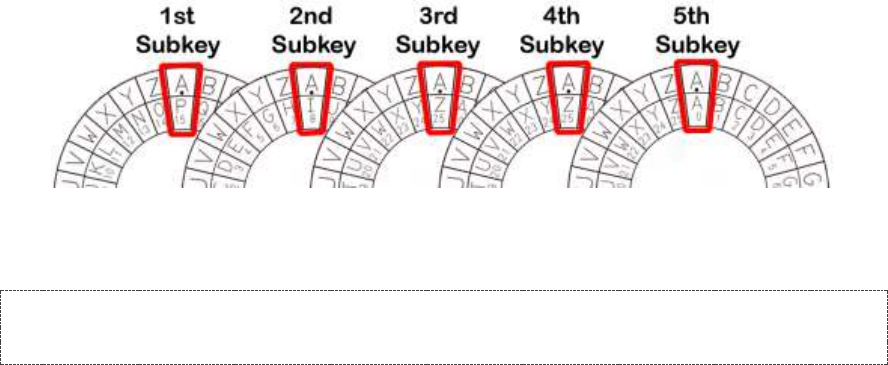
Chapter 19 – The Vigenère Cipher 289
The key in a Vigenère cipher is a series of letters, such as a single English word. This single
word key will be split into multiple subkeys. If we use a Vigenère key of “PIZZA”, then the
first subkey is P, the second subkey is I, the third and fourth subkeys are both Z and the fifth
subkey is A. We will use the first subkey to encrypt the first letter of the plaintext, and the second
subkey to encrypt the second letter, and so on. When we get to the sixth letter of the plaintext, we
will go back to using the first subkey.
The Vigenère cipher is the same as using multiple Caesar ciphers in the same message.
Figure 19-3. Multiple Caesar ciphers combine to make the Vigenère cipher
The following shows which subkey will encrypt which letters in the message, “Common sense is
not so common.” with the Vigenère key, “PIZZA”.
COMMONSENSEISNOTSOCOMMON
PIZZAPIZZAPIZZAPIZZAPIZZ
To encrypt the first C with the subkey P, encrypt it with the Caesar cipher using numeric key 15
(15 is the number for the letter P) which creates the ciphertext R, and so on. Do this for each of
the letters of the plaintext. The following table shows this process:

290 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Table 19-1. Numbers of the letters before and after encryption.
Plaintext
Letter
Subkey
Ciphertext
Letter
C (2)
P (15)
→
R (17)
O (14)
I (8)
→
W (22)
M (12)
Z (25)
→
L (11)
M (12)
Z (25)
→
L (11)
O (14)
A (0)
→
O (14)
N (13)
P (15)
→
C (2)
S (18)
I (8)
→
A (0)
E (4)
Z (25)
→
D (3)
N (13)
Z (25)
→
M (12)
S (18)
A (0)
→
S (18)
E (4)
P (15)
→
T (19)
I (8)
I (8)
→
Q (16)
S (18)
Z (25)
→
R (17)
N (13)
Z (25)
→
M (12)
O (14)
A (0)
→
O (14)
T (19)
P (15)
→
I (8)
S (18)
I (8)
→
A (0)
O (14)
Z (25)
→
N (13)
C (2)
Z (25)
→
B (1)
O (14)
A (0)
→
O (14)
M (12)
P (15)
→
B (1)
M (12)
I (8)
→
U (20)
O (14)
Z (25)
→
N (13)
N (13)
Z (25)
→
M (12)
So using the Vigenère cipher with the key “PIZZA” (which is made up of the subkeys 15, 8, 25,
25, 0) the plaintext “Common sense is not so common.” becomes the ciphertext “Rwlloc admst qr
moi an bobunm.”
The more letters in the Vigenère key, the stronger the encrypted message will be against a brute-
force attack. The choice of “PIZZA” is a poor one for a Vigenère key, because it only has five
letters. A key with only five letters has 11,881,376 possible combinations. (26 ^ 5 = 26 × 26 × 26
× 26 × 26 = 11,881,376) Eleven million keys is far too many for a human to try out, but a
computer could try them all in a few hours. It would first try to decrypt the message with the key
“AAAAA” and check if the resulting decryption was in English. Then it could try “AAAAB”,
then “AAAAC”, until it got to “PIZZA”.

Chapter 19 – The Vigenère Cipher 291
The good news is that for every additional letter the key has, the number of possible keys
multiplies by 26. Once there are quadrillions of possible keys, it would take a computer years to
break. Table 19-2 shows how many possible keys there are for each length:
Table 19-2. Number of possible keys based on Vigenère key length.
Key Length
Equation
Possible Keys
1
26
= 26
2
26 × 26
= 676
3
676 × 26
= 17,576
4
17,576 × 26
= 456,976
5
456,976 × 26
= 11,881,376
6
11,881,376 × 26
= 308,915,776
7
308,915,776 × 26
= 8,031,810,176
8
8,031,810,176 × 26
= 208,827,064,576
9
208,827,064,576 × 26
= 5,429,503,678,976
10
5,429,503,678,976 × 26
= 141,167,095,653,376
11
141,167,095,653,376 × 26
= 3,670,344,486,987,776
12
3,670,344,486,987,776 × 26
= 95,428,956,661,682,176
13
95,428,956,661,682,176 × 26
= 2,481,152,873,203,736,576
14
2,481,152,873,203,736,576 × 26
= 64,509,974,703,297,150,976
Once we get to keys that are twelve or more letters long, then it becomes impossible for most
consumer laptops to crack in a reasonable amount of time.
A Vigenère key does not have to be a word like “PIZZA”. It can be any combination of letters,
such as “DURIWKNMFICK”. In fact, it is much better not to use a word that can be found in the
dictionary. The word “RADIOLOGISTS” is a 12-letter key that is easier to remember than
“DURIWKNMFICK” even though they have the same number of letters. But a cryptanalyst
might anticipate that the cryptographer is being lazy by using an English word for the Vigenère
key. There are 95,428,956,661,682,176 possible 12-letter keys, but there are only about 1,800 12-
letter words in our dictionary file. If you are using a 12-letter English word, it would be easier to
brute-force that ciphertext than it would be to brute-force the ciphertext from a 3-letter random
key.
Of course, the cryptographer is helped by the fact that the cryptanalyst does not know how many
letters long the Vigenère key is. But the cryptanalyst could try all 1-letter keys, then all 2-letter
keys, and so on.
Source Code of Vigenère Cipher Program
Open a new file editor window by clicking on File ► New Window. Type in the following code
into the file editor, and then save it as vigenereCipher.py. Press F5 to run the program. Note that

292 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
first you will need to download the pyperclip.py module and place this file in the same directory
as the vigenereCipher.py file. You can download this file from http://invpy.com/pyperclip.py.
Source code for vigenereCipher.py
1. # Vigenere Cipher (Polyalphabetic Substitution Cipher)
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import pyperclip
5.
6. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
7.
8. def main():
9. # This text can be copy/pasted from http://invpy.com/vigenereCipher.py
10. myMessage = """Alan Mathison Turing was a British mathematician,
logician, cryptanalyst, and computer scientist. He was highly influential in
the development of computer science, providing a formalisation of the concepts
of "algorithm" and "computation" with the Turing machine. Turing is widely
considered to be the father of computer science and artificial intelligence.
During World War II, Turing worked for the Government Code and Cypher School
(GCCS) at Bletchley Park, Britain's codebreaking centre. For a time he was head
of Hut 8, the section responsible for German naval cryptanalysis. He devised a
number of techniques for breaking German ciphers, including the method of the
bombe, an electromechanical machine that could find settings for the Enigma
machine. After the war he worked at the National Physical Laboratory, where he
created one of the first designs for a stored-program computer, the ACE. In
1948 Turing joined Max Newman's Computing Laboratory at Manchester University,
where he assisted in the development of the Manchester computers and became
interested in mathematical biology. He wrote a paper on the chemical basis of
morphogenesis, and predicted oscillating chemical reactions such as the
Belousov-Zhabotinsky reaction, which were first observed in the 1960s. Turing's
homosexuality resulted in a criminal prosecution in 1952, when homosexual acts
were still illegal in the United Kingdom. He accepted treatment with female
hormones (chemical castration) as an alternative to prison. Turing died in
1954, just over two weeks before his 42nd birthday, from cyanide poisoning. An
inquest determined that his death was suicide; his mother and some others
believed his death was accidental. On 10 September 2009, following an Internet
campaign, British Prime Minister Gordon Brown made an official public apology
on behalf of the British government for "the appalling way he was treated." As
of May 2012 a private member's bill was before the House of Lords which would
grant Turing a statutory pardon if enacted."""
11. myKey = 'ASIMOV'
12. myMode = 'encrypt' # set to 'encrypt' or 'decrypt'
13.
14. if myMode == 'encrypt':
15. translated = encryptMessage(myKey, myMessage)
16. elif myMode == 'decrypt':

Chapter 19 – The Vigenère Cipher 293
17. translated = decryptMessage(myKey, myMessage)
18.
19. print('%sed message:' % (myMode.title()))
20. print(translated)
21. pyperclip.copy(translated)
22. print()
23. print('The message has been copied to the clipboard.')
24.
25.
26. def encryptMessage(key, message):
27. return translateMessage(key, message, 'encrypt')
28.
29.
30. def decryptMessage(key, message):
31. return translateMessage(key, message, 'decrypt')
32.
33.
34. def translateMessage(key, message, mode):
35. translated = [] # stores the encrypted/decrypted message string
36.
37. keyIndex = 0
38. key = key.upper()
39.
40. for symbol in message: # loop through each character in message
41. num = LETTERS.find(symbol.upper())
42. if num != -1: # -1 means symbol.upper() was not found in LETTERS
43. if mode == 'encrypt':
44. num += LETTERS.find(key[keyIndex]) # add if encrypting
45. elif mode == 'decrypt':
46. num -= LETTERS.find(key[keyIndex]) # subtract if decrypting
47.
48. num %= len(LETTERS) # handle the potential wrap-around
49.
50. # add the encrypted/decrypted symbol to the end of translated.
51. if symbol.isupper():
52. translated.append(LETTERS[num])
53. elif symbol.islower():
54. translated.append(LETTERS[num].lower())
55.
56. keyIndex += 1 # move to the next letter in the key
57. if keyIndex == len(key):
58. keyIndex = 0
59. else:
60. # The symbol was not in LETTERS, so add it to translated as is.
61. translated.append(symbol)
62.

294 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
63. return ''.join(translated)
64.
65.
66. # If vigenereCipher.py is run (instead of imported as a module) call
67. # the main() function.
68. if __name__ == '__main__':
69. main()
Sample Run of the Vigenère Cipher Program
Encrypted message:
Adiz Avtzqeci Tmzubb wsa m Pmilqev halpqavtakuoi, lgouqdaf, kdmktsvmztsl, izr
xoexghzr kkusitaaf. Vz wsa twbhdg ubalmmzhdad qz hce vmhsgohuqbo ox kaakulmd
gxiwvos, krgdurdny i rcmmstugvtawz ca tzm ocicwxfg jf "stscmilpy" oid
...skipped for brevity...
uiydviyv, Nfdtaat Dmiem Ywiikbqf Bojlab Wrgez avdw iz cafakuog pmjxwx ahwxcby
gv nscadn at ohw Jdwoikp scqejvysit xwd "hce sxboglavs kvy zm ion tjmmhzd." Sa
at Haq 2012 i bfdvsbq azmtmd'g widt ion bwnafz tzm Tcpsw wr Zjrva ivdcz eaigd
yzmbo Tmzubb a kbmhptgzk dvrvwz wa efiohzd.
The message has been copied to the clipboard.
How the Program Works
vigenereCipher.py
1. # Vigenere Cipher (Polyalphabetic Substitution Cipher)
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import pyperclip
5.
6. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
The beginning of the program has the usual comments to describe the program, an import
statement for the pyperclip module, and creates a variable called LETTERS with a string of
every uppercase letter.
vigenereCipher.py
8. def main():
9. # This text can be copy/pasted from http://invpy.com/vigenereCipher.py
10. myMessage = """Alan Mathison Turing was a British mathematician,
...skipped for brevity...

Chapter 19 – The Vigenère Cipher 295
grant Turing a statutory pardon if enacted."""
11. myKey = 'ASIMOV'
12. myMode = 'encrypt' # set to 'encrypt' or 'decrypt'
13.
14. if myMode == 'encrypt':
15. translated = encryptMessage(myKey, myMessage)
16. elif myMode == 'decrypt':
17. translated = decryptMessage(myKey, myMessage)
18.
19. print('%sed message:' % (myMode.title()))
20. print(translated)
21. pyperclip.copy(translated)
22. print()
23. print('The message has been copied to the clipboard.')
The main() function for the Vigenère cipher is exactly like the other main() functions in this
book: there are variables for message, key, and mode. The user sets these variables on lines
10, 11, and 12 before running the program. The encrypted or decrypted message (depending on
what myMode is set to) is stored in a variable named translated so that it can be printed to
the screen (on line 20) and copied to the clipboard (on line 21).
The code that does the actual encryption and decryption is in translateMessage(), which is
explained later.
vigenereCipher.py
26. def encryptMessage(key, message):
27. return translateMessage(key, message, 'encrypt')
28.
29.
30. def decryptMessage(key, message):
31. return translateMessage(key, message, 'decrypt')
Since the encryption and decryption use much of the same code as the other, we put them both in
translateMessage(). The encryptMessage() and decryptMessage() functions
are wrapper functions for translateMessage(). (Wrapper functions were covered in
Chapter 17.)
vigenereCipher.py
34. def translateMessage(key, message, mode):
35. translated = [] # stores the encrypted/decrypted message string
36.
37. keyIndex = 0

296 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
38. key = key.upper()
In the translateMessage() function, we will slowly build the encrypted (or decrypted)
string one character at a time. The list in translated will store these characters so that they
can be joined together once the string building is done. (The reason we use a list instead of just
appending the characters to a string is explained in the “Building Strings in Python with Lists”
section in Chapter 18.)
Remember, the Vigenère cipher is just the Caesar cipher except that a different key is used
depending on the position of the letter in the message. The keyIndex variable keeps track of
which subkey to use. The keyIndex variable starts off as 0, because the letter used to encrypt
or decrypt the first character of the message will be the one at key[0].
Our code assumes that the key has only uppercase letters. To make sure the key is valid, line 38
sets the key to be the uppercase version of it.
vigenereCipher.py
40. for symbol in message: # loop through each character in message
41. num = LETTERS.find(symbol.upper())
42. if num != -1: # -1 means symbol.upper() was not found in LETTERS
43. if mode == 'encrypt':
44. num += LETTERS.find(key[keyIndex]) # add if encrypting
45. elif mode == 'decrypt':
46. num -= LETTERS.find(key[keyIndex]) # subtract if decrypting
The rest of the code in translateMessage() is similar to the Caesar cipher code. The for
loop on line 40 sets the characters in message to the variable symbol on each iteration of the
loop. On line 41 we find the index of the uppercase version of this symbol in LETTERS. (This is
how we translate a letter into a number).
If num was not set to -1 on line 41, then the uppercase version of symbol was found in
LETTERS (meaning that symbol is a letter). The keyIndex variable keeps track of which
subkey to use, and the subkey itself will always be what key[keyIndex] evaluates to.
Of course, this is just a single letter string. We need to find this letter’s index in the LETTERS to
convert the subkey into an integer. This integer is then added (if encrypting) to the symbol’s
number on line 44 or subtracted (if decrypting) to the symbol’s number on line 46.
vigenereCipher.py
48. num %= len(LETTERS) # handle the potential wrap-around

Chapter 19 – The Vigenère Cipher 297
In the Caesar cipher code, we checked if the new value of num was less than 0 (in which case, we
added len(LETTERS) to it) or if the new value of num was len(LETTERS) or greater (in
which case, we subtracted len(LETTERS) from it). This handles the “wrap-around” cases.
However, there is a simpler way that handles both of these cases. If we mod the integer stored in
num by len(LETTERS), then this will do the exact same thing except in a single line of code.
For example, if num was -8 we would want to add 26 (that is, len(LETTERS)) to it to get 18.
Or if num was 31 we would want to subtract 26 to get 5. However -8 % 26 evaluates to 18
and 31 % 26 evaluates to 5. The modular arithmetic on line 48 handles both “wrap-around”
cases for us.
vigenereCipher.py
50. # add the encrypted/decrypted symbol to the end of translated.
51. if symbol.isupper():
52. translated.append(LETTERS[num])
53. elif symbol.islower():
54. translated.append(LETTERS[num].lower())
The encrypted (or decrypted) character exists at LETTERS[num]. However, we want the
encrypted (or decrypted) character’s case to match symbol’s original case. So if symbol is an
uppercase letter, the condition on line 51 will be True and line 52 will append the character at
LETTERS[num] to translated. (Remember, all the characters in the LETTERS string are
already uppercase.)
However, if symbol is a lowercase letter, than the condition on line 53 will be True instead and
line 54 will append the lowercase form of LETTERS[num] to translated instead. This is
how we can get the encrypted (or decrypted) message to match the casing of the original
message.
vigenereCipher.py
56. keyIndex += 1 # move to the next letter in the key
57. if keyIndex == len(key):
58. keyIndex = 0
Now that we have translated the symbol, we want to make sure that on the next iteration of the
for loop we use the next subkey. Line 56 increments keyIndex by one. This way when the
next iteration uses key[keyIndex] to get the subkey, it will be the index to the next subkey.
298 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
However, if we were on the last subkey in the key, then keyIndex would be equal to the length
of key. Line 57 checks for this condition, and resets keyIndex back to 0 on line 58. That way
key[keyIndex] will point back to the first subkey.
vigenereCipher.py
59. else:
60. # The symbol was not in LETTERS, so add it to translated as is.
61. translated.append(symbol)
From the indentation you can tell that the else statement on line 59 is paired with the if
statement on line 42. The code on line 61 executes if the symbol was not found in the LETTERS
string. This happens if symbol is a number or punctuation mark such as '5' or '?'. In this
case, line 61 will just append the symbol untranslated.
vigenereCipher.py
63. return ''.join(translated)
Now that we are done building the string in translated, we call the join() method on the
blank string to join together all the strings in translated (with a blank in between them).
vigenereCipher.py
66. # If vigenereCipher.py is run (instead of imported as a module) call
67. # the main() function.
68. if __name__ == '__main__':
69. main()
Lines 68 and 69 call the main() function if this program was run by itself, rather than imported
by another program that wants to use its encryptMessage() and decryptMessage()
functions.
Summary
We are close to the end of the book, but notice how the Vigenère cipher isn’t that much more
complicated than the second cipher program in this book, the Caesar cipher. With just a few
changes, we can create a cipher that has exponentially many more possible keys than can be
brute-forced.
The Vigenère cipher is not vulnerable to the dictionary word pattern attack that our Simple
Substitution hacker program uses. The “indecipherable cipher” kept secret messages secret for
hundreds of years. The attack on the Vigenère cipher was not widely known until the early 20th
century. But of course, this cipher too eventually fell. In the next couple of chapters, we will learn
new “frequency analysis” techniques to hack the Vigenère cipher.

Chapter 20 – Frequency Analysis 299
FREQUENCY ANALYSIS
Topics Covered In This Chapter:
Letter Frequency and ETAOIN
The sort() Method’s key and reverse Keyword Arguments
Passing Functions as Values Instead of Calling Functions
Converting Dictionaries to Lists with the keys(), values(), items() Dictionary
Methods
The ineffable talent for finding patterns in chaos
cannot do its thing unless he immerses himself in
the chaos first. If they do contain patterns, he does
not see them just now, in any rational way. But
there may be some subrational part of his mind
that can go to work, now that the letters have
passed before his eyes and through his pencil, and
that may suddenly present him with a gift-wrapped
clue--or even a full solution--a few weeks from
now while he is shaving or antenna-twiddling.
“Cryptonomicon” by Neal Stephenson
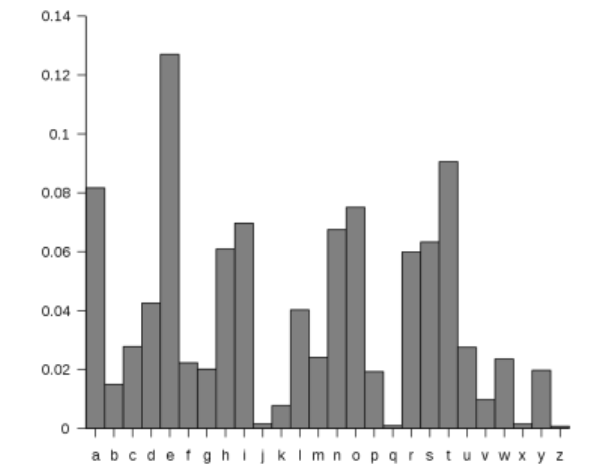
300 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
A coin has 2 sides, and when you flip a coin, about half the time it will come up heads and half of
the time it comes up tails. The frequency (that is, how often) that the coin flip ends up heads is
the same as the frequency that it ends up tails: about one-half or 50%.
There are 26 letters in the English alphabet, but they don’t each appear an equal amount of the
time in English text. Some letters are used more often than others. For example, if you look at the
letters in this book you will find that the letters E, T, A and O occur very frequently in English
words. But the letters J, X, Q, and Z are rarely found in English text. We can use this fact to help
crack Vigenère-encrypted messages. This technique is called frequency analysis.
Here are the frequencies of the 26 letters in average English text. This graph is compiled by
grabbing English text from books, newspapers, and other sources to count often each letter
appears:
Figure 20-1. Letter frequency of normal English.
If we sort these in order of greatest frequency to least, we find that E is the most frequent letter,
followed by T, followed by A, and so on:
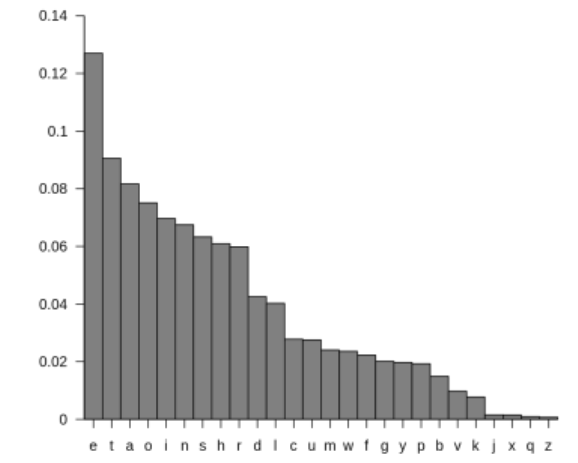
Chapter 20 – Frequency Analysis 301
Figure 20-2. Letter frequency of normal English, sorted.
The word “ETAOIN” is a handy way to remember the six most frequent letters. The full list of
letters ordered by frequency is “ETAOINSHRDLCUMWFGYPBVKJXQZ”.
Think about the transposition cipher: Messages encrypted with the transposition cipher contain all
the original letters of the original English plaintext, except in a different order. But the frequency
of each letter in the ciphertext remains the same: E, T, and A should occur much more often than
Q and Z. Because they are the same letters, the frequencies of these letters in the ciphertext are
the same as the plaintext.
The Caesar and simple substitution ciphers have their letters replaced, but you can still count the
frequency of the letters. The letters may be different but the frequencies are the same. There
should be letters that occur the most often in the ciphertext. These letters are good candidates for
being cipherletters for the E, T, or A letters. The letters in the ciphertext that occur least are more
likely to be X, Q, and Z.
This counting of letters and how frequently they appear in both plaintexts and ciphertexts is
called frequency analysis.
Since the Vigenère cipher is essentially multiple Caesar cipher keys used in the same message,
we can use frequency analysis to hack each subkey one at a time based on the letter frequency of
the attempted decryptions. We can’t use English word detection, since any word in the ciphertext
will have been encrypted with multiple subkeys. But we don’t need full words, we can analyze

302 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
the letter frequency of each subkey’s decrypted text. (This will be explained more in the next
chapter.)
Matching Letter Frequencies
By “matching the letter frequency of regular English” we could try several different algorithms.
The one used in our hacking program will simply order the letters from most frequent to least
frequent. We will calculate what we will call in this book a frequency match score for this
ordering of frequencies. To calculate the frequency match score for a string, the score starts at 0
and each time one of the letters E, T, A, O, I, N appears among the six most frequent letters of the
string, we add a point to the score. And each time one of the letters V, K, J, X, Q, or Z appears
among the six least frequent letters of the string, we add a point to the score. The frequency match
score for a string will be an integer from 0 (meaning the letter frequency of the string is
completely unlike regular English’s letter frequency) to 12 (meaning it is identical to regular
English’s letter frequency).
An Example of Calculating Frequency Match Score
For example, look at this ciphertext which was encrypted with a simple substitution cipher:
“Sy l nlx sr pyyacao l ylwj eiswi upar lulsxrj isr sxrjsxwjr, ia esmm
rwctjsxsza sj wmpramh, lxo txmarr jia aqsoaxwa sr pqaceiamnsxu, ia esmm caytra
jp famsaqa sj. Sy, px jia pjiac ilxo, ia sr pyyacao rpnajisxu eiswi lyypcor l
calrpx ypc lwjsxu sx lwwpcolxwa jp isr sxrjsxwjr, ia esmm lwwabj sj aqax px jia
rmsuijarj aqsoaxwa. Jia pcsusx py nhjir sr agbmlsxao sx jisr elh. -Facjclxo
Ctrramm”
If we count the frequency of each letter and then arrange them by order of its frequency, we end
up with this ordering: ASRXJILPWMCYOUEQNTHBFZGKVD. That is, A is the most frequent
letter, S is the 2nd most frequent letter, and so on down to the letter D, which appears the least
frequently.
The six most frequent letters in this ordering are A, S, R, X, J, and I. Only two of these letters (A
and I) appear in the ETAOIN set of letters. The six least frequent letters in the ordering are F, Z,
G, K, V, and D. Only three of these letters (Z, K, and V) appear in the VKJXQZ set of letters. So
the frequency ordering ASRXJILPWMCYOUEQNTHBFZGKVD (which comes from the above
ciphertext) has a frequency match score of 5.

Chapter 20 – Frequency Analysis 303
Figure 20-3. How the frequency match score of ASRXJILPWMCYOUEQNTHBFZGKVD is calculated.
The above ciphertext was encrypted with a simple substitution cipher, which is why the
frequency match score isn’t very high. The letter frequencies of simple substitution ciphertext
won’t match regular English’s letter frequencies.
Another Example of Calculating Frequency Match Score
For another example, look at this ciphertext which was encrypted with a transposition cipher:
“I rc ascwuiluhnviwuetnh,osgaa ice tipeeeee slnatsfietgi tittynecenisl. e fo f
fnc isltn sn o a yrs sd onisli ,l erglei trhfmwfrogotn,l stcofiit.aea
wesn,lnc ee w,l eIh eeehoer ros iol er snh nl oahsts ilasvih tvfeh rtira id
thatnie.im ei-dlmf i thszonsisehroe, aiehcdsanahiec gv gyedsB affcahiecesd d
lee onsdihsoc nin cethiTitx eRneahgin r e teom fbiotd n
ntacscwevhtdhnhpiwru”
The ordering of most to least frequent letters in the above ciphertext is:
EISNTHAOCLRFDGWVMUYBPZXQJK. (That is, E is the most frequent letter, I the 2nd most
frequent letter, and so on.)
Of the top and bottom six letters in this ordering, the four letters E, I, N, and T appear in ETAOIN
and the five letters Z, X, Q, J, and K appear in VKJXQZ. This gives the ordering a frequency
match score of 9.
Figure 20-4. How the frequency match score of EISNTHAOCLRFDGWVMUYBPZXQJK is calculated.

304 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The above ciphertext was encrypted with a transposition cipher, so it has all the same letters as
the original English plaintext (their order has just been switched around.) This is why the
frequency ordering has a much higher frequency match score.
Hacking Each Subkey
When hacking the Vigenère cipher, we try to decrypt the letters for the first subkey with each of
the 26 possible letters and find out which decrypted ciphertext produces a letter frequency that
closest matches that of regular English. This is a good indication that we have found the correct
subkey.
We can do this same thing for the second, third, fourth, and fifth subkey as well. Since we are
only doing 26 decryptions for each subkey individually, our computer only has to perform 26 +
26 + 26 + 26 + 26, or 156, decryptions. This is much easier than trying to do 11,881,376
decryptions!
So, hacking the Vigenère cipher sounds simple in theory. Just try all 26 possible subkeys for each
subkey in the key, and see which one produces decrypted text that has a letter frequency that
closest matches the letter frequency of English.
It turns out that there are a few more steps than this, though, but we can cover them when we
write the hacking program in the next chapter. For this chapter, we will write a module with
several helpful functions that perform frequency analysis. This module will have these functions:
getLetterCount() – This function will take a string parameter and return a dictionary
that has the count of how often each letter appears in the string.
getFrequencyOrder() – This function will take a string parameter and return a string of
the 26 letters ordered from those that appear most frequently to least frequently in the string
parameter.
englishFreqMatchScore() – This function will take a string parameter and return an
integer from 0 to 12 of the string’s letter frequency match score.
The Code for Matching Letter Frequencies
Type in the following code into the file editor, and then save it as freqAnalysis.py. Press F5 to run
the program.
Source code for freqAnalysis.py
1. # Frequency Finder
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4.

Chapter 20 – Frequency Analysis 305
5.
6. # frequency taken from http://en.wikipedia.org/wiki/Letter_frequency
7. englishLetterFreq = {'E': 12.70, 'T': 9.06, 'A': 8.17, 'O': 7.51, 'I':
6.97, 'N': 6.75, 'S': 6.33, 'H': 6.09, 'R': 5.99, 'D': 4.25, 'L': 4.03, 'C':
2.78, 'U': 2.76, 'M': 2.41, 'W': 2.36, 'F': 2.23, 'G': 2.02, 'Y': 1.97, 'P':
1.93, 'B': 1.29, 'V': 0.98, 'K': 0.77, 'J': 0.15, 'X': 0.15, 'Q': 0.10, 'Z':
0.07}
8. ETAOIN = 'ETAOINSHRDLCUMWFGYPBVKJXQZ'
9. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
10.
11.
12.
13. def getLetterCount(message):
14. # Returns a dictionary with keys of single letters and values of the
15. # count of how many times they appear in the message parameter.
16. letterCount = {'A': 0, 'B': 0, 'C': 0, 'D': 0, 'E': 0, 'F': 0, 'G': 0,
'H': 0, 'I': 0, 'J': 0, 'K': 0, 'L': 0, 'M': 0, 'N': 0, 'O': 0, 'P': 0, 'Q': 0,
'R': 0, 'S': 0, 'T': 0, 'U': 0, 'V': 0, 'W': 0, 'X': 0, 'Y': 0, 'Z': 0}
17.
18. for letter in message.upper():
19. if letter in LETTERS:
20. letterCount[letter] += 1
21.
22. return letterCount
23.
24.
25. def getItemAtIndexZero(x):
26. return x[0]
27.
28.
29. def getFrequencyOrder(message):
30. # Returns a string of the alphabet letters arranged in order of most
31. # frequently occurring in the message parameter.
32.
33. # first, get a dictionary of each letter and its frequency count
34. letterToFreq = getLetterCount(message)
35.
36. # second, make a dictionary of each frequency count to each letter(s)
37. # with that frequency
38. freqToLetter = {}
39. for letter in LETTERS:
40. if letterToFreq[letter] not in freqToLetter:
41. freqToLetter[letterToFreq[letter]] = [letter]
42. else:
43. freqToLetter[letterToFreq[letter]].append(letter)
44.

306 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
45. # third, put each list of letters in reverse "ETAOIN" order, and then
46. # convert it to a string
47. for freq in freqToLetter:
48. freqToLetter[freq].sort(key=ETAOIN.find, reverse=True)
49. freqToLetter[freq] = ''.join(freqToLetter[freq])
50.
51. # fourth, convert the freqToLetter dictionary to a list of tuple
52. # pairs (key, value), then sort them
53. freqPairs = list(freqToLetter.items())
54. freqPairs.sort(key=getItemAtIndexZero, reverse=True)
55.
56. # fifth, now that the letters are ordered by frequency, extract all
57. # the letters for the final string
58. freqOrder = []
59. for freqPair in freqPairs:
60. freqOrder.append(freqPair[1])
61.
62. return ''.join(freqOrder)
63.
64.
65. def englishFreqMatchScore(message):
66. # Return the number of matches that the string in the message
67. # parameter has when its letter frequency is compared to English
68. # letter frequency. A "match" is how many of its six most frequent
69. # and six least frequent letters is among the six most frequent and
70. # six least frequent letters for English.
71. freqOrder = getFrequencyOrder(message)
72.
73. matchScore = 0
74. # Find how many matches for the six most common letters there are.
75. for commonLetter in ETAOIN[:6]:
76. if commonLetter in freqOrder[:6]:
77. matchScore += 1
78. # Find how many matches for the six least common letters there are.
79. for uncommonLetter in ETAOIN[-6:]:
80. if uncommonLetter in freqOrder[-6:]:
81. matchScore += 1
82.
83. return matchScore
How the Program Works
freqAnalysis.py
1. # Frequency Finder
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.

Chapter 20 – Frequency Analysis 307
4.
5.
6. # frequency taken from http://en.wikipedia.org/wiki/Letter_frequency
7. englishLetterFreq = {'E': 12.70, 'T': 9.06, 'A': 8.17, 'O': 7.51, 'I':
6.97, 'N': 6.75, 'S': 6.33, 'H': 6.09, 'R': 5.99, 'D': 4.25, 'L': 4.03, 'C':
2.78, 'U': 2.76, 'M': 2.41, 'W': 2.36, 'F': 2.23, 'G': 2.02, 'Y': 1.97, 'P':
1.93, 'B': 1.29, 'V': 0.98, 'K': 0.77, 'J': 0.15, 'X': 0.15, 'Q': 0.10, 'Z':
0.07}
The englishLetterFreq dictionary will contain strings of the letters of the alphabet as keys
and a float for their percentage frequency as the value. (These values come from the Wikipedia
article for letter frequency: https://en.wikipedia.org/wiki/Letter_frequency) The
englishLetterFreq value isn’t actually used by our program. It is simply here for your
future reference in case you write a program that needs it.
The Most Common Letters, “ETAOIN”
freqAnalysis.py
8. ETAOIN = 'ETAOINSHRDLCUMWFGYPBVKJXQZ'
We will create a variable named ETAOIN on line 8 which will have the 26 letters of the alphabet
in order of most frequent to least frequent. The word ETAOIN is a handy way to remember the
six most common letters in English. Of course, this ordering isn’t always going to be perfect. You
could easily find a book that has a set of letter frequencies where Z is used more often than Q, for
example. Gadsby by Ernest Vicent Wright is a novel that never uses the letter E, which gives it a
very odd set of letter frequencies. But in most cases, the “ETAOIN order” will be accurate.
freqAnalysis.py
9. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
Our module will also need a string of all the uppercase letters of the alphabet for a few different
functions, so we set the LETTERS constant variable on line 9.
The Program’s getLettersCount() Function
freqAnalysis.py
13. def getLetterCount(message):
14. # Returns a dictionary with keys of single letters and values of the
15. # count of how many times they appear in the message parameter.
16. letterCount = {'A': 0, 'B': 0, 'C': 0, 'D': 0, 'E': 0, 'F': 0, 'G': 0,
'H': 0, 'I': 0, 'J': 0, 'K': 0, 'L': 0, 'M': 0, 'N': 0, 'O': 0, 'P': 0, 'Q': 0,
'R': 0, 'S': 0, 'T': 0, 'U': 0, 'V': 0, 'W': 0, 'X': 0, 'Y': 0, 'Z': 0}

308 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The getLetterCount() function returns a dictionary value where the keys are single
uppercase letter strings, and the values are an integer showing how many times that letter occurs
in the message parameter. For example, a certain string value for the message parameter with
135 A’s, 30 B’s, and so on will cause getLetterCount() to return {'A': 135, 'B': 30,
'C': 74, 'D': 58, 'E': 196, 'F': 37, 'G': 39, 'H': 87, 'I': 139, 'J': 2,
'K': 8, 'L': 62, 'M': 58, 'N': 122, 'O': 113, 'P': 36, 'Q': 2, 'R': 106,
'S': 89, 'T': 140, 'U': 37, 'V': 14, 'W': 30, 'X': 3, 'Y': 21, 'Z': 1}
Line 16 starts the letterCount variable with a dictionary that has all keys with a value of 0.
freqAnalysis.py
18. for letter in message.upper():
19. if letter in LETTERS:
20. letterCount[letter] += 1
The for loop on line 18 iterates through each character in the uppercase version of message.
On line 19, if the character exists in the LETTERS string, we know it is an uppercase letter. In
that case line 20 will increment the value at letterCount[letter].
freqAnalysis.py
22. return letterCount
After the for loop on line 18 finishes, the letterCount dictionary will have a count of how
often each letter appeared in message. This dictionary is returned from getLetterCount().
The Program’s getItemAtIndexZero() Function
freqAnalysis.py
25. def getItemAtIndexZero(x):
26. return x[0]
The getItemAtIndexZero() function is very simple: it is passed a tuple and returns the
items at index 1. This function will be passed as the key keyword argument for the sort()
method. (The reason for this will be explained later.)
The Program’s getFrequencyOrder() Function
freqAnalysis.py
29. def getFrequencyOrder(message):
30. # Returns a string of the alphabet letters arranged in order of most

Chapter 20 – Frequency Analysis 309
31. # frequently occurring in the message parameter.
32.
33. # first, get a dictionary of each letter and its frequency count
34. letterToFreq = getLetterCount(message)
The getFrequencyOrder() function will return a string with the 26 uppercase letters of the
alphabet arranged in order of how frequently they appear in the message parameter. If
message is readable English instead of random gibberish, this string will most likely be similar
(if not identical to) the string in the ETAOIN constant.
For example, if the “Alan Mathison Turing was a British mathematician…” text from Chapter
19’s vigenereCipher.py program was passed as a string to getFrequencyOrder(), the
function would return the string 'ETIANORSHCLMDGFUPBWYVKXQJZ' because E is the most
common letter in that paragraph, followed by T, then I, then A, and so on.
This function is somewhat complicated, but it breaks down to five simple steps.
The first step of getFrequencyOrder(), line 34 gets a dictionary value of the letter
frequency count from getLetterCount() for the string in the message parameter. (The
getLetterCount() function was described previously.)
If the “Alan Mathison Turing…” text was passed as a string value for the message parameter,
then line 34 would assign letterToFreq the dictionary value, {'A': 135, 'C': 74,
'B': 30, 'E': 196, 'D': 58, 'G': 39, 'F': 37, 'I': 139, 'H': 87, 'K': 8,
'J': 2, 'M': 58, 'L': 62, 'O': 113, 'N': 122, 'Q': 2, 'P': 36, 'S': 89,
'R': 106, 'U': 37, 'T': 140, 'W': 30, 'V': 14, 'Y': 21, 'X': 3, 'Z': 1}.
freqAnalysis.py
36. # second, make a dictionary of each frequency count to each letter(s)
37. # with that frequency
38. freqToLetter = {}
39. for letter in LETTERS:
40. if letterToFreq[letter] not in freqToLetter:
41. freqToLetter[letterToFreq[letter]] = [letter]
42. else:
43. freqToLetter[letterToFreq[letter]].append(letter)
For the second step of getFrequencyOrder(), while the letterToFreq dictionary has
keys of each of the 26 letters and values of their frequency count, what we need is a dictionary
value that maps the opposite: a dictionary where the keys are the frequency count and values are a
list of letters that appear that many times. While the letterToFreq dictionary maps letter keys

310 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
to frequency values, the freqToLetter dictionary will map frequency keys to list of letter
values.
Line 38 creates a blank dictionary. Line 39 loops over all the letters in LETTERS. The if
statement on line 40 checks if the letter’s frequency (that is, letterToFreq[letter])
already exists as a key in freqToLetter. If not, then line 41 adds this key with a list of the
letter as the value. Or else, line 43 appends the letter to the end of the list that is already at
letterToFreq[letter].
If we continue to use our “Alan Mathison Turing…” example value of letterToFreq then
freqToLetter would end up looking like this: {1: ['Z'], 2: ['J', 'Q'], 3: ['X'],
135: ['A'], 8: ['K'], 139: ['I'], 140: ['T'], 14: ['V'], 21: ['Y'], 30:
['B', 'W'], 36: ['P'], 37: ['F', 'U'], 39: ['G'], 58: ['D', 'M'], 62:
['L'], 196: ['E'], 74: ['C'], 87: ['H'], 89: ['S'], 106: ['R'], 113:
['O'], 122: ['N']}
The sort() Method’s key and reverse Keyword Arguments
freqAnalysis.py
45. # third, put each list of letters in reverse "ETAOIN" order, and then
46. # convert it to a string
47. for freq in freqToLetter:
48. freqToLetter[freq].sort(key=ETAOIN.find, reverse=True)
49. freqToLetter[freq] = ''.join(freqToLetter[freq])
The third step of getFrequencyOrder() to is sort the letter strings in each list in
freqToLetter in reverse ETAOIN order (as opposed to alphabetical order).
Remember that freqToLetter[freq] will evaluate to a list of letters that have a frequency
count of freq. A list is used because it’s possible that two or more letters have the exact same
frequency count, in which case this list will have two-or-more-letters strings in it.
When multiple letters are tied for frequency, we want these tied letters to be sorted in the reverse
order that they appear in the ETAOIN string. We need this so that we have a consistent way of
breaking ties. Otherwise messages with the same letter frequencies might produce different return
values from getFrequencyOrder()!
For example, if E appears 15 times, D and W appear 8 times each, and H appears 4 times, we
would want them to be sorted as 'EWDH' and not 'EDWH'. This is because while E is the most
frequent, D and W have the same frequency count but W comes after D in the ETAOIN string.

Chapter 20 – Frequency Analysis 311
Python’s sort() function can do this sorting for us if we pass it a function or method for its
key keyword argument. Normally the sort() function simply sorts the list it is called on into
alphabetical (or numeric) order. However, we can change this by passing the find() method of
the ETAOIN string as the key keyword argument. This will sort the items in the
freqToLetter[freq] list by the integer returned from the ETAOIN.find() method, that
is, the order that they appear in the ETAOIN string.
Normally the sort() method sorts the values in a list in ascending order (that is, lowest to
highest or the letter A first and letter Z last). If we pass True for the sort() method’s
reverse keyword argument, it will sort the items in descending order instead. The reason we
want to sort the letters in reverse ETAOIN order is so that ties result in lower match scores in the
englishFreqMatchScore() function rather than higher match scores. (This function is
explained later.)
If we continue using our “Alan Mathison Turing…” example value for freqToLetter, then
after the loop finishes the value stored in freqToLetter would be: {1: 'Z', 2: 'QJ', 3:
'X', 135: 'A', 8: 'K', 139: 'I', 140: 'T', 14: 'V', 21: 'Y', 30: 'BW', 36:
'P', 37: 'FU', 39: 'G', 58: 'MD', 62: 'L', 196: 'E', 74: 'C', 87: 'H', 89:
'S', 106: 'R', 113: 'O', 122: 'N'}
Notice that the strings for the 30, 37, and 58 keys are all sorted in reverse ETAOIN order.
Passing Functions as Values
freqAnalysis.py
48. freqToLetter[freq].sort(key=ETAOIN.find, reverse=True)
If you look on line 47, you’ll notice that we are not calling the find() method but instead using
the find method itself as a value that is passed to the sort() method call. In Python, functions
themselves are values just like any other values. For example, try typing this into the interactive
shell:
>>> def foo():
... print('Hello!')
...
>>> bar = foo
>>> bar()
Hello!
In the above code, we define a function named foo() that prints out the string 'Hello!'. But
this is basically defining a function and then storing it in a variable named foo. Then we copy

312 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
the function in foo to the variable bar. This means we can call bar() just like we can call
foo()! Note that in this assignment statement we do not have parentheses after foo. If we did,
we would be calling the function foo() and setting bar to its return value. Just like spam[42]
has the [42] index operating on spam, the parentheses means, “Call the value in foo as a
function.”
You can also pass functions as values just like any other value. Try typing the following into the
interactive shell:
>>> def doMath(func):
... return func(10, 5)
...
>>> def adding(a, b):
... return a + b
...
>>> def subtracting(a, b):
... return a - b
...
>>> doMath(adding)
15
>>> doMath(subtracting)
5
>>>
When the function in adding is passed to the doMath() call, the func(10, 5) line is
calling adding() and passing 10 and 5 to it. So the call func(10, 5) is effectively the
same as the call adding(10, 5). This is why doMath(adding) returns 15.
When subtracting is passed to the doMath() call, func(10, 5) is the same as
subtracting(10, 5). This is why doMath(subtracting) returns 5.
Passing a function or method to a function or method call is how the sort() method lets you
implement different sorting behavior. The function or method that is passed to sort() should
accept a single parameter and returns a value that is used to alphabetically sort the item.
To put it another way: normally sort() sorts the values in a list by the alphabetical order of the
list values.. But if we pass a function (or method) for the key keyword argument, then the values
in the list are sorted by the alphabetical or numeric order of the return value of the function when
the value in the list is passed to that function.
You can think of a normal sort() call such as this:

Chapter 20 – Frequency Analysis 313
someListVariable.sort()
…as being equivalent to this:
def func(x):
return x # sorting based on the value itself
someListVariable.sort(key=func)
So when the sort() method call is passed ETAOIN.find, instead of sorting the strings like
'A', 'B', and 'C' by the alphabetical order the sort() method sorts them by the numeric
order of the integers returned from ETAOIN.find('A'), ETAOIN.find('B'), and
ETAOIN.find('C'): that is, 2, 19, and 11 respectively. So the 'A', 'B', and 'C' strings
get sorted as 'A', 'C', and then 'B' (the order they appear in ETAOIN).
Converting Dictionaries to Lists with the keys(), values(), items()
Dictionary Methods
If you want to get a list value of all the keys in a dictionary, the keys() method will return a
dict_keys object that can be passed to list() to get a list of all the keys. There is a similar
dictionary method named values() that returns a dict_values object. Try typing the following
into the interactive shell:
>>> spam = {'cats': 10, 'dogs': 3, 'mice': 3}
>>> spam.keys()
dict_keys(['mice', 'cats', 'dogs'])
>>> list(spam.keys())
['mice', 'cats', 'dogs']
>>> list(spam.values())
[3, 10, 3]
>>>
Remember, dictionaries do not have any ordering associated with the key-value pairs they
contain. When getting a list of the keys or values, they will be in a random order in the list. If you
want to get the keys and values together, the items() dictionary method returns a dict_items
object that can be passed to list(). The list() function will then return a list of tuples
where the tuples contain a key and value pair of values. Try typing the following into the
interactive shell:
>>> spam = {'cats': 10, 'dogs': 3, 'mice': 3}
>>> list(spam.items())

314 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
[('mice', 3), ('cats', 10), ('dogs', 3)]
We will be using the items() method in our getFrequencyOrder() function, but you
should know about the keys() and values() methods too. Remember, in order to use the
return values from these methods as lists, they must be passed to the list() function. The
list() function then returns a list version of the dict_keys, dict_values, or dict_items object.

Chapter 20 – Frequency Analysis 315
Sorting the Items from a Dictionary
freqAnalysis.py
51. # fourth, convert the freqToLetter dictionary to a list of tuple
52. # pairs (key, value), then sort them
53. freqPairs = list(freqToLetter.items())
The fourth step of getFrequencyOrder() is to sort the strings from the freqToLetter
dictionary by the frequency count. Remember that the freqToLetter dictionary has integer
frequency counts for the keys and lists of single-letter strings for the values. But since dictionaries
do not have an ordering for the key-value pairs in them, we will call the items() method and
list() function to create a list of tuples of the dictionary’s key-value pairs. This list of tuples
(stored in a variable named freqPairs on line 53) is what we will sort.
freqAnalysis.py
54. freqPairs.sort(key=getItemAtIndexZero, reverse=True)
The sort() method call is passed the getItemAtIndexZero function value itself. This
means the items in the freqPairs will be sorted by the numeric order of the value at index 0 of
the tuple value, which is the frequency count integer. Line 54 also passes True for the reverse
keyword argument so that the tuples are reverse ordered from largest frequency count to smallest.
If we continue using the previous “Alan Mathison Turing…” example, the value of freqPairs
will be [(196, 'E'), (140, 'T'), (139, 'I'), (135, 'A'), (122, 'N'), (113,
'O'), (106, 'R'), (89, 'S'), (87, 'H'), (74, 'C'), (62, 'L'), (58,
'MD'), (39, 'G'), (37, 'FU'), (36, 'P'), (30, 'BW'), (21, 'Y'), (14,
'V'), (8, 'K'), (3, 'X'), (2, 'QJ'), (1, 'Z')]
freqAnalysis.py
56. # fifth, now that the letters are ordered by frequency, extract all
57. # the letters for the final string
58. freqOrder = []
59. for freqPair in freqPairs:
60. freqOrder.append(freqPair[1])
The fifth step is to create a list of all the strings from the sorted list in freqPairs. The variable
freqOrder will start as a blank list on line 58, and the string at index 1 of the tuple in
freqPairs will be appended to the end of freqOrder.
If we continue with the “Alan Mathison Turing was a British mathematician...” example from
before, after this loop has finished, freqOrder will contain the value ['E', 'T', 'I',

316 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
'A', 'N', 'O', 'R', 'S', 'H', 'C', 'L', 'MD', 'G', 'FU', 'P', 'BW', 'Y',
'V', 'K', 'X', 'QJ', 'Z']
freqAnalysis.py
62. return ''.join(freqOrder)
Line 62 creates a string from the list of strings in freqOrder by joining them together with the
join() method. If we continue using the previous example, getFrequencyOrder() will
return the string 'ETIANORSHCLMDGFUPBWYVKXQJZ'. According to this ordering, E is the
most frequent letter in the “Alan Mathison Turing…” example string, T is the second most
frequent letter, I is the third most frequent, and so on.
The Program’s englishFreqMatchScore() Function
freqAnalysis.py
65. def englishFreqMatchScore(message):
66. # Return the number of matches that the string in the message
67. # parameter has when its letter frequency is compared to English
68. # letter frequency. A "match" is how many of its six most frequent
69. # and six least frequent letters is among the six most frequent and
70. # six least frequent letters for English.
71. freqOrder = getFrequencyOrder(message)
The englishFreqMatchScore() function takes a string for message, and then returns an
integer between 0 and 12 to show message’s frequency match score with readable English’s
letter frequency. The higher the integer, the more that the frequency of the letters in message
matches the frequency of normal English text.
The first step in calculating the match score is to get the letter frequency ordering of message
by calling the getFrequencyOrder() function.
freqAnalysis.py
73. matchScore = 0
74. # Find how many matches for the six most common letters there are.
75. for commonLetter in ETAOIN[:6]:
76. if commonLetter in freqOrder[:6]:
77. matchScore += 1
The matchScore variable starts off at 0 on line 73. The for loop on line 75 goes through each
of the first 6 letters of the ETAOIN string. Remember that the [:6] slice is the same thing as
[0:6]. If one of these E, T, A, O, I, or N letters is in the first six letters in the freqOrder
string, then line 76’s condition is True and line 77 will increment matchScore.
Chapter 20 – Frequency Analysis 317
freqAnalysis.py
78. # Find how many matches for the six least common letters there are.
79. for uncommonLetter in ETAOIN[-6:]:
80. if uncommonLetter in freqOrder[-6:]:
81. matchScore += 1
Lines 79 to 81 are much like lines 75 to 77, except the last six letters in ETAOIN (V, K, J, X, Q,
and Z) are checked to see if they are in the last six letters in the freqOrder string. If they are,
then matchScore is incremented.
freqAnalysis.py
83. return matchScore
The integer in matchScore is returned on line 83.
The 14 letters in the middle of the frequency ordering are ignored with our frequency match score
calculation. This approach to comparing letter frequencies is pretty simple, but it works well
enough for our hacking program in the next chapter.
Summary
The sort() function is useful for sorting the values in a list. Normally sort() will sort them
in alphabetical or numerical order. But the reverse and key keyword arguments can be used to
sort them in different orders. This chapter also explains how functions themselves can be passed
as values in function calls.
Let’s use the frequency analysis module to hack the Vigenère cipher, a cipher that perplexed
cryptanalysts for hundreds of years!

318 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
HACKING THE VIGENÈRE CIPHER
Topics Covered In This Chapter:
The extend() list method
The Set data type and set() function
The itertools.product() function
Alan says, “When we want to sink a convey, we send out an
observation plane first. It is ostensibly an observation plane. Of
course, to observe is not its real duty—We already know exactly
where the convoy is. Its real duty is to be observed—That is, to fly
close enough to the convoy that it will be noticed by the lookouts on
the ships. The ships will then send out a radio message to the effect
that they have been sighted by an Allied observation plane. Then,
when we come round and sink them, the Germans will not find it
suspicious—At least, not quite so monstrously suspicious that we
knew exactly where to go.”
...
Alan says, “Unless we continue to do stunningly idiotic things like
sinking convoys in the fog, they will never receive any clear and
unmistakable indications that we have broken Enigma.”
“Cryptonomicon” by Neal Stephenson

Chapter 21 – Hacking the Vigenère Cipher 319
There are two different methods to hack the Vigenère cipher. The first is a brute-force attack that
tries every word in the dictionary file as the Vigenère key. This method will only work if an
English word like “RAVEN” or “DESK” was used for the key instead of a random key like
“VUWFE” or “PNFJ”. The second is a more sophisticated method that works even if a random
key was used. The earliest record of its use was by the mathematician Charles Babbage in the 19th
century.
The Dictionary Attack
If the Vigenère key is an English word it is very easy to memorize. But never use an English
word for the encryption key. This makes your ciphertext vulnerable to a dictionary attack.
A dictionary attack is a brute-force technique where a hacker attempts to decrypt the ciphertext
using the words from a dictionary file as the keys. The dictionary.txt dictionary file available on
this book’s website (at http://invpy.com/dictionary.txt) has about 45,000 English words. It takes
less than 5 minutes for my computer to run through all of these decryptions for a message the size
of a long paragraph.
Source Code for a Vigenère Dictionary Attack Program
Open a new file editor window by clicking on File ► New Window. Type in the following code
into the file editor, and then save it as vigenereDictionaryHacker.py. Press F5 to run the program.
Note that first you will need to download the pyperclip.py module and place this file in the same
directory as the vigenereDictionaryHacker.py file. You can download this file from
http://invpy.com/pyperclip.py.
Source code for vigenereDictionaryHacker.py
1. # Vigenere Cipher Dictionary Hacker
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import detectEnglish, vigenereCipher, pyperclip
5.
6. def main():
7. ciphertext = """Tzx isnz eccjxkg nfq lol mys bbqq I lxcz."""
8. hackedMessage = hackVigenere(ciphertext)
9.
10. if hackedMessage != None:
11. print('Copying hacked message to clipboard:')
12. print(hackedMessage)
13. pyperclip.copy(hackedMessage)
14. else:
15. print('Failed to hack encryption.')
16.

320 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
17.
18. def hackVigenere(ciphertext):
19. fo = open('dictionary.txt')
20. words = fo.readlines()
21. fo.close()
22.
23. for word in words:
24. word = word.strip() # remove the newline at the end
25. decryptedText = vigenereCipher.decryptMessage(word, ciphertext)
26. if detectEnglish.isEnglish(decryptedText, wordPercentage=40):
27. # Check with user to see if the decrypted key has been found.
28. print()
29. print('Possible encryption break:')
30. print('Key ' + str(word) + ': ' + decryptedText[:100])
31. print()
32. print('Enter D for done, or just press Enter to continue
breaking:')
33. response = input('> ')
34.
35. if response.upper().startswith('D'):
36. return decryptedText
37.
38. if __name__ == '__main__':
39. main()
Sample Run of the Vigenère Dictionary Hacker Program
When you run this program the output will look like this:
Possible encryption break:
Key ASTROLOGY: The recl yecrets crk not the qnks I tell.
Enter D for done, or just press Enter to continue breaking:
>
Possible encryption break:
Key ASTRONOMY: The real secrets are not the ones I tell.
Enter D for done, or just press Enter to continue breaking:
> d
Copying hacked message to clipboard:
The real secrets are not the ones I tell.
The first keyword it suggests (“ASTROLOGY”) doesn’t quite work, so the user presses Enter to
let the hacking program continue until it gets the correct decryption key (“ASTRONOMY”).

Chapter 21 – Hacking the Vigenère Cipher 321
The readlines() File Object Method
20. words = fo.readlines()
File objects returned from open() have a readlines() method. Unlike the read() method
which returns the full contents of the file as a single string, the readlines() method will
return a list of strings, where each string is a single line from the file. Note that each of the strings
in the list will end with a \n newline character (except for possibly the very last string, since the
file might not have ended with a newline).
The source code for this program isn’t anything we haven’t seen in previous hacking programs in
this book, aside from the new readlines() method. The hackVigenere() function reads
in the contents of the dictionary file, uses each word in that file to decrypt the ciphertext, and if
the decrypted text looks like readable English it will prompt the user to quit or continue.
As such, we won’t do a line-by-line explanation for this program, and instead continue on with a
program that can hack the Vigenère cipher even when the key was not a word that can be found
in the dictionary.
The Babbage Attack & Kasiski Examination
Charles Babbage is known to have broken the Vigenère cipher, but he never published his results.
Later studies revealed he used a method that was later published by early 20th-century
mathematician Friedrich Kasiski.
“Kasiski Examination” is a process used to determine how long the Vigenère key used to encrypt
a ciphertext was. After this is determined, frequency analysis can be used to break each of the
subkeys.
Kasiski Examination, Step 1 – Find Repeat Sequences’ Spacings
The first part of Kasiski Examination is to find every repeated set of letters at least three letters
long in the ciphertext. These are significant, because they could indicate that they were the same
letters of plaintext encrypted with the same subkeys of the key. For example, if the ciphertext is
“Ppqca xqvekg ybnkmazu ybngbal jon i tszm jyim. Vrag voht vrau c tksg. Ddwuo xitlazu vavv
raz c vkb qp iwpou.” and we remove the non-letters, the ciphertext looks like this:
PPQCAXQVEKGYBNKMAZUYBNGBALJONITSZMJYIMVRAGVOHTVRAUCTKSGDDWUOXITLA
ZUVAVVRAZCVKBQPIWPOU
You can see that the sequences VRA, AZU, and YBN repeat in this ciphertext:

322 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
PPQCAXQVEKGYBNKMAZUYBNGBALJONITSZMJYIMVRAGVOHTVRAUCTKSGDDWUOXITLA
ZUVAVVRAZCVKBQPIWPOU
PPQCAXQVEKGYBNKMAZUYBNGBALJONITSZMJYIMVRAGVOHTVRAUCTKSGDDWUOXITLA
ZUVAVVRAZCVKBQPIWPOU
PPQCAXQVEKGYBNKMAZUYBNGBALJONITSZMJYIMVRAGVOHTVRAUCTKSGDDWUOXITLA
ZUVAVVRAZCVKBQPIWPOU
After finding the repeated sequences, get a count of the spacing between the sequences. If we
count the number of letters between the start of each of these sequences, we find that:
Between the first and second VRA sequences there are 8 letters.
Between the second and third VRA sequences there are 24 letters.
Between the first and third VRA sequences there are 32 letters.
Between the first and second AZU there are 48 letters.
Between the first and second YBN there are 8 letters.
Kasiski Examination, Step 2 – Get Factors of Spacings
So the spacings are 8, 8, 24, 32, and 48. Let’s find the factors of each of these numbers (not
including one):
The factors of 8 are 2, 4, and 8.
The factors of 24 are 2, 4, 6, 8, 12, and 24.
The factors of 32 are 2, 4, 8, and 16.
The factors of 48 are 2, 4, 6, 8, 12, 24, and 48.
So the spacings of 8, 8, 24, 32, and 48 expand to this list of factors: 2, 2, 2, 2, 4, 4, 4, 4, 6, 6, 8, 8,
8, 8, 12, 12, 16, 24, 24, and 48. If we do a count of these factors, we get this:
Table 21-1. Factor count from our “Ppqca xqvekg...” example.
Factor
Count
2
Appears 4 times.
4
Appears 4 times.
6
Appears 2 times.
8
Appears 4 times.
12
Appears 2 times.
16
Appears 1 time.
24
Appears 2 times.
48
Appears 1 time.

Chapter 21 – Hacking the Vigenère Cipher 323
The factors that have the highest count are the most likely lengths of the Vigenère key. In
our example above, these are 2, 4, and 8. The Vigenère key is probably 2, 4, or 8 letters long.
Get Every Nth Letters from a String
For this example, we will guess that the key length is 4. Next we will want to split up the
ciphertext into every 4th letter. This means we want the following underlined letters as a separate
string:
Every 4th letter starting with the first letter:
PPQCAXQVEKGYBNKMAZUYBNGBALJONITSZMJYIMVRAGVOHTVRAUCTKSGDDWUOXITLAZUVAVVRAZCVKBQPIWPOU
Every 4th letter starting with the second letter:
PPQCAXQVEKGYBNKMAZUYBNGBALJONITSZMJYIMVRAGVOHTVRAUCTKSGDDWUOXITLAZUVAVVRAZCVKBQPIWPOU
Every 4th letter starting with the third letter:
PPQCAXQVEKGYBNKMAZUYBNGBALJONITSZMJYIMVRAGVOHTVRAUCTKSGDDWUOXITLAZUVAVVRAZCVKBQPIWPOU
Every 4th letter starting with the fourth lettter:
PPQCAXQVEKGYBNKMAZUYBNGBALJONITSZMJYIMVRAGVOHTVRAUCTKSGDDWUOXITLAZUVAVVRAZCVKBQPIWPOU
When combined, they become these four strings:
Every 4th letter starting with the first letter:
PAEBABANZIAHAKDXAAAKIU
Every 4th letter starting with the second letter:
PXKNZNLIMMGTUSWIZVZBW
Every 4th letter starting with the third letter:
QQGKUGJTJVVVCGUTUVCQP
Every 4th letter starting with the fourth letter:
CVYMYBOSYRORTDOLVRVPO
If our guess from Kasiski Examination was correct and the decryption key was in fact 4
characters long, then the first subkey of the key would have been used to encrypt the characters in
the first string above, the second subkey of the key would have been used to encrypt the
characters in the second string above, and so on.
Frequency Analysis
Remember, the Vigenère cipher is the same as the Caesar cipher, except it uses multiple subkeys.
Kasiski Examination tells us how many subkeys were used for the ciphertext, now we just have to
hack each subkey one at a time. Let’s try to hack the first of these four ciphertext strings:
PAEBABANZIAHAKDXAAAKIU
We will decrypt this string 26 times, once for each of the 26 possible subkeys, and then see what
English frequency match score the decrypted text has. In the table below, the first column is the
subkey used to decrypt the PAEBABANZIAHAKDXAAAKIU string. The second column is the
returned decrypted text value from vigenereCipher.decryptMessage(subkey,

324 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
'PAEBABANZIAHAKDXAAAKIU') where subkey is the subkey from the first column. The
third column is the returned value from
freqAnalysis.englishFreqMatchScore(decryptedText) where
decryptedText is the value from the second column.
Table 21-2. English frequency match score for each decryption.
Subkey
Text When PAEB… is Decrypted
with the Subkey
English
Frequency
Match
Score
'A'
'PAEBABANZIAHAKDXAAAKIU'
2
'B'
'OZDAZAZMYHZGZJCWZZZJHT'
1
'C'
'NYCZYZYLXGYFYIBVYYYIGS'
1
'D'
'MXBYXYXKWFXEXHAUXXXHFR'
0
'E'
'LWAXWXWJVEWDWGZTWWWGEQ'
1
'F'
'KVZWVWVIUDVCVFYSVVVFDP'
0
'G'
'JUYVUVUHTCUBUEXRUUUECO'
1
'H'
'ITXUTUTGSBTATDWQTTTDBN'
1
'I'
'HSWTSTSFRASZSCVPSSSCAM'
2
'J'
'GRVSRSREQZRYRBUORRRBZL'
0
'K'
'FQURQRQDPYQXQATNQQQAYK'
1
'L'
'EPTQPQPCOXPWPZSMPPPZXJ'
0
'M'
'DOSPOPOBNWOVOYRLOOOYWI'
1
'N'
'CNRONONAMVNUNXQKNNNXVH'
2
'O'
'BMQNMNMZLUMTMWPJMMMWUG'
1
'P'
'ALPMLMLYKTLSLVOILLLVTF'
1
'Q'
'ZKOLKLKXJSKRKUNHKKKUSE'
0
'R'
'YJNKJKJWIRJQJTMGJJJTRD'
1
'S'
'XIMJIJIVHQIPISLFIIISQC'
1
'T'
'WHLIHIHUGPHOHRKEHHHRPB'
1
'U'
'VGKHGHGTFOGNGQJDGGGQOA'
1
'V'
'UFJGFGFSENFMFPICFFFPNZ'
1
'W'
'TEIFEFERDMELEOHBEEEOMY'
2
'X'
'SDHEDEDQCLDKDNGADDDNLX'
2
'Y'
'RCGDCDCPBKCJCMFZCCCMKW'
0
'Z'
'QBFCBCBOAJBIBLEYBBBLJV'
0
Chapter 21 – Hacking the Vigenère Cipher 325
The subkeys that produce decryptions with the closest frequency match to English are the ones
that are most likely to be the real subkey. In the above decryptions (for the 1st of the four
ciphertext strings), 'A', 'I', 'N', 'W', and 'X' are the subkeys that have the highest
frequency matches with English. Note that these scores are low in general because there isn’t
enough ciphertext to give us a large sample of text, but it still ends up working well.
We need to repeat this 26-decryptions-and-frequency-match for the other three strings to
find out their most likely subkeys. After this frequency analysis, we find:
The most likely subkeys for the first string are:
A, I, N, W, and X
The most likely subkeys for the second string are:
I and Z
The most likely subkey for the third string is:
C
The most likely subkeys for the fourth string are:
K, N, R, V, and Y
Brute-Force through the Possible Keys
Next we will brute-force the key by trying out every combination of subkey. Because there are 5
possible subkeys for the first subkey, 2 for the second subkey, 1 for the third subkey, and 5 for the
fourth subkey, the number of combinations is 5 × 2 × 1 × 5 or 50 possible keys to brute-force
through. This is much better than the 26 × 26 × 26 × 26 or 456,976 possible keys we would have
to brute-force through if we had not narrowed the list of possible subkeys. This difference
becomes even greater if the Vigenère key had been longer!
AICK
IICK
NICK
WICK
XICK
AICN
IICN
NICN
WICN
XICN
AICR
IICR
NICR
WICR
XICR
AICV
IICV
NICV
WICV
XICV
AICY
IICY
NICY
WICY
XICY
AZCK
IZCK
NZCK
WZCK
XZCK
AZCN
IZCN
NZCN
WZCN
XZCN
AZCR
IZCR
NZCR
WZCR
XZCR
AZCV
IZCV
NZCV
WZCV
XZCV
AZCY
IZCY
NZCY
WZCY
XZCY
Now it’s just a matter of going through all 50 of these decryption keys for the full ciphertext and
seeing which one produces a readable English plaintext. If you do this, you’ll find that the key to
the “Ppqca xqvekg…” ciphertext is “WICK”.

326 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Source Code for the Vigenère Hacking Program
Open a new file editor window by clicking on File ► New Window. Type in the following code
into the file editor, and then save it as vigenereHacker.py. Press F5 to run the program. Note that
first you will need to download the pyperclip.py module and place this file in the same directory
as the vigenereHacker.py file. You can download this file from http://invpy.com/pyperclip.py.
The ciphertext in this program may be difficult to copy from the book, but you can copy & paste
it from http://invpy.com/vigenereHacking.py. You can see if there are any differences between
the text in your program to the text of the program in this book by using the online diff tool at
http://invpy.com/hackingdiff.
Source code for vigenereHacker.py
1. # Vigenere Cipher Hacker
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import itertools, re
5. import vigenereCipher, pyperclip, freqAnalysis, detectEnglish
6.
7. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
8. SILENT_MODE = False # if set to True, program doesn't print attempts
9. NUM_MOST_FREQ_LETTERS = 4 # attempts this many letters per subkey
10. MAX_KEY_LENGTH = 16 # will not attempt keys longer than this
11. NONLETTERS_PATTERN = re.compile('[^A-Z]')
12.
13.
14. def main():
15. # Instead of typing this ciphertext out, you can copy & paste it
16. # from http://invpy.com/vigenereHacker.py
17. ciphertext = """Adiz Avtzqeci Tmzubb wsa m Pmilqev halpqavtakuoi,
lgouqdaf, kdmktsvmztsl, izr xoexghzr kkusitaaf. Vz wsa twbhdg ubalmmzhdad qz
hce vmhsgohuqbo ox kaakulmd gxiwvos, krgdurdny i rcmmstugvtawz ca tzm ocicwxfg
jf "stscmilpy" oid "uwydptsbuci" wabt hce Lcdwig eiovdnw. Bgfdny qe kddwtk
qjnkqpsmev ba pz tzm roohwz at xoexghzr kkusicw izr vrlqrwxist uboedtuuznum.
Pimifo Icmlv Emf DI, Lcdwig owdyzd xwd hce Ywhsmnemzh Xovm mby Cqxtsm Supacg
(GUKE) oo Bdmfqclwg Bomk, Tzuhvif'a ocyetzqofifo ositjm. Rcm a lqys ce oie vzav
wr Vpt 8, lpq gzclqab mekxabnittq tjr Ymdavn fihog cjgbhvnstkgds. Zm psqikmp o
iuejqf jf lmoviiicqg aoj jdsvkavs Uzreiz qdpzmdg, dnutgrdny bts helpar jf lpq
pjmtm, mb zlwkffjmwktoiiuix avczqzs ohsb ocplv nuby swbfwigk naf ohw Mzwbms
umqcifm. Mtoej bts raj pq kjrcmp oo tzm Zooigvmz Khqauqvl Dincmalwdm, rhwzq vz
cjmmhzd gvq ca tzm rwmsl lqgdgfa rcm a kbafzd-hzaumae kaakulmd, hce SKQ. Wi
1948 Tmzubb jgqzsy Msf Zsrmsv'e Qjmhcfwig Dincmalwdm vt Eizqcekbqf Pnadqfnilg,
ivzrw pq onsaafsy if bts yenmxckmwvf ca tzm Yoiczmehzr uwydptwze oid tmoohe
avfsmekbqr dn eifvzmsbuqvl tqazjgq. Pq kmolm m dvpwz ab ohw ktshiuix pvsaa at
hojxtcbefmewn, afl bfzdakfsy okkuzgalqzu xhwuuqvl jmmqoigve gpcz ie hce

Chapter 21 – Hacking the Vigenère Cipher 327
Tmxcpsgd-Lvvbgbubnkq zqoxtawz, kciup isme xqdgo otaqfqev qz hce 1960k. Bgfdny'a
tchokmjivlabk fzsmtfsy if i ofdmavmz krgaqqptawz wi 1952, wzmz vjmgaqlpad iohn
wwzq goidt uzgeyix wi tzm Gbdtwl Wwigvwy. Vz aukqdoev bdsvtemzh rilp rshadm
tcmmgvqg (xhwuuqvl uiehmalqab) vs sv mzoejvmhdvw ba dmikwz. Hpravs rdev qz
1954, xpsl whsm tow iszkk jqtjrw pug 42id tqdhcdsg, rfjm ugmbddw xawnofqzu. Vn
avcizsl lqhzreqzsy tzif vds vmmhc wsa eidcalq; vds ewfvzr svp gjmw wfvzrk
jqzdenmp vds vmmhc wsa mqxivmzhvl. Gv 10 Esktwunsm 2009, fgtxcrifo mb Dnlmdbzt
uiydviyv, Nfdtaat Dmiem Ywiikbqf Bojlab Wrgez avdw iz cafakuog pmjxwx ahwxcby
gv nscadn at ohw Jdwoikp scqejvysit xwd "hce sxboglavs kvy zm ion tjmmhzd." Sa
at Haq 2012 i bfdvsbq azmtmd'g widt ion bwnafz tzm Tcpsw wr Zjrva ivdcz eaigd
yzmbo Tmzubb a kbmhptgzk dvrvwz wa efiohzd."""
18. hackedMessage = hackVigenere(ciphertext)
19.
20. if hackedMessage != None:
21. print('Copying hacked message to clipboard:')
22. print(hackedMessage)
23. pyperclip.copy(hackedMessage)
24. else:
25. print('Failed to hack encryption.')
26.
27.
28. def findRepeatSequencesSpacings(message):
29. # Goes through the message and finds any 3 to 5 letter sequences
30. # that are repeated. Returns a dict with the keys of the sequence and
31. # values of a list of spacings (num of letters between the repeats).
32.
33. # Use a regular expression to remove non-letters from the message.
34. message = NONLETTERS_PATTERN.sub('', message.upper())
35.
36. # Compile a list of seqLen-letter sequences found in the message.
37. seqSpacings = {} # keys are sequences, values are list of int spacings
38. for seqLen in range(3, 6):
39. for seqStart in range(len(message) - seqLen):
40. # Determine what the sequence is, and store it in seq
41. seq = message[seqStart:seqStart + seqLen]
42.
43. # Look for this sequence in the rest of the message
44. for i in range(seqStart + seqLen, len(message) - seqLen):
45. if message[i:i + seqLen] == seq:
46. # Found a repeated sequence.
47. if seq not in seqSpacings:
48. seqSpacings[seq] = [] # initialize blank list
49.
50. # Append the spacing distance between the repeated
51. # sequence and the original sequence.
52. seqSpacings[seq].append(i - seqStart)
53. return seqSpacings

328 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
54.
55.
56. def getUsefulFactors(num):
57. # Returns a list of useful factors of num. By "useful" we mean factors
58. # less than MAX_KEY_LENGTH + 1. For example, getUsefulFactors(144)
59. # returns [2, 72, 3, 48, 4, 36, 6, 24, 8, 18, 9, 16, 12]
60.
61. if num < 2:
62. return [] # numbers less than 2 have no useful factors
63.
64. factors = [] # the list of factors found
65.
66. # When finding factors, you only need to check the integers up to
67. # MAX_KEY_LENGTH.
68. for i in range(2, MAX_KEY_LENGTH + 1): # don't test 1
69. if num % i == 0:
70. factors.append(i)
71. factors.append(int(num / i))
72. if 1 in factors:
73. factors.remove(1)
74. return list(set(factors))
75.
76.
77. def getItemAtIndexOne(x):
78. return x[1]
79.
80.
81. def getMostCommonFactors(seqFactors):
82. # First, get a count of how many times a factor occurs in seqFactors.
83. factorCounts = {} # key is a factor, value is how often if occurs
84.
85. # seqFactors keys are sequences, values are lists of factors of the
86. # spacings. seqFactors has a value like: {'GFD': [2, 3, 4, 6, 9, 12,
87. # 18, 23, 36, 46, 69, 92, 138, 207], 'ALW': [2, 3, 4, 6, ...], ...}
88. for seq in seqFactors:
89. factorList = seqFactors[seq]
90. for factor in factorList:
91. if factor not in factorCounts:
92. factorCounts[factor] = 0
93. factorCounts[factor] += 1
94.
95. # Second, put the factor and its count into a tuple, and make a list
96. # of these tuples so we can sort them.
97. factorsByCount = []
98. for factor in factorCounts:
99. # exclude factors larger than MAX_KEY_LENGTH

Chapter 21 – Hacking the Vigenère Cipher 329
100. if factor <= MAX_KEY_LENGTH:
101. # factorsByCount is a list of tuples: (factor, factorCount)
102. # factorsByCount has a value like: [(3, 497), (2, 487), ...]
103. factorsByCount.append( (factor, factorCounts[factor]) )
104.
105. # Sort the list by the factor count.
106. factorsByCount.sort(key=getItemAtIndexOne, reverse=True)
107.
108. return factorsByCount
109.
110.
111. def kasiskiExamination(ciphertext):
112. # Find out the sequences of 3 to 5 letters that occur multiple times
113. # in the ciphertext. repeatedSeqSpacings has a value like:
114. # {'EXG': [192], 'NAF': [339, 972, 633], ... }
115. repeatedSeqSpacings = findRepeatSequencesSpacings(ciphertext)
116.
117. # See getMostCommonFactors() for a description of seqFactors.
118. seqFactors = {}
119. for seq in repeatedSeqSpacings:
120. seqFactors[seq] = []
121. for spacing in repeatedSeqSpacings[seq]:
122. seqFactors[seq].extend(getUsefulFactors(spacing))
123.
124. # See getMostCommonFactors() for a description of factorsByCount.
125. factorsByCount = getMostCommonFactors(seqFactors)
126.
127. # Now we extract the factor counts from factorsByCount and
128. # put them in allLikelyKeyLengths so that they are easier to
129. # use later.
130. allLikelyKeyLengths = []
131. for twoIntTuple in factorsByCount:
132. allLikelyKeyLengths.append(twoIntTuple[0])
133.
134. return allLikelyKeyLengths
135.
136.
137. def getNthSubkeysLetters(n, keyLength, message):
138. # Returns every Nth letter for each keyLength set of letters in text.
139. # E.g. getNthSubkeysLetters(1, 3, 'ABCABCABC') returns 'AAA'
140. # getNthSubkeysLetters(2, 3, 'ABCABCABC') returns 'BBB'
141. # getNthSubkeysLetters(3, 3, 'ABCABCABC') returns 'CCC'
142. # getNthSubkeysLetters(1, 5, 'ABCDEFGHI') returns 'AF'
143.
144. # Use a regular expression to remove non-letters from the message.
145. message = NONLETTERS_PATTERN.sub('', message)

330 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
146.
147. i = n - 1
148. letters = []
149. while i < len(message):
150. letters.append(message[i])
151. i += keyLength
152. return ''.join(letters)
153.
154.
155. def attemptHackWithKeyLength(ciphertext, mostLikelyKeyLength):
156. # Determine the most likely letters for each letter in the key.
157. ciphertextUp = ciphertext.upper()
158. # allFreqScores is a list of mostLikelyKeyLength number of lists.
159. # These inner lists are the freqScores lists.
160. allFreqScores = []
161. for nth in range(1, mostLikelyKeyLength + 1):
162. nthLetters = getNthSubkeysLetters(nth, mostLikelyKeyLength,
ciphertextUp)
163.
164. # freqScores is a list of tuples like:
165. # [(<letter>, <Eng. Freq. match score>), ... ]
166. # List is sorted by match score. Higher score means better match.
167. # See the englishFreqMatchScore() comments in freqAnalysis.py.
168. freqScores = []
169. for possibleKey in LETTERS:
170. decryptedText = vigenereCipher.decryptMessage(possibleKey,
nthLetters)
171. keyAndFreqMatchTuple = (possibleKey,
freqAnalysis.englishFreqMatchScore(decryptedText))
172. freqScores.append(keyAndFreqMatchTuple)
173. # Sort by match score
174. freqScores.sort(key=getItemAtIndexOne, reverse=True)
175.
176. allFreqScores.append(freqScores[:NUM_MOST_FREQ_LETTERS])
177.
178. if not SILENT_MODE:
179. for i in range(len(allFreqScores)):
180. # use i + 1 so the first letter is not called the "0th" letter
181. print('Possible letters for letter %s of the key: ' % (i + 1),
end='')
182. for freqScore in allFreqScores[i]:
183. print('%s ' % freqScore[0], end='')
184. print() # print a newline
185.
186. # Try every combination of the most likely letters for each position
187. # in the key.

Chapter 21 – Hacking the Vigenère Cipher 331
188. for indexes in itertools.product(range(NUM_MOST_FREQ_LETTERS),
repeat=mostLikelyKeyLength):
189. # Create a possible key from the letters in allFreqScores
190. possibleKey = ''
191. for i in range(mostLikelyKeyLength):
192. possibleKey += allFreqScores[i][indexes[i]][0]
193.
194. if not SILENT_MODE:
195. print('Attempting with key: %s' % (possibleKey))
196.
197. decryptedText = vigenereCipher.decryptMessage(possibleKey,
ciphertextUp)
198.
199. if detectEnglish.isEnglish(decryptedText):
200. # Set the hacked ciphertext to the original casing.
201. origCase = []
202. for i in range(len(ciphertext)):
203. if ciphertext[i].isupper():
204. origCase.append(decryptedText[i].upper())
205. else:
206. origCase.append(decryptedText[i].lower())
207. decryptedText = ''.join(origCase)
208.
209. # Check with user to see if the key has been found.
210. print('Possible encryption hack with key %s:' % (possibleKey))
211. print(decryptedText[:200]) # only show first 200 characters
212. print()
213. print('Enter D for done, or just press Enter to continue
hacking:')
214. response = input('> ')
215.
216. if response.strip().upper().startswith('D'):
217. return decryptedText
218.
219. # No English-looking decryption found, so return None.
220. return None
221.
222.
223. def hackVigenere(ciphertext):
224. # First, we need to do Kasiski Examination to figure out what the
225. # length of the ciphertext's encryption key is.
226. allLikelyKeyLengths = kasiskiExamination(ciphertext)
227. if not SILENT_MODE:
228. keyLengthStr = ''
229. for keyLength in allLikelyKeyLengths:
230. keyLengthStr += '%s ' % (keyLength)

332 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
231. print('Kasiski Examination results say the most likely key lengths
are: ' + keyLengthStr + '\n')
232.
233. for keyLength in allLikelyKeyLengths:
234. if not SILENT_MODE:
235. print('Attempting hack with key length %s (%s possible
keys)...' % (keyLength, NUM_MOST_FREQ_LETTERS ** keyLength))
236. hackedMessage = attemptHackWithKeyLength(ciphertext, keyLength)
237. if hackedMessage != None:
238. break
239.
240. # If none of the key lengths we found using Kasiski Examination
241. # worked, start brute-forcing through key lengths.
242. if hackedMessage == None:
243. if not SILENT_MODE:
244. print('Unable to hack message with likely key length(s).
Brute-forcing key length...')
245. for keyLength in range(1, MAX_KEY_LENGTH + 1):
246. # don't re-check key lengths already tried from Kasiski
247. if keyLength not in allLikelyKeyLengths:
248. if not SILENT_MODE:
249. print('Attempting hack with key length %s (%s possible
keys)...' % (keyLength, NUM_MOST_FREQ_LETTERS ** keyLength))
250. hackedMessage = attemptHackWithKeyLength(ciphertext,
keyLength)
251. if hackedMessage != None:
252. break
253. return hackedMessage
254.
255.
256. # If vigenereHacker.py is run (instead of imported as a module) call
257. # the main() function.
258. if __name__ == '__main__':
259. main()
Sample Run of the Vigenère Hacking Program
When you run the vigenereHacker.py program, the output will look like this:
Kasiski Examination results say the most likely key lengths are: 3 2 6 4 12
Attempting hack with key length 3 (27 possible keys)...
Possible letters for letter 1 of the key: A L M
Possible letters for letter 2 of the key: S N O
Possible letters for letter 3 of the key: V I Z

Chapter 21 – Hacking the Vigenère Cipher 333
Attempting with key: ASV
Attempting with key: ASI
Attempting with key: ASZ
Attempting with key: ANV
Attempting with key: ANI
Attempting with key: ANZ
Attempting with key: AOV
Attempting with key: AOI
Attempting with key: AOZ
Attempting with key: LSV
Attempting with key: LSI
Attempting with key: LSZ
Attempting with key: LNV
Attempting with key: LNI
Attempting with key: LNZ
Attempting with key: LOV
Attempting with key: LOI
Attempting with key: LOZ
Attempting with key: MSV
Attempting with key: MSI
Attempting with key: MSZ
Attempting with key: MNV
Attempting with key: MNI
Attempting with key: MNZ
Attempting with key: MOV
Attempting with key: MOI
Attempting with key: MOZ
Attempting hack with key length 2 (9 possible keys)...
Possible letters for letter 1 of the key: O A E
Possible letters for letter 2 of the key: M S I
Attempting with key: OM
Attempting with key: OS
Attempting with key: OI
Attempting with key: AM
Attempting with key: AS
Attempting with key: AI
Attempting with key: EM
Attempting with key: ES
Attempting with key: EI
Attempting hack with key length 6 (729 possible keys)...
Possible letters for letter 1 of the key: A E O
Possible letters for letter 2 of the key: S D G
Possible letters for letter 3 of the key: I V X
Possible letters for letter 4 of the key: M Z Q
Possible letters for letter 5 of the key: O B Z
Possible letters for letter 6 of the key: V I K

334 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Attempting with key: ASIMOV
Possible encryption hack with key ASIMOV:
ALAN MATHISON TURING WAS A BRITISH MATHEMATICIAN, LOGICIAN, CRYPTANALYST, AND
COMPUTER SCIENTIST. HE WAS HIGHLY INFLUENTIAL IN THE DEVELOPMENT OF COMPUTER
SCIENCE, PROVIDING A FORMALISATION OF THE CON
Enter D for done, or just press Enter to continue hacking:
> d
Copying hacked message to clipboard:
Alan Mathison Turing was a British mathematician, logician, cryptanalyst, and
computer scientist. He was highly influential in the development of computer
...skipped for brevity...
his death was accidental. On 10 September 2009, following an Internet campaign,
British Prime Minister Gordon Brown made an official public apology on behalf
of the British government for "the appalling way he was treated." As of May
2012 a private member's bill was before the House of Lords which would grant
Turing a statutory pardon if enacted.
How the Program Works
vigenereHacker.py
1. # Vigenere Cipher Hacker
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import itertools, re
5. import vigenereCipher, pyperclip, freqAnalysis, detectEnglish
6.
7. LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
8. SILENT_MODE = False # if set to True, program doesn't print attempts
9. NUM_MOST_FREQ_LETTERS = 4 # attempts this many letters per subkey
10. MAX_KEY_LENGTH = 16 # will not attempt keys longer than this
11. NONLETTERS_PATTERN = re.compile('[^A-Z]')
The hacking program imports many different modules, including a new module named
itertools. The constants will be explained as they are used in the program.
vigenereHacker.py
14. def main():
15. # Instead of typing this ciphertext out, you can copy & paste it
16. # from http://invpy.com/vigenereHacker.py
17. ciphertext = """Adiz Avtzqeci Tmzubb wsa m Pmilqev halpqavtakuoi,
lgouqdaf, kdmktsvmztsl, izr xoexghzr kkusitaaf. Vz wsa twbhdg ubalmmzhdad qz

Chapter 21 – Hacking the Vigenère Cipher 335
...skipped for brevity...
at Haq 2012 i bfdvsbq azmtmd'g widt ion bwnafz tzm Tcpsw wr Zjrva ivdcz eaigd
yzmbo Tmzubb a kbmhptgzk dvrvwz wa efiohzd."""
18. hackedMessage = hackVigenere(ciphertext)
19.
20. if hackedMessage != None:
21. print('Copying hacked message to clipboard:')
22. print(hackedMessage)
23. pyperclip.copy(hackedMessage)
24. else:
25. print('Failed to hack encryption.')
The main() function of the hacking program is similar to the main() functions of previous
hacking functions. The ciphertext is passed to the hackVigenere() cipher, which either
returns the decrypted string (if the hack was successful) or the None value (if the hack failed). If
successful, the hacked message is printed to the screen and copied to the clipboard.
Finding Repeated Sequences
vigenereHacker.py
28. def findRepeatSequencesSpacings(message):
29. # Goes through the message and finds any 3 to 5 letter sequences
30. # that are repeated. Returns a dict with the keys of the sequence and
31. # values of a list of spacings (num of letters between the repeats).
32.
33. # Use a regular expression to remove non-letters from the message.
34. message = NONLETTERS_PATTERN.sub('', message.upper())
35.
36. # Compile a list of seqLen-letter sequences found in the message.
37. seqSpacings = {} # keys are sequences, values are list of int spacings
38. for seqLen in range(3, 6):
The findRepeatSequencesSpacings() locates all the repeated sequences of letters in the
message string and counts the spacings (that is, the number of letters) between the sequences.
First, line 34 converts the message to uppercase and removes any non-letter characters from
message using the sub() regular expression method.
The seqSpacings dictionary will have keys of the sequence strings and values of a list with
the integer number of letters between all the occurrences of that sequence in the key. The
previous “PPQCAXQV…” example string from earlier in the “Kasiski Examination, Step 1”
section, if passed as message, would cause findRepeatSequenceSpacings() to return
{'VRA': [8, 24, 32], 'AZU': [48], 'YBN': [8]}.
336 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The code inside line 38’s for loop will find the repeated sequences in message and calculate
the spacings. On the first iteration, it will find sequences that are exactly 3 letters long. On the
next iteration it will find sequences exactly 4 letters long, and then 5 letters long. (You can
change what sequence lengths the code searches for by modifying the range(3, 6) call on
line 38, but finding repeated sequences of length 3, 4 and 5 seems to work for most ciphertexts.)
vigenereHacker.py
39. for seqStart in range(len(message) - seqLen):
40. # Determine what the sequence is, and store it in seq
41. seq = message[seqStart:seqStart + seqLen]
The for loop on line 39 makes sure that we iterate over every possible substring of length
seqLen in the message string. Line 41 sets the seq variable with the sequence we are looking
for. For example, if seqLen is 3 and message is 'PPQCAXQ', we would want to search for the
following sequences (notice the indexes at the top of the 'PPQCAXQ' string):
Table 21-3. Values of seq from message depending on the value in seqStart.
Indexes:
0123456
On 1st iteration, seqStart is 0:
'PPQCAXQ'
(PPQ starts at index 0.)
On 2nd iteration, seqStart is 1:
'PPQCAXQ'
(PQC starts at index 1.)
On 3rd iteration, seqStart is 2:
'PPQCAXQ'
(QCA starts at index 2.)
On 4th iteration, seqStart is 3:
'PPQCAXQ'
(CAX starts at index 3.)
On 5th iteration, seqStart is 4:
'PPQCAXQ'
(AXQ starts at index 4, which is
what len(message) - seqLen
evaluates to and is the last index.)
vigenereHacker.py
43. # Look for this sequence in the rest of the message
44. for i in range(seqStart + seqLen, len(message) - seqLen):
45. if message[i:i + seqLen] == seq:
The for loop on line 44 is inside line 39’s for loop and sets i to be the indexes of every
possible sequence of length seqLen in message. These indexes start at seqStart +
seqLen (that is, after the sequence currently in seq) and go up to len(message) -
seqLen (which is the last index where a sequence of length seqLen can be found).
The expression message[i:i + seqLen] will evaluate to the substring of message that
gets checked for being a repeat of seq on line 45. If it is, then we need to calculate the spacing
and add it to the seqSpacings dictionary. This is done on lines 46 to 52.

Chapter 21 – Hacking the Vigenère Cipher 337
vigenereHacker.py
46. # Found a repeated sequence.
47. if seq not in seqSpacings:
48. seqSpacings[seq] = [] # initialize blank list
49.
50. # Append the spacing distance between the repeated
51. # sequence and the original sequence.
52. seqSpacings[seq].append(i - seqStart)
The spacing between the sequence we’ve found at message[i:i + seqLen] and the
original sequence at message[seqStart:seqStart+seqLen] is simply i -
seqStart. Notice that i and seqStart are the beginning indexes before the colons. So the
integer that i - seqStart evaluates to is the spacing between the two sequences, which is
appended to the list stored at seqSpacings[seq].
(Lines 47 and 48 guarantee there is a list at this key by checking beforehand if seq exists as a
key in seqSpacings. If it does not, then seqSpacings[seq] is set as a key with a blank
list as its value.)
vigenereHacker.py
53. return seqSpacings
By the time all these for loops have finished, the seqSpacings dictionary will contain every
repeated sequence of length 3, 4, and 5 and their spacings. This dictionary is returned from
findRepeatSequencesSpacings() on line 53.
Calculating Factors
vigenereHacker.py
56. def getUsefulFactors(num):
57. # Returns a list of useful factors of num. By "useful" we mean factors
58. # less than MAX_KEY_LENGTH + 1. For example, getUsefulFactors(144)
59. # returns [2, 72, 3, 48, 4, 36, 6, 24, 8, 18, 9, 16, 12]
60.
61. if num < 2:
62. return [] # numbers less than 2 have no useful factors
63.
64. factors = [] # the list of factors found
The only useful factors for the hacking program’s Kasiski Examination code are of length
MAX_KEY_LENGTH and under, not including 1. The getUsefulFactors() takes a num

338 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
parameter and returns a list of “useful” factors. The function does not necessarily return all the
factors of num in this list.
Line 61 checks for the special case where num is less than 2. In this case, line 62 returns the
empty list because these numbers have no useful factors.
vigenereHacker.py
66. # When finding factors, you only need to check the integers up to
67. # MAX_KEY_LENGTH.
68. for i in range(2, MAX_KEY_LENGTH + 1): # don't test 1
69. if num % i == 0:
70. factors.append(i)
71. factors.append(int(num / i))
The for loop on line 68 loops through the integers 2 up to MAX_KEY_LENGTH (including the
value in MAX_KEY_LENGTH itself, since the second argument to range() is
MAX_KEY_LENGTH + 1).
If num % i is equal to 0, then we know that i evenly divides (that is, has 0 remainder) num and
is a factor of num. In this case, line 70 appends i to the list of factors in the factors variable.
Line 71 also appends num / i (after converting it from a float to an int, since the / operator
always evaluates to a float value).
vigenereHacker.py
72. if 1 in factors:
73. factors.remove(1)
The value 1 is not a useful factor, so we remove it from the factors list. (If the Vigenère key
had a length of 1, the Vigenère cipher would be no different from the Caesar cipher!)
Removing Duplicates with the set() Function
vigenereHacker.py
74. return list(set(factors))
The factors list might contain duplicates. For example, if getUsefulFactors() was
passed 9 for the num parameter, then 9 % 3 == 0 would be True and both i and int(num
/ i) (both of which evaluate to 3) would have been appended to factors. But we don’t want
duplicate numbers to appear in our factors list.
Line 74 passes the list value in factors to set() which returns a set form of the list. The set
data type is similar to the list data type, except a set value can only contain unique values. You

Chapter 21 – Hacking the Vigenère Cipher 339
can pass a list value to the set() function and it will return a set value form of the list. This set
value will not have any duplicate values in it. If you pass this set value to list(), it will return
a list value version of the set. This is how line 74 removes duplicate values from the factors list.
Try typing the following into the interactive shell:
>>> set([1, 2, 3, 3, 4])
set([1, 2, 3, 4])
>>> spam = list(set([2, 2, 2, 'cats', 2, 2]))
>>> spam
[2, 'cats']
>>>
This list(set(factors)) code is an easy way to remove duplicate factors from the
factors list. The final list value is then returned from the function.
vigenereHacker.py
77. def getItemAtIndexOne(x):
78. return x[1]
The getItemAtIndexOne() is almost identical to getItemAtIndexZero() from the
freqAnalysis.py program in the previous chapter. This function is passed to sort() to sort based
on the item at index 1 of the items being sorted. (See the “The Program’s
getItemAtIndexZero() Function” section in Chapter 20.)
vigenereHacker.py
81. def getMostCommonFactors(seqFactors):
82. # First, get a count of how many times a factor occurs in seqFactors.
83. factorCounts = {} # key is a factor, value is how often if occurs
84.
85. # seqFactors keys are sequences, values are lists of factors of the
86. # spacings. seqFactors has a value like: {'GFD': [2, 3, 4, 6, 9, 12,
87. # 18, 23, 36, 46, 69, 92, 138, 207], 'ALW': [2, 3, 4, 6, ...], ...}
Remember, we need to know the most common factor of the sequence spacings as a part of the
Kasiski Examination because the most common factor is most likely going to be the length of the
Vigenère key.
The seqFactors parameter is a dictionary value created in the kasiskiExamination()
function, which is explained later. This dictionary has strings of sequences for keys and a list of
integer factors for the value of each key. (These are factors of the spacing integers found by
findRepeatSequencesSpacings().) For example, seqFactors could contain a

340 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
dictionary value like {'VRA': [8, 2, 4, 2, 3, 4, 6, 8, 12, 16, 8, 2, 4],
'AZU': [2, 3, 4, 6, 8, 12, 16, 24], 'YBN': [8, 2, 4]}.
The getMostCommonFactors() function will find the most common factors in
seqFactors and return a list of two-integer tuples. The first integer in the tuple will be the
factor and the second integer will be how many times it was in seqFactors.
For example, getMostCommonFactors() may return a list value such as [(3, 556),
(2, 541), (6, 529), (4, 331), (12, 325), (8, 171), (9, 156), (16,
105), (5, 98), (11, 86), (10, 84), (15, 84), (7, 83), (14, 68),
(13, 52)]. This means that in the seqFactors dictionary passed to
getMostCommonFactors(), the factor 3 showed up 556 times, the factor 2 showed up 541
times, the factor 5 showed up 529 times, and so on. Note that 3 is the most frequent factor in the
list and appears first in the list. 13 is the least frequent factor and is last in the list.
vigenereHacker.py
88. for seq in seqFactors:
89. factorList = seqFactors[seq]
90. for factor in factorList:
91. if factor not in factorCounts:
92. factorCounts[factor] = 0
93. factorCounts[factor] += 1
For the first step of getMostCommonFactors() the for loop on line 88 loops over every
sequence in seqFactors, storing it in a variable named seq on each iteration. The list of
factors in seqFactors for seq is stored in a variable named factorList on line 89.
The factors in this list are looped over with a for loop on line 90. If a factor does not exist as a
key in factorCounts, it is added on line 92 with a value of 0. On line 93,
factorCounts[factor] (that is, the factor’s value in factorCounts) is incremented.
vigenereHacker.py
95. # Second, put the factor and its count into a tuple, and make a list
96. # of these tuples so we can sort them.
97. factorsByCount = []
98. for factor in factorCounts:
99. # exclude factors larger than MAX_KEY_LENGTH
100. if factor <= MAX_KEY_LENGTH:
101. # factorsByCount is a list of tuples: (factor, factorCount)
102. # factorsByCount has a value like: [(3, 497), (2, 487), ...]
103. factorsByCount.append( (factor, factorCounts[factor]) )

Chapter 21 – Hacking the Vigenère Cipher 341
For the second step of getMostCommonFactors(), we need to sort the values in the
factorCounts dictionary by their count. But dictionaries do not have an order, so we must
first convert the dictionary into a list of two-integer tuples. (We did something similar in Chapter
20 in the getFrequencyOrder() function of the freqAnalaysis.py module.) This list value
will be stored in a variable named factorsByCount, which starts as an empty list on line 97.
The for loop on line 98 goes through each of the factors in factorCounts and appends this
(factor, factorCounts[factor]) tuple to the factorsByCount list as long as the
factor is less than or equal to MAX_KEY_LENGTH.
vigenereHacker.py
105. # Sort the list by the factor count.
106. factorsByCount.sort(key=getItemAtIndexOne, reverse=True)
107.
108. return factorsByCount
After the for loop finishes adding all the tuples to factorsByCount, the last step of
getMostCommonFactors() is that the factorsByCount list is sorted on line 106.
Because the getItemAtIndexOne function is passed for the key keyword argument and
True is passed for the reverse keyword argument, the list is sorted in descending order by the
factor counts.
After being sorted, the list in factorsByCount is returned on line 108.
The Kasiski Examination Algorithm
vigenereHacker.py
111. def kasiskiExamination(ciphertext):
112. # Find out the sequences of 3 to 5 letters that occur multiple times
113. # in the ciphertext. repeatedSeqSpacings has a value like:
114. # {'EXG': [192], 'NAF': [339, 972, 633], ... }
115. repeatedSeqSpacings = findRepeatSequencesSpacings(ciphertext)
The kasiskiExamination() function returns a list of the most likely key lengths for the
given ciphertext argument. The key lengths are integers in a list, with the first integer in the
list being the most likely key length, the second integer the second most likely, and so on.
The first step is to find the spacings between repeated sequences in the ciphertext. This is
returned from findRepeatSequencesSpacings() as a dictionary with keys of the
sequence strings and values of a list with the spacings as integers.

342 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The extend() List Method
The extend() list method is very similar to the append() list method. While the append()
method adds a single value passed to it to the end of the list, the extend() method will add
every item in a list argument to the end of the list. Try typing the following into the interactive
shell:
>>> spam = []
>>> eggs = ['cat', 'dog', 'mouse']
>>> spam.extend(eggs)
>>> spam
['cat', 'dog', 'mouse']
>>> spam.extend([1, 2, 3])
>>> spam
['cat', 'dog', 'mouse', 1, 2, 3]
>>>
Notice the difference if you pass a list to the append() list method. The list itself gets appended
to the end instead of the values in the list:
>>> spam = []
>>> eggs = ['cat', 'dog', 'mouse']
>>> spam.append(eggs)
>>> spam
[['cat', 'dog', 'mouse']]
>>> spam.append([1, 2, 3])
>>> spam
[['cat', 'dog', 'mouse'], [1, 2, 3]]
>>>
vigenereHacker.py
117. # See getMostCommonFactors() for a description of seqFactors.
118. seqFactors = {}
119. for seq in repeatedSeqSpacings:
120. seqFactors[seq] = []
121. for spacing in repeatedSeqSpacings[seq]:
122. seqFactors[seq].extend(getUsefulFactors(spacing))
While repeatedSeqSpacings is a dictionary that maps sequence strings to lists of integer
spacings, we actually need a dictionary that maps sequence strings to lists of factors of those
integer spacings. Lines 118 to 122 do this.

Chapter 21 – Hacking the Vigenère Cipher 343
Line 118 starts with an empty dictionary in seqFactors. The for loop on line 119 iterates
over every key (which is a sequence string) in repeatedSeqSpacings. For each key, line
120 sets a blank list to be the value in seqFactors.
The for loop on line 121 iterates over all the spacing integers, which are each passed to a
getUsefulFactors() call. The list returned from getUsefulFactors() has each of its
items appended to seqFactors[seq].
When all the for loops are finished, seqFactors is a dictionary that maps sequence strings to
lists of factors of integer spacings.
vigenereHacker.py
123. # See getMostCommonFactors() for a description of factorsByCount.
124. factorsByCount = getMostCommonFactors(seqFactors)
The seqFactors dictionary is passed to getMostCommonFactors() on line 124. A list of
two-integer tuples (the first integer in the tuple being the factor, the second integer being the
count of how often that factor appeared in seqFactors) is returned and stored in
factorsByCount.
vigenereHacker.py
126. # Now we extract the factor counts from factorsByCount and
127. # put them in allLikelyKeyLengths so that they are easier to
128. # use later.
129. allLikelyKeyLengths = []
130. for twoIntTuple in factorsByCount:
131. allLikelyKeyLengths.append(twoIntTuple[0])
132.
133. return allLikelyKeyLengths
The kasiskiExamination() function doesn’t return a list of two-integer tuples though, it
returns a list of integer factors. These integer factors are in the first item of the two-integer tuples
list in factorsByCount, so we need code to pull these integer factors out and put them in a
separate list.
This separate list will be stored in allLikelyKeyLengths, which to begin with is set to an
empty list on line 129. The for loop on line 130 iterates over each of the tuples in
factorsByCount, and appends the tuple’s index 0 item to the end of
allLikelyKeyLengths.

344 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
After this for loop completes, the allLikelyKeyLengths variable contains all the factor
integers that were in factorsByCount. This list is returned from
kasiskiExamination().
vigenereHacker.py
137. def getNthSubkeysLetters(n, keyLength, message):
138. # Returns every Nth letter for each keyLength set of letters in text.
139. # E.g. getNthSubkeysLetters(1, 3, 'ABCABCABC') returns 'AAA'
140. # getNthSubkeysLetters(2, 3, 'ABCABCABC') returns 'BBB'
141. # getNthSubkeysLetters(3, 3, 'ABCABCABC') returns 'CCC'
142. # getNthSubkeysLetters(1, 5, 'ABCDEFGHI') returns 'AF'
143.
144. # Use a regular expression to remove non-letters from the message.
145. message = NONLETTERS_PATTERN.sub('', message)
In order to pull out the letters from a ciphertext that were encrypted with the same subkey, we
need a function that can create a string for the 1st, 2nd, or “N th” subkey’s letters from a message.
The first part of getting these letters is to remove the non-letter characters from message using a
regular expression object and its sub() method on line 145. (Regular expressions were first
discussed in Chapter 18’s “A Brief Intro to Regular Expressions and the sub() Regex Method”.)
This letters-only string is stored as the new value in message.
vigenereHacker.py
147. i = n - 1
148. letters = []
149. while i < len(message):
150. letters.append(message[i])
151. i += keyLength
152. return ''.join(letters)
Next we will build up a string by appending the letter strings to a list and using the join() list
method to create the final string value. This approach executes much faster than string
concatenation with the + operator. (This approach was first discussed in Chapter 18’s “Building
Strings in Python with Lists” section.)
The i variable will point to the index of the letter in message that we want to append to our
string-building list. This list is stored in a variable named letters. The i variable starts with
the value n - 1 on line 147 and the letters variable starts with a blank list on line 148.
The while loop on line 149 keeps looping while i is less than the length of message. On each
iteration the letter at message[i] is appended to the list in letters. Then i is updated to
point to the next of the subkey’s letters by adding keyLength to i on line 151.

Chapter 21 – Hacking the Vigenère Cipher 345
After this loop finishes, the code on line 152 joins the single-letter string values in the letters
list together to form a single string, and this string is returned from
getNthSubkeysLetters().
vigenereHacker.py
155. def attemptHackWithKeyLength(ciphertext, mostLikelyKeyLength):
156. # Determine the most likely letters for each letter in the key.
157. ciphertextUp = ciphertext.upper()
Recall that our kasiskiExamination() function isn’t guaranteed to return the one true
integer length of the Vigenère key, but rather the function returns a list of several lengths sorted
in order of most likely to be the key length. If our code has guessed the wrong key length, then it
will have to try again with a different key length. The attemptHackWithKeyLength()
function is passed the ciphertext and the key length guess. If successful, this function returns a
string of the hacked message. If the hacking fails, the function returns None.
The hacking code works on uppercase letters but the original string will also be needed, so the
uppercase form of the ciphertext string will be stored in a separate variable named
ciphertextUp.
vigenereHacker.py
158. # allFreqScores is a list of mostLikelyKeyLength number of lists.
159. # These inner lists are the freqScores lists.
160. allFreqScores = []
161. for nth in range(1, mostLikelyKeyLength + 1):
162. nthLetters = getNthSubkeysLetters(nth, mostLikelyKeyLength,
ciphertextUp)
If we assume the value in the mostLikelyKeyLength is the correct key length, the hack
algorithm calls getNthSubkeysLetters() for each subkey and then brute-forces through
the 26 possible letters for each subkey to find the one that produces decrypted text whose letter
frequency closest matches the letter frequency of English.
First, an empty list is stored in allFreqScores on line 160. What this list stores will be
explained a little later.
The for loop on line 161 sets the nth variable to each integer from 1 to the
mostLikelyKeyLength value. (Remember, that when range() is passed two arguments,
the range goes up to, but not including, the second argument. The + 1 is put into the code so that
the integer value in mostLikelyKeyLength itself is included in the range object returned.)

346 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The letters of the Nth subkey are returned from getNthSubkeysLetters() on line 162.
vigenereHacker.py
164. # freqScores is a list of tuples like:
165. # [(<letter>, <Eng. Freq. match score>), ... ]
166. # List is sorted by match score. Higher score means better match.
167. # See the englishFreqMatchScore() comments in freqAnalysis.py.
168. freqScores = []
169. for possibleKey in LETTERS:
170. decryptedText = vigenereCipher.decryptMessage(possibleKey,
nthLetters)
171. keyAndFreqMatchTuple = (possibleKey,
freqAnalysis.englishFreqMatchScore(decryptedText))
172. freqScores.append(keyAndFreqMatchTuple)
Next, a list of English frequency match scores is stored in a list in a variable named
freqScores. This variable starts as an empty list on line 168 and then the for loop on line
169 loops through each of the 26 uppercase letter from the LETTERS string. The possibleKey
value is used to decrypt the ciphertext by calling vigenereCipher.decryptMessage()
on line 170. The subkey in possibleKey is only one letter, but the string in nthLetters is
made up of only the letters from message that would have been encrypted with that subkey if
we’ve guessed the key length correctly.
The decrypted text is then passed to freqAnalysis.englishFreqMatchScore() to see
how closely the frequency of the letters in decryptedText matches the letter frequency of
regular English. (Remember from the last chapter that the return value will be an integer between
0 and 12, with a higher number meaning a closer match.)
This frequency match score, along with the key used to decrypt, are put into a tuple that is stored
in a variable named keyAndFreqMatchTuple on line 171. This tuple is appended to the end
of freqScores on line 172.
vigenereHacker.py
173. # Sort by match score
174. freqScores.sort(key=getItemAtIndexOne, reverse=True)
After the for loop on line 169 completes, the freqScores list will contain 26 key-and-
frequency-match-score tuples: one tuple for each of the 26 subkeys. We need to sort this so that
the tuples with the largest English frequency match scores are first in the list.
This means that we want to sort by the value at index 1 of the tuples in freqScores and in
reverse (that is, descending) order. We call the sort() method on the freqScores list,

Chapter 21 – Hacking the Vigenère Cipher 347
passing the function value getItemAtIndexOne (not calling the function: note the lack of
parentheses) for the key keyword argument. The value True is passed for the reverse
keyword argument to sort in reverse (that is, descending) order.
vigenereHacker.py
176. allFreqScores.append(freqScores[:NUM_MOST_FREQ_LETTERS])
The NUM_MOST_FREQ_LETTERS constant was set to the integer value 3 on line 9. Once the
tuples in freqScores are sorted, a list containing only the first 3 tuples (that is, the tuples with
the three highest English frequency match scores) is appended to allFreqScores.
After the for loop on line 161 completes, allFreqScores will contain a number of list
values equal to the integer value in mostLikelyKeyLength. (For example, since
mostLikelyKeyLength was 3, allFreqScores would be a list of three lists.) The first
list value will hold the tuples for the top three highest matching subkeys for the first subkey of the
full Vigenère key. The second list value will hold the tuples for the top three highest matching
subkeys for the second subkey of the full Vigenère key, and so on.
Originally, if we wanted to brute-force through the full Vigenère key, there would be (26 ^ key
length) number of possible keys. For example, if the key was ROSEBUD (with a length of 7)
there would be 26 ^ 7 (that is, 8,031,810,176) possible keys.
But by checking the English frequency matching, we’ve narrowed it down to the 4 most likely
letters for each subkey, meaning that there are now only (4 ^ key length) possible keys. Using the
example of ROSEBUD (with a length of 7) for a Vigenère key, now we only need to check 4 ^ 7
(that is, 16,384) possible keys. This is a huge improvement over 8 billion!
The end Keyword Argument for print()
vigenereHacker.py
178. if not SILENT_MODE:
179. for i in range(len(allFreqScores)):
180. # use i + 1 so the first letter is not called the "0th" letter
181. print('Possible letters for letter %s of the key: ' % (i + 1),
end='')
182. for freqScore in allFreqScores[i]:
183. print('%s ' % freqScore[0], end='')
184. print() # print a newline

348 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
At this point, the user might want to know which letters are in the top three most likely list for
each subkey. If the SILENT_MODE constant was set to False, then the code on lines 178 to 184
will print out the values in allFreqScores to the screen.
Whenever the print() function is called, it will print the string passed to it on the screen along
with a newline character. If we want something else printed at the end of the string instead of a
newline character, we can specify the string for the print() function’s end keyword argument.
Try typing the following into the interactive shell:
>>> print('HEllo', end='\n')
HEllo
>>> print('Hello', end='\n')
Hello
>>> print('Hello', end='')
Hello>>> print('Hello', end='XYZ')
HelloXYZ>>>
(The above was typed into the python.exe interactive shell rather than IDLE. IDLE will always
add a newline character before printing the >>> prompt.)
The itertools.product() Function
The itertools.product() function produces every possible combination of items in a list
or list-like value, such as a string or tuple. (Though the itertools.product() function
returns a “itertools product” object value, this can be converted to a list by passing it to list().)
This combination of things is called a Cartesian product, which is where the function gets its
name. Try typing the following into the interactive shell:
>>> import itertools
>>> itertools.product('ABC', repeat=4)
<itertools.product object at 0x02C40170>
>>> list(itertools.product('ABC', repeat=4))
[('A', 'A', 'A', 'A'), ('A', 'A', 'A', 'B'), ('A', 'A', 'A', 'C'), ('A', 'A',
'B', 'A'), ('A', 'A', 'B', 'B'), ('A', 'A', 'B', 'C'), ('A', 'A', 'C', 'A'),
('A', 'A', 'C', 'B'), ('A', 'A', 'C', 'C'), ('A', 'B', 'A', 'A'), ('A', 'B',
'A', 'B'), ('A', 'B', 'A', 'C'), ('A', 'B', 'B', 'A'), ('A', 'B', 'B', 'B'),
...skipped for brevity...
('C', 'B', 'C', 'B'), ('C', 'B', 'C', 'C'), ('C', 'C', 'A', 'A'), ('C', 'C',
'A', 'B'), ('C', 'C', 'A', 'C'), ('C', 'C', 'B', 'A'), ('C', 'C', 'B', 'B'),
('C', 'C', 'B', 'C'), ('C', 'C', 'C', 'A'), ('C', 'C', 'C', 'B'), ('C', 'C',
'C', 'C')]

Chapter 21 – Hacking the Vigenère Cipher 349
As you can see, by passing 'ABC' and the integer 4 for the repeat keyword argument,
itertools.product() returns an “itertools product” object that, when converted to a list,
has tuples of four values with every possible combination of 'A', 'B', and 'C'. (This results in
a list with a total of 3 ^ 4 or 81 tuples in it.)
Since range objects returned from range() are also list-like, they can be passed to
itertools.product() as well. Try typing the following into the interactive shell:
>>> import itertools
>>> list(itertools.product(range(8), repeat=5))
[(0, 0, 0, 0, 0), (0, 0, 0, 0, 1), (0, 0, 0, 0, 2), (0, 0, 0, 0, 3), (0, 0, 0,
0, 4), (0, 0, 0, 0, 5), (0, 0, 0, 0, 6), (0, 0, 0, 0, 7), (0, 0, 0, 1, 0), (0,
0, 0, 1, 1), (0, 0, 0, 1, 2), (0, 0, 0, 1, 3), (0, 0, 0, 1, 4),
...skipped for brevity...
(7, 7, 7, 6, 6), (7, 7, 7, 6, 7), (7, 7, 7, 7, 0), (7, 7, 7, 7, 1), (7, 7, 7,
7, 2), (7, 7, 7, 7, 3), (7, 7, 7, 7, 4), (7, 7, 7, 7, 5), (7, 7, 7, 7, 6), (7,
7, 7, 7, 7)]
When the range object returned from range(8) is passed to itertools.product() (along
with 5 for the repeat keyword argument), the list that is generated has tuples of 5 values, and
each value are from the integers 0 to 7.
The itertools.product() function is an easy way to generate a list with every possible
combination of some group of values. This is how our hacking program will create integer
indexes to test every possible combination of possible subkeys.
vigenereHacker.py
186. # Try every combination of the most likely letters for each position
187. # in the key.
188. for indexes in itertools.product(range(NUM_MOST_FREQ_LETTERS),
repeat=mostLikelyKeyLength):
The allFreqScores variable is a list of lists of tuples such that allFreqScores[i] will
evaluate to a list of tuples of possible letters for a single subkey. That is, allFreqScores[0]
has a list of tuples for the first subkey, allFreqScores[1] has a list of tuples for the second
subkey, and so on.
Also, since the NUM_MOST_FREQ_LETTERS constant is set to 4,
itertools.product(range(NUM_MOST_FREQ_LETTERS),
repeat=mostLikelyKeyLength) will cause the for loop to have a tuple of integers (from
0 to 3) for the indexes variable. If 5 was passed for mostLikelyKeyLength, then the
following values would be set to indexes for each iteration:

350 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Table 21-4. Value of indexes on each iteration.
On the 1st iteration, indexes is set to:
(0, 0, 0, 0, 0)
On the 2nd iteration, indexes is set to:
(0, 0, 0, 0, 1)
On the 3rd iteration, indexes is set to:
(0, 0, 0, 0, 2)
On the 4th iteration, indexes is set to:
(0, 0, 0, 1, 0)
On the 5th iteration, indexes is set to:
(0, 0, 0, 1, 1)
And so on…
vigenereHacker.py
189. # Create a possible key from the letters in allFreqScores
190. possibleKey = ''
191. for i in range(mostLikelyKeyLength):
192. possibleKey += allFreqScores[i][indexes[i]][0]
The full Vigenère key will be constructed from the subkeys in allFreqScores using the
indexes supplied by indexes. The key starts off as a blank string on line 190, and the for loop
on line 191 will iterate through the integers from 0 up to, but not including,
mostLikelyKeyLength.
As the i variable changes for each iteration of the for loop, the value at indexes[i] will be
the index of the tuple we want to use in allFreqScores[i]. This is why
allFreqScores[i][indexes[i]] evaluates to the correct tuple we want (and the subkey
we want is at index 0 in that tuple).
vigenereHacker.py
194. if not SILENT_MODE:
195. print('Attempting with key: %s' % (possibleKey))
If SILENT_MODE is False, the key created by the for loop on line 191 is printed to the
screen.
vigenereHacker.py
197. decryptedText = vigenereCipher.decryptMessage(possibleKey,
ciphertextUp)
198.
199. if detectEnglish.isEnglish(decryptedText):
200. # Set the hacked ciphertext to the original casing.
201. origCase = []
202. for i in range(len(ciphertext)):
203. if ciphertext[i].isupper():
204. origCase.append(decryptedText[i].upper())
205. else:
206. origCase.append(decryptedText[i].lower())

Chapter 21 – Hacking the Vigenère Cipher 351
207. decryptedText = ''.join(origCase)
Now that we have a complete Vigenère key, lines 197 to 208 will decrypt the ciphertext and
check if the decrypted text is readable English. If it is, then it is printed to the screen for the user
to confirm it is English (since isEnglish() might produce a false positive).
But decryptedText is in all uppercase letters. The code on lines 201 to 207 builds a new
string by appending the origCase list with an uppercase or lowercase form of the letters in
decryptedText. The for loop on line 202 goes through each of the indexes in the
ciphertext string (which, unlike ciphertextUp, has the original casing of the
ciphertext). If ciphertext[i] is uppercase, then the uppercase form of
decryptedText[i] is appended to origCase. Otherwise, the lowercase form of
decryptedText[i] is appended. The list in origCase is then joined together on line 207 to
become the new value of decryptedText.
This table shows how the ciphertext and decryptedText values produce the strings that
go into origCase:
ciphertext
Adiz Avtzqeci Tmzubb wsa m Pmilqev halpqavtakuoi
decryptedText
ALAN MATHISON TURING WAS A BRITISH MATHEMATICIAN
''.join(origCase)
Alan Mathison Turing was a British mathematician
vigenereHacker.py
209. # Check with user to see if the key has been found.
210. print('Possible encryption hack with key %s:' % (possibleKey))
211. print(decryptedText[:200]) # only show first 200 characters
212. print()
213. print('Enter D for done, or just press Enter to continue
hacking:')
214. response = input('> ')
215.
216. if response.strip().upper().startswith('D'):
217. return decryptedText
The correctly-cased decrypted text is printed to the screen for the user to confirm it is English. If
the user enters 'D' then the function returns the decryptedText string.
vigenereHacker.py
219. # No English-looking decryption found, so return None.
220. return None

352 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Otherwise, after the for loop on line 188 iterates through all of the possible indexes to use and
none of the decryptions look like English, the hacking has failed and the None value is returned.
vigenereHacker.py
223. def hackVigenere(ciphertext):
224. # First, we need to do Kasiski Examination to figure out what the
225. # length of the ciphertext's encryption key is.
226. allLikelyKeyLengths = kasiskiExamination(ciphertext)
Now we define the hackVigenere() function, which calls all of the previous functions.
We’ve already defined all the work it will do. Let’s run through the steps it goes through to
perform the hacking. The first step is to get the most likely lengths of the Vigenère key based on
Kasiski Examination of ciphertext.
vigenereHacker.py
227. if not SILENT_MODE:
228. keyLengthStr = ''
229. for keyLength in allLikelyKeyLengths:
230. keyLengthStr += '%s ' % (keyLength)
231. print('Kasiski Examination results say the most likely key lengths
are: ' + keyLengthStr + '\n')
The likely key lengths are printed to the screen if SILENT_MODE is False.
The break Statement
Similar to how the continue statement is used inside of a loop to continue back to the start of
the loop, the break statement (which is just the break keyword by itself) is used inside of a
loop to immediately exit the loop. When the program execution “breaks out of a loop”, it
immediately moves to the first line of code after the loop ends.
vigenereHacker.py
233. for keyLength in allLikelyKeyLengths:
234. if not SILENT_MODE:
235. print('Attempting hack with key length %s (%s possible
keys)...' % (keyLength, NUM_MOST_FREQ_LETTERS ** keyLength))
236. hackedMessage = attemptHackWithKeyLength(ciphertext, keyLength)
237. if hackedMessage != None:
238. break
For each possible key length, the code calls the attemptHackWithKeyLength() function
on line 236. If attemptHackWithKeyLength() does not return None, then the hack was
successful and the program execution should break out of the for loop on line 238.

Chapter 21 – Hacking the Vigenère Cipher 353
vigenereHacker.py
240. # If none of the key lengths we found using Kasiski Examination
241. # worked, start brute-forcing through key lengths.
242. if hackedMessage == None:
243. if not SILENT_MODE:
244. print('Unable to hack message with likely key length(s).
Brute-forcing key length...')
245. for keyLength in range(1, MAX_KEY_LENGTH + 1):
246. # don't re-check key lengths already tried from Kasiski
247. if keyLength not in allLikelyKeyLengths:
248. if not SILENT_MODE:
249. print('Attempting hack with key length %s (%s possible
keys)...' % (keyLength, NUM_MOST_FREQ_LETTERS ** keyLength))
250. hackedMessage = attemptHackWithKeyLength(ciphertext,
keyLength)
251. if hackedMessage != None:
252. break
If the hack had failed for all the possible key lengths that kasiskiExamination() returned,
hackedMessage will be set to None when the if statement on line 242 executes. In this case,
all the other key lengths up to MAX_KEY_LENGTH are tried. If Kasiski Examination failed to
calculate the correct key length, then we can just brute-force through the key lengths.
Line 245 starts a for loop that will call attemptHackWithKeyLength() for each value of
keyLength (which ranges from 1 to MAX_KEY_LENGTH) as long as it was not in
allLikelyKeyLengths. (This is because the key lengths in allLikelyKeyLengths
have already been tried in the code on lines 233 to 238.)
vigenereHacker.py
253. return hackedMessage
Finally, the value in hackedMessage is returned on line 253.
vigenereHacker.py
256. # If vigenereHacker.py is run (instead of imported as a module) call
257. # the main() function.
258. if __name__ == '__main__':
259. main()
Lines 258 and 259 call the main() function if this program was run by itself rather than
imported by another program.

354 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
That’s the full Vigenère hacking program. Whether it is successful or not depends on the
characteristics of the ciphertext. Also, the closer the original plaintext’s letter frequency is to
regular English’s letter frequency and the longer the plaintext, the more likely our hacking
program will work.
Practice Exercises, Chapter 21, Set A
Practice exercises can be found at http://invpy.com/hackingpractice21A.
Modifying the Constants of the Hacking Program
There are a few things we can modify if the hacking program doesn’t work though. There are
three constants we set on lines 8 to 10 that affect how our hacking program runs:
vigenereHacker.py
8. MAX_KEY_LENGTH = 16 # will not attempt keys longer than this
If the Vigenère key was longer than the integer in MAX_KEY_LENGTH, there is no possible way
the hacking program will find the correct key. However, if we have MAX_KEY_LENGTH set very
high and the kasiskiExamination() function mistakenly thinks that the key length could
be a very large integer, the program could be spending hours (or days or months) attempting to
hack the ciphertext with wrong key lengths.
Trying to hack the wrong key length that is small is not that big of a problem: it will only take
seconds or minutes to go through the likely keys of that length. If the hacking program fails to
hack the ciphertext, try increasing this value and running the program again.
vigenereHacker.py
9. NUM_MOST_FREQ_LETTERS = 3 # attempts this many letters per subkey
The NUM_MOST_FREQ_LETTERS limits the number of possible letters tried for each subkey.
By increasing this value, the hacking program tries many more keys (which is needed if the
freqAnalysis.englishFreqMatchScore() was inaccurate for the original plaintext
message), but this will also cause the program to slow down. And setting
NUM_MOST_FREQ_LETTERS to 26 will cause the program to not narrow down the number of
possible letters for each subkey at all!
Table 21-5. Tradeoffs for the MAX_KEY_LENGTH and NUM_MOST_FREQ_LETTERS.
Smaller value:
Larger value:
Faster to execute.
Slower to execute.
Less likely to hack.
More likely to hack.

Chapter 21 – Hacking the Vigenère Cipher 355
vigenereHacker.py
10. SILENT_MODE = False # if set to True, program doesn't print attempts
While your computer can perform calculations very fast, displaying characters on the screen is
relatively slow. If you want to speed up your program, you can set SILENT_MODE to True so
that the program does not waste time printing information to the screen. On the downside, you
will not know how the program is doing until it has completely finished running.
Summary
Hacking the Vigenère cipher requires several detailed steps to follow. There are also many parts
where our hacking program could fail: perhaps the Vigenère key used for encryption was larger
in length than MAX_KEY_LENGTH, or perhaps the English frequency matching function got
inaccurate results because the plaintext doesn’t follow normal letter frequency, or maybe the
plaintext has too many words that aren’t in our dictionary file and isEnglish() doesn’t
recognize it as English.
If you identify different ways that the hacking program could fail, you could change the code to
become ever more sophisticated to handle these other cases. But the hacking program in this book
does a pretty good job at reducing billions or trillions of possible keys to brute-force through to
mere thousands.
However, there is one trick to make the Vigenère cipher mathematically impossible to break, no
matter how powerful your computer or how clever your hacking program is. We’ll learn about
these “one-time pads” in the next chapter.

356 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
THE ONE-TIME PAD CIPHER
Topics Covered In This Chapter:
The Unbreakable One-Time Pad Cipher
The Two-Time Pad is the Vigenère Cipher
“I’ve been over it a thousand times,” Waterhouse
says, “and the only explanation I can think of is
that they are converting their messages into large
binary numbers and then combining them with
other large binary numbers —one-time pads, most
likely —to produce the ciphertext.”
“In which case your project is doomed," Alan says,
"because you can't break a one-time pad.”
“Cryptonomicon” by Neal Stephenson
Chapter 22 – The One-Time Pad Cipher 357
The Unbreakable One-Time Pad Cipher
There is one cipher that is impossible to crack, no matter how powerful your computer is, how
much time you have to crack it, or how clever of a hacker you are. We won’t have to write a new
program to use it either. Our Vigenère program can implement this cipher without any changes.
But this cipher is so inconvenient to use on a regular basis that it is often only used for the most
top-secret of messages.
The one-time pad cipher is an unbreakable cipher. It is a Vigenère cipher where:
1. The key is exactly as long as the message that is encrypted.
2. The key is made up of truly random symbols.
3. The key is used one time only, and never used again for any other message.
By following these three rules, your encrypted message will be invulnerable to any cryptanalyst’s
attack. Even with literally an infinite amount of computing power, the cipher cannot be broken.
The key for the one-time pad cipher is called a pad because they were printed on pads of paper.
The top sheet of paper would be torn off the pad after it was used to reveal the next key to use.
Why the One-Time Pad is Unbreakable
To see why the one-time pad (OTP) cipher is unbreakable, let’s think about why the regular
Vigenère cipher is vulnerable to breaking. Our Vigenère cipher hacking program works by doing
frequency analysis. But if the key is the same length as the message, then every possible
ciphertext letter is equally probable to be for the same plaintext letter.
Say that we want to encrypt the message, “If you want to survive out here, you've got to know
where your towel is.” If we remove the spaces and punctuation, this message has 55 letters. So to
encrypt it with a one-time pad, we need a key that is also 55 letters long. Let’s use the key
“kcqyzhepxautiqekxejmoretzhztrwwqdylbttvejmedbsanybpxqik”. Encrypting the string looks like
this:
Plaintext
ifyouwanttosurviveouthereyouvegottoknowwhereyourtowelis
Key
kcqyzhepxautiqekxejmoretzhztrwwqdylbttvejmedbsanybpxqik
Ciphertext
shomtdecqtilchzssixghyikdfnnmacewrzlghraqqvhzguerplbbqc
Now imagine a cryptanalyst got a hold of the ciphertext (“shomtdec...”). How could she attack
the cipher? Brute-forcing through the keys would not work, because there are too many even for a
computer. The number of keys is 26 ^ (number of letters in the message), so if the message has 55
letters, there would be a total of 26 ^ 55, or 666,091,878,431,395,624,153,823,182,526,730,590,
376,250,379,52 8,249,805,353,030,484,209,594,192,101,376 possible keys.

358 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
But it turns out that even if she had a computer that was powerful enough to try all the keys, it
still would not break the one-time pad cipher. This is because for any ciphertext, all possible
plaintext messages are equally likely.
For example, given the ciphertext “shomtdec...”, we could easily say the original plaintext was
“The myth of Osiris was of importance in ancient Egyptian religion.” encrypted with the key
“zakavkxolfqdlzhwsqjbzmtwmmnakwurwexdcuywksgorghnnedvtcp”:
Plaintext
themythofosiriswasofimportanceinancientegyptianreligion
Key
zakavkxolfqdlzhwsqjbzmtwmmnakwurwexdcuywksgorghnnedvtcp
Ciphertext
shomtdecqtilchzssixghyikdfnnmacewrzlghraqqvhzguerplbbqc
The way we are able to hack encryption is because there is usually only one key that can be used
to decrypt the message to sensible English. But we’ve just shown that the same ciphertext could
have been made from two very different plaintext messages. For the one-time pad, the
cryptanalyst has no way of telling which was the original message. In fact, any readable English
plaintext message that is exactly 55 letters long is just as likely to be the original plaintext. Just
because a certain key can decrypt the ciphertext to readable English does not mean it was
the original encryption key.
Since any English plaintext could have been used to create a ciphertext with equal likelihood, it is
completely impossible to hack a message encrypted with a one-time pad.
Beware Pseudorandomness
The random module that comes with Python does not generate truly random numbers. They are
computed from an algorithm that creates numbers that only appear random (which is often good
enough). If the pad is not generated from a truly random source, then it loses its mathematically-
perfect secrecy.
The os.urandom() function can provide truly random numbers but is a bit more difficult to
use. For more information about this function, see http://invpy.com/random.
Beware the Two-Time Pad
If you do use the same one-time pad key to encrypt two different messages, you have introduced
a weakness into your encryption. Using the one-time pad cipher this way is sometimes called a
“two-time pad cipher”. It’s a joke name though, the two-time pad cipher is really just using the
one-time pad cipher incorrectly.
Just because a key decrypts the one-time pad ciphertext to readable English does not mean it is
the correct key. However, if you use the same key for two different messages, now the hacker can
Chapter 22 – The One-Time Pad Cipher 359
know that if a key decrypts the first ciphertext to readable English, but that same key decrypts the
second message to random garbage text, it must not be the original key. In fact, it is highly likely
that there is only one key that will decrypt both messages to English.
If the hacker only had one of the two messages, then it is still perfectly encrypted. But, you must
always assume that all of your encrypted messages are being intercepted by hackers and/or
governments (otherwise, you wouldn’t need to bother encrypting your messages.) Remember
Shannon’s Maxim: The enemy knows the system! This includes knowing the ciphertext.
The Two-Time Pad is the Vigenère Cipher
To see why the two-time pad is hackable just like the Vigenère Cipher, let’s think about how the
Vigenère cipher works when it encrypts a message that is longer than the key. Once we run out of
characters in the key to encrypt with, we go back to the first character of the key and continue
encrypting. So to encrypt a 20-character message like “AABBCCDDEEVVWWXXYYZZ” with
a 10-character long key such as “PRECOCIOUS”, the first ten characters (AABBCCDDEE) are
encrypted with “PRECOCIOUS” and then the next ten characters (VVWWXXYYZZ) are also
encrypted with “PRECOCIOUS”.
Plaintext
AABBCCDDEEVVWWXXYYZZ
Vigenère Key
PRECOCIOUSPRECOCIOUS
Vigenère Ciphertext
PRFDQELRYWKMAYLZGMTR
We have already learned how to break Vigenère ciphers. If we can show that a two-time pad
cipher is the same thing as a Vigenère cipher, then we can prove that it is breakable using the
same techniques used to break Vigenère cipher.
Using the one-time pad cipher, let’s say the 10-character message “AABBCCDDEE” was
encrypted with the one-time pad key “PRECOCIOUS”. Then the cryptographer makes the
mistake of encrypting a second 10-character message “VVWWXXYYZZ” with the same one-
time pad key, “PRECOCIOUS”.
Message 1 Message 2
Plaintext
AABBCCDDEE VVWWXXYYZZ
One-Time Pad Key
PRECOCIOUS PRECOCIOUS
One-Time Pad Ciphertext
PRFDQELRYW KMAYLZGMTR
If we compare the ciphertext of the Vigenère cipher and the ciphertexts of the one-time pad
cipher, we can see they are the exact same. The two-time pad cipher has the same properties as
the Vigenère cipher, which means that the same techniques could be used to hack it!
This also tells us that if we do the Vigenère cipher but use a key that is as long as the message it
is encrypting (and only use this key once for this message), then it will be perfectly unbreakable.

360 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
This is why we don’t need to write a separate one-time pad cipher program. Our Vigenère cipher
program already does it!
Practice Exercises, Chapter 22, Set A
Practice exercises can be found at http://invpy.com/hackingpractice22A.
Summary
In short, a one-time pad is just the Vigenère cipher with a key that is the same length as the
message and is only used once. As long as these two conditions are followed, it is literally
impossible to break the one-time pad. However, it is so inconvenient to use the one-time pad that
it is not generally used except for the most top-secret of secrets. Usually a large list of one-time
pad keys are generated and shared in person, with the keys marked for specific dates. This way, if
you receive a message from your collaborator on October 31st, you can just look through the list
of one-time pads to find the one for that day. But be sure this list doesn’t fall into the wrong
hands!

Chapter 23 – Finding Prime Numbers 361
FINDING PRIME NUMBERS
Topics Covered In This Chapter:
Prime and Composite Numbers
The Sieve of Eratosthenes
The Rabin-Miller Primality Test
“Mathematicians have tried in vain to this day to
discover some order in the sequence of prime
numbers, and we have reason to believe that it is a
mystery into which the human mind will never
penetrate.”
Leonhard Euler, 18th century mathematician
All of the ciphers described in this book so far have been around for hundreds of years, and all of
them (with the exception of the one-time pad) are easily broken by computers. These ciphers
worked very well when hackers had to rely on pencil and paper to hack them, but computers can
now manipulate data trillions of times faster than a person with a pencil.
The RSA cipher has several improvements over these old ciphers, and it will be detailed in the
next chapter. However, the RSA cipher will require us to learn about prime numbers first.

362 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Prime Numbers
A prime number is an integer (that is, a whole number) that is greater than 1 and has only two
factors: 1 and itself. Remember that the factors of a number are the numbers that can be
multiplied to equal the original number. The numbers 3 and 7 are factors of 21. The number 12
has factors 2 and 6, but also 3 and 4.
Every number has factors of 1 and itself. The numbers 1 and 21 are factors of 21. The numbers 1
and 12 are factors of 12. This is because 1 times any number will always be that same number.
But if no other factors exist for that number, then that number is prime.
Here’s a list of prime numbers (note that 1 is not considered a prime number):
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103,
107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199,
211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281 …and so on, FOREVER.
There are an infinite number of prime numbers. This means there is no “largest” prime. They just
keep getting bigger and bigger, just like regular numbers do. (See http://invpy.com/infiniteprimes
for a proof of this.) The RSA cipher makes use of very large prime numbers in the keys it uses.
Because of this, there will be far too many keys to brute-force through.
A googol is the number that has a one with a hundred zeros behind it:
10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,00
0,000,000,000,000,000,000,000,000,000,000,000
(As a bit of history: the name of the search engine company Google came from misspelling
“googol”, but they decided they liked that spelling better and kept it.)
A billion billion billion googols has twenty-seven more zeros than a googol:
10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,00
0,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
But these are tiny numbers. A typical prime number used in our RSA program will have hundreds
of digits:
112,829,754,900,439,506,175,719,191,782,841,802,172,556,768,253,593,054,977,186,2355,84,9
79,780,304,652,423,405,148,425,447,063,090,165,759,070,742,102,132,335,103,295,947,000,71
8,386,333,756,395,799,633,478,227,612,244,071,875,721,006,813,307,628,061,280,861,610,153,
485,352,017,238,548,269,452,852,733,818,231,045,171,038,838,387,845,888,589,411,762,622,0
41,204,120,706,150,518,465,720,862,068,595,814,264,819

Chapter 23 – Finding Prime Numbers 363
The above number is so big, I’m going to guess you didn’t even read it to notice the typo in it.
Composite Numbers
Integers that are not prime numbers are called composite numbers, because they are composed
of at least two factors besides 1 and the number itself. They are called composite numbers
because these number are composed of prime numbers multiplied together, such as the composite
number 1,386 being composed of the prime numbers in 2 × 3 × 3 × 7 × 11.
Here are four facts about prime numbers:
1. Prime numbers are integers greater than 1that have only 1 and themselves as factors.
2. Two is the only even prime number. (Though I guess that makes two a very odd
prime number.)
3. There are an infinite number of prime numbers. There is no “largest prime number”.
4. Multiplying two prime numbers will give a number that only has two pairs of
factors, 1 and itself (like all numbers do), and the two prime numbers that were
multiplied. For example, 3 and 7 are prime numbers. 3 times 7 is 21. The only
factors for 21 are 1, 21, 3, and 7.
Source Code for The Prime Sieve Module
First we will create a module that has functions related to prime numbers:
isPrime() will return either True or False if the number passed to it is prime or not. It will
use the “divides test” algorithm.
primeSieve() will use the “Sieve of Eratosthenes” algorithm (explained later) to generate
numbers.
Like cryptomath.py, the primeSieve.py program is only meant to be imported as a module to our
other programs. It does not do anything when run on its own.
Open a new file editor window by clicking on File ► New Window. Type in the following code
into the file editor, and then save it as primeSieve.py.
Source code for primeSieve.py
1. # Prime Number Sieve
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import math
5.
6.
7. def isPrime(num):

364 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
8. # Returns True if num is a prime number, otherwise False.
9.
10. # Note: Generally, isPrime() is slower than primeSieve().
11.
12. # all numbers less than 2 are not prime
13. if num < 2:
14. return False
15.
16. # see if num is divisible by any number up to the square root of num
17. for i in range(2, int(math.sqrt(num)) + 1):
18. if num % i == 0:
19. return False
20. return True
21.
22.
23. def primeSieve(sieveSize):
24. # Returns a list of prime numbers calculated using
25. # the Sieve of Eratosthenes algorithm.
26.
27. sieve = [True] * sieveSize
28. sieve[0] = False # zero and one are not prime numbers
29. sieve[1] = False
30.
31. # create the sieve
32. for i in range(2, int(math.sqrt(sieveSize)) + 1):
33. pointer = i * 2
34. while pointer < sieveSize:
35. sieve[pointer] = False
36. pointer += i
37.
38. # compile the list of primes
39. primes = []
40. for i in range(sieveSize):
41. if sieve[i] == True:
42. primes.append(i)
43.
44. return primes
How the Program Works
primeSieve.py
1. # Prime Number Sieve
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import math

Chapter 23 – Finding Prime Numbers 365
The only module primeSieve.py needs is the math module.
How to Calculate if a Number is Prime
primeSieve.py
7. def isPrime(num):
8. # Returns True if num is a prime number, otherwise False.
9.
10. # Note: Generally, isPrime() is slower than primeSieve().
11.
12. # all numbers less than 2 are not prime
13. if num < 2:
14. return False
We will program the isPrime() function to return False if the num parameter is a composite
number and True if the num parameter is a prime number. If num is less than 2 we know it is
not prime and can simply return False.
primeSieve.py
16. # see if num is divisible by any number up to the square root of num
17. for i in range(2, int(math.sqrt(num)) + 1):
18. if num % i == 0:
19. return False
20. return True
A prime number has no factors besides 1 and itself. So to find out if a given number is prime or
not, we just have to keep dividing it by integers and see if any of them evenly divide the number
with 0 remainder.
The math.sqrt() function will return a float value of the square root of the number it is
passed. The square root of a number can be multiplied by itself to get the number. For example,
the square root of 49 is 7, because 7 × 7 is 49.
For example, to find out if 49 is prime, divide it by the integers starting with 2:
49 ÷ 2 = 24 remainder 1
49 ÷ 3 = 16 remainder 1
49 ÷ 4 = 12 remainder 1
49 ÷ 5 = 9 remainder 4
49 ÷ 6 = 8 remainder 1
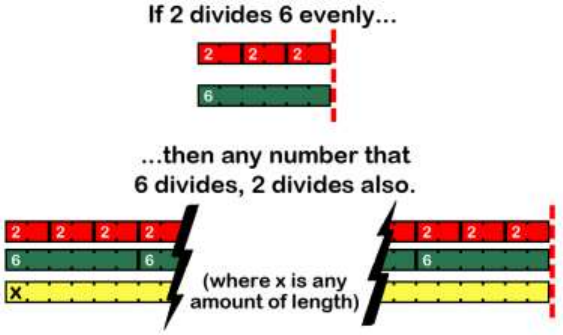
366 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
49 ÷ 7 = 7 remainder 0
Actually, you only need to divide the number by prime numbers. For example, there’s no reason
to see if 6 divides 49, because if it did then 2 would have divided 49 since 2 is a factor of 6. Any
number that 6 divides evenly can also be divided by 2 evenly:
Figure 23-1. 2 divides 6, and 6 divides X, therefore 2 divides X.
Because there’s an integer (that is not 1 or 49) that evenly divides 49 (that is, has a remainder of
0), we know that 49 is not a prime number. For another example, let’s try 13:
13 ÷ 2 = 6 remainder 1
13 ÷ 3 = 4 remainder 1
13 ÷ 4 = 3 remainder 1
No integer divides 13 with a remainder of 0 (except for 1 and 13, which don’t count). Actually,
we don’t even have to divide all the numbers up to 13. We only have to test the integers up to
(and including) the square root of the number we are testing for primality. The square root of a
number is the number that is multiplied by itself to get that first number. The square root of 25 is
5, because 5 × 5 = 25. The square root of 13 is about 3.6055512754639, because
3.6055512754639 × 3.6055512754639 = 13. This means that when we were testing 13 for
primality, we only had to divide 2 and 3 because 4 is larger than the square root of 13.
Line 18 checks if the remainder of division is 0 by using the % mod operator. If line 17’s for
loop never returns False, the function will return True on line 20.
The Sieve of Eratosthenes
The sieve of Eratosthenes (pronounced “era, taws, thuh, knees”) is an algorithm for calculating
prime numbers. Imagine a bunch of boxes for each integer, all marked “prime”:

Chapter 23 – Finding Prime Numbers 367
Table 23-1. A blank sieve of Eratosthenes, with each number marked as “prime”.
Prime
1
Prime
2
Prime
3
Prime
4
Prime
5
Prime
6
Prime
7
Prime
8
Prime
9
Prime
10
Prime
11
Prime
12
Prime
13
Prime
14
Prime
15
Prime
16
Prime
17
Prime
18
Prime
19
Prime
20
Prime
21
Prime
22
Prime
23
Prime
24
Prime
25
Prime
26
Prime
27
Prime
28
Prime
29
Prime
30
Prime
31
Prime
32
Prime
33
Prime
34
Prime
35
Prime
36
Prime
37
Prime
38
Prime
39
Prime
40
Prime
41
Prime
42
Prime
43
Prime
44
Prime
45
Prime
46
Prime
47
Prime
48
Prime
49
Prime
50
Mark 1 as “Not Prime” (since one is never prime). Then mark all the multiples of two (except for
two itself) as “Not Prime”. This means we will mark the integers 4 (2 × 2), 6 (2 × 3), 8 (2 × 4),
10, 12, and so on up to 50 (the largest number we have) are all marked as “Not Prime”:
Table 23-2. The sieve with one and the multiples of 2 (except 2 itself) marked as “not prime”.
Not
Prime
1
Prime
2
Prime
3
Not
Prime
4
Prime
5
Not
Prime
6
Prime
7
Not
Prime
8
Prime
9
Not
Prime
10
Prime
11
Not
Prime
12
Prime
13
Not
Prime
14
Prime
15
Not
Prime
16
Prime
17
Not
Prime
18
Prime
19
Not
Prime
20
Prime
21
Not
Prime
22
Prime
23
Not
Prime
24
Prime
25
Not
Prime
26
Prime
27
Not
Prime
28
Prime
29
Not
Prime
30
Prime
31
Not
Prime
32
Prime
33
Not
Prime
34
Prime
35
Not
Prime
36
Prime
37
Not
Prime
38
Prime
39
Not
Prime
40
Prime
41
Not
Prime
42
Prime
43
Not
Prime
44
Prime
45
Not
Prime
46
Prime
47
Not
Prime
48
Prime
49
Not
Prime
50
Then repeat this with all the multiples of three, except for three itself: 6, 9, 12, 15, 18, 21, and so
on are all marked “Not Prime”. Then do this for all of the multiples of four (except for four
itself), and all of the multiples of five (except for five itself), up until eight. We stop at 8 because

368 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
it is larger than 7.071, the square root of 50). We can do this because all the multiples of 9, 10,
11, and so on will already have been marked.
The completed sieve looks like this:
Table 23-3. A completed sieve of Eratosthenes.
Not
Prime
1
Prime
2
Prime
3
Not
Prime
4
Prime
5
Not
Prime
6
Prime
7
Not
Prime
8
Not
Prime
9
Not
Prime
10
Prime
11
Not
Prime
12
Prime
13
Not
Prime
14
Not
Prime
15
Not
Prime
16
Prime
17
Not
Prime
18
Prime
19
Not
Prime
20
Not
Prime
21
Not
Prime
22
Prime
23
Not
Prime
24
Not
Prime
25
Not
Prime
26
Not
Prime
27
Not
Prime
28
Prime
29
Not
Prime
30
Prime
31
Not
Prime
32
Not
Prime
33
Not
Prime
34
Not
Prime
35
Not
Prime
36
Prime
37
Not
Prime
38
Not
Prime
39
Not
Prime
40
Prime
41
Not
Prime
42
Prime
43
Not
Prime
44
Not
Prime
45
Not
Prime
46
Prime
47
Not
Prime
48
Not
Prime
49
Not
Prime
50
By using the sieve of Erastothenes, we’ve calculated that the prime numbers under 50 are 2, 3, 5,
7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, and 47. This sieve algorithm is good when we want to
quickly find out all the prime numbers in a certain range of numbers. It is much faster than using
the previous “divides test” algorithm to test if 2 is prime, then test if 3 is prime, then test if 4 is
prime, and so on.
The primeSieve() Function
23. def primeSieve(sieveSize):
24. # Returns a list of prime numbers calculated using
25. # the Sieve of Eratosthenes algorithm.
26.
27. sieve = [True] * sieveSize
28. sieve[0] = False # zero and one are not prime numbers
29. sieve[1] = False
The primeSieve() function returns a list of all prime numbers between 1 and sieveSize.
First, line 27 creates a list of Boolean True values that is the length of sieveSize. The 0 and
1 indexes are marked as False because 0 and 1 are not prime numbers.

Chapter 23 – Finding Prime Numbers 369
31. # create the sieve
32. for i in range(2, int(math.sqrt(sieveSize)) + 1):
33. pointer = i * 2
34. while pointer < sieveSize:
35. sieve[pointer] = False
36. pointer += i
The for loop on line 32 goes through each integer from 2 up to the square root of sieveSize.
The variable pointer will start at the first multiple of i after i (which will be i * 2). Then
the while loop will set the pointer index in the sieve list to False, and line 36 will
change pointer to point to the next multiple of i.
38. # compile the list of primes
39. primes = []
40. for i in range(sieveSize):
41. if sieve[i] == True:
42. primes.append(i)
After the for loop on line 32 completes, the sieve list will contain True for each index that is
a prime number. We can create a new list (which starts as an empty list in primes) and loop over
the entire sieve list, and appends and numbers if sieve[i] is True (meaning i is prime).
44. return primes
The list of prime numbers is returned on line 44.
Detecting Prime Numbers
The isPrime() function in primeSieve.py checks if the number can be divided evenly by a
range of numbers from 2 to the square root of the number. But what about a number like
1,070,595,206,942,983? If you pass this integer to isPrime(), it takes several seconds to
determine if it is prime or not. And if the number is hundreds of digits long (like the prime
numbers in next chapter’s RSA cipher program are), it would take over a trillion years to figure
out if that one number is prime or not.
The isPrime() function in primeSieve.py is too slow for the large numbers we will use in the
RSA cipher. Fortunately there is an algorithm called the Rabin-Miller Primality Test than can
calculate if such large numbers are prime or not. We will create a new isPrime() function in
rabinMiller.py that makes use of this better algorithm.

370 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The code for this algorithm uses advanced mathematics, and how the algorithm works is beyond
the scope of this book. Like the gcd() function in cryptomath.py, this book will just present the
code for the algorithm for you to use without explanation.
Source Code for the Rabin-Miller Module
Open a new file editor window and type in the following code. Save this file as rabinMiller.py.
This program will be a module that is meant to be imported by other programs.
Instead of typing out the list of numbers on line 43, just temporarily add the lines import
pyperclip and pyperclip.copy(primeSieve(1000)) in the primeSieve.py file and
run it. This will copy the list of primes to the clipboard, and then you can paste it into the
rabinMiller.py file.
Open a new file editor window by clicking on File ► New Window. Type in the following code
into the file editor, and then save it as rabinMiller.py.
Source code for rabinMiller.py
1. # Primality Testing with the Rabin-Miller Algorithm
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import random
5.
6.
7. def rabinMiller(num):
8. # Returns True if num is a prime number.
9.
10. s = num - 1
11. t = 0
12. while s % 2 == 0:
13. # keep halving s while it is even (and use t
14. # to count how many times we halve s)
15. s = s // 2
16. t += 1
17.
18. for trials in range(5): # try to falsify num's primality 5 times
19. a = random.randrange(2, num - 1)
20. v = pow(a, s, num)
21. if v != 1: # this test does not apply if v is 1.
22. i = 0
23. while v != (num - 1):
24. if i == t - 1:
25. return False
26. else:

Chapter 23 – Finding Prime Numbers 371
27. i = i + 1
28. v = (v ** 2) % num
29. return True
30.
31.
32. def isPrime(num):
33. # Return True if num is a prime number. This function does a quicker
34. # prime number check before calling rabinMiller().
35.
36. if (num < 2):
37. return False # 0, 1, and negative numbers are not prime
38.
39. # About 1/3 of the time we can quickly determine if num is not prime
40. # by dividing by the first few dozen prime numbers. This is quicker
41. # than rabinMiller(), but unlike rabinMiller() is not guaranteed to
42. # prove that a number is prime.
43. lowPrimes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137,
139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227,
229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313,
317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419,
421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509,
521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617,
619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727,
733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829,
839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947,
953, 967, 971, 977, 983, 991, 997]
44.
45. if num in lowPrimes:
46. return True
47.
48. # See if any of the low prime numbers can divide num
49. for prime in lowPrimes:
50. if (num % prime == 0):
51. return False
52.
53. # If all else fails, call rabinMiller() to determine if num is a prime.
54. return rabinMiller(num)
55.
56.
57. def generateLargePrime(keysize=1024):
58. # Return a random prime number of keysize bits in size.
59. while True:
60. num = random.randrange(2**(keysize-1), 2**(keysize))
61. if isPrime(num):
62. return num
372 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Sample Run of the Rabin Miller Module
If you run the interactive shell, you can import the rabinMiller.py module and call the functions
in it. Try typing the following into the interactive shell:
>>> import rabinMiller
>>> rabinMiller.generateLargePrime()
1228811683422110410305236835154432390074842906007015553694882717483780547440094
6375131251147129101194573241337844666680914050203700367321105215349360768161999
0563076859566835016382556518967124921538212397036345815983641146000671635019637
218348455544435908428400192565849620509600312468757953899553441648428119
>>> rabinMiller.isPrime(45943208739848451)
False
>>> rabinMiller.isPrime(13)
True
>>>
How the Program Works
rabinMiller.py
1. # Primality Testing with the Rabin-Miller Algorithm
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import random
The Rabin-Miller algorithm uses random numbers, so we import the random module on line 4.
The Rabin-Miller Primality Algorithm
rabinMiller.py
7. def rabinMiller(num):
8. # Returns True if num is a prime number.
9.
10. s = num - 1
11. t = 0
12. while s % 2 == 0:
13. # keep halving s while it is even (and use t
14. # to count how many times we halve s)
15. s = s // 2
16. t += 1
17.
18. for trials in range(5): # try to falsify num's primality 5 times
19. a = random.randrange(2, num - 1)
20. v = pow(a, s, num)
21. if v != 1: # this test does not apply if v is 1.

Chapter 23 – Finding Prime Numbers 373
22. i = 0
23. while v != (num - 1):
24. if i == t - 1:
25. return False
26. else:
27. i = i + 1
28. v = (v ** 2) % num
29. return True
The mathematics of the Rabin-Miller Primality algorithm are beyond the scope of this book, so
the code in this function will not be explained.
The Rabin-Miller algorithm is also not a surefire test for primality; however, you can be
extremely certain that it is accurate. (Although this is not good enough for commercial encryption
software, it is good enough for the purposes of the programs in this book.) The main benefit of
the Rabin-Miller algorithm is that it is a relatively simple primality test and only takes a few
seconds to run on a normal computer.
If rabinMiller() returns True, then the num argument is extremely likely to be prime. If
rabinMiller() returns False, then num is definitely composite.
The New and Improved isPrime() Function
rabinMiller.py
32. def isPrime(num):
33. # Return True if num is a prime number. This function does a quicker
34. # prime number check before calling rabinMiller().
35.
36. if (num < 2):
37. return False # 0, 1, and negative numbers are not prime
All numbers that are less than two (such as one, zero, and negative numbers) are all not prime, so
we can immediately return False.
rabinMiller.py
39. # About 1/3 of the time we can quickly determine if num is not prime
40. # by dividing by the first few dozen prime numbers. This is quicker
41. # than rabinMiller(), but unlike rabinMiller() is not guaranteed to
42. # prove that a number is prime.
43. lowPrimes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137,
139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227,
229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313,
317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419,

374 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509,
521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617,
619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727,
733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829,
839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947,
953, 967, 971, 977, 983, 991, 997]
44.
45. if num in lowPrimes:
46. return True
The numbers in the lowPrimes list are primes. (Duh.) We can immediately return True if num
is in the lowPrimes list.
rabinMiller.py
48. # See if any of the low prime numbers can divide num
49. for prime in lowPrimes:
50. if (num % prime == 0):
51. return False
Line 49 loops through each of the prime numbers in the lowPrimes list. The integer in num is
modded with the % mod operator by each prime number on line 50, and if this evaluates to 0 then
we know that prime divides num and so num is not prime. In that case, line 51 returns False.
Checking if num is divisible by all the primes under 1000 won’t tell us if the number is prime, but
it might tell us if the number is composite. About 30% of the random numbers that
generateLargePrime() creates that are composite will be detected as composite by
dividing by the low prime numbers. Dividing by the low prime numbers is much faster than
executing the full Rabin-Miller algorithm on the number, so this shortcut can make our program
execute much more quickly.
rabinMiller.py
53. # If all else fails, call rabinMiller() to determine if num is a prime.
54. return rabinMiller(num)
Those are all the quick tests to determine if a number is prime or not. But if num does not match
any of those tests, then it is passed to the rabinMiller() function to check if it is prime or
not. The return value of rabinMiller() will be returned by isPrime().
The comment on line 53 means call the rabinMiller() function to determine if the number is
prime. Please do not call Dr. Rabin or Dr. Miller personally to ask them if your number is prime.
rabinMiller.py

Chapter 23 – Finding Prime Numbers 375
57. def generateLargePrime(keysize=1024):
58. # Return a random prime number of keysize bits in size.
59. while True:
60. num = random.randrange(2**(keysize-1), 2**(keysize))
61. if isPrime(num):
62. return num
The generateLargePrime() function will return an integer that is prime. It does this by
coming up with a large random number, storing it in num, and then passing num to isPrime().
The isPrime() function will then test to see if num is composite and then pass the num to
rabinMiller() for a more thorough (and computationally expensive) primality test.
If the number num is prime, then line 62 returns num. Otherwise the infinite loop goes back to
line 60 to try a new random number. This loop keeps trying over and over again until it finds a
number that the isPrime() function says is prime.
Summary
Prime numbers have fascinating properties in mathematics. As you will learn in the next chapter,
they are also the backbone of ciphers used in actual professional encryption software. The
definition of a prime number is simple enough: a number that only has one and itself as factors.
But determining which numbers are prime and which are composite (that is, not prime) takes
some clever code.
Modding a number with all the numbers from two up to the square root of the number is how our
isPrime() function determines if that number is prime or not. A prime number will never have
a remainder of 0 when it is modded by any number (besides its factors, 1 and itself.) But this can
take a while for the computer to calculate when testing large numbers for primality.
The sieve of Erastothenes can be used to quickly tell if a range of numbers is prime or not, but
this requires a lot of memory.
The RSA cipher makes use of extremely large prime numbers that are hundreds of digits long.
The Sieve of Erastothenes and the basic isPrime() function we have in primeSieve.py aren’t
sophisticated enough to handle numbers this large.
The Rabin-Miller algorithm uses some mathematics which has simple code (but the mathematical
reasoning behind it is too complex for this book), but it allows us to determine if a number that is
hundreds of digits long is prime.
376 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
In the next chapter, we will use the prime number code we developed for the rabinMiller.py
module in our RSA Cipher program. At last, we will have a cipher easier to use than the one-time
pad cipher but that cannot be hacked by the simple hacker techniques in this book!

Chapter 24 – Public Key Cryptography and the RSA Cipher 377
Warning to Time Travelers:
Should you travel back to the early 1990’s with this book, the contents of Chapter 24 would be
illegal to possess in the United States. Strong crypto (that is, cryptography strong enough not to
be hacked) was regulated at the same level as tanks, missiles, and flamethrowers and the export of
encryption software would require State Department approval. They said that this was a matter of
national security.
Daniel J. Bernstein, a student at the University of California, Berkeley at the time, wanted to
publish an academic paper and associated source code on his “Snuffle” encryption system. He
was told by the U.S. government that he would first need to become a licensed arms dealer before
he could post his source code on the Internet. They also told him that they would deny him an
export license if he actually applied for one, because his technology was too secure.
The Electronic Frontier Foundation, in its second major case as a young digital civil liberties
organization, brought about the Bernstein v. United States court cases. The court ruled, for the
first time ever, that written software code is speech protected by the First Amendment, and that
the export control laws on encryption violated Bernstein’s First Amendment rights by prohibiting
his constitutionally protected speech.
Today, strong crypto is used to safeguard businesses and e-commerce used by millions of Internet
shoppers everyday. Cryptography is at the foundation of a large part of the global economy. But
in the 1990’s, spreading this knowledge freely (as this book does) would have landed you in
prison for arms trafficking.
A more detailed history of the legal battle for cryptography can be found in Steven Levy’s book,
Crypto: How the Code Rebels Beat the Government, Saving Privacy in the Digital Age.
The fears and predictions made by the “experts” of the intelligence community that encryption
software would become a grave national security threat turned out to be… less than well-founded.

378 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
PUBLIC KEY CRYPTOGRAPHY
AND THE RSA CIPHER
Topics Covered In This Chapter:
Public key cryptography
Man-in-the-middle attacks
ASCII
The chr() and ord() functions
The bytes data type and bytes() function
The encode() string and decode() bytes method
The min() and max() functions
The insert() list method
The pow() function
“Why shouldn’t I work for the NSA? That’s a tough one, but I’ll take a
shot. Say I’m working at the NSA and somebody puts a code on my desk,
something no one else can break. Maybe I take a shot at it, and maybe I
break it. I’m real happy with myself, ‘cause I did my job well. But maybe
that code was the location of some rebel army in North Africa or the
Middle East and once they have that location they bomb the village where
the rebels are hiding. Fifteen hundred people that I never met, never had
no problem with, get killed.
Chapter 24 – Public Key Cryptography and the RSA Cipher 379
Now the politicians are saying ‘Oh, send in the Marines to secure the
area,’ ‘cause they don’t give a shit. It won’t be their kid over there getting
shot just like it wasn’t them when their number got called ‘cause they
were pulling a tour in the National Guard. It’ll be some kid from Southie
over there taking shrapnel in the ass. He comes back to find that the plant
he used to work at got exported to the country he just got back from, and
the guy that put the shrapnel in his ass got his old job, ‘cause he’ll work
for fifteen cents a day and no bathroom breaks.
Meanwhile he realizes that the only reason he was over there in the first
place was so we could install a government that would sell us oil at a good
price. And of course the oil companies use the little skirmish to scare up
domestic oil prices, a cute little ancillary benefit for them, but it ain’t
helping my buddy at two-fifty a gallon. They’re taking their sweet time
bringing the oil back, of course, and maybe they took the liberty of hiring
an alcoholic skipper who likes to drink martinis and fucking play slalom
with the icebergs. It ain’t too long until he hits one, spills the oil, and kills
all the sea life in the North Atlantic.
So now my buddy’s out of work, he can’t afford to drive, so he’s walking
to the fucking job interviews which sucks because the shrapnel in his ass
is giving him chronic hemorrhoids. And meanwhile he’s starving ‘cause
any time he tries to get a bite to eat the only Blue Plate Special they’re
serving is North Atlantic Scrod with Quaker State.
So what did I think? I’m holding out for something better.”
“Good Will Hunting”
Public Key Cryptography
All of the ciphers in this book so far have one thing in common: the key used for encryption is the
same key used for decryption. This leads to a tricky problem: How do you share encrypted
messages with someone you’ve never talked to before?
380 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Say someone on the other side of the world wants to communicate with you. But you both know
that spy agencies are monitoring all emails, letters, texts, and calls that you send. You could send
them encrypted messages, however you would both have to agree on a secret key to use. But if
one of you emailed the other a secret key to use, then the spy agency would be able to see this key
and then decrypt any future messages you send with that key. Normally you would both secretly
meet in person and exchange the key then. But you can’t do this if the person is on the other side
of the world. You could try encrypting the key before you send it, but then you would have to
send the secret key for that message to the other person and it would also be intercepted.
This is a problem solved by public key cryptography. Public key cryptography ciphers have
two keys, one used for encryption and one used for decryption. A cipher that uses different keys
for encryption and decryption is called an asymmetric cipher, while the ciphers that use the
same key for encryption and decryption (like all the previous ciphers in this book) are called
symmetric ciphers.
The important thing to know is that a message encrypted with one key can only be decrypted
with the other key. So even if someone got their hands on the encryption key, they would not be
able to read an encrypted message because the encryption key can only encrypt; it cannot be used
to decrypt messages that it encrypted.
So when we have these two keys, we call one the public key and one the private key. The public
key is shared with the entire world. However, the private key must be kept secret.
If Alice wants to send Bob a message, Alice finds Bob’s public key (or Bob can give it to her).
Then Alice encrypts her message to Bob with Bob’s public key. Since the public key cannot
decrypt a message that was encrypted with it, it doesn’t matter that everyone else has Bob’s
public key.
When Bob receives the encrypted message, he uses his private key to decrypt it. If Bob wants to
reply to Alice, he finds her public key and encrypts his reply with it. Since only Alice knows her
own private key, Alice will be the only person who can decrypt the encrypted message.
Remember that when sending encrypted messages using a public key cipher:
The public key is used for encrypting.
The private key is used for decrypting.
To go back to the example of communicating with someone across the world, now it doesn’t
matter if you send them your public key. Even if the spy agency has your public key, they cannot
read messages that were encrypted with the public key. Only your private key can decrypt those
messages, and you keep that key a secret.

Chapter 24 – Public Key Cryptography and the RSA Cipher 381
The particular public key cipher that we will implement is called the RSA cipher, which was
invented in 1977 and named after its inventors: Ron Rivest, Adi Shamir and Leonard Adleman.
The Dangers of “Textbook” RSA
While we don’t write a hacking program for the RSA cipher program in this book, don’t make the
mistake of thinking the rsaCipher.py program featured in this chapter is secure. Getting
cryptography right is very hard and requires a lot of experience to know if a cipher (and a
program that implements it) is truly secure.
The RSA program in this chapter is known as textbook RSA because, while it does implement
the RSA algorithm correctly using large prime numbers, there are several subtle faults with it that
can lead to its encrypted messages being hacked. The difference between pseudorandom and truly
random number generation functions is one such fault. But there are many others.
So while you might not be able to hack the ciphertext created by rsaCipher.py, don’t think that no
one else can. The highly accomplished cryptographer Bruce Schneier once said, “Anyone, from
the most clueless amateur to the best cryptographer, can create an algorithm that he himself can’t
break. It’s not even hard. What is hard is creating an algorithm that no one else can break, even
after years of analysis. And the only way to prove that is to subject the algorithm to years of
analysis by the best cryptographers around.”
The program in this book is a fun example, but stick to professional encryption software to secure
your files. You can find a list of (usually free) encryption software here:
http://invpy.com/realcrypto.
A Note About Authentication
There is a slight problem with public key ciphers. Imagine you got an email that said this:
“Hello. I am Emmanuel Goldstein, leader of the resistance. I would
like to communicate secretly with you about very important matters.
Attached is my public key.”
Using the public key, you can be sure that the messages you send cannot be read by anyone other
than “Emmanuel Goldstein”. But how do you know the person who sent you this is actually
Emmanuel Goldstein? Maybe it is Emmanuel Goldstein that you are sending encrypted messages
to, or maybe it is a spy agency that is pretending to be Emmanuel Goldstein to lure you into a
trap.
382 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
So while public key ciphers (and, in fact, all the ciphers in this book) can provide
confidentiality (that is, keeping the message a secret), they don’t provide authentication (that
is, proof that who you are communicating with really is who they say they are).
Normally this isn’t a problem with symmetric ciphers, because when you exchange keys with the
person you can see them for yourself. However, you don’t need to see a person in order to get
their public key and begin sending them encrypted messages. This is something to keep in mind
when using public key cryptography.
There is an entire field called PKI (Public Key Infrastructure) that deals with authentication so
that you can match public keys to people with some level of security; however, PKI is beyond the
scope of this book.
The Man-In-The-Middle Attack
Even more insidious than hacking our encrypted messages is a man-in-the-middle attack. Say
Emmanuel Goldstein really did want to communicate with you and sent you the above message,
but the spy agency intercepted it. They could then replace the public key Emmanuel attached to
the email with their own public key, and then send it on to you. You would think the spy agency’s
key was Emmanuel’s key!
Now when you encrypt a reply to Emmanuel, they intercept that message, decrypt it (since you
really encrypted the message with the spy agency’s public key, not Emmanuel’s public key) and
read it, and then they re-encrypt it with Emmanuel’s actual public key and send it to him. They do
the same thing with any messages that Emmanuel sends to you.
Figure 24-1. A man-in-the-middle attack.

Chapter 24 – Public Key Cryptography and the RSA Cipher 383
To both you and Emmanuel, it looks like you are communicating secretly with each other. But
actually, the spy agency is doing a man-in-the-middle attack and reading all of your messages.
You and Emmanuel are actually encrypting your messages public keys generated by the spy
agency! Again, this problem is caused by the fact that the public key cipher only provides
confidentiality, but does not provide authentication.
Generating Public and Private Keys
A key in the RSA scheme is made of two numbers. There are three steps to creating the keys:
1. Create two random, very large prime numbers. These numbers will be called p and q.
Multiply these numbers to get a number which we will call n.
2. Create a random number, called e, which is relatively prime with (p – 1) × (q – 1).
3. Calculate the modular inverse of e. This number will be called d.
The public key will be the two numbers n and e. The private key will be the two numbers n and d.
(Notice that both keys have the number n in them.) We will cover how to encrypt and decrypt
with these numbers when the RSA cipher program is explained. First let’s write a program to
generate these keys.
Source Code for the RSA Key Generation Program
Open a new file editor window by clicking on File ► New Window. Type in the following code
into the file editor, and then save it as makeRsaKeys.py.
Source code for makeRsaKeys.py
1. # RSA Key Generator
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import random, sys, os, rabinMiller, cryptomath
5.
6.
7. def main():
8. # create a public/private keypair with 1024 bit keys
9. print('Making key files...')
10. makeKeyFiles('al_sweigart', 1024)
11. print('Key files made.')
12.
13. def generateKey(keySize):
14. # Creates a public/private key pair with keys that are keySize bits in
15. # size. This function may take a while to run.
16.
17. # Step 1: Create two prime numbers, p and q. Calculate n = p * q.
18. print('Generating p prime...')

384 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
19. p = rabinMiller.generateLargePrime(keySize)
20. print('Generating q prime...')
21. q = rabinMiller.generateLargePrime(keySize)
22. n = p * q
23.
24. # Step 2: Create a number e that is relatively prime to (p-1)*(q-1).
25. print('Generating e that is relatively prime to (p-1)*(q-1)...')
26. while True:
27. # Keep trying random numbers for e until one is valid.
28. e = random.randrange(2 ** (keySize - 1), 2 ** (keySize))
29. if cryptomath.gcd(e, (p - 1) * (q - 1)) == 1:
30. break
31.
32. # Step 3: Calculate d, the mod inverse of e.
33. print('Calculating d that is mod inverse of e...')
34. d = cryptomath.findModInverse(e, (p - 1) * (q - 1))
35.
36. publicKey = (n, e)
37. privateKey = (n, d)
38.
39. print('Public key:', publicKey)
40. print('Private key:', privateKey)
41.
42. return (publicKey, privateKey)
43.
44.
45. def makeKeyFiles(name, keySize):
46. # Creates two files 'x_pubkey.txt' and 'x_privkey.txt' (where x is the
47. # value in name) with the the n,e and d,e integers written in them,
48. # delimited by a comma.
49.
50. # Our safety check will prevent us from overwriting our old key files:
51. if os.path.exists('%s_pubkey.txt' % (name)) or
os.path.exists('%s_privkey.txt' % (name)):
52. sys.exit('WARNING: The file %s_pubkey.txt or %s_privkey.txt already
exists! Use a different name or delete these files and re-run this program.' %
(name, name))
53.
54. publicKey, privateKey = generateKey(keySize)
55.
56. print()
57. print('The public key is a %s and a %s digit number.' %
(len(str(publicKey[0])), len(str(publicKey[1]))))
58. print('Writing public key to file %s_pubkey.txt...' % (name))
59. fo = open('%s_pubkey.txt' % (name), 'w')
60. fo.write('%s,%s,%s' % (keySize, publicKey[0], publicKey[1]))

Chapter 24 – Public Key Cryptography and the RSA Cipher 385
61. fo.close()
62.
63. print()
64. print('The private key is a %s and a %s digit number.' %
(len(str(publicKey[0])), len(str(publicKey[1]))))
65. print('Writing private key to file %s_privkey.txt...' % (name))
66. fo = open('%s_privkey.txt' % (name), 'w')
67. fo.write('%s,%s,%s' % (keySize, privateKey[0], privateKey[1]))
68. fo.close()
69.
70.
71. # If makeRsaKeys.py is run (instead of imported as a module) call
72. # the main() function.
73. if __name__ == '__main__':
74. main()
Sample Run of the RSA Key Generation Program
When you run the makeRsaKeys.py program, the output will look something like this (of course,
the numbers for your keys will be different since they are random numbers):
Making key files...
Generating p prime...
Generating q prime...
Generating e that is relatively prime to (p-1)*(q-1)...
Calculating d that is mod inverse of e...
Public key:
(210902406316700502401968491406579417405090396754616926135810621216116191338086
5678407459875355468897928072386270510720443827324671435893274858393749685062411
6776147241821152026946322876869404394483922202407821672864242478920813182699000
8473526711744296548563866768454251404951960805224682425498975230488955908086491
8521163487778495362706850854469709529156400505222122042218037444940658810103314
8646830531744960702788478777031572995978999471326531132766377616771007701834003
6668306612665759417207845823479903440572724068125211002329298338718615859542093
72109725826359561748245019920074018549204468791300114315056117093,
1746023076917516102173184545923683355383240391086912905495420037367858093524760
6622265764388235752176654737805849023006544732896308685513669509917451195822611
3980989513066766009588891895645995814564600702703936932776834043548115756816059
906591453170741270845572335375041024799371425300216777273298110097435989)
Private key:
(210902406316700502401968491406579417405090396754616926135810621216116191338086
5678407459875355468897928072386270510720443827324671435893274858393749685062411
6776147241821152026946322876869404394483922202407821672864242478920813182699000
8473526711744296548563866768454251404951960805224682425498975230488955908086491
8521163487778495362706850854469709529156400505222122042218037444940658810103314

386 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
8646830531744960702788478777031572995978999471326531132766377616771007701834003
6668306612665759417207845823479903440572724068125211002329298338718615859542093
72109725826359561748245019920074018549204468791300114315056117093,
4767673579813771041216688491698376504317312028941690434129597155228687099187466
6099933371008075948549008551224760695942666962465968168995404993934508399014283
0537106767608359489023128886399384026861870750523607730623641626642761449656525
5854533116668173598098138449334931305875025941768372702963348445191139635826000
8181223734862132564880771928931192572481077942568188460364002867327313529283117
0178614206817165802812291528319562200625082557261680470845607063596018339193179
7437503163601143217769616471700002543036826990539739057474642785416933878499897
014777481407371328053001838085314443545845219087249544663398589)
The public key is a 617 and a 309 digit number.
Writing public key to file al_sweigart_pubkey.txt...
The private key is a 617 and a 309 digit number.
Writing private key to file al_sweigart_privkey.txt...
These two keys are written out to two different files, al_sweigart_pubkey.txt and
al_sweigart_privkey.txt. These filenames are used because the string 'al_sweigart' was
passed to the makeKeyFiles() function. You can specify a different filenames by passing a
different string. These key files will be used by the RSA cipher program to encrypt and decrypt
messages.
If you try to run makeRsaKeys.py again with the same string being passed to
makeKeyFiles(), the output of the program will look like this:
Making key files...
WARNING: The file al_sweigart_pubkey.txt or al_sweigart_privkey.txt already
exists! Use a different name or delete these files and re-run this program.
This warning is here so you don’t accidentally overwrite your key files, making any files you
encrypted with them impossible to recover. Keep your keys safe!
How the Key Generation Program Works
makeRsaKeys.py
1. # RSA Key Generator
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import random, sys, os, rabinMiller, cryptomath
The program imports the rabinMiller and cryptomath modules that we created in the last
chapter, along with a few others.

Chapter 24 – Public Key Cryptography and the RSA Cipher 387
makeRsaKeys.py
7. def main():
8. # create a public/private keypair with 1024 bit keys
9. print('Making key files...')
10. makeKeyFiles('al_sweigart', 1024)
11. print('Key files made.')
When makeRsaKeys.py is run, the main() function is called, which will create the key files.
Since the keys might take a while for the computer to generate, we print a message on line 9
before the makeKeyFiles() call so the user knows what the program is doing.
The makeKeyFiles() call on line 10 passes the string 'al_sweigart' and the integer
1024. This will generate keys with a size of 1024 bits and store them in files named
al_sweigart_pubkey.txt and al_sweigart_privkey.txt.
The Program’s generateKey() Function
makeRsaKeys.py
13. def generateKey(keySize):
14. # Creates a public/private key pair with keys that are keySize bits in
15. # size. This function may take a while to run.
16.
17. # Step 1: Create two prime numbers, p and q. Calculate n = p * q.
18. print('Generating p prime...')
19. p = rabinMiller.generateLargePrime(keySize)
20. print('Generating q prime...')
21. q = rabinMiller.generateLargePrime(keySize)
22. n = p * q
The first step of creating keys is coming up with two random prime numbers which are called p
and q. The generateLargePrime() function we wrote in the last chapter’s rabinMiller.py
program will return a prime number (as an integer value) of the size determined by the value in
keySize on line 19 and line 21. These integer values are stored in variables named p and q.
On line 22, the number n is calculated by multiplying p and q, and stored in n.
makeRsaKeys.py
24. # Step 2: Create a number e that is relatively prime to (p-1)*(q-1).
25. print('Generating e that is relatively prime to (p-1)*(q-1)...')
26. while True:
27. # Keep trying random numbers for e until one is valid.
28. e = random.randrange(2 ** (keySize - 1), 2 ** (keySize))
29. if cryptomath.gcd(e, (p - 1) * (q - 1)) == 1:

388 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
30. break
The second step is calculating a number e which is relatively prime to the product of p – 1 and
q – 1. The while loop on line 26 is an infinite loop. The random.randrange() call on
line 28 returns a random integer (stored in the e variable) and line 29 tests if this random number
is relatively prime to (p - 1) * (q - 1). If it is, the break statement on line 30 breaks
out of the infinite loop. Otherwise, the program execution jumps back to line 26 and will keep
trying different random numbers until it finds one that is relatively prime with (p - 1) * (q -
1).
This way we can guarantee that when the program execution gets past this while loop, the
variable e will contain a number that is relatively prime to (p - 1) * (q - 1).
makeRsaKeys.py
32. # Step 3: Calculate d, the mod inverse of e.
33. print('Calculating d that is mod inverse of e...')
34. d = cryptomath.findModInverse(e, (p - 1) * (q - 1))
The third step is to find the mod inverse of e. The findModInverse() function that we wrote
for our cryptomath module in Chapter 14 will do this calculation for us. The mod inverse of e
is stored in a variable named d.
makeRsaKeys.py
36. publicKey = (n, e)
37. privateKey = (n, d)
In the RSA cipher, each key is made up of two numbers. The public key will be the integers
stored in n and e, and the private key will be the integers stored in n and d. Lines 36 and 37 store
these integers as tuples in the variables publicKey and privateKey.
There’s no reason e has to be in the public key and d in the private key, and you could swap
them. However, once you make the public key public, you must keep the private key a secret.
makeRsaKeys.py
39. print('Public key:', publicKey)
40. print('Private key:', privateKey)
41.
42. return (publicKey, privateKey)

Chapter 24 – Public Key Cryptography and the RSA Cipher 389
The remaining lines in the generateKey() function print the keys on the screen with
print() calls on lines 39 and 40. Then line 42’s generateKey() call returns a tuple with
publicKey and privateKey.
makeRsaKeys.py
45. def makeKeyFiles(name, keySize):
46. # Creates two files 'x_pubkey.txt' and 'x_privkey.txt' (where x is the
47. # value in name) with the the n,e and d,e integers written in them,
48. # delimited by a comma.
While the generateKey() function will generate the actual integers for the public and private
keys, we need to store these numbers in a file so that our RSA cipher program can use them later
to encrypt and decrypt. Each of the keys are made of two integers that are hundreds of digits long;
that’s too many to memorize or conveniently write down. The easiest way to store them is as text
files on your computer.
This means that you have to be sure that nobody hacks your computer and copies these key files.
It might be a good idea to store these files on a USB thumb drive instead of on your computer.
However, this is also risky. If someone borrows the thumb drive then they could copy the key
files, or if you accidentally break or lose the thumb drive then you will lose your own private key!
makeRsaKeys.py
50. # Our safety check will prevent us from overwriting our old key files:
51. if os.path.exists('%s_pubkey.txt' % (name)) or
os.path.exists('%s_privkey.txt' % (name)):
52. sys.exit('WARNING: The file %s_pubkey.txt or %s_privkey.txt already
exists! Use a different name or delete these files and re-run this program.' %
(name, name))
To prevent us from accidentally deleting our key files by running the program again, line 51
checks to see if the public or private key files with the given name already exist. If they do, the
program will exit with a warning message.
makeRsaKeys.py
54. publicKey, privateKey = generateKey(keySize)
After the check, line 54 has a call to generateKey() to get the public and private keys using
the multiple assignment trick. The generateKey() function returns a tuple of two tuples. The
first tuple has two integers for the public key and the second tuple has two integers for the private
key. These are stored in the variables publicKey and privateKey.

390 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
RSA Key File Format
makeRsaKeys.py
56. print()
57. print('The public key is a %s and a %s digit number.' %
(len(str(publicKey[0])), len(str(publicKey[1]))))
58. print('Writing public key to file %s_pubkey.txt...' % (name))
59. fo = open('%s_pubkey.txt' % (name), 'w')
60. fo.write('%s,%s,%s' % (keySize, publicKey[0], publicKey[1]))
61. fo.close()
Line 57 prints some information about the public key. It can tell how many digits are in the
integer in publicKey[0] and publicKey[1] by converting those values to strings with the
str() function, and then finding the length of the string with the len() function.
The key file’s contents will be the key size, a comma, the n integer, another comma, and the e (or
d) integer. The file’s contents will look like: <key size integer>,<n integer>,<e or d integer>
Lines 59 to 61 open a file in write mode, as you can tell from the 'w' string passed to open().
makeRsaKeys.py
63. print()
64. print('The private key is a %s and a %s digit number.' %
(len(str(publicKey[0])), len(str(publicKey[1]))))
65. print('Writing private key to file %s_privkey.txt...' % (name))
66. fo = open('%s_privkey.txt' % (name), 'w')
67. fo.write('%s,%s,%s' % (keySize, privateKey[0], privateKey[1]))
68. fo.close()
Lines 63 to 68 do the exact same thing as lines 56 and 61, except for writing the private key out to
a file.
makeRsaKeys.py
71. # If makeRsaKeys.py is run (instead of imported as a module) call
72. # the main() function.
73. if __name__ == '__main__':
74. main()
Lines 73 and 74 are at the bottom of the program, and call main() if makeRsaKeys.py is being
run as a program instead of imported as a module by another program.

Chapter 24 – Public Key Cryptography and the RSA Cipher 391
Hybrid Cryptosystems
In real life, the complicated mathematics make RSA and public-key encryption slow to compute.
This is especially true for servers that need to make hundreds or thousands of encrypted
connections a second. Instead, the RSA cipher is often used to encrypt the key for a symmetric
key cipher. The encrypted key is then sent to the other person, and that key is used to pass
messages that are encrypted using the (faster) symmetric cipher. Using a symmetric key cipher
and an asymmetric key cipher to securely communicate like this is called a hybrid
cryptosystem. More information about hybrid cryptosystems can be found at
https://en.wikipedia.org/wiki/Hybrid_cryptosystem.
It’s not recommended to use the rsaCipher.py program to encrypt the keys for, say, the
vigenereCipher.py program. We’ve already proven that the Vigenère cipher is hackable. A strong
symmetric key cipher isn’t covered in this book, but you can still use rsaCipher.py to encrypt
your files anyway.
Source Code for the RSA Cipher Program
Now that you can create key files, let’s write the program that does encryption and decryption
with the RSA cipher. Open a new file editor window by clicking on File ► New Window. Type
in the following code into the file editor, and then save it as rsaCipher.py.
Source code for rsaCipher.py
1. # RSA Cipher
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import sys
5.
6. # IMPORTANT: The block size MUST be less than or equal to the key size!
7. # (Note: The block size is in bytes, the key size is in bits. There
8. # are 8 bits in 1 byte.)
9. DEFAULT_BLOCK_SIZE = 128 # 128 bytes
10. BYTE_SIZE = 256 # One byte has 256 different values.
11.
12. def main():
13. # Runs a test that encrypts a message to a file or decrypts a message
14. # from a file.
15. filename = 'encrypted_file.txt' # the file to write to/read from
16. mode = 'encrypt' # set to 'encrypt' or 'decrypt'
17.
18. if mode == 'encrypt':
19. message = '''"Journalists belong in the gutter because that is
where the ruling classes throw their guilty secrets." -Gerald Priestland "The

392 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Founding Fathers gave the free press the protection it must have to bare the
secrets of government and inform the people." -Hugo Black'''
20. pubKeyFilename = 'al_sweigart_pubkey.txt'
21. print('Encrypting and writing to %s...' % (filename))
22. encryptedText = encryptAndWriteToFile(filename, pubKeyFilename,
message)
23.
24. print('Encrypted text:')
25. print(encryptedText)
26.
27. elif mode == 'decrypt':
28. privKeyFilename = 'al_sweigart_privkey.txt'
29. print('Reading from %s and decrypting...' % (filename))
30. decryptedText = readFromFileAndDecrypt(filename, privKeyFilename)
31.
32. print('Decrypted text:')
33. print(decryptedText)
34.
35.
36. def getBlocksFromText(message, blockSize=DEFAULT_BLOCK_SIZE):
37. # Converts a string message to a list of block integers. Each integer
38. # represents 128 (or whatever blockSize is set to) string characters.
39.
40. messageBytes = message.encode('ascii') # convert the string to bytes
41.
42. blockInts = []
43. for blockStart in range(0, len(messageBytes), blockSize):
44. # Calculate the block integer for this block of text
45. blockInt = 0
46. for i in range(blockStart, min(blockStart + blockSize,
len(messageBytes))):
47. blockInt += messageBytes[i] * (BYTE_SIZE ** (i % blockSize))
48. blockInts.append(blockInt)
49. return blockInts
50.
51.
52. def getTextFromBlocks(blockInts, messageLength,
blockSize=DEFAULT_BLOCK_SIZE):
53. # Converts a list of block integers to the original message string.
54. # The original message length is needed to properly convert the last
55. # block integer.
56. message = []
57. for blockInt in blockInts:
58. blockMessage = []
59. for i in range(blockSize - 1, -1, -1):
60. if len(message) + i < messageLength:
61. # Decode the message string for the 128 (or whatever

Chapter 24 – Public Key Cryptography and the RSA Cipher 393
62. # blockSize is set to) characters from this block integer.
63. asciiNumber = blockInt // (BYTE_SIZE ** i)
64. blockInt = blockInt % (BYTE_SIZE ** i)
65. blockMessage.insert(0, chr(asciiNumber))
66. message.extend(blockMessage)
67. return ''.join(message)
68.
69.
70. def encryptMessage(message, key, blockSize=DEFAULT_BLOCK_SIZE):
71. # Converts the message string into a list of block integers, and then
72. # encrypts each block integer. Pass the PUBLIC key to encrypt.
73. encryptedBlocks = []
74. n, e = key
75.
76. for block in getBlocksFromText(message, blockSize):
77. # ciphertext = plaintext ^ e mod n
78. encryptedBlocks.append(pow(block, e, n))
79. return encryptedBlocks
80.
81.
82. def decryptMessage(encryptedBlocks, messageLength, key,
blockSize=DEFAULT_BLOCK_SIZE):
83. # Decrypts a list of encrypted block ints into the original message
84. # string. The original message length is required to properly decrypt
85. # the last block. Be sure to pass the PRIVATE key to decrypt.
86. decryptedBlocks = []
87. n, d = key
88. for block in encryptedBlocks:
89. # plaintext = ciphertext ^ d mod n
90. decryptedBlocks.append(pow(block, d, n))
91. return getTextFromBlocks(decryptedBlocks, messageLength, blockSize)
92.
93.
94. def readKeyFile(keyFilename):
95. # Given the filename of a file that contains a public or private key,
96. # return the key as a (n,e) or (n,d) tuple value.
97. fo = open(keyFilename)
98. content = fo.read()
99. fo.close()
100. keySize, n, EorD = content.split(',')
101. return (int(keySize), int(n), int(EorD))
102.
103.
104. def encryptAndWriteToFile(messageFilename, keyFilename, message,
blockSize=DEFAULT_BLOCK_SIZE):
105. # Using a key from a key file, encrypt the message and save it to a

394 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
106. # file. Returns the encrypted message string.
107. keySize, n, e = readKeyFile(keyFilename)
108.
109. # Check that key size is greater than block size.
110. if keySize < blockSize * 8: # * 8 to convert bytes to bits
111. sys.exit('ERROR: Block size is %s bits and key size is %s bits.
The RSA cipher requires the block size to be equal to or less than the key
size. Either increase the block size or use different keys.' % (blockSize * 8,
keySize))
112.
113.
114. # Encrypt the message
115. encryptedBlocks = encryptMessage(message, (n, e), blockSize)
116.
117. # Convert the large int values to one string value.
118. for i in range(len(encryptedBlocks)):
119. encryptedBlocks[i] = str(encryptedBlocks[i])
120. encryptedContent = ','.join(encryptedBlocks)
121.
122. # Write out the encrypted string to the output file.
123. encryptedContent = '%s_%s_%s' % (len(message), blockSize,
encryptedContent)
124. fo = open(messageFilename, 'w')
125. fo.write(encryptedContent)
126. fo.close()
127. # Also return the encrypted string.
128. return encryptedContent
129.
130.
131. def readFromFileAndDecrypt(messageFilename, keyFilename):
132. # Using a key from a key file, read an encrypted message from a file
133. # and then decrypt it. Returns the decrypted message string.
134. keySize, n, d = readKeyFile(keyFilename)
135.
136.
137. # Read in the message length and the encrypted message from the file.
138. fo = open(messageFilename)
139. content = fo.read()
140. messageLength, blockSize, encryptedMessage = content.split('_')
141. messageLength = int(messageLength)
142. blockSize = int(blockSize)
143.
144. # Check that key size is greater than block size.
145. if keySize < blockSize * 8: # * 8 to convert bytes to bits
146. sys.exit('ERROR: Block size is %s bits and key size is %s bits.
The RSA cipher requires the block size to be equal to or less than the key

Chapter 24 – Public Key Cryptography and the RSA Cipher 395
size. Did you specify the correct key file and encrypted file?' % (blockSize *
8, keySize))
147.
148. # Convert the encrypted message into large int values.
149. encryptedBlocks = []
150. for block in encryptedMessage.split(','):
151. encryptedBlocks.append(int(block))
152.
153. # Decrypt the large int values.
154. return decryptMessage(encryptedBlocks, messageLength, (n, d),
blockSize)
155.
156.
157. # If rsaCipher.py is run (instead of imported as a module) call
158. # the main() function.
159. if __name__ == '__main__':
160. main()
Sample Run of the RSA Cipher Program
Once you have a public and private key file, you can send anyone your public file (or post it
somewhere online) so others can send you messages. If you want to send a secret message to
someone, first get their public key file and place it in the same directory as the rsaCipher.py
program. Set the message variable on line 19 to the string of the message to encrypt.
Make sure the mode variable is set to the string 'encrypt' on line 16, and set the
pubKeyFilename variable to the public key file’s filename on line 20. The filename
variable holds a string of the file that the ciphertext will be written to.
When you run the program, the output will look like this:
Encrypting and writing to encrypted_file.txt...
Encrypted text:
262_128_99261588918914129248869521413561361425429438626950729912505980066002708
9830015533870663668185646157509007528457226336261821873976954531347724960840148
5234147843064609273929706353514554444810285427183303767133366827434264155196422
0917826499299282445350219039270525853857169256807439317455881433369973441896615
9641434946805896304802494813292321784924727694126957902732539670170912919151008
4539012275457327046892059514600198713235394985023008043572425418307615110483262
2796568393228930000619315738939341534920563203314816419962044702016227849752350
41470244964996075123464854629954207517620745550909143567815440815430367,6684261
3553841756289795361296785769122909029892643608575548034344009592725547265584325
2331933112765122922637923600156910575424723444966430139306688707256391991191466
4504822721492217530056774346964092597494522555496959638903763181124233744530745

396 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
2041948917261094688708004245747998030244635761849845611609053856921438831555343
2751213283486646600584040245146570901217502941710992503572482408074196762322544
6680099823178790059243202224297039960462494558200472899766913932921695002362188
1996217713713494770944644417894970293643840346744192412614346008019737829011867
03144271104078294839144290043228508639879193883889311384,7277016624458973047704
0806680156575455285570435553143790299815533233656061333313422971390933175290260
5817773458688756774589737014227054621841244485285514206025269405528441594535085
0536174716382559790627193026256934316461174349640238168693204610463496242533658
4736211406286896178786120454116459075038688037119234659059503824465257190001591
9094263967757274610514128826270203357049019841335033192183418122067029417580137
3024013553583624428117568253845170657841567369678118510784447456725765265002966
2854459043617323327066630863887606386875040688709377112851144150781493772858323
25922978358897651126143551277531003851780
At the start of the text is 262 (which is the original message length), followed by an underscore
and then 128 (which is the “block size”; block sizes are explained later). If you look carefully at
the long string of digits after that, you will find two commas. The message is encrypted into three
very large integers, separated by commas. These integers are the encrypted form of the string in
the message variable on line 19.
To decrypt, change the mode variable to 'decrypt' and run the program again. Make sure
privKeyFilename on line 28 is set to the filename of the private key file and that this file is
in the same folder as rsaCipher.py. When you run the program, the output on the screen will look
like this:
Reading from encrypted_file.txt and decrypting...
Decrypted text:
"Journalists belong in the gutter because that is where the ruling classes
throw their guilty secrets." -Gerald Priestland "The Founding Fathers gave the
free press the protection it must have to bare the secrets of government and
inform the people." -Hugo Black
Note that the way the RSA cipher program is implemented, it can only encrypt and decrypt
plaintext files. A plaintext file (not to be confused with “plaintext” in the cryptography sense) is
a file that only contains text characters (like the kind that you can type on your keyboard). For
example, the .py files that you type for your Python programs are plaintext files. Plaintext files
are the type created with text editor software such as Notepad (on Windows), TextMate (on OS
X), or Gedit (on Ubuntu). Specifically, plaintext files are files that only contain ASCII values
(which are described later in this chapter).
Files such as images, videos, executable programs, or word processor files are called binary
files.(Word processor files are binary files because their text has font, color, and size information

Chapter 24 – Public Key Cryptography and the RSA Cipher 397
bundled with the text.) More information about plaintext files and binary files can be found at
http://invpy.com/plainvsbinary.
Practice Exercises, Chapter 24, Set A
Practice exercises can be found at http://invpy.com/hackingpractice24A.
Digital Signatures
Digital signatures is a very large topic of its own, but we can cover a little of it here. Let’s say
Alice sent this email to Bob:
From: alice@inventwithpython.com
To: bob@coffeeghost.net
Subject: Our agreement.
Dear Bob,
I promise to buy your old broken laptop for one
million dollars.
Sincerely,
Alice
This is great news to Bob, who wants to get rid of his worthless laptop for any price. But what if
Alice later claims that she didn’t make this promise, and that the email Bob has is a forgery that
didn’t really come from her. The email just exists as some file on Bob’s computer. Bob could
have easily created this file himself.
If they had met in person, Alice and Bob could have signed a contract. The handwritten signature
is not easy to forge and provides some proof that Alice really did make this promise. But even if
Alice signed such a paper, took a photo of it with her digital camera, and sent Bob the image file,
it is still believable for Alice to say that the image was photoshopped.
The RSA cipher (and any public key cipher) not only provides encryption, but it can also provide
a way to digitally sign a file or string. Remember that RSA has a public key and a private key,
and that any string that is encrypted with one key produces ciphertext that can only be decrypted
with the other key. Normally we encrypt with the public key, so that only the owner of the private
key can decrypt this ciphertext.
But we can also do the reverse. If Alice writes this message, and then “encrypts” it with her
private key, this will produce “ciphertext” that only Alice’s public key can decrypt. This
“ciphertext” isn’t really so secret since everyone in the world has access to Alice’s public key to

398 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
decrypt it. But by encrypting a message with her own private key, Alice has digitally signed
the message in a way that cannot be forged. Everyone can decrypt this signed message with her
public key, and since only Alice has access to her private key, only Alice could have produced
this ciphertext. Alice has to stick to her digital signature; she can’t say that Bob forged or
photoshopped it!
This feature is called nonrepudiation. Nonrepudiation is where someone who has made a
statement or claim cannot later refute that they made that statement or claim. Alice could always
claim that her computer was hacked and somebody else had access to her private key, but this
would mean that any other documents she signed could be called into question. (And it would be
very suspicious if Alice’s computer kept “getting hacked” each time she wanted to back out of a
promise.)
Digital signatures can also provide authentication, which allows someone to prove they are who
they say they are. If Alice gets an email claiming to be from the President but wants to be sure it
really is the President, she could always respond with, “Prove you’re the President! Encrypt the
string 'SIMTAVOKXVAHXXSLBGZXVPKNMQMHOYGWFQMXEBCC' with the President’s
private key.” and Alice would be able to decrypt the reply with the President’s public key to see if
it decrypted to her random string. This is called a challenge-response authentication system.
Digital signatures can be used to do many important things, including digital cash, authentication
of public keys, or anonymous web surfing. If you’d like to find out more, go to
http://invpy.com/digitalsignatures.
How the RSA Cipher Program Works
rsaCipher.py
1. # RSA Cipher
2. # http://inventwithpython.com/hacking (BSD Licensed)
3.
4. import sys
5.
6. # IMPORTANT: The block size MUST be less than or equal to the key size!
7. # (Note: The block size is in bytes, the key size is in bits. There
8. # are 8 bits in 1 byte.)
9. DEFAULT_BLOCK_SIZE = 128 # 128 bytes
10. BYTE_SIZE = 256 # One byte has 256 different values.
A single “byte” can hold a number between 0 and 255, that is, 256 different numbers. We will use
this fact in some of the block-related math explained later. This is why the BYTE_SIZE constant
is set to 256. The DEFAULT_BLOCK_SIZE constant is set to 128 because we will be using
block sizes of 128 bytes by default in our program. (Block sizes are explained later.)

Chapter 24 – Public Key Cryptography and the RSA Cipher 399
rsaCipher.py
12. def main():
13. # Runs a test that encrypts a message to a file or decrypts a message
14. # from a file.
15. filename = 'encrypted_file.txt' # the file to write to/read from
16. mode = 'encrypt' # set to 'encrypt' or 'decrypt'
If mode is set to 'encrypt' the program encrypts a message (and writes it to the file that is
named in filename). If mode is set to 'decrypt' the program reads the contents of an
encrypted file (specified by the string in filename) to decrypt it.
rsaCipher.py
18. if mode == 'encrypt':
19. message = '''"Journalists belong in the gutter because that is
where the ruling classes throw their guilty secrets." -Gerald Priestland "The
Founding Fathers gave the free press the protection it must have to bare the
secrets of government and inform the people." -Hugo Black'''
20. pubKeyFilename = 'al_sweigart_pubkey.txt'
21. print('Encrypting and writing to %s...' % (filename))
22. encryptedText = encryptAndWriteToFile(filename, pubKeyFilename,
message)
23.
24. print('Encrypted text:')
25. print(encryptedText)
The message variable contains the text to be encrypted, and pubKeyFilename contains the
filename of the public key file. Line 22 calls the encryptAndWriteToFile() function,
which will encrypt message using the key, and write the encrypted message to the file named in
filename.
rsaCipher.py
27. elif mode == 'decrypt':
28. privKeyFilename = 'al_sweigart_privkey.txt'
29. print('Reading from %s and decrypting...' % (filename))
30. decryptedText = readFromFileAndDecrypt(filename, privKeyFilename)
31.
32. print('Decrypted text:')
33. print(decryptedText)
The code that handles calling the decryption function is similar to the code on lines 18 to 33. The
filename of the private key file is set in privKeyFilename. The encrypted file’s filename is
stored in the filename variable. These two variables are passed to a call to

400 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
readFromFileAndDecrypt(). The return value is stored in decryptedText and then
printed to the screen.
ASCII: Using Numbers to Represent Characters
All data is stored on your computer as numbers. A code called the American Standard Code for
Information Interchange, or ASCII (pronounced “ask-ee”) maps numbers to characters. Table 24-
1 shows how ASCII maps numbers and characters (only numbers 32 to 126 are used):
Table 24-1. The ASCII table.
32
(space)
48
0
64
@
80
P
96
`
112
p
33
!
49
1
65
A
81
Q
97
a
113
q
34
"
50
2
66
B
82
R
98
b
114
r
35
#
51
3
67
C
83
S
99
c
115
s
36
$
52
4
68
D
84
T
100
d
116
t
37
%
53
5
69
E
85
U
101
e
117
u
38
&
54
6
70
F
86
V
102
f
118
v
39
'
55
7
71
G
87
W
103
g
119
w
40
(
56
8
72
H
88
X
104
h
120
x
41
)
57
9
73
I
89
Y
105
i
121
y
42
*
58
:
74
J
90
Z
106
j
122
z
43
+
59
;
75
K
91
[
107
k
123
{
44
,
60
<
76
L
92
\
108
l
124
|
45
-
61
=
77
M
93
]
109
m
125
}
46
.
62
>
78
N
94
^
110
n
126
~
47
/
63
?
79
O
95
_
111
o
A single ASCII character uses one byte of memory to store. A byte is enough memory to store a
number from 0 to 255 (for a total of 256 different values.) So the string 'Hello' is actually
stored on your computer as the numbers 72, 101, 108, 108, and 111. These numbers take up 5
bytes. ASCII provides a standard way to convert string characters to numbers and back.
ASCII works fine for English messages, but not so much for other European languages that have
special characters such as the è in “Vigenère”, or languages such as Chinese and Arabic. ASCII
doesn’t even work well outside of America, since ASCII includes the $ dollar sign but not the €
euro or £ pound signs. If you want to learn about Unicode, the international system of character
encoding, go to http://invpy.com/unicode. But this book will use ASCII for simplicity.
The chr() and ord() Functions
Remember from the first chapter where a code was a publicly-known way of translating
information from one format to another format? For example, Morse code was a way of
Chapter 24 – Public Key Cryptography and the RSA Cipher 401
translating English letters into electric pulses of dots and dashes. ASCII is just a code. We can
encode characters into ASCII numbers and decode ASCII numbers back to characters.
The chr() function (pronounced “char”, short for “character”) takes an integer ASCII number
as the argument and returns a single-character string. The ord() function (short for “ordinal”)
takes a single-character string as the argument, and returns the integer ASCII value for that
character. Try typing the following into the interactive shell:
>>> chr(65)
'A'
>>> ord('A')
65
>>> chr(73)
'I'
>>> chr(65+8)
'I'
>>> chr(52)
'4'
>>> chr(ord('F'))
'F'
>>> ord(chr(68))
68
>>>
But if you have a string with many letters, it may be easier to use the encode() and
decode() string methods explained later in this chapter.
Practice Exercises, Chapter 24, Set B
Practice exercises can be found at http://invpy.com/hackingpractice24B.
Blocks
In cryptography, a “block” is a fixed length of bits. In our RSA cipher program, a block is
represented by an integer. We’ve set the block size to 128 bytes, or 1024 bits (since there are 8
bits in 1 byte). Our message string value will be converted into several integer values (i.e. several
blocks).
It is important to note that the RSA encryption algorithm requires that the block size be
equal or less than the key size. Otherwise, the math doesn’t work and you won’t be able
to decrypt the ciphertext the program produced.
402 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
So a cryptographic block is really just a very large integer. Since our block size is 128 bytes, it
can represent any integer between 0 and up to (but not including) 256 ^ 128, which is
179,769,313,486,231,590,772,930,519,078,902,473,361,797,697,894,230,657,273,430,081,157,7
32,675,805,500,963,132,708,477,322,407,536,021,120,113,879,871,393,357,658,789,768,814,41
6,622,492,847,430,639,474,124,377,767,893,424,865,485,276,302,219,601,246,094,119,453,082,
952,085,005,768,838,150,682,342,462,881,473,913,110,540,827,237,163,350,510,684,586,298,2
39,947,245,938,479,716,304,835,356,329,624,224,137,216.
(You might have noticed that the RSA cipher uses a lot of big numbers.)
The reason RSA needs to work on a block (which represents multiple characters) is because if we
used the RSA encryption algorithm on a single character, the same plaintext characters would
always encrypt to the same ciphertext characters. In that case, the RSA cipher just becomes a
simple substitution cipher with fancy mathematics, kind of like the affine and Caesar ciphers.
The RSA cipher works by encrypting an integer that is hundreds of digits long (that is, a block)
into a new integer that is hundreds of digits long (that is, a new block). The mathematics of
encrypting a large plaintext integer to a large ciphertext integer are simple enough. But first we
will need a way to convert between a string and a large integer (that is, a block).
We can use ASCII as a system to convert between a single character and a small integer (between
0 and 255). But we will also need a way to combine several small integers into a large integer that
we perform RSA encryption on.
Remember how the affine cipher in Chapter 15 had two keys, Key A and Key B, but they were
combined by multiplying Key A by the symbol set size (which was 95) and then adding Key B?
This was how we combined two small key integers into one larger key integer.
This worked because the ranges of both Key A and Key B were from 0 to 94. In the RSA
program, each character’s ASCII integer ranges from 0 to 255. To combine ASCII integers
together into one large number we use the following formula:
Take the ASCII integer of the character at index 0 of the string and multiply it by 256 ^ 0 (but
since 256 ^ 0 is 1, and multiplying by 1 leaves you with just the original number, this one is
easy). Take the ASCII integer of the character at index 1 and multiply it by 256 ^ 1. Take the
ASCII integer of the character at index 2 and multiply it by 256 ^ 2, and so on and so on. To get
the final large integer, add all of these products together. This integer is the ciphertext’s block.
Table 24-2 has an example using the string, 'Hello world!':

Chapter 24 – Public Key Cryptography and the RSA Cipher 403
Table 24-2. Encoding a string into a block.
Index
Character
ASCII
Number
Multiplied
By
Number
0
H
72
× 256 ^ 0
= 72
1
e
101
× 256 ^ 1
= 25,856
2
l
108
× 256 ^ 2
= 7,077,888
3
l
108
× 256 ^ 3
= 1,811,939,328
4
o
111
× 256 ^ 4
= 476,741,369,856
5
(space)
32
× 256 ^ 5
= 35,184,372,088,832
6
w
119
× 256 ^ 6
= 33,495,522,228,568,064
7
o
111
× 256 ^ 7
= 7,998,392,938,210,000,896
8
r
114
× 256 ^ 8
= 2,102,928,824,402,888,884,224
9
l
108
× 256 ^ 9
= 510,015,580,149,921,683,079,168
10
d
100
× 256 ^ 10
= 120,892,581,961,462,917,470,617,600
11
!
33
× 256 ^ 11
= 10,213,005,324,104,387,267,917,774,848
SUM:
10,334,410,032,606,748,633,331,426,632
(You might have noticed that the RSA cipher does a lot of math with big numbers.)
So the string 'Hello world!' when put into a single large integer “block” becomes the
integer 10,334,410,032,606,748,633,331,426,632. This integer uniquely refers to the string
'Hello world!'. By continuing to use larger and larger powers of 256, any string possible
has exactly one large integer. For example, 2,175,540 is the integer for '42!' and
17,802,628,493,700,941 is the integer for 'Moose??' and
23,071,981,395,336,227,453,293,155,570,939,985,398,502,658,016,284,755,880,397,214,576,11
0,064,091,578,359,739,349,325 is the integer for 'My cat's breath smells like cat
food.'.
Because our block size is 128 bytes, we can only encrypt up to 128 characters in a single block.
But we can just use more blocks if the message is longer than 128 characters. The RSA cipher
program will separate the blocks it outputs with commas so we can tell when one block ends and
the next one begins.
As an example, here’s a message that is split into blocks, and the integer that represents each
block (calculated using the same method in Table 24-2.). Each block has at most 128 characters
of the message.

404 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Table 24-3. A message split into blocks, with each block’s integer.
Message
Block Integer
1st Block
(128 characters)
Alan Mathison Turing
was a British
mathematician,
logician, cryptanalyst,
and computer scientist.
He was highly
influential in t
81546931218178010029845817915569188970228
63503588092404856861189798874246340656702
38839432215827478831941988018897629951268
20043055718365161172430048774726604180301
48768604258244651074200425332013985856895
55969506391783606289711328048889254351125
31133886746309774148590001157056903849858
716430520524535327809
2nd Block
(128 characters)
he development of
computer science,
providing a
formalisation of the
concepts of "algorithm"
and "computation" with
the Turing m
76631289268154712859022451851447083030531
65677349319343558638588471345037404319956
45932085093160422349968619052225062492420
68799766044149679741160521638235464390814
93343748091892111084834682008279498952509
54725768834415584340223896902248947030025
14434767442075089828357797890134106785932
701869224970151814504
3rd Block
(128 characters)
achine. Turing is
widely considered to be
the father of computer
science and artificial
intelligence. During
World War II, Turin
77533874832922662837221187157031815413218
69665618828947923728504232931792998759025
56568632161704130179292825376098664640739
13897327838474709028475738093888688583459
78166272494460147358283858671447396525449
89137517820478280435270940014295674175014
93130489686652467441331220556610652015232
230994266943673361249
4th Block
(107 characters)
g worked for the
Government Code and
Cypher School (GCCS)
at Bletchley Park,
Britain's codebreaking
centre.
87080208891262703930798322686594857958157
73519113112470129994578811890430257029137
88108716196921960428416274796671334547332
64625727703476738415017881880631980435061
77034123161704448596151119133333044771426
77343891157354079822547964726407323487308
38206586983
Converting Strings to Blocks with getBlocksFromText()
rsaCipher.py
36. def getBlocksFromText(message, blockSize=DEFAULT_BLOCK_SIZE):
37. # Converts a string message to a list of block integers. Each integer
38. # represents 128 (or whatever blockSize is set to) string characters.
The getBlocksFromText() function takes the message and returns a list of blocks (that is, a
list of very large integer values) that represents the message. It is trivially easy to convert between

Chapter 24 – Public Key Cryptography and the RSA Cipher 405
strings to blocks and blocks to strings, so this step isn’t encrypting anything. The encryption will
be done later in the encryptMessage() function.
The encode() String Method and the Bytes Data Type
rsaCipher.py
40. messageBytes = message.encode('ascii') # convert the string to bytes
First, we need to convert the characters in the message string into ASCII integers. The
encode() string method will return a “bytes” object. Because a byte is represented as a number
from 0 to 255, a bytes value is like a list of integers (although these integers have a very limited
range of 0 to 255). The len() function and indexing work with a bytes object in the same way a
list of integers would. A bytes value can be turned into a list value of integer values by passing it
to the list() function. Try typing the following into the interactive shell:
>>> spam = 'hello'.encode('ascii')
>>> spam
b'hello'
>>> list(spam)
[104, 101, 108, 108, 111]
>>> len(spam)
5
>>> spam[2]
108
>>>
Note that a single bytes value is a collection of values, just like a single list value can contain
multiple values. If you try to get a single “byte” from a bytes object (like spam[2] does above),
this just evaluates to an integer value.
Line 40 places the bytes form of the message string in a variable named messageBytes.
The bytes() Function and decode() Bytes Method
Just like you can create a list by calling the list() function, you can also create a bytes object
by calling the bytes() function. The bytes() function is passed a list of integers for the byte
values. Try typing the following into the interactive shell:
>>> spam = bytes([104, 101, 108, 108, 111])
>>> spam
b'hello'
>>> list(spam)
[104, 101, 108, 108, 111]

406 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
>>>
You can also directly type a bytes object into your source code just like you type a string or list.
A bytes object has the letter b right before what looks like an ordinary string value. But
remember, the letter b right before the quotes means that this is a bytes value, not a string value.
Try typing the following into the interactive shell, making sure that there is no space between the
b and the quote characters:
>>> spam = b'hello'
>>> list(spam)
[104, 101, 108, 108, 111]
>>>
We don’t use the decode() bytes method in this program, but you should know about it. It does
the opposite of the encode() string method. When called on a bytes object, the decode()
method returns a string made from the values stored in the bytes object. Try typing the following
into the interactive shell:
>>> spam = bytes([104, 101, 108, 108, 111])
>>> spam.decode('ascii')
'hello'
>>>
Practice Exercises, Chapter 24, Set C
Practice exercises can be found at http://invpy.com/hackingpractice24C.
Back to the Code
rsaCipher.py
42. blockInts = []
43. for blockStart in range(0, len(messageBytes), blockSize):
The blockInts list will contain the large integer “blocks” form of the characters in message.
The blockSize parameter is set to DEFAULT_BLOCK_SIZE by default, and the
DEFAULT_BLOCK_SIZE constant was set to 128 (meaning, 128 bytes) on line 9. This means
that each large integer block can only store 128 string characters at most (since 1 ASCII character
takes up 1 byte). See Table 24-3 for an example of a message split into 128-character blocks.
Line 43’s for loop will set the value in blockStart so that on each iteration it will be set to
the index of the block being created. For example, if blockSize is set to 128, then the index of

Chapter 24 – Public Key Cryptography and the RSA Cipher 407
the start of the first block will be 0, the index of the start of the second block will be 128, the
index of the start of the third block will be 256, and so on as long as the index is less than
len(messageBytes).
The min() and max() Functions
The min() function returns the smallest (that is, the minimum) value of its arguments. Try
typing the following into the interactive shell:
>>> min(13, 32, 13, 15, 17, 39)
13
>>> min(21, 45, 18, 10)
10
You can also pass min() a single argument if the argument is a list or tuple value. In this case,
min() returns the smallest value in that list or tuple. Try typing the following into the interactive
shell:
>>> min([31, 26, 20, 13, 12, 36])
12
>>> spam = (10, 37, 37, 43, 3)
>>> min(spam)
3
>>>
The max() function will return the largest (that is, the maximum) value of its arguments:
>>> max(18, 15, 22, 30, 31, 34)
34
>>>
rsaCipher.py
44. # Calculate the block integer for this block of text
45. blockInt = 0
46. for i in range(blockStart, min(blockStart + blockSize,
len(messageBytes))):
The code inside line 43’s for loop will create the very large integer for a single block. Recall
from earlier in this chapter that this is done by multiplying the ASCII value of the character by
(256 ^ index-of-character).
408 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
The very large integer will eventually be stored in blockInt, which starts at 0 on line 45. (This
is much like how our previous cipher programs had a translated variable that started as a
blank string but eventually held the encrypted or decrypted message by the end of the program.)
Line 46’s for loop sets i to be the index of all the characters in message for this block. This
index should start at blockStart and go up to blockStart + blockSize (that is,
blockSize characters after blockStart) or len(messageBytes), whichever is smaller.
The min() call on line 46 will return the smaller of these two expressions.
The second argument to range() on line 46 should be the smaller of these values because each
block will always be made up of 128 (or whatever value is in blockSize) characters, except for
the last block. The last block might be exactly 128 characters, but more likely it is less than the
full 128 characters. In that case we want i to stop at len(messageBytes) because that will
be the last index in messageBytes.
rsaCipher.py
47. blockInt += messageBytes[i] * (BYTE_SIZE ** (i % blockSize))
The value that is added to the block integer in blockInt is the ASCII value of the character
(which is what messageBytes[i] evaluates to) multiplied by (256 ^ index-of-character).
The variable i cannot directly be used for the index-of-character part of the equation, because it
is the index in the entire messageBytes object which has indexes from 0 up to
len(messageBytes). We only want the index relative to the current iteration’s block, which
will always be from 0 to blockSize. This table shows the difference between these indexes:
Table 24-4. The indexes of the full message on top, and indexes relative to the block on bottom.
1st Block’s Indexes
2nd Block’s Indexes
3rd Block’s Indexes
0
1
2
…
127
129
130
…
255
257
258
…
511
0
1
2
…
127
0
1
…
127
0
1
…
127
By modding i by blockSize, we can get the position relative to the block. This is why line 47
is BYTE_SIZE ** (i % blockSize) instead of BYTE_SIZE ** i.
rsaCipher.py
48. blockInts.append(blockInt)
49. return blockInts
After line 46’s for loop completes, the very large integer for the block has been calculated. We
want to append this block integer to the blockInts list. The next iteration of line 43’s for
loop will calculate the block integer for the next block of the message.

Chapter 24 – Public Key Cryptography and the RSA Cipher 409
After line 43’s for loop has finished, all of the block integers have been calculated and are
stored in the blockInts list. Line 49 returns blockInts from getBlocksFromText().
rsaCipher.py
52. def getTextFromBlocks(blockInts, messageLength,
blockSize=DEFAULT_BLOCK_SIZE):
53. # Converts a list of block integers to the original message string.
54. # The original message length is needed to properly convert the last
55. # block integer.
56. message = []
57. for blockInt in blockInts:
The getTextFromBlocks() function does the opposite of getBlocksFromText(). This
function is passed a list of block integers (as the blockInts parameter) and returns the string
value that these blocks represent. The function needs the length of the message encoded in
messageLength, since this information is needed to get the string from the last block integer if
it is not a full 128 characters in size.
Just as before, blockSize will default to DEFAULT_BLOCK_SIZE if no third argument is
passed to getTextFromBlocks(), and DEFAULT_BLOCK_SIZE was set to 128 on line 9.
The message list (which starts as blank on line 56) will contain a string value for each character
that was computed from each block integer in blockInts. (This list of strings will be joined
together to form the complete string at the end of getTextFromBlocks().) The message
list starts off empty on line 56. The for loop on line 57 iterates over each block integer in the
blockInts list.
rsaCipher.py
58. blockMessage = []
59. for i in range(blockSize - 1, -1, -1):
Inside the for loop, the code from lines 58 to 65 calculates the letters that are in the current
iteration’s block. Recall from Chapter 15’s affine cipher program how one integer key was split
into two integer keys:
24. def getKeyParts(key):
25. keyA = key // len(SYMBOLS)
26. keyB = key % len(SYMBOLS)
27. return (keyA, keyB)
The code in getTextFromBlocks() works in a similar way, except the single integer (i.e. the
block integer) is split into 128 integers (and each is the ASCII value for a single character). The

410 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
way the ASCII numbers are extracted from blockInt has to work backwards, which is why the
for loop on line 59 starts at blockSize - 1, and then subtracts 1 on each iteration down to
(but not including) -1. This means the value of i on the last iteration will be 0.
rsaCipher.py
60. if len(message) + i < messageLength:
61. # Decode the message string for the 128 (or whatever
62. # blockSize is set to) characters from this block integer.
63. asciiNumber = blockInt // (BYTE_SIZE ** i)
64. blockInt = blockInt % (BYTE_SIZE ** i)
The length of the message list will be how many characters have been translated from blocks so
far. The if statement on line 60 makes sure the code does not keep computing text from the
block after i has reached the end of the message.
The ASCII number of the next character from the block is calculated by integer dividing
blockInt by (BYTE_SIZE ** i). Now that we have calculated this character, we can
“remove” it from the block by setting blockInt to the remainder of blockInt divided by
(BYTE_SIZE ** i). The % mod operator is used to calculate the remainder.
The insert() List Method
While the append() list method only adds values to the end of a list, the insert() list
method can add a value anywhere in the list. The arguments to insert() are an integer index
of where in the list to insert the value, and the value to be inserted. Try typing the following into
the interactive shell:
>>> spam = [2, 4, 6, 8]
>>> spam.insert(0, 'hello')
>>> spam
['hello', 2, 4, 6, 8]
>>> spam.insert(2, 'world')
>>> spam
['hello', 2, 'world', 4, 6, 8]
>>>
rsaCipher.py
65. blockMessage.insert(0, chr(asciiNumber))
Using the chr() function, the character that asciiNumber is the ASCII number of is inserted
to the beginning of the list at index 0.

Chapter 24 – Public Key Cryptography and the RSA Cipher 411
rsaCipher.py
66. message.extend(blockMessage)
After the for loop on line 59 completes, blockMessage will be a list of single-character
strings that were computed from the current block integer. The strings in this list are appended to
the end of the message list with the extend() method.
rsaCipher.py
67. return ''.join(message)
After the for loop on line 57 completes, the single-character strings in message are joined
together into a single string which is the complete message. This string is then returned from the
getTextFromBlocks() function.
The Mathematics of RSA Encrypting and Decrypting
With the numbers for e, d, and n from the public and private keys, the mathematics done on the
block integers to encrypt and decrypt them can be summarized as follows:
Encrypted Block = Plaintext Block ^ e mod n
Decrypted Block = Ciphertext Block ^ d mod n
rsaCipher.py
70. def encryptMessage(message, key, blockSize=DEFAULT_BLOCK_SIZE):
71. # Converts the message string into a list of block integers, and then
72. # encrypts each block integer. Pass the PUBLIC key to encrypt.
73. encryptedBlocks = []
74. n, e = key
The encryptMessage() function is passed the plaintext string along with the two-integer
tuple of the private key. The function returns a list of integer blocks of the encrypted ciphertext.
First, the encryptedBlocks variable starts as an empty list that holds the integer blocks and
the two integers in key are assigned to variables n and e.
The pow() Function
While the ** operator does exponents, the pow() function handles exponents and mod. The
expression pow(a, b, c) is equivalent to (a ** b) % c. However, the code inside the
pow() function knows how to intelligently handle very large integers and is much faster than
typing the expression (a ** b) % c. Try typing the following into the interactive shell:
>>> pow(2, 8)

412 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
256
>>> (2 ** 8)
256
>>> pow(2, 8, 10)
6
>>> (2 ** 8) % 10
6
>>>
rsaCipher.py
76. for block in getBlocksFromText(message, blockSize):
77. # ciphertext = plaintext ^ e mod n
78. encryptedBlocks.append(pow(block, e, n))
79. return encryptedBlocks
While creating the public and private keys involved a lot of math, the actual math of the
encryption is simple. The very large integer of the block created from the string in message is
raised to e and then modded by n. This expression evaluates to the encrypted block integer, and
is then appended to encryptedBlocks on line 78.
After all the blocks have been encrypted, the function returns encryptedBlocks on line 79.
rsaCipher.py
82. def decryptMessage(encryptedBlocks, messageLength, key,
blockSize=DEFAULT_BLOCK_SIZE):
83. # Decrypts a list of encrypted block ints into the original message
84. # string. The original message length is required to properly decrypt
85. # the last block. Be sure to pass the PRIVATE key to decrypt.
86. decryptedBlocks = []
87. n, d = key
The math used in the decryptMessage() function is also simple. The decryptedBlocks
variable will store a list of the decrypted integer blocks, and the two integers of the key tuple are
placed in n and d respectively using the multiple assignment trick.
rsaCipher.py
88. for block in encryptedBlocks:
89. # plaintext = ciphertext ^ d mod n
90. decryptedBlocks.append(pow(block, d, n))
The math of the decryption on line 90 is the same as the encryption’s math, except the integer
block is being raised to d instead of e.

Chapter 24 – Public Key Cryptography and the RSA Cipher 413
rsaCipher.py
91. return getTextFromBlocks(decryptedBlocks, messageLength, blockSize)
The decrypted blocks along with the messageLength and blockSize parameters are passed
getTextFromBlocks() so that the decrypted plaintext as a string is returned from
decryptMessage().
Reading in the Public & Private Keys from their Key Files
rsaCipher.py
94. def readKeyFile(keyFilename):
95. # Given the filename of a file that contains a public or private key,
96. # return the key as a (n,e) or (n,d) tuple value.
97. fo = open(keyFilename)
98. content = fo.read()
99. fo.close()
The key files that makeRsakeys.py creates look like this:
<key size as an integer>,<big integer for N>,<big integer for E or D>
The readKeyFile() function is called to read the key size, n, and e (for the public key) or d
(for the private key) values from the key file. Lines 97 to 99 open this file and read in the contents
as a string into the content variable.
rsaCipher.py
100. keySize, n, EorD = content.split(',')
101. return (int(keySize), int(n), int(EorD))
The split() string method splits up the string in content along the commas. The list that
split() returns will have three items in it, and the multiple assignment trick will place each of
these items into the keySize, n, and EorD variables respectively on line 100.
Remember that content was a string when it was read from the file, and the items in the list
that split() returns will also be string values. So before returning the keySize, n, and EorD
values, they are each passed to int() to return an integer form of the value. This is how
readKeyFile() returns three integers that were read from the key file.
The Full RSA Encryption Process
rsaCipher.py
104. def encryptAndWriteToFile(messageFilename, keyFilename, message,
blockSize=DEFAULT_BLOCK_SIZE):

414 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
105. # Using a key from a key file, encrypt the message and save it to a
106. # file. Returns the encrypted message string.
107. keySize, n, e = readKeyFile(keyFilename)
The encryptAndWriteToFile() function is passed three string arguments: a filename to
write the encrypted message in, a filename of the public key to use, and a message to be
encrypted. This function handles not just encrypting the string with the key, but also creating the
file that contains the encrypted contents. (The blockSize parameter can also be specified, but
it will be set to DEFAULT_BLOCK_SIZE by default, which is 128.)
The first step is to read in the values for keySize, n, and e from the key file by calling
readKeyFile() on line 107.
rsaCipher.py
109. # Check that key size is greater than block size.
110. if keySize < blockSize * 8: # * 8 to convert bytes to bits
111. sys.exit('ERROR: Block size is %s bits and key size is %s bits.
The RSA cipher requires the block size to be equal to or less than the key
size. Either increase the block size or use different keys.' % (blockSize * 8,
keySize))
In order for the mathematics of the RSA cipher to work, the key size must be equal to or greater
than the block size. The blockSize value is in bytes, while the key size that was stored in the
key file was in bits, so we multiply the integer in blockSize by 8 on line 110 so that both of
these values represent number of bits.
If keySize is less than blockSize * 8, the program exits with an error message. The user
will either have to decrease the value passed for blockSize or use a larger key.
rsaCipher.py
114. # Encrypt the message
115. encryptedBlocks = encryptMessage(message, (n, e), blockSize)
Now that we have the n and e values for the key, we call the encryptMessage() function
which returns a list of integer blocks on line 115. The encryptMessage() is expecting a two-
integer tuple for the key, which is why the n and e variables are placed inside a tuple that is then
passed as the second argument for encryptMessage().
rsaCipher.py
117. # Convert the large int values to one string value.
118. for i in range(len(encryptedBlocks)):

Chapter 24 – Public Key Cryptography and the RSA Cipher 415
119. encryptedBlocks[i] = str(encryptedBlocks[i])
120. encryptedContent = ','.join(encryptedBlocks)
The join() method will return a string of the blocks separated by commas, but join() only
works on lists with string values, and encryptedBlocks is a list of integers. These integers
will have to first be converted into strings.
The for loop on line 118 iterates through each index in encryptedBlocks, replacing the
integer at encryptedBlocks[i] with a string form of the integer. When the loop completes,
encryptedBlocks now contains a list of string values instead of a list of integer values.
The list of string values is passed to the join() method, which returns a single string of the
list’s strings joined together with commas. Line 120 stores this string in a variable named
encryptedContent.
rsaCipher.py
122. # Write out the encrypted string to the output file.
123. encryptedContent = '%s_%s_%s' % (len(message), blockSize,
encryptedContent)
We want to write out more than just the encrypted integer blocks to the file though, so line 123
changes the encryptedContent variable to include the size of the message (as an integer),
followed by an underscore, followed by the blockSize (which is also an integer), followed by
another underscore, and then followed by the encrypted integer blocks.
rsaCipher.py
124. fo = open(messageFilename, 'w')
125. fo.write(encryptedContent)
126. fo.close()
The last step is to write out the contents of the encrypted file. The filename provided by the
messageFilename parameter is created with the call to open() on line 124. (The 'w'
argument tells open() to open the file in “write mode”.) Note that if a file with this name
already exists, then it will be overwritten by the new file.
The string in encryptedContent is written to the file by calling the write() method on
line 125. Now that we are done writing the file’s contents, line 126 closes the file object in fo.
rsaCipher.py
127. # Also return the encrypted string.
128. return encryptedContent

416 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Finally, the string in encryptedContent is returned from the
encryptAndWriteToFile() function on line 128. (This is so that the code that calls the
function can use this string to, for example, print it on the screen.)
The Full RSA Decryption Process
rsaCipher.py
131. def readFromFileAndDecrypt(messageFilename, keyFilename):
132. # Using a key from a key file, read an encrypted message from a file
133. # and then decrypt it. Returns the decrypted message string.
134. keySize, n, d = readKeyFile(keyFilename)
The readFromFileAndDecrypt() function, like encryptAndWriteToFile(), has
parameters for the encrypted message file’s filename and the key file’s filename. (Be sure to pass
the filename of the private key for keyFilename, not the public key.)
The first step is the same as encryptAndWriteToFile(): the readKeyFile() function
is called to get the values for the keySize, n, and d variables.
rsaCipher.py
137. # Read in the message length and the encrypted message from the file.
138. fo = open(messageFilename)
139. content = fo.read()
140. messageLength, blockSize, encryptedMessage = content.split('_')
141. messageLength = int(messageLength)
142. blockSize = int(blockSize)
The second step is to read in the contents of the file. The messageFilename file is opened for
reading (the lack of a second argument means open() will use “read mode”) on line 138. The
read() method call on line 139 will return a string of the full contents of the file.
Remember that the encrypted file’s format has an integer of the message length, an integer for the
block size used, and then the encrypted integer blocks (all separated by underscore characters).
Line 140 calls the split() method to return a list of these three values, and the multiple
assignment trick places the three values into the messageLength, blockSize, and
message variables respectively.
Because the values returned by split() will be strings, lines 141 and 142 will set
messageLength and blockSize to their integer form, respectively.
rsaCipher.py
144. # Check that key size is greater than block size.

Chapter 24 – Public Key Cryptography and the RSA Cipher 417
145. if keySize < blockSize * 8: # * 8 to convert bytes to bits
146. sys.exit('ERROR: Block size is %s bits and key size is %s bits.
The RSA cipher requires the block size to be equal to or less than the key
size. Did you specify the correct key file and encrypted file?' % (blockSize *
8, keySize))
The readFromFileAndDecrypt() function also has a check that the block size is equal to
or less than the key size. This should always pass, because if the block size was too small, then it
would have been impossible to create this encrypted file. Most likely the wrong private key file
was specified for the keyFilename parameter, which means the key would not have decrypted
the file correctly anyway.
rsaCipher.py
148. # Convert the encrypted message into large int values.
149. encryptedBlocks = []
150. for block in encryptedMessage.split(','):
151. encryptedBlocks.append(int(block))
The encryptedMessage string contains many integer characters joined together with
commas. Line 150’s for loop iterates over the list returned by the split() method. This list
contains strings of individual blocks. The integer form of these strings is appended to the
encryptedBlocks list (which starts as an empty list on line 149) each time line 151 is
executed. After the for loop on line 150 completes, the encryptedBlocks list contains
integer values of the numbers that were in the encryptedMessage string.
rsaCipher.py
153. # Decrypt the large int values.
154. return decryptMessage(encryptedBlocks, messageLength, (n, d),
blockSize)
The list in encryptedBlocks is passed to decryptMessage(), along with
messageLength, the private key (which is a tuple value of the two integers in n and d), and
the block size. The decryptMessage() function returns a single string value of the decrypted
message, which itself is returned from readFileAndDecrypt() on line 154.
rsaCipher.py
157. # If rsaCipher.py is run (instead of imported as a module) call
158. # the main() function.
159. if __name__ == '__main__':
160. main()

418 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
Lines 159 and 160 call the main() function if this program was run by itself rather than
imported by another program.
Practice Exercises, Chapter 24, Set D
Practice exercises can be found at http://invpy.com/hackingpractice24D.
Why Can’t We Hack the RSA Cipher
All the different types of cryptographic attacks we’ve used in this book can’t be used against the
RSA cipher:
1. The brute-force attack won’t work. There are too many possible keys to go through.
2. A dictionary attack won’t work because the keys are based on numbers, not words.
3. A word pattern attack can’t be used because the same plaintext word can be encrypted
differently depending on where in the block it appears.
4. Frequency analysis can’t be used. Since a single encrypted block represents several
characters, we can’t get a frequency count of the individual characters.
There are no mathematical tricks that work, either. Remember, the RSA decryption equation is:
M = C^d mod n
Where M is the message block integer, C is the ciphertext block integer, and the private key is
made up of the two numbers (d, n). Everyone (including a cryptanalyst) has the public key file,
which provides (e, n), so the n number is known. If the cryptanalyst can intercept the ciphertext
(which we should always assume is possible), then she knows C as well. But without knowing d,
it is impossible to do the decryption and calculate M, the original message.
A cryptanalyst knows that d is the inverse of e mod (p – 1) × (q – 1) and also knows e from the
public key. But there’s no way she knows what (p – 1) × (q – 1) is. There are some hints to figure
it out though.
The key sizes are known (it’s in the public key file), so the cryptanalyst knows that p and q are
less than 2 ^ 1024 and that e is relatively prime with (p – 1) × (q – 1). But e is relatively prime
with a lot of numbers, and with a range of 0 to 2 ^ 1024 possible numbers, it is too large to brute-
force.
The cryptanalyst has another hint from the public key, though. The public key is two numbers (e,
n). And from the RSA algorithm she knows that n = p × q. And since p and q are both prime
numbers, for the given n number there can be only two numbers for p and q.

Chapter 24 – Public Key Cryptography and the RSA Cipher 419
(Remember, prime numbers have no factors besides 1 and themselves. If you multiply two prime
numbers, that new number will only have the factors of 1 and itself, and also the two prime
numbers.)
So to solve everything and hack the RSA cipher, all we need to do is figure out what the factors
are for n. Since there are two and only two numbers that multiply to n, we won’t have several
different numbers to choose from. Then we can calculate (p – 1) × (q – 1) and then calculate d.
This seems pretty easy. We already have code that finds factors in primeSieve.py’s isPrime()
function:
Source code from primeSieve.py
7. def isPrime(num):
8. # Returns True if num is a prime number, otherwise False.
9.
10. # Note: Generally, isPrime() is slower than primeSieve().
11.
12. # all numbers less than 2 are not prime
13. if num < 2:
14. return False
15.
16. # see if num is divisible by any number up to the square root of num
17. for i in range(2, int(math.sqrt(num)) + 1):
18. if num % i == 0:
19. return False
20. return True
We can just modify this code to return the first factors it finds (since we know that there can be
only two factors for n besides 1 and n):
def isPrime(num):
# Returns (p,q) where p and q are factors of num
# see if num is divisible by any number up to the square root of num
for i in range(2, int(math.sqrt(num)) + 1):
if num % i == 0:
return (i, num / i)
return None # no factors exist for num, num must be prime
We can just call this function, pass it n (which we get from the public key file), and wait for it to
find our factors, p and q. Then we can know what (p – 1) × (q – 1) is, which means we can
calculate the mod inverse of e mod (p – 1) × (q – 1), which is d, the decryption key. Then it
would be easy to calculate M, the plaintext message.
420 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
There’s a problem, though. Remember that n is a number that is around 600 digits long. In fact,
Python’s math.sqrt() function can’t even handle a number that big (it will give you an error
message). But even if it could, Python would be executing that for loop for a very, very long
time.
Our Sun doesn’t have enough mass to eventually go supernova, but in 5 billion years it will
expand into a red giant star and utterly destroy the Earth. Even if your computer was still running
then, there’s still no chance that 5 billion years is long enough to find the factors of n. That is how
big the numbers we are dealing with are.
And here’s where the strength of the RSA cipher comes from: Mathematically, there is no
shortcut to finding the factors of a number. It’s easy to look at a small number like 15 and say,
“Oh, 5 and 3 are two numbers that multiply to 15. Those are factors of 15.” But it’s another thing
entirely to take a (relatively small) number like 178,565,887,643,607,245,654,502,737 and try to
figure out the factors for it. The only way we can try is by brute-forcing through numbers, but
there are too many numbers.
It is really easy to come up with two prime numbers p and q and multiply them together to get n.
But it is reasonably impossible to take a number n and figure out what p and q are. These facts
make the RSA cipher usable as a cryptographic cipher.
Summary
That’s it! This is the last chapter of the book! There is no “Hacking the RSA Cipher” chapter
because there’s no straightforward attack on the mathematics behind the RSA cipher. And any
brute-force attack would fail, because there are far too many possible keys to try: the keys are
literally hundreds of digits long. If you had a trillion buildings each with a trillion computers that
each tried a trillion keys every nanosecond, it would still take longer than the universe as been in
existence to go through a fraction of the possible keys. (And the electric bill for all those
computers would bankrupt every industrialized nation on the planet.)
That’s a lot of possible keys.
The RSA algorithm is a real encryption cipher used in professional encryption software. When
you log into a website or buy something off the Internet, the RSA cipher (or one like it) is used to
keep passwords and credit card numbers secret from anyone who may be intercepting your
network traffic.
Actually, while the basic mathematics used for professional encryption software are the same as
described in this chapter, you probably don’t want to use this program for your secret files. The
hacks against an encryption program like rsaCipher.py are pretty sophisticated, but they do exist.
(For example, the “random” numbers returned from random.randint() aren’t truly random

Chapter 24 – Public Key Cryptography and the RSA Cipher 421
and can be predicted, meaning that a hacker could figure out which “random” numbers were used
for the prime numbers of your private key.)
You’ve seen how all the previous ciphers in this book have each been hacked and rendered
worthless. In general, you don’t want to write your own cryptography code for things you want to
keep secret, because you will probably make subtle mistakes in the implementation of these
programs. And hackers and spy agencies use these mistakes to hack your encrypted messages.
A cipher is only secure if everything but the key can be revealed but still keep the message a
secret. You cannot rely on a cryptanalyst not having access to the same encryption software or
knowing what cipher you used. Remember Shannon’s Maxim: The enemy knows the system!
Professional encryption software is written by cryptographers who have spent years studying the
mathematics and potential weaknesses of various ciphers. Even then, the software they write is
inspected by other cryptographers to check for mistakes or potential weaknesses. You are
perfectly capable of learning about these cipher systems and cryptographic mathematics too. It’s
not about being the smartest hacker, but spending the time to study to become the most
knowledgeable hacker.
I hope you’ve found this book to be a helpful start on becoming an elite hacker and programmer.
There is a lot more to learn about programming and cryptography than what is in this book, but I
encourage you explore and learn more! One great book about the general history of cryptography
that I highly recommend is “The Code Book” by Simon Singh. You can go to
http://invpy.com/morehacking for a list of other books and websites to learn more about
cryptography. Feel free to email me your programming or cryptography questions at
al@inventwithpython.com.
Good luck!

422 http://inventwithpython.com/hacking
Email questions to the author: al@inventwithpython.com
ABOUT THE AUTHOR
Albert Sweigart (but you can call him Al), is a software developer in San Francisco, California
who enjoys haunting coffee shops and making useful software. Hacking Secret Ciphers with
Python is his third book.
His first two books, Invent Your Own Computer Games with Python and Making Games with
Python & Pygame can be read online for free at http://inventwithpython.com.
He is originally from Houston, Texas. He laughs out loud when watching park squirrels, which
makes people think he’s a simpleton.
Email: al@inventwithpython.com
Twitter: @AlSweigart