Howard Anton Student Solutions Manual Set For Calculus Early Transcendentals Single Variable 8th E
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 676 [warning: Documents this large are best viewed by clicking the View PDF Link!]
CONTENTS
Introduction .............................................................. 1
Chapter 1. Functions ..................................................... 2
Chapter 2. Limits and Continuity ......................................... 43
Chapter 3. The Derivative ................................................ 65
Chapter 4. Logarithmic and Exponential Functions ......................... 99
Chapter 5. Analysis of Functions and Their Graphs ........................139
Chapter 6. Applications of the Derivative .................................177
Chapter 7. Integration ...................................................209
Chapter 8. Applications of the Definite Integral
in Geometry, Science, and Engineering .........................256
Chapter 9. Principles of Integral Evaluation ...............................292
Chapter 10. Mathematical Modeling with Differential Equations ..............343
Chapter 11. Infinite Series ................................................361
Chapter 12. Analytic Geometry in Calculus .................................408
Chapter 13. Three-Dimensional Space; Vectors .............................448
Chapter 14. Vector-Valued Functions ......................................490
Chapter 15. Partial Derivatives ............................................524
Chapter 16. Multiple Integrals .............................................573
Chapter 17. Topics in Vector Calculus .....................................608
Appendix A. Real Numbers, Intervals, and Inequalities .......................640
Appendix B. Absolute Value ...............................................647
Appendix C. Coordinate Planes and Lines ...................................650
Appendix D. Distance, Circles, and Quadratic Equations ......................658
Appendix E. Trigonometry Review .........................................668
Appendix F. Solving Polynomial Equations .................................674

CALCULUS:
A New Horizon from Ancient Roots
EXERCISE SET FOR INTRODUCTION
1. (a) x=0.123123123 ...; 1000x= 123.123123123 ...= 123 + x; 999x= 123; x=123
999 =41
333
(b) x=12.7777 ...;10x= 127.7777 ...,so9x=10x−x= 115; x=115
9
(c) x=38.07818181 ...; 100x= 3807.818181 ...;99x= 3769.74;
x=3769.74
99 =376974
9900 =41886
1100 =20943
550
(d) 0.4296000 ...=0.4296 = 4296
10000 =537
1250
2. (a) πis irrational, and thus has a nonrepeating decimal expansion, whereas 22
7=3.
repeats
z }| {
142857 ...
(b) 22
7>π
3. (a) 223
71 <333
106 <63
25 Ã17+15
√
5
7+15
√
5!<355
113 <22
7(b) 63
25 Ã17+15
√
5
7+15
√
5!
(c) 333
106 (d) 63
25 Ã17+15
√
5
7+15
√
5!
4. (a) If ris the radius, then D=2rso µ8
9D¶2
=µ16
9r¶2
=256
81 r2. The area of a circle of radius ris
πr2so 256/81 was the approximation used for π.
(b) 256/81 ≈3.16049, 22/7≈3.14268, and π≈3.14159 so 256/81 is worse than 22/7.
5. The first series, taken to ten terms, adds to 3.0418; the second, as printed, adds to 3.1416.
6. (a) 1
9=0.111111 ...=1
10 +1
100 +1
1000 +1
10000 +1
100000 +1
1000000 +...
(b) 2
27 =0.185185 ...=1
10 +8
100 +5
1000 +1
10000 +8
100000 +5
1000000 +...
(c) 14
45 =0.311111 ...=3
10 +1
100 +1
1000 +1
10000 +1
100000 +1
1000000 +...
7. (a) 7
11 =0.636363 ...=6
10 +3
100 +6
1000 +3
10000 +6
100000 +3
1000000 +...
(b) 8
33 =0.242424 ...=2
10 +4
100 +2
1000 +4
10000 +2
100000 +4
1000000 +...
(c) 5
12 =0.416666 ...=4
10 +1
100 +6
1000 +6
10000 +6
100000 +6
1000000 +...
8. (a) 1, 2, 1.75, 1.7321 (b) 1, 3, 2.33, 2.238, 2.2361
9. (a) 1, 4, 2.875, 2.6549, 2.6458 (b) 1, 25.5, 13.7, 8.69, 7.22, 7.0726, 7.0711
10. (a) Let x1=1
2(a+b), x2=1
2(a+x1), x3=1
2(a+x2), etc. Then b>x
1>x
2>···>x
n−1>x
n>a
so all the xi’s are distinct, there are infinitely many of them and they all lie between aand b.
(b) x=0.99999 ...,10x=9.99999 ...,9x=9,x=1
(c) (1.999999 ...)/2=0.999999 ...= 1; yes it is consistent, as all three are equal.
(d) 10x=9+x,sox=9/9 = 1. They are equal.
1
CHAPTER 1
Functions
EXERCISE SET 1.1
1. (a) around 1943 (b) 1960; 4200
(c) no; you need the year’s population (d) war; marketing techniques
(e) news of health risk; social pressure, antismoking campaigns, increased taxation
2. (a) 1989; $35,600 (b) 1983; $32,000 (c) the first two years; the curve is steeper (downhill)
3. (a) −2.9,−2.0,2.35,2.9(b) none (c) y=0
(d) −1.75 ≤x≤2.15 (e) ymax =2.8atx=−2.6; ymin =−2.2atx=1.2
4. (a) x=−1,4(b) none (c) y=−1
(d) x=0,3,5(e) ymax =9atx=6;y
min =−2atx=0
5. (a) x=2,4(b) none (c) x≤2; 4 ≤x(d) ymin =−1; no maximum value
6. (a) x=9 (b) none (c) x≥25 (d) ymin = 1; no maximum value
7. (a) Breaks could be caused by war, pestilence, flood, earthquakes, for example.
(b) Cdecreases for eight hours, takes a jump upwards, and then repeats.
8. (a) Yes, if the thermometer is not near a window or door or other source of sudden temperature
change.
(b) The number is always an integer, so the changes are in movements (jumps) of at least one unit.
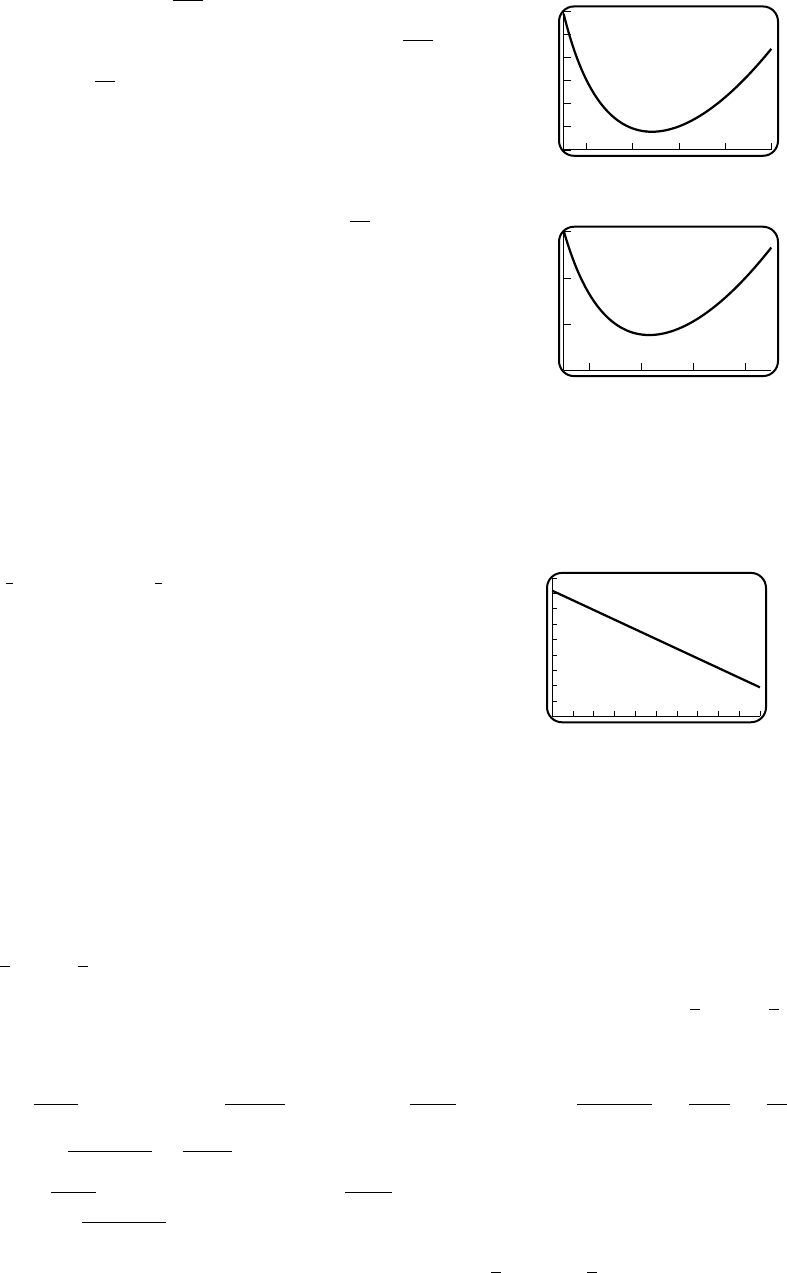
9. (a) If the side adjacent to the building has length xthen L=x+2y. Since A=xy = 1000,
L=x+ 2000/x.
(b) x>0 and xmust be smaller than the width of the building, which was not given.
(c) 120
80
20 80
(d) Lmin ≈89.44
10. (a) V=lwh =(6−2x)(6 −2x)x(b) From the figure it is clear that 0 <x<3.
(c) 20
0
03
(d) Vmax ≈16
2
3 Chapter 1
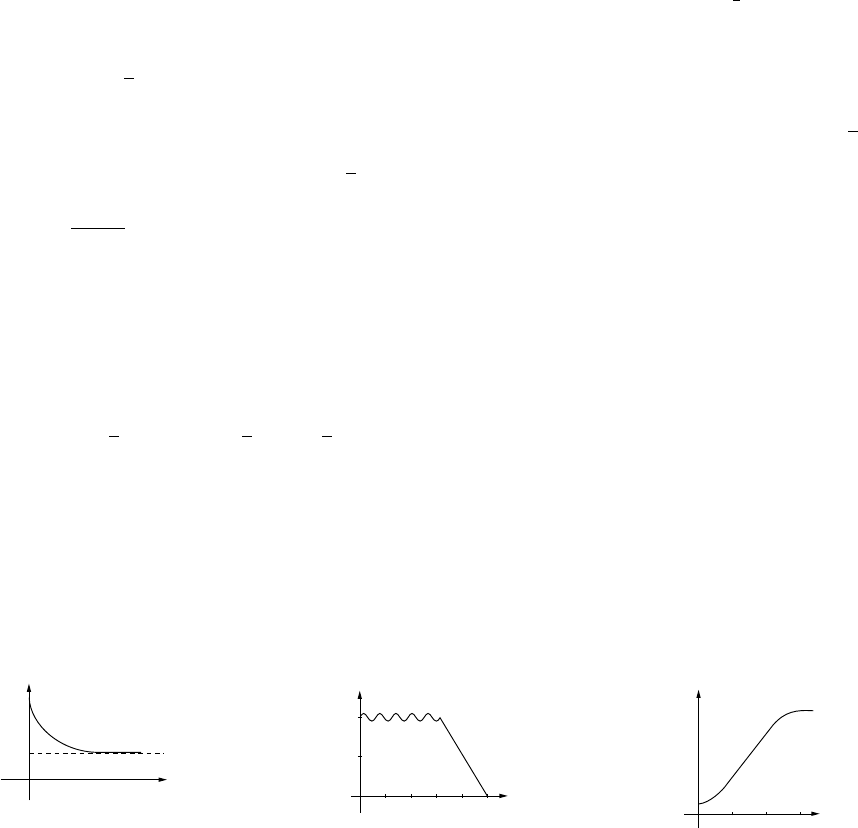
11. (a) V= 500 = πr2hso h=500
πr2. Then
C=(0.02)(2)πr2+(0.01)2πrh =0.04πr2+0.02πr 500
πr2
=0.04πr2+10
r;Cmin ≈4.39 at r≈3.4,h≈13.8.
7
4
1.5 6
(b) C=(0.02)(2)(2r)2+(0.01)2πrh =0.16r2+10
r. Since
0.04π<0.16, the top and bottom now get more weight.
Since they cost more, we diminish their sizes in the solution,
and the cans become taller.
7
4
1.5 5.5
(c) r≈3.1, h≈16.0, C≈4.76
12. (a) The length of a track with straightaways of length Land semicircles of radius ris
P= (2)L+ (2)(πr) ft. Let L= 360 and r=80togetP= 720 + 160π= 1222.65 ft.
Since this is less than 1320 ft (a quarter-mile), a solution is possible.
(b) P=2L+2πr = 1320 and 2r=2x+ 160, so
L=1
2(1320 −2πr)=1
2(1320 −2π(80 + x)) = 660 −80π−πx.
450
0
0 100
(c) The shortest straightaway is L= 360, so x=15.49 ft.
(d) The longest straightaway occurs when x=0,soL= 660 −80π= 408.67 ft.
EXERCISE SET 1.2
1. (a) f(0) = 3(0)2−2=−2; f(2) = 3(2)2−2 = 10; f(−2)=3(−2)2−2 = 10; f(3) = 3(3)2−2 = 25;
f(√2)=3(
√
2)2−2=4;f(3t) = 3(3t)2−2=27t
2−2
(b) f(0) = 2(0) = 0; f(2) = 2(2) = 4; f(−2)=2(−2)=−4; f(3) = 2(3) = 6; f(√2)=2
√
2;
f(3t)=1/3tfor t>1 and f(3t)=6tfor t≤1.
2. (a) g(3) = 3+1
3−1=2; g(−1) = −1+1
−1−1=0;g(π)= π+1
π−1;g(−1.1) = −1.1+1
−1.1−1=−0.1
−2.1=1
21;
g(t2−1) = t2−1+1
t
2−1−1=t
2
t
2−2
(b) g(3) = √3+1=2;g(−1)=3;g(π)=√
π+1;g(−1.1)=3;g(t
2−1)=3ift
2<2 and
g(t2−1) = √t2−1+1=|t|if t2≥2.
3. (a) x6=3 (b) x≤−
√
3orx≥√
3
Exercise Set 1.2 4
(c) x2−2x+ 5 = 0 has no real solutions so x2−2x+ 5 is always positive or always negative. If
x= 0, then x2−2x+5=5>0; domain: (−∞,+∞).
(d) x6=0 (e) sin x6=1,sox6=(2n+1
2)π,
n=0,±1,±2,...
4. (a) x6=−7
5
(b) x−3x2must be nonnegative; y=x−3x2is a parabola that crosses the x-axis at x=0,1
3and
opens downward, thus 0 ≤x≤1
3
(c) x2−4
x−4>0, so x2−4>0 and x−4>0, thus x>4; or x2−4<0 and x−4<0, thus
−2<x<2
(d) x6=−1
(e) cos x≤1<2, 2 −cos x>0, all x
5. (a) x≤3(b) −2≤x≤2(c) x≥0(d) all x(e) all x
6. (a) x≥2
3(b) −3
2≤x≤3
2(c) x≥0(d) x6=0 (e) x≥0
7. (a) yes (b) yes
(c) no (vertical line test fails) (d) no (vertical line test fails)
8. The sine of θ/2is(L/2)/10 (side opposite over hypotenuse), so that L= 20 sin(θ/2).
9. The cosine of θis (L−h)/L (side adjacent over hypotenuse), so h=L(1 −cos θ).
10. T
t
11.
t
h12.
51015
t
w
13. (a) If x<0, then |x|=−xso f(x)=−x+3x+1=2x+1. If x≥0, then |x|=xso
f(x)=x+3x+1=4x+1;
f(x)=½2x+1,x<0
4x+1,x≥0
(b) If x<0, then |x|=−xand |x−1|=1−xso g(x)=−x+1−x=1−2x.If0≤x<1, then
|x|=xand |x−1|=1−xso g(x)=x+1−x=1. Ifx≥1, then |x|=xand |x−1|=x−1
so g(x)=x+x−1=2x−1;
g(x)=
1−2x, x < 0
1,0≤x<1
2x−1,x≥1
14. (a) If x<5/2, then |2x−5|=5−2xso f(x) = 3+(5−2x)=8−2x.Ifx≥5/2, then |2x−5|=2x−5
so f(x)=3+(2x−5)=2x−2;
f(x)=½8−2x, x < 5/2
2x−2,x≥5/2

5 Chapter 1
(b) If x<−1, then |x−2|=2−xand |x+1|=−x−1sog(x) = 3(2 −x)−(−x−1)=7−2x.If
−1≤x<2, then |x−2|=2−xand |x+1|=x+1 sog(x) = 3(2 −x)−(x+1)=5−4x.If
x≥2, then |x−2|=x−2 and |x+1|=x+1so g(x)=3(x−2) −(x+1)=2x−7;
g(x)=
7−2x, x < −1
5−4x, −1≤x<2
2x−7,x≥2
15. (a) V=(8−2x)(15 −2x)x(b) −∞ <x<+∞,−∞ <V <+∞(c) 0<x<4
(d) minimum value at x= 0 or at x= 4; maximum value somewhere in between (can be approxi-
mated by zooming with graphing calculator)
16. (a) x= 3000 tan θ(b) θ6=nπ +π/2 for nan integer, −∞ <n<∞
(c) 0≤θ<π/2, 0 ≤x<+∞(d) 3000 ft
6000
0
06
17. (i) x=1,−2 causes division by zero (ii) g(x)=x+ 1, all x
18. (i) x= 0 causes division by zero (ii) g(x)=√
x+ 1 for x≥0
19. (a) 25◦F(b) 2◦F(c) −15◦F
20. If v= 48 then −60=WCI=1.6T−55; thus T=(−60 + 55)/1.6≈−3
◦F.
21. If v= 8 then −10=WCI=91.4 + (91.4−T)(0.0203(8) −0.304√8−0.474); thus
T=91.4+(10+91.4)/(0.0203(8) −0.304√8−0.474) and T=5
◦F
22. The WCI is given by three formulae, but the first and third don’t work with the data. Hence
−15=WCI=91.4 + (91.4−20)(0.0203v−0.304√v−0.474); set x=√vso that v=x2and obtain
0.0203x2−0.304x−0.474+(15+91.4)/(91.4−20) = 0. Use the quadratic formula to find the two
roots. Square them to get vand discard the spurious solution, leaving v≈25.
23. Let tdenote time in minutes after 9:23 AM. Then D(t) = 1000 −20tft.
EXERCISE SET 1.3
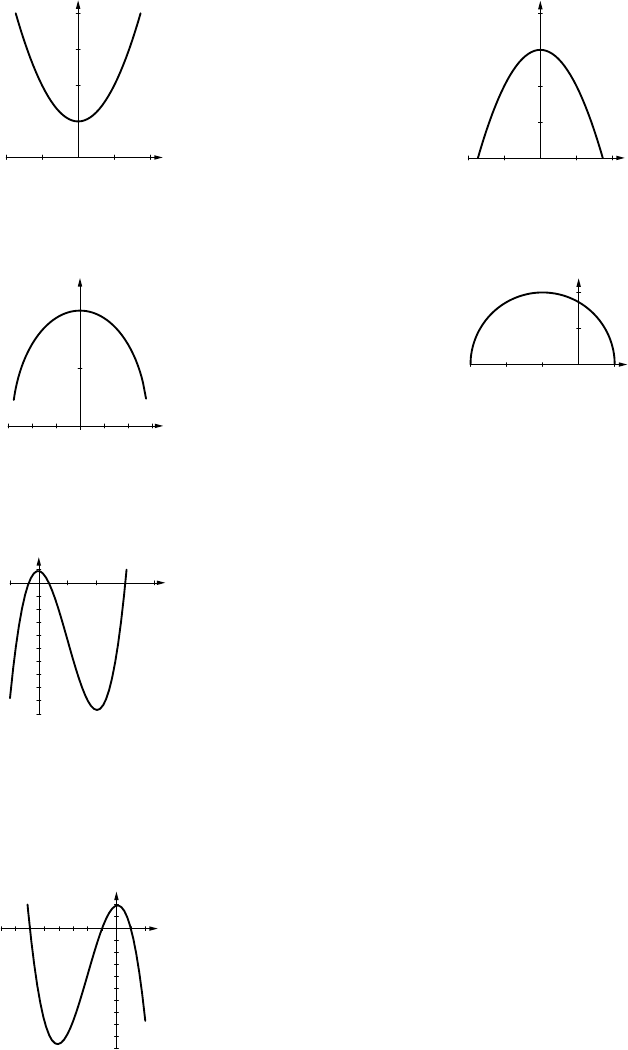
1. (e) seems best, though only (a) is bad.
-0.5
0.5
y
-1 1 x
2. (e) seems best, though only (a) is bad and (b) is
not good.
-0.5
0.5
y
-1 1 x
Exercise Set 1.3 6
3. (b) and (c) are good; (a) is very bad.
12
13
14
15
y
-2 -1 0 1 2 x
4. (b) and (c) are good; (a) is very bad.
-14
-13
-12
-11
y
-2 -1 0 1 2 x
5. [−3,3] ×[0,5]
2
4
y
-3 -2 -1 1 2 3 x
6. [−4,2] ×[0,3]
1
2
y
-3 -2 -1 1 x
7. (a) window too narrow, too short (b) window wide enough, but too short
(c) good window, good spacing
-500
-400
-300
-200
-100
y
-5 5 101520
x
(d) window too narrow, too short
(e) window too narrow, too short
8. (a) window too narrow (b) window too short
(c) good window, good tick spacing
-250
-200
-150
-100
-50
50
y
-16 -12 -8 -4 4
x
(d) window too narrow, too short
(e) shows one local minimum only, window too narrow, too short
7 Chapter 1
9. [−5,14] ×[−60,40]
-60
-40
-20
20
40
y
-5 5 10 x
10. [6,12] ×[−100,100]
-100
-50
50
100
y
81012
x
11. [−0.1,0.1] ×[−3,3]
-3
-2
-1
1
2
3
y
-0.1 x
0.1
12. [−1000,1000] ×[−13,13]
-10
-5
5
10
y
-1000 x
1000
13. [−250,1050] ×[−1500000,600000]
-500000
y
-1000 1000 x
14. [−3,20] ×[−3500,3000]
-2000
-1000
1000
51015
x
y
15. [−2,2] ×[−20,20]
-20
-10
10
20
y
x
-2 -1 1 2
16. [1.6,2] ×[0,2]
0.5
1
1.5
2
y
1.6 1.7 1.8 1.9 2 x
17. depends on graphing utility
-6
-4
-2
2
4
6
y
-4 -2 2 4 x
18. depends on graphing utility
-6
-4
-2
2
4
6
y
-4 -2 2 4 x
Exercise Set 1.3 8
19. (a) f(x)=√
16 −x2
1
2
3
4
-4 -2 2 4 x
y
(b) f(x)=−
√
16 −x2
-4
-3
-2
-1
x
y
-4 -2 2 4
(c)
-4
-2
2
4
x
y
-4 -2 2 4
(d)
1
2
3
4
1234
y
(e) No; the vertical line test fails.
20. (a) y=±3p1−x2/4(b) y=±√x2+1
-4
-2
2
4
-4 -2 2 4 x
y
21. (a)
-1 1 x
y
1
(b)
1x
1
2
y(c)
-1 1x
-1
y
(d)
2π
π
1
y
x
(e)
π
1
y
x
−π
—1
(f)
1x
1
-1
y
-1
22.
1
x
y
-1 1
-1
23. The portions of the graph of y=f(x) which lie below the x-axis are reflected over the x-axis to give the
graph of y=|f(x)|.
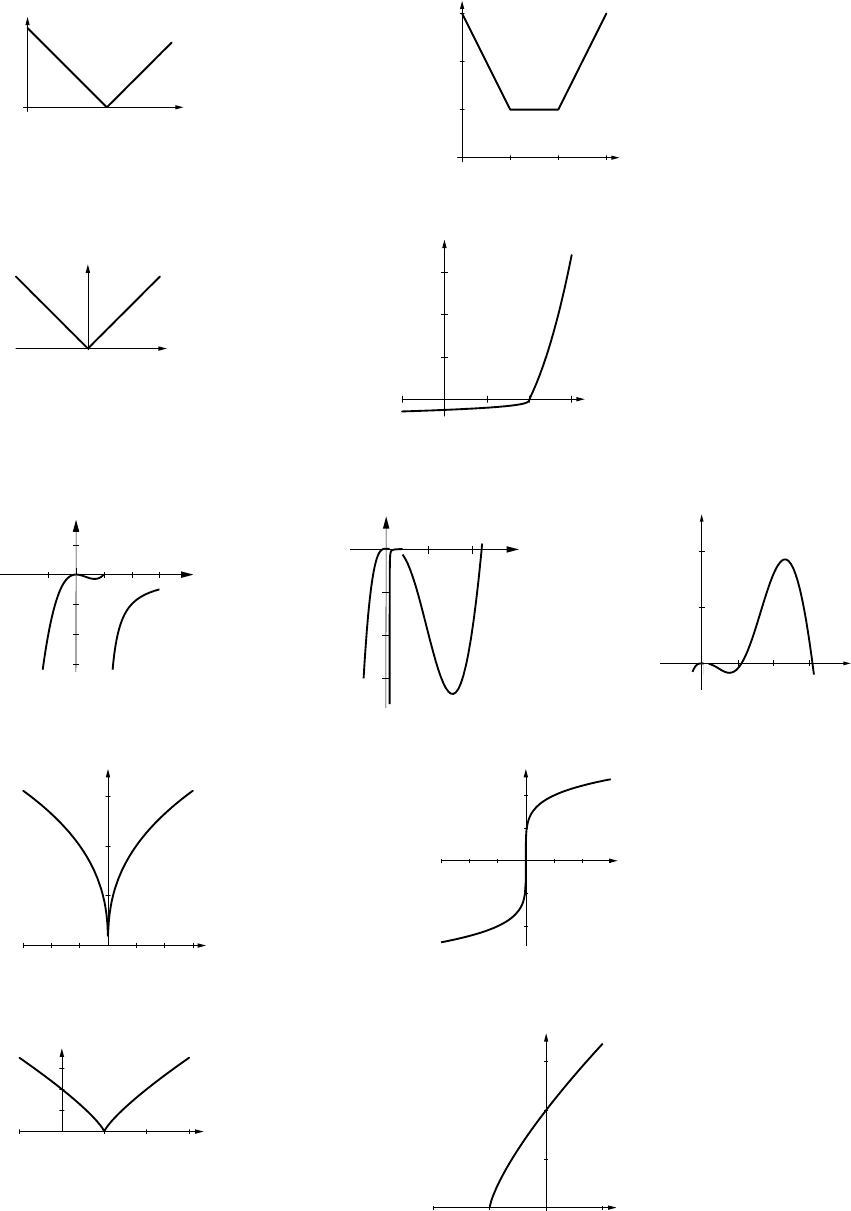
9 Chapter 1
24. Erase the portion of the graph of y=f(x) which lies in the left-half plane and replace it with the reflection
over the y-axis of the portion in the right-half plane (symmetry over the y-axis) and you obtain the graph
of y=f(|x|).
25. (a) for example, let a=1.1
µ
y
(b)
1
2
3
y
123
x
26. They are identical.
x
y
27.
5
10
15
y
-1 123
x
28. This graph is very complex. We show three views, small (near the origin), medium and large:
(a) y
x
-1
-1 2
(b)
-50
y
x
10
(c)
1000
y
40 x
29. (a)
0.5
1
1.5
y
-3 -2 -1 123x
(b)
-1
-0.5
0.5
1
-3 -2 -1 1 23
x
y
(c)
0.5
1
1.5
y
-1 1 2 3 x
(d)
0.5
1
1.5
-2 -1 1 x
y
Exercise Set 1.3 10
30. y
1
2x
31. (a) stretches or shrinks the graph in the
y-direction; flips it if cchanges sign
-2
2
4c = 2
c = 1
c = -1.5
-1 1 x
y
(b) As cincreases, the parabola moves down
and to the left. If cincreases, up and right.
2
4
6
8
-2 -1 1 2 x
c = 2
c = 1
c = -1.5
y
(c) The graph rises or falls in the y-direction with changes in c.
2
4
6
8
-2 -1 1 2 x
c = +2
c = .5
c = -1
y
32. (a) y
—2
2
12 x
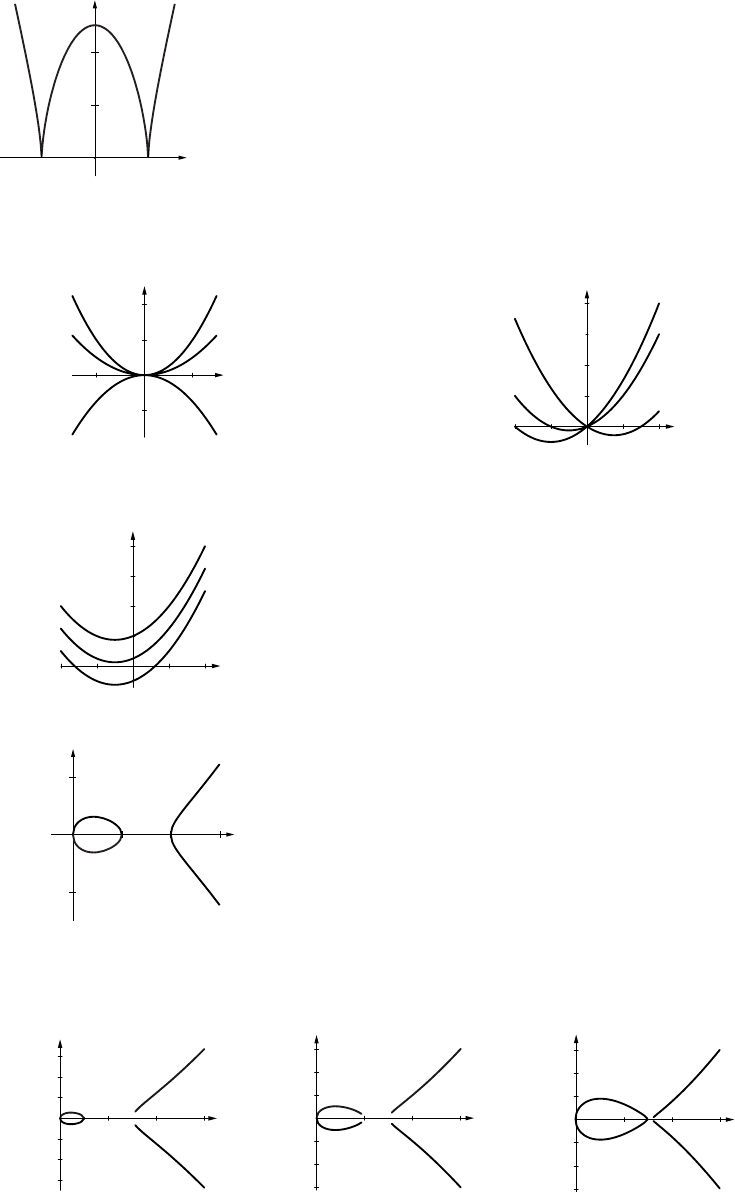
(b) x-intercepts at x=0,a,b. Assume a<band let aapproach b. The two branches of the curve
come together. If amoves past bthen aand bswitch roles.
-3
-2
-1
1
2
3
123
x
a = 0.5
b = 1.5
y
-3
-2
-1
1
2
3
123
x
a = 1
b = 1.5
y
-3
-2
-1
1
2
3
123
x
a = 1.5
b = 1.6
y
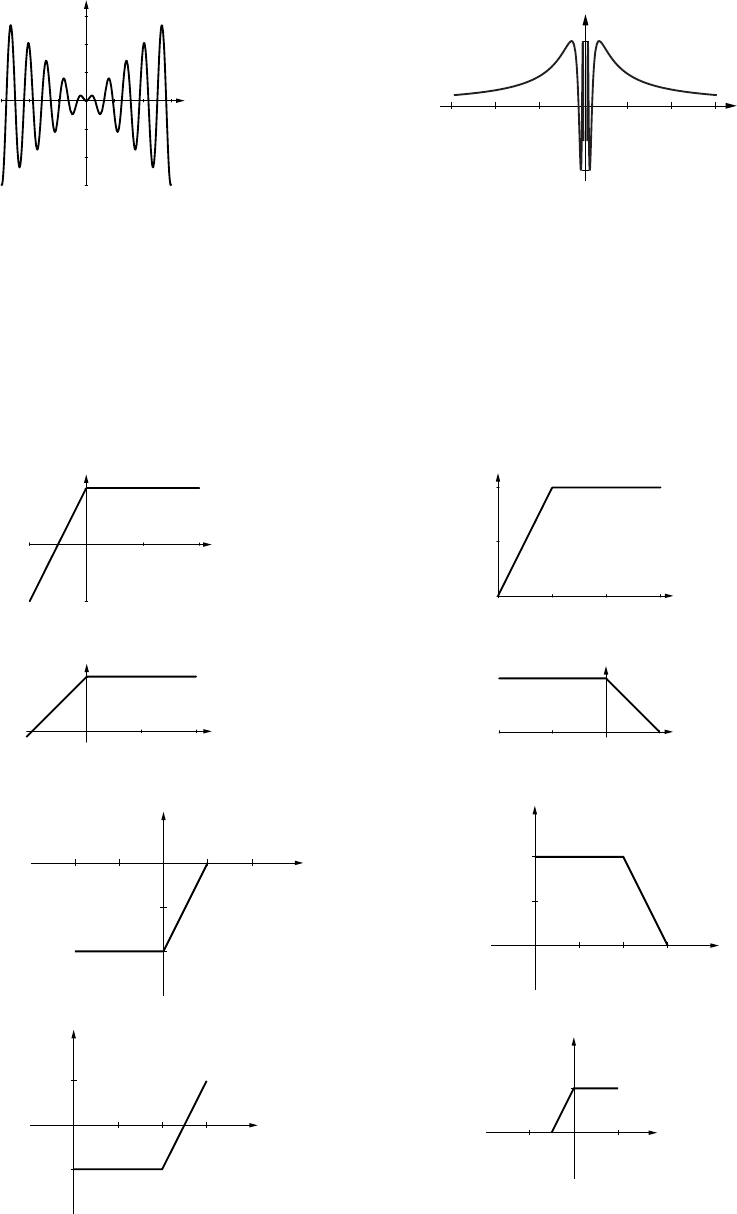
11 Chapter 1
33. The curve oscillates between the lines
y=xand y=−xwith increasing ra-
pidity as |x|increases.
-30
-20
-10
10
20
30
y
-30 -20 -10 10 20 30 x
34. The curve oscillates between the lines
y= +1 and y=−1, infinitely many times
in any neighborhood of x=0.
y
—1
4—2
—1
x
35. Plot f(x)on[−10,10]; then on [−1,0], [−0.7,−0.6], [−0.65,−0.64], [−0.646,−0.645]; for the other
root use [4,5], [4.6,4.7], [4.64,4.65], [4.645,4.646]; roots −0.6455,4.6455.
36. Plot f(x)on[−10,10]; then on [−4,−3], [−3.7,−3.6], [−3.61,−3.60], [−3.606,−3.605]; for the other
root use [3,4], [3.6,3.7], [3.60,3.61], [3.605,3.606]; roots 3.6055,−3.6055.
EXERCISE SET 1.4
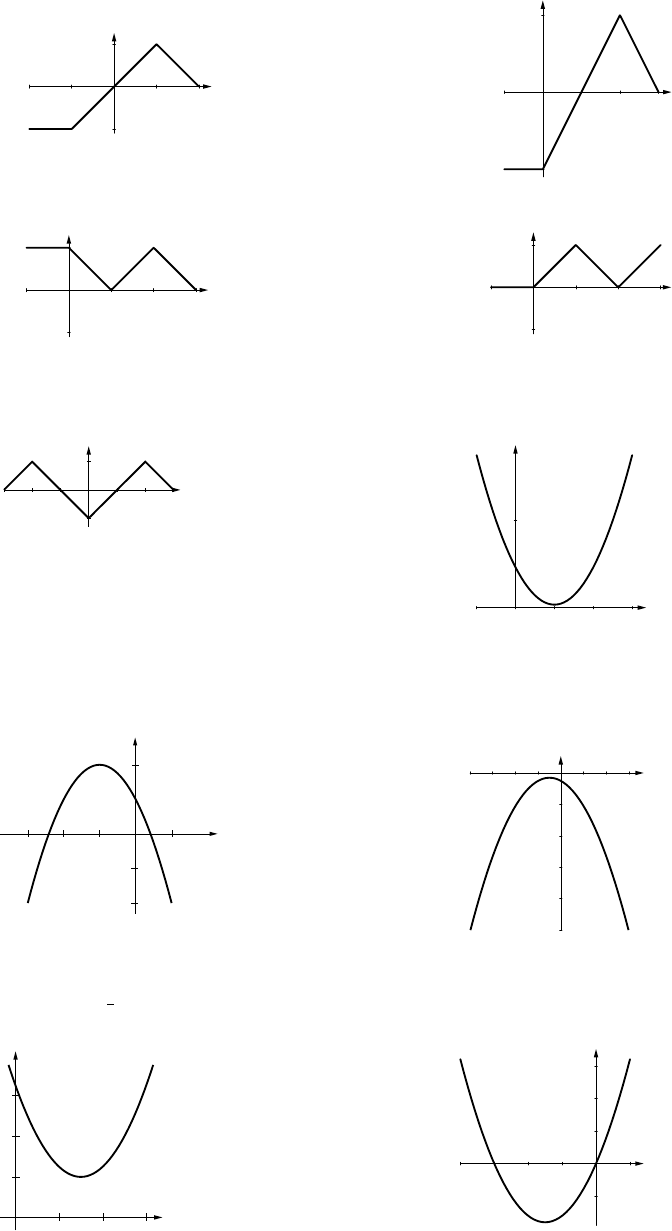
1. (a)
-1
0
1
y
-1 1 2 x
(b)
2
1
y
123x
(c)
1
y
-1 1 2 x
(d)
2
y
-4 -2 2 x
2. (a)
x
y
1
-2
-2
(b)
x
y
3
2
2
(c)
x
2
y
-1
3
1
(d)
x
y
1
1
-1
Exercise Set 1.4 12
3. (a)
-1
1
y
-2 -1 1 2 x
(b)
-1
1
y
-0.5 0.5 1 1.5 x
(c)
-1
1
y
-1 1 2 3 x
(d)
-1
1
y
-1 1 2 3 x
4.
1
y
-2 2 x
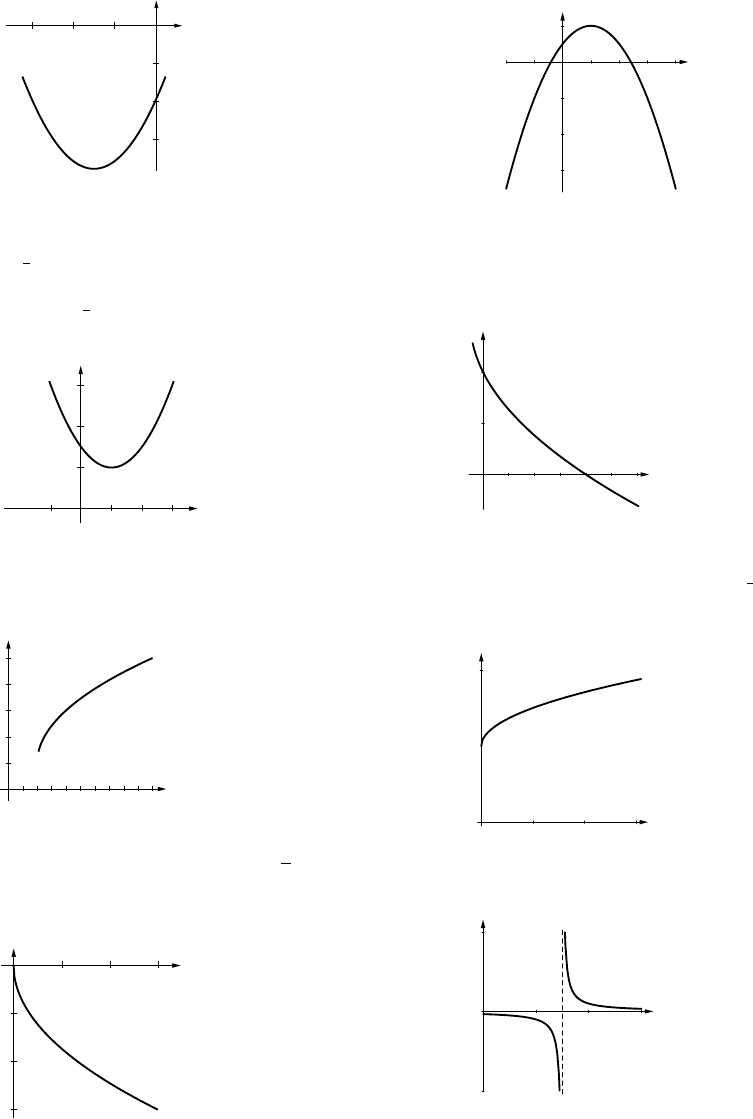
5. Translate right 2 units, and up one unit.
10
-2 2 4 6x
y
6. Translate left 1 unit, reflect over x-axis, and
translate up 2 units.
y
x
–2
1
7. Translate left 1 unit, stretch vertically by
a factor of 2, reflect over x-axis, translate
down 3 units.
-100
-80
-60
-40
-20
-8 -6 -4 -2 2 4 6 x
y
8. Translate right 3 units, compress vertically
by a factor of 1
2, and translate up 2 units.
y
x
2
4
9. y=(x+3)
2−9; translate left 3 units and
down 9 units.
-5
5
10
15
-8 -6 -4 -2 2 x
y
13 Chapter 1
10. y=(x+3)
2−19; translate left 3 units
and down 19 units.
y
x
–5
–4
11. y=−(x−1)2+ 2; translate right 1 unit,
reflect over x-axis, translate up 2 units.
-6
-4
-2
2
-2 -1 1 2 3 4 x
y
12. y=1
2[(x−1)2+ 2]; translate left 1 unit
and up 2 units, compress vertically by
a factor of 1
2.
y
x
1
2
1
13. Translate left 1 unit, reflect over x-axis,
translate up 3 units.
1
2
2 4 6 8 10 12 x
y
14. Translate right 4 units and up 1 unit.
y
x
1
4
410
15. Compress vertically by a factor of 1
2,
translate up 1 unit.
2
y
123
x
16. Stretch vertically by a factor of √3 and
reflect over x-axis.
y
x
-1
2
17. Translate right 3 units.
-10
10
y
246
x
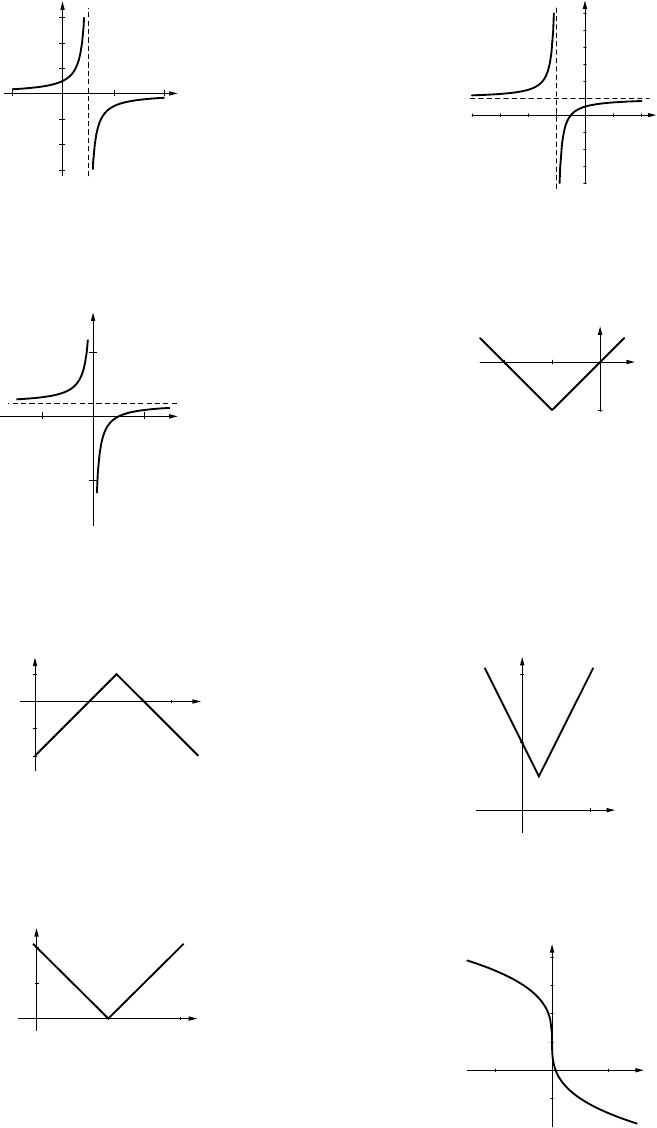
Exercise Set 1.4 14
18. Translate right 1 unit and reflect
over x-axis.
y
x
-4
2
-2 2
19. Translate left 1 unit, reflect over x-axis,
translate up 2 units.
-8
-6
-4
-2
2
4
6
8
10
12
y
-4 -3 -2 -1 1 2 x
20. y=1−1/x; reflect over x-axis, translate
up 1 unit.
y
x
-5
5
2
21. Translate left 2 units and down 2 units.
-2
-4 -2 x
y
22. Translate right 3 units, reflect over x-axis,
translate up 1 unit.
y
x
-1
1
5
23. Stretch vertically by a factor of 2, translate
right 1 unit and up 1 unit.
y
x
2
4
2
24. y=|x−2|; translate right 2 units.
y
x
1
2
24
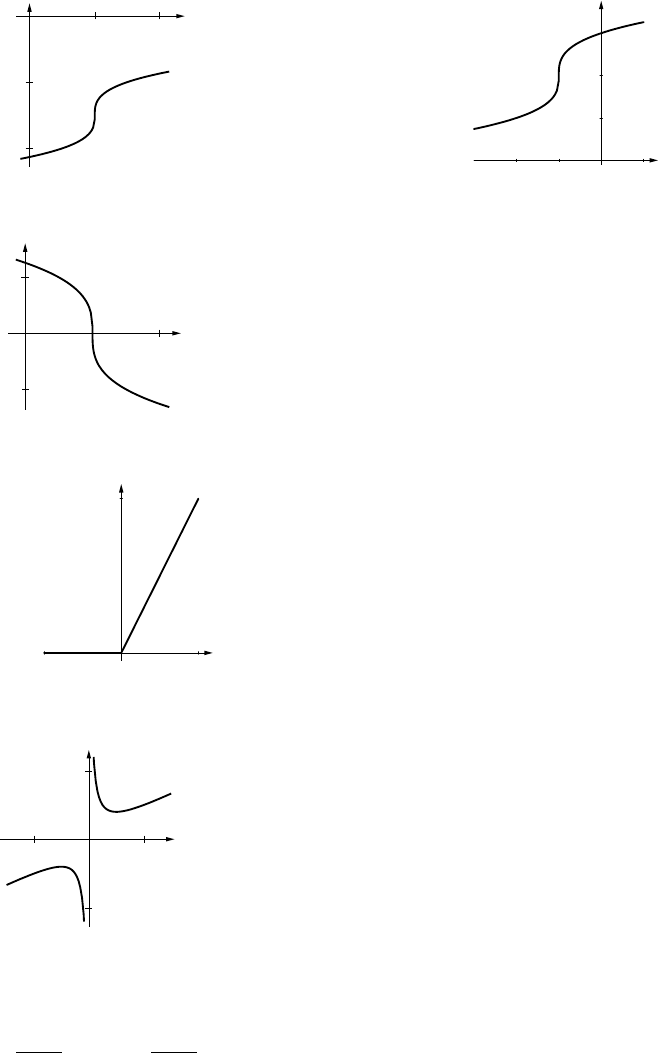
25. Stretch vertically by a factor of 2, reflect
over x-axis, translate up 2 units.
-1
1
2
3
4
-2 2 x
y
15 Chapter 1
26. Translate right 2 units and down 3 units.
y
x
–2
2
27. Translate left 1 unit and up 2 units.
1
2
3
y
-3 -2 -1 1 x
28. Translate right 2 units, reflect over x-axis.
y
x
–1
1
4
29. (a)
2
y
-1 1 x
(b) y=½0ifx≤0
2xif 0 <x
30. y
x
–5
2
31. x2+2x+ 1, all x;2x−x
2−1, all x;2x
3+2x, all x;2x/(x2+ 1), all x
32. 3x−2+|x|, all x;3x−2−|x|, all x;3x|x|−2|x|, all x;(3x−2)/|x|, all x6=0
33. 3√x−1, x≥1; √x−1, x≥1; 2x−2, x≥1; 2, x>1
34. (2x2+1)/x(x2+ 1), all x6=0;−1/x(x2+ 1), all x6=0;1/(x
2+ 1), all x6=0;x
2
/(x
2+ 1), all x6=0
35. (a) 3(b) 9(c) 2(d) 2
36. (a) π−1(b) 0(c) −π2+3π−1(d) 1

Exercise Set 1.4 16
37. (a) t4+1 (b) t2+4t+5 (c) x2+4x+5 (d) 1
x2+1
(e) x2+2xh +h2+1 (f) x2+1 (g) x+1 (h) 9x2+1
38. (a) √5s+2 (b) p√x+2 (c) 3√5x(d) 1/√x
(e) 4
√x(f) 0(g) 1/4
√x(h) |x−1|
39. 2x2−2x+1, all x;4x
2+2x, all x40. 2−x6, all x;−x6+6x
4−12x2+ 8, all x
41. 1−x,x≤1; √1−x2,|x|≤142. p√x2+3−3, |x|≥√
6; √x,x≥3
43. 1
1−2x,x6=1
2,1; −1
2x−1
2,x6=0,144. x
x2+1,x6=0; 1
x+x,x6=0
45. x−6+1 46. x
x+1
47. (a) g(x)=√
x,h(x)=x+2 (b) g(x)=|x|,h(x)=x
2−3x+5
48. (a) g(x)=x+1,h(x)=x
2(b) g(x)=1/x,h(x)=x−3
49. (a) g(x)=x
2
,h(x) = sin x(b) g(x)=3/x,h(x) = 5 + cos x
50. (a) g(x)=3sinx,h(x)=x
2(b) g(x)=3x
2+4x,h(x) = sin x
51. (a) f(x)=x
3
,g(x) = 1 + sin x,h(x)=x
2(b) f(x)=√
x,g(x)=1−x,h(x)= 3
√
x
52. (a) f(x)=1/x,g(x)=1−x,h(x)=x
2(b) f(x)=|x|,g(x)=5+x,h(x)=2x
53. y
x
-4
-3
-2
-1
1
2
-3 -2 -1 1 2 3
54. {−2,−1,0,1,2,3}
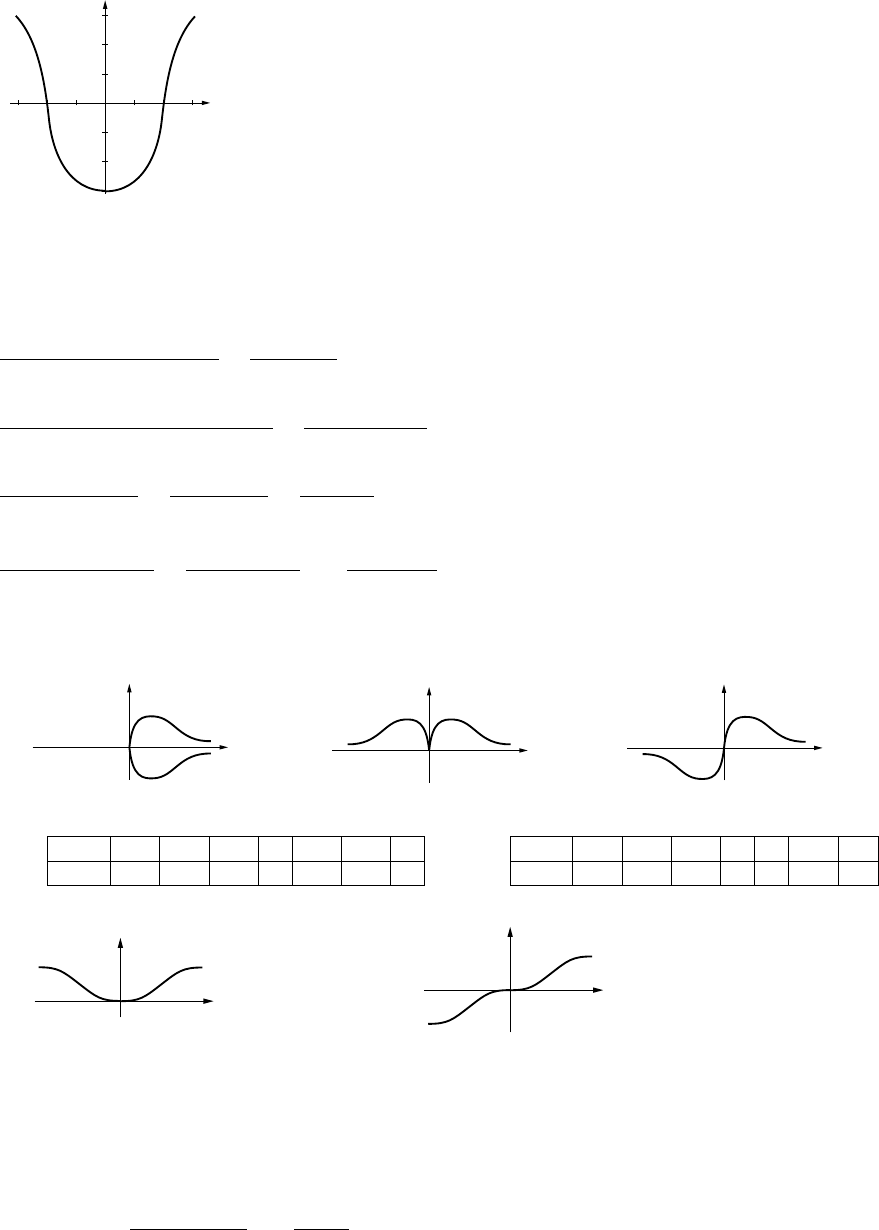
55. Note that f(g(−x)) = f(−g(x)) = f(g(x)), so f(g(x)) is even.
f(g(x))
x
y
1
–3 –1 –1
–3
1
17 Chapter 1
56. Note that g(f(−x)) = g(f(x)), so g(f(x)) is even.
x
y
–1
–2
1
3
–1
1
3
–3
g(f(x))
57. f(g(x)) = 0 when g(x)=±2, so x=±1.4; g(f(x)) = 0 when f(x)=0,sox=±2.
58. f(g(x))=0atx=−1 and g(f(x))=0atx=−1
59. 3(x+h)2−5−(3x2−5)
h=6xh +3h
2
h=6x+3h
60. (x+h)2+6(x+h)−(x
2+6x)
h=2xh +h2+6h
h=2x+h+6
61. 1/(x+h)−1/x
h=x−(x+h)
xh(x+h)=−1
x(x+h)
62. 1/(x+h)2−1/x2
h=x2−(x+h)2
x2h(x+h)2=−2x+h
x2(x+h)2
63. (a) the origin (b) the x-axis (c) the y-axis (d) none
64. (a)
x
y(b)
x
y(c)
x
y
65. (a) x−3−2−1 0 1 2 3
f(x) 1 −5−1 0 −1−5 1 (b) x−3−2−1 0 1 2 3
f(x) 1 5 −1 0 1 −5 -1
66. (a)
x
y(b)
x
y
67. (a) even (b) odd (c) odd (d) neither
68. neither; odd; even
69. (a) f(−x)=(−x)
2=x
2=f(x), even (b) f(−x)=(−x)
3=−x
3=−f(x), odd
(c) f(−x)=|−x|=|x|=f(x), even (d) f(−x)=−x+ 1, neither
(e) f(−x)=(−x)
3−(−x)
1+(−x)
2=−x
3+x
1+x
2=−f(x), odd
(f) f(−x)=2=f(x), even
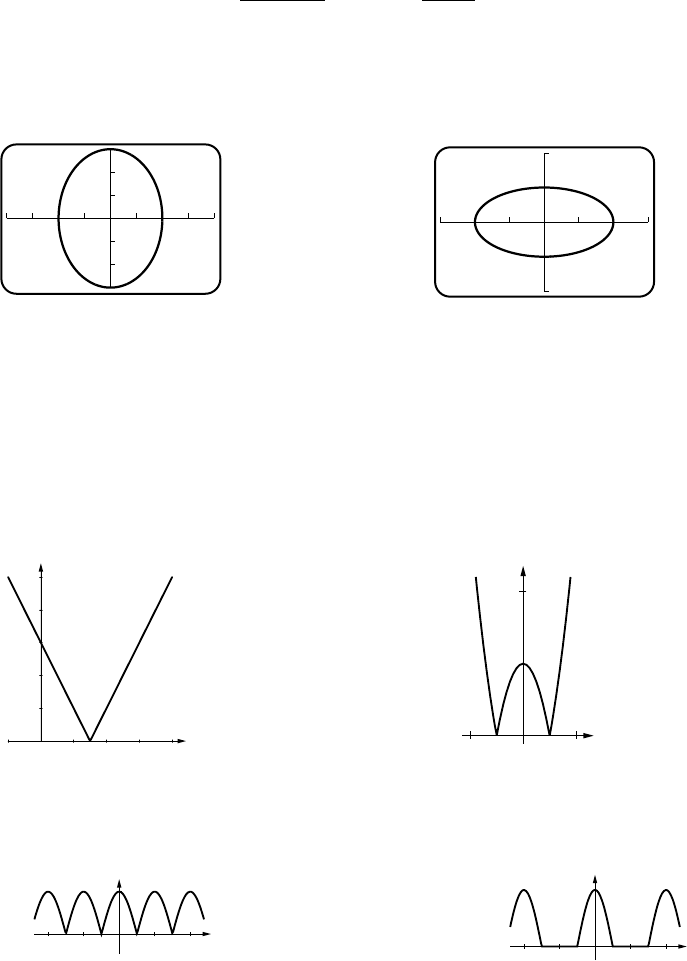
Exercise Set 1.4 18
70. (a) x-axis, because x=5(−y)
2+ 9 gives x=5y
2+9
(b) x-axis, y-axis, and origin, because x2−2(−y)2=3,(−x)
2−2y
2= 3, and
(−x)2−2(−y)2= 3 all give x2−2y2=3
(c) origin, because (−x)(−y) = 5 gives xy =5
71. (a) y-axis, because (−x)4=2y
3+ygives x4=2y
3+y
(b) origin, because (−y)= (−x)
3+(−x)
2gives y=x
3+x
2
(c) x-axis, y-axis, and origin because (−y)2=|x|−5, y2=|−x|−5,and (−y)2=|−x|−5 all give
y2=|x|−5
72. 3
–3
-4 4
73. 2
-2
-3 3
74. (a) Whether we replace xwith −x,ywith −y, or both, we obtain the same equation, so by Theorem
1.4.3 the graph is symmetric about the x-axis, the y-axis and the origin.
(b) y=(1−x
2/3
)
3/2
(c) For quadrant II, the same; for III and IV use y=−(1 −x2/3)3/2. (For graphing it may be helpful
to use the tricks that precede Exercise 29 in Section 1.3.)
75.
1
2
3
4
5
y
-1 1 2 3 4 x
76. y
x
2
2
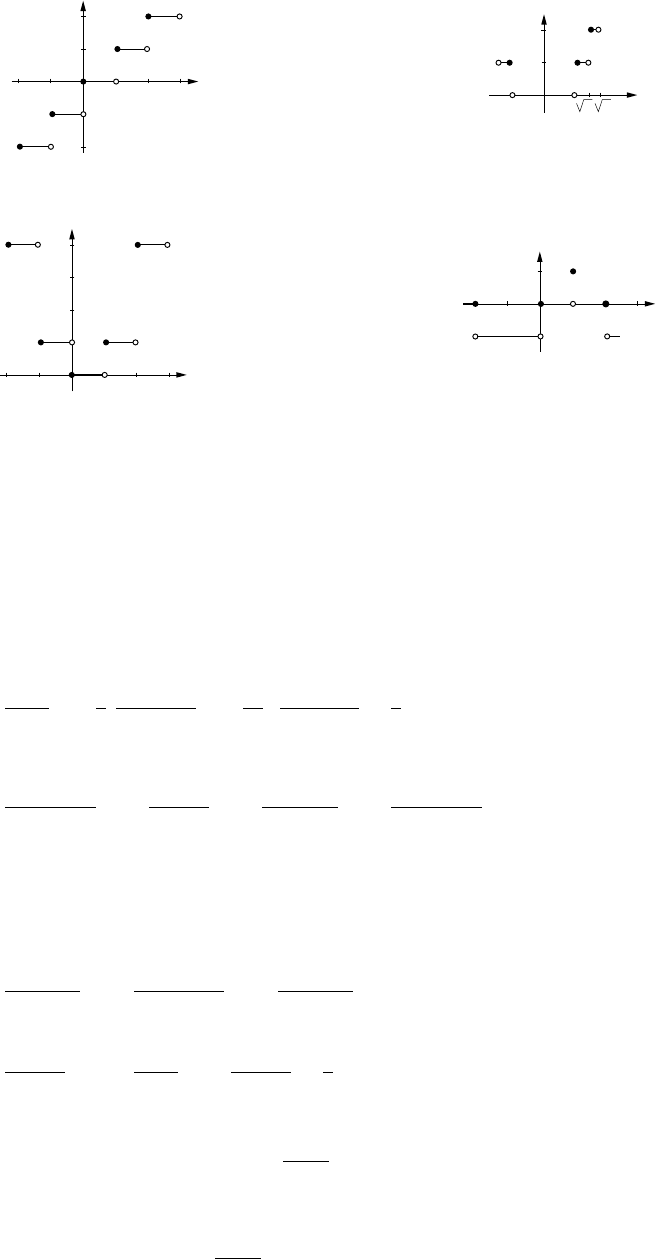
77. (a)
1
y
Cx
Oco
(b)
2
y
Ox
Cco
19 Chapter 1
78. (a)
x
1
y
1
-1
-1
(b)
x
1
y
1
-1
23
(c)
x
1
y
1
-1
3
(d)
x
y
1
-1
π/2
−π
79. Yes, e.g. f(x)=x
kand g(x)=x
nwhere kand nare integers.
80. If x≥0 then |x|=xand f(x)=g(x). If x<0 then f(x)=|x|
p/q if pis even and f(x)=−|x|p/q if p
is odd; in both cases f(x) agrees with g(x).
EXERCISE SET 1.5
1. (a) 3−0
0−2=−3
2,3−(8/3)
0−6=−1
18,0−(8/3)
2−6=2
3
(b) Yes; the first and third slopes above are negative reciprocals of each other.
2. (a) −1−(−1)
−3−5=0, −1−3
5−7=2, 3−3
7−(−1) =0, −1−3
−3−(−1) =2
(b) Yes; there are two pairs of equal slopes, so two pairs of parallel lines.
3. III <II <IV <I
4. III <IV <I<II
5. (a) 1−(−5)
1−(−2) =2, −5−(−1)
−2−0=2, 1−(−1)
1−0= 2. Since the slopes connecting all pairs of points are
equal, they lie on a line.
(b) 4−2
−2−0=−1, 2−5
0−1=3, 4−5
−2−1=1
3
. Since the slopes connecting the pairs of points are not
equal, the points do not lie on a line.
6. The slope, m=−2, is obtained from y−5
x−7, and thus y−5=−2(x−7).
(a) If x= 9 then y=1. (b) If y= 12 then x=7/2.
7. The slope, m= 3, is equal to y−2
x−1, and thus y−2=3(x−1).
(a) If x= 5 then y= 14. (b) If y=−2 then x=−1/3.
Exercise Set 1.5 20
8. (a) Compute the slopes: y−0
x−0=1
2or y=x/2. Also y−5
x−7=2ory=2x−9. Solve simultaneously
to obtain x=6,y =3.
9. (a) The first slope is 2−0
1−xand the second is 5−0
4−x. Since they are negatives of each other we get
2(4 −x)=−5(1 −x)or7x= 13, x=13/7.
10. (a) 27◦(b) 135◦(c) 63◦(d) 91◦
11. (a) 153◦(b) 45◦(c) 117◦(d) 89◦
12. (a) m= tan φ=−√3/3, so φ= 150◦(b) m= tan φ=4,soφ=76
◦
13. (a) m= tan φ=√3, so φ=60
◦(b) m= tan φ=−2, so φ= 117◦
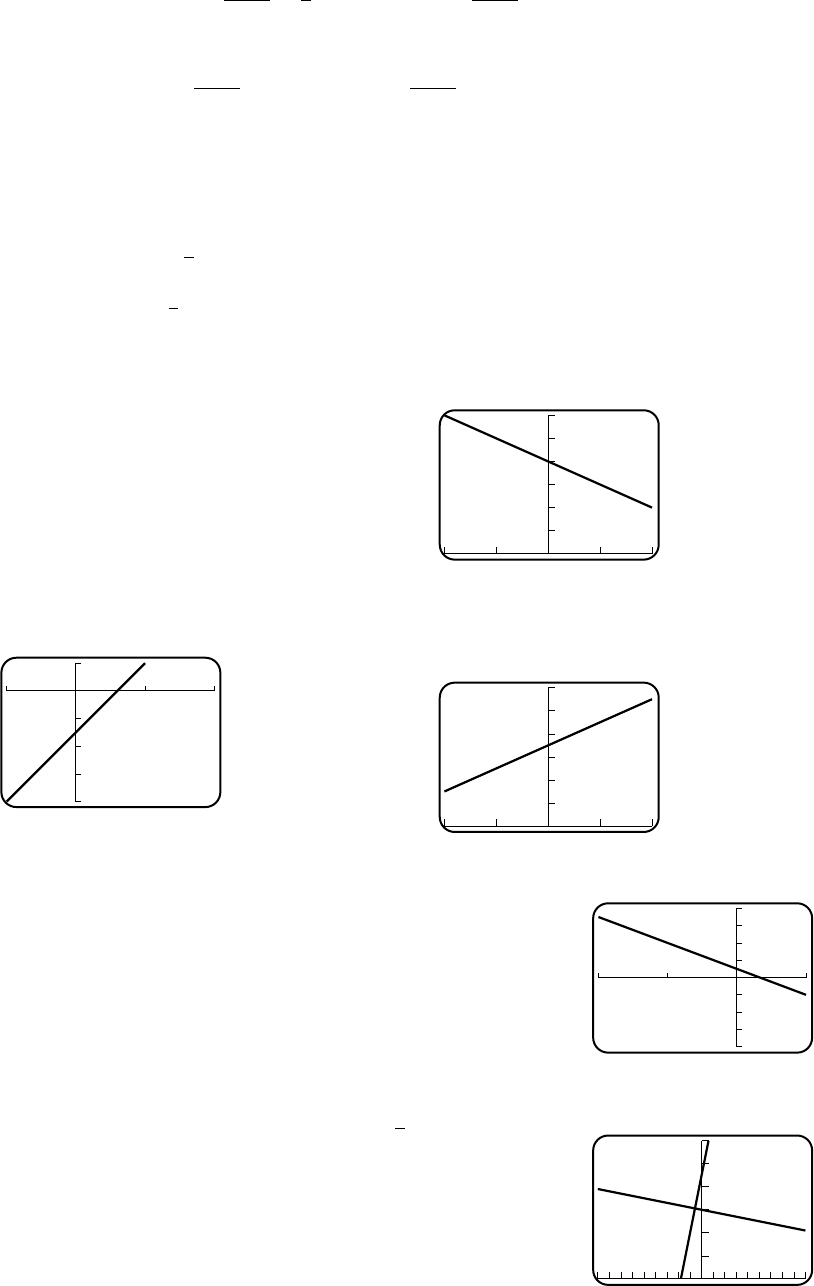
14. y= 0 and x= 0 respectively 15. y=−2x+4
6
0
-1 1
16. y=5x−3
2
–8
–1 2
17. Parallel means the lines have equal slopes, so
y=4x+7.
12
0
-1 1
18. The slope of both lines is −3/2, so y−2=(−3/2)(x−(−1)),
or 3x+2y=1
4
–4
-2 1
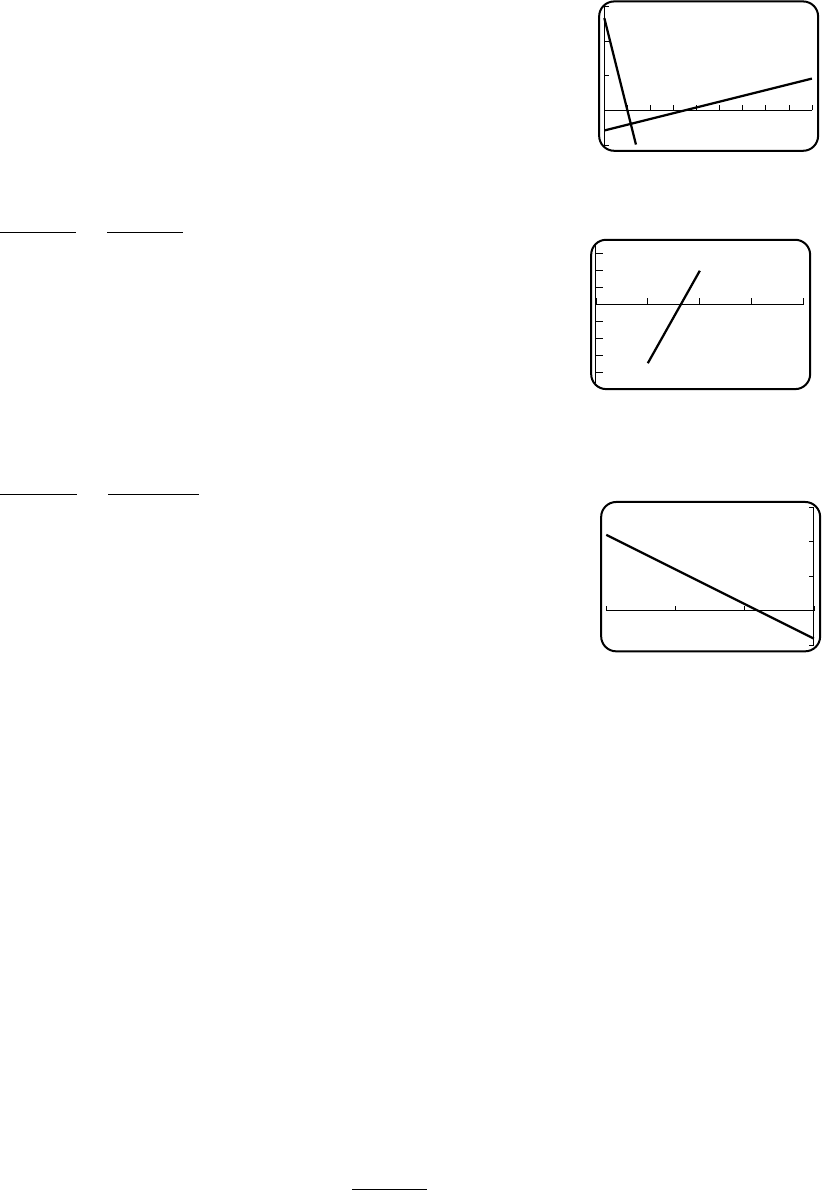
19. The negative reciprocal of 5 is −1/5, so y=−1
5x+6. 12
0
-9 9
21 Chapter 1
20. The slope of x−4y= 7 is 1/4 whose negative reciprocal
is −4, so y−(−4) = −4(x−3) or y+4x=8.
9
–3
018
21. y−(−7)
x−1=4−(−7)
2−1,ory=11x−18 7
-9
04
22. y−1
x−(−2) =6−1
−3−(−2),ory=−5x−915
–5
–4 0
23. (a) m1=m2= 4, parallel (b) m1=2=−1/m2, perpendicular
(c) m1=m2=5/3, parallel
(d) If A6= 0 and B6= 0 then m1=−A/B =−1/m2, perpendicular; if A=0orB= 0 (not both)
then one line is horizontal, the other vertical, so perpendicular.
(e) neither
24. (a) m1=m2=−5, parallel (b) m1=2=−1/m2, perpendicular
(c) m1=−4/5=−1/m2, perpendicular (d) If B6=0,m
1=m
2=−A/B;ifB= 0 both
are vertical, so parallel
(e) neither
25. (a) m=(0−(−3))/(2 −0))=3/2soy=3x/2−3
(b) m=(−3−0)/(4 −0) = −3/4soy=−3x/4
26. (a) m=(0−2)/(2 −0)) = −1soy=−x+2
(b) m=(2−0)/(3 −0)=2/3soy=2x/3
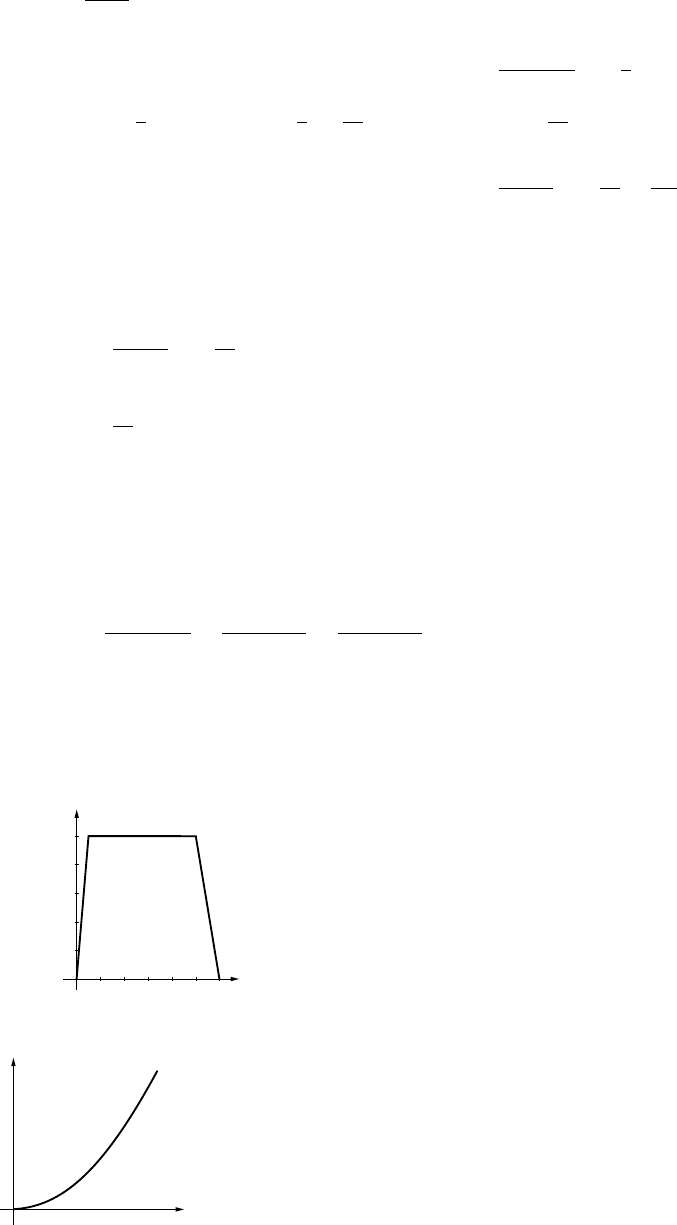
27. (a) The velocity is the slope, which is 5−(−4)
10 −0=9/10 ft/s.
(b) x=−4
(c) The line has slope 9/10 and passes through (0,−4), so has equation x=9t/10 −4; at t=2,
x=−2.2.
(d) t=80/9
Exercise Set 1.5 22
28. (a) v=5−1
4−2= 2 m/s (b) x−1=2(t−2) or x=2t−3(c) x=−3
29. (a) The acceleration is the slope of the velocity, so a=3−(−1)
1−4=−4
3ft/s2.
(b) v−3=−4
3
(t−1), or v=−4
3t+13
3(c) v=13
3ft/s
30. (a) The acceleration is the slope of the velocity, so a=0−5
10 −0=−5
10 =−1
2ft/s2.
(b) v= 5 ft/s (c) v= 4 ft/s (d) t=4s
31. (a) It moves (to the left) 6 units with velocity v=−3 cm/s, then remains motionless for 5 s, then
moves 3 units to the left with velocity v=−1 cm/s.
(b) vave =0−9
10 −0=−9
10 cm/s
(c) Since the motion is in one direction only, the speed is the negative of the velocity, so
save =9
10 cm/s.
32. It moves right with constant velocity v= 5 km/h; then accelerates; then moves with constant, though
increased, velocity again; then slows down.
33. (a) If x1denotes the final position and x0the initial position, then v=(x
1−x
0
)/(t
1−t
0
) = 0 mi/h,
since x1=x0.
(b) If the distance traveled in one direction is d, then the outward journey took t=d/40 h. Thus
save =total dist
total time =2d
t+(2/3)t=80t
t+(2/3)t= 48 mi/h.
(c) t+(2/3)t=5,sot= 3 and 2d=80t= 240 mi round trip
34. (a) down, since v<0(b) v=0att=2 (c) It’s constant at 32 ft/s2.
35. (a) v
t
20
40
60
80
100
20 40 60 80 100 120
(b) v=
10tif 0 ≤t≤10
100 if 10 ≤t≤100
600 −5tif 100 ≤t≤120
36. x
t
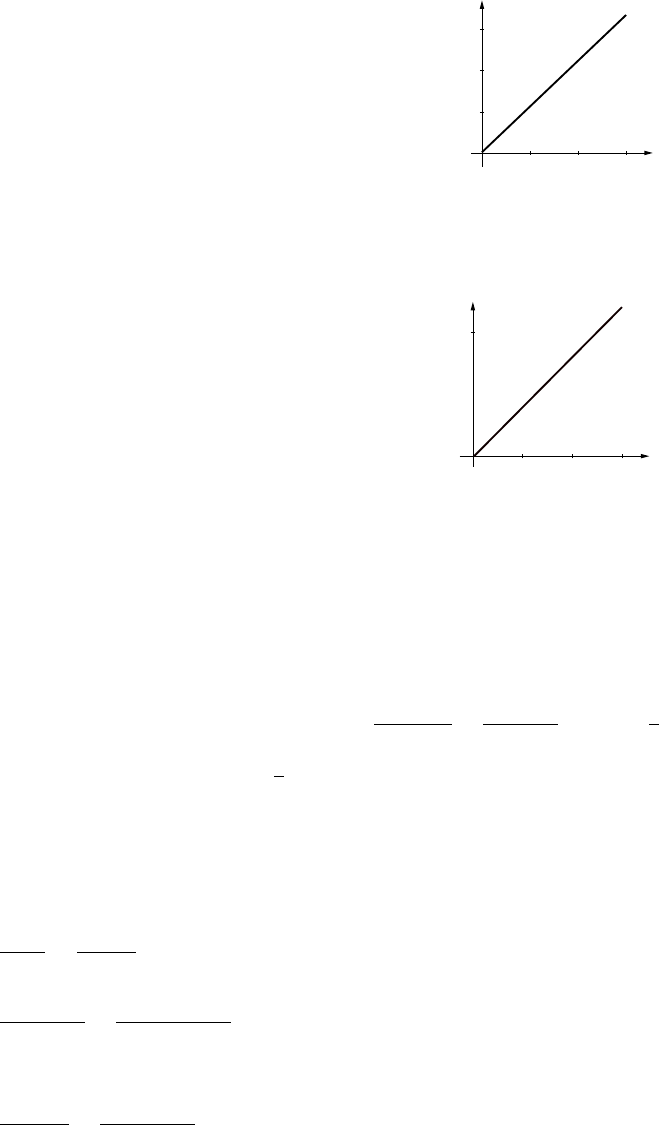
23 Chapter 1
37. (a) y=20−15 = 5 when x= 45, so 5 = 45k,
k=1/9, y=x/9
(b) y
x
0.2
0.4
0.6
246
(c) l=15+y= 15 + 100(1/9)=26.11 in. (d) If ymax = 15 then solve 15 = kx =x/9 for
x= 135 lb.
38. (a) Since y=0.2 = (1)k,k=1/5 and y=x/5(b) y
x
1
246
(c) y=3k=3/5so0.6 ft. (d) ymax =(1/2)3=1.5 so solve 1.5=x/5 for
x=7.5 tons
39. Each increment of 1 in the value of xyields the increment of 1.2 for y, so the relationship is linear. If
y=mx +bthen m=1.2; from x=0,y= 2, follows b=2,soy=1.2x+2
40. Each increment of 1 in the value of xyields the increment of −2.1 for y, so the relationship is linear.
If y=mx +bthen m=−2.1; from x=0,y=10.5 follows b=10.5, so y=−2.1x+10.5
41. (a) With TFas independent variable, we have TC−100
TF−212 =0−100
32 −212,soT
C=5
9
(T
F−32).
(b) 5/9 (c) Set TF=TC=5
9(TF−32) and solve for TF:TF=TC=−40◦(F or C).
(d) 37◦C
42. (a) One degree Celsius is one degree Kelvin, so the slope is the ratio 1/1=1. ThusT
C=T
K−273.15.
(b) TC=0−273.15 = −273.15◦C
43. (a) p−1
h−0=5.9−1
50 −0,orp=0.098h+1 (b) when p=2,orh=1/0.098 ≈10.20 m
44. (a) R−123.4
T−20 =133.9−123.4
45 −20 ,soR=0.42T+ 115.
(b) T=32.38◦C
45. (a) r−0.80
t−0=0.75 −0.80
4−0,sor=−0.0125t+0.8
(b) 64 days
46. (a) Let the position at rest be y0. Then y0+y=y0+kx; with x=11wegety
0+kx =y0+11k= 40,
and with x=24wegety
0+kx =y0+24k= 60. Solve to get k=20/13 and y0= 300/13.
(b) 300/13 + (20/13)W= 30, so W= (390 −300)/20=9/2g.
Exercise Set 1.6 24
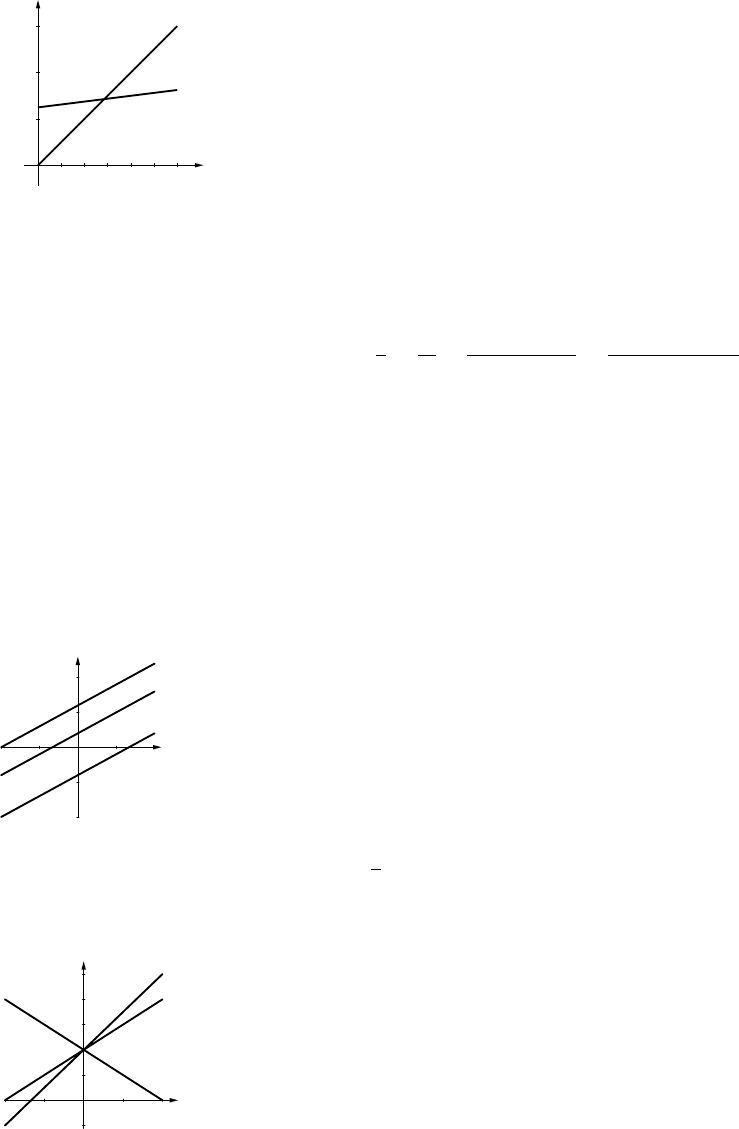
47. (a) For xtrips we have C1=2xand
C2=25+x/4
C
x
20
40
60
510 15 20 25 30
(b) 2x=25+x/4, or x= 100/7, so the com-
muter pass becomes worthwhile at x= 15.
48. If the student drives xmiles, then the total costs would be CA= 4000 + (1.25/20)xand
CB= 5500 + (1.25/30)x. Set 4000 + 5x/80 = 5500 + 5x/120 and solve for x=72,000 mi.
49. (a) H≈20000/110 ≈181
(b) One light year is 9.408 ×1012 km and t=d
v=1
H=1
20km/s/Mly =9.408 ×1018km
20km/s
=4.704 ×1017 s=1.492 ×1010 years.
(c) The Universe would be even older.
EXERCISE SET 1.6
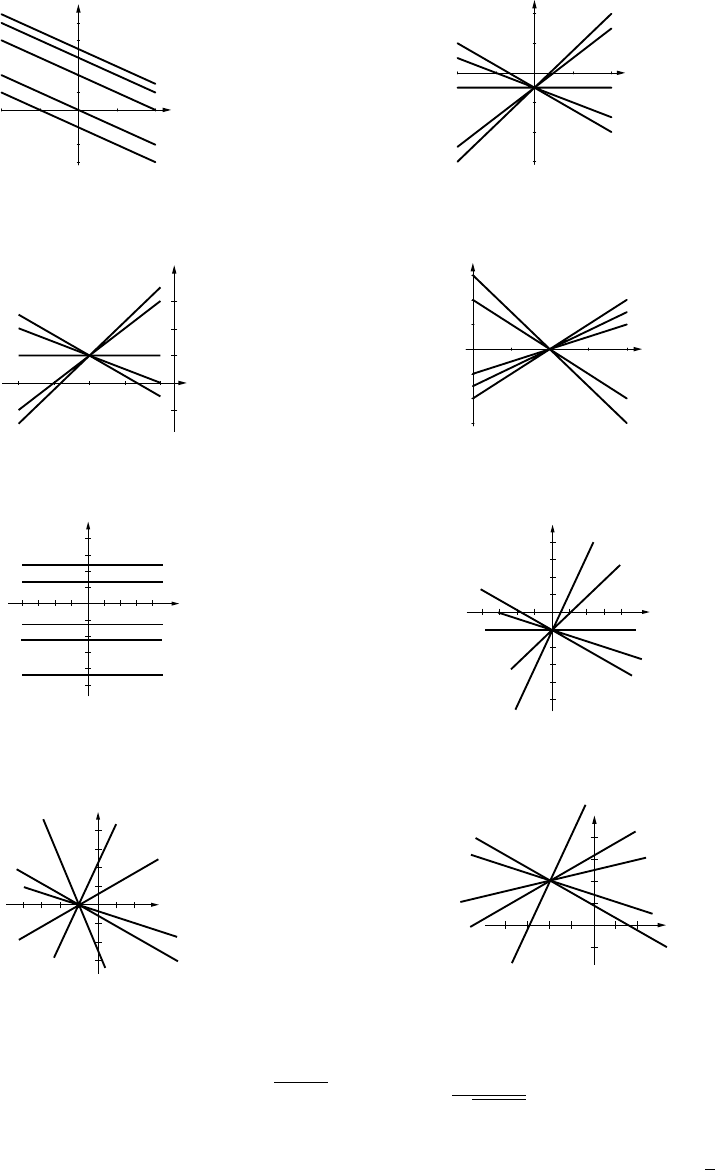
1. (a) y=3x+b(b) y=3x+6
(c)
-10
-5
5
10
y
-2 -1 1 2 x
y = 3x + 6
y = 3x + 2
y = 3x - 4
2. Since the slopes are negative reciprocals, y=−1
3x+b.
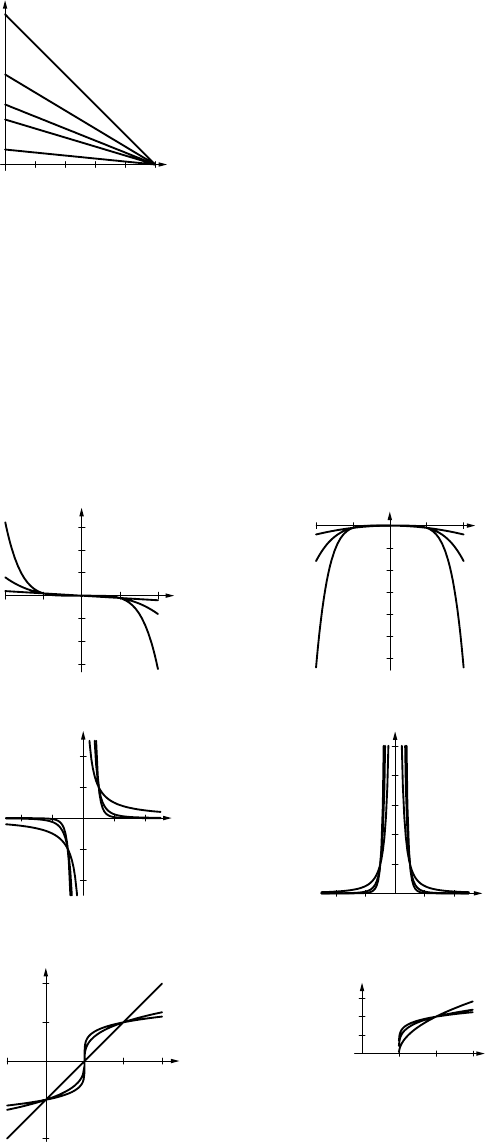
3. (a) y=mx +2 (b) m= tan φ= tan 135◦=−1, so y=−x+2
(c)
-1
1
2
3
4
5
-2 -1 1 2 x
y
m = –1
m = 1
m = 1.5
4. (a) y=mx (b) y=m(x−1)
(c) y=−2+m(x−1) (d) 2x+4y=C
25 Chapter 1
5. (a) The slope is −1.
-3
-2
-1
1
2
3
4
5
-2 -1 1 2 x
y
(b) The y-intercept is y=−1.
-6
-4
-2
2
4
-2 -1 1 2 x
y
(c) They pass through the point (−4,2).
y
x
-2
2
4
6
-6 -4 -2
(d) The x-intercept is x=1.
-3
-2
-1
1
2
3
0.5 11.5 2x
y
6. (a) horizontal lines
x
y
(b) The y-intercept is y=−1/2.
x
y
-1
2
2
(c) The x-intercept is x=−1/2.
x
y
1
1
(d) They pass through (−1,1).
x
y
-2
1
1
(-1,1)
7. Let the line be tangent to the circle at the point (x0,y
0) where x2
0+y2
0= 9. The slope of the tangent
line is the negative reciprocal of y0/x0(why?), so m=−x0/y0and y=−(x0/y0)x+b. Substituting
the point (x0,y
0) as well as y0=±p9−x2
0we get y=±9−x0x
p9−x2
0
.
8. Solve the simultaneous equations to get the point (−2,1/3) of intersection. Then y=1
3+m(x+ 2).
Exercise Set 1.6 26
9. The x-intercept is x= 10 so that with depreciation at 10% per year the final value is always zero, and
hence y=m(x−10). The y-intercept is the original value.
y
246810
x
10. A line through (6,−1) has the form y+1 = m(x−6). The intercepts are x= 6+1/m and y=−6m−1.
Set −(6+1/m)(6m+1)=3,or36m
2+15m+1 = (12m+1)(3m+1) = 0 with roots m=−1/12,−1/3;
thus y+1=−(1/3)(x−6) and y+1=−(1/12)(x−6).
11. (a) VI (b) IV (c) III (d) V(e) I(f) II
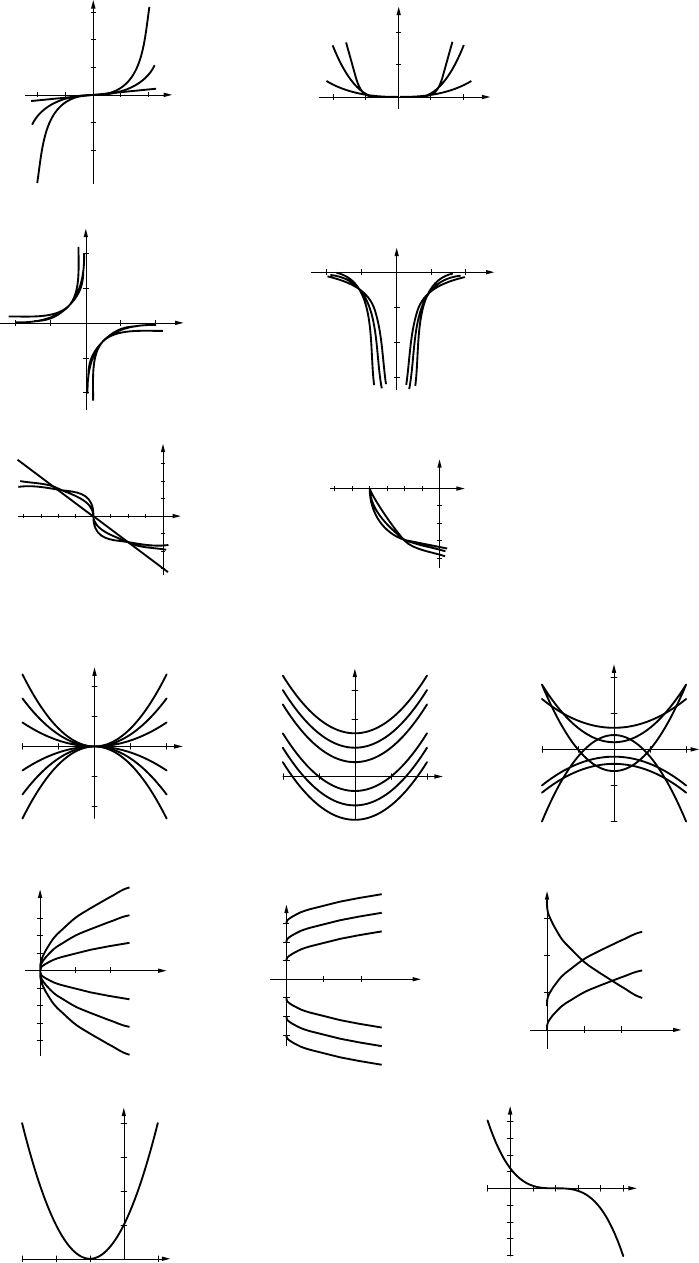
12. In all cases kmust be positive, or negative values would appear in the chart. Only kx−3decreases, so
that must be f(x). Next, kx2grows faster than kx3/2, so that would be g(x), which grows faster than
h(x) (to see this, consider ratios of successive values of the functions). Finally, experimentation (a
spreadsheet is handy) for values of kyields (approximately) f(x)=10x
−3
,g(x)=x
2
/2, h(x)=2x
1.5
.
13. (a)
-30
-20
-10
10
20
30
-2 -1 1 2 x
y
-60
-50
-40
-30
-20
-10
-2 -1 1 2 x
y
(b)
-4
-2
2
4
y
-4 -2 2 4 x
2
4
6
8
10
y
-4 -2 2 4 x
(c)
-2
-1
1
2
-1 1 2 3 x
y
0.5
1
1.5
y
123
x
27 Chapter 1
14. (a)
x
y
2
40
-2
-40
x
y
2
40
-2
80
(b)
x
y
2
4
-2
-4
x
y
2
-2
-2
-4
(c)
x
y
-1 -2
4
-3
x
y
-1
-2
15. (a)
-10
-5
5
10
y
-2 -1 1 2 x
(b)
-2
2
4
6
y
-2 -1 1 2 x
(c)
-10
-5
5
10
y
-2 -1 1 2 x
16. (a)
x
y
2
3
(b)
x
y
2
2
(c)
x
y
2
2
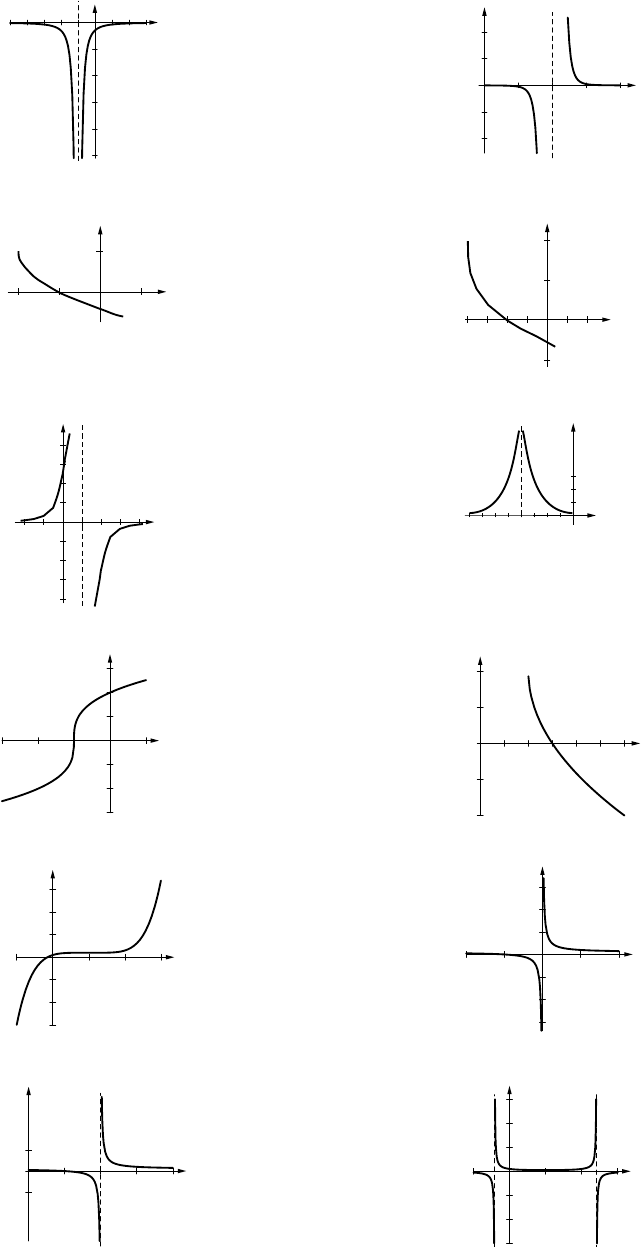
17. (a)
2
4
6
8
y
-3 -2 -1 1 x
(b)
-80
-60
-40
-20
20
40
60
80
y
-1 1 2 3 4 5x
Exercise Set 1.6 28
(c)
-50
-40
-30
-20
-10
y
-5 -4 -3 -2 -1 1 2 3 x
(d)
-40
-20
20
40
y
12 3 4 5
x
18. (a)
x
y
1
1
(b)
x
y
1
1
-2
(c)
x
y
2
4
-2
-4
(d)
x
y
-2
4
-6
19. (a)
-1.5
-1
-0.5
0.5
1
1.5
y
-3 -2 -1 1 x
(b)
-1
-0.5
0.5
1
y
123456x
(c)
-30
-20
-10
10
20
30
y
-1 1 2 3 x
(d)
-30
-20
-10
10
20
30
y
-2 -1 1 2 x
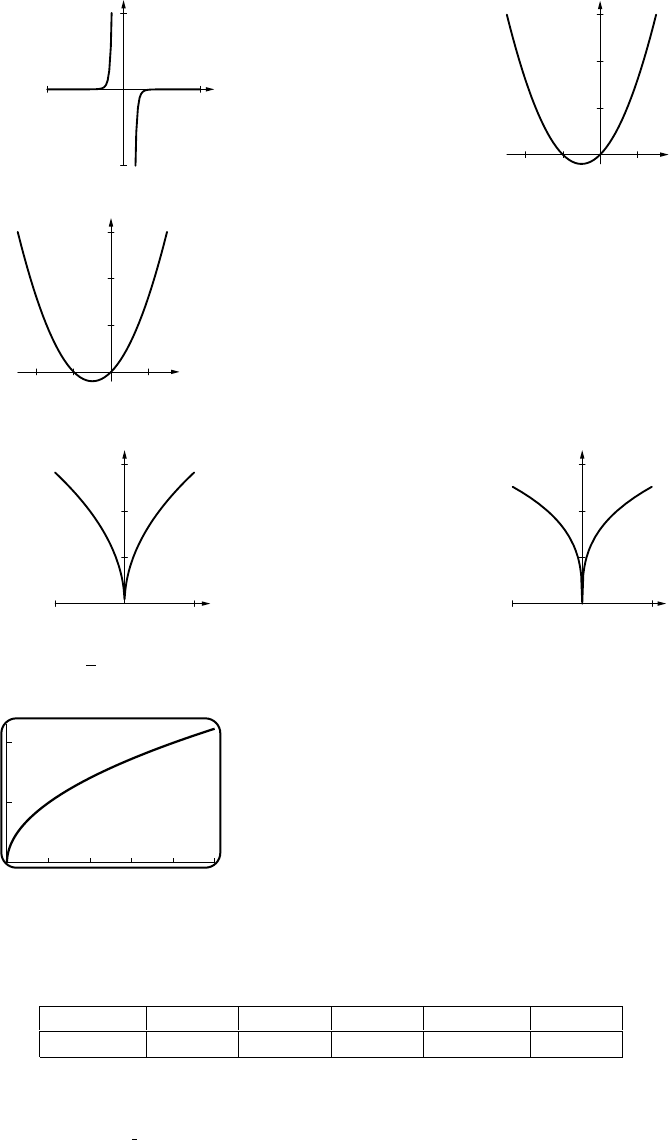
20. (a)
-10
10
y
134
x
(b)
-30
-20
-10
10
20
30
y
-1 1 2 3 x
29 Chapter 1
(c)
-106
106
y
-1 1 x
(d)
5
10
15
y
-4 -2 2 x
21.
5
10
15
y
-4 -2 2 x
22. (a)
0.5
1
1.5
y
-2 2 x
(b)
0.5
1
1.5
y
-2 2 x
23. t=0.445√d
2.3
0
025
24. (a) t=0.373r1.5(b) 238,000 km (c) 1.89 days
25. (a) N·m(b) 20 N·m
(c) V(L) 0.25 0.5 1.0 1.5 2.0
P(N/m2) 80 ×10340 ×10320 ×10313.3×10310 ×103
26. If the side of the square base is xand the height of the container is ythen V=x2y= 100; minimize
A=2x
2+4xy =2x
2+ 400/x. A graphing utility with a zoom feature suggests that the solution is a
cube of side 1001
3cm.
27. (a) F=k/x2so 0.0005 = k/(0.3)2and
k=0.000045 N·m2.
(b) 0.000005 N
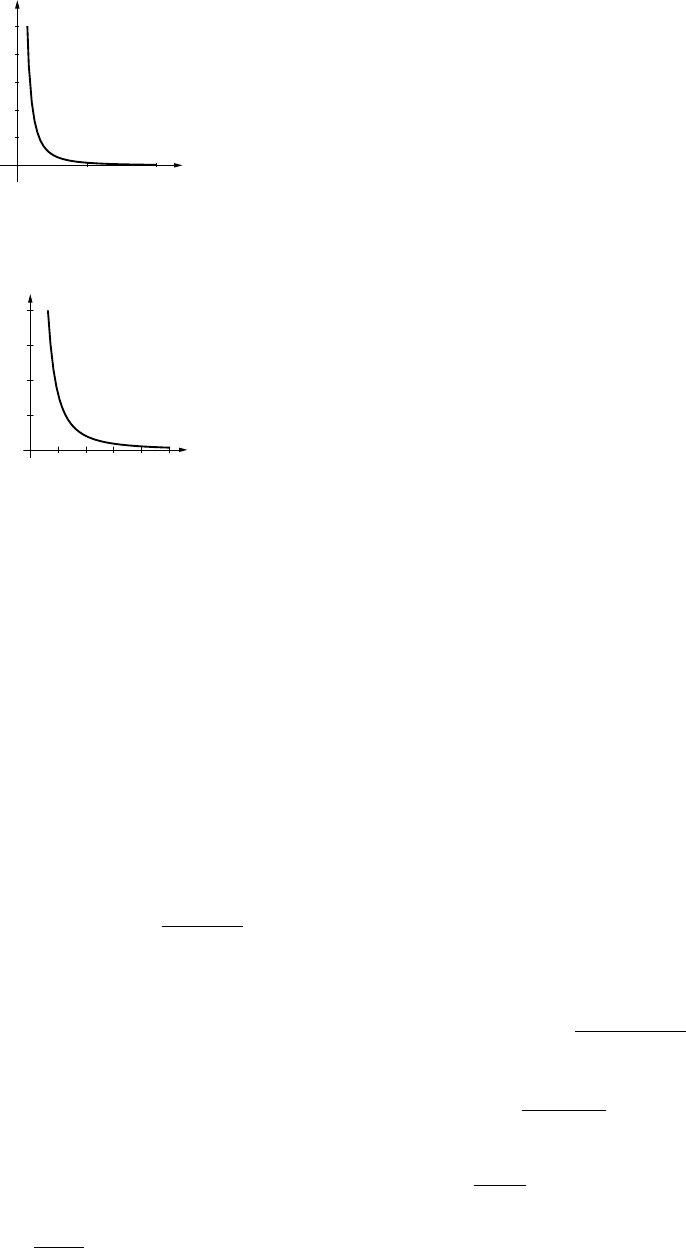
Exercise Set 1.6 30
(c)
d
510
F
10-5
(d) When they approach one another, the force
becomes infinite; when they get far apart it
tends to zero.
28. (a) 2000 = C/(4000)2,soC=3.2×1010 lb·mi2(b) W=C/50002=(3.2×1010)/(25 ×106)=
1280 lb.
(c)
5000
10000
15000
20000
W
2000 4000 6000 8000 10000
x
(d) No, but Wis very small when xis large.
29. (a) II; y=1,x=−1,2(b) I; y=0,x=−2,3
(c) IV; y=2 (d) III; y=0,x=−2
30. The denominator has roots x=±1, so x2−1 is the denominator. To determine kuse the point (0,−1)
to get k=1,y=1/(x
2−1).
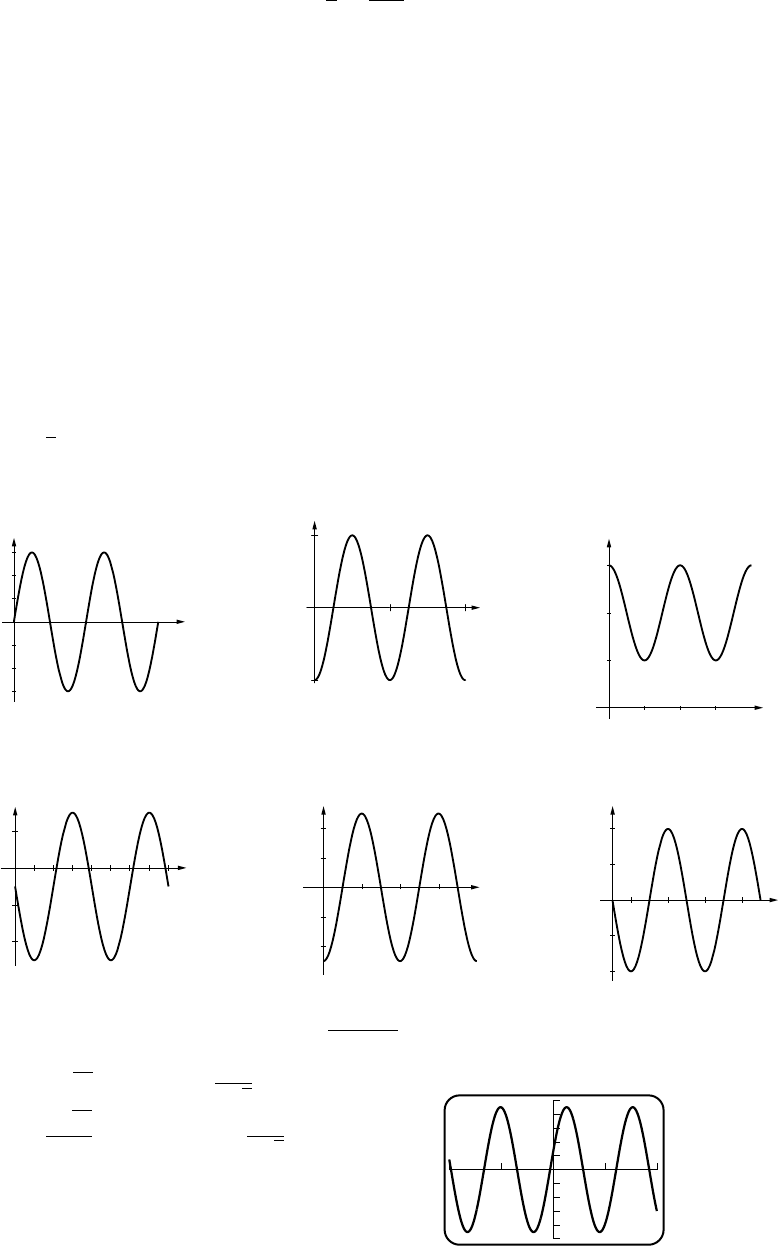
31. Order the six trigonometric functions as sin, cos, tan, cot, sec, csc:
(a) pos, pos, pos, pos, pos, pos (b) neg, zero, undef, zero, undef, neg
(c) pos, neg, neg, neg, neg, pos (d) neg, pos, neg, neg, pos, neg
(e) neg, neg, pos, pos, neg, neg (f) neg, pos, neg, neg, pos, neg
32. (a) neg, zero, undef, zero, undef, neg (b) pos, neg, neg, neg, neg, pos
(c) zero, neg, zero, undef, neg, undef (d) pos, zero, undef, zero, undef, pos
(e) neg, neg, pos, pos, neg, neg (f) neg, neg, pos, pos, neg, neg
33. (a) sin(π−x) = sin x; 0.588 (b) cos(−x) = cos x; 0.924
(c) sin(2π+x) = sin x; 0.588 (d) cos(π−x)=−cos x;−0.924
(e) sin 2x=±2 sin xp1−sin2x; use the +
sign for xsmall and positive; 0.951
(f) cos2x=1−sin2x; 0.654
34. (a) sin(3π+x)=−sin x;−0.588 (b) cos(−x−2π) = cos x; 0.924
(c) sin(8π+x) = sin x; 0.588 (d) sin(x/2) = ±p(1 −cos x)/2; use the nega-
tive sign for xsmall and negative; −0.195
(e) cos(3π+3x)=−4 cos3x+ 3 cos x;−0.384 (f) tan2x=1−cos2x
cos2x; 0.172
35. (a) −a(b) b
(c) −c(d) ±√1−a2
(e) −b(f) −a
(g) ±2b√1−b2(h) 2b2−1
(i) 1/b (j) −1/a
(k) 1/c (l) (1 −b)/2
31 Chapter 1
36. (a) The distance is 36/360=1/10th of a great
circle, so it is (1/10)2πr =2,513.27 mi.
(b) 36/360=1/10
37. If the arc length is 1, then solve the ratio x
1=2πr
29.5to get x≈80,936 km.
38. The distance travelled is equal to the length of that portion of the circumference of the wheel which
touches the road, and that is the fraction 225/360 of a circumference, so a distance of (225/360)(2π)3 =
11.78 ft
39. The second quarter revolves twice (720◦) about its own center.
40. Add rto itself until you exceed 2πr; since 6r<2πr < 7r, you can cut off 6 pieces of pie, but there’s
not enough for a full seventh piece. We conclude that there is no exact solution of the equation
‘One pie = 2πr’.
41. (a) y= 3 sin(x/2) (b) y= 4 cos 2x(c) y=−5 sin 4x
42. (a) y= 1 + cos πx (b) y=1+2sinx(c) y=−5 cos 4x
43. (a) y= sin(x+π/2)
(b) y= 3 + 3 sin(2x/9)
(c) y= 1 + 2 sin(2(x−π/4))
44. V= 120√2 sin(120πt)
45. (a) 3,π/2,0
y
x
-2
1
3
π/2
(b) 2,2,0
-2
2
24
x
(c) 1,4π, 0
y
x
1
2
3
2π4π6π
46. (a) 4,π,0
y
x
-4
-2
2
π/4 3π/4 5π/4 7π/4
(b) 1/2,2π/3,π/3
y
x
-0.2
0.4
π/3 2π/3 π
(c) 4,6π, −6π
y
x
-4
-2
2
4
3π/2 9π/2 15π/2 21π/2
47. (a) Asin(ωt +θ)=Asin(ωt) cos θ+Acos(ωt) sin θ=A1sin(ωt)+A
2cos(ωt)
(b) A1=Acos θ, A2=Asin θ,soA=pA
2
1+A
2
2and θ= tan−1(A2/A1).
(c) A=5
√
13/2, θ= tan−11
2√3;
x=5√13
2sin µ2πt + tan−11
2√3¶
10
-10
^6
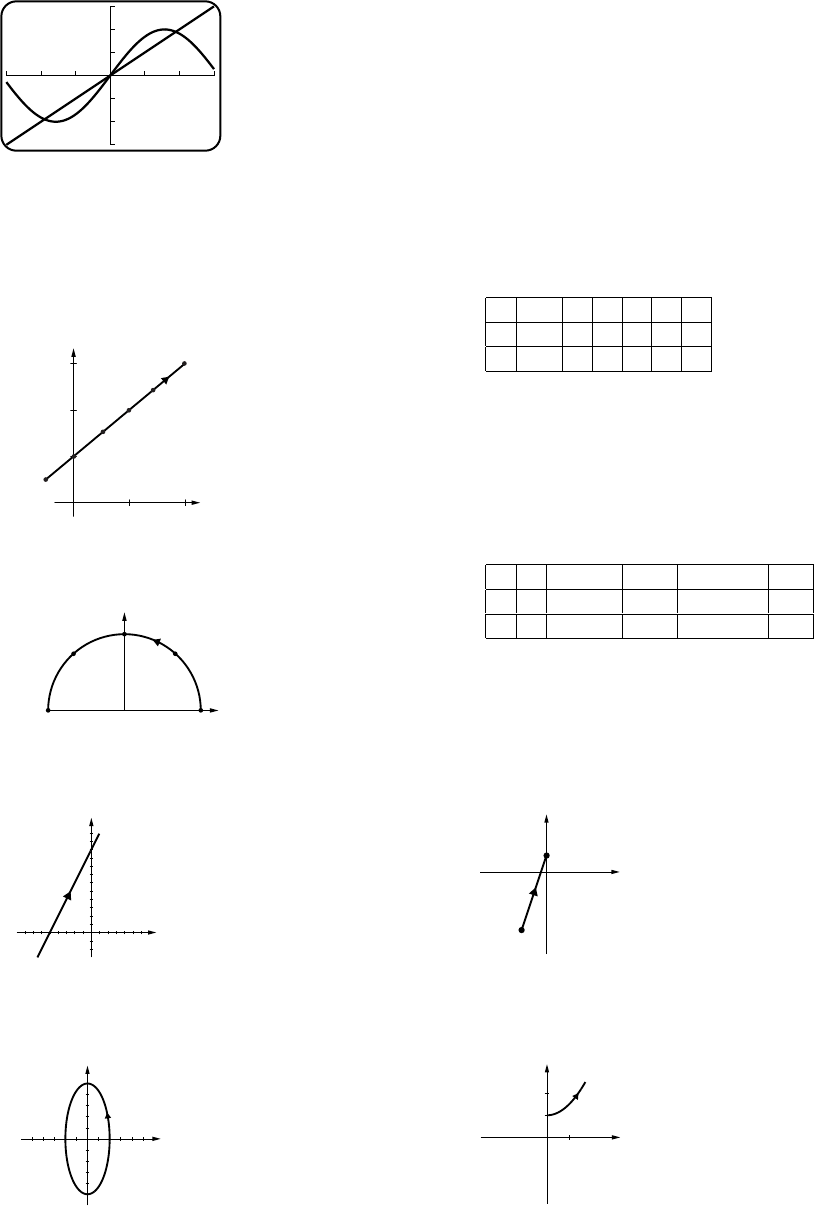
Exercise Set 1.7 32
48. three; x=0,x=±1.8955
3
–3
-3 3
EXERCISE SET 1.7
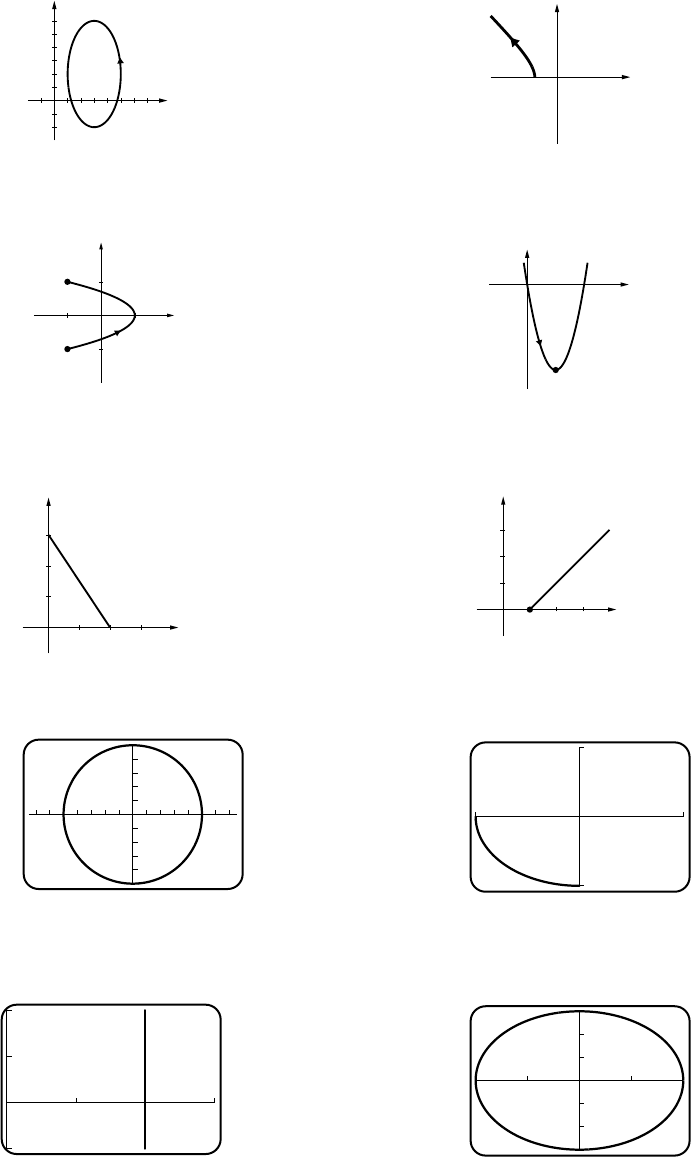
1. (a) x+1=t=y−1, y=x+2
2
4
6
y
24
t=0
t=1
t=2
t=3
t=4
t=5
x
(c) t012345
x−101234
y123456
2. (a) x2+y2=1
1
y
-1 1 x
t=1
t=.5
t=.75 t=.25
t=0
(c) t0 0.2500 0.50 0.7500 1
x1 0.7071 0.00 −0.7071 −1
y0 0.7071 1.00 0.7071 0
3. t=(x+4)/3; y=2x+10
-8 6
12
x
y
4. t=x+3;y=3x+2,−3≤x≤0
x
y
(0, 2)
(-3, -7)
5. cos t=x/2,sin t=y/5; x2/4+y
2
/25=1
-5 5
-5
5
x
y
6. t=x2;y=2x
2+4,x≥0
1
4
8
x
y
33 Chapter 1
7. cos t=(x−3)/2,sin t=(y−2)/4;
(x−3)2/4+(y−2)2/16=1
7
-2
6
x
y
8. sec2t−tan2t=1;x
2
−y
2=1,
x≤−1 and y≥0
-1 x
y
9. cos 2t=1−2 sin2t;x=1−2y
2
,−1≤y≤1
-1 1
-1
1
x
y
10. t=(x−3)/4; y=(x−3)2−9
x
y
(3, -9)
11. x/2+y/3=1,0≤x≤2,0≤y≤3
x
y
2
3
12. y=x−1,x≥1,y ≥0
1
1
x
y
13. x= 5 cos t,y=−5 sin t,0≤t≤2π
5
-5
-7.5 7.5
14. x= cos t,y= sin t,π≤t≤3π/2
1
–1
-1 1
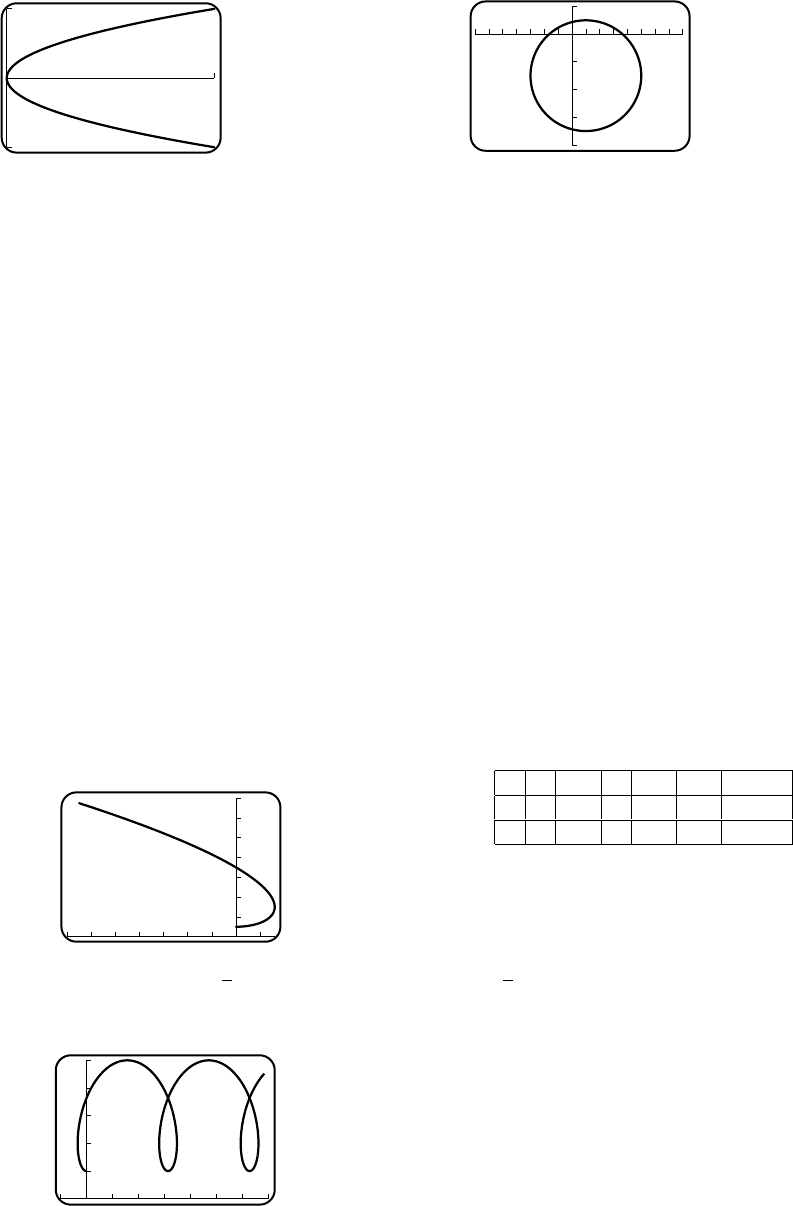
15. x=2,y=t
2
-1
03
16. x= 2 cos t,y= 3 sin t,0≤t≤2π
3
–3
-2 2
Exercise Set 1.7 34
17. x=t2,y=t,−1≤t≤1
1
-1
01
18. x=1+4cost,y=−3+4sint,0≤t≤2π
2
-8
-7 8
19. (a) IV, because xalways increases whereas yoscillates.
(b) II, because (x/2)2+(y/3)2= 1, an ellipse.
(c) V, because x2+y2=t2increases in magnitude while xand ykeep changing sign.
(d) VI; examine the cases t<−1 and t>−1 and you see the curve lies in the first, second and
fourth quadrants only.
(e) III because y>0.
(f) I; since xand yare bounded, the answer must be I or II; but as truns, say, from 0 to π,xgoes
directly from 2 to −2, but ygoesfrom0to1to0to−1 and back to 0, which describes I but
not II.
20. (a) from left to right
(b) counterclockwise
(c) counterclockwise
(d) As ttravels from −∞ to −1, the curve goes from (near) the origin in the third quadrant and
travels up and left. As ttravels from −1to+∞the curve comes from way down in the second
quadrant, hits the origin at t= 0, and then makes the loop clockwise and finally approaches the
origin again as t→+∞.
(e) from left to right
(f) Starting, say, at (1,0), the curve goes up into the first quadrant, loops back through the origin
and into the third quadrant, and then continues the figure-eight.
21. (a) 14
0
-35 8
(b) t0 1 2 3 4 5
x0 5.5 8 4.5−8−32.5
y1 1.5 3 5.5 9 13.5
(c) x= 0 when t=0,2
√
3. (d) for 0 <t<2
√
2(e) at t=2
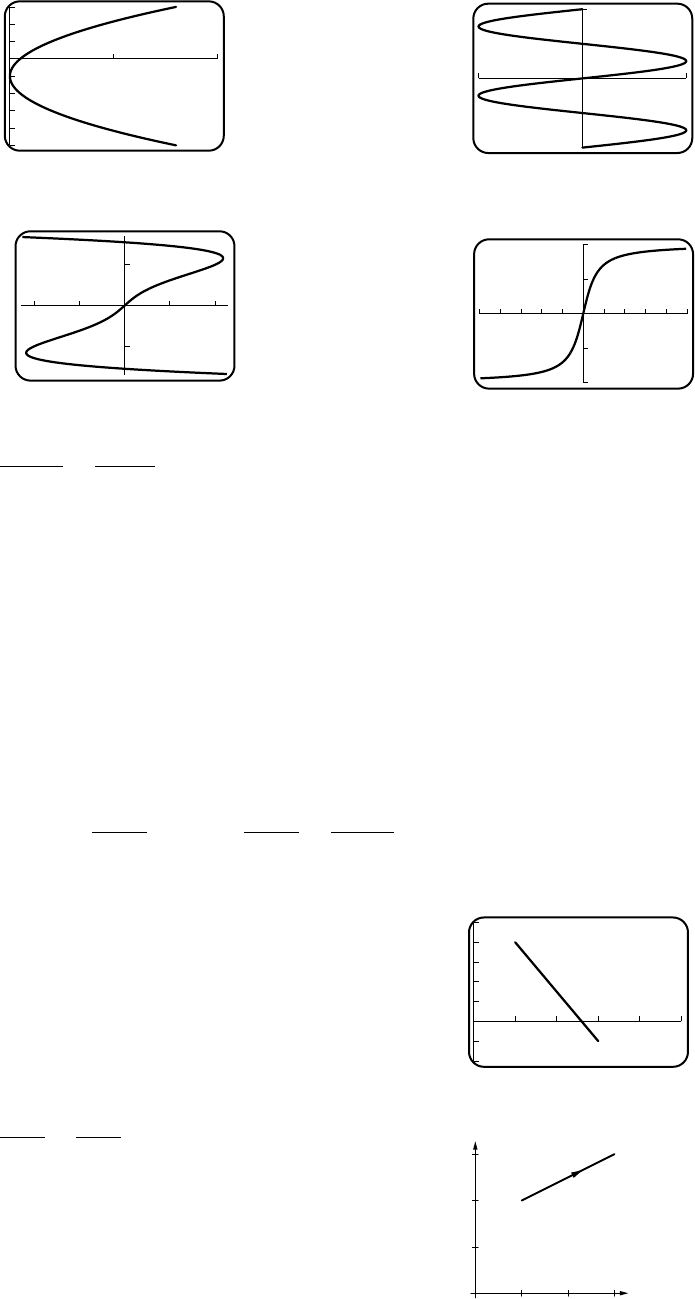
22. (a) 5
0
-2 14
(b) yis always ≥1 since cos t≤1
(c) greater than 5, since cos t≥−1
35 Chapter 1
23. (a) 3
-5
020
(b) o
O
-1 1
24. (a) 1.7
-1.7
-2.3 2.3
(b)
-10 10
^
6
25. (a) x−x0
x1−x0
=y−y0
y1−y0
(b) Set t= 0 to get (x0,y
0); t= 1 for (x1,y
1).
(c) x=1+t,y=−2+6t(d) x=2−t,y=4−6t
26. (a) x=−3−2t,y=−4+5t(b) x=at,y=b(1 −t)
27. (a) |R−P|2=(x−x
0
)
2+(y−y
0)
2=t
2[(x1−x0)2+(y
1−y
0)
2] and |Q−P|2=(x
1−x
0
)
2+(y
1−y
0)
2,
so r=|R−P|=|Q−P|t=qt.
(b) t=1/2(c) t=3/4
28. x=2+t,y=−1+2t
(a) (5/2,0) (b) (9/4,−1/2) (c) (11/4,1/2)
29. The two branches corresponding to −1≤t≤0 and 0 ≤t≤1 coincide.
30. (a) Eliminate t−t0
t1−t0
to obtain y−y0
x−x0
=y1−y0
x1−x0
.
(b) from (x0,y
0)to(x
1
,y
1)(c) x=3−2(t−1), y=−1+5(t−1)
5
-2
05
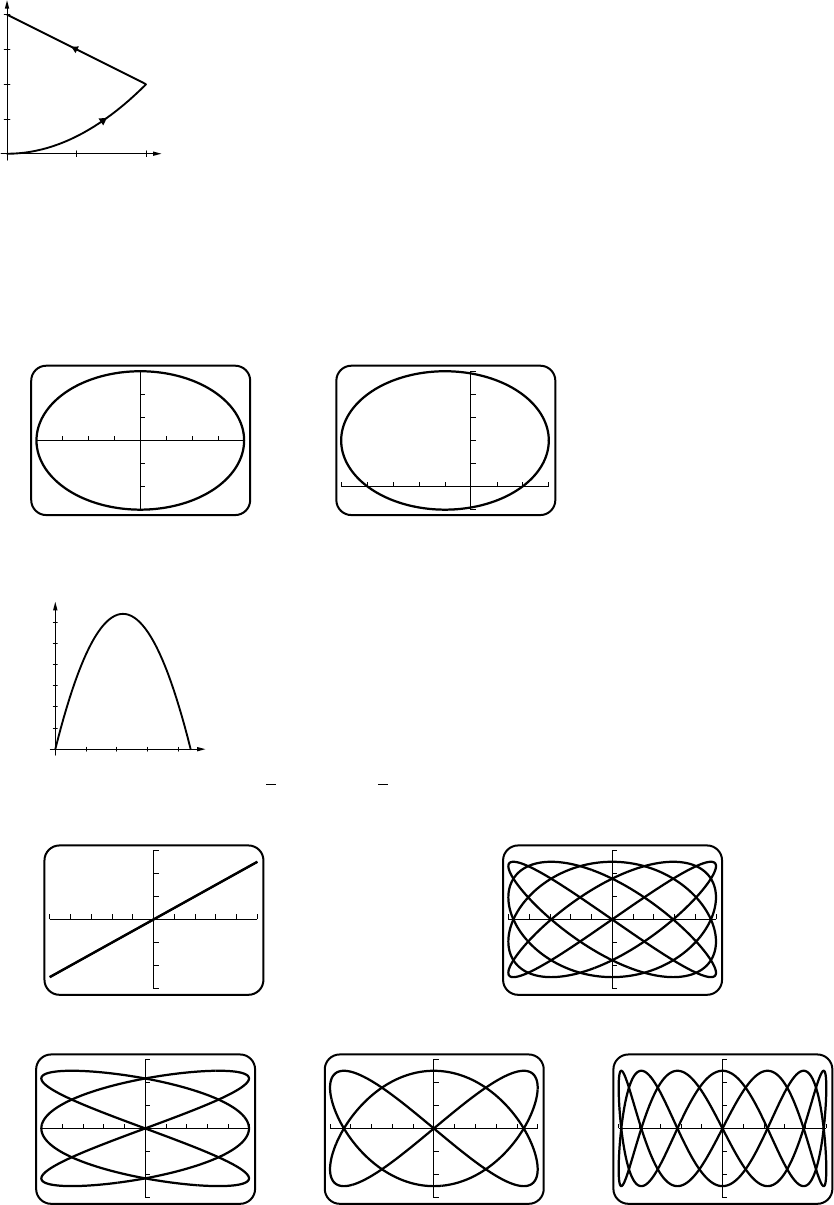
31. (a) x−b
a=y−d
c(b)
1
2
3
y
123
x
Exercise Set 1.7 36
32. (a) If a= 0 the line segment is vertical; if c= 0 it is horizontal.
(b) The curve degenerates to the point (b, d).
33.
0.5
1
1.5
2
y
0.5 1 x
34. x=1/2−4t, y =1/2 for 0 ≤t≤1/4
x=−1/2,y=1/2−4(t−1/4) for 1/4≤t≤1/2
x=−1/2+4(t−1/2),y=−1/2 for 1/2≤t≤3/4
x=1/2,y=−1/2+4(t−3/4) for 3/4≤t≤1
35. (a) x= 4 cos t,y= 3 sin t(b) x=−1+4cost,y=2+3sint
(c) 3
-3
-4 4
5
-1
-5 3
36. (a) t=x/(v0cos α), so y=xtan α−gx2/(2v2
0cos2α).
(b)
2000
4000
6000
8000
10000
12000
40000 80000 x
y
37. (a) From Exercise 36, x= 400√2t,y= 400√2t−4.9t2.(b) 16,326.53 m (c) 65,306.12 m
38. (a) 15
–15
-25 25
(b) 15
–15
-25 25
(c) 15
–15
-25 25
a = 3, b = 2
15
–15
-25 25
a = 2, b = 3
15
–15
-25 25
a = 2, b = 7

37 Chapter 1
39. Assume that a6= 0 and b6= 0; eliminate the parameter to get (x−h)2/a2+(y−k)
2/b2=1. If|a|=|b|
the curve is a circle with center (h, k) and radius |a|;if|a|6=|b|the curve is an ellipse with center
(h, k) and major axis parallel to the x-axis when |a|>|b|, or major axis parallel to the y-axis when
|a|<|b|.
(a) ellipses with a fixed center and varying axes of symmetry
(b) (assume a6= 0 and b6= 0) ellipses with varying center and fixed axes of symmetry
(c) circles of radius 1 with centers on the line y=x−1
40. Refer to the diagram to get bθ =aφ,θ=aφ/b but θ−α=φ+π/2
so α=θ−φ−π/2=(a/b −1)φ−π/2
x=(a−b) cos φ−bsin α
=(a−b) cos φ+bcos µa−b
b¶φ,
y=(a−b) sin φ−bcos α
=(a−b) sin φ−bsin µa−b
b¶φ.
x
y
θ
α
φφ
a
θ
b
a − b
41. (a)
-a
a
-a a
y
x
(b) Use b=a/4 in the equations of Exercise 40 to get
x=3
4acos φ+1
4acos 3φ,y=3
4asin φ−1
4asin 3φ;
but trigonometric identities yield cos 3φ= 4 cos3φ−3 cos φ, sin 3φ= 3 sin φ−4 sin3φ,
so x=acos3φ,y=asin3φ.
(c) x2/3+y2/3=a2/3(cos2φ+ sin2φ)=a
2/3
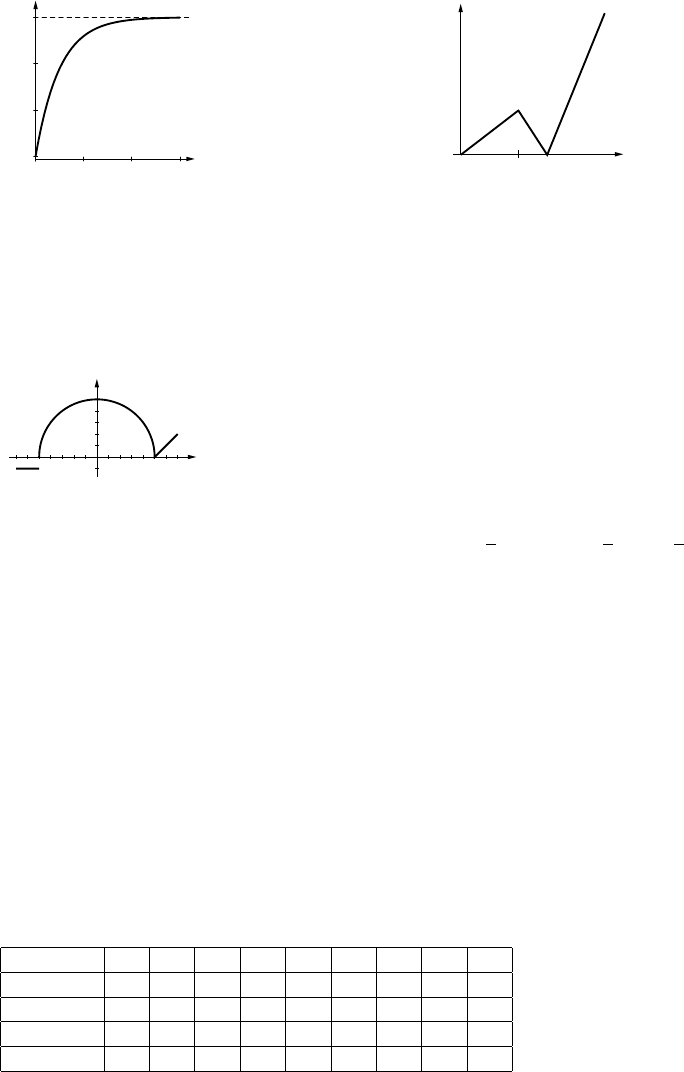
42.
-50
0
50
y
-3 -2 -1 x
a=−2
-50
50
y
-2 -1 x
a=−1
-1
1
y
-1 1 x
a=0
-50
50
y
12
x
a=1
-50
0
50
y
12 3
x
a=2
Supplementary Exercises 1 38
CHAPTER 1 SUPPLEMENTARY EXERCISES
1. 1940-45; the greatest five-year slope
2. (a) f(−1)=3.3,g(3)=2 (b) x=−3,3
(c) x<−2,x>3(d) the domain is −5≤x≤5 and the range is
−5≤y≤4
(e) the domain is −4≤x≤4.1, the range is
−3≤y≤5
(f) f(x)=0atx=−3,5; g(x)=0at
x=−3,2
3.
40
50
60
70
0246
t
T4. x
58 13 t
5. If the side has length xand height h, then V=8=x
2
h,soh=8/x2. Then the cost C=5x
2+
2(4)(xh)=5x
2+64/x.
6. Assume that the paint is applied in a thin veneer of uniform thickness, so that the quantity of paint
to be used is proportional to the area covered. If P is the amount of paint to be used, P=kπr2. The
constant kdepends on physical factors, such as the thickness of the paint, absorption of the wood,
etc.
7. y
x
-1
5
-5 5
8. Suppose the radius of the uncoated ball is rand that of the coated ball is r+h. Then the plastic has
volume equal to the difference of the volumes, i.e. V=4
3π(r+h)3−4
3πr3=4
3πh[3r2+3rh +h2]in
3
.
9. (a) The base has sides (10 −2x)/2 and 6 −2x, and the height is x,soV=(6−2x)(5 −x)xft3.
(b) From the picture we see that x<5 and 2x<6, so 0 <x<3.
(c) 3.57 ft ×3.79 ft ×1.21 ft
10. {x6=0}and ∅(the empty set)
11. impossible; we would have to solve 2(3x−2) −5 = 3(2x−5) −2, or −9=−17
12. (a) (3 −x)/x (b) no; f(g(x)) can be defined at x=1,
whereas g, and therefore f◦g, requires
x6=1
13. 1/(2 −x2)14. g(x)=x
2+2x
15. x−4−3−2−1 0 1 2 3 4
f(x) 0 −1 2 1 3 −2−3 4 −4
g(x) 3 2 1 −3−1−4 4 −2 0
(f◦g)(x) 4 −3−2−1 1 0 −4 2 3
(g◦f)(x)−1−3 4 −4−2 1 2 0 3

39 Chapter 1
16. (a) y=|x−1|,y=|(−x)−1|=|x+1|,
y=2|x+1|,y=2|x+1|−3,
y=−2|x+1|+3
(b) y
x
-1
1
3
-3 -1 2
17. (a) even ×odd=odd (b) a square is even
(c) even + odd is neither (d) odd ×odd=even
18. (a) y= cos x−2 sin xcos x=(1−2 sin x) cos x,sox=±π
2
,±3π
2,π
6
,5π
6,−7π
6,−11π
6
(b) (±π
2,0),(±3π
2,0),(π
6,√3/2),(5π
6,−√3/2),(−7π
6,−√3/2),(−11π
6,√3/2)
19. (a) If xdenotes the distance from Ato the base of the tower, and ythe distance from Bto the
base, then x2+d2=y2. Moreover h=xtan α=ytan β,sod
2=y
2−x
2=h
2
(cot2β−cot2α),
h2=d2
cot2β−cot2α=d2sin2αsin2β
sin2αcos2β−cos2αsin2β. The trigonometric identity
sin(α+β) sin(α−β) = sin2αcos2β−cos2αsin2βyields h=dsin αsin β
psin(α+β) sin(α−β).
(b) 295.72 ft.
20. (a)
-20
20
40
60
y
100 200 300 t
(b) when 2π
365(t−101) = 3π
2,ort= 374.75,
which is the same date as t=9.75, so dur-
ing the night of January 10th-11th
(c) from t=0tot=70.58 and from t= 313.92 to t= 365 (the same date as t= 0) , for a total of
about 122 days
21. Cis the highest nearby point on the graph; zoom to find that the coordinates of Care (2.0944,1.9132).
Similarly, Dis the lowest nearby point, and its coordinates are (4.1888,1.2284). Since f(x)=1
2x−sin x
is an odd function, the coordinates of Bare (−2.0944,−1.9132) and those of Aare (−4.1888,−1.2284).
22. Let y=A+Bsin(at +b). Since the maximum and minimum values of yare 35 and 5, A+B=35
and A−B=5,soA= 20, B= 15. The period is 12 hours, so 12a=2πand a=π/6. The
maximum occurs at t= 2, so 1 = sin(2a+b) = sin(π/3+b), π/3+b=π/2, b=π/2−π/3=π/6 and
y= 20 + 15 sin(πt/6+π/6).
23. (a) The circle of radius 1 centered at (a, a2); therefore, the family of all circles of radius 1 with
centers on the parabola y=x2.
(b) All parabolas which open up, have latus rectum equal to 1 and vertex on the line y=x/2.
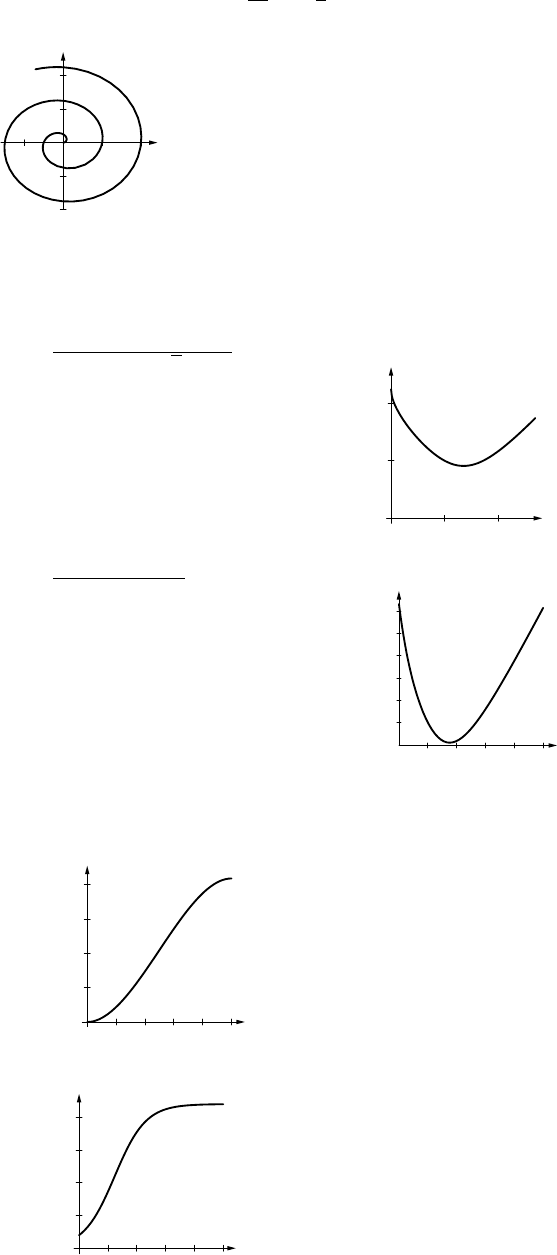
24. (a) x=f(1 −t),y =g(1 −t)25.
-2
-1
1
2
y
-2 -1 1 2 x
Supplementary Exercises 1 40
26. Let y=ax2+bx +c. Then 4a+2b+c=0,64a+8b+c=18,64a−8b+c= 18, from which b=0
and 60a= 18, or finally y=3
10x2−6
5.
27.
-2
-1
1
2
y
-1 1 2 x
28. (a) R=R0is the R-intercept, R0kis the slope,
and T=−1/k is the T-intercept
(b) −1/k =−273, or k=1/273
(c) 1.1=R
0
(1+20/273), or R0=1.025 (d) T= 126.55◦C
29. d=p(x−1)2+(
√
x−2)2;
d=9.1atx=1.358094
1
2
y
12
x
30. d=p(x−1)2+1/x2;
d=0.82 at x=1.380278
0.8
1
1.2
1.4
1.6
1.8
2
0.5 1 1.5 2 2.5 3
y
31. w=63.9V,w=63.9πh2(5/2−h/3); h=0.48 ft when w= 108 lb
32. (a)
1000
2000
3000
4000
W
12345
h
(b) w=63.9πh2(5/2−h/3); at h=5/2,
w= 2091.12 lb
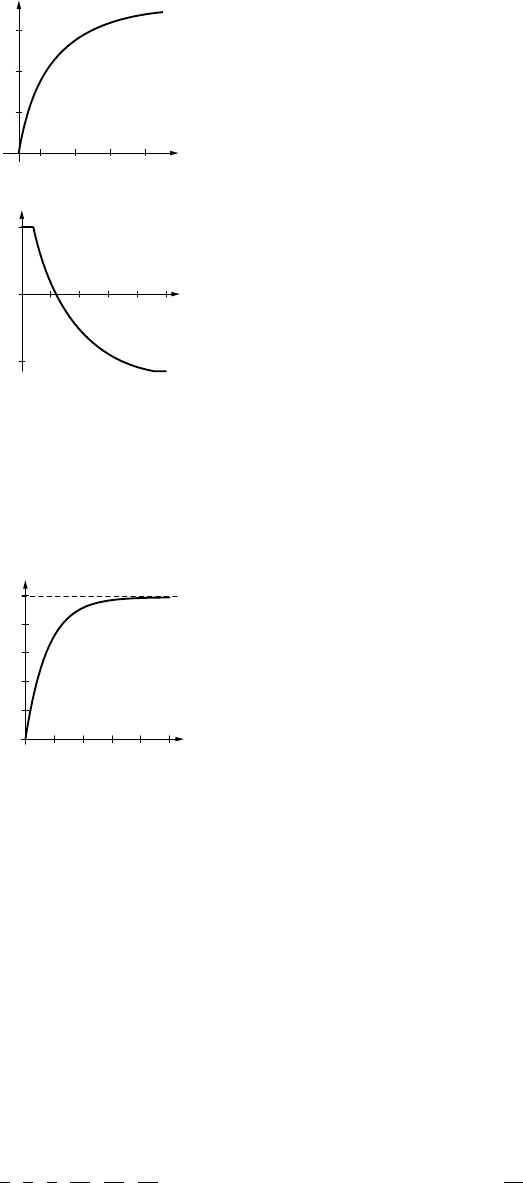
33. (a)
50
100
150
200
N
10 20 30 40 50 t
(b) N= 80 when t=9.35 yrs
(c) 220 sheep
41 Chapter 1
34. (a) T
v
10
20
(b) T=17
◦F, 27◦F, 32◦F
35. (a)
-20
20
WCI
10 20 30 40 50 v
(b) T=3
◦F, −11◦F, −18◦F, −22◦F
(c) v=35,19,12,7 mi/h
36. The domain is the set of all x, the range is −0.1746 ≤y≤0.1227.
37. The domain is the set −0.7245 ≤x≤1.2207, the range is −1.0551 ≤y≤1.4902.
38. (a) The potato is done in the interval
27.65 <t<32.71.
(b) 91.54 min.
39. (a)
5
10
15
20
25
v
12345
t
(b) As t→∞,(0.273)t→0, and thus
v→24.61 ft/s.
(c) For large tthe velocity approaches c.(d) No; but it comes very close (arbitrarily
close).
(e) 3.013 s
CHAPTER 1 HORIZON MODULE
1. (a) 0.25,6.25 ×10−2,3.91 ×10−3,1.53 ×10−5,2.32 ×10−10,5.42 ×10−20,2.94 ×10−39,8.64 ×10−78,
7.46 ×10−155,5.56 ×10−309;
1,1,1,1,1,1,1,1,1,1;
4,16,256,65536,4.29 ×109,1.84 ×1019,3.40 ×1038,1.16 ×1077,1.34 ×10154,1.80 ×10308
2. 2,2.25,2.2361111,2.23606798,2.23606798,...
3. (a) 1
2,1
4,1
8,1
16,1
32,1
64 (b) yn=1
2n
4. (a) yn+1 =1.05yn
(b) y0=$1000, y1=$1050, y2=$1102.50, y3=$1157.62, y4=$1215.51, y5=$1276.28
(c) yn+1 =1.05ynfor n≥1(d) yn=(1.05)n1000; y15 =$2078.93
Horizon Module 1 42
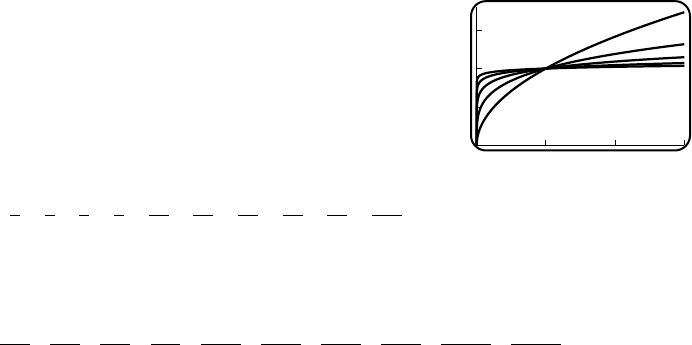
5. (a) x1/2,x
1/4,x
1/8,x
1/16,x
1/32 (b) They tend to the horizontal line y= 1, with
a hole at x=0.
1.8
0
03
6. (a) 1
2
2
3
3
5
5
8
8
13
13
21
21
34
34
55
55
89
89
144
(b) 1,2,3,5,8,13,21,34,55,89 ;
each new numerator is the sum of the previous two numerators.
(c) 144
233,233
377,377
610,610
987,987
1597,1597
2584,2584
4181,4181
6765,6765
10946,10946
17711
(d) F0=1,F
1=1,F
n=F
n−1+F
n−2for n≥2.
(e) the positive solution
7. (a) y1=cr,y2=cy1=cr2,y3=cr3,y4=cr4
(b) yn=crn
(c) If r= 1 then yn=cfor all n;ifr<1 then yntends to zero; if r>1, then yngets ever larger
(tends to +∞).
8. The first point on the curve is (c, kc(1 −c)), so y1=kc(1 −c) and hence y1is the first iterate. The
point on the line to the right of this point has equal coordinates (y1,y
1), and so the point above it on
the curve has coordinates (y1,ky
1(1 −y1)); thus y2=ky1(1 −y1), and y2is the second iterate, etc.
9. (a) 0.261,0.559,0.715,0.591,0.701
(b) It appears to approach a point somewhere near 0.65.
CHAPTER 2
Limits and Continuity
EXERCISE SET 2.1
1. (a) −1(b) 3(c) does not exist
(d) 1(e) −1(f) 3
2. (a) 2(b) 0(c) does not exist
(d) 2(e) 0(f) 2
3. (a) 1(b) 1(c) 1(d) 1(e) −∞ (f ) +∞
4. (a) 3(b) 3(c) 3(d) 3(e) +∞(f ) +∞
5. (a) 0(b) 0(c) 0(d) 3(e) +∞(f ) +∞
6. (a) 2(b) 2(c) 2(d) 3(e) −∞ (f ) +∞
7. (a) −∞ (b) +∞(c) does not exist
(d) undef (e) 2(f) 0
8. (a) +∞(b) +∞(c) +∞(d) undef (e) 0(f ) −1
9. (a) −∞ (b) −∞ (c) −∞ (d) 1(e) 1(f ) 2
10. (a) 1(b) −∞ (c) does not exist
(d) −2(e) +∞(f) +∞
11. (a) 0(b) 0(c) 0
(d) 0(e) does not exist (f) does not exist
12. (a) 3(b) 3(c) 3
(d) 3(e) does not exist (f) 0
13. for all x06=−414. for all x06=−6,3
15. (a) At x= 3 the one-sided limits fail to exist.
(b) At x=−2 the two-sided limit exists but is not equal to F(−2).
(c) At x= 3 the limit fails to exist.
16. (a) At x= 2 the two-sided limit fails to exist.
(b) At x= 3 the two-sided limit exists but is not equal to F(3).
(c) At x= 0 the two-sided limit fails to exist.
43
Exercise Set 2.1 44
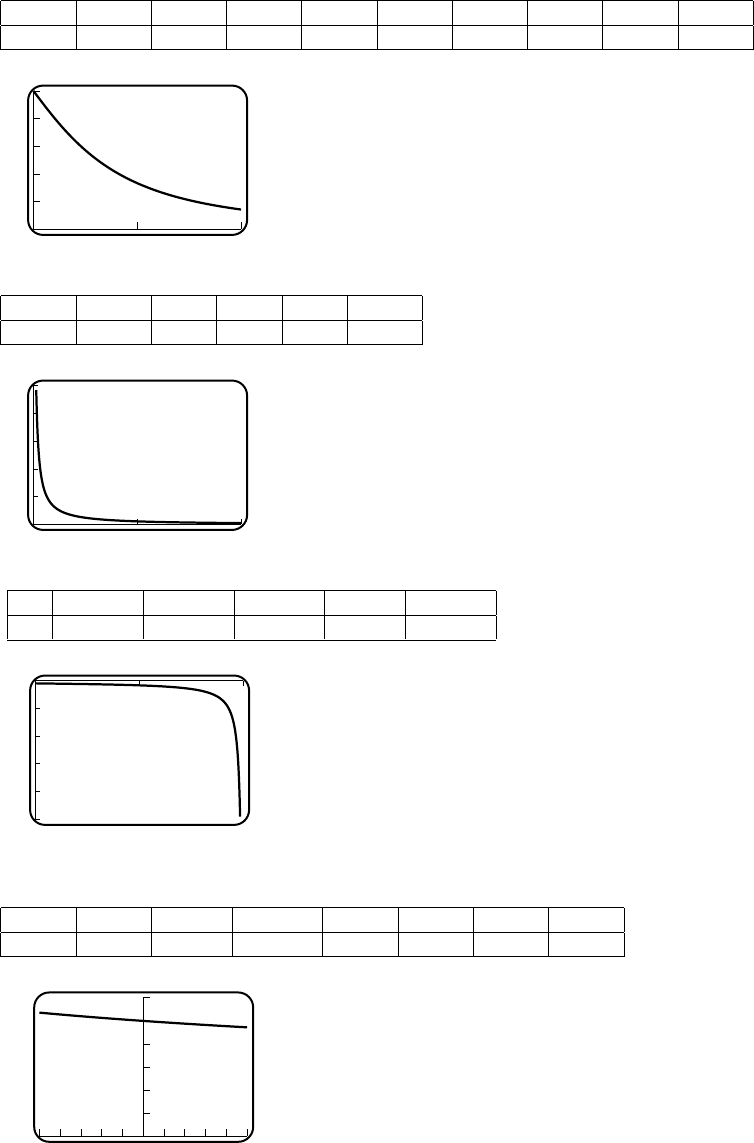
17. (a) 2 1.5 1.1 1.01 1.001 0 0.5 0.9 0.99 0.999
0.1429 0.2105 0.3021 0.3300 0.3330 1.0000 0.5714 0.3690 0.3367 0.3337
1
0
02
The limit is 1/3.
(b) 2 1.5 1.1 1.01 1.001 1.0001
0.4286 1.0526 6.344 66.33 666.3 6666.3
50
0
12
The limit is +∞.
(c) 0 0.5 0.9 0.99 0.999 0.9999
−1−1.7143 −7.0111 −67.001 −667.0−6667.0
0
-50
01
The limit is −∞.
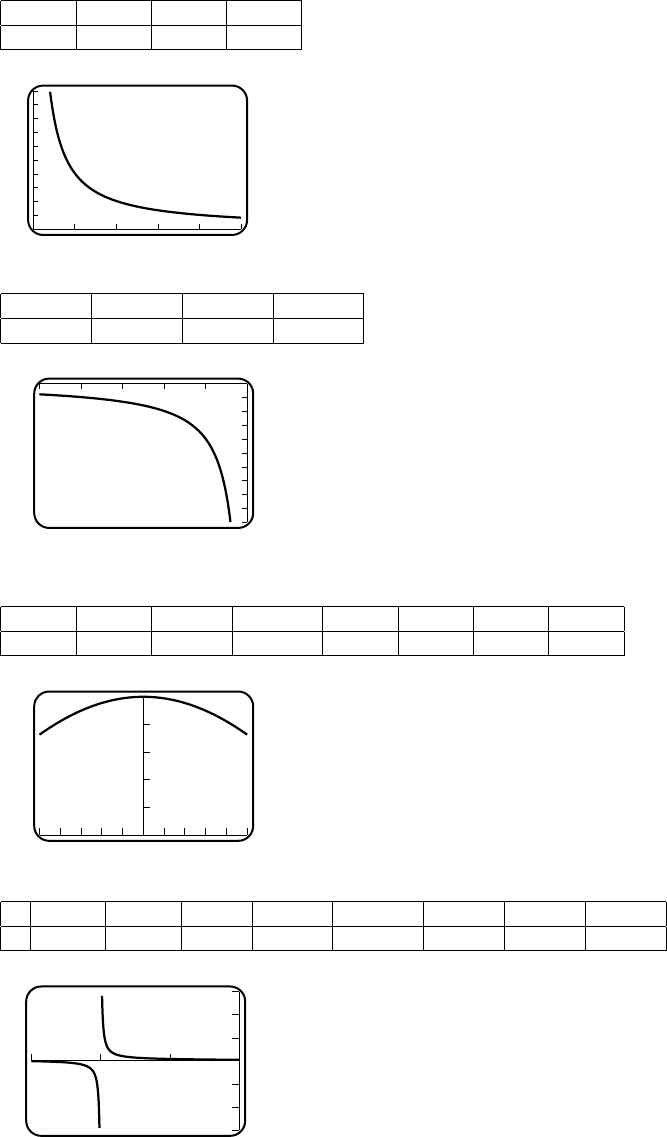
18. (a) −0.25 −0.1−0.001 −0.0001 0.0001 0.001 0.1 0.25
0.5359 0.5132 0.5001 0.5000 0.5000 0.4999 0.4881 0.4721
0.6
0
-0.25 0.25
The limit is 1/2.
45 Chapter 2
(b) 0.25 0.1 0.001 0.0001
8.4721 20.488 2000.5 20001
100
0
0 0.25
The limit is +∞.
(c) −0.25 −0.1−0.001 −0.0001
−7.4641 −19.487 −1999.5−20000
0
-100
-0.25 0 The limit is −∞.
19. (a) −0.25 −0.1−0.001 −0.0001 0.0001 0.001 0.1 0.25
2.7266 2.9552 3.0000 3.0000 3.0000 3.0000 2.9552 2.7266
3
2
-0.25 0.25
The limit is 3.
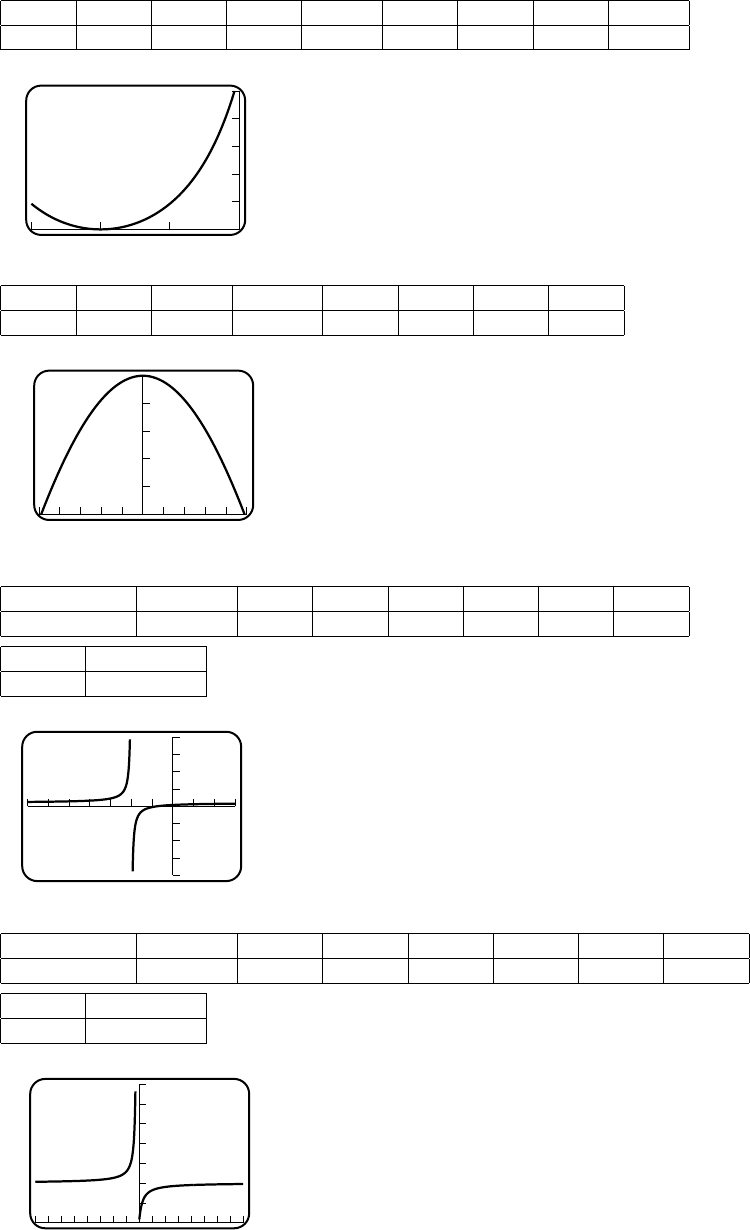
(b) 0−0.5−0.9−0.99 −0.999 −1.5−1.1−1.01 −1.001
1 1.7552 6.2161 54.87 541.1−0.1415 −4.536 −53.19 −539.5
60
-60
-1.5 0
The limit does not exist.
Exercise Set 2.1 46
20. (a) 0−0.5−0.9−0.99 −0.999 −1.5−1.1−1.01 −1.001
1.5574 1.0926 1.0033 1.0000 1.0000 1.0926 1.0033 1.0000 1.0000
1.5
1
-1.5 0
The limit is 1.
(b) −0.25 −0.1−0.001 −0.0001 0.0001 0.001 0.1 0.25
1.9794 2.4132 2.5000 2.5000 2.5000 2.5000 2.4132 1.9794
2.5
2
-0.25 0.25
The limit is 5/2.
21. (a) −100,000,000 −100,000 −1000 −100 −10 10 100 1000
2.0000 2.0001 2.0050 2.0521 2.8333 1.6429 1.9519 1.9950
100,000 100,000,000
2.0000 2.0000
40
-40
-14 6
asymptote y=2asx→±∞
(b) −100,000,000 −100,000 −1000 −100 −10 10 100 1000
20.0855 20.0864 20.1763 21.0294 35.4013 13.7858 19.2186 19.9955
100,000 100,000,000
20.0846 20.0855
70
0
-160 160
asymptote y=20.086.
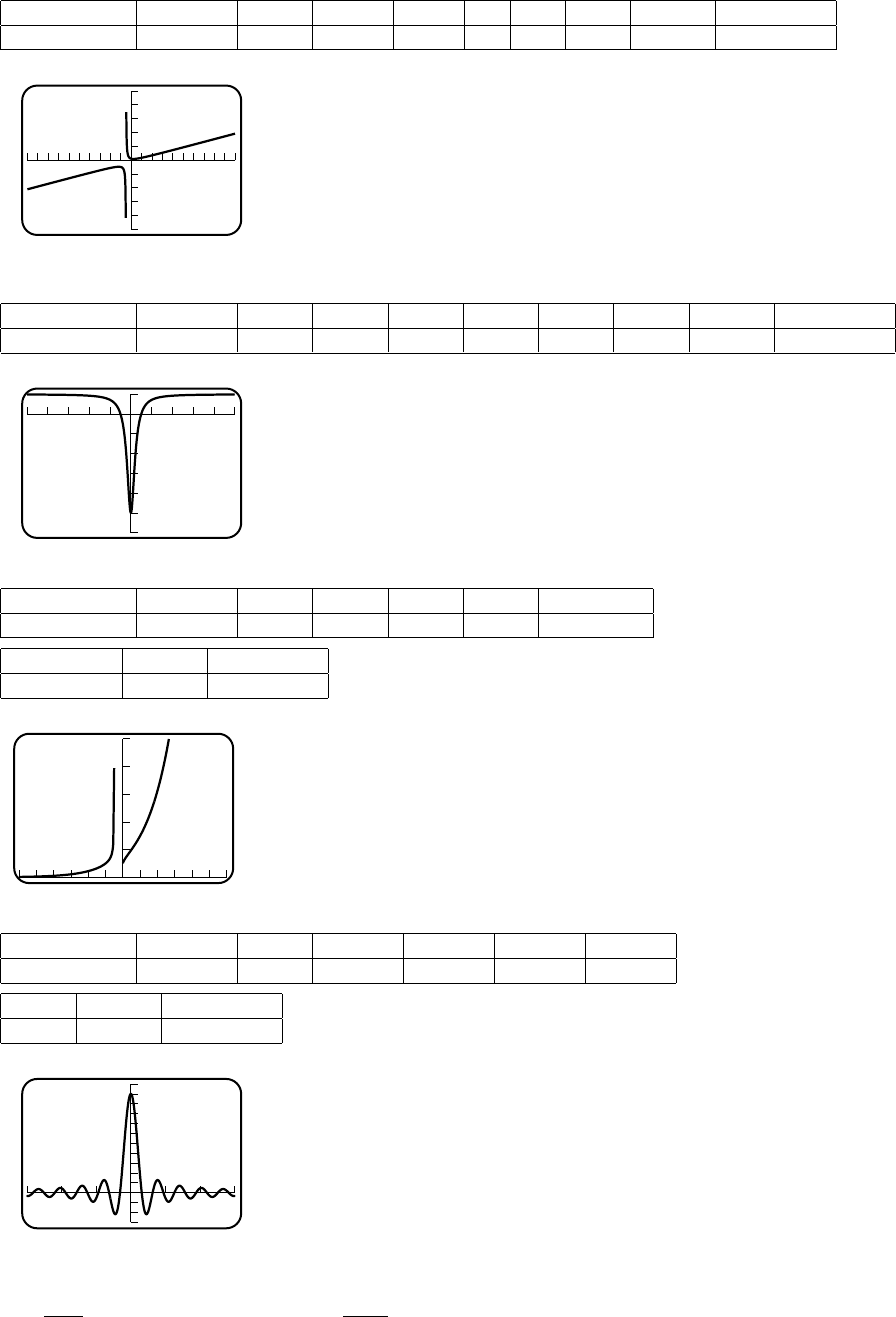
47 Chapter 2
(c) −100,000,000 −100,000 −1000 −100 −10 10 100 1000 100,000 100,000,000
−100,000,001 −100,000 −1001 −101.0−11.2 9.2 99.0 999.0 99,999 99,999,999
50
–50
-20 20
no horizontal asymptote
22. (a) −100,000,000 −100,000 −1000 −100 −10 10 100 1000 100,000 100,000,000
0.2000 0.2000 0.2000 0.2000 0.1976 0.1976 0.2000 0.2000 0.2000 0.2000
0.2
-1.2
-10 10 asymptote y=1/5asx→±∞
(b) −100,000,000 −100,000 −1000 −100 −10 10 100
0.0000 0.0000 0.0000 0.0000 0.0016 1668.0 2.09 ×1018
1000 100,000 100,000,000
1.77 ×10301 ? ?
10
0
-6 6
asymptote y=0asx→−∞, none as
x→+∞
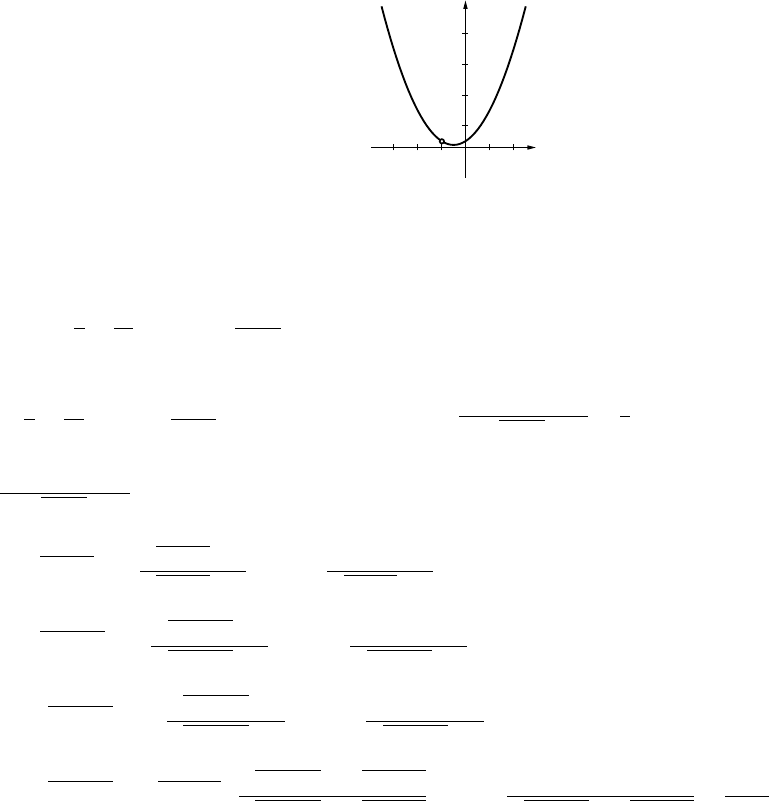
(c) −100,000,000 −100,000 −1000 −100 −10 10 100
0.0000 0.0000 0.0008 −0.0051 −0.0544 −0.0544 −0.0051
1000 100,000 100,000,000
0.0008 0.0000 0.0000
1.1
-0.3
-30 30
asymptote y=0asx→±∞
23. (a) lim
x→0+
sin x
x(b) lim
x→0+
x−1
x+1 (c) lim
x→0−(1+2x)
1/x

Exercise Set 2.2 48
24. (a) lim
x→0+
cos x
x(b) lim
x→0+
1
x+1 (c) lim
x→0−µ1+ 2
x¶x
25. (a) y
x
(b) yes; for example f(x) = (sin x)/x
26. (a) no
(b) yes; tan xand sec xat x=nπ +π/2, and cot xand csc xat x=nπ,n=0,±1,±2,...
29. (a) The plot over the interval [−a, a] becomes subject to catastrophic subtraction if ais small enough
(the size depending on the machine).
(c) It does not.
EXERCISE SET 2.2
1. (a) −6(b) 13 (c) −8(d) 16 (e) 2(f ) −1/2
(g) The limit doesn’t exist because the denominator tends to zero but the numerator doesn’t.
(h) The limit doesn’t exist because the denominator tends to zero but the numerator doesn’t.
2. (a) 0
(b) The limit doesn’t exist because lim fdoesn’t exist and lim gdoes.
(c) 0(d) 3(e) 0
(f) The limit doesn’t exist because the denominator tends to zero but the numerator doesn’t.
(g) The limit doesn’t exist because pf(x) is not defined for 0 ≤x<2.
(h) 1
3. (a) 7(b) −3(c) π(d) −6(e) 36 (f ) −∞
4. (a) 1(b) −1(c) 1(d) −1(e) 1(f ) −1
5. 06. 3/4 7. 88. −39. 4
10. 12 11. −4/512. 013. 3/2 14. 4/3
15. 016. 017. 018. 5/3 19. −√5
20. 3
p3/221. 1/√622. √523. √324. −1/√6
25. +∞26. √327. does not exist 28. −∞ 29. −∞
30. +∞31. +∞32. does not exist 33. does not exist 34. −∞
35. +∞36. −∞ 37. −∞ 38. does not exist 39. −1/7
40. +∞41. 642. +∞43. +∞44. 4
49 Chapter 2
45. +∞46. +∞47. −∞ 48. +∞
49. (a) 2(b) 2(c) 2
50. (a) −2(b) 0(c) does not exist
51. (a) 3(b) y
x
4
1
52. (a) −6(b) F(x)=x−3
53. (a) Theorem 2.2.2(a) doesn’t apply; moreover one cannot add/subtract infinities.
(b) lim
x→0+µ1
x−1
x2¶= lim
x→0+µx−1
x2¶=−∞
54. lim
x→0−µ1
x+1
x2¶= lim
x→0−
x+1
x
2=+∞55. lim
x→0
x
x¡√x+4+2
¢=1
4
56. lim
x→0
x2
x¡√x+4+2
¢=0
57. lim
x→+∞(px2+3−x)√
x
2+3+x
√
x
2+3+x= lim
x→+∞
3
√x2+3+x=0
58. lim
x→+∞(px2−3x−x)√x2−3x+x
√x2−3x+x= lim
x→+∞−3x
√x2−3x+x=−3/2
59. lim
x→+∞³px2+ax −x´√x2+ax +x
√x2+ax +x= lim
x→+∞
ax
√x2+ax +x=a/2
60. lim
x→+∞³px2+ax −px2+bx´√x2+ax +√x2+bx
√x2+ax +√x2+bx = lim
x→+∞
(a−b)x
√x2+ax +√x2+bx =a−b
2
61. lim
x→+∞p(x)=(−1)n∞and lim
x→−∞ p(x)=+∞
62. If m>nthe limits are both zero. If m=nthe limits are both 1. If n>mthe limits are (−1)n+m∞
and +∞, respectively.
63. If m>nthe limits are both zero. If m=nthe limits are both equal to am, the leading coefficient of
p.Ifn>mthe limits are ±∞ where the sign depends on the sign of amand whether nis even or
odd.
64. (a) p(x)=q(x)=x(b) p(x)=x,q(x)=x
2
(c) p(x)=x
2
,q(x)=x(d) p(x)=x+3,q(x)=x
65. The left and/or right limits could be plus or minus infinity; or the limit could exist, or equal any
preassigned real number. For example, let q(x)=x−x
0and let p(x)=a(x−x
0
)
nwhere ntakes on
the values 0,1,2.
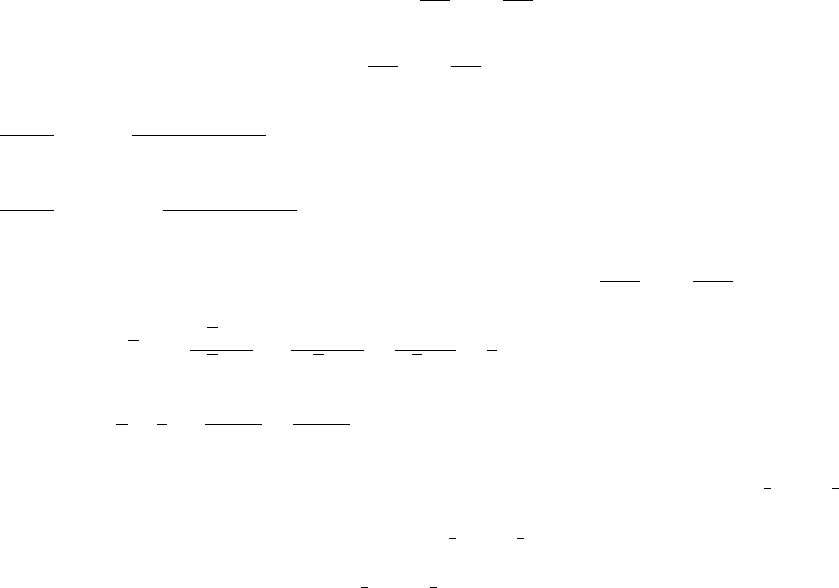
Exercise Set 2.3 50
66. If m>nthe limit is zero. If m=nthe limit is cm/dm.Ifn>mthe limit is ±∞, where the sign
depends on the signs of cnand dm.
EXERCISE SET 2.3
1. (a) |f(x)−f(0)|=|x+2−2|=|x|<0.1 if and only if |x|<0.1
(b) |f(x)−f(3)|=|(4x−5) −7|=4|x−3|<0.1 if and only if |x−3|<(0.1)/4=0.0025
(c) |f(x)−f(4)|=|x2−16|<²if |x−4|<δ. We get f(x)=16+²=16.001 at x=4.000124998,
which corresponds to δ=0.000124998; and f(x)=16−²=15.999 at x=3.999874998, for
which δ=0.000125002. Use the smaller δ:thus|f(x)−16|<²provided |x−4|<0.000125 (to
six decimals).
2. (a) |f(x)−f(0)|=|2x+3−3|=2|x|<0.1 if and only if |x|<0.05
(b) |f(x)−f(0)|=|2x+3−3|=2|x|<0.01 if and only if |x|<0.005
(c) |f(x)−f(0)|=|2x+3−3|=2|x|<0.0012 if and only if |x|<0.0006
3. (a) x1=(1.95)2=3.8025,x
2=(2.05)2=4.2025
(b) δ= min ( |4−3.8025|,|4−4.2025|)=0.1975
4. (a) x1=1/(1.1)=0.909090 ...,x
2=1/(0.9)=1.111111 ...
(b) δ= min( |1−0.909090|,|1−1.111111|)=0.0909090 ...
5. |2x−8|=2|x−4|<0.1if|x−4|<0.05, δ=0.05
6. |x/2+1|=(1/2)|x−(−2)|<0.1if|x+2|<0.2, δ=0.2
7. |7x+5−(−2)|=7|x−(−1)|<0.01 if |x+1|<1
700,δ=1
700
8. |5x−2−13|=5|x−3|<0.01 if |x−3|<1
500,δ=1
500
9. ¯¯¯¯
x2−4
x−2−4¯¯¯¯
=¯¯¯¯
x2−4−4x+8
x−2¯
¯
¯
¯
=|x−2|<0.05 if |x−2|<0.05, δ=0.05
10. ¯¯¯¯
x2−1
x+1 −(−2)¯¯¯¯
=¯¯¯¯
x2−1+2x+2
x+1 ¯
¯
¯
¯
=|x+1|<0.05 if |x+1|<0.05, δ=0.05
11. if δ<1 then ¯¯x2−16¯¯=|x−4||x+4|<9|x−4|<0.001 if |x−4|<1
9000,δ=1
9000
12. if δ<1 then |√x−3|¯¯¯¯
√x+3
√
x+3¯
¯
¯
¯
=|x−9|
|
√
x+3|<|x−9|
√
8+3 <1
4|x−9|<0.001 if |x−9|<0.004, δ=0.004
13. if δ≤1 then ¯¯¯¯
1
x−1
5¯¯¯¯
=|x−5|
5|x|≤|x−5|
20 <0.05 if |x−5|<1, δ=1
14. |x−0|=|x|<0.05 if |x|<0.05, δ=0.05 15. |3x−15|=3|x−5|<²if |x−5|<1
3²,δ=1
3²
16. |(4x−5) −7|=|4x−12|=4|x−3|<²if |x−3|<1
4²,δ=1
4²
17. |2x−7−(−3)|=2|x−2|<²if |x−2|<1
2²,δ=1
2²

51 Chapter 2
18. |2−3x−5|=3|x+1|<²if |x+1|<1
3²,δ=1
3²
19. ¯¯¯¯
x2+x
x−1¯¯¯¯
=|x|<²if |x|<²,δ=²20. ¯¯¯¯
x2−9
x+3 −(−6)¯¯¯¯
=|x+3|<²if |x+3|<²,δ=²
21. if δ<1 then |2x2−2|=2|x−1||x+1|<6|x−1|<²if |x−1|<1
6²,δ= min(1,1
6²)
22. if δ<1 then |x2−5−4|=|x−3||x+3|<7|x−3|<²if |x−3|<1
7²,δ= min(1,1
7²)
23. if δ<1
6then ¯¯¯¯
1
x−3¯¯¯¯
=
3|x−1
3|
|x|<18|x−1
3|<²if |x−1
3|<1
18²,δ= min( 1
6,1
18 ²)
24. If δ<1
2and |x−(−2)|<δthen −5
2<x<−3
2
,x+1<−1
2,|x+1|>1
2; then
¯¯¯¯
1
x+1−(−1)¯¯¯¯
=|x+2|
|x+1|<2|x+2|<²if |x+2|<1
2²,δ= min( 1
2,1
2²)
25. |√x−2|=¯¯¯¯
(√x−2)√x+2
√
x+2¯
¯
¯
¯
=¯
¯
¯
¯
x−4
√
x+2¯
¯
¯
¯
<1
2|x−4|<²if |x−4|<2²,δ=2²
26. |√x+3−3|¯
¯
¯
¯
√
x+3+3
√
x+3+3¯
¯
¯
¯
=|x−6|
√
x+3+3 ≤1
3|x−6|<²if |x−6|<3²,δ=3²
27. |f(x)−3|=|x+2−3|=|x−1|<²if 0 <|x−1|<²,δ=²
28. If δ<1 then |(x2+3x−1) −9|=|(x−2)(x+5)|<8|x−2|<²if |x−2|<1
8²,δ= min (1,1
8²)
29. (a) |f(x)−L|=1
x2<0.1ifx>√
10, N=√10
(b) |f(x)−L|=|x
x+1−1|=|1
x+1|<0.01 if x+1>100, N=99
(c) |f(x)−L|=¯¯¯¯
1
x3¯¯¯¯
<1
1000 if |x|>10, x<−10, N=−10
(d) |f(x)−L|=¯¯¯¯
x
x+1−1
¯
¯
¯
¯
=¯
¯
¯
¯
1
x+1¯
¯
¯
¯
<0.01 if |x+1|>100, −x−1>100, x<−101, N=−101
30. (a) ¯¯¯¯
1
x3¯¯¯¯
<0.1, x>101/3,N=10
1/3(b) ¯¯¯¯
1
x3¯¯¯¯
<0.01, x>1001/3,N= 1001/3
(c) ¯¯¯¯
1
x3¯¯¯¯
<0.001, x>10, N=10
31. (a) x2
1
1+x
2
1
=1−²,x
1=−
r1−²
²;x
2
2
1+x
2
2
=1−²,x
2=r1−²
²
(b) N=r1−²
²(c) N=−r1−²
²
32. (a) x1=−1/²3;x2=1/²3(b) N=1/²3(c) N=−1/²3
33. 1
x2<0.01 if |x|>10, N=10
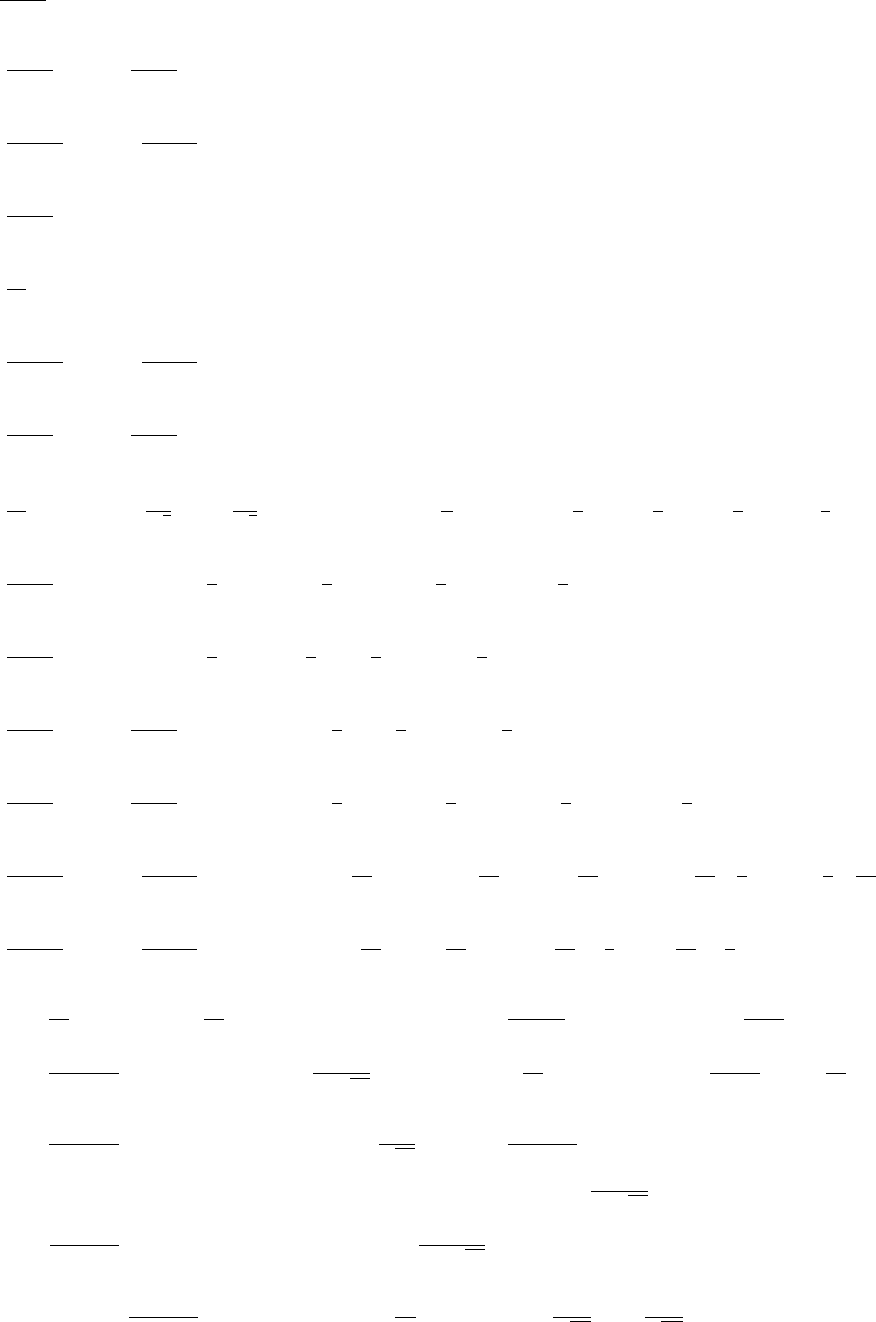
Exercise Set 2.3 52
34. 1
x+2 <0.005 if |x+2|>200, x>198, N= 198
35. ¯¯¯¯
x
x+1−1
¯
¯
¯
¯
=¯
¯
¯
¯
1
x+1¯
¯
¯
¯
<0.001 if |x+1|>1000, x>999, N= 999
36. ¯¯¯¯
4x−1
2x+5−2
¯
¯
¯
¯
=¯
¯
¯
¯
11
2x+5¯
¯
¯
¯
<0.1if|2x+5|>110, 2x>105, N=52.5
37. ¯¯¯¯
1
x+2−0
¯
¯
¯
¯
<0.005 if |x+2|>200, −x−2>200, x<−202, N=−202
38. ¯¯¯¯
1
x2¯¯¯¯
<0.01 if |x|>10, −x>10, x<−10, N=−10
39. ¯¯¯¯
4x−1
2x+5−2
¯
¯
¯
¯
=¯
¯
¯
¯
11
2x+5¯
¯
¯
¯
<0.1if|2x+5|>110, −2x−5>110, 2x<−115, x<−57.5, N=−57.5
40. ¯¯¯¯
x
x+1−1
¯
¯
¯
¯
=¯
¯
¯
¯
1
x+1¯
¯
¯
¯
<0.001 if |x+1|>1000, −x−1>1000, x<−1001, N=−1001
41. ¯¯¯¯
1
x2¯¯¯¯
<²if |x|>1
√²,N=1
√²42. ¯¯¯¯
1
x¯¯¯¯
<²if |x|>1
²,−x>1
²,x<−1
²,N=−1
²
43. ¯¯¯¯
1
x+2¯
¯
¯
¯
<²if |x+2|>1
²,−x−2<1
²,x>−2−1
²,N=−2−1
²
44. ¯¯¯¯
1
x+2¯
¯
¯
¯
<²if |x+2|>1
²,x+2>1
²,x>1
²−2, N=1
²−2
45. ¯¯¯¯
x
x+1−1
¯
¯
¯
¯
=¯
¯
¯
¯
1
x+1¯
¯
¯
¯
<²if |x+1|>1
²,x>1
²−1, N=1
²−1
46. ¯¯¯¯
x
x+1−1
¯
¯
¯
¯
=¯
¯
¯
¯
1
x+1¯
¯
¯
¯
<²if |x+1|>1
²,−x−1>1
²,x<−1−1
²,N=−1−1
²
47. ¯¯¯¯
4x−1
2x+5−2
¯
¯
¯
¯
=¯
¯
¯
¯
11
2x+5¯
¯
¯
¯
<²if |2x+5|>11
²,−2x−5>11
²,2x<−11
²−5, x<−11
2²−5
2,N=−5
2−11
2²
48. ¯¯¯¯
4x−1
2x+5−2
¯
¯
¯
¯
=¯
¯
¯
¯
11
2x+5¯
¯
¯
¯
<²if |2x+5|>11
²,2x> 11
²−5, x>11
2²−5
2,N=11
2²−5
2
49. (a) 1
x2>100 if |x|<1
10 (b) 1
|x−1|>1000 if |x−1|<1
1000
(c) −1
(x−3)2<−1000 if |x−3|<1
10√10 (d) −1
x4<−10000 if x4<1
10000,|x|<1
10
50. (a) 1
(x−1)2>10 if and only if |x−1|<1
√10 (b) 1
(x−1)2>1000 if and only if
|x−1|<1
10√10
(c) 1
(x−1)2>100000 if and only if |x−1|<1
100√10
51. if M>0 then 1
(x−3)2>M,0<(x−3)2<1
M,0<|x−3|<1
√
M,δ=1
√
M
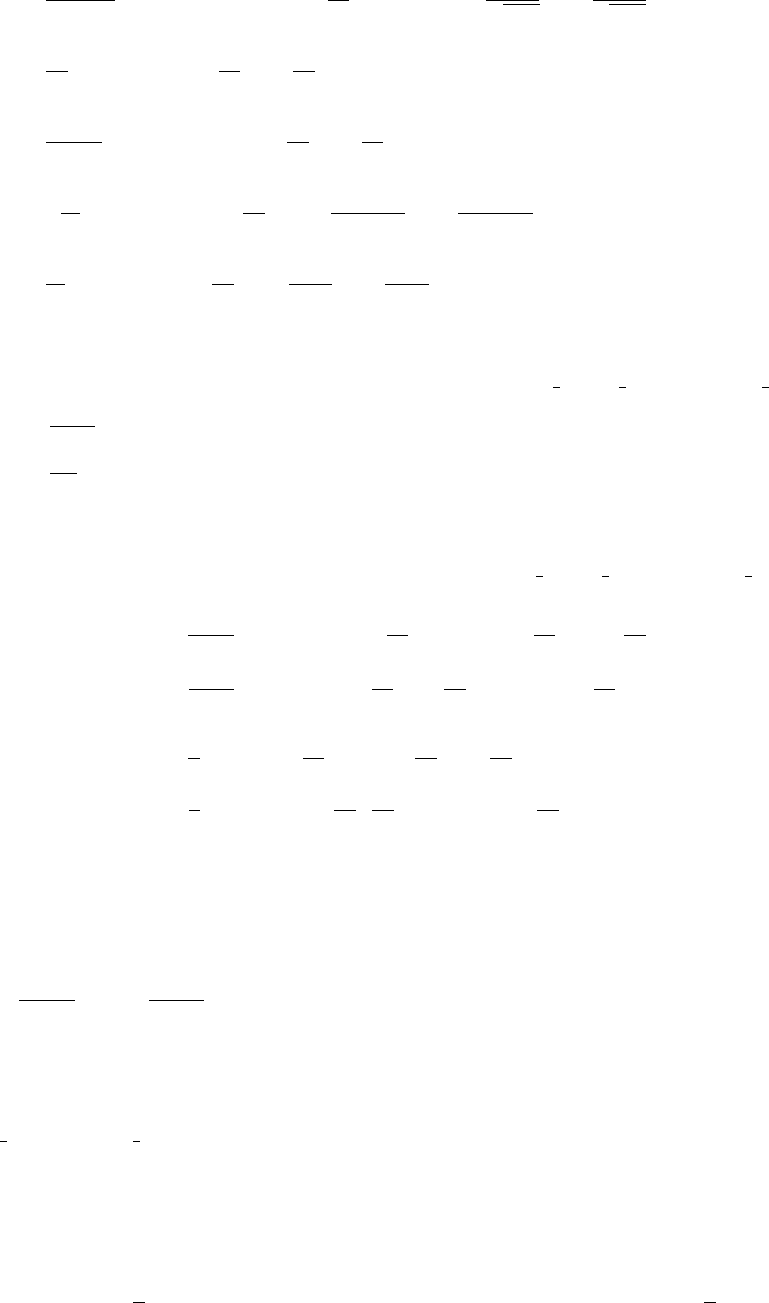
53 Chapter 2
52. if M<0 then −1
(x−3)2<M,0<(x−3)2<−1
M,0<|x−3|<1
√
−M,δ=1
√
−M
53. if M>0 then 1
|x|>M,0<|x|<1
M,δ=1
M
54. if M>0 then 1
|x−1|>M,0<|x−1|<1
M,δ=1
M
55. if M<0 then −1
x4<M,0<x
4<−1
M,|x|<1
(−M)
1/4,δ=1
(−M)
1/4
56. if M>0 then 1
x4>M,0<x
4<1
M,x< 1
M
1/4,δ=1
M
1/4
57. if x>2 then |x+1−3|=|x−2|=x−2<²if 2 <x<2+²,δ=²
58. if x<1 then |3x+2−5|=|3x−3|=3|x−1|= 3(1 −x)<²if 1 −x<1
3²,1−1
3
²<x<1, δ=1
3²
59. if x>4 then √x−4<²if x−4<²
2
,4<x<4+²
2
,δ=²
2
60. if x<0 then √−x<²if −x<²
2
,−²
2<x<0, δ=²2
61. if x>2 then |f(x)−2|=|x−2|=x−2<²if 2 <x<2+²,δ=²
62. if x<2 then |f(x)−6|=|3x−6|=3|x−2|= 3(2 −x)<²if 2 −x< 1
3²,2−1
3
²<x<2, δ=1
3²
63. (a) if M<0 and x>1 then 1
1−x<M,x−1<−1
M,1<x<1−1
M,δ=−1
M
(b) if M>0 and x<1 then 1
1−x>M,1−x< 1
M,1−1
M<x<1, δ=1
M
64. (a) if M>0 and x>0 then 1
x>M,x< 1
M,0<x< 1
M,δ=1
M
(b) if M<0 and x<0 then 1
x<M,−x<−1
M,1
M<x<0, δ=−1
M
65. (a) Given any M>0 there corresponds N>0 such that if x>N then f(x)>M,x+1>M,
x>M−1, N=M−1.
(b) Given any M<0 there corresponds N<0 such that if x<N then f(x)<M,x+1 <M,
x<M−1, N=M−1.
66. (a) Given any M>0 there corresponds N>0 such that if x>N then f(x)>M,x
2−3>M,
x>√
M+3,N=√
M+3.
(b) Given any M<0 there corresponds N<0 such that if x<N then f(x)<M,x
3+5<M,
x<(M−5)1/3,N=(M−5)1/3.
67. if δ≤2 then |x−3|<2, −2<x−3<2, 1 <x<5, and |x2−9|=|x+3||x−3|<8|x−3|<²if
|x−3|<1
8²,δ= min ¡2,1
8²¢
68. (a) We don’t care about the value of fat x=a, because the limit is only concerned with values of
xnear a. The condition that fbe defined for all x(except possibly x=a) is necessary, because
if some points were excluded then the limit may not exist; for example, let f(x)=xif 1/x is
not an integer and f(1/n) = 6. Then lim
x→0f(x) does not exist but it would if the points 1/n were
excluded.
(b) when x<0 then √xis not defined (c) yes; if δ≤0.01 then x>0, so √xis defined
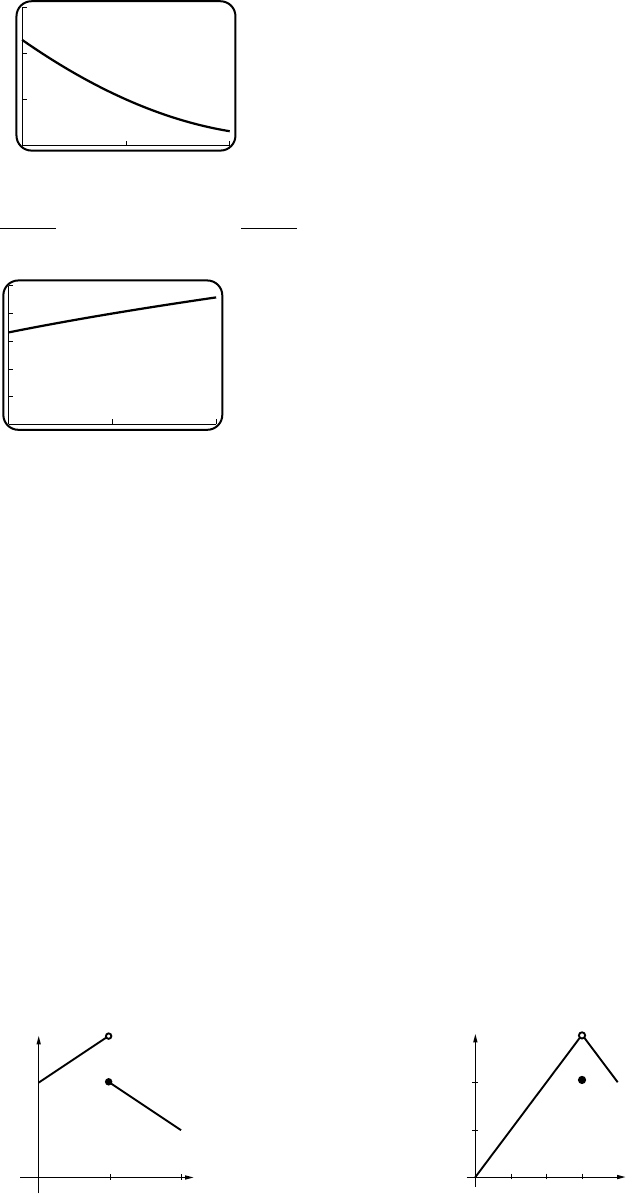
Exercise Set 2.4 54
69. |(x3−4x+5)−2|<0.05, −0.05 <(x3−4x+5)−2<0.05, 1.95 <x
3−4x+5 <2.05; x3−4x+5=1.95
at x=1.0616, x3−4x+5=2.05 at x=0.9558; δ= min (1.0616 −1,1−0.9558) = 0.0442
2.2
1.9
0.9 1.1
70. √5x+1=3.5atx=2.25, √5x+1=4.5atx=3.85, so δ= min(3 −2.25,3.85 −3)=0.75
5
0
24
EXERCISE SET 2.4
1. (a) no, x=2 (b) no, x=2 (c) no, x=2 (d) yes
(e) yes (f) yes
2. (a) no, x=2 (b) no, x=2 (c) no, x=2 (d) yes
(e) no, x=2 (f) yes
3. (a) no, x=1,3(b) yes (c) no, x=1 (d) yes
(e) no, x=3 (f) yes
4. (a) no, x=3 (b) yes (c) yes (d) yes
(e) no, x=3 (f) yes
5. (a) 3(b) 3
6. −2/5
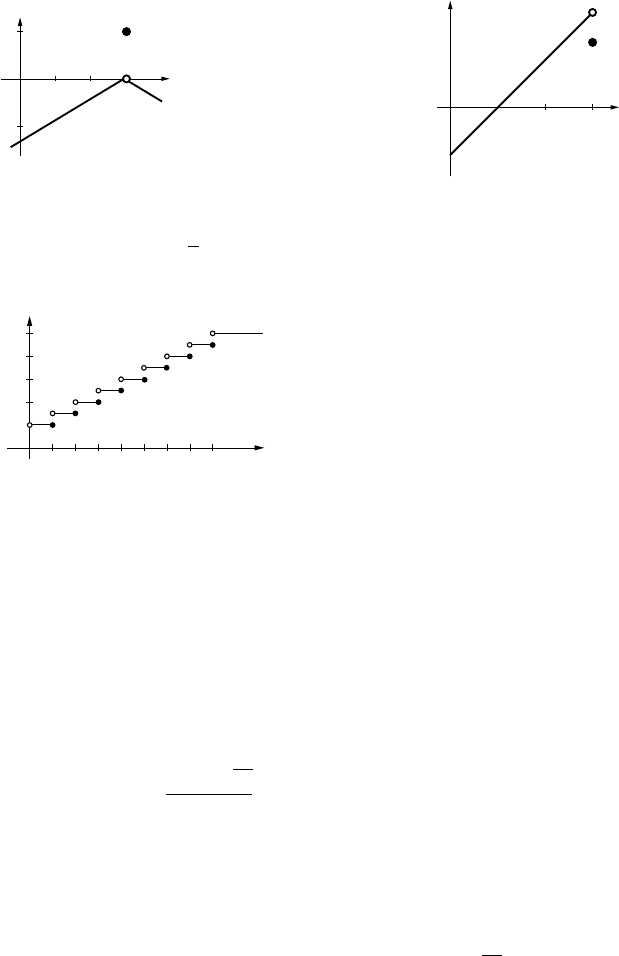
7. (a) y
x
3
(b) y
x
1
13
55 Chapter 2
(c) y
x
-1
1
1
(d) y
x
23
8. f(x)=1/x,g(x)=(0ifx=0
sin 1
xif x6=0
9. (a) C
t
1
$4
2
(b) One second could cost you one dollar.
10. (a) no; disasters (war, flood, famine, pestilence, for example) can cause discontinuities
(b) continuous
(c) not usually continuous; see Exercise 9
(d) continuous
11. none 12. none 13. none
14. fis not defined at x=±115. fis not defined at x=±4
16. fis not defined at x=−7±√57
2
17. fis not defined at x=±3
18. fis not defined at x=0,−419. none
20. fis not defined at x=0,−3
21. none; f(x)=2x+ 3 is continuous on x<4 and f(x)=7+16
xis continuous on 4 <x;
lim
x→4−f(x) = lim
x→4+f(x)=f(4)=11sofis continuous at x=4
22. lim
x→1f(x) does not exist so fis discontinuous at x=1
23. (a) fis continuous for x<1, and for x>1; lim
x→1−f(x)=5, lim
x→1
+f(x)=k,soifk= 5 then fis
continuous for all x
(b) fis continuous for x<2, and for x>2; lim
x→2−f(x)=4k, lim
x→2+f(x)=4+k,soif4k=4+k,
k=4/3 then fis continuous for all x
24. (a) no, fis not defined at x=2 (b) no, fis not defined for x≤2
(c) yes (d) no, fis not defined for x≤2
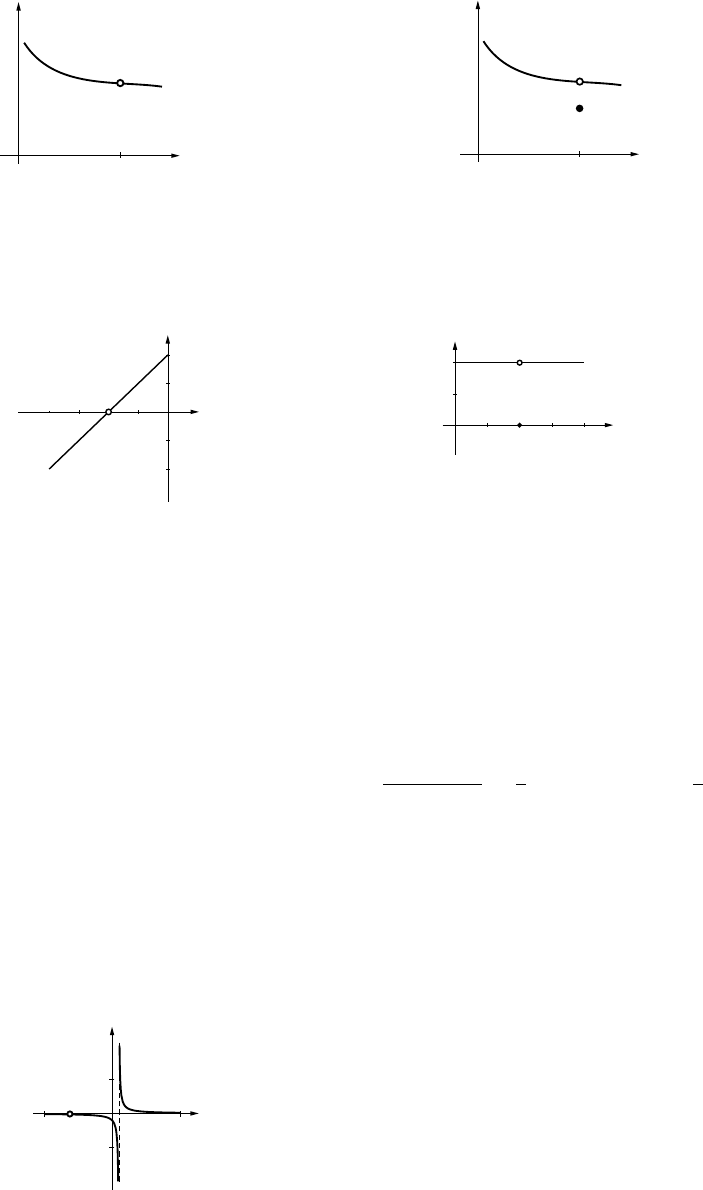
Exercise Set 2.4 56
25. (a) y
x
c
(b) y
x
c
26. (a) f(c) = lim
x→cf(x)
(b) lim
x→1f(x)=2
y
x
1
-1
lim
x→1g(x)=1
y
x
1
1
(c) Define f(1) = 2 and redefine g(1)=1.
27. (a) x= 0, lim
x→0−f(x)=−16=+1= lim
x→0
+f(x) so the discontinuity is not removable
(b) x=−3; define f(−3) = −3 = lim
x→−3f(x), then the discontinuity is removable
(c) fis undefined at x=±2; at x= 2, lim
x→2f(x) = 1, so define f(2) = 1 and fbecomes continuous
there; at x=−2, lim
x→−2does not exist, so the discontinuity is not removable
28. (a) fis not defined at x= 2; lim
x→2f(x) = lim
x→2
x+2
x
2+2x+4 =1
3, so define f(2) = 1
3and fbecomes
continuous there
(b) lim
x→2−f(x)=16=4= lim
x→2
+f(x), so fhas a nonremovable discontinuity at x=2
(c) lim
x→1f(x)=86=f(1), so fhas a removable discontinuity at x=1
29. (a) discontinuity at x=1/2, not removable; at
x=−3, removable
y
x
-5
5
5
(b) 2x2+5x−3=(2x−1)(x+3)
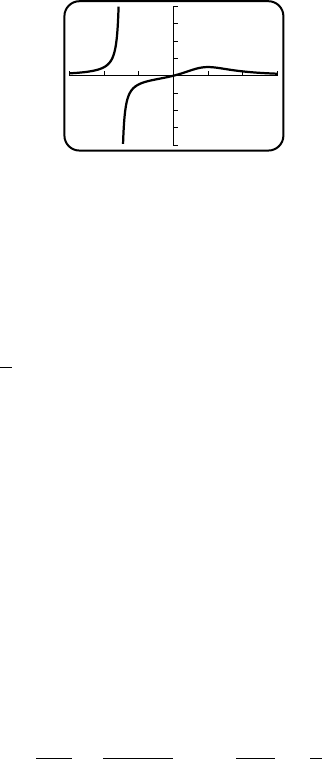
57 Chapter 2
30. (a) there appears to be one discontinuity near
x=−1.52
4
–4
-3 3
(b) one discontinuity at x=−1.52
31. For x>0, f(x)=x
3/5=(x
3
)
1/5is the composition (Theorem 2.4.6) of the two continuous functions
g(x)=x
3and h(x)=x
1/5and is thus continuous. For x<0, f(x)=f(−x) which is the composition
of the continuous functions f(x) (for positive x) and the continuous function y=−x. Hence f(−x)is
continuous for all x>0. At x=0,f(0) = lim
x→0f(x)=0.
32. x4+7x
2+1≥1>0, thus f(x) is the composition of the polynomial x4+7x
2+ 1, the square root
√x, and the function 1/x and is therefore continuous by Theorem 2.4.6.
33. (a) Let f(x)=kfor x6=cand f(c)=0;g(x)=lfor x6=cand g(c)=0. Ifk=−lthen f+gis
continuous; otherwise it’s not.
(b) f(x)=kfor x6=c,f(c)=1;g(x)=l6= 0 for x6=c,g(c)=1. Ifkl = 1, then fg is continuous;
otherwise it is not.
34. A rational function is the quotient f(x)/g(x) of two polynomials f(x) and g(x). By Theorem 2.4.2 f
and gare continuous everywhere; by Theorem 2.4.3 f/g is continuous except when g(x)=0.
35. Since fand gare continuous at x=cwe know that lim
x→cf(x)=f(c) and lim
x→cg(x)=g(c). In the
following we use Theorem 2.2.2.
(a) f(c)+g(c) = lim
x→cf(x) + lim
x→cg(x) = lim
x→c(f(x)+g(x)) so f+gis continuous at x=c.
(b) same as (a) except the + sign becomes a −sign
(c) f(c)
g(c)=
lim
x→cf(x)
lim
x→cg(x)= lim
x→c
f(x)
g(x)so f
gis continuous at x=c
36. h(x)=f(x)−g(x) satisfies h(a)>0, h(b)<0. Use the Intermediate Value Theorem or Theorem
2.4.9.
37. Of course such a function must be discontinuous. Let f(x)=1on0≤x<1, and f(x)=−1on
1≤x≤2.
38. A square whose diagonal has length rhas area f(r)=r
2
/2. Note that
f(r)=r
2
/2<πr
2
/2<2r
2=f(2r). By the Intermediate Value Theorem there must be a value
cbetween rand 2rsuch that f(c)=πr2/2, i.e. a square of diagonal cwhose area is πr2/2.
39. The cone has volume πr2h/3. The function V(r)=πr2h(for variable rand fixed h) gives the volume
of a right circular cylinder of height hand radius r, and satisfies V(0) <πr
2
h/3<V(r). By the
Intermediate Value Theorem there is a value cbetween 0 and rsuch that V(c)=πr2h/3, so the
cylinder of radius c(and height h) has volume equal to that of the cone.
40. If f(x)=x
3−4x+ 1 then f(0)=1,f(1) = −2. Use Theorem 2.4.9.
41. If f(x)=x
3+x
2−2xthen f(−1)=2,f(1) = 0. Use the Intermediate Value Theorem.
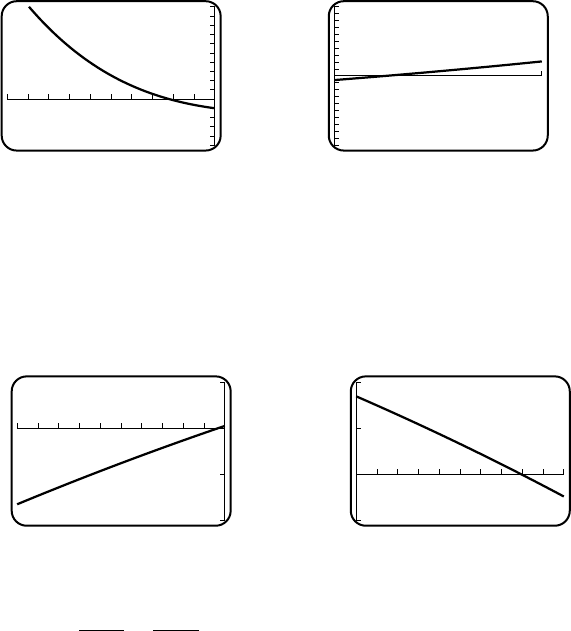
Exercise Set 2.4 58
42. Since lim
x→−∞ p(x)=−∞ and lim
x→+∞p(x)=+∞(or vice versa, if the leading coefficient of pis negative),
it follows that for M=−1 there corresponds N1<0, and for M= 1 there is N2>0, such that
p(x)<−1 for x<N
1and p(x)>1 for x>N
2
. Choose x1<N
1and x2>N
2and use Theorem 2.4.9
on the interval [x1,x
2] to find a solution of p(x)=0.
43. For the negative root, use intervals on the x-axis as follows: [−2,−1]; since f(−1.3) <0 and
f(−1.2) >0, the midpoint x=−1.25 of [−1.3,−1.2] is the required approximation of the root.
For the positive root use the interval [0,1]; since f(0.7) <0 and f(0.8) >0, the midpoint x=0.75 of
[0.7,0.8] is the required approximation.
44. x=−1.25 and x=0.75.
10
-5
-2 -1
1
-1
0.7 0.8
45. For the negative root, use intervals on the x-axis as follows: [−2,−1]; since f(−1.7) <0 and
f(−1.6) >0, use the interval [−1.7,−1.6]. Since f(−1.61) <0 and f(−1.60) >0 the midpoint
x=−1.605 of [−1.61,−1.60] is the required approximation of the root. For the positive root use
the interval [1,2]; since f(1.3) >0 and f(1.4) <0, use the interval [1.3,1.4]. Since f(1.37) >0 and
f(1.38) <0, the midpoint x=1.375 of [1.37,1.38] is the required approximation.
46. x=−1.605 and x=1.375.
1
-2
-1.7 -1.6
1
-0.5
1.3 1.4
47. x=2.24.
48. Set f(x)= a
x−1+b
x−3
. Since lim
x→1+f(x)=+∞and lim
x→3−f(x)=−∞ there exist x1>1 and x2<3
(with x2>x
1
) such that f(x)>1 for 1 <x<x
1and f(x)<−1 for x2<x<3. Choose x3in (1,x
1)
and x4in (x2,3) and apply Theorem 2.4.9 on [x3,x
4].
49. The uncoated sphere has volume 4π(x−1)3/3 and the coated sphere has volume 4πx3/3. If the volume
of the uncoated sphere and of the coating itself are the same, then the coated sphere has twice the
volume of the uncoated sphere. Thus 2(4π(x−1)3/3)=4πx3/3, or x3−6x2+6x−2 = 0, with the
solution x=4.847 cm.
50. Let g(t) denote the altitude of the monk at time tmeasured in hours from noon of day one, and let f(t)
denote the altitude of the monk at time tmeasured in hours from noon of day two. Then g(0) <f(0)
and g(12) >f(12). Use Exercise 36.
51. We must show lim
x→cf(x)=f(c). Let ²>0; then there exists δ>0 such that if |x−c|<δthen
|f(x)−f(c)|<². But this certainly satisfies Definition 2.3.3.
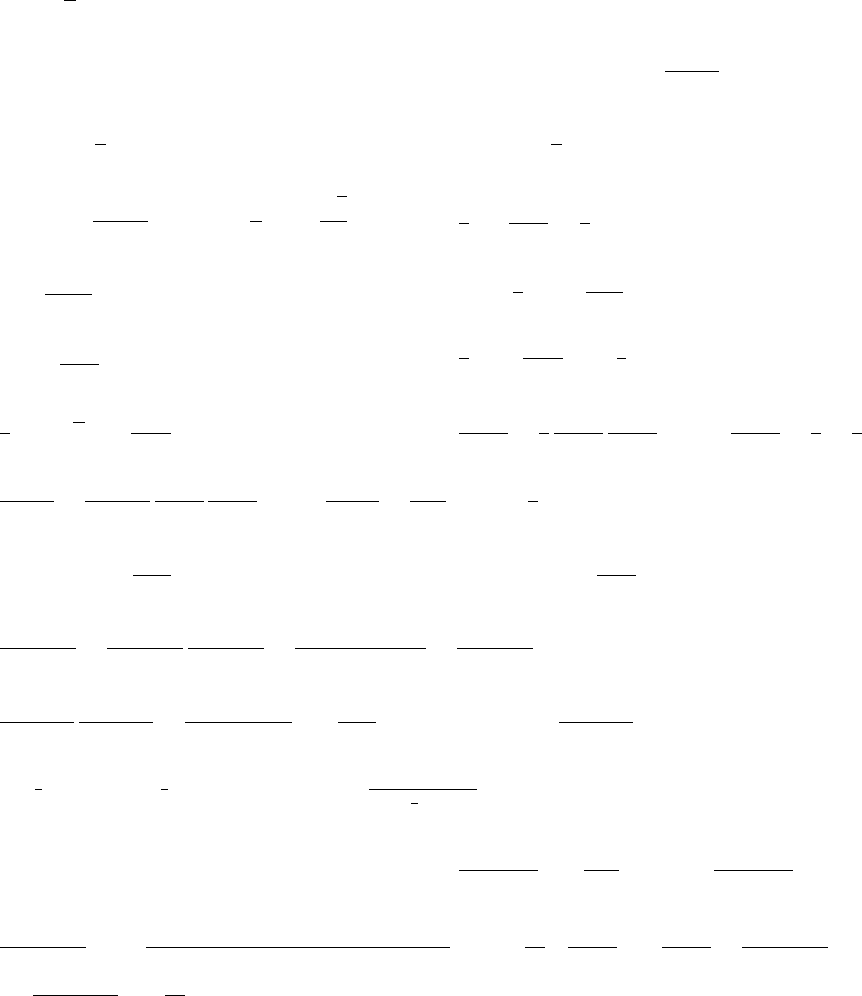
59 Chapter 2
EXERCISE SET 2.5
1. none 2. x=π3. x=nπ,n=0,±1,±2,...
4. x=nπ +π/2, n=0,±1,±2,... 5. x=nπ,n=0,±1,±2,...
6. none 7. none 8. x=nπ +π/2, n=0,±1,±2,...
9. 2nπ +π/6,2nπ +5π/6, n=0,±1,±2,... 10. none
11. (a) sin x, x3+7x+1 (b) |x|,sin x(c) x3,cos x, x +1
(d) √x, 3+x, sin x, 2x(e) sin x, sin x(f) x5−2x3+1,cos x
12. (a) Use Theorem 2.4.6. (b) g(x) = cos x,g(x)= 1
x
2+1,g(x)=x
2+1
13. cos µlim
x→+∞
1
x¶=cos0=1 14. sin µlim
x→+∞
2
x¶=sin0=0
15. sin µlim
x→+∞
πx
2−3x¶= sin ³−π
3´=−√3
216. 1
2lim
h→0
sin h
h=1
2
17. 3 lim
θ→0
sin 3θ
3θ=3 18. µlim
θ→0+
1
θ¶lim
θ→0+
sin θ
θ=+∞
19. −lim
x→0−
sin x
x=−120. 1
3µlim
x→0
sin x
x¶2
=1
3
21. 1
5lim
x→0+√xlim
x→0+
sin x
x=0 22. sin 6x
sin 8x=6
8
sin 6x
6x
8x
sin 8x, so lim
x→0
sin 6x
sin 8x=6
8=3
4
23. tan 7x
sin 3x=7
3 cos 7x
sin 7x
7x
3x
sin 3xso lim
x→0
tan 7x
sin 3x=7
3(1)(1)(1) = 7
3
24. µlim
θ→0sin θ¶lim
θ→0
sin θ
θ=0 25. µlim
h→0cos h¶lim
h→0
h
sin h=1
26. sin h
1−cos h=sin h
1−cos h
1 + cos h
1 + cos h=sin h(1 + cos h)
1−cos2h=1 + cos h
sin h; no limit
27. θ2
1−cos θ
1 + cos θ
1 + cos θ=θ2(1 + cos θ)
1−cos2θ=µθ
sin θ¶2
(1 + cos θ) so lim
θ→0
θ2
1−cos θ= (1)22=2
28. cos(1
2π−x) = sin(1
2π) sin x= sin x, so lim
x→0
x
cos ¡1
2π−x¢=1
29. 030. t2
1−cos2t=µt
sin t¶2
,solim
t→0
t
2
1−cos2t=1
31. 1−cos 5h
cos 7h−1=(1 −cos 5h)(1 + cos 5h)(1 + cos 7h)
(cos 7h−1)(1 + cos 5h)(1 + cos 7h)=−25
49 µsin 5h
5h¶2µ7h
sin 7h¶21 + cos 7h
1 + cos 5hso
lim
h→0
1−cos 5h
cos 7h−1=−25
49
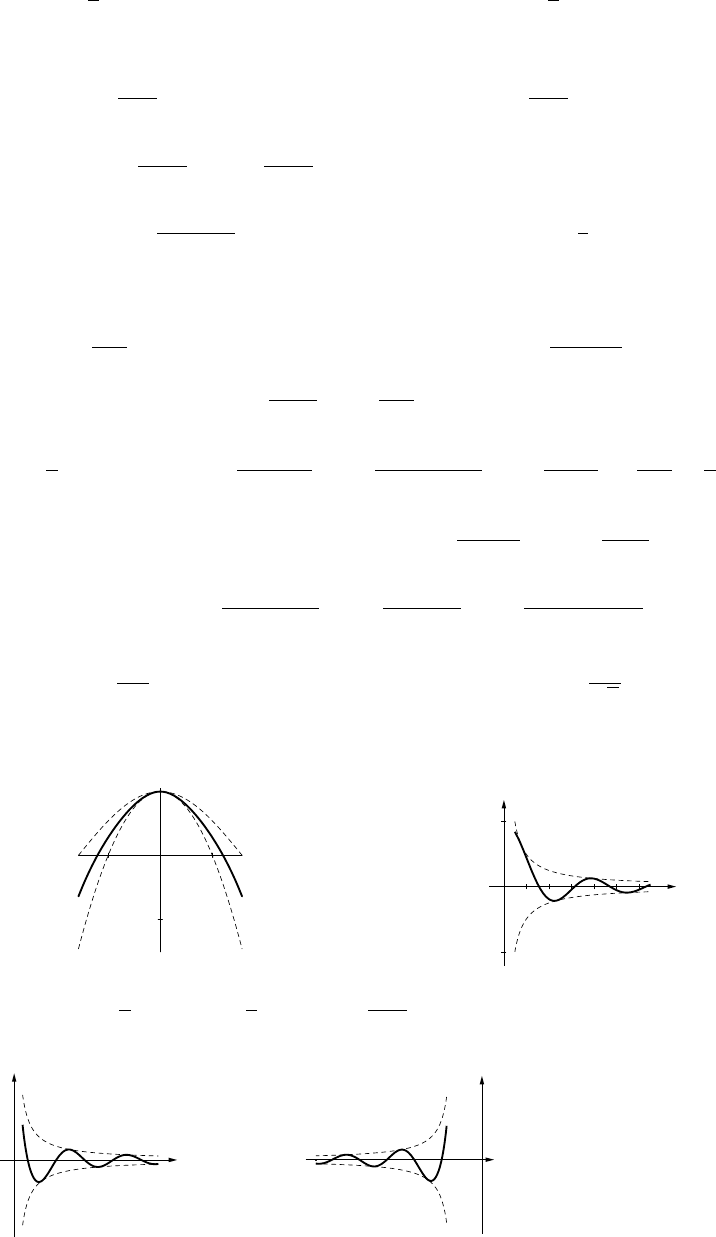
Exercise Set 2.5 60
32. lim
x→0+sin µ1
x¶= lim
t→+∞sin t;
limit does not exist
33. lim
x→0+cos µ1
x¶= lim
t→+∞cos t;
limit does not exist
34. lim
x→0x−3 lim
x→0
sin x
x=−335. 2 + lim
x→0
sin x
x=3
36. k=f(0) = lim
x→0
sin 3x
x= 3 lim
x→0
sin 3x
3x=3,sok=3
37. lim
x→0−f(x)=klim
x→0
sin kx
kx cos kx =k, lim
x→0+f(x)=2k
2
,sok=2k
2
,k=1
2
38. No; sin x/|x|has unequal one-sided limits.
39. (a) lim
t→0+
sin t
t=1 (b) lim
t→0−
1−cos t
t= 0 (Theorem 2.5.3)
(c) sin(π−t) = sin t, so lim
x→π
π−x
sin x= lim
t→0
t
sin t=1
40. cos ³π
2−t´= sin t, so lim
x→2
cos(π/x)
x−2= lim
t→0
(π−2t) sin t
4t= lim
t→0
π−2t
4lim
t→0
sin t
t=π
4
41. t=x−1; sin(πx) = sin(πt +π)=−sin πt; and lim
x→1
sin(πx)
x−1=−lim
t→0
sin πt
t=−π
42. t=x−π/4; tan x−1= 2 sin t
cos t−sin t; lim
x→π/4
tan x−1
x−π/4= lim
t→0
2 sin t
t(cos t−sin t)=2
43. −x≤xcos µ50π
x¶≤x44. −x2≤x2sin µ50π
3
√x¶≤x2
45. lim
x→0f(x) = 1 by the Squeezing Theorem
-1
0
1
-1 1 x
y = cos x
y = 1 – x2
y = f(x)
46. lim
x→+∞f(x) = 0 by the Squeezing Theorem
y
x
-1
4
47. Let g(x)=−1
xand h(x)= 1
x
; thus lim
x→+∞
sin x
x= 0 by the Squeezing Theorem.
48. y
x
y
x
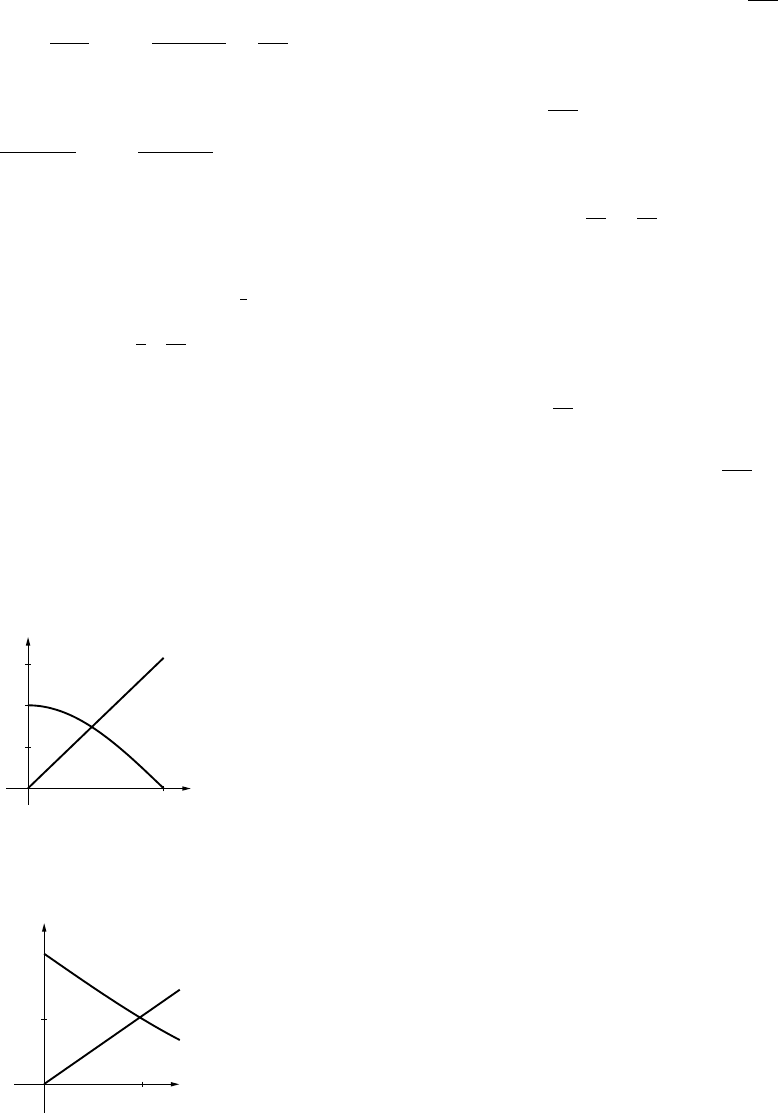
61 Chapter 2
49. (a) sin x= sin twhere xis measured in degrees, tis measured in radians and t=πx
180.Thus
lim
x→0
sin x
x= lim
t→0
sin t
(180t/π)=π
180.
50. cos x= cos twhere xis measured in degrees, tin radians, and t=πx
180.Thus
lim
x→0
1−cos x
x= lim
t→0
1−cos t
(180t/π)=0.
51. (a) sin 10◦=0.17365 (b) sin 10◦= sin π
18 ≈π
18 =0.17453
52. (a) cos θ= cos 2α=1−2 sin2(θ/2)
≈1−2(θ/2)2=1−1
2θ
2
(b) cos 10◦=0.98481
(c) cos 10◦=1−1
2³π
18´2≈0.98477
53. (a) 0.08749 (b) tan 5◦≈π
36 =0.08727
54. (a) h=52.55 ft (b) Since αis small, tan α◦≈πα
180 isagood
approximation.
(c) h≈52.36 ft
55. (a) Let f(x)=x−cos x;f(0) = −1, f(π/2)=π/2. By the IVT there must be a solution of
f(x)=0.
(b) y
x
0
0.5
1
1.5
y = cos x
π/2
y = x
(c) 0.739
56. (a) f(x)=x+ sin x−1; f(0) = −1, f(π/6) = π/6−1/2>0. By the IVT there must be a solution
of f(x)=0.
(b) y
x
0
0.5
π/6
y = x
y = 1– sin x
(c) x=0.511.
57. (a) There is symmetry about the equatorial plane.
(b) Let g(φ) be the given function. Then g(38) <9.8 and g(39) >9.8, so by the Intermediate Value
Theorem there is a value cbetween 38 and 39 for which g(c)=9.8 exactly.
58. (a) does not exist
(b) the limit is zero
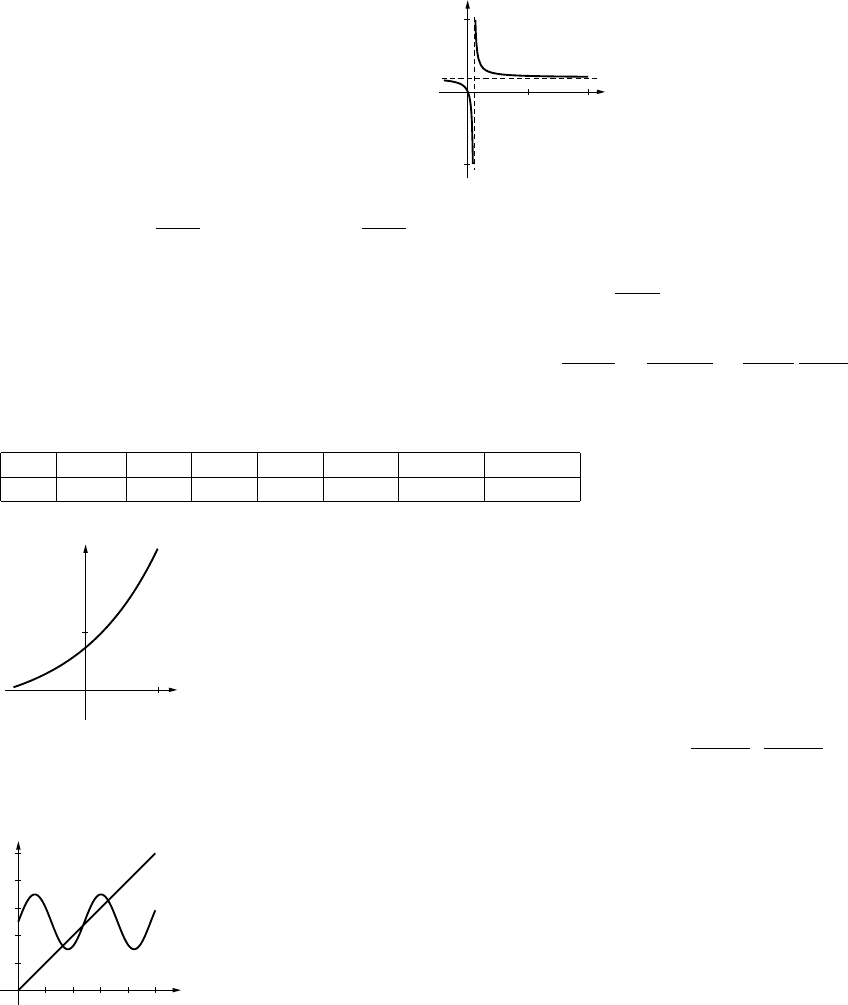
Supplementary Exercises 2 62
(c) For part (a) consider the fact that given any δ>0 there are infinitely many rational numbers x
satisfying |x|<δand there are infinitely many irrational numbers satisfying the same condition.
Thus if the limit were to exist, it could not be zero because of the rational numbers, and it could
not be 1 because of the irrational numbers, and it could not be anything else because of all the
numbers. Hence the limit cannot exist. For part (b) use the Squeezing Theorem with +xand
−xas the ‘squeezers’.
CHAPTER 2 SUPPLEMENTARY EXERCISES
1. (a) 1(b) no limit (c) no limit (d) 1(e) 3
(f) 0(g) 0(h) 2(i) 1/2
2. (a) f(x)=2x/(x−1) (b) y
x
10
10
4. f(x)=−1 for a≤x< a+b
2and f(x)=1for a+b
2≤x≤b.
5. (a) 0.222 ...,0.24390,0.24938,0.24994,0.24999,0.25000; for x6=2,f(x)= 1
x+2, so the limit is 1/4;
the limit is 4.
(b) 1.15782,4.22793,4.00213,4.00002,4.00000,4.00000; to prove, use tan 4x
x=sin 4x
xcos 4x=4
cos 4x
sin 4x
4x.
6. (a) y=0 (b) none (c) y=2
7. (a) x 1 0.1 0.01 0.001 0.0001 0.00001 0.000001
f(x) 1.000 0.443 0.409 0.406 0.406 0.405 0.405
(b) y
x
0.5
-1 1
8. (a) 0.4 amperes (b) [0.3947,0.4054] (c) ·3
7.5+δ,3
7.5−δ¸
(d) 0.0187 (e) It becomes infinite.
9. (a) y
x
0.4
1
0.2 0.8
(b) Let g(x)=x−f(x). Then g(1) ≥0 and
g(0) ≤0; by the Intermediate Value Theo-
rem there is a solution cin [0,1] of g(c)=0.
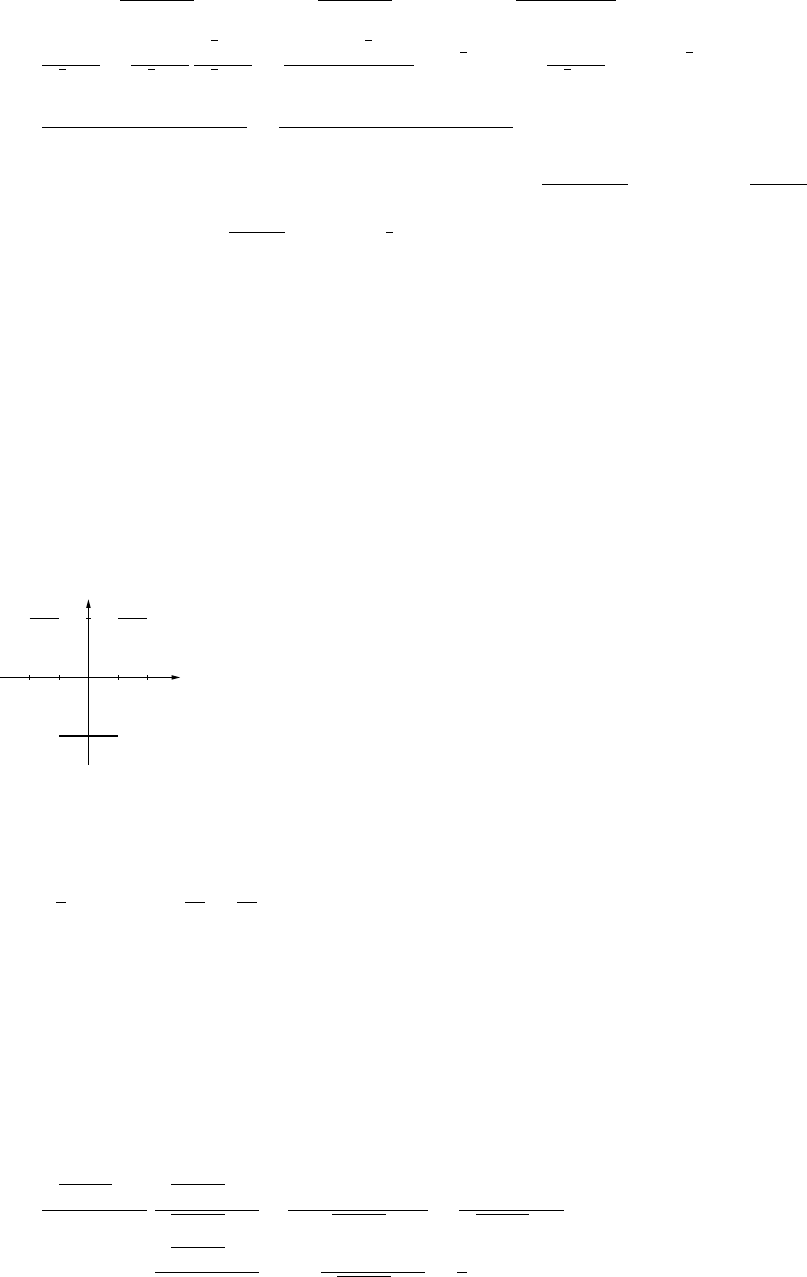
63 Chapter 2
10. (a) lim
θ→0tan µ1−cos θ
θ¶= tan µlim
θ→0
1−cos θ
θ¶= tan µlim
θ→0
1−cos2θ
θ(1 + cos θ)¶=tan0=0
(b) t−1
√t−1=t−1
√t−1
√t+1
√
t+1 =(t−1)(√t+1)
t−1=√
t+ 1; lim
t→1
t−1
√t−1= lim
t→1(√t+1)=2
(c) (2x−1)5
(3x2+2x−7)(x3−9x)=(2 −1/x)5
(3+2/x −7/x2)(1 −9/x2)→25/3=32/3asx→+∞
(d) sin(θ+π) = sin θcos π−cos θsin π=−sin θ, so lim
θ→0cos µsin(θ+π)
2θ¶= lim
θ→0cos µ−sin θ
2θ¶
= cos µlim
θ→0−sin θ
2θ¶= cos ¡−1
2¢
11. If, on the contrary, f(x0)<0 for some x0in [0,1], then by the Intermediate Value Theorem we would
have a solution of f(x) = 0 in [0,x
0], contrary to the hypothesis.
12. For x<2fis a polynomial and is continuous; for x>2fis a polynomial and is continuous. At
x=2,f(2) = −13 6=13= lim
x→2
+f(x)sofis not continuous there.
13. f(−6) = 185, f(0) = −1, f(2) = 65; apply Theorem 2.4.9 twice, once on [−6,0] and once on [0,2]
14. 3.317
15. Let ²=f(x0)/2>0; then there corresponds δ>0 such that if |x−x0|<δthen |f(x)−f(x0)|<²,
−²<f(x)−f(x
0
)<²,f(x)>f(x
0
)−²=f(x
0
)/2>0 for x0−δ<x<x
0+δ.
16. y
x
1
4
17. (a) 1.449 (xmust be ≥−1) (b) x=0,±1.896
18. Since lim
x→0sin(1/x) does not exist, no conclusions can be drawn.
19. (a) √5, no limit, √10, √10, no limit, +∞,
no limit
(b) 5,10,0,0,10,−∞,+∞
20. (a) −1/5,+∞,−1/10,−1/10, no limit, 0, 0 (b) −1,+1,−1,−1, no limit, −1,+1
21. a/b 22. 123. does not exist
24. 225. 026. k227. 3−k
28. The numerator satisfies: |2x+xsin 3x|≤|2x|+|x|=3|x|. Since the denominator grows like x2, the
limit is 0.
30. (a) √x2+4−2
x
2
√
x
2+4+2
√
x
2+4+2=x
2
x
2
(
√
x
2+4+2) =1
√
x
2+4+2,so
lim
x→0
√x2+4−2
x
2= lim
x→0
1
√x2+4+2 =1
4
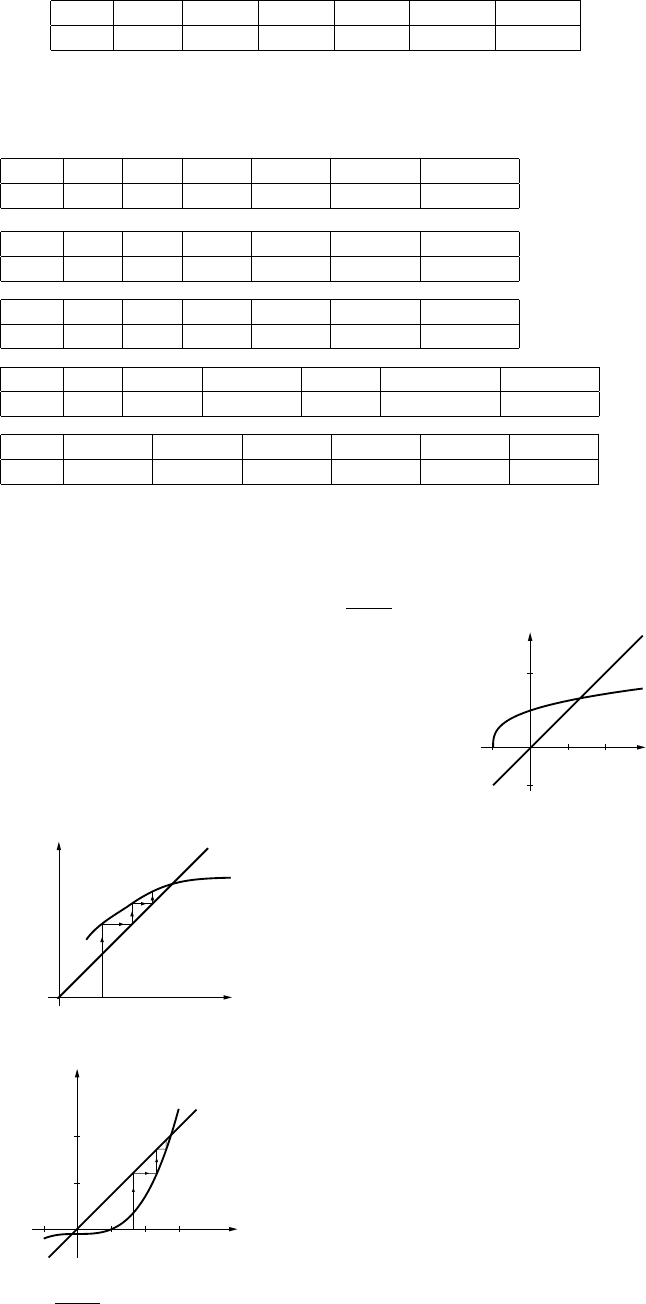
Supplementary Exercises 2 64
(b) x1 0.1 0.01 0.001 0.0001 0.00001
f(x) 0.236 0.2498 0.2500 0.2500 0.25000 0.00000
The division may entail division by zero (e.g. on an HP 42S), or the numerator may be inaccurate
(catastrophic subtraction, e.g.).
(c) in the 3d picture, catastrophic subtraction
31. x0.1 0.01 0.001 0.0001 0.00001 0.000001
f(x) 2.59 2.70 2.717 2.718 2.7183 2.71828
32. x3.1 3.01 3.001 3.0001 3.00001 3.000001
f(x) 5.74 5.56 5.547 5.545 5.5452 5.54518
33. x1.1 1.01 1.001 1.0001 1.00001 1.000001
f(x) 0.49 0.54 0.540 0.5403 0.54030 0.54030
34. x0.1 0.01 0.001 0.0001 0.00001 0.000001
f(x) 99.0 9048.8 368063.3 4562.7 3.9×10−34 0
35. x100 1000 104105106107
f(x) 0.48809 0.49611 0.49876 0.49961 0.49988 0.49996
36. For large values of x(not much more than 100) the computer can’t handle 5xor 3x, yet the limit is 5.
37. δ=0.07747 38. $2,001.60, $2,009.66, $2,013.62, $2013.75
39. (a) x3−x−1=0,x
3=x+1,x=3
√
x+1. (b) y
x
-1
2
-1 1
(c) y
x
x1x2x3
(d) 1,1.26,1.31,1.322,1.324,1.3246,1.3247
40. (a) y
x
10
20
-1 1 32
x1x2
(b) 0,−1,−2,−9,−730
41. x=5
√x+ 2; 1.267168 42. x= cos x; 0.739085 (after 33 iterations!).
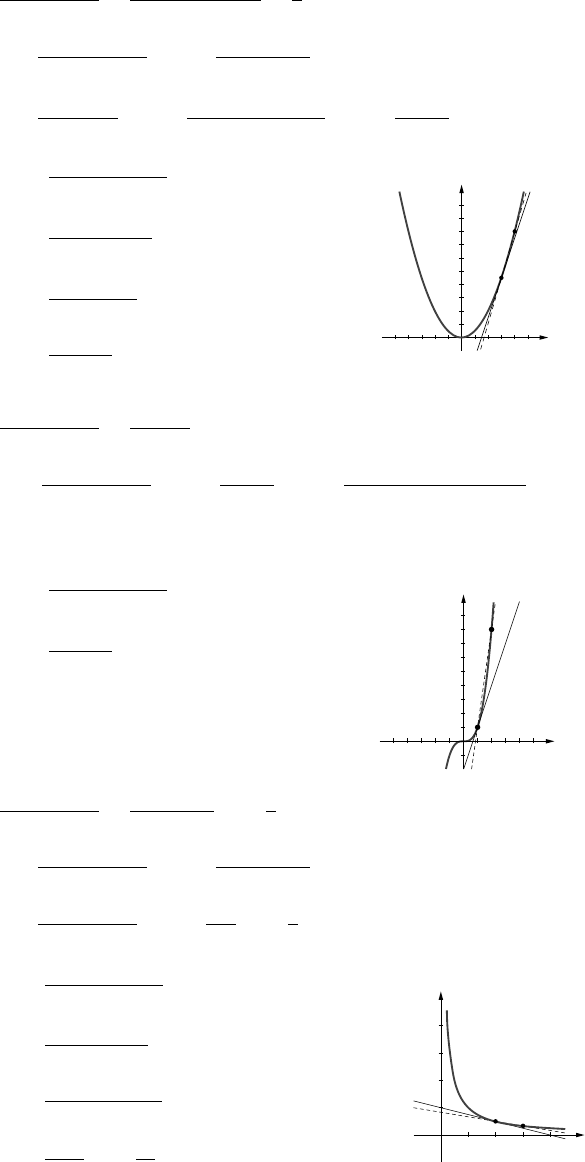
CHAPTER 3
The Derivative
EXERCISE SET 3.1
1. (a) msec =f(4) −f(3)
4−3=(4)2/2−(3)2/2
1=7
2
(b) mtan = lim
x1→3
f(x1)−f(3)
x1−3= lim
x1→3
x2
1/2−9/2
x1−3
= lim
x1→3
x2
1−9
2(x1−3) = lim
x1→3
(x1+ 3)(x1−3)
2(x1−3) = lim
x1→3
x1+3
2=3
(c) mtan = lim
x1→x0
f(x1)−f(x0)
x1−x0
= lim
x1→x0
x2
1/2−x2
0/2
x1−x0
= lim
x1→x0
x2
1−x2
0
2(x1−x0)
= lim
x1→x0
x1+x0
2=x0
(d)
x
y
Tangent
Secant
5
10
2. (a) msec =f(2) −f(1)
2−1=23−13
1=7
(b) mtan = lim
x1→1
f(x1)−f(1)
x1−1= lim
x1→1
x3
1−1
x1−1= lim
x1→1
(x1−1)(x2
1+x1+1)
x
1−1
= lim
x1→1(x2
1+x1+1)=3
(c) mtan = lim
x1→x0
f(x1)−f(x0)
x1−x0
= lim
x1→x0
x3
1−x3
0
x1−x0
= lim
x1→x0
(x2
1+x1x0+x2
0)
=3x
2
0
(d)
x
y
Secant
Tangent
5
9
3. (a) msec =f(3) −f(2)
3−2=1/3−1/2
1=−1
6
(b) mtan = lim
x1→2
f(x1)−f(2)
x1−2= lim
x1→2
1/x1−1/2
x1−2
= lim
x1→2
2−x1
2x1(x1−2) = lim
x1→2−1
2x1
=−1
4
(c) mtan = lim
x1→x0
f(x1)−f(x0)
x1−x0
= lim
x1→x0
1/x1−1/x0
x1−x0
= lim
x1→x0
x0−x1
x0x1(x1−x0)
= lim
x1→x0
−1
x0x1
=−1
x2
0
(d)
x
y
Secant
Tangent
1
4
65

Exercise Set 3.1 66
4. (a) msec =f(2) −f(1)
2−1=1/4−1
1=−3
4
(b) mtan = lim
x1→1
f(x1)−f(1)
x1−1= lim
x1→1
1/x2
1−1
x1−1
= lim
x1→1
1−x2
1
x2
1(x1−1) = lim
x1→1−(x1+1)
x
2
1
=−2
(c) mtan = lim
x1→x0
f(x1)−f(x0)
x1−x0
= lim
x1→x0
1/x2
1−1/x2
0
x1−x0
= lim
x1→x0
x2
0−x2
1
x2
0x2
1(x1−x0)
= lim
x1→x0
−(x1+x0)
x2
0x2
1
=−2
x3
0
(d)
x
y
Tangent Secant
1
2
5. (a) mtan = lim
x1→x0
f(x1)−f(x0)
x1−x0
= lim
x1→x0
(x2
1+1)−(x
2
0+1)
x
1−x
0
= lim
x1→x0
x2
1−x2
0
x1−x0
= lim
x1→x0
(x1+x0)=2x
0
(b) mtan =2(2)=4
6. (a) mtan = lim
x1→x0
f(x1)−f(x0)
x1−x0
= lim
x1→x0
(x2
1+3x
1+2)−(x
2
0+3x
0+2)
x
1−x
0
= lim
x1→x0
(x2
1−x2
0)+3(x
1−x
0
)
x
1−x
0
= lim
x1→x0
(x1+x0+3)=2x
0+3
(b) mtan =2(2)+3=7
7. (a) mtan = lim
x1→x0
f(x1)−f(x0)
x1−x0
= lim
x1→x0
√x1−√x0
x1−x0
= lim
x1→x0
1
√x1+√x0
=1
2√x0
(b) mtan =1
2√1=1
2
8. (a) mtan = lim
x1→x0
f(x1)−f(x0)
x1−x0
= lim
x1→x0
1/√x1−1/√x0
x1−x0
= lim
x1→x0
√x0−√x1
√x0√x1(x1−x0)= lim
x1→x0
−1
√x0√x1(√x1+√x0)=−1
2x3/2
0
(b) mtan =−1
2(4)3/2=−1
16
9. (a) mtan = (50 −10)/(15 −5)
=40/10
= 4 m/s
(b)
t (s)
4
10 20
Velocity
(m/s)

67 Chapter 3
10. (a) (10 −10)/(3 −0) = 0 cm/s
(b) t=0,t= 2, and t=4.2 (horizontal tangent line)
(c) maximum: t= 1 (slope >0) minimum: t= 3 (slope <0)
(d) (3 −18)/(4 −2) = −7.5 cm/s (slope of estimated tangent line to curve at t=3)
11. From the figure:
t
s
t0t1t2
(a) The particle is moving faster at time t0because the slope of the tangent to the curve at t0is
greater than that at t2.
(b) The initial velocity is 0 because the slope of a horizontal line is 0.
(c) The particle is speeding up because the slope increases as tincreases from t0to t1.
(d) The particle is slowing down because the slope decreases as tincreases from t1to t2.
12.
t
s
t0t1
13. It is a straight line with slope equal to the velocity.
14. (a) decreasing (slope of tangent line decreases with increasing time)
(b) increasing (slope of tangent line increases with increasing time)
(c) increasing (slope of tangent line increases with increasing time)
(d) decreasing (slope of tangent line decreases with increasing time)
15. (a) 72◦F at about 4:30 P.M. (b) about (67 −43)/6=4
◦F/h
(c) decreasing most rapidly at about 9 P.M.; rate of change of temperature is about −7◦F/h (slope
of estimated tangent line to curve at 9 P.M.)
16. For V= 10 the slope of the tangent line is about −0.25 atm/L, for V= 25 the slope is
about −0.04 atm/L.
17. (a) during the first year after birth
(b) about 6 cm/year (slope of estimated tangent line at age 5)
(c) the growth rate is greatest at about age 14; about 10 cm/year
(d)
t (yrs)
Growth rate
(cm/year)
5101520
10
20
30
40
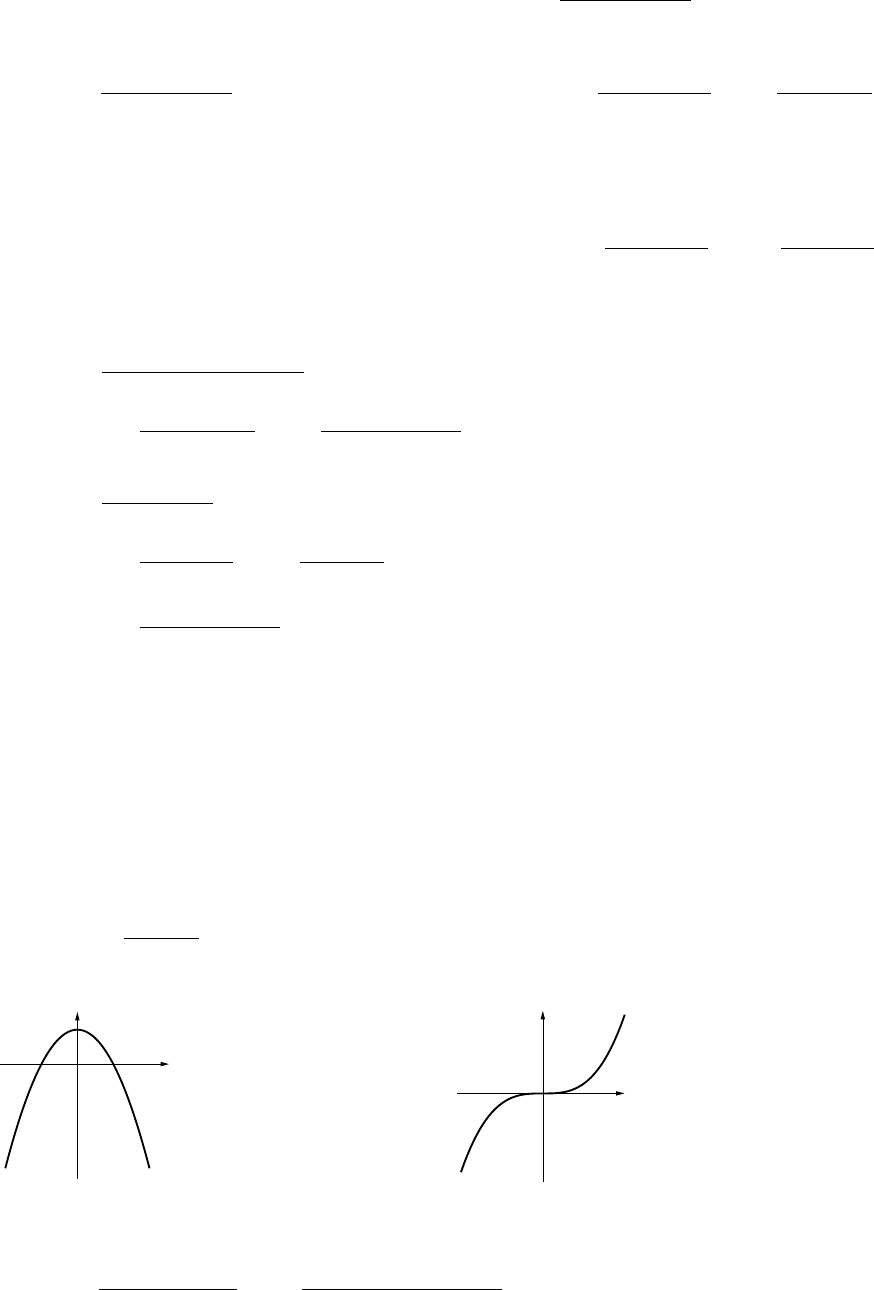
Exercise Set 3.2 68
18. (a) The rock will hit the ground when
16t2= 576, t2= 36, t= 6 s (only t≥0
is meaningful)
(b) vave =16(6)2−16(0)2
6−0= 96 ft/s
(c) vave =16(3)2−16(0)2
3−0= 48 ft/s (d) vinst = lim
t1→6
16t2
1−16(6)2
t1−6= lim
t1→6
16(t2
1−36)
t1−6
= lim
t1→616(t1+ 6) = 192 ft/s
19. (a) 5(40)3= 320,000 ft (b) vave = 320,000/40=8,000 ft/s
(c) 5t3= 135 when the rocket has gone 135 ft,
so t3= 27, t=3s;
v
ave = 135/3 = 45 ft/s.
(d) vinst = lim
t1→40
5t3
1−5(40)3
t1−40 = lim
t1→40
5(t3
1−403)
t1−40
= lim
t1→40 5(t2
1+40t
1+ 1600) = 24,000 ft/s
20. (a) vave =[3(3)2+3]−[3(1)2+1]
3−1= 13 mi/h
(b) vinst = lim
t1→1
(3t2
1+t1)−4
t1−1= lim
t1→1
(3t1+ 4)(t1−1)
t1−1= lim
t1→1(3t1+ 4) = 7 mi/h
21. (a) vave =6(4)4−6(2)4
4−2= 720 ft/min
(b) vinst = lim
t1→2
6t4
1−6(2)4
t1−2= lim
t1→2
6(t4
1−16)
t1−2
= lim
t1→2
6(t2
1+ 4)(t2
1−4)
t1−2= lim
t1→26(t2
1+ 4)(t1+ 2) = 192 ft/min
EXERCISE SET 3.2
1. f0(1)=2,f
0(3)=0,f
0(5) = −2, f0(6) = −1/2
2. f0(4) <f
0(0) <f
0(2) <0<f
0(−3)
3. (b) f0(2) = m=3 (c) the same, f0(2)=3
4. f0(−1) = m=4−3
0−(−1) =1
5. y
x
0
1
6. y
x
7. y−(−1)=5(x−3),y=5x−16 8. y−3=−4(x+2),y=−4x−5
9. f0(x) = lim
h→0
f(x+h)−f(x)
h= lim
h→0
3(x2+2xh +h2)−3x2
h= lim
h→03(2x+h)=6x;f(3) = 3(3)2= 27,
f0(3)=18soy−27 = 18(x−3), y=18x−27
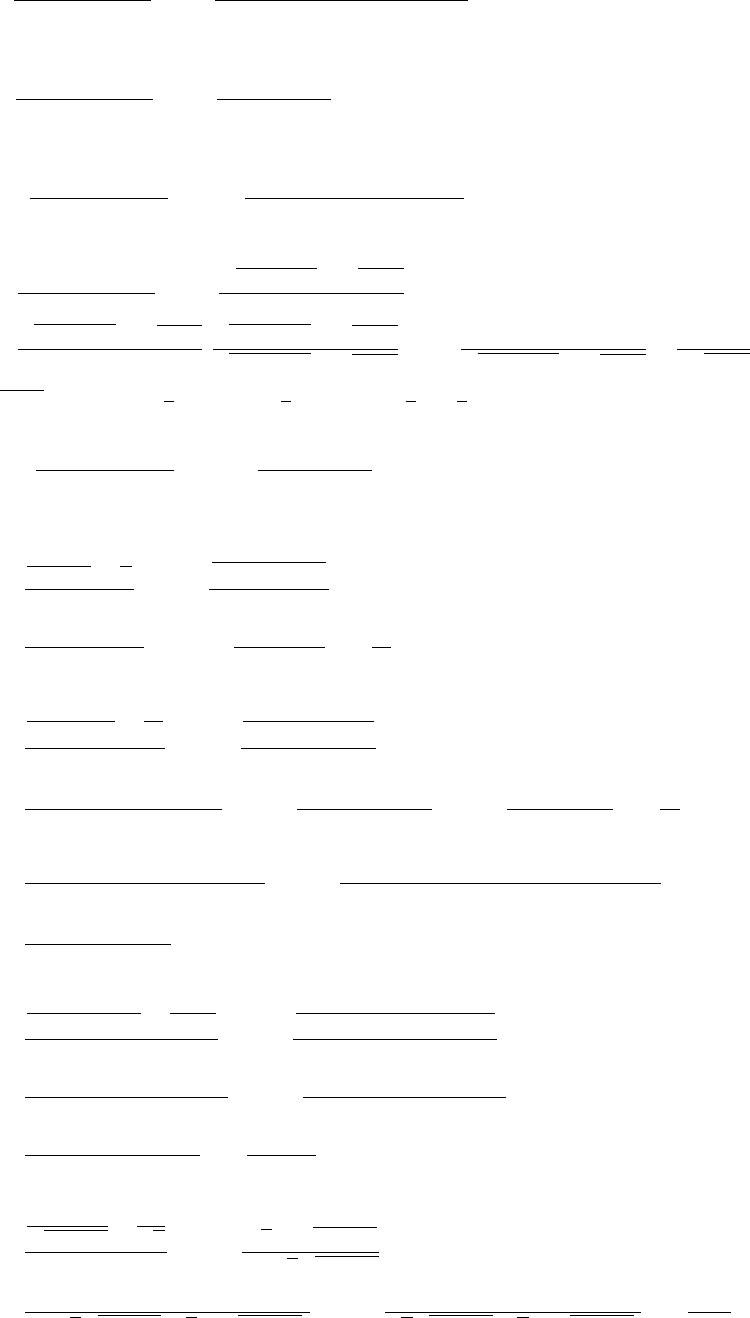
69 Chapter 3
10. f0(x) = lim
h→0
f(x+h)−f(x)
h= lim
h→0
(x+h)2−(x+h)−(x2−x)
h= lim
h→0(2x+h−1)=2x−1;
f(2) = 22−2=2,f
0
(2) = 3 so y−2=3(x−2),y=3x−4
11. f0(x) = lim
h→0
f(x+h)−f(x)
h= lim
h→0
(x+h)3−x3
h=3x
2
;f(0)=0
3=0,
f
0(0) = 0 so y−0 = (0)(x−0), y=0
12. f0(x) = lim
h→0
f(x+h)−f(x)
h= lim
h→0
2(x+h)3+1−(2x3+1)
h= lim
h→0(6x2+6xh +2h
2
)=6x
2
;
f(−1)=2(−1)3+1=−1, f0(−1)=6soy+1=6(x+ 1), y=6x+5
13. f0(x) = lim
h→0
f(x+h)−f(x)
h= lim
h→0
√x+1+h−√
x+1
h
= lim
h→0
√x+1+h−√
x+1
h
√
x+1+h+√
x+1
√
x+1+h+√
x+1 = lim
h→0
1
√x+1+h+√
x+1 =1
2
√
x+1;
f(8) = √8+1=3,f
0(8) = 1
6so y−3=1
6
(x−8), y=1
6x+5
3
14. f0(x) = lim
h→0
f(x+h)−f(x)
h= lim
h→0
(x+h)4−x4
h= lim
h→0(4x3+6x
2
h+4xh2+h3)=4x
3
;
f(−2)=(−2)4= 16, f0(−2) = −32 so y−16 = −32(x+ 2), y=−32x−48
15. f0(x) = lim
∆x→0
1
x+∆x−1
x
∆x= lim
∆x→0
x−(x+∆x)
x(x+∆x)
∆x
= lim
∆x→0−∆x
x∆x(x+∆x)= lim
∆x→0−1
x(x+∆x)=−1
x
2
16. f0(x) = lim
∆x→0
1
(x+∆x)
2−1
x
2
∆x= lim
∆x→0
x2−(x+∆x)
2
x
2
(x+∆x)
2
∆x
= lim
∆x→0
x2−x2−2x∆x−∆x2
x2∆x(x+∆x)
2= lim
∆x→0−2x∆x−∆x2
x2∆x(x+∆x)
2= lim
∆x→0−2x−∆x
x2(x+∆x)
2=−2
x
3
17. f0(x) = lim
∆x→0
[a(x+∆x)
2+b]−[ax2+b]
∆x= lim
∆x→0
ax2+2ax∆x+a(∆x)2+b−ax2−b
∆x
= lim
∆x→0
2ax∆x+a(∆x)2
∆x= lim
∆x→0(2ax +a∆x)=2ax
18. f0(x) = lim
∆x→0
1
(x+∆x)+1 −1
x+1
∆x= lim
∆x→0
(x+1)−(x+∆x+1)
(x+ 1)(x+∆x+1)
∆x
= lim
∆x→0
x+1−x−∆x−1
∆x(x+ 1)(x+∆x+1) = lim
∆x→0−∆x
∆x(x+ 1)(x+∆x+1)
= lim
∆x→0−1
(x+ 1)(x+∆x+1) =−1
(x+1)
2
19. f0(x) = lim
∆x→0
1
√x+∆x−1
√
x
∆x= lim
∆x→0
√x−√x+∆x
∆x
√
x
√
x+∆x
= lim
∆x→0
x−(x+∆x)
∆x
√
x
√
x+∆x(
√
x+√
x+∆x)= lim
∆x→0−1
√x√x+∆x(
√
x+√
x+∆x)=−1
2x
3/2
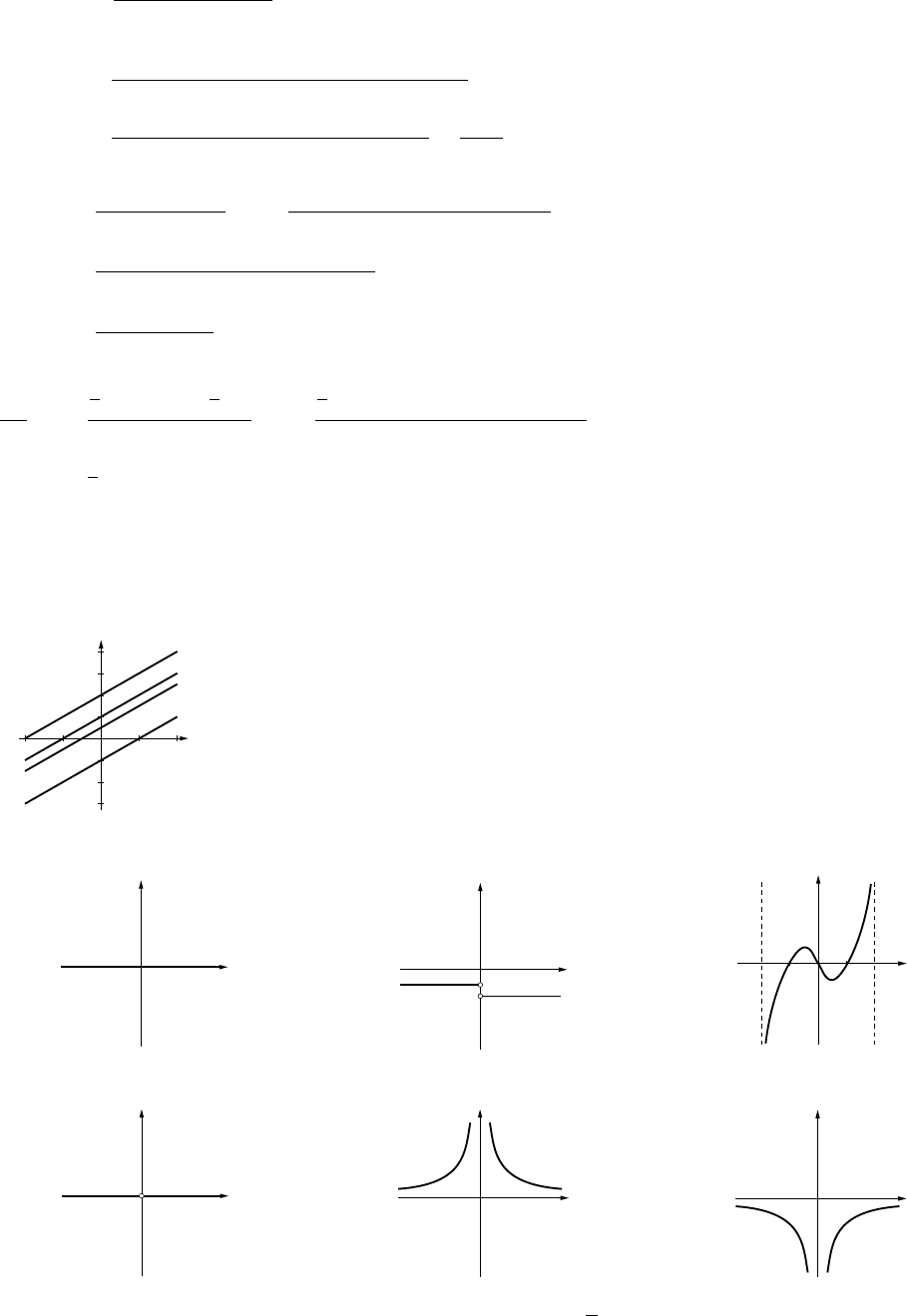
Exercise Set 3.2 70
20. f0(x) = lim
∆x→0
(x+∆x)
1/3−x
1/3
∆x, but a3−b3=(a−b)(a2+ab +b2) so with a=(x+∆x)
1/3
and b=x1/3
f0(x) = lim
∆x→0
(x+∆x)−x
∆x[(x+∆x)
2/3+(x+∆x)
1/3
x
1/3+x
2/3
]
= lim
∆x→0
1
(x+∆x)
2/3+(x+∆x)
1/3
x
1/3+x
2/3=1
3x
2/3
21. f0(t) = lim
h→0
f(t+h)−f(t)
h= lim
h→0
[4(t+h)2+(t+h)] −[4t2+t]
h
= lim
h→0
4t2+8th +4h
2+t+h−4t
2−t
h
= lim
h→0
8th +4h
2+h
h= lim
h→0(8t+4h+1)=8t+1
22. dV
dr = lim
h→0
4
3π(r+h)3−4
3πr3
h= lim
h→0
4
3π(r3+3r
2
h+3rh2+h3−r3)
h
= lim
h→0
4
3π(3r2+3rh +h2)=4πr2
23. (a) D(b) F(c) B(d) C(e) A(f ) E
24. Any function of the form f(x)=x+khas slope 1, and thus the derivative must be equal to 1
everywhere.
y
x
1
-2
3
-2
25. (a)
x
y(b)
x
y
-1
(c)
x
y
12
26. (a)
x
y(b)
x
y(c)
x
y
27. (a) f(x)=x
2and a=3 (b) f(x)=√
xand a=1
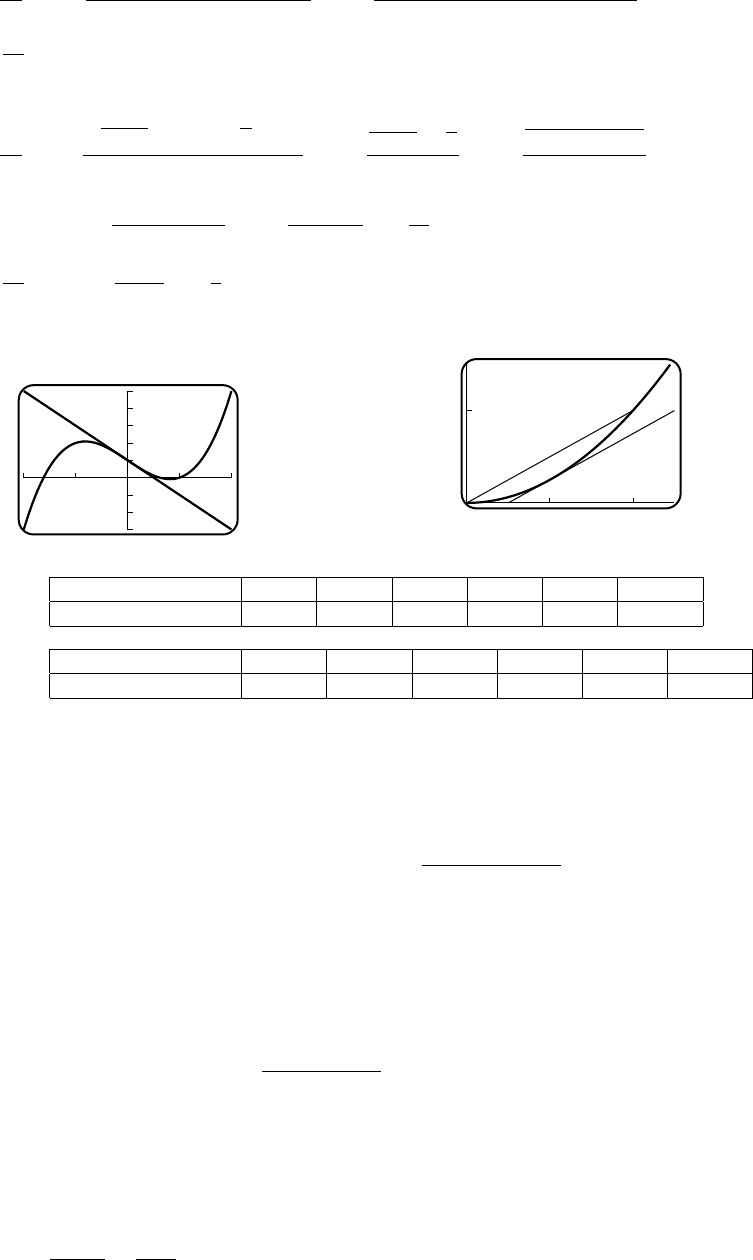
71 Chapter 3
28. (a) f(x) = cos xand a=π(b) f(x)=x
7and a=1
29. dy
dx = lim
h→0
[4(x+h)2+1]−[4x2+1]
h= lim
h→0
4x2+8xh +4h
2+1−4x
2−1
h= lim
h→0(8x+4h)=8x
dy
dx¯¯¯¯x=1
=8(1)=8
30. dy
dx = lim
h→0µ5
x+h+1
¶−µ5
x+1
¶
h= lim
h→0
5
x+h−5
x
h= lim
h→0
5x−5(x+h)
x(x+h)
h
= limh→0
5x−5x−5h
hx(x+h)= lim
h→0−5
x(x+h)=−5
x2
dy
dx¯¯¯¯x=−2
=−5
(−2)2=−5
4
31. y=−2x+1
5
-2 2
-3
32. 1.5
0
0 2.5
33. (b) h0.5 0.1 0.01 0.001 0.0001 0.00001
(f(1+h)−f(1))/h 1.6569 1.4355 1.3911 1.3868 1.3863 1.3863
34. (b) h0.5 0.1 0.01 0.001 0.0001 0.00001
(f(1+h)−f(1))/h 0.50489 0.67060 0.70356 0.70675 0.70707 0.70710
35. (a) dollars/ft
(b) As you go deeper the price per foot may increase dramatically, so f0(x) is roughly the price per
additional foot.
(c) If each additional foot costs extra money (this is to be expected) then f0(x) remains positive.
(d) From the approximation 1000 = f0(300) ≈f(301) −f(300)
301 −300 we see that f(301) ≈f(300) + 1000,
so the extra foot will cost around $1000.
36. (a) gallons/dollar
(b) The increase in the amount of paint that would be sold for one extra dollar.
(c) It should be negative since an increase in the price of paint would decrease the amount of paint
sold.
(d) From −100 = f0(10) ≈f(11) −f(10)
11 −10 we see that f(11) ≈f(10) −100, so an increase of one
dollar would decrease the amount of paint sold by around 100 gallons.
37. (a) F≈200 lb, dF/dθ ≈60 lb/rad (b) µ=(dF/dθ)/F ≈60/200=0.3
38. (a) dN/dt ≈34 million/year; in 1950 the world population was increasing at the rate of about 34
million per year.
(b) dN/dt
N≈34
2490 ≈0.014=1.4 %/year
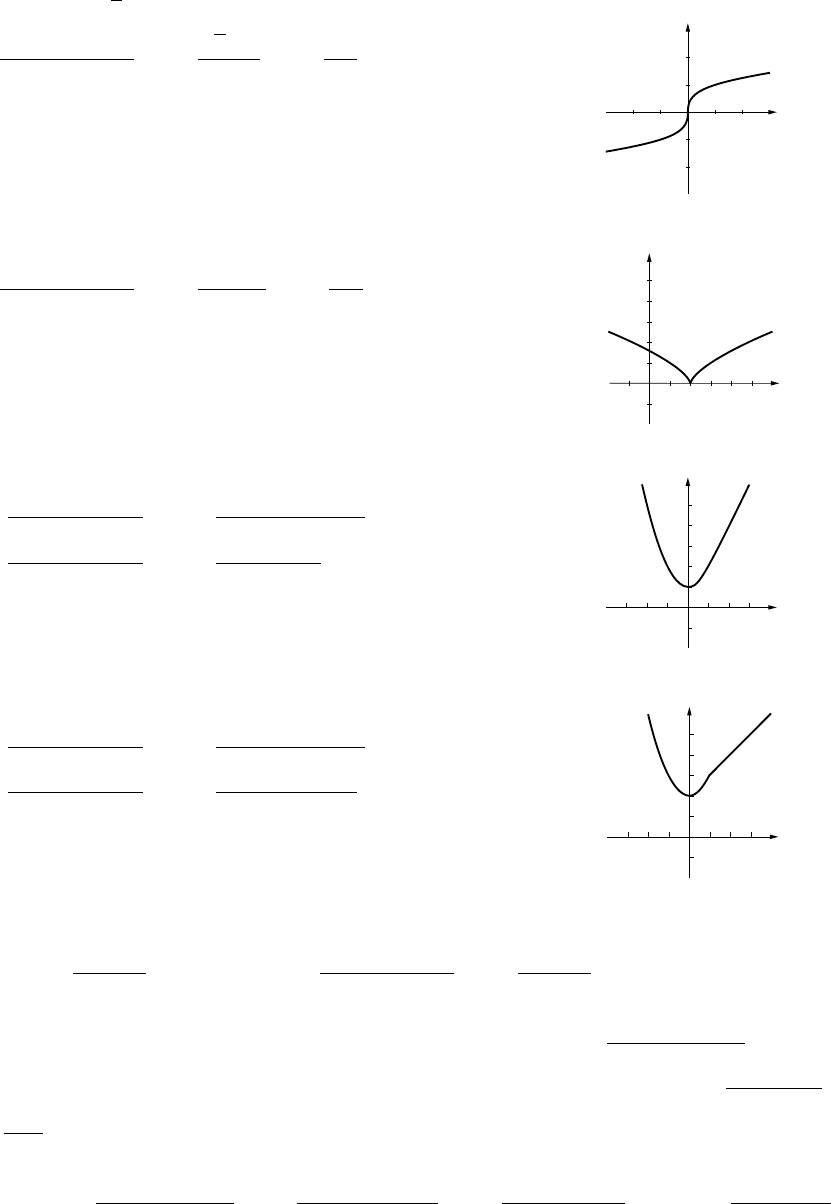
Exercise Set 3.2 72
39. (a) T≈120◦F, dT/dt ≈−4.5
◦F/min
(b) k=(dT /dt)/(T−T0)≈(−4.5)/(120 −75) = −0.1
41. lim
x→0f(x) = lim
x→0
3
√x=0=f(0), so fis continuous at x=0.
lim
h→0
f(0+h)−f(0)
h= lim
h→0
3
√h−0
h= lim
h→0
1
h2/3=+∞,so
f
0
(0) does not exist. x
y
2-2
2
42. lim
x→2f(x) = lim
x→2(x−2)2/3=0=f(2) so fis continuous at x=2.
lim
h→0
f(2+h)−f(2)
h= lim
h→0
h2/3−0
h= lim
h→0
1
h1/3which does not exist
so f0(2) does not exist.
x
y
2
5
43. lim
x→1−f(x) = lim
x→1+f(x)=f(1), so fis continuous at x=1.
lim
h→0−
f(1+h)−f(1)
h= lim
h→0−
[(1 + h)2+1]−2
h= lim
h→0−(2+h)=2;
lim
h→0+
f(1+h)−f(1)
h= lim
h→0+
2(1 + h)−2
h= lim
h→0+2=2,sof
0(1)=2.
x
y
3-3
5
44. lim
x→1−f(x) = lim
x→1+f(x)=f(1) so fis continuous at x=1.
lim
h→0−
f(1+h)−f(1)
h= lim
h→0−
[(1 + h)2+2]−3
h= lim
h→0−(2+h)=2;
lim
h→0+
f(1+h)−f(1)
h= lim
h→0+
[(1 + h)+2]−3
h= lim
h→0+1=1,sof
0(1)
does not exist. x
y
3-3
5
45. fis continuous at x= 1 because it is differentiable there, thus lim
h→0f(1+h)=f(1) and so f(1)=0
because lim
h→0
f(1+h)
hexists; f0(1) = lim
h→0
f(1+h)−f(1)
h= lim
h→0
f(1+h)
h=5.
46. Let x=y= 0 to get f(0) = f(0) + f(0) + 0 so f(0)=0. f
0
(x) = lim
h→0
f(x+h)−f(x)
h, but (with
y=h)f(x+h)=f(x)+f(h)+5xh so f(x+h)−f(x)=f(h)+5xh and f0(x) = lim
h→0
f(h)+5xh
h=
lim
h→0(f(h)
h+5x)=3+5x.
47. f0(x) = limh→0
f(x+h)−f(x)
h= lim
h→0
f(x)f(h)−f(x)
h= lim
h→0
f(x)[f(h)−1]
h=f(x) lim
h→0
f(h)−f(0)
h
=f(x)f0(0) = f(x)
73 Chapter 3
EXERCISE SET 3.3
1. 28x62. −36x11 3. 24x7+2 4. 2x3
5. 06. √27. −1
3(7x6+2) 8. 2
5x
9. 3ax2+2bx +c10. 1
aµ2x+1
b¶11. 24x−9+1/
√
x12. −42x−7−5
2√x
13. −3x−4−7x−814. 1
2√x−1
x2
15. f0(x)=(3x
2+6) d
dx µ2x−1
4¶+µ2x−1
4¶d
dx(3x2+6)=(3x
2+ 6)(2) + µ2x−1
4¶(6x)
=18x
2−3
2x+12
16. f0(x)=(2−x−3x
3)d
dx(7+x5)+(7+x
5
)d
dx(2 −x−3x3)=(2−x−3x
3
)(5x4)+(7+x
5
)(−1−9x2)
=−24x7−6x5+10x
4−63x2−7
17. f0(x)=(x
3+7x
2−8) d
dx(2x−3+x−4)+(2x
−3+x
−4
)d
dx(x3+7x
2−8)
=(x
3+7x
2−8)(−6x−4−4x−5)+(2x
−3+x
−4
)(3x2+14x)=−15x−2−14x−3+48x
−4+32x
−5
18. f0(x)=(x
−1+x
−2)d
dx(3x3+27)+(3x
3+ 27) d
dx(x−1+x−2)
=(x
−1+x
−2
)(9x2)+(3x
3+ 27)(−x−2−2x−3)=3+6x−27x−2−54x−3
19. 12x(3x2+1) 20. f(x)=x
10 +4x
6+4x
2
,f0(x)=10x
9+24x
5+8x
21. dy
dx =
(5x−3) d
dx(1) −(1) d
dx(5x−3)
(5x−3)2=−5
(5x−3)2;y0(1) = −5/4
22. dy
dx =
(√x+2) d
dx(3) −3d
dx(√x+2)
(
√
x+2)
2=−3/(2√x(√x+2)
2
;y
0(1) = −3/18 = −1/6
23. dx
dt =
(2t+1)d
dt(3t)−(3t)d
dt(2t+1)
(2t+1)
2=(2t+ 1)(3) −(3t)(2)
(2t+1)
2=3
(2t+1)
2
24. dx
dt =
(3t)d
dt(t2+1)−(t
2+1)d
dt(3t)
(3t)2=(3t)(2t)−(t2+ 1)(3)
9t2=t2−1
3t2
25. dy
dx =
(x+3) d
dx(2x−1) −(2x−1) d
dx(x+3)
(x+3)
2=(x+ 3)(2) −(2x−1)(1)
(x+3)
2=7
(x+3)
2;dy
dx¯¯¯¯x=1
=7
16
26. dy
dx =
(x2−5) d
dx(4x+1)−(4x+1) d
dx(x2−5)
(x2−5)2=(x2−5)(4) −(4x+ 1)(2x)
(x2−5)2=−4x2+2x+20
(x
2−5)2;
dy
dx¯¯¯¯x=1
=13
8
Exercise Set 3.3 74
27. dy
dx =µ3x+2
x¶d
dx ¡x−5+1
¢+¡x
−5+1
¢d
dx µ3x+2
x¶
=µ3x+2
x¶¡−5x
−6
¢+¡x
−5+1
¢·x(3) −(3x+ 2)(1)
x2¸=µ3x+2
x¶¡−5x
−6
¢+¡x
−5+1
¢µ−2
x
2¶;
dy
dx¯¯¯¯x=1
=5(−5)+2(−2) = −29
28. dy
dx =(2x
7−x
2
)d
dx µx−1
x+1¶+µx−1
x+1¶d
dx(2x7−x2)
=(2x
7−x
2
)·(x+ 1)(1) −(x−1)(1)
(x+1)
2¸+µx−1
x+1¶(14x6−2x)
=(2x
7−x
2
)·2
(x+1)
2+µx−1
x+1¶(14x6−2x);
dy
dx¯¯¯¯x=1
=(2−1)2
4+ 0(14 −2) = 1
2
29. 32t30. 2π31. 3πr232. −2α−2+1
33. (a) dV
dr =4πr2(b) dV
dr ¯¯¯¯r=5
=4π(5)2= 100π
35. (a) g0(x)=√
xf0(x)+ 1
2
√
xf(x), g0(4) = (2)(−5) + 1
4(3) = −37/4
(b) g0(x)=xf0(x)−f(x)
x2,g0(4) = (4)(−5) −3
16 =−23/16
36. (a) g0(x)=6x−5f
0(x), g0(3) = 6(3) −5(4) = −2
(b) g0(x)=2f(x)−(2x+1)f0(x)
f2
(x),g
0(3) = 2(−2) −7(4)
(−2)2=−8
37. (a) F0(x)=5f
0(x)+2g
0(x),F0(2) = 5(4) + 2(−5)=10
(b) F0(x)=f
0(x)−3g
0(x),F0(2)=4−3(−5)=19
(c) F0(x)=f(x)g
0(x)+g(x)f0(x),F0(2)=(−1)(−5) + (1)(4) = 9
(d) F0(x)=[g(x)f
0(x)−f(x)g
0(x)]/g2(x),F0(2) = [(1)(4) −(−1)(−5)]/(1)2=−1
38. dy
dx =(1+x)(−1) −(1 −x)(1)
(1+x)2=−2
(1+x)2,dy
dx¯¯¯¯x=2
=−2
9and y=−1
3for x= 2 so an equation of
the tangent line is y−µ−1
3¶=−2
9(x−2), or y=−2
9x+1
9.
39. y−2=5(x+ 3), y=5x+17
40. d
dλ ·λλ0+λ6
2−λ0¸=1
2−λ0
d
dλ(λλ0+λ6)= 1
2−λ
0
(λ
0+6λ
5
)=λ
0+6λ
5
2−λ
0
41. (a) dy/dx =21x
2−10x+1,d
2
y/dx2=42x−10
(b) dy/dx =24x−2, d2y/dx2=24
(c) dy/dx =−1/x2,d2y/dx2=2/x3
(d) y=35x
5−16x3−3x,dy/dx = 175x4−48x2−3, d2y/dx2= 700x3−96x
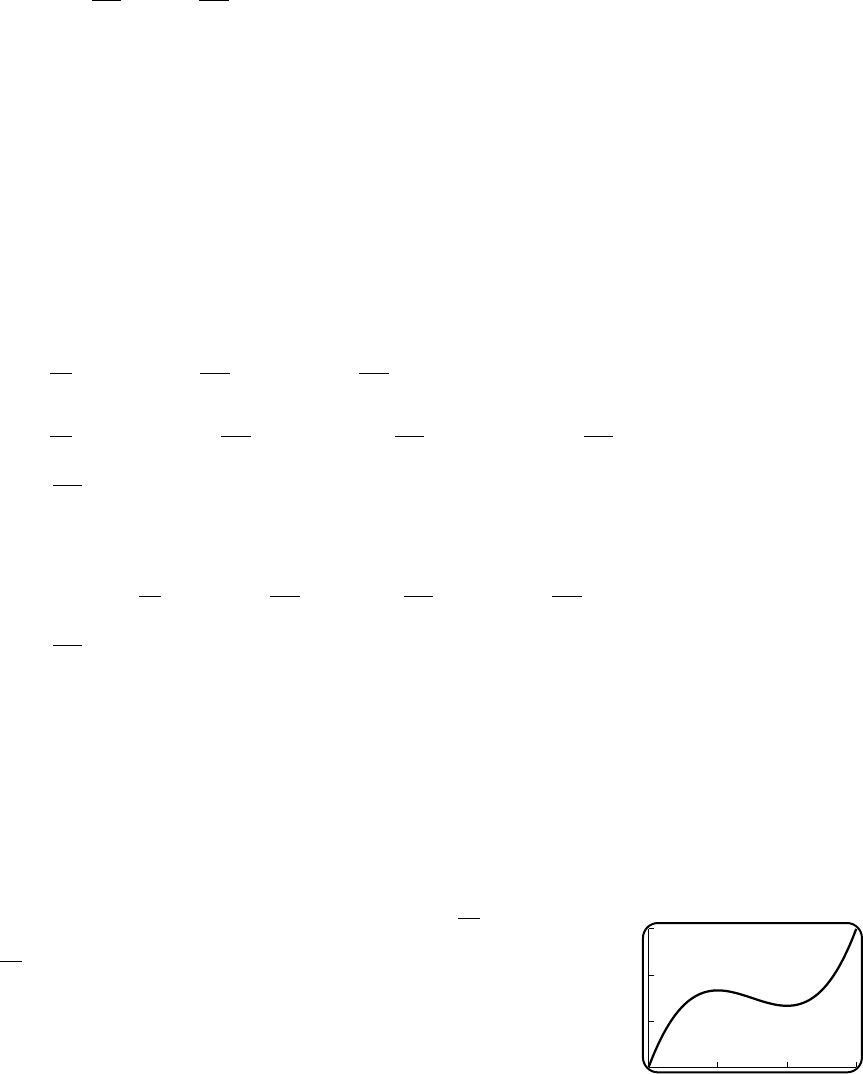
75 Chapter 3
42. (a) y0=28x
6−15x2+2,y
00 = 168x5−30x
(b) y0=3,y
00 =0
(c) y0=2
5x2,y00 =−4
5x3
(d) y=2x
4+3x
3−10x−15, y0=8x
3+9x
2−10, y00 =24x
2+18x
43. (a) y0=−5x−6+5x
4
,y
00 =30x
−7+20x
3
,y
000 =−210x−8+60x
2
(b) y=x−1,y0=−x−2,y00 =2x
−3
,y
000 =−6x−4
(c) y0=3ax2+b,y00 =6ax,y000 =6a
44. (a) dy/dx =10x−4, d2y/dx2= 10, d3y/dx3=0
(b) dy/dx =−6x−3−4x−2+1,d
2
y/dx2=18x
−4+8x
−3
,d
3
y/dx3=−72x−5−24x−4
(c) dy/dx =4ax3+2bx,d2y/dx2=12ax2+2b,d
3
y/dx3=24ax
45. (a) f0(x)=6x,f
00(x)=6,f
000(x)=0,f
000(2)=0
(b) dy
dx =30x
4−8x,d
2
y
dx2= 120x3−8, d2y
dx2¯¯¯¯x=1
= 112
(c) d
dx £x−3¤=−3x−4,d2
dx2£x−3¤=12x
−5
,d
3
dx3£x−3¤=−60x−6,d4
dx4£x−3¤= 360x−7,
d4
dx4£x−3¤¯¯¯¯x=1
= 360
46. (a) y0=16x
3+6x
2
,y
00 =48x
2+12x,y
000 =96x+ 12, y000(0)=12
(b) y=6x
−4
,dy
dx =−24x−5,d2y
dx2= 120x−6,d3y
dx3=−720x−7,d4y
dx4= 5040x−8,
d4y
dx4¯¯¯¯x=1
= 5040
47. y0=3x
2+3,y
00 =6x, and y000 =6so
y
000 +xy00 −2y0=6+x(6x)−2(3x2+3)=6+6x
2−6x
2−6=0
48. y=x−1,y0=−x−2,y00 =2x
−3so
x3y00 +x2y0−xy =x3(2x−3)+x
2
(−x
−2
)−x(x
−1
)=2−1−1=0
49. F0(x)=xf0(x)+f(x), F00(x)=xf 00(x)+f0(x)+f0(x)=xf00(x)+2f0(x)
51. The graph has a horizontal tangent at points where dy
dx = 0, but
dy
dx =x2−3x+2=(x−1)(x−2)=0ifx=1,2. The
corresponding values of yare 5/6 and 2/3 so the tangent line is
horizontal at (1,5/6) and (2,2/3).
1.5
0
03
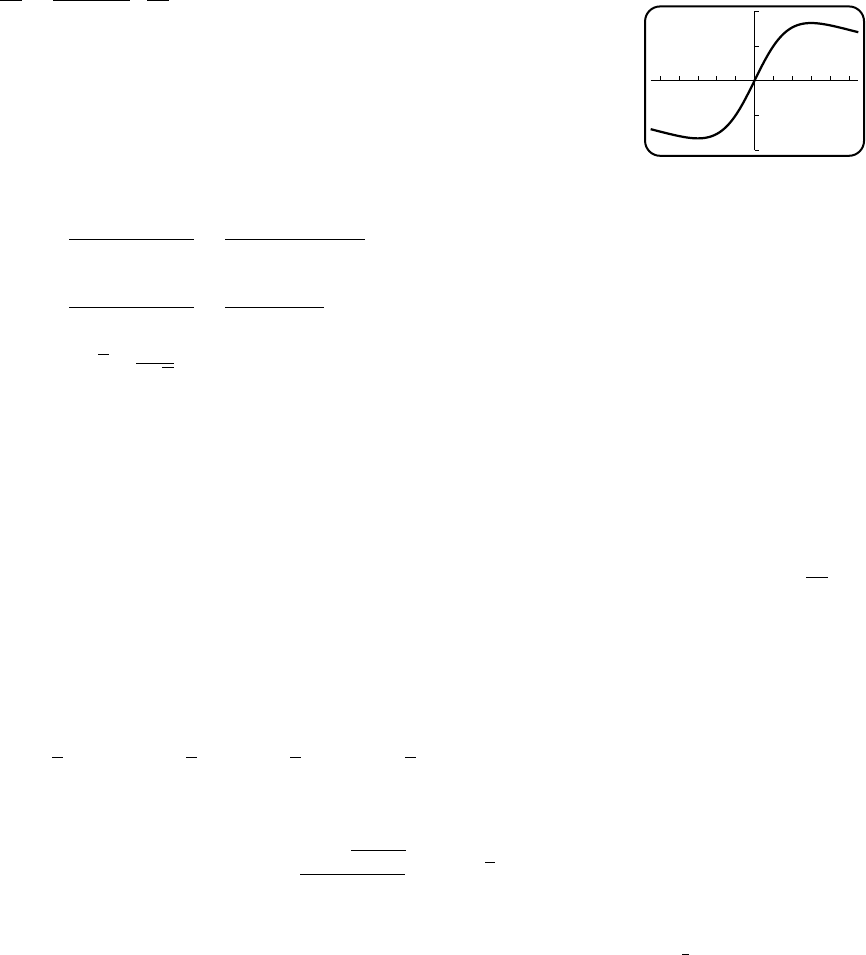
Exercise Set 3.3 76
52. dy
dx =9−x2
(x2+9)
2;dy
dx = 0 when x2=9sox=±3. The points are
(3,1/6) and (−3,−1/6).
0.2
-0.2
-5.5 5.5
53. f0(1) ≈f(1.01) −f(1)
0.01 =0.999699 −(−1)
0.01 =0.0301, and by differentiation, f0(1) = 3(1)2−3=0
54. f0(1) ≈f(1.01) −f(1)
0.01 =1.01504 −1
0.01 =1.504, and by differentiation,
f0(1) = µ√x+x
2√x¶¯¯¯x=1 =1.5
55. f0(1)=0 56. f0(1)=1
57. The y-intercept is −2 so the point (0,−2) is on the graph; −2=a(0)2+b(0) + c,c=−2. The
x-intercept is 1 so the point (1,0) is on the graph; 0 = a+b−2. The slope is dy/dx =2ax +b;at
x= 0 the slope is bso b=−1, thus a= 3. The function is y=3x
2−x−2.
58. Let P(x0,y
0) be the point where y=x2+kis tangent to y=2x. The slope of the curve is dy
dx =2x
and the slope of the line is 2 thus at P,2x
0=2sox
0= 1. But Pis on the line, so y0=2x
0=2.
Because Pis also on the curve we get y0=x2
0+kso k=y0−x2
0=2−(1)2=1.
59. The points (−1,1) and (2,4) are on the secant line so its slope is (4 −1)/(2 + 1) = 1. The slope of
the tangent line to y=x2is y0=2xso 2x=1,x=1/2.
60. The points (1,1) and (4,2) are on the secant line so its slope is 1/3. The slope of the tangent line to
y=√xis y0=1/(2√x)so1/(2√x)=1/3, 2√x=3,x=9/4.
61. y0=−2x,soatanypoint(x
0
,y
0)ony=1−x
2the tangent line is y−y0=−2x0(x−x0), or
y=−2x0x+x2
0+ 1. The point (2,0) is to be on the line, so 0 = −4x0+x2
0+1, x
2
0−4x
0+1=0. Use
the quadratic formula to get x0=4±√16 −4
2=2±√
3.
62. Let P1(x1,ax
2
1) and P2(x2,ax
2
2) be the points of tangency. y0=2ax so the tangent lines at P1and P2
are y−ax2
1=2ax1(x−x1) and y−ax2
2=2ax2(x−x2). Solve for xto get x=1
2(x1+x2) which is the
x-coordinate of a point on the vertical line halfway between P1and P2.
63. y0=3ax2+b; the tangent line at x=x0is y−y0=(3ax2
0+b)(x−x0) where y0=ax3
0+bx0. Solve
with y=ax3+bx to get
(ax3+bx)−(ax3
0+bx0)=(3ax2
0+b)(x−x0)
ax3+bx −ax3
0−bx0=3ax2
0x−3ax3
0+bx −bx0
x3−3x2
0x+2x
3
0=0
(x−x
0
)(x2+xx0−2x2
0)=0
(x−x
0)
2(x+2x
0
)=0,so x=−2x0.
64. Let (x0,y
0) be the point of tangency. Refer to the solution to Exercise 65 to see that the endpoints of
the line segment are at (2x0,0) and (0,2y0), so (x0,y
0) is the midpoint of the segment.
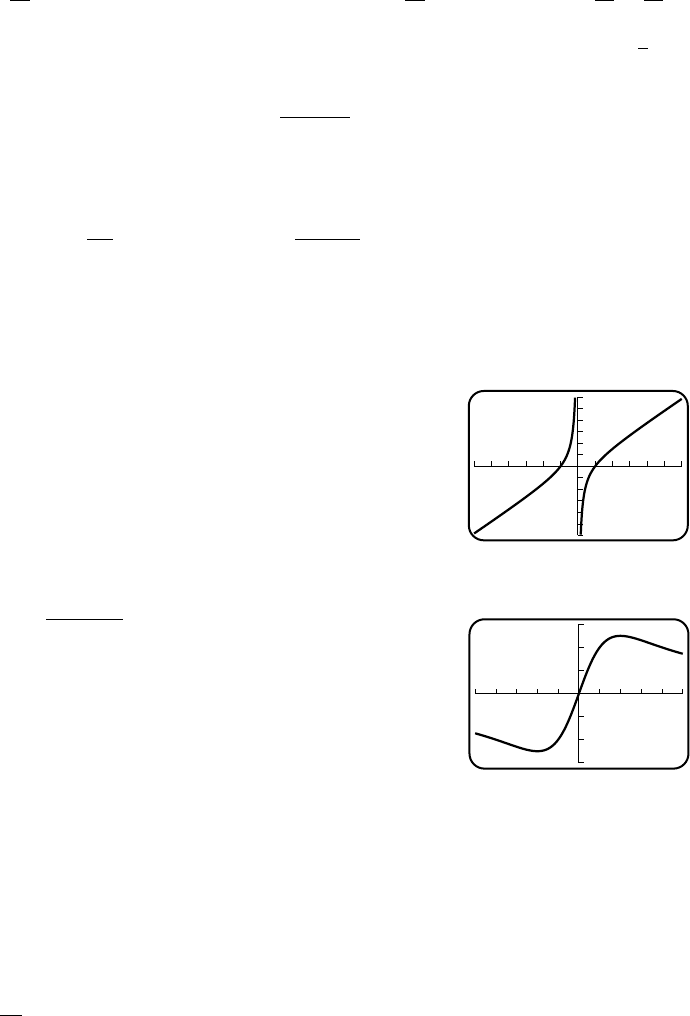
77 Chapter 3
65. y0=−1
x2; the tangent line at x=x0is y−y0=−1
x2
0
(x−x0), or y=−x
x2
0
+2
x0
. The tangent line
crosses the x-axis at 2x0, the y-axis at 2/x0, so that the area of the triangle is 1
2(2/x0)(2x0)=2.
66. f0(x)=3ax2+2bx +c; there is a horizontal tangent where f0(x) = 0. Use the quadratic formula on
3ax2+2bx +c= 0 to get x=(−b±√
b
2−3ac)/(3a) which gives two real solutions, one real solution,
or none if
(a) b2−3ac > 0(b) b2−3ac =0 (c) b2−3ac < 0
67. F=GmMr−2,dF
dr =−2GmMr−3=−2GmM
r3
68. dR/dT =0.04124 −3.558 ×10−5Twhich decreases as Tincreases from 0 to 700. When T=0,
dR/dT =0.04124 Ω/◦C; when T= 700, dR/dT =0.01633 Ω/◦C. The resistance is most sensitive to
temperature changes at T=0
◦C, least sensitive at T= 700◦C.
69. f0(x)=1+1/x2>0 for all x6
-6 6
-6
70. f0(x)=−5x
2−4
(x
2+4)
2;
f0(x)>0 when x2<4, i.e. on −2<x<2
1.5
-1.5
-5 5
71. (f·g·h)0=[(f·g)·h]
0=(f·g)h
0+h(f·g)
0=(f·g)h
0+h[fg0+f0g]=fgh0+fg0h+f0gh
72. (f1f2···f
n)
0=(f
0
1
f
2···f
n)+(f
1
f0
2···f
n)+···+(f
1
f
2···f0
n)
73. (a) 2(1 + x−1)(x−3+7)+(2x+ 1)(−x−2)(x−3+7)+(2x+ 1)(1 + x−1)(−3x−4)
(b) (x7+2x−3)3=(x
7+2x−3)(x7+2x−3)(x7+2x−3) so
d
dx(x7+2x−3)3=(7x
6+ 2)(x7+2x−3)(x7+2x−3)
+(x7+2x−3)(7x6+ 2)(x7+2x−3)
+(x7+2x−3)(x7+2x−3)(7x6+2)
= 3(7x6+ 2)(x7+2x−3)2
74. (a) −5x−6(x2+2x)(4 −3x)(2x9+1)+x
−5
(2x+ 2)(4 −3x)(2x9+1)
+x
−5
(x
2+2x)(−3)(2x9+1)+x
−5
(x
2+2x)(4 −3x)(18x8)

Exercise Set 3.3 78
(b) (x2+1)
50 =(x
2+ 1)(x2+1)···(x
2+ 1), where (x2+ 1) occurs 50 times so
d
dx(x2+1)
50 = [(2x)(x2+1)···(x
2+1)]+[(x
2+ 1)(2x)···(x
2+ 1)]
+···+[(x
2+ 1)(x2+1)···(2x)]
=2x(x
2+1)
49 +2x(x
2+1)
49 +···+2x(x
2+1)
49
= 100x(x2+1)
49 because 2x(x2+1)
49 occurs 50 times.
75. fis continuous at 1 because lim
x→1−f(x) = lim
x→1+f(x)=f(1), also lim
x→1−f0(x) = lim
x→1−2x= 2 and
lim
x→1+f0(x) = lim
x→1+
1
2√x=1
2so fis not differentiable at 1.
76. fis continuous at 1/2 because lim
x→1/2−f(x) = lim
x→1/2+f(x)=f(1/2), also
lim
x→1/2−f0(x) = lim
x→1/2−3x2=3/4 and lim
x→1/2+f0(x) = lim
x→1/2+3x/2=3/4sof
0
(1/2)=3/4.
77. If fis differentiable at x= 1, then fis continuous there;
lim
x→1+f(x) = lim
x→1−f(x)=f(1)=3,a+b= 3; lim
x→1+f0(x)=aand
lim
x→1−f0(x)=6soa= 6 and b=3−6=−3.
78. (a) lim
x→0−f0(x) = lim
x→0−2x= 0 and lim
x→0+f0(x) = lim
x→0+2x=0;f
0
(0) does not exist because fis not
continuous at x=0.
(b) lim
x→0−f0(x) = lim
x→0+f0(x)=0andfis continuous at x=0,sof
0(0)=0;
lim
x→0−f00(x) = lim
x→0−(2) = 2 and lim
x→0+f00(x) = lim
x→0+6x=0,sof
00(0) does not exist.
79. (a) f(x)=3x−2ifx≥2/3, f(x)=−3x+2 if x<2/3sofis differentiable everywhere except
perhaps at 2/3. fis continuous at 2/3, also lim
x→2/3−f0(x) = lim
x→2/3−(−3)=−3 and lim
x→2/3+f0(x)=
lim
x→2/3+(3) = 3 so fis not differentiable at x=2/3.
(b) f(x)=x
2−4if|x|≥2, f(x)=−x
2+4 if |x|<2sofis differentiable everywhere except
perhaps at ±2. fis continuous at −2 and 2, also lim
x→2−f0(x) = lim
x→2−(−2x)=−4 and lim
x→2+f0(x)=
lim
x→2+(2x)=4sofis not differentiable at x= 2. Similarly, fis not differentiable at x=−2.
80. (a) f0(x)=−(1)x−2,f00(x)=(2·1)x−3,f000(x)=−(3 ·2·1)x−4
f(n)(x)=(−1)nn(n−1)(n−2) ···1
x
n+1
(b) f0(x)=−2x
−3
,f
00(x)=(3·2)x−4,f000(x)=−(4 ·3·2)x−5
f(n)(x)=(−1)n(n+ 1)(n)(n−1) ···2
x
n+2
81. (a) d2
dx2[cf(x)] = d
dx ·d
dx[cf (x)]¸=d
dx ·cd
dx[f(x)]¸=cd
dx ·d
dx[f(x)]¸=cd2
dx2[f(x)]
d2
dx2[f(x)+g(x)] = d
dx ·d
dx[f(x)+g(x)]¸=d
dx ·d
dx[f(x)] + d
dx[g(x)]¸=d2
dx2[f(x)] + d2
dx2[g(x)]
(b) yes, by repeated application of the procedure illustrated in part (a)
82. (f·g)0=fg0+gf0,(f·g)00 =fg00 +g0f0+gf00 +f0g0=f00g+2f0g
0+fg00
83. (a) f0(x)=nxn−1,f00(x)=n(n−1)xn−2,f000(x)=n(n−1)(n−2)xn−3,...,
f(n)(x)=n(n−1)(n−2) ···1
(b) from part (a), f(k)(x)=k(k−1)(k−2) ···1sof
(k+1)(x) = 0 thus f(n)(x)=0ifn>k
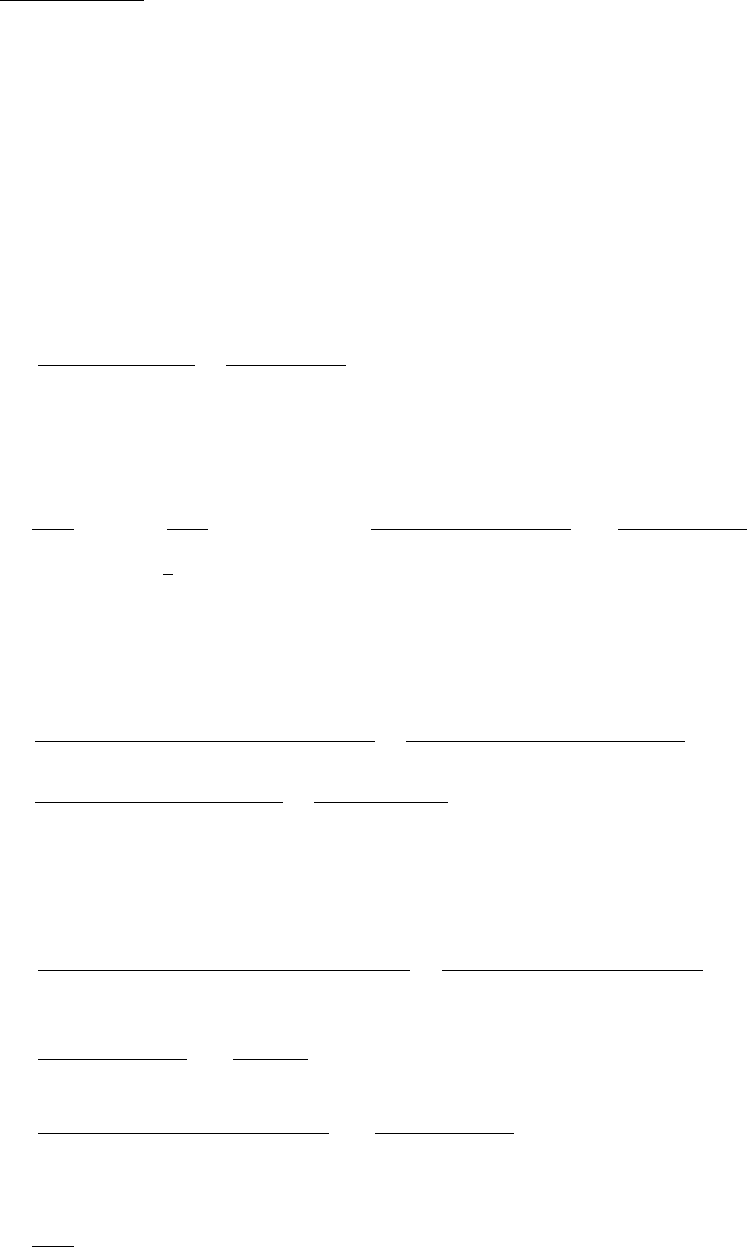
79 Chapter 3
(c) from parts (a) and (b), f(n)(x)=a
n
n(n−1)(n−2) ···1
84. lim
h→0
f0(2+h)−f0(2)
h=f00(2); f0(x)=8x
7−2, f00(x)=56x
6
,sof
00(2) = 56(26) = 3584.
85. (a) If a function is differentiable at a point then it is continuous at that point, thus f0is continuous
on (a, b) and consequently so is f.
(b) fand all its derivatives up to f(n−1)(x) are continuous on (a, b)
EXERCISE SET 3.4
1. f0(x)=−2 sin x−3 cos x
2. f0(x) = sin x(−sin x) + cos x(cos x) = cos2x−sin2x= cos 2x
3. f0(x)=x(cos x)−sin x(1)
x2=xcos x−sin x
x2
4. f0(x)=x
2
(−sin x) + (cos x)(2x)=−x
2sin x+2xcos x
5. f0(x)=x
3
(cos x) + (sin x)(3x2)−5(−sin x)=x
3cos x+(3x
2+ 5) sin x
6. f(x)=cot x
x(because cos x
sin x= cot x), f0(x)= x(−csc2x)−(cot x)(1)
x2=−xcsc2x+ cot x
x2
7. f0(x) = sec xtan x−√2 sec2x
8. f0(x)=(x
2+ 1) sec xtan x+ (sec x)(2x)=(x
2+ 1) sec xtan x+2xsec x
9. f0(x) = sec x(sec2x) + (tan x)(sec xtan x) = sec3x+ sec xtan2x
10. f0(x)= (1 + tan x)(sec xtan x)−(sec x)(sec2x)
(1 + tan x)2=sec xtan x+ sec xtan2x−sec3x
(1 + tan x)2
=sec x(tan x+ tan2x−sec2x)
(1 + tan x)2=sec x(tan x−1)
(1 + tan x)2
11. f0(x) = (csc x)(−csc2x) + (cot x)(−csc xcot x)=−csc3x−csc xcot2x
12. f0(x)=1+4cscxcot x−2 csc2x
13. f0(x)=(1 + csc x)(−csc2x)−cot x(0 −csc xcot x)
(1 + csc x)2=csc x(−csc x−csc2x+ cot2x)
(1 + csc x)2but
1 + cot2x= csc2x(identity) thus cot2x−csc2x=−1so
f
0
(x)= csc x(−csc x−1)
(1 + csc x)2=−csc x
1 + csc x
14. f0(x)=tan x(−csc xcot x)−csc x(sec2x)
tan2x=−csc x(1 + sec2x)
tan2x
15. f(x) = sin2x+ cos2x= 1 (identity) so f0(x)=0
16. f(x)= 1
cot x= tan x,sof
0
(x) = sec2x
Exercise Set 3.4 80
17. f(x)= tan x
1+xtan x(because sin xsec x= (sin x)(1/cos x) = tan x),
f0(x)= (1+xtan x)(sec2x)−tan x[x(sec2x) + (tan x)(1)]
(1+xtan x)2
=sec2x−tan2x
(1+xtan x)2=1
(1+xtan x)2(because sec2x−tan2x=1)
18. f(x)= (x
2+ 1) cot x
3−cot x(because cos xcsc x= (cos x)(1/sin x) = cot x),
f0(x)= (3 −cot x)[2xcot x−(x2+ 1) csc2x]−(x2+ 1) cot xcsc2x
(3 −cot x)2
=6xcot x−2xcot2x−3(x2+ 1) csc2x
(3 −cot x)2
19. dy/dx =−xsin x+ cos x,d2y/dx2=−xcos x−sin x−sin x=−xcos x−2 sin x
20. dy/dx =−csc xcot x,d2y/dx2=−[(csc x)(−csc2x) + (cot x)(−csc xcot x)] = csc3x+ csc xcot2x
21. dy/dx =x(cos x) + (sin x)(1) −3(−sin x)=xcos x+ 4 sin x,
d2y/dx2=x(−sin x) + (cos x)(1) + 4 cos x=−xsin x+ 5 cos x
22. dy/dx =x2(−sin x) + (cos x)(2x)+4cosx=−x
2sin x+2xcos x+ 4 cos x,
d2y/dx2=−[x2(cos x) + (sin x)(2x)]+2[x(−sin x) + cos x]−4 sin x=(2−x
2
) cos x−4(x+ 1) sin x
23. dy/dx = (sin x)(−sin x) + (cos x)(cos x) = cos2x−sin2x,
d2y/dx2= (cos x)(−sin x) + (cos x)(−sin x)−[(sin x)(cos x) + (sin x)(cos x)] = −4 sin xcos x
24. dy/dx = sec2x;d2y/dx2= 2 sec2xtan x
26. Let f(x) = sin x, then f0(x) = cos x.
(a) f(0) = 0 and f0(0) = 1 so y−0 = (1)(x−0), y=x
(b) f(π)=0andf
0(π)=−1soy−0=(−1)(x−π), y=−x+π
(c) f³π
4´=1
√2and f0³π
4´=1
√2so y−1
√2=1
√2³x−π
4´,y=1
√2x−π
4√2+1
√2
27. Let f(x) = tan x, then f0(x) = sec2x.
(a) f(0) = 0 and f0(0) = 1 so y−0 = (1)(x−0), y=x.
(b) f³π
4´= 1 and f0³π
4´=2soy−1=2³x−π
4´,y=2x−π
2+1.
(c) f³−π
4´=−1 and f0³−π
4´=2soy+1=2³x+π
4´,y=2x+π
2−1.
28. (a) If y= cos xthen y0=−sin xand y00 =−cos xso y00 +y=(−cos x) + (cos x)=0;
if y= sin xthen y0= cos xand y00 =−sin xso y00 +y=(−sin x) + (sin x)=0.
(b) y0=Acos x−Bsin x,y00 =−Asin x−Bcos xso
y00 +y=(−Asin x−Bcos x)+(Asin x+Bcos x)=0.
29. (a) f0(x) = cos x=0atx=±π/2,±3π/2.
(b) f0(x)=1−sin x=0atx=−3π/2,π/2.
(c) f0(x) = sec2x≥1 always, so no horizontal tangent line.
(d) f0(x) = sec xtan x= 0 when sin x=0,x=±2π, ±π, 0

81 Chapter 3
30. (a) 0.5
-0.5
02p
(b) y= sin xcos x=(1/2) sin 2xand y0= cos 2x.Soy
0= 0 when 2x=(2n+1)π/2 for n=0,1,2,3
or x=π/4,3π/4,5π/4,7π/4
31. x= 10 sin θ,dx/dθ = 10 cos θ;ifθ=60
◦, then
dx/dθ = 10(1/2) = 5 ft/rad = π/36 ft/deg ≈0.087 ft/deg
32. s= 3800 csc θ, ds/dθ =−3800 csc θcot θ;ifθ=30
◦, then
ds/dθ =−3800(2)(√3) = −7600√3 ft/rad = −380√3π/9 ft/deg ≈−230 ft/deg
33. D= 50 tan θ, dD/dθ = 50 sec2θ;ifθ=45
◦, then
dD/dθ = 50(√2)2= 100 m/rad = 5π/9m/deg ≈1.75 m/deg
34. (a) From the right triangle shown, sin θ=r/(r+h)sor+h=rcsc θ,h=r(csc θ−1).
(b) dh/dθ =−rcsc θcot θ;ifθ=30
◦, then
dh/dθ =−6378(2)(√3) ≈−22,094 km/rad ≈−386 km/deg
35. (a) d4
dx4sin x= sin x,so d
4k
dx4ksin x= sin x;d87
dx87 sin x=d3
dx3
d4·21
dx4·21 sin x=d3
dx3sin x=−cos x
(b) d100
dx100 cos x=d4k
dx4kcos x= cos x
36. d
dx[xsin x]=xcos x+ sin xd2
dx2[xsin x]=−xsin x+ 2 cos x
d3
dx3[xsin x]=−xcos x−3 sin xd4
dx4[xsin x]=xsin x−4 cos x
By mathematical induction one can show
d4k
dx4k[xsin x]=xsin x−(4k) cos x;d4k+1
dx4k+1 [xsin x]=xcos x+(4k+ 1) sin x;
d4k+2
dx4k+2 [xsin x]=−xsin x+(4k+ 2) cos x;d4k+3
dx4k+3 [xsin x]=−xcos x−(4k+ 3) sin x;
Since 17 = 4 ·4+1, d
17
dx17 [xsin x]=xcos x+ 17 sin x
37. (a) all x(b) all x
(c) x6=π/2+nπ,n=0,±1,±2,... (d) x6=nπ,n=0,±1,±2,...
(e) x6=π/2+nπ,n=0,±1,±2,... (f) x6=nπ,n=0,±1,±2,...
(g) x6=(2n+1)π,n=0,±1,±2,... (h) x6=nπ/2, n=0,±1,±2,...
(i) all x
Exercise Set 3.5 82
38. (a) d
dx[cos x] = lim
h→0
cos(x+h)−cos x
h= lim
h→0
cos xcos h−sin xsin h−cos x
h
= lim
h→0·cos xµcos h−1
h¶−sin xµsin h
h¶¸= (cos x)(0) −(sin x)(1) = −sin x
(b) d
dx[sec x]= d
dx ·1
cos x¸=cos x(0) −(1)(−sin x)
cos2x=sin x
cos2x= sec xtan x
(c) d
dx[cot x]= d
dx hcos x
sin xi=sin x(−sin x)−cos x(cos x)
sin2x
=−sin2x−cos2x
sin2x=−1
sin2x=−csc2x
(d) d
dx[csc x]= d
dx ·1
sin x¸=sin x(0) −(1)(cos x)
sin2x=−cos x
sin2x=−csc xcot x
39. f0(x)=−sin x,f00(x)=−cos x,f000(x) = sin x, and f(4)(x) = cos xwith higher order derivatives
repeating this pattern, so f(n)(x) = sin xfor n=3,7,11,...
40. (a) lim
h→0
tan h
h= lim
h→0µsin h
cos h¶
h= lim
h→0µsin h
h¶
cos h=1
1=1
(b) d
dx[tan x] = lim
h→0
tan(x+h)−tan x
h= lim
h→0
tan x+ tan h
1−tan xtan h−tan x
h
= lim
h→0
tan x+ tan h−tan x+ tan2xtan h
h(1 −tan xtan h)= lim
h→0
tan h(1 + tan2x)
h(1 −tan xtan h)
= lim
h→0
tan hsec2x
h(1 −tan xtan h)= sec2xlim
h→0
tan h
h
1−tan xtan h
= sec2x
lim
h→0
tan h
h
lim
h→0(1 −tan xtan h)= sec2x
41. lim
x→0
tan(x+y)−tan y
x= lim
h→0
tan(y+h)−tan y
h=d
dy (tan y) = sec2y
43. Let tbe the radian measure, then h=180
πtand cos h= cos t, sin h= sin t.
(a) lim
h→0
cos h−1
h= lim
t→0
cos t−1
180t/π =π
180 lim
t→0
cos t−1
t=0
(b) lim
h→0
sin h
h= lim
t→0
sin t
180t/π =π
180 lim
t→0
sin t
t=π
180
(c) d
dx[sin x] = sin xlim
h→0
cos h−1
h+ cos xlim
h→0
sin h
h= sin x(0) + cos x(π/180) = π
180 cos x
EXERCISE SET 3.5
1. f0(x) = 37(x3+2x)
36 d
dx(x3+2x) = 37(x3+2x)
36(3x2+2)
2. f0(x) = 6(3x2+2x−1)5d
dx(3x2+2x−1) = 6(3x2+2x−1)5(6x+ 2) = 12(3x2+2x−1)5(3x+1)
83 Chapter 3
3. f0(x)=−2µx
3−7
x
¶
−3d
dx µx3−7
x¶=−2µx3−7
x¶−3µ3x2+7
x2¶
4. f(x)=(x
5−x+1)
−9
,
f0(x)=−9(x5−x+1)
−10 d
dx(x5−x+1)=−9(x5−x+1)
−10(5x4−1) = −9(5x4−1)
(x5−x+1)
10
5. f(x) = 4(3x2−2x+1)
−3
,
f0(x)=−12(3x2−2x+1)
−4d
dx(3x2−2x+1)=−12(3x2−2x+1)
−4
(6x−2) = 24(1 −3x)
(3x2−2x+1)
4
6. f0(x)= 1
2
√
x
3−2x+5
d
dx(x3−2x+5)= 3x
2−2
2
√
x
3−2x+5
7. f0(x)= 1
2
p4+3
√
x
d
dx(4+3
√
x)= 3
4
√
x
p4+3
√
x
8. f0(x)=3sin
2xd
dx(sin x)=3sin
2xcos x
9. f0(x) = cos(x3)d
dx(x3)=3x
2cos(x3)
10. f0(x) = 2 cos(3√x)d
dx[cos(3√x)] = −2 cos(3√x) sin(3√x)d
dx(3√x)=−3 cos(3√x) sin(3√x)
√x
11. f0(x) = sec2(4x2)d
dx(4x2)=8xsec2(4x2)
12. f0(x)=12cot
3xd
dx(cot x)=12cot
3x(−csc2x)=−12 cot3xcsc2x
13. f0(x)=20cos
4xd
dx(cos x)=20cos
4x(−sin x)=−20 cos4xsin x
14. f0(x)=−csc(x3) cot(x3)d
dx(x3)=−3x
2csc(x3) cot(x3)
15. f0(x) = cos(1/x2)d
dx(1/x2)=−2
x
3cos(1/x2)
16. f0(x)=4tan
3
(x
3
)d
dx[tan(x3)] = 4 tan3(x3) sec2(x3)d
dx(x3)=12x
2tan3(x3) sec2(x3)
17. f0(x) = 4 sec(x7)d
dx[sec(x7)] = 4 sec(x7) sec(x7) tan(x7)d
dx(x7)=28x
6sec2(x7) tan(x7)
18. f0(x)=3cos
2µx
x+1¶d
dx cos µx
x+1¶= 3 cos2µx
x+1¶·−sin µx
x+1¶¸(x+ 1)(1) −x(1)
(x+1)
2
=−3
(x+1)
2cos2µx
x+1¶sin µx
x+1¶
19. f0(x)= 1
2
pcos(5x)
d
dx[cos(5x)] = −5 sin(5x)
2pcos(5x)
20. f0(x)= 1
2
p3x−sin2(4x)
d
dx[3x−sin2(4x)] = 3−8 sin(4x) cos(4x)
2p3x−sin2(4x)
Exercise Set 3.5 84
21. f0(x)=−3£x+ csc(x3+3)
¤−4d
dx £x+ csc(x3+3)
¤
=−3£x+ csc(x3+3)
¤−4·1−csc(x3+ 3) cot(x3+3) d
dx(x3+3)
¸
=−3£x+ csc(x3+3)
¤−4£1−3x
2csc(x3+ 3) cot(x3+3)
¤
22. f0(x)=−4£x
4−sec(4x2−2)¤−5d
dx £x4−sec(4x2−2)¤
=−4£x4−sec(4x2−2)¤−5·4x3−sec(4x2−2) tan(4x2−2) d
dx(4x2−2)¸
=−16x£x4−sec(4x2−2)¤−5£x2−2 sec(4x2−2) tan(4x2−2)¤
23. f0(x)=x
2·−2x
2
√
5−x
2+2x
p5−x
2=x(10 −3x2)
√5−x2
24. f0(x)=√
1−x
2
(1) −x(−x/√1−x2)
1−x2=1
(1 −x2)3/2
25. dy
dx =x3(2 sin 5x)d
dx(sin 5x)+3x
2sin25x=10x
3sin 5xcos 5x+3x
2sin25x
26. dy
dx =√x·3 tan2(√x) sec2(√x)1
2√x¸+1
2√xtan3(√x)=3
2tan2(√x) sec2(√x)+ 1
2
√
xtan3(√x)
27. dy
dx =x5sec µ1
x¶tan µ1
x¶d
dx µ1
x¶+ sec µ1
x¶(5x4)=x
5sec µ1
x¶tan µ1
x¶µ−1
x
2¶+5x
4sec µ1
x¶
=−x3sec µ1
x¶tan µ1
x¶+5x
4sec µ1
x¶
28. dy
dx =sec(3x+ 1) cos x−3 sin xsec(3x+ 1) tan(3x+1)
sec2(3x+1) =cos x−3 sin xtan(3x+1)
sec(3x+1)
29. dy
dx =−sin(cos x)d
dx(cos x)=−sin(cos x)(−sin x) = sin(cos x) sin x
30. dy
dx = cos(tan 3x)d
dx(tan 3x)=3sec
23xcos(tan 3x)
31. dy
dx = 3 cos2(sin 2x)d
dx[cos(sin 2x)] = 3 cos2(sin 2x)[−sin(sin 2x)] d
dx(sin 2x)
=−6 cos2(sin 2x) sin(sin 2x) cos 2x
32. dy
dx =(1 −cot x2)(−2xcsc x2cot x2)−(1 + csc x2)(2xcsc2x2)
(1 −cot x2)2=−2xcsc x21 + cot x2csc x2
(1 −cot x2)2
33. dy
dx =(5x+8)
1312(x3+7x)
11 d
dx(x3+7x)+(x
3+7x)
1213(5x+8)
12 d
dx(5x+8)
= 12(5x+8)
13(x3+7x)
11(3x2+7)+65(x
3+7x)
12(5x+8)
12
34. dy
dx =(2x−5)23(x2+4)
2
(2x)+(x
2+4)
3
2(2x−5)(2) = 6x(2x−5)2(x2+4)
2+ 4(2x−5)(x2+4)
3
= 2(2x−5)(x2+4)
2
(8x2−15x+8)
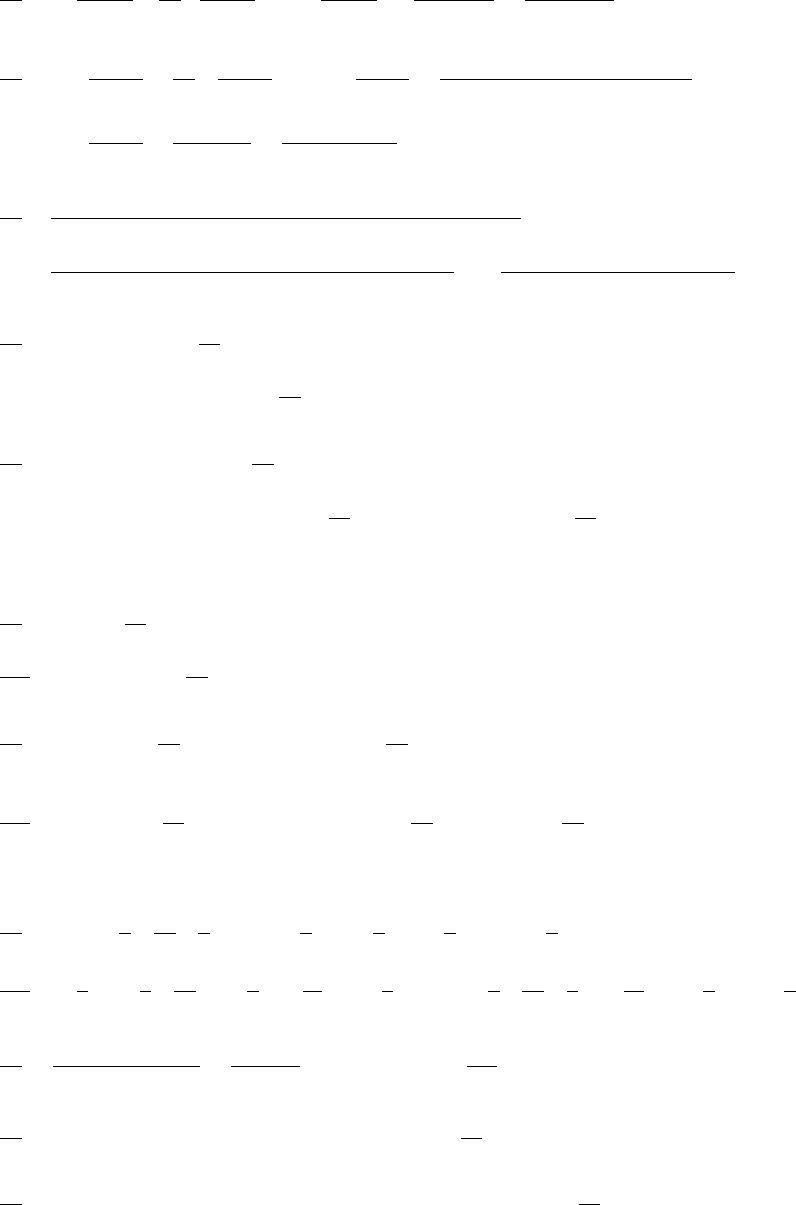
85 Chapter 3
35. dy
dx =3·x−5
2x+1¸2d
dx ·x−5
2x+1¸=3·x−5
2x+1¸2
·11
(2x+1)
2=33(x−5)2
(2x+1)
4
36. dy
dx =17µ1+x
2
1−x
2¶
16 d
dx µ1+x
2
1−x
2¶=17µ1+x
2
1−x
2¶
16 (1 −x2)(2x)−(1+x2)(−2x)
(1 −x2)2
=17µ1+x
2
1−x
2¶
16 4x
(1 −x2)2=68x(1+x2)16
(1 −x2)18
37. dy
dx =(4x2−1)8(3)(2x+3)
2
(2) −(2x+3)
3
(8)(4x2−1)7(8x)
(4x2−1)16
=2(2x+3)
2
(4x2−1)7[3(4x2−1) −32x(2x+ 3)]
(4x2−1)16 =−2(2x+3)
2
(52x2+96x+3)
(4x2−1)9
38. dy
dx = 12[1 + sin3(x5)]11 d
dx[1 + sin3(x5)]
= 12[1 + sin3(x5)]113 sin2(x5)d
dx sin(x5) = 180x4[1 + sin3(x5)]11 sin2(x5) cos(x5)
39. dy
dx =5£xsin 2x+ tan4(x7)¤4d
dx £xsin 2xtan4(x7)¤
=5£xsin 2x+ tan4(x7)¤4·xcos 2xd
dx(2x) + sin 2x+ 4 tan3(x7)d
dx tan(x7)¸
=5£xsin 2x+ tan4(x7)¤4£2xcos 2x+ sin 2x+28x
6tan3(x7) sec2(x7)¤
40. dy
dx = cos(3x2)d
dx(3x2)=6xcos(3x2),
d2y
dx2=6x(−sin(3x2)) d
dx(3x2) + 6 cos(3x2)=−36x2sin(3x2) + 6 cos(3x2)
41. dy
dx =x(−sin(5x)) d
dx(5x) + cos(5x)−2 sin xd
dx(sin x)
=−5xsin(5x) + cos(5x)−2 sin xcos x=−5xsin(5x) + cos(5x)−sin(2x),
d2y
dx2=−5xcos(5x)d
dx(5x)−5 sin(5x)−sin(5x)d
dx(5x)−cos(2x)d
dx(2x)
=−25xcos(5x)−10 sin(5x)−2 cos(2x)
42. dy
dx =xsec2µ1
x¶d
dx µ1
x¶+ tan µ1
x¶=−1
xsec2µ1
x¶+ tan µ1
x¶,
d2y
dx2=−2
xsec µ1
x¶d
dx sec µ1
x¶+1
x2sec2µ1
x¶+ sec2µ1
x¶d
dx µ1
x¶=2
x3sec2µ1
x¶tan µ1
x¶
43. dy
dx =(1 −x)+(1+x)
(1 −x)2=2
(1 −x)2= 2(1 −x)−2and d2y
dx2=−2(2)(−1)(1 −x)−3= 4(1 −x)−3
45. dy
dx =−3xsin 3x+ cos 3x;ifx=πthen y=−πand dy
dx =−1soy+π=−(x−π), y=−x
46. dy
dx =3x
2cos(1 + x3); if x=−3 then y= sin(−26) = −sin 26 and dy
dx = 27 cos 26
so y+ sin 26 = 27(cos 26)(x+3)
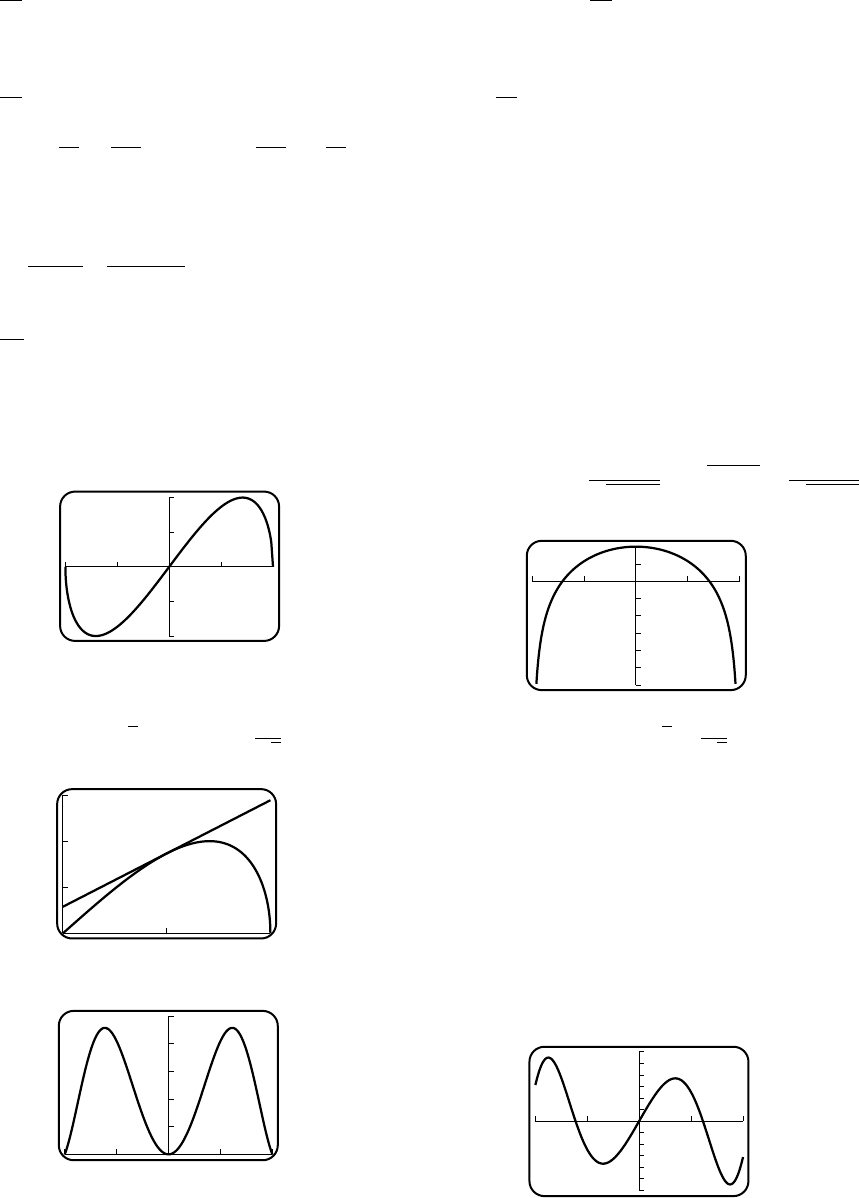
Exercise Set 3.5 86
47. dy
dx =−3 sec3(π/2−x) tan(π/2−x); if x=−π/2 then y=−1 and dy
dx =0
so y+ 1 = (0)(x+π/2), y=−1
48. dy
dx =3(x−1/x)2(1+1/x2); if x= 2 then y=27/8 and dy
dx = 135/16
so y−27
8=135
16 (x−2), y=135
16 x−27
2
49. y= cot3(π−θ)=−cot3θso dy/dx = 3 cot2θcsc2θ
50. 6µau +b
cu +d¶5ad −bc
(cu +d)2
51. d
dω [acos2πω +bsin2πω]=−2πa cos πω sin πω +2πb sin πω cos πω
=π(b−a)(2 sin πω cos πω)=π(b−a) sin 2πω
52. 2 csc2(π/3−y) cot(π/3−y)
53. (a) 2
-2 2
-2
(c) f0(x)=x−x
√
4−x
2+p4−x
2=4−2x
2
√
4−x
2
2
-2 2
-6
(d) f(1) = √3 and f0(1) = 2
√3so the tangent line has the equation y−√3= 2
√
3
(x−1).
3
0
02
54. (a) 0.5
0
^6
(c) f0(x)=2xcos x2cos x−sin xsin x2
1.2
-1.2
^6

87 Chapter 3
(d) f(1) = sin 1 cos 1 and f0(1) = 2 cos21−sin21, so the tangent line has the equation
y−sin 1 cos 1 = (2 cos21−sin21)(x−1).
0.8
0
^6
55. (a) dy/dt =−Aω sin ωt, d2y/dt2=−Aω2cos ωt =−ω2y
(b) one complete oscillation occurs when ωt increases over an interval of length 2π,oriftincreases
over an interval of length 2π/ω
(c) f=1/T
(d) amplitude = 0.6 cm, T=2π/15 s/oscillation, f=15/(2π) oscillations/s
56. dy/dt =3Acos 3t, d2y/dt2=−9Asin 3t,so−9Asin 3t+2Asin 3t= 4 sin 3t,
−7Asin 3t= 4 sin 3t, −7A=4,A=−4/7
57. (a) p≈10 lb/in2,dp/dh ≈−2 lb/in2/mi
(b) dp
dt =dp
dh
dh
dt ≈(−2)(0.3) = −0.6 lb/in2/s
58. (a) F=45
cos θ+0.3 sin θ,dF
dθ =−45(−sin θ+0.3 cos θ)
(cos θ+0.3 sin θ)2;
if θ=30
◦, then dF/dθ ≈10.5 lb/rad ≈0.18 lb/deg
(b) dF
dt =dF
dθ
dθ
dt ≈(0.18)(−0.5) = −0.09 lb/s
59. With u= sin x,d
dx(|sin x|)= d
dx(|u|)= d
du(|u|)du
dx =d
du(|u|) cos x=½cos x, u > 0
−cos x, u < 0
=½cos x, sin x>0
−cos x, sin x<0=½cos x, 0<x<π
−cos x, −π<x<0
60. d
dx(cos x)= d
dx[sin(π/2−x)] = −cos(π/2−x)=−sin x
61. (a) for x6=0,f
0(x)=xµcos 1
x¶µ−1
x
2¶+ sin 1
x=−1
xcos 1
x+ sin 1
x
(b) lim
x→0xsin 1
x=0=f(0)
(c) lim
h→0
f(0+h)−f(0)
h= lim
h→0
hsin 1
h
h= lim
h→0sin 1
h, which does not exist
62. (a) f0(x)=x
2µcos 1
x¶µ−1
x
2¶+2xsin 1
x=−cos 1
x+2xsin 1
x,x6=0
(b) lim
x→0x2sin 1
x=0=f(0)

Exercise Set 3.5 88
(c) f0(0) = lim
h→0
f(0+h)−f(0)
h= lim
h→0
h2sin 1
h
h= lim
h→0hsin 1
h=0
(d) lim
x→0f0(x) does not exist because cos 1
xoscillates between 1 and −1
63. (a) g0(x)=3[f(x)]2f0(x), g0(2)=3[f(2)]2f0(2) = 3(1)2(7)=21
(b) h0(x)=f
0(x
3
)(3x2), h0(2) = f0(8)(12) = (−3)(12) = −36
64. (a) F0(x)=f
0(g(x))g0(x), F0(−1) = f0(g(−1))g0(−1) = f0(2)(−3) = (4)(−3) = −12
(b) G0(x)=g
0(f(x))f0(x), G0(−1) = g0(f(−1))f0(−1) = g0(2)(3) = (−5)(3) = −15
65. (f◦g)0(x)=f
0(g(x))g0(x)so(f◦g)
0
(0) = f0(g(0))g0(0) = f0(0)(3) = (2)(3) = 6
66. F0(x)=f
0(g(x))g0(x)=p3(x2−1) + 4(2x)=2x
√
3x
2+1
67. F0(x)=f
0(g(x))g0(x)=f
0(
√
3x−1) 3
2√3x−1=√3x−1
(3x−1)+1
3
2
√
3x−1=1
2x
68. d
dx[f(x2)] = f0(x2)(2x), thus f0(x2)(2x)=x
2so f0(x2)=x/2ifx6=0
69. d
dx[f(3x)] = f0(3x)d
dx(3x)=3f
0(3x)=6x,sof
0
(3x)=2x. Let u=3xto get f0(u)=2
3
u;
d
dx[f(x)] = f0(x)= 2
3
x.
70. (a) If f(−x)=f(x), then d
dx[f(−x)] = d
dx[f(x)], f0(−x)(−1) = f0(x), f0(−x)=−f
0(x)so
f
0is odd.
(b) If f(−x)=−f(x), then d
dx[f(−x)] = −d
dx[f(x)], f0(−x)(−1) = −f0(x), f0(−x)=f
0(x)so
f
0is even.
71. For an even function, the graph is symmetric about the y-axis; the slope of the tangent line at
(a, f(a)) is the negative of the slope of the tangent line at (−a, f(−a). For an odd function, the graph
is symmetric about the origin; the slope of the tangent line at (a, f(a)) is the same as the slope of the
tangent line at (−a, f(−a).
y
x
f(x)
f'(x)
y
x
f(x)
f'(x)
72. dy
dx =dy
du
du
dv
dv
dw
dw
dx
73. d
dx[f(g(h(x)))] = d
dx[f(g(u))],u=h(x)
=
d
du[f(g(u))] du
dx =f0(g(u))g0(u)du
dx =f0(g(h(x)))g0(h(x))h0(x)
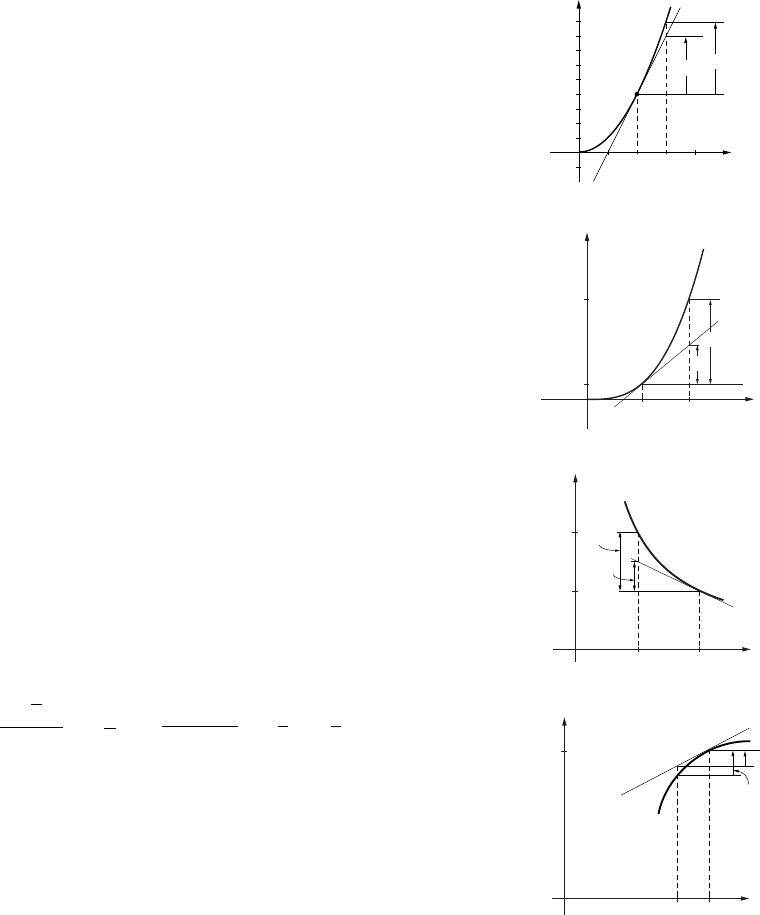
89 Chapter 3
EXERCISE SET 3.6
1. (a) dy =f0(x)dx =2xdx = 4(1) = 4 and
∆y=(x+∆x)
2−x
2=(2+1)
2−2
2=5
(b)
x
y
dy ∆y
4
23
2. (a) dy =3x
2
dx = 3(1)2(1) = 3 and
∆y=(x+∆x)
3−x
3=(1+1)
3−1
3=7
(b)
1
y
x
8
1 2
(1,1) dx
∆y
dy
3. (a) dy =(−1/x2)dx =(−1)(−0.5)=0.5 and
∆y=1/(x+∆x)−1/x =1/(1 −0.5) −1/1=2−1=1
(b) y
x
1
2
0.5 1
dy=0.5
y∆=1
4. (a) dy =(1/2
√
x)dx =(1/(2 ·3))(−1) = −1/6≈−0.167 and
∆y=√x+∆x−√
x=p9+(−1) −√9=√
8−3≈−0.172
(b) y
x
3
89
dy = –0.167
∆y = –0.171
5. dy =3x
2
dx;
∆y=(x+∆x)
3−x
3=x
3+3x
2
∆x+3x(∆x)2+(∆x)
3−x
3=3x
2
∆x+3x(∆x)2+(∆x)
3
6. dy =8dx;∆y= [8(x+∆x)−4] −[8x−4]=8∆x
7. dy =(2x−2)dx;
∆y=[(x+∆x)
2−2(x+∆x)+1]−[x
2−2x+1]
=x
2+2x∆x+(∆x)
2−2x−2∆x+1−x
2+2x−1=2x∆x+(∆x)
2−2∆x
8. dy = cos xdx;∆y= sin(x+∆x)−sin x
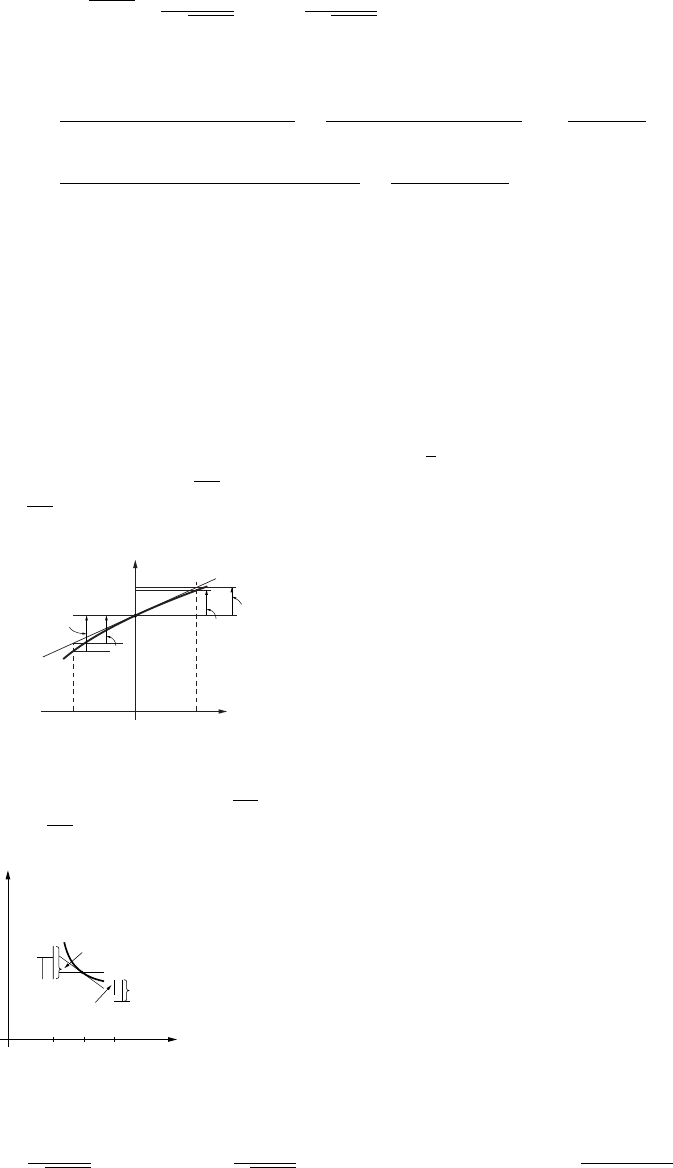
Exercise Set 3.6 90
9. (a) dy = (12x2−14x)dx
(b) dy =xd(cos x) + cos xdx=x(−sin x)dx + cos xdx =(−xsin x+ cos x)dx
10. (a) dy =(−1/x2)dx (b) dy = 5 sec2xdx
11. (a) dy =µ√1−x−x
2√1−x¶dx =2−3x
2√1−xdx
(b) dy =−17(1 + x)−18dx
12. (a) dy =(x3−1)d(0) −(1)d(x3−1)
(x3−1)2=(x3−1)(0) −(1)3x2dx
(x3−1)2=−3x2
(x3−1)2dx
(b) dy =(2 −x)(−3x2)dx −(1 −x3)(−1)dx
(2 −x)2=2x3−6x2+1
(2 −x)2dx
13. (a) f(x)≈f(1) + f0(1)(x−1)=1+3(x−1) (b) f(1+∆x)≈f(1) + f0(1)∆x=1+3∆x
(c) From part (a), (1.02)3≈1 + 3(0.02)=1.06. From part (b), (1.02)3≈1 + 3(0.02)=1.06.
14. (a) f(x)≈f(2) + f0(2)(x−2)=1/2+(−1/2
2
)(x−2)=(1/2) −(1/4)(x−2)
(b) f(2+∆x)≈f(2) + f0(2)∆x=1/2−(1/4)∆x
(c) From part (a), 1/2.05 ≈0.5−0.25(0.05)=0.4875, and from part (b),
1/2.05 ≈0.5−0.25(0.05)=0.4875.
15. (a) f(x)≈f(x0)+f
0
(x
0
)(x−x0) = 1+(1/(2√1)(x−0) = 1+(1/2)x, so with x0= 0 and
x=−0.1, we have √0.9=f(−0.1) ≈1+(1/2)(−0.1)=1−0.05=0.95. With x=0.1 we have
√1.1=f(0.1) ≈1+(1/2)(0.1)=1.05.
(b) y
x
dy
0.1
–0.1
∆y
∆ydy
16. (a) f(x)≈f(x0)+f
0(x
0
)(x−x0)=1/2−£1/(2 ·43/2)¤(x−4)=1/2−(x−4)/16, so with x0=4
and x=3.9wehave1/
√
3.9=f(3.9) ≈0.5−(−0.1)/16=0.50625. If x0= 4 and x=4.1 then
1/√4.1=f(4.1) ≈0.5−(0.1)/16=0.49375
(b)
x
y
43.9 4.1
∆y
∆y
dy
dy
17. f(x)=(1+x)
15 and x0=0. Thus(1+x)
15 ≈f(x0)+f0(x
0
)(x−x0) = 1 + 15(1)14(x−0)=1+15x.
18. f(x)= 1
√
1−xand x0=0,so 1
√
1−x≈f(x
0
)+f0(x
0
)(x−x0)=1+ 1
2(1 −0)3/2(x−0)=1+x/2
91 Chapter 3
19. tan x≈tan(0) + sec2(0)(x−0) = x20. 1
1+x≈1+ −1
(1+0)
2(x−0)=1−x
21. x4≈(1)4+ 4(1)3(x−1). Set ∆x=x−1; then x=∆+1 and(1+∆x)
4=1+4∆x.
22. √x≈√1+ 1
2
√
1(x−1), and x=1+∆x,so√
1+∆x≈1+∆x/2
23. 1
2+x=1
2+1−1
(2+1)
2(x−1), and 2 + x=3+∆x,so 1
3+∆x=1
3−1
9∆x
24. (4+x)3=(4+1)
3+3(4+1)
2
(x−1) so, with 4 + x=5+∆xwe get (5 + ∆x)3= 125 + 75∆x
25. (a) The local linear approximation sin x≈xgives sin 1◦= sin(π/180) ≈π/180=0.0174533 and
a calculator gives sin 1◦=0.0174524. The relative error |sin(π/180) −(π/180)|/(sin π/180) =
0.000051 is very small, so for such a small value of xthe approximation is very good.
(b) Use x0=45
◦(this assumes you know, or can approximate, √2/2).
(c) 44◦=44π
180 radians, and 45◦=45π
180 =π
4radians. With x=44π
180 and x0=π
4we obtain
sin 44◦= sin 44π
180 ≈sin π
4+³cos π
4´µ44π
180 −π
4¶=√2
2+√2
2µ−π
180¶=0.694765. With a
calculator, sin 44◦=0.694658.
26. (a) tan x≈tan 0 + sec20(x−0)=x, so tan 2◦= tan(2π/180) ≈2π/180=0.034907, and with a
calculator tan 2◦=0.034921
(b) use x0=π/3 because we know tan 60◦= tan(π/3) = √3
(c) with x0=π
3=60π
180 and x=61π
180 we have tan 61◦= tan 61π
180 ≈tan π
3+³sec2π
3´µ61π
180 −π
3¶=
√3+4 π
180 =1.8019, and with a calculator tan 61◦=1.8040
27. f(x)=x
4
,f
0(x)=4x
3
,x
0=3,∆x=0.02; (3.02)4≈34+ (108)(0.02)=81+2.16=83.16
28. f(x)=x
3
,f
0(x)=3x
2
,x
0=2,∆x=−0.03; (1.97)3≈23+ (12)(−0.03)=8−0.36=7.64
29. f(x)=√
x,f
0(x)= 1
2
√
x
,x
0= 64, ∆x=1;√
65 ≈√64 + 1
16(1)=8+ 1
16 =8.0625
30. f(x)=√
x,f
0(x)= 1
2
√
x
,x
0= 25, ∆x=−1; √24 ≈√25 + 1
10(−1)=5−0.1=4.9
31. f(x)=√
x,f
0(x)= 1
2
√
x
,x
0= 81, ∆x=−0.1; √80.9≈√81 + 1
18(−0.1) ≈8.9944
32. f(x)=√
x,f
0(x)= 1
2
√
x
,x
0= 36, ∆x=0.03; √36.03 ≈√36 + 1
12(0.03)=6+0.0025 = 6.0025
33. f(x) = sin x,f0(x) = cos x,x0=0,∆x=0.1; sin 0.1≈sin 0 + (cos 0)(0.1)=0.1
34. f(x) = tan x,f0(x) = sec2x,x0=0,∆x=0.2; tan 0.2≈tan 0 + (sec20)(0.2)=0.2
35. f(x) = cos x,f0(x)=−sin x,x0=π/6, ∆x=π/180;
cos 31◦≈cos 30◦+µ−1
2¶³π
180´=√3
2−π
360 ≈0.8573
Exercise Set 3.6 92
36. (a) Let f(x)=(1+x)
kand x0= 0. Then (1 + x)k≈1k+k(1)k−1(x−0)=1+kx. Set k= 37 and
x=0.001 to obtain (1.001)37 ≈1.037.
(b) With a calculator (1.001)37 =1.03767.
(c) The approximation is (1.1)37 ≈1 + 37(0.1)=4.7, and the calculator value is 34.004. The error
is due to the relative largeness of f0(1)∆x= 37(0.1)=3.7.
37. f(x)=√
x+ 3 and x0=0,so
√
x+3≈√
3+ 1
2
√
3(x−0) = √3+ 1
2
√
3x, and
¯¯¯¯
f(x)−µ√3+ 1
2
√
3x
¶¯
¯
¯
¯
<0.1if|x|<1.692.
0
-0.1
-2 2
|
f(x) – ( 3 + x)
|
1
2 3
38. f(x)= 1
√
9−xso 1
√9−x≈1
√9+1
2(9 −0)3/2(x−0) = 1
3+1
54x,
and ¯¯¯¯
f(x)−µ1
3+1
54x¶¯¯¯¯
<0.1if|x|<5.5114
0.06
0
-6 6
|
f(x) – ( + x)
|
1
31
54
39. tan x≈tan 0 + (sec20)(x−0) = x, and |tan x−x|<0.1if
|x|<0.6316
0.06
0
-0.8 0.8
|f(x) – x|
40. 1
(1+2x)
5≈1
(1+2·0)5+−5(2)
(1+2·0)6(x−0)=1−10x, and
|f(x)−(1 −10x)|<0.1if|x|<0.0372
0.06
0
-0.8 0.8
|f(x) – x|
41. dy =3
2√3x−2dx,x=2,dx =0.03; ∆y≈dy =3
4(0.03)=0.0225
42. dy =x
√x2+8dx,x=1,dx =−0.03; ∆y≈dy =(1/3)(−0.03) = −0.01
93 Chapter 3
43. dy =1−x2
(x2+1)
2dx,x=2,dx =−0.04; ∆y≈dy =µ−3
25¶(−0.04)=0.0048
44. dy =µ4x
√8x+1+√
8x+1
¶dx,x=3,dx =0.05; ∆y≈dy = (37/5)(0.05)=0.37
45. (a) A=x2where xis the length of a side; dA =2xdx= 2(10)(±0.1) = ±2ft
2
.
(b) relative error in xis ≈dx
x=±0.1
10 =±0.01 so percentage error in xis ≈±1%; relative error in
Ais ≈dA
A=2xdx
x
2=2
dx
x=2(±0.01) = ±0.02 so percentage error in Ais ≈±2%
46. (a) V=x3where xis the length of a side; dV =3x
2
dx = 3(25)2(±1) = ±1875 cm3.
(b) relative error in xis ≈dx
x=±1
25 =±0.04 so percentage error in xis ≈±4%; relative error in V
is ≈dV
V=3x2dx
x3=3
dx
x=3(±0.04) = ±0.12 so percentage error in Vis ≈±12%
47. (a) x= 10 sin θ,y= 10 cos θ(see figure),
dx = 10 cos θdθ =10¡cos π
6¢¡±π
180 ¢=10³√
3
2´¡±π
180 ¢
≈±0.151 in,
dy =−10(sin θ)dθ =−10 ¡sin π
6¢¡±π
180 ¢=−10 ¡1
2¢¡±π
180 ¢
≈±0.087 in
10″x
y
θ
(b) relative error in xis ≈dx
x= (cot θ)dθ =³cot π
6´³±π
180´=√3³±π
180´≈±0.030
so percentage error in xis ≈±3.0%;
relative error in yis ≈dy
y=−tan θdθ =−³tan π
6´³±π
180´=−1
√3³±π
180´≈±0.010
so percentage error in yis ≈±1.0%
48. (a) x= 25 cot θ,y= 25 csc θ(see figure);
dx =−25 csc2θdθ =−25 ³csc2π
3´³±π
360´
=−25 µ4
3¶³±π
360´≈±0.291 cm,
dy =−25 csc θcot θdθ =−25 ³csc π
3´³cot π
3´³±π
360´
=−25 µ2
√3¶µ1
√3¶³±π
360´≈±0.145 cm
25 cm
x
y
θ
(b) relative error in xis ≈dx
x=−csc2θ
cot θdθ =−4/3
1/√3³±π
360´≈±0.020 so percentage
error in xis ≈±2.0%; relative error in yis ≈dy
y=−cot θdθ =−1
√3³±π
360´≈±0.005
so percentage error in yis ≈±0.5%
49. dR
R=(−2k/r3)dr
(k/r2)=−2dr
r, but dr
r≈±0.05 so dR
R≈−2(±0.05) = ±0.10; percentage error in Ris
≈±10%
50. h= 12 sin θthus dh = 12 cos θdθ so, with θ=60
◦=π/3 radians and dθ =−1◦=−π/180 radians,
dh = 12 cos(π/3)(−π/180) = −π/30 ≈−0.105 ft
Supplementary Exercises 3 94
51. A=1
4(4)2sin 2θ= 4 sin 2θthus dA = 8 cos 2θdθ so, with θ=30
◦=π/6 radians and
dθ =±150=±1/4◦=±π/720 radians, dA = 8 cos(π/3)(±π/720) = ±π/180 ≈±0.017 cm2
52. A=x2where xis the length of a side; dA
A=2xdx
x
2=2
dx
x, but dx
x≈±0.01 so
dA
A≈2(±0.01) = ±0.02; percentage error in Ais ≈±2%
53. V=x3where xis the length of a side; dV
V=3x2dx
x3=3
dx
x, but dx
x≈±0.02
so dV
V≈3(±0.02) = ±0.06; percentage error in Vis ≈±6%.
54. dV
V=4πr2dr
4πr3/3=3
dr
r, but dV
V≈±0.03 so 3dr
r≈±0.03, dr
r≈±0.01; maximum permissible
percentage error in ris ≈±1%.
55. A=1
4πD2where Dis the diameter of the circle; dA
A=(πD/2)dD
πD2/4=2
dD
D, but dA
A≈±0.01 so
2dD
D≈±0.01, dD
D≈±0.005; maximum permissible percentage error in Dis ≈±0.5%.
56. V=x3where xis the length of a side; approximate ∆Vby dV if x= 1 and dx =∆x=0.02,
dV =3x
2
dx = 3(1)2(0.02)=0.06 in3.
57. V= volume of cylindrical rod = πr2h=πr2(15) = 15πr2; approximate ∆Vby dV if r=2.5 and
dr =∆r=0.001. dV =30πr dr =30π(2.5)(0.001) ≈0.236 cm3.
58. P=2π
√g√L,dP =2π
√g
1
2√LdL =π
√g√LdL,dP
P=1
2
dL
Lso the relative error in P≈1
2the relative
error in L. Thus the percentage error in Pis ≈1
2the percentage error in L.
59. (a) α=∆L/(L∆T)=0.006/(40 ×10)=1.5×10−5
/◦C
(b) ∆L=2.3×10−5(180)(25) ≈0.1 cm, so the pole is about 180.1 cm long.
60. ∆V=7.5×10−4(4000)(−20) = −60 gallons; the truck delivers 4000 −60 = 3940 gallons.
CHAPTER 3 SUPPLEMENTARY EXERCISES
4. (a) dy
dx = lim
h→0p9−4(x+h)−√9−4x
h= lim
h→0
(9 −4(x+h)−(9 −4x)
h(p9−4(x+h)+√
9−4x)
= lim
h→0−4h
h(p9−4(x+h)+√
9−4x)=−4
2
√
9−4x=−2
√
9−4x
(b) dy
dx = lim
h→0
x+h
x+h+1−x
x+1
h= lim
h→0
(x+h)(x+1)−x(x+h+1)
h(x+h+ 1)(x+1)
= lim
h→0
h
h(x+h+ 1)(x+1) =1
(x+1)
2
95 Chapter 3
5. Set f0(x)=0: f
0
(x) = 6(2)(2x+7)
5
(x−2)5+ 5(2x+7)
6
(x−2)4=0,so2x+7=0orx−2=0
or, factoring out (2x+7)
5
(x−2)4, 12(x−2) + 5(2x+ 7) = 0. This reduces to x=−7/2, x=2,or
22x+ 11 = 0, so the tangent line is horizontal at x=−7/2,2,−1/2.
6. Set f0(x)=0: f
0(x)=4(x2+2x)(x−3)3−(2x+ 2)(x−3)4
(x2+2x)
2, and a fraction can equal zero only if its
numerator equals zero. So either x−3 = 0 or, after factoring out (x−3)3,4(x
2
+2x)−(2x+2)(x−3)=0,
2x
2+12x+ 6 = 0, whose roots are (by the quadratic formula) x=−6±√36 −4·3
2=−3±√6. So
the tangent line is horizontal at x=3,−3±√
6.
7. Set f0(x)= 3
2
√
3x+1(x−1)2+2
√
3x+1(x−1)=0. Ifx= 1 then y0=0. Ifx6= 1 then divide out
x−1 and multiply through by 2√3x+ 1 (at points where fis differentiable we must have √3x+16=0)
to obtain 3(x−1) + 4(3x+1)=0,or15x+ 1 = 0. So the tangent line is horizontal at x=1,−1/15.
8. f0(x)=3
µ3x+1
x
2¶2d
dx
3x+1
x
2=3
µ3x+1
x
2¶2x
2
(3) −(3x+ 1)(2x)
x4=−3µ3x+1
x
2¶23x
2+2x
x
4=0.
If f0(x) = 0 then (3x+1)
2
(3x2+2x) = 0. The tangent line is horizontal at x=−1/3,−2/3(x=0is
ruled out from the definition of f).
9. (a) x=−2,−1,1,3(b) (−∞,−2), (−1,1), (3,+∞)(c) (−2,−1), (1,3)
(d) g00(x)=f
00(x) sin x+2f0(x) cos x−f(x) sin x;g00(0)=2f
0(0) cos 0 = 2(2)(1) = 4
10. (a) f0(1)g(1) + f(1)g0(1)=3(−2)+1(−1) = −7
(b) g(1)f0(1) −f(1)g0(1)
g(1)2=−2(3) −1(−1)
(−2)2=−5
4
(c) 1
2pf(1)f0(1) = 1
2√13=3
2(d) 0 (because f(1)g0(1) is constant)
11. The equations of such a line has the form y=mx. The points (x0,y
0) which lie on both the line and
the parabola and for which the slopes of both curves are equal satisfy y0=mx0=x3
0−9x2
0−16x0,
so that m=x2
0−9x0−16. By differentiating, the slope is also given by m=3x
2
0−18x0−16.
Equating, we have x2
0−9x0−16=3x
2
0−18x0−16, or 2x2
0−9x0= 0. The root x0= 0 corresponds
to m=−16,y
0= 0 and the root x0=9/2 corresponds to m=−145/4,y
0=−1305/8. So the line
y=−16xis tangent to the curve at the point (0,0), and the line y=−145x/4 is tangent to the curve
at the point (9/2,−1305/8).
12. The slope of the line x+4y=10ism
1=−1/4, so we set the negative reciprocal
4=m
2=d
dx(2x3−x2)=6x
2−2xand obtain 6x2−2x−4 = 0 with roots x=1±√1+24
6=1,−2/3.
13. The line y−x= 2 has slope m1= 1 so we set m2=d
dx(3x−tan x)=3−sec2x= 1, or sec2x=2,
sec x=±√2sox=nπ ±π/4 where n=0,±1,±2,....
14. f(x) is continuous and differentiable at any x6= 1, so we consider x=1.
(a) lim
x→1−(x2−1) = lim
x→1+k(x−1)=0=f(1), so any value of kgives continuity at x=1.
(b) lim
x→1−f0(x) = lim
x→1−2x= 2, and lim
x→1+f0(x) = lim
x→1+k=k, so only if k=2isf(x) differentiable at
x=1.
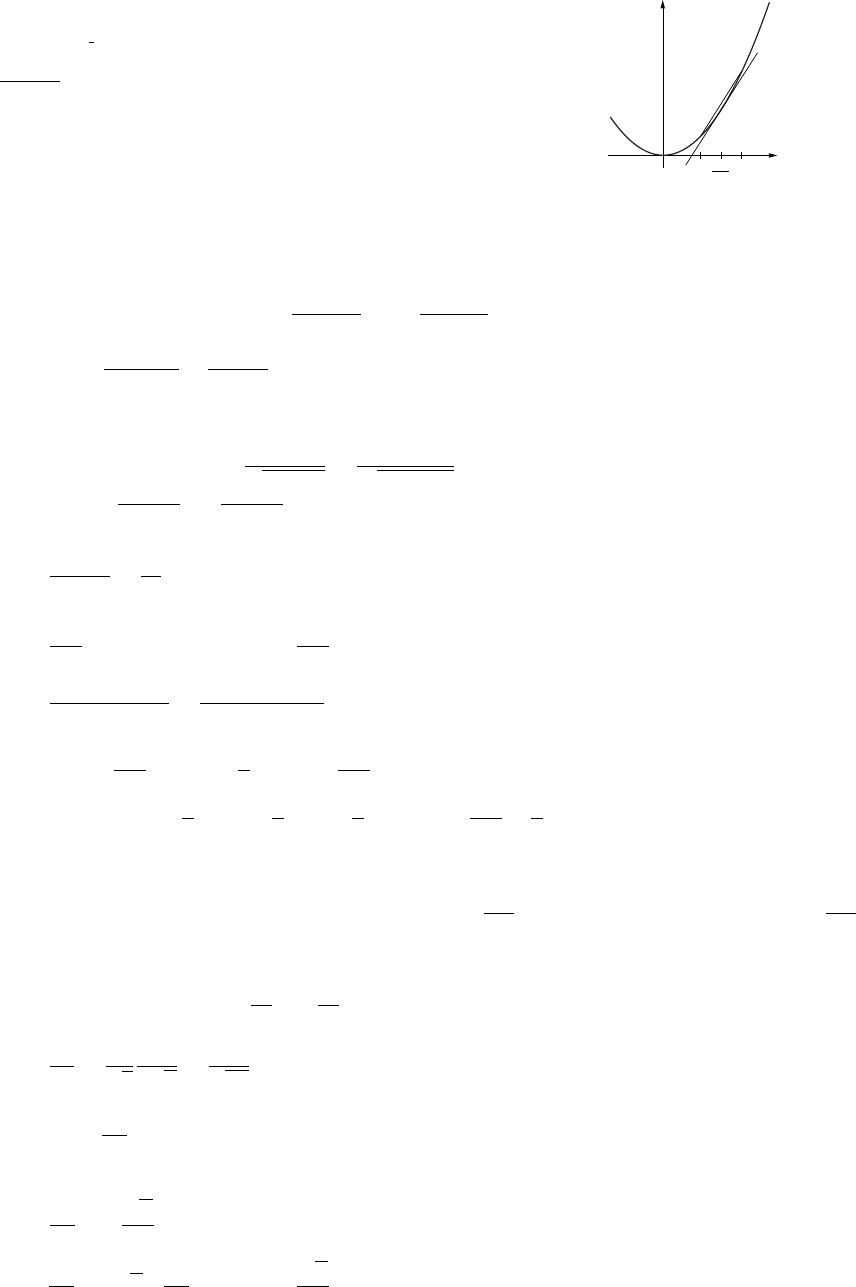
Supplementary Exercises 3 96
15. The slope of the tangent line is the derivative
y0=2x
¯
¯
¯x=1
2(a+b)=a+b. The slope of the secant is
a2−b2
a−b=a+b, so they are equal.
y
x
ab
a+b
2
(a,a)
2
(b,b)
2
16. To average 60 mi/h one would have to complete the trip in two hours. At 50 mi/h, 100 miles are
completed after two hours. Thus time is up, and the speed for the remaining 20 miles would have to
be infinite.
17. (a) ∆x=1.5−2=−0.5; dy =−1
(x−1)2∆x=−1
(2 −1)2(−0.5)=0.5; and
∆y=1
(1.5−1) −1
(2 −1) =2−1=1.
(b) ∆x=0−(−π/4) = π/4; dy =¡sec2(−π/4)¢(π/4) = π/2; and ∆y= tan 0 −tan(−π/4)=1.
(c) ∆x=3−0=3;dy =−x
√25 −x2=−0
p25 −(0)2(3) = 0; and
∆y=√25 −32−√25 −02=4−5=−1.
18. (a) 43−23
4−2=56
2=28 (b) (dV /d`)|`=5 =3`
2
¯
¯`=5 = 3(5)2=75
19. (a) dW
dt = 200(t−15); at t=5, dW
dt =−2000; the water is running out at the rate of 2000 gal/min.
(b) W(5) −W(0)
5−0=10000 −22500
5=−2500; the average rate of flow out is 2500 gal/min.
20. cot 46◦= cot 46π
180 ; let x0=π
4and x=46π
180 . Then
cot 46◦= cot x= cot π
4−³csc2π
4´³x−π
4´=1−2µ46π
180 −π
4¶=0.9651;
with a calculator, cot 46◦=0.9657.
21. (a) h= 115 tan φ,dh = 115 sec2φdφ; with φ=51
◦=51
180πradians and dφ =±0.5◦=±0.5³π
180´
radians, h±dh = 115(1.2349) ±2.5340 = 142.0135 ±2.5340, so the height lies between
139.48 m and 144.55 m.
(b) If |dh|≤5 then |dφ|≤ 5
115 cos251
180 π≈0.017 radians, or |dφ|≤0.98◦.
22. (a) dT
dL =2
√g
1
2√L=1
√gL (b) s/m
(c) Since dT
dL >0 an increase in Lgives an increase in T, which is the period. To speed up a clock,
decrease the period; to decrease T, decrease L.
(d) dT
dg =−√L
g3/2<0; a decrease in gwill increase Tand the clock runs slower
(e) dT
dg =2
√
Lµ−1
2¶g
−3/2=−√
L
g
3/2(f) s3/m
97 Chapter 3
23. (a) f0(x)=2x, f0(1.8)=3.6
(b) f0(x)=(x
2−4x)/(x−2)2,f0(3.5) ≈−0.777778
24. (a) f0(x)=3x
2−2x, f 0(2.3)=11.27 (b) f0(x)=(1−x
2
)/(x
2+1)
2
,f0(−0.5)=0.48
25. f0(x)=2
xln 2; f0(2) ≈2.772589
26. f0(x)=x
sin x(cos xln x+ sin x/x); f0(2)=0.312141
27. vinst = lim
h→0
3(h+1)
2.5+ 580h−3
10h=58+ 1
10
d
dx3x2.5¯¯¯¯x=1
=58+ 1
10(2.5)(3)(1)1.5=58.75 ft/s
28. 164 ft/s
2500
0
120
29. Solve 3x2−cos x= 0 to get x=±0.535428.
30. When x4−x−1>0, f(x)=x
4−2x−1; when x4−x−1<0,
f(x)=−x
4+ 1, and fis differentiable in both cases. The roots of
x4−x−1=0arex
1=−0.724492, x2=1.220744. So x4−x−1>0
on (−∞,x
1) and (x2,+∞), and x4−x−1<0on(x
1
,x
2). Then
lim
x→x−
1
f0(x) = lim
x→x−
1
(4x3−2)=4x
3
1−2 and
lim
x→x+
1
f0(x) = lim
x→x+
1−4x3=−4x3
1which is not equal to 4x3
1−2, so
fis not differentiable at x=x1; similarly fis not differentiable at
x=x2.
1.5
-1.5
-1.5 2
31. (a) f0(x)=5x
4(b) f0(x)=−1/x2(c) f0(x)=−1/2x
3/2
(d) f0(x)=−3/(x−1)2(e) f0(x)=3x/√3x2+5 (f ) f0(x) = 3 cos 3x
32. f0(x)=2xsin x+x2cos x33. f0(x)= 1−2
√
xsin 2x
2√x
34. f0(x)=6x
2+8x−17
(3x+2)
235. f0(x)=(1+x2) sec2x−2xtan x
(1+x2)2
36. f0(x)=x
2cos √x−2x3/2sin √x
2x7/2
37. f0(x)=−2x
5sin x−2x4cos x+4x
4+6x
2sin x+6x−3xcos x−4xsin x+ 4 cos x−8
2x2√x4−3+2(2−cos x)2
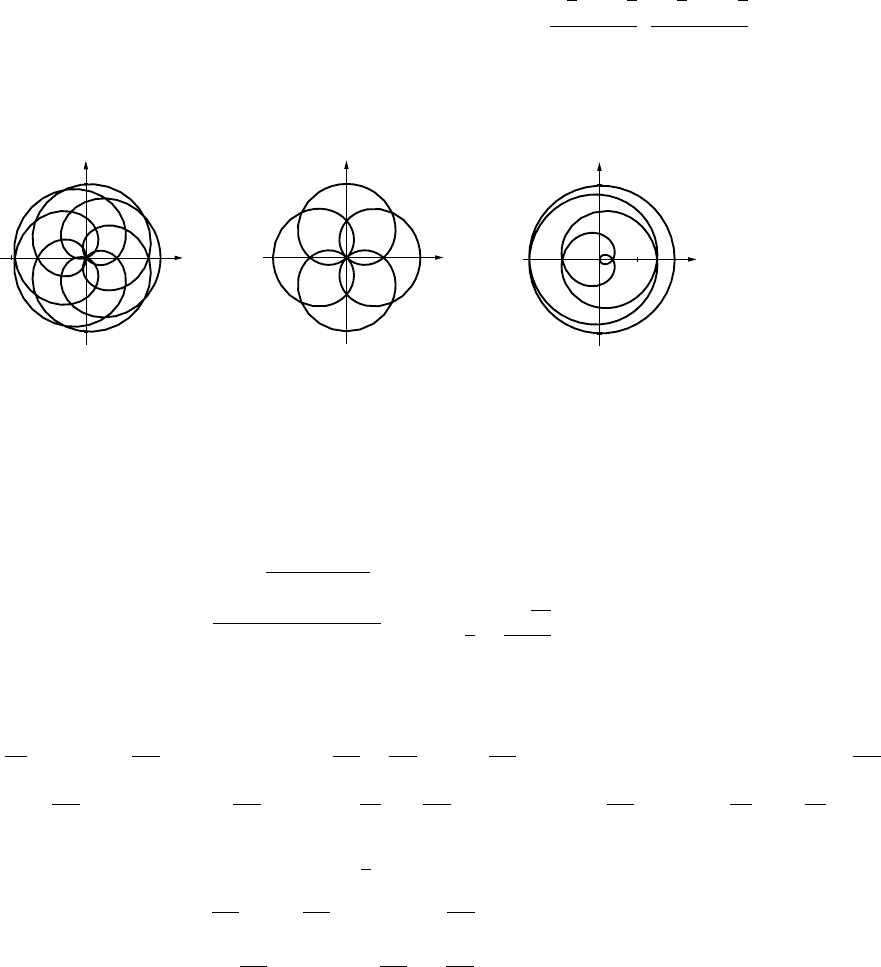
Horizon Module 3 98
CHAPTER 3 HORIZON MODULE
1. x1=l1cos θ1,x
2=l
2cos(θ1+θ2), so x=x1+x2=l1cos θ1+l2cos(θ1+θ2) (see Figure 3 in text);
similarly y1=l1sin θ1+l2sin(θ1+θ2).
2. Fix θ1for the moment and let θ2vary; then the distance rfrom (x, y) to the origin (see Figure 3 in
text) is at most l1+l2and at least l1−l2if l1≥l2and l2−l1otherwise. For any fixed θ2let θ1vary
and the point traces out a circle of radius r.
(a) {(x, y):0≤x
2+y
2≤2l
1
}
(b) {(x, y):l
1−l
2≤x
2+y
2≤l
1+l
2
}
(c) {(x, y):l
2−l
1≤x
2+y
2≤l
1+l
2
}
3. (x, y)=(l
1cos θ+l2cos(θ1+θ2),l
1sin θ1+l2sin(θ1+θ2))
= (cos(π/4) + 3 cos(5π/12),sin(π/4) + 3 sin(5π/12)) = Ã√2+3
√
6
4,7
√
2+3
√
6
4!
4. x= (1) cos 2t+ (1) cos(2t+3t) = cos 2t+ cos 5t,
y= (1) sin 2t+ (1) sin(2t+3t) = sin 2t+ sin 5t
5. y
x
-2
2
-2 2
v1 = 3, v2 = 5
y
x
-2
2
-2 2
v1 = 1, v2 = 4
y
x
-2
2
12
v
1
= 4, v2 = 1
6. x= 2 cos t,y= 2 sin t, a circle of radius 2
7. (a) 9 = [3 sin(θ1+θ2)]2+ [3 cos(θ1+θ2)]2=[5−3 sin θ1]2+[3−3 cos θ1]2
=25−30 sin θ1+ 9 sin2θ1+9−18 cos θ1+ 9 cos2θ1=43−30 sin θ1−18 cos θ1,
so 15 sin θ1+ 9 cos θ1=17
(b) 1 = sin2θ1+ cos2θ2=µ17 −9 cos θ1
15 ¶2
+ cos θ1, or 306 cos2θ1−306 cos θ1=−64
(c) cos θ1=³153 ±p(153)2−4(153)(32)´/306 = 1
2±5√17
102
(e) If θ1=0.792436 rad, then θ2=0.475882 rad ≈27.2660◦;
if θ1=1.26832 rad, then θ2=−0.475882 rad ≈−27.2660◦.
8. dx
dt =−3 sin θ1
dθ1
dt −(3 sin(θ1+θ2)) µdθ1
dt +dθ2
dt ¶=−3dθ1
dt (sin θ1+ sin(θ1+θ2)) −3 (sin(θ1+θ2)) dθ2
dt
=−ydθ1
dt −3(sin(θ1+θ2))dθ2
dt ; similarly dy
dt =xdθ1
dt + 3(cos(θ1+θ2))dθ2
dt . Now set dx
dt =0, dy
dt =1.
9. (a) x= 3 cos(π/3) + 3 cos(−π/3)=6
1
2= 3 and y= 3 sin(π/3) −3 sin(π/3) = 0; equations (4)
become 3 sin(π/3)dθ2
dt =0,3
dθ1
dt + 3 cos(π/3)dθ2
dt = 1 with solution dθ2/dt =0,dθ1/dt =1/3.
(b) x=−3, y=3,so−3
dθ1
dt = 0 and −3dθ1
dt −3dθ2
dt = 1, with solution dθ1/dt =0,dθ2/dt =−1/3.
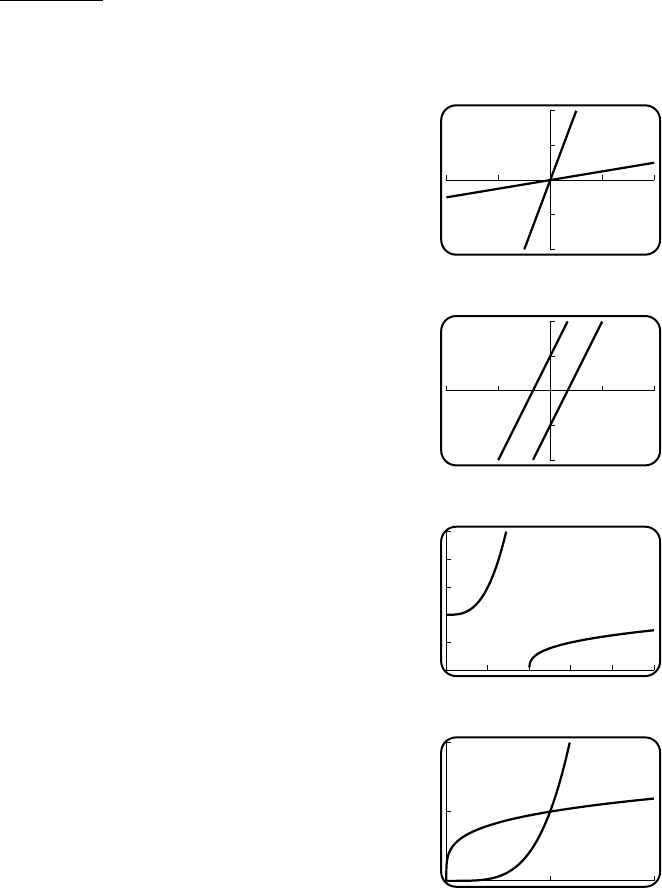
CHAPTER 4
Logarithmic and Exponential Functions
EXERCISE SET 4.1
1. (a) f(g(x))=4(x/4) = x,g(f(x))=(4x)/4=x,fand gare inverse functions
(b) f(g(x)) = 3(3x−1)+1=9x−26=xso fand gare not inverse functions
(c) f(g(x)) = 3
p(x3+2)−2=x,g(f(x))=(x−2)+2=x,fand gare inverse functions
(d) f(g(x))=(x
1/4
)
4=x,g(f(x))=(x
4
)
1/4=|x|6=x,fand gare not inverse functions
2. (a) They are inverse functions. 2
-2
-2 2
(b) The graphs are not reflections of each other
about the line y=x.
2
-2
-2 2
(c) They are inverse functions provided the domain of
gis restricted to [0,+∞)
5
0
05
(d) They are inverse functions provided the domain of f(x)
is restricted to [0,+∞)
2
0
02
3. (a) yes; all outputs (the elements of row two) are distinct
(b) no; f(1) = f(6)
4. (a) no; it is easy to conceive of, say, 8 people in line at two different times
(b) no; perhaps your weight remains constant for more than a year
(c) yes, since the function is increasing, in the sense that the greater the volume, the greater the
weight
99
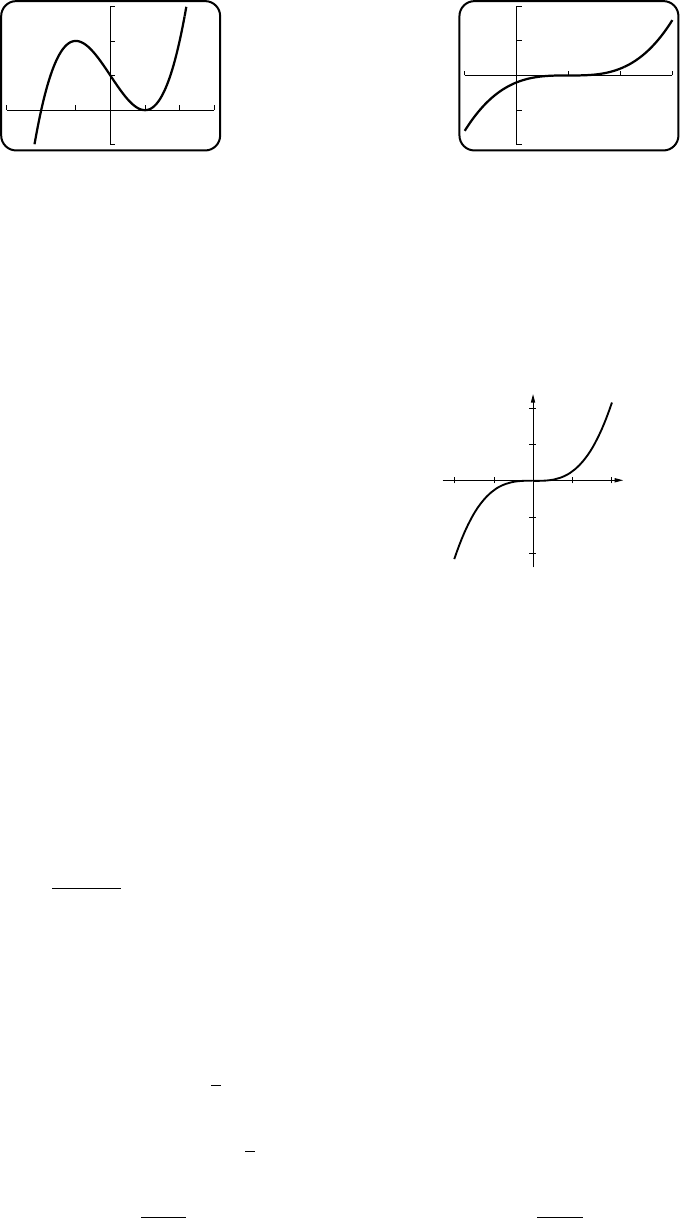
Exercise Set 4.1 100
5. (a) yes (b) yes (c) no (d) yes (e) no (f ) no
6. (a) no, the horizontal line test fails
6
-2
-3 3
(b) yes, horizontal line test
10
-10
-1 3
7. (a) no, the horizontal line test fails
(b) no, the horizontal line test fails
(c) yes, horizontal line test
8. (a) no, the horizontal line test fails
(b) no, the horizontal line test fails
(c) yes, horizontal line test
9. (a) fhas an inverse because the graph passes the horizontal line test. To compute f−1(2) start at
2onthey-axis and go to the curve and then down, so f−1(2) = 8; similarly, f−1(−1) = −1 and
f−1(0)=0.
(b) domain of f−1is [−2,2], range is [−8,8] (c)
-2 -1 1 2
-8
-4
4
8
y
x
10. (a) the horizontal line test fails
(b) −∞ <x≤−1; −1≤x≤2; and 2 ≤x<+∞.
11. (a) f0(x)=2x+8;f0<0on(−∞,−4) and f0>0on(−4,+∞); not one-to-one
(b) f0(x)=10x
4+3x
2+3≥3>0; f0(x) is positive for all x,sofis one-to-one
(c) f0(x) = 2 + cos x≥1>0 for all x,sofis one-to-one
12. (a) f0(x)=3x
2+6x=x(3x+ 6) changes sign at x=−2,0, so fis not one-to-one
(b) f0(x)=5x
4+24x
2+2≥2>0; f0is positive for all x,sofis one-to-one
(c) f0(x)= 1
(x+1)
2;fis one-to-one because:
if x1<x
2<−1 then f0>0on[x
1
,x
2], so f(x1)6=f(x2)
if −1<x
1<x
2then f0>0on[x
1
,x
2], so f(x1)6=f(x2)
if x1<−1<x
2then f(x1)>1>f(x
2
) since f(x)>1on(−∞,−1) and f(x)<1on(−1,+∞)
13. y=f−1(x), x=f(y)=y
5
,y=x
1/5=f
−1
(x)
14. y=f−1(x), x=f(y)=6y,y=1
6
x=f
−1
(x)
15. y=f−1(x), x=f(y)=7y−6, y=1
7(x+6)=f−1
(x)
16. y=f−1(x), x=f(y)=y+1
y−1,xy −x=y+1,(x−1)y=x+1,y=x+1
x−1=f−1
(x)
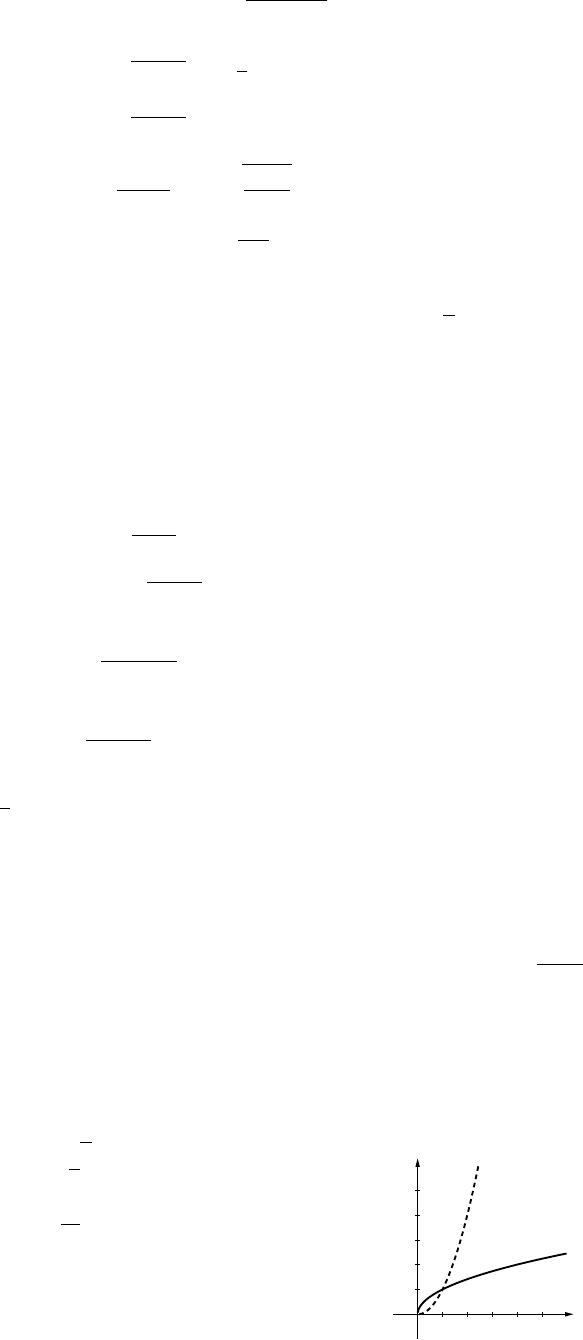
101 Chapter 4
17. y=f−1(x), x=f(y)=3y
3−5, y=3
p(x+5)/3=f
−1
(x)
18. y=f−1(x), x=f(y)= 5
√
4y+2,y=1
4(x
5−2) = f−1(x)
19. y=f−1(x), x=f(y)= 3
√
2y−1, y=(x
3+1)/2=f
−1
(x)
20. y=f−1(x), x=f(y)= 5
y
2+1,y=r5−x
x=f−1
(x)
21. y=f−1(x), x=f(y)=3/y2,y=−p3/x =f−1(x)
22. y=f−1(x), x=f(y)=½2y, y ≤0
y2,y>0
,y=f
−1
(x)=½x/2,x≤0
√
x, x > 0
23. y=f−1(x),x=f(y)=½5/2−y, y < 2
1/y, y ≥2,y=f
−1
(x)=½5/2−x, x > 1/2
1/x, 0<x≤1/2
24. y=p−1(x), x=p(y)=y
3−3y
2+3y−1=(y−1)3,y=x1/3+1=p
−1
(x)
25. y=f−1(x), x=f(y)=(y+2)
4for y≥0, y=f−1(x)=x
1/4−2 for x≥16
26. y=f−1(x), x=f(y)=√
y+ 3 for y≥−3, y=f−1(x)=x
2−3 for x≥0
27. y=f−1(x), x=f(y)=−
√
3−2yfor y≤3/2, y=f−1(x)=(3−x
2
)/2 for x≤0
28. y=f−1(x), x=f(y)=3y
2+5y−2 for y≥0, 3y2+5y−2−x= 0 for y≥0,
y=f−1(x)=(−5+√
12x+ 49)/6 for x≥−2
29. y=f−1(x), x=f(y)=y−5y
2for y≥1, 5y2−y+x= 0 for y≥1,
y=f−1(x)=(1+√
1−20x)/10 for x≤−4
30. (a) C=5
9(F−32)
(b) how many degrees Celsius given the Fahrenheit temperature
(c) C=−273.15◦C is equivalent to F=−459.67◦F, so the domain is F≥−459.67, the range is
C≥−273.15
31. (a) y=f(x)=(6.214 ×10−4)x(b) x=f−1(y)= 104
6.214y
(c) how many meters in ymiles
32. fand f−1are continuous so f(3) = lim
x→3f(x) = 7; then f−1(7) = 3, and
lim
x→7f−1(x)=f
−1³lim
x→7x´=f−1(7)=3
33. (a) f(g(x)) = f(√x)
=(
√
x)
2=x, x > 1;
g(f(x)) = g(x2)
=√x2=x, x > 1
(b)
x
y
y = f(x)
y = g(x)
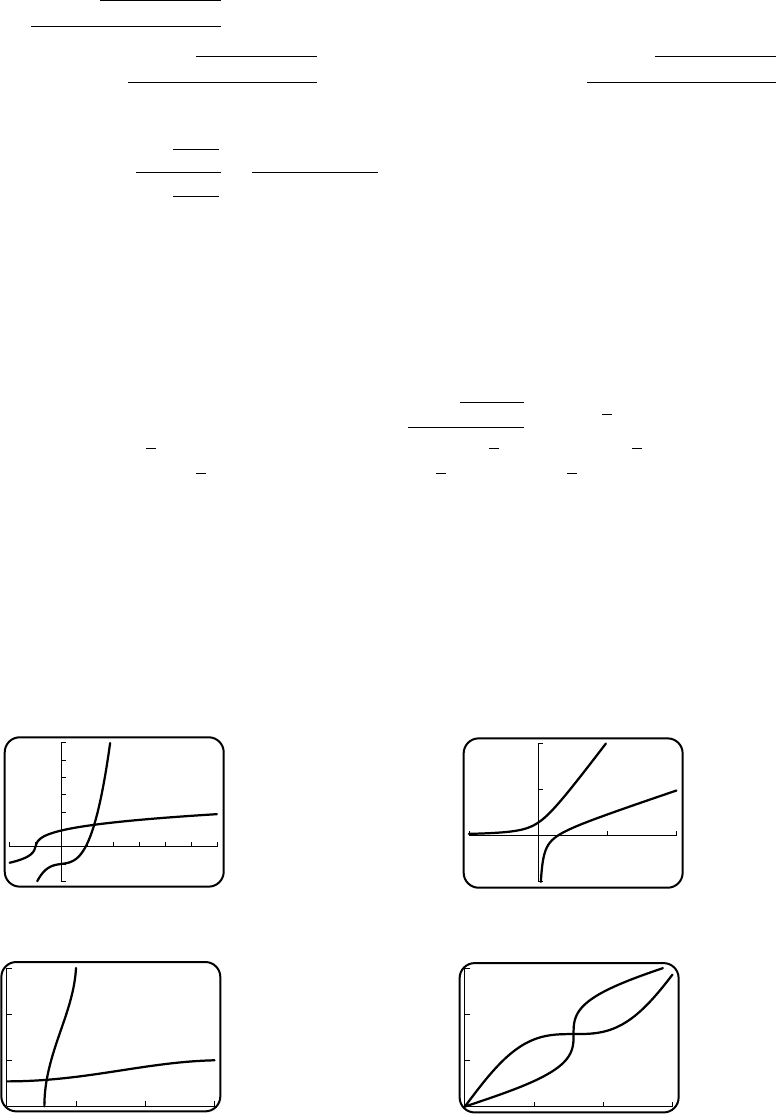
Exercise Set 4.1 102
(c) no, because f(g(x)) = xfor every xin the domain of gis not satisfied (the domain of gis x≥0)
34. y=f−1(x), x=f(y)=ay2+by +c,ay2+by +c−x= 0, use the quadratic formula to get
y=−b±pb2−4a(c−x)
2a;
(a) f−1(x)=−b+pb
2−4a(c−x)
2a(b) f−1(x)= −b−pb
2−4a(c−x)
2a
35. (a) f(f(x)) =
3−3−x
1−x
1−3−x
1−x
=3−3x−3+x
1−x−3+x=xso f=f−1
(b) symmetric about the line y=x
36. y=m(x−x0) is an equation of the line. The graph of the inverse of f(x)=m(x−x
0
) will be the
reflection of this line about y=x. Solve y=m(x−x0) for xto get x=y/m +x0=f−1(y)so
y=f
−1
(x)=x/m +x0.
37. (a) f(x)=x
3−3x
2+2x=x(x−1)(x−2) so f(0) = f(1) = f(2) = 0 thus fis not one-to-one.
(b) f0(x)=3x
2−6x+2, f0(x) = 0 when x=6±√36 −24
6=1±√
3/3. f0(x)>0(fis increasing)
if x<1−√
3/3, f0(x)<0(fis decreasing) if 1 −√3/3<x<1+√3/3, so f(x) takes on values
less than f(1 −√3/3) on both sides of 1 −√3/3thus1−√
3/3 is the largest value of k.
38. (a) f(x)=x
3
(x−2) so f(0) = f(2) = 0 thus fis not one to one.
(b) f0(x)=4x
3−6x
2=4x
2
(x−3/2),f0(x) = 0 when x= 0 or 3/2; fis decreasing on (−∞,3/2]
and increasing on [3/2,+∞)so3/2 is the smallest value of k.
39. if f−1(x) = 1, then x=f(1) = 2(1)3+ 5(1) + 3 = 10
40. if f−1(x) = 2, then x=f(2) = (2)3/[(2)2+1]=8/5
41. 6
-2
-2 6
42. 10
-5
-5 10
43. 3
0
03
44. 6
0
06
45. f(f(x)) = xthus f=f−1so the graph is symmetric about y=x.
46. (a) Suppose x16=x2where x1and x2are in the domain of gand g(x1), g(x2) are in the domain of f
then g(x1)6=g(x2) because gis one-to-one so f(g(x1)) 6=f(g(x2)) because fis one-to-one thus
f◦gis one-to-one because (f◦g)(x1)6=(f◦g)(x2)ifx
16=x
2
.
103 Chapter 4
(b) f,g, and f◦gall have inverses because they are all one-to-one. Let h=(f◦g)
−1then
(f◦g)(h(x)) = f[g(h(x))] = x, apply f−1to both sides to get g(h(x)) = f−1(x), then apply g−1
to get h(x)=g
−1
(f
−1
(x))=(g
−1◦f
−1
)(x), so h=g−1◦f−1
47.
x
y
48. Suppose that gand hare both inverses of fthen f(g(x)) = x,h[f(g(x))] = h(x), but h[f(g(x))] = g(x)
because his an inverse of fso g(x)=h(x).
49. F0(x)=2f
0
(2g(x))g0(x)soF
0
(3)=2f
0
(2g(3))g0(3). By inspection f(1)=3,sog(3) = f−1(3)=1
and g0(3)=(f
−1
)
0
(3)=1/f 0(f−1(3)) = 1/f 0(1)=1/7 because f0(x)=4x
3+3x
2
.Thus
F
0
(3)=2f
0(2)(1/7) = 2(44)(1/7)=88/7.
EXERCISE SET 4.2
1. (a) −4(b) 4(c) 1/4
2. (a) 1/16 (b) 8(c) 1/3
3. (a) 2.9690 (b) 0.0341
4. (a) 1.8882 (b) 0.9381
5. (a) log216 = log2(24)=4 (b) log2µ1
32¶= log2(2−5)=−5
(c) log44=1 (d) log93 = log9(91/2)=1/2
6. (a) log10(0.001) = log10(10−3)=−3(b) log10(104)=4
(c) ln(e3)=3 (d) ln(√e) = ln(e1/2)=1/2
7. (a) 1.3655 (b) −0.3011
8. (a) −0.5229 (b) 1.1447
9. (a) 2lna+1
2ln b+1
2ln c=2r+s/2+t/2(b) ln b−3lna−ln c=s−3r−t
10. (a) 1
3ln c−ln a−ln b=t/3−r−s(b) 1
2(ln a+3lnb−2lnc)=r/2+3s/2−t
11. (a) 1 + log x+1
2log(x−3) (b) 2ln|x|+ 3 ln sin x−1
2ln(x2+1)
12. (a) 1
3log(x+2)−log cos 5x(b) 1
2ln(x2+1)−1
2ln(x3+5)
13. log 24(16)
3= log(256/3) 14. log √x−log(sin32x) + log 100 = log 100√x
sin32x
Exercise Set 4.2 104
15. ln
3
√x(x+1)
2
cos x16. 1+x=10
3= 1000, x= 999
17. √x=10
−1=0.1, x=0.01 18. x2=e4,x=±e2
19. 1/x =e−2,x=e220. x=7
21. 2x=8,x=4 22. log10 x3= 30, x3=10
30,x=10
10
23. log10 x=5,x=10
5
24. ln 4x−ln x6=ln2,ln 4
x
5=ln2, 4
x
5=2,x
5=2,x=5
√
2
25. ln 2x2=ln3,2x
2=3,x
2=3/2, x=p3/2 (we discard −p3/2 because it does not satisfy the original
equation)
26. ln 3x=ln2,xln3=ln2,x=ln 2
ln 3
27. ln 5−2x=ln3,−2xln5=ln3,x=−ln 3
2ln5
28. e−2x=5/3,−2x= ln(5/3),x=−
1
2
ln(5/3)
29. e3x=7/2,3x= ln(7/2),x=1
3
ln(7/2)
30. ex(1 −2x)=0soe
x= 0 (impossible) or 1 −2x=0,x=1/2
31. e−x(x+2)=0soe
−x= 0 (impossible) or x+2=0,x=−2
32. e2x−ex−6=(e
x−3)(ex+2)=0soe
x=−2 (impossible) or ex=3,x=ln3
33. e−2x−3e−x+2=(e
−x−2)(e−x−1)=0soe
−x=2,x=−ln 2 or e−x=1,x=0
34. (a) y
x
-2
2
26
(b) y
x
2
-2 2
35. (a) y
x
2
4
6
-2 2 4
(b) y
x
-4
2
-4 2
105 Chapter 4
36. (a) y
x
-10
-1
(b) y
x
-1
3
37. log27.35 = (log 7.35)/(log 2) = (ln 7.35)/(ln 2) ≈2.8777;
log50.6 = (log 0.6)/(log 5) = (ln 0.6)/(ln 5) ≈−0.3174
38. 10
-5
02
39. 2
-3
03
40. (a) Let X= logbxand Y= logax. Then bX=xand aY=xso aY=bX,ora
Y/X =b, which means
logab=Y/X. Substituting for Yand Xyields logax
logbx= logab, logbx=logax
logab.
(b) Let x=ato get logba= (logaa)/(logab)=1/(logab) so (logab)(logba)=1.
(log281)(log332) = (log2[34])(log3[25]) = (4 log23)(5 log32) = 20(log23)(log32)=20
41. x=3.6541,y =1.2958
2
0.6
26
42. Since the units are billions, one trillion is 1,000 units. Solve 1000 = 0.051517(1.1306727)xfor xby
taking common logarithms, resulting in 3 = log 0.051517 + xlog 1.1306727, which yields x≈77.4, so
the debt first reached one trillion dollars around 1977.
43. (a) no, the curve passes through the origin (b) y=2
x/4
(c) y=2
−x(d) y=(
√
5)x
5
0
-1 2

Exercise Set 4.2 106
44. (a) As x→+∞the function grows very slowly,
but it is always increasing and tends to +∞.
As x→1+the function tends to −∞.
(b) y
x
-2
150
45. log(1/2) <0 so 3 log(1/2) <2 log(1/2)
46. Let x= logbaand y= logbc,soa=b
xand c=by.
First, ac =bxby=bx+yor equivalently, logb(ac)=x+y= logba+logbc.
Secondly, a/c =bx/by=bx−yor equivalently, logb(a/c)=x−y= logba−logbc.
Next, ar=(b
x
)
r=b
rx or equivalently, logbar=rx =rlogba.
Finally, 1/c =1/by=b−yor equivalently, logb(1/c)=−y=−logbc.
47. 75e−t/125 =15,t=−125 ln(1/5) = 125 ln 5 ≈201 days.
48. (a) If t= 0, then Q= 12 grams (b) Q=12e
−0.055(4) =12e
−0.22 ≈9.63 grams
(c) 12e−0.055t=6,e
−0.055t=0.5,t=−(ln 0.5)/(0.055) ≈12.6 hours
49. (a) 7.4; basic (b) 4.2; acidic (c) 6.4; acidic (d) 5.9; acidic
50. (a) log[H+]=−2.44,[H+]=10
−2.44 ≈3.6×10−3mol/L
(b) log[H+]=−8.06,[H+]=10
−8.06 ≈8.7×10−9mol/L
51. (a) 140 dB; damage (b) 120 dB; damage
(c) 80 dB; no damage (d) 75 dB; no damage
52. Suppose that I1=3I
2and β1= 10 log10 I1/I0,β2= 10 log10 I2/I0. Then
I1/I0=3I
2
/I0, log10 I1/I0= log10 3I2/I0= log10 3 + log10 I2/I0,β1= 10 log10 3+β
2
,
β
1−β
2= 10 log10 3≈4.8 decibels.
53. Let IAand IBbe the intensities of the automobile and blender, respectively. Then
log10 IA/I0= 7 and log10 IB/I0=9.3, IA=10
7
I
0and IB=10
9.3
I
0
,soI
B
/IA=10
2.3≈200.
54. The decibel level of the nth echo is 120(2/3)n;
120(2/3)n<10 if (2/3)n<1/12,n> log(1/12)
log(2/3) =log 12
log 1.5≈6.13 so 6 echoes can be heard.
55. (a) log E=4.4+1.5(8.2)=16.7,E =10
16.7≈5×1016 J
(b) Let M1and M2be the magnitudes of earthquakes with energies of Eand 10E,
respectively. Then 1.5(M2−M1) = log(10E)−log E= log 10 = 1,
M2−M1=1/1.5=2/3≈0.67.
56. Let E1and E2be the energies of earthquakes with magnitudes Mand M+ 1, respectively. Then
log E2−log E1= log(E2/E1)=1.5,E
2/E1=10
1.5≈31.6.
57. If t=−2x, then x=−t/2 and lim
x→0(1 −2x)1/x = lim
t→0(1+t)−2/t = lim
t→0[(1 + t)1/t]−2=e−2.
58. If t=3/x, then x=3/t and lim
x→+∞(1+3/x)x= lim
t→0+(1+t)3/t = lim
t→0+[(1 + t)1/t]3=e3.
107 Chapter 4
EXERCISE SET 4.3
1. y=(2x−5)1/3;dy/dx =2
3(2x−5)−2/3
2. dy/dx =1
3£2 + tan(x2)¤−2/3sec2(x2)(2x)=2
3
xsec2(x2)£2 + tan(x2)¤−2/3
3. dy/dx =3
2·x−1
x+2¸1/2d
dx ·x−1
x+2¸=9
2(x+2)
2·x−1
x+2¸1/2
4. dy/dx =1
2·x2+1
x
2−5¸−1/2d
dx ·x2+1
x
2−5¸=1
2·x
2+1
x
2−5¸−1/2−12x
(x2−5)2=−6x
(x2−5)2·x2+1
x
2−5¸−1/2
5. dy/dx =x3µ−2
3¶(5x2+1)
−5/3
(10x)+3x
2
(5x2+1)
−2/3=1
3x
2
(5x2+1)
−5/3
(25x2+9)
6. dy/dx =
x24
3(3 −2x)1/3(−2) −(3 −2x)4/3(2x)
x4=2(3 −2x)1/3(2x−9)
3x3
7. dy/dx =5
2[sin(3/x)]3/2[cos(3/x)](−3/x2)=−15[sin(3/x)]3/2cos(3/x)
2x2
8. dy/dx =−1
2£cos(x3)¤−3/2£−sin(x3)¤(3x2)=3
2
x
2sin(x3)£cos(x3)¤−3/2
9. (a) 3x2+xdy
dx +y−2=0, dy
dx =2−3x2−y
x
(b) y=1+2x−x
3
x=1
x+2−x
2so dy
dx =−1
x2−2x
(c) from part (a), dy
dx =2−3x2−y
x=2−3x2−(1/x +2−x
2
)
x=−2x−1
x
2
10. (a) 1
2y−1/2dy
dx −ex=0or dy
dx =2e
x
√
y
(b) y=(2+e
x
)
2=2+4e
x+e
2xso dy
dx =4e
x+2e
2x
(c) from part (a), dy
dx =2e
x
√
y=2e
x
(2+ex)=4e
x+2e
2x
11. 2x+2ydy
dx =0so dy
dx =−x
y
12. 3x2−3y2dy
dx =6(x
dy
dx +y), −(3y2+6x)dy
dx =6y−3x
2so dy
dx =x2−2y
y2+2x
13. x2dy
dx +2xy +3x(3y2)dy
dx +3y
3−1=0
(x
2+9xy2)dy
dx =1−2xy −3y3so dy
dx =1−2xy −3y3
x2+9xy2
14. x3(2y)dy
dx +3x
2
y
2−5x
2dy
dx −10xy +1=0
(2x3y−5x2)dy
dx =10xy −3x2y2−1so dy
dx =10xy −3x2y2−1
2x3y−5x2
Exercise Set 4.3 108
15. −1
y2
dy
dx −1
x2=0so dy
dx =−y2
x2
16. 2x=(x−y)(1 + dy/dx)−(x+y)(1 −dy/dx)
(x−y)2,
2x(x−y)2=−2y+2xdy
dx so dy
dx =x(x−y)2+y
x
17. cos(x2y2)·x2(2y)dy
dx +2xy2¸=1, dy
dx =1−2xy2cos(x2y2)
2x2ycos(x2y2)
18. 2x=(1 + csc y)(−csc2y)(dy/dx)−(cot y)(−csc ycot y)(dy/dx)
(1 + csc y)2,
2x(1 + csc y)2=−csc y(csc y+ csc2y−cot2y)dy
dx,
but csc2y−cot2y=1,so dy
dx =−2x(1 + csc y)
csc y
19. 3 tan2(xy2+y) sec2(xy2+y)µ2xy dy
dx +y2+dy
dx¶=1
so dy
dx =1−3y2tan2(xy2+y) sec2(xy2+y)
3(2xy + 1) tan2(xy2+y) sec2(xy2+y)
20. (1 + sec y)[3xy2(dy/dx)+y
3
]−xy3(sec ytan y)(dy/dx)
(1 + sec y)2=4y
3dy
dx,
multiply through by (1 + sec y)2and solve for dy
dx
to get dy
dx =y(1 + sec y)
4y(1 + sec y)2−3x(1 + sec y)+xy sec ytan y
21. dy
dx =3x
4y,d2y
dx2=(4y)(3) −(3x)(4dy/dx)
16y2=12y−12x(3x/(4y))
16y2=12y2−9x2
16y3=−3(3x2−4y2)
16y3,
but 3x2−4y2=7so d
2
y
dx2=−3(7)
16y3=−21
16y3
22. dy
dx =−x2
y2,d2y
dx2=−y2(2x)−x2(2ydy/dx)
y4=−2xy2−2x2y(−x2/y2)
y4=−2x(y3+x3)
y5,
but x3+y3=1so d
2
y
dx2=−2x
y5
23. dy
dx =−y
x,d2y
dx2=−x(dy/dx)−y(1)
x2=−x(−y/x)−y
x2=2y
x2
24. dy
dx =y
y−x,
d2y
dx2=(y−x)(dy/dx)−y(dy/dx −1)
(y−x)2=
(y−x)µy
y−x¶−yµy
y−x−1¶
(y−x)2
=y2−2xy
(y−x)3but y2−2xy =−3,so d2y
dx2=−3
(y−x)3
25. dy
dx = (1 + cos y)−1,d2y
dx2=−(1 + cos y)−2(−sin y)dy
dx =sin y
(1 + cos y)3
109 Chapter 4
26. dy
dx =cos y
1+xsin y,
d2y
dx2=(1+xsin y)(−sin y)(dy/dx)−(cos y)[(xcos y)(dy/dx) + sin y]
(1+xsin y)2
=−2 sin ycos y+(xcos y)(2 sin2y+ cos2y)
(1+xsin y)3,
but xcos y=y, 2 sin ycos y= sin 2y, and sin2y+ cos2y=1so
d
2
y
dx2=−sin 2y+y(sin2y+1)
(1+xsin y)3
27. By implicit differentiation, 2x+2y(dy/dx)=0,dy
dx =−x
y;at(1/
√
2,1/
√
2), dy
dx =−1; at (1/√2,−1/√2),
dy
dx = +1. Directly, at the upper point y=√1−x2,dy
dx =−x
√1−x2=−1 and at the lower point
y=−√1−x2,dy
dx =x
√1−x2= +1.
28. If y2−x+ 1 = 0, then y=√x−1 goes through the point (10,3) so dy/dx =1/(2√x−1). By
implicit differentiation dy/dx =1/(2y). In both cases, dy/dx|(10,3) =1/6. Similarly y=−√x−1
goes through (10,−3) so dy/dx =−1/(2√x−1) = −1/6 which yields dy/dx =1/(2y)=−1/6.
29. 4x3+4y
3dy
dx =0,so dy
dx =−x3
y3=−1
153/4≈−0.1312.
30. 3y2dy
dx +x2dy
dx +2xy +2x−6ydy
dx =0,so dy
dx =−2xy+1
3y
2+x
2−6y=0atx=0
31. 4(x2+y2)µ2x+2ydy
dx¶=25µ2x−2ydy
dx¶,
dy
dx =x[25 −4(x2+y2)]
y[25+4(x
2+y
2
)] ;at(3,1) dy
dx =−9/13
32. 2
3µx−1/3+y−1/3dy
dx¶=0, dy
dx =−y1/3
x1/3=√3at(−1,3
√
3)
34. (a) y
–2
0
2
12 x
(b) 2ydy
dx =(x−a)(x−b)+x(x−b)+x(x−a)=3x
2−2(a+b)x+ab.If
dy
dx = 0 then
3x2−2(a+b)x+ab = 0. By the quadratic formula
x=2(a+b)±p4(a+b)2−4·3ab
6=1
3ha+b±(a2+b2−ab)1/2i.
(c) y=±px(x−a)(x−b). The square root is only defined for nonnegative arguments, so it is
necessary that all three of the factors x,x−a,x−bbe nonnegative, or that two of them be
nonpositive. If, for example, 0 <a<bthen the function is defined on the disjoint intervals
0<x<aand b<x<+∞, so there are two parts.
Exercise Set 4.3 110
35. (a) y
x
2
-2 2
2
(b) ±1.1547
(c) Implicit differentiation yields 2x−xdy
dx −y+2ydy
dx = 0. Solve for dy
dx =y−2x
2y−x.Ifdy
dx = 0 then
y−2x=0ory=2x.Thus4=x
2−xy +y2=x2−2x2+4x
2=3x
2
,x=±2
√
3
.
36. 1
2u−1/2du
dv +1
2v−1/2=0so du
dv =−√u
√v
37. 4a3da
dt −4t3=6µa
2+2at da
dt ¶, solve for da
dt to get da
dt =2t3+3a
2
2a
3−6at
38. 1 = (cos x)dx
dy so dx
dy =1
cos x= sec x39. 2a2ωdω
dλ +2b
2
λ=0so dω
dλ =−b2λ
a2ω
40. Let P(x0,y
0) be the required point. The slope of the line 4x−3y+1=0is4/3 so the slope of
the tangent to y2=2x
3at Pmust be −3/4. By implicit differentiation dy/dx =3x
2
/y,soatP,
3x
2
0
/y0=−3/4, or y0=−4x2
0. But y2
0=2x
3
0because Pis on the curve y2=2x
3
. Elimination of y0
gives 16x4
0=2x
3
0
,x
3
0
(8x0−1) = 0, so x0= 0 or 1/8. From y0=−4x2
0it follows that y0= 0 when
x0= 0, and y0=−1/16 when x0=1/8. It does not follow, however, that (0,0) is a solution because
dy/dx =3x
2
/y (the slope of the curve as determined by implicit differentiation) is valid only if y6=0.
Further analysis shows that the curve is tangent to the x-axis at (0,0), so the point (1/8,−1/16) is
the only solution.
41. The point (1,1) is on the graph, so 1 + a=b. The slope of the tangent line at (1,1) is −4/3; use
implicit differentiation to get dy
dx =−2xy
x2+2ay so at (1,1), −2
1+2a=−4
3, 1+2a=3/2, a=1/4 and
hence b=1+1/4=5/4.
42. Use implicit differentiation to get dy/dx =(y−3x
2
)/(3y2−x), so dy/dx =0ify=3x
2
. Substitute
this into x3−xy +y3= 0 to obtain 27x6−2x3=0,x
3=2/27, x=3
√2/3 and hence y=3
√4/3.
43. Let P(x0,y
0) be a point where a line through the origin is tangent to the curve
x2−4x+y2+ 3 = 0. Implicit differentiation applied to the equation of the curve gives
dy/dx =(2−x)/y.AtPthe slope of the curve must equal the slope of the line so
(2 −x0)/y0=y0/x0,ory
2
0=2x
0−x
2
0
. But x2
0−4x0+y2
0+ 3 = 0 because (x0,y
0) is on the curve,
and elimination of y2
0in the latter two equations gives x2
0−4x0+(2x
0−x
2
0
)+3=0,x
0=3/2 which
when substituted into y2
0=2x
0−x
2
0yields y2
0=3/4, so y0=±√3/2. The slopes of the lines are
(±√3/2)/(3/2) = ±√3/3 and their equations are y=(
√
3/3)xand y=−(√3/3)x.
44. By implicit differentiation, dy/dx =k/(2y) so the slope of the tangent to y2=kx at (x0,y
0)is
k/(2y0)ify
06= 0. The tangent line in this case is y−y0=k
2y0
(x−x0), or 2y0y−2y2
0=kx −kx0.
But y2
0=kx0because (x0,y
0) is on the curve y2=kx, so the equation of the tangent line becomes
2y0y−2kx0=kx −kx0which gives y0y=k(x+x0)/2. If y0= 0, then x0= 0; the graph of y2=kx
has a vertical tangent at (0,0) so its equation is x= 0, but y0y=k(x+x0)/2 gives the same result
when x0=y0=0.

111 Chapter 4
45. By the chain rule, dy
dx =dy
dt
dt
dx. Use implicit differentiation on 2y3t+t3y= 1 to get
dy
dt =−2y3+3t
2
y
6ty2+t3, but dt
dx =1
cos tso dy
dx =−2y3+3t
2
y
(6ty2+t3) cos t.
46. 2x3ydy
dt +3x
2
y
2dx
dt +dy
dt =0,dy
dt =−3x2y2
2x3y+1
dx
dt
47. 2xy dy
dt =y2dx
dt = 3(cos 3x)dx
dt ,dy
dt =3 cos 3x−y2
2xy
dx
dt
48. (a) f0(x)= 4
3
x
1/3
,f
00(x)=4
9
x
−2/3
(b) f0(x)=7
3
x
4/3
,f
00(x)=28
9x1/3,f000(x)=28
27x−2/3
(c) generalize parts (a) and (b) with k=(n−1)+1/3=n−2/3
49. y0=rxr−1,y
00 =r(r−1)xr−2so 3x2£r(r−1)xr−2¤+4x¡rxr−1¢−2xr=0,
3r(r−1)xr+4rxr−2xr=0,(3r2+r−2)xr=0,
3r
2+r−2=0,(3r−2)(r+1)=0;r=−1,2/3
50. y0=rxr−1,y
00 =r(r−1)xr−2so 16x2£r(r−1)xr−2¤+24x¡rxr−1¢+xr=0,
16r(r−1)xr+24rxr+xr=0,(16r2+8r+1)x
r=0,
16r2+8r+1=0,(4r+1)
2=0;r=−1/4
51. We shall find when the curves intersect and check that the slopes are negative reciprocals. For the
intersection solve the simultaneous equations x2+(y−c)
2=c
2and (x−k)2+y2=k2to obtain
cy =kx =1
2(x2+y2). Thus x2+y2=cy +kx,ory
2−cy =−x2+kx, and y−c
x=−x−k
y.
Differentiating the two families yields (black) dy
dx =−x
y−c, and (gray) dy
dx =−x−k
y. But it was
proven that these quantities are negative reciprocals of each other.
52. Differentiating, we get the equations (black) xdy
dx +y= 0 and (gray) 2x−2ydy
dx = 0. The first says
the (black) slope is = −y
xand the second says the (gray) slope is x
y, and these are negative reciprocals
of each other.
53. y=f−1(x), x=f(y)=5y
3+y−7, dx
dy =15y
2+1, dy
dx =1
15y2+1;
check: 1 = 15y2dy
dx +dy
dx,dy
dx =1
15y2+1
54. y=f−1(x), x=f(y)=1/y2,dx
dy =−2y−3,dy
dx =−y3/2;
check: 1 = −2y−3dy
dx,dy
dx =−y3/2
55. y=f−1(x), x=f(y)=2y
5+y
3+1, dx
dy =10y
4+3y
2
,dy
dx =1
10y4+3y
2;
check: 1 = 10y4dy
dx +3y
2dy
dx,dy
dx =1
10y4+3y
2
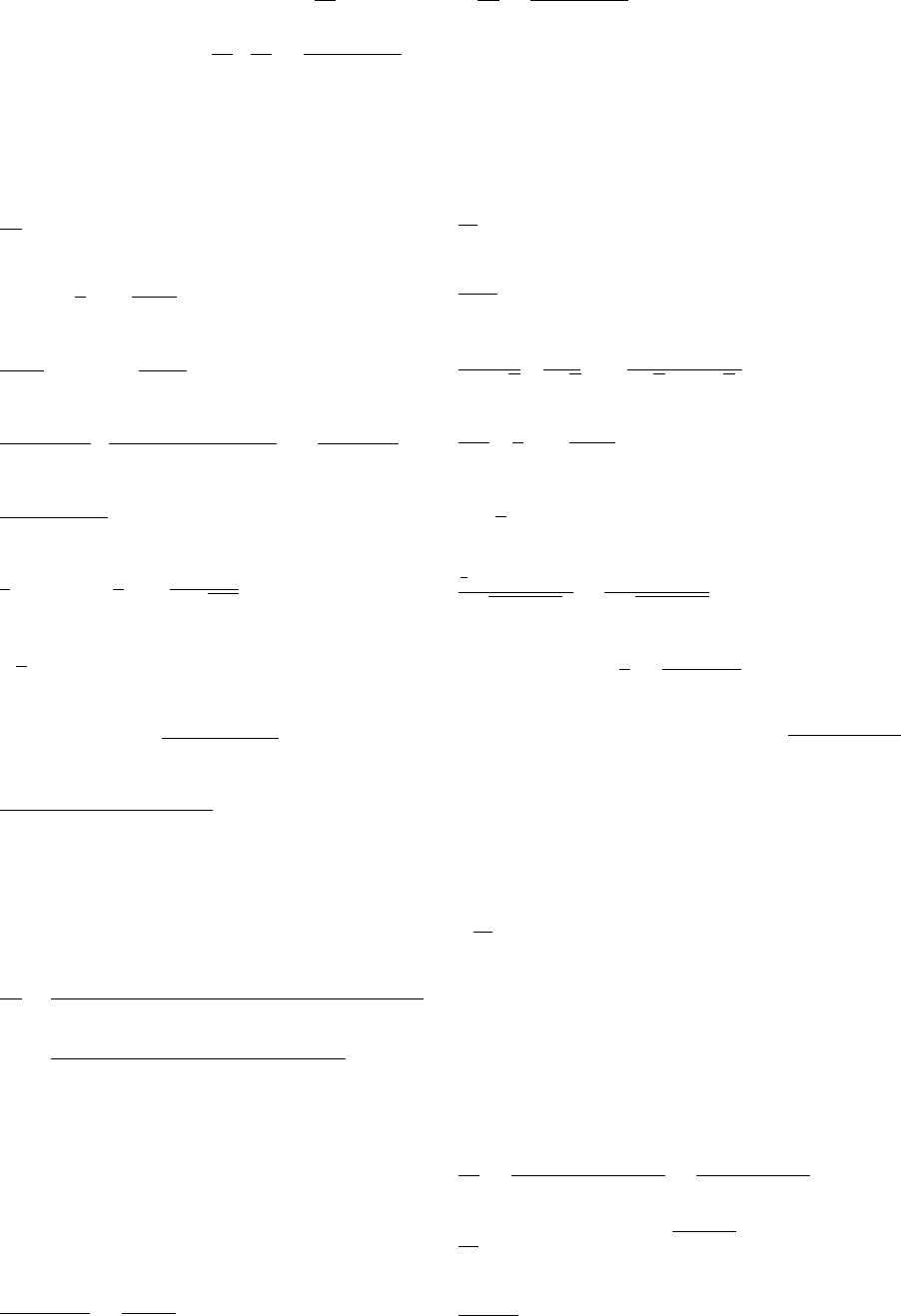
Exercise Set 4.4 112
56. y=f−1(x), x=f(y)=5y−sin 2y,dx
dy =5−2 cos 2y,dy
dx =1
5−2 cos 2y;
check: 1 = (5 −2 cos 2y)dy
dx,dy
dx =1
5−2 cos 2y
EXERCISE SET 4.4
1. 1
2x(2)=1/x 2. 1
x3(3x2)=3/x
3. 2(ln x)µ1
x¶=2lnx
x4. 1
sin x(cos x) = cot x
5. 1
tan x(sec2x)=sec2x
tan x6. 1
2+√
xµ1
2
√
x¶=1
2
√
x(2+√x)
7. 1
x/(1+x2)·(1+x2)(1) −x(2x)
(1+x2)2¸=1−x2
x(1+x2)8. 1
ln xµ1
x¶=1
xln x
9. 3x2−14x
x3−7x2−310. x3µ1
x¶+(3x
2
)lnx=x
2(1+3lnx)
11. 1
2(ln x)−1/2µ1
x¶=1
2x√ln x12.
1
22(ln x)(1/x)
p1+ln
2x=ln x
xp1+ln
2x
13. −1
xsin(ln x)14. 2 sin(ln x) cos(ln x)1
x=sin(ln x2)
x
15. 3x2log2(3 −2x)+ −2x
3
(ln 2)(3 −2x)16. £log2(x2−2x)¤3+3x£log2(x2−2x)¤22x−2
(x2−2x)ln2
17. 2x(1 + log x)−x/(ln 10)
(1 + log x)218. 1/[x(ln 10)(1 + log x)2]
19. 7e7x20. −10xe−5x2
21. x3ex+3x
2
e
x=x
2
e
x
(x+3) 22. −1
x2e1/x
23. dy
dx =(ex+e−x)(ex+e−x)−(ex−e−x)(ex−e−x)
(ex+e−x)2
=(e2x+2+e
−2x
)−(e
2x−2+e
−2x
)
(e
x+e
−x
)
2=4/(e
x+e
−x
)
2
24. excos(ex)
25. (xsec2x+ tan x)extan x26. dy
dx =(ln x)ex−ex(1/x)
(ln x)2=ex(xln x−1)
x(ln x)2
27. (1 −3e3x)e(x−e3x)28. 15
2x2(1+5x
3
)
−1/2exp(p1+5x
3
)
29. (x−1)e−x
1−xe−x=x−1
ex−x30. 1
cos(ex)[−sin(ex)]ex=−extan(ex)
113 Chapter 4
31. dy
dx +1
xy µxdy
dx +y¶=0, dy
dx =−y
x(y+1)
32. dy
dx =1
xtan yµxsec2ydy
dx + tan y¶,dy
dx =tan y
x(tan y−sec2y)
33. d
dx ·ln cos x−1
2ln(4 −3x2)¸=−tan x+3x
4−3x2
34. d
dx µ1
2[ln(x−1) −ln(x+ 1)]¶=1
2µ1
x−1−1
x+1¶
35. ln |y|=ln|x|+1
3ln |1+x
2
|,dy
dx =x3
p1+x
2·1
x+2x
3(1 + x2)¸
36. ln |y|=1
5[ln |x−1|−ln |x+1|], dy
dx =1
5
5
rx−1
x+1·1
x−1−1
x+1¸
37. ln |y|=1
3ln |x2−8|+1
2ln |x3+1|−ln |x6−7x+5|
dy
dx =(x2−8)1/3√x3+1
x
6−7x+5 ·2x
3(x2−8) +3x2
2(x3+1) −6x
5−7
x
6−7x+5¸
38. ln |y|=ln|sin x|+ln|cos x|+3ln|tan x|−1
2ln |x|
dy
dx =sin xcos xtan3x
√x·cot x−tan x+3 sec2x
tan x−1
2x¸
39. f0(x)=2
xln 2; y=2
x
,lny=xln 2, 1
yy0=ln2,y
0=yln2=2
xln 2
40. f0(x)=−3
−xln 3; y=3
−x
,lny=−xln 3, 1
yy0=−ln 3, y0=−yln 3 = −3−xln 3
41. f0(x)=π
sin x(ln π) cos x;
y=πsin x,lny= (sin x)lnπ,1
yy
0= (ln π) cos x,y0=πsin x(ln π) cos x
42. f0(x)=π
xtan x(ln π)(xsec2x+ tan x);
y=πxtan x,lny=(xtan x)lnπ,1
yy
0= (ln π)(xsec2x+ tan x)
y0=πxtan x(ln π)(xsec2x+ tan x)
43. ln y= (ln x) ln(x3−2x), 1
y
dy
dx =3x2−2
x3−2xln x+1
xln(x3−2x),
dy
dx =(x
3−2x)
ln x·3x2−2
x3−2xln x+1
xln(x3−2x)¸
44. ln y= (sin x)lnx,1
y
dy
dx =sin x
x+ (cos x)lnx,dy
dx =xsin x·sin x
x+ (cos x)lnx
¸
45. ln y= (tan x) ln(ln x), 1
y
dy
dx =1
xln xtan x+ (sec2x) ln(ln x),
dy
dx = (ln x)tan x·tan x
xln x+ (sec2x) ln(ln x)¸
Exercise Set 4.4 114
46. ln y= (ln x) ln(x2+ 3), 1
y
dy
dx =2x
x2+3ln x+1
xln(x2+ 3),
dy
dx =(x
2+3)
ln x·2x
x2+3ln x+1
xln(x2+3)
¸
47. y=Ae2x+Be−4x,y0=2Ae2x−4Be−4x,y00 =4Ae2x+16Be−4xso
y00 +2y
0−8y=(4Ae2x+16Be−4x) + 2(2Ae2x−4Be−4x)−8(Ae2x+Be−4x)=0
48. y=Aekt,dy/dt =kAekt =k(Aekt)=ky
49. (a) f0(x)=kekx,f00(x)=k
2
e
kx,f000(x)=k
3
e
kx,...,f(n)(x)=k
n
e
kx
(b) f0(x)=−ke−kx,f00(x)=k
2
e
−kx,f000(x)=−k
3
e
−kx,...,f(n)(x)=(−1)nkne−kx
50. dy
dt =e−λt(ωA cos ωt −ωB sin ωt)+(−λ)e
−λt(Asin ωt +Bcos ωt)
=e−λt[(ωA −λB) cos ωt −(ωB +λA) sin ωt]
51. f0(x)= 1
√2πσ exp "−1
2µx−µ
σ¶2#d
dx "−1
2µx−µ
σ¶2#
=1
√2πσ exp "−1
2µx−µ
σ¶2#·−µx−µ
σ¶µ1
σ¶¸
=−1
√2πσ3(x−µ) exp "−1
2µx−µ
σ¶2#
52. (a) y0=−xe−x+e−x=e−x(1 −x), xy0=xe−x(1 −x)=y(1 −x)
(b) y0=−x2e−x2/2+e−x2/2=e−x2/2(1 −x2), xy0=xe−x2/2(1 −x2)=y(1 −x2)
53. (a) logxe=ln e
ln x=1
ln x,d
dx[logxe]=−1
x(ln x)2
(b) logx2= ln 2
ln x,d
dx[logx2] = −ln 2
x(ln x)2
54. β= 10 log I−10 log I0,dβ
dI =10
Iln 10
(a) dβ
dI ¸I=10I0
=1
I0ln 10 db/W/m2(b) dβ
dI ¸I=100I0
=1
10I0ln 10 db/W/m2
(c) dβ
dI ¸I=100I0
=1
100I0ln 10 db/W/m2
55. dk
dT =k0exp ·−q(T−T0)
2T0T¸³−q
2T2´=−qk0
2T2exp ·−q(T−T0)
2T0T¸
56. (a) because xxis not of the form axwhere ais constant
(b) y=xx,lny=xln x,1
yy0=1+lnx,y
0=x
x
(1+lnx)
57. f0(x)=exe−1
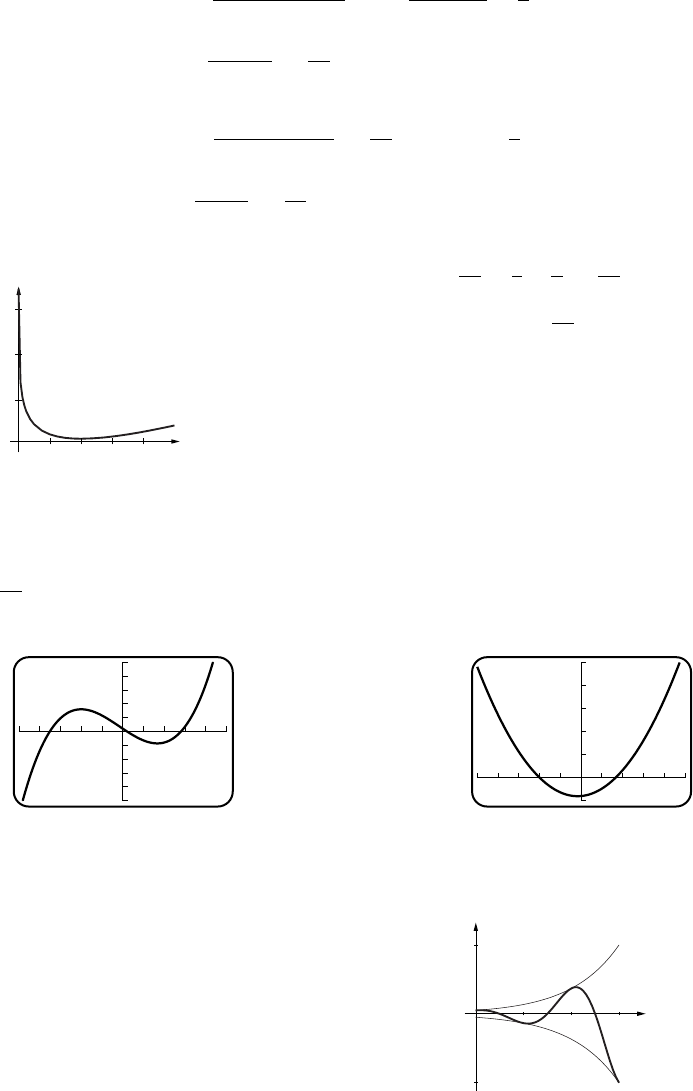
115 Chapter 4
58. Let P(x0,y
0)beapointony=e
3xthen y0=e3x0.dy/dx =3e
3xso mtan =3e
3x
0at Pand an equation
of the tangent line at Pis y−y0=3e
3x
0(x−x
0
), y−e3x0=3e
3x
0(x−x
0
). If the line passes through
the origin then (0,0) must satisfy the equation so −e3x0=−3x0e3x0which gives x0=1/3 and thus
y0=e. The point is (1/3,e).
59. (a) f(x)=lnx;f
0(1) = lim
h→0
ln(1 + h)−ln 1
h= lim
h→0
ln(1 + h)
h=1
x¯¯¯¯x=1
=1
(b) f(x)=10
x
;f
0(0) = lim
h→0
10h−1
h=d
dx(10x)¯¯¯¯x=0
=10
xln 10¯¯¯¯x=0
=ln10
60. (a) f(x)=lnx;f
0(e
2
) = lim
h→0
ln(e2+h)−2
h=d
dx(ln x)¯¯¯¯x=e2
=1
x¯¯¯¯x=e2
=e−2
(b) f(x)=2
x
;f
0(1) = lim
x→1
2x−2
x−1=d
dx(2x)¯¯¯¯x=1
=2
xln 2¯¯¯¯x=1
= 2 ln 2
61. (b) y
x
2
4
6
1234
(c) dy
dx =1
2−1
xso dy
dx <0at
x= 1 and dy
dx >0atx=e
(d) The slope is a continuous function which goes from a negative value to a positive value; therefore
it must take the value zero in between, by the Intermediate Value Theorem.
(e) dy
dx = 0 when x=2
62. (a) 100
-100
-5 5
(c) 125
-25
-5 5
(d) x=−2,5/3
63. (a) excos πx oscillates between +exand −ex
as cos πx oscillates between −1 and +1.
(b) y
x
-20
20
123
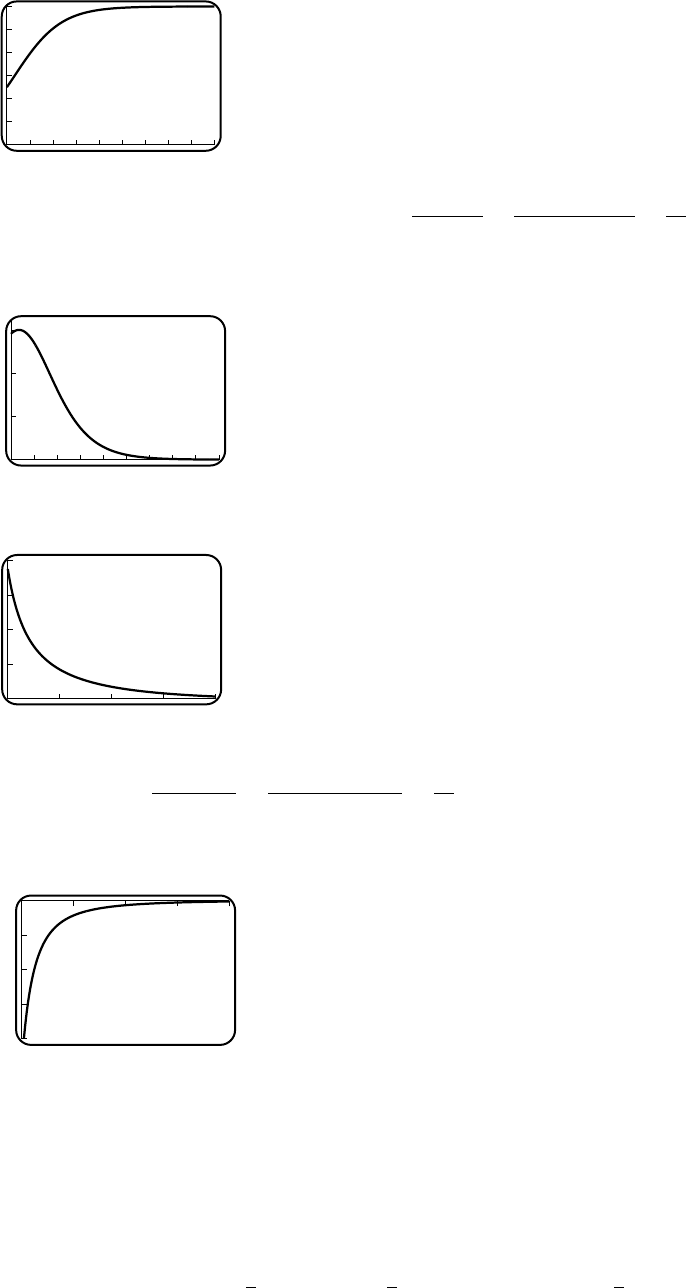
Exercise Set 4.5 116
64. (a) 12
0
09
(b) Ptends to 12 as tgets large; lim
t→+∞P(t) = lim
t→+∞
60
5+7e
−t=60
5+7 lim
t→+∞e
−t=60
5=12
(c) the rate of population growth tends to zero
3.2
0
09
65. (a) 100
20
08
(b) as ttends to +∞, the population tends to 19
lim
t→+∞P(t) = lim
t→+∞
95
5−4e−t/4=95
5−4 lim
t→+∞e−t/4=95
5=19
(c) the rate of population growth tends to zero
0
-80
08
EXERCISE SET 4.5
1. (a) −π/2(b) π(c) −π/4(d) 0
2. (a) π/3(b) π/3(c) π/4(d) 4π/3
3. θ=−π/3; cos θ=1/2, tan θ=−√3, cot θ=−1/√3, sec θ= 2, csc θ=−2/√3
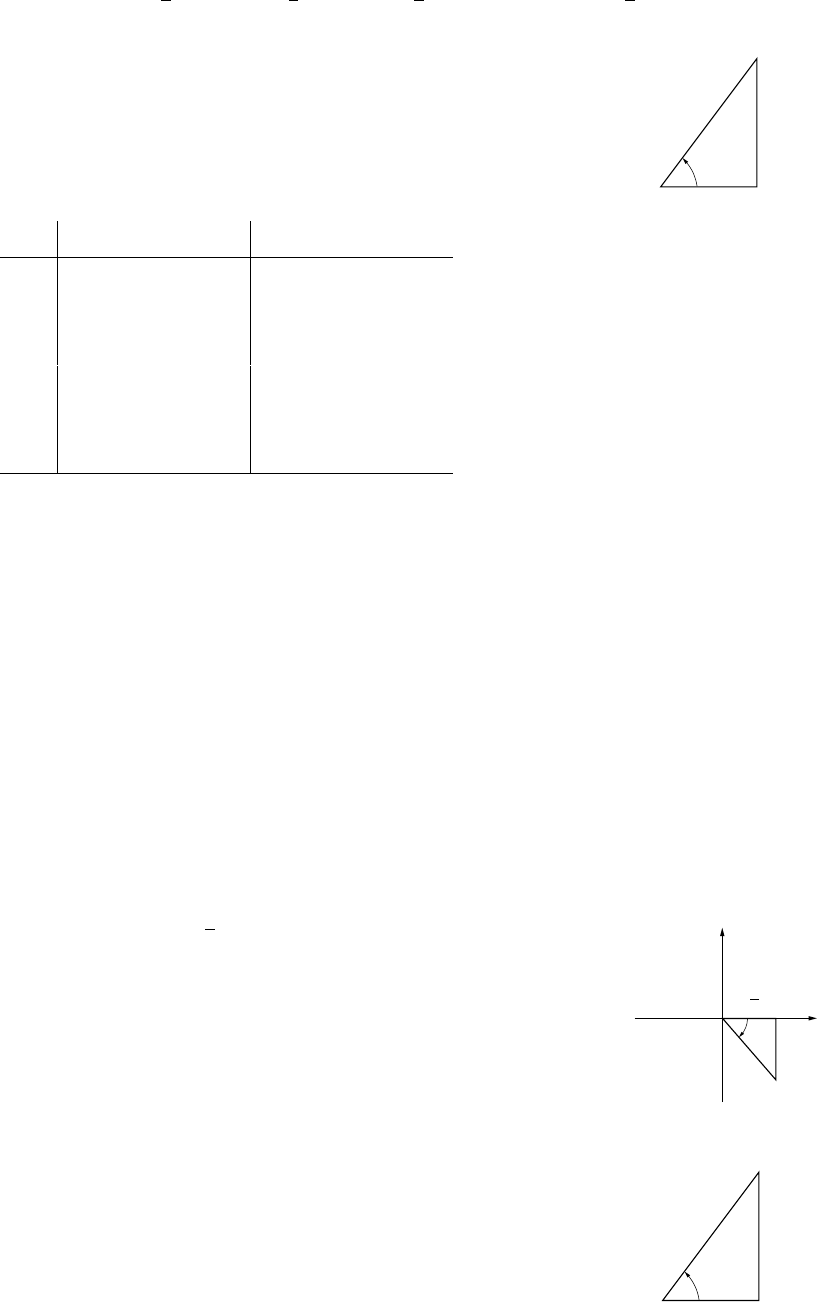
117 Chapter 4
4. θ=π/3; sin θ=√3/2, tan θ=√3, cot θ=1/
√
3, sec θ= 2, csc θ=2/
√
3
5. tan θ=4/3, 0 <θ<π/2; use the triangle shown to get sin θ=4/5,
cos θ=3/5, cot θ=3/4, sec θ=5/3, csc θ=5/4
θ
3
4
5
6. domain range
sin−1[−1,1] [−π/2,π/2]
cos−1[−1,1] [0,π]
tan−1(−∞,+∞) (−π/2,π/2)
cot−1(−∞,+∞) (0,π)
sec−1(−∞,−1] ∪[1,+∞) [0,π/2) ∪[π, 3π/2)
csc−1(−∞,−1] ∪[1,+∞) (0,π/2] ∪(−π, −π/2]
7. (a) π/7(b) sin−1(sin π) = sin−1(sin 0) = 0
(c) sin−1(sin(5π/7)) = sin−1(sin(2π/7))=2π/7
(d) Note that π/2<630 −200π<πso
sin(630) = sin(630 −200π) = sin(π−(630 −200π)) = sin(201π−630) where
0<201π−630 <π/2; sin−1(sin 630) = sin−1(sin(201π−630)) = 201π−630.
8. (a) π/7(b) π
(c) cos−1(cos(12π/7)) = cos−1(cos(2π/7))=2π/7
(d) Note that −π/2<200 −64π<0 so cos(200) = cos(200 −64π) = cos(64π−200) where
0<64π−200 <π/2; cos−1(cos 200) = cos−1(cos(64π−200)) = 64π−200.
9. (a) 0≤x≤π(b) −1≤x≤1
(c) −π/2<x<π/2(d) −∞ <x<+∞
10. Let θ= sin−1(−3/4) then sin θ=−3/4, −π/2<θ<0 and
(see figure) sec θ=4/
√
7
θ
−3
4
÷7
11. Let θ= cos−1(3/5), sin 2θ= 2 sin θcos θ= 2(4/5)(3/5)=24/25
θ
3
4
5
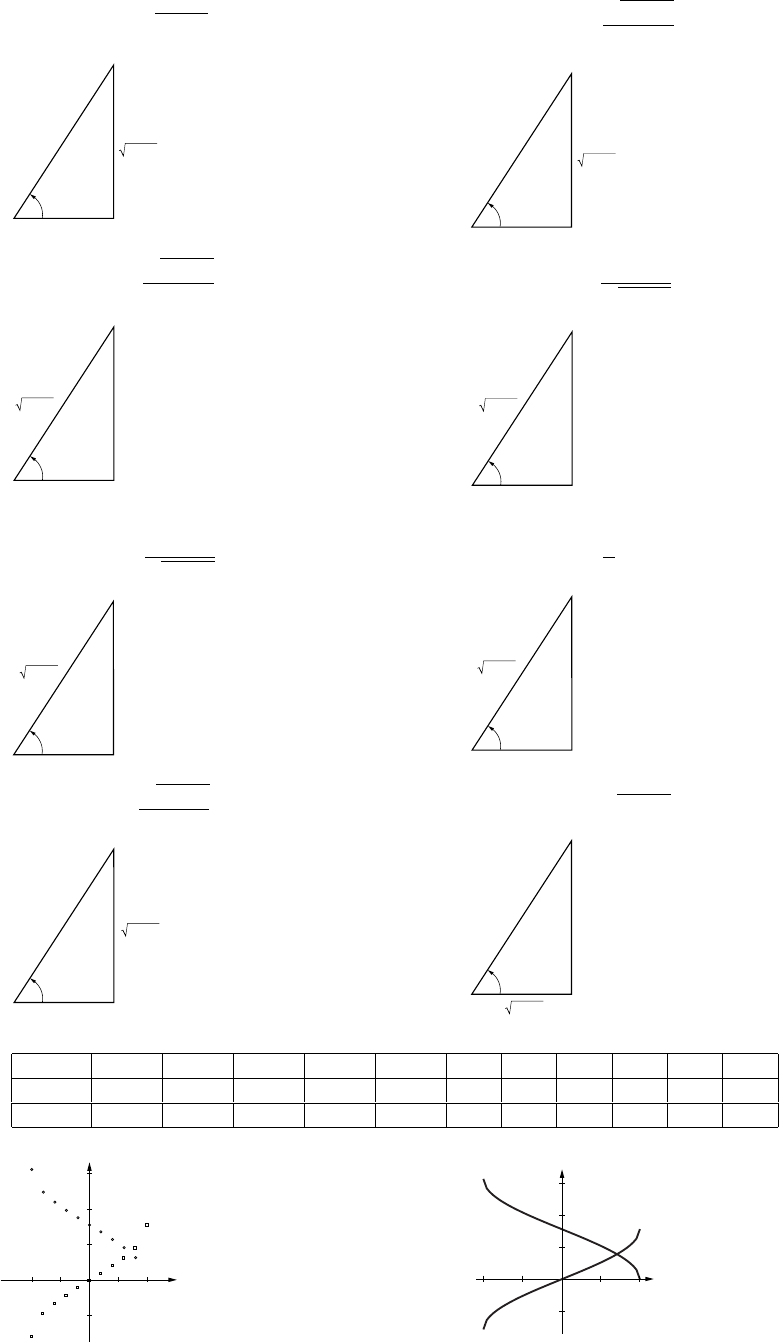
Exercise Set 4.5 118
12. (a) sin(cos−1x)=√
1−x
2
1
x
1 − x
2
cos−1x
(b) tan(cos−1x)=√
1−x
2
x
1
x
cos−1x
1 − x
2
(c) csc(tan−1x)=√
1+x
2
x
1
x
tan−1x
1 + x
2
(d) sin(tan−1x)= x
√
1+x
2
1
x
tan−1x
1 + x
2
13. (a) cos(tan−1x)= 1
√
1+x
2
1
x
tan−1x
1 + x
2
(b) tan(cot−1x)= 1
x
x
1
cot−1x
1 + x
2
(c) sin(sec−1x)=√
x
2−1
x
1
x
sec−1x
x
2
− 1
(d) cot(csc−1x)=px
2−1
1
x
csc−1x
x
2
− 1
14. (a) x−1.00 −0.80 −0.6−0.40 −0.20 0.00 0.20 0.40 0.60 0.80 1.00
sin−1x−1.57 −0.93 −0.64 −0.41 −0.20 0.00 0.20 0.41 0.64 0.93 1.57
cos−1x3.14 2.50 2.21 1.98 1.77 1.57 1.37 1.16 0.93 0.64 0.00
(b) y
x
1
1
(c) y
x
-1
1
2
3
0.5 1
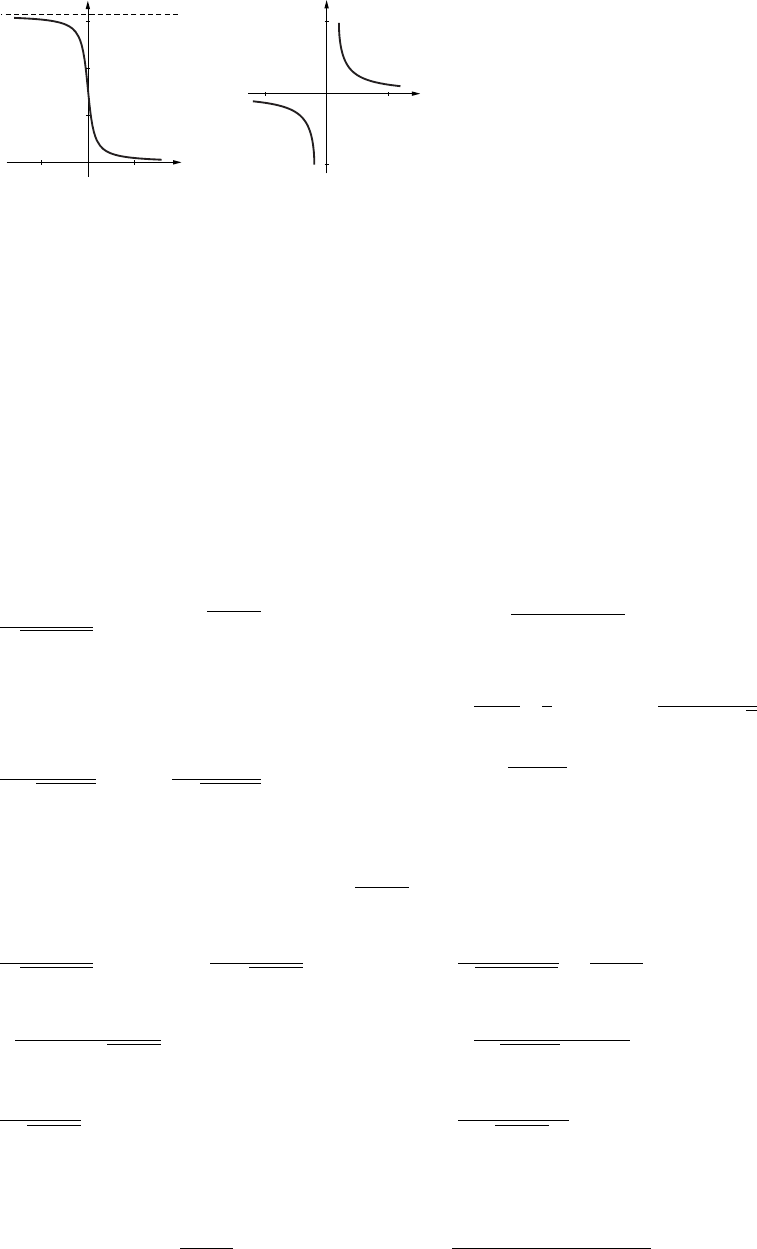
119 Chapter 4
15. (a) y
x
1
3
-10 10
y
x
-π/2
π/2
-5 51
(b) The domain of cot−1xis (−∞,+∞), the range is (0,π); the domain of csc−1xis
(−∞,−1] ∪[1,+∞), the range is [−π/2,0) ∪(0,π/2].
16. (a) y= cot−1x,x= cot y, tan y=1/x,y= tan−1(1/x)
(b) y= sec−1x,x= sec y, cos y=1/x,y= cos−1(1/x)
(c) y= csc−1x,x= csc y, sin y=1/x,y= sin−1(1/x)
17. (a) 55.0◦(b) 33.6◦(c) 25.8◦
18. (a) x=π−sin−1(0.37) ≈2.7626 rad (b) θ= 180◦+ sin−1(0.61) ≈217.6◦
19. (a) x=π+ cos−1(0.85) ≈3.6964 rad (b) θ=−cos−1(0.23) ≈−76.7◦
20. (a) x= tan−1(3.16) −π≈−1.8773 (b) θ= 180◦−tan−1(0.45) ≈155.8◦
21. (a) 1
p1−x2/9(1/3)=1/
p9−x
2(b) −2/p1−(2x+1)
2
22. (a) 2x/(1+x4)(b) −1
1+xµ1
2x
−1/2
¶=−1
2(1 + x)√x
23. (a) 1
x7√x14 −1(7x6)= 7
x
√
x
14 −1(b) −1/√e2x−1
24. (a) y=1/tan x= cot x,dy/dx =−csc2x
(b) y= (tan−1x)−1,dy/dx =−(tan−1x)−2µ1
1+x
2¶
25. (a) 1
p1−1/x2(−1/x2)=−1
|x|
√
x
2−1(b) sin x
√1−cos2x=sin x
|sin x|=½1,sin x>0
−1,sin x<0
26. (a) −1
(cos−1x)√1−x2(b) −1
2√cot−1x(1+x2)
27. (a) ex
x√x2−1+exsec−1x(b) 3x2(sin−1x)2
√1−x2+2x(sin−1x)3
28. (a) 0(b) 0
29. x3+xtan−1y=ey,3x
2+x
1+y
2y
0+ tan−1y=eyy0,y0=(3x2+ tan−1y)(1 + y2)
(1+y2)ey−x
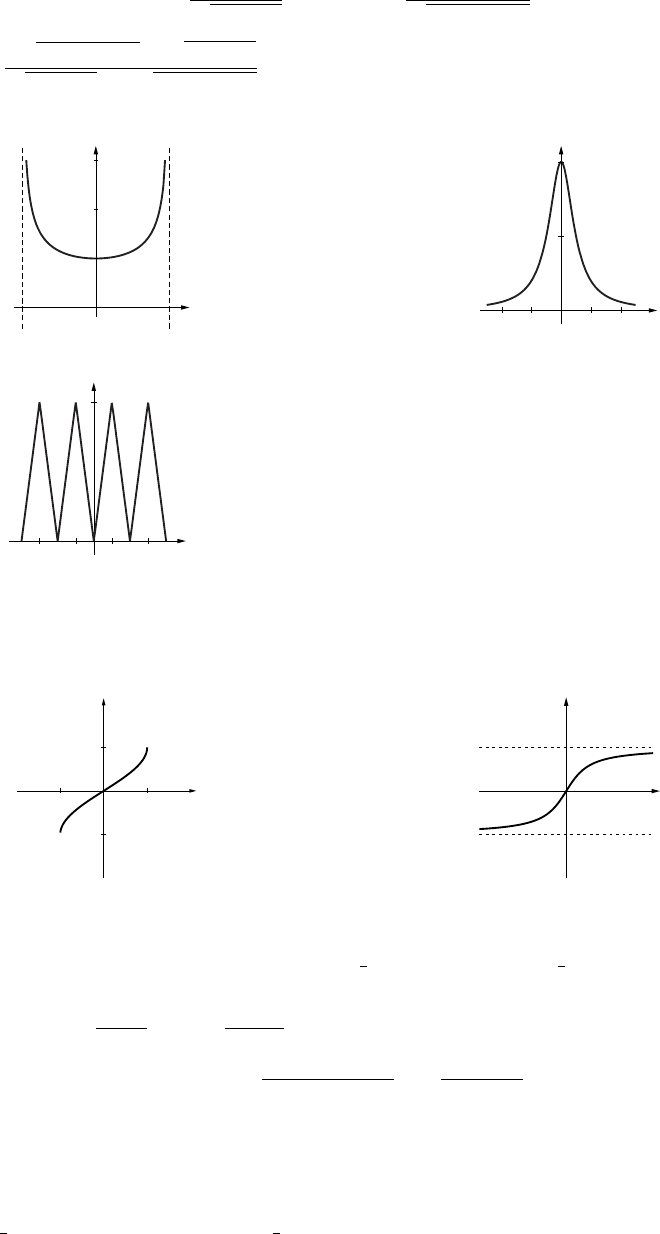
Exercise Set 4.5 120
30. sin−1(xy) = cos−1(x−y), 1
p1−x2y2(xy0+y)=−1
p1−(x−y)
2(1 −y0),
y0=yp1−(x−y)2+p1−x2y2
p1−x2y2−xp1−(x−y)2
31. (a) y
x
1
2
3
-1 1
32. (a) y
x
1
2
33. (a) y
x
π
−2π4π
34. (a) sin−10.9>1, so it is not in the domain of sin−1x
(b) −1≤sin−1x≤1 is necessary, or −0.841471 ≤x≤0.841471
35. (a)
-0.5 0.5
-6
6
x
y(b)
-6
6
x
y
36. (a) x=2π−cos−1k(b) x=π+ tan−1k
(c) 2x= sin−1kor 2x=π−sin−1kso x=1
2sin−1kor x=π/2−1
2sin−1k
37. (b) θ= sin−1R
R+h= sin−16378
16,378 ≈23◦
38. (a) If γ=90
◦, then sin γ=1,p1−sin2φsin2γ=p1−sin2φ= cos φ,
D= tan φtan λ= (tan 23.55◦)(tan 65◦)≈0.934684245 so h≈21.2 hours.
(b) If γ= 270◦, then sin γ=−1, D=−tan φtan λ≈−0.934684245 so h≈2.8 hours.
39. sin 2θ=gR/v2=(9.8)(18)/(14)2=0.9, 2θ= sin−1(0.9) or 2θ= 180◦−sin−1(0.9) so
θ=1
2sin−1(0.9) ≈32◦or θ=90
◦−1
2sin−1(0.9) ≈58◦. The ball will have a lower
parabolic trajectory for θ=32
◦and hence will result in the shorter time of flight.
40. 42=2
2+3
2−2(2)(3) cos θ, cos θ=−1/4, θ= cos−1(−1/4) ≈104◦

121 Chapter 4
41. y= 0 when x2= 6000v2/g,x=10v
p60/g = 1000√30 for v= 400 and g= 32;
tan θ= 3000/x =3/
√
30, θ= tan−1(3/√30) ≈29◦.
42. θ=α−β, cot α=x
a+band cot β=x
bso
θ= cot−1x
a+b−cot−1x
b
a
θ
αβ
b
x
43. (a) Let θ= sin−1(−x) then sin θ=−x,−π/2≤θ≤π/2. But sin(−θ)=−sin θand
−π/2≤−θ≤π/2 so sin(−θ)=−(−x)=x,−θ= sin−1x,θ=−sin−1x.
(b) proof is similar to that in part (a)
44. (a) Let θ= cos−1(−x) then cos θ=−x,0≤θ≤π. But cos(π−θ)=−cos θand
0≤π−θ≤πso cos(π−θ)=x,π−θ= cos−1x,θ=π−cos−1x
(b) Let θ= sec−1(−x) for x≥1; then sec θ=−xand π/2<θ≤π.So0≤π−θ<π/2 and
π−θ= sec−1sec(π−θ) = sec−1(−sec θ) = sec−1x,orsec
−1
(−x)=π−sec−1x.
45. (a) sin−1x= tan−1x
√1−x2
x
1
÷1
− x
2
sin−1x
(b) sin−1x+ cos−1x=π/2; cos−1x=π/2−sin−1x=π/2−tan−1x
√1−x2
46. tan(α+β)= tan α+ tan β
1−tan αtan β,
tan(tan−1x+ tan−1y)= tan(tan−1x) + tan(tan−1y)
1−tan(tan−1x) tan(tan−1y)=x+y
1−xy
so tan−1x+ tan−1y= tan−1x+y
1−xy
47. (a) tan−11
2+ tan−11
3= tan−11/2+1/3
1−(1/2) (1/3) = tan−11=π/4
(b) 2 tan−11
3= tan−11
3+ tan−11
3= tan−11/3+1/3
1−(1/3) (1/3) = tan−13
4,
2 tan−11
3+ tan−11
7= tan−13
4+ tan−11
7= tan−13/4+1/7
1−(3/4) (1/7) = tan−11=π/4
48. sin(sec−1x) = sin(cos−1(1/x)) = s1−µ1
x¶2
=√x2−1
|x|
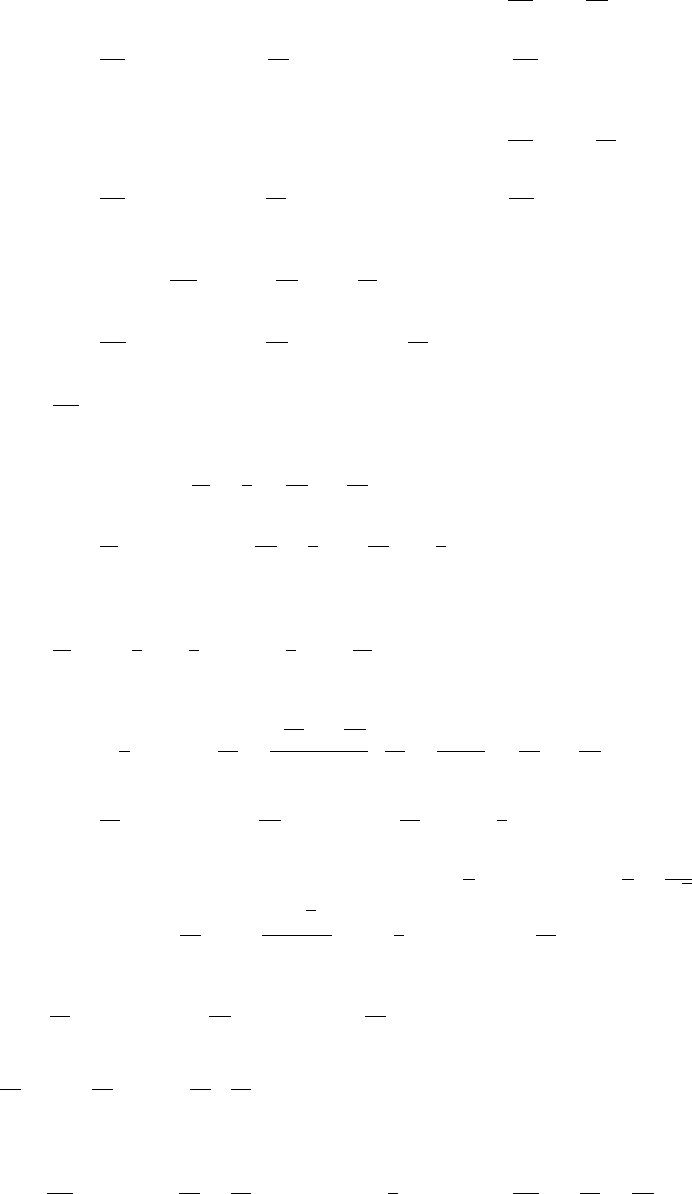
Exercise Set 4.6 122
EXERCISE SET 4.6
1. (b) A=x2(c) dA
dt =2x
dx
dt
(d) Find dA
dt ¯¯¯¯x=3
given that dx
dt ¯¯¯¯x=3
= 2. From part (c), dA
dt ¯¯¯¯x=3
= 2(3)(2) = 12 ft2/min.
2. (b) A=πr2(c) dA
dt =2πr dr
dt
(d) Find dA
dt ¯¯¯¯r=5
given that dr
dt ¯¯¯¯r=5
= 2. From part (c), dA
dt ¯¯¯¯r=5
=2π(5)(2) = 20πcm2/s.
3. (a) V=πr2h,so dV
dt =πµr2dh
dt +2rhdr
dt ¶.
(b) Find dV
dt ¯¯¯¯h=6,
r=10
given that dh
dt ¯¯¯¯h=6,
r=10
= 1 and dr
dt ¯¯¯¯h=6,
r=10
=−1. From part (a),
dV
dt ¯¯¯¯h=6,
r=10
=π[102(1) + 2(10)(6)(−1)] = −20πin3/s; the volume is decreasing.
4. (a) `2=x2+y2,sod`
dt =1
`µxdx
dt +ydy
dt ¶.
(b) Find d`
dt ¯¯¯¯x=3,
y=4
given that dx
dt =1
2and dy
dt =−1
4.
From part (a) and the fact that `= 5 when x= 3 and y=4,
d`
dt ¯¯¯¯x=3,
y=4
=1
5·3µ1
2¶+4µ−1
4¶¸=1
10 ft/s; the diagonal is increasing.
5. (a) tan θ=y
x,sosec
2θ
dθ
dt =
xdy
dt −ydx
dt
x2,dθ
dt =cos2θ
x2µxdy
dt −ydx
dt ¶
(b) Find dθ
dt ¯¯¯¯x=2,
y=2
given that dx
dt ¯¯¯¯x=2,
y=2
= 1 and dy
dt ¯¯¯¯x=2,
y=2
=−1
4.
When x= 2 and y= 2, tan θ=2/2=1soθ=π
4and cos θ= cos π
4=1
√2.Thus
from part (a), dθ
dt ¯¯¯¯x=2,
y=2
=(1/√2)2
22·2µ−1
4¶−2(1)¸=−5
16 rad/s; θis decreasing.
6. Find dz
dt ¯¯¯¯x=1,
y=2
given that dx
dt ¯¯¯¯x=1,
y=2
=−2 and dy
dt ¯¯¯¯x=1,
y=2
=3.
dz
dt =2x
3
ydy
dt +3x
2
y
2dx
dt ,dz
dt ¯¯¯¯x=1,
y=2
= (4)(3) + (12)(−2) = −12 units/s; zis decreasing
7. Let Abe the area swept out, and θthe angle through which the minute hand has rotated.
Find dA
dt given that dθ
dt =π
30 rad/min; A=1
2r2θ=8θ,so dA
dt =8
dθ
dt =4π
15 in2/min.
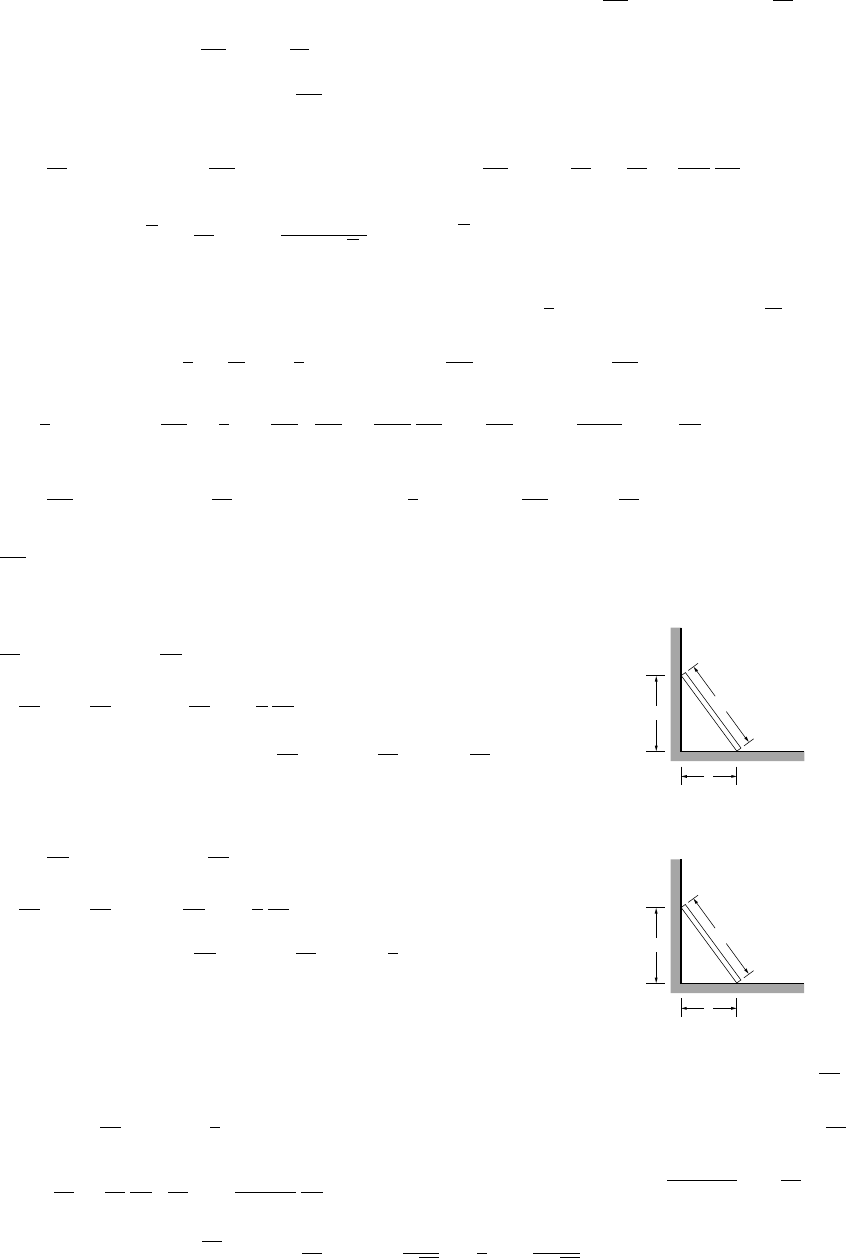
123 Chapter 4
8. Let rbe the radius and Athe area enclosed by the ripple. We want dA
dt ¯¯¯¯t=10
given that dr
dt =3. We
know that A=πr2,so dA
dt =2πrdr
dt . Because ris increasing at the constant rate of 3 ft/s, it follows
that r= 30 ft after 10 seconds so dA
dt ¯¯¯¯t=10
=2π(30)(3) = 180πft2/s.
9. Find dr
dt ¯¯¯¯A=9
given that dA
dt = 6. From A=πr2we get dA
dt =2πr dr
dt so dr
dt =1
2πr
dA
dt .IfA= 9 then
πr2=9,r=3/
√
πso dr
dt ¯¯¯¯A=9
=1
2π(3/√π)(6)=1/
√
πmi/h.
10. The volume Vof a sphere of radius ris given by V=4
3πr3or, because r=D
2where D
is the diameter, V=4
3πµD
2¶3
=1
6πD3. We want dD
dt ¯¯¯¯r=1
given that dV
dt = 3. From
V=1
6πD3we get dV
dt =1
2πD2dD
dt ,dD
dt =2
πD2
dV
dt ,so dD
dt ¯¯¯¯r=1
=2
π(2)2(3) = 3
2πft/min.
11. Find dV
dt ¯¯¯¯r=9
given that dr
dt =−15. From V=4
3πr3we get dV
dt =4πr2dr
dt so
dV
dt ¯¯¯¯r=9
=4π(9)2(−15) = −4860π. Air must be removed at the rate of 4860πcm3/min.
12. Let xand ybe the distances shown in the diagram. We want to find
dy
dt ¯¯¯¯y=8
given that dx
dt = 5. From x2+y2=17
2we get
2xdx
dt +2ydy
dt =0,so dy
dt =−x
y
dx
dt . When y=8,x
2+8
2=17
2
,
x
2= 289 −64 = 225, x=15so dy
dt ¯¯¯¯y=8
=−15
8(5) = −75
8ft/s; the
top of the ladder is moving down the wall at a rate of 75/8 ft/s.
17
x
y
13. Find dx
dt ¯¯¯¯y=5
given that dy
dt =−2. From x2+y2=13
2we get
2xdx
dt +2ydy
dt =0so dx
dt =−y
x
dy
dt . Use x2+y2= 169 to find that
x= 12 when y=5so dx
dt ¯¯¯¯y=5
=−5
12(−2) = 5
6ft/s.
13
x
y
14. Let θbe the acute angle, and xthe distance of the bottom of the plank from the wall. Find dθ
dt ¯¯¯¯x=2
given that dx
dt ¯¯¯¯x=2
=−1
2ft/s. The variables θand xare related by the equation cos θ=x
10 so
−sin θdθ
dt =1
10
dx
dt ,dθ
dt =−1
10 sin θ
dx
dt . When x= 2, the top of the plank is √102−22=√96 ft above
the ground so sin θ=√96/10 and dθ
dt ¯¯¯¯x=2
=−1
√96 µ−1
2¶=1
2√96 ≈0.051 rad/s.
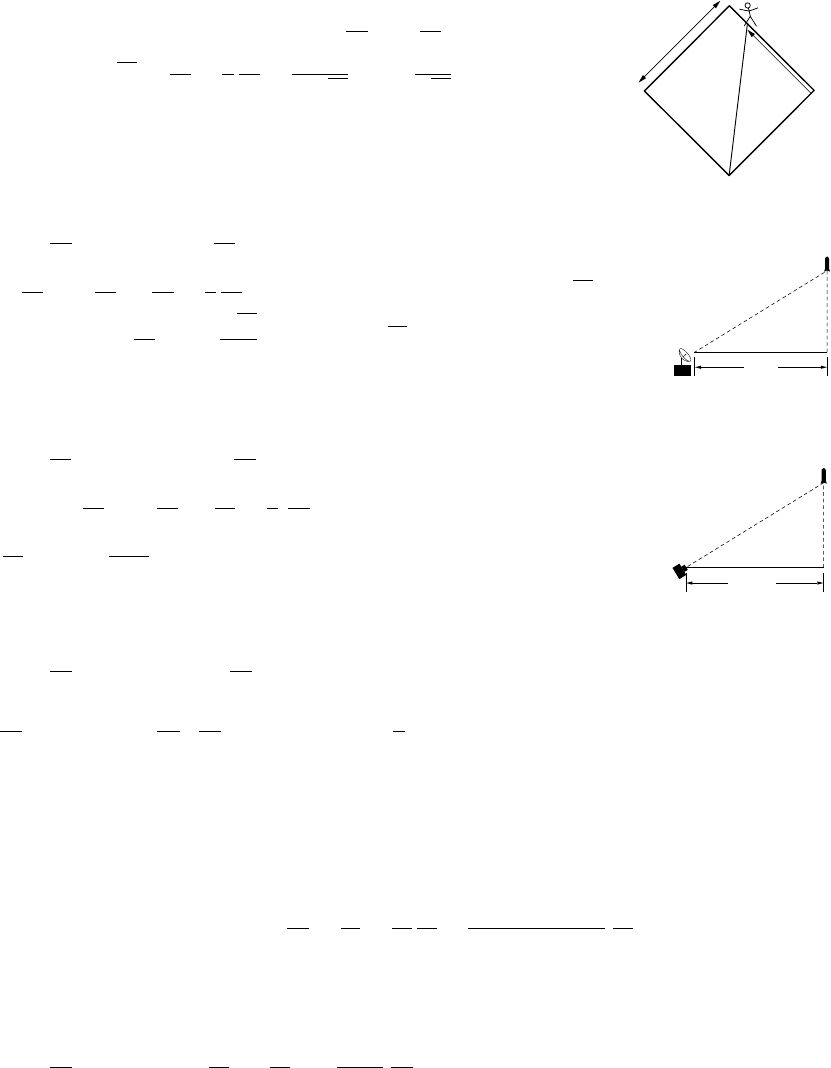
Exercise Set 4.6 124
15. Let xdenote the distance from first base and ythe distance from
home plate. Then x2+60
2=y
2and 2xdx
dt =2ydy
dt . When x=50
then y=10
√
61 so dy
dt =x
y
dx
dt =50
10√61(25) = 125
√61 ft/s.
60 ft
y
x
Home
First
16. Find dx
dt ¯¯¯¯x=4
given that dy
dt ¯¯¯¯x=4
= 2000. From x2+5
2=y
2we get
2xdx
dt =2ydy
dt so dx
dt =y
x
dy
dt . Use x2+25=y
2to find that y=√41
when x=4so dx
dt ¯¯¯¯x=4
=√41
4(2000) = 500√41 mi/h.
Rocket
yx
5 mi
Radar
station
17. Find dy
dt ¯¯¯¯x=4000
given that dx
dt ¯¯¯¯x=4000
= 880. From y2=x2+ 30002
we get 2ydy
dt =2x
dx
dt so dy
dt =x
y
dx
dt .Ifx= 4000, then y= 5000 so
dy
dt ¯¯¯¯x=4000
=4000
5000(880) = 704 ft/s.
Rocket
Camera
3000 ft
yx
18. Find dx
dt ¯¯¯¯φ=π/4
given that dφ
dt ¯¯¯¯φ=π/4
=0.2. But x= 3000 tan φso
dx
dt = 3000(sec2φ)dφ
dt ,dx
dt ¯¯¯¯φ=π/4
= 3000 ³sec2π
4´(0.2) = 1200 ft/s.
19. (a) If xdenotes the altitude, then r−x= 3960, the radius of the Earth. θ= 0 at perigee, so
r= 4995/1.12 ≈4460; the altitude is x= 4460 −3960 = 500 miles. θ=πat apogee, so
r= 4995/0.88 ≈5676; the altitude is x= 5676 −3960 = 1716 miles.
(b) If θ= 120◦, then r= 4995/0.94 ≈5314; the altitude is 5314 −3960 = 1354 miles. The rate of
change of the altitude is given by
dx
dt =dr
dt =dr
dθ
dθ
dt =4995(0.12 sin θ)
(1+0.12 cos θ)2
dθ
dt .
Use θ= 120◦and dθ/dt =2.7
◦/min = (2.7)(π/180) rad/min to get dr/dt ≈27.7 mi/min.
20. (a) Let xbe the horizontal distance shown in the figure. Then x= 4000 cot θand
dx
dt =−4000 csc2θdθ
dt ,so dθ
dt =−sin2θ
4000
dx
dt . Use θ=30
◦and
dx/dt = 300 mi/h = 300(5280/3600) ft/s = 440 ft/s to get
dθ/dt =−0.0275 rad/s ≈−1.6
◦/s; θis decreasing at the rate of 1.6◦/s.
(b) Let ybe the distance between the observation point and the aircraft. Then y= 4000 csc θso
dy/dt =−4000(csc θcot θ)(dθ/dt). Use θ=30
◦and dθ/dt =−0.0275 rad/s to get dy/dt ≈381
ft/s.
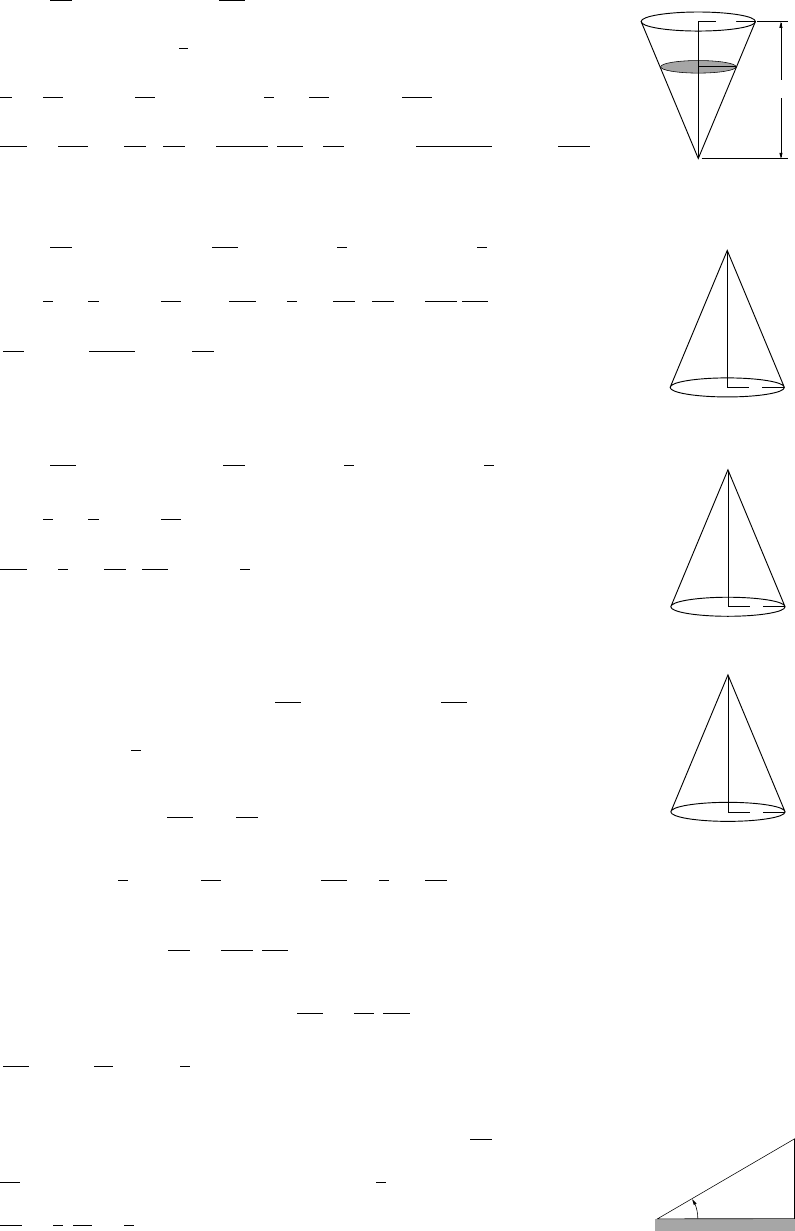
125 Chapter 4
21. Find dh
dt ¯¯¯¯h=16
given that dV
dt = 20. The volume of water in the tank
at a depth his V=1
3πr2h. Use similar triangles (see figure) to get
r
h=10
24 so r=5
12hthus V=1
3πµ5
12h¶2
h=25
432πh3,
dV
dt =25
144πh2dh
dt ;dh
dt =144
25πh2
dV
dt ,dh
dt ¯¯¯¯h=16
=144
25π(16)2(20) = 9
20π
ft/min.
h
r
24
10
22. Find dh
dt ¯¯¯¯h=6
given that dV
dt =8. V=1
3
πr2h, but r=1
2hso
V=1
3πµh
2¶2
h=1
12πh3,dV
dt =1
4πh2dh
dt ,dh
dt =4
πh2
dV
dt ,
dh
dt ¯¯¯¯h=6
=4
π(6)2(8) = 8
9πft/min.
h
r
23. Find dV
dt ¯¯¯¯h=10
given that dh
dt =5. V=1
3
πr2h, but r=1
2hso
V=1
3πµh
2¶2
h=1
12πh3,
dV
dt =1
4πh2dh
dt ,dV
dt ¯¯¯¯h=10
=1
4π(10)2(5) = 125πft3/min.
h
r
24. Let rand hbe as shown in the figure. If Cis the circumference of
the base, then we want to find dC
dt ¯¯¯¯h=8
given that dV
dt = 10. It is
given that r=1
2h,thusC=2πr =πh so
dC
dt =πdh
dt (1)
Use V=1
3πr2h=1
12πh3to get dV
dt =1
4πh2dh
dt ,so
dh
dt =4
πh2
dV
dt (2)
Substitution of (2) into (1) gives dC
dt =4
h2
dV
dt so
dC
dt ¯¯¯¯h=8
=4
64(10) = 5
8ft/min.
h
r
25. With sand has shown in the figure, we want to find dh
dt given that
ds
dt = 500. From the figure, h=ssin 30◦=1
2sso
dh
dt =1
2
ds
dt =1
2(500) = 250 mi/h.
sh
Ground
30°
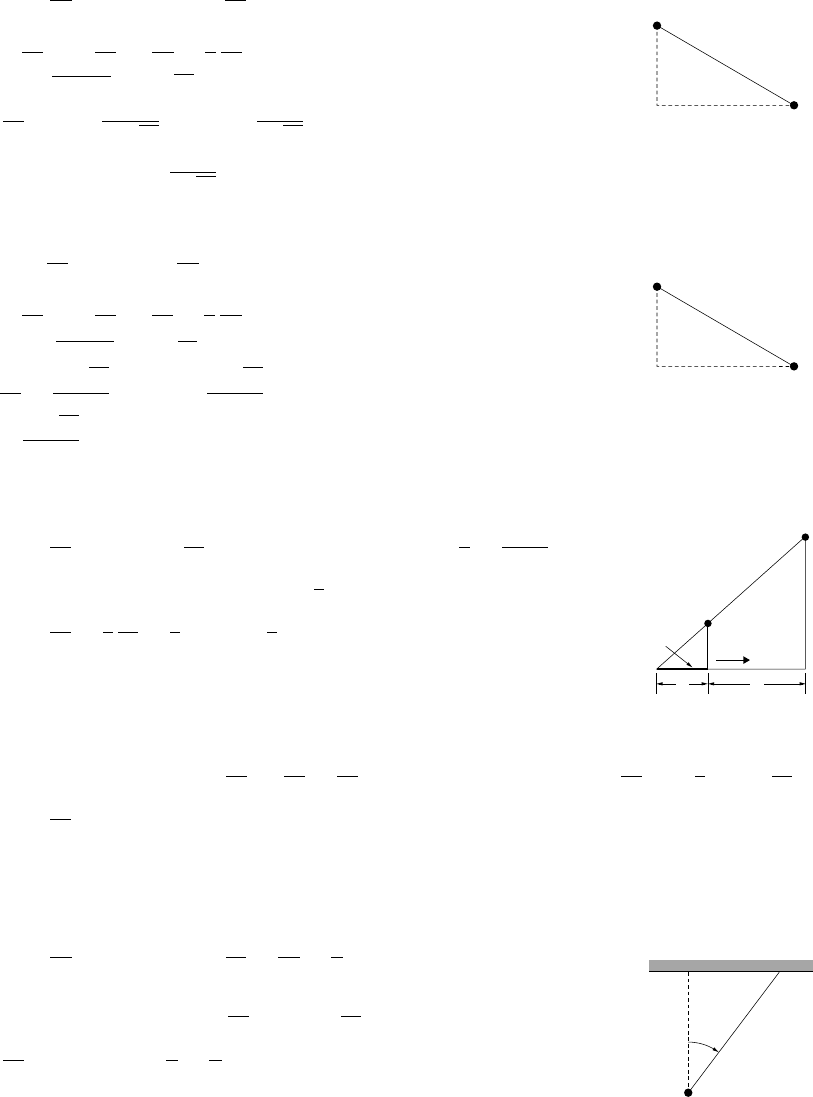
Exercise Set 4.6 126
26. Find dx
dt ¯¯¯¯y=125
given that dy
dt =−20. From x2+10
2=y
2we get
2xdx
dt =2ydy
dt so dx
dt =y
x
dy
dt . Use x2+ 100 = y2to find that
x=√15,525=15
√
69 when y= 125 so
dx
dt ¯¯¯¯y=125
=125
15√69(−20) = −500
3√69. The boat is approaching the
dock at the rate of 500
3√69 ft/min.
y
xBoat
Pulley
10
27. Find dy
dt given that dx
dt ¯¯¯¯y=125
=−12. From x2+10
2=y
2we get
2xdx
dt =2ydy
dt so dy
dt =x
y
dx
dt . Use x2+ 100 = y2to find that
x=p15,525=15
√
69 when y= 125 so
dy
dt =15√69
125 (−12) = −36√69
25 . The rope must be pulled at the rate
of 36√69
25 ft/min.
y
xBoat
Pulley
10
28. (a) Let xand ybe as shown in the figure. It is required to find
dx
dt , given that dy
dt =−3. By similar triangles, x
6=x+y
18 ,
18x=6x+6y,12x=6y,x=1
2
y,so
dx
dt =1
2
dy
dt =1
2(−3) = −3
2ft/s. 6
18
Man
Shadow
Light
yx
(b) The tip of the shadow is z=x+yfeet from the street light, thus the rate at which it is
moving is given by dz
dt =dx
dt +dy
dt . In part (a) we found that dx
dt =−3
2when dy
dt =−3so
dz
dt =(−3/2)+(−3) = −9/2 ft/s; the tip of the shadow is moving at the rate of 9/2 ft/s toward
the street light.
29. Find dx
dt ¯¯¯¯θ=π/4
given that dθ
dt =2π
10 =π
5rad/s. Then
x= 4 tan θ(see figure) so dx
dt = 4 sec2θdθ
dt ,
dx
dt ¯¯¯¯θ=π/4
=4³sec2π
4´³π
5´=8π/5 km/s.
x
4
Ship
θ

127 Chapter 4
30. If x,y, and zare as shown in the figure, then we want dz
dt ¯¯¯¯x=2,
y=4
given
that dx
dt =−600 and dy
dt ¯¯¯¯x=2,
y=4
=−1200. But z2=x2+y2so
2zdz
dt =2x
dx
dt +2ydy
dt ,dz
dt =1
zµxdx
dt +ydy
dt ¶. When x= 2 and
y=4,z
2=2
2+4
2= 20, z=√20=2
√
5so
dz
dt ¯¯¯¯x=2,
y=4
=1
2√5[2(−600) + 4(−1200)] = −3000
√5=−600√5 mi/h; the
distance between missile and aircraft is decreasing at the rate of
600√5 mi/h.
Aircraft
P
Missile
x
y
z
31. We wish to find dz
dt ¯¯¯¯x=2,
y=4
given dx
dt =−600 and dy
dt ¯¯¯¯x=2,
y=4
=−1200 (see
figure). From the law of cosines,
z2=x2+y2−2xy cos 120◦=x2+y2−2xy(−1/2) = x2+y2+xy,so
2z
dz
dt =2x
dx
dt +2ydy
dt +xdy
dt +ydx
dt ,
dz
dt =1
2z·(2x+y)dx
dt +(2y+x)dy
dt ¸. When x= 2 and y=4,
z
2=2
2+4
2+ (2)(4) = 28, so z=√28=2
√
7, thus
dz
dt ¯¯¯¯x=2,
y=4
=1
2(2√7)[(2(2) + 4)(−600) + (2(4) + 2)(−1200)] = −4200
√7=
−600√7 mi/h; the distance between missile and aircraft is
decreasing at the rate of 600√7 mi/h.
Aircraft
P
Missile
x
y
z
120°
32. (a) Let x,y, and zbe the distances shown in the first figure. Find dz
dt ¯¯¯¯x=2,
y=0
given that dx
dt =−75 and
dy
dt =−100. In order to find an equation relating x,y, and z, first draw the line segment that
joins the point Pto the car, as shown in the second figure. Because triangle OPC is a right
triangle, it follows that PC has length px2+(1/2)2; but triangle HPC is also a right triangle
so z2=³px2+(1/2)2´2+y2=x2+y2+1/4 and 2zdz
dt =2x
dx
dt +2ydy
dt +0,
dz
dt =1
zµxdx
dt +ydy
dt ¶. Now, when x= 2 and y=0,z
2= (2)2+ (0)2+1/4=17/4, z=√17/2
so dz
dt ¯¯¯¯x=2,
y=0
=1
(√17/2)[2(−75)+0(−100)] = −300/√17 mi/h
West East
North
Car
Helicopter
x
z
y
P
mi
1
2
C
H
x
O
z
y
P
mi
1
2
(b) decreasing, because dz
dt <0.
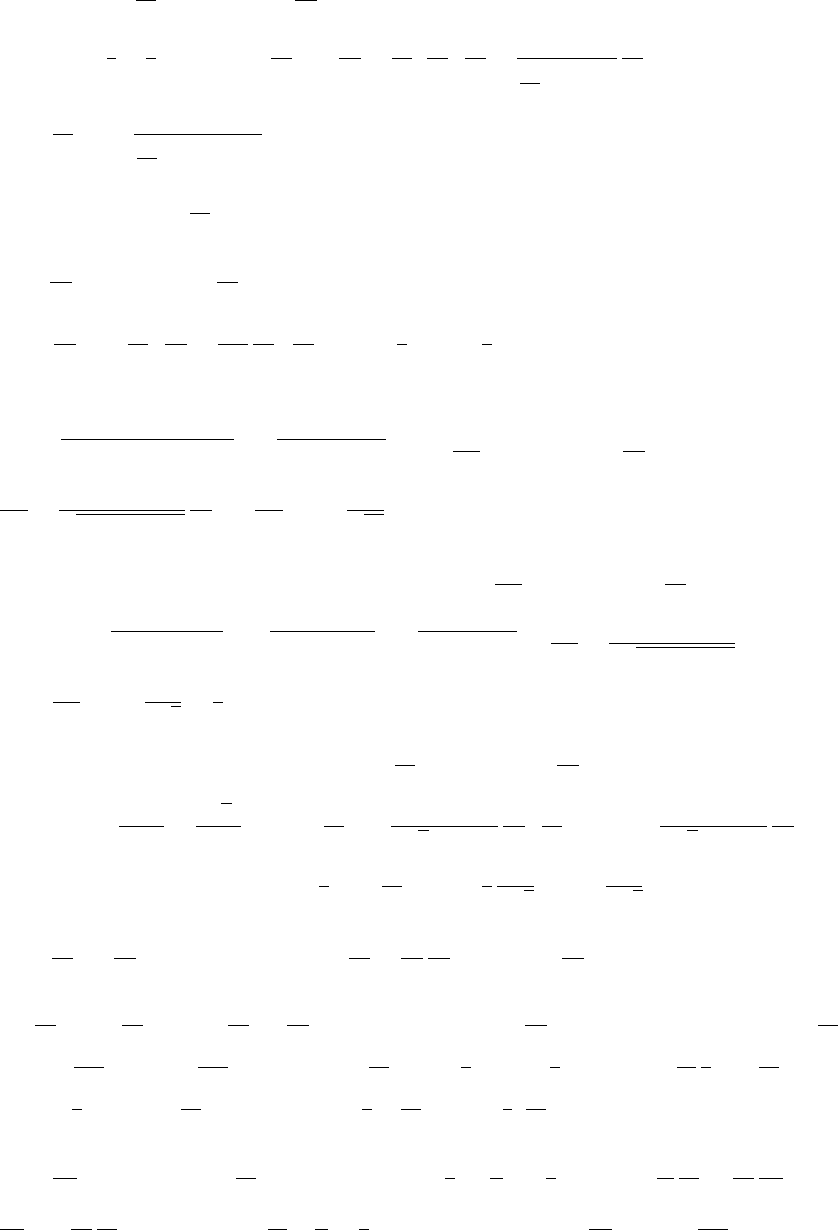
Exercise Set 4.6 128
33. (a) We want dy
dt ¯¯¯¯x=1,
y=2
given that dx
dt ¯¯¯¯x=1,
y=2
= 6. For convenience, first rewrite the equation as
xy3=8
5+8
5y2then 3xy2dy
dt +y3dx
dt =16
5ydy
dt ,dy
dt =y3
16
5y−3xy2
dx
dt so
dy
dt ¯¯¯¯x=1,
y=2
=23
16
5(2) −3(1)22
(6) = −60/7 units/s.
(b) falling, because dy
dt <0
34. Find dx
dt ¯¯¯¯(2,5)
given that dy
dt ¯¯¯¯(2,5)
= 2. Square and rearrange to get x3=y2−17
so 3x2dx
dt =2ydy
dt ,dx
dt =2y
3x2
dy
dt ,dx
dt ¯¯¯¯(2,5)
=µ5
6¶(2) = 5
3units/s.
35. The coordinates of Pare (x, 2x), so the distance between Pand the point (3,0) is
D=p(x−3)2+(2x−0)2=√5x2−6x+ 9. Find dD
dt ¯¯¯¯x=3
given that dx
dt ¯¯¯¯x=3
=−2.
dD
dt =5x−3
√5x2−6x+9
dx
dt ,so dD
dt ¯¯¯¯x=3
=12
√36(−2) = −4 units/s.
36. (a) Let Dbe the distance between Pand (2,0). Find dD
dt ¯¯¯¯x=3
given that dx
dt ¯¯¯¯x=3
=4.
D=p(x−2)2+y2=p(x−2)2+x=√x2−3x+4 so dD
dt =2x−3
2√x2−3x+4;
dD
dt ¯¯¯¯x=3
=3
2√4=3
4units/s.
(b) Let θbe the angle of inclination. Find dθ
dt ¯¯¯¯x=3
given that dx
dt ¯¯¯¯x=3
=4.
tan θ=y
x−2=√x
x−2so sec2θdθ
dt =−x+2
2
√
x(x−2)2
dx
dt ,dθ
dt =−cos2θx+2
2
√
x(x−2)2
dx
dt .
When x=3,D= 2 so cos θ=1
2and dθ
dt ¯¯¯¯x=3
=−1
4
5
2√3(4) = −5
2√3rad/s.
37. Solve dy
dt =3
dx
dt given y=xln x. Then dy
dt =dy
dx
dx
dt =(1+lnx)dx
dt ,so1+lnx=3,lnx=2,x=e
2
.
38. 32xdx
dt +18ydy
dt =0;ifdy
dt =dx
dt 6= 0, then (32x+18y)
dx
dt =0,32x+18y=0,y=−
16
9xso
16x2+9256
81 x2= 144, 400
9x2= 144, x2=81
25,x=±9
5.Ifx=9
5
, then y=−16
9
9
5=−16
5. Similarly,
if x=−9
5, then y=16
5. The points are (9
5,−16
5) and (−9
5,16
5).
39. Find dS
dt ¯¯¯¯s=10
given that ds
dt ¯¯¯¯s=10
=−2. From 1
s+1
S=1
6we get −1
s2
ds
dt −1
S2
dS
dt =0,so
dS
dt =−S2
s2
ds
dt .Ifs= 10, then 1
10 +1
S=1
6which gives S= 15. So dS
dt ¯¯¯¯s=10
=−225
100(−2)=4.5 cm/s.
The image is moving away from the lens.
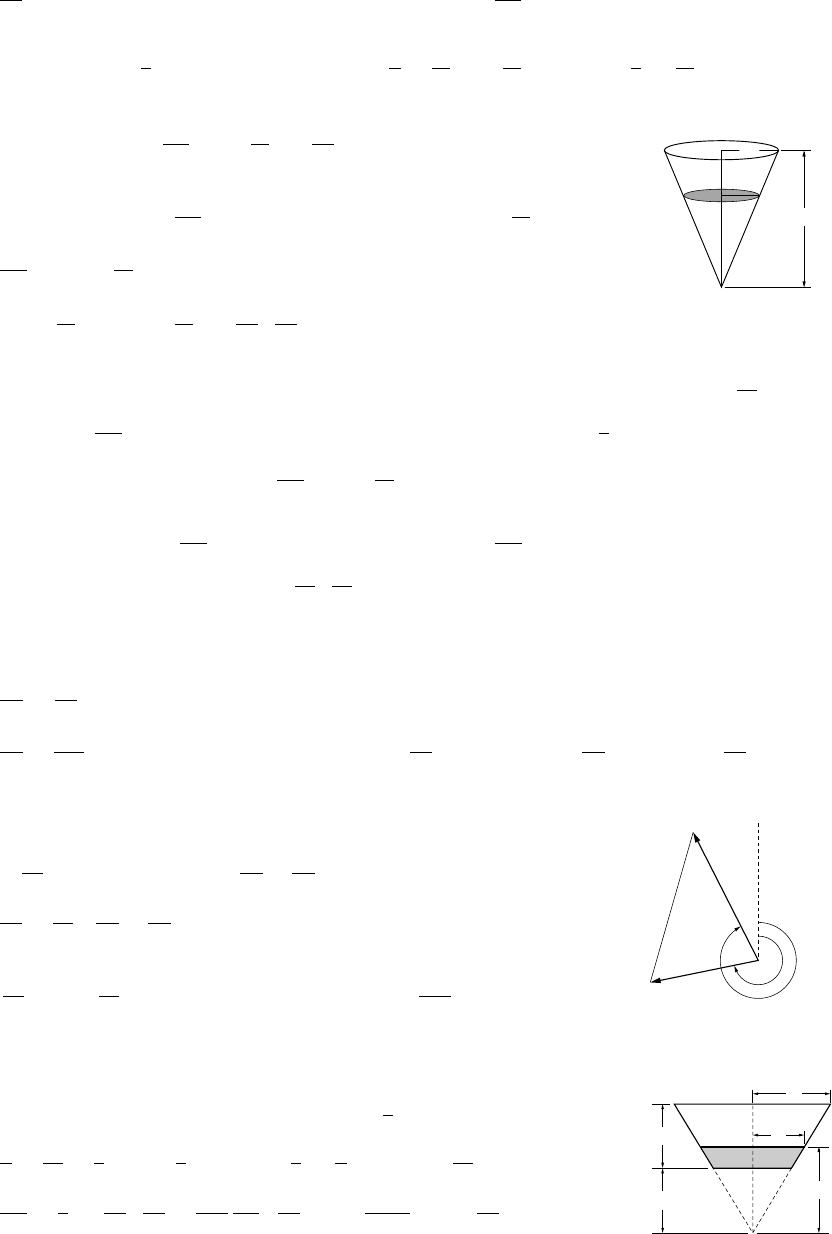
129 Chapter 4
40. Suppose that the reservoir has height Hand that the radius at the top is R. At any instant of time
let hand rbe the corresponding dimensions of the cone of water (see figure). We want to show that
dh
dt is constant and independent of Hand R, given that dV
dt =−kA where Vis the volume of water,
Ais the area of a circle of radius r, and kis a positive constant. The volume of a cone of radius rand
height his V=1
3πr2h. By similar triangles r
h=R
H,r=R
Hhthus V=1
3πµR
H¶2
h3so
dV
dt =πµR
H¶2
h2dh
dt (1)
But it is given that dV
dt =−kA or, because A=πr2=πµR
H¶
2
h2,
dV
dt =−kπ µR
H¶
2
h2, which when substituted into equation (1) gives
−kπ µR
H¶
2
h2=πµR
H¶
2
h2dh
dt ,dh
dt =−k.
h
r
H
R
41. Let rbe the radius, Vthe volume, and Athe surface area of a sphere. Show that dr
dt is a constant
given that dV
dt =−kA, where kis a positive constant. Because V=4
3πr3,
dV
dt =4πr2dr
dt (1)
But it is given that dV
dt =−kA or, because A=4πr2,dV
dt =−4πr2kwhich when substituted into
equation (1) gives −4πr2k=4πr2dr
dt ,dr
dt =−k.
42. Let xbe the distance between the tips of the minute and hour hands, and αand βthe angles shown
in the figure. Because the minute hand makes one revolution in 60 minutes,
dα
dt =2π
60 =π/30 rad/min; the hour hand makes one revolution in 12 hours (720 minutes), thus
dβ
dt =2π
720 =π/360 rad/min. We want to find dx
dt ¯¯¯¯α=2π,
β=3π/2
given that dα
dt =π/30 and dβ
dt =π/360.
Using the law of cosines on the triangle shown in the figure,
x2=3
2+4
2−2(3)(4) cos(α−β)=25−24 cos(α−β), so
2xdx
dt = 0 + 24 sin(α−β)µdα
dt −dβ
dt ¶,
dx
dt =12
xµdα
dt −dβ
dt ¶sin(α−β). When α=2πand β=3π/2,
x2=25−24 cos(2π−3π/2) = 25, x=5;so
dx
dt ¯¯¯¯α=2π,
β=3π/2
=12
5(π/30 −π/360) sin(2π−3π/2) = 11π
150 in/min. 3
4
a
x
b
43. Extend sides of cup to complete the cone and let V0be the volume
of the portion added, then (see figure) V=1
3πr2h−V0where
r
h=4
12 =1
3so r=1
3hand V=1
3πµh
3¶2
h−V0=1
27πh3−V0,
dV
dt =1
9πh2dh
dt ,dh
dt =9
πh2
dV
dt ,dh
dt ¯¯¯¯h=9
=9
π(9)2(20) = 20
9πcm/s.
r
4
2h
6
6
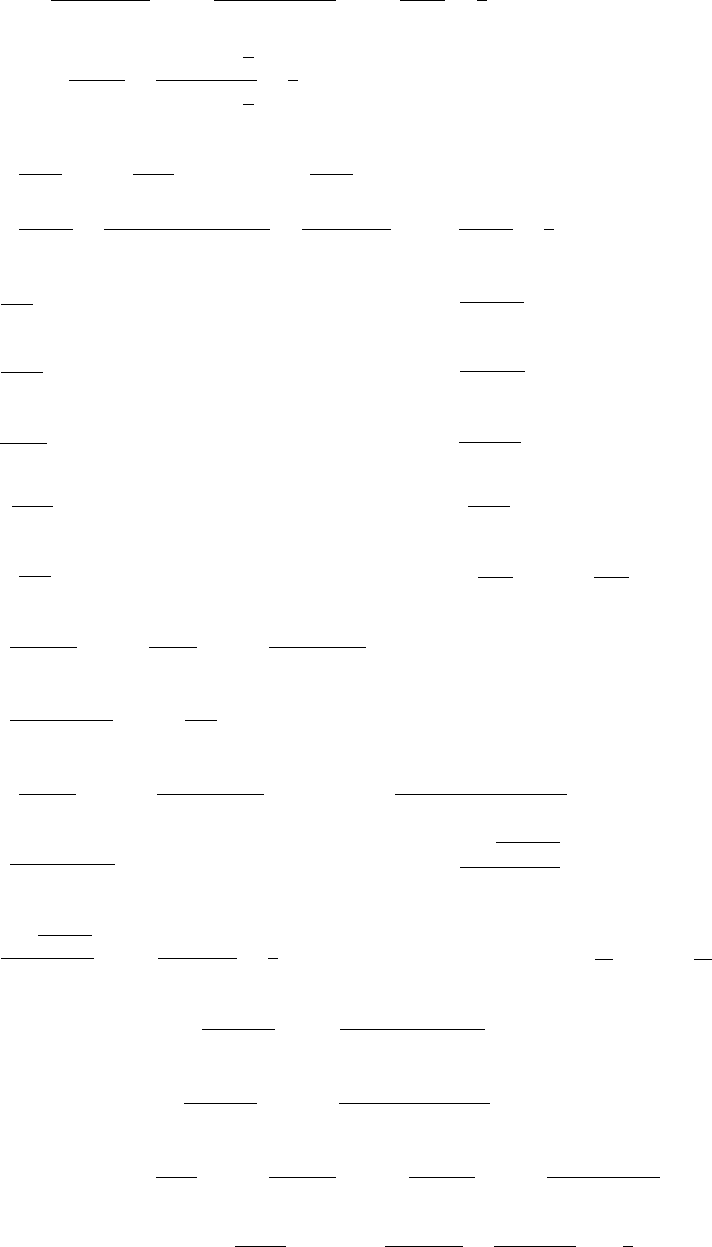
Exercise Set 4.7 130
EXERCISE SET 4.7
1. (a) lim
x→2
x2−4
x2+2x−8= lim
x→2
(x−2)(x+2)
(x+ 4)(x−2) = lim
x→2
x+2
x+4 =2
3
(b) lim
x→+∞
2x−5
3x+7 =
2−lim
x→+∞
5
x
3 + lim
x→+∞
7
x
=2
3
2. (a) sin x
tan x= sin xcos x
sin x= cos xso lim
x→0
sin x
tan x=0
(b) x2−1
x3−1=(x−1)(x+1)
(x−1)(x2+x+1) =x+1
x
2+x+1 so lim
x→1
x2−1
x3−1=2
3
3. lim
x→1
1/x
1=1 4. lim
x→0
2 cos 2x
5 cos 5x=2/5
5. lim
x→0
ex
cos x=1 6. lim
x→3
1
6x−13 =1/5
7. lim
θ→0
sec2θ
1=1 8. lim
t→0
tet+et
−et=−1
9. lim
x→π+
cos x
1=−110. lim
x→0+
cos x
2x=+∞
11. lim
x→+∞
1/x
1=0 12. lim
x→+∞
3e3x
2x= lim
x→+∞
9e3x
2=+∞
13. lim
x→0+−csc2x
1/x = lim
x→0+−x
sin2x= lim
x→0+−1
2 sin xcos x=−∞
14. lim
x→0+−1/x
(−1/x2)e1/x = lim
x→0+
x
e1/x =0
15. lim
x→+∞
100x99
ex= lim
x→+∞
(100)(99)x98
ex=···= lim
x→+∞
(100)(99)(98) ···(1)
ex=0
16. lim
x→0+
cos x/ sin x
sec2x/ tan x= lim
x→0+cos2x=1 17. lim
x→0
2/√1−4x2
1=2
18. lim
x→0
1−1
1+x
2
3x
2= lim
x→0
1
3(1 + x2)=1
319. lim
x→+∞xe−x= lim
x→+∞
x
ex= lim
x→+∞
1
ex=0
20. lim
x→π(x−π) tan(x/2) = lim
x→π
x−π
cot(x/2) = lim
x→π
1
−(1/2) csc2(x/2) =−2
21. lim
x→+∞xsin(π/x) = lim
x→+∞
sin(π/x)
1/x = lim
x→+∞
(−π/x2) cos(π/x)
−1/x2= lim
x→+∞πcos(π/x)=π
22. lim
x→0+tan xln x= lim
x→0+
ln x
cot x= lim
x→0+
1/x
−csc2x= lim
x→0+−sin2x
x= lim
x→0+−2 sin xcos x
1=0
23. lim
x→(π/2)−sec 3xcos 5x= lim
x→(π/2)−
cos 5x
cos 3x= lim
x→(π/2)−−5 sin 5x
−3 sin 3x=−5(+1)
(−3)(−1) =−5
3
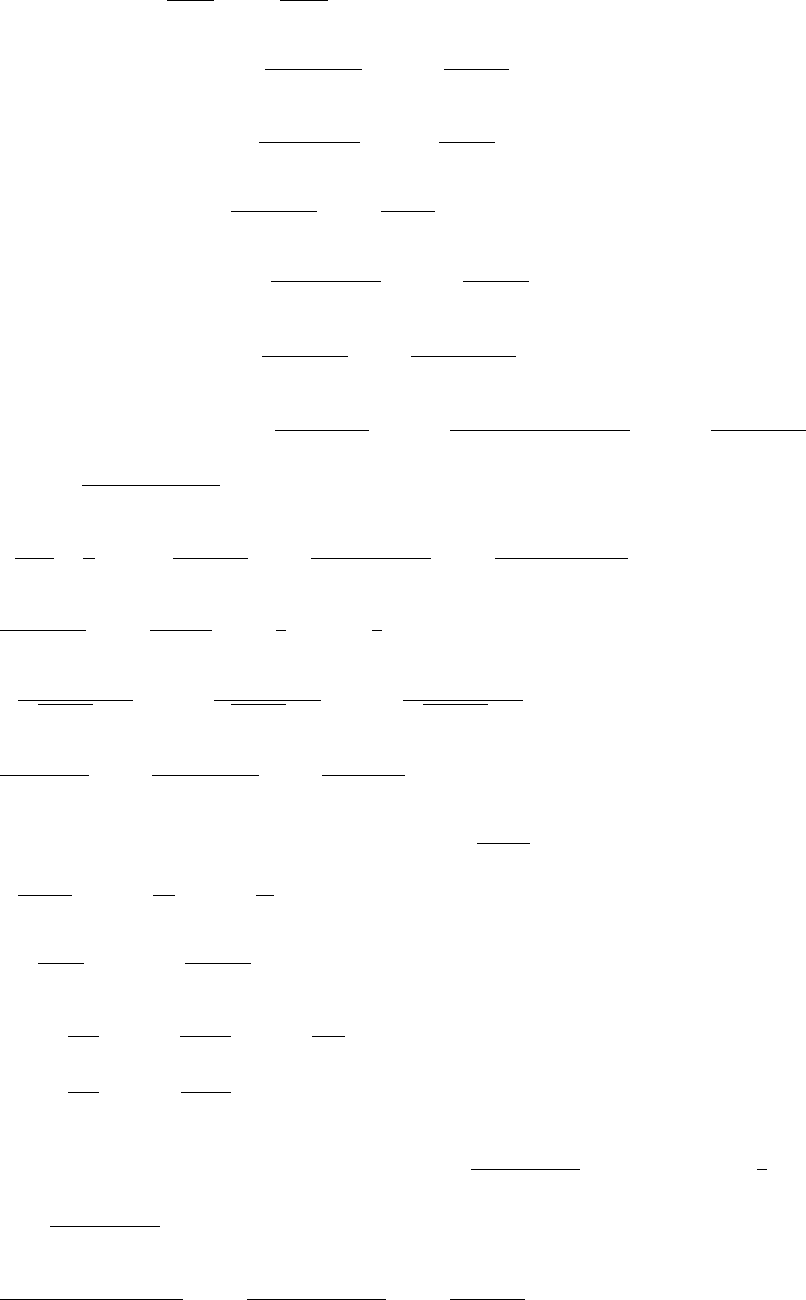
131 Chapter 4
24. lim
x→π(x−π) cot x= lim
x→π
x−π
tan x= lim
x→π
1
sec2x=1
25. y=(1−3/x)x, lim
x→+∞ln y= lim
x→+∞
ln(1 −3/x)
1/x = lim
x→+∞−3
1−3/x =−3, lim
x→+∞y=e−3
26. y=(1+2x)
−3/x, lim
x→0ln y= lim
x→0−3 ln(1 + 2x)
x= lim
x→0−6
1+2x=−6, lim
x→0y=e−6
27. y=(e
x+x)
1/x, lim
x→0ln y= lim
x→0
ln(ex+x)
x= lim
x→0
ex+1
e
x+x= 2, lim
x→0y=e2
28. y=(1+a/x)bx, lim
x→+∞ln y= lim
x→+∞
bln(1 + a/x)
1/x = lim
x→+∞
ab
1+a/x =ab, lim
x→+∞y=eab
29. y=(2−x)
tan(πx/2), lim
x→1ln y= lim
x→1
ln(2 −x)
cot(πx/2) = lim
x→1
2 sin2(πx/2)
π(2 −x)=2/π, lim
x→1y=e2/π
30. y= [cos(2/x)]x2,lim
x→+∞ln y= lim
x→+∞
ln cos(2/x)
1/x2= lim
x→+∞
(−2/x2)(−tan(2/x))
−2/x3= lim
x→+∞−tan(2/x)
1/x
= limx→+∞
(2/x2) sec2(2/x)
−1/x2=−2,lim
x→+∞y=e−2
31. lim
x→0µ1
sin x−1
x¶= lim
x→0
x−sin x
xsin x= lim
x→0
1−cos x
xcos x+ sin x= lim
x→0
sin x
2 cos x−xsin x=0
32. lim
x→0
1−cos 3x
x2= lim
x→0
3 sin 3x
2x= lim
x→0
9
2cos 3x=9
2
33. lim
x→+∞
(x2+x)−x2
√x2+x+x= lim
x→+∞
x
√x2+x+x= lim
x→+∞
1
p1+1/x +1 =1/2
34. lim
x→0
ex−1−x
xex−x= lim
x→0
ex−1
xex+ex−1= lim
x→0
ex
xex+2e
x=1/2
35. lim
x→+∞[x−ln(x2+ 1)] = lim
x→+∞[ln ex−ln(x2+ 1)] = lim
x→+∞ln ex
x2+1,
lim
x→+∞
ex
x2+1 = lim
x→+∞
ex
2x= lim
x→+∞
ex
2=+∞so lim
x→+∞[x−ln(x2+1)]=+∞
36. lim
x→+∞ln x
1+x= lim
x→+∞ln 1
1/x +1 = ln(1) = 0
38. (a) lim
x→+∞
ln x
xn= lim
x→+∞
1/x
nxn−1= lim
x→+∞
1
nxn=0
(b) lim
x→+∞
xn
ln x= lim
x→+∞
nxn−1
1/x = lim
x→+∞nxn=+∞
39. (a) L’Hˆopital’s Rule does not apply to the problem lim
x→1
3x2−2x+1
3x
2−2xbecause it is not a 0
0form
(b) lim
x→1
3x2−2x+1
3x
2−2x=2
40. lim
x→1
4x3−12x2+12x−4
4x
3−9x
2+6x−1= lim
x→1
12x2−24x+12
12x2−18x+6 = lim
x→1
24x−24
24x−18 =0
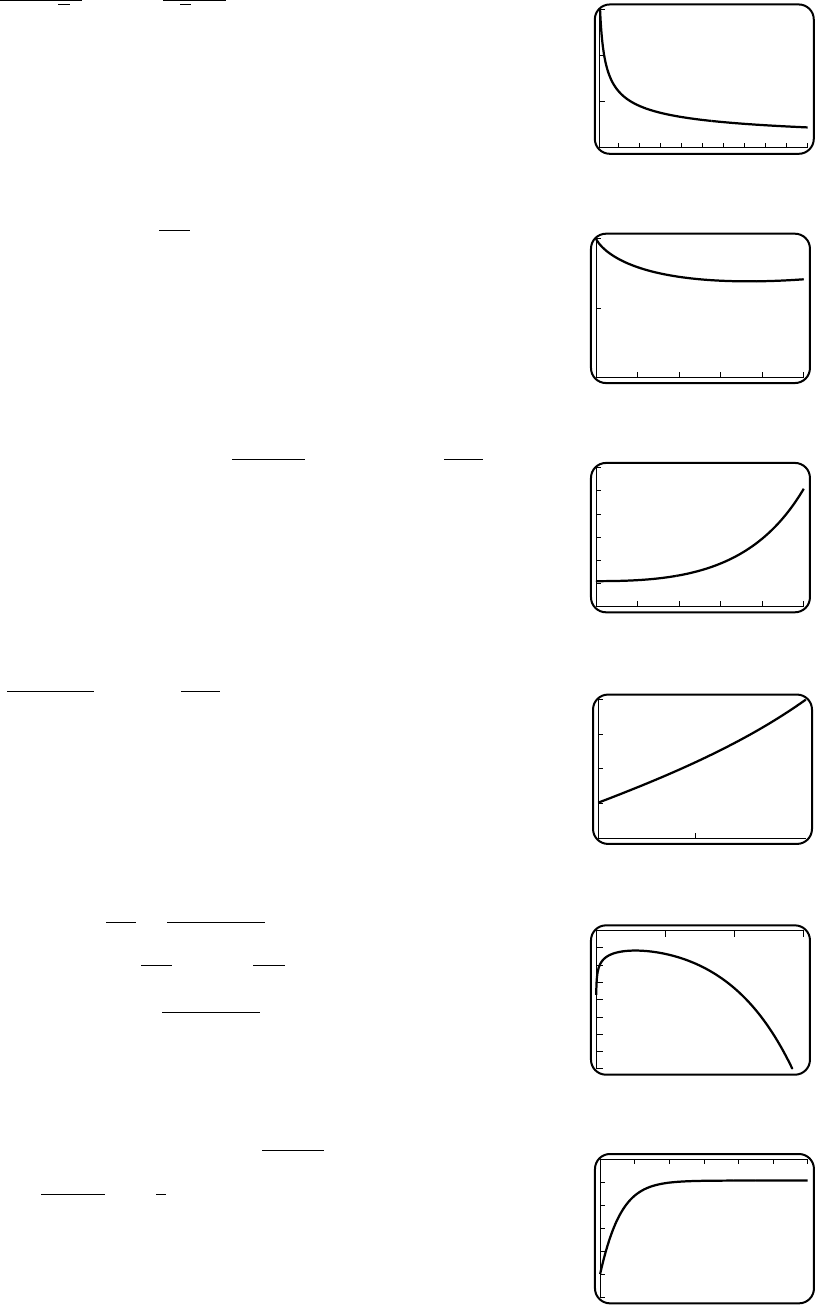
Exercise Set 4.7 132
41. lim
x→+∞
1/(xln x)
1/(2√x)= lim
x→+∞
2
√xln x=0 0.15
0
100 10000
42. y=xx, lim
x→0+ln y= lim
x→0+
ln x
1/x = lim
x→0+−x= 0, lim
x→0+y=1 1
0
0 0.5
43. y= (sin x)3/ln x, lim
x→0+ln y= lim
x→0+
3lnsinx
ln x= lim
x→0+(3 cos x)x
sin x=3,
lim
x→0+y=e3
25
19
0 0.5
44. lim
x→π/2−
4 sec2x
sec xtan x= lim
x→π/2−
4
sin x=4 4
0
0.5 p/2
45. ln x−ex=lnx−1
e
−x=e
−xln x−1
e−x;
lim
x→+∞e−xln x= lim
x→+∞
ln x
ex= lim
x→+∞
1/x
ex= 0 by L’Hˆopital’s Rule, so
lim
x→+∞[ln x−ex] = lim
x→+∞
e−xln x−1
e−x=−∞
0
-16
03
46. lim
x→+∞[ln ex−ln(1 + 2ex)] = lim
x→+∞ln ex
1+2e
x
= lim
x→+∞ln 1
e−x+2 =ln1
2
;
horizontal asymptote y=−ln 2
-0.6
-1.2
012
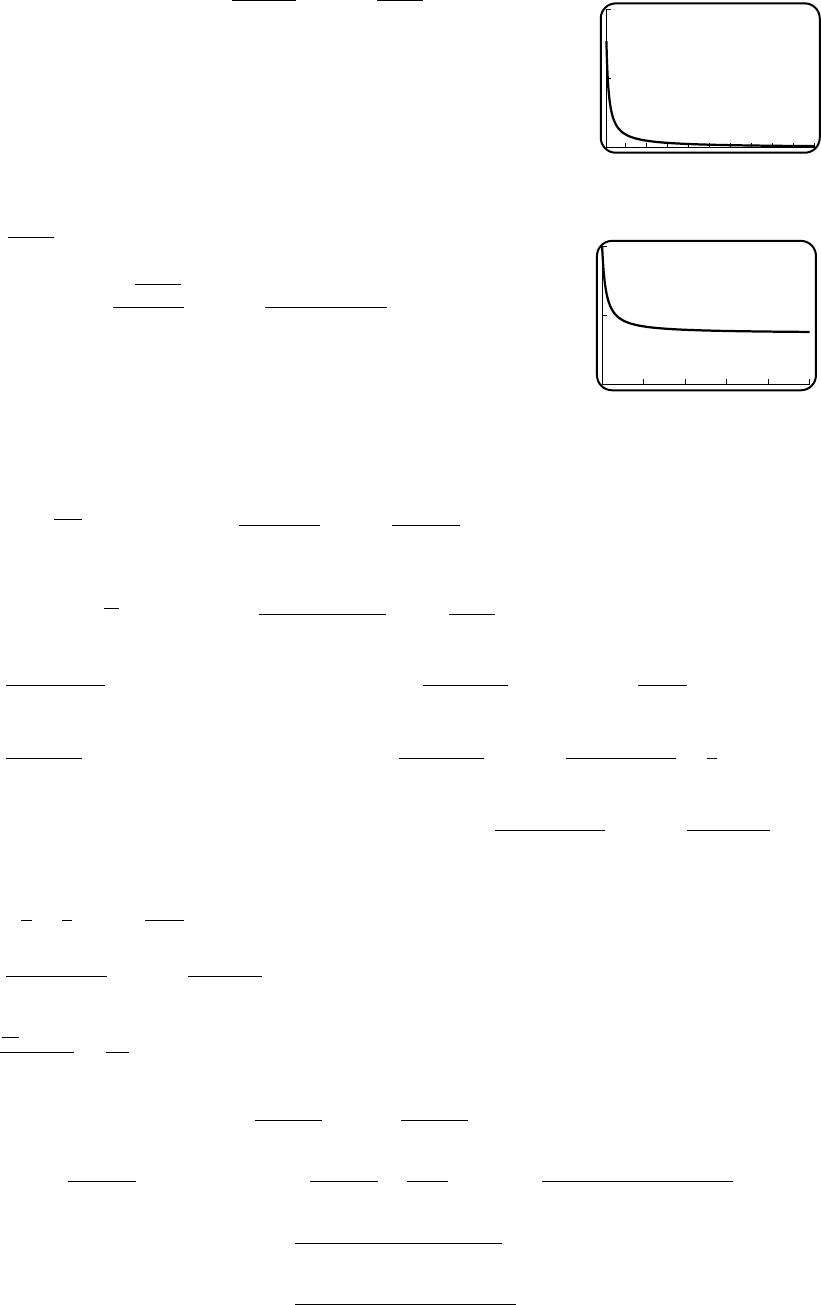
133 Chapter 4
47. y= (ln x)1/x, lim
x→+∞ln y= lim
x→+∞
ln(ln x)
x= lim
x→+∞
1
xln x=0;
lim
x→+∞y=1,y= 1 is the horizontal asymptote
1.02
1
100 10000
48. y=µx+1
x+2¶
x
,
lim
x→+∞ln y= lim
x→+∞
ln x+1
x+2
1/x = lim
x→+∞−x2
(x+ 1)(x+2) =−1;
lim
x→+∞y=e−1is the horizontal asymptote
1
0
050
49. (a) 0(b) +∞(c) 0(d) −∞ (e) +∞(f ) −∞
50. (a) y=xln a
1+ln x; lim
x→0+ln y= lim
x→0+
(ln a)lnx
1+lnx= lim
x→0+
(ln a)/x
1/x = lim
x→0+ln a=lna, lim
x→0+y=eln a=a
(b) same as part (a) with x→+∞
(c) y=(x+1)ln a
x, lim
x→0ln y= lim
x→0
(ln a) ln(x+1)
x= lim
x→0
ln a
x+1 =lna, lim
x→0y=eln a=a
51. lim
x→+∞
1 + 2 cos 2x
1does not exist, nor is it ±∞; lim
x→+∞
x+ sin 2x
x= lim
x→+∞µ1+sin 2x
x¶=1
52. lim
x→+∞
2−cos x
3 + cos xdoes not exist, nor is it ±∞; lim
x→+∞
2x−sin x
3x+ sin x= lim
x→+∞
2−(sin x)/x
3 + (sin x)/x =2
3
53. lim
x→+∞(2 + xcos 2x+ sin 2x) does not exist, nor is it ±∞; lim
x→+∞
x(2 + sin 2x)
x+1 = lim
x→+∞
2 + sin 2x
1+1/x , which
does not exist because sin 2xoscillates between −1and1asx→+∞
54. lim
x→+∞µ1
x+1
2cos x+sin x
2x¶does not exist, nor is it ±∞;
lim
x→+∞
x(2 + sin x)
x2+1 = lim
x→+∞
2 + sin x
x+1/x =0
55. lim
R→0+
Vt
Le
−Rt/L
1=Vt
L
56. (a) lim
x→π/2(π/2−x) tan x= lim
x→π/2
π/2−x
cot x= lim
x→π/2−1
−csc2x= lim
x→π/2sin2x=1
(b) lim
x→π/2µ1
π/2−x−tan x¶= lim
x→π/2µ1
π/2−x−sin x
cos x¶= lim
x→π/2
cos x−(π/2−x) sin x
(π/2−x) cos x
= lim
x→π/2−(π/2−x) cos x
−(π/2−x) sin x−cos x
= lim
x→π/2
(π/2−x) sin x+ cos x
−(π/2−x) cos x+ 2 sin x=0
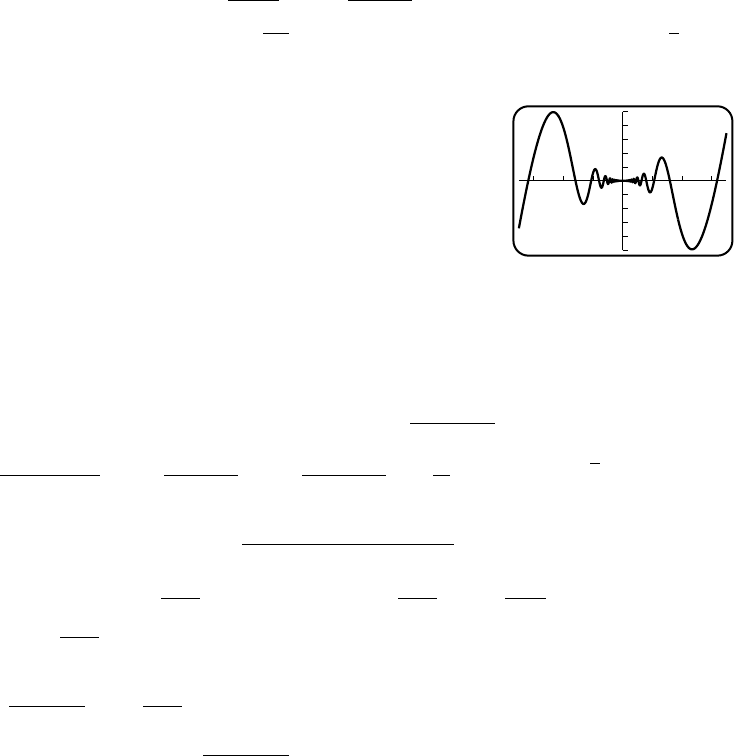
Supplementary Exercises 4 134
(c) 1/(π/2−1.57) ≈1255.765849,tan 1.57 ≈1255.765592;
1/(π/2−1.57) −tan 1.57 ≈0.000265
57. (b) lim
x→+∞x(k1/x −1) = lim
t→0+
kt−1
t= lim
t→0+
(ln k)kt
1=lnk
(c) ln 0.3=−1.20397, 1024 ¡1024
√0.3−1¢=−1.20327; ln 2 = 0.69315, 1024 ¡1024
√2−1¢=0.69338
58. (a) No; sin(1/x) oscillates as x→0. (b) 0.05
-0.05
-0.35 0.35
(c) For the limit as x→0+use the Squeezing Theorem together with the inequalities −x2≤
x2sin(1/x)≤x2.Forx→0
−do the same; thus lim
x→0f(x)=0.
59. If k6=−1 then lim
x→0(k+ cos `x)=k+16= 0, so lim
x→0
k+ cos `x
x2=±∞. Hence k=−1, and by the rule
lim
x→0−1 + cos `x
x2= lim
x→0−`sin `x
2x= lim
x→0−`2cos `x
2=−`2
2=4if`=±2
√
2.
60. (a) Apply the rule to get lim
x→0−cos(1/x)+2xsin(1/x)
cos xwhich does not exist (nor is it ±∞).
(b) Rewrite as lim
x→0hx
sin xi[xsin(1/x)], but lim
x→0
x
sin x= lim
x→0
1
cos x= 1 and lim
x→0xsin(1/x)=0,thus
lim
x→0hx
sin xi[xsin(1/x)] = (1)(0) = 0
61. lim
x→0+
sin(1/x)
(sin x)/x, lim
x→0+
sin x
x= 1 but lim
x→0+sin(1/x) does not exist because sin(1/x) oscillates between −1
and1asx→+∞, so lim
x→0+
xsin(1/x)
sin xdoes not exist.
CHAPTER 4 SUPPLEMENTARY EXERCISES
1. (a) f(g(x)) = xfor all xin the domain of g, and g(f(x)) = xfor all xin the domain of f.
(b) They are reflections of each other through the line y=x.
(c) The domain of one is the range of the other and vice versa.
(d) The equation y=f(x) can always be solved for xas a function of y. Functions with no inverses
include y=x2,y= sin x.
(e) Yes, gis continuous; this is evident from the statement about the graphs in part (b) above.
(f) Yes, gmust be differentiable (where f06= 0); this can be inferred from the graphs. Note that if
f0= 0 at a point then g0cannot exist (infinite slope).
2. (a) For sin x,−π/2≤x≤π/2; for cos x,0≤x≤π; for tan x,−π/2<x<π/2; for sec x,
0≤x<π/2orπ/2<x≤π.
135 Chapter 4
(b) y
x
-1
1
π/2
y = sin-1x
y = sinx
y
x
-1
π
y = cos-1x
y = cosx
y
x
-2
2
π/2
-π/2
y = tan-1x
y = tanx
y
x
-1
2
π/2
y = sec-1xy = sec x
y = sec-1x
y = secx
3. (a) when the limit takes the form 0/0or∞/∞
(b) Not necessarily; only if lim f(x) = 0. Consider g(x)=x; lim
x→0g(x)=0. Forf(x) choose
cos x,x2, and |x|1/2. There are three possibilities; lim
x→0
cos x
xdoes not exist; lim
x→0
x2
x= 0, and
lim
x→0|x|1/2
x2=+∞.
4. In the case +∞−(−∞) the limit is +∞; in the case −∞−(+∞) the limit is −∞, because large positive
(negative) quantities are being added to large positive (negative) quantities. The cases +∞−(+∞)
and −∞−(−∞) are indeterminate; large numbers of opposite sign are being subtracted, and more
information about the sizes is needed.
5. (a) x=f(y)=8y
3−1; y=f−1(x)=µx+1
8¶1/3
=1
2(x+1)
1/3
(b) f(x)=(x−1)2;fdoes not have an inverse because fis not one-to-one, for example
f(0) = f(2)=1.
(c) x=f(y)=(e
y
)
2+1;y=f−1
(x)=ln√
x−1=1
2ln(x−1)
(d) x=f(y)=y+2
y−1;y=f−1
(x)= x+2
x−1
6. f0(x)= ad −bc
(cx +d)2;ifad−bc = 0 then the function represents a horizontal line, no inverse. If ad−bc 6=0
then f0(x)>0orf
0
(x)<0sofis invertible. If x=f(y)= ay +b
cy +dthen y=f−1(x)= b−xd
xc −a.
7. (a) Differentiating, 2
3x−1/3−2
3y−1/3y0−y0=0. Atx= 1 and y=−1, y0= 2. The tangent line is
y+1=2(x−1).
(b) (xy0+y) cos xy =y0. With x=π/2 and y= 1 this becomes y0= 0, so the equation of the
tangent line is y−1=0(x−π/2) or y=1.
8. Draw equilateral triangles of sides 5, 12, 13, and 3, 4, 5. Then sin[cos−1(4/5)]=3/5,
sin[cos−1(5/13)] = 12/13, cos[sin−1(4/5)]=3/5, cos[sin−1(5/13)] = 12/13
(a) cos[cos−1(4/5) + sin−1(5/13)] = cos(cos−1(4/5)) cos(sin−1(5/13)) −sin(cos−1(4/5)) sin(sin−1(5/13))
=4
5
12
13 −3
5
5
13 =33
65.
Supplementary Exercises 4 136
(b) sin[sin−1(4/5) + cos−1(5/13)] = sin(sin−1(4/5)) cos(cos−1(5/13)) + cos(sin−1(4/5)) sin(cos−1(5/13))
=4
5
5
13 +3
5
12
13 =56
65.
9. 3ln¡e
2x(e
x)
3¢+ 2 exp(ln 1) = 3 ln e2x+ 3 ln(ex)3+2·1 = 3(2x)+(3·3)x+2=15x+2
10. Y= ln(Cekt)=lnC+lne
kt =lnC+kt, a line with slope kand Y-intercept ln C
11. (a) lim
x→+∞(ex−x2) = lim
x→+∞x2(ex/x2−1), but lim
x→+∞
ex
x2= lim
x→+∞
ex
2x= lim
x→+∞
ex
2=+∞
so lim
x→+∞(ex/x2−1)=+∞and thus lim
x→+∞x2(ex/x2−1)=+∞
(b) lim
x→1
ln x
x4−1= lim
x→1
1/x
4x3=1
4; lim
x→1rln x
x4−1=rlim
x→1
ln x
x4−1=1
2
(c) lim
x→0axln a=lna
12. y0=aeax sin bx +beax cos bx and y00 =(a
2−b
2
)e
ax sin bx +2abeax cos bx,soy
00 −2ay0+(a
2+b
2
)y
=(a
2−b
2
)e
ax sin bx +2abeax cos bx −2a(aeax sin bx +beax cos bx)+(a
2+b
2
)e
ax sin bx =0.
13. sin(tan−1x)=x/√1+x
2and cos(tan−1x)=1/
√
1+x
2
, and y0=1
1+x
2,y
00 =−2x
(1+x2)2, hence
y00 + 2 sin ycos3y=−2x
(1+x2)2+2 x
√
1+x
2
1
(1+x2)3/2=0.
14. ln y=2xln3+7xln 5; dy
dx/y = 2 ln 3 + 7 ln 5, or dy
dx = (2 ln 3 + 7 ln 5)y
15. Find dθ
dt ¯¯¯¯x=1
y=1
given dz
dt =aand dy
dt =−b. From the figure
sin θ=y/z; when x=y=1,z=√
2. So θ= sin−1(y/z) and
dθ
dt =1
p1−y2/z2µ1
z
dy
dt −y
z2
dz
dt ¶=−b−a
√2when x=y=1.
y
x
z
θ
16. (a) f0(x)=−3/(x+1)
2
.Ifx=f(y)=3/(y+ 1) then y=f−1(x)=(3/x)−1, so d
dxf−1(x)= −3
x
2;
and 1
f0(f−1(x)) =−(f−1(x)+1)
2
3=−(3/x)2
3=−3
x2.
(b) f(x)=e
x/2,f0(x)=1
2
e
x/2.Ifx=f(y)=e
y/2then y=f−1(x)=2lnx,so d
dxf−1(x)= 2
x
; and
1
f0(f−1(x)) =2e
−f
−1
(x)/2=2e
−ln x=2x
−1=2
x
17. (a) y
x
-2
2
24
(b) The curve y=e−x/2sin 2xhas x-intercepts
at x=0,π/2. It intersects the curve y=
e−x/2at x=π/4, and it intersects the curve
y=−e−x/2at x=−π/4,3π/4.
137 Chapter 4
18. (a) y
x
π/2
1
(b) y
x
π/2
1
(c) y
x
−π/2
5
(d) y
x
π/2
1
19. (a) ln y=ln(1 + x)
x,y0
y=x/(1+x)−ln(1 + x)
x2=1
x(1+x)−ln(1 + x)
x2,
dy
dx =1
x(1+x)(1/x)−1−(1+x)(1/x)
x2ln(1 + x)
(b) ln y=exln x,y0
y=exµ1
x+lnx
¶,dy
dx =xexexµ1
x+lnx
¶=e
x£x
e
x−1+x
e
xln x¤
(c) y=x3+1so y
0=3x
2
.
(d) y0=abe−x
(1+be−x)2
(e) 2
3xy−1/3dy
dx +y2/3+2
3yx−1/3+x2/3dy
dx =2x. Multiply by 3x1/3y1/3:
2x4/3dy
dx +3x
1/3
y+2y
4/3+3xy1/3dy
dx =6x
4/3
y
1/3
. Regroup:
dy
dx ³2x4/3+3xy1/3´=6x
4/3
y
1/3−3x
1/3
y−2y
4/3
,dy
dx =6x4/3y1/3−3x1/3y−2y4/3
2x4/3+3xy1/3.
(f) y=1
2ln x+1
3ln(x+1)−ln sin x+ ln cos x,so
y
0=1
2x+1
3(x+1) −cos x
sin x−sin x
cos x=5x+3
6x(x+1) −cot x−tan x.
20. (a) Find xwhen y=5·12 = 60 in. Since y= log x,x=10
y=10
60 in. This is approximately
2.68 ×1042 light-years, so even in astronomical terms it is a fabulously long distance.
(b) Find xwhen y= 100(5280)(12) in. Since y=10
x
,x= log y=6.80 in or 0.57 ft, approximately.
21. (a) The function ln x−x0.2is negative at x= 1 and positive at x= 4, so it must be zero in between
(IVT).
(b) x=3.654
Supplementary Exercises 4 138
22. (a) If xk=exthen kln x=x,or ln x
x=1
k. The steps are reversible.
(b) By zooming it is seen that the maximum value of yis
approximately 0.368 (actually, 1/e), so there are two distinct
solutions of xk=exwhenever k>1/0.368 ≈2.717.
y
x
-2
2
(c) x=1.155
23. Set y= logbxand solve y0=1: y
0=1
xln b=1sox=1
ln b. The
curves intersect when (x, x) lies on the graph of y= logbx,so
x= logbx. From Formula (9), Section 4.2, logbx=ln x
ln bfrom which
ln x=1,x=e,lnb=1/e,b=e1/e ≈1.4447.
y
x
2
2
24. (a) Find the point of intersection: f(x)=√
x+k=lnx. The
slopes are equal, so m1=1
x=m2=1
2√x,√x=2,x=4.
Then ln 4 = √4+k,k=ln4−2.
y
x
2
2
(b) Since the slopes are equal m1=k
2√x=m2=1
x,sok
√
x=2.
At the point of intersection k√x=lnx,2=lnx,x=e
2
,
k=2/e.
y
x
0
2
5
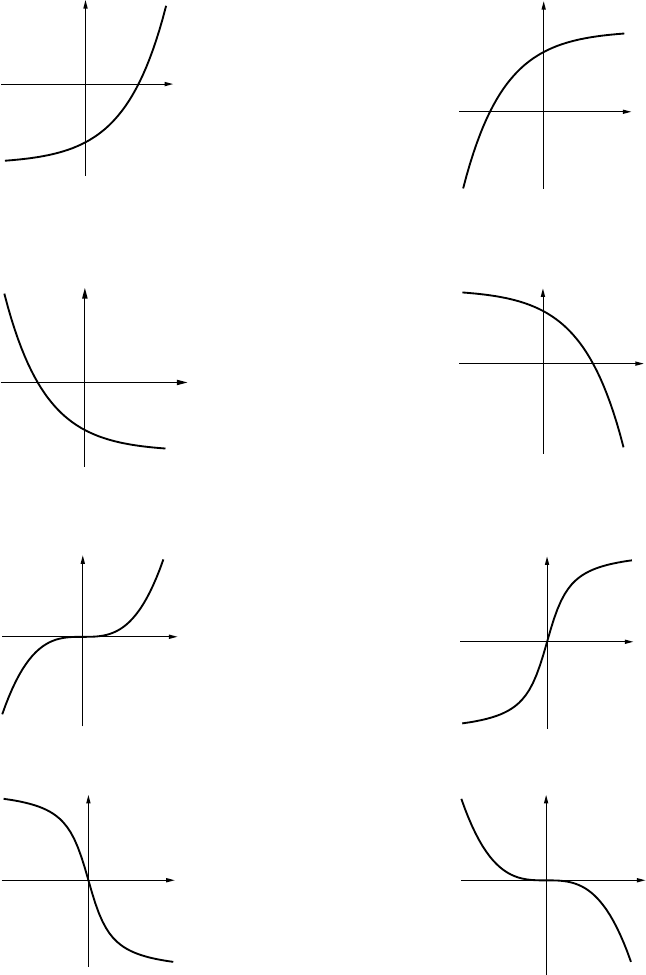
CHAPTER 5
Analysis of Functions and Their Graphs
EXERCISE SET 5.1
1. (a) f0>0 and f00 >0
y
x
(b) f0>0 and f00 <0
y
x
(c) f0<0 and f00 >0
y
x
(d) f0<0 and f00 <0
y
x
2. (a) y
x
(b) y
x
(c) y
x
(d) y
x
3. A:dy/dx < 0,d
2
y/dx2>0
B:dy/dx > 0,d
2
y/dx2<0
C:dy/dx < 0,d
2
y/dx2<0
4. A:dy/dx < 0,d
2
y/dx2<0
B:dy/dx < 0,d
2
y/dx2>0
C:dy/dx > 0,d
2
y/dx2<0
139
Exercise Set 5.1 140
5. An inflection point occurs when f00 changes sign: at x=−1,0,1 and 2.
6. (a) f(0) <f(1) since f0>0on(0,1). (b) f(1) >f(2) since f0<0on(1,2).
(c) f0(0) >0 by inspection. (d) f0(1) = 0 by inspection.
(e) f00(0) <0 since f0is decreasing there. (f) f00(2) = 0 since f0has a minimum there.
7. (a) [4,6] (b) [1,4] and [6,7] (c) (1,2) and (3,5)
(d) (2,3) and (5,7) (e) x=2,3,5
8. (1,2) (2,3) (3,4) (4,5) (5,6) (6,7)
f0− − − ++−
f00 +−+ + − −
9. f0(x)=2x−5
f
00(x)=2
(a) [5/2,+∞)(b) (−∞,5/2]
(c) (−∞,+∞)(d) none
(e) none
10. f0(x)=−2(x+3/2)
f00(x)=−2
(a) (−∞,−3/2] (b) [−3/2,+∞)
(c) none (d) (−∞,+∞)
(e) none
11. f0(x)=3(x+2)
2
f00(x)=6(x+2)
(a) (−∞,+∞)(b) none
(c) (−2,+∞)(d) (−∞,−2)
(e) −2
12. f0(x) = 3(4 −x2)
f00(x)=−6x
(a) [−2,2] (b) (−∞,−2], [2,+∞)
(c) (−∞,0) (d) (0,+∞)
(e) 0
13. f0(x)=12x
2
(x−1)
f00(x)=36x(x−2/3)
(a) [1,+∞)(b) (−∞,1]
(c) (−∞,0), (2/3,+∞)(d) (0,2/3)
(e) 0,2/3
14. f0(x)=4x(x
2−4)
f00(x) = 12(x2−4/3)
(a) [−2,0], [2,+∞)(b) (−∞,−2], [0,2]
(c) (−∞,−2/√3), (2/√3,+∞)(d) (−2/√3,2/√3)
(e) −2/√3, 2/√3
15. f0(x)= 4x
(x
2+2)
2f00(x)=−43x
2−2
(x
2+2)
3
(a) [0,+∞)(b) (−∞,0] (c) (−p2/3,+p2/3)
(d) (−∞,−p2/3), (+p2/3,+∞)(e) −p2/3,p2/3
16. f0(x)= 2−x
2
(x
2+2)
2f00(x)=2x(x
2−6)
(x2+2)
3
(a) [−√2,√2] (b) (−∞,−√2], [√2,+∞)(c) (−√6,0), (√6,+∞)
(d) (−∞,−√6), (0,√6) (e) −√6,0,√6
17. f0(x)=1
3(x+2)
−2/3
f00(x)=−2
9(x+2)
−5/3
(a) (−∞,+∞)(b) none
(c) (−∞,−2) (d) (−2,+∞)
(e) −2
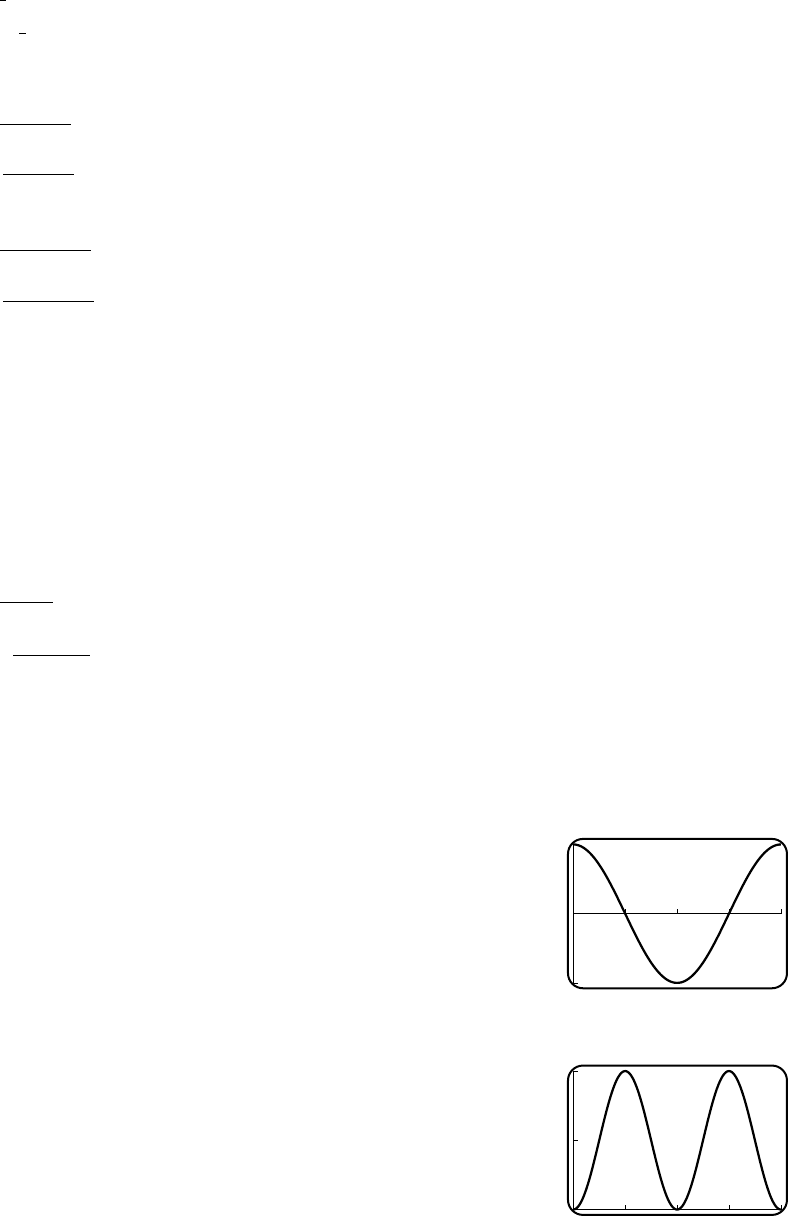
141 Chapter 5
18. f0(x)=2
3x
−1/3
f
00(x)=−2
9x
−4/3
(a) [0,+∞)(b) (−∞,0]
(c) none (d) (−∞,0), (0,+∞)
(e) none
19. f0(x)=4(x+1)
3x
2/3
f00(x)=4(x−2)
9x5/3
(a) [−1,+∞)(b) (−∞,−1]
(c) (−∞,0), (2,+∞)(d) (0,2)
(e) 0,2
20. f0(x)=4(x−1/4)
3x2/3
f00(x)=4(x+1/2)
9x5/3
(a) [1/4,+∞)(b) (−∞,1/4]
(c) (−∞,−1/2), (0,+∞)(d) (−1/2,0)
(e) −1/2,0
21. f0(x)=−xe−x2/2
f00(x)=(−1+x
2
)e
−x
2/2
(a) (−∞,0] (b) [0,+∞)
(c) (−∞,−1), (1,+∞)(d) (−1,1)
(e) −1,1
22. f0(x)=(2x
2+1)e
x
2
f00(x)=2x(2x2+3)e
x
2
(a) (−∞,+∞)(b) none
(c) (0,+∞)(d) (−∞,0)
(e) 0
23. f0(x)= 2x
1+x
2
f00(x)=2 1−x
2
(1+x2)2
(a) [0,+∞)(b) (−∞,0]
(c) (−1,1) (d) (−∞,−1),(1,+∞)
(e) −1,1
24. f0(x)=x(2 ln x+1)
f00(x)=2lnx+3
(a) [e−1/2,+∞)(b) (0,e
−1/2]
(c) (e−3/2,+∞)(d) (0,e
−3/2)
(e) e−3/2
25. f0(x)=−sin x
f00(x)=−cos x
(a) [π, 2π](b) [0,π]
(c) (π/2,3π/2) (d) (0,π/2), (3π/2,2π)
(e) π/2, 3π/2
1
-1
02p
26. f0(x) = 2 sin 4x
f00(x) = 8 cos 4x
(a) (0,π/4], [π/2,3π/4] (b) [π/4,π/2], [3π/4,π]
(c) (0,π/8), (3π/8,5π/8), (7π/8,π)(d) (π/8,3π/8), (5π/8,7π/8)
(e) π/8, 3π/8, 5π/8, 7π/8
1
0
0p
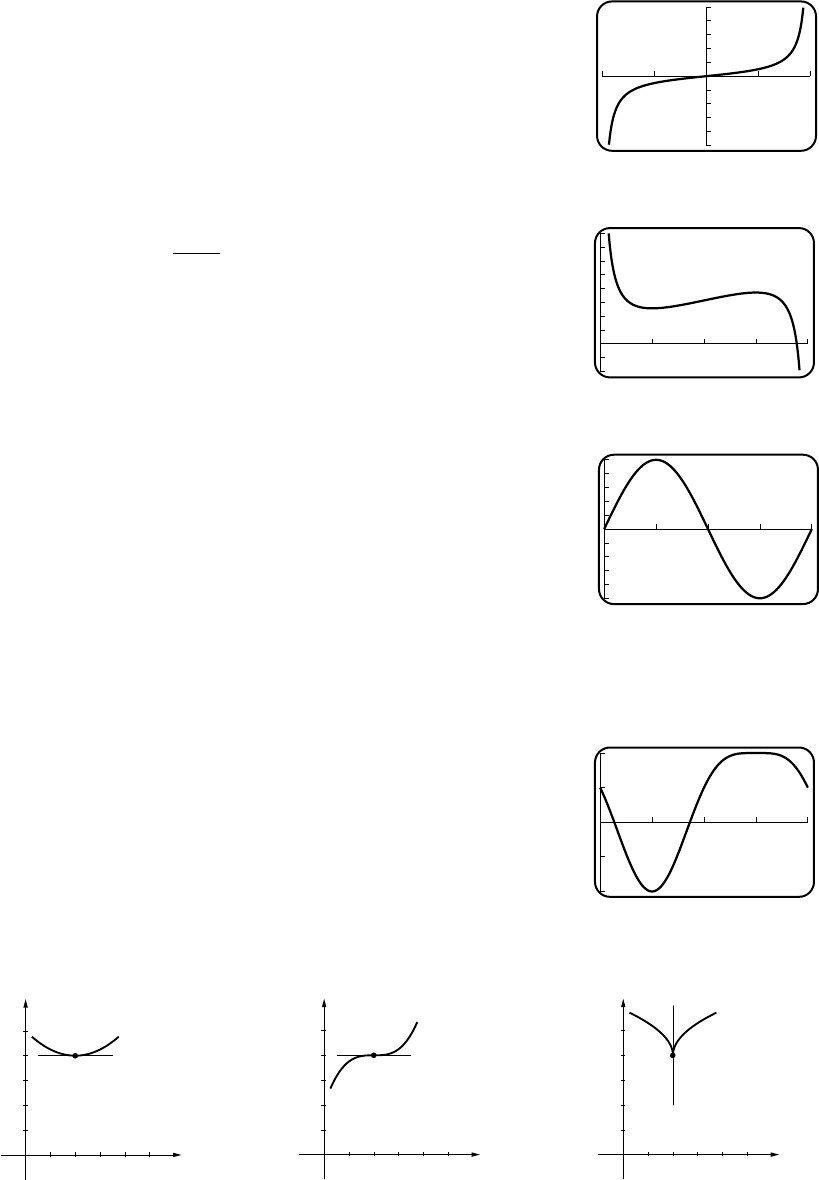
Exercise Set 5.1 142
27. f0(x) = sec2x
f00(x)=2sec
2xtan x
(a) (−π/2,π/2) (b) none
(c) (0,π/2) (d) (−π/2,0)
(e) 0
10
-10
^6
28. f0(x)=2−csc2x
f00(x)=2csc
2xcot x=2cos x
sin3x
(a) [π/4,3π/4] (b) (0,π/4],[3π/4,π)
(c) (0,π/2) (d) (π/2,π)
(e) π/2
8
-2
0p
29. f0(x) = cos 2x
f00(x)=−2 sin 2x
(a) [0,π/4], [3π/4,π](b) [π/4,3π/4]
(c) (π/2,π)(d) (0,π/2)
(e) π/2
0.5
-0.5
0p
30. f0(x)=−2 cos xsin x−2 cos x=−2 cos x(1 + sin x)
f00(x)=2sinx(sin x+1)−2 cos2x= 2 sin x(sin x+1)−2+2sin
2x= 4(1 + sin x)(sin x−1/2)
Note: 1 + sin x≥0
(a) [π/2,3π/2] (b) [0,π/2], [3π/2,2π]
(c) (π/6,5π/6) (d) (0,π/6), (5π/6,2π)
(e) π/6, 5π/6
2
-2
0o
31. (a)
2
4
x
y(b)
2
4
x
y(c)
2
4
x
y
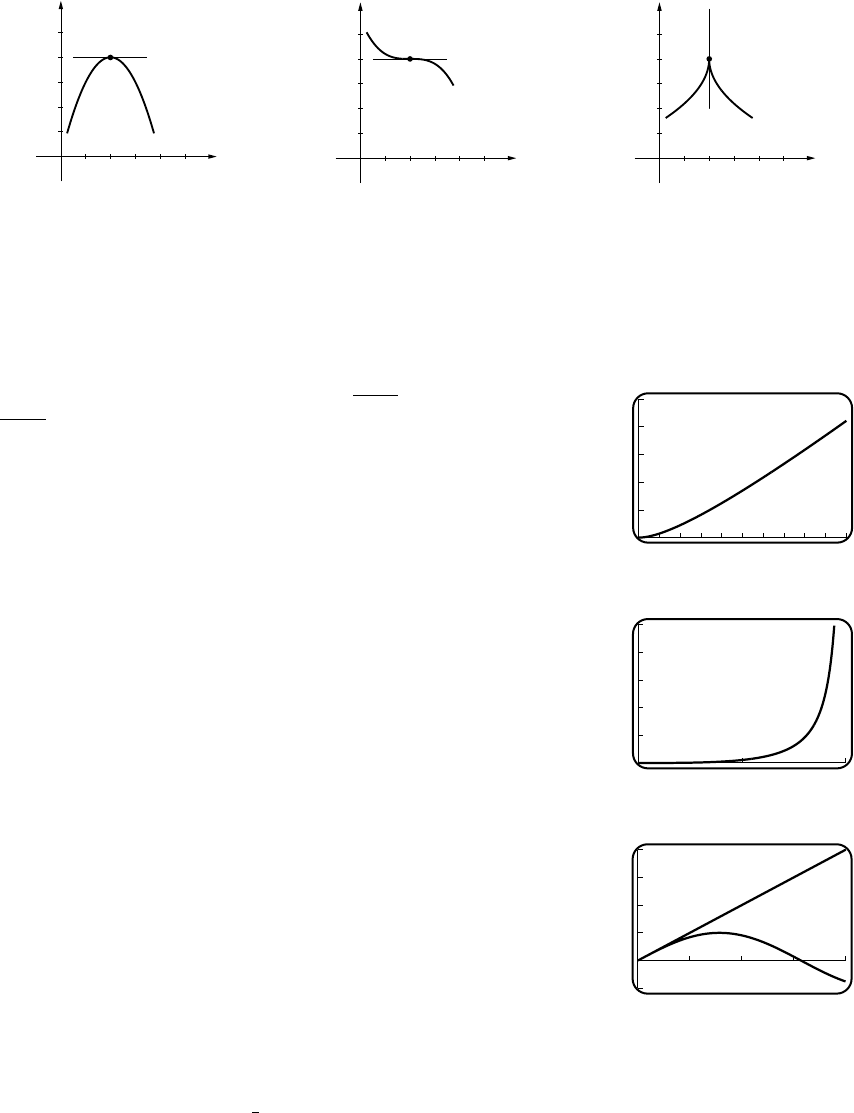
143 Chapter 5
32. (a)
2
4
x
y(b)
2
4
x
y(c)
2
4
x
y
33. (a) f0(x)=3(x−a)
2
,f
00(x)=6(x−a); inflection point is (a, 0)
(b) f0(x)=4(x−a)
3
,f
00(x) = 12(x−a)2; no inflection points
34. For n≥2, f00(x)=n(n−1)(x−a)n−2; there is a sign change of f00 (point of inflection) at (a, 0) if and
only if nis odd. For n=1,y=x−a, so there is no point of inflection.
35. f0(x)=1/3−1/[3(1 + x)2/3]sofis increasing on [0,+∞)thusif
x>0, then f(x)>f(0)=0,1+x/3−3
√1+x>0,
3
√1+x<1+x/3.
2.5
0
010
36. f0(x) = sec2x−1sofis increasing on [0,π/2) thus if 0 <x<π/2,
then f(x)>f(0) = 0, tan x−x>0, x<tan x.
10
0
06
37. x≥sin xon [0,+∞): let f(x)=x−sin x. Then f(0) = 0 and
f0(x)=1−cos x≥0, so f(x) is increasing on [0,+∞).
4
-1
04
38. (a) Let h(x)=e
x−1−xfor x≥0. Then h(0) = 0 and h0(x)=e
x−1≥0 for x≥0, so h(x)is
increasing.
(b) Let h(x)=e
x−1−x−1
2x
2
. Then h(0) = 0 and h0(x)=e
x−1−x. By part (a), ex−1−x≥0
for x≥0, so h(x) is increasing.
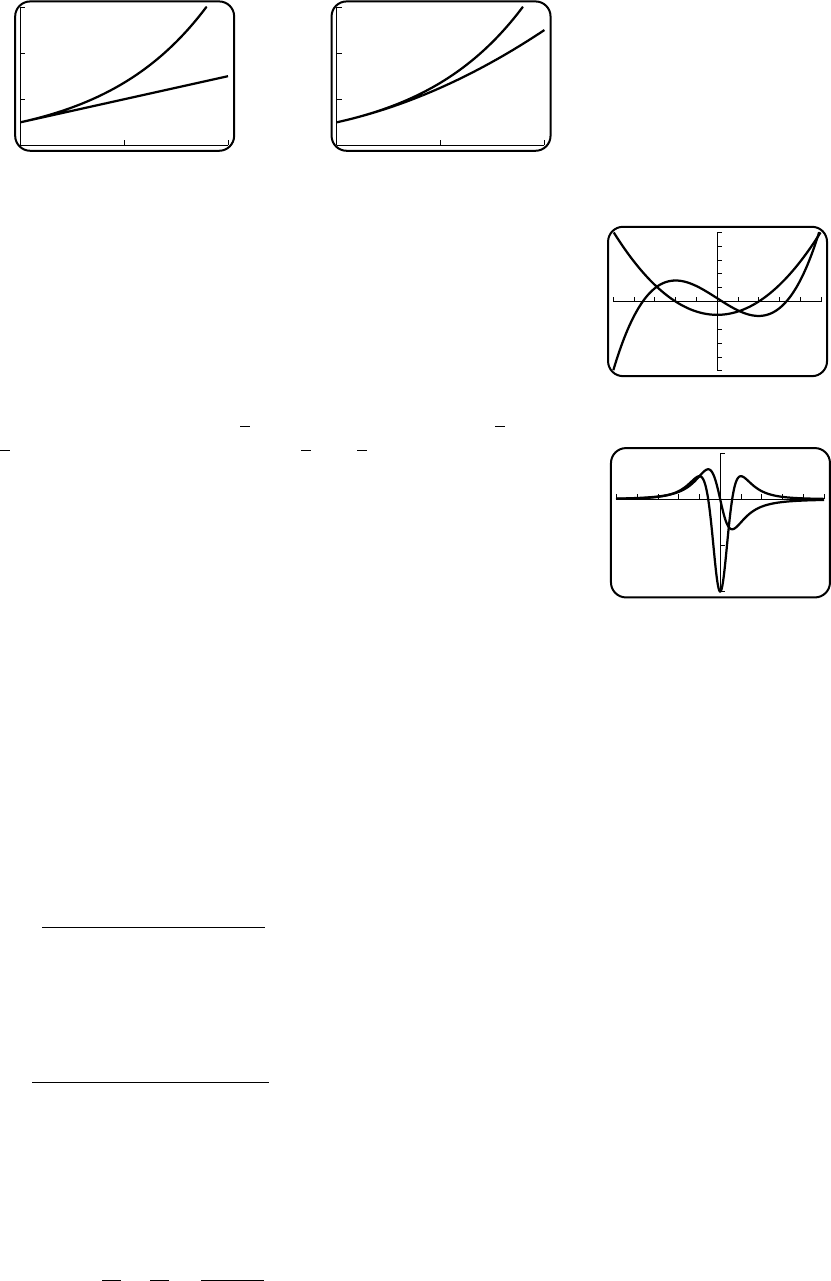
Exercise Set 5.1 144
(c) 6
0
02
6
0
02
39. Points of inflection at x=−2,+2. Concave up on (−5,−2) and
(2,5); concave down on (−2,2). Increasing on [−3.5829,0.2513] and
[3.3316,5] , and decreasing on [−5,−3.5829] and [0.2513,3.3316].
250
-250
-5 5
40. Points of inflection at x=±1/√3. Concave up on (−5,−1/√3) and
(1/√3,5), and concave down on (−1/√3,1/√3). Increasing on
[−5,0] and decreasing on [0,5].
1
-2
-5 5
41. Break the interval [−5,5] into ten subintervals and check f00(x) at each endpoint. We find f00(−1) >0
and f00(0) <0. Refine [−1,0] into ten subintervals; f00(−0.2) >0, f00(−0.1) <0; repeat, f00(−0.18) >0,
f00(−0.17) <0, so x=−0.175 is correct to two decimal places. Note also that f00(1) = 0 so there are
two inflection points.
42. Break the interval [−5,5] into ten subintervals and check f00(x) at each endpoint. We discover
f00(−1) >0, f00(0) <0 and f00(1) >0. Refine [−1,0] into ten subintervals and we see that f00(−0.6) >0,
f00(−0.5) <0. Subdivide [−0.6,−0.5] into 10 subintervals and we see that f00(−0.58) >0 and
f00(−0.57) <0. Thus x=−0.575 is within 0.005 of the true root and is thus correct to two dec-
imal places. For the other root we could proceed in a similar manner, but it easier to note that f00(x)
is an even function and thus the other root is x=0.575 to two decimal places.
43. f00(x)=2
90x3−81x2−585x+ 397
(3x2−5x+8)
3.The denominator has complex roots, so is always positive; hence
the x-coordinates of the points of inflection of f(x) are the roots of the numerator (if it changes sign).
A plot of the numerator over [−5,5] shows roots lying in [−3,−2], [0,1], and [2,3]. Breaking each of
these intervals into ten subintervals locates the roots in [−2.5,−2.4], [0.6,0.7] and [2.7,2.8]. Thus to
one decimal place the roots are x=−2.45,0.65,2.75.
44. f00(x)=2x
5+5x
3+14x
2+30x−7
(x
2+1)
5/2. Points of inflection will occur when the numerator changes sign,
since the denominator is always positive. A plot of y=2x
5+5x
3+14x
2+30x−7 suggests that there
is only one root and it lies in [0,1]. Subdivide into ten subintervals and determine that the root lies
between x=0.2 and x=0.3. Thus to one decimal place the point of inflection is located at x=0.25.
45. f(x1)−f(x2)=x
2
1−x
2
2=(x
1+x
2
)(x1−x2)<0ifx
1<x
2for x1,x2in [0,+∞), so f(x1)<f(x
2
)
and fis thus increasing.
46. f(x1)−f(x2)= 1
x
1−1
x
2
=x
2−x
1
x
1
x
2
>0ifx
1<x
2for x1,x2in (0,+∞), so f(x1)>f(x
2
) and thus f
is decreasing.
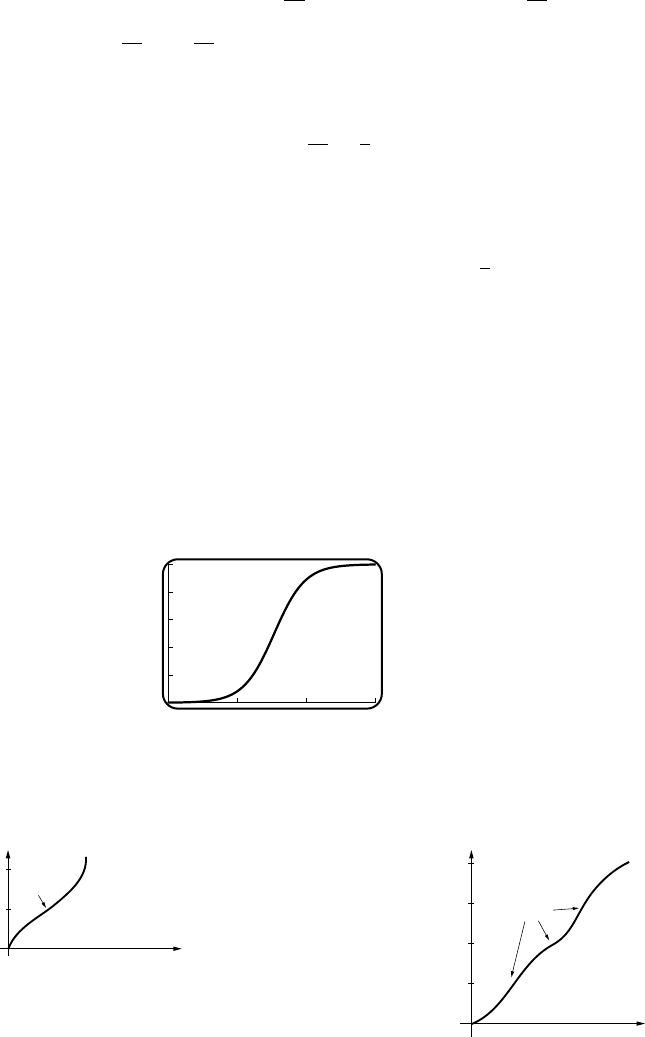
145 Chapter 5
47. (a) If x1<x
2where x1and x2are in I, then f(x1)<f(x
2
) and g(x1)<g(x
2
), so f(x1)+g(x
1
)<
f(x
2
)+g(x
2
), (f+g)(x1)<(f+g)(x2). Thus f+gis increasing on I.
(b) Case I: If fand gare ≥0onI, and if x1<x
2where x1and x2are in I, then 0 <f(x
1
)<f(x
2
)
and 0 <g(x
1
)<g(x
2
), so f(x1)g(x1)<f(x
2
)g(x
2
), (f·g)(x1)<(f·g)(x2). Thus f·gis
increasing on I.
Case II: If fand gare not necessarily positive on Ithen no conclusion can be drawn: for example,
f(x)=g(x)=xare both increasing on (−∞,0), but (f·g)(x)=x
2is decreasing there.
48. (a) f(x)=x,g(x)=2x(b) f(x)=x,g(x)=x+6 (c) f(x)=2x,g(x)=x
49. (a) f00(x)=6ax +2b=6a(x+b
3a
), f00(x) = 0 when x=−b
3a.fchanges its direction of concavity
at x=−b
3aso −b
3ais an inflection point.
(b) If f(x)=ax3+bx2+cx +dhas three x-intercepts, then it has three roots, say x1,x2and x3,so
we can write f(x)=a(x−x
1
)(x−x2)(x−x3)=ax3+bx2+cx +d, from which it follows that
b=−a(x1+x2+x3). Thus −b
3a=1
3(x1+x2+x3), which is the average.
(c) f(x)=x(x
2−3x
2+2)=x(x−1)(x−2) so the intercepts are 0, 1, and 2 and the average is 1.
f00(x)=6x−6=6(x−1) changes sign at x=1.
50. f00(x)=6x+2b, so the point of inflection is at x=−b
3. Thus an increase in bmoves the point of
inflection to the left.
51. (a) Let x1<x
2belong to (a, b). If both belong to (a, c] or both belong to [c, b) then we have
f(x1)<f(x
2
) by hypothesis. So assume x1<c<x
2
. We know by hypothesis that f(x1)<f(c),
and f(c)<f(x
2
). We conclude that f(x1)<f(x
2
).
(b) Use the same argument as in part (a), but with inequalities reversed.
52. By Theorem 5.1.2, fis increasing on any interval ((2n−1)π, 2(n+1)π)(n=0,±1,±2,···), because
f0(x) = 1+ cos x>0on[(2n−1)π, (2n+1)π]. By Exercise 51 (a) we can piece these intervals together
to show that f(x) is increasing on (−∞,+∞).
53. t=7.67 1000
0
015
54. By zooming on the graph of y0(t), maximum increase is at x=−0.577 and maximum decrease is at
x=0.577.
55.
t
1
2
y
infl pt
56. y
x
infl pts
1
2
3
4
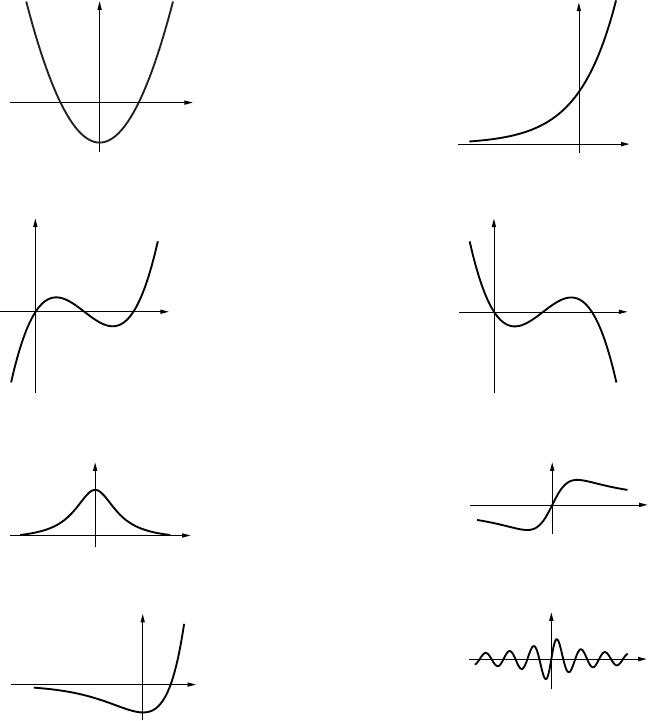
Exercise Set 5.2 146
EXERCISE SET 5.2
1. (a)
f(x)
x
y(b)
f(x)
x
y
(c)
f(x)
x
y(d)
f(x)
x
y
2. (a) y
x
(b) y
x
(c) y
x
(d) y
x
3. (a) f0(x)=6x−6 and f00(x) = 6, with f0(1) = 0. For the first derivative test, f0<0 for x<1 and
f0>0 for x>1. For the second derivative test, f00(1) >0.
(b) f0(x)=3x
2−3 and f00(x)=6x.f
0
(x)=0atx=±1. First derivative test: f0>0 for x<−1
and x>1, and f0<0 for −1<x<1, so there is a relative maximum at x=−1, and a relative
minimum at x= 1. Second derivative test: f00 <0atx=−1, a relative maximum; and f00 >0
at x= 1, a relative minimum.
4. (a) f0(x)=2sinxcos x= sin 2x(so f0(0) = 0) and f00(x) = 2 cos 2x. First derivative test: if xis
near 0 then f0<0 for x<0 and f0>0 for x>0, so a relative minimum at x= 0. Second
derivative test: f00(0)=2>0, so relative minimum at x=0.
(b) g0(x)=2tanxsec2x(so g0(0) = 0) and g00(x)=2sec
2x(sec2x+ 2 tan2x). First derivative test:
g0<0 for x<0 and g0>0 for x>0, so a relative minimum at x= 0. Second derivative test:
g00(0)=2>0, relative minimum at x=0.
(c) Both functions are squares, and so are positive for values of xnear zero; both functions are zero
at x= 0, so that must be a relative minimum.
5. (a) f0(x)=4(x−1)3,g0(x)=3x
2−6x+3 sof0(1) = g0(1)=0.
(b) f00(x) = 12(x−1)2,g00(x)=6x−6, so f00(1) = g00(1) = 0, which yields no information.
(c) f0<0 for x<1 and f0>0 for x>1, so there is a relative minimum at x=1;
g
0
(x)=3(x−1)2>0 on both sides of x= 1, so there is no relative extremum at x=1.

147 Chapter 5
6. (a) f0(x)=−5x
4
,g
0(x)=12x
3−24x2so f0(0) = g0(0)=0.
(b) f00(x)=−20x3,g00(x)=36x
2−48x,sof
00(0) = g00(0) = 0, which yields no information.
(c) f0<0 on both sides of x= 0, so there is no relative extremum there; g0(x)=12x
2
(x−2) <0
on both sides of x= 0 (for xnear 0), so again there is no relative extremum there.
7. (a) f0(x)=3x
2+6x−9=3(x+ 3)(x−1), f0(x) = 0 when x=−3,1 (stationary points).
(b) f0(x)=4x(x
2−3), f0(x) = 0 when x=0,±
√
3 (stationary points).
8. (a) f0(x)=6(x
2−1), f0(x) = 0 when x=±1 (stationary points).
(b) f0(x)=12x
3−12x2=12x
2
(x−1), f0(x) = 0 when x=0,1 (stationary points).
9. (a) f0(x)=(2−x
2
)/(x
2+2)
2
,f0(x) = 0 when x=±√2 (stationary points).
(b) f0(x)=2
3x
−1/3=2/(3x1/3), f0(x) does not exist when x=0.
10. (a) f0(x)=8x/(x2+1)
2
,f0(x) = 0 when x= 0 (stationary point).
(b) f0(x)=1
3(x+2)
−2/3
,f0(x) does not exist when x=−2.
11. (a) f0(x)= 4(x+1)
3x
2/3,f0(x) = 0 when x=−1 (stationary point), f0(x) does not exist when x=0.
(b) f0(x)=−3 sin 3x, f0(x) = 0 when sin 3x=0,3x=nπ, n =0,±1,±2,···
x=nπ/3,n=0,±1,±2,··· (stationary points)
12. (a) f0(x)=4(x−3/2)
3x2/3,f0(x) = 0 when x=3/2 (stationary point), f0(x) does not exist when x=0.
(b) f(x)=|sin x|=½sin x, sin x≥0
−sin x, sin x<0so f0(x)=½cos x, sin x>0
−cos x, sin x<0and f0(x)doesnot
exist when x=nπ,n=0,±1,±2,···(sin x= 0) because limx→nπ−f0(x)6= limx→nπ+f0(x) (see
Theorem preceding Exercise 75, Section 3.3). Now f0(x) = 0 when ±cos x= 0 provided sin x6=0
so x=π/2+nπ,n=0,±1,±2,···are stationary points.
13. (a) x= 2 because f0(x) changes sign from −to + there.
(b) x= 0 because f0(x) changes sign from + to −there.
(c) x=1,3 because f00(x) (the slope of the graph of f0(x)) changes sign at these points.
14. (a) x=1 (b) x=5 (c) x=−1,0,3
15. (a) critical points x=0,±
√
5; f0:00
0
0
−−−− ++
++
5
5
−
x= 0: relative maximum; x=±√5: relative minimum
(b) critical point x=0;f
0:0
0
−+−+−+
x= 0: relative minimum
16. (a) critical points x=0,−1/2,1; f0:00
0
0
−1
−−−+++ +
−
1
2
x= 0: neither; x=−1/2: relative maximum; x= 1: relative minimum

Exercise Set 5.2 148
(b) critical points: x=±3/2,−1; f0:0?
−1
0
++++ −−
−−
−
3
23
2
x=±3/2: relative maximum; x=−1: relative minimum
17. f0(x)=−2(x+ 2); critical point x=−2; f0(x): 0
-2
−−+++−
f
00(x)=−2; f00(−2) <0, f(−2) = 5; relative max of 5 at x=−2
18. f0(x)=6(x−2)(x−1); critical points x=1,2; f0(x): 00
12
−+++ ++
+−−
f
00(x)=12x−18; f00(1) <0, f00(2) >0, f(1)=5,f(2) = 4; relative min of 4 at x= 2, relative max
of5atx=1
19. f0(x)=2sinxcos x= sin 2x; critical points x=π/2, π,3π/2; f0(x): 00
π
0
++++ −−
−−
ππ
22
3
f
00(x) = 2 cos 2x;f00(π/2) <0, f00(π)>0, f00(3π/2) <0, f(π/2) = f(3π/2)=1,
f(π) = 0; relative min of 0 at x=π, relative max of 1 at x=π/2, 3π/2
20. f0(x)=1/2−cos x; critical points x=π/3, 5π/3; f0(x): 00
++−− −−
+++
ππ
3 3
5
f
00(x)=−sin x;f00(π/3) <0, f00(5π/3) >0
f(π/3) = π/6−√3/2, f(5π/3)=5π/6+√
3/2;
relative min of π/6−√3/2atx=π/3, relative max of 5π/6+√
3/2atx=5π/3
21. f0(x)=3x
2+ 5; no relative extrema because there are no critical points.
22. f0(x)=4x(x
2−1); critical points x=0,1,−1
f
00(x)=12x
2−4; f00(0) <0, f00(1) >0, f00(−1) >0
relative min of 6 at x=1,−1, relative max of 7 at x=0
23. f0(x)=(x−1)(3x−1); critical points x=1,1/3
f
00(x)=6x−4; f00(1) >0, f00(1/3) <0
relative min of 0 at x= 1, relative max of 4/27 at x=1/3
24. f0(x)=2x
2
(2x+ 3); critical points x=0,−3/2
relative min of −27/16 at x=−3/2 (first derivative test)
25. f0(x)=4x(1 −x2); critical points x=0,1,−1
f
00(x)=4−12x2;f00(0) >0, f00(1) <0, f00(−1) <0
relative min of 0 at x= 0, relative max of 1 at x=1,−1
26. f0(x) = 10(2x−1)4; critical point x=1/2; no relative extrema (first derivative test)
27. f0(x)=4
5x
−1/5
; critical point x= 0; relative min of 0 at x= 0 (first derivative test)
28. f0(x)=2+2
3x
−1/3
; critical points x=0,−1/27
relative min of 0 at x= 0, relative max of 1/27 at x=−1/27
29. f0(x)=2x/(x2+1)
2
; critical point x= 0; relative min of 0 at x=0
149 Chapter 5
30. f0(x)=2/(x+2)
2
; no critical points (x=−2 is not in the domain of f) no relative extrema
31. f0(x)=2x/(1+x2); critical point at x= 0; relative min of 0 at x= 0 (first derivative test)
32. f0(x)=x(2 + x)ex; critical points at x=0,−2; relative min of 0 at x= 0 and relative max of 4/e2at
x=−2 (first derivative test)
33. f0(x)=2xif |x|>2, f0(x)=−2xif |x|<2,
f0(x) does not exist when x=±2; critical points x=0,2,−2
relative min of 0 at x=2,−2, relative max of 4 at x=0
34. f0(x)=−1ifx<3, f0(x)=2xif x>3, f0(3) does not exist;
critical point x= 3, relative min of 6 at x=3
35. f0(x) = 2 cos 2xif sin 2x>0, f0(x)=−2 cos 2xif sin 2x<0,
f0(x) does not exist when x=π/2,π,3π/2;
critical points x=π/4,3π/4,5π/4,7π/4,π/2,π,3π/2
relative min of 0 at x=π/2,π,3π/2; relative max of 1 at
x=π/4,3π/4,5π/4,7π/4
1
0
0o
36. f0(x)=√
3+2cosx; critical points x=5π/6,7π/6
relative min of 7√3π/6−1atx=7π/6; relative max of
5√3π/6+1atx=5π/6
12
0
0o
37. f0(x)=−sin 2x; critical points x=π/2,π,3π/2
relative min of 0 at x=π/2,3π/2; relative max of 1 at x=π
1
0
0o
38. f0(x)=(2cosx−1)/(2 −cos x)2; critical points x=π/3,5π/3
relative max of √3/3atx=π/3, relative min of
−√3/3atx=5π/3
0.8
0o
-0.8
Exercise Set 5.2 150
39. f0(x)=lnx+1, f00(x)=1/x;f0(1/e)=0,f
00(1/e)>0;
relative min of −1/e at x=1/e
2.5
-0.5
0 2.5
40. f0(x)=−2e
x−e
−x
(e
x+e
−x
)
2= 0 when x= 0. By the first derivative test
f0(x)>0 for x<0 and f0(x)<0 for x>0; relative max of 1 at
x=0
1
0
-2 2
41. f0(x)=2x(1 −x)e−2x=0atx=0,1. f00(x)=(4x
2−8x+2)e
−2x
;
f00(0) >0 and f00(1) <0, so a relative min of 0 at x= 0 and a
relative max of 1/e2at x=1.
0.14
0
-0.3 4
42. f0(x)=10/x −1=0atx= 10; f00(x)=−10/x2<0;
relative max of 10(ln(10) −1) ≈13.03 at x=10
14
-4
020
43. Relative minima at x=−3.58,3.33; relative max at x=0.25 250
-250
-5 5
44. Relative min at x=−0.84; relative max at x=0.84 1.2
-1.2
-66
151 Chapter 5
45. relative max at x=0.255 46. relative max at x=0.845
47. Relative min at x=−1.20 and a relative max at x=1.80 y
x
-2
-1
1
-4 -2 2 4
f'(x)
f''(x)
48. Relative max at x=−0.78 and a relative min at x=1.55 y
x
-5
5
-4 -2 2 4
f'(x)
f''(x)
49. (a) Let f(x)=x
2+k
x
, then f0(x)=2x−k
x
2=2x
3−k
x
2.fhas a relative extremum when 2x3−k=0,
so k=2x
3= 2(3)3= 54.
(b) Let f(x)= x
x
2+k
, then f0(x)= k−x
2
(x
2+k)
2
.fhas a relative extremum when k−x2=0,so
k=x
2=3
2=9.
50. (a) one relative maximum, located at x=n0.3
0
014
(b) f0(x)=cxn−1(−x+n)e−x=0atx=n. Since f0(x)>0 for x<nand f0(x)<0 for
x>nit’s a maximum.
51. (a) f0(x)=−xf(x). Since f(x)isalways
positive, f0(x)=0atx=0,f
0(x)>0
for x<0 and f0(x)<0 for x>0, so
x= 0 is a maximum.
(b) y
x
µ
1
µ,
()
2π
1
2π
Exercise Set 5.3 152
52. (a) relative minima at x=±0.6436,
relative max at x=0
y
x
1
1.2
1.4
1.6
1.8
2
-1.5 -1 -0.5 0.5 1 1.5
(b) x=±0.6436,0
53. f0(x)=3ax2+2bx +cand f0(x) has roots at x=0,1, so f0(x) must be of the form f0(x)=3ax(x−1);
thus c= 0 and 2b=−3a,b=−3a/2. f00(x)=6ax +2b=6ax −3a,sof
00(0) >0 and f00(1) <0
provided a<0. Finally f(0) = d,sod= 0; and f(1) = a+b+c+d=a+b=−a/2soa=−2. Thus
f(x)=−2x
3+3x
2
.
54. (a) Because hand ghave relative maxima at x0,h(x)≤h(x0) for all xin I1and g(x)≤g(x0) for all
xin I2, where I1and I2are open intervals containing x0.Ifxis in I1∩I2then both inequalities
are true and by addition so is h(x)+g(x)≤h(x
0)+g(x
0) which shows that h+ghas a relative
maximum at x0.
(b) By counterexample; both h(x)=−x
2and g(x)=−2x
2have relative maxima at x= 0 but
h(x)−g(x)=x
2has a relative minimum at x= 0 so in general h−gdoes not necessarily have
a relative maximum at x0.
55. (a)
x
y
)( x0
f(x0) is not an extreme value.
(b)
x
y
)( x0
f(x0) is a relative maximum.
(c)
x
y
)( x0
f(x0) is a relative minimum.
EXERCISE SET 5.3
1. y=x2−2x−3;
y0=2(x−1);
y00 =2
1
-4
x
y
(1, -4)

153 Chapter 5
2. y=1+x−x
2
;
y
0=−2(x−1/2);
y00 =−2
1
1
x
y
1
25
4
()
,
3. y=x3−3x+1;
y
0=3(x
2−1);
y00 =6x
x
y
(1, -1)
(0, 1)
(-1, 3)
4. y=2x
3−3x
2+12x+9;
y
0=6(x
2−x+ 2);
y00 = 12(x−1/2)
1
10
x
y
1
229
2
()
,
5. y=x4+2x
3−1;
y0=4x
2
(x+3/2);
y00 =12x(x+1) x
y
3
243
16
, -
(-1, -2)
(0, -1)
-
()
6. y=x4−2x2−12;
y0=4x(x
2−1);
y00 = 12(x2−1/3)
1
10
x
y
1
3
113
9
-1 113
9
(1, -13)
(-1, -13)
(0, -12)
, - , -
()()
3

Exercise Set 5.3 154
7. y=x3(3x2−5);
y0=15x
2
(x
2−1);
y00 =30x(2x2−1)
x
y
(-1, 2)
(0, 0)
(1, -2)
178
178
, -
()
-
,
()
3
3
3
3
8. y=3x
3
(x+4/3);
y0=12x
2
(x+ 1);
y00 =36x(x+2/3)
x
y
(-1, -1)
(0, 0)
2
316
27
-, -
()
9. y=x(x−1)3;
y0=(4x−1)(x−1)2;
y00 = 6(2x−1)(x−1) 0.1
-0.1
x
y
1
427
256
1
21
16
(1, 0)
, -
()
, -
()
10. y=x4(x+ 5);
y0=5x
3
(x+ 4);
y00 =20x
2
(x+3)
300
x
y
(0, 0)
(-4, 256)
(-3, 162)
11. y=2x/(x−3);
y0=−6/(x−3)2;
y00 =12/(x−3)3
x
y
y = 2
x = 3
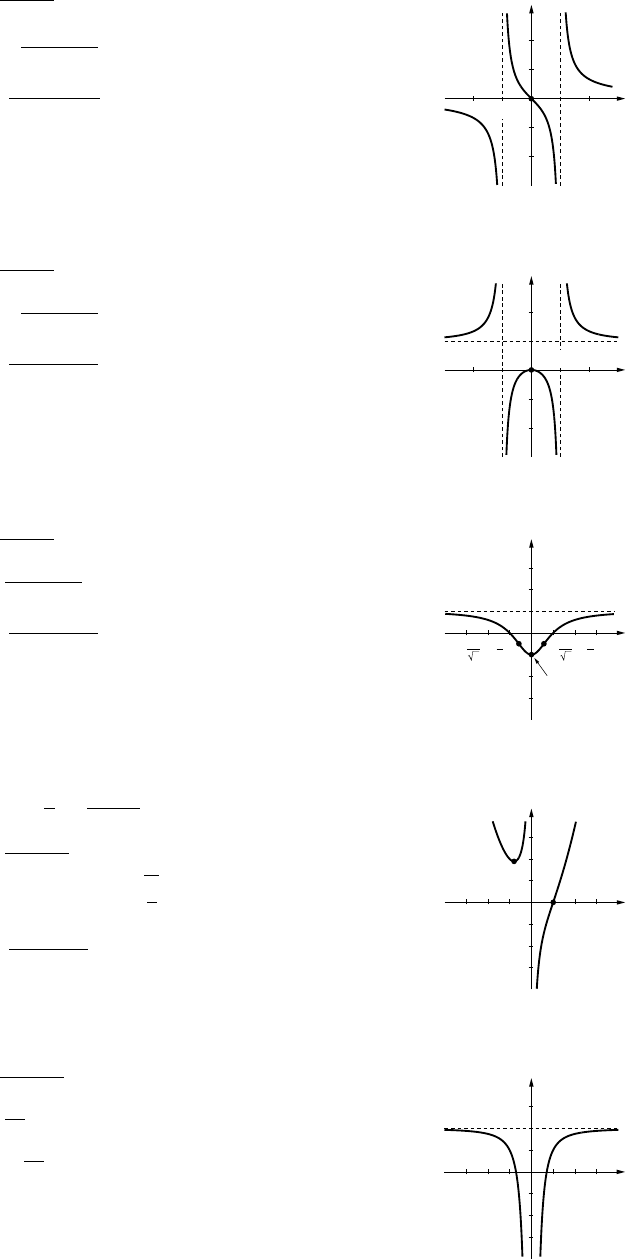
155 Chapter 5
12. y=x
x2−1;
y0=−x2+1
(x
2−1)2;
y00 =2x(x2+3)
(x
2−1)3x
y
x = 1
x = -1
1
(0, 0)
13. y=x2
x2−1;
y0=−2x
(x2−1)2;
y00 =2(3x2+1)
(x
2−1)3x
y
x = 1
y = 1
x = -1
(0, 0)
14. y=x2−1
x2+1;
y
0=4x
(x
2+1)
2;
y
00 =4(1 −3x2)
(x2+1)
3x
y
11
211
2
(0, -1)
y = 1
, -
(
-
()
, -
)
3 3
15. y=x2−1
x=x3−1
x;
y0=2x3+1
x
2,
y
0= 0 when x=−3
r1
2≈−0.8;
y00 =2(x3−1)
x3
x
y
≈(-0.8, 1.9)
(1, 0)
16. y=2x2−1
x2;
y0=2
x3;
y00 =−6
x4x
y
y = 2
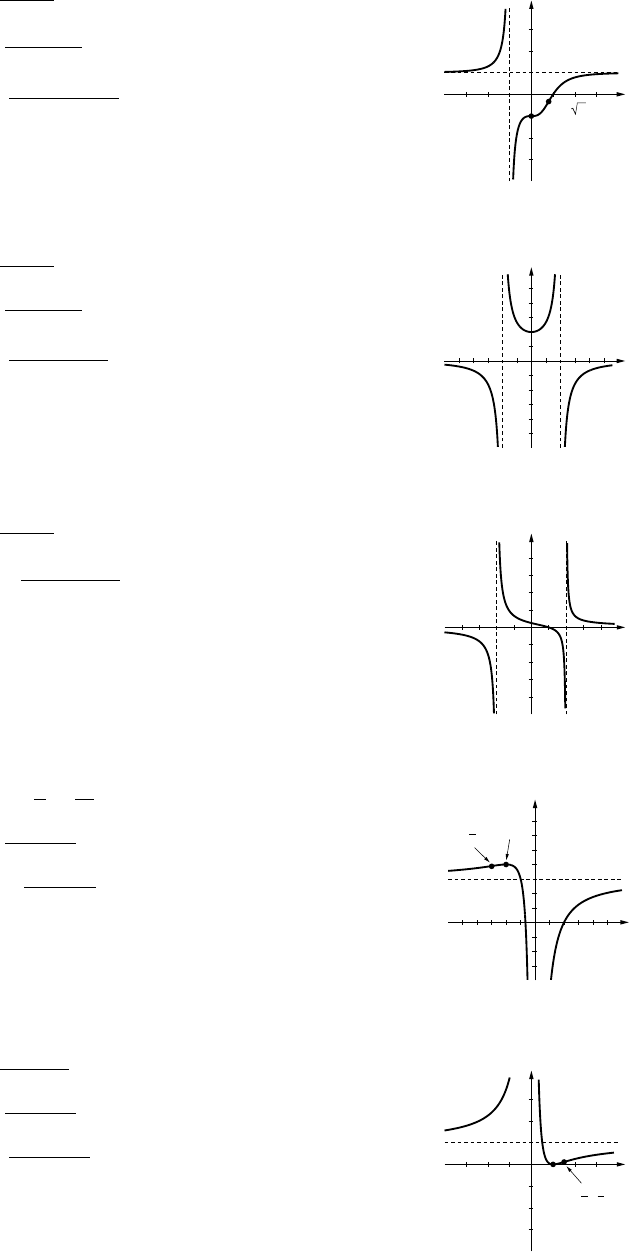
Exercise Set 5.3 156
17. y=x3−1
x3+1;
y
0=6x
2
(x
3+1)
2;
y
00 =12x(1 −2x3)
(x3+1)
3x
y
(0, -1)
(1/ 2 , -1/3)
3
y = 1
x = -1
18. y=8
4−x2;
y0=16x
(4 −x2)2;
y00 =16(3x2+4)
(4 −x2)3x
y
x = 2x = -2
1
19. y=x−1
x2−4;
y0=−x2−2x+4
(x
2−4)2
x
y
x = 2
x = -2 4
20. y=3−4
x−4
x
2;
y
0=4(x+2)
x
3;
y
00 =−8(x+3)
x
4
x
y
(-2, 4)
y = 3
-3,
()
35
9
21. y=(x−1)2
x2;
y0=2(x−1)
x3;
y00 =2(3 −2x)
x4
y
x
(1, 0)
1
9
3
2
y = 1
,
()
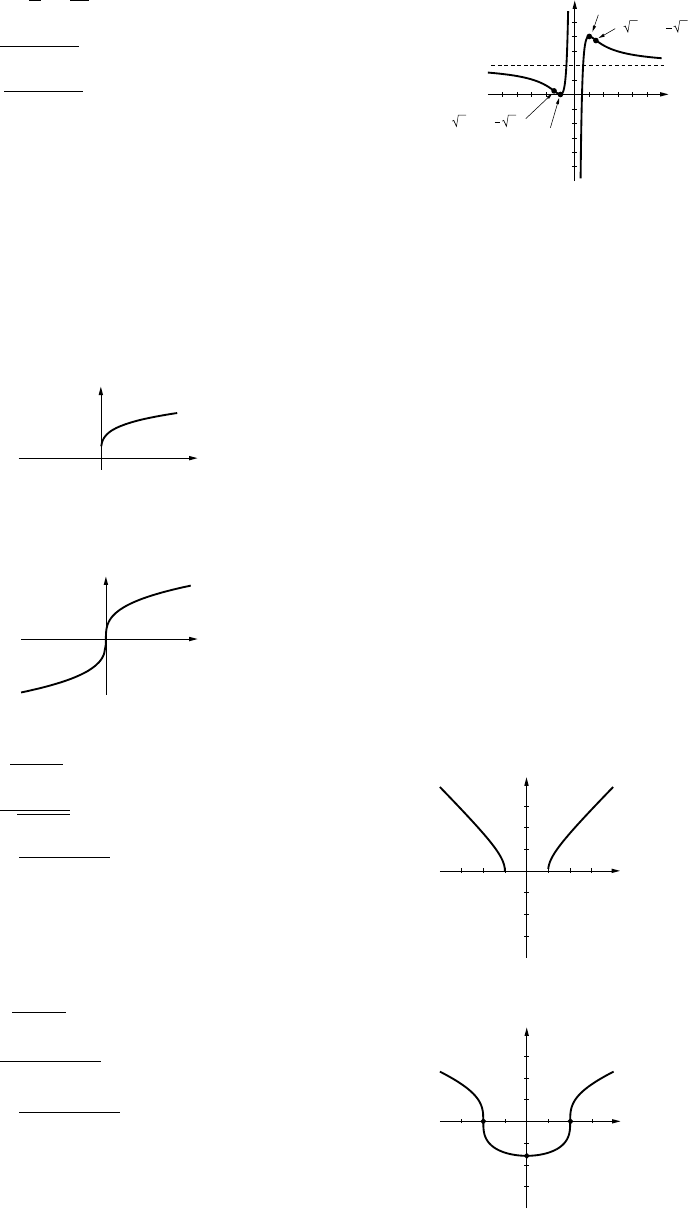
157 Chapter 5
22. y=2+3
x−1
x
3;
y
0=3(1 −x2)
x4;
y00 =6(x2−2)
x5x
y
(–1, 0)
(1, 4)
y = 2
2, 2 + 2
)(
5
4
−2, 2 – 2
)(
5
4
23. (a) VI (b) I(c) III (d) V(e) IV (f ) II
24. (a) When nis even the function is defined only for x≥0; as nincreases the graph approaches the
line y= 1 for x>0.
y
x
(b) When nis odd the graph is symmetric with respect to the origin; as nincreases the graph
approaches the line y= 1 for x>0 and the line y=−1 for x<0.
y
x
25. y=√x2−1;
y0=x
√x2−1;
y00 =−1
(x2−1)3/2-1 1 x
y
3
26. y=3
px2−4;
y0=2x
3(x2−4)2/3;
y00 =−2(3x2+4)
9(x2−4)5/3-2
(-2, 0) (2, 0)
(0, -2)
2x
y
3
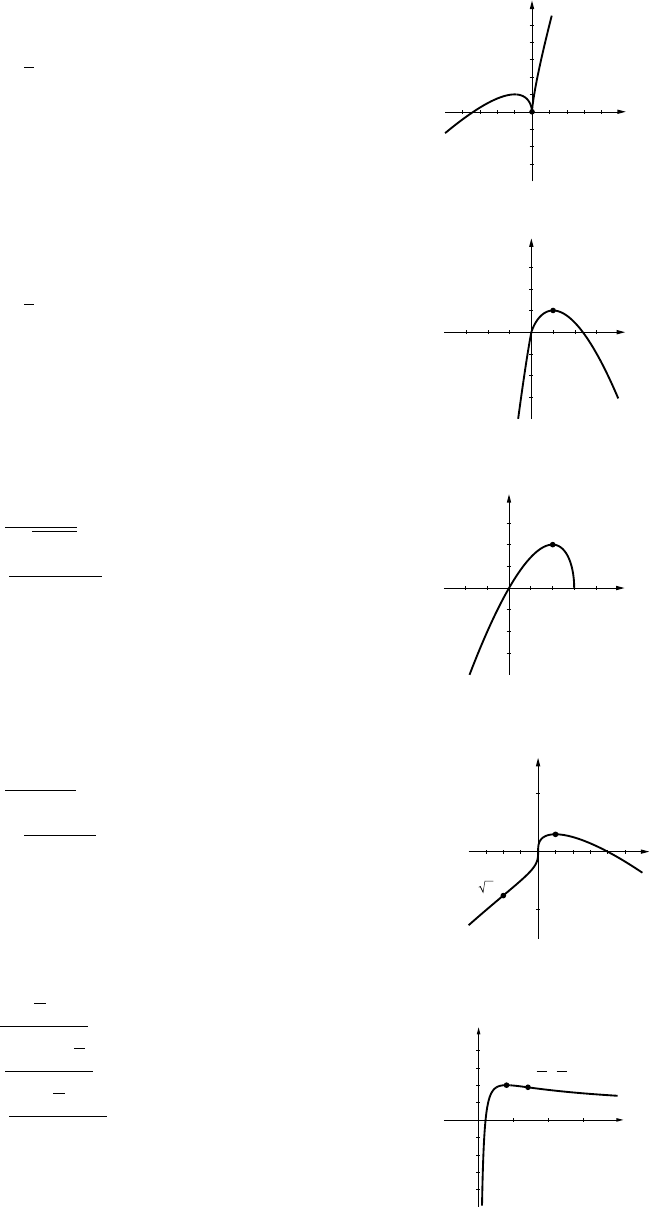
Exercise Set 5.3 158
27. y=2x+3x
2/3
;
y
0=2+2x
−1/3
;
y
00 =−2
3x−4/3
x
y
4
5
(0, 0)
28. y=4x−3x
4/3
;
y
0=4−4x
1/3
;
y
00 =−4
3x−2/3
x
y
1
(1, 1)
3
29. y=x(3 −x)1/2;
y0=3(2 −x)
2√3−x;
y00 =3(x−4)
4(3 −x)3/2x
y
(2, 2)
30. y=x1/3(4 −x);
y0=4(1 −x)
3x2/3;
y00 =−4(x+2)
9x
5/3
-10
10
x
y
(1, 3)
(-2, -6 )2
3
31. y=8(√x−1)
x;
y0=4(2 −√x)
x2;
y00 =2(3√x−8)
x315 x
y
(4, 2) 64
915
8
,
4
()
159 Chapter 5
32. y=1+√
x
1−√
x;
y
0=1
2
√
x(1−√x);
y00 =3√x−1
2x3/2(1 −√x)3
2
-2
x
y
x = 1
y = -1
1
9, 2
()
33. y=x+ sin x;
y0= 1 + cos x,y0= 0 when x=π+2nπ;
y00 =−sin x;y00 = 0 when x=nπ
n=0,±1,±2,... c
c
x
y
34. y=x−cos x;
y0= 1 + sin x;
y0= 0 when x=−π/2+2nπ;
y00 = cos x;
y00 = 0 when x=π/2+nπ
n=0,±1,±2,...
c
c
x
y
35. y= sin x+ cos x;
y0= cos x−sin x;
y0= 0 when x=π/4+nπ;
y00 =−sin x−cos x;
y00 = 0 when x=3π/4+nπ
-oo
-2
2
x
y
36. y=√3 cos x+ sin x;
y0=−√3 sin x+ cos x;
y0= 0 when x=π/6+nπ;
y00 =−√3 cos x−sin x;
y00 = 0 when x=2π/3+nπ
o
-2
2
x
y
Exercise Set 5.3 160
37. y= sin2x, 0≤x≤2π;
y0= 2 sin xcos x= sin 2x;
y00 = 2 cos 2x
co
x
y
1
38. y=xtan x, −π/2<x<π/2;
y0=xsec2x+ tan x;
y0= 0 when x=0;
y
00 = 2 sec2x(xtan x+ 1), which is always
positive for −π/2<x<π/2-6 6
x
y
39. (a) lim
x→+∞xex=+∞, lim
x→−∞ xex=0
(b) y=xex;
y0=(x+1)e
x
;
y
00 =(x+2)e
x
-1
-1-3-5
1
x
y
(-2, -0.27)
(-1, -0.37)
40. (a) lim
x→+∞xe−2x= 0, lim
x→−∞ xe−2x=−∞
(b) y=xe−2x;y0=−2µx−1
2¶e−2x;y00 =4(x−1)e−2x
-3 -1 1 3
-0.3
-0.1
0.1
0.3
x
y
(0.5, 0.18)
(1, 0.14)
41. (a) lim
x→+∞
x2
e2x= 0, lim
x→−∞
x2
e2x=+∞
(b) y=x2/e2x=x2e−2x;
y0=2x(1 −x)e−2x;
y00 = 2(2x2−4x+1)e
−2x
;
y
00 = 0 if 2x2−4x+ 1 = 0, when
x=4±√16 −8
4=1±√
2/2≈0.29,1.71
123
0.3
x
y
(0, 0)
(0.29, 0.05)
(1, 0.14)
(1.71, 0.10)
42. (a) lim
x→+∞x2e2x=+∞, lim
x→−∞ x2e2x=0.
161 Chapter 5
(b) y=x2e2x;
y0=2x(x+1)e
2x
;
y
00 = 2(2x2+4x+1)e
2x
;
y
00 = 0 if 2x2+4x+1=0,when
x=−4±√16 −8
4=−1±√2/2≈−0.29,−1.71
-3 -2 -1
y
x
0.2
0.3
(-1.71, 0.10)
(-1, 0.14)
(0, 0)
(-0.29, 0.05)
43. (a) lim
x→+∞f(x)=+∞, lim
x→−∞ f(x)=−∞
(b) y=xex2;
y0=(1+2x
2
)e
x
2;
y
00 =2x(3+2x
2
)e
x
2
no relative extrema, inflection point at (0,0)
y
x
-100
100
-2 2
(0,0)
44. (a) lim
x→±∞ f(x)=1
(b) f0(x)=2x
−3
e
−1/x2so f0(x)<0 for x<0 and f0(x)>0 for
x>0. By L’Hˆopital’s Rule limx→0f0(x) = 0, so (by the first
derivative test) f(x) has a minimum at x=0.
f
00(x)=(−6x
−4+4x
−6
)e
−1/x2,sof(x) has points of inflection
at x=±p2/3
.y
x
0.4
0.8
1
-10 -5 5 10
(0, 0)
2/3, e−3/2
−
()
2/3, e−3/2
()
45. (a) lim
x→0+y= lim
x→0+xln x= lim
x→0+
ln x
1/x = lim
x→0+
1/x
−1/x2=0;
lim
x→+∞y=+∞
(b) y=xln x,
y0=1+lnx,y
00 =1/x,
y0= 0 when x=e−1
1x
y
(e-1, -e-1)
46. (a) lim
x→0+y= lim
x→0+
ln x
1/x2= lim
x→0+
1/x
−2/x3=0,
lim
x→+∞y=+∞
(b) y=x2ln x, y0=x(1+2lnx),
y
00 =3+2lnx,
y0=0ifx=e
−1/2
,
y
00 =0ifx=e
−3/2
,
lim
x→0+y0=0
1
-0.2
-0.1
0.1
0.2
x
y
(
e-1/2, - e-1
)
1
2
(
e-3/2, - e-3
)
3
2
Exercise Set 5.3 162
47. (a) lim
x→0+y= lim
x→0+
ln x
x2=−∞;
lim
x→+∞y= lim
x→+∞
ln x
x2= lim
x→+∞
1/x
2x=0
(b) y=ln x
x2,y
0=1−2lnx
x
3,
y
00 =6lnx−5
x
4,
y
0=0ifx=e
1/2
,
y
00 =0ifx=e
5/6
123
-0.4
-0.3
-0.2
-0.1
0.1
0.2
0.3
0.4
x
y
(
e1/2, e-1
)
1
2
(
e5/6, e-5/3
)
5
6
48. (a) lim
x→0+(ln x)/√x=−∞ by inspection, lim
x→+∞(ln x)/√x= lim
x→+∞
1/x
1/2√x= lim
x→+∞
2
√x= 0, L’Hˆopital’s
Rule.
(b) y=ln x
√x,y0=2−ln x
2x3/2
y00 =−8+3lnx
4x
5/2
y
0=0ifx=e
2
,
y
00 =0ifx=e
8/3
y
x
-1
0.5
2 6 10 14
(e2, 2/e)
(
e8/3, e-4/3
)
8
3
49. (a) lim
x→−∞ y=−∞, lim
x→+∞y=+∞;
curve crosses x-axis at x=0,1,−1
y
x
-6
-4
-2
2
4
-2 -1 1
(b) lim
x→±∞ y=+∞;
curve never crosses x-axis
y
x
0.1
0.2
-1 1
(c) lim
x→−∞ y=−∞, lim
x→+∞y=+∞;
curve crosses x-axis at x=−1
y
x
-0.2
0.2
0.4
-1 1
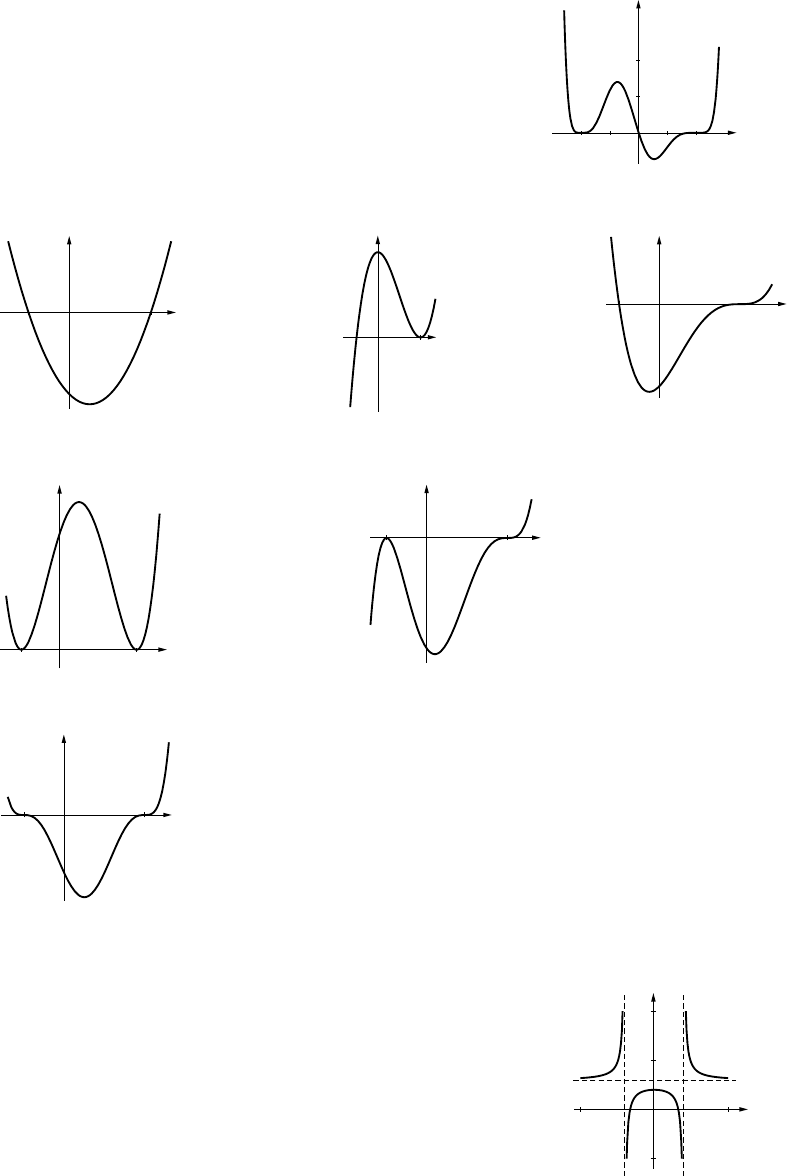
163 Chapter 5
(d) lim
x→±∞ y=+∞;
curve crosses x-axis at x=0,1
y
x
0.2
0.4
-1 1
50. (a) y
x
ab
y
x
ab
y
x
ab
(b) y
x
ab
y
x
ab
(c) y
x
ab
51. (a) horizontal asymptote y=3asx→±∞, vertical asymptotes of
x=±2
y
x
-5
5
10
-5 5
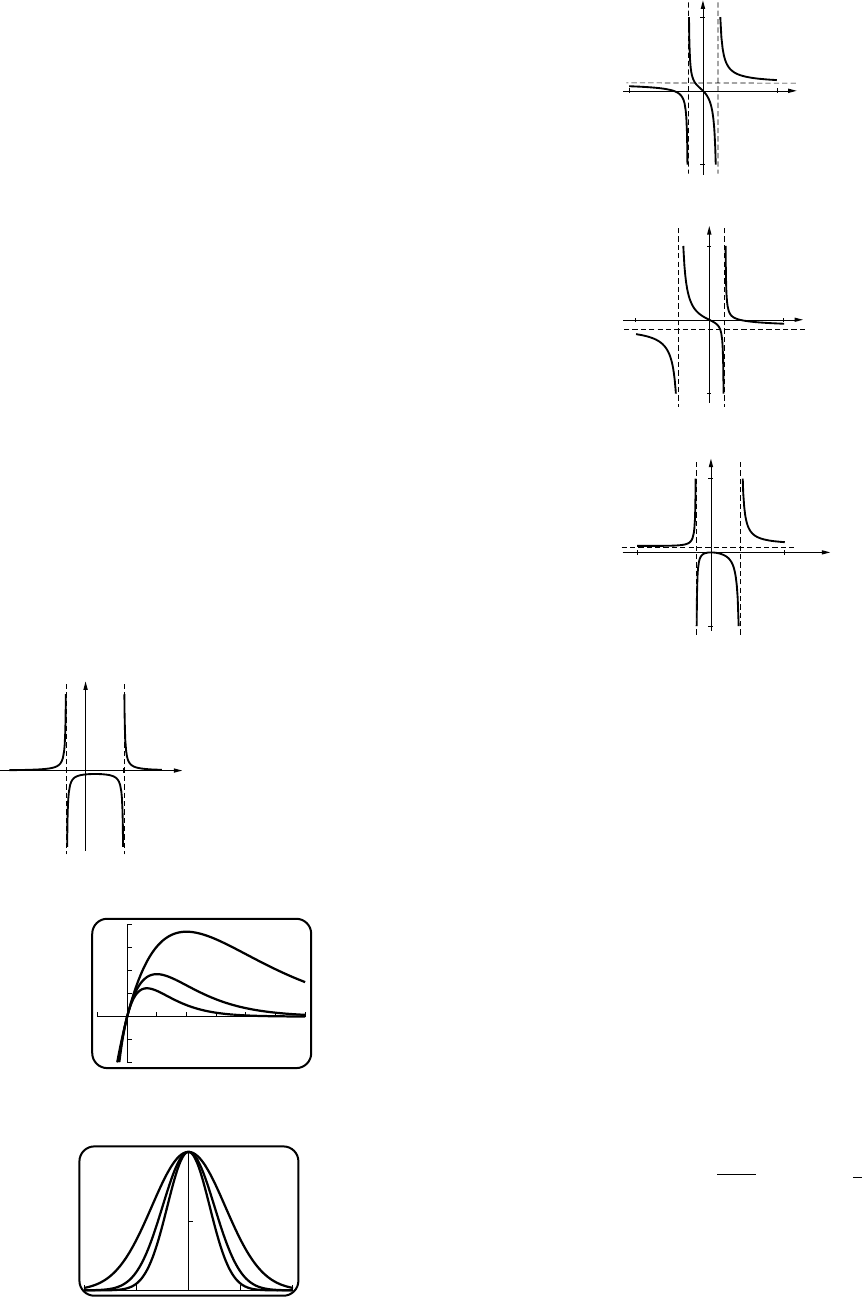
Exercise Set 5.3 164
(b) horizontal asymptote of y=1asx→±∞, vertical asymptotes
at x=±1
y
x
-10
10
-5 5
(c) horizontal asymptote of y=−1asx→±∞, vertical
asymptotes at x=−2,1
y
x
-10
10
-5 5
(d) horizontal asymptote of y=1asx→±∞,
vertical asymptote at x=−1,2
y
x
-10
10
-5 5
52. y
x
ab
53. (a) 0.4
-0.2
-0.5 3
(b) y0=(1−bx)e−bx,y00 =b2(x−2/b)e−bx;
relative max at x=1/b,y=1/be;pointof
inflection at x=2/b,y=2/be2. Increasing
bmoves the relative max and the point of
inflection to the left and down, i.e. towards
the origin.
54. (a) 1
0
-2 2
(b) y0=−2bxe−bx2,y00 =2b(−1+2bx2)e−bx2;
relative max at x=0,y= 1; points
of inflection at x=±p1/2b,y=1/
√
e.
Increasing bmoves the points of inflection
towards the y-axis; the relative max doesn’t
move.
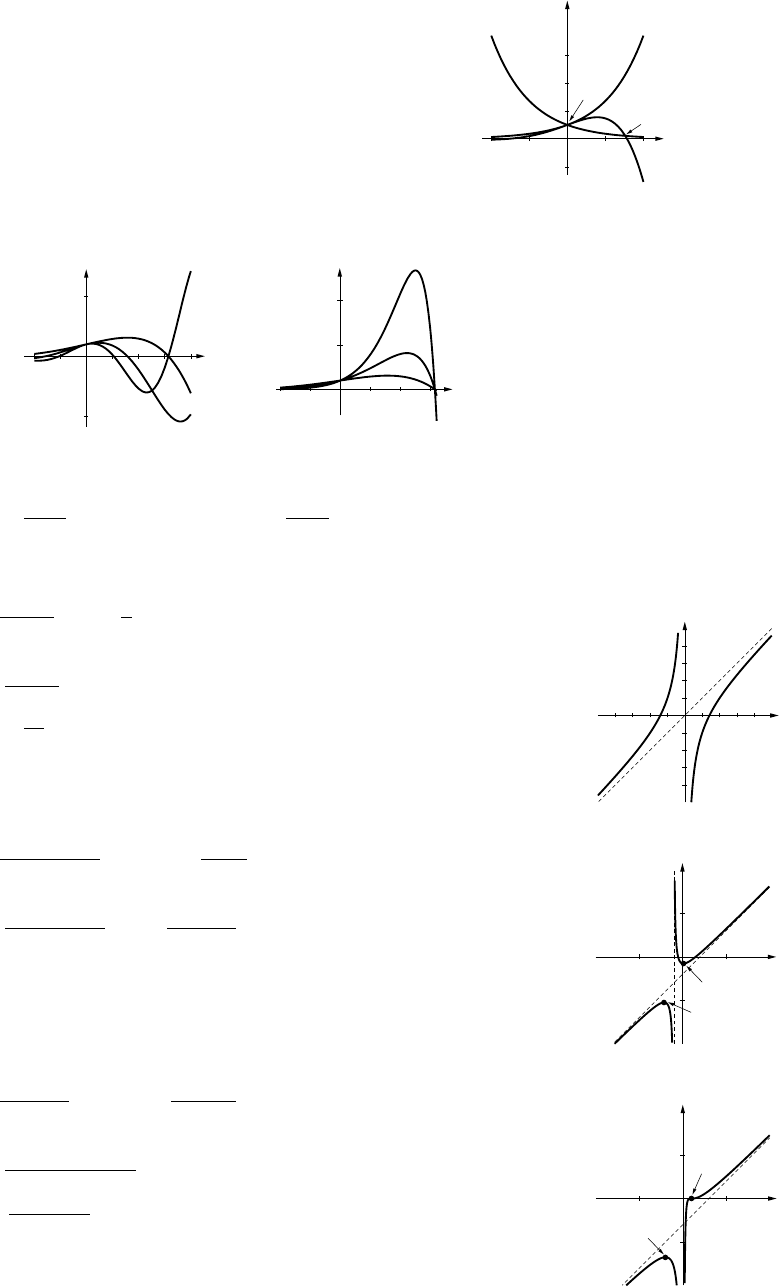
165 Chapter 5
55. (a) The oscillations of excos xabout zero
increase as x→±∞so the limit does not
exist.
(b) y
x
-2
4
6
-2 -1 1 2
(0,1)
(1.52, 0.22)
(c) The curve y=eax cos bx oscillates between y=eax and y=−eax. The frequency of oscillation
increases when bincreases.
y
x
-5
5
-1 1 2
a = 1
b = 1
b = 2
b = 3
y
x
5
10
-1 0.5 1
b = 1
a = 1
a = 2
a = 3
56. lim
x→±∞ ·P(x)
Q(x)−(ax +b)¸= lim
x→±∞
R(x)
Q(x)= 0 because the degree of R(x) is less than
the degree of Q(x).
57. y=x2−2
x=x−2
xso
y=xis an oblique asymptote;
y0=x2+2
x
2,
y
00 =−4
x3
x
y
y = x
4
4
58. y=x2−2x−3
x+2 =x−4+ 5
x+2 so
y=x−4 is an oblique asymptote;
y0=x2+4x−1
(x+2)
2,y
00 =10
(x+2)
3
≈(-4.24, -10.48)
≈(0.24, -1.52)
x = -2
y = x - 4
-10 10 x
y
59. y=(x−2)3
x2=x−6+12x−8
x2so
y=x−6 is an oblique asymptote;
y0=(x−2)2(x+4)
x
3,
y
00 =24(x−2)
x4
x
y
-10
(-4, -13.5)
y = x - 6
(2, 0)
10
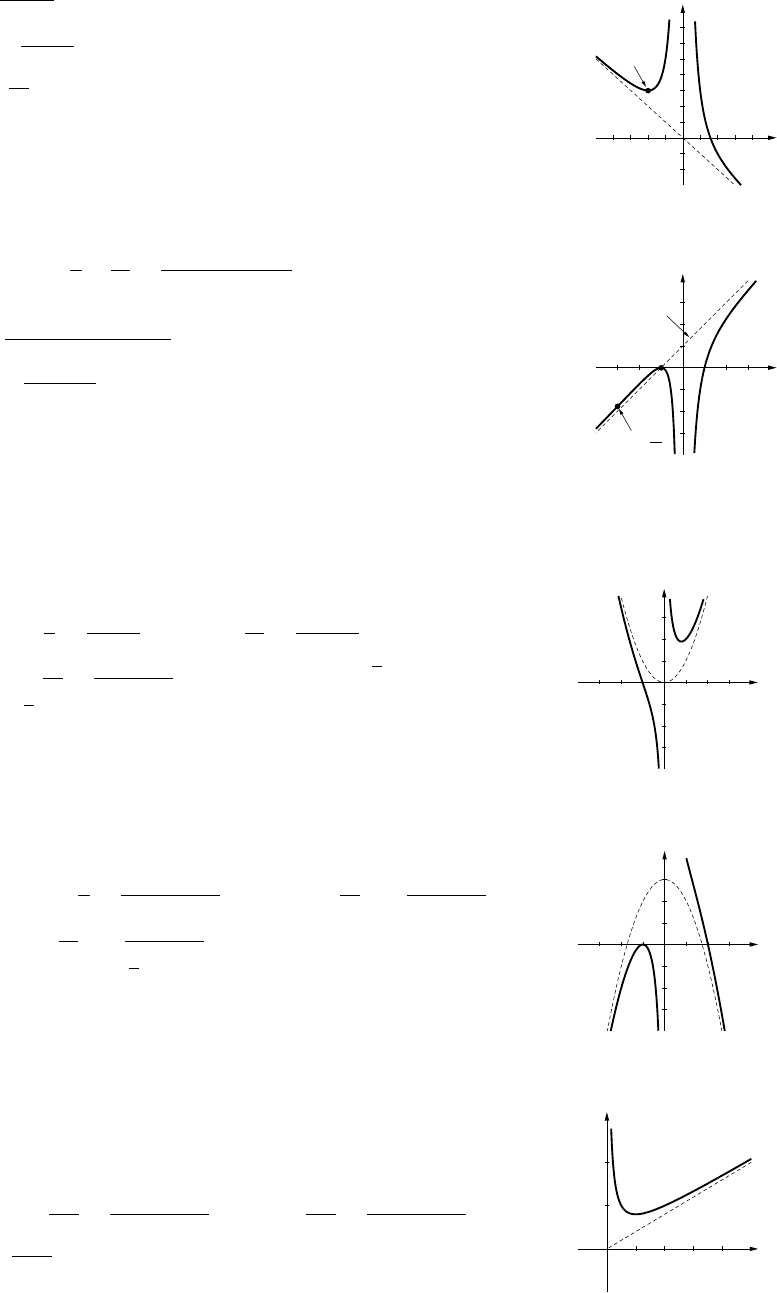
Exercise Set 5.3 166
60. y=4−x3
x2,
y0=−x3+8
x
3,
y
00 =24
x4
x
y
(-2, 3)
y = -x
61. y=x+1−1
x−1
x
2=(x−1)(x+1)
2
x
2,
y=x+ 1 is an oblique asymptote;
y0=(x+ 1)(x2−x+2)
x
3,
y
00 =−2(x+3)
x
4
x
y
y = x + 1
(-1, 0)
16
9
-3, -
)(
62. The oblique asymptote is y=2xso (2x3−3x+4)/x2=2x,−3x+4=0,x=4/3.
63. lim
x→±∞[f(x)−x2] = lim
x→±∞(1/x)=0
y=x
2+1
x=x
3+1
x,y
0=2x−1
x
2=2x
3−1
x
2,
y
00 =2+ 2
x
3=2(x3+1)
x
3,y
0= 0 when x=1/3
√
2≈0.8,
y=33
√
2/2≈1.9; y00 = 0 when x=−1,y =0
x
y
y = x2
3
3
64. lim
x→±∞[f(x)−(3 −x2)] = lim
x→±∞(2/x)=0
y=3−x
2+2
x=2+3x−x
3
x,y
0=−2x−2
x
2=−2(x3+1)
x
2,
y
00 =−2+ 4
x
3=−2(x3−2)
x3,y0= 0 when x=−1,y =0;
y
00 = 0 when x=3
√2≈1.3, y=3
x
y
y = 3 - x2
3
1
65. Let ybe the length of the other side of the rectangle, then
L=2x+2yand xy = 400 so y= 400/x and hence L=2x+ 800/x.
L=2xis an oblique asymptote (see Exercise 48)
L=2x+800
x=2(x2+ 400)
x,L0=2−800
x2=2(x2−400)
x2,
L00 =1600
x3,L0= 0 when x=20,L =80 20
100
x
L
167 Chapter 5
66. Let ybe the height of the box, then S=x2+4xy and x2y= 500 so
y= 500/x2and hence S=x2+ 2000/x.
The graph approaches the curve S=x2asymptotically
(see Exercise 63)
S=x2+2000
x=x3+ 2000
x,S0=2x−2000
x2=2(x3−1000)
x2,
S00 =2+4000
x3=2(x3+ 2000)
x3,S00 = 0 when x=10,S = 300
30
1000
x
S
67. y0=0.1x
4
(6x−5);
critical points: x=0,x=5/6;
relative minimum at x=5/6,
y≈−6.7×10−3
-1 1
0.01
x
y
68. y0=0.1x
4
(x+ 1)(7x+ 5);
critical points: x=0,x=−1, x=−5/7,
relative maximum at x=−1, y=0;
relative minimum at x=−5/7, y≈−1.5×10−3
1
0.001
x
y
69. (a) P0(t)= kL2Ae−kLt
(1+Ae−kLt)2S,soP
0
(0) = kL2A
(1+A)2
(b) The rate of growth increases to its maximum, which occurs when Pis halfway between 0 and
L, or when t=1
Lk ln A; it then decreases back towards zero.
(c) From (6) one sees that dP
dt is maximized when Plies half way between 0 and L, i.e. P=L/2.
This follows since the right side of (6) is a parabola (with Pas independent variable) with
P-intercepts P=0,L. The value P=L/2 corresponds to t=1
Lk ln A, from (8).
70. Since 0 <P <Lthe right-hand side of (7) can change sign only if the factor L−2Pchanges sign,
which it does when P=L/2. From (5) we have L
2=L
1+Ae−kLt ,1=Ae−kLt,t=1
Lk ln A.
SUPPLEMENTARY EXERCISES FOR CHAPTER 5
4. (a) False; an example is y=x3
3−x2
2on [−2,2]; x= 0 is a relative maximum and x= 1 is a relative
minimum, buty=0isnotthelargest value of yon the interval, nor is y=−1
6the smallest.
Supplementary Exercises 168
(b) true
(c) False; for example y=x3on (−1,1) which has a critical point but no relative extrema
6. (a)
2
4
x
y(b)
2
4
x
y(c)
2
4
x
y
7. (a) f0(x)= 7(x−7)(x−1)
3x2/3; critical points at x=0,1,7;
neither at x= 0, relative max at x= 1, relative min at x= 7 (first derivative test)
(b) f0(x)=2cosx(1 + 2 sin x); critical points at x=π/2,3π/2,7π/6,11π/6;
relative max at x=π/2,3π/2, relative min at x=7π/6,11π/6
(c) f0(x)=3−3
√
x−1
2; critical points at x= 5; relative max at x=5
8. (a) f0(x)= x−9
18x3/2,f00(x)=27 −x
36x5/2; critical point at x=9;f
00(9) >0, relative min at x=9
(b) f0(x)=2
x
3−4
x
2,f
00(x)=2
x
3+8
x
3;
critical point at x=4
1/3
,f
00(41/3)>0, relative min at x=4
1/3
(c) f0(x) = sin x(2 cos x+ 1), f00(x)=2cos
2x−2 sin2x+ cos x; critical points at x=2π/3,π,4π/3;
f00(2π/3) <0, relative max at x=2π/3; f00(π)>0, relative min at x=π;f00(4π/3) <0, relative
max at x=4π/3
9. lim
x→−∞ f(x)=+∞, lim
x→+∞f(x)=+∞
f
0(x)=x(4x2−9x+ 6), f00(x) = 6(2x−1)(x−1)
relative min at x=0,
points of inflection when x=1/2,1,
no asymptotes
y
x
1
2
3
4
12
(0,1)
)(
(1,2)
1
2,23
16
10. lim
x→−∞ f(x)=−∞, lim
x→+∞f(x)=+∞
f(x)=x
3
(x−2)2,f0(x)=x
2
(5x−6)(x−2),
f00(x)=4x(5x2−12x+6)
critical points at x=0,8±2
√
31
5
relative max at x=8−2√31
5=−0.63
relative min at x=8+2
√
31
5=3.83
points of inflection at x=0,6±√
66
5=0,−0.42,2.82
no asymptotes
y
x
-200
-100
-1 1234
(0,0)
(-0.42,0.16)
(2.82,-165.00) (3.83,-261.31)
(-0.63,0.27)
169 Chapter 5
11. lim
x→±∞ f(x) doesn’t exist
f0(x)=2xsec2(x2+ 1),
f00(x)=2sec
2
(x
2+1)£1+4x
2tan(x2+1)
¤
critical point at x= 0; relative min at x=0
point of inflection when 1 + 4x2tan(x2+1)=0
vertical asymptotes at x=±qπ(n+1
2)−1, n=0,1,2,...
y
x
-4
-2
2
4
-2 -1 1 2
12. lim
x→−∞ f(x)=−∞, lim
x→+∞f(x)=+∞
f
0(x) = 1 + sin x,f00(x) = cos x
critical points at x=2nπ +π/2, n=0,±1,±2,...,
no extrema because f0≥0 and by Exercise 51 of Section 5.1,
fis increasing on (−∞,+∞)
inflections points at x=nπ +π/2, n=0,±1,±2,...
no asymptotes
y
x
-6
-4
-2
2
4
−π π
13. f0(x)=2 x(x+5)
(x
2+2x+5)
2,f00(x)=−2
2x
3+15x
2−25
(x2+2x+5)
3
critical points at x=−5,0;
relative max at x=−5,
relative min at x=0
points of inflection at x=−7.26,−1.44,1.20
horizontal asymptote y=1asx→±∞
y
x
0.2
0.4
0.6
0.8
1
-20 -10 10 20
14. f0(x)=3
3x
2−25
x4,f00(x)=−6
3x
2−50
x5
critical points at x=±5√3/3;
relative max at x=−5√3/3,
relative min at x=+5
√
3/3
inflection points at x=±5p2/3
horizontal asymptote of y=0asx→±∞,
vertical asymptote x=0
y
x
-5
5
-4 6
15. lim
x→−∞ f(x)=+∞, lim
x→+∞f(x)=−∞
f0(x)=½x
−2xif ½x≤0
x>0
critical point at x= 0, no extrema
inflection point at x=0(fchanges concavity)
no asymptotes
y
x
-2
1
2
-2 1
Supplementary Exercises 170
16. f0(x)= 5−3x
3(1 + x)1/3(3 −x)2/3,
f00(x)= −32
9(1 + x)4/3(3 −x)5/3
critical point at x=5/3;
relative max at x=5/3
cusp at x=−1;
point of inflection at x=3
oblique asymptote y=−xas x→±∞
y
x
-3
-1
2
4
-4 -2 2
17. lim
x→+∞f(x)=+∞
f
0(x)=1+lnx,f00(x)=1/x
lim
x→0+f(x)=0, lim
x→0
+f
0(x)=−∞
critical point at x=1/e;
relative min at x=1/e
no points of inflection, no asymptotes
y
x
1
12
18. lim
x→+∞f(x)=+∞
f
0(x)=x(2 ln x+ 1), f00(x)=2lnx+3
lim
x→0+f(x)=0, lim
x→0
+f
0(x)=0
critical point at x=e−1/2;
relative min at x=e−1/2
point of inflection at x=e−3/2
y
x
-0.1
0.2 0.4 0.6
19. f0(x)=1−2lnx
x
3,f00(x)=6lnx−5
x
4
critical point at x=e1/2,
relative max at x=e1/2
point of inflection at x=e5/6
horizontal asymptote y=0asx→+∞
y
x
-2
-1
12
20. lim
x→±∞ f(x)=+∞
f
0(x)= 2x
x
2+1,f00(x)=2 1−x
2
(x
2+1)
2
critical point at x=0;
relative min at x=0
points of inflection at x=±1
no asymptotes
y
x
1
2
-2 2
171 Chapter 5
21. lim
x→+∞f(x)=+∞
f
0(x)=e
xx−1
x
2,f
00(x)=e
xx
2−2x+2
x
3
critical point at x=1;
relative min at x=1
no points of inflection
vertical asymptote x=0,
horizontal asymptote y= 0 for x→−∞
y
x
-2
2
6
-2 1 3
22. f0(x)=(1−x)e
−x
,f
00(x)=(x−2)e−x
critical point at x= 1; relative max at x=1
point of inflection at x=2
horizontal asymptote y=0asx→+∞, lim
x→−∞ f(x)=−∞
y
x
-0.8
0.2
12
23. f0(x)=x(2 −x)e1−x,f00(x)=(x
2−4x+2)e
1−x
critical points at x=0,2;
relative min at x=0,
relative max at x=2
points of inflection at x=2±√
2
horizontal asymptote y=0asx→+∞,
lim
x→−∞ f(x)=+∞
y
x
0.6
1
1.8
1234
24. f0(x)=x
2
(3+x)ex−1,f00(x)=x(x
2+6x+6)e
x−1
critical points at x=−3,0;
relative min at x=−3
points of inflection at x=0,−3±√
3
horizontal asymptote y=0asx→−∞
lim
x→+∞f(x)=+∞
y
x
-0.4
0.4
1
-4 -2 1
25. (a) 40
-40
-5 5
(b) f0(x)=x
2−1
400,f00(x)=2x
critical points at x=±1
20;
relative max at x=−1
20,
relative min at x=1
20
Supplementary Exercises 172
(c) The finer details can be seen when graphing over
a much smaller x-window.
0.0001
-0.0001
-0.1 0.1
26. (a) 200
-200
-5 5
(b) critical points at x=±√2,3
2,2;
relative max at x=−√2,
relative min at x=√2,
relative max at x=3
2,
relative min at x=2
(c) 10
-4
-2.2 3.5
-2.909
-2.912
1.3 1.6
27. (a) 6
-6
-5 5
(b) Divide y=x2+ 1 into y=x3−8 to get the
asymptote ax +b=x
28. (a) p(x)=x
3−x(b) p(x)=x
4−x
2
(c) p(x)=x
5−x
4−x
3+x
2(d) p(x)=x
5−x
3
29. f0(x)=4x
3−18x2+24x−8, f00(x) = 12(x−1)(x−2)
f00(1)=0,f
0(1)=2,f(1)=2;f
00(2)=0,f
0(2)=0,f(2)=3,
so the tangent lines at the inflection points are y=2xand y=3.
30. cos x−(sin y)dy
dx =2
dy
dx;dy
dx = 0 when cos x= 0. Use the first derivative test: dy
dx =cos x
2 + sin yand
2 + sin y>0, so critical points when cos x= 0, relative maxima when x=2nπ +π/2, relative minima
when x=2nπ −π/2, n=0,±1,±2,...
173 Chapter 5
31. f(x)= (2x−1)(x2+x−7)
(2x−1)(3x2+x−1) =x2+x−7
3x2+x−1,x6=1/2
horizontal asymptote: y=1/3,
vertical asymptotes: x=(−1±√
13)/6
y
x
-5
5
10
-4 -2 2 4
32. (a) f(x)= (x−2)(x2+x+ 1)(x2−2)
(x−2)(x2−2)2(x2+1)
=x
2+x+1
(x
2−2)(x2+1)
(b)
y
x
-2
4
-2 1 3
33. (a) sin x=−1 yields the smallest values, and
sin x= +1 yields the largest
3
0
Oo
(b) f0(x)=e
sin xcos x; relative maxima at x=2nπ +π/2, y=e; relative minima at x=2nπ −π/2,
y=1/e;n=0,±1,±2,... (first derivative test)
(c) f00(x)=(1−sin x−sin2x)esin x;f00(x) = 0 when sin x=t,arootoft
2+t−1=0,
t=−1±√
5
2; sin x=−1−√5
2is impossible. So the points of inflection on 0 <x<2πoccur
when sin x=−1+√
5
2,orx=0.66624,2.47535
34. f0(x)=3ax2+2bx +c;f0(x)>0orf
0
(x)<0on(−∞,+∞)iff
0
(x) = 0 has no real solutions so
from the quadratic formula (2b)2−4(3a)c<0, 4b2−12ac < 0, b2−3ac < 0. If b2−3ac = 0, then
f0(x) = 0 has only one real solution at, say, x=cso fis always increasing or always decreasing on
both (−∞,c] and [c, +∞), and hence on (−∞,+∞) because fis continuous everywhere. Thus fis
always increasing or decreasing if b2−3ac ≤0.
35. (a) relative minimum −0.232466 at x=0.450184 2
-0.5
-1 1.5
Supplementary Exercises 174
(b) relative maximum 0 at x=0;
relative minimum −0.107587 at x=±0.674841
0.2
-0.15
-1.2 1.2
(c) relative maximum 0.876839; at x=0.886352;
relative minimum −0.355977 at x=−1.244155
1
-0.4
-1.5 1.5
36. (a) f0(x) = 2+3x2−4x3has one real root at x=1.14, a relative max; so fis one-to-one for x≤1.14
(b) f(1.14)=3.07 so the domain of f−1is (−∞,3.07) and the range is (−∞,1.14); f−1(−1) = −0.70
37. (a) 0.5
0
05
(b) y=0atx= 0; lim
x→+∞y=0
(c) relative max at x=1/a, inflection point at x=2/a
(d) As aincreases, the x-coordinate of the maximum and the inflection point move towards the
origin.
38. (a) 4
0
-2 2
4
0
-2 2
(b) y=1atx=a; lim
x→−∞ y=+∞, lim
x→+∞y=0
(c) Since y0is always negative and y00 is always positive, there are
no relative extrema and no inflection points.
(d) An increase in bmakes the graph flatter.
(e) An increase in ashifts the graph to the right.
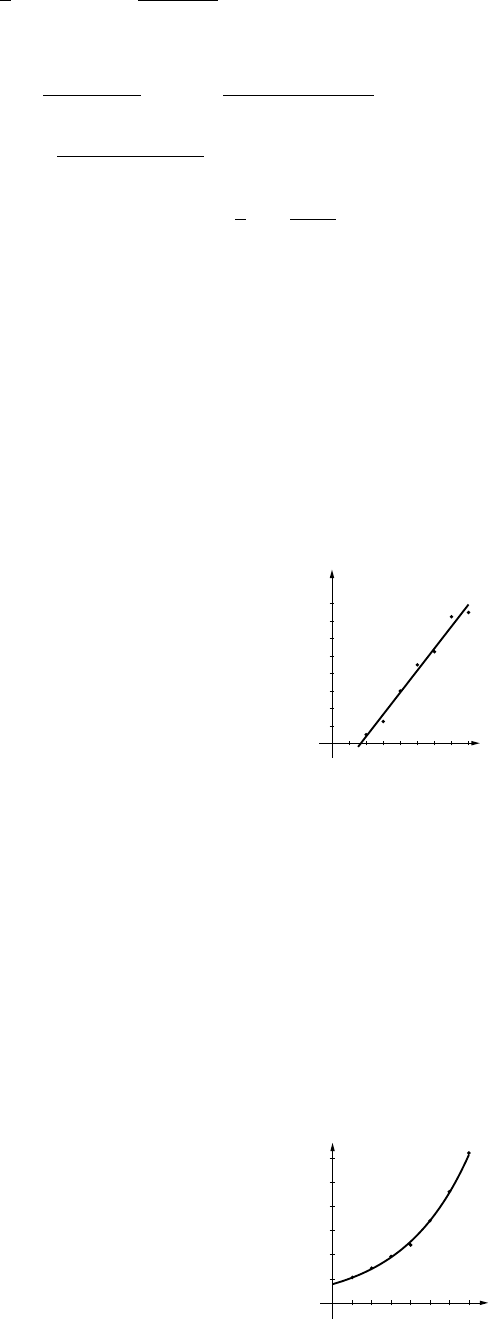
175 Chapter 5
39. f0(x) = ln(1 + 1/x)−1
xand f00(x)= 1
x
2
(x+1);sof
00 >0ifx>1 and therefore f0is increasing on
[1,+∞). Next, f0(1)=ln2−1<0. Then by L’Hˆopital’s Rule,
lim
x→+∞xln(1 + 1/x) = lim
x→+∞
ln(1 + 1/x)
1/x = lim
x→+∞−1/x2
(1+1/x)(−1/x2)=1
and thus lim
x→+∞f0(x) = lim
x→+∞
xln(1 + 1/x)−1
xis indeterminate.
By L’Hˆopital’s Rule lim
x→+∞f0(x) = lim
x→+∞·ln µ1+ 1
x¶−1
x+1¸=0.
Thus on [1,+∞) the function f0starts negative and increases towards zero, so it is negative
on the whole interval. So f(x) is decreasing, and f(x)>f(x+ 1). Set x=nand obtain
ln(1 + 1/n)n+1 >ln(1 + 1/(n+ 1))n+2. Since ln xand its inverse function exare both increasing,
it follows that (1 + 1/n)n+1 >(1+1/(n+ 1))n+2.
CALCULUS HORIZON MODULE CHAPTER 5
1. The sum of the squares for the residuals for line I is approximately 12+12+12+02+22+12+12+12= 10,
and the same for line II is approximately 02+(0.4)2+(1.2)2+0
2+(2.2)2+(0.6)2+(0.2)2+0
2=6.84;
line II is the regression line.
2. (a) y=5.035714286x−4.232142857 (b) y
x
2
6
10
14
1234
4. r=0.9907002406
5. (a) S=2.155239850t+ 190.3600714; r=0.9569426456
(b) yes, because ris close to 1
(c) 244.241068 mi/h
(d) It is assumed that the line still gives a good estimate in the year 2000.
6. (a) Y=lny=bx +lnahas slope band Y-intercept ln a.
(b) y=a+bX has slope band y-intercept a.
(c) Y=lny=bln x+lna=bX +lnahas slope band Y-intercept ln a.
(d) The same algebraic rules hold.
7. (a) y=3.923208367 + e0.2934589528x(b) y
x
5
10
15
20
25
30
1234567
Calculus Horizon Module 176
8. (a) It appears that log T=a+blog d,soT=10
a
d
b
, an exponential model.
(b) log T=1.719666407 ×10−4+1.499661719 log d
(c) T=1.000396046 d1.499661719
(d) “The squares of the periods of revolution of the planets are proportional to the cubes of their
mean distances”
9. (a) T=27+57.8e
−0.046t(b) T0=84.9
◦C(c) 53.19 min
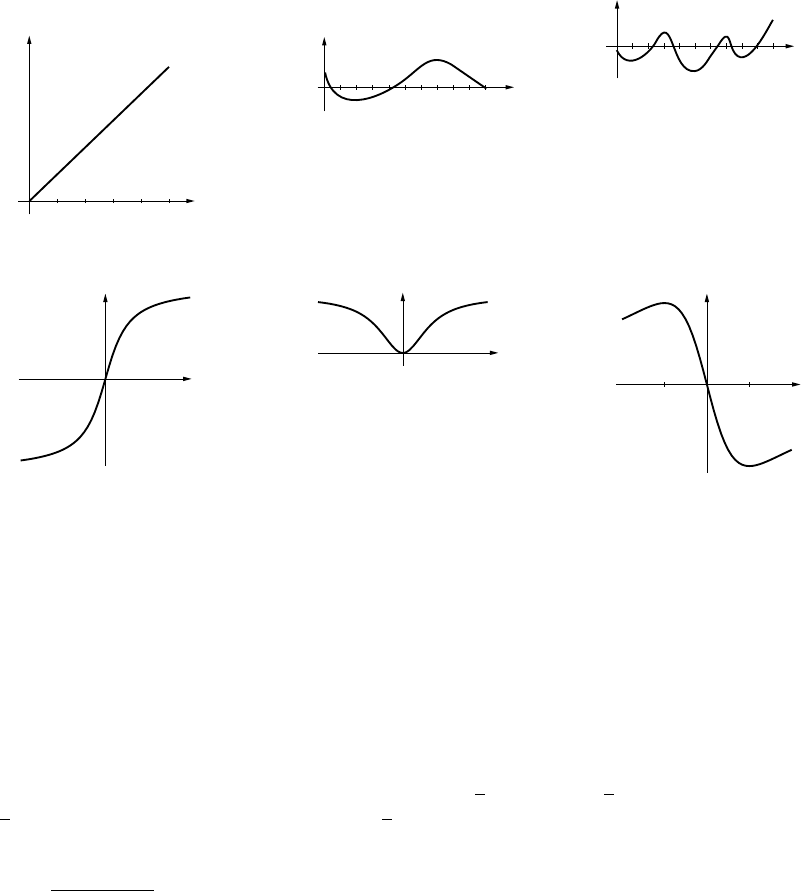
CHAPTER 6
Applications of the Derivative
EXERCISE SET 6.1
1. relative maxima at x=2,6; absolute maximum at x= 6; relative and absolute minimum at x=4
2. relative maximum at x= 3; absolute maximum at x= 7; relative minima at x=1,5; absolute minima
at x=1,5
3. (a) y
x
10
(b) y
x
27
(c)
y
x
53 7
4. (a) y
x
(b) y
x
(c) y
x
-5 5
5. f0(x)=8x−4, f0(x) = 0 when x=1/2; f(0)=1,f(1/2)=0,f(1) = 1 so the maximum value is 1
at x=0,1 and the minimum value is 0 at x=1/2.
6. f0(x)=8−2x,f
0
(x) = 0 when x=4;f(0)=0,f(4) = 16, f(6) = 12 so the maximum value is 16 at
x= 4 and the minimum value is 0 at x=0.
7. f0(x)=3(x−1)2,f0(x) = 0 when x=1;f(0) = −1, f(1)=0,f(4) = 27 so the maximum value is 27
at x= 4 and the minimum value is −1atx=0.
8. f0(x)=6x
2−6x−12=6(x+ 1)(x−2), f0(x) = 0 when x=−1,2; f(−2) = −4, f(−1)=7,
f(2) = −20, f(3) = −9 so the maximum value is 7 at x=−1 and the minimum value is −20 at x=2.
9. f0(x)=3/(4x2+1)
3/2
, no critical points; f(−1)=−3/√5, f(1)=3/
√
5 so the maximum value is
3/√5atx= 1 and the minimum value is −3/√5atx=−1.
10. f0(x)= 2(2x+1)
3(x2+x)1/3,f0(x) = 0 when x=−1/2 and f0(x) does not exist when x=−1,0;
f(−2)=2
2/3
,f(−1)=0,f(−1/2)=4
−2/3
,f(0)=0,f(3)=12
2/3so the maximum value is 122/3at
x= 3 and the minimum value is 0 at x=−1,0.
11. f0(x)=1−sec2x,f0(x)=0forxin (−π/4,π/4) when x=0;f(−π/4)=1−π/4, f(0)=0,
f(π/4) = π/4−1 so the maximum value is 1 −π/4atx=−π/4 and the minimum value is π/4−1
at x=π/4.
177
Exercise Set 6.1 178
12. f0(x) = cos x+ sin x,f0(x)=0forxin (0,π) when x=3π/4; f(0) = −1, f(3π/4)=√2, f(π)=1so
the maximum value is √2atx=3π/4 and the minimum value is −1atx=0.
13. f(x)=1+|9−x
2
|=½10 −x2,|x|≤3
−8+x
2
,|x|>3,f0(x)=½−2x, |x|<3
2x, |x|>3thus f0(x) = 0 when x=0,
f
0
(x) does not exist for xin (−5,1) when x=−3 because lim
x→−3−f0(x)6= lim
x→−3+f0(x) (see Theorem
preceding Exercise 75, Section 3.3); f(−5) = 17, f(−3)=1,f(0) = 10, f(1) = 9 so the maximum
value is 17 at x=−5 and the minimum value is 1 at x=−3.
14. f(x)=|6−4x|=½6−4x, x ≤3/2
−6+4x, x > 3/2,f0(x)=½−4,x<3/2
4,x>3/2
,f
0
(x) does not exist when
x=3/2thus3/2 is the only critical point in (−3,3); f(−3) = 18, f(3/2)=0,f(3) = 6 so the
maximum value is 18 at x=−3 and the minimum value is 0 at x=3/2.
15. f0(x)=2x−3; critical point x=3/2. Minimum value f(3/2) = −13/4, no maximum.
16. f0(x)=−4(x+ 1); critical point x=−1. Maximum value f(−1) = 5, no minimum.
17. f0(x)=12x
2
(1 −x); critical points x= 0, 1. Maximum value f(1) = 1, no minimum because
lim
x→+∞f(x)=−∞.
18. f0(x)=4(x
3+ 1); critical point x=−1. Minimum value f(−1) = −3, no maximum.
19. No maximum or minimum because lim
x→+∞f(x)=+∞and lim
x→−∞ f(x)=−∞.
20. No maximum or minimum because lim
x→+∞f(x)=+∞and lim
x→−∞ f(x)=−∞.
21. f0(x)=x(x+2)/(x+1)
2
; critical point x=−2in(−5,−1). Maximum value f(−2) = −4, no
minimum.
22. f0(x)=−6/(x−3)2; no critical points in [−5,5] (x= 3 is not in the domain of f). No maximum or
minimum because lim
x→3+f(x)=+∞and lim
x→3−f(x)=−∞.
23. (x2−1)2can never be less than zero because it is the square of
x2−1; the minimum value is 0 for x=±1, no maximum because
lim
x→+∞f(x)=+∞.
10
0
-2 2
24. (x−1)2(x+2)
2can never be less than zero because it is the product
of two squares; the minimum value is 0 for x=1or−2, no
maximum because lim
x→+∞f(x)=+∞.
15
0
-3 2
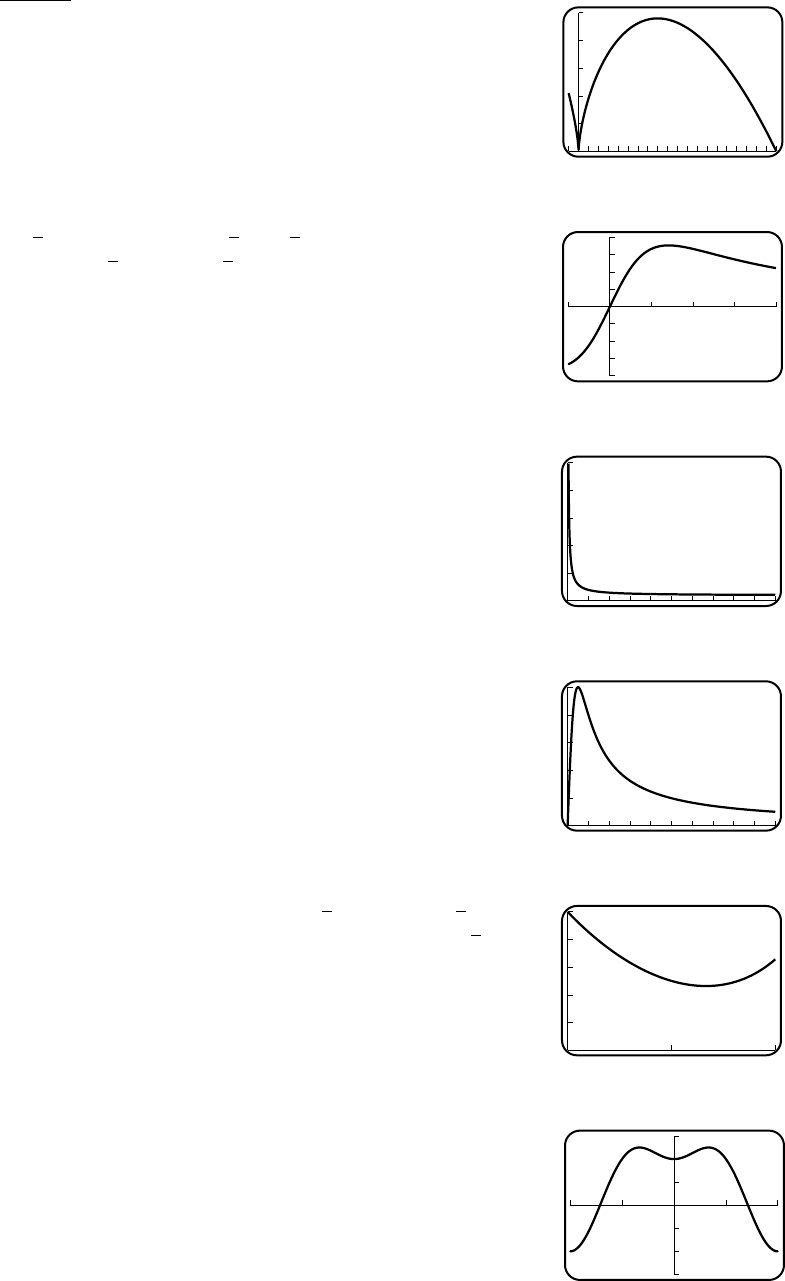
179 Chapter 6
25. f0(x)=5(8 −x)
3x1/3,f0(x) = 0 when x= 8 and f0(x) does not exist
when x=0;f(−1) = 21, f(0)=0,f(8) = 48, f(20) = 0 so the
maximum value is 48 at x= 8 and the minimum value is 0 at
x=0,20.
50
0
-1 20
26. f0(x)=(2−x
2
)/(x
2+2)
2
,f0(x)=0forxin the interval (−1,4)
when x=√2; f(−1) = −1/3, f(√2) = √2/4, f(4)=2/9sothe
maximum value is √2/4atx=√
2 and the minimum value is
−1/3atx=−1.
0.4
-0.4
-1 4
27. f0(x)=−1/x2; no maximum or minimum because there are no
critical points in (0,+∞).
25
0
010
28. f0(x)=(1−x
2
)/(x
2+1)
2
; critical point x= 1. Maximum value
f(1)=1/2, minimum value 0 because f(x) is never less than zero
on [0,+∞) and f(0)=0.
0.5
0
020
29. f0(x)=2secxtan x−sec2x= (2 sin x−1)/cos2x,f0(x)=0forxin
(0,π/4) when x=π/6; f(0)=2,f(π/6) = √3, f(π/4)=2
√
2−1so
the maximum value is 2 at x= 0 and the minimum value is √3at
x=π/6.
2
1.5
03
30. f0(x)=2sinxcos x−sin x= sin x(2 cos x−1), f0(x)=0forxin
(−π, π) when x=0,±π/3; f(−π)=−1, f(−π/3)=5/4, f(0)=1,
f(π/3)=5/4, f(π)=−1 so the maximum value is 5/4at
x=±π/3 and the minimum value is −1atx=±π.
1.5
-1.5
Cc
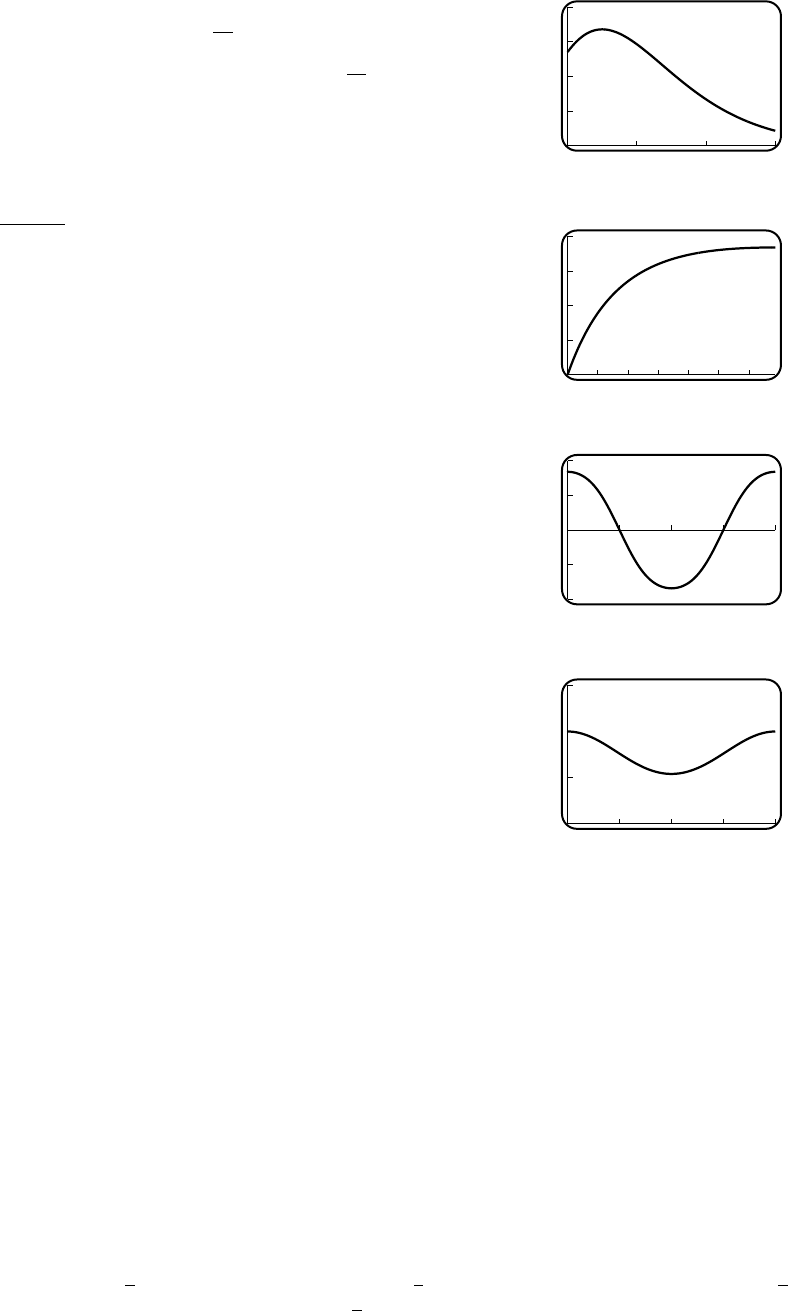
Exercise Set 6.1 180
31. f0(x)=x
2
(2x−3)e−2x,f0(x)=0forxin [1,4] when x=3/2;
if x=1,3/2,4, then f(x)=e
−2
,27
8e−3,64e−8;
critical point at x=3/2; absolute maximum of 27
8e−3at x=3/2,
absolute minimum of 64e−8at x=4
0.2
0
14
32. f0(x)=1−ln x
x2,f0(x) = 0 when x=e;
absolute minimum of 0 at x=1;
absolute maximum of 1/e at x=e
0.4
0
1e
33. f0(x)=−[cos(cos x)] sin x;f0(x) = 0 if sin x= 0 or if cos(cos x)=0.
If sin x= 0, then x=πis the critical point in (0,2π); cos(cos x)=0
has no solutions because −1≤cos x≤1. Thus f(0) = sin(1),
f(π) = sin(−1) = −sin(1), and f(2π) = sin(1) so the maximum
value is sin(1) ≈0.84147 and the minimum value is
−sin(1) ≈−0.84147.
1
-1
0o
34. f0(x)=−[sin(sin x)] cos x;f0(x) = 0 if cos x= 0 or if sin(sin x)=0.
If cos x= 0, then x=π/2 is the critical point in (0,π);
sin(sin x) = 0 if sin x= 0, which gives no critical points in (0,π).
Thus f(0)=1,f(π/2) = cos(1), and f(π) = 1 so the maximum
value is 1 and the minimum value is cos(1) ≈0.54030.
1.5
0
0c
35. f0(x)=½4,x<1
2x−5,x>1so f0(x) = 0 when x=5/2, and f0(x) does not exist when x= 1 because
lim
x→1−f0(x)6= lim
x→1+f0(x) (see Theorem preceding Exercise 75, Section 3.3); f(1/2)=0,f(1)=2,
f(5/2) = −1/4, f(7/2)=3/4 so the maximum value is 2 and the minimum value is −1/4.
36. f0(x)=2x+pwhich exists throughout the interval (0,2) for all values of pso f0(1) = 0 because
f(1) is an extreme value, thus 2 + p=0,p=−2. f(1) = 3 so 12+(−2)(1) + q=3,q= 4 thus
f(x)=x
2−2x+ 4 and f(0)=4,f(2) = 4 so f(1) is the minimum value.
37. sin 2xhas a period of π, and sin 4xa period of π/2sof(x) is periodic with period π. Consider the
interval [0,π]. f0(x) = 4 cos 2x+ 4 cos 4x,f0(x) = 0 when cos 2x+ cos 4x= 0, but cos 4x= 2 cos22x−1
(trig identity) so
2 cos22x+ cos 2x−1=0
(2 cos 2x−1)(cos 2x+1)=0
cos 2x=1/2 or cos 2x=−1.
From cos 2x=1/2, 2x=π/3or5π/3sox=π/6or5π/6. From cos 2x=−1, 2x=πso x=π/2.
f(0)=0,f(π/6)=3
√
3/2, f(π/2)=0,f(5π/6) = −3√3/2, f(π) = 0. The maximum value is 3√3/2
at x=π/6+nπ and the minimum value is −3√3/2atx=5π/6+nπ,n=0,±1,±2,···.
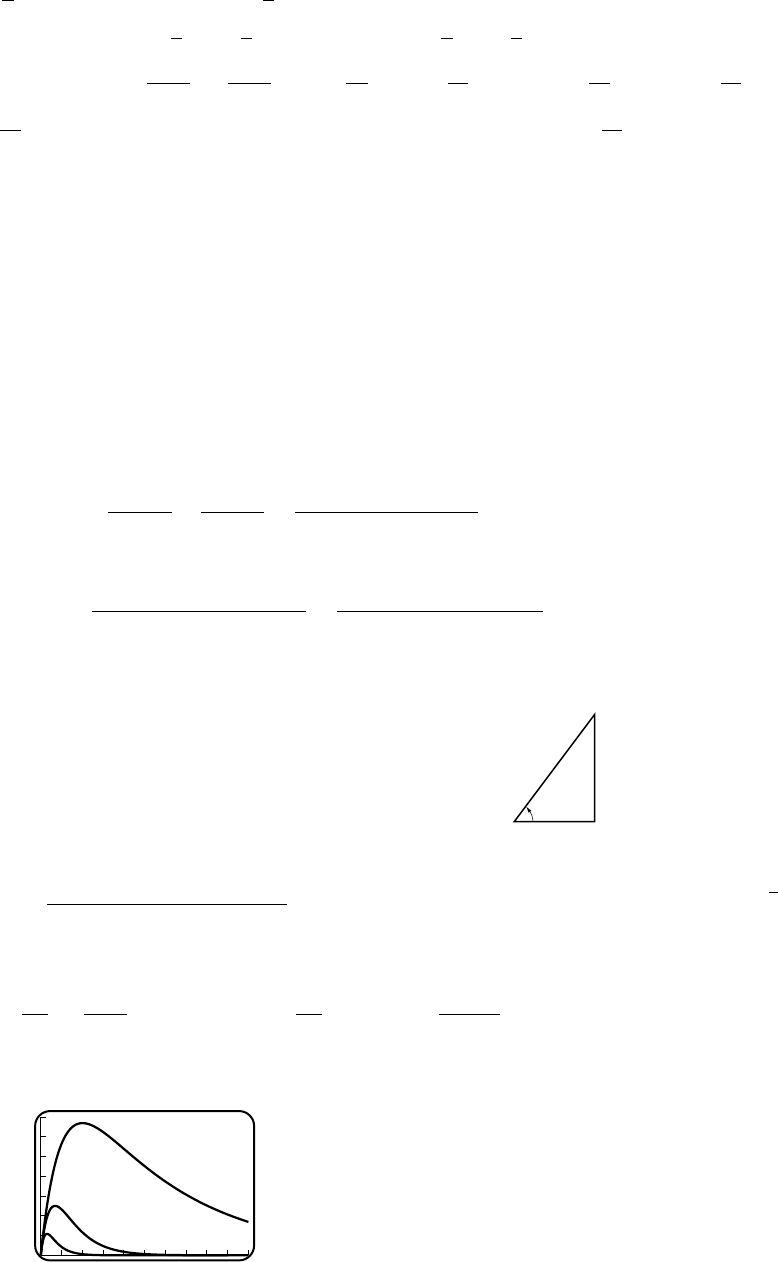
181 Chapter 6
38. cos x
3has a period of 6π, and cos x
2a period of 4π,sof(x) has a period of 12π. Consider the interval
[0,12π]. f0(x)=−sin x
3−sin x
2,f0(x) = 0 when sin x
3+ sin x
2= 0 thus, by use of the trig identity
sin a+ sin b= 2 sin a+b
2cos a−b
2, 2 sin µ5x
12 ¶cos ³−x
12´=0sosin
5x
12 =0orcosx
12 = 0. Solve
sin 5x
12 = 0 to get x=12π/5, 24π/5, 36π/5, 48π/5 and then solve cos x
12 = 0 to get x=6π. The
corresponding values of f(x) are −4.0450,1.5450,1.5450,−4.0450,1,5,5 so the maximum value is 5
and the minimum value is −4.0450 (approximately).
39. Let f(x)=x−sin x, then f0(x)=1−cos xand so f0(x) = 0 when cos x= 1 which has no solution
for 0 <x<2πthus the minimum value of fmust occur at 0 or 2π.f(0)=0,f(2π)=2πso0isthe
minimum value on [0,2π]thusx−sin x≥0, sin x≤xfor all xin [0,2π].
40. Let f(x)=lnx−x+ 1, then f0(x)=1/x −1 and so f0(x)=0atx= 1. Since lim
x→0+f(x)=−∞ and
lim
x→+∞f(x)=−∞,f(x) has a maximum of f(1) = 0 at x= 1 and so f(x)≤0 for 0 <x<+∞,so
ln x≤x−1on(0,+∞).
41. Let m= slope at x, then m=f0(x)=3x
2−6x+5, dm/dx =6x−6; critical point for mis x=1,
minimum value of mis f0(1)=2
42. (a) f0(x)=−64 cos x
sin2x+27 sin x
cos2x=−64 cos3x+ 27 sin3x
sin2xcos2x,f0(x) = 0 when
27 sin3x= 64 cos3x, tan3x=64/27, tan x=4/3 so the critical point is x=x0where
tan x0=4/3 and 0 <x
0<π/2. To test x0first rewrite f0(x)as
f
0
(x)= 27 cos3x(tan3x−64/27)
sin2xcos2x=27 cos x(tan3x−64/27)
sin2x;
if x<x
0then tan x<4/3 and f0(x)<0, if x>x
0then tan x>4/3 and f0(x)>0sof(x
0
)is
the minimum value. fhas no maximum because lim
x→0+f(x)=+∞.
(b) If tan x0=4/3 then (see figure)
sin x0=4/5 and cos x0=3/5
so f(x0)=64/sin x0+27/cos x0
=64/(4/5)+27/(3/5)
=80+45=125
3
45
x
0
43. f0(x)=2x(x
3−24x2+ 192x−640)
(x−8)3; real root of x3−24x2+ 192x−640 at x= 4(2 + 3
√2). Since
lim
x→8+f(x) = lim
x→+∞f(x)=+∞and there is only one relative extremum, it must be a minimum.
44. (a) dC
dt =K
a−b¡ae−at −be−bt¢so dC
dt =0att=ln(a/b)
a−b. This is the only stationary point and
C(0) = 0, lim
x→+∞C(t)=0,C(t)>0 for 0 <t<+∞, so it is an absolute maximum.
(b) 0.7
0
010
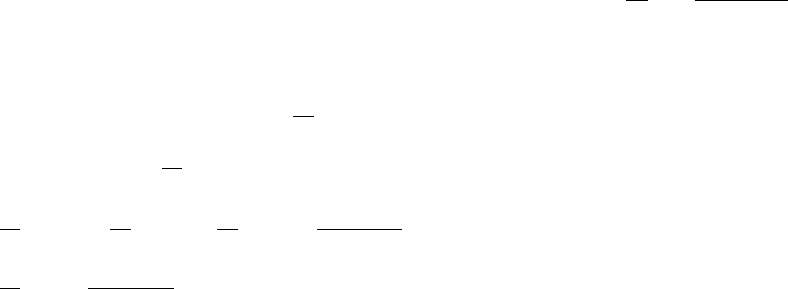
Exercise Set 6.2 182
45. The slope of the line is −1, and the slope of the tangent to y=−x2is −2xso −2x=−1, x=1/2.
The line lies above the curve so the vertical distance is given by F(x)=2−x+x
2
;F(−1)=4,
F(1/2)=7/4, F(3/2)=11/4. The point (1/2,−1/4) is closest, the point (−1,−1) farthest.
46. The slope of the line is 4/3; and the slope of the tangent to y=x3is 3x2so 3x2=4/3, x2=4/9,
x=±2/3. The line lies below the curve so the vertical distance is given by F(x)=x
3−4x/3+1;
F(−1)=4/3, F(−2/3)=43/27, F(2/3)=11/27, F(1)=2/3. The closest point is (2/3,8/27), the
farthest is (−2/3,−8/27).
47. The absolute extrema of y(t) can occur at the endpoints t=0,12 or when dy/dt = 2 sin t= 0, i.e.
t=0,12,kπ,k=1,2,3; the absolute maximum is y=4att=π, 3π; the absolute minimum is y=0
at t=0,2π.
48. (a) The absolute extrema of y(t) can occur at the endpoints t=0,2πor when
dy/dt = 2 cos 2t−4 sin tcos t= 2 cos 2t−2 sin 2t=0,t=0,2π, π/8,5π/8,9π/8,13π/8;
the absolute maximum is y=3.4142 at t=π/8,9π/8; the absolute minimum is y=0.5859
at t=5π/8,13π/8.
(b) The absolute extrema of x(t) occur at the endpoints t=0,2πor when dx
dt =−2 sin t+1
(2 + sin t)2=0,
t=7π/6,11π/6. The absolute maximum is x=0.5774 at t=11π/6 and the absolute minimum
is x=−0.5774 at t=7π/6.
49. f0(x)=2ax +b; critical point is x=−b
2a
f00(x)=2a>0sofµ−b
2a
¶is the minimum value of f, but
fµ−b
2a¶=aµ−b
2a¶2
+bµ−b
2a¶+c=−b2+4ac
4athus f(x)≥0 if and only if
fµ−b
2a¶≥0, −b2+4ac
4a≥0, −b2+4ac ≥0, b2−4ac ≤0
50. Use the proof given in the text, replacing “maximum” by “minimum” and “largest” by “smallest” and
reversing the order of all inequality symbols.
EXERCISE SET 6.2
1. Let x= one number, y= the other number, and P=xy where x+y= 10. Thus y=10−xso
P=x(10 −x)=10x−x
2for xin [0,10]. dP/dx =10−2x,dP/dx = 0 when x=5. Ifx=0,5,10
then P=0,25,0soPis maximum when x= 5 and, from y=10−x, when y=5.
2. Let xand ybe nonnegative numbers and zthe sum of their squares, then z=x2+y2. But x+y=1,
y=1−xso z=x2+(1−x)
2=2x
2−2x+ 1 for 0 ≤x≤1. dz/dx =4x−2, dz/dx = 0 when x=1/2.
If x=0,1/2,1 then z=1,1/2,1so
(a) zis as large as possible when one number is 0 and the other is 1.
(b) zis as small as possible when both numbers are 1/2.
3. If y=x+1/x for 1/2≤x≤3/2 then dy/dx =1−1/x2=(x
2−1)/x2,dy/dx = 0 when x=1. If
x=1/2,1,3/2 then y=5/2,2,13/6so
(a) yis as small as possible when x=1. (b) yis as large as possible when x=1/2.
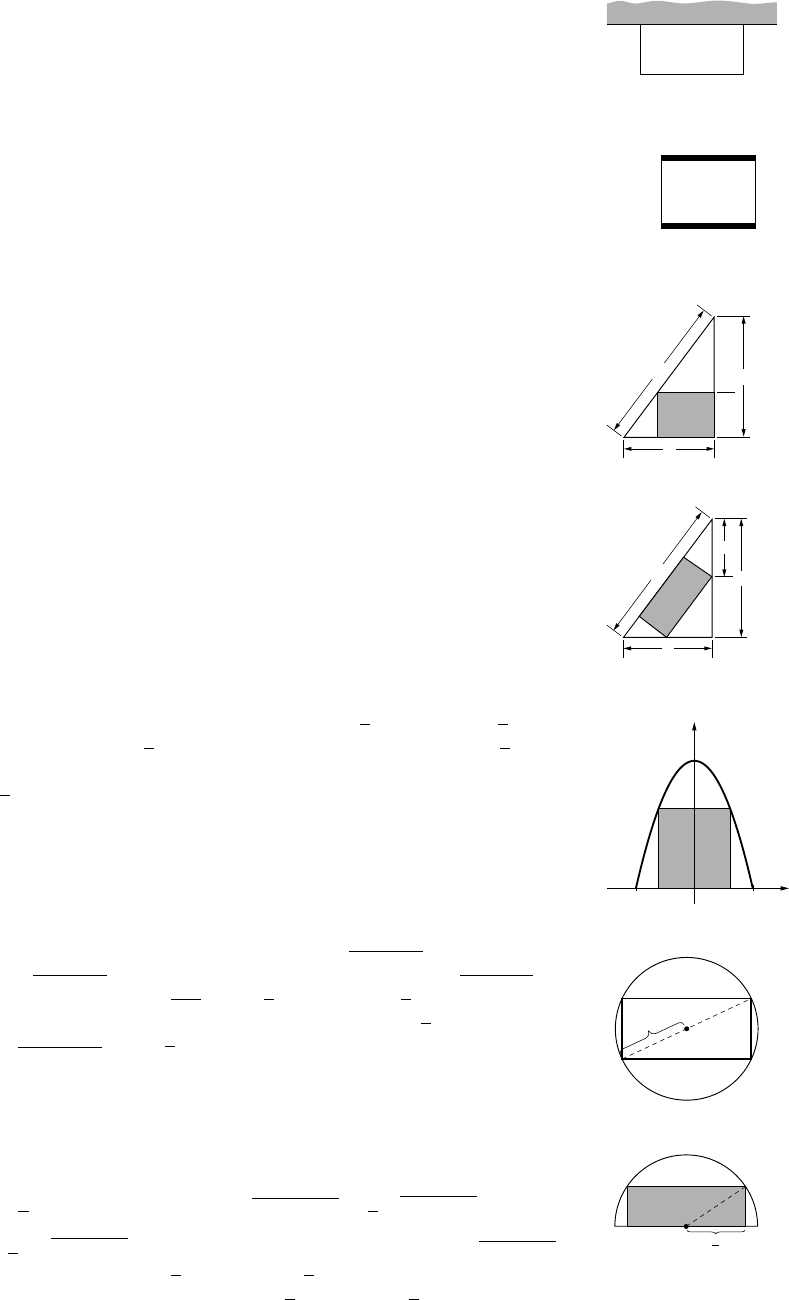
183 Chapter 6
4. A=xy where x+2y= 1000 so y= 500 −x/2 and A= 500x−x2/2
for xin [0,1000]; dA/dx = 500 −x,dA/dx = 0 when x= 500. If
x= 0 or 1000 then A=0,ifx= 500 then A= 125,000 so the area
is maximum when x= 500 ft and y= 500 −500/2 = 250 ft.
x
y
Stream
5. Let xand ybe the dimensions shown in the figure and Athe area,
then A=xy subject to the cost condition 3(2x) + 2(2y) = 6000, or
y= 1500 −3x/2. Thus A=x(1500 −3x/2) = 1500x−3x2/2 for xin
[0,1000]. dA/dx = 1500 −3x,dA/dx = 0 when x= 500. If x=0or
1000 then A=0,ifx= 500 then A= 375,000 so the area is greatest
when x= 500 ft and (from y= 1500 −3x/2) when y= 750 ft.
Heavy-duty
Standard
x
y
6. Let xand ybe the dimensions shown in the figure and Athe area of
the rectangle, then A=xy and, by similar triangles,
x/6=(8−y)/8, y=8−4x/3soA=x(8 −4x/3)=8x−4x
2
/3 for
xin [0,6]. dA/dx =8−8x/3, dA/dx = 0 when x=3. Ifx=0,3,6
then A=0,12,0 so the area is greatest when x= 3 in and (from
y=8−4x/3) y= 4 in.
8
y
x
6
10
7. Let x,y, and zbe as shown in the figure and Athe area of the
rectangle, then A=xy and, by similar triangles, z/10 = y/6,
z=5y/3; also x/10=(8−z)/8=(8−5y/3)/8thus
y=24/5−12x/25 so A=x(24/5−12x/25)=24x/5−12x2/25 for
xin [0,10]. dA/dx =24/5−24x/25, dA/dx = 0 when x=5. If
x=0,5,10 then A=0,12,0 so the area is greatest when x= 5 in.
and y=12/5 in.
8
z
x
y
6
10
8. A=(2x)y=2xy where y=16−x
2so A=32x−2x
3for 0 ≤x≤4;
dA/dx =32−6x
2
,dA/dx = 0 when x=4/
√
3. If x=0,4/
√
3,4
then A=0,256/(3√3),0 so the area is largest when x=4/
√
3 and
y=32/3. The dimensions of the rectangle with largest area are
8/√3by32/3.
-4 4
16
x
y
y
x
9. A=xy where x2+y2=20
2= 400 so y=√400 −x2and
A=x√400 −x2for 0 ≤x≤20; dA/dx = 2(200 −x2)/√400 −x2,
dA/dx = 0 when x=√200=10
√
2. If x=0,10√2,20 then
A=0,200,0 so the area is maximum when x=10
√
2 and
y=√400 −200=10
√
2. x
y
10
10. Let xand ybe the dimensions shown in the figure, then the area of
the rectangle is A=xy.
But ³x
2´2+y2=R2,thusy=pR
2−x
2
/4= 1
2
p4R
2−x
2so
A=1
2xp4R2−x2for 0 ≤x≤2R.dA/dx =(2R
2−x
2
)/
√
4R
2−x
2
,
dA/dx = 0 when x=√2R.Ifx=0,√
2R, 2Rthen A=0,R
2,0so
the greatest area occurs when x=√2Rand y=√2R/2.
x
y
R
x
2
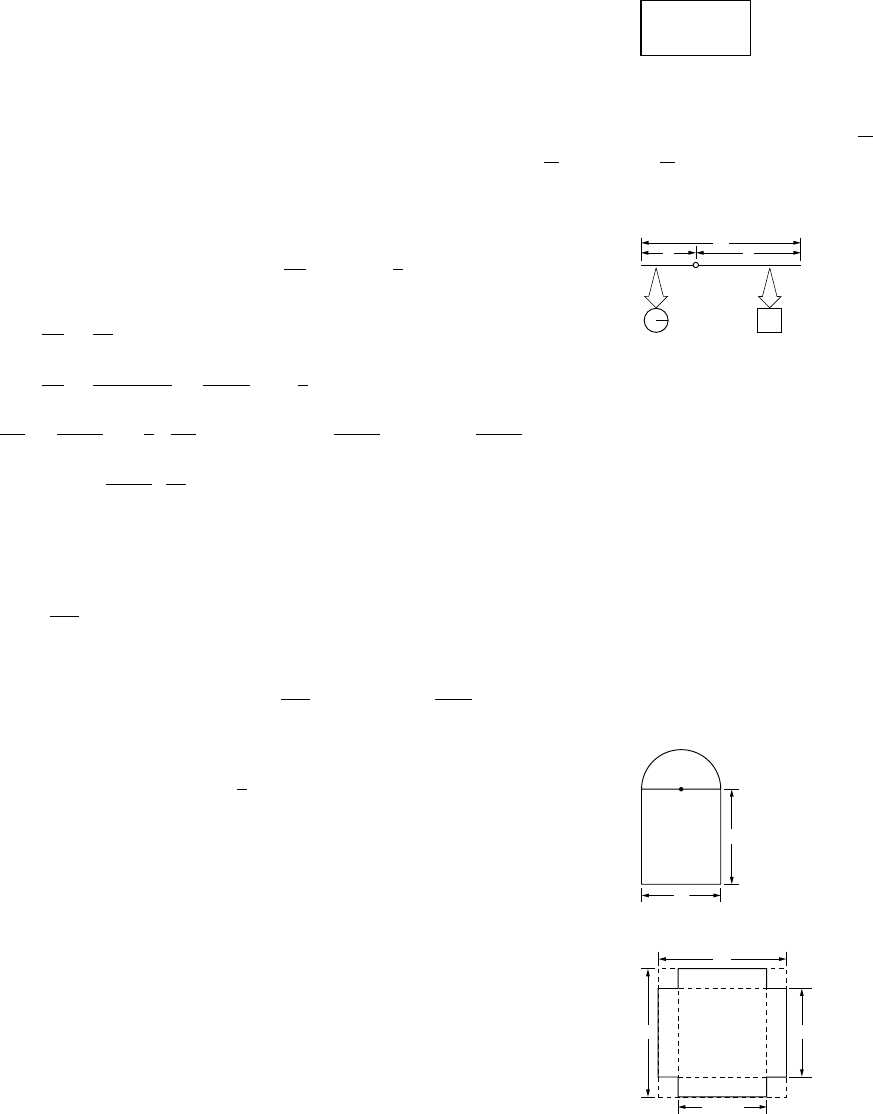
Exercise Set 6.2 184
11. Let x= length of each side that uses the $1 per foot fencing,
y= length of each side that uses the $2 per foot fencing.
The cost is C= (1)(2x) + (2)(2y)=2x+4y, but A=xy = 3200 thus y= 3200/x so
C=2x+ 12800/x for x>0,
dC/dx =2−12800/x2, dC/dx = 0 when x=80,d
2
C/dx2>0so
Cis least when x= 80, y= 40.
12. A=xy where 2x+2y=pso y=p/2−xand A=px/2−x2for x
in [0,p/2]; dA/dx =p/2−2x,dA/dx = 0 when x=p/4. If x=0or
p/2 then A=0,ifx=p/4 then A=p2/16 so the area is maximum
when x=p/4 and y=p/2−p/4=p/4, which is a square. x
y
13. Let xand ybe the dimensions of a rectangle; the perimeter is p=2x+2y. But A=xy thus
y=A/x so p=2x+2A/x for x>0, dp/dx =2−2A/x2=2(x
2−A)/x2,dp/dx = 0 when x=√A,
d2p/dx2=4A/x3>0ifx>0sopis a minimum when x=√Aand y=√Aand thus the rectangle
is a square.
14. With x,y,r, and sas shown in the figure, the sum of the enclosed
areas is A=πr2+s2where r=x
2πand s=y
4because xis the
circumference of the circle and yis the perimeter of the square, thus
A=x2
4π+y2
16. But x+y= 12, so y=12−xand
A=x2
4π+(12 −x)2
16 =π+4
16πx2−3
2x+ 9 for 0 ≤x≤12.
dA
dx =π+4
8πx−3
2,dA
dx = 0 when x=12π
π+4.Ifx=0,12π
π+4,12
then A=9,36
π+4,36
πso the sum of the enclosed areas is
x y
12
rs
cut
(a) a maximum when x= 12 in. (when all of the wire is used for the circle)
(b) a minimum when x=12π/(π+ 4) in.
15. (a) dN
dt = 250(20 −t)e−t/20 =0att= 20, N(0) = 125000, N(20) ≈161788, and N(100) ≈128,369;
the absolute maximum is N= 161788 at t= 20, the absolute minimum is N= 125000 at t=0.
(b) The absolute minimum of dN
dt occurs when d2N
dt2=12.5(t−40)e−t/20 =0,t= 40.
16. The area of the window is A=2rh +πr2/2, the perimeter is
p=2r+2h+πr thus h=1
2[p−(2+π)r]so
A=r[p−(2+π)r]+πr2/2
=pr −(2+π/2)r2for 0 ≤r≤p/(2+π),
dA/dr =p−(4+π)r,dA/dr = 0 when r=p/(4+π) and
d2A/dr2<0, so Ais maximum when r=p/(4+π). 2r
r
h
17. V=x(12 −2x)2for 0 ≤x≤6; dV/dx = 12(x−2)(x−6),
dV/dx = 0 when x= 2 for 0 <x<6. If x=0,2,6 then
V=0,128,0 so the volume is largest when x= 2 in.
x
xx
x
x
x
x
x
12
12
12 − 2x
12 − 2x
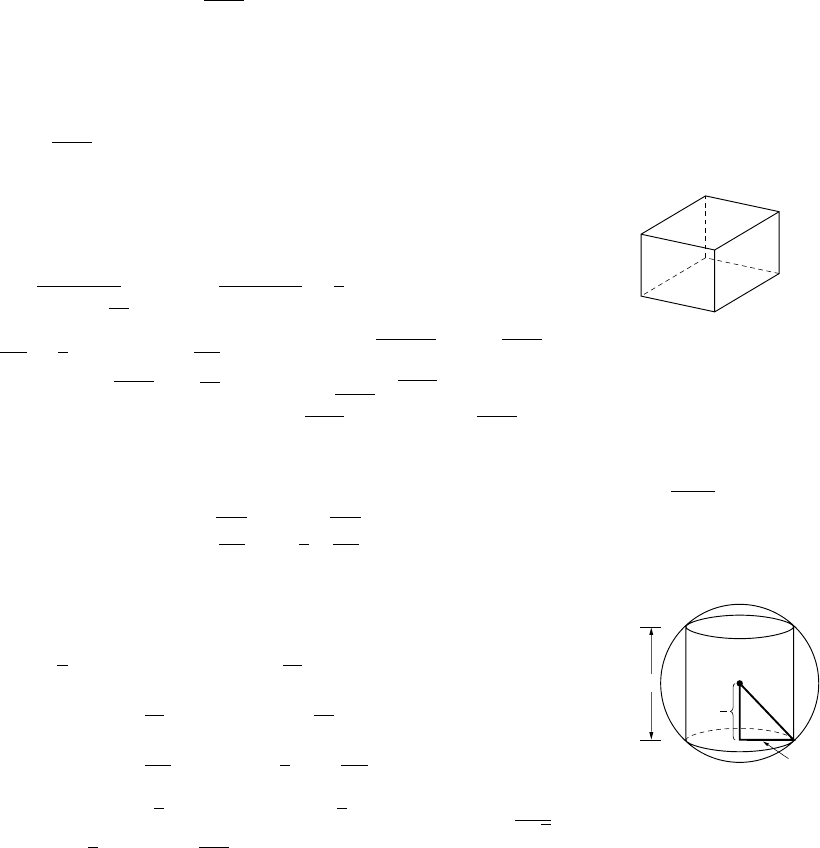
185 Chapter 6
18. The dimensions of the box will be (k−2x)by(k−2x)byxso V=(k−2x)
2
x=4x
3−4kx2+k2xfor
xin [0,k/2]. dV/dx =12x
2−8kx +k2=(6x−k)(2x−k), dV /dx = 0 for xin (0,k/2) when x=k/6.
If x=0,k/6,k/2 then V=0,2k
3
/27,0soVis maximum when x=k/6. The squares should have
dimensions k/6byk/6.
19. Let xbe the length of each side of a square, then V=x(3 −2x)(8 −2x)=4x
3−22x2+24xfor
0≤x≤3/2; dV/dx =12x
2−44x+ 24 = 4(3x−2)(x−3), dV/dx = 0 when x=2/3 for 0 <x<3/2.
If x=0,2/3,3/2 then V=0,200/27,0 so the maximum volume is 200/27 ft3.
20. Let x= length of each edge of base, y= height. The cost is
C= (cost of top and bottom) + (cost of sides) = (2)(2x2) + (3)(4xy)=4x
2+12xy, but
V=x2y= 2250 thus y= 2250/x2so C=4x
2+ 27000/x for x>0, dC/dx =8x−27000/x2,
dC/dx = 0 when x=3
√3375 = 15, d2C/dx2>0soCis least when x= 15, y= 10.
21. Let x= length of each edge of base, y= height, k=$/cm2for the sides. The cost is
C=(2k)(2x2)+(k)(4xy)=4k(x
2+xy), but V=x2y= 2000 thus y= 2000/x2so
C=4k(x
2+ 2000/x) for x>0dC/dx =4k(2x−2000/x2), dC/dx = 0 when
x=3
√1000 = 10, d2C/dx2>0soCis least when x= 10, y= 20.
22. Let xand ybe the dimensions shown in the figure and Vthe
volume, then V=x2y. The amount of material is to be 1000 ft2,
thus (area of base) + (area of sides) = 1000, x2+4xy = 1000,
y=1000 −x2
4xso V=x21000 −x2
4x=1
4(1000x−x3) for
0<x≤10√10.
dV
dx =1
4(1000 −3x2), dV
dx = 0 when x=p1000/3=10
p10/3.
If x=0,10p10/3,10√10 then V=0,5000
3p10/3,0;
the volume is greatest for x=10
p10/3ftandy=5
p10/3 ft.
xx
y
23. Let x= height and width, y= length. The surface area is S=2x
2+3xy where x2y=V,soy=V/x2
and S=2x
2+3V/x for x>0; dS/dx =4x−3V/x2,dS/dx = 0 when x=3
p3V/4, d2S/dx2>0soS
is minimum when x=3
r3V
4,y=4
3
3
r3V
4.
24. Let rand hbe the dimensions shown in the figure, then the volume
of the inscribed cylinder is V=πr2h. But
r2+µh
2¶2
=R2thus r2=R2−h2
4
so V=πµR2−h2
4¶h=πµR2h−h3
4¶
for 0 ≤h≤2R.dV
dh =πµR2−3
4h2¶,dV
dh =0
h
2
h
r
R
when h=2R/√3. If h=0,2R/√3,2Rthen V=0,4π
3
√
3
R
3
,0 so the volume is largest when
h=2R/√3 and r=p2/3R.
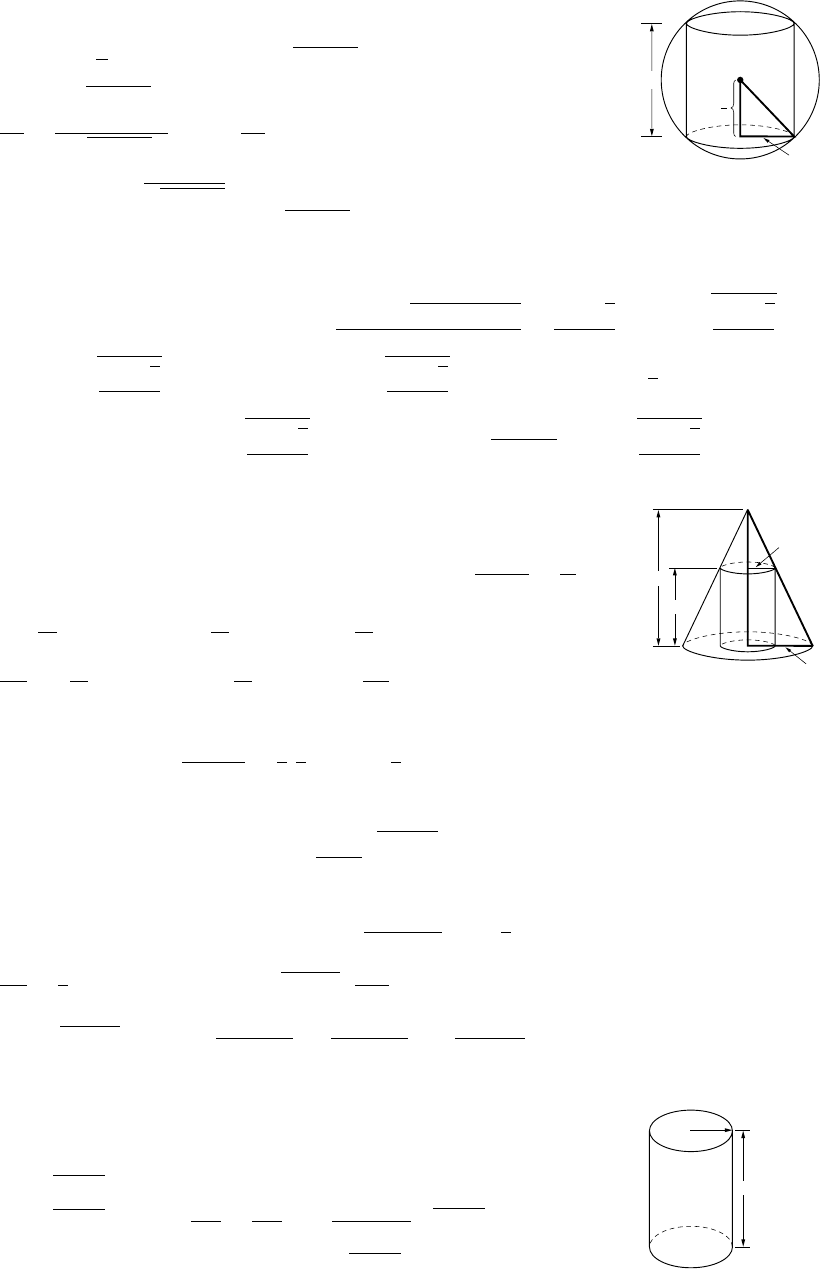
Exercise Set 6.2 186
25. Let rand hbe the dimensions shown in the figure, then the surface
area is S=2πrh +2πr2.
But r2+µh
2¶2
=R2thus h=2
√
R
2−r
2so
S=4πr√R2−r2+2πr2for 0 ≤r≤R,
dS
dr =4π(R2−2r2)
√R2−r2+4πr;dS
dr = 0 when
R2−2r2
√R2−r2=−r(i)
R2−2r2=−r√R2−r2
R4−4R2r2+4r
4=r
2
(R
2−r
2
)
5r
4−5R
2
r
2+R
4=0
h
2
h
r
R
and using the quadratic formula r2=5R2±√25R4−20R4
10 =5±√5
10 R2,r=s5±√5
10 R, of which
only r=s5+√
5
10 Rsatisfies (i). If r=0,s5+√
5
10 R, 0 then S=0,(5 + √5)πR2,2πR2so the surface
area is greatest when r=s5+√
5
10 Rand, from h=2
pR
2−r
2
,h=2
s5−√
5
10 R.
26. Let Rand Hbe the radius and height of the cone, and rand hthe
radius and height of the cylinder (see figure), then the volume of the
cylinder is V=πr2h. By similar triangles (see figure) H−h
H=r
R
thus
h=H
R(R−r)soV=π
H
R
(R−r)r
2=π
H
R
(Rr2−r3) for 0 ≤r≤R.
dV
dr =πH
R(2Rr −3r2)=πH
Rr(2R−3r), dV
dr = 0 for 0 <r<R
when r=2R/3. If r=0,2R/3,R then V=0,4πR2H/27,0sothe
maximum volume is 4πR2H
27 =4
9
1
3πR2H=4
9·(volume of cone).
R
r
H
h
27. From (13), S=2πr2+2πrh. But V=πr2hthus h=V/(πr2) and so S=2πr2+2V/r for r>0.
dS/dr =4πr −2V/r2, dS/dr =0ifr=3
pV/(2π). Since d2S/dr2=4π+4V/r3>0, the minimum
surface area is achieved when r=3
pV/2πand so h=V/(πr2)=[V/(πr3)]r=2r.
28. V=πr2hwhere S=2πr2+2πrh so h=S−2πr2
2πr ,V=1
2(Sr −2πr3) for r>0.
dV
dr =1
2(S−6πr2)=0ifr=pS/(6π), d2V
dr2=−6πr < 0soVis maximum when
r=pS/(6π) and h=S−2πr2
2πr =S−2πr2
2πr2r=S−S/3
S/3r=2r, thus the height is equal to the
diameter of the base.
29. The surface area is S=πr2+2πrh where V=πr2h= 500 so
h= 500/(πr2) and S=πr2+ 1000/r for r>0;
dS/dr =2πr −1000/r2=(2πr3−1000)/r2,dS/dr = 0 when
r=3
p500/π,d2S/dr2>0 for r>0soSis minimum when
r=3
p500/π and h=500
πr2=500
πr3r=500
π(500/π)
3
p500/π
=3
p500/π.
r
h

187 Chapter 6
30. The total area of material used is
A=Atop +Abottom +Aside =(2r)
2+(2r)
2+2πrh =8r
2+2πrh.
The volume is V=πr2hthus h=V/(πr2)soA=8r
2+2V/r for r>0,
dA/dr =16r−2V/r2= 2(8r3−V)/r2,dA/dr = 0 when r=3
√V/2. This is the only critical point,
d2A/dr2>0 there so the least material is used when r=3
√V/2, r
h=r
V/(πr2)=π
Vr3and, for
r=3
√V/2, r
h=π
V
V
8=π
8.
31. Let xbe the length of each side of the squares and ythe height of the frame, then the volume is V=x2y.
The total length of the wire is Lthus 8x+4y=L,y=(L−8x)/4soV=x
2
(L−8x)/4=(Lx2−8x3)/4
for 0 ≤x≤L/8. dV /dx =(2Lx −24x2)/4, dV/dx = 0 for 0 <x<L/8 when x=L/12. If
x=0,L/12,L/8 then V=0,L
3/1728,0 so the volume is greatest when x=L/12 and y=L/12.
32. (a) Let x= diameter of the sphere, y= length of an edge of the cube. The combined volume is
V=1
6πx3+y3and the surface area is S=πx2+6y
2= constant. Thus y=(S−πx2)1/2
61/2and
V=π
6x3+(S−πx2)3/2
63/2for 0 ≤x≤rS
π;
dV
dx =π
2x2−3π
63/2x(S−πx2)1/2=π
2√6x(√6x−pS−πx2). dV
dx = 0 when x= 0, or when
√6x=√S−πx2,6x
2=S−πx2,x2=S
6+π,x=rS
6+π.Ifx=0,rS
6+π,rS
π, then
V=S3/2
63/2,S3/2
6√6+π,S
3/2
6
√
πso that Vis smallest when x=rS
6+π, and hence when y=rS
6+π,
thus x=y.
(b) From part (a), the sum of the volumes is greatest when there is no cube.
33. Let hand rbe the dimensions shown in the figure, then the volume
is V=1
3πr2h. But r2+h2=L2thus r2=L2−h2so
V=1
3π(L2−h2)h=1
3π(L2h−h3) for 0 ≤h≤L.
dV
dh =1
3π(L2−3h2). dV
dh = 0 when h=L/√3. If h=0,L/
√3,0
then V=0,2π
9
√
3
L
3
,0 so the volume is as large as possible when
h=L/√3 and r=p2/3L.
hL
r
34. Let rand hbe the radius and height of the cone (see figure). The
slant height of any such cone will be R, the radius of the circular
sheet. Refer to the solution of Exercise 33 to find that the largest
volume is 2π
9√3R3.hR
r
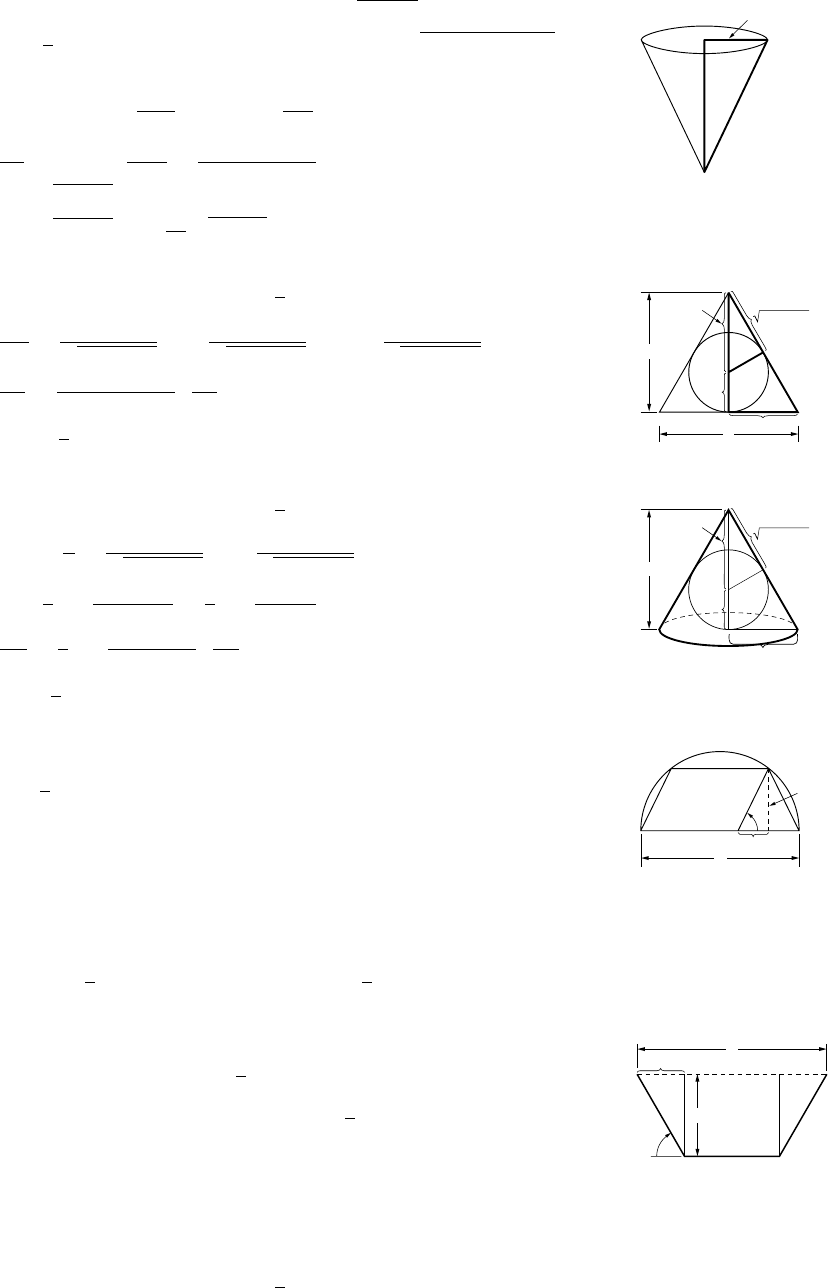
Exercise Set 6.2 188
35. The area of the paper is A=πrL =πr√r2+h2, but
V=1
3πr2h=10thush=30/(πr2)soA=πrpr2+ 900/(π2r4).
To simplify the computations let S=A2,
S=π2r2µr2+900
π2r4¶=π2r4+900
r2for r>0,
dS
dr =4π
2
r
3−1800
r3=4(π2r6−450)
r3,dS/dr = 0 when
r=6
p450/π2,d2S/dr2>0, so Sand hence Ais least when
r=6
p450/π2,h=30
π
3
pπ2/450.
hL
r
36. The area of the triangle is A=1
2hb. By similar triangles (see figure)
b/2
h=R
√h2−2Rh,b=2Rh
√h2−2Rh so A=Rh2
√h2−2Rh for h>2R,
dA
dh =Rh2(h−3R)
(h2−2Rh)3/2,dA
dh = 0 for h>2Rwhen h=3R, by the first
derivative test Ais minimum when h=3R.Ifh=3Rthen
b=2
√
3R(the triangle is equilateral).
R
h − R
R
h
bb/2
h2 − 2Rh
37. The volume of the cone is V=1
3πr2h. By similar triangles (see
figure) r
h=R
√h2−2Rh,r=Rh
√h2−2Rh so
V=1
3πR2h3
h2−2Rh =1
3πR2h2
h−2Rfor h>2R,
dV
dh =1
3πR2h(h−4R)
(h−2R)2,dV
dh = 0 for h>2Rwhen h=4R,bythe
first derivative test Vis minimum when h=4R.Ifh=4Rthen
r=√2R.
r
R
h − R
R
h
h2 − 2Rh
38. The area is (see figure)
A=1
2(2 sin θ)(4 + 4 cos θ)
= 4(sin θ+ sin θcos θ)
for 0 ≤θ≤π/2;
dA/dθ = 4(cos θ−sin2θ+ cos2θ)
= 4(cos θ−[1 −cos2θ] + cos2θ)
= 4(2 cos2θ+ cos θ−1)
= 4(2 cos θ−1)(cos θ+1)
dA/dθ = 0 when θ=π/3 for 0 <θ<π/2. If θ=0,π/3,π/2 then
A=0,3
√
3,4 so the maximum area is 3√3.
42 cos
θ
θ
4 cos
θ
2 sin
θ
2
39. Let band hbe the dimensions shown in the figure, then the
cross-sectional area is A=1
2h(5+b). But h= 5 sin θand
b= 5 + 2(5 cos θ)=5+10cosθso A=5
2sin θ(10 + 10 cos θ)
= 25 sin θ(1 + cos θ) for 0 ≤θ≤π/2.
dA/dθ =−25 sin2θ+ 25 cos θ(1 + cos θ)
= 25(−sin2θ+ cos θ+ cos2θ)
= 25(−1 + cos2θ+ cos θ+ cos2θ)
= 25(2 cos2θ+ cos θ−1) = 25(2 cos θ−1)(cos θ+1).
dA/dθ = 0 for 0 <θ<π/2 when cos θ=1/2, θ=π/3. If
θ=0,π/3,π/2 then A=0,75√3/4,25 so the cross-sectional area is
greatest when θ=π/3.
b
5 cos
θ
θ
5
5
5
h = 5 sin
θ

189 Chapter 6
40. I=kcos φ
`2,kthe constant of proportionality. If his the height of the lamp above the table then
cos φ=h/` and `=√h2+r2so I=kh
`3=kh
(h2+r2)3/2for h>0, dI
dh =kr2−2h2
(h2+r2)5/2,dI
dh =0
when h=r/√2, by the first derivative test Iis maximum when h=r/√2.
41. Let L,L1, and L2be as shown in the figure, then
L=L1+L2= 8 csc θ+ sec θ,
dL
dθ =−8 csc θcot θ+ sec θtan θ, 0<θ<π/2
=−8 cos θ
sin2θ+sin θ
cos2θ=−8 cos3θ+ sin3θ
sin2θcos2θ;
dL
dθ = 0 if sin3θ= 8 cos3θ, tan3θ= 8, tan θ= 2 which gives the
absolute minimum for Lbecause lim
θ→0+L= lim
θ→π/2−L=+∞.If
tan θ= 2, then csc θ=√5/2 and sec θ=√5so
L=8(
√
5/2)+√5=5
√
5 ft.
1
8
θ
L2
L1
L
42. Let x= number of steers per acre
w= average market weight per steer
T= total market weight per acre
then T=xw where w= 2000 −50(x−20) = 3000 −50x
so T=x(3000 −50x) = 3000x−50x2for 0 ≤x≤60,
dT/dx = 3000 −100xand dT/dx = 0 when x= 30. If x=0,30,60 then T=0,45000,0 so the total
market weight per acre is largest when 30 steers per acre are allowed.
43. (a) The daily profit is
P= (revenue) −(production cost) = 100x−(100,000+50x+0.0025x2)
=−100,000+50x−0.0025x2
for 0 ≤x≤7000, so dP/dx =50−0.005xand dP/dx = 0 when x=10,000. Because 10,000
is not in the interval [0,7000], the maximum profit must occur at an endpoint. When x=0,
P=−100,000; when x= 7000, P= 127,500 so 7000 units should be manufactured and sold
daily.
(b) Yes, because dP/dx > 0 when x= 7000 so profit is increasing at this production level.
44. (a) R(x)=px but p= 1000 −xso R(x) = (1000 −x)x
(b) P(x)=R(x)−C(x) = (1000 −x)x−(3000 + 20x)=−3000 + 980x−x2
(c) P0(x) = 980 −2x,P0(x) = 0 for 0 <x<500 when x= 490; test the points 0,490,500 to find
that the profit is a maximum when x= 490.
(d) P(490) = 237,100
(e) p= 1000 −x= 1000 −490 = 510.
45. The profit is
P= (profit on nondefective) −(loss on defective) = 100(x−y)−20y= 100x−120y
but y=0.01x+0.00003x2so P= 100x−120(0.01x+0.00003x2)=98.8x−0.0036x2for x>0,
dP/dx =98.8−0.0072x,dP/dx = 0 when x=98.8/0.0072 ≈13,722, d2P/dx2<0 so the profit is
maximum at a production level of about 13,722 pounds.
Exercise Set 6.2 190
46. The total cost Cis
C=c·(hours to travel 3000 mi at a speed of vmi/h)
=c·3000
v=(a+bvn)3000
v= 3000(av−1+bvn−1) for v>0,
dC/dv = 3000[−av−2+b(n−1)vn−2] = 3000[−a+b(n−1)vn]/v2,
dC/dv = 0 when v=·a
b(n−1)¸1/n
. This is the only critical point and dC/dv changes sign from −to
+ at this point so the total cost is least when v=·a
b(n−1)¸1/n
mi/h.
47. The distance between the particles is D=p(1 −t−t)2+(t−2t)
2=√
5t
2−4t+ 1 for t≥0. For
convenience, we minimize D2instead, so D2=5t
2−4t+1, dD2/dt =10t−4, which is 0 when t=2/5.
d2D2/dt2>0soD
2and hence Dis minimum when t=2/5. The minimum distance is D=1/
√
5.
48. The distance between the particles is D=p(2t−t)2+(2−t
2
)
2=√
t
4−3t
2+ 4 for t≥0. For
convenience we minimize D2instead so D2=t4−3t2+4,dD2/dt =4t
3−6t=4t(t
2−3/2), which is
0 for t>0 when t=p3/2. d2D2/dt2=12t
2−6>0 when t=p3/2soD
2and hence Dis minimum
there. The minimum distance is D=√7/2.
49. Let P(x, y) be a point on the curve x2+y2= 1. The distance between P(x, y) and P0(2,0) is
D=p(x−2)2+y2, but y2=1−x
2so D=p(x−2)2+1−x
2=√
5−4xfor −1≤x≤1,
dD
dx =−2
√5−4xwhich has no critical points for −1<x<1. If x=−1,1 then D=3,1sothe
closest point occurs when x= 1 and y=0.
50. Let P(x, y)beapointony=√
x, then the distance Dbetween Pand (2,0) is
D=p(x−2)2+y2=p(x−2)2+x=√x2−3x+ 4, for 0 ≤x≤3. For convenience we find the
extrema for D2instead, so D2=x2−3x+4, dD2/dx =2x−3 = 0 when x=3/2. If x=0,3/2,3
then D2=4,7/4,4soD=2,√
7/2,2. The points (0,0) and (3,√3) are at the greatest distance, and
(3/2,p3/2) the shortest distance from (2,0).
51. Let (x, y) be a point on the curve, then the square of the distance between (x, y) and (0,2) is
S=x2+(y−2)2where x2−y2=1,x
2=y
2+1so
S=(y
2+1)+(y−2)2=2y
2−4y+ 5 for any y,dS/dy =4y−4, dS/dy = 0 when y=1,
d
2
S/dy2>0soSis least when y= 1 and x=±√2.
52. The square of the distance between a point (x, y) on the curve and the point (0,9) is
S=x2+(y−9)2where x=2y
2so S=4y
4+(y−9)2for any y,
dS/dy =16y
3+2(y−9) = 2(8y3+y−9), dS/dy = 0 when y= 1 (which is the only real solution),
d2S/dy2>0soSis least when y=1,x=2.
53. If P(x0,y
0) is on the curve y=1/x2, then y0=1/x2
0.AtPthe slope of the tangent line is −2/x3
0so its
equation is y−1
x2
0
=−2
x3
0
(x−x0), or y=−2
x3
0
x+3
x2
0
. The tangent line crosses the y-axis at 3
x2
0
, and
the x-axis at 3
2x0. The length of the segment then is L=s9
x4
0
+9
4x2
0for x0>0. For convenience,
we minimize L2instead, so L2=9
x4
0
+9
4x2
0,dL2
dx0
=−36
x5
0
+9
2x0=9(x6
0−8)
2x5
0
, which is 0 when x6
0=8,
x
0=√
2. d2L2
dx2
0
>0soL
2and hence Lis minimum when x0=√2, y0=1/2.

191 Chapter 6
54. If P(x0,y
0) is on the curve y=1−x
2
, then y0=1−x
2
0
.AtPthe slope of the tangent line is −2x0so
its equation is y−(1 −x2
0)=−2x
0
(x−x
0
), or y=−2x0x+x2
0+ 1. The y-intercept is x2
0+ 1 and the
x-intercept is 1
2(x0+1/x0) so the area Aof the triangle is A=1
4(x2
0+1)(x0+1/x0)=1
4
(x
3
0
+2x0+1/x0)
for 0 ≤x0≤1.
dA/dx0=1
4(3x2
0+2−1/x2
0)=1
4
(3x4
0+2x
2
0−1)/x2
0which is 0 when x2
0=−1 (reject), or
when x2
0=1/3sox
0=1/
√
3. d2A/dx2
0=1
4(6x0+2/x3
0)>0atx
0=1/
√
3 so a relative minimum and
hence the absolute minimum occurs there.
55. At each point (x, y) on the curve the slope of the tangent line is m=dy
dx =−2x
(1+x2)2for any x,
dm
dx =2(3x2−1)
(1+x2)3,dm
dx = 0 when x=±1/√3, by the first derivative test the only relative maximum
occurs at x=−1/√3, which is the absolute maximum because lim
x→±∞ m= 0. The tangent line has
greatest slope at the point (−1/√3,3/4).
56. Let xbe how far Pis upstream from where the man starts
(see figure), then the total time to reach Tis
t= (time from Mto P) + (time from Pto T)
=√x2+1
r
R
+1−x
r
W
for 0 ≤x≤1,
where rRand rWare the rates at which he can row and walk,
respectively. M
TP
1
1
x
(a) t=√x2+1
3+1−x
5,dt
dx =x
3√x2+1−1
5so dt
dx = 0 when 5x=3
px
2+1,
25x2=9(x
2+1),x
2=9/16, x=3/4. If x=0,3/4,1 then t=8/15,7/15,√2/3 so the time is a
minimum when x=3/4 mile.
(b) t=√x2+1
4+1−x
5,dt
dx =x
4√x2+1−1
5so dt
dx = 0 when x=4/3 which is not in the interval
[0,1]. Check the endpoints to find that the time is a minimum when x= 1 (he should row
directly to the town).
57. With xand yas shown in the figure, the maximum length of pipe
will be the smallest value of L=x+y. By similar triangles
y
8=x
√x2−16,y=8x
√x2−16 so
L=x+8x
√x2−16 for x>4, dL
dx =1−128
(x2−16)3/2,dL
dx = 0 when
(x2−16)3/2= 128
x2−16 = 1282/3= 16(22/3)
x2= 16(1 + 22/3)
x=4(1+2
2/3
)
1/2
,
8
4
x
y
x
2
− 16
d2L/dx2= 384x/(x2−16)5/2>0ifx>4soLis smallest when x=4(1+2
2/3
)
1/2
.
For this value of x,L=4(1+2
2/3
)
3/2ft.
Exercise Set 6.2 192
58. s=(x
1−¯x)
2+(x
2−¯x)
2+···+(x
n−¯x)
2
,
ds/d¯x=−2(x1−¯x)−2(x2−¯x)−···−2(xn−¯x),
ds/d¯x= 0 when
(x1−¯x)+(x
2−¯x)+···+(x
n−¯x)=0
(x
1+x
2+···x
n)−(¯x+¯x+···+¯x)=0
(x
1+x
2+···+x
n)−n¯x=0
¯x=1
n
(x
1+x
2+···+x
n),
d
2s/d¯x2=2+2+···+2=2n>0, so sis minimum when ¯x=1
n(x1+x2+···+x
n).
59. Let x= distance from the weaker light source, I= the intensity at that point, and kthe constant of
proportionality. Then
I=kS
x2+8kS
(90 −x)2if 0 <x<90;
dI
dx =−2kS
x3+16kS
(90 −x)3=2kS[8x3−(90 −x)3]
x3(90 −x)3=18
kS(x−30)(x2+ 2700)
x3(x−90)3,
which is 0 when x= 30; dI
dx <0ifx<30, and dI
dx >0ifx>30, so the intensity is minimum at a
distance of 30 cm from the weaker source.
60. If f(x0) is a maximum then f(x)≤f(x0) for all xin some open interval containing x0thus
pf(x)≤pf(x0) because √xis an increasing function, so pf(x0) is a maximum of pf(x)at
x
0
. The proof is similar for a minimum value, simply replace ≤by ≥.
61. Let v= speed of light in the medium. The total time required for the light to travel from Ato Pto
Bis
t= (total distance from Ato Pto B)/v =1
v(p(c−x)2+a2+px2+b2),
dt
dx =1
v"−c−x
p(c−x)2+a2+x
√x2+b2#
and dt
dx = 0 when x
√x2+b2=c−x
p(c−x)2+a2. But x/√x2+b2= sin θ2and
(c−x)/p(c−x)2+a2= sin θ1thus dt/dx = 0 when sin θ2= sin θ1so θ2=θ1.
62. The total time required for the light to travel from Ato Pto Bis
t= (time from Ato P) + (time from Pto B)= √
x
2+a
2
v
1
+p(c−x)
2+b
2
v
2
,
dt
dx =x
v1√x2+a2−c−x
v2p(c−x)2+b2but x/√x2+a2= sin θ1and
(c−x)/p(c−x)2+b2= sin θ2thus dt
dx =sin θ1
v1−sin θ2
v2
so dt
dx = 0 when sin θ1
v1
=sin θ2
v2
.
63. (a) The rate at which the farmer walks is analogous to the speed of light in Fermat’s principle.
(b) the best path occurs when θ1=θ2
(see figure).
x1 − x
3
4
1
4
θ
2
θ
1
House
Barn
(c) by similar triangles,
x/(1/4) = (1 −x)/(3/4)
3x=1−x
4x=1
x=1/4mi.
193 Chapter 6
EXERCISE SET 6.3
1. (a) positive, negative, slowing down (b) positive, positive, speeding up
(c) negative, positive, slowing down
2. (a) positive, slowing down (b) negative, slowing down
(c) positive, speeding up
3. (a) left because v=ds/dt < 0att
0
(b) negative because a=d2s/dt2and the curve is concave down at t0(d2s/dt2<0)
(c) speeding up because vand ahave the same sign
(d) v<0 and a>0att
1so the particle is slowing down because vand ahave opposite signs.
4. (a) C(b) A(c) B
5.
t(s)
s(m)
6. (a) when s≥0, so 0 <t<2 and 4 <t≤8(b) when the slope is zero, at t=3
(c) when sis decreasing, so 0 ≤t<3
7.
6
25
t
s
6t
a
–15
–15
8. (a) v≈(30 −10)/(15 −10)=20/5=4m/s
(b)
t
v
t
a
2525
(1) (2)
9. (a) At 60 mi/h the slope of the estimated tangent line is about 4.6 mi/h/s. Use 1 mi = 5,280 ft
and 1 h = 3600 s to get a=dv/dt ≈4.6(5,280)/(3600) ≈6.7 ft/s2.
(b) The slope of the tangent to the curve is maximum at t=0s.

Exercise Set 6.3 194
10. (a) t1 2 3 4 5
s0.71 1.00 0.71 0.00 −0.71
v0.56 0.00 −0.56 −0.79 −0.56
a−0.44 −0.62 −0.44 0.00 0.44
(b) to the right at t= 1, stopped at t= 2, otherwise to the left
(c) speeding up at t= 3; slowing down at t=1,5; neither at t=2,4
11. (a) v(t)=3t
2−12t,a(t)=6t−12
(b) s(1) = −5 ft, v(1) = −9 ft/s, speed = 9 ft/s, a(1) = −6 ft/s2
(c) v=0att=0,4
(d) for t≥0, v(t) changes sign at t= 4, and a(t) changes sign at t= 2; so the particle is speeding
up for 0 <t<2 and 4 <tand is slowing down for 2 <t<4
(e) total distance = |s(4) −s(0)|+|s(5) −s(4)|=|−32 −0|+|−25 −(−32)|=39ft
12. (a) v(t)=4t
3−4, a(t)=12t
2
(b) s(1) = −1 ft, v(1) = 0 ft/s, speed = 0 ft/s, a(1) = 12 ft/s2
(c) v=0att=1
(d) speeding up for t>1, slowing down for 0 <t<1
(e) total distance = |s(1) −s(0)|+|s(5) −s(1)|=|−1−2|+|607 −(−1)|= 611 ft
13. (a) v(t)=−(3π/2) sin(πt/2), a(t)=−(3π2/4) cos(πt/2)
(b) s(1) = 0 ft, v(1) = −3π/2 ft/s, speed = 3π/2 ft/s, a(1) = 0 ft/s2
(c) v=0att=0,2,4
(d) vchanges sign at t=0,2,4 and achanges sign at t=1,3,5, so the particle is speeding up for
0<t<1, 2 <t<3 and 4 <t<5, and it is slowing down for 1 <t<2 and 3 <t<4
(e) total distance = |s(2) −s(0)|+|s(4) −s(2)|+|s(5) −s(4)|
=|−3−3|+|3−(−3)|+|0−3|=15ft
14. (a) v(t)= 4−t
2
(t
2+4)
2,a(t)= 2t(t
2−12)
(t2+4)
3
(b) s(1)=1/5 ft, v(1)=3/25 ft/s, speed = 3/25 ft/s, a(1) = −22/125 ft/s2
(c) v=0att=2
(d) achanges sign at t=2
√
3, so the particle is speeding up for 2 <t<2
√
3 and it is slowing down
for 0 <t<2 and for 2√3<t
(e) total distance = |s(2) −s(0)|+|s(5) −s(2)|=¯¯¯¯
1
4−0¯¯¯¯
+¯¯¯¯
5
29 −1
4¯¯¯¯
=19
58 ft
15. v(t)= 5−t
2
(t
2+5)
2,a(t)= 2t(t
2−15)
(t2+5)
3
0.25
0
020
s(t)
0.2
-0.05
020
v(t)
0.01
-0.15
010
a(t)
195 Chapter 6
(a) v=0att=√
5(b) s=√5/10 at t=√5
(c) achanges sign at t=√15, so the particle is speeding up for √5<t<√
15 and slowing down
for 0 <t<√
5 and √15 <t
16. v(t)=(1−t)e
−t
,a(t)=(t−2)e−t
0.4
0
010
s(t)
1
-0.2
08
v(t)
0.1
-2
06
a(t)
(a) v=0att=1 (b) s=1/e at t=1
(c) achanges sign at t= 2, so the particle is speeding up for 1 <t<2 and slowing down for
0<t<1 and 2 <t
17. s=−3t+2
v=−3
a=0
2
Constant speed t = 0 s
18. s=t3−6t2+9t+1
v=3(t−1)(t−3)
a=6(t−2) 531
t = 1 (Stopped)
t = 0
(Stopped) t = 3t = 2
s
Speeding up
Slowing down
19. s=t3−9t2+24t
v=3(t−2)(t−4)
a=6(t−3)
2018160
t = 2 (Stopped)
t = 0
(Stopped) t = 4
t = 3
s
Speeding up
Slowing down
Slowing down
20. s=t+9
t+1
v=(t+ 4)(t−2)
(t+1)
2
a=18
(t+1)
3
95
(Stopped) t = 2
s
Speeding up
Slowing down
21. s=½cos t, 0≤t≤2π
1,t>2π
v=
½
−sin t, 0≤t≤2π
0, t>2π
a=
½
−cos t, 0≤t<2π
0,t>2π
10-1 s
Speeding up
t = π
t = π/2
t = 3π/2 t = 2π
t = 0
(Stopped
permanently)
Slowing down
22. v(t)=5t
2−6t+2
√
tis always positive, a(t)=15t2−6t−2
2t3/2has a positive root at t=3+√
39
15
0s
Slowing down Speeding up
3 +
15 39

Exercise Set 6.3 196
23. (a) v=10t−22, speed = |v|=|10t−22|.d|v|/dt does not exist at t=2.2 which is the only critical
point. If t=1,2.2,3 then |v|=12,0,8. The maximum speed is 12 ft/s.
(b) the distance from the origin is |s|=|5t2−22t|=|t(5t−22)|, but t(5t−22) <0 for
1≤t≤3so|s|=−(5t2−22t)=22t−5t
2
,d|s|/dt =22−10t, thus the only critical point is
t=2.2. d2|s|/dt2<0 so the particle is farthest from the origin when t=2.2. Its position is
s= 5(2.2)2−22(2.2) = −24.2.
24. v=−200t
(t2+ 12)2, speed = |v|=200t
(t2+ 12)2for t≥0. d|v|
dt =600(4 −t2)
(t2+ 12)3= 0 when t= 2, which is the
only critical point in (0,+∞). By the first derivative test there is a relative maximum, and hence an
absolute maximum, at t= 2. The maximum speed is 25/16 ft/s to the left.
25. s(t)=s
0−1
2gt2=s0−4.9t2m, v=−9.8tm/s, a=−9.8 m/s2
(a) |s(1.5) −s(0)|=11.025 m
(b) v(1.5) = −14.7 m/s
(c) |v(t)|= 12 when t=12/9.8=1.2245 s
(d) s(t)−s0=−100 when 4.9t2= 100, t=4.5175 s
26. (a) s(t)=s
0−1
2gt2= 800 −16t2ft, s(t) = 0 when t=r800
16 =5
√
2
(b) v(t)=−32tand v(5√2) = −160√2≈226.27 ft/s = 154.28 mi/h
27. s(t)=s
0+v
0
t−1
2gt2=60t−4.9t
2m and v(t)=v
0−gt =60−9.8tm/s
(a) v(t) = 0 when t=60/9.8≈6.12 s
(b) s(60/9.8) ≈183.67 m
(c) another 6.12 s; solve for tin s(t) = 0 to get this result, or use the symmetry of the parabola
s=60t−4.9t
2about the line t=6.12 in the t-splane
(d) also 60 m/s, as seen from the symmetry of the parabola (or compute v(6.12))
28. (a) they are the same
(b) s(t)=v
0
t−1
2gt2and v(t)=v
0−gt;s(t) = 0 when t=0,2v
0
/g;
v(0) = v0and v(2v0/g)=v
0−g(2v0/g)=−v
0so the speed is the same
at launch (t= 0) and at return (t=2v
0
/g).
29. Ifg=32ft/s2,s0= 7 and v0is unknown, then s(t)=7+v
0
t−16t2and v(t)=v
0−32t;s=smax when
v=0,ort=v
0
/32; and smax = 208 yields 208 = s(v0/32)=7+v
0
(v
0
/32) −16(v0/32)2=7+v
2
0
/64,
so v0=8
√
201 ≈113.42 ft/s.
30. (a) Use (6) and then (5) to get v2=v2
0−2v0gt +g2t2=v2
0−2g(v0t−1
2gt2)=v
2
0−2g(s−s
0
).
(b) Add v0to both sides of (6): 2v0−gt =v0+v,v0−1
2gt =1
2(v0+v);
from (5) s=s0+t(v0−1
2gt)=s
0+1
2(v
0+v)t
(c) Add vto both sides of (6): 2v+gt =v0+v,v+1
2gt =1
2(v0+v); from part (b), s=s0+1
2(v0+v)t=
s0+vt +1
2gt2
31. v0= 0 and g=9.8, so v2=−19.6(s−s0); since v= 24 when s= 0 it follows that 19.6s0=24
2or
s0=29.39 m.
32. s= 1000 + vt +1
2(32)t2= 1000 + vt +16t
2;s= 0 when t=5,sov=−(1000 + 16 ·52)/5=−280 ft/s.
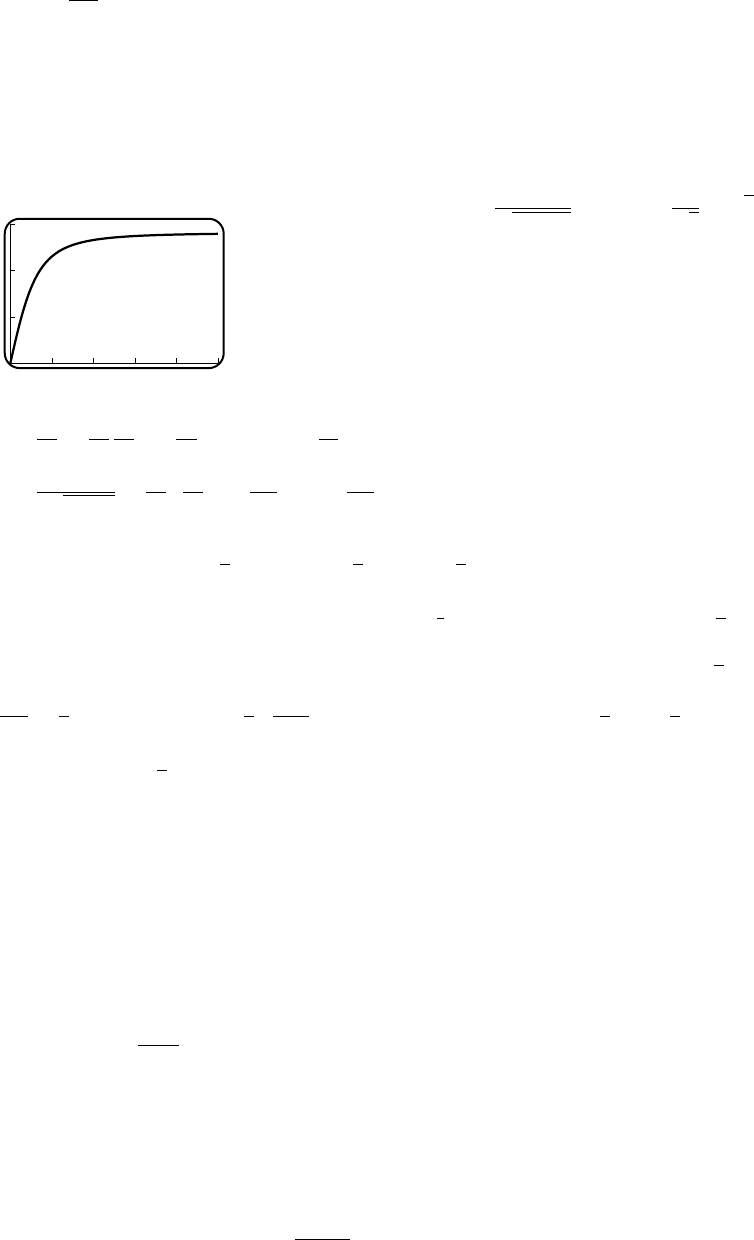
197 Chapter 6
33. (a) s=smax when v=0,so0=v
2
0−2g(s
max −s0), smax =v2
0/2g+s0.
(b) s0=7,s
max = 208, g= 32 and v0is unknown, so from part (a) v2
0=2g(208 −7)=64·201,
v0=8
√
201 ≈113.42 ft/s.
34. s=t3−6t2+1,v=3t
2−12t,a=6t−12.
(a) a= 0 when t=2;s=−15, v=−12.
(b) v= 0 when 3t2−12t=3t(t−4)=0,t=0ort=4. Ift= 0, then s= 1 and a=−12; if t=4,
then s=−31 and a= 12.
35. (a) 1.5
0
05
(b) v=2t
√2t2+1, lim
t→+∞v=2
√2=√2
36. (a) a=dv
dt =dv
ds
ds
dt =vdv
ds because v=ds
dt
(b) v=3
2√3t+7 =3
2s;dv
ds =−3
2s2;a=−9
4s3=−9/500
37. (a) s1=s2if they collide, so 1
2t2−t+3= −1
4t
2+t+1, 3
4t
2−2t+ 2 = 0 which has no real solution.
(b) Find the minimum value of D=|s1−s2|=¯¯3
4t2−2t+2
¯
¯. From part (a), 3
4t2−2t+2
is never zero, and for t= 0 it is positive, hence it is always positive, so D=3
4t2−2t+2.
dD
dt =3
2t−2 = 0 when t=4
3.d2D
dt2>0soDis minimum when t=4
3,D=2
3.
(c) v1=t−1, v2=−1
2t+1. v
1<0if0≤t<1, v1>0ift>1; v2<0ift>2, v2>0if0≤t<2.
They are moving in opposite directions during the intervals 0 ≤t<1 and t>2.
38. (a) sA−sB=20−0=20ft
(b) sA=sB,15t
2+10t+20=5t
2+40t,10t
2−30t+20=0,(t−2)(t−1)=0,t=1ort=2s.
(c) vA=vB,30t+10=10t+ 40, 20t= 30, t=3/2 s. When t=3/2, sA= 275/4 and sB= 285/4
so car Bis ahead of car A.
39. (a) From the estimated tangent to the graph at the point where v= 2000, dv/ds ≈−1.25 ft/s/ft.
(b) a=v dv/ds ≈(2000)(−1.25) = −2500 ft/s2
40. r0(t)=2v(t)v
0(t)/[2pv2(t)] = v(t)a(t)/|v(t)|so r0(t)>0 (speed is increasing) if vand ahave the same
sign, and r0(t)<0 (speed is decreasing) if vand ahave opposite signs.
EXERCISE SET 6.4
1. f(x)=x
2−2, f0(x)=2x,x
n+1 =xn−x2
n−2
2xn
x1=1,x
2=1.5, x3=1.416666667,···,x
5=x
6=1.414213562
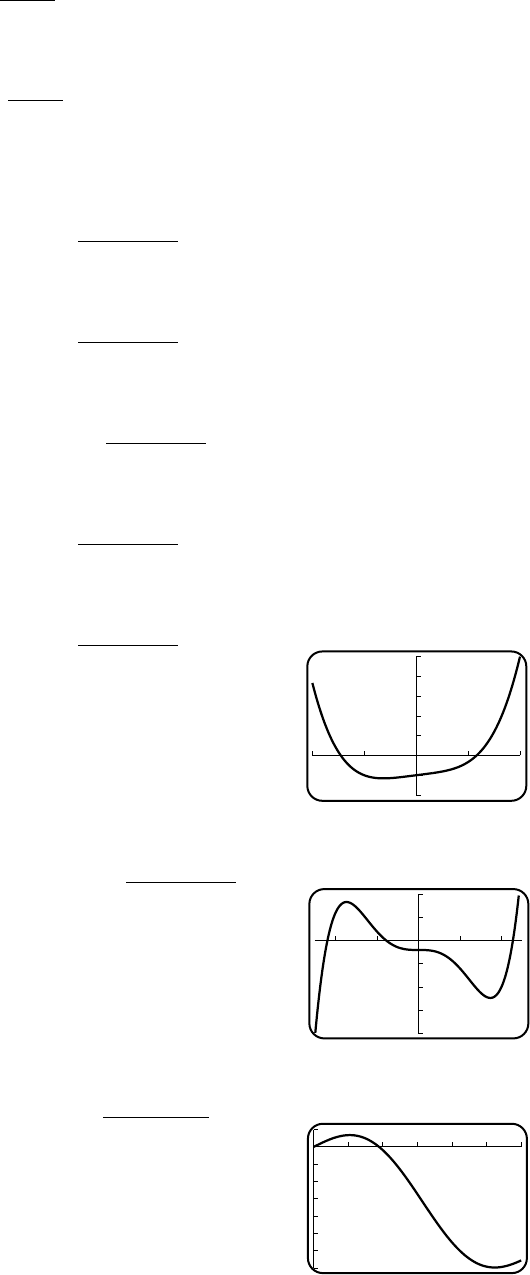
Exercise Set 6.4 198
2. f(x)=x
2−7, f0(x)=2x,x
n+1 =xn−x2
n−7
2xn
x1=3,x
2=2.666666667, x3=2.645833333,···,x
5=x
6=2.645751311
3. f(x)=x
3−6, f0(x)=3x
2
,x
n+1 =xn−x3
n−6
3x2
n
x1=2,x
2=1.833333333, x3=1.817263545,···,x
5=x
6=1.817120593
4. xn−a=0
5. f(x)=x
3−x+3,f0(x)=3x
2−1, xn+1 =xn−x3
n−xn+3
3x
2
n−1
x
1=−2, x2=−1.727272727, x3=−1.673691174,···,x
5=x
6=−1.671699882
6. f(x)=x
3+x−1, f0(x)=3x
2+1,x
n+1 =xn−x3
n+xn−1
3x2
n+1
x
1=1,x
2=0.75, x3=0.686046512,···,x
5=x
6=0.682327804
7. f(x)=x
5+x
4−5, f0(x)=5x
4+4x
3
,x
n+1 =xn−x5
n+x4
n−5
5x4
n+4x
3
n
x
1=1,x
2=1.333333333, x3=1.239420573,···,x
6=x
7=1.224439550
8. f(x)=x
5−x+1,f0(x)=5x
4−1, xn+1 =xn−x5
n−xn+1
5x
4
n−1
x
1=−1, x2=−1.25, x3=−1.178459394,···,x
6=x
7=−1.167303978
9. f(x)=x
4+x−3, f0(x)=4x
3+1,x
n+1 =xn−x4
n+xn−3
4x3
n+1
x
1=−2, x2=−1.645161290,
x3=−1.485723955,···,x
6=x
7=−1.452626879
15
-6
-2 2
10. f(x)=x
5−5x
3−2, f0(x)=5x
4−15x2,xn+1 =xn−x5
n−5x3
n−2
5x4
n−15x2
n
x1=2,x
2=2.5, x3=2.327384615,···,x
7=x
8=2.273791732
10
-20
-2.5 2.5
11. f(x)=2sinx−x,f
0(x)=2cosx−1, xn+1 =xn−2 sin xn−xn
2 cos xn−1
x1=2,x
2=1.900995594, x3=1.895511645, x4=x5=1.895494267
1
–7
06
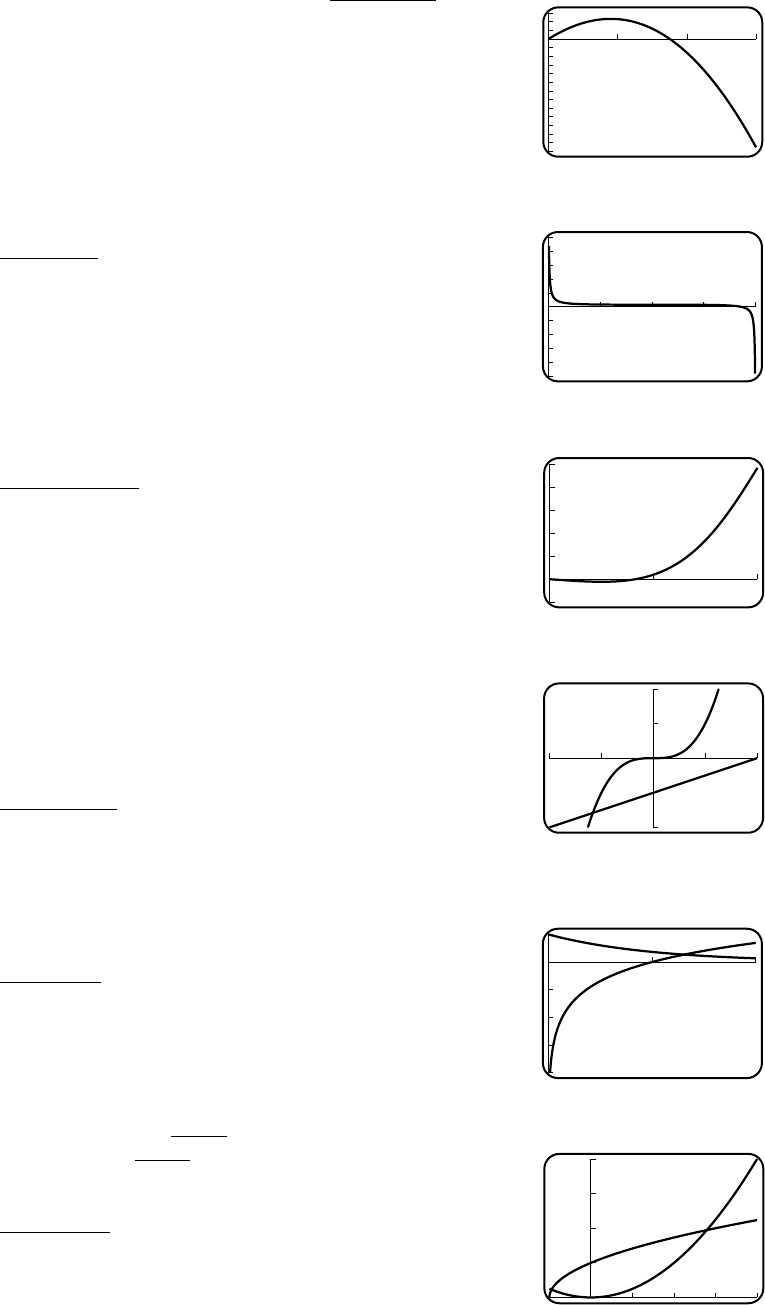
199 Chapter 6
12. f(x) = sin x−x2,f0(x) = cos x−2x,xn+1 =xn−sin xn−x2
n
cos xn−2xn
x1=1,x
2=0.891395995,
x3=0.876984845,···,x
5=x
6=0.876726215
0.3
–1.3
0 1.5
13. f(x)=x−tan x,f0(x)=1−sec2x=−tan2x,
xn+1 =xn+xn−tan xn
tan2xn
x1=4.5, x2=4.493613903, x3=4.493409655,
x4=x5=4.493409458
100
–100
6i
14. f(x)=1−e
xcos x,f0(x)=e
x
(sin x−cos x),
xn+1 =xn+1−excos x
ex(sin x−cos x)
x1=1,x
2=1.572512605, x3=1.363631415, x7=x8=1.292695719
25
-5
0c
15. At the point of intersection, x3=0.5x−1, x3−0.5x+1=0. Let
f(x)=x
3−0.5x+ 1. By graphing y=x3and y=0.5x−1itis
evident that there is only one point of intersection and it occurs in
the interval [−2,−1]; note that f(−2) <0 and f(−1) >0.
f0(x)=3x
2−0.5so
x
n+1 =xn−x3
n−0.5x+1
3x
2
n−0.5;x
1=−1, x2=−1.2,
x3=−1.166492147,···,
x
5=x
6=−1.165373043
2
-2
-2 2
16. The graphs of y=e−xand y=lnxintersect near x=1.3; let
f(x)=e
−x−ln x,f0(x)=−e
−x−1/x,x1=1.3,
xn+1 =xn+e−xn−ln xn
e−xn+1/xn
,x2=1.309759929, x4=x5=1.309799586
1
-4
02
17. The graphs of y=x2and y=√2x+ 1 intersect at points near
x=−0.5 and x=1;x
2=√
2x+1,x
4−2x−1=0. Let
f(x)=x
4−2x−1, then f0(x)=4x
3−2so
x
n+1 =xn−x4
n−2xn−1
4x3
n−2.
If x1=−0.5, then x2=−0.475, x3=−0.474626695,
x4=x5=−0.474626618; if x1= 1, then x2=2,
x
3=1.633333333,···,x
8=x
9=1.395336994.
4
0
-0.5 2

Exercise Set 6.4 200
18. The graphs of y=x3/8+1and y= cos 2xintersect at x= 0 and at
a point near x=−2;
x3/8 + 1 = cos 2x,x3−8 cos 2x+8=0. Letf(x)=x
3−8 cos 2x+8,
then f0(x)=3x
2+ 16 sin 2xso xn+1 =xn−x3
n−8 cos 2xn+8
3x
2
n+ 16 sin 2xn
.
x1=−2, x2=−2.216897577,
x3=−2.193821581,···,x
5=x
6=−2.193618950.
2
-2
-3 2
19. (a) f(x)=x
2−a,f
0(x)=2x,x
n+1 =xn−x2
n−a
2xn
=1
2µxn+a
xn¶
(b) a= 10; x1=3,x
2=3.166666667, x3=3.162280702, x4=x5=3.162277660
20. (a) f(x)= 1
x−a,f
0(x)=−1
x
2,x
n+1 =xn(2 −axn)
(b) a= 17; x1=0.05, x2=0.0575, x3=0.058793750, x5=x6=0.058823529
21. f0(x)=x
3+2x+ 5; solve f0(x) = 0 to find the critical points. Graph y=x3and y=−2x−5tosee
that they intersect at a point near x=−1; f00(x)=3x
2+2so x
n+1 =xn−x3
n+2x
n+5
3x
2
n+2 .
x
1=−1, x2=−1.4, x3=−1.330964467,···,x
5=x
6=−1.328268856 so the minimum value of f(x)
occurs at x≈−1.328268856 because f00(x)>0; its value is approximately −4.098859132.
22. From a rough sketch of y=xsin xwe see that the maximum occurs at a point near x= 2, which will
be a point where f0(x)=xcos x+ sin x=0. f
00(x)=2cosx−xsin xso
xn+1 =xn−xncos xn+ sin xn
2 cos xn−xnsin xn
=xn−xn+ tan xn
2−xntan xn
.
x1=2,x
2=2.029048281, x3=2.028757866, x4=x5=2.028757838; the maximum value is approxi-
mately 1.819705741.
23. Let f(x) be the square of the distance between (1,0) and any point (x, x2) on the parabola, then
f(x)=(x−1)2+(x
2−0)2=x4+x2−2x+ 1 and f0(x)=4x
3+2x−2. Solve f0(x) = 0 to find
the critical points; f00(x)=12x
2+2 so x
n+1 =xn−4x3
n+2x
n−2
12x2
n+2 =x
n−2x
3
n+x
n−1
6x
2
n+1 .x
1=1,
x
2=0.714285714, x3=0.605168701,···,x
6=x
7=0.589754512; the coordinates are approximately
(0.589754512,0.347810385).
24. The area is A=xy =xcos xso dA/dx = cos x−xsin x. Find xso that dA/dx =0;
d
2
A/dx2=−2 sin x−xcos xso xn+1 =xn+cos xn−xnsin xn
2 sin xn+xncos xn
=xn+1−xntan xn
2 tan xn+xn
.
x1=1,x
2=0.864536397, x3=0.860339078, x4=x5=0.860333589; y≈0.652184624.
25. (a) Let sbe the arc length, and Lthe length of the chord, then s=1.5L. But s=rθ and
L=2rsin(θ/2) so rθ =3rsin(θ/2), θ−3 sin(θ/2)=0.
(b) Let f(θ)=θ−3 sin(θ/2), then f0(θ)=1−1.5 cos(θ/2) so θn+1 =θn−θn−3 sin(θn/2)
1−1.5 cos(θn/2).
θ1=3,θ
2=2.991592920, θ3=2.991563137, θ4=θ5=2.991563136 rad so θ≈171◦.
26. r2(θ−sin θ)/2=πr2/4soθ−sin θ−π/2=0. Letf(θ)=θ−sin θ−π/2, then f0(θ)=1−cos θso
θn+1 =θn−sin θn−π/2
1−cos θn
.
θ1=2,θ
2=2.339014106, θ3=2.310063197,···,θ
5=θ
6=2.309881460 rad; θ≈132◦.
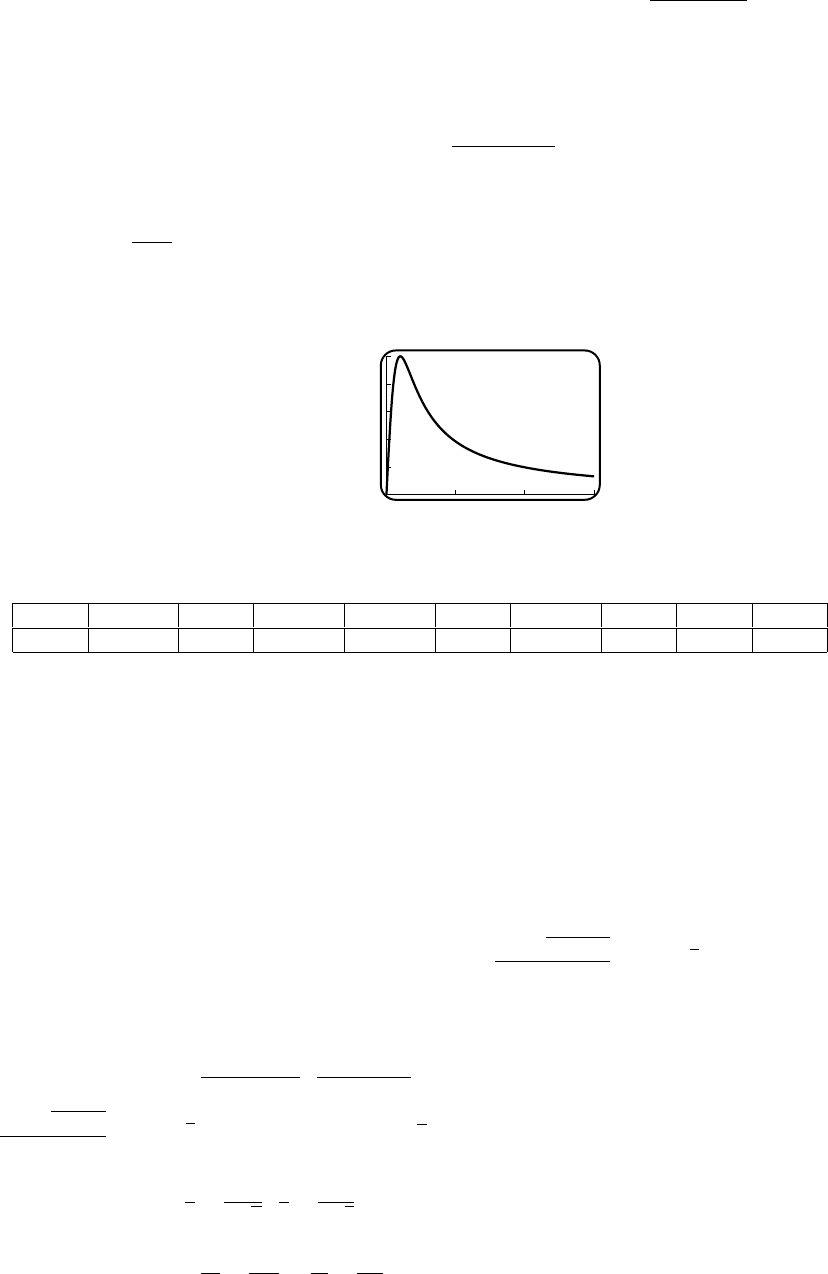
201 Chapter 6
27. If x= 1, then y4+y=1,y
4+y−1 = 0. Graph z=y4and z=1−yto see that they intersect near
y=−1 and y= 1. Let f(y)=y
4+y−1, then f0(y)=4y
3+1so y
n+1 =yn−y4
n+yn−1
4y3
n+1 .
If y1=−1, then y2=−1.333333333, y3=−1.235807860,···,y
6=y
7=−1.220744085;
if y1= 1, then y2=0.8, y3=0.731233596,···,y
6=y
7=0.724491959.
28. If x= 1, then 2y−cos y= 0. Graph z=2yand z= cos yto see that they intersect near y=0.5. Let
f(y)=2y−cos y, then f0(y) = 2 + sin yso yn+1 =yn−2yn−cos yn
2 + sin yn
.
y1=0.5, y2=0.450626693, y3=0.450183648, y4=y5=0.450183611.
29. S(25) = 250000 = 5000
i£(1+i)25 −1¤; set f(i)=50i−(1 + i)25 +1, f
0(i)=50−25(1 + i)24; solve
f(i)=0. Seti
0=.06 and ik+1 =ik−£50i−(1+i)25 +1
¤/£50 −25(1 + i)24¤. Then i1=0.05430,
i2=0.05338, i3=0.05336, ···,i=0.053362.
30. (a) x1=2,x
2=5.3333,
x3=11.055, x4=22.293,
x5=44.676
0.5
0
015
(b) x1=0.5, x2=−0.3333, x3=0.0833, x4=−0.0012, x5=0.0000 (and xn= 0 for n≥6)
31. (a) x1x2x3x4x5x6x7x8x9x10
0.5000 −0.7500 0.2917 −1.5685 −0.4654 0.8415 −0.1734 2.7970 1.2197 0.1999
(b) The sequence xnmust diverge, since if it did converge then f(x)=x
2+ 1 = 0 would have a
solution. It seems the xnare oscillating back and forth in a quasi-cyclical fashion.
EXERCISE SET 6.5
1. f(0) = f(4)=0;f
0(3)=0;[0,4], c=3 2. f(−3) = f(3)=0;f
0(0)=0
3. f(2) = f(4)=0,f
0(x)=2x−6, 2c−6=0,c=3
4. f(0) = f(2)=0,f
0(x)=3x
2−6x+2,3c
2−6c+2=0;c=6±√
36 −24
6=1±√
3/3
5. f(π/2) = f(3π/2)=0,f
0(x)=−sin x,−sin c=0,c=π
6. f(−1) = f(1)=0,f
0(x)=x
2−4x+1
(x−2)2,c2−4c+1
(c−2)2=0,c
2−4c+1=0
c=4±√
16 −4
2=2±√
3, of which only c=2−√
3isin(−1,1)
7. f(0) = f(4)=0,f
0(x)=1
2−1
2
√
x
,1
2−1
2
√
c=0,c=1
8. f(1) = f(3)=0,f
0(x)=−2
x
3+4
3x
2,−2
c
3+4
3c
2=0,−6+4c=0,c=3/2
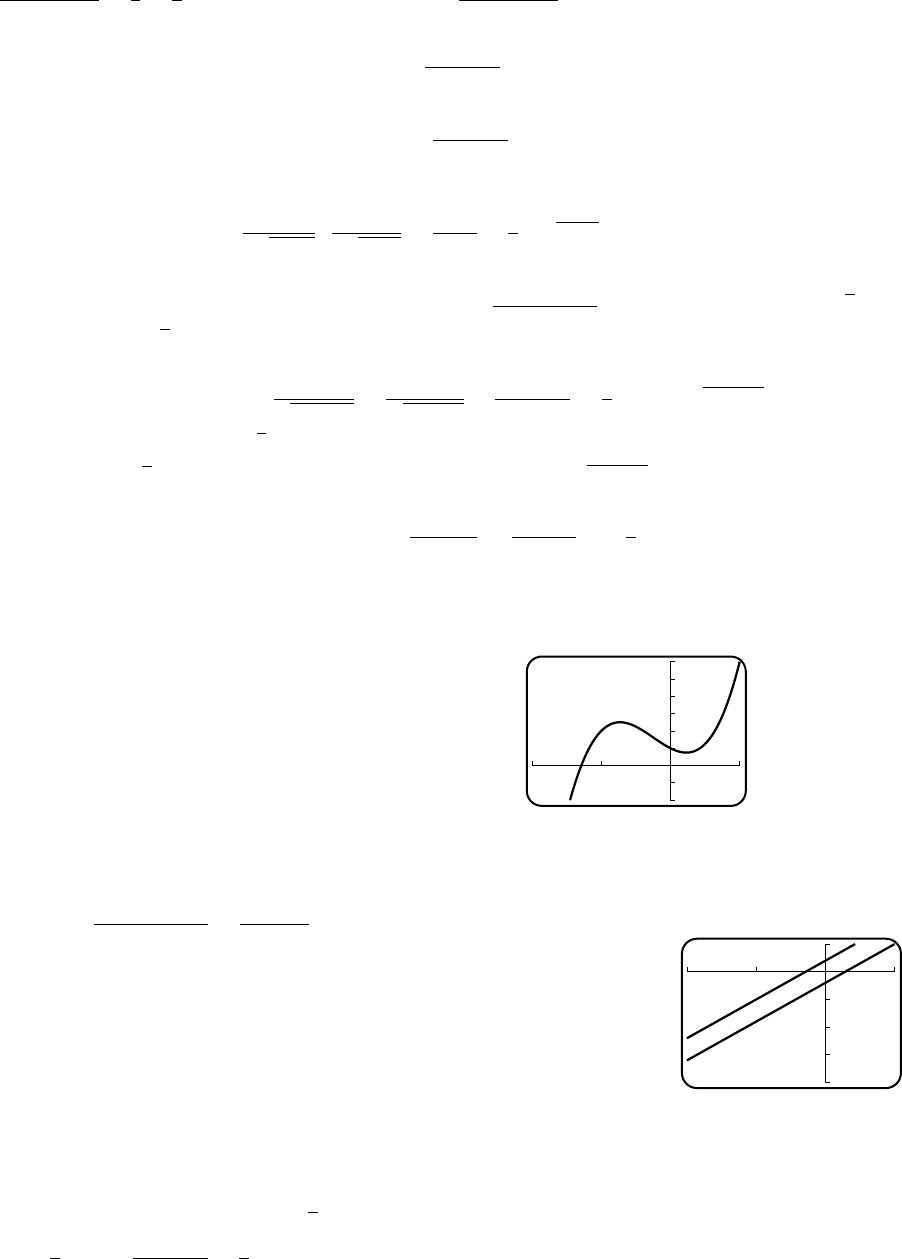
Exercise Set 6.5 202
9. f(8) −f(0)
8−0=6
8=3
4=f0(1.54); c=1.54 10. f(4) −f(0)
4−0=1.19 = f0(0.77)
11. f(−4) = 12, f(6) = 42, f0(x)=2x+1, 2c+1= 42 −12
6−(−4) =3,c=1
12. f(−1) = −6, f(2)=6,f
0(x)=3x
2+1, 3c
2+1= 6−(−6)
2−(−1) =4,c
2=1,c=±1 of which only c=1is
in (−1,2)
13. f(0)=1,f(3)=2,f
0(x)= 1
2
√
x+1,1
2
√
c+1 =2−1
3−0=1
3,√
c+1=3/2, c+1=9/4, c=5/4
14. f(3)=10/3, f(4)=17/4, f0(x)=1−1/x2,1−1/c2=17/4−10/3
4−3=11/12, c2= 12, c=±2√3of
which only c=2
√
3isin(3,4)
15. f(−5)=0,f(3)=4,f
0(x)=−x
√
25 −x2,−c
√25 −c2=4−0
3−(−5) =1
2,−2c=√25 −c2,
4c2=25−c
2
,c
2=5,c=−
√
5
(we reject c=√5 because it does not satisfy the equation −2c=√25 −c2)
16. f(2)=1,f(5)=1/4, f0(x)=−1/(x−1)2,−1
(c−1)2=1/4−1
5−2=−1
4,(c−1)2=4,c−1=±2,
c=−1 (reject), or c=3
17. (a) f(−2) = f(1)=0 (b) c=−1.29
6
-2
-2 1
(c) x0=−1, x1=−1.5, x2=−1.32, x3=−1.290, x4=−1.2885843
18. (a) m=f(−2) −f(1)
−2−1=−16 −5
−3=7soy−5=7(x−1),
y=7x−2
(b) f0(x)=3x
2+ 4 = 7 has solutions x=±1;
discard x=1,soc=−1
(c) y−f(−1)=7(x−(−1)) or y=7x+2
(d) 5
-20
-2 1
19. (a) f0(x) = sec2x, sec2c= 0 has no solution (b) tan xis not continuous on [0,π]
20. (a) f(−1)=1,f(8)=4,f
0(x)=2
3
x
−1/3
2
3
c
−1/3=4−1
8−(−1) =1
3,c1/3=2,c= 8 which is not in (−1,8).
(b) x2/3is not differentiable at x= 0, which is in (−1,8).

203 Chapter 6
21. (a) Two x-intercepts of fdetermine two solutions aand bof f(x) = 0; by Rolle’s Theorem there
exists a point cbetween aand bsuch that f0(c) = 0, i.e. cis an x-intercept for f0.
(b) f(x) = sin x=0atx=nπ, and f0(x) = cos x=0atx=nπ +π/2, which lies between nπ and
(n+1)π,(n=0,±1,±2,...)
22. f(x1)−f(x0)
x1−x0
is the average rate of change of ywith respect to xon the interval [x0,x
1]. By the
Mean-Value Theorem there is a value cin (x0,x
1) such that the instantaneous rate of change f0(c)=
f(x
1
)−f(x
0
)
x
1−x
0
.
23. Let s(t) be the position function of the automobile for 0 ≤t≤5, then by the Mean-Value Theorem
there is at least one point cin (0,5) where
s0(c)=v(c)=[s(5) −s(0)]/(5 −0)=4/5=0.8 mi/min = 48 mi/h.
24. Let T(t) denote the temperature at time with t= 0 denoting 11 AM, then T(0) = 76 and T(12) = 52.
(a) By the Mean-Value Theorem there is a value cbetween 0 and 12 such that
T0(c)=[T(12) −T(0)]/(12 −0) = (52 −76)/(12) = −2◦F/h.
(b) Assume that T(t1)=88
◦F where 0 <t
1<12, then there is at least one point cin (t1,12) where
T0(c)=[T(12) −T(t1)]/(12 −t1) = (52 −88)/(12 −t1)=−36/(12 −t1). But 12 −t1<12 so
T0(c)<−36/12 = −3◦F/h.
25. Let f(t) and g(t) denote the distances from the first and second runners to the starting point, and let
h(t)=f(t)−g(t). Since they start (at t= 0) and finish (at t=t1) at the same time, h(0) = h(t1)=0,
so by Rolle’s Theorem there is a time t2for which h0(t2) = 0, i.e. f0(t2)=g
0
(t
2
); so they have the
same velocity at time t2.
26. f(x)=x
6−2x
2+xsatisfies f(0) = f(1) = 0, so by Rolle’s Theorem f0(c) = 0 for some cin (0,1).
27. (a) By the Constant Difference Theorem f(x)−g(x)=kfor some k; since f(x0)=g(x
0
), k=0,so
f(x)=g(x) for all x.
(b) Set f(x) = sin2x+ cos2x,g(x) = 1; then f0(x)=2sinxcos x−2 cos xsin x=0=g
0
(x). Since
f(0)=1=g(0), f(x)=g(x) for all x.
28. (a) By the Constant Difference Theorem f(x)−g(x)=kfor some k; since f(x0)−g(x0)=c,k=c,
so f(x)−g(x)=cfor all x.
(b) Set f(x)=(x−1)3,g(x)=(x
2+ 3)(x−3). Then
f0(x)=3(x−1)2,g0(x)=(x
2+3)+2x(x−3)=3x
2−6x+3=3(x
2−2x+1)=3(x−1)2,
so f0(x)=g
0(x) and hence f(x)−g(x)=k. Expand f(x) and g(x)toget
h(x)=f(x)−g(x)=(x
3−3x
2+3x−1) −(x3−3x2+3x−9)=8.
(c) h(x)=x
3−3x
2+3x−1−(x
3−3x
2+3x−9)=8
29. (a) If x, y belong to Iand x<ythen for some cin I,f(y)−f(x)
y−x=f0(c),
so |f(x)−f(y)|=|f0(c)||x−y|≤M|x−y|;ifx>yexchange xand y;ifx=ythe inequality
also holds.
(b) f(x) = sin x,f0(x) = cos x,|f0(x)|≤1=M,so|f(x)−f(y)|≤|x−y|or |sin x−sin y|≤|x−y|.
30. (a) If x, y belong to Iand x<ythen for some cin I,f(y)−f(x)
y−x=f0(c),
so |f(x)−f(y)|=|f0(c)||x−y|≥M|x−y|;ifx>yexchange xand y;if
x=ythe inequality also holds.
(b) If xand ybelong to (−π/2,π/2) and f(x) = tan x, then |f0(x)|= sec2x≥1 and
|tan x−tan y|≥|x−y|
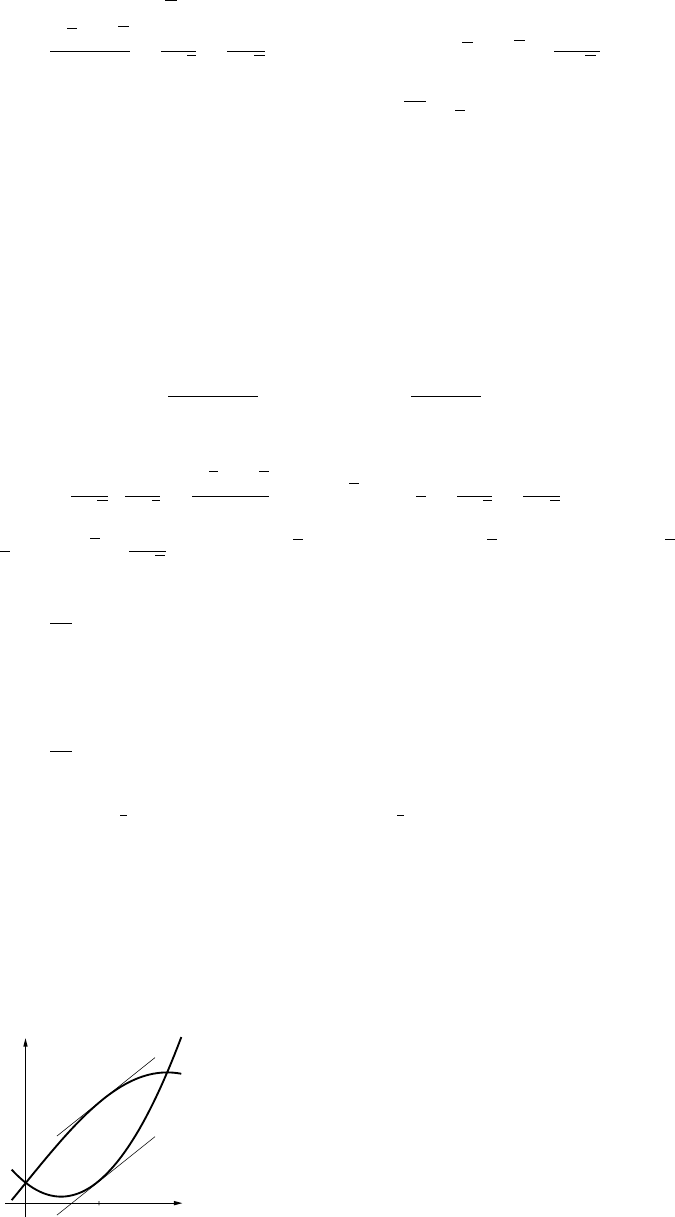
Exercise Set 6.5 204
(c) ylies in (−π/2,π/2) if and only if −ydoes; use part (b) and replace ywith −y
31. (a) Let f(x)=√
x. By the Mean-Value Theorem there is a number cbetween xand ysuch that
√y−√x
y−x=1
2√c<1
2√xfor cin (x, y), thus √y−√x<y−x
2
√
x
(b) multiply through and rearrange to get √xy < 1
2(x+y).
32. Suppose that f(x) has at least two distinct real solutions r1and r2in I. Then
f(r1)=f(r
2
) = 0 so by Rolle’s Theorem there is at least one number between r1and r2where
f0(x) = 0, but this contradicts the assumption that f0(x)6=0,sof(x) = 0 must have fewer than two
distinct solutions in I.
33. (a) If f(x)=x
3+4x−1 then f0(x)=3x
2+ 4 is never zero, so by Exercise 32 fhas at most one real
root; since fis a cubic polynomial it has at least one real root, so it has exactly one real root.
(b) Let f(x)=ax3+bx2+cx +d.Iff(x) = 0 has at least two distinct real solutions r1and r2, then
f(r1)=f(r
2
) = 0 and by Rolle’s Theorem there is at least one number between r1and r2where
f0(x)=0. Butf
0(x)=3ax2+2bx +c= 0 for
x=(−2b±√
4b
2−12ac)/(6a)=(−b±√
b
2−3ac)/(3a), which are not real if b2−3ac < 0
so f(x) = 0 must have fewer than two distinct real solutions.
34. f0(x)= 1
2
√
x
,1
2
√
c=√
4−√
3
4−3=2−√
3. But 1
4<1
2√c<1
2√3for cin (3,4) so
1
4<2−√3<1
2√3,0.25 <2−√3<0.29, −1.75 <−√3<−1.71, 1.71 <√3<1.75.
35. (a) d
dx[f2(x)+g
2
(x)]=2f(x)f
0(x)+2g(x)g
0(x)=2f(x)g(x)+2g(x)[−f(x)]=0,
so f2(x)+g
2
(x) is constant.
(b) f(x) = sin xand g(x) = cos x
36. (a) d
dx[f2(x)−g2(x)]=2f(x)f
0(x)−2g(x)g
0(x)=2f(x)g(x)−2g(x)f(x)=0sof
2
(x)−g
2
(x)
is constant.
(b) f0(x)=1
2(e
x−e
−x
)=g(x) and g0(x)=1
2(e
x+e
−x
)=f(x)
37. If f0(x)=g
0(x), then f(x)=g(x)+k. Let x=1,
f(1) = g(1) + k= (1)3−4(1)+6+k=3+k=2,sok=−1. f(x)=x
3−4x+5.
38. Let h=f−g, then his continuous on [a, b], differentiable on (a, b), and h(a)=f(a)−g(a)=0,
h(b)=f(b)−g(b) = 0. By Rolle’s Theorem there is some cin (a, b) where h0(c)=0. But
h
0(c)=f
0(c)−g
0(c)sof
0
(c)−g
0
(c)=0,f
0(c)=g
0(c).
39. y
x
c
205 Chapter 6
40. (a) Suppose f0(x) = 0 more than once in (a, b), say at c1and c2. Then f0(c1)=f
0
(c
2
)=0and
by using Rolle’s Theorem on f0, there is some cbetween c1and c2where f00(c) = 0, which
contradicts the fact that f00(x)>0sof
0
(x) = 0 at most once in (a, b).
(b) If f00(x)>0 for all xin (a, b), then fis concave up on (a, b) and has at most one relative
extremum, which would be a relative minimum, on (a, b).
41. similar to the proof of part (a) with f0(c)<0
42. similar to the proof of part (a) with f0(c)=0
CHAPTER 6 SUPPLEMENTARY EXERCISES
3. (a) If fhas an absolute extremum at a point of (a, b) then it must, by Theorem 6.1.4, be at a critical
point of f; since fis differentiable on (a, b) the critical point is a stationary point.
(b) It could occur at a critical point which is not a stationary point: for example, f(x)=|x|on
[−1,1] has an absolute minimum at x= 0 but is not differentiable there.
4. No; speeding up means the velocity and acceleration have the same sign, i.e. av > 0; the velocity is
increasing when the acceleration is positive, i.e. a>0. These are not the same thing. An example is
s=t−t2at t= 1, where v=−1 and a=−2, so av > 0 but a<0.
5. Yes; by the Mean Value Theorem there is a point cin (a, b) such that f0(c)=f(b)−f(a)
b−a=0.
7. (a) f0(x)=−1/x26= 0, no critical points; by inspection M=−1/2atx=−2; m=−1atx=−1
(b) f0(x)=3x
2−4x
3=0atx=0,3/4; f(−1) = −2,f(0)=0,f(3/4)=27/256,f(3/2) = −27/16,
so m=−2atx=−1, M=27/256 at x=3/4
(c) f0(x)= x(7x−12)
3(x−2)2/3, critical points at x=12/7,2; m=f(12/7) = 144
49 µ−2
7¶1/3
≈−1.9356 at
x=12/7, M=9atx=3
(d) lim
x→0+f(x) = lim
x→+∞f(x)=+∞and f0(x)= e
x
(x−2)
x3, stationary point at x= 2; by Theorem
6.1.5 f(x) has an absolute minimum at x= 2, and m=e2/4.
8. (a) f0(x)=2 3−x
2
(x
2+3)
2, critical point at x=√3. Since lim
x→0+f(x)=0,f(x) has no minimum, and
M=√3/3atx=√
3.
(b) f0(x)=10x
3
(x−2), critical points at x=0,2; lim
x→3−f(x) = 88, so f(x) has no maximum; m=−9
at x=2
(c) critical point at x=2;m=−3atx=3,M=0atx=2
(d) f0(x)=(1+lnx)x
x
, critical point at x=1/e; lim
x→0+f(x) = lim
x→0+exln x= 1, lim
x→+∞f(x)=+∞;no
absolute maximum, absolute minimum m=e−1/e at x=1/e
9. x=2.3561945 10. x=−2.11491,0.25410,1.86081
11. (a) yes; f0(0)=0 (b) no, fis not differentiable on (−1,1)
(c) yes, f0(pπ/2)=0
12. (a) no, fis not differentiable on (−2,2) (b) yes, f(3) −f(2)
3−2=−1=f
0(1+√2)
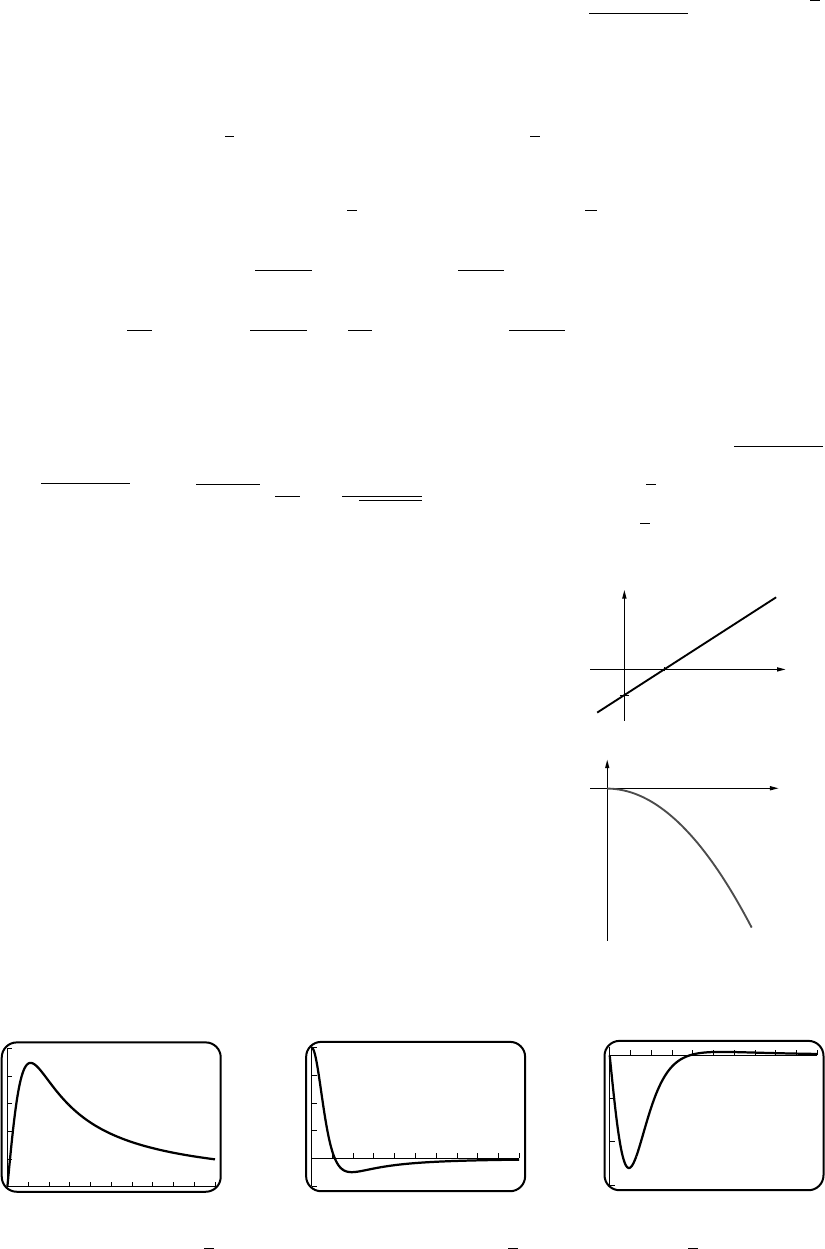
Supplementary Exercises 6 206
(c) lim
x→1−f(x) = 2, lim
x→1+f(x)=2sofis continuous on [0,2]; lim
x→1−f0(x) = lim
x→1−−2x=−2 and
lim
x→1+f0(x) = lim
x→1+(−2/x2)=−2, so fis differentiable on (0,2); and f(2) −f(0)
2−0=−1=f
0(
√
2)
13. Let kbe the amount of light admitted per unit area of clear glass. The total amount of light admitted
by the entire window is
T=k·(area of clear glass) + 1
2k·(area of blue glass) = 2krh +1
4πkr2.
But P=2h+2r+πr which gives 2h=P−2r−πr so
T=kr(P−2r−πr)+1
4πkr2=khPr−³2+π−π
4´r
2
i
=k·Pr−8+3π
4r
2
¸for 0 <r< P
2+π,
dT
dr =kµP−8+3π
2r
¶,dT
dr = 0 when r=2P
8+3π.
This is the only critical point and d2T/dr2<0 there so the most light is admitted when
r=2P/(8+3π) ft.
14. If one corner of the rectangle is at (x, y) with x>0, y>0, then A=4xy,y=3
p
1−(x/4)2,
A=12x
p1−(x/4)2=3x
√
16 −x2,dA
dx =6 8−x
2
√
16 −x2, critical point at x=2
√
2. Since A= 0 when
x=0,4 and A>0 otherwise, there is an absolute maximum A=24atx=2
√
2.
15. (a) If a=k, a constant, then v=kt +bwhere bis constant; so
the velocity changes sign at t=−b/k.
v
t
b-b/k
(b) Consider the equation s=5−t
3
/6, v=−t2/2, a=−t. Then
for t>0, ais decreasing and av > 0, so the particle is
speeding up.
v
t
16. s(t)=t/(t2+ 5), v(t)=(5−t
2
)/(t
2+5)
2
,a(t)=2t(t
2−15)/(t2+5)
3
(a) 0.25
0
020
s(t)
0.2
-0.05
020
v(t)
0.01
-0.15
010
a(t)
(b) vchanges sign at t=√5(c) s=√5/10, v=0,a=−
√
5/50
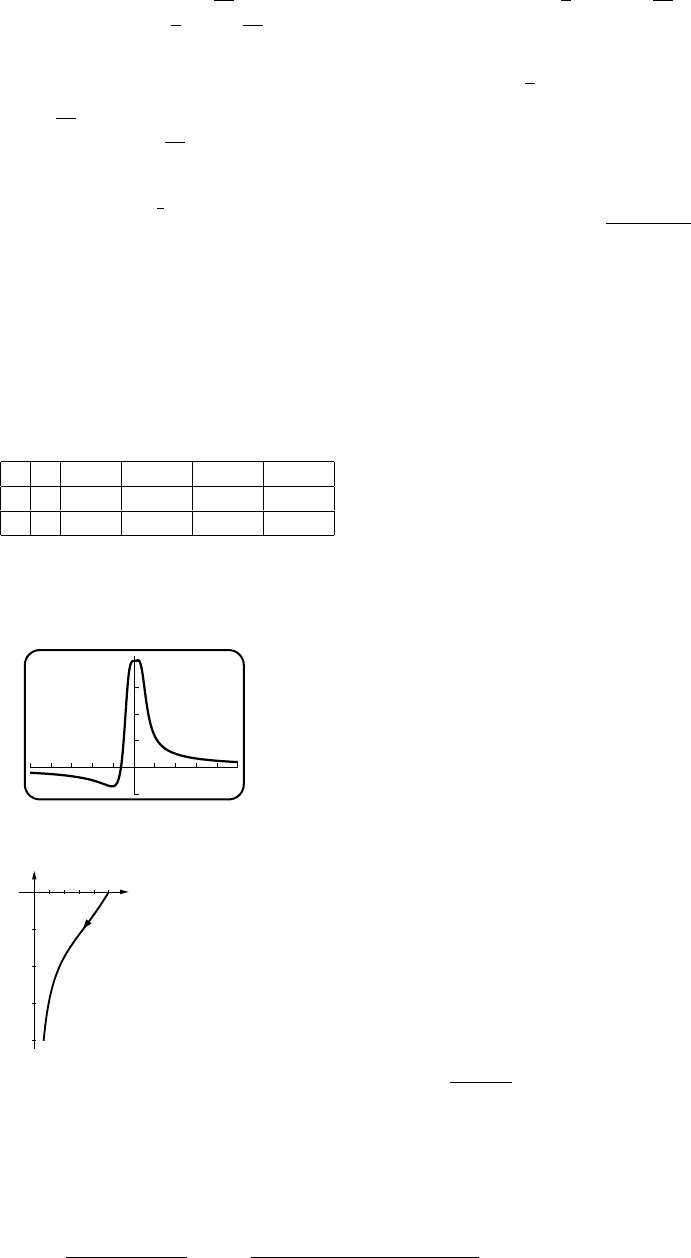
207 Chapter 6
(d) achanges sign at t=√15, so the particle is speeding up for √5<t<√
15, and it is slowing
down for 0 <t<√
5 and √15 <t
(e) v(0)=1/5, lim
t→+∞v(t)=0,v(t) has one t-intercept at t=√5 and v(t) has one critical point at
t=√15. Consequently the maximum velocity occurs when t= 0 and the minimum velocity
occurs when t=√15.
17. (a) s(t)=s
0+v
0
t−1
2
gt2=v0t−4.9t2,v(t)=v
0−9.8t;s
max occurs when v= 0, i.e. t=v0/9.8,
and then 0.76 = smax =v0(v0/9.8) −4.9(v0/9.8)2=v2
0/19.6, so v0=√0.76 ·19.6=3.86 m/s and
s(t)=3.86t−4.9t2. Then s(t) = 0 when t=0,0.7878, s(t)=0.15 when t=0.0410,0.7468, and
s(t)=0.76−0.15=0.61 when t=0.2188,0.5689, so the player spends 0.5689−0.2188 = 0.3501 s
in the top 15.0 cm of the jump and 0.0410 + (0.7878 −0.7468) = 0.0820 s in the bottom
15.0 cm.
(b) The height vs time plot is a parabola that opens down, and the slope is smallest near the top
of the parabola, so a given change ∆hin height corresponds to a large time change ∆tnear the
top of the parabola and a narrower time change at points farther away from the top.
18. (a) s(t)=s
0+v
0−4.9t
2
; assume s0=v0=0,sos(t)=−4.9t
2
,v(t)=−9.8t
t0 1 2 3 4
s0−4.9−19.6−44.1−78.4
v0−9.8−19.6−29.4−39.2
(b) The formula for vis linear (with no constant term).
(c) The formula for sis quadratic (with no linear or constant term).
19. (a) 2.1
-0.5
-10 10
(b) minimum: (−2.111985,−0.355116)
maximum: (0.372591,2.012931)
20. (a) y
x
-2
-1.5
-1
-0.5
0.2 0.6 1
(b) The distance between the boat and the origin is px2+y2, where y=(x
10/3−1)/(2x2/3). The
minimum distance is 0.8247 mi when x=0.6598 mi. The boat gets swept downstream.
(c) Use the equation of the path to obtain dy/dt =(dy/dx)(dx/dt), dx/dt =(dy/dt)/(dy/dx). Let
dy/dt =−4 and find the value of dy/dx for the value of xobtained in part (b) to get
dx/dt =−3 mi/h.
21. (a) v=−2t(t4+2t
2−1)
(t4+1)
2,a=2
3t
8+10t
6−12t4−6t2+1
(t
4+1)
3
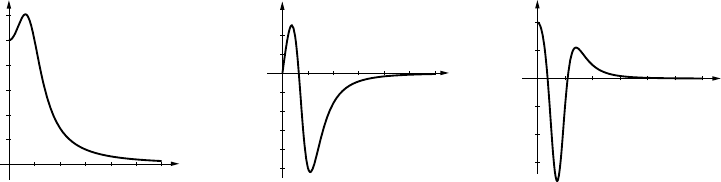
Supplementary Exercises 6 208
(b) s
t
0.2
0.4
0.6
0.8
1
1.2
123456
v
t
-1
-0.8
-0.6
-0.4
-0.2
0.2
0.4
123456
a
t
-3
-2
-1
1
2
123456
(c) It is farthest from the origin at approximately t=0.64 (when v= 0) and s=1.2
(d) Find tso that the velocity v=ds/dt > 0. The particle is moving in the positive direction for
0≤t≤0.64 s.
(e) It is speeding up when a, v > 0ora, v < 0, so for 0 ≤t<0.36 and 0.64 <t<1.1, otherwise it
is slowing down.
(f) Find the maximum value of |v|to obtain: maximum speed = 1.05 m/s when t=1.10 s.
22. Find tso that N0(t) is maximum. The size of the population is increasing most rapidly when t=8.4
years.
23. Solve φ−0.0167 sin φ=2π(90)/365 to get φ=1.565978 so
r= 150 ×106(1 −0.0167 cos φ) = 149.988 ×106km.
24. Solve φ−0.0934 sin φ=2π(1)/1.88 to get φ=3.325078 so
r= 228 ×106(1 −0.0934 cos φ) = 248.938 ×106km.
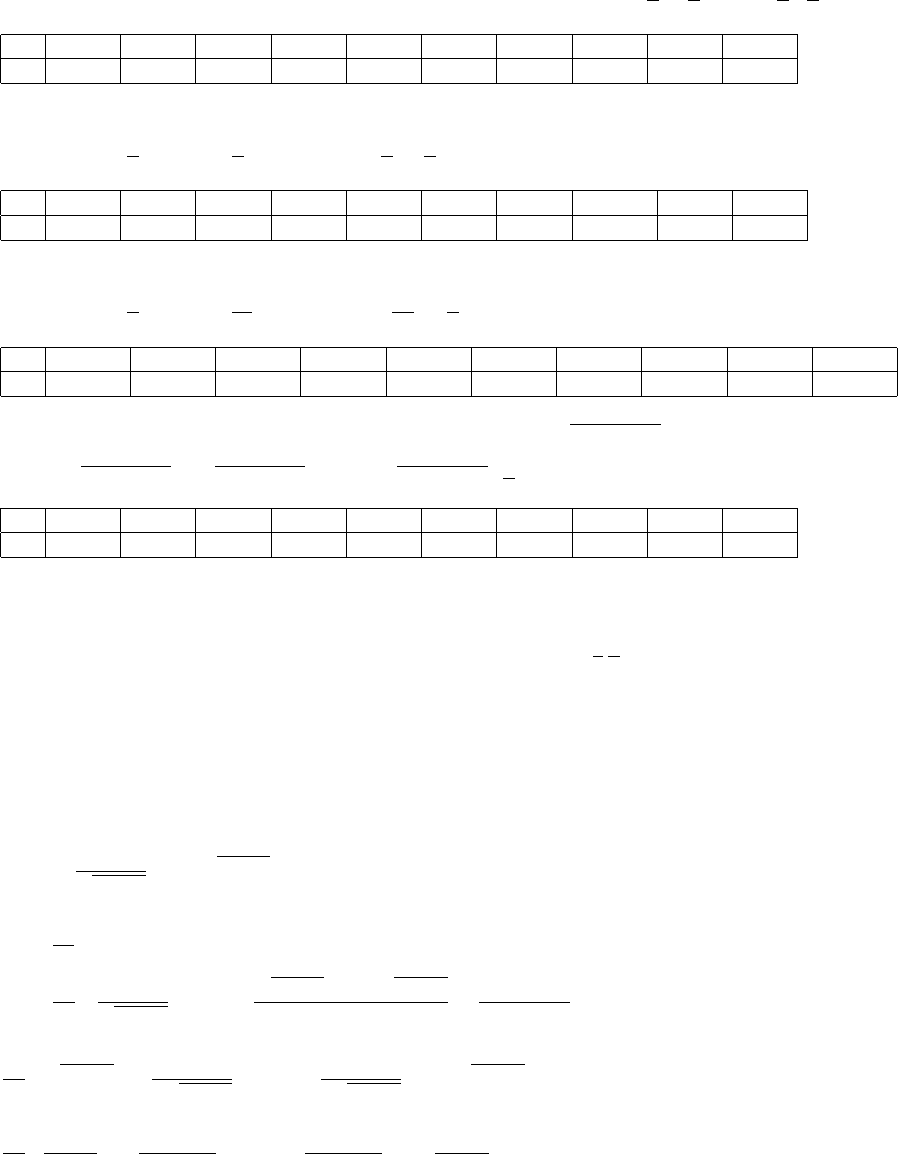
CHAPTER 7
Integration
EXERCISE SET 7.1
1. A= 1(1)/2=1/2; ∆x=(b−a)/n =1/n,x∗
k=k/n,f(x∗
k)=k/n,An=·1
n+2
n+···+n
n¸1
n
n12345678910
An1.0000 0.7500 0.6666 0.6250 0.6000 0.5833 0.5714 0.5625 0.5556 0.5500
2. A= 4(2)/2=4;∆x=(b−a)/n =2/n,x∗
k=2k/n,f(x∗
k)=4−2(2k/n)=4−4k/n = 4(1 −k/n),
An=4·µ1−1
n¶+µ1−2
n¶+···+³1−n
n´¸2
n
n1 2 3 4 5 6 7 8 9 10
An0.0000 2.0000 2.6667 3.0000 3.2000 3.3333 3.4286 3.50000 3.5556 3.6000
3. A= 2(2 + 14)/2 = 16; ∆x=(b−a)/n =2/n,x∗
k=2k/n,f(x∗
k)=2+12k/n = 2(1+6k/n),
An=2·µ1+ 6
n¶+µ1+ 12
n¶+···+µ1+6n
n¶¸2
n
n12345678910
An28.0000 22.0000 20.0000 19.0000 18.4000 18.0000 17.7143 17.5000 17.3333 17.2000
4. A=π(1)2/4=π/4; ∆x=(b−a)/n =1/n,x∗
k=k/n,f(x∗
k)=p1−(k/n)2,
An=hp1+(1/n)2+p1+(2/n)2+···+p1+(n/n)2i1
n
n1 2 3 4 5 6 7 8 9 10
An0.0000 0.4330 0.5627 0.6239 0.6593 0.6822 0.6982 0.7100 0.7190 0.7261
5. A(1) −A(0)=1/26. A(2) −A(0)=4
7. A(2) −A(0)=16 8. A(1) −A(0) = 1
2
π
2=π/4
9. A(x)=e
x
, area = A(1) −A(0) = e−110. A(x)=−cos x, area = A(π)−A(0)=2
EXERCISE SET 7.2
1. (a) Zx
√1+x
2dx =p1+x
2+C(b) Z(x+1)e
x
dx =xex+C
2. (a) d
dx(sin x−xcos x+C) = cos x−cos x+xsin x=xsin x
(b) d
dx µx
√1−x2+C¶=√1−x2+x2/√1−x2
1−x2=1
(1 −x2)3/2
3. d
dx hpx3+5
i=3x
2
2
√
x
3+5 so Z3x2
2√x3+5dx =px3+5+C
4. d
dx ·x
x2+3¸=3−x
2
(x
2+3)
2so Z3−x2
(x2+3)
2dx =x
x2+3+C
209
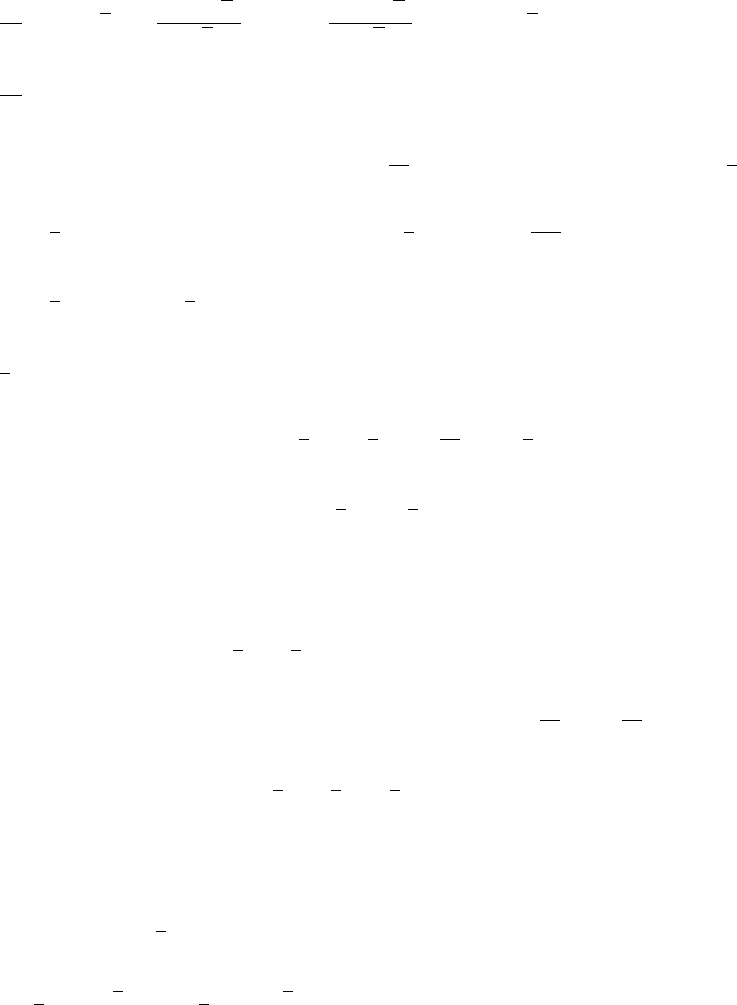
Exercise Set 7.2 210
5. d
dx £sin ¡2√x¢¤=cos (2√x)
√xso Zcos (2√x)
√xdx = sin ¡2√x¢+C
6. d
dx[sin x−xcos x]=xsin xso Zxsin xdx= sin x−xcos x+C
7. (a) x9/9+C(b) 7
12x12/7+C(c) 2
9x9/2+C
8. (a) 3
5x5/3+C(b) −1
5x−5+C=−1
5x5+C(c) 8x1/8+C
9. (a) 1
2Zx−3dx =−1
4x−2+C(b) u4/4−u2+7u+C
10. 3
5x5/3−5x4/5+4x+C
11. Z(x−3+x1/2−3x1/4+x2)dx =−1
2x−2+2
3x3/2−12
5x5/4+1
3x3+C
12. Z(7y−3/4−y1/3+4y
1/2
)dy =28y
1/4−3
4
y
4/3+8
3
y
3/2+C
13. Z(x+x4)dx =x2/2+x
5
/5+C
14. Z(4+4y
2+y
4
)dy =4y+4
3
y
3+1
5
y
5+C
15. Zx1/3(4 −4x+x2)dx =Z(4x1/3−4x4/3+x7/3)dx =3x
4/3−12
7x7/3+3
10x10/3+C
16. Z(2 −x+2x
2−x
3
)dx =2x−1
2
x
2+2
3
x
3−1
4
x
4+C
17. Z(x+2x
−2−x
−4
)dx =x2/2−2/x +1/(3x3)+C
18. Z(t−3−2)dt =−1
2t−2−2t+C19. 2lnx+3e
x+C
20. Z·1
2t−1−√2et¸dt =1
2ln t−√2et+C21. −4 cos x+ 2 sin x+C
22. 4 tan x−csc x+C23. Z(sec2x+ sec xtan x)dx = tan x+ sec x+C
24. Z(sec xtan x+1)dx = sec x+x+C25. ln θ−2eθ+ cot θ+C
26. Zsin ydy =−cos y+C27. Zsec xtan xdx= sec x+C
28. Z(φ+ 2 csc2φ)dφ =φ2/2−2 cot φ+C29. Z(1 + sin θ)dθ =θ−cos θ+C
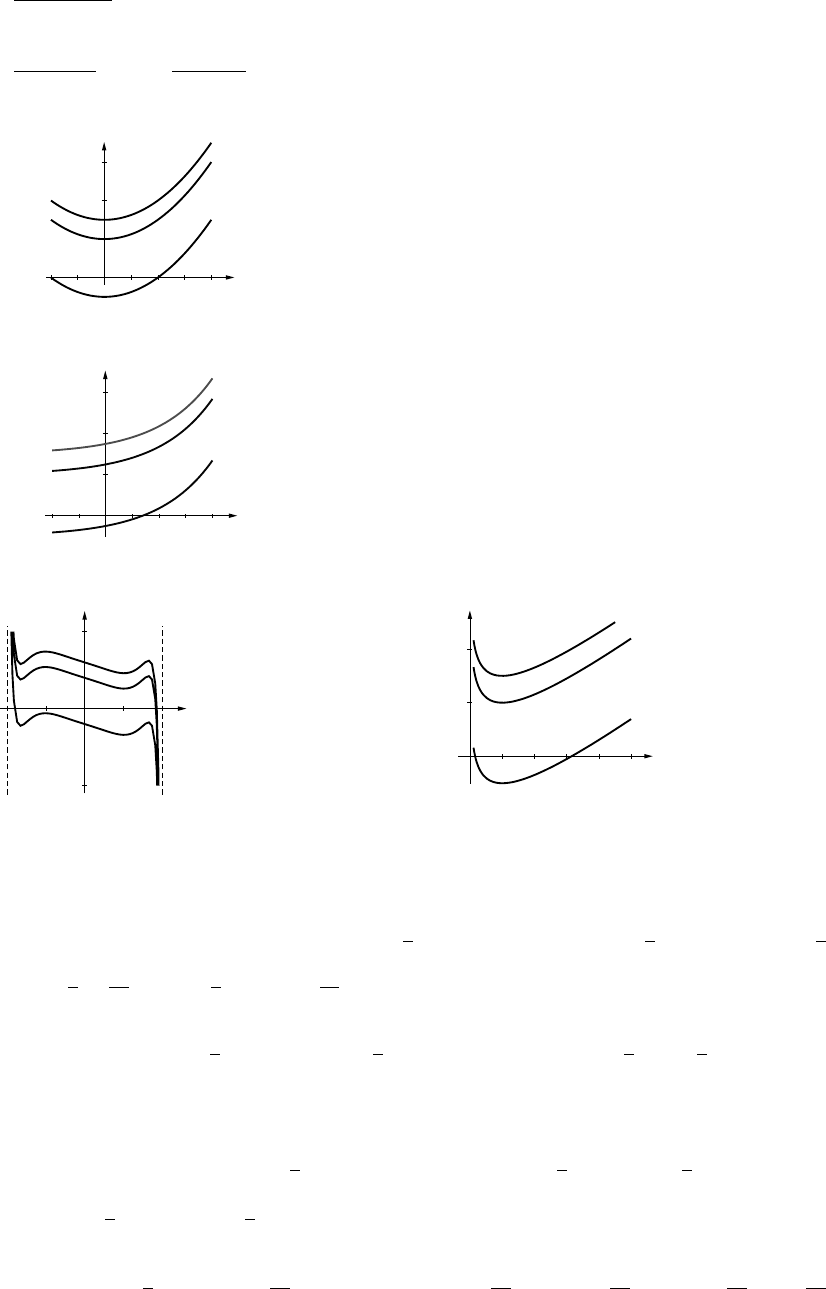
211 Chapter 7
30. Z2 sin xcos x
cos xdx =2Zsin xdx=−2 cos x+C
31. Z1−sin x
1−sin2xdx =Z1−sin x
cos2x=Z¡sec2x−sec xtan x¢dx = tan x−sec x+C
33. (a) y
x
2
4
6
-1 1 2
(b) f(x)=x
2
/2+5
34. (a) y
x
2
4
6
-1 1 2
(b) f(x)=e
x
/2+1/2
35. y
x
-5
5
π/4π/2
36. y
x
2
4
12345
37. f0(x)=m=−sin xso f(x)=Z(−sin x)dx = cos x+C;f(0)=2=1+Cso C=1,f(x) = cos x+1
38. f0(x)=m=(x+1)2,sof(x)=Z(x+1)2dx =1
3(x+1)3+C;f(−2)=8= 1
3
(−2+1)3+C=−1
3+C,
C=8+1
3=25
3,f(x)=1
3
(x+1)
3+25
3
39. (a) y(x)=Zx
1/3
dx =3
4x4/3+C,y(1) = 3
4+C=2,C=5/4; y(x)=3
4
x
4/3+5
4
(b) y(t)=Zt
−1
dt =ln|t|+C,y(−1) = C=5,C=5;y(t)=ln|t|+5
(c) y(x)=Z(x
1/2+x
−1/2
)dx =2
3x3/2+2x
1/2+C,y(1)=0=8
3+C,C=−8
3
,
y(x)=2
3
x
3/2+2x
1/2−8
3
40. (a) y(x)=Zµ1
8
x
−3
¶dx =−1
16x−2+C,y(1)=0=−1
16 +C,C=1
16;y(x)=−1
16x−2+1
16

Exercise Set 7.2 212
(b) y(t)=Z(sec2t−sin t)dt = tan t+ cos t+C,y(π
4)=1=1+
√
2
2+C,C=−
√
2
2;
y(t) = tan t+ cos t−√2
2
(c) y(x)=Zx
7/2
dx =2
9x9/2+C,y(0)=0=C,C=0;y(x)=2
9
x
9/2
41. f0(x)=2
3
x
3/2+C
1
;f(x)= 4
15x5/2+C1x+C2
42. f0(x)=x
2
/2 + sin x+C1, use f0(0) = 2 to get C1=2sof
0(x)=x
2
/2 + sin x+2,
f(x)=x
3
/6−cos x+2x+C
2
, use f(0) = 1 to get C2=2sof(x)=x
3
/6−cos x+2x+2
43. dy/dx =2x+1,y =Z(2x+1)dx =x2+x+C;y= 0 when x=−3
so (−3)2+(−3)+C=0,C =−6thusy=x
2+x−6
44. dy/dx =x2,y =Zx
2dx =x3/3+C;y= 2 when x=−1so(−1)3/3+C=2,C =7/3
thus y=x3/3+7/3
45. dy/dx =Z6xdx =3x
2+C
1
. The slope of the tangent line is −3sody/dx =−3 when x=1. Thus
3(1)2+C1=−3, C1=−6sody/dx =3x
2−6, y=Z(3x2−6)dx =x3−6x+C2;Ifx= 1, then
y=5−3(1) = 2 so (1)2−6(1) + C2=2,C
2= 7 thus y=x3−6x+7.
46. dT/dx =C1,T=C1x+C2;T= 25 when x=0soC
2= 25, T=C1x+ 25. T= 85 when x=50so
50C1+ 25 = 85, C1=1.2, T=1.2x+25
47. (a) F0(x)=G
0(x)=3x+4
(b) F(0)=16/6=8/3, G(0)=0,soF(0) −G(0)=8/3
(c) F(x)=(9x
2+24x+ 16)/6=3x
2
/2+4x+8/3=G(x)+8/3
48. (a) F0(x)=G
0(x)=10x/(x2+5)
2
(b) F(0)=0,G(0) = −1, so F(0) −G(0)=1
(c) F(x)= x
2
x
2+5 =(x
2+5)−5
x
2+5 =1−5
x
2+5 =G(x)+1
49. Z(sec2x−1)dx = tan x−x+C50. Z(csc2x−1)dx =−cot x−x+C
51. (a) 1
2Z(1 −cos x)dx =1
2(x−sin x)+C(b) 1
2Z(1 + cos x)dx =1
2(x+ sin x)+C
52. (a) F0(x)=G
0(x)=f(x), where f(x)=½1,x>0
−1,x<0
(b) G(x)−F(x)=½2,x>0
3,x<0so G(x)6=F(x) plus a constant
(c) no, because (−∞,0) ∪(0,+∞) is not an interval
53. v=1087
2√273 ZT−1/2dT =1087
√273T1/2+C,v(273) = 1087 = 1087 + Cso C=0,v=1087
√273T1/2ft/s
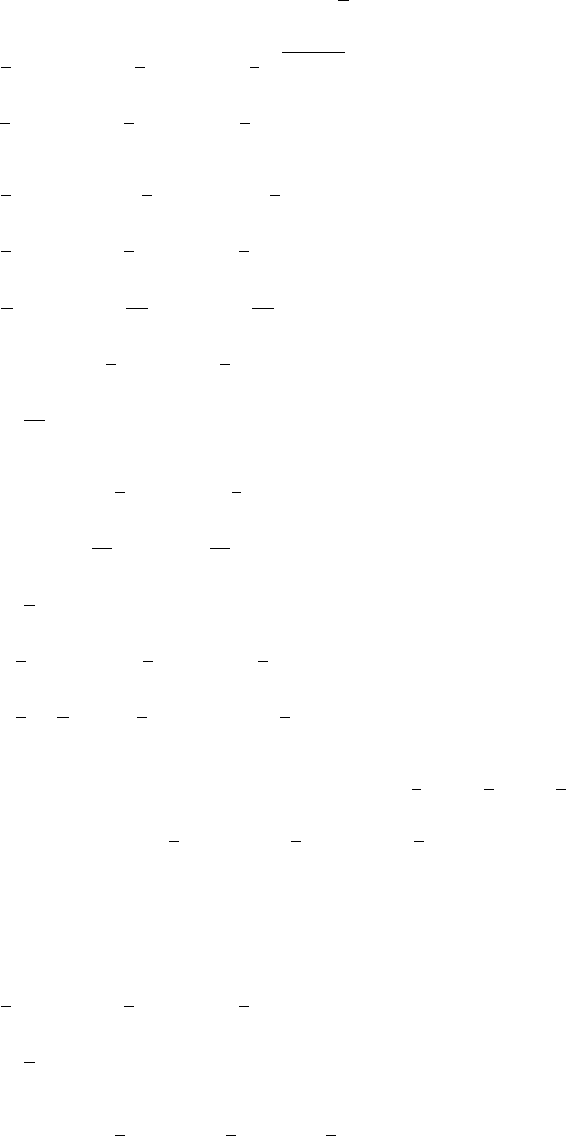
213 Chapter 7
EXERCISE SET 7.3
1. (a) Zu23du =u24/24+C=(x
2+1)
24/24+C
(b) −Zu3du =−u4/4+C=−(cos4x)/4+C
(c) 2Zsin udu=−2 cos u+C=−2 cos √x+C
(d) 3
8Zu−1/2du =3
4u1/2+C=3
4p4x2+5+C
(e) 1
3Zu−1du =1
3ln u+C=1
3ln(x3−4)+C
2. (a) 1
4Zsec2udu=1
4tan u+C=1
4tan(4x+1)+C
(b) 1
4Zu1/2du =1
6u3/2+C=1
6(1+2y
2
)
3/2+C
(c) 1
πZu1/2du =2
3πu3/2+C=2
3πsin3/2πθ +C
(d) Zu4/5du =5
9u9/5+C=5
9(x2+7x+3)
9/5+C
(e) Zdu
u=lnu+C= ln(1 + ex)+C
3. (a) −Zudu=−1
2u
2+C=−1
2cot2x+C
(b) Zu9du =1
10u10 +C=1
10(1 + sin t)10 +C
(c) Z1
udu =ln|u|+C=ln|ln x|+C
(d) −1
5Zeudu =−1
5eu+C=−1
5e−5x+C
(e) −1
3Z1
udu =−1
3ln |u|+C=−1
3ln |(1 + cos 3θ)|+C
4. (a) Z(u−1)2u1/2du =Z(u5/2−2u3/2+u1/2)du =2
7u7/2−4
5u5/2+2
3u3/2+C
=2
7(1+x)7/2−4
5(1+x)5/2+2
3(1+x)3/2+C
(b) Zcsc2udu=−cot u+C=−cot(sin x)+C
(c) Zeudu =eu+C=etan x+C
(d) 1
2Zu1/2du =1
3u3/2+C=1
3(1+e2t)3/2+C
(e) Z1
udu =ln|u|+C=ln¯
¯x
5+1
¯
¯+C
5. u=2x,du =2dx;1
2Zeudu =1
2eu+C=1
2e2x+C
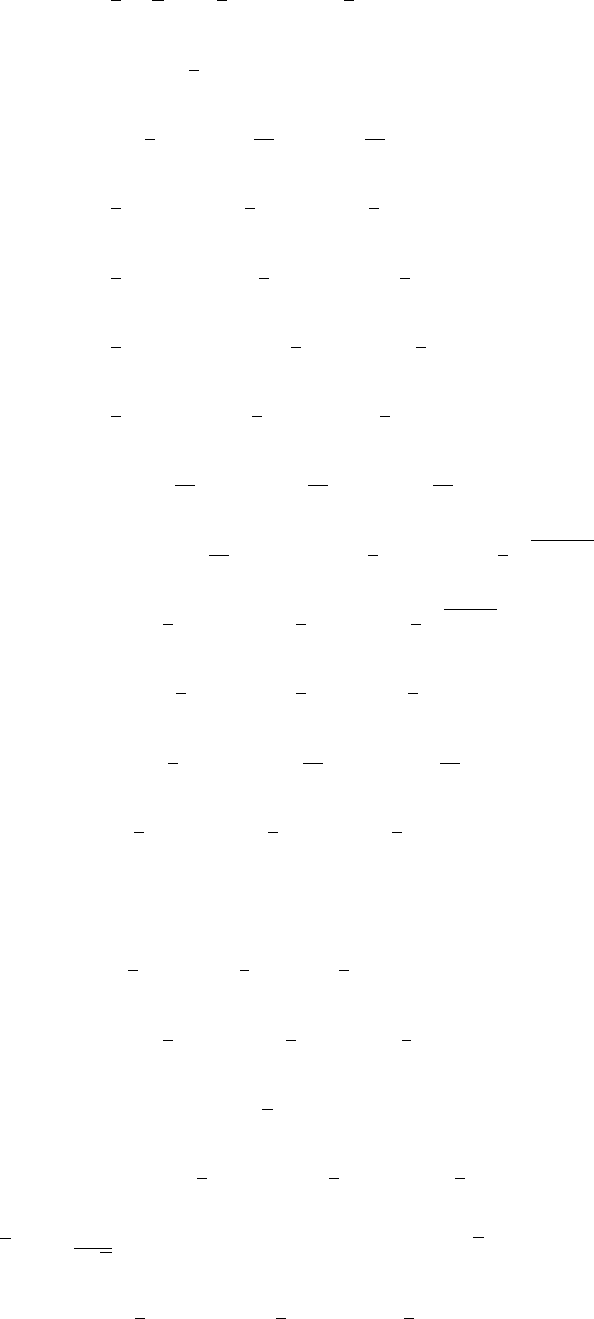
Exercise Set 7.3 214
6. u=2x,du =2dx;1
2Z1
udu =1
2ln |u|+C=1
2ln |2x|+C
7. u=2−x
2
,du =−2xdx;−1
2Zu
3du =−u4/8+C=−(2 −x2)4/8+C
8. u=3x−1, du =3dx;1
3Zu5du =1
18u6+C=1
18(3x−1)6+C
9. u=8x,du =8dx;1
8Zcos udu=1
8sin u+C=1
8sin 8x+C
10. u=3x,du =3dx;1
3Zsin udu=−1
3cos u+C=−1
3cos 3x+C
11. u=4x,du =4dx;1
4Zsec utan udu=1
4sec u+C=1
4sec 4x+C
12. u=5x,du =5dx;1
5Zsec2udu=1
5tan u+C=1
5tan 5x+C
13. u=7t
2+ 12, du =14tdt;1
14 Zu1/2du =1
21u3/2+C=1
21(7t2+ 12)3/2+C
14. u=4−5x
2
,du =−10xdx;−1
10 Zu−1/2du =−1
5u1/2+C=−1
5p4−5x2+C
15. u=x3+1,du =3x
2
dx;1
3Zu−1/2du =2
3u1/2+C=2
3px3+1+C
16. u=1−3x,du =−3dx;−1
3Zu−2du =1
3u−1+C=1
3(1 −3x)−1+C
17. u=4x
2+1,du =8xdx;1
8Zu
−3du =−1
16u−2+C=−1
16(4x2+1)
−2+C
18. u=3x
2
,du =6xdx;1
6Zcos udu=1
6sin u+C=1
6sin(3x2)+C
19. u= sin x,du = cos xdx;Ze
udu =eu+C=esin x+C
20. u=x4,du =4x
3
dx;1
4Zeudu =1
4eu+C=1
4ex4+C
21. u=−2x3,du =−6x2,−1
6Zeudu =−1
6eu+C=−1
6e−2x3+C
22. u=ex−e−x,du =(e
x+e
−x
)dx,Z1
udu =ln|u|+C=ln¯
¯e
x−e
−x
¯
¯+C
23. u=5/x,du =−(5/x2)dx;−1
5Zsin udu=1
5cos u+C=1
5cos(5/x)+C
24. u=√x,du =1
2√xdx;2
Zsec2udu= 2 tan u+C= 2 tan √x+C
25. u=x3,du =3x
2
dx;1
3Zsec2udu=1
3tan u+C=1
3tan(x3)+C
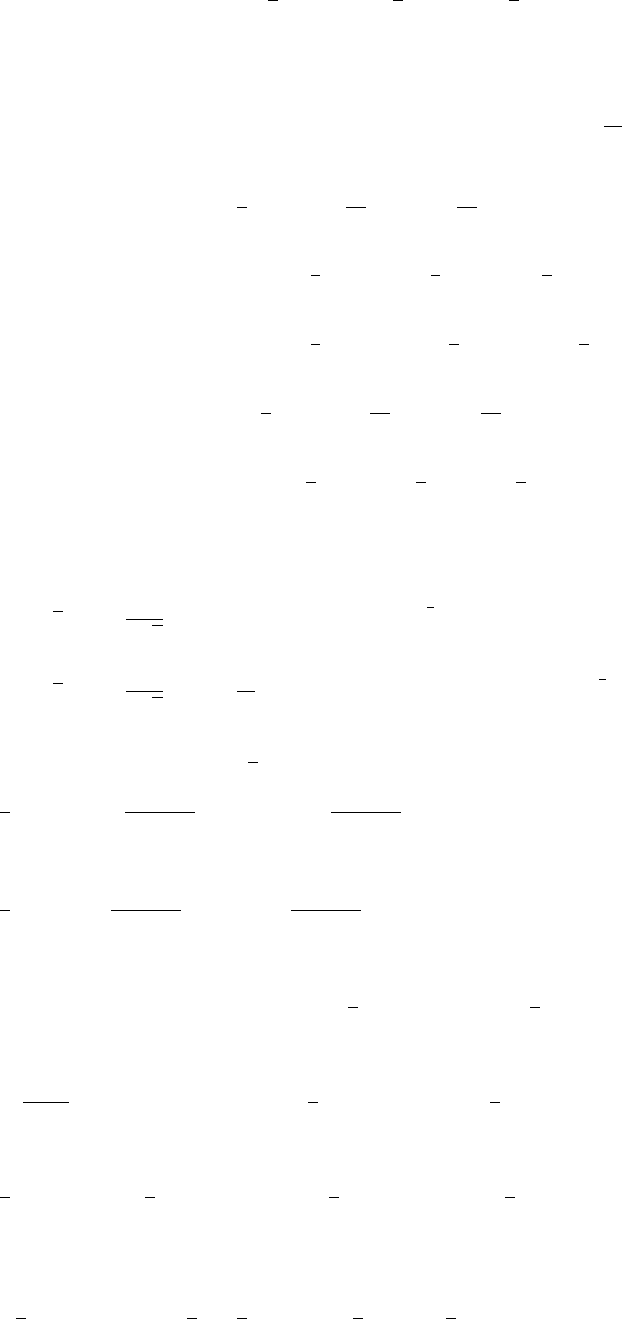
215 Chapter 7
26. u= cos 2t,du =−2 sin 2tdt;−1
2Zu
3du =−1
8u4+C=−1
8cos42t+C
27. Ze−xdx;u=−x,du =−dx;−Zeudu =−eu+C=−e−x+C
28. Zex/2dx;u=x/2, du =dx/2; 2 Zeudu =2e
u+C=2e
x/2+C=2
√
e
x+C
29. u= sin 3t,du = 3 cos 3tdt;1
3Zu
5du =1
18u6+C=1
18 sin63t+C
30. u= 5 + cos 2θ,du =−2 sin 2θdθ;−1
2Zu
−3du =1
4u−2+C=1
4(5 + cos 2θ)−2+C
31. u=2−sin 4θ,du =−4 cos 4θdθ;−1
4Zu
1/2du =−1
6u3/2+C=−1
6(2 −sin 4θ)3/2+C
32. u= tan 5x,du = 5 sec25xdx;1
5Zu
3du =1
20u4+C=1
20 tan45x+C
33. u= sec 2x,du = 2 sec 2xtan 2xdx;1
2Zu
2du =1
6u3+C=1
6sec32x+C
34. u= sin θ,du = cos θdθ;Zsin udu =−cos u+C=−cos(sin θ)+C
35. u=√y,du =1
2√ydy,2
Ze
u
du =2e
u+C=2e
√
y+C
36. u=√y,du =1
2√ydy,2
Z1
e
udu =2Ze
−u
du =−2e−u+C=−2e−√y+C
38. u=a+bx,du =bdx,dx =1
bdu
1
bZu1/ndu =n
b(n+1)u
(n+1)/n +C=n
b(n+1)(a+bx)(n+1)/n +C
39. u= sin(a+bx), du =bcos(a+bx)dx
1
bZundu =1
b(n+1)u
n+1 +C=1
b(n+1)sinn+1(a+bx)+C
41. u=x−3, x=u+3,dx =du
Z(u+3)u
1/2
du =Z(u3/2+3u
1/2
)du =2
5u5/2+2u
3/2+C=2
5(x−3)5/2+2(x−3)3/2+C
42. u=y+1,y=u−1, dy =du
Zu−1
u1/2du =Z(u1/2−u−1/2)du =2
3u3/2−2u1/2+C=2
3(y+1)
3/2−2(y+1)
1/2+C
43. u=3θ,du =3dθ
1
3Ztan2udu=1
3Z(sec2u−1)du =1
3(tan u−u)+C=1
3(tan 3θ−3θ)+C
44. Zsin22θsin 2θdθ=Z(1 −cos22θ) sin 2θdθ;u= cos 2θ,du =−2 sin 2θdθ,
−1
2Z(1 −u2)du =−1
2u+1
6u3+C=−1
2cos 2θ+1
6cos32θ+C
Exercise Set 7.3 216
45. Zµ1+1
t¶dt =t+ln|t|+C
46. e2lnx=e
ln x2=x2,x>0, so Ze2lnxdx =Zx2dx =1
3x3+C
47. ln(ex) + ln(e−x) = ln(exe−x)=ln1=0soZ[ln(ex) + ln(e−x)]dx =C
48. Zcos x
sin xdx;u= sin x,du = cos xdx;Z1
udu =ln|u|+C=ln|sin x|+C
49. (a) with u= sin x,du = cos xdx;Zudu =1
2u
2+C
1=1
2sin2x+C1;
with u= cos x,du =−sin xdx;−Zudu =−1
2u
2+C
2=−1
2cos2x+C2
(b) because they differ by a constant:
µ1
2sin2x+C1¶−µ−1
2cos2x+C2¶=1
2(sin2x+ cos2x)+C
1−C
2=1/2+C
1−C
2
50. (a) First method: Z(25x2−10x+1)dx =25
3x3−5x2+x+C1;
second method: 1
5Zu2du =1
15u3+C2=1
15(5x−1)3+C2
(b) 1
15(5x−1)3+C2=1
15(125x3−75x2+15x−1)+C2=25
3x3−5x2+x−1
15 +C2;
the answers differ by a constant.
51. y(x)=Z√
3x+1dx =2
9(3x+1)
3/2+C,
y(1) = 16
9+C=5,C=29
9so y(x)=2
9
(3x+1)
3/2+29
9
52. y(x)=Z(6 −5 sin 2x)dx =6x+5
2cos 2x+C,
y(0) = 5
2+C=3,C=1
2so y(x)=6x+5
2cos 2x+1
2
53. f0(x)=m=√
3x+1, f(x)=Z(3x+1)
1/2
dx =2
9(3x+1)
3/2+C;f(0)=1=2
9+C,C=7
9
,so
f(x)=2
9
(3x+1)
3/2+7
9
54. y
x
4
-4 4

217 Chapter 7
55. p(t)=Z(4+0.15t)3/2dt =8
3(4+0.15t)5/2+C;p(0) = 100,000 = 8
345/2+C=256
3+C,
C= 100,000 −256
3≈99,915, p(t)=8
3
(4+0.15t)5/2+99,915, p(5) = 8
3(4.75)5/2+99,915 ≈100,416
56. dr
dt =−k√t,r=−kZt1/2dt =−2
3kt3/2+C;r(0)=10,000 = Cso C=10,000 and
r=−2
3kt3/2+10,000; r(25) = 9,000 = −2
3k(25)3/2+10,000=10,000 −250
3k,so
k= 12, r=−8t3/2+10,000, and r(60) = 6281.94 m
EXERCISE SET 7.4
1. (a) 1+8+27=36 (b) 5+8+11+14+17=55
(c) 20+12+6+2+0+0=40 (d) 1+1+1+1+1+1=6
(e) 1−2+4−8+16=11 (f) 0+0+0+0+0+0=0
2. (a) 1+0−3+0=−2(b) 1−1+1−1+1−1=0
(c) e2+e2+···+e
2=14e
2
(14 terms)
(d) 24+2
5+2
6= 112
(e) ln 1 + ln 2 + ln 3 + ln 4 + ln 5 + ln 6 = ln(1 ·2·3·4·5·6) = ln 720
(f) 1−1+1−1+1−1+1−1+1−1+1=1
3.
10
X
k=1
k4.
20
X
k=1
3k5.
49
X
k=1
k(k+1) 6.
4
X
k=0
2k
7.
10
X
k=1
2k8.
8
X
k=1
(2k−1) 9.
6
X
k=1
(−1)k+1(2k−1)
10.
5
X
k=1
(−1)k+1 1
k11.
5
X
k=1
(−1)k1
k12.
3
X
k=0
cos kπ
7
13. (a)
50
X
1
2k(b)
50
X
1
(2k−1)
14. (a)
5
X
k=1
(−1)k+1ak(b)
5
X
k=0
(−1)k+1bk(c)
n
X
k=0
akxk(d)
5
X
k=0
a5−kbk
15. 1
2(100)(100 + 1) = 5050
16.
100
X
k=1
k−
2
X
k=1
k=1
2(100)(100 + 1) −(1 + 2) = 5050 −3 = 5047
17. 1
6(20)(21)(41) = 2,870 18. 7
100
X
k=1
k+
100
X
k=1
1=7
2
(100)(101) + 100 = 35,450
19. 4
6
X
k=1
k3−2
6
X
k=1
k+
6
X
k=1
1=4·1
4
(6)2(7)2¸−2·1
2(6)(7)¸+ 6 = 1728

Exercise Set 7.4 218
20.
20
X
k=1
k2−
3
X
k=1
k2=2,870 −14=2,856
21.
30
X
k=1
k(k2−4) =
30
X
k=1
(k3−4k)=
30
X
k=1
k3−4
30
X
k=1
k=1
4(30)2(31)2−4·1
2(30)(31) = 214,365
22.
6
X
k=1
k−
6
X
k=1
k3=1
2(6)(7) −1
4(6)2(7)2=−420
23.
n
X
k=1
(4k−3)=4
n
X
k=1
k−
n
X
k=1
3=4·1
2
n(n+1)−3n=2n
2−n
24.
n−1
X
k=1
k2=1
6(n−1)[(n−1) + 1][2(n−1)+1]= 1
6n(n−1)(2n−1)
25.
n
X
k=1
3k
n=3
n
n
X
k=1
k=3
n·1
2n(n+1)= 3
2(n+1)
26.
n−1
X
k=1
k2
n=1
n
n−1
X
k=1
k2=1
n·1
6(n−1)(n)(2n−1) = 1
6(n−1)(2n−1)
27.
n−1
X
k=1
k3
n2=1
n2
n−1
X
k=1
k3=1
n2·1
4(n−1)2n2=1
4(n−1)2
28.
n
X
k=1 µ5
n−2k
n¶=5
n
n
X
k=1
1−2
n
n
X
k=1
k=5
n(n)−2
n·1
2n(n+1)=4−n
30. S−rS =
n
X
k=0
ark−
n
X
k=0
ark+1
=(a+ar +ar2+···+arn)−(ar +ar2+ar3+···+arn+1)
=a−arn+1 =a(1 −rn+1)
so (1 −r)S=a(1 −rn+1), hence S=a(1 −rn+1)/(1 −r)
31. (a)
19
X
k=0
3k+1 =
19
X
k=0
3(3k)=3(1 −320)
1−3=3
2(320 −1)
(b)
25
X
k=0
2k+5 =
25
X
k=0
252k=25(1 −226)
1−2=2
31 −25
(c)
100
X
k=0
(−1) µ−1
2¶k
=(−1)(1 −(−1/2)101)
1−(−1/2) =−2
3(1+1/2
101)
32. (a) 1.999023438,1.999999046,2.000000000; 2 (b) 2.831059456,2.990486364,2.999998301; 3
33. 1+2+3+···+n
n
2=
n
X
k=1
k
n2=1
n2
n
X
k=1
k=1
n2·1
2n(n+1)= n+1
2n; lim
n→+∞
n+1
2n=1
2
219 Chapter 7
34. 12+2
2+3
2+···+n
2
n
3=
n
X
k=1
k2
n3=1
n3
n
X
k=1
k2=1
n3·1
6n(n+ 1)(2n+1)= (n+ 1)(2n+1)
6n
2;
lim
n→+∞
(n+ 1)(2n+1)
6n
2= lim
n→+∞
1
6(1+1/n)(2+1/n)=1
3
35.
n
X
k=1
5k
n2=5
n2
n
X
k=1
k=5
n2·1
2n(n+1)= 5(n+1)
2n; lim
n→+∞
5(n+1)
2n=5
2
36.
n−1
X
k=1
2k2
n3=2
n3
n−1
X
k=1
k2=2
n3·1
6(n−1)(n)(2n−1) = (n−1)(2n−1)
3n2;
lim
n→+∞
(n−1)(2n−1)
3n2= lim
n→+∞
1
3(1 −1/n)(2 −1/n)=2
3
37. (a)
5
X
j=0
2j(b)
6
X
j=1
2j−1(c)
7
X
j=2
2j−2
38. (a)
5
X
k=1
(k+ 4)2k+8 (b)
13
X
k=9
(k−4)2k
39. (a)
18
X
k=1
sin ³π
k´(b)
6
X
k=0
ek=e7−1
e−1
40. 1+3+5+···+(2n−1) =
n
X
k=1
(2k−1)=2
n
X
k=1
k−
n
X
k=1
1=2·1
2
n(n+1)−n=n
2
41. For 1 ≤k≤nthe k-th L-shaped strip consists of the corner square, a strip above and a strip to the
right for a combined area of 1 + (k−1)+(k−1)=2k−1, so the total area is
n
X
k=1
(2k−1) = n2.
42. n(n+1)
2= 465, n2+n−930=0,(n+ 31)(n−30)=0,n= 30.
43. (35−34)+(3
6−3
5
)+···+(3
17 −316)=3
17 −34
44. µ1−1
2¶+µ1
2−1
3¶+···+µ1
50 −1
51¶=50
51
45. µ1
22−1
12¶+µ1
32−1
22¶+···+µ1
202−1
192¶=1
202−1=−399
400
46. (22−2)+(2
3−2
2
)+···+(2
101 −2100)=2
101 −2
47. (a)
n
X
k=1
1
(2k−1)(2k+1)=1
2
n
X
k=1 µ1
2k−1−1
2k+1¶
=1
2·µ1−1
3¶+µ1
3−1
5¶+µ1
5−1
7¶+···+µ1
2n−1−1
2n+1¶¸
=1
2·1−1
2n+1¸=n
2n+1
(b) lim
n→+∞
n
2n+1 =1
2
Exercise Set 7.4 220
48. (a)
n
X
k=1
1
k(k+1)=
n
X
k=1 µ1
k−1
k+1¶
=µ1−1
2¶+µ1
2−1
3¶+µ1
3−1
4¶+···+µ1
n−1
n+1¶
=1−1
n+1 =n
n+1
(b) lim
n→+∞
n
n+1 =1
49. both are valid 50. none is valid
51.
n
X
i=1
(xi−¯x)=
n
X
i=1
xi−
n
X
i=1
¯x=
n
X
i=1
xi−n¯xbut ¯x=1
n
n
X
i=1
xithus
n
X
i=1
xi=n¯xso
n
X
i=1
(xi−¯x)=n¯x−n¯x=0
52.
n
X
k=1
(ak−bk)=(a
1−b
1)+(a
2−b
2
)+···+(a
n−b
n
)
=(a
1+a
2+···+a
n)−(b
1+b
2+···+b
n)=
n
X
k=1
ak−
n
X
k=1
bk
53.
n
X
k=1 £(k+1)
4−k
4
¤=(n+1)
4−1 (telescoping sum), expand the
quantity in brackets to get
n
X
k=1
(4k3+6k
2+4k+1)=(n+1)
4−1,
4
n
X
k=1
k3+6
n
X
k=1
k2+4
n
X
k=1
k+
n
X
k=1
1=(n+1)
4−1
n
X
k=1
k3=1
4"(n+1)
4−1−6
n
X
k=1
k2−4
n
X
k=1
k−
n
X
k=1
1#
=1
4[(n+1)
4−1−n(n+ 1)(2n+1)−2n(n+1)−n]
=1
4(n+ 1)[(n+1)
3−n(2n+1)−2n−1]
=1
4(n+ 1)(n3+n2)=1
4
n
2
(n+1)
2
54. If n=2mthen 2m+2(m−1)+···+2·2+2=2
m
X
k=1
k=2·m(m+1)
2=m(m+1)= n
2+2n
4;
if n=2m+ 1 then (2m+1)+(2m−1)+···+5+3+1=
m+1
X
k=1
(2k−1)
=2
m+1
X
k=1
k−
m+1
X
k=1
1=2·(m+ 1)(m+2)
2−(m+1)=(m+1)
2=n
2+2n+1
4
55. 50·30+49·29+···+22·2+21·1=
30
X
k=1
k(k+20) =
30
X
k=1
k2+20
30
X
k=1
k=30 ·31 ·61
6+2030 ·31
2=18,755
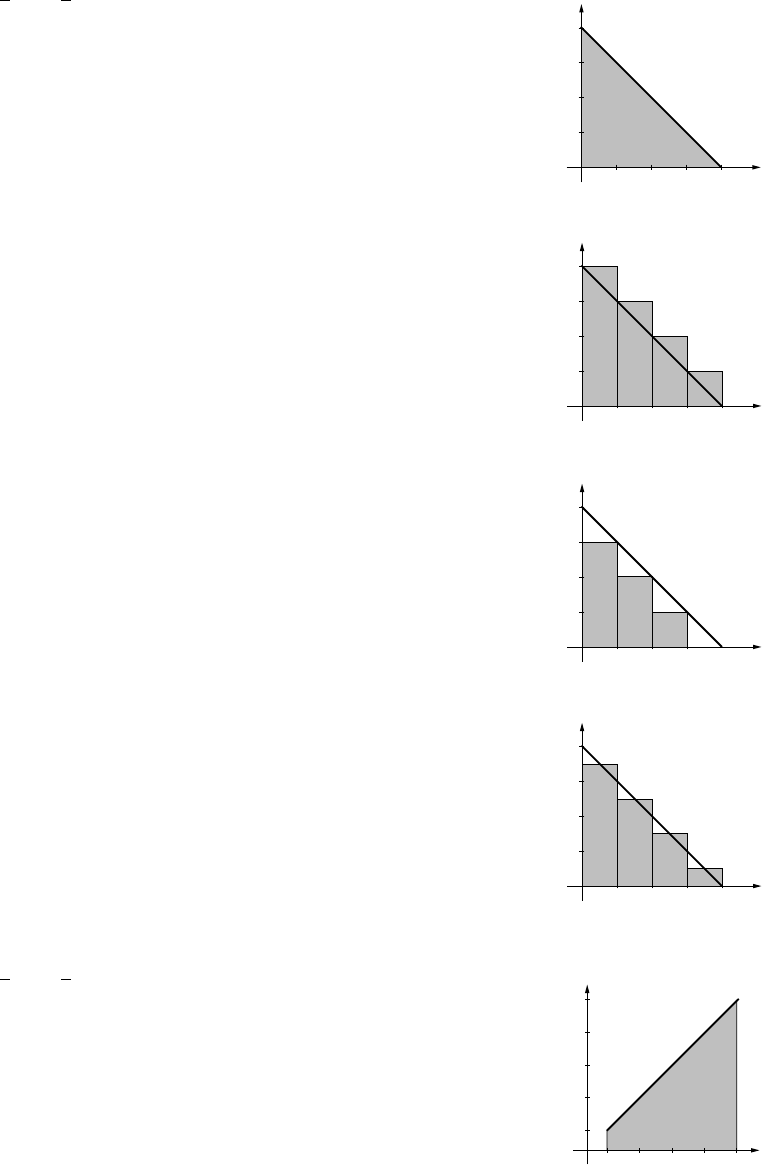
221 Chapter 7
EXERCISE SET 7.5
1. (a) 1
2bh =1
2·4·4=8 y
x
1
1A
(b) The approximation is greater than A,
as the rectangles extend beyond the area.
4
X
k=1
f(x∗
k)∆x=(4+3+2+1)(1) = 10
y
x
1
1
(c) The approximation is less than A,
as the rectangles lie inside the area.
4
X
k=1
f(x∗
k)∆x=(3+2+1+0)(1) = 6
y
x
1
1
(d) The approximation is equal to A,
as can be seen by measuring congruent triangles.
4
X
k=1
f(x∗
k)∆x=(3.5+2.5+1.5+0.5)(1) = 8
y
x
1
1
2. (a) 1
2bh =1
24·12=24 y
x
2
6
3
9
18
6
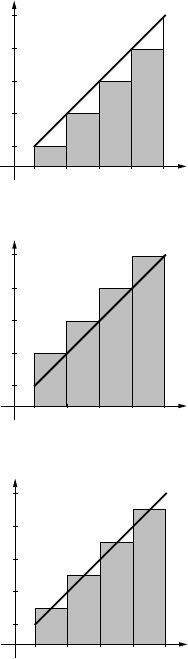
Exercise Set 7.5 222
(b) The approximation is less than A,
as the rectangles lie inside the area.
4
X
k=1
f(x∗
k)∆x=(6+9+12+15)(1) = 42
y
x
2
6
3
9
18
6
(c) The approximation is greater than A,
as the rectangles extend beyond the area.
4
X
k=1
f(x∗
k)∆x= (9 + 12 + 15 + 18)(1) = 54
y
x
2
6
3
9
18
6
(d) The approximation is equal to A,
as can be seen by measuring congruent triangles.
4
X
k=1
f(x∗
k)∆x=(7.5+10.5+13.5+16.5)(1) = 48
y
x
2
6
3
9
18
6
3. (a) x∗
k=0,1,2,3,4
5
X
k=1
f(x∗
k)∆x=(1+2+5+10+17)(1) = 35
(b) x∗
k=1,2,3,4,5
5
X
k=1
f(x∗
k)∆x=(2+5+10+17+26)(1) = 60
(c) x∗
k=1/2,3/2,5/2,7/2,9/2
5
X
k=1
f(x∗
k)∆x=(5/4+13/4+29/4+53/4+85/4)(1) = 185/4=46.25
4. (a) x∗
k=1,2,3,4,5
5
X
k=1
f(x∗
k)∆x=(1+8+27+64+125)(1) = 225
(b) x∗
k=2,3,4,5,6
5
X
k=1
f(x∗
k)∆x= (8 + 27 + 64 + 125 + 216)(1) = 440
(c) x∗
k=3/2,5/2,7/2,9/2,11/2
5
X
k=1
f(x∗
k)∆x= (27/8 + 125/8 + 343/8 + 729/8 + 1331/8)(1) = 2555/8 = 319.375
223 Chapter 7
5. (a) x∗
k=−π/2,−π/4,0,π/4
4
X
k=1
f(x∗
k)∆x=(0+1/
√
2+1+1/
√
2)(π/4)=(1+√
2)π/4≈1.896
(b) x∗
k=−π/4,0,π/4,π/2
4
X
k=1
f(x∗
k)∆x=(1/
√
2+1+1/
√
2 + 0)(π/4)=(1+√
2)π/4≈1.896
(c) x∗
k=−3π/8,−π/8,π/8,3π/8
4
X
k=1
f(x∗
k)∆x=·cos 3π
8+ cos π
8+ cos π
8+ cos 3π
8¸π
4=πcos π
4cos π
8=³π√2 cos π
8´/2≈2.052
6. (a) x∗
k=0,1,2,3,4
4
X
k=1
f(x∗
k)∆x=¡e0+e1+e2+e3+e4¢(1)=(1−e
5
)/(1 −e)=85.791
(b) x∗
k=1,2,3,4,5
4
X
k=1
f(x∗
k)∆x=¡e1+e2+e3+e4+e5¢(1) = e(1 −e5)/(1 −e) = 233.204
(c) x∗
k=1/2,3/2,5/2,7/2,9/2
4
X
k=1
f(x∗
k)∆x=³e1/2+e3/2+e5/2+e7/2+e9/2´(1) = e1/2(1 −e5)/(1 −e) = 141.446
7. left endpoints: x∗
k=1,2,3,4;
4
X
k=1
f(x∗
k)∆x=(2+3+2+1)(1) = 8
right endpoints: x∗
k=2,3,4,5;
4
X
k=1
f(x∗
k)∆x=(3+2+1+2)(1) = 8
8. (a) A=1
2(h1+h2)w=1
2(4 + 16)(4) = 40 y
x
1
4
2
7
16
5
(b) (left) x∗
k=1,2,3,4;
4
X
k=1
f(x∗
k)∆x=(4+7+10+13)(1) = 34
(right) x∗
k=2,3,4,5;
4
X
k=1
f(x∗
k)∆x= (7 + 10 + 13 + 16)(1) = 46; the average is 1
2(34 + 46) = 40
(c) The right endpoint approximation exceeds the true area by four triangles; the true area exceeds
the left endpoint approximation by four different, but congruent, triangles.
9. 0.718771403, 0.668771403, 0.692835360 10. 0.761923639, 0.584145862, 0.663501867
11. 0.919403170, 1.07648280, 1.001028825 12. 4.884074732, 5.684074732, 5.347070728
13. 0.351220577, 0.420535296, 0.386502483 14. 1.63379940, 1.805627583, 1.717566087
Exercise Set 7.5 224
15. n1/x 1/x2sin x√xln x ex
(a) 25 0.693097198 0.666154270 1.000164512 5.336963538 0.386327689 1.718167282
(b) 50 0.693134682 0.666538346 1.000041125 5.334644416 0.386302694 1.718253191
(c) 100 0.693144056 0.666634573 1.000010281 5.333803776 0.3862964444 1.718274669
17. (a) A=1
2(3)(3) = 9/2
3x
y
A
(b) −A=−1
2(1)(1 + 2) = −3/2
-2 -1 x
y
A
(c) −A1+A2=−1
2+8=15/2
-1
4x
y
A1
A2
(d) −A1+A2=0
-5
5x
y
A1
A2
18. (a) A=1
2(1)(2) = 1
2
1
x
y
A
(b) A=1
2(2)(3/2+1/2)=2
-1 1
1
x
y
A
(c) −A=−1
2(1/2)(1) = −1/4
2
1
x
y
A
(d) A1−A2=1−1/4=3/4
2
1
x
y
A
2
A
1
225 Chapter 7
19. (a) A=2(5)=10
y
x
1
2
12345
A
(b) 0; A1=A2by symmetry
6
cx
y
A1
A2
(c) A1+A2=1
2(5)(5/2) + 1
2(1)(1/2)
=13/2
-1
5
2x
y
3
2
A1A2
(d) 1
2[π(1)2]=π/2
y
x
1
-1 1
A
20. (a) A= (6)(5) = 30
-10 -5
6
x
y
A
(b) −A1+A2= 0 because
A1=A2by symmetry
$
4x
y
A1
A2
(c) A1+A2=1
2(2)(2) + 1
2(1)(1) = 5/2
2
2
3x
y
A1A2
(d) 1
4π(2)2=π
y
x
2
2
A
21. (a) 0.8(b) −2.6(c) −1.8(d) −0.3
22. (a) Z1
0
f(x)dx =Z1
0
2xdx =x2¸1
0
=1
(b) Z1
−1
f(x)dx =Z1
−1
2xdx =x2¸1
−1
=1
2−(−1)2=0
Exercise Set 7.5 226
(c) Z10
1
f(x)dx =Z10
1
2dx =2x
¸10
1
=18
(d) Z5
1/2
f(x)dx =Z1
1/2
2xdx +Z5
1
2dx =x2¸1
1/2
+2x
#5
1
=1
2−(1/2)2+2·5−2·1=3/4+8=35/4
23. Z2
−1
f(x)dx +2Z2
−1
g(x)dx =5+2(−3) = −1
24. 3Z4
1
f(x)dx −Z4
1
g(x)dx = 3(2) −10 = −4
25. Z5
1
f(x)dx =Z5
0
f(x)dx −Z1
0
f(x)dx =1−(−2)=3
26. Z−2
3
f(x)dx =−Z3
−2
f(x)dx =−·Z1
−2
f(x)dx +Z3
1
f(x)dx¸=−(2 −6)=4
27. (a) Z1
0
xdx +2Z1
0p1−x
2
dx =1/2+2(π/4)=(1+π)/2
(b) 4Z3
−1
dx −5Z3
−1
xdx =4·4−5(−1/2+(3·3)/2) = −4
28. (a) Z0
−3
2dx +Z0
−3p9−x2dx =2·3+(π(3)2)/4=6+9π/4
(b) Z2
−2
dx −3Z2
−2|x|dx =4·1−3(2)(2 ·2)/2=−8
29. (a) √x>0, 1 −x<0on[2,3] so the integral is negative
(b) x2>0, 3 −cos x>0 for all xso the integral is positive
30. (a) x4>0, √3−x>0on[−3,−1] so the integral is positive
(b) x3−9<0, |x|+1>0on[−2,2] so the integral is negative
31. Z10
0p25 −(x−5)2dx =π(5)2/2=25π/2
32. Z3
0p9−(x−3)2dx =π(3)2/4=9π/4
33. (a) Z3
−3
4x(1 −3x)dx (b) Z1
0
exdx
34. (a) Z2
1
x3dx (b) Zπ/2
0
sin2xdx
35. Z1
0
(3x+1)dx =5/236. Z2
−2p4−x2dx =π(2)2/2=2π
37. (a) lim
max ∆xk→0
n
X
k=1
2x∗
k∆xk;a=1,b=2 (b) lim
max ∆xk→0
n
X
k=1
x∗
k
x∗
k+1∆x
k;a=0,b=1
227 Chapter 7
38. (a) lim
max ∆xk→0
n
X
k=1
ln x∗
k∆xk,a=1,b=2
(b) lim
max ∆xk→0
n
X
k=1
(1 + cos x∗
k)∆x
k,a=−π/2, b=π/2
39. (a) x∗
k+1 =x∗
k+1
nand x∗
1=1+1
n
,sox
∗
2=x
∗
1+1
n=1+2
n
,x
∗
k+1 =x∗
k+1
n=1+k+1
nfor
k=2,3,···,n−1
(b) f(x∗
k)=1+k
nand ∆x=1
n
(c) 1
n
n
X
k=1
1+ 1
n
2
n
X
k=1
k=1
nn+1
n2
n(n+1)
2=3
2+1
2n
(d) lim
n→+∞µ3
2+1
2n¶=3
2which is the area of the trapezoid with base 1 and sides 1 and 2
40. f(x∗
k)=1+k−1
n,
n
X
k=1
f(x∗
k)∆x=
n
X
k=1 µ1+k−1
n¶1
n=1
nn+1
n
2
(n−1)n
2=3
2−1
2n;
lim
n→+∞µ3
2−1
2n¶=3
2
41. (a) (right) ∆x=b−a
n=1
n,x∗
k=k
n,
n
X
k=1
f(x∗
k)∆x=
n
X
k=1 µk
n¶21
n=1
n3
n
X
k=1
k2=1
n3
n(n+ 1)(2n+1)
6; lim
n→+∞
n
X
k=1
f(x∗
k)∆x=2
6=1
3
(b) (left) ∆x=b−a
n=1
n,x∗
k=k−1
n,
n
X
k=1
f(x∗
k)∆x=
n
X
k=1 µk−1
n¶21
n=1
n3
n
X
k=1
(k−1)2=1
n3
(n−1)n(2n−1)
6;
lim
n→+∞
n
X
k=1
f(x∗
k)∆x=2
6=1
3
42. (a) (right) ∆x=b−a
n=3
n,x∗
k=3k
n,
n
X
k=1
f(x∗
k)∆x=
n
X
k=1 Ã4−1
4µ3k
n¶2!3
n=12
n
n
X
k=1
1−27
4n3
n
X
k=1
k2=12−27
4n3
n(n+ 1)(2n+1)
6;
lim
n→+∞
n
X
k=1
f(x∗
k)∆x=12−27(2)
4(6) =39
4
(b) (left) ∆x=b−a
n=3
n,x∗
k=3(k−1)
n,
n
X
k=1
f(x∗
k)∆x=
n
X
k=1 Ã4−1
4µ3(k−1)
n¶2!3
n=12
n
n
X
k=1
1−27
4n3
n
X
k=1
(k−1)2=12−27
4n3
(n−1)n(2n−1)
6;
lim
n→+∞
n
X
k=1
f(x∗
k)∆x=12−27(2)
4(6) =39
4
Exercise Set 7.5 228
43. (a) (right) ∆x=b−a
n=4
n,x∗
k=2+4k
n,
n
X
k=1
f(x∗
k)∆x=
n
X
k=1 µ2+4k
n¶34
n= 32+192
n2
n(n+1)
2+384
n3
n(n+ 1)(2n+1)
6+256
n4µn(n+1)
2¶2
;
lim
n→+∞
n
X
k=1
f(x∗
k)∆x=32+192
2+384(2)
6+256
4= 320
(b) (left) ∆x=b−a
n=4
n,x∗
k=2+4(k−1)
n,
n
X
k=1
f(x∗
k)∆x=
n
X
k=1 µ2+4(k−1)
n¶34
n= 32+192
n2
(n−1)n
2+384
n3
(n−1)n(2n−1)
6+256
n4µ(n−1)n
2¶2
;
lim
n→+∞
n
X
k=1
f(x∗
k)∆x=32+192
2+384(2)
6+256
4= 320
44. (a) (right) ∆x = b−a
n=2
n,x∗
k=−3+2k
n,
n
X
k=1
f(x∗
k)∆x=
n
X
k=1 Ã1−µ2k
n−3¶3!2
n=56
n
n
X
k=1
1−108
n2
n
X
k=1
k+72
n3
n
X
k=1
k2−16
n4
n
X
k=1
k3
=56−108
n2
n(n+1)
2+72
n3
n(n+ 1)(2n+1)
6−16
n4µn(n+1)
2¶2
;
lim
n→+∞
n
X
k=1
f(x∗
k)∆x=56−54 + 72(2)
6−16
4=22
(b) (left) ∆x = b−a
n=2
n,x∗
k=−3+2(k−1)
n,
n
X
k=1
f(x∗k)∆x=
n
X
k=1 Ã1−µ2(k−1)
n−3¶3!2
n
=56
n
n
X
k=1
1−108
n2
n
X
k=1
(k−1) + 72
n3
n
X
k=1
(k−1)2−16
n4
n
X
k=1
(k−1)3
=56−108
n2
(n−1)n
2+72
n3
(n−1)n(2n−1)
6−16
n4µ(n−1)n
2¶2
;
lim
n→+∞
n
X
k=1
f(x∗
k)∆x=56−108
2+72(2)
6−16
4=22
45. (a) fis continuous on [−1,1] so fis integrable there by part (a) of Theorem 7.5.8
(b) |f(x)|≤1sofis bounded on [−1,1], and fhas one point of discontinuity, so by part (b) of
Theorem 7.5.8 fis integrable on [−1,1]
(c) fis not bounded on [-1,1] because lim
x→0f(x)=+∞,sofis not integrable on [0,1]
(d) f(x) is discontinuous at the point x= 0 because lim
x→0sin 1
xdoes not exist. fis continuous
elsewhere. −1≤f(x)≤1 for xin [−1,1] so fis bounded there. By part (b), Theorem 7.5.8, f
is integrable on [−1,1].
46. Each subinterval of a partition of [a, b] contains both rational and irrational numbers. If all x∗
kare
chosen to be rational then
n
X
k=1
f(x∗
k)∆xk=
n
X
k=1
(1)∆xk=
n
X
k=1
∆xk=b−aso lim
max ∆xk→0
n
X
k=1
f(x∗
k)∆xk=b−a.
If all x∗
kare irrational then lim
max ∆xk→0
n
X
k=1
f(x∗
k)∆xk=0. fis not integrable on [a, b] because the
preceding limits are not equal.

229 Chapter 7
47. (a) Let Sn=
n
X
k=1
f(x∗
k)∆xkand S=Zb
a
f(x)dx then
n
X
k=1
cf(x∗
k)∆xk=cSnand we want to prove
that lim
max ∆xk→0cSn=cS.Ifc= 0 the result follows immediately, so suppose that c6= 0 then for
any ²>0, |cSn−cS|=|c||Sn−S|<²if |Sn−S|<²/|c|. But because fis integrable on [a, b],
there is a number δ>0 such that |Sn−S|<²/|c|whenever max ∆xk<δso |cSn−cS|<²and
hence lim
max ∆xk→0cSn=cS.
(b) Let Rn=
n
X
k=1
f(x∗
k)∆xk,Sn=
n
X
k=1
g(x∗
k)∆xk,Tn=
n
X
k=1
[f(x∗
k)+g(x
∗
k
)]∆xk,R=Zb
a
f(x)dx, and
S=Zb
a
g(x)dx then Tn=Rn+Snand we want to prove that lim
max ∆xk→0Tn=R+S.
|Tn−(R+S)|=|(Rn−R)+(S
n−S)|≤|R
n−R|+|S
n−S|
so for any ²>0|T
n−(R+S)|<²if |Rn−R|+|Sn−S|<².
Because fand gare integrable on [a, b], there are numbers δ1and δ2such that
|Rn−R|<²/2 for max ∆xk<δ
1and |Sn−S|<²/2 for max ∆xk<δ
2
.
If δ= min(δ1,δ
2) then |Rn−R|<²/2 and |Sn−S|<²/2 for max ∆xk<δthus
|Rn−R|+|Sn−S|<²and so |Tn−(R+S)|<²for max ∆xk<δwhich shows that
lim
max ∆xk→0Tn=R+S.
48. For the smallest, find x∗
kso that f(x∗
k) is minimum on each subinterval: x∗
1=1,x
∗
2=3/2, x∗
3=3so
(2)(1)+(7/4)(2) +(4)(1) = 9.5. For the largest, find x∗
kso that f(x∗
k) is maximum on each subinterval:
x∗
1=0,x
∗
2=3,x
∗
3= 4 so (4)(1) + (4)(2) + (8)(1) = 20.
EXERCISE SET 7.6
1. (a) Z2
0
(2 −x)dx =(2x−x
2
/2)¤2
0=4−4/2=2
(b) Z1
−1
2dx =2x
¸1
−1
= 2(1) −2(−1)=4
(c) Z3
1
(x+1)dx =(x
2
/2+x)
i3
1=9/2+3−(1/2+1)=6
2. (a) Z5
0
xdx =x2/2¸5
0
=25/2(b) Z9
3
5dx =5x
¸9
3
= 5(9) −5(3) = 30
(c) Z2
−1
(x+3)dx =(x
2
/2+3x)
¸2
−1
=4/2+6−(1/2−3)=21/2
3. Z3
2
x3dx =x4/4¸3
2
=81/4−16/4=65/44. Z1
−1
x4dx =x5/5¸1
−1
=1/5−(−1)/5=2/5
5. Z9
1
√xdx =2
3x3/2¸9
1
=2
3(27 −1)=52/36. Z4
1
x−3/5dx =5
2x2/5¸4
1
=5
2(42/5−1)
7. Z3
1
exdx =ex¸3
1
=e3−e8. Z5
1
1
xdx =lnx
¸5
1
=ln5−ln1=ln5
9. µ1
3x3−2x2+7x
¶¸0
−3
=48 10. µ1
2x2+1
5x5¶¸2
−1
=81/10

Exercise Set 7.6 230
11. Z3
1
x−2dx =−1
x¸3
1
=2/312. Z2
1
x−6dx =−1
5x5¸2
1
=31/160
13. 4
5x5/2¸9
4
= 844/514. µ3x5/3+4
x¶¸8
1
= 179/2
15. −cos θiπ/2
−π/2=0 16. tan θiπ/4
0=1
17. sin xiπ/4
−π/4=√218. µ1
2x2−sec x¶¸1
0
=3/2−sec(1)
19. 5exi3
ln 2 =5e
3−5(2) = 5e3−10 20. (ln x)/2i1
1/2= (ln 2)/2
21. µ6√t−10
3t3/2+2
√t¶¸4
1
=−55/322. µ8√y+4
3y3/2−2
3y3/2¶¸9
4
= 10819/324
23. µ1
2x2−2 cot x¶¸π/2
π/6
=π2/9+2
√
3
24. ³ln x+√2ex+ csc x´i2
1=ln2+√
2(e2−e) + csc 2 −csc 1
26. µa1/2x−2
3x3/2¶#4a
a
=−5
3a3/2
27. (a) Z3/2
0
(3 −2x)dx +Z2
3/2
(2x−3)dx =(3x−x
2
)
¸3/2
0
+(x
2−3x)
¸2
3/2
=9/4+1/4=5/2
(b) Zπ/2
0
cos xdx+Z3π/4
π/2
(−cos x)dx = sin x¸π/2
0−sin x¸3π/4
π/2
=2−√
2/2
28. (a) Z0
−1
√2−xdx+Z2
0
√2+xdx=−2
3(2 −x)3/2¸0
−1
+2
3(2+x)3/2¸2
0
=−2
3(2√2−3√3) + 2
3(8 −2√2) = 2
3(8 −4√2+3
√
3)
(b) Z0
−1
(1−ex)dx+Z1
0
(ex−1)dx =(x−e
x
)
¸0
−1
+(ex−x)¸1
0
=−1−(−1−e−1)+e−1−1=e+1/e−2
29. Z0
−2
x2dx +Z3
0
(−x)dx =1
3x3¸0
−2−1
2x2¸3
0
=−11/6
30. Z1
0
√xdx+Z4
1
1
x
2dx =2
3x3/2¸1
0−1
x¸4
1
=17/12
31. 0.665867079; Z3
1
1
x2dx =−1
x¸3
1
=2/3
32. 1.000257067; Zπ/2
0
sin xdx =−cos x¸π/2
0
=1
231 Chapter 7
33. 1.098242635; Z3
1
1
xdx =lnx
¸3
1
=ln3≈1.098612289
35. A=Z3
0
(x2+1)dx =µ1
3x3+x¶¸3
0
=12
36. A=Z2
1
(−x2+3x−2)dx =µ−1
3x3+3
2x2−2x¶¸2
1
=1/6
37. A=Z2π/3
0
3 sin xdx=−3 cos x#2π/3
0
=9/238. A=−Z−1
−2
x3dx =−1
4x4¸−1
−2
=15/4
39. A1=Z−2
−3
(x2−3x−10)dx =µ1
3x3−3
2x2−10x¶¸−2
−3
=23/6,
A
2=−Z5
−2
(x
2−3x−10)dx = 343/6,
A3=Z8
5
(x2−3x−10)dx = 243/6, A=A1+A2+A3= 203/2
-3
-2
85
10
x
y
A1
A2
A3
40. (a) the area is positive
(b) Z5
−2µ1
100x3−1
20x2−1
25x+1
5¶dx =µ1
400x4−1
60x3−1
50x2+1
5x¶¸5
−2
=343
1200
41. (a) the area between the curve and the x-axis breaks into equal parts, one above and one below the
x-axis, so the integral is zero
(b) Z1
−1
x3dx =1
4x4¸1
−1
=1
4(14−(−1)4)=0;
Zπ/2
−π/2
sin xdx =−cos x#π/2
−π/2
=−cos(π/2) + cos(−π/2)=0+0=0
(c) The area on the left side of the y-axis is equal to the area on the right side, so
Za
−a
f(x)dx =2Za
0
f(x)dx
(d) Z1
−1
x2dx =1
3x3¸1
−1
=1
3(13−(−1)3)=2
3=2Z1
0
x
2
dx;
Zπ/2
−π/2
cos xdx = sin x#π/2
−π/2
= sin(π/2) −sin(−π/2)=1+1=2=2Zπ/2
0
cos xdx
42. The numerator is an odd function and the denominator is an even function, so the integrand is an
odd function and the integral is zero.
43. (a) x3+1 (b) F(x)=µ1
4
t
4+t
¶¸x
1
=1
4x4+x−5
4;F0(x)=x
3+1
44. (a) cos 2x(b) F(x)= 1
2sin 2t¸x
π/4
=1
2sin 2x−1
2,F0(x) = cos 2x
45. (a) sin √x(b) ex2
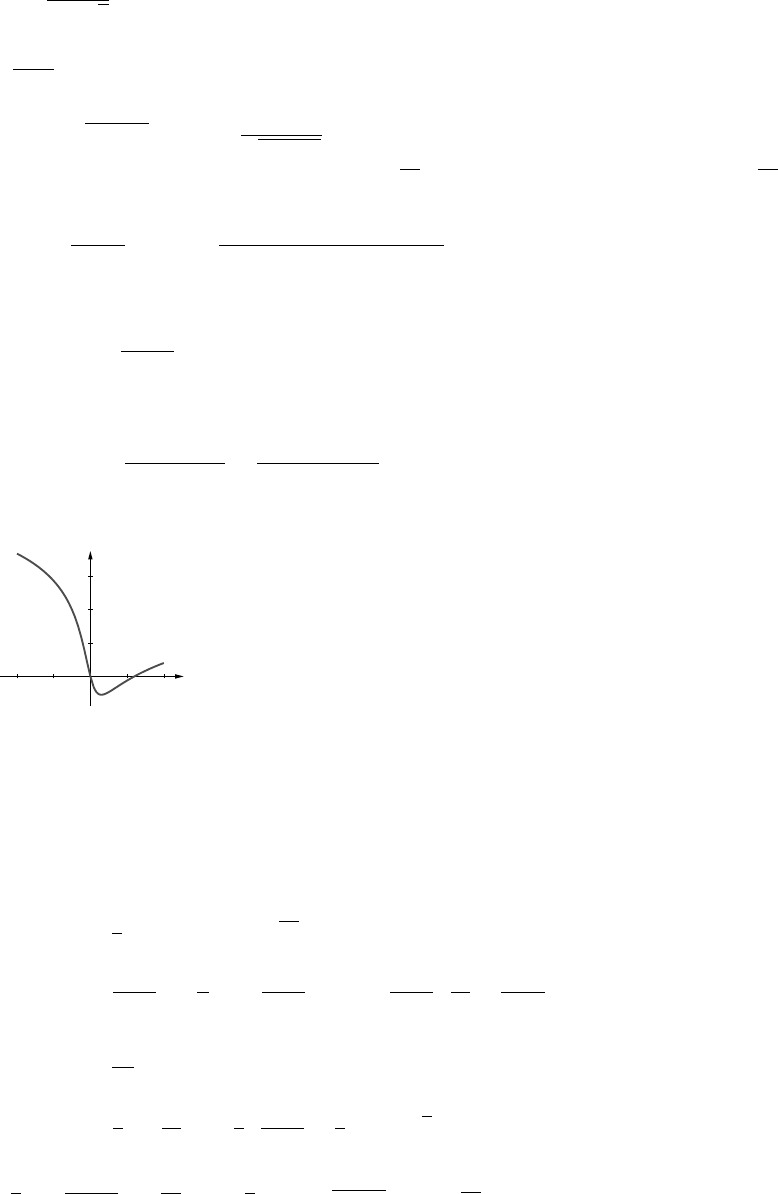
Exercise Set 7.6 232
46. (a) 1
1+√
x(b) ln x
47. −x
cos x48. |u|
49. F0(x)=√
3x
2+1,F00(x)= 3x
√
3x
2+1
(a) 0(b) √13 (c) 6/√13
50. F0(x)= cos x
x2+3,F00(x)=−(x
2+ 3) sin x−2xcos x
(x2+3)
2
(a) 0(b) 1/3(c) 0
51. (a) F0(x)= x−3
x
2+7 = 0 when x= 3, which is a relative minimum, and hence the absolute minimum,
by the first derivative test.
(b) increasing on [3,+∞), decreasing on (−∞,3]
(c) F00(x)=7+6x−x
2
(x
2+7)
2=(7 −x)(1 + x)
(x2+7)
2; concave up on (−1,7), concave down on (−∞,−1) and
on (7,+∞)
52. F
t
2
3
-20 -10 10 20
53. (a) (0,+∞) because fis continuous there and 1 is in (0,+∞)
(b) at x= 1 because F(1)=0
54. (a) (−3,3) because fis continuous there and 1 is in (−3,3)
(b) at x= 1 because F(1)=0
55. (a) fave =1
9Z9
0
x1/2dx =2;√
x
∗=2,x
∗=4
(b) fave =1
e−1Ze
1
1
xdx =1
e−1ln x¸e
1
=1
e−1;1
x∗=1
e−1,x∗=e−1
56. (a) fave =1
2πZπ
−π
sin xdx= 0; sin x∗=0,x
∗=−π, 0,π
(b) fave =1
2Z3
1
1
x2dx =1
3;1
(x∗)2=1
3,x∗=√3
57. √2≤√x3+2≤√
29, so 3√2≤Z3
0px3+2dx ≤3√29
58. Let f(x)=xsin x,f(0) = f(1)=0,f
0
(x) = sin x+xcos x= 0 when x=−tan x,x≈2.0288,
so fhas an absolute maximum at x≈2.0288; f(2.0288) ≈1.8197, so 0 ≤xsin x≤1.82 and
0≤Zπ
0
xsin xdx ≤1.82π=5.72
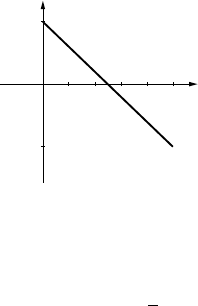
233 Chapter 7
59. 0≤ln x≤ln 5 for xin [1,5], so 0 ≤Z5
1
ln xdx ≤4ln5
60. (a) £cF (x)¤b
a=cF (b)−cF (a)=c[F(b)−F(a)] = c£F(x)¤b
a
(b) £F(x)+G(x)
¤b
a=[F(b)+G(b)] −[F(a)+G(a)]
=[F(b)−F(a)]+[G(b)−G(a)] = F(x)¤b
a+G(x)¤b
a
(c) £F(x)−G(x)¤b
a=[F(b)−G(b)] −[F(a)−G(a)]
=[F(b)−F(a)] −[G(b)−G(a)] = F(x)¤b
a−G(x)¤b
a
EXERCISE SET 7.7
1. (a) the increase in height in inches, during the first ten years
(b) the change in the radius in centimeters, during the time interval t=1tot= 2 seconds
(c) the change in the speed of sound in ft/s, during an increase in temperature from t=32
◦
Fto
t= 100◦F
(d) the displacement of the particle in cm, during the time interval t=t1to t=t2seconds
2. (a) Z1
0
V(t)dt gal
(b) the change f(x1)−f(x2) in the values of fover the interval
3. (a) displ = s(3) −s(0)
=Z3
0
v(t)dt =Z2
0
(1 −t)dt +Z3
2
(t−3)dt =(t−t
2
/2)¸2
0
+(t
2
/2−3t)
¸3
2
=−1/2;
dist = Z3
0|v(t)|dt =(t−t
2
/2)¸1
0
+(t
2
/2−t)
¸2
1
+(t
2
/2−3t)
¸3
2
=1/2
(b) displ = s(3) −s(0)
=Z3
0
v(t)dt =Z1
0
tdt +Z2
1
dt +Z3
2
(5 −2t)dt =t2/2¸2
0
+t¸3
2
+(5t−t
2
)
¸3
2
=5;
dist = Z1
0
tdt +Z2
1
dt +Z5/2
2
(5 −2t)dt +Z3
5/2
(2t−5)dt
=t2/2¸1
0
+t¸2
1
+(5t−t
2
)
¸5/2
2
+(t
2−5t)
¸3
5/2
=5/2
4. v
t
-1
1
246810
5. (a) v(t)=20+Zt
0
a(u)du; add areas of the small blocks to get
v(5) ≈20 + 1
2(1.5+2.7+4.6+6.2+7.6)=31.3
Exercise Set 7.7 234
(b) v(10) = v(4) + Z10
5
a(u)du ≈31.3+1
2(8.6+9.3+9.7+10+10.1)=55.15
6. a>0 and therefore (Theorem 7.5.6(a)) v>0, so the particle is always speeding up for 0 <t<10
7. (a) s(t)=Z(t
3−2t
2+1)dt =1
4t4−2
3t3+t+C,
s(0) = 1
4(0)4−2
3(0)3+0+C=1,C=1,s(t)= 1
4
t
4−2
3
t
3+t+1
(b) v(t)=Z4 cos 2tdt= 2 sin 2t+C1,v(0) = 2 sin 0 + C1=−1, C1=−1,
v(t) = 2 sin 2t−1, s(t)=Z(2 sin 2t−1)dt =−cos 2t−t+C2,
s(0) = −cos 0 −0+C
2=−3, C2=−2, s(t)=−cos 2t−t−2
8. (a) s(t)=Z(1 + sin t)dt =t−cos t+C,s(0)=0−cos 0 + C=−3, C=−2, s(t)=t−cos t−2
(b) v(t)=Z(t
2−3t+1)dt =1
3t3−3
2t2+t+C1,
v(0) = 1
3(0)3−3
2(0)2+0+C
1=0,C
1=0,v(t)=1
3
t
3−3
2
t
2+t,
s(t)=Zµ1
3
t
3−3
2
t
2+t
¶dt =1
12t4−1
2t3+1
2t2+C2,
s(0) = 1
12(0)4−1
2(0)3+1
2(0)2+C2=0,C
2=0,s(t)= 1
12t4−1
2t3+1
2t2
9. (a) s(t)=Z(2t−3)dt =t2−3t+C,s(1) = (1)2−3(1) + C=5,C=7,s(t)=t
2−3t+7
(b) v(t)=Zcos tdt = sin t+C1,v(π/2)=2=1+C
1
,C
1=1,v(t) = sin t+1,
s(t)=Z(sin t+1)dt =−cos t+t+C2,s(π/2)=0=π/2+C2,C2=−π/2, s(t)=−cos t+t−π/2
10. (a) s(t)=Zt
2/3
dt =3
5t5/3+C,s(8)=0=3
5
32+C,C=−96
5,s(t)=3
5
t
5/3−96
5
(b) v(t)=Z√
tdt =2
3t3/2+C1,v(4)=1=2
3
8+C
1
,C
1=−13
3,v(t)=2
3
t
3/2−13
3,
s(t)=Zµ2
3
t
3/2−13
3¶dt =4
15t5/2−13
3t+C2,s(4) = −5= 4
1532 −13
34+C
2=−44
5+C2,
C2=19
5,s(t)= 4
15t5/2−13
3t+19
5
11. (a) displacement = s(π/2) −s(0) = Zπ/2
0
sin tdt =−cos t¸π/2
0
=1
distance = Zπ/2
0|sin t|dt =1
(b) displacement = s(2π)−s(π/2) = Z2π
π/2
cos tdt = sin t¸2π
π/2
=−1
distance = Z2π
π/2|cos t|dt =−Z3π/2
π/2
cos tdt +Z2π
3π/2
cos tdt =3
235 Chapter 7
12. (a) displacement = s(6) −s(0) = Z6
0
(2t−4)dt =(t
2−4t)
¸6
0
=12
distance Z6
0|2t−4|dt =Z2
0
(4 −2t)dt +Z6
2
(2t−4)dt =(4t−t
2
)
¸2
0
+(t
2−4t)
¸6
2
=20
(b) displacement = Z5
0|t−3|dt =Z3
0−(t−3)dt +Z5
3
(t−3)dt =13/2
distance = Z5
0|t−3|dt =13/2
13. (a) v(t)=t
3−3t
2+2t=t(t−1)(t−2)
displacement = Z3
0
(t3−3t2+2t)dt =9/4
distance = Z3
0|v(t)|dt =Z1
0
v(t)dt +Z2
1−v(t)dt +Z3
2
v(t)dt =11/4
(b) displacement = Z3
0
(et−2)dt =e3−7
distance = Z3
0|v(t)|dt =−Zln 2
0
v(t)dt +Z3
ln 2
v(t)dt =e3−9+4ln2
14. (a) displacement = Z3
1
(1
2−1
t)dt =1−ln 3
distance = Z3
1|v(t)|dt =−Z2
1
v(t)dt +Z3
2
v(t)dt = 2 ln 2 −ln 3
(b) displacement = Z9
4
3t−1/2dt =6
distance = Z9
4|v(t)|dt =Z9
4
v(t)dt =6
15. v(t)=−2t+3
displacement = Z4
1
(−2t+3)dt =−6
distance = Z4
1|−2t+3|dt =Z3/2
1
(−2t+3)dt +Z4
3/2
(2t−3)dt =13/2
16. v(t)= 1
2t
2−2t
displacement = Z5
1µ1
2t2−2t¶dt =−10/3
distance = Z5
1¯¯¯¯
1
2t2−2t¯¯¯¯
dt =Z4
1−µ1
2t2−2t¶dt +Z5
4µ1
2t2−2t¶dt =17/3
17. v(t)= 2
5√5t+1+8
5
displacement = Z3
0µ2
5√5t+1+8
5¶dt =4
75(5t+1)
3/2+8
5t
¸3
0
= 204/25
distance = Z3
0|v(t)|dt =Z3
0
v(t)dt = 204/25
Exercise Set 7.7 236
18. v(t)=−cos t+2
displacement = Zπ/2
π/4
(−cos t+2)dt =(π+√
2−2)/2
distance = Zπ/2
π/4|−cos t+2|dt =Zπ/2
π/4
(−cos t+2)dt =(π+√
2−2)/2
19. (a) s=Zsin 1
2πt dt =−2
πcos 1
2πt +C
s= 0 when t= 0 which gives C=2
πso s=−2
πcos 1
2πt +2
π.
a=dv
dt =π
2cos 1
2πt. When t=1:s=2/π,v=1,|v|=1,a=0.
(b) v=−3Ztdt =−3
2t
2+C
1,v= 0 when t= 0 which gives C1=0sov=−3
2
t
2
s=−3
2Zt
2
dt =−1
2t3+C2,s= 1 when t= 0 which gives C2=1sos=−1
2
t
3+1.
When t=1:s=1/2, v=−3/2, |v|=3/2, a=−3.
20. (a) negative, because vis decreasing
(b) speeding up when av > 0, so 2 <t<5; slowing down when 1 <t<2
(c) negative, because the area between the graph of v(t) and the t-axis appears to be greater where
v<0 compared to where v>0
21. A=A1+A2=Z1
0
(1 −x2)dx +Z3
1
(x2−1)dx =2/3+20/3=22/3
22. A=A1+A2=Zπ
0
sin xdx −Z3π/2
π
sin xdx =2+1=3
23. A=A1+A2=Z0
−1
(1 −ex)dx +Z1
0
(ex−1)dx =1/e +e−2
24. A=A1+A2=Z1
1/2
1−x
xdx +Z2
1
x−1
xdx =−µ1
2−ln 2¶+(1−ln 2) = 1/2
25. s(t)=20
3t3−50t2+50t+s
0
,s(0) = 0 gives s0=0,sos(t)= 20
3t3−50t2+50t,a(t)=40t−100
150
-100
06
150
-100
06
50
0
06
237 Chapter 7
26. v(t)=2t
2−30t+v0,v(0)=3=v
0
,sov(t)=2t
2−30t+3, s(t)=2
3
t
3−15t2+3t+s
0,s(0) = −5=s
0
,
so s(t)=2
3
t
3−15t2+3t−5
1200
-1200
025
s(t)
500
-200
025
v(t)
70
-30
025
a(t)
27. (a) from the graph the velocity is positive, so the displacement is
always increasing and is therefore positive
v
t
0.2
0.3
0.4
0.5
12345
(b) s(t)=t/2+(t+1)e
−t
28. (a) If t0<1 then the area between the velocity curve and the
t-axis, between t= 0 and t=t0, will always be negative, so
the displacement will be negative.
v
t
-0.2
-0.1
0.1
0.2 0.4 0.6 0.8 1
(b) s(t)=µt
2
2−1
200¶ln(t+0.1) −t2
4+t
20 −1
200 ln 10
29. (a) a(t)=½0,t<4
−10,t>4
a
t
-10
-5
24 12
(b) v(t)=½25,t<4
65 −10t, t > 4
v
t
-40
-20
20
2 4 6 8 10 12
(c) x(t)=½25t, t < 4
65t−5t2−80,t>4
,sox(8) = 120, x(12) = −20
(d) x(6.5) = 131.25
Exercise Set 7.7 238
30. (a) From exercise 30 part (a), in Section 3 of Chapter 6, v2=v2
0−2g(s−s0), so a=−g=v2−v2
0
2(s−s0)
(b) From exercise 30 part (b), in Section 3 of Chapter 6, s=s0+1
2(v0+v)t,sot=2(s−s0)
v0+v
(c) From exercise 30 part (c), in Section 3 of Chapter 6, s=s0+vt +1
2gt2=s0+vt −1
2at2
31. (a) a=−1 mi/h/s = −22/15 ft/s2(b) a= 30 km/h/min = 1/7200 km/s2
32. Take t= 0 when deceleration begins, then a=−10 so v=−10t+C1, but v= 88 when t= 0 which
gives C1=88thusv=−10t+ 88, t≥0
(a) v= 45 mi/h = 66 ft/s, 66 = −10t+ 88, t=2.2s
(b) v= 0 (the car is stopped) when t=8.8s
s=Zvdt =Z(−10t+ 88)dt =−5t2+88t+C
2
, and taking s= 0 when t=0,C
2=0so
s=−5t
2+88t.Att=8.8, s= 387.2. The car travels 387.2 ft before coming to a stop.
33. a=a0ft/s2,v=a0t+v0=a0t+ 132 ft/s, s=a0t2/2 + 132t+s0=a0t2/2 + 132tft; s= 200 ft
when v= 88 ft/s. Solve 88 = a0t+ 132 and 200 = a0t2/2 + 132tto get a0=−121
5when t=20
11,so
s=−12.1t2+ 132t,v=−121
5t+ 132.
(a) a0=−121
5ft/s2(b) v= 55 mi/h = 242
3ft/s when t=70
33 s
(c) v= 0 when t=60
11 s
34. dv/dt =3,v=3t+C
1
, but v=v0when t=0soC
1=v
0
,v=3t+v
0
. From ds/dt =v=3t+v
0we
get s=3t
2
/2+v
0
t+C
2and, with s= 0 when t=0,C
2=0sos=3t
2
/2+v
0
t.s= 40 when t=4
thus 40 = 3(4)2/2+v
0
(4), v0= 4 m/s
35. Suppose s=s0=0,v=v
0=0att=t
0=0;s=s
1= 120, v=v1at t=t1; and s=s2,v=v2=12
at t=t2. From Exercise 30(a),
2.6=a=v
2
1−v
2
0
2(s1−s0),v
2
1=2as1=5.2(120) = 624. Applying the formula again,
−1.5=a=v
2
2−v
2
1
2(s2−s1),v
2
2=v
2
1−3(s2−s1), so
s2=s1−(v2
2−v2
1)/3 = 120 −(144 −624)/3 = 280 m.
36. a(t)=½4,t<2
0,t>2
, so, with v0=0,v(t)=½4t, t < 2
8,t>2
and, since s0=0,s(t)=½2t
2
,t<2
8t−8,t>2
s= 100 when 8t−8 = 100, t= 108/8=13.5s
37. The truck’s velocity is vT= 50 and its position is sT=50t+ 5000. The car’s acceleration is aC=2,
so vC=2t,s
C=t
2(initial position and initial velocity of the car are both zero). sT=sCwhen
50t+ 5000 = t2,t2−50t−5000 = (t+ 50)(t−100) = 0, t= 100 s and sC=sT=t2=10,000 ft
38. Let t= 0 correspond to the time when the leader is 100 m from the finish line; let s= 0 correspond to
the finish line. Then vC= 12, sC=12t−115; aL=0.5 for t>0, vL=0.5t+8, s
L=0.25t2+8t−100.
sC=0att= 115/12 ≈9.58 s, and sL=0att=−16+4
√
41 ≈9.61, so the challenger wins.
39. s= 0 and v= 112 when t=0sov(t)=−32t+ 112, s(t)=−16t2+ 112t
(a) v(3) = 16 ft/s, v(5) = −48 ft/s
(b) v= 0 when the projectile is at its maximum height so −32t+112=0,t=7/2s,
s(7/2) = −16(7/2)2+ 112(7/2) = 196 ft.

239 Chapter 7
(c) s= 0 when it reaches the ground so −16t2+ 112t=0,−16t(t−7)=0,t=0,7 of which t=7
is when it is at ground level on its way down. v(7) = −112, |v|= 112 ft/s.
40. s= 112 when t=0sos(t)=−16t2+v0t+ 112. But s= 0 when t= 2 thus
−16(2)2+v0(2) + 112 = 0, v0=−24 ft/s.
41. (a) s(t) = 0 when it hits the ground, s(t)=−16t2+16t=−16t(t−1) = 0 when t=1s.
(b) The projectile moves upward until it gets to its highest point where v(t)=0,
v(t)=−32t+ 16 = 0 when t=1/2s.
42. (a) s(t) = 0 when the rock hits the ground, s(t)=−16t2+ 555 = 0 when t=√555/4s
(b) v(t)=−32t,v(√555/4) = −8√555, the speed at impact is 8√555 ft/s
43. (a) s(t) = 0 when the package hits the ground,
s(t)=−16t2+20t+ 200 = 0 when t=(5+5
√
33)/8s
(b) v(t)=−32t+ 20, v[(5+5
√
33)/8] = −20√33, the speed at impact is 20√33 ft/s
44. (a) s(t) = 0 when the stone hits the ground,
s(t)=−16t2−96t+ 112 = −16(t2+6t−7) = −16(t+ 7)(t−1) = 0 when t=1s
(b) v(t)=−32t−96, v(1) = −128, the speed at impact is 128 ft/s
45. s(t)=−4.9t
2+49t+ 150 and v(t)=−9.8t+49
(a) the projectile reaches its maximum height when v(t)=0,−9.8t+49=0,t=5s
(b) s(5) = −4.9(5)2+ 49(5) + 150 = 272.5m
(c) the projectile reaches its starting point when s(t) = 150, −4.9t2+49t+ 150 = 150,
−4.9t(t−10)=0,t=10s
(d) v(10) = −9.8(10) + 49 = −49 m/s
(e) s(t) = 0 when the projectile hits the ground, −4.9t2+49t+ 150 = 0 when (use the quadratic
formula) t≈12.46 s
(f) v(12.46) = −9.8(12.46)+49≈−73.1, the speed at impact is about 73.1 m/s
46. take s= 0 at the water level and let hbe the height of the bridge, then s=hand v= 0 when t=0
so s(t)=−16t2+h
(a) s= 0 when t= 4 thus −16(4)2+h=0,h= 256 ft
(b) First, find how long it takes for the stone to hit the water (find tfor s=0):−16t2+h=0,
t=√
h/4. Next, find how long it takes the sound to travel to the bridge: this time is h/1080
because the speed is constant at 1080 ft/s. Finally, use the fact that the total of these two
times must be 4 s: h
1080 +√h
4=4,h+ 270√h= 4320, h+ 270√h−4320 = 0, and by the
quadratic formula √h=−270 ±p(270)2+ 4(4320)
2, reject the negative value to get √h≈15.15,
h≈229.5 ft.
47. g=9.8/6=4.9/3 m/s2,sov=−(4.9/3)t,s=−(4.9/6)t2+5,s= 0 when t=p30/4.9 and
v=−(4.9/3)p30/4.9≈−4.04, so the speed of the module upon landing is 4.04 m/s
48. s(t)=−1
2gt2+v0t;s= 1000 when v=0,so0=v=−gt +v0,t=v0/g,
1000 = s(v0/g)=−1
2g(v
0
/g)2+v0(v0/g)=1
2v
2
0
/g,sov
2
0= 2000g,v0=√2000g.
The initial velocity on the Earth would have to be √6 times faster than that on the Moon.
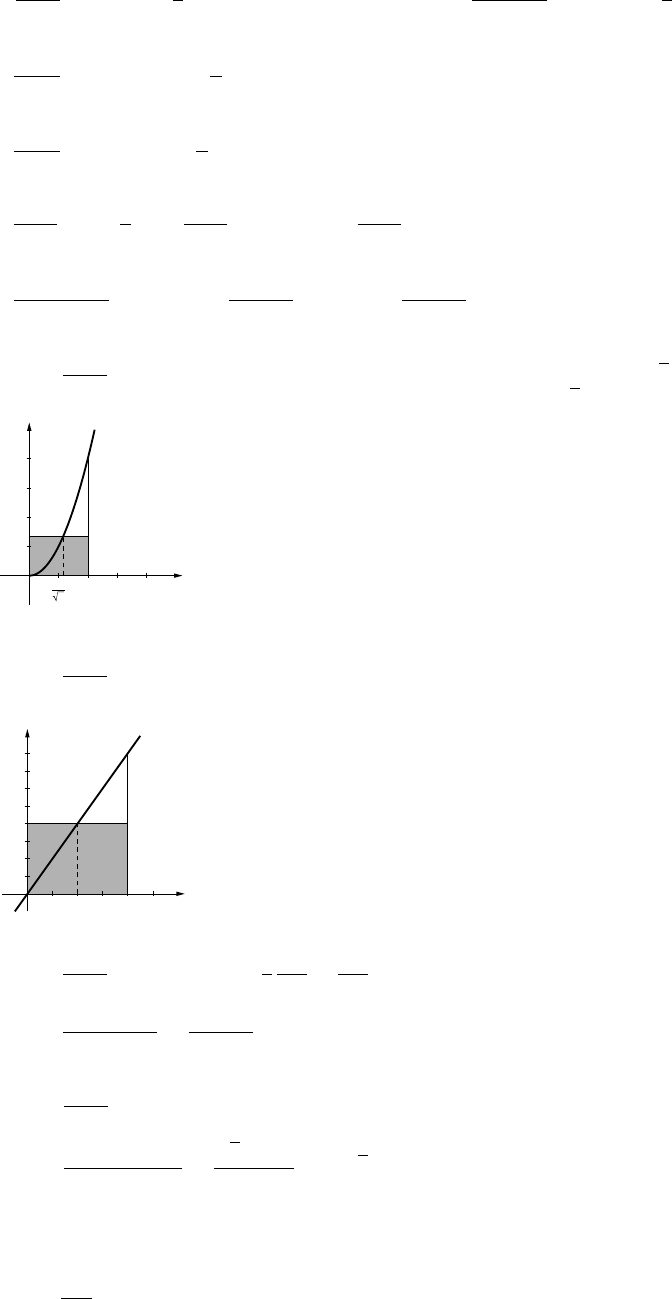
Exercise Set 7.7 240
49. fave =1
3−1Z3
1
3xdx=3
4x
2¸3
1
=6 50. fave =1
2−(−1) Z2
−1
x2dx =1
9x3¸2
−1
=1
51. fave =1
π−0Zπ
0
sin xdx=−1
πcos x¸π
0
=2/π
52. fave =1
π−0Zπ
0
cos xdx=1
πsin x¸π
0
=0
53. fave =1
e−1=Ze
1
1
xdx =1
1−e(ln e−ln 1) = 1
e−1
54. fave =1
ln 5 −(−1) Zln 5
−1
exdx =1
ln5+1(5 −e−1)= 5−e
−1
1+ln5
55. (a) fave =1
2−0Z2
0
x2dx =4/3(b) (x∗)2=4/3,x
∗=±2/
√3,
but only 2/√3isin[0,2]
(c)
2
4
x
y
2
3
56. (a) fave =1
4−0Z4
0
2xdx=4 (b) 2x∗=4,x
∗=2
(c)
24
4
8
x
y
57. (a) vave =1
4−1Z4
1
(3t3+2)dt =1
3
789
4=263
4
(b) vave =s(4) −s(1)
4−1=100 −7
3=31
58. (a) aave =1
5−0Z5
0
(t+1)dt =7/2
(b) aave =v(π/4) −v(0)
π/4−0=√2/2−1
π/4=(2
√
2−4)/π
59. time to fill tank = (volume of tank)/(rate of filling) = [π(3)25]/(1)=45π, weight of water in tank at
time t= (62.4) (rate of filling)(time) = 62.4t,
weightave =1
45πZ45π
0
62.4tdt= 1404πlb
241 Chapter 7
60. (a) If xis the distance from the cooler end, then the temperature is T(x)= (15+1.5x)
◦C, and
Tave =1
10 −0Z10
0
(15+1.5x)dx =22.5
◦C
(b) By the Mean-Value Theorem for Integrals there exists x∗in [0,10] such that
f(x∗)= 1
10 −0Z10
0
(15+1.5x)dx =22.5, 15 + 1.5x∗=22.5, x∗=5
61. (a) amount of water = (rate of flow)(time) = 4tgal, total amount = 4(30) = 120 gal
(b) amount of water = Z60
0
(4+t/10)dt = 420 gal
(c) amount of water = Z120
0
(10 + √t)dt = 1200 + 160√30 ≈2076.36 gal
62. (a) The maximum value of Roccurs at 4:30 P.M. when t=0.
(b) Z60
0
100(1 −0.0001t2)dt = 5280 cars
63. (a) Zb
a
[f(x)−fave]dx =Zb
a
f(x)dx −Zb
a
favedx =Zb
a
f(x)dx −fave(b−a)=0
because fave(b−a)=Zb
a
f(x)dx
(b) no, because if Zb
a
[f(x)−c]dx = 0 then Zb
a
f(x)dx −c(b−a)=0so
c=1
b−aZb
a
f(x)dx =fave is the only value
EXERCISE SET 7.8
1. (a) Z3
1
u7du (b) −1
2Z4
7
u1/2du (c) 1
πZπ
−π
sin udu (d) Z0
−3
(u+5)u
20du
2. (a) 1
2Z1
−1
eudu (b) Z2
1
udu
(c) Z1
0
u2du (d) 1
2Z4
3
(u−3)u1/2du
3. u=2x+1, 1
2Z3
1
u
4
du =1
10u5¸3
1
= 121/5, or 1
10(2x+1)
5
¸1
0
= 121/5
4. u=4x−2, 1
4Z6
2
u3du =1
16u4¸6
2
= 80, or 1
16(4x−2)4¸2
1
=80
5. u=1−2x,−1
2Z1
3
u
3
du =−1
8u4¸1
3
= 10, or −1
8(1 −2x)4¸0
−1
=10
6. u=4−3x,−1
3Z−2
1
u
8
du =−1
27u9¸−2
1
= 19, or −1
27(4 −3x)9¸2
1
=19
Exercise Set 7.8 242
7. u=1+x,Z9
1
(u−1)u1/2du =Z9
1
(u3/2−u1/2)du =2
5u5/2−2
3u3/2¸9
1
= 1192/15,
or 2
5(1+x)5/2−2
3(1+x)3/2¸8
0
= 1192/15
8. u=4−x,Z4
9
(u−4)u1/2du =Z4
9
(u3/2−4u1/2)du =2
5u5/2−8
3u3/2¸4
9
=−506/15
or 2
5(4 −x)5/2−8
3(4 −x)3/2¸0
−5
=−506/15
9. u=x/2, 8 Zπ/4
0
sin udu=−8 cos u¸π/4
0
=8−4
√
2, or −8 cos(x/2)¸π/2
0
=8−4
√
2
10. u=3x,2
3Zπ/2
0
cos udu=2
3sin u¸π/2
0
=2/3, or 2
3sin 3x¸π/6
0
=2/3
11. u=ex+4,du =exdx,u=e−ln 3 +4= 1
3+4= 13
3when x=−ln 3,
u=eln 3 + 4 = 3 + 4 = 7 when x=ln3,Z7
13/3
1
udu =lnu
¸7
13/3
= ln(7) −ln(13/3) = ln(21/13)
12. u=3−4e
x
,du =−4exdx,u=−1 when x=0,u=−17 when x=ln5
−1
4Z−17
−1
udu=−1
8u
2¸−17
−1
=−36
13. 1
3Z5
0p25 −u2du =1
3·1
4π(5)2¸=25
12π
14. 1
2Z4
0p16 −u2du =1
2·1
4π(4)2¸=2π
15. −1
2Z0
1p1−u2du =1
2Z1
0p1−u2du =1
2·1
4[π(1)2]=π/8
16. Z6
−6p36 −u2du =π(6)2/2=18π
17. Z1
0
sin πxdx =−1
πcos πx¸1
0
=−1
π(−1−1)=2/π
18. A=Zπ/8
0
3 cos 2xdx=3
2sin 2x¸π/8
0
=3
√
2/4
19. Z7
3
(x+5)
−2=−(x+5)
−1
¸7
3
=−1
12 +1
8=1
24
20. A=Z1
0
dx
(3x+1)
2=−1
3(3x+1)¸1
0
=1
4
21. fave =1
4−0Z4
0
e−2xdx =−1
8e−2x¸4
0
=1−e−8
8
243 Chapter 7
22. fave =1
1/4−(−1/4) Z1/4
−1/4
sec2πxdx =2
πtan πx#1/4
−1/4
=4
π
23. 2
3(3x+1)
1/2
¸1
0
=2/324. 2
15(5x−1)3/2¸2
1
=38/15
25. 2
3(x3+9)
1/2
¸1
−1
=2
3(
√
10 −2√2) 26. 1
10(t3+1)
20¸0
−1
=1/10
27. u=x2+4x+7, 1
2Z28
12
u−1/2du =u1/2¸28
12
=√28 −√12=2(
√
7−√
3)
28. Z2
1
1
(x−3)2dx =−1
x−3¸2
1
=1/2
29. 1
2sin2x¸π/4
−3π/4
=0 30. 2
3(tan x)3/2¸π/4
0
=2/331. 5
2sin(x2)¸√π
0
=0
32. u=√x,2
Z2π
π
sin udu=−2 cos u¸2π
π
=−4
33. u=3θ,1
3Zπ/3
π/4
sec2udu=1
3tan u¸π/3
π/4
=(
√
3−1)/3
34. u= sin 3θ,1
3Z−1
0
u2du =1
9u3¸−1
0
=−1/9
35. u=4−3y,y=1
3
(4 −u), dy =−1
3du
−1
27 Z1
4
16 −8u+u2
u1/2du =1
27 Z4
1
(16u−1/2−8u1/2+u3/2)du
=1
27 ·32u1/2−16
3u3/2+2
5u5/2¸4
1
= 106/405
36. u=5+x,Z9
4
u−5
√
udu =Z9
4
(u1/2−5u−1/2)du =2
3u3/2−10u1/2¸9
4
=8/3
37. ln(x+e)ie
0= ln(2e)−ln e=ln2 38. −1
2e−x2¸√2
1
=(e
−1−e
−2
)/2
40. Z2
−2p4−u2du =1
2[π(2)2]=2π
41. (a) u=3x+1,1
3Z4
1
f(u)du =5/3(b) u=3x,1
3Z9
0
f(u)du =5/3
(c) u=x2,1/2Z0
4
f(u)du =−1/2Z4
0
f(u)du =−1/2
42. u=1−x,Z1
0
x
m
(1 −x)ndx =−Z0
1
(1 −u)mundu =Z1
0
un(1 −u)mdu =Z1
0
xn(1 −x)mdx
Exercise Set 7.8 244
43. sin x= cos(π/2−x),
Zπ/2
0
sinnxdx=Zπ/2
0
cosn(π/2−x)dx =−Z0
π/2
cosnudu (u=π/2−x)
=Zπ/2
0
cosnudu=Zπ/2
0
cosnxdx (by replacing uby x)
44. u=1−x,−Z0
1
(1 −u)undu =Z1
0
(1 −u)undu =Z1
0
(un−un+1)du =1
n+1−1
n+2 =1
(n+ 1)(n+2)
45. y(t) = (802.137) Ze1.528tdt = 524.959e1.528t+C;y(0) = 750 = 524.959 + C,C= 225.041,
y(t) = 524.959e1.528t+ 225.041, y(12) = 48,233,525,650
46. Vave =275000
10 −0Z10
0
e−0.17tdt =−161764.7059e−0.17t¸10
0
= $132,212.96
47. s(t)=Z(25+10e
−0.05t)dt =25t−200e−0.05t+C
(a) s(10) −s(0) = 250 −200(e−0.5−1) = 450 −200/√e≈328.69 ft
(b) yes; without it the distance would have been 250 ft
48. Zk
0
e2xdx =3,1
2
e
2x
¸k
0
=3,1
2
(e
2k−1)=3,e
2k=7,k =1
2ln 7
49. (a) V2
rms =1
1/f −0Z1/f
0
V2
psin2(2πft)dt =1
2fV2
pZ1/f
0
[1 −cos(4πft)]dt
=1
2fV2
p[t−1
4πf sin(4πft)]¸1/f
0
=1
2V2
p,so Vrms =Vp/√2
(b) Vp/√2 = 120,V
p= 120√2≈169.7V
50. Let u=t−x, then du =−dx and
Zt
0
f(t−x)g(x)dx =−Z0
t
f(u)g(t−u)du =Zt
0
f(u)g(t−u)du;
the result follows by replacing uby xin the last integral.
51. (a) I=−Z0
a
f(a−u)
f(a−u)+f(u)du =Za
0
f(a−u)+f(u)−f(u)
f(a−u)+f(u)du
=Za
0
du −Za
0
f(u)
f(a−u)+f(u)du, I =a−Iso 2I=a, I =a/2
(b) 3/2(c) π/4
52. x=1
u,dx =−1
u2du,I=Z1
−1
1
1+1/u2(−1/u2)du =−Z1
−1
1
u2+1du =−Iso I= 0 which is impossible
because 1
1+x
2is positive on [−1,1]. The substitution u=1/x is not valid because uis not continuous
for all xin [−1,1].
53. Z1
0
sin πxdx =2/π
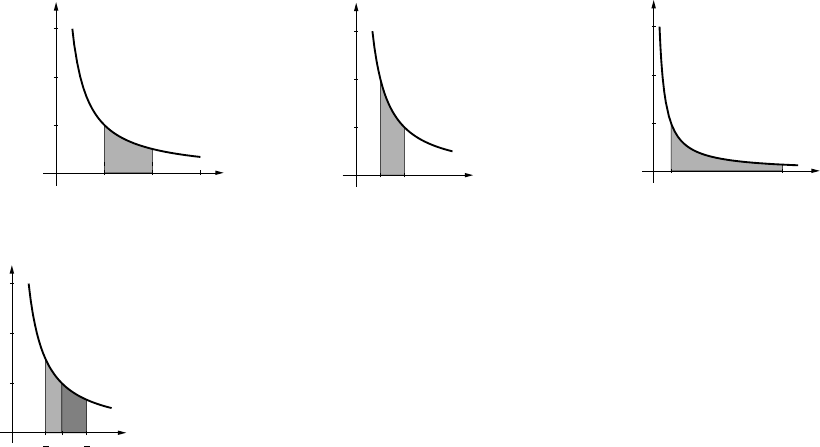
245 Chapter 7
55. (a) Let u=−xthen
Za
−a
f(x)dx =−Z−a
a
f(−u)du =Za
−a
f(−u)du =−Za
−a
f(u)du
so, replacing uby xin the latter integral,
Za
−a
f(x)dx =−Za
−a
f(x)dx,2
Za
−a
f(x)dx =0,Za
−a
f(x)dx =0
The graph of fis symmetric about the origin so Z0
−a
f(x)dx is the negative of Za
0
f(x)dx thus
Za
−a
f(x)dx =Z0
−a
f(x)+Za
0
f(x)dx =0
(b) Za
−a
f(x)dx =Z0
−a
f(x)dx +Za
0
f(x)dx, let u=−xin Z0
−a
f(x)dx to get
Z0
−a
f(x)dx =−Z0
a
f(−u)du =Za
0
f(−u)du =Za
0
f(u)du =Za
0
f(x)dx
so Za
−a
f(x)dx =Za
0
f(x)dx +Za
0
f(x)dx =2Za
0
f(x)dx
The graph of f(x) is symmetric about the y-axis so there is as much signed area to the left of
the y-axis as there is to the right.
EXERCISE SET 7.9
1. (a) y
t
1
2
3
123
(b) y
t
1
2
3
0.5 1
(c) y
t
1
2
3
1e2
2. y
t
1
2
3
1
2
33
2
3. (a) ln tiac
1= ln(ac)=lna+lnc=7 (b) ln ti1/c
1= ln(1/c)=−5
(c) ln tia/c
1= ln(a/c)=2−5=−3(d) ln tia3
1=lna
3=3lna=6
Exercise Set 7.9 246
4. (a) ln ti√a
1=lna
1/2=2 (b) ln ti2a
1=ln2+4
(c) ln ti2/a
1=ln2−4(d) ln tia
2=4−ln 2
5. ln 5 ≈1.603210678; ln 5 = 1.609437912; magnitude of error is <0.0063
6. ln 3 ≈1.098242635; ln 3 = 1.098612289; magnitude of error is <0.0004
7. (a) x−1,x>0(b) x2,x6=0
(c) −x2,−∞ <x<+∞(d) −x,−∞ <x<+∞
(e) x3,x>0(f) ln x+x,x>0
(g) x−3
√x,−∞ <x<+∞(h) ex
x,x>0
8. (a) f(ln 3) = e−2ln3 =e
ln(1/9) =1/9
(b) f(ln 2) = eln 2 +3e
−ln 2 =2+3e
ln(1/2) =2+3/2=7/2
9. (a) 3π=eπln 3 (b) 2√2=e√2ln2
10. (a) π−x=e−xln π(b) x2x=e2xln x
11. (a) lim
x→+∞·µ1+ 1
x¶x
¸2
=·lim
x→+∞µ1+ 1
x¶x
¸2
=e
2
(b) y=2x, lim
y→0(1+y)2/y = lim
y→0h(1+y)1/yi2=e2
12. (a) y=3x, lim
y→+∞µ1+ 1
y¶y/3
= lim
y→+∞·µ1+ 1
y¶y¸1/3
=·lim
y→+∞µ1+ 1
y¶y¸1/3
=e
1/3
(b) lim
x→0(1+x)1/3x= lim
x→0h(1+x)1/xi1/3=e1/3
13. g0(x)=x
2−x14. g0(x)=1−cos x
15. (a) 1
x3(3x2)= 3
x(b) eln x1
x=1
16. (a) 2x√x2+1 (b) −µ1
x2¶sin µ1
x¶
17. F0(x)= cos x
x2+3,F00(x)=−(x
2+ 3) sin x−2xcos x
(x2+3)
2
(a) 0(b) 1/3(c) 0
18. F0(x)=√
3x
2+1,F00(x)= 3x
√
3x
2+1
(a) 0(b) √13 (c) 6/√13
19. (a) d
dx Zx2
1
t√1+tdt =x2p1+x
2
(2x)=2x
3
p1+x
2
(b) Zx2
1
t√1+tdt =−2
3(x2+1)
3/2+2
5(x
2+1)
5/2−4
√
2
15

247 Chapter 7
20. (a) d
dx Za
x
f(t)dt =−d
dx Zx
a
f(t)dt =−f(x)
(b) d
dx Za
g(x)
f(t)dt =−d
dx Zg(x)
a
f(t)dt =−f(g(x))g0(x)
21. (a) −sin x2(b) −tan2x
1 + tan2xsec2x=−tan2x
22. (a) −(x2+1)
40 (b) −cos3µ1
x¶µ−1
x
2¶=cos3(1/x)
x2
23. −33x−1
9x2+1+2xx
2−1
x
4+1
24. If fis continuous on an open interval Iand g(x), h(x), and aare in Ithen
Zg(x)
h(x)
f(t)dt =Za
h(x)
f(t)dt +Zg(x)
a
f(t)dt =−Zh(x)
a
f(t)dt +Zg(x)
a
f(t)dt
so d
dx Zg(x)
h(x)
f(t)dt =−f(h(x))h0(x)+f(g(x))g0(x)
25. (a) sin2(x3)(3x2)−sin2(x2)(2x)=3x
2sin2(x3)−2xsin2(x2)
(b) 1
1+x(1) −1
1−x(−1) = 2
1−x2
26. F0(x)= 1
3x
(3) −1
x(1) = 0 so F(x) is constant on (0,+∞). F(1) = ln 3 so F(x) = ln 3 for all x>0.
27. from geometry, Z3
0
f(t)dt =0,Z5
3
f(t)dt =6,Z7
5
f(t)dt =0;andZ10
7
f(t)dt =Z10
7
(4t−37)/3dt =−3
(a) F(0)=0,F(3)=0,F(5)=6,F(7)=6,F(10) = 3
(b) Fis increasing where F0=fis positive, so on [3/2,6] and [37/4,10], decreasing on [0,3/2] and
[6,37/4]
(c) critical points when F0(x)=f(x)=0,sox=3/2,6,37/4; maximum 15/2 at x= 6, minimum
−9/4atx=3/2
(d) F(x)
x
-2
2
4
6
246810
28. fave =1
10 −0Z10
0
f(t)dt =1
10F(10) = 0.3
29. x<0:F(x)=Zx
−1
(−t)dt =−1
2t2¸x
−1
=1
2(1 −x2),
x≥0:F(x)=Z0
−1
(−t)dt +Zx
0
tdt=1
2+1
2x
2;F(x)=((1 −x2)/2,x<0
(1+x2)/2,x≥0

Exercise Set 7.9 248
30. 0≤x≤2:F(x)=Zx
0
tdt=1
2x
2,
x>2:F(x)=Z2
0
tdt+Zx
2
2dt =2+2(x−2)=2x−2; F(x)=(x
2
/2,0≤x≤2
2x−2,x>2
31. y(x)=2+Zx
1
t
1/3
dt =2+3
4
t
4/3
¸x
1
=5
4+3
4
x
4/3
32. y(x)=Zx
1
(t
1/2+t
−1/2
)dt =2
3x3/2−2
3+2x
1/2−2
33. y(x)=1+Zx
π/4
(sec2t−sin t)dt = tan x+ cos x−√2/2
34. y(x)=Zx
0
tet2dt =1
2e−x2−1
235. P(x)=P
0+Zx
0
r(t)dt individuals
36. s(T)=s
1+ZT
1
v(t)dt
37. II has a minimum at x= 1, and I has a zero there, so I could be the derivative of II; on the other
hand I has a minimum near x=1/3, but II is not zero there, so II could not be the derivative of I
38. (b) lim
k→0
1
k(xk−1)=lnxlim
k→0xk=lnxby L’Hˆopital’s rule (with respect to k)
39. (a) where f(t) = 0; by the first derivative test, at t=3
(b) where f(t) = 0; by the first derivative test, at t=1
(c) at t=0,1 or 5; from the graph it is evident that it is at t=5
(d) at t=0,3 or 5; from the graph it is evident that it is at t=3
(e) Fis concave up when F00 =f0is positive, i.e. where fis increasing, so on (0,1/2) and (2,4);
it is concave down on (1/2,2) and (4,5)
(f) F(x)
x
-1
-0.5
0.5
1
12345
40. (a)
x
-1
1
-4 -2 2 4
erf(x)
(c) erf0(x)>0 for all x, so there are no relative extrema
(e) erf00(x)=−4xe−x2/√πchanges sign only at x= 0 so that is the only point of inflection
(g) lim
x→+∞erf(x) = +1, lim
x→−∞ erf(x)=−1
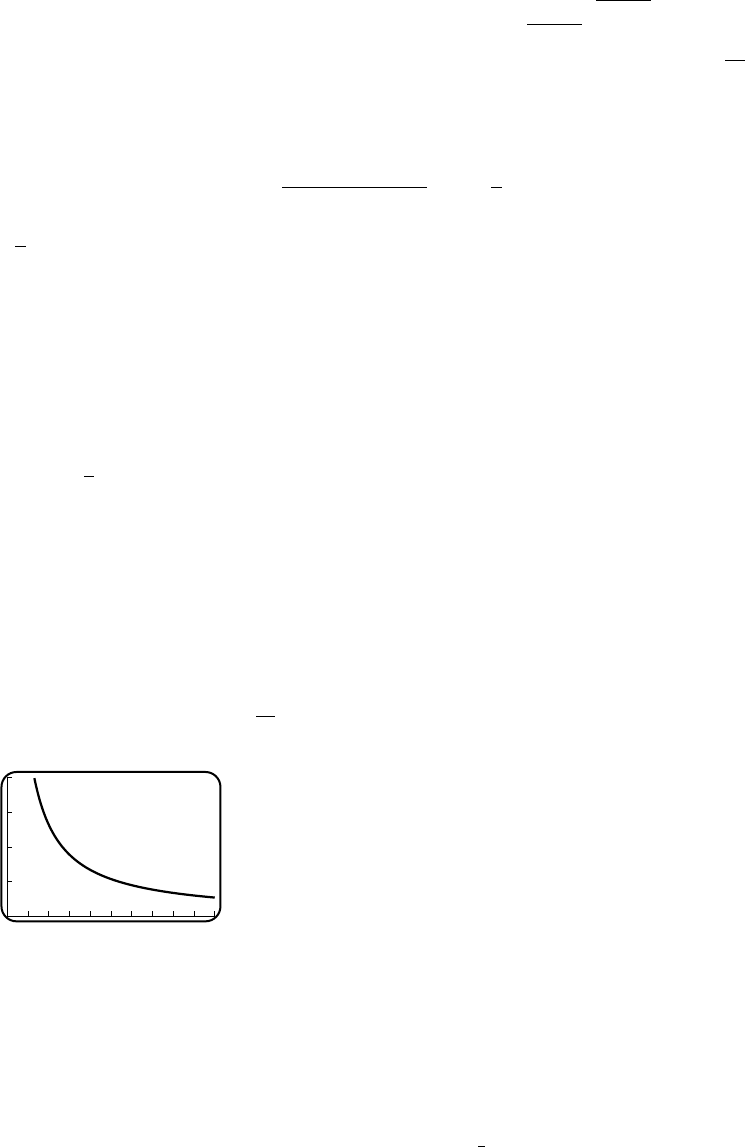
249 Chapter 7
41. C0(x) = cos(πx2/2), C00(x)=−πx sin(πx2/2)
(a) cos tgoes from negative to positive at 2kπ −π/2, and from positive to negative at t=2kπ +π/2,
so C(x) has relative minima when πx2/2=2kπ −π/2, x=±√4k−1, k=1,2,..., and C(x)
has relative maxima when πx2/2=(4k+1)π/2, x=±√4k+1,k=0,1,....
(b) sin tchanges sign at t=kπ,soC(x) has inflection points at πx2/2=kπ,x=±√2k,k=1,2,...;
the case k= 0 is distinct due to the factor of xin C00(x), but xchanges sign at x= 0 and
sin(πx2/2) does not, so there is also a point of inflection at x=0
42. Let F(x)=Zx
1
ln tdt,F0(x) = lim
h→0
F(x+h)−F(x)
h= lim
h→0
1
hZx+h
x
ln tdt; but F0(x)=lnxso
lim
h→0
1
hZx+h
x
ln tdt =lnx
43. Differentiate: f(x)=3e
3x
,so2+Zx
a
f(t)dt =2+Zx
a
3e
3t
dt =2+e
3t
¸x
a
= 2+e
3x−e
3a=e
3xprovided
e3a=2,a= (ln 2)/3.
44. (a) The area under 1/t for x≤t≤x+ 1 is less than the area of the rectangle with altitude 1/x and
base 1, but greater than the area of the rectangle with altitude 1/(x+ 1) and base 1.
(b) Zx+1
x
1
tdt =lnt
¸x+1
x
= ln(x+1)−ln x= ln(1 + 1/x), so
1/(x+1)<ln(1 + 1/x)<1/x for x>0.
(c) from part (b), e1/(x+1) <e
ln(1+1/x)<e
1/x,e1/(x+1) <1+1/x<e
1/x,
ex/(x+1) <(1+1/x)x<e; by the Squeezing Theorem, lim
x→+∞(1+1/x)x=e.
(d) Use the inequality ex/(x+1) <(1+1/x)xto get e<(1+1/x)x+1 so
(1+1/x)x<e<(1+1/x)x+1.
45. From Exercise 44(d) ¯¯¯¯¯
e−µ1+ 1
50¶50¯¯¯¯¯
<y(50), and from the graph y(50) <0.06
0.2
0
0 100
46. F0(x)=f(x), thus F0(x) has a value at each xin Ibecause fis continuous on Iso Fis continuous
on Ibecause a function that is differentiable at a point is also continuous at that point
CHAPTER 7 SUPPLEMENTARY EXERCISES
5. If the acceleration a= const, then v(t)=at +v0,s(t)=1
2at2+v0t+s0
6. (a) Divide the base into nequal subintervals. Above each subinterval choose the lowest and highest
points on the curved top. Draw a rectangle above the subinterval going through the lowest point,
and another through the highest point. Add the rectangles that go through the lowest points to
obtain a lower estimate of the area; add the rectangles through the highest points to obtain an
upper estimate of the area.
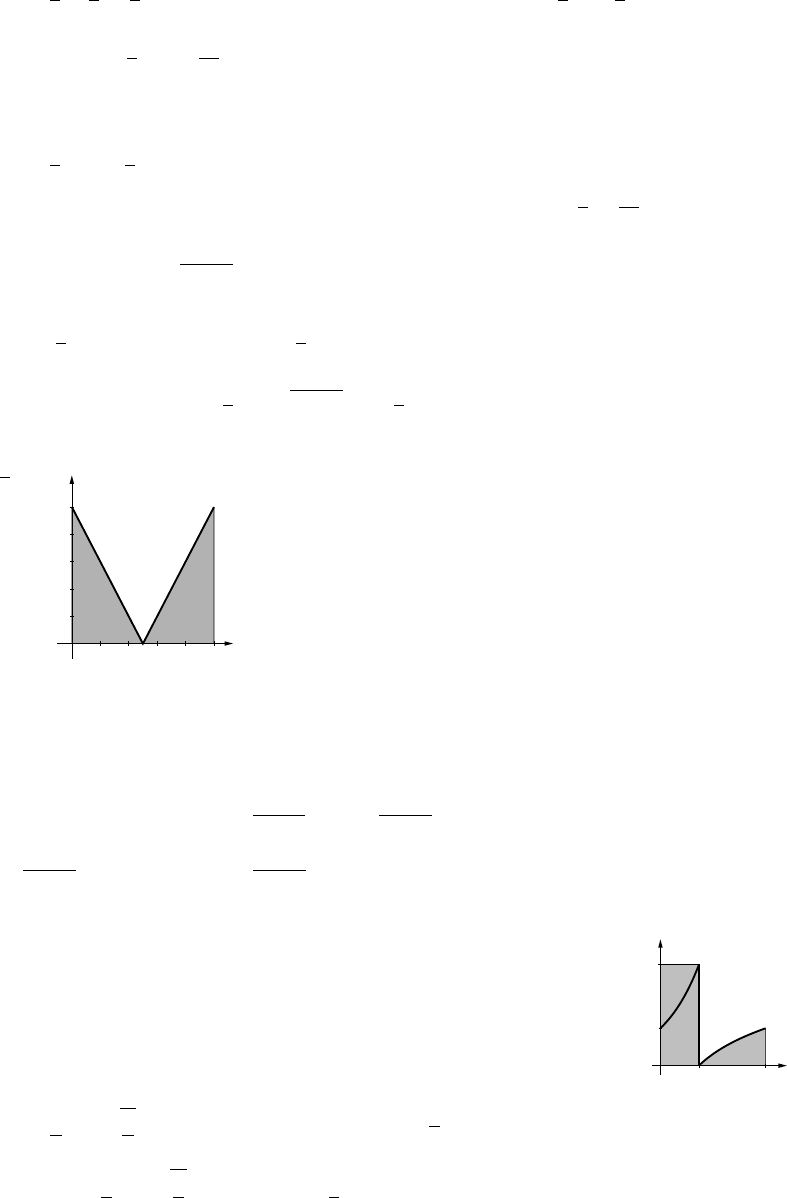
Supplementary Exercises 7 250
(b) n= 10: 25.0 cm, 22.4cm
(c) n= 20: 24.4 cm, 23.1cm
7. (a) 1
2+1
4=3
4(b) −1−1
2=−3
2
(c) 5µ−1−3
4¶=−35
4(d) −2
(e) not enough information (f) not enough information
8. (a) 1
2+2= 5
2(b) not enough information
(c) not enough information (d) 4(2) −31
2=13
2
9. (a) Z1
−1
dx +Z1
−1p1−x2dx = 2(1) + π(1)2/2=2+π/2
(b) 1
3(x2+1)
3/2
¸3
0−π(3)2/4=1
3
(103/2−1) −9π/4
(c) u=x2,du =2xdx;1
2Z1
0p1−u2du =1
2π(1)2/4=π/8
10. 1
2
y
x
0.2
0.4
0.6
0.8
1
0.2 0.6 1
11. The rectangle with vertices (0,0), (π, 0), (π, 1) and (0,1) has area πand is much too large; so is the
triangle with vertices (0,0), (π, 0) and (π, 1) which has area π/2; 1 −πis negative; so the answer is
35π/128.
12. Divide ex+ 3 into e2xto get e2x
ex+3 =e
x−3e
x
e
x+3 so
Ze2x
ex+3dx =Zexdx −3Zex
ex+3dx =ex−3 ln(ex+3)+C
13. Since y=exand y=lnxare inverse functions, their graphs are
symmetric with respect to the line y=x; consequently the areas A1
and A3are equal (see figure). But A1+A2=e,so
Ze
1
ln xdx +Z1
0
exdx =A2+A3=A2+A1=e
y
x
1
e
1e
A3
A1
A2
14. (a) 1
n
n
X
k=1 rk
n=
n
X
k=1
f(x∗
k)∆xwhere f(x)=√
x,x
∗
k=k/n, and ∆x=1/n for 0 ≤x≤1. Thus
lim
n→+∞
1
n
n
X
k=1 rk
n=Z1
0
x1/2dx =2
3
251 Chapter 7
(b) 1
n
n
X
k=1 µk
n¶4
=
n
X
k=1
f(x∗
k)∆xwhere f(x)=x
4
,x
∗
k=k/n, and ∆x=1/n for 0 ≤x≤1. Thus
lim
n→+∞
1
n
n
X
k=1 µk
n¶4
=Z1
0
x4dx =1
5
(c)
n
X
k=1
ek/n
n=
n
X
k=1
f(x∗
k)∆xwhere f(x)=e
x
,x
∗
k=k/n, and ∆x=1/n for 0 ≤x≤1. Thus
lim
n→+∞
n
X
k=1
ek/n
n= lim
n→+∞
n
X
k=1
f(x∗
k)∆x=Z1
0
exdx =e−1.
15. Since f(x)= 1
xis positive and increasing on the interval [1,2], the left endpoint approximation
overestimates the integral of 1
xand the right endpoint approximation underestimates it.
(a) For n= 5 this becomes
0.2·1
1.2+1
1.4+1
1.6+1
1.8+1
2.0¸<Z2
1
1
xdx < 0.2·1
1.0+1
1.2+1
1.4+1
1.6+1
1.8¸
(b) For general nthe left endpoint approximation to Z2
1
1
xdx =ln2is
1
n
n
X
k=1
1
1+(k−1)/n =
n
X
k=1
1
n+k−1=
n−1
X
k=0
1
n+kand the right endpoint approximation is
n
X
k=1
1
n+k. This yields
n
X
k=1
1
n+k<Z2
1
1
xdx <
n−1
X
k=0
1
n+kwhich is the desired inequality.
(c) By telescoping, the difference is 1
n−1
2n=1
2nso 1
2n≤0.1, n≥5
(d) n≥1,000
16. The direction field is clearly an even function, which means that the solution is even, its derivative
is odd. Since sin xis periodic and the direction field is not, that eliminates all but x, the solution of
which is the family y=x2/2+C.
17. (a) 1·2+2·3+···+n(n+1)=
n
X
k=1
k(k+1)=
n
X
k=1
k2+
n
X
k=1
k
=1
6n(n+ 1)(2n+1)+ 1
2n(n+1)= 1
3n(n+ 1)(n+2)
(b)
n−1
X
k=1 µ9
n−k
n2¶=9
n
n−1
X
k=1
1−1
n2
n−1
X
k=1
k=9
n(n−1) −1
n2·1
2(n−1)(n)=17
2µn−1
n¶;
lim
n→+∞
17
2µn−1
n¶=17
2
(c)
3
X
i=1 "2
X
j=1
i+
2
X
j=1
j#=
3
X
i=1 ·2i+1
2(2)(3)¸=2
3
X
i=1
i+
3
X
i=1
3=2·1
2
(3)(4) + (3)(3) = 21
18. (a)
14
X
k=0
(k+ 4)(k+1) (b)
19
X
k=5
(k−1)(k−4)
Supplementary Exercises 7 252
19. (a) If u= sec x,du = sec xtan xdx,Zsec2xtan xdx =Zudu =u2/2+C
1= (sec2x)/2+C
1
;
if u= tan x,du = sec2xdx,Zsec2xtan xdx =Zudu =u2/2+C
2= (tan2x)/2+C
2
.
(b) They are equal only if sec2xand tan2xdiffer by a constant, which is true.
20. 1
2sec2xiπ/4
0=1
2(2 −1)=1/2 and 1
2tan2xiπ/4
0=1
2(1 −0)=1/2
21. Zp1+x
−2/3
dx =Zx−1/3px2/3+1dx;u=x2/3+1,du =2
3x−1/3dx
3
2Zu1/2du =u3/2+C=(x
2/3+1)
3/2+C
22. (a) Zb
a
n
X
k=1
fk(x)dx =
n
X
k=1 Zb
a
fk(x)dx
(b) yes; substitute ckfk(x) for fk(x) in part (a), and then use Zb
a
ckfk(x)dx =ckZb
a
fk(x)dx from
Theorem 7.5.4
23. (a) Zx
1
1
1+t
2dt
(b) Zx
tan(π/4−2)
1
1+t
2dt
24. (a) F0(x)= x−3
x
2+7; increasing on [3,+∞), decreasing on (−∞,3]
(b) F00(x)=7+6x−x
2
(x
2+7)
2=(7 −x)(1 + x)
(x2+7)
2; concave up on (−1,7), concave down on (−∞,−1) and
(7,+∞)
(c) F0(x)= x−3
x
2+7 = 0 when x= 3, which is a relative minimum, and hence the absolute minimum,
by the first derivative test.
(d) F(x)
x
1
2
3
-10 10 20
25. F0(x)= 1
1+x
2+1
1+(1/x)2(−1/x2)=0soFis constant on (0,+∞).
26. (−3,3) because fis continuous there and 1 is in (−3,3)
27. (a) The domain is (−∞,+∞); F(x)is0ifx= 1, positive if x>1, and negative if x<1, because
the integrand is positive, so the sign of the integral depends on the orientation (forwards or
backwards).
(b) The domain is [−2,2]; F(x)is0ifx=−1, positive if −1<x≤2, and negative if −2≤x<−1;
same reasons as in part (a).
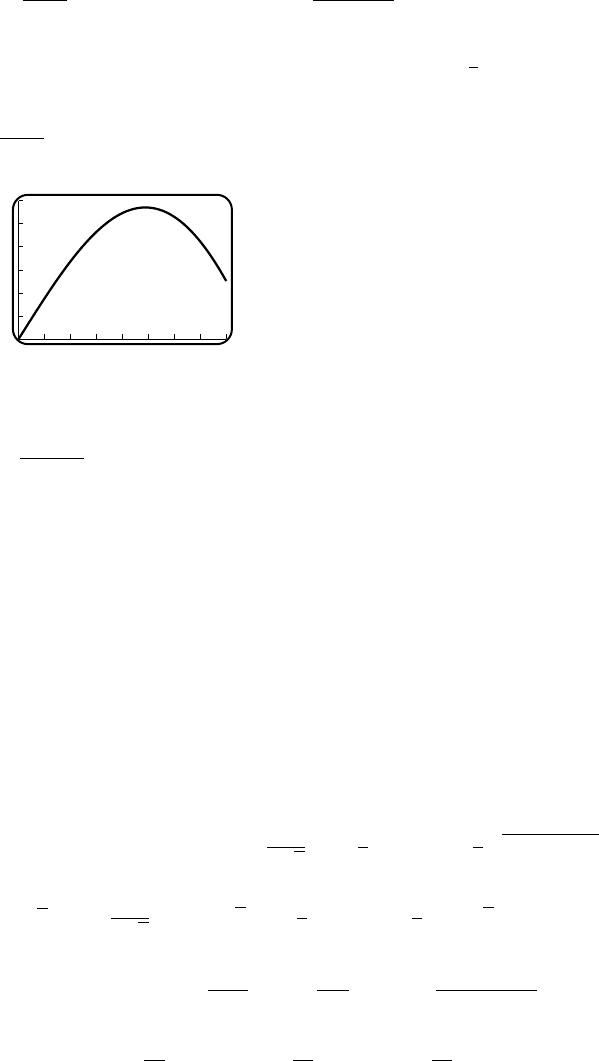
253 Chapter 7
28. The left endpoint of the top boundary is ((b−a)/2,h) and the right endpoint of the top boundary is
((b+a)/2,h)so
f(x)=
2hx/(b−a),x<(b−a)/2
h, (b−a)/2<x<(b+a)/2
2h(x−b)/(a−b),x>(a+b)/2
The area of the trapezoid is given by
Z(b−a)/2
0
2hx
b−adx +Z(b+a)/2
(b−a)/2
hdx +Zb
(b+a)/2
2h(x−b)
a−bdx =(b−a)h/4+ah +(b−a)h/4=h(a+b)/2.
29. (a) Z24
0³2000e−t/48 + 500 sin(πt/12)´dt = 96000(1 −1/√e)≈37,773.06
(b) 1
8−0Z8
0³2000e−t/48 + 500 sin(πt/12)dt´= 1125/π + 12000(1 −e−1/6)≈2,200.32
(c) 2300
2000
08
(d) maximum rate is 2285.32 kW/h at t=4.8861
30. wave =1
52 −26 Z52
26
(t/7)dt =39/7; t∗/7=39/7, t∗=39
31. (a) no, since the velocity curve is not a straight line
(b) 25 <t<40
(c) 3.54 ft/s
(d) 141.5ft
(e) no since the velocity is positive and the acceleration is never negative
(f) need the position at any one given time (e.g. s0)
32. (a) x=aekt +be−kt,dx/dt =akekt −bke−kt,
d2x/dt2=ak2ekt +bk2e−kt =k2(aekt +be−kt)=k
2
x
(b) At t=0,v=ak −bk =(a−b)k=v
0so k=v0/(a−b) and a=k2x=v2
0x/(a−b)2.
33. u= 5 + 2 sin 3x,du = 6 cos 3xdx;Z1
6√udu =1
3u1/2+C=1
3√5 + 2 sin 3x+C
34. u=3+√
x,du =1
2√xdx;Z2√udu =4
3u3/2+C=4
3(3+√x)3/2+C
35. u=ax3+b,du =3ax2dx;Z1
3au2du =−1
3au +C=−1
3a2x3+3ab +C
36. u=ax2,du =2axdx;1
2aZsec2udu =1
2atan u+C=1
2atan(ax2)+C
37. ln(ex) + ln(e−x) = ln(exe−x)=ln1=0soZ[ln(ex) + ln(e−x)]dx =C

Supplementary Exercises 7 254
38. µ−1
3u3−3
u+1
4u4¶¸−1
−2
= 389/192
39. u=lnx,du =(1/x)dx;Z2
1
1
udu =lnu
¸2
1
=ln2
40. Z1
0
e−x/2dx = 2(1 −1/√e)
41. u=e−2x,du =−2e−2xdx;−1
2Z1/4
1
(1 + cos u)du =3
8+1
2µsin 1 −sin 1
4¶
42. 1
3πsin3πx¸1
0
=0
43. With b=1.618034, area = Zb
0
(x+x2−x3)dx =1.007514.
44. (a) f(x)= 1
3
x
2sin 3x−2
27 sin 3x+2
9xcos 3x−0.251607
(b) f(x)=p4+x
2+4
√
4+x
2−6
45. (a) Solve 1
4k4−k−k2+7
4= 0 to get k=2.073948.
(b) Solve −1
2cos 2k+1
3k3+1
2= 3 to get k=1.837992.
46. F(x)=Zx
−1
t
√
2+t
3dt,F0(x)= x
√
2+x
3,soFis increasing on [1,3]; Fmax =F(3) ≈1.152082854
and Fmin =F(1) ≈−0.07649493141
47. (a)
12345678
-0.5
0.5
1
y = J0(x)
x
y(b) 0.7651976866 (c) J0(x)=0ifx=2.404826
48. (a) A=Z1
0
x2dx =1
3x3¸1
0
=1/3
(b)
n
X
k=1 µk−1
n¶21
n=1
n3"n
X
k=1
k2−2
n
X
k=1
k+
n
X
k=1
1#=1
n3µn(n+ 1)(2n+1)
6−2n(n+1)
2+n
¶,
lim
n→+∞
n
X
k=1 µk−1
n¶21
n=2
6=1
3
(c)
n
X
k=1 µk
n¶21
n=1
n3
n
X
k=1
k2=1
n3
n(n+ 1)(2n+1)
6and lim
n→+∞
n
X
k=1 µk
n¶21
n=2
6=1
3
49. 100,000/(ln 100,000) ≈8,686; Z100,000
2
1
ln tdt ≈9,629, so the integral is better
255 Chapter 7
CHAPTER 7 HORIZON MODULE
1. vx(0) = 35 cos α, so from Equation (1), x(t) = (35 cos α)t;vy(0) = 35 sin α, so from Equation (2),
y(t) = (35 sin α)t−4.9t2.
2. (a) vx(t)= dx(t)
dt = 35 cos α,vy(t)= dy(t)
dt = 35 sin α−9.8t
(b) vy(t)=35sinα−9.8t,v
y
(t) = 0 when t= 35 sin α/9.8;
y=vy(0)t−4.9t2= (35 sin α)(35 sin α)/9.8−4.9((35 sin α)/9.8)2=62.5 sin2α,so
y
max =62.5 sin2α.
3. t=x/(35 cos α)soy= (35 sin α)(x/(35 cos α)) −4.9(x/(35 cos α))2= (tan α)x−0.004
cos2αx2;
the trajectory is a parabola because yis a quadratic function of x.
4. 15◦25◦35◦45◦55◦65◦75◦85◦
no yes no no no yes no no
65
0
0 120
5. y(t) = (35 sin αs)t−4.9t2= 0 when t= 35 sin α/4.9, at which time
x= (35 cos α)(35 sin α/4.9) = 125 sin 2α; this is the maximum value of x,soR= 125 sin 2αm.
6. (a) R= 95 when sin 2α=95/125=0.76, α=0.4316565575,1.139139769 rad ≈24.73◦,65.27◦.
(b) y(t)<50 is required; but y(1.139) ≈51.56 m, so his height would be 56.56 m.
7. 0.4019 <α<0.4636 (radians), or 23.03◦<α<26.57◦
256
CHAPTER 8
Applications of the Definite Integral
in Geometry, Science, and Engineering
EXERCISE SET 8.1
1. A=Z2
−1(x2+1−x)dx =(x
3
/3+x−x
2/2)2
−1
=9/2
2. A=Z4
0(√x+x/4)dx =(2x
3/2
/3+x
2/8)4
0
=22/3
3. A=Z2
1(y−1/y2)dy =(y
2
/2+1/y)2
1
=1
4. A=Z2
0(2 −y2+y)dy =(2y−y
3
/3+y
2/2)2
0
=10/3
5. (a) A=Z4
0(4x−x2)dx =32/3(b) A=Z16
0(√y−y/4)dy =32/3
5
1
(4, 16)
y = 4x
y = x2
x
y
(4, 4)
(1, -2)
x
y
y2 = 4x
y = 2x – 4
6. Eliminate xto get y2=4(y+4)/2,y
2−2y−8=0,
(y−4)(y+2)=0;y=−2,4 with corresponding
values of x=1,4.
(a) A=Z1
0[2√x−(−2√x)]dx +Z4
1[2√x−(2x−4)]dx
=Z1
04√xdx +Z4
1(2√x−2x+4)dx =8/3+19/3=9
(b) A=Z4
−2[(y/2+2)−y
2/4]dy =9
1
4
(1, 1)
x
y
y = x2
y = √x
7. A=Z1
1/4(√x−x2)dx =49/192
257 Chapter 8
8. A=Z2
0[0 −(x3−4x)]dx
=Z2
0(4x−x3)dx =4
2
x
y
y = 2x3 – 4x
9. A=Zπ/2
π/4(0 −cos 2x)dx
=−Zπ/2
π/4cos 2xdx=1/2
36
-1
1
x
y
y = cos 2x
10. Equate sec2xand 2 to get sec2x=2,
1
2
x
y
y = sec2 x
(#, 2)(3
, 2)
sec x=±√2, x=±π/4
A=Zπ/4
−π/4(2 −sec2x)dx =π−2
11. A=Z3π/4
π/4sin ydy=√2
3
9
x
y
x = sin y
12. A=Z2
−1[(x+2)−x
2]dx =9/2
(2, 4)
(–1, 1)
x
y
y = x2
x = y – 2
13. A=Zln 2
0e2x−exdx =1
2e2x−ex#ln 2
0
=1/2
2
4
x
y
ln 2
y = e2x
y = ex
1/e1
1
e
x
y
14. A=Ze
1
dy
y=lny
ie
1=1
Exercise Set 8.1 258
(–5, 8)
(5, 6)
y = 3 – xy = 1 + x
y = – x + 7
1
5
x
y
15. y=2+|x−1|=(3−x, x ≤1
1+x, x ≥1,
A=Z1
−5−1
5x+7
−(3 −x)dx
+Z5
1−1
5x+7
−(1+x)dx
=Z1
−54
5x+4
dx +Z5
16−6
5xdx
=72/5+48/5=24
16. A=Z2/5
0(4x−x)dx
+Z1
2/5(−x+2−x)dx
=Z2/5
03xdx+Z1
2/5(2 −2x)dx =3/5
(1, 1)
2
5
8
5
(, )
x
y
y = 4x
y = x
y = −x + 2
17. A=Z1
0(x3−4x2+3x)dx
+Z3
1[−(x3−4x2+3x)]dx
=5/12+32/12=37/12
4
-8
-1 4
9
-2
-1 3
18. Equate y=x3−2x2and y=2x
2−3x
to get x3−4x2+3x=0,
x(x−1)(x−3)=0;x=0,1,3
with corresponding values of y=0,−1.9.
A=Z1
0[(x3−2x2)−(2x2−3x)]dx
+Z3
1[(2x3−3x)−(x3−2x2)]dx
=Z1
0(x3−4x2+3x)dx +Z3
1(−x3+4x
2−3x)dx
=5
12 +8
3=37
12
1
-1
0o
19. From the symmetry of the region
A=2Z5π/4
π/4(sin x−cos x)dx =4
√
2
259 Chapter 8
20. The region is symmetric about the
origin so
A=2Z0
−2
(x
3−4x)dx =8
3.1
-3.1
-3 3
21. A=Z0
−1(y3−y)dy +Z1
0−(y3−y)dy
=1/2
1
-1
-1 1
4.1
0
-2.2 12.1
22. A=Z1
0y3−4y2+3y−(y
2−y)
dy
+Z4
1y2−y−(y3−4y2+3y)
dy
=7/12+45/4=71/6
23. Solve 3−2x=x6+2x5−3x4+x2to find the real roots x=−3,1; from a plot it is seen that the line
is above the polynomial when −3<x<1, so A=Z1
−3(3−2x−(x6+2x5−3x4+x2)) dx = 9152/105
24. Solve x5−2x3−3x=x3to find the roots x=0,±1
2
q6+2
√
21. Thus, by symmetry,
A=2Z√
(6+2√21)/2
0(x3−(x5−2x3−3x)) dx =27
4+7
4√21
25. Zk
02√ydy =Z9
k
2√ydy
Zk
0y1/2dy =Z9
k
y1/2dy
2
3k3/2=2
3(27 −k3/2)
k3/2=27/2
k= (27/2)2/3=9/3
√
4
y = 9
y = k
x
y
26. Zk
0x2dx =Z2
k
x2dx
1
3k3=1
3(8 −k3)
k3=4
k=3
√
4
2
x
y
x = √y
x = k
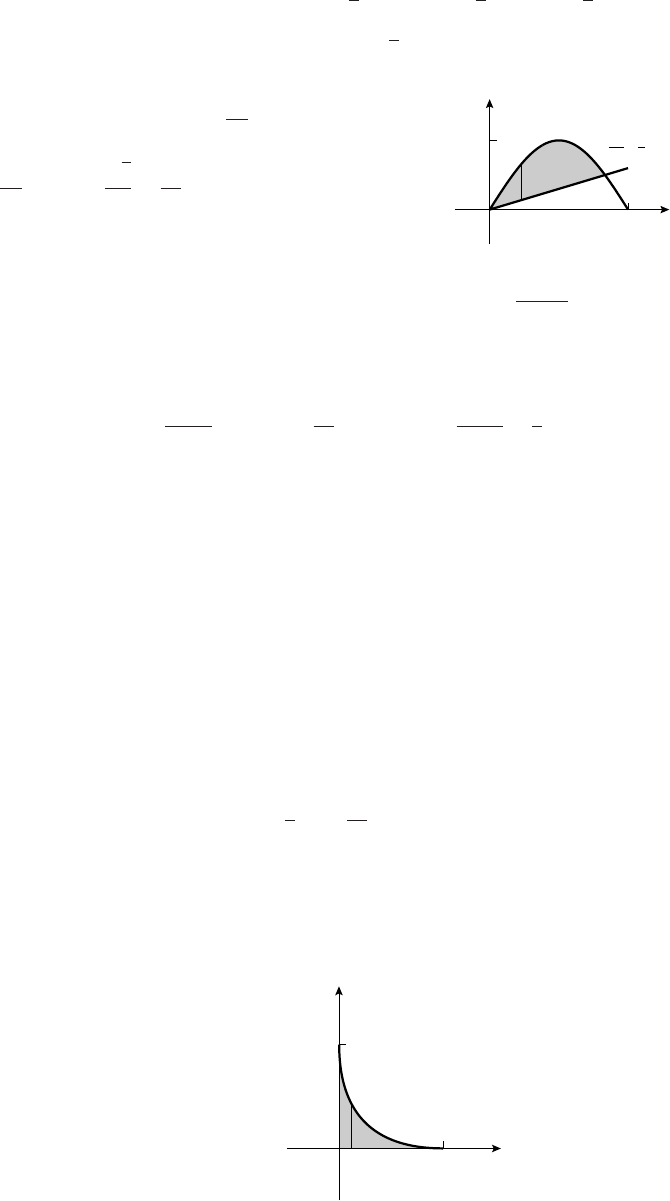
Exercise Set 8.1 260
27. (a) A=Z2
0(2x−x2)dx =4/3
(b) y=mx intersects y=2x−x
2where mx =2x−x
2
,x
2+(m−2)x=0,x(x+m−2)=0so
x=0orx=2−m. The area below the curve and above the line is
Z2−m
0(2x−x2−mx)dx =Z2−m
0[(2 −m)x−x2]dx =1
2(2 −m)x2−1
3x32−m
0
=1
6(2 −m)3
so (2 −m)3/6=(1/2)(4/3)=2/3,(2 −m)3=4,m=2−3
√
4.
c
11
2
c5
6,
( )
x
y
y = sin x
28. The line through (0,0) and (5π/6,1/2) is y=3
5πx;
A=Z5π/6
0sin x−3
5πxdx =√3
2−5
24π+1
29. (a) It gives the area of the region that is between fand gwhen f(x)>g(x) minus the area of
the region between fand gwhen f(x)<g(x), for a≤x≤b.
(b) It gives the area of the region that is between fand gfor a≤x≤b.
30. (b) lim
n→+∞Z1
0(x1/n −x)dx = lim
n→+∞n
n+1x
(n+1)/n −x2
21
0
= lim
n→+∞n
n+1−1
2=1/2
31. The curves intersect at x= 0 and, by Newton’s Method, at x≈2.595739080 = b,so
A≈Zb
0(sin x−0.2x)dx =−cos x+0.1x
2b
0≈1.180898334
32. By Newton’s Method, the points of intersection are at x≈±0.824132312, so with
b=0.824132312 we have A≈2Zb
0(cos x−x2)dx = 2(sin x−x3/3)b
0≈1.094753609
33. distance = R|v|dt,so
(a) distance = Z60
0(3t−t2/20) dt = 1800 ft.
(b) If T≤60 then distance = ZT
0(3t−t2/20) dt =3
2T2−1
60T3ft.
34. Since a1(0) = a2(0)=0,A=
ZT
0(a
2
(t)−a
1
(t)) dt =v2(T)−v1(T) is the difference in the velocities
of the two cars at time T.
a
a
x
y
35. Solve x1/2+y1/2=a1/2for yto get
y=(a
1/2−x
1/2
)
2=a−2a
1/2
x
1/2+x
A=Za
0(a−2a
1/2
x
1/2+x)dx =a2/6
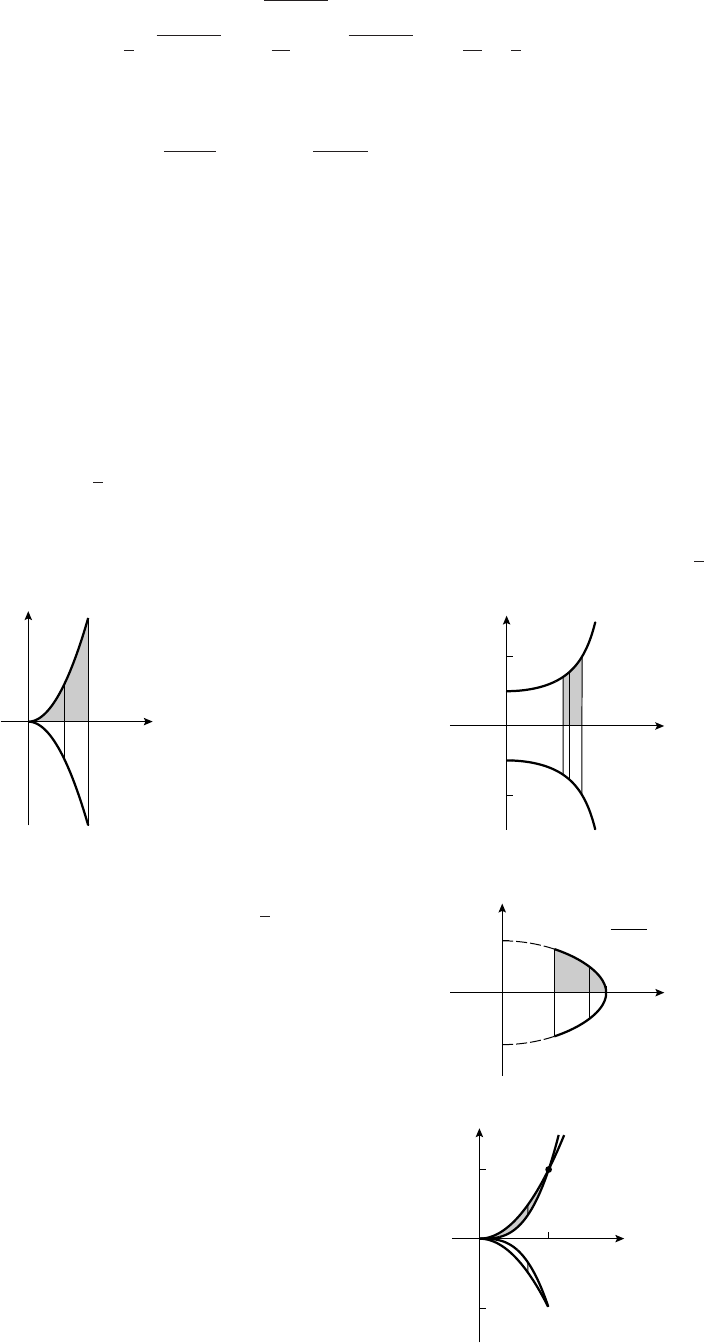
261 Chapter 8
36. Solve for yto get y=(b/a)√a2−x2for the upper half of the ellipse; make use of symmetry to
get A=4Za
0
b
a
pa
2−x
2
dx =4b
aZa
0pa2−x2dx =4b
a×1
4πa2=πab.
37. Let Abe the area between the curve and the x-axis and ARthe area of the rectangle, then
A=Zb
0kxmdx =k
m+1x
m+1b
0
=kbm+1
m+1,A
R=b(kbm)=kbm+1,soA/AR=1/(m+ 1).
EXERCISE SET 8.2
1. V=πZ3
−1(3 −x)dx =8π2. V=πZ1
0[(2 −x2)2−x2]dx
=πZ1
0(4 −5x2+x4)dx
=38π/15
3. V=πZ2
0
1
4(3 −y)2dy =13π/64. V=πZ2
1/2(4 −1/y2)dy =9π/2
5. V=πZ2
0x4dx =32π/5
2
x
y
y = x2
6. V=πZπ/3
π/4sec2xdx=π(
√3−1)
34
-2
-1
1
2
x
y
y = sec x
36
-1
1
x
y
y = √cos x
7. V=πZπ/2
π/4cos xdx=(1−√
2/2)π
1
1(1, 1)
y = x2
y = x3
x
y
8. V=πZ1
0[(x2)2−(x3)2]dx
=πZ1
0(x4−x6)dx =2π/35
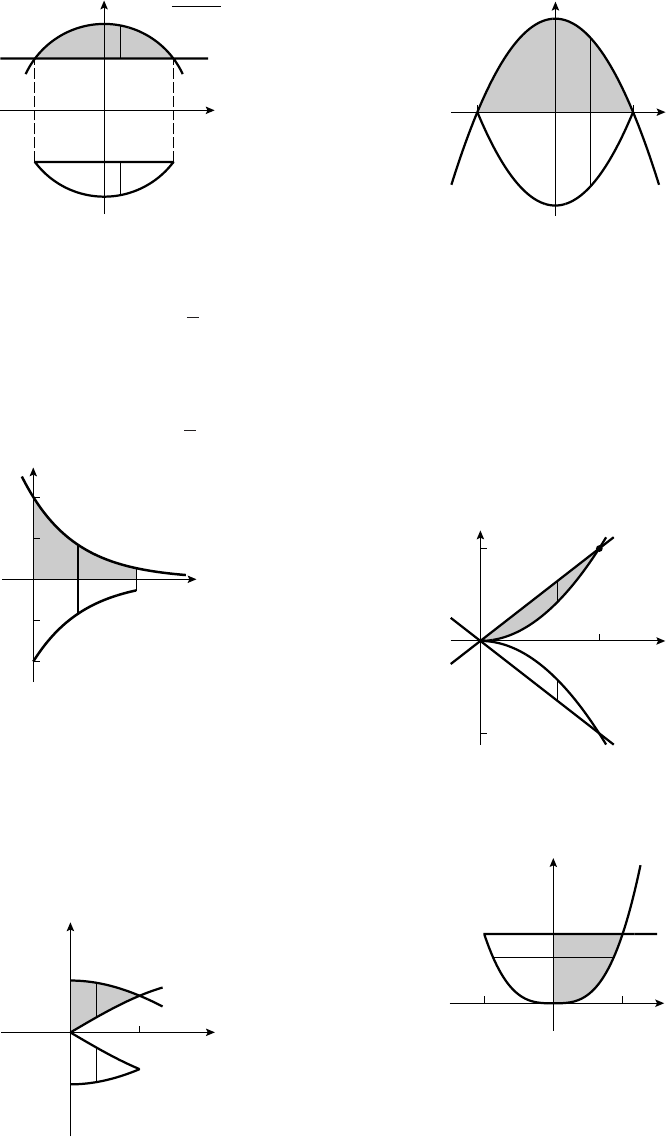
Exercise Set 8.2 262
9. V=πZ4
−4[(25 −x2)−9]dx
=2πZ4
0(16 −x2)dx = 256π/3
5
x
yy = √25 – x2
y = 3
10. V=πZ3
−3(9 −x2)2dx
=πZ3
−3(81 −18x2+x4)dx = 1296π/5
-3 3
9
x
y
y = 9 – x2
11. V=πZln 3
0e2xdx =π
2e2xln 3
0
=4π
12. V=πZ1
0e−4xdx =π
4(1 −e−4)
1
-1
1
x
y
13. V=πZ4
0[(4x)2−(x2)2]dx
=πZ4
0(16x2−x4)dx = 2048π/15
4
16 (4, 16)
x
y
y = x2
y = 4x
14. V=πZπ/4
0(cos2x−sin2x)dx
=πZπ/4
0cos 2xdx=π/2
3
-1
1
x
y
y = cos x
y = sin x
15. V=πZ1
0y2/3dy =3π/5
-1 1
1
x
y
y = x3
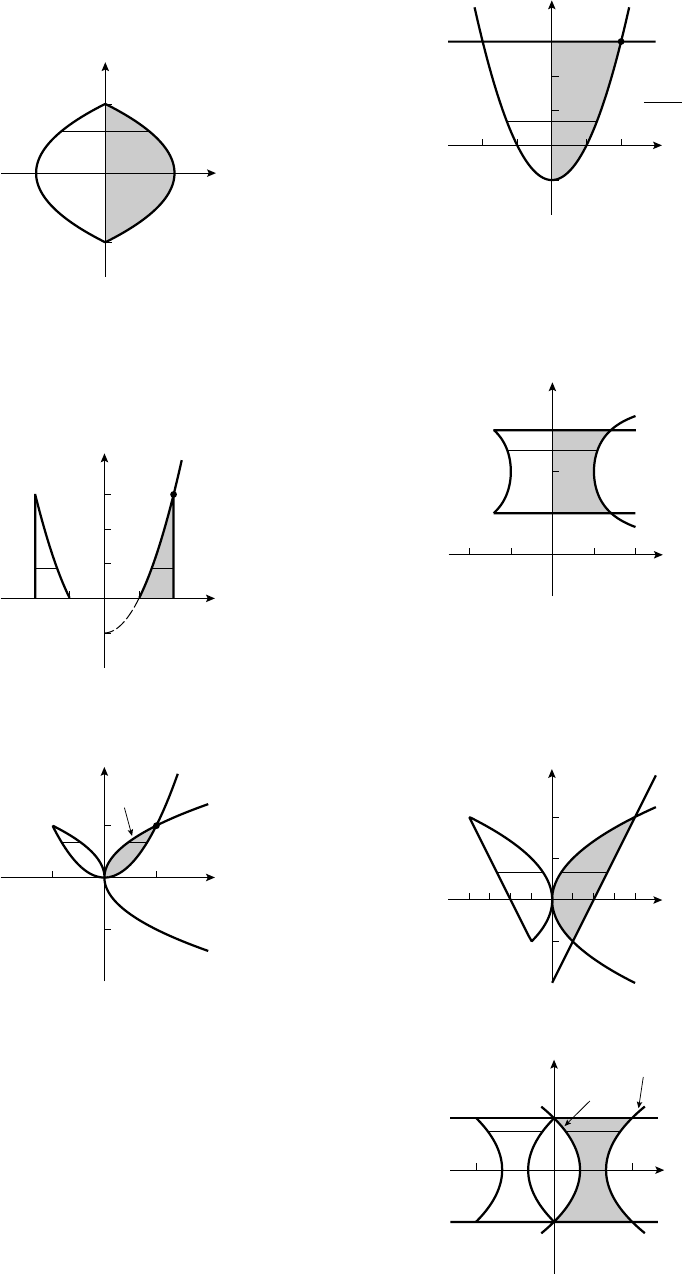
263 Chapter 8
16. V=πZ1
−1(1 −y2)2dy
=πZ1
−1(1 −2y2+y4)dy =16π/15
-1 1
-1
1
x
y
x = 1 – y2
17. V=πZ3
−1(1+y)dy =8π
3
2
x
y
x = √1 + y
18. V=πZ3
0[22−(y+ 1)]dy
=πZ3
0(3 −y)dy =9π/2
3(2, 3)
x
yy = x2 – 1
19. V=πZ3π/4
π/4csc2ydy=2π
-2 -1 1 2
3
6
9
x
y
x = csc y
20. V=πZ1
0(y−y4)dy =3π/10
-1 1
-1
1(1, 1)
x
y
y = x2
x = y2
21. V=πZ2
−1[(y+2)
2−y
4]dy =72π/5
(4, 2)
x
y
x = y2
x = y + 2
(1, –1)
12
-1
1
x
yx = 2 + y2
x = 1 – y2
22. V=πZ1
−1(2+y2)2−(1 −y2)2dy
=πZ1
−1(3+6y
2)dy =10π
Exercise Set 8.2 264
23. V=πZa
−a
b2
a2(a2−x2)dx =4πab2/3
–aa
b
x
y
b
a
y = √a2 – x2
24. V=πZ2
b
1
x2dx =π(1/b −1/2); π(1/b −1/2)=3,b=2π/(π+6)
25. V=πZ0
−1(x+1)dx
+πZ1
0[(x+1)−2x]dx
=π/2+π/2=π
-1 1
1
x
y
y = √2x
(1, √2)
y = √x + 1
26. V=πZ4
0xdx+πZ6
4(6 −x)2dx
=8π+8π/3=32π/3
46
x
y
y = √xy = 6 – x
27. V=πZ3
0(9 −y2)2dy
=πZ3
0(81 −18y2+y4)dy
= 648π/5
9
3
x
y
x = y2
28. V=πZ9
0[32−(3 −√x)2]dx
=πZ9
0(6√x−x)dx
= 135π/2
9
x
y
y = √x
y = 3
1
1
x
y
x = y2
x = y
y = −1
29. V=πZ1
0[(√x+1)
2−(x+1)
2]dx
=πZ1
0(2√x−x−x2)dx =π/2
265 Chapter 8
30. V=πZ1
0[(y+1)
2−(y
2+1)
2]dy
=πZ1
0(2y−y2−y4)dy =7π/15
1
1
x
y
x = y2
x = y
x = –1
31. A(x)=π(x
2
/4)2=πx4/16,
V=Z20
0(πx4/16)dx =40,000πft3
32. V=πZ1
0(x−x4)dx =3π/10
33. V=Z1
0(x−x2)2dx
=Z1
0(x2−2x3+x4)dx =1/30
Square
(1, 1)
1
y = x
y = x2
x
y
34. A(x)=1
2
π1
2
√
x
2
=1
8
πx,
V=Z4
0
1
8πx dx =π
4x
y
y = √x
35. On the upper half of the circle, y=√1−x2, so:
(a) A(x) is the area of a semicircle of radius y,so
A(x)=πy2/2=π(1 −x2)/2; V=π
2Z1
−1(1 −x2)dx =πZ1
0(1 −x2)dx =2π/3
1
-1
y = √1 – x2
x
yy
(b) A(x) is the area of a square of side 2y,so
A(x)=4y
2= 4(1 −x2); V=4Z1
−1
(1 −x2)dx =8Z1
0(1 −x2)dx =16/3
1
-1
y = √1 – x2x
y
2y
Exercise Set 8.2 266
(c) A(x) is the area of an equilateral triangle with sides 2y,so
A(x)=√
3
4(2y)2=√3y2=√3(1 −x2);
V=Z1
−1
√3(1 −x2)dx =2
√
3Z1
0(1 −x2)dx =4
√
3/3
x
y
1
-1
y = √1 – x2
2y
2y2y
y
R
r
h
36. By similar triangles, R/r =y/h so
R=ry/h and A(y)=πr2y2/h2.
V=(πr2/h2)Zh
0y2dy =πr2h/3
37. The two curves cross at x=b≈1.403288534, so
V=πZb
0((2x/π)2−sin16 x)dx +πZπ/2
b
(sin16 x−(2x/π)2)dx =0.710172176.
38. V=πZe
1(1 −(ln y)2)dy =π
39. (a) V=πZr
r−h
(r2−y2)dy =π(rh2−h3/3) = 1
3πh2(3r−h)
r
h
rx
y
x2 + y2 = r2
(b) By the Pythagorean Theorem,
r2=(r−h)
2+ρ
2
,2hr =h2+ρ2; from part (a),
V=πh
3(3hr −h2)=πh
33
2(h2+ρ2)−h2)
=1
6πh(h2+3ρ
2).
10
h – 10
−10
h
x
y
x = √100 – y2
40. Find the volume generated by revolving
the shaded region about the y-axis.
V=πZ−10+h
−10 (100 −y2)dy =π
3h2(30 −h)
Find dh/dt when h= 5 given that dV/dt =1/2.
V=π
3(30h2−h3), dV
dt =π
3(60h−3h2)dh
dt ,
1
2=π
3(300 −75)dh
dt ,dh
dt =1/(150π) ft/min
267 Chapter 8
41. (b) ∆x=5
10 =0.5; {y0,y
1,···,y
10}={0,2.00,2.45,2.45,2.00,1.46,1.26,1.25,1.25,1.25,1.25};
left = π
9
X
i=0 yi
22∆x≈11.157;
right = π
10
X
i=1 yi
22∆x≈11.771; V≈average = 11.464 cm3
r
2
x
y
x = √r2 – y2
√3r
2
√3r
2
–
42. If x=r/2 then from y2=r2−x2we get y=±√3r/2
as limits of integration; for −√3≤y≤√3,
A(y)=π[(r2−y2)−r2/4] = π(3r2/4−y2), thus
V=πZ√3r/2
−√3r/2(3r2/4−y2)dy
=2πZ√
3r/2
0(3r2/4−y2)dy =√3πr3/2.
43. (a)
h
-4
x
y
0 ≤ h < 2
h – 4
(b)
-4
-2 h
2 ≤ h ≤ 4
h – 4 x
y
If the cherry is partially submerged then 0 ≤h<2 as shown in Figure (a); if it is totally sub-
merged then 2 ≤h≤4 as shown in Figure (b). The radius of the glass is 4 cm and that of the
cherry is 1 cm so points on the sections shown in the figures satisfy the equations x2+y2=16
and x2+(y+3)
2= 1. We will find the volumes of the solids that are generated when the shaded
regions are revolved about the y-axis.
For 0 ≤h<2,
V=πZh−4
−4[(16 −y2)−(1 −(y+3)
2)]dy =6πZh−4
−4(y+4)dy =3πh2;
for 2 ≤h≤4,
V=πZ−2
−4[(16 −y2)−(1 −(y+3)
2)]dy +πZh−4
−2(16 −y2)dy
=6πZ−2
−4(y+4)dy +πZh−4
−2(16 −y2)dy =12π+1
3
π(12h2−h3−40)
=1
3π(12h2−h3−4)
so
V=
3πh2if 0 ≤h<2
1
3
π(12h2−h3−4) if 2 ≤h≤4
Exercise Set 8.3 268
44. x=h±pr2−y2,
V=πZr
−rh(h+pr2−y2)2−(h−pr2−y2)2idy
=4πh Zr
−rpr2−y2dy
=4πh 1
2πr2=2π
2
r
2
h
x
y
(x – h2) + y2 = r2
x
h
u
45. tan θ=h/x so h=xtan θ,
A(y)=1
2
hx =1
2x2tan θ=1
2(r2−y2) tan θ
because x2=r2−y2,
V=1
2tan θZr
−r
(r2−y2)dy
= tan θZr
0(r2−y2)dy =2
3r3tan θ
46. A(x)=(xtan θ)(2pr2−x2)
= 2(tan θ)xpr2−x2,
V= 2 tan θZr
0xpr2−x2dx
=2
3r3tan θ
yx
√r2 – x2
x tan u
47. Each cross section perpendicular to the
y-axis is a square so
A(y)=x
2=r
2−y
2
,
1
8
V=Zr
0(r
2−y
2
)dy
V= 8(2r3/3)=16r
3
/3
r
x = √r2 – y2
x
y
48. The regular cylinder of radius rand height hhas the same circular cross sections as do those of
the oblique clinder, so by Cavalieri’s Principle, they have the same volume: πr2h.
EXERCISE SET 8.3
1. V=Z2
12πx(x2)dx =2πZ2
1x
3
dx =15π/2
2. V=Z√2
02πx(p4−x2−x)dx =2πZ√
2
0(x
p4−x
2−x
2
)dx =8π
3(2 −√2)
3. V=Z1
02πy(2y−2y2)dy =4πZ1
0(y
2−y
3
)dy =π/3
269 Chapter 8
4. V=Z2
02πy[y−(y2−2)]dy =2πZ2
0(y
2−y
3+2y)dy =16π/3
5. V=Z1
02π(x)(x3)dx
=2πZ1
0x
4
dx =2π/5
-1 1
-1
1
x
y
y = x3
6. V=Z9
42πx(√x)dx
=2πZ9
4x
3/2
dx = 844π/5
-9 -4 4 9
1
2
3
x
y
y = √x
7. V=Z3
12πx(1/x)dx =2πZ3
1dx =4π
-3 -1 1 3
y = x
1
x
y
8. V=Z√π/2
02πx cos(x2)dx =π/√2
√p
2
x
y
y = cos (x2)
9. V=Z2
12πx[(2x−1) −(−2x+ 3)]dx
=8πZ2
1(x
2−x)dx =20π/3
(2, 3)
(2, –1)
(1, 1)
x
y
10. V=2πZ1
0
x
x
2+1dx
=πln(x2+1)
i1
0=πln 2
-1 1
1
x
y
y = 1
x2 + 1
-√3-1 1 √
3
10
20
x
y
y = ex2
11. V=Z√3
12πxex2dx =πex2i√3
1=π(e3−e)
Exercise Set 8.3 270
12. V=Z2
02πx(2x−x2)dx
=2πZ2
0(2x2−x3)dx =8
3π
2
x
y
y = 2x – x2
13. V=Z1
02πy3dy =π/2
1
x
y
x = y2
14. V=Z3
22πy(2y)dy =4πZ3
2y
2
dy =76π/3
2
3
x
y
x = 2y
15. V=Z1
02πy(1 −√y)dy
=2πZ1
0(y−y
3/2
)dy =π/5
1
x
y
y = √x
16. V=Z4
12πy(5 −y−4/y)dy
=2πZ4
1(5y−y2−4)dy =9π
(1, 4)
(4, 1)
x
y
x = 5 – y
x = 4/y
17. V=2πZπ
0xsin xdx =2π
218. V=2πZπ/2
0xcos xdx =π2−2π
19. (a) V=Z1
02πx(x3−3x2+2x)dx =7π/30
(b) much easier; the method of slicing would require that xbe expressed in terms of y.
-1 1
x
y
y = x3 – 3x2 + 2x
271 Chapter 8
20. V=Z2
12π(x+ 1)(1/x3)dx
=2πZ2
1(x
−2+x
−3
)dx =7π/4
-1 x21
x
y
y = 1/x3
x + 1
1
x
y
1 – yx = y1/3
21. V=Z1
02π(1 −y)y1/3dy
=2πZ1
0(y
1/3−y
4/3
)dy =9π/14
22. (a) Zb
a
2πx[f(x)−g(x)]dx (b) Zd
c
2πy[f(y)−g(y)]dy
x
y
(0, r)
(h, 0)
23. x=h
r(r−y) is an equation of the line
through (0,r) and (h, 0) so
V=Zr
02πy h
r(r−y)dy
=2πh
rZr
0(ry −y2)dy =πr2h/3
x
y
x = k/2
k/2 – x
x = k/4
y = √kx
y = –√kx
24. V=Zk/4
02π(k/2−x)2√kxdx
=2π
√
kZk/4
0(kx1/2−2x3/2)dx =7πk3/60
a
x
y
y = √r2 – x2
y = –√r2 – x2
25. V=Za
02πx(2pr2−x2)dx =4πZa
0x(r
2−x
2
)
1/2
dx
=−4π
3(r2−x2)3/2a
0
=4π
3hr3−(r2−a2)3/2i
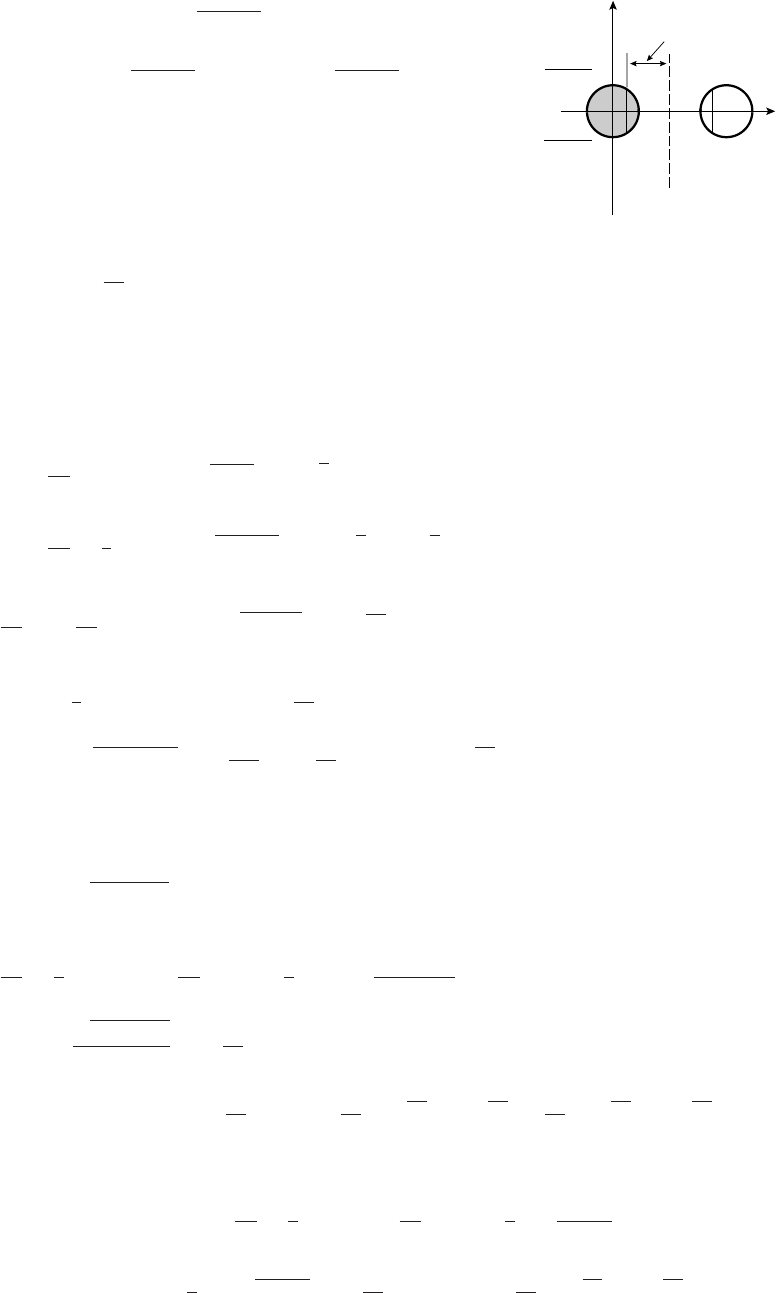
Exercise Set 8.4 272
26. V=Za
−a
2π(b−x)(2pa2−x2)dx
=4πb Za
−apa2−x2dx −4πZa
−a
xpa2−x2dx
=4πb ·(area of a semicircle of radius a)−4π(0)
=2π
2
a
2
b
a–a
x
y
√
a
2
– x2
–√a2 – x2
b − x
x = b
27. Vx=πZb
1/2
1
x2dx =π(2 −1/b), Vy=2πZb
1/2dx =π(2b−1);
Vx=Vyif 2 −1/b =2b−1, 2b2−3b+ 1 = 0, solve to get b=1/2 (reject) or b=1.
EXERCISE SET 8.4
1. (a) dy
dx =2,L=Z2
1
√
1+4dx =√5
(b) dx
dy =1
2,L=Z4
2p1+1/4dy =2
√
5/2=√
5
2. dx
dt =1, dy
dt =5,L=Z1
0p1
2+5
2dt =√26
3. f0(x)=9
2
x
1/2
,1+[f0(x)]2=1+81
4x,
L=Z1
0p1+81x/4dx =8
243 1+81
4x3/2#1
0
= (85√85 −8)/243
4. g0(y)=y(y
2+2)
1/2,1+[g
0(y)]2=1+y
2
(y
2+2)=y
4+2y
2+1=(y
2+1)
2,
L=Z1
0p(y
2+1)
2dy =Z1
0(y2+1)dy =4/3
5. dy
dx =2
3x−1/3,1+dy
dx2
=1+4
9
x
−2/3=9x
2/3+4
9x
2/3,
L=Z8
1
√
9x
2/3+4
3x
1/3dx =1
18 Z40
13 u1/2du, u =9x
2/3+4
=1
27u3/240
13
=1
27(40√40 −13√13) = 1
27(80√10 −13√13)
or (alternate solution)
x=y3/2,dx
dy =3
2y1/2,1+dx
dy 2
=1+9
4
y=4+9y
4,
L=1
2Z4
1p4+9ydy=1
18 Z40
13 u1/2du =1
27(80√10 −13√13)
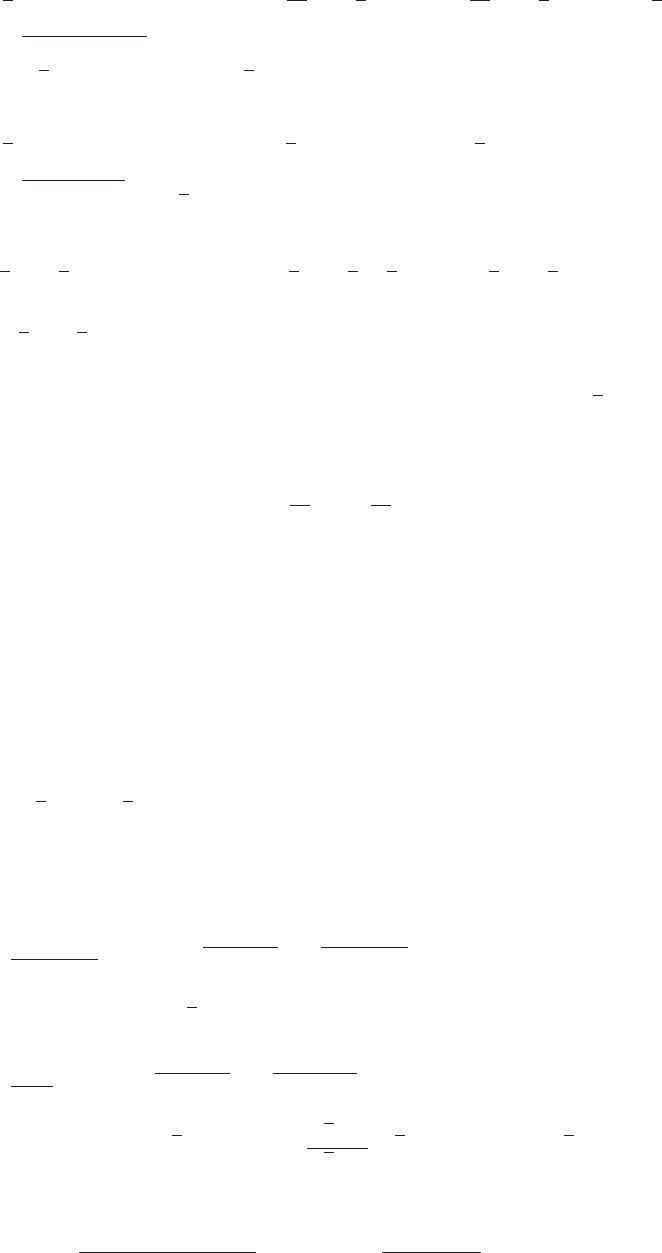
273 Chapter 8
6. f0(x)=1
4
x
3−x
−3
, 1+[f0(x)]2=1+1
16x6−1
2+x−6=1
16x6+1
2+x−6=1
4x3+x−32
,
L=Z3
2s1
4x3+x−32
dx =Z3
21
4x3+x−3dx = 595/144
7. f0(x)=1
2e
x−e
−x
,1+[f0(x)]2=1+1
4e
2x−2+e
−2x
=1
4e
2x+2+e
−2x
,so
L=Z3
0p1+(f0(x))2dx =1
2Z3
0ex+e−xdx =(e
3−e
−3
)/2
8. g0(y)=1
2
y
3−1
2
y
−3
,1+[g
0(y)]2=1+1
4
y
6−1
2+1
4
y
−6
=1
2
y
3+1
2
y
−3
2
,
L=Z4
11
2
y
3+1
2
y
−3
dy = 2055/64
9. (dx/dt)2+(dy/dt)2=(t
2
)
2+(t)
2=t
2(t
2+ 1), L=Z1
0t(t2+1)
1/2dt =(2
√
2−1)/3
10. (dx/dt)2+(dy/dt)2= [2(1 + t)]2+ [3(1 + t)2]2=(1+t)
2
[4+9(1+t)2],
L=Z1
0(1+t)[4 + 9(1 + t)2]1/2dt = (80√10 −13√13)/27
11. (dx/dt)2+(dy/dt)2=(−2 sin 2t)2+ (2 cos 2t)2=4,L=Zπ/2
02dt =π
12. (dx/dt)2+(dy/dt)2=(−sin t+ sin t+tcos t)2+ (cos t−cos t+tsin t)2=t2,
L=Zπ
0tdt=π
2/2
13. (dx/dt)2+(dy/dt)2=[e
t
(cos t−sin t)]2+[e
t
(cos t+ sin t)]2=2e
2t
,
L=Zπ/2
0
√2etdt =√2(eπ/2−1)
14. (dx/dt)2+(dy/dt)2=(2e
tcos t)2+(−2e
tsin t)2=4e
2t
,L=Z4
12e
t
dt =2(e
4−e)
15. dy/dx =sec xtan x
sec x= tan x,p1+(y
0)
2=√
1 + tan2x= sec xwhen 0 <x<π/4, so
L=Zπ/4
0sec xdx= ln(1 + √2)
16. dy/dx =cos x
sin x= cot x,p1+(y
0)
2=√
1 + cot2x= csc xwhen π/4<x<π/2, so
L=Zπ/2
π/4csc xdx=−ln(√2−1) = −ln √2−1
√2+1(
√
2+1)
!= ln(1 + √2)
17. (a) (dx/dθ)2+(dy/dθ)2=(a(1 −cos θ))2+(asin θ)2=a2(2 −2 cos θ), so
L=Z2π
0p(dx/dθ)2+(dy/dθ)2dθ =aZ2π
0p2(1 −cos θ)dθ
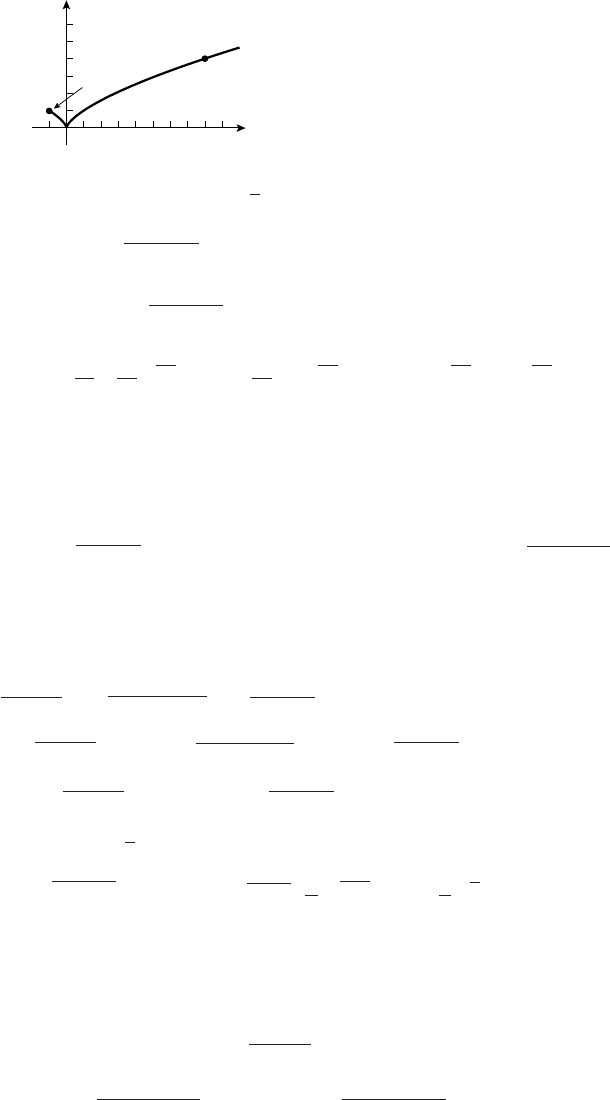
Exercise Set 8.4 274
18. (a) Use the interval 0 ≤φ<2π.
(b) (dx/dφ)2+(dy/dφ)2=(−3acos2φsin φ)2+(3asin2φcos φ)2
=9a
2cos2φsin2φ(cos2φ+ sin2φ)=(9a
2
/4) sin22φ, so
L=(3a/2) Z2π
0|sin 2φ|dφ =6aZπ/2
0sin 2φdφ=−3acos 2φπ/2
0
=6a
19. (a)
(-1, 1)
(8, 4)
x
y(b) dy/dx does not exist at x=0.
(c) x=g(y)=y
3/2
,g
0(y)=3
2y
1/2
,
L=Z1
0p1+9y/4dy (portion for −1≤x≤0)
+Z4
0p1+9y/4dy (portion for 0 ≤x≤8)
=8
27 13
8√13 −1+8
27(10√10 −1) = (13√13+80
√
10 −16)/27
20. For (4), express the curve y=f(x) in the parametric form x=t, y =f(t)sodx/dt = 1 and
dy/dt =f0(t)=f
0(x)=dy/dx. For (5), express x=g(y)asx=g(t),y =tso
dx/dt =g0(t)=g
0(y)=dx/dy and dy/dt =1.
21. L=Z2
0p1+4x
2dx ≈4.645975301 22. L=Zπ
0p1 + cos2ydy≈3.820197789
23. Numerical integration yields: in Exercise 21, L≈4.646783762; in Exercise 22, L≈3.820197788.
24. 0≤m≤f0(x)≤M,so m
2≤[f
0
(x)]2≤M2, and 1 + m2≤1+[f0(x)]2≤1+M2;thus
√
1+m
2≤p1+[f0(x)]2≤√1+M2,
Zb
ap1+m
2dx ≤Zb
ap1+[f0(x)]2dx ≤Zb
ap1+M2dx, and
(b−a)p1+m
2≤L≤(b−a)
p1+M2
25. f0(x) = cos x,√2/2≤cos x≤1 for 0 ≤x≤π/4so
(π/4)p1+1/2≤L≤(π/4)√1+1, π
4p3/2≤L≤π
4√
2.
26. (dx/dt)2+(dy/dt)2=(−asin t)2+(bcos t)2=a2sin2t+b2cos2t
=a2(1 −cos2t)+b
2cos2t=a2−(a2−b2) cos2t
=a21−a2−b2
a2cos2t=a2[1 −k2cos2t],
L=Z2π
0ap1−k2cos2tdt=4aZπ/2
0p1−k2cos2tdt
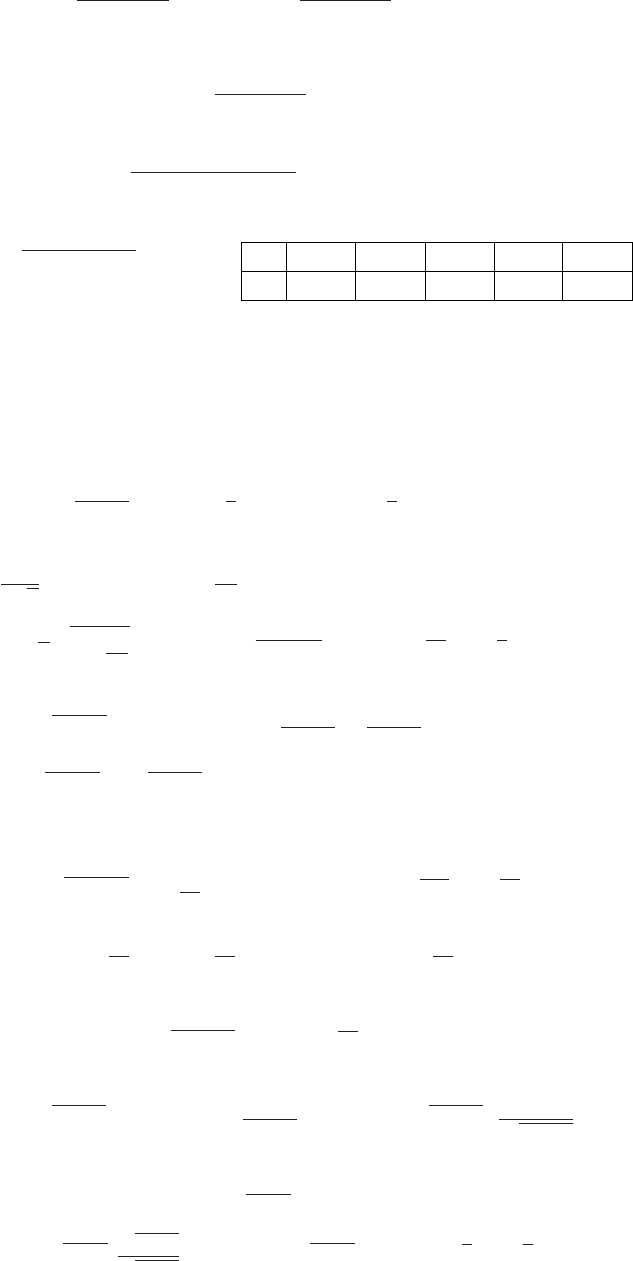
275 Chapter 8
27. (a) (dx/dt)2+(dy/dt)2= 4 sin2t+ cos2t= 4 sin2t+(1−sin2t)=1+3sin
2t,
L=Z2π
0p1+3sin
2tdt=4Zπ/2
0p1+3sin
2tdt
(b) 9.69
(c) distance traveled = Z4.8
1.5p1+3sin
2tdt≈5.16 cm
28. The distance is Z4.6
0p1+(2.09 −0.82x)2dx ≈6.65 m
1 2 1.84 1.83 1.832
3.8202 5.2704 5.0135 4.9977 5.0008
k
L
29. L=Zπ
0p1+(kcos x)2dx
Experimentation yields the values in the table, which by the Intermediate-Value Theorem show
that the true solution kto L= 5 lies between k=1.83 and k=1.832, so k=1.83 to two decimal
places.
EXERCISE SET 8.5
1. S=Z1
02π(7x)√1+49dx =70π
√
2Z1
0xdx=35π
√
2
2. f0(x)= 1
2
√
x
,1+[f0(x)]2=1+ 1
4x
S=Z4
12π
√
x
r1+ 1
4xdx =2πZ4
1px+1/4dx =π(17√17 −5√5)/6
3. f0(x)=−x/√4−x2,1+[f0(x)]2=1+ x
2
4−x
2=4
4−x
2,
S=Z1
−12π
p4−x
2
(2/p4−x2)dx =4πZ1
−1dx =8π
4. y=f(x)=x
3for 1 ≤x≤2, f0(x)=3x
2
,
S=Z2
12πx3p1+9x
4dx =π
27(1+9x
4)
3/22
1
=5π(29√145 −2√10)/27
5. S=Z2
02π(9y+1)
√
82dy =2π
√
82 Z2
0(9y+1)dy =40π
√
82
6. g0(y)=3y
2
,S=Z1
02πy3p1+9y
4dy =π(10√10 −1)/27
7. g0(y)=−y/p9−y2,1+[g
0(y)]2=9
9−y2,S=Z2
−22πp9−y2·3
p9−y2dy =6πZ2
−2dy =24π
8. g0(y)=−(1 −y)−1/2,1+[g
0(y)]2=2−y
1−y,
S=Z0
−12π(2p1−y)√2−y
√1−ydy =4πZ0
−1p2−ydy=8π(3√3−2√2)/3
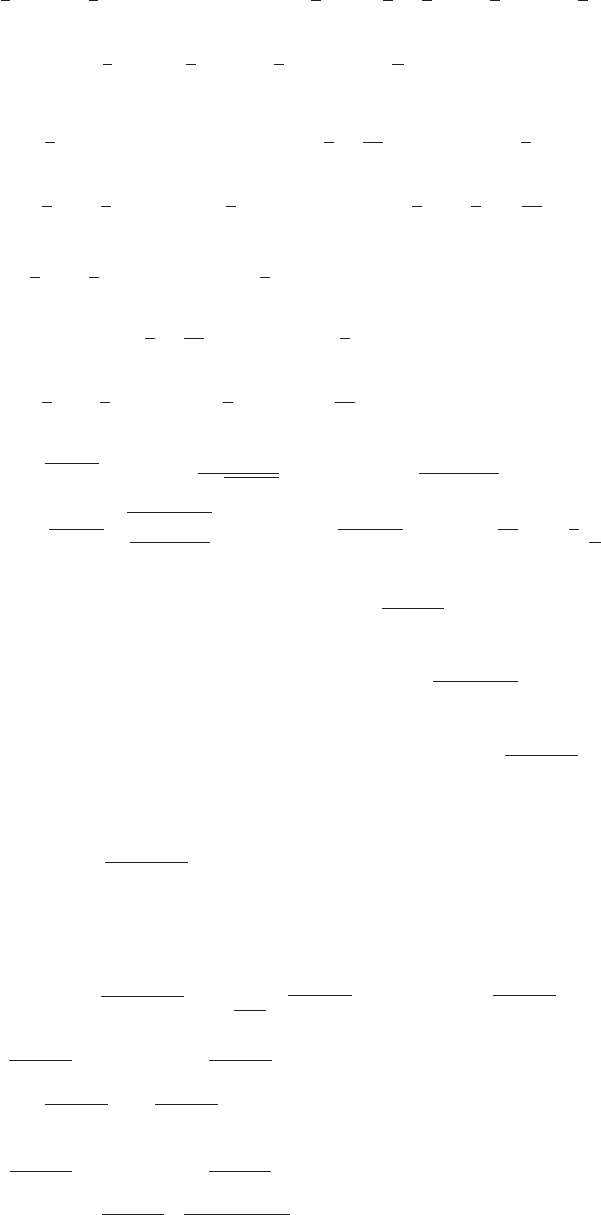
Exercise Set 8.5 276
9. f0(x)=1
2
x
−1/2−1
2
x
1/2
,1+[f0(x)]2=1+1
4
x
−1−1
2+1
4
x=1
2
x
−1/2+1
2
x
1/2
2
,
S=Z3
12πx
1/2−1
3
x
3/2
1
2x
−1/2+1
2x
1/2dx =π
3Z3
1(3+2x−x
2)dx =16π/9
10. f0(x)=x
2−1
4
x
−2
,1+[f0(x)]2=1+x
4−1
2+1
16x−4=x2+1
4x−22
,
S=Z2
12π1
3x3+1
4x−1x
2+1
4x
−2dx =2πZ2
11
3
x
5+1
3
x+1
16x−3dx = 515π/64
11. x=g(y)=1
4
y
4+1
8
y
−2
,g
0(y)=y
3−1
4
y
−3
,
1+[g
0(y)]2=1+y
6−1
2+1
16y−6=y3+1
4y−32
,
S=Z2
12π1
4y4+1
8y−2y
3+1
4y
−3dy =π
16 Z2
1(8y7+6y+y
−5)dy =16,911π/1024
12. x=g(y)=√
16 −y;g0(y)=−1
2
√
16 −y,1+[g
0(y)]2=65 −4y
4(16 −y),
S=Z15
02πp16 −ys65 −4y
4(16 −y)dy =πZ15
0p65 −4ydy = (65√65 −5√5)π
6
13. f0(x)=e
x
, 1+[f0(x)]2=1+e
2x
,S=Z1
02πexp1+e
2xdx ≈22.94
14. f0(x) = cos x, 1+[f0(x)]2= 1 + cos2x,S=Zπ
02πsin xp1 + cos2xdx≈14.42
15. x=g(y)=lny, g0(y)=1/y, 1+[g
0(y)]2=1+1/y2;S=Ze
12πp1+1/y2ln ydy ≈7.05
16. x=g(y) = tan y, g0(y) = sec2y, 1+[g
0(y)]2= 1 + sec4y;
S=Zπ/4
02πtan yp1 + sec4ydy ≈3.84
17. Revolve the line segment joining the points (0,0) and (h, r) about the x-axis. An equation of the
line segment is y=(r/h)xfor 0 ≤x≤hso
S=Zh
02π(r/h)xp1+r
2/h2dx =2πr
h2pr2+h2Zh
0xdx=πrpr2+h2
18. f(x)=√
r
2−x
2
,f
0(x)=−x/√r2−x2,1+[f0(x)]2=r2/(r2−x2),
S=Zr
−r
2πpr2−x2(r/pr2−x2)dx =2πr Zr
−r
dx =4πr2
19. g(y)=pr
2−y
2
,g
0(y)=−y/pr2−y2,1+[g
0(y)]2=r2/(r2−y2),
(a) S=Zr
r−h
2πpr2−y2pr2/(r2−y2)dy =2πr Zr
r−h
dy =2πrh
(b) From part (a), the surface area common to two polar caps of height h1>h
2is
2πrh1−2πrh2=2πr(h1−h2).

277 Chapter 8
20. For (4), express the curve y=f(x) in the parametric form x=t, y =f(t)sodx/dt = 1 and
dy/dt =f0(t)=f
0(x)=dy/dx. For (5), express x=g(y)asx=g(t),y =tso
dx/dt =g0(t)=g
0(y)=dx/dy and dy/dt =1.
21. x0=2t, y0=2,(x
0)
2+(y
0)
2=4t
2+4
S=2πZ4
0(2t)p4t2+4dt =8πZ4
0t
pt
2+1dt =8π
3(17√17 −1)
22. x0=et(cos t−sin t),y
0=e
t(cos t+ sin t),(x0)2+(y
0)
2=2e
2t
S=2πZπ/2
0(etsin t)√2e2tdt =2
√
2πZπ/2
0e2tsin tdt
=2
√
2π1
5
e
2t
(2 sin t−cos t)π/2
0
=2√2
5π(2eπ+1)
23. x0=1,y
0=4t,(x
0
)
2+(y
0)
2=1+16t
2,S=2πZ1
0t
p1+16t
2dt =π
24(17√17 −1)
24. x0=−2 sin tcos t, y0= 2 sin tcos t, (x0)2+(y
0)
2= 8 sin2tcos2t
S=2πZπ/2
0cos2tp8 sin2tcos2tdt=4
√
2πZπ/2
0cos3tsin tdt=√2π
25. x0=−rsin t,y0=rcos t,(x
0
)
2+(y
0)
2=r
2,
S=2πZπ
0rsin t√r2dt =2πr2Zπ
0sin tdt=4πr2
26. dx
dφ =a(1 −cos φ), dy
dφ =asin φ,dx
dφ2
+dy
dφ2
=2a
2
(1 −cos φ)
S=2πZ2π
0a(1 −cos φ)p2a2(1 −cos φ)dφ =2
√
2πa2Z2π
0(1 −cos φ)3/2dφ,
but 1 −cos φ= 2 sin2φ
2so (1 −cos φ)3/2=2
√
2 sin3φ
2for 0 ≤φ≤πand, taking advantage of the
symmetry of the cycloid, S=16πa2Zπ
0sin3φ
2dφ =64πa2/3.
27. (a) length of arc of sector = circumference of base of cone,
`θ =2πr, θ =2πr/`;S= area of sector = 1
2`2(2πr/`)=πr`
(b) S=πr2`2−πr1`1=πr2(`1+`)−πr1`1=π[(r2−r1)`1+r2`];
Using similar triangles `2/r2=`1/r1,r
1`
2=r
2`
1,r
1(`
1+`)=r
2
`
1
,(r
2−r
1
)`
1=r
1
`
so S=π(r1`+r2`)=π(r
1+r
2
)`.
r
1
r
2
l
2
l
1
l

Exercise Set 8.6 278
28. 2πkp1+[f0(x)]2≤2πf(x)p1+[f0(x)]2≤2πKp1+[f0(x)]2,so
Zb
a
2πkp1+[f0(x)]2dx ≤Zb
a
2πf(x)p1+[f0(x)]2dx ≤Zb
a
2πKp1+[f0(x)]2dx,
2πk Zb
ap1+[f0(x)]2dx ≤S≤2πK Zb
ap1+[f0(x)]2dx,2πkL ≤S≤2πKL
29. (a) 1≤p1+[f0(x)]2so 2πf(x)≤2πf(x)p1+[f0(x)]2,
Zb
a
2πf(x)dx ≤Zb
a
2πf(x)p1+[f0(x)]2dx,2π
Zb
a
f(x)dx ≤S, 2πA ≤S
(b) 2πA =Sif f0(x) = 0 for all xin [a, b]sof(x) is constant on [a, b].
EXERCISE SET 8.6
1. (a) W=F·d= 30(7) = 210 ft·lb
(b) W=Z6
1F(x)dx =Z6
1x−2dx =−1
x6
1
=5/6ft·lb
2. W=Z5
0F(x)dx =Z2
040 dx −Z5
2
40
3(x−5) dx =80+60=140J
3. distance traveled = Z5
0v(t)dt =Z5
0
4t
5dt =2
5t2i5
0= 10 ft. The force is a constant 10 lb, so the
work done is 10 ·10 = 100 ft·lb.
4. (a) F(x)=kx, F(0.05)=0.05k=45,k = 900 N/m
(b) W=Z0.03
0900xdx=0.405 J (c) W=Z0.10
0.05 900xdx=3.375 J
5. F(x)=kx,F(0.2)=0.2k= 100, k= 500 N/m, W=Z0.8
0500xdx = 160 J
6. F(x)=kx,F(1/2) = k/2=6,k= 12 N/m, W=Z2
012xdx=24J
7. W=Z1
0kx dx =k/2 = 10, k= 20 lb/ft
9 - x
x
0
6
95
8. W=Z6
0(9 −x)62.4(25π)dx
= 1560πZ6
0(9 −x)dx =56,160πft·lb
9. W=Z6
0(9 −x)ρ(25π)dx = 900πρ ft·lb
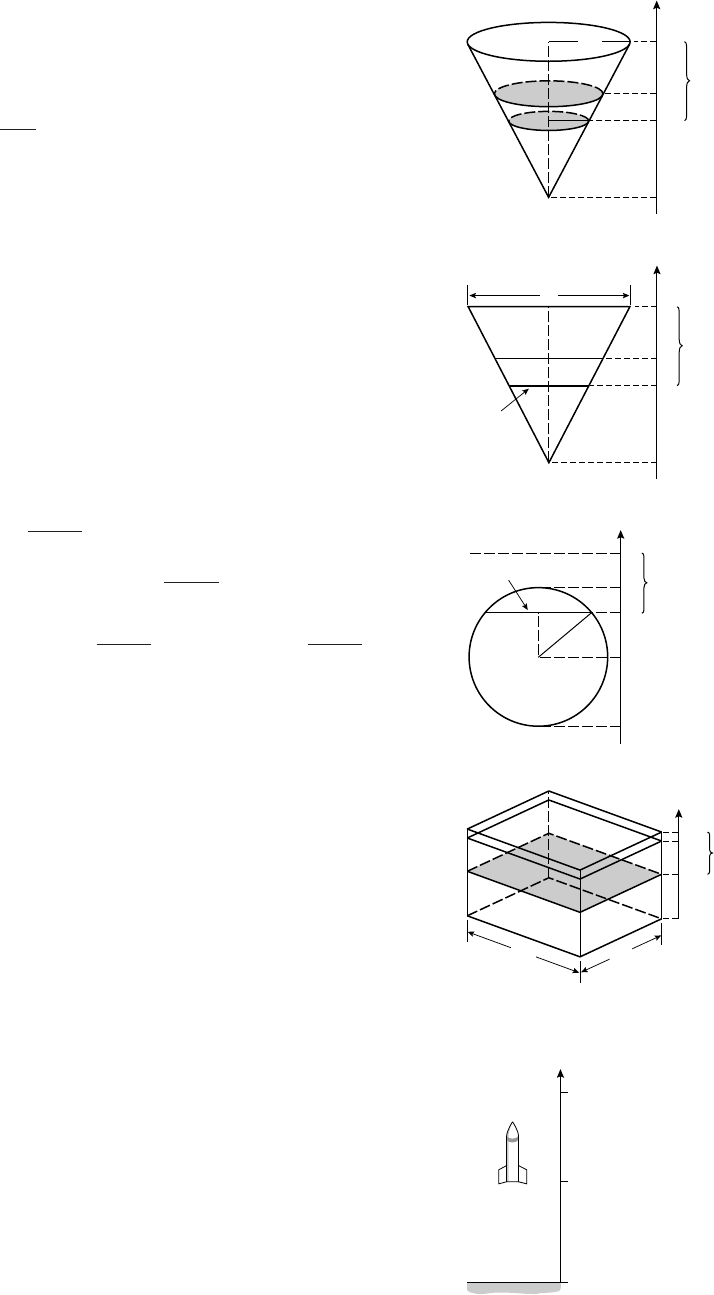
279 Chapter 8
15 - x
x
0
10
1510
r
10. r/10 = x/15, r=2x/3,
W=Z10
0(15 −x)62.4(4πx2/9)dx
=83.2
3πZ10
0(15x2−x3)dx
= 208,000π/3ft·lb
3 - x
x
0
2
3
4
w(x)
11. w/4=x/3,w =4x/3,
W=Z2
0(3 −x)(9810)(4x/3)(6)dx
= 78480 Z2
0(3x−x2)dx
= 261,600 J
3
2
0
-2
3 - x
x
w(x)
2
12. w=2
p4−x
2
W=Z2
−2
(3 −x)(50)(2p4−x2)(10)dx
= 3000 Z2
−2p4−x2dx −1000 Z2
−2xp4−x2dx
= 3000[π(2)2/2] −0 = 6000πft·lb
0
10
910 - x
x
20 15
13. (a) W=Z9
0(10 −x)62.4(300)dx
=18,720 Z9
0(10 −x)dx
= 926,640 ft·lb
(b) to empty the pool in one hour would require
926,640/3600 = 257.4ft·lb of work per second
so hp of motor = 257.4/550=0.468
3000
0
x
Rocket
14. When the rocket is xft above the ground
total weight = weight of rocket
+ weight of fuel
= 3 + [40 −2(x/1000)]
=43−x/500 tons,
W=Z3000
0(43 −x/500)dx = 120,000 ft·tons

Exercise Set 8.7 280
15. W=Z100
015(100 −x)dx
=75,000 ft·lb
100
0
100 - x
x
Pulley
Chain
16. Let F(x) be the force needed to hold
charge Aat position x, then
F(x)= c
(a−x)
2,F(−a)= c
4a
2=k,
so c=4a
2
k.
W=Z0
−a
4a
2
k(a−x)
−2
dx =2ak J
0−aax
BA
17. (a) 150 = k/(4000)2,k=2.4×109,w(x)=k/x2=2,400,000,000/x2lb
(b) 6000 = k/(4000)2,k=9.6×1010,w(x)=9.6×1010/(x+ 4000)2lb
(c) W=Z5000
4000 9.6(1010)x−2dx =4,800,000 mi·lb = 2.5344 ×1010 ft·lb
18. (a) 20 = k/(1080)2,k=2.3328 ×107, weight = w(x+ 1080) = 2.3328 ·107/(x+ 1080)2lb
(b) W=Z10.8
0[2.3328 ·107/(x+ 1080)2]dx = 213.86 mi·lb = 1,129,188 ft·lb
19. W=F·d=(6.40 ×105)(3.00 ×103)=1.92 ×109J; from Theorem 8.6.4,
v2
f=2W/m +v2
i= 2(1.92 ·109)/(4 ·105)+20
2=10,000, vf= 100 m/s
20. W=F·d=(2.00 ×105)(2.00 ×105)=4×1010 J; from Theorem 8.6.4,
v2
f=2W/m +v2
i=8·1010/(2 ·103)+10
8≈11.832 m/s.
21. (a) The kinetic energy would have decreased by 1
2mv2=1
24·106(15000)2=4.5×1014 J
(b) (4.5×1014)/(4.2×1015)≈0.107 (c) 1000
13 (0.107) ≈8.24 bombs
EXERCISE SET 8.7
1. (a) F=ρhA =62.4(5)(100) = 31,200 lb
P=ρh =62.4(5) = 312 lb/ft2
(b) F=ρhA = 9810(10)(25) = 2,452,500 N
P=ρh = 9810(10) = 98.1kPa
2. (a) F=PA =6·105(160) = 9.6×107N(b) F=PA = 100(60) = 6000 lb
3. F=Z2
062.4x(4)dx
= 249.6Z2
0xdx= 499.2lb
2
04
x
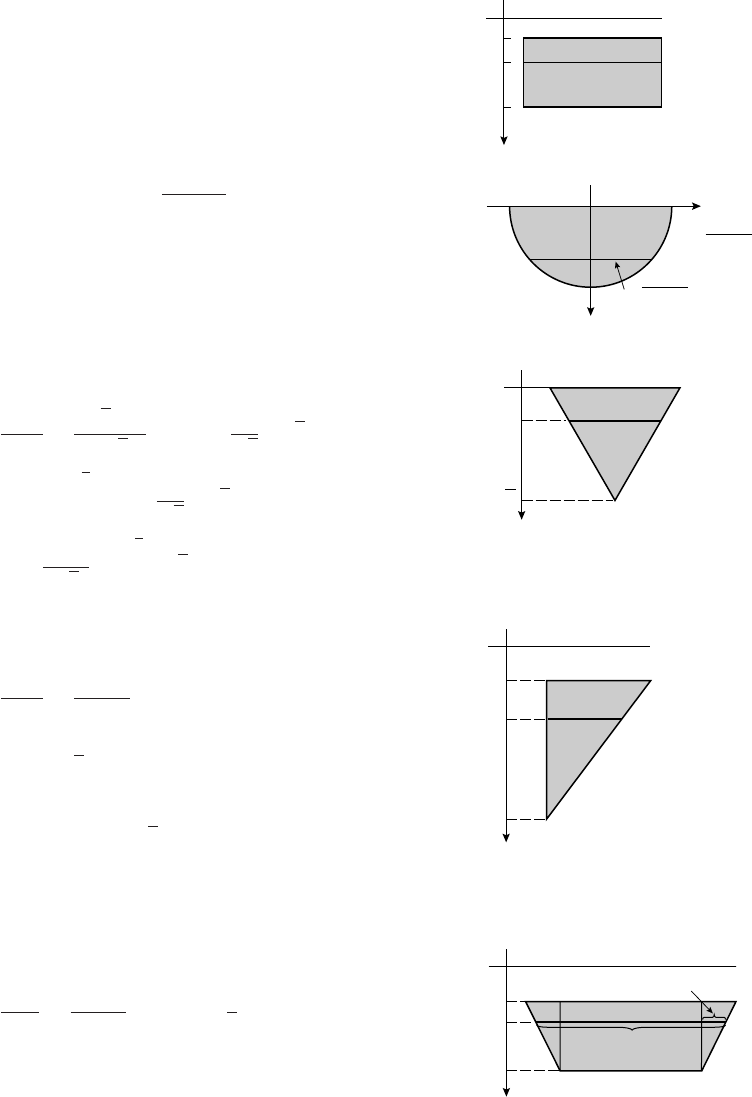
281 Chapter 8
4. F=Z3
19810x(4)dx
= 39240 Z3
1xdx
= 156,960 N 3
1
0
4
x
50
5
xy = √25 – x2
y
2√25 – x2
5. F=Z5
09810x(2p25 −x2)dx
=19,620 Z5
0x(25 −x2)1/2dx
=8.175 ×105N
2√3
04
44
xw(x)
6. By similar triangles
w(x)
4=2√3−x
2√3,w(x)= 2
√
3
(2√3−x),
F=Z2√3
062.4x2
√3(2√3−x)dx
=124.8
√3Z2√3
0(2√3x−x2)dx = 499.2lb
10
2
0
xw(x)
8
6
7. By similar triangles
w(x)
6=10 −x
8
w(x)=3
4
(10 −x),
F=Z10
29810x3
4(10 −x)dx
= 7357.5Z10
2(10x−x2)dx =1,098,720 N
12
44
16
4
0
x
w(x)
u(x)
8. w(x)=16+2u(x),but
u(x)
4=12 −x
8so u(x)=1
2
(12 −x),
w(x)=16+(12−x)=28−x,
F=Z12
462.4x(28 −x)dx
=62.4Z12
4(28x−x2)dx =77,209.6 lb.
9. Yes: if ρ2=2ρ
1then F2=Zb
a
ρ2h(x)w(x)dx =Zb
a
2ρ1h(x)w(x)dx =2Zb
a
ρ
1
h(x)w(x)dx =2F
1
.
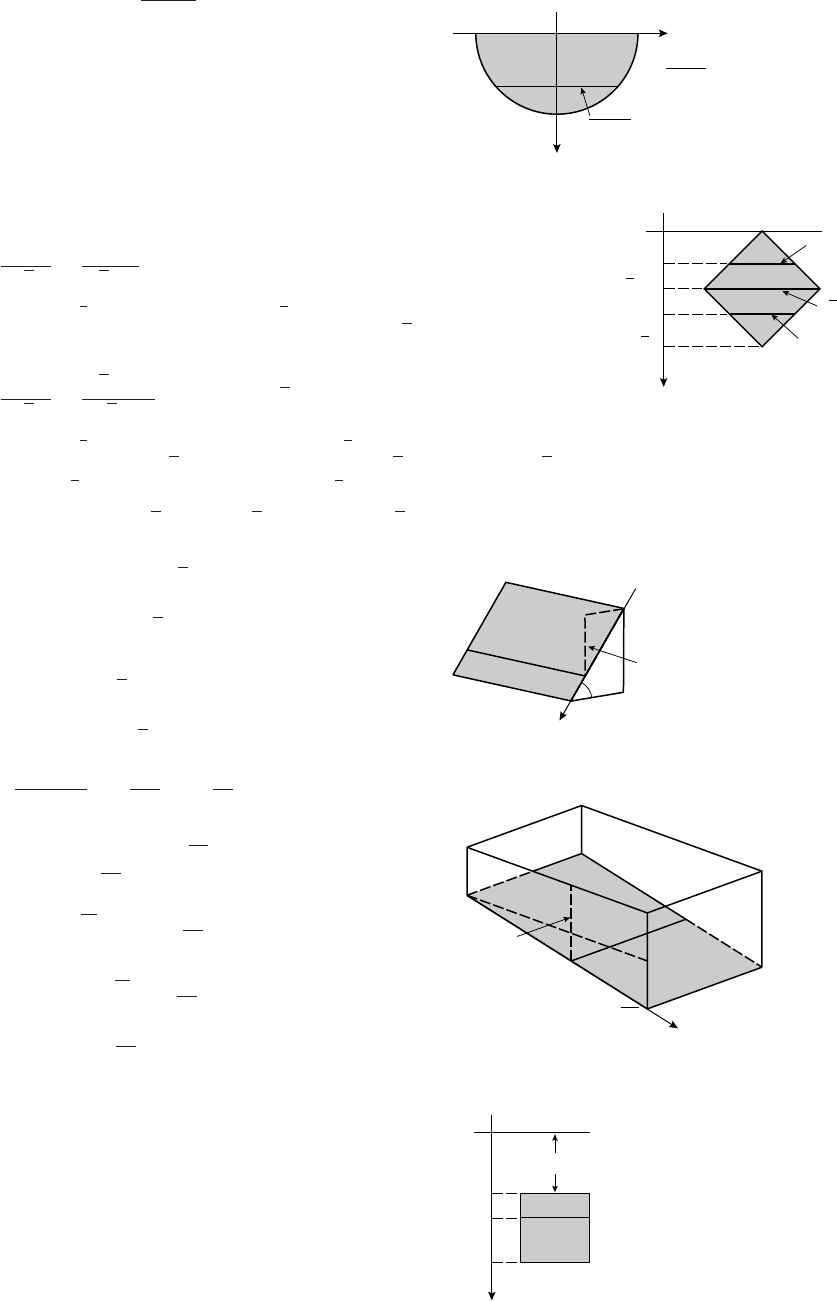
Exercise Set 8.7 282
10. F=Z2
050x(2p4−x2)dx
= 100 Z2
0x(4 −x2)1/2dx
= 800/3lb
20
x
y
2
√4 – x2
y = √4 – x2
0
x
x
√2a
√2a
√2a/2
w1(x)
w2(x)
a
a
a
a
11. Find the forces on the upper and lower halves and add them:
w1(x)
√2a=x
√2a/2,w1(x)=2x
F
1=Z√
2a/2
0ρx(2x)dx =2ρZ√
2a/2
0x2dx =√2ρa3/6,
w2(x)
√2a=√2a−x
√2a/2,w2(x)=2(
√
2a−x)
F
2=Z√
2a
√
2a/2ρx[2(√2a−x)]dx =2ρZ√
2a
√
2a/2(√2ax −x2)dx =√2ρa3/3,
F=F1+F2=√2ρa3/6+√
2ρa3/3=ρa3/√2lb
xh(x)
200
100
0
60°
12. h(x)=xsin 60◦=√3x/2,
F=Z100
09810(√3x/2)(200)dx
= 981000√3Z100
0xdx
=4,905,000√3N
16
10
4
4
0
4
4√17
x
h(x)
13. √162+4
2=√
272=4
√
17 is the
other dimension of the bottom.
(h(x)−4)/4=x/(4√17)
h(x)=x/√17+4,
F=Z4
√
17
062.4(x/√17 + 4)10dx
= 624 Z4√17
0(x/√17+4)dx
=14,976√17 lb
h + 2
h
0
2
2
x
h
14. F=Zh+2
h
ρ0x(2)dx
=2ρ
0Zh+2
h
xdx
=4ρ
0
(h+1)
283 Chapter 8
15. (a) From Exercise 14, F=4ρ
0
(h+ 1) so (assuming that ρ0is constant) dF/dt =4ρ
0
(dh/dt)
which is a positive constant if dh/dt is a positive constant.
(b) If dh/dt = 20 then dF/dt =80ρ
0lb/min from part (a).
EXERCISE SET 8.8
1. (a) sinh 3 ≈10.0179
(b) cosh(−2) ≈3.7622
(c) tanh(ln 4) = 15/17 ≈0.8824
(d) sinh−1(−2) ≈−1.4436
(e) cosh−13≈1.7627
(f) tanh−13
4≈0.9730
2. (a) csch(−1) ≈−0.8509
(b) sech(ln 2) = 0.8
(c) coth 1 ≈1.3130
(d) sech−11
2≈1.3170
(e) coth−13≈0.3466
(f) csch−1(−√3) ≈−0.5493
3. (a) sinh(ln 3) = 1
2(eln 3 −e−ln 3)=1
23−1
3
=4
3
(b) cosh(−ln 2) = 1
2(e−ln 2 +eln 2)=1
21
2+2
=5
4
(c) tanh(2 ln 5) = e2ln5 −e
−2ln5
e
2ln5 +e
−2ln5 =25 −1/25
25+1/25 =312
313
(d) sinh(−3ln2)= 1
2(e
−3ln2 −e
3ln2)=1
21
8−8
=−63
16
4. (a) 1
2(eln x+e−ln x)=1
2x+1
x
=x
2+1
2x,x>0
(b) 1
2(eln x−e−ln x)=1
2x−1
x
=x
2−1
2x,x>0
(c) e2lnx−e
−2lnx
e
2lnx+e
−2lnx=x
2−1/x2
x2+1/x2=x4−1
x4+1,x>0
(d) 1
2(e−ln x+eln x)=1
21
x+x
=1+x
2
2x,x>0
5. sinh x0 cosh x0 tanh x0 coth x0 sech x0 csch x0
2√52
/√
5
√
5
/
21
/√
5
1
/
2
3
/
45
/
43
/
55
/
34
/
5
4
/
3
4
/
3
(a)
(b)
(c) 5/34
/
55
/
43
/
5
3
/
4
(a) cosh2x0= 1 + sinh2x0= 1 + (2)2= 5, cosh x0=√5
(b) sinh2x0= cosh2x0−1=25
16 −1= 9
16, sinh x0=3
4(because x0>0)
(c) sech2x0=1−tanh2x0=1−4
5
2
=1−16
25 =9
25, sech x0=3
5,
cosh x0=1
sech x0=5
3, from sinh x0
cosh x0= tanh x0we get sinh x0=5
34
5=4
3
Exercise Set 8.8 284
6. d
dx cschx=d
dx
1
sinh x=−cosh x
sinh2x=−coth xcsch xfor x6=0
d
dx sech x=d
dx
1
cosh x=−sinh x
cosh2x=−tanh xsech xfor all x
d
dx coth x=d
dx
cosh x
sinh x=sinh2x−cosh2x
sinh2x=−csch2xfor x6=0
7. (a) y= sinh−1xif and only if x= sinh y;1=dy
dx
dx
dy =dy
dx cosh y;so
d
dx[sinh−1x]= dy
dx =1
cosh y=1
p1 + sinh2y=1
√1+x
2for all x.
(b) Let x≥1. Then y= cosh−1xif and only if x= cosh y;1=dy
dx
dx
dy =dy
dx sinh y,so
d
dx[cosh−1x]= dy
dx =1
sinh y=1
pcosh2y−1=1
x2−1for x≥1.
(c) Let −1<x<1. Then y= tanh−1xif and only if x= tanh y;thus
1=dy
dx
dx
dy =dy
dx sech2y=dy
dx(1 −tanh2y)=1−x
2
,so d
dx[tanh−1x]= dy
dx =1
1−x2.
9. 4 cosh(4x−8) 10. 4x3sinh(x4)11. −1
xcsch2(ln x)
12. 2sech22x
tanh 2x13. 1
x2csch(1/x) coth(1/x)14. −2e2xsech(e2x) tanh(e2x)
15. 2 + 5 cosh(5x) sinh(5x)
q4x+ cosh2(5x)16. 6 sinh2(2x) cosh(2x)
17. x5/2tanh(√x) sech2(√x)+3x
2tanh2(√x)
18. −3 cosh(cos 3x) sin 3x19. 1
p1+x
2/91
3=1/
p9+x
2
20. 1
p1+1/x2(−1/x2)=−1
|x|
√
x
2+1 21. 1/(cosh−1x)√x2−1
22. 1/q(sinh−1x)2−1√1+x
223. −(tanh−1x)−2/(1 −x2)
24. 2(coth−1x)/(1 −x2)25. sinh x
pcosh2x−1=sinh x
|sinh x|=1,x>0
−1,x<0
26. (sech2x)/p1 + tanh2x27. −ex
2x√1−x+exsech−1x
28. 10(1 + xcsch−1x)9−x
|x|√1+x
2+ csch−1x
31. 1
7sinh7x+C32. 1
2sinh(2x−3)+C33. 2
3(tanh x)3/2+C
285 Chapter 8
34. −1
3coth(3x)+C35. ln(cosh x)+C36. −1
3coth3x+C
37. −1
3sech3xln 3
ln 2
=37/375 38. ln(cosh x)iln 3
0=ln5−ln 3
39. u=3x,1
3Z1
√
1+u
2du =1
3sinh−13x+C
40. x=√2u,Z√2
√2u2−2du =Z1
√u2−1du = cosh−1(x/√2)+C
41. u=ex,Z1
u√1−u2du =−sech−1(ex)+C
42. u= cos θ,−Z1
√1+u
2du =−sinh−1(cos θ)+C
43. u=2x,Zdu
u√1+u
2=−csch−1|u|+C=−csch−1|2x|+C
44. x=5u/3, Z5/3
√25u2−25du =1
3Z1
√u2−1du =1
3cosh−1(3x/5)+C
45. tanh−1xi1/2
0= tanh−1(1/2) −tanh−1(0) = 1
2ln 1+1/2
1−1/2=1
2ln 3
46. sinh−1ti√3
0= sinh−1√3−sinh−10 = ln(√3+2)
49. A=Zln 3
0sinh 2xdx=1
2cosh 2xln 3
0
=1
2[cosh(2 ln 3) −1],
but cosh(2 ln 3) = cosh(ln 9) = 1
2(eln 9 +e−ln 9)=1
2
(9+1/9)=41/9soA=1
2
[41/9−1]=16/9.
50. V=πZln 2
0sech2xdx=πtanh xln 2
0
=πtanh(ln 2) = 3π/5
51. V=πZ5
0(cosh22x−sinh22x)dx =πZ5
0dx =5π
52. Z1
0cosh ax dx =2,1
asinh ax1
0
=2,1
asinh a=2,sinh a=2a;
let f(a) = sinh a−2a, then an+1 =an−sinh an−2an
cosh an−2,a
1=2.2,...,a
4=a
5=2.177318985.
53. y0= sinh x,1+(y
0)
2= 1 + sinh2x= cosh2x
L=Zln 2
0cosh xdx= sinh xln 2
0
= sinh(ln 2) = 1
2(eln 2 −e−ln 2)=1
22−1
2
=3
4

Exercise Set 8.8 286
54. y0= sinh(x/a),1+(y
0)
2= 1 + sinh2(x/a) = cosh2(x/a)
L=Zx1
0cosh(x/a)dx =asinh(x/a)x1
0
=asinh(x1/a)
55. sinh(−x)=1
2
(e
−x−e
x
)=−1
2
(e
x−e
−x
)=−sinh x
cosh(−x)=1
2
(e
−x+e
x
)=1
2
(e
x+e
−x
) = cosh x
56. (a) cosh x+ sinh x=1
2(ex+e−x)+1
2(e
x−e
−x
)=e
x
(b) cosh x−sinh x=1
2(ex+e−x)−1
2(ex−e−x)=e
−x
(c) sinh xcosh y+ cosh xsinh y=1
4(ex−e−x)(ey+e−y)+1
4(e
x+e
−x
)(ey−e−y)
=1
4[(ex+y−e−x+y+ex−y−e−x−y)+(e
x+y+e
−x+y−e
x−y−e
−x−y)]
=1
2[e(x+y)−e−(x+y)] = sinh(x+y)
(d) Let y=xin part (c).
(e) The proof is similar to part (c), or: treat xas variable and yas constant, and differentiate
the result in part (c) with respect to x.
(f) Let y=xin part (e).
(g) Use cosh2x= 1 + sinh2xtogether with part (f).
(h) Use sinh2x= cosh2x−1 together with part (f).
57. (a) Divide cosh2x−sinh2x= 1 by cosh2x.
(b) tanh(x+y)=sinh xcosh y+ cosh xsinh y
cosh xcosh y+ sinh xsinh y=
sinh x
cosh x+sinh y
cosh y
1+ sinh xsinh y
cosh xcosh y
=tanh x+ tanh y
1 + tanh xtanh y
(c) Let y=xin part (b).
58. (a) Let y= cosh−1x; then x= cosh y=1
2(ey+e−y), ey−2x+e−y=0,e
2y−2xey+1=0,
e
y=2x±√
4x
2−4
2=x±px
2−1. To determine which sign to take, note that y≥0
so e−y≤ey,x=(e
y+e
−y
)/2≤(e
y+e
y
)/2=e
y
, hence ey≥xthus ey=x+√x2−1,
y= cosh−1x= ln(x+√x2−1).
(b) Let y= tanh−1x; then x= tanh y=ey−e−y
ey+e−y=e2y−1
e2y+1,xe2y+x=e2y−1,
1+x=e
2y(1 −x), e2y=(1+x)/(1 −x), 2y=ln1+x
1−x,y=1
2ln 1+x
1−x.
59. (a) d
dx(cosh−1x)=1+x/√x2−1
x+√x2−1=1/
px
2−1
(b) d
dx(tanh−1x)= d
dx 1
2(ln(1 + x)−ln(1 −x))=1
21
1+x+1
1−x=1/(1 −x2)
287 Chapter 8
60. Let y= sech−1xthen x= sech y=1/cosh y, cosh y=1/x,y= cosh−1(1/x); the proofs for the
remaining two are similar.
61. If |u|<1 then, by Theorem 8.8.6, Zdu
1−u2= tanh−1u+C.
For |u|>1,Zdu
1−u2= coth−1u+C= tanh−1(1/u)+C.
62. (a) d
dx(sech−1|x|)= d
dx(sech−1√x2)=−1
√
x
2
√
1−x
2
x
√
x
2=−1
x
√
1−x
2
(b) Similar to solution of part (a)
63. (a) lim
x→+∞sinh x= lim
x→+∞
1
2(ex−e−x)=+∞−0=+∞
(b) lim
x→−∞ sinh x= lim
x→−∞
1
2(ex−e−x)=0−∞=−∞
(c) lim
x→+∞tanh x= lim
x→+∞
ex−e−x
ex+e−x=1
(d) lim
x→−∞ tanh x= lim
x→−∞
ex−e−x
ex+e−x=−1
(e) lim
x→+∞sinh−1x= lim
x→+∞ln(x+px2+1)=+∞
(f) lim
x→1−tanh−1x= lim
x→1−
1
2[ln(1 + x)−ln(1 −x)]=+∞
64. (a) lim
x→+∞(cosh−1x−ln x) = lim
x→+∞[ln(x+px2−1) −ln x]
= lim
x→+∞ln x+√x2−1
x= lim
x→+∞ln(1 + p1−1/x2)=ln2
(b) lim
x→+∞
cosh x
ex= lim
x→+∞
ex+e−x
2ex= lim
x→+∞
1
2(1+e−2x)=1/2
65. For |x|<1, y= tanh−1xis defined and dy/dx =1/(1 −x2)>0; y00 =2x/(1 −x2)2changes sign
at x= 0, so there is a point of inflection there.
66. Let x=−u,Z1
√u2−1du =−Z1
√x2−1dx =−cosh−1x+C=−cosh−1(−u)+C.
−cosh−1(−u)=−ln(−u+pu2−1)=ln 1
−u+√
u
2−1
= ln(−u−pu2−1)=ln|u+pu
2−1|
67. Using sinh x+ cosh x=ex(Exercise 56a), (sinh x+ cosh x)n=(e
x
)
n=e
nx = sinh nx + cosh nx.
68. Za
−a
etxdx =1
tetxa
−a
=1
t(eat −e−at)=2 sinh at
tfor t6=0.
69. (a) y0= sinh(x/a),1+(y
0)
2= 1 + sinh2(x/a) = cosh2(x/a)
L=2Zb
0cosh(x/a)dx =2asinh(x/a)b
0
=2asinh(b/a)
(b) The highest point is at x=b, the lowest at x=0,
so S=acosh(b/a)−acosh(0) = acosh(b/a)−a.
Chapter 8 Supplementary Exercises 288
70. From part (a) of Exercise 69, L=2asinh(b/a)so120=2asinh(50/a),asinh(50/a) = 60. Let
u=50/a, then a=50/u so (50/u) sinh u=60,sinh u=1.2u.Iff(u) = sinh u−1.2u, then
un+1 =un−sinh un−1.2un
cosh un−1.2;u1=1,...,u
5=u
6=1.064868548 ≈50/a so a≈46.95415231.
From part (b), S=acosh(b/a)−a≈46.95415231[cosh(1.064868548) −1] ≈29.2 ft.
71. From part (b) of Exercise 69, S=acosh(b/a)−aso 30 = acosh(200/a)−a. Let u= 200/a,
then a= 200/u so 30 = (200/u)[cosh u−1],cosh u−1=0.15u.Iff(u) = cosh u−0.15u−1,
then un+1 =un−cosh un−0.15un−1
sinh un−0.15 ;u1=0.3,...,u
4=u
5=0.297792782 ≈200/a so
a≈671.6079505. From part (a), L=2asinh(b/a)≈2(671.6079505) sinh(0.297792782) ≈405.9 ft.
72. (a) When the bow of the boat is at the point (x, y) and the person has walked a distance D,
then the person is located at the point (0,D), the line segment connecting (0,D) and (x, y)
has length a;thusa
2=x
2+(D−y)
2,D=y+√
a
2−x
2=asech−1(x/a).
(b) Find Dwhen a= 15, x= 10: D= 15 sech−1(10/15)=15ln 1+p5/9
2/3!≈14.44 m.
(c) dy/dx =−a2
x√a2−x2+x
√a2−x2=1
√a2−x2−a2
x+x=−1
xpa2−x2,
1+[y
0]
2=1+a
2−x
2
x
2=a
2
x
2; with a= 15 and x=5,L=Z15
5
225
x2dx =−225
x15
5
=30m.
CHAPTER 8 SUPPLEMENTARY EXERCISES
6. (a) A=Z2
0(2+x−x2)dx (b) A=Z2
0√ydy+Z4
2[(√y−(y−2)] dy
(c) V=πZ2
0[(2 + x)2−x4]dx
(d) V=2πZ2
0y
√
ydy+2πZ4
2y[
√
y−(y−2)] dy
(e) V=2πZ2
0x(2+x−x2)dx (f) V=πZ2
0ydy+Z4
2π(y−(y−2)2)dy
7. (a) A=Zb
a
(f(x)−g(x)) dx +Zc
b
(g(x)−f(x)) dx +Zd
c
(f(x)−g(x)) dx
(b) A=Z0
−1(x3−x)dx +Z1
0(x−x3)dx +Z2
1(x3−x)dx =1
4+1
4+9
4=11
4
8. (a) S=Z8/27
02πxp1+x
−4/3dx (b) S=Z2
02πy3
27p1+y
4/81 dy
(c) S=Z2
02π(y+2)
p1+y
4/81 dy
9. By implicit differentiation dy
dx =−y
x1/3,so1+dy
dx2
=1+y
x
2/3=x
2/3+y
2/3
x
2/3=a
2/3
x
2/3,
L=Z−a/8
−a
a1/3
(−x1/3)dx =−a1/3Z−a/8
−a
x−1/3dx =9a/8.
289 Chapter 8
10. The base of the dome is a hexagon of side r. An equation of the circle of radius rthat lies in a
vertical x-yplane and passes through two opposite vertices of the base hexagon is x2+y2=r2.
A horizontal, hexagonal cross section at height yabove the base has area
A(y)=3
√
3
2x
2=3
√
3
2(r
2−y
2
), hence the volume is V=Zr
0
3√3
2(r2−y2)dy =√3r3.
11. Let the sphere have radius R, the hole radius r. By the Pythagorean Theorem, r2+(L/2)2=R2.
Use cylindrical shells to calculate the volume of the solid obtained by rotating about the y-axis
the region r<x<R, −
√
R
2−x
2<y<√
R
2−x
2
:
V=ZR
r
(2πx)2pR2−x2dx =−4
3π(R2−x2)3/2R
r
=4
3π(L/2)3,
so the volume is independent of R.
12. V=2ZL/2
0π16R2
L4(x2−L2/4)2=4π
15 LR2
13. Set a=68.7672, b=0.0100333, c= 693.8597, d= 299.2239.
(a) 650
0
-300 300
(b) L=2Zd
0p1+a
2b
2sinh2bx dx
= 1480.2798 ft
(c) x= 283.6249 ft (d) 82◦
14. y=0atx=b=30.585; distance = Zb
0p1 + (12.54 −0.82x)2dx = 196.306 yd
15. Let u=ax then du =adx,Z1
√a
2+u
2du =Za
√a2+a2x2dx =Z1
√1+x
2dx = sinh−1(u/a)+C,
Z1
√u2−a2du =Z1
√x2−1dx = cosh−1(u/a)+C,u>a,
Z1
a
2−u
2du =1
aZ1
1−x2dx =
1
atanh−1(u/a)+C, |u|<a
1
acoth−1(u/a)+C, |u|>a
=1
2aln
a+u
a−u+C
(a) sinh−1(x/2)+C
(b) cosh−1(x/3)+C
(c)
1
√2tanh−1(x/√2)+C, |x|<√2
1
√2coth−1(x/√2)+C, |x|>√2
=1
2√2ln
√2+x
√
2−x
+C
(d) Zdx
√16+5x
2=1
√
5Zdx
p16/5+x
2dx =1
√5sinh−1 √5x
4!+C
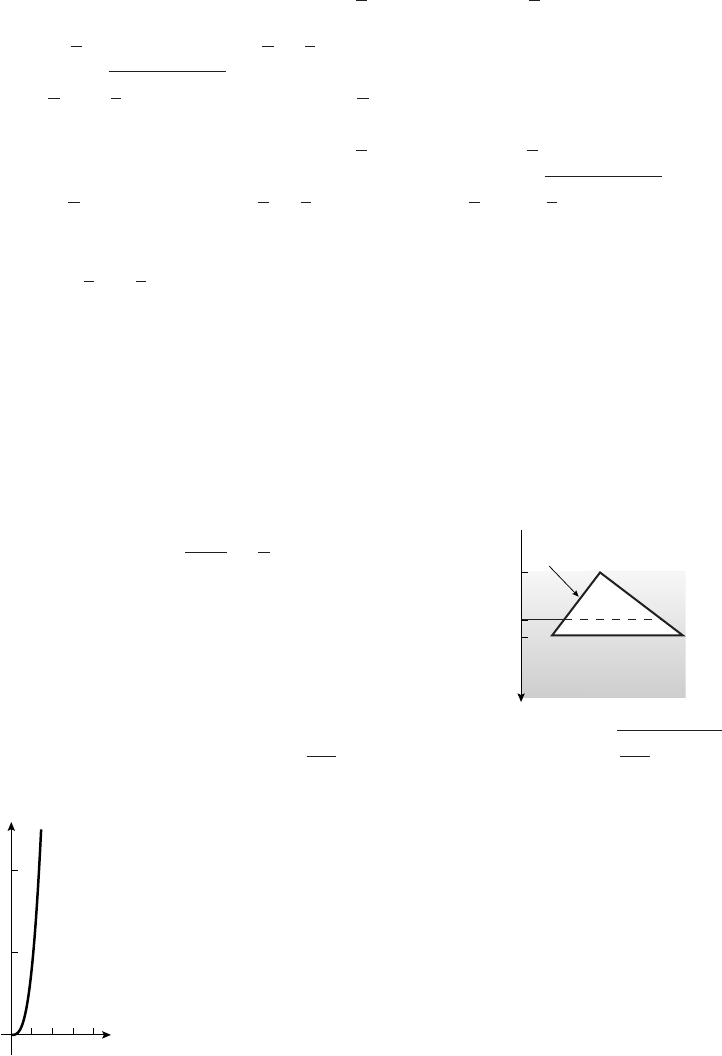
Chapter 8 Supplementary Exercises 290
16. (a) cosh 3x= cosh(2x+x) = cosh 2xcosh x+ sinh 2xsinh x
= (2 cosh2x−1) cosh x+ (2 sinh xcosh x) sinh x
= 2 cosh3x−cosh x+ 2 sinh2xcosh x
= 2 cosh3x−cosh x+ 2(cosh2x−1) cosh x= 4 cosh3x−3 cosh x
(b) from Theorem 8.8.2 with xreplaced by x
2: cosh x= 2 cosh2x
2−1,
2 cosh2x
2= cosh x+ 1, cosh2x
2=1
2(cosh x+ 1),
cosh x
2=r1
2(cosh x+ 1) (because cosh x
2>0)
(c) from Theorem 8.8.2 with xreplaced by x
2: cosh x= 2 sinh2x
2+1,
2 sinh2x
2= cosh x−1, sinh2x
2=1
2(cosh x−1), sinh x
2=±r1
2(cosh x−1)
17. (a) F=kx,1
2=k1
4,k=2,W=Z1/4
0kx dx =1/16 J
(b) 25 = ZL
0kx dx =kL2/2, L=5m
18. F=30x+ 2000, W=Z150
0(30x+ 2000) dx =15·1502+ 2000 ·150 = 637,500 lb·ft
19. (a) F=Z1
0ρx3dx N
0
4
2
h(x) = 1 + x
w(x)
x
(b) By similar triangles w(x)
4=x
2,w(x)=2x,so
F=Z4
1ρ(1+x)2xdx lb/ft2.
(c) A formula for the parabola is y=8
125x2−10, so F=Z0
−10 9810|y|2r125
8(y+ 10) dy N.
20. (a)
1
1
2
t
r(b) r= 1 when t≈0.673080 s.
(c) dr/dt =4.48 m/s.
291 Chapter 8
21. (a)
100 200
-1.6
-1.2
-0.8
-0.4
x
y(b) The maximum deflection occurs at
x= 96 inches (the midpoint
of the beam) and is about 1.42 in.
(c) The length of the centerline is
Z192
0p1+(dy/dx)2dx = 192.026 in.
22. The x-coordinates of the points of intersection are a≈−0.423028 and b≈1.725171; the area is
Zb
a
(2 sin x−x2+1)dx ≈2.542696.
23. Let (a, k), where π/2<a<π, be the coordinates of the point of intersection of y=kwith
y= sin x.Thusk= sin aand if the shaded areas are equal,
Za
0(k−sin x)dx =Za
0(sin a−sin x)dx =asin a+ cos a−1=0
Solve for ato get a≈2.331122, so k= sin a≈0.724611.
24. The volume is given by 2πZk
0xsin xdx=2π(sin k−kcos k) = 8; solve for kto get
k=1.736796.
25. (a) Za+2
a
x
√1+x
3dx
(b) Use the result in Exercise 24, Section 7.9, to obtain
d
da Za+2
a
x
√1+x
3dx=a+2
p1+(a+2)
3−a
√
1+a
3= 0; solve for ato get a≈0.683772.
The maximum work is Za+2
a
x
√1+x
3dx ≈1.347655 J.
292
CHAPTER 9
Principles of Integral Evaluation
EXERCISE SET 9.1
1. u=3−2x, du =−2dx, −1
2Zu3du =−1
8u4+C=−1
8(3 −2x)4+C
2. u=4+9x, du =9dx, 1
9Zu1/2du =2
3·9u3/2+C=2
27(4+9x)
3/2+C
3. u=x2,du=2xdx, 1
2Zsec2udu=1
2tan u+C=1
2tan(x2)+C
4. u=x2,du=2xdx, 2Ztan udu=−2ln|cos u|+C=−2ln|cos(x2)|+C
5. u= 2 + cos 3x, du =−3 sin 3xdx, −1
3Zdu
u=−1
3ln |u|+C=−1
3ln(2 + cos 3x)+C
6. u=3x
2,du=3
2dx, 2
3Zdu
4+4u
2=1
6Zdu
1+u
2=1
6tan−1u+C=1
6tan−1(3x/2)+C
7. u=ex,du=e
xdx, Zsinh udu= cosh u+C= cosh ex+C
8. u=lnx, du =1
xdx, Zsec utan udu= sec u+C= sec(ln x)+C
9. u= cot x, du =−csc2xdx, −Zeudu =−eu+C=−ecot x+C
10. u=x2,du=2xdx, 1
2Zdu
√1−u2=1
2sin−1u+C=1
2sin−1(x2)+C
11. u= cos 7x, du =−7 sin 7xdx, −1
7Zu5du =−1
42u6+C=−1
42 cos67x+C
12. u= sin x, du = cos x dx, Zdu
u√u2+1 =−ln
1+√
1+u
2
u
+C=−ln
1+p1 + sin2x
sin x+C
13. u=ex,du=e
xdx, Zdu
√4+u
2=lnu+pu
2+4
+C=lne
x+pe
2x+4
+C
14. u= tan−1x, du =1
1+x
2dx, Zeudu =eu+C=etan−1x+C
15. u=√x−2,du=1
2
√x−2dx, 2Zeudu =2e
u+C=2e
√
x−2+C
16. u=3x
2+2x, du =(6x+2)dx, 1
2Zcot udu=1
2ln |sin u|+C=1
2ln sin |3x2+2x|+C
293 Chapter 9
17. u=√x, du =1
2√xdx, Z2 cosh udu= 2 sinh u+C= 2 sinh √x+C
18. u=lnx, du =dx
x,Zdu
u=ln|u|+C=ln|ln x|+C
19. u=√x, du =1
2√xdx, Z2du
3u=2Ze
−uln 3 du =−2
ln 3e−uln 3 +C=−2
ln 33−√x+C
20. u= sin θ, du = cos θdθ, Zsec utan udu= sec u+C= sec(sin θ)+C
21. u=2
x,du=−2
x
2dx, −1
2Zcsch2udu=1
2coth u+C=1
2coth 2
x+C
22. Zdx
√x2−3=ln
x+px
2−3
+C
23. u=e−x,du=−e
−xdx, −Zdu
4−u2=−1
4ln
2+u
2−u
+C=−1
4ln
2+e
−x
2−e
−x
+C
24. u=lnx, du =1
xdx, Zcos udu= sin u+C= sin(ln x)+C
25. u=ex,du=e
xdx, Zexdx
√1−e2x=Zdu
√1−u2= sin−1u+C= sin−1ex+C
26. u=x−1/2,du=−1
2x
3/2dx, −Z2 sinh udu=−2 cosh u+C=−2 cosh(x−1/2)+C
27. u=x2,du=2xdx, 1
2Zdu
sec u=1
2Zcos udu=1
2sin u+C=1
2sin(x2)+C
28. 2u=ex,2du =exdx, Z2du
√4−4u2= sin−1u+C= sin−1(ex/2)+C
29. 4−x2=e−x2ln 4,u=−x
2ln 4,du=−2xln 4 dx =−xln 16 dx,
−1
ln 16 Zeudu =−1
ln 16eu+C=−1
ln 16e−x2ln 4 +C=−1
ln 164−x2+C
30. 2πx =eπx ln 2,Z2πx dx =1
πln 2eπx ln 2 +C=1
πln 22πx +C
31. (a) With u=xwe get
from (15), Zdx
√1−x2= sin−1x+C(|x|<1)
from (17), Zdx
1+x
2= tan−1x+C
from (19), Zdx
x√x2−1= sec−1x+C(x>1)
Exercise Set 9.2 294
(b) With u=ax, du =adx, we get (for a>0)
Zdu
√a2−u2=Zadx
a√1−x2= sin−1x+C= sin−1(u/a)+C
Zdu
a2+u2=1
a2Zadx
1+x
2=1
atan−1x+C=1
atan−1(u/a)+C
Zdu
u√u2−a2=Zadx
a2x√x2−1=1
asec−1x+C=1
asec−1(u/a)+C
EXERCISE SET 9.2
1. u=x,dv =e−xdx,du =dx,v=−e−x;Zxe−xdx =−xe−x+Ze−xdx =−xe−x−e−x+C
2. u=x,dv =e3xdx,du =dx,v=1
3e3x;Zxe3xdx =1
3xe3x−1
3Ze3xdx =1
3xe3x−1
9e3x+C
3. u=x2,dv =exdx,du =2xdx,v=e
x;Zx
2e
xdx =x2ex−2Zxexdx.
For Zxexdx use u=x,dv =exdx,du =dx,v=exto get
Zxexdx =xex−ex+C1so Zx2exdx =x2ex−2xex+2e
x+C
4. u=x2,dv =e−2xdx,du =2xdx,v=−1
2e
−2x;Zx
2e
−2xdx =−1
2x2e−2x+Zxe−2xdx
For Zxe−2xdx use u=x,dv =e−2xdx to get
Zxe−2xdx =−1
2xe−2x+1
2Ze−2xdx =−1
2xe−2x−1
4e−2x+C
so Zx2e−2xdx =−1
2x2e−2x−1
2xe−2x−1
4e−2x+C
5. u=x,dv = sin 2xdx,du =dx,v=−1
2cos 2x;
Zxsin 2xdx=−1
2xcos 2x+1
2Zcos 2xdx=−1
2xcos 2x+1
4sin 2x+C
6. u=x,dv = cos 3xdx,du =dx,v=1
3sin 3x;
Zxcos 3xdx=1
3xsin 3x−1
3Zsin 3xdx=1
3xsin 3x+1
9cos 3x+C
7. u=x2,dv = cos xdx,du =2xdx,v= sin x;Zx2cos xdx=x
2sin x−2Zxsin xdx
For Zxsin xdx use u=x,dv = sin xdx to get
Zxsin xdx=−xcos x+ sin x+C1so Zx2cos xdx=x
2sin x+2xcos x−2 sin x+C
295 Chapter 9
8. u=x2,dv = sin xdx,du =2xdx,v=−cos x;
Zx2sin xdx=−x
2cos x+2Zxcos xdx; for Zxcos xdx use u=x,dv = cos xdx to get
Zxcos xdx=xsin x+ cos x+C1so Zx2sin xdx=−x
2cos x+2xsin x+ 2 cos x+C
9. u=lnx,dv =√xdx,du =1
xdx,v=2
3x3/2;
Z√xln xdx=2
3x
3/2ln x−2
3Zx1/2dx =2
3x3/2ln x−4
9x3/2+C
10. u=lnx,dv =xdx,du =1
xdx,v=1
2x2;Zxln xdx=1
2x
2ln x−1
2Zxdx=1
2x
2ln x−1
4x2+C
11. u= (ln x)2,dv =dx,du =2
ln x
xdx,v=x;Z(ln x)2dx =x(ln x)2−2Zln xdx.
Use u=lnx,dv =dx to get Zln xdx=xln x−Zdx =xln x−x+C1so
Z(ln x)2dx =x(ln x)2−2xln x+2x+C
12. u=lnx,dv =1
√xdx,du =1
xdx,v=2
√
x;Zln x
√xdx =2
√
xln x−2Z1
√xdx =2
√
xln x−4√x+C
13. u= ln(2x+ 3), dv =dx,du =2
2x+3dx,v=x;Zln(2x+3)dx =xln(2x+3)−Z2x
2x+3dx
but Z2x
2x+3dx =Z1−3
2x+3dx =x−3
2ln(2x+3)+C
1so
Zln(2x+3)dx =xln(2x+3)−x+3
2ln(2x+3)+C
14. u= ln(x2+ 4), dv =dx,du =2x
x2+4dx,v=x;Zln(x2+4)dx =xln(x2+4)−2Zx
2
x
2+4dx
but Zx2
x2+4dx =Z1−4
x2+4dx =x−2 tan−1x
2+C1so
Zln(x2+4)dx =xln(x2+4)−2x+ 4 tan−1x
2+C
15. u= sin−1x,dv =dx,du =1/
√
1−x
2
dx,v=x;
Zsin−1xdx=xsin−1x−Zx/p1−x2dx =xsin−1x+p1−x2+C
16. u= cos−1(2x), dv =dx,du =−2
√1−4x2dx,v=x;
Zcos−1(2x)dx =xcos−1(2x)+Z2x
√
1−4x
2dx =xcos−1(2x)−1
2p1−4x2+C

Exercise Set 9.2 296
17. u= tan−1(2x), dv =dx,du =2
1+4x
2dx,v=x;
Ztan−1(2x)dx =xtan−1(2x)−Z2x
1+4x
2dx =xtan−1(2x)−1
4ln(1 + 4x2)+C
18. u= tan−1x,dv =xdx,du =1
1+x
2dx,v=1
2x2;Zxtan−1xdx=1
2x
2tan−1x−1
2Zx2
1+x
2dx
but Zx2
1+x
2dx =Z1−1
1+x
2dx =x−tan−1x+C1so
Zxtan−1xdx=1
2x
2tan−1x−1
2x+1
2tan−1x+C
19. u=ex,dv = sin xdx,du =exdx,v=−cos x;Zexsin xdx=−e
xcos x+Zexcos xdx.
For Zexcos xdx use u=ex,dv = cos xdx to get Zexcos x=exsin x−Zexsin xdx so
Zexsin xdx=−e
xcos x+exsin x−Zexsin xdx,
2Ze
xsin xdx=e
x(sin x−cos x)+C
1,Ze
xsin xdx=1
2e
x(sin x−cos x)+C
20. u=e2x,dv = cos 3xdx,du =2e
2x
dx,v=1
3sin 3x;
Ze2xcos 3xdx=1
3e
2xsin 3x−2
3Ze2xsin 3xdx. Use u=e2x,dv = sin 3xdx to get
Ze2xsin 3xdx=−1
3e
2xcos 3x+2
3Ze2xcos 3xdx so
Ze2xcos 3xdx=1
3e
2xsin 3x+2
9e2xcos 3x−4
9Ze2xcos 3xdx,
13
9Ze2xcos 3xdx=1
9e
2x(3 sin 3x+2 cos 3x)+C1,Ze2xcos 3xdx=1
13e2x(3 sin 3x+2 cos 3x)+C
21. u=eax,dv = sin bx dx,du =aeaxdx,v=−1
bcos bx (b6= 0);
Zeax sin bx dx =−1
beax cos bx +a
bZeax cos bx dx. Use u=eax,dv = cos bx dx to get
Zeax cos bx dx =1
beax sin bx −a
bZeax sin bx dx so
Zeax sin bx dx =−1
beax cos bx +a
b2eax sin bx −a2
b2Zeax sin bx dx,
Zeax sin bx dx =eax
a2+b2(asin bx −bcos bx)+C
22. From Exercise 21 with a=−3,b=5,x =θ, answer = e−3θ
√34 (−3 sin 5θ−5 cos 5θ)+C

297 Chapter 9
23. u= sin(ln x), dv =dx,du =cos(ln x)
xdx,v=x;
Zsin(ln x)dx =xsin(ln x)−Zcos(ln x)dx. Use u= cos(ln x), dv =dx to get
Zcos(ln x)dx =xcos(ln x)+Zsin(ln x)dx so
Zsin(ln x)dx =xsin(ln x)−xcos(ln x)−Zsin(ln x)dx,
Zsin(ln x)dx =(x/2)[sin(ln x)−cos(ln x)]+C
24. u= cos(ln x), dv =dx,du =−1
xsin(ln x)dx,v=x;
Zcos(ln x)dx =xcos(ln x)+Zsin(ln x)dx. Use u= sin(ln x), dv =dx to get
Zsin(ln x)dx =xsin(ln x)−Zcos(ln x)dx so
Zcos(ln x)dx =xcos(ln x)+xsin(ln x)−Zcos(ln x)dx,
Zcos(ln x)dx =1
2x[cos(ln x) + sin(ln x)]+C
25. u=x,dv = sec2xdx,du =dx,v= tan x;
Zxsec2xdx=xtan x−Ztan xdx=xtan x−Zsin x
cos xdx =xtan x+ln|cos x|+C
26. u=x,dv = tan2xdx= (sec2x−1)dx,du =dx,v= tan x−x;
Zxtan2xdx=xtan x−x2−Z(tan x−x)dx
=xtan x−x2+ln|cos x|+1
2x2+C=xtan x−1
2x2+ln|cos x|+C
27. u=x2,dv =xex2dx,du =2xdx,v=1
2e
x
2;
Zx
3e
x
2dx =1
2x2ex2−Zxex2dx =1
2x2ex2−1
2ex2+C
28. u=xex,dv =1
(x+1)
2dx,du =(x+1)e
xdx,v=−1
x+1;
Zxex
(x+1)
2dx =−xex
x+1+Ze
x
dx =−xex
x+1+e
x+C=e
x
x+1+C
Exercise Set 9.2 298
29. u=x,dv =e−5xdx,du =dx,v=−1
5e−5x;
Z1
0xe−5xdx =−1
5xe−5x1
0
+1
5Z1
0e−5xdx
=−1
5e−5−1
25e−5x1
0
=−1
5e−5−1
25(e−5−1)=(1−6e
−5
)/25
30. u=x,dv =e2xdx,du =dx,v=1
2e2x;
Z2
0xe2xdx =1
2xe2x2
0−1
2Z2
0e2xdx =e4−1
4e2x2
0
=e4−1
4(e4−1)=(3e
4+1)/4
31. u=lnx,dv =x2dx,du =1
xdx,v=1
3x3;
Ze
1x2ln xdx=1
3x
3ln xe
1−1
3Ze
1x2dx =1
3e3−1
9x3e
1
=1
3e3−1
9(e3−1)=(2e
3+1)/9
32. u=lnx,dv =1
x2dx,du =1
xdx,v=−1
x;
Ze
√e
ln x
x2dx =−1
xln xe
√e
+Ze
√e
1
x2dx
=−1
e+1
√eln √e−1
xe
√e
=−1
e+1
2√e−1
e+1
√e=3√e−4
2e
33. u= ln(x+ 3), dv =dx,du =1
x+3dx,v=x;
Z2
−2ln(x+3)dx =xln(x+3)
2
−2−Z2
−2
x
x+3dx = 2 ln 5 + 2 ln 1 −Z2
−21−3
x+3dx
= 2 ln 5 −[x−3 ln(x+ 3)]2
−2= 2 ln 5 −(2 −3ln5)+(−2−3ln1)=5ln5−4
34. u= sin−1x,dv =dx,du =1
√1−x2dx,v=x;
Z1/2
0sin−1xdx=xsin−1x1/2
0−Z1/2
0
x
√1−x2dx =1
2sin−11
2+p1−x21/2
0
=1
2π
6+r3
4−1= π
12 +√3
2−1
35. u= sec−1√θ,dv =dθ,du =1
2θ√θ−1dθ,v=θ;
Z4
2sec−1√θdθ =θsec−1√θ4
2−1
2Z4
2
1
√θ−1dθ = 4 sec−12−2 sec−1√2−√θ−14
2
=4π
3−2π
4−√
3+1= 5π
6−√
3+1
299 Chapter 9
36. u= sec−1x,dv =xdx,du =1
x√x2−1dx,v=1
2x2;
Z2
1xsec−1xdx=1
2x
2sec−1x2
1−1
2Z2
1
x
√x2−1dx
=1
2[(4)(π/3) −(1)(0)] −1
2px2−12
1
=2π/3−√3/2
37. u=x,dv = sin 4xdx,du =dx,v=−1
4cos 4x;
Zπ/2
0xsin 4xdx=−1
4xcos 4xπ/2
0
+1
4Zπ/2
0cos 4xdx=−π/8+ 1
16 sin 4xπ/2
0
=−π/8
38. Zπ
0(x+xcos x)dx =1
2x2π
0
+Zπ
0xcos xdx=π
2
2+Zπ
0xcos xdx;
u=x,dv = cos xdx,du =dx,v= sin x
Zπ
0xcos xdx=xsin xπ
0−Zπ
0sin xdx= cos xπ
0
=−2soZπ
0(x+xcos x)dx =π2/2−2
39. u= tan−1√x,dv =√xdx,du =1
2√x(1+x)dx,v=2
3x3/2;
Z3
1
√xtan−1√xdx =2
3x3/2tan−1√x3
1−1
3Z3
1
x
1+xdx
=2
3x3/2tan−1√x3
1−1
3Z3
11−1
1+xdx
=2
3x3/2tan−1√x−1
3x+1
3ln |1+x|
3
1
=(2
√
3π−π/2−2+ln2)/3
40. u= ln(x2+ 1), dv =dx,du =2x
x2+1dx,v=x;
Z2
0ln(x2+1)dx =xln(x2+1)
2
0−Z2
0
2x
2
x
2+1dx = 2 ln 5 −2Z2
01−1
x2+1dx
= 2 ln 5 −2(x−tan−1x)i2
0= 2 ln 5 −4+2tan
−12
41. t=√x, t2=x, dx =2tdt
(a) Ze√xdx =2Ztetdt;u=t, dv =etdt, du =dt, v =et,
Ze√xdx =2tet−2Zetdt =2(t−1)et+C=2(
√
x−1)e√x+C
(b) Zcos √xdx=2Ztcos tdt;u=t, dv = cos tdt, du =dt, v = sin t,
Zcos √xdx=2tsin t−2Zsin tdt =2tsin t+ 2 cos t+C=2
√
xsin √x+ 2 cos √x+C
Exercise Set 9.2 300
43. (a) A=Ze
1ln xdx=(xln x−x)e
1
=1
(b) V=πZe
1(ln x)2dx =πh(x(ln x)2−2xln x+2x)
ie
1=π(e−2)
44. A=Zπ/2
0(x−xsin x)dx =1
2x2π/2
0−Zπ/2
0xsin xdx=π
2
8−(−xcos x+ sin x)π/2
0
=π2/8−1
45. V=2πZπ
0xsin xdx=2π(−xcos x+ sin x)π
0
=2π
2
46. V=2πZπ/2
0xcos xdx=2π(cos x+xsin x)π/2
0
=π(π−2)
47. distance = Z5
0t2e−tdt;u=t2,dv =e
−tdt, du =2tdt, v =−e−t,
distance = −t2e−ti5
0+2Z5
0te−tdt;u=2t, dv =e−tdt, du =2dt, v =−e−t,
distance = −25e−5−2te−ti5
0+2Z5
0e
−t
dt =−25e−5−10e−5−2e−ti5
0
=−25e−5−10e−5−2e−5+2=−37e−5+2
48. u=2t, dv = sin(kωt)dt, du =2dt, v =−1
kω cos(kωt); the integrand is an even function of tso
Zπ/ω
−π/ω
tsin(kωt)dt =2Zπ/ω
0tsin(kωt)dt =−2
kω tcos(kωt)π/ω
0
+2Zπ/ω
0
1
kω cos(kωt)dt
=2π(−1)k+1
kω2+2
k2ω2sin(kωt)π/ω
0
=2π(−1)k+1
kω2
49. (a) Zsin3xdx =−1
3sin2xcos x+2
3Zsin xdx=−1
3sin2xcos x−2
3cos x+C
(b) Zsin4xdx=−1
4sin3xcos x+3
4Zsin2xdx,Zsin2xdx=−1
2sin xcos x+1
2x+C1so
Zπ/4
0sin4xdx=−1
4sin3xcos x−3
8sin xcos x+3
8xπ/4
0
=−1
4(1/√2)3(1/√2) −3
8(1/√2)(1/√2)+3π/32=3π/32 −1/4
50. (a) Zcos5xdx=1
5cos4xsin x+4
5Zcos3xdx=1
5cos4xsin x+4
51
3cos2xsin x+2
3sin x+C
=1
5cos4xsin x+4
15 cos2xsin x+8
15 sin x+C

301 Chapter 9
(b) Zcos6xdx=1
6cos5xsin x+5
6Zcos4xdx
=1
6cos5xsin x+5
61
4cos3xsin x+3
4Zcos2xdx
=1
6cos5xsin x+5
24 cos3xsin x+5
81
2cos xsin x+1
2x+C,
1
6cos5xsin x+5
24 cos3xsin x+5
16 cos xsin x+5
16xπ/2
0
=5π/32
51. u= sinn−1x,dv = sin xdx,du =(n−1) sinn−2xcos xdx,v=−cos x;
Zsinnxdx=−sinn−1xcos x+(n−1) Zsinn−2xcos2xdx
=−sinn−1xcos x+(n−1) Zsinn−2x(1 −sin2x)dx
=−sinn−1xcos x+(n−1) Zsinn−2xdx−(n−1) Zsinnx dx,
nZsinnxdx=−sinn−1xcos x+(n−1) Zsinn−2x dx,
Zsinnxdx=−1
nsinn−1xcos x+n−1
nZsinn−2xdx
52. (a) u= secn−2x,dv = sec2xdx,du =(n−2) secn−2xtan xdx,v= tan x;
Zsecnxdx= secn−2xtan x−(n−2) Zsecn−2xtan2xdx
= secn−2xtan x−(n−2) Zsecn−2x(sec2x−1)dx
= secn−2xtan x−(n−2) Zsecnxdx+(n−2) Zsecn−2x dx,
(n−1) Zsecnxdx= secn−2xtan x+(n−2) Zsecn−2xdx,
Zsecnxdx=1
n−1secn−2xtan x+n−2
n−1Zsecn−2xdx
(b) Ztannxdx=Ztann−2x(sec2x−1) dx =Ztann−1xsec2xdx−Ztann−2xdx
=1
n−1tann−1x−Ztann−2xdx
(c) u=xn,dv =exdx,du =nxn−1dx,v=ex;Zxnexdx =xnex−nZxn−1exdx
53. (a) Ztan4xdx =1
3tan3x−Ztan2xdx=1
3tan3x−tan x+Zdx =1
3tan3x−tan x+x+C
(b) Zsec4xdx=1
3sec2xtan x+2
3Zsec2xdx=1
3sec2xtan x+2
3tan x+C

Exercise Set 9.2 302
(c) Zx3exdx =x3ex−3Zx2exdx =x3ex−3x2ex−2Zxexdx
=x3ex−3x2ex+6xex−Zexdx=x3ex−3x2ex+6xex−6ex+C
54. (a) u=3x,
Zx
2
e
3x
dx =1
27 Zu2eudu =1
27 u2eu−2Zueudu=1
27u2eu−2
27 ueu−Zeudu
=1
27u2eu−2
27ueu+2
27eu+C=1
3x2e3x−2
9xe3x+2
27e3x+C
(b) u=−√x,
Z1
0xe−√xdx =2Z−1
0u
3
e
u
du,
Zu3eudu =u3eu−3Zu2eudu =u3eu−3u2eu−2Zueudu
=u3eu−3u2eu+6ueu−Zeudu=u3eu−3u2eu+6ueu−6eu+C,
2Z−1
0u3eudu =2(u
3−3u
2+6u−6)eu−1
0
=12−32e−1
55. u=x,dv =f00(x)dx,du =dx,v=f0(x);
Z1
−1xf00(x)dx =xf 0(x)1
−1−Z1
−1f0(x)dx
=f0(1) + f0(−1) −f(x)1
−1
=f0(1) + f0(−1) −f(1) + f(−1)
56. (a) u=f(x),dv =dx, du =f0(x),v =x;
Zb
a
f(x)dx =xf(x)b
a−Zb
a
xf0(x)dx =bf(b)−af(a)−Zb
a
xf0(x)dx
(b) Substitute y=f(x),dy =f0(x)dx, x =awhen y=f(a), x=bwhen y=f(b),
Zb
a
xf0(x)dx =Zf(b)
f(a)xdy =Zf(b)
f(a)f−1(y)dy
(c) From a=f−1(α) and b=f−1(β)weget
bf(b)−af(a)=βf−1(β)−αf−1(α); then
Zβ
α
f−1(x)dx =Zβ
α
f−1(y)dy =Zf(b)
f(a)f−1(y)dy,
which, by part (b), yields
a
b
a = f–1(a) b = f–1(b)
x
y
A1
A2
Zβ
α
f−1(x)dx =bf(b)−af(a)−Zb
a
f(x)dx
=βf−1(β)−αf−1(α)−Zf−1(β)
f−1(α)f(x)dx
303 Chapter 9
Note from the figure that A1=Zβ
α
f−1(x)dx, A2=Zf−1(β)
f−1(α)f(x)dx, and
A1+A2=βf−1(β)−αf−1(α), a ”picture proof”.
57. (a) Use Exercise 56(c);
Z1/2
0sin−1xdx=1
2sin−11
2−0·sin−10−Zsin−1(1/2)
sin−1(0) sin xdx=1
2sin−11
2−Zπ/6
0sin xdx
(b) Use Exercise 56(b);
Ze2
e
ln xdx=e
2ln e2−eln e−Zln e2
ln e
f−1(y)dy =2e
2−e−Z2
1e
ydy =2e
2−e−Z2
1e
xdx
58. (a) Zxexdx =x(ex+C1)−Z(ex+C1)dx =xex+C1x−ex−C1x+C=xex−ex+C
(b) u(v+C1)−Z(v+C1)du =uv +C1u−Zvdu−C
1u=uv −Zvdu
EXERCISE SET 9.3
1. u= cos x,−Zu5du =−1
6cos6x+C2. u= sin 3x,1
3Zu4du =1
15 sin53x+C
3. u= sin ax,1
aZudu=1
2asin2ax +C,a6=0
4. Zcos23xdx=1
2Z(1 + cos 6x)dx =1
2x+1
12 sin 6x+C
5. Zsin25θdθ=1
2Z(1 −cos 10θ)dθ =1
2θ−1
20 sin 10θ+C
6. Zcos3at dt =Z(1 −sin2at) cos at dt
=Zcos at dt −Zsin2at cos at dt =1
asin at −1
3asin3at +C(a6=0)
7. Zcos5θdθ =Z(1 −sin2θ)2cos θdθ =Z(1 −2 sin2θ+ sin4θ) cos θdθ
= sin θ−2
3sin3θ+1
5sin5θ+C
8. Zsin3xcos3xdx=Zsin3x(1 −sin2x) cos xdx
=Z(sin3x−sin5x) cos xdx=1
4sin4x−1
6sin6x+C
9. Zsin22tcos32tdt=Zsin22t(1 −sin22t) cos 2tdt=Z(sin22t−sin42t) cos 2tdt
=1
6sin32t−1
10 sin52t+C
Exercise Set 9.3 304
10. Zsin32xcos22xdx=Z(1 −cos22x) cos22xsin 2xdx
=Z(cos22x−cos42x) sin 2xdx=−1
6cos32x+1
10 cos52x+C
11. Zsin2xcos2xdx=1
4Zsin22xdx=1
8Z(1 −cos 4x)dx =1
8x−1
32 sin 4x+C
12. Zsin2xcos4xdx=1
8Z(1 −cos 2x)(1 + cos 2x)2dx =1
8Z(1 −cos22x)(1 + cos 2x)dx
=1
8Zsin22xdx+1
8Zsin22xcos 2xdx=1
16 Z(1 −cos 4x)dx +1
48 sin32x
=1
16x−1
64 sin 4x+1
48 sin32x+C
13. Zsin xcos 2xdx=1
2Z(sin 3x−sin x)dx =−1
6cos 3x+1
2cos x+C
14. Zsin 3θcos 2θdθ =1
2Z(sin 5θ+ sin θ)dθ =−1
10 cos 5θ−1
2cos θ+C
15. Zsin xcos(x/2)dx =1
2Z[sin(3x/2) + sin(x/2)]dx =−1
3cos(3x/2) −cos(x/2)+C
16. u= cos x,−Zu1/5du =−5
6cos6/5x+C
17. Zπ/4
0cos3xdx=Zπ/4
0(1 −sin2x) cos xdx
=sin x−1
3sin3xπ/4
0
=(
√
2/2) −1
3(√2/2)3=5
√
2/12
18. Zπ/2
0sin2(x/2) cos2(x/2)dx =1
4Zπ/2
0sin2xdx=1
8Zπ/2
0(1 −cos 2x)dx
=1
8x−1
2sin 2xπ/2
0
=π/16
19. Zπ/3
0sin43xcos33xdx=Zπ/3
0sin43x(1 −sin23x) cos 3xdx=1
15 sin53x−1
21 sin73xπ/3
0
=0
20. Zπ
−π
cos25θdθ=1
2Zπ
−π
(1 + cos 10θ)dθ =1
2θ+1
10 sin 10θπ
−π
=π
21. Zπ/6
0sin 2xcos 4xdx=1
2Zπ/6
0(sin 6x−sin 2x)dx =−1
12 cos 6x+1
4cos 2xπ/6
0
=[(−1/12)(−1)+(1/4)(1/2)] −[−1/12+1/4]=1/24
22. Z2π
0sin2kx dx =1
2Z2π
0(1 −cos 2kx)dx =1
2x−1
2ksin 2kx2π
0
=π−1
4ksin 4πk (k6=0)
305 Chapter 9
23. 1
3tan(3x+1)+C24. −1
5ln |cos 5x|+C
25. u=e−2x,du=−2e
−2xdx;−1
2Ztan udu=1
2ln |cos u|+C=1
2ln |cos(e−2x)|+C
26. 1
3ln |sin 3x|+C27. 1
2ln |sec 2x+ tan 2x|+C
28. u=√x, du =1
2√xdx;Z2 sec udu=2ln|sec u+ tan u|+C=2ln|sec √x+ tan √x|+C
29. u= tan x,Zu2du =1
3tan3x+C
30. Ztan5x(1 + tan2x) sec2xdx=Z(tan5x+ tan7x) sec2xdx=1
6tan6x+1
8tan8x+C
31. Ztan34x(1 + tan24x) sec24xdx=Z(tan34x+ tan54x) sec24xdx=1
16 tan44x+1
24 tan64x+C
32. Ztan4θ(1 + tan2θ) sec2θdθ=1
5tan5θ+1
7tan7θ+C
33. Zsec4x(sec2x−1) sec xtan xdx=Z(sec6x−sec4x) sec xtan xdx=1
7sec7x−1
5sec5x+C
34. Z(sec2θ−1)2sec θtan θdθ =Z(sec4θ−2 sec2θ+ 1) sec θtan θdθ =1
5sec5θ−2
3sec3θ+ sec θ+C
35. Z(sec2x−1)2sec xdx=Z(sec5x−2 sec3x+ sec x)dx =Zsec5xdx−2Zsec3xdx+Zsec xdx
=1
4sec3xtan x+3
4Zsec3xdx−2Zsec3xdx+ln|sec x+ tan x|
=1
4sec3xtan x−5
41
2sec xtan x+1
2ln |sec x+ tan x|+ln|sec x+ tan x|+C
=1
4sec3xtan x−5
8sec xtan x+3
8ln |sec x+ tan x|+C
36. Z[sec2(x/2) −1] sec3(x/2)dx =Z[sec5(x/2) −sec3(x/2)]dx
=2Zsec5udu−Zsec3udu
(u=x/2)
=21
4sec3utan u+3
4Zsec3udu
−Zsec3udu
(equation (20))
=1
2sec3utan u−1
2Zsec3udu
=1
2sec3utan u−1
4sec utan u−1
4ln |sec u+ tan u|+C(equation (20), (22))
=1
2sec3x
2tan x
2−1
4sec x
2tan x
2−1
4ln sec x
2+ tan x
2+C
Exercise Set 9.3 306
37. Zsec22t(sec 2ttan 2t)dt =1
6sec32t+C38. Zsec4x(sec xtan x)dx =1
5sec5x+C
39. Zsec4xdx=Z(1 + tan2x) sec2xdx =Z(sec2x+ tan2xsec2x)dx = tan x+1
3tan3x+C
40. Using equation (20),
Zsec5xdx=1
4sec3xtan x+3
4Zsec3xdx
=1
4sec3xtan x+3
8sec xtan x+3
8ln |sec x+ tan x|+C
41. Use equation (19) to get Ztan4xdx=1
3tan3x−tan x+x+C
42. u=4x, use equation (19) to get
1
4Ztan3udu=1
41
2tan2u+ln|cos u|+C=1
8tan24x+1
4ln |cos 4x|+C
43. Z√tan x(1 + tan2x) sec2xdx=2
3tan3/2x+2
7tan7/2x+C
44. Zsec1/2x(sec xtan x)dx =2
3sec3/2x+C
45. Zπ/6
0(sec22x−1)dx =1
2tan 2x−xπ/6
0
=√3/2−π/6
46. Zπ/6
0sec2θ(sec θtan θ)dθ =1
3sec3θπ/6
0
=(1/3)(2/√3)3−1/3=8
√
3/27 −1/3
47. u=x/2,
2Zπ/4
0tan5udu=1
2tan4u−tan2u−2ln|cos u|π/4
0
=1/2−1−2 ln(1/√2) = −1/2+ln2
48. u=πx, 1
πZπ/4
0sec utan udu=1
πsec uπ/4
0
=(
√
2−1)/π
49. Z(csc2x−1) csc2x(csc xcot x)dx =Z(csc4x−csc2x)(csc xcot x)dx =−1
5csc5x+1
3csc3x+C
50. Zcos23t
sin23t·1
cos 3tdt =Zcsc 3tcot 3tdt=−1
3csc 3t+C
51. Z(csc2x−1) cot xdx=Zcsc x(csc xcot x)dx −Zcos x
sin xdx =−1
2csc2x−ln |sin x|+C
52. Z(cot2x+ 1) csc2xdx=−1
3cot3x−cot x+C
307 Chapter 9
53. (a) Z2π
0sin mx cos nx dx =1
2Z2π
0[sin(m+n)x+sin(m−n)x]dx =−cos(m+n)x
2(m+n)−cos(m−n)x
2(m−n)2π
0
but cos(m+n)x2π
0
=0,cos(m−n)x2π
0
=0.
(b) Z2π
0cos mx cos nx dx =1
2Z2π
0[cos(m+n)x+ cos(m−n)x]dx;
since m6=n, evaluate sin at integer multiples of 2πto get 0.
(c) Z2π
0sin mx sin nx dx =1
2Z2π
0[cos(m−n)x−cos(m+n)x]dx;
since m6=n, evaluate sin at integer multiples of 2πto get 0.
55. y0= tan x,1+(y
0)
2= 1 + tan2x= sec2x,
L=Zπ/4
0
√sec2xdx=Zπ/4
0sec xdx=ln|sec x+ tan x|π/4
0
= ln(√2+1)
56. V=πZπ/4
0(1 −tan2x)dx =πZπ/4
0(2 −sec2x)dx =π(2x−tan x)π/4
0
=1
2π(π−2)
57. V=πZπ/4
0(cos2x−sin2x)dx =πZπ/4
0cos 2xdx=1
2πsin 2x#π/4
0
=π/2
58. V=πZπ
0sin2xdx=π
2Zπ
0(1 −cos 2x)dx =π
2x−1
2sin 2xπ
0
=π2/2
59. With 0 <α<β,D=D
β
−D
α=L
2πZβ
α
sec xdx=L
2πln |sec x+ tan x|#β
α
=L
2πln
sec β+ tan β
sec α+ tan α
60. (a) D=100
2πln(sec 25◦+ tan 25◦)=7.18 cm (b) D=100
2πln
sec 50◦+ tan 50◦
sec 30◦+ tan 30◦=7.34 cm
61. (a) Zcsc xdx =Zsec(π/2−x)dx =−ln |sec(π/2−x) + tan(π/2−x)|+C
=−ln |csc x+ cot x|+C
(b) −ln |csc x+ cot x|=ln 1
|csc x+ cot x|=ln |csc x−cot x|
|csc2x−cot2x|=ln|csc x−cot x|,
−ln |csc x+ cot x|=−ln
1
sin x+cos x
sin x=ln
sin x
1 + cos x
=ln
2 sin(x/2) cos(x/2)
2 cos2(x/2) =ln|tan(x/2)|
62. sin x+ cos x=√2[(1/√2) sin x+(1/
√
2) cos x]
=√2[sin xcos(π/4) + cos xsin(π/4)] = √2 sin(x+π/4),
Zdx
sin x+ cos x=1
√2Zcsc(x+π/4)dx =−1
√2ln |csc(x+π/4) + cot(x+π/4)|+C
=−1
√2ln
√2 + cos x−sin x
sin x+ cos x+C

Exercise Set 9.4 308
63. asin x+bcos x=pa2+b2a
√a2+b2sin x+b
√a2+b2cos x=pa2+b2(sin xcos θ+ cos xsin θ)
where cos θ=a/√a2+b2and sin θ=b/√a2+b2so asin x+bcos x=√a2+b2sin(x+θ)
and Zdx
asin x+bcos x=1
√a2+b2Zcsc(x+θ)dx =−1
√a2+b2ln |csc(x+θ) + cot(x+θ)|+C
=−1
√a2+b2ln
√a2+b2+acos x−bsin x
asin x+bcos x+C
64. (a) Zπ/2
0sinnxdx=−1
nsinn−1xcos xπ/2
0
+n−1
nZπ/2
0sinn−2xdx=n−1
nZπ/2
0sinn−2xdx
(b) By repeated application of the formula in part (a)
Zπ/2
0sinnxdx=n−1
nn−3
n−2Zπ/2
0sinn−4xdx
=
n−1
nn−3
n−2n−5
n−4···1
2Zπ/2
0dx, n even
n−1
nn−3
n−2n−5
n−4···2
3Zπ/2
0sin x dx, n odd
=
1·3·5···(n−1)
2·4·6···n·π
2,n even
2·4·6···(n−1)
3·5·7···n,n odd
65. (a) Zπ/2
0sin3xdx=2
3(b) Zπ/2
0sin4xdx=1·3
2·4·π
2=3π/16
(c) Zπ/2
0sin5xdx=2·4
3·5=8/15 (d) Zπ/2
0sin6xdx=1·3·5
2·4·6·π
2=5π/32
66. Similar to proof in Exercise 64.
EXERCISE SET 9.4
1. x= 2 sin θ,dx = 2 cos θdθ,
4Zcos2θdθ=2Z(1 + cos 2θ)dθ =2θ+ sin 2θ+C
=2θ+ 2 sin θcos θ+C= 2 sin−1(x/2) + 1
2xp4−x2+C
2. x=1
2sin θ,dx =1
2cos θdθ,
1
2Zcos2θdθ=1
4Z(1 + cos 2θ)dθ =1
4θ+1
8sin 2θ+C
=1
4θ+1
4sin θcos θ+C=1
4sin−12x+1
2xp1−4x2+C
309 Chapter 9
3. x= 3 sin θ,dx = 3 cos θdθ,
9Zsin2θdθ=9
2Z(1 −cos 2θ)dθ =9
2θ−9
4sin 2θ+C=9
2θ−9
2sin θcos θ+C
=9
2sin−1(x/3) −1
2xp9−x2+C
4. x= 4 sin θ,dx = 4 cos θdθ,
1
16 Z1
sin2θdθ =1
16 Zcsc2θdθ=−1
16 cot θ+C=−√16 −x2
16x+C
5. x= 2 tan θ,dx = 2 sec2θdθ,
1
8Z1
sec2θdθ =1
8Zcos2θdθ=1
16 Z(1 + cos 2θ)dθ =1
16θ+1
32 sin 2θ+C
=1
16θ+1
16 sin θcos θ+C=1
16 tan−1x
2+x
8(4 + x2)+C
6. x=√5 tan θ,dx =√5 sec2θdθ,
5Ztan2θsec θdθ=5Z(sec3θ−sec θ)dθ =51
2sec θtan θ−1
2ln |sec θ+ tan θ|+C1
=1
2xp5+x
2−5
2ln √5+x
2+x
√
5+C
1=1
2x
p5+x
2−5
2ln(p5+x
2+x)+C
7. x= 3 sec θ,dx = 3 sec θtan θdθ,
3Ztan2θdθ=3Z(sec2θ−1)dθ = 3 tan θ−3θ+C=px2−9−3 sec−1x
3+C
8. x= 4 sec θ,dx = 4 sec θtan θdθ,
1
16 Z1
sec θdθ =1
16 Zcos θdθ=1
16 sin θ+C=√x2−16
16x+C
9. x=√2 sin θ,dx =√2 cos θdθ,
2
√2Zsin3θdθ=2
√
2Z1−cos2θsin θdθ
=2
√
2−cos θ+1
3cos3θ+C=−2p2−x2+1
3(2 −x2)3/2+C
10. x=√5 sin θ,dx =√5 cos θdθ,
25√5Zsin3θcos2θdθ=25
√
5−1
3cos3θ+1
5cos5θ+C=−5
3(5 −x2)3/2+1
5(5 −x2)5/2+C
11. x=3
2sec θ,dx =3
2sec θtan θdθ,2
9Z1
sec θdθ =2
9Zcos θdθ=2
9sin θ+C=√4x2−9
9x+C
12. t= tan θ,dt = sec2θdθ,
Zsec3θ
tan θdθ =Ztan2θ+1
tan θsec θdθ=Z(sec θtan θ+ csc θ)dθ
= sec θ+ln|csc θ−cot θ|+C=p1+t
2+ln√
1+t
2−1
|t|+C
Exercise Set 9.4 310
13. x= sin θ,dx = cos θdθ,Z1
cos2θdθ =Zsec2θdθ= tan θ+C=x/p1−x2+C
14. x= 5 tan θ,dx = 5 sec2θdθ,1
25Zsec θ
tan2θdθ =1
25Zcsc θcot θdθ =−1
25 csc θ+C=−√x2+25
25x+C
15. x= sec θ,dx = sec θtan θdθ,Zsec θdθ=ln|sec θ+ tan θ|+C=ln
x+px
2−1
+C
16. 1+2x
2+x
4=(1+x
2
)
2
,x= tan θ,dx = sec2θdθ,
Z1
sec2θdθ =Zcos2θdθ=1
2Z(1 + cos 2θ)dθ =1
2θ+1
4sin 2θ+C
=1
2θ+1
2sin θcos θ+C=1
2tan−1x+x
2(1 + x2)+C
17. x=1
3sec θ,dx =1
3sec θtan θdθ,
1
3Zsec θ
tan2θdθ =1
3Zcsc θcot θdθ=−1
3csc θ+C=−x/p9x2−1+C
18. x= 5 sec θ,dx = 5 sec θtan θdθ,
25 Zsec3θdθ=25
2sec θtan θ+25
2ln |sec θ+ tan θ|+C1
=1
2xpx2−25 + 25
2ln |x+px2−25|+C
19. ex= sin θ,exdx = cos θdθ,
Zcos2θdθ=1
2Z(1 + cos 2θ)dθ =1
2θ+1
4sin 2θ+C=1
2sin−1(ex)+1
2e
x
p1−e
2x+C
20. u= sin θ,Z1
√2−u2du = sin−1sin θ
√2+C
21. x= 4 sin θ,dx = 4 cos θdθ,
1024 Zπ/2
0sin3θcos2θdθ= 1024 −1
3cos3θ+1
5cos5θπ/2
0
= 1024(1/3−1/5) = 2048/15
22. x=2
3sin θ,dx =2
3cos θdθ,
1
24 Zπ/6
0
1
cos3θdθ =1
24 Zπ/6
0sec3θdθ=1
48 sec θtan θ+1
48 ln |sec θ+ tan θ|π/6
0
=1
48[(2/√3)(1/√3)+ln|2/
√
3+1/
√
3|]= 1
48 2
3+1
2ln 3
23. x= sec θ,dx = sec θtan θdθ,Zπ/3
π/4
1
sec θdθ =Zπ/3
π/4cos θdθ= sin θπ/3
π/4
=(
√
3−√
2)/2
24. x=√2 sec θ,dx =√2 sec θtan θdθ,2
Zπ/4
0tan2θdθ=2 tan θ−2θπ/4
0
=2−π/2
311 Chapter 9
25. x=√3 tan θ,dx =√3 sec2θdθ,
1
9Zπ/3
π/6
sec θ
tan4θdθ =1
9Zπ/3
π/6
cos3θ
sin4θdθ =1
9Zπ/3
π/6
1−sin2θ
sin4θcos θdθ=1
9Z√3/2
1/2
1−u
2
u
4du (u= sin θ)
=1
9Z√3/2
1/2(u−4−u−2)du =1
9−1
3u3+1
u√3/2
1/2
=10√3+18
243
26. x=√3 tan θ,dx =√3 sec2θdθ,
√3
3Zπ/3
0
tan3θ
sec3θdθ =√3
3Zπ/3
0sin3θdθ=√3
3Zπ/3
01−cos2θsin θdθ
=√3
3−cos θ+1
3cos3θπ/3
0
=√3
3−1
2+1
24−−1+1
3=5
√
3/72
27. u=x2+4,du =2xdx,
1
2Z1
udu =1
2ln |u|+C=1
2ln(x2+4)+C;orx= 2 tan θ,dx = 2 sec2θdθ,
Ztan θdθ=ln|sec θ|+C1=ln√
x
2+4
2+C
1= ln(x2+4)
1/2−ln 2 + C1
=1
2ln(x2+4)+Cwith C=C1−ln 2
29. y0=1
x,1+(y
0)
2=1+ 1
x
2=x
2+1
x
2,
L=Z2
1rx
2+1
x
2dx =Z2
1
√x2+1
xdx;x= tan θ,dx = sec2θdθ,
L=Ztan−1(2)
π/4
sec3θ
tan θdθ =Ztan−1(2)
π/4
tan2θ+1
tan θsec θdθ=Ztan−1(2)
π/4(sec θtan θ+ csc θ)dθ
=sec θ+ln|csc θ−cot θ|tan−1(2)
π/4
=√5+ln √
5
2−1
2!−h√
2+ln|
√
2−1|
i
=√
5−√
2+ln2+2
√
2
1+√
5
30. y0=2x,1+(y
0)
2=1+4x
2,
L=Z1
0p1+4x
2dx;x=1
2tan θ,dx =1
2sec2θdθ,
L=1
2Ztan−12
0sec3θdθ=1
21
2sec θtan θ+1
2ln |sec θ+ tan θ|tan−12
0
=1
4(√5)(2) + 1
4ln |√5+2|=1
2√
5+1
4ln(2 + √5)
31. y0=2x,1+(y
0)
2=1+4x
2,
S=2πZ1
0x
2
p1+4x
2dx;x=1
2tan θ,dx =1
2sec2θdθ,
Exercise Set 9.4 312
S=π
4Ztan−12
0tan2θsec3θdθ=π
4Ztan−12
0(sec2θ−1) sec3θdθ=π
4Ztan−12
0(sec5θ−sec3θ)dθ
=π
41
4sec3θtan θ−1
8sec θtan θ−1
8ln |sec θ+ tan θ|tan−12
0
=π
32[18√5−ln(2 + √5)]
32. V=πZ1
0y2p1−y2dy;y= sin θ,dy = cos θdθ,
V=πZπ/2
0sin2θcos2θdθ=π
4Zπ/2
0sin22θdθ=π
8Zπ/2
0(1 −cos 4θ)dθ =π
8θ−1
4sin 4θπ/2
0
=π2
16
33. (a) x= 3 sinh u,dx = 3 cosh udu,Zdu =u+C= sinh−1(x/3)+C
(b) x= 3 tan θ,dx = 3 sec2θdθ,
Zsec θdθ=ln|sec θ+ tan θ|+C= ln(px2+9/3+x/3)+C
but sinh−1(x/3) = ln(x/3+px
2/9+1)=ln(x/3+√
x
2+9/3) so the results agree.
(c) x= cosh u,dx = sinh udu,
Zsinh2udu=1
2Z(cosh 2u−1)du =1
4sinh 2u−1
2u+C
=1
2sinh ucosh u−1
2u+C=1
2xpx2−1−1
2cosh−1x+C
because cosh u=x, and sinhu=pcosh2u−1=√
x
2−1
34. A=4b
aZa
0pa2−x2dx;x=acos θ, dx =−asin θdθ,
A=−4b
aZ0
π/2a2sin2θdθ=4ab Zπ/2
0sin2θdθ=2ab Zπ/2
0(1 −cos 2θ)dθ =πab
35. Z1
(x−2)2+9dx =1
3tan−1x−2
3+C36. Z1
p1−(x−1)2dx = sin−1(x−1)+C
37. Z1
p9−(x−1)2dx = sin−1x−1
3+C
38. Z1
16(x+1/2)2+1dx =1
16 Z1
(x+1/2)2+1/16dx =1
4tan−1(4x+2)+C
39. Z1
p(x−3)2+1dx =lnx−3+p(x−3)2+1
+C
40. Zx
(x+3)
2+1dx, let u=x+3,
Zu−3
u
2+1du =Zu
u2+1−3
u
2+1du =1
2ln(u2+1)−3 tan−1u+C
=1
2ln(x2+6x+ 10) −3 tan−1(x+3)+C
313 Chapter 9
41. Zp4−(x+1)
2dx, let x+1=2sinθ,
4Zcos2θdθ=2θ+ sin 2θ+C=2θ+ 2 sin θcos θ+C
= 2 sin−1x+1
2+1
2(x+1)
p3−2x−x
2+C
42. Zex
p(ex+1/2)2+3/4dx, let u=ex+1/2,
Z1
pu2+3/4du = sinh−1(2u/√3)+C= sinh−12ex+1
√
3+C
Alternate solution: let ex+1/2=√
3
2tan θ,
Zsec θdθ=ln|sec θ+ tan θ|+C=ln 2
√
e
2x+e
x+1
√
3+2e
x+1
√
3!+C
1
= ln(2pe2x+ex+1+2e
x+1)+C
43. Z1
2(x+1)
2+5dx =1
2Z1
(x+1)
2+5/2dx =1
√10 tan−1p2/5(x+1)+C
44. Z2x+3
4(x+1/2)2+4dx, let u=x+1/2,
Z2u+2
4u
2+4du =1
2Zu
u2+1+1
u
2+1du =1
4ln(u2+1)+1
2tan−1u+C
=1
4ln(x2+x+5/4) + 1
2tan−1(x+1/2)+C
45. Z2
1
1
√4x−x2dx =Z2
1
1
p4−(x−2)2dx = sin−1x−2
22
1
=π/6
46. Z1
0p4x−x2dx =Z1
0p4−(x−2)2dx, let x−2=2sinθ,
4Z−π/6
−π/2cos2θdθ =2θ+ sin 2θ−π/6
−π/2
=2π
3−√3
2
48. u=xsin x, du =(xcos x+ sin x)dx;
Zp1+u
2du =1
2up1+u
2+1
2sinh−1u+C=1
2xsin xp1+x
2sin2x+1
2sinh−1(xsin x)+C
49. u= sin2x, du = 2 sin xcos xdx;
1
2Zp1−u
2du =1
4hup1−u2+ sin−1ui+C=1
4hsin2xp1−sin4x+ sin−1(sin2x)i+C
Exercise Set 9.5 314
50. u=3
x=e
xln 3,du= (ln 3)3xdx;
1
ln 3 Z3
1pu2−1du =1
2ln3u
pu
2−1−ln u+pu2−13
1
=6√2−ln(3 + 2√2)
2ln3
EXERCISE SET 9.5
1. A
(x−2) +B
(x+5) 2. 5
x(x−3)(x+3) =A
x+B
x−3+C
x+3
3. 2x−3
x2(x−1) =A
x+B
x2+C
x−14. A
x+2+B
(x+2)
2+C
(x+2)
3
5. A
x+B
x2+C
x3+Dx +E
x2+1 6. A
x−1+Bx +C
x2+5
7. Ax +B
x2+5 +Cx +D
(x2+5)
28. A
x−2+Bx +C
x2+1 +Dx +E
(x2+1)
2
9. 1
(x+ 4)(x−1) =A
x+4+B
x−1;A=−1
5,B=1
5so
−1
5Z1
x+4dx +1
5Z1
x−1dx =−1
5ln |x+4|+1
5ln |x−1|+C=1
5ln
x−1
x+4
+C
10. 1
(x+ 1)(x+7) =A
x+1+B
x+7;A=1
6,B=−1
6so
1
6Z1
x+1dx −1
6Z1
x+7dx =1
6ln |x+1|−1
6ln |x+7|+C=1
6ln
x+1
x+7
+C
11. 11x+17
(2x−1)(x+4) =A
2x−1+B
x+4;A=5,B=3so
5Z1
2x−1
dx +3Z1
x+4dx =5
2ln |2x−1|+3ln|x+4|+C
12. 5x−5
(x−3)(3x+1) =A
x−3+B
3x+1;A=1,B=2so
Z1
x−3
dx +2Z1
3x+1dx =ln|x−3|+2
3ln |3x+1|+C
13. 2x2−9x−9
x(x+ 3)(x−3) =A
x+B
x+3+C
x−3;A=1,B=2,C=−1so
Z1
x
dx +2Z1
x+3dx −Z1
x−3dx =ln|x|+2ln|x+3|−ln |x−3|+C=ln
x(x+3)
2
x−3
+C
Note that the symbol Chas been recycled; to save space this recycling is usually not mentioned.
315 Chapter 9
14. 1
x(x+ 1)(x−1) =A
x+B
x+1+C
x−1;A=−1, B=1
2,C=1
2so
−Z1
xdx +1
2Z1
x+1dx +1
2Z1
x−1dx =−ln |x|+1
2ln |x+1|+1
2ln |x−1|+C
=1
2ln
(x+ 1)(x−1)
x2+C=1
2ln |x2−1|
x2+C
15. x2+2
x+2 =x−2+ 6
x+2,Zx−2+ 6
x+2dx =1
2x2−2x+6 ln|x+2|+C
16. x2−4
x−1=x+1−3
x−1,Zx+1−3
x−1dx =1
2x2+x−3ln|x−1|+C
17. 3x2−10
x2−4x+4 =3+ 12x−22
x2−4x+4,12x−22
(x−2)2=A
x−2+B
(x−2)2;A= 12, B=2so
Z3dx +12Z1
x−2dx +2Z1
(x−2)2dx =3x+12ln|x−2|−2/(x−2)+C
18. x2
x2−3x+2 =1+ 3x−2
x
2−3x+2,3x−2
(x−1)(x−2) =A
x−1+B
x−2;A=−1, B=4so
Zdx −Z1
x−1dx +4Z1
x−2dx =x−ln |x−1|+4ln|x−2|+C
19. x5+2x
2+1
x
3−x=x
2+1+2x
2+x+1
x
3−x,
2x
2+x+1
x(x+ 1)(x−1) =A
x+B
x+1+C
x−1;A=−1, B=1,C=2so
Z(x
2+1)dx −Z1
xdx +Z1
x+1dx +2Z1
x−1dx
=1
3x3+x−ln |x|+ln|x+1|+2ln|x−1|+C=1
3x
3+x+ln
(x+ 1)(x−1)2
x+C
20. 2x5−x3−1
x3−4x=2x
2+7+28x−1
x3−4x,
28x−1
x(x+ 2)(x−2) =A
x+B
x+2+C
x−2;A=1
4,B=−57
8,C=55
8so
Z(2x2+7)dx +1
4Z1
xdx −57
8Z1
x+2dx +55
8Z1
x−2dx
=2
3x3+7x+1
4ln |x|−57
8ln |x+2|+55
8ln |x−2|+C
21. 2x2+3
x(x−1)2=A
x+B
x−1+C
(x−1)2;A=3,B=−1, C=5so
3Z1
x
dx −Z1
x−1dx +5Z1
(x−1)2dx =3ln|x|−ln |x−1|−5/(x−1)+C
Exercise Set 9.5 316
22. 3x2−x+1
x
2(x−1) =A
x+B
x2+C
x−1;A=0,B=−1, C=3so
−Z1
x
2dx +3Z1
x−1dx =1/x +3ln|x−1|+C
23. x2+x−16
(x+ 1)(x−3)2=A
x+1+B
x−3+C
(x−3)2;A=−1, B=2,C=−1so
−Z1
x+1dx +2Z1
x−3dx −Z1
(x−3)2dx
=−ln |x+1|+2ln|x−3|+1
x−3+C=ln(x−3)2
|x+1|+1
x−3+C
24. 2x2−2x−1
x2(x−1) =A
x+B
x2+C
x−1;A=3,B=1,C=−1so
3
Z1
x
dx +Z1
x2dx −Z1
x−1dx =3ln|x|−1
x−ln |x−1|+C
25. x2
(x+2)
3=A
x+2+B
(x+2)
2+C
(x+2)
3;A=1,B=−4, C=4so
Z1
x+2dx −4Z1
(x+2)
2dx +4Z1
(x+2)
3dx =ln|x+2|+4
x+2−2
(x+2)
2+C
26. 2x2+3x+3
(x+1)
3=A
x+1+B
(x+1)
2+C
(x+1)
3;A=2,B=−1, C=2so
2Z1
x+1dx −Z1
(x+1)
2dx +2Z1
(x+1)
3dx =2ln|x+1|+1
x+1−1
(x+1)
2+C
27. 2x2−1
(4x−1)(x2+1) =A
4x−1+Bx +C
x2+1 ;A=−14/17, B=12/17, C=3/17 so
Z2x2−1
(4x−1)(x2+1)dx =−7
34 ln |4x−1|+6
17 ln(x2+1)+ 3
17 tan−1x+C
28. 1
x(x2+1) =A
x+Bx +C
x2+1 ;A=1,B=−1, C=0so
Z1
x
3+x
dx =ln|x|−1
2ln(x2+1)+C=1
2ln x2
x2+1+C
29. x3+3x
2+x+9
(x
2+ 1)(x2+3) =Ax +B
x2+1 +Cx +D
x2+3 ;A=0,B=3,C=1,D=0so
Zx
3+3x
2+x+9
(x
2+ 1)(x2+3)dx = 3 tan−1x+1
2ln(x2+3)+C
30. x3+x2+x+2
(x
2+ 1)(x2+2) =Ax +B
x2+1 +Cx +D
x2+2 ;A=D=0,B=C=1so
Zx
3+x
2+x+2
(x
2+ 1)(x2+2)dx = tan−1x+1
2ln(x2+2)+C
317 Chapter 9
31. x3−3x2+2x−3
x
2+1 =x−3+ x
x
2+1,
Zx
3−3x
2+2x−3
x
2+1 dx =1
2x2−3x+1
2ln(x2+1)+C
32. x4+6x
3+10x
2+x
x
2+6x+10 =x
2+x
x
2+6x+10,
Zx
x
2+6x+10dx =Zx
(x+3)
2+1dx =Zu−3
u2+1du, u =x+3
=1
2ln(u2+1)−3 tan−1u+C1
so Zx4+6x
3+10x
2+x
x
2+6x+10 dx =1
3x3+1
2ln(x2+6x+ 10) −3 tan−1(x+3)+C
33. Let x= sin θto get Z1
x2+4x−5dx, and 1
(x+ 5)(x−1) =A
x+5+B
x−1;A=−1/6,
B=1/6soweget−1
6Z1
x+5dx +1
6Z1
x−1dx =1
6ln
x−1
x+5
+C=1
6ln 1−sin θ
5 + sin θ+C.
34. Let x=et; then Zet
e2t−4dt =Z1
x2−4dx,
1
(x+ 2)(x−2) =A
x+2+B
x−2;A=−1/4, B=1/4so
−1
4Z1
x+2dx +1
4Z1
x−2dx =1
4ln
x−2
x+2
+C=1
4ln
et−2
et+2
+C.
35. V=πZ2
0
x4
(9 −x2)2dx,x4
x4−18x2+81 =1+ 18x2−81
x4−18x2+81,
18x2−81
(9 −x2)2=18x2−81
(x+3)
2(x−3)2=A
x+3+B
(x+3)
2+C
x−3+D
(x−3)2;
A=−9
4,B=9
4,C=9
4,D=9
4so
V=πx−9
4ln |x+3|− 9/4
x+3+9
4ln |x−3|− 9/4
x−32
0
=π19
5−9
4ln 5
36. Let u=exto get Zln 5
−ln 5
dx
1+e
x=Zln 5
−ln 5
exdx
ex(1+ex)=Z5
1/5
du
u(1+u),
1
u(1+u)=A
u+B
1+u;A=1,B=−1; Z5
1/5
du
u(1+u)= (ln u−ln(1 + u))5
1/5
=ln5
37. x2+1
(x
2+2x+3)
2=Ax +B
x2+2x+3+Cx +D
(x2+2x+3)
2;A=0,B=1,C=D=−2so
Zx
2+1
(x
2+2x+3)
2dx =Z1
(x+1)
2+2dx −Z2x+2
(x
2+2x+3)
2dx
=1
√2tan−1x+1
√
2+1/(x
2+2x+3)+C
Exercise Set 9.5 318
38. x5+x4+4x
3+4x
2+4x+4
(x
2+2)
3=Ax +B
x2+2 +Cx +D
(x2+2)
2+Ex +F
(x2+2)
3;
A=B=1,C=D=E=F=0so
Zx+1
x
2+2dx =1
2ln(x2+2)+ 1
√
2tan−1(x/√2)+C
39. x4−3x3−7x2+27x−18=(x−1)(x−2)(x−3)(x+ 3),
1
(x−1)(x−2)(x−3)(x+3) =A
x−1+B
x−2+C
x−3+D
x+3;
A=1/8, B=−1/5, C=1/12, D=−1/120 so
Zdx
x4−3x3−7x2+27x−18 =1
8ln |x−1|−1
5ln |x−2|+1
12 ln |x−3|− 1
120 ln |x+3|+C
40. 16x3−4x2+4x−1=(4x−1)(4x2+ 1),
1
(4x−1)(4x2+1) =A
4x−1+Bx +C
4x2+1;A=4/5, B=−4/5, C=−1/5so
Zdx
16x3−4x2+4x−1=1
5ln |4x−1|− 1
10 ln(4x2+1)−1
10 tan−1(2x)+C
41. (a) x4+1=(x
4+2x
2+1)−2x
2=(x
2+1)
2−2x
2
=[(x
2+1)+√
2x][(x2+1)−√
2x]
=(x
2+√
2x+ 1)(x2−√2x+ 1); a=√2,b =−√2
(b) x
(x2+√2x+ 1)(x2−√2x+1) =Ax +B
x2+√2x+1+Cx +D
x2−√2x+1;
A=0,B=−√
2
4,C=0,D=√
2
4so
Z1
0
x
x4+1dx =−√2
4Z1
0
1
x2+√2x+1dx +√2
4Z1
0
1
x2−√2x+1dx
=−√2
4Z1
0
1
(x+√2/2)2+1/2dx +√2
4Z1
0
1
(x−√2/2)2+1/2dx
=−√2
4Z1+√2/2
√2/2
1
u2+1/2du +√2
4Z1−√2/2
−√2/2
1
u2+1/2du
=−1
2tan−1√2u1+√2/2
√2/2
+1
2tan−1√2u1−√2/2
−√2/2
=−1
2tan−1(√2+1)+1
2π
4+1
2tan−1(√2−1) −1
2−π
4
=π
4−1
2[tan−1(√2+1)−tan−1(√2−1)]
=π
4−1
2[tan−1(1+√2) + tan−1(1 −√2)]
=π
4−1
2tan−1"(1+√2)+(1−√
2)
1−(1+√2)(1 −√2)#(Exercise 46, Section 4.5)
=π
4−1
2tan−11=π
4−1
2π
4=π
8
319 Chapter 9
42. 1
a2−x2=A
a−x+B
a+x;A=1
2a,B =1
2aso
1
2aZ1
a−x+1
a+xdx =1
2a(−ln |a−x|+ln|a+x|)+C=1
2aln
a+x
a−x+C
EXERCISE SET 9.6
1. Formula (60): 3
16h4x+ln|−1+4x|i+C2. Formula (62): 1
92
2−3x+ln|2−3x|
+C
3. Formula (65): 1
5ln
x
5+2x
+C4. Formula (66): −1
x−5ln
1−5x
x
+C
5. Formula (102): 1
5(x+ 1)(−3+2x)
3/2+C6. Formula (105): 2
3(−x−4)√2−x+C
7. Formula (108): 1
2ln
√4−3x−2
√4−3x+2
+C8. Formula (108): tan−1√3x−4
2+C
9. Formula (69): 1
2√5ln
x+√5
x−√5+C10. Formula (70): 1
6ln
x−3
x+3
+C
11. Formula (73): x
2px2−3−3
2ln x+px2−3+C
12. Formula (93): −√x2+5
x+ ln(x+px2+5)+C
13. Formula (95): x
2px2+4−2 ln(x+px2+4)+C
14. Formula (90): −√x2−2
2x+C15. Formula (74): x
2p9−x2+9
2sin−1x
3+C
16. Formula (80): −√4−x2
x−sin−1x
2+C
17. Formula (79): √3−x2−√3ln
√3+√
9−x
2
x
+C
18. Formula (117): −√6x−x2
3x+C19. Formula (38): −1
10 sin(5x)+1
2sin x+C
20. Formula (40): −1
14 cos(7x)+1
6cos(3x)+C
21. Formula (50): x4
16 [4 ln x−1]+C22. Formula (50): 4√x1
2ln x−1+C
23. Formula (42): e−2x
13 (−2 sin(3x)−3 cos(3x))+C
Exercise Set 9.6 320
24. Formula (43): ex
5(cos(2x) + 2 sin(2x))+C
25. u=e2x,du=2e
2x
dx, Formula (62): 1
2Zudu
(4 −3u)2=1
18 4
4−3e2x+ln
4−3e
2x
+C
26. u= sin 2x, du = 2 cos 2xdx, Formula (116): Zdu
2u(3 −u)=1
6ln
sin 2x
3−sin 2x+C
27. u=3
√
x, du =3
2√xdx, Formula (68): 2
3Zdu
u2+4 =1
3tan−13√x
2+C
28. u= sin 4x, du = 4 cos 4xdx, Formula (68): 1
4Zdu
9+u
2=1
12 tan−1sin 4x
3+C
29. u=3x, du =3dx, Formula (76): 1
3Zdu
√u2−4=1
3ln 3x+p9x2−4+C
30. u=√2x2,du=2
√
2xdx, Formula (72):
1
2√2Zpu2+3du =x2
4p2x4+3+ 3
4
√
2ln √2x2+p2x4+3
+C
31. u=3x
2
,du=6xdx, u2du =54x
5
dx, Formula (81):
1
54 Zu2du
√5−u2=−x2
36p5−9x4+5
108 sin−13x2
√5+C
32. u=2x, du =2dx, Formula (83): 2 Zdu
u2√3−u2=−1
3xp3−4x2+C
33. u=lnx, du =dx/x, Formula (26): Zsin2udu=1
2ln x+1
4sin(2 ln x)+C
34. u=e−2x,du=−2e
−2x, Formula (27): −1
2Zcos2udu=−1
4e
−2x−1
8sin 2e−2x+C
35. u=−2x, du =−2dx, Formula (51): 1
4Zueudu =1
4(−2x−1)e−2x+C
36. u=5x−1,du=5dx, Formula (50): 1
5Zln udu=1
5(uln u−u)+C=1
5(5x−1)[ln(5x−1)−1]+C
37. u= cos 3x, du =−3 sin 3x, Formula (67): −Zdu
u(u+1)
2=−1
31
1 + cos 3x+ln
cos 3x
1 + cos 3x+C
38. u=lnx, du =1
xdx, Formula (105): Zudu
√4u−1=1
12(2 ln x+1)
√
4lnx−1+C
39. u=4x
2
,du=8xdx, Formula (70): 1
8Zdu
u2−1=1
16 ln
4x2−1
4x2+1
+C
40. u=2e
x
,du=2e
x
dx, Formula (69): 1
2Zdu
3−u2=1
4√3ln
2ex+√3
2ex−√3+C
321 Chapter 9
41. u=2e
x
,du=2e
x
dx, Formula (74):
1
2Zp3−u2du =1
4up3−u2+3
4sin−1(u/√3)+C=1
2exp3−4e2x+3
4sin−1(2ex/√3)+C
42. u=3x, du =3dx, Formula (80):
3Z√4−u2du
u2=−3√4−u2
u−3 sin−1(u/2)+C=−√4−9x2
x−3 sin−1(3x/2)+C
43. u=3x, du =3dx, Formula (112):
1
3Zr5
3u−u2du =1
6u−5
6r5
3u−u2+25
216 sin−1u−5
5+C
=18x−5
36 p5x−9x2+25
216 sin−118x−5
5+C
44. u=√5x, du =√5dx, Formula (117):
Zdu
uq(u/√5) −u2=−q(u/√5) −u2
u/(2√5) +C=−2√x−5x2
x+C
45. u=3x, du =3dx, Formula (44):
1
9Zusin udu=1
9(sin u−ucos u)+C=1
9(sin 3x−3xcos 3x)+C
46. u=√x, u2=x, 2udu =dx, Formula (45): 2 Zucos udu= 2 cos √x+2
√
xsin √x+C
47. u=−√x, u2=x, 2udu =dx, Formula (51): 2 Zueudu =−2(√x+1)e
−
√
x+C
48. u=2−3x
2
,du=−6xdx, Formula (50):
−1
6Zln udu=−1
6(uln u−u)+C=−1
6((2 −3x2) ln(2 −3x2)+1
6(2 −3x2)+C
49. x2+4x−5=(x+2)
2−9; u=x+2,du=dx, Formula (70):
Zdu
u2−9=1
6ln
u−3
u+3
+C=1
6ln
x−1
x+5
+C
50. x2+2x−3=(x+1)
2−4,u=x+1,du=dx, Formula (77):
Zp4−u2du =1
2up4−u2+ 2 sin−1(u/2)+C
=1
2(x+1)
p3−2x−x
2+ 2 sin−1((x+1)/2)+C
51. x2−4x−5=(x−2)2−9,u =x−2,du=dx, Formula (77):
Zu+2
√
9−u
2du =Zudu
√9−u
2+2Zdu
√9−u2=−p9−u2+ 2 sin−1u
3+C
=−p5+4x−x
2+ 2 sin−1x−2
3+C
Exercise Set 9.6 322
52. x2+6x+13=(x+3)
2+4,u=x+3,du=dx, Formula (71):
Z(u−3) du
u2+4 =1
2ln(u2+4)−3
2tan−1(u/2)+C=1
2ln(x2+6x+ 13) −3
2tan−1((x+3)/2)+C
53. u=√x−2, x=u2+2,dx =2udu;
Z2u
2(u
2+2)du =2Z(u
4+2u
2)du =2
5u5+4
3u3+C=2
5(x−2)5/2+4
3(x−2)3/2+C
54. u=√x+1,x=u
2−1, dx =2udu;
2Z(u
2−1)du =2
3u3−2u+C=2
3(x+1)
3/2−2
√
x+1+C
55. u=√x3+1,x
3=u
2−1, 3x2dx =2udu;
2
3Zu
2(u
2−1)du =2
3Z(u4−u2)du =2
15u5−2
9u3+C=2
15(x3+1)
5/2−2
9(x
3+1)
3/2+C
56. u=√x3−1, x3=u2+1,3x
2dx =2udu;
2
3Z1
u
2+1du =2
3tan−1u+C=2
3tan−1px3−1+C
57. u=x1/6,x=u6,dx =6u
5
du;
Z6u5
u3+u2du =6Zu
3
u+1du =6Zu
2−u+1−1
u+1du
=2x
1/2−3x
1/3+6x
1/6−6 ln(x1/6+1)+C
58. u=x1/5,x=u5,dx =5u
4
du;Z5u4
u5−u3du =5Zu
u
2−1
du =5
2ln |x2/5−1|+C
59. u=x1/4,x=u4,dx =4u
3
du;4
Z1
u(1 −u)du =4Z1
u+1
1−u
du =4ln x
1/4
|1−x
1/4
|+C
60. u=x1/3,x=u3,dx =3u
2
du;3
Zu
4
u
3+1du =3Z(u−u
u
3+1)du,
u
u3+1 =u
(u+ 1)(u2−u+1) =−1/3
u+1+(1/3)u+1/3
u
2−u+1 so
3Zu−u
u3+1du =Z3u+1
u+1−u+1
u
2−u+1du
=3
2u2+ln|u+1|−1
2ln(u2−u+1)−√
3 tan−12u−1
√3+C
=3
2x2/3+ln|x
1/3+1|−1
2ln(x2/3−x1/3+1)−√
3 tan−12x1/3−1
√3+C
61. u=x1/6,x=u6,dx =6u
5
du;
6Zu3
u−1du =6Zu
2+u+1+ 1
u−1du =2x
1/2+3x
1/3+6x
1/6+6 ln|x
1/6−1|+C
323 Chapter 9
62. u=√x,x=u2,dx =2udu;
−2Zu
2+u
u−1du =−2Zu+2+ 2
u−1du =−x−4√x−4ln|√x−1|+C
63. u=√1+x
2,x
2=u
2−1, 2xdx=2udu,xdx=udu;
Z(u
2−1)du =1
3(1+x2)3/2−(1+x2)1/2+C
64. u=(x+3)
1/5,x=u
5−3, dx =5u
4
du;
5Z(u8−3u3)du =5
9(x+3)
9/5−15
4(x+3)
4/5+C
65. u=√x,x=u2,dx =2udu, Formula (44): 2 Zusin udu= 2 sin √x−2√xcos √x+C
66. u=√x,x=u2,dx =2udu, Formula (51): 2 Zueudu =2
√
xe√x−2e√x+C
67. Z1
1+ 2u
1+u
2+1−u
2
1+u
2
2
1+u
2du =Z1
u+1du =ln|tan(x/2)+1|+C
68. Z1
2+ 2u
1+u
2
2
1+u
2du =Z1
u2+u+1du
=Z1
(u+1/2)2+3/4du =2
√3tan−12 tan(x/2)+1
√
3+C
69. u= tan(θ/2), Zdθ
1−cos θ=Z1
u2du =−1
u+C=−cot(θ/2)+C
70. u= tan(x/2),
Z2
3u2+8u−3du =2
3Z1
(u+4/3)2−25/9du =2
3Z1
z2−25/9dz (z=u+4/3)
=1
5ln
z−5/3
z+5/3
+C=1
5ln
tan(x/2) −1/3
tan(x/2)+3
+C
71. u= tan(x/2), 2 Z1−u2
(3u2+ 1)(u2+1)du;
1−u2
(3u2+ 1)(u2+1) =(0)u+2
3u
2+1 +(0)u−1
u2+1 =2
3u
2+1−1
u
2+1 so
Zcos x
2−cos xdx =4
√3tan−1[√3 tan(x/2)] −x+C
72. u= tan(x/2), 1
2Z1−u2
udu =1
2Z(1/u −u)du =1
2ln |tan(x/2)|−1
4tan2(x/2)+C
Exercise Set 9.6 324
73. Zx
2
1
t(4 −t)dt =1
4ln t
4−tx
2
(Formula (65), a=4,b =−1)
=1
4ln x
4−x−ln 1=1
4ln x
4−x,1
4ln x
4−x=0.5,ln x
4−x=2,
x
4−x=e
2
,x=4e
2−e
2
x,x(1+e2)=4e
2
,x=4e
2
/(1+e2)≈3.523188312
74. Zx
1
1
t√2t−1dt = 2 tan−1√2t−1x
1
(Formula (108), a=−1,b=2)
=2tan−1√2x−1−tan−11=2tan−1√2x−1−π/4,
2(tan−1√2x−1−π/4) = 1, tan−1√2x−1=1/2+π/4, √2x−1 = tan(1/2+π/4),
x= [1 + tan2(1/2+π/4)]/2≈6.307993516
75. A=Z4
0p25 −x2dx =1
2xp25 −x2+25
2sin−1x
54
0
(Formula (74), a=5)
=6+25
2sin−14
5≈17.59119023
76. A=Z2
2/3p9x2−4dx;u=3x,
A=1
3Z6
2pu
2−4du =1
31
2upu2−4−2ln
u+pu
2−4
6
2
(Formula (73), a2=4)
=1
33
√
32 −2 ln(6 + √32) + 2 ln 2=4
√
2−2
3ln(3 + 2√2) ≈4.481689467
77. A=Z1
0
1
25 −16x2dx;u=4x,
A=1
4Z4
0
1
25 −u2du =1
40 ln
u+5
u−5
4
0
=1
40 ln 9 ≈0.054930614 (Formula (69), a=5)
78. A=Z4
1
√xln xdx=4
9x
3/23
2ln x−14
1
(Formula (50), n=1/2)
=4
9(12 ln 4 −7) ≈4.282458815
79. V=2πZπ/2
0xcos xdx=2π(cos x+xsin x)π/2
0
=π(π−2) ≈3.586419094 (Formula (45))
80. V=2πZ8
4x
√
x−4dx =4π
15 (3x+ 8)(x−4)3/28
4
(Formula (102), a=−4,b=1)
=1024
15 π≈214.4660585
81. V=2πZ3
0xe−xdx;u=−x,
V=2πZ−3
0ueudu =2πeu(u−1)−3
0
=2π(1 −4e−3)≈5.031899801 (Formula (51))
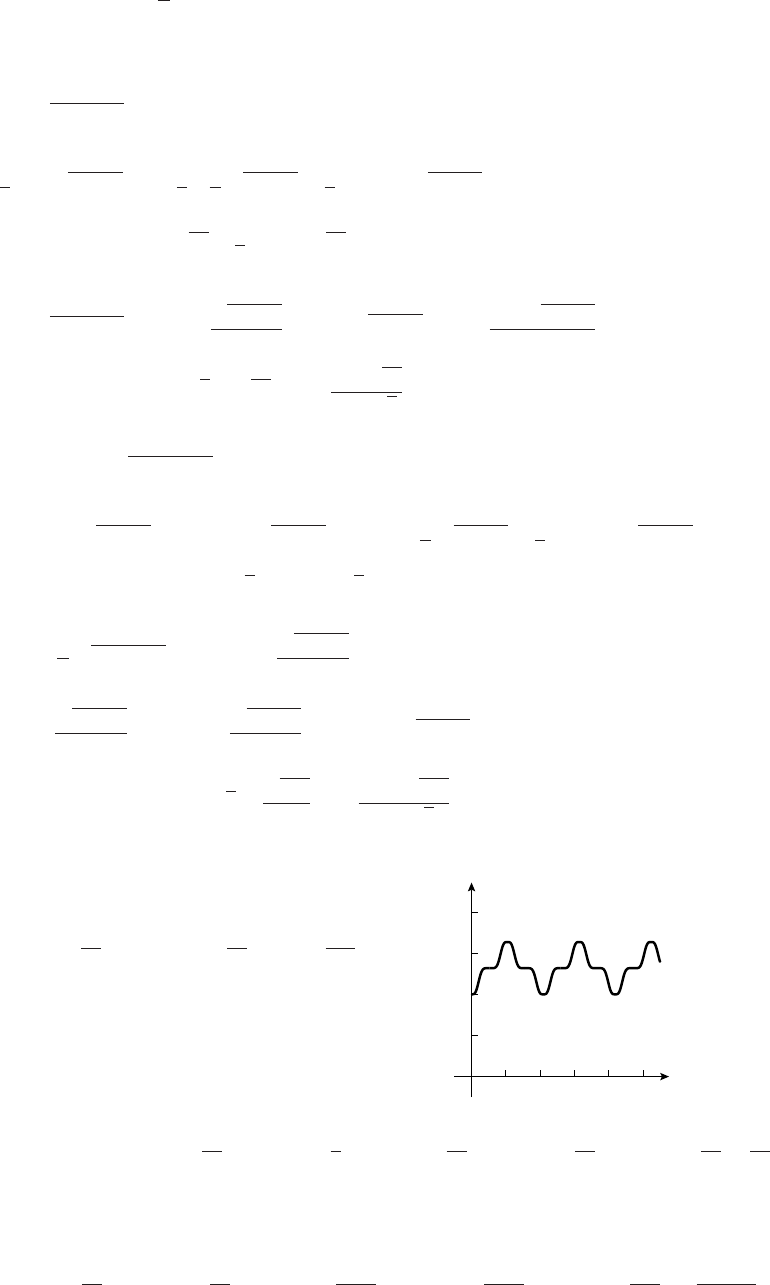
325 Chapter 9
82. V=2πZ5
1xln xdx=π
2x
2(2 ln x−1)5
1
=π(25 ln 5 −12) ≈88.70584621 (Formula (50), n=1)
83. L=Z2
0p1+16x
2dx;u=4x,
L=1
4Z8
0p1+u
2du =1
4u
2p1+u
2+1
2ln u+p1+u
28
0
(Formula (72), a2=1)
=√
65 + 1
8ln(8 + √65) ≈8.409316783
84. L=Z3
1p1+9/x2dx =Z3
1
√x2+9
xdx = px2+9−3ln
3+√
x
2+9
x
!#3
1
=3
√
2−√
10+3ln3+√
10
1+√
2≈3.891581644 (Formula (89), a=3)
85. S=2πZπ
0(sin x)p1 + cos2xdx;u= cos x,
S=−2πZ−1
1p1+u
2du =4πZ1
0p1+u
2du =4πu
2p1+u
2+1
2ln u+p1+u
21
0
a2=1)
=2π[
√
2+ln(1+√2)] ≈14.42359945 (Formula (72)
86. S=2πZ4
1
1
x
p1+1/x4dx =2πZ4
1
√
x
4+1
x
3dx;u=x2,
S=πZ16
1
√u2+1
u
2du =π −√u2+1
u+lnu+pu
2+1!#16
1
=π √2−√257
16 +ln16+√257
1+√
2!≈9.417237485 (Formula (93), a2=1)
87. (a) s(t)=2+Zt
020 cos6usin3udu
=−20
9sin2tcos7t−40
63 cos7t+166
63
(b)
3 6 9 12 15
1
2
3
4
t
s(t)
88. (a) v(t)=Zt
0a(u)du =−1
10e−tcos 2t+1
5e−tsin 2t+1
74e−tcos 6t−3
37e−tsin 6t+1
10 −1
74
s(t)=10+Zt
0v(u)du
=−3
50e−tcos 2t−2
25e−tsin 2t+35
2738e−tcos 6t+6
1369e−tsin 6t+16
185t+343866
34225

Exercise Set 9.7 326
(b)
2 6 10 14 18
2
4
6
8
10
12
t
s(t)
89. (a) Zsec xdx =Z1
cos xdx =Z2
1−u2du =ln
1+u
1−u
+C=ln
1 + tan(x/2)
1−tan(x/2)+C
=ln
cos(x/2) + sin(x/2)
cos(x/2) −sin(x/2)
cos(x/2) + sin(x/2)
cos(x/2) + sin(x/2)+C=ln
1 + sin x
cos x+C
=ln|sec x+ tan x|+C
(b) tan π
4+x
2=tan π
4+ tan x
2
1−tan π
4tan x
2
=1 + tan x
2
1−tan x
2
90. Zcsc xdx=Z1
sin xdx =Z1/u du =ln|tan(x/2)|+Cbut
ln |tan(x/2)|=1
2ln sin2(x/2)
cos2(x/2) =1
2ln (1 −cos x)/2
(1 + cos x)/2=1
2ln 1−cos x
1 + cos x; also,
1−cos x
1 + cos x=1−cos2x
(1 + cos x)2=1
(csc x+ cot x)2so 1
2ln 1−cos x
1 + cos x=−ln |csc x+ cot x|
91. Let u= tanh(x/2) then cosh(x/2)=1/sech(x/2)=1/
q1−tanh2(x/2)=1/
√
1−u
2
,
sinh(x/2) = tanh(x/2) cosh(x/2) = u/√1−u2, so sinh x= 2 sinh(x/2) cosh(x/2)=2u/(1 −u2),
cosh x= cosh2(x/2) + sinh2(x/2)=(1+u
2
)/(1 −u2), x= 2 tanh−1u, dx =[2/(1 −u2)]du;
Zdx
2 cosh x+ sinh x=Z1
u2+u+1du =2
√3tan−12u+1
√
3+C=2
√
3tan−12 tanh(x/2)+1
√
3+C.
EXERCISE SET 9.7
1. exact value = 14/3≈4.666666667
(a) 4.667600663, |EM|≈0.000933996
(b) 4.664795679, |ET|≈0.001870988
(c) 4.666651630, |ES|≈0.000015037
2. exact value = 2
(a) 1.998377048, |EM|≈0.001622952
(b) 2.003260982, |ET|≈0.003260982
(c) 2.000072698, |ES|≈0.000072698
3. exact value = 2
(a) 2.008248408, |EM|≈0.008248408
(b) 1.983523538, |ET|≈0.016476462
(c) 2.000109517, |ES|≈0.000109517
4. exact value = sin(1) ≈0.841470985
(a) 0.841821700, |EM|≈0.000350715
(b) 0.840769642, |ET|≈0.000701343
(c) 0.841471453, |ES|≈0.000000468
5. exact value = e−1−e−3≈0.318092373
(a) 0.317562837, |EM|≈0.000529536
(b) 0.319151975, |ET|≈0.001059602
(c) 0.318095187, |ES|≈0.000002814
6. exact value = 1
2ln 5 ≈0.804718956
(a) 0.801605339, |EM|≈0.003113617
(b) 0.811019505, |ET|≈0.006300549
(c) 0.805041497, |ES|≈0.000322541

327 Chapter 9
7. f(x)=√
x+1,f00(x)=−1
4
(x+1)
−3/2,f(4)(x)=−15
16(x+1)
−7/2;K
2=1/4, K4=15/16
(a) |EM|≤ 27
2400(1/4)=0.002812500 (b) |ET|≤ 27
1200(1/4)=0.005625000
(c) |ES|≤ 243
180 ×104(15/16) ≈0.000126563
8. f(x)=1/
√
x,f
00(x)=3
4
x
−5/2
,f
(4)(x)=105
16 x−9/2;K2=3/4, K4= 105/16
(a) |EM|≤ 27
2400(3/4)=0.008437500 (b) |ET|≤ 27
1200(3/4)=0.016875000
(c) |ES|≤ 243
180 ×104(105/16) ≈0.000885938
9. f(x) = sin x,f00(x)=−sin x,f(4)(x) = sin x;K2=K4=1
(a) |EM|≤ π
3
2400(1) ≈0.012919282 (b) |ET|≤ π
3
1200(1) ≈0.025838564
(c) |ES|≤ π
5
180 ×104(1) ≈0.000170011
10. f(x) = cos x,f00(x)=−cos x,f(4)(x) = cos x;K2=K4=1
(a) |EM|≤ 1
2400(1) ≈0.000416667 (b) |ET|≤ 1
1200(1) ≈0.000833333
(c) |ES|≤ 1
180 ×104(1) ≈0.000000556
11. f(x)=e
−x
,f
00(x)=f
(4)(x)=e
−x
;K
2=K
4=e
−1
(a) |EM|≤ 8
2400(e−1)≈0.001226265 (b) |ET|≤ 8
1200(e−1)≈0.002452530
(c) |ES|≤ 32
180 ×104(e−1)≈0.000006540
12. f(x)=1/(2x+ 3), f00(x) = 8(2x+3)
−3,f(4)(x) = 384(2x+3)
−5;K
2=8,K
4= 384
(a) |EM|≤ 8
2400(8) ≈0.026666667 (b) |ET|≤ 8
1200(8) ≈0.053333333
(c) |ES|≤ 32
180 ×104(384) ≈0.006826667
13. (a) n>(27)(1/4)
(24)(5 ×10−4)1/2
≈23.7; n=24 (b) n>
(27)(1/4)
(12)(5 ×10−4)1/2
≈33.5; n=34
(c) n>(243)(15/16)
(180)(5 ×10−4)1/4
≈7.1; n=8
14. (a) n>(27)(3/4)
(24)(5 ×10−4)1/2
≈41.1; n=42 (b) n>
(27)(3/4)
(12)(5 ×10−4)1/2
≈58.1; n=59
(c) n>(243)(105/16)
(180)(5 ×10−4)1/4
≈11.5; n=12

Exercise Set 9.7 328
15. (a) n>(π
3
)(1)
(24)(10−3)1/2
≈35.9; n=36 (b) n>(π
3
)(1)
(12)(10−3)1/2
≈50.8; n=51
(c) n>(π
5
)(1)
(180)(10−3)1/4
≈6.4; n=8
16. (a) n>(1)(1)
(24)(10−3)1/2
≈6.5; n=7 (b) n>(1)(1)
(12)(10−3)1/2
≈9.1; n=10
(c) n>(1)(1)
(180)(10−3)1/4
≈1.5; n=2
17. (a) n>(8)(e−1)
(24)(10−6)1/2
≈350.2; n= 351 (b) n>(8)(e−1)
(12)(10−6)1/2
≈495.2; n= 496
(c) n>(32)(e−1)
(180)(10−6)1/4
≈15.99; n=16
18. (a) n>(8)(8)
(24)(10−6)1/2
≈1632.99; n= 1633 (b) n>(8)(8)
(12)(10−6)1/2
≈2309.4; n= 2310
(c) n>(32)(384)
(180)(10−6)1/4
≈90.9; n=92
19. 0.746824948,
0.746824133 20. 1.137631378,
1.137630147 21. 2.129861595,
2.129861293
22. 2.418388347,
2.418399152 23. 0.805376152,
0.804776489 24. 1.536963087,
1.544294774
25. (a) 3.142425985, |EM|≈0.000833331
(b) 3.139925989, |ET|≈0.001666665
(c) 3.141592614, |ES|≈0.000000040
26. (a) 3.152411433, |EM|≈0.010818779
(b) 3.104518326, |ET|≈0.037074328
(c) 3.127008159, |ES|≈0.014584495
27. S14 =0.693147984, |ES|≈0.000000803 = 8.03 ×10−7; the method used in Example 5 results
in a value of nwhich ensures that the magnitude of the error will be less than 10−6, this is not
necessarily the smallest value of n.
28. (a) greater, because the graph of e−x2is concave up on the interval (1,2)
(b) less, because the graph of e−x2is concave down on the interval (0,0.5)
29. f(x)=xsin x,f00(x)=2cosx−xsin x,|f00(x)|≤2|cos x|+|x||sin x|≤2+2=4soK
2≤4,
n>(8)(4)
(24)(10−4)1/2
≈115.5; n= 116 (a smaller nmight suffice)
30. f(x)=e
cos x,f00(x) = (sin2x)ecos x−(cos x)ecos x,|f00(x)|≤e
cos x(sin2x+|cos x|)≤2eso
K2≤2e,n>(1)(2e)
(24)(10−4)1/2
≈47.6; n= 48 (a smaller nmight suffice)
31. f(x)=√
x,f
00(x)=−1
4x
3/2, lim
x→0+|f00(x)|=+∞
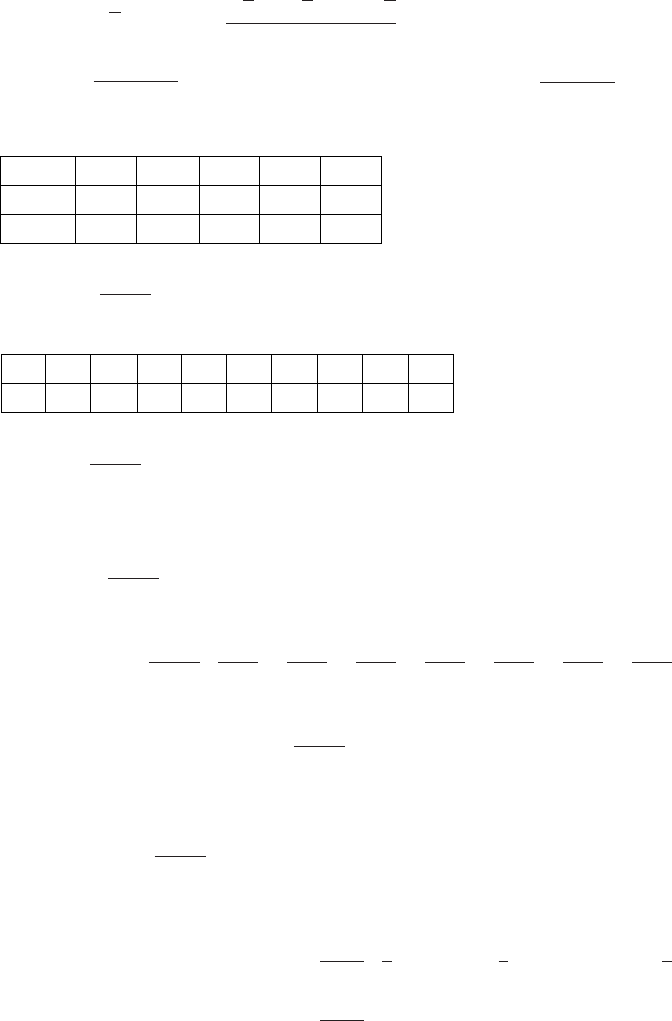
329 Chapter 9
32. f(x) = sin √x,f00(x)=−√
xsin √x+ cos √x
4x3/2, lim
x→0+|f00(x)|=+∞
33. L=Zπ
0p1 + cos2xdx≈3.820187623 34. L=Z3
1p1+1/x4dx ≈2.146822803
35. 0
0
0
5
40
58.67
10
60
88
15
73
107.07
20
84
123.2
t (s)
v (mi/hr)
v (ft/s)
Z20
0vdt≈20
(3)(4)[0 + 4(58.67) + 2(88) + 4(107.07) + 123.2] ≈1604 ft
36. 0
0
1
0.02
2
0.08
3
0.20
4
0.40
t
a
5
0.60
6
0.70
7
0.60
8
0
Z8
0adt≈8
(3)(8)[0 + 4(0.02) + 2(0.08) + 4(0.20) + 2(0.40) + 4(0.60) + 2(0.70) + 4(0.60)+0]
≈2.7 cm/s
37. Z180
0vdt≈180
(3)(6)[0.00 + 4(0.03) + 2(0.08) + 4(0.16) + 2(0.27) + 4(0.42)+0.65]=37.9mi
38. Z1800
0(1/v)dx ≈1800
(3)(6) 1
3100 +4
2908 +2
2725 +4
2549 +2
2379 +4
2216 +1
2059≈0.71 s
39. V=Z16
0πr2dy =πZ16
0r2dy ≈π16
(3)(4)[(8.5)2+ 4(11.5)2+ 2(13.8)2+ 4(15.4)2+ (16.8)2]
≈9270 cm3≈9.3L
40. A=Z600
0hdx≈600
(3)(6)[0 + 4(7) + 2(16) + 4(24) + 2(25) + 4(16) + 0] = 9000 ft2,
V=75A≈75(9000) = 675,000 ft3
41. Zb
a
f(x)dx ≈A1+A2+···+A
n=b−a
n1
2(y
0+y
1)+1
2(y
1+y
2)+···+1
2(y
n−1+y
n)
=b−a
2n[y
0+2y
1+2y
2+···+2y
n−1+y
n
]
42. right endpoint, trapezoidal, midpoint, left endpoint
43. (a) The maximum value of |f00(x)|is approximately 3.844880.
(b) n=18
(c) 0.904741
44. (a) The maximum value of |f00(x)|is approximately 1.467890.
(b) n=12
(c) 1.112062
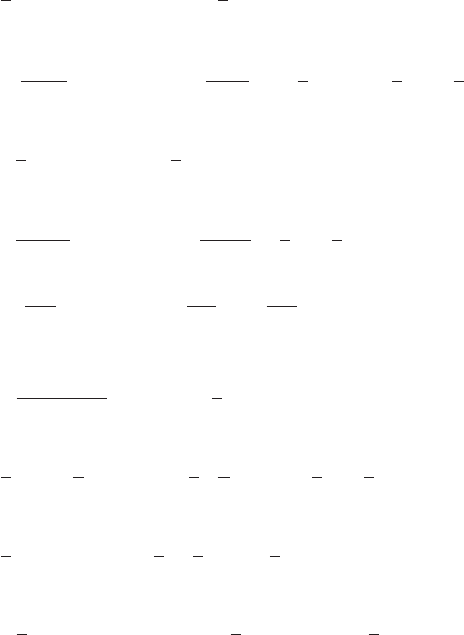
Exercise Set 9.8 330
45. (a) The maximum value of |f(4)(x)|is approximately 42.551816.
(b) n=8
(c) 0.904524
46. (a) The maximum value of |f(4)(x)|is approximately 7.022710.
(b) n=8
(c) 1.111443
EXERCISE SET 9.8
1. (a) improper; infinite discontinuity at x=3
(b) continuous integrand, not improper
(c) improper; infinite discontinuity at x=0
(d) improper; infinite interval of integration
(e) improper; infinite interval of integration and infinite discontinuity at x=1
(f) continuous integrand, not improper
2. (a) improper if p>0(b) improper if 1 <p<2
(c) integrand is continuous for all p, not improper
3. lim
`→+∞(−e−x)`
0
= lim
`→+∞(−e−`+1)=1
4. lim
`→+∞
1
2ln(1 + x2)`
−1
= lim
`→+∞
1
2[ln(1 + `2)−ln 2] = +∞, divergent
5. lim
`→+∞ln x−1
x+1`
4
= lim
`→+∞ln `−1
`+1−ln 3
5=−ln 3
5=ln5
3
6. lim
`→+∞−1
2e−x2`
0
= lim
`→+∞
1
2−e−`2+1
=1/2
7. lim
`→+∞−1
2ln
2x`
e
= lim
`→+∞−1
2ln
2`+1
2=1
2
8. lim
`→+∞2√ln x`
2
= lim
`→+∞(2√ln `−2√ln 2) = +∞, divergent
9. lim
`→−∞ −1
4(2x−1)20
`
= lim
`→−∞
1
4[−1+1/(2`−1)2]=−1/4
10. lim
`→−∞
1
2tan−1x
22
`
= lim
`→−∞
1
2π
4−tan−1`
2=1
2[π/4−(−π/2)]=3π/8
11. lim
`→−∞
1
3e3x0
`
= lim
`→−∞ 1
3−1
3e3`=1
3
12. lim
`→−∞ −1
2ln(3 −2ex)0
`
= lim
`→−∞
1
2ln(3 −2e`)=1
2ln 3
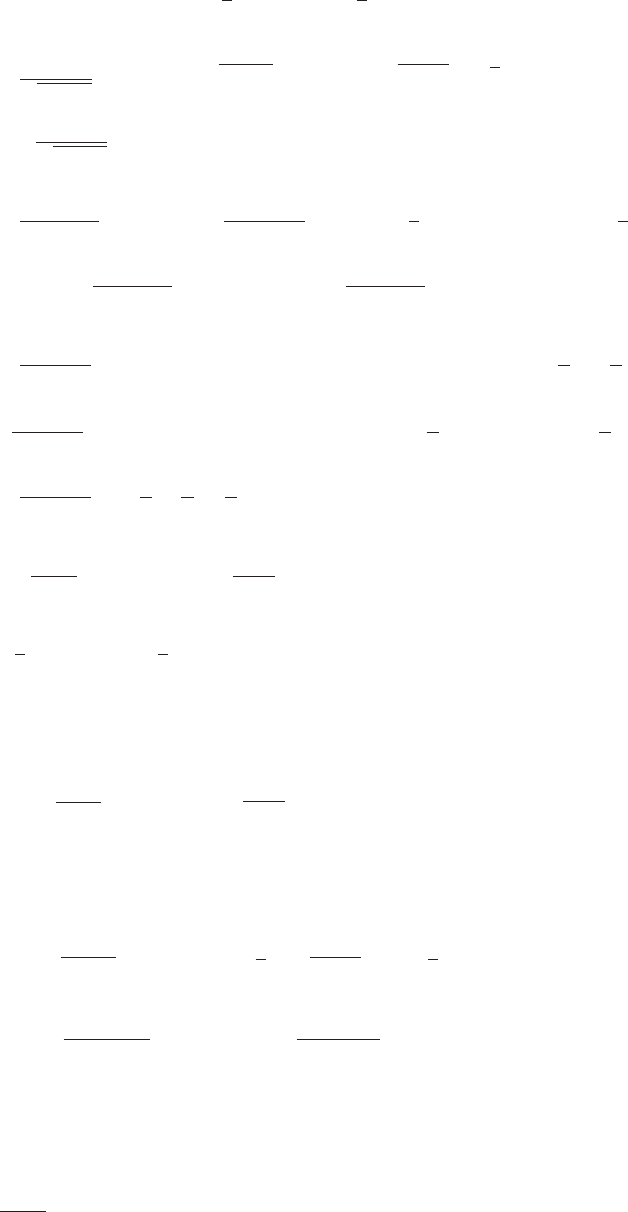
331 Chapter 9
13. Z+∞
−∞
x3dx converges if Z0
−∞
x3dx and Z+∞
0x3dx both converge; it diverges if either (or both)
diverge. Z+∞
0x3dx = lim
`→+∞
1
4x4`
0
= lim
`→+∞
1
4`4=+∞so Z+∞
−∞
x3dx is divergent.
14. Z+∞
0
x
√x2+2dx = lim
`→+∞px2+2
`
0
= lim
`→+∞(p`2+2−√
2)=+∞
so Z∞
−∞
x
√x2+2dx is divergent.
15. Z+∞
0
x
(x2+3)
2dx = lim
`→+∞−1
2(x2+3)`
0
= lim
`→+∞
1
2[−1/(`2+3)+1/3] = 1
6,
similarly Z0
−∞
x
(x2+3)
2dx =−1/6soZ∞
−∞
x
(x2+3)
2dx =1/6+(−1/6)=0
16. Z+∞
0
e−t
1+e
−2tdt = lim
`→+∞−tan−1(e−t)`
0
= lim
`→+∞h−tan−1(e−`)+π
4i=π
4,
Z0
−∞
e−t
1+e
−2tdt = lim
`→−∞ −tan−1(e−t)0
`
= lim
`→−∞ h−π
4+ tan−1(e−`)i=π
4,
Z+∞
−∞
e−t
1+e
−2tdt =π
4+π
4=π
2
17. lim
`→3+−1
x−34
`
= lim
`→3+−1+ 1
`−3=+∞, divergent
18. lim
`→0+
3
2x2/38
`
= lim
`→0+
3
2(4 −`2/3)=6
19. lim
`→π/2−−ln(cos x)`
0
= lim
`→π/2−−ln(cos `)=+∞, divergent
20. lim
`→9−−2√9−x`
0
= lim
`→9−2(−√9−`+3)=6
21. lim
`→1−sin−1x`
0
= lim
`→1−sin−1`=π/2
22. lim
`→−3+−p9−x21
`
= lim
`→−3+(−√8+p9−`
2)=−
√
8
23. lim
`→π/6−−√1−2 sin x`
0
= lim
`→π/6−(−√1−2 sin `+1)=1
24. lim
`→π/4−−ln(1 −tan x)`
0
= lim
`→π/4−−ln(1 −tan `)=+∞, divergent
25. Z2
0
dx
x−2= lim
`→2−ln |x−2|`
0
= lim
`→2−(ln |`−2|−ln 2) = −∞, divergent
Exercise Set 9.8 332
26. Z2
0
dx
x2= lim
`→0+−1/x2
`
= lim
`→0+(−1/2+1/`)=+∞so Z2
−2
dx
x2is divergent
27. Z8
0x−1/3dx = lim
`→0+
3
2x2/38
`
= lim
`→0+
3
2(4 −`2/3)=6,
Z0
−1x
−1/3
dx = lim
`→0−
3
2x2/3`
−1
= lim
`→0−
3
2(`2/3−1) = −3/2
so Z8
−1x−1/3dx =6+(−3/2)=9/2
28. Z2
0
dx
(x−2)2/3= lim
`→2−3(x−2)1/3`
0
= lim
`→2−3[(`−2)1/3−(−2)1/3]=33
√
2,
similarly Z4
2
dx
(x−2)2/3= lim
`→2+3(x−2)1/34
`
=33
√
2soZ4
0
dx
(x−2)2/3=63
√
2
29. Define Z+∞
0
1
x2dx =Za
0
1
x2dx +Z+∞
a
1
x2dx where a>0; take a= 1 for convenience,
Z1
0
1
x2dx = lim
`→0+(−1/x)1
`
= lim
`→0+(1/` −1)=+∞so Z+∞
0
1
x2dx is divergent.
30. Define Z+∞
1
dx
x√x2−1=Za
1
dx
x√x2−1+Z+∞
a
dx
x√x2−1where a>1,
take a= 2 for convenience to get
Z2
1
dx
x√x2−1= lim
`→1+sec−1x2
`
= lim
`→1+(π/3−sec−1`)=π/3,
Z+∞
2
dx
x√x2−1= lim
`→+∞sec−1x`
2
=π/2−π/3soZ+∞
1
dx
x√x2−1=π/2.
31. Z+∞
0
e−√x
√xdx =2Z+∞
0e
−u
du = 2 lim
`→+∞−e−u`
0
= 2 lim
`→+∞1−e−`=2
32. Z+∞
0
dx
√x(x+4) =2Z+∞
0
du
u2+4 = 2 lim
`→+∞
1
2tan−1u
2`
0
= lim
`→+∞tan−1`
2=π
2
33. Z+∞
0
e−x
√1−e−xdx =Z1
0
du
√u= lim
`→0+2√u1
`
= lim
`→0+2(1 −√`)=2
34. Z+∞
0
e−x
√1−e−2xdx =−Z0
1
du
√1−u2=Z1
0
du
√1−u2= lim
`→1sin−1u`
0
= lim
`→1sin−1`=π
2
36. A=Z+∞
0xe−3xdx = lim
`→+∞−1
9(3x+1)e
−3x
`
0
=1/3
37. lim
`→+∞Z`
0e−xcos xdx= lim
`→+∞
1
2e−x(sin x−cos x)`
0
=1/2
39. (a) 2.726585 (b) 2.804364 (c) 0.219384 (d) 0.504067
333 Chapter 9
40. 1+dy
dx2
=1+ 16x2
9−4x2=9+12x
2
9−4x
2; the arc length is Z3/2
0s9+12x
2
9−4x
2dx ≈3.633168
41. Zln xdx=xln x−x+C,
Z1
0ln xdx= lim
`→0+Z1
`
ln xdx= lim
`→0+(xln x−x)1
`
= lim
`→0+(−1−`ln `+`),
but lim
`→0+`ln `= lim
`→0+
ln `
1/` = lim
`→0+(−`)=0soZ1
0ln xdx=−1
42. Zln x
x2dx =−ln x
x−1
x+C,
Z+∞
1
ln x
x2dx = lim
`→+∞Z`
1
ln x
x2dx = lim
`→+∞−ln x
x−1
x`
1
= lim
`→+∞−ln `
`−1
`+1
,
but lim
`→+∞
ln `
`= lim
`→+∞
1
`=0soZ+∞
1
ln x
x2=1
43. Zxe−3xdx =−1
3xe−3x−1
9e−3x+C,
Z+∞
0xe−3xdx = lim
`→+∞Z`
0xe−3xdx = lim
`→+∞−1
3xe−3x−1
9e−3x`
0
= lim
`→+∞−1
3`e−3`−1
9e−3`+1
9
but lim
`→+∞`e−3`= lim
`→+∞
`
e3`= lim
`→+∞
1
3e3`=0soZ+∞
0xe−3xdx =1/9
44. A=Z+∞
3
8
x2−4dx = lim
`→+∞2lnx−2
x+2`
3
= lim
`→+∞2ln `−2
`+2−ln 1
5= 2 ln 5
45. (a) V=πZ+∞
0e−2xdx =−π
2lim
`→+∞e−2x`
0
=π/2
(b) S=2πZ+∞
0e
−x
p1+e
−2x
dx, let u=e−xto get
S=−2πZ0
1p1+u
2du =2πu
2p1+u
2+1
2ln |u+p1+u
2|
1
0
=πh√
2+ln(1+√2)i
47. (a) For x≥1,x
2≥x, e−x2≤e−x
(b) Z+∞
1e−xdx = lim
`→+∞Z`
1e−xdx = lim
`→+∞−e−xi`
1= lim
`→+∞(e−1−e−`)=1/e
(c) By parts (a) and (b) and Exercise 46(b), Z+∞
1e−x2dx is convergent and is ≤1/e.
48. (a) If x≥0 then ex≥1,1
2x+1 ≤e
x
2x+1
(b) lim
`→+∞Z`
0
dx
2x+1 = lim
`→+∞
1
2ln(2x+1)
`
0
=+∞
(c) By parts (a) and (b) and Exercise 46(a), Z+∞
0
ex
2x+1dx is divergent.
Exercise Set 9.8 334
49. V= lim
`→+∞Z`
1(π/x2)dx = lim
`→+∞−(π/x)i`
1= lim
`→+∞(π−π/`)=π
A= lim
`→+∞Z`
12π(1/x)p1+1/x4dx; use Exercise 46(a) with f(x)=2π/x,g(x)=(2π/x)p1+1/x4
and a= 1 to see that the area is infinite.
50. (a) 1≤√x3+1
xfor x≥2, Z+∞
21dx =+∞
(b) Z+∞
2
x
x5+1dx ≤Z+∞
2
dx
x4= lim
`→+∞−1
3x3`
2
=1/24
(c) 1
2x+1 ≤e
x
2x+1 for x≥0, Z+∞
0
1
2x+1dx = lim
`→+∞
1
2ln(2x+1)
`
0
=+∞
51. Z2x
0p1+t
3dt ≥Z2x
0t3/2dt =2
5t5/22x
0
=2
5(2x)5/2,
lim
x→+∞Z2x
0t3/2dt = lim
x→+∞
2
5(2x)5/2=+∞so Z+∞
0p1+t
3dt =+∞; by L’Hˆopital’s Rule
lim
x→+∞Z2x
0p1+t
3dt
x5/2= lim
x→+∞
2p1+(2x)
3
(5/2)x3/2= lim
x→+∞
2p1/x3+8
5/2=8
√
2/5
52. (b) u=√x, Z+∞
0
cos √x
√xdx =2Z+∞
0cos udu;Z+∞
0cos udu diverges by part (a).
53. Let x=rtan θto get Zdx
(r2+x2)3/2=1
r2Zcos θdθ=1
r
2sin θ+C=x
r2√r2+x2+C
so u=2πNIr
klim
`→+∞
x
r2√r2+x2`
a
=2πNI
kr lim
`→+∞(`/pr2+`2−a/pr2+a2)
=2πNI
kr (1 −a/pr2+a2).
54. Let a2=M
2RT to get
(a) ¯v=4
√πM
2RT 3/21
2M
2RT −2
=2
√πr2RT
M=r8RT
πM
(b) v2
rms =4
√πM
2RT 3/23√π
8M
2RT −5/2
=3RT
Mso vrms =r3RT
M
55. (a) Satellite’s weight = w(x)=k/x2lb when x= distance from center of Earth; w(4000) = 6000
so k=9.6×1010 and W=Z4000+`
4000 9.6×1010x−2dx mi·lb.
(b) Z+∞
4000 9.6×1010x−2dx = lim
`→+∞−9.6×1010/x`
4000
=2.4×107mi·lb
56. (a) L{1}=Z+∞
0e−stdt = lim
`→+∞−1
se−st`
0
=1
s
(b) L{e2t}=Z+∞
0e−ste2tdt =Z+∞
0e−(s−2)tdt = lim
`→+∞−1
s−2e−(s−2)t`
0
=1
s−2
335 Chapter 9
(c) L{sin t}=Z+∞
0e−st sin tdt= lim
`→+∞
e−st
s2+1(−ssin t−cos t)`
0
=1
s2+1
(d) L{cos t}=Z+∞
0e−st cos tdt= lim
`→+∞
e−st
s2+1(−scos t+ sin t)`
0
=s
s2+1
57. (a) L{f(t)}=Z+∞
0te−st dt = lim
`→+∞−(t/s +1/s2)e−st`
0
=1
s2
(b) L{f(t)}=Z+∞
0t2e−st dt = lim
`→+∞−(t2/s +2t/s2+2/s3)e−st`
0
=2
s3
(c) L{f(t)}=Z+∞
3e−stdt = lim
`→+∞−1
se−st`
3
=e−3s
s
58. 10 100 1000 10,000
0.8862269 0.8862269 0.8862269 0.8862269
59. (a) u=√ax, du =√a dx, 2Z+∞
0e−ax2dx =2
√aZ+∞
0e−u2du =pπ/a
(b) x=√2σu, dx =√2σ du, 2
√2πσ Z+∞
0e−x2/2σ2dx =2
√πZ+∞
0e−u2du =1
60. (a) Z3
0e−x2dx ≈0.8862; √π/2≈0.8862
(b) Z+∞
0e−x2dx =Z3
0e−x2dx +Z+∞
3e−x2dx so E=Z+∞
3e−x2dx < Z+∞
3xe−x2dx =1
2e−9<7×10−5
61. (a) Z4
0
1
x6+1dx ≈1.047; π/3≈1.047
(b) Z+∞
0
1
x6+1dx =Z4
0
1
x6+1dx +Z+∞
4
1
x6+1dx so
E=Z+∞
4
1
x6+1dx < Z+∞
4
1
x6dx =1
5(4)5<2×10−4
62. If p= 0, then Z+∞
0(1)dx = lim
`→+∞x`
0
=+∞,
if p6= 0, then Z+∞
0epxdx = lim
`→+∞
1
pepx`
0
= lim
`→+∞
1
p(ep` −1) = −1/p, p < 0
+∞,p>0
.
63. If p= 1, then Z1
0
dx
x= lim
`→0+ln x1
`
=+∞;
if p6= 1, then Z1
0
dx
xp= lim
`→0+
x1−p
1−p1
`
= lim
`→0+[(1 −`1−p)/(1 −p)] = 1/(1 −p),p<1
+∞, p>1
.
64. u=√1−x, u2=1−x, 2udu=−dx;
−2Z0
1p2−u2du =2Z1
0p2−u
2du =hup2−u2+ 2 sin−1(u/√2)i1
0=√2+π/2
65. 2Z1
0cos(u2)du ≈1.809 66. −2Z0
1sin(1 −u2)du =2Z1
0sin(1 −u2)du ≈1.187
Chapter 9 Supplementary Exercises 336
CHAPTER 9 SUPPLEMENTARY EXERCISES
1. (a) integration by parts, u=x,dv = sin xdx (b) u-substitution: u= sin x
(c) reduction formula (d) u-substitution: u= tan x
(e) u-substitution: u=x3+1 (f) u-substitution: u=x+1
(g) integration by parts: dv =dx, u = tan−1x(h) trigonometric substitution: x= 2 sin θ
(i) u-substitution: u=4−x
2
2. (a) x= 3 tan θ(b) x= 3 sin θ(c) x=1
3sin θ
(d) x= 3 sec θ(e) x=√3 tan θ(f) x=1
9tan θ
5. (a) #40 (b) #57 (c) #113
(d) #108 (e) #52 (f) #71
6. (a) u=x2,dv =x
√x2+1dx,du =2xdx,v=√x
2+1;
Z1
0
x
3
√
x
2+1dx =x2px2+1
i1
0−2Z1
0x(x
2+1)
1/2dx
=√2−2
3(x2+1)
3/21
0
=√
2−2
3[2√2−1]=(2−√
2)/3
(b) u2=x2+1,x
2=u
2−1, 2xdx=2udu,xdx=udu;
Z1
0
x
3
√x
2+1dx =Z1
0
x2
√x2+1xdx=Z√2
1
u
2−1
uudu
=Z√2
1(u
2−1)du =1
3u3−u√2
1
=(2−√
2)/3
7. (a) u=2x,
Zsin42xdx=1
2Zsin4udu=1
2−1
4sin3ucos u+3
4Zsin2udu
=−1
8sin3ucos u+3
8−1
2sin ucos u+1
2Zdu
=−1
8sin3ucos u−3
16 sin ucos u+3
16u+C
=−1
8sin32xcos 2x−3
16 sin 2xcos 2x+3
8x+C
(b) u=x2,
Zxcos4(x2)dx =1
2Zcos4udu=1
21
4cos3usin u+3
4Zcos2udu
=1
8cos3usin u+3
81
2cos usin u+1
2Zdu
=1
8cos3usin u+3
16 cos usin u+3
16u+C
=1
8cos3(x2) sin(x2)+ 3
16 cos(x2) sin(x2)+ 3
16x2+C
8. (a) With x= sec θ:
Z1
x3−xdx =Zcot θdθ=ln|sin θ|+C=ln√
x
2−1
|x|+C; valid for |x|>1.
337 Chapter 9
(b) With x= sin θ:
Z1
x3−xdx =−Z1
sin θcos θdθ =−Z2 csc 2θdθ
=−ln |csc 2θ−cot 2θ|+C=ln|cot θ|+C=ln√
1−x
2
|x|+C, 0<|x|<1.
(c) By partial fractions:
Z−1
x+1/2
x+1+1/2
x−1dx =−ln |x|+1
2ln |x+1|+1
2ln |x−1|+C
=lnp|x
2−1|
|x|+C; valid for all xexcept x=0,±1.
9. (a) With u=√x:
Z1
√x√2−xdx =2Z1
√
2−u
2du = 2 sin−1(u/√2)+C= 2 sin−1(px/2)+C;
with u=√2−x:
Z1
√x√2−xdx =−2
Z1
√2−u2du =−2 sin−1(u/√2)+C=−2 sin−1(√2−x/√2)+C;
completing the square:
Z1
p1−(x−1)2dx = sin−1(x−1)+C.
(b) In the three results in part (a) the antiderivatives differ by a constant, in particular
2 sin−1(px/2) = π−2 sin−1(√2−x/√2) = π/2 + sin−1(x−1).
10. A=Z2
1
3−x
x3+x2dx,3−x
x2(x+1) =A
x+B
x
2+C
x+1;A=−4, B=3,C=4
A=−4ln|x|−3
x+4ln|x+1|
2
1
=(−4ln2−3
2+ 4 ln 3) −(−4ln1−3 + 4 ln 2) = 3
2−8ln2+4ln3= 3
2+4ln3
4
11. Solve y=1/(1+x2) for xgetting
x=r1−y
yand integrate with respect to
to yto get A=Z1
0r1−y
ydy (see figure)
1y = 1/(1 + x2)
x
y
12. A=Z+∞
e
ln x−1
x2dx = lim
`→+∞−ln x
x`
e
=1/e
13. V=2πZ+∞
0xe−xdx =2πlim
`→+∞−e−x(x+1)
`
0
=2πlim
`→+∞1−e−`(`+1)
but lim
`→+∞e−`(`+ 1) = lim
`→+∞
`+1
e
`= lim
`→+∞
1
e`=0soV=2π
14. Z+∞
0
dx
x2+a2= lim
`→+∞
1
atan−1(x/a)`
0
= lim
`→+∞
1
atan−1(`/a)= π
2a=1,a=π/2
Chapter 9 Supplementary Exercises 338
15. u= cos θ,−Zu1/2du =−2
3cos3/2θ+C
16. Use Endpaper Formula (31) to get Ztan7θdθ =1
6tan6θ−1
4tan4θ+1
2tan2θ+ln|cos θ|+C.
17. u= tan(x2), 1
2Zu2du =1
6tan3(x2)+C
18. x=(1/
√
2) sin θ,dx =(1/
√
2) cos θdθ,
1
√2Zπ/2
−π/2cos4θdθ =1
√2(1
4cos3θsin θπ/2
−π/2
+3
4Zπ/2
−π/2cos2θdθ
)
=3
4
√2(1
2cos θsin θπ/2
−π/2
+1
2Zπ/2
−π/2dθ)=3
4√2
1
2π=3π
8√2
19. x=√3 tan θ,dx =√3 sec2θdθ,
1
3Z1
sec θdθ =1
3Zcos θdθ=1
3sin θ+C=x
3√3+x
2+C
20. Zcos θ
(sin θ−3)2+3dθ, let u= sin θ−3, Z1
u2+3du =1
√3tan−1[(sin θ−3)/√3]+C
21. Zx+3
p(x+1)
2+1dx, let u=x+1,
Zu+2
√
u
2+1du =Zu(u2+1)
−1/2+2
√
u
2+1du =pu2+1+2sinh−1u+C
=px2+2x+2+2sinh−1(x+1)+C
Alternate solution: let x+ 1 = tan θ,
Z(tan θ+ 2) sec θdθ=Zsec θtan θdθ+2Zsec θdθ= sec θ+2ln|sec θ+ tan θ|+C
=px2+2x+2+2ln(
px
2+2x+2+x+1)+C.
22. Let x= tan θto get Z1
x3−x2dx.
1
x2(x−1) =A
x+B
x2+C
x−1;A=−1, B=−1, C=1so
−Z1
x
dx −Z1
x2dx +Z1
x−1dx =−ln |x|+1
x+ln|x−1|+C
=1
x+ln
x−1
x
+C= cot θ+ln
tan θ−1
tan θ+C= cot θ+ln|1−cot θ|+C
23. 1
(x−1)(x+ 2)(x−3) =A
x−1+B
x+2+C
x−3;A=−1
6,B=1
15,C=1
10 so
−1
6Z1
x−1dx +1
15 Z1
x+2dx +1
10 Z1
x−3dx
=−1
6ln |x−1|+1
15 ln |x+2|+1
10 ln |x−3|+C
339 Chapter 9
24. 1
x(x2+x+1) =A
x+Bx +C
x2+x+1;A=1,B=C=−1so
Z−x−1
x
2+x+1dx =−Zx+1
(x+1/2)2+3/4dx =−Zu+1/2
u
2+3/4du, u =x+1/2
=−1
2ln(u2+3/4) −1
√3tan−12u/√3+C
1
so Zdx
x(x2+x+1) =ln|x|−1
2ln(x2+x+1)−1
√
3tan−12x+1
√
3+C
25. u=√x−4, x=u2+4,dx =2udu,
Z2
0
2u
2
u
2+4du =2Z2
01−4
u
2+4du =2u−4 tan−1(u/2)2
0
=4−π
26. u=√x,x=u2,dx =2udu,
2Z3
0
u
2
u
2+9du =2Z3
01−9
u
2+9du =2u−6 tan−1u
33
0
=6−3
2
π
27. u=√ex+1,e
x=u
2−1, x= ln(u2−1), dx =2u
u2−1du,
Z2
u2−1du =Z1
u−1−1
u+1du =ln|u−1|−ln |u+1|+C=ln√
e
x+1−1
√
e
x+1+1+C
28. u=√ex−1, ex=u2+1,x= ln(u2+ 1), dx =2u
u2+1du,
Z1
0
2u2
u2+1du =2Z1
01−1
u
2+1du =(2u−2 tan−1u)1
0
=2−π
2
29. lim
`→+∞−1
2(x2+1)`
a
= lim
`→+∞−1
2(`2+1)+1
2(a2+1)=1
2(a2+1)
30. lim
`→+∞
1
ab tan−1bx
a`
0
= lim
`→+∞
1
ab tan−1b`
a=π
2ab
31. Let u=x4to get 1
4Z1
√1−u2du =1
4sin−1u+C=1
4sin−1(x4)+C.
32. Z(cos32 xsin30 x−cos30 xsin32 x)dx =Zcos30 xsin30 x(cos2x−sin2x)dx
=1
230 Zsin30 2xcos 2xdx=sin31 2x
31(231)+C
33. Zqx−px2−4dx =1
√2Z(√x+2−√
x−2)dx =√2
3[(x+2)
3/2−(x−2)3/2]+C
34. Z1
x10(1+x−9)dx =−1
9Z1
udu =−1
9ln |u|+C=−1
9ln |1+x
−9|+C

Chapter 9 Supplementary Exercises 340
35. (a) (x+ 4)(x−5)(x2+1)
2;A
x+4+B
x−5+Cx +D
x2+1 +Ex +F
(x2+1)
2
(b) −3
x+4+2
x−5−x−2
x
2+1−3
(x
2+1)
2
(c) −3ln|x+4|+2ln|x−5|+ 2 tan−1x−1
2ln(x2+1)−3
2x
x
2+1+ tan−1x
36. (a) Γ(1) = Z+∞
0e−tdt = lim
`→+∞−e−t`
0
= lim
`→+∞(−e−`+1)=1
(b) Γ(x+1)=Z+∞
0t
x
e
−t
dt; let u=tx,dv =e−tdt to get
Γ(x+1)= −t
x
e
−t
+∞
0+xZ+∞
0t
x−1e
−t
dt =−txe−t+∞
0+xΓ(x)
lim
t→+∞txe−t= lim
t→+∞
tx
et= 0 (by multiple applications of L’Hˆopital’s rule)
so Γ(x+1)=xΓ(x)
(c) Γ(2) = (1)Γ(1) = (1)(1) = 1, Γ(3) = 2Γ(2) = (2)(1) = 2, Γ(4) = 3Γ(3) = (3)(2) = 6
It appears that Γ(n)=(n−1)! if nis a positive integer.
(d) Γ1
2=Z+∞
0t−1/2e−tdt =2Z+∞
0e
−u
2du (with u=√t)=2(
√
π/2) = √π
(e) Γ3
2=1
2Γ1
2=1
2√π,Γ
5
2
=3
2
Γ
3
2
=3
4
√
π
37. (a) t=−ln x, x =e−t,dx=−e
−tdt,
Z1
0(ln x)ndx =−Z0
+∞
(−t)ne−tdt =(−1)nZ+∞
0tne−tdt =(−1)nΓ(n+1)
(b) t=xn,x=t
1/n,dx=(1/n)t1/n−1dt,
Z+∞
0e−xndx =(1/n)Z+∞
0t1/n−1e−tdt =(1/n)Γ(1/n) = Γ(1/n +1)
38. (a) pcos θ−cos θ0=q2sin2(θ0/2) −sin2(θ/2)=q2(k2−k2sin2φ)=p2k
2cos2φ
=√2kcos φ;ksin φ= sin(θ/2) so kcos φdφ=1
2cos(θ/2) dθ =1
2q1−sin2(θ/2) dθ
=1
2q1−k2sin2φdθ,thusdθ =2kcos φ
p1−k2sin2φdφ and hence
T=s8L
gZπ/2
0
1
√2kcos φ·2kcos φ
p1−k2sin2φdφ =4
sL
gZπ/2
0
1
p1−k2sin2φdφ
(b) If L=1.5ftandθ
0=(π/180)(20) = π/9, then
T=√3
2Zπ/2
0
dφ
q1−sin2(π/18) sin2φ≈1.37 s.

341 Chapter 9
CHAPTER 9 HORIZON MODULE
1. The depth of the cut equals the terrain elevation minus the track elevation. From Figure 2, the
cross sectional area of a cut of depth Dmeters is 10D+2·1
2D
2=D
2+10Dsquare meters.
Distance from
town A (m) Terrain elevation
(m)
0
2000
4000
6000
8000
10,000
12,000
14,000
16,000
18,000
20,000
100
105
108
110
104
106
120
122
124
128
130
Track elevation
(m)
100
101
102
103
104
105
106
107
108
109
110
Depth of cut
(m)
0
4
6
7
0
1
14
15
16
19
20
Cross-sectional area
f(x) of cut (m2)
0
56
96
119
0
11
336
375
416
551
600
The total volume of dirt to be excavated, in cubic meters, is Z2000
0f(x)dx.
By Simpson’s Rule, this is approximately
20,000 −0
3·10 [0+4·56+2·96+4·119+2·0+4·11+2·336+4·375+2·416+4·551 + 600]
=4,496,000 m3.
Excavation costs $4 per m3, so the ttal cost of the railroad from kAto Mis about
4·4,496,000=17,984,000 dollars.
2. (a) Distance from
town A (m) Terrain elevation
(m)
20,000
20,100
20,200
20,300
20,400
20,500
20,600
20,700
20,800
20,900
21,000
130
135
139
142
145
147
148
146
143
139
133
Track elevation
(m)
110
109.8
109.6
109.4
109.2
109
108.8
108.6
108.4
108.2
108
Depth of cut
(m)
20
25.2
29.4
32.6
35.8
38
39.2
37.4
34.6
30.8
25
Cross-sectional area
f(x) of cut (m2)
300
887.04
1158.36
1388.76
1639.64
1824
1928.64
1772.76
1543.16
1256.64
875
The total volume of dirt to be excavated, in cubic meters, is Z21,000
20,000 f(x)dx.
By Simpson’s Rule this is approximately
21,000 −20,000
3·10 [600 + 4 ·887.04+2·1158.36+...+4·1256.64 + 875] = 1,417,713.33 m3.
The total cost of a trench from Mto Nis about 4 ·1,417,713.33 ≈5,670,853 dollars.
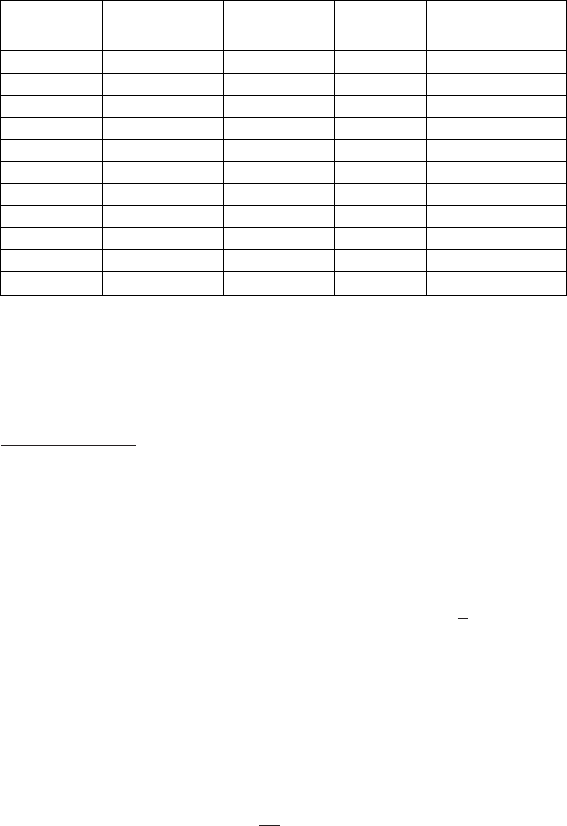
Chapter 9 Horizon Module 342
(b) Distance from
town A (m) Terrain elevation
(m)
21,000
22,000
23,000
24,000
25,000
26,000
27,000
28,000
29,000
30,000
31,000
133
120
106
108
106
98
100
102
96
91
88
Track elevation
(m)
108
106
104
102
100
98
96
94
92
90
88
Depth of cut
(m)
25
14
2
6
6
0
4
8
4
1
0
Cross-sectional area
f(x) of cut (m2)
875
336
24
96
96
0
56
144
56
11
0
The total volume of dirt to be excavated, in cubic meters, is Z31,000
21,000 f(x)dx. By Simpson’s
Rule this is approximately
31,000 −21,000
3·10 [875 + 4 ·336+2·24+...+4·11+0]=1,229,000 m3.
The total cost of the railroad from Nto Bis about 4 ·1,229,000 ≈4,916,000 dollars.
3. The total cost if trenches are used everywhere is about
17,984,000+5,670,853+4,916,000=28,570,853 dollars.
4. (a) The cross-sectional area of a tunnel is AT=80+1
2
π5
2≈119.27 m2. The length of the
tunnel is 1000 m, so the volume of dirt to be removed is about 1000AT≈1,119,269.91 m3,
and the drilling and dirt-piling costs are 8 ·1000AT≈954,159 dollars.
(b) To extend the tunnel from a length of xmeters to a length of x+dx meters, we must move
a volume of ATdx cubic meters of dirt a distance of about xmeters. So the cost of this
extension is about 0.06 ×ATdx dollars. The cost of moving all of the dirt in the tunnel is
therefore
Z1000
00.06 ×ATdx =0.06AT
x2
21000
0
=30,000AT≈3,578,097 dollars.
(c) The total cost of the tunnel is about 954,159+3,578,097 ≈4,532,257 dollars.
5. The total cost of the railroad, using a tunnel, is 17,894,000+4,532,257+4,916,000+27,432,257
dollars, which is smaller than the cost found in Exercise 3. It will be cheaper to build the railroad
if a tunnel is used.
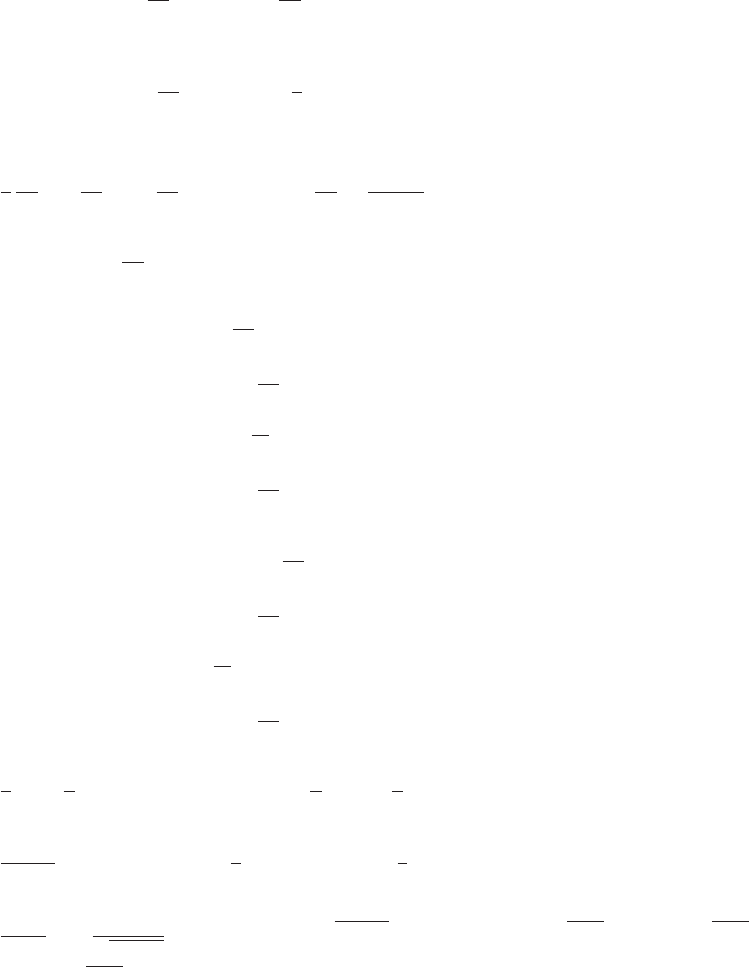
343
CHAPTER 10
Mathematical Modeling with Differential
Equations
EXERCISE SET 10.1
1. y0=2x
2
e
x
3
/3=x
2
yand y(0) = 2 by inspection.
2. y0=x3−2 sin x, y(0) = 3 by inspection.
3. (a) first order; dy
dx =c;(1+x)dy
dx =(1+x)c=y
(b) second order; y0=c1cos t−c2sin t, y00 +y=−c1sin t−c2cos t+(c
1sin t+c2cos t)=0
4. (a) first order; 2dy
dx +y=2
−c
2
e
−x/2+1
+ce−x/2+x−3=x−1
(b) second order; y0=c1et−c2e−t,y
00 −y=c1et+c2e−t−c1et+c2e−t=0
5. 1
y
dy
dx =xdy
dx +y, dy
dx(1 −xy)=y
2
,dy
dx =y2
1−xy
6. 2x+y2+2xy dy
dx = 0, by inspection.
7. (a) IF: µ=e3Rdx =e3x,d
dxye3x=0,ye
3x=C, y =Ce−3x
separation of variables: dy
y=−3dx, ln |y|=−3x+C1,y =±e
−3xe
C
1=Ce−3x
(b) IF: µ=e−2Rdt =e−2t,d
dt[ye−2t]=0,ye
−2t=C, y =Ce2t
separation of variables: dy
y=2dt, ln |y|=2t+C
1
,y=±e
C
1
e
2t=Ce2t
8. (a) IF: µ=e−4Rxdx =e
−2x
2,d
dx hye−2x2i=0,y=Ce2x2
separation of variables: dy
y=4x dx, ln |y|=2x
2+C
1
,y=±e
C
1
e
2x
2=Ce2x2
(b) IF: µ=eRdt =et,d
dt yet=0,y=Ce−t
separation of variables: dy
y=−dt, ln |y|=−t+C1,y =±e
C
1e
−t=Ce−t
9. 1
ydy =1
xdx,ln|y|=ln|x|+C
1
,ln
y
x
=C
1
,y
x=±e
C
1=C,y=Cx
10. dy
1+y
2=x
2dx, tan−1y=1
3x3+C, y = tan 1
3x3+C
11. dy
1+y=−x
√
1+x
2dx, ln |1+y|=−
p1+x
2+C
1,1+y=±e
−
√
1+x2eC1=Ce−√1+x2,
y=Ce−√1+x2−1
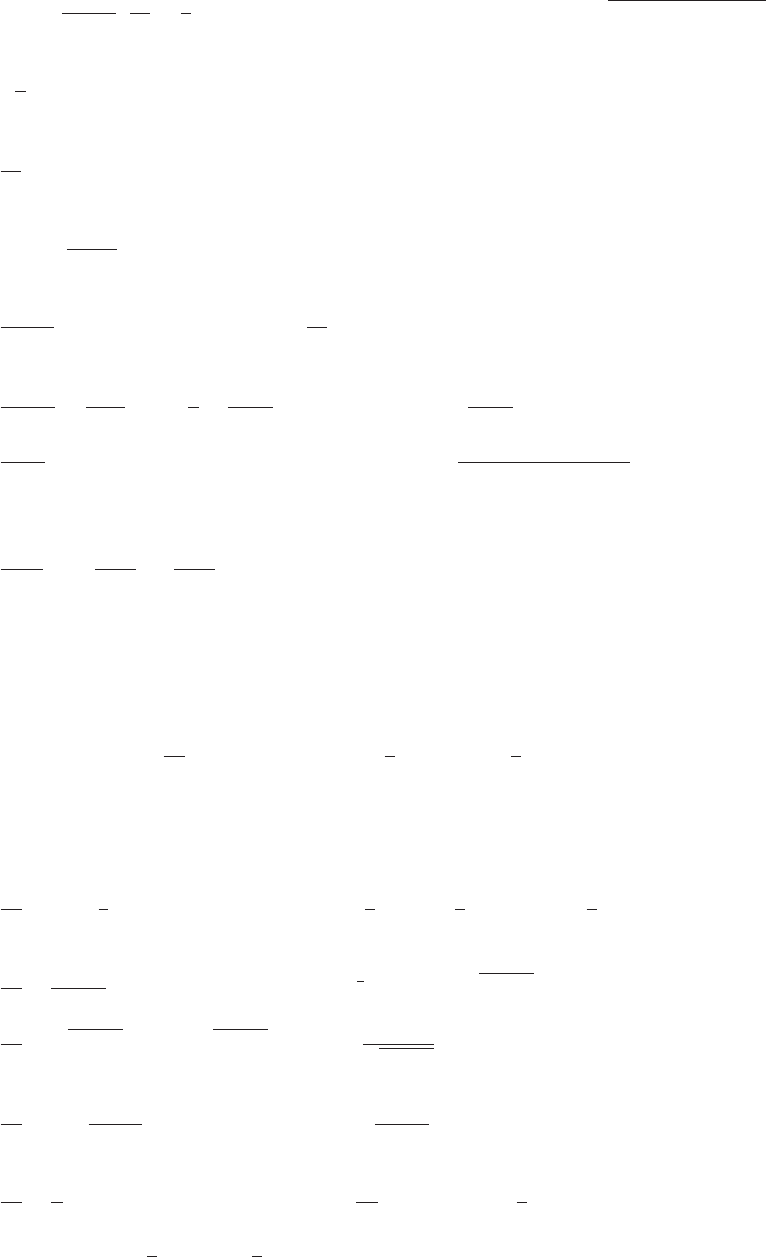
Exercise Set 10.1 344
12. ydy =x
3dx
1+x
4,y
2
2=1
4ln(1 + x4)+C
1,2y
2= ln(1 + x4)+C, y =±p[ln(1 + x4)+C]/2
13. 1
y+ydy =exdx, ln |y|+y2/2=e
x+C; by inspection, y=0
14. dy
y=−x dx, ln |y|=−x2/2+C
1,y=±e
C
1
e
−x
2
/2=Ce−x2/2
15. eydy =sin x
cos2xdx = sec xtan xdx,e
y= sec x+C,y= ln(sec x+C)
16. dy
1+y
2=(1+x)dx, tan−1y=x+x2
2+C, y = tan(x+x2/2+C)
17. dy
y2−y=dx
sin x,Z−1
y+1
y−1dy =Zcsc x dx, ln
y−1
y=ln|csc x−cot x|+C1,
y−1
y=±eC1(csc x−cot x)=C(csc x−cot x),y=1
1−C(csc x−cot x);
by inspection, y= 0 is also a solution.
18. 1
tan ydy =3
sec xdx,cos y
sin ydy = 3 cos xdx,ln|sin y|= 3 sin x+C1,
sin y=±e3 sin x+C1=±eC1e3 sin x=Ce3 sin x
19. µ=eR3dx =e3x,e3xy=Zexdx =ex+C,y=e−2x+Ce−3x
20. µ=e2Rxdx =e
x
2,d
dxhyex2i=xex2,ye
x
2=1
2e
x
2+C, y =1
2+Ce−x2
21. µ=eRdx =ex,exy=Zexcos(ex)dx = sin(ex)+C,y=e
−xsin(ex)+Ce−x
22. dy
dx +2y=1
2,µ=e
R2dx =e2x,e2xy=Z1
2e2xdx =1
4e2x+C,y=1
4+Ce−2x
23. dy
dx +x
x2+1y=0,µ=e
R(x/(x2+1))dx =e1
2ln(x2+1) =px2+1,
d
dx hypx2+1
i=0,y
px
2+1=C, y =C
√x2+1
24. dy
dx +y=1
1+e
x,µ=e
Rdx =ex,exy=Zex
1+e
xdx = ln(1 + ex)+C,y=e
−xln(1 + ex)+Ce−x
25. dy
dx +1
xy=1,µ=e
R(1/x)dx =eln x=x, d
dx[xy]=x, xy =1
2x2+C, y =x/2+C/x
(a) 2=y(1) = 1
2+C, C =3
2,y =x/2+3/(2x)
(b) 2=y(−1) = −1/2−C, C =−5/2,y =x/2−5/(2x)
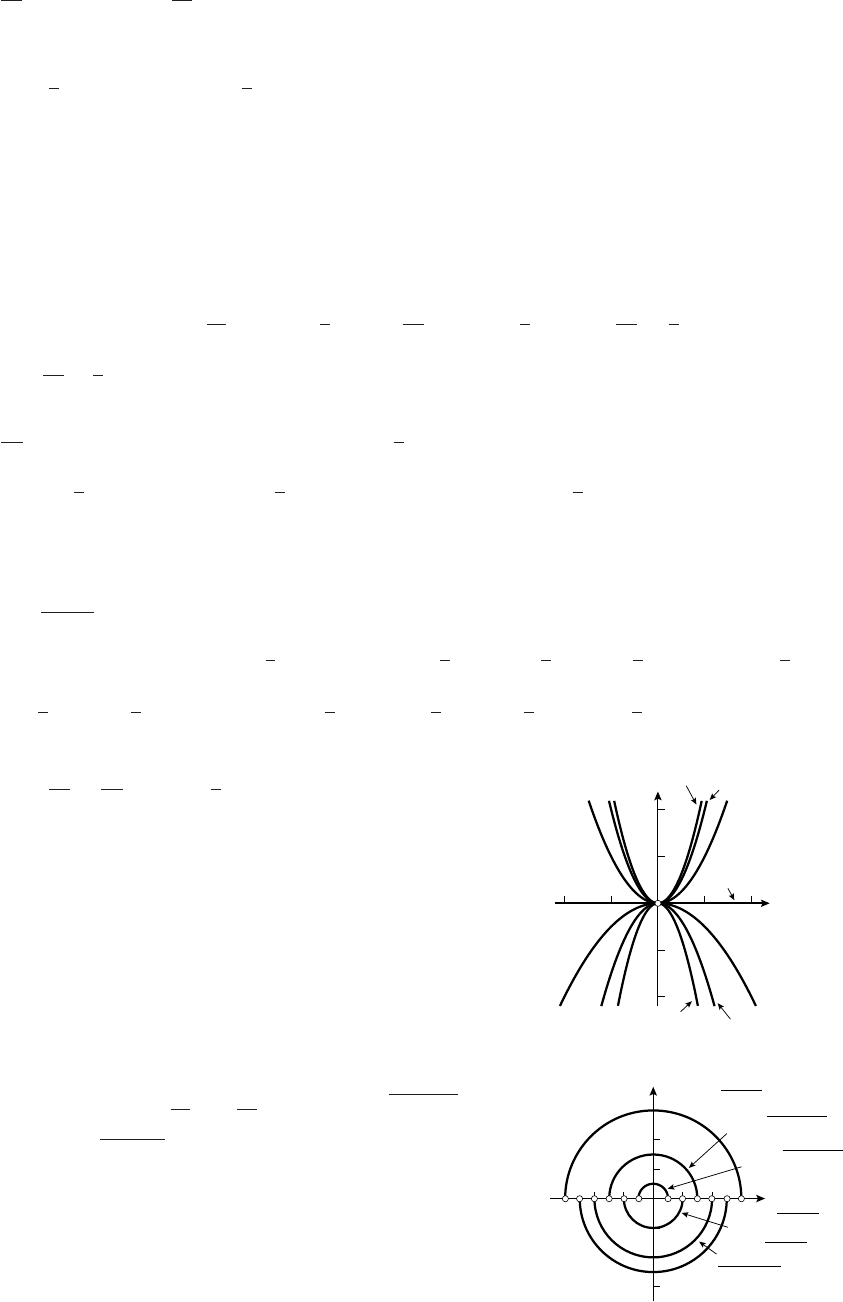
345 Chapter 10
26. dy
y=x dx, ln |y|=x2
2+C1,y=±e
C
1
e
x
2
/2=Cex2/2
(a) 1=y(0) = Cso C=1,y=e
x
2
/2
(b) 1
2=y(0) = C,soy=1
2
e
x
2
/2
27. µ=e−Rxdx =e
−x
2/2,e
−x
2/2y=Zxe−x2/2dx =−e−x2/2+C,
y=−1+Cex2/2,3=−1+C,C=4,y=−1+4e
x
2/2
28. µ=eRdt =et,ety=Z2etdt =2e
t+C,y=2+Ce−t,1=2+C,C=−1, y=2−e
−t
29. (y+ cos y)dy =4x
2dx, y2
2+ sin y=4
3x3+C, π2
2+ sin π=4
3(1)3+C, π2
2=4
3+C,
C=π2
2−4
3,3y2+ 6 sin y=8x
3+3π
2−8
30. dy
dx =(x+2)e
y,e
−ydy =(x+2)dx,−e−y=1
2x2+2x+C,−1=C,
−e
−y=1
2
x
2+2x−1, e−y=−1
2x2−2x+1,y=−ln 1−2x−1
2x2
31. 2(y−1) dy =(2t+1)dt, y2−2y=t2+t+C, 1+2=C, C =3,y
2−2y=t
2+t+3
32. y0+sinh x
cosh xy= cosh x,µ=eR(sinh x/ cosh x)dx =eln cosh x= cosh x,
(cosh x)y=Zcosh2xdx=Z1
2(cosh 2x+1)dx =1
4sinh 2x+1
2x+C=1
2sinh xcosh x+1
2x+C,
y=1
2sinh x+1
2xsech x+Csech x,1
4=C,y=1
2sinh x+1
2xsech x+1
4sech x
-2 2
-2
2
x
y
y = –0.5x2
y = –1.5x2
y = x2
y = 2x2
y = 2.5x2
y = 0
y = –3x2
33. (a) dy
y=dx
2x,ln |y|=1
2ln |x|+C1,|y|=C|x|1/2;
by inspection y= 0 is also a solution.
(b) 2=C(1)2,C =2,x =2y
2
-3 3
-3
3
x
yy = √9 – x2
y = –√6.25 – x2
y = –√4 – x2
y = –√1 – x2
y = √2.25 – x2
y = √0.25 – x2
34. (a) ydy =−x dx, y2
2=−x2
2+C1,y =±pC2−x
2
(b) y=√25 −x2
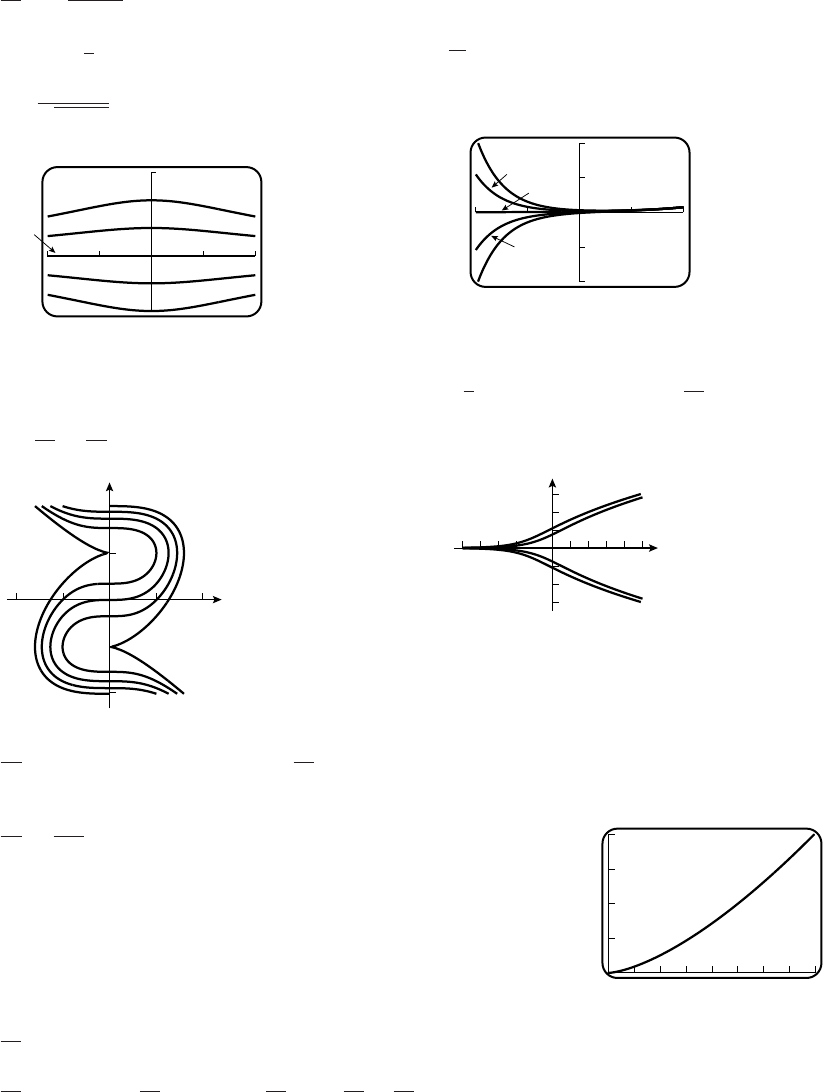
Exercise Set 10.1 346
35. dy
y=−xdx
x
2+4,
ln |y|=−1
2ln(x2+4)+C
1,
y=C
√
x
2+4
1.5
-1
-2 2
C = –1
C = 1
C = 0 C = 2
C = –2
36. y0+2y=3e
t
,µ=e
2Rdt =e2t,
d
dtye2t=3e
3t
,ye
2t=e
3t+C,
y=et+Ce−2t
C = 2
C = 1
C = 0
C = –1
C = –2
100
-100
-2 2
37. (1 −y2)dy =x2dx,
y−y3
3=x3
3+C1,x
3+y
3−3y=C
-2 2
-2
2
x
y
38. 1
y+ydy =dx, ln |y|+y2
2=x+C1,
yey2/2=±eC1ex=Cex
-5 5
-3
3
x
y
41. dy
dx =xey,e
−ydy =x dx, −e−y=x2
2+C, x = 2 when y=0so−1=2+C, C =−3,x
2+2e
−y=6
2
0
0 1.6
42. dy
dx =3x2
2y,2ydy =3x
2dx, y2=x3+C, 1=1+C, C =0,
y
2=x
3
,y=x
3/2passes through (1,1).
43. dy
dt = rate in −rate out, where yis the amount of salt at time t,
dy
dt = (4)(2) −y
50(2)=8−1
25y, so dy
dt +1
25y= 8 and y(0) = 25.
µ=eR(1/25)dt =et/25,et/25y=Z8et/25dt = 200et/25 +C,
y= 200 + Ce−t/25, 25 = 200 + C,C=−175,
(a) y= 200 −175e−t/25 oz (b) when t= 25, y= 200 −175e−1≈136 oz
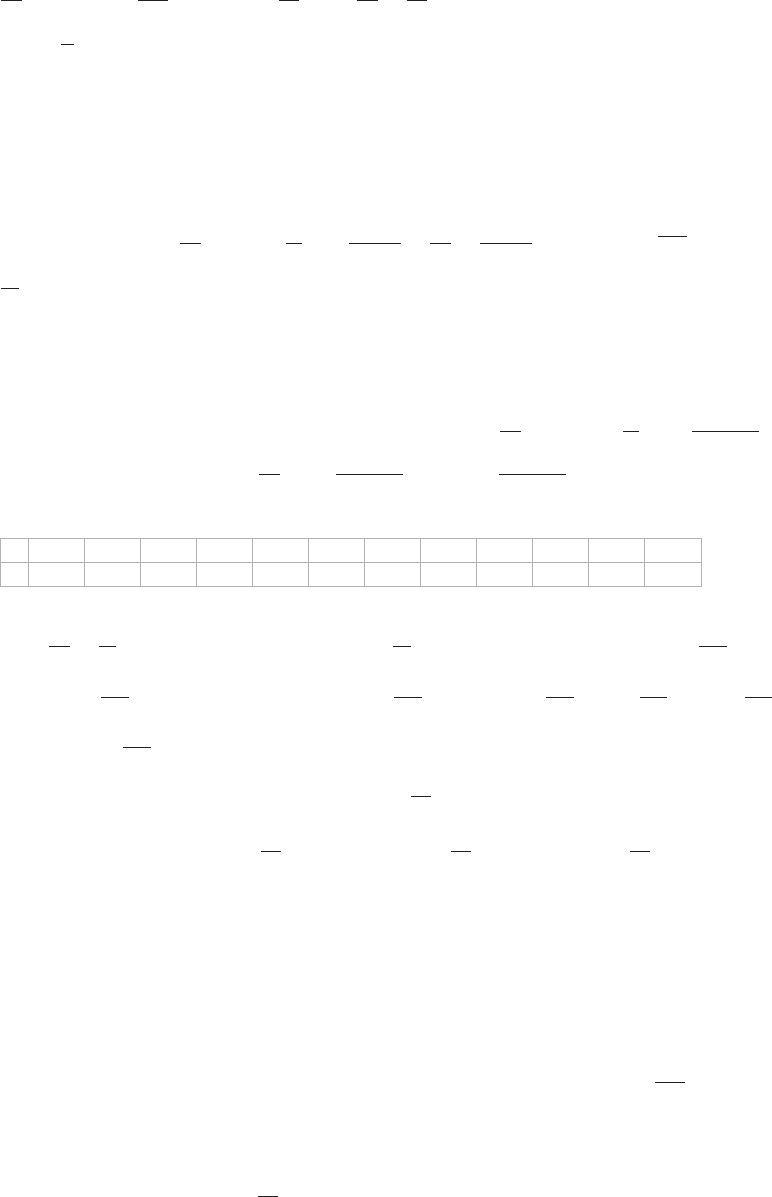
347 Chapter 10
44. dy
dt = (5)(10) −y
200(10) = 50 −1
20y, so dy
dt +1
20y= 50 and y(0)=0.
µ=e
R1
20 dt =et/20,et/20y=Z50et/20dt = 1000et/20 +C,
y= 1000 + Ce−t/20, 0 = 1000 + C,C=−1000;
(a) y= 1000 −1000e−t/20 lb (b) when t= 30, y= 1000 −1000e−1.5≈777 lb
45. The volume Vof the (polluted) water is V(t) = 500 + (20 −10)t=500+10t;
if y(t) is the number of pounds of particulate matter in the water,
then y(0) = 50, and dy
dt =0−10 y
V=−1
50+ty, dy
dt +1
50+ty=0; µ=e
Rdt
50+t=50+t;
d
dt[(50 + t)y]=0,(50 + t)y=C, 2500 = 50y(0) = C, y(t) = 2500/(50 + t).
The tank reaches the point of overflowing when V=500+10t= 1000, t= 50 min, so
y= 2500/(50 + 50) = 25 lb.
46. The volume of the lake (in gallons) is V= 246πr2h= 246π(15)23 = 166,050π. Let y(t) denote
the number of pounds of mercury salts at time t, then dy
dt =0−103y
V=−y
166.05πlb/h and
y0=10
−5
V=1.6605πlb; dy
y=−dt
166.05π,ln y=−t
166.05π+C1,y=Ce−t/(166.05π), and
C=y(0) = y0=1.6605π,y=1.6605πe−t/(166.05π).
t
y(t)
1
5.2066
2
5.1967
3
5.1867
4
5.1768
5
5.1669
6
5.1570
7
5.1471
8
5.1372
9
5.1274
10
5.1176
11
5.1078
12
5.0980
47. (a) dv
dt +c
mv=−g, µ =e(c/m)Rdt =ect/m,d
dt hvect/mi=−gect/m,ve
ct/m =−gm
cect/m +C,
v=−gm
c+Ce−ct/m, but v0=v(0) = −gm
c+C, C =v0+gm
c,v =−gm
c+v0+gm
ce−ct/m
(b) Replace mg
cwith vτand −ct/m with −gt/vτin (23).
(c) From part (b), s(t)=C−v
τt−(v
0+v
τ)
v
τ
ge
−gt/vτ;
s0=s(0) = C−(v0+vτ)vτ
g,C=s
0
+(v0+vτ)vτ
g,s(t)=s
0−v
τt+v
τ
g(v
0+v
τ)1−e
−gt/vτ
48. Given m= 240,g =32,v
τ=mg/c: with a closed parachute vτ= 120 so c= 64, and with an open
parachute vτ= 24, c= 320.
(a) Let tdenote time elapsed in seconds after the moment of the drop. From Exercise 47(b),
while the parachute is closed
v(t)=e
−gt/vτ(v0+vτ)−vτ=e−32t/120 (0 + 120) −120 = 120 e−4t/15 −1and thus
v(25) = 120 e−20/3−1≈−119.85, so the parachutist is falling at a speed of 119.85 ft/s
when the parachute opens. From Exercise 47(c), s(t)=s
0−120t+120
32 120 1−e−4t/15,
s(25) = 10000 −120 ·25 + 450 1−e−20/3≈7449.43 ft.
(b) If tdenotes time elapsed after the parachute opens, then, by Exercise 47(c),
s(t) = 7449.43 −24t+24
32 (−119.85 + 24) 1−e−32t/24= 0, with the solution (Newton’s
Method) t= 310.42 s, so the sky diver is in the air for about 25 + 310 = 335 s.
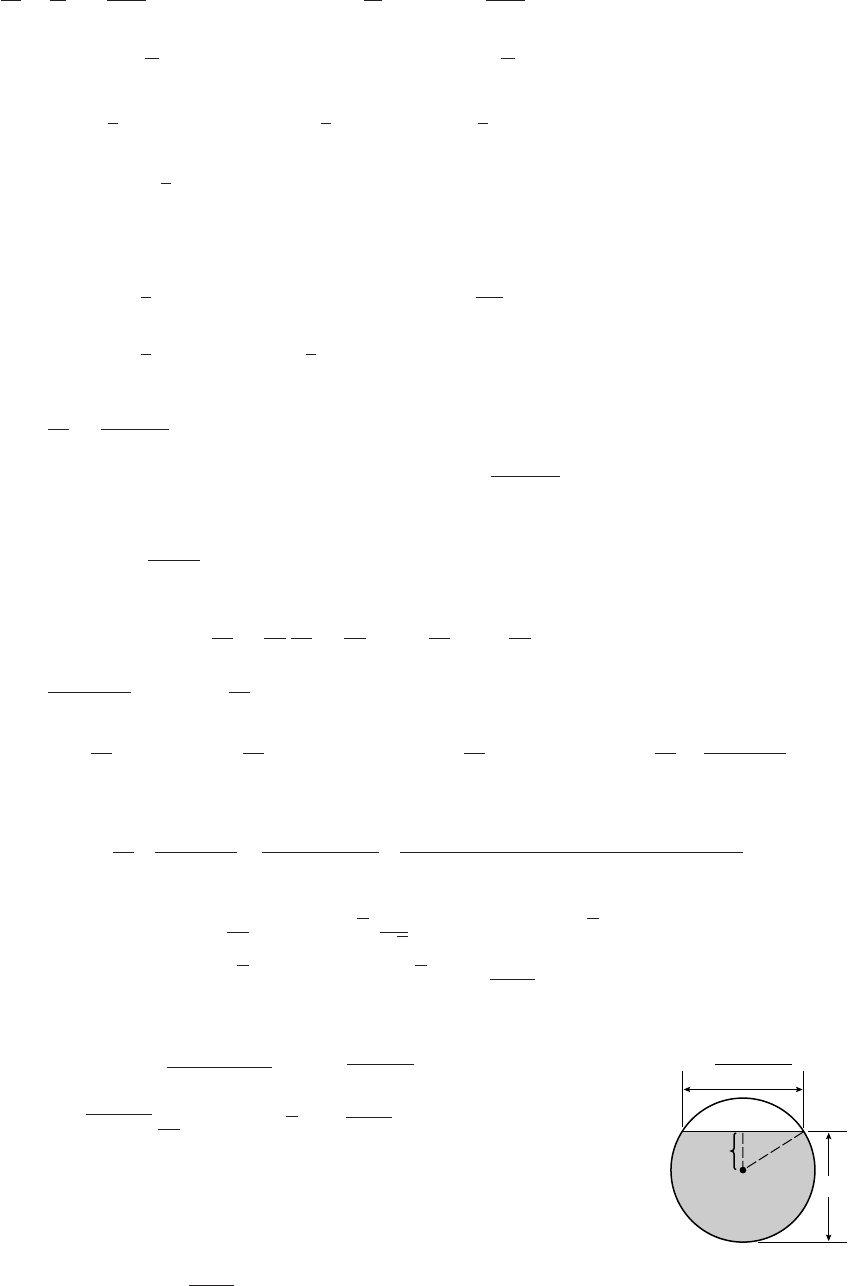
Exercise Set 10.1 348
49. dI
dt +R
LI=V(t)
L,µ=e
(R/L)Rdt =eRt/L,d
dt(eRt/LI)=V(t)
Le
Rt/L,
IeRt/L =I(0) + 1
LZt
0V(u)eRu/Ldu, I(t)=I(0)e−Rt/L +1
Le−Rt/L Zt
0V(u)eRu/Ldu.
(a) I(t)=1
4
e
−5t/2Zt
012e5u/2du =6
5e−5t/2e5u/2t
0
=6
51−e−5t/2A.
(b) lim
t→+∞I(t)=6
5A
50. From Exercise 49 and Endpaper Table #42,
I(t)=15e
−2t+1
3
e
−2tZt
03e
2usin udu=15e
−2t+e
−2te
2u
5(2 sin u−cos u)t
0
=15e
−2t+1
5
(2 sin t−cos t)+1
5e
−2t
.
51. (a) dv
dt =ck
m0−kt −g, v =−cln(m0−kt)−gt +C;v= 0 when t=0so0=−cln m0+C,
C=cln m0,v =cln m0−cln(m0−kt)−gt =cln m0
m0−kt −gt.
(b) m0−kt =0.2m
0when t= 100 so
v= 2500 ln m0
0.2m0−9.8(100) = 2500 ln 5 −980 ≈3044 m/s.
52. (a) By the chain rule, dv
dt =dv
dx
dx
dt =dv
dxvso mdv
dt =mv dv
dx.
(b) mv
kv2+mg dv =−dx, m
2kln(kv2+mg)=−x+C;v=v
0when x=0so
C=m
2kln(kv2
0+mg),m
2kln(kv2+mg)=−x+m
2kln(kv2
0+mg),x=m
2kln kv2
0+mg
kv2+mg .
(c) x=xmax when v=0so
x
max =m
2klnkv2
0+mg
mg =3.56 ×10−3
2(7.3×10−6)ln(7.3×10−6)(988)2+(3.56 ×10−3)(9.8)
(3.56 ×10−3)(9.8) ≈1298 m
53. (a) A(h)=π(1)2=π, π dh
dt =−0.025√h, π
√hdh =−0.025dt, 2π√h=−0.025t+C;h= 4 when
t=0,so4π=C, 2π√h=−0.025t+4π, √h=2−0.025
2πt, h ≈(2 −0.003979t)2.
(b) h= 0 when t≈2/0.003979 ≈502.6s≈8.4 min.
h − 22
2√4 − (h − 2)2
h
54. (a) A(h)=6h2
p4−(h−2)2i=12
p4h−h
2
,
12p4h−h2dh
dt =−0.025√h,12
√
4−hdh=−0.025dt,
−8(4 −h)3/2=−0.025t+C;h= 4 when t=0soC=0,
(4 −h)3/2=(0.025/8)t,4−h=(0.025/8)2/3t2/3,
h≈4−0.021375t2/3ft
(b) h= 0 when t=8
0.025(4 −0)3/2= 2560 s ≈42.7 min
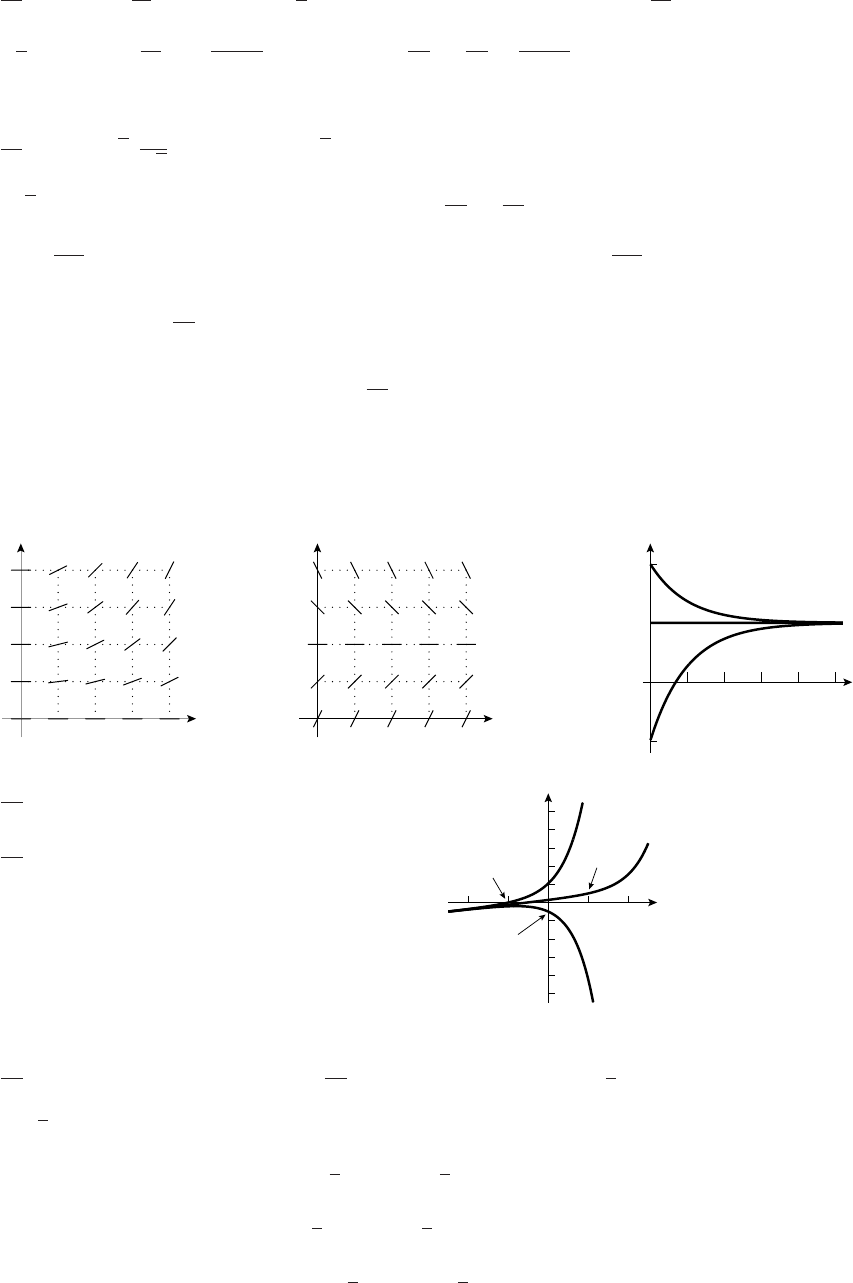
349 Chapter 10
55. dv
dt =−0.04v2,1
v2dv =−0.04dt, −1
v=−0.04t+C;v= 50 when t=0so−1
50 =C,
−1
v=−0.04t−1
50,v =50
2t+1 cm/s. But v=dx
dt so dx
dt =50
2t+1,x = 25 ln(2t+1)+C
1;x=0
when t=0soC
1=0,x = 25 ln(2t+ 1) cm.
56. dv
dt =−0.02√v, 1
√vdv =−0.02dt, 2√v=−0.02t+C;v= 9 when t=0so6=C,
2
√
v=−0.02t+6,v =(3−0.01t)2cm/s. But v=dx
dt so dx
dt =(3−0.01t)2,
x=−100
3(3 −0.01t)3+C1;x= 0 when t=0soC
1= 900,x= 900 −100
3(3 −0.01t)3cm.
57. Differentiate to get dy
dx =−sin x+e−x2,y(0)=1.
58. Zh(y)dy =Zh(y(x))y0(x)dx; since h(y)dy
dx =g(x) it follows that Zh(y)dy =Zg(x)dx.
EXERCISE SET 10.2
1.
1234
1
2
3
4
x
y2.
1234
1
2
3
4
x
y3.
5
-1
2
x
y
y(0) = 1
y(0) = 2
y(0) = –1
4. dy
dx +y=1,µ =e
Rdx =ex,
d
dx[yex]=e
x
,
yex=ex+C, y =1+Ce−x
(a) −1=1+C, C =−2,y =1−2e
−x
(b) 1=1+C, C =0,y =1
(c) 2=1+C, C =1,y =1+e
−x
5.
-2 2
-10
10
x
y
y(0) = –1
y(–1) = 0 y(1) = 1
6. dy
dx −2y=−x, µ =e−2Rdx =e−2x,d
dx ye−2x=−xe−2x,ye
−2x=1
4
(2x+1)e
−2x+C,
y=1
4(2x+1)+Ce2x
(a) 1=3/4+Ce2,C=1/4e
2
,y=1
4
(2x+1)+1
4e
2x−2
(b) −1=1/4+C, C =−5/4,y =1
4(2x+1)−5
4e
2x
(c) 0=−1/4+Ce−2,C=e
2
/4,y=1
4
(2x+1)+1
4e
2x+2
Exercise Set 10.2 350
7. lim
x→+∞y=1 8. lim
x→+∞y=(+∞if y0≥1/4
−∞,if y0<1/4
9. (a) IV, since the slope is positive for x>0 and negative for x<0.
(b) VI, since the slope is positive for y>0 and negative for y<0.
(c) V, since the slope is always positive.
(d) II, since the slope changes sign when crossing the lines y=±1.
(e) I, since the slope can be positive or negative in each quadrant but is not periodic.
(f) III, since the slope is periodic in both xand y.
11. (a) y0=1,
y
n+1 =yn+(x
n+y
n
)(0.2)=(x
n+6y
n
)/5 n
x
n
y
n
0
0
1
1
0.2
1.20
2345
0.4
1.48
0.6
1.86
0.8
2.35
1.0
2.98
(b) y0−y=x, µ =e−x,d
dx ye−x=xe−x,
ye−x=−(x+1)e
−x+C, 1=−1+C,
C=2,y =−(x+1)+2e
x
x
n
y(x
n
)
abs. error
perc. error
0
1
0
03
0.2
1.24
0.04
7 9 11 13
0.4
1.58
0.10
0.6
2.04
0.19
0.8
2.65
0.30
1.0
3.44
0.46
(c)
0.2 0.4 0.6 0.8 1
3
x
y
12. h=0.1,y
n+1 =(x
n+11y
n
)/10
n
xn
yn
0
0
1.00
1
0.1
1.10
2345
0.2
1.22
0.3
1.36
0.4
1.53
0.5
1.72
6
0.6
1.94
7
0.7
2.20
8
0.8
2.49
9
0.9
2.82
10
1.0
3.19
In Exercise 11, y(1) ≈2.98; in Exercise 12, y(1) ≈3.19; the true solution is y(1) ≈3.44; so the
absolute errors are approximately 0.46 and 0.25 respectively.
2413
9
x
y
13. y0=1,y
n+1 =yn+√yn/2
n
xn
yn
0
0
1
1
0.5
1.50
2
1
34
2
5
2.11
1.5
2.84 3.68
2.5
4.64
6
3
5.72
7
3.5
6.91
8
4
8.23
351 Chapter 10
14. y0=1,y
n+1 =yn+(x
n−y
2
n
)/4
n
x
n
y
n
0
0
1
1
0.25
0.75
2345
0.50
0.67
0.75
0.68
1.00
0.75
1.25
0.86
6
1.50
0.99
7
1.75
1.12
8
2.00
1.24
0.5 1 1.5 2
0.5
1
1.5
2
x
y
3
3
t
y
15. y0=1,y
n+1 =yn+1
2sin yn
n
tn
yn
0
0
1
1
0.5
1.42
2
1
34
2
1.92
1.5
2.39 2.73
1
1
t
y
16. y0=0,y
n+1 =yn+e−yn/10
n
tn
yn
0
0
0
1
0.1
0.10
2345
0.2
0.19
0.3
0.27
0.4
0.35
0.5
0.42
6
0.6
0.49
7
0.7
0.55
8
0.8
0.60
9
0.9
0.66
10
1.0
0.71
17. h=1/5,y
0=1,y
n+1 =yn+1
5cos(2πn/5)
n
tn
yn
0
0
1.00
1
0.2
1.06
0.4
0.90
234
0.6
0.74
0.8
0.80
1.0
1.00
5
18. (a) By inspection, dy
dx =e−x2and y(0)=0.
(b) yn+1 =yn+e−x2
n/20 = yn+e−(n/20)2/20 and y20 =0.7625. From a CAS, y(1)=0.7468.
19. (b) ydy =−x dx, y2/2=−x
2
/2+C
1,x
2+y
2=C;ify(0) = 1 then C=1soy(1/2) = √3/2.
20. (a) y0=1,y
n+1 =yn+(
√
y
n
/2)h
h=0.2: y
n+1 =yn+√yn/10; y5≈1.5489
h=0.1:y
n+1 =yn+√yn/20; y10 ≈1.5556
h=0.05 : yn+1 =yn+√yn/40; y20 ≈1.5590
(c) dy
√y=1
2dx, 2√y=x/2+C, 2=C,
√y=x/4+1,y =(x/4+1)
2,
y(1)=25/16=1.5625
Exercise Set 10.3 352
EXERCISE SET 10.3
1. (a) dy
dt =ky2,y(0) = y0,k > 0(b) dy
dt =−ky2,y(0) = y0,k > 0
3. (a) ds
dt =1
2s(b) d2s
dt2=2
ds
dt
4. (a) dv
dt =−2v2(b) d2s
dt2=−2ds
dt 2
5. (a) dy
dt =0.01y, y0=10,000 (b) y=10,000et/100
(c) T=1
kln 2 = 1
0.01 ln 2 ≈69.31 hr (d) 45,000=10,000et/100,
t= 100 ln 45,000
10,000 ≈150.41 hr
6. k=1
Tln 2 = 1
20 ln 2
(a) dy
dt = ((ln 2)/20)y, y(0)=1 (b) y(t)=e
t(ln 2)/20 =2
t/20
(c) y(120) = 26=64 (d) 1,000,000=2
t/20,
t=20
ln 106
ln 2 ≈398.63 min
7. (a) dy
dt =−ky, y(0)=5.0×107;3.83 = T=1
kln 2, so k=ln 2
3.83 ≈0.1810
(b) y=5.0×107e−0.181t
(c) y(30) = 5.0×107e−0.1810(30) ≈219,297
(d) y(t)=0.1y
0=y
0
e
−kt,−kt =ln0.1,t=−ln 0.1
0.1810 =12.72 days
8. (a) k=1
Tln 2 = 1
140 ln 2 ≈0.0050, so dy
dt =−0.0050y, y0= 10.
(b) y=10e
−0.0050t
(c) 10weeks=70dayssoy=10e
−0.35 ≈7 mg.
(d) 0.3y0=y0e−kt,t=−ln 0.3
0.0050 ≈243.2days
9. 100e0.02t= 5000, e0.02t= 50, t=1
0.02 ln 50 ≈196 days
10. y=10,000ekt, but y=12,000 when t=10so10,000e10k=12,000, k=1
10 ln 1.2. y=20,000 when
2=e
kt,t=ln 2
k=10 ln 2
ln 1.2≈38, in the year 2025.
11. y(t)=y
0
e
−kt =10.0e
−kt,3.5=10.0e
−k(5),k=−
1
5
ln 3.5
10.0≈0.2100,T=1
k
ln 2 ≈3.30 days

353 Chapter 10
12. dy
dt =y0e−kt,0.6y0=y0e−5k,k=−
1
5
ln 0.6≈0.10
(a) T=ln 2
k≈6.8yr
(b) y(t)≈y0e−0.10t,y
y0≈e−0.10t,soe
−0.10t×100 percent will remain.
13. (a) k=ln 2
5≈0.1386; y≈2e0.1386t(b) y(t)=5e
0.015t
(c) y=y0ekt,1=y
0
e
k
,100 = y0e10k. Divide: 100 = e9k,k=1
9
ln 100 ≈0.5117,
y≈y0e0.5117t; also y(1)=1,so y0=e−0.5117 ≈0.5995,y ≈0.5995e0.5117t.
(d) k=ln 2
T≈0.1386,1=y(1) ≈y0e0.1386,y
0≈e
−0.1386 ≈0.8706,y≈0.8706e0.1386t
14. (a) k=ln 2
T≈0.1386,y≈10e−0.1386t(b) y=10e
−0.015t
(c) 100 = y0e−k,1=y
0
e
−10k. Divide: e9k= 100,k=1
9
ln 100 ≈0.5117;
y0=e10k≈e5.117 ≈166.81,y= 166.81e−0.5117t.
(d) k=ln 2
T≈0.1386,10 = y(1) ≈y0e−0.1386,y
0≈10e0.1386 ≈11.4866,y≈11.4866e−0.1386t
16. (a) None; the half-life is independent of the initial amount.
(b) kT =ln2,soTis inversely proportional to k.
17. (a) T=ln 2
k; and ln 2 ≈0.6931. If kis measured in percent, k0= 100k,
then T=ln 2
k≈69.31
k0≈70
k0.
(b) 70 yr (c) 20 yr (d) 7%
18. Let y=y0ekt with y=y1when t=t1and y=3y
1when t=t1+T; then y0ekt1=y1(i) and
y0ek(t1+T)=3y
1(ii). Divide (ii) by (i) to get ekT =3,T=1
kln 3.
19. From (12), y(t)=y
0
e
−0.000121t.If0.27 = y(t)
y0=e−0.000121tthen t=−ln 0.27
0.000121 ≈10,820 yrs,
and if 0.30 = y(t)
y0then t=−ln 0.30
0.000121 ≈9950, or roughly between 9000 B.C. and 8000 B.C.
20. (a) 1
0
0 50000
(b) t= 1988 yields
y/y0=e−0.000121(1988) ≈79%.
21. y0≈2,L≈8; since the curve y=2·8
2+6e
−kt passes through the point (2,4), 4 = 16
2+6e
−2k,
6e
−2k=2,k=1
2
ln 3 ≈0.5493.
Exercise Set 10.3 354
22. y0≈400,L≈1000; since the curve y=400,000
400 + 600e−kt passes through the point (200,600),
600 = 400,000
400 + 600e−200k,600e−200k=800
3,k=1
200 ln 2.25 ≈0.00405.
23. (a) y0=5 (b) L=12 (c) k=1
(d) L/2=6= 60
5+7e
−t,5+7e
−t=10,t=−ln(5/7) ≈0.3365
(e) dy
dt =1
12y(12 −y),y(0)=5
24. (a) y0=1 (b) L= 1000 (c) k=0.9
(d) 750 = 1000
1 + 999e−0.9t,3(1 + 999e−0.9t)=4,t=1
0.9
ln(3 ·999) ≈8.8949
(e) dy
dt =0.9
1000y(1000 −y),y(0)=1
25. See (13):
(a) L=10 (b) k=10
(c) dy
dt = 10(1 −0.1y)y=25−(y−5)2is maximized when y=5.
26. dy
dt =50y1−1
50,000y; from (13), k=50,L=50,000.
(a) L=50,000 (b) k=50
(c) dy
dt is maximized when 0 = d
dy dy
dt =50−y/500,y =25,000
27. Assume y(t) students have had the flu tdays after semester break. Then y(0)=20,y(5) = 35.
(a) dy
dt =ky(L−y)=ky(1000 −y),y
0=20
(b) Part (a) has solution y=20000
20 + 980e−1000kt =1000
1+49e
−1000kt ;
35 = 1000
1+49e
−5000k,k=0.000115,y≈1000
1+49e
−0.115t.
(c) t
y(t)
0
20
1
22
2
25
3
28
4
31
5
35
6
39
7
44
8
49
9
54
10
61
11
67
12
75
13
83
14
93
(d)
36912
25
50
75
100
t
y

355 Chapter 10
28. (a) dp
dh =−kh, p(0) = p0
(b) p0=1,sop=e
−kh, but p=0.83 when h= 5000 thus e−5000k=0.83,
k=−ln 0.83
5000 ≈0.0000373,p≈e
−0.0000373hatm.
29. (a) dT
dt =−k(T−21),T(0)=95,dT
T−21 =−k dt, ln(T−21) = −kt +C1,
T=21+e
C
1e
−kt =21+Ce−kt,95 = T(0)=21+C, C =74,T=21+74e
−kt
(b) 85 = T(1)=21+74e
−k
,k=−ln 64
74 =−ln 32
37,T=21+74e
tln(32/37) =21+7432
37t
,
T= 51 when 30
74 =32
37t
,t=ln(30/74)
ln(32/37) ≈6.22 min
30. dT
dt =k(70 −T),T(0) = 40; −ln(70 −T)=kt +C, 70 −T=e−kte−C,T= 40 when t=0,so
30 = e−C,T=70−30e−kt;52=T(1)=70−30e−k,k=−ln 70 −52
30 =ln5
3≈0.5,
T≈70 −30e−0.5t
31. Let Tdenote the body temperature of McHam’s body at time t, the number of hours elapsed after
10:06 P.M.; then dT
dt =−k(T−72),dT
T−72 =−kdt, ln(T−72) = −kt +C, T =72+e
C
e
−kt,
77.9=72+e
C
,e
C=5.9,T=72+5.9e
−kt,75.6=72+5.9e
−k
,k=−ln 3.6
5.9≈0.4940,
T= 72+5.9e−0.4940t. McHam’s body temperature was last 98.6◦when t=−ln(26.6/5.9)
0.4940 ≈−3.05,
so around 3 hours and 3 minutes before 10:06; the death took place at approximately 7:03 P.M.,
while Moore was on stage.
32. If T0<T
athen dT
dt =k(Ta−T) where k>0. If T0>T
athen dT
dt =−k(T−Ta) where k>0;
both cases yield T(t)=T
a+(T
0−T
a
)e
−kt with k>0.
33. k/m =0.25/1=0.25
(a) From (21), y=0.3 cos(t/2) (b) T=2π·2=4πs, f=1/T =1/(4π)Hz
(c)
6cio
-0.3
0.3
t
y(d) y= 0 at the equilibrium position,
so t/2=π/2,t=πs.
(e) t/2=πat the maximum position below
the equlibrium position, so t=2πs.
34. 64 = w=−mg, m =2,k/m=0.25/2=1/8,pk/m =1/(2√2)
(a) From (21), y= cos(t/(2√2)) (b) T=2π
rm
k=2π(2√2)=4π
√
2s,
f=1/T =1/(4π√2) Hz
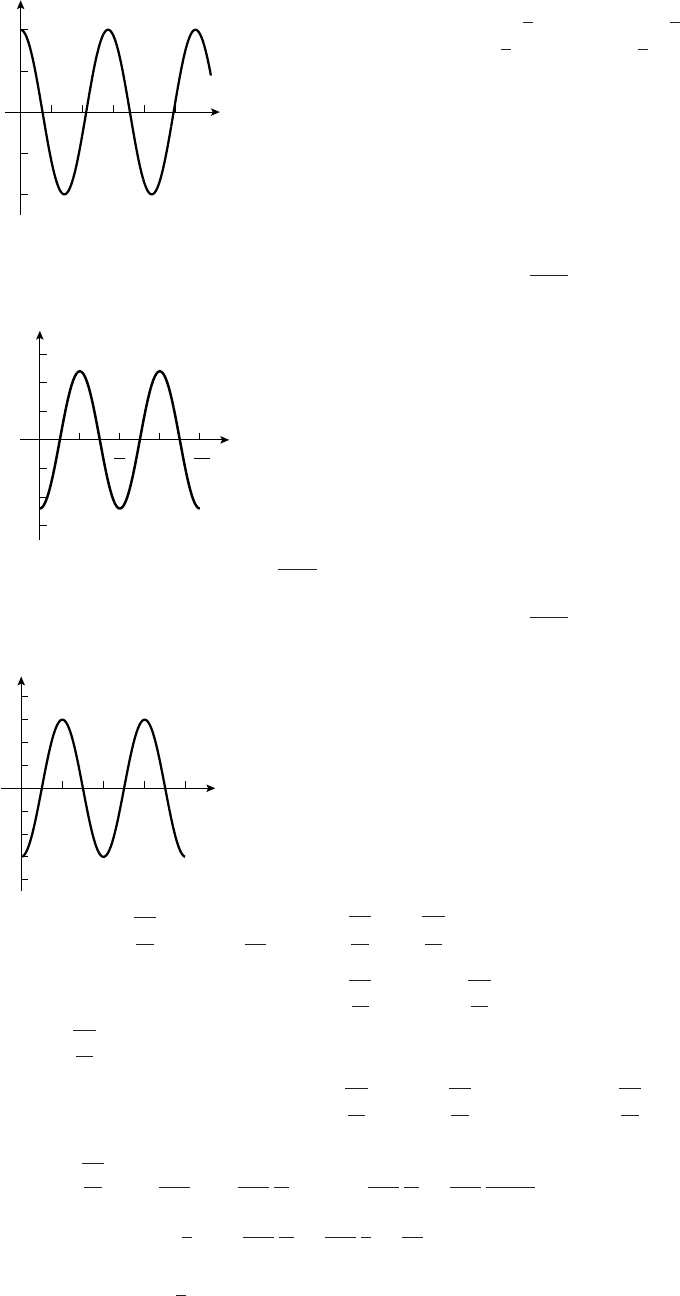
Exercise Set 10.3 356
(c)
-1
1
t
y
2p6p10p
(d) y= 0 at the equilibrium position,
so t/(2√2) = π/2,t=π
√2s
(e) t/(2√2) = π, t =2π
√
2s
35. l=0.05,k/m=g/l =9.8/0.05 = 196 s−2
(a) From (21), y=−0.12 cos 14t.(b) T=2π
pm/k =2π/14 = π/7s,
f=7/π Hz
(c)
-0.15
0.15
t
y
π
7
π
7
2
(d) 14t=π/2,t=π/28 s
(e) 14t=π, t =π/14 s
36. l=0.5,k/m=g/l =32/0.5=64,pk/m =8
(a) From (21), y=−1.5 cos 8t.(b) T=2π
pm/k =2π/8=π/4s;
f=1/T =4/π Hz
(c)
36
-2
2
t
y(d) 8t=π/2,t=π/16 s
(e) 8t=π, t =π/8s
37. Assume y=y0cos rk
mt, so v=dy
dt =−y0rk
msin rk
mt
(a) The maximum speed occurs when sin rk
mt=±1,rk
mt=nπ +π/2,
so cos rk
mt=0,y=0.
(b) The minimum speed occurs when sin rk
mt=0,rk
mt=nπ,socos
rk
mt=±1,y=±y
0
.
38. (a) T=2π
rm
k,k=4π
2
T
2m=4π
2
T
2
w
g
,sok=4π
2
g
w
9=4π
2
g
w+4
25 ,25w=9(w+4),
25w=9w+36,w =9
4,k =4π
2
g
w
9=4π
2
32
1
4=π2
32
(b) From part (a), w=1
4

357 Chapter 10
39. By Hooke’s Law, F(t)=−kx(t), since the only force is the restoring force of the spring. Newton’s
Second Law gives F(t)=mx00(t), so mx00(t)+kx(t)=0,x(0) = x0,x
0(0)=0.
40. 0=v(0) = y0(0) = c2rk
m,soc
2=0; y
0=y(0) = c1,soy=y
0cos rk
mt.
41. (a) y=y0bt=y0etln b=y0ekt with k=lnb>0 since b>1.
(b) y=y0bt=y0etln b=y0e−kt with k=−ln b>0 since 0 <b<1.
(c) y= 4(2t)=4e
tln 2 (d) y= 4(0.5t)=4e
tln 0.5=4e
−tln 2
42. If y=y0ekt and y=y1=y0ekt1then y1/y0=ekt1,k=ln(y1/y0)
t1;ify=y
0
e
−kt and
y=y1=e−kt1then y1/y0=e−kt1,k=−
ln(y1/y0)
t1.
CHAPTER 10 SUPPLEMENTARY EXERCISES
4. The differential equation in part (c) is not separable; the others are.
5. (a) linear (b) linear and separable (c) separable (d) neither
6. IF: µ=e−2x2,d
dx hye−2x2i=xe−2x2,ye
−2x
2=−
1
4
e
−2x
2+C, y =−1
4+Ce2x2
Sep of var: dy
4y+1 =x dx, 1
4ln |4y+1|=x
2
2+C
1,4y+1 = ±e
4C
1e
2x
2=C
2e
2x
2;y=−1
4+Ce2x2
7. The parabola ky(L−y) opens down and has its maximum midway between the y-intercepts, that
is, at the point y=1
2(0+L)=L/2, where dy
dt =k(L/2)2=kL2/4.
8. (a) If y=y0ekt,then y1=y0ekt1,y
2=y
0
e
kt2, divide: y2/y1=ek(t2−t1),k=1
t
2−t
1ln(y2/y1),
T=ln 2
k=(t2−t1)ln2
ln(y2/y1).Ify=y
0
e
−kt, then y1=y0e−kt1,y
2=y
0
e
−kt2,
y2/y1=e−k(t2−t1),k =−1
t
2−t
1ln(y2/y1),T=ln 2
k=−(t2−t1)ln2
ln(y2/y1).
In either case, Tis positive, so T=
(t2−t1)ln2
ln(y2/y1).
(b) In part (a) assume t2=t1+ 1 and y2=1.25y1. Then T=ln 2
ln 1.25 ≈3.1h.
9. dV
dt =−kS; but V=4π
3r3,dV
dt =4πr2dr
dt ,S=4πr2,sodr/dt =−k, r =−kt +C, 4=C,
r=−kt +4,3=−k+4,k =1,r =4−tm.
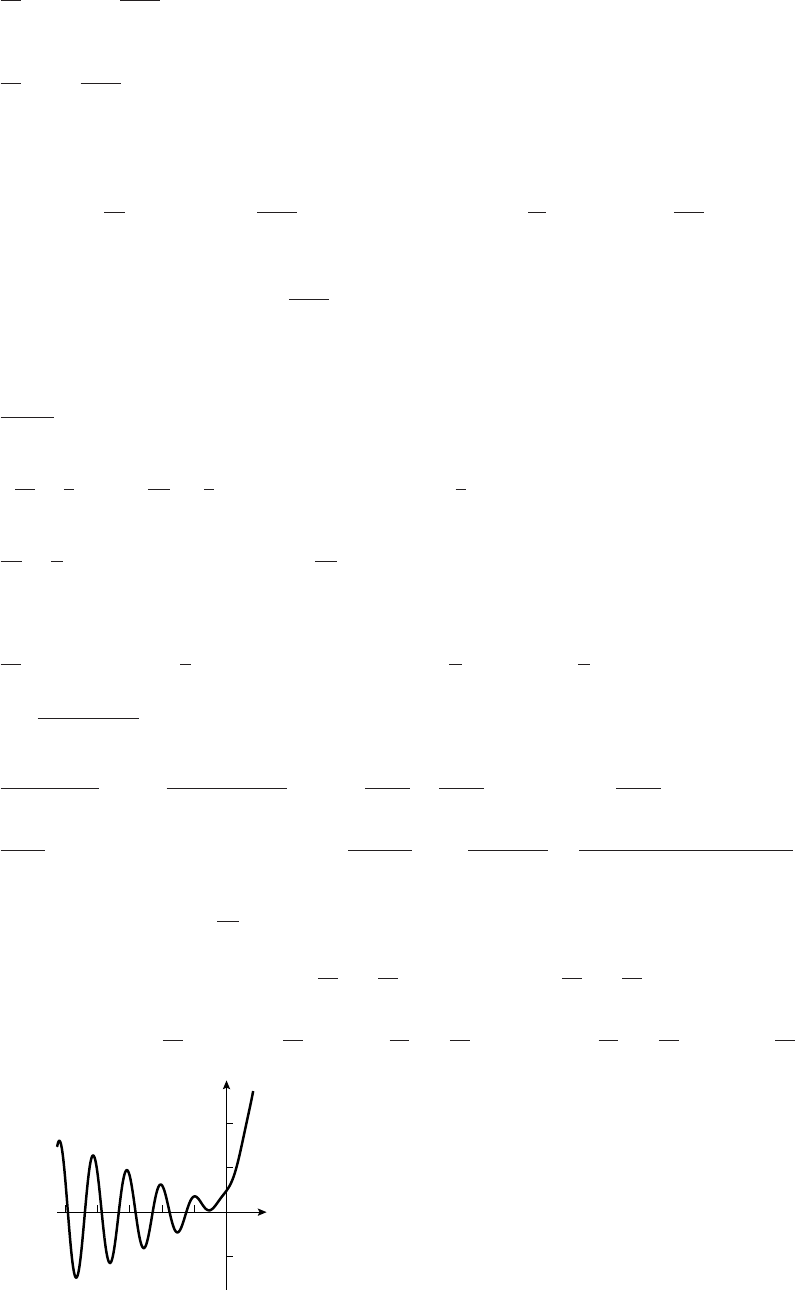
Chapter 10 Supplementary Exercises 358
10. Assume the tank contains y(t) oz of salt at time t. Then y0= 0 and for 0 <t<15,
dy
dt =5·10 −y
100010 = (50 −y/100) oz/min, with solution y= 5000 + Ce−t/100. But y(0) = 0 so
C=−5000, y= 5000(1 −e−t/100) for 0 ≤t≤15, and y(15) = 5000(1 −e−0.15). For 15 <t<30,
dy
dt =0−y
10005,y=C
1
e
−t/200,C
1
e
−0.075 =y(15) = 5000(1−e−0.15),C
1= 5000(e0.075 −e−0.075),
y= 5000(e0.075 −e−0.075)e−t/100,y(30) = 5000(e0.075 −e−0.075)e−0.3≈556.13 oz.
11. (a) Assume the air contains y(t)ft
3of carbon monoxide at time t. Then y0= 0 and for
t>0, dy
dt =0.04(0.1) −y
1200(0.1)=1/250 −y/12000,d
dt hyet/12000i=1
250et/12000,
yet/12000 =48e
t/12000 +C, y(0)=0,C=−48; y= 48(1 −e−t/12000). Thus the percentage
of carbon monoxide is P=y
1200100 = 4(1 −e−t/12000) percent.
(b) 0.012 = 4(1 −e−t/12000),t=35.95 min
12. dy
y2+1 =dx, tan−1y=x+C, π/4=C;y= tan(x+π/4)
13. 1
y5+1
ydy =dx
x,−1
4y−4+ln|y|=ln|x|+C;−1
4=C, y−4+ 4 ln(x/y)=1
14. dy
dx +2
xy=4x, µ =eR(2/x)dx =x2,d
dx yx2=4x
3
,yx
2=x
4+C, y =x2+Cx−2,
2=y(1)=1+C, C =1,y=x
2+1/x2
15. dy
y2= 4 sec22x dx, −1
y= 2 tan 2x+C, −1 = 2 tan 2π
8+C= 2 tan π
4+C=2+C, C =−3,
y=1
3−2 tan 2x
16. dy
y2−5y+6 =dx, dy
(y−3)(y−2) =dx, 1
y−3−1
y−2dy =dx, ln
y−3
y−2=x+C1,
y−3
y−2=Cex;y=ln2ifx=0,so C=ln 2 −3
ln 2 −2;y=3−2Cex
1−cex=3ln2−6−(2 ln 2 −6)ex
ln 2 −2−(ln 2 −3)ex
17. (a) µ=e−Rdx =e−x,d
dx ye−x=xe−xsin 3x,
ye−x=Zxe−xsin 3xdx =−3
10x−3
50e−xcos 3x+−1
10x+2
25e−xsin 3x+C;
1=y(0) = −3
50 +C, C =53
50,y=
−3
10x−3
50cos 3x+−1
10x+2
25sin 3x+53
50ex
(c)
-10 -2
-2
4
x
y
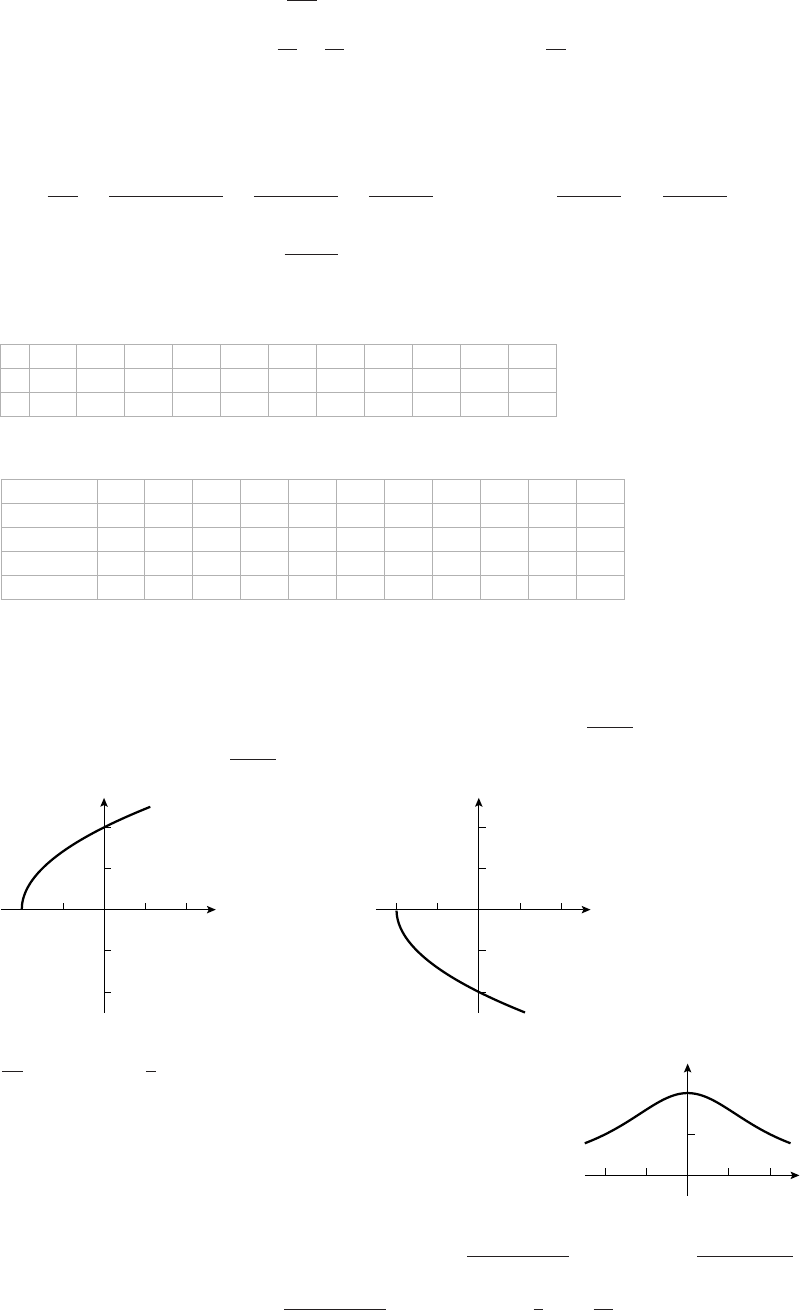
359 Chapter 10
19. (a) Let T1= 5730 −40 = 5690,k
1=ln 2
T1≈0.00012182; T2= 5730 + 40 = 5770,k
2≈0.00012013.
With y/y0=0.92,0.93,t
1=−1
k
1ln y
y0= 684.5,595.7; t2=−1
k2ln(y/y0) = 694.1,604.1; in
1988 the shroud was at most 695 years old, which places its creation in or after the year 1293.
(b) If the true half-life is Twith decay rate kand solution y(t)=y
0
e
−kt, and if the half-life is
taken to be T1=T(1+r/100) with decay rate k1and solution y1(t)=y
0
e
−k
1
t
, then
k1=ln 2
T1=ln 2
T(1+r/100) =k
1+r/100 =100k
100 + r;k−k1=k−100k
100 + r=kr
100 + rand the
percentage error is given by 100
y1−y
y= 100 e(k−k1)t−1= 100 ektr/(100+r)−1percent.
20. (a) yn+1 =yn+0.1(1+5t
n−y
n
),y
0=5
n
t
n
y
n
0
1
5.00
1
1.1
5.10
2345
1.2
5.24
1.3
5.42
1.4
5.62
1.5
5.86
6
1.6
6.13
7
1.7
6.41
8
1.8
6.72
9
1.9
7.05
10
2
7.39
(b) The true solution is y(t)=5t−4+4e
1−t
, so the percentage errors are given by
tn
yn
y(tn)
abs. error
rel. error (%)
1
5.00
5.00
0.00
0.00
1.1
5.10
5.12
0.02
0.38
1.2
5.24
5.27
0.03
0.66
1.3
5.42
5.46
0.05
0.87
1.4
5.62
5.68
0.06
1.00
1.5
5.86
5.93
0.06
1.08
1.6
6.13
6.20
0.07
1.12
1.7
6.41
6.49
0.07
1.13
1.8
6.72
6.80
0.08
1.11
1.9
7.05
7.13
0.08
1.07
2
7.39
7.47
0.08
1.03
21. (b) y=C1ex+C2e−x
(c) 1=y(0) = C1+C2,1=y
0(0) = C1−C2;C2=0,C
1=1,y =e
x
22. (a) 2ydy =dx, y2=x+C;ify(0) = 1 then C=1,y
2=x+1,y =√x+1; ify(0) = −1 then
C=1,y
2=x+1,y =−√x+1.
-1 1
-1
1
x
y
-1 1
-1
1
x
y
-1 1
1
x
y
(b) dy
y2=−2x dx, −1
y=−x2+C, −1=C, y =1/(x
2+1)
23. (a) Use (15) in Section 10.3 with y0=19,L= 95: y(t)= 1805
19+76e
−kt ,25 = y(1) = 1805
19+76e
−k,
k≈0.3567; when 0.8L=y(t)= y
0
L
19+76e
−kt ,19+76e
−kt =5
4y0=95
4,t≈7.77 yr.
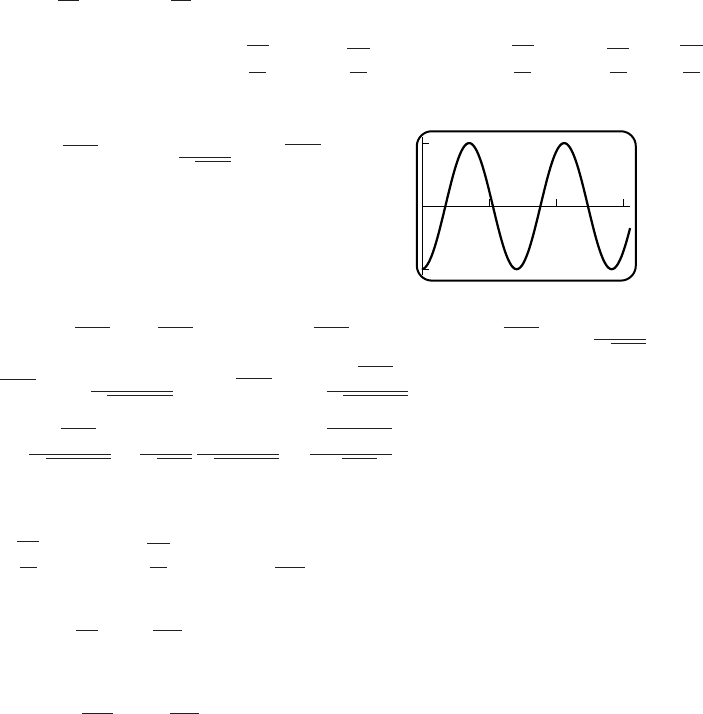
Chapter 10 Supplementary Exercises 360
(b) From (13), dy
dt =k1−y
95y, y(0) = 19.
24. (a) y0=y(0) = c1,v
0=y
0
(0) = c2rk
m,c
2=
rm
k
v
0
,y=y
0cos rk
mt+v0rm
ksin rk
mt
1.1
-1.1
0 3.1
(b) l=0.5,k/m=g/l =9.8/0.5=19.6,
y=−cos(√19.6t)+0.25 1
√19.6sin(√19.6t)
(c) v=y0(t)=√
19.6 sin √19.6t+0.25 cos √19.6t= 0 when tan √19.6t=−0.25
√19.6,so
sin √19.6t=±0.25
√19.6625,cos √19.6t=∓√19.6
√19.6625,
|y(t)|=√19.6
√19.6625 +0.25
√19.6
0.25
√19.6625 =√19.6625
√19.6
≈1.0016 m is the maximum displacement.
25. y=y0cos rk
mt, T =2π
rm
k,y=y
0cos 2πt
T
(a) v=y0(t)=−2π
Ty
0sin 2πt
Thas maximum magnitude 2π|y0|/T and occurs when
2πt/T =nπ +π/2,y=y
0cos(nπ +π/2)=0.
(b) a=h00(t)=−4π
2
T
2y
0cos 2πt
Thas maximum magnitude 4π2|y0|/T 2and occurs when
2πt/T =jπ, y =y0cos jπ =±y0.
26. (a) In tyears the interest will be compounded nt times at an interest rate of r/n each time. The
value at the end of 1 interval is P+(r/n)P=P(1 + r/n), at the end of 2 intervals it is
P(1+r/n)+(r/n)P(1+r/n)=P(1+r/n)2, and continuing in this fashion the value at the
end of nt intervals is P(1+r/n)nt.
(b) Let x=r/n, then n=r/x and
lim
n→+∞P(1+r/n)nt = lim
x→0+P(1+x)rt/x = lim
x→0+P[(1 + x)1/x]rt =Pe
rt.
(c) The rate of increase is dA/dt =rPert =rA.
27. (a) A= 1000e(0.08)(5) = 1000e0.4≈$1,491.82
(b) Pe
(0.08)(10) =10,000, Pe
0.8=10,000, P=10,000e−0.8≈$4,493.29
(c) From (11) with k=r=0.08, T= (ln 2)/0.08 ≈8.7 years.

361
CHAPTER 11
Infinite Series
EXERCISE SET 11.1
1. (a) 1
3n−1(b) (−1)n−1
3n−1(c) 2n−1
2n(d) n2
π1/(n+1)
2. (a) (−r)n−1;(−r)
n(b) (−1)n+1rn;(−1)nrn+1
3. (a) 2,0,2,0(b) 1,−1,1,−1(c) 2(1+(−1)n); 2 + 2 cos nπ
4. (a) (2n)! (b) (2n−1)!
5. 1/3, 2/4, 3/5, 4/6, 5/7,...; lim
n→+∞
n
n+2 = 1, converges
6. 1/3, 4/5, 9/7, 16/9, 25/11,...; lim
n→+∞
n2
2n+1 =+∞, diverges
7. 2,2,2,2,2,...; lim
n→+∞2 = 2, converges
8. ln 1, ln 1
2,ln1
3
,ln1
4
,ln1
5
,...; lim
n→+∞ln(1/n)=−∞, diverges
9. ln 1
1,ln 2
2,ln 3
3,ln 4
4,ln 5
5,...;
lim
n→+∞
ln n
n= lim
n→+∞
1
n=0apply L’Hˆopital’s Rule to ln x
x, converges
10. sin π, 2 sin(π/2), 3 sin(π/3), 4 sin(π/4), 5 sin(π/5),...;
lim
n→+∞nsin(π/n) = lim
n→+∞
sin(π/n)
1/n = lim
n→+∞
(−π/n2) cos(π/n)
−1/n2=π, converges
11. 0,2,0,2,0,...; diverges
12. 1, −1/4, 1/9, −1/16, 1/25,...; lim
n→+∞
(−1)n+1
n2= 0, converges
13. −1, 16/9, −54/28, 128/65, −250/126,...; diverges because odd-numbered terms approach
−2, even-numbered terms approach 2.
14. 1/2, 2/4, 3/8, 4/16, 5/32,...; lim
n→+∞
n
2n= lim
n→+∞
1
2nln 2 = 0, converges
15. 6/2, 12/8, 20/18, 30/32, 42/50,...; lim
n→+∞
1
2(1+1/n)(1+2/n)=1/2, converges
16. π/4, π2/42,π3/43,π4/44,π5/45,...; lim
n→+∞(π/4)n= 0, converges
17. cos(3), cos(3/2), cos(1), cos(3/4), cos(3/5),...; lim
n→+∞cos(3/n) = 1, converges
18. 0, −1, 0, 1, 0,...; diverges

Exercise Set 11.1 362
19. e−1,4e
−2
,9e
−3
,16e
−4
,25e
−5
,...; lim
x→+∞x2e−x= lim
x→+∞
x2
ex= 0, so lim
n→+∞n2e−n= 0, converges
20. 1, √10 −2, √18 −3, √28 −4, √40 −5,...;
lim
n→+∞(pn2+3n−n) = lim
n→+∞
3n
√n2+3n+n= lim
n→+∞
3
p1+3/n +1 =3
2, converges
21. 2, (5/3)2,(6/4)3,(7/5)4,(8/6)5,...; let y=x+3
x+1x
, converges because
lim
x→+∞ln y= lim
x→+∞
ln x+3
x+1
1/x = lim
x→+∞
2x2
(x+ 1)(x+3) = 2, so lim
n→+∞n+3
n+1n
=e
2
22. −1, 0, (1/3)3,(2/4)4,(3/5)5,...; let y=(1−2/x)x, converges because
lim
x→+∞ln y= lim
x→+∞
ln(1 −2/x)
1/x = lim
x→+∞−2
1−2/x =−2, lim
n→+∞(1 −2/n)n= lim
x→+∞y=e−2
23. 2n−1
2n+∞
n=1
; lim
n→+∞
2n−1
2n= 1, converges
24. n−1
n2+∞
n=1
; lim
n→+∞
n−1
n2= 0, converges 25. 1
3n+∞
n=1
; lim
n→+∞
1
3n= 0, converges
26. {(−1)nn}+∞
n=1; diverges because odd-numbered terms tend toward −∞,
even-numbered terms tend toward +∞.
27. 1
n−1
n+1+∞
n=1
; lim
n→+∞1
n−1
n+1= 0, converges
28. 3/2n−1+∞
n=1; lim
n→+∞3/2n−1= 0, converges
29. √n+1−√
n+2
+∞
n=1; converges because
lim
n→+∞(√n+1−√
n+ 2) = lim
n→+∞
(n+1)−(n+2)
√
n+1+√
n+2 = lim
n→+∞−1
√n+1+√
n+2 =0
30. (−1)n+1/3n+4+∞
n=1; lim
n→+∞(−1)n+1/3n+4 = 0, converges
32. lim
n→+∞
n
√n= 1, so lim
n→+∞
n
√n3=1
3=1
33. (a) 1,2,1,4,1,6(b) an=(n, n odd
1/2n,neven (c) an=(1/n, n odd
1/(n+1),neven
(d) In part (a) the sequence diverges, since the even terms diverge to +∞and the odd terms
equal 1; in part (b) the sequence diverges, since the odd terms diverge to +∞and the even
terms tend to zero; in part (c) lim
n→+∞an=0.
34. The even terms are zero, so the odd terms must converge to zero, and this is true if and only if
lim
n→+∞bn=0,or−1<b<1.

363 Chapter 11
35. lim
n→+∞yn+1 = lim
n→+∞
1
2(yn+p/yn), L=1
2(L+p/L), L2=p,L=±√p;
L=−√p(reject, because the terms in the sequence are positive) or L=√p; lim
n→+∞yn=√p.
36. (a) an+1 =√6+a
n
(b) lim
n→+∞an+1 = lim
n→+∞√6+a
n
,L=√
6+L,L
2−L−6=0,(L−3)(L+2)=0,
L=−2 (reject, because the terms in the sequence are positive) or L= 3; lim
n→+∞an=3.
37. (a) 1, 1
4+2
4,1
9+2
9+3
9,1
16 +2
16 +3
16 +4
16 =1,3
4
,2
3
,5
8
(c) an=1
n2(1+2+···+n)= 1
n
2
1
2
n(n+1)= 1
2
n+1
n,lim
n→+∞an=1/2
38. (a) 1, 1
8+4
8,1
27 +4
27 +9
27,1
64 +4
64 +9
64 +16
64 =1,5
8
,14
27,15
32
(c) an=1
n3(12+2
2+···+n
2)= 1
n
3
1
6
n(n+ 1)(2n+1)= 1
6
(n+ 1)(2n+1)
n
2,
lim
n→+∞an= lim
n→+∞
1
6(1+1/n)(2+1/n)=1/3
39. Let an=0,b
n=sin2n
n,c
n=1
n; then an≤bn≤cn, lim
n→+∞an= lim
n→+∞cn= 0, so lim
n→+∞bn=0.
40. Let an=0,b
n=1+n
2nn
,c
n=3
4n
; then (for n≥2), an≤bn≤n/2+n
2nn
=c
n
,
lim
n→+∞an= lim
n→+∞cn= 0, so lim
n→+∞bn=0.
41. (a) a1=(0.5)2,a
2=a
2
1=(0.5)4,...,a
n=(0.5)2n
(c) lim
n→+∞an= lim
n→+∞e2nln(0.5) = 0, since ln(0.5) <0.
(d) Replace 0.5 in part (a) with a0; then the sequence converges for −1≤a0≤1, because if
a0=±1, then an= 1 for n≥1; if a0= 0 then an= 0 for n≥1; and if 0 <|a0|<1 then
a1=a2
0>0 and lim
n→+∞an= lim
n→+∞e2n−1ln a1= 0 since 0 <a
1<1.
42. f(0.2)=0.4,f(0.4)=0.8,f(0.8)=0.6,f(0.6)=0.2 and then the cycle repeats, so the sequence
does not converge.
43. (a) 30
0
05
(b) Let y=(2
x+3
x
)
1/x, lim
x→+∞ln y= lim
x→+∞
ln(2x+3
x
)
x= lim
x→+∞
2xln2+3
xln 3
2x+3
x
= lim
x→+∞
(2/3)xln2+ln3
(2/3)x+1 = ln 3, so lim
n→+∞(2n+3
n
)
1/n =eln 3 =3
Exercise Set 11.2 364
44. Let f(x)=1/(1+x), 0 ≤x≤1. Take ∆xk=1/n and x∗
k=k/n then
an=
n
X
k=1
1
1+(k/n)(1/n)=
n
X
k=1
1
1+x
∗
k
∆x
kso lim
n→+∞an=Z1
0
1
1+xdx = ln(1 + x)1
0
=ln2
45. an=1
n−1Zn
1
1
xdx =ln n
n−1, lim
n→+∞an= lim
n→+∞
ln n
n−1= lim
n→+∞
1
n=0,
apply L’Hˆopital’s Rule to ln n
n−1, converges
46. (a) If n≥1, then an+2 =an+1 +an,soa
n+2
an+1 =1+ a
n
a
n+1 .
(c) With L= lim
n→+∞(an+2/an+1) = lim
n→+∞(an+1/an), L=1+1/L,L2−L−1=0,
L=(1±√
5)/2, so L=(1+√
5)/2 because the limit cannot be negative.
47.
1
n−0=1
n<if n>1/
(a) 1/ =1/0.5=2,N=3 (b) 1/ =1/0.1 = 10, N=11
(c) 1/ =1/0.001 = 1000, N= 1001
48.
n
n+1−1
=1
n+1 <if n+1>1/,n>1/ −1
(a) 1/ −1=1/0.25 −1=3,N=4 (b) 1/ −1=1/0.1−1=9,N=10
(c) 1/ −1=1/0.001 −1 = 999, N= 1000
49. (a)
1
n−0=1
n<if n>1/, choose any N>1/.
(b)
n
n+1−1
=1
n+1 <if n>1/ −1, choose any N>1/ −1.
50. If |r|<1 then lim
n→+∞rn=0;ifr>1 then lim
n→+∞rn=+∞,ifr<−1 then rnoscillates between
positive and negative values that grow in magnitude so lim
n→+∞rndoes not exist for |r|>1; if r=1
then lim
n→+∞1n=1;ifr=−1 then (−1)noscillates between −1 and 1 so lim
n→+∞(−1)ndoes not exist.
EXERCISE SET 11.2
1. an+1 −an=1
n+1−1
n=−1
n(n+1) <0 for n≥1, so strictly decreasing.
2. an+1 −an=(1−1
n+1)−(1 −1
n)= 1
n(n+1) >0 for n≥1, so strictly increasing.
3. an+1 −an=n+1
2n+3−n
2n+1 =1
(2n+ 1)(2n+3) >0 for n≥1, so strictly increasing.

365 Chapter 11
4. an+1 −an=n+1
4n+3−n
4n−1=−1
(4n−1)(4n+3) <0 for n≥1, so strictly decreasing.
5. an+1 −an=(n+1−2
n+1)−(n−2n)=1−2
n<0 for n≥1, so strictly decreasing.
6. an+1 −an=[(n+1)−(n+1)
2]−(n−n
2)=−2n<0 for n≥1, so strictly decreasing.
7. an+1
an
=(n+1)/(2n+3)
n/(2n+1) =(n+ 1)(2n+1)
n(2n+3) =2n
2+3n+1
2n
2+3n>1 for n≥1, so strictly increasing.
8. an+1
an
=2n+1
1+2
n+1 ·1+2
n
2
n=2+2
n+1
1+2
n+1 =1+ 1
1+2
n+1 >1 for n≥1, so strictly increasing.
9. an+1
an
=(n+1)e
−(n+1)
ne−n=(1+1/n)e−1<1 for n≥1, so strictly decreasing.
10. an+1
an
=10n+1
(2n+ 2)! ·(2n)!
10n=10
(2n+ 2)(2n+1) <1 for n≥1, so strictly decreasing.
11. an+1
an
=(n+1)
n+1
(n+ 1)! ·n!
nn=(n+1)
n
n
n=(1+1/n)n>1 for n≥1, so strictly increasing.
12. an+1
an
=5n+1
2(n+1)2·2n2
5n=5
22n+1 <1 for n≥1, so strictly decreasing.
13. f(x)=x/(2x+ 1), f0(x)=1/(2x+1)
2>0 for x≥1, so strictly increasing.
14. f(x)=3−1/x,f0(x)=1/x2>0 for x≥1, so strictly increasing.
15. f(x)=1/(x+lnx), f0(x)=−1+1/x
(x+lnx)
2<0 for x≥1, so strictly decreasing.
16. f(x)=xe−2x,f0(x)=(1−2x)e
−2x<0 for x≥1, so strictly decreasing.
17. f(x)=ln(x+2)
x+2 ,f0(x)=1−ln(x+2)
(x+2)
2<0 for x≥1, so strictly decreasing.
18. f(x) = tan−1x,f0(x)=1/(1+x2)>0 for x≥1, so strictly increasing.
19. f(x)=2x
2−7x,f
0(x)=4x−7>0 for x≥2, so eventually strictly increasing.
20. f(x)=x
3−4x
2
,f
0(x)=3x
2−8x=x(3x−8) >0 for x≥3, so eventually strictly increasing.
21. f(x)= x
x
2+10,f0(x)= 10 −x2
(x2+ 10)2<0 for x≥4, so eventually strictly decreasing.
22. f(x)=x+17
x,f0(x)=x
2−17
x2>0 for x≥5, so eventually strictly increasing.
23. an+1
an
=(n+ 1)!
3n+1 ·3n
n!=n+1
3>1 for n≥3, so eventually strictly increasing.
24. f(x)=x
5
e
−x
,f
0(x)=x
4
(5 −x)e−x<0 for x≥6, so eventually strictly decreasing.
Exercise Set 11.2 366
25. (a) Yes: a monotone sequence is increasing or decreasing; if it is increasing, then it is increas-
ing and bounded above, so by Theorem 11.2.3 it converges; if decreasing, then use Theo-
rem 11.2.4. The limit lies in the interval [1,2].
(b) Such a sequence may converge, in which case, by the argument in Part (a), its limit is ≤2.
But convergence may not happen: for example, the sequence {−n}+∞
n=1 diverges.
26. (a) an+1 =|x|n+1
(n+ 1)! =|x|
n+1|x|
n
n!=|x|
n+1a
n
(b) an+1/an=|x|/(n+1)<1ifn>|x|−1.
(c) From Part (b) the sequence is eventually decreasing, and it is bounded below by 0, so by
Theorem 11.2.4 it converges.
(d) If lim
n→+∞an=Lthen from Part (a), L=|x|
lim
n→+∞(n+1)L=0.
(e) lim
n→+∞|x|n
n!= lim
n→+∞an=0
27. (a) √2, q2+√
2, r2+q2+√
2
(b) a1=√2<2soa
2=√
2+a
1<√
2+2=2,a
3=√
2+a
2<√
2 + 2 = 2, and so on
indefinitely.
(c) a2
n+1 −a2
n=(2+a
n
)−a
2
n=2+a
n−a
2
n=(2−a
n
)(1 + an)
(d) an>0 and, from Part (b), an<2so2−a
n>0 and 1 + an>0 thus, from Part (c),
a2
n+1 −a2
n>0, an+1 −an>0, an+1 >a
n
;{a
n
}is a strictly increasing sequence.
(e) The sequence is increasing and has 2 as an upper bound so it must converge to a limit L,
lim
n→+∞an+1 = lim
n→+∞√2+a
n
,L=√
2+L,L
2−L−2=0,(L−2)(L+1)=0
thus lim
n→+∞an=2.
28. (a) If f(x)=1
2(x+3/x), then f0(x)=(x
2−3)/(2x2) and f0(x)=0forx=√
3; the minimum
value of f(x) for x>0isf(
√
3) = √3. Thus f(x)≥√3 for x>0 and hence an≥√3 for
n≥2.
(b) an+1 −an=(3−a
2
n
)/(2an)≤0 for n≥2 since an≥√3 for n≥2; {an}is eventually
decreasing.
(c) √3 is a lower bound for anso {an}converges; lim
n→+∞an+1 = lim
n→+∞
1
2(an+3/an),
L=1
2(L+3/L), L2−3=0,L=√
3.
29. (a) The altitudes of the rectangles are ln kfor k=2ton, and their bases all have length 1 so
the sum of their areas is ln 2 + ln 3 + ···+lnn= ln(2 ·3···n)=lnn!. The area under the
curve y=lnxfor xin the interval [1,n]isZn
1ln xdx, and Zn+1
1ln xdx is the area for xin
the interval [1,n+ 1] so, from the figure, Zn
1ln xdx< ln n!<Zn+1
1ln xdx.
(b) Zn
1ln xdx=(xln x−x)n
1
=nln n−n+ 1 and Zn+1
1ln xdx=(n+ 1) ln(n+1)−nso from
Part (a), nln n−n+1<ln n!<(n+ 1) ln(n+1)−n,e
nln n−n+1 <n!<e
(n+1) ln(n+1)−n,
enln ne1−n<n!<e
(n+1) ln(n+1)e−n,nn
en−1<n!<(n+1)
n+1
en

367 Chapter 11
(c) From part (b), nn
en−11/n
<n
√n!<(n+1)
n+1
en1/n
,
n
e1−1/n <n
√n!<(n+1)
1+1/n
e,1
e1−1/n <
n
√n!
n<(1+1/n)(n+1)
1/n
e,
but 1
e1−1/n →1
eand (1+1/n)(n+1)
1/n
e→1
eas n→+∞(why?), so lim
n→+∞
n
√n!
n=1
e.
30. n!>nn
en−1,n
√n!>n
e1−1/n , lim
n→+∞
n
e1−1/n =+∞so lim
n→+∞
n
√n!=+∞.
EXERCISE SET 11.3
1. (a) s1=2,s
2=12/5, s3=62
25,s4=312
125 sn=2−2(1/5)n
1−1/5=5
2−5
2(1/5)n,
lim
n→+∞sn=5
2, converges
(b) s1=1
4,s2=3
4,s3=7
4,s4=15
4sn=(1/4) −(1/4)2n
1−2=−1
4+1
4(2n),
lim
n→+∞sn=+∞, diverges
(c) 1
(k+ 1)(k+2) =1
k+1−1
k+2,s
1=1
6,s
2=1
4,s
3=3
10,s4=1
3;
sn=1
2−1
n+2, lim
n→+∞sn=1
2, converges
2. (a) s1=1/4,s
2=5/16,s
3=21/64,s
4=85/256
sn=1
4 1+1
4+···+1
4n−1!=1
4
1−(1/4)n
1−1/4=1
31−1
4n
; lim
n→+∞sn=1
3
(b) s1=1,s
2=5,s
3=21,s
4= 85; sn=4n−1
3, diverges
(c) s1=1/20,s
2=1/12,s
3=3/28,s
4=1/8;
sn=
n
X
k=1 1
k+3−1
k+4=1
4−1
n+4, lim
n→+∞sn=1/4
3. geometric, a=1,r=−3/4, sum = 1
1−(−3/4) =4/7
4. geometric, a=(2/3)3,r=2/3, sum = (2/3)3
1−2/3=8/9
5. geometric, a=7,r=−1/6, sum = 7
1+1/6=6
6. geometric, r=−3/2, diverges
7. sn=
n
X
k=1 1
k+2−1
k+3=1
3−1
n+3, lim
n→+∞sn=1/3
Exercise Set 11.3 368
8. sn=
n
X
k=1 1
2k−1
2k+1 =1
2−1
2n+1 , lim
n→+∞sn=1/2
9. sn=
n
X
k=1 1/3
3k−1−1/3
3k+2=1
6−1/3
3n+2, lim
n→+∞sn=1/6
10. sn=
n+1
X
k=2 1/2
k−1−1/2
k+1=1
2"n+1
X
k=2
1
k−1−
n+1
X
k=2
1
k+1#
=1
2"n+1
X
k=2
1
k−1−
n+3
X
k=4
1
k−1#=1
21+1
2−1
n+1−1
n+2; lim
n→+∞sn=3
4
11. ∞
X
k=3
1
k−2=∞
X
k=1
1/k, the harmonic series, so the series diverges.
12. geometric, a=(e/π)4,r=e/π < 1, sum = (e/π)4
1−e/π =e4
π3(π−e)
13. ∞
X
k=1
4k+2
7k−1=∞
X
k=1
64 4
7k−1
; geometric, a= 64, r=4/7, sum = 64
1−4/7= 448/3
14. geometric, a= 125,r = 125/7, diverges
15. 0.4444 ···=0.4+0.04+0.004 + ···=0.4
1−0.1=4/9
16. 0.9999 ···=0.9+0.09+0.009 + ···=0.9
1−0.1=1
17. 5.373737 ···=5+0.37+0.0037 + 0.000037 + ···=5+ 0.37
1−0.01 =5+37/99 = 532/99
18. 0.159159159 ···=0.159+0.000159 + 0.000000159 + ···=0.159
1−0.001 = 159/999=53/333
19. 0.782178217821 ···=0.7821 + 0.00007821 + 0.000000007821 + ···=0.7821
1−0.0001 =7821
9999 =869
1111
20. 0.451141414 ···=0.451+0.00014 + 0.0000014 + 0.000000014 + ···=0.451 + 0.00014
1−0.01 =44663
99000
22. (a) geometric; 18/5 (b) geometric; diverges (c) ∞
X
k=1
1
21
2k−1−1
2k+1=1/2
23. d=10+2·3
4·10+2·3
4·3
4·10+2·3
4·3
4·3
4·10+···
=10+203
4+203
42
+203
43
+···=10+20(3/4)
1−3/4= 10 + 60 = 70 meters
369 Chapter 11
24. volume = 13+1
23
+1
43
+···+1
2
n3
+···=1+1
8+1
8
2
+···+1
8n
+···
=1
1−(1/8) =8/7
25. (a) sn=ln1
2+ln2
3+ln3
4+···+ln n
n+1 =ln1
2·2
3·3
4··· n
n+1=ln 1
n+1 =−ln(n+1),
lim
n→+∞sn=−∞, series diverges.
(b) ln(1 −1/k2)=lnk
2−1
k
2=ln(k−1)(k+1)
k
2=lnk−1
k+lnk+1
k=lnk−1
k−ln k
k+1,
s
n=
n+1
X
k=2 ln k−1
k−ln k
k+1
=ln 1
2−ln 2
3+ln 2
3−ln 3
4+ln 3
4−ln 4
5+···+ln n
n+1−ln n+1
n+2
=ln1
2−ln n+1
n+2,lim
n→+∞sn=ln1
2=−ln 2
26. (a) ∞
X
k=0
(−1)kxk=1−x+x
2−x
3+···=1
1−(−x)=1
1+xif |−x|<1, |x|<1, −1<x<1.
(b) ∞
X
k=0
(x−3)k=1+(x−3)+(x−3)2+···=1
1−(x−3) =1
4−xif |x−3|<1, 2 <x<4.
(c) ∞
X
k=0
(−1)kx2k=1−x
2+x
4−x
6+···=1
1−(−x
2)=1
1+x
2if |−x2|<1, |x|<1, −1<x<1.
27. (a) Geometric series, a=x,r=−x2. Converges for |−x
2|<1, |x|<1;
S=x
1−(−x2)=x
1+x
2.
(b) Geometric series, a=1/x2,r=2/x. Converges for |2/x|<1, |x|>2;
S=1/x2
1−2/x =1
x2−2x.
(c) Geometric series, a=e−x,r=e−x. Converges for |e−x|<1, e−x<1, ex>1, x>0;
S=e−x
1−e−x=1
ex−1.
28. √k+1−√
k
√
k
2+k=√
k+1−√
k
√
k
√
k+1 =1
√
k−1
√
k+1,
s
n=
n
X
k=1 1
√k−1
√k+1=1
√
1−1
√
2+1
√
2−1
√
3+1
√
3−1
√
4
+···+1
√n−1
√n+1=1−1
√
n+1; lim
n→+∞sn=1
29. sn=(1−1/3)+(1/2−1/4)+(1/3−1/5)+(1/4−1/6)+···+[1/n −1/(n+ 2)]
=(1+1/2+1/3+···+1/n)−(1/3+1/4+1/5+···+1/(n+ 2))
=3/2−1/(n+1)−1/(n+2),lim
n→+∞sn=3/2
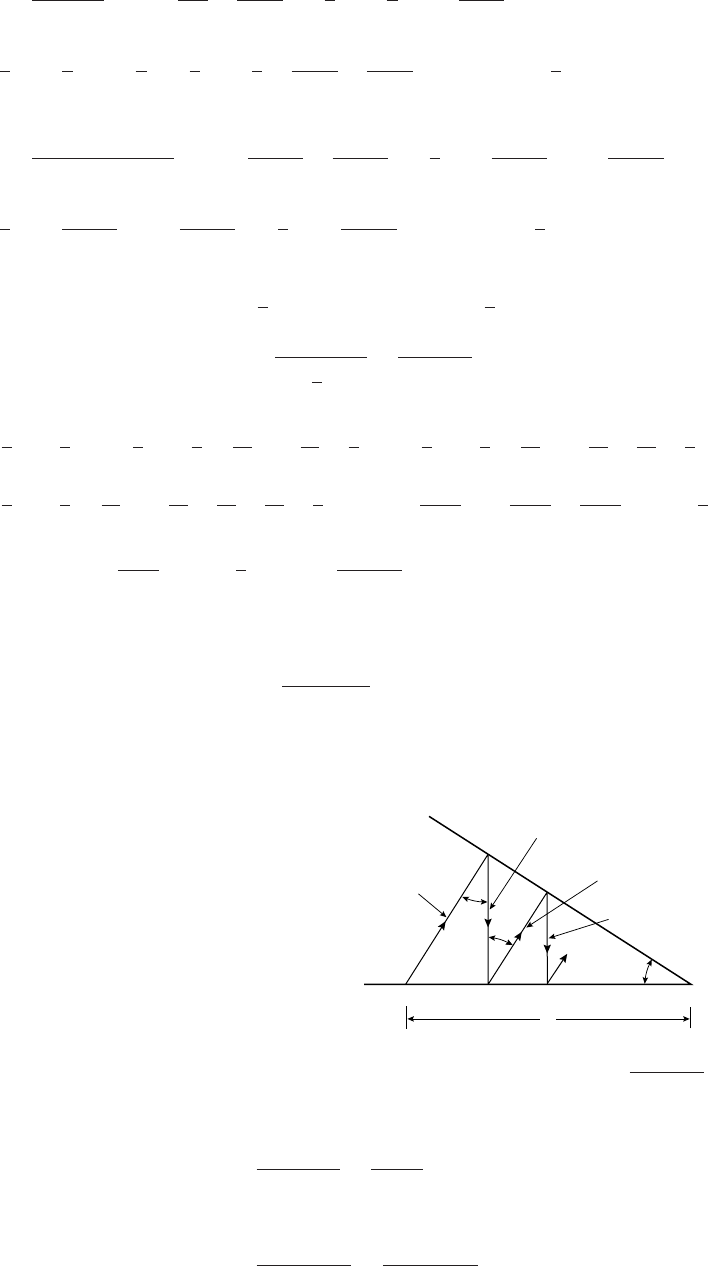
Exercise Set 11.3 370
30. sn=
n
X
k=1
1
k(k+2) =
n
X
k=1 1/2
k−1/2
k+2=1
2"n
X
k=1
1
k−
n
X
k=1
1
k+2#
=1
2"n
X
k=1
1
k−
n+2
X
k=3
1
k#=1
21+1
2−1
n+1−1
n+2; lim
n→+∞sn=3
4
31. sn=
n
X
k=1
1
(2k−1)(2k+1) =
n
X
k=1 1/2
2k−1−1/2
2k+1=1
2"n
X
k=1
1
2k−1−
n
X
k=1
1
2k+1#
=1
2"n
X
k=1
1
2k−1−
n+1
X
k=2
1
2k−1#=1
21−1
2n+1; lim
n→+∞sn=1
2
32. Geometric series, a= sin x,r=−1
2sin x. Converges for |−1
2sin x|<1, |sin x|<2,
so converges for all values of x.S=sin x
1+1
2sin x
=2 sin x
2 + sin x.
33. a2=1
2a1+1
2,a3=1
2a2+1
2=1
22a1+1
22+1
2,a4=1
2a3+1
2=1
23a1+1
23+1
22+1
2,
a5=1
2a4+1
2=1
24a1+1
24+1
23+1
22+1
2,...,a
n=1
2
n−1a
1+1
2
n−1+1
2
n−2+···+1
2,
lim
n→+∞an= lim
n→+∞
a1
2n−1+∞
X
n=1 1
2n
=0+ 1/2
1−1/2=1
34. 0.a1a2···a
n9999 ···=0.a1a2···a
n+0.9 (10−n)+0.09 (10−n)+···
=0.a1a2···a
n+0.9 (10−n)
1−0.1=0.a1a2···a
n+10
−n
=0.a1a2···(a
n+1)=0.a1a2···(a
n+ 1) 0000 ···
35. The series converges to 1/(1 −x) only if −1<x<1.
36. P0P1=asin θ,
P1P2=asin θcos θ,
P2P3=asin θcos2θ,
P3P4=asin θcos3θ,...
(see figure)
Each sum is a geometric series.
a
P
uu
u
a sin u cos3 u
a sin u cos2 u
a sin u cos u
a sin u
P1
P0P2P4
P3
(a) P0P1+P1P2+P2P3+···=asin θ+asin θcos θ+asin θcos2θ+···=asin θ
1−cos θ
(b) P0P1+P2P3+P4P5+···=asin θ+asin θcos2θ+asin θcos4θ+···
=asin θ
1−cos2θ=asin θ
sin2θ=acsc θ
(c) P1P2+P3P4+P5P6+···=asin θcos θ+asin θcos3θ+···
=asin θcos θ
1−cos2θ=asin θcos θ
sin2θ=acot θ
371 Chapter 11
37. By inspection, θ
2−θ
4+θ
8−θ
16 +···=θ/2
1−(−1/2) =θ/3
38. A1+A2+A3+···=1+1/2+1/4+···=1
1−(1/2) =2
39. (b) 2kA
3k−2k+2kB
3k+1 −2k+1 =2k3k+1 −2k+1A+2
k3
k−2
k
B
(3k−2k)(3
k+1 −2k+1)
=3·6k−2·22kA+6k−22kB
(3k−2k)(3
k+1 −2k+1)=(3A+B)6k−(2A+B)22k
(3k−2k)(3
k+1 −2k+1)
so 3A+B= 1 and 2A+B=0,A= 1 and B=−2.
(c) sn=
n
X
k=1 2k
3k−2k−2k+1
3k+1 −2k+1 =
n
X
k=1
(ak−ak+1) where ak=2k
3k−2k.
But sn=(a
1−a
2
)+(a
2−a
3)+(a
3−a
4)+···+(a
n−a
n+1) which is a telescoping sum,
sn=a1−an+1 =2−2
n+1
3n+1 −2n+1 , lim
n→+∞sn= lim
n→+∞2−(2/3)n+1
1−(2/3)n+1 =2.
EXERCISE SET 11.4
1. (a) ∞
X
k=1
1
2k=1/2
1−1/2=1; ∞
X
k=1
1
4k=1/4
1−1/4=1/3; ∞
X
k=1 1
2k+1
4k=1+1/3=4/3
(b) ∞
X
k=1
1
5k=1/5
1−1/5=1/4; ∞
X
k=1
1
k(k+1) = 1 (Example 5, Section 11.3);
∞
X
k=1 1
5k−1
k(k+1)=1/4−1=−3/4
2. (a) ∞
X
k=2
1
k2−1=3/4 (Exercise 10, Section 11.3); ∞
X
k=2
7
10k−1=7/10
1−1/10 =7/9;
so ∞
X
k=2 1
k2−1−7
10k−1=3/4−7/9=−1/36
(b) with a=9/7,r =3/7, geometric, ∞
X
k=1
7−k3k+1 =9/7
1−(3/7) =9/4;
with a=4/5,r =2/5, geometric, ∞
X
k=1
2k+1
5k=4/5
1−(2/5) =4/3;
∞
X
k=1 7−k3k+1 −2k+1
5k=9/4−4/3=11/12
3. (a) p=3, converges (b) p=1/2, diverges (c) p=1, diverges (d) p=2/3, diverges
4. (a) p=4/3, converges (b) p=1/4, diverges (c) p=5/3, converges (d) p=π, converges
Exercise Set 11.4 372
5. (a) lim
k→+∞
k2+k+3
2k
2+1 =1
2; the series diverges. (b) lim
k→+∞1+1
kk
=e; the series diverges.
(c) lim
k→+∞cos kπ does not exist;
the series diverges.
(d) lim
k→+∞
1
k!= 0; no information
6. (a) lim
k→+∞
k
ek= 0; no information (b) lim
k→+∞ln k=+∞; the series diverges.
(c) lim
k→+∞
1
√k= 0; no information (d) lim
k→+∞
√k
√k+3 = 1; the series diverges.
7. (a) Z+∞
1
1
5x+2 = lim
`→+∞
1
5ln(5x+2)
`
1
=+∞, the series diverges by the Integral Test.
(b) Z+∞
1
1
1+9x
2dx = lim
`→+∞
1
3tan−13x`
1
=1
3π/2−tan−13,
the series converges by the Integral Test.
8. (a) Z+∞
1
x
1+x
2dx = lim
`→+∞
1
2ln(1 + x2)`
1
=+∞, the series diverges by the Integral Test.
(b) Z+∞
1(4+2x)
−3/2dx = lim
`→+∞−1/√4+2x
`
1
=1/
√
6,
the series converges by the Integral Test.
9. ∞
X
k=1
1
k+6 =∞
X
k=7
1
k, diverges because the harmonic series diverges.
10. ∞
X
k=1
3
5k=∞
X
k=1
3
51
k, diverges because the harmonic series diverges.
11. ∞
X
k=1
1
√k+5 =∞
X
k=6
1
√k, diverges because the p-series with p=1/2≤1 diverges.
12. lim
k→+∞
1
e1/k = 1, the series diverges because lim
k→+∞uk=16=0.
13. Z+∞
1(2x−1)−1/3dx = lim
`→+∞
3
4(2x−1)2/3`
1
=+∞, the series diverges by the Integral Test.
14. ln x
xis decreasing for x≥e, and Z+∞
3
ln x
x= lim
`→+∞
1
2(ln x)2`
3
=+∞,
so the series diverges by the Integral Test.
15. lim
k→+∞
k
ln(k+1) = lim
k→+∞
1
1/(k+1) =+∞, the series diverges because lim
k→+∞uk6=0.
16. Z+∞
1xe−x2dx = lim
`→+∞−1
2e−x2`
1
=e−1/2, the series converges by the Integral Test.

373 Chapter 11
17. lim
k→+∞(1+1/k)−k=1/e 6= 0, the series diverges.
18. lim
k→+∞
k2+1
k
2+3 =16= 0, the series diverges.
19. Z+∞
1
tan−1x
1+x
2dx = lim
`→+∞
1
2tan−1x2`
1
=3π
2
/32, the series converges by the Integral Test, since
d
dx
tan−1x
1+x
2=1−2xtan−1x
1+x
2<0 for x≥1.
20. Z+∞
1
1
√x2+1dx = lim
`→+∞sinh−1x`
1
=+∞, the series diverges by the Integral Test.
21. lim
k→+∞k2sin2(1/k)=16= 0, the series diverges.
22. Z+∞
1x2e−x3dx = lim
`→+∞−1
3e−x3`
1
=e−1/3,
the series converges by the Integral Test (x2e−x3is decreasing for x≥1).
23. 7∞
X
k=5
k−1.01,p-series with p>1, converges
24. Z+∞
1sech2xdx= lim
`→+∞tanh x`
1
=1−tanh(1), the series converges by the Integral Test.
25. 1
x(ln x)pis decreasing for x≥e−p, so use the Integral Test with Z+∞
e−p
dx
x(ln x)pto get
lim
`→+∞ln(ln x)`
e−p
=+∞if p= 1, lim
`→+∞
(ln x)1−p
1−p`
e−p
=
+∞if p<1
−1
(−1)ppp(p−1) if p>1
Thus the series converges for p>1.
26. Set g(x)=x(ln x)[ln(ln x)]p,g
0(x)=(1+lnx) ln(ln x)+p, so for fixed pthere exists A>0 such
that g0(x)>0,1/g(x) is decreasing for x>A; use the Integral Test with Z+∞
A
dx
x(ln x)[ln(ln x)]p
to get
lim
`→+∞ln[ln(ln x)]`
A
=+∞if p= 1, lim
`→+∞
[ln(ln x)]1−p
1−p`
A
=
+∞if p<1,
1
(p−1)[ln(ln A)]p−1if p>1
Thus the series converges for p>1.
27. (a) 3∞
X
k=1
1
k2−∞
X
k=1
1
k4=π2/2−π4/90 (b) ∞
X
k=1
1
k2−1−1
22=π2/6−5/4
(c) ∞
X
k=2
1
(k−1)4=∞
X
k=1
1
k4=π4/90
Exercise Set 11.4 374
28. (a) Suppose Σ(uk+vk) converges; then so does Σ[(uk+vk)−uk], but Σ[(uk+vk)−uk]=Σv
k
,
so Σvkconverges which contradicts the assumption that Σvkdiverges. Suppose Σ(uk−vk)
converges; then so does Σ[uk−(uk−vk)]=Σv
kwhich leads to the same contradiction as
before.
(b) Let uk=2/k and vk=1/k; then both Σ(uk+vk) and Σ(uk−vk) diverge; let uk=1/k and
vk=−1/k then Σ(uk+vk) converges; let uk=vk=1/k then Σ(uk−vk) converges.
29. (a) diverges because ∞
X
k=1
(2/3)k−1converges and ∞
X
k=1
1/k diverges.
(b) diverges because ∞
X
k=1
1/(3k+ 2) diverges and ∞
X
k=1
1/k3/2converges.
(c) converges because both ∞
X
k=2
1
k(ln k)2(Exercise 25) and ∞
X
k=2
1/k2converge.
30. (a) If S=∞
X
k=1
ukand sn=
n
X
k=1
uk, then S−sn=∞
X
k=n+1
uk. Interpret uk,k=n+1,n+2,...,as
the areas of inscribed or circumscribed rectangles with height ukand base of length one for
the curve y=f(x) to obtain the result.
(b) Add sn=
n
X
k=1
ukto each term in the conclusion of part (a) to get the desired result:
sn+Z+∞
n+1 f(x)dx <
+∞
X
k=1
uk<s
n+Z+∞
n
f(x)dx
31. (a) In Exercise 30 above let f(x)= 1
x
2. Then Z+∞
n
f(x)dx =−1
x+∞
n
=1
n;
use this result and the same result with n+ 1 replacing nto obtain the desired result.
(b) s3=1+1/4+1/9=49/36; 58/36 = s3+1
4<1
6π2<s
3+1
3=61/36
(d) 1/11 <1
6π2−s10 <1/10
32. Apply Exercise 30 with f(x)= 1
(2x+1)
2,Z+∞
n
f(x)dx =1
2(2n+1):
(a) 1
46 <∞
X
k=1
1
(2k+1)
2−s
10 <1
42
(b) π/2−tan−1(11) <∞
X
k=1
1
k2+1−s
10 <π/2−tan−1(10)
(c) 12e−11 <∞
X
k=1
k
ek<11e−10
33. (a) Z+∞
n
1
x3dx =1
2n2; use Exercise 30(b)
(b) 1
2n2−1
2(n+1)
2<0.01 for n=5.
(c) From Part (a) with n= 5 obtain 1.1995 <S<1.2057, so S≈1.203.
375 Chapter 11
34. (a) Z+∞
n
1
x4dx =1
3n3; choose nso that 1
3n3−1
3(n+1)
3<0.005,n=4; S≈1.084
35. (a) Let F(x)= 1
x
, then Zn
1
1
xdx =lnnand Zn+1
1
1
xdx = ln(n+ 1), u1=1so
ln(n+1)<s
n<1+lnn.
(b) ln(1,000,001) <s
1,000,000 <1 + ln(1,000,000), 13 <s
1,000,000 <15
(c) s109<1+ln10
9= 1 + 9 ln 10 <22
(d) sn>ln(n+1)≥100, n≥e100 −1≈2.688 ×1043;n=2.69 ×1043
36. p-series with p=lna; convergence for p>1,a>e
37. x2e−xis decreasing and positive for x>2 so the Integral Test applies:
Z∞
1x2e−xdx =(x
2+2x+2)e
−x
∞
1
=5e
−1so the series converges.
38. (a) f(x)=1/(x
3+ 1) is decreasing and continuous on the interval [1,+∞], so the Integral Test
applies.
(c) n
sn
10
0.681980
20
0.685314
30
0.685966
40
0.686199
50
0.686307
n
sn
60
0.686367
70
0.686403
80
0.686426
90
0.686442
100
0.686454
(e) Set g(n)=Z+∞
n
1
x
3+1dx =√3
6π+1
6
n3+1
(n+1)
3−√
3
3tan−12n−1
√3; for n≥10,
g(n)−g(n+1) ≤0.001; s10 +(g(10) + g(11))/2≈0.6865, so the sum ≈0.6865 to three
decimal places.
EXERCISE SET 11.5
1. (a) f(k)(x)=(−1)ke−x,f
(k)
(0)=(−1)k;e−x≈1−x+x2/2 (quadratic), e−x≈1−x(linear)
(b) f0(x)=−sin x, f00(x)=−cos x, f(0)=1,f0(0)=0,f00(0) = −1,
cos x≈1−x2/2 (quadratic), cos x≈1 (linear)
(c) f0(x) = cos x, f00(x)=−sin x, f(π/2)=1,f0(π/2)=0,f00(π/2) = −1,
sin x≈1−(x−π/2)2/2 (quadratic), sin x≈1 (linear)
(d) f(1)=1,f0(1)=1/2,f00(1) = −1/4;
√x=1+1
2
(x−1) −1
8(x−1)2(quadratic), √x≈1+1
2(x−1) (linear)
2. (a) p2(x)=1+x+x
2
/2, p1(x)=1+x
(b) p2(x)=3+1
6
(x−9) −1
216(x−9)2,p1(x)=3+1
6
(x−9)
(c) p2(x)=π
3+√
3
6(x−2) −7
72√3(x−2)2,p1(x)=π
3+√
3
6(x−2)
(d) p2(x)=x,p
1
(x)=x
Exercise Set 11.5 376
3. (a) f0(x)=1
2
x
−1/2
,f
00(x)=−1
4
x
−3/2
;f(1)=1,f0(1) = 1
2,f00(1) = −1
4;
√x≈1+1
2(x−1) −1
8(x−1)2
(b) x=1.1,x
0=1,√
1.1≈1+1
2(0.1) −1
8(0.1)2=1.04875, calculator value ≈1.0488088
4. (a) cos x≈1−x2/2
(b) 2◦=π/90 rad, cos 2◦= cos(π/90) ≈1−π2
2·902≈0.99939077, calculator value ≈0.99939083
5. f(x) = tan x, 61◦=π/3+π/180 rad; x0=π/3,f
0
(x) = sec2x, f00(x)=2sec
2xtan x;
f(π/3) = √3,f0(π/3)=4,f00(x)=8
√
3; tan x≈√3+4(x−π/3)+4
√
3(x−π/3)2,
tan 61◦= tan(π/3+π/180) ≈√3+4π/180+4
√
3(π/180)2≈1.80397443,
calculator value ≈1.80404776
6. f(x)=√
x, x0=36,f0(x)=1
2
x
−1/2
,f
00(x)=−1
4
x
−3/2
;
f(36) = 6,f0(36) = 1
12,f00(36) = −1
864;√x≈6+ 1
12(x−36) −1
1728(x−36)2;
√36.03 ≈6+0.03
12 −(0.03)2
1728 ≈6.00249947917, calculator value ≈6.00249947938
7. f(k)(x)=(−1)ke−x,f(k)(0)=(−1)k;p0(x)=1,p
1
(x)=1−x, p2(x)=1−x+1
2
x
2
,
p
3
(x)=1−x+1
2
x
2−1
3!x3,p
4
(x)=1−x+1
2
x
2−1
3!x3+1
4!x4;∞
X
k=0
(−1)k
k!xk
8. f(k)(x)=a
k
e
ax,f(k)(0) = ak;p0(x)=1,p
1
(x)=1+ax, p2(x)=1+ax +a2
2x2,
p3(x)=1+ax +a2
2x2+a3
3! x3,p
4
(x)=1+ax +a2
2x2+a3
3! x3+a4
4! x4;∞
X
k=0
ak
k!xk
9. f(k)(0) = 0 if kis odd, f(k)(0) is alternately πkand −πkif kis even; p0(x)=1,p
1
(x)=1,
p
2
(x)=1−π
2
2! x2;p3(x)=1−π
2
2! x2,p
4
(x)=1−π
2
2! x2+π4
4! x4;∞
X
k=0
(−1)kπ2k
(2k)! x2k
10. f(k)(0) = 0 if kis even, f(k)(0) is alternately πkand −πkif kis odd; p0(x)=0,p
1
(x)=πx,
p2(x)=πx;p3(x)=πx −π3
3! x3,p
4
(x)=πx −π3
3! x3;∞
X
k=0
(−1)kπ2k+1
(2k+ 1)! x2k+1
11. f(0)(0) = 0; for k≥1, f(k)(x)=(−1)k+1(k−1)!
(1+x)k,f(k)(0)=(−1)k+1(k−1)!; p0(x)=0,
p
1
(x)=x, p2(x)=x−1
2
x
2
,p
3
(x)=x−1
2
x
2+1
3
x
3
,p
4
(x)=x−1
2
x
2+1
3
x
3−1
4
x
4
;∞
X
k=1
(−1)k+1
kxk
12. f(k)(x)=(−1)kk!
(1+x)k+1 ;f(k)(0)=(−1)kk!; p0(x)=1,p
1
(x)=1−x,
p2(x)=1−x+x
2
,p
3
(x)=1−x+x
2−x
3
,p
4
(x)=1−x+x
2−x
3+x
4
;∞
X
k=0
(−1)kxk

377 Chapter 11
13. f(k)(0) = 0 if kis odd, f(k)(0) = 1 if kis even; p0(x)=1,p
1(x)=1,
p
2
(x)=1+x
2
/2,p
3
(x)=1+x
2
/2,p
4
(x)=1+x
2
/2+x
4/4!; ∞
X
k=0
1
(2k)!x2k
14. f(k)(0) = 0 if kis even, f(k)(0) = 1 if kis odd; p0(x)=0,p
1
(x)=x, p2(x)=x,
p3(x)=x+x
3
/3!,p
4
(x)=x+x
3
/3!; ∞
X
k=0
1
(2k+ 1)!x2k+1
15. f(k)(x)=((−1)k/2(xsin x−kcos x)keven
(−1)(k−1)/2(xcos x+ksin x)kodd ,f
(k)
(0) = ((−1)1+k/2kkeven
0kodd
p0(x)=0,p
1
(x)=0,p
2
(x)=x
2
,p
3(x)=x
2
,p
4
(x)=x
2−1
6
x
4
;∞
X
k=0
(−1)k
(2k+ 1)!x2k+2
16. f(k)(x)=(k+x)e
x
,f
(k)
(0) = k;p0(x)=0,p
1
(x)=x, p2(x)=x+x
2
,
p
3
(x)=x+x
2+1
2
x
3
,p
4
(x)=x+x
2+1
2
x
3+1
3!x4;∞
X
k=1
1
(k−1)!xk
17. (a) f(0)=1,f0(0)=2,f00(0) = −2,f000(0)=6,f(k)(0) = 0 for k≥4;
the Maclaurin series for f(x)isf(x).
(b) f(k)(0) = k!ckfor k≤n, and f(k)(0) = 0 for k>n; the Maclaurin series for f(x)isf(x).
19. f(k)(x0)=e;p
0
(x)=e, p1(x)=e+e(x−1),
p2(x)=e+e(x−1) + e
2(x−1)2,p
3
(x)=e+e(x−1) + e
2(x−1)2+e
3!(x−1)3,
p4(x)=e+e(x−1) + e
2(x−1)2+e
3!(x−1)3+e
4!(x−1)4;∞
X
k=0
e
k!(x−1)k
20. f(k)(x)=(−1)ke−x,f
(k)
(ln 2) = (−1)k1
2;p0(x)=1
2
,p
1
(x)=1
2−1
2
(x−ln 2),
p2(x)=1
2−1
2
(x−ln 2)+ 1
2·2(x−ln 2)2,p
3
(x)=1
2−1
2
(x−ln 2)+ 1
2·2(x−ln 2)2−1
2·3!(x−ln 2)3,
p4(x)=1
2−1
2
(x−ln 2) + 1
2·2(x−ln 2)2−1
2·3!(x−ln 2)3+1
2·4!(x−ln 2)4;
∞
X
k=0
(−1)k
2·k!(x−ln 2)k
21. f(k)(x)=(−1)kk!
xk+1 ,f(k)(−1) = −k!; p0(x)=−1; p1(x)=−1−(x+ 1);
p2(x)=−1−(x+1)−(x+1)
2;p
3(x)=−1−(x+1)−(x+1)
2−(x+1)
3;
p
4(x)=−1−(x+1)−(x+1)
2−(x+1)
3−(x+1)
4;∞
X
k=0
(−1)(x+1)
k
Exercise Set 11.5 378
22. f(k)(x)= (−1)kk!
(x+2)
k+1 ,f(k)(3) = (−1)kk!
5k+1 ;p0(x)=1
5
;p
1
(x)=1
5−1
25(x−3);
p2(x)=1
5−1
25(x−3) + 1
125(x−3)2;p3(x)=1
5−1
25(x−3) + 1
125(x−3)2−1
625(x−3)3;
p4(x)=1
5−1
25(x−3) + 1
125(x−3)2−1
625(x−3)3+1
3025(x−3)4;∞
X
k=0
(−1)k
5k+1 (x−3)k
23. f(k)(1/2)=0ifkis odd, f(k)(1/2) is alternately πkand −πkif kis even;
p0(x)=p
1
(x)=1,p
2(x)=p
3
(x)=1−π
2
2(x−1/2)2,
p4(x)=1−π
2
2(x−1/2)2+π4
4! (x−1/2)4;∞
X
k=0
(−1)kπ2k
(2k)! (x−1/2)2k
24. f(k)(π/2)=0ifkis even, f(k)(π/2) is alternately −1and1ifkis odd; p0(x)=0,
p
1
(x)=−(x−π/2),p
2
(x)=−(x−π/2),p
3
(x)=−(x−π/2) + 1
3!(x−π/2)3,
p4(x)=−(x−π/2) + 1
3!(x−π/2)3;∞
X
k=0
(−1)k+1
(2k+ 1)!(x−π/2)2k+1
25. f(1) = 0, for k≥1,f(k)(x)=(−1)k−1(k−1)!
xk;f(k)(1)=(−1)k−1(k−1)!;
p0(x)=0,p
1
(x)=(x−1); p2(x)=(x−1) −1
2(x−1)2;p3(x)=(x−1) −1
2(x−1)2+1
3(x−1)3,
p4(x)=(x−1) −1
2(x−1)2+1
3(x−1)3−1
4(x−1)4;∞
X
k=1
(−1)k−1
k(x−1)k
26. f(e)=1,fork≥1,f(k)(x)=(−1)k−1(k−1)!
xk;f(k)(e)=(−1)k−1(k−1)!
ek;
p0(x)=1,p
1
(x)=1+1
e
(x−e); p2(x)=1+1
e
(x−e)−1
2e
2(x−e)
2
;
p
3
(x)=1+1
e
(x−e)−1
2e
2(x−e)
2+1
3e
3(x−e)
3
,
p
4
(x)=1+1
e
(x−e)−1
2e
2(x−e)
2+1
3e
3(x−e)
3−1
4e
4(x−e)
4
;1+
∞
X
k=1
(−1)k−e
kek(x−e)k
27. (a) f(1)=1,f0(1)=2,f00(1) = −2,f000(1)=6,f(k)(1) = 0 for k≥4;
the Taylor series for f(x)isf(x).
(b) f(k)(x0)=k!c
kfor k≤n; for k > n, f(k)(x0) = 0; the Taylor series for f(x)isf(x).

379 Chapter 11
29. f(k)(0)=(−2)k;p0(x)=1,p
1
(x)=1−2x,
p2(x)=1−2x+2x
2,p
3
(x)=1−2x+2x
2−4
3x
3
4
-1
-0.6 0.6
30. f(k)(π/2)=0ifkis odd, f(k)(π/2) is alternately 1
and −1ifkis even; p0(x)=1,p
2
(x)=1−1
2
(x−π/2)2,
p4(x)=1−1
2
(x−π/2)2+1
24(x−π/2)4,
p6(x)=1−1
2
(x−π/2)2+1
24(x−π/2)4−1
720(x−π/2)6
1.25
-1.25
^i
31. f(k)(π)=0ifkis odd, f(k)(π/2) is alternately −1
and1ifkis even; p0(x)=−1,p
2
(x)=−1+1
2(x−π)
2,
p
4(x)=−1+1
2(x−π)
2−1
24(x−π)4,
p6(x)=−1+1
2(x−π)
2−1
24(x−π)4+1
720(x−π)6
1.25
-1.25
0o
32. f(0) = 0; for k≥1,f(k)(x)=(−1)k−1(k−1)!
(x+1)
k,
f(k)(0)=(−1)k−1(k−1)!; p0(x)=0,p
1
(x)=x,
p
2
(x)=x−1
2
x
2
,p
3
(x)=x−1
2
x
2+1
3
x
3
1.5
-1.5
-1 1
33. p(0)=1,p(x) has slope −1atx= 0, and p(x) is concave up at x= 0, eliminating I, II and III
respectively and leaving IV.
34. Let p0(x)=2,p
1(x)=p
2
(x)=1−3x, p3(x)=1−3x+x
3
, and, for any arbitrary integer n≥4
and constants c4,c
5,...,c
n, let pn(x)=2−3(x−1)+(x−1)3+
n
X
k=4
ck(x−1)k; then any of the
polynomials p0,p
1,...,p
nis a possible Taylor polynomial for fabout x=1.
35. f(k)(ln 4) = 15/8 for keven, f(k)(ln4) = 17/8 for kodd, which can be written as
f(k)(ln 4) = 16 −(−1)k
8;∞
X
k=0
16 −(−1)k
8k!(x−ln 4)k
Exercise Set 11.6 380
36. (a) cos α≈1−α2/2; x=r−rcos α=r(1 −cos α)≈rα2/2
(b) In Figure Ex-36 let r= 4000 mi and α=1/80 so that the arc has length 2rα = 100 mi.
Then x≈rα2/2= 4000
2·802=5/16 mi.
37. From Exercise 2(a), p1(x)=1+x,p
2
(x)=1+x+x
2
/2
(a) 3
-1
-1 1
(b) x
f(x)
p1(x)
p2(x)
–1.000
0.431
0.000
0.500
–0.750
0.506
0.250
0.531
–0.500
0.619
0.500
0.625
–0.250
0.781
0.750
0.781
0.000
1.000
1.000
1.000
0.250
1.281
1.250
1.281
0.500
1.615
1.500
1.625
0.750
1.977
1.750
2.031
1.000
2.320
2.000
2.500
(c) |esin x−(1+x)|<0.01
for −0.14 <x<0.14
0.01
0
-0.15 0.15
(d) |esin x−(1+x+x2/2)|<0.01
for −0.50 <x<0.50
0.015
0
-0.6 0.6
EXERCISE SET 11.6
1. (a) 1
5k2−k≤1
5k2−k2=1
4k2,∞
X
k=1
1
4k2converges
(b) 3
k−1/4>3
k,∞
X
k=1
3/k diverges
2. (a) k+1
k
2−k>k
k
2=1
k,∞
X
k=2
1/k diverges (b) 2
k4+k<2
k4,∞
X
k=1
2
k4converges
3. (a) 1
3k+5 <1
3
k,∞
X
k=1
1
3kconverges (b) 5 sin2k
k!<5
k!,∞
X
k=1
5
k!converges
4. (a) ln k
k>1
kfor k≥3, ∞
X
k=1
1
kdiverges
(b) k
k3/2−1/2>k
k3/2=1
√k;∞
X
k=1
1
√kdiverges
381 Chapter 11
5. compare with the convergent series ∞
X
k=1
1/k5,ρ= lim
k→+∞
4k7−2k6+6k
5
8k
7+k−8=1/2, converges
6. compare with the divergent series ∞
X
k=1
1/k,ρ= lim
k→+∞
k
9k+6 =1/9, diverges
7. compare with the convergent series ∞
X
k=1
5/3k,ρ= lim
k→+∞
3k
3k+1 = 1, converges
8. compare with the divergent series ∞
X
k=1
1/k,ρ= lim
k→+∞
k2(k+3)
(k+ 1)(k+ 2)(k+5) = 1, diverges
9. compare with the divergent series ∞
X
k=1
1
k2/3,
ρ= lim
k→+∞
k2/3
(8k2−3k)1/3= lim
k→+∞
1
(8 −3/k)1/3=1/2, diverges
10. compare with the convergent series ∞
X
k=1
1/k17,
ρ= lim
k→+∞
k17
(2k+3)
17 = lim
k→+∞
1
(2+3/k)17 =1/2
17, converges
11. ρ= lim
k→+∞
3k+1/(k+ 1)!
3k/k!= lim
k→+∞
3
k+1 = 0, the series converges
12. ρ= lim
k→+∞
4k+1/(k+1)
2
4
k
/k2= lim
k→+∞
4k2
(k+1)
2= 4, the series diverges
13. ρ= lim
k→+∞
k
k+1 = 1, the result is inconclusive
14. ρ= lim
k→+∞
(k+ 1)(1/2)k+1
k(1/2)k= lim
k→+∞
k+1
2k=1/2, the series converges
15. ρ= lim
k→+∞
(k+ 1)!/(k+1)
3
k!/k3= lim
k→+∞
k3
(k+1)
2=+∞, the series diverges
16. ρ= lim
k→+∞
(k+1)/[(k+1)
2+1]
k/(k2+1) = lim
k→+∞
(k+ 1)(k2+1)
k(k
2+2k+2) = 1, the result is inconclusive.
17. ρ= lim
k→+∞
3k+2
2k−1=3/2, the series diverges
18. ρ= lim
k→+∞k/100=+∞, the series diverges
19. ρ= lim
k→+∞
k1/k
5=1/5, the series converges
20. ρ= lim
k→+∞(1 −e−k) = 1, the result is inconclusive

Exercise Set 11.6 382
21. Ratio Test, ρ= lim
k→+∞7/(k+ 1) = 0, converges
22. Limit Comparison Test, compare with the divergent series ∞
X
k=1
1/k
23. Ratio Test, ρ= lim
k→+∞
(k+1)
2
5k
2=1/5, converges
24. Ratio Test, ρ= lim
k→+∞(10/3)(k+1)=+∞, diverges
25. Ratio Test, ρ= lim
k→+∞e−1(k+1)
50/k50 =e−1<1, converges
26. Limit Comparison Test, compare with the divergent series ∞
X
k=1
1/k
27. Limit Comparison Test, compare with the convergent series ∞
X
k=1
1/k5/2,ρ= lim
k→+∞
k3
k3+1 =1,
converges
28. 4
2+3
k
k<4
3
k
k,∞
X
k=1
4
3kkconverges (Ratio Test) so ∞
X
k=1
4
2+k3
kconverges by the Comparison Test
29. Limit Comparison Test, compare with the divergent series ∞
X
k=1
1/k,ρ= lim
k→+∞
k
√k2+k=1,
diverges
30. 2+(−1)k
5k≤3
5k,∞
X
k=1
3/5kconverges so ∞
X
k=1
2+(−1)k
5kconverges
31. Limit Comparison Test, compare with the convergent series ∞
X
k=1
1/k5/2,
ρ= lim
k→+∞
k3+2k
5/2
k
3+3k
2+3k= 1, converges
32. 4+|cos k|
k3<5
k3,∞
X
k=1
5/k3converges so ∞
X
k=1
4+|cos k|
k3converges
33. Limit Comparison Test, compare with ∞
X
k=1
1/√k
34. Ratio Test, ρ= lim
k→+∞(1+1/k)−k=1/e < 1, converges
35. Ratio Test, ρ= lim
k→+∞
ln(k+1)
eln k= lim
k→+∞
k
e(k+1) =1/e < 1, converges
36. Ratio Test, ρ= lim
k→+∞
k+1
e
2k+1 = lim
k→+∞
1
2e2k+1 = 0, converges
37. Ratio Test, ρ= lim
k→+∞
k+5
4(k+1) =1/4, converges
383 Chapter 11
38. Root Test, ρ= lim
k→+∞(k
k+1)
k= lim
k→+∞
1
(1+1/k)k=1/e, converges
39. diverges because lim
k→+∞
1
4+2
−k=1/46=0
40. ∞
X
k=1
√kln k
k3+1 =∞
X
k=2
√kln k
k3+1 because ln1 = 0, √kln k
k3+1 <kln k
k3=ln k
k2,
Z+∞
2
ln x
x2dx = lim
`→+∞−ln x
x−1
x`
2
=1
2(ln 2+1) so ∞
X
k=2
ln k
k2converges and so does ∞
X
k=1
√kln k
k3+1.
41. tan−1k
k2<π/2
k2,∞
X
k=1
π/2
k2converges so ∞
X
k=1
tan−1k
k2converges
42. 5k+k
k!+3 <5
k+5
k
k!=25
k
k!,∞
X
k=1
25k
k!converges (Ratio Test) so ∞
X
k=1
5k+k
k!+3 converges
43. Ratio Test, ρ= lim
k→+∞
(k+1)
2
(2k+ 2)(2k+1) =1/4, converges
44. Ratio Test, ρ= lim
k→+∞
2(k+1)
2
(2k+ 4)(2k+3) =1/2, converges
45. uk=k!
1·3·5···(2k−1), by the Ratio Test ρ= lim
k→+∞
k+1
2k+1 =1/2; converges
46. uk=1·3·5···(2k−1)
(2k−1)! , by the Ratio Test ρ= lim
k→+∞
1
2k= 0; converges
47. Root Test: ρ= lim
k→+∞
1
3(ln k)1/k =1/3, converges
48. Root Test: ρ= lim
k→+∞
π(k+1)
k
1+1/k = lim
k→+∞πk+1
k=π, diverges
49. (b) ρ= lim
k→+∞
sin(π/k)
π/k = 1 and ∞
X
k=1
π/k diverges
50. (a) cos x≈1−x2/2,1−cos 1
k≈1
2k2(b) ρ= lim
k→+∞
1−cos(1/k)
1/k2= 2, converges
51. Set g(x)=√
x−ln x;d
dxg(x)= 1
2
√
x−1
x= 0 when x= 4. Since lim
x→0+ g(x) = lim
x→+∞g(x)=+∞
it follows that g(x) has its minimum at x=4,g(4) = √4−ln 4 >0, and thus √x−ln x>0 for
x>0.
(a) ln k
k2<√k
k2=1
k3/2,∞
X
k=1
1
k3/2converges so ∞
X
k=1
ln k
k2converges.
(b) 1
(ln k)2>1
k,∞
X
k=2
1
kdiverges so ∞
X
k=2
1
(ln k)2diverges.
Exercise Set 11.7 384
52. By the Root Test, ρ= lim
k→+∞
α
(k1/k)α=α
1α=α, the series converges if α<1 and diverges
if α>1. If α= 1 then the series is ∞
X
k=1
1/k which diverges.
53. (a) If Pbkconverges, then set M=Pbk. Then a1+a2+···+a
n≤b
1+b
2+···+b
n≤M;
apply Theorem 11.4.6 to get convergence of Pak.
(b) Assume the contrary, that Pbkconverges; then use part (a) of the Theorem to show that
Pakconverges, a contradiction.
54. (a) If lim
k→+∞(ak/bk) = 0 then for k≥K,ak/bk<1, ak<b
kso Pakconverges by the Comparison
Test.
(b) If lim
k→+∞(ak/bk)=+∞then for k≥K,ak/bk>1, ak>b
kso Pakdiverges by the
Comparison Test.
EXERCISE SET 11.7
1. ak+1 <a
k
,lim
k→+∞ak=0,a
k>0
2. ak+1
ak
=k
3(k+1) <1
3for k>0, so {ak}is decreasing and tends to zero.
3. diverges because lim
k→+∞ak= lim
k→+∞
k+1
3k+1 =1/36=0
4. diverges because lim
k→+∞ak= lim
k→+∞
k+1
√
k+1 =+∞6=0
5. {e−k}is decreasing and lim
k→+∞e−k= 0, converges
6. ln k
kis decreasing and lim
k→+∞
ln k
k= 0, converges
7. ρ= lim
k→+∞
(3/5)k+1
(3/5)k=3/5,converges absolutely
8. ρ= lim
k→+∞
2
k+1 = 0, converges absolutely
9. ρ= lim
k→+∞
3k2
(k+1)
2= 3, diverges
10. ρ= lim
k→+∞
k+1
5k=1/5, converges absolutely
11. ρ= lim
k→+∞
(k+1)
3
ek3=1/e, converges absolutely
12. ρ= lim
k→+∞
(k+1)
k+1k!
(k+ 1)!kk= lim
k→+∞(1+1/k)k=e, diverges
385 Chapter 11
13. conditionally convergent, ∞
X
k=1
(−1)k+1
3kconverges by the Alternating Series Test but ∞
X
k=1
1
3kdiverges
14. absolutely convergent, ∞
X
k=1
1
k4/3converges
15. divergent, lim
k→+∞ak6=0
16. absolutely convergent, Ratio Test for absolute convergence
17. ∞
X
k=1
cos kπ
k=∞
X
k=1
(−1)k
kis conditionally convergent, ∞
X
k=1
(−1)k
kconverges by the Alternating Series
Test but ∞
X
k=1
1/k diverges.
18. conditionally convergent, ∞
X
k=3
(−1)kln k
kconverges by the Alternating Series Test but ∞
X
k=3
ln k
k
diverges (Limit Comparison Test with P1/k).
19. conditionally convergent, ∞
X
k=1
(−1)k+1 k+2
k(k+3) converges by the
Alternating Series Test but ∞
X
k=1
k+2
k(k+3) diverges (Limit Comparison Test with P1/k)
20. conditionally convergent, ∞
X
k=1
(−1)k+1k2
k3+1 converges by the Alternating Series Test but
∞
X
k=1
k2
k3+1 diverges (Limit Comparison Test with P(1/k))
21. ∞
X
k=1
sin(kπ/2)=1+0−1+0+1+0−1+0+···, divergent ( lim
k→+∞sin(kπ/2) does not exist)
22. absolutely convergent, ∞
X
k=1
|sin k|
k3converges (compare with P1/k3)
23. conditionally convergent, ∞
X
k=2
(−1)k
kln kconverges by the Alternating Series Test but ∞
X
k=2
1
kln kdiverges
(Integral Test)
24. conditionally convergent, ∞
X
k=1
(−1)k
pk(k+1) converges by the Alternating Series Test but
∞
X
k=1
1
pk(k+1) diverges (Limit Comparison Test with P1/k)
25. absolutely convergent, ∞
X
k=2
(1/ln k)kconverges by the Root Test
Exercise Set 11.7 386
26. conditionally convergent, ∞
X
k=1
(−1)k+1
√k+1+√
kconverges by the Alternating Series Test but
∞
X
k=1
1
√k+1+√
kdiverges (Limit Comparison Test with P1/√k)
27. conditionally convergent, let f(x)=x
2+1
x
3+2 then f0(x)=x(4 −3x−x3)
(x3+2)
2≤0 for x≥2so
{a
k
}
+∞
k=2 =k2+1
k
3+2+∞
k=2
is nonincreasing, lim
k→+∞ak= 0; the series converges by the
Alternating Series Test but ∞
X
k=2
k2+1
k
3+2 diverges (Limit Comparison Test with P1/k)
28. ∞
X
k=1
kcos kπ
k2+1 =∞
X
k=1
(−1)kk
k2+1 is conditionally convergent, ∞
X
k=1
(−1)kk
k2+1 converges by the
Alternating Series Test but ∞
X
k=1
k
k2+1 diverges
29. absolutely convergent by the Ratio Test, ρ= lim
k→+∞
k+1
(2k+ 1)(2k)=0
30. divergent, lim
k→+∞ak=+∞31. |error|<a
8=1/8=0.125
32. |error|<a
6=1/6! <0.0014 33. |error|<a
100 =1/
√
100=0.1
34. |error|<a
4=1/(5 ln 5) <0.125
35. |error|<0.0001 if an+1 ≤0.0001, 1/(n+1)≤0.0001, n+1≥10,000, n≥9,999, n=9,999
36. |error|<0.00001 if an+1 ≤0.00001, 1/(n+ 1)! ≤0.00001, (n+ 1)! ≥100,000. But 8! = 40,320,
9! = 362,880 so (n+ 1)! ≥100,000 if n+1≥9, n≥8, n=8
37. |error|<0.005 if an+1 ≤0.005, 1/√n+1≤0.005, √n+1 ≥200, n+1≥40,000, n≥39,999,
n=39,999
38. |error|<0.05 if an+1 ≤0.05, 1/[(n+ 2) ln(n+ 2)] ≤0.05, (n+ 2) ln(n+2)≥20. But 9 ln 9 ≈19.8
and 10 ln 10 ≈23.0so(n+ 2) ln(n+2)≥20 if n+2≥10, n≥8, n=8
39. ak=3
2k+1 ,|error|<a
11 =3
212 <0.00074; s10 ≈0.4995; S=3/4
1−(−1/2) =0.5
40. ak=2
3k−1
,|error|<a
11 =2
310
<0.01735; s10 ≈0.5896; S=1
1−(−2/3) =0.6
41. ak=1
(2k−1)!,an+1 =1
(2n+ 1)! ≤0.005, (2n+ 1)! ≥200, 2n+1≥6, n≥2.5; n=3,
s
3=1−1/6+1/120 ≈0.84
42. ak=1
(2k−2)!,an+1 =1
(2n)! ≤0.005, (2n)! ≥200, 2n≥6, n≥3; n=3,s
3≈0.54

387 Chapter 11
43. ak=1
k2k,an+1 =1
(n+ 1)2n+1 ≤0.005, (n+ 1)2n+1 ≥200, n+1≥6, n≥5; n=5,s
5≈0.41
44. ak=1
(2k−1)5+ 4(2k−1),an+1 =1
(2n+1)
5+ 4(2n+1) ≤0.005,
(2n+1)
5+ 4(2n+1)≥200, 2n+1≥3, n≥1; n=1,s
1=0.20
45. (c) ak=1
2k−1,an+1 =1
2n+1 ≤10−2,2n+1≥100, n≥49.5; n=50
46. P(1/kp) converges if p>1 and diverges if p≤1, so ∞
X
k=1
(−1)k1
kpconverges absolutely if p>1,
and converges conditionally if 0 <p≤1 since it satisfies the Alternating Series Test; it diverges
for p≤0 since lim
k→+∞ak6=0.
47. 1+ 1
3
2+1
5
2+···=1+ 1
2
2+1
3
2+···−1
2
2+1
4
2+1
6
2+···
=π
2
6−1
2
21+ 1
2
2+1
3
2+···=π
2
6−1
4
π
2
6=π
2
8
48. 1+ 1
3
4+1
5
4+···=1+ 1
2
4+1
3
4+···−1
2
4+1
4
4+1
6
4+···
=π
4
90 −1
241+ 1
2
4+1
3
4+···=π
4
90 −1
16
π4
90 =π4
96
49. Every positive integer can be written in exactly one of the three forms 2k−1or4k−2or4k,
so a rearrangement is
1−1
2−1
4+1
3−1
6−1
8+1
5−1
10 −1
12+···+1
2k−1−1
4k−2−1
4k+···
=1
2−1
4+1
6−1
8+1
10 −1
12+···+1
4k−2−1
4k+···=1
2ln 2
50. (a) 1.5
0
010
(b) Yes; since f(x) is decreasing for x≥1
and lim
x→+∞f(x) = 0, so the series
satisfies the Alternating Series Test.
51. (a) The distance dfrom the starting point is
d= 180 −180
2+180
3−···− 180
1000 = 180 1−1
2+1
3−···− 1
1000.
From Theorem 11.7.2, 1 −1
2+1
3−···− 1
1000 differs from ln 2 by less than 1/1001 so
180(ln 2 −1/1001) <d<180 ln 2, 124.58 <d<124.77.
Exercise Set 11.8 388
(b) The total distance traveled is s= 180 + 180
2+180
3+···+180
1000, and from inequality (2) in
Section 11.4,
Z1001
1
180
xdx<s<180 + Z1000
1
180
xdx
180 ln 1001 <s<180(1 + ln 1000)
1243 <s<1424
52. (a) Suppose Σ|ak|converges, then lim
k→+∞|ak|=0so|a
k
|<1 for k≥Kand thus |ak|2<|ak|,
a2
k<|ak|hence Σa2
kconverges by the Comparison Test.
(b) Let ak=1
k, then Pa2
kconverges but Pakdiverges.
EXERCISE SET 11.8
1. geometric series, ρ= lim
k→+∞
uk+1
uk=|x|, so the interval of convergence is −1<x<1, converges
there to 1
1+x(the series diverges for x=±1)
2. geometric series, ρ= lim
k→+∞
uk+1
uk=|x|2, so the interval of convergence is −1<x<1, converges
there to 1
1−x2(the series diverges for x=±1)
3. geometric series, ρ= lim
k→+∞
uk+1
uk=|x−2|, so the interval of convergence is 1 <x<3, converges
there to 1
1−(x−2) =1
3−x(the series diverges for x=1,3)
4. geometric series, ρ= lim
k→+∞
uk+1
uk=|x+3|, so the interval of convergence is −4<x<−2,
converges there to 1
1+(x+3) =1
4+x(the series diverges for x=−4,−2)
5. (a) geometric series, ρ= lim
k→+∞
uk+1
uk=|x/2|, so the interval of convergence is −2<x<2,
converges there to 1
1+x/2=2
2+x; (the series diverges for x=−2,2)
(b) f(0)=1; f(1)=2/3
6. (a) geometric series, ρ= lim
k→+∞
uk+1
uk=
x−5
3, so the interval of convergence is 2 <x<8,
converges to 1
1+(x−5)/3=3
x−2(the series diverges for x=2,8)
(b) f(3)=3,f(6)=3/4
389 Chapter 11
7. ρ= lim
k→+∞
k+1
k+2|x|=|x|, the series converges if |x|<1 and diverges if |x|>1. If x=−1,
∞
X
k=0
(−1)k
k+1 converges by the Alternating Series Test; if x=1, ∞
X
k=0
1
k+1 diverges. The radius of
convergence is 1, the interval of convergence is [−1,1).
8. ρ= lim
k→+∞3|x|=3|x|, the series converges if 3|x|<1or|x|<1/3 and diverges if |x|>1/3. If
x=−1/3, ∞
X
k=0
(−1)kdiverges, if x=1/3, ∞
X
k=0
(1) diverges. The radius of convergence is 1/3, the
interval of convergence is (−1/3, 1/3).
9. ρ= lim
k→+∞|x|
k+1 = 0, the radius of convergence is +∞, the interval is (−∞,+∞).
10. ρ= lim
k→+∞
k+1
2|x|=+∞, the radius of convergence is 0, the series converges only if x=0.
11. ρ= lim
k→+∞
5k2|x|
(k+1)
2=5|x|, converges if |x|<1/5 and diverges if |x|>1/5. If x=−1/5, ∞
X
k=1
(−1)k
k2
converges; if x=1/5, ∞
X
k=1
1/k2converges. Radius of convergence is 1/5, interval of convergence is
[−1/5,1/5].
12. ρ= lim
k→+∞
ln k
ln(k+1)|x|=|x|, the series converges if |x|<1 and diverges if |x|>1. If x=−1,
∞
X
k=2
(−1)k
ln kconverges; if x=1, ∞
X
k=2
1/(ln k) diverges (compare to P(1/k)). Radius of convergence
is 1, interval of convergence is [−1,1).
13. ρ= lim
k→+∞
k|x|
k+2 =|x|, converges if |x|<1, diverges if |x|>1. If x=−1, ∞
X
k=1
(−1)k
k(k+1) converges;
if x=1, ∞
X
k=1
1
k(k+1) converges. Radius of convergence is 1, interval of convergence is [−1,1].
14. ρ= lim
k→+∞2k+1
k+2|x|=2|x|, converges if |x|<1/2, diverges if |x|>1/2. If x=−1/2, ∞
X
k=0
−1
2(k+1)
diverges; if x=1/2, ∞
X
k=0
(−1)k
2(k+1) converges. Radius of convergence is 1/2, interval of convergence
is (−1/2,1/2].
15. ρ= lim
k→+∞
√k
√k+1|x|=|x|, converges if |x|<1, diverges if |x|>1. If x=−1, ∞
X
k=1
−1
√kdiverges; if
x=1, ∞
X
k=1
(−1)k−1
√kconverges. Radius of convergence is 1, interval of convergence is (−1,1].
Exercise Set 11.8 390
16. ρ= lim
k→+∞|x|2
(2k+ 2)(2k+1) = 0, radius of convergence is +∞, interval of convergence is (−∞,+∞).
17. ρ= lim
k→+∞|x|2
(2k+ 3)(2k+2) = 0, radius of convergence is +∞, interval of convergence is (−∞,+∞).
18. ρ= lim
k→+∞
k3/2|x|3
(k+1)
3/2=|x|
3, converges if |x|<1, diverges if |x|>1. If x=−1, ∞
X
k=0
1
k3/2converges;
if x=1, ∞
X
k=0
(−1)k
k3/2converges. Radius of convergence is 1, interval of convergence is [−1,1].
19. ρ= lim
k→+∞
3|x|
k+1 = 0, radius of convergence is +∞, interval of convergence is (−∞,+∞).
20. ρ= lim
k→+∞
k(ln k)2|x|
(k+ 1)[ln(k+ 1)]2=|x|, converges if |x|<1, diverges if |x|>1. If x=−1, then, by
Exercise 11.4.25, ∞
X
k=2
−1
k(ln k)2converges; if x=1, ∞
X
k=2
(−1)k+1
k(ln k)2converges. Radius of convergence
is 1, interval of convergence is [−1,1].
21. ρ= lim
k→+∞
1+k
2
1+(k+1)
2|x|=|x|, converges if |x|<1, diverges if |x|>1. If x=−1, ∞
X
k=0
(−1)k
1+k
2
converges; if x=1, ∞
X
k=0
1
1+k
2converges. Radius of convergence is 1, interval of convergence is
[−1,1].
22. ρ= lim
k→+∞
1
2|x−3|=1
2|x−3|, converges if |x−3|<2, diverges if |x−3|>2. If x=1, ∞
X
k=0
(−1)k
diverges; if x=5, ∞
X
k=0
1 diverges. Radius of convergence is 2, interval of convergence is (1,5).
23. ρ= lim
k→+∞
k|x+1|
k+1 =|x+1|, converges if |x+1|<1, diverges if |x+1|>1. If x=−2, ∞
X
k=1
−1
k
diverges; if x=0, ∞
X
k=1
(−1)k+1
kconverges. Radius of convergence is 1, interval of convergence is
(−2,0].
24. ρ= lim
k→+∞
(k+1)
2
(k+2)
2|x−4|=|x−4|, converges if |x−4|<1, diverges if |x−4|>1. If x=3,
∞
X
k=0
1/(k+1)2converges; if x=5, ∞
X
k=0
(−1)k/(k+1)2converges. Radius of convergence is 1, interval
of convergence is [3,5].

391 Chapter 11
25. ρ= lim
k→+∞(3/4)|x+5|=3
4
|x+5|, converges if |x+5|<4/3, diverges if |x+5|>4/3. If
x=−19/3, ∞
X
k=0
(−1)kdiverges; if x=−11/3, ∞
X
k=0
1 diverges. Radius of convergence is 4/3, interval
of convergence is (−19/3,−11/3).
26. ρ= lim
k→+∞
(2k+ 3)(2k+2)k
3
(k+1)
3|x−2|=+∞, radius of convergence is 0,
series converges only at x=2.
27. ρ= lim
k→+∞
k2+4
(k+1)
2+4|x+1|2=|x+1|2, converges if |x+1|<1, diverges if |x+1|>1. If x=−2,
∞
X
k=1
(−1)3k+1
k2+4 converges; if x=0, ∞
X
k=1
(−1)k
k2+4 converges. Radius of convergence is 1, interval of
convergence is [−2,0].
28. ρ= lim
k→+∞
kln(k+1)
(k+1)lnk|x−3|=|x−3|, converges if |x−3|<1, diverges if |x−3|>1. If
x=2, ∞
X
k=1
(−1)kln k
kconverges; if x=4, ∞
X
k=1
ln k
kdiverges. Radius of convergence is 1, interval of
convergence is [2,4).
29. ρ= lim
k→+∞
π|x−1|2
(2k+ 3)(2k+2) = 0, radius of convergence +∞, interval of convergence (−∞,+∞).
30. ρ= lim
k→+∞
1
16|2x−3|=1
16|2x−3|, converges if 1
16|2x−3|<1or|x−3/2|<8, diverges if
|x−3/2|>8. If x=−13/2, ∞
X
k=0
(−1)kdiverges; if x=19/2, ∞
X
k=0
1 diverges. Radius of convergence
is 8, interval of convergence is (−13/2,19/2).
31. ρ= lim
k→+∞
k
p|uk|= lim
k→+∞|x|
ln k= 0, the series converges absolutely for all xso the interval of
convergence is (−∞,+∞).
32. ρ= lim
k→+∞
2k+1
(2k)(2k−1)|x|=0
so R=+∞.
33. (a) 10
-1
-1 1

Exercise Set 11.8 392
34. Ratio Test: ρ= lim
k→+∞|x|2
4(k+ 1)(k+2) =0,R=+∞
35. By the Ratio Test for absolute convergence,
ρ= lim
k→+∞
(pk +p)!(k!)p
(pk)![(k+ 1)!]p|x|= lim
k→+∞
(pk +p)(pk +p−1)(pk +p−2) ···(pk +p−[p−1])
(k+1)
p|x|
= lim
k→+∞pp−1
k+1p−2
k+1···p−p−1
k+1|x|=p
p
|x|,
converges if |x|<1/pp, diverges if |x|>1/pp. Radius of convergence is 1/pp.
36. By the Ratio Test for absolute convergence,
ρ= lim
k→+∞
(k+1+p)!k!(k+q)!
(k+p)!(k+ 1)!(k+1+q)!|x|= lim
k→+∞
k+1+p
(k+ 1)(k+1+q)|x|=0,
radius of convergence is +∞.
37. (a) By Theorem 11.4.3(b) both series converge or diverge together, so they have the same radius
of convergence.
(b) By Theorem 11.4.3(a) the series P(ck+dk)(x−x0)kconverges if |x−x0|<R;if|x−x
0
|>R
then P(ck+dk)(x−x0)kcannot converge, as otherwise Pck(x−x0)kwould converge by
the same Theorem. Hence the radius of convergence of P(ck+dk)(x−x0)kis R.
(c) Let rbe the radius of convergence of P(ck+dk)(x−x0)k.If|x−x
0
|<min(R1,R
2)
then Pck(x−x0)kand Pdk(x−x0)kconverge, so P(ck+dk)(x−x0)kconverges. Hence
r≥min(R1,R
2) (to see that r>min(R1,R
2) is possible consider the case ck=−dk= 1).
If in addition R16=R2, and R1<|x−x0|<R
2(or R2<|x−x0|<R
1
) then
P(ck+dk)(x−x0)kcannot converge, as otherwise all three series would converge. Thus
in this case r= min(R1,R
2).
38. By the Root Test for absolute convergence,
ρ= lim
k→+∞|ck|1/k|x|=L|x|,L|x|<1if|x|<1/L so the radius of convergence is 1/L.
39. By assumption ∞
X
k=0
ckxkconverges if |x|<Rso ∞
X
k=0
ckx2k=∞
X
k=0
ck(x2)kconverges if |x2|<R,
|x|<√
R. Moreover, ∞
X
k=0
ckx2k=∞
X
k=0
ck(x2)kdiverges if |x2|>R,|x|>√
R.Thus∞
X
k=0
ckx2k
has radius of convergence √R.
40. The assumption is that ∞
X
k=0
ckRkis convergent and ∞
X
k=0
ck(−R)kis divergent. Suppose that ∞
X
k=0
ckRk
is absolutely convergent then ∞
X
k=0
ck(−R)kis also absolutely convergent and hence convergent
because |ckRk|=|ck(−R)k|, which contradicts the assumption that ∞
X
k=0
ck(−R)kis divergent so
∞
X
k=0
ckRkmust be conditionally convergent.
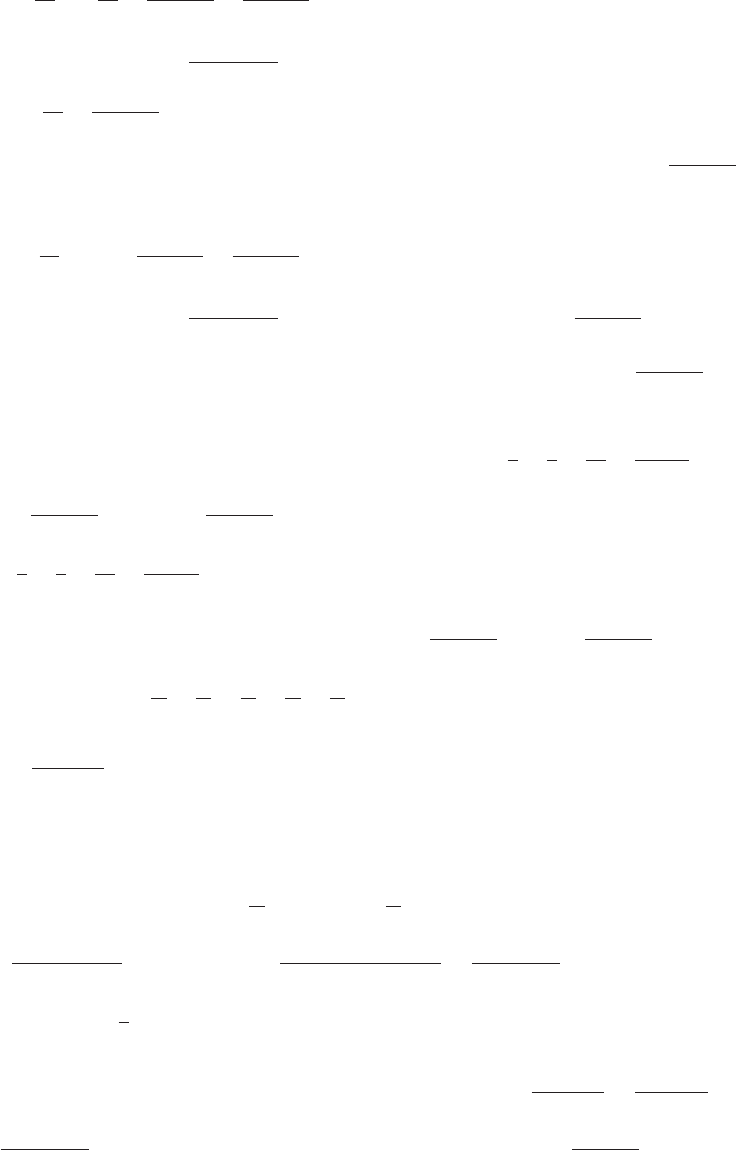
393 Chapter 11
EXERCISE SET 11.9
1. sin 4◦= sin π
45=π
45 −(π/45)3
3! +(π/45)5
5! −···
(a) Method 1: |Rn(π/45)|≤(π/45)n+1
(n+ 1)! <0.000005 for n+1=4,n =3;
sin 4◦≈π
45 −(π/45)3
3! ≈0.069756
(b) Method 2: The first term in the alternating series that is less than 0.000005 is (π/45)5
5! ,so
the result is the same as in part (a).
2. cos 3◦= cos π
60=1−(π/60)2
2+(π/60)4
4! −···
(a) Method 1: |Rn(π/60)|≤(π/60)n+1
(n+ 1)! <0.0005 for n= 2; cos 3◦≈1−(π/60)2
2≈0.9986.
(b) Method 2: The first term in the alternating series that is less than 0.0005 is (π/60)4
4! , so the
result is the same as in part (a).
3. f(k)(x)=e
x
,|f
(k)
(x)|≤e
1/2<2on[0,1/2],let M=2,e
1/2=1+1
2+1
8+1
48 +1
24 ·16 +···;
|R
n(1/2)|≤ M
(n+ 1)!(1/2)n+1 ≤2
(n+ 1)!(1/2)n+1 ≤0.00005 for n=5;
e
1/2≈1+1
2+1
8+1
48 +1
24 ·16 ≈1.64844, calculator value 1.64872
4. f(x)=e
x
,f(k)(x)=e
x
,|f
(k)
(x)|≤1on[−1,0], |Rn(x)|≤ 1
(n+ 1)!(1)n+1 =1
(n+ 1)! <0.5×10−3
if n=6,soe
−1≈1−1+ 1
2! −1
3! +1
4! −1
5! +1
6! ≈0.3681, calculator value 0.3679
5. |Rn(0.1)|≤(0.1)n+1
(n+ 1)! ≤0.000005 for n= 3; cos 0.1≈1−(0.1)2/2=0.99500, calculator value
0.995004 ...
6. (0.1)3/3<0.5×10−3so tan−1(0.1) ≈0.100, calculator value ≈0.0997
7. Expand about π/2 to get sinx=1−1
2!(x−π/2)2+1
4!(x−π/2)4−···,85
◦=17π/36 radians,
|Rn(x)|≤|x−π/2|n+1
(n+ 1)! ,|Rn(17π/36)|≤|17π/36 −π/2|n+1
(n+ 1)! =(π/36)n+1
(n+ 1)! <0.5×10−4
if n= 3, sin 85◦≈1−1
2(−π/36)2≈0.99619, calculator value 0.99619 ...
8. −175◦=−π+π/36 rad; x0=−π, x =−π+π/36,cos x=−1+(x+π)
2
2−(x+π)
4
4! −···;
|R
n|≤(π/36)n+1
(n+ 1)! ≤0.00005 for n= 3; cos(−π+π/36) = −1+(π/36)2
2≈−0.99619,
calculator value −0.99619 ...
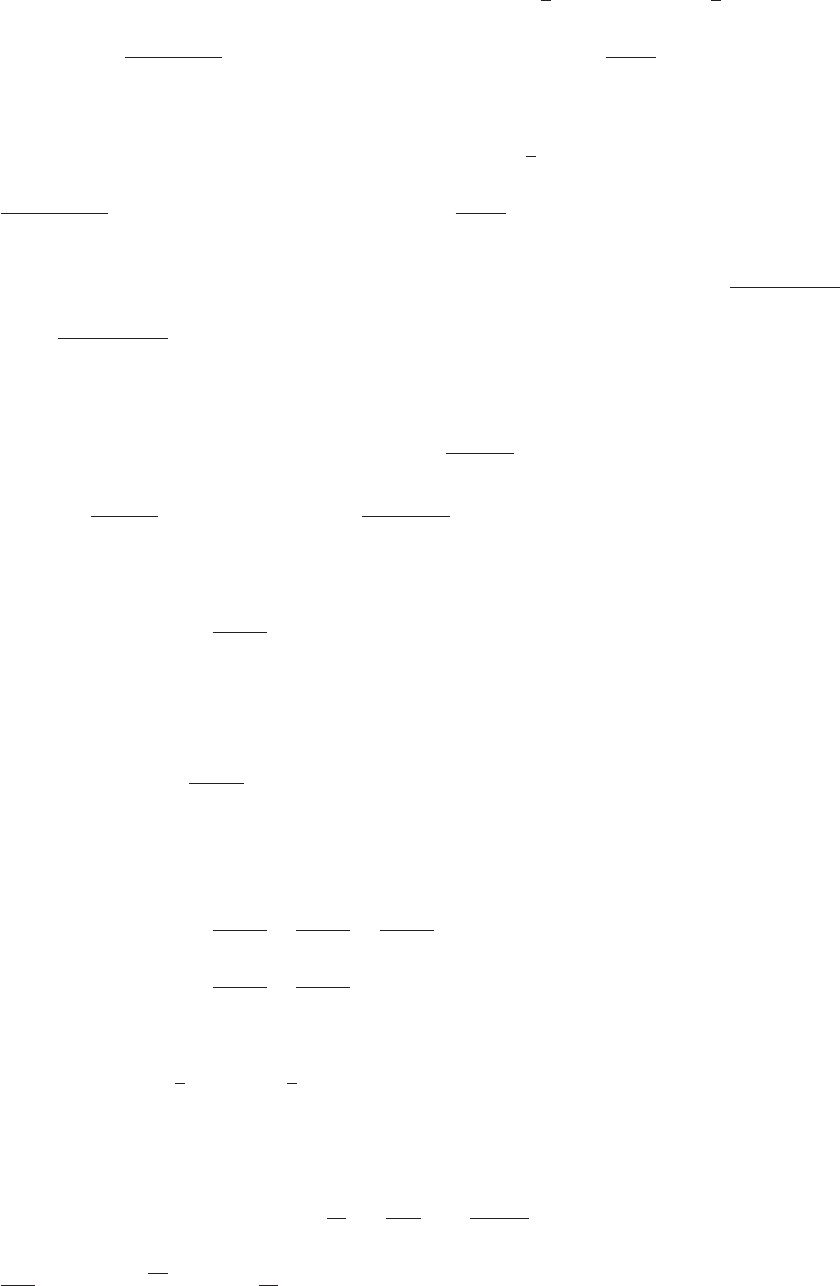
Exercise Set 11.9 394
9. f(k)(x) = cosh xor sinh x, |f(k)(x)|≤cosh x≤cosh 0.5=1
2
e
0.5+e
−0.5
<1
2
(2+1) = 1.5
so |Rn(x)|<1.5(0.5)n+1
(n+ 1)! ≤0.5×10−3if n= 4, sinh 0.5≈0.5+(0.5)3
3! ≈0.5208, calculator
value 0.52109 ...
10. f(k)(x) = cosh xor sinh x, |f(k)(x)|≤cosh x≤cosh 0.1=1
2e
0.1+e
−0.1
<1.06 so |Rn(x)|<
1.06(0.1)n+1
(n+ 1)! ≤0.5×10−3for n= 2, cosh 0.1≈1+(0.1)2
2! =1.005, calculator value 1.0050 ...
11. f(x) = sin x,f(n+1)(x)=±sin xor ±cos x,|f(n+1)(x)|≤1, |Rn(x)|≤|x−π/4|n+1
(n+ 1)! ,
lim
n→+∞|x−π/4|n+1
(n+ 1)! = 0; by the Squeezing Theorem, lim
n→+∞|Rn(x)|=0
so lim
n→+∞Rn(x) = 0 for all x.
12. f(x)=e
x
,f
(n+1)(x)=e
x
;ifx>1 then |Rn(x)|≤ e
x
(n+ 1)!|x−1|n+1;ifx<1 then
|Rn(x)|≤ e
(n+ 1)!|x−1|n+1. But lim
n→+∞|x−1|n+1
(n+ 1)! = 0 so lim
n→+∞Rn(x)=0.
13. (a) Let x=1/9 in series (17).
(b) ln 1.25 ≈21/9+(1/9)3
3= 2(1/9+1/3
7)≈0.223, which agrees with the calculator value
0.22314 ... to three decimal places.
14. (a) Let x=1/2 in series (17).
(b) ln 3 ≈21/2+(1/2)3
3= 2(1/2+1/24)=13/12 ≈1.083; the calculator value is 1.099 to
three decimal places.
15. (a) (1/2)9/9<0.5×10−3and (1/3)7/7<0.5×10−3so
tan−11/2≈1/2−(1/2)3
3+(1/2)5
5−(1/2)7
7≈0.4635
tan−11/3≈1/3−(1/3)3
3+(1/3)5
5≈0.3218
(b) From Formula (21), π≈4(0.4635 + 0.3218) = 3.1412
(c) Let a= tan−11
2,b= tan−11
3; then |a−0.4635|<0.0005 and |b−0.3218|<0.0005, so
|4(a+b)−3.140|≤4|a−0.4635|+4|b−0.3218|<0.004, so two decimal-place accuracy is
guaranteed, but not three.
16. (27+x)1/3= 3(1+x/33)1/3=31+ 1
3
4x−1·2
3
82x
2+1·2·5
3
123! x3+...
, alternates after first term,
3·2
382<0.0005, √28 ≈31+ 1
3
4≈3.0370
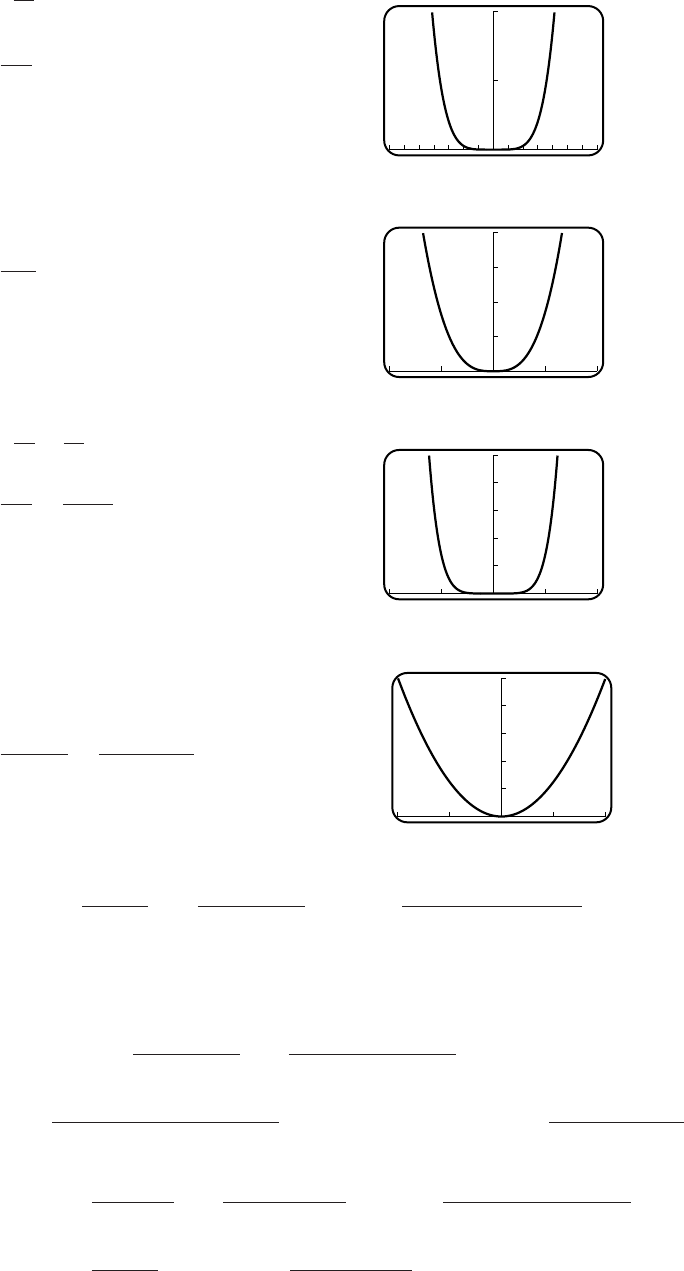
395 Chapter 11
17. (a) sin x=x−x3
3! +0·x
4+R
4(x),
|R
4(x)|≤|x|
5
5! <0.5×10−3if |x|5<0.06,
|x|<(0.06)1/5≈0.569,(−0.569,0.569)
(b) 0.0001
0
-0.7 0.7
18. (a) f(k)(x)=e
x≤e
b
,
|R
2
(x)|≤e
b
b
3
3! <0.0005,
ebb3<0.003 if b<0.137 (by trial and
error with a hand calculator), so [0,0.136].
(b) 0.0004
0
-0.2 0.2
19. (a) cos x=1−x
2
2! +x4
4! + (0)x5+R5(x),
|R5(x)|≤|x|
6
6! ≤(0.2)6
6! <9×10−8
(b) 0.000000005
0
-0.2 0.2
20. (a) f00(x)=−1/(1+x)2,
f00(x)<1/(0.99)2≤1.03,
|R1(x)|≤1.03|x|2
2≤1.03(0.01)2
2
≤5.11 ×10−5for −0.01 ≤x≤0.01
(b) 0.00005
0
-0.01 0.01
21. (a) (1+x)−1=1−x+−1(−2)
2! x2+−1(−2)(−3)
3! x3+···+−1(−2)(−3) ···(−k)
k!x
k+···
=∞
X
k=0
(−1)kxk
(b) (1+x)1/3=1+(1/3)x+(1/3)(−2/3)
2! x2+(1/3)(−2/3)(−5/3)
3! x3+···
+(1/3)(−2/3) ···(4 −3k)/3
k!xk+···=1+x/3+ ∞
X
k=2
(−1)k−12·5···(3k−4)
3kk!xk
(c) (1+x)−3=1−3x+(−3)(−4)
2! x2+(−3)(−4)(−5)
3! x3+···+(−3)(−4) ···(−2−k)
k!x
k+···
=∞
X
k=0
(−1)k(k+ 2)!
2·k!xk=∞
X
k=0
(−1)k(k+ 2)(k+1)
2x
k

Exercise Set 11.9 396
22. (1+x)m=m
0+∞
X
k=1 m
kxk=∞
X
k=0 m
kxk
23. (a) d
dx ln(1 + x)= 1
1+x,d
k
dxkln(1 + x)=(−1)k−1(k−1)!
(1+x)k; similarly d
dx ln(1 −x)=−(k−1)!
(1 −x)k,
so f(n+1)(x)=n!(−1)n
(1+x)n+1 +1
(1 −x)n+1 .
(b) f(n+1)(x)≤n!
(−1)n
(1+x)n+1 +n!
1
(1 −x)n+1 =n!1
(1+x)n+1 +1
(1 −x)n+1
(c) If f(n+1)(x)≤Mon the interval [0,1/3] then |Rn(1/3)|≤ M
(n+ 1)! 1
3n+1
.
(d) If 0 ≤x≤1/3 then 1 + x≥1,1−x≥2/3,f(n+1)(x)≤M=n!1+ 1
(2/3)n+1 .
(e) 0.000005 ≥M
(n+ 1)! 1
3n+1
=1
n+1"1
3n+1
+(1/3)n+1
(2/3)n+1 #=1
n+1"1
3n+1
+1
2n+1#
24. Set x=1/4 in Formula (17). Follow the argument of Exercise 23: parts (a) and (b) remain
unchanged; in part (c) replace (1/3) with (1/4): M
(n+ 1)! 1
4n+1
≤0.000005 for xin the interval
[0,1/4]. From part (b), together with 0 ≤x≤1/4,1+x≥1,1−x≥3/4, follows
part (d): M=n!1+ 1
(3/4)n+1 . Part (e) now becomes 0.000005 ≥M
(n+ 1)! 1
4n+1
=1
n+1"1
4n+1
+1
3n+1#, which is true for n=9.
25. f(x) = cos x, f(n+1)(x)=±sin xor ±cos x, |f(n+1)(x)|≤1,set M=1,
|R
n
(x)|≤ 1
(n+ 1)!|x−a|n+1,lim
n→+∞|x−a|n+1
(n+ 1)! = 0 so lim
n→+∞Rn(x) = 0 for all x.
26. f(x) = sin x, f(n+1)(x)=±sin xor ±cos x, |f(n+1)(x)|≤1, follow Exercise 25.
27. (a) From Machin’s formula and a CAS, π
4≈0.7853981633974483096156609,accurate to the 25th
decimal place.
(b) n
0
1
2
3
1/p
sn
0.3183098 78 . . .
0.3183098 861837906 067 . . .
0.3183098 861837906 7153776 695 . . .
0.3183098 861837906 7153776 752674502 34 . . .
0.3183098 861837906 7153776 752674502 87 . . .
28. (a) f0(0) = lim
h→0
f(h)−f(0)
h= lim
h→0
e−1/h2
h, let t=1/h then h=1/t and
lim
h→0+
e−1/h2
h= lim
t→+∞te−t2= lim
t→+∞
t
et2= lim
t→+∞
1
2tet2= 0, similarly lim
h→0−
e−1/h2
h=0so
f
0
(0)=0.
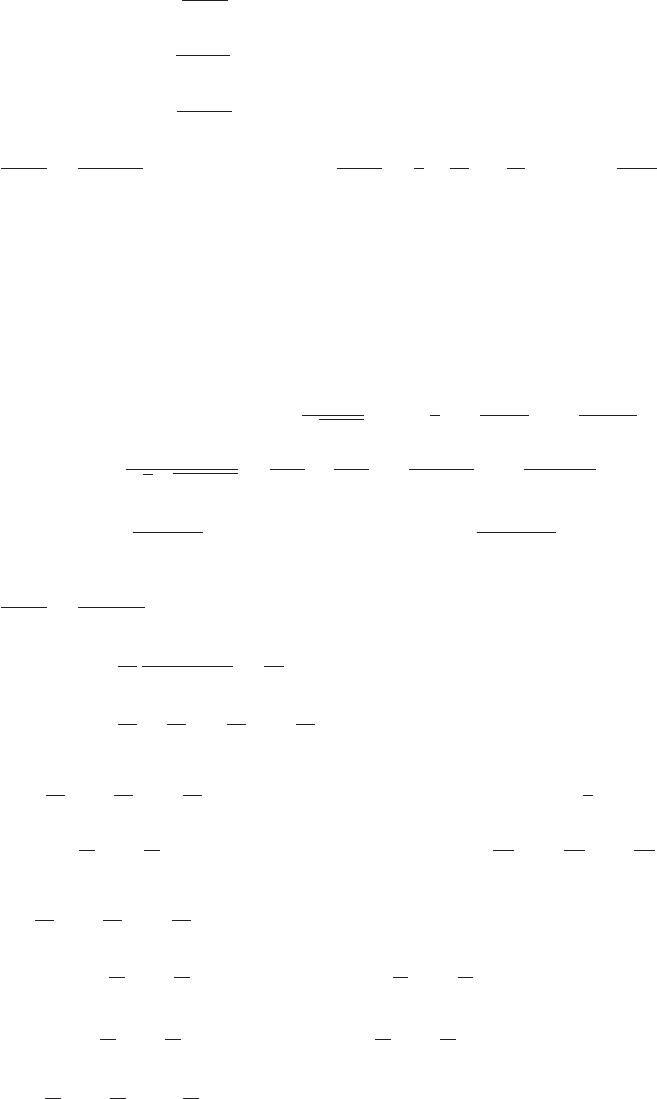
397 Chapter 11
(b) The Maclaurin series is 0 + 0 ·x+0·x
2+···= 0, but f(0) = 0 and f(x)>0ifx6= 0 so the
series converges to f(x) only at the point x=0.
EXERCISE SET 11.10
1. (a) Replace xwith −x:1
1+x=1−x+x
2−···+(−1)kxk+···;R=1.
(b) Replace xwith x2:1
1−x2=1+x
2+x
4+···+x
2k+···;R=1.
(c) Replace xwith 2x:1
1−2x=1+2x+4x
2+···+2
k
x
k+···;R=1/2.
(d) 1
2−x=1/2
1−x/2; replace xwith x/2: 1
2−x=1
2+1
2
2x+1
2
3x
2+···+1
2
k+1 xk+···;R=2.
2. (a) Replace xwith −x: ln(1 −x)=−x−x
2
/2−x
3
/3−···−x
k/k −···;R=1.
(b) Replace xwith x2: ln(1 + x2)=x
2−x
4
/2+x
6/3−···+(−1)k−1x2k/k +···;R=1.
(c) Replace xwith 2x: ln(1+2x)=2x−(2x)2/2+(2x)3/3−···+(−1)k−1(2x)k/k+···;R=1/2.
(d) ln(2 + x) = ln 2 + ln(1 + x/2); replace xwith x/2:
ln(2 + x)=ln2+x/2−(x/2)2/2+(x/2)3/3+···+(−1)k−1(x/2)k/k +···;R=2.
3. (a) From Section 11.9, Example 5(b), 1
√1+x=1−1
2
x+1·3
2
2·2!x2−1·3·5
23·3! x3+···,so
(2+x)−1/2=1
√2p1+x/2=1
21/2−1
25/2x+1·3
29/2·2!x2−1·3·5
213/2·3!x3+···
(b) Example 5(a): 1
(1+x)2=1−2x+3x
2−4x
3+···,so 1
(1 −x2)2=1+2x
2+3x
4+4x
6+···
4. (a) 1
a−x=1/a
1−x/a =1/a +x/a2+x2/a3+···+x
k/ak+1 +···;R=|a|.
(b) 1/(a+x)2=1
a2
1
(1+x/a)2=1
a21−2(x/a)+3(x/a)2−4(x/a)3+···
=1
a
2−2
a
3x+3
a
4x
2−4
a
5x
3+···
5. (a) 2x−23
3! x3+25
5! x5−27
7! x7+···;R=+∞(b) 1−2x+2x
2−4
3x
3+···;R=+∞
(c) 1+x
2+1
2!x4+1
3!x6+···;R=+∞(d) x2−π2
2x4+π4
4! x6−π6
6! x8+···;R=+∞
6. (a) 1−22
2! x2+24
4! x4−26
6! x6+···;R=+∞
(b) x21+x+1
2!x2+1
3!x3+···=x
2+x
3+1
2!x4+1
3!x5+···;R=+∞
(c) x1−x+1
2!x2−1
3!x3+···=x−x
2+1
2!x3−1
3!x4+···;R=+∞
(d) x2−1
3!x6+1
5!x10 −1
7!x14 +···;R=+∞
Exercise Set 11.10 398
7. (a) x21−3x+9x
2−27x3+···=x
2−3x
3+9x
4−27x5+···;R=1/3
(b) x2x+23
3! x3+25
5! x5+27
7! x7+···=2x
2+2
3
3! x4+25
5! x6+27
7! x8+···;R=+∞
(c) Substitute 3/2 for mand −x2for xin Equation (22) of Section 11.9, then multiply by x:
x−3
2x3+3
8x5+1
16x7+···;R=1
8. (a) x
x−1=−x
1−x=−x1+x+x
2+x
3+···=−x−x
2−x
3−x
4−···;R=1.
(b) 3+ 3
2!x4+3
4!x8+3
6!x12 +···;R=+∞
(c) From Table 11.9 with m=−3,(1+x)−3=1−3x+6x
2−10x3+···,so
x(1+2x)
−3=x−6x
2+24x
3−80x4+···;R=1/2
9. (a) sin2x=1
2(1 −cos 2x)=1
21−1−2
2
2! x2+24
4! x4−26
6! x6+···
=x2−23
4! x4+25
6! x6−27
8! x8+···
(b) ln (1+x3)12= 12 ln(1 + x3)=12x
3−6x
6+4x
9−3x
12 +···
10. (a) cos2x=1
2(1 + cos 2x)=1
21+1−2
2
2! x2+24
4! x4−26
6! x6+···
=1−x
2+2
3
4! x4−25
6! x6+···
(b) In Equation (17) of Section 11.9 replace xwith −x:ln
1−x
1+x=−2x+1
3x
3+1
5x
5+···
11. (a) 1
x=1
1−(1 −x)=1+(1−x)+(1−x)
2+···+(1−x)
k+···
=1−(x−1)+(x−1)2−···+(−1)k(x−1)k+···
(b) (0,2)
12. (a) 1
x=1/x0
1+(x−x
0)/x0=1/x0−(x−x0)/x2
0+(x−x
0)
2/x3
0−···+(−1)k(x−x0)k/xk+1
0+···
(b) (0,2x0)
13. (a) (1+x+x2/2+x
3/3!+x4/4!+···)(x−x3/3!+x5/5! −···)=x+x
2+x
3
/3−x
5
/30+···
(b) (1+x/2−x2/8+x
3/16 −(5/128)x4+···)(x−x2/2+x
3/3−x
4/4+x
5/5−···)
=x−x
3/24+x4/24 −(71/1920)x5+···
14. (a) (1 −x2+x4/2−x6/6+···)1−1
2x
2+1
24x4−1
720x6···=1−3
2
x
2+25
24x4−331
720x6+···
(b) 1+4
3x
2+···1+1
3x−1
9x
2+5
81x3−···=1+1
3
x+11
9x2+41
81x3+···

399 Chapter 11
15. (a) 1
cos x=1
1−1
2!x2+1
4!x4−1
6!x6+···=1+1
2
x
2+5
24x4+61
720x6+···
(b) sin x
ex=x−x3
3! +x5
5! −···1+x+x
2
2! +x3
3! +x4
4! +···=x−x
2+1
3x
3−1
30x5+···
16. (a) tan−1x
1+x=x−x
3/3+x
5/5−···/(1+x)=x−x
2+2
3
x
3−2
3
x
4···
(b) ln(1 + x)
1−x=x−x2/2+x
3/3−x
4/4+···/(1 −x)=x+1
2
x
2+5
6
x
3+7
12x4+···
17. ex=1+x+x
2
/2+x
3/3! + ···+x
k/k!+···,e
−x=1−x+x
2
/2−x
3
/3! + ···+(−1)kxk/k!+···;
sinh x=1
2ex−e−x=x+x3/3!+x5/5!+···+x
2k+1/(2k+1)!+···,R=+∞
cosh x=1
2ex+e−x=1+x
2
/2+x
4/4!+···+x
2k/(2k)!+···,R=+∞
18. tanh x=x+x3/3!+x5/5!+···
1+x
2/2+x
4/4!+··· =x−1
3x
3+2
15x5−17
315x7+···
19. 4x−2
x2−1=−1
1−x+3
1+x=−1+x+x
2+x
3+x
4+···+31−x+x
2−x
3+x
4+···
=2−4x+2x
2−4x
3+2x
4+···
20. x3+x2+2x−2
x
2−1=x+1−1
1−x+2
1+x
=x+1−1+x+x
2+x
3+x
4+···+21−x+x
2−x
3+x
4+···
=2−2x+x
2−3x
3+x
4−···
21. (a) d
dx 1−x2/2!+x4/4! −x6/6!+···=−x+x
3/3! −x5/5!+···=−sin x
(b) d
dx x−x2/2+x
3/3−···=1−x+x
2−···=1/(1+x)
22. (a) d
dx x+x3/3!+x5/5!+···=1+x
2
/2!+x4/4!+···= cosh x
(b) d
dx x−x3/3+x
5/5−x
7/7+···=1−x
2+x
4−x
6+···=1
1+x
2
23. (a) Z1+x+x
2/2!+···dx =(x+x
2
/2!+x3/3!+···)+C
1
=1+x+x
2/2!+x3/3!+···+C
1−1=e
x+C
(b) Zx+x3/3!+x5/5!+···=x
2/2!+x4/4!+···+C
1
=1+x
2
/2!+x4/4!+···+C
1−1 = cosh x+C
Exercise Set 11.10 400
24. (a) Zx−x3/3!+x5/5! −···dx =x2/2! −x4/4!+x6/6! −···+C
1
=−1−x
2/2!+x4/4! −x6/6!+···+C
1+1
=−cos x+C
(b) Z1−x+x2−···dx =x−x2/2+x
3/3−···+C= ln(1 + x)+C
(Note: −1<x<1, so |1+x|=1+x)
25. (a) Substitute x2for xin the Maclaurin Series for 1/(1 −x) (Table 11.9.1)
and then multiply by x:x
1−x2=x∞
X
k=0
(x2)k=∞
X
k=0
x2k+1
(b) f(5)(0)=5!c
5=5,f
(6)(0)=6!c
6=0 (c) f(n)(0) = n!cn=(n!ifnodd
0ifneven
26. x2cos 2x=∞
X
k=0
(−1)k22k
(2k)! x2k+2;f(99)(0) = 0 because c99 =0.
27. (a) lim
x→0
sin x
x= lim
x→01−x2/3!+x4/5! −···=1
(b) lim
x→0
tan−1x−x
x3= lim
x→0x−x3/3+x
5/5−x
7/7+···−x
x
3=−1/3
28. (a) 1−cos x
sin x=1−1−x2/2!+x4/4! −x6/6!+···
x−x
3/3!+x5/5! −··· =x
2/2! −x4/4!+x6/6! −···
x−x
3/3!+x5/5! −···
=x/2! −x3/4!+x5/6! −···
1−x
2/3!+x4/5! −··· ,x6= 0; lim
x→0
1−cos x
sin x=0
1=0
(b) lim
x→0
1
xln √1+x−sin 2x= lim
x→0
1
x1
2ln(1 + x)−sin 2x
= lim
x→0
1
x1
2x−1
2x2+1
3x3−···−2x−4
3x
3+4
15x5−···
= lim
x→0−3
2−1
4x+3
2x2+···=−3/2
29. Z1
0sin x2dx =Z1
0x2−1
3!x6+1
5!x10 −1
7!x14 +···dx
=1
3x3−1
7·3!x7+1
11 ·5!x11 −1
15 ·7!x15 +···1
0
=1
3−1
7·3! +1
11 ·5! −1
15 ·7! +···,
but 1
15 ·7! <0.5×10−3so Z1
0sin(x2)dx ≈1
3−1
7·3! +1
11 ·5! ≈0.3103
401 Chapter 11
30. Z1/2
0tan−12x2dx =Z1/2
02x2−8
3x6+32
5x10 −128
7x14 +···dx
=2
3x3−8
21x7+32
55x11 −128
105x15 +···1/2
0
=2
3
1
2
3−8
21
1
27+32
55
1
211 −128
105
1
215 −···,
but 128
105 ·215 <0.5×10−4so Z1/2
0tan−1(2x2)dx ≈2
3·23−8
21 ·27+32
55 ·211 ≈0.0806
31. Z0.2
01+x
41/3dx =Z0.2
01+1
3x
4−1
9x
8+···dx
=x+1
15x5−1
81x9+···0.2
0
=0.2+ 1
15(0.2)5−1
81(0.2)9+···,
but 1
15(0.2)5<0.5×10−3so Z0.2
0(1+x4)1/3dx ≈0.200
32. Z1/2
0(1+x2)−1/4dx =Z1/2
01−1
4x2+5
32x4−15
128x6+···dx
=x−1
12x3+1
32x5−15
896x7+···1/2
0
=1/2−1
12(1/2)3+1
32(1/2)5−15
896(1/2)7+···,
but 15
896(1/2)7<0.5×10−3so Z1/2
0(1+x2)−1/4dx ≈1/2−1
12(1/2)3+1
32(1/2)5≈0.4906
33. (a) x
(1 −x)2=xd
dx 1
1−x=xd
dx "∞
X
k=0
xk#=x"∞
X
k=1
kxk−1#=∞
X
k=1
kxk
(b) −ln(1 −x)=Z1
1−xdx −C=Z"∞
X
k=0
xk#dx −C
=∞
X
k=0
xk+1
k+1−C=∞
X
k=1
xk
k−C, −ln(1 −0)=0soC=0.
(c) Replace xwith −xin part (b): ln(1 + x)=−
+∞
X
k=1
(−1)k
kxk=
+∞
X
k=1
(−1)k+1
kxk
(d)
+∞
X
k=1
(−1)k+1
kconverges by the Alternating Series Test.
(e) By parts (c) and (d) and the remark,
+∞
X
k=1
(−1)k+1
kxkconverges to ln(1 + x) for −1<x≤1.

Exercise Set 11.10 402
34. (a) In Exercise 33(a), set x=1
3,S=1/3
(1 −1/3)2=3
4
(b) In part (b) set x=1/4,S = ln(4/3) (c) In part (e) set x=1,S =ln2
35. (a) sinh−1x=Z1+x
2−1/2dx −C=Z1−1
2x2+3
8x4−5
16x6+···dx −C
=x−1
6x3+3
40x5−5
112x7+···−C; sinh−10=0soC=0.
(b) 1+x
2−1/2=1+ ∞
X
k=1
(−1/2)(−3/2)(−5/2) ···(−1/2−k+1)
k!(x
2)
k
=1+ ∞
X
k=1
(−1)k1·3·5···(2k−1)
2kk!x2k,
sinh−1x=x+∞
X
k=1
(−1)k1·3·5···(2k−1)
2kk!(2k+1) x
2k+1
(c) R=1
36. (a) sin−1x=Z(1 −x2)−1/2dx −C=Z1+1
2x
2+3
8x
4+5
16x6+···dx −C
=x+1
6x3+3
40x5+5
112x7+···−C, sin−10=0soC=0
(b) 1−x2−1/2=1+ ∞
X
k=1
(−1/2)(−3/2)(−5/2) ···(−1/2−k+1)
k!−x
2k
=1+ ∞
X
k=1
(−1)k(1/2)k(1)(3)(5) ···(2k−1)
k!(−1)kx2k
=1+ ∞
X
k=1
1·3·5···(2k−1)
2kk!x2k
sin−1x=x+∞
X
k=1
1·3·5···(2k−1)
2kk!(2k+1) x
2k+1
(c) R=1
37. (a) y(t)=y
0
∞
X
k=0
(−1)k(0.000121)ktk
k!
(b) y(1) ≈y0(1 −0.000121t)it=1 =0.999879y0
(c) y0e−0.000121 ≈0.9998790073y0
38. (a) If ct
m≈0 then e−ct/m ≈1−ct
m, and v(t)≈1−ct
mv0+mg
c−mg
c=v0−cv0
m+gt.
(b) The quadratic approximation is
v0≈1−ct
m+(ct)2
2m2v0+mg
c−mg
c=v0−cv0
m+gt+c2
2m2v0+mg
ct2.
403 Chapter 11
39. θ0=5
◦=π/36 rad, k= sin(π/72)
(a) T≈2πrL
g=2π
p1/9.8≈2.00709 (b) T≈2πrL
g1+k
2
4≈2.008044621
(c) 2.008045644
40. The third order model gives the same result as the second, because there is no term of degree three
in (5). By the Wallis sine formula, Zπ/2
0sin4φdφ=1·3
2·4
π
2, and
T≈4rL
gZπ/2
01+1
2k
2sin2φ+1·3
222!k4sin4φdφ =4
sL
gπ
2+k
2
2
π
4+3k
4
8
3π
16
=2π
sL
g1+k
2
4+9k
4
64
41. (a) F=mgR2
(R+h)2=mg
(1+h/R)2=mg 1−2h/R +3h
2/R2−4h3/R3+···
(b) If h= 0, then the binomial series converges to 1 and F=mg.
(c) Sum the series to the linear term, F≈mg −2mgh/R.
(d) mg −2mgh/R
mg =1−2h
R=1−2·29,028
4000 ·5280 ≈0.9973, so about 0.27% less.
42. (a) We can differentiate term-by-term:
y0=∞
X
k=1
(−1)kx2k−1
22k−1k!(k−1)! =∞
X
k=0
(−1)k+1x2k+1
22k+1(k+ 1)!k!,y
00 =∞
X
k=0
(−1)k+1(2k+1)x
2k
2
2k+1(k+ 1)!k!, and
xy00 +y0+xy =∞
X
k=0
(−1)k+1(2k+1)x
2k+1
22k+1(k+ 1)!k!+∞
X
k=0
(−1)k+1x2k+1
22k+1(k+ 1)!k!+∞
X
k=0
(−1)kx2k+1
22k(k!)2,
xy00 +y0+xy =∞
X
k=0
(−1)k+1x2k+1
22k(k!)22k+1
2(k+1)+1
2(k+1)−1
=0
(b) y0=∞
X
k=0
(−1)k(2k+1)x
2k
2
2k+1k!(k+ 1)! ,y
00 =∞
X
k=1
(−1)k(2k+1)x
2k−1
2
2k
(k−1)!(k+ 1)! .
Since J1(x)= ∞
X
k=0
(−1)kx2k+1
22k+1k!(k+ 1)! and x2J1(x)= ∞
X
k=1
(−1)k−1x2k+1
22k−1(k−1)!k!, it follows that
x2y00 +xy0+(x
2−1)y
=∞
X
k=1
(−1)k(2k+1)x
2k+1
22k(k−1)!(k+ 1)! +∞
X
k=0
(−1)k(2k+1)x
2k+1
22k+1(k!)(k+ 1)! +∞
X
k=1
(−1)k−1x2k+1
22k−1(k−1)!k!
−∞
X
k=0
(−1)kx2k+1
22k+1k!(k+ 1)!
=x
2−x
2+∞
X
k=1
(−1)kx2k+1
22k−1(k−1)!k!2k+1
2(k+1)+2k+1
4k(k+1)−1−1
4k(k+1)=0.

Chapter 11 Supplementary Exercises 404
(c) From part (a), J0
0(x)= ∞
X
k=0
(−1)k+1x2k+1
22k+1(k+ 1)!k!=−J1(x).
43. If ∞
X
k=0
akxk=∞
X
k=0
bkxkfor xin (−r,r) then ∞
X
k=0
(ak−bk)xk= 0 so by Theorem 11.10.6 ∞
X
k=0
(ak−bk)xk
is the Taylor series for f(x) = 0 about 0 and hence ak−bk=0,a
k=b
kfor all k.
CHAPTER 11 SUPPLEMENTARY EXERCISES
4. (a) ∞
X
k=0
f(k)(0)
k!xk(b) ∞
X
k=0
f(k)(x0)
k!(x−x0)k
9. (a) always true by Theorem 11.4.2
(b) sometimes false, for example the harmonic series diverges but P(1/k2) converges
(c) sometimes false, for example f(x) = sin πx, ak=0,L =0
(d) always true by Example 3(d) of Section 11.1
(e) sometimes false, for example an=1
2+(−1)n1
4
(f) sometimes false, for example uk=1/2
(g) always false by Theorem 11.4.3
(h) sometimes false, for example uk=vk=(2/k)
(i) always true by the Comparison Test
(j) always true by the Comparison Test
(k) sometimes false, for example P(−1)k/k
(l) sometimes false, for example P(−1)k/k
10. (a) false, f(x) is not differentiable at x= 0, Definition 11.5.4
(b) true: sn=1ifnis odd and s2n=1+1/(n+ 1); lim
n→+∞sn=1
(c) false, lim ak6=0
11. (a) geometric, r=1/5, converges (b) 1/(5k+1)<1/5
k
, converges
(c) 9
√k+1 ≥9
√
k+√
k=9
2
√
k,∞
X
k=1
9
2√kdiverges
12. (a) converges by Alternating Series Test
(b) absolutely convergent, ∞
X
k=1 k+2
3k−1k
converges by the Root Test.
(c) k−1/2
2 + sin2k>k−1
2+1 =1
3k,∞
X
k=1
1
3kdiverges
13. (a) 1
k3+2k+1 <1
k
3,∞
X
k=1
1/k3converges, so ∞
X
k=1
1
k3+2k+1 converges by the Comparison Test
(b) Limit Comparison Test, compare with the divergent series ∞
X
k=1
1
k2/5, diverges
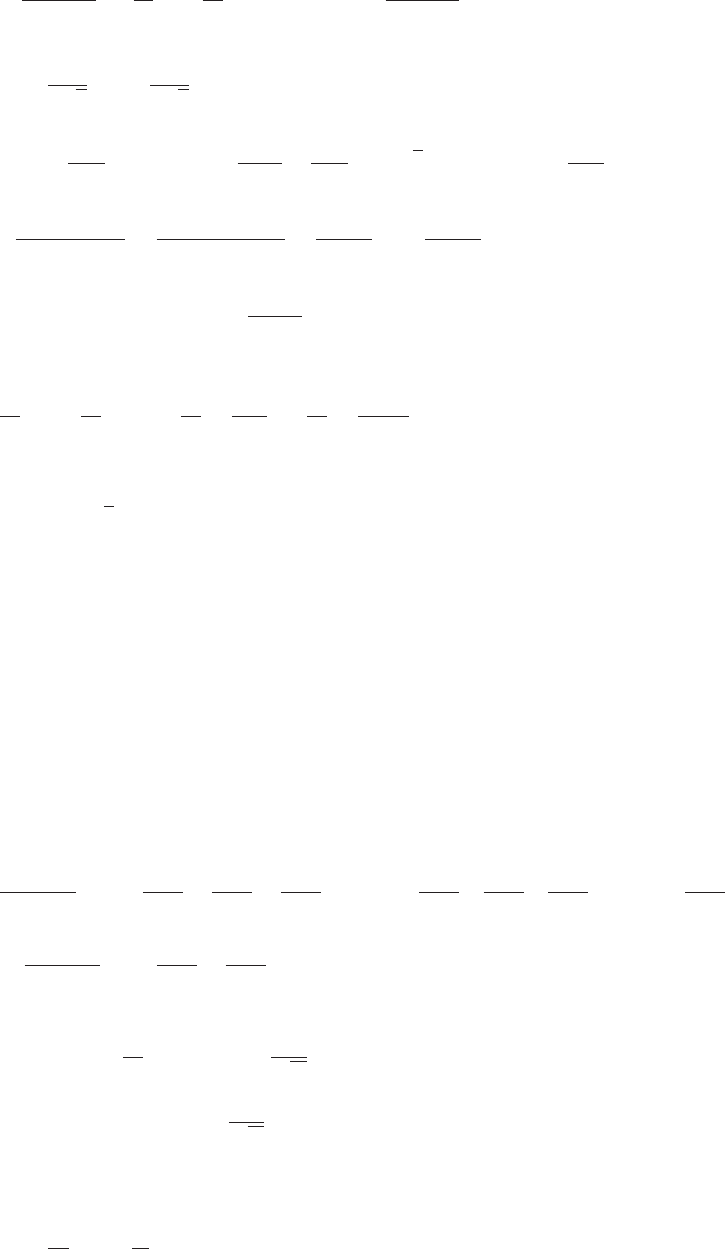
405 Chapter 11
(c)
cos(1/k)
k2<1
k2,∞
X
k=1
1
k2converges, so ∞
X
k=1
cos(1/k)
k2converges absolutely
14. (a) ∞
X
k=1
ln k
k√k=∞
X
k=2
ln k
k√kbecause ln1 = 0,
Z+∞
2
ln x
x3/2dx = lim
`→+∞−2lnx
x
1/2−4
x
1/2`
2
=√2(ln2 + 2) so ∞
X
k=2
ln k
k3/2converges
(b) k4/3
8k2+5k+1 ≥k
4/3
8k
2+5k
2+k
2=1
14k2/3,∞
X
k=1
1
14k2/3diverges
(c) absolutely convergent, ∞
X
k=1
1
k2+1 converges (compare with P1/k2)
15. ∞
X
k=0
1
5k−
99
X
k=0
1
5k=∞
X
k=100
1
5k=1
5100
∞
X
k=0
1
5k=1
4·599
16. no, lim
k→+∞ak=1
26= 0 (Divergence Test)
17. (a) p0(x)=1,p
1(x)=1−7x, p2(x)=1−7x+5x
2
,p
3(x)=1−7x+5x
2−4x
3
,
p
4
(x)=1−7x+5x
2−4x
3
(b) If f(x) is a polynomial of degree nand k≥nthen the Maclaurin polynomial of degree kis
the polynomial itself; if k<nthen it is the truncated polynomial.
18. ln(1 + x)=x−x
2
/2+···;so|ln(1 + x)−x|≤x
2
/2 by Theorem 11.7.2.
19. sin x=x−x3/3!+x5/5! −x7/7!+···is an alternating series, so
|sin x−x+x3/3! −x5/5!|≤x
7
/7! ≤π7/(477!) ≤0.00005
20. Z1
0
1−cos x
xdx =x2
2·2! −x4
4·4! +x6
6·6! −···1
0
=1
2·2! −1
4·4! +1
6·6! −···, and 1
6·6! <0.0005,
so Z1
0
1−cos x
xdx =1
2·2! −1
4·4! =0.2396 to three decimal-place accuracy.
21. (a) ρ= lim
k→+∞2k
k!1/k
= lim
k→+∞
2
k
√k!= 0, converges
(b) ρ= lim
k→+∞u1/k
k= lim
k→+∞
k
k
√k!=e, diverges
22. (a) 11≥1!; if kk≥k!,then (k+1)k+1 ≥(k+1)kk≥(k+1)k!=(k+1)!; mathematical induction
(b) X1
kk≤X1
k!, converges

Chapter 11 Supplementary Exercises 406
(c) lim
k→+∞1
kk1/k
= lim
k→+∞
1
k= 0, converges
23. (a) u100 =
100
X
k=1
uk−
99
X
k=1
uk=2−1
100−2−1
99=1
9900
(b) u1= 1; for k≥2,u
k=2−1
k−2−1
k−1=1
k(k−1),lim
k→+∞uk=0
(c) ∞
X
k=1
uk= lim
n→+∞
n
X
k=1
uk= lim
n→+∞2−1
n=2
24. (a) ∞
X
k=1 3
2k−2
3k=∞
X
k=1
3
2k−∞
X
k=1
2
3k=3
21
1−(1/2) −2
31
1−(1/3) = 2 (geometric series)
(b)
n
X
k=1
[ln(k+1)−ln k] = ln(n+ 1), so ∞
X
k=1
[ln(k+1)−ln k] = lim
n→+∞ln(n+1)=+∞, diverges
(c) lim
n→+∞
n
X
k=1
1
21
k−1
k+2= lim
n→+∞
1
21+1
2−1
n+1−1
n+2=3
4
(d) lim
n→+∞
n
X
k=1 tan−1(k+1)−tan−1k= lim
n→+∞tan−1(n+1)−tan−1(1)=π
2−π
4=π
4
25. (a) e2−1(b) sin π=0 (c) cos e(d) e−ln 3 =1/3
26. ak+1 =√ak=a1/2
k=a1/4
k−1=···=a
1/2
k
1=c
1/2
k+1
(a) If c=1/2 then lim
k→+∞ak=1. (b) if c=3/2 then lim
k→+∞ak=1.
27. Expand in a Maclaurin Series about x= 100 : e−[(x−100)/16]2=1−(x−100)2
162+(x−100)4
2·164,so
p≈1
16√2πZ110
100 1−(x−100)2
162+(x−100)4
2·164dx =1
16√2π10 −103
3·162+105
2·5·164
≈0.220678, or about 22.07%.
28. f(x)=xex=x+x2+x3
2! +x4
3! +···=∞
X
k=0
xk+1
k!,
f0(x)=(x+1)e
x=1+2x+3x
2
2! +4x3
3! +···=∞
X
k=0
k+1
k!x
k
;∞
X
k=0
k+1
k!=f0(1)=2e.
29. Let A=1−1
2
2+1
3
2−1
4
2+···; since the series all converge absolutely,
π2
6−A=21
2
2+21
4
2+21
6
2+···=1
21+ 1
2
2+1
3
2+···=1
2
π
2
6,soA=1
2
π
2
6=π
2
12.
30. Compare with 1/kp: converges if p>1, diverges otherwise.
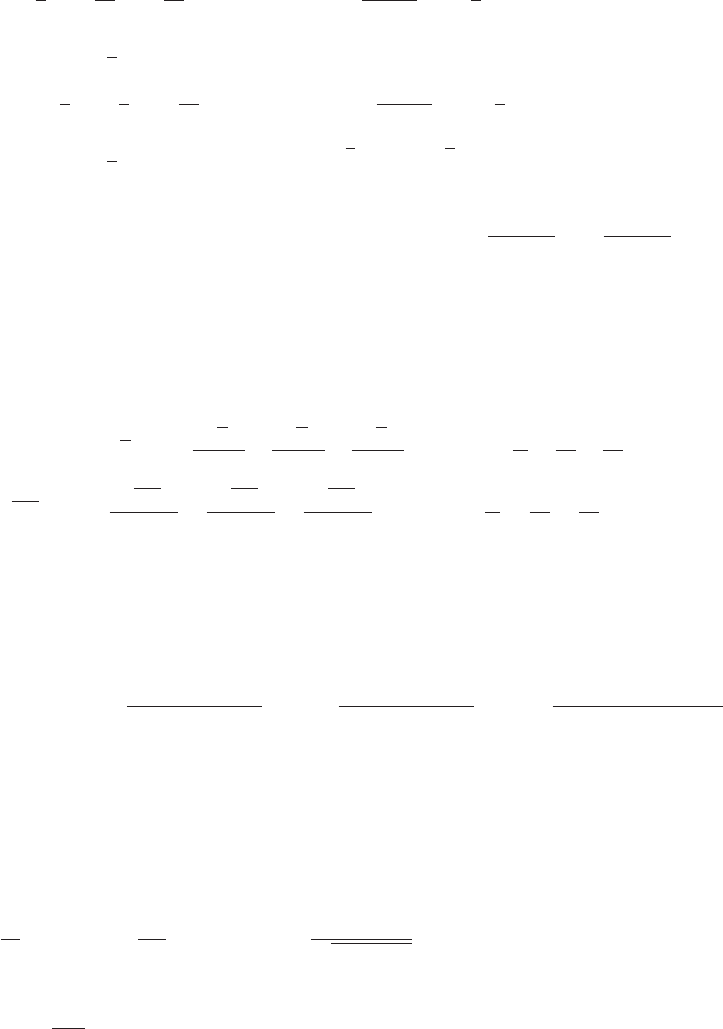
407 Chapter 11
31. (a) x+1
2x2+3
14x3+3
35x4+···;ρ= lim
k→+∞
k+1
3k+1|x|=1
3|x|,
converges if 1
3|x|<1, |x|<3soR=3.
(b) −x3+2
3x5−2
5x7+8
35x9−···;ρ= lim
k→+∞
k+1
2k+1|x|
2=1
2|x|
2,
converges if 1
2|x|2<1, |x|2<2, |x|<√2soR=√
2.
32. By the Ratio Test for absolute convergence, ρ= lim
k→+∞|x−x0|
b=|x−x0|
b; converges if
|x−x0|<b, diverges if |x−x0|>b.Ifx=x
0
−b,∞
X
k=0
(−1)kdiverges; if x=x0+b,
∞
X
k=0
1 diverges. The interval of convergence is (x0−b, x0+b).
33. If x≥0, then cos √x=1−(
√
x)
2
2! +(√x)4
4! −(√x)6
6! +···=1−x
2! +x2
4! −x3
6! +···;ifx≤0, then
cosh(√−x)=1+(
√
−x)
2
2! +(√−x)4
4! +(√−x)6
6! +···=1−x
2! +x2
4! −x3
6! +···.
34. By Exercise 70 of Section 3.5, the derivative of an odd (even) function is even (odd); hence all
odd-numbered derivatives of an odd function are even, all even-numbered derivatives of an odd
function are odd; a similar statement holds for an even function.
(a) If f(x) is an even function, then
2f0(0) = lim
h→0+
f(0+h)−f(0)
h+ lim
h→0+
f(0) −f(0 −h)
h= lim
h→0+
f(0+h)−f(0 −h)
h=0,so
f
0(0)=0. Iff(x) is even then so is f(2k),thusf
(2k+1)(0)=0,k=0,1,2,.... Hence
c2k+1 =f(2k+1)(0)/(2k+1)!=0.
(b) If f(x) is an odd function, then f(2k−1) is even (k=1,2,...), and thus by Part (a),
f(2k)(0)=0,c
2k=f
(2k)(0)/(2k)!=0.
35. 1−v2
c2−1/2
≈1+ v
2
2c
2,soK=m
0
c
2"1
p1−v
2
/c2−1#≈m0c2(v2/(2c2)=m
0
v
2
/2
36. (a) Z+∞
n
1
x3.7dx < (0.5)10−5if n>63.7; let n= 64.
(b) sn≈1.10628342; CAS: 1.10628824
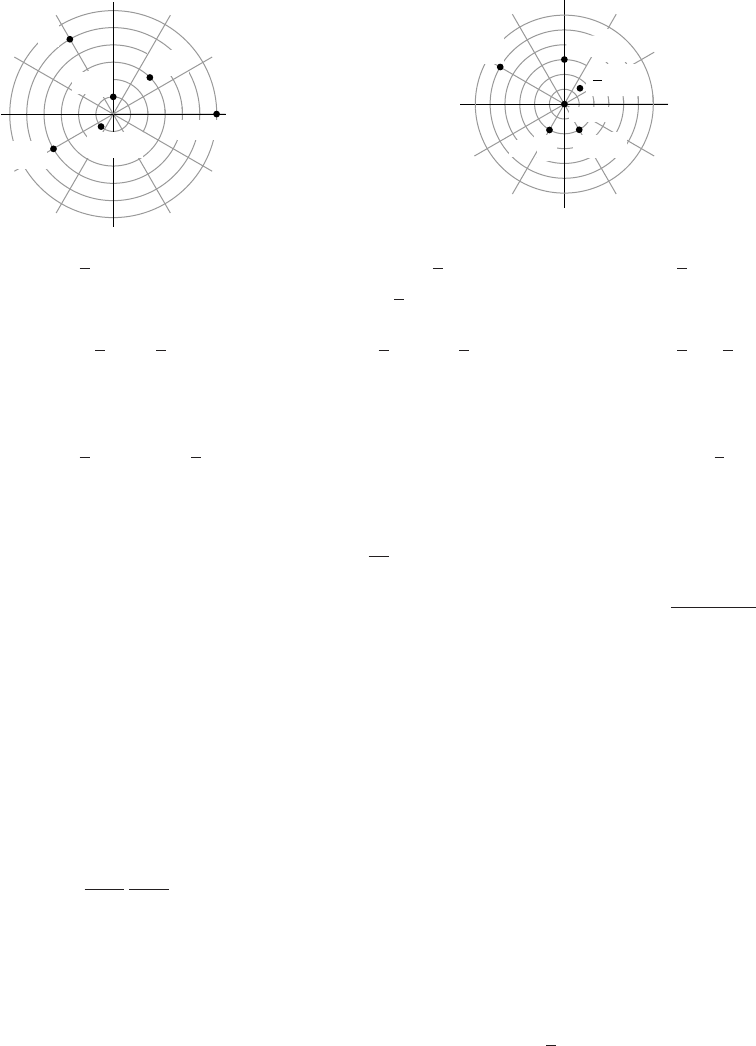
408
CHAPTER 12
Analytic Geometry in Calculus
EXERCISE SET 12.1
1.
(1, 6)
(3, 3)
(4, e)(–1, r)
0
p/2
(5, 8)
(–6, –p)
2.
( , L)
3
20
p/2
(–3, i)
(–5, @)
(2, $)
(0, c)
(2, g)
3. (a) (3√3,3) (b) (−7/2,7√3/2) (c) (3√3,3)
(d) (0,0) (e) (−7√3/2,7/2) (f) (−5,0)
4. (a) (−4√2,−4√2) (b) (7√2/2,−7√2/2) (c) (4√2,4√2)
(d) (5,0) (e) (0,−2) (f) (0,0)
5. (a) both (5,π)(b) (4,11π/6),(4,−π/6) (c) (2,3π/2),(2,−π/2)
(d) (8√2,5π/4),(8√2,−3π/4) (e) both (6,2π/3) (f) both (√2,π/4)
6. (a) (2,5π/6) (b) (−2,11π/6) (c) (2,−7π/6) (d) (−2,−π/6)
7. (a) (5,0.6435) (b) (√29,5.0929) (c) (1.2716,0.6658)
8. (a) (5,2.2143) (b) (3.4482,2.6260) (c) (p4+π
2/36,0.2561)
9. (a) r2=x2+y2= 4; circle (b) y= 4; horizontal line
(c) r2=3rcos θ,x2+y2=3x,(x−3/2)2+y2=9/4; circle
(d) 3rcos θ+2rsin θ=6,3x+2y= 6; line
10. (a) rcos θ=5,x= 5; vertical line
(b) r2=2rsin θ,x2+y2=2y,x
2+(y−1)2= 1; circle
(c) r2=4rcos θ+4rsin θ, x2+y2=4x+4y, (x−2)2+(y−2)2= 8; circle
(d) r=1
cos θ
sin θ
cos θ,rcos2θ= sin θ,r2cos2θ=rsin θ,x2=y; parabola
11. (a) rcos θ=7 (b) r=3
(c) r2−6rsin θ=0,r= 6 sin θ
(d) 4(rcos θ)(rsin θ)=9,4r
2sin θcos θ=9,r
2sin 2θ=9/2
12. (a) rsin θ=−3(b) r=√5
(c) r2+4rcos θ=0,r=−4 cos θ
(d) r4cos2θ=r2sin2θ,r2= tan2θ,r= tan θ
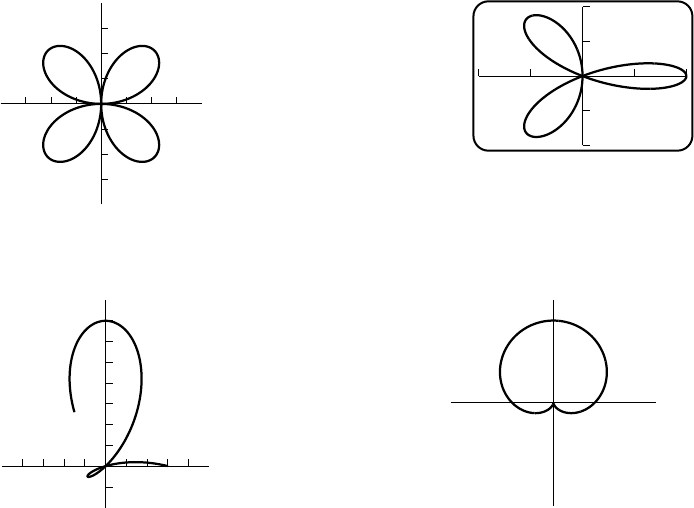
409 Chapter 12
13.
0
p/2
-3
-3
3
3
r= 3 sin 2θ
14. 2
-2
-2 2
r= 2 cos 3θ
15.
0
p/2
-4 4
-1
r=3−4 sin 3θ
16.
0
p/2
r=2+2sinθ
17. (a) r=5
(b) (x−3)2+y2=9,r= 6 cos θ
(c) Example 6, r=1−cos θ
18. (a) From (8-9), r=a±bsin θor r=a±bcos θ. The curve is not symmetric about the y-axis,
so Theorem 12.2.1(a) eliminates the sine function, thus r=a±bcos θ. The cartesian point
(−3,0) is either the polar point (3,π)or(−3,0), and the cartesian point (−1,0) is either
the polar point (1,π)or(−1,0). A solution is a=1,b =−2; we may take the equation as
r=1−2 cos θ.
(b) x2+(y+3/2)2=9/4,r =−3 sin θ
(c) Figure 12.1.18, a=1,n =3,r = sin 3θ
19. (a) Figure 12.1.18, a=3,n =2,r = 3 sin 2θ
(b) From (8-9), symmetry about the y-axis and Theorem 12.1.1(b), the equation is of the form
r=a±bsin θ. The cartesian points (3,0) and (0,5) give a=3and5=a+b,sob= 2 and
r=3+2sinθ.
(c) Example 8, r2= 9 cos 2θ
20. (a) Example 6 rotated through π/2 radian: a=3,r =3−3 sin θ
(b) Figure 12.1.18, a=1,r = cos 5θ
(c) x2+(y−2)2=4,r= 4 sin θ
Exercise Set 12.1 410
21.
Line
2
22.
Line
(
23.
Circle
3
24. 4
Circle
25.
6
Circle
26.
1
2
Cardioid
27.
Circle
1
2
28.
4
2
Cardioid
29.
Cardioid
3
6
30.
5
10
Cardioid
31. 4
8
Cardioid
32.
1
3
1
Limaçon
33.
1
2
Cardioid
34.
17
4
Limaçon
35.
3
2
1
Limaçon
36.
42
3
Limaçon
37.
Limaçon
3
17
38.
2
5
8
Limaçon
411 Chapter 12
39.
3
5
Limaçon
7
40.
3
1
7
Limaçon
41.
Lemniscate
3
42. 1
Lemniscate
43.
Lemniscate
444.
Spiral
2p
4p
6p
8p
45.
Spiral
2p4p
6p
8p
46. 2p
6p
4p
Spiral
47.
1
Four-petal rose
48.
3
Four-petal rose
49.
9
Eight-petal rose
50.
2
Three-petal rose
52. 1
-1
-1 1
53. 3
-3
-3 3
54. 2
-2
-2 2
55. 1
-1
-1 1

Exercise Set 12.1 412
56. 0≤θ≤8π57. (a) −4π<θ<4π
58. In I, along the x-axis, x=rgrows ever slower with θ.InIIx=rgrows linearly with θ.
Hence I: r=√θ;II:r=θ.
59. (a) r=a/ cos θ, x =rcos θ=a, a family of vertical lines
(b) r=b/ sin θ, y =rsin θ=b, a family of horizontal lines
60. The image of (r0,θ
0) under a rotation through an angle αis (r0,θ
0+α). Hence (f(θ),θ) lies on
the original curve if and only if (f(θ),θ+α) lies on the rotated curve, i.e. (r, θ) lies on the rotated
curve if and only if r=f(θ−α).
61. (a) r= 1 + cos(θ−π/4)=1+√
2
2(cos θ+ sin θ)
(b) r= 1 + cos(θ−π/2) = 1 + sin θ
(c) r= 1 + cos(θ−π)=1−cos θ
(d) r= 1 + cos(θ−5π/4)=1−√
2
2(cos θ+ sin θ)
62. r2= 4 cos 2(θ−π/2) = −4 cos 2θ
63. Either r−1=0orθ−1=0,
so the graph consists of the
circle r= 1 and the line θ=1.
0
p
/
2
r = 1
u = 1
64. (a) r2=Ar sin θ+Br cos θ,x2+y2=Ay +Bx, (x−B/2)2+(y−A/2)2=(A
2+B
2
)/4, which
is a circle of radius 1
4pA2+B2.
(b) Formula (4) follows by setting A=0,B =2a, (x−a)2+y2=a2, the circle of radius aabout
(a, 0). Formula (5) is derived in a similar fashion.
65. y=rsin θ= (1 + cos θ) sin θ= sin θ+ sin θcos θ,
dy/dθ = cos θ−sin2θ+ cos2θ= 2 cos2θ+ cos θ−1=(2cosθ−1)(cos θ+ 1);
dy/dθ = 0 if cos θ=1/2orifcosθ=−1; θ=π/3orπ.
If θ=π/3,π, then y=3
√
3/4,0 so the maximum value of yis 3√3/4 and the polar coordinates
of the highest point are (3/2,π/3).
66. x=rcos θ= (1 + cos θ) cos θ= cos θ+ cos2θ,dx/dθ =−sin θ−2 sin θcos θ=−sin θ(1 + 2 cos θ),
dx/dθ = 0 if sin θ= 0 or if cos θ=−1/2; θ=0,2π/3, or π.Ifθ=0,2π/3, π, then x=2,−1/4,0
so the minimum value of xis −1/4. The leftmost point has polar coordinates (1/2,2π/3).
67. (a) Let (x1,y
1) and (x2,y
2) be the rectangular coordinates of the points (r1,θ
1) and (r2,θ
2) then
d=p(x2−x1)2+(y
2−y
1)
2=p(r
2cos θ2−r1cos θ1)2+(r
2sin θ2−r1sin θ1)2
=pr2
1+r2
2−2r1r2(cos θ1cos θ2+ sin θ1sin θ2)=pr
2
1+r
2
2−2r
1
r
2cos(θ1−θ2).
(b) Let Pand Qhave polar coordinates (r1,θ
1),(r
2,θ
2), respectively, then the perpendicular
from OQ to OP has length h=r2sin(θ2−θ1) and A=1
2hr1=1
2r1r2sin(θ2−θ1).
413 Chapter 12
(c) From Part (a), d=p9+4−2·3·2 cos(π/6−π/3) = p13 −6√3≈1.615
(d) A=1
22 sin(5π/6−π/3)=1
68. (a) 0=(x
2+y
2+a
2
)
2−a
4−4a
2
x
2=x
4+y
4+a
4+2x
2y
2+2x
2a
2+2y
2a
2−a
4−4a
2x
2
=x
4+y
4+2x
2y
2−2x
2a
2+2y
2a
2=(x
2+y
2
)
2+2a
2(y
2−x
2)
=r
4+2a
2r
2(sin2θ−cos2θ)=r
4−2a
2
r
2cos 2θ, so r2=2a
2cos 2θ
(b) (x2+a2+y2)2−4x2a2=a4;(x−a)2+y2(x+a)2+y2=a4;
p(x+a)2+y2p(x−a)+y
2=a
2
69. lim
θ→0+y= lim
θ→0+rsin θ= lim
θ→0+
sin θ
θ=1
70. lim
θ→0±y= lim
θ→0±rsin θ= lim
θ→0±
sin θ
θ2= lim
θ→0±
sin θ
θlim
θ→0±
1
θ=1·lim
θ→0±
1
θ, so lim
θ→0±ydoes not exist.
71. Note that r→±∞as θapproaches odd multiples of π/2;
x=rcos θ= 4 tan θcos θ= 4 sin θ,
y=rsin θ= 4 tan θsin θ
so x→±4 and y→±∞as θapproaches
odd multiples of π/2.4
-4
u
r
72. lim
θ→(π/2)−x= lim
θ→(π/2)−rcos θ= lim
θ→(π/2)−2 sin2θ=2,x= 2 is a vertical asymptote.
73. Let r=asin nθ (the proof for r=acos nθ is similar). If θstarts at 0, then θwould have to increase
by some positive integer multiple of πradians in order to reach the starting point and begin to
retrace the curve. Let (r, θ) be the coordinates of a point Pon the curve for 0 ≤θ<2π.Now
asin n(θ+2π)=asin(nθ +2πn)=asin nθ =rso Pis reached again with coordinates (r, θ +2π)
thus the curve is traced out either exactly once or exactly twice for 0 ≤θ<2π. If for 0 ≤θ<π,
P(r, θ) is reached again with coordinates (−r, θ +π) then the curve is traced out exactly once for
0≤θ<π, otherwise exactly once for 0 ≤θ<2π. But
asin n(θ+π)=asin(nθ +nπ)=asin nθ, n even
−asin nθ, n odd
so the curve is traced out exactly once for 0 ≤θ<2πif nis even, and exactly once for 0 ≤θ<π
if nis odd.
EXERCISE SET 12.2
1. (a) dy/dx =1/2
2t=1/(4t); dy/dxt=−1=−1/4; dy/dxt=1 =1/4
(b) x=(2y)
2+1, dx/dy =8y, dy/dxy=±(1/2) =±1/4
2. (a) dy/dx = (4 cos t)/(−3 sin t)=−(4/3) cot t;dy/dxt=π/4=−4/3, dy/dxt=7π/4=4/3
(b) (x/3)2+(y/4)2=1,2x/9+(2y/16)(dy/dx)=0, dy/dx =−16x/9y,
dy/dxx=3/√2
y=4/√2
=−4/3; dy/dxx=3/√2
y=−4/√2
=4/3
Exercise Set 12.2 414
3. d2y
dx2=d
dx
dy
dx =d
dt dy
dxdt
dx =−1
4t2(1/2t)=−1/(8t3); positive when t=−1,
negative when t=1
4. d2y
dx2=d
dt dy
dxdt
dx =−(4/3)(−csc2t)
−3 sin t=−4
9csc3t; negative at t=π/4, positive at t=7π/4.
5. dy/dx =2
1/(2√t)=4
√
t,d
2
y/dx2=2/√t
1/(2√t)=4,dy/dxt=1 =4, d
2
y/dx2t=1 =4
6. dy/dx =t2
t=t,d2y/dx2=1
t,dy/dxt=2 =2, d
2
y/dx2t=2 =1/2
7. dy/dx =sec2t
sec ttan t= csc t,d2y/dx2=−csc tcot t
sec ttan t=−cot3t,
dy/dxt=π/3=2/
√
3, d2y/dx2t=π/3=−1/(3√3)
8. dy/dx =sinh t
cosh t= tanh t,d2y
dx2= sech2t/ cosh t= sech3t,dy/dxt=0 =0,d
2y/dx2t=0 =1
9. dy
dx =dy/dθ
dx/dθ =−cos θ
2−sin θ;d2y
dx2=d
dθ dy
dx/dx
dθ =2
(2 −sin θ)2
1
2−sin θ=1
(2 −sin θ)3;
dy
dxθ=π/3=−1/2
2−√3/2=−1
4−√3;d2y
dx2θ=π/3=1
(2 −√3/2)3=8
(4 −√3)3
10. dy
dx =3 cos φ
−sin φ=−3 cot φ;d2y
dx2=d
dφ(−3 cot φ)dφ
dx =−3(−csc2φ)(−csc φ)=−3 csc3φ;
dy
dxφ=5π/6
=3
√
3; d2y
dx2φ=5π/6
=−24
11. (a) dy/dx =−e−t
et=−e−2t; for t=1,dy/dx =−e−2,(x, y)=(e, e−1); y−e−1=−e−2(x−e),
y=−e−2x+2e
−1
(b) y=1/x, dy/dx =−1/x2,m=−1/e2,y−e
−1=−1
e
2(x−e),y =−1
e
2x+2
e
12. dy/dx =16t−2
2=8t−1; for t=1,dy/dx =7,(x, y)=(6,10); y−10=7(x−6), y=7x−32
13. dy/dx =4 cos t
−2 sin t=−2 cot t
(a) dy/dx = 0 if cot t=0,t=π/2+nπ for n=0,±1,···
(b) dx/dy =−1
2tan t= 0 if tan t=0,t=nπ for n=0,±1,···
14. dy/dx =2t+1
6t
2−30t+24 =2t+1
6(t−1)(t−4)
(a) dy/dx =0ift=−1/2
(b) dx/dy =6(t−1)(t−4)
2t+1 =0ift=1,4
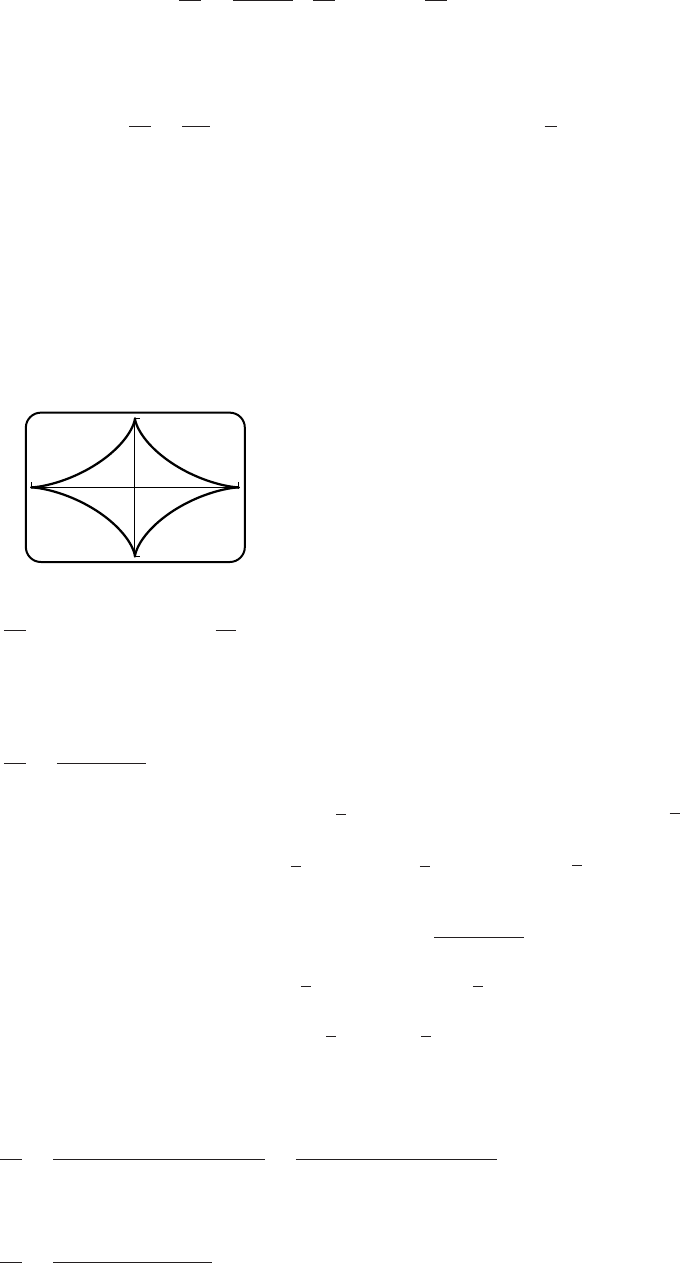
415 Chapter 12
15. x=y= 0 when t=0,π;dy
dx =2 cos 2t
cos t;dy
dxt=0
=2,dy
dxt=π
=−2,the equations of the tangent
lines are y=−2x, y =2x.
16. y(t) = 0 has three solutions, t=0,±π/2; the last two correspond to the crossing point.
For t=±π/2, m=dy
dx =2
±π; the tangent lines are given by y=±2
π(x−2).
17. If y= 4 then t2=4,t=±2, x= 0 for t=±2so(0,4) is reached when t=±2.
dy/dx =2t/(3t2−4). For t=2,dy/dx =1/2 and for t=−2, dy/dx =−1/2. The tangent lines
are y=±x/2+4.
18. If x= 3 then t2−3t+5=3,t
2−3t+2=0,(t−1)(t−2)=0,t= 1 or 2. If t= 1 or 2 then
y= 1 so (3,1) is reached when t= 1 or 2. dy/dx =(3t
2+2t−10)/(2t−3). For t=1,dy/dx =5,
the tangent line is y−1=5(x−3), y=5x−14. For t=2,dy/dx = 6, the tangent line is
y−1=6(x−3), y=6x−17.
19. (a) 1
-1
-1 1
(b) dx
dt =−3 cos2tsin tand dy
dt = 3 sin2tcos tare both zero when t=0,π/2,π,3π/2,2π,
so singular points occur at these values of t.
20. (a) when y=0
(b) dy
dx =asin θ
a−acos θ= 0 when θ=2nπ +π/2,n=0,1,... (which is when y= 0).
21. Substitute θ=π/3, r= 1, and dr/dθ =−√3 in equation (7) gives slope m=1/
√
3.
22. As in Exercise 21, θ=π/4, dr/dθ =√2/2, r=1+√
2/2, m=−1−√2
23. As in Exercise 21, θ=2,dr/dθ =−1/4, r=1/2, m=tan 2 −2
2 tan 2 + 1
24. As in Exercise 21, θ=π/6, dr/dθ =4
√
3a,r=2a,m=3
√
3/5
25. As in Exercise 21, θ=3π/4, dr/dθ =−3√2/2, r=√2/2, m=−2
26. As in Exercise 21, θ=π,dr/dθ =3,r=4,m=4/3
27. m=dy
dx =rcos θ+ (sin θ)(dr/dθ)
−rsin θ+ (cos θ)(dr/dθ)=cos θ+ 2 sin θcos θ
−sin θ+ cos2θ−sin2θ;ifθ=0,π/2,π,
then m=1,0,−1.
28. m=dy
dx =cos θ(4 sin θ−1)
4 cos2θ+ sin θ−2;ifθ=0,π/2,π then m=−1/2,0,1/2.
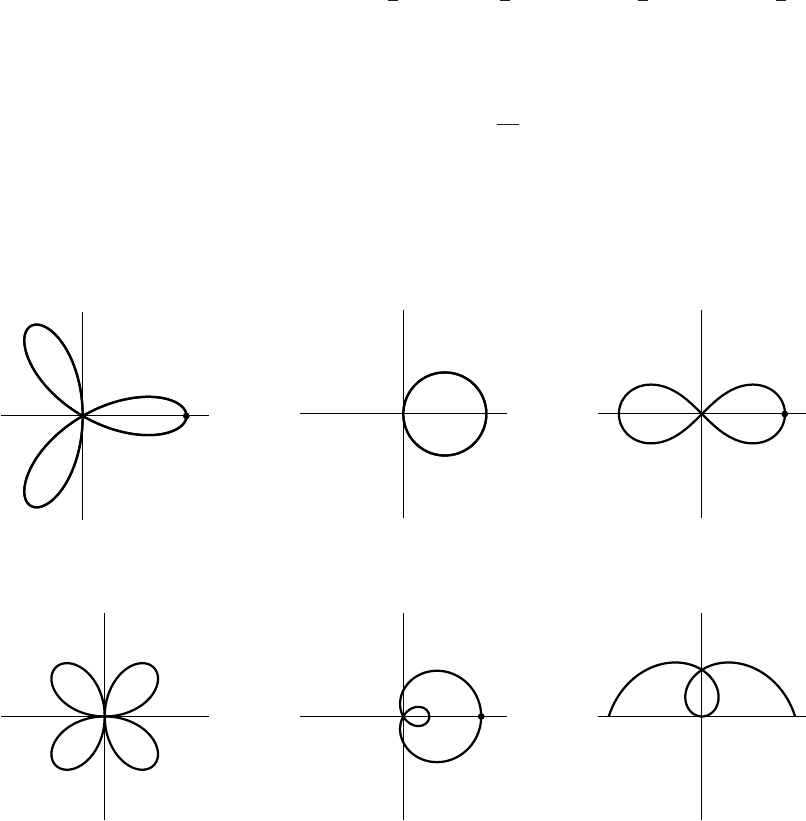
Exercise Set 12.2 416
29. dx/dθ =−asin θ(1 + 2 cos θ), dy/dθ =a(2 cos θ−1)(cos θ+1)
(a) horizontal if dy/dθ = 0 and dx/dθ 6=0.dy/dθ = 0 when cos θ=1/2orcosθ=−1soθ=π/3,
5π/3, or π;dx/dθ 6= 0 for θ=π/3 and 5π/3. For the singular point θ=πwe find that
lim
θ→πdy/dx = 0. There is a horizontal tangent line at (3a/2,π/3),(0,π), and (3a/2,5π/3).
(b) vertical if dy/dθ 6= 0 and dx/dθ =0. dx/dθ = 0 when sin θ= 0 or cos θ=−1/2soθ=0,π,
2π/3, or 4π/3; dy/dθ 6= 0 for θ=0,2π/3, and 4π/3. The singular point θ=πwas discussed
in part (a). There is a vertical tangent line at (2a, 0),(a/2,2π/3), and (a/2,4π/3).
30. dx/dθ =a(cos2θ−sin2θ)=acos 2θ, dy/dθ =2asin θcos θ=asin 2θ
(a) horizontal if dy/dθ = 0 and dx/dθ 6=0. dy/dθ = 0 when θ=0,π/2,π,3π/2,2π;dx/dθ 6=0
for (0,0),(a, π/2),(0,π),(−a, 3π/2),(0,2π); in reality only two distinct points
(b) vertical if dy/dθ 6= 0 and dx/dθ =0. dx/dθ = 0 when θ=π/4,3π/4,5π/4,7π/4; dy/dθ 6=0
there, so vertical tangent line at (a/√2,π/4),(a/√2,3π/4),(−a/√2,5π/4),(−a/√2,7π/4),
only two distinct points
31. dy/dθ =(d/dθ)(sin2θcos2θ) = (sin 4θ)/2=0atθ=0,π/4,π/2,3π/4,π; at the same points,
dx/dθ =(d/dθ)(sin θcos3θ) = cos2θ(4 cos2θ−3). Next, dx
dθ =0atθ=π/2, a singular point; and
θ=0,π both give the same point, so there are just three points with a horizontal tangent.
32. dx/dθ = 4 sin2θ−sin θ−2, dy/dθ = cos θ(1 −4 sin θ). dy/dθ = 0 when cos θ= 0 or sin θ=1/4so
θ=π/2, 3π/2, sin−1(1/4), or π−sin−1(1/4); dx/dθ 6= 0 at these points, so there is a horizontal
tangent at each one.
33.
0
p/2
2
θ0=π/6,π/2,5π/6
34.
0
p/2
θ0=π/2
35.
0
p/2
4
θ0=±π/4
36.
0
p/2
θ0=0,π/2
37.
0
p/2
3
θ0=2π/3,4π/3
38.
0
p/2
θ0=0
39. r2+(dr/dθ)2=a2+0
2=a
2,L=Z2π
0adθ =2πa
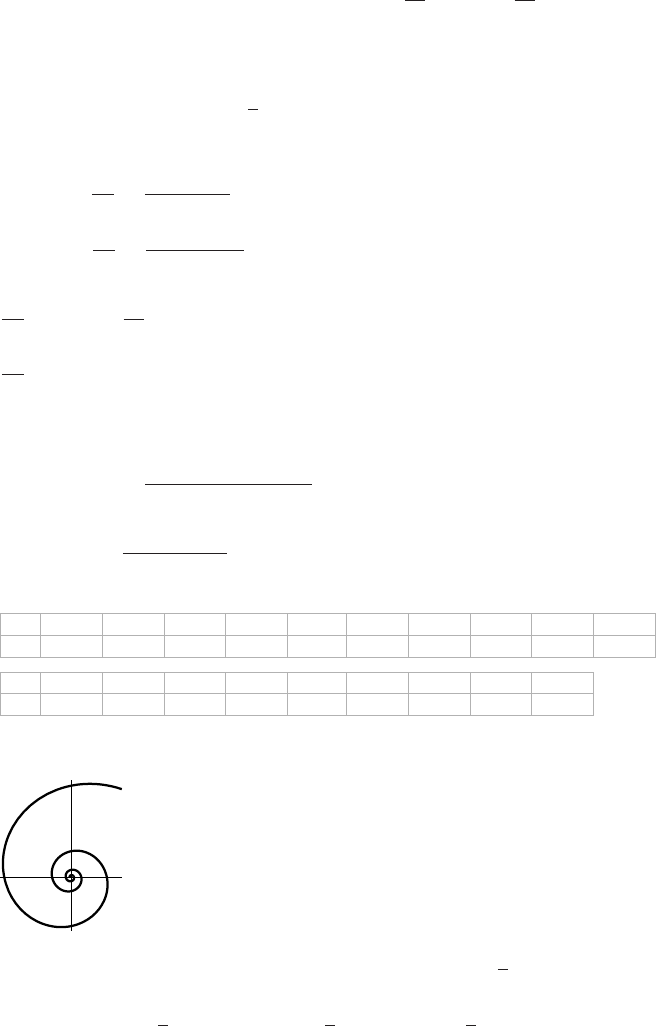
417 Chapter 12
40. r2+(dr/dθ)2=(2acos θ)2+(−2asin θ)2=4a
2
,L=Zπ/2
−π/22adθ =2πa
41. r2+(dr/dθ)2=[a(1 −cos θ)]2+[asin θ]2=4a
2sin2(θ/2), L=2Zπ
02asin(θ/2)dθ =8a
42. r2+(dr/dθ)2= [sin2(θ/2)]2+ [sin(θ/2) cos(θ/2)]2= sin2(θ/2), L=Zπ
0sin(θ/2)dθ =2
43. r2+(dr/dθ)2=(e
3θ
)
2+(3e
3θ)
2=10e
6θ
,L=Z2
0
√
10e3θdθ =√10(e6−1)/3
44. r2+(dr/dθ)2= [sin3(θ/3)]2+ [sin2(θ/3) cos(θ/3)]2= sin4(θ/3),
L=Zπ/2
0sin2(θ/3)dθ =(2π−3
√
3)/8
45. (a) From (3), dy
dx =3 sin t
1−3 cos t
(b) At t=10,dy
dx =3 sin 10
1−3 cos 10 ≈−0.4640,θ ≈tan−1(−0.4640) = −0.4344
46. (a) dy
dx = 0 when dy
dt = 2 sin t=0,t=0,π,2π, 3π
(b) dx
dt = 0 when 1 −2 cos t=0,cos t=1/2,t =π/3,5π/3,7π/3
47. (a) r2+(dr/dθ)2= (cos nθ)2+(−nsin nθ)2= cos2nθ +n2sin2nθ
=(1−sin2nθ)+n
2sin2nθ =1+(n
2−1) sin2nθ,
L=2Zπ/(2n)
0q1+(n
2−1) sin2nθdθ
(b) L=2Zπ/4
0p1+3sin
22θdθ ≈2.42
(c) n
L
2
2.42211
3
2.22748
4
2.14461
5
2.10100
6
2.07501
7
2.05816
8
2.04656
9
2.03821
10
2.03199
11
2.02721
n
L
12
2.02346
13
2.02046
14
2.01802
15
2.01600
16
2.01431
17
2.01288
18
2.01167
19
2.01062
20
2.00971
48. (a)
0
p/2
(b) r2+(dr/dθ)2=(e
−θ
)
2+(−e
−θ)
2=2e
−2θ
,L=
Z+∞
0
√
2e
−θ
dθ
(c) L= lim
θ0→+∞Zθ0
0
√2e−θdθ = lim
θ0→+∞
√2(1 −e−θ0)=√
2
Exercise Set 12.2 418
49. x0=2t,y
0=2,(x
0)
2+(y
0)
2=4t
2+4
S=2πZ4
0(2t)p4t2+4dt =8πZ4
0t
pt
2+1dt =8π
3(t2+1)
7/24
0
=8π
3(17√17 −1)
50. x0=et(cos t−sin t), y0=et(cos t+ sin t), (x0)2+(y
0)
2=2e
2t
S=2πZπ/2
0(etsin t)√2e2tdt =2
√
2πZπ/2
0e2tsin tdt
=2
√
2π1
5
e
2t
(2 sin t−cos t)π/2
0
=2√2
5π(2eπ+1)
51. x0=−2 sin tcos t,y0= 2 sin tcos t,(x
0
)
2+(y
0)
2= 8 sin2tcos2t
S=2πZπ/2
0cos2tp8 sin2tcos2tdt=4
√
2πZπ/2
0cos3tsin tdt=−√2πcos4tπ/2
0
=√2π
52. x0=1,y
0=4t,(x
0
)
2+(y
0)
2=1+16t
2,S=2πZ1
0t
p1+16t
2dt =π
24(17√17 −1)
53. x0=−rsin t,y0=rcos t,(x
0
)
2+(y
0)
2=r
2,S=2πZπ
0rsin t√r2dt =2πr2Zπ
0sin tdt=4πr2
54. dx
dφ =a(1 −cos φ), dy
dφ =asin φ,dx
dφ2
+dy
dφ2
=2a
2
(1 −cos φ)
S=2πZ2π
0a(1 −cos φ)p2a2(1 −cos φ)dφ =2
√
2πa2Z2π
0(1 −cos φ)3/2dφ,
but 1 −cos φ= 2 sin2φ
2so (1 −cos φ)3/2=2
√
2 sin3φ
2for 0 ≤φ≤πand, taking advantage of the
symmetry of the cycloid, S=16πa2Zπ
0sin3φ
2dφ =64πa2/3
55. (a) dr
dt = 2 and dθ
dt =1sodr
dθ =dr/dt
dθ/dt =2
1=2,r=2θ+C,r= 10 when θ=0so
10 = C, r =2θ+ 10.
(b) r2+(dr/dθ)2=(2θ+ 10)2+ 4, during the first 5 seconds the rod rotates through an angle
of (1)(5) = 5 radians so L=Z5
0p(2θ+ 10)2+4dθ, let u=2θ+10toget
L=1
2Z20
10 pu2+4du =1
2hu
2pu2+4+2ln|u+pu
2+4|
i20
10
=1
2"10√404 −5√104 + 2 ln 20+√404
10+√104#≈75.7mm
56. x=rcos θ, y =rsin θ, dx
dθ =dr
dθ cos θ−rsin θ, dy
dθ =rcos θ+dr
dθ sin θ,
dx
dθ 2
+dy
dθ 2
=r2+dr
dθ 2
, and Formula (6) of Section 8.4 becomes
L=Zβ
αsr2+dr
dθ 2
dθ

419 Chapter 12
EXERCISE SET 12.3
1. (a) Zπ
π/2
1
2(1 −cos θ)2dθ (b) Zπ/2
0
1
24 cos2θdθ (c) Zπ/2
0
1
2sin22θdθ
(d) Z2π
0
1
2θ2dθ (e) Zπ/2
−π/2
1
2(1 −sin θ)2dθ (f) 2Zπ/4
0
1
2cos22θdθ
2. (a) 3π/8+1 (b) π/2(c) π/8
(d) 4π3/3(e) 3π/4(f) π/8
3. (a) A=Z2π
0
1
2a2dθ =πa2(b) A=Zπ
0
1
24a2sin2θdθ=πa2
(c) A=Zπ/2
−π/2
1
24a2cos2θdθ =πa2
4. (a) r2=rsin θ+rcos θ, x2+y2−y−x=0,x−1
2
2
+y−1
2
2
=1
2
(b) A=Z3π/4
−π/4
1
2(sin θ+ cos θ)2dθ =π/2
5. A=2Zπ
0
1
2
(2 + 2 cos θ)2dθ =6π6. A=Zπ/2
0
1
2(1 + sin θ)2dθ =3π/8+1
7. A=6Zπ/6
0
1
2(16 cos23θ)dθ =4π
8. The petal in the first quadrant has area Zπ/2
0
1
24 sin22θdθ=π/2, so total area = 2π.
9. A=2Zπ
2π/3
1
2(1 + 2 cos θ)2dθ =π−3√3/210. A=Z3
1
2
θ2dθ =4/3
11. area = A1−A2=Zπ/2
0
1
24 cos2θdθ−Zπ/4
0
1
2cos 2θdθ=π/2−1
4
12. area = A1−A2=Zπ
0
1
2(1 + cos θ)2dθ −Zπ/2
0
1
2cos2θdθ=5π/8
13. The circles intersect when cos t=√3 sin t, tan t=1/
√
3,t =π/6, so
A=A1+A2=Zπ/6
0
1
2(4√3 sin t)2dt+Zπ/2
π/6
1
2(4 cos t)2dt =2π−3
√
3+4π/3−√3=10π/3−4√3.
14. The curves intersect when 1 + cos t= 3 cos t, cos t=1/2,t=±π/3, and hence
total area = 2 Zπ/3
0
1
2(1+cos t)2dt+2 Zπ/2
π/3
1
29 cos2tdt=2(π/4+9√3/16+3π/8−9√3/16)=5π/4.

Exercise Set 12.3 420
15. A=2Zπ/2
π/6
1
2[25 sin2θ−(2 + sin θ)2]dθ =8π/3+√
3
16. A=2Zπ
0
1
2
[16 −(2 −2 cos θ)2]dθ =10π
17. A=2Zπ/3
0
1
2[(2 + 2 cos θ)2−9]dθ =9
√
3/2−π
18. A=2Zπ/4
0
1
2(16 sin2θ)dθ =2π−4
19. A=2"Z2π/3
0
1
2(1/2 + cos θ)2dθ −Zπ
2π/3
1
2(1/2 + cos θ)2dθ#=(π+3
√
3)/4
20. A=2Zπ/3
0
1
2(2 + 2 cos θ)2−9
4sec2θdθ =2π+9
4
√
3
21. A=2Zcos−1(3/5)
0
1
2(100 −36 sec2θ)dθ = 100 cos−1(3/5) −48
22. A=8Zπ/8
0
1
2(4a2cos22θ−2a2)dθ =2a
2
23. (a) ris not real for π/4<θ<3π/4 and 5π/4<θ<7π/4
(b) A=4Zπ/4
0
1
2a2cos 2θdθ=a
2
(c) A=4Zπ/6
0
1
2h4 cos 2θ−2idθ =2
√
3−2π
3
24. A=2Zπ/2
0
1
2sin 2θdθ=1 25. A=Z4π
2π
1
2a2θ2dθ −Z2π
0
1
2a2θ2dθ =8π
3
a
2
26. (a) x=rcos θ, y =rsin θ,
(dx/dθ)2+(dy/dθ)2=(f
0(θ) cos θ−f(θ) sin θ)2+(f0(θ) sin θ+f(θ) cos θ)2=f0(θ)2+f(θ)2;
S=Zβ
α
2πf(θ) sin θpf0(θ)2+f(θ)2dθ if about θ= 0; similarly for θ=π/2
(b) f0,g
0are continuous and no segment of the curve is traced more than once.
27. r2+dr
dθ 2
= cos2θ+ sin2θ=1,
so S=Zπ/2
−π/22πcos2θdθ =π
2.
421 Chapter 12
28. S=Zπ/2
02πeθcos θ√2e2θdθ
=2
√
2πZπ/2
0e2θcos θdθ=2
√2π
5(e
π−2)
29. S=Zπ
02π(1 −cos θ) sin θp1−2 cos θ+ cos2θ+ sin2θdθ
=2
√
2πZπ
0sin θ(1 −cos θ)3/2dθ =2
52√2π(1 −cos θ)5/2
π
0=32π/5
30. S=Zπ
02πa sin(θ)adθ =4πa2
31. (a) r3cos3θ−3r2cos θsin θ+r3sin3θ=0,r=3 cos θsin θ
cos3θ+ sin3θ
32. (a) A=2Zπ/(2n)
0
1
2a2cos2nθ dθ =πa2
4n(b) A=2Zπ/(2n)
0
1
2a2cos2nθ dθ =πa2
4n
(c) 1
2n×total area = πa2
4n(d) 1
n×total area = πa2
4n
33. If the upper right corner of the square is the point (a, a) then the large circle has equation r=√2a
and the small circle has equation (x−a)2+y2=a2,r=2acos θ,so
area of crescent = 2 Zπ/4
0
1
2h(2acos θ)2−(√2a)2idθ =a2= area of square.
Exercise Set 12.4 422
34. A=Z2π
0
1
2(cos 3θ+2)
2dθ =9π/2
3
-3
-3 3
35. A=Zπ/2
0
1
24 cos2θsin4θdθ=π/16
1
–1
01
EXERCISE SET 12.4
1. (a) 4px =y2,point(1,1),4p=1,x=y
2(b) −4py =x2,point(3,−3),12p=9,−3y=x
2
(c) a=3,b =2,x
2
9+y
2
4=1 (d) a=3,b =2,x
2
4+y
2
9=1
(e) asymptotes: y=±x,soa=b;point(0,1), so y2−x2=1
(f) asymptotes: y=±x,sob=a;point(2,0), so x2
4−y2
4=1
2. (a) part (a), vertex (0,0),p=1/4; focus (1/4,0), directrix: x=−1/4
part (b), vertex (0,0),p=3/4; focus (0,−3/4), directrix: y=3/4
(b) part (c), c=√a2−b2=√5, foci (±√5,0)
part (d), c=√a2−b2=√5, foci (0,±√5)
(c) part (e), c=√a2+b2=√2, foci at (0,±√2); asymptotes: y2−x2=0,y =±x
part (f), c=√a2+b2=√8=2
√
2, foci at (±2√2,0); asymptotes: x2
4−y2
4=0,y =±x
3. (a)
-3 3
-3
3
3
2
F( , 0)x
y
3
2
x = –
(b)
x
y
9
4
F(0, –
)
9
4
y =
-5 5
-5
5
4. (a)
5
2
x =
5
2
F(– , 0)x
y(b)
x
y
F(0, 1)
y = –1
423 Chapter 12
5. (a)
6
6
x
y1
2
x =
V(2, 3)
7
2
F( , 3)
(b)
-4
-4
x
y
9
4
F(–2, –
)
7
4
y = –
V(–2, –2)
6. (a) 23
4
x =
x
y
9
4
F( , –1)V(4, –1)
(b)
1
2
y =
F( , )
1
2
3
2
V( , 1)
1
2
x
y
7. (a)
4
4
x
y
5
2
V(2,
)
F(2, 2)
y = 3
(b)
2
4
x
y
V(–2, 2) 7
4
F(– , 2)
9
4
x = –
8. (a)
x
y
9
2
x = –
7
2
F(– , 3)
V(–4, 3)
(b)
15
16
y =
17
16
F(–1, )
x
y
V (–1, 1)
9. (a) c2=16−9=7,c=√
7
(4, 0)
(0, 3)
(0, –3)
(–4, 0) x
y
(–√7, 0)
(√7, 0)
(b) x2
1+y2
9=1
c
2=9−1=8,c=√8
(0, 3)
(0, –3)
(–1, 0) (1, 0)
x
y
(0, √8)
(0, –√8)
Exercise Set 12.4 424
10. (a) c2=25−4 = 21, c=√21
(0, 5)
(0, –5)
(–2, 0) (2, 0)
x
y
(0, –√21)
(0, √21)
(b) x2
9+y2
4=1
c
2=9−4=5,c=√5
(0, 2)
(0, –2)
(–3, 0)
(3, 0)
x
y
(–√5, 0)
(√5, 0)
11. (a) (x−1)2
16 +(y−3)2
9=1
c
2=16−9=7,c=√7
(1, 6)
(1, 0)
x
y
(1 – √7, 3) (1 + √7, 3)
(5, 3)(–3, 3)
(b) (x+2)
2
4+(y+1)
2
3=1
c
2=4−3=1,c=1
(–4, –1) (–3, –1)
(–1, –1) (0, –1)
x
y
(–2, –1 + √3)
(–2, –1 – √3)
12. (a) (x+3)
2
16 +(y−5)2
4=1
c
2=16−4=12,c=2
√
3
(1, 5)
(–3, 7)
(–3, 3)
(–7, 5)
x
y
(–3 –2√3, 5)
(–3 +2√3, 5)
(b) x2
4+(y+2)
2
9=1
c
2=9−4=5,c=√5
(0, –5)
(0, 1) (0, –2 + √5)
(0, –2 – √5)
(–2, –2) (2, –2)
x
y
425 Chapter 12
13. (a) (x+1)
2
9+(y−1)2
1=1
c
2=9−1=8,c=√8
(–1, 2)
(–1, 0)
(–4, 1)
(2, 1)
x
y
(–1 – √8, 1)
(–1 + √8, 1)
(b) (x+1)
2
4+(y−5)2
16 =1
c
2=16−4=12,c=2
√
3
(1, 5)(–3, 5)
(–1, 1)
(–1, 9)
x
y
(–1, 5 + 2√3)
(–1, 5 – 2√3)
14. (a) (x+1)
2
4+(y−3)2
9=1
c
2=9−4=5,c=√5
(–1, 3 + √5)
(–1, 3 – √5)
(1, 3)
(–1, 6)
(–1, 0)
(–3, 3)
x
y
(b) (x−2)2
9+(y+3)
2
5=1
c
2=9−5=4,c=2
(2, –3 + √5)
(2, –3 – √5)
(4, –3)
(–1, –3) (5, –3)
(0, –3)
x
y
15. (a) c2=a2+b2=16+4=20,c=2
√
5
(0, –2)
(0, 2)
x
y
2
3
y = – x2
3
y = x
(0, √13)
(0, –√13)
(b) y2/4−x2/9=1
c
2=4+9=13,c=√13
(–4, 0) (4, 0)
x
y
1
2
y = – x1
2
y = x
(–2√5, 0) (2√5, 0)
Exercise Set 12.4 426
16. (a) c2=a2+b2=9+25=34,c=√34
(0, –3)
(0, 3)
x
y
(0, √34)
(0, –√34)
3
5
y = – x3
5
y = x
(b) x2/25 −y2/16=1
c
2=25+16=41,c=√41
(–5, 0) (5, 0)
x
y
4
5
y = – x4
5
y = x
(–√41, 0) (√41, 0)
17. (a) c2=9+4=13,c=√13
(5, 4)
x
y
(2 – √13, 4) (2 + √13, 4)
(–1, 4)
y – 4 = – (x – 2)
2
3
y – 4 = (x – 2)
2
3
(b) (y+3)
2/36 −(x+2)
2/4=1
c
2=36+4=40,c =2
√
10
(–2, 3)
(–2, –9)
y + 3 = –3(x + 2) y + 3 = 3(x + 2)
x
y
(–2, –3 + 2√10)
(–2, –3 – 2√10)
18. (a) c2=3+5=8,c=2
√
2
x
y
(2, –4 + √3)
(2, –4 – √3)
(2, –4 – 2√2)
(2, –4 + 2√2)
√
3
5
y + 4 = (x – 2)
√
3
5
y + 4 = – (x – 2)
(b) (x+1)
2/1−(y−3)2/2=1
c
2=1+2=3,c =√3
(–2, 3)
(-1 + √3, 3)(-1 − √3, 3)
(0, 3)
y − 3 = √2(x + 1)
y − 3 = −√2(x + 1)
x
y
427 Chapter 12
19. (a) (x+1)
2/4−(y−1)2/1=1
c
2=4+1=5,c =√5
(–3, 1)
(1, 1)
x
y
y – 1 = – (x + 1)
1
2
y – 1 = (x + 1)
1
2
(–1 – √5, 1)
(–1 + √5, 1)
(b) (x−1)2/4−(y+3)
2/64=1
c
2=4+64=68,c =2
√
17
(–1, –3) (3, –3) x
y
y + 3 = –4(x –1)
y + 3 = 4(x –1)
(1 + 2√17, –3)(–1 – 2√17, –3)
20. (a) (y−3)2/4−(x+2)
2/9=1
c
2=4+9=13,c=√13
(-2, 5)
(-2, 1)
x
y
2
3
y – 3 = – (x + 2)
2
3
y – 3 = (x + 2)
(–2, 3 – √13)
(–2, 3 + √13)
(b) (y+5)
2/9−(x+2)
2/36=1
c
2=9+36=45,c =3
√
5
(–2, –8)
(–2, –2) x
y
1
2
y + 5 = – (x + 2)
1
2
y + 5 = (x + 2)
(–2, –5 + 3√5)
(–2, –5 – 3√5)
21. (a) y2=4px,p=3,y
2=12x(b) y2=−4px,p=7,y
2=−28x
22. (a) x2=−4py,p=4,x
2=−16y(b) x2=−4py,p=1/2, x2=−2y
23. (a) x2=−4py,p=3,x
2=−12y
(b) The vertex is 3 units above the directrix so p=3,(x−1)2= 12(y−1).
24. (a) y2=4px,p=6,y
2=24x
(b) The vertex is half way between the focus and directrix so the vertex is at (2,4), the focus is 3
units to the left of the vertex so p=3,(y−4)2=−12(x−2)
25. y2=a(x−h), 4 = a(3 −h) and 9 = a(2 −h), solve simultaneously to get h=19/5, a=−5so
y
2=−5(x−19/5)
26. (x−5)2=a(y+ 3), (9 −5)2=a(5+3)soa=2,(x−5)2=2(y+3)
27. (a) x2/9+y
2/4=1
(b) a=26/2 = 13, c=5,b
2=a
2−c
2= 169 −25 = 144; x2/169 + y2/144=1
Exercise Set 12.4 428
28. (a) x2+y2/5=1
(b) b=8,c=6,a
2=b
2+c
2= 64 + 36 = 100; x2/64+y2/100=1
29. (a) c=1,a
2=b
2+c
2=2+1=3;x
2
/3+y
2/2=1
(b) b2=16−12=4;x
2
/16+y2/4=1andx
2
/4+y
2/16=1
30. (a) c=3,b
2=a
2−c
2=16−9=7;x
2
/16+y2/7=1
(b) a2=9+16=25;x
2/25+y2/9=1andx
2
/9+y
2/25=1
31. (a) a=6,(2,3) satisfies x2/36+y2/b2= 1 so 4/36+9/b2=1,b
2=81/8; x2/36+y2/(81/8)=1
(b) The center is midway between the foci so it is at (1,3), thus c=1,b=1,a
2=1+1=2;
(x−1)2+(y−3)2/2=1
32. (a) Substitute (3,2) and (1,6) into x2/A +y2/B = 1 to get 9/A +4/B = 1 and 1/A +36/B =1
which yields A= 10, B= 40; x2/10+y2/40=1
(b) The center is at (2,−1) thus c=2,a=3,b
2=9−4=5;(x−2)2/5+(y+1)
2/9=1
33. (a) a=2,c=3,b
2=9−4=5;x
2
/4−y
2
/5=1
(b) a=1,b/a =2,b=2;x
2−y
2
/4=1
34. (a) a=3,c=5,b
2=25−9 = 16; y2/9−x2/16=1
(b) a=3,a/b =1,b=3;y
2
/9−x
2
/9=1
35. (a) vertices along x-axis: b/a =3/2soa=8/3; x2/(64/9) −y2/16=1
vertices along y-axis: a/b =3/2soa=6;y
2
/36 −x2/16=1
(b) c=5,a/b = 2 and a2+b2= 25, solve to get a2= 20, b2=5;y
2
/20 −x2/5=1
36. (a) foci along the x-axis: b/a =3/4 and a2+b2= 25, solve to get a2= 16, b2=9;
x
2
/16 −y2/9=1
foci along the y-axis: a/b =3/4 and a2+b2= 25 which results in y2/9−x2/16=1
(b) c=3,b/a = 2 and a2+b2=9soa
2=9/5, b2=36/5; x2/(9/5) −y2/(36/5)=1
37. (a) the center is at (6,4), a=4,c=5,b
2=25−16=9;(x−6)2/16 −(y−4)2/9=1
(b) The asymptotes intersect at (1/2,2) which is the center, (y−2)2/a2−(x−1/2)2/b2=1is
the form of the equation because (0,0) is below both asymptotes, 4/a2−(1/4)/b2= 1 and
a/b = 2 which yields a2=3,b
2=3/4; (y−2)2/3−(x−1/2)2/(3/4)=1.
38. (a) the center is at (1,−2); a=2,c= 10, b2= 100 −4 = 96; (y+2)
2/4−(x−1)2/96=1
(b) the center is at (1,−1); 2a=5−(−3)=8,a =4,(x−1)2
16 −(y+1)
2
16 =1
39. (a) y=ax2+b, (20,0) and (10,12) are on the curve so
400a+b= 0 and 100a+b= 12. Solve for bto get
b= 16 ft = height of arch.
(b) x2
a2+y2
b2=1,400 = a2,a = 20; 100
400 +144
b2=1,
b=8
√
3 ft = height of arch.
-20 -10 10 20
(10, 12)
x
y
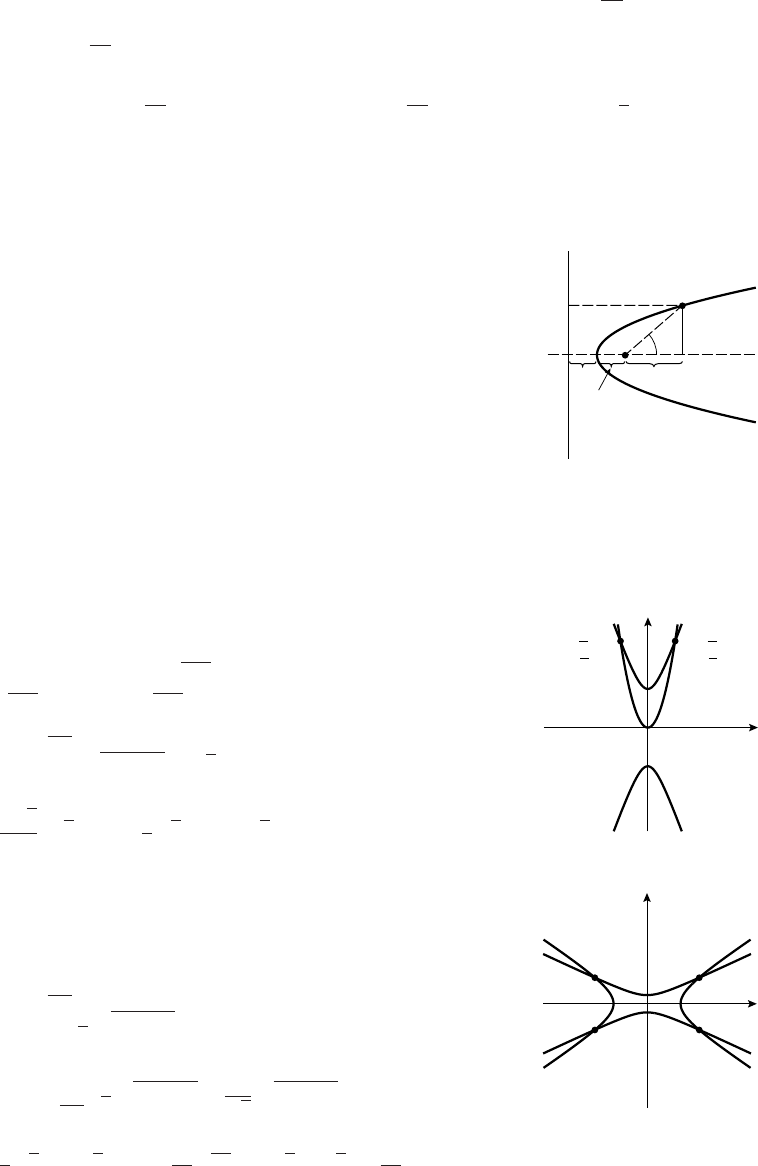
429 Chapter 12
40. (a) (x−b/2)2=a(y−h), but (0,0) is on the parabola so b2/4=−ah,a=−b2
4h,
(x−b/2)2=−b2
4h(y−h)
(b) As in part (a), y=−4h
b2(x−b/2)2+h,A=Zb
0−4h
b2(x−b/2)2+hdx =2
3bh
41. We may assume that the vertex is (0,0) and the parabola opens to the right. Let P(x0,y
0)bea
point on the parabola y2=4px, then by the definition of a parabola, PF = distance from Pto
directrix x=−p,soPF =x
0+pwhere x0≥0 and PF is a minimum when x0= 0 (the vertex).
42. Let p= distance (in millions of miles) between
the vertex (closest point) and the focus F,
then PD =PF,2p+ 20 = 40, p= 10 million miles.
40 60°
40 cos 60° = 20
p
DP
p
Directrix
43. Use an xy-coordinate system so that y2=4px is an equation of the parabola, then (1,1/2) is a
point on the curve so (1/2)2=4p(1), p=1/16. The light source should be placed at the focus
which is 1/16 ft. from the vertex.
44. (a) Substitute x2=y/2intoy
2−8x
2= 5 to get y2−4y−5=0;
y=−1,5. Use x2=y/2 to find that there is no solution if
y=−1 and that x=±p5/2ify= 5. The curves intersect
at (p5/2,5) and (−p5/2,5), and thus the area is
A=2Z√
5/2
0(
p5+8x
2−√
2x)dx
=5√2
2(√5−1) + 5
4√2 ln(2 + √5)
5
2
(
–
√
, 5
)
5
2
(
√
, 5
)
x
y
(b) Eliminate xto get y2=1,y=±1. Use either equation
to find that x=±2ify= 1 or if y=−1. The curves
intersect at (2,1), (2,−1), (−2,1), and (−2,−1),
and thus the area is
A=4Z√
5/3
0
1
3
p1+2x
2dx
+4Z2
√
5/31
3
p1+2x
2−1
√
7p3x
2−5
dx
=1
3√2 ln(2√2+3)+10
21√21 ln(2√3+√
7) −5
21 ln 5
(–2, 1)
(–2, –1) (2, –1)
(2, 1)
x
y
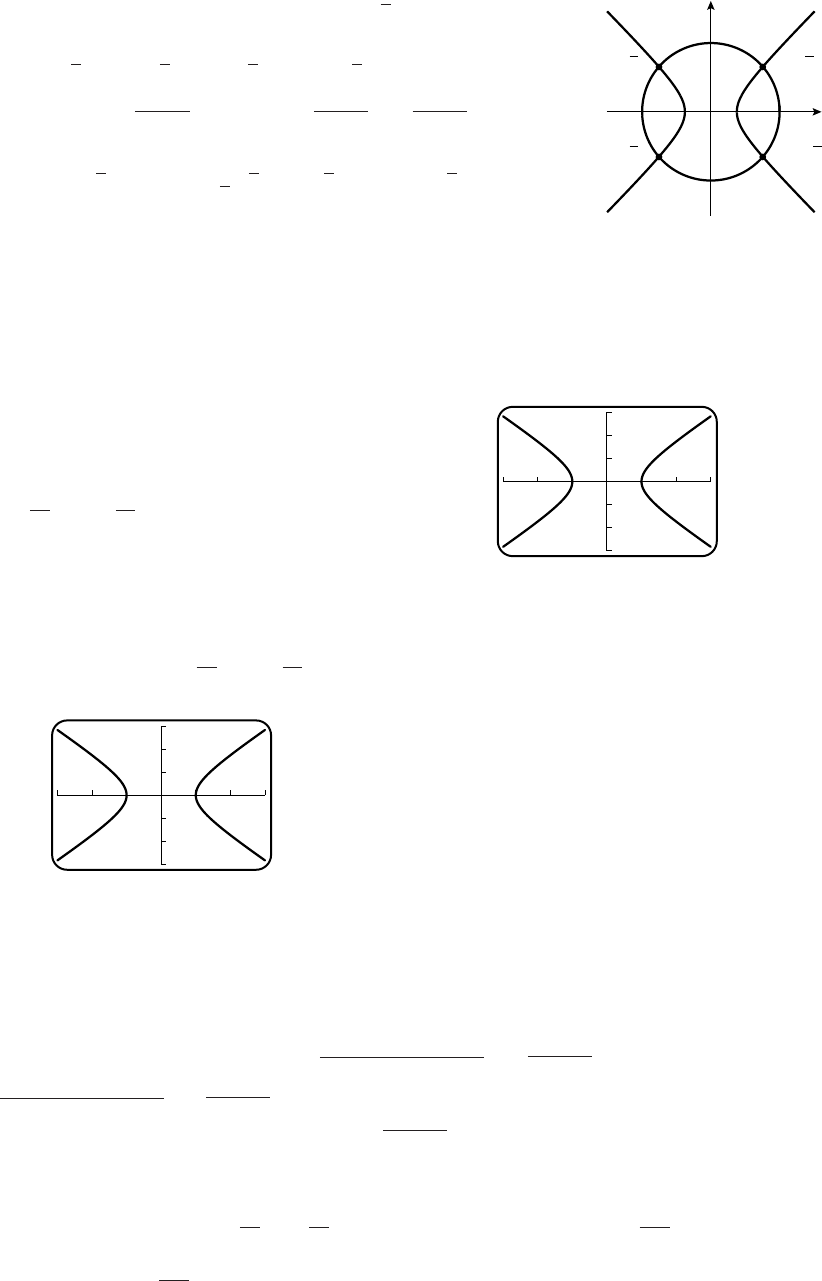
Exercise Set 12.4 430
(c) Add both equations to get x2=4,x=±2.
Use either equation to find that y=±√3ifx=2
or if x=−2. The curves intersect at
(2,√3), (2,−√3), (−2,√3), (−2,−√3) and thus
A=4Z1
0p7−x
2dx +4Z2
1hp7−x
2−px
2−1
idx
=4
√
3+14sin
−12
7√
7
−4
√
3 + 2 ln(2 + √3)
x
y
(–2, √3) (2, √3)
(–2, –√3) (2, –√3)
45. (a) P:(bcos t, b sin t); Q:(acos t, a sin t); R:(acos t, b sin t)
(b) For a circle, tmeasures the angle between the positive x-axis and the line segment joining
the origin to the point. For an ellipse, tmeasures the angle between the x-axis and OPQ,
not OR.
46. (a) Foranypoint(x, y),the equation
y=bsinh thas a unique solution t,
−∞ <t<+∞. On the hyperbola,
x2
a2=1+y
2
b
2= 1 + sinh2t
= cosh2t,sox=±acosh t.
(b) 3
-3
-3 3
47. (a) Foranypoint(x, y), the equation y=btan thas a unique solution twhere −π/2<t<π/2.
On the hyperbola, x2
a2=1+y
2
b
2= 1 + tan2t= sec2t,sox=±asec t.
(b) 3
-3
-3 3
48. By Definition 12.4.1, (x+1)
2+(y−4)2=(y−1)2,(x+1)
2=6y−15,(x+1)
2=6(y−5/2)
49. (4,1) and (4,5) are the foci so the center is at (4,3) thus c=2,a=12/2=6,b
2=36−4 = 32;
(x−4)2/32+(y−3)2/36=1
50. From the definition of a hyperbola, p(x−1)2+(y−1)2−px2+y2=1,
p(x−1)2+(y−1)2−px2+y2=±1, transpose the second radical to the right hand side of the
equation and square and simplify to get ±2px2+y2=−2x−2y+ 1, square and simplify again
to get 8xy −4x−4y+1=0.
51. Let the ellipse have equation 4
81x2+y2
4= 1, then A(x)=(2y)
2=161−4x
2
81 ,
V=2Z9/2
016 1−4x2
81 dx =96
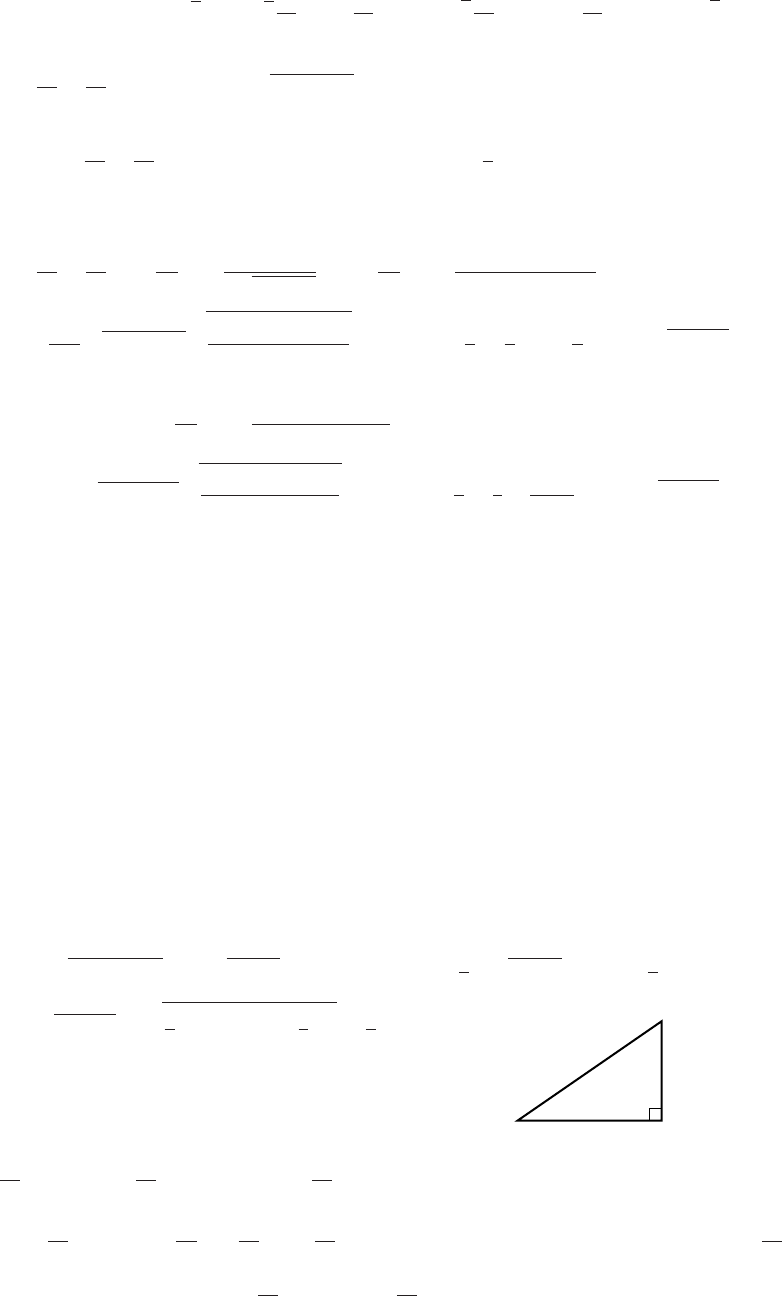
431 Chapter 12
52. See Exercise 51, A(y)=√
3x
2=√
3
81
41−y2
4,V =√381
2Z2
01−y2
4dy =54
√
3
53. Assume x2
a2+y2
b2=1,A =4Za
0b
p1−x
2
/a2dx =πab
54. (a) Assume x2
a2+y2
b2=1,V =2Za
0πb21−x2/a2dx =4
3πab2
(b) In Part (a) interchange aand bto obtain the result.
55. Assume x2
a2+y2
b2=1,dy
dx =−bx
a√a2−x2,1+dy
dx2
=a4−(a2−b2)x2
a2(a2−x2),
S=2Za
0
2πb
ap1−x2/a2sa4−(a2−b2)x2
a2−x2dx =2πab b
a+a
csin−1c
a,c=pa
2−b
2
56. As in Exercise 55, 1 + dx
dy 2
=b4+(a
2−b
2)y
2
b
2(b
2−y
2),
S=2Zb
02πap1−y2/b2sb4+(a
2−b
2)y
2
b
2(b
2−y
2)dy =2πab a
b+b
cln a+c
b,c=pa
2−b
2
57. Open the compass to the length of half the major axis, place the point of the compass at an end
of the minor axis and draw arcs that cross the major axis to both sides of the center of the ellipse.
Place the tacks where the arcs intersect the major axis.
58. Let Pdenote the pencil tip, and let R(x, 0) be the point below Qand Pwhich lies on the line L.
Then QP +PF is the length of the string and QR =QP +PR is the length of the side of the
triangle. These two are equal, so PF =PR. But this is the definition of a parabola according to
Definition 12.4.1.
59. Let Pdenote the pencil tip, and let kbe the difference between the length of the ruler and that
of the string. Then QP +PF
2+k=QF1, and hence PF
2+k=PF
1,PF
1−PF
2=k. But this
is the definition of a hyperbola according to Definition 12.4.3.
60. In the x0y0-plane an equation of the circle is x02+y02=r2where ris the radius of the cylinder. Let
P(x, y) be a point on the curve in the xy-plane, then x0=xcos θand y0=yso x2cos2θ+y2=r2
which is an equation of an ellipse in the xy-plane.
61. L=2a=pD
2+p
2
D
2=D
p1+p
2(see figure), so a=1
2Dp1+p
2, but b=1
2D,
T=c=pa2−b2=r1
4D2(1+p2)−1
4D2=1
2pD.
D
pD
62. y=1
4px2,dy/dx =1
2px,dy/dxx=x0
=1
2px0, the tangent line at (x0,y
0) has the formula
y−y0=x0
2p(x−x0)=x
0
2p
x−x
2
0
2p
, but x2
0
2p=2y
0because (x0,y
0) is on the parabola y=1
4px2.
Thus the tangent line is y−y0=x0
2px−2y0,y=x0
2px−y0.
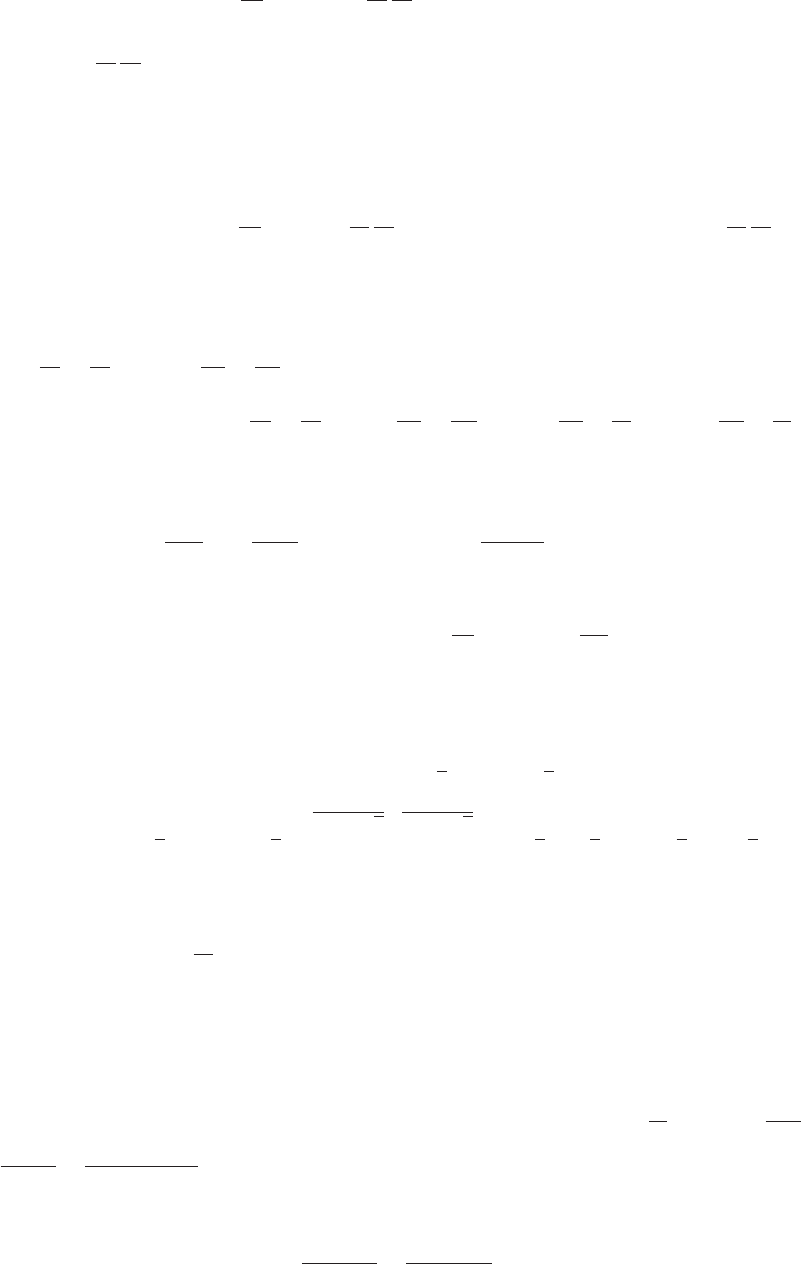
Exercise Set 12.4 432
63. By implicit differentiation, dy
dx(x0,y0)
=−b2
a2
x0
y0if y06= 0, the tangent line is
y−y0=−b2
a2
x0
y0(x−x0), a2y0y−a2y2
0=−b2x0x+b2x2
0,b2x0x+a2y0y=b2x2
0+a2y2
0,
but (x0,y
0) is on the ellipse so b2x2
0+a2y2
0=a2b2; thus the tangent line is b2x0x+a2y0y=a2b2,
x0x/a2+y0y/b2=1. Ify
0= 0 then x0=±aand the tangent lines are x=±awhich also follows
from x0x/a2+y0y/b2=1.
64. By implicit differentiation, dy
dx(x0,y0)
=b2
a2
x0
y0if y06= 0, the tangent line is y−y0=b2
a2
x0
y0(x−x0),
b2x0x−a2y0y=b2x2
0−a2y2
0=a2b2,x0x/a2−y0y/b2=1. Ify
0= 0 then x0=±aand the tangent
lines are x=±awhich also follow from x0x/a2−y0y/b2=1.
65. Use x2
a2+y2
b2= 1 and x2
A2−y2
B2= 1 as the equations of the ellipse and hyperbola. If (x0,y
0)is
a point of intersection then x2
0
a2+y2
0
b2=1= x
2
0
A
2−y
2
0
B
2,sox
2
01
A
2−1
a
2
=y
2
01
B
2+1
b
2
and
a2A2y2
0(b2+B2)=b
2
B
2
x
2
0
(a
2−A
)
. Since the conics have the same foci, a2−b2=c2=A2+B2,
so a2−A2=b2+B2. Hence a2A2y2
0=b2B2x2
0. From Exercises 63 and 64, the slopes of the
tangent lines are −b2x0
a2y0and B2x0
A2y0, whose product is −b2B2x2
0
a2A2y2
0
=−1. Hence the tangent lines are
perpendicular.
66. Use implicit differentiation on x2+4y
2= 8 to get dy
dx(x0,y0)
=−x0
4y0where (x0,y
0) is the point
of tangency, but −x0/(4y0)=−1/2 because the slope of the line is −1/2sox
0=2y
0
.(x
0
,y
0)is
on the ellipse so x2
0+4y2
0= 8 which when solved with x0=2y
0yields the points of tangency (2,1)
and (−2,−1). Substitute these into the equation of the line to get k=±4.
67. Let (x0,y
0) be such a point. The foci are at (−√5,0) and (√5,0),the lines are perpendicular if
the product of their slopes is −1so y
0
x
0+√
5·y
0
x
0−√
5=−1,y
2
0=5−x
2
0and 4x2
0−y2
0=4.Solve
to get x0=±3/√5,y
0=±4/
√5. The coordinates are (±3/√5,4/√5),(±3/√5,−4/√5).
68. Let (x0,y
0) be one of the points; then dy/dx(x0,y0)=4x
0
/y0, the tangent line is y=(4x
0
/y0)x+4,
but (x0,y
0) is on both the line and the curve which leads to 4x2
0−y2
0+4y
0= 0 and 4x2
0−y2
0= 36,
solve to get x0=±3√13/2, y0=−9.
69. Let d1and d2be the distances of the first and second observers, respectively, from the point
where the gun was fired. Then t= (time for sound to reach the second observer) −(time for
sound to reach the first observer) = d2/v −d1/v so d2−d1=vt. For constant vand tthe
difference of distances, d2and d1is constant so the gun was fired somewhere on a branch of a
hyperbola whose foci are where the observers are. Since d2−d1=2a, a =vt
2,b
2=c
2−v
2t
2
4, and
x2
v2t2/4−y2
c2−(v2t2/4) =1.
70. As in Exercise 69, d2−d1=2a=vt = 299,792,458 ×10−7,a
2=(vt/2)2≈224.6888; c2= (50)2
= 2500,b
2=c
2−a
2≈2275.3112,x2
224.6888 −y2
2275.3112 = 1. But y= 200 km, so x≈64.6 km.

433 Chapter 12
71. (a) Use x2
9+y2
4=1,x=3
2
p4−y
2
,
V=Z−2+h
−2(2)(3/2)p4−y2(18)dy =54Z−2+h
−2p4−y2dy
=54y
2p4−y
2+ 2 sin−1y
2−2+h
−2
=274 sin−1h−2
2+(h−2)p4h−h2+2π
ft3
(b) When h= 4 ft, Vfull = 108 sin−11+54π= 108πft3, so solve for hwhen V=(k/4)Vfull,
k=1,2,3, to get h=1.19205,2,2.80795 ft or 14.30465,24,33.69535 in.
72. We may assume A>0, since if A<0 then one can multiply the equation by −1, and if A=0
then one can exchange Awith C(Ccannot be zero simultaneously with A). Then
Ax2+Cy2+Dx +Ey +F=Ax+D
2A2
+Cy+E
2C2
+F−D2
4A−E2
4C=0.
(a) Let AC > 0. If F<D
2
4A
+
E
2
4Cthe equation represents an ellipse (a circle if A=C);
if F=D2
4A+E2
4C, the point x=−D/(2A),y =−E/(2C); and if F>D
2
4A+E
2
4Cthen there is
no graph.
(b) If AC < 0 and F=D2
4A+E2
4C, then
√Ax+D
2A+√−Cy+E
2C√Ax+D
2A−√−Cy+E
2C= 0, a pair of lines;
otherwise a hyperbola
(c) Assume C=0,soAx2+Dx+Ey+F=0.IfE6= 0, parabola; if E= 0 then Ax2+Dx+F=0.
If this polynomial has roots x=x1,x
2with x16=x2then a pair of parallel lines; if x1=x2
then one line; if no roots, then no graph. If A=0,C 6= 0 then a similar argument applies.
73. (a) (x−1)2−5(y+1)
2= 5, hyperbola
(b) x2−3(y+1)
2=0,x =±√3(y+ 1), two lines
(c) 4(x+2)
2+8(y+1)
2= 4, ellipse
(d) 3(x+2)
2+(y+1)
2= 0, the point (−2,−1) (degenerate case)
(e) (x+4)
2+2y= 2, parabola
(f) 5(x+4)
2+2y=−14, parabola
74. distance from the point (x, y) to the focus (0,p) = distance to the directrix y=−p,sox
2+(y−p)2
=(y+p)
2
,x
2=4py
75. distance from the point (x, y) to the focus (0,−c) plus distance to the focus (0,c) = const = 2a,
px2+(y+c)
2+px
2+(y−c)
2=2a, x2+(y+c)
2=4a
2+x
2+(y−c)
2−4a
px
2+(y−c)
2,
px
2+(y−c)
2=a−c
ay, and since a2−c2=b2,x2
b2+y2
a2=1
76. distance from the point (x, y) to the focus (−c, 0) less distance to the focus (c, 0) is equal to 2a,
p(x+c)2+y2−p(x−c)2+y2=±2a, (x+c)2+y2=(x−c)
2+y
2+4a
2±4a
p(x−c)
2+y
2,
p(x−c)
2+y
2=±cx
a−a, and, since c2−a2=b2,x2
a2−y2
b2=1
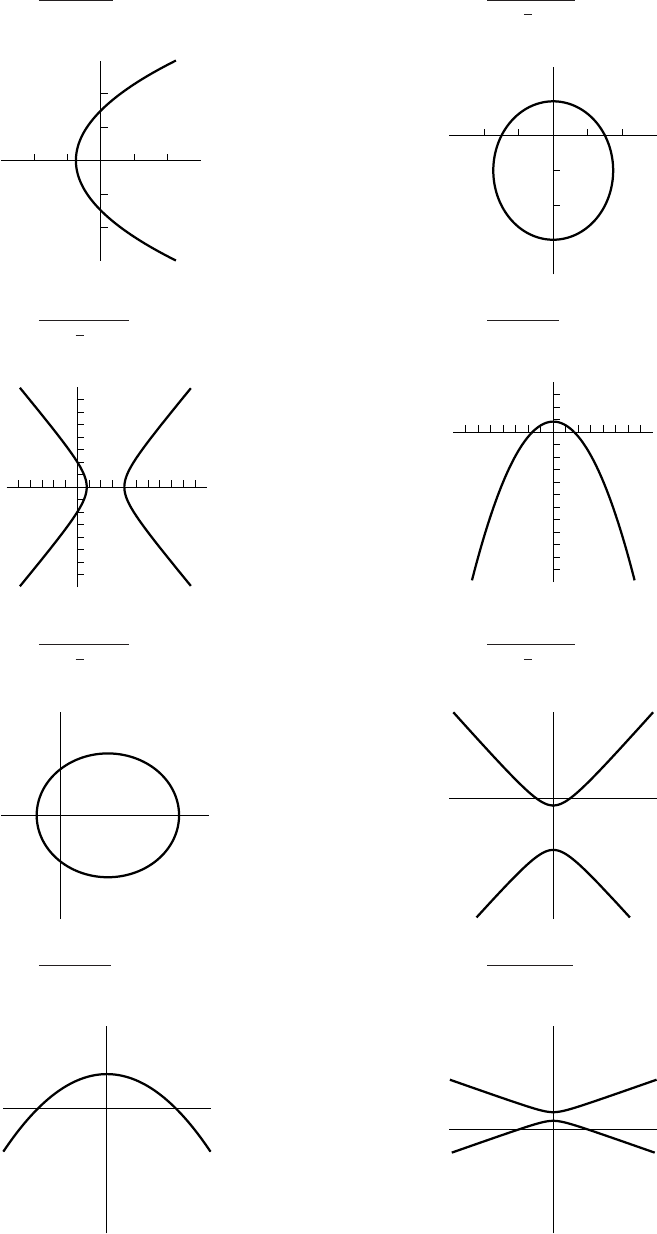
Exercise Set 12.5 434
EXERCISE SET 12.5
1. (a) r=3/2
1−cos θ,e=1,d=3/2
0
p
/
2
-2
-2
2
2
(b) r=3/2
1+1
2sin θ,e=1/2,d=3
0
p
/
2
–2
–2 2
(c) r=2
1+3
2cos θ,e=3/2,d=4/3
0
p
/
2
-5 10
-7
7
(d) r=5/3
1 + sin θ,e=1,d=5/3
0
p
/
2
-11
3
-7 7
2. (a) r=4/3
1−2
3cos θ,e=2/3,d=2
0
p
/
2
(b) r=1
1−4
3sin θ,e=4/3,d=3/4
0
p
/
2
(c) r=1/3
1 + sin θ,e=1,d=1/3
0
p
/
2
(d) r=1/2
1+3sinθ,e =3,d =1/6
0
p
/
2
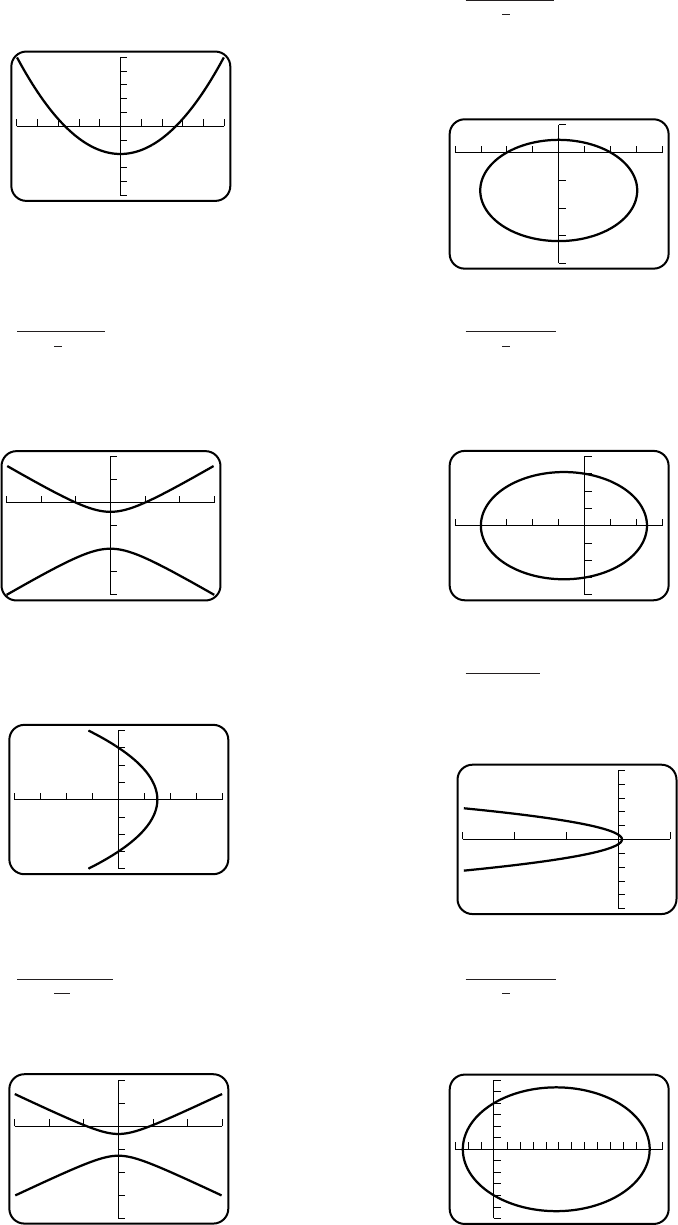
435 Chapter 12
3. (a) e=1,d=8,parabola, opens up
10
-10
-15 15
(b) r=4
1+3
4sin θ,e=3/4,d=16/3,
ellipse, directrix 16/3 units
above the pole
5
-20
-8 8
(c) r=2
1−3
2sin θ,e=3/2,d=4/3,
hyperbola, directrix 4/3 units
below the pole
4
-8
-6 6
(d) r=3
1+1
4cos θ,e=1/4,d=12,
ellipse, directrix 12 units
to the right of the pole
4
-4
-5 3
4. (a) e=1,d=15,parabola, opens left
20
-20
-20 20
(b) r=2/3
1 + cos θ,e=1,
d=2/3,parabola, opens left
10
-10
-15 5
(c) r=64/7
1−12
7sin θ,e=12/7,d=16/3,
hyperbola, directrix 16/3 units below pole
20
-40
-30 30
(d) r=4
1−2
3cos θ,e=2/3,d=6,
ellipse, directrix 6 units left of the pole
6
-6
-3 13
Exercise Set 12.5 436
5. (a) d=1,r =ed
1+ecos θ=2/3
1+2
3cos θ=2
3+2cosθ
(b) e=1,d =1,r =ed
1−ecos θ=1
1−cos θ
(c) e=3/2,d =1,r =ed
1+esin θ=3/2
1+3
2sin θ=3
2+3sinθ
6. (a) e=2/3,d =1,r =ed
1−esin θ=2/3
1−2
3sin θ=2
3−2 sin θ
(b) e=1,d =1,r =ed
1+esin θ=1
1 + sin θ
(c) e=4/3,d =1,r =ed
1−ecos θ=4/3
1−4
3cos θ=4
3−4 cos θ
7. (a) r=ed
1±ecos θ,θ =0:6= ed
1±e,θ =π:4= ed
1∓e,6±6e=4∓4e, 2=∓10e, use bottom
sign to get e=1/5,d =24,r=24/5
1−cos θ=24
5−5 cos θ
(b) e=1,r =d
1−sin θ,1=d
2,d=2,r =2
1−sin θ
(c) r=ed
1±esin θ,θ =π/2:3= ed
1±e,θ =3π/2:−7= ed
1∓e,ed=3±3e=−7±7e, 10 = ±4e,
e=5/2,d =21/5,r =21/2
1+(5/2) sin θ=21
2+5sinθ
8. (a) r=ed
1±esin θ,1= ed
1±e,4= ed
1∓e,1±e=4∓4e, upper sign yields e=3/5,d=8/3,
r=8/5
1+3
5sin θ=8
5+3sinθ
(b) e=1,r =d
1−cos θ,3=d
2,d=6,r=6
1−cos θ
(c) a=b=5,e =c/a =√50/5=√
2,r =√2d
1+√
2 cos θ;r= 5 when θ=0,sod=5+ 5
√
2
,
r=5
√
2+5
1+√
2 cos θ.
9. (a) r=3
1+1
2sin θ,e=1/2,d= 6, directrix 6 units above pole; if θ=π/2:r
0=2;
if θ=3π/2:r
1=6,a =(r
0+r
1
)/2=4,b =√r
0r
1=2
√
3, center (0,−2) (rectangular
coordinates), x2
12 +(y+2)
2
16 =1
(b) r=1/2
1−1
2cos θ,e=1/2,d= 1, directrix 1/2 unit left of pole; if θ=π:r0=1/2
3/2=1/3;
if θ=0:r
1=1,a =2/3,b =1/
√
3, center = (1/3,0) (rectangular coordinates),
9
4(x−1/3)2+3y
2=1
437 Chapter 12
10. (a) r=6/5
1+2
5cos θ,e=2/5,d= 3, directrix 3 units right of pole, if θ=0:r
0=6/7,
if θ=π:r1=2,a =10/7,b=2
√
3/
√
7, center (−4/7,0) (rectangular coordinates),
49
100(x+4/7)2+7
12y2=1
(b) r=2
1−3
4sin θ,e=3/4,d=8/3, directrix 8/3 units below pole, if θ=3π/2:r
0=8/7,
if θ=π/2; r1=8,a=32/7,b =8/
√
7, center: (0,24/7) (rectangular coordinates),
7
64x2+49
1024 y−24
72
=1
11. (a) r=2
1+3sinθ,e =3,d =2/3, hyperbola, directrix 2/3 units above pole, if θ=π/2:
r
0=1/2; θ=3π/2:r
1= 1, center (0,3/4),a=1/4,b =1/
√
2,−2x
2+16y−3
42
=1
(b) r=5/3
1−3
2cos θ,e=3/2,d=10/9, hyperbola, directrix 3/2 units left of pole, if θ=π:
r0=2/3; θ=0:r
1=5/3
1/2=10/3, center (−2,0),a=4/3,b =p20/9,9
16(x+2)2−9
20y2=1
12. (a) r=4
1−2 sin θ,e=2,d= 2, hyperbola, directrix 2 units below pole, if θ=3π/2:r
0=4/3;
θ=π/2:r
1=
4
1−2
= 4, center (0,−8/3),a=4/3,b =4/
√
3,9
16 y+8
32
−3
16x2=1
(b) r=15/2
1+4cosθ,e =4,d =15/8, hyperbola, directrix 15/8 units right of pole, if θ=0:
r
0=3/2; θ=π:r1=−5
2=5/2,a=1/2,b =√15
2, center (2,0),4(x−2)2−4
15y2=1
13. (a) r=1
2d
1+1
2cos θ=d
2 + cos θ,ifθ=0:r
0=d/3; θ=π, r1=d,
8=a=1
2
(r
1+r
0
)=2
3
d, d =12,r=12
2 + cos θ
(b) r=3
5d
1−3
5sin θ=3d
5−3 sin θ,ifθ=3π/2:r
0=3
8
d;θ=π/2,r
1=3
2d,
4=a=1
2
(r
1+r
0
)=15
16d, d =64
15,r =3(64/15)
5−3 sin θ=64
25 −15 sin θ
(c) r=3
5d
1−3
5cos θ=3d
5−3 cos θ,ifθ=π:r
0=3
8
d;θ=0,r
1=3
2d, 4=b=3
4
d,
d=16/3,r=16
5−3 cos θ
(d)
1
5d
1+1
5sin θ=d
5 + sin θ,ifθ=π/2:r
0=d/6; θ=3π/2,r
1=d/4,
5=c=1
2
d1
4−1
6
=1
24d, d = 120,r=120
5 + sin θ

Exercise Set 12.5 438
14. (a) r=1
2d
1+1
2sin θ=d
2 + sin θ,ifθ=π/2:r
0=d/3; θ=3π/2:r
1=d,
10 = a=1
2(r0+r1)=2
3
d, d =15,r=15
2 + sin θ
(b) r=1
5d
1−1
5cos θ=d
5−cos θ,ifθ=π:r
0=d/6,θ =0:r
1=d/4,
6=a=1
2
(r
1+r
0
)=1
2
d1
4+1
6
=5
24d, d = 144/5,r=144/5
5−cos θ=144
25 −5 cos θ
(c) r=3
4d
1−3
4sin θ=3d
4−3 sin θ,ifθ=3π/2:r
0=3
7
d, θ =π/2:r
1=3d, 4=b=3d/√7,
d=4
3√7,r=4
√
7
4−3 sin θ
(d) r=4
5d
1+4
5cos θ=4d
5+4cosθ,ifθ=0:r
0=4
9
d;θ=π:r
1=4d,
c=10=1
2
(r
1−r
0
)=1
2
d4−4
9
=16
9d, d =45
8,r=45/2
5+4cosθ=45
10 + 8 cos θ
15. (a) e=c/a =1
2(r1−r0)
1
2(r1+r0)=r1−r0
r1+r0
(b) e=r1/r0−1
r1/r0+1,e(r
1/r0+1)=r
1/r0−1,r1
r0=1+e
1−e
16. (a) e=c/a =1
2(r1+r0)
1
2(r1−r0)=r1+r0
r1−r0
(b) e=r1/r0+1
r
1/r0−1,e(r
1/r0−1) = r1/r0+1,r
1
r
0=e+1
e−1
17. (a) T=a3/2=39.5
1.5≈248 yr
(b) r0=a(−e)=39.5(1 −0.249) = 29.6645 AU ≈4,449,675,000 km
r1=a(1+e)=39.5(1+0.249) = 49.3355 AU ≈7,400,325,000 km
(c) r=a(1 −e2)
1+ecos θ≈39.5(1 −(0.249)2)
1+0.249 cos θ≈37.05
1+0.249 cos θAU
(d)
0
p/2
-50
50
-30 20
18. (a) In yr and AU, T=a3/2; in days and km, T
365 =a
150 ×1063/2
,
so T= 365 ×10−9a
1503/2days.
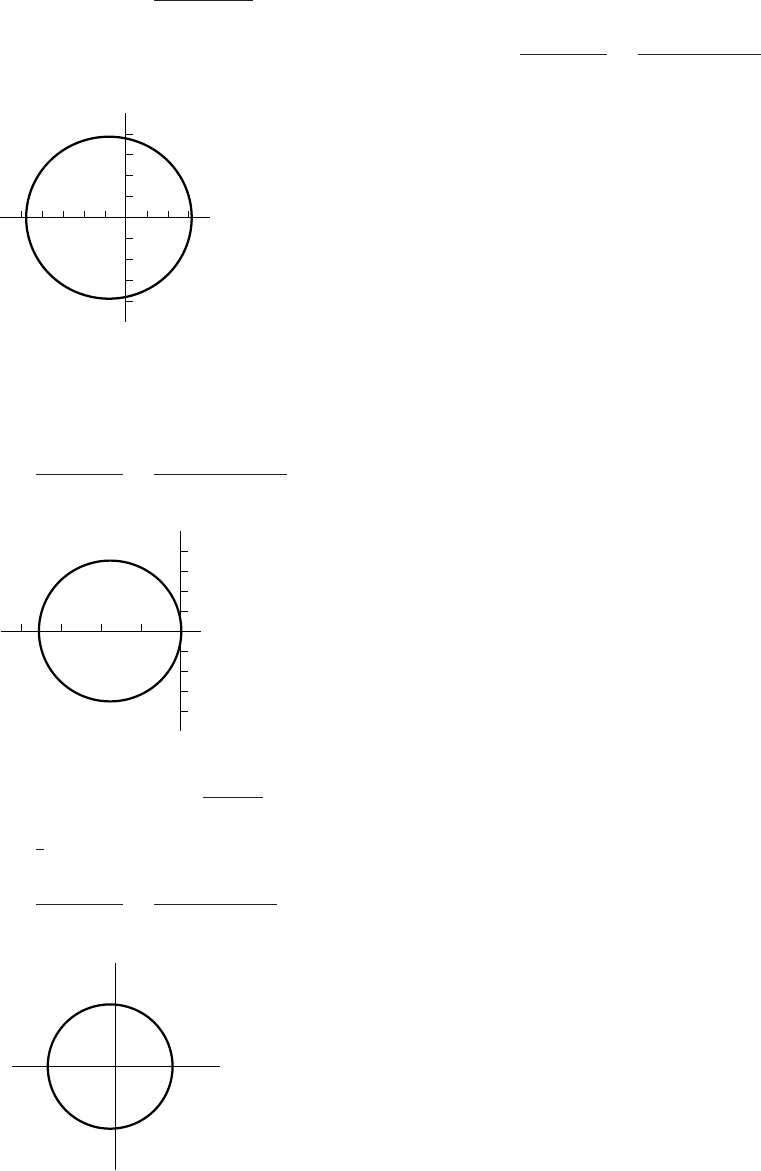
439 Chapter 12
(b) T= 365 ×10−957.95 ×106
150 3/2
≈87.6days
(c) From (17) the polar equation of the orbit has the form r=a(1 −e2)
1+ecos θ=37.82
1+0.205 cos θ
(d)
0
p/2
20-50
-40
40
19. (a) a=T2/3= 23802/3≈178.26 AU
(b) r0=a(1 −e)≈0.8735 AU,r
1=a(1+e)≈355.64 AU
(c) r=a(1 −e2)
1+ecos θ≈1.74
1+0.9951 cos θAU
(d)
0
p/2
-400
-20
20
20. (a) By Exercise 15(a), e=r1−r0
r1+r0≈0.093
(b) r=1
2(a0+a1) = 225,400,000 km ≈1.503 AU, so T=a3/2≈1.84 yr
(c) r=a(1 −e2)
1+ecos θ≈1.49
1+0.093 cos θAU
(d)
0
p/2
1.3632
1.49
1.49
1.6428
21. r0=a(1 −e)≈7003 km, hmin ≈7003 −6440 = 563 km,
r1=a(1+e)≈10,726 km, hmax ≈10,726 −6440 = 4286 km
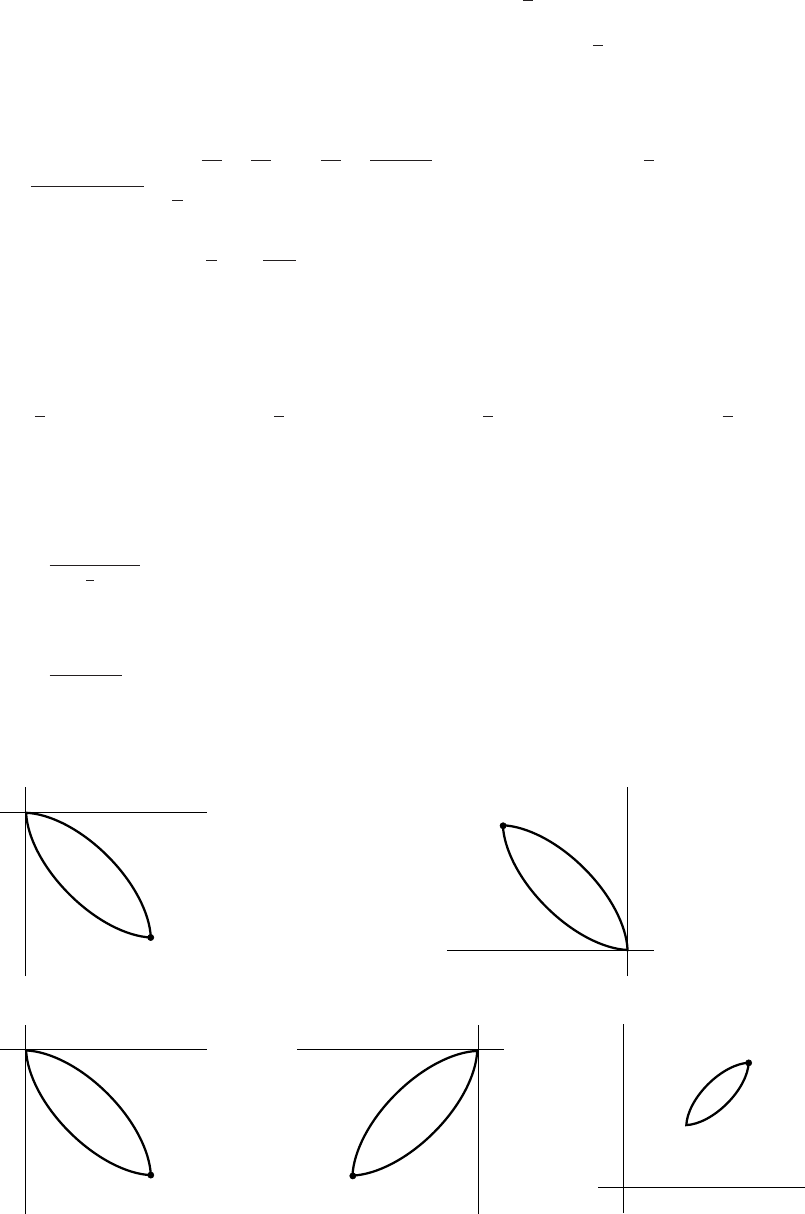
Chapter 12 Supplementary Exercises 440
22. r0=a(1 −e)≈651,736 km, hmin ≈581,736 km; r1=a(1+e)≈6,378,102 km,
hmax ≈6,308,102 km
23. Since the foci are fixed, ais constant; since e→0, the distance a
e→+∞.
Let dbe the distance between the directrix and the focus, then d=a1
e−eand lim
e→0d=+∞;
but the center and the focus come together, so distance between the directrix and the center also
tends to +∞.
24. (a) From Figure 12.4.22, x2
a2−y2
b2=1,x
2
a
2−y
2
c
2−a
2=1,(x−c)
2+y
2=c
a
x−a
2,
p(x−c)
2+y
2=c
a
x−afor x>0.
(b) From Part (a), PF =c
aPD, PF
PD =c/a.
CHAPTER 12 SUPPLEMENTARY EXERCISES
2. (a) (√2,3π/4) (b) (−√2,7π/4) (c) (√2,3π/4) (d) (−√2,−π/4)
3. (a) circle (b) rose (c) line (d) lima¸con
(e) lima¸con (f) none (g) none (h) spiral
4. (a) r=1/3
1+1
3cos θ, ellipse, right of pole, distance = 1
(b) hyperbola, left of pole, distance = 1/3
(c) r=1/3
1 + sin θ, parabola, above pole, distance = 1/3
(d) parabola, below pole, distance = 3
5. (a) p/2
0
(b) p/2
0
(1, 9)
(c) p/2
0
(1, #)
(d) p/2
0
(–1, 3)
(e) p/2
0
(1, 3)
(2, 3)
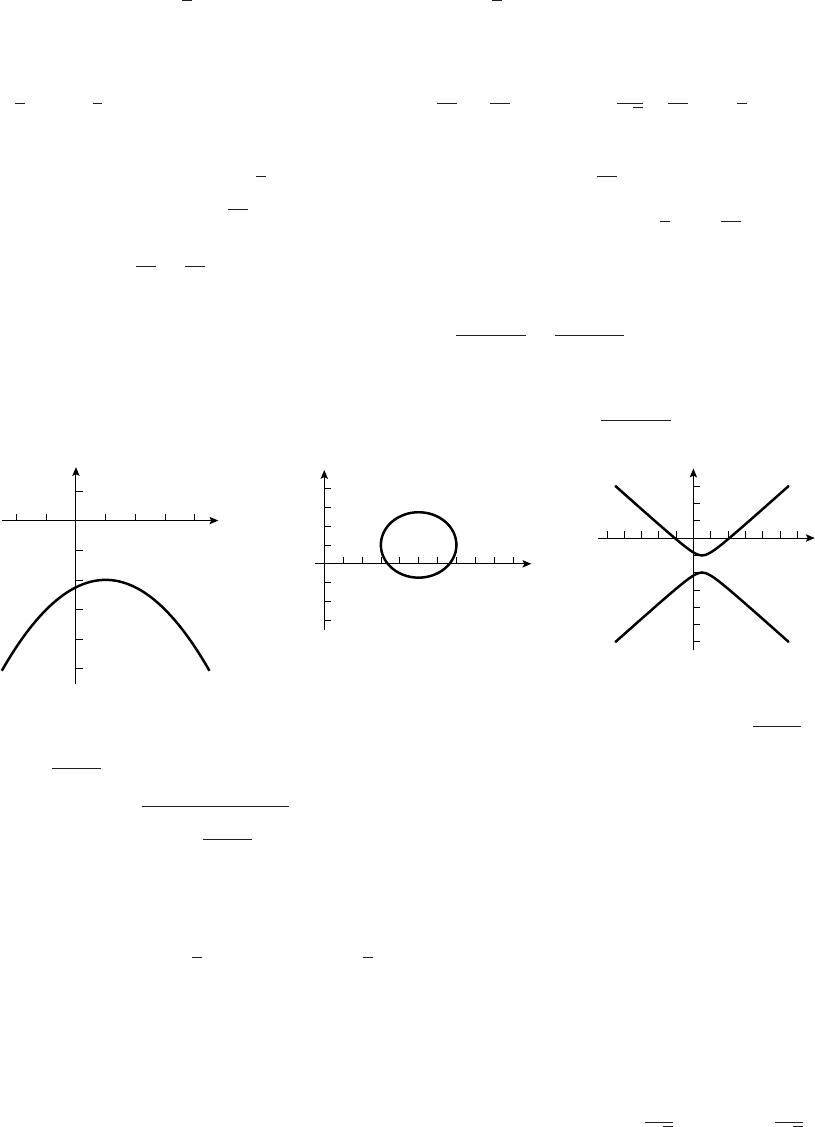
441 Chapter 12
6. Family I: x2+(y−b)
2=b
2
,b < 0, or r=2bsin θ; Family II: (x−a)2+y2=a2,a < 0, or
r=2acos θ
7. (a) r=2a/(1 + cos θ),r+x=2a, x2+y2=(2a−x)
2
,y
2=−4ax +4a
2, parabola
(b) r2(cos2θ−sin2θ)=x
2−y
2=a
2
, hyperbola
(c) rsin(θ−π/4)=(
√
2/2)r(sin θ−cos θ)=4,y−x=4
√
2, line
(d) r2=4rcos θ+8rsin θ, x2+y2=4x+8y, (x−2)2+(y−4)2= 20, circle
9. (a) c
a=e=2
7and 2b=6,b =3,a
2=b
2+c
2=9+ 4
49a2,45
49a2=9,a=7
√5,5
49x2+1
9y2=1
(b) x2=−4py, directrix y= 4, focus (−4,0),2p=8,x
2=−16y
(c) For the ellipse, a=4,b =√3,c
2=a
2−b
2=16−3 = 13, foci (±√13,0);
for the hyperbola, c=√13, b/a =2/3,b =2a/3,13 = c2=a2+b2=a2+4
9a2=13
9a2,
a=3,b =2,x
2
9−y
2
4=1
10. (a) e=4/5=c/a, c =4a/5, but a=5soc=4,b=3,(x+3)
2
25 +(y−2)2
9=1
(b) directrix y=2,p =2,(x+2)
2=−8y
(c) center (−1,5), vertices (−1,7) and (−1,3),a=2, a/b =8,b=1/4,(y−5)2
4−16(x+1)2=1
11. (a)
-4 8
-10
2x
y(b)
210
-3
4
x
y(c)
-8 8
-12
4
x
y
13. (a) The equation of the parabola is y=ax2and it passes through (2100,470), thus a=470
21002,
y=470
21002x2.
(b) L=2Z2100
0s1+2470
21002x2
dx ≈4336.3ft
14. (a) As truns from 0 to π, the upper portion of the curve is traced out from right to left; as t
runs from πto 2πthe bottom portion of the curve is traced out from right to left. The loop
occurs for π+ sin−11
4<t<2π−sin−11
4.
(b) lim
t→0+x=+∞,lim
t→0+y= 1; lim
t→π−x=−∞,lim
t→π−y= 1; lim
t→π+x=+∞,lim
t→π+y=1;
lim
t→2π−x=−∞,lim
t→2π−y= 1; the horizontal asymptote is y=1.
(c) horizontal tangent line when dy/dx =0,ordy/dt =0,socost=0,t=π/2,3π/2;
vertical tangent line when dx/dt =0,so−csc2t−4 sin t=0,t=π+sin−11
3
√4,2π−sin−11
3
√4,
t=3.823,5.602

Chapter 12 Supplementary Exercises 442
(d) r2=x2+y2= (cot t+ 4 cos t)2+(1+4sint)
2= (4 + csc t)2,r = 4 + csc t; with t=θ,
f(θ) = 4 + csc θ;m=dy/dx =(f(θ) cos θ+f0(θ) sin θ)/(−f(θ) sin θ+f0(θ) cos θ); when
θ=π+ sin−1(1/4),m =√15/15, when θ=2π−sin−1(1/4),m =−√15/15, so the tangent
lines to the conchoid at the pole have polar equations θ=±√15/15.
15. A
2=Zπ/6
0
1
2(2 sin θ)2dθ +Zπ/4
π/6
1
212,dθ =2θ−1
4sin 2θπ/6
0
+π
24,A =5π
12 −√3
2
16. The circle has radius a/2 and lies entirely inside the cardioid, so
A=Z2π
0
1
2a2(1 + sin θ)2dθ −πa2/4=3a
2
2π−a
2
4π=5a
2
4π
17. (a) r=1/θ, dr/dθ =−1/θ2,r
2+(dr/dθ)2=1/θ2+1/θ4,L=
Zπ/2
π/4
1
θ2p1+θ
2dθ ≈0.9457 by
Endpaper Table Formula 93.
(b) The integral Z+∞
1
1
θ2p1+θ
2dθ diverges by the comparison test (with 1/θ), and thus the
arc length is infinite.
18. (a) When the point of departure of the thread from the circle has traversed an angle θ, the
amount of thread that has been unwound is equal to the arc length traversed by the point of
departure, namely aθ. The point of departure is then located at (acos θ, a sin θ), and the tip of
the string, located at (x, y), satisfies the equations x−acos θ=aθ sin θ, y−asin θ=−aθ cos θ;
hence x=a(cos θ+θsin θ),y =a(sin θ−θcos θ).
(b) Assume for simplicity that a= 1. Then dx/dθ =θcos θ, dy/dθ =θsin θ;dx/dθ = 0 has
solutions θ=0,π/2,3π/2; and dy/dθ = 0 has solutions θ=0,π,2π.Atθ=π/2, dy/dθ > 0,
so the direction is North; at θ=π, dx/dθ < 0, so West; at θ=3π/2, dy/dθ < 0, so South; at
θ=2π, dx/dθ > 0, so East. Finally, lim
θ→0+dy/dx = lim
θ→0+tan θ= 0, so East.
(c) u
x
y
0
1
0
p/2
p/2
1
p
–1
p
3p/2
–3p/2
–1
2p
1
–2p
Note that the parameter θin these equations does not satisfy equations (1) and (2) of Section
12.1, since it measures the angle of the point of departure and not the angle of the tip of the
thread.
4
-8
-5 2
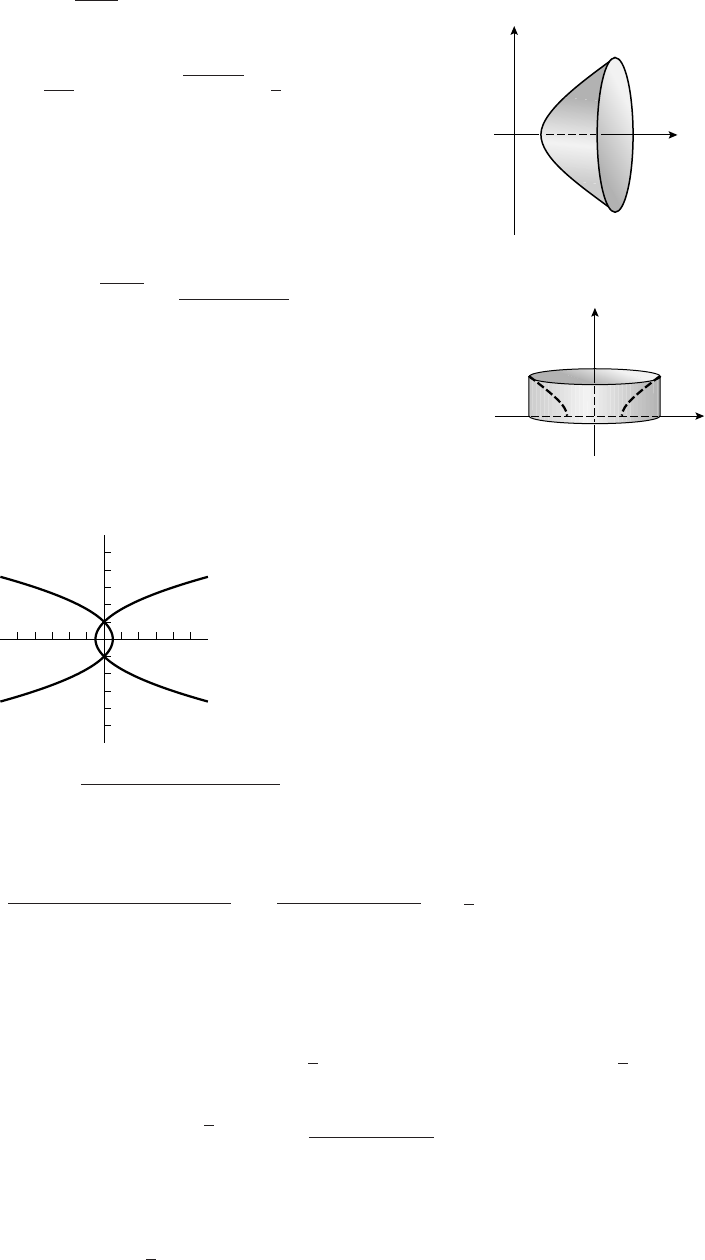
443 Chapter 12
19. (a) V=Z√a2+b2
a
πb2x2/a2−b2dx
=πb2
3a2(b2−2a2)pa2+b2+2
3ab2π
x
y
(b) V=2πZ√
a
2
+b
2
a
x
pb
2
x
2
/a2−b2dx =(2b
4
/3a)π
x
y
20. (a)
-5 5
-5
5
0
p/2(b) θ=π/2,3π/2,r =1
(c) dy/dx =rcos θ+(dr/dθ) sin θ
−rsin θ+(dr/dθ) cos θ;atθ=π/2,m
1=(−1)/(−1)=1,m
2=1/(−1) = −1,
m1m2=−1; and at θ=3π/2,m
1=−1,m
2=1,m
1m
2=−1
22. The tips are located at r=1,θ =π/6,5π/6,3π/2 and, for example,
d=p1+1−2 cos(5π/6−π/6) = p2(1 −cos(2π/3)) = √3
23. (a) x=rcos θ= cos θ+cos2θ, dx/dθ =−sin θ−2 sin θcos θ=−sin θ(1 +2 cos θ) = 0 if sin θ=0
or cos θ=−1/2, so θ=0,π,2π/3,4π/3; maximum x=2atθ= 0, minimum x=−1/4at
θ=π
(b) y=rsin θ= sin θ+ sin θcos θ, dy/dθ = 2 cos2θ+ cos θ−1 = 0 at cos θ=1/2,−1, so
θ=π/3,5π/3,π; maximum y=3
√
3/4atθ=π/3, minimum y=−3√3/4atθ=5π/3
24. (a) y=rsin θ= (sin θ)/√θ, dy/dθ =2θcos θ−sin θ
2θ3/2=0if2θcos θ= sin θ, tan θ=2θwhich
only happens once on (0,π]. Since lim
θ→0+y= 0 and y=0atθ=π,yhas a maximum when
tan θ=2θ.
(b) θ≈1.16556
(c) ymax = (sin θ)/√θ≈0.85124
Chapter 12 Supplementary Exercises 444
25. The width is twice the maximum value of yfor 0 ≤θ≤π/4:
y=rsin θ= sin θcos 2θ= sin θ−2 sin3θ, dy/dθ = cos θ−6 sin2θcos θ= 0 when cos θ=0or
sin θ=1/
√
6,y =1/
√
6−2/(6√6) = √6/9, so the width of the petal is 2√6/9.
26. (a) x2
225 −y2
1521 =1,soV=2Zh/2
0225π1+ y
2
1521dy =25
2028πh3+ 225πh ft3.
(b) S=2Zh/2
02πxp1+(dx/dy)2dy =4πZh/2
0v
u
u
t225 + y2 225
1521 +225
15212!dy
=5
26πhp6084 + h2+ 1170πln "h+√6084 + h2
78 #ft2
27. (a) The end of the inner arm traces out the circle x1= cos t, y1= sin t. Relative to the end of
the inner arm, the outer arm traces out the circle x2= cos 2t, y2=−sin 2t. Add to get the
motion of the center of the rider cage relative to the center of the inner arm:
x= cos t+ cos 2t, y = sin t−sin 2t.
(b) Same as part (a), except x2= cos 2t, y2= sin 2t,sox= cos t+ cos 2t, y = sin t+ sin 2t
(c) L1=Z2π
0"dx
dt 2
+dy
dt 2#1/2
dt =Z2π
0
√5−4 cos 3tdt≈13.36489321,
L2=Z2π
0
√5+4costdt≈13.36489322; L1and L2appear to be equal, and indeed, with the
substitution u=3t−πand the periodicity of cos u,
L1=1
3Z5π
−πp5−4 cos(u+π)du =Z2π
0
√5+4cosudu=L
2.
29. C=4Zπ/2
0"dx
dt 2
+dy
dt 2#1/2
dt =4Zπ/2
0(a2sin2t+b2cos2t)1/2dt
=4Zπ/2
0(a2sin2t+(a
2−c
2) cos2t)1/2dt =4aZπ/2
0(1 −e2cos2t)1/2dt
30. a=3,b =2,c =√5,C= 4(3) Zπ/2
0p1−(5/9) cos2udu ≈15.86543959
31. (a) r0
r1=59
61 =1−e
1+e,e=1
60
(b) a=93×106,r
0=a(1 −e)=59
60 93 ×106=91,450,000 mi
(c) C=4×93 ×106Zπ/2
0"1−cos θ
60 2#1/2
dθ ≈584,295,652.5mi
32. (a) y=y0+(v
0sin α)x
v0cos α−g
2x
v0cos α2
=y0+xtan α−g
2v2
0cos2αx2
(b) dy
dx = tan α−g
v2
0cos2αx, dy/dx =0atx=v
2
0
gsin αcos α,
y=y0+v2
0
gsin2α−g
2v2
0cos2αv2
0sin αcos α
g2
=y0+v2
0
2gsin2α
445 Chapter 12
33. α=π/4,y
0=3,x =v
0t/√2,y =3+v
0
t/√2−16t2
(a) Assume the ball passes through x= 391,y = 50, then 391 = v0t/√2,50 = 3 + 391 −16t2,
16t2= 344,t=√21.5,v
0=√2x/t ≈119.3 ft/s
(b) dy
dt =v0
√2−32t= 0 when t=v0
32√2,y
max =3+ v
0
√
2
v
0
32√2−16 v2
0
211 =3+ v
2
0
128 ≈114.2ft
(c) y= 0 when t=−v0/√2±pv2
0/2 + 192
−32 ,t≈−0.04 (discard) and 5.31, dist = 447.9ft
34. (a)
x
y
-1 1
-1
1
(c) L=Z1
−1cos2πt2
2+ sin2πt2
2dt =2
35. tan ψ= tan(φ−θ)= tan φ−tan θ
1 + tan φtan θ=
dy
dx −y
x
1+y
x
dy
dx
=
rcos θ+(dr/dθ) sin θ
−rsin θ+(dr/dθ) cos θ−sin θ
cos θ
1+rcos θ+(dr/dθ) sin θ)
−rsin θ+(dr/dθ) cos θ)sin θ
cos θ=r
dr/dθ
36. (a) From Exercise 35,
tan ψ=r
dr/dθ =1−cos θ
sin θ= tan θ
2,
so ψ=θ/2.
(b)
0
p/2
(c) At θ=π/2,ψ =θ/2=π/4. At θ=3π/2,ψ =θ/2=3π/4.
37. tan ψ=r
dr/dθ =aebθ
abebθ =1
bis constant, so ψis constant.

Chapter 12 Horizon Module 446
CHAPTER 12 HORIZON MODULE
1. For the Earth, aE(1 −e2
E) = 1(1 −0.0172)=0.999711, so the polar equation is
r=aE(1 −e2
E)
1−eEcos θ=0.999711
1−0.017 cos θ.
For Rogue 2000, aR(1 −e2
R) = 5(1 −0.982)=0.198, so the polar equation is
r=aR(1 −e2
R)
1−eRcos θ=0.198
1−0.98 cos θ.
2. 1
-1
-1 10
3. At the intersection point A,kE
1−eEcos θ=kR
1−eRcos θ,sok
E−k
E
e
Rcos θ=kR−kReEcos θ.
Solving for cos θgives cos θ=kE−kR
kEeR−kReE
.
4. From Exercise 1, kE=0.999711 and kR=0.198, so
cos θ=kE−kR
kEeR−kReE
=0.999711 −0.198
0.999711(0.98) −0.198(0.017) ≈0.821130
and θ= cos−10.821130 ≈0.607408 radian.
5. Substituting cos θ≈0.821130 into the polar equation for the Earth gives
r≈0.999711
1−0.017(0.821130) ≈1.013864,
so the polar coordinates of intersection Aare approximately (1.013864,0.607408).
6. By Theorem 12.3.2 the area of the elliptic sector is ZθF
θI
1
2r2dθ. By Exercise 12.4.53 the area of
the entire ellipse is πab, where ais the semimajor axis and bis the semiminor axis. But
b=√a2−c2=pa2−(ea)2=a√1−e2,
so Formula (1) becomes t
T=ZθF
θI
r2dθ
2πa2√1−e2, which implies Formula (2).
7. In Formula (2) substitute T=1,θ
I= 0, and θF≈0.607408, and use the polar equation of the
Earth’s orbit found in Exercise 1:
t=ZθF
0kE
1−eEcos θ2
dθ
2πp1−e2
E≈Z0.607408
00.999711
1−0.017 cos θ2
dθ
2π√0.999711 ≈0.099792 yr.

447 Chapter 12
Note: This calculation can be done either by numerical integration or by using the integration
formula
Zdθ
(1 −ecos θ)2=
2 tan−1r1+e
1−etan θ
2
(1 −e2)3/2+esin θ
(1 −e2)(1 −ecos θ)+C,
obtained by using a CAS or by the substitution u= tan(θ/2).
8. In Formula (2) we substitute T=5
√
5 and θI=0.45, and use the polar equation of Rogue 2000’s
orbit found in Exercise 1:
t=
TZθF
θIaR(1 −e2
R)
1−eRcos θ2
dθ
2πa2
Rp1−e2
R
=
5√5ZθF
0.45 aR(1 −e2
R)
1−eRcos θ2
dθ
2πa2
Rp1−e2
R
,
so
ZθF
0.45 aR(1 −e2
R)
1−eRcos θ2
dθ =2tπa2
Rp1−e2
R
5√5.
9. (a) A CAS shows that
ZaR(1 −e2
R)
1−eRcos θ2
dθ =a2
R2q1−e2
Rtan−1r1+e
R
1−e
R
tan θ
2+eR(1 −e2
R) sin θ
1−eRcos θ+C
(b) Evaluating the integral above from θ=0.45 to θ=θF, setting the result equal to the right
side of (3), and simplifying gives
tan−1r1+R
1−eR
tan θ
2+eRp1−e2
Rsin θ
2(1 −eRcos θ)θF
0.45
=tπ
5√5.
Using the known values of eRand t, and solving numerically, θF≈0.611346.
10. Substituting θF≈0.611346 in the equation for Rogue 2000’s orbit gives r≈1.002525 AU. So the
polar coordinates of Rogue 2000 when the Earth is at intersection Aare about (1.002525,0.611346).
11. Substituting the values found in Exercises 5 and 10 into the distance formula in Supplementary
Exercise 22 gives d=pr2
1+r2
2−2r1r2cos(θ1−θ2)≈0.012013 AU ≈1.797201 ×106km.
Since this is less than 4 million kilometers, a notification should be issued. (Incidentally, Rogue
2000’s closest approach to the Earth does not occur when the Earth is at A, but about 9 hours
earlier, at t≈0.098768 yr, at which time the distance is about 1.219435 million kilometers.)
448
CHAPTER 13
Three-Dimensional Space; Vectors
EXERCISE SET 13.1
1. (a) (0,0,0),(3,0,0),(3,5,0),(0,5,0),(0,0,4),(3,0,4),(3,5,4),(0,5,4)
(b) (0,1,0),(4,1,0),(4,6,0),(0,6,0),(0,1,−2),(4,1,−2),(4,6,−2),(0,6,−2)
2. corners: (2,2,±2), (2,−2,±2),
(−2,2,±2), (−2,−2,±2)
y
x
z
(–2, –2, 2) (–2, 2, 2)
(–2, 2, –2)(–2, –2, –2)
(2, 2, –2)(2, –2, –2)
(2, –2, 2) (2, 2, 2)
3. corners: (4,2,−2), (4,2,1), (4,1,1), (4,1,−2),
(−6,1,1), (−6,2,1), (−6,2,−2), (−6,1,−2)
(–6, 2, 1)
(–6, 2, –2)
y
x
z
(–6, 1, –2)
(4, 1, 1)
(4, 1, –2)
(4, 2, 1)
4. (a) (x2,y
1
,z
1
),(x
2
,y
2
,z
1
),(x
1
,y
2
,z
1
)(x1,y
1
,z
2
),(x
2
,y
1
,z
2
),(x
1
,y
2
,z
2
)
(b) The midpoint of the diagonal has coordinates which are the coordinates of the midpoints
of the edges. The midpoint of the edge (x1,y
1
,z
1
) and (x2,y
1
,z
1
)is1
2
(x
1+x
2
),y
1
,z
1
;
the midpoint of the edge (x2,y
1
,z
1
) and (x2,y
2
,z
1
)is
x
2
,
1
2
(y
1+y
2
),z
1
; the midpoint
of the edge (x2,y
2
,z
1
) and (x2,y
2
,z
2
)) is x2,y
2
,1
2(z
1+z
2
)
. Thus the coordinates of the
midpoint of the diagonal are 1
2(x1+x2),1
2(y1+y2),1
2(z1+z2).
5. The diameter is d=p(1 −3)2+(−2−4)2+(4+12)
2=√
296, so the radius is √296/2=√
74.
The midpoint (2,1,−4) of the endpoints of the diameter is the center of the sphere.
6. Each side has length √14 so the triangle is equilateral.
7. (a) The sides have lengths 7, 14, and 7√5; it is a right triangle because the sides satisfy the
Pythagorean theorem, (7√5)2=7
2+14
2
.
(b) (2,1,6) is the vertex of the 90◦angle because it is opposite the longest side
(the hypotenuse).
(c) area = (1/2)(altitude)(base) = (1/2)(7)(14) = 49
8. (a) 3(b) 2(c) 5
(d) p(2)2+(−3)2=√13 (e) p(−5)2+(−3)2=√34 (f ) p(−5)2+ (2)2=√29
9. (a) (x−1)2+y2+(z+1)
2=16
(b) r=p(−1−0)2+(3−0)2+(2−0)2=√14, (x+1)
2+(y−3)2+(z−2)2=14
449 Chapter 13
(c) r=1
2p(−1−0)2+(2−2)2+(1−3)2=1
2√5, center (−1/2,2,2),
(x+1/2)2+(y−2)2+(z−2)2=5/4
10. r=|[distance between (0,0,0) and (3,−2,4)] ±1|=√29 ±1,
x2+y2+z2=r2=√29 ±12=30±2
√
29
11. (x−2)2+(y+1)
2+(z+3)
2=r
2
,
(a) r2=3
2=9 (b) r2=1
2=1 (c) r2=2
2=4
12. (a) The sides have length 1, so the radius is 1
2; hence (x+2)
2+(y−1)2+(z−3)2=1
4
(b) The diagonal has length √1+1+1=√
3 and is a diameter, so (x+2)2+(y−1)2+(z−3)2=3
4.
13. (x+5)
2+(y+2)
2+(z+1)
2= 49; sphere, C(−5,−2,−1), r=7
14. x2+(y−1/2)2+z2=1/4; sphere, C(0,1/2,0), r=1/2
15. (x−1/2)2+(y−3/4)2+(z+5/4)2=54/16; sphere, C(1/2,3/4,−5/4), r=3
√
6/4
16. (x+1)
2+(y−1)2+(z+1)
2= 0; the point (−1,1,−1)
17. (x−3/2)2+(y+2)
2+(z−4)2=−11/4; no graph
18. (x−1)2+(y−3)2+(z−4)2= 25; sphere, C(1,3,4), r=5
19. (a)
y
x
z(b)
y
x
z(c)
y
x
z
20. (a)
y
x
z
x = 1
(b)
y
x
zy = 1
(c)
y
x
z
z = 1
21. (a)
5
y
x
z(b)
5
y
x
z(c)
5
y
x
z
Exercise Set 13.1 450
22. (a)
y
x
z(b)
y
x
z(c)
y
x
z
23. (a) −2y+z=0 (b) −2x+z=0
(c) (x−1)2+(y−1)2=1 (d) (x−1)2+(z−1)2=1
24. (a) (x−a)2+(z−a)
2=a
2
(b) (x−a)2+(y−a)
2=a
2
(c) (y−a)2+(z−a)
2=a
2
25.
y
x
z
26.
y
x
z27.
1
1
x
y
z
28.
y
x
z29.
3
3
2
y
x
z
30.
2
3
y
x
z31.
2-3
3
x
y
z32.
3
√3
y
x
z
451 Chapter 13
33.
-2 2
x
y
z34.
y
x
z
35. (a)
1.4-1.4
-1.4
1.4 (b) z
y
x
36. (a) 1
-1
-2 2
(b)
y
x
z
37. Complete the square to get (x+1)
2+(y−1)2+(z−2)2= 9; center (−1,1,2), radius 3. The
distance between the origin and the center is √6<3 so the origin is inside the sphere. The largest
distance is 3 + √6, the smallest is 3 −√6.
38. (x−1)2+y2+(z+4)
2≤25; all points on and inside the sphere of radius 5 with center
at (1,0,−4).
39. (y+3)
2+(z−2)2>16; all points outside the circular cylinder (y+3)
2+(z−2)2= 16.
40. p(x−1)2+(y+2)
2+z
2=2
px
2+(y−1)2+(z−1)2, square and simplify to get
3x2+3y
2+3z
2+2x−12y−8z+ 3 = 0, then complete the square to get
(x+1/3)2+(y−2)2+(z−4/3)2=44/9; center (−1/3,2,4/3), radius 2√11/3.
41. Let rbe the radius of a styrofoam sphere. The distance from the origin to the center of the bowling
ball is equal to the sum of the distance from the origin to the center of the styrofoam sphere nearest
the origin and the distance between the center of this sphere and the center of the bowling ball so
√3R=√3r+r+R,(
√
3+1)r=(
√
3−1)R,r=√3−1
√3+1R=(2−√
3)R.
42. (a) Complete the square to get (x+G/2)2+(y+H/2)2+(z+I/2)2=K/4, so the equation
represents a sphere when K>0, a point when K= 0, and no graph when K<0.
(b) C(−G/2,−H/2,−I/2), r=√K/2
Exercise Set 13.2 452
43. (asin φcos θ)2+(asin φsin θ)2+(acos φ)2=a2sin2φcos2θ+a2sin2φsin2θ+a2cos2φ
=a2sin2φ(cos2θ+ sin2θ)+a
2cos2φ
=a2sin2φ+a2cos2φ=a2(sin2φ+ cos2φ)=a
2
EXERCISE SET 13.2
1. (a–c)
〈2, 5〉
〈–5, –4〉
〈2, 0〉
x
y(d–f)
x
y
-5i + 3j
3i - 2j
-6j
2. (a–c)
〈0, -8〉
〈6, -2〉
〈-3, 7〉
x
y(d–f)
-2 i - j
4i + 2 j
4i
x
y
3. (a–b)
〈1, -2, 2〉
〈2, 2, –1〉
y
x
z(c–d)
y
x
z–i + 2j + 3k
2i + 3j – k
4. (a–b)
〈-1, 3, 2 〉
〈3, 4, 2 〉
y
x
z(c–d)
i - j + 2 k
2j - k
y
x
z
453 Chapter 13
5. (a) h4−1,1−5i=h3,−4i
x
y
3i – 4j
(b) h0−2,0−3,4−0i=h−2,−3,4i
y
x
–2i – 3j + 4kz
6. (a) h−3−2,3−3i=h−5,0i
–5i
x
y
(b) h0−3,4−0,4−4i=h−3,4,0i
y
x
– 3i + 4j
z
7. (a) h2−3, 8 −5i=h−1,3i
(b) h0−7, 0 −(−2)i=h−7,2i
(c) h−3,6,1i
8. (a) h−4−(−6), −1−(−2)i=h2,1i
(b) h−1,6,1i
(c) h5,0,0i
9. (a) Let (x, y) be the terminal point, then x−1=3,x= 4 and y−(−2) = −2, y=−4.
The terminal point is (4,−4).
(b) Let (x, y, z) be the initial point, then 5 −x=−3, −y= 1, and −1−z=2sox=8,
y=−1, and z=−3. The initial point is (8,−1,−3).
10. (a) Let (x, y) be the terminal point, then x−2=7,x= 9 and y−(−1)=6,y=5.
The terminal point is (9,5).
(b) Let (x, y, z) be the terminal point, then x+2=1,y−1=2,andz−4=−3sox=−1,
y= 3, and z= 1. The terminal point is (−1,3,1).
11. (a) −i+4j−2k (b) 18i+12j−6k (c) −i−5j−2k
(d) 40i−4j−4k (e) −2i−16j−18k(f)−i+13j−2k
12. (a) h1,−2,0i(b) h28,0,−14i+h3,3,9i=h31,3,−5i
(c) h3,−1,−5i(d) 3(h2,−1,3i−h28,0,−14i)=3h−26,−1,17i=h−78,−3,51i
(e) h−12,0,6i−h8,8,24i=h−20,−8,−18i
(f) h8,0,−4i−h3,0,6i=h5,0,−10i
13. (a) kvk=√1+1=√
2(b) kvk=√1+49=5
√
2
(c) kvk=√21 (d) kvk=√14
14. (a) kvk=√9+16=5 (b) kvk=√2+7=3
(c) kvk=3 (d) kvk=√3
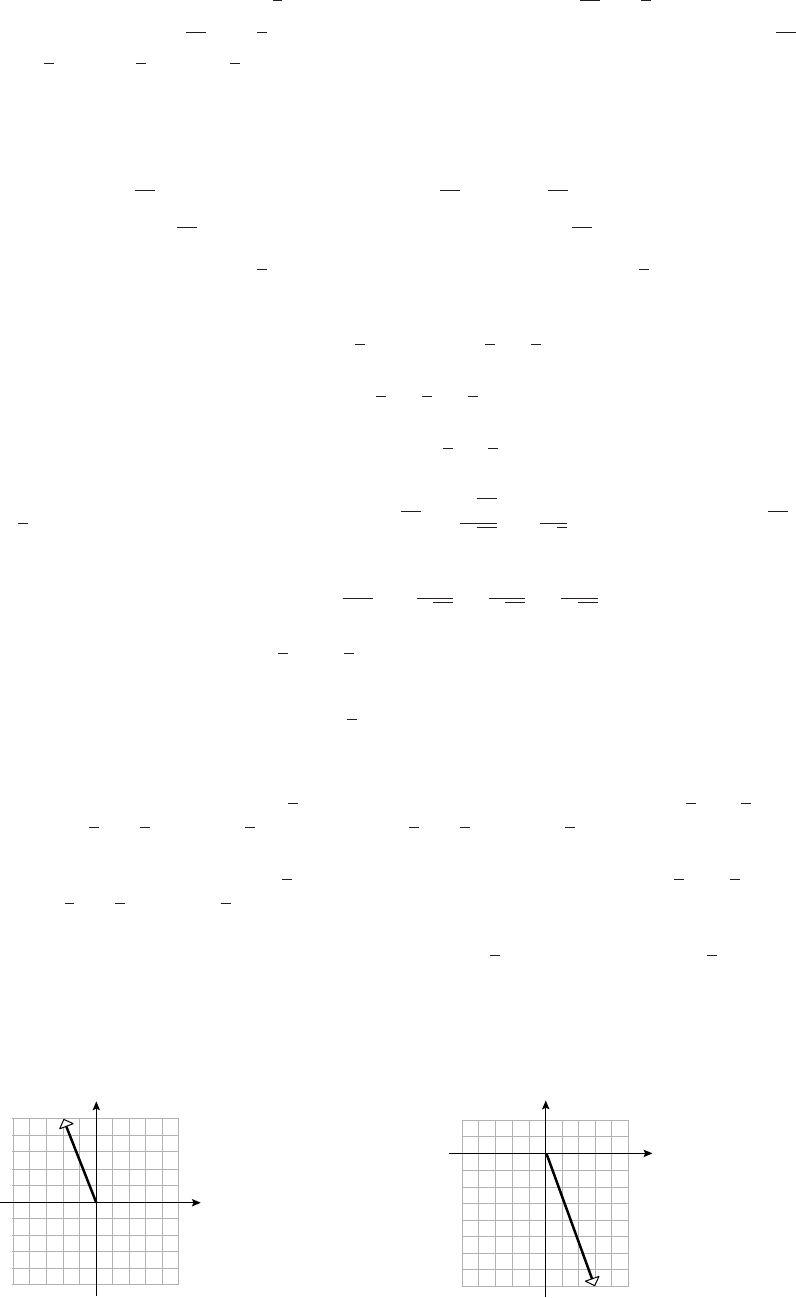
Exercise Set 13.2 454
15. (a) ku+vk=k2i−2j+2kk=2
√
3(b) kuk+kvk=√14+√2
(c) k−2uk+2kvk=2
√
14+2
√
2(d) k3u−5v+wk=k−12j+2kk=2
√
37
(e) (1/√6)i+(1/
√
6)j−(2/√6)k(f)1
16. If one vector is a positive multiple of the other, say u=αvwith α>0, then u,vand u+vare
parallel and ku+vk=(1+α)kvk=kuk+kvk.
17. (a) k−i+4jk=√
17 so the required vector is −1/√17i+4/√17j
(b) k6i−4j+2kk=2
√
14 so the required vector is (−3i+2j−k)/
√
14
(c) −→
AB=4i+j−k,k−→
AB k=3
√
2 so the required vector is (4i+j−k)/3√2
18. (a) k3i−4jk= 5 so the required vector is −1
5(3i−4j)=−3
5
i+4
5
j
(b) k2i−j−2kk= 3 so the required vector is 2
3i−1
3j−2
3k
(c) −→
AB =4i−3j,k−→
AB k= 5 so the required vector is 4
5i−3
5j
19. (a) −1
2v=h−3/2,2i(b) kvk=√85, so √17
√85v=1
√5h7,0,−6ihas length √17
20. (a) 3v=−6i+9j (b) −2
kvkv=6
√26i−8
√26j−2
√26k
21. (a) v =kvkhcos π/4,sin π/4i=h3√2/2,3√2/2i
(b) v =kvkhcos 90◦,sin 90◦i=h0,2i
(c) v =kvkhcos 120◦,sin 120◦i=h−5/2,5√3/2i
(d) v =kvkhcos π, sin πi=h−1,0i
22. From (12), v=hcos π/6,sin π/6i=h√3/2,1/2iand w=hcos 3π/4,sin 3π/4i=h−√2/2,√2/2i,
so v+w=((
√
3−√
2)/2,(1+√2)/2,v−w=((
√
3+√
2)/2,(1 −√2)/2)
23. From (12), v=hcos 30◦,sin 30◦i=h√3/2,1/2iand w=hcos 135◦,sin 135◦i=h−√2/2,√2/2i,so
v+w=((
√
3−√
2)/2,(1+√2)/2)
24. w =h1,0i, and from (12), v=hcos 120◦,sin 120◦i=h−1/2,√3/2i,sov+w=h1/2,
√
3/2i
25. (a) The initial point of u+v+w
is the origin and the endpoint
is (−2,5), so u+v+w=h−2,5i.
-5 5
-5
5
x
y
–2i + 5j
(b) The initial point of u+v+w
is (−5,4) and the endpoint
is (−2,−4), so u+v+w=h3,−8i.
-5 5
-8
2
x
y
3i – 8j
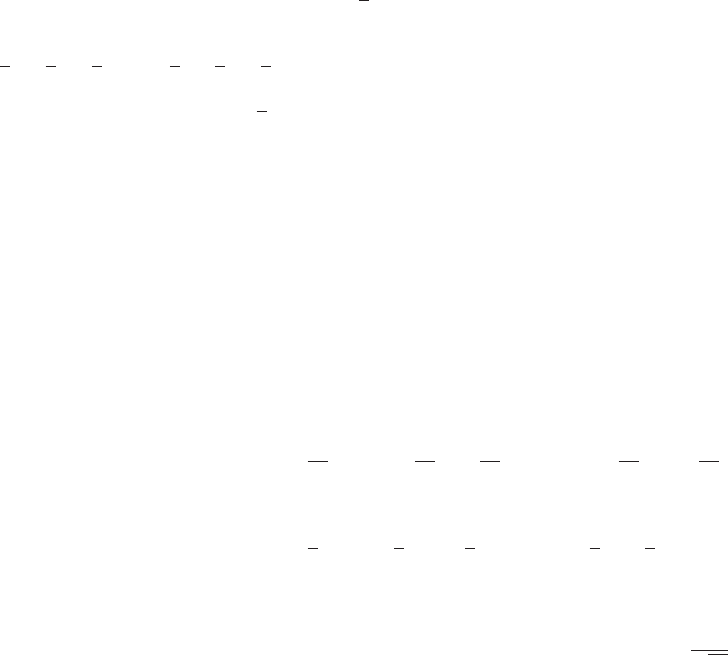
455 Chapter 13
26. (a) v =h−10,2iby inspection, so u−v+w=u+v+w−2v=h−2,5i+h20,−4i=h18,1i.
(b) v =h−3,8iby inspection, so u−v+w=u+v+w−2v=h3,−8i+h6,−16i=h9,−24i.
27. 6x=2u−v−w=h−4,6i,x=h−2/3,1i
28. u −2x=x−w+3v,3x=u+w−3v,x=1
3
(u+w−3v)=h2/3,2/3i
29. u =5
7i+2
7j+1
7k,v=8
7i−1
7j−4
7k 30. u =h−5,8i,v=h7,−11i
31. k(i+j)+(i−2j)k=k2i−jk=√
5,k(i+j−(i−2j)k=k3jk=3
32. Let A, B,Cbe the vertices (0,0), (1,3), (2,4) and Dthe fourth vertex (x, y). For the parallelogram
ABCD, −→
AD =−→
BC,hx, yi=h1,1iso x=1,y= 1 and Dis at (1,1). For the parallelogram ACBD,
−→
AD =−→
CB,hx, yi=h−1,−1iso x=−1, y=−1 and Dis at (−1,−1). For the parallelogram
ABDC, −→
AC=−→
BD,hx−1,y−3i=h2,4i,sox=3,y = 7 and Dis at (3,7).
33. (a) 5=kkvk=|k|kvk=±3k,sok=±5/3
(b) 6=kkvk=|k|kvk=2kvk,sokvk=3
34. If kkvk= 0 then |k|kvk= 0 so either k=0orkvk= 0; in the latter case, by (9) or (10), v=0.
35. (a) Choose two points on the line, for example P1(0,2) and P2(1,5); then −→
P 1P 2=h1 ,3 iis
parallel to the line, kh1,3ik =√10, so h1/√10,3/√10iand h−1/√10,−3/√10iare unit
vectors parallel to the line.
(b) Choose two points on the line, for example P1(0,4) and P2(1,3); then −→
P 1P 2=h1 ,−1 iis
parallel to the line, kh1,−1ik =√2soh1/
√
2,−1/
√
2iand h−1/√2,1/√2iare unit vectors
parallel to the line.
(c) Pick any line that is perpendicular to the line x+y= 4, for example y=x/5; then P1(0,0)
and P2(5,1) are on the line, so −→
P 1P 2=h5 ,1 iis perpendicular to the line, so ±1
√26h5,1iare
unit vectors perpendicular to the line.
36. (a) ±k (b) ±j (c) ±i
37. (a) the circle of radius 1 about the origin
(b) the solid disk of radius 1 about the origin
(c) all points outside the solid disk of radius 1 about the origin
38. (a) the circle of radius 1 about the tip of r0
(b) the solid disk of radius 1 about the tip of r0
(c) all points outside the solid disk of radius 1 about the tip of r0
39. (a) the (hollow) sphere of radius 1 about the origin
(b) the solid ball of radius 1 about the origin
(c) all points outside the solid ball of radius 1 about the origin
40. The sum of the distances between (x, y) and the points (x1,y
1
), (x2,y
2
) is the constant k,so
the set consists of all points on the ellipse with foci at (x1,y
1
) and (x2,y
2
), and major axis of
length k.

Exercise Set 13.2 456
41. Since φ=π/2, from (13) we get kF1+F2k2=kF1k2+kF2k2= 3600 + 900,
so kF1+F2k=30
√
5 lb, and sin α=kF2k
kF1+F2ksin φ=30
30√5,α≈26.57◦,θ =α≈26.57◦.
42. kF1+F2k2=kF1k2+kF2k2+2kF
1
kkF2kcos φ=14,400+10,000 + 2(120)(100)1
2=36,400, so
kF1+F2k=20
√
91 N, sin α=kF2k
kF1+F2ksin φ=100
20√91 sin 60◦=5√3
2√91,α ≈27.16◦,
θ=α≈27.16◦.
43. kF1+F2k2=kF1k2+kF2k2+2kF
1
kkF2kcos φ= 160,000 + 160,000 −2(400)(400)√3
2,
so kF1+F2k≈207.06 N, and sin α=kF2k
kF1+F2ksin φ≈400
207.06 1
2,α=75.00◦,
θ=α−30◦=45.00◦.
44. kF1+F2k2=kF1k2+kF2k2+2kF
1
kkF2kcos φ=16+4+2(4)(2) cos 77◦,so
kF
1
+F
2
k≈4.86 lb, and sin α=kF2k
kF1+F2ksin φ=2
4.86 sin 77◦,α≈23.64◦,θ =α−27◦≈−3.36◦.
45. Let F1,F2,F3be the forces in the diagram with magnitudes 40,50,75 respectively. Then
F1+F2+F3=(F
1+F
2
)+F
3
. Following the examples, F1+F2has magnitude 45.83 N and
makes an angle 79.11◦with the positive x-axis. Then
k(F1+F2)+F3k2≈45.832+752+2(45.83)(75) cos 79.11◦,soF
1+F
2+F
3has magnitude ≈94.995
N and makes an angle θ=α≈28.28◦with the positive x-axis.
46. Let F1,F2,F3be the forces in the diagram with magnitudes 150,200,100 respectively. Then
F1+F2+F3=(F
1+F
2
)+F
3
. Following the examples, F1+F2has magnitude 279.34 N and
makes an angle 91.24◦with the positive x-axis. Then
kF1+F2+F3k2≈279.342+ 1002+ 2(279.34)(100) cos(270 −91.24)◦, and F1+F2+F3has
magnitude ≈179.37 N and makes an angle 91.94◦with the positive x-axis.
47. Let F1,F2be the forces in the diagram with magnitudes 8,10 respectively. Then kF1+F2khas
magnitude √82+10
2+2·8·10 cos 120◦=2
√
21 ≈9.165 lb, and makes an angle
60◦+sin−1kF1k
kF1+F2ksin 120 ≈109.11◦with the positive x-axis, so Fhas magnitude 9.165 lb and
makes an angle −70.89◦with the positive x-axis.
48. kF1+F2k=√1202+ 1502+2·120 ·150 cos 75◦= 214.98 N and makes an angle 92.63◦with the
positive x-axis, and kF1+F2+F3k= 232.90 N and makes an angle 67.23◦with the positive x-axis,
hence Fhas magnitude 232.90 N and makes an angle −112.77◦with the positive x-axis.
49. F1+F2+F=0, where Fhas magnitude 250 and makes an angle −90◦with the positive x-axis.
Thus kF1+F2k2=kF1k2+kF2k2+2kF
1
kkF2kcos 105◦= 2502and
45◦=α= sin−1kF2k
250 sin 105◦,so√
2
2≈kF
2
k
250 0.9659,kF2k≈183.02 lb,
kF1k2+ 2(183.02)(−0.2588)kF1k+ (183.02)2=62,500,kF1k= 224.13 lb.
50. Similar to Exercise 49, kF1k= 100√3N,kF
2
k= 100 N
51. (a) c1v1+c2v2=(2c
1+4c
2
)i+(−c
1+2c
2
)j=−4j,so2c
1+4c
2= 0 and −c1+2c
2=−4
which gives c1=2,c
2=−1.
(b) c1v1+c2v2=hc1−2c2,−3c1+6c
2
i=h3,5i,so c1−2c2= 3 and −3c1+6c
2=5
which has no solution.
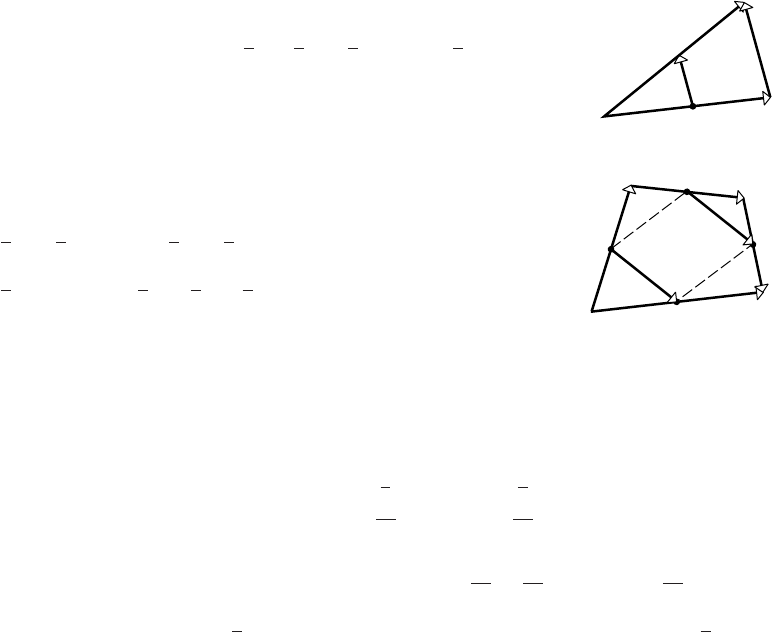
457 Chapter 13
52. (a) Equate corresponding components to get the system of equations c1+3c
2=−1,
2c2+c3= 1, and c1+c3= 5. Solve to get c1=2,c
2=−1, and c3=3.
(b) Equate corresponding components to get the system of equations c1+3c
2+4c
3=2,
−c
1−c
3= 1, and c2+c3=−1. From the second and third equations, c1=−1−c3and
c2=−1−c3; substitute these into the first equation to get −4 = 2, which is nonsense so the
system has no solution.
53. Place uand vtip to tail so that u+vis the vector from the initial point of uto the terminal
point of v. The shortest distance between two points is along the line joining these points so
ku+vk≤kuk+kvk.
54. (a): u+v=(u
1
i+u
2j)+(v
1
i+v
2j)=(v
1
i+v
2j)+u
1
i+u
2j=v+u
(c): u+0=u1i+u2j+0i+0j=u
1
i+u
2j=u
(e): k(lu)=k(l(u
1
i+u
2j)) = k(lu1i+lu2j)=klu1i+klu2j=(kl)u
55. (d): u+(−u)=u
1
i+u
2j+(−u
1
i−u
2j)=(u
1−u
1
)i+(u
1−u
1
)j=0
(g): (k+l)u=(k+l)(u1i+u2j)=ku1i+ku2j+lu1i+lu2j=ku+lu
(h): 1u=1(u
1
i+u
2j)=1u
1
i+1u
2j=u
1
i+u
2j=u
56. Draw the triangles with sides formed by the vectors u,v,u+vand ku,kv,ku+kv. By similar
triangles, k(u+v)=ku+kv.
57. Let a,b,cbe vectors along the sides of the triangle and A,B the
midpoints of aand b, then u=1
2a−1
2b=1
2(a−b)=1
2
cso uis
parallel to cand half as long.
A
B
u
c
b
a
58. Let a,b,c,dbe vectors along the sides of the quadrilateral
and A, B, C, D the corresponding midpoints, then
u=1
2b+1
2cand v=1
2d−1
2abut d=a+b+cso
v=1
2(a+b+c)−1
2a=1
2b+1
2c=uthus ABCD
is a parallelogram because sides AD and BC are equal
and parallel.
v
a
b
c
d
u
A
B
C
D
EXERCISE SET 13.3
1. (a) (1)(6) + (2)(−8) = −10; cos θ=(−10)/[(√5)(10)] = −1/√5
(b) (−7)(0) + (−3)(1) = −3; cos θ=(−3)/[(√58)(1)] = −3/√58
(c) (1)(8) + (−3)(−2) + (7)(−2) = 0; cos θ=0
(d) (−3)(4) + (1)(2) + (2)(−5) = −20; cos θ=(−20)/[(√14)(√45)] = −20/(3√70)
2. (a) u ·v= 1(2) cos(π/6) = √3(b) u ·v= 2(3) cos 135◦=−3√2
3. (a) u ·v=−34 <0, obtuse (b) u ·v=6>0, acute
(c) u ·v=−1<0, obtuse (d) u ·v= 0, orthogonal
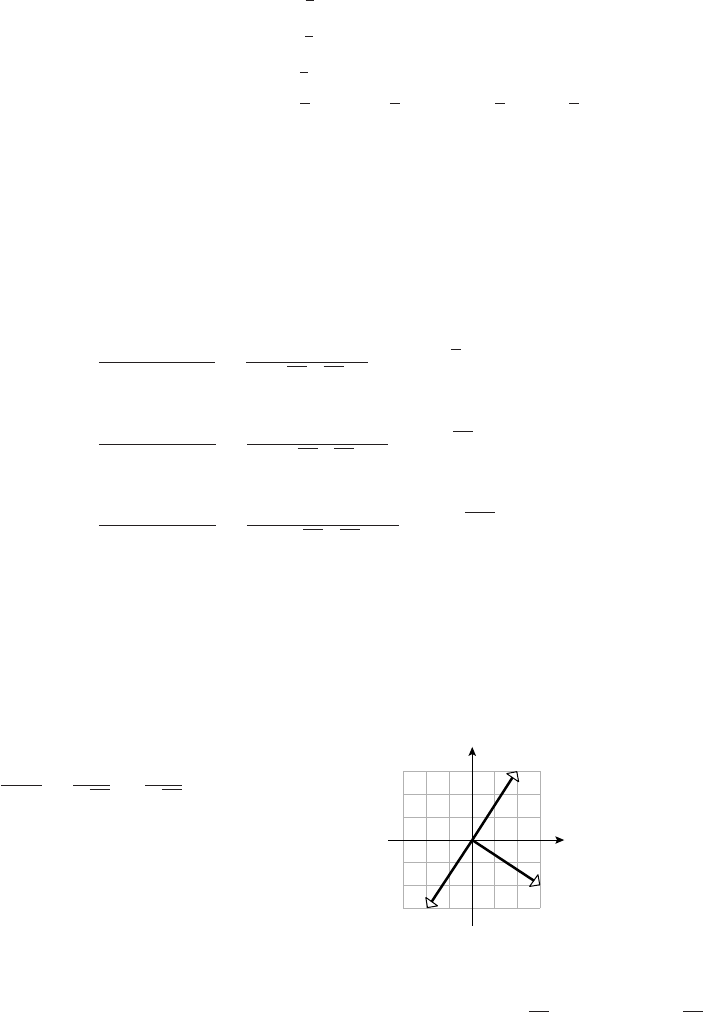
Exercise Set 13.3 458
4. Let the points be P, Q, R in order, then −→
PQ=h2−(−1),−2−2,0−3i=h3,−4,−3i,
−→
QR=h3−2,1−(−2),−4−0i=h1,3,−4i,−→
RP =h−1−3,2−1,3−(−4)i=h−4,1,7i;
since −→
QP ·
−→
QR=−3(1) + 4(3) + 3(−4) = −3<0,6PQR is obtuse;
since −→
RP ·
−→
RQ=−4(−1)+(−3) + 7(4) = 29 >0,6PRQ is acute;
since −→
PR ·
−→
PQ= 4(3) −1(−4) −7(−3)=37>0,6RP Q is acute
5. Since v1·vi= cos φi, the answers are, in order, √2/2,0,−√2/2,−1,−√2/2,0,√2/2
6. Proceed as in Exercise 5; 25/2,−25/2,−25,−25/2,25/2
7. (a) −→
AB =h1,3,−2i,−→
BC =h4,−2,−1i,−→
AB ·
−→
BC =0so −→
AB and −→
BC are orthogonal; it is a right
triangle with the right angle at vertex B.
(b) Let A, B, and Cbe the vertices (−1,0), (2,−1), and (1,4) with corresponding interior angles
α,β, and γ, then
cos α=
−→
AB ·
−→
AC
k−→
AB kk−→
AC k
=h3,−1i·h2,4i
√10√20 =1/(5√2),α≈82◦
cos β=
−→
BA ·
−→
BC
k−→
BAkk−→
BC k
=h−3,1i·h−1,5i
√10√26 =4/
√
65,β≈60◦
cos γ=
−→
CA ·
−→
CB
k−→
CAkk−→
CBk
=h−2,−4i·h1,−5i
√20√26 =9/
√
130,γ≈38◦
8. −→
AB ·
−→
AP =[2i+j+2k]·[(k−1)i+(k+1)j+(k−3)k]
=2(k−1)+(k+1)+2(k−3)=5k−7=0,k =7/5.
9. (a) v ·v1=−ab +ba =0;v·v
2=ab +b(−a)=0
(b) Let v1=2i+3j,v
2=−2i−3j;
take u1=v1
kv1k=2
√13i+3
√13j,u2=−u1.
-3 3
-3
3
x
y
v
u1
u2
10. By inspection, 3i−4jis orthogonal to and has the same length as 4i+3j
so u1=(4i+3j)+(3i−4j)=7i−jand u2=(4i+3j)+(−1)(3i−4j)=i+7jeach make an angle
of 45◦with 4i+3j; unit vectors in the directions of u1and u2are (7i−j)/√50 and (i+7j)/
√50.
11. (a) The dot product of a vector uand a scalar v·wis not defined.
(b) The sum of a scalar u·vand a vector wis not defined.
(c) u ·vis not a vector.
(d) The dot product of a scalar kand a vector u+vis not defined.
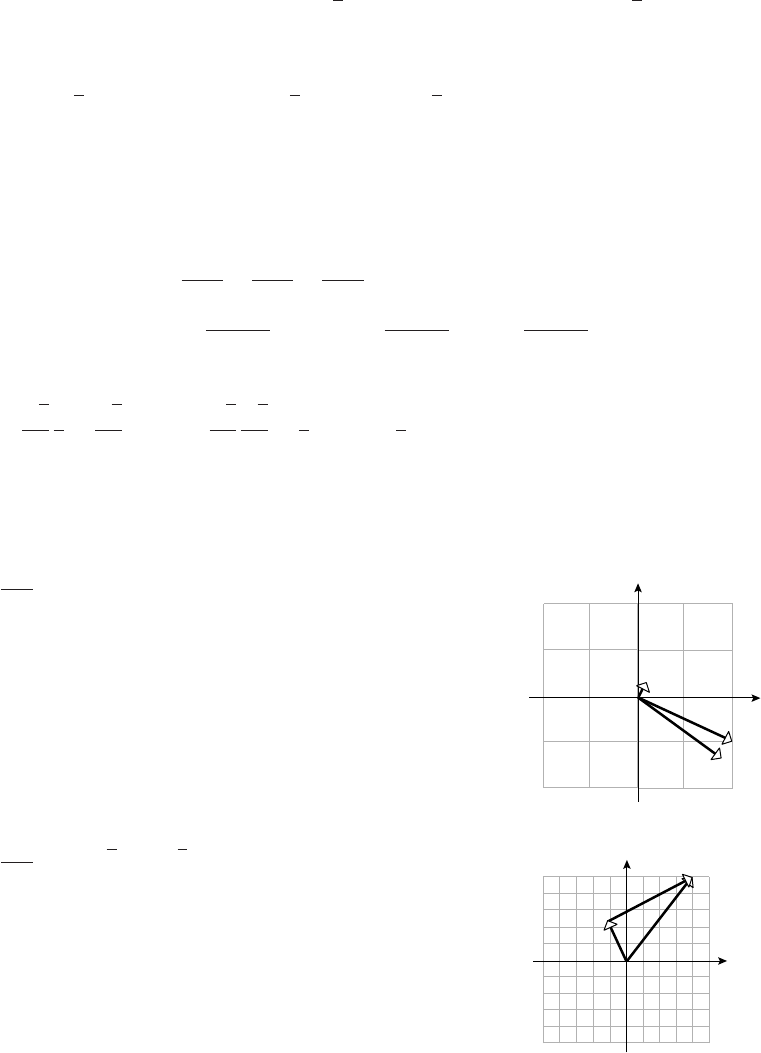
459 Chapter 13
12. (b): u·(v+w)=(6i−j+2k)·((2i+7j+4k)+(i+j−3k))=(6i−j+2k)·(3i+8j+k) = 12;
u·v+u·w=(6i−j+2k)·(2i+7j+4k)+(6i−j+2k)·(i+j−3k)=13−1=12
(c): k(u·v)=−5(13) = −65; (ku)·v=(−30i+5j−10k)·(2i+7j+4k)=−65;
u·(kv)=(6i−j+2k)·(−10i−35j−20k)=−65
13. (a) h1,2i·(h28,−14i+h6,0i)=h1,2i·h34,−14i=6
(b) k6wk=6kwk=36 (c) 24√5(d) 24√5
14. false, for example a=h1,2i,b=h−1,0i,c=h5,−3i
15. (a) kvk=√3socosα= cos β=1/
√
3, cos γ=−1/√3, α=β≈55◦,γ≈125◦
(b) kvk= 3 so cos α=2/3, cos β=−2/3, cos γ=1/3, α≈48◦,β≈132◦,γ≈71◦
16. (a) kvk= 7 so cos α=3/7, cos β=−2/7, cos γ=−6/7, α≈65◦,β≈107◦,γ≈149◦
(b) kvk= 5, cos α=3/5, cos β= 0, cos γ=−4/5, α≈53◦,β≈90◦,γ≈143◦
17. cos2α+ cos2β+ cos2γ=v2
1
kvk2+v2
2
kvk2+v2
3
kvk2=v2
1+v2
2+v2
3/kvk2=kvk2/kvk2=1
18. Let v=hx, y, zi, then x=px2+y2cos θ, y =px2+y2sin θ, px2+y2=kvkcos λ, and
z=kvksin λ,sox/kvk= cos θcos λ, y/kvk= sin θcos λ, and z/kvk= sin λ.
19. cos α=√3
2
1
2=√3
4,cos β=√3
2
√3
2=3
4,cos γ=1
2;α≈64◦,β ≈41◦,γ =60
◦
20. Let u1=ku1khcos α1,cos β1,cos γ1i,u2=ku2khcos α2,cos β2,cos γ2i,u1and u2are perpendicular
if and only if u1·u2=0soku
1
kku
2
k(cos α1cos α2+ cos β1cos β2+ cos γ1cos γ2)=0,
cos α1cos α2+ cos β1cos β2+ cos γ1cos γ2=0.
21. (a) b
kbk=h3/5,4/5i, so projbv=h6/25,8/25i
and v−projbv=h44/25,−33/25i
2
-2
-2
2
x
y
v
v – projbv
projbv
(b) b
kbk=h1/√5,−2/√5i, so projbv=h−6/5,12/5i
and v−projbv=h26/5,13/5i
x
y
-5 5
-5
5
v
v – projbv
projbv

Exercise Set 13.3 460
(c) b
kbk=h2/√5,1/√5i, so projbv=h−16/5,−8/5i
and v−projbv=h1/5,−2/5ix
y
-4
-4
v
v – projbv
projbv
22. (a) b
kbk=h1/3,2/3,2/3i, so projbv=h2/3,4/3,4/3iand v−projbv=h4/3,−7/3,5/3i
(b) b
kbk=h2/7,3/7,−6/7i, so projbv=h−74/49,−111/49,222/49i
and v−projbv=h270/49,62/49,121/49i
23. (a) projbv=h−1,−1i,sov=h−1,−1i+h3,−3i
(b) projbv=h16/5,0,−8/5i,sov=h16/5,0,−8/5i+h−1/5,1,−2/5i
24. (a) projbv=h1,1i,sov=h1,1i+h−4,4i
(b) projbv=h0,−8/5,4/5i,sov=h0,−8/5,4/5i+h−2,13/5,26/5i
25. −→
AP =−i+3j,−→
AB=3i+4j,kproj−→
AB
−→
AP k=|−→
AP ·
−→
AB |/k−→
AB k=9/5
k−→
AP k=√10,p10 −81/25=13/5
26. −→
AP =−4i+2k,−→
AB =−3i+2j−4k,kproj−→
AB
−→
AP k=|−→
AP ·
−→
AB |/k−→
AB k=4/
√
29.
k−→
AP k=√20, p20 −16/29 = p564/29
27. Let Fbe the downward force of gravity on the block, then kFk= 10(9.8) = 98 N, and if F1and
F2are the forces parallel to and perpendicular to the ramp, then kF1k=kF2k=49
√
2N.Thus
the block exerts a force of 49√2 N against the ramp and it requires a force of 49√2 N to prevent
the block from sliding down the ramp.
28. Let xdenote the magnitude of the force in the direction of Q. Then the force Facting on the
block is F=xi−10j. Let u=−1
√2(i+j) and v=1
√2(i−j) be the unit vectors in the directions
along and against the ramp. Then Fdecomposes as F=−x−10
√2u+x+10
√
2v, and thus the block
will not slide down the ramp provided x≥10 N.
29. Three forces act on the block: its weight −300j; the tension in cable A, which has the form
a(−i+j); and the tension in cable B, which has the form b(√3i−j), where a, b are positive
constants. The sum of these forces is zero, which yields a= 450 + 150√3,b= 150 + 150√3. Thus
the forces along cables A and B are, respectively,
k150(3 + √3)(i−j)k= 450√2 + 150√6 lb, and k150(√3 + 1)(√3i−j)k= 300 + 300√3 lb.
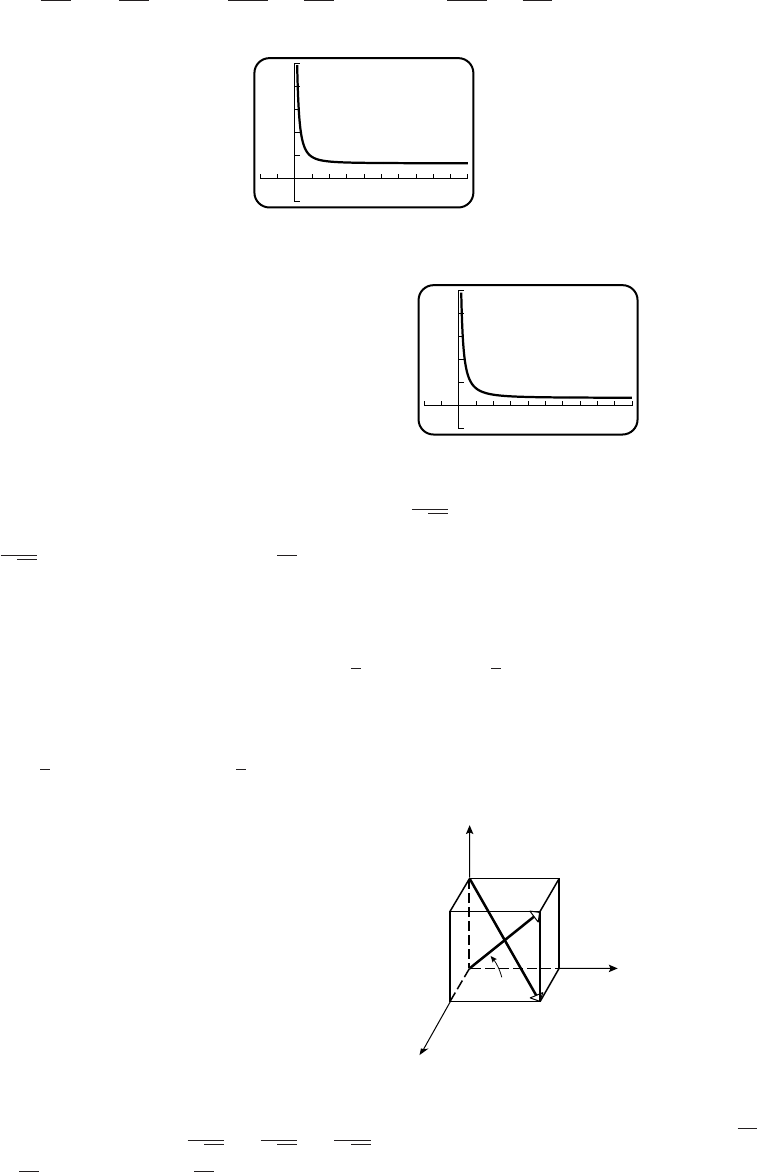
461 Chapter 13
30. (a) Let T
Aand T
Bbe the forces exerted on the block by cables Aand B. Then
T
A=a(−10i+dj) and T
B=b(20i+dj) for some positive a, b. Since T
A+T
B−100j=0,we
find a=200
3d,b=100
3d,T
A=−2000
3di+200
3j, and T
B=2000
3di+100
3j.
500
-100
-20 100
(b) An increase in dwill decrease both forces. 500
-100
-20 100
(c) The inequality kT
Ak≤150 is equivalent to d≥40
√65, and kT
Bk≤150 is equivalent to
d≥40
√77. Hence we must have d≥40
65.
31. Let Pand Qbe the points (1,3) and (4,7) then −→
PQ=3i+4jso W=F·
−→
PQ=−12 ft ·lb.
32. W=F·
−→
PQ=kFkk−→
PQkcos 45◦= (500)(100) √2/2=25,000√2N·m
33. W=F·15i=15·50 cos 60◦= 375 ft ·lb.
34. W=F·(15/√3)(i+j+k)=−15/√3N·m
35. With the cube as shown in the diagram,
and athe length of each edge,
d1=ai+aj+ak,d2=ai+aj−ak,
cos θ=(d
1·d
2
)/(kd
1
kkd
2
k)=1/3,θ ≈71◦
d1
d2
y
x
z
36. Take i,j, and kalong adjacent edges of the box, then 10i+15j+25kis along a diagonal, and a
unit vector in this direction is 2
√38i+3
√38j+5
√38k. The direction cosines are cos α=2/
√
38,
cos β=3/
√
38, and cos γ=5/
√
38 so α≈71◦,β≈61◦, and γ≈36◦.

Exercise Set 13.3 462
37. u +vand u−vare vectors along the diagonals,
(u+v)·(u−v)=u·u−u·v+v·u−v·v=kuk
2−kvk
2so (u+v)·(u−v)=0
if and only if kuk=kvk.
38. The diagonals have lengths ku+vkand ku−vkbut
ku+vk2=(u+v)·(u+v)=kuk
2+2u·v+kvk
2
, and
ku−vk2=(u−v)·(u−v)=kuk
2−2u·v+kvk
2
. If the parallelogram is a rectangle then
u·v=0soku+vk
2=ku−vk
2
; the diagonals are equal. If the diagonals are equal, then
4u·v=0,u·v=0souis perpendicular to vand hence the parallelogram is a rectangle.
39. ku+vk2=(u+v)·(u+v)=kuk
2+2u·v+kvk
2and
ku−vk2=(u−v)·(u−v)=kuk
2−2u·v+kvk
2
, add to get
ku+vk2+ku−vk2=2kuk
2+2kvk
2
The sum of the squares of the lengths of the diagonals of a parallelogram is equal to twice the sum
of the squares of the lengths of the sides.
40. ku+vk2=(u+v)·(u+v)=kuk
2+2u·v+kvk
2and
ku−vk2=(u−v)·(u−v)=kuk
2−2u·v+kvk
2
, subtract to get
ku+vk2−ku−vk
2=4u·v, the result follows by dividing both sides by 4.
41. v =c1v1+c2v2+c3v3so v·vi=civi·vibecause vi·vj=0ifi6=j,
thus v·vi=cikvik2,c
i=v·v
i/kv
ik2for i=1,2,3.
42. v1·v2=v1·v3=v2·v3= 0 so they are mutually perpendicular. Let v=i−j+k, then
c1=v·v1
kv1k2=3
7,c2=v·v2
kv2k2=−1
3, and c3=v·v3
kv3k2=1
21.
43. (a) u =xi+(x
2+1)j,v=xi−(x+1)j,θ = cos−1[(u·v)/(kukkvk)].
Solve dθ/dx = 0 to find that the minimum value of θoccurs when x≈−3.136742 so the
minimum angle is about 40◦.
(b) Solve u·v= 0 for xto get x≈−0.682328.
44. (a) u = cos θ1i±sin θ1j,v=±sin θ2j+ cos θ2k,cos θ=u·v=±sin θ1sin θ2
(b) cos θ=±sin245◦=±1/2,θ=60
◦
(c) Let θ(t) = cos−1(sin tsin 2t); solve θ0(t)=0fortto find that θmax ≈140◦(reject, since θ
is acute) when t≈2.186276 and that θmin ≈40◦when t≈0.955317; for θmax check the
endpoints t=0,π/2 to obtain θmax = cos−1(0) = π/2.
45. Let u=hu1,u
2
,u
3
i,v=hv
1
,v
2
,v
3
i,w=hw
1
,w
2
,w
3
i. Then
u·(v+w)=hu
1
(v
1+w
1
),u
2
(v
2+w
2
),u
3
(v
3+w
3
)i=hu
1
v
1+u
1
w
1
,u
2
v
2+u
2
w
2
,u
3
v
3+u
3
w
3
i
=hu
1
v
1
,u
2
v
2
,u
3
v
3
i+hu
1
w
1
,u
2
w
2
,u
3
w
3
i=u·v+u·w
0·v=0·v
1+0·v
2+0·v
3=0
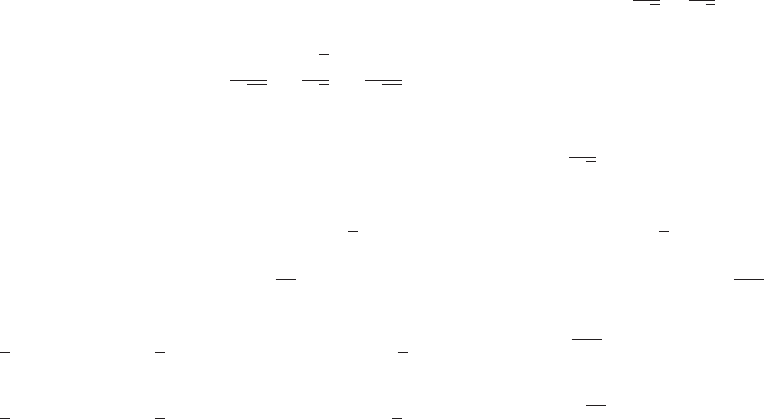
463 Chapter 13
EXERCISE SET 13.4
1. (a) i ×(i+j+k)=
ijk
100
111
=−j+k
(b) i ×(i+j+k)=(i×i)+(i×j)+(i×k)=−j+k
2. (a) j ×(i+j+k)=
ijk
010
111
=i−k
j×(i+j+k)=(j×i)+(j×j)+(j×k)=i−k
(b) k ×(i+j+k)=
ijk
001
111
=−i+j
k×(i+j+k)=(k×i)+(k×j)+(k×k)=j−i+0=−i+j
3. h7,10,9i4. −i−2j−7k5.h−4,−6,−3i6. i +2j−4k
7. (a) v ×w=h−23,7,−1i,u×(v×w)=h−20,−67,−9i
(b) u ×v=h−10,−14,2i,(u×v)×w=h−78,52,−26i
(c) (u×v)×(v×w)=h−10,−14,2i×h−23,7,−1i=h0,−56,−392i
(d) (v×w)×(u×v)=h0,56,392i
9. u ×v=(i+j)×(i+j+k)=k−j−k+i=i−j, the direction cosines are 1
√2,−1
√2,0
10. u ×v=12i+30j−6k,so± 2
√
30i+√5
√6j−1
√30k!
11. n =−→
AB ×−→
AC =h1,1,−3i×h−1,3,−1i=h8,4,4i, unit vectors are ±1
√6h2,1,1i
12. A vector parallel to the yz-plane must be perpendicular to i;
i×(3i −j+2k)=−2j−k,k−2j−kk=√
5, the unit vectors are ±(2j+k)/√5.
13. A=ku×vk=k−7i−j+3kk=√
59 14. A=ku×vk=k−6i+4j+7kk=√
101
15. A=1
2k−→
PQ ×−→
PRk=1
2kh−1,−5,2i×h2,0,3ik =1
2kh−15,7,10ik =√374/2
16. A=1
2k−→
PQ ×−→
PRk=1
2kh−1,4,8i×h5,2,12ik =1
2kh32,52,−22ik =9
√
13
17. 80 18. 29 19. −320. 1
21. V=|u·(v×w)|=|−16|=16 22. V=|u·(v×w)|=|45|=45
23. (a) u ·(v×w)=0,yes (b) u ·(v×w)=0,yes (c) u ·(v×w) = 245, no
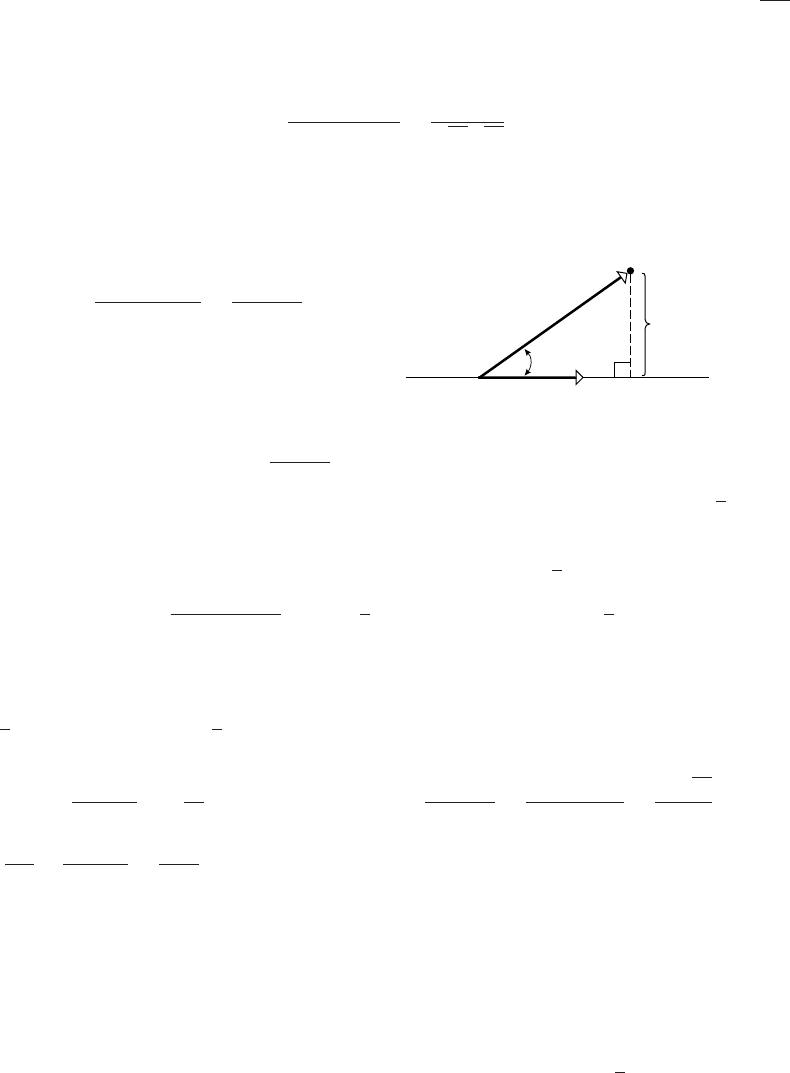
Exercise Set 13.4 464
24. (a) u ·(w×v)=−u·(v×w)=−3(b) (v×w)·u=u·(v×w)=3
(c) w ·(u×v)=u·(v×w)=3 (d) v ·(u×w)=u·(w×v)=−3
(e) (u×w)·v=u·(w×v)=−3(f ) v ·(w×w) = 0 because w×w=0
25. (a) V=|u·(v×w)|=|−9|=9 (b) A=ku×wk=k3i−8j+7kk=√
122
(c) v ×w=−3i−j+2kis perpendicular to the plane determined by vand w; let θbe the
angle between uand v×wthen
cos θ=u·(v×w)
kukkv×wk=−9
√
14√14 =−9/14
so the acute angle φthat umakes with the plane determined by vand wis
φ=θ−π/2 = sin−1(9/14).
26. From the diagram,
d=kuksin θ=kukkvksin θ
kvk=ku×vk
kvku
v
d
P
θ
27. (a) u =−→
AP =−4i+2k,v=−→
AB =−3i+2j−4k,u×v=−4i−22j−8k;
distance = ku×vk/kvk=2
p141/29
(b) u =−→
AP =2i+2j,v=−→
AB =−2i+j,u×v=6k; distance = ku×vk/kvk=6/
√
5
28. Take vand was sides of the (triangular) base, then area of base = 1
2kv×wkand
height = kprojv×wuk=|u·(v×w)|
kv×wkso V=1
3(area of base) (height) = 1
6|u·(v×w)|
29. −→
PQ=h3,−1,−3i,−→
PR=h2,−2,1i,−→
PS=h4,−4,3i,
V=1
6|−→
PQ ·(−→
PR ×−→
PS)|=1
6|−4|=2/3
30. (a) cos θ=u·v
kukkvk=−23
49 (b) sin θ=ku×vk
kukkvk=k36i−24jk
49 =12√13
49
(c) 232
492+144 ·13
492=2401
492=1
31. From Theorems 13.3.3 and 13.4.5a it follows that sin θ= cos θ,soθ=π/4.
32. ku×vk2=kuk2kvk2sin2θ=kuk2kvk2(1 −cos2θ)=kuk
2
kvk
2−(u·v)
2
33. (a) F =10jand −→
PQ=i+j+k, so the vector moment of Fabout Pis
−→
PQ ×F=
ijk
111
0100
=−10i+10k, and the scalar moment is 10√2lb·ft.
The direction of rotation of the cube about Pis counterclockwise looking along
−→
PQ ×F=−10i+10ktoward its initial point.

465 Chapter 13
(b) F =10jand −→
PQ=j+k, so the vector moment of Fabout Pis
−→
PQ ×F=
ijk
011
0100
=−10i, and the scalar moment is 10 lb·ft. The direction of rotation
of the cube about Pis counterclockwise looking along −10itoward its initial point.
(c) F =10jand −→
PQ=j, so the vector moment of Fabout Pis
−→
PQ ×F=
ijk
010
0100
=0, and the scalar moment is 0 lb·ft. Since the force is parallel to
the direction of motion, there is no rotation about P.
34. (a) F =1000
√2(−i+k) and −→
PQ=2j−k, so the vector moment of Fabout Pis
−→
PQ ×F= 500√2
ijk
02−1
−10 1
= 500√2(2i+j+2k), and the scalar moment is
1500√2N·m.
(b) The direction angles of the vector moment of Fabout the point Pare
cos−1(2/3) ≈48◦,cos−1(1/3) ≈71◦, and cos−1(2/3) ≈48◦.
35. F makes an angle 72◦with the positive x-axis, and ~
PQ =0.2i+0.03jmakes an angle
α= tan−1(0.03/0.2) with the x-axis, so φ≈72◦−8.53◦=63.47◦and kFk= 200 N, so
k−→
PQ ×Fk=k~
PQkkFk|sin 63.47◦|= 200k(0.2i+0.030j)k|sin 63.47◦|≈36.19 N·m.
36. Part (b) : let u=hu1,u
2
,u
3
i,v=hv
1
,v
2
,v
3
i,and w=hw1,w
2
,w
3
i; show that
u×(v+w) and (u×v)+(u×w) are the same.
Part (c) : (u+v)×w=−[w×(u+v)] from part (a)
=−[(w×u)+(w×v)] from part (b)
=(u×w)+(v×w) from part (a)
37. Let u=hu1,u
2
,u
3
iand v=hv1,v
2
,v
3
i; show that k(u×v), (ku)×v, and u×(kv) are all the
same; Part (e) is proved in a similar fashion.
38. Suppose the first two rows are interchanged. Then by definition,
b1b2b3
a1a2a3
c1c2c3
=b1
a2a3
c2c3−b2
a1a3
c1c3
+b3
a1a2
c1c2
=b1(a2c3−a3c2)−b2(a1c3−a3c1)+b
3
(a
1
c
2−a
2
c
1
),
which is the negative of the right hand side of (2) after expansion. If two other rows were to be
exchanged, a similar proof would hold. Finally, suppose ∆ were a determinant with two identical
rows. Then the value is unchanged if we interchange those two rows, yet ∆ = −∆ by Part (b) of
Theorem 13.4.1. Hence ∆ = −∆,∆=0.
39. −8i−20j+2k,−8i−8k
40. (a) From the first formula in Exercise 39 it follows that u×(v×w) is a linear combination of
vand wand hence lies in the plane determined by them.
(b) Similar to (a).
Exercise Set 13.5 466
41. If a,b,c, and dlie in the same plane then a×band c×dare parallel so (a×b)×(c×d)=0
42. Let uand vbe the vectors from a point on the curve to the points (2,−1,0) and (3,2,2), respec-
tively. Then u=(2−x)i+(−1−lnx)jand v=(3−x)i+(2−lnx)j+2k.The area of the triangle
is given by A=(1/2)ku×vk; solve dA/dx = 0 for xto get x=2.091581. The minimum area is
1.887850.
43.
−→
PQ
0×F=−→
PQ ×F+−→
QQ0×F=−→
PQ ×F, since Fand −→
QQ0are parallel.
EXERCISE SET 13.5
In many of the Exercises in this section other answers are also possible.
1. (a) L1:P(1,0),v=j,x=1,y =t
L
2
:P(0,1),v=i,x=t, y =1
L
3
:P(0,0),v=i+j,x=t, y =t
(b) L1:P(1,1,0),v=k,x=1,y =1,z =t
L
2
:P(0,1,1),v=i,x=t, y =1,z =1
L
3
:P(1,0,1),v=j,x=1,y =t, z =1
L
4
:P(0,0,0),v=i+j+k,x=t,
y=t, z =t
2. (a) L1:x=t, y =1,0≤t≤1
L
2
:x=1,y =t, 0≤t≤1
L3:x=t, y =t, 0≤t≤1
(b) L1:x=1,y =1,z =t, 0≤t≤1
L2:x=t, y =1,z =1,0≤t≤1
L
3
:x=1,y =t, z =1,0≤t≤1
L
4
:x=t, y =t, z =t, 0≤t≤1
3. (a) −→
P 1P 2=h2 ,3 iso x=3+2t,y=−2+3tfor the line; for the line segment add the condition
0≤t≤1.
(b) −→
P 1P 2=h−3,6,1iso x=5−3t,y=−2+6t,z=1+tfor the line; for the line segment add
the condition 0 ≤t≤1.
4. (a) −→
P 1P 2=h−3,−5iso x=−3t,y=1−5tfor the line; for the line segment add the condition
0≤t≤1.
(b) −→
P 1P 2=h0 ,0 ,−3 iso x=−1, y=3,z=5−3tfor the line; for the line segment add the
condition 0 ≤t≤1.
5. (a) x=2+t, y =−3−4t(b) x=t, y =−t, z =1+t
6. (a) x=3+2t, y =−4+t(b) x=−1−t, y =3t, z =2
7. (a) r0=2i−jso P(2,−1) is on the line, and v=4i−jis parallel to the line.
(b) At t=0,P(−1,2,4) is on the line, and v=5i+7j−8kis parallel to the line.
8. (a) At t=0,P(−1,5) is on the line, and v=2i+3jis parallel to the line.
(b) r0=i+j−2kso P(1,1,−2) is on the line, and v=jis parallel to the line.
9. (a) hx, yi=h−3,4i+th1,5i;r=−3i+4j+t(i+5j)
(b) hx, y, zi=h2,−3,0i+th−1,5,1i;r=2i−3j+t(−i+5j+k)
10. (a) hx, yi=h0,−2i+th1,1i;r=−2j+t(i+j)
(b) hx, y, zi=h1,−7,4i+th1,3,−5i;r=i−7j+4k+t(i+3j−5k)
11. x=−5+2t,y=2−3t12. x=t,y=3−2t

467 Chapter 13
13. 2x+2yy0=0,y
0=−x/y =−(3)/(−4)=3/4, v=4i+3j;x=3+4t,y=−4+3t
14. y0=2x=2(−2) = −4, v=i−4j;x=−2+t,y=4−4t
15. x=−1+3t,y=2−4t,z=4+t16. x=2−t,y=−1+2t,z=5+7t
17. The line is parallel to the vector h2,−1,2iso x=−2+2t,y=−t,z=5+2t.
18. The line is parallel to the vector h1,1,0iso x=t,y=t,z=0.
19. (a) y=0,2−t=0,t =2,x=7 (b) x=0,1+3t=0,t=−1/3,y =7/3
(c) y=x2,2−t=(1+3t)
2
,9t
2+7t−1=0,t=−7±√85
18 ,x=−1±√85
6,y =43 ∓√85
18
20. (4t)2+(3t)
2=25,25t2=25,t=±1, the line intersects the circle at ±h4,3i
21. (a) z= 0 when t= 3 so the point is (−2,10,0)
(b) y= 0 when t=−2sothepointis(−2,0,−5)
(c) xis always −2 so the line does not intersect the yz-plane
22. (a) z= 0 when t= 4 so the point is (7,7,0)
(b) y= 0 when t=−3sothepointis(−7,0,7)
(c) x= 0 when t=1/2sothepointis(0,7/2,7/2)
23. (1 + t)2+(3−t)
2= 16, t2−2t−3=0,(t+ 1)(t−3)=0;t=−1, 3. The points of intersection
are (0,4,−2) and (4,0,6).
24. 2(3t)+3(−1+2t)=6,12t=9;t=3/4. The point of intersection is (5/4,9/4,1/2).
25. The lines intersect if we can find values of t1and t2that satisfy the equations 2 + t1=2+t
2
,
2+3t
1=3+4t
2
, and 3 + t1=4+2t
2
. Solutions of the first two of these equations are t1=−1,
t2=−1 which also satisfy the third equation so the lines intersect at (1,−1,2).
26. Solve the equations −1+4t
1=−13+12t
2
,3+t
1=1+6t
2
, and 1 = 2 + 3t2. The third equation
yields t2=−1/3 which when substituted into the first and second equations gives t1=−4inboth
cases; the lines intersect at (−17,−1,1).
27. The lines are parallel, respectively, to the vectors h7,1,−3iand h−1,0,2i. These vectors are not
parallel so the lines are not parallel. The system of equations 1 + 7t1=4−t
2
,3+t
1= 6, and
5−3t1=7+2t
2has no solution so the lines do not intersect.
28. The vectors h8,−8,10iand h8,−3,1iare not parallel so the lines are not parallel. The lines do not
intersect because the system of equations 2 + 8t1=3+8t
2
,6−8t
1=5−3t
2
,10t
1=6+t
2has no
solution.
29. The lines are parallel, respectively, to the vectors v1=h−2,1,−1iand v2=h−4,2,−2i;
v2=2v
1
,v
1and v2are parallel so the lines are parallel.
30. The lines are not parallel because the vectors h3,−2,3iand h9,−6,8iare not parallel.
31. −→
P 1P2=h3 ,−7 ,−7 i ,−→
P 2P 3=h−9,−7,−3i; these vectors are not parallel so the points do not lie on
the same line.
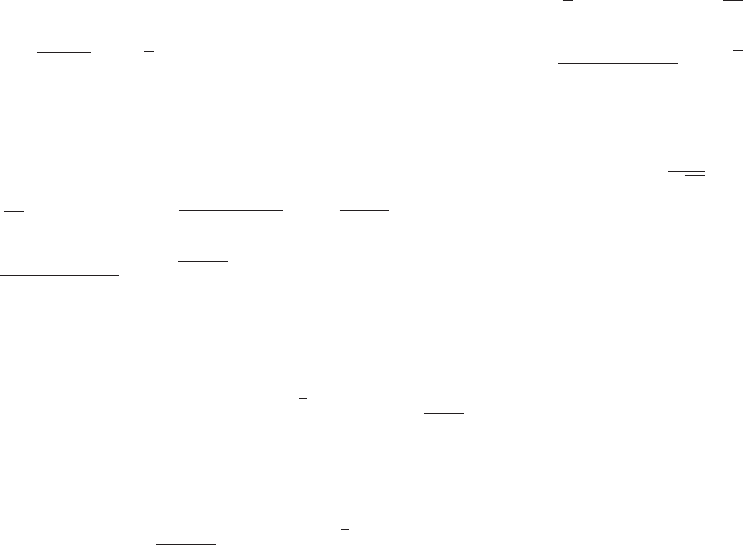
Exercise Set 13.5 468
32. −→
P 1P 2=h2 ,−4 ,−4 i ,−→
P2P 3=h1 ,−2 ,−2 i ;−→
P 1P 2=2 −→
P2P 3so the vectors are parallel and the points
lie on the same line.
33. If t2gives the point h−1+3t
2
,9−6t
2
ion the second line, then t1=4−3t
2yields the point
h3−(4 −3t2),1 + 2(4 −3t2)i=h−1+3t
2
,9−6t
2
ion the first line, so each point of L2is a point
of L1; the converse is shown with t2=(4−t
1
)/3.
34. If t1gives the point h1+3t
1
,−2+t
1
,2t
1
ion L1, then t2=(1−t
1
)/2 gives the point
h4−6(1 −t1)/2,−1−2(1 −t1)/2,2−4(1 −t1)/2i=h1+3t
1
,−2+t
1
,2t
1
ion L2, so each point of
L1isapointofL
2
; the converse is shown with t1=1−2t
2
.
35. The line segment joining the points (1,0) and (−3,6).
36. The line segment joining the points (−2,1,4) and (7,1,1).
37. A(3,0,1) and B(2,1,3) are on the line, and (method of Exercise 25)
−→
AP =−5i+j,−→
AB=−i+j+2k,kproj−→
AB
−→
AP k=|−→
AP ·
−→
AB |/k−→
AB k=√6 and k−→
AP k=√26,
so distance = √26 −6=4
√
5. Using the method of Exercise 26, distance = k−→
AP ×−→
AB k
k−→
AB k
=2
√
5.
38. A(2,−1,0) and B(3,−2,3) are on the line, and (method of Exercise 25)
−→
AP =−i+5j−3k,−→
AB=i−j+3k,kproj−→
AB
−→
AP k=|−→
AP ·
−→
AB |/k−→
AB k=15
√11 and
k−→
AP k=√35, so distance = p35 −225/11=4
p10/11. Using the method of Exercise 26,
distance = k−→
AP ×−→
AB k
k−→
AB k
=4
p10/11.
39. The vectors v1=−i+2j+kand v2=2i−4j−2kare parallel to the lines, v2=−2v1so v1and
v2are parallel. Let t= 0 to get the points P(2,0,1) and Q(1,3,5) on the first and second lines,
respectively. Let u=−→
PQ=−i+3j+4k,v=1
2v
2=i−2j−k;u×v=5i+3j−k; by the method
of Exercise 26 of Section 13.4, distance = ku×vk/kvk=p35/6.
40. The vectors v1=2i+4j−6kand v2=3i+6j−9kare parallel to the lines, v2=(3/2)v1so v1
and v2are parallel. Let t= 0 to get the points P(0,3,2) and Q(1,0,0) on the first and second
lines, respectively. Let u=−→
PQ=i−3j−2k,v=1
2v
1=i+2j−3k;u×v=13i+j+5k,
distance = ku×vk/kvk=p195/14 (Exer. 26, Section 13.4).
41. (a) The line is parallel to the vector hx1−x0,y
1−y
0
,z
1−z
0
iso
x=x0+(x
1−x
0
)t,y=y
0+(y
1−y
0
)t,z=z
0+(z
1−z
0
)t
(b) The line is parallel to the vector ha, b, ciso x=x1+at,y=y1+bt,z=z1+ct
42. Solve each of the given parametric equations (2) for tto get t=(x−x
0
)/a,t=(y−y
0
)/b,
t=(z−z
0
)/c,so(x, y, z) is on the line if and only if (x−x0)/a =(y−y
0
)/b =(z−z
0
)/c.
43. (a) It passes through the point (1,−3,5) and is parallel to v=2i+4j+k
(b) hx, y, zi=h1+2t, −3+4t, 5+ti
44. Let the desired point be P(x0,y
0
,z
0
), then −→
P 1P=(2/3) −→
P1P 2,
hx0−1 ,y
0−4,z
0+3i=(2/3)h0,1,2i=h0,2/3,4/3i; equate corresponding components to get
x0=1,y
0=14/3, z0=−5/3.

469 Chapter 13
45. (a) Let t= 3 and t=−2, respectively, in the equations for L1and L2.
(b) u =2i−j−2kand v=i+3j−kare parallel to L1and L2,
cos θ=u·v/(kukkvk)=1/(3√11),θ ≈84◦.
(c) u ×v=7i+7kis perpendicular to both L1and L2, and hence so is i+k,thusx=7+t,
y=−1, z=−2+t.
46. (a) Let t=1/2 and t= 1, respectively, in the equations for L1and L2.
(b) u =4i−2j+2kand v=i−j+4kare parallel to L1and L2,
cos θ=u·v/(kukkvk)=14/
√
432,θ ≈48◦.
(c) u ×v=−6i−14j−2kis perpendicular to both L1and L2, and hence so is 3i+7j+k,
thus x=2+3t,y=7t,z=3+t.
47. (0,1,2) is on the given line (t=0)sou=j−kis a vector from this point to the point (0,2,1),
v=2i−j+kis parallel to the given line. u×v=−2j−2k, and hence w=j+k, is perpendicular
to both lines so v×w=−2i−2j+2k, and hence i+j−k, is parallel to the line we seek. Thus
x=t,y=2+t,z=1−tare parametric equations of the line.
48. (−2,4,2) is on the given line (t=0)sou=5i−3j−4kis a vector from this point to the point
(3,1,−2), v=2i+2j+kis parallel to the given line. u×v=5i−13j+16kis perpendicular to
both lines so v×(u×v)=45i−27j−36k, and hence 5i−3j−4kis parallel to the line we seek.
Thus x=3+5t,y=1−3t,z=−2−4tare parametric equations of the line.
49. (a) When t= 0 the bugs are at (4,1,2) and (0,1,1) so the distance between them is
√42+0
2+1
2=√
17 cm.
(b)
5
0
0
10 (c) The distance has a minimum value.
(d) Minimize D2instead of D(the distance between the bugs).
D2=[t−(4 −t)]2+[(1+t)−(1+2t)]2+[(1+2t)−(2+t)]2=6t
2−18t+ 17,
d(D2)/dt =12t−18 = 0 when t=3/2; the minimum
distance is p6(3/2)2−18(3/2)+17=√
14/2 cm.
50. The line intersects the xz-plane when t=−1, the xy-plane when t=3/2. Along the line,
T=25t
2
(1 + t)(3 −2t) for −1≤t≤3/2. Solve dT/dt = 0 for tto find that the maximum value
of Tis about 50.96 when t≈1.073590.
EXERCISE SET 13.6
1. x=3,y =4,z =5 2. x=x0,y =y
0
,z =z
0
3. (x−2)+4(y−6)+2(z−1)=0,x+4y+2z=28
4. −(x+1)+7(y+1)+6(z−2)=0,−x+7y+6z=6

Exercise Set 13.6 470
5. z=0 6. 2x−3y−4z=0 7. n =i−j,x−y=0
8. n =i+j,P(1,0,0),(x−1)+y=0,x+y=1
9. n =j+k,P(0,1,0),(y−1)+z=0,y+z=1 10. n =j−k,y−z=0
11. −→
P 1P 2×−→
P 1P 3=h2 ,1 ,2 i×h3,−1,−2i=h0,10,−5i,for convenience choose h0,2,−1iwhich is also
normal to the plane. Use any of the given points to get 2y−z=1
12. −→
P 1P 2×−→
P 1P 3=h−1,−1,−2i×h−4,1,1i=h1,9,−5i,x+9y−5z=16
13. (a) parallel, because h2,−8,−6iand h−1,4,3iare parallel
(b) perpendicular, because h3,−2,1iand h4,5,−2iare orthogonal
(c) neither, because h1,−1,3iand h2,0,1iare neither parallel nor orthogonal
14. (a) neither, because h3,−2,1iand h6,−4,3iare neither parallel nor orthogonal
(b) parallel, because h4,−1,−2iand h1,−1/4,−1/2iare parallel
(c) perpendicular, because h1,4,7iand h5,−3,1iare orthogonal
15. (a) parallel, because h2,−1,−4iand h3,2,1iare orthogonal
(b) neither, because h1,2,3iand h1,−1,2iare neither parallel nor orthogonal
(c) perpendicular, because h2,1,−1iand h4,2,−2iare parallel
16. (a) parallel, because h−1,1,−3iand h2,2,0iare orthogonal
(b) perpendicular, because h−2,1,−1iand h6,−3,3iare parallel
(c) neither, because h1,−1,1iand h1,1,1iare neither parallel nor orthogonal
17. (a) 3t−2t+t−5=0,t=5/2sox=y=z=5/2, the point of intersection is (5/2,5/2,5/2)
(b) 2(2 −t)+(3+t)+t= 1 has no solution so the line and plane do not intersect
18. (a) 2(3t)−5t+(−t)+1=0,1 = 0 has no solution so the line and the plane do not intersect.
(b) (1+t)−(−1+3t)+4(2+4t)=7,t=−3/14 so x=1−3/14=11/14,
y=−1−9/14 = −23/14, z=2−12/14=8/7, the point is (11/14,−23/14,8/7)
19. n1=h1,0,0i,n2=h2,−1,1i,n1·n2=2so
cos θ=n1·n2
kn1kkn
2
k=2
√
1
√
6=2/
√
6,θ = cos−1(2/√6) ≈35◦
20. n1=h1,2,−2i,n2=h6,−3,2i,n1·n2=−4so
cos θ=(−n1)·n2
k−n
1
kkn
2
k=4
(3)(7) =4/21,θ = cos−1(4/21) ≈79◦
(Note: −n1is used instead of n1to get a value of θin the range [0,π/2])
21. h4,−2,7iis normal to the desired plane and (0,0,0) is a point on it; 4x−2y+7z=0
22. v =h3,2,−1iis parallel to the line and n=h1,−2,1iis normal to the given plane so
v×n=h0,−4,−8iis normal to the desired plane. Let t= 0 in the line to get (−2,4,3) which is
also a point on the desired plane, use this point and (for convenience) the normal h0,1,2ito find
that y+2z= 10.
471 Chapter 13
23. Find two points P1and P2on the line of intersection of the given planes and then find an equation
of the plane that contains P1,P2, and the given point P0(−1,4,2). Let (x0,y
0
,z
0
)beonthe
line of intersection of the given planes; then 4x0−y0+z0−2 = 0 and 2x0+y0−2z0−3=0,
eliminate y0by addition of the equations to get 6x0−z0−5=0;ifx
0= 0 then z0=−5, if x0=1
then z0= 1. Substitution of these values of x0and z0into either of the equations of the planes
gives the corresponding values y0=−7 and y0=3soP
1
(0,−7,−5) and P2(1,3,1) are on the
line of intersection of the planes. −→
P 0P 1×−→
P 0P 2=h4 ,−13,21iis normal to the desired plane whose
equation is 4x−13y+21z=−14.
24. h1,2,−1iis parallel to the line and hence normal to the plane x+2y−z=10
25. n1=h2,1,1iand n2=h1,2,1iare normals to the given planes, n1×n2=h−1,−1,3iso h1,1,−3i
is normal to the desired plane whose equation is x+y−3z=6.
26. n =h4,−1,3iis normal to the given plane, −→
P 1P 2=h3 ,−1 ,−1 iis parallel to the line,
n×−→
P 1P 2=h4 ,13,−1iis normal to the desired plane whose equation is 4x+13y−z=1.
27. n1=h2,−1,1iand n2=h1,1,−2iare normals to the given planes,
n1×n2=h1,5,3iis normal to the desired plane whose equation is x+5y+3z=−6.
28. Let t= 0 and t= 1 to get the points P1(−1,0,−4) and P2(0,1,−2) that lie on the line. Denote the
given point by P0, then −→
P 0P 1×−→
P 0P 2=h7 ,−1 ,−3 iis normal to the desired plane whose equation
is 7x−y−3z=5.
29. The plane is the perpendicular bisector of the line segment that joins P1(2,−1,1) and P2(3,1,5).
The midpoint of the line segment is (5/2,0,3) and −→
P 1P 2=h1 ,2 ,4 iis normal to the plane so an
equation is x+2y+4z=29/2.
30. n1=h2,−1,1iand n2=h0,1,1iare normals to the given planes, n1×n2=h−2,−2,2iso
n=h1,1,−1iis parallel to the line of intersection of the planes. v=h3,1,2iis parallel to the
given line, v×n=h−3,5,2iso h3,−5,−2iis normal to the desired plane. Let t= 0 to find the
point (0,1,0) that lies on the given line and hence on the desired plane. An equation of the plane
is 3x−5y−2z=−5.
31. The line is parallel to the line of intersection of the planes if it is parallel to both planes. Normals
to the given planes are n1=h1,−4,2iand n2=h2,3,−1iso n1×n2=h−2,5,11iis parallel to
the line of intersection of the planes and hence parallel to the desired line whose equations are
x=5−2t,y=5t,z=−2+11t.
32. Denote the points by A,B,C, and D, respectively. The points lie in the same plane if −→
AB ×−→
AC
and −→
AB ×−→
AD are parallel (method 1). −→
AB ×−→
AC =h0,−10,5i,−→
AB ×−→
AD =h0,16,−8i, these
vectors are parallel because h0,−10,5i=(−10/16)h0,16,−8i. The points lie in the same plane
if Dlies in the plane determined by A, B, C (method 2), and since −→
AB ×−→
AC =h0,−10,5i,an
equation of the plane is −2y+z+1=0,2y−z= 1 which is satisfied by the coordinates of D.
33. v =h0,1,1iis parallel to the line.
(a) For any t, 6·0+4t−4t=0,so(0,t,t) is in the plane.
(b) n =h5,−3,3iis normal to the plane, v·n= 0 so the line is parallel to the plane. (0,0,0) is
on the line, (0,0,1/3) is on the plane. The line is below the plane because (0,0,0) is below
(0,0,1/3).
Exercise Set 13.6 472
(c) n =h6,2,−2i,v·n= 0 so the line is parallel to the plane. (0,0,0) is on the line, (0,0,−3/2)
is on the plane. The line is above the plane because (0,0,0) is above (0,0,−3/2).
34. The intercepts correspond to the points A(a, 0,0),B(0,b,0), and C(0,0,c). −→
AB ×−→
AC =hbc, ac, abi
is normal to the plane so bcx +acy +abz =abc or x/a +y/b +z/c =1.
35. v1=h1,2,−1iand v2=h−1,−2,1iare parallel, respectively, to the given lines and to each
other so the lines are parallel. Let t= 0 to find the points P1(−2,3,4) and P2(3,4,0) that lie,
respectively, on the given lines. v1×−→
P 1P 2=h−7,−1,−9iso h7,1,9iis normal to the desired plane
whose equation is 7x+y+9z= 25.
36. The system 4t1−1=12t
2−13, t1+3=6t
2+1,1=3t
2+ 2 has the solution (Exercise 26,
Section 13.5) t1=−4, t2=−1/3so(−17,−1,1) is the point of intersection. v1=h4,1,0iand
v2=h12,6,3iare (respectively) parallel to the lines, v1×v2=h3,−12,12iso h1,−4,4iis normal
to the desired plane whose equation is x−4y+4z=−9.
37. n1=h−2,3,7iand n2=h1,2,−3iare normals to the planes, n1×n2=h−23,1,−7iis parallel
to the line of intersection. Let z= 0 in both equations and solve for xand yto get x=−11/7,
y=−12/7so(−11/7,−12/7,0) is on the line, a parametrization of which is
x=−11/7−23t,y=−12/7+t,z=−7t.
38. Similar to Exercise 37 with n1=h3,−5,2i,n2=h0,0,1i,n1×n2=h−5,−3,0i.z=0so
3x−5y= 0, let x= 0 then y= 0 and (0,0,0) is on the line, a parametrization of which is
x=−5t,y=−3t,z=0.
39. D=|2(1) −2(−2) + (3) −4|/√4+4+1=5/3
40. D=|3(0) + 6(1) −2(5) −5|/√9+36+4=9/7
41. (0,0,0) is on the first plane so D=|6(0) −3(0) −3(0) −5|/√36+9+9=5/
√
54.
42. (0,0,1) is on the first plane so D=|(0)+(0)+(1)+1|/
√
1+1+1=2/
√
3.
43. (1,3,5) and (4,6,7) are on L1and L2, respectively. v1=h7,1,−3iand v2=h−1,0,2iare,
respectively, parallel to L1and L2,v1×v2=h2,−11,1iso the plane 2x−11y+z+51=0
contains L2and is parallel to L1,D=|2(1) −11(3) + (5) + 51|/√4+121+1=25/
√
126.
44. (3,4,1) and (0,3,0) are on L1and L2, respectively. v1=h−1,4,2iand v2=h1,0,2iare parallel to
L1and L2,v1×v2=h8,4,−4i=4h2,1,−1iso 2x+y−z−3 = 0 contains L2and is parallel to
L1,D=|2(3) + (4) −(1) −3|/√4+1+1=√
6.
45. The distance between (2,1,−3) and the plane is |2−3(1)+2(−3)−4|/√1+9+4=11/
√
14 which
is the radius of the sphere; an equation is (x−2)2+(y−1)2+(z+3)
2= 121/14.
46. The vector 2i+j−kis normal to the plane and hence parallel to the line so parametric equations
of the line are x=3+2t,y=1+t,z=−t. Substitution into the equation of the plane yields
2(3+2t)+(1+t)−(−t)=0,t=−7/6; the point of intersection is (2/3,−1/6,7/6).
47. v =h1,2,−1iis parallel to the line, n=h2,−2,−2iis normal to the plane, v·n=0sovis
parallel to the plane because vand nare perpendicular. (−1,3,0) is on the line so
D=|2(−1) −2(3) −2(0) + 3|/√4+4+4=5/
√
12
473 Chapter 13
48. (a)
P(x0, y0)P(x, y)
n
r0
r – r0
r
O
(b) n ·(r−r0)=a(x−x
0
)+b(y−y
0
)=0
(c) See the proof of Theorem 13.6.1. Since aand bare not both zero, there is at least one point
(x0,y
0
) that satisfies ax+by +d=0,soax0+bx0+d=0. If(x, y) also satisfies ax+by+d=0
then, subtracting, a(x−x0)+b(y−y
0
) = 0, which is the equation of a line with n=ha, bi
as normal.
(d) Let Q(x1,y
1
) be a point on the line, and position the normal n=ha, bi, with length √a2+b2,
so that its initial point is at Q. The distance is the orthogonal projection of
−→
QP0=hx0−x1,y
0−y
1
ionto n. Then
D=kprojn
−→
QP 0k=
−→
QP0·n
knk2n
=|ax0+by0+d|
√a2+b2.
49. D=|2(−3) + (5) −1|/√4+1=2/
√
5
50. (a) If hx0,y
0
,z
0
ilies on the second plane, so that ax0+by0+cz0+d2= 0, then by Theorem
13.6.2, the distance between the planes is D=|ax0+by0+cz0+d1|
√a2+b2+c2=|−d
2+d
1
|
√
a
2+b
2+c
2
(b) The distance between the planes −2x+y+z= 0 and −2x+y+z+5
3=0is
D=|0−5/3|
√
4+1+1 =5
3
√
6.
EXERCISE SET 13.7
1. (a) elliptic paraboloid, a=2,b=3
(b) hyperbolic paraboloid, a=1,b =5
(c) hyperboloid of one sheet, a=b=c=4
(d) circular cone, a=b=1
(e) elliptic paraboloid, a=2,b=1
(f) hyperboloid of two sheets, a=b=c=1
2. (a) ellipsoid, a=√2/2,b=1/2,e =√3/3
(b) hyperbolic paraboloid, a=b=1
(c) hyperboloid of one sheet, a=1,b=3,c =1
(d) hyperboloid of two sheets, a=1,b=2,c=1
(e) elliptic paraboloid, a=√2,b=√2/2
(f) elliptic cone, a=2,b=√3
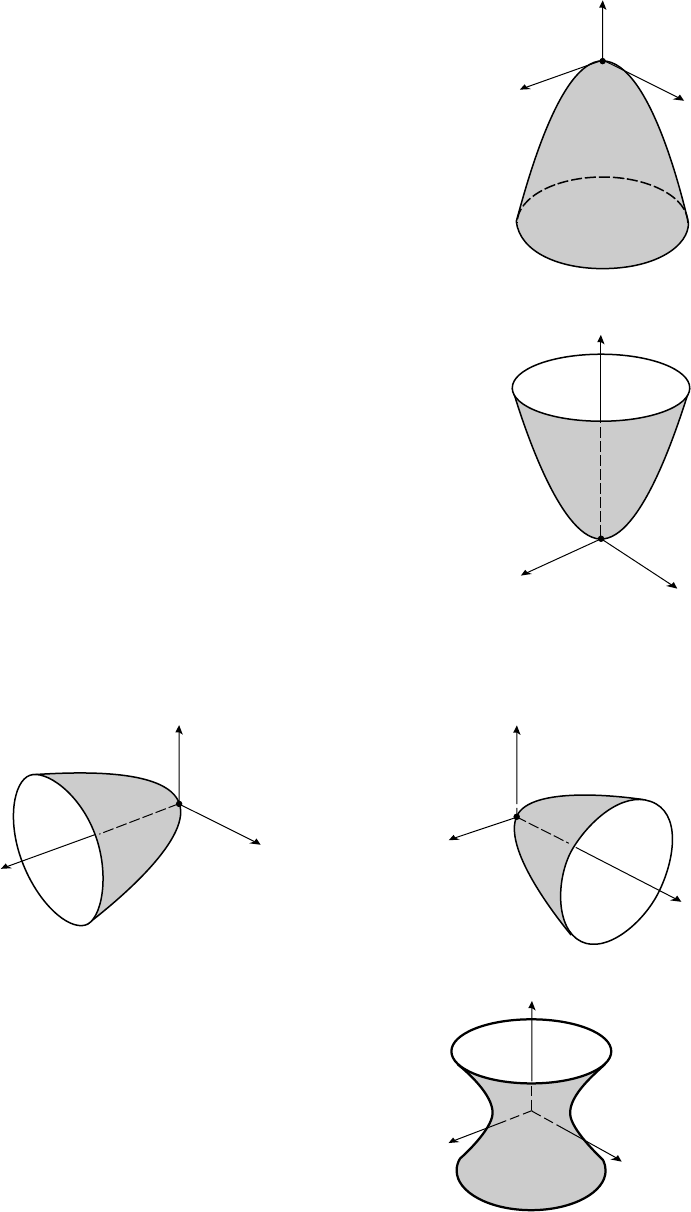
Exercise Set 13.7 474
3. (a) −z=x2+y2, circular paraboloid
opening down the negative z-axis
z
y
x
(b) z=x2+y2, circular paraboloid, no change
(c) z=x2+y2, circular paraboloid, no change
(d) z=x2+y2, circular paraboloid, no change
y
x
z
(e) x=y2+z2, circular paraboloid
opening along the positive x-axis
z
y
x
(f) y=x2+z2, circular paraboloid
opening along the positive y-axis
z
y
x
4. (a) x2+y2−z2= 1, no change
(b) x2+y2−z2= 1, no change
(c) x2+y2−z2= 1, no change
(d) x2+y2−z2= 1, no change
z
y
x
475 Chapter 13
(e) −x2+y2+z2= 1, hyperboloid
of one sheet with x-axis as axis
z
y
x
(f) x2−y2+z2= 1, hyperboloid
of one sheet with y-axis as axis
z
y
x
5. (a) hyperboloid of one sheet, axis is y-axis
(b) hyperboloid of two sheets separated by yz-plane
(c) elliptic paraboloid opening along the positive x-axis
(d) elliptic cone with x-axis as axis
(e) hyperbolic paraboloid straddling x- and z-axes
(f) paraboloid opening along the negative y-axis
6. (a) same (b) same (c) same
(d) same (e) y=x2
a2−z2
c2(f) y=x2
a2+z2
c2
7. (a) x=0:y
2
25 +z2
4=1;y=0:x
2
9+z
2
4=1;
z=0:x
2
9+y
2
25 =1
y
2
25
z2
4
+= 1
x2
9
z2
4
+= 1
x2
9
y2
25
+= 1
y
x
z
(b) x=0:z=4y
2
;y=0:z=x
2
;
z=0:x=y=0
xy
z
z = x2
x2 + 4y2 = 0
z = 4y2
(0, 0, 0)
Exercise Set 13.7 476
(c) x=0:y
2
16 −z2
4=1;y=0:x
2
9−z
2
4=1;
z=0:x
2
9+y
2
16 =1
y
x
z
y
2
16
z2
4
–= 1
x2
9
z2
4
–= 1
x2
9
y2
16
+= 1
8. (a) x=0:y=z=0;y=0:x=9z
2
;z=0:x=y
2z
y
x
x = 9z2
x = y2
(b) x=0:−y
2+4z
2=4;y=0:x
2+z
2=1;
z=0:4x
2−y
2=4 z
y
x
y = 0
x = 0
z = 0
(c) x=0:z=±y
2;y=0:z=±x;z=0:x=y=0 z
y
x
x = 0
y = 0
z = 0
9. (a) 4x2+z2= 3; ellipse (b) y2+z2= 3; circle (c) y2+z2= 20; circle
(d) 9x2−y2= 20; hyperbola (e) z=9x
2+ 16; parabola (f) 9x2+4y
2= 4; ellipse
10. (a) y2−4z2= 27; hyperbola (b) 9x2+4z
2= 25; ellipse (c) 9z2−x2= 4; hyperbola
(d) x2+4y
2= 9; ellipse (e) z=1−4y
2
; parabola (f) x2−4y2= 4; hyperbola
477 Chapter 13
11.
(0, 2, 0)
(0, 0, 3)
(1, 0, 0)
Ellipsoid
xy
z12.
(0, 3, 0)
(0, 0, 2)
(6, 0, 0)
Ellipsoid
xy
z13.
(0, 3, 0)
(2, 0, 0)
Hyperboloid
of one sheet
y
x
z
14.
(0, 3, 0)
(3, 0, 0)
Hyperboloid
of one sheet
xy
z15.
Elliptic cone
y
x
z16.
Elliptic cone
xy
z
17.
(0, 0, 2) (0, 0, –2)
Hyperboloid
of two sheets
xy
z18. z
y
x
Hyperboloid
of two sheets
19.
Hyperbolic paraboloid
x
y
z
20. z
y
xHyperbolic
paraboloid
21.
Elliptic paraboloid
xy
z22.
Circular paraboloid
x
z
y
Exercise Set 13.7 478
23.
Circular cone
xy
z24.
Elliptic paraboloid
xy
z25.
(0, 0, 2)
(0, 2, 0)
Hyperboloid
of one sheet
xy
z
26.
(3, 0, 0)
Hyperboloid
of two sheets
(-3, 0, 0)
y
x
z27.
Hyperbolic
paraboloid
y
x
z28.
(0, 0, 2)
(2, 0, 0)
Hyperboloid
of one sheet
y
x
z
29. z
y
x
30.
(0, 1, 0)
(0, 0, 1)
(1, 0, 0)
y
x
z
31.
(1, 0, 0)
(0, 1, 0)
z
y
x
32.
(0, 0, 1)
xy
z
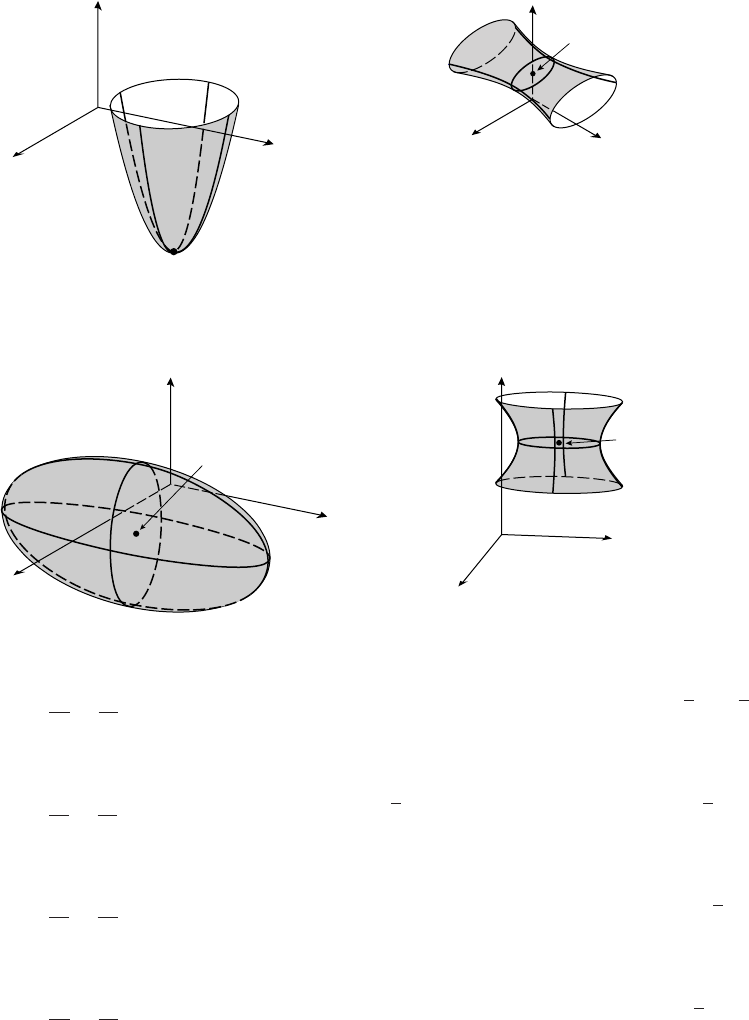
479 Chapter 13
33.
Circular paraboloid
z
y
x
(–2, 3, –9)
34.
Hyperboloid
of one sheet
(0, 0, 2)
y
x
z
35.
Ellipsoid
z
y
x
(1, –1, –2)
36.
Hyperboloid
of one sheet
(-1, 1, 2)
y
x
z
37. (a) x2
9+y2
4=1 (b) 6,4(c) (±√5,0,√2)
(d) The focal axis is parallel to the x-axis.
38. (a) y2
4+z2
2=1 (b) 4,2√2(c) (3,±√2,0)
(d) The focal axis is parallel to the y-axis.
39. (a) y2
4−x2
4=1 (b) (0,±2,4) (c) (0,±2√2,4)
(d) The focal axis is parallel to the y-axis.
40. (a) x2
4−y2
4=1 (b) (±2,0,−4) (c) (±2√2,0,−4)
(e) The focal axis is parallel to the x-axis.
41. (a) z+4=y
2(b) (2,0,−4) (c) (2,0,−15/4)
(d) The focal axis is parallel to the z-axis.
42. (a) z−4=−x
2(b) (0,2,4) (c) (0,2,15/4)
(d) The focal axis is parallel to the z-axis.
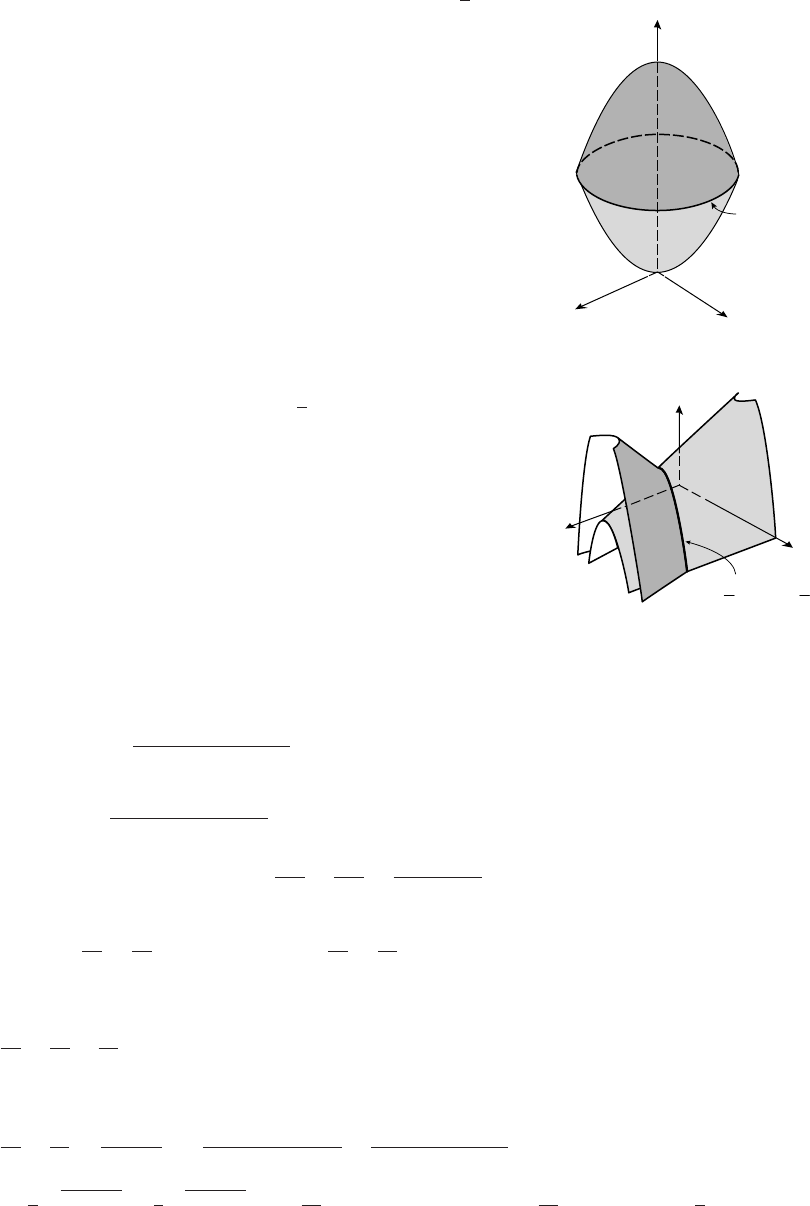
Exercise Set 13.7 480
43. x2+y2=4−x
2−y
2
,x
2+y
2= 2; circle of radius √2
in the plane z= 2, centered at (0,0,1)
xy
x2 + y2 = 2
(z = 2)
4
z
44. y2+z=4−2(y2+z),y
2+z=4/3;
parabolas in the planes x=±2/√3
which open in direction of the negative y-axis
z
y
x
z = – y2, x =
4
3
4
3
45. y=4(x
2+z
2
)46. y2=4(x
2+z
2
)
47. |z−(−1)|=px2+y2+(z−1)2,z2+2z+1=x
2+y
2+z
2−2z+1,z=(x
2+y
2
)/4; circular
paraboloid
48. |z+1|=2
px
2+y
2+(z−1)2,z2+2z+1=4x
2+y
2+z
2−2z+1
,
4x
2+4y
2+3z
2−10z+3=0, x
2
4/3+y
2
4/3+(z−5/3)2
16/9= 1; ellipsoid, center at (0,0,5/3).
49. If z=0, x
2
a
2+y
2
a
2=1;ify= 0 then x2
a2+z2
c2= 1; since c<athe major axis has length 2a, the
minor axis length 2c.
50. x2
a2+y2
a2+z2
b2= 1, where a= 6378.1370,b = 6356.5231.
51. Each slice perpendicular to the z-axis for |z|<cis an ellipse whose equation is
x2
a2+y2
b2=c2−z2
c2,or x
2
(a
2
/c2)(c2−z2)+y2
(b2/c2)(c2−z2)= 1, the area of which is
πa
cpc2−z2b
cpc2−z2=πab
c2c2−z2so V=2Zc
0
πab
c2c2−z2dz =4
3πabc.
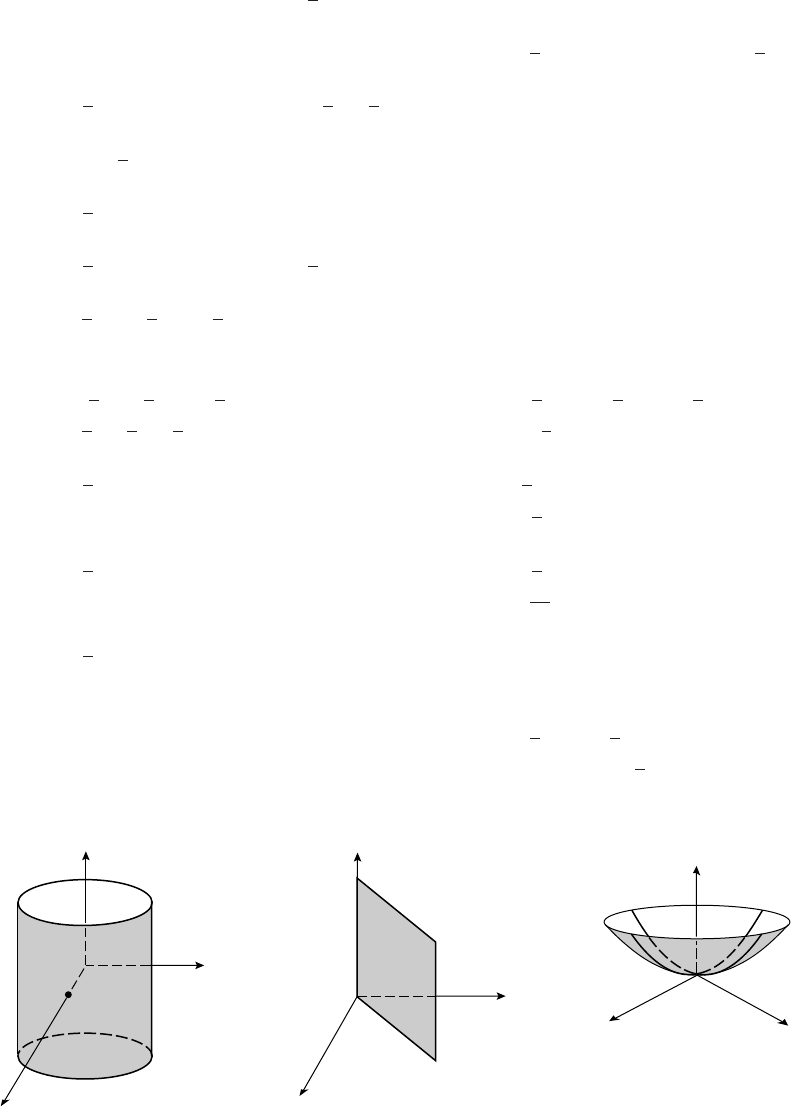
481 Chapter 13
EXERCISE SET 13.8
1. (a) (8,π/6,−4) (b) 5√2,3π/4,6(c) (2,π/2,0) (d) (8,5π/3,6)
2. (a) (2,7π/4,1) (b) (1,π/2,1) (c) (4√2,3π/4,−7) (d) (2√2,7π/4,−2)
3. (a) 2√3,2,3(b) −4√2,4√2,−2(c) (5,0,4) (d) (−7,0,−9)
4. (a) 3,−3√3,7(b) (0,1,0) (c) (0,3,5) (d) (0,4,−1)
5. (a) 2√2,π/3,3π/4(b) (2,7π/4,π/4) (c) (6, π/2, π/3) (d) (10,5π/6, π/2)
6. (a) 8√2,π/4,π/6
(b) 2√2,5π/3,3π/4(c) (2,0,π/2) (d) (4,π/6,π/6)
7. (a) (5√6/4,5√2/4,5√2/2) (b) (7,0,0)
(c) (0,0,1) (d) (0,−2,0)
8. (a) −√2/4,√6/4,−√2/2(b) 3√2/4,−3√2/4,−3√3/2
(c) (2√6,2√2,4√2) (d) 0,2√3,2
9. (a) 2√3,π/6,π/6
(b) √2,π/4,3π/4
(c) (2,3π/4,π/2) (d) 4√3,1,2π/3
10. (a) 4√2,5π/6,π/4
(b) 2√2,0,3π/4
(c) (5,π/2,tan−1(4/3)) (d) (2√10,π,tan−13)
11. (a) 5√3/2,π/4,−5/2
(b) (0,7π/6,−1)
(c) (0,0,3) (d) (4,π/6,0)
12. (a) (0,π/2,−5/2) (b) (3√2,0,−3√2)
(c) (0,3π/4,−3) (d) (5/2,2π/3,−5√3/2)
15.
y
x
z
(3, 0, 0)
x2 + y2 = 9
16.
y = x, x ≥ 0
y
x
z17.
y
x
z
z = x2 + y2
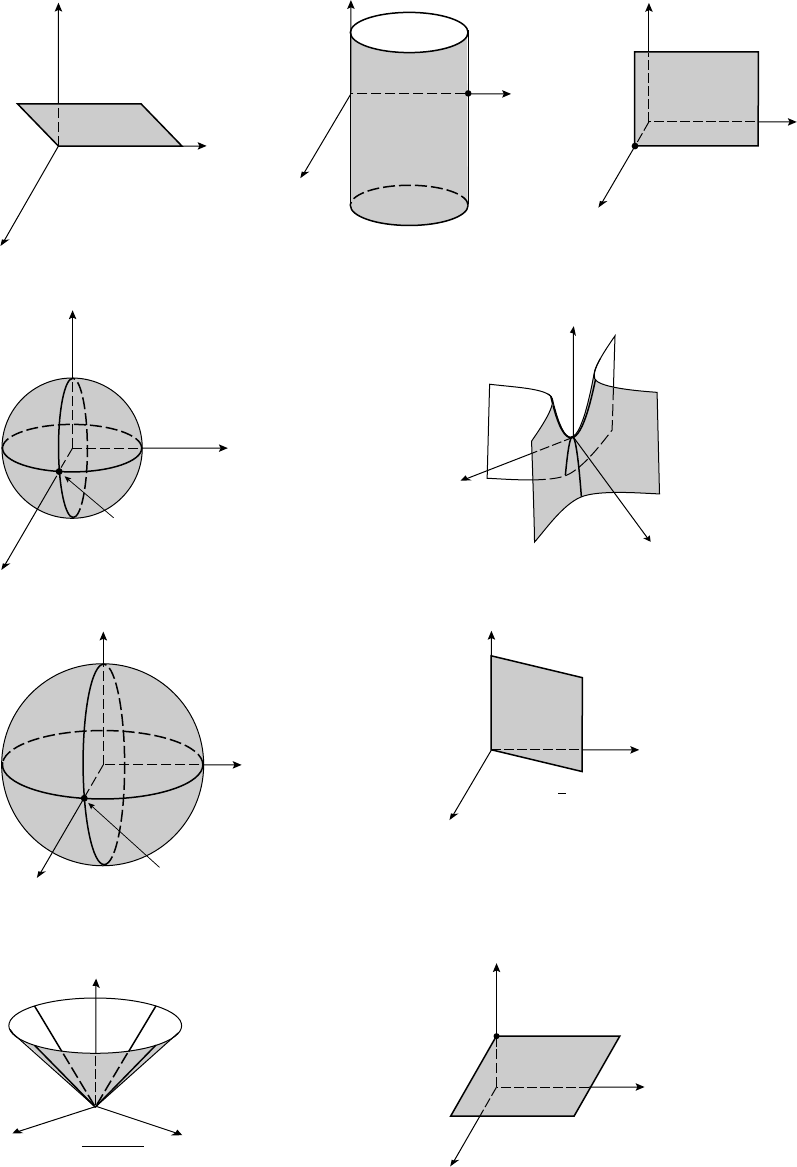
Exercise Set 13.8 482
18.
z = x
y
x
z19.
y
x
z
(0, 4, 0)
x2 + (y – 2)2 = 4
20.
x = 2
(2, 0, 0)
y
x
z
21.
(1, 0, 0)
y
x
z
x2 + y2 + z2 = 1
22. z
y
x
x2 – y2 = z
23.
(3, 0, 0)
y
x
z
x2 + y2 + z2 = 9
24.
y
x
z
y = √3x
25. z
y
x
z = √x2 + y2
26.
(0, 0, 2)
z = 2
y
x
z
483 Chapter 13
27. (0, 0, 2)
y
x
z
x2 + y2 + (z – 2)2 = 4
28.
(1, 0, 0)
y
x
z
x2 + y2 = 1
29.
(1, 0, 0)
y
x
z
(x – 1)2 + y2 = 1
30.
(1, 0, 0)
y
x
z
(x – 1)2 + y2 + z2 = 1
31. (a) z=3 (b) ρcos φ=3,ρ= 3 sec φ
32. (a) rsin θ=2,r = 2 csc θ(b) ρsin φsin θ=2,ρ= 2 csc φcsc θ
33. (a) z=3r
2(b) ρcos φ=3ρ
2sin2φ, ρ =1
3csc φcot φ
34. (a) z=√3r(b) ρcos φ=√3ρsin φ, tan φ=1
√3,φ=π
6
35. (a) r=2 (b) ρsin φ=2,ρ= 2 csc φ
36. (a) r2−6rsin θ=0,r= 6 sin θ(b) ρsin φ= 6 sin θ, ρ = 6 sin θcsc φ
37. (a) r2+z2=9 (b) ρ=3
38. (a) z2=r2cos2θ−r2sin2θ=r2(cos2θ−sin2θ), z2=r2cos 2θ
(b) Use the result in part (a) with r=ρsin φ,z=ρcos φto get ρ2cos2φ=ρ2sin2φcos 2θ,
cot2φ= cos 2θ
39. (a) 2rcos θ+3rsin θ+4z=1
(b) 2ρsin φcos θ+3ρsin φsin θ+4ρcos φ=1
40. (a) r2−z2=1
(b) Use the result of part (a) with r=ρsin φ,z=ρcos φto get ρ2sin2φ−ρ2cos2φ=1,
ρ
2cos 2φ=−1
Exercise Set 13.8 484
41. (a) r2cos2θ=16−z
2
(b) x2=16−z
2
,x
2+y
2+z
2=16+y
2
,ρ
2=16+ρ
2sin2φsin2θ,ρ21−sin2φsin2θ=16
42. (a) r2+z2=2z(b) ρ2=2ρcos φ,ρ= 2 cos φ
43. all points on or above the paraboloid z=x2+y2, that are also on or below the plane z=4
44. a right circular cylindrical solid of height 3 and radius 1 whose axis is the line x=0,y =1
45. all points on or between concentric spheres of radii 1 and 3
46. all points on or above the cone φ=π/6, that are also on or below the sphere ρ=2
47. θ=π/6, φ=π/6, spherical (4000,π/6, π/6), rectangular 1000√3,1000,2000√3
48. (a) y=rsin θ=asin θbut az =asin θso y=az, which is a plane that contains the curve of
intersection of z= sin θand the circular cylinder r=a. From Exercise 60, Section 12.4, the
curve of intersection of a plane and a circular cylinder is an ellipse.
(b) z = sin
θ
y
x
z
49. (a) (10,π/2,1) (b) (0,10,1) (c) (√101,π/2,tan−110)
50. 20
0
030
51. Using spherical coordinates: for point A,θA= 360◦−60◦= 300◦,φ
A=90
◦−40◦=50
◦
; for point
B,θB= 360◦−40◦= 320◦,φ
B=90
◦−20◦=70
◦
. Unit vectors directed from the origin to the
points Aand B, respectively, are
uA= sin 50◦cos 300◦i+ sin 50◦sin 300◦j+ cos 50◦k,
uB= sin 70◦cos 320◦i+ sin 70◦sin 320◦j+ cos 70◦k
The angle αbetween uAand uBis α= cos−1(uA·uB)≈0.459486 so the shortest distance is
6370α≈2,927 km.

485 Chapter 13
CHAPTER 13 SUPPLEMENTARY EXERCISES
2. (c) F =−i−j
(d) kh1,−2,2ik =3,sokr−h1,−2,2ik =3,or(x−1)2+(y+2)
2+(z−2)2=9
3. (b) x= cos 120◦=−1/2,y =±sin 120◦=±√3/2
(d) true: ku×vk=kukkvk|sin(θ)|=1
4. (d) x+2y−z=0
5. (b) (y, x, z),(x, z, y),(z, y, x)
(c) circle of radius 5 in plane z= 1 with center at (0,0,1) (rectangular coordinates)
(d) the two half-lines z=±x,x≥0inthexz-plane
6. (x+3)
2+(y−5)2+(z+4)
2=r
2
,
(a) r2=4
2=16 (b) r2=5
2=25 (c) r2=3
2=9
7. (a) −→
AB =−i+2j+2k,−→
AC =i+j−k,−→
AB ×−→
AC=−4i+j−3k, area = 1
2k−→
AB ×−→
AC k=√26/2
(b) area = 1
2hk−→
AB k=3
2h=1
2√26, h=√26/3
8. The sphere x2+(y−1)2+(z+3)
2= 16 has center Q(0,1,−3) and radius 4, and
k−→
PQ k=√12+4
2=√
17, so minimum distance is √17 −4, maximum distance is √17+4.
9. (a) a ·b=0,4c+3=0,c=−3/4
(b) Use a·b=kakkbkcos θto get 4c+3=pc
2+ 1(5) cos(π/4), 4c+3=5
pc
2+1/
√
2
Square both sides and rearrange to get 7c2+48c−7=0,(7c−1)(c+7)=0soc=−7
(invalid) or c=1/7.
(c) Proceed as in (b) with θ=π/6 to get 11c2−96c+ 39 = 0 and use the quadratic formula to
get c=48 ±25√3/11.
(d) a must be a scalar multiple of b,soci+j=k(4i+3j),k =1/3,c=4/3.
10. −→
OS =−→
OP +−→
PS=3i+4j+−→
QR =3i+4j+(4i+j)=7i+5j
11. (a) the plane through the origin which is perpendicular to r0
(b) the plane through the tip of r0which is perpendicular to r0
12. The normals to the planes are given by ha1,b
1
,c
1
iand ha2,b
2
,c
2
i, so the condition is
a1a2+b1b2+c1c2=0.
13. Since −→
AC ·(−→
AB ×−→
AD)=
−→
AC ·(−→
AB ×−→
CD)+−→
AC ·(−→
AB ×−→
AC)=0+0=0, the volume of the
parallelopiped determined by −→
AB, −→
AC, and −→
AD is zero, thus A, B, C, and Dare coplanar (lie in
the same plane). Since −→
AB ×−→
CD6=0, the lines are not parallel. Hence they must intersect.
14. The points Plie on the plane determined by A, B and C.
15. (a) false, for example i·j=0 (b) false, for example i×i=0
(c) true; 0 = kuk·kvkcos θ=kuk·kvksin θ, so either u=0or v=0since cos θ= sin θ=0is
impossible.
Chapter 13 Supplementary Exercises 486
16. (a) Replace uwith a×b,vwith c, and wwith din the first formula of Exercise 39.
(b) From the second formula of Exercise 39,
(a×b)×c+(b×c)×a+(c×a)×b
=(c·a)b−(c·b)a+(a·b)c−(a·c)b+(b·c)a−(b·a)c=0
17. ku−vk2=(u−v)·(u−v)=kuk
2+kvk
2−2kukkvkcos θ= 2(1 −cos θ)=4sin
2
(θ/2), so
ku−vk= 2 sin(θ/2)
18. −→
AB=i−2j−2k,−→
AC=−2i−j−2k,−→
AD=i+2j−3k
(a) From Theorem 13.4.6 and formula (9) of Section 13.4,
1−2−2
−2−1−2
12−3
= 29, so V= 29.
(b) The plane containing A, B, and Chas normal −→
AB ×−→
AC=2i+6j−5k, so the equation of
the plane is 2(x−1)+6(y+1)−5(z−2)=0,2x+6y−5z=−14. From Theorem 13.6.2,
D=|2(2) + 6(1) −5(−1)|
√65 =15
√65.
19. (a) h2,1,−1i×h1,2,1i=h3,−3,3i, so the line is parallel to i−j+k. By inspection, (0,2,−1)
lies on both planes, so the line has an equation r=2j−k+t(i−j+k), that is,
x=t, y =2−t, z =−1+t.
(b) cos θ=h2,1,−1i·h1,2,1i
kh2,1,−1ikkh1,2,1ik =1/2, so θ=π/3
20. Let α=50
◦
,β =70
◦
, then γ= cos−1p1−cos2α−cos2β≈47◦.
21. 5hcos 60◦,cos 120◦,cos 135◦i=h5/2,−5/2,−5√2/2i
22. (a) Let kbe the length of an edge and introduce a coordinate system as shown in the figure,
then d=hk, k, ki,u=hk, k, 0i, cos θ=d·u
kdkkuk=2k
2
k
√
3
k
√2
=2/
√
6
so θ= cos−1(2/√6) ≈35◦
d
u
θ
y
x
z
(b) v =h−k, 0,ki,cos θ=d·v
kdkkvk=0soθ=π/2 radians.
23. (a) (x−3)2+4(y+1)
2−(z−2)2= 9, hyperboloid of one sheet
(b) (x+3)
2+(y−2)2+(z+6)
2= 49, sphere
(c) (x−1)2+(y+2)
2−z
2= 0, circular cone
24. (a) perpendicular, since h2,1,2i·h−1,−2,2i=0
(b) L1:hx, y, zi=h1+2t, −3
2+t, −1+2ti;L
2
:hx, y, zi=h4−t, 3−2t, −4+2ti
487 Chapter 13
(c) Solve simultaneously 1 + 2t1=4−t
2
,−3
2+t
1=3−2t
2
,−1+2t
1=−4+2t
2
, solution
t1=1
2,t
2=2,x =2,y =−1,z =0
25. (a) r2=z;ρ2sin2φ=ρcos φ, ρ = cot φcsc φ
(b) r2(cos2θ−sin2θ)−z2=0,z2=r
2cos 2θ;
ρ2sin2φcos2θ−ρ2sin2φsin2θ−ρ2cos2φ=0,cos 2θ= cot2φ
26. (a) z=r2cos2θ−r2sin2θ=x2−y2(b) (ρsin φcos θ)(ρcos φ)=1,xz =1
27. (a) z
y
x
(2, 0, 0)
(0, 0, 2)
(0, 2, 0)
(b) z
y
x
p/6
(c)
p/6
y
x
z(0, 0, 2)
28. (a) z
y
x5
5
5
(b)
y
x
z
z = 2
f
(c) z
y
x
2
2
Chapter 13 Supplementary Exercises 488
29. (a) z
y
x
r = 1
r = 2 (b)
y
x
z
z = 3
z = 2
(c) z
y
x
u = p/6 u = p/3
(d) z
y
x
u = p/6 u = p/3
r = 1
z = 2
z = 3
r = 2
30. (a)
y
x
z
2
2
2
(b)
y
x
z
1(c)
y
x
z
2
2
2
1
31. (a) At x=cthe trace of the surface is the circle y2+z2=[f(c)]2, so the surface is given by
y2+z2=[f(x)]2
(b) y2+z2=e2x(c) y2+z2=4−3
4
x
2
,soletf(x)=r4−3
4
x
2
32. (a) Permute xand yin Exercise 31a: x2+z2=[f(y)]2
(b) Permute xand zin Exercise 31a: x2+y2=[f(z)]2
(c) Permute yand zin Exercise 31a: y2+z2=[f(x)]2
33. z
y
x
34. −→
PQ=h1,−1,6i, and W=F·
−→
PQ =13lb·ft

489 Chapter 13
35. F =F1+F2=2i−j+3k,−→
PQ=i+4j−3k,W =F·−→
PQ=−11 N·m
36. F1= 250 cos 38◦i+ 250 sin 38◦j,F= 1000i,F2=F−F1= (1000 −250 cos 38◦)i−250 sin 38◦j;
kF2k= 1000r17
16 −1
2cos 38◦≈817.62 N·m, θ= tan−1250 sin 38◦
250 cos 38◦−1000 ≈−11◦
37. (a) F =−6i+3j−6k
(b) −→
OA=h5,0,2i, so the vector moment is −→
OA ×F=−6i+18j+15k
490
CHAPTER 14
Vector-Valued Functions
EXERCISE SET 14.1
1. (−∞,+∞); r(π)=−i−3πj2.[−1/3,+∞); r(1) = h2,1i
3. [2,+∞); r(3) = −i−ln 3j+k4.[−1,1); r(0) = h2,0,0i
5. r = 3 cos ti+(t+ sin t)j6.r=(t
2+1)i+e
−2t
j
7. r =2ti+ 2 sin 3tj+ 5 cos 3tk8.r=tsin ti+lntj+ cos2tk
9. x=3t
2
,y=−2, z=0 10. x= sin2t,y=1−cos 2t,z=0
11. x=2t−1, y=−3√t,z= sin 3t12. x=te−t,y=0,z=−5t
2
13. the line in 2-space through the point (2,0) and parallel to the vector −3i−4j
14. the circle of radius 3 in the xy-plane, with center at the origin
15. the line in 3-space through the point (0,−3,1) and parallel to the vector 2i+3k
16. the circle of radius 2 in the plane x= 3, with center at (3,0,0)
17. an ellipse in the plane z=−1, center at (0,0,−1), major axis of length 6 parallel to x-axis, minor
axis of length 4 parallel to y-axis
18. a parabola in the plane x=−2, vertex at (−2,0,−1), opening upward
19. (a) The line is parallel to the vector −2i+3j; the slope is −3/2.
(b) y= 0 in the xz-plane so 1 −2t=0,t=1/2thusx=2+1/2=5/2 and z= 3(1/2)=3/2;
the coordinates are (5/2,0,3/2).
20. (a) x=3+2t=0,t=−3/2soy=5(−3/2) = −15/2
(b) x=t,y=1+2t,z=−3tso 3(t)−(1+2t)−(−3t)=2,t=3/4; the point of intersection is
(3/4,5/2,−9/4).
21. (a)
x
y
(1, 0)
(0, 1) (b)
x
y
(1, -1)
(1, 1)
491 Chapter 14
22. (a)
y
x
z
(0, 0, 1)
(1, 1, 0)
(b)
y
x
z
(1, 1, 0)
(1, 1, 1)
23. r =(1−t)(3i+4j),0≤t≤124. r =(1−t)4k+t(2i+3j),0≤t≤1
25. x=2
2
x
y
26. y=2x+10
-5
10
x
y
27. (x−1)2+(y−3)2=1
1
3
x
y
28. x2/4+y
2
/25=1
2
5
x
y
29. x2−y2=1,x≥1
1
2
x
y
30. y=2x
2+4,x≥0
1
4
x
y
Exercise Set 14.1 492
31.
(0, 2,
π
/2)
(2, 0, 0)
y
x
z32.
(9, 0, 0)
(0, 4,
π
/2)
y
x
z
33.
2
y
x
z34.
c
oy
x
z
35. x=t, y =t, z =2t
2
z
x
y
36. x=t, y =−t, z =√2√1−t2
y
x
zy + x = 0
z = √2 – x2 – y2
37. r =ti+t2j±1
3p81 −9t2−t4k
x
y
z
38. r =ti+tj+(1−2t)ks
z
x
y
x + y + z = 1
y = x
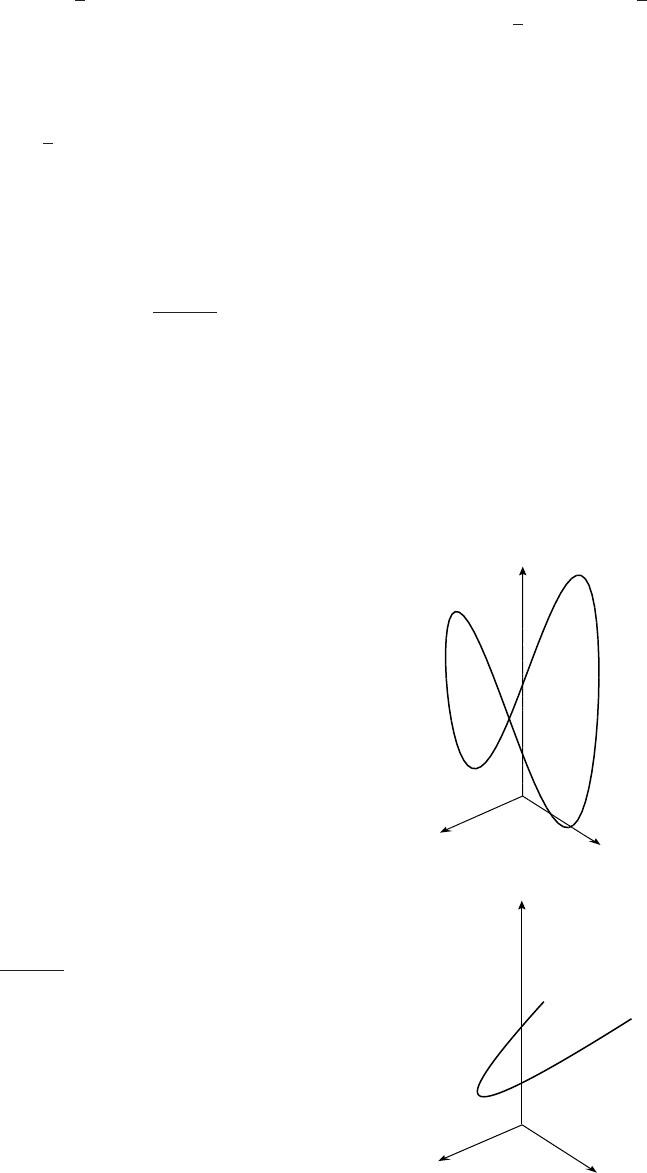
493 Chapter 14
39. x2+y2=(tsin t)2+(tcos t)2=t2(sin2t+ cos2t)=t
2=z
40. x−y+z+1=t−(1+t)/t +(1−t
2
)/t +1=[t
2−(1+t)+(1−t
2
)+t]/t =0
41. x= sin t,y= 2 cos t,z=√3 sin tso x2+y2+z2= sin2t+ 4 cos2t+ 3 sin2t= 4 and z=√3x;it
is the curve of intersection of the sphere x2+y2+z2= 4 and the plane z=√3x, which is a circle
with center at (0,0,0) and radius 2.
42. x= 3 cos t,y= 3 sin t,z= 3 sin tso x2+y2= 9 cos2t+ 9 sin2t= 9 and z=y; it is the curve
of intersection of the circular cylinder x2+y2= 9 and the plane z=y, which is an ellipse with
major axis of length 6√2 and minor axis of length 6.
43. The helix makes one turn as tvaries from 0 to 2πso z=c(2π)=3,c=3/(2π).
44. 0.2t= 10, t= 50; the helix has made one revolution when t=2πso when t= 50 it has made
50/(2π)=25/π ≈7.96 revolutions.
45. x2+y2=t2cos2t+t2sin2t=t2,px2+y2=t=z; a conical helix.
46. The curve wraps around an elliptic cylinder with axis along the z-axis; an elliptical helix.
47. (a) III, since the curve is a subset of the plane y=−x
(b) IV, since only xis periodic in t, and y, z increase without bound
(c) II, since all three components are periodic in t
(d) I, since the projection onto the yz-plane is a circle and the curve increases without bound in
the x-direction
49. (a) Let x= 3 cos tand y= 3 sin t, then z= 9 cos2t.(b) z
y
x
50. The plane is parallel to a line on the surface of
the cone and does not go through the vertex so
the curve of intersection is a parabola. Eliminate
zto get y+2=px
2+y
2
,(y+2)
2=x
2+y
2
,
y=x
2
/4−1; let x=t, then y=t2/4−1
and z=t2/4+1.
z
y
x
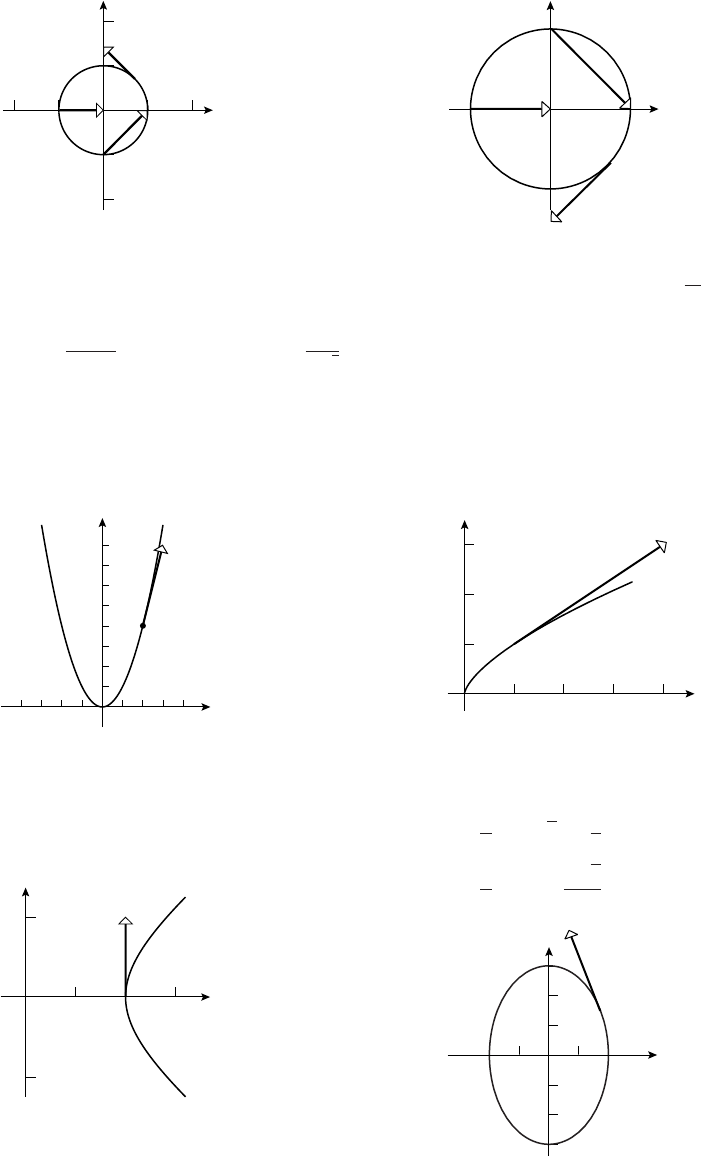
Exercise Set 14.2 494
EXERCISE SET 14.2
1.
-2 2
-2
2
x
y2.
x
y
r'(p/4)
r''(p)
r(2p) – r(3p/2)
3. r0(t)=5i+(1−2t)j4.r
0
(t) = sin tj5.r
0
(t)=−1
t
2i+sec2tj+2e2tk
6. r0(t)= 1
1+t
2i+ (cos t−tsin t)j−1
2√tk
7. r0(t)=h1,2ti,
r
0
(2) = h1,4i,
r(2) = h2,4i
2
4
〈1, 4 〉
x
y
8. r0(t)=3t
2
i+2tj,
r
0
(1)=3i+2j
r(1) = i+j
1 2 3 4
1
2
3
x
y
9. r0(t) = sec ttan ti+ sec2tj,
r0(0) = j
r(0) = i
1.5
x
y
-1
1
10. r0(t)=2costi−3 sin tj,
r0π
6=√3i−3
2j
rπ
6=i+3√3
2j
-2 -1 1 2
-3
-2
-1
1
2
3
x
y
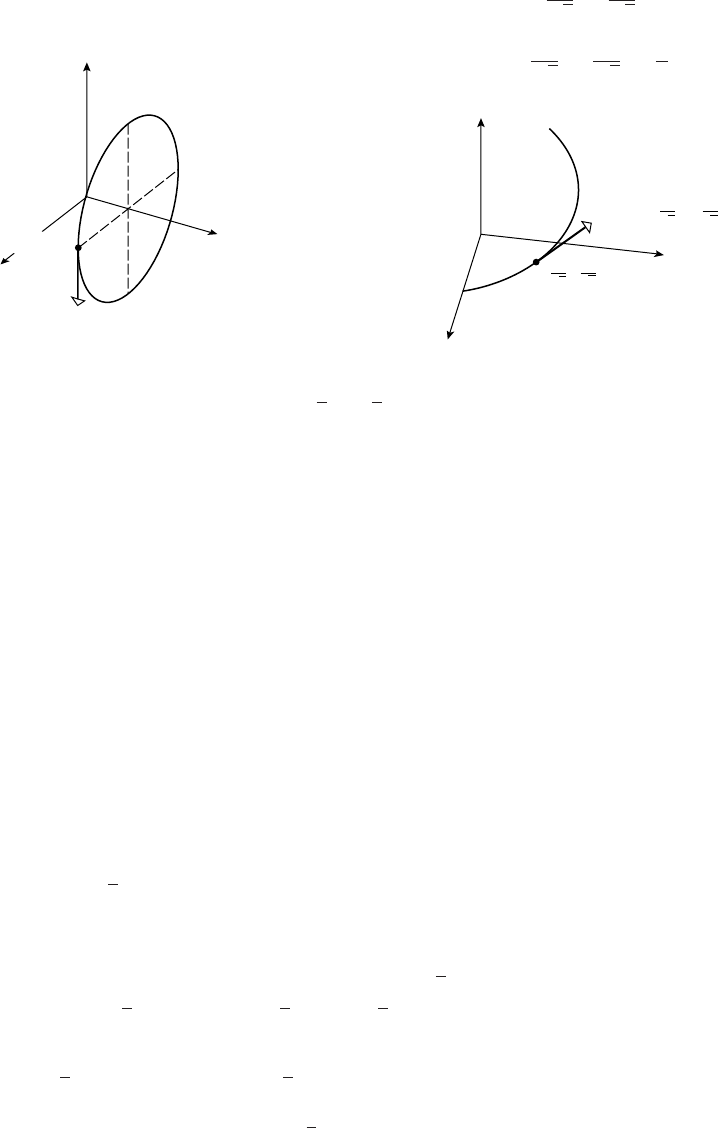
495 Chapter 14
11. r0(t)=2costi−2 sin tk,
r0(π/2) = −2k,
r(π/2) = 2i+j
r′(
6
) = -2k
y
x
z
(2, 1, 0)
12. r0(t)=−sin ti+ cos tj+k,
r0(π/4) = −1
√2i+1
√2j+k,
r(π/4) = 1
√2i+1
√2j+π
4k
1
√
2
1
√
2
−
i + j + k
r′(
3
) =
1
√2
1
√2
( , ,
3
)y
x
z
13. 9i+6j 14. h√2/2,√2/2i15. h1/3,0i
16. j 17. 2i−3j+4k 18. h3,1/2,sin 2i
19. (a) continuous, lim
t→0r(t)=0=r(0) (b) not continuous, lim
t→0r(t) does not exist
20. (a) not continuous, lim
t→0r(t) does not exist. (b) continuous, lim
t→0r(t)=5i−j+k=r(0)
21. (a) lim
t→0(r(t)−r0(t)) = i−j+k
(b) lim
t→0(r(t)×r0(t)) = lim
t→0(−cos ti−sin tj+k)=−i+k
(c) lim
t→0(r(t)·r0(t))=0
22. r(t)·(r0(t)×r00 (t)) =
tt
2t
3
12t3t
2
026t
=2t
3
, so lim
t→1r(t)·(r0(t)×r00 (t))=2
23. r0(t)=2ti−1
tj,r
0
(1)=2i−j,r(1) = i+2j;x=1+2t,y=2−t,z=0
24. r0(t)=2e
2t
i+ 6 sin 3tj,r0(0)=2i,r(0) = i−2j;x=1+2t,y=−2, z=0
25. r0(t)=−2πsin πti+2πcos πtj+3k,r
0
(1/3) = −√3πi+πj+3k,
r(1/3) = i+√3j+k;x=1−√
3πt,y=√3+πt,z=1+3t
26. r0(t)=1
ti−e
−t
j+3t
2
k,r
0
(2) = 1
2i−e−2j+12k,
r(2)=ln2i+e
−2
j+8k;x=ln2+1
2
t,y=e
−2−e
−2
t,z=8+12t
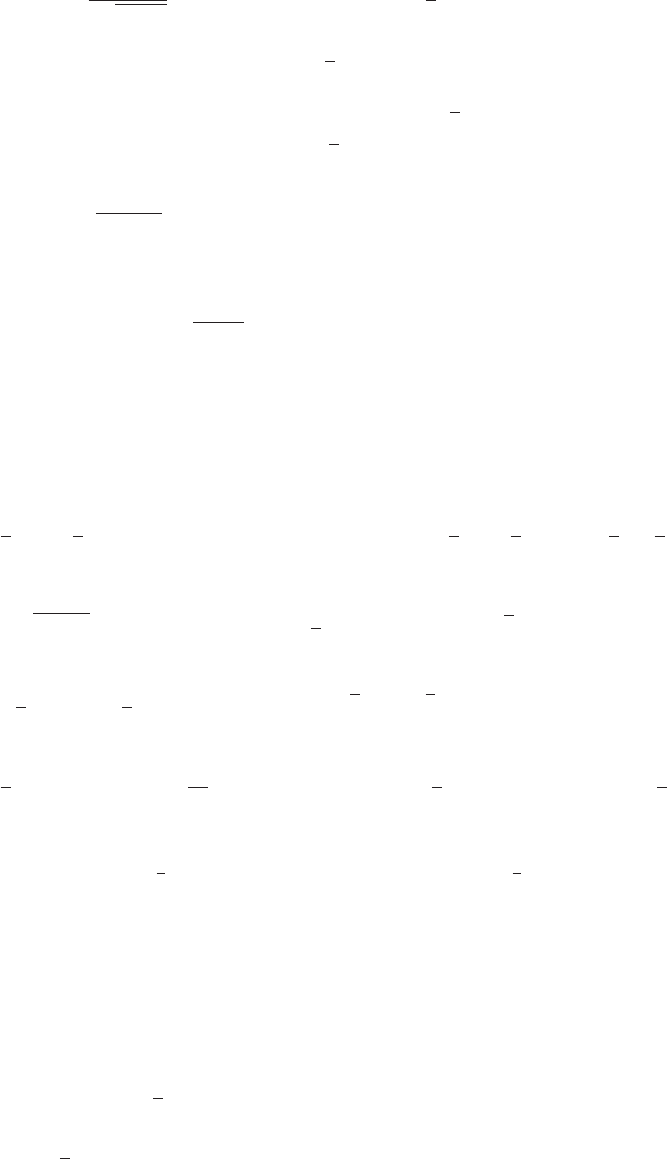
Exercise Set 14.2 496
27. r0(t)=2i+3
2
√
3t+4j,t=0atP
0so r0(0)=2i+3
4
j,
r(0) = −i+2j;r=(−i+2j)+t2i+3
4j
28. r0(t)=−4 sin ti−3j,t=π/3atP
0so r0(π/3) = −2√3i−3j,
r(π/3)=2i−πj;r=(2i−πj)+t(−2
√
3i−3j)
29. r0(t)=2ti+1
(t+1)
2j−2tk,t=−2atP
0so r0(−2) = −4i+j+4k,
r(−2)=4i+j;r=(4i+j)+t(−4i+j+4k)
30. r0(t) = cos ti+ sinh tj+1
1+t
2k,t=0atP
0so r0(0) = i+k,r(0) = j;r=ti+j+tk
31. 3ti+2t
2
j+C 32. (sin t)i−(cos t)j+C 33. (−tcos t+ sin t)i+tj+C
34. h(t−1)et,t(ln t−1)i+C 35. (t3/3)i−t2j+ln|t|k+C 36. h−e−t,e
t,t
3i+C
37. 1
3sin 3t, 1
3cos 3tπ/3
0
=h0,−2/3i38. 1
3t3i+1
4t4j1
0
=1
3i+1
4j
39. Z2
0pt2+t4dt =Z2
0
t(1+t2)1/2dt =1
31+t
2
3/22
0
=(5
√
5−1)/3
40. −2
5(3 −t)5/2,2
5(3+t)5/2,t
3
−3
=h72√6/5,72√6/5,6i
41. 2
3t3/2i+2t
1/2
j
9
1
=52
3i+4j 42. 1
2(e2−1)i+(1−e
−1
)j+1
2k
43. y(t)=Zy
0
(t)dt =1
3t3i+t2j+C,y(0) = C=i+j,y(t)=(
1
3
t
3+1)i+(t
2+1)j
44. y(t)=Zy
0
(t)dt = (sin t)i−(cos t)j+C,
y(0) = −j+C=i−jso C=iand y(t)=(1+sint)i−(cos t)j.
45. y0(t)=Zy
00 (t)dt =ti+etj+C1,y0(0) = j+C1=jso C1=0and y0(t)=ti+e
t
j.
y(t)=Zy
0
(t)dt =1
2t2i+etj+C2,y(0) = j+C2=2iso C2=2i−jand
y(t)=1
2
t
2+2
i+(e
t−1)j
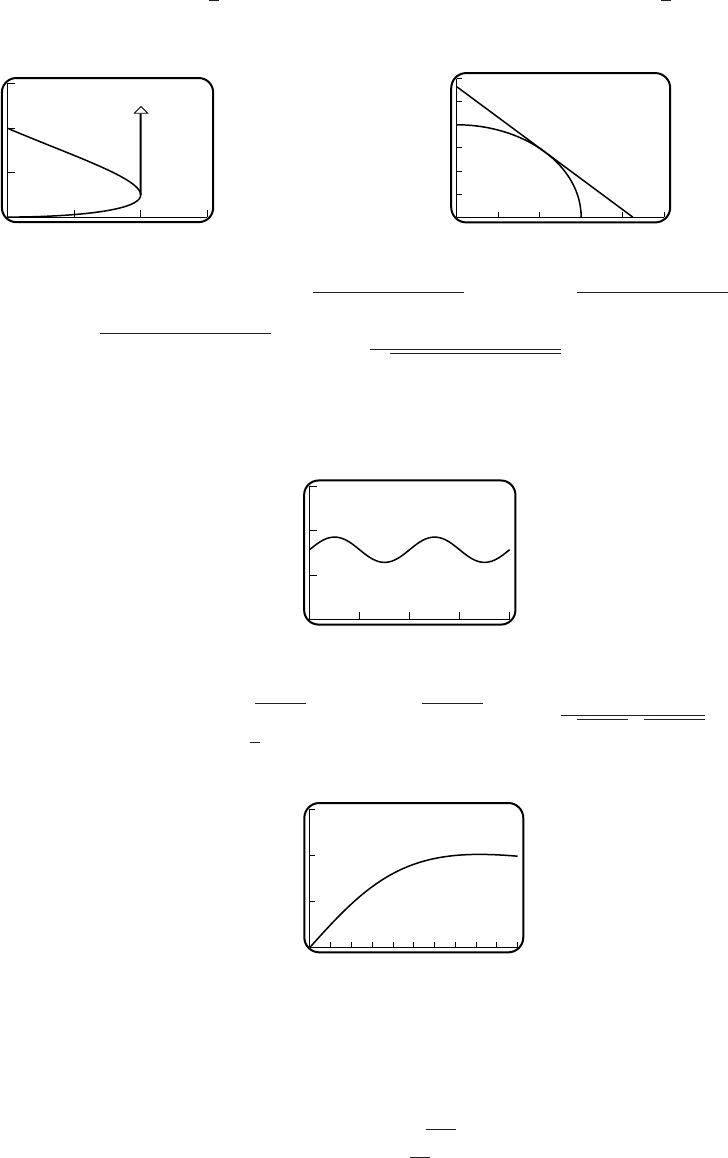
497 Chapter 14
46. y0(t)=Zy
00 (t)dt =4t
3
i−t
2
j+C
1
,y
0
(0) = C1=0,y0(t)=4t
3
i−t
2
j
y(t)=Zy
0
(t)dt =t4i−1
3t3j+C2,y(0) = C2=2i−4j,y(t)=(t
4+2)i−(1
3t
3+4)j
47.
1.50
0
1.5 48. 6
0
05
49. r0(t)=−4 sin ti+ 3 cos tj,kr(t)k=p16 cos2t+ 9 sin2t, kr0(t)k=p16 sin2t+ 9 cos2t,
krkkr0k=p144 + 49 sin2tcos2t, θ = cos−1−7 sin tcos t
p144 + 49 sin2tcos2t
rand r0are parallel when θ=0,sot=0,π/2,π,3π/2,2π; the angle between rand r0is greatest at
θmax =0.28 (t≈2.23,5.53) and θmin =−0.28, (t≈0.77,3.95), so rand r0are never perpendicular.
o0
0
3
50. r0(t)=2ti+3t
2
j,kr(t)k=t
2
√
1+t
2
,kr
0
(t)k=t
√
4+9t
2
,cos θ=2+3t
2
√
1+t
2
√
4+9t
2
cos θ= 1 when t=0,±2
3/4
/
√
3 and rand r0are parallel; cos θ>0, so they are never perpendicular.
0.3
0
01
51. (a) 2t−t2−3t=−2, t2+t−2=0,(t+ 2)(t−1)=0sot=−2,1. The points of intersection
are (−2,4,6) and (1,1,−3).
(b) r0=i+2tj−3k;r
0
(−2) = i−4j−3k,r0(1) = i+2j−3k, and n=2i−j+kis normal to
the plane. Let θbe the acute angle, then
for t=−2: cos θ=|n·r0|/(knkkr
0
k)=3/
√
156, θ≈76◦;
for t= 1: cos θ=|n·r0|/(knkkr
0
k)=3/
√
84, θ≈71◦.
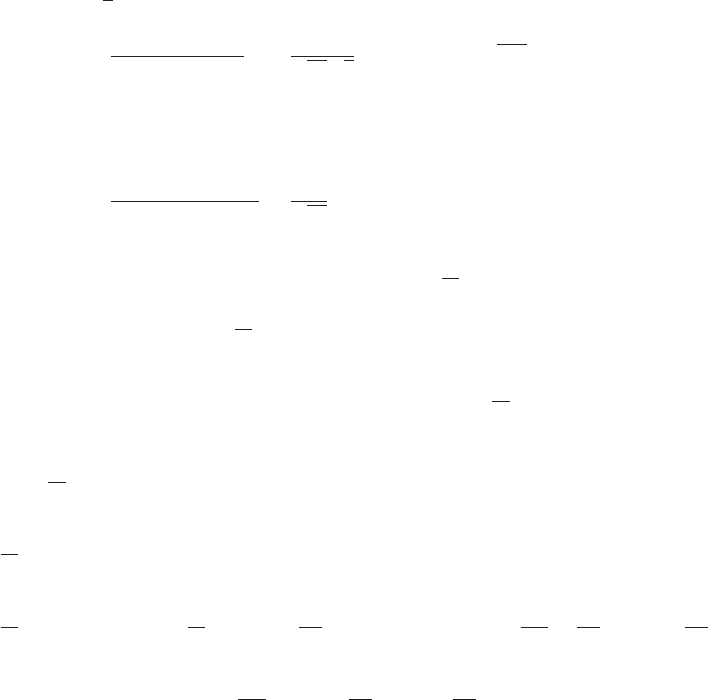
Exercise Set 14.2 498
52. r0=−2e−2ti−sin tj+3 cos tk,t= 0 at the point (1,1,0) so r0(0) = −2i+3kand hence the tangent
line is x=1−2t,y=1,z=3t. But x= 0 in the yz-plane so 1 −2t=0,t=1/2. The point of
intersection is (0,1,3/2).
53. r1(1) = r2(2) = i+j+3kso the graphs intersect at P; r0
1(t)=2ti+j+9t
2
kand
r0
2(t)=i+1
2
tj−kso r0
1(1)=2i+j+9kand r0
2(2) = i+j−kare tangent to the graphs at P,
thus cos θ=r0
1(1) ·r0
2(2)
kr0
1(1)kkr
0
2
(2)k=−6
√86√3,θ= cos−1(6/√258) ≈68◦.
54. r1(0) = r2(−1)=2i+j+3kso the graphs intersect at P; r0
1(t)=−2e
−t
i−(sin t)j+2tkand
r0
2(t)=−i+2tj+3t
2
kso r0
1(0) = −2iand r0
2(−1) = −i−2j+3kare tangent to the graphs at P,
thus cos θ=r0
1(0) ·r0
2(−1)
kr0
1(0)kkr
0
2
(−1)k=1
√14,θ≈74◦.
55. (a) r0
1=2i+6tj+3t
2
k,r
0
2=4t
3
k,r
1·r
2=t
7
;d
dt(r1·r2)=7t
6=r
1·r
0
2+r
0
1·r
2
(b) r1×r2=3t
6
i−2t
5
j,d
dt(r1×r2)=18t
5
i−10t4j=r1×r0
2+r0
1×r2
56. (a) r0
1=−sin ti+cos tj+k,r0
2=k,r1·r2= cos t+t2;d
dt(r1·r2)=−sin t+2t=r1·r0
2+r0
1·r2
(b) r1×r2=tsin ti+t(1 −cos t)j−sin tk,
d
dt(r1×r2) = (sin t+tcos t)i+(1+tsin t−cos t)j−cos tk=r1×r0
2+r0
1×r2
57. d
dt[r(t)×r0(t)] = r(t)×r00 (t)+r
0
(t)×r
0
(t)=r(t)×r
00 (t)+0=r(t)×r
00 (t)
58. d
dt[u·(v×w)] = u·
d
dt[v×w]+du
dt
·[v×w]=u·v×dw
dt +dv
dt ×w+du
dt
·[v×w]
=u·v×dw
dt +u·dv
dt ×w+du
dt
·[v×w]
59. In Exercise 60, write each scalar triple product as a determinant.
60. Let c=c1i+c2j,r(t)=x(t)i+y(t)j,r
1
(t)=x
1
(t)i+y
1
(t)j,r
2
(t)=x
2
(t)i+y
2
(t)jand use
properties of derivatives.
61. Let r1(t)=x
1
(t)i+y
1
(t)j+z
1
(t)kand r2(t)=x
2
(t)i+y
2
(t)j+z
2
(t)k, in both (8) and (9); show
that the left and right members of the equalities are the same.
62. (a) Zkr(t)dt =Zk(x(t)i+y(t)j+z(t)k)dt
=kZx(t)dt i+kZy(t)dt j+kZz(t)dt k=kZr(t)dt
(b) Similar to Part (a) (c) Use Part (a) on Part (b) with k=−1
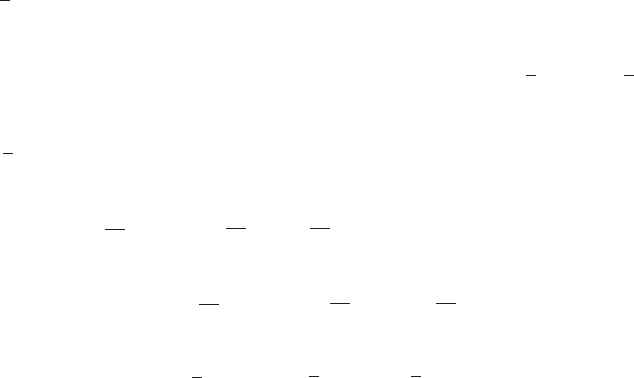
499 Chapter 14
EXERCISE SET 14.3
1. (a) The tangent vector reverses direction at the four cusps.
(b) r0(t)=−3 cos2tsin ti+ 3 sin2tcos tj=0when t=0,π/2,π,3π/2,2π.
2. r0(t) = cos ti+ 2 sin tcos tj=0when t=π/2,3π/2. The tangent vector reverses direction at (1,1)
and (−1,1).
3. r0(t)=3t
2
i+(6t−2)j+2tk; smooth
4. r0(t)=−2tsin(t2)i+2tcos(t2)j−e−tk; smooth
5. r0(t)=(1−t)e
−t
i+(2t−2)j−πsin(πt)k; not smooth, r0(1) = 0
6. r0(t)=πcos(πt)i+(2−1/t)j+(2t−1)k; not smooth, r0(1/2) = 0
7. (dx/dt)2+(dy/dt)2+(dz/dt)2=(−3 cos2tsin t)2+ (3 sin2tcos t)2+0
2= 9 sin2tcos2t,
L=Zπ/2
0
3 sin tcos tdt=3/2
8. (dx/dt)2+(dy/dt)2+(dz/dt)2=(−3 sin t)2+ (3 cos t)2+16=25,L=Zπ
0
5dt =5π
9. r0(t)=he
t
,−e
−t
,√
2i,kr
0
(t)k=e
t+e
−t
,L=Z1
0
(e
t+e
−t
)dt =e−e−1
10. (dx/dt)2+(dy/dt)2+(dz/dt)2=1/4+(1−t)/4+(1+t)/4=3/4, L=Z1
−1
(√3/2)dt =√3
11. r0(t)=3t
2
i+j+√
6tk,kr
0
(t)k=3t
2+1,L=Z3
1
(3t2+1)dt =28
12. r0(t)=3i−2j+k,kr
0
(t)k=√
14, L=Z4
3
√14 dt =√14
13. r0(t)=−3 sin ti+ 3 cos tj+k,kr0(t)k=√10, L=Z2π
0
√10 dt =2π
√
10
14. r0(t)=2ti+tcos tj+tsin tk,kr0(t)k=√5t, L =Zπ
0
√5tdt=π
2√5/2
15. (dr/dt)(dt/dτ)=(i+2tj)(4) = 4i+8tj=4i+ 8(4τ+1)j;
r(τ)=(4τ+1)i+(4τ+1)
2
j,r
0
(τ)=4i+ 2(4)(4τ+1)
16. (dr/dt)(dt/dτ)=h−3 sin t, 3 cos ti(π)=h−3πsin πτ,3πcos πτi;
r(τ)=h3 cos πτ, 3 sin πτi,r0(τ)=h−3πsin πτ, 3πcos πτi
17. (dr/dt)(dt/dτ)=(e
t
i−4e
−t
j)(2τ)=2τeτ2i−8τe−τ2j;
r(τ)=e
τ
2i+4e
−τ2j,r
0
(τ)=2τeτ2i−4(2)τe−τ2j
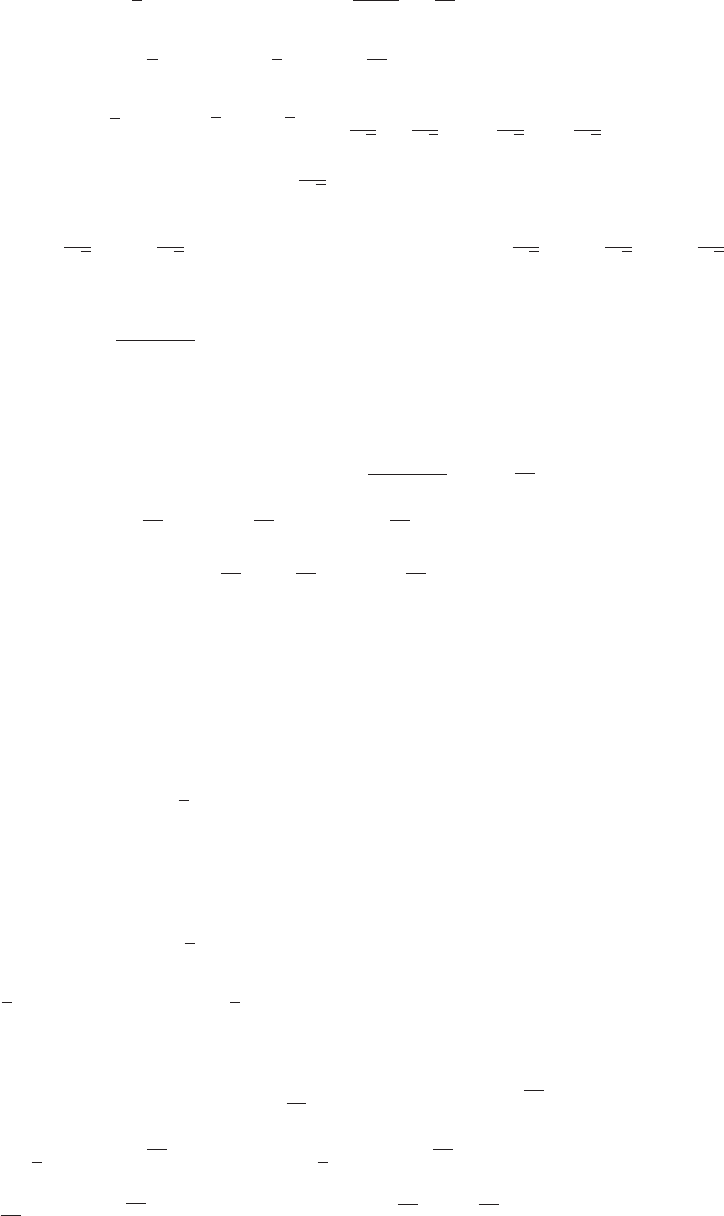
Exercise Set 14.3 500
18. (dr/dt)(dt/dτ)=9
2
t
1/2
j+k
(−1/τ 2)=−9
2τ
5/2j−1
τ
2k;
r(τ)=i+3τ−3/2
j+1
τk,r
0
(τ)=−9
2
τ
−5/2
j−1
τ
2k
19. (a) kr0(t)k=√2,s=Zt
0
√2dt =√2t;r=s
√2i+s
√2j,x=s
√2,y =s
√2
(b) Similar to Part (a), x=y=z=s
√3
20. (a) x=−s
√2,y =−s
√2(b) x=−s
√3,y =−s
√3,z =−s
√3
21. (a) r(t)=h1,3,4iwhen t=0,
so s=Zt
0
√1+4+4du =3t, x =1+s/3,y =3−2s/3,z =4+2s/3
(b) rs=25
=h28/3,−41/3,62/3i
22. (a) r(t)=h−5,0,1iwhen t=0,sos=Zt
0
√
9+4+1du =√14t,
x=−5+3s/√14,y =2s/√14,z =5+s/√14
(b) r(s)s=10
=h−5+30/
√
14,20/√14,5+10/
√
14i
23. x= 3 + cos t,y= 2 + sin t,(dx/dt)2+(dy/dt)2=1,
s=Zt
0
du =tso t=s,x= 3 + cos s,y= 2 + sin sfor 0 ≤s≤2π.
24. x= cos3t,y= sin3t,(dx/dt)2+(dy/dt)2= 9 sin2tcos2t,
s=Zt
0
3 sin ucos udu=3
2sin2tso sin t=(2s/3)1/2, cos t=(1−2s/3)1/2,
x=(1−2s/3)3/2,y=(2s/3)3/2for 0 ≤s≤3/2
25. x=t3/3, y=t2/2, (dx/dt)2+(dy/dt)2=t2(t2+ 1),
s=Zt
0
u(u2+1)
1/2
du =1
3[(t2+1)
3/2−1] so t= [(3s+1)
2/3−1]1/2,
x=1
3[(3s+1)
2/3−1]3/2,y=1
2[(3s+1)
2/3−1] for s≥0
26. x=(1+t)
2
,y=(1+t)
3
,(dx/dt)2+(dy/dt)2=(1+t)
2
[4+9(1+t)2],
s=Zt
0
(1+u)[4 + 9(1 + u)2]1/2du =1
27([4 + 9(1 + t)2]3/2−13√13) so
1+t=1
3[(27s+13
√
13)2/3−4]1/2,x=1
9[(27s+13
√
13)2/3−4],
y=1
27[(27s+13
√
13)2/3−4]3/2for 0 ≤s≤(80√10 −13√13)/27
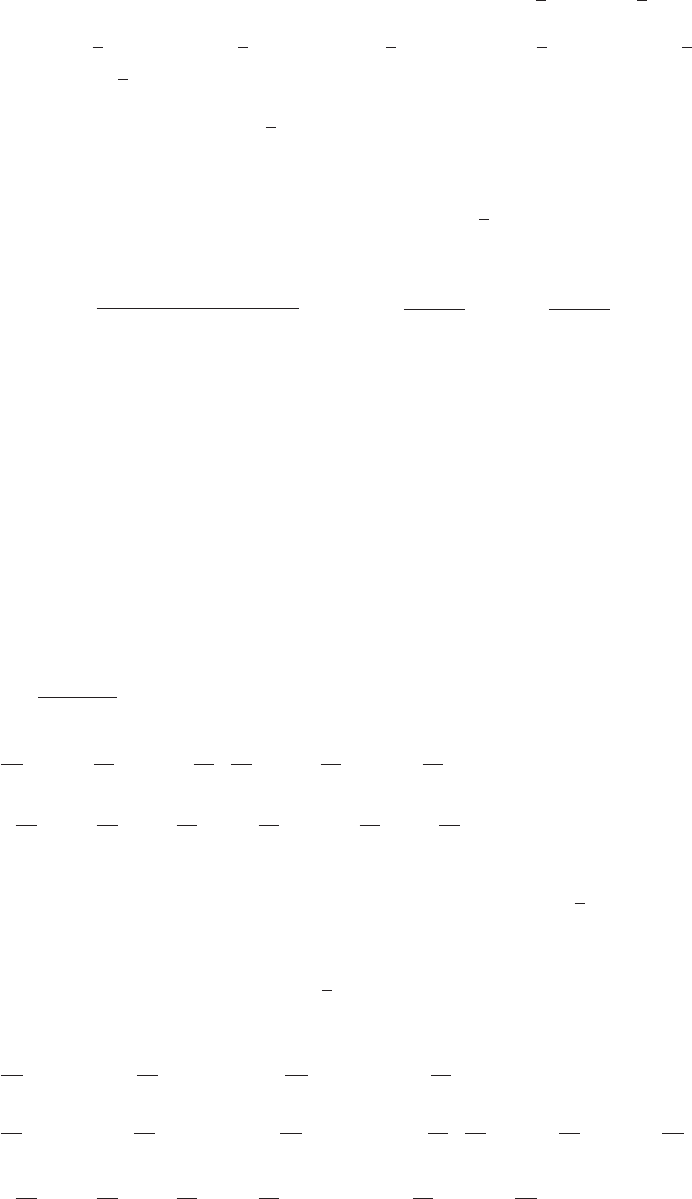
501 Chapter 14
27. x=etcos t,y=etsin t,(dx/dt)2+(dy/dt)2=2e
2t
,s=Zt
0
√
2e
udu =√2(et−1) so
t= ln(s/√2 + 1), x=(s/√2 + 1) cos[ln(s/√2 + 1)], y=(s/√2 + 1) sin[ln(s/√2 + 1)]
for 0 ≤s≤√2(eπ/2−1)
28. x= sin(et), y= cos(et), z=√3et,
(dx/dt)2+(dy/dt)2+(dz/dt)2=4e
2t
,s=Zt
0
2e
udu =2(e
t−1) so
et=1+s/2; x= sin(1 + s/2), y= cos(1 + s/2), z=√3(1 + s/2) for s≥0
29. dx/dt =−asin t,dy/dt =acos t,dz/dt =c,
L=Zt0
0pa2sin2t+a2cos2t+c2dt =Zt0
0pa2+c2dt =t0pa2+c2
30. x=acos t,y=asin t,z=ct,(dx/dt)2+(dy/dt)2+(dz/dt)2=a2+c2=w2,
s=Zt
0
wdu=wt so t=s/w;x=acos(s/w), y=asin(s/w), z=cs/w for s≥0
31. x=at −asin t,y=a−acos t,(dx/dt)2+(dy/dt)2=4a
2sin2(t/2),
s=Zt
0
2asin(u/2)du =4a[1 −cos(t/2)] so cos(t/2)=1−s/(4a), t= 2 cos−1[1 −s/(4a)],
cos t= 2 cos2(t/2) −1 = 2[1 −s/(4a)]2−1,
sin t= 2 sin(t/2) cos(t/2) = 2(1 −[1 −s/(4a)]2)1/2(2[1 −s/(4a)]2−1),
x=2acos−1[1 −s/(4a)] −2a(1 −[1 −s/(4a)]2)1/2(2[1 −s/(4a)]2−1),
y=s(8a−s)
8afor 0 ≤s≤8a
32. dx
dt = cos θdr
dt −rsin θdθ
dt ,dy
dt = sin θdr
dt +rcos θdθ
dt ,
dx
dt
2
+dy
dt
2
+dz
dt
2
=dr
dt
2
+r2dθ
dt
2
+dz
dt
2
33. (a) (dr/dt)2+r2(dθ/dt)2+(dz/dt)2=9e
4t
,L=Zln 2
0
3e2tdt =3
2e2tln 2
0
=9/2
(b) (dr/dt)2+r2(dθ/dt)2+(dz/dt)2=5t
2+t
4=t
2
(5+t2),
L=Z2
1
t(5+t2)1/2dt =9−2
√
6
34. dx
dt = sin φcos θdρ
dt +ρcos φcos θdφ
dt −ρsin φsin θdθ
dt ,
dy
dt = sin φsin θdρ
dt +ρcos φsin θdφ
dt +ρsin φcos θdθ
dt ,dz
dt = cos φdρ
dt −ρsin φdφ
dt ,
dx
dt
2
+dy
dt
2
+dz
dt
2
=dρ
dt
2
+ρ2sin2φdθ
dt
2
+ρ2dφ
dt
2
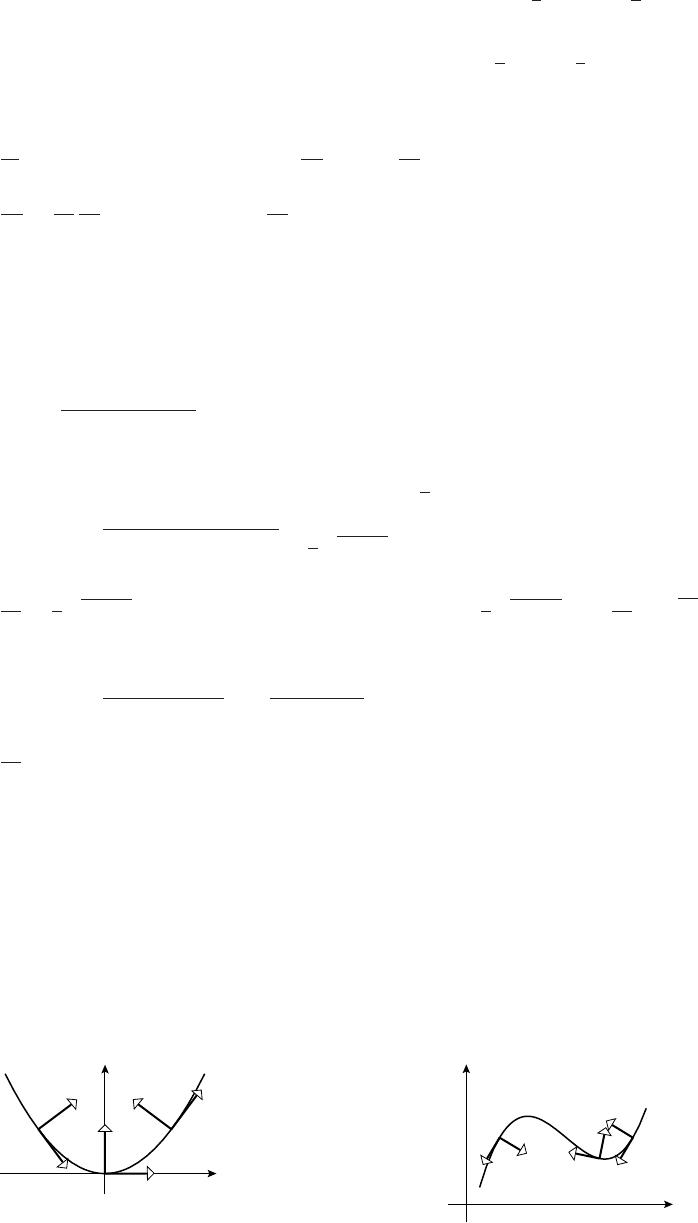
Exercise Set 14.4 502
35. (a) (dρ/dt)2+ρ2sin2φ(dθ/dt)2+ρ2(dφ/dt)2=3e
−2t
,L=Z2
0
√
3e
−t
dt =√3(1 −e−2)
(b) (dρ/dt)2+ρ2sin2φ(dθ/dt)2+ρ2(dφ/dt)2=5,L=Z5
1
√
5dt =4
√
5
36. (a) d
dtr(t)=i+2tjis never zero, but d
dτ r3(τ)= d
dτ (τ3i+τ6j)=3τ
2
i+6τ5
jis zero at τ=0.
(b) dr
dτ =dr
dt
dt
dτ , and since t=τ3,dt
dτ = 0 when τ=0.
37. (a) g(τ)=πτ (b) g(τ)=π(1 −τ)38. t=1−τ
39. Represent the helix by x=acos t,y=asin t,z=ct with a=6.25 and c=10/π, so that the
radius of the helix is the distance from the axis of the cylinder to the center of the copper cable,
and the helix makes one turn in a distance of 20 in. (t=2π). From Exercise 29 the length of the
helix is 2πp6.252+ (10/π)2≈44 in.
40. r(t) = cos ti+ sin tj+t3/2k,r0(t)=−sin ti+ cos tj+3
2t1/2k
(a) kr0(t)k=qsin2t+ cos2t+9t/4=1
2
√
4+9t
(b) ds
dt =1
2√4+9t(c) Z2
0
1
2√4+9tdt=2
27(11√22 −4)
41. r0(t)=(1/t)i+2j+2tk
(a) kr0(t)k=p1/t2+4+4t
2=p(2t+1/t)2=2t+1/t
(b) ds
dt =2t+1/t (c) Z3
1
(2t+1/t)dt =8+ln3
42. If r(t)=x(t)i+y(t)j+z(t)kis smooth, then kr0(t)kis continuous and nonzero. Thus the angle
between r0(t) and i, given by cos−1(x0(t)/kr0(t)k), is a continuous function of t. Similarly, the
angles between r0(t) and the vectors jand kare continuous functions of t.
43. Let r(t)=x(t)i+y(t)jand use the chain rule.
EXERCISE SET 14.4
1. (a)
x
y(b)
x
y
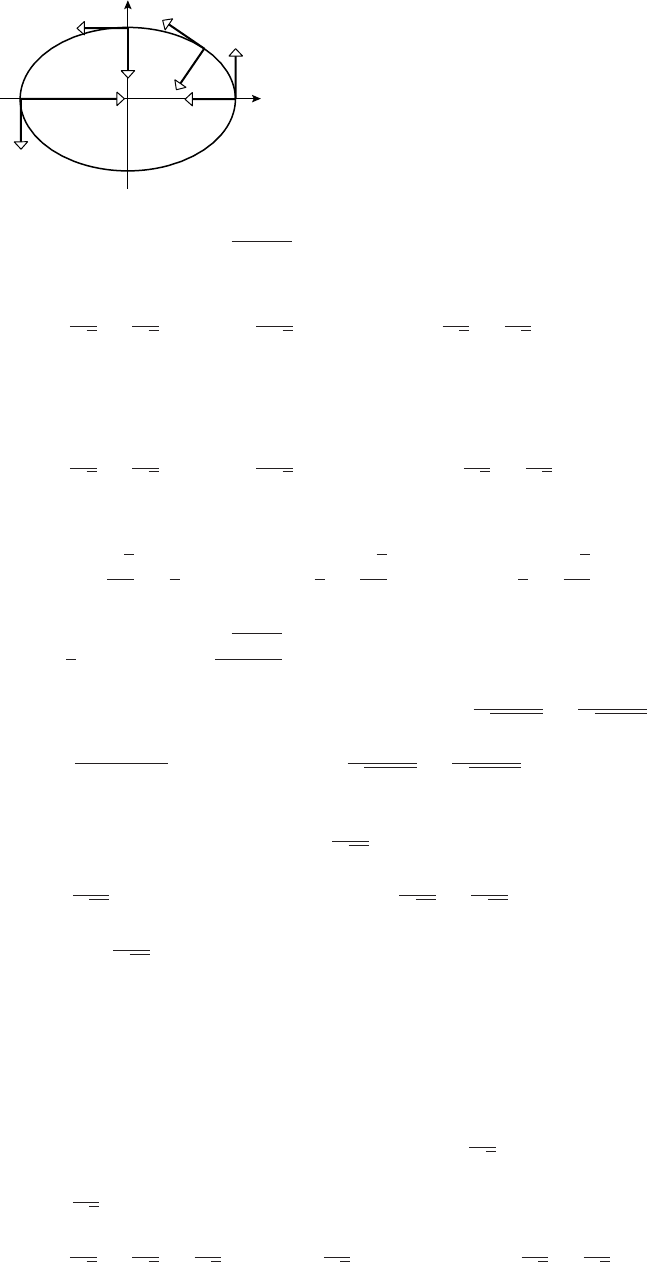
503 Chapter 14
2.
x
y
3. r0(t)=2ti+j,kr
0
(t)k=√
4t
2+1,T(t)=(4t
2+1)
−1/2
(2ti+j),
T0(t)=(4t
2+1)
−1/2
(2i)−4t(4t2+1)
−3/2
(2ti+j);
T(1) = 2
√5i+1
√5j,T0(1) = 2
5√5(i−2j), N(1) = 1
√5i−2
√5j.
4. r0(t)=ti+t
2
j,T(t)=(t
2+t
4
)
−1/2
(ti+t
2
j),
T0(t)=(t
2+t
4
)
−1/2
(i+2tj)−(t+2t
3
)(t2+t4)−3/2(ti+t2j);
T(1) = 1
√2i+1
√2j,T0(1) = 1
2√2(−i+j), N(1) = −1
√2i+1
√2j
5. r0(t)=−5 sin ti+ 5 cos tj,kr0(t)k=5,T(t)=−sin ti+ cos tj,T0(t)=−cos ti−sin tj;
T(π/3) = −√3
2i+1
2j,T0(π/3) = −1
2i−√3
2j,N(π/3) = −1
2i−√3
2j
6. r0(t)=1
ti+j,kr
0
(t)k=√
1+t
2
t,T(t)=(1+t
2
)
−1/2
(i+tj),
T0(t)=(1+t
2
)
−1/2
(j)−t(1+t2)−3/2(i+tj); T(e)= 1
√
1+e
2i+e
√
1+e
2j,
T
0
(e)= 1
(1+e2)3/2(−ei+j), N(e)=−e
√
1+e
2i+1
√
1+e
2j
7. r0(t)=−4 sin ti+ 4 cos tj+k,T(t)= 1
√
17(−4 sin ti+ 4 cos tj+k),
T0(t)= 1
√
17(−4 cos ti−4 sin tj), T(π/2) = −4
√17i+1
√17k
T0(π/2) = −4
√17j,N(π/2) = −j
8. r0(t)=i+tj+t
2
k,T(t)=(1+t
2+t
4
)
−1/2
(i+tj+t
2
k),
T0(t)=(1+t
2+t
4
)
−1/2
(j+2tk)−(t+2t
3
)(1 + t2+t4)−3/2(i+tj+t2k),
T(0) = i,T0(0) = j=N(0)
9. r0(t)=e
t
[(cos t−sin t)i+ (cos t+ sin t)j+k], T(t)= 1
√
3
[(cos t−sin t)i+ (cos t+ sin t)j+k],
T0(t)= 1
√
3
[(−sin t−cos t)i+(−sin t+ cos t)j],
T(0) = 1
√3i+1
√3j+1
√3k,T0(0) = 1
√3(−i+j), N(0) = −1
√2i+1
√2j
Exercise Set 14.4 504
10. r0(t) = sinh ti+ cosh tj+k,kr0(t)k=psinh2t+ cosh2t+1=√
2 cosh t,
T(t)= 1
√
2
(tanh ti+j+ sech tk), T0(t)= 1
√
2
(sech2ti−sech ttanh tk), at t=ln2,
tanh(ln 2) = 3
5and sech(ln 2) = 4
5so T(ln 2) = 3
5√2i+1
√2j+4
5√2k,
T0(ln 2) = 4
25√2(4i−3k), N(ln 2) = 4
5i−3
5k
11. From the remark, the line is parametrized by normalizing v, but T(t0)=v/kvk,sor=r(t
0
)+tv
becomes r=r(t0)+sT(t
0
).
12. r0(t)it=1 =h1,2tiit=1 =h1,2i, and T(1) = h1
√5,2
√5i, so the tangent line can be parametrized as
r=h1,1i+s1
√5,2
√5,sox=1+ s
√
5
,y =1+ 2s
√
5
.
13. r0(t) = cos ti−sin tj+tk,r0(0) = i,r(0) = j,T(0) = i, so the tangent line has the parametrization
x=s, y =1.
14. r(1) = i+j+√8k,r0(t)=i+j−t
√
9−t
2k,r
0
(1) = i+j−1
√8k,kr0(1)k=√17
√8, so the tangent
line has parametrizations r=i+j+√8k+ti+j−1
√8k=i+j+√8k+s√8
√17 i+j−1
√8k.
15. T =3
5cos ti−3
5sin tj+4
5k,N=−sin ti−cos tj,B=T×N=4
5cos ti−4
5sin tj−3
5k
16. T0(t)= 1
√
2
[(cos t+ sin t)i+(−sin t+ cos t)j],N=1
√2[(−sin t+ cos t)i−(cos t+ sin t)j],
B=T×N=−k
17. r0(t)=tsin ti+tcos tj,kr0k=t, T= sin ti+ cos tj,N= cos ti−sin tj,B=T×N=−k
18. T =(−asin ti+acos tj+bk)/√a2+b2,N=−cos ti−sin tj,
B=T×N=(bsin ti−bcos tj+ak)/√a2+b2
19. r(π/4) = √2
2i+√2
2j+k,T=−sin ti+ cos tj=√2
2(−i+j),N=−(cos ti+ sin tj)=−√
2
2(i+j),
B=k; the rectifying, osculating, and normal planes are given (respectively) by x+y=√2,
z=1,−x+y=0.
20. r(0) = i+j,T=1
√3(i+j+k),N=1
√2(−j+k),B=1
√6(2i−j−k); the rectifying, osculating,
and normal planes are given (respectively) by −y+z=−1,2x−y−z=1,x+y+z=2.
21. (a) By formulae (1) and (11), N(t)=B(t)×T(t)= r
0
(t)×r
00 (t)
kr0(t)×r00 (t)k×r0(t)
kr0(t)k.
(b) Since r0is perpendicular to r0×r00 it follows from Lagrange’s Identity (Exercise 32 of Section
13.4) that k(r0(t)×r00 (t)) ×r0(t)k=kr0(t)×r00 (t)kkr0(t)k, and the result follows.
(c) From Exercise 39 of Section 13.4, (r0(t)×r00 (t)) ×r0(t)=kr
0
(t)k
2
r
00 (t)−(r0(t)·r00 (t))r0(t)=
u(t), so N(t)=u(t)/ku(t)k

505 Chapter 14
22. (a) r0(t)=2ti+j,r
0
(1)=2i+j,r
00 (t)=2i,u=2i−4j,N=1
√
5
i−2
√
5
j
(b) r0(t)=−4 sin ti+ 4 cos tj+k,r0(π
2)=−4i+k,r
00 (t)=−4 cos ti−4 sin tj,
r00 (π
2)=−4j,u= 17(−4j),N=−j
23. r0(t) = cos ti−sin tj+k,r00 (t)=−sin ti−cos tj,u=−2(sin ti+cos tj),kuk=2,N=−sin ti−cos tj
24. r0(t)=i+2tj+3t
2
k,r
00 (t)=2j+6tk,u(t)=−(4t+18t
3
)i+(2−18t4)j+(6t+12t
3
)k,
N=1
2
√
81t8+ 117t6+54t
4+13t
2+1−(4t+18t
3
)i+(2−18t4)j+(6t+12t
3
)k
EXERCISE SET 14.5
1. κ≈1
0.5=2 2. κ≈1
4/3=3
4
3. r0(t)=2ti+3t
2
j,r
00 (t)=2i+6tj,κ=kr
0
(t)×r
00 (t)k/kr0(t)k3=6
t(4+9t
2
)
3/2
4. r0(t)=−4 sin ti+cos tj,r00 (t)=−4 cos ti−sin tj,κ=kr0(t)×r00 (t)k/kr0(t)k3=4
(16 sin2t+ cos2t)3/2
5. r0(t)=3e
3t
i−e
−t
j,r
00 (t)=9e
3t
i+e
−t
j,κ=kr
0
(t)×r
00 (t)k/kr0(t)k3=12e2t
(9e6t+e−2t)3/2
6. r0(t)=−3t
2
i+(1−2t)j,r
00 (t)=−6ti−2j,κ=kr
0
(t)×r
00 (t)k/kr0(t)k3=6pt2(t−1)2
(9t4+4t
2−4t+1)
3/2
7. r0(t)=−4 sin ti+ 4 cos tj+k,r00 (t)=−4 cos ti−4 sin tj,
κ=kr0(t)×r00 (t)k/kr0(t)k3=4/17
8. r0(t)=i+tj+t
2
k,r
00 (t)=j+2tk,κ=kr
0
(t)×r
00 (t)k/kr0(t)k3=√t4+4t
2+1
(t
4+t
2+1)
3/2
9. r0(t) = sinh ti+ cosh tj+k,r00 (t) = cosh ti+ sinh tj,κ=kr0(t)×r00 (t)k/kr0(t)k3=1
2 cosh2t
10. r0(t)=j+2tk,r
00 (t)=2k,κ=kr
0
(t)×r
00 (t)k/kr0(t)k3=2
(4t2+1)
3/2
11. r0(t)=−3 sin ti+ 4 cos tj+k,r00 (t)=−3 cos ti−4 sin tj,
r0(π/2) = −3i+k,r00 (π/2) = −4j;κ=k4i+12kk/k−3i+kk
3=2/5,ρ =5/2
12. r0(t)=e
t
i−e
−t
j+k,r
00 (t)=e
t
i+e
−t
j,
r
0
(0) = i−j+k,r00 (0) = i+j;κ=k−i+j+2kk/ki−j+kk
3=√
2/3,ρ =3/
√
2
13. r0(t)=e
t
(cos t−sin t)i+et(cos t+ sin t)j+etk,
r00 (t)=−2e
tsin ti+2e
tcos tj+etk,r0(0) = i+j+k,
r00 (0)=2j+k;κ=k−i−j+2kk/ki+j+kk
3=√
2/3,ρ =3
√
2/2
Exercise Set 14.5 506
14. r0(t) = cos ti−sin tj+tk,r00 (t)=−sin ti−cos tj+k,
r0(0) = i,r00 (0) = −j+k;κ=k−j−kk/kik
3=√
2,ρ=√2/2
15. r0(s)=1
2cos 1+s
2i−1
2sin 1+s
2j+√
3
2k,kr
0
(s)k=1,so
dT
ds =−1
4sin 1+s
2i−1
4cos 1+s
2j,κ=
dT
ds
=1
16
16. r0(s)=−
r3−2s
3si+r2s
3j,kr
0
(s)k=1,so
dT
ds =1
√9−6si+1
√6sj,κ=
dT
ds
=r1
9−6s+1
6s=s3
2s(9 −6s)
17. (a) r0=x0i+y0j,r00 =x00 i+y00 j,kr0×r00 k=|x0y00 −x00 y0|,κ=|x
0
y
00 −y0x00 |
(x02+y02)3/2
(b) r =xi+y(x)j,r0(x)=i+(dy/dx)j,r00 (x)=(d
2
y/dx2)j,so
κ(x)=k(d
2
y/dx2)kk/ki+(dy/dx)jk3=|d2y/dx2|/[1+(dy/dx)2]3/2.
18. dy
dx = tan φ, (1 + tan2φ)3/2= (sec2φ)3/2=|sec φ|3,κ(x)= |y
00 |
|sec φ|3=|y00 cos3φ|
19. κ(x)= |sin x|
(1 + cos2x)3/2,κ(π/2)=1 20. κ(x)= 2|x|
(1+x4)3/2,κ(0)=0
21. κ(x)= 2|x|
3
(x
4+1)
3/2,κ(1)=1/
√
222. κ(x)= e
−x
(1+e−2x)3/2,κ(1) = e−1
(1+e−2)3/2
23. κ(x)= 2 sec2x|tan x|
(1 + sec4x)3/2,κ(π/4)=4/(5√5)
24. By implicit differentiation, dy/dx =4x/y,d2y/dx2=36/y3so κ=36/|y|3
(1+16x
2
/y2)3/2;
if (x, y)=(2,5) then κ=36/125
(1+64/25)3/2=36
89√89
25. x0(t)=2t,y
0
(t)=3t
2
,x
00 (t)=2,y
00 (t)=6t,
x
0
(1/2)=1,y
0
(1/2)=3/4, x00 (1/2)=2,y
00 (1/2)=3;κ=96/125
26. x0(t)=−4 sin t,y0(t) = cos t,x00 (t)=−4 cos t,y00 (t)=−sin t,
x0(π/2) = −4, y0(π/2)=0,x
00 (π/2)=0,y
00 (π/2) = −1; κ=1/16
27. x0(t)=3e
3t
,y
0
(t)=−e
−t
,x
00 (t)=9e
3t
,y
00 (t)=e
−t
,
x
0
(0)=3,y
0
(0) = −1, x00 (0)=9,y
00 (0)=1;κ=6/(5√10)
28. x0(t)=−3t
2
,y
0
(t)=1−2t,x
00 (t)=−6t,y
00 (t)=−2,
x0(1) = −3, y0(1) = −1, x00 (1) = −6, y00 (1) = −2; κ=0

507 Chapter 14
29. x0(t)=1,y
0
(t)=−1/t2,x
00 (t)=0,y
00 (t)=2/t3
x0(1)=1,y
0
(1) = −1,x
00 (1)=0,y
00 (1)=2;κ=1/
√
2
30. x0(t) = 4 cos 2t, y0(t)=3cost, x00 (t)=−8 sin 2t, y00 (t)=−3 sin t,
x0(π/2) = −4,y
0
(π/2)=0,x
00 (π/2)=0,y
00 (π/2) = −3,κ=12/4
3/2=3/2
31. (a) κ(x)= |cos x|
(1 + sin2x)3/2,
ρ(x)=(1 + sin2x)3/2
|cos x|
ρ(0) = ρ(π)=1.
c
(0) = ( ) = 1
c
x
y
rr
(b) κ(t)= 2
(4 sin2t+ cos2t)3/2,
ρ(t)=1
2
(4 sin2t+ cos2t)3/2,
ρ(0)=1/2, ρ(π/2)=4
1
2
ρ
(
6
)
= 4
ρ
(0) =
1
2
x
y
32. x0(t)=−e
−t
(cos t+ sin t),
y0(t)=e
−t
(cos t−sin t),
x00 (t)=2e
−tsin t,
y00 (t)=−2e
−tcos t;
using the formula of Exercise 17(a),
κ=1
√2et.
3-3
t
κ
6
33. (a) At x= 0 the curvature of I has a large value, yet the value of II there is zero, so II is not the
curvature of I; hence I is the curvature of II.
(b) I has points of inflection where the curvature is zero, but II is not zero there, and hence is
not the curvature of I; so I is the curvature of II.
34. (a) II takes the value zero at x= 0, yet the curvature of I is large there; hence I is the curvature
of II.
(b) I has constant zero curvature; II has constant, positive curvature; hence I is the curvature
of II.
35. (a)
5
00
1(b) 1
0
05
Exercise Set 14.5 508
36. (a) 4
-4
-1 1
(b) 4
-4
-1 1
37. (a) κ=|12x2−4|
(1+(4x
3−4x)
2
)
3/2(b)
f(x)
k
-2 2
8
x
y
(c) f0(x)=4x
3−4x=0atx=0,±1,f00 (x)=12x
2−4, so extrema at x=0,±1, and ρ=1/4
for x= 0 and ρ=1/8 when x=±1.
38. (a)
-30 30
-30
30
x
y(c) κ(t)= t
2+2
(t
2+1)
3/2(d) lim
t→+∞κ(t)=0
39. r0(θ)=−rsin θ+ cos θdr
dθ i+rcos θ+ sin θdr
dθ j;
r00 (θ)=−rcos θ−2 sin θdr
dθ + cos θd2r
dθ2i+−rsin θ+ 2 cos θdr
dθ + sin θd2r
dθ2j;
κ=
r2+2dr
dθ
2
−rd2r
dθ2
"r2+dr
dθ
2#3/2.
40. Let r=abe the circle, so that dr/dθ = 0, and κ(θ)=1
r=1
a
41. κ(θ)= 3
2
√
2(1 + cos θ)1/2,κ(π/2) = 3
2√242. κ(θ)= 1
√
5e
2θ,κ(1) = 1
√5e2
43. κ(θ)= 10 + 8 cos23θ
(1 + 8 cos2θ)3/2,κ(0) = 2
344. κ(θ)= θ
2+2
(θ
2+1)
3/2,κ(1) = 3
2√2

509 Chapter 14
45. The radius of curvature is zero when θ=π, so there is a cusp there.
46. dr
dθ =−sin θ,d2r
dθ2=−cos θ,κ(θ)= 3
2
3/2
√
1 + cos θ
47. Let y=t, then x=t2
4pand κ(t)= 1/|2p|
[t
2
/(4p2)+1]
3/2;
t= 0 when (x, y)=(0,0) so κ(0)=1/|2p|,ρ=2|p|.
48. κ(x)= e
x
(1+e2x)3/2,κ0(x)=e
x
(1 −2e2x)
(1+e2x)5/2;κ0(x) = 0 when e2x=1/2, x=−(ln 2)/2. By the first
derivative test, κ(−1
2ln 2) is maximum so the point is (−1
2ln 2,1/√2).
49. Let x= 3 cos t,y= 2 sin tfor 0 ≤t<2π,κ(t)= 6
(9 sin2t+ 4 cos2t)3/2so
ρ(t)=1
6
(9 sin2t+ 4 cos2t)3/2=1
6(5 sin2t+4)
3/2which, by inspection, is minimum when
t=0orπ. The radius of curvature is minimum at (3,0) and (−3,0).
50. κ(x)= 6x
(1+9x
4
)
3/2for x>0, κ0(x)= 6(1 −45x4)
(1+9x
4
)
5/2;κ
0
(x) = 0 when x=45
−1/4which, by the
first derivative test, yields the maximum.
51. r0(t)=−sin ti+ cos tj−sin tk,r00 (t)=−cos ti−sin tj−cos tk,
kr0(t)×r00 (t)k=k−i+kk=√
2, kr0(t)k= (1 + sin2t)1/2;κ(t)=√
2/(1 + sin2t)3/2,
ρ(t)=(1+sin
2t)
3/2
/
√
2. The minimum value of ρis 1/√2; the maximum value is 2.
52. r0(t)=e
t
i−e
−t
j+√
2k,r
00 (t)=e
t
i+e
−t
j;
κ(t)= √
2
e
2t+e
−2t+2,ρ(t)= 1
√
2
(e
t+e
−t
)
2=2
√
2 cosh2t. The minimum value of ρis 2√2.
53. From Exercise 39: dr/dθ =aeaθ =ar,d2r/dθ2=a2eaθ =a2r;κ=1/[
p1+a
2r].
54. Use implicit differentiation on r2=a2cos 2θto get 2rdr
dθ =−2a2sin 2θ,rdr
dθ =−a2sin 2θ, and
again to get rd2r
dθ2+dr
dθ
2
=−2a2cos 2θso rd2r
dθ2=−dr
dθ
2
−2a2cos 2θ=−dr
dθ
2
−2r2,thus
r
2+2dr
dθ
2
−rd2r
dθ2
=3"r
2+dr
dθ
2#,κ=3
[r2+(dr/dθ)2]1/2;dr
dθ =−a2sin 2θ
rso
r2+dr
dθ
2
=r2+a4sin22θ
r2=r4+a4sin22θ
r2=a4cos22θ+a4sin22θ
r2=a4
r2, hence κ=3r
a2.
Exercise Set 14.5 510
55. (a) d2y/dx2=2,κ(φ)=|2 cos3φ|
(b) dy/dx = tan φ=1,φ=π/4,κ(π/4) = |2 cos3(π/4)|=1/
√
2,ρ=
√
2
(c)
-2 1
3
x
y
56. (a) 5
3,0,0,−5
2(b) clockwise (c) it is a point, namely the center of the circle
57. κ= 0 along y= 0; along y=x2,κ(x)=2/(1+4x
2
)
3/2
,κ(0) = 2. Along y=x3,
κ(x)=6|x|/(1+9x
4
)
3/2
,κ(0)=0.
58. (a)
2-2
4
x
y(b) For y=x2,κ(x)= 2
(1+4x
2
)
3/2
so κ(0) = 2; for y=x4,
κ(x)= 12x2
(1+16x
6
)
3/2so κ(0)=0.
κis not continuous at x=0.
59. κ=1/r along the circle; along y=ax2,κ(x)=2a/(1+4a
2
x
2
)
3/2
,κ(0)=2aso 2a=1/r,
a=1/(2r).
60. κ(x)= |y
00 |
(1+y02)3/2so the transition will be smooth if the values of yare equal, the values of y0
are equal, and the values of y00 are equal at x=0.Ify=e
x
, then y0=y00 =ex;ify=ax2+bx +c,
then y0=2ax +band y00 =2a. Equate y,y0, and y00 at x= 0 to get c=1,b= 1, and a=1/2.
61. The result follows from the definitions N=T0(s)
kT0(s)kand κ=kT0(s)k.
62. (a) B ·
dB
ds = 0 because kB(s)k=1so dB
ds is perpendicular to B(s).
(b) B(s)·T(s)=0,B(s)·
dT
ds +dB
ds
·T(s)=0,butdT
ds =κN(s)soκB(s)·N(s)+dB
ds
·
T(s)=0, dB
ds
·T(s) = 0 because B(s)·N(s)=0;thus dB
ds is perpendicular to T(s).
(c) dB
ds is perpendicular to both B(s) and T(s) but so is N(s), thus dB
ds is parallel to N(s) and
hence a scalar multiple of N(s).
(d) If Clies in a plane, then T(s) and N(s) also lie in the plane; B(s)=T(s)×N(s)soB(s)is
always perpendicular to the plane and hence dB/ds =0,thusτ=0.
511 Chapter 14
63. dN
ds =B×dT
ds +dB
ds ×T=B×(κN)+(−τN)×T=κB×N−τN×T, but B×N=−Tand
N×T=−Bso dN
ds =−κT+τB
64. r00 (s)=dT/ds =κNso r000 (s)=κdN/ds +(dκ/ds)Nbut dN/ds =−κT+τBso
r000 (s)=−κ
2
T+(dκ/ds)N+κτB,r0(s)×r00 (s)=T×(κN)=κT×N=κB,
[r
0
(s)×r
00 (s)] ·r000 (s)=−κ
3
B·T+κ(dκ/ds)B·N+κ2τB·B=κ2τ,
τ=[r
0
(s)×r
00 (s)] ·r000 (s)/κ2=[r
0
(s)×r
00 (s)] ·r000 (s)/kr00 (s)k2and
B=T×N=[r
0
(s)×r
00 (s)]/kr0(s)k
65. r =acos(s/w)i+asin(s/w)j+(cs/w)k,r0=−(a/w) sin(s/w)i+(a/w) cos(s/w)j+(c/w)k,
r00 =−(a/w2) cos(s/w)i−(a/w2) sin(s/w)j,r000 =(a/w3) sin(s/w)i−(a/w3) cos(s/w)j,
r0×r00 =(ac/w3) sin(s/w)i−(ac/w3) cos(s/w)j+(a
2
/w3)k,(r
0×r
00 )·r000 =a2c/w6,
kr00 (s)k=a/w2,soτ=c/w2and B=(c/w) sin(s/w)i−(c/w) cos(s/w)j+(a/w)k
66. (a) T0=dT
dt =dT
ds
ds
dt =(κN)s
0=κs0N,
N0=dN
dt =dN
ds
ds
dt =(−κT+τB)s
0=−κs0T+τs0B.
(b) kr0(t)k=s0so r0(t)=s
0
Tand r00 (t)=s
00 T+s0T0=s00 T+s0(κs0N)=s
00 T+κ(s0)2N.
(c) r000 (t)=s
00 T0+s000 T+κ(s0)2N0+[2κs0s00 +κ0(s0)2]N
=s00 (κs0N)+s
000 T+κ(s0)2(−κs0T+τs0B)+[2κs0s00 +κ0(s0)2]N
=[s
000 −κ2(s0)3]T+[3κs0s00 +κ0(s0)2]N+κτ(s0)3B.
(d) r0(t)×r00 (t)=s
0
s
00 T×T+κ(s0)3T×N=κ(s0)3B,[r
0
(t)×r
00 (t)] ·r000 (t)=κ
2
τ(s
0
)
6so
τ=[r0(t)×r00 (t)] ·r000 (t)
κ2(s0)6=[r0(t)×r00 (t)] ·r000 (t)
kr0(t)×r00 (t)k2
67. r0=2i+2tj+t
2
k,r
00 =2j+2tk,r
000 =2k,r
0×r
00 =2t
2
i−4tj+4k,kr
0×r
00 k=2(t
2+ 2),
τ=8/[2(t2+ 2)]2=2/(t
2+2)
2
68. r0=−asin ti+acos tj+bk,r00 =−acos ti−asin tj,r000 =asin ti−acos tj,
r0×r00 =ab sin ti−ab cos tj+a2k,kr0×r00 k=pa2(a2+b2),
τ=a2b/[a2(a2+b2)] = b/(a2+b2)
69. r0=eti−e−tj+√2k,r00 =eti+e−tj,r000 =eti−e−tj,r0×r00 =−√2e−ti+√2etj+2k,
kr
0×r
00 k=√2(et+e−t), τ=(−2
√
2)/[2(et+e−t)2]=−
√
2/(e
t+e
−t
)
2
70. r0=(1−cos t)i+ sin tj+k,r00 = sin ti+ cos tj,r000 = cos ti−sin tj,
r0×r00 =−cos ti+ sin tj+ (cos t−1)k,
kr0×r00 k=qcos2t+ sin2t+ (cos t−1)2=q1+4sin
4
(t/2), τ=−1/[1 + 4 sin4(t/2)]
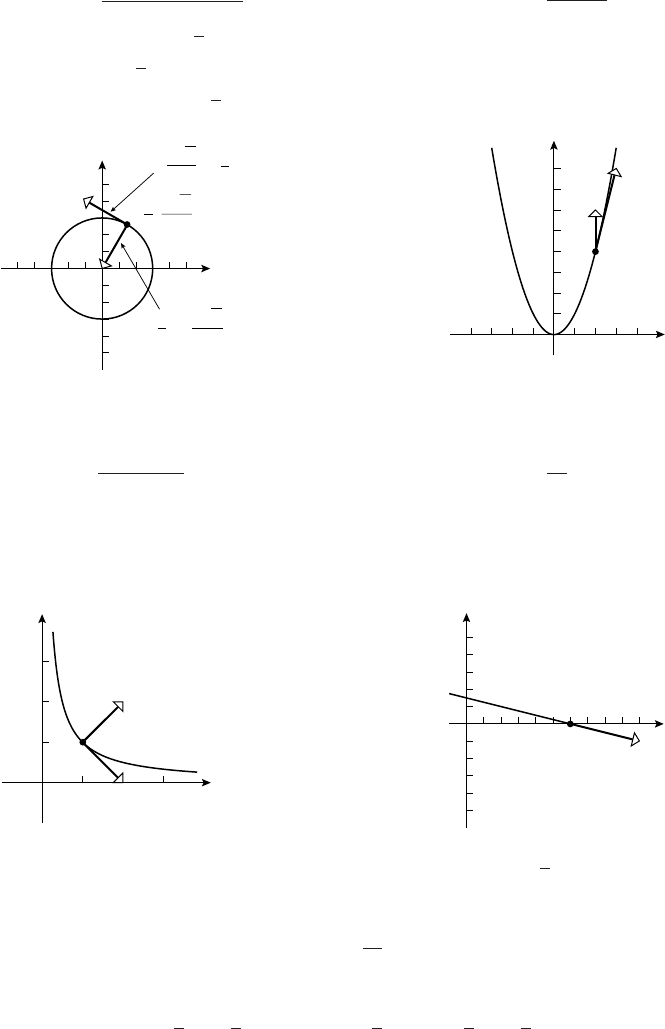
Exercise Set 14.6 512
EXERCISE SET 14.6
1. v(t)=−3 sin ti+ 3 cos tj
a(t)=−3 cos ti−3 sin tj
kv(t)k=p9 sin2t+ 9 cos2t=3
r(π/3)=(3/2)i+(3
√
3/2)j
v(π/3) = −(3√3/2)i+(3/2)j
a(π/3) = −(3/2)i−(3√3/2)j
3
3
23√3
2
()
,
3
23√3
2
a = − i − j
x
y
3√3
2
v = − i + j
3
2
2. v(t)=i+2tj
a(t)=2j
kv(t)k=√
1+4t
2
r(2)=2i+4j
v(2) = i+4j
a(2)=2j
(2, 4)
a = 2j
v = i + 4j
8
4
x
y
3. v(t)=e
t
i−e
−t
j
a(t)=e
t
i+e
−t
j
kv(t)k=√
e
2t+e
−2t
r(0) = i+j
v(0) = i−j
a(0) = i+j
(1, 1)
v = i − j
a = i + j
x
y
4. v(t)=4i−j
a(t)=0
kv(t)k=√
17
r(1)=6i
v(1)=4i−j
a(1) = 0
(6, 0)
v = 4i − j
a = 0
x
y
5. v =i+tj+t2k,a=j+2tk;att=1,v=i+j+k,kvk=√
3, a=j+2k
6. r =(1+3t)i+(2−4t)j+(7+t)k,v=3i−4j+k,
a=0;att=2,v=3i−4j+k,kvk=√
26, a=0
7. v =−2 sin ti+ 2 cos tj+k,a=−2 cos ti−2 sin tj;
at t=π/4, v=−√2i+√2j+k,kvk=√5, a=−√2i−√2j
8. v =et(cos t+ sin t)i+et(cos t−sin t)j+k,a=2e
tcos ti−2etsin tj;att=π/2,
v=eπ/2i−eπ/2j+k,kvk=(1+2e
π)
1/2
,a=−2e
π/2j
513 Chapter 14
9. (a) v =−aω sin ωti+bω cos ωtj,a=−aω2cos ωti−bω2sin ωtj=−ω2r
(b) From Part (a), kak=ω2krk
10. (a) v =16πcos πti−8πsin 2πtj,a=−16π2sin πti−16π2cos 2πtj;
at t=1,v=−16πi,kvk=16π,a=−16π2j
(b) x= 16 sin πt, y = 4 cos 2πt = 4 cos2πt −4 sin2πt =4−8 sin2πt, y =4−x
2
/32
(c) Both x(t) and y(t) are periodic and have period 2, so after 2 s the particle retraces its path.
11. v =(6/
√
t)i+(3/2)t1/2j,kvk=p36/t +9t/4,dkvk/dt =(−36/t2+9/4)/(2p36/t +9t/4)=0
if t= 4 which yields a minimum by the first derivative test. The minimum speed is 3√2 when
r=24i+8j.
12. v =(1−2t)i−2tj,kvk=p(1 −2t)2+4t
2=√
8t
2−4t+1,
d
dtkvk=8t−2
√8t2−4t+1 =0ift=1
4which yields a minimum by the first derivative test. The
minimum speed is 1/√2 when the particle is at r=3
16i−1
16j.
13. (a)
803
6
(b) v = 3 cos 3ti+ 6 sin 3tj,kvk=p9 cos23t+ 36 sin23t=3
p1+3sin
23t; by inspection, maxi-
mum speed is 6 and minimum speed is 4
(d) d
dtkvk=9 sin 6t
2p1+3sin
23t= 0 when t=0,π/6,π/3,π/2,2π/3; the maximum speed is 6 which
occurs first when sin3t=1,t=π/6.
14. (a) 8
0
0c
(d) v =−6 sin 2ti+2 cos 2tj+4k,kvk=p36 sin22t+ 4 cos22t+16=2
p8 sin2t+ 5; by inspec-
tion the maximum speed is 2√13 when t=π, the minimum speed is 2√5 when t=π/2.
15. v(t)=−sin ti+ cos tj+C1,v(0) = j+C1=i,C1=i−j,v(t)=(1−sin t)i+ (cos t−1)j;
r(t)=(t+ cos t)i+ (sin t−t)j+C2,r(0) = i+C2=j,
C2=−i+jso r(t)=(t+ cos t−1)i+ (sin t−t+1)j
Exercise Set 14.6 514
16. v(t)=ti−e
−t
j+C
1
,v(0) = −j+C1=2i+j;C
1=2i+2jso
v(t)=(t+2)i+(2−e
−t
)j;r(t)=(t
2
/2+2t)i+(2t+e
−t
)j+C
2
r(0) = j+C2=i−j,C2=i−2jso r(t)=(t
2
/2+2t+1)i+(2t+e
−t−2)j
17. v(t)=−cos ti+ sin tj+etk+C1,v(0) = −i+k+C1=kso
C1=i,v(t)=(1−cos t)i+ sin tj+etk;r(t)=(t−sin t)i−cos tj+etk+C2,
r(0) = −j+k+C2=−i+kso C2=−i+j,r(t)=(t−sin t−1)i+(1−cos t)j+etk.
18. v(t)=−1
t+1j+1
2e
−2t
k+C
1
,v(0) = −j+1
2k+C1=3i−jso
C1=3i−1
2
k,v(t)=3i−1
t+1j+1
2e
−2t−1
2k;
r(t)=3ti−ln(t+1)j−1
4e
−2t+1
2t
k+C
2
,
r(0) = −1
4k+C2=2kso C2=9
4k,r(t)=3ti−ln(t+1)j+9
4−1
4e
−2t−1
2t
k.
19. If a=0then x00 (t)=y
00 (t)=z
00 (t)=0,sox(t)=x
1
t+x
0
,y(t)=y
1
t+y
0
,z(t)=z
1
t+z
0
, the
motion is along a straight line and has constant speed.
20. (a) If krkis constant then so is krk2, but then x2+y2=c2(2-space) or x2+y2+z2=c2
(3-space), so the motion is along a circle or a sphere of radius ccentered at the origin, and
the velocity vector is always perpendicular to the locating vector.
(b) If kvkis constant then by the Theorem, v(t)·a(t) = 0, so the velocity is always perpendicular
to the acceleration.
21. v =3t
2
i+2tj,a=6ti+2j;v=3i+2jand a=6i+2jwhen t=1so
cos θ=(v·a)/(kvkkak)=11/
√
130, θ≈15◦.
22. v =et(cos t−sin t)i+et(cos t+ sin t)j,a=−2etsin ti+2e
tcos tj,v·a=2e
2t
,kvk=√
2e
t
,
kak=2e
t
, cos θ=(v·a)/(kvkkak)=1/
√
2, θ=45
◦
.
23. (a) displacement = r1−r0=0.7i+2.7j−3.4k
(b) ∆r=r1−r0,sor
0=r
1−∆r=−0.7i−2.9j+4.8k.
24. (a)
-4 -2 2 4
-4
-2
2
4
x
y(b) distance = p50(1 −cos 2πt)
25. ∆r=r(3) −r(1)=8i+26/3j;v=2ti+t
2
j,s=Z3
1
t
p4+t
2
dt = (13√13 −5√5)/3.
26. ∆r=r(3π/2) −r(0)=3i−3j;v= 3 cos ti−3 sin tj,s=Z3π/2
0
3dt =9π/2.
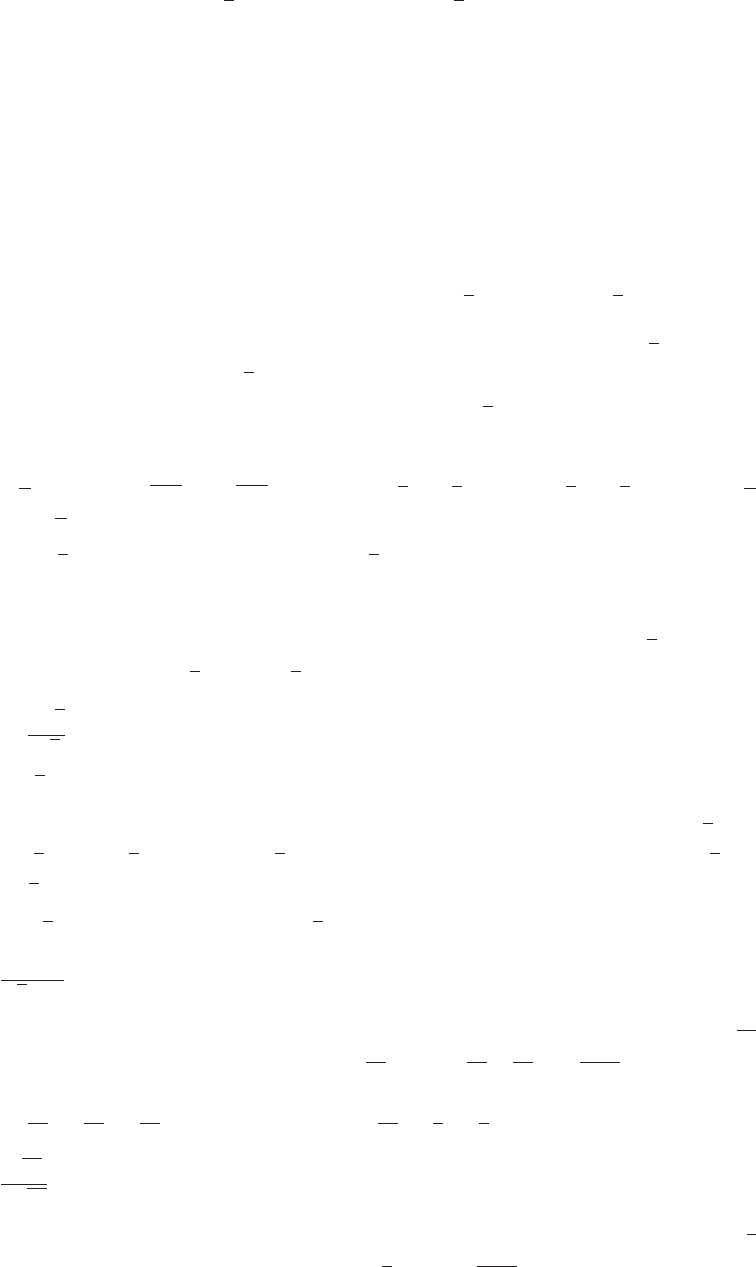
515 Chapter 14
27. ∆r=r(ln 3) −r(0)=2i−2/3j+√
2ln3k;v=e
ti−e
−tj+√2k,s=Zln 3
0
(et+e−t)dt =8/3.
28. ∆r=r(π)−r(0) = 0;v=−2 sin 2ti+ 2 sin 2tj−sin 2tk,
kvk=3|sin 2t|,s=Zπ
0
3|sin 2t|dt =6Zπ/2
0
sin 2tdt=6.
29. In both cases, the equation of the path in rectangular coordinates is x2+y2= 4, the particles
move counterclockwise around this circle; v1=−6 sin 3ti+ 6 cos 3tjand
v2=−4tsin(t2)i+4tcos(t2)jso kv1k= 6 and kv2k=4t.
30. Let u=1−t
3in r2to get r2(u)=(3+2u)i+uj+(1−u)kso both particles move along the same
line; v1=2i+j−kand v2=−6t2i−3t2j+3t
2
kso kv1k=√6 and kv2k=3
√
6t
2
.
31. (a) v =−e−ti+etj,a=e−ti+etj; when t=0,v=−i+j,a=i+j,kvk=√
2, v·a=0,
v×a=−2kso aT=0,a
N=√
2.
(b) aTT=0,a
NN=a−a
TT=i+j (c) κ=1/
√
2
32. (a) v =−2tsin(t2)i+2tcos(t2)j,a=[−4t
2cos(t2)−2 sin(t2)]i+[−4t
2sin(t2) + 2 cos(t2)]j; when
t=√π/2, v=−pπ/2i+pπ/2j,a=(−π/√2−√2)i+(−π/√2+√
2)j,kvk=√π,
v·a=2
√
π,v×a=π
3/2
kso aT=2,a
N=π
(b) aTT=−√2(i−j),a
N
N=a−a
T
T=−(π/√2)(i+j)
(c) κ=1
33. (a) v =(3t
2−2)i+2tj,a=6ti+2j; when t=1,v=i+2j,a=6i+2j,kvk=√
5, v·a= 10,
v×a=−10kso aT=2
√
5, aN=2
√
5
(b) aTT=2√5
√5(i+2j)=2i+4j,a
N
N=a−a
T
T=4i−2j
(c) κ=2/
√
5
34. (a) v =et(−sin t+cos t)i+et(cos t+sin t)j,a=−2etsin ti+2etcos tj; when t=π/4, v=√2eπ/4j,
a=−√2eπ/4i+√2eπ/4j,kvk=√2eπ/4,v·a=2e
π/2,v×a=2e
π/2kso aT=√2eπ/4,
aN=√2eπ/4
(b) aTT=√2eπ/4j,a
N
N=a−a
T
T=−
√
2e
π/4i
(c) κ=1
√2eπ/4
35. (a) v =i+2tj+3t
2
k,a=2j+6tk; when t=1,v=i+2j+3k,a=2j+6k,kvk=√
14,
v·a= 22, v×a=6i−6j+2kso aT=22/
√
14, aN=√76/√14 = p38/7
(b) aTT=11
7i+22
7j+33
7k,a
N
N=a−a
T
T=−
11
7i−8
7j+9
7k
(c) κ=√19
7√14
36. (a) v =eti−2e−2tj+k,a=eti+4e
−2t
j; when t=0,v=i−2j+k,a=i+4j,kvk=√
6,
v·a=−7, v×a=−4i+j+6kso aT=−7/√6, aN=p53/6
Exercise Set 14.6 516
(b) aTT=−7
6(i−2j+k),a
NN=a−a
TT=13
6i+19
3j+7
6k
(c) κ=√53
6√6
37. (a) v = 3 cos ti−2 sin tj−2 cos 2tk,a=−3 sin ti−2 cos tj+4 sin 2tk; when t=π/2, v=−2j+2k,
a=−3i,kvk=2
√
2, v·a=0,v×a=−6j−6kso aT=0,a
N=3
(b) aTT=0,a
NN=a=−3i
(c) κ=3
8
38. (a) v =3t
2
j−(16/t)k,a=6tj+ (16/t2)k; when t=1,v=3j−16k,a=6j+16k,kvk=√265,
v·a=−238, v×a= 144iso aT=−238/√265, aN= 144/√265
(b) aTT=−714
265j+3808
265 k,a
N
N=a−a
T
T=2304
265 j+432
265k
(c) κ=144
2653/2
39. kvk=4,v·a=−12, v×a=8kso aT=−3, aN=2,T=−j,N=(a−a
TT)/aN=i
40. kvk=√5, v·a=3,v×a=−6kso aT=3/
√
5, aN=6/
√
5, T=(1/
√
5)(i+2j),
N=(a−a
TT)/aN=(1/
√
5)(2i−j)
41. kvk=3,v·a=4,v×a=4i−3j−2kso aT=4/3, aN=√29/3, T=(1/3)(2i+2j+k),
N=(a−a
TT)/aN=(i−8j+14k)/(3√29)
42. kvk=5,v·a=−5, v×a=−4i−10j−3kso aT=−1, aN=√5, T=(1/5)(3i−4k),
N=(a−a
TT)/aN=(8i−5j+6k)/(5√5)
43. aT=d2s
dt2=d
dtp3t2+4=3t/p3t2+ 4 so when t=2,a
T=3/2.
44. aT=d2s
dt2=d
dtpt2+e−3t=(2t−3e
−3t
)/[2pt2+e−3t] so when t=0,a
T=−3/2.
45. aT=d2s
dt2=d
dtp(4t−1)2+ cos2πt =[4t−1−πcos πt sin πt]/p(4t−1)2+ cos2πt so when
t=1/4, aT=−π/√2.
46. aT=d2s
dt2=d
dtpt4+5t
2+3=(2t
3+5t)/
pt
4+5t
2+ 3 so when t=1,a
T=7/3.
47. aN=κ(ds/dt)2=(1/ρ)(ds/dt)2=(1/1)(2.9×105)2=8.41 ×1010 km/s2
48. a =(d
2
s/dt2)T+κ(ds/dt)2Nwhere κ=|d2y/dx2|
[1+(dy/dx)2]3/2.Ifd
2
y/dx2= 0, then κ= 0 and
a=(d
2
s/dt2)Tso ais tangent to the curve.
49. aN=κ(ds/dt)2=[2/(1+4x
2
)
3/2
](3)2=18/(1+4x
2
)
3/2
50. y=ex,a
N=κ(ds/dt)2=[e
x
/(1+e2x)3/2](2)2=4e
x
/(1+e2x)3/2
517 Chapter 14
51. a =aTT+aNN; by the Pythagorean Theorem aN=pkak2−a2
T=√9−9=0
52. As in Exercise 51, kak2=a2
T+a2
N,81=9+a
2
N,a
N=√72=6
√
2.
53. Let c=ds/dt, aN=κds
dt 2
,a
N=1
1000c2,soc
2= 1000aN,c≤10√10√1.5≈38.73 m/s.
54. 10 km/h is the same as 100
36 m/s, so kFk= 500 1
15 100
36 2
≈257.20 N.
55. (a) v0= 320, α=60
◦
,s
0=0sox= 160t,y= 160√3t−16t2.
(b) dy/dt = 160√3−32t,dy/dt = 0 when t=5
√
3so
y
max = 160√3(5√3) −16(5√3)2= 1200 ft.
(c) y=16t(10√3−t), y= 0 when t= 0 or 10√3sox
max = 160(10√3) = 1600√3 ft.
(d) v(t) = 160i+ (160√3−32t)j,v(10√3) = 160(i−√3j), kv(10√3)k= 320 ft/s.
56. (a) v0= 980, α=45
◦
,s
0=0sox= 490√2t,y= 490√2t−4.9t2
(b) dy/dt = 490√2−9.8t,dy/dt = 0 when t=50
√
2so
y
max = 490√2(50√2) −4.9(50√2)2=24,500 m.
(c) y=4.9t(100√2−t), y= 0 when t= 0 or 100√2so
x
max = 490√2(100√2)=98,000 m.
(d) v(t) = 490√2i+ (490√2−9.8t)j,v(100√2) = 490√2(i−j), kv(100√2)k= 980 m/s.
57. v0= 80, α=−60◦,s0= 168 so x=40t,y= 168 −40√3t−16t2;y= 0 when
t=−7√3/2 (invalid) or t=√3sox(
√
3)=40
√
3 ft.
58. v0= 80, α=0
◦
,s
0= 168 so x=80t,y= 168 −16t2;y= 0 when t=−√42/2 (invalid) or
t=√42/2sox(
√
42/2)=40
√
42 ft.
59. α=30
◦
,s
0=0sox=√
3v
0
t/2, y=v0t/2−16t2;dy/dt =v0/2−32t,dy/dt = 0 when t=v0/64
so ymax =v2
0/256 = 2500, v0= 800 ft/s.
60. α=45
◦
,s
0=0sox=√
2v
0
t/2, y=√2v0t/2−4.9t2;y= 0 when t=0or√
2v
0
/9.8so
x
max =v2
0/9.8=24,500, v0= 490 m/s.
61. v0= 800, s0=0sox= (800 cos α)t,y= (800 sin α)t−16t2=16t(50 sin α−t); y= 0 when t=0
or 50 sin αso xmax =40,000 sin αcos α=20,000 sin 2α=10,000, 2α=30
◦or 150◦,α=15
◦
or 75◦.
62. (a) v0=5,α=0
◦
,s
0=4sox=5t,y=4−16t2;y= 0 when t=−1/2 (invalid) or 1/2soit
takes the ball 1/2 s to hit the floor.
(b) v(t)=5i−32tj,v(1/2)=5i−16j,kv(1/2)k=√281 so the ball hits the floor with a speed
of √281 ft/s.
(c) v0=0,α=−90◦,s0=4sox=0,y=4−16t2;y= 0 when t=1/2 so both balls would hit
the ground at the same instant.
Exercise Set 14.6 518
63. (a) v0=40,α=60,s
0=4,sox=20t, y =4+20
√
3t−16t2; when x=15,t=3
4,
y=4+20
√
33
4−16 3
42
≈20.98 ft, so the water clears the corner point Awith 0.98 ft to
spare.
(b) y= 20 when −16t2+25
√
3t−16=0,t =0.668 (reject) or 1.500,x(1.500) ≈30 ft, so the
water hits the roof.
(c) about 15 ft
64. x=(v
0
/2)t, y =4+(v
0
√
3/2)t−16t2, solve x=15,y = 20 simultaneously for v0and t,
v0/2=15/t, t2=15
16√3−1,t ≈0.7898,v
0≈30/0.7898 ≈37.98 ft/s.
65. (a) x= (35√2/2)t, y = (35√2/2)t−4.9t2, from Exercise 17a in Section 14.5
κ=|x0y00 −x00 y0|
[(x0)2+(y
0
)
2
]
3/2,κ(0) = 9.8
352√2=0.004√2≈0.00566
(b) y0(t) = 0 when t=25
14√2,y =125
4m
66. (a) a =aTT+aNN,a
T=d
2s
dt2=−7.5 ft/s2,aN=κds
dt 2
=1
ρ(132)2=1322
3000 ft/s2,
kak=pa2
T+a2
N=s(7.5)2+1322
30002
≈9.49 ft/s2
(b) cos θ=a·T
kakkTk=aT
kak≈−7.5
9.49 ≈−0.79,θ ≈2.48 radians ≈142◦
67. s0=0sox=(v
0cos α)t,y=(v
0sin α)t−gt2/2
(a) dy/dt =v0sin α−gt so dy/dt = 0 when t=(v
0sin α)/g,ymax =(v
0sin α)2/(2g)
(b) y= 0 when t= 0 or (2v0sin α)/g,sox=R=(2v
2
0sin αcos α)/g =(v
2
0sin 2α)/g when
t=(2v
0sin α)/g;Ris maximum when 2α=90
◦
,α=45
◦
, and the maximum value of R
is v2
0/g.
68. The range is (v2
0sin 2α)/g and the maximum range is v2
0/g so (v2
0sin 2α)/g =(3/4)v2
0/g,
sin 2α=3/4, α=(1/2) sin−1(3/4) ≈24.3◦or α=(1/2)[180◦−sin−1(3/4)] ≈65.7◦.
69. v0= 80, α=30
◦
,s
0=5sox=40
√
3t,y=5+40t−16t2
(a) y= 0 when t=(−40±p(40)2−4(−16)(5))/(−32)=(5±√
30)/4, reject (5 −√30)/4toget
t=(5+√
30)/4≈2.62 s.
(b) x≈40√3(2.62) ≈181.5 ft.
70. (a) v0=v,s0=hso x=(vcos α)t,y=h+(vsin α)t−1
2gt2.Ifx=R, then (vcos α)t=R,
t=R
vcos αbut y= 0 for this value of tso h+(vsin α)[R/(vcos α)] −1
2g[R/(vcos α)]2=0,
h+ (tan α)R−g(sec2α)R2/(2v2)=0,g(sec2α)R2−2v2(tan α)R−2v2h=0.

519 Chapter 14
(b) 2gsec2αtan αR2+2gsec2αRdR
dα −2v2sec2αR −2v2tan αdR
dα =0;ifdR
dα = 0 and α=α0
when R=R0, then 2gsec2α0tan α0R2
0−2v2sec2α0R0=0,gtan α0R0−v2=0,
tan α0=v2/(gR0).
(c) If α=α0and R=R0, then from part (a) g(sec2α0)R2
0−2v2(tan α0)R0−2v2h= 0, but from
part (b) tan α0=v2/(gR0)sosec
2
α
0= 1 + tan2α0=1+v
4
/(gR0)2thus
g[1+v4/(gR0)2]R2
0−2v2[v2/(gR0)]R0−2v2h=0,gR2
0−v4/g −2v2h=0,
R
2
0=v
2
(v
2+2gh)/g2,R0=(v/g)pv2+2gh and
tan α0=v2/(vpv2+2gh)=v/pv2+2gh,α0= tan−1(v/pv2+2gh).
71. (a) v0(cos α)(2.9) = 259 cos 23◦so v0cos α≈82.21061, v0(sin α)(2.9) −16(2.9)2=−259 sin 23◦
so v0sin α≈11.50367; divide v0sin αby v0cos αto get tanα≈0.139929, thus α≈8◦
and v0≈82.21061/cos 8◦≈83 ft/s.
(b) From part (a), x≈82.21061tand y≈11.50367t−16t2for 0 ≤t≤2.9; the distance traveled
is Z2.9
0p(dx/dt)2+(dy/dt)2dt ≈268.76 ft.
EXERCISE SET 14.7
1. The results follow from formulae (1) and (7) of Section 12.5.
2. (a) (rmax −rmin)/(rmax +rmin)=2ae/(2a)=e
(b) rmax/rmin =(1+e)/(1 −e), and the result follows.
3. (a) From (15) and (6), at t=0,
C=v
0×b
0−GMu=v0j×r0v0k−GMu=r0v2
0i−GMi=(r
0
v
2
0−GM)i
(b) From (22), r0v2
0−GM =GMe, so from (7) and (17), v×b=GM(cos θi+ sin θj)+GMei,
and the result follows.
(c) From (10) it follows that bis perpendicular to v, and the result follows.
(d) From Part (c) and (10), kv×bk=kvkkbk=vr0v0. From Part (b),
kv×bk=GMq(e+ cos θ)2+ sin2θ=GM√e2+2ecos θ+1.By (10) and
Part (d), kv×bk=kvkkbk=v(r0v0)thusv=GM
r0v0pe2+2ecos θ+ 1. From (22),
r0v2
0/(GM)=1+e,GM/(r0v0)=v
0
/(1+e)sov=v
0
1+epe
2+2ecos θ+1.
4. At the end of the minor axis, cos θ=−c/a =−eso
v=v0
1+epe
2+2e(−e)+1= v
0
1+ep1−e
2=v
0
r1−e
1+e.
5. vmax occurs when θ=0sov
max =v0;vmin occurs when θ=πso
vmin =v0
1+epe
2−2e+1=v
max
1−e
1+e,thusv
max =vmin
1+e
1−e.
6. If the orbit is a circle then e= 0 so from Part (e) of Exercise 3, v=v0at all points on the orbit.
Use (22) with e= 0 to get v0=pGM/r0so v=pGM/r0.
Chapter 14 Supplementary Exercises 520
7. r0= 6440 + 200 = 6640 km so v=p3.99 ×105/6640 ≈7.75 km/s.
8. From Example 1, the orbit is 22,352 mi above the Earth, thus v≈s1.24 ×1012
26,352 ≈6859.68 mi/h.
9. From (23) with r0= 6440 + 300 = 6740 km, vesc =r2(3.99) ×105
6740 ≈10.88 km/s.
10. From (29), T=2π
√GM a3/2. But T= 1 yr = 365 ·24 ·3600 s, thus M=4π2a3
GT 2≈1.99 ×1030 kg.
11. (a) At perigee, r=rmin =a(1 −e) = 238,900 (1 −0.055) ≈225,760 mi; at apogee,
r=rmax =a(1+e) = 238,900(1 + 0.055) ≈252,040 mi. Subtract the sum
of the radius of the moon and the radius of the Earth to get
minimum distance = 225,760 −5080 = 220,680 mi,
and maximum distance = 252,040 −5080 = 246,960 mi.
(b) T=2π
pa
3
/(GM)=2π
p(238,900)3/(1.24 ×1012)≈659 hr ≈27.5 days.
12. (a) rmin = 6440 + 649 = 7,089 km, rmax = 6440 + 4,340 = 10,780 km so
a=(r
min +rmax)/2 = 8934.5 km.
(b) e= (10,780 −7,089)/(10,780 + 7,089) ≈0.207.
(c) T=2π
pa
3
/(GM)=2π
p(8934.5)3/(3.99 ×105)≈8400 s ≈140 min
13. (a) r0= 4000 + 180 = 4180 mi, v=p1.24 ×1012/4180 ≈17,224 mph
(b) r0= 4180 mi, v0=17,224+600 = 17,824 mi/h; e=r0v2
0
GM −1=(4180)(17,824)2
1.24 ×1012 −1≈0.07094.
rmax = 4180(1 + 0.07094)/(1 −0.07094) ≈4818 mi; the apogee altitude
is 4818 −4000 = 818 mi.
14. By equation (20), r=k
1+ecos θ, where k>0. By assumption, ris minimal when θ=0,
hence e≥0.
CHAPTER 14 SUPPLEMENTARY EXERCISES
2. (a) the line through the tips of r0and r1
(b) the line segment connecting the tips of r0and r1
(c) the line through the tip of r0which is parallel to r0(t0)
4. (a) speed (b) distance traveled (c) distance of the particle from the origin
7. (a) r(t)=Zt
0
cos πu2
2du i+Zt
0
sin πu2
2du j;
dr
dt
2
=x0(t)2+y0(t)2= cos2πt2
2+ sin2πt2
2= 1 and r(0) = 0
521 Chapter 14
(b) r0(s) = cos πs2
2i+ sin πs2
2j,r00 (s)=−πs sin πs2
2i+πs cos πs2
2j,
κ=kr00 (s)k=π|s|
(c) κ(s)→+∞, so the spiral winds ever tighter.
8. (a) The tangent vector to the curve is always tangent to the sphere.
(b) kvk= const, so v·a= 0; the acceleration vector is always perpendicular to the velocity
vector
(c) kr(t)k2=1−1
4cos2t(cos2t+ sin2t)+1
4cos2t=1
9. (a) kr(t)k= 1, so by Theorem 14.2.7, r0(t) is always perpendicular to the vector r(t). Then
v(t)=Rω(−sin ωti+ cos ωtj),v =kv(t)k=Rω
(b) a =−Rω2(cos ωti+ sin ωtj),a =kak=Rω2, and a=−ω2ris directed toward the origin.
(c) The smallest value of tfor which r(t)=r(0) satisfies ωt =2π,soT=t=2π
ω.
10. (a) F=kFk=mkak=mRω2=mR v2
R2=mv2
R
(b) R= 6440 + 3200 = 9600 km, 6.5=v=Rω = 9600ω, ω =6.5
9600 =13
19,200,
a=−ar
krk=−Rω2r
R=−Rω2(cos ωti+sin ωtj)=−13
2cos 13t
19,200i+ sin 13t
19,200j
(c) F=ma =702
13 kg ·km/s2≈10.77 N
11. (a) Let r=xi+yj+zk, then x2+z2=t2(sin2πt + cos2πt)=t
2=y
2
xy
z
(b) Let x=t, then y=t2,z =±p4−t
2/3−t
4/6
x
y
z
Chapter 14 Supplementary Exercises 522
12.
x
y
t = 0
t = 1 t = 1
3
t = 2
3
13. (a) ker(t)k2= cos2θ+sin2θ=1,soe
r
(t) is a unit vector; r(t)=r(t)e(t), so they have the same
direction if r(t)>0, opposite if r(t)<0. eθ(t) is perpendicular to er(t) since er(t)·eθ(t)=0,
and it will result from a counterclockwise rotation of er(t) provided e(t)×eθ(t)=k, which
is true.
(b) d
dter(t)=dθ
dt (−sin θi+ cos θj)=dθ
dt eθ(t) and d
dteθ(t)=−dθ
dt (cos θi+ sin θj)=−dθ
dt er(t), so
v(t)= d
dtr(t)= d
dt(r(t)er(t)) = r0(t)er(t)+r(t)dθ
dt eθ(t)
(c) From Part (b), a=d
dtv(t)
=r00 (t)er(t)+r
0
(t)dθ
dt eθ(t)+r
0
(t)dθ
dt eθ(t)+r(t)d
2
θ
dt2eθ(t)−r(t)dθ
dt 2
er(t)
="d2r
dt2−rdθ
dt 2#er(t)+rd
2
θ
dt2+2dr
dt
dθ
dt eθ(t)
14. The height y(t) of the rocket satisfies tan θ=y/b, y =btan θ, v =dy
dt =dy
dθ
dθ
dt =bsec2θdθ
dt .
15. r =r0+t
−→
PQ=(t−1)i+(4−2t)j+(3+2t)k;
dr
dt
=3,r(s)=s−3
3i+12 −2s
3j+9+2s
3k
16. By equation (26) of Section 14.6, r(t) = (60 cos α)ti+ ((60 sin α)t−16t2+4)j, and the maximum
height of the baseball occurs when y0(t)=0,60 sin α=32t, t =15
8sin α, so the ball clears the
ceiling if ymax = (60 sin α)15
8sin α−16152
82sin2α+4≤25,152sin2α
4≤21,sin2α≤28
75. The ball
hits the wall when x=60,t = sec α, and y(sec α)=60sinαsec α−16 sec2α+ 4. Maximize the
height h(α)=y(sec α)=60tanα−16 sec2α+ 4, subject to the constraint sin2α≤28
75. Then
h0(α)=60sec
2
α−32 sec2αtan α=0,tan α=60
32 =15
8, so sin α=15
√82+15
2=15
17, but for
this value of αthe constraint is not satisfied (the ball hits the ceiling). Hence the maximum
value of hoccurs at one of the endpoints of the α-interval on which the ball clears the ceiling, i.e.
h0,sin−1p28/75i. Since h0(0) = 60, it follows that his increasing throughout the interval, since
h0>0 inside the interval. Thus hmax occurs when sin2α=28
75,hmax = 60 tan α−16 sec2α+4=
60√28
√47 −1675
47 +4= 120√329 −1012
47 ≈24.78 ft. Note: the possibility that the baseball keeps
climbing until it hits the wall can be rejected as follows: if so, then y0(t) = 0 after the ball hits
the wall, i.e. t=15
8sin αoccurs after t= sec α, hence 15
8sin α≥sec α, 15 sin αcos α≥8,
15 sin 2α≥16, impossible.

523 Chapter 14
17. r0(1)=3i+10j+10k,soifr
0
(t)=3t
2
i+10j+10tkis perpendicular to r0(1), then
9t2+ 100 + 100t=0,t =−10,−10/9,
so r=−1000i−100j+ 500k,−(1000/729)i−(100/9)j+ (500/81)k.
18. Let r(t)=x(t)i+y(t)j, then dx
dt =x(t),dy
dt =y(t),x(0) = x0,y(0) = y0,so
x(t)=x
0
e
t
,y(t)=y
0
e
t
,r(t)=e
t
r
0
19. (a) dv
dt =2t
2
i+j+ cos 2tk,v0=i+2j−k,sox
0
(t)=2
3
t
3+1,y
0
(t)=t+2,z0
(t)=1
2sin 2t−1,
x(t)=1
6
t
4+t, y(t)=1
2
t
2+2t, z(t)=−1
4cos 2t−t+1
4, since r(0) = 0. Hence
r(t)=1
6
t
4+t
i+1
2
t
2+2t
j−1
4cos 2t+t−1
4k
(b) ds
dt it=1 =kr0(t)kit=1p(5/3)2+9+(1−(sin 2)/2)2≈3.475
20. kvk2=v(t)·v(t),2kvkd
dtkvk=2v·a,d
dt (kvk)= 1
kvk(v·a)
524
CHAPTER 15
Partial Derivatives
EXERCISE SET 15.1
1. (a) f(2,1) = (2)2(1)+1=5 (b) f(1,2) = (1)2(2)+1=3
(c) f(0,0) = (0)2(0)+1=1 (d) f(1,−3) = (1)2(−3)+1=−2
(e) f(3a, a)=(3a)
2
(a)+1=9a
3+1 (f) f(ab,a−b)=(ab)2(a−b)+1=a
3
b
2−a
2
b
3+1
2. (a) 2t(b) 2x(c) 2y2+2y
3. (a) f(x+y, x −y)=(x+y)(x−y)+3=x
2−y
2+3
(b) fxy, 3x2y3=(xy)3x2y3+3=3x
3
y
4+3
4. (a) (x/y) sin(x/y)(b) xy sin(xy)(c) (x−y) sin(x−y)
5. F(g(x),h(y)) = Fx3,3y+1
=x
3
e
x
3
(3y+1)
6. g(u(x, y),v(x, y)) = gx2y3,πxy
=πxy sin hx2y32(πxy)i=πxy sin πx5y7
7. (a) t2+3t
10 (b) 0(c) 3076
8. √te−3ln
(
t
2+1)=√t
(t2+1)
3
9. (a) 19 (b) −9(c) 3
(d) a6+3 (e) −t8+3 (f) (a+b)(a−b)2b3+3
10. (a) x2(x+y)(x−y)+(x+y)=x
2x
2−y
2
+(x+y)=x
4−x
2
y
2+x+y
(b) (xz)(xy)(y/x)+xy =xy2z+xy
11. Fx2,y+1,z2=(y+1)e
x
2
(y+1)z2
12. gx2z3, πxyz, xy/z=(xy/z) sin πx3yz4
13. (a) f(√5,2,π,−3π)=80
√
π(b) f(1,1,...,1) =
n
X
k=1
k=n(n+1)/2
14. (a) f(−2,2,0,π/4)=1
(b) f(1,2,...,n)=n(n+ 1)(2n+1)/6, see (Theorem 2(b), Section 7.4)
15.
1
x
y16.
2
x
y
525 Chapter 15
17.
x
y18.
x
y
19. (a) all points above or on the line y=−2
(b) all points on or within the sphere x2+y2+z2=25
(c) all points in 3-space
20. (a) all points on or between the vertical lines x=±2.
(b) all points above the line y=2x
(c) all points not on the plane x+y+z=0
21.
3
x
y
z22.
(0, 3, 0)
z
y
x
23. z
y
x
24. z
y
x
25. z
y
x
26.
(2, 0, 0)
(0, 2, 0)
(0, 0, 4)
z
y
x

Exercise Set 15.1 526
27. z
y
x
(0, 0, 1)
28.
(0, 1, 0)
(1, 0, 0)
z
y
x
29. z
y
x
(0, 0, 1)
(0, –1, 0)
30. z
y
x
31.
1234k = 0
x
y32.
k = -1
k = -2 k = 2
k = 1
k = 0x
y
33.
x
y
k = 2
k = 1
k = 0
k = –1
k = –2
34.
1234
k = 0
x
y
527 Chapter 15
35.
x
y
k = 2
k = 2
k = 1
k = 1
k = 0
k = 0
k = –1
k = –1
k = –2
k = –2
-2
-2
2
2
36.
2
co
k = -2
k = 2
k = -1
k = 0
k = 1
x
y
37.
(0, 4, 0)
(0, 0, 2)
(2, 0, 0)
z
y
x
38. z
y
x
39.
(0, 0, 3)
z
xy
40.
(0, 0, 1)
( , 0, 0)
1
4
(0, − , 0)
1
2
z
x
y
41. concentric spheres, common center at (2,0,0)
42. parallel planes, common normal 3i−j+2k
43. concentric cylinders, common axis the y-axis
44. circular paraboloids, common axis the z-axis, all the same shape but with different vertices along
z-axis.
45. (a) f(−1,1)=0;x
2−2x
3+3xy =0 (b) f(0,0)=0;x
2−2x
3+3xy =0
(c) f(2,−1) = −18; x2−2x3+3xy =−18
Exercise Set 15.1 528
46. (a) f(ln 2, 1) = 2; yex=2 (b) f(0,3)=3;yex=3
(c) f(1,−2) = −2e;yex=−2e
47. (a) f(1,−2,0)=5;x
2+y
2−z=5 (b) f(1,0,3) = −2; x2+y2−z=−2
(c) f(0,0,0)=0;x
2+y
2−z=0
48. (a) f(1,0,2)=3;xyz +3=3,xyz =0 (b) f(−2,4,1) = −5; xyz +3=−5, xyz =−8
(c) f(0,0,0)=3;xyz =0
49. (a)
4
4
x
y
T = 1
T = 2
T = 3
(b) At (1,4) the temperature is
T(1,4) = 4 so the temperature
will remain constant along
the path xy =4.
50. V=8/
p16+x2+y2p16+x2+y2
=8/V x2+y2=64/V 2−16
the equipotential curves are circles.
10 20
20 V = 2.0
V = 1.0
V = 0.5x
y
51. (a) f(x, y)=1−x
2−y
2
, because f=cis a circle of radius √1−c(provided c≤1), and the
radii in (a) decrease as cincreases.
(b) f(x, y)=p
x
2+y
2because f=cis a circle of radius c, and the radii increase uniformly.
(a) is the contour plot of f(x, y)=1−x
2−y
2
, because f=cis a circle of radius √1−c
(provided c≤1), and the radii in (a) decrease as cincreases.
(c) f(x, y)=x
2+y
2because f=cis a circle of radius √cand the radii in the plot grow like
the square root function.
52. (a) III (b) IV (c) I(d) II
53. (a) A(b) B(c) increase
(d) decrease (e) increase (f) decrease
54. (a) Calgary, since the contour lines are closer together near Calgary than they are near Chicago.
(b) The change in atmospheric pressure is about ∆p≈1012 −999 = 13, so the average rate of
change is ∆p/1600 ≈0.0081.
529 Chapter 15
55. (a)
5-5
-3
2(b)
4
-4
-3
1
56. (a) 10
-10
-10 10
(b) 10
-10
-10 10
57. (a) z
xy
(b)
-2 -1 0 1 2
-2
-1
0
1
2
58. (a)
0
1
2
3
4 x
0y
-5
0
5
z
6cio
(b)
0 1 2 3 4
0
3
6
9
c
f
i
l
o
59. (a) The graph of gis the graph of fshifted one unit in the positive x-direction.
(b) The graph of gis the graph of fshifted one unit up the z-axis.
(c) The graph of gis the graph of fshifted one unit down the y-axis and then inverted with
respect to the plane z=0.
Exercise Set 15.2 530
60. (a) z
y
x
(b) If ais positive and increasing then the graph of gis more pointed, and in the limit as a→+∞
the graph approaches a ’spike’ on the z-axis of height 1. As adecreases to zero the graph of
ggets flatter until it finally approaches the plane z=1.
EXERCISE SET 15.2
1.
-1
x
y2.
y = x
x
y3.
5
x
y
4.
1
y = 2x + 1
x
y5.
x
y6.
x
y
7.
x
y
xy = –1
xy = 1
xy = 1
xy = –1
8.
x
y
9. all of 3-space

531 Chapter 15
10. all points inside the sphere with radius 2 and center at the origin
11. all points not on the cylinder x2+z2=1 12. all of 3-space
13. 35 14. π2/215. −8
16. e−717. 018. 0
19. (a) Along x= 0 lim
(x,y)→(0,0)
3
x2+2y
2= lim
y→0
3
2y2does not exist.
(b) Along x=0,lim
(x,y)→(0,0)
x+y
x+y2= lim
y→0
1
ydoes not exist.
20. (a) Along y=0:lim
x→0
x
x
2= lim
x→0
1
xdoes not exist because
1
x→+∞as x→0 so the original
limit does not exist.
(b) Along y=0:lim
x→0
1
xdoes not exist, so the original limit does not exist.
21. Let z=x2+y2, then lim
(x,y)→(0,0)
sin x2+y2
x2+y2= lim
z→0+
sin z
z=1
22. Let z=x2+y2, then lim
(x,y)→(0,0)
1−cos x2+y2
x2+y2= lim
z→0+
1−cos z
z= lim
z→0+
sin z
1=0
23. Let z=x2+y2, then lim
(x,y)→(0,0) e−1/(x2+y2)= lim
z→0+e−1/z =0
24. With z=1
x2+y2, lim
z→+∞
1
√ze−1/√z; let w=1
√z,lim
w→+∞
w
ew=0
25. lim
(x,y)→(0,0) x2+y2x
2−y
2
x
2+y
2= lim
(x,y)→(0,0) x2−y2=0
26. lim
(x,y)→(0,0) x2+4y
2
x
2−4y
2
x
2+4y
2= lim
(x,y)→(0,0) x2−4y2=0
27. along y=0:lim
x→0
0
3x
2= lim
x→00 = 0; along y=x: lim
x→0
x2
5x2= lim
x→01/5=1/5
so the limit does not exist.
28. Let z=x2+y2, then lim
(x,y)→(0,0)
1−x2−y2
x2+y2= lim
z→0+
1−z2
z2=+∞so the limit does not exist.
29. 8/330. ln 5
31. Let t=px2+y2+z2, then lim
(x,y,z)→(0,0,0)
sin x2+y2+z2
px2+y2+z2= lim
t→0+
sin t2
t=0
Exercise Set 15.2 532
32. With t=px2+y2+z2, lim
t→0+
sin t
t2= lim
t→0+
cos t
2t=+∞so the limit does not exist.
33. yln(x2+y2)=rsin θln r2=2r(ln r) sin θ, so lim
(x,y)→(0,0) yln(x2+y2) = lim
r→0+2r(ln r) sin θ=0
34. x2y2
px2+y2=(r2cos2θ)(r2sin2θ)
r=r3cos2θsin2θ, so lim
(x,y)→(0,0)
x2y2
px2+y2=0
35. e√x2+y2+z2
px2+y2+z2=eρ
ρ, so lim
(x,y,z)→(0,0,0)
e√x2+y2+z2
px2+y2+z2= lim
ρ→0+
eρ
ρdoes not exist.
36. lim
(x,y,z)→(0,0,0) tan−11
x2+y2+z2= lim
ρ→0+tan−11
ρ2=π
2
37. (a) No, since there seem to be points near (0,0) with z= 0 and other points near (0,0) with
z≈1/2.
(b) lim
x→0
mx3
x4+m2x2= lim
x→0
mx
x2+m2=0 (c) lim
x→0
x4
2x4= lim
x→01/2=1/2
(d) A limit must be unique if it exists, so f(x, y) cannot have a limit as (x, y)→(0,0).
38. (a) Along y=mx : lim
x→0
mx4
2x6+m2x2= lim
x→0
mx2
2x4+m2=0;
along y=kx2: lim
x→0
kx5
2x6+k2x4= lim
x→0
kx
2x2+k2=0.
(b) lim
x→0
x6
2x6+x6= lim
x→0
1
3=1
36=0
39. (a) lim
t→0
abct3
a2t2+b4t4+c4t4= lim
t→0
abct
a2+b4t2+c4t2=0
(b) lim
t→0
t4
t4+t4+t4= lim
t→01/3=1/3
40. π/2 because x2+1
x
2+(y−1)2→+∞as (x, y)→(0,1)
41. −π/2 because x2−1
x2+(y−1)2→−∞as (x, y)→(0,1)
42. with z=x2+y2, lim
z→0+
sin z
z=1=f(0,0)
43. No, because lim
(x,y)→(0,0)
x2
x2+y2does not exist.
Along x=0:lim
y→00/y2= lim
y→00 = 0; along y=0:lim
x→0x
2
/x2= lim
x→01=1.
44. Using polar coordinates with r>0, xy =r2sin θcos θand x2+y2=r2so
|xy ln x2+y2|=|r2sin θcos θln r2|≤|2r
2ln r|, but lim
r→0+2r2ln r= 0 thus
lim
(x,y)→(0,0) xy ln x2+y2=0;f(x, y) will be continuous at (0,0) if we define f(0,0)=0.
533 Chapter 15
EXERCISE SET 15.3
1. (a) 9x2y2(b) 6x3y(c) 9y2(d) 9x2
(e) 6y(f) 6x3(g) 36 (h) 12
2. (a) 2e2xsin y(b) e2xcos y(c) 2 sin y(d) 0
(e) cos y(f) e2x(g) 0(h) 4
3. (a) −1
4x3/2cos y(b) −√xcos y(c) −sin y
2√x(d) −sin y
2√x
4. (a) 8+84x
2
y
5(b) 140x4y3(c) 140x3y4(d) 140x3y4
5. (a) ∂z
∂x =3
2√3x+2y; slope = 3
8(b) ∂z
∂y =1
√3x+2y; slope = 1
4
6. (a) ∂z
∂x =e−y; slope = 1 (b) ∂z
∂y =−xe−y+ 5; slope = 2
7. (a) ∂z
∂x =−4 cos(y2−4x); rate of change = −4 cos 7
(b) ∂z
∂y =2ycos(y2−4x); rate of change = 2 cos 7
8. (a) ∂z
∂x =−1
(x+y)2; rate of change = −1
4(b) ∂z
∂y =−1
(x+y)2; rate of change = −1
4
9. ∂z/∂x = slope of line parallel to xz-plane = −4; ∂z/∂y = slope of line parallel to yz-plane = 1/2
10. The slope at Pin the positive x-direction is negative, the slope in the positive y-direction is
negative, thus ∂z/∂x < 0,∂z/∂y < 0; the curve through Pwhich is parallel to the x-axis is
concave down, so ∂2z/∂x2<0; the curve parallel to the y-axis is concave down, so ∂2z/∂y2<0.
11. ∂z/∂x =8xy3ex2y3,∂z/∂y =12x
2
y
2
e
x
2
y
3
12. ∂z/∂x =−5x4y4sin(x5y4), ∂z/∂y =−4x5y3sin x5y4
13. ∂z/∂x =x3/(y3/5+x)+3x
2ln(1 + xy−3/5),∂z/∂y=−(3/5)x4/(y8/5+xy)
14. ∂z/∂x =yexy sin(4y2),∂z/∂y=8yexy cos(4y2)+xexy sin(4y2)
15. ∂z
∂x =−y(x2−y2)
(x2+y2)2,∂z
∂y =x(x2−y2)
(x2+y2)216. ∂z
∂x =xy3(3x+4y)
2(x+y)3/2,∂z
∂y =x2y2(6x+5y)
2(x+y)3/2
17. fx(x, y)=(3/2)x2y5x2−73x
5y−7x
3y
−1/2
f
y(x, y)=(1/2)x33x2−73x
5y−7x
3y
−1/2
18. fx(x, y)=−2y/(x−y)2,fy(x, y)=2x/(x−y)2
19. fx(x, y)= y
−1/2
y
2+x
2,f
y
(x, y)=−xy−3/2
y2+x2−3
2y−5/2tan−1(x/y)

Exercise Set 15.3 534
20. fx(x, y)=3x
2
e
−y+(1/2)x−1/2y3sec √xtan √x,fy(x, y)=−x
3
e
−y+3y
2sec √x
21. fx(x, y)=−(4/3)y2sec2xy2tan x−7/3,fy(x, y)=−(8/3)ytan xy2tan x−7/3
22. fx(x, y)=2y
2cosh √xsinh xy2cosh xy2+1
2x−1/2sinh √xsinh2xy2
fy(x, y)=4xy cosh √xsinh xy2cosh xy2
23. fx(x, y)=−2x, fx(3,1) = −6; fy(x, y)=−21y2,f
y
(3,1) = −21
24. ∂f/∂x =x2y2exy +2xyexy,∂f/∂x
(1,1) =3e;∂f/∂y =x3yexy +x2exy,∂f/∂y
(1,1) =2e
25. ∂z/∂x =x(x2+4y2)−1/2,∂z/∂x
(1,2) =1/
√
17 ; ∂z/∂y =4y(x
2+4y2)−1/2,∂z/∂y
(1,2) =8/
√
17
26. ∂w/∂x =−x2ysin xy +2xcos xy, ∂w
∂x (1/2,π)=−π/4; ∂w/∂y =−x3sin x, ∂w
∂y (1/2,π)=−1/8
27. fx=8x−8y
4
,f
y=−32xy3+35y
4
,f
xy =fyx =−32y3
28. fx=x/px2+y2,f
y=y/px2+y2,f
xy =fyx =−xy(x2+y2)−3/2
29. fx=excos y, fy=−exsin y, fxy =fyx =−exsin y
30. fx=ex−y2,f
y=−2yex−y2,f
xy =fyx =−2yex−y2
31. fx=4/(4x−5y),f
y=−5/(4x−5y),f
xy =fyx =20/(4x−5y)2
32. fx=4xy2/(x2+y2)2,f
y=−4x
2
y/(x2+y2)2,f
xy =fyx =8xy(x2−y2)/(x2+y2)3
35. (a) 2x−2z(∂z/∂x)=0,∂z/∂x=x/z =±3/(2√6) = ±√6/4,∂z/∂x=±
√
6/4
(b) z=±px2+y2−1,∂z/∂x=±x/px2+y2−1=±
√
6/4
36. (a) 2y−2z(∂z/∂y)=0,∂z/∂y=y/z =±4/(2√6) = ±√6/3
(b) z=±px2+y2−1,∂z/∂y=±y/px2+y2−1=±
√
6/3
37. 3
2x2+y2+z21/22x+2z∂z
∂x=0,∂z/∂x =−x/z; similarly, ∂z/∂y =−y/z
38. 4x−3z2(∂z/∂x)
2x2+y−z3=1, ∂z
∂x =4x−2x2−y+z3
3z2;1−3z2(∂z/∂y)
2x2+y−z3=1, ∂z
∂y =1−2x2−y+z3
3z2
39. 2x+zxy ∂z
∂x +yzcos xyz +∂z
∂x sin xyz =0, ∂z
∂x =−2x+yz2cos xyz
xyz cos xyz + sin xyz ;
zxy ∂z
∂y +xzcos xyz +∂z
∂y sin xyz =0, ∂z
∂y =−xz2cos xyz
xyz cos xyz + sin xyz
40. exy(cosh z)∂z
∂x +yexy sinh z−z2−2xz ∂z
∂x =0, ∂z
∂x =z2−yexy sinh z
exy cosh z−2xz ;
exy(cosh z)∂z
∂y +xexy sinh z−2xz ∂z
∂y =0, ∂z
∂y =−xexy sinh z
exy cosh z−2xz
535 Chapter 15
41. III is a plane, and its partial derivatives are constants, so III cannot be f(x, y). If I is the graph
of z=f(x, y) then (by inspection) fyis constant as yvaries, but neither II nor III is constant as
yvaries. Hence z=f(x, y) has II as its graph, and as II seems to be an odd function of xand an
even function of y,fxhas I as its graph and fyhas III as its graph.
42. Moving to the right from (x0,y
0) decreases f(x, y), so fx<0; moving up increases f,sof
y>0.
43. (a) 30xy4−4(b) 60x2y3(c) 60x3y2
44. (a) 120(2x−y)2(b) −240(2x−y)2(c) 480(2x−y)
45. (a) fxyy(0,1) = −30 (b) fxxx(0,1) = −125 (c) fyyxx(0,1) = 150
46. (a) ∂3w
∂y2∂x =−eysin x,∂3w
∂y2∂x
(π/4,0)
=−1/√2
(b) ∂3w
∂x2∂y =−eycos x,∂3w
∂x2∂y
(π/4,0)
=−1/√2
47. (a) ∂3f
∂x3(b) ∂3f
∂y2∂x (c) ∂4f
∂x2∂y2(d) ∂4f
∂y3∂x
48. (a) fxyy (b) fxxxx (c) fxxyy (d) fyyyxx
49. (a) 2xy4z3+y(b) 4x2y3z3+x(c) 3x2y4z2+2z
(d) 2y4z3+y(e) 32z3+1 (f) 438
50. (a) 2xy cos z(b) x2cos z(c) −x2ysin z
(d) 4ycos z(e) 4 cos z(f) 0
51. fx=2z/x,fy=z/y,fz= ln(x2ycos z)−ztan z
52. fx=y−5/2zsec(xz/y) tan(xz/y), fy=−xy−7/2zsec(xz/y) tan(xz/y)−(3/2)y−5/2sec(xz/y),
fz=xy−5/2sec(xz/y) tan(xz/y)
53. fx=−y2z3/1+x
2
y
4
z
6
,f
y=−2xyz3/1+x
2
y
4
z
6
,f
z=−3xy2z2/1+x
2
y
4
z
6
54. fx=4xyz cosh √zsinh x2yzcosh x2yz,fy=2x
2
zcosh √zsinh x2yzcosh x2yz,
fz=2x
2
ycosh √zsinh x2yzcosh x2yz+(1/2)z−1/2sinh √zsinh2x2yz
55. ∂w/∂x =yzezcos xz,∂w/∂y =ezsin xz,∂w/∂z =yez(sin xz +xcos xz)
56. ∂w/∂x =2x/ y2+z2,∂w/∂y =−2yx2+z2/y2+z22,∂w/∂z =2zy
2−x
2
/y
2+z
2
2
57. ∂w/∂x =x/px2+y2+z2,∂w/∂y =y/px2+y2+z2,∂w/∂z =z/px2+y2+z2
58. ∂w/∂x =2y
3
e
2x+3z,∂w/∂y =3y
2
e
2x+3z,∂w/∂z =3y
3
e
2x+3z
59. (a) e(b) 2e(c) e
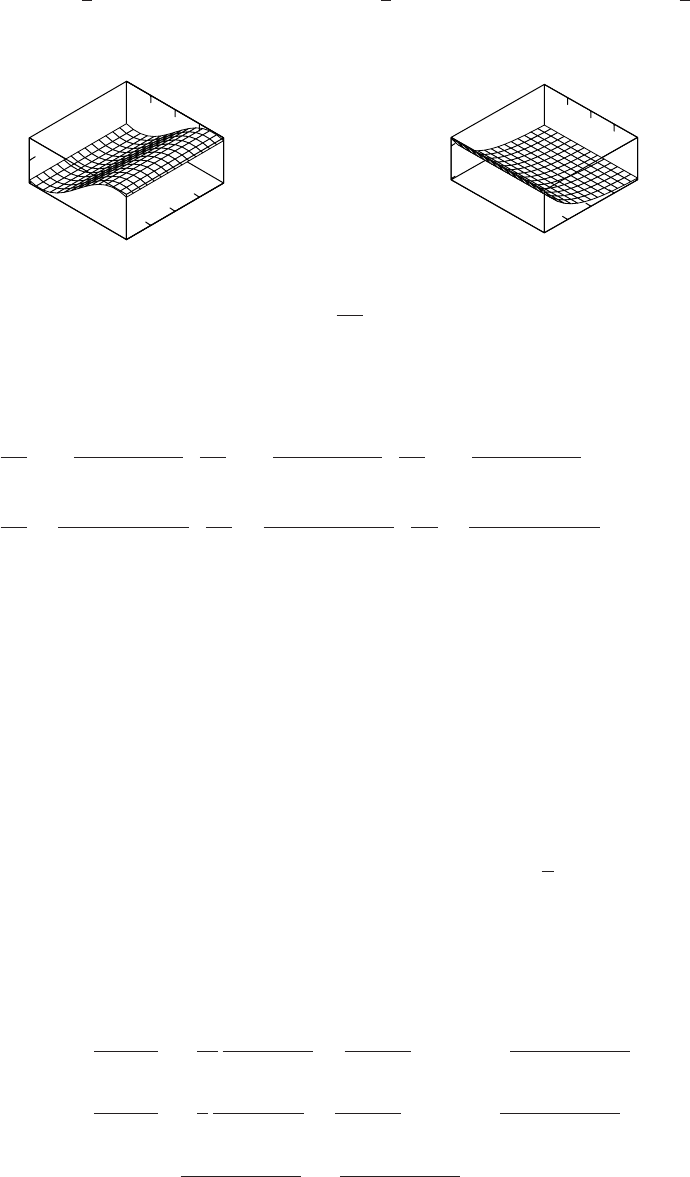
Exercise Set 15.3 536
60. (a) 2/√7(b) 4/√7(c) 1/√7
62.
-2
-1
0
1
2
x
-2
-1
0
1
2
-1
0
1
z
y
-2
-1
0
1
2
x
-2
-1
0
1
2
0
6
z
y
63. (3/2) x2+y2+z2+w21/22x+2w∂w
∂x =0,∂w/∂x =−x/w; similarly, ∂w/∂y =−y/w
and ∂w/∂z =−z/w
64. ∂w/∂x =−4x/3, ∂w/∂y =−1/3, ∂w/∂z =(2x
2+y−z
3+3z
2+3w)/3
65. ∂w
∂x =−yzw cos xyz
2w+ sin xyz ,∂w
∂y =−xzw cos xyz
2w+ sin xyz ,∂w
∂z =−xyw cos xyz
2w+ sin xyz
66. ∂w
∂x =yexy sinh w
z2−exy cosh w,∂w
∂y =xexy sinh w
z2−exy cosh w,∂w
∂z =2zw
exy cosh w−z2
67. (a) fxy =15x
2
y
4
z
7+2y(b) fyz =35x
3
y
4
z
6+3y
2
(c) fxz =21x
2
y
5
z
6(d) fzz =42x
3
y
5
z
5
(e) fzyy = 140x3y3z6+6y(f) fxxy =30xy4z7
(g) fzyx = 105x2y4z6(h) fxxyz = 210xy4z6
68. (a) 160(4x−3y+2z)
3(b) −1440(4x−3y+2z)
2(c) −5760(4x−3y+2z)
69. fx=ex2,f
y=−e
y
270. fx=yex2y2,f
y=xex2y2
71. ∂w/∂xi=−isin(x1+2x
2+...+nxn)72. ∂w/∂xi=1
n n
X
k=1
xk!(1/n)−1
73. (a) fx=2x+2y, fxx =2,f
y=−2y+2x, fyy =−2; fxx +fyy =2−2=0
(b) zx=exsin y−eysin x, zxx =exsin y−eycos x, zy=excos y+eycos x,
zyy =−exsin y+eycos x;zxx +zyy =exsin y−eycos x−exsin y+eycos x=0
(c) zx=2x
x2+y2−2y
x2
1
1+(y/x)2=2x−2y
x2+y2,z
xx =−2x2−y2−2xy
(x2+y2)2,
zy=2y
x2+y2+21
x
1
1+(y/x)2=2y+2x
x
2+y
2,z
yy =−2y2−x2+2xy
(x2+y2)2;
zxx +zyy =−2x2−y2−2xy
(x2+y2)2−2y2−x2+2xy
(x2+y2)2=0
537 Chapter 15
74. (a) zt=−e−tsin(x/c),z
x=(1/c)e−tcos(x/c),z
xx =−(1/c2)e−tsin(x/c);
zt−c2zxx =−e−tsin(x/c)−c2(−(1/c2)e−tsin(x/c))=0
(b) zt=−e−tcos(x/c),z
x=−(1/c)e−tsin(x/c),z
xx =−(1/c2)e−tcos(x/c);
zt−c2zxx =−e−tcos(x/c)−c2(−(1/c2)e−tcos(x/c))=0
75. ux=ωsin cωtcos ωx, uxx =−ω2sin cωtsin ωx, ut=cωcos cωtsin ωx, utt =−c2ω2sin cωtsin ωx;
uxx −1
c2utt =−ω2sin cωtsin ωx −1
c2(−c2)ω2sin cωtsin ωx =0
76. (a) ∂u/∂x =∂v/∂y =2x,∂u/∂y =−∂v/∂x =−2y
(b) ∂u/∂x =∂v/∂y =excos y,∂u/∂y =−∂v/∂x =−exsin y
(c) ∂u/∂x =∂v/∂y =2x/(x2+y2), ∂u/∂y =−∂v/∂x =2y/(x2+y2)
77. ∂u/∂x =∂v/∂y and ∂u/∂y =−∂v/∂x so ∂2u/∂x2=∂2v/∂x∂y, and ∂2u/∂y2=−∂2v/∂y∂x,
∂2u/∂x2+∂2u/∂y2=∂2v/∂x∂y −∂2v/∂y∂x,if∂
2
v/∂x∂y =∂2v/∂y∂x then
∂2u/∂x2+∂2u/∂y2=0;thususatisfies Laplace’s equation. The proof that vsatisfies Laplace’s
equation is similar. Adding Laplace’s equations for uand vgives Laplaces’ equation for u+v.
78. ∂z/∂y =6y,∂z/∂y (2,1) =6
79. ∂z/∂x =−x29 −x2−y2−1/2,∂z/∂x](4,3) =−2
80. (a) ∂z/∂y =8y,∂z/∂y](−1,1) =8 (b) ∂z/∂x =2x,∂z/∂x](−1,1) =−2
81. (a) ∂V/∂r =2πrh (b) ∂V/∂h =πr2
(c) ∂V/∂r]r=6,h=4 =48π(d) ∂V/∂h]r=8,h=10 =64π
82. (a) ∂V/∂s =πsd2
6√4s2−d2(b) ∂V/∂d =πd(8s2−3d2)
24√4s2−d2
(c) ∂V/∂s]s=10,d=16 = 320π/9(d) ∂V/∂d]s=10,d=16 =16π/9
83. (a) P=10T/V,∂P/∂T =10/V ,∂P/∂T ]T=80,V=50 =1/5 lb/(in2K)
(b) V=10T/P, ∂V/∂P =−10T/P2,if V= 50 and T= 80 then
P= 10(80)/(50) = 16,∂V/∂P]
T=80,P=16 =−25/8(in5/lb3)
84. (a) ∂z/∂y =x2,∂z/∂y](1,3) =1,j+kis parallel to the tangent line so x=1,y=3+t,
z=3+t
(b) ∂z/∂x =2xy,∂z/∂x](1,3) =6,i+6kis parallel to the tangent line so x=1+t,y=3,
z=3+6t
85. 1+∂z
∂xcos(x+z) + cos(x−y)=0, ∂z
∂x =−1−cos(x−y)
cos(x+z);∂z
∂y cos(x+z)−cos(x−y)=0,
∂z
∂y =cos(x−y)
cos(x+z);∂2z
∂x∂y =−cos(x+z) sin(x−y) + cos(x−y) sin(x+z)(1 + ∂z/∂x)
cos2(x+z),
substitute for ∂z/∂x and simplify to get ∂2z
∂x∂y =−cos2(x+z) sin(x−y) + cos2(x−y) sin(x+z)
cos3(x+z).

Exercise Set 15.4 538
86. ∂V/∂r =2
3πrh =2
r(1
3πr2h)=2V/r
87. (a) ∂T/∂x =3x
2+1, ∂T /∂x](1,2) =4 (b) ∂T /∂y =4y,∂T/∂y](1,2) =8
88. ∂2R/∂R2
1=−2R2
2/(R1+R2)3,∂
2
R/∂R2
2=−2R2
1/(R1+R2)3,
∂2R/∂R2
1∂2R/∂R2
2=4R
2
1
R
2
2
/(R
1+R
2
)
6=h4/(R
1+R
2
)
4
i[R
1
R
2
/(R
1+R
2
)]2
=4R
2
/(R
1+R
2
)
4
89. f(x+∆x, y)−f(x, y)
∆x=2(x+∆x)
2−3(x+∆x)y+y
2−(2x2−3xy +y2)
∆x=4x+2∆x−3y,
fx= lim
∆x→0
f(x+∆x, y)−f(x, y)
∆x= lim
∆x→0(4x+2∆x−3y)=4x−3y;f
x
(2,−1)=11
f(x, y +∆y)−f(x, y)
∆y=2x2−3x(y+∆y)+(y+∆y)
2−(2x2−3xy +y2)
∆y=−3x+2y+∆y,
fy= lim
∆y→0
f(x, y +∆y)−f(x, y)
∆y=−3x+2y;f
y(2,−1) = −8
90. fx(x, y)=2
3
(x
2+y
2
)
−1/3
(2x)= 4x
3(x2+y2)1/3,(x, y)6=(0,0);
fx(0,0) = d
dx[f(x, 0)]x=0
=d
dx[x4/3]x=0
=4
3x1/3x=0
=0.
91. (a) fy(0,0) = d
dy [f(0,y)]y=0
=d
dy [y]y=0
=1
(b) If (x, y)6=(0,0), then fy(x, y)=1
3
(x
3+y
3
)
−2/3
(3y2)= y
2
(x
3+y
3
)
2/3;
f
y
(x, y) does not exist where y=−x,x6=0.
EXERCISE SET 15.4
1. 42t13 2. 2(3 + t−1/3)
3(2t+t2/3)
3. 3t−2sin(1/t)4. 1−2t4−8t4ln t
2t√1+lnt−2t
4ln t
5. −10
3t7/3e1−t10/36. (1+t)etcosh (tet/2) sinh (tet/2)
7. ∂z/∂u =24u
2
v
2−16uv3−2v+3,∂z/∂v=16u
3
v−24u2v2−2u−3
8. ∂z/∂u =2u/v2−u2vsec2(u/v)−2uv2tan(u/v)
∂z/∂v =−2u2/v3+u3sec2(u/v)−2u2vtan(u/v)
9. ∂z/∂u =−2 sin u
3 sin v,∂z/∂v=−
2 cos ucos v
3 sin2v
10. ∂z/∂u =3+3v/u −4u, ∂z/∂v =2+3lnu+2lnv
539 Chapter 15
11. ∂z/∂u =eu,∂z/∂v =0
12. ∂z/∂u =−sin(u−v) sin u2+v2+2ucos(u−v) cos u2+v2
∂z/∂v = sin(u−v) sin u2+v2+2vcos(u−v) cos u2+v2
13. ∂T/∂r =3r
2sin θcos2θ−4r3sin3θcos θ
∂T/∂θ =−2r3sin2θcos θ+r4sin4θ+r3cos3θ−3r4sin2θcos2θ
14. dR/dφ =5e
5φ
15. ∂t/∂x =x2+y2/4x2y3,∂t/∂y =y2−3x2/4xy4
16. ∂w/∂u =2v2u2v2−(u−2v)2
[u2v2+(u−2v)
2
]
2,∂w/∂v =u2(u−2v)2−u2v2
[u2v2+(u−2v)
2
]
2
17. −π18. 351/2, −168
19. √3e√3,2−4√3e√320. 1161
21. F(x, y)=x
2
y
3+ cos y,dy
dx =−2xy3
3x2y2−sin y
22. F(x, y)=x
3−3xy2+y3−5, dy
dx =−3x2−3y2
−6xy +3y
2=x
2−y
2
2xy −y2
23. F(x, y)=e
xy +yey−1, dy
dx =−yexy
xexy +yey+ey
24. F(x, y)=x−(xy)1/2+3y−4, dy
dx =−1−(1/2)(xy)−1/2y
−(1/2)(xy)−1/2x+3 =2
√
xy −y
x−6√xy
25. D=x2+y21/2where xand yare the distances of cars A and B, respectively, from the
intersection and Dis the distance between them.
dD/dt =hx/ x2+y21/2i(dx/dt)+hy/ x2+y21/2i(dy/dt), dx/dt =−25 and dy/dt =−30
when x=0.3 and y=0.4sodD/dt =(0.3/0.5)(−25)+(0.4/0.5)(−30) = −39 mph.
26. T=(1/10)PV,dT/dt =(V/10)(dP/dt)+(P/10)(dV /dt), dV/dt = 4 and dP/dt =−1 when
V= 200 and P=5sodT/dt = (20)(−1)+(1/2)(4) = −18 K/s.
27. A=1
2ab sin θbut θ=π/6 when a= 4 and b=3soA=1
2
(4)(3) sin(π/6)=3.
Solve 1
2ab sin θ= 3 for θto get θ= sin−16
ab,0≤θ≤π/2.
dθ
dt =∂θ
∂a
da
dt +∂θ
∂b
db
dt =1
r1−36
a2b2−6
a2bda
dt +1
r1−36
a2b2−6
ab2db
dt
=−6
√a2b2−36 1
a
da
dt +1
b
db
dt ,da
dt = 1 and db
dt =1
when a= 4 and b=3so dθ
dt =−6
√144 −36 1
4+1
3=−7
12√3=−7
36√3 radians/s
Exercise Set 15.4 540
28. From the law of cosines, c=√a2+b2−2ab cos θwhere cis the length of the third side.
θ=π/3soc=√
a
2+b
2−ab,
dc
dt =∂c
∂a
da
dt +∂c
∂b
db
dt =1
2(a2+b2−ab)−1/2(2a−b)da
dt +1
2a2+b2−ab−1/2(2b−a)db
dt
=1
2√a2+b2−ab (2a−b)da
dt +(2b−a)db
dt ,da
dt = 2 and db
dt = 1 when a= 5 and b=10
so dc
dt =1
2√75[(0)(2) + (15)(1)] = √3/2 cm/s. The third side is increasing.
29. V=(π/4)D2hwhere Dis the diameter and his the height, both measured in inches,
dV/dt =(π/2)Dh(dD/dt)+(π/4)D2(dh/dt), dD/dt = 3 and dh/dt = 24 when D= 30 and
h= 240, so dV /dt =(π/2)(30)(240)(3) + (π/4)(30)2(24) = 16,200πin3/year.
30. dT
dt =∂T
∂x
dx
dt +∂T
∂y
dy
dt =y2
x
dx
dt +2yln xdy
dt ,dx/dt = 1 and dy/dt =−4 at (3,2) so
dT/dt =(4/3)(1) + (4 ln 3)(−4)=4/3−16 ln 3◦C/s.
31. (a) xy-plane, fx=12x
2
y+6xy, fy=4x
3+3x
2
,f
xy =fyx =12x
2+6x
(b) y6=0,f
x=3x
2
/y, fy=−x3/y2,f
xy =fyx =−3x2/y2
32. (a) x2+y2>1, (the exterior of the circle of radius 1 about the origin);
fx=x/px2+y2−1,f
y=y/px2+y2−1,f
xy =fyx =−xy x2+y2−1−3/2
(b) xy-plane, fx=2xcos(x2+y3),f
y=3y
2cos(x2+y3),f
xy =fyx =−6xy2sin x2+y3
33. (a) 4: f
xxx,f
xxy =fxyx =fyxx,f
xyy =fyxy =fyyx,f
yyy
(b) 5: f
xxxx,f
xxxy =fxxyx =fxyxx =fyxxx,
fxxyy =fxyxy =fxyyx =fyxyx =fyyxx =fyxxy,
fxyyy =fyxyy =fyyxy =fyyyx,f
yyyy
34. (a) Since ewhas infinitely many continuous derivatives, as does xy2, by the Chain Rule the
function exy2has infinitely many continuous derivatives, hence by Theorem 15.4.6,
fxyx =fxxy ; since fxy =fyx if follows that fxyx =fyxx.
(b) fxyx =fxxy =fyxx =2xy5exy2+4y
3
e
xy2
35. (a) f(tx, ty)=3t
2
x
2+t
2
y
2=t
2
f(x, y); n=2
(b) f(tx, ty)=pt
2
x
2+t
2
y
2=tf(x, y); n=1
(c) f(tx, ty)=t
3
x
2
y−2t
3
y
3=t
3
f(x, y); n=3
(d) f(tx, ty)=5/t
2
x
2+2t
2
y
2
2=t
−4
f(x, y); n=−4
36. (a) If f(u, v)=t
n
f(x, y), then ∂f
∂u
du
dt +∂f
∂v
dv
dt =ntn−1f(x, y), x∂f
∂u +y∂f
∂v =ntn−1f(x, y);
let t= 1 to get x∂f
∂x +y∂f
∂y =nf(x, y).
541 Chapter 15
(b) If f(x, y)=3x
2+y
2then xfx+yfy=6x
2+2y
2=2f(x, y);
If f(x, y)=px
2+y
2then xfx+yfy=x2/px2+y2+y2/px2+y2=px2+y2=f(x, y);
If f(x, y)=x
2
y−2y
3then xfx+yfy=3x
2
y−6y
3=3f(x, y);
If f(x, y)= 5
(x
2+2y
2
)
2then xfx+yfy=x5(−2)2x
(x2+2y
2
)
3+y5(−2)4y
(x2+2y
2
)
3=−4f(x, y)
37. (a) ∂z
∂x =dz
du
∂u
∂x,∂z
∂y =dz
du
∂u
∂y
(b) ∂2z
∂x2=dz
du
∂2u
∂x2+∂
∂x dz
du∂u
∂x =dz
du
∂2u
∂x2+d2z
du2∂u
∂x2
;
∂2z
∂y∂x =dz
du
∂2u
∂y∂x +∂
∂y dz
du∂u
∂x =dz
du
∂2u
∂y∂x +d2z
du2
∂u
∂x
∂u
∂y
∂2z
∂y2=∂z
∂u
∂2u
∂y2+∂
∂y ∂z
∂u∂u
∂y =dz
du
∂2u
∂y2+d2z
du2∂u
∂z 2
38. (a) z=f(u), u=x2−y2;∂z/∂x =(dz/du)(∂u/∂x)=2xdz/du
∂z/∂y =(dz/du)(∂u/∂y)=−2ydz/du, y∂z/∂x +x∂z/∂y =2xydz/du −2xydz/du =0
(b) z=f(u), u=xy;∂z
∂x =dz
du
∂u
∂x =ydz
du,∂z
∂y =dz
du
∂u
∂y =xdz
du,
x∂z
∂x −y∂z
∂y =xy dz
du −xy dz
du =0.
(c) yzx+xzy=y(2xcos(x2−y2)) −x(2ycos(x2−y2))=0
(d) xzx−yzy=xyexy −yxexy =0
39. (a) 1=−rsin θ∂θ
∂x + cos θ∂r
∂x and 0 = rcos θ∂θ
∂x + sin θ∂r
∂x; solve for ∂r/∂x and ∂θ/∂x.
(b) 0=−rsin θ∂θ
∂y + cos θ∂r
∂y and 1 = rcos θ∂θ
∂y + sin θ∂r
∂y; solve for ∂r/∂y and ∂θ/∂y.
(c) ∂z
∂x =∂z
∂r
∂r
∂x +∂z
∂θ
∂θ
∂x =∂z
∂r cos θ−1
r
∂z
∂θ sin θ.
∂z
∂y =∂z
∂r
∂r
∂y +∂z
∂θ
∂θ
∂y =∂z
∂r sin θ+1
r
∂z
∂θ cos θ.
(d) Square and add the results of parts (a) and (b).
(e) From Part (c),
∂2z
∂x2=∂
∂r ∂z
∂r cos θ−1
r
∂z
∂θ sin θ∂r
∂x +∂
∂θ ∂z
∂r cos θ−1
r
∂z
∂θ sin θ∂θ
∂x
=∂2z
∂r2cos θ+1
r2
∂z
∂θ sin θ−1
r
∂2z
∂r∂θ sin θcos θ
+∂2z
∂θ∂r cos θ−∂z
∂r sin θ−1
r
∂2z
∂θ2sin θ−1
r
∂z
∂θ cos θ−sin θ
r
=∂2z
∂r2cos2θ+2
r2
∂z
∂θ sin θcos θ−2
r
∂2z
∂θ∂r sin θcos θ+1
r2
∂2z
∂θ2sin2θ+1
r
∂z
∂r sin2θ.
Exercise Set 15.4 542
Similarly, from Part (c),
∂2z
∂y2=∂2z
∂r2sin2θ−2
r2
∂z
∂θ sin θcos θ+2
r
∂2z
∂θ∂r sin θcos θ+1
r2
∂2z
∂θ2cos2θ+1
r
∂z
∂r cos2θ.
Add to get ∂2z
∂x2+∂2z
∂y2=∂2z
∂r2+1
r2
∂2z
∂θ2+1
r
∂z
∂r.
40. zx=−2y
x2+y2,z
xx =4xy
(x2+y2)2,z
y=2x
x
2+y
2,z
yy =−4xy
(x2+y2)2,z
xx +zyy =0;
z= tan−12r2cos θsin θ
r2(cos2θ−sin2θ)= tan−1tan 2θ=2θ, zr=0,z
θθ =0
41. (a) By the chain rule, ∂u
∂r =∂u
∂x cos θ+∂u
∂y sin θand ∂v
∂θ =−∂v
∂xrsin θ+∂v
∂yrcos θ, use the
Cauchy-Riemann conditions ∂u
∂x =∂v
∂y and ∂u
∂y =−∂v
∂x in the equation for ∂u
∂r to get
∂u
∂r =∂v
∂y cos θ−∂v
∂x sin θand compare to ∂v
∂θ to see that ∂u
∂r =1
r
∂v
∂θ. The result ∂v
∂r =−1
r
∂u
∂θ
can be obtained by considering ∂v
∂r and ∂u
∂θ .
(b) ux=2x
x2+y2,v
y=21
x
1
1+(y/x)2=2x
x2+y2=ux;
uy=2y
x2+y2,v
x=−2y
x
2
1
1+(y/x)2=−2y
x2+y2=−uy;
u=lnr
2
,v =2θ, ur=2/r, vθ=2,sou
r=1
rv
θ
,u
θ=0,v
r=0,sov
r=−1
ru
θ
42. z=f(u, v) where u=x−yand v=y−x,
∂z
∂x =∂z
∂u
∂u
∂x +∂z
∂v
∂v
∂x =∂z
∂u −∂z
∂v and ∂z
∂y =∂z
∂u
∂u
∂y +∂z
∂v
∂v
∂y =−∂z
∂u +∂z
∂v so ∂z
∂x +∂z
∂y =0
43. (a) ux=f0(x+ct),u
xx =f00(x+ct),u
t=cf0(x+ct),u
tt =c2f00(x+ct); utt =c2uxx
(b) Substitute gfor fand −cfor cin Part (a).
(c) Since the sum of derivatives equals the derivative of the sum, the result follows from Parts
(a) and (b).
(d) sin tsin x=1
2(−cos(x+t) + cos(x−t))
44. fx(x0,y
0)=y
0
,f
y
(x
0
,y
0)=x
0
,
∆f=(x
0+∆x)(y0+∆y)−x
0
y
0=y
0
∆x+x
0
∆y+∆x∆y
=f
x
(x
0
,y
0)∆x+fy(x0,y
0)∆y+ (0)∆x+(∆x)∆ywhere 1= 0 and 2=∆x.
45. fx(x0,y
0)=2x
0
,f
y
(x
0
,y
0)=2y
0
,
∆f=(x
0+∆x)
2+(y
0+∆y)
2−x
2
0+y
2
0=2x
0
∆x+(∆x)
2+2y
0
∆y+(∆y)
2
=f
x
(x
0
,y
0)∆x+fy(x0,y
0)∆y+(∆x)∆x+(∆y)∆ywhere 1=∆xand 2=∆y.

543 Chapter 15
46. fx(x0,y
0)=2x
0
y
0
,f
y
(x
0
,y
0)=x
2
0
,
∆f=(x
0+∆x)
2
(y
0+∆y)−x
2
0
y
0=2x
0
y
0
∆x+x
2
0
∆y+y
0
(∆x)2+(∆x)
2
∆y+2x
0
∆x∆y
=f
x
(x
0
,y
0)∆x+fy(x0,y
0)∆y+(y
0
∆x+∆x∆y)∆x+(2x
0
∆x)∆y
where 1=y0∆x+∆x∆yand 2=2x
0
∆x.
47. fx(x0,y
0)=3,f
y
(x
0
,y
0)=2y
0
,
∆f=3(x
0+∆x)+(y
0+∆y)
2−3x
0−y
2
0=3∆x+2y
0
∆y+(∆y)
2
=f
x
(x
0
,y
0)∆x+fy(x0,y
0)∆y+ (0)∆x+(∆y)∆ywhere 1= 0 and 2=∆y.
48. (a) lim
(x,y)→(0,0) f(x, y)=0=f(0,0)
(b) lim
∆x→0
f(0+∆x, 0) −f(0,0)
∆x= lim
∆x→0
f(∆x, 0)
∆x= lim
∆x→0|∆x|
∆x, which does not exist because
lim
∆x→0+|∆x|/∆x= 1 and lim
∆x→0−|∆x|/∆x=−1.
49. fx(0,0) = lim
∆x→0
f(∆x, 0) −f(0,0)
∆x= lim
∆x→0−3∆x
∆x=−3,
fy(0,0) = lim
∆y→0
f(0,∆y)−f(0,0)
∆y= lim
∆y→0−2∆y
∆y=−2;
lim
(x,y)→(0,0) f(x, y) does not exist because f(x, y)→5if(x, y)→(0,0) where x≥0ory≥0, but
f(x, y)→0if(x, y)→(0,0) where x<0 and y<0, so fis not continuous at (0,0).
50. fx(0,0) = lim
∆x→0
f(∆x, 0) −f(0,0)
∆x= lim
∆x→0
0−0
∆x= lim
∆x→00=0
f
y
(0,0) = lim
∆y→0
f(0,∆y)−f(0,0)
∆y= lim
∆y→0
0−0
∆y= 0; along y= 0, lim
x→0
0
x2= lim
x→00=0,
along y=x, lim
x→0
x2
2x2= lim
x→01/2=1/2 so lim
(x,y)→(0,0) f(x, y) does not exist.
51. (a) fx(0,0) = lim
∆x→0
f(∆x, 0) −f(0,0)
∆x= 0; similarly, fy(0,0)=0
(b) fx(0,y) = lim
∆x→0
f(∆x, y)−f(0,y)
∆x= lim
∆x→0
y(∆x2−y2)
∆x2+y2=−y
fy(x, 0) = lim
∆y→0
f(x, ∆y)−f(x, 0)
∆y= lim
∆y→0
x(x2−∆y2)
x2+∆y
2=x
(c) fxy(0,0) = lim
∆y→0
fx(0,∆y)−fx(0,0)
∆y= lim
∆y→0−∆y
∆y=−1
fyx(0,0) = lim
∆x→0
fy(∆x, 0) −fy(0,0)
∆x= lim
∆x→0
∆x
∆x=1
(d) No, since fxy and fyx are not continuous.
52. Represent the line segment Cthat joins Aand Bby x=x0+(x
1−x
0
)t,y=y
0+(y
1−y
0
)t
for 0 ≤t≤1. Let F(t)=f(x
0+(x
1−x
0
)t, y0+(y
1−y
0
)t) for 0 ≤t≤1; then
f(x1,y
1)−f(x
0,y
0)=F(1) −F(0). Apply the Mean Value Theorem to F(t) on the interval [0,1]
to get [F(1) −F(0)]/(1 −0) = F0(t∗), F(1) −F(0) = F0(t∗) for some t∗in (0,1) so
f(x1,y
1)−f(x
0,y
0)=F
0(t
∗
). By the chain rule, F0(t)=f
x
(x, y)(dx/dt)+f
y
(x, y)(dy/dt)=
f
x
(x, y)(x1−x0)+f
y(x, y)(y1−y0). Let (x∗,y
∗) be the point on Cfor t=t∗then
f(x1,y
1)−f(x
0,y
0)=F
0(t
∗
)=f
x(x
∗
,y
∗)(x
1−x
0)+f
y(x
∗,y
∗)(y
1−y
0).
Exercise Set 15.5 544
53. Let (a, b) be any point in the region, if (x, y) is in the region then by the result of Exercise 52
f(x, y)−f(a, b)=f
x
(x
∗
,y
∗)(x−a)+f
y(x
∗,y
∗)(y−b) where (x∗,y
∗) is on the line segment joining
(a, b) and (x, y). If fx(x, y)=f
y
(x, y) = 0 throughout the region then
f(x, y)−f(a, b) = (0)(x−a)+ (0)(y−b)=0,f(x, y)=f(a, b)sof(x, y) is constant on the region.
EXERCISE SET 15.5
1. At P,∂z/∂x = 48 and ∂z/∂y =−14, tangent plane 48x−14y−z= 64, normal line x=1+48t,
y=−2−14t,z=12−t.
2. At P,∂z/∂x = 14 and ∂z/∂y =−2, tangent plane 14x−2y−z= 16, normal line x=2+14t,
y=4−2t,z=4−t.
3. At P,∂z/∂x = 1 and ∂z/∂y =−1, tangent plane x−y−z= 0, normal line x=1+t,y=−t,
z=1−t.
4. At P,∂z/∂x =−1 and ∂z/∂y = 0, tangent plane x+z=−1, normal line x=−1−t,y=0,
z=−t.
5. At P,∂z/∂x = 0 and ∂z/∂y = 3, tangent plane 3y−z=−1, normal line x=π/6, y=3t,
z=1−t.
6. At P,∂z/∂x =1/4 and ∂z/∂y =1/6, tangent plane 3x+2y−12z=−30, normal line x=4+t/4,
y=9+t/6, z=5−t.
7. By implicit differentiation ∂z/∂x =−x/z,∂z/∂y =−y/z so at P,∂z/∂x =3/4 and
∂z/∂y = 0, tangent plane 3x−4z=−25, normal line x=−3+3t/4, y=0,z=4−t.
8. By implicit differentiation ∂z/∂x =(xy)/(4z), ∂z/∂y =x2/(8z)soatP,∂z/∂x =3/8 and
∂z/∂y =−9/16, tangent plane 6x−9y−16z= 5, normal line x=−3+3t/8, y=1−9t/16,
z=−2−t.
9. The tangent plane is horizontal if the normal ∂z/∂xi+∂z/∂yj−kis parallel to kwhich occurs
when ∂z/∂x =∂z/∂y =0.
(a) ∂z/∂x =3x
2
y
2
,∂z/∂y =2x
3
y;3x
2
y
2= 0 and 2x3y= 0 for all (x, y)onthex-axis or y-axis,
and z= 0 for these points, the tangent plane is horizontal at all points on the x-axis or
y-axis.
(b) ∂z/∂x =2x−y−2, ∂z/∂y =−x+2y+ 4; solve the system 2x−y−2=0,−x+2y+4=0,
to get x=0,y=−2. z=−4at(0,−2), the tangent plane is horizontal at (0,−2,−4).
10. ∂z/∂x =6x,∂z/∂y =−2y,so6x
0
i−2y
0
j−kis normal to the surface at a point (x0,y
0,z
0)on
the surface. 6i+4j−kis normal to the given plane. The tangent plane and the given plane are
parallel if their normals are parallel so 6x0=6,x
0= 1 and −2y0=4,y
0=−2. z=−1at(1,−2),
the point on the surface is (1,−2,−1).
11. ∂z/∂x =−6x,∂z/∂y =−4yso −6x0i−4y0j−kis normal to the surface at a point (x0,y
0,z
0)on
the surface. This normal must be parallel to the given line and hence to the vector
−3i+8j−kwhich is parallel to the line so −6x0=−3, x0=1/2 and −4y0=8,y
0=−2.
z=−3/4at(1/2,−2). The point on the surface is (1/2,−2,−3/4).
12. (3,4,5) is a point of intersection because it satisfies both equations. Both surfaces have
(3/5)i+(4/5)j−kas a normal so they have a common tangent plane at (3,4,5).
545 Chapter 15
13. df =2xydx +x2dy =0.6+0.2=0.8,∆f=(x+∆x)
2(y+∆y)−x
2y=(1.1)2(3.2) −12·3=0.872
14. dz =6xdx −2dy =−12(0.02) −2(−0.03) = −0.18,
∆z=3(−2+0.02)2−2(4 −0.03) −(3(−2)2−2(4)) = −0.1788
15. 3/1−(−1)/2=7/216. 2(4)(−2) −(−2)3−(0 −13)=−7
17. dz =3x
2
y
2
dx +2x
3
ydy, ∆z=(x+∆x)
3
(y+∆y)
2−x
3
y
2
18. dz =yexydx +xexy dy, ∆z=e(x+∆x)(y+∆y)−exy
19. dz =7dx −2dy 20. dz = (10xy5−2)dx + (25x2y4+4)dy
21. dz =y/ 1+x
2
y
2
dx +x/ 1+x
2
y
2
dy
22. dz = 2 sec2(x−3y) tan(x−3y)dx −6 sec2(x−3y) tan(x−3y)dy
23. (a) Let f(x, y)=e
xsin y;f(0,0)=0,f
x(0,0)=0,f
y(0,0)=1,soe
xsin y≈y
(b) Let f(x, y)=2x+1
y+1 ;f(0,0)=1,f
x(0,0)=2,f
y(0,0) = −1, so 2x+1
y+1 ≈1+2x−y
24. f(1,1)=1,f
x(x, y)=αxα−1yβ,f
x(1,1) = α, fy(x, y)=βxαyβ−1,f
y(1,1) = β,so
x
α
y
β≈1+α(x−1)+β(y−1)
25. dT =Txdx +Tydy ≈2(−0.02) −(0.02) = −0.06,T≈T(1,3)+dT ≈93 −0.06=92.94◦
26. p(104,103) ≈p(100,98) −px(100,98)(104 −100) −py(100,98)(103 −98)
= 1008 + (−2)4 + (1)5 = 1005 mb
27. f(x, y)=(x
2+y
2
)
−1/2
,f
x
(4,3) = −x
(x2+y2)3/2=−4
125,f
y
(4,3) = −y
(x2+y2)3/2=−3
125,
1
p(3.92)2+(3.01)2≈1
√42+3
2−4
125(−0.08) −3
125(0.01)=0.20232; actual value ≈0.202334.
28. From Exercise 24, x0.5y0.3≈1+0.5(x−1)+0.3(y−1), so
(1.05)0.5(0.97)0.3≈1+0.5(0.05)+0.3(−0.03)=1.016, actual value ≈1.01537
29. df =(2x+2y−4)dx +2xdy;x=1,y=2,dx =0.01, dy =0.04 so df =0.10
30. df =(1/3)x−2/3y1/2dx +(1/2)x1/3y−1/2dy;x=8,y=9,dx =−0.02, dy =0.03 so df =0.005
31. df =−x −2dx −y−2dy;x=−1, y=−2, dx =−0.02, dy =−0.04 so df =0.03
32. df =y
2(1 + xy)dx +x
2(1 + xy)dy;x=0,y=2,dx =−0.09, dy =−0.02 so df =−0 . 09
33. z=px2+y2,dz =xx2+y2−1/2dx +yx2+y2−1/2dy;x=3,y=4,dx =0.2,
dy =−0.04 so dz =0.088 cm.
34. dV =(2/3)πrhdr +(1/3)πr2dh;r=4,h= 20, dr =0.05, dh =−0.05 so dV =2.4π≈7.54 in3.
Exercise Set 15.5 546
35. A=xy,dA =ydx +xdy,dA/A =dx/x +dy/y,|dx/x|≤0.03 and |dy/y|≤0.05,
|dA/A|≤|dx/x|+|dy/y|≤0.08=8%
36. V=(1/3)πr2h,dV =(2/3)πrhdr +(1/3)πr2dh,dV/V =2(dr/r)+dh/h,|dr/r|≤0.01 and
|dh/h|≤0.04, |dV/V |≤2|dr/r|+|dh/h|≤0.06 = 6%.
37. z=px2+y2,dz =x
px2+y2dx +y
px2+y2dy,
dz
z=x
x2+y2dx +y
x2+y2dy =x2
x2+y2dx
x+y2
x2+y2dy
y,
dz
z≤x2
x2+y2
dx
x
+y2
x2+y2
dy
y
,if
dx
x≤r/100 and
dy
y≤r/100 then
dz
z≤x2
x2+y2(r/100) + y2
x2+y2(r/100) = r
100 so the percentage error in zis at most about r%.
38. (a) z=px2+y2,dz =xx2+y2−1/2dx +yx2+y2−1/2dy,
|dz|≤xx
2+y
2
−1/2|dx|+yx2+y2−1/2|dy|;ifx=3,y=4,|dx|≤0.05, and
|dy|≤0.05 then |dz|≤(3/5)(0.05)+(4/5)(0.05)=0.07 cm
(b) A=(1/2)xy,dA =(1/2)ydx +(1/2)xdy,
|dA|≤(1/2)y|dx|+(1/2)x|dy|≤2(0.05)+(3/2)(0.05)=0.175 cm2.
39. dR =R2
2
(R1+R2)2dR1+R2
1
(R1+R2)2dR2,dR
R=R2
R1+R2dR1
R1+R1
R1+R2dR2
R2,
dR
R≤R2
R1+R2
dR1
R1
+R1
R1+R2
dR2
R2
;ifR
1= 200, R2= 400, |dR1/R1|≤0.02, and
|dR2/R2|≤0.02 then |dR/R|≤(400/600)(0.02) + (200/600)(0.02)=0.02 = 2%.
40. dP =(k/V )dT −(kT/V 2)dV ,dP/P =dT/T −dV /V ;ifdT/T =0.03 and dV/V =0.05 then
dP/P =−0.02 so there is about a 2% decrease in pressure.
41. dθ =1
√c2−a2da −a
c√c2−a2dc;ifa=3,c=5,|da|≤0.01, and |dc|≤0.01 then
|dθ|≤(1/4)(0.01)+(3/20)(0.01)=0.004 radians.
42. V=πr2h,dV =2πrhdr +πr2dh;r=2,h=5,dr =0.01, and dh =0.01 so
dV = (20π)(0.01)+(4π)(0.01)=0.24π, or about 0.754 cm3.
43. dT =π
gpL/g dL −πL
g2pL/g dg,dT
T=1
2
dL
L−1
2
dg
g;|dL/L|≤0.005 and |dg/g|≤0.001 so
|dT/T |≤(1/2)(0.005) + (1/2)(0.001) = 0.003=0.3%
44. Let hbe the height of the building, xthe distance to the building, and θthe angle of elevation,
then h=xtan θ,dh = tan θdx +xsec2θdθ;ifx= 100, θ=60
◦
,|dx|≤1/6 ft, and
|dθ|≤(0.2)(π/180) = π/900 radians, then |dh|≤√
3
(1/6) + (100)(4)(π/900) <1.7 ft.
45. (a) z=xy,dz =ydx +xdy,dz/z =dx/x +dy/y;(r+s)%.
(b) z=x/y,dz =dx/y −xdy/y2,dz/z =dx/x −dy/y;(r+s)%.
547 Chapter 15
(c) z=x2y3,dz =2xy3dx +3x
2
y
2
dy,dz/z =2dx/x +3dy/y;(2r+3s)%.
(d) z=x3y1/2,dz =3x
2
y
1/2
dx +x3dy/ 2y1/2,dz/z =3dx/x +(1/2)dy/y;(3r+s/2)%.
46. z=k
xy ; at a point a, b, k
abon the surface, −k
a2b,−k
ab2,−1and hence bk, ak, a2b2is
normal to the surface so the tangent plane is bkx +aky +a2b2z=3abk. The plane cuts the x,
y, and z-axes at the points 3a, 3b, and 3k
ab , respectively, so the volume of the tetrahedron that is
formed is V=1
33k
ab 1
2(3a)(3b)=9
2k, which does not depend on a and b.
47. (a) 2t+7=(−1+t)
2+(2+t)
2
,t
2=1,t=±1 so the points of intersection are (−2,1,5) and
(0,3,9).
(b) ∂z/∂x =2x,∂z/∂y =2yso at (−2,1,5) the vector n=−4i+2j−kis normal to the surface.
v=i+j+2kis parallel to the line; n·v=−4 so the cosine of the acute angle is
[n·(−v)]/(knkk−vk)=4/√
21√6=4/3
√
14. Similarly, at (0,3,9) the vector
n=6j−kis normal to the surface, n·v= 4 so the cosine of the acute angle is
4/√37√6=4/
√
222.
48. z=xf(u) where u=x/y,∂z/∂x =xf 0(u)∂u/∂x +f(u)=(x/y)f0(u)+f(u)=uf0(u)+f(u),
∂z/∂y =xf 0(u)∂u/∂y =−(x2/y2)f0(u)=−u
2
f
0
(u). If (x0,y
0,z
0) is on the surface then, with
u0=x0/y0,[u
0
f
0(u
0
)+f(u
0
)] i−u2
0f0(u0)j−kis normal to the surface so the tangent plane is
[u0f0(u0)+f(u
0
)] x−u2
0f0(u0)y−z=[u
0
f
0
(u
0
)+f(u
0
)]x0−u2
0f0(u0)y0−z0
=x0
y0
f0(u0)+f(u
0
)
x
0−x
2
0
y
2
0
f0(u
0
)y
0−z
0
=x
0
f(u
0
)−z
0=0
so all tangent planes pass through the origin.
49. Use implicit differentiation to get ∂z/∂x =−c2x/ a2z,∂z/∂y =−c2y/ b2z.At(x
0
,y
0,z
0),
z06= 0, a normal to the surface is −c2x0/a2z0i−c2y0/b2z0j−kso the tangent plane is
−c2x0
a2z0
x−c2y0
b2z0
y−z=−c2x2
0
a2z0−c2y2
0
b2z0−z0,x0x
a2+y0y
b2+z0z
c2=x2
0
a2+y2
0
b2+z2
0
c2=1
50. ∂z/∂x =2x/a2,∂z/∂y =2y/b2.At(x
0
,y
0,z
0) the vector 2x0/a2i+2y0/b2j−kis normal
to the surface so the tangent plane is 2x0/a2x+2y0/b2y−z=2x
2
0
/a2+2y
2
0/b2−z0, but
z0=x2
0/a2+y2
0/b2so 2x0/a2x+2y0/b2y−z=2z
0−z
0=z
0
,2x
0
x/a2+2y
0
y/b2=z+z0
51. n1=fx(x0,y
0)i+f
y(x
0,y
0)j−kand n2=gx(x0,y
0)i+g
y(x
0,y
0)j−kare normal, respectively,
to z=f(x, y) and z=g(x, y)atP;n
1and n2are perpendicular if and only if n1·n2=0,
f
x
(x
0
,y
0)g
x(x
0,y
0)+f
y(x
0
,y
0)g
y(x
0,y
0)+1=0,
f
x(x
0
,y
0)g
x(x
0,y
0)+f
y(x
0
,y
0)g
y(x
0,y
0)=−1.
52. n1=fxi+fyj−k=x0
px2
0+y2
0
i+y0
px2
0+y2
0
j−k; similarly n2=−x0
px2
0+y2
0
i−y0
px2
0+y2
0
j−k;
since a normal to the sphere is N=x0i+y0j+z0k, and n1·N=px2
0+y2
0−z0=0,
n
2·N=−
px
2
0+y
2
0−z
0= 0, the result follows.
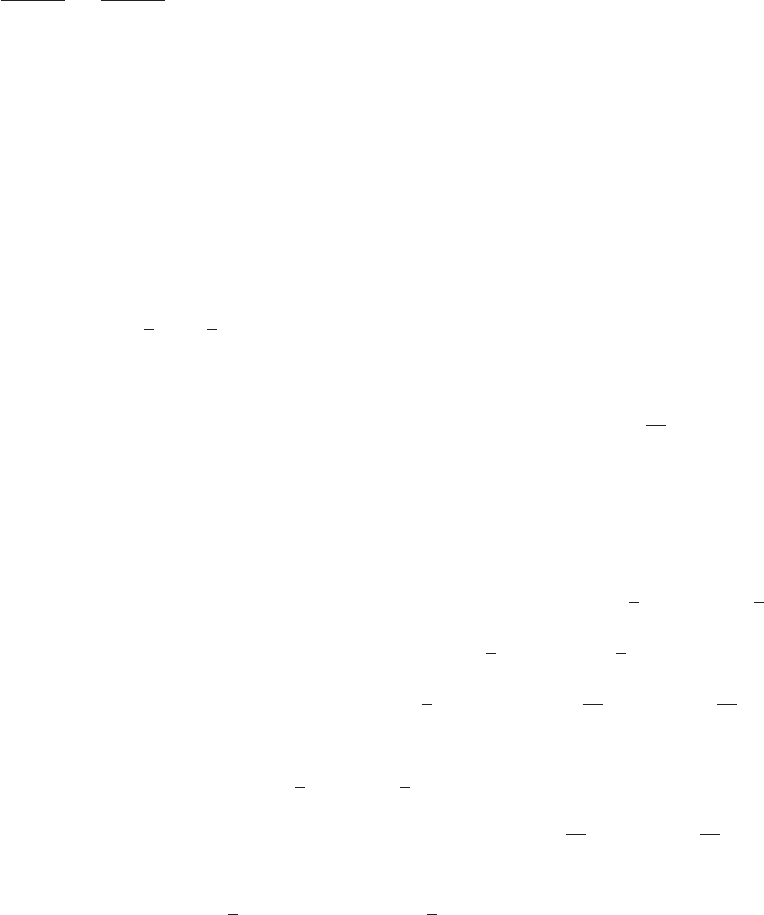
Exercise Set 15.6 548
EXERCISE SET 15.6
1. fincreases the most in the direction of III.
2. The contour lines are closer at P, so the function is increasing more rapidly there, hence ∇fis
larger at P.
3. ∇z=4i−8j4.∇z=−4e
−3y
sin 4xi−3e−3ycos 4xj
5. ∇z=x
x2+y2i+y
x2+y2j
6. ∇z=e−5xsec x2y2xy tan x2y−5i+x2tan x2yj
7. ∇f(x, y) = 3(2x+y)x2+xy2i+3xx
2+xy2j,∇f(−1,−1) = −36i−12j
8. ∇f(x, y)=−xx
2+y
2
−3/2i−yx
2+y
2
−3/2j,∇f(3,4) = −(3/125)i−(4/125)j
9. ∇f(x, y)=[y/(x+y)]i+[y/(x+y) + ln(x+y)]j,∇f(−3,4)=4i+4j
10. ∇f(x, y)=3y
2tan2xsec2xi+2ytan3xj,∇f(π/4,−3)=54i−6j
11. ∇f(x, y)=(3y/2)(1 + xy)1/2i+(3x/2)(1 + xy)1/2j,∇f(3,1)=3i+9j,
D
u
f=∇f·u=12/
√
2=6
√
2
12. ∇f(x, y)=2ye2xyi+2xe2xy j,∇f(4,0)=8j,D
u
f=∇f·u=32/5
13. ∇f(x, y)=2x/ 1+x
2+y
i+1/1+x
2+y
j,∇f(0,0) = j,Duf=−3/√10
14. ∇f(x, y)=−(c+d)y/(x−y)2i+(c+d)x/(x−y)2j,
∇f(3,4) = −4(c+d)i+3(c+d)j,D
u
f=−(7/5)(c+d)
15. ∇f(x, y)=12x
2
y
2
i+8x
3
yj,∇f(2,1)=48i+64j,u=(4/5)i−(3/5)j,Duf=∇f·u=0
16. ∇f(x, y)=(2x−3y)i+−3x+12y
2
j,∇f(−2,0) = −4i+6j,u=(i+2j)/
√
5, Duf=8/
√
5
17. ∇f(x, y)=y
2
/xi+2yln xj,∇f(1,4)=16i,u=(−i+j)/
√
2, Duf=−8√2
18. ∇f(x, y)=e
xcos yi−exsin yj,∇f(0,π/4)=(i−j)/
√
2, u=(5i−2j)/
√
29, Duf=7/
√
58
19. ∇f(x, y)=−y/ x2+y2i+x/ x2+y2j,
∇f(−2,2) = −(i+j)/4, u=−(i+j)/√2, Duf=√2/4
20. ∇f(x, y)=(e
y−yex)i+(xey−ex)j,∇f(0,0) = i−j,u=(5i−2j)/
√
29, Duf=7/
√
29
21. ∇f(x, y)=(y/2)(xy)−1/2i+(x/2)(xy)−1/2j,∇f(1,4) = i+(1/4)j,
u= cos θi+ sin θj=(1/2)i+√3/2j,Duf=1/2+√
3/8
22. ∇f(x, y)=[2y/(x+y)2]i−[2x/(x+y)2]j,∇f(−1,−2) = −(4/9)i+(2/9)j,u=j,Duf=2/9
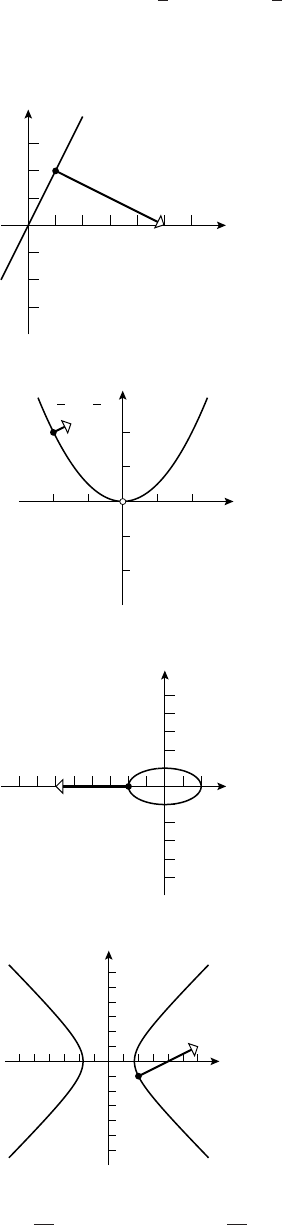
549 Chapter 15
23. ∇f(x, y)=2sec
2
(2x+y)i+ sec2(2x+y)j,∇f(π/6,π/3)=8i+4j,u=(i−j)/
√
2, Duf=2
√
2
24. ∇f(x, y) = cosh xcosh yi+ sinh xsinh yj,∇f(0,0) = i,u=−i,Duf=−1
25. f(1,2) = 3, level curve 4x−2y+3=3,2x−y=0;
∇f(x, y)=4i−2j
∇f(1,2)=4i−2j(1, 2)
4i – 2jx
y
26. f(−2,2)=1/2, level curve y/x2=1/2,y=x
2
/2 for x6=0.
∇f(x, y)=−2y/x3i+1/x2j
∇f(−2,2)=(1/2)i+(1/4)j
1
21
4
i + j
(−2, 2)
x
y
27. f(−2,0) = 4, level curve x2+4y
2=4,x
2
/4+y
2=1.
∇f(x, y)=2xi+8yj
∇f(−2,0) = −4i
-4i
1
2
x
y
28. f(2,−1) = 3, level curve x2−y2=3.
∇f(x, y)=2xi−2yj
∇f(2,−1)=4i+2j
(2, −1)
4i + 2j
x
y
29. ∇f(x, y)=12x
2
y
2
i+8x
3
yj,∇f(−1,1)=12i−8j,u=(3i−2j)/
√
13, k∇f(−1,1)k=4
√
13

Exercise Set 15.6 550
30. ∇f(x, y)=3i−(1/y)j,∇f(2,4)=3i−(1/4)j,u= (12i−j)/√145, k∇f(2,4)k=√145/4
31. ∇f(x, y)=xx
2+y
2
−1/2i+yx
2+y
2
−1/2j,
∇f(4,−3)=(4i−3j)/5, u=(4i−3j)/5, k∇f(4,−3)k=1
32. ∇f(x, y)=y(x+y)
−2
i−x(x+y)
−2
j,∇f(0,2)=(1/2)i,u=i,k∇f(0,2)k=1/2
33. ∇f(x, y)=−2xi−2yj,∇f(−1,−3)=2i+6j,u=−(i+3j)/
√
10, −k∇f(−1,−3)k=−2√10
34. ∇f(x, y)=yexyi+xexy j;∇f(2,3) = e6(3i+2j), u=−(3i+2j)/
√
13, −k∇f(2,3)k=−√13e6
35. ∇f(x, y)=−3 sin(3x−y)i+ sin(3x−y)j,
∇f(π/6,π/4)=(−3i+j)/
√
2, u=(3i−j)/
√
10, −k∇f(π/6,π/4)k=−√5
36. ∇f(x, y)= y
(x+y)
2rx+y
x−yi−x
(x+y)
2rx+y
x−yj,∇f(3,1)=(
√
2/16)(i−3j),
u=−(i−3j)/√10, −k∇f(3,1)k=−√5/8
37. ∇f(x, y)=y(x+y)
−2
i−x(x+y)
−2
j,∇f(1,0) = −j,−→
PQ=−2i−j,u=(−2i−j)/
√
5,
Duf=1/
√
5
38. ∇f(x, y)=−e
−xsec yi+e−xsec ytan yj,
∇f(0,π/4) = √2(−i+j), −→
PO=−(π/4)j,u=−j,Duf=−√2
39. ∇f(x, y)= yey
2√xy i+√xyey+xey
2√xy j,∇f(1,1)=(e/2)(i+3j), u=−j,Duf=−3e/2
40. ∇f(x, y)=−y(x+y)
−2
i+x(x+y)
−2
j,∇f(2,3)=(−3i+2j)/25, if Duf= 0 then uand ∇fare
orthogonal, by inspection 2i+3jis orthogonal to ∇f(2,3) so u=±(2i+3j)/
√
13.
41. ∇f(x, y)=8xyi+4x
2
j,∇f(1,−2) = −16i+4jis normal to the level curve through Pso
u=±(−4i+j)/√17.
42. ∇f(x, y)=(6xy −y)i+3x2−xj,∇f(2,−3)=−33i+10jis normal to the level curve through
Pso u=±(−33i+10j)/
√
1189.
43. Solve the system (3/5)fx(1,2) −(4/5)fy(1,2) = −5, (4/5)fx(1,2)+(3/5)fy(1,2) = 10 for
fx(1,2) and fy(1,2) to get fx(1,2)=5,f
y
(1,2) = 10. For (c), ∇f(1,2)=5i+10j,
u=(−i−2j)/
√
5, Duf=−5√5.
44. ∇f(−5,1) = −3i+2j,−→
PQ=i+2j,u=(i+2j)/
√
5, Duf=1/
√
5
45. ∇f(4,−5)=2i−j,u=(5i+2j)/
√
29, Duf=8/
√
29
46. Let u=u1i+u2jwhere u2
1+u2
2= 1, but Duf=∇f·u=u1−2u2=−2sou
1=2u
2−2,
(2u2−2)2+u2
2=1,5u
2
2−8u
2+3=0,u
2=1oru
2=3/5thusu
1=0oru
1=−4/5; u=jor
u=−4
5i+3
5j.
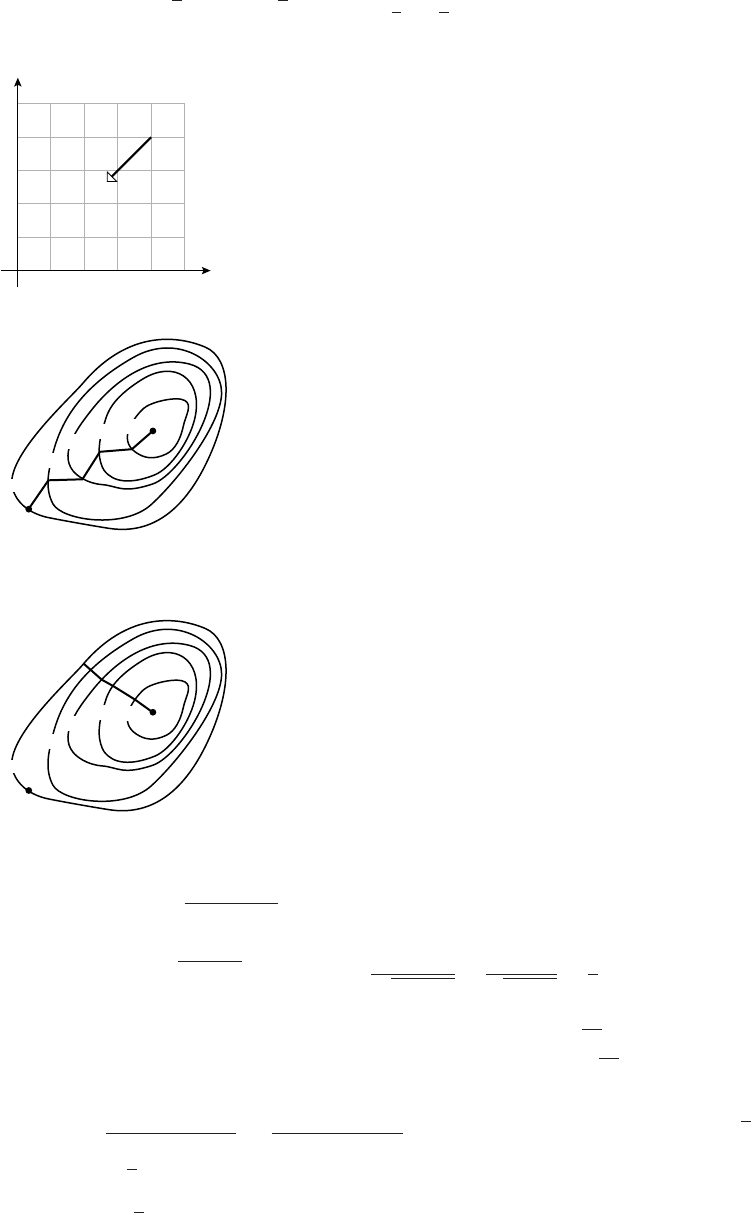
551 Chapter 15
47. (a) At (1,2) the steepest ascent seems to be in the direction i+jand the slope in that direction
seems to be 0.5/(√2/2)=1/
√
2, so ∇f≈1
2i+1
2j, which has the required direction and
magnitude.
(b)
5
5
x
y
−∇f(4, 4)
48. (a)
500
P
0 ft
100200 300 400
Depart from each contour line in a direction orthogonal to that contour line, as an approxi-
mation to the optimal path.
(b)
500
P
0 ft
100200 300 400
At the top there is no contour line, so head for the nearest contour line. From then on depart
from each contour line in a direction orthogonal to that countour line, as in Part (a).
49. ∇z=6xi−2yj,k∇zk=p36x2+4y
2=6if36x
2+4y2= 36; all points on the ellipse 9x2+y2=9.
50. ∇z=3i+2yj,k∇zk=p9+4y
2
,so∇k∇zk=4y
p9+4y
2=8
√
9+16 =8
5
51. r =ti−t2j,dr/dt =i−2tj=i−4jat the point (2,−4), u=(i−4j)/
√
17;
∇z=2xi+2yj=4i−8jat (2,−4), hence dz/ds =Duz=∇z·u=36/
√
17.
52. (a) ∇T(x, y)=y1−x
2+y
2
(1+x2+y2)2i+x1+x
2−y
2
(1+x2+y2)2j,∇T(1,1)=(i+j)/9, u=(2i−j)/
√
5,
DuT=1/9
√
5
(b) u =−(i+j)/√2, opposite to ∇T(1,1)

Exercise Set 15.6 552
53. (a) ∇V(x, y)=−2e
−2xcos 2yi−2e−2xsin 2yj,E=−∇V(π/4,0)=2e
−π/2i
(b) V(x, y) decreases most rapidly in the direction of −∇V(x, y) which is E.
54. ∇z=−4xi−8yj,ifx=−20 and y= 5 then ∇z=80i−40j.
(a) u =−ipoints due west, Duz=−80, the climber will descend because zis decreasing.
(b) u =(i+j)/
√
2 points northeast, Duz=20
√
2, the climber will ascend at the rate of 20√2
ftperftoftravelinthexy−plane.
(c) The climber will travel a level path in a direction perpendicular to ∇z=80i−40j,by
inspection ±(i+2j)/
√
5 are unit vectors in these directions; (i+2j)/
√
5 makes an angle of
tan−1(1/2) ≈27◦with the positive y-axis so −(i+2j)/√5 makes the same angle with the
negative y-axis. The compass direction should be N 27◦EorS27
◦W.
55. (a) ∇r=x
px2+y2i+y
px2+y2j=r/r
(b) ∇f(r)=∂f(r)
∂x i+∂f(r)
∂y j=f0(r)∂r
∂xi+f0(r)∂r
∂yj=f0(r)∇r
56. (a) ∇re−3r=(1 −3r)
re−3rr
(b) 3r2r=f0(r)
rrso f0(r)=3r
3
,f(r)=3
4
r
4+C,f(2)=12+C=1,C=−11; f(r)=3
4
r
4−11
57. ur= cos θi+ sin θj,uθ=−sin θi+ cos θj,
∇z=∂z
∂xi+∂z
∂yj=∂z
∂r cos θ−1
r
∂z
∂θ sin θi+∂z
∂r sin θ+1
r
∂z
∂θ cos θj
=∂z
∂r(cos θi+ sin θj)+1
r
∂z
∂θ(−sin θi+ cos θj)=∂z
∂rur+1
r
∂z
∂θuθ
58. (a) ∇(f+g)=(f
x+g
x
)i+(f
y+g
y)j=(f
x
i+f
y
j)+(g
x
i+g
yj)=∇f+∇g
(b) ∇(cf)=(cfx)i+(cfy)j=c(fxi+fyj)=c∇f
(c) ∇(fg)=(fgx+gfx)i+(fgy+gfy)j=f(gxi+gyj)+g(f
x
i+f
yj)=f∇g+g∇f
(d) ∇(f/g)=gfx−fgx
g2i+gfy−fgy
g2j=g(fxi+fyj)−f(gxi+gyj)
g2=g∇f−f∇g
g2
(e) ∇(fn)=nf n−1fxi+nfn−1fyj=nfn−1(fxi+fyj)=nfn−1∇f
59. r0(t)=v(t)=k(x, y)∇T=−8k(x, y)xi−2k(x, y)yj;dx
dt =−8kx, dy
dt =−2ky. Divide and solve
to get y4= 256x; one parametrization is x(t)=e
−8t
,y(t)=4e
−2t
.
60. r0(t)=v(t)=k∇T=−2k(x, y)xi−4k(x, y)yj. Divide and solve to get y=3
25x2; one parametriza-
tion is x(t)=5e
−2t
,y(t)=3e
−4t
.
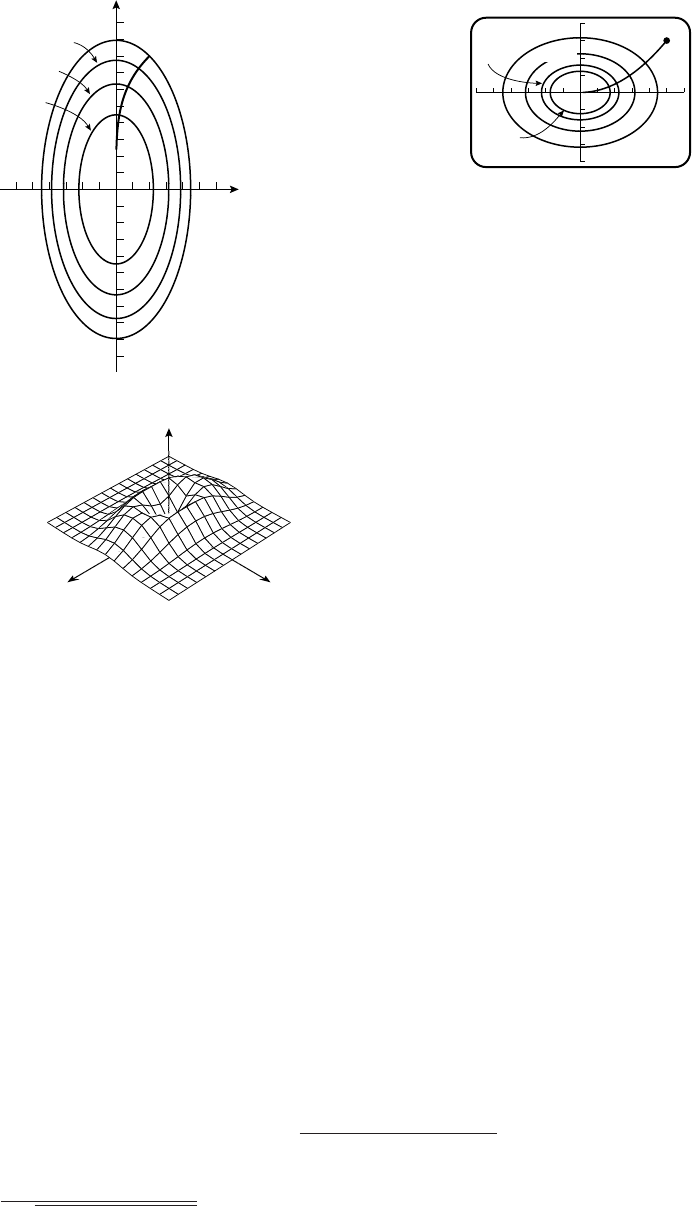
553 Chapter 15
61.
-3 3
-5
5
x
y
C = 0
C = –5
C = –10
C = –15
62. 4
-4
-6 6
T = 80
T = 95
T = 97
(5, 3)
T = 90
63. (a) z
xy
(c) ∇f=[2x−2x(x
2+3y
2
)]e−(x2+y2)i+[6y−2y(x
2+3y
2
)]e−(x2+y2)j
(d) ∇f=0if x=y=0orx=0,y =±1orx=±1,y =0.
64. dz/dt =(∂z/∂x)(dx/dt)+(∂z/∂y)(dy/dt)
=(∂z/∂xi+∂z/∂yj)·(dx/dti+dy/dtj)=∇z·r
0
(t)
65. ∇f(x, y)=f
x
(x, y)i+fy(x, y)j,if∇f(x, y) = 0 throughout the region then
fx(x, y)=f
y
(x, y) = 0 throughout the region, the result follows from Exercise 51, Section 15.4.
66. Let u1and u2be nonparallel unit vectors for which the directional derivative is zero. Let ube
any other unit vector, then u=c1u1+c2u2for some choice of scalars c1and c2,
Duf(x, y)=∇f(x, y)·u=c1∇f(x, y)·u1+c2∇f(x, y)·u2
=c1Du1f(x, y)+c
2
D
u
2f(x, y)=0.
EXERCISE SET 15.7
1. 165t32 2. 3−(4/3)t−1/3−24t−7
3t−2t2/3+4t
−63. −2tcos t2
4. 1−512t5−2560t5ln t
2t√1+lnt−512t5ln t5. 3264 6. 0
7. ∇f(x, y, z)=20x
4
y
2
z
3
i+8x
5
yz3j+12x
5
y
2
z
2
k,∇f(2,−1,1) = 320i−256j+ 384k,Duf=−320

Exercise Set 15.7 554
8. ∇f(x, y, z)=yzexzi+exzj+(xyexz +2z)k,∇f(0,2,3)=6i+j+6k,D
u
f=45/7
9. ∇f(x, y, z)= 2x
x
2+2y
2+3z
2i+4y
x
2+2y
2+3z
2j+6z
x
2+2y
2+3z
2k,
∇f(−1,2,4)=(−2/57)i+(8/57)j+ (24/57)k,Duf=−314/741
10. ∇f(x, y, z)=yz cos xyzi+xz cos xyzj+xy cos xyzk,
∇f(1/2,1/3,π)=(π
√
3/6)i+(π
√
3/4)j+(
√
3/12)k,Duf=(1−π)/12
11. ∇f(x, y, z)=3x
2
z−2xyi−x2j+x3+2z
k,∇f(2,−1,1)=16i−4j+10k,
u=(3i−j+2k)/
√
14, Duf=72/
√
14
12. ∇f(x, y, z)=−xx
2+z
2
−1/2i+j−zx
2+z
2
−1/2k,∇f(−3,1,4)=(3/5)i+j−(4/5)k,
u=(2i−2j−k)/3, Duf=0
13. ∇f(x, y, z)=−1
z+yi−z−x
(z+y)
2j+y+x
(z+y)
2k,∇f(1,0,−3)=(1/3)i+(4/9)j+(1/9)k,
u=(−6i+3j−2k)/7, Duf=−8/63
14. ∇f(x, y, z)=e
x+y+3z(i+j+3k), ∇f(−2,2,−1) = e−3(i+j+3k), u= (20i−4j+5k)/21,
Duf= (31/21)e−3
15. ∇f(1,1,−1)=3i−3j,u=(i−j)/
√
2, k∇f(1,1,−1)k=3
√
2
16. ∇f(0,−3,0)=(i−3j+4k)/6, u=(i−3j+4k)/√26, k∇f(0,−3,0)k=√26/6
17. ∇f(1,2,−2)=(−i+j)/2, u=(−i+j)/
√
2, k∇f(1,2,−2)k=1/
√
2
18. ∇f(4,2,2)=(i−j−k)/8, u=(i−j−k)/
√
3, k∇f(4,2,2)k=√3/8
19. ∇f(5,7,6) = −i+11j−12k,u=(i−11j+12k)/
√
266, −k∇f(5,7,6)k=−√266
20. ∇f(0,1,π/4)=2
√
2(i−k), u=−(i−k)/√2, −k∇f(0,1,π/4)k=−4
21. ∇f(2,1,−1) = −i+j−k.−→
PQ=−3i+j+k,u=(−3i+j+k)/
√
11, Duf=3/
√
11
22. ∇f(−1,−2,1)=13i+5j−20k,u=−k,Duf=20
23. Let ube the unit vector in the direction of a, then
Duf(3,−2,1)=∇f(3,−2,1) ·u=k∇f(3,−2,1)kcos θ= 5 cos θ=−5, cos θ=−1, θ=πso
∇f(3,−2,1) is oppositely directed to u;∇f(3,−2,1) = −5u=−10/3i+5/3j+10/3k.
24. (a) ∇T(1,1,1)=(i+j+k)/8, u=−(i+j+k)/√3, DuT=−√3/8
(b) (i+j+k)/√3(c) √3/8
25. (a) f(x, y, z)=x
2+y
2+4z
2
,∇f=2xi+2yj+8zk,∇f(2,2,1)=4i+4j+8k,
n=i+j+2k,x+y+2z=6
(b) r(t)=2i+2j+k+t(i+j+2k),x(t)=2+t, y(t)=2+t, z(t)=1+2t
(c) cos θ=n·k
knk=√2
√3,θ ≈35.26◦
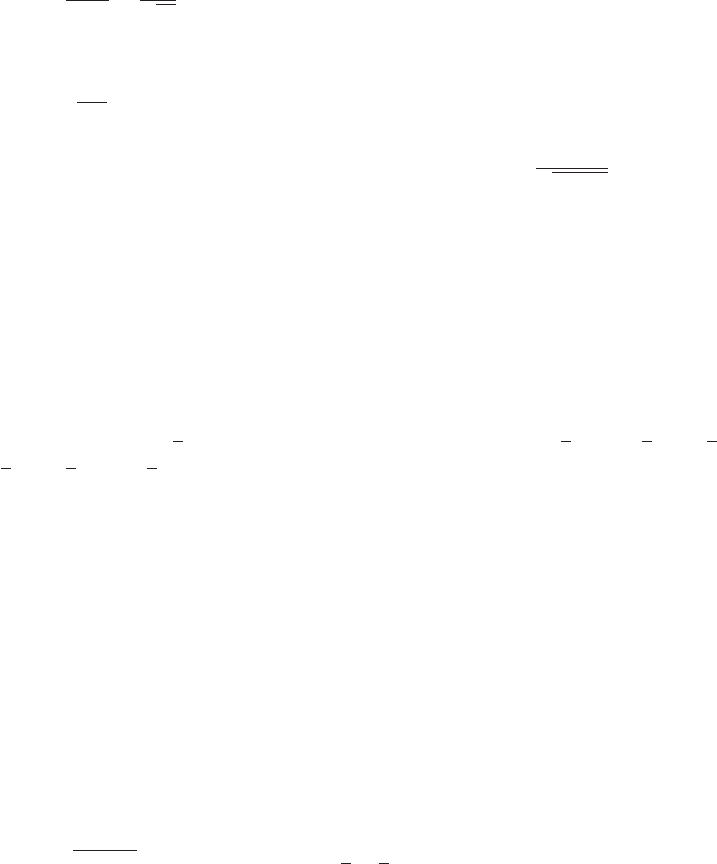
555 Chapter 15
26. (a) f(x, y, z)=xz −yz3+yz2,n=∇f(2,−1,1) = i+3k; tangent plane x+3z=5
(b) normal line x=2+t,y=−1, z=1+3t
(c) cos θ=n·k
knk=3
√10,θ ≈18.43◦
27. Set f(x, y)=z+x−z
4
(y−1), then f(x, y, z)=0,n=±∇f(3,5,1) = ±(i−j−19k),
unit vectors ±1
363(i−j−19k)
28. f(x, y, z) = sin xz −4 cos yz,∇f(π, π, 1) = −i−πk; unit vectors ±1
√1+π
2(i+πk)
29. f(x, y, z)=x
2+y
2+z
2
,if(x
0
,y
0,z
0) is on the sphere then ∇f(x0,y
0,z
0)=2(x
0
i+y
0
j+z
0
k)
is normal to the sphere at (x0,y
0,z
0), the normal line is x=x0+x0t,y=y0+y0t,z=z0+z0t
which passes through the origin when t=−1.
30. f(x, y, z)=2x
2+3y
2+4z
2
,if(x
0
,y
0,z
0) is on the ellipsoid then
∇f(x0,y
0,z
0)=2(2x
0
i+3y
0
j+4z
0
k) is normal there and hence so is n1=2x
0
i+3y
0
j+4z
0
k;
n
1must be parallel to n2=i−2j+3kwhich is normal to the given plane so n1=cn2
for some constant c. Equate corresponding components to get x0=c/2, y0=−2c/3, and
z0=3c/4; substitute into the equation of the ellipsoid yields 2 c2/4+34c
2/9+49c
2/16=9,
c
2= 108/49, c=±6√3/7. The points on the ellipsoid are 3√3/7,−4√3/7,9√3/14and
−3√3/7,4√3/7,−9√3/14.
31. f(x, y, z)=x
2+y
2−z
2
,if(x
0
,y
0,z
0) is on the surface then ∇f(x0,y
0,z
0)=2(x
0
i+y
0
j−z
0
k)
is normal there and hence so is n1=x0i+y0j−z0k;n1must be parallel to −→
PQ=3i+2j−2kso
n1=c−→
PQ for some constant c. Equate components to get x0=3c,y
0=2cand z0=2cwhich
when substituted into the equation of the surface yields 9c2+4c
2−4c
2=1,c
2=1/9, c=±1/3
so the points are (1,2/3,2/3) and (−1,−2/3,−2/3).
32. f1(x, y, z)=2x
2+3y
2+z
2
,f
2
(x, y, z)=x
2+y
2+z
2−6x−8y−8z+ 24,
n1=∇f1(1,1,2)=4i+6j+4k,n
2=∇f
2
(1,1,2) = −4i−6j−4k,n1=−n2so n1and n2are
parallel.
33. n1=2i−2j−k,n
2=2i−8j+4k,n
1×n
2=16i−10j−12kis tangent to the line, so
x(t)=1+8t, y(t)=−1+5t, z(t)=2+6t
34. f(x, y, z)=px
2+y
2
−z,n1=∇f(4,3,5) = 4
5i+3
5j−k,n2=i+2j+2k,n1×n2= (16i−13j+5k)/5
is tangent to the line, x(t)=4+16t, y(t)=3−13t, z(t)=5+5t
35. f(x, y, z)=x
2+z
2−25,g(x, y, z)=y
2+z
2−25,n1=∇f(3,−3,4)=6i+8k,
n
2=∇g(3,−3,4) = −6j+8k,n
1×n
2=48i−48j−36kis tangent to the line,
x(t)=3+4t, y(t)=−3−4t, z(t)=4−3t
36. (a) f(x, y, z)=z−8+x
2+y
2
,g(x, y, z)=4x+2y−z, n1=4j+k,n
2=4i+2j−k,
n
1×n
2=−6i+4j−16kis tangent to the line, x(t)=3t, y(t)=2−2t, z(t)=4+8t
37. dw =3x
2
y
2
zdx +2x
3
yzdy +x3y2dz, ∆w=(x+∆x)
3
(y+∆y)
2
(z+∆z)−x
3
y
2
z
38. dw =yzexyzdx +xzexyzdy +xyexyz dz, ∆w=e(x+∆x)(y+∆y)(z+∆z)−exyz
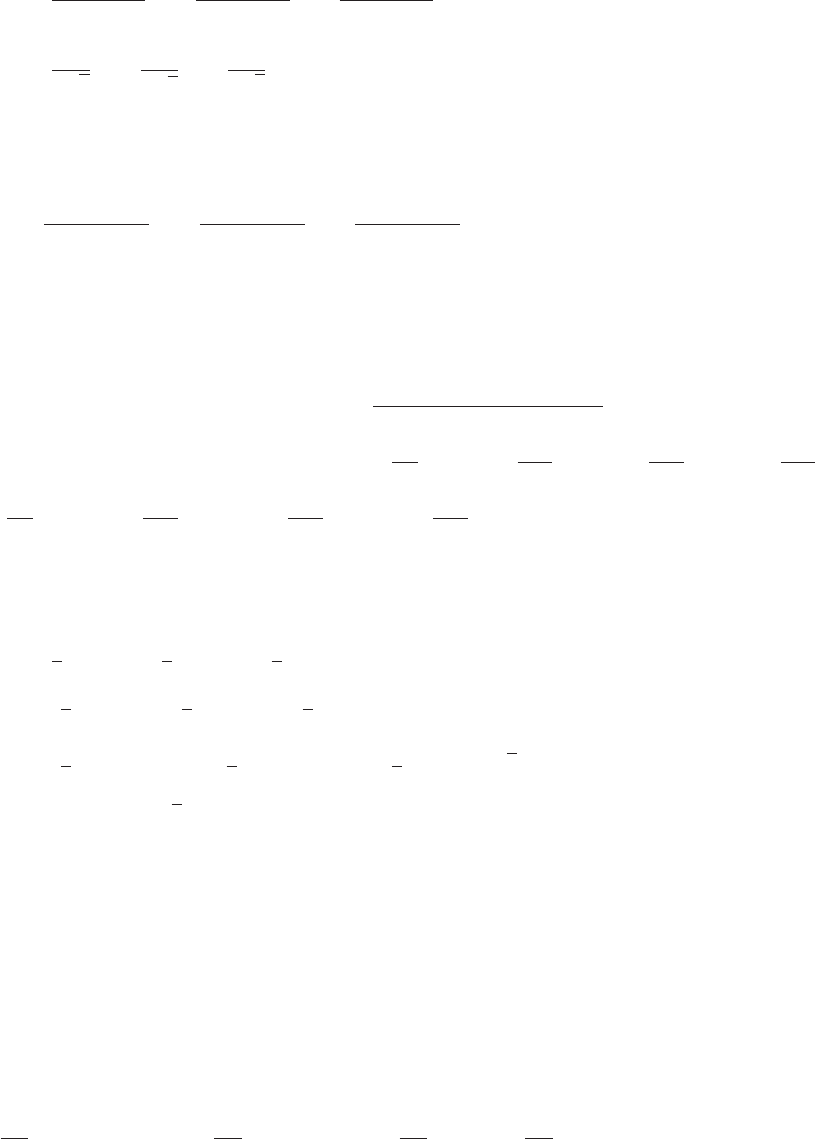
Exercise Set 15.7 556
39. dw =8dx −3dy +4dz
40. dw =8xy3z7−3ydx +12x2y2z7−3xdy +28x2y3z6+1
dz
41. dw =yz
1+x
2
y
2
z
2dx +xz
1+x
2
y
2
z
2dy +xy
1+x
2
y
2
z
2dz
42. dw =1
2√xdx +1
2√ydy +1
2√zdz
43. df =2y
2
z
3
dx +4xyz3dy +6xy2z2dz
=2(−1)2(2)3(−0.01) + 4(1)(−1)(2)3(−0.02) + 6(1)(−1)2(2)2(0.02)=0.96
44. df =yz(y+z)
(x+y+z)2dx +xz(x+z)
(x+y+z)2dy +xy(x+y)
(x+y+z)2dz
=(−16)(−0.04)+(−12)(0.02)+(−6)(−0.03)=0.58
45. V=`wh,dV =wh d` +`h dw +`w dh,
|dV |≤wh|d`|+`h|dw|+`w|dh|≤(4)(5)(0.05) + (3)(5)(0.05) + (3)(4)(0.05)=2.35 cm3
46. R=1/(1/R1+1/R2+1/R3), ∂R/∂R1=1
R2
1(1/R1+1/R2+1/R3)2=R2/R2
1, similarly
∂R/∂R2=R2/R2
2and ∂R/∂R3=R2/R2
3so dR
R=(R/R1)dR1
R1
+(R/R2)dR2
R2
+(R/R3)dR3
R3
,
dR
R≤(R/R1)
dR1
R1
+(R/R2)
dR2
R2
+(R/R3)
dR3
R3
≤(R/R1)(0.10)+(R/R2)(0.10)+(R/R3)(0.10)
=R(1/R1+1/R2+1/R3)(0.10) = (1)(0.10)=0.10 = 10%
47. dA =1
2bsin θda +1
2asin θdb +1
2ab cos θdθ,
|dA|≤ 1
2bsin θ|da|+1
2asin θ|db|+1
2ab cos θ|dθ|
≤1
2(50)(1/2)(1/2) + 1
2(40)(1/2)(1/4) + 1
2(40)(50) √3/2(π/90)
=35/4+50π
√
3/9≈39 ft2
48. V=`wh,dV =whd` +`hdw +`wdh,|dV/V |≤|d`/`|+|dw/w|+|dh/h|≤3(r/100) = 3r%
49. ∂f/∂v =8vw3x4y5,∂f/∂w =12v
2
w
2
x
4
y
5
,∂f/∂x =16v
2
w
3
x
3
y
5
,∂f/∂y =20v
2
w
3
x
4
y
4
50. ∂w/∂r = cos st +ueucos ur,∂w/∂s =−rt sin st,
∂w/∂t =−rs sin st,∂w/∂u =reucos ur +eusin ur
51. ∂f/∂v1=2v
1
/v
2
3+v
2
4
,∂f/∂v2=−2v2/v2
3+v2
4,∂f/∂v3=−2v3v2
1−v2
2/v2
3+v2
42,
∂f/∂v4=−2v4v2
1−v2
2/v2
3+v2
42
52. ∂V
∂x =2xe2x−y+e2x−y,∂V
∂y =−xe2x−y+w,∂V
∂z =w2ezw,∂V
∂w =wzezw +ezw +y

557 Chapter 15
53. (a) 0(b) 0(c) 0(d) 0
(e) 2(yw +1)e
yw sin zcos z(f) 2xw(yw +2)e
yw sin zcos z
54. 128, −512, 32, 64/3
55. ∂z/∂r =(dz/dx)(∂x/∂r)=2rcos2θ/ r2cos2θ+1
,
∂z/∂θ =(dz/dx)(∂x/∂θ)=−2r
2sin θcos θ/ r2cos2θ+1
56. ∂u/∂x =(∂u/∂r)(dr/dx)+(∂u/∂t)(∂t/∂x)
=s2ln t(2x)+rs2/ty
3=x(4y+1)
21+2lnxy3
∂u/∂y =(∂u/∂s)(ds/dy)+(∂u/∂t)(∂t/∂y)
=(2rs ln t)(4) + rs2/t3xy2=8x
2
(4y+1)lnxy3+3x
2
(4y+1)
2
/y
57. ∂w/∂ρ =2ρ4 sin2φ+ cos2φ,∂w/∂φ =6ρ
2sin φcos φ,∂w/∂θ =0
58. dw
dx =∂w
∂x +∂w
∂y
dy
dx +∂w
∂z
dz
dx =3y
2
z
3+(6xyz3)(6x)+9xy2z21
2√x−1
= 3(3x2+2)
2
(x−1)3/2+36x
2
(3x2+ 2)(x−1)3/2+9
2x(3x2+2)
2
√
x−1
=3
2(3x2+ 2)(39x3−30x2+10x−4)√x−1
59. (a) V=`wh, dV
dt =∂V
∂`
d`
dt +∂V
∂w
dw
dt +∂V
∂h
dh
dt =whd`
dt +`hdw
dt +`w dh
dt
= (3)(6)(1) + (2)(6)(2) + (2)(3)(3) = 60 in3/s
(b) D=p`2+w2+h2;dD/dt =(`/D)d`/dt +(w/D)dw/dt +(h/D)dh/dt
=(2/7)(1) + (3/7)(2) + (6/7)(3) = 26/7 in/s
60. (a) ∂A/∂a =(1/2)bsin θ=(1/2)(10) √3/2=5
√
3/2
(b) ∂A/∂θ =(1/2)ab cos θ=(1/2)(5)(10)(1/2)=25/2
(c) b=(2Acsc θ)/a,∂b/∂a =−(2Acsc θ)/a2=−b/a =−2
61. Let z=f(u) where u=x+2y; then ∂z/∂x =(dz/du)(∂u/∂x)=dz/du,
∂z/∂y =(dz/du)(∂u/∂y)=2dz/du so 2∂z/∂x −∂z/∂y =2dz/du −2dz/du =0
62. Let z=f(u) where u=x2+y2; then ∂z/∂x =(dz/du)(∂u/∂x)=2x dz/du,
∂z/∂y =(dz/du)(∂u/∂y)=2ydz/du so y∂z/∂x−x∂z/∂y =2xydz/du −2xydz/du =0
63. ∂w/∂x =(dw/dρ)(∂ρ/∂x)=(x/ρ)dw/dρ, similarly ∂w/∂y =(y/ρ)dw/dρ and
∂w/∂z =(z/ρ)dw/dρ so (∂w/∂x)2+(∂w/∂y)2+(∂w/∂z)2=(dw/dρ)2
64. Let w=f(r, s, t) where r=x−y,s=y−z,t=z−x;
∂w/∂x =(∂w/∂r)(∂r/∂x)+(∂w/∂t)(∂t/∂x)=∂w/∂r −∂w/∂t, similarly
∂w/∂y =−∂w/∂r +∂w/∂s and ∂w/∂z =−∂w/∂s +∂w/∂t so ∂w/∂x +∂w/∂y +∂w/∂z =0
65. ∂w/∂ρ = sin φcos θ∂w/∂x + sin φsin θ∂w/∂y + cos φ∂w/∂z
∂w/∂φ =ρcos φcos θ∂w/∂x +ρcos φsin θ∂w/∂y −ρsin φ∂w/∂z
∂w/∂θ =−ρsin φsin θ∂w/∂x +ρsin φcos θ∂w/∂y

Exercise Set 15.7 558
66. ∂F
∂x +∂F
∂z
∂z
∂x =0so ∂z
∂x =−∂F/∂x
∂F/∂z ,∂F
∂y +∂F
∂z
∂z
∂y =0so ∂z
∂y =−∂F/∂y
∂F/∂z .
67. ∂z
∂x =2x+yz
6yz −xy ,∂z
∂y =xz −3z2
6yz −xy
68. ln(1 + z)+xy2+z−1=0; ∂z
∂x =−y2(1+z)
2+z,∂z
∂y =−2xy(1+z)
2+z
69. yex−5 sin 3z−3z=0; ∂z
∂x =−yex
−15 cos 3z−3=yex
15 cos 3z+3,∂z
∂y =ex
15 cos 3z+3
70. ∂z
∂x =−zeyz cos xz −yexy cos yz
yexy sin yz +xeyz cos xz +yeyz sin xz ,∂z
∂y =−zexy sin yz −xexy cos yz +zeyz sin xz
yexy sin yz +xeyz cos xz +yeyz sin xz
71. ∇f(u, v, w)= ∂f
∂xi+∂f
∂y j+∂f
∂z k
=∂f
∂u
∂u
∂x +∂f
∂v
∂v
∂x +∂f
∂w
∂w
∂x i+∂f
∂u
∂u
∂y +∂f
∂v
∂v
∂y +∂f
∂w
∂w
∂y j
+∂f
∂u
∂u
∂z +∂f
∂v
∂v
∂z +∂f
∂w
∂w
∂z k=∂f
∂u∇u+∂f
∂v ∇v+∂f
∂w∇w
72. (a) ∂w
∂x =∂f
∂x +∂f
∂z
∂z
∂x (b) ∂w
∂y =∂f
∂y +∂f
∂z
∂z
∂y
73. wr=er/(er+es+et+eu), wrs =−eres/(er+es+et+eu)2,
wrst =2e
r
e
s
e
t
/(e
r+e
s+e
t+e
u
)
3,
w
rstu =−6ereseteu/(er+es+et+eu)4=−6er+s+t+u/e4w=−6er+s+t+u−4w
74. ∂w/∂y1=a1∂w/∂x1+a2∂w/∂x2+a3∂w/∂x3,
∂w/∂y2=b1∂w/∂x1+b2∂w/∂x2+b3∂w/∂x3
75. (a) dw/dt =
4
X
i=1
(∂w/∂xi)(dxi/dt)
(b) ∂w/∂vj=
4
X
i=1
(∂w/∂xi)(∂xi/∂vj) for j=1,2,3
76. Let u=x2
1+x2
2+...+x
2
n
; then w=uk,∂w/∂xi=kuk−1(2xi)=2kx
i
u
k−1
,
∂
2
w/∂x2
i=2k(k−1)xiuk−2(2xi)+2kuk−1=4k(k−1)x2
iuk−2+2kuk−1for i=1,2,...,n
so
n
X
i=1
∂2w/∂x2
i=4k(k−1) uk−2
n
X
i=1
x2
i+2kn uk−1
=4k(k−1)uk−2u+2kn uk−1=2kuk−1[2(k−1)+n]
which is 0 if k= 0 or if 2(k−1)+n=0,k=1−n/2.
77. dF/dx =(∂F/∂u)(du/dx)+(∂F/∂v)(dv/dx)
=f(u)g0(x)−f(v)h0(x)=f(g(x))g0(x)−f(h(x))h0(x)
559 Chapter 15
78. ∇f=fxi+fyj+fzkand ∇g=gxi+gyj+gzkevaluated at (x0,y
0,z
0) are normal, respectively,
to the surfaces f(x, y, z)=0andg(x, y, z)=0at(x
0
,y
0,z
0). The surfaces are orthogonal at
(x0,y
0,z
0) if and only if ∇f·∇g=0sof
x
g
x+f
y
g
y+f
z
g
z=0.
79. f(x, y, z)=x
2+y
2+z
2−a
2=0,g(x, y, z)=z
2−x
2−y
2=0,
f
x
g
x+f
y
g
y+f
z
g
z=−4x
2−4y
2+4z
2=4g(x, y, z)=0
EXERCISE SET 15.8
1. (a) minimum at (2,−1), no maxima (b) maximum at (0,0), no minima
(c) no maxima or minima
2. (a) maximum at (−1,5), no minima (b) no maxima or minima
(c) no maxima or minima
3. f(x, y)=(x−3)2+(y+2)
2
, minimum at (3,−2), no maxima
4. f(x, y)=−(x+1)
2−2(y−1)2+ 4, maximum at (−1,1), no minima
5. fx=6x+2y=0,f
y=2x+2y= 0; critical point (0,0); D=8>0 and fxx =6>0 at (0,0),
relative minimum.
6. fx=3x
2−3y=0,f
y=−3x−3y
2= 0; critical points (0,0) and (−1,1); D=−9<0 at (0,0),
saddle point; D=27>0 and fxx =−6<0at(−1,1), relative maximum.
7. fx=2x−2xy =0,f
y=4y−x
2= 0; critical points (0,0) and (±2,1); D=8>0 and fxx =2>0
at (0,0), relative minimum; D=−16 <0at(±2,1), saddle points.
8. fx=3x
2−3=0,f
y=3y
2−3 = 0; critical points (−1,±1) and (1,±1); D=−36 <0at(−1,1)
and (1,−1), saddle points; D=36>0 and fxx =6>0 at (1,1), relative minimum; D=36>0
and fxx =−36 <0at(−1,−1), relative maximum.
9. fx=y+2=0,f
y=2y+x+ 3 = 0; critical point (1,−2); D=−1<0at(1,−2), saddle point.
10. fx=2x+y−2=0,f
y=x−2 = 0; critical point (2,−2); D=−1<0at(2,−2), saddle point.
11. fx=2x+y−3=0,f
y=x+2y= 0; critical point (2,−1); D=3>0 and fxx =2>0at(2,−1),
relative minimum.
12. fx=y−3x2=0,f
y=x−2y= 0; critical points (0,0) and (1/6,1/12); D=−1<0 at (0,0),
saddle point; D=1>0 and fxx =−1<0at(1/6,1/12), relative maximum.
13. fx=2x−2/
x
2
y
=0,f
y=2y−2/
xy2= 0; critical points (−1,−1) and (1,1); D=32>0
and fxx =6>0at(−1,−1) and (1,1), relative minima.
14. fx=ey= 0 is impossible, no critical points.
15. fx=2x=0,f
y=1−e
y= 0; critical point (0,0); D=−2<0at(0,0), saddle point.
16. fx=y−2/x2=0,f
y=x−4/y2= 0; critical point (1,2); D=3>0 and fxx =−4>0at(1,2),
relative minimum.
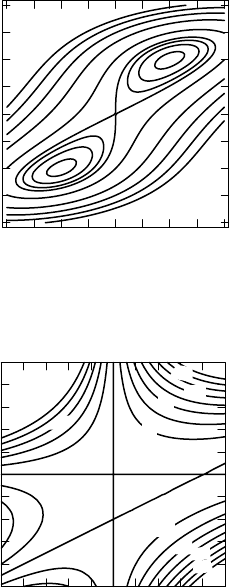
Exercise Set 15.8 560
17. fx=exsin y=0,f
y=e
xcos y= 0, sin y= cos y= 0 is impossible, no critical points.
18. fx=ycos x=0,f
y= sin x= 0; sin x=0ifx=nπ for n=0,±1,±2,... and cos x6= 0 for these
values of xso y= 0; critical points (nπ, 0) for n=0,±1,±2,...;D=−1<0at(nπ, 0), saddle
points.
19. fx=−2(x+1)e
−
(
x
2
+y
2
+2x)=0,f
y=−2ye−(x2+y2+2x)= 0; critical point (−1,0); D=4e
2>0
and fxx =−2e<0at(−1,0), relative maximum.
20. fx=y−a3/x2=0,f
y=x−b
3
/y2= 0; critical point a2/b, b2/a;ifab>0 then D=3>0 and
fxx =2b
3
/a3>0ata
2
/b, b2/a, relative minimum; if ab < 0 then D=3>0 and
fxx =2b
3
/a3<0ata
2
/b, b2/a, relative maximum.
21.
-2 -1 0 1 2
-2
-1
0
1
2
∇f=(4x−4y)i−(4x−4y3)j=0when x=y, x =y3,sox=y=0orx=y=±1. At
(0,0),D =−16, a saddle point; at (1,1) and (−1,−1),D =32>0,f
xx = 4, a relative minimum.
22.
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5
-4
-3
-2
-1
0
1
2
3
4
5140
100
140
100
60
60
40 20
20
20
0
0
0
-20
-20
-40
-60
-100
∇f=(2y
2−2xy +4y)i+(4xy −x2+4x)j=0when 2y2−2xy +4y=0,4xy −x2+4x= 0, with
solutions (0,0),(0,−2),(4,0),(4/3,−2/3). At (0,0), D=−16, a saddle point. At (0,−2),
D=−16, a saddle point. At (4,0),D =−16, a saddle point. At (4/3,−2/3),D =16/3,
fxx =4/3>0, a relative minimum.
23. (a) critical point (0,0); D=0
(b) f(0,0)=0,x
4+y
4≥0sof(x, y)≥f(0,0), relative minimum.
24. (a) critical point (0,0); D=0
(b) f(0,0) = 0, inside any circle centered at (0,0) there are points where f(x, y)>0 (along the
x-axis) and points where f(x, y)<0 (along the y-axis) so (0,0) is a saddle point.
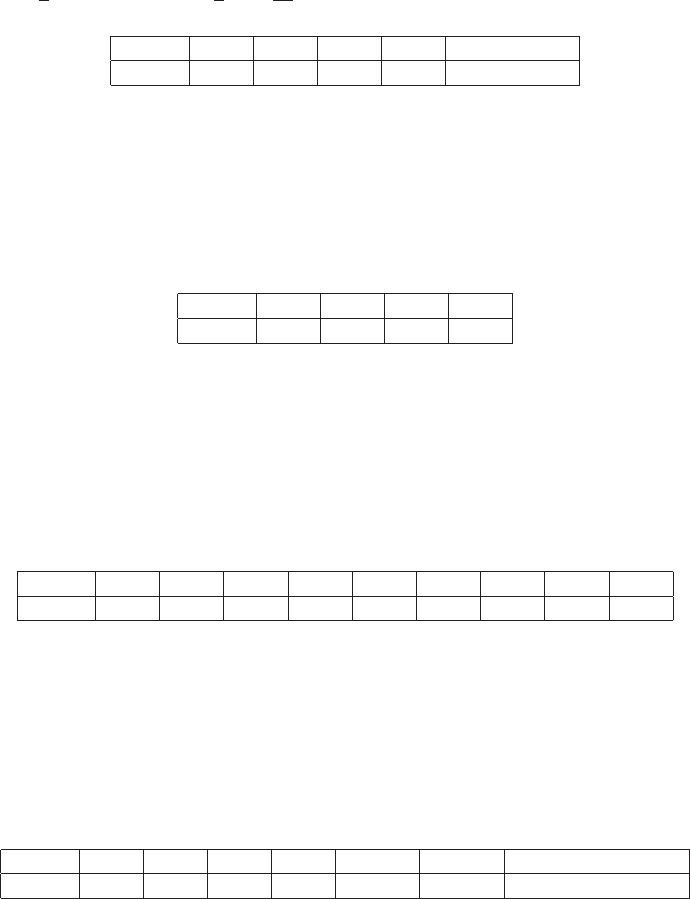
561 Chapter 15
25. (a) fx=3e
y−3x
2=3e
y−x
2
=0,f
y=3xey−3e3y=3e
yx−e
2y
=0,e
y=x
2and
e2y=x,x4=x,xx3−1=0sox=0,1; critical point (1,0); D=27>0 and fxx =−6<0
at (1,0), relative maximum.
(b) lim
x→−∞ f(x, 0) = lim
x→−∞ 3x−x3−1=+∞so no absolute maximum.
26. fx=8xey−8x3=8x(e
y−x
2
)=0,f
y=4x
2
e
y−4e
4y=4e
y
(x
2−e
3y
)=0,x
2=e
yand
x2=e3y,e3y=ey,e2y=1,soy= 0 and x=±1; critical points (1,0) and (−1,0). D= 128 >0
and fxx =−16 <0 at both points so a relative maximum occurs at each one.
27. fx=y−1=0,f
y=x−3 = 0; critical point (3,1).
Along y=0: u(x)=−x; no critical points,
along x=0: v(y)=−3y; no critical points,
along y=−4
5x+4: w(x)=−4
5
x
2+27
5x−12; critical point (27/8,13/10).
(x, y) (3,1) (0,0) (5,0) (0,4) (27/8,13/10)
f(x, y)−3 0 −5−12 −231/80
Absolute maximum value is 0, absolute minimum value is −12.
28. fx=y−2=0,f
y=x= 0; critical point (0,2), but (0,2) is not in the interior of R.
Along y=0: u(x)=−2x; no critical points,
along x=0: v(y) = 0; no critical points,
along y=4−x:w(x)=2x−x
2
; critical point (1,3).
(x, y) (0,0) (0,4) (4,0) (1,3)
f(x, y) 0 0 −8 1
Absolute maximum value is 1, absolute minimum value is −8.
29. fx=2x−2=0,f
y=−6y+ 6 = 0; critical point (1,1).
Along y=0: u
1
(x)=x
2−2x; critical point (1,0),
along y=2: u
2
(x)=x
2−2x; critical point (1,2)
along x=0: v
1
(y)=−3y
2+6y; critical point (0,1),
along x=2: v
2
(y)=−3y
2+6y; critical point (2,1)
(x, y) (1,1) (1,0) (1,2) (0,1) (2,1) (0,0) (0,2) (2,0) (2,2)
f(x, y) 2 −1−1330000
Absolute maximum value is 3, absolute minimum value is −1.
30. fx=ey−2x=0,f
y=xey−ey=ey(x−1) = 0; critical point (1,ln 2).
Along y=0: u
1
(x)=x−x
2−1; critical point (1/2,0),
along y=1: u
2
(x)=ex −x2−e; critical point (e/2,1),
along x=0: v
1
(y)=−e
y
; no critical points,
along x=2: v
2
(y)=e
y−4; no critical points (for 0 <y<1).
(x, y) (0,0) (0,1) (2,1) (2,0) (1,ln 2) (1/2,0) (e/2,1)
f(x, y)−1−e e −4−3−1−3/4e(e−4)/4≈−0.87
Absolute maximum value is −3/4, absolute minimum value is −3.
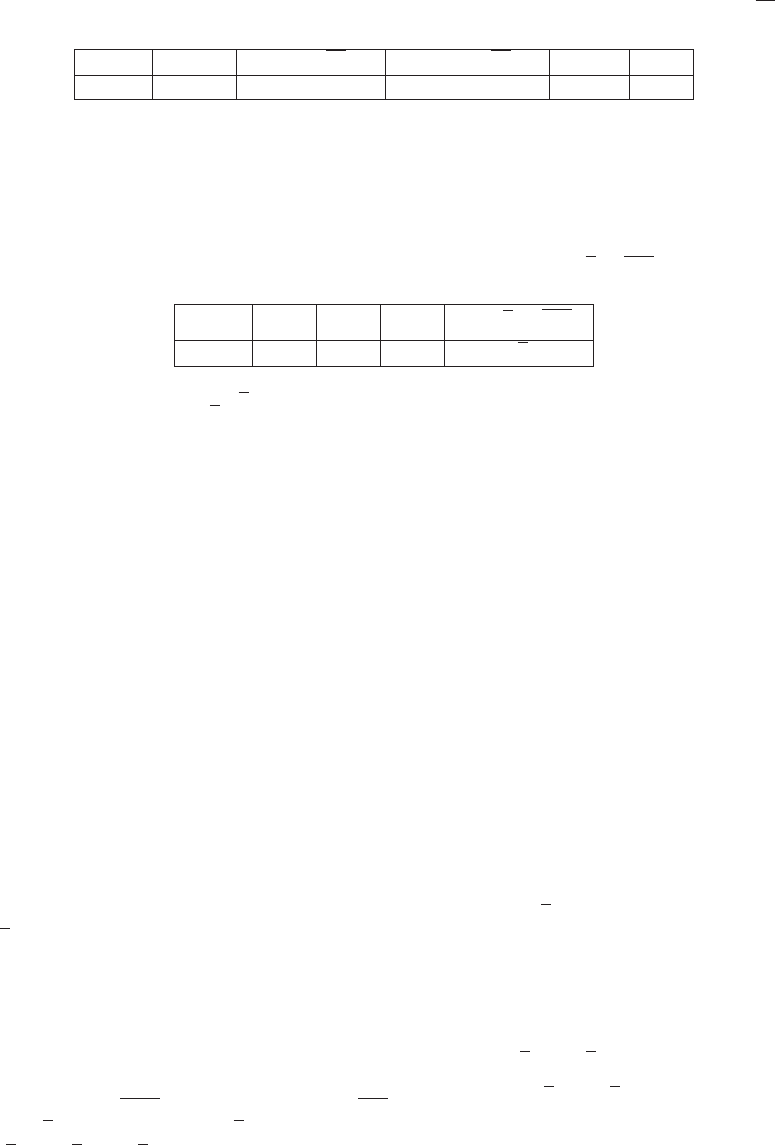
Exercise Set 15.8 562
31. fx=2x−1=0,f
y=4y= 0; critical point (1/2,0).
Along x2+y2=4:y
2=4−x
2
,u(x)=8−x−x
2for −2≤x≤2; critical points (−1/2,±√15/2).
(x, y) (1/2,0) −1/2,√15/2−1/2,−√15/2(−2,0) (2,0)
f(x, y)−1/4 33/4 33/4 6 2
Absolute maximum value is 33/4, absolute minimum value is −1/4.
32. fx=y2=0,f
y=2xy = 0; no critical points in the interior of R.
Along y=0: u(x) = 0; no critical points,
along x=0: v(y) = 0; no critical points
along x2+y2=1: w(x)=x−x
3for 0 ≤x≤1; critical point 1/√3,p2/3.
(x, y) (0,0) (0,1) (1,0) 1/√3,p2/3
f(x, y) 0 0 0 2√3/9
Absolute maximum value is 2
9√3, absolute minimum value is 0.
33. Maximize P=xyz subject to x+y+z= 48, x>0, y>0, z>0. z=48−x−yso
P=xy(48 −x−y)=48xy −x2y−xy2,Px=48y−2xy −y2=0,P
y=48x−x
2−2xy = 0. But
x6= 0 and y6= 0 so 48 −2x−y= 0 and 48 −x−2y= 0; critical point (16,16). PxxPyy −P2
xy >0
and Pxx <0 at (16,16), relative maximum. z= 16 when x=y= 16, the product is maximum for
the numbers 16,16,16.
34. Minimize S=x2+y2+z2subject to x+y+z= 27, x>0, y>0, z>0. z=27−x−yso
S=x2+y2+ (27 −x−y)2,Sx=4x+2y−54=0,S
y=2x+4y−54 = 0; critical point (9,9);
SxxSyy −S2
xy =12>0 and Sxx =4>0 at (9,9), relative minimum. z= 9 when x=y= 9, the
sum of the squares is minimum for the numbers 9,9,9.
35. Maximize w=xy2z2subject to x+y+z=5,x>0, y>0, z>0. x=5−y−zso
w=(5−y−z)y
2
z
2=5y
2
z
2−y
3
z
2−y
2
z
3
,w
y=10yz2−3y2z2−2yz3=yz2(10 −3y−2z)=0,
w
z=10y
2
z−2y
3
z−3y
2
z
2=y
2
z(10−2y−3z)=0,10−3y−2z= 0 and 10−2y−3z= 0; critical
point when y=z=2;w
yywzz −w2
yz = 320 >0 and wyy =−24 <0 when y=z= 2, relative
maximum. x= 1 when y=z=2,xy2z2is maximum at (1,2,2).
36. Minimize w=D2=x2+y2+z2subject to x2−yz =5. x
2=5+yz so w=5+yz +y2+z2,
wy=z+2y=0,w
z=y+2z= 0; critical point when y=z=0;w
yywzz −w2
yz =3>0 and
wyy =2>0 when y=z= 0, relative minimum. x2=5,x=±
√
5 when y=z= 0. The points
±√5,0,0are closest to the origin.
37. The diagonal of the box must equal the diameter of the sphere, thus we maximize V=xyz or, for
convenience, w=V2=x2y2z2subject to x2+y2+z2=4a
2
,x>0,y>0,z>0; z2=4a
2
−x
2
−y
2
hence w=4a
2
x
2
y
2−x
4
y
2−x
2
y
4
,w
x=2xy2(4a2−2x2−y2)=0,w
y=2x
2
y4a
2−x
2−2y
2
=0,
4a
2−2x
2−y
2= 0 and 4a2−x2−2y2= 0; critical point 2a/√3,2a/√3;
wxxwyy −w2
xy =4096
27 a8>0 and wxx =−128
9a4<0at
2a/√3,2a/√3, relative maximum.
z=2a/√3 when x=y=2a/√3, the dimensions of the box of maximum volume are
2a/√3,2a/√3,2a/√3.
38. Maximize V=xyz subject to x+y+z=1,x>0, y>0, z>0. z=1−x−yso V=xy−x2y−xy2,
Vx=y(1 −2x−y)=0,V
y=x(1 −x−2y)=0,1−2x−y= 0 and 1 −x−2y= 0; critical point
(1/3,1/3); VxxVyy −V2
xy =1/3>0 and Vxx =−2/3<0at(1/3,1/3), relative maximum. The
maximum volume is V=(1/3)(1/3)(1/3)=1/27.
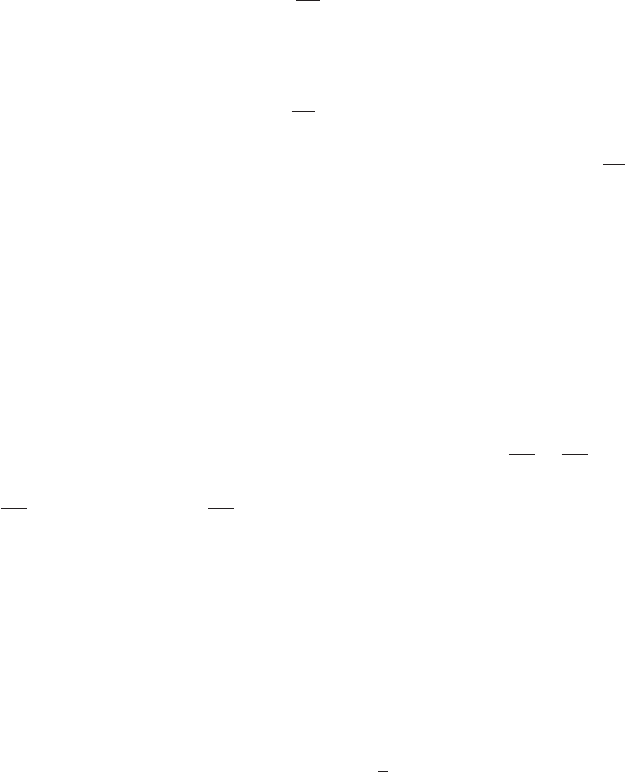
563 Chapter 15
39. Let x,y, and zbe, respectively, the length, width, and height of the box. Minimize
C= 10(2xy) + 5(2xz +2yz) = 10(2xy +xz +yz) subject to xyz = 16. z=16/(xy)
so C= 20(xy +8/y +8/x), Cx= 20(y−8/x2)=0,C
y= 20(x−8/y2)=0;
critical point (2,2); CxxCyy −C2
xy = 1200 >0
and Cxx =40>0 at (2,2), relative minimum. z= 4 when x=y= 2. The cost of materials is
minimum if the length and width are 2 ft and the height is 4 ft.
40. Maximize the profit P= 500(y−x)(x−40) + [45,000 + 500(x−2y)](y−60)
= 500(−x2−2y2+2xy −20x+ 170y−5400).
Px= 1000(−x+y−10)=0,P
y= 1000(−2y+x+ 85) = 0; critical point (65,75);
PxxPyy −P2
xy =1,000,000 >0 and Pxx =−1000 <0 at (65,75), relative maximum. The profit
will be maximum when x= 65 and y= 75.
41. (a) x=0:f(0,y)=−3y
2
, minimum −3, maximum 0;
x=1,f(1,y)=4−3y
2+2y, ∂f
∂y (1,y)=−6y+2=0aty=1/3, minimum 3,
maximum 13/3;
y=0,f(x, 0)=4x
2
, minimum 0, maximum 4;
y=1,f(x, 1)=4x
2+2x−3,∂f
∂x(x, 1)=8x+2 6= 0 for 0 <x<1, minimum −3, maximum 3
(b) f(x, x)=3x
2
, minimum 0, maximum 3; f(x, 1−x)=−x
2
+8x−3,d
dxf(x, 1−x)=−2x+8 6=0
for 0 <x<1, maximum 4, minimum −3
(c) fx(x, y)=8x+2y=0,f
y(x, y)=−3y+2x= 0, solution is (0,0), which is not an interior
point of the square, so check the sides: minimum −3, maximum 14/3.
42. Maximize A=ab sin αsubject to 2a+2b=`,a>0, b>0, 0 <α<π.b=(`−2a)/2so
A=(1/2)(`a −2a2) sin α,Aa=(1/2)(`−4a) sin α,Aα=(a/2)(`−2a) cos α; sin α6= 0 so from
Aa= 0 we get a=`/4 and then from Aα= 0 we get cosα=0,α=π/2. AaaAαα −A2
aα =`2/8>0
and Aaa =−2<0 when a=`/4 and α=π/2, the area is maximum.
43. Minimize S=xy +2xz +2yz subject to xyz =V,x>0, y>0, z>0 where x,y, and zare,
respectively, the length, width, and height of the box. z=V/(xy)soS=xy +2V/y +2V/x,
Sx=y−2V/x2=0,S
y=x−2V/y2= 0; critical point ( 3
√2V, 3
√
2V); SxxSyy −S2
xy =3>0 and
Sxx =2>0 at this point so there is a relative minimum there. The length and width are each
3
√2V, the height is z=3
√2V/2.
44. The altitude of the trapezoid is xsin φand the lengths of the lower and upper bases are, respectively,
27 −2xand 27 −2x+2xcos φso we want to maximize
A=(1/2)(xsin φ)[(27 −2x)+(27−2x+2xcos φ)]=27xsin φ−2x2sin φ+x2sin φcos φ.
Ax= sin φ(27 −4x+2xcos φ),
Aφ=x(27 cos φ−2xcos φ−xsin2φ+xcos2φ)=x(27 cos φ−2xcos φ+2xcos2φ−x).
sin φ6= 0 so from Ax= 0 we get cosφ=(4x−27)/(2x), x6= 0 so from Aφ= 0 we get
(27 −2x+2xcos φ) cos φ−x= 0 which, for cos φ=(4x−27)/(2x), yields 4x−27 −x=0,
x=9. Ifx= 9 then cosφ=1/2, φ=π/3. The critical point occurs when x= 9 and φ=π/3;
AxxAφφ −A2
xφ = 729/2>0 and Axx =−3√3/2<0 there, the area is maximum when x= 9 and
φ=π/3.
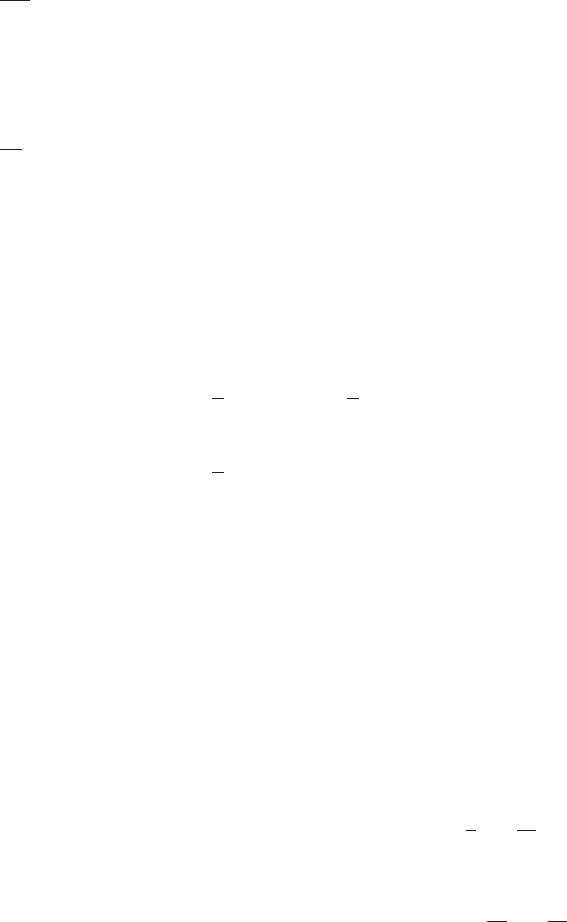
Exercise Set 15.8 564
45. (a) ∂g
∂m =
n
X
i=1
2(mxi+b−yi)xi=2 m
n
X
i=1
x2
i+b
n
X
i=1
xi−
n
X
i=1
xiyi!=0if
n
X
i=1
x2
i!m+ n
X
i=1
xi!b=
n
X
i=1
xiyi,
∂g
∂b =
n
X
i=1
2(mxi+b−yi)=2 m
n
X
i=1
xi+bn −
n
X
i=1
yi!=0if n
X
i=1
xi!m+nb =
n
X
i=1
yi
(b) The function z=g(m, b), as a function of mand b, has only one critical point, found in part
(a), and tends to +∞as either |m|or |b|tends to infinity. Thus the only critical point must
be a minimum.
46. (a)
n
X
i=1
(xi−¯x)2=
n
X
i=1 x2
i−2¯xxi+¯x
2
=
n
X
i=1
x2
i−2¯x
n
X
i=1
xi+n¯x2
=
n
X
i=1
x2
i−2
n n
X
i=1
xi!2
+1
n n
X
i=1
xi!2
=
n
X
i=1
x2
i−1
n n
X
i=1
xi!2
>0son
n
X
i=1
x2
i− n
X
i=1
xi!2
>0
(b) gmm =2
n
X
i=1
x2
i,g
bb =2n, gmb =2
n
X
i=1
xi,
D=gmmgbb −g2
mb =4
n
n
X
i=1
x2
i− n
X
i=1
xi!2
>0 and gmm >0
(c) g(m, b) is of the second-degree in mand bso the graph of z=g(m, b) is a quadric surface.
(d) The only quadric surface of this form having a relative minimum is a paraboloid that opens
upward where the relative minimum is also the absolute minimum.
47. n=3,
3
X
i=1
xi=3,
3
X
i=1
yi=7,
3
X
i=1
xiyi=13,
3
X
i=1
x2
i=11,y =3
4x+19
12
48. n=4,
4
X
i=1
xi=7,
4
X
i=1
yi=4,
4
X
i=1
x2
i=21,
4
X
i=1
xiyi=−2,y =−36
35x+14
5
49.
4
X
i=1
xi=10,
4
X
i=1
yi=8.2,
4
X
i=1
x2
i=30,
4
X
i=1
xiyi=23,n=4; m=0.5,b=0.8,y=0.5x+0.8.
50.
5
X
i=1
xi=15,
5
X
i=1
yi=15.1,
5
X
i=1
x2
i=55,
5
X
i=1
xiyi=39.8,n=5;m=−0.55,b =4.67,y =4.67−0.55x
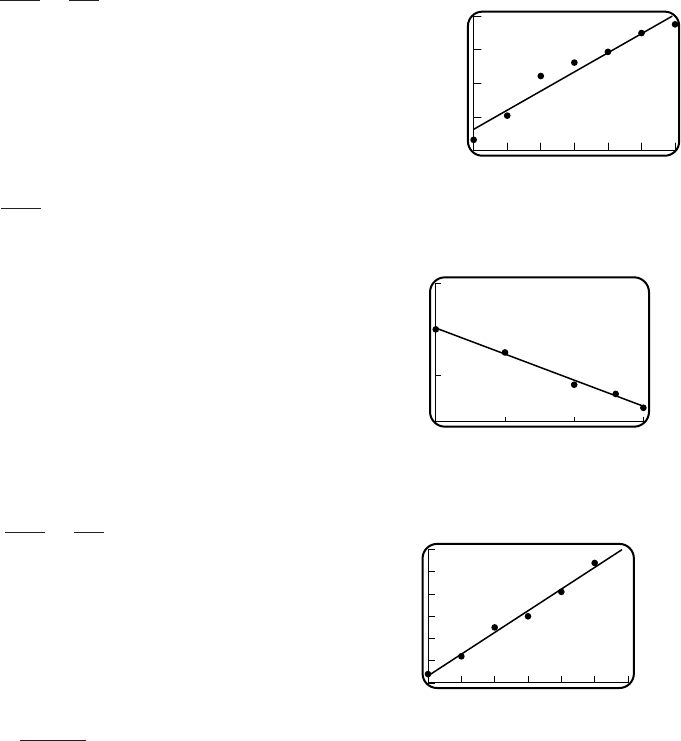
565 Chapter 15
51. (a) y=8843
140 +57
200t≈63.1643 + 0.285t(b)
600(1930)
60
80
(c) y=2909
35 ≈83.1143
52. (a) y≈119.84 −1.13x(b) 90
60
35 50
(c) about 52 units
53. (a) P=2798
21 +171
350T≈133.2381 + 0.4886T(b)
1200
130
190
(c) T≈−139,900
513 =≈−272.7096◦C
54. (a) for example, z=y
(b) For example, on 0 ≤x≤1,0≤y≤1 let z=(yif 0 <x<1,0<y<1
1/2ifx=0,1ory=0,1
55. f(x0,y
0)≥f(x, y) for all (x, y) inside a circle centered at (x0,y
0) by virtue of Definition 15.8.1.
If ris the radius of the circle, then in particular f(x0,y
0)≥f(x, y0) for all xsatisfying
|x−x0|<rso f(x, y0) has a relative maximum at x0. The proof is similar for the function
f(x0,y).
EXERCISE SET 15.9
1. (a) xy = 4 is tangent to the line, so the maximum value of fis 4.
(b) xy = 2 intersects the curve and so gives a smaller value of f.
(c) Maximize f(x, y)=xy subject to the constraint g(x, y)=x+y−4=0,∇f=λ∇g,
yi+xj=λ(i+j), so solve the equations y=λ, x =λwith solution x=y=λ, but x+y=4,
so x=y= 2, and the maximum value of fis f=xy =4.

Exercise Set 15.9 566
2. (a) x2+y2= 25 is tangent to the line at (3,4), so the minimum value of fis 25.
(b) A smaller value of fyields a circle of a smaller radius, and hence does not intersect the line.
(c) Minimize f(x, y)=x
2+y
2subject to the constraint g(x, y)=3x+4y−25=0,∇f=λ∇g,
2xi+2yj=3λi+4λj, so solve 2x=3λ, 2y=4λ; solution is x=3,y = 4, minimum = 25.
3. y=8xλ,x=16yλ;y/(8x)=x/(16y), x2=2y
2so 4 2y2+8y
2= 16, y2=1,y=±1. Test
±√2,−1and (±√2,1). f−√2,−1=f√2,1=√2, f−√2,1=f√2,−1=−√2.
Maximum √2at−
√
2,−1
and √2,1, minimum −√2at−
√
2,1
and √2,−1.
4. 2x=2xλ, −1=2yλ.Ifx6= 0 then λ= 1 and y=−1/2sox
2+(−1/2)2= 25,
x2=99/4, x=±3√11/2. If x= 0 then 02+y2= 25, y=±5. Test ±3√11/2,−1/2and (0,±5).
f±3√11/2,−1/2= 101/4, f(0,−5)=5,f(0,5) = −5. Maximum 101/4at±3
√
11/2,−1/2,
minimum −5 at (0,5).
5. 12x2=4xλ,2y=2yλ.Ify6= 0 then λ= 1 and 12x2=4x,12x(x−1/3)=0,x=0orx=1/3
so from 2x2+y2= 1 we find that y=±1 when x=0,y=±
√
7/3 when x=1/3. If y=0
then 2x2+ (0)2=1,x=±1/
√
2. Test (0,±1), 1/3,±√7/3, and ±1/√2,0.f(0,±1)=1,
f
1/3,±
√
7/3
=25/27, f1/√2,0=√2, f−1/√2,0=−√2. Maximum √2at
1/
√
2,0
,
minimum −√2at−1/
√
2,0
.
6. 1=2xλ,−3=6yλ;1/(2x)=−1/(2y), y=−xso x2+3(−x)
2= 16, x=±2. Test (−2,2) and
(2,−2). f(−2,2) = −9, f(2,−2) = 7. Maximum 7 at (2,−2), minimum −9at(−2,2).
7. 2=2xλ, 1=2yλ, −2=2zλ;1/x =1/(2y)=−1/z thus x=2y,z=−2yso
(2y)2+y2+(−2y)
2=4,y
2=4/9, y=±2/3. Test (−4/3,−2/3,4/3) and (4/3,2/3,−4/3).
f(−4/3,−2/3,4/3) = −6, f(4/3,2/3,−4/3) = 6. Maximum 6 at (4/3,2/3,−4/3), minimum −6
at (−4/3,−2/3,4/3).
8. 3=4xλ,6=8yλ,2=2zλ;3/(4x)=3/(4y)=1/z thus y=x,z=4x/3, so
2x2+4(x)
2+(4x/3)2= 70, x2=9,x=±3. Test (−3,−3,−4) and (3,3,4).
f(−3,−3,−4) = −35, f(3,3,4) = 35. Maximum 35 at (3, 3, 4), minimum −35 at (−3,−3,−4).
9. yz =2xλ,xz =2yλ,xy =2zλ;yz/(2x)=xz/(2y)=xy/(2z)thusy
2=x
2
,z
2=x
2so
x2+x2+x2=1,x=±1/
√
3. Test the eight possibilities with x=±1/√3, y=±1/√3, and
z=±1/√3 to find the maximum is 1/3√3at 1/√3,1/√3,1/√3,1/√3,−1/√3,−1/√3,
−1/√3,1/√3,−1/√3, and −1/√3,−1/√3,1/√3; the minimum is −1/3√3at
1/√3,1/√3,−1/√3,1/√3,−1/√3,1/√3,−1/√3,1/√3,1/√3, and −1/√3,−1/√3,−1/√3.
10. 4x3=λ, 4y3=λ, 4z3=λ,sox=y=z;x+y+z=3x=1,x =y=z=1/3, minimum value
1/27, no maximum
11. f(x, y)=x
2+y
2
;2x=2λ,2y=−4λ;y=−2xso 2x−4(−2x)=3,x=3/10. The point is
(3/10,−3/5).
12. f(x, y)=(x−4)2+(y−2)2,g(x, y)=y−2x−3; 2(x−4) = −2λ,2(y−2) = λ;x−4=−2(y−2),
x=−2y+8soy=2(−2y+8)+3,y=19/5. The point is (2/5,19/5).
13. f(x, y, z)=x
2+y
2+z
2
;2x=λ,2y=2λ,2z=λ;y=2x,z=xso x+ 2(2x)+x=1,x=1/6.
The point is (1/6,1/3,1/6).
14. f(x, y, z)=(x−1)2+(y+1)
2+(z−1)2;2(x−1)=4λ,2(y+1)=3λ,2(z−1) = λ;x=4z−3,
y=3z−4so4(4z−3) + 3(3z−4)+z=2,z= 1. The point is (1,−1,1).
567 Chapter 15
15. f(x, y)=(x−1)2+(y−2)2;2(x−1)=2xλ,2(y−2)=2yλ;(x−1)/x =(y−2)/y,y=2x
so x2+(2x)
2= 45, x=±3. f(−3,−6) = 80 and f(3,6) = 20 so (3,6) is closest and (−3,−6) is
farthest.
16. f(x, y, z)=x
2+y
2+z
2
;2x=yλ,2y=xλ,2z=−2zλ.Ifz6= 0 then λ=−1so2x=−yand
2y=−x,x=y= 0; substitute into xy −z2= 1 to get z2=−1 which has no real solution. If
z= 0 then xy −(0)2=1,y=1/x, and also (from 2x=yλ and 2y=xλ), 2x/y =2y/x,y2=x2
so (1/x)2=x2,x4=1,x=±1. Test (1,1,0) and (−1,−1,0) to see that they are both closest to
the origin.
17. f(x, y, z)=x+y+z,x
2+y
2+z
2= 25 where x,y, and zare the components of the vector;
1=2xλ,1=2yλ,1=2zλ;1/(2x)=1/(2y)=1/(2z); y=x,z=xso x2+x2+x2= 25,
x=±5/√3. f−5/√3,−5/√3,−5/√3=−5√3 and f5/√3,5/√3,5/√3=5
√
3 so the vector
is 5(i+j+k)/√3.
18. x2+y2= 25 is the constraint; 8x−4y=2xλ,−4x+2y=2yλ;(4x−2y)/x =(−2x+y)/y,
2x2+3xy −2y2=0,(2x−y)(x+2y)=0,y=2xor x=−2y.Ify=2xthen x2+(2x)
2= 25,
x=±√5. If x=−2ythen −2y2+y2= 25, y=±√5. T−√5,−2√5=T√5,2√5= 0 and
T2√5,−√5=T−2√5,√5= 125. The highest temperature is 125 and the lowest is 0.
19. (a)
31.5
-31.5
-27
15 (b) minimum value −5,
maximum value 101/4
(c) Find the minimum and maximum values of f(x, y)=x
2−ysubject to the constraint
g(x, y)=x
2+y
2−25=0,∇f=λ∇g, 2xi−j=2λxi+2λyj, so solve 2x=2λx, −1=2λy.
If x= 0 then y=±5,f =∓5, and if x6= 0 then λ=1,y =−1/2,x
2=25−1/4=99/4,
f=99/4+1/2 = 101/4, so the maximum value of fis 101/4at(±3
√
11/2,−1/2) and the
minimum value of fis −5at(0,5).
20. (a)
0 1 2 3 4 5 6
0
1
2
3
4
5
6(b) f≈15
(d) Set f(x, y)=x
3+y
3−3xy, g(x, y)=(x−4)2+(y−4)2−25; minimize fsubject to the
constraint g=0: ∇f=λg, (3x2−3y)i+(3y
2−3x)j=2λ(x−4)i+2λ(y−4)j, so solve
(use a CAS) 3x2−3y=2λ(x−4),3y2−3x=2λ(y−4); minimum value f=14.52 at
(2.5858,2.5858)
21. Minimize f=x2+y2+z2subject to g(x, y, z)=x+y+z−27=0. ∇f=λ∇g,
2xi+2yj+2zk=λi+λj+λk, solution x=y=z= 9, minimum value 243

Exercise Set 15.9 568
22. Maximize f(x, y, z)=xy2z2subject to g(x, y, z)=x+y+z−5=0,∇f=λ∇g=λ(i+j+k),
λ=y
2
z
2=2xyz2=2xy2z, λ = 0 is impossible, hence x, y, z 6= 0, and z=y=2x, 5x−5=0,
x=1,y =z= 2, maximum value 8 at (1,2,2)
23. Minimize f=x2+y2+z2subject to x2−yz =5,∇f=λ∇g, 2x=2xλ, 2y=−zλ,2z=−yλ.
If λ6=±2, then y=z=0,x =±√5,f =5;ifλ=±2 then x= 0, and since −yz =5,
y=−z=±
√
5,f = 10, thus the minimum value is 5 at (±√5,0,0).
24. The diagonal of the box must equal the diameter of the sphere so maximize V=xyz or, for
convenience, maximize f=V2=x2y2z2subject to g(x, y, z)=x
2+y
2+z
2−4a
2=0,∇f=λ∇g,
2xy2z2=2λx, 2x2yz2=2λy, 2x2y2z=2λz. Since V6= 0 it follows that x, y, z 6= 0, hence
x=±y=±z,3x2=4a
2
,x=±2a/√3, maximum volume 8a3/(3√3).
25. Let x,y, and zbe, respectively, the length, width, and height of the box. Minimize
f(x, y, z) = 10(2xy) + 5(2xz +2yz) = 10(2xy +xz +yz) subject to g(x, y, z)=xyz −16=0,
∇f=λ∇g, 20y+10z=λyz, 20x+10z=λxz, 10x+10y=λz. Since V=xyz =16,x,y,z 6=0,
thus λz = 20 + 10(z/y)=20+10(z/x)=10x+10y,sox=y. Then z=16/x2,thus
20 + 10(16/x3)=20x, x3+8=x
4
, the only real solution of which is x= 2,thus x=y=2,z =4,
minimum value 240.
26. Minimize f(p, q, r)=2pq +2pr+2qr, subject to g(p, q, r)=p+q+r−1=0,∇
(p,q,r)f=λ∇(p,q,r)g,
2(q+r)=λ, 2(p+r)=λ, 2(p+q)=λ, solution p=q=r=1/3, minimum value 2/3.
27. Maximize A(a, b, α)=ab sin αsubject to g(a, b, α)=2a+2b−`=0,∇
(a,b,α)f=λ∇(a,b,α)g,
bsin α=2λ, a sin α=2λ, ab cos α= 0 with solution a=b, α =π/2 maximum value if parallelogram
is a square.
28. Minimize f(x, y, z)=xy +2xz +2yz subject to g(x, y, z)=xyz −V=0,∇f=λ∇g,
y+2z=λyz, x +2z=λxz, 2x+2y=λxy;λ= 0 leads to x=y=z= 0, impossible, so solve for
λ=1/z +2/x =1/z +2/y =2/y +2/x,sox=y=2z, x3=2V, minimum value 3(2V)2/3
29. (a) Maximize f(α, β, γ) = cos αcos βcos γsubject to g(α, β, γ)=α+β+γ−π=0,
∇f=λ∇g, −sin αcos βcos γ=λ, −cos αsin βcos γ=λ, −cos αcos βsin γ=λwith solution
α=β=γ=π/3, maximum value 3√3/8
(b) for example, f(α, β) = cos αcos βcos(π−α−β)
z
xy
30. Find maxima and minima z=x2+4y
2subject to the constraint g(x, y)=x
2+y
2−1=0,
∇z=λ∇g, 2xi+8yj=2λxi+2λyj, solve 2x=2λx, 8y=2λy.Ify6= 0 then λ=4,x =0,y
2=1
and z=x2+4y
2=4. Ify= 0 then x2= 1 and z= 1, so the maximum height is obtained for
(x, y)=(0,±1),z = 4 and the minimum height is z= 1 at (±1,0).
569 Chapter 15
CHAPTER 15 SUPPLEMENTARY EXERCISES
1. (a) They approximate the profit per unit of any additional sales of the standard or high-resolution
monitors, respectively.
(b) The rates of change with respect to the two directions xand y, and with respect to time.
3. z=px2+y2=cimplies x2+y2=c2, which is the equation of a circle; x2+y2=cis also the
equation of a circle (for c>0).
-3 3
-3
3
x
y
z = x2 + y2
-3 3
-3
3
x
y
z = √x2 + y2
5. (b) f(x, y, z)=z−x
2−y
2
7. (a) f(ln y, ex)=e
ln yln ex=xy (b) er+sln rs
8. (a)
x
y
y = 1
x
(b)
x
y
–1 1
9. wx=2xsec2(x2+y2)+√
y, wxy =8xy sec2(x2+y2) tan(x2+y2)+1
2y
−1/2
,
w
y=2ysec2(x2+y2)+1
2xy−1/2,w
yx =8xy sec2(x2+y2) tan(x2+y2)+1
2y
−1/2
10. ∂w/∂x =1
x−y−sin(x+y),∂2w/∂x2=−1
(x−y)2−cos(x+y),
∂w/∂y =−1
x−y−sin(x+y),∂
2
w/∂y2=−1
(x−y)2−cos(x+y)=∂
2
w/∂x2
11. Fx=−6xz, Fxx =−6z,Fy=−6yz, Fyy =−6z,Fz=6z
2−3x
2−3y
2
,
F
zz =12z,Fxx +Fyy +Fzz =−6z−6z+12z=0
12. fx=yz +2x, fxy =z, fxyz =1,f
xyzx =0; f
z=xy −(1/z),f
zx =y, fzxx =0,f
zxxy =0
Chapter 15 Supplementary Exercises 570
13. (a) P=10T
V,dP
dT =10
V
dT
dt = 12 K/(m2min) (b) dP
dt =−10 P
V2
dV
dt = 240 K/(m2min)
14. (a) z=1−y
2
, slope = ∂z
∂y =−2y=4 (b) z=1−4x
2
,∂z
∂x =−8x=−8
15. x4−x+y−x3y=(x
3−1)(x−y), limit = −1, continuous
16. x4−y4
x2+y2=x2−y2, limit = lim
(x,y)→(0,0)(x2−y2) = 0, continuous
17. Use the unit vectors u=h1
√2,1
√2i,v=h0,−1i,w=h− 1
√5,−2
√5i=−√2
√5u+1
√5v, so that
Dwf=−√2
√5Duf+1
√5Dvf=−√2
√52√2+ 1
√
5(−3) = −7
√5
18. (a) n =zxi+zyj−k=8i+8j−k, tangent plane 8x+8y−z= 4 + 8 ln 2, normal line
x(t)=1+8t, y(t)=ln2+8t, z(t)=4−t
(b) n =3i+10j−14k, tangent plane 3x+10y−14z= 30, normal line
x(t)=2+3t, y(t)=1+10t, z(t)=−1−14t
19. The origin is not such a point, so assume that the normal line at (x0,y
0,z
0)6=(0,0,0) passes
through the origin, then n=zxi+zyj−k=−y0i−x0j−k; the line passes through the origin and
is normal to the surface if it has the form r(t)=−y
0
ti−x
0
tj−tkand (x0,y
0,z
0)=(x
0
,y
0,2−x
0y
0)
lies on the line if −y0t=x0,−x0t=y0,−t=2−x
0
y
0
, with solutions x0=y0=−1,
x0=y0=1,x
0=y
0= 0; thus the points are (0,0,2),(1,1,1),(−1,−1,1).
20. n =2
3x−1/3
0i+2
3y−1/3
0j+2
3z−1/3
0k, tangent plane x−1/3
0x+y−1/3
0y+z−1/3
0z=x2/3
0+y2/3
0+z2/3
0=1;
intercepts are x=x1/3
0,y =y
1/3
0,z =z1/3
0, sum of squares of intercepts is x2/3
0+y2/3
0+z2/3
0=1.
21. A tangent to the line is 6i+4j+k, a normal to the surface is n=18xi+8yj−k, so solve
18x=6k, 8y=4k, −1=k;k=−1,x =−1/3,y =−1/2,z =2
22. ∆w=(1.1)2(−0.1) −2(1.1)(−0.1)+(−0.1)2(1.1) −0=0.11,
dw =(2xy −2y+y2)dx +(x
2−2x+2yx)dy =−(−0.1)=0.1
23. dV =2
3xhdx +1
3x2dh =2
32(−0.1) + 1
3(0.2) = −0.06667 m3;∆V=−0.07267 m3
24. ∇f=(2x+3y−6)i+(3x+6y+3)j=0if 2x+3y=6,x+2y=−1,x=15,y =−8,D =3>0,
f
xx =2>0, so fhas a relative minimum at (15,−8).
25. ∇f=(2xy −6x)i+(x
2−12y)j=0if 2xy −6x=0,x
2−12y=0;ifx= 0 then y= 0, and
if x6= 0 then y=3,x =±6, thus the gradient vanishes at (0,0),(−6,3),(6,3); fxx = 0 at all
three points, fyy =−12 <0,D =−4x
2,so(±6,3) are saddle points, and near the origin we write
f(x, y)=(y−3)x2−6y2; since y−3<0 when |y|<3, fhas a maximum by inspection.
26. ∇f=(3x
2−3y)i−(3x−y)j=0if y=x2,3x=y,sox=y=0orx=3,y =9;at
x=y=0,D =−9, saddle point; at x=3,y =9,D =9,f
xx =18>0, relative minimum

571 Chapter 15
27. (a)
P = 1
P = 3
P = 2
12345
1
2
3
4
5
L
K(b)
012345
0
1
2
3
4
5
28. (a) ∂P/∂L =cαLα−1Kβ,∂P/∂K =cβLαKβ−1
(b) the rates of change of output with respect to labor and capital equipment, respectively
(c) K(∂P/∂K)+L(∂P/∂L)=cβLαKβ+cαLαKβ=(α+β)P=P
29. (a) L+K= 200,000,P = 1000L0.6(200,000 −L)0.4,
dP/dL = 600(200,000 −L)0.4
L4−400 L6
(200,000 −L)0.6= 0 when L= 120,000,
P= 102,033,960.1, which is a maximum because P=0atL=0,200,000, P>0 in between,
and dP/dL = 0 has only the one solution.
(b) Since L+K= 200,000 and L= 120,000,K =80,000
30. (a) y2=8−4x
2
, find extrema of f(x)=x
2
(8 −4x2)=−4x
4+8x
2defined for −√2≤x≤√2.
Then f0(x)=−16x3+16x= 0 when x=0,±1,f00(x)=−48x2+ 16, so fhas a relative
maximum at x=±1,y =±2 and a relative minimum at x=0,y =±2
√2. At the endpoints
x=±√2,y = 0 we obtain the minimum f= 0 again.
(b) f(x, y)=x
2
y
2
,g(x, y)=4x
2+y
2−8=0,∇f=2xy2i+2x
2
yj=λ∇g=8λxi+2λyj,so
solve 2xy2=λ8x, 2x2y=λ2y.Ifx= 0 then y=±2√2, and if y= 0 then x=±√2. In
either case fhas a relative and absolute minimum. Assume x, y 6= 0, then y2=4λ, x2=λ,
use g= 0 to obtain x2=1,x =±1,y =±2, and f= 4 is a relative and absolute maximum
at (±1,±2).
31. Let a corner of the box be at (x, y, z), so that (x/a)2+(y/b)2+(z/c)2= 1. Maximize V=xyz
subject to g(x, y, z)=(x/a)2+(y/b)2+(z/c)2=1,solve ∇V=λ∇g,or
yzi+xzj+xyk=(2λx/a2)i+(2λy/b2)j+(2λz/c2)k,a
2yz =2λx, b2xz =2λy, c2xy =2λz. For the
maximum volume, x, y, z 6= 0; divide the first and second equations to obtain a2y2=b2x2; the first
and third to obtain a2z2=c2x2, and finally b2z2=c2y2. From g= 0 get 3(x/a)2=1,x =±a/√3,
and then y=±b/√3,z =±c/√3. The dimensions of the box are 2a
√3×2b
√3×2c
√3, and the
maximum volume is 8abc/(3√3).
32. (a) Let f(x, y)=3x
2−5xy + tan xy = 0. Then
df
dx =6x−5y+ysec2xy +(−5x+xsec2xy)dy
dx =0,so dy
dx =6x−5y+ysec2xy
5x−xsec2xy .
(b) Let g(x, y)=xln y+ sin(x−y)=π, dg
dx =lny+ cos(x−y)+x
y−cos(x−y)dy
dx =0,
dy
dx =ln y+ cos(x−y)
−x/y + cos(x−y)
Chapter 15 Supplementary Exercises 572
33. F(x, y)=0,F
x+F
y
dy
dx =0,F
xx +Fxy
dy
dx +Fyx
dy
dx +Fy
d2y
dx2=0,thus
dy
dx =−Fx
Fy
,d2y
dx2=−Fxx +2F
xy(dy/dx)
Fy
=−FxxFy−2FxFxy
F2
y
34. Denote the currents I1,I
2,I
3by x, y, z respectively. Then minimize F(x, y, z)=x
2
R
1
+y
2
R
2
+z
2
R
3
subject to g(x, y, z)=x+y+z−I= 0, so solve ∇F=λ∇g, 2xR1i+2yR2j+2zR3k=λ(i+j+k),
λ=2xR1=2yR2=2zR3, so the minimum value of Foccurs when I1:I2:I3=1
R1
:1
R2
:1
R3
.
35. Solve (t−1)2/4+16e
−2t+(2−√
t)
2= 1 for tto get t=1.8332,2.83984; the particle strikes
the surface at the points P1(0.8332,0.63959,0.64603),P
2(1.83984,0.23374,0.31482). The velocity
vectors are given by v=dx
dt i+dy
dt j+dz
dt k=i−4e−tj−1/(2√t)k, and a normal to the surface is
n=∇(x2/4+y
2+z
2
)=x/2i+2yj+2zk. At the points Pithese are
v1=i−0.639589j−0.369286k,v2=i−0.23374j+0.29670k;
n1=0.41661i+1.27918j+1.29207kand n2=0.91992i+0.46748j+0.62963kso
cos−1[(vi·ni)/(kvikkn
ik)] = 112.3◦,61.1◦; the acute angles are 67.7◦,61.1◦.
36. (a) F0(x)=Z1
0
e
ycos(xey)dy =sin(ex)−sin x
x
(b) Use a CAS to get x=π
e+1 so the maximum value of F(x)is
Fπ
e+1=Z1
0
sin π
e+1e
ydy ≈0.909026.
37. Let x, y, z be the lengths of the sides opposite angles α, β, γ, located at A, B, C respectively. Then
x2=y2+z2−2yz cos αand x2= 100 + 400 −2(10)(20)/2 = 300,x =10
√
3 and
2xdx
dt =2ydy
dt +2zdz
dt −2ydz
dt cos α+zdy
dt cos α−yz(sin α)dα
dt
= 2(10)(4) + 2(20)(2) −2 10(2)1
2+ 20(4)1
2−10(20)√3
2
π
60!=60+10π
√3
so dx
dt =√3+π
6, the length of BC is increasing.
38. (a) d
dt ∂z
∂x=∂
∂x ∂z
∂xdx
dt +∂
∂y ∂z
∂xdy
dt =∂2z
∂x2
dx
dt +∂2z
∂y∂x
dy
dt by the Chain Rule, and
d
dt ∂z
∂y=∂
∂x ∂z
∂ydx
dt +∂
∂y ∂z
∂ydy
dt =∂2z
∂x∂y
dx
dt +∂2z
∂y2
dy
dt
(b) dz
dt =∂z
∂x
dx
dt +∂z
∂y
dy
dt ,
d2z
dt2=dx
dt ∂2z
∂x2
dx
dt +∂2z
∂y∂x
dy
dt +∂z
∂x
d2x
dt2+dy
dt ∂2z
∂x∂y
dx
dt +∂2z
∂y2
dy
dt +∂z
∂y
d2y
dt2

573
CHAPTER 16
Multiple Integrals
EXERCISE SET 16.1
1. Z1
0Z2
0
(x+3)dy dx =Z1
0
(2x+6)dx =7 2. Z3
1Z1
−1
(2x−4y)dy dx =Z3
1
4xdx=16
3. Z4
2Z1
0
x2ydxdy=Z4
2
1
3ydy =2 4. Z0
−2Z2
−1
(x2+y2)dx dy =Z0
−2
(3+3y
2
)dy =14
5. Zln 3
0Zln 2
0
ex+ydy dx =Zln 3
0
exdx =2
6. Z2
0Z1
0
ysin xdydx=Z2
0
1
2sin xdx=(1−cos 2)/2
7. Z0
−1Z5
2
dx dy =Z0
−1
3dy =3 8. Z6
4Z7
−3
dy dx =Z6
4
10dx =20
9. Z1
0Z1
0
x
(xy +1)
2dy dx =Z1
01−1
x+1dx =1−ln 2
10. Zπ
π/2Z2
1
xcos xy dy dx =Zπ
π/2
(sin 2x−sin x)dx =−2
11. Zln 2
0Z1
0
xy ey2xdy dx =Zln 2
0
1
2(ex−1)dx =(1−ln 2)/2
12. Z4
3Z2
1
1
(x+y)2dy dx =Z4
31
x+1−1
x+2dx = ln(25/24)
13. Z1
−1Z2
−2
4xy3dy dx =Z1
−1
0dx =0
14. Z1
0Z1
0
xy
px2+y2+1dy dx =Z1
0
[x(x2+2)
1/2−x(x
2+1)
1/2
]dx =(3
√
3−4
√
2+1)/3
15. Z1
0Z3
2
xp1−x2dy dx =Z1
0
x(1 −x2)1/2dx =1/3
16. Zπ/2
0Zπ/3
0
(xsin y−ysin x)dy dx =Zπ/2
0x
2−π2
18 sin xdx =π2/144
19. V=Z5
3Z2
1
(2x+y)dy dx =Z5
3
(2x+3/2)dx =19
20. V=Z3
1Z2
0
(3x3+3x
2
y)dy dx =Z3
1
(6x3+6x
2
)dx = 172
Exercise Set 16.1 574
21. V=Z2
0Z3
0
x2dy dx =Z2
0
3x2dx =8
22. V=Z3
0Z4
0
5(1 −x/3)dy dx =Z3
0
5(4 −4x/3)dx =30
23. (a)
(1, 0, 4)
(2, 5, 0)
x
y
z(b)
(0, 0, 5)
(3, 4, 0)
z
x
y
24. (a)
(1, 1, 0)
(0, 0, 2)
x
y
z(b)
(2, 2, 0)
(2, 2, 8)
x
y
z
25. Z1/2
0Zπ
0
xcos(xy) cos2πx dy dx =Z1/2
0
cos2πx sin(xy)iπ
0dx
=Z1/2
0
cos2πx sin πx dx =−1
3cos3πxi1/2
0=1
3π
26. (a)
y
x
z
5
3
(b) The projection onto the xy-plane consists of R1:[0,5] ×[0,1], over which lie each of the two
skew planes, and R2:[0,5] ×[1,3], over which is only the plane z=−2y+6,so
V=Z5
0Z1
0
((−2y+6)−y)dy dx +Z5
0Z3
1
(−2y+6)dy dx =45
2+20= 85
2
27. fave =2
πZπ/2
0Z1
0
ysin xy dy dx =2
πZπ/2
0−cos xyi1
0dx =2
πZπ/2
0
(1 −cos x)dx =1−2
π

575 Chapter 16
28. average = 1
3Z3
0Z1
0
x(x2+y)1/2dx dy =Z3
0
1
9[(1 + y)3/2−y3/2]dy = 2(31 −9√3)/45
29. Tave =1
2Z1
0Z2
010 −8x2−2y2dy dx =1
2Z1
044
3−16x2dx =14
3◦
30. fave =1
A(R)Zb
aZd
c
kdydx=1
A(R)(b−a)(d−c)k=k
31. 0.6211310829 32. 2.230985141
33. ZZ
R
f(x, y)dA =Zb
a"Zd
c
g(x)h(y)dy#dx =Zb
a
g(x)"Zd
c
h(y)dy#dx
="Zb
a
g(x)dx#"Zd
c
h(y)dy#
34. The integral of tan x(an odd function) over the interval [−1,1] is zero.
35. The first integral equals 1/2, the second equals −1/2. No, because the integrand is not continuous.
36. (a)
16
X
k=1
f(x∗
k,y
∗
k)∆A∗
k=
4
X
i=1
4
X
j=1 i
2−1
4−2j
2−1
41
22
=−4
(b) Z2
0Z2
0
(x−2y)dy dx =Z2
0
(2x−4) dx =−4
EXERCISE SET 16.2
1. Z1
0Zx
x2
xy2dy dx =Z1
0
1
3(x4−x7)dx =1/40
2. Z3/2
1Z3−y
y
ydxdy=Z3/2
1
(3y−2y2)dy =7/24
3. Z3
0Z√9−y2
0
ydxdy=Z3
0
y
p9−y
2dy =9
4. Z1
1/4Zx
x2px/y dy dx =Z1
1/4Zx
x2
x1/2y−1/2dy dx =Z1
1/4
2(x−x3/2)dx =13/80
5. Z√2π
√πZx3
0
sin(y/x)dy dx =Z√2π
√π
[−xcos(x2)+x]dx =π/2
6. Z1
−1Zx2
−x2
(x2−y)dy dx =Z1
−1
2x4dx =4/57. Zπ
π/2Zx2
0
1
xcos(y/x)dy dx =Zπ
π/2
sin xdx=1
Exercise Set 16.2 576
8. Z1
0Zx
0
ex2dy dx =Z1
0
xex2dx =(e−1)/29. Z1
0Zx
0
ypx2−y2dy dx =Z1
0
1
3x3dx =1/12
10. Z2
1Zy2
0
ex/y2dx dy =Z2
1
(e−1)y2dy =7(e−1)/3
11. (a) Z2
0Zx2
0
xy dy dx =Z2
0
1
2x5dx =16
3
(b) Z3
1Z(y+7)/2
−(y−5)/2
xy dx dy =Z3
1
(3y2+3y)dy =38
12. (a) Z1
0Z√x
x2
(x+y)dy dx =Z1
0
(x3/2+x/2−x3−x4/2)dx =3/10
(b) Z1
−1Z√1−x2
−√1−x2
xdydx+Z1
−1Z√1−x
2
−√1−x
2
ydydx=Z1
−1
2x
p1−x
2dx +0=0
13. Z8
4Zx
16/x
x2dy dx =Z8
4
(x3−16x)dx = 576 14. Z2
1Zy
0
xy2dx dy =Z2
1
1
2y4dy =31/10
15. Z4
0Z√y
0
x(1+y2)−1/2dx dy =Z4
0
1
2y(1+y2)−1/2dy =(
√
17 −1)/2
16. Zπ
0Zx
0
xcos ydydx=Zπ
0
xsin xdx=π
17. Z1
−1Z√1−x2
−√1−x2
(3x−2y)dy dx =Z1
−1
6xp1−x2dx =0
18. Z5
0Z√25−x2
5−x
ydydx=Z5
0
(5x−x2)dx = 125/6
19. Z2
0Z6−y
y2
xy dx dy =Z2
0
1
2(36y−12y2+y3−y5)dy =50/3
20. Zπ/4
0Z1/√2
sin y
xdxdy =Zπ/4
0
1
4cos 2ydy=1/8
21. Z0
−1Zx3
x
(x−1)dy dx +Z1
0Zx
x3
(x−1)dy dx
=Z0
−1
(x4−x3−x2+x)dx +Z1
0
(−x4+x3+x2−x)dx =−1/2
22. Z1/√2
0Z2x
x
x2dy dx +Z1
1/√2Z1/x
x
x2dy dx =Z1/√2
0
x3dx +Z1
1/√2
(x−x3)dx =1/8

577 Chapter 16
24. (a)
1 2 3
5
15
25
x
y
R
(b) (1,3),(3,27)
(c) Z3
1Z4x3−x4
3−4x+4x2
xdydx=Z3
1
x[(4x3−x4)−(3 −4x+4x
2
)] dx =224
15
25. A=Zπ/4
0Zcos x
sin x
dy dx =Zπ/4
0
(cos x−sin x)dx =√2−1
26. A=Z1
−4Z−y2
3y−4
dx dy =Z1
−4
(−y2−3y+4)dy = 125/6
27. A=Z3
−3Z9−y2
1−y2/9
dx dy =Z3
−3
8(1 −y2/9)dy =32
28. A=Z1
0Zcosh x
sinh x
dy dx =Z1
0
(cosh x−sinh x)dx =1−e
−1
29. Z4
0Z6−3x/2
0
(3 −3x/4−y/2) dy dx =Z4
0
[(3 −3x/4)(6 −3x/2) −(6 −3x/2)2/4] dx =12
30. Z2
0Z√4−x2
0p4−x2dy dx =Z2
0
(4 −x2)dx =16/3
31. V=Z3
−3Z√9−x2
−√9−x2
(3 −x)dy dx =Z3
−3
(6p9−x2−2xp9−x2)dx =27π
32. V=Z1
0Zx
x2
(x2+3y
2
)dy dx =Z1
0
(2x3−x4−x6)dx =11/70
33. V=Z3
0Z2
0
(9x2+y2)dy dx =Z3
0
(18x2+8/3)dx = 170
34. V=Z1
−1Z1
y2
(1 −x)dx dy =Z1
−1
(1/2−y2+y4/2)dy =8/15
35. V=Z3/2
−3/2Z√9−4x2
−√9−4x2
(y+3)dy dx =Z3/2
−3/2
6p9−4x2dx =27π/2
36. V=Z3
0Z3
y2/3
(9 −x2)dx dy =Z3
0
(18 −3y2+y6/81)dy = 216/7
Exercise Set 16.2 578
37. V=8Z5
0Z√
25−x2
0p25 −x2dy dx =8Z5
0
(25 −x2)dx = 2000/3
38. V=2Z2
0Z√
1−(y−1)2
0
(x2+y2)dx dy =2Z2
01
3
[1 −(y−1)2]3/2+y2[1 −(y−1)2]1/2dy,
let y−1 = sin θto get V=2
Zπ/2
−π/21
3cos3θ+(1+sinθ)
2cos θcos θdθ which eventually yields
V=3π/2
39. V=4Z1
0Z√
1−x
2
0
(1 −x2−y2)dy dx =8
3Z1
0
(1 −x2)3/2dx =π/2
40. V=Z2
0Z√4−x2
0
(x2+y2)dy dx =Z2
0x2p4−x2+1
3(4 −x2)3/2dx =2π
41. Z√2
0Z2
y2
f(x, y)dx dy 42. Z8
0Zx/2
0
f(x, y)dy dx 43. Ze2
1Z2
ln x
f(x, y)dy dx
44. Z1
0Ze
ey
f(x, y)dx dy 45. Zπ/2
0Zsin x
0
f(x, y)dy dx 46. Z1
0Z√x
x2
f(x, y)dy dx
47. Z4
0Zy/4
0
e−y2dx dy =Z4
0
1
4ye−y2dy =(1−e
−16)/8
48. Z1
0Z2x
0
cos(x2)dy dx =Z1
0
2xcos(x2)dx = sin 1
49. Z2
0Zx2
0
ex3dy dx =Z2
0
x2ex3dx =(e
8−1)/3
50. Zln 3
0Z3
ey
xdxdy =1
2Zln 3
0
(9 −e2y)dy =1
2(9 ln 3 −4)
51. Z2
0Zy2
0
sin(y3)dx dy =Z2
0
y2sin(y3)dy =(1−cos 8)/3
52. Z1
0Ze
ex
xdydx=Z1
0
(ex −xex)dx =e/2−1
53. (a) Z4
0Z2
√x
sin πy3dy dx; the inner integral is non-elementary.
Z2
0Zy2
0
sin πy3dx dy =Z2
0
y2sin πy3dy =−1
3πcos πy32
0
=0

579 Chapter 16
(b) Z1
0Zπ/2
sin−1y
sec2(cos x)dx dy ; the inner integral is non-elementary.
Zπ/2
0Zsin x
0
sec2(cos x)dy dx =Zπ/2
0
sec2(cos x) sin xdx= tan 1
54. V=4Z2
0Z√
4−x
2
0
(x
2+y
2
)dy dx =4Z2
0x
2
p4−x
2+1
3
(4 −x2)3/2dx (x= 2 sin θ)
=Zπ/2
064
3+64
3sin2θ−128
3sin4θdθ =64
3
π
2+64
3
π
4−128
3
π
2
1·3
2·4=8π
55. Z−1
−2Z2
0
xy2dy dx +Z1
−1Z2
1
xy2dy dx +Z2
1Z2
0
xy2dy dx
=Z−1
−2
8
3xdx+Z1
−1
7
3xdx+Z2
1
8
3xdx=0
56. This is the volume in the first octant under the surface z=p1−x2−y2, so 1/8 of the volume of
the sphere of radius 1, thus π
6.
57. Area of triangle is 1/2, so ¯
f=2Z1
0Z1
x
1
1+x
2dy dx =2Z1
01
1+x
2−x
1+x
2dx =π
2−ln 2
58. Area = Z2
0
(3x−x2−x)dx =4/3, so
¯
f=3
4Z2
0Z3x−x2
x
(x2−xy)dy dx =3
4Z2
0
(−2x3+2x
4−x
5
/2)dx =−3
4
8
15 =−2
5
59. y= sin xand y=x/2 intersect at x= 0 and x=a=1.895494, so
V=Za
0Zsin x
x/2p1+x+ydydx=0.676089
EXERCISE SET 16.3
1. Zπ/2
0Zsin θ
0
rcos θdr dθ =Zπ/2
0
1
2sin2θcos θdθ=1/6
2. Zπ
0Z1+cos θ
0
rdrdθ=Zπ
0
1
2(1 + cos θ)2dθ =3π/4
3. Zπ/2
0Zasin θ
0
r2dr dθ =Zπ/2
0
a3
3sin3θdθ=2
9a
3
4. Zπ/3
0Zcos 3θ
0
rdrdθ=Zπ/3
0
1
2cos23θdθ=π/12
5. Zπ
0Z1−sin θ
0
r2cos θdrdθ=Zπ
0
1
3(1 −sin θ)3cos θdθ=0
Exercise Set 16.3 580
6. Zπ
0Zcos θ
0
r3dr dθ =Zπ
0
1
4cos4θdθ=3π/32
7. A=Z2π
0Z1−cos θ
0
rdrdθ=Z2π
0
1
2(1 −cos θ)2dθ =3π/2
8. A=4Zπ/2
0Zsin 2θ
0
rdrdθ=2Zπ/2
0
sin22θdθ=π/2
9. A=Zπ/2
π/4Z1
sin 2θ
rdrdθ=Zπ/2
π/4
1
2(1 −sin22θ)dθ =π/16
10. A=2Zπ/3
0Z2
sec θ
rdrdθ=Zπ/3
0
(4 −sec2θ)dθ =4π/3−√3
11. A=2Zπ/2
π/6Z4 sin θ
2
rdrdθ=Zπ/2
π/6
(16 sin2θ−4)dθ =4π/3+2
√
3
12. A=2Zπ
π/2Z1
1+cos θ
rdrdθ=Zπ
π/2
(−2 cos θ−cos2θ)dθ =2−π/4
13. V=8Zπ/2
0Z3
1
rp9−r2dr dθ =128
3√2Zπ/2
0
dθ =64
3√2π
14. V=2Zπ/2
0Z2 sin θ
0
r2dr dθ =16
3Zπ/2
0
sin3θdθ=32/9
15. V=2Zπ/2
0Zcos θ
0
(1 −r2)rdrdθ=1
2Zπ/2
0
(1 −sin4θ)dθ =5π/32
16. V=4Zπ/2
0Z3
1
dr dθ =8Zπ/2
0
dθ =4π
17. V=Zπ/2
0Z3 sin θ
0
r2sin θdrdθ=9Zπ/2
0
sin4θdθ=27π/16
18. V=4Zπ/2
0Z2 cos θ
0
rp4−r2dr dθ =32
3Zπ/2
0
(1 −sin3θ)dθ =16
9(3π−4)
19. Z2π
0Z1
0
e−r2rdrdθ=1
2(1 −e−1)Z2π
0
dθ =(1−e
−1
)π
20. Zπ/2
0Z3
0
rp9−r2dr dθ =9Zπ/2
0
dθ =9π/2
21. Zπ/4
0Z2
0
1
1+r
2rdrdθ=1
2ln 5 Zπ/4
0
dθ =π
8ln 5
22. Zπ/2
π/4Z2 cos θ
0
2r2sin θdrdθ=16
3Zπ/2
π/4
cos3θsin θdθ=1/3
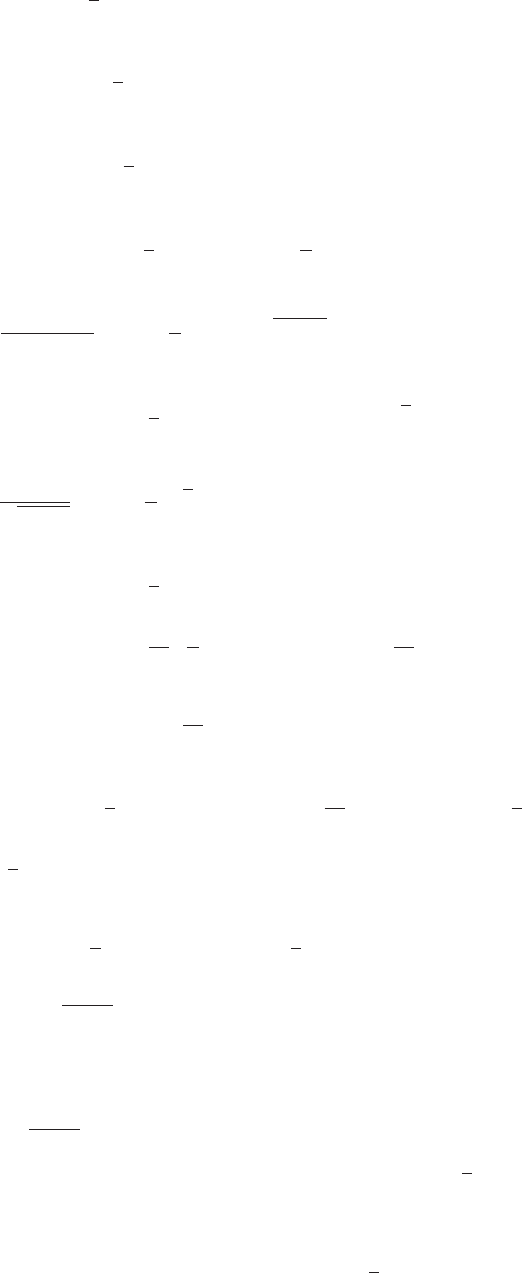
581 Chapter 16
23. Zπ/2
0Z1
0
r3dr dθ =1
4Zπ/2
0
dθ =π/8
24. Z2π
0Z2
0
e−r2rdrdθ=1
2(1 −e−4)Z2π
0
dθ =(1−e
−4
)π
25. Zπ/2
0Z2 cos θ
0
r2dr dθ =8
3Zπ/2
0
cos3θdθ=16/9
26. Zπ/2
0Z1
0
cos(r2)rdrdθ=1
2sin 1 Zπ/2
0
dθ =π
4sin 1
27. Zπ/2
0Za
0
r
(1+r2)3/2dr dθ =π
21−1/p1+a
2
28. Zπ/4
0Zsec θtan θ
0
r2dr dθ =1
3Zπ/4
0
sec3θtan3θdθ=2(
√
2+1)/45
29. Zπ/4
0Z2
0
r
√1+r
2dr dθ =π
4(√5−1)
30. Zπ/2
tan−1(3/4) Z5
3 csc θ
rdrdθ=1
2Zπ/2
tan−1(3/4)
(25 −9 csc2θ)dθ
=25
2hπ
2−tan−1(3/4)i−6=25
2tan−1(4/3) −6
31. V=Z2π
0Za
0
hr dr dθ =Z2π
0
ha2
2dθ =πa2h
32. (a) V=8Zπ/2
0Za
0
c
a(a2−r2)1/2rdrdθ =−4c
3aπ(a
2−r
2)
3/2a
0
=4
3πa2c
(b) V≈4
3π(6378.1370)26356.5231 ≈1,083,168,200,000 km3
33. V=2Zπ/2
0Zasin θ
0
c
a(a2−r2)1/2rdrdθ=2
3a
2cZπ/2
0
(1 −cos3θ)dθ =(3π−4)a2c/9
34. A=4Zπ/4
0Za√2 cos 2θ
0
rdrdθ=4a
2Zπ/4
0
cos 2θdθ=2a
2
35. A=Zπ/4
π/6Z4 sin θ
√8 cos 2θ
rdrdθ+Zπ/2
π/4Z4 sin θ
0
rdrdθ
=Zπ/4
π/6
(8 sin2θ−4 cos 2θ)dθ +Zπ/2
π/4
8 sin2θdθ=4π/3+2
√
3−2
36. A=Zφ
0Z2asin θ
0
rdrdθ=2a
2Zφ
0
sin2θdθ=a
2φ−1
2a
2sin 2φ
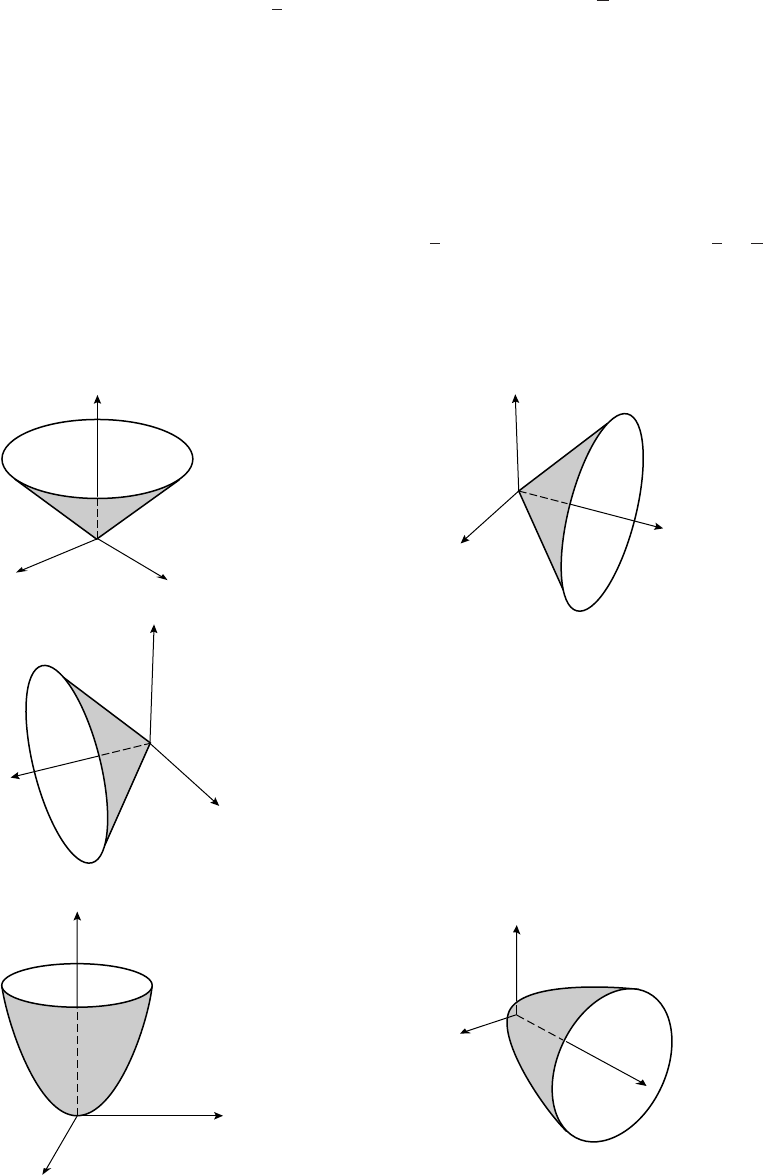
Exercise Set 16.4 582
37. (a) I2=Z+∞
0
e−x2dxZ+∞
0
e
−y
2dy=Z+∞
0Z+∞
0
e−x2dxe−y2dy
=Z+∞
0Z+∞
0
e−x2e−y2dx dy =Z+∞
0Z+∞
0
e−(x2+y2)dx dy
(b) I2=Zπ/2
0Z+∞
0
e−r2rdrdθ=1
2Zπ/2
0
dθ =π/4(c) I=√π/2
38. (a) 1.173108605 (b) Zπ
0Z1
0
re−r4dr dθ =πZ1
0
re−r4dr ≈1.173108605
39. V=Z2π
0ZR
0
D(r)rdrdθ=Z2π
0ZR
0
ke−rrdrdθ =−2πk(1+r)e−rR
0
=2πk[1 −(R+1)e
−R
]
40. Ztan−1(2)
tan−1(1/3) Z2
0
r3cos2θdrdθ=4Ztan−1(2)
tan−1(1/3)
cos2θdθ=1
5+ 2[tan−1(2) −tan−1(1/3)] = 1
5+π
2
EXERCISE SET 16.4
1. (a) z
xy
(b)
xy
z
(c)
x
y
z
2. (a)
y
x
z(b) z
y
x
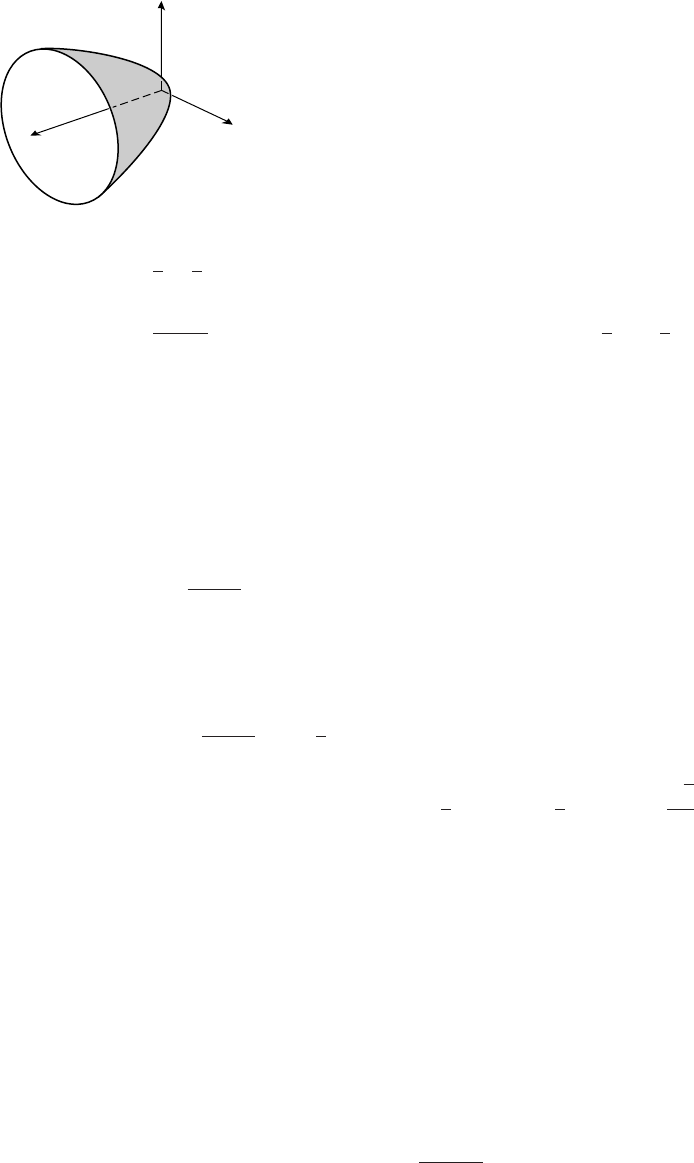
583 Chapter 16
(c) z
y
x
3. (a) x=u, y =v, z =5
2+3
2u−2v(b) x=u, y =v, z =u2
4. (a) x=u, y =v, z =v
1+u
2(b) x=u, y =v, z =1
3v2−5
3
5. (a) x= 5 cos u, y = 5 sin u, z =v;0≤u≤2π, 0≤v≤1
(b) x= 2 cos u, y =v, z = 2 sin u;0≤u≤2π, 1≤v≤3
6. (a) x=u, y =1−u, z =v;−1≤v≤1(b) x=u, y =5+2v, z =v;0≤u≤3
7. x=u, y = sin ucos v, z = sin usin v8. x=u, y =eucos v, z =eusin v
9. x=rcos θ, y =rsin θ, z =1
1+r
210. x=rcos θ, y =rsin θ, z =e−r2
11. x=rcos θ, y =rsin θ, z =2r
2cos θsin θ
12. x=rcos θ, y =rsin θ, z =r2(cos2θ−sin2θ)
13. x=rcos θ, y =rsin θ, z =√9−r2;r≤√5
14. x=rcos θ, y =rsin θ, z =r;r≤315. x=1
2ρcos θ, y =1
2ρsin θ, z =√3
2ρ
16. x= 3 cos θ, y = 3 sin θ, z = 3 cot φ17. z=x−2y; a plane
18. y=x2+z2,0≤y≤4; part of a circular paraboloid
19. (x/3)2+(y/2)2=1;2≤z≤4; part of an elliptic cylinder
20. z=x2+y2;0≤z≤4; part of a circular paraboloid
21. (x/3)2+(y/4)2=z2;0≤z≤1; part of an elliptic cone
22. x2+(y/2)2+(z/3)2= 1; part of an ellipsoid
23. (a) x=rcos θ, y =rsin θ, z =r;x=u, y =v, z =√u2+v2;0≤z≤2
24. (a) I: x=rcos θ, y =rsin θ, z =r2;II:x=u, y =v, z =u2+v2;u2+v2≤2
25. (a) 0≤u≤3,0≤v≤π(b) 0≤u≤4,−π/2≤v≤π/2

Exercise Set 16.4 584
26. (a) 0≤u≤6,−π≤v≤0(b) 0≤u≤5,π/2≤v≤3π/2
27. (a) 0≤φ≤π/2,0≤θ≤2π(b) 0≤φ≤π, 0≤θ≤π
28. (a) π/2≤φ≤π(b) 0≤θ≤π/2,0≤φ≤π/2
29. u=1,v =2,r
u×r
v=−2i−4j+k;2x+4y−z=5
30. u=1,v =2,r
u×r
v=−4i−2j+8k;2x+y−4z=−6
31. u=0,v =1,r
u×r
v=6k;z=0 32. ru×rv=2i−j−3k;2x−y−3z=−4
33. ru×rv=(
√
2/2)i−(√2/2)j+(1/2)k;x−y+√2
2z=π√2
8
34. ru×rv=2i−ln 2k;2x−(ln 2)z=0
35. z=p9−y2,zx=0,z
y=−y/p9−y2,z2
x+z2
y+1=9/(9 −y2),
S=Z2
0Z3
−3
3
p9−y2dy dx =Z2
0
3πdx=6π
36. z=8−2x−2y,z
2
x+z
2
y+1=4+4+1=9,S=Z4
0Z4−x
0
3dy dx =Z4
0
3(4 −x)dx =24
37. z2=4x
2+4y
2
,2zzx=8xso zx=4x/z, similarly zy=4y/z thus
z2
x+z2
y+ 1 = (16x2+16y
2
)/z2+1=5,S=Z1
0Zx
x
2
√
5dy dx =√5Z1
0
(x−x2)dx =√5/6
38. z2=x2+y2,zx=x/z,zy=y/z,z2
x+z2
y+1=(z
2+y
2
)/z2+1=2,
S=ZZ
R
√2dA =2Zπ/2
0Z2 cos θ
0
√2rdrdθ=4
√
2Zπ/2
0
cos2θdθ=√2π
39. zx=−2x,zy=−2y,z2
x+z2
y+1=4x
2+4y
2+1,
S=ZZ
Rp4x2+4y
2+1dA =Z2π
0Z1
0
rp4r2+1dr dθ
=1
12(5√5−1) Z2π
0
dθ =(5
√
5−1)π/6
40. zx=2,z
y=2y,z
2
x+z
2
y+1=5+4y
2
,
S=Z1
0Zy
0p5+4y
2dx dy =Z1
0
yp5+4y
2dy = (27 −5√5)/12
41. ∂r/∂u = cos vi+ sin vj+2uk,∂r/∂v =−usin vi+ucos vj,
k∂r/∂u ×∂r/∂vk=u√4u2+1; S=Z2π
0Z2
1
u
p4u
2+1du dv = (17√17 −5√5)π/6
42. ∂r/∂u = cos vi+ sin vj+k,∂r/∂v =−usin vi+ucos vj,
k∂r/∂u ×∂r/∂vk=√2u;S=Zπ/2
0Z2v
0
√2ududv=√
2
12 π3
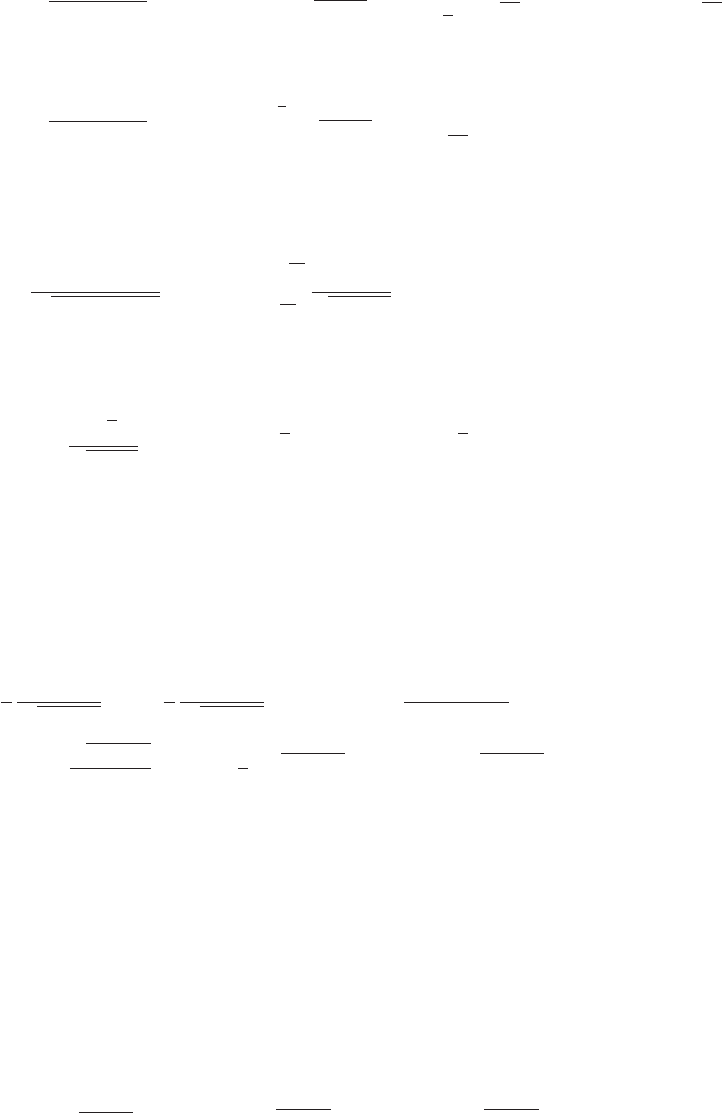
585 Chapter 16
43. zx=y,zy=x,z2
x+z2
y+1=x
2+y
2+1,
S=ZZ
Rpx2+y2+1dA =Zπ/6
0Z3
0
rpr2+1dr dθ =1
3(10√10−1) Zπ/6
0
dθ = (10√10−1)π/18
44. zx=x,zy=y,z2
x+z2
y+1=x
2+y
2+1,
S=ZZ
Rpx2+y2+1dA =Z2π
0Z√8
0
rpr2+1dr dθ =26
3Z2π
0
dθ =52π/3
45. On the sphere, zx=−x/z and zy=−y/z so z2
x+z2
y+1=(x
2+y
2+z
2
)/z2=16/(16 −x2−y2);
the planes z= 1 and z= 2 intersect the sphere along the circles x2+y2= 15 and x2+y2= 12;
S=ZZ
R
4
p16 −x2−y2dA =Z2π
0Z√15
√12
4r
√16 −r2dr dθ =4Z2π
0
dθ =8π
46. On the sphere, zx=−x/z and zy=−y/z so z2
x+z2
y+1=(x
2+y
2+z
2
)/z2=8/(8 −x2−y2);
the cone cuts the sphere in the circle x2+y2=4;
S=Z2π
0Z2
0
2
√
2r
√
8−r
2dr dθ =(8−4
√
2) Z2π
0
dθ = 8(2 −√2)π
47. r(u, v)=acos usin vi+asin usin vj+acos vk,kru×rvk=a2sin v,
S=Zπ
0Z2π
0
a2sin vdudv=2πa2Zπ
0
sin vdv =4πa2
48. r =rcos ui+rsin uj+vk,kru×rvk=r;S=Zh
0Z2π
0
rdudv =2πrh
49. zx=h
a
x
px2+y2,zy=h
a
y
px2+y2,z2
x+z2
y+1= h
2
x
2+h
2
y
2
a
2
(x
2+y
2
)+1=(a
2+h
2
)/a2,
S=Z2π
0Za
0
√a2+h2
ardrdθ=1
2a
pa
2+h
2Z2π
0
dθ =πapa2+h2
50. Revolving a point (a0,0,b
0)ofthexz-plane around the z-axis generates a circle, an equation of
which is r=a0cos ui+a0sin uj+b0k,0≤u≤2π. A point on the circle (x−a)2+z2=b2which
generates the torus can be written r=(a+bcos v)i+bsin vk,0≤v≤2π. Set a0=a+bcos v
and b0=a+bsin vand use the first result: any point on the torus can thus be written in the form
r=(a+bcos v) cos ui+(a+bcos v) sin uj+bsin vk, which yields the result.
51. ∂r/∂u =−(a+bcos v) sin ui+(a+bcos v) cos uj,
∂r/∂v =−bsin vcos ui−bsin vsin uj+bcos vk,k∂r/∂u ×∂r/∂vk=b(a+bcos v);
S=Z2π
0Z2π
0
b(a+bcos v)du dv =4π
2
ab
52. kru×rvk=√u2+1;S=Z4π
0Z5
0pu
2+1du dv =4πZ5
0pu
2+1du = 174.7199011
53. z=−1 when v≈0.27955,z = 1 when v≈2.86204,kru×rvk=|cos v|;
S=Z2π
0Z2.86204
0.27955 |cos v|dv du ≈9.099

Exercise Set 16.5 586
54. (a) x=vcos u, y =vsin u, z =f(v), for example (b) x=vcos u, y =vsin u, z =1/v2
(c) z
y
x
55. (x/a)2+(y/b)2+(z/c)2= cos2v(cos2u+ sin2u) + sin2v= 1, ellipsoid
56. (x/a)2+(y/b)2−(z/c)2= cos2ucosh2v+ sin2ucosh2v−sinh2v= 1, hyperboloid of one sheet
57. (x/a)2+(y/b)2−(z/c)2= sinh2v+ cosh2v(sinh2u−cosh2u)=−1, hyperboloid of two sheets
EXERCISE SET 16.5
1. Z1
−1Z2
0Z1
0
(x2+y2+z2)dx dy dz =Z1
−1Z2
0
(1/3+y
2+z
2
)dy dz =Z1
−1
(10/3+2z
2
)dz =8
2. Z1/2
1/3Zπ
0Z1
0
zxsin xy dz dy dx =Z1/2
1/3Zπ
0
1
2xsin xy dy dx =Z1/2
1/3
1
2(1−cos πx)dx =1
12 +√3−2
4π
3. Z2
0Zy2
−1Zz
−1
yz dx dz dy =Z2
0Zy2
−1
(yz2+yz)dz dy =Z2
01
3y7+1
2y5−1
6ydy =47
3
4. Zπ/4
0Z1
0Zx2
0
xcos ydzdxdy=Zπ/4
0Z1
0
x3cos ydxdy=Zπ/4
0
1
4cos ydy =√2/8
5. Z3
0Z√9−z2
0Zx
0
xy dy dx dz =Z3
0Z√9−z2
0
1
2x3dx dz =Z3
0
1
8(81 −18z2+z4)dz =81/5
6. Z3
1Zx2
xZln z
0
xeydy dz dx =Z3
1Zx2
x
(xz −x)dz dx =Z3
11
2x5−3
2x3+x2dx = 118/3
7. Z2
0Z√4−x2
0Z3−x2−y2
−5+x2+y2
xdzdydx=Z2
0Z√4−x
2
0
[2x(4 −x2)−2xy2]dy dx
=Z2
0
4
3x(4 −x2)3/2dx = 128/15
8. Z2
1Z2
zZ√3y
0
y
x2+y2dx dy dz =Z2
1Z2
z
π
3dy dz =Z2
1
π
3(2 −z)dz =π/6

587 Chapter 16
9. Zπ
0Z1
0Zπ/6
0
xy sin yz dz dy dx =Zπ
0Z1
0
x[1 −cos(πy/6)]dy dx =Zπ
0
(1 −3/π)xdx =π(π−3)/2
10. Z1
−1Z1−x2
0Zy
0
ydzdydx=Z1
−1Z1−x
2
0
y
2
dy dx =Z1
−1
1
3(1 −x2)3dx =32/105
11. Z√2
0Zx
0Z2−x2
0
xyzdzdydx=Z√
2
0Zx
0
1
2xy(2 −x2)2dy dx =Z√2
0
1
4x3(2 −x2)2dx =1/6
12. Zπ/2
π/6Zπ/2
yZxy
0
cos(z/y)dz dx dy =Zπ/2
π/6Zπ/2
y
ysin xdxdy =Zπ/2
π/6
ycos ydy =(5π−6
√
3)/12
14. 8Z1
0Z√1−x2
0Z√1−x2−y2
0
e−x2−y2−z2dz dy dx ≈2.381
15. V=Z4
0Z(4−x)/2
0Z(12−3x−6y)/4
0
dz dy dx =Z4
0Z(4−x)/2
0
1
4(12 −3x−6y)dy dx
=Z4
0
3
16(4 −x)2dx =4
16. V=Z1
0Z1−x
0Z√y
0
dz dy dx =Z1
0Z1−x
0
√ydydx=Z1
0
2
3(1 −x)3/2dx =4/15
17. V=2Z2
0Z4
x
2Z4−y
0
dz dy dx =2Z2
0Z4
x
2
(4 −y)dy dx =2Z2
08−4x
2+1
2
x
4
dx = 256/15
18. V=Z1
0Zy
0Z√1−y2
0
dz dx dy =Z1
0Zy
0p1−y2dx dy =Z1
0
yp1−y2dy =1/3
19. The projection of the curve of intersection onto the xy-plane is x2+y2=1,
V=4Z1
0Z√
1−x
2
0Z4−3y
2
4x
2
+y
2
dz dy dx
20. The projection of the curve of intersection onto the xy-plane is 2x2+y2=4,
V=4Z√
2
0Z√
4−2x
2
0Z8−x
2
−y
2
3x
2
+y
2
dz dy dx
21. V=2Z3
−3Z√
9−x
2
/3
0Zx+3
0
dz dy dx 22. V=8Z1
0Z√
1−x
2
0Z√
1−x
2
0
dz dy dx
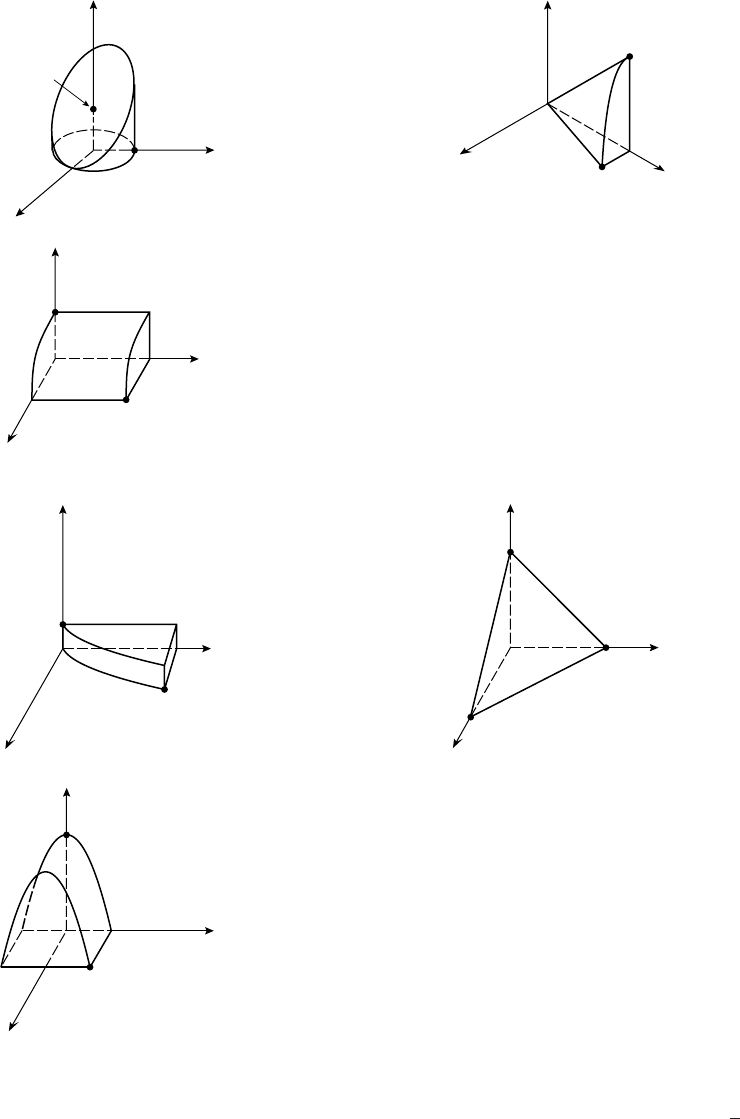
Exercise Set 16.5 588
23. (a)
(0, 0, 1)
(1, 0, 0)
z
y
x
(b)
(0, 9, 9)
(3, 9, 0)
z
xy
(c)
(0, 0, 1)
(1, 2, 0)
x
y
z
24. (a)
(3, 9, 0)
(0, 0, 2)
x
y
z(b)
(0, 0, 2)
(0, 2, 0)
(2, 0, 0)
x
y
z
(c)
(2, 2, 0)
(0, 0, 4)
x
y
z
25. V=Z1
0Z1−x
0Z1−x−y
0
dz dy dx =1/6,f
ave =6Z1
0Z1−x
0Z1−x−y
0
(x+y+z)dz dy dx =3
4
26. The integrand is an odd function of each of x, y, and z, so the answer is zero.

589 Chapter 16
27. (a) Za
0Zb(1−x/a)
0Zc(1−x/a−y/b)
0
dz dy dx,Zb
0Za(1−y/b)
0Zc(1−x/a−y/b)
0
dz dx dy,
Zc
0Za(1−z/c)
0Zb(1−x/a−z/c)
0
dy dx dz,Za
0Zc(1−x/a)
0Zb(1−x/a−z/c)
0
dy dz dx,
Zc
0Zb(1−z/c)
0Za(1−y/b−z/c)
0
dx dy dz,Zb
0Zc(1−y/b)
0Za(1−y/b−z/c)
0
dx dz dy
(b) Use the first integral in part (a) to get
Za
0Zb(1−x/a)
0
c1−x
a−y
bdy dx =Za
0
1
2bc 1−x
a2dx =1
6abc
28. (a) Z3
0Z√9−x2
0Z√9−x2−y2
0
f(x, y, z)dz dy dx
(b) Z4
0Zx/2
0Z2
0
f(x, y, z)dz dy dx (c) Z2
0Z4−x2
0Z4−y
x2
f(x, y, z)dz dy dx
29. V=8Za
0Zb
√
1−x
2
/a2
0Zc√1−x2/a2−y2/b2
0
dz dy dx
30. Zb
aZd
cZ`
k
f(x)g(y)h(z)dz dy dx =Zb
aZd
c
f(x)g(y)"Z`
k
h(z)dz#dy dx
="Zb
a
f(x)"Zd
c
g(y)dy#dx#"Z`
k
h(z)dz#
="Zb
a
f(x)dx#"Zd
c
g(y)dy#"Z`
k
h(z)dz#
31. (a) Z1
−1
xdx
Z1
0
y
2dy"Zπ/2
0
sin zdz
#= (0)(1/3)(1) = 0
(b) Z1
0
e2xdx"Zln 3
0
eydy#"Zln 2
0
e−zdz#=[(e
2−1)/2](2)(1/2)=(e
2−1)/2
32. (a) At any point outside the closed sphere {x2+y2+z2≤1}the integrand is negative, so to
maximize the integral it suffices to include all points inside the sphere; hence the maximum
value is taken on the region G={x2+y2+z2≤1}.
(b) 8π
15
EXERCISE SET 16.6
1. Let abe the unknown coordinate of the fulcrum; then the total moment about the fulcrum is
5(0 −a) + 10(5 −a) + 20(10 −a) = 0 for equilibrium, so 250 −35a=0,a=50/7. The fulcrum
should be placed 50/7 ft to the right of m1.
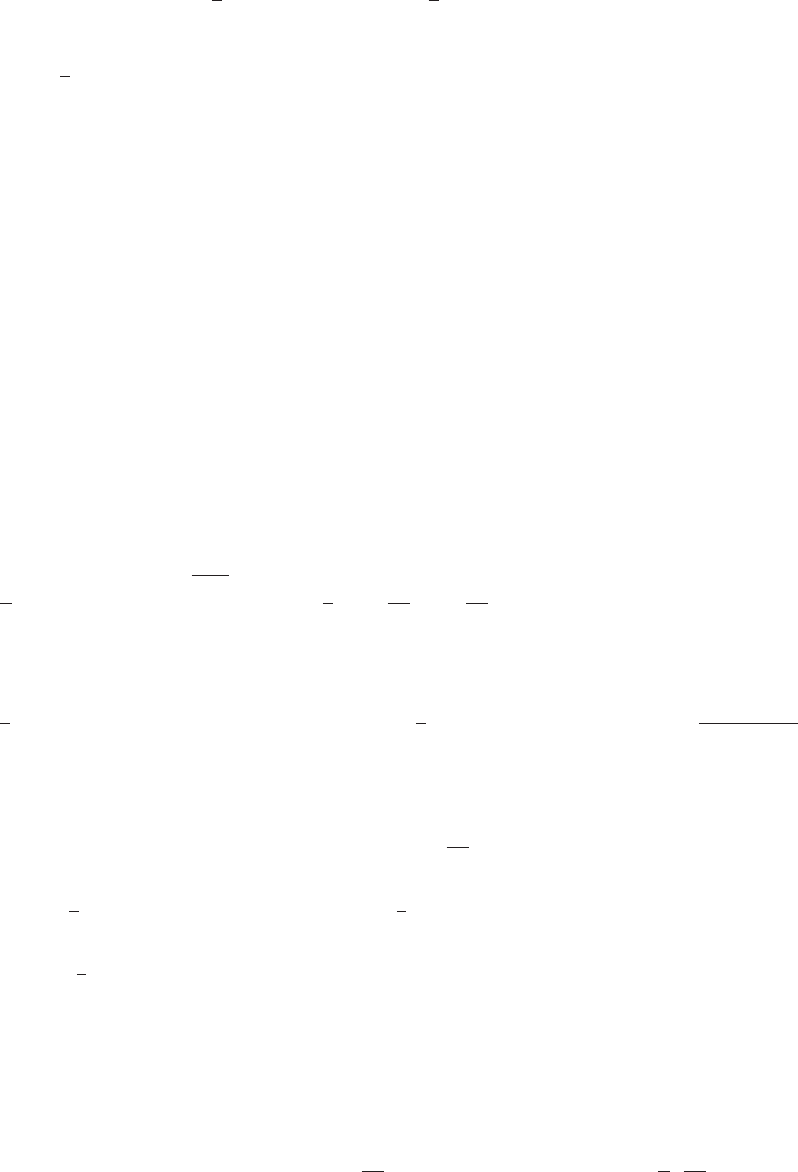
Exercise Set 16.6 590
2. At equilibrium, 10(0 −4) + 3(2 −4) + 4(3 −4)+m(6 −4)=0,m=25
3. A=1,¯x=Z1
0Z1
0
xdydx=1
2,¯y=Z1
0Z1
0
ydydx=1
2
4. A=2,¯x=1
2Z0
−1Z1+x
−1−x
xdydx+Z1
0Z1−x
−1+x
xdydx= 0, similarly ¯y=0.
5. A=1/2, ZZ
R
xdA=Z1
0Zx
0
xdydx=1/3, ZZ
R
ydA=Z1
0Zx
0
ydydx=1/6;
centroid (2/3,1/3)
6. A=Z1
0Zx2
0
dy dx =1/3, ZZ
R
xdA=Z1
0Zx
2
0
xdydx=1/4,
ZZ
R
ydA=Z1
0Zx
2
0
ydydx=1/10; centroid (3/4,3/10)
7. A=Z1
0Z2−x2
x
dy dx =7/6, ZZ
R
xdA=Z1
0Z2−x
2
x
xdydx=5/12,
ZZ
R
ydA=Z1
0Z2−x
2
x
ydydx=19/15; centroid (5/14,38/35)
8. A=π
4,ZZ
R
xdA=Z1
0Z√1−x
2
0
xdydx=1
3,¯x=4
3π
,¯y=4
3πby symmetry
9. ¯x= 0 from the symmetry of the region,
A=1
2π(b2−a2), ZZ
R
ydA=Zπ
0Zb
a
r
2sin θdrdθ=2
3(b
3−a
3); centroid ¯x=0,¯y=4(b3−a3)
3π(b2−a2).
10. ¯y= 0 from the symmetry of the region, A=πa2/2,
ZZ
R
xdA=Zπ/2
−π/2Za
0
r2cos θdrdθ=2a
3
/3; centroid 4a
3π,0
11. M=Z1
0Z√x
0
(x+y)dy dx =13/20, Mx=Z1
0Z√x
0
(x+y)ydydx=3/10,
My=Z1
0Z√x
0
(x+y)xdydx=19/42, ¯x=My/M = 190/273, ¯y=Mx/M =6/13;
the mass is 13/20 and the center of gravity is at (190/273,6/13).
12. M=Zπ
0Zsin x
0
ydydx=π/4, ¯x=π/2 from the symmetry of the density and the region,
Mx=Zπ
0Zsin x
0
y2dy dx =4/9, ¯y=Mx/M =16
9π; mass π/4, center of gravity π
2,16
9π.

591 Chapter 16
13. M=Zπ/2
0Za
0
r3sin θcos θdrdθ =a
4/8, ¯x=¯yfrom the symmetry of the density and the
region, My=Zπ/2
0Za
0
r4sin θcos2θdrdθ =a
5/15, ¯x=8a/15; mass a4/8, center of gravity
(8a/15,8a/15).
14. M=Zπ
0Z1
0
r3dr dθ =π/4, ¯x= 0 from the symmetry of density and region,
Mx=Zπ
0Z1
0
r4sin θdrdθ=2/5, ¯y=8
5π; mass π/4, center of gravity 0,8
5π.
15. V=1,¯x=Z1
0Z1
0Z1
0
xdzdydx=1
2, similarly ¯y=¯z=1
2
; centroid 1
2,1
2,1
2
16. V=πr2h=2π,¯x=¯y= 0 by symmetry, ZZZ
G
zdzdydx=Z2
0Z2π
0Z1
0
rz dr dθ dz =2π,
centroid = (0,0,1)
17. ¯x=¯y=¯zfrom the symmetry of the region, V=1/6,
¯x=1
VZ1
0Z1−x
0Z1−x−y
0
xdzdydx= (6)(1/24)=1/4; centroid (1/4,1/4,1/4)
18. The solid is described by −1≤y≤1,0≤z≤1−y2,0≤x≤1−z;
V=Z1
−1Z1−y2
0Z1−z
0
dx dz dy =4
5,¯x=1
VZ1
−1Z1−y2
0Z1−z
0
xdxdzdy =5
14,¯y= 0 by symmetry,
¯z=1
VZ1
−1Z1−y2
0Z1−z
0
zdxdzdy=2
7; the centroid is 5
14,0,2
7.
19. ¯x=1/2 and ¯y= 0 from the symmetry of the region,
V=Z1
0Z1
−1Z1
y2
dz dy dx =4/3, ¯z=1
VZZZ
G
zdV =(3/4)(4/5)=3/5; centroid (1/2,0,3/5)
20. ¯x=¯yfrom the symmetry of the region,
V=Z2
0Z2
0Zxy
0
dz dy dx =4,¯x=1
VZZZ
G
xdV =(1/4)(16/3)=4/3,
¯z=1
VZZZ
G
zdV =(1/4)(32/9)=8/9; centroid (4/3,4/3,8/9)
21. ¯x=¯y=¯zfrom the symmetry of the region, V=πa3/6,
¯x=1
VZa
0Z√a2−x2
0Z√a2−x2−y2
0
xdzdydx=1
VZa
0Z√a
2−x
2
0
x
pa
2−x
2−y
2dy dx
=1
VZπ/2
0Za
0
r2pa2−r2cos θdrdθ =6
πa3(πa4/16)=3a/8; centroid (3a/8,3a/8,3a/8)
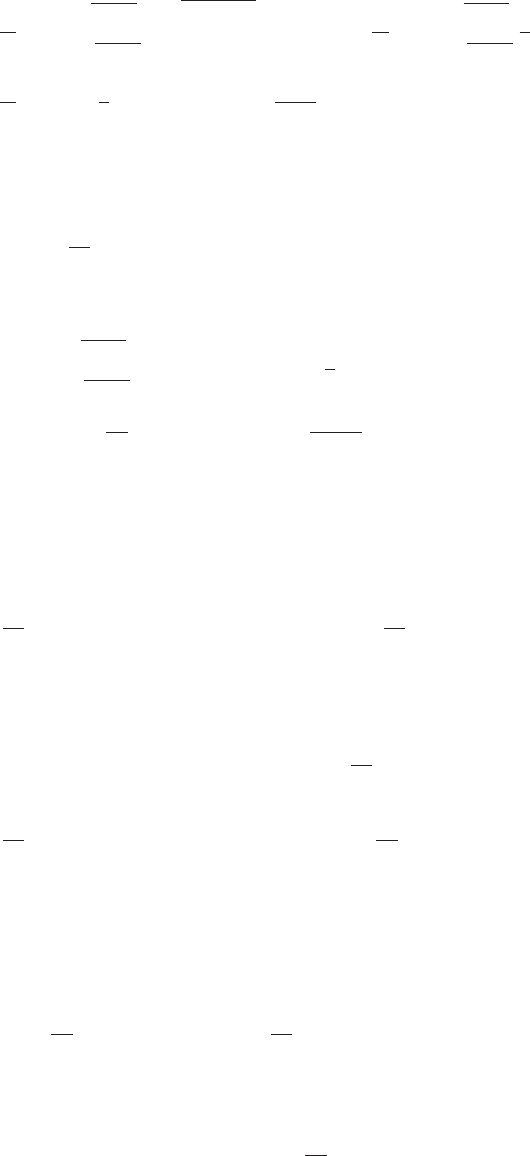
Exercise Set 16.6 592
22. ¯x=¯y= 0 from the symmetry of the region, V=2πa3/3
¯z=1
VZa
−aZ√a2−x2
−√a2−x2Z√a2−x2−y2
0
zdzdydx=1
VZa
−aZ√
a
2
−x
2
−
√
a
2
−x
2
1
2(a
2−x
2−y
2
)dy dx
=1
VZ2π
0Za
0
1
2(a2−r2)rdrdθ=3
2πa3(πa4/4)=3a/8; centroid (0,0,3a/8)
23. M=Za
0Za
0Za
0
(a−x)dz dy dx =a4/2, ¯y=¯z=a/2 from the symmetry of density and
region, ¯x=1
MZa
0Za
0Za
0
x(a−x)dz dy dx =(2/a4)(a5/6) = a/3;
mass a4/2, center of gravity (a/3,a/2,a/2)
24. M=Za
−aZ√a2−x2
−√a2−x2Zh
0
(h−z)dz dy dx =1
2πa2h2,¯x=¯y= 0 from the symmetry of density
and region, ¯z=1
MZZZ
G
z(h−z)dV =2
πa2h2(πa2h3/6) = h/3;
mass πa2h2/2, center of gravity (0,0,h/3)
25. M=Z1
−1Z1
0Z1−y2
0
yz dz dy dx =1/6, ¯x= 0 by the symmetry of density and region,
¯y=1
MZZZ
G
y2zdV = (6)(8/105) = 16/35, ¯z=1
MZZZ
G
yz2dV = (6)(1/12)=1/2;
mass 1/6, center of gravity (0,16/35,1/2)
26. M=Z3
0Z9−x2
0Z1
0
xz dz dy dx =81/8, ¯x=1
MZZZ
G
x2zdV =(8/81)(81/5)=8/5,
¯y=1
MZZZ
G
xyz dV =(8/81)(243/8)=3,¯z=1
MZZZ
G
xz2dV =(8/81)(27/4)=2/3;
mass 81/8, center of gravity (8/5,3,2/3)
27. (a) M=Z1
0Z1
0
k(x2+y2)dy dx =2k/3, ¯x=¯yfrom the symmetry of density and region,
¯x=1
MZZ
R
kx(x2+y2)dA =3
2k(5k/12)=5/8; center of gravity (5/8,5/8)
(b) ¯y=1/2 from the symmetry of density and region,
M=Z1
0Z1
0
kx dy dx =k/2, ¯x=1
MZZ
R
kx2dA =(2/k)(k/3)=2/3,
center of gravity (2/3,1/2)

593 Chapter 16
28. (a) ¯x=¯y=¯zfrom the symmetry of density and region,
M=Z1
0Z1
0Z1
0
k(x2+y2+z2)dz dy dx =k,
¯x=1
MZZZ
G
kx(x2+y2+z2)dV =(1/k)(7k/12)=7/12; center of gravity (7/12,7/12,7/12)
(b) ¯x=¯y=¯zfrom the symmetry of density and region,
M=Z1
0Z1
0Z1
0
k(x+y+z)dz dy dx =3k/2,
¯x=1
MZZZ
G
kx(x+y+z)dV =2
3k(5k/6)=5/9; center of gravity (5/9,5/9,5/9)
29. V=ZZZ
G
dV =Zπ
0Zsin x
0Z1/(1+x2+y2)
0
dz dy dx =0.666633,
x=1
VZZZ
G
xdV =1.177406, y=1
VZZZ
G
ydV =0.353554, z=1
VZZZ
G
zdV =0.231557
30. (b) Use cylindrical coordinates to get
V=ZZZ
G
dV =Z2π
0Za
0Z1/(1+r2)
0
rdzdrdθ=πln(1 + a2),
z=1
VZZZ
G
zdV =a2
2(1 + a2) ln(1 + a2)
(c) lim
a→0+¯z=1
2; lim
a→+∞¯z= 0; solve z=1/4 for ato obtain a≈1.980291.
31. Let x=rcos θ,y=rsin θ, and dA =rdrdθ in formulas (10) and (11).
32. ¯x= 0 from the symmetry of the region, A=Z2π
0Za(1+sin θ)
0
rdrdθ=3πa2/2,
¯y=1
AZ2π
0Za(1+sin θ)
0
r2sin θdrdθ=2
3πa2(5πa3/4)=5a/6; centroid (0,5a/6)
33. ¯x=¯yfrom the symmetry of the region, A=Zπ/2
0Zsin 2θ
0
rdrdθ=π/8,
¯x=1
AZπ/2
0Zsin 2θ
0
r2cos θdrdθ=(8/π)(16/105) = 128
105π; centroid 128
105π,128
105π
34. ¯x=3/2 and ¯y= 1 from the symmetry of the region,
ZZ
R
xdA=¯xA =(3/2)(6) = 9, ZZ
R
ydA=¯yA = (1)(6) = 6
35. ¯x= 0 from the symmetry of the region, πa2/2 is the area of the semicircle, 2π¯yis the distance
traveled by the centroid to generate the sphere so 4πa3/3=(πa2/2)(2π¯y), ¯y=4a/(3π)

Exercise Set 16.7 594
36. (a) V=1
2πa22πa+4a
3π=1
3π(3π+4)a
3
(b) the distance between the centroid and the line is √2
2a+4a
3πso
V=1
2πa2"2π√2
2a+4a
3π#=1
6√2π(3π+4)a
3
37. ¯x=kso V=(πab)(2πk)=2π
2
abk
38. ¯y= 4 from the symmetry of the region,
A=Z2
−2Z8−x2
x2
dy dx =64/3soV= (64/3)[2π(4)] = 512π/3
39. The region generates a cone of volume 1
3πab2when it is revolved about the x-axis, the area of the
region is 1
2ab so 1
3πab2=1
2ab(2π¯y), ¯y=b/3. A cone of volume 1
3πa2bis generated when the
region is revolved about the y-axis so 1
3πa2b=1
2ab(2π¯x), ¯x=a/3. The centroid is (a/3,b/3).
40. Ix=Za
0Zb
0
y2δdydx=1
3δab3,I
y=
Za
0Zb
0
x
2
δdydx=1
3δa3b,
Iz=Za
0Zb
0
(x2+y2)δdydx=1
3δab(a2+b2)
41. Ix=Z2π
0Za
0
r3sin2θ δ dr dθ =δπa4/4; Iy=Z2π
0Za
0
r3cos2θ δ dr dθ =δπa4/4=I
x
;
I
z=I
x+I
y=δπa4/2
EXERCISE SET 16.7
1. Z2π
0Z1
0Z√1−r2
0
zr dz dr dθ =Z2π
0Z1
0
1
2(1 −r2)rdrdθ=Z2π
0
1
8dθ =π/4
2. Zπ/2
0Zcos θ
0Zr2
0
rsin θdzdrdθ =Zπ/2
0Zcos θ
0
r3sin θdrdθ=Zπ/2
0
1
4cos4θsin θdθ=1/20
3. Zπ/2
0Zπ/2
0Z1
0
ρ3sin φcos φdρdφdθ =Zπ/2
0Zπ/2
0
1
4sin φcos φdφdθ =Zπ/2
0
1
8dθ =π/16
4. Z2π
0Zπ/4
0Zasec φ
0
ρ2sin φdρdφdθ =Z2π
0Zπ/4
0
1
3a3sec3φsin φdφdθ =Z2π
0
1
6a
3dθ =πa3/3
5. V=Z2π
0Z3
0Z9
r2
rdzdrdθ =Z2π
0Z3
0
r(9 −r2)dr dθ =Z2π
0
81
4dθ =81π/2

595 Chapter 16
6. V=2Z2π
0Z2
0Z√
9−r
2
0
rdzdrdθ =2Z2π
0Z2
0
r
p9−r
2
dr dθ
=2
3(27 −5√5) Z2π
0
dθ = 4(27 −5√5)π/3
7. r2+z2= 20 intersects z=r2in a circle of radius 2,
V=Z2π
0Z2
0Z√20−r2
r2
rdzdrdθ=Z2π
0Z2
0
(r
p20 −r2−r3)dr dθ
=4
3(10√5−19) Z2π
0
dθ = 8(10√5−19)π/3
8. z=hr/a intersects z=hin a circle of radius a,
V=Z2π
0Za
0Zh
hr/a
rdzdrdθ =Z2π
0Za
0
h
a(ar −r2)dr dθ =Z2π
0
1
6a2hdθ =πa2h/3
9. V=Z2π
0Zπ/3
0Z4
0
ρ2sin φdρdφdθ =Z2π
0Zπ/3
0
64
3sin φdφdθ =32
3Z2π
0
dθ =64π/3
10. V=Z2π
0Zπ/4
0Z2
1
ρ2sin φdρdφdθ =Z2π
0Zπ/4
0
7
3sin φdφdθ =7
6(2−√2) Z2π
0
dθ = 7(2−√2)π/3
11. In spherical coordinates the sphere and the plane z=aare ρ=2aand ρ=asec φ, respectively.
They intersect at φ=π/3,
V=Z2π
0Zπ/3
0Zasec φ
0
ρ2sin φdρdφdθ+Z2π
0Zπ/2
π/3Z2a
0
ρ2sin φdρdφdθ
=Z2π
0Zπ/3
0
1
3a3sec3φsin φdφdθ+Z2π
0Zπ/2
π/3
8
3a3sin φdφdθ
=1
2a
3Z2π
0
dθ +4
3a3Z2π
0
dθ =11πa3/3
12. V=Z2π
0Zπ/2
π/4Z3
0
ρ2sin φdρdφdθ =Z2π
0Zπ/2
π/4
9 sin φdφdθ =9
√2
2Z2π
0
dθ =9
√
2π
13. Zπ/2
0Za
0Za2−r2
0
r3cos2θdzdrdθ =Zπ/2
0Za
0
(a2r3−r5) cos2θdrdθ
=1
12a6Zπ/2
0
cos2θdθ=πa6/48
14. Zπ
0Zπ/2
0Z1
0
e−ρ3ρ2sin φdρdφdθ =1
3(1 −e−1)Zπ
0Zπ/2
0
sin φdφdθ =(1−e
−1
)π/3
15. Zπ/2
0Zπ/4
0Z√8
0
ρ4cos2φsin φdρdφdθ = 32(2√2−1)π/15
16. Z2π
0Zπ
0Z3
0
ρ3sin φdρdφdθ =81π
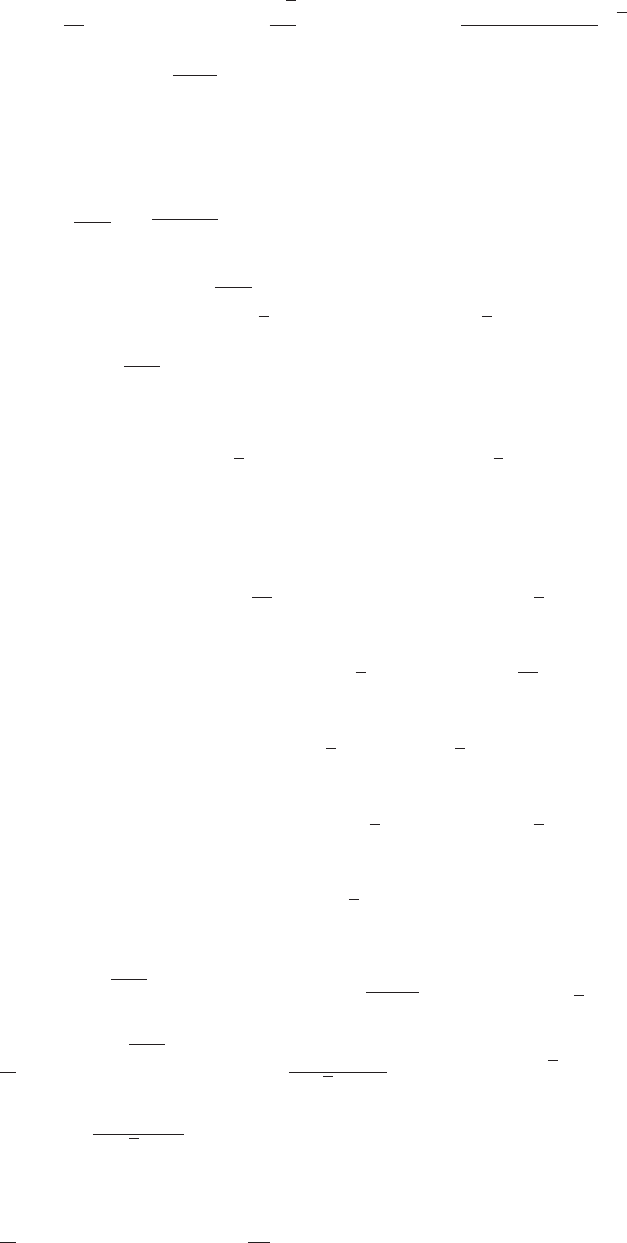
Exercise Set 16.7 596
18. Zπ/2
0Zπ/4
0
1
18 cos37 θcos φdφdθ =√2
36 Zπ/2
0
cos37 θdθ=4,294,967,296
755,505,013,725√2≈0.008040
19. (a) V=2Z2π
0Za
0Z√
a
2
−r
2
0
rdzdrdθ =4πa3/3
(b) V=Z2π
0Zπ
0Za
0
ρ2sin φdρdφdθ =4πa3/3
20. (a) Z2
0Z√4−x2
0Z√4−x2−y2
0
xyzdzdydx
=Z2
0Z√
4−x
2
0
1
2xy(4 −x2−y2)dy dx =1
8Z2
0
x(4 −x2)2dx =4/3
(b) Zπ/2
0Z2
0Z√4−r2
0
r3zsin θcos θdzdrdθ
=Zπ/2
0Z2
0
1
2(4r3−r5) sin θcos θdrdθ=8
3Zπ/2
0
sin θcos θdθ=4/3
(c) Zπ/2
0Zπ/2
0Z2
0
ρ5sin3φcos φsin θcos θdρdφdθ
=Zπ/2
0Zπ/2
0
32
3sin3φcos φsin θcos θdφdθ=8
3Zπ/2
0
sin θcos θdθ=4/3
21. M=Z2π
0Z3
0Z3
r
(3 −z)rdzdrdθ =Z2π
0Z3
0
1
2r(3 −r)2dr dθ =27
8Z2π
0
dθ =27π/4
22. M=Z2π
0Za
0Zh
0
kzrdzdrdθ =Z2π
0Za
0
1
2kh2rdrdθ=1
4ka2h2Z2π
0
dθ =πka2h2/2
23. M=Z2π
0Zπ
0Za
0
kρ3sin φdρdφdθ =Z2π
0Zπ
0
1
4ka4sin φdφdθ =1
2ka4Z2π
0
dθ =πka4
24. M=Z2π
0Zπ
0Z2
1
ρsin φdρdφdθ =Z2π
0Zπ
0
3
2sin φdφdθ =3Z2π
0
dθ =6π
25. ¯x=¯y= 0 from the symmetry of the region,
V=Z2π
0Z1
0Z√2−r2
r2
rdzdrdθ =Z2π
0Z1
0
(r
p2−r
2−r
3)dr dθ =(8
√
2−7)π/6,
¯z=1
VZ2π
0Z1
0Z√2−r2
r2
zr dz dr dθ =6
(8√2−7)π(7π/12)=7/(16√2−14);
centroid 0,0,7
16√2−14
26. ¯x=¯y= 0 from the symmetry of the region, V=8π/3,
¯z=1
VZ2π
0Z2
0Z2
r
zr dz dr dθ =3
8π(4π)=3/2; centroid (0,0,3/2)
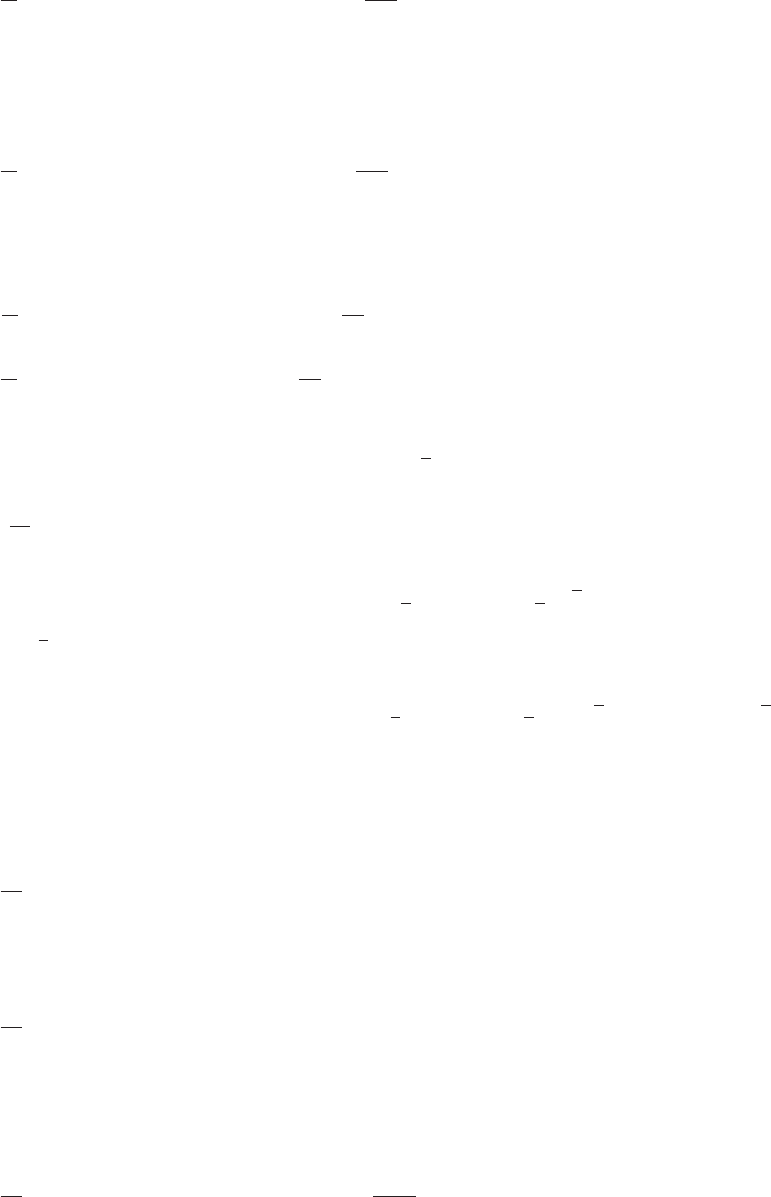
597 Chapter 16
27. ¯x=¯y=¯zfrom the symmetry of the region, V=πa3/6,
¯z=1
VZπ/2
0Zπ/2
0Za
0
ρ3cos φsin φdρdφdθ =6
πa3(πa4/16)=3a/8;
centroid (3a/8,3a/8,3a/8)
28. ¯x=¯y= 0 from the symmetry of the region, V=Z2π
0Zπ/3
0Z4
0
ρ2sin φdρdφdθ =64π/3,
¯z=1
VZ2π
0Zπ/3
0Z4
0
ρ3cos φsin φdρdφdθ =3
64π(48π)=9/4; centroid (0,0,9/4)
29. ¯y= 0 from the symmetry of the region, V=2Zπ/2
0Z2 cos θ
0Zr2
0
rdzdrdθ =3π/2,
¯x=2
VZπ/2
0Z2 cos θ
0Zr2
0
r2cos θdzdrdθ =4
3π(π)=4/3,
¯z=2
VZπ/2
0Z2 cos θ
0Zr2
0
rz dz dr dθ =4
3π(5π/6)=10/9; centroid (4/3,0,10/9)
30. M=Zπ/2
0Z2 cos θ
0Z4−r2
0
zr dz dr dθ =Zπ/2
0Z2 cos θ
0
1
2r(4 −r2)2dr dθ
=16
3Zπ/2
0
(1 −sin6θ)dθ = (16/3)(11π/32)=11π/6
31. V=Zπ/2
0Zπ/3
π/6Z2
0
ρ2sin φdρdφdθ =Zπ/2
0Zπ/3
π/6
8
3sin φdφdθ =4
3(
√3−1) Zπ/2
0
dθ
=2(
√
3−1)π/3
32. M=Z2π
0Zπ/4
0Z1
0
ρ3sin φdρdφdθ =Z2π
0Zπ/4
0
1
4sin φdφdθ =1
8(2 −√2) Z2π
0
dθ =(2−√
2)π/4
33. ¯x=¯y= 0 from the symmetry of density and region,
M=Z2π
0Z1
0Z1−r2
0
(r2+z2)rdzdrdθ =π/4,
¯z=1
MZ2π
0Z1
0Z1−r2
0
z(r2+z2)rdzdrdθ =(4/π)(11π/120) = 11/30; center of gravity (0,0,11/30)
34. ¯x=¯y= 0 from the symmetry of density and region, M=Z2π
0Z1
0Zr
0
zr dz dr dθ =π/4,
¯z=1
MZ2π
0Z1
0Zr
0
z2rdzdrdθ =(4/π)(2π/15)=8/15; center of gravity (0,0,8/15)
35. ¯x=¯y= 0 from the symmetry of density and region,
M=Z2π
0Zπ/2
0Za
0
kρ3sin φdρdφdθ =πka4/2,
¯z=1
MZ2π
0Zπ/2
0Za
0
kρ4sin φcos φdρdφdθ =2
πka4(πka5/5)=2a/5; center of gravity (0,0,2a/5)
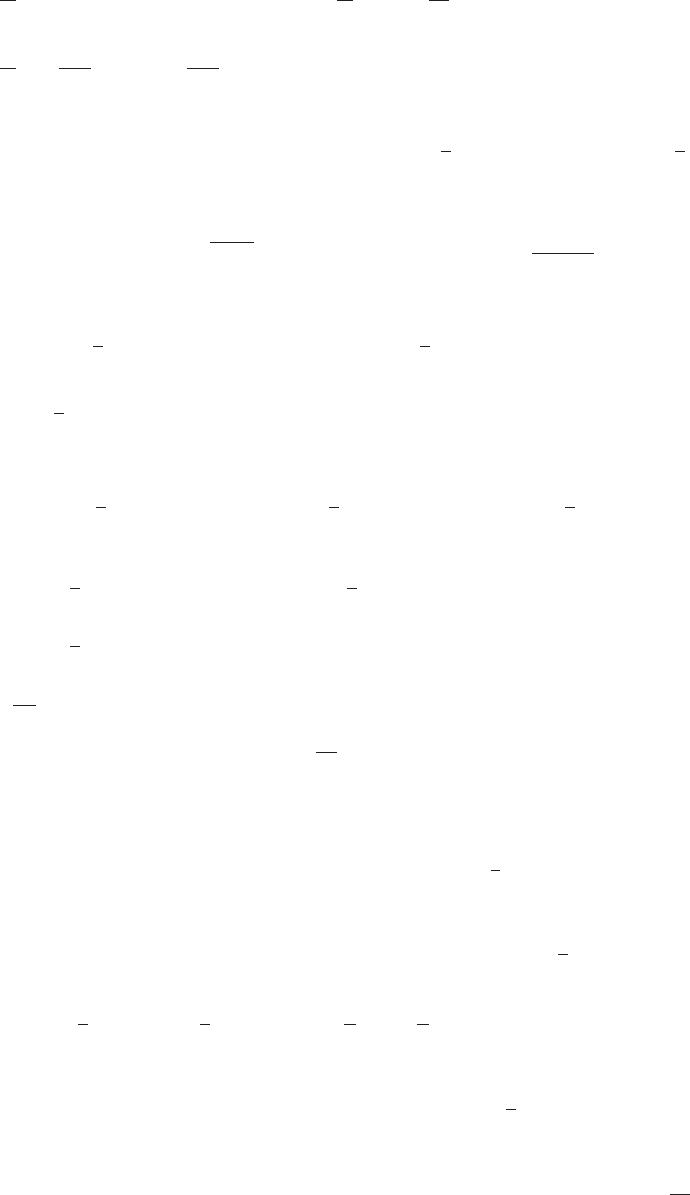
Exercise Set 16.7 598
36. ¯x=¯z= 0 from the symmetry of the region, V=54π/3−16π/3=38π/3,
¯y=1
VZπ
0Zπ
0Z3
2
ρ3sin2φsin θdρdφdθ =1
VZπ
0Zπ
0
65
4sin2φsin θdφdθ
=1
VZπ
0
65π
8sin θdθ=3
38π(65π/4) = 195/152; centroid (0,195/152,0)
37. M=Z2π
0Zπ
0ZR
0
δ0e(ρ/R)3ρ2sin φdρdφdθ =Z2π
0Zπ
0
1
3(e−1)R3δ0sin φdφdθ =4
3π(e−1)δ0R3
38. (a) The sphere and cone intersect in a circle of radius ρ0sin φ0,
V=Zθ2
θ1Zρ0sin φ0
0Z√ρ2
0−r2
rcot φ0
rdzdrdθ =Zθ
2
θ
1Zρ
0sin φ0
0rqρ2
0−r2−r2cot φ0dr dθ
=Zθ2
θ1
1
3ρ3
0(1 −cos3φ0−sin3φ0cot φ0)dθ =1
3ρ3
0(1 −cos3φ0−sin2φ0cos φ0)(θ2−θ1)
=1
3ρ3
0(1 −cos φ0)(θ2−θ1).
(b) From part (a), the volume of the solid bounded by θ=θ1,θ=θ2,φ=φ1,φ=φ2, and
ρ=ρ0is 1
3ρ3
0(1 −cos φ2)(θ2−θ1)−1
3ρ3
0(1 −cos φ1)(θ2−θ1)=1
3
ρ
3
0
(cos φ1−cos φ2)(θ2−θ1)
so the volume of the spherical wedge between ρ=ρ1and ρ=ρ2is
∆V=1
3ρ3
2(cos φ1−cos φ2)(θ2−θ1)−1
3ρ3
1(cos φ1−cos φ2)(θ2−θ1)
=1
3(ρ3
2−ρ3
1)(cos φ1−cos φ2)(θ2−θ1)
(c) d
dφ cos φ=−sin φso from the Mean-Value Theorem cosφ2−cos φ1=−(φ2−φ1) sin φ∗where
φ∗is between φ1and φ2. Similarly d
dρρ3=3ρ
2so ρ3
2−ρ3
1=3ρ
∗2
(ρ
2−ρ
1
) where ρ∗is between
ρ1and ρ2. Thus cos φ1−cos φ2= sin φ∗∆φand ρ3
2−ρ3
1=3ρ
∗2
∆ρso ∆V=ρ∗2sin φ∗∆ρ∆φ∆θ.
39. Iz=Z2π
0Za
0Zh
0
r2δ r dz dr dθ =δZ2π
0Za
0Zh
0
r3dz dr dθ =1
2δπa4h
40. Iy=Z2π
0Za
0Zh
0
(r2cos2θ+z2)δr dz dr dθ =δZ2π
0Za
0
(hr3cos2θ+1
3h3r)dr dθ
=δZ2π
01
4a4hcos2θ+1
6a2h3dθ =δπ
4a4h+π
3a2h3
41. Iz=Z2π
0Za2
a1Zh
0
r2δ r dz dr dθ =δZ2π
0Za2
a1Zh
0
r3dz dr dθ =1
2δπh(a4
2−a4
1)
42. Iz=Z2π
0Zπ
0Za
0
(ρ2sin2φ)δρ
2sin φdρdφdθ =δZ2π
0Zπ
0Za
0
ρ
4sin3φdρdφdθ =8
15δπa5
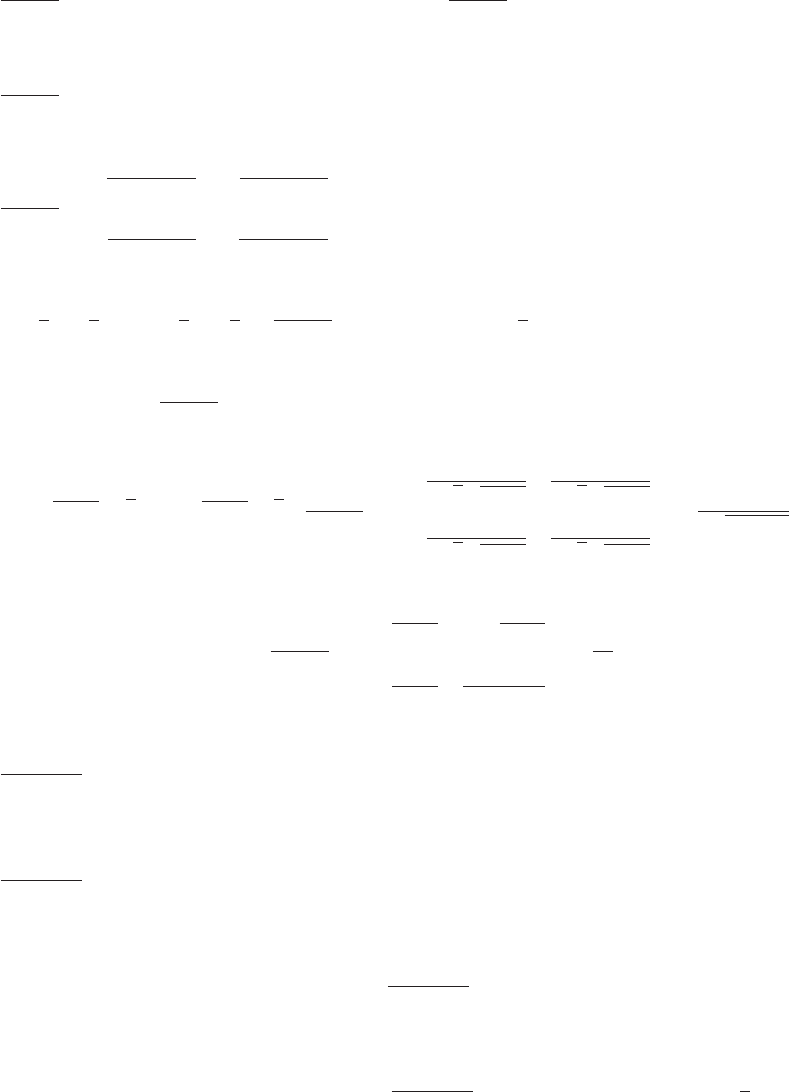
599 Chapter 16
EXERCISE SET 16.8
1. ∂(x, y)
∂(u, v)=
14
3−5
=−17 2. ∂(x, y)
∂(u, v)=
14v
4u−1
=−1−16uv
3. ∂(x, y)
∂(u, v)=
cos u−sin v
sin ucos v
= cos ucos v+ sin usin v= cos(u−v)
4. ∂(x, y)
∂(u, v)=
2(v2−u2)
(u2+v2)2−4uv
(u2+v2)2
4uv
(u2+v2)2
2(v2−u2)
(u2+v2)2
=4/(u
2+v
2
)
2
5. x=2
9u+5
9v,y=−1
9u+2
9v;∂(x, y)
∂(u, v)=
2/95/9
−1/92/9
=
1
9
6. x=lnu,y=uv;∂(x, y)
∂(u, v)=
1/u 0
vu
=1
7. x=√u+v/√2, y=√v−u/√2; ∂(x, y)
∂(u, v)=
1
2√2√u+v
1
2√2√u+v
−1
2√2√v−u
1
2√2√v−u
=1
4√v2−u2
8. x=u3/2/v1/2,y=v1/2/u1/2;∂(x, y)
∂(u, v)=
3u1/2
2v1/2−u3/2
2v3/2
−v1/2
2u3/2
1
2u1/2v1/2
=1
2v
9. ∂(x, y, z)
∂(u, v, w)=
31 0
10−2
01 1
=5
10. ∂(x, y, z)
∂(u, v, w)=
1−v−u0
v−vw u −uw −uv
vw uw uv
=u2v
11. y=v, x =u/y =u/v, z =w−x=w−u/v;∂(x, y, z)
∂(u, v, w)=
1/v −u/v20
010
−1/v u/v21
=1/v
12. x=(v+w)/2,y =(u−w)/2,z =(u−v)/2,∂(x, y, z)
∂(u, v, w)=
01/21/2
1/20−1/2
1/2−1/20
=−
1
4
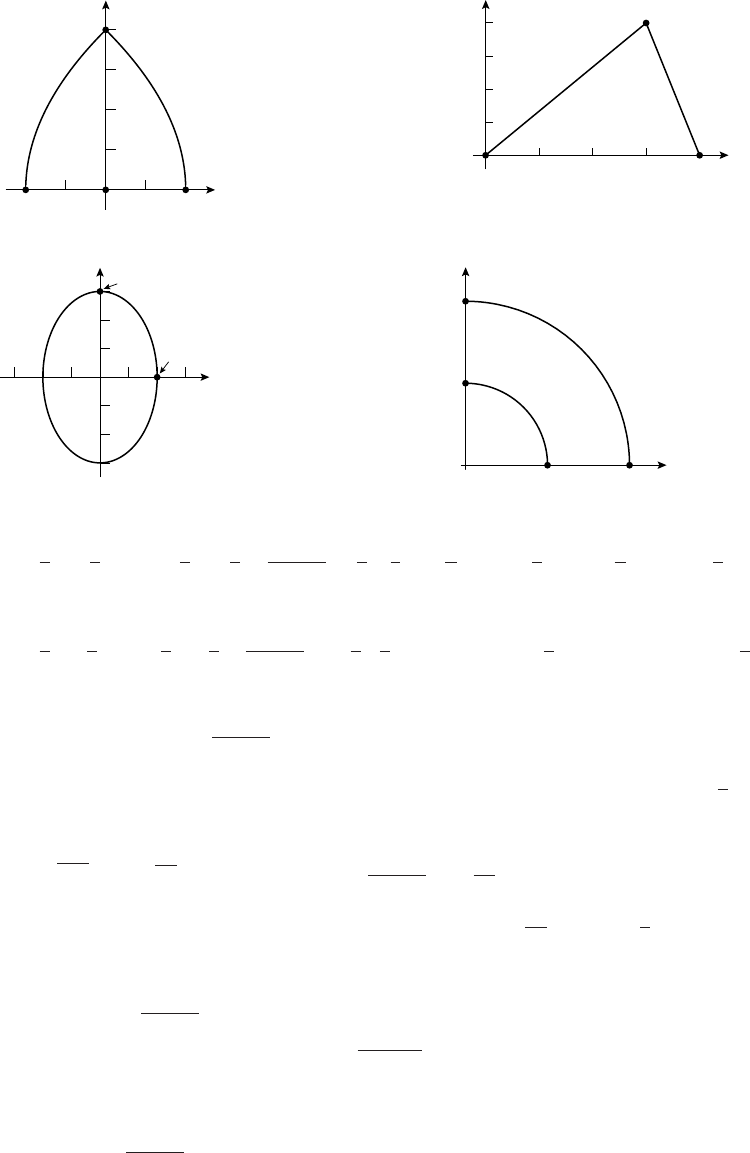
Exercise Set 16.8 600
13.
x
y
(0, 2)
(–1, 0) (1, 0)
(0, 0)
14.
1 2 3
1
2
3
4
x
y
(0, 0) (4, 0)
(3, 4)
15.
-3 3
-3
3
x
y
(2, 0)
(0, 3) 16.
1 2
1
2
x
y
17. x=1
5u+2
5v,y=−2
5u+1
5v,∂(x, y)
∂(u, v)=1
5;1
5ZZ
S
u
vdAuv =1
5Z3
1Z4
1
u
vdu dv =3
2ln 3
18. x=1
2u+1
2v,y=1
2u−1
2v,∂(x, y)
∂(u, v)=−1
2;1
2ZZ
S
veuvdAuv =1
2Z4
1Z1
0
veuvdu dv =1
2(e4−e−3)
19. x=u+v,y=u−v,∂(x, y)
∂(u, v)=−2; the boundary curves of the region Sin the uv-plane are
v=0,v =u, and u= 1 so 2 ZZ
S
sin ucos vdAuv =2Z1
0Zu
0
sin ucos vdvdu=1−1
2sin 2
20. x=pv/u,y=√uv so, from Example 3, ∂(x, y)
∂(u, v)=−1
2u; the boundary curves of the region Sin
the uv-plane are u=1,u=3,v = 1, and v=4soZZ
S
uv21
2udAuv =1
2Z4
1Z3
1
v2du dv =21
21. x=3u, y =4v, ∂(x, y)
∂(u, v)= 12; Sis the region in the uv-plane enclosed by the circle u2+v2=1.
Use polar coordinates to obtain ZZ
S
12pu2+v2(12) dAuv = 144 Z2π
0Z1
0
r2dr dθ =96π
22. x=2u, y =v, ∂(x, y)
∂(u, v)=2;Sis the region in the uv-plane enclosed by the circle u2+v2= 1. Use
polar coordinates to obtain ZZ
S
e−(4u2+4v2)(2) dAuv =2Z2π
0Z1
0
re−4r2dr dθ =(1−e
−4
)π/2
601 Chapter 16
23. Let Sbe the region in the uv-plane bounded by u2+v2=1,sou=2x, v =3y,
x=u/2,y =v/3,∂(x, y)
∂(u, v)=
1/20
01/3
=1/6, use polar coordinates to get
1
6ZZ
S
sin(u2+v2)du dv =1
6Zπ/2
0Z1
0
rsin r2dr dθ =π
24(−cos r2)i1
0=π
24(1 −cos 1)
24. u=x/a, v =y/b, x =au, y =bv;∂(x, y)
∂(u, v)=ab;A=ab Z2π
0Z1
0
rdrdθ=πab
25. x=u/3,y =v/2,z =w, ∂(x, y, z)
∂(u, v, w)=1/6; Sis the region in uvw-space enclosed by the sphere
u2+v2+w2=36so
ZZZ
S
u2
9
1
6dVuvw =1
54 Z2π
0Zπ
0Z6
0
(ρsin φcos θ)2ρ2sin φdρdφdθ
=1
54 Z2π
0Zπ
0Z6
0
ρ4sin3φcos2θdρdφdθ=192
5π
26. Let G1be the region u2+v2+w2≤1, let x=au, y =bv, z =cw, ∂(x, y, z)
∂(u, v, w)=abc;
Ix=ZZZ
G
(y2+z2)dx dy dz =ZZZ
G1
(b2v2+c2w2)du dv dw
=Z2π
0Zπ
0Z1
0
abc(b2sin2φsin2θ+c2cos2φ)ρ4sin φdρdφdθ
=Z2π
0
abc
15 (4b2sin2θ+2c
2
)dθ =4
15πabc(b2+c2)
27. Let u=y−4x, v =y+4x, then x=1
8(v−u),y =1
2(v+u)so∂(x, y)
∂(u, v)=−1
8;
1
8ZZ
S
u
vdAuv =1
8Z5
2Z2
0
u
vdu dv =1
4ln 5
2
28. Let u=y+x, v =y−x, then x=1
2(u−v),y =1
2(u+v)so∂(x, y)
∂(u, v)=1
2;
−1
2ZZ
S
uv dAuv =−1
2Z2
0Z1
0
uv du dv =−1
2
29. Let u=x−y, v =x+y, then x=1
2(v+u),y =1
2(v−u)so∂(x, y)
∂(u, v)=1
2; the boundary curves of
the region Sin the uv-plane are u=0,v =u, and v=π/4; thus
1
2ZZ
S
sin u
cos vdAuv =1
2Zπ/4
0Zv
0
sin u
cos vdu dv =1
2[ln(√2+1)−π/4]
Exercise Set 16.8 602
30. Let u=y−x, v =y+x, then x=1
2(v−u),y =1
2(u+v)so∂(x, y)
∂(u, v)=−1
2; the boundary
curves of the region Sin the uv-plane are v=−u, v =u, v = 1, and v=4;thus
1
2ZZ
S
eu/v dAuv =1
2Z4
1Zv
−v
eu/vdu dv =15
4(e−e−1)
31. Let u=y/x, v =x/y2, then x=1/(u
2
v),y =1/(uv)so∂(x, y)
∂(u, v)=1
u4v3;
ZZ
S
1
u4v3dAuv =Z4
1Z2
1
1
u4v3du dv =35/256
32. Let x=3u, y =2v,∂(x, y)
∂(u, v)=6;Sis the region in the uv-plane enclosed by the circle u2+v2=1
so ZZ
R
(9 −x−y)dA =ZZ
S
6(9 −3u−2v)dAuv =6Z2π
0Z1
0
(9 −3rcos θ−2rsin θ)rdrdθ=54π
33. x=u, y =w/u, z =v+w/u, ∂(x, y, z)
∂(u, v, w)=−1
u;
ZZZ
S
v2w
udVuvw =Z4
2Z1
0Z3
1
v2w
udu dv dw = 2 ln 3
34. u=xy, v =yz, w =xz, 1≤u≤2,1≤v≤3,1≤w≤4,
x=puw/v, y =puv/w, z =pvw/u, ∂(x, y, z)
∂(u, v, w)=1
2√uvw
V=ZZZ
G
dV =Z2
1Z3
1Z4
1
1
2√uvw dw dv du =4(
√
2−1)(√3−1)
35. (b) If x=x(u, v),y =y(u, v) where u=u(x, y),v =v(x, y), then by the chain rule
∂x
∂u
∂u
∂x +∂x
∂v
∂v
∂x =∂x
∂x =1,∂x
∂u
∂u
∂y +∂x
∂v
∂v
∂y =∂x
∂y =0
∂y
∂u
∂u
∂x +∂y
∂v
∂v
∂x =∂y
∂x =0,∂y
∂u
∂u
∂y +∂y
∂v
∂v
∂y =∂y
∂y =1
36. (a) ∂(x, y)
∂(u, v)=
1−v−u
vu
=u;u=x+y, v =y
x+y,
∂(u, v)
∂(x, y)=
11
−y/(x+y)2x/(x+y)2
=x
(x+y)2+y
(x+y)2=1
x+y=1
u;
∂(u, v)
∂(x, y)
∂(x, y)
∂(u, v)=1
(b) ∂(x, y)
∂(u, v)=
vu
02v
=2v
2
;u=x/√y, v =√y,
∂(u, v)
∂(x, y)=
1/√y−x/(2y−3/2)
01/(2√y)
=1
2y=1
2v2;∂(u, v)
∂(x, y)
∂(x, y)
∂(u, v)=1

603 Chapter 16
(c) ∂(x, y)
∂(u, v)=
uv
u−v
=−2uv;u=√x+y, v =√x−y,
∂(u, v)
∂(x, y)=
1/(2√x+y)1/(2√x+y)
1/(2√x−y)−1/(2√x−y)
=−1
2px2−y2=−1
2uv ;∂(u, v)
∂(x, y)
∂(x, y)
∂(u, v)=1
37. ∂(u, v)
∂(x, y)=3xy4=3vso ∂(x, y)
∂(u, v)=1
3v;1
3ZZ
S
sin u
vdAuv =1
3Z2
1Z2π
π
sin u
vdu dv =−2
3ln 2
38. ∂(u, v)
∂(x, y)=8xy so ∂(x, y)
∂(u, v)=1
8xy ;xy
∂(x, y)
∂(u, v)
=xy 1
8xy =1
8so
1
8ZZ
S
dAuv =1
8Z16
9Z4
1
du dv =21/8
39. ∂(u, v)
∂(x, y)=−2(x2+y2)so∂(x, y)
∂(u, v)=−1
2(x2+y2);
(x4−y4)exy
∂(x, y)
∂(u, v)
=x4−y4
2(x2+y2)exy =1
2(x2−y2)exy =1
2veuso
1
2ZZ
S
veudAuv =1
2Z4
3Z3
1
veudu dv =7
4(e3−e)
40. Set u=x+y+2z, v =x−2y+z,w =4x+y+z, then ∂(u, v, w)
∂(x, y, z)=
112
1−21
411
= 18, and
V=ZZZ
R
dx dy dz =Z6
−6Z2
−2Z3
−3
∂(x, y, z)
∂(u, v, w)du dv dw = 6(4)(12) 1
18 =16
41. (a) Let u=x+y, v =y, then the triangle Rwith vertices (0,0),(1,0) and (0,1) becomes the
triangle in the uv-plane with vertices (0,0),(1,0),(1,1), and
ZZ
R
f(x+y)dA =Z1
0Zu
0
f(u)∂(x, y)
∂(u, v)dv du =Z1
0
uf(u)du
(b) Z1
0
ueudu =(u−1)eui1
0=1
42. (a) ∂(x, y)
∂(r, θ)=
cos θ−rsin θ
sin θrcos θ
=r,
∂(x, y)
∂(r, θ)
=r
(b) ∂(x, y, z)
∂(ρ, θ, φ)=
sin φcos θ−ρsin φsin θρcos φcos θ
sin φsin θρsin φcos θρcos φsin θ
cos φ0−ρsin φ
=−ρ2sin φ;
∂(x, y, z)
∂(ρ, θ, φ)
=ρ2sin φ

Chapter 16 Supplementary Exercises 604
CHAPTER 16 SUPPLEMENTARY EXERCISES
3. (a) ZZ
R
dA (b) ZZZ
G
dV (c) ZZ
Rs∂z
∂x2
+∂z
∂y2
dA
4. (a) x=asin φcos θ, y =asin φsin θ, z =ρcos φ, 0≤θ≤2π, 0≤φ≤π
(b) x=acos θ, y =asin θ, z =z,0≤θ≤2π, 0≤z≤h
7. Z1
0Z1+√1−y2
1−√1−y2
f(x, y)dx dy 8. Z2
0Z2x
x
f(x, y)dy dx +Z3
2Z6−x
x
f(x, y)dy dx
9. (a) (1,2)=(b, d),(2,1)=(a, c), so a=2,b =1,c=1,d=2
(b) ZZ
R
dA =Z1
0Z1
0
∂(x, y)
∂(u, v)du dv =Z1
0Z1
0
3du dv =3
10. 0<sin √xy < 1 for 0 < x,y < π,so
0=Zπ
0Zπ
0
0dy dx < Zπ
0Zπ
0
sin √xy dy dx < Zπ
0Zπ
0
1dy dx =π2
11. Z1
1/2
2xcos(πx2)dx =1
πsin(πx2)i1
1/2=−1/(√2π)
12. Z2
0
x2
2ey3x=2y
x=−y
dy =3
2Z2
0
y2ey3dy =1
2ey32
0
=1
2e8−1
13. Z1
0Z2
2y
exeydx dy 14. Zπ
0Zx
0
sin x
xdy dx
15.
6
1
x
y
y = sin x
y = tan (x/2)
16.
0
p/2
p/6
r = a
r = a(1 + cos u)
17. 2Z8
0Zy1/3
0
x2sin y2dx dy =2
3Z8
0
ysin y2dy =−1
3cos y28
0
=1
3(1 −cos 64) ≈0.20271
18. Zπ/2
0Z2
0
(4 −r2)rdrdθ=2π
605 Chapter 16
19. sin 2θ= 2 sin θcos θ=2xy
x2+y2, and r=2asin θis the circle x2+(y−a)
2=a
2
,so
Za
0Za+
√
a
2
−x
2
a−
√
a
2
−x
2
2xy
x2+y2dy dx =Za
0
xhln a+pa2−x2−ln a−pa2−x2idx =a2
20. Zπ/2
π/4Z2
0
4r2(cos θsin θ)rdrdθ=−4 cos 2θπ/2
π/4
=4
21. Z2π
0Z2
0Z16
r4
r2cos2θrdzdrdθ =Z2π
0
cos2θdθZ2
0
r
3(16 −r4)dr =32π
22. Zπ/2
0Zπ/2
0Z1
0
1
1+ρ
2ρ
2sin φdρdφdθ =1−π
4π
2Zπ/2
0
sin φdφ
=1−π
4π
2(−cos φ)iπ/2
0=1−π
4π
2
23. (a) Z2π
0Zπ/3
0Za
0
(ρ2sin2φ)ρ2sin φdρdφdθ =Z2π
0Zπ/3
0Za
0
ρ4sin3φdρdφdθ
(b) Z2π
0Z√3a/2
0Z√a2−r2
r/√3
r2dz rdr dθ =Z2π
0Z√3a/2
0Z√a2−r2
r/√3
r3dz dr dθ
(c) Z√3a/2
−√3a/2Z√(3a2/4)−x2
−√(3a2/4)−x2Z√a2−x2−y2
√x2+y2/√3
(x2+y2)dz dy dx
24. (a) Z4
0Z√4x−x2
−√4x−x2Z4x
x2+y2
dz dy dx
(b) Zπ/2
−π/2Z4 cos θ
0Z4rcos θ
r2
rdzdrdθ
25. Z2
0Z2−y/2
(y/2)1/3
dx dy =Z2
02−y
2−y
21/3dy =2y−y2
4−3
2y
24/32
0
=3
2
26. A=6Zπ/6
0Zcos 3θ
0
rdrdθ=3Zπ/6
0
cos23θ=π/4
27. V=Z2π
0Za/√3
0Za
√3r
rdzdrdθ =2πZa/√3
0
r(a−√3r)dr =πa3
9
28. The intersection of the two surfaces projects onto the yz-plane as 2y2+z2=1,so
V=4Z1/
√
2
0Z√
1−2y
2
0Z1−y
2
y
2
+z
2
dx dz dy
=4Z1/
√
2
0Z√
1−2y
2
0
(1 −2y2−z2)dz dy =4Z1/
√
2
0
8
3
(1 −2x2)3/2dx =√2π
4
29. kru×rvk=√2u2+2v
2+4,
S=ZZ
u2+v2≤4p2u2+2v
2+4dA =Z2π
0Z2
0
√2pr2+2rdrdθ =8π
3(3√3−1)
Chapter 16 Supplementary Exercises 606
30. kru×rvk=√1+u
2
,S=
Z2
0Z3u
0p
1+u
2
dv du =Z2
0
3up1+u
2
du =5
3/2−1
31. (ru×rv)iu=1
v=2
=h−2,−4,1i, tangent plane 2x+4y−z=5
32. u=−3,v =0,(r
u×r
v
)
iu=−3
v=0
=h−18,0,−3i, tangent plane 6x+z=−9
33. A=Z4
−4Z2+y2/8
y2/4
dx dy =Z4
42−y2
8dy =32
3;¯y= 0 by symmetry;
Z4
−4Z2+y2/8
y2/4
xdxdy =Z4
−42+1
4y
2−3
128y4dy =256
15 ,¯x=3
32
256
15 =8
5; centroid 8
5,0
34. A=πab/2,¯x= 0 by symmetry,
Za
−aZb√1−x2/a2
0
ydydx=1
2Za
−a
b
2
(1 −x2/a2)dx =2ab2/3, centroid 0,4b
3π
35. V=1
3πa2h, ¯x=¯y= 0 by symmetry,
Z2π
0Za
0Zh−rh/a
0
rz dz dr dθ =πZa
0
rh21−r
a2dr =πa2h2/12, centroid (0,0,h/4)
36. V=Z2
−2Z4
x2Z4−y
0
dz dy dx =Z2
−2Z4
x2
(4 −y)dy dx =Z2
−28−4x2+1
2x4dx =256
15 ,
Z2
−2Z4
x2Z4−y
0
ydzdydx=Z2
−2Z4
x
2
(4y−y2)dy dx =Z2
−21
3x6−2x4+32
3dx =1024
35
Z2
−2Z4
x2Z4−y
0
zdzdydx=Z2
−2Z4
x
2
1
2(4 −y)2dy dx =Z2
−2−x6
6+2x
4−8x
2+32
3dx =2048
105
¯x= 0 by symmetry, centroid 0,8
7,4
37. The two quarter-circles with center at the origin and of radius Aand √2Alie inside and outside
of the square with corners (0,0),(A, 0),(A, A),(0,A), so the following inequalities hold:
Zπ/2
0ZA
0
1
(1+r2)2rdr dθ ≤ZA
0ZA
0
1
(1+x2+y2)2dx dy ≤Zπ/2
0Z√2A
0
1
(1+r2)2rdr dθ
The integral on the left can be evaluated as πA2
4(1 + A2)and the integral on the right equals
2πA2
4(1+2A
2
). Since both of these quantities tend to π
4, it follows by sandwiching that
Z+∞
0Z+∞
0
1
(1+x2+y2)2dx dy =π
4.
38. The centroid of the circle which generates the tube travels a distance
s=Z4π
0qsin2t+ cos2t+1/16 dt =√17π,soV=π(1/2)2√17π=√17π2/4.
607 Chapter 16
39. (a) The values of xin the formula of the astroidal sphere lie between −aand a; and the same is
true for x=(acos ucos v)3; similarly for yand z. Moreover,
x2/3+y2/3+z2/3=a2/3cos2ucos2v+a2/3sin2ucos2v+a2/3sin2v
=a2/3cos2v+a2/3sin2v=a2/3
(b) S=8Zπ/2
0Zπ/2
0kru×rvkdu dv
=72Zπ/2
0Zπ/2
0
sin ucos usin vcos4vpsin2v+ sin2ucos2ucos2vdu dv ≈4.451
(c) 8Z(1−x2/3)3/2
0Z1
0p1−x2/3−y2/3dy dx ≈0.3590
(d) Let x=tcos3u, y =tsin3u, 0≤t≤1,0≤u≤π/2, then J=∂(x, y)
∂(t, u)=3tsin2ucos2u,
V=8Z1
0Zπ/2
0
(1 −t2/3)3/23tsin2ucos2ududt=3π
2Z1
0
t(1 −t2/3)3/2dt =4π
35
40. V=4
3πa3,¯
d=3
4πa3ZZZ
ρ≤a
ρdV =3
4πa3Zπ
0Z2π
0Za
0
ρ3sin φdρdθdφ =3
4πa32π(2)a4
4=3
4a
41. (a) (x/a)2+(y/b)2+(z/c)2= sin2φcos2θ+sin2φsin2θ+cos2φ= sin2φ+cos2φ= 1, an ellipsoid
(b) r(φ, θ)=h2 sin φcos θ, 3 sin φsin θ, 4 cos φi;rφ×rθ=2h6 sin2φcos θ, 4 sin2φsin θ, 3 cos φsin φi,
krφ×rθk=2
p16 sin4φ+ 20 sin4φcos2θ+ 9 sin2φcos2φ,
S=Z2π
0Zπ
0
2q16 sin4φ+ 20 sin4φcos2θ+ 9 sin2φcos2φdφdθ ≈111.5457699
608
CHAPTER 17
Topics in Vector Calculus
EXERCISE SET 17.1
1. (a) III because the vector field is independent of yand the direction is that of the negative x-axis
for negative x, and positive for positive
(b) IV, because the y-component is always positive, and the x-component is positive for positive
x, negative for negative x
2. (a) I, since the vector field is constant
(b) II, since the vector field points away from the origin
3. (a) true (b) true (c) true
4. (a) false, the lengths are equal to 1 (b) false, the y-component is then zero
(c) false, the x-component is then zero
5.
x
y6.
x
y7.
x
y
8.
x
y9.
x
y10.
x
y
11. (a) ∇φ=φxi+φyj=y
1+x
2
y
2i+x
1+x
2
y
2j=F,soFis conservative for all x, y
(b) ∇φ=φxi+φyj=2xi−6yj+8zk=Fso Fis conservative for all x, y
12. (a) ∇φ=φxi+φyj=(6xy −y3)i+(4y+3x
2−3xy2)j=F,soFis conservative for all x, y
(b) ∇φ=φxi+φyj+φzk= (sin z+ycos x)i+ (sin x+zcos y)j+(xcos z+ sin y)k=F,soFis
conservative for all x, y
609 Chapter 17
13. div F=2x+y, curl F=zi
14. div F=z3+8y
3
x
2+10zy, curl F=5z
2
i+3xz2j+4xy4k
15. div F= 0, curl F= (40x2z4−12xy3)i+ (14y3z+3y
4
)j−(16xz5+21y
2
z
2
)k
16. div F=yexy + sin y+ 2 sin zcos z, curl F=−xexyk
17. div F=2
px2+y2+z2, curl F=0
18. div F=1
x+xzexyz +x
x2+z2, curl F=−xyexyz i+z
x2+z2j+yzexyzk
19. ∇·(F×G)=∇·(−(z+4y
2
)i+(4xy +2xz)j+(2xy −x)k)=4x
20. ∇·(F×G)=∇·((x2yz2−x2y2)i−xy2z2j+xy2zk)=−xy2
21. ∇·(∇×F)=∇·(−sin(x−y)k)=0
22. ∇·(∇×F)=∇·(−zeyzi+xexzj+3e
yk)=0
23. ∇×(∇×F)=∇×(xzi−yzj+yk)=(1+y)i+xj
24. ∇×(∇×F)=∇×((x+3y)i−yj−2xyk)=−2xi+2yj−3k
25. div (kF)=k
∂f
∂x +k∂q
∂y +k∂h
∂z =kdiv F
26. curl (kF)=k∂h
∂y −∂g
∂zi+k∂f
∂z −∂h
∂xj+k∂g
∂x −∂f
∂y k=kcurl F
27. Let F=f(x, y, z)i+g(x, y, z)j+h(x, y, z)kand G=P(x, y, z)i+Q(x, y, z)j+R(x, y, z)k, then
div (F+G)=∂f
∂x +∂P
∂x +∂g
∂y +∂Q
∂y +∂h
∂z +∂R
∂z
=∂f
∂x +∂g
∂y +∂h
∂z +∂P
∂x +∂Q
∂y +∂R
∂z = div F+ div G
28. Let F=f(x, y, z)i+g(x, y, z)j+h(x, y, z)kand G=P(x, y, z)i+Q(x, y, z)j+R(x, y, z)k, then
curl (F+G)=∂
∂y(h+R)−∂
∂z(g+Q)i+∂
∂z(f+P)−∂
∂x(h+R)j
+∂
∂x(g+Q)−∂
∂y(f+P)k;
expand and rearrange terms to get curl F+ curl G.
29. div (φF)=φ
∂f
∂x +∂φ
∂xf+φ∂g
∂y +∂φ
∂y g+φ∂h
∂z +∂φ
∂z h
=φ∂f
∂x +∂g
∂y +∂h
∂z +∂φ
∂xf+∂φ
∂y g+∂φ
∂z h
=φdiv F+∇φ·F
Exercise Set 17.1 610
30. curl (φF)=∂
∂y(φh)−∂
∂z(φg)i+∂
∂z(φf)−∂
∂x(φh)j+∂
∂x(φg)−∂
∂y(φf )k; use the product
rule to expand each of the partial derivatives, rearrange to get φcurl F+∇φ×F
31. div(curl F)= ∂
∂x ∂h
∂y −∂g
∂z+∂
∂y ∂f
∂z −∂h
∂x+∂
∂z ∂g
∂x −∂f
∂y
=∂2h
∂x∂y −∂2g
∂x∂z +∂2f
∂y∂z −∂2h
∂y∂x +∂2g
∂z∂x −∂2f
∂z∂y =0,
assuming equality of mixed second partial derivatives
32. curl (∇φ)=∂
2
φ
∂y∂z −∂2φ
∂z∂yi+∂2φ
∂z∂x −∂2φ
∂x∂z j+∂2φ
∂x∂y −∂2φ
∂y∂xk=0, assuming equality
of mixed second partial derivatives
33. ∇·(kF)=k∇·F,∇·(F+G)=∇·F+∇·G,∇·(φF)=φ∇·F+∇φ·F,∇·(∇×F)=0
34. ∇×(kF)=k∇×F,∇×(F+G)=∇×F+∇×G,∇×(φF)=φ∇×F+∇φ×F,∇×(∇φ)=0
37. (a) curl r=0i+0j+0k=0
(b) ∇krk=∇px2+y2+z2=x
px2+y2+z2i+y
px2+y2+z2j+z
px2+y2+z2k=r
krk
38. (a) div r=1+1+1=3
(b) ∇1
krk=∇(x2+y2+z2)−1/2=−xi+yj+zk
(x2+y2+z2)3/2=−r
krk3
39. (a) ∇f(r)=f
0
(r)∂r
∂xi+f0(r)∂r
∂yj+f0(r)∂r
∂zk=f0(r)∇r=f0(r)
rr
(b) div[f(r)r]=f(r)div r+∇f(r)·r=3f(r)+f0(r)
rr·r=3f(r)+rf0(r)
40. (a) curl[f(r)r]=f(r)curl r+∇f(r)×r=f(r)0+f0(r)
rr×r=0+0=0
(b) ∇2f(r) = div[∇f(r)] = div f0(r)
rr=f0(r)
rdiv r+∇f0(r)
r
·r
=3
f
0
(r)
r+rf00(r)−f0(r)
r3r·r=2
f
0
(r)
r+f
00(r)
41. f(r)=1/r3,f0(r)=−3/r4, div(r/r3) = 3(1/r3)+r(−3/r4)=0
42. Multiply 3f(r)+rf0(r) = 0 through by r2to obtain 3r2f(r)+r
3
f0(r)=0,
d[r
3
f(r)]/dr =0,r
3
f(r)=C, f(r)=C/r3,soF=Cr/r3(an inverse-square field).
43. (a) At the point (x, y) the slope of the line along which the vector −yi+xjlies is −x/y; the
slope of the tangent line to Cat (x, y)isdy/dx,sody/dx =−x/y.
(b) ydy =−xdx, y2/2=−x
2
/2+K
1
,x
2+y
2=K
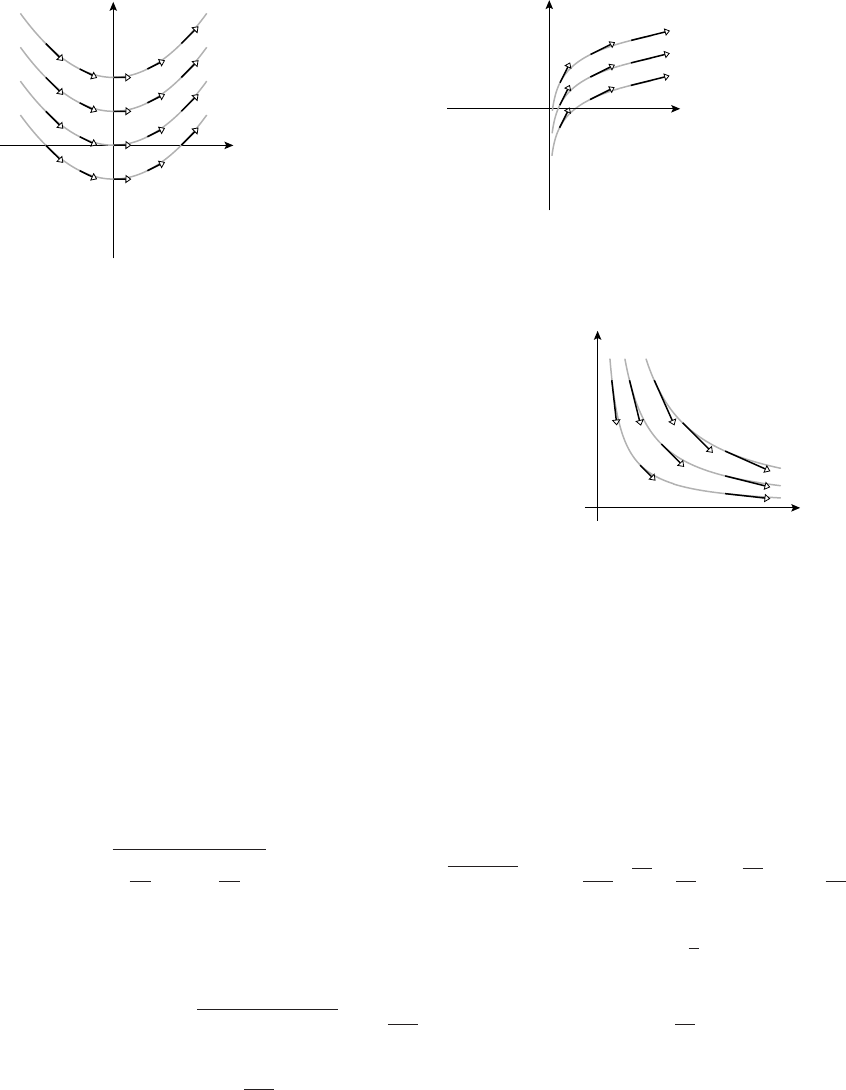
611 Chapter 17
44. dy/dx =x, y =x2/2+K
x
y
45. dy/dx =1/x, y =lnx+K
x
y
46. dy/dx =−y/x, (1/y)dy =(−1/x)dx, ln y=−ln x+K1,
y=eK1e−ln x=K/x
x
y
EXERCISE SET 17.2
1. (a) Z1
0
dy = 1 because s=yis arclength measured from (0,0)
(b) 0, because sinxy = 0 along C
2. (a) Z
C
ds = length of line segment = 2 (b) 0, because xis constant and dx =0
3. (a) ds =sdx
dt 2
+dy
dt 2
dt,soZ1
0
(2t−3t2)p4+36t
2dt =−11
108√10 −1
36 ln(√10−3) −4
27
(b) Z1
0
(2t−3t2)2 dt =0 (c) Z1
0
(2t−3t2)6tdt=−1
2
4. (a) Z1
0
t(3t2)(6t3)2p1+36t
2+ 324t4dt =864
5(b) Z1
0
t(3t2)(6t3)2dt =54
5
(c) Z1
0
t(3t2)(6t3)26tdt=648
11 (d) Z1
0
t(3t2)(6t3)218t2dt = 162
5. (a) C:x=t,y=t,0≤t≤1; Z1
0
6tdt=3
(b) C:x=t,y=t2,0≤t≤1; Z1
0
(3t+6t
2−2t
3
)dt =3

Exercise Set 17.2 612
(c) C:x=t,y= sin(πt/2), 0 ≤t≤1;
Z1
0
[3t+ 2 sin(πt/2)+πt cos(πt/2) −(π/2) sin(πt/2) cos(πt/2)]dt =3
(d) C:x=t3,y=t,0≤t≤1; Z1
0
(9t5+8t
3−t)dt =3
6. (a) C:x=t, y =t, z =t, 0≤t≤1; Z1
0
(t+t−t)dt =1
2
(b) C:x=t, y =t2,z =t
3,0≤t≤1; Z1
0
(t2+t3(2t)−t(3t2)) dt =−1
60
(c) C:x= cos πt, y = sin πt, z =t, 0≤t≤1; Z1
0
(−πsin2πt +πt cos πt −cos πt)dt =−π
2−2
π
7. Z3
0
√1+t
1+tdt =Z3
0
(1+t)−1/2dt =2 8. √5Z1
0
1+2t
1+t
2dt =√5(π/4+ln2)
9. Z1
0
3(t2)(t2)(2t3/3)(1 + 2t2)dt =2Z1
0
t
7
(1+2t
2
)dt =13/20
10. √5
4Z2π
0
e−tdt =√5(1 −e−2π)/411. Zπ/4
0
(8 cos2t−16 sin2t−20 sin tcos t)dt =1−π
12. Z1
−12
3t−2
3t5/3+t2/3dt =6/5
13. C:x=(3−t)
2
/3, y=3−t,0≤t≤3; Z3
0
1
3(3 −t)2dt =3
14. C:x=t2/3,y=t,−1≤t≤1; Z1
−12
3t2/3−2
3t1/3+t7/3dt =4/5
15. C:x= cos t,y= sin t,0≤t≤π/2; Zπ/2
0
(−sin t−cos2t)dt =−1−π/4
16. C:x=3−t,y=4−3t,0≤t≤1; Z1
0
(−37+41t−9t
2
)dt =−39/2
17. Z1
0
(−3)e3tdt =1−e
3
18. Zπ/2
0
(sin2tcos t−sin2tcos t+t4(2t)) dt =π6
192
20. (a) Zπ/2
0
cos21 tsin9tq(−3 cos2tsin t)2+ (3 sin2tcos t)2dt
=3
Zπ/2
0
cos22 tsin10 tdt=61,047
4,294,967,296π
(b) Ze
1t5ln t+7t
2
(2t)+t
4
(ln t)1
tdt =5
36e6+59
16e4−491
144
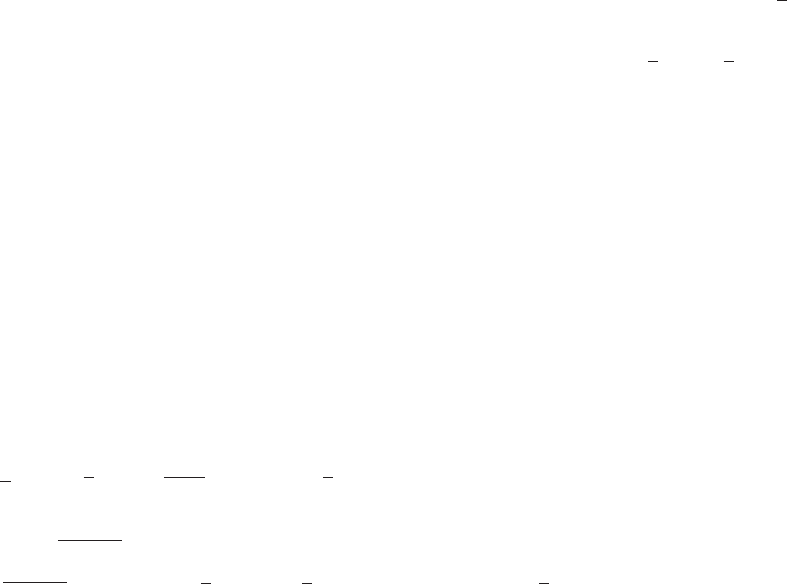
613 Chapter 17
21. (a) C1:(0,0) to (1,0); x=t, y =0,0≤t≤1
C
2:(1,0) to (0,1); x=1−t, y =t, 0≤t≤1
C3:(0,1) to (0,0); x=0,y =1−t, 0≤t≤1
Z1
0
(0)dt +Z1
0
(−1)dt +Z1
0
(0)dt =−1
(b) C1:(0,0) to (1,0); x=t, y =0,0≤t≤1
C
2:(1,0) to (1,1); x=1,y =t, 0≤t≤1
C3:(1,1) to (0,1); x=1−t, y =1,0≤t≤1
C
4:(0,1) to (0,0); x=0,y =1−t, 0≤t≤1
Z1
0
(0)dt +Z1
0
(−1)dt +Z1
0
(−1)dt +Z1
0
(0)dt =−2
22. (a) C1:(0,0) to (1,1); x=t, y =t, 0≤t≤1
C2:(1,1) to (2,0); x=1+t, y =1−t, 0≤t≤1
C3:(2,0) to (0,0); x=2−2t, y =0,0≤t≤1
Z1
0
(0)dt +Z1
0
2dt +Z1
0
(0)dt =2
(b) C1:(−5,0) to (5,0); x=t, y =0,−5≤t≤5
C
2:x= 5 cos t, y = 5 sin t, 0≤t≤π
Z5
−5
(0)dt +Zπ
0
(−25)dt =−25π
23. C1:x=t, y =z=0,0≤t≤1,Z1
0
0dt =0; C
2:x=1,y =t, z =0,0≤t≤1,Z1
0
(−t)dt =−1
2
C3:x=1,y =1,z =t, 0≤t≤1,Z1
0
3dt =3; ZC
x
2
zdx−yx2dy +3dz =0−1
2+3= 5
2
24. C1:(0,0,0) to (1,1,0); x=t, y =t, z =0,0≤t≤1
C
2:(1,1,0) to (1,1,1); x=1,y =1,z =t, 0≤t≤1
C3:(1,1,1) to (0,0,0); x=1−t, y =1−t, z =1−t, 0≤t≤1
Z1
0
(−t3)dt +Z1
0
3dt +Z1
0−3dt =−1/4
25. Zπ
0
(0)dt =0 26. Z1
0
(e2t−4e−t)dt =e2/2+4e
−1−9/2
27. Z1
0
e−tdt =1−e
−128. Zπ/2
0
(7 sin2tcos t+ 3 sin tcos t)dt =23/6
29. Represent the circular arc by x= 3 cos t, y = 3 sin t, 0≤t≤π/2.
ZC
x√yds =9
√
3Zπ/2
0
√sin tcos tdt=6
√
3
30. δ(x, y)=k
px
2+y
2where kis the constant of proportionality,
ZC
kpx2+y2ds =kZ1
0
et(√2et)dt =√2kZ1
0
e2tdt =(e
2−1)k/√2
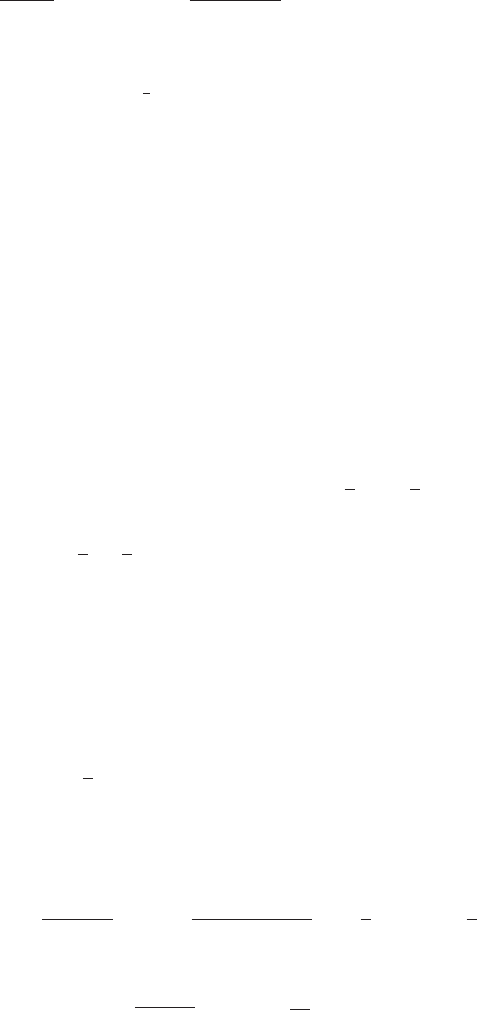
Exercise Set 17.2 614
31. ZC
kx
1+y
2ds =15kZπ/2
0
cos t
1+9sin
2tdt =5ktan−13
32. δ(x, y, z)=kz where kis the constant of proportionality,
ZC
kzds =Z4
1
k(4√t)(2+1/t)dt = 136k/3
33. C:x=t2,y=t,0≤t≤1; W=Z1
0
3t4dt =3/5
34. W=Z3
1
(t2+1−1/t3+1/t)dt =92/9+ln3 35. W=Z1
0
(t3+5t
6
)dt =27/28
36. C1:(0,0,0) to (1,3,1); x=t,y=3t,z=t,0≤t≤1
C
2:(1,3,1) to (2,−1,4); x=1+t,y=3−4t,z=1+3t,0≤t≤1
W=Z1
0
(4t+8t
2
)dt +Z1
0
(−11 −17t−11t2)dt =−37/2
37. Since Fand rare parallel, F·r=kFkkrk, and since Fis constant,
ZF·dr=Z
C
d(F·r)=Z
C
d(kFkkrk)=√
2Z4
−4
√
2dt =16
Z
C
F·r=√
2(4√2)
38. Z
C
F·r= 0, since Fis perpendicular to the curve
39. C:x= 4 cos t, y = 4 sin t, 0≤t≤π/2
Zπ/2
0−1
4sin t+ cos tdt =3/4
40. C1:(0,3) to (6,3); x=6t, y =3,0≤t≤1
C
2:(6,3) to (6,0); x=6,y =3−3t, 0≤t≤1
Z1
0
6
36t2+9dt +Z1
0
−12
36 + 9(1 −t)2dt =1
3tan−12−2
3tan−1(1/2)
41. Represent the parabola by x=t, y =t2,0≤t≤2.
ZC
3xds =Z2
0
3tp1+4t
2dt = (17√17 −1)/4
42. Represent the semicircle by x= 2 cos t, y = 2 sin t, 0≤t≤π.
ZC
x2yds =Zπ
0
16 cos2tsin tdt=32/3
43. (a) 2πrh =2π(1)2 = 4π(b) S=ZC
z(t)dt
(c) C:x= cos t, y = sin t, 0≤t≤2π;S=Z2π
0
(2+(1/2) sin 3t)dt =4π

615 Chapter 17
44. C:x=acos t, y =asin t, 0≤t≤2π,Z−C
dt =−ZC
dt =−Z2π
0
dt =−2π
45. W=Z1
0
λ[(1 −λ)t+(3λ−1)t2−(1+2λ)t
3
]dt =−λ/12, W= 1 when λ=−12
46. The force exerted by the farmer is F=150+20−1
10zk=170 −3
4πtk,so
F·dr=170 −1
10zdz, and W=Z60
0170 −1
10zdz =10,020. Note that the functions
x(z),y(z) are irrelevant.
EXERCISE SET 17.3
1. ∂x/∂y =0=∂y/∂x, conservative so ∂φ/∂x =xand ∂φ/∂y =y,φ=x2/2+k(y), k0(y)=y,
k(y)=y
2
/2+K,φ=x
2
/2+y
2
/2+K
2. ∂(3y2)/∂y =6y=∂(6xy)/∂x, conservative so ∂φ/∂x =3y
2and ∂φ/∂y =6xy,
φ=3xy2+k(y), 6xy +k0(y)=6xy,k0(y)=0,k(y)=K,φ=3xy2+K
3. ∂(x2y)/∂y =x2and ∂(5xy2)/∂x =5y
2
, not conservative
4. ∂(excos y)/∂y =−exsin y=∂(−exsin y)/∂x, conservative so ∂φ/∂x =excos yand
∂φ/∂y =−exsin y,φ=excos y+k(y), −exsin y+k0(y)=−e
xsin y,
k0(y)=0,k(y)=K,φ=e
xcos y+K
5. ∂(cos y+ycos x)/∂y =−sin y+ cos x=∂(sin x−xsin y)/∂x, conservative so
∂φ/∂x = cos y+ycos xand ∂φ/∂y = sin x−xsin y,φ=xcos y+ysin x+k(y),
−xsin y+ sin x+k0(y) = sin x−xsin y,k0(y)=0,k(y)=K,φ=xcos y+ysin x+K
6. ∂(xln y)/∂y =x/y and ∂(yln x)/∂x =y/x, not conservative
7. (a) ∂(y2)/∂y =2y=∂(2xy)/∂x, independent of path
(b) C:x=−1+2t,y=2+t,0≤t≤1; Z1
0
(4+14t+6t
2
)dt =13
(c) ∂φ/∂x =y2and ∂φ/∂y =2xy,φ=xy2+k(y), 2xy +k0(y)=2xy,k0(y)=0,k(y)=K,
φ=xy2+K. Let K= 0 to get φ(1,3) −φ(−1,2)=9−(−4)=13
8. (a) ∂(ysin x)/∂y = sin x=∂(−cos x)/∂x, independent of path
(b) C1:x=πt,y=1−2t,0≤t≤1; Z1
0
(πsin πt −2πt sin πt + 2 cos πt)dt =0
(c) ∂φ/∂x =ysin xand ∂φ/∂y =−cos x,φ=−ycos x+k(y), −cos x+k0(y)=−cos x,
k0(y)=0,k(y)=K,φ=−ycos x+K. Let K= 0 to get φ(π, −1)−φ(0,1)=(−1)−(−1)=0
9. ∂(3y)/∂y =3=∂(3x)/∂x,φ=3xy,φ(4,0) −φ(1,2) = −6
10. ∂(exsin y)/∂y =excos y=∂(excos y)/∂x,φ=exsin y,φ(1,π/2) −φ(0,0) = e
11. ∂(2xey)/∂y =2xey=∂(x2ey)/∂x,φ=x2ey,φ(3,2) −φ(0,0)=9e
2

Exercise Set 17.3 616
12. ∂(3x−y+1)/∂y =−1=∂[−(x+4y+ 2)]/∂x,
φ=3x
2
/2−xy +x−2y2−2y,φ(0,1) −φ(−1,2)=11/2
13. ∂(2xy3)/∂y =6xy2=∂(3x2y2)/∂x,φ=x2y3,φ(−1,0) −φ(2,−2)=32
14. ∂(exln y−ey/x)/∂y =ex/y −ey/x =∂(ex/y −eyln x)/∂x,
φ=exln y−eyln x,φ(3,3) −φ(1,1)=0
15. φ=x2y2/2, W=φ(0,0) −φ(1,1) = −1/216. φ=x2y3,W =φ(4,1) −φ(−3,0)=16
17. φ=exy,W=φ(2,0) −φ(−1,1)=1−e
−1
18. φ=e−ysin x, W =φ(−π/2,0) −φ(π/2,1) = −1−1/e
19. ∂(ey+yex)/∂y =ey+ex=∂(xey+ex)/∂x so Fis conservative, φ(x, y)=xey+yexso
ZC
F·dr=φ(0,ln 2) −φ(1,0)=ln2−1
20. ∂(2xy)/∂y =2x=∂(x
2+ cos y)/∂x so Fis conservative, φ(x, y)=x
2
y+ sin yso
ZC
F·dr =φ(π, π/2) −φ(0,0) = π3/2+1
21. F ·dr=[(e
y+yex)i+(xey+ex)j]·[(π/2) cos(πt/2)i+(1/t)j]dt
=π
2cos(πt/2)(ey+yex)+(xey+ex)/tdt,
so ZC
F·dr=Z2
1π
2cos(πt/2) eln t+ (ln t)esin(πt/2)+sin(πt/2)eln t+esin(πt/2)dt ≈−0.307
22. F ·dr=2t2cos(t/3)+[t
2+ cos(tcos(t/3))](cos(t/3) −(t/3) sin(t/3))dt,so
ZC
F·dr=Zπ
02t
2cos(t/3)+[t
2+ cos(tcos(t/3))](cos(t/3) −(t/3) sin(t/3))dt ≈16.503
23. No; a closed loop can be found whose tangent everywhere makes an angle <πwith the vector
field, so the line integral ZC
F·dr>0, and by Theorem 17.3.2 the vector field is not conservative.
24. The vector field is constant, say F=ai+bj,soletφ(x, y)=ax +by and Fis conservative.
25. If Fis conservative, then F=∇φ=∂φ
∂xi+∂φ
∂y j+∂φ
∂z kand hence f=∂φ
∂x,g =∂φ
∂y , and h=∂φ
∂z .
Thus ∂f
∂y =∂2φ
∂y∂x and ∂g
∂x =∂2φ
∂x∂y,∂f
∂z =∂2φ
∂z∂x and ∂h
∂x =∂2φ
∂x∂z ,∂g
∂z =∂2φ
∂z∂y and ∂h
∂y =∂2φ
∂y∂z.
The result follows from the equality of mixed second partial derivatives.
26. Let f(x, y, z)=yz, g(x, y, z)=xz, h(x, y, z)=yx2, then ∂f/∂z =y, ∂h/∂x =2xy 6=∂f/∂z,thus
by Exercise 25, F=fi+gj+hkis not conservative, and by Theorem 17.3.2, ZC
yz dx+xz dy+yx2dz
is not independent of the path.

617 Chapter 17
27. ∂
∂y(h(x)[xsin y+ycos y]) = h(x)[xcos y−ysin y+ cos y]
∂
∂x(h(x)[xcos y−ysin y]) = h(x) cos y+h0(x)[xcos y−ysin y],
equate these two partial derivatives to get (xcos y−ysin y)(h0(x)−h(x)) = 0 which holds for all
xand yif h0(x)=h(x), h(x)=Cexwhere Cis an arbitrary constant.
28. (a) ∂
∂y
cx
(x2+y2)3/2=−3cxy
(x2+y2)−5/2=∂
∂x
cy
(x2+y2)3/2when (x, y)6=(0,0),
so by Theorem 17.3.3, Fis conservative. Set ∂φ/∂x =cx/(x2+y2)−3/2,
then φ(x, y)=−c(x
2+y
2
)
−1/2+k(y), ∂φ/∂y =cy/(x2+y2)−3/2+k0(y), so k0(y)=0.
Thus φ(x, y)=−c
(x
2+y
2
)
1/2is a potential function.
(b) curl F=0is similar to part (a), so Fis conservative. Let
φ(x, y, z)=Zcx
(x2+y2+z2)3/2dx =−c(x2+y2+z2)−1/2+k(y, z). As in part (a),
∂k/∂y =∂k/∂z =0,soφ(x, y, z)=−c/(x2+y2+z2)1/2is a potential function for F.
29. (a) See Exercise 28, c=1;W=ZQ
P
F·dr=φ(3,2,1) −φ(1,1,2) = −1
√14 +1
√6
(b) Cbegins at P(1,1,2) and ends at Q(3,2,1) so the answer is again W=−1
√14 +1
√6.
(c) Cbegins at, say, (3,0) and ends at the same point so W=0.
30. (a) F ·dr=ydx
dt −xdy
dt dt for points on the circle x2+y2=1,so
C
1:x= cos t, y = sin t, 0≤t≤π, ZC1
F·dr=Zπ
0
(−sin2t−cos2t)dt =−π
C2:x= cos t, y =−sin t, 0≤t≤π, ZC2
F·dr=Zπ
0
(sin2t+ cos2t)dt =π
(b) ∂f
∂y =x2−y2
(x2+y2)2,∂g
∂x =−y2−x2
(x2+y2)2=∂f
∂y
(c) The circle about the origin of radius 1, which is formed by traversing C1and then traversing
C2in the reverse direction, does not lie in an open simply connected region inside which F
is continuous, since Fis not defined at the origin, nor can it be defined there in such a way
as to make the resulting function continuous there.
31. If Cis composed of smooth curves C1,C
2,...,C
nand curve Ciextends from (xi−1,y
i−1)to(x
i
,y
i)
then ZC
F·dr=
n
X
i=1 ZCi
F·dr=
n
X
i=1
[φ(xi,y
i)−φ(x
i−1,y
i−1)] = φ(xn,y
n)−φ(x
0,y
0)
where (x0,y
0) and (xn,y
n) are the endpoints of C.
32. ZC1
F·dr+Z−C2
F·dr= 0, but Z−C2
F·dr=−ZC2
F·drso ZC1
F·dr=ZC2
F·dr,thus
Z
C
F·dris independent of path.

Exercise Set 17.4 618
33. Let C1be an arbitrary piecewise smooth curve from (a, b)toapoint(x, y1) in the disk, and C2
the vertical line segment from (x, y1)to(x, y). Then
φ(x, y)=ZC
1
F·dr+ZC
2
F·dr=Z(x,y1)
(a,b)
F·dr+ZC2
F·dr.
The first term does not depend on y;
hence ∂φ
∂y =∂
∂y ZC2
F·dr=∂
∂y ZC2
f(x, y)dx +g(x, y)dy.
However, the line integral with respect to xis zero along C2,so∂φ
∂y =∂
∂y ZC2
g(x, y)dy.
Express C2as x=x, y =twhere tvaries from y1to y, then ∂φ
∂y =∂
∂y Zy
y1
g(x, t)dt =g(x, y).
EXERCISE SET 17.4
1. ZZ
R
(2x−2y)dA =Z1
0Z1
0
(2x−2y)dy dx = 0; for the line integral, on x=0,y
2dx =0,x
2dy =0;
on y=0,y
2dx =x2dy =0;onx=1,y
2dx +x2dy =dy; and on y=1,y
2dx +x2dy =dx,
hence I
C
y2dx +x2dy =Z1
0
dy +Z0
1
dx =1−1=0
2. ZZ
R
(1 −1)dA = 0; for the line integral let x= cos t, y = sin t,
I
C
ydx+xdy =Z2π
0
(−sin2t+ cos2t)dt =0
3. Z4
−2Z2
1
(2y−3x)dy dx =0 4. Z2π
0Z3
0
(1+2rsin θ)rdrdθ =9π
5. Zπ/2
0Zπ/2
0
(−ycos x+xsin y)dy dx =0 6. ZZ
R
(sec2x−tan2x)dA =ZZ
R
dA =π
7. ZZ
R
[1 −(−1)]dA =2ZZ
R
dA =8π8. Z1
0Zx
x2
(2x−2y)dy dx =1/30
9. ZZ
R−y
1+y−1
1+ydA =−ZZ
R
dA =−4
10. Zπ/2
0Z4
0
(−r2)rdrdθ =−32π
11. ZZ
R−y2
1+y
2−1
1+y
2dA =−ZZ
R
dA =−1

619 Chapter 17
12. ZZ
R
(cos xcos y−cos xcos y)dA =0 13. Z1
0Z√x
x2
(y2−x2)dy dx =0
15. (a) C:x= cos t, y = sin t, 0≤t≤2π;
IC
=Z2π
0esin t(−sin t) + sin tcos tecos tdt ≈−3.550999378;
ZZ
R∂
∂x(yex)−∂
∂yeydA =ZZ
R
[yex−ey]dA
=Z2π
0Z1
0rsin θercos θ−ersin θrdrdθ≈−3.550999378
(b) C1:x=t, y =t2,0≤t≤1; Z
C1
[eydx +yexdy]=Z1
0he
t
2+2t
3
e
t
idt ≈2.589524432
C2:x=t2,y =t, 0≤t≤1; Z
C2
[eydx +yexdy]=Z1
0h2tet+tet2idt =e+3
2≈2.859140914
Z
C1
−Z
C2
≈−0.269616482; ZZ
R
=Z1
0Z√x
x2
[yex−ey]dy dx ≈−0.269616482
16. (a) IC
xdy =Z2π
0
ab cos2tdt=πab (b) IC−ydx=Z2π
0
ab sin2tdt=πab
17. A=1
2IC−ydx+xdy=1
2Z2π
0
(3a2sin4φcos2φ+3a
2cos4φsin2φ)dφ
=3
2a2Z2π
0
sin2φcos2φdφ=3
8a
2Z2π
0
sin22φdφ=3πa2/8
18. C1:(0,0) to (a, 0); x=at, y =0,0≤t≤1
C
2:(a, 0) to (0,b); x=a−at, y =bt, 0≤t≤1
C3:(0,b)to(0,0); x=0,y=b−bt, 0≤t≤1
A=IC
xdy =Z1
0
(0)dt +Z1
0
ab(1 −t)dt +Z1
0
(0)dt =1
2ab
19. C1:(0,0) to (a, 0); x=at,y=0,0≤t≤1
C
2:(a, 0) to (acos t0,bsin t0); x=acos t,y=bsin t,0≤t≤t
0
C
3:(acos t0,bsin t0)to(0,0); x=−a(cos t0)t,y=−b(sin t0)t,−1≤t≤0
A=1
2IC−ydx+xdy =1
2Z1
0
(0) dt +1
2Zt0
0
ab dt +1
2Z0
−1
(0) dt =1
2ab t0
20. C1:(0,0) to (a, 0); x=at,y=0,0≤t≤1
C
2:(a, 0) to (acosh t0,bsinh t0); x=acosh t,y=bsinh t,0≤t≤t
0
C
3:(acosh t0,bsinh t0)to(0,0); x=−a(cosh t0)t,y=−b(sinh t0)t,−1≤t≤0
A=1
2IC−ydx+xdy =1
2Z1
0
(0) dt +1
2Zt0
0
ab dt +1
2Z0
−1
(0) dt =1
2ab t0
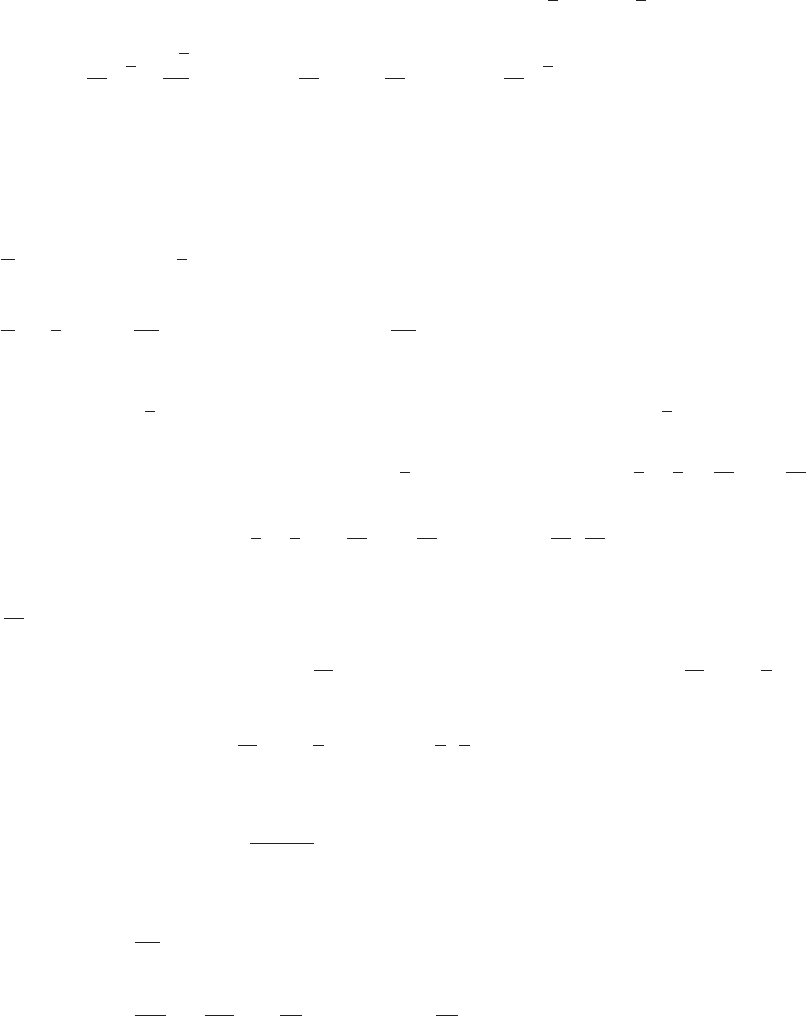
Exercise Set 17.4 620
21. W=ZZ
R
ydA=Zπ
0Z5
0
r
2sin θdrdθ= 250/3
22. We cannot apply Green’s Theorem on the region enclosed by the closed curve C, since Fdoes not
have first order partial derivatives at the origin. However, the curve C, consisting of
y=x3
0/4,x
0≤x≤2; x=2,x
0≤y≤2; and y=x3/4,x
0≤x≤2 encloses a region Rin which
Green’s Theorem does hold, and
W=I
C
F·dr= lim
→0+I
C
F·dr= lim
→0+ZZ
R
∇·FdA =Z2
x0Zx3/4
x3
0/41
2x−1/2−1
2y−1/2dy dx
= lim
→0+ −18
35√2−√2
4x3
0+x3/2
0+3
14x7/2
0−3
10x5/2
0!=−18
35√2
23. IC
ydx−xdy =ZZ
R
(−2)dA =−2Z2π
0Za(1+cos θ)
0
rdrdθ=−3πa2
24. ¯x=1
AZZ
R
xdA, but IC
1
2x2dy =ZZ
R
xdA from Green’s Theorem so
¯x=1
AIC
1
2x2dy =1
2AIC
x2dy. Similarly, ¯y=−1
2AIC
y2dx.
25. A=Z1
0Zx
x3
dy dx =1
4;C1:x=t, y =t3,0≤t≤1,ZC1
x2dy =Z1
0
t2(3t2)dt =3
5
C2:x=t, y =t, 0≤t≤1; ZC2
x2dy =Z1
0
t2dt =1
3,IC
x2dy =ZC1−ZC2
=3
5−1
3=4
15,¯x=8
15
ZC
y2dx =Z1
0
t6dt −Z1
0
t2dt =1
7−1
3=−4
21,¯y=8
21,centroid 8
15,8
21
26. A=a2
2;C1:x=t, y =0,0≤t≤a, C2:x=a−t, y =t, 0≤t≤a;C3:x=0,y =a−t, 0≤t≤a;
Z
C1
x2dy =0,Z
C
2
x
2dy =Za
0
(a−t)2dt =a3
3,Z
C3
x2dy =0,I
C
x
2dy =Z
C1
+Z
C2
+Z
C3
=a3
3,¯x=a
3;
Z
C
y2dx =0−Za
0
t
2dt +0=−a
3
3,¯y=a
3,centroid a
3,a
3
27. ¯x= 0 from the symmetry of the region,
C1:(a, 0) to (−a, 0) along y=√a2−x2;x=acos t,y=asin t,0≤t≤π
C
2:(−a, 0) to (a, 0); x=t,y=0,−a≤t≤a
A=πa2/2,¯y=−1
2AZπ
0−a3sin3tdt+Za
−a
(0)dt
=−1
πa2−4a3
3=4a
3π; centroid 0,4a
3π
621 Chapter 17
28. A=ab
2;C1:x=t, y =0,0≤t≤a, C2:x=a, y =t, 0≤t≤b;
C3:x=a−t, y =b−bt/a, 0≤t≤a;
ZC1
x2dy =0,ZC
2
x
2dy =Zb
0
a2dt =ba2,ZC3
x2dy =Za
0
(a−t)2(−b/a)dt =−ba2
3,
IC
x2dy =ZC1
+ZC2
+ZC3
=2ba2
3,¯x=2a
3;
ZC
y2dx =0+0−Za
0
b
2a−t
adt =−ab2
3,¯y=b
3,centroid 2a
3,b
3
29. From Green’s Theorem, the given integral equals ZZ
R
(1−x2−y2)dA where Ris the region enclosed
by C. The value of this integral is maximum if the integration extends over the largest region for
which the integrand 1 −x2−y2is nonnegative so we want 1 −x2−y2≥0, x2+y2≤1. The
largest region is that bounded by the circle x2+y2= 1 which is the desired curve C.
30. (a) C:x=a+(c−a)t,y=b+(d−b)t,0≤t≤1
ZC−ydx+xdy =Z1
0
(ad −bc)dt =ad −bc
(b) Let C1,C2, and C3be the line segments from (x1,y
1)to(x
2
,y
2), (x2,y
2)to(x
3
,y
3), and
(x3,y
3)to(x
1
,y
1), then if Cis the entire boundary consisting of C1,C
2,and C3
A=1
2ZC−ydx+xdy =1
2
3
X
i=1 ZCi−ydx+xdy
=1
2[(x1y2−x2y1)+(x
2
y
3−x
3
y
2
)+(x
3
y
1−x
1
y
3
)]
(c) A=1
2[(x1y2−x2y1)+(x
2
y
3−x
3
y
2
)+···+(x
n
y
1−x
1
y
n
)]
(d) A=1
2[(0 −0)+(6+8)+(0+2)+(0−0)]=8
31. ZC
F·dr=ZC
(x2+y)dx +(4x−cos y)dy =3ZZ
R
dA = 3(25 −2)=69
32. ZC
F·dr=ZC
(e−x+3y)dx +xdy =−2ZZ
R
dA =−2[π(4)2−π(2)2]=−24π
EXERCISE SET 17.5
1. Ris the annular region between x2+y2= 1 and x2+y2=4;
ZZ
σ
z2dS =ZZ
R
(x2+y2)sx2
x2+y2+y2
x2+y2+1dA
=√2ZZ
R
(x2+y2)dA =√2Z2π
0Z2
1
r3dr dθ =15
2π√2.

Exercise Set 17.5 622
2. z=1−x−y,Ris the triangular region enclosed by x+y=1,x= 0 and y=0;
ZZ
σ
xy dS =ZZ
R
xy√3dA =√3Z1
0Z1−x
0
xy dy dx =√3
24 .
3. Let r(u, v) = cos ui+vj+ sin uk,0≤u≤π, 0≤v≤1. Then ru=−sin ui+ cos uk,rv=j,
ru×rv=−cos ui+ sin uk,kru×rvk=1,ZZσ
x2ydS =Z1
0Zπ
0
vcos2ududv =π/4
4. z=p4−x2−y2,Ris the circular region enclosed by x2+y2=3;
ZZ
σ
(x2+y2)zdS=ZZ
R
(x2+y2)p4−x2−y2sx2
4−x2−y2+y2
4−x2−y2+1dA
=ZZ
R
2(x2+y2)dA =2Z2π
0Z√
3
0
r
3
dr dθ =9π.
5. If we use the projection of σonto the xz-plane then y=1−xand Ris the rectangular region in
the xz-plane enclosed by x=0,x=1,z= 0 and z=1;
ZZ
σ
(x−y−z)dS =ZZ
R
(2x−1−z)√2dA =√2Z1
0Z1
0
(2x−1−z)dz dx =−√2/2
6. Ris the triangular region enclosed by 2x+3y=6,x= 0, and y=0;
ZZ
σ
(x+y)dS =ZZ
R
(x+y)√14 dA =√14 Z3
0Z(6−2x)/3
0
(x+y)dy dx =5
√
14.
7. There are six surfaces, parametrized by projecting onto planes:
σ1:z=0;0≤x≤1, 0 ≤y≤1 (onto xy-plane), σ2:x=0;0≤y≤1, 0 ≤z≤1 (onto yz-plane),
σ3:y=0;0≤x≤1, 0 ≤z≤1 (onto xz-plane), σ4:z=1;0≤x≤1, 0 ≤y≤1 (onto xy-plane),
σ5:x=1;0≤y≤1, 0 ≤z≤1 (onto yz-plane), σ6:y=1;0≤x≤1, 0 ≤z≤1 (onto xz-plane).
By symmetry the integrals over σ1,σ
2and σ3are equal, as are those over σ4,σ
5and σ6, and
ZZ
σ1
(x+y+z)dS =Z1
0Z1
0
(x+y)dx dy =1; ZZ
σ4
(x+y+z)dS =Z1
0Z1
0
(x+y+1)dx dy =2,
thus, ZZ
σ
(x+y+z)dS =3·1+3·2=9.
8. Let r(φ, θ) = sinφcos θi+ sin φsin θj+ cos φk,
0≤θ≤2π, 0≤φ≤π/2; krφ×rθk=p1−cos2φ= sin φ,
ZZ
σ
(1+p1−x2−y2)dS =Z2π
0Zπ/2
0
(1+q1−sin2φ) sin φdφdθ
=2πZπ/2
0
(1 + cos φ) sin φdφ=3π
623 Chapter 17
9. Ris the circular region enclosed by x2+y2=1;
ZZ
σpx2+y2+z2dS =ZZ
Rp2(x2+y2)sx2
x2+y2+y2
x2+y2+1dA
= lim
r0→0+2ZZ
R0px2+y2dA
where R0is the annular region enclosed by x2+y2= 1 and x2+y2=r2
0with r0slightly larger
than 0 because sx2
x2+y2+y2
x2+y2+ 1 is not defined for x2+y2=0,so
ZZ
σpx2+y2+z2dS = lim
r0→0+2Z2π
0Z1
r0
r2dr dθ = lim
r0→0+
4π
3(1 −r3
0)=4π
3.
10. Let r(φ, θ)=asin φcos θi+asin φsin θj+acos φk,
0≤θ≤2π, 0≤φ≤π/2; krφ×rθk=a2p1−cos2φ,
ZZ
σ
f(x, y, z)=a
2Z2π
0Zπ
0
a
2sin2φp1−cos2φdφdθ =8
3πa4
11. (a) √29
16 Z6
0Z(12−2x)/3
0
xy(12 −2x−3y)dy dx
(b) √29
4Z3
0Z(12−4z)/3
0
yz(12 −3y−4z)dy dz
(c) √29
9Z3
0Z6−2z
0
xz(12 −2x−4z)dx dz
12. (a) aZa
0Z√a2−x2
0
xdydx (b) aZa
0Z√a2−z2
0
zdydz
(c) aZa
0Z√a2−z2
0
xz
√a2−x2−z2dx dz
13. 18√29/514. a4/3
15. Z4
0Z2
1
y3zp4y2+1dy dz;1
2Z4
0Z4
1
xz√1+4xdxdz
16. aZ9
0Za/√2
a/√5
x2y
pa2−y2dy dx,aZ2a/√5
a/√2Z9
0
x2dx dz 17. 391√17/15 −5√5/3
18. The region R:3x
2+2y
2= 5 is symmetric in y. The integrand is
x2yz dS =x2y(5 −3x2−2y2)p1+36x
2+16y
2dy dx, which is odd in y, henceZZZ
σ
x2yz dS =0.

Exercise Set 17.5 624
19. z=√4−x2,∂z
∂x =−x
√4−x2,∂z
∂y =0;
ZZ
σ
δ0dS =δ0ZZ
Rrx2
4−x2+1dA =2δ
0Z4
0Z1
0
1
√
4−x
2dx dy =4
3πδ0.
20. z=1
2(x2+y2), Ris the circular region enclosed by x2+y2=8;
ZZ
σ
δ0dS =δ0ZZ
Rpx2+y2+1dA =δ0Z2π
0Z√8
0pr2+1rdrdθ =52
3πδ0.
21. z=4−y
2
,Ris the rectangular region enclosed by x=0,x=3,y= 0 and y=3;
ZZ
σ
ydS =ZZ
R
yp4y2+1dA =Z3
0Z3
0
yp4y2+1dy dx =1
4(37√37 −1).
22. Ris the annular region enclosed by x2+y2= 1 and x2+y2= 16;
ZZ
σ
x2zdS=ZZ
R
x2px2+y2sx2
x2+y2+y2
x2+y2+1dA
=√2ZZ
R
x2px2+y2dA =√2Z2π
0Z4
1
r4cos2θdrdθ=1023√2
5π.
23. M=ZZ
σ
δ(x, y, z)dS =ZZ
σ
δ0dS =δ0ZZ
σ
dS =δ0S
24. δ(x, y, z)=|z|; use z=pa2−x2−y2, let Rbe the circular region enclosed by x2+y2=a2, and
σthe hemisphere above R. By the symmetry of both the surface and the density function with
respect to the xy-plane we have
M=2ZZ
σ
zdS =2ZZ
Rpa2−x2−y2sx2
a2−x2−y2+y2
a2−x2−y2+1dA = lim
r0→a−2aZZ
Rr
0
dA
where Rr0is the circular region with radius r0that is slightly less than a. But ZZ
Rr
0
dA is simply
the area of the circle with radius r0so M= lim
r0→a−2a(πr2
0)=2πa3.
25. By symmetry ¯x=¯y=0.
ZZ
σ
dS =ZZ
Rpx2+y2+1dA =Z2π
0Z√8
0pr2+1rdrdθ =52π
3,
ZZ
σ
zdS=ZZ
R
zpx2+y2+1dA =1
2ZZ
R
(x2+y2)px2+y2+1dA
=1
2Z2π
0Z√8
0
r3pr2+1dr dθ =596π
15
so ¯z=596π/15
52π/3=149
65 . The centroid is (¯x, ¯y, ¯z)=(0,0,149/65).
625 Chapter 17
26. By symmetry ¯x=¯y=0.
ZZ
σ
dS =ZZ
R
2
p4−x2−y2dA =2Z2π
0Z√
3
0
r
√
4−r
2dr dθ =4π,
ZZ
σ
zdS =ZZ
R
2dA = (2)(area of circle of radius √3)=6π
so ¯z=6π
4π=3
2. The centroid is (¯x, ¯y, ¯z)=(0,0,3/2).
27. ∂r/∂u = cos vi+ sin vj+3k,∂r/∂v =−usin vi+ucos vj,k∂r/∂u ×∂r/∂vk=√10u;
3√10 ZZ
R
u4sin vcos vdA=3
√
10 Zπ/2
0Z2
1
u4sin vcos vdudv=93/
√
10
28. ∂r/∂u =j,∂r/∂v =−2 sin vi+ 2 cos vk,k∂r/∂u ×∂r/∂vk=2;
8ZZ
R
1
udA =8Z2π
0Z3
1
1
u
du dv =16πln 3
29. ∂r/∂u = cos vi+ sin vj+2uk,∂r/∂v =−usin vi+ucos vj,k∂r/∂u ×∂r/∂vk=u√4u2+1;
ZZ
R
udA=Zπ
0Zsin v
0
ududv =π/4
30. ∂r/∂u = 2 cos ucos vi+ 2 cos usin vj−2 sin uk,∂r/∂v =−2 sin usin vi+ 2 sin ucos vj;
k∂r/∂u ×∂r/∂vk= 4 sin u;
4ZZ
R
e−2 cos usin udA=4Z2π
0Zπ/2
0
e−2 cos usin ududv =4π(1 −e−2)
31. ∂z/∂x =−2xe−x2−y2,∂z/∂y =−2ye−x2−y2,
(∂z/∂x)2+(∂z/∂y)2+1=4(x
2+y
2
)e
−2(x2+y2)+ 1; use polar coordinates to get
M=Z2π
0Z3
0
r2p4r2e−2r2+1dr dθ ≈57.895751
32. (b) A=ZZ
σ
dS =Z2π
0Z1
−1
1
2p40ucos(v/2)+u2+4u
2cos2(v/2) + 100du dv ≈62.93768644;
¯x≈0.01663836266; ¯y=¯z= 0 by symmetry
EXERCISE SET 17.6
1. (a) zero (b) zero (c) positive
(d) negative (e) zero (f) zero
2. (a) positive (b) zero (c) zero
(d) zero (e) negative (f) zero

Exercise Set 17.6 626
3. (a) positive (b) zero (c) positive
(d) zero (e) positive (f) zero
4. 0; the flux is zero on the faces y=0,1 and z=0,1; it is 1 on x= 1 and −1onx=0
5. (a) n =−cos vi−sin vj (b) inward, by inspection
6. (a) −rcos θi−rsin θj+rk (b) inward, by inspection
7. n =−zxi−zyj+k,ZZ
R
F·ndS =ZZ
R
(2x2+2y
2+ 2(1 −x2−y2)) dS =Z2π
0Z1
0
2rdrdθ=2π
8. With z=1−x−y,Ris the triangular region enclosed by x+y=1,x= 0 and y= 0; use upward
normals to get
ZZ
σ
F·ndS =2ZZ
R
(x+y+z)dA =2ZZ
R
dA = (2)(area of R)=1.
9. Ris the annular region enclosed by x2+y2= 1 and x2+y2=4;
ZZ
σ
F·ndS =ZZ
R −x2
px2+y2−y2
px2+y2+2z
!dA
=ZZ
Rpx2+y2dA =Z2π
0Z2
1
r2dr dθ =14π
3.
10. Ris the circular region enclosed by x2+y2=4;
ZZ
σ
F·ndS =ZZ
R
(2y2−1)dA =Z2π
0Z2
0
(2r2sin2θ−1)rdrdθ=4π.
11. Ris the circular region enclosed by x2+y2−y=0;ZZ
σ
F·ndS =ZZ
R
(−x)dA = 0 since the
region Ris symmetric across the y-axis.
12. With z=1
2(6 −6x−3y), Ris the triangular region enclosed by 2x+y=2,x= 0, and y=0;
ZZ
σ
F·ndS =ZZ
R3x2+3
2yx +zxdA =3ZZ
R
xdA=3Z1
0Z2−2x
0
xdydx=1.
13. ∂r/∂u = cos vi+ sin vj−2uk,∂r/∂v =−usin vi+ucos vj,
∂r/∂u ×∂r/∂v =2u
2cos vi+2u
2sin vj+uk;
ZZ
R
(2u3+u)dA =Z2π
0Z2
1
(2u3+u)du dv =18π
14. ∂r/∂u =k,∂r/∂v =−2 sin vi+ cos vj,∂r/∂u ×∂r/∂v =−cos vi−2 sin vj;
ZZ
R
(2 sin2v−e−sin vcos v)dA =Z2π
0Z5
0
(2 sin2v−e−sin vcos v)du dv =10π

627 Chapter 17
15. ∂r/∂u = cos vi+ sin vj+2k,∂r/∂v =−usin vi+ucos vj,
∂r/∂u ×∂r/∂v =−2ucos vi−2usin vj+uk;
ZZ
R
u2dA =Zπ
0Zsin v
0
u2du dv =4/9
16. ∂r/∂u = 2 cos ucos vi+ 2 cos usin vj−2 sin uk,∂r/∂v =−2 sin usin vi+ 2 sin ucos vj;
∂r/∂u ×∂r/∂v = 4 sin2ucos vi+ 4 sin2usin vj+ 4 sin ucos uk;
ZZ
R
8 sin udA=8Z2π
0Zπ/3
0
sin ududv =8π
17. In each part, divide σinto the six surfaces
σ1:x=−1 with |y|≤1, |z|≤1, and n=−i,σ2:x= 1 with |y|≤1, |z|≤1, and n=i,
σ3:y=−1 with |x|≤1, |z|≤1, and n=−j,σ4:y= 1 with |x|≤1, |z|≤1, and n=j,
σ5:z=−1 with |x|≤1, |y|≤1, and n=−k,σ6:z= 1 with |x|≤1, |y|≤1, and n=k,
(a) ZZ
σ1
F·ndS =ZZ
σ1
dS =4,ZZ
σ2
F·ndS =ZZ
σ2
dS = 4, and ZZ
σi
F·ndS = 0 for
i=3,4,5,6soZZ
σ
F·ndS =4+4+0+0+0+0=8.
(b) ZZ
σ1
F·ndS =ZZ
σ1
dS = 4, similarly ZZ
σi
F·ndS = 4 for i=2,3,4,5,6so
ZZ
σ
F·ndS =4+4+4+4+4+4=24.
(c) ZZ
σ1
F·ndS =−ZZ
σ1
dS =−4, ZZ
σ2
F·ndS = 4, similarly ZZ
σi
F·ndS =−4 for i=3,5
and ZZ
σi
F·ndS = 4 for i=4,6soZZ
σ
F·ndS =−4+4−4+4−4+4=0.
18. Decompose σinto a top σ1(the disk) and a bottom σ2(the portion of the paraboloid). Then
n1=k,ZZ
σ1
F·n1dS =−ZZ
σ1
ydS =−Z2π
0Z1
0
r
2sin θdrdθ=0,
n
2=(2xi+2yj−k)/
p1+4x
2+4y
2
,ZZ
σ2
F·n2dS =ZZ
σ2
y(2x2+2y
2+1)
p1+4x
2+4y
2dS =0,
because the surface σ2is symmetric with respect to the xy-plane and the integrand is an odd
function of y. Thus the flux is 0.
19. Ris the circular region enclosed by x2+y2=1;
ZZ
σ
F·ndS =ZZ
R x
px2+y2+y
px2+y2−1!dA =ZZ
R
x+y−px2+y2
px2+y2dA
= lim
r0→0+Z2π
0Z1
r0
(rcos θ+rsin θ−r)dr dθ = lim
r0→0+π(r2
0−1) = −π.
Exercise Set 17.6 628
20. Let r= cos vi+uj+ sin vk,−2≤u≤1,0≤v≤2π;ru×rv= cos vi+ sin vk,
ZZ
σ
F·ndS =ZZ
R
(cos2v+ sin2v)dA = area of R=3·2π=6π
21. (a) ZZ
σ
F·ndS =ZZ
R
F·i−∂x
∂yj−∂x
∂z kdA,ifσis oriented by front normals, and
ZZ
σ
F·ndS =ZZ
R
F·−i+∂x
∂yj+∂x
∂z kdA,ifσis oriented by back normals,
where Ris the projection of σonto the yz-plane.
(b) Ris the semicircular region in the yz-plane enclosed by z=p1−y2and z=0;
ZZ
σ
F·ndS =ZZ
R
(−y−2yz +16z)dA =Z1
−1Z√1−y2
0
(−y−2yz +16z)dz dy =32
3.
22. (a) ZZ
R
F·∂y
∂xi−j+∂y
∂zkdA,σoriented by right normals,
and ZZ
R
F·−∂y
∂xi+j−∂y
∂zkdA,σoriented by left normals,
where Ris the projection of σonto the xz-plane.
(b) Ris the semicircular region in the xz-plane enclosed by z=√1−x2and z=0;
ZZ
σ
F·ndS =ZZ
R
(2x2−(x2+z2)+z
2
)dA =Z1
−1Z√1−x2
0
(x2+z2)dz dx =π
4.
23. (a) On the sphere, krk=aso F=akrand F·n=akr·(r/a)=a
k−1
krk
2=a
k−1
a
2=a
k+1,
hence ZZ
σ
F·ndS =ak+1 ZZ
σ
dS =ak+1(4πa2)=4πak+3.
(b) If k=−3, then ZZ
σ
F·ndS =4π.
24. Let r= sin ucos vi+ sin usin vj+ cos uk,ru×rv= sin2ucos vi+ sin2usin vj+ sin ucos uk,
F·(ru×rv)=a
2sin3ucos2v+1
9sin3usin2v+asin ucos3u,
ZZ
σ
F·ndS =Z2π
0Zπ
0
(a2sin3ucos2v+1
9sin3usin2v+asin ucos3u)du dv
=a2Zπ
0
sin3uduZ2π
0
cos2vdv+1
aZπ
0
sin3udu
+Z2π
0
sin2vdv+2πa Zπ
0
sin ucos3udu
=4π
3a
2+1
a=10ifa≈−1.722730,0.459525,1.263205

629 Chapter 17
EXERCISE SET 17.7
1. σ1:x=0,F·n=−x=0,ZZ
σ1
(0)dA =0 σ
2:x=1,F·n=x=1,ZZ
σ2
(1)dA =1
σ
3:y=0,F·n=−y=0,ZZ
σ3
(0)dA =0 σ
4:y=1,F·n=y=1,ZZ
σ4
(1)dA =1
σ
5:z=0,F·n=−z=0,ZZ
σ5
(0)dA =0 σ
6:z=1,F·n=z=1,ZZ
σ6
(1)dA =1
ZZσ
F·n=3; ZZZ
G
div FdV =ZZZ
G
3dV =3
2. For any point r=xi+yj+zkon σlet n=xi+yj+zk; then F·n=x2+y2+z2=1,so
ZZ
σ
F·ndS =ZZ
σ
dS =4π; also ZZZ
G
div FdV =ZZZ
G
3dV = 3(4π/3)=4π
3. σ1:z=1,n=k,F·n=z
2=1,ZZ
σ1
(1)dS =π,
σ2:n=2xi+2yj−k,F·n=4x
2−4x
2
y
2−x
4−3y
4
,
ZZ
σ2
F·ndS =Z2π
0Z1
04r2cos2θ−4r4cos2θsin2θ−r4cos4θ−3r4sin4θrdrdθ=π
3;
ZZ
σ
=4π
3
ZZZ
G
div FdV =ZZZ
G
(2+z)dV =Z2π
0Z1
0Z1
r2
(2+z)dzrdrdθ =4π/3
4. σ1:x=0,F·n=−xy =0,ZZ
σ1
(0)dA =0 σ
2:x=2,F·n=xy =2y, ZZ
σ2
(2y)dA =8
σ
3:y=0,F·n=−yz =0,ZZ
σ3
(0)dA =0 σ
4:y=2,F·n=yz =2z,ZZ
σ4
(2z)dA =8
σ
5:z=0,F·n=−xz =0,ZZ
σ5
(0)dA =0 σ
6:z=2,F·n=xz =2x, ZZ
σ6
(2x)dA =8
ZZ
σ
F·n= 24; also ZZZ
G
div FdV =ZZZ
G
(y+z+x)dV =24
5. Gis the rectangular solid; ZZZ
G
div FdV =Z2
0Z1
0Z3
0
(2x−1) dx dy dz = 12.
6. Gis the spherical solid enclosed by σ;ZZZ
G
div FdV =ZZZ
G
0dV =0ZZZ
G
dV =0.

Exercise Set 17.7 630
7. Gis the cylindrical solid;
ZZZ
G
div FdV =3ZZZ
G
dV = (3)(volume of cylinder) = (3)[πa2(1)] = 3πa2.
8. Gis the solid bounded by z=1−x
2−y
2and the xy-plane;
ZZZ
G
div FdV =3ZZZ
G
dV =3Z2π
0Z1
0Z1−r
2
0
rdzdrdθ =3π
2.
9. Gis the cylindrical solid;
ZZZ
G
div FdV =3ZZZ
G
(x2+y2+z2)dV =3Z2π
0Z2
0Z3
0
(r
2+z
2
)rdzdrdθ= 180π.
10. Gis the tetrahedron; ZZZ
G
div FdV =ZZZ
G
xdV =Z1
0Z1−x
0Z1−x−y
0
xdzdydx=1
24.
11. Gis the hemispherical solid bounded by z=p4−x2−y2and the xy-plane;
ZZZ
G
div FdV =3ZZZ
G
(x2+y2+z2)dV =3Z2π
0Zπ/2
0Z2
0
ρ4sin φdρdφdθ =192π
5.
12. Gis the hemispherical solid;
ZZZ
G
div FdV =5ZZZ
G
zdV =5Z2π
0Zπ/2
0Za
0
ρ3sin φcos φdρdφdθ =5πa4
4.
13. Gis the conical solid;
ZZZ
G
div FdV =2ZZZ
G
(x+y+z)dV =2Z2π
0Z1
0Z1
r
(rcos θ+rsin θ+z)rdzdrdθ=π
2.
14. Gis the solid bounded by z=2xand z=x2+y2;
ZZZ
G
div FdV =ZZZ
G
dV =2Zπ/2
0Z2 cos θ
0Z2rcos θ
r2
rdzdrdθ =π
2.
15. Gis the solid bounded by z=4−x
2
,y+z= 5, and the coordinate planes;
ZZZ
G
div FdV =4ZZZ
G
x2dV =4Z2
−2Z4−x
2
0Z5−z
0
x
2
dy dz dx =4608
35 .
16. ZZ
σ
F·ndS =ZZZ
G
div FdV =ZZZ
G
0dV =0;
since the vector field is constant, the same amount enters as leaves.
17. ZZ
σ
r·ndS =ZZZ
G
div rdV =3ZZZ
G
dV = 3vol(G)

631 Chapter 17
18. ZZ
σ
F·ndS =3[π(32)(5)] = 135π
19. ZZ
σ
curl F·ndS =ZZZ
G
div(curl F)dV =ZZZ
G
(0)dV =0
20. ZZ
σ∇f·ndS =ZZZ
G
div (∇f)dV =ZZZ
G
∇2fdV
21. ZZ
σ
(f∇g)·n=ZZZ
G
div (f∇g)dV =ZZZ
G
(f∇2g+∇f·∇g)dV by Exercise 29, Section 17.1.
22. ZZ
σ
(f∇g)·ndS =ZZZ
G
(f∇2g+∇f·∇g)dV by Exercise 29, Section 17.1;
ZZ
σ
(g∇f)·ndS =ZZZ
G
(g∇2f+∇g·∇f)dV by interchanging fand g;
subtract to obtain the result.
23. Let the normal n=n1i+n2j+n3k, then we have to show that
ZZ
σ
(fn1i+fn2j+fn3k)dS =ZZZ
G
(fxi+fyj+fzk)dV . We shall show that
ZZ
σ
fn1idS =ZZZ
G
fxidV , i.e. that ZZ
σ
fn1dS =ZZZ
G
fxdV ; the other parts will follow in a
similar manner. Let F(x, y, z)=f(x, y, z)i, then by the Divergence Theorem
ZZ
σ
fn1dS =ZZ
σ
F·ndS =ZZZ
G
∇·FdV =ZZZ
G
fxdV .
24. div r=c∂
∂x
x
(x2+y2+z2)3/2+∂
∂y
y
(x2+y2+z2)3/2+∂
∂z
z
(x2+y2+z2)3/2
=c(−2x2+y2+z2)+(−2y
2+x
2+z
2
)+(−2z
2+x
2+y
2
)
(x
2+y
2+z
2
)
5/2=0
25. (a) The flux through any cylinder whose axis is the z-axis is positive by inspection; by the
Divergence Theorem, this says that the divergence cannot be negative at the origin, else
the flux through a small enough cylinder would also be negative (impossible), hence the
divergence at the origin must be ≥0.
(b) Similar to Part (a), ≤0.
26. (a) F =xi+yj+zk, div F=3 (b) F =−xi−yj−zk, div F=−3
27. div F= 0; no sources or sinks.
28. div F=y−x; sources where y>x, sinks where y<x.
29. div F=3x
2+3y
2+3z
2
; sources at all points except the origin, no sinks.

Exercise Set 17.8 632
30. div F=3(x
2+y
2+z
2−1); sources outside the sphere x2+y2+z2= 1, sinks inside the sphere
x2+y2+z2=1.
31. Let σ1be the portion of the paraboloid z=1−x
2−y
2for z≥0, and σ2the portion of the plane
z= 0 for x2+y2≤1. Then
ZZ
σ1
F·ndS =ZZ
R
F·(2xi+2yj+k)dA
=Z1
−1Z√1−x2
−√1−x2
(2x[x2y−(1 −x2−y2)2]+2y(y
3−x)+(2x+2−3x
2−3y
2
)) dy dx
=3π/4;
z= 0 and n=−kon σ2so F·n=1−2x,ZZ
σ2
F·ndS =ZZ
σ2
(1 −2x)dS =π.Thus
ZZ
σ
F·ndS =3π/4+π=7π/4. But div F=2xy +3y
2+3so
ZZZ
G
div FdV =Z1
−1Z√1−x2
−√1−x2Z1−x2−y2
0
(2xy +3y
2+3)dz dy dx =7π/4.
EXERCISE SET 17.8
1. (a) The flow is independent of zand has no component in the direction of k, and so by inspection
the only nonzero component of the curl is in the direction of k. However both sides of (9)
are zero, as the flow is orthogonal to the curve Ca. Thus the curl is zero.
(b) Since the flow appears to be tangential to the curve Ca, it seems that the right hand side of
(9) is nonzero, and thus the curl is nonzero, and points in the positive z-direction.
2. (a) The only nonzero vector component of the vector field is in the direction of i, and it increases
with yand is independent of x. Thus the curl of Fis nonzero, and points in the negative
z-direction.
(b) By inspection the vector field is constant, and thus its curl is zero.
3. If σis oriented with upward normals then Cconsists of three parts parametrized as
C1:r(t)=(1−t)i+tjfor 0 ≤t≤1, C2:r(t)=(1−t)j+tkfor 0 ≤t≤1,
C3:r(t)=ti+(1−t)kfor 0 ≤t≤1.
ZC1
F·dr=ZC2
F·dr=ZC3
F·dr=Z1
0
(3t−1)dt =1
2so
IC
F·dr=1
2+1
2+1
2=3
2. curl F=i+j+k,z=1−x−y,Ris the triangular region in
the xy-plane enclosed by x+y=1,x= 0, and y=0;
ZZ
σ
(curl F)·ndS =3ZZ
R
dA = (3)(area of R) = (3) 1
2(1)(1)=3
2.

633 Chapter 17
4. If σis oriented with upward normals then Ccan be parametrized as r(t) = cos ti+ sin tj+kfor
0≤t≤2π.
IC
F·dr=Z2π
0
(sin2tcos t−cos2tsin t)dt =0;
curl F=0so ZZ
σ
(curl F)·ndS =ZZ
σ
0dS =0.
5. If σis oriented with upward normals then Ccan be parametrized as r(t)=acos ti+asin tjfor
0≤t≤2π.
IC
F·dr=Z2π
0
0dt = 0; curl F=0so ZZ
σ
(curl F)·ndS =ZZ
σ
0dS =0.
6. If σis oriented with upward normals then Ccan be parametrized as r(t)=3costi+ 3 sin tjfor
0≤t≤2π.
IC
F·dr=Z2π
0
(9 sin2t+ 9 cos2t)dt =9Z2π
0
dt =18π.
curl F=−2i+2j+2k,Ris the circular region in the xy-plane enclosed by x2+y2=9;
ZZ
σ
(curl F)·ndS =ZZ
R
(−4x+4y+2)dA =Z2π
0Z3
0
(−4rcos θ+4rsin θ+2)rdrdθ =18π.
7. Take σas the part of the plane z= 0 for x2+y2≤1 with n=k; curl F=−3y2i+2zj+2k,
ZZ
σ
(curl F)·ndS =2ZZ
σ
dS = (2)(area of circle) = (2)[π(1)2]=2π.
8. curl F=xi+(x−y)j+6xy2k;
ZZ
σ
(curl F)·ndS =ZZ
R
(x−y−6xy2)dA =Z1
0Z3
0
(x−y−6xy2)dy dx =−30.
9. Cis the boundary of Rand curl F=2i+3j+4k,so
IF·r=ZZR
curl F·ndS =ZZR
4dA = 4(area of R)=16π
10. curl F=−4i−6j+6yk,z=y/2 oriented with upward normals, Ris the triangular region in the
xy-plane enclosed by x+y=2,x= 0, and y=0;
ZZ
σ
(curl F)·ndS =ZZ
R
(3+6y)dA =Z2
0Z2−x
0
(3+6y)dy dx = 14.
11. curl F=xk, take σas part of the plane z=yoriented with upward normals, Ris the circular
region in the xy-plane enclosed by x2+y2−y=0;
ZZ
σ
(curl F)·ndS =ZZ
R
xdA=Zπ
0Zsin θ
0
r2cos θdrdθ=0.
12. curl F=−yi−zj−xk,z=1−x−yoriented with upward normals, Ris the triangular region in
the xy-plane enclosed by x+y=1,x= 0 and y=0;
ZZ
σ
(curl F)·ndS =ZZ
R
(−y−z−x)dA =−ZZ
R
dA =−1
2(1)(1) = −1
2.
Exercise Set 17.8 634
13. curl F=i+j+k, take σas the part of the plane z= 0 with x2+y2≤a2and n=k;
ZZ
σ
(curl F)·ndS =ZZ
σ
dS = area of circle = πa2.
14. curl F=i+j+k, take σas the part of the plane z=1/
√
2 with x2+y2≤1/2 and n=k.
ZZ
σ
(curl F)·ndS =ZZ
σ
dS = area of circle = π
2.
15. (a) Take σas the part of the plane 2x+y+2z= 2 in the first octant, oriented with downward
normals; curl F=−xi+(y−1)j−k,
IC
F·Tds =ZZ
σ
(curl F)·ndS
=ZZ
Rx−1
2y+3
2dA =Z1
0Z2−2x
0x−1
2y+3
2dy dx =3
2.
(b) At the origin curl F=−j−kand with n=k, curl F(0,0,0) ·n=(−j−k)·k=−1.
(c) The rotation of Fhas its maximum value at the origin about the unit vector in the same
direction as curl F(0,0,0) so n=−1
√2j−1
√2k.
16. (a) div(curl F)= ∂
∂x ∂h
∂y −∂g
∂z+∂
∂y ∂f
∂z −∂h
∂x+∂
∂z ∂g
∂x −∂f
∂y
=∂2h
∂x∂y −∂2g
∂x∂z +∂2f
∂y∂z −∂2h
∂y∂x +∂2g
∂z∂x −∂2f
∂z∂y =0,
assuming equality of mixed second partial derivatives
(b) By the Divergence Theorem
ZZ
σ
(curl F)·ndS =ZZZ
G
div(curl F)dV =ZZZ
G
0dV =0.
(c) The flux of the curl field through the boundary of a solid is zero.
17. Since I
C
E·rdr=ZZ
σ
curl E·ndS, it follows that ZZ
σ
curl E·ndS =−ZZ
σ
∂B
∂t
·ndS. This
relationship holds for any volume σ, hence curl E=−∂B
∂t .
18. Parametrize Cby x= cos t, y = sin t, 0≤t≤2π. But F=x2yi+(y
3−x)j+(2x−1)kalong C
so IC
F·dr=−5π/4. Since curl F=(−2z−2)j+(−1−x
2
)k,
ZZ
σ
(curl F)·ndS =ZZ
R
(curl F)·(2xi+2yj+k)dA
=Z1
−1Z√1−x2
−√1−x2
[2y(2x2+2y
2−4) −1−x2]dy dx =−5π/4
635 Chapter 17
CHAPTER 17 SUPPLEMENTARY EXERCISES
2. (b) c
kr−r0k3(r−r0)(c) cxi+yj+zk
px2+y2+z2
3. (a) Zb
af(x(t),y(t))dx
dt +g(x(t),y(t))dy
dt dt
(b) Zb
a
f(x(t),y(t))px0(t)2+y0(t)2dt
4. (a) M=Z
C
δ(x, y, z)ds (b) L=Z
C
ds (c) S=ZZ
σ
dS
(d) A=I
C
xdy =−I
C
ydx=1
2I
C
−ydx+xdy
11. ZZ
σ
f(x, y, z)dS =ZZ
R
f(x(u, v),y(u, v),z(u, v))kru×rvkdu dv
13. C1:(0,0) to (1,0); x=t,y=0,0≤t≤1
C
2:(1,0) to (cosh t0,sinh t0); x= cosh t,y= sinh t,0≤t≤t
0
C
3: (cosh t0,sinh t0)to(0,0); x=−(cosh t0)t,y=−(sinh t0)t,−1≤t≤0
A=1
2IC−ydx+xdy =1
2Z1
0
(0) dt +1
2Zt0
0
dt +1
2Z0
−1
(0) dt =1
2t0
14. (a) F(x, y, z)= qQ(xi+yj+zk)
4π0(x2+y2+z2)3/2
(b) F =∇φ, where φ=−qQ
4π0(x2+y2+z2)1/2,soW=φ(3,1,5)−φ(3,0,0) = qQ
4π01
3−1
√35.
C:x=3,y =t, z =5t, 0≤t≤1; F·dr=qQ[0+t+25t]dt
4π0(9+t2+25t
2
)
3/2
W=Z1
0
26qQt dt
4π0(26t2+9)
3/2=qQ
4π01
√35 −1
3
15. (a) Assume the mass Mis located at the origin and the mass mat (x, y, z), then
r=xi+yj+zk,F(x, y, z)=−GmM
(x2+y2+z2)3/2r,
W=−Zt2
t1
GmM
(x2+y2+z2)3/2xdx
dt +ydy
dt +zdz
dt dt
=GmM(x2+y2+z2)−1/2it2
t1
=GmM 1
r2−1
r1
(b) W=3.99 ×105×1031
7200 −1
7000≈−1.597 ×109J
Chapter 17 Supplementary Exercises 636
16. Let g(x, y)=x
2
, then Z
C
gdy =ZZ
R
2xdA,so¯x=1
AZZ
R
xdA=1
2AZ
C
gdy =1
2AZ
C
x
2dy,
similarly for ¯y.
17. ¯x= 0 by symmetry; by Exercise 16, ¯y=1
2AZ
C
y2dx;C1:y=0,−a≤x≤a, y2dx =0;
C
2:x=acos θ, y =asin θ, 0≤θ≤π,so
¯y=−1
2(πa2/2) Zπ
0
a2sin2θ(−asin θ)dθ =4a
3π
18. ¯y=¯xby symmetry; by Exercise 16, ¯x=1
2AZ
C
x2dy;C1:y=0,0≤x≤a, x2dy =0;
C
2:x=acos θ, y =asin θ, 0≤θ≤π/2; C3:x=0,x
2dy =0;
¯x=1
2(πa2/4) Zπ/2
0
a2(cos2θ)acos θdθ=4a
3π
19. ¯y= 0 by symmetry; ¯x=1
2AZ
C
x2dy;A=αa2;C1:x=tcos α, y =−tsin α, 0≤t≤a;
C2:x=acos θ, y =asin θ, −α≤θ≤α;C3:x=tcos α,
y=tsin α, 0≤t≤a(reverse orientation);
2A¯x=−Za
0
t2cos2αsin αdt+Zα
−α
a
3cos3θdθ−Za
0
t
2cos2αsin α dt,
=−2a3
3cos2αsin α+2a
3Zα
0
cos3θdθ=−2a
3
3cos2αsin α+2a3
3cos2αsin α=4
3a3sin α;
¯x=2a
3
sin α
α
20. A=Za
0b−b
a2x2dx =2ab
3,C
1:x=t, y =bt2/a2,0≤t≤a;
C2:x=a−t, y =b, 0≤t≤a, x2dy =0;C
3:x=0,y =b−t, 0≤t≤b, x2dy =y2dx =0;
2A¯x=Za
0
t
2
(2bt/a2)dt =a2b
2,¯x=3a
8;
2A¯y=−Za
0
(bt2/a2)2dt +Za
0
b2dt =−ab2
5+ab2=4ab2
5,¯y=3b
5
21. (a) Z
C
f(x)dx +g(y)dy =ZZ
R∂
∂xg(y)−∂
∂yf(x)dA =0
(b) W=Z
C
F·dr=Z
C
f(x)dx +g(y)dy = 0, so the work done by the vector field around any
simple closed curve is zero. The field is conservative.

637 Chapter 17
22. (a) Let r=dcos θi+dsin θj+zkin cylindrical coordinates, so
dr
dt =dr
dθ
dθ
dt =ω(−dsin θi+dcos θj),v=dr
dt =ωk×r=ω×r.
(b) From Part (a), v=ωd(−sin θi+ cos θj)=−ωyi+ωxj
(c) From Part (b), curl v=2ωk=2ω
(d) No; from Exercise 32 in Section 17.1, if φwere a potential function for v, then
curl (∇φ) = curl v= 0, contradicting Part (c) above.
23. Yes; by imagining a normal vector sliding around the surface it is evident that the surface has two
sides.
24. Dnφ=n·∇φ,soZZ
σ
DnφdS =ZZ
σ
n·∇φdS =ZZZ
G
∇·(∇φ)dV
=ZZZ
G∂2φ
∂x2+∂2φ
∂y2+∂2φ
∂z2dV
25. By Exercise 24, ZZ
σ
DnfdS=−ZZZ
G
[fxx +fyy +fzz]dV =−6ZZZ
G
dV =−6vol(G)=−8π
26. (a) fy−gx=exy +xyexy −exy −xyexy = 0 so the vector field is conservative.
(b) φx=yexy −1,φ=e
xy −x+k(x),φ
y=xexy, let k(x)=0;φ(x, y)=e
xy −x
(c) W=Z
C
F·dr=φ(x(8π),y(8π)) −φ(x(0),y(0)) = φ(8π, 0) −φ(0,0) = −8π
27. (a) If h(x)Fis conservative, then ∂
∂y(yh(x)) = ∂
∂x(−2xh(x)), or h(x)=−2h(x)−2xh0(x) which
has the general solution x3h(x)2=C1,h(x)=Cx−3/2,soCy
x
3/2i−C2
x
1/2jis conservative,
with potential function φ=−2Cy/√x.
(b) If g(y)F(x, y) is conservative then ∂
∂y(yg(y)) = ∂
∂x(−2xg(y)), or g(y)+yg0(y)=−2g(y),
with general solution g(y)=C/y3,soF=C1
y
2
i−C
2x
y
3
jis conservative, with potential
function Cx/y2.
28. A computation of curl Fshows that curl F=0if and only if the three given equations hold.
Moreover the equations hold if Fis conservative, so it remains to show that Fis conservative if
curl F=0. Let Cby any simple closed curve in the region. Since the region is simply connected,
there is a piecewis smooth, oriented surface σin the region with boundary C. By Stokes’ Theorem,
I
C
F·r=ZZ
σ
(curl F)·ndS =ZZ
σ
0dS =0.
By the 3-space analog of Theorem 17.3.2, Fis conservative.
29. (a) conservative, φ(x, y, z)=xz2−e−y(b) not conservative, fy6=gx(for example)
30. (a) conservative, φ(x, y, z)=−cos x+yz (b) not conservative, fz6=hx

Chapter 17 Horizon Module 638
CHAPTER 17 HORIZON MODULE
1. (a) If r=xi+yjdenotes the position vector, then F1·r= 0 by inspection, so the velocity field
is tangent to the circle. The relationship F1×r=−k
2πkindicates that r,F1,kis a right-
handed system, so the flow is counterclockwise. The polar form F1=−k
2πr(sin θi−cos θj)
shows that the speed is the constant k
2πr on a circle of radius r; and it also shows that the
speed is proportional to 1
rwith constant of proportionality 2kπ.
(b) Since kF1k=k
2πr, when r= 1 we get k=2πkF
1
k
2.
x
y
–1
–1
1
1
3. (a) F2=−q
2πkrk2rso F2is directed toward the origin, and kF2k=q
2πr is constant for constant
r, and the speed is proportional to the distance from the origin (constant of proportionality
q
2π). Since the velocity vector is directed toward the origin, the fluid flows towards the origin,
which must therefore be a sink.
(b) From Part (a) when r=1,q=2πkF
2
k.
4.
x
y
–1
–1
1
1
5. (b) The magnitudes of the field vectors increase, and their directions become more tangent to
circles about the origin.
(c) The magnitudes of the field vectors increase, and their directions tend more towards the
origin.
639 Chapter 17
6. (a) The inward component is F2,soatr=20,15 = kF2k=q
2π(20),soq= 600π; the tangential
component is F1,soatr=20,45 = kF1k=k
2π(20),sok= 1800π.
(b) F =−1
x2+y2[(300x+ 900y)i+ (300y−900x)j]
(c) kFk=300√10
r≤5 km/hr if r≥60√10 ≈189.7 km.
7. F =−1
2πr[(qcos θ+ksin θ)i+(qsin θ−kcos θ)j]=−q
2πr ur+k
2πruθ=−1
2πr(qur−kuθ)
8. F ·∇ψ=−1
2πr(qur−kuθ)·(−1
2π(kur+quθ)) = 1
(2πr)2(qk −kq) = 0, since urand uθare unit
orthogonal vectors.
9. From the hypotheses of Exercise 8, ψ=−1
2πkln r+α(θ),∂
∂θψ=α0(θ)=−q
2π,
α=−q
2πθ, ψ =−1
2π(kln r+qθ)
10. The streamline ψ=cbecomes kln r+qθ =−2πc, ln r=−qθ/k −2πc/k,
r=e−qθ/ke−2πc/k =κe−qθ, where κ>0.
11.
321
1
x
y
12. q= 600π, k = 1800π, r =κe−θ/3;atr=20,θ =π/4,κ =reθ/3=20e
π/12 ≈25.985; the desired
streamline has the polar equation r=25.985e−θ/3.
25
10
20
x
y
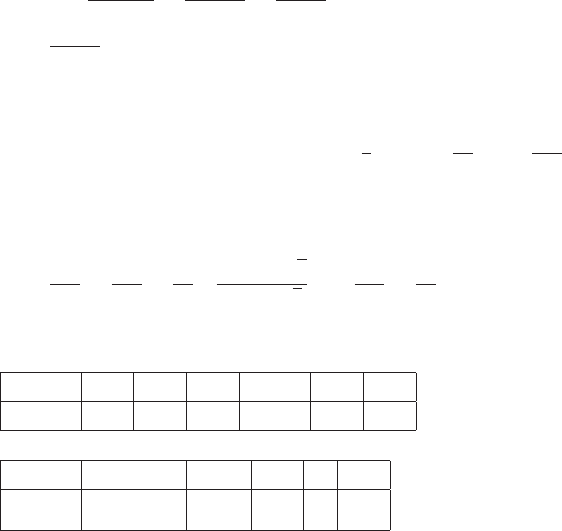
640
APPENDIX A
Real Numbers, Intervals, and Inequalities
EXERCISE SET A
1. (a) rational (b) integer, rational (c) integer, rational
(d) rational (e) integer, rational (f) irrational
(g) rational (h) integer, rational
2. (a) irrational (b) rational (c) rational (d) rational
3. (a) x=0.123123123 ..., 1000x= 123 + x,x= 123/999=41/333
(b) x=12.7777 ..., 10(x−12)=7+(x−12), 9x= 115, x= 115/9
(c) x=38.07818181 ..., 100x= 3807.81818181 ...,99x= 100x−x= 3769.74,
x=3769.74
99 =376974
9900 =20943
550
(d) 4296
10000
4. x=0.99999 ...,10x=9+x,9x=9,x=1
5. (a) If ris the radius, then D=2rso 8
9D2
=16
9r2
=256
81 r2. The area of a circle of radius
ris πr2so 256/81 was the approximation used for π.
(b) 22/7≈3.1429 is better than 256/81 ≈3.1605.
6. (a) 223
71 <333
106 <63
25 17+15
√
5
7+15
√
5!<355
113 <22
7
(b) Ramanujan’s (c) Athoniszoon’s (d) Ramanujan’s
7. Line 2 3 4 5 6 7
Blocks 3,4 1,2 3,4 2,4,5 1,2 3,4
8. Line 1 2 3 4 5
Blocks all blocks none 2,4 2 2,3
9. (a) always correct (add −3 to both sides of a≤b)
(b) not always correct (correct only if a=b)
(c) not always correct (correct only if a=b)
(d) always correct (multiply both sides of a≤bby 6)
(e) not always correct (correct only if a≥0)
(f) always correct (multiply both sides of a≤bby the nonnegative quantity a2)
10. (a) always correct
(b) not always correct (for example let a=b=0,c=1,d=2)
(c) not always correct (for example let a=1,b=2,c=d=0)
11. (a) all values because a=ais always valid (b) none
12. a=b, because if a6=bthen a<band b<aare contradictory
641 Appendix A
13. (a) yes, because a≤bis true if a<b (b) no, because a<bis false if a=bis true
14. (a) x2−5x=0,x(x−5)=0sox=0orx=5
(b) −1,0,1,2 are the only integers that satisfy −2<x<3
15. (a) {x:xis a positive odd integer}(b) {x:xis an even integer}
(c) {x:xis irrational}(d) {x:xis an integer and 7 ≤x≤10}
16. (a) not equal to Abecause 0 is not in A(b) equal to A
(c) equal to Abecause (x−3)(x2−3x+2)=0,(x−3)(x−2)(x−1)=0sox=1,2,or3
17. (a) false, there are points inside the triangle that are not inside the circle
(b) true, all points inside the triangle are also inside the square
(c) true (d) false (e) true
(f) true, ais inside the circle (g) true
18. (a) ∅,{a1},{a2},{a3},{a1,a
2
},{a
1
,a
3
},{a
2
,a
3
},{a
1
,a
2
,a
3
}(b) ∅
19. (a) 4(b) −3
(c) −17
(d) −33
(e) −33
(f) −33
20. (a)
84
(b)
52
(c)
3
(d) none
21. (a) [−2,2] (b) (−∞,−2) ∪(2,+∞)
22. (a) −34
(b)
41168
(c) −51
(d)
274
(e)
04
(f)
1 2.3
(g) (h)
05
Exercise Set A 642
23. 3x<10; (−∞,10/3)
10
3
24. 1
5x≥8; [40,+∞)
40
25. 2x≤−11; (−∞,−11/2]
11
2
−
26. 9x<−10; (−∞,−10/9)
10
9
−
27. 2x≤1 and 2x>−3; (−3/2,1/2]
1
2
3
2
−
28. 8x≥5 and 8x≤14; [5
8,7
4]
7
4
5
8
29. x
x−3−4<0,12 −3x
x−3<0,4−x
x−3<0;
(−∞,3) ∪(4,+∞)4
3
34
0
0
0
34
−−−
+++++
+++
++
+++++++
−−−−−−
−−−
4 − x
x − 3
x − 3
4 − x
30. x
8−x+2= 16 −x
8−x≥0;
(−∞,8) ∪[16,+∞)16
8
816
0
0
0
816
−−−
−−−−−
−−−
−−
+++++++
++++++
+++
16 − x
8 − x
16 − x
8 − x
31. 3x+1
x−2−1=2x+3
x−2<0,x+3/2
x−2<0;
(−3
2,2)
0
0
0
2
+++
+−−−−
−−−
++
+−−−+++
++++++
−−− x − 2
3
2
−
2
3
2
−
2
3
2
x + 3
2
x − 2
x + 3
2
−
643 Appendix A
32. x/2−3
4+x−1>0,x−6
4+x−2>0,x+14
x+4 <0;
(−14,−4)
0
0
0
−4
+++
+−−−−
−−−
++
+−−−+++
++++++
−−−
x + 14
x + 4
x + 4
−4
−4
x + 14
−14
−14
−14
33. 4
2−x−1=x+2
2−x≤0; (−∞,−2] ∪(2,+∞)0
0
0
2
+++
−++++
+++
−−
+−−−+++
−−−−−−
+++
x + 2
2 − x
2
2
2 − x
x + 2
−2
−2
−2
34. 3
x−5−2=13 −2x
x−5≤0,13/2−x
x−5≤0;
(−∞,5) ∪[13
2,+∞)
0
0
0
−−−
+++++
+++
++
+++++++
−−−−−−
−−− x − 5
5
5
13
2
13
2
513
2
− x
13
2
x − 5
− x
13
2
35. x2−9=(x+ 3)(x−3) >0;
(−∞,−3) ∪(3,+∞)
0
0
00
3−3
−3
−3
+++
+−−−−
−−−
++
+−−−+++
++++++
−−−
x + 3
x − 3
3
3
(x + 3)(x − 3)
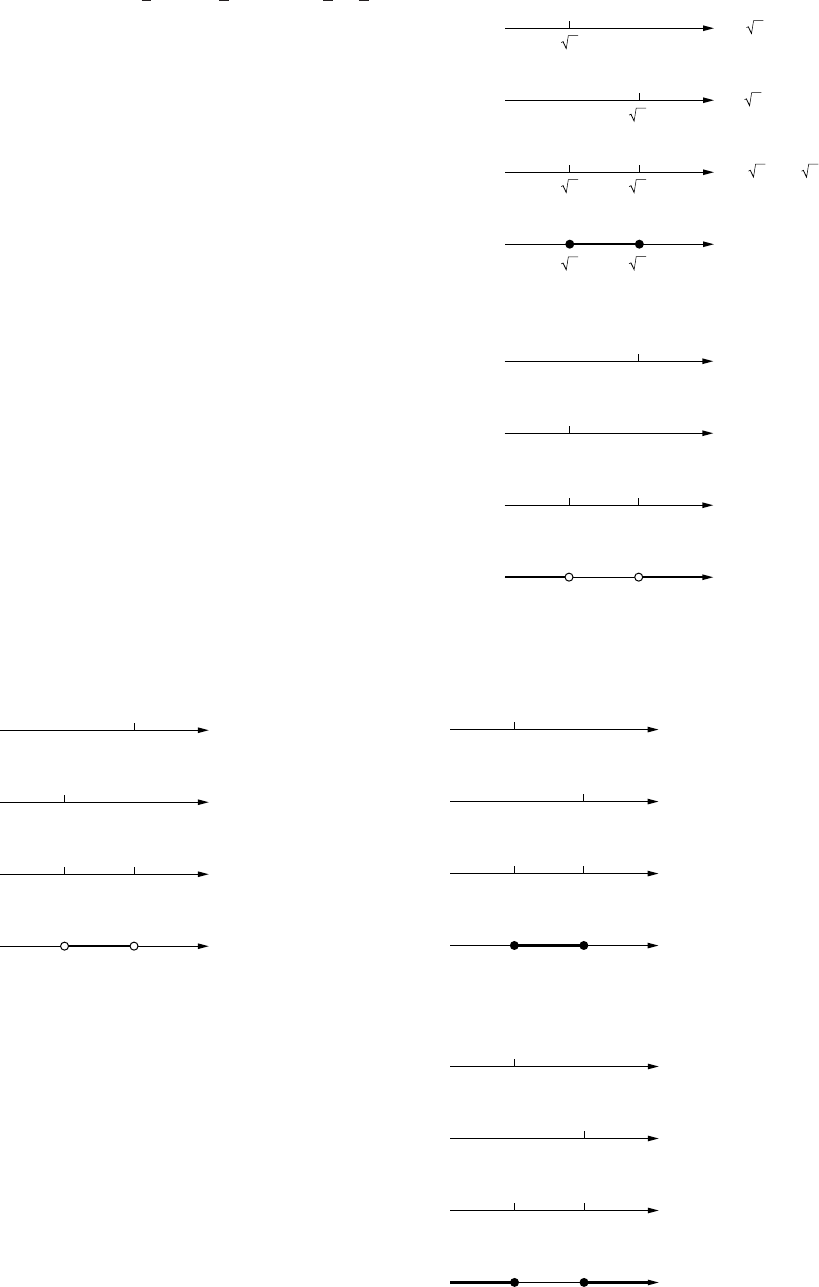
Exercise Set A 644
36. x2−5=(x−√
5)(x+√5) ≤0; [−√5,√5] 0
0
00
+++
+−−−−
−−−
++
+−−−+++
++++++
−−−
−
5x + 5
x − 5
()()
x + 5 x − 5
−
5
− 5
5
5
5
37. (x−4)(x+2)>0; (−∞,−2) ∪(4,+∞)
00
4−2
−2
++++++
0
−2
++++−−−+++x + 2
4
0+−−−−
−−−
++−−− x − 4
4
(x − 4)(x + 2)
38. (x−3)(x+4)<0; (−4,3)
3
−4
−4 3
−43
0
0
00
+++
+++++
−−−
++
−−−−−−−
++++++
−−−
x − 3
x + 4
(x − 3)(x + 4)
39. (x−4)(x−5) ≤0; [4,5]
4 5
45
0
0
−−−++++++
5
0+++−−−−−−− x − 5
4
0+++++++−−− x − 4
(x − 4)(x − 5)
40. (x−2)(x−1) ≥0; (−∞,1] ∪[2,+∞)
1 2
12
00
−−−++++++
2
0+++−−−−−−− x − 2
1
0+++++++−−− x − 1
(x − 1)(x − 2)

645 Appendix A
41. 3
x−4−2
x=x+8
x(x−4) >0; (−8,0) ∪(4,+∞)
−−+++++−−
4
0
4
++−−−−−−−−x − 4
0
0
0
++−−−−−−++
x
−8
0
−8
40−8
0
+++++++−− + x + 8
x(x − 4)
(x + 8)
42. 1
x+1−3
x−2=−2x−5
(x+ 1)(x−2) ≥0,
x+5/2
(x+ 1)(x−2) ≤0;
(−∞,−5
2]∪(−1,2)
0
0
0
2
+++
−−−−−
−−−
++
++−−+++
+++−−
−−− x − 2
5
2
−
2
5
2
−
2
++++−
−−−
++−−− x + 1
0
−1
−1
−1
x + 5
2
(x + 1)(x − 2)
x + 5
2
5
2
−
43. By trial-and-error we find that x= 2 is a root of the equation x3−x2−x−2=0sox−2
is a factor of x3−x2−x−2. By long division we find that x2+x+ 1 is another factor so
x3−x2−x−2=(x−2)(x2+x+ 1). The linear factors of x2+x+ 1 can be determined by first
finding the roots of x2+x+ 1 = 0 by the quadratic formula. These roots are complex numbers
so x2+x+1 6= 0 for all real x;thusx
2+x+ 1 must be always positive or always negative.
Since x2+x+ 1 is positive when x= 0, it follows that x2+x+1 >0 for all real x. Hence
x3−x2−x−2>0, (x−2)(x2+x+1)>0, x−2>0, x>2, so S=(2,+∞).
44. By trial-and-error we find that x= 1 is a root of the equation x3−3x+2=0sox−1
is a factor of x3−3x+ 2. By long division we find that x2+x−2 is another factor so
x3−3x+2=(x−1)(x2+x−2)=(x−1)(x−1)(x+2)=(x−1)2(x+ 2). Therefore we
want to solve (x−1)2(x+2)≤0. Now if x6= 1, then (x−1)2>0 and so x+2≤0, x≤−2. By
inspection, x= 1 is also a solution so S=(−∞,−2] ∪{1}.
45. √x2+x−6 is real if x2+x−6≥0. Factor to get (x+ 3)(x−2) ≥0 which has as its solution
x≤−3orx≥2.
46. x+2
x−1≥0; (−∞,−2] ∪(1,+∞)
47. 25 ≤5
9(F−32) ≤40, 45 ≤F−32 ≤72, 77 ≤F≤104
48. (a) n=2k,n
2=4k
2= 2(2k2) where 2k2is an integer.
(b) n=2k+1,n
2=4k
2+4k+ 1 = 2(2k2+2k) + 1 where 2k2+2kis an integer.
Exercise Set A 646
49. (a) Assume mand nare rational, then m=p
qand n=r
swhere p,q,r, and sare integers so
m+n=p
q+r
s=ps +rq
qs which is rational because ps +rq and qs are integers.
(b) (proof by contradiction) Assume mis rational and nis irrational, then m=p
qwhere pand
qare integers. Suppose that m+nis rational, then m+n=r
swhere rand sare integers
so n=r
s−m=r
s−p
q=rq −ps
sq . But rq −ps and sq are integers, so nis rational which
contradicts the assumption that nis irrational.
50. (a) Assume mand nare rational, then m=p
qand n=r
swhere p,q,r, and sare integers so
mn =p
q·r
s=pr
qs which is rational because pr and qs are integers.
(b) (proof by contradiction) Assume mis rational and nonzero and that nis irrational, then
m=p
qwhere pand qare integers and p6= 0. Suppose that mn is rational, then mn =r
s
where rand sare integers so n=r/s
m=r/s
p/q =rq
ps. But rq and ps are integers, so nis
rational which contradicts the assumption that nis irrational.
51. a=√2,b =√3,c =√6,d =−√2 are irrational, and a+d= 0, a rational; a+a=2
√
2, an
irrational; ad =−2, a rational; and ab =c, an irrational.
52. (a) irrational (Exercise 49(b)) (b) irrational (Exercise 50(b))
(c) rational by inspection; Exercise 51 gives no information
(d) √πmust be irrational, for if it were rational, then so would be π=(
√
π)
2by Exercise 50(a);
but πis known to be irrational.
53. The average of aand bis 1
2(a+b); if aand bare rational then so is the average, by Exercise 49(a)
and Exercise 50(a). On the other hand if a=b=√2 then the average of aand bis irrational, but
the average of aand −bis rational.
54. If 10x= 3, then x>0 because 10x≤1 for x≤0. If 10p/q = 3 with p, q integers, then 10p=3
q
,
so 3qmust be even (as well as 10podd), a contradiction to Exercise 48(b).
55. 8x3−4x2−2x+ 1 can be factored by grouping terms:
(8x3−4x2)−(2x−1)=4x
2
(2x−1)−(2x−1)=(2x−1)(4x2−1)=(2x−1)2(2x+1). The problem,
then, is to solve (2x−1)2(2x+1)<0. By inspection, x=1/2 is not a solution. If x6=1/2, then
(2x−1)2>0 and it follows that 2x+1<0, 2x<−1, x<−1/2, so S=(−∞,−1/2).
56. First, rewrite the inequality as 12x3−20x2+11x−2≥0. Now, if a polynomial in xwith integer
coefficients has a rational zero p
q, then pwill be a factor of the constant term and qwill be a factor
of the coefficient of the highest power of x. By trial-and-error we find that x=1/2 is a zero, thus
(x−1/2) is a factor so
12x3−20x2+11x−2=(x−1/2) 12x2−14x+4
=2(x−1/2) 6x2−7x+2
=2(x−1/2)(2x−1)(3x−2)=(2x−1)2(3x−2).
Now to solve (2x−1)2(3x−2) ≥0 we first note that x=1/2 is a solution. If x6=1/2 then
(2x−1)2>0 and 3x−2≥0, 3x≥2, x≥2/3soS=[2/3,+∞)∪{1/2}.
57. If a<b, then ac<bcbecause cis positive; if c<d, then bc<bdbecause bis positive, so ac<bd
(Theorem A.1(a)).
58. no, since the decimal representation is not repeating (the string of zeros does not have constant
length)
647
APPENDIX B
Absolute Value
EXERCISE SET B
1. (a) 7(b) √2(c) k2(d) k2
2. p(x−6)2=x−6ifx≥6, p(x−6)2=−(x−6) = −x+6ifx<6
3. |x−3|=|3−x|=3−xif 3 −x≥0, which is true if x≤3
4. |x+2|=x+2ifx+2≥0sox≥−2. 5. All real values of xbecause x2+9>0.
6. |x2+5x|=x
2+5xif x2+5x≥0sox(x+5)≥0 which is true for x≤−5orx≥0.
7. |3x2+2x|=|x(3x+2)|=|x||3x+2|.If|x||3x+2|=x|3x+2|, then |x||3x+2|−x|3x+2|=0,
(|x|−x)|3x+2|= 0, so either |x|−x=0or|3x+2|=0. If|x|−x= 0, then |x|=x, which is
true for x≥0. If |3x+2|= 0, then x=−2/3. The statement is true for x≥0orx=−2/3.
8. |6−2x|=|2(3 −x)|=|2||3−x|=2|x−3|for all real values of x.
9. p(x+5)
2=|x+5|=x+5ifx+5≥0, which is true if x≥−5.
10. p(3x−2)2=|3x−2|=|2−3x|=2−3xif 2 −3x≥0sox≤2/3.
13. (a) |7−9|=|−2|=2 (b) |3−2|=|1|=1
(c) |6−(−8)|=|14|=14 (d) |−3−√
2|=|−(3+√2)|=3+√
2
(e) |−4−(−11)|=|7|=7 (f) |−5−0|=|−5|=5
14. √a4=p(a2)2=|a2|, but |a2|=a2because a2≥0 so it is valid for all values of a.
15. (a) Bis 6 units to the left of A;b=a−6=−3−6=−9.
(b) Bis 9 units to the right of A;b=a+9=−2+9=7.
(c) Bis 7 units from A; either b=a+7=5+7=12orb=a−7=5−7=−2. Since it is
given that b>0, it follows that b= 12.
16. In each case we solve for ein terms of f:
(a) e=f−4; eis to the left of f.(b) e=f+4;eis to the right of f.
(c) e=f+6;eis to the right of f.(d) e=f−7; eis to the left of f.
17. |6x−2|=7
Case 1: Case 2:
6x−2=7 6x−2=−7
6x=9 6x=−5
x=3/2x=−5/6
18. |3+2x|=11
Case 1: Case 2:
3+2x=11 3+2x=−11
2x=8 2x=−14
x=4 x=−7
19. |6x−7|=|3+2x|
Case 1: Case 2:
6x−7=3+2x6x−7=−(3+2x)
4x=10 8x=4
x=5/2x=1/2
20. |4x+5|=|8x−3|
Case 1: Case 2:
4x+5=8x−34x+5=−(8x−3)
−4x=−812x=−2
x=2 x=−1/6

Exercise Set B 648
21. |9x|−11 = x
Case 2:
9x−11 = x−9x−11 = x
8x=11 −10x=11
x=11/8x=−11/10
22. 2x−7=|x+1|
Case 1: Case 2:
2x−7=x+1 2x−7=−(x+1)
x=8 3x=6
x= 2; not a solution
because xmust also
satisfy x<−1
23.
x+5
2−x
=6
Case 1: Case 2:
x+5
2−x=6 x+5
2−x=−6
x+5=12−6xx+5=−12+6x
7x=7 −5x=−17
x=1 x=17/5
24.
x−3
x+4
=5
Case 1: Case 2:
x−3
x+4=5 x−3
x+4=−5
x−3=5x+20 x−3=−5x−20
−4x=23 6x=−17
x=−23/4x=−17/6
25. |x+6|<3
−3<x+6<3
−9<x<−3
S=(−9,−3)
26. |7−x|≤5
−5≤7−x≤5
−12 ≤−x≤−2
12 ≥x≥2
S=[2,12]
27. |2x−3|≤6
−6≤2x−3≤6
−3≤2x≤9
−3/2≤x≤9/2
S=[−3/2,9/2]
28. |3x+1|<4
−4<3x+1<4
−5<3x<3
−5/3<x<1
S=(−5/3,1)
29. |x+2|>1
Case 1: Case 2:
x+2>1x+2<−1
x>−1x<−3
S=(−∞,−3) ∪(−1,+∞)
30.
1
2x−1≥2
Case 1: Case 2:
1
2x−1≥21
2x−1≤−2
1
2
x≥31
2
x≤−1
x≥6x≤−2
S=(−∞,−2] ∪[6,+∞)
31. |5−2x|≥4
Case 1: Case 2:
5−2x≥45−2x≤−4
−2x≥−1−2x≤−9
x≤1/2x≥9/2
S=(−∞,1/2] ∪[9/2,+∞)
32. |7x+1|>3
Case 1: Case 2:
7x+1>37x+1<−3
7x>27x<−4
x>2/7x< −4/7
S=(−∞,−4/7) ∪(2/7,+∞)
649 Appendix B
33. 1
|x−1|<2,x6=1
|x−1|>1/2
Case 1: Case 2:
x−1>1/2x−1<−1/2
x>3/2x< 1/2
S=(−∞,1/2) ∪(3/2,+∞)
34. 1
|3x+1|≥5,x6=−1/3
|3x+1|≤1/5
−1/5≤3x+1≤1/5
−6/5≤3x≤−4/5
−2/5≤x≤−4/15
S=[−2/5,−1/3) ∪(−1/3,−4/15]
35. 3
|2x−1|≥4,x6=1/2
|2x−1|
3≤1
4
|2x−1|≤3/4
−3/4≤2x−1≤3/4
1/4≤2x≤7/4
1/8≤x≤7/8
S=[1/8,1/2) ∪(1/2,7/8]
36. 2
|x+3|<1,x6=−3
|x+3|
2>1
|x+3|>2
Case 1: Case 2:
x+3>2x+3<−2
x>−1x<−5
S=(−∞,−5) ∪(−1,+∞)
37. p(x2−5x+6)
2=x
2−5x+6ifx
2−5x+6≥0 or, equivalently, if (x−2)(x−3) ≥0;
x∈(−∞,2] ∪[3,+∞).
38. If x≥2 then 3 ≤x−2≤7so5≤x≤9; if x<2 then 3 ≤2−x≤7so−5≤x≤−1.
S=[−5,−1] ∪[5,9].
39. If u=|x−3|then u2−4u= 12, u2−4u−12=0,(u−6)(u+2)=0,sou=6oru=−2. If
u= 6 then |x−3|=6,sox=9orx=−3. If u=−2 then |x−3|=−2 which is impossible. The
solutions are −3 and 9.
41. |a−b|=|a+(−b)|
≤|a|+|−b|(triangle inequality)
=|a|+|b|.
42. a=(a−b)+b
|a|=|(a−b)+b|
|a|≤|a−b|+|b|(triangle inequality)
|a|−|b|≤|a−b|.
43. From Exercise 42
(i) |a|−|b|≤|a−b|; but |b|−|a|≤|b−a|=|a−b|, so (ii) |a|−|b|≥−|a−b|.
Combining (i) and (ii): −|a−b|≤|a|−|b|≤|a−b|,so||a|−|b||≤|a−b|.
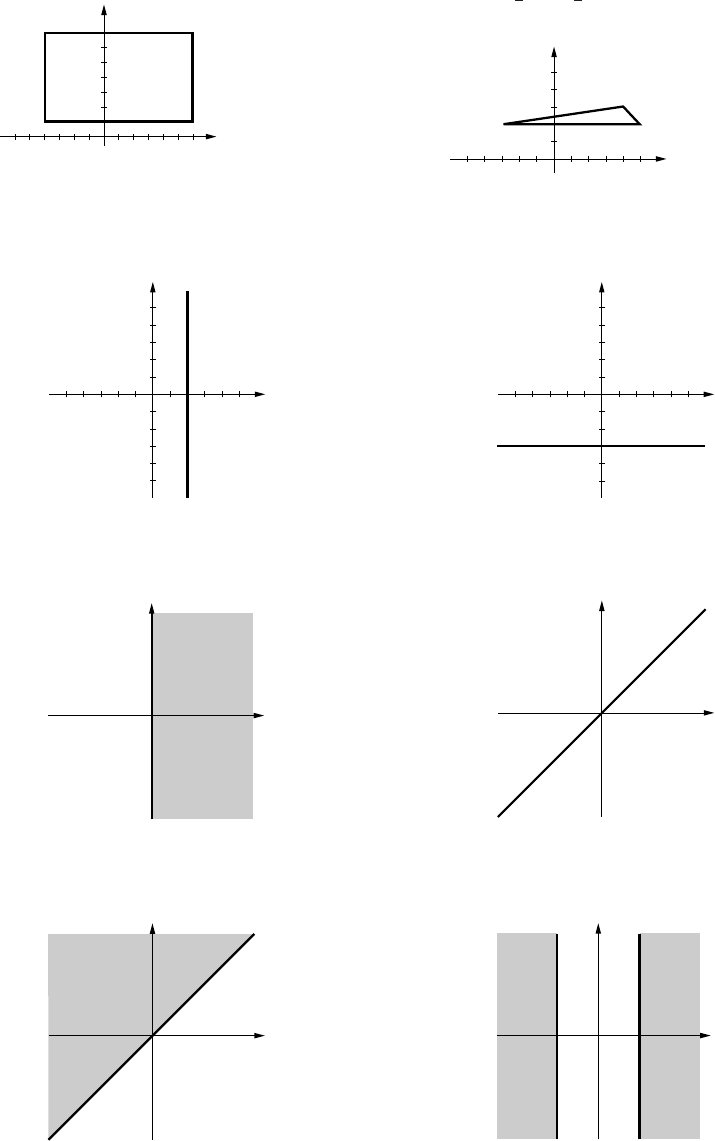
650
APPENDIX C
Coordinate Planes and Lines
EXERCISE SET C
1.
x
y
(-4, 1)
(-4, 7) (6, 7)
(6, 1)
2. area = 1
2bh =1
2(5 −(−3))(1) = 4
x
y
(-3, 2)
(4, 3)
(5, 2)
3. (a) x=2
2x
y
(b) y=−3
-3
x
y
(c) x≥0
x
y
(d) y=x
x
y
(e) y≥x
x
y
(f) |x|≥1
x
y
-1 1
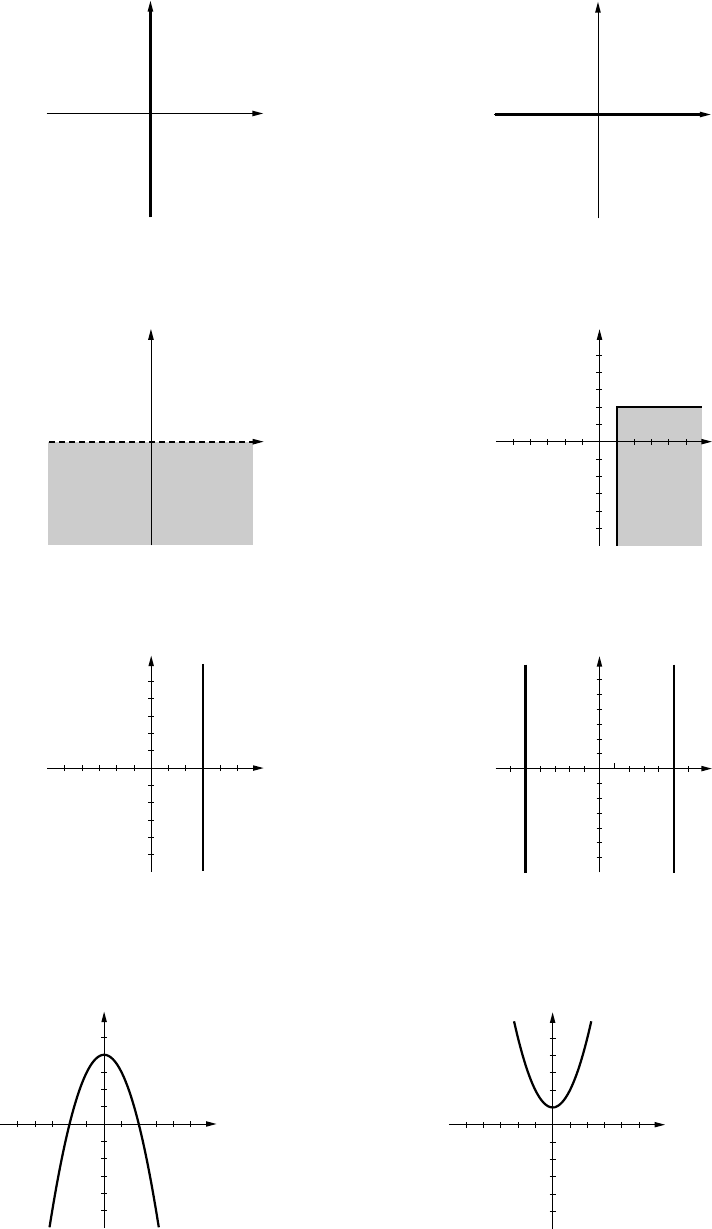
651 Appendix C
4. (a) x=0
x
y
(b) y=0
x
y
(c) y<0
x
y
(d) x≥1 and y≤2
x
y
1
2
(e) x=3
x
y
3
(f) |x|=5
x
y
5-5
5. y=4−x
2
x
y
4
5-5
6. y=1+x
2
x
y
5
5-5
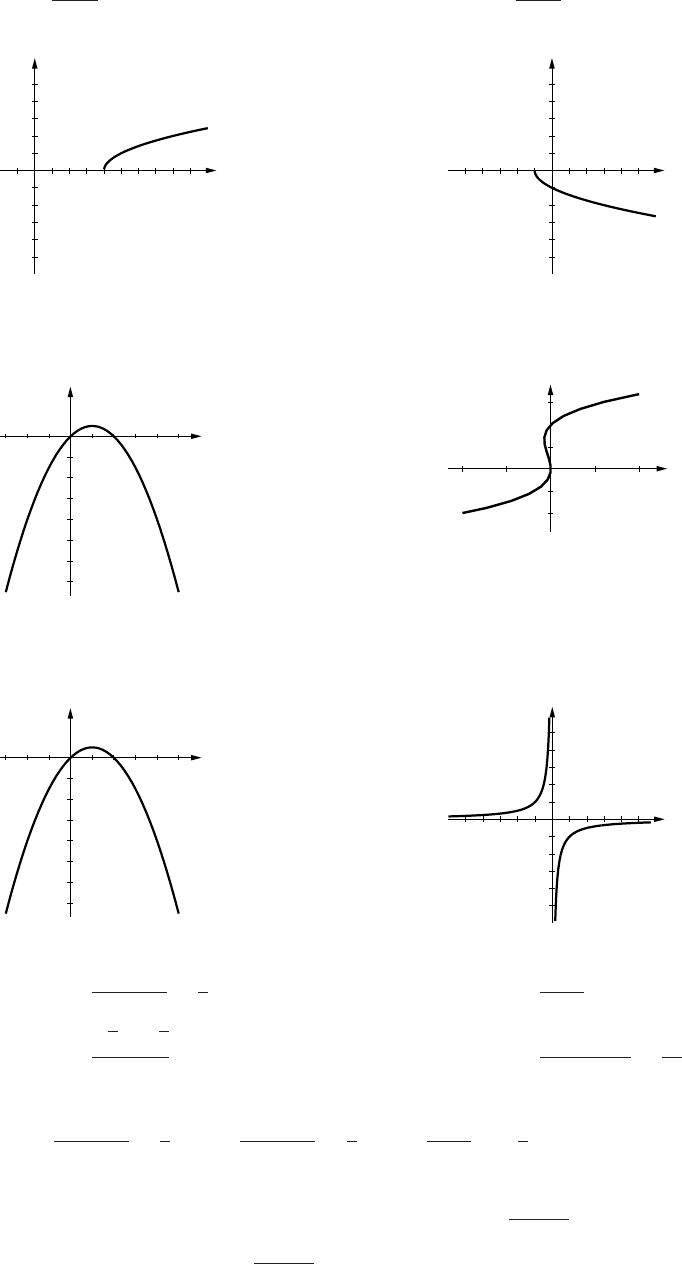
Exercise Set C 652
7. y=√x−4
x
y
4
5
8. y=−√x+1
x
y
-5 5
5
9. x2−x+y=0
y
x
-3
-2
-1
-1 1 2
10. x=y3−y2
y
x
-1
1
-2 -1 1 2
11. x2y=2
y
x
-3
-2
-1
-1 1 2
12. xy =−1
x
y
1
1
13. (a) m=4−2
3−(−1) =1
2(b) m=1−3
7−5=−1
(c) m=√2−√2
−3−4=0 (d) m=12 −(−6)
−2−(−2) =18
0, not defined
14. m1=5−2
6−(−1) =3
7,m2=7−2
2−(−1) =5
3,m3=7−5
2−6=−1
2
15. (a) The line through (1,1) and (−2,−5) has slope m1=−5−1
−2−1= 2, the line through (1,1) and
(0,−1) has slope m2=−1−1
0−1= 2. The given points lie on a line because m1=m2.
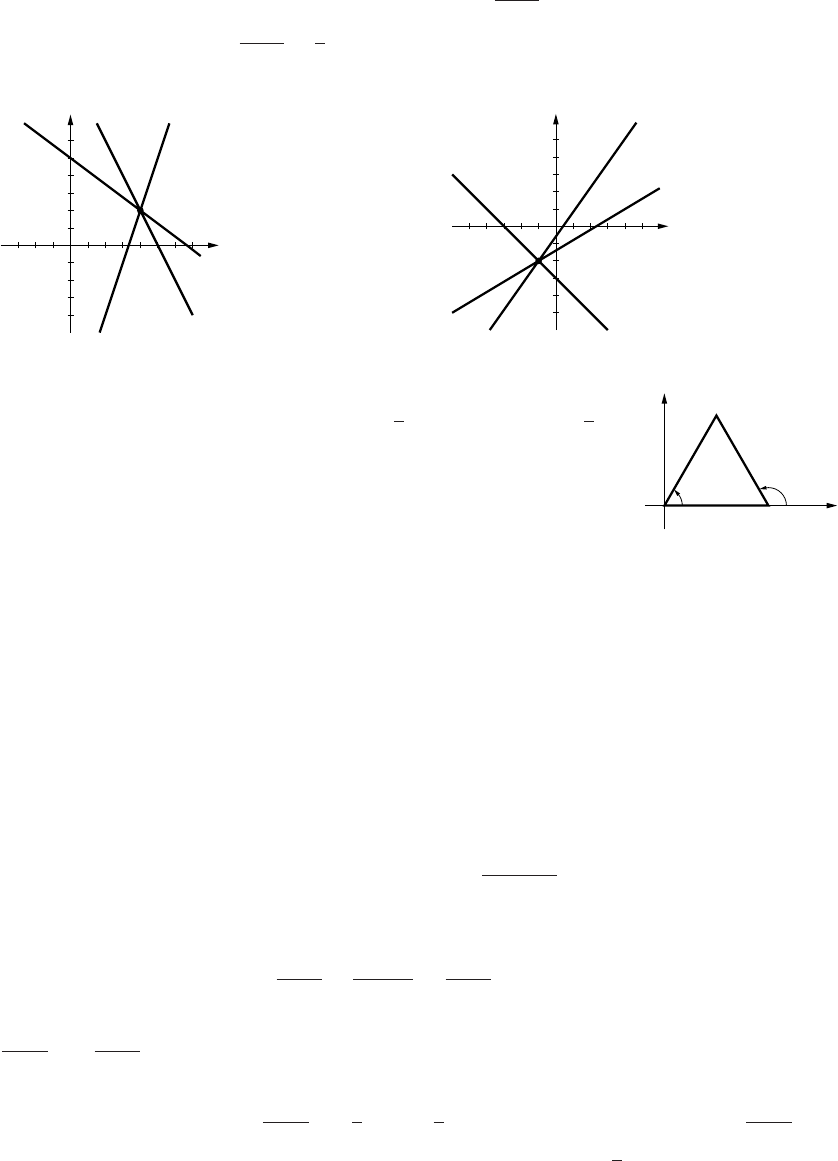
653 Appendix C
(b) The line through (−2,4) and (0,2) has slope m1=2−4
0+2 =−1, the line through (−2,4) and
(1,5) has slope m2=5−4
1+2 =1
3. The given points do not lie on a line because m16=m2.
16.
x
y
(4, 2)
(a)
(b)
(c)
17.
x
y
(-1, -2)
(b)
(a)
(c)
18. The triangle is equiangular because it is equilateral. The angles of
inclination of the sides are 0◦,60
◦
, and 120◦(see figure), thus the
slopes of its sides are tan0◦= 0, tan 60◦=√3, and tan 120◦=−√3.
x
y
120°
60°
19. III <II <IV <I20. III <IV <I<II
21. Use the points (1,2) and (x, y) to calculate the slope: (y−2)/(x−1)=3
(a) if x= 5, then (y−2)/(5 −1)=3,y−2 = 12, y=14
(b) if y=−2, then (−2−2)/(x−1)=3,x−1=−4/3, x=−1/3
22. Use (7,5) and (x, y) to calculate the slope: (y−5)/(x−7) = −2
(a) if x= 9, then (y−5)/(9 −7) = −2, y−5=−4, y=1
(b) if y= 12, then (12 −5)/(x−7) = −2, x−7=−7/2, x=7/2
23. Using (3,k) and (−2,4) to calculate the slope, we find k−4
3−(−2) =5,k−4 = 25, k= 29.
24. The slope obtained by using the points (1,5) and (k, 4) must be the same as that obtained from
the points (1,5) and (2,−3) so 4−5
k−1=−3−5
2−1,−1
k−1=−8, k−1=1/8, k=9/8.
25. 0−2
x−1=−0−5
x−4,−2x+8=5x−5, 7x= 13, x=13/7
26. Use (0,0) and (x, y)togety−0
x−0=1
2
,y=1
2
x. Use (7,5) and (x, y)togety−5
x−7=2,
y−5=2(x−7), y=2x−9. Solve the system of equations y=1
2xand y=2x−9toget
x=6,y=3.
27. Show that opposite sides are parallel by showing that they have the same slope:
using (3,−1) and (6,4), m1=5/3; using (6,4) and (−3,2), m2=2/9;
using (−3,2) and (−6,−3), m3=5/3; using (−6,−3) and (3,−1), m4=2/9.
Opposite sides are parallel because m1=m3and m2=m4.
Exercise Set C 654
28. The line through (3,1) and (6,3) has slope m1=2/3, the line through (3,1) and (2,9) has slope
m2=−8, the line through (6,3) and (2,9) has slope m3=−3/2. Because m1m3=−1, the
corresponding lines are perpendicular so the given points are vertices of a right triangle.
29. (a)
8
3
x
y(b)
3x
y
(c)
-2
x
y(c)
4
-7
x
y
30. (a)
3
-4
x
y(b)
-8 x
y
(c)
x
y(d)
2
5
x
y

655 Appendix C
31. (a)
-1
x
y
5-5
(b)
3
x
y
5-5
(c)
x
y
5-5
5
32. (a)
2
x
y
5-5
(b)
x
y
5-5
5
(c)
x
y
5-5
5
33. (a) m=3,b=2 (b) m=−1
4,b=3
(c) y=−3
5x+8
5so m=−3
5,b=8
5(d) m=0,b=1
(e) y=−b
ax+bso m=−b
a,y-intercept b
34. (a) m=−4, b=2 (b) y=1
3x−2
3so m=1
3,b=−2
3
(c) y=−3
2x+3som=−3
2,b=3 (d) y=3som=0,b=3
(e) y=−a0
a1
xso m=−a0
a1
,b=0
35. (a) m=(0−(−3))/(2 −0))=3/2soy=3x/2−3
(b) m=(−3−0)/(4 −0) = −3/4soy=−3x/4
36. (a) m=(0−2)/(2 −0)) = −1soy=−x+2
(b) m=(2−0)/(3 −0)=2/3soy=2x/3
37. y=−2x+4 38. y=5x−3
39. The slope mof the line must equal the slope of y=4x−2, thus m= 4 so the equation is y=4x+7.
40. The slope of the line 3x+2y=5is−3/2 so the line through (−1,2) with this slope
is y−2=−3
2
(x+ 1); y=−3
2x+1
2.
41. The slope mof the line must be the negative reciprocal of the slope of y=5x+9,thusm=−1/5
and the equation is y=−x/5+6.

Exercise Set C 656
42. The slope of the line x−4y= 7 is 1/4 so a line perpendicular to it must have a slope of −4;
y+4=−4(x−3); y=−4x+8.
43. y−4=−7−4
1−2(x−2) = 11(x−2), y=11x−18.
44. y−6= 1−6
−2−(−3)(x−(−3)), y−6=−5(x+ 3), y=−5x−9.
45. The line passes through (0,2) and (−4,0), thus m=0−2
−4−0=1
2so y=1
2x+2.
46. The line passes through (0,b) and (a, 0), thus m=0−b
a−0=−b
a, so the equation is
y=−b
ax+b.
47. y=1 48. y=−8
49. (a) m1=4,m
2= 4; parallel because m1=m2
(b) m1=2,m
2=−1/2; perpendicular because m1m2=−1
(c) m1=5/3, m2=5/3; parallel because m1=m2
(d) If A6= 0 and B6= 0, then m1=−A/B,m2=B/A and the lines are perpendicular because
m1m2=−1. If either Aor B(but not both) is zero, then the lines are perpendicular because
one is horizontal and the other is vertical.
(e) m1=4,m
2=1/4; neither
50. (a) m1=−5, m2=−5; parallel because m1=m2
(b) m1=2,m
2=−1/2; perpendicular because m1m2=−1.
(c) m1=−4/5, m2=5/4; perpendicular because m1m2=−1.
(d) If B6= 0, then m1=m2=−A/B and the lines are parallel because m1=m2.IfB= 0 (and
A6= 0), then the lines are parallel because they are both perpendicular to the x-axis.
(e) m1=1/2, m2= 2; neither
51. y=(−3/k)x+4/k,k6=0
(a) −3/k =2,k=−3/2
(b) 4/k =5,k=4/5
(c) 3(−2)+k(4)=4,k=5/2
(d) The slope of 2x−5y= 1 is 2/5so−3/k =2/5, k=−15/2.
(e) The slope of 4x+3y=2is−4/3 so the slope of the line perpendicular to it is 3/4;
−3/k =3/4, k=−4.
52. y2=3x: the union of the graphs of y=√3xand y=−√3x
x
y
5-5
5

657 Appendix C
53. (x−y)(x+y) = 0: the union of the graphs of
x−y= 0 and x+y=0
x
y
5-5
5
54. F=9
5C+32
-30 30
-30
50
C
F
55. u=3v
2
u
v
8
5
56. Y=4X+5
5
-1 Y
X
57. Solve x=5t+ 2 for tto get t=1
5x−2
5,soy=1
5
x−2
5
−3=1
5
x−17
5, which is a line.
58. Solve x=1+3t
2for t2to get t2=1
3x−1
3,soy=2−1
3
x−1
3
=−1
3
x+7
3
, which is a line;
1+3t
2≥1 for all tso x≥1.
59. An equation of the line through (1,4) and (2,1) is y=−3x+7. It crosses the y-axis at y= 7, and
the x-axis at x=7/3, so the area of the triangle is 1
2(7)(7/3)=49/6.
60. (2x−3y)(2x+3y)=0,so2x−3y=0,y=2
3
xor 2x+3y=0,
y=−2
3
x. The graph consists of the lines y=±2
3x.
x
y
5-5
5
61. (a) yes (b) yes (c) no (d) yes (e) yes (f) yes (g) no
658
APPENDIX D
Distance, Circles, and Quadratic Equations
EXERCISE SET D
1. in the proof of Theorem D.1
2. (a) d=p(−1−2)2+(1−5)2=√9+16=√
25=5
(b) 2+(−1)
2,5+1
2=(1/2,3)
3. (a) d=p(1 −7)2+(9−1)2=√36+64=√
100=10
(b) 7+1
2,1+9
2=(4,5)
4. (a) d=p(−3−2)2+(6−0)2=√25+36=√
61
(b) 2+(−3)
2,0+6
2=(−1/2,3)
5. (a) d=p[−7−(−2)]2+[−4−(−6)]2=√25+4=√
29
(b) −2+(−7)
2,−6+(−4)
2=(−9/2,−5)
6. Let A(1,1), B(−2,−8), and C(4,10) be the given points
(see diagram). A,B, and Clie on a straight line if and only if
d1+d2=d3, where d1,d2, and d3are the lengths of the line
segments AB,AC, and BC. But
d1=p(−2−1)2+(−8−1)2=3
√
10,
d2=p(4 −1)2+ (10 −1)2=3
√
10,
d3=p(4+2)
2+(10+8)
2=6
√
10; because d1+d2=d3,
it follows that A,B, and Clie on a straight line.
x
y
C(4, 10)
A(1, 1)
B(-2, -8)
d3
d2
d1
7. Let A(5,−2), B(6,5), and C(2,2) be the given vertices and a,b, and cthe lengths of the sides
opposite these vertices; then
a=p(2 −6)2+(2−5)2=√25 = 5 and b=p(2 −5)2+(2+2)
2=√
25=5.
Triangle ABC is isosceles because it has two equal sides (a=b).
8. A triangle is a right triangle if and only if the square of the longest side is equal to the sum of the
squares of the other two sides (Pythagorean theorem). With A(1,3), B(4,2), and C(−2,−6) as ver-
tices and s1,s2, and s3the lengths of the sides opposite these vertices we find that
s2
1=(−2−4)2+(−6−2)2= 100, s2
2=(−2−1)2+(−6−3)2= 90, s2
3=(4−1)2+(2−3)2= 10,
and that s2
1=s2
2+s2
3,soABC is a right triangle.
9. P1(0,−2), P2(−4,8), and P3(3,1) all lie on a circle whose center is C(−2,3) if the points P1,
P2and P3are equidistant from C. Denoting the distances between P1,P2,P3and Cby d1,d2
and d3we find that d1=p(0+2)
2+(−2−3)2=√29, d2=p(−4+2)
2+(8−3)2=√29, and
d3=p(3+2)
2+(1−3)2=√29, so P1,P2and P3lie on a circle whose center is C(−2,3) because
d1=d2=d3.

659 Appendix D
10. The distance between (t, 2t−6) and (0,4) is
p(t−0)2+(2t−6−4)2=pt2+(2t−10)2=√5t2−40t+ 100;
the distance between (t, 2t−6) and (8,0) is p(t−8)2+(2t−6)2=√5t2−40t+ 100,
so (t, 2t−6) is equidistant from (0,4) and (8,0).
11. If (2,k) is equidistant from (3,7) and (9,1), then
p(2 −3)2+(k−7)2=p(2 −9)2+(k−1)2,1+(k−7)2=49+(k−1)2,
1+k
2−14k+49=49+k
2−2k+1,−12k=0,k=0.
12. (x−3)/2 = 4 and (y+2)/2=−5sox= 11 and y=−12.
13. The slope of the line segment joining (2,8) and (−4,6) is 6−8
−4−2=1
3so the slope of the perpen-
dicular bisector is −3. The midpoint of the line segment is (−1,7) so an equation of the bisector is
y−7=−3(x+ 1); y=−3x+4.
14. The slope of the line segment joining (5,−1) and (4,8) is 8−(−1)
4−5=−9 so the slope of the perpen-
dicular bisector is 1
9. The midpoint of the line segment is (9/2,7/2) so an equation of the bisector is
y−7
2=1
9x−9
2;y=1
9x+3.
15. Method (see figure): Find an equation of the perpendicular bisector of the line segment joining
A(3,3) and B(7,−3). All points on this perpendicular bisector are equidistant from Aand B,thus
find where it intersects the given line.
The midpoint of AB is (5,0), the slope of AB is −3/2thusthe
slope of the perpendicular bisector is 2/3 so an equation is
y−0=2
3
(x−5)
3y=2x−10
2x−3y−10=0.
The solution of the system
(4x−2y+3=0
2x−3y−10=0
gives the point (−29/8,−23/4).
x
y
A(3, 3)
B(7, -3)
4x - 2y + 3 = 0
16. (a) y= 4 is a horizontal line, so the vertical distance is |4−(−2)|=|6|=6.
(b) x=−1 is a vertical line, so the horizontal distance is |−1−3|=|−4|=4.
17. Method (see figure): write an equation of the line that goes through
the given point and that is perpendicular to the given line; find the
point Pwhere this line intersects the given line; find the
distance between Pand the given point.
The slope of the given line is 4/3, so the slope of a line
perpendicular to it is −3/4. x
y
4x – 3y + 10 = 0
(2, 1)
P

Exercise Set D 660
The line through (2,1) having a slope of −3/4isy−1=−
3
4
(x−2) or, after simplification,
3x+4y= 10 which when solved simultaneously with 4x−3y+ 10 = 0 yields (−2/5,14/5) as the
point of intersection. The distance dbetween (−2/5,14/5) and (2,1) is
d=p(2+2/5)2+(1−14/5)2=3.
18. (See the solution to Exercise 17 for a description of the method.) The slope of the line
5x+12y−36=0is−5/12. The line through (8,4) and perpendicular to the given line is
y−4=12
5(x−8) or, after simplification, 12x−5y= 76. The point of intersection of this line with
the given line is found to be 84
13,4
13and the distance between it and (8,4) is 4.
19. If B= 0, then the line Ax +C= 0 is vertical and x=−C/A for each point on the line. The line
through (x0,y
0
) and perpendicular to the given line is horizontal and intersects the given line at
the point (−C/A,y0). The distance dbetween (−C/A,y0) and (x0,y
0
)is
d=p(x
0+C/A)2+(y
0−y
0
)
2=r(Ax0+C)2
A2=|Ax0+C|
√A2
which is the value of |Ax0+By0+C|
√A2+B2for B=0.
If B6= 0, then the slope of the given line is −A/B and the line through (x0,y
0
) and perpendicular
to the given line is
y−y0=B
A(x−x0), Ay −Ay0=Bx −Bx0,Bx −Ay =Bx0−Ay0.
The point of intersection of this line and the given line is obtained by solving
Ax +By =−Cand Bx −Ay =Bx0−Ay0.
Multiply the first equation through by Aand the second by Band add the results to get
(A2+B2)x=B2x0−ABy0−AC so x=B2x0−ABy0−AC
A2+B2
Similarly, by multiplying by Band −A,wegety=−ABx0+A2y0−BC
A2+B2.
The square of the distance dbetween (x, y) and (x0,y
0
)is
d
2=x
0−B
2
x
0−ABy0−AC
A2+B22
+y0−−ABx0+A2y0−BC
A2+B22
=(A2x0+ABy0+AC)2
(A2+B2)2+(ABx0+B2y0+BC)2
(A2+B2)2
=A2(Ax0+By0+C)2+B2(Ax0+By0+C)2
(A2+B2)2
=(Ax0+By0+C)2(A2+B2)
(A2+B2)2=(Ax0+By0+C)2
A2+B2
so d=|Ax0+By0+C|
√A2+B2.
20. d=|4(2) −3(1) + 10|
p42+(−3)2=|15|
√25 =15
5=3. 21. d=|5(8) + 12(4) −36|
√52+12
2=|52|
√169 =52
13 =4.
661 Appendix D
22. Method (see figure): Let A(0,a), B(b, 0), and C(c, 0) be the given
vertices; find equations for the perpendicular bisectors L1,L2, and
L3and show that they all intersect at the same point.
x
y
L3
L1
L2
B(b, 0)
A(0, a)
C(c, 0)
line L1: The midpoint of BC is b+c
2,0and since L1is vertical,
an equation for L1is x=b+c
2;
line L2: The midpoint of AB is b
2,a
2; the slope of AB is −a
b
(if b6= 0) so the slope of
L2is b
a(even if b= 0) and an equation of L2is y−a
2=b
ax−b
2;
line L3: The midpoint of AC is c
2,a
2; the slope of AC is −a
c(if c6= 0) so the slope of
L3is c
a(even if c= 0) and an equation of L3is y−a
2=c
ax−c
2.
For the point of intersection of L1and L2, solve x=b+c
2and y−a
2=b
ax−b
2.
The point is found to be b+c
2,a2+bc
2. The point of intersection of L1and L3is obtained by
solving the system x=b+c
2and y−a
2=c
ax−c
2, its solution yields the point b+c
2,a2+bc
2.
So L1L2, and L3all intersect at the same point.
23. (a) center (0,0), radius 5 (b) center (1,4), radius 4
(c) center (−1,−3), radius √5(d) center (0,−2), radius 1
24. (a) center (0,0), radius 3 (b) center (3,5), radius 6
(c) center (−4,−1), radius √8(d) center (−1,0), radius 1
25. (x−3)2+(y−(−2))2=4
2
,(x−3)2+(y+2)
2=16
26. (x−1)2+(y−0)2=(
√
8/2)2,(x−1)2+y2=2
27. r= 8 because the circle is tangent to the x-axis, so (x+4)
2+(y−8)2= 64.
28. r= 5 because the circle is tangent to the y-axis, so (x−5)2+(y−8)2= 25.
29. (0,0) is on the circle, so r=p(−3−0)2+(−4−0)2=5;(x+3)
2+(y+4)
2= 25.
30. r=p(4 −1)2+(−5−3)2=√73; (x−4)2+(y+5)
2= 73.
31. The center is the midpoint of the line segment joining (2,0) and (0,2) so the center is at (1,1).
The radius is r=p(2 −1)2+(0−1)2=√2, so (x−1)2+(y−1)2=2.
32. The center is the midpoint of the line segment joining (6,1) and (−2,3), so the center is at (2,2).
The radius is r=p(6 −2)2+(1−2)2=√17, so (x−2)2+(y−2)2= 17.
33. (x2−2x)+(y
2−4y) = 11, (x2−2x+1)+(y
2−4y+4)=11+1+4,(x−1)2+(y−2)2= 16;
center (1,2) and radius 4
Exercise Set D 662
34. (x2+8x)+y
2=−8, (x2+8x+16)+y2=−8 + 16, (x+4)
2+y
2= 8; center (−4,0) and radius
2√2
35. 2(x2+2x)+2(y
2−2y)=0,2(x
2+2x+1)+2(y
2−2y+1)=2+2,(x+1)
2+(y−1)2=2;
center (−1,1) and radius √2
36. 6(x2−x)+6(y
2+y)=3,6(x
2−x+1/4)+6(y
2+y+1/4)=3+6/4+6/4,
(x−1/2)2+(y+1/2)2= 1; center (1/2,−1/2) and radius 1
37. (x2+2x)+(y
2+2y)=−2, (x2+2x+1)+(y
2+2y+1)=−2+1+1,(x+1)
2+(y+1)
2=0;
the point (−1,−1)
38. (x2−4x)+(y
2−6y)=−13, (x2−4x+4)+(y
2−6y+9)=−13+4+9,(x−2)2+(y−3)2=0;
the point (2,3)
39. x2+y2=1/9; center (0,0) and radius 1/3
40. x2+y2= 4; center (0,0) and radius 2
41. x2+(y
2+10y)=−26, x2+(y
2+10y+ 25) = −26 + 25, x2+(y+5)
2=−1; no graph
42. (x2−10x)+(y
2−2y)=−29, (x2−10x+25)+(y
2−2y+1)=−29+25+1,
(x−5)2+(y−1)2=−3; no graph
43. 16 x2+5
2x+ 16(y2+y)=7,16x
2+5
2
x+25
16+16y
2+y+1
4=7+25+4,
(x+5/4)2+(y+1/2)2=9/4; center (−5/4,−1/2) and radius 3/2
44. 4(x2−4x)+4(y
2−6y)=9,4(x
2−4x+4)+4(y
2−6y+9)=9+16+36,
(x−2)2+(y−3)2=61/4; center (2,3) and radius √61/2
45. (a) y2=16−x
2
,soy=±
√
16 −x2. The bottom half is y=−√16 −x2.
(b) Complete the square in yto get (y−2)2=3−2x−x
2
,soy−2=±
√
3−2x−x
2
,
or y=2±√
3−2x−x
2
. The top half is y=2+√
3−2x−x
2
.
46. (a) x2=9−y
2so x=±p9−y2. The right half is x=p9−y2.
(b) Complete the square in xto get (x−2)2=1−y
2so x−2=±
p1−y
2
,x=2±p1−y
2
.
The left half is x=2−p1−y
2
.
47. (a)
-5 5
5
x
y(b) y=√5+4x−x
2
=p5−(x
2−4x)
=p5+4−(x
2−4x+4)
=p9−(x−2)2
-1 5
3
x
y

663 Appendix D
48. (a)
-2
-2
2
x
y(b)
35
-2
2
x
y
49. The tangent line is perpendicular to the radius at the point. The slope of the radius is 4/3, so
the slope of the perpendicular is −3/4. An equation of the tangent line is y−4=−3
4
(x−3), or
y=−3
4x+25
4.
50. (a) (x+1)
2+y
2= 10, center at C(−1,0). The slope of CP is −1/3 so the slope of the tangent
is 3; y+1=3(x−2), y=3x−7.
(b) (x−3)2+(y+2)
2= 26, center at C(3,−2). The slope of CP is 5 so the slope of the tangent
is −1
5;y−3=−1
5
(x−4), y=−1
5x+19
5.
51. (a) The center of the circle is at (0,0) and its radius is √20=2
√
5. The distance between Pand
the center is p(−1)2+ (2)2=√5 which is less than 2√5, so Pis inside the circle.
(b) Draw the diameter of the circle that passes through P, then the shorter segment of the
diameter is the shortest line that can be drawn from Pto the circle, and the longer segment
is the longest line that can be drawn from Pto the circle (can you prove it?). Thus, the
smallest distance is 2√5−√5=√
5, and the largest is 2√5+√
5=3
√
5.
52. (a) x2+(y−1)2= 5, center at C(0,1) and radius √5. The distance between Pand Cis 3√5/2
so Pis outside the circle.
(b) The smallest distance is 3
2√5−√5=1
2
√
5, the largest distance is 3
2√5+√
5=5
2
√
5.
53. Let (a, b) be the coordinates of T(or T0). The radius from (0,0) to T(or T0) will be perpendicular
to L(or L0) so, using slopes, b/a =−(a−3)/b,a2+b2=3a. But (a, b) is on the circle so a2+b2=1,
thus 3a=1,a=1/3. Let a=1/3ina
2+b
2= 1 to get b2=8/9, b=±√8/3. The coordinates of
Tand T0are (1/3,√8/3) and (1/3,−√8/3).
54. (a) p(x−2)2+(y−0)2=√2p(x−0)2+(y−1)2; square both sides and expand to get
x2−4x+4+y
2=2(x
2+y
2−2y+ 1), x2+y2+4x−4y−2 = 0, which is a circle.
(b) (x2+4x)+(y
2−4y)=2,(x
2+4x+4)+(y
2−4y+4)=2+4+4,(x+2)
2+(y−2)2= 10;
center (−2,2), radius √10.
55. (a) [(x−4)2+(y−1)2]+[(x−2)2+(y+5)
2
]=45
x
2−8x+16+y
2−2y+1+x
2−4x+4+y
2+10y+25=45
2x
2+2y
2−12x+8y+ 1 = 0, which is a circle.
(b) 2(x2−6x)+2(y
2+4y)=−1, 2(x2−6x+9)+2(y
2+4y+4)=−1+18+8,
(x−3)2+(y+2)
2=25/2; center (3,−2), radius 5/√2.
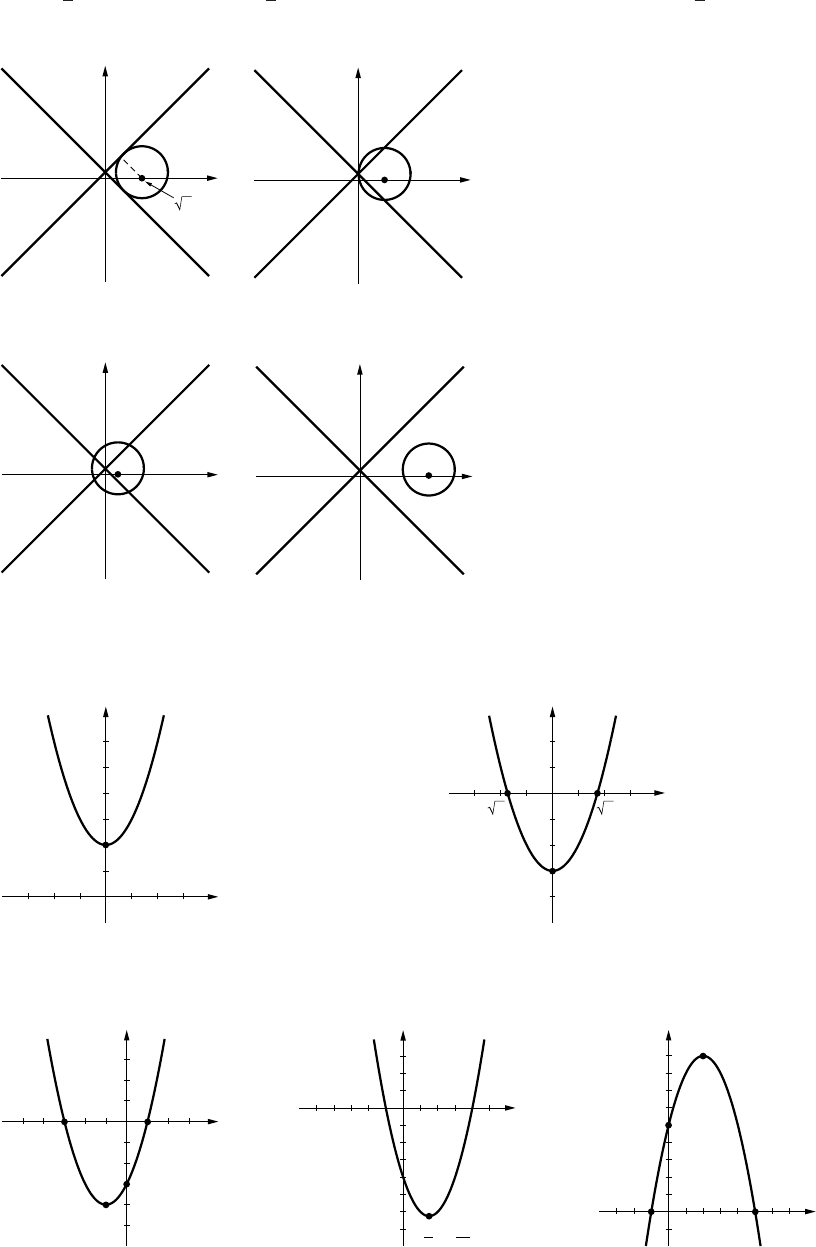
Exercise Set D 664
56. If x2−y2= 0, then y2=x2so y=xor y=−x. The graph of x2−y2= 0 consists of the graphs
of the two lines y=±x. The graph of (x−c)2+y2= 1 is a circle of radius 1 with center at (c, 0).
Examine the figure to see that the system cannot have just one solution, and has 0 solutions if
|c|>√2, 2 solutions if |c|=√2, 3 solutions if |c|= 1, and 4 solutions if |c|<√2, |c|6=1.
x
y
1x
y
1
2 solutions 3 solutions
x
y
x
y
4 solutions 0 solutions
2
57. y=x2+2
x
y
(0, 2)
58. y=x2−3
x
y
(0, -3)
3– 3
59. y=x2+2x−3
-3 1
-3
x
y
(-1, -4)
60. y=x2−3x−4
-1 4
-4
x
y
3
225
4
()
, –
61. y=−x2+4x+5
-1 5
5
x
y
(2, 9)
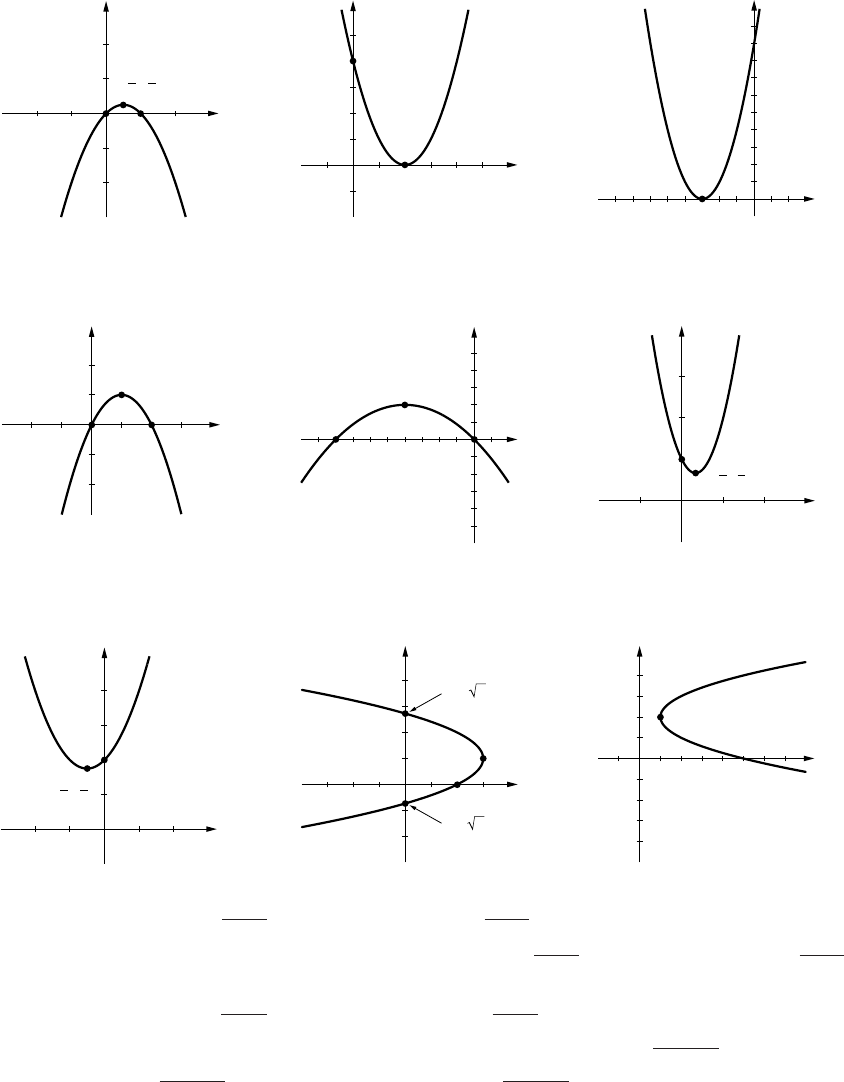
665 Appendix D
62. y=−x2+x
1x
y
1
21
4
()
,
63. y=(x−2)2
4
x
y
(2, 0)
64. y=(3+x)
2
9
x
y
(-3, 0)
65. x2−2x+y=0
2x
y
(1, 1)
66. x2+8x+8y=0
-8 x
y
(-4, 2)
67. y=3x
2−2x+1
1
x
y
2
3
1
3
()
,
68. y=x2+x+2
2
x
y
7
4
1
2
()
, –
69. x=−y2+2y+2
2x
y
(3, 1)
1 – 3
1 + 3
70. x=y2−4y+5
5x
y
(1, 2)
71. (a) x2=3−y,x=±
√
3−y. The right half is x=√3−y.
(b) Complete the square in xto get (x−1)2=y+1, x=1±
√
y+ 1. The left half is x=1−
√
y+1.
72. (a) y2=x+5,y=±
√
x+ 5. The upper half is y=√x+5.
(b) Complete the square in yto get (y−1/2)2=x+9/4, y−1/2=±
px+9/4,
y=1/2±px+9/4. The lower half is y=1/2−px+9/4.
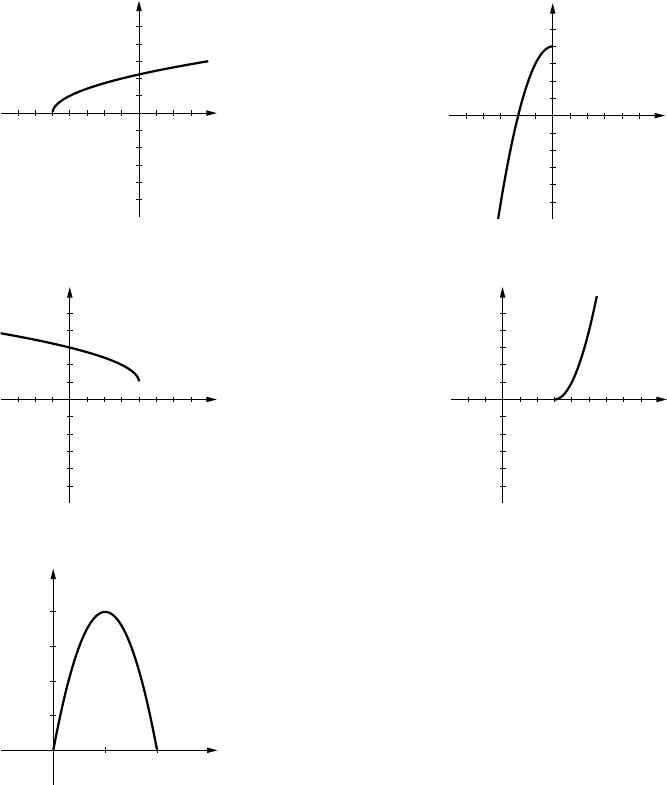
Exercise Set D 666
73. (a)
x
y
-5
5
(b)
4
x
y
5
74. (a)
4x
y
5
(b)
3x
y
5
75. (a)
12
8
16
t
s(b) The ball will be at its highest point
when t= 1 sec; it will rise 16 ft.
76. (a) 2x+y= 500, y= 500 −2x.(b) A=xy =x(500 −2x) = 500x−2x2.
(c) The graph of Aversus xis a parabola with its vertex (high point) at
x=−b/(2a)=−500/(−4) = 125, so the maximum value of Ais
A= 500(125) −2(125)2= 31,250 ft2.
77. (a) (3)(2x) + (2)(2y) = 600, 6x+4y= 600, y= 150 −3x/2
(b) A=xy =x(150 −3x/2) = 150x−3x2/2
(c) The graph of Aversus xis a parabola with its vertex (high point) at
x=−b/(2a)=−150/(−3) = 50, so the maximum value of Ais
A= 150(50) −3(50)2/2 = 3,750 ft2.
667 Appendix D
78. (a) y=ax2+bx +c=ax2+b
ax+c
=ax2+b
ax+b2
4a2+c−b2
4a=ax+b
2a2
+c−b2
4a
(b) If a<0 then yis always less than c−b2
4aexcept when x=−b
2a, so the graph has its high
point there. If a>0 then yis always greater than c−b2
4aexcept when x=−b
2a, so the
graph has its low point there.
79. (a) The parabola y=2x
2+5x−1 opens upward and has x-intercepts of x=(−5±√
33)/4, so
2x2+5x−1<0if(−5−√
33)/4<x<(−5+√
33)/4.
(b) The parabola y=x2−2x+ 3 opens upward and has no x-intercepts, so x2−2x+3>0if
−∞ <x<+∞.
80. (a) The parabola y=x2+x−1 opens upward and has x-intercepts of x=(−1±√
5)/2, so
x2+x−1>0ifx<(−1−√
5)/2orx>(−1+√
5)/2.
(b) The parabola y=x2−4x+ 6 opens upward and has no x-intercepts, so x2−4x+6<0 has
no solution.
81. (a) The t-coordinate of the vertex is t=−40/[(2)(−16)] = 5/4, so the maximum height is
s= 5 + 40(5/4) −16(5/4)2= 30 ft.
(b) s=5+40t−16t2=0ift≈2.6s
(c) s=5+40t−16t2>12 if 16t2−40t+7<0, which is true if (5−3√2)/4<t<(5+3
√2)/4.
The length of this interval is (5 + 3√2)/4−(5 −3√2)/4=3
√
2/2≈2.1s.
82. x+3−x
2>0, x2−x−3<0, (1 −√13)/2<x<(1+√13)/2
668
APPENDIX E
Trigonometry Review
EXERCISE SET E
1. (a) 5π/12 (b) 13π/6(c) π/9(d) 23π/30
2. (a) 7π/3(b) π/12 (c) 5π/4(d) 11π/12
3. (a) 12◦(b) (270/π)◦(c) 288◦(d) 540◦
4. (a) 18◦(b) (360/π)◦(c) 72◦(d) 210◦
5. sin θcos θtan θcsc θsec θcot θ
(a) √21/5 2/5√21/2 5/√21 5/2 2/√21
(b) 3/4√7/4 3/√7 4/3 4/√7√7/3
(c) 3/√10 1/√10 3 √10/3√10 1/3
6. sin θcos θtan θcsc θsec θcot θ
(a) 1/√2 1/√2 1 √2√2 1
(b) 3/5 4/5 3/4 5/3 5/4 4/3
(c) 1/4√15/4 1/√15 4 4/√15 √15
7. sin θ=3/
√
10, cos θ=1/
√
10 8. sin θ=√5/3, tan θ=√5/2
9. tan θ=√21/2, csc θ=5/
√
21 10. cot θ=√15, sec θ=4/
√
15
11. Let xbe the length of the side adjacent to θ, then cos θ=x/6=0.3, x=1.8.
12. Let xbe the length of the hypotenuse, then sinθ=2.4/x =0.8, x=2.4/0.8=3.
13. θsin θcos θtan θcsc θsec θcot θ
(a) 225◦−1/√2−1/√2 1 −√2−√2 1
(b) −210◦1/2−√3/2−1/√32−2/√3−√3
(c) 5π/3−√3/2 1/2−√3−2/√3 2 −1/√3
(d) −3π/2 1 0 — 1 — 0
14. θsin θcos θtan θcsc θsec θcot θ
(a) 330◦−1/2√3/2−1/√3−2 2/√3−√3
(b) −120◦−√3/2−1/2√3−2/√3−2 1/√3
(c) 9π/4 1/√2 1/√2 1 √2√2 1
(d) −3π0−1 0 — −1 —
669 Appendix E
15. sin θcos θtan θcsc θsec θcot θ
(a) 4/5 3/5 4/3 5/4 5/3 3/4
(b) −4/5 3/5−4/3−5/4 5/3−3/4
(c) 1/2−√3/2−1/√3 2 −2√3−√3
(d) −1/2√3/2−1/√3−2 2/√3−√3
(e) 1/√21/√21√2√21
(f) 1/√2−1/√2−1√2−√2−1
16. sin θcos θtan θcsc θsec θcot θ
(a) 1/4√15/4 1/√15 4 4/√15 √15
(b) 1/4−√15/4−1/√15 4 −4/√15 −√15
(c) 3/√10 1/√10 3 √10/3√10 1/3
(d) −3/√10 −1/√10 3 −√10/3−√10 1/3
(e) √21/5−2/5−√21/2 5/√21 −5/2−2/√21
(f) −√21/5−2/5√21/2−5/√21 −5/2 2/√21
17. (a) x= 3 sin 25◦≈1.2679 (b) x=3/tan(2π/9) ≈3.5753
18. (a) x=2/sin 20◦≈5.8476 (b) x=3/cos(3π/11) ≈4.5811
19. sin θcos θtan θcsc θsec θcot θ
(a) a/3√9−a2/3a/√9−a23/a 3/√9−a2√9−a2/a
(b) a/√a2+25 5/
√
a
2+25 a/5√a2+25/a √a2+25/5 5/a
(c) √a2−1/a 1/a √a2−1a/√a2−1a1/√a2−1
20. (a) θ=3π/4±2nπ and θ=5π/4±2nπ,n=0,1,2,...
(b) θ=5π/4±2nπ and θ=7π/4±2nπ,n=0,1,2,...
21. (a) θ=3π/4±nπ,n=0,1,2,...
(b) θ=π/3±2nπ and θ=5π/3±2nπ,n=0,1,2,...
22. (a) θ=7π/6±2nπ and θ=11π/6±2nπ,n=0,1,2,...
(b) θ=π/3±nπ,n=0,1,2,...
23. (a) θ=π/6±nπ,n=0,1,2,...
(b) θ=4π/3±2nπ and θ=5π/3±2nπ,n=0,1,2,...
24. (a) θ=3π/2±nπ,n=0,1,2,... (b) θ=π±2nπ,n=0,1,2,...
25. (a) θ=3π/4±nπ,n=0,1,2,... (b) θ=π/6±nπ,n=0,1,2,...
26. (a) θ=2π/3±2nπ and θ=4π/3±2nπ,n=0,1,2,...
(b) θ=7π/6±2nπ and θ=11π/6±2nπ,n=0,1,2,...
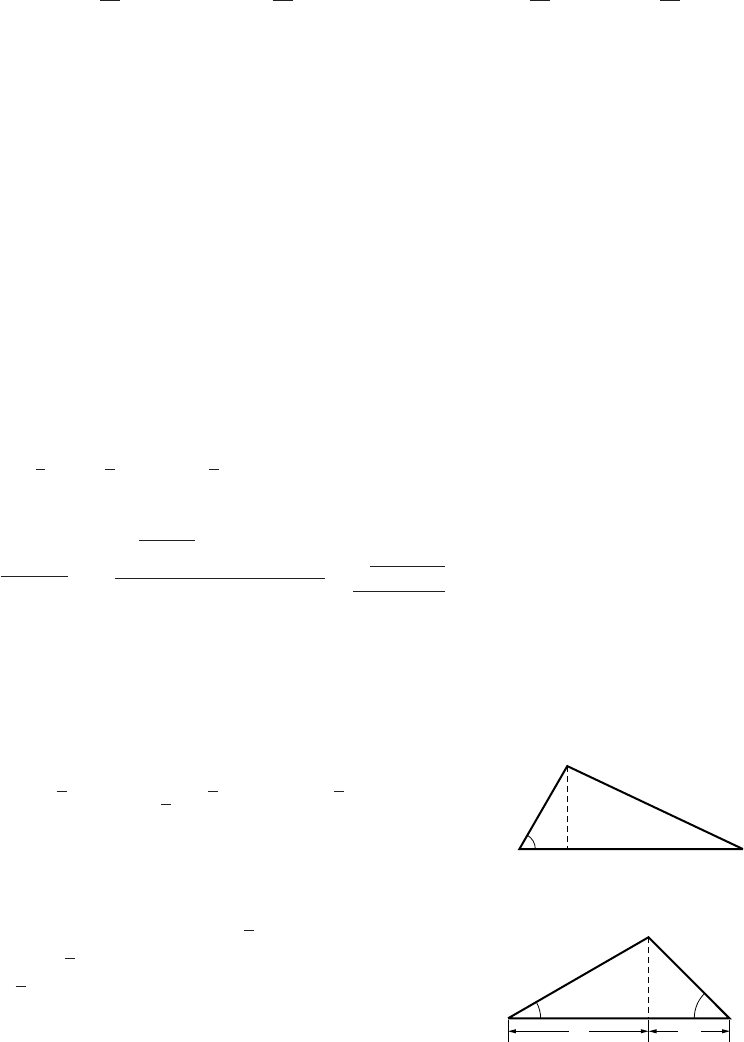
Exercise Set E 670
27. (a) θ=π/3±2nπ and θ=2π/3±2nπ,n=0,1,2,...
(b) θ=π/6±2nπ and θ=11π/6±2nπ,n=0,1,2,...
28. sin θ=−3/5, cos θ=−4/5, tan θ=3/4, csc θ=−5/3, sec θ=−5/4, cot θ=4/3
29. sin θ=2/5, cos θ=−√21/5, tan θ=−2/√21, csc θ=5/2, sec θ=−5/√21, cot θ=−√21/2
30. (a) θ=π/2±2nπ,n=0,1,2,... (b) θ=±2nπ,n=0,1,2,...
(c) θ=π/4±nπ,n=0,1,2,... (d) θ=π/2±2nπ,n=0,1,2,...
(e) θ=±2nπ,n=0,1,2,... (f) θ=π/4±nπ,n=0,1,2,...
31. (a) θ=±nπ,n=0,1,2,... (b) θ=π/2±nπ,n=0,1,2,...
(c) θ=±nπ,n=0,1,2,... (d) θ=±nπ,n=0,1,2,...
(e) θ=π/2±nπ,n=0,1,2,... (f) θ=±nπ,n=0,1,2,...
32. Construct a right triangle with one angle equal to 17◦, measure the lengths of the sides and
hypotenuse and use formula (6) for sin θand cos θto approximate sin 17◦and cos 17◦.
33. (a) s=rθ =4(π/6)=2π/3cm (b) s=rθ = 4(5π/6)=10π/3cm
34. r=s/θ =7/(π/3)=21/π 35. θ=s/r =2/5
36. θ=s/r so A=1
2r2θ=1
2r2(s/r)=1
2
rs
37. (a) 2πr =R(2π−θ), r=2π−θ
2πR
(b) h=pR2−r2=pR2−(2π−θ)2R2/(4π2)=√
4πθ −θ2
2πR
38. The circumference of the circular base is 2πr. When cut and flattened, the cone becomes a circular
sector of radius L.Ifθis the central angle that subtends the arc of length 2πr, then θ=(2πr)/L
so the area Sof the sector is S=(1/2)L2(2πr/L)=πrL which is the lateral surface area of the
cone.
39. Let hbe the altitude as shown in the figure, then
h= 3 sin 60◦=3
√
3/2soA=1
2
(3√3/2)(7) = 21√3/4.
60°
h
3
7
40. Draw the perpendicular from vertex Cas shown in the figure, then
h= 9 sin 30◦=9/2, a=h/ sin 45◦=9
√
2/2,
c1= 9 cos 30◦=9
√
3/2, c2=acos 45◦=9/2,
c1+c2=9(
√
3+1)/2,angle C= 180◦−(30◦+45
◦
) = 105◦
A
C
30°45°
h
9a
c1c2B
41. Let xbe the distance above the ground, then x= 10 sin 67◦≈9.2 ft.
42. Let xbe the height of the building, then x= 120 tan 76◦≈481 ft.
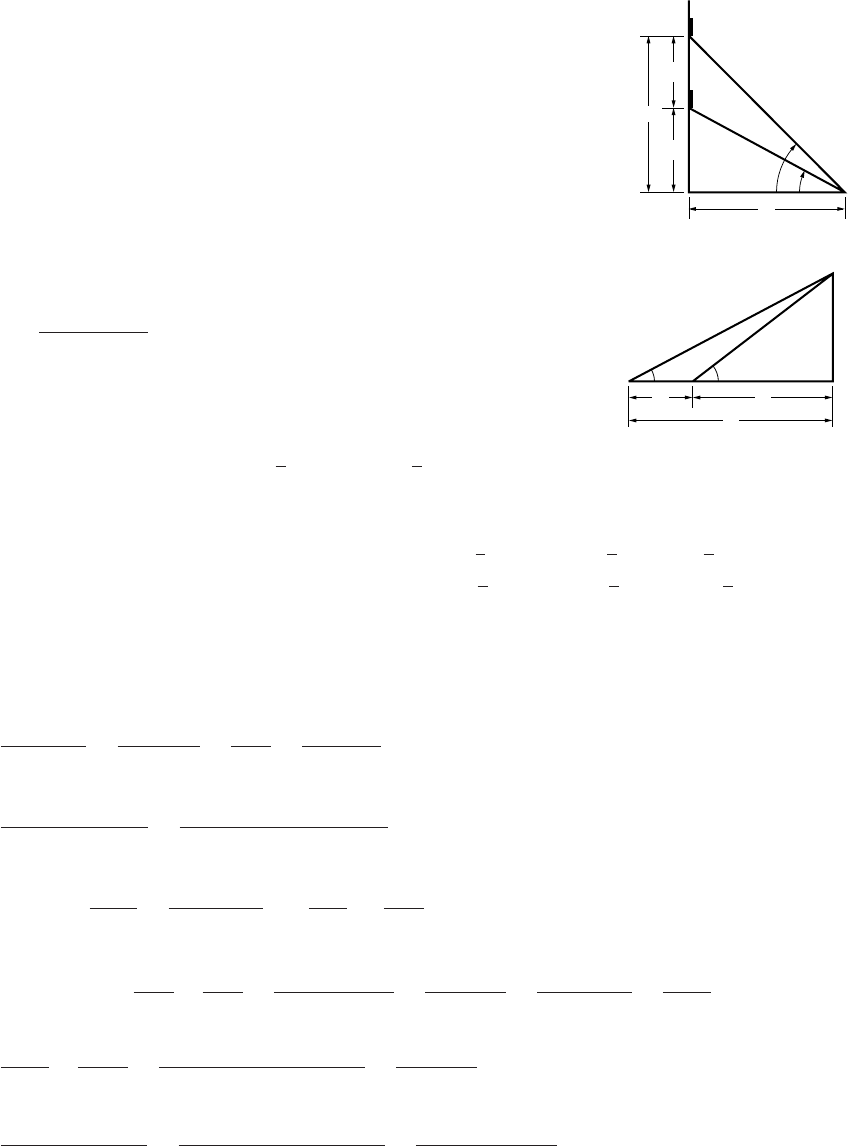
671 Appendix E
43. From the figure, h=x−ybut x=dtan β,
y=dtan αso h=d(tan β−tan α).
x
h
y
α
β
d
44. From the figure, d=x−ybut x=hcot α,
y=hcot βso d=h(cot α−cot β),
h=d
cot α−cot β.
d
x
y
h
αβ
45. (a) sin 2θ= 2 sin θcos θ=2(
√
5/3)(2/3)=4
√
5/9
(b) cos 2θ= 2 cos2θ−1 = 2(2/3)2−1=−1/9
46. (a) sin(α−β) = sin αcos β−cos αsin β=(3/5)(1/√5) −(4/5)(2/√5) = −1/√5
(b) cos(α+β) = cos αcos β−sin αsin β=(4/5)(1/√5) −(3/5)(2/√5) = −2/(5√5)
47. sin 3θ= sin(2θ+θ) = sin 2θcos θ+ cos 2θsin θ= (2 sin θcos θ) cos θ+ (cos2θ−sin2θ) sin θ
= 2 sin θcos2θ+ sin θcos2θ−sin3θ= 3 sin θcos2θ−sin3θ; similarly, cos 3θ= cos3θ−3 sin2θcos θ
48. cos θsec θ
1 + tan2θ=cos θsec θ
sec2θ=cos θ
sec θ=cos θ
(1/cos θ)= cos2θ
49. cos θtan θ+ sin θ
tan θ=cos θ(sin θ/ cos θ) + sin θ
sin θ/ cos θ= 2 cos θ
50. 2 csc 2θ=2
sin 2θ=2
2 sin θcos θ=1
sin θ 1
cos θ= csc θsec θ
51. tan θ+ cot θ=sin θ
cos θ+cos θ
sin θ=sin2θ+ cos2θ
sin θcos θ=1
sin θcos θ=2
2 sin θcos θ=2
sin 2θ= 2 csc 2θ
52. sin 2θ
sin θ−cos 2θ
cos θ=sin 2θcos θ−cos 2θsin θ
sin θcos θ=sin θ
sin θcos θ= sec θ
53. sin θ+ cos 2θ−1
cos θ−sin 2θ=sin θ+(1−2 sin2θ)−1
cos θ−2 sin θcos θ=sin θ(1 −2 sin θ)
cos θ(1 −2 sin θ)= tan θ
54. Using (47), 2 sin 2θcos θ= 2(1/2)(sin θ+ sin 3θ) = sin θ+ sin 3θ
55. Using (47), 2 cos 2θsin θ= 2(1/2)[sin(−θ) + sin 3θ] = sin 3θ−sin θ
Exercise Set E 672
56. tan(θ/2) = sin(θ/2)
cos(θ/2) =2 sin2(θ/2)
2 sin(θ/2) cos(θ/2) =1−cos θ
sin θ
57. tan(θ/2) = sin(θ/2)
cos(θ/2) =2 sin(θ/2) cos(θ/2)
2 cos2(θ/2) =sin θ
1 + cos θ
58. From (52), cos(π/3+θ) + cos(π/3−θ) = 2cos(π/3) cos θ= 2(1/2) cos θ= cos θ
59. From the figure, area = 1
2hc but h=bsin A
so area = 1
2bc sin A. The formulas
area = 1
2ac sin Band area = 1
2ab sin C
follow by drawing altitudes from vertices Band C, respectively. A
C
ha
c
b
B
60. From right triangles ADC and BDC,
h1=bsin A=asin Bso a/ sin A=b/ sin B.
From right triangles AEB and CEB,
h2=csin A=asin Cso a/ sin A=c/ sin C
thus a/ sin A=b/ sin B=c/ sin C.
A
E
B
C
D
h1
h2
a
c
b
61. (a) sin(π/2+θ) = sin(π/2) cos θ+ cos(π/2) sin θ= (1) cos θ+ (0) sin θ= cos θ
(b) cos(π/2+θ) = cos(π/2) cos θ−sin(π/2) sin θ= (0) cos θ−(1) sin θ=−sin θ
(c) sin(3π/2−θ) = sin(3π/2) cos θ−cos(3π/2) sin θ=(−1) cos θ−(0) sin θ=−cos θ
(d) cos(3π/2+θ) = cos(3π/2) cos θ−sin(3π/2) sin θ= (0) cos θ−(−1) sin θ= sin θ
62. tan(α+β)= sin(α+β)
cos(α+β)=sin αcos β+ cos αsin β
cos αcos β−sin αsin β, divide numerator and denominator by
cos αcos βand use tan α=sin α
cos αand tan β=sin β
cos βto get (38);
tan(α−β) = tan(α+(−β)) = tan α+ tan(−β)
1−tan αtan(−β)=tan α−tan β
1 + tan αtan βbecause
tan(−β)=−tan β.
63. (a) Add (34) and (36) to get sin(α−β) + sin(α+β)=2sinαcos βso
sin αcos β=(1/2)[sin(α−β) + sin(α+β)].
(b) Subtract (35) from (37).
(c) Add (35) and (37).
64. (a) From (47), sin A+B
2cos A−B
2=1
2(sin B+ sin A)so
sin A+ sin B= 2 sin A+B
2cos A−B
2.
(b) Use (49) (c) Use (48)

673 Appendix E
65. sin α+ sin(−β)=2sinα−β
2cos α+β
2, but sin(−β)=−sin βso
sin α−sin β= 2 cos α+β
2sin α−β
2.
66. (a) From (34), Csin(α+φ)=Csin αcos φ+Ccos αsin φso Ccos φ= 3 and Csin φ=5,
square and add to get C2(cos2φ+sin2φ) = 9+ 25, C2= 34. If C=√34 then cos φ=3/
√
34
and sin φ=5/
√
34 so φis the first-quadrant angle for which tanφ=5/3.
3 sin α+ 5 cos α=√34 sin(α+φ).
(b) Follow the procedure of part (a) to get Ccos φ=Aand Csin φ=B,C=√A2+B2,
tan φ=B/A where the quadrant in which φlies is determined by the signs of Aand Bbecause
cos φ=A/C and sin φ=B/C,soAsin α+Bcos α=√A2+B2sin(α+φ).
67. Consider the triangle having a,b, and das sides. The angle formed by sides aand bis π−θso
from the law of cosines, d2=a2+b2−2ab cos(π−θ)=a
2+b
2+2ab cos θ,d=√a2+b2+2ab cos θ.

674
APPENDIX F
Solving Polynomial Equations
EXERCISE SET F
1. (a) q(x)=x
2+4x+2,r(x)=−11x+6 (b) q(x)=2x
2+4,r(x)=9
(c) q(x)=x
3−x
2+2x−2,r(x)=2x+1
2. (a) q(x)=2x
2−x+2,r(x)=5x+5 (b) q(x)=x
3+3x
2−x+2,r(x)=3x−1
(c) q(x)=5x
3−5,r(x)=4x
2+10
3. (a) q(x)=3x
2+6x+8,r(x)=15 (b) q(x)=x
3−5x
2+20x−100,r(x) = 504
(c) q(x)=x
4+x
3+x
2+x+1,r(x)=0
4. (a) q(x)=2x
2+x−1,r(x)=0 (b) q(x)=2x
3−5x
2+3x−39,r(x) = 147
(c) q(x)=x
6+x
5+x
4+x
3+x
2+x+1,r(x)=2
5. x0 1 −3 7
p(x)−4−3 101 5001
6. x1−1 3 −3 7 −7 21 −21
p(x)−24 −12 12 0 420 −168 10416 −7812
7. (a) q(x)=x
2+6x+13,r =20 (b) q(x)=x
2+3x−2,r =−4
8. (a) q(x)=x
4−x
3+x
2−x+1,r =−2(b) q(x)=x
4+x
3+x
2+x+1,r =0
9. Assume r=a/b a and bintegers with a>0:
(a) bdivides 1, b=±1; adivides 24, a=1,2,3,4,6,8,12,24;
the possible candidates are {±1,±2,±3,±4,±6,±8,±12,±24}
(b) bdivides 3 so b=±1,±3; adivides −10 so a=1,2,5,10;
the possible candidates are {±1,±2,±5,±10,±1/3,±2/3,±5/3,±10/3}
(c) bdivides 1 so b=±1; adivides 17 so a=1,17;
the possible candidates are {±1,±17}
10. An integer zero cdivides −21, so c=±1,±3,±7,±21 are the only possibilities; substitution of
these candidates shows that the integer zeros are −7,−1,3
11. (x+ 1)(x−1)(x−2) 12. (x+ 2)(3x+ 1)(x−2)
13. (x+3)
3
(x+1) 14. 2x4+x3−19x2+9
15. (x+ 3)(x+ 2)(x+1)
2
(x−3) 17. −3 is the only real root.
18. x=−3/2 is the only real root. 19. x=−2,−2/3 are the only real roots.

675 Appendix F
20. −2,−1,1/2,321. −2,2,3 are the only real roots.
23. If x−1 is a factor then p(1)=0,sok
2−7k+10=0,k
2−7k+10=(k−2)(k−5), so k=2,5.
24. (−3)7=−2187, so −3 is a root and thus by Theorem F.4(a), x+ 3 is a factor of x7+ 2187.
25. If the side of the cube is xthen x2(x−3) = 196; the only real root of this equation is x= 7 cm.
26. (a) Try to solve a
b>a
b3+ 1. The polynomial p(x)=x
3−x+ 1 has only one real root
c≈−1.325, and p(0) = 1 so p(x)>0 for all x>c; hence there is no positive rational
solution of a
b>a
b3+1.
(b) From part (a), any real x<cis a solution.
27. Use the Factor Theorem with xas the variable and yas the constant c.
(a) For any positive integer nthe polynomial xn−ynhas x=yas a root.
(b) For any positive even integer nthe polynomial xn−ynhas x=−yas a root.
(c) For any positive odd integer nthe polynomial xn+ynhas x=−yas a root.