Anton_FM_ELA W/A Howard Anton, Chris Rorres Elementary Linear Algebra With Applications, Student Solutions Manual Wiley%2
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 386 [warning: Documents this large are best viewed by clicking the View PDF Link!]

STUDENT SOLUTIONS MANUAL
TO ACCOMPANY
Elementary Linear Algebra
with Applications
NINTH EDITION
Howard Anton
Chris Rorres
Drexel University
Prepared by
Christine Black
Seattle University
Blaise DeSesa
Kutztown University
Molly Gregas
Duke University
Elizabeth M. Grobe
Charles A. Grobe, Jr.
Bowdoin College
JOHN WILEY & SONS, INC.

Cover Photo: ©John Marshall/Stone/Getty Images
Copyright © 2005 John Wiley & Sons, Inc. All rights reserved.
No part of this publication may be reproduced, stored in a retrieval system or
transmitted in any form or by any means, electronic, mechanical,
photocopying, recording, scanning, or otherwise, except as permitted under
Sections 107 or 108 of the 1976 United States Copyright Act, without either
the prior written permission of the Publisher, or authorization through payment
of the appropriate per-copy fee to the Copyright Clearance Center, Inc., 222
Rosewood Drive, Danvers, MA 01923, or on the web at www.copyright.com.
Requests to the Publisher for permission should be addressed to the
Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken,
NJ 07030-5774, (201) 748-6011, fax (201) 748-6008, or online at
http://www.wiley.com/go/permissions.
To order books or for customer service call 1-800-CALL-WILEY (225-5945).
ISBN-13 978- 0-471-43329-3
ISBN-10 0-471-43329-2
Printed in the United States of America
10 9 8 7 6 5 4 3 2 1
Printed and bound by Bind-Rite Graphics, Inc.

TABLE OF CONTENTS
Chapter 1
Exercise Set 1.1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
Exercise Set 1.2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Exercise Set 1.3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
Exercise Set 1.4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
Exercise Set 1.5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
Exercise Set 1.6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
Exercise Set 1.7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
Supplementary Exercises 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
Chapter 2
Exercise Set 2.1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
Exercise Set 2.2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
Exercise Set 2.3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
Exercise Set 2.4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
Supplementary Exercises 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
Technology Exercises 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
Chapter 3
Exercise Set 3.1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
Exercise Set 3.2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
Exercise Set 3.3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
Exercise Set 3.4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
Exercise Set 3.5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
Chapter 4
Exercise Set 4.1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
Exercise Set 4.2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
Exercise Set 4.3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119
Exercise Set 4.4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 125
Chapter 5
Exercise Set 5.1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
Exercise Set 5.2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135
Exercise Set 5.3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 141
Exercise Set 5.4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145
Exercise Set 5.5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 151
Exercise Set 5.6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155
Supplementary Exercises 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157

Chapter 6
Exercise Set 6.1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 159
Exercise Set 6.2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 165
Exercise Set 6.3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171
Exercise Set 6.4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 179
Exercise Set 6.5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 185
Exercise Set 6.6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 189
Supplementary Exercises 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191
Chapter 7
Exercise Set 7.1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 195
Exercise Set 7.2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203
Exercise Set 7.3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 207
Supplementary Exercises 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 209
Chapter 8
Exercise Set 8.1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 215
Exercise Set 8.2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 219
Exercise Set 8.3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 223
Exercise Set 8.4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 227
Exercise Set 8.5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231
Exercise Set 8.6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 239
Supplementary Exercises 8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 243
Chapter 9
Exercise Set 9.1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 251
Exercise Set 9.2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 261
Exercise Set 9.3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 265
Exercise Set 9.4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 267
Exercise Set 9.5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 271
Exercise Set 9.6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 275
Exercise Set 9.7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 281
Exercise Set 9.8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 287
Exercise Set 9.9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 291
Chapter 10
Exercise Set 10.1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 299
Exercise Set 10.2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 303
Exercise Set 10.3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 309
Exercise Set 10.4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 315
Exercise Set 10.5. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 321
Exercise Set 10.6. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 329
Supplementary Exercises 10 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 339

Chapter 11
Exercise Set 11.1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 343
Exercise Set 11.2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 347
Exercise Set 11.3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 351
Exercise Set 11.4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 355
Exercise Set 11.5. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 357
Exercise Set 11.6. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 365
Exercise Set 11.7. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 369
Exercise Set 11.8. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 373
Exercise Set 11.9. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 375
Exercise Set 11.10. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 379
Exercise Set 11.11. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 381
Exercise Set 11.12. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 387
Exercise Set 11.13. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 391
Exercise Set 11.14. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 401
Exercise Set 11.15. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 405
Exercise Set 11.16. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 417
Exercise Set 11.17. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 425
Exercise Set 11.18. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 429
Exercise Set 11.19. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 431
Exercise Set 11.20. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 433
Exercise Set 11.21. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 435


EXERCISE SET 1.1
1. (b) Not linear because of the term x1x3.
(d) Not linear because of the term x–2
1.
(e) Not linear because of the term x3/5
1.
7. Since each of the three given points must satisfy the equation of the curve, we have the
system of equations
ax2
1+ bx1+ c= y1
ax2
2+ bx2+ c= y2
ax2
3+ bx3+ c= y3
If we consider this to be a system of equations in the three unknowns a, b, and c, the
augmented matrix is clearly the one given in the exercise.
9. The solutions of x1+ kx2= care x1= c– kt, x2= twhere tis any real number. If these
satisfy x1+ x2= d, then c– kt + t= d, or (– k)t= d– cfor all real numbers t. In
particular, if t= 0, then d= c, and if t= 1, then = k.
11. If x– y= 3, then 2x– 2y= 6. Therefore, the equations are consistent if and only if k= 6;
that is, there are no solutions if k≠6. If k= 6, then the equations represent the same line,
in which case, there are infinitely many solutions. Since this covers all of the possibilities,
there is never a unique solution.
1


EXERCISE SET 1.2
1. (e) Not in reduced row-echelon form because Property 2 is not satisfied.
(f) Not in reduced row-echelon form because Property 3 is not satisfied.
(g) Not in reduced row-echelon form because Property 4 is not satisfied.
5. (a) The solution is
x3= 5
x2= 2 – 2 x3= –8
x1= 7 – 4 x3+ 3x2= –37
(b) Let x4= t. Then x3= 2 – t. Therefore
x2= 3 + 9t– 4x3= 3 + 9t– 4(2 – t) = –5 + 13t
x1= 6 + 5t– 8x3= 6 + 5t– 8(2 – t) = –10 + 13t
7. (a) In Problem 6(a), we reduced the augmented matrix to the following row-echelon
matrix:
By Row 3, x3= 2. Thus by Row 2, x2= 5x3– 9 = 1. Finally, Row 1 implies that x1= –
x2– 2 x3+ 8 = 3. Hence the solution is
x1= 3
x2= 1
x3= 2
11 28
01 59
00 12
−−
3

(c) According to the solution to Problem 6(c), one row-echelon form of the augmented
matrix is
Row 2 implies that y= 2z. Thus if we let z= s, we have y= 2s. Row 1 implies that x
= –1 + y– 2z+ w. Thus if we let w= t, then x= –1 + 2s– 2s+ tor x= –1 + t. Hence
the solution is
x= –1 + t
y= 2s
z= s
w= t
9. (a) In Problem 8(a), we reduced the augmented matrix of this system to row-echelon
form, obtaining the matrix
Row 3 again yields the equation 0 = 1 and hence the system is inconsistent.
(c) In Problem 8(c), we found that one row-echelon form of the augmented matrix is
Again if we let x2= t, then x1= 3 + 2x2= 3 + 2t.
123
000
000
−
132 1
0134
00 1
−−
/
/
11211
01200
00000
00000
−−−
−
4Exercise Set 1.2

11. (a) From Problem 10(a), a row-echelon form of the augmented matrix is
If we let x3= t, then Row 2 implies that x2= 5 – 27t. Row 1 then implies that x1=
(–6/5)x3+ (2/5)x2= 2 – 12t. Hence the solution is
x1= 2 – 12t
x2= 5 – 27t
x3= t
(c) From Problem 10(c), a row-echelon form of the augmented matrix is
If we let y= t, then Row 3 implies that x= 3 + t. Row 2 then implies that
w= 4 – 2x+ t= –2 – t.
Now let v= s. By Row 1, u= 7/2 – 2s– (1/2)w– (7/2)x= –6 – 2s– 3t. Thus we have
the same solution which we obtained in Problem 10(c).
13. (b) The augmented matrix of the homogeneous system is
This matrix may be reduced to
31110
04140
31110
51110−−
121272 072
00 1 2 1 4
00 0 1 1 3
00 0 0 0 0
−
−
125650
01 275
−
Exercise Set 1.2 5

If we let x3= 4sand x4= t, then Row 2 implies that
4x2= –4t– 4sor x2= –t– s
Now Row 1 implies that
3x1= –x2– 4s– t= t+ s– 4s– t= –3sor x1= –s
Therefore the solution is
x1= –s
x2= –(t+ s)
x3= 4s
x4= t
15. (a) The augmented matrix of this system is
Its reduced row-echelon form is
Hence the solution is
I1= –1
I2= 0
I3= 1
I4= 2
1000 1
0100 0
0010 1
0001 2
−
21349
102711
33158
214410
−
−
−
6Exercise Set 1.2

(b) The reduced row-echelon form of the augmented matrix is
If we let Z2= sand Z5= t, then we obtain the solution
Z1= –s– t
Z2= s
Z3= –t
Z4= 0
Z5= t
17. The Gauss-Jordan process will reduce this system to the equations
x+ 2y– 3z= 4
y– 2z= 10/7
(a2– 16)z= a– 4
If a= 4, then the last equation becomes 0 = 0, and hence there will be infinitely many
solutions—for instance, z= t, y= 2 t+ 10
—
7 , x= –2 (2t+ 10
—
7 ) + 3t+ 4. If a= – 4, then the last
equation becomes 0 = –8, and so the system will have no solutions. Any other value of awill
yield a unique solution for zand hence also for yand x.
19. One possibility is
13
27
13
01
→
110010
001010
000100
000000
Exercise Set 1.2 7
Another possibility is
21. If we treat the given system as linear in the variables sin α, cos β, and tan γ, then the
augmented matrix is
This reduces to
so that the solution (for α, β, γbetween 0 and 2 π) is
sin α= 0 ⇒α= 0, π, 2π
cos β= 0 ⇒β= π/2, 3π/2
tan γ= 0 ⇒γ= 0, π, 2π
That is, there are 3•2•3 = 18 possible triples α, β, γwhich satisfy the system of equations.
23. If λ= 2, the system becomes
– x2= 0
2x1– 3x2+ x3= 0
–2x1+ 2x2– x3= 0
Thus x2= 0 and the third equation becomes –1 times the second. If we let x1= t, then x3
= –2t.
10 0 0
010 0
00 1 0
1230
2530
1550−−
13
27
27
13
172
13
172
→
→
→001
8Exercise Set 1.2
25. Using the given points, we obtain the equations
d= 10
a+ b+ c+ d= 7
27a+ 9b+ 3c+ d= –11
64a+ 16b+ 4c+ d= –14
If we solve this system, we find that a= 1, b= –6, c= 2, and d= 10.
27. (a) If a= 0, then the reduction can be accomplished as follows:
If a= 0, then b≠0 and c≠0, so the reduction can be carried out as follows:
Where did you use the fact that ad – bc ≠0? (This proof uses it twice.)
0
0
1
0
1
01
b
cd
cd
b
d
c
b
d
c
→
→
→
→
10
01
ab
cd
b
a
cd
b
a
ad bc
a
→
→−
11
0
→
→
1
01
10
01
b
a
Exercise Set 1.2 9

29. There are eight possibilities. They are
(a)
(b)
1000
01 00
0010
0001
100
01 0
001
,
p
q
rr
p
q
0000
10 0
01 0
0001
000 0
,
,
100
0010
00 01
00 00
p
,
001 00
0010
0001
0000
10
01
00
,
pq
rs
000
000 0
10
001
00 00
00 00
,
pq
r
,,
10
00 01
00 00
00 00
pq 01 0
001
0000
0000
01 0
0001
00
p
q
p
,
000
000 0
0010
0001
0000
0000
,
,
1
00 00
00 00
00 00
pqr
,,
,
01
000 0
000 0
000 0
001
0000
0
pq p
0000
0000
0001
0000
0000
0000
,
,and
0000
0000
0000
0000
100
01 0
001
10
01
000
,,
p
q
110
001
00 0
01 0
001
000
1
p
,
,
ppq p
00 0
00 0
01
000
000
00
,,
11
000
000
,,,where are any realpq nnumbers,
and
000
000
000
10 Exercise Set 1.2

31. (a) False. The reduced row-echelon form of a matrix is unique, as stated in the remark in
this section.
(b) True. The row-echelon form of a matrix is not unique, as shown in the following
example:
but
(c) False. If the reduced row-echelon form of the augmented matrix for a system of 3
equations in 2 unknowns is
then the system has a unique solution. If the augmented matrix of a system of 3
equations in 3 unknowns reduces to
then the system has no solutions.
(d) False. The system can have a solution only if the 3 lines meet in at least one point
which is common to all 3.
1110
0001
0000
10
01
000
a
b
12
13
13
12
13
01
13
01
→
→−
→
12
13
12
01
→
Exercise Set 1.2 11


EXERCISE SET 1.3
1. (c) The matrix AE is 4 ×4. Since Bis 4 ×5, AE + Bis not defined.
(e) The matrix A+ Bis 4 ×5. Since Eis 5 ×4, E(A+ B)is 5 ×5.
(h) Since ATis 5 ×4 and Eis 5 ×4, their sum is also 5 ×4. Thus (AT+ E)Dis 5 ×2.
3. (e) Since 2Bis a 2 ×2 matrix and Cis a 2 ×3 matrix, 2B– Cis not defined.
(g) We have
(j) We have tr(D– 3E) = (1 – 3(6)) + (0 – 3(1)) + (4 – 3(3)) = –25.
5. (b) Since Bis a 2 ×2 matrix and Ais a 3 ×2 matrix, BA is not defined (although AB is).
(d) We have
AB =
−
−
12 3
45
41
=–3
13 7 8
32 5
11 4 10
39 21 24
96−
=
−−−
–−−
−−−
15
33 12 30
–( ) –32 3
152
101
324
DE+= −
+
112 2 6
224
826
−
13

Hence
(e) We have
(f) We have
(j) We have tr(4ET– D) = tr(4E– D) = (4(6) – 1) + (4(1) – 0) + (4(3) – 4) = 35.
7. (a) The first row of Ais
A1= [3 -2 7]
Thus, the first row of AB is
(c) The second column of Bis
B2
2
1
7
=
−
AB
1327 624
0
=[6741 41]
=−
[– ]
113
775
CCT=142
31 5
13
41
25
21 17
=117 35
ABC()=−
=
30
12
11
115 3
6210
33459
11 11 17
71713
−
()AB C =−
3459
11 11 17
71713
14 Exercise Set 1.3

Thus, the second column of AB is
(e) The third row of Ais
A3= [0 4 9]
Thus, the third row of AA is
9. (a) The product yAis the matrix
[y1a11 + y2a21 + …+ ymam1y1a12 + y2a22 + …+ ymam2…
y1a1n+ y2a2n+ …+ ymamn]
We can rewrite this matrix in the form
y1[a11 a12 …a1n] + y2[a21 a22 …a2n] + …+ ym[am1 am2 … amn]
which is, indeed, a linear combination of the row matrices of Awith the scalar
coefficients of y.
(b) Let y= [y1, y2, …, ym]
by 9a, yA
y
y
y
A
A
A
mm
=
1
2
1
2
and = be the rowsAA
A
Am
1
2
mof .A
AA
3049
327
654
049
[]=
−
=[[]24 56 97
AB2
327
654
049
2
1
7
=
−
=
–441
21
67
Exercise Set 1.3 15

Taking transposes of both sides, we have
(yA)T= ATyT= (A1|A2|…|Am)
= (y1A1 | y2A2 | … | ymAm
11. Let fij denote the entry in the ith row and jth column of C(DE). We are asked to find f23. In
order to compute f23, we must calculate the elements in the second row of Cand the third
column of DE. According to Equation (3), we can find the elements in the third column of
DE by computing DE3where E3is the third column of E. That is,
f23 315
152
101
324
3
=−
[] 22
3
19
0
25
=[315]
=182
=
y
y
y
A
A
A
mm
T
1
2
1
2
y
1
ym
16 Exercise Set 1.3

15. (a) By block multiplication,
17. (a) The partitioning of Aand Bmakes them each effectively 2 ×2 matrices, so block
multiplication might be possible. However, if
then the products A11B11, A12B21, A11B12, A12B22, A21B11, A22B21, A21B12, and A22B22 are
all undefined. If even one of these is undefined, block multiplication is impossible.
21. (b) If i> j, then the entry aij has row number larger than column number; that is, it lies
below the matrix diagonal. Thus [aij] has all zero elements below the diagonal.
(d) If |i– j|> 1, then either i– j> 1 or i– j< –1; that is, either i> j+ 1 or j> i+ 1. The
first of these inequalities says that the entry aij lies below the diagonal and also below
the “subdiagonal“ consisting of all entries immediately below the diagonal ones. The
second inequality says that the entry aij lies above the diagonal and also above the
entries immediately above the diagonal ones. Thus we have
[a
aa
aaa
aaa
ij ]=
11 12
21 22 23
32 33 34
0000
000
000
000 0
000
0000
43 44 45
54 55 56
65 66
aaa
aaa
aa
AAA
AA BBB
B
=
=
11 12
21 22
11 12
21
and BB22
AB =
−
−
−
+
12
03
21
35
15
42
−
−
−
71
03
12
03
4
2
+
−
15
42
5
3
15 21
35 61 71
03 15
−
+
−
+
−
4
261 5
3
=
−
−
+
89
915
714
28 2
−
+−
−
+
0
6
10
14
13 26 442 3 14 27
123
−
+
=
−−110
37 13 8
29 23 41
−
Exercise Set 1.3 17
23.
27. The only solution to this system of equations is, by inspection,
A=−
110
110
000
xf (x)
x
x
x
f (x) =
f (x)
f (x)
)= 2
1
fx
)= 2
0
fx
)= 7
4
fx
)= 0
–2
fx
fx
x
xx
x
1
2
1
2
=2
+
x=
1
1
x=
2
0
x=
4
3
x=−
2
2
(
(
(
(
18 Exercise Set 1.3
(a)
(b)
(c)
(d)

29. (a) Let B= . Then B2= Aimplies that
(*)
a2+ bc = 2 ab + bd = 2
ac + cd = 2 bc + d2= 2
One might note that a= b= c= d= 1 and a= b= c= d= –1 satisfy (*). Solving the
first and last of the above equations simultaneously yields a2= d2. Thus a= ±d. Solving
the remaining 2 equations yields c(a+ d) = b(a+ d) = 2. Therefore a≠–dand aand
dcannot both be zero. Hence we have a= d≠0, so that ac = ab = 1, or b= c= 1/a.
The first equation in (*) then becomes a2+ 1/a2= 2 or a4– 2a2+ 1 = 0. Thus a= ±1.
That is,
and
are the only square roots of A.
(b) Using the reasoning and the notation of Part (a), show that either a= –dor b= c= 0.
If a= –d, then a2+ bc = 5 and bc + a2= 9. This is impossible, so we have b= c= 0.
This implies that a2= 5 and d2= 9. Thus
are the 4 square roots of A.
Note that if Awere , say, then B= would be a square root of Afor
every nonzero real number rand there would be infinitely many other square roots as well.
(c) By an argument similar to the above, show that if, for instance,
A=and B=
where BB = A, then either a= –dor b= c= 0. Each of these alternatives leads to a
contradiction. Why?
ab
cd
−
10
01
1
41
r
r−
50
05
50
03
50
03
50
03
−
−
−
−
50
03
−−
−−
11
11
11
11
ab
cd
Exercise Set 1.3 19

31. (a) True. If Ais an m×nmatrix, then ATis n×m. Thus AATis m×mand AT Ais n×n.
Since the trace is defined for every square matrix, the result follows.
(b) True. Partition Ainto its row matrices, so that
A=and AT=
Then
Since each of the rows riis a 1 ×nmatrix, each rT
iis an n×1 matrix, and therefore
each matrix rirT
jis a 1 ×1 matrix. Hence
tr(AAT) = r1rT
1+ r2rT
2+ …+ rmrT
m
Note that since rirT
iis just the sum of the squares of the entries in the ith row of A, r1
rT
1+ r2rT
2+ …+ rmrT
mis the sum of the squares of all of the entries of A.
A similar argument works for ATA, and since the sum of the squares of the entries of AT
is the same as the sum of the squares of the entries of A, the result follows.
31. (c) False. For instance, let A=and B= .
(d) True. Every entry in the first row of AB is the matrix product of the first row of Awith
a column of B. If the first row of Ahas all zeros, then this product is zero.
11
11
01
01
AA
rr rr rr
rr rr rr
T
TT
m
T
TT
m
T
=
⋅⋅⋅
⋅⋅⋅
11 12 1
21 22 2
rr rr rr
m
T
m
T
mm
T
12
⋅⋅⋅
rr r
TT
m
T
12
⋅⋅⋅
r
r
rm
1
2
20 Exercise Set 1.3

EXERCISE SET 1.4
1. (a) We have
Hence,
On the other hand,
Hence,
ABC++=
−
−
+()
21
04
21
3
5
4
8852
186
7215
10 6 1
1121
−−
−
=
−
11
5119−
BC+=
−−
−
852
186
7215
=
−
−
10 6 1
11211
5119
()AB C++=
−−
−
+
10 4
05
26
2
7
10
0−−
23
174
359
A+ B=
10 4 2
057
2610
−−
−
21

1. (c) Since a+ b= –3, we have
Also
3. (b) Since
and
the two matrices are equal.
AB
TT
+=
−
−
−
+
20 2
14 1
35 4
880 4
31 7
52 6
10 0 2
45 6−−
−
=− −
−−
2710
()AB
T
T
+=
−−
−
=
10 4 2
057
2610
10 0 2
−−−
−
45 6
2710
aC bC+=
−
+
0812
42816
12 20 36
014−−
−− −
−−−
=
−
−−
21
74928
21 35 63
06 9
321−−
−− −
12
91527
()()abC+=−
−
3
23
74
59
0
1
3
==
−
−− −
−− −
06 9
321 12
915 27
22 Exercise Set 1.4

3. (d) Since
and
the two matrices are equal.
5. (b)
7. (b)
Thus,
A=
27 1
17 37
77 37
12
27
13
11
1
AA(( ) )==
−
−
=
−− −
We are given that Th() .737
12
1
A−=−
−
eerefore
()BT
T
−=−
=
11
20
43
42
1
20
43
42
1
20
44
32−
=−
T
()BT−−
=−
=−
1
1
24
34
1
20
44
32
BA
TT
=− −
−
−80 4
31 7
52 6
20 2
−−
=−14 1
35 4
28 20 0
228 31 21
63836
−−
()AB T
T
=
−
−
−
=
28 28 6
20 31 38
02136
28 20 0
28 31 21
63836
−−−
Exercise Set 1.4 23

7. (d)
9. (b) We have
11. Call the matrix A. By Theorem 1.4.5,
since cos2
θ
+ sin2
θ
= 1.
=−
cos sin
sin cos
θθ
θθ
A−=+
−
1
22
1
cos sin
cos sin
sin cos
θθ
θθ
θθ
=
20 7
14 6
=
−
+
22 8
16 6
31
21
10
01
=
−
+
211 4
83
31
21
10
01
pA()=
−
+231
21
31
21 110
01
2
2
5
13
2
13
4
13
1
13
10
01
A=−
−
=−
−
,
18
13
2
13
4
13
12
13
so that A.=−
−
9
13
1
13
2
13
6
13
If then() ,IA I+=
−
+
−
212
45
122 12
45
5
13
2
13
4
13
1
13
1
A=−
=−
−
.Hence
24 Exercise Set 1.4

13. If a11a22 …ann ≠0, then aii ≠0, and hence 1/aii is defined for i= 1,2, . . ., n. It is now easy
to verify that
15. Let Adenote a matrix which has an entire row or an entire column of zeros. Then if Bis any
matrix, either AB has an entire row of zeros or BA has an entire column of zeros,
respectively. (See Exercise 18, Section 1. 3.) Hence, neither AB nor BA can be the identity
matrix; therefore, Acannot have an inverse.
17. Suppose that AB = 0and Ais invertible. Then A–1(AB) = A–10or IB = 0. Hence, B= 0.
19. (a) Using the notation of Exercise 18, let
Then
so that
C=− −
−
1
4
11
11
11
11
11
11
=−
=−
1
4
00
40
00
10
A−=−
11
2
11
11
AB=−
=
11
11
11
11
and
A
a
a
ann
−=
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
1
11
22
10 0
01 0
00 1
Exercise Set 1.4 25

Thus the inverse of the given matrix is
21. We use Theorem 1.4.9.
(a) If A= BBT, then
AT= (BBT)T= (BT)TBT= BBT= A
Thus Ais symmetric. On the other hand, if A= B+ BT, then
AT= (B+ BT)T= BT+ (BT)T= BT+ B= B+ BT= A
Thus Ais symmetric.
(b) If A= B– BT, then
AT= (B– BT)T= [B+ (–1)BT]T= BT+ [(–1)BT]T
= BT+ (–1)(BT)T= BT+ (–1)B= BT– B= –A
Thus Ais skew-symmetric.
23. Let
A
xxx
xxx
xxx
−=
1
11 12 13
21 22 23
31 32 33
1
2
1
200
1
2
1
200
00
1
2
1
2
10
1
2
1
−
−
−22
26 Exercise Set 1.4

Then
Since AA–1 = I, we equate corresponding entries to obtain the system of equations
The solution to this system of equations gives
25. We wish to show that A(B– C) = AB – AC. By Part (d) of Theorem 1.4.1, we have
A(B– C) = A(B+ (–C)) = AB + A(–C). Finally by Part (m), we have A(–C) = –AC and
the desired result can be obtained by substituting this result in the above equation.
A−=
−
−
−
1
12 12 12
12 12 12
12 12 12
xx
xx
xx
xx
xx
11 31
12 32
13 33
11 21
12 22
1
0
0
0
+=
+=
+=
+=
+==
+=
+=
+=
+=
1
0
0
0
1
13 23
21 31
22 32
23 33
xx
xx
xx
xx
AA
xxx
xx
−=
1
11 12 13
21 2
101
110
011
2223
31 32 33
11 31 12 32 1
x
xxx
xx xx x
=
++
3333
11 21 12 22 13 23
21 31 22 32 2
+
+++
++
x
xx xx xx
xx xx x
3333
+
x
Exercise Set 1.4 27

27. (a) We have
On the other hand,
(b) Suppose that r< 0 and s< 0; let
ρ
= –rand
σ
= –s, so that
ArAs= A–
ρ
A–
σ
= (A–1)
ρ
(A–1)
σ
(by the definition)
= (A–1)
ρ
+
σ
(by Part (a))
= A–(
ρ
+
σ
)(by the definition)
= A–
ρ
–
σ
= Ar+s
() )( ) (AAAAAAAAAA
rs
rrr
=()
factors ffactors aactors
factors
factor
s
rs
AA A=
ss
AA AA A AA A
rs
rs
=((
factors
)
factors
))
==
+
+
AA A A
rs
rs
factors
28 Exercise Set 1.4

Also
(Ar)s= (A–
ρ
)–
σ
= [(A–1)
ρ
]–
σ
(by the definition)
= ([(A–1)
ρ
]–1)
σ
(by the definition)
= ([(A–1)–1)]
ρ
)
σ
(by Theorem 1.4.8b)
= ([A]
ρ
)
σ
(by Theorem 1.4.8a)
= A
ρσ
(by Part (a))
= A(–
ρ
)(–
σ
)
= Ars
29. (a) If AB = AC, then
A–1(AB) = A–1(AC)
or
(A–1 A)B= (A–1 A)C
or
B= C
(b) The matrix Ain Example 3 is not invertible.
31. (a) Any pair of matrices that do not commute will work. For example, if we let
then
()AB+=
=
2
2
11
01
12
01
AB=
10
00 ==
01
01
Exercise Set 1.4 29

whereas
(b) In general,
(A+ B)2= (A+ B)(A+ B) = A2+ AB + BA + B2
33. If
Thus, A2= Iif and only if a2
11 = a2
22 = a2
33 = 1, or a11 = ±1, a22 = ±1, and a33 = ±1. There are
exactly eight possibilities:
35. (b) The statement is true, since (A– B)2= (–(B– A))2= (B– A)2.
(c) The statement is true only if A–1 and B–1 exist, in which case
(AB–1)(BA–1) = A(B–1B)A–1 = AInA–1 = AA–1 = In
100
010
001
100
010
001
10
−
00
010
001
100
010
001
1
−
−
−
−000
010
001
100
010
001
−
−
−
−
−100
010
001
1100
010
001
−
−
A
a
a
a
A
a
=
=
11
22
33
2
00
00
00
then
111
2
22
2
33
2
00
00
00
a
a
AABB
22
213
01
++=
30 Exercise Set 1.4

EXERCISE SET 1.5
1. (a) The matrix may be obtained from I2by adding –5 times Row 1 to Row 2. Thus, it is
elementary.
(c) The matrix may be obtained from I2by multiplying Row 2 of I2by 3. Thus it is
elementary.
(e) This is not an elementary matrix because it is not invertible.
(g) The matrix may be obtained from I4only by performing two elementary row operations
such as replacing Row 1 of I4by Row 1 plus Row 4, and then multiplying Row 1 by 2.
Thus it is not an elementary matrix.
3. (a) If we interchange Rows 1 and 3 of A, then we obtain B. Therefore, E1must be the
matrix obtained from I3by interchanging Rows 1 and 3 of I3, i.e.,
(c) If we multiply Row 1 of Aby –2 and add it to Row 3, then we obtain C. Therefore, E3
must be the matrix obtained from I3by replacing its third row by –2 times Row 1 plus
Row 3, i.e.,
5. (a) R1↔R2, Row 1 and Row 2 are swapped
(b) R1→2R1
R2→–3R2
(c) R2→–2R1+ R2
E3
100
010
201
=
−
E1
001
010
100
=
31
7. (a)
Thus, the desired inverse is
3
2
11
10
6
5
111
1
2
7
10
2
5
−−
−
−
34 1100
10 3010
25 4001
10 3010
34 1
−
−
−
−1100
25 4001
10 30 10
04 101 30
0
−
−−
5510021
10 3 0 10
04 10 1
−−
−−
330
01 0 1 11
10 3 0 1 0
01
−
0111
00 10 5 7 4
100 3
2
−
−−−
−−−
−
−
11
10
6
5
010 1 1 1
001 1
2
7
10
2
5
32 Exercise Set 1.5
Interchange Rows
1 and 2.
Add –3 times Row 1
to Row 2 and –2 times
Row 1 to 3.
Add –4 times Row 3
to Row 2 and inter-
change Rows 2 and 3.
Multiply Row 3 by
–1/10. Then add –3
times Row 3 to Row 1.
Add –1 times Row 2
to Row 3.
7. (c)
Thus
101
011
110
1
2
1
2
1
2
1
2
1
2
1
1
=
−
−
−
22
1
2
1
2
1
2
−
101100
011010
110001
10 1 100
01 1
010
01 1 101
1011 0 0
0110 1
−−
00
0011
2
1
2
1
2
100 1
2
1
2
1
−
−22
010 1
2
1
2
1
2
110 1
2
1
2
1
2
−
−
Exercise Set 1.5 33
Subtract Row 1
from Row 3.
Subtract Row 2 from
Row 3 and multiply
Row 3 by –1/2.
Subtract Row 3
from Rows 1 and 2.

(e)
Thus
9. (b) Multiplying Row iof
000 1000
00 00100
0000010
0000001
1
2
3
4
k
k
k
k
101
111
010
1
2
1
2
1
2
00
1
−
=
−
−
1
1
2
1
2
1
2
−
101100
111010
010001
10 1 1
−
000
01 2 1 10
00 2 1 11
1011 0 0
0
−−−
1100 0 1
0011
2
1
2
1
2
1001
2
1
2
1
2
0
−
−
1100 0 1
0011
2
1
2
1
2
−
34 Exercise Set 1.5
Add Row 1 to Row 2
and subtract the new
Row 2 from Row 3.
Add Row 3 to Row 2
and then multiply
Row 3 by -1/2.
Subtract Row 3
from Row 1.

by 1/kifor i= 1, 2, 3, 4 and then reversing the order of the rows yields I4on the left
and the desired inverse
on the right.
(c) To reduce
we multiply Row iby 1/kand then subtract Row ifrom Row (i+ 1) for i= 1, 2, 3.
Then multiply Row 4 by 1/k. This produces I4on the left and the inverse,
on the right.
13. (a) E3E2E1A=
100
0140
001
10 0
01 3
00 1
−
−
102
010
001
10 2
04 3
00 1
=I3
1000
11 00
1110
1111
2
32
432
/k
kk
kkk
kkkk
−
−
−
k
k
k
k
0001000
1000100
01 00010
001 0001
0001
001 0
01 0 0
1000
4
3
2
1
k
k
k
k
Exercise Set 1.5 35

(b) A= (E3E2E1)–1 = E1
–1E2
–1E3
–1
15. If Ais an elementary matrix, then it can be obtained from the identity matrix Iby a single
elementary row operation. If we start with Iand multiply Row 3 by a nonzero constant, then
a= b= 0. If we interchange Row 1 or Row 2 with Row 3, then c= 0. If we add a nonzero
multiple of Row 1 or Row 2 to Row 3, then either b= 0 or a= 0. Finally, if we operate only
on the first two rows, then a= b= 0. Thus at least one entry in Row 3 must equal zero.
17. Every m×nmatrix Acan be transformed into reduced row-echelon form Bby a sequence
of row operations. From Theorem 1.5.1,
B= EkEk–1 …E1A
where E1, E2,…, Ekare the elementary matrices corresponding to the row operations. If we
take C= EkEk–1 …E1, then Cis invertible by Theorem 1.5.2 and the rule following Theorem
1.4.6.
19. (a) First suppose that Aand Bare row equivalent. Then there are elementary matrices
E1,…, Epsuch that A= E1…EpB. There are also elementary matrices Ep+1,…, Ep+q
such that Ep+1 …Ep+qAis in reduced row-echelon form. Therefore, the matrix Ep+1 …
Ep+qE1…EpBis also in (the same) reduced row-echelon form. Hence we have found,
via elementary matrices, a sequence of elementary row operations which will put Bin
the same reduced row-echelon form as A.
Now suppose that Aand Bhave the same reduced row-echelon form. Then
there are elementary matrices E1,…, Epand Ep+1,…, Ep+qsuch that E1…EpA= Ep+1
…Ep+qB. Since elementary matrices are invertible, this equation implies that
A= Ep
–1 …E–1
1Ep+1 …Ep+qB. Since the inverse of an elementary matrix is also an
elementary matrix, we have that Aand Bare row equivalent.
21. The matrix A, by hypothesis, can be reduced to the identity matrix via a sequence of
elementary row operations. We can therefore find elementary matrices E1, E2,…Eksuch
that
Ek…E2•E1•A= In
Since every elementary matrix is invertible, it follows that
A= E1
–1E2
–1 …Ek
–1In
=
−
10 2
01 0
00 1
100
013
001
100
040
001
36 Exercise Set 1.5

23. (a) True. Suppose we reduce Ato its reduced row-echelon form via a sequence of
elementary row operations. The resulting matrix must have at least one row of zeros,
since otherwise we would obtain the identity matrix and Awould be invertible. Thus
at least one of the variables in xmust be arbitrary and the system of equations will
have infinitely many solutions.
(b) See Part (a).
(d) False. If B= EA for any elementary matrix E, then A= E–1B. Thus, if Bwere
invertible, then Awould also be invertible, contrary to hypothesis.
Exercise Set 1.5 37


EXERCISE SET 1.6
1. This system of equations is of the form Ax = b, where
By Theorem 1.4.5,
Thus
That is,
x1= 3 and x2= –1
3. This system is of the form Ax = b, where
By direct computation we obtain
A
x
x
x
=
=
131
221
231
1
2
3
xx
=−
and bb
4
1
3
x== −
−
=
−
A161
51
2
9
bb 3
1−
A−=−
−
161
51
Ax
x
=
11
56
1
2
x= aand bb=
2
9
39

so that
That is,
x1= –1, x2= 4, and x3= –7
5. The system is of the form Ax = b, where
By direct computation, we obtain
Thus,
That is, x1= 1, x2= 5, and x3= –1.
x==
−
−
A1
1
5
1
bb
A−=
−
−
11
5
101
311
110
A
x
x
x
=−
−
11 1
11 4
41 1
1
2
3
x=
=
and bb
5
10
0
x==
−
−
−
A1
1
4
7
bb
A−=
−
−
−
1
101
011
234
40 Exercise Set 1.6

7. The system is of the form Ax = bwhere
By Theorem 1.4.5, we have
Thus
That is,
x1= 2b1– 5b2and x2= –b1+ 3b2
9. The system is of the form Ax = b, where
We compute
so that
xxbb=
−
()
+
()
+
()
−
−
A
bbb
b
1
123
1
13 13
13 133
23 13
2
123
()
()
+
()
−
b
bbb
A−=
−
−
−
1
13 13 1
13 13 0
23 13 1
A
x
x
x
=−
=
121
111
110
1
2
3
xx
=
and bb
b
b
b
1
2
3
xxbb==
−
−+
−
Abb
bb
112
12
25
3
A−=−
−
125
13
Ax
x
=
=
35
12
1
2
xannd bb=
b
b
1
2
Exercise Set 1.6 41

9. (a) In this case, we let
Then
That is, x1= 16/3, x2= –4/3, and x3= –11/3.
(c) In this case, we let
Then
That is, x1= 3, x2= 0, and x3= –4.
x=
−
−
A1
3
0
4
bb
bb =
−
−
1
1
3
x=−
−
−
A1
16 3
43
11 3
bb
bb =
−
1
3
4
42 Exercise Set 1.6
11. The coefficient matrix, augmented by the two bmatrices, yields
This reduces to
or
Thus the solution to Part (a) is x1= 22/17, x2= 1/17, and to Part (b) is x1= 21/17,
x2= 11/17.
15. As above, we set up the matrix
This reduces to
or
121 21
011 53
000 00
−−
−
12121
01153
01153
−−
−− −
−− −
12121
251 11
372 10
−−
−−
−−
10
01
22 17 21 17
117 1117
1512
017111
−−
1512
3245
−−
Exercise Set 1.6 43
Add –3 times Row 1
to Row 2.
Divide Row 2 by 17 and add
5 times Row 2 to Row 1.
Add appropriate
multiples of Row 1
to Rows 2 and 3.
Add –1 times Row 2 to
Row 3 and multiply
Row 2 by –1.

or
Thus if we let x3= t, we have for Part (a) x1= –12 – 3tand x2= –5 – t, while for
Part (b) x1= 7 – 3tand x2= 3 – t.
17. The augmented matrix for this system of equations is
If we reduce this matrix to row-echelon form, we obtain
The third row implies that b3= b1– b2. Thus, Ax = bis consistent if and only if bhas the
form
23. Since Ax = has only x = 0as a solution, Theorem 1.6.4 guarantees that Ais invertible. By
Theorem 1.4.8 (b), Akis also invertible. In fact,
(Ak)–1 = (A–1)k
bb =
−
b
b
bb
1
2
12
125
014
1
34
000
1
21
123
−
−−
()
−+ +
b
bb
bbb
125
458
333
1
2
3
−
−
−−
b
b
b
103 127
011 53
000 00
−
−
44 Exercise Set 1.6
Add twice Row 2
to Row 3.

Since the proof of Theorem 1.4.8 (b) was omitted, we note that
Because Akis invertible, Theorem 1.6.4 allows us to conclude that Akx = 0has only the
trivial solution.
25. Suppose that x1is a fixed matrix which satisfies the equation Ax1= b. Further, let x be any
matrix whatsoever which satisfies the equation Ax = b. We must then show that there is a
matrix x0which satisfies both of the equations x = x1+ x0and Ax0= 0.
Clearly, the first equation implies that
x0= x – x1
This candidate for x0will satisfy the second equation because
Ax0= A(x – x1) = Ax – Ax1= b– b= 0
We must also show that if both Ax1= band Ax0= 0, then A(x1+ x0) = b. But
A(x1+ x0) = Ax1+ Ax0= b+ 0= b
27. (a) x ≠0 and x ≠y
(b) x ≠0 and y≠0
(c) x ≠yand x ≠–y
Gaussian elimination has to be performed on (AI) to find A–1. Then the product
A–1Bis performed, to find x. Instead, use Gaussian elimination on (AB) to find x. There
are fewer steps in the Gaussian elimination, since (AB) is a m×(n+1) matrix in general,
or n×(n+1) where Ais square (n×n). Compare this with (AI) which is n×(2n) in the
inversion approach. Also, the inversion approach only works for An×nand invertible.
Exercise Set 1.6 45

29. No. The system of equations Ax = x is equivalent to the system (A– I)x = 0. For this
system to have a unique solution, A– Imust be invertible. If, for instance, A= I, then
any vector x will be a solution to the system of equations Ax = x.
Note that if x ≠0is a solution to the equation Ax = x, then so is kx for any real number k.
A unique solution can only exist if A– Iis invertible, in which case, x = 0.
31. Let Aand Bbe square matrices of the same size. If either Aor Bis singular, then AB is
singular.
46 Exercise Set 1.6

EXERCISE SET 1.7
7. The matrix Afails to be invertible if and only if a+ b– 1 = 0 and the matrix Bfails to be
invertible if and only if 2a– 3b– 7 = 0. For both of these conditions to hold, we must have
a= 2 and b= –1.
9. We know that Aand Bwill commute if and only if
is symmetric. So 2b+ d= a– 5b, from which it follows that a– d= 7b.
11. (b) Clearly
for any real number k= 0.
A
ka ka ka
ka ka ka
ka ka ka
=
11 12 13
21 22 23
31 32 33
300
05 0
007
k
k
k
AB ab
bd
ab bd
abb
=−
=++
−
21
15
22
5−−
5d
47
13. We verify the result for the matrix Aby finding its inverse.
Thus A–1 is indeed upper triangular.
15. (a) If Ais symmetric, then AT= A. Then (A2)T= (AA)T= ATAT= A.A= A2, so A2
is symmetric.
(b) We have from part (a) that
(2A2– 3A+ I)T= 2(A2)T– 3AT+ IT= 2A2– 3A+ I
17. From Theorem 1.7.1(b), we have if Ais an n×nupper triangular matrix, so is A2. By
induction, if Ais an n×nupper triangular matrix, so is Ak, k= 1, 2, 3, . . . We note that the
identity matrix In= A0is also upper triangular. Next, if Ais n×nupper triangular, and K
is any (real) scalar, then KA is upper triangular. Also, if Aand Bare n×nupper triangular
matrices, then so is A+B. These facts allow us to conclude if p(x) is any (real) polynomial,
and Ais n×nupper triangular, then P(A) is an n×nupper triangular matrix.
101 1 2 0
01 0 0 1 34
001 0 0 14
100 1 214
01 0
−
−
−
00134
001 0 0 14−
−
−
−−−
12 51 0 0
01 30 1 0
00 40 0 1
12510 0
01 30
110
0010014−
48 Exercise Set 1.7
Multiply Row 1 by –1
and Row 3 by –1/4.
Add –1 times Row
3 to Row 1.
Add 2 times Row 2 to
Row 1 and –3 times
Row 3 to Row 2.

19. Let
Then if A2– 3A– 4I= O, we have
This leads to the system of equations
x2– 3x– 4 = 0
y2– 3y– 4 = 0
z2– 3z– 4 = 0
which has the solutions x= 4, –1, y= 4, –1, z= 4, –1. Hence, there are 8 possible choices
for x, y, and z, respectively, namely (4, 4, 4), (4, 4, –1), (4, –1, 4), (4, –1, –1), (–1, 4, 4),
(–1, 4, –1), (–1, –1, 4), and (–1, –1, –1).
23. The matrix
is skew-symmetric but
is not skew-symmetric. Therefore, the result does not hold.
In general, suppose that Aand Bare commuting skew-symmetric matrices. Then
(AB)T= (BA)T= ATBT= (–A)(–B) = AB, so that AB is symmetric rather than skew-
symmetric. [We note that if Aand Bare skew-symmetric and their product is symmetric,
then AB = (AB)T= BTAT= (–B)(–A) = BA, so the matrices commute and thus skew-
symmetric matrices, too, commute if and only if their product is symmetric.]
AA A==
−
−
210
01
A=−
01
10
x
y
z
x
y
z
2
2
2
00
00
00
3
00
00
00
−
−
=4
100
010
001
O
A
x
y
z
=
00
00
00
Exercise Set 1.7 49

25. Let
Then
Hence, x3= 1 which implies that x= 1, and z3= –8 which implies that z= –2. Therefore,
3y= 30 and thus y= 10.
27. To multiply two diagonal matrices, multiply their corresponding diagonal elements to obtain
a new diagonal matrix. Thus, if D1and D2are diagonal matrices with diagonal elements
d1,..., dnand e1,..., enrespectively, then D1D2is a diagonal matrix with diagonal elements
d1e1,..., dnen. The proof follows directly from the definition of matrix multiplication.
29. In general, let A= [aij]n × ndenote a lower triangular matrix with no zeros on or below the
diagonal and let Ax = bdenote the system of equations where b= [b1, b2,..., bn]T. Since A
is lower triangular, the first row of Ayields the equation a11x1= b1. Since a11 ≠0, we can
solve for x1. Next, the second row of Ayields the equation a21x1+ a22x2= b2. Since we
know x1and since a22 ≠0, we can solve for x2. Continuing in this way, we can solve for
successive values of xiby back substituting all of the previously found values x1, x2,..., xi–1.
Axyxxzz
z
3
32 2
3
0
130
08
=++
()
=−
Axy
z
=
0
50 Exercise Set 1.7
SUPPLEMENTARY EXERCISES 1
1.
3
5
4
5
4
5
3
5
14
3
5
3
4
5
3
5
−
−
x
y
x
y
−
−+
−
14
3
5
3
05
3
4
3
1
x
xy
44
3
5
3
01 4
5
3
5
10 3
5
4
5
01 4
5
x
xy
xy
−+
+
−xxy+
3
5
51
Multiply Row 1 by 5/3.
Multiply Row 2 by 3/5.
Add –4/5 times Row 1
to Row 2.
Add –4/3 times Row 2
to Row 1.

Thus,
x′=3
–
5x+ 4
–
5y
y′= – 4
–
5x+ 3
–
5y
3. We denote the system of equations by
a11x1+ a12x2+ a13x3+ a14x4= 0
a21x1+ a22x2+ a23x3+ a24x4= 0
If we substitute both sets of values for x1, x2, x3, and x4into the first equation, we obtain
a11 – a12 + a13 + 2a14 = 0
2a11 + 3a13 – 2a14 = 0
where a11, a12, a13, and a14 are variables. If we substitute both sets of values for x1, x2, x3,
and x4into the second equation, we obtain
a21 – a22 + a23 + 2a24 = 0
2a21 + 3a23 –a24 = 0
where a21, a22, a23, and a24 are again variables. The two systems above both yield the matrix
which reduces to
This implies that
a11 = –(3/2)a13 + (1/2)a14
a12 = –(1/2)a13 + (5/2)a14
1032 120
0112 520
−
−
11120
20310
−
−
52 Supplementary Exercises 1
and similarly,
a21 = (–3/2)a23 + (1/2)a24
a22 = (–1/2)a23 + (5/2)a24
As long as our choice of values for the numbers aij is consistent with the above, then
the system will have a solution. For simplicity, and to insure that neither equation is a
multiple of the other, we let a13 = a14 = –1 and a23 = 0, a24 = 2. This means that
a11 = 1, a12 = –2, a21 = 1, and a22 = 5, so that the system becomes
x1– 2x2– x3– x4= 0
x1+ 5x2+2x4= 0
Of course, this is just one of infinitely many possibilities.
5. As in Exercise 4, we reduce the system to the equations
Since x, y, and zmust all be positive integers, we have z> 0 and 35 – 9z> 0 or 4 > z. Thus
we need only check the three values z= 1, 2, 3 to see whether or not they produce integer
solutions for xand y. This yields the unique solution x= 4, y= 2, z= 3.
9. Note that Kmust be a 2 ×2 matrix. Let
Then
14
23
12
20 0
01 1
−
−
−
ab
cd ==
−
−
−
866
611
400
Kab
cd
=
xz
yz
=1+5
4
=35 – 9
4
Supplementary Exercises 1 53

or
or
Thus
2a+ 8c= 8
b+ 4d= 6
– 4a+ 6c= 6
– 2b+ 3d= –1
2a– 4c= –4
b– 2d= 0
Note that we have omitted the 3 equations obtained by equating elements of the last
columns of these matrices because the information so obtained would be just a repeat of
that gained by equating elements of the second columns. The augmented matrix of the
above system is
20808
01046
40606
02031
20404
01020
−
−−
−−
−
28 4 4
46 23 23
24 2
ac bd bd
ac bd bd
ac bd b
++−−
−+ −+ −
−−−+22
866
611
400d
=
−
−
−
14
23
12
2
2
866
6−
−
−
−
=
−
ab b
cd d −−
−
11
400
54 Supplementary Exercises 1

The reduced row-echelon form of this matrix is
Thus a= 0, b= 2, c= 1, and d= 1.
11. The matrix Xin Part (a) must be 2 ×3 for the operations to make sense. The matrices in
Parts (b) and (c) must be 2 ×2.
(b) Let X= . Then
If we equate matrix entries, this gives us the equations
x+ 3y=–5 x+ 3w= 6
– x=–1 – z= –3
2x+ y= 0 2z+ w= 7
Thus x= 1 and z= 3, so that the top two equations give y= –2 and w= 1. Since
these values are consistent with the bottom two equations, we have that
11. (c) As above, let X= , so that the matrix equation becomes
33
22
24
24
xz yw
xz yw
xy x
zw z
++
−+ −+
−+
+
=−
22
54
xy
zw
X=−
12
31
Xxy x xy
zw z zw
112
301
32
32
−
=+− +
+− +
xy
zw
10000
01 00 2
00101
00011
00000
00000
Supplementary Exercises 1 55

This yields the system of equations
2x– 2y+ z=2
–4x+ 3y+ w=–2
–x+ z– 2w=5
–y– 4z+ 2w=4
with matrix
which reduces to
Hence, x= –113/37, y= –160/37, z= –20/37, and w= –46/37.
15. Since the coordinates of the given points must satisfy the polynomial, we have
p(1) = 2 ⇒a+ b+ c= 2
p(–1) = 6 ⇒a– b+ c= 6
p(2) = 3 ⇒4a+ 2b+ c= 3
The reduced row-echelon form of the augmented matrix of this system of equations is
Thus, a= 1, b= – 2, and c= 3.
1001
0102
0013
−
1000 11337
01 00 160 37
0010 20 37
0001 4637
−
−
−
−
22102
43012
10125
01424
−
−−
−−
−−
56 Supplementary Exercises 1

17. We must show that (I– Jn)
(
I– n–1
1 Jn
)
= Ior that
(
I– n–1
1 Jn
)
(I– Jn) = I. (By virtue of
Theorem 1.6.3, we need only demonstrate one of these equalities.) We have
But Jn
2= nJ
n(think about actually squaring Jn), so that the right-hand side of the above
equation is just I, as desired.
19. First suppose that AB–1 = B–1 A. Note that all matrices must be square and of the same
size. Therefore
(AB–1)B= (B–1 A)B
or
A= B–1 AB
so that
BA = B(B–1 AB) = (BB–1)(AB) = AB
It remains to show that if AB = BA then AB–1 = B–1 A. An argument similar to the one given
above will serve, and we leave the details to you.
21. (b) Let the ijth entry of Abe aij. Then tr(A) = a11 + a22 + …+ ann, so that
tr(kA) = ka11 + ka22 + …+ kann
= k(a11 + a22 + …+ ann)
= ktr(A)
(d) Let the ijth entries of Aand Bbe aij and bij, respectively. Then
tr(AB) = a11b11 + a12b21 + …+ a1nbn1
+ a21b12 + a22b22 + …+ a2nbn2
+ …
+ an1b1n+ an2b2n+ …+ annbnn
IJ I nJI
nIJ J I
nn nn
−
()
−−
=−−−+
1
1
1
1
1
2
nn J
In
nJnJ
n
nn
−
=− −+−
1
1
1
1
2
2
Supplementary Exercises 1 57

and
tr(BA) = b11a11 + b12a21 + …+ b1nan1
+ b21a12 + b22a22 + …+ b2nan2
+ …
+ bn1a1n+ bn2a2n+ …+ bnnann
If we rewrite each of the terms bijaji in the above expression as ajibij and list the terms
in the order indicated by the arrows below,
tr(BA) = a11b11 + a21b12 + …+ an1b1n
+ a12b21 + a22b22 + …+ an2b2n
+ …
+ a1nbn1+ a2nbn2+ …+ annbnn
then we have tr(AB) = tr(BA).
25. Suppose that Ais a square matrix whose entries are differentiable functions of x. Suppose
also that Ahas an inverse, A–1. Then we shall show that A–1 also has entries which are
differentiable functions of xand that
dA–1
——
dx = –A–1 dA
—
dx A–1
Since we can find A–1 by the method used in Chapter 1, its entries are functions of xwhich
are obtained from the entries of Aby using only addition together with multiplication and
division by constants or entries of A. Since sums, products, and quotients of differentiable
functions are differentiable wherever they are defined, the resulting entries in the inverse
will be differentiable functions except, perhaps, for values of xwhere their denominators
are zero. (Note that we never have to divide by a function which is identically zero.) That
is, the entries of A–1 are differentiable wherever they are defined. But since we are assuming
that A–1 is defined, its entries must be differentiable. Moreover,
or
dA
dx AA
dA
dx
−−
+=
11
0
d
dx AA d
dx I() ()
−==
10
58 Supplementary Exercises 1

Therefore
so that
27. (b) Let Hbe a Householder matrix, so that H= I– 2PPTwhere Pis an n×1 matrix. Then
using Theorem 1.4.9,
HT= (I– 2PPT)T
= IT– (2PPT)T
= I– 2(PT)TPT
= I– 2 PPT
= H
and (using Theorem 1.4.1)
HTH= H2(by the above result)
= (I– 2PPT)2
= I2– 2PPT– 2PPT+ (–2PPT)2
= I– 4PPT+ 4PPTPPT
= I– 4PPT+ 4PPT(because PTP= I)
= I
29. (b) A bit of experimenting and an application of Part (a) indicates that
An
n
n
n
a
b
dc
=
00
00
0
–
–––
dA
dx AdA
dx A
111
=
–
–
AdA
dx =dA
dx A
1
1
Supplementary Exercises 1 59

where
d= an–1 + an–2 c+ …+ acn–2 + cn–1 = if a≠c
If a= c, then d= nan–1. We prove this by induction. Observe that the result holds
when n= 1. Suppose that it holds when n= N. Then
Here
Thus the result holds when n= N+ 1 and so must hold for all values of n.
acd
ac
ac
ac
aacacc
ac
N
N
NN N N N N
++−
−=−+−
−=
++
=
11
aac
ac ac
aaNa N a a
NN
NN N
++
−
−
−≠
+
()
=+
()
=
11
11
if
if cc
AAAA
a
b
dc
a
NN
N
N
N
+==
=
1
00
00
0
NN
N
NN
b
acd c
+
+
+
+
1
1
1
00
00
0
ac
ac
nn
–
–
60 Supplementary Exercises 1
EXERCISE SET 2.1
1. (a) M11 = 7 • 4–(–1) • 1 = 29, M12 = 21, M13 = 27, M21 = –11, M22 = 13, M23 = –5, M31 = –19,
M32 = –19, M33 = 19
(b) C11 = 29, C12 = –21, C13 = 27, C21 = 11, C22 = 13, C23 = 5, C31 = –19, C32 = 19, C33 = 19
3. (a)
(b) |A|= 1 • M11 – 6 • M21 – 3 • M23 = 152
(c) |A= 6 • M21 + 7 • M22 + 1 • M23 = 152
(d) |A|= 2 • M12 + 7 • M22 + 1 • M32 = 152
(e) |A|= –3 • M31 – 1 • M32 + 4 • M33 = 152
(f) |A|= 3 • M13 + 1 • M23 + 4 • M33 = 152
5. Second column:
A=⋅
−
−=⋅−=−537
15 58 40
A=⋅ −+⋅ −
−+⋅
−
171
14 261
34367
331 29 42 81 152=++=
61
7. First column:
9. Third column:
11.
13.
15. (a)
(b) Same as (a).
(c) Gaussian elimination is significantly more efficient for finding inverses.
A−=
−−
−
−−
1
4301
2100
7018
6017−
adj(A) =
264
046
002
41
==
−
;;AA
112 32 1
0132
0012
//
/
/
adj(A) =
−
−−
−
355
345
223
;;AA=− =
−−
−
−−
−
1
355
34 5
223
1
A=− ⋅ − − ⋅ −3
33 5
22 2
210 2
3
33 5
22 2
4110
240=−
Ak kkk
kk() ( ) ()=− − ⋅ + − ⋅ +−+124
5315
71⋅⋅ +k17
24
Akk
kk
kk
kk
kk
kk
=⋅ −⋅ +⋅ =1110
2
2
2
2
2
2
62 Exercise Set 2.1

17.
|A1|= –36, |A2|= –24, |A3|= –12
x1= –36/–132 = 3/11, x2= –24/–132 = 2/11, x3= 12/–132 = –1/11
19.
|A1|= 30, |A2|= 38, |A3|= –40
x1= 30/–11 = –30/11, x2= 38/–11 = –38/11, x3= 40/–11 = –40/11
21.
The method is not applicable to this problem because the determinant of the coefficient
matrix is zero.
23.
A=−
−
=
41 11
37 11
73 58
11 12
,bb ;
6
1
3
3
424
−
=−A
A,=
−
−
−
=
311
172
261
4
1
5
bb
=;A0
A=
−
−
−
=−
,
131
210
403
4
2
0
bb ;; A=−11
A,=
=
450
11 1 2
152
2
3
1
bb
=−;A132
Exercise Set 2.1 63

y= 0/–424 = 0
25. This follows from Theorem 2.1.2 and the fact that the cofactors of Aare integers if A has
only integer entries.
27. Let Abe an upper (not lower) triangular matrix. Consider AX = I; the solution Xof this
equation is the inverse of A. To solve for column 1 of X, we could use Cramer’s Rule. Note
that if we do so then A2,..., Anare each upper triangular matrices with a zero on the main
diagonal; hence their determinants are all zero, and so x2,1,..., xn,1 are all zero. In a similar
way, when solving for column 2 of Xwe find that x3,2,..., xn,2 are all zero, and so on. Hence,
Xis upper triangular; the inverse of an invertible upper triangular matrix is itself upper
triangular. Now apply Theorem 1.4.10 to obtain the corresponding result for lower triangular
matrices.
29. Expanding the determinant gives x(b1– b2) – y(a1– a2) + a1b2– a2b1= 0
which is the slope-intercept form of the line through these two points, assuming that a1≠a2.
31. (a) |A|= A11|• |A22|= (2 • 3 – 4 • –1) • (1 • 2 – 3 • –10 + • –28) = –1080
(b.) Expand along the first column; |A|= –1080.
33. From I4we see that such a matrix can have at least 12 zero entries (i.e., 4 nonzero entries).
If a 4 ×4 matrix has only 3 nonzero entries, some row has only zero entries. Expanding
along that row shows that its determinant is necessarily zero.
35. (a) True (see the proof of Theorem 2.1.2).
(b) False (requires an invertible, and hence in particular square, coefficient matrix).
(c) True (Theorem 2.1.2).
(d) True (a row of all zeroes will appear in every minor’s submatrix).
xb b ya a ab ab
y
()( )
12 1 2 11 21
0−− −+ − =
== −
−+−
−
bb
aa
xab ab
aa
12
12
12 21
12
A2
4611
3111
7358
1312
=−
−−
=;A20
64 Exercise Set 2.1
EXERCISE SET 2.2
1. (b) We have
3. (b) Since this matrix is just I4with Row 2 and Row 3 interchanged, its determinant is –1.
det( )A=
−
−
=
−−
−−
=
213
124
536
05 5
124
01314
(()()
()()
−−
−−
=− −
−
15
124
01 1
01314
15
12 4
01 1
00 1
==− − − =−
=− − =
()()()
det( )
151 5
215
123
346
05
AT
−−
−−
−
=−
−−
−
1
123
010 3
1
12 3
05 1
00
()
−−
=− − − =−
1
1151 5()()()()
65
By Theorem 2.2.2.
Add 13 times
Row 2 to Row 3.
Factor –5 from Row 1
and interchange
Row 1 and Row 2.
Add 2 times Row 2
to Row 1 and 3 times
Row 2 to Row 3.
Add –2 times Row 1 to
Row 3, and interchange
Row 1 and Row 2.
By Theorem 2.2.2.
Add –2 times Row 2 to
Row 1 and –5 times
Row 2 to Row 3.
5.
If we factor –5/3 from Row 3 and apply Theorem 2.2.2 we fInd that
det(A) = –3(–5/3)(1) = 5
7.
(=3))( )3
12 3
0143
00113
911
3
1
−
=
−−
==
23
0143
001
9113 1 33()()
det( )A=
−
−−=
−369
272
015
3
123
034
015
det( )A==−
()
031
112
324
1
112
031
3224
1
112
031
012
13
11 2
0113
01
()
()()
=−
−−
=−
−−
22
3
11 2
0113
0053
=−
−
66 Exercise Set 2.2
Interchange
Row 1 and
Row 2.
Add –3 times Row 1
to Row 3.
Factor 3
from Row 2.
Add Row 2
to Row 3.
Factor 3 from
Row 1 and Add
twice Row 1
to Row 2.
Factor 3 from
Row 2 and
subtract Row 2
from Row 3.
Factor 11/3
from Row 3.
9.
11.
Hence, det(A) = (–1)(2)(1) = –2.
det( )A=
−− −
13153
27042
00101
002111
00011
13153
01268
00101
00011
000
=
−
−
111
13153
01268
00101
00011
00002
=
−
−
det( )A==−
()
2131
1011
0210
0123
1
1011
2131
0210
01233
1
10 1 1
01 1 1
02 1 0
01 2 3
1
1011
01
=− −
=−
()
() 111
0012
0014
1
10 1 1
01 1 1
00 1 2
0
−
−
=− −
−
()
0006
11616=− − =()()()()
Exercise Set 2.2 67
Interchange
Row 1 and
Row 2.
Add –2 times Row 1
to Row 2.
Add –2 times Row 2
to Row 3; subtract
Row 2 from Row 4.
Add Row 3 to Row 4.
Add 2 times Row 1 to
Row 2; add –2 times
Row 3 to Row 4.
Add –1 times
Row 4 to Row 5.

13.
Since b2– a2= (b– a)(b+ a), we add –(b+ a) times Row 2 to Row 3 to obtain
=(b–a)[(c2– a2) – (c– a)(b+ a)]
= (b– a)(c–a)[(c+ a) – (b+ a)]
= (b– a)(c– a)(c– b)
15. In each case, dwill denote the determinant on the left and, as usual, det(A) =
∑±a1j1a2j2a3j3, where ∑denotes the sum of all such elementary products.
(a) d= ∑±(ka1j1)a2j2a3j3= k ∑±a1j1a2j2a3j3= kdet(A)
(b) d= ∑±a2j1a1j2a3j3= ∑±a1j2a2j1a3j3
det( )Aba ca
ca ca
=− −
−
()
−−
11 1
0
00 22
(()
+
()
ba
det( )Aabc
abc
ba ca
ba ca
=
=−−
−−
111
11 1
0
0
222
22 222
68 Exercise Set 2.2
Add –atimes Row 1 to
Row 2; add –a2times
Row 1 to Row 3.

= (a11 + ka21)(a22)(a33) + (a12 + ka22)(a23)(a31)
+ (a13 + ka23)(a21)(a32) – (a13 + ka23)(a22)(a31)
– (a12 + ka22)(a21)(a33) – (a11 + ka21)(a23)(a32)
= a11 a22 a33 + a12 a23 a31 + a13 a21 a32 – a13 a22 a31
– a12 a22 a33 – a11 a23 a32
+ ka21 a22 a33 + ka22 a23 a31 + ka23 a21 a32
– ka23 a22 a31 – ka22 a21 a33 – ka21 a23 a32
17. (8)
R2→R2– 2R1
R3→R3+ 2R1
R4→R4– 2R1
R3→R3+ R1
=
−
−
−
=
−
−=−=3
351
120
012 1
3
351
120
370
312
37
39
1231
5963
1262
2861
1231
3501
1200
0
−
−
−−−
=
−
−
−
112 0 1−
=
aaa
aaa
aaa
11 12 13
21 22 23
31 32 33
aka aka aka
aa a
aa a
11 21 12 22 13 23
21 22 23
31 32 3
+++
33
Exercise Set 2.2 69
69

(9)
R1→R1– 2R2R3→R3+ 3R1
(10)
R1→R1– 2R2
R1→R1+ 3R2
=−+
=−1
6
2
3
1
3
1
6
=
−−
−
=
−
=
1
2
10 1
231313
13230
1
2
110
231313
13230
1213
11
1323
()
−
()
−
0111
1212112
2313130
132300
10 10
1212112
23
−
=
−−
113130
132300−
=−
−
=−
()
−
()
=()1
111
210
450
11
21
45 6
2131
1011
0210
0123
01 1 1
10 1 1
02 1 0
01 2 3
1
11
=
−
=−
()
−−1
21 0
12 3
70 Exercise Set 2.2
(11)
R2→R2– R3
19. Since the given matrix is upper triangular, its determinant is the product of the diagonal
elements. That is, the determinant is x(x+ 1)(2x– 1). This product is zero if and only if
x= 0, x= – 1, or x= 1/2.
13153
27042
00101
00211
00011
13153
01268
0
−− −
=
−
00101
00211
00011
1268
0101
0211
0011
2
22
=
−
→+RRR
11
1
101
211
011
1
101
200
011
12
01
11
=−
()
=−
()
=−
()
−
()
==−2
Exercise Set 2.2 71


EXERCISE SET 2.3
1. (a) We have
and
5. (a) By Equation (1),
det(3A) = 33det(A) = (27)(–7) = –189
(c) Again, by Equation (1), det(2A–1) = 23det(A–1). By Theorem 2.3.5, we have
det(2A–1) = 8
det(A)= –8
7
(d) Again, by Equation (1), det(2A) = 23det(A) = –56. By Theorem 2.3.5, we have
det[(2A)–1] = 1
det(2A)= – 1
56
det( ) ( )( )()() ( )224
68 28 46 402 10
2
A=−=− − =− = −
det( )A=−=− − =−
12
34 46 10
73

(e)
7. If we replace Row 1 by Row 1 plus Row 2, we obtain
because the first and third rows are proportional.
13. By adding Row 1 to Row 2 and using the identity sin2x+ cos2x= 1, we see that the
determinant of the given matrix can be written as
But this is zero because two of its rows are identical. Therefore the matrix is not invertible.
15. We work with the system from Part (b).
(i) Here
so the characteristic equation is λ2– 5λ– 6 = 0.
det( ) ( )( )
λλ
λλλ λ
IA−=−
−−
=− −−=−
23
43 2312
2556
λ
−
sin sin sin
222
111
111
αβγ
bc ca ba
ab c
f
abc bca cba
abc
f
+++
=
++ ++ ++
=
11 1 1
0
agd
bhe
ci f
adg
beh
cfi
abc
de f
gh i
=−
=− .
=7
74 Exercise Set 2.3
Interchange Columns
2 and 3.
Take the transpose of
the matrix.

(ii) The eigenvalues are just the solutions to this equation, or λ= 6 and λ= –1.
(iii) If λ= 6, then the corresponding eigenvectors are the nonzero solutions
to the equation
The solution to this system is x1= (3/4)t, x2= t, so is an eigenvector
whenever t≠0.
If λ= –1, then the corresponding eigenvectors are the nonzero solutions
to the equation
If we let x1= t, then x2= –t, so is an eigenvector whenever t≠0.
It is easy to check that these eigenvalues and their corresponding eigenvectors satisfy
the original system of equations by substituting for x1, x2, and λ. The solution is valid for all
values of t.
17. (a) We have, for instance,
The answer is clearly not unique.
ab cd
ab cd
ab cd
ac
a
11 1 1
22 2 2
11 1 1
22
1
++
++
=++
++bbcd
bd
ac
ac
bd
ac
ac
bd
111
22
11
22
11
22
11
22
+
=+ + +bd
bd
11
22
x=−
t
t
−−
−−
=
33
44
0
0
1
2
x
x
x=
x
x
1
2
x=
(
)
34 t
t
62 3
463
43
43
1
2
−−
−−
=−
−
x
x
x
x
1
2
0
0
=
x=
x
x
1
2
Exercise Set 2.3 75

19. Let Bbe an n×nmatrix and Ebe an n×nelementary matrix.
Case 2: Let Ebe obtained by interchanging two rows of In. Then det(E) = –1 and EA is
just Awith (the same) two rows interchanged. By Theorem 2.2.3, det(EA) = –det(A) =
det(E) det(A).
Case 3: Let Ebe obtained by adding a multiple of one row of Into another. Then det(E)
= 1 and det(EA) = det(A). Hence det(EA) = det(A) = det(E) det(A).
21. If either Aor Bis singular, then either det(A) or det(B) is zero. Hence, det(AB) = det(A)
det(B) = 0. Thus AB is also singular.
23. (a) False. If det(A) = 0, then Acannot be expressed as the product of elementary
matrices. If it could, then it would be invertible as the product of invertible matrices.
(b) True. The reduced row echelon form of Ais the product of Aand elementary matrices,
all of which are invertible. Thus for the reduced row echelon form to have a row of
zeros and hence zero determinant, we must also have det(A) = 0.
(c) False. Consider the 2 ×2 identity matrix. In general, reversing the order of the
columns may change the sign of the determinant.
(d) True. Since det(AAT) = det(A) det(AT) = [det(A)]2, det(AAT) cannot be negative.
76 Exercise Set 2.3

EXERCISE SET 2.4
1. (a) The number of inversions in (4,1,3,5,2) is 3 + 0 + 1 + 1 = 5.
(d) The number of inversions in (5,4,3,2,1) is 4 + 3 + 2 + 1 = 10.
3.
5.
7.
9.
11.
()( )
300
215
194
12 0 0 0 135 0−
−
=++−++==−123
−
−=−−+ − ++=−
214
357
162
20 7 72 20846 65()()
a
aaa aa
−
−−
=− −−− =−+
35
32 3235 521
2
()()()()
−
−−
=− − −− =
56
72 52 7652()()()()
35
24 12 10 22
−=−− =()
77

13. (a)
= λ2+ 2λ– 3 = (λ– 1)(λ+ 3)
Hence, det(A) = 0 if and only if λ= 1 or λ= –3.
15. If Ais a 4 ×4 matrix, then
det(A) = ∑(–1)pa1i1a2i2a3i3a4i4
where p= 1 if (i1, i2, i3, i4) is an odd permutation of {1,2,3,4} and p= 2 otherwise. There
are 24 terms in this sum.
17. (a) The only nonzero product in the expansion of the determinant is
a15a24a33a42a51 = (–3)(–4)(–1)(2)(5) = –120
Since (5,4,3,2,1) is even, det(A) = –120.
(b) The only nonzero product in the expansion of the determinant is
a11a25a33a44a52 = (5)(–4)(3)(1)(–2) = 120
Since (1,5,3,4,2) is odd, det(A) = –120.
19. The value of the determinant is
sin2
θ
– (–cos2
θ
) = sin2
θ
+ cos2
θ
= 1
The identity sin2
θ
+ cos2
θ
= 1 holds for all values of
θ
.
21. Since the product of integers is always an integer, each elementary product is an integer.
The result then follows from the fact that the sum of integers is always an integer.
23. (a) Since each elementary product in the expansion of the determinant contains a factor
from each row, each elementary product must contain a factor from the row of zeros.
Thus, each signed elementary product is zero and det(A) = 0.
det ( ) ( )( )A=−
−+
=− ++
λ
λλλ
21
54 245
78 Exercise Set 2.4

25. Let U= [aij] be an nby nupper triangular matrix. That is, suppose that aij = 0 whenever
i> j. Now consider any elementary product a1j1a2j2
…anjn. If k> jkfor any factor akjkin this
product, then the product will be zero. But if k≤jkfor all k= 1, 2, …, n, then k= jkfor all
kbecause j1, j2,…, jnis just a permutation of the integers 1, 2, …, n. Hence, a11a22 …ann
is the only elementary product which is not guaranteed to be zero. Since the column indices
in this product are in natural order, the product appears with a plus sign. Thus, the
determinant of Uis the product of its diagonal elements. A similar argument works for
lower triangular matrices.
Exercise Set 2.4 79

SUPPLEMENTARY EXERCISES 2
1.
3. The determinant of the coefficient matrix is
The system of equations has a nontrivial solution if and only if this determinant is zero;
that is, if and only if
α
=
β
. (See Theorem 2.3.6.)
11 11 11
α
β
αβ
α
βα
αβ
βαβ
11
1
=0 0 −
1
==–( – )a––( – )( – )
ββ
aa
′=
−
−
=+
+
=x
x
yxy
4
5
3
5
3
5
4
5
4
5
3
5
3
5
4
5
9
25
16
25
3
5
4
5
3
5
4
5
3
5
4
5
4
5
3
5
3
5
4
5
1
xy
y
x
yyx
+
′=
−
=−=−+
4
5
3
5
xy
81
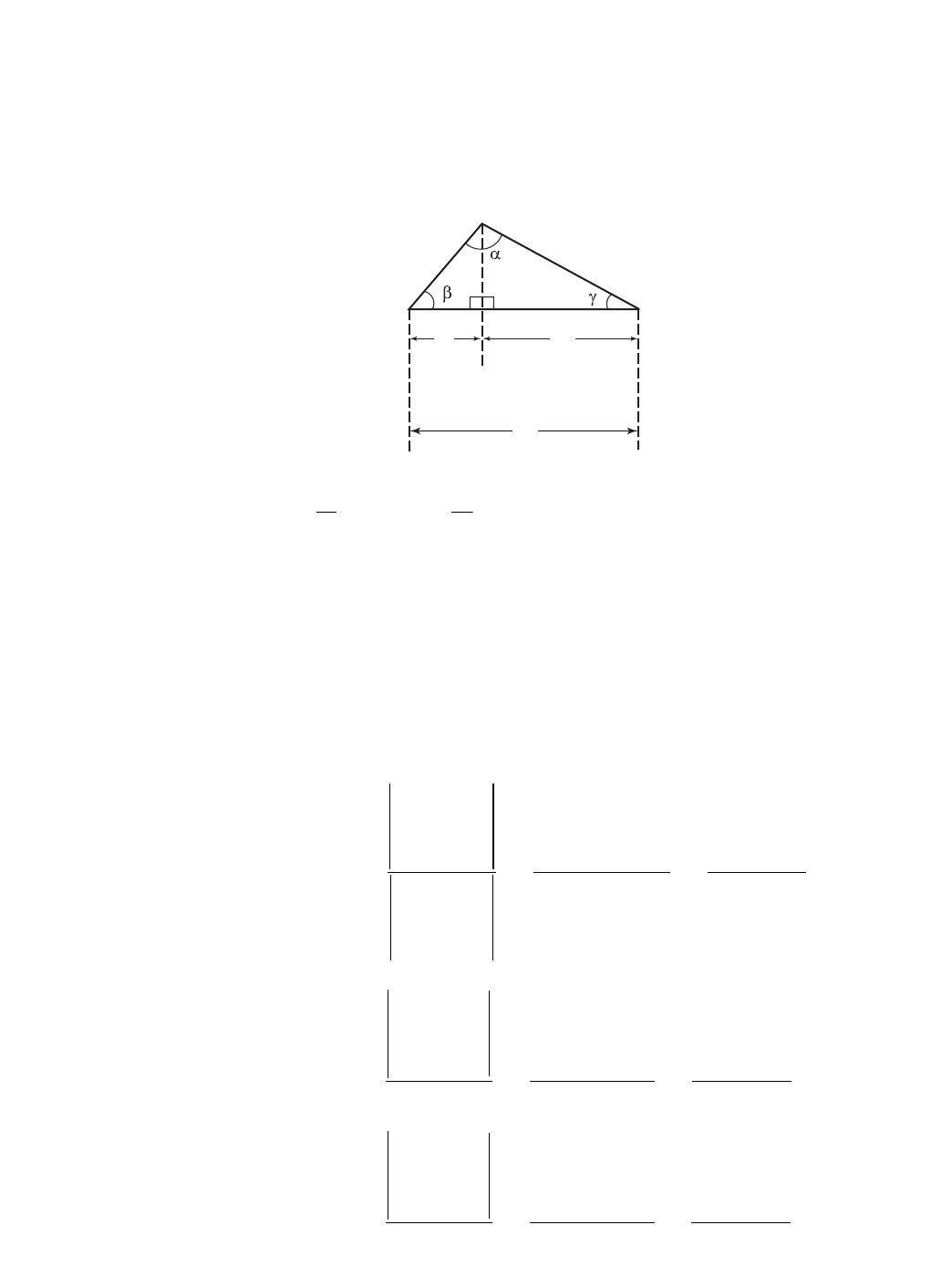
5. (a) If the perpendicular from the vertex of angle
α
to side ameets side abetween angles
β
and
γ
, then we have the following picture:
Thus cos and cos and hence
a= a1+ a2= ccos
β
+ bcos
γ
This is the first equation which you are asked to derive. If the perpendicular intersects
side aoutside of the triangle, the argument must be modified slightly, but the same
result holds. Since there is nothing sacred about starting at angle
α
, the same
argument starting at angles
β
and
γ
will yield the second and third equations.
Cramer’s Rule applied to this system of equations yields the following results:
(b.)
cos
α
(–
==
++
acb
ba
ca
cb
ca
ba
aa b c
0
0
0
0
0
2222222
22
0
2
)
abc
bca
bc
ab
cba
bca
=+−
=cos
β
aabc
ba b c
abc
acb
ac
()
=−+ =+−
222 222
22
cos
γ
()
==
+−
0
0
22
222
ca
cb
bac
abc
ca b c
abc == +−abc
ab
222
2
γ
=a
b
2
β
=a
c
1
a
a1a2
cb
82 Supplementary Exercises 2

7. If Ais invertible, then adj(A), or adj(A) = [det(A)]A–1. Thus
That is, adj(A) is invertible and
It remains only to prove that A= det(A)adj(A–1). This follows from Theorem 2.4.2 and
Theorem 2.3.5 as shown:
9. We simply expand W. That is,
= d
dx (f1(x)g2(x) – f2(x)g1(x))
= f ′
1(x)g2(x) + f1(x)g′
2(x) – f′
2(x)g1(x) – f2(x)g′
1(x)
= [f′
1(x)g2(x) – f′
2(x)g1(x)] + [f1(x)g′
2(x) – f2(x)g′
1(x)]
=′′
+′
fx fx
gx gx
fx fx
gx
12
12
12
1
() ()
() ()
() ()
() ′′
gx
2()
dW
dx
d
dx
fx fx
gx gx
() ()
() ()
=12
12
AA
A
AAA== =[] det ( ) ()det()()
––
–
––11
1
11
1adj adj
[adj( )] det ( )
–
AAA
11
=
adj ( ) det ( )
AA
AI==
AA
–
det ( )
11
=
Supplementary Exercises 2 83

11. Let Abe an n×nmatrix for which the entries in each row add up to zero and let xbe the
n×1 matrix each of whose entries is one. Then all of the entries in the n×1 matrix
Ax are zero since each of its entries is the sum of the entries of one of the rows of A.
That is, the homogeneous system of linear equations
has a nontrivial solution. Hence det(A) = 0. (See Theorem 2.3.6.)
13. (a) If we interchange the ith and jth rows of A, then we claim that we must interchange the
ith and jth columns of A–1. To see this, let
where AA–1 = I. Thus, the sum of the products of corresponding entries from Row sin
Aand from Column rin A–1 must be 0 unless s= r, in which case it is 1. That is, if
Rows iand jare interchanged in A, then Columns iand jmust be interchanged in A–1
in order to insure that only 1’s will appear on the diagonal of the product AA–1.
(b) If we multiply the ith row of Aby a nonzero scalar c, then we must divide the ith
column of A–1 by c. This will insure that the sum of the products of corresponding
entries from the ith row of Aand the ith column of A–1 will remain equal to 1.
(c) Suppose we add ctimes the ith row of Ato the jth row of A. Call that matrix B. Now
suppose that we add –ctimes the jth column of A–1 to the ith column of A–1. Call that
matrix C. We claim that C= B–1. To see that this is so, consider what happens when
Row j→Row j+ cRow i[in A]
Column i→Column i– cColumn j[in A–1]
The sum of the products of corresponding entries from the jth row of Band any kth
column of Cwill clearly be 0 unless k= ior k= j. If k= i, then the result will be c–
c= 0. If k= j, then the result will be 1. The sum of the products of corresponding
entries from any other row of B—say the rth row—and any column of C—say the kth
column—will be 1 if r= kand 0 otherwise. This follows because there have been no
changes unless k= i. In case k= i, the result is easily checked.
AA=
−
Row 1
Row 2
Row n
and = Co
1ll. 1, Col. 2, , Col. n⋅⋅⋅
Ax=
0
0
84 Supplementary Exercises 2
15. (a) We have
If we calculate this determinant by any method, we find that
det(λI– A)= (λ– a11)(λ– a22)(λ– a33) – a23a32 (λ– a11)
–a13a31(λ– a22) – a12a21(λ– a33)
–a13a21a32 – a12a23a31
= λ3+ (–a11 – a22 – a33)λ2
+ (a11a22 + a11a33 + a22a33 – a12a21 – a13a31 – a23a32)λ
+ (a11a23a32 + a12a21a33 + a13a22a31
–a11a22a33 – a12a23a31 – a13a21a32)
(b) From Part (a) we see that b= –tr(A) and d= –det(A). (It is less obvious that cis the
trace of the matrix of minors of the entries of A; that is, the sum of the minors of the
diagonal entries of A.)
17. If we multiply Column 1 by 104, Column 2 by 103, Column 3 by 102, Column 4 by 10, and
add the results to Column 5, we obtain a new Column 5 whose entries are just the 5
numbers listed in the problem. Since each is divisible by 19, so is the resulting determinant.
det( )
λ
λ
λ
IA
aa a
aaa−=
−− −
−−−
−
11 12 13
21 22 23
aaa a
31 32 33
−−
λ
Supplementary Exercises 2 85


TECHNOLOGY EXERCISES 2
T3. Let y= ax3+ bx3+ cx + dbe the polynomial of degree three to pass through the four
given points. Substitution of the xand ycoordinates of these points into the equation of the
polynomial yields the system
7 = 27a+ 9b+ 3c+ d
–1 = 8a+ 4b+ 2c+ d
–1 = a+ b+ c+ d
1 = 0a+ 0b+ 0c+ d
Using Cramer’s Rule,
Plot. y= x3– 2x2– x+ 1
a=
−
−
=
7931
1421
1111
1001
27931
8421
1111
0001
12
122 1
27 7 3 1
8121
1111
0
,==
−
−
b1101
12
24
12 2
27 9 7 1
84 1 1
11 1 1
=−=−
=
−
−
c000 1 1
12
12
12 1
27 9 3 7
842 1
,=−=− =
−
d
1111 1
000 1
12
12
12 1
−
==
87
(1, −1) (2, −1)
(3, 7)
(0, 1)
88 Technology Exercises 2
EXERCISE SET 3.1
1.
3. (a) →= (3 – 4, 7 – 8) = (–1, –1)
(e) →
→= (–2 – 3, 5 + 7, –4 –2) = (–5, 12, –6)
5. (a) Let P= (x, y, z) be the initial point of the desired vector and assume that this vector
has the same length as v. Since has the same direction as v= (4, –2, –1), we have
the equation
= (3 – x, 0 – y, –5 – z) = (4, –2, –1)
PQ
→
PQ
→
PP
12
→
PP
12
→
89
x
(3, 4, 5)
y
z
x
y
z
(3, 4, 5)
x
(3, 4, 5)
y
z
x
z
y
(3, 0, 3)
(a) (c)
(e) ( j)

If we equate components in the above equation, we obtain
x= –1, y= 2, and z= –4
Thus, we have found a vector which satisfies the given conditions. Any positive
multiple kwill also work provided the terminal point remains fixed at Q. Thus, P
could be any point (3 – 4k, 2k, k– 5) where k> 0.
(b) Let P= (x, y, z) be the initial point of the desired vector and assume that this vector
has the same length as v. Since is oppositely directed to v= (4, –2, –1), we
have the equation
= (3 – x, 0 – y, –5 –z) = (–4, 2, 1)
If we equate components in the above equation, we obtain
x= 7, y= –2, and z= –6
Thus, we have found a vector which satisfies the given conditions. Any positive
multiple k will also work, provided the terminal point remains fixed at Q. Thus,
Pcould be any point (3 + 4k, –2k, –k– 5) where k> 0.
7. Let x= (x1, x2, x3). Then
2u– v+ x = (–6, 2, 4) – (4, 0, –8) + (x1, x2, x3)
= (–10 + x1, 2 + x2, 12 + x3)
On the other hand,
7x + w= 7(x1, x2, x3) + (6, –1, –4)
= (7x1+ 6, 7x2– 1, 7 x3– 4)
If we equate the components of these two vectors, we obtain
7x1+ 6 = x1– 10
7x2– 1 = x2+ 2
7x3– 4 = x3+ 12
Hence, x= (–8/3, 1/2, 8/3).
PQ
→
PQ
→
PQ
→
PQ
→
PQ
→
PQ
→
90 Exercise Set 3.1
9. Suppose there are scalars c1, c2, and c3which satisfy the given equation. If we equate
components on both sides, we obtain the following system of equations:
–2c1– 3c2+ c3= 0
9c1+ 2c2+ 7c3= 5
6c1+ c2+ 5c3= 4
The augmented matrix of this system of equations can be reduced to
The third row of the above matrix implies that 0c1+ 0c2+ 0c3= –1. Clearly, there do not
exist scalars c1, c2, and c3which satisfy the above equation, and hence the system is
inconsistent.
11. We work in the plane determined by the three points O= (0, 0, 0), P= (2, 3, –2), and Q=
(7, –4, 1). Let Xbe a point on the line through Pand Qand let t(where tis a positive,
real number) be the vector with initial point Pand terminal point X. Note that the length
of t→is ttimes the length of . Referring to the figure below, we see that
and
Q
O
PX
tPQ
OP PQ OQ
→→→
+=
OP t PQ OX
→→→
+=
PQ
→
PQ
→
PQ
→
23 1 0
02 2 1
00 0 1
−
−−
−
Exercise Set 3.1 91

Therefore,
(a) To obtain the midpoint of the line segment connecting Pand Q, we set t=1/2. This
gives
(b) Now set t= 3/4.This gives
13. Q= (7, –3, –19)
17. The vector uhas terminal point Qwhich is the midpoint of the line segment connecting P1
and P2.
−OP1
OP2 − OP1
(OP2 − OP1)
O
QP2
P1
OP1OP2
1
2
OX
→=−+−=−
1
423 2 3
4741 23
4
9
4
1
4
(,, ) (, ,) , ,
OX OP OQ
→→→
=+
=−+−
1
2
1
2
1
223 2 1
2741(,, ) (, ,)
==−−
9
2
1
2
1
2
,,
OX OP t OQ OP
tOP tOQ
→→→→
→→
=+
=+
(– )
(–)1
92 Exercise Set 3.1

19. Geometrically, given 4 nonzero vectors attach the “tail” of one to the “head” of another and
continue until all 4 have been strung together.The vector from the “tail” of the first vector
to the “head” of the last one will be their sum.
x
y
z
w
x + y + z + w
Exercise Set 3.1 93


EXERCISE SET 3.2
1. (a) v= (42+ (–3)2)1/2 = 5
(c) v= [(–5)2+ 02]1/2 = 5
(e) v= [(–7)2+ 22+ (–1)2]1/2 = 54
3. (a) Since u+ v= (3, –5, 7), then
u+ v= [32+ (–5)2+ 72]1/2 = 83
(c) Since
– 2u= [(–4)2+ 42+ (–6)2]1/2 = 2 17
and
2u= 2 [22+ (–2)2+ 32]1/2 = 2 17
then
–2u+ 2u= 4 17
(e) Since w= [32+ 62+ (–4)2]1/2 = 61, then
5. (a) k= 1, l= 3
(b) no possible solution
7. Since kv= (–k, 2k, 5k), then
kv= [k2+ 4k2+ 25k2]1/2 = |k|30
If kv= 4, it follows that |k|30 = 4 or k= ±4/ 30.
,,
–1
ww=3
61
6
61
4
61
95

9. (b) From Part (a), we know that the norm of v/vis 1. But if v= (3, 4), then v= 5.
Hence u= v/v= (3/5, 4/5) has norm 1 and has the same direction as v.
11. Note that p– p0= 1 if and only if p– p02= 1. Thus
(x– x0)2+ (y– y0)2+ (z– z0)2= 1
The points (x, y, z) which satisfy these equations are just the points on the sphere of radius
1 with center (x0, y0, z0); that is, they are all the points whose distance from (x0, y0, z0)
is 1.
13. These proofs are for vectors in 3-space. To obtain proofs in 2-space, just delete the 3rd
component. Let u= (u1, u2, u3) and v= (v1, v2, v3). Then
(a) u + v= (u1+ v1, u2+ v2, u3+ v3)
= (v1+ u1, v2+ u2, v3+ u3) = v+ u
(c) u + 0= (u1+ 0, u2+ 0, u3+ 0)
= (0+ u1, 0 + u2, 0 + u3)
= (u1, u2, u3) =0+u =u
(e) k(lu) = k(lu1, lu2, lu3) = (klu1, klu2, klu3) = (kl)u
15. See Exercise 9. Equality occurs only when uand vhave the same direction or when one is
the zero vector.
17. (a) If x< 1, then the point xlies inside the circle or sphere of radius one with center at
the origin.
(b) Such points xmust satisfy the inequality x– x0> 1.
96 Exercise Set 3.2

97
EXERCISE SET 3.3
1. (a) u •v= (2)(5) + (3)(–7) = –11
(c) u •v= (1)(3) + (–5)(3) + (4)(3) = 0
3. (a) u •v= (6)(2)+ (1)(0)+ (4)(–3) =0. Thus the vectors are orthogonal.
(b) u •v= –1 < 0. Thus θis obtuse.
5. (a) From Problem 4(a), we have
w2= u– w1= u= (6, 2)
(c) From Problem 4(c), we have
w2= (3, 1, –7) – (–16/13, 0, –80/13) = (55/13, 1, –11/13)
13. Let w= (x, y, z) be orthogonal to both uand v. Then u•w= 0 implies that x+ z= 0 and
v•w= 0 implies that y+ z= 0. That is w= (x, x, –x). To transform into a unit vector, we
divide each component by w= 3x2. Thus either (1/ 3, 1/ 3, –1/ 3) or (–1/ 3,
–1/ 3, 1/ 3) will work.
The minus sign in the above equation is extraneous because it yields an angle of 2π/3.
17. (b) Here
D=+−−
+=
42 1 5 2
41
1
17
22
() ( )
() ()

19. If we subtract Equation (**) from Equation (*) in the solution to Problem 18, we obtain
u+ v2– u– v2= 4(u•v)
If we then divide both sides by 4, we obtain the desired result.
21. (a) Let i= (1, 0, 0), j= (0, 1, 0), and k= (0, 0, 1) denote the unit vectors along the x, y,
and zaxes, respectively. If vis the arbitrary vector (a, b, c), then we can write v= ai+ bj
+ ck. Hence, the angle αbetween vand iis given by
since i= 1 and i•j= i•k= 0.
23. By the results of Exercise 21, we have that if vi= (ai, bi, ci) for i= 1 and 2, then cos αi=
, cos βi= , and cos γi= . Now
25. Note that
v•(k1w1+ k2w2) = k1(v•w1) + k2(v•w2) = 0
because, by hypothesis, v•w1= v•w2= 0. Therefore vis orthogonal to k1w1+ k2w2for any
scalars k1and k2.
27. (a) The inner product x•yis defined only if both xand yare vectors, but here v•wis a
scalar.
(b) We can add two vectors or two scalars, but not one of each.
(c) The norm of xis defined only for xa vector, but u•vis a scalar.
(d) Again, the dot product of a scalar and a vector is undefined.
vv
12 12
and are orthogonal ⇔=
⇔+
•vvvv0
12 1
aa bbbcc
aa bb cc
212
12
12
12
12
12
1
0+=
⇔++
vvvvvvvvvv
cos cos cos
vv2
12 12 12
0=
⇔++=cos cos
αα ββ γγ
cos 00
ci
i
vv
b
i
i
vv
ai
i
vv
cos
α
==
++ =
•vvii
vvii vv
a
abc
a
222
98 Exercise Set 3.3
29. If, for instance, u= (1, 0, 0), v= (0, 1, 0) and w= (0, 0, 1), we have u•v= u•w= 0, but
v≠w.
31. This is just the Pythagorean Theorem.
u
u + v v
Exercise Set 3.3 99


EXERCISE SET 3.4
1. (a)
(c) Since
we have
(e) Since
v– 2w= (0, 2, –3) – (4, 12, 14) = (–4, –10, –17)
we have
3. (a) Since u×v= (–7, –1, 3), the area of the parallelogram is u×v= 59.
(c) Since uand vare proportional, they lie on the same line and hence the area of the
parallelogram they determine is zero, which is, of course, u×v.
uuvvww(–2)×=−
−−−−
−− −−
,,
21
10 17
31
417
32
4110 44 55 22
=− −(,, )
()uuvvww××= −
−−
=,,
96
67
46
27
49
26 ((, , )27 40 42−
uuvv×= −
−−−
−
=−,, (,
21
23
31
03
32
02 4996,)
vvww×= −−−
=−,, (,,
23
67
03
27
02
26 32 6 )−4
101

7. Choose any nonzero vector wwhich is not parallel to u. For instance, let w= (1, 0, 0) or
(0, 1, 0). Then v= u×wwill be orthogonal to u. Note that if uand wwere parallel, then
v= u×wwould be the zero vector.
Alternatively, let w= (x, y, z). Then worthogonal to uimplies 2x– 3y+ 5z= 0. Now
assign nonzero values to any two of the variables x, y, and zand solve for the remaining
variable.
9. (e) Since (u×w) •v= v•(u×w) is a determinant whose rows are the components of v,
u, and w, respectively, we interchange Rows 1 and 2 to obtain the determinant which
represents u•(v×w). Since the value of this determinant is 3, we have (u×
w) •v= –3.
11. (a) Since the determinant
the vectors do not lie in the same plane.
15. By Theorem 3.4.2, we have
(u+ v) × (u– v)= u×(u– v) + v×(u– v)
= (u×u) + (u×(–v)) + (v×u) + (v×(–v))
= 0– (u×v) – (u×v) – (v– v)
= –2(u×v)
17. (a) The area of the triangle with sides and is the same as the area of the triangle
with sides (–1, 2, 2) and (1, 1, –1) where we have “moved” Ato the origin and
translated Band Caccordingly. This area is 1
2(–1, 2, 2) ×(1, 1, –1)= 1
2(–4, 1, –3)=
26/2.
19. (a) Let u= = (–4, 0, 2) and v= = (–3, 2, –4). Then the distance we want is
(–4, 0, 2) ×(–3, 2, –4)/(–3, 2, –4)= (–4, –22, –8)/ 29. = 2 141/ 29
AB
→
AP
→
AC
→
AB
→
−−
−
−
=≠
121
302
540
16 0
102 Exercise Set 3.4
21. (b) One vector nwhich is perpendicular to the plane containing vand wis given by
n= w×v= (1, 3, 3) ×(1, 1, 2) = (3, 1, –2)
Therefore the angle φbetween uand nis given by
Hence the angle θbetween uand the plane is given by
θ= π
2 – φ≈.6982 radians (or 40°19′)
If we had interchanged the roles of vand win the formula for nso that
n= v×w= (–3, –1, 2), then we would have obtained φ= cos–1 ≈2.269
radians or 130.0052°. In this case, θ= φ≈– π
2.
In either case, note that θmay be computed using the formula
25. (a) By Theorem 3.4.1, we know that the vector v×wis perpendicular to both vand w.
Hence v×wis perpendicular to every vector in the plane determined by vand w;
moreover the only vectors perpendicular to v×wwhich share its initial point must be
in this plane. But also by Theorem 3.4.1, u×(v×w) is perpendicular to v×wfor any
vector u≠0and hence must lie in the plane determined by vand w.
(b) The argument is completely similar to Part (a), above.
29. If a, b, c, and dlie in the same plane, then (a×b) and (c×d) are both perpendicular to
this plane, and are therefore parallel. Hence, their cross-product is zero.
θ
cos .=
−•
1un
un
−
9
14
φ
=
=
≈
−−
•
cos cos
.
11
9
14
08726
uunn
uunn
rradians or(.)49 99ο
Exercise Set 3.4 103

31. (a) The required volume is
= 2/3
33. Let u= (u1, u2, u3), v= (v1, v2, v3), and w= (w1, w2, w3).
For Part (c), we have
u×w= (u2w3– u3w2, u3w1– u1w3, u1w2– u2w1)
and
v×w= (v2w3– v3w2, v3w1– v1w3, v1w2– v2w1)
Thus
(u×w) + (v×w)
= ([u2+ v2]w3– [u3+ v3]w2, [u3+ v3]w1– [u1+ v1]w3, [u1+ v1]w2– [u2+ v2]w1)
But, by definition, this is just (u+ v) ×w.
For Part (d), we have
k(u×v) = (k[u2v3– u3v2], k[u3v1– u1v3], k[u1v2– u2v1])
and
(ku) ×v= (ku2v3– ku3v3, ku3v1– ku1v3, ku1v2– ku2v1)
Thus, k(u×v) = (ku) ×v. The identity k(u×v) = u×(kv) may be proved in an analogous
way.
35. (a) Observe that u×vis perpendicular to both uand v, and hence to all vectors in the
plane which they determine. Similarly, w= v×(u×v) is perpendicular to both vand
to u×v. Hence, it must lie on the line through the origin perpendicular to vand in the
plane determined by uand v.
1
6132203 2312 33 13021(– – , , – ) (( – ,,––)(–,,++×+
•––))
(– , , – ) ( , , )
3
1
644 3 6104
()
=
()
•
104 Exercise Set 3.4

(b) From the above, v•w= 0. Applying Part (d) of Theorem 3.7.1, we have
w= v×(u×v) = (v•v)u– (v•u)v
so that
u•w= (v•v)(u•u) – (v•u)(u•v)
= v2u2– (u•v)2
37. The expression u•(v×w) is clearly well-defined.
Since the cross product is not associative, the expression u×v×wis not well-defined
because the result is dependent upon the order in which we compute the cross products,
i.e., upon the way in which we insert the parentheses. For example, (i×j) ×j= k×j= –i
but i×(j×j) = i×0= 0.
The expression u•v×wmay be deemed to be acceptable because there is only one
meaningful way to insert parenthesis, namely, u•(v×w). The alternative, (u• v) ×w,
does not make sense because it is the cross product of a scalar with a vector.
Exercise Set 3.4 105


EXERCISE SET 3.5
5. (a) Normal vectors for the planes are (4, –1, 2) and (7, –3, 4). Since these vectors are not
multiples of one another, the planes are not parallel.
(b) Normal vectors are (1, –4, –3) and (3, –12, –9). Since one vector is three times the
other, the planes are parallel.
7. (a) Normal vectors for the planes are (3, –1, 1) and (1, 0, 2). Since the inner product of
these two vectors is not zero, the planes are not perpendicular.
11. (a) As in Example 6, we solve the two equations simultaneously. If we eliminate y, we
have x+ 7z+ 12 = 0. Let, say, z= t, so that x= –12 – 7t, and substitute these values
into the equation for either plane to get y= –41 – 23t.
Alternatively, recall that a direction vector for the line is just the cross-product of
the normal vectors for the two planes, i.e.,
(7, –2, 3) ×(–3, 1, 2) = (–7, –23, 1)
Thus if we can find a point which lies on the line (that is, any point whose coordinates
satisfy the equations for both planes), we are done. If we set z= 0 and solve the two
equations simultaneously, we get x= –12 and y= –41, so that x= –12 – 7t, y= –41 –
23t, z= 0 + tis one set of equations for the line (see above).
13. (a) Since the normal vectors (–1, 2, 4) and (2, –4, –8) are parallel, so are the planes.
(b) Since the normal vectors (3, 0, –1) and (–1, 0, 3) are not parallel, neither are the
planes.
17. Since the plane is perpendicular to a line with direction (2, 3, –5), we can use that vector
as a normal to the plane. The point-normal form then yields the equation 2(x+ 2) + 3(y–1)
– 5(z–7) = 0, or 2x+ 3y– 5z+ 36 = 0.
19. (a) Since the vector (0, 0, 1) is perpendicular to the xy-plane, we can use this as the
normal for the plane. The point-normal form then yields the equation z– z0= 0. This
equation could just as well have been derived by inspection, since it represents the set
of all points with fixed zand xand yarbitrary.
107

21. A normal to the plane is n= (5, –2, 1) and the point (3, –6, 7) is in the desired plane.
Hence, an equation for the plane is 5(x– 3) – 2(y+ 6) + (z–7) = 0 or 5x– 2y+ z– 34 = 0.
25. Call the points A, B, C, and D, respectively. Since the vectors = (–1, 2, 4) and =
(–2, –1, –2) are not parallel, then the points A, B, and Cdo determine a plane (and not just
a line). A normal to this plane is ×= (0, –10, 5). Therefore an equation for the
plane is
2y– z+ 1 = 0
Since the coordinates of the point Dsatisfy this equation, all four points must lie in the
same plane.
Alternatively, it would suffice to show that (for instance) ×and ×
are parallel, so that the planes determined by A, B, and Cand A, D, and Care parallel.
Since they have points in common, they must coincide.
27. Normals to the two planes are (4, –2, 2) and (3, 3, –6) or, simplifying, n1= (2, –1, 1) and
n2= (1, 1, –2). A normal nto a plane which is perpendicular to both of the given planes
must be perpendicular to both n1and n2. That is, n= n1×n2= (1, 5, 3). The plane with this
normal which passes through the point (–2, 1, 5) has the equation
(x+ 2) + 5(y– 1) + 3(z– 5) = 0
or
x+ 5y+ 3z– 18 = 0
31. If, for instance, we set t= 0 and t= –1 in the line equation, we obtain the points (0, 1, –3)
and (–1, 0, –5). These, together with the given point and the methods of Example 2, will
yield an equation for the desired plane.
33. The plane we are looking for is just the set of all points P= (x, y, z) such that the distances
from Pto the two fixed points are equal. If we equate the squares of these distances, we
have
(x+ 1)2+ (y+ 4)2+ (z+ 2)2= (x– 0)2+ (y+ 2)2+ (z– 2)2
or
2x+ 1 + 8y+ 16 + 4z+ 4 = 4y+ 4 – 4z+ 4
or
2x+ 4y+ 8z+ 13 = 0
DC
→
AD
→
BC
→
AB
→
BC
→
AB
→
BC
→
AB
→
108 Exercise Set 3.5
35. We change the parameter in the equations for the second line from tto s. The two lines will
then intersect if we can find values of sand tsuch that the x, y, and zcoordinates for the
two lines are equal; that is, if there are values for sand tsuch that
4t+ 3 = 12s– 1
t+ 4 = 6s+ 7
1 = 3s+ 5
This system of equations has the solution t= –5 and s= –4/3. If we then substitute t= –5
into the equations for the first line or s= –4/3 into the equations for the second line, we find
that x= –17, y= –1, and z= 1 is the point of intersection.
37. (a) If we set z= tand solve for xand yin terms of z, then we find that
39. (b) By Theorem 3.5.2, the distance is
41. (a)
(b)
(c)
45. (a) Normals to the two planes are (1, 0, 0) and (2, –1, 1). The angle between them is
given by
Thus θ= cos–1 (2/ 6) ≈35°15′52′′.
cos ,, , ,
θ
=
()
−
()
++ =
•100 2 11
1411
2
6
d
d
d
=
=
=
30
11
382
11
0sincepoint is on the linne
D=−
()
+
()
−
()
−
++−
()
=
21 32 41 1
23 4
1
29
22 2
xty tzt=+ =−− =
11
23
7
23
41
23
1
23
,,
Exercise Set 3.5 109

47. If we substitute any value of the parameter—say t0—into r= r0+ tvand –t0into r= r0– tv,
we clearly obtain the same point. Hence, the two lines coincide. They both pass through the
point r0and both are parallel to v.
49. The equation r= (1 – t)r1+ tr2can be rewritten as r= r1+ t(r2– r1). This represents a line
through the point P1with direction r2– r1. If t= 0, we have the point P1. If t= 1, we have
the point P2. If 0 < t< 1, we have a point on the line segment connecting P1and P2. Hence
the given equation represents this line segment.
110 Exercise Set 3.5

EXERCISE SET 4.1
3. We must find numbers c1, c2, c3, and c4such that
c1(–1, 3, 2, 0) + c2(2, 0, 4, –1) + c3(7, 1, 1, 4) + c4(6, 3, 1, 2) = (0, 5, 6, –3)
If we equate vector components, we obtain the following system of equations:
–c1+2c2+ 7c3+ 6c4= 0
3c1+ c3+ 3c4= 5
2c1+ 4c2+c3+ c4= 6
–c2+ 4c3+ 2c4= 3
The augmented matrix of this system is
The reduced row-echelon form of this matrix is
Thus c1= 1, c2= 1, c3= –1, and c4= 1.
1000 1
0100 1
0010 1
0001 1
−
−
−−
12760
30135
24116
01423
111

5. (c) v= [32+ 42+ 02+ (–12)2]1/2 = 169 = 13
9. (a) (2,5) •(–4,3) = (2)(–4) + (5)(3) = 7
(c) (3, 1, 4, –5) •(2, 2, –4, –3) = 6 + 2 –16 + 15 = 7
11. (a) d(u,v) = [(1 – 2)2+ (–2 – 1)2]1/2 = 10
(c) d(u, v) = [(0 + 3)2+ (–2 – 2)2+ (–1 – 4)2+ (1 – 4)2]1/2 = 59
15. (a) We look for values of ksuch that
u•v= 2 + 7 + 3k= 0
Clearly k= –3 is the only possiblity.
17. (a) We have |u•v| = |3(4) + 2(–1)| = 10, while
uv= [32+ 22]1/2[42+ (–1)2]1/2 = 221.
(d) Here |u•v| = 0 + 2 + 2 + 1 = 5, while
uv= [02+ (–2)2+ 22+ 12]1/2[(–1)2+ (–1)2+ 12+ 12]1/2 = 6.
23. We must see if the system
3 + 4t= s
2 + 6t= 3 – 3s
3 + 4t= 5 – 4s
–1 – 2t= 4 – 2s
is consistent. Solving the first two equations yield t= – 4/9, s= 11/9. Substituting into the
3rd equation yields 5/3 = 1/9. Thus the system is inconsistent, so the lines are skew.
25. This is just the Cauchy-Schwarz inequality applied to the vectors vTATand uTATwith both
sides of the inequality squared. Why?
112 Exercise Set 4.1
27. Let u= (u1,…, un), v= (v1,…, vn), and w= (w1,…, wn).
(a) u •(kv) = (u1,…, un) •(kv1,…, kvn)
= u1kv1+ …+ unkvn
= k(u1v1+ …+ unvn)
= k(u•v)
(b) u •(v+ w) = (u1,…, un) •(v1+ w1,…, vn+ wn)
= u1(v1+ w1) + …+ un(vn+ wn)
= (u1v1+ …+ unvn) + (u1w1+ …+ unwn)
= u•v+ u•w
35. (a) By theorem 4.1.7, we have
37. (a) True. In general, we know that
u+ v2= u2+ v2+ 2(u•v)
So in this case u•v= 0 and the vectors are orthogonal.
(b) True. We are given that u•v= u•w= 0. But since u•(v+ w) = u•v+ u•w, it
follows that uis orthogonal to v+ w.
(c) False. To obtain a counterexample, let u= (1, 0, 0), v= (1, 1, 0), and w= (–1, 1, 0).
d() .uv u v u v,, ––==+=
22
2
Exercise Set 4.1 113


EXERCISE SET 4.2
1. (b) Since the transformation maps (x1, x2) to (w1, w2, w3), the domain is R2and the
codomain is R3. The transformation is not linear because of the terms 2x1x2and 3x1x2.
3. The standard matrix is A, where
so that
5. (a) The standard matrix is
Note that T(1, 0) = (0, –1, 1, 1) and T(0, 1) = (1, 0, 3, –1).
01
10
13
11
−
−
T(,,)−=
−
−
−
−
124
351
411
321
1
2
4
=−
−
3
2
3
ww= Ax=
−
−
−
351
411
321
1
2
3
x
x
x
115

7. (b) Here
9. (a) In this case,
so the reflection of (2, –5, 3) is (2, –5, –3).
13. (b) The image of (–2, 1, 2) is (0, 1, 2 2), since
15. (b) The image of (–2, 1, 2) is (0, 1, 2 2), since
=
−
−
1
201
2
010
1
201
2
2
1
2
=
0
1
22
cos sin
sin cos
−°
()
−−°
()
−°
()
−°
()
45 0 45
01 0
45 0 45
−
2
1
2
cos sin
sin cos
45 0 45
010
45 0 45
°
()
°
()
−°
()
°
()
−
=
−
2
1
2
1
201
2
010
1
201
2
−
=
2
1
2
0
1
22
T(, , )253
10 0
01 0
00 1
2
5
3
−=
−
−
=−
−
2
5
3
T(, )21
211
011
00 0
2
1
3
3−=
−
−
=−
0
2
0
116 Exercise Set 4.2

17. (a) The standard matrix is
(c) The standard matrix for a counterclockwise rotation of 15° + 105° + 60° = 180° is
19. (c) The standard matrix is
21. (a) Geometrically, it doesn’t make any difference whether we rotate and then dilate or
whether we dilate and then rotate. In matrix terms, a dilation or contraction is
represented by a scalar multiple of the identity matrix. Since such a matrix commutes
with any square matrix of the appropriate size, the transformations commute.
=−
−
010
001
100
=
−
−
−
100
010
001
001
010
100
100
001
010−
cos sin
sin cos
180 180 0
180 180 0
001
°
()
−°
()
°
()
°
()
°
()
°
()
−°
()
cos sin
sin c
90 0 90
010
90 0 oos
cos sin
90
10 0
0270 270
°
()
°
()
−°
()
00 270 270sin cos°
()
°
()
cos sin
sin cos
180 180
180 180
°
()
−°
()
°
()
°
()
=−
−
10
01
01
10
10
00
1
2
3
2
3
2
1
2
−
=−
00
1
2
3
2
Exercise Set 4.2 117

23. Set (a, b, c) equal to (1, 0, 0), (0, 1, 0), and (0, 0, 1) in turn.
25. (a) Since T2(T1(x1, x2)) = (3(x1+ x2), 2(x1+ x2) + 4(x1– x2)) = (3x1+ 3x2, 6x1– 2x2),
we have
We also have
27. Compute the trace of the matrix given in Formula (17) and use the fact that (a, b, c) is a
unit vector.
29. (a) This is an orthogonal projection on the x-axis and a dilation by a factor of 2.
(b) This is a reflection about the x-axis and a dilation by a factor of 2.
31. Since cos(2
θ
) = cos2θ– sin2θand sin(2
θ
) = 2 sin
θ
cos
θ
, this represents a rotation
through an angle of 2
θ
.
[][]TT
21
30
24
11
11
33
62
=
−
=−
[]TT
21
33
62
=−
118 Exercise Set 4.2

EXERCISE SET 4.3
1. (a) Projections are not one-to-one since two distinct vectors can have the same image
vector.
(b) Since a reflection is its own inverse, it is a one-to-one mapping of R2or R3onto itself.
3. If we reduce the system of equations to row-echelon form, we find that w1= 2w2, so that any
vector in the range must be of the form (2w, w). Thus (3, 1), for example, is not in the range.
5. (a) Since the determinant of the matrix
is 3, the transformation Tis one-to-one with
(b) Since the determinant of the matrix
is zero, Tis not one-to-one.
[]T=−
−
46
23
Thus Tww w w w w
−=− +
1
12 1 2 12
1
3
2
3
1
3
1
3
(, ) , .
[]T−=−
1
1
3
2
3
1
3
1
3
[]T=−
12
11
119

9. (a) Tis linear since
T((x1, y1) + (x2, y2) ) = (2(x1+ x2) + (y1+ y2), (x1+ x2) – (y1+ y2))
= (2x1+ y1, x1– y1) + (2x2+ y2, x2– y2)
= T(x1, y1) + T(x2, y2)
and
T(k(x, y)) = (2kx + ky, kx – ky)
= k(2x+ y, x– y) = kT(x, y)
(b) Since
T((x1, y1) + (x2, y2))= (x1+ x2+ 1, y1+ y2)
= (x1+ 1, y1) + (x2, y2)
≠T(x1, y1) + T(x2, y2)
and T(k(x, y)) = (kx + 1, ky) ≠kT (x, y) unless k= 1, Tis nonlinear.
13. (a) The projection sends e1to itself and the reflection sends e1to –e1, while the projection
sends e2to the zero vector, which remains fixed under the reflection. Therefore
T(e1) = (–1, 0) and T(e2) = (0, 0), so that
(b) We have e1= (1, 0) →(0, 1) →(0, –1) = 0e1– e2while e2= (0, 1) →(1, 0) →(1, 0)
= e1+ 0e2. Hence
(c) Here e1= (1, 0) →(3, 0) →(0, 3) →(0, 3) = 0e1+ 3e2and e2= (0, 1) →(0, 3) →
(3, 0) →(0, 0) = 0e1+ 0e2. Therefore
[]T=
00
30
[]T=−
01
10
[]T=−
10
00
120 Exercise Set 4.3

17. (a) By the result of Example 5,
or T(–1, 2) = (1/2, 1/2)
19. (a)
Eigenvalue λ1= –1, eigenvector
Eigenvalue λ2= 1, eigenvector
(b)
λ1= 0,
λ2= 1,
(c) This transformation doubles the length of each vector while leaving its direction
unchanged. Therefore λ= 2 is the only eigenvalue and every nonzero vector in R3is a
corresponding eigenvector. To verify this, observe that the characteristic equation is
λ−
λ−
λ−
20 0
020
00 2
0=
ξξ
21 22
1
0
0
0
0
1
=
=
,,orinn general
s
t
0
ξ1=
0
1
0
A=
100
000
001
ξξ
2221
0
1
0
0
0
1
=
=
,
ξ1
1
0
0
=
A=
−
100
010
001
T−
=
() ()()
()()(
1
2
12 1212
1212 12
2
))
−
=
2
1
2
12
12
Exercise Set 4.3 121
or (λ– 2)3= 0. Thus the only eigenvalue is λ= 2. If (x, y, z) is a corresponding
eigenvector, then
Since the above equation holds for every vector (x, y, z), every nonzero vector is an
eigenvector.
(d) Since the transformation leaves all vectors on the z-axis unchanged and alters (but
does not reverse) the direction of all other vectors, its only eigenvalue is λ= 1 with
corresponding eigenvectors (0, 0, z) with z≠0. To verify this, observe that the
characteristic equation is
or
Since the quadratic (λ– 1/ 2)2+ 1/2 = 0 has no real roots, λ= 1 is the only real
eigenvalue. If (x, y, z) is a corresponding eigenvector, then
You should verify that the above equation is valid if and only if x= y= 0. Therefore the
corresponding eigenvectors are all of the form (0, 0, z) with z≠0.
21. Since T(x, y) = (0, 0) has the standard matrix , it is linear. If T(x, y) = (1, 1) were
linear, then we would have
(1, 1) = T(0, 0) = T(0 + 0, 0 + 0) = T(0, 0) + T(0, 0) = (1, 1) + (1, 1) = (2, 2)
Since this is a contradiction, Tcannot be linear.
00
00
10
10
000
−
−−
12 12
12 12
x
y
z
=
−
(
)
+
(
)
−
(
)
+
(
)
112 12
12 1−12
xy
xy
0
0
0
0
=
() ()
λλλ
−=−−
()
+
()
111212
22
λ−
−λ−
12 12
12 12
=0
λ−1 2
λ−1 2
λ−1
12 0
12 0
00
0−=
000
000
000
0
0
0
=
x
y
z
122 Exercise Set 4.3
23. From Figure 1, we see that T(e1) = (cos 2
θ
, sin 2
θ
) and from Figure 2, that T(e2) =
Figure 1 Figure 2
This, of course, should be checked for all possible diagrams, and in particular for the case
π
2<
θ
< π. The resulting standard matrix is
25. (a) False. The transformation T(x1, x2) = x2
1from R2to R1is not linear, but T(0) = 0.
(b) True. If not, T(u) = T(v) where uand vare distinct. Why?
(c) False. One must also demand that x≠0.
(d) True. If c1= c2= 1, we obtain equation (a) of Theorem 4.3.2 and if c2= 0, we obtain
equation (b).
27. (a) The range of Tcannot be all of Rn, since otherwise Twould be invertible and det(A)
≠0. For instance, the matrix sends the entire xy-plane to the x-axis.
(b) Since det(A) = 0, the equation T(x) = Ax= 0will have a non-trivial solution and
hence, Twill map infinitely many vectors to 0.
10
00
cos sin
sin cos
22
22
θθ
θθ
−
l
l
y
y
x
x
(1, 0)
(0, 1)
(cos 2 , sin 2 )
θ
θ
θ
2θ
3
22
πθ
θθ
+
2
πθ
−
2
πθ
−
3
223
22
πθπ
cos , sin+
+
θθ
cos , sin(sin
3
223
222
πθπθ
+
+
=
θθθ
,cos )−2
Exercise Set 4.3 123


EXERCISE SET 4.4
1. (a) (x2+ 2x– 1) – 2(3x2+ 2) = –5x2+ 2x– 5
(b) 5/4x2+ 3x) + 6(x2+ 2x+ 2) = 26x2+ 27x+ 6
(c) (x4+ 2x3+ x2– 2x+ 1) – (2x3– 2x) = x4+ x2+ 1
(d) π(4x3– 3x2+ 7x+ 1) = 4πx3– 3πx2+ 7πx+ π
3. (a) Note that the mapping fR3→Rgiven by f(a, b, c) = |a|has f(1, 0, 0) = 1, f(0, 1, 0) =
0, and f(0, 0, 1) = 0. So If fwere a linear mapping, the matrix would be A= (1, 0, 0).
Thus, f(–1, 0, 0) would be found as . Yet, f(–1, 0, 0) = |–1| = 1 ≠–1.
Thus fis not linear.
(b) Yes, and here A= (1, 0, 0) by reasoning as in (a).
5. (a)
A=
3000
0200
0010
40000
003000
00200
00010
500000
040000
003
0000
000200
000010
100
1
0
0
1
,,
(
)
−
=−
125
7. (a) T(ax + b) = (a+ b)x+ (a– b)
TP1→P1
(b) T(ax + b) = ax2+ (a+ b)x+ (2a– b)
TP1→P2
(c) T(ax3+ bx2+ cx + d) = (a+ 2c– d)x+ (2a+ b+ c+ 3d)
TP3→P1
(d) T(ax2+ bx + c) = bx
TP2→P2
(e) T(ax2+ bx + c) = b
T
P2
→
P0
9. (a) 3et+ 3e–t
(b) Yes, since cosh t= 1
2et+ 1
2e–t, cosh tcorresponds to the vector (0, 0, 1
2, 1
2).
(c)
11. If S(u) = T(u) + f, f≠0, then S(0) = T(0) + f= f≠0. Thus Sis not linear.
13. (a) The Vandermonde system is
Solving: a0= 1, a1= 2, a2= 1
p(x) = x2+ 2x+ 1 = (x+ 1)2
124
100
111
0
1
2
−
a
a
a
==
1
1
4
Aa=
−
0100
0000
0010
0001
(,,,, ) (,,, )bcd b c d→−0
126 Exercise Set 4.4

(b) The system is:
Solving: b0= 1, b1= 0, b2= 1.
Thus, p(x) = 1 •(x+ 2)(x) + 0 •(x+ 2) + 1 = (x+ 2) •x+ 1
= (x+ 2) •x+ 1
= x2+ 2x+ 1
15. (a) The Vandermonde system is
Thus, p(x) = 2x3– 2x+ 2
(b) The system is
Thus, p(x) = 2(x + 2)(x + 1)(x – 1) – 4(x + 2)(x + 1) + 12(x + 2) – 10
(c) We have
a
a
a
a
0
1
2
3
122 2
013 1
00
=
−
−
112
000 1
10
12
4
2
−
−
=−
2
2
0
2
10 0 0 10
11 0 0 2
13 6 0 2
141212 14
−
=−
=
=−
=
Solving, b
b
b
b
0
1
2
3
10
12
4
2
124810
1111 2
1111 2
124
−−−
−−
814
2
2
0
0
1
2
=
=−
=
Solving, a
a
a
a33 2=
100
120
133
1
1
4
0
1
2
=
b
b
b
Exercise Set 4.4 127

(d) We have
17. (a)
(b)
(c)
where
= –(x1x2x3+ x0x2x3+ x0x1x3+ x0x1x2)
= x0x1+ x0x2+ x0x3+ x1x2+ x1x3+ x2x3
19. (a) D2= (2 0 0)
(b)
(c) No. For example, the matrix for first differentiation from P3→P2is
D2
1cannot be formed.
D2
3000
0200
0010
=
D2
6000
0200
=
2
1
a
a
a
a
a
xxx xx
0
1
2
3
4
001 0
1
=
−−
112 0123
01 120201 1
01
00 1
xxxxx
xx xxxx xx
x
−+
()
++
−
0012 2
23
00 0 1
00 0 0 1
++
()
−+
()
xx
xx
b
b
b
b
b
0
1
2
3
4
a
a
a
xxx
xx
0
1
2
001
01
1
01
00 1
=
−
−+
()
b
b
b
0
1
2
a
a
xb
b
0
1
00
1
1
01
=−
b
b
b
b
0
1
2
3
1248
0137
0
=
−−
−
0012
0001
2
2
0
2
−
−
=
−
−
10
12
4
2
128 Exercise Set 4.4

21. (a) We first note P= yi. Hence the Vandermonde system has a unique solution that are the
coefficients of the polynomial of nth degree through the n+ 1 data points. So, there
is exactly one polynomial of the nth degree through n+ 1 data points with the xi
unique. Thus, the Lagrange expression must be algebraically equivalent to the
Vandermonde form.
(b) Since ci= yi, i= 0, 1, …, n, then the linear systems for the Vandermonde and Newtons
method remain the same.
(c) Newton’s form allows for the easy addition of another point (xn+1, yn+1) that does not
have to be in any order with respect to the other xivalues. This is done by adding a
next term to p(i), pe.
pn+1(x) = bn+1(x– x0)(x– x1)(x– x2)… (x– xn)
+ bn(x– x0)(x– x1)(x– x2)… (x– xn–1)
+ …+ b1(x– x0) + b0,
where Pn(x) = bn(x– x0)(x– x1)(x– x2)… (x– xn–1) + … +b1(x– x0) + b0is the
interpolant to the points (x0, y0)… (xn, yn). The coefficients for pn+1(x) are found as
in (4), giving an n+ 1 degree polynomial. The extra point (xn+1, yn+1) may be the
desired interpolating value.
23. We may assume in all cases that x= 1, since
Let (x1, x2) = (cos
θ
, sin
θ
) = since x= 1.
(a)
(b)
(c)
(d)
Txxxx=+
+−
max 1
2
1
2
1
2
1
2
12
2
12
=+=
2
1
2
2
21max xx
Txx=+=+=max max sin49 45 3
1
2
2
22
θ
Txx=+=max 1
2
2
21
T=+=+=max cos sin max cos4132
22 2
θθ θ
x
Tx
x
Tx
x
Tx
x
2
2
2
2
()
=
()
=
()
Exercise Set 4.4 129


EXERCISE SET 5.1
11. This is a vector space. We shall check only four of the axioms because the others follow
easily from various properties of the real numbers.
(1) If fand gare real-valued functions defined everywhere, then so is f+ g. We must
also check that if f(1) = g(1) = 0, then (f+ g)(1) = 0. But (f+ g)(1) = f(1) + g(1)
= 0 + 0 = 0.
(4) The zero vector is the function zwhich is zero everywhere on the real line. In
particular, z(1) = 0.
(5) If fis a function in the set, then –fis also in the set since it is defined for all real
numbers and –f(1) = –0 = 0. Moreover, f+ (–f) = (–f) + f= z.
(6) If fis in the set and kis any real number, then kf is a real valued function defined
everywhere. Moreover, kf(1) = k0 = 0.
13. This is a vector space with 0= (1, 0) and –x= (1, –x). The details are easily checked.
15. We must check all ten properties:
(1) If xand yare positive reals, so is x+ y= xy.
(2) x+ y= xy = yx = y+ x
(3) x+ (y+ z) = x(yz) = (xy)z= (x+ y) + z
(4) There is an object 0, the positive real number 1, which is such that
1 + x= 1 •x= x= x•1 = x+ 1
for all positive real numbers x.
(5) For each positive real x, the positive real 1/xacts as the negative:
x+ (1/x) = x(1/x) = 1 = 0= 1 = (1/x)x= (1/x) + x
(6) If kis a real and xis a positive real, then kx = xkis again a positive real.
(7) k(x+ y) = (xy)k= xkyk= kx + ky
(8) (k+ )x= xk+= xkx= kx + x
(9) k(x) = (x)k= (x)k= xk= xk= (k)x
(10) 1x= x1= x
131

17. (a) Only Axiom 8 fails to hold in this case. Let kand mbe scalars. Then
(k+ m)(x, y, z) = ((k+ m)2x, (k+ m)2y, (k+ m)2z) = (k2x, k2y, k2z) + (2kmx, 2kmy,
2kmz) + (m2x, m2y, m2z)
= k(x, y, z) + m(x, y, z) + (2kmx, 2kmy, 2kmz)
≠k(x, y, z) + m(x, y, z),
and Axiom 8 fails to hold.
(b) Only Axioms 3 & 4 fail for this set.
Axiom 3: Using the obvious notation, we have
u+ (v+ w) = (u1, u2, u3) + (v3+ w3, v2+ w2, v1+ w1)
= (u3+ v1+ w1, u2+ v2+ w2, u1+ v3+ w3)
whereas
(u+ v) + w= (u3+ v3, u2+ v2, u1+ v1) + (w1, w2, w3)
= (u1+ v1+ w3, u2+ v2+ w2, u3+ v3+ w1)
Thus, u+ (v+ w) ≠(u+ w) + w.
Axiom 4: There is no zero vector in this set. If we assume that there is, and let 0
= (z1, z2, z3), then for any vector (a, b, c), we have (a, b, c) + (z1, z2, z3)
= (c+ z3, b+ z2, a+ z1) = (a, b, c). Solving for the z′
is, we have z3= a
– c, z2= 0 and z1= c– a. Thus, there is no one zero vector that will
work for every vector (a, b, c) in R3.
(c) Let Vbe the set of all 2 ×2 invertible matrices and let Abe a matrix in V. Since we are
using standard matrix addition and scalar multiplication, the majority of axioms hold.
However, the following axioms fail for this set V:
Axiom 1: Clearly if Ais invertible, then so is –A. However, the matrix A+ (–A) =
0is not invertible, and thus A+ (–A) is not in V, meaning Vis not closed
under addition.
Axiom 4: We’ve shown that the zero matrix is not in V, so this axiom fails.
Axiom 6: For any 2 ×2 invertible matrix A, det(kA) = k2det(A), so for k≠0, the
matrix kA is also invertible. However, if k= 0, then kA is not invertible,
so this axiom fails.
Thus, Vis not a vector space.
19. (a) Let Vbe the set of all ordered pairs (x, y) that satisfy the equation ax + by = c, for
fixed constants a, band c. Since we are using the standard operations of addition and
scalar multiplication, Axioms 2, 3, 5, 7, 8, 9, 10 will hold automatically. However, for
Axiom 4 to hold, we need the zero vector (0, 0) to be in V. Thus a0 + b0 = c, which
forces c= 0. In this case, Axioms 1 and 6 are also satisfied. Thus, the set of all points
in R2lying on a line is a vector space exactly in the case when the line passes through
the origin.
132 Exercise Set 5.1

(b) Let Vbe the set of all ordered triples (x, y, z) that satisfy the equation ax + by + cz
= d, for fixed constants a, b, cand d. Since we are using the standard operations of
addition and scalar multiplication, Axioms 2, 3, 5, 7, 8, 9, 10 will hold automatically.
However, for Axiom 4 to hold, we need the zero vector (0, 0, 0) to be in V. Thus a0 +
b0 + c0 = d, which forces d= 0. In this case, Axioms 1 and 6 are also satisfied. Thus,
the set of all points in R3lying on a plane is a vector space exactly in the case when
the plane passes through the origin.
25. No. Planes which do not pass through the origin do not contain the zero vector.
27. Since this space has only one element, it would have to be the zero vector. In fact, this is
just the zero vector space.
33. Suppose that uhas two negatives, (–u)1and (–u)2. Then
(–u)1= (–u)1+ 0= (–u)1+ (u+ (–u)2) = ((–u)1+ u) + (–u)2= 0+ (–u)2= (–u)2
Axiom 5 guarantees that umust have at least one negative. We have proved that it has at
most one.
Exercise Set 5.1 133


EXERCISE SET 5.2
1. (a) The set is closed under vector addition because
(a, 0, 0) + (b, 0, 0) = (a+ b, 0, 0)
It is closed under scalar multiplication because
k(a, 0, 0) = (ka, 0, 0)
Therefore it is a subspace of R3.
(b) This set is not closed under either vector addition or scalar multiplication. For
example, (a, 1, 1) + (b, 1, 1) = (a+ b, 2, 2) and (a+ b, 2, 2) does not belong to the
set. Thus it is not a subspace.
(c) This set is closed under vector addition because
(a1, b1, 0) + (a2, b2, 0) = (a1+ a2, b1+ b2, 0).
It is also closed under scalar multiplication because
k(a, b, 0) = (ka, kb, 0).
Therefore, it is a subspace of R3.
3. (a) This is the set of all polynominals with degree ≤3 and with a constant term which is
equal to zero. Certainly, the sum of any two such polynomials is a polynomial with
degree ≤3 and with a constant term which is equal to zero. The same is true of a
constant multiple of such a polynomial. Hence, this set is a subspace of P3.
(c) The sum of two polynomials, each with degree ≤3 and each with integral coefficients,
is again a polynomial with degree ≤3 and with integral coefficients. Hence, the subset
is closed under vector addition. However, a constant multiple of such a polynomial
will not necessarily have integral coefficients since the constant need not be an integer.
Thus, the subset is not closed under scalar multiplication and is therefore not a
subspace.
135

5. (b) If Aand Bare in the set, then aij = –aji and bij = –bji for all iand j. Thus aij + bij =
–(aji + bji) so that A+ Bis also in the set. Also aij = –aji implies that kaij = –(kaji), so
that kA is in the set for all real k. Thus the set is a subspace.
(c) For Aand Bto be in the set it is necessary and sufficient for both to be invertible, but
the sum of 2 invertible matrices need not be invertible. (For instance, let B= –A.)
Thus A+ Bneed not be in the set, so the set is not a subspace.
7. (a) We look for constants aand bsuch that au+ bv= (2, 2, 2), or
a(0, –2, 2) + b(1, 3, –1) = (2, 2, 2)
Equating corresponding vector components gives the following system of equations:
b= 2
–2a+ 3b= 2
2a– b= 2
From the first equation, we see that b= 2. Substituting this value into the remaining
equations yields a= 2. Thus (2, 2, 2) is a linear combination of uand v.
(c) We look for constants aand bsuch that au+ bv= (0, 4, 5), or
a(0, –2, 2) + b(1, 3, –1) = (0, 4, 5)
Equating corresponding components gives the following system of equations:
b= 0
–2a+ 3b= 4
2a– b= 5
From the first equation, we see that b= 0. If we substitute this value into the
remaining equations, we find that a= –2 and a= 5/2. Thus, the system of equations is
inconsistent and therefore (0, 4, 5) is not a linear combination of uand v.
9. (a) We look for constants a, b, and csuch that
ap1+ bp2+ cp3= –9– 7x – 15x2
136 Exercise Set 5.2

If we substitute the expressions for p1, p2, and p3into the above equation and equate
corresponding coefficients, we find that we have exactly the same system of equations
that we had in Problem 8(a), above. Thus, we know that a= –2, b= 1, and c= –2 and
thus –2p1+ 1p2– 2p3= –9 – 7x– 15x2.
(c) Just as Problem 9(a) was Problem 8(a) in disguise, Problem 9(c) is Problem 8(c) in
different dress. The constants are the same, so that 0= 0p1+ 0p2+ 0p3.
11. (a) Given any vector (x, y, z) in R3, we must determine whether or not there are
constants a, b, and csuch that
(x, y, z) = av1+ bv2+ cv3
= a(2, 2, 2) + b(0, 0, 3) + c(0, 1, 1)
= (2a, 2a+ c, 2a+ 3b+ c)
or
x= 2a
y= 2a+ c
z= 2a+ 3b+ c
This is a system of equations for a, b, and c. Since the determinant of the system is
nonzero, the system of equations must have a solution for any values of x, y, and z,
whatsoever. Therefore, v1, v2, and v3do indeed span R3.
Note that we can also show that the system of equations has a solution by solving
for a, b, and cexplicitly.
(c) We follow the same procedure that we used in Part (a). This time we obtain the
system of equations
3a+ 2b+ 5c+ d=x
a– 3b– 2c+ 4d= y
4a+ 5b+ 9c– d= z
The augmented matrix of this system is
3251
1324
4591
x
y
z
−−
−
Exercise Set 5.2 137

which reduces to
Thus the system is inconsistent unless the last entry in the last row of the above
matrix is zero. Since this is not the case for all values of x, y, and z, the given vectors
do not span R3.
13. Given an arbitrary polynomial a0+ a1x+ a2x2in P2, we ask whether there are numbers a,
b, cand dsuch that
a0+ a1x+ a2x2= ap1+ bp2+ cp3+ dp4
If we equate coefficients, we obtain the system of equations:
a0=a+ 3b+ 5c– 2d
a1=–a+ b– c– 2d
a2=2a+ 4c+ 2d
A row-echelon form of the augmented matrix of this system is
Thus the system is inconsistent whenever –a0+ 3a1+ 2a2≠0 (for example, when a0= 0,
a1= 0, and a2= 1). Hence the given polynomials do not span P2.
135 2
011 1 4
000 0 3
0
01
0
−
−+
−+
a
aa
aaaa
12
2+
1324
011 1 3
11
0000
−−
−−
−
y
xy
z44
17
3
11
yx y
−−
138 Exercise Set 5.2

15. The plane has the vector u×v= (0, 7, –7) as a normal and passes through the point
(0,0,0). Thus its equation is y– z= 0.
Alternatively, we look for conditions on a vector (x, y, z) which will insure that it lies
in span {u, v}. That is, we look for numbers aand bsuch that
(x, y, z)= au+ bv
= a(–1, 1, 1) + b(3, 4, 4)
If we expand and equate components, we obtain a system whose augmented matrix is
This reduces to the matrix
Thus the system is consistent if and only if = 0 or y= z.
17. The set of solution vectors of such a system does not contain the zero vector. Hence it
cannot be a subspace of Rn.
19. Note that if we solve the system v1= aw1+ bw2, we find that v1= w1+ w2. Similarly, v2=
2w1+ w2, v3= –w1+ 0w2, w1= 0v1+ 0v2– v3, and w2= v1+ 0v2+ v3.
21. (a) We simply note that the sum of two continuous functions is a continuous function and
that a constant times a continuous function is a continuous function.
(b) We recall that the sum of two differentiable functions is a differentiable function and
that a constant times a differentiable function is a differentiable function.
7
−+yz
13
01 7
00 7
−−
+
−+
x
xy
yz
−
13
14
14
x
y
z
Exercise Set 5.2 139

23. (a) False. The system has the form Ax= bwhere bhas at least one nonzero entry.
Suppose that x1and x2are two solutions of this system; that is, Ax1= band Ax2= b.
Then
A(x1+ x2) = Ax1+ Ax2= b+ b≠b
Thus the solution set is not closed under vector addition and so cannot form a subspace
of Rn. Alternatively, we could show that it is not closed under scalar multiplication.
(b) True. Let uand vbe vectors in W. Then we are given that ku+ vis in Wfor all scalars
k. If k= 1, this shows that Wis closed under addition. If k= –1 and u= v, then the
zero vector of Vmust be in W. Thus, we can let v= 0to show that Wis closed under
scalar multiplication.
(d) True. Let W1and W2be subspaces of V. Then if uand vare in W1∩W2, we know that
u+ vmust be in both W1and W2, as must kufor every scalar k. This follows from the
closure of both W1and W2under vector addition and scalar multiplication.
(e) False. Span{v} = span{2v}, but v≠2 vin general.
25. No. For instance, (1, 1) is in W1and (1, –1) is in W2, but (1, 1) + (1, –1) = (2, 0) is in
neither W1nor W2.
27. They cannot all lie in the same plane.
140 Exercise Set 5.2

EXERCISE SET 5.3
3. (a) Following the technique used in Example 4, we obtain the system of equations
3k1+ k2+ 2k3+ k4= 0
8k1+ 5k2– k3+ 4k4= 0
7k1+ 3k2+ 2k3= 0
–3k1– k2+ 6k3+ 3k4= 0
Since the determinant of the coefficient matrix is nonzero, the system has only the
trivial solution. Hence, the four vectors are linearly independent.
(b) Again following the technique of Example 4, we obtain the system of equations
3k2+ k3= 0
3k2+ k3= 0
2k1= 0
2k1– k3= 0
The third equation, above, implies that k1= 0. This implies that k3and hence k2must
also equal zero. Thus the three vectors are linearly independent.
5. (a) The vectors lie in the same plane through the origin if and only if they are linearly
dependent. Since the determinant of the matrix
is not zero, the matrix is invertible and the vectors are linearly independent. Thus
they do not lie in the same plane.
26 2
21 0
04 4
−
−
141

7. (a) Note that 7v1– 2v2+ 3v3= 0.
9. If there are constants a, b, and csuch that
a(λ, –1/2, –1/2) + b(–1/2, λ, –1/2) + c(–1/2, –1/2, λ) = (0, 0, 0)
then
The determinant of the coefficient matrix is
This equals zero if and only if λ= 1 or λ= –1/2. Thus the vectors are linearly dependent for
these two values of λand linearly independent for all other values.
11. Suppose that Shas a linearly dependent subset T. Denote its vectors by w1,…, wm. Then
there exist constants ki, not all zero, such that
k1w1+ …+ kmwm= 0
But if we let u1,…, un–mdenote the vectors which are in Sbut not in T, then
k1w1+ …+ kmwm+ 0u1+ …+ 0un–m= 0
Thus we have a linear combination of the vectors v1,…, vnwhich equals 0. Since not all of
the constants are zero, it follows that Sis not a linearly independent set of vectors, contrary
to the hypothesis. That is, if Sis a linearly independent set, then so is every non-empty
subset T.
λλ λλ
3
2
3
4
1
411
2
()−−=− +
λ
λ
λ
−−
−−
−−
12 12
12 12
12 12
a
b
c
=
0
0
0
142 Exercise Set 5.3

13. This is similar to Problem 10. Since {v1, v2,…, vr} is a linearly dependent set of vectors,
there exist constants c1, c2,…, crnot all zero such that
c1v1+ c2v2+ …+ crvr= 0
But then
c1v1+ c2v2+ …+ crvr+ 0vr+1 + …+ 0vn= 0
The above equation implies that the vectors v1,…, vnare linearly dependent.
15. Suppose that {v1, v2, v3} is linearly dependent. Then there exist constants a, b, and cnot all
zero such that
(*)av1+ bv2+ cv3= 0
Case 1: c= 0. Then (*) becomes
av1+ bv2= 0
where not both aand bare zero. But then {v1, v2} is linearly dependent, contrary to
hypothesis.
Case 2: c≠0. Then solving (*) for v3yields
v3= – a
cv1– b
cv2
This equation implies that v3is in span{v1, v2}, contrary to hypothesis. Thus, {v1, v2, v3}
is linearly independent.
21. (a) The Wronskian is
Thus the vectors are linearly independent.
1
01
00
0
xe
e
e
e
x
x
x
x
=≡
Exercise Set 5.3 143
(b) The Wronskian is
Thus the vectors are linearly independent.
23. Use Theorem 5.3.1, Part (a).
sin cos sin
cos sin sin cos
sin cos
xx xx
xxxxx
xx
−+
−−2ccos sin
sin cos sin
cos sin sin cos
xx x
xx xx
xxxx
−
=− +
xx
x
xxx x
00 2
220
22
cos
cos sin cos ) cos=−−=−≡(
144 Exercise Set 5.3

EXERCISE SET 5.4
3. (a) This set has the correct number of vectors and they are linearly independent because
= 6 ≠0
Hence, the set is a basis.
(c) The vectors in this set are linearly dependent because
= 0
Hence, the set is not a basis.
5. The set has the correct number of vectors. To show that they are linearly independent, we
consider the equation
ab c
36
36
01
10
08
12 4−
+−
−
+−
−−
+−
=
d10
12
00
00
24 0
31 7
11 1
−−
123
023
003
145

If we add matrices and equate corresponding entries, we obtain the following system of
equations:
3a+ d= 0
6a– b– 8c= 0
3a– b– 12c– d = 0
–6a– 4c+ 2d= 0
Since the determinant of the coefficient matrix is nonzero, the system of equations has
only the trivial solution; hence, the vectors are linearly independent.
7. (a) Clearly w= 3u1– 7u2, so the coordinate vector relative to {u1, u2} is (3, –7).
(b) If w= au1+ bu2, then equating coordinates yields the system of equations
2a+ 3b= 1
–4a+ 8b= 1
This system has the solution a= 5/28, b= 3/14. Thus the desired coordinate vector is
(5/28, 3/14).
9. (a) If v= av1+ bv2+ cv3, then
a+ 2b+ 3c=2
2b+ 3c=–1
3c=3
From the third equation, c= 1. Plugging this value into the second equation yields b
= –2, and finally, the first equation yields a= 3. Thus the desired coordinate vector is
(3, –2, 1).
15. If we reduce the augmented matrix to row-echelon form, we obtain
1310
0000
0000
−
146 Exercise Set 5.4

Thus x1= 3r– s, x2= r, and x3= s, and the solution vector is
Since (3, 1, 0) and (–1, 0, 1) are linearly independent, they form a basis for the solution
space and the dimension of the solution space is 2.
19. (a) Any two linearly independent vectors in the plane form a basis. For instance, (1, –1,
–1) and (0, 5, 2) are a basis because they satisfy the plane equation and neither is a
multiple of the other.
(c) Any nonzero vector which lies on the line forms a basis. For instance, (2, –1, 4) will
work, as will any nonzero multiple of this vector.
(d) The vectors (1, 1, 0) and (0, 1, 1) form a basis because they are linearly independent
and
a(1, 1, 0) + c(0, 1, 1) = (a, a+ c, c)
21. (a) We consider the three linear systems
which give rise to the matrix
A row-echelon form of the matrix is
111 00
013 01
001120
−−
−
−
−
11100
22010
32001
−+ =
−=
−=
kk
kk
kk
12
12
12
100
22 010
32 001
x
x
x
rs
r
s
1
2
3
33
1
0
=
−
=
+
−
rs
1
0
1
Exercise Set 5.4 147

from which we conclude that e3is in the span of {v1, v2}, but e1and e2are not. Thus
{v1, v2, e1} and {v1, v2, e2} are both bases for R3.
23. Since {u1, u2, u3} has the correct number of vectors, we need only show that they are
linearly independent. Let
au1+ bu2+ cu3= 0
Thus
av1+ b(v1+ v2) + c(v1+ v2+ v3) = 0
or
(a+ b+ c)v1+ (b+ c)v2+ cv3= 0
Since {v1, v2, v3} is a linearly independent set, the above equation implies that a+ b+ c=
b+ c= c= 0. Thus, a= b= c= 0 and {u1, u2, u3} is also linearly independent.
25. First notice that if vand ware vectors in Vand aand bare scalars, then (av+ bw)S=
a(v)S+ b(w)S. This follows from the definition of coordinate vectors. Clearly, this result
applies to any finite sum of vectors. Also notice that if (v)S= (0)S, then v= 0. Why?
Now suppose that k1v1+ …+ krvr= 0. Then
(k1v1+ …+ krvr)S= k1(v1)S+ …+ kr(vr)S
= (0)S
Conversely, if k1(v1)S+ …+ kr(vr)S, = (0)S, then
(k1v1+ …+ krvr)S= (0)S,or k1v1+ …+ krvr= 0
Thus the vectors v1,…, vrare linearly independent in Vif and only if the coordinate vectors
(v1)S,…, (vr)Sare linearly independent in Rn.
27. (a) Let v1, v2, and v3denote the vectors. Since S= {1, x, x2} is the standard basis for P2,
we have (v1)S= (–1, 1, –2), (v2)S= (3, 3, 6), and (v3)S= (9, 0, 0). Since {(–1, 1, –2),
(3, 3, 6), (9, 0, 0)} is a linearly independent set of three vectors in R3, then it spans R3.
Thus, by Exercises 24 and 25, {v1, v2, v3} is linearly independent and spans P2. Hence
it is a basis for P2.
148 Exercise Set 5.4

31. There is. Consider, for instance, the set of matrices
Each of these matrices is clearly invertible. To show that they are linearly independent,
consider the equation
aA + bB + cC + dD =
This implies that
The above 4 ×4 matrix is invertible, and hence a= b= c= d= 0 is the only solution. And
since the set {A, B, C, and D} consists of 4 linearly independent vectors, it forms a basis for
M22.
33. (a) The set has 10 elements in a 9 dimensional space.
0111
1011
1101
1110
a
b
c
d
=
0
0
0
0
00
00
AB
CD
=
=
=
=
01
11
10
11
1111
01 and 110
Exercise Set 5.4 149

35. (b) The equation x1+ x2+ …+ xn= 0 can be written as x1= –x2–x3– …–xnwhere x2,
x3,…, xncan all be assigned arbitrary values. Thus, its solution space should have
dimension n– 1. To see this, we can write
The n– 1 vectors in the above equation are linearly independent, so the vectors do
form a basis for the solution space.
=
−
+
−
xx
23
1
1
0
0
0
1
0
1
0
0
++
−
xn
1
0
0
0
1
x
x
x
x
xx x
n
n1
2
3
23
=
−−−−
x
x
2
3
xn
150 Exercise Set 5.4

EXERCISE SET 5.5
3. (b) Since the equation Ax= bhas no solution, bis not in the column space of A.
(c) Since A= b, we have b= c1– 3c2+ c3.
(d) Since A= b, we have b= c1+ (t– 1)c2+ tc3for all real numbers t.
5. (a) The general solution is x1= 1 + 3t, x2= t. Its vector form is
Thus the vector form of the general solution to Ax= 0is
(c) The general solution is x1= – 1 + 2r– s– 2t, x2= r, x3= s, x4= t. Its vector form is
−
+
+
−1
0
0
0
2
1
0
0
rs
11
0
1
0
2
0
0
1
+
−
t
t3
1
1
0
3
1
+
t
1
1t
t
−
1
3
1
−
151

Thus the vector form of the general solution to Ax= 0is
9. (a) One row-echelon form of ATis
Thus a basis for the column space of Ais
(c) One row-echelon form of ATis
Thus a basis for the column space of Ais
11. (a) The space spanned by these vectors is the row space of the matrix
1143
2022
2132
−−
−
−
1
2
1
0
1
1−
−
and
12 1
01 1
00 0
00 0
−
−
1
5
7
0
1
1
and
157
011
000
rs t
2
1
0
0
1
0
1
1
+
−
+
−22
0
0
1
152 Exercise Set 5.5

One row-echelon form of the above matrix is
and the reduced row-echelon form is
Thus {(1, 1, –4, –3), (0, 1, –5, –2), (0, 0, 1, –1/2)} is one basis. Another basis is {(1, 0,
0, –1/2), (0, 1, 0, –9/2), (0, 0, 1, –1/2)}.
13. Let Abe an n×ninvertible matrix. Since ATis also invertible, it is row equivalent to In. It
is clear that the column vectors of Inare linearly independent. Hence, by virtue of Theorem
5.5.5, the column vectors of AT, which are just the row vectors of A, are also linearly
independent. Therefore the rows of Aform a set of nlinearly independent vectors in Rn,
and consequently form a basis for Rn.
15. (a) We are looking for a matrix so that the only solution to the equation Ax= 0is x= 0.
Any invertible matrix will satisfy this condition. For example, the nullspace of the
matrix A=is the single point (0, 0, 0).
(b) In this case, we are looking for a matrix so that the solution of Ax= 0is
one-dimensional. Thus, the reduced row-echelon form of Ahas one column without
a leading one. As an example, the nullspace of the matrix A=is
span , a line in R3.
1
1
1
10 1
01 1
00 0
−
−
100
010
001
100 12
010 92
001 12
−
−
−
11 4 3
01 5 2
00 1 12
−−
−−
−
Exercise Set 5.5 153

(c) In this case, we are looking for a matrix so that the solution space of Ax= 0is
two-dimensional. Thus, the reduced row-echelon form of Ahas two columns without
leading ones. As an example, the nullspace of the matrix A=is
span , a plane in R3.
17. (a) The matrices will all have the form where sand
tare any real numbers.
(b) Since Aand Bare invertible, their nullspaces are the origin. The nullspace of Cis the
line 3x+ y= 0. The nullspace of Dis the entire xy-plane.
19. Theorem: If Aand Bare n×nmatrices and Ais invertible, then the row space of AB is the
row space of B.
Proof: If Ais invertible, then there exist elementary matrices E1, E2,…, Eksuch that
A= E1E2… EkIn
or
AB = E1E2… EkB
Thus, Theorem 5.5.4 guarantees that AB and Bwill have the same row spaces.
35
35
35
00
00
35
ss
tt st
−
−
=−
+−
−
1
1
0
1
0
1
,
11 1
00 0
00 0
−
154 Exercise Set 5.5

EXERCISE SET 5.6
7. Use Theorems 5.6.5 and 5.6.7.
(a) The system is consistent because the two ranks are equal. Since n= r= 3, n– r= 0
and therefore the number of parameters is 0.
(b) The system is inconsistent because the two ranks are not equal.
(d) The system is consistent because the two ranks are equal. Here n= 9 and r= 2, so
that n– r= 7 parameters will appear in the solution.
(f) Since the ranks are equal, the system is consistent. However Amust be the zero
matrix, so the system gives no information at all about its solution. This is reflected in
the fact that n– r= 4 – 0 = 4, so that there will be 4 parameters in the solution for the
4 variables.
9. The system is of the form Ax= bwhere rank(A) = 2. Therefore it will be consistent if and
only if rank([A|b]) = 2. Since [A|b] reduces to
the system will be consistent if and only if b3= 4b2– 3b1, b4= –b2+ 2b1, and b5= 8b2– 7b1,
where b1and b2can assume any values.
11. If the nullspace of Ais a line through the origin, then it has the form x= at, y= bt, z= ct
where tis the only parameter. Thus nullity(A) = 3 – rank(A) = 1. That is, the row and
column spaces of Ahave dimension 2, so neither space can be a line. Why?
13
01
00 4 3
00 2
00 8
1
21
321
42 1
52
−
−
−+
+−
−
b
bb
bbb
bb b
bb++
71
b
155

13. Call the matrix A. If r= 2 and s= 1, then clearly rank(A) = 2. Otherwise, either r– 2 or s
– 1 ≠0 and rank(A) = 3. Rank(A) can never be 1.
17. (a) False. Let A=
(c) True. If Awere an m×nmatrix where, say, m> n, then it would have mrows, each
of which would be a vector in Rn. Thus, by Theorem 5.4.2, they would form a linearly
dependent set.
100
010
156 Exercise Set 5.6

SUPPLEMENTARY EXERCISES 5
1. (b) The augmented matrix of this system reduces to
Therefore, the solution space is a plane with equation 2x– 3y+ z= 0
(c) The solution is x= 2t, y= t, z= 0, which is a line.
5. (a) We look for constants a, b, and csuch that v= av1+ bv2+ cv3, or
a+ 3b+ 2c= 1
–a+ c= 1
This system has the solution
a= t– 1 b= 2
3– tc= t
where tis arbitrary. If we set t= 0 and t= 1, we obtain v= (–1)v1+ (2/3)v2and v=
(–1/3)v2+ v3, respectively. There are infinitely many other possibilities.
(b) Since v1, v2, and v3all belong to R2and dim(R2) = 2, it follows from Theorem 5.4.2 that
these three vectors do not form a basis for R2. Hence, Theorem 5.4.1 does not apply.
7. Consider the polynomials xand x+ 1 in P1. Verify that these polynomials form a basis for
P1.
2310
0000
0000
−
157

13. (a) Since = – 1≠0, the rank is 2.
(b) Since all three 2 ×2 subdeterminants are zero, the rank is 1.
(c) Since the determinant of the matrix is zero, its rank is less than 3. Since = –1
≠0, the rank is 2.
(d) Since the determinant of the 3 ×3 submatrix obtained by deleting the last column is
30 ≠0, the rank of the matrix is 3.
15. (b) Let S= {v1,…, vn} and let u= u1v1+ …+ unvn. Thus (u)S= (u1,…, un). We have
ku= ku1v1+ …+ kunvn
so that (ku)S= (ku1,…, kun) = k(u1,…, un). Therefore (ku)S= k(u)S.
10
21−
10
21−
158 Supplementary Exercises 5

EXERCISE SET 6.1
1. (c) Since v+ w= (3, 11), we have
〈u, v+ w〉= 3(3) + (–2)(11) = –13
On the other hand,
〈u, v〉= 3(4) + (–2)(5) = 2
and
〈u, w〉= 3(–1) + (–2)(6) = –15
(d) Since ku= (–12, 8) and kv= (–16, –20) , we have
〈ku, v〉= (–12)(4) + (8)(5) = –8
and
〈u, kv〉= 3(–16) + (–2)(–20) = –8
Since 〈u,v〉= 2, k〈u, v〉= –8.
3. (a) 〈u, v〉= 3(–1) – 2(3) + 4(1) + 8(1) = 3
159

5. (a) By Formula (4),
(b) We have 〈u, v〉= 9(–3)(1) + 4(2)(7) = 29.
7. (a) By Formula (4), we have 〈u, v〉= vTATAuwhere
9. (b) Axioms 1 and 4 are easily checked. However, if w= (w1, w2, w3), then
〈u+ v, w〉= (u1+ v1)2w1
2+ (u2+ v2)2w2
2+ (u3+ v3)2w3
2
= 〈u, w〉+ 〈v, w〉+ 2u1v1w1
2+ 2u2v2w2
2+ 2u3v3w3
2
If, for instance, u= v= w= (1, 0, 0), then Axiom 2 fails.
To check Axiom 3, we note that 〈ku, v〉= k2〈u, v〉. Thus 〈ku, v〉≠k〈u, v〉unless k
= 0 or k= 1, so Axiom 3 fails.
(c) (1) Axiom 1 follows from the commutativity of multiplication in R.
(2) If w= (w1, w2, w3), then
〈u+ v, w〉= 2(u1+ v1)w1+ (u2+ v2)w2+ 4(u3+ v3)w3
= 2u1w1+ u2w2+ 4u3w3+ 2v1w1+ v2w2+ 4v3w3
= 〈u, w〉+ 〈v, w〉
(3) 〈ku, v〉= 2(ku1)v1+ (ku2)v2+ 4(ku3)v3= k〈u, v〉
(4) 〈v, v〉= 2v1
2+ v2
2+ 4v3
2≥0
= 0 if and only if v1= v2= v3= 0, or v= 0
Thus this is an inner product for R3.
A=
30
05
uu,, vv=
=
vv u
u
12
1
2
30
02
30
02
vvv u
u
vv
u
u
12
1
2
12
1
90
04
94
=
22
11 22
94
=+uv uv
160 Exercise Set 6.1

11. We have u– v= (–3, –3).
(b) d(u, v) = (–3, –3)= [3(9) + 2(9)]1/2 = 45 = 3 5
(c) From Problem 10(c), we have
Thus
d(u, v) = 117 = 3 13
13. (a) A= [(–2)2+ (5)2+ (3)2+ (6)2]1/2 = 74
15. (a) Since , we have
d(A, B) = 〈A– B, A– B〉1/2 = [62+ (–1)2+ 82+ (–2)2]1/2 = 105
17. (a) For instance,
(b) We have
d(p, q)= p– q
= 1 – x
=−
=−+
−
−
∫
∫
()
()
/
1
12
2
1
112
2
1
1
xdx
xxdx
=−+
=
−
12
23
1
112
3
22
3
/
/
xx x
=
12 2
36
/
xxdx x
=
=
=
−−
∫2
1
112 3
1
112
3
2
3
12
AB−= −
−
61
82
d(, )uv
[]
=− −
−
−
−
−
233 21
113
3
3
=117
Exercise Set 6.1 161

21. If, in the solution to Exercise 20, we subtract (**) from (*) and divide by 4, we obtain the
desired result.
23. Axioms 1 and 3 are easily verified. So is Axiom 2, as shown: Let r= r(x) be a polynomial
in P2. Then
〈p+ q, r〉= [(p+ q)(0)]r(0) + [(p+ q)(1/2)]r(1/2) + [(p+ q)(1)]r(1)
= p(0)r(0) + p(1/2)r(1/2) + p(1)r(1) + q(0)r(0) + q(1/2)r(1/2) + q(1)r(1)
= 〈p, r〉+ 〈q, r〉
It remains to verify Axiom 4:
〈p, p〉= [p(0)]2+ [p(1/2)]2+ [p(1)]2≥0
and
〈p, p〉= 0 if and only if p(0) = p(1/2) = p(1) = 0
But a quadratic polynomial can have at most two zeros unless it is identically zero. Thus
〈p, p〉= 0 if and only if pis identically zero, or p= 0.
27. (b) 〈p, q〉=(x– 5x3) (2 + 8x2) dx = (2x– 2x3– 40x5) dx
= x2– x4/2 – 20x6/3]1
-1= 0
29. We have 〈U, V〉= u1v1+ u2v2+ u3v3+ u4v4and
which does, indeed, equal 〈U, V〉.
tr tr 1
()UV uu
uu
vv
vv
T=
3
24
12
34
=++
++
tr uv uv uv uv
uv uv uv u
11 33 12 34
21 4 3 2 2 4
vv
uv uv uv uv
4
11 33 22 44
=+++
-1
1
∫
-1
1
∫
162 Exercise Set 6.1

31. Calling the matrix A, we have
〈u, v〉= vTATAu= vTA2u= w1u1v1+ …+ wnunvn
33. To prove Part (a) of Theorem 6.1.1 first observe that 〈0, v〉= 〈v, 0〉by the symmetry axiom.
Moreover,
〈0, v〉= 〈00, v〉by Theorem 5.1.1
= 0〈0, v〉by the homogeneity axiom
= 0
Alternatively,
〈0, v〉+ 〈0, v〉= 〈0+ 0, v〉by additivity
= 〈0, v〉by definition of the zero vector
But 〈0, v〉= 2〈0, v〉only if 〈0, v〉= 0.
To prove Part (d), observe that, by Theorem 5.1.1, –v(the inverse of v) and (–1)vare
the same vector. Thus,
〈u– v, w〉= 〈u+ (–v), w〉
= 〈u, w〉+ 〈–v, w〉by additivity
= 〈u, w〉– 〈v, w〉by homogeneity
Exercise Set 6.1 163

EXERCISE SET 6.2
1. (e) Since u•v= 0 + 6 + 2 + 0 = 8, the vectors are not orthogonal.
3. We have ku+ v= (k+ 6, k+ 7, –k– 15), so
ku+ v= 〈(ku+ v), (ku+ v)〉1/2
= [(k+ 6)2+ (k+ 7)2+ (–k– 15)2]1/2
= (3k2+ 56k+ 310)1/2
Since ku+ v= 13 exactly when ku+ v2= 169, we need to solve the quadratic equation
3k2+ 56k+ 310 = 169 to find k. Thus, values of kthat give ku+ v= 13 are k= –3 or k=
–47/3.
5. (a)
(c)
(e)
7. 〈p, q〉= (1)(0) + (–1)(2) + (2)(1) = 0
9. (b) = (2)(1) + (1)(1) + (–1)(0) + (3)(–1) = 0
Thus the matrices are orthogonal.
21
13
11
01−
−
,
cos (, ,, ),( ,,,)
(, ,, ) ( ,
θ
=−−−−
−
1010 3333
1010 3−−−− =−− =−
333
33
236
1
2
,,)
cos (,,),(,, )
(,,)(,, )
θ
=−−
−−
=
152 24 9
152 24 9
−+ − =
22018
30 101 0
cos (, ),( , )
(, ) ( , )
θ
=−
−=−
13 24
13 24
212
10 20 =−1
2
165

(d) = 4 + 1 – 5 + 6 = 6 ≠0
Thus the matrices are not orthogonal.
11. We must find two vectors x= (x1, x2, x3, x4) such that 〈x, x〉= 1 and 〈x, u〉= 〈x, v〉= 〈x,
w〉= 0. Thus x1, x2, x3, and x4must satisfy the equations
x1
2+ x2
2+ x3
2+ x4
2=1
2x1+ x2– 4x3=0
–x1– x2+ 2x3+ 2x4=0
3x1+ 2x2+ 5x3+ 4x4=0
The solution to the three linear equations is x1= –34t, x2= 44t, x3= –6t, and x4= 11t. If we
substitute these values into the quadratic equation, we get
[(–34)2+ (44)2+ (–6)2+ (11)2] t2= 1
or
Therefore, the two vectors are
13. (a) Here 〈u, v〉2= (3(–2)(1) + 2(1)(0))2= 36, while, on the other hand, 〈u, u〉〈v, v〉=
(3(–2)2+ 2(1)2) (3(1)2+ 2(0)2) = 42.
15. (a) Here W is the line which is normal to the plane and which passes through the origin.
By inspection, a normal vector to the plane is (1, –2, –3). Hence this line has
parametric equations x= t, y= –2t, z= –3t.
±− −
1
57 34 44 6 11(,,,)
t=± 1
57
21
13
21
52−
,
166 Exercise Set 6.2

17. (a) The subspace of R3spanned by the given vectors is the row space of the matrix
which reduces to
The space we are looking for is the nullspace of this matrix. From the reduced form,
we see that the nullspace consists of all vectors of the form (16, 19, 1)t, so that the
vector (16, 19, 1) is a basis for this space.
Alternatively the vectors w1= (1, –1, 3) and w2= (0, 1, –19) form a basis for the
row space of the matrix. They also span a plane, and the orthogonal complement of
this plane is the line spanned by the normal vector w1×w2= (16, 19, 1).
19. If uand vare orthogonal vectors with norm 1, then
u– v= 〈u– v, u– v〉1/2
= [〈u, u〉– 2〈u, v〉+ 〈v, v〉]1/2
= [1 – 2(0) + 1]1/2
= 2
21. By definition, uis in span {u1, u2,…, ur} if and only if there exist constants c1, c2,…, crsuch
that
u= c1u1+ c2u2+ …+ crur
But if 〈w, u1〉= 〈w, u2〉= …= 〈w, ur〉= 0, then 〈w, u〉= 0.
23. We have that W= span{w1, w2,…, wk}
Suppose that wis in W. Then, by definition, 〈w, wi〉= 0 for each basis vector wiof W.
Conversely, if a vector wof Vis orthogonal to each basis vector of W, then, by Problem
20, it is orthogonal to every vector in W.
25. (c) By Property (3) in the definition of inner product, we have
ku2= 〈ku, ku〉= k2〈u, u〉= k2u2
Therefore ku= |k|u.
11 3
0119
00 0
−
−
113
544
762
−
−−
−
Exercise Set 6.2 167

27. This is just the Cauchy-Schwarz inequality using the inner product on Rngenerated by A
(see Formula (4) of Section 6.1).
31. We wish to show that ABC is a right angle, or that and are orthogonal. Observe
that = u– (–v) and = v– uwhere uand vare radii of the circle, as shown in the
figure. Thus u= v. Hence
〈, 〉= 〈u+ v, v– u〉
= 〈u, v〉+ 〈v, v〉+ 〈u, –u〉+ 〈v, –u〉
= 〈v, u〉+ 〈v, v〉– 〈u, u〉– 〈v, u〉
= v2– u2
= 0
33. (a) As noted in Example 9 of Section 6.1, 0
1f(x)g(x)dx is an inner product on C[0, 1].
Thus the Cauchy-Schwarz Inequality must hold, and that is exactly what we’re asked
to prove.
(b) In the inner product notation, we must show that
〈f+ g, f+ g〉1/2 ≤〈f, f〉1/2 + 〈g, g〉1/2
or, squaring both sides, that
〈f+ g, f+ g〉≤〈f, f〉+ 2〈f, f〉1/2 〈g, g〉1/2 + 〈g, g〉
For any inner product, we know that
〈f+ g, f+ g〉= 〈f, f〉+ 2〈f, g〉+ 〈g, g〉
By the Cauchy-Schwarz Inequality
〈f, g〉2≤〈f, f〉〈g, g〉
or
〈f, g〉≤〈f, f〉1/2 〈g, g〉1/2
BC
AB
BC
AB
BC
AB
168 Exercise Set 6.2

If we substitute the above inequality into the equation for 〈f+ g, f+ g〉,we obtain
〈f+ g, f+ g〉≤〈f, f〉+ 2〈f, f〉1/2 〈g, g〉1/2 + 〈g, g〉
as required.
35. (a) Wis the line y= –x.
(b) Wis the xz-plane.
(c) Wis the x-axis.
37. (b) False. Let n= 3, let Vbe the xy-plane, and let Wbe the x-axis. Then V is the z-axis
and W is the yz-plane. In fact V is a subspace of W
(c) True. The two spaces are orthogonal complements and the only vector orthogonal to
itself is the zero vector.
(d) False. For instance, if Ais invertible, then both its row space and its column space are
all of Rn.
Exercise Set 6.2 169


EXERCISE SET 6.3
5. See Exercise 3, Parts (b) and (c).
7. (b) Call the vectors u1, u2and u3. Then 〈u1, u2〉= 2 – 2 = 0 and 〈u1, u3〉= 〈u2, u3〉= 0. The
set is therefore orthogonal. Moreover, u1= 2, u2= 8 = 2 2, and u3= 25
= 5. Thus is an orthonormal set.
9. It is easy to verify that v1•v2= v1•v3= v2•v3= 0 and that v3= 1. Moreover, v12=
(–3/5)2+ (4/5)2= 1 and v2= (4/5)2+ (3/5)2= 1. Thus {v1, v2, v3} is an orthonormal set in
R3. It will be an orthonormal basis provided that the three vectors are linearly independent,
which is guaranteed by Theorem 6.3.3.
(b) By Theorem 6.3.1, we have
11. (a) We have (w)S= (〈w, u1〉, 〈w, u2〉).
17. (a) Let
vv uu
uu
11
1
1
3
1
3
1
3
,,==
=−
=−
()
4
2
10
22252
,,
(, , )374 9
5
28
5012
5
21
5
1
−=−−+
+−+vv 004
37 5 9 5 4
23
123
+
=−
(
)
+−
(
)
+
vvvv
vvvvvv
1
2
1
22
1
5
123
uuu,,
171
Since 〈u2, v1〉= 0, we have
Since 〈u3, v1〉=and 〈u3, v2〉=, we have
u3– 〈u3, v1〉v1– 〈u3, v2〉v2
This vector has norm Thus
and {v1, v2, v3} is the desired orthonormal basis.
19. Since the third vector is the sum of the first two, we ignore it. Let u1= (0, 1, 2) and u2=
(–1, 0, 1). Then
Since 〈u2, v1〉=, then
uuuuvvvv
2211 12
5
1
5
,,,−=−−
2
5
vv uu
uu
11
1
01
5
2
5
,,==
vv3
1
6
1
6
2
6
,,=−
1
6
1
6
1
3
1
6
,, .−
=
=−
1
6
1
6
1
3
,,
=−
−−(, , ) , , ,121 4
3
1
3
1
3
1
3
1
2
1
2
1
22 0,
1
2
4
3
vv uu
uu
22
2
1
2
1
20,,==−
172 Exercise Set 6.3

where . Hence
Thus {v1, v2} is an orthonormal basis.
21. Note that u1and u2are orthonormal. Thus we apply Theorem 6.3.5 to obtain
and
25. By Theorem 6.3.1, we know that
w= a1v1+ a2v2+ a3v3
where ai= 〈w, vi〉. Thus
w2= 〈w, w〉
But 〈vi, vj〉= 0 if i≠jand 〈vi, vi〉= 1 because the set {v1, v2, v3} is orthonormal. Hence
w2= a1
2+ a2
2+ a3
2
= 〈w, v1〉2+ 〈w, v2〉2+ 〈w, v3〉2
=+
=≠
∑∑
,,aaa
iii
i
ij i j
i
2
1
3
1
vvvvvvvv
wwwwww
21
9
5012
5
=−
=
,,
wwwwuuuuwwuuuu
11122
4
503
5201
=+
=− −
+
,,
,, ,,
00
4
523
5
(
)
=−
,,
vv2
5
30
2
30
1
30
=− −
,,
,,−−
=12
5
1
5
30
5
Exercise Set 6.3 173

27. Suppose the contrary; that is, suppose that
(*)u3– 〈u3, v1〉v1– 〈u3, v2〉v2= 0
Then (*) implies that u3is a linear combination of v1and v2. But v1is a multiple of u1
while v2is a linear combination of u1and u2. Hence, (*) implies that u3is a linear
combination of u1and u2and therefore that {u1, u2, u3} is linearly dependent, contrary to
the hypothesis that {u1,…, un} is linearly independent. Thus, the assumption that (*) holds
leads to a contradiction.
29. We have u1= 1, u2= x, and u3= x2. Since
we let
Then
and thus v2= u2/u2where
Hence
In order to compute v3, we note that
uuvv
31
2
1
1
1
2
2
3
,==
−
∫xdx
vv2
3
2
=x
uu2
2
1
12
3
==
−
∫xdx
uuvv
21 1
1
1
20, ==
−
∫xdx
vv1
1
2
=
uuuuuu
1
2
11
112===
−
∫
,1dx
174 Exercise Set 6.3
and
Thus
and
Hence,
31. This is similar to Exercise 29 except that the lower limit of integration is changed from –1
to 0. If we again set u1= 1, u2= x, and u3= x2, then u1= 1 and thus
v1= 1
Then 〈u2, v1〉= x dx = 1
2and thus
Finally,
uuvv
31
2
0
11
3
,==
∫xdx
vv
vv
2
or
=−
−=−
=−
(
)
x
xx
x
12
12 12 1 2
32 1
2
()
0
1
∫
vv33
or=−
=−
(
)
45
8
1
3
5
22 31
22
xxvv
xxdx
2
2
2
2
1
1
1
3
1
3
8
45
−= −
=
−
∫
uuuuvvvvuuvv
331132
21
3
−− =−,,vv2x
uuvv
32
3
1
1
3
20, ==
−
∫xdx
Exercise Set 6.3 175

and
Thus
or
v3= 5 (6x2– 6x+ 1)
33. Let Wbe a finite dimensional subspace of the inner product space Vand let {v1, v2,…, vr}
be an orthonormal basis for W. Then if uis any vector in V, we know from Theorem 6.3.4
that u= w1+ w2where w1is in Wand w2is in W. Moreover, this decomposition of uis
unique. Theorem 6.3.5 gives us a candidate for w1. To prove the theorem, we must show
that if w1= 〈u, v1〉v1+ …+ 〈u, vr〉vrand, therefore, that w2= u– w1then
(i) w1is in W
and
(ii) w2is orthogonal to W.
That is, we must show that this candidate “works.” Then, since w1is unique, it will be
projWu.
Part (i) follows immediately because w1is, by definition, a linear combination of the
vectors v1, v2,…, vr.
〈w2, vi〉= 〈u– w1, vi〉
= 〈u, vi〉– 〈w1, vi〉
= 〈u, vi〉– 〈u, vi〉〈vi, vi〉
= 〈u, vi〉– 〈u, vi〉
= 0
vv3
2
2
2
1
3
1
221
1
3
1
221
65 1
6
=−− −
(
)
−− −
(
)
=−+
xx
xx
xx
uuvv
32
32
0
1
32 3
6
,()=−=
∫xxdx
176 Exercise Set 6.3
Thus, w2is orthogonal to each of the vectors v1, v2,…, vrand hence w2is in W.
If the vectors viform an orthogonal set, not necessarily orthonormal, then we must
normalize them to obtain Part (b) of the theorem.
35. The vectors x= (1/ 3, 0) and y= (0, 1/ 2) are orthonormal with respect to the given
inner product. However, although they are orthogonal with respect to the Euclidean
inner product, they are not orthonormal.
The vectors x= (2/ 30, 3/ 30) and y= (1/ 5, –1/ 5) are orthonormal with respect
to the given inner product. However, they are neither orthogonal nor of unit length with
respect to the Euclidean inner product.
37. (a) True. Suppose that v1, v2,…, vnis an orthonormal set of vectors. If they were linearly
dependent, then there would be a linear combination
c1v1+ c2v2+ …+ cnvn= 0
where at least one of the numbers ci≠0. But
ci= 〈vi, c1v1+ c2v2+ …+ cnvn〉= 〈vi, 0〉= 0
for i= 1, …, n. Thus, the orthonormal set of vectors cannot be linearly dependent.
(b) False. The zero vector space has no basis 0. This vector cannot be linearly independent.
(c) True, since projWuis in Wand projWuis in W.
(d) True. If Ais a (necessarily square) matrix with a nonzero determinant, then Ahas
linearly independent column vectors. Thus, by Theorem 6.3.7, Ahas a QR
decomposition.
Exercise Set 6.3 177


EXERCISE SET 6.4
1. (a) If we call the system Ax= b, then the associated normal system is ATAx= ATb, or
which simplifies to
3. (a) The associated normal system is ATAx= ATb,or
or
This system has solution x1= 5, x2= 1/2, which is the least squares solution of
Ax= b.
The orthogonal projection of bon the column space of Ais Ax, or
11
11
12
5
12
11 2
92
4
−
−
=−
−
32
26
14
7
1
2
−
−
=−
x
x
111
112
11
11
12
1
2
−−
−
−
x
x
=−−
−
111
112
7
0
7
21 25
25 35
20
20
1
2
=
x
x
124
135
11
23
45
1
2
−
−
x
x =−
−
124
135
2
1
5
179

3. (c) The associated normal system is
or
This system has solution x1= 12, x2= –3, x3= 9, which is the least squares solution of
Ax= b.
The orthogonal projection of bon the column space of Ais Ax, or
which can be written as (3, 3, 9, 0).
5. (a) First we find a least squares solution of Ax= uwhere A= [v1
T|v2
T|v3
T]. The associated
normal system is
2111
1011
2101
21 2
10 1
11 0
11 1
−− −
−
−
−
x
x
x
1
2
3
10 1
21 2
11 0
11 1
12
3
9
−
−
−
−
=
3
3
9
0
746
433
636
1
1
2
3
−
−
−−
=
x
x
x
88
12
9−
=
−− −
1211
0111
1201
6
0
9
3
1211
0111
1201
10 1
21 2
11 0
11 1
−− −
−
−
−
x
x
x
1
2
3
180 Exercise Set 6.4

or
This system has solution x1= 6, x2= 3, x3= 4, which is the least squares solution. The
desired orthogonal projection is Ax, or
or (7, 2, 9, 5).
7. (a) If we use the vector (1, 0) as a basis for the x-axis and let , then we have
[P] = A(ATA)–1 AT=[1] [1 0] =
10
00
1
0
A=
1
0
21 2
10 1
11 0
11 1
6
3
4
−
−
−
==
7
2
9
5
746
433
636
1
2
3
−
−
−−
=
x
x
x
30
21
21−
=
−− −
2111
1011
2101
6
3
9
6
Exercise Set 6.4 181
11. (a) The vector v= (2, –1, 4) forms a basis for the line W.
(b) If we let A= [vT], then the standard matrix for the orthogonal projection on Wis
(c) By Part (b), the point (x0, y0, z0) projects to the point on the line Wgiven by
(d) By the result in Part (c), the point (2, 1, –3) projects to the point (–6/7, 3/7, –12/7).
The distance between these two points is 497/7.
13. (a) Using horizontal vector notation, we have b= (7, 0, –7) and Ax= (11/2, –9/2, –4).
Therefore Ax– b= (–3/2, –9/2, 3), which is orthogonal to both of the vectors (1, –1,
–1) and (1, 1, 2) which span the column space of A. Hence the error vector is
orthogonal to the column space of A.
(c) In horizontal vector notation, b= (6, 0, 9, 3) and Ax= (3, 3, 9, 0). Hence Ax– b=
(–3, 3, 0, –3), which is orthogonal to the three vectors (1, 2, 1, 1), (0, 1, 1, 1), and (–1,
–2, 0, –1) which span the column space of A. Therefore Ax– bis orthogonal to the
column space of A.
15. Recall that if bis orthogonal to the column space of A, then projWb= 0.
17. If Ais an m×nmatrix with linearly independent row vectors, then ATis an n×mmatrix
with linearly independent column vectors which span the row space of A. Therefore, by
Formula (6) and the fact that (AT)T= A, the standard matrix for the orthogonal projection,
S, of Rnon the row space of Ais [S] = AT(AAT)–1 A.
1
21
428
214
8416
0
0
0
−
−−
−
x
y
z
=
−+
−+−
−
()
()
(
42821
2421
84
000
00 0
0
xyz
xy z
xyyz
00
16 21+
)
=
−
−−
−
1
21
428
214
8416
=−
−
2
1
4
1
21 214
PAA A A
TT
[]
==−
−
−
−
()
1
2
1
4
214
2
11
4
214
1
−
−
182 Exercise Set 6.4

19. If we assume a relationship V= IR + c, we have the linear system
1 = 0.1 R+ c
2.1 = 0.2 R+ c
2.9 = 0.3 R+ c
4.2 = 0.4 R+ c
5.1 = 0.5 R+ c
This system can be written as Ax= b, where
Then, we have the least squares solution
.
Thus, we have the relationship V= 10.3 R– 0.03.
xb==
−−
() ..
.
.
.
AA A
TT1
1
055 155
15 5
562
15 33
10 3
003
=−
.
..
Aand
.
.
.
.
.
=
01 1
02 1
03 1
04 1
05 1
bbbb =
.
.
.
.
.
1
21
29
42
51
Exercise Set 6.4 183


EXERCISE SET 6.5
1. (b) We have (w)S= (a, b) where w= au1+ bu2. Thus
2a+ 3b= 1
–4a+ 8b= 1
3. (b) Let p= ap1+ bp2+ cp3. Then
a+ b=2
a+ c=–1
b+ c=1
or a= 0, b= 2, and c= –1. Thus (v)S= (0, 2, –1) and
vv
[]
=
−
S
0
2
1
or and Hence (w)ab s
.== =
5
28
3
14
5
28 ,3
14
and
w
[]
=
s
5
28
3
14
185

5. (a) We have w= 6v1– v2+ 4v3= (16, 10, 12).
(c) We have B= –8A1+ 7A2+ 6A3+ 3A4=
7. (a) Since v1= 13
10u1– 2
5u2and v2= – 1
2u1+ 0u2, the transition matrix is
(b) Since u1= 0v1– 2v2and u2= – 5
2v1– 13
2 v2, the transition matrix is
Note that P= Q–1.
(c) We find that w= – 17
10 u1+ 8
5u2; that is
and hence
(d) Verify that w= (–4)v1+ (–7)v2.
ww
[]
=−
−−
−
B′
05
2
213
2
17
10
8
5
=−
−
4
7
ww
[]
=−
B
17
10
8
5
P=−
−−
05
2
213
2
Q=−
−
13
10
1
2
2
50
15 1
63
−
.
186 Exercise Set 6.5

11. (a) By hypothesis, f1and f2span V. Since neither is a multiple of the other, then {f1, f2} is
a linearly independent set and hence is a basis for V. Now by inspection,
. Therefore, {g1, g2} must also be a basis for V
because it is a spanning set which contains the correct number of vectors.
(b) The transition matrix is
(c) From the observations in Part (a), we have
(d) Since h= 2f1+ (–5)f2, we have [h]B=; thus
[]hh B′=
−
−
=−
1
20
1
6
1
3
2
5
1
2
2
5−
P=
−
1
20
1
6
1
3
1
20
1
6
1
3
20
13
1
−
=
−
ffggggffgg
1111222222
=+−
=
1
2
1
6
1
3
and
Exercise Set 6.5 187


EXERCISE SET 6.6
3. (b) Since the row vectors form an orthonormal set, the matrix is orthogonal. Therefore its
inverse is its transpose,
(c) Since the Euclidean inner product of Column 2 and Column 3 is not zero, the column
vectors do not form an orthonormal set and the matrix is not orthogonal.
(f) Since the norm of Column 3 is not 1, the matrix is not orthogonal.
9. The general transition matrix will be
In particular, if we rotate through
θ
= π
3, then the transition matrix is
11. (a) See Exercise 19, above.
13. Since the row vectors (and the column vectors) of the given matrix are orthogonal, the
matrix will be orthogonal provided these vectors have norm 1. A necessary and sufficient
condition for this is that a2+ b2= 1/2. Why?
1
203
2
01 0
3
201
2
−
cos sin
sin cos
θθ
θθ
0
01 0
0
−
12 12
12 12−
189

15. Multiplication by the first matrix Ain Exercise 24 represents a rotation and det(A) = 1. The
second matrix has determinant –1 and can be written as
Thus it represents a rotation followed by a reflection about the x-axis.
19. Note that Ais orthogonal if and only if ATis orthogonal. Since the rows of ATare the
columns of A, we need only apply the equivalence of Parts (a) and (b) to ATto obtain the
equivalence of Parts (a) and (c).
21. If Ais the standard matrix associated with a rigid transformation, then Theorem 6.5.3
guarantees that Amust be orthogonal. But if Ais orthogonal, then Theorem 6.5.2
guarantees that det(A) = ±1.
cos sin
sin cos
cos s
θθ
θθ
θ
−
−−
=−
−10
01
iin
sin cos
θ
θθ
190 Exercise Set 6.6

SUPPLEMENTARY EXERCISES 6
1. (a) We must find a vector x= (x1, x2, x3, x4) such that
The first two conditions guarantee that x1= x4= 0. The third condition implies that x2
= x3. Thus any vector of the form (0, a, a, 0) will satisfy the given conditions provided
a≠0.
(b) We must find a vector x= (x1, x2, x3, x4) such that x•u1= x•u4= 0. This implies
that x1= x4= 0. Moreover, since x= u2= u3= 1, the cosine of the angle between
xand u2is x•u2and the cosine of the angle between xand u3is x•u3. Thus we are
looking for a vector xsuch that x•u2= 2x•u3, or x2= 2x3. Since x= 1, we have x
= (0, 2x3, x3, 0) where 4x3
2+ x3
2= 1 or x3= ±1/ 5. Therefore
7. Let
(*)〈u, v〉=w1u1v1+ w2u2v2+ …+ wnunvn
be the weighted Euclidean inner product. Since 〈vi, vj〉= 0 whenever i≠j, the vectors {v1,
v2,…, vn} form an orthogonal set with respect to (*) for any choice of the constants w1, w2,
…, wn. We must now choose the positive constants w1, w2,…, wnso that vk= 1 for all k.
But vk2= kwk. If we let wk= 1/kfor k= 1, 2, …, n, the given vectors will then form an
orthonormal set with respect to (*).
x=±
02
5
1
50,,,
xxuuxxuuxxuu
xxuu
xxuu
xxuu
⋅⋅ ⋅⋅
14 2
2
3
3
=0, =0, and =
191

9. Let Q= [aij] be orthogonal. Then Q–1 = QTand det(Q) = ±1. If Cij is the cofactor of aij, then
so that aij = det(Q)Cij.
11. (a) The length of each “side” of this “cube” is |k|. The length of the “diagonal” is n|k|.
The inner product of any “side” with the “diagonal” is k2. Therefore,
(b) As n→+ ∞, cos
θ
→0, so that
θ
→π/2.
13. Recall that ucan be expressed as the linear combination
u= a1v1+ …+ anvn
where ai= 〈u, vi〉for i= 1, …, n. Thus
Therefore
cos cos
2
1
21
2
2
22
1
2
2
22
αα
++ = +++
+++ =
n
n
n
aa a
aa a
11
cos ,
2
2
2
1
α
i
i
i
i
i
a
=
=
=
()
=
uuvv
uuvv
uu vv
aa
aa a
i
n
2
1
2
2
22
++
...+(Why?)
cos
θ
==
k
knk n
21
Qa Q QCQ
ij
T
ij
T
T
== =
=
−
[( )] ( ) det( ) () det(
11))( )Cij
192 Supplementary Exercises 6

15. Recall that Ais orthogonal provided A–1 = AT. Hence
〈u, v〉= vTATAu
= vTA–1 Au= vTu
which is the Euclidean inner product.
Supplementary Exercises 6 193


EXERCISE SET 7.1
1. (a) Since
the characteristic equation is λ2– 2λ– 3 = 0.
(e) Since
the characteristic equation is λ2= 0.
3. (a) The equation (λI– A)x= 0becomes
The eigenvalues are λ= 3 and λ= –1. Substituting λ= 3 into (λI– A)x= 0yields
or
–8x1+ 4x2= 0
00
84
0
0
1
2
−
=
x
x
λ
λ
−
−+
=
30
81
0
0
1
2
x
x
det( ) det
λλ
λλ
IA−=
=
0
0
2
det( ) det ( )( )
λλ
λλλ
IA−= −
−+
=− +
30
81 31
195

Thus x1= 1
–
2sand x2= swhere sis arbitrary, so that a basis for the eigenspace
corresponding to λ= 3 is . Of course, and are also bases.
Substituting λ= –1 into (λI– A)x= 0yields
or
–4x1= 0
–8x1= 0
Hence, x1= 0 and x2= swhere sis arbitrary. In particular, if s= 1, then a basis for the
eigenspace corresponding to λ= –1 is .
3. (e) The equation (λI– A)x= 0becomes
Clearly, λ= 0 is the only eigenvalue. Substituting λ= 0 into the above equation yields
x1= sand x2= twhere sand tare arbitrary. In particular, if s= t= 1, then we find
that and form a basis for the eigenspace associated with λ= 0.
5. (c) From the solution to 4(c), we have
λ3+ 8λ2+ λ+ 8 = (λ+ 8)(λ2+ 1)
Since λ2+ 1 = 0 has no real solutions, then λ= –8 is the only (real) eigenvalue.
0
1
1
0
λ
λ
0
0
0
0
1
2
=
x
x
0
1
−
−
=
40
80
0
0
1
2
x
x
π
π2
1
2
12
1
196 Exercise Set 7.1

7. (a) Since
=λ
4+ λ3– 3λ2– λ+ 2
=(λ– 1)2(λ+ 2)(λ+ 1)
the characteristic equation is
(λ– 1)2(λ+ 2)(λ+ 1) = 0
9. (a) The eigenvalues are λ= 1, λ= –2, and λ= –1. If we set λ= 1, then (λI– A)x= 0
becomes
The augmented matrix can be reduced to
Thus, x1= 2s, x2= 3s, x3= s, and x4= tis a solution for all sand t. In particular, if we
let s= t= 1, we see that
form a basis for the eigenspace associated with λ= 1.
2
3
1
0
0
0
0
1
and
10 2 0 0
01300
00000
00000
−
−
1020
1110
0130
0000
−
−−
−
=
x
x
x
x
1
2
3
4
0
0
0
0
det( ) det
λ
λ
λ
λ
IA−=
−
−−
−+
02 0
110
01 20
00 0
λ
−
1
Exercise Set 7.1 197

If we set λ= –2, then (λI– A)x= 0becomes
The augmented matrix can be reduced to
This implies that x1= –s, x2= x4= 0, and x3= s. Therefore the vector
forms a basis for the eigenspace associated with λ= –2.
Finally, if we set λ= –1, then (λI– A)x= 0becomes
The augmented matrix can be reduced to
10 2 00
01 100
00 0 10
00 0 00
−
−−
−−−
−
−
1020
1110
0110
0002
1
2
3
x
x
x
xx4
0
0
0
0
=
−
1
0
1
0
10100
01000
00010
00000
−−
−−−
−
−
2020
1210
0100
0003
=
x
x
x
x
1
2
3
4
0
0
0
0
198 Exercise Set 7.1

Thus, x1= –2s, x2= s, x3= s, and x4= 0 is a solution. Therefore the vector
forms a basis for the eigenspace associated with λ= –1.
11. By Theorem 7.1.1, the eigenvalues of Aare 1, 1/2, 0, and 2. Thus by Theorem 7.1.3, the
eigenvalues of A9are 19= 1, (1/2)9= 1/512, 09= 0, and 29= 512.
13. The vectors Axand xwill lie on the same line through the origin if and only if there exists
a real number λsuch that Ax= λx, that is, if and only if λis a real eigenvalue for Aand x
is the associated eigenvector.
(a) In this case, the eigenvalues are λ= 3 and λ= 2, while associated eigenvectors are
respectively. Hence the lines y= xand y= 2xare the only lines which are invariant
under A.
(b) In this case, the characteristic equation for Ais λ2+ 1 = 0. Since Ahas no real
eigenvalues, there are no lines which are invariant under A.
15. Let aij denote the ijth entry of A. Then the characteristic polynomial of Ais det(λI– A) or
This determinant is a sum each of whose terms is the product of nentries from the given
matrix. Each of these entries is either a constant or is of the form λ– aij. The only term
with a λin each factor of the product is
(λ– a11)(λ– a22) …(λ– ann)
Therefore, this term must produce the highest power of λin the characteristic polynomial.
This power is clearly nand the coefficient of λnis 1.
det
λ
λ
−−
−− −
−−
aa a
aa a
aa
n
n
nn
11 12 1
21 22 2
12
λλ
−
ann
1
1
1
2
and
−
2
1
1
0
Exercise Set 7.1 199
17. The characteristic equation of Ais
λ2– (a+ d)λ+ ad – bc = 0
This is a quadratic equation whose discriminant is
(a+ d)2– 4ad + 4bc = a2– 2ad + d2+ 4bc
= (a– d)2+ 4bc
The roots are
If the discriminant is positive, then the equation has two distinct real roots; if it is zero, then
the equation has one real root (repeated); if it is negative, then the equation has no real
roots. Since the eigenvalues are assumed to be real numbers, the result follows.
19. As in Exercise 17, we have
Alternate Solution: Recall that if r1and r2are roots of the quadratic equation
x2+ Bx + C= 0, then B= –(r1+ r2) and C= r1r2. The converse of this result is also true.
Thus the result will follow if we can show that the system of equations
λ1+ λ2= a+ d
λ1λ2= ad – bc
is satisfied by λ1= a+ band λ2= a– c. This is a straightforward computation and we leave
it to you.
λ
()
()
=+± − +
=+± − +
ad ad bc
ad cb
2
2
4
2
44
2
2
2
bc adcb
ad cb
a
because −=−
=+± +
=+
()
ddcd abcd
ab ac
++ −−+
=+ −
22
or
or
λ
=+±−+
1
24()()
2
ad ab bc
200 Exercise Set 7.1

21. Suppose that Ax= λx. Then
(A– sI)x= Ax– sIx= λx– sx= (λ– s)x
That is, λ– sis an eigenvalue of A– sI and xis a corresponding eigenvector.
23. (a) For any square matrix B, we know that det(B) = det(BT). Thus
det(λI– A) = det(λI– A)T
= det(λIT– AT)
= det(λI– AT)
from which it follows that Aand AThave the same eigenvalues because they have the
same characteristic equation.
(b) Consider, for instance, the matrix which has λ= 1 as a (repeated) eigen-
value. Its eigenspace is spanned by the vector , while the eigenspace of its
transpose is spanned by the vector
25. (a) Since p(λ) has degree 6, Ais 6 ×6.
(b) Yes, Ais invertible because λ= 0 is not an eigenvalue.
(c) Awill have 3 eigenspaces corresponding to the 3 eigenvalues.
1
1
−
1
1
21
10−
Exercise Set 7.1 201

EXERCISE SET 7.2
1. The eigenspace corresponding to λ= 0 can have dimension 1 or 2. The eigenspace
corresponding to λ= 1 must have dimension 1. The eigenspace corresponding to λ= 2 can
have dimension 1, 2, or 3.
5. Call the matrix A. Since Ais triangular, the eigenvalues are λ= 3 and λ= 2. The matrices
3I– Aand 2I– Aboth have rank 2 and hence nullity 1. Thus Ahas only 2 linearly
independent eigenvectors, so it is not diagonalizable.
13. The characteristic equation is λ3– 6λ2+ 11λ– 6 = 0, the eigenvalues are λ= 1, λ= 2, and
λ= 3, and the eigenspaces are spanned by the vectors
Thus, one possibility is
and
PAP
−=
1
100
020
003
P=
121
133
134
1
1
1
23
1
1
14
34
1
203

15. The characteristic equation is λ2(λ– 1) = 0; thus λ= 0 and λ= 1 are the only eigenvalues.
The eigenspace associated with λ= 0 is spanned by the vectors and ; the
eigenspace associated with λ= 1 is spanned by . Thus, one possibility is
and hence
21. The characteristic equation of Ais (λ– 1)(λ– 3)(λ– 4) = 0 so that the eigenvalues are
λ= 1, 3, and 4. Corresponding eigenvectors are [1 2 1]T, [1 0 –1]T, and [1 –1 1]T,
respectively, so we let
Hence
and therefore
An
n
n
n
=−
−
111
201
111
100
030
00 4
−
−
///
//
///
16 13 16
12 0 12
13 13 13
P−=−
−
1
16 13 16
12 0 12
13 13 13
///
//
///
P=−
−
111
201
111
PAP
−=
1
000
000
001
P=
−
100
010
301
0
0
1
0
1
0
1
0
3−
204 Exercise Set 7.2

25. (a) False. For instance the matrix , which has linearly independent column
vectors, has characteristic polynomial (λ– 1)2. Thus λ= 1 is the only eigenvalue.
The corresponding eigenvectors all have the form . Thus this 2 ×2 matrix has
only 1 linearly independent eigenvector, and hence is not diagonalizable.
(b) False. Any matrix Qwhich is obtained from Pby multiplying each entry by a nonzero
number kwill also work. Why?
(c) True by Theorem 7.2.2.
(d) True. Suppose that Ais invertible and diagonalizable. Then there is an invertible
matrix Psuch that P–1 AP = Dwhere Dis diagonal. Since Dis the product of invertible
matrices, it is invertible, which means that each of its diagonal elements diis nonzero
and D–1 is the diagonal matrix with diagonal elements 1/di. Thus we have
(P–1 AP)–1 = D–1
or
P–1 A–1 P= D–1
That is, the same matrix Pwill diagonalize both Aand A–1.
27. (a) Since Ais diagonalizable, there exists an invertible matrix Psuch that P–1 AP = D
where Dis a diagonal matrix containing the eigenvalues of Aalong its diagonal.
Moreover, it easily follows that P–1 AkP= Dkfor ka positive integer. In addition,
Theorem 7.1.3 guarantees that if λis an eigenvalue for A, then λkis an eigenvalue for
Ak. In other words, Dkdisplays the eigenvalues of Akalong its diagonal.
Therefore, the sequence
P–1 AP = D
P–1 A2P= D2
.
.
.
P–1 AkP= Dk
.
.
.
will converge if and only if the sequence A, A2,..., Ak,... converges. Moreover, this
will occur if and only if the sequences λi, λi
2,..., λi
k,... converges for each of the n
eigenvalues λiof A.
t1
1
01
12−
Exercise Set 7.2 205

(b) In general, a given sequence of real numbers a, a2, a3,... will converge to 0 if and only
if –1 < a< 1 and to 1 if a= 1. The sequence diverges for all other values of a.
Recall that P–1 AkP= Dkwhere Dkis a diagonal matrix containing the eigenvalues
λ1
k, λ2
k,..., λn
kon its diagonal. If |λi|< 1 for all i= 1, 2, . . ., n, then Dk= 0
and hence Ak= 0.
If λi= 1 is an eigenvalue of Afor one or more values of iand if all of the other
eigenvalues satisfy the inequality |λj|< 1, then Akexists and equals PDLP–1 where
DLis a diagonal matrix with only 1’s and 0’s on the diagonal.
If Apossesses one or more eigenvalues λwhich do not satisfy the inequality
–1 < λ≤1, then Akdoes not exist.
29. The Jordan block matrix is
Since this is an upper triangular matrix, we can see that the only eigenvalue is λ= 1, with
algebraic multiplicity n. Solving for the eigenvectors leads to the system
()
λ
IJ
n
−=
x
01 0 00
00 1 00
00 0 10
00 0 01
x.
Jn=
11 0 00
01 1 00
00 1 10
00 0 11
.
lim
k→∞
lim
k→∞
lim
k→∞
lim
k→∞
206 Exercise Set 7.2

EXERCISE SET 7.3
1. (a) The characteristic equation is λ(λ– 5) = 0. Thus each eigenvalue is repeated once
and hence each eigenspace is 1-dimensional.
(c) The characteristic equation is λ2(λ– 3) = 0. Thus the eigenspace corresponding to λ
= 0 is 2-dimensional and that corresponding to λ= 3 is 1-dimensional.
(e) The characteristic equation is λ3(λ– 8) = 0. Thus the eigenspace corresponding to λ
= 0 is 3-dimensional and that corresponding to λ= 8 is 1-dimensional.
13. By the result of Exercise 17, Section 7.1, the eigenvalues of the symmetric 2 ×2 matrix
, are Since (a– d)2+ 4b2cannot be negative,
the eigenvalues are real.
15. Yes. Notice that the given vectors are pairwise orthogonal, so we consider the equation
P–1 AP = D
or
A= PDP–1
where the columns of Pconsist of the given vectors each divided by its norm and where D
is the diagonal matrix with the eigenvalues of Aalong its diagonal. That is,
PD=
−
=
−
010
12 012
12 012
100
030
0
and
007
λ
()=+±−
()
+
1
24
22
ad ad b
ab
ba
207

From this, it follows that
Alternatively, we could just substitute the appropriate values for λand xin the equation
Ax= λxand solve for the matrix A.
APDP
–
==
1
300
034
043
208 Exercise Set 7.3

SUPPLEMENTARY EXERCISES 7
1. (a) The characteristic equation of Ais λ2– 2 cos
θ
+ 1 = 0. The discriminant of this
equation is 4 (cos2
θ
– 1), which is negative unless cos2
θ
= 1. Thus Acan have no real
eigenvalues or eigenvectors in case 0 <
θ
< π.
3. (a) If
then D= S2, where
Of course, this makes sense only if a1≥0, . . ., an≥0.
(b) If Ais diagonalizable, then there are matrices Pand Dsuch that Dis diagonal and D
= P–1 AP. Moreover, if Ahas nonnegative eigenvalues, then the diagonal entries of D
are nonnegative since they are all eigenvalues. Thus there is a matrix T, by virtue of
Part (a), such that D= T2. Therefore,
A= PDP–1 = PT2P–1 = PTP–1 PTP–1 = (PTP–1)2
That is, if we let S= PTP–1, then A= S2.
S
a
a
an
=
1
2
00
00
00
D
a
a
an
=
1
2
00
00
00
209

3. (c) The eigenvalues of Aare λ= 9, λ= 1, and λ= 4. The eigenspaces are spanned by the
vectors
Thus, we have
while
Therefore
5. Since det(λI– A) is a sum of signed elementary products, we ask which terms involve λn–1.
Obviously the signed elementary product
q= (λ– a11)(λ– a22) …. (
λ
– ann)
= λn– (a11 + a22 + …. + ann)λn–1
+ terms involving λrwhere r< n– 1
has a term – (trace of A)λn–1. Any elementary product containing fewer than n– 1 factors
of the form λ– aii cannot have a term which contains λn–1. But there is no elementary
product which contains exactly n– 1 of these factors (Why?). Thus the coefficient of λn–1
is the negative of the trace of A.
SPTP==
−1
110
021
003
DT=
=
900
010
004
300
010
002
and
PP=
=−
−
111
201
200
0012
1112
01
1
and
−−
1
1
2
2
1
0
0
1
1
0
210 Supplementary Exercises 7

7. (b) The characteristic equation is
p(λ) = –1 + 3λ– 3λ2+ λ3= 0
Moreover,
and
It then follows that
p(A) = –I+ 3A– 3A2+ A3= 0
=
+P
a
a
a
a
0
0
0
1
00
00
00
λλ
λ
λ
1
12
00
00
00 1
a
an
+
aa
a
an
21
2
22
2
2
2
00
00
00
λ
λ
λ
++
a
a
a
n
n
n
n
nn
n
λ
λ
λ
1
2
00
00
00
=
+++
−
P
P
aa
1
011
λ
aa
aa a
aa
n
n
n
n
n
λ
λλ
λ
1
012 2
01
00
00
00
+++
++++
=
a
P
p
p
nn
n
λ
λ
λ
()
(
–
P1
100
0
22 1
0
00
)
()
p
P
n
λ
−
A3
133
386
61510
=
−
−
−
A2
001
133
386
=−
−
Supplementary Exercises 7 211

However, each λiis a root of the characteristic polynomial, so p(λi) = 0 for i= 1, . . ., n.
Then,
=0.
Thus, a diagonalizable matrix satisfies its characteristic polynomial.
9. Since c0= 0 and c1= –5, we have A2= 5A, and, in general, An= 5n–1 A.
11. Call the matrix Aand show that A2= (c1+ c2+ . . . + cn)A= [tr(A)]A. Thus Ak=
[tr(A)]k–1 Afor k= 2, 3, .... Now if λis an eigenvalue of A, then λkis an eigenvalue of Ak,
so that in case tr(A) ≠0, we have that λk[tr(A)]k–1 = [λ/tr(A)]k–1 λis an eigenvalue of A
for k= 2, 3, .... Why? We know that Ahas at most neigenvalues, so that this expression
can take on only finitely many values. This means that either λ= 0 or λ= tr(A). Why?
In case tr(A) = 0, then all of the eigenvalues of Aare 0. Why? Thus the only possible
eigenvalues of Aare zero and tr(A). It is easy to check that each of these is, in fact, an
eigenvalue of A.
Alternatively, we could evaluate det(Iλ– A) by brute force. If we add Column 1 to
Column 2, the new Column 2 to Column 3, the new Column 3 to Column 4, and so on, we
obtain the equation
det( ) detIA
cccccc c
λ
λλ λ λ
−=
−−−−−− −−
112123 1
ccc
cccccc ccc
c
n
n
2
112123 12
−−
−−−−−− −−−−
−
λλ λ
1112 123 12
11
−− − − − −− −−
−−−
cc ccc cc c
ccc
n
λλ
22123 12
−− − −− −−
ccc cc c
n
λ
pA P P()=
−
00 0
00 0
00 0
1
212 Supplementary Exercises 7

If we subtract Row 1 from each of the other rows and then expand by cofactors along the
nth column, we have
= (–1)n+1 (λ– tr(A))(–λ)n–1 because the above matrix is triangular
= (–1)2n(λ– tr(A))λn–1
= λn–1(λ– tr(A))
Thus λ= tr(A) and λ= 0 are the eigenvalues, with λ= 0 repeated n– 1 times.
17. Since every odd power of Ais again A, we have that every odd power of an eigenvalue of
Ais again an eigenvalue of A. Thus the only possible eigenvalues of Aare λ= 0, ±1.
det( ) det
()
IA
cccccc A
−=
−−−−−− −
λλ λ λ
112123
tr
−−
−−
−− −
=
λ
λλ
λλ λ
00 0
00
0
() ( ())det−−
−
−−
−−−
+
1
00 0
00
0
1ntr A
λ
λ
λλ
λλλ
−−− −
λλλ λ
Supplementary Exercises 7 213


EXERCISE SET 8.1
3. Since T(–u) = –u= u= T(u) ≠–T(u) unless u= 0, the function is not linear.
5. We observe that
T(A1+ A2) = (A1+ A2)B= A1B+ A2B= T(A1) + T(A2)
and
T(cA) = (cA)B= c(AB) = cT(A)
Hence, Tis linear.
17. (a) Since T1is defined on all of R2, the domain of T2T1is R2. We have T2T1(x, y) =
T2(T1(x, y)) = T2(2x, 3y) = (2x– 3y, 2x+ 3y). Since the system of equations
2x– 3y= a
2x+ 3y= b
can be solved for all values of aand b, the codomain is also all of R2.
(d) Since T1is defined on all of R2, the domain of T2T1is R2. We have
T2(T1(x, y)) = T2(x– y, y+ z, x– z) = (0, 2x)
Thus the codomain of T2T1is the y-axis.
215

19. (a) We have
(b) Since the range of T1is not contained in the domain of T2, T2T1is not well defined.
25. Since (1, 0, 0) and (0, 1, 0) form an orthonormal basis for the xy-plane, we have T(x, y, z)
= (x, 0, 0) + (0, y, 0) = (x, y, 0), which can also be arrived at by inspection. Then T(T(x,
y, z)) = T(x, y, 0) = (x, y, 0) = T(x, y, z). This says that Tleaves every point in the x-y
plane unchanged.
31. (b) We have
(c) We have
33. (a) True. Let c1= c2= 1 to establish Part (a) of the definition and let c2= 0 to establish
Part (b).
(b) False. All linear transformations have this property, and, for instance there is more
than one linear transformation from R2to R2.
(c) True. If we let u= 0, then we have T(v) = T(–v) = –T(v). That is, T(v) = 0for all
vectors vin V. But there is only one linear transformation which maps every vector to
the zero vector.
(d) False. For this operator T, we have
T(v+ v) = T(2v) = v0+ 2 v
But
T(v) + T(v) = 2T(v) = 2v0+ 2v
Since v0≠0, these two expressions cannot be equal.
()( )()JDe e dte
xxx
x
ο+= +
′=−
∫
331
0
()(sin ) (sin ) sin( ) – sin( ) sin( )JD x tdt x x
ο=′==0
0
xx
∫
()()()TT A A ac
bd ad
T
12
==
=+tr tr
216 Exercise Set 8.1
35. Yes. Let TPn→Pmbe the given transformation, and let TRRn+1 →Rm+1 be the
corresponding linear transformation in the sense of Section 4.4. Let nPn→Rn+1 be the
function that maps a polynomial in Pnto its coordinate vector in Rn+1, and let mPm→
Rm+1 be the function that maps a polynomial in Pmto its coordinate vector in Rm+1.
By Example 7, both nand mare linear transformations. Theorem 5.4.1 implies that a
coordinate map is invertible, so m
–1 is also a linear transformation.
We have T=m
–1 TRn, so T is a composition of linear transformations. Refer to the
diagram below:
Thus, by Theorem 8.1.2., Tis itself a linear transformation.
T
TR
Pn
n
ϕϕ
m
–1
Pm
Rm+1
Rn+1
Exercise Set 8.1 217


EXERCISE SET 8.2
1. (a) If (1, –4) is in R(T), then there must be a vector (x, y) such that T(x, y) = (2x– y,
–8x+ 4y) = (1, –4). If we equate components, we find that 2x– y= 1 or y= tand x
= (1 + t)/2. Thus Tmaps infinitely many vectors into (1, –4).
(b) Proceeding as above, we obtain the system of equations
2x– y= 5
–8x+ 4y= 0
Since 2x– y= 5 implies that –8x+ 4y= –20, this system has no solution. Hence
(5, 0) is not in R(T).
3. (b) The vector (1, 3, 0) is in R(T) if and only if the following system of equations has a
solution:
4x+ y– 2z– 3w= 1
2x+ y+ z– 4w= 3
6x–9z+ 9w= 0
This system has infinitely many solutions x= (3/2)(t– 1), y= 10 – 4t, z= t, w= 1
where tis arbitrary. Thus (1, 3, 0) is in R(T).
5. (a) Since T(x2) = x3≠0, the polynomial x2is not in ker(T).
7. (a) We look for conditions on xand ysuch that 2x– y= and –8x+ 4y= 0. Since these
equations are satisfied if and only if y= 2x, the kernel will be spanned by the vector
(1, 2), which is then a basis.
(c) Since the only vector which is mapped to zero is the zero vector, the kernel is {0} and
has dimension zero so the basis is the empty set.
219

9. (a) Here n= dim(R2) = 2, rank(T) = 1 by the result of Exercise 8(a), and nullity(T) = 1
by Exercise 7(a). Recall that 1 + 1 = 2.
(c) Here n= dim(P2) = 3, rank(T) = 3 by virtue of Exercise 8(c), and nullity(T) = 0 by
Exercise 7(c). Thus we have 3 = 3 + 0.
19. By Theorem 8.2.1, the kernel of Tis a subspace of R3. Since the only subspaces of R3are
the origin, a line through the origin, a plane through the origin, or R3itself, the result
follows. It is clear that all of these possibilities can actually occur.
21. (a) If
then x= –t, y= –t, z= t. These are parametric equations for a line through the origin.
(b) Using elementary column operations, we reduce the given matrix to
Thus, (1, 3, –2)Tand (0, –5, 8)Tform a basis for the range. That range, which we can
interpret as a subspace of R3, is a plane through the origin. To find a normal to that
plane, we compute
(1, 3, –2) ×(0, –5, 8) = (14, –8, –5)
Therefore, an equation for the plane is
14x– 8y– 5z= 0
Alternatively, but more painfully, we can use elementary row operations to reduce
the matrix
134
347
220
x
y
z−
100
350
280
−
−
134
347
220
0
0
0
−
=
x
y
z
220 Exercise Set 8.2

to the matrix
Thus the vector (x, y, z)is in the range of Tif and only if 14x– 8y– 5z= 0.
23. The rank of Tis at most 1, since dimR= 1 and the image of Tis a subspace of R. So, we
know that either rank(T) = 0 or rank(T) = 1. If rank(T) = 0, then every matrix Ais in the
kernel of T, so every n×nmatrix Ahas diagonal entries that sum to zero. This is clearly
false, so we must have that rank(T) = 1. Thus, by the Dimension Theorem (Theorem 8.2.3),
dim (ker(T)) = n2– 1.
27. If f(x) is in the kernel of DD, then f ′′(x) = 0 or f(x) = ax + b. Since these are the only
eligible functions f(x) for which f ′′(x) = 0 (Why?), the kernel of DDis the set of all
functions f(x) = ax + b, or all straight lines in the plane. Similarly, the kernel of DD
Dis the set of all functions f(x) = ax2+ bx + c, or all straight lines except the y-axis
and certain parabolas in the plane.
29. (a) Since the range of Thas dimension 3 minus the nullity of T, then the range of Thas
dimension 2. Therefore it is a plane through the origin.
(b) As in Part (a), if the range of Thas dimension 2, then the kernel must have dimension
1. Hence, it is a line through the origin.
101 4 3 5
011 3 5
00014 85
−+
()
−
()
−−
xy
xy
xyz
Exercise Set 8.2 221


EXERCISE SET 8.3
1. (a) Clearly ker(T) = {(0, 0)}, so Tis one-to-one.
(c) Since T(x, y) = (0, 0) if and only if x= yand x= –y, the kernel is {0, 0} and Tis one-
to-one.
(e) Here T(x, y) = (0, 0, 0) if and only if xand ysatisfy the equations x– y= 0, –x+ y
= 0, and 2x– 2y= 0. That is, (x, y) is in ker(T) if and only if x= y, so the kernel of
Tis this line and Tis not one-to-one.
3. (a) Since det(A) = 0, or equivalently, rank(A) < 3, Thas no inverse.
(c) Since Ais invertible, we have
T
x
x
x
A
x
x
x
−−
=
=
1
1
2
3
1
1
2
3
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
−
−
−
x
x
x
1
2
3
=
−+
1
212
xxx
33
123
123
1
2
1
2
()
−+ +
()
+−
()
xxx
xxx
223

5. (a) The kernel of Tis the line y= –xsince all points on this line (and only those points)
map to the origin.
(b) Since the kernel is not {0, 0}, the transformation is not one-to-one.
7. (b) Since nullity(T) = n– rank(T) = 1, Tis not one-to-one.
(c) Here Tcannot be one-to-one since rank(T) ≤n< m, so nullity(T) ≥1.
11. (a) We know that Twill have an inverse if and only if its kernel is the zero vector, which
means if and only if none of the numbers ai= 0.
13. (a) By inspection, T1
–1(p(x)) = p(x)/x, where p(x) must, of course, be in the range of T1
and hence have constant term zero. Similarly T2
–1(p(x)) = p(x– 1), where, again, p(x)
must be in the range of T2. Therefore (T2T1)–1(p(x)) = p(x– 1)/xfor appropriate
polynomials p(x).
17. (a) Since Tsends the nonzero matrix to the zero matrix, it is not one-to-one.
(c) Since Tsends only the zero matrix to the zero matrix, it is one-to-one. By inspection,
T–1(A) = T(A).
Alternative Solution: Tcan be represented by the matrix
By direct calculation, TB= (TB)–1, so T= T–1.
19. Suppose that w1and w2are in R(T). We must show that
T–1(w1+ w2) = T–1(w1) + T–1(w2)
TB=−
−
0001
0100
0010
1000
01
00
224 Exercise Set 8.3

and
T–1(kw1) = kT–1(w1)
Because Tis one-to-one, the above equalities will hold if and only if the results of applying
Tto both sides are indeed valid equalities. This follows immediately from the linearity of the
transformation T.
21. It is easy to show that Tis linear. However, Tis not one-to-one, since, for instance, it sends
the function f(x) = x– 5 to the zero vector.
25. Yes. The transformation is linear and only (0, 0, 0) maps to the zero polynomial. Clearly
distinct triples in R3map to distinct polynomials in P2.
27. No. Tis a linear operator by Theorem 3.4.2. However, it is not one-to-one since T(a) = a
×a= 0= T(0). That is, Tmaps ato the zero vector, so if Tis one-to-one, amust be the
zero vector. But then Twould be the zero transformation, which is certainly not one-to-one.
Exercise Set 8.3 225


EXERCISE SET 8.4
9. (a) Since Ais the matrix of Twith respect to B, then we know that the first and second
columns of Amust be [T(v1)]Band [T(v2)]B, respectively. That is
Alternatively, since v1= 1v1+ 0v2and v2= 0v1+ 1v2, we have
and
(b) From Part (a),
and
T()vvvvvv
212
35 2
29
=+=
−
T()vvvvvv
11 2
23
5
=− =
−
()TA
B
vv2
0
1
3
5
=
=
TA
B
()vv1
=
=−
1
0
1
2
T
T
B
B
()
()
vv
vv
1
2
1
2
3
5
=−
=
227

(c) Since we already know T(v1) and T(v2), all we have to do is express [x1x2]Tin terms
of v1and v2. If
then
x1= a– b
x2= 3a+ 4b
or
a= (4x1+ x2)/7
b= (–3x1+ x2)/7
Thus
(d) By the above formula,
11. (a) The columns of A, by definition, are [T(v1)]B, [T(v2)]B, and [T(v3)]B, respectively.
(b) From Part (a),
T(v1) = v1+ 2v2+ 6v3= 16 + 51x+ 19x2
T(v2) = 3v1–2v3= –6 – 5x+ 5x2
T(v3) = –v1+ 5v2+ 4v3= 7 + 40x+ 15x2
T1
1
19 7
83 7
=−
x
x
xx
1
2
12
4
7
3
5
3
=+
−
+−xxx
xx
xx
12
12
12
7
2
29
18
7
107 24
7
+−
=
+
−+
x
xab a b
1
2
12
1
3
1
4
=+=
+−
vvvv
228 Exercise Set 8.4

(c) Let a0+ a1x+ a2x2= b0v1+ b1v2+ b2v3. Then
a0=– b1+ 3b2
a1=3b0+ 3b1+ 7b2
a2=3b0+ 2b1+ 2b2
This system of equations has the solution
b0= (a0– a1+ 2a2)/3
b1= (–5a0+ 3a1– 3a2)/8
b2= (a0+ a1– a2)/8
Thus
T(a0+ a1x+ a2x2) = b0T(v1) + b1T(v2) + b2T(v3)
(d) By the above formula,
T(1 + x2) = 2 + 56x+ 14x2
13. (a) Since
T1(1) = 2 and T1(x) = –3x2
T2(1) = 3xT
2(x) = 3x2and T2(x2) = 3x3
T2°T1(1) = 6xand T2°T1(x) = –9x3
we have
=−+
+−+
+
239 161 247
24
201 111 247
8
01 2
01 2
aaa
aaa
x
61 31 107
12
01 2
2
aa a
x
−+
Exercise Set 8.4 229

and
(b) We observe that here
[T2°T1]B′,B= [T2]B′,B′′ [T1]B′′,B
15. If Tis a contraction or a dilation of V, then Tmaps any basis B= {v1,…, vn} of Vto
{kv1,…, kvn} where kis a nonzero constant. Therefore the matrix of Twith respect to Bis
17. The standard matrix for Tis just the m×nmatrix whose columns are the transforms of the
standard basis vectors. But since Bis indeed the standard basis for Rn, the matrices are the
same. Moreover, since B′is the standard basis for Rm, the resulting transformation will yield
vector components relative to the standard basis, rather than to some other basis.
19. (c) Since D(f1) = 2f1, D(f2) = f1+ 2f2, and D(f3) = 2f2+ 2f3, we have the matrix
210
022
002
k
k
k
k
00 0
00 0
00 0
000
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
TT
BB
21
00
60
00
09
°′,
=
−
[] []
,,
TT
BB BB12
20
00
03
000
30
′′ ′ ′′
=
−
=00
030
003
230 Exercise Set 8.4

EXERCISE SET 8.5
1. First, we find the matrix of Twith respect to B. Since
and
then
In order to find P, we note that v1= 2u1+ u2and v2= –3u1+ 4u2. Hence the transition
matrix from B′to Bis
Thus
P−=
1
4
11
3
11
1
11
2
11
P=−
23
14
AT
B
=
=−
−
12
01
T()uu2=−
−
2
1
T()uu1
1
0
=
231

and therefore
3. Since T(u1) = (1/ 2, 1/ 2) and T(u2) = (–1/ 2, 1/ 2), then the matrix of Twith
respect to Bis
From Exercise 1, we know that
Thus
5. Since T(e1) = (1, 0, 0), T(e2) = (0, 1, 0), and T(e3) = (0, 0, 0), we have
In order to compute P, we note that v1= e1, v2= e1+ e2, and v3= e1+ e2+ e3. Hence,
P=
111
011
001
AT
B
=
=
100
010
000
AT PAP
B
′=
== −
−
'
11
11 2
13 25
59
PP=−
=−
−
23
14
1
11
43
12
1
and
AT
B
=
=−
12 12
12 12
′== =−
−
−
′−
AT PTP
BB
[] []
11
11
43
12
12
01
−
=−−
−
23
14
3
11
56
11
2
11
3
11
232 Exercise Set 8.5

and
Thus
7. Since
and
we have
We note that
P=−
−
2
9
7
9
1
3
1
6
qqppppqqpppp
112 212
2
9
1
3
7
9
1
6
=− + = − .and Hence
TB
=−
2
3
2
9
1
2
4
3
Tx()pppppp
212
12 2 2
9
4
3
=+ =− +
Tx()pppppp
112
93 2
3
1
2
=+ = +
TB
=
−
−
′
110
011
001
100
0110
000
111
011
001
100
0
=111
000
P−=
−
−
1
110
011
001
Exercise Set 8.5 233

and
Therefore
9. (a) If Aand Care similar n×nmatrices, then there exists an invertible n×nmatrix P
such that A= P–1CP. We can interpret Pas being the transition matrix from a basis B′
for Rnto a basis B. Moreover, Cinduces a linear transformation TRn→Rnwhere C
= [T]B. Hence A= [T]B′. Thus Aand Care matrices for the same transformation with
respect to different bases. But from Theorem 8.2.2, we know that the rank of Tis
equal to the rank of Cand hence to the rank of A.
Alternate Solution:We observe that if Pis an invertible n×nmatrix, then P
represents a linear transformation of Rnonto Rn. Thus the rank of the transformation
represented by the matrix CP is the same as that of C. Since P–1 is also invertible, its
null space contains only the zero vector, and hence the rank of the transformation
represented by the matrix P–1 CP is also the same as that of C. Thus the ranks of A
and Care equal. Again we use the result of Theorem 8.2.2 to equate the rank of a
linear transformation with the rank of a matrix which represents it.
Second Alternative:Since the assertion that similar matrices have the same rank deals
only with matrices and not with transformations, we outline a proof which involves
only matrices. If A= P–1 CP, then P–1 and Pcan be expressed as products of
elementary matrices. But multiplication of the matrix Cby an elementary matrix is
equivalent to performing an elementary row or column operation on C. From Section
5.5, we know that such operations do not change the rank of C. Thus Aand Cmust
have the same rank.
TB
=
−
′
3
4
7
2
3
21
2
3
2
9
1
2
4
3
−
−
=
2
9
7
9
1
3
1
6
11
01
P−=
1
3
4
7
2
3
21
234 Exercise Set 8.5

11. (a) The matrix for Trelative to the standard basis Bis
The eigenvalues of [T]Bare λ= 2 and λ= 3, while corresponding eigenvectors are
(1, –1) and (1, –2), respectively. If we let
and
is diagonal. Since Prepresents the transition matrix from the basis B′to the standard
basis B, we have
as a basis which produces a diagonal matrix for [T]B′.
13. (a) The matrix of Twith respect to the standard basis for P2is
The characteristic equation of Ais
λ3– 2λ2– 15λ+ 36 = (λ– 3)2(λ+ 4) = 0
and the eigenvalues are therefore λ= –4 and λ= 3.
A=−−
−
562
018
102
B′= ,
1
1
1
2−
−
PTP
B
−=
120
03
[]
PP=−−
=−−
11
12
21
11
then –1
TB
=−
11
24
Exercise Set 8.5 235

(b) If we set λ= –4, then (λI– A)x= 0becomes
The augmented matrix reduces to
and hence x1= –2s, x2= 8
–
3s, and x3= s. Therefore the vector
is a basis for the eigenspace associated with λ= –4. In P2, this vector represents the
polynomial –2 + 8
–
3x+ x2.
If we set λ= 3 and carry out the above procedure, we find that x1= 5 s, x2= –2s,
and x3= s. Thus the polynomial 5 – 2x+ x2is a basis for the eigenspace associated
with λ= 3.
15. If vis an eigenvector of Tcorresponding to λ, then vis a nonzero vector which satisfies
the equation T(v) = λvor (λI– T)v= 0. Thus λI– Tmaps vto 0, or vis in the kernel of
λI– T.
17. Since C[x]B= D[x]Bfor all xin V, we can, in particular, let x= vifor each of the basis
vectors v1,…, vnof V. Since [vi]B= eifor each iwhere {e1,…,en} is the standard basis for
Rn, this yields Cei=Deifor i= 1, … , n. But Ceiand Deiare just the ith columns of Cand
D, respectively. Since corresponding columns of Cand Dare all equal, we have C= D.
19. (a) False. Every matrix is similar to itself, since A= I–1 AI.
(b) True. Suppose that A= P–1 BP and B= Q–1 CQ. Then
A= P–1(Q–1 CQ)P= (P–1Q–1)C(QP) = (QP)–1C(QP)
Therefore Aand Care similar.
−
2
83
1
10 2 0
01 83 0
00 0 0
−
−−−
−
−−
962
038
102
1
2
3
x
x
x
=
0
0
0
236 Exercise Set 8.5

(c) True. By Table 1, Ais invertible if and only if Bis invertible, which guarantees that A
is singular if and only if Bis singular.
Alternatively, if A= P–1 BP, then B= PAP–1. Thus, if Bis singular, then so is A.
Otherwise, Bwould be the product of 3 invertible matrices.
(d) True. If A= P–1 BP, then A–1=(P–1 BP)–1 = P–1 B–1(P–1)–1 = P–1B–1P, so A–1 and B–1 are
similar.
25. First, we need to prove that for any square matrices Aand B, the trace satisfies tr(A) =
tr(B). Let
Then,
Thus,
tr(AB) = [AB]11 + [AB]22 + …+ [AB]nn
=++⋅⋅⋅+
=
== =
∑∑ ∑
ab ab ab
a
j
j
n
jjj
j
n
nj jn
j
n
k
1
1
122
11
jj
j
n
kj
k
n
b
== ∑∑ 11
.
[]AB a b a b ab a b a
nn j
j
11 11 11 12 21 13 31 1 1 1
1
=++++ =
=
…nn
j
nn
b
AB a b a b ab a b
∑
=++++ =
1
22 21 12 22 22 23 32 2 2
[] …aab
AB a b ab ab
j
j
n
j
nn n n nn nn
2
1
2
11 2 2 33
=
∑
=++++
[] …aab ab
nn nn nj
j
n
jn
=
=
∑
1
.
A
aa a
aa a
aa a
n
n
nn nn
=
⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
11 12 1
21 22 2
12
⯗⯗ ⯗
=
⋅⋅⋅
⋅⋅⋅
and
b11
B
bb
bb b
n
n
12 1
21 22 2
⯗⯗⯗ ⯗
bb b
nn nn12
⋅⋅⋅
Exercise Set 8.5 237

Reversing the order of summation and the order of multiplication, we have
Now, we show that the trace is a similarity invariant. Let B= P–1 AP. Then
tr(B) = tr(P–1 AP)
= tr((P–1 A)P)
= tr(P(P–1 A))
= tr(PP–1)A)
= tr(I A)
= tr(A).
tr( )AB b a
ba b
jk
k
n
jk
j
n
k
k
n
kk
k
n
=
=+
==
==
∑∑
∑
11
1
1
12
1
∑∑∑
++
=+++
=
=
aba
BA BA BA
knk
k
n
kn
nn
2
1
11 22
[] [] []
ttr( ).BA
238 Exercise Set 8.5

EXERCISE SET 8.6
1. (a) This transformation is onto because for any ordered pair (a, b) in R2, T(b, a) = (a, b).
(b) We use a counterexample to show that this transformation is not onto. Since there is
no pair (x, y) that satisfies T(x, y) = (1, 0), Tis not onto.
(c) This transformation is onto. For any ordered pair (a, b) in R2, T= (a, b).
(d) This is not an onto transformation. For example, there is no
pair (x, y) that satisfies T(x, y) = (1, 1, 0).
(e) The image of this transformation is all vectors in R3of the form (a, –a, 2a). Thus, the
image of Tis a one-dimensional subspace of R3and cannot be all of R3. In particular,
there is no vector (x, y) that satisfies T(x, y) = (1, 1, 0), and this transformation is not
onto.
(f) This is an onto transformation. For any point (a, b) in R2, there are an infinite number
of points that map to it. One such example is T= (a, b).
3. (a) We find that rank(A) = 2, so the image of Tis a two-dimensional subspace of R3. Thus,
Tis not onto.
(b) We find that rank(A) = 3, so the image of Tis all of R3. Thus, Tis not onto.
(c) We find that rank(A) = 3, so the image of Tis all of R3. Thus, Tis onto.
(d) We find that rank(A) = 3, so the image of Tis all of R3. Thus, Tis onto.
5. (a) The transformation Tis not a bijection because it is not onto. There is no p(x) in
P2(x) so that xp(x) = 1.
(b) The transformation T(A) = ATis one-to-one, onto, and linear, so it is a bijection.
(c) By Theorem 8.6.1, there is no bijection between R4and R3, so Tcannot be a bijection. In
particular, it fails being one-to-one. As an example, T(1, 1, 2, 2) = T(1, 1, 0, 0) = (1, 1, 0).
abab+−
22
0,,
abab+−
22
,
239

(d) Because dim P3= 4 and dim R3= 3, Theorem 8.6.1 states that there is no bijection
between P3and R3, so Tcannot be a bijection. In particular, it fails being one-to-one.
As an example, T(x+ x2+ x3) = T(1 + x+ x2+ x3) = (1, 1, 1).
7. Assume there exists a surjective (onto) linear transformation TV→W, where dim W>
dim V. Let m= dim Vand n= dim W, with m< n. Then, the matrix ATof the
transformation is an n×mmatrix, with m< n. The maximal rank of ATis m, so the
dimension of the image of Tis at most m. Since the dimension of the image of Tis smaller
than the dimension of the codomain Rn, Tis not onto. Thus, there cannot be a surjective
transformation from Vonto Wif dim V< dim W.
If n= dim W≤dim V= m, then the matrix ATof the transformation is an n×mmatrix
with maximim possible rank n. If rank(AT) = n, then Tis a surjective transformation.
Thus, it is only possible for TV→Wto be a surjective linear transformation if dim W
≤dim V.
9. Let TV→Rnbe defined by T(v) = (v)S, where S= {u1, u2,…, un} is a basis of V. We
know from Example 7 in Section 8.1 that the coordinate map is a linear transformation.
Let (a1, a2,…, an) be any point in Rn. Then, for the vector v= a1u1+ a2u2+ …+ anun, we
have
T(v) = T(a1u1+ a2u2+ …+ anun) = (a1, a2,…, an)
so Tis onto.
Also, let v1= a1u1+ a2u2+ …+ anunand v2= b1u1+ b2u2+ …+ bnun. If T(v1) =
T(v2), then (v1)S= (v2)S, and thus (a1, a2,…, an) = (b1, b2,…, bn). It follows that a1= b1,
a2= b2,…, an= bn, and thus
v1= a1u1+ a2u2+ …+ anun= v2.
So, Tis one-to-one and is thus an isomorphism.
11. Let V= Span{1, sin x, cos x, sin 2x, cos 2x}. Differentiation is a linear transformation (see
Example 11, Section 8.1). In this case, Dmaps functions in Vinto other functions in V. To
construct the matrix of the linear transformation with respect to the basis B= {1, sin x,
cos x, sin 2x, cos 2x}, we look at coordinate vectors of the derivatives of the basis vectors:
D(1) = 0 D(sin x) = cos xD(cos x) = –sin xD(sin 2x) = 2 cos 2x
D(cos 2x) = 2 sin 2x
The coordinate matrices are:
[()] [(sin)]DDx
BB
1
0
0
0
0
0
0
0
1
=
=
00
0
0
1
0
0
=
−
[(cos)]Dx
B
00
2
0
0
0
0
2
=
[(sin )]Dx
B
=
−
[(cos )]Dx
B
2
0
0
0
2
0
.
240 Exercise Set 8.6

Thus, the matrix of the transformation is
Then, differentiation of a function in Vcan be accomplished by matrix multiplication by the
formula
[D(f)]B= AD[f]B.
The final vector, once transformed back to Vfrom coordinates in R5, will be the desired
derivative.
For example,
Thus, D(3 – 4 sin x+ sin 2 x+ 5 cos 2x) = –4 cos x– 10 sin 2x+ 2 cos 2x.
[( sin sin cos )]DxxxA
BD
34 2 5 2
3
4
−++ =
−
0
1
5
00000
0010
=
−0
01000
00002
00020
−
−
=
3
4
0
1
5
0
.
0
4
10
2
−
−
AD=
−
−
00000
00100
01000
00002
000020
Exercise Set 8.6 241


SUPPLEMENTARY EXERCISES 8
3. By the properties of an inner product, we have
T(v+ w) = 〈v+ w, v0〉v0
= (〈v, v0〉+ 〈w, v0〉)v0
= 〈v, v0〉v0+ 〈w, v0〉v0
= T(v) + T(w)
and
T(kv) = 〈kv, v0〉v0= k〈v, v0〉v0= kT(v)
Thus Tis a linear operator on V.
5. (a) The matrix for Twith respect to the standard basis is
We first look for a basis for the range of T; that is, for the space of vectors Bsuch that
Ax= b. If we solve the system of equations
x+ z+ w= b1
2x+ y+ 3x+ w= b2
x+ w= b3
we find that = z= b1– b3and that any one of x, y, or wwill determine the other two.
Thus, T(e3) and any two of the remaining three columns of Ais a basis for R(T).
A=
1011
21 31
1001
243

Alternate Solution :We can use the method of Section 5.5 to find a basis for the
column space of Aby reducing ATto row-echelon form. This yields
so that the three vectors
form a basis for the column space of Tand hence for its range.
Second Alternative:Note that since rank(A) = 3, then R(T) is a 3-dimensional
subspace of R3and hence is all of R3. Thus the standard basis for R3is also a basis for
R(T).
To find a basis for the kernel of T, we consider the solution space of Ax= 0. If we set
b1= b2= b3= 0 in the above system of equations, we find that z= 0, x= –w, and y=
w. Thus the vector (–1, 1, 0, 1) forms a basis for the kernel.
7. (a) We know that Tcan be thought of as multiplication by the matrix
where reduction to row-echelon form easily shows that rank([T]B) = 2. Therefore the
rank of Tis 2 and the nullity of Tis 4 – 2 = 2.
(b) Since [T]Bis not invertible, Tis not one-to-one.
[]TB=
−
−−
−
−
1122
1146
1256
3232
1
2
1
0
1
0
0
0
1
11
01 0
001
000
2
244 Supplementary Exercises 8

9. (a) If A= P–1 BP, then
AT= (P–1 BP)T
= PTBT(P–1)T
= ((PT)–1)–1 BT(P–1)T
= ((P–1)T)TB (P–1)T
Therefore ATand BTare similar. You should verify that if Pis invertible, then so is PT
and that (PT)–1 = (P–1)T.
11. If we let then we have
The matrix Xis in the kernel of Tif and only if T(X) = 0, i.e., if and only if
a+ b+ c = 0
2b + d= 0
d= 0
Hence
The space of all such matrices Xis spanned by the matrix and therefore has
dimension 1. Thus the nullity is 1. Since the dimension of M22 is 4, the rank of Tmust
therefore be 3.
,
10
10−
Xa
a
=−
0
0
Tab
cd
ac bd b b
dd
=++
+
00
=++ +
abc bd
dd
2
Xab
cd
=
,
Supplementary Exercises 8 245

Alternate Solution.Using the computations done above, we have that the matrix for this
transformation with respect to the standard basis in M22 is
Since this matrix has rank 3, the rank of Tis 3, and therefore the nullity must be 1.
13. The standard basis for M22 is the set of matrices
If we think of the above matrices as the vectors
[1 000]
T,[0100]
T,[0010]
T,[0001]
T
then Ltakes these vectors to
[1 000]
T,[0010]
T,[0100]
T,[0001]
T
Therefore the desired matrix for Lis
15. The transition matrix Pfrom B′to Bis
Therefore, by Theorem 8.5.2, we have
[] []TPTP
BB
′−
==
−
−
1
409
102
011
P=
111
011
001
1000
0010
01 00
0001
10
00
01
00
00
10
00
01
,,,
1110
0201
0001
0001
246 Supplementary Exercises 8

Alternate Solution:We compute the above result more directly. It is easy to show that u1
= v1, u2= –v1+ v2, and u3= –v2+ v3. So
T(v1) = T(u1) = –3u1+ u2= –4v1+ v2
T(v2) = T(u1+ u2) = T(u1) + T(u2)
= u1+ u2+ u3= v3
T(v3) = T(u1+ u2+ u3) = T(u1) + T(u2) + T(u3)
= 8u1– u2+ u3
= 9v1– 2v2+ v3
17. Since
we have
In fact, this result can be read directly from [T(X)]B.
19. (a) Recall that D(f+ g) = (f(x) + g(x))′′ = f ′′(x) + g′′(x) and D(cf) = (cf(x))′′ = cf ′′(x).
(b) Recall that D(f) = 0if and only if f′(x) = afor some constant aif and only if f(x) = ax
+ bfor constants aand b. Since the functions f(x) = xand g(x) = 1 are linearly
independent, they form a basis for the kernel of D.
(c) Since D(f) = f(x) if and only if f ′′(x) = f(x) if and only if f(x) = aex+ be–xfor aand
barbitrary constants, the functions f(x) = exand g(x) = e–xspan the set of all such
functions. This is clearly a subspace of C2(–∞, ∞) (Why?), and to show that it has
dimension 2, we need only check that exand e–xare linearly independent functions.
To this end, suppose that there exist constants c1and c2such that c1ex+ c2e–x= 0. If
we let x= 0 and x= 1, we obtain the equations c1+ c2= 0 and c1e+ c2e–1 = 0. These
imply that c1= c2= 0, so exand e–xare linearly independent.
[]TB=
−
−
11 1
010
10 1
T,
1
0
0
1
0
1
=
T
0
1
0
1
1
0
=
−
,andT
0
0
1
=
−
1
0
1
Supplementary Exercises 8 247

21. (a) We have
and
(b) Since Tis defined for quadratic polynomials only, and the numbers x1, x2, and x3are
distinct, we can have p(x1) = p(x2) = p(x3) = 0 if and only if pis the zero polynomial.
(Why?) Thus ker(T) = {0}, so Tis one-to-one.
(c) We have
T(a1P1(x) + a2P2(x) + a3P3(x)) = a1T(P1(x)) + a2T(P2(x)) + a3T(P3(x))
(d) From the above calculations, we see that the points must lie on the curve.
23. Since
Dx k
kx k n
k
k
() ,, ,
==
=
−
00
12
1
if
if
=
+
+
aaa
123
1
0
0
0
1
0
0
0
1
=
a
a
a
1
2
3
Tkpx
kp x
kp x
kp x
k(())
()
()
()
=
=
1
2
3
()
()
()
(())
px
px
px
kT p x
1
2
3
=
Tpx qx
px qx
px qx(() ())
() ()
() ()+=
+
+
11
22
ppx qx
px
px
px() ()
()
()
()
33
1
2
3
+
=
+
=
()
()
()
(
qx
qx
qx
T
1
2
3
ppx Tqx()) (())+
248 Supplementary Exercises 8

then
where the above vectors all have n+ 1 components. Thus the matrix of Dwith respect to
Bis
25. Let Bnand Bn+1 denote the bases for Pnand Pn+1, respectively. Since
J(xk) = xk+1
——
k+ 1 for k= 0, … , n
we have
[( )] , , ,, (Jx B kn
k
n+=+
+
101
102
)components
(
↑
+k22)nd component
0100
0
0020 0
0003 0
0000
0000 0
n
[( )] (, , )
(, , , ,) ,,
Dx k
kk
k
B==
=
00 0
0012
if
if ,n
↑↑
kth component
Supplementary Exercises 8 249

where [xk]Bn= [0, … , 1,…, 0]
Twith the entry 1 as the (k+ 1)st component out of a total
of n+ 1 components. Thus the matrix of Jwith respect to Bn+1 is
with n+ 2 rows and n+ 1 columns.
00 0 0
10 0 0
012 0 0
0013 0
00 0 1 1()
n+
250 Supplementary Exercises 8

EXERCISE SET 9.1
1. (a) The system is of the form y′= Aywhere
The eigenvalues of Aare λ= 5 and λ= –1 and the corresponding eigenspaces are
spanned by the vectors
respectively. Thus if we let
we have
Let y= Puand hence y′= Pu′. Then
or
u′1= 5u1
u′2= –u2
′−
uuuu= 50
01
DPAP==
−
−150
01
P=−
12
11
1
1
2
1
−
and
A=
14
23
251

Therefore
u1= c1e5x
u2= c2e–x
Thus the equation y= Puis
or
y1=c1e5x– 2c2e–x
y2=c1e5x+ c2e–x
1. (b) If y1(0) = y2(0) = 0 , then
c1– 2c2= 0
c1+ c2= 0
so that c1= c2= 0. Thus y1= 0 and y2= 0.
3. (a) The system is of the form y′= Aywhere
The eigenvalues of Aare λ= 1, λ= 2, and λ= 3 and the corresponding eigenspaces are
spanned by the vectors
respectively. Thus, if we let
P
/
=
−−
0121
111
011
0
1
0
12
1
1
1
1
1
−
−
/
A=−
−
401
210
201
y
y
ce
ce
c
x
x
1
1
1
5
2
12
11
=−
=
−
11
5
2
1
5
2
2ece
ce ce
xx
xx
−
+
−
−
252 Exercise Set 9.1

then
Let y= Puand hence y′= Pu′. Then
so that
u′1= u1
u′2= 2u2
u′3= 3u3
Therefore
u1= c1ex
u2= c2e2x
u3= c3e3x
Thus the equation y= Puis
or
y1= – 1
2c2e2x– c3e3x
y2= c1ex+ c2e2x+ c3e3x
y3= c2e2x+ c3e3x
y
y
y
1
2
3
=
−−
/0121
111
011
ce
ce
ce
x
x
x
1
2
2
3
3
′
uuuu=
100
020
003
DPAP=
−1
100
020
003
Exercise Set 9.1 253

Note: If we use
as basis vectors for the eigenspaces, then
and
y1= –c2e2x+ c3e3x
y2= c1ex+ 2c2e2x– c3e3x
y3= 2c2e2x– c3e3x
There are, of course, infinitely many other ways of writing the answer, depending upon
what bases you choose for the eigenspaces. Since the numbers c1, c2, and c3are
arbitrary, the “different” answers do, in fact, represent the same functions.
3. (b) If we set x= 0, then the initial conditions imply that
– 1
2c2– c3=–1
c1+ c2+ c3=1
c2+ c3=0
or, equivalently, that c1= 1, c2= –2, and c3= 2. If we had used the “different” solution
we found in Part (a), then we would have found that c1= 1, c2= –1, and c3= –2. In
either case, when we substitute these values into the appropriate equations, we find
that
y1= e2x– 2e3x
y
2= ex– 2e2x+ 2e3x
y3= –2e2x+ 2e3x
P=
−
−
−
011
121
021
0
1
0
1
2
2
1
1
1
−
−
−
254 Exercise Set 9.1

5. Following the hint, let y= f(x) be a solution to y′= ay, so that f ′(x) = af(x). Now consider
the function g(x) = f(x)e–ax. Observe that
g′(x) = f ′(x)e–ax – af(x)e–ax
= af(x)e–ax – af(x)e–ax
= 0
Thus g(x) must be a constant; say g(x) = c. Therefore,
f(x)e–ax = c
or
f(x) = ceax
That is, every solution of y′= ay has the form y= ceax.
.. . .
7. If y1= yand y2= y′, then y1
′= y2and y2
′= y′′ = y′+ 6y= y2+ 6y1. That is,
y1
′=y2
y2
′= 6y1+ y2
or y′= Aywhere
The eigenvalues of Aare λ= –2 and λ= 3 and the corresponding eigenspaces are spanned
by the vectors
respectively. Thus, if we let
P=−
11
23
−
1
2and 1
3
A=
01
61
Exercise Set 9.1 255

then
Let y= Puand hence y′= Pu′. Then
or
y1= –c1e–2x+ c2e3x
y2= 2c1e–2x+ 3c2e3x
Therefore
u1= c1e–2x
u2= c2e3x
Thus the equation y= Puis
or
y1= –c1e–2x+ c2e3x
y2= 2c1e–2x+ 3c2e3x
Note that y1
′= y2, as required, and, since y1= y, then
y= –c1e–2x+ c2e3x
Since c1and c2are arbitrary, any answer of the form y= ae–2x+ be3xis correct.
y
y
ce
ce
x
x
1
2
1
2
2
3
11
23
=−
−
′=−
uuuu
20
03
PAP
−=−
120
03
256 Exercise Set 9.1

9. If we let y1= y, y2= y′, and y3= y′′, then we obtain the system
y1
′= y2
y2
′= y3
y3
′= 6y1–11y2+ 6y3
The associated matrix is therefore
The eigenvalues of Aare λ= 1, λ= 2, and λ= 3 and the corresponding eigenvectors are
The solution is, after some computation,
y= c1ex+ c2e2x+ c3e3x
11. Consider y′= Ay, where , with aij real. Solving the system
yields the quadratic equation
λ2– (a11 + a22) λ+ a11a22 – a21 a12 = 0, or
λ2– (TrA)λ+ det A= 0.
Let λ1, λ2be the solutions of the characteristic equation. Using the quadratic formula yields
λλ
12
24
2
,
det
=±−Tr A Tr A A
det( )
λλ
λ
I– Aaa
aa
=−−
−−
=
11 12
21 21
0
Aaa
aa
=
11 12
21 22
1
1
1
1
2
4
1
3
9
,and
A=
−
010
001
6116
Exercise Set 9.1 257

Now the solutions y1(t) and y2(t) to the system y′= Ay will approach zero as t→∞if
and only if Re(λ1, λ2) < 0. (Both are < 0)
Case I: Tr2A– 4 det A< 0.
In this case Re(λ1) = Re(λ2) = TrA
2. Thus y1(t), y2(t) →0 if and only if TrA < 0.
Case II: Tr2A– 4 det A= 0. Then λ1= λ2, and Re(λ1, λ2) = TrA
2, so y1, y2→0 if and only
if TrA < 0.
Case III: Tr2A– 4 det A> 0. Then λ1, λ2are both real.
Subcase 1: det A> 0.
If TrA > 0, then both (λ1, λ2) > 0, so y1, y20.
If TrA < 0, then both (λ1, λ2) < 0, so y1, y2→0. TrA = 0 is not possible in this case.
Subcase 2: det A< 0
If TrA > 0, then one root (say λ1) is positive, the other is negative, so y1, y20.
If TrA = 0, then again λ1> 0, λ2< 0, so y1, y20.
Subcase 3: det A= 0. Then λ1= 0 or λ2= 0, so y1, y20.
→
→
→
Then TTA
2
rA A r−> ≥40det
→
Then T A > T 2
rrAA−>40det
258 Exercise Set 9.1

13. The system
can be put into the form
The eigenvalues and eigenvectors of Aare:
Solving:
y
yce ce
tt
1
2
12
3
1
1
1
1
=−
+
+−
+
−
t0
1
1
3
2
3
/
/
λλ
12
11
131
1
,,==
−
==
xx
12
′
′
=
+
y
y
y
yt
1
2
1
2
21
12
1
22
+=Ay f
′=++
′=+ +
yyyt
yy y t
112
21 2
2
22
Exercise Set 9.1 259


EXERCISE SET 9.2
1. (a) Since T(x, y) = (–y, –x), the standard matrix is
(b)
(c) Since T(x, y) = (x, 0), the standard matrix is
(d)
3. (b) Since T(x, y, z) = (x, –y, z), the standard matrix is
010
100
001
−
A=
00
01
10
00
A=−
−
10
01
A=−
−
10
01
261

5. (a) This transformation leaves the z-coordinate of every point fixed. However it sends (1,
0, 0) to (0, 1, 0) and (0, 1, 0) to (–1, 0, 0). The standard matrix is therefore
(c) This transformation leaves the y-coordinate of every point fixed. However it sends (1,
0, 0) to (0, 0, –1) and (0, 0, 1) to (1, 0, 0). The standard matrix is therefore
13. (a)
(c)
15. (b) The matrices which represent compressions along the x- and y- axes are
and , respectively, where 0 < k< 1. But
and
Since 0 < k< 1 implies that 1/k> 1, the result follows.
(c) The matrices which represent reflections about the x- and y- axes are and
, respectively. Since these matrices are their own inverses, the
result follows.
−
10
01
10
01−
10
0
10
01
1
kk
=
−
/
kk0
01
10
01
1
=
−/
10
0k
k0
01
−
−
=−
−
10
01
01
10
01
10
10
05
12 0
01
12 0
05
=
//
001
010
100−
010
100
001
−
262 Exercise Set 9.2

17. (a) The matrix which represents this shear is ; its inverse is . Thus,
points(x′, y′) on the image line must satisfy the
equations
x= x′– 3y′
y=y′
where y= 2x. Hence y′= 2x′– 6y′, or 2x′– 7y′= 0. That is, the equation of the image
line is 2x– 7y= 0.
Alternatively, we could note that the transformation leaves (0, 0) fixed and sends
(1, 2) to (7, 2). Thus (0, 0) and (7, 2) determine the image line which has the
equation 2x– 7y= 0.
(c) The reflection and its inverse are both represented by the matrix . Thus the
point (x′, y′) on the image line must satisfy the equations
x= y′
y= x′
where y= 2x. Hence x′= 2y′, so the image line has the equation x– 2y= 0.
(e) The rotation can be represented by the matrix . This sends the
origin to itself and the point (1, 2) to the point ((1 – 2 3 )/2, (2 + 3)/2). Since both
(0, 0) and (1, 2) lie on the line y= 2x, their images determine the image of the line
under the required rotation. Thus, the image line is represented by the equation (2 +
3)x+ (2 3 – 1)y= 0.
Alternatively, we could find the inverse of the matrix, , and
proceed as we did in Parts (a) and (c).
12 32
32 12
//
//−
12 32
32 12
//
//
−
01
10
13
01
−
13
01
Exercise Set 9.2 263

21. We use the notation and the calculations of Exercise 20. If the line Ax + By + C= 0 passes
through the origin, then C= 0, and the equation of the image line reduces to (dA – cB)x+
(–bA + aB)y= 0. Thus it also must pass through the origin.
The two lines A1x+ B1y+ C1= 0 and A2x+ B2y+ C2= 0 are parallel if and only
if A1B2= A2B1. Their image lines are parallel if and only if
(dA1– cB1)(–bA2+ aB2) = (dA2– cB2)(–bA1+ aB1)
or
bcA2B1+ adA1B2= bcA1B2+ adA2B1
or
(ad – bc)(A1B2– A2B1) = 0
or
A1B2– A2B1= 0
Thus the image lines are parallel if and only if the given lines are parallel.
23. (a) The matrix which transforms (x, y, z) to (x+ kz, y+ kz, z) is
10
01
001
k
k
264 Exercise Set 9.2

EXERCISE SET 9.3
1. We have
Thus the desired line is y= –1/2 + (7/2)x.
3. Here
M=
124
139
1525
1636
a
b
T
=
10
11
12
10
11
12
=
−1
10
11
12
0
2
7
T
33
35
9
16
5
6
1
2
1
2
1
2
1
=−
−
−
=−
/
9
16
12
72
265

and
Thus the desired quadratic is y= 2 + 5x– 3x2.
5. The two column vectors of Mare linearly independent if and only if neither is a nonzero
multiple of the other. Since all of the entries in the first column are equal, the columns are
linearly independent if and only if the second column has at least two different entries, or
if and only if at least two of the numbers xiare distinct.
a
b
c
MM MT
T
=−
−
−
−
()
1
0
10
48
76
=
416 74
16 74 376
74 376 2018
−
−
−
=
−
−1134
726
4026
221
10
62
55
3
2
62
5
649
90
8
9
3
2
8
9
1
9
−−
−
−
−
−
=
−
134
726
4026
2
5
3
266 Exercise Set 9.3

EXERCISE SET 9.4
1. (a) Since f(x) = 1 + x, we have
Using Example 1 and some simple integration, we obtain
k= 1, 2, . . .
Thus, the least squares approximation to 1 + xon [0, 2π] by a trigonometric polynomial
of order ≤2 is
1 + x(1 + π) – 2 sin x– sin 2x
3. (a) The space Wof continuous functions of the form a+ bexover [0, 1] is spanned by the
functions u1= 1 and u2= ex. First we use the Gram-Schmidt process to find an
orthonormal basis {v1, v2} for W.
Since 〈f, g〉=f(x)g(x)dx, then u1= 1 and hence
v1= 1
Thus
v2=
ee
ee
ee
xx
xx
x
−
−=−+(,)
(,)
11
11
1
α
0
1
∫
bxkxdx
k
k()sin()=+ =−
∫
112
0
2
π
π
axkxdx
k()cos()=+ =
∫
110
0
2
π
π
axdx
00
2
1122()=+=+
∫
ππ
π
267

where αis the constant
Therefore the orthogonal projection of xon Wis
(b) The mean square error is
The answer above is deceptively short since a great many calculations are involved.
To shortcut some of the work, we derive a different expression for the mean square
error (m.s.e.). By definition,
m.s.e. = ∫a
b
[f(x) – g(x)]2dx
= f– g2
= 〈f– g, f– g〉
= 〈f, f– g〉– 〈g, f– g〉
xeedx e
e
x
−− + −
=++
−
(()
1
2
1
1
13
12
1
21
2
==+ −
−
∫1
2
3
21
0
1e
e()
projW
xx
xx x
ee ee
xd
,,=+−+ −+
=
11 11
αα
xx ee xee dx
ee
xx
x
+−+ −+
=+ −+
∫∫
11
1
2
1
0
1
0
1
αα
α
()
(
3
2
1
2
1
1
−
=+ −
−+
e
eee
x
α
11
1
2
1
1
)
=− + −
eex
α
()
(
/
=−+ =−+
=
∫
ee ee dx
xx
112
0
112
331
2
12
−−
ee)( ) /
268 Exercise Set 9.4

Recall that g= projWf, so that gand f– gare orthogonal. Therefore,
m.s.e. = 〈f, f– g〉
= 〈f, f〉– 〈fg〉
But g= 〈f, v1〉v1+ 〈f, v2〉v2, so that
(*)m.s.e. = 〈f, f〉– 〈f, v1〉2– 〈f, v2〉2
Now back to the problem at hand. We know 〈f, v1〉and 〈f, v2〉from Part (a). Thus,
in this case,
Clearly the formula (*) above can be generalized. If Wis an n-dimensional space with
orthonormal basis {v1, v2,…, vn}, then
(**)m.s.e. = f2– 〈f, v1〉2– …– 〈f, vn〉2
5. (a) The space Wof polynomials of the form a0+ a1x+ a2x2over [–1, 1] has the basis {1,
x, x2}. Using the inner product 〈u, v〉=u(x)v(x)dx and the Gram-Schmidt
process, we obtain the orthonormal basis
(See Exercise 29, Section 6.3.) Thus
sin , sin( )
sin , s
ππ
π
xxdx
xx
vv
vv
11
1
2
1
20
3
2
==
=
−
∫
iin( )
sin , ( )sin
ππ
π
xdx
xx
−
∫=
=−
1
1
3
2
23
2
1
2
5
231vv(()
π
xdx
−
∫=
1
10
1
2
3
2
1
2
5
231
2
,, ( )xx−
−
∫1
1
m.s.e. =−
−−
∫xdx e
2
2
0
12
1
2
3
2
α
==−−
−≈
()
.
1
12
3
21 0014
e
e
Exercise Set 9.4 269
Therefore,
(b) From Part (a) and (**) in the solution to 3(b), we have
9.
(note a slight correction to definition of f(x) as stated on pg. 479.)
Then
So the Fourier Series is
1
2
111
1
+−−
=
∞
∑()sin
kkx
k
k
π
afxdxdx
afxkxdx
k
000
2
11
1
1
===
==
∫∫
ππ
π
ππ
()
()cos 11 0
1
00
2
π
π
ππ
cos
()sin
kx dx
k
bfxkx
k
=
=
=
∫∫
1, 2,
ddx kx dx
k
k
=
=−−
∫∫ 1
111
00
2
π
π
ππ
sin
().
Let ( ) ,
,
fx x
x
=≤<
≤≤
10
02
π
ππ
m.s.e. =−=−≈
−
∫sin ( ) .
2
22
1
161639
πππ
xdx
sin
ππ
xx3
270 Exercise Set 9.4

EXERCISE SET 9.5
1. (d) Since one of the terms in this expression is the product of 3 rather than 2 variables,
the expression is not a quadratic form.
5. (b) The quadratic form can be written as
The characteristic equation of Ais (λ– 7)(λ– 4) – 1/4 = 0 or
4λ2– 44λ+ 111 = 0
which gives us
If we solve for the eigenvectors, we find that for
x1= (3 + 10)x2
and
x1= (3 - 10)x2
Therefore the normalized eigenvectors are
310
20 6 10
1
20 6 10
310
20 6 1
+
+
+
−
−
and 00
1
20 6 10−
λ
=−11 10
2
λ
=+11 10
2
λ
=±11 10
2
[]xx x
xxAx
T
12
1
2
712
12 4
=
271
or, if we simplify,
Thus the maximum value of the given form with its constraint is
The minimum value is
7. (b) The eigenvalues of this matrix are the roots of the equation λ2– 10λ+ 24 = 0. They
are λ= 6 and λ= 4 which are both positive. Therefore the matrix is positive definite.
9. (b) The characteristic equation of this matrix is λ3– 3λ+ 2 = (λ+ 1)2(λ– 2). Since two
of the eigenvalues are negative, the matrix is not positive definite.
11. (a) Since x1
2+ x2
2> 0 unless x1= x2= 0, the form is positive definite.
(c) Since (x1– x2)2≥0, the form is positive semidefinite. It is not positive definite because
it can equal zero whenever x1= x2even when x1= x2≠0.
(e) If |x1|> |x2|, then the form has a positive value, but if |x1|< |x2|, then the form has a
negative value. Thus it is indefinite.
11 10
2
1
20 6 10
1
20 6 10
12
−=−
+=−
at andxx
11 10
2
1
20 6 10
1
20 6 10
12
+=−=+
at andxx
1
20 6 10
1
20 6 10
1
20 6 10
1
20
−
+
−
+
−
and
6610
272 Exercise Set 9.5

13. (a) By definition,
T(x+ y) = (x+ y)TA(x+ y)
= (xT+ yT)A(x+ y)
= xTAx+ xTAy+ yTAx+ yTAy
= T(x) + xTAy+ (xTATTy)T+ T(y)
= T(x) + xT
Α
y+ xTATy+ T(y)
(The transpose of a 1 ×1 matrix is itself.)
= T(x) + 2xTAy+ T(y)
(Assuming that Ais symmetric, AT= A.)
(b) We have
T(kx) = (kx)TA(kx)
= k2xTAx(Every term has a factor of k2.)
= k2T(x)
(c) The transformation is not linear because T(kx) ≠kT(x) unless k= 0 or 1 by Part (b).
15. If we expand the quadratic form, it becomes
c1
2x1
2+ c2
2x2
2+ …+ cn
2xn
2+ 2c1c2x1x2+ 2c1c3x1x3+
…+ 2c1cnx1xn+ 2c2c3x2x3+ …+ 2cn–1cnxn–1xn
Thus we have
and the quadratic form is given by xTAxwhere x= [x1x2…xn]T.
A
ccccc cc
cc c cc cc
cc
n
n
=
⋅⋅⋅
⋅⋅⋅
1
2
12 13 1
12 2
2
13 2
13323 3
2
3
123
cc c cc
cc cc cc
n
nnn
⋅⋅⋅
⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅
⋅⋅⋅⋅
cn
2
Exercise Set 9.5 273

17. To show that λn≤xTAxif x= 1, we use the equation from the proof dealing with λ1and
the fact that λnis the smallest eigenvalue. This gives
xTAx= 〈x, Ax〉= λ1〈x, v1〉2+ λ2〈x, v2〉2+ …+ λn〈x, vn〉2
≥λ
n〈x, v1〉2+ λn〈x, v2〉2+ …+ λn〈x, vn〉2
= λn(〈x, v1〉2+ …+ 〈x, vn〉2)
= λn
Now suppose that xis an eigenvector of Acorresponding to λn. As in the proof dealing
with λ1, we have
xTAx= 〈x, Ax〉= 〈x, λnx〉= λn〈x, x〉= λnx2= λn
274 Exercise Set 9.5

EXERCISE SET 9.6
1. (a) The quadratic form xTAxcan be written as
The characteristic equation of Ais λ2– 4λ+ 3 = 0. The eigenvalues are λ= 3 and λ=
1. The corresponding eigenspaces are spanned by the vectors
respectively. These vectors are orthogonal. If we normalize them, we can use the result
to obtain a matrix Psuch that the substitution x= Pyor
will eliminate the cross-product term. This yields the new quadratic form
or 3y1
2+ y2
2.
7. (a) If we complete the squares, then the equation 9x2+ 4y2– 36x– 24y+ 36 = 0 becomes
9(x2– 4x+ 4) + 4(y2– 6y+ 9) = –36 + 9(4) + 4(9)
yy y
y
12
1
2
30
01
x
x
y
y
1
2
1
2
1212
1212
=−
1
1
1
1−
and
xx x
x
12
1
2
21
12
−
−
275
or
9(x– 2)2+ 4(y– 3)2= 36
or
This is an ellipse.
(c) If we complete the square, then y2– 8x– 14y+ 49 = 0 becomes
y2– 14y+ 49 = 8x
or
(y– 7)2= 8x
This is the parabola (y′)2= 8x′.
(e) If we complete the squares, then 2x2– 3y2+ 6x+ 2y= –41 becomes
or
or
12(x′)2– 18(y′)2= –419
This is a hyperbola.
9. The matrix form for the conic 9x2– 4xy + 6y2– 10x– 20y= 5 is
xTAx+ Kx= 5
23
2310
3
419
6
22
xy+
−−
=−
23
9
4320
3
100
941 9
22
xx y y++
−−+
=− +22
100
3
−
′
()
+′
()
=
xy
22
49
1
276 Exercise Set 9.6

where
and K= [ – 10 – 20]
The eigenvalues of Aare λ1= 5 and λ2= 1 and the eigenspaces are spanned by the vectors
Thus we can let
Note that det(P) = 1. If we let x= Px′, then
(x′)T(PTAP)x′+ KPx′= 5
where
Thus we have the equation
5(x′)2+ 10(y′)2– 10 5x′= 5
If we complete the square, we obtain the equation
5((x′)2– 2 5x′+ 5)+ 10 (y′)2= 5 + 25
or
(x′′)2+ 2(y′′)2= 6
PAP KP
T=
=−
50
010 10 5 0and
P=
−
1
5
2
5
2
5
1
5
1
2
2
1
−
and
A=−
−
92
26
Exercise Set 9.6 277

where x′′ = x′– 5 and y′′ = y′. This is the ellipse
Of course we could also rotate to obtain the same ellipse in the form 2(x′′)2+ (y′′)2= 6,
which is just the other standard position.
11. The matrix form for the conic 2x2– 4xy – y2– 4x– 8y= –14 is
xTAx+ Kx= –14
where
The eigenvalues of Aare λ1= 3, λ2= –2 and the eigenspaces are spanned by the vectors
Thus we can let
Note that det(P) = 1. If we let x= Px′, then
(x′)T(PTAP)x′+ KPx′= –14
where
PAP KP
T=−
=−
30
02 045
and
P=−
2
5
1
5
1
5
2
5
−
2
1
1
2
and
AK=−
−−
=−−
[]
22
21 48
and
′′
()
+′′
()
=
xy
22
63
1
278 Exercise Set 9.6

Thus we have the equation
3(x′)2– 2(y′)2– 4 5y′= –14
If we complete the square, then we obtain
3(x′)2– 2((y′)2+ 2 5y′+ 5)= –14 – 10
or
3(x′′)2– 2(y′′)2= –24
where x′′ = x′and y′′ = y′+ 5. This is the hyperbola
We could also rotate to obtain the same hyperbola in the form 2(x′′)2– 3(y′′)2= 24.
15. (a) The equation x2– y2= 0 can be written as (x– y)(x+ y) = 0. Thus it represents the
two intersecting lines x±y= 0.
(b) The equation x2+ 3y2+ 7 = 0 can be written as x2+ 3y2= –7. Since the left side of
this equation cannot be negative, then there are no points (x, y) which satisfy the
equation.
(c) If 8x2+ 7y2= 0, then x= y= 0. Thus the graph consists ofthe single point (0, 0).
(d) This equation can be rewritten as (x– y)2= 0. Thus it represents the single line y=
x.
(e) The equation 9x2+ 12xy + 4y2– 52 = 0 can be written as (3x+ 2y)2= 52 or 3x+ 2y
= ± 52. Thus its graph is the two parallel lines 3x+ 2y±2 13 = 0.
(f) The equation x2+ y2– 2x– 4y= –5 can be written as x2– 2x+ 1 + y2– 4y+ 4 = 0 or
(x– 1)2+ (y– 2)2= 0. Thus it represents the point (1, 2).
′′
(
)
−′′
(
)
=
yx
22
12 8 1
Exercise Set 9.6 279


EXERCISE SET 9.7
5. (a) ellipse 36x2+ 9y2= 32
(b) ellipse 2x2+ 6y2= 21
(c) hyperbola 6x2– 3y2= 8
(d) ellipse 9x2+ 4y2= 1
(e) ellipse 16x2+ y2= 16
(f) hyperbola 3y2– 7x2= 1
(g) circle x2+ y2= 24
7. (a) If we complete the squares, the quadratic becomes
9(x2– 2x+ 1) + 36(y2– 4y+ 4) + 4(z2– 6z+ 9)
= –153 + 9 + 144 + 36
or
9(x– 1) 2+ 36(y– 2) 2+ 4(z– 3) 2= 36
or
This is an ellipsoid.
(c) If we complete the square, the quadratic becomes
3(x2+ 14z+ 49) – 3y2– z2= 144 + 147
() () ()
′+′−′=
xyz
22
419
1
281

or
3(x+ 7) 2– 3y2– z2= 3
or
This is a hyperboloid of two sheets.
7. (e) If we complete the squares, the quadric becomes
(x2+ 2x+ 1) + 16(y2– 2y+ 1) – 16z= 15 + 1 + 16
or
(x+ 1)2+ 16(y– 1)2– 16(z+ 2) = 0
or
This is an elliptic paraboloid.
(g) If we complete the squares, the quadric becomes
(x2– 2x+ 1) + (y2+ 4y+ 4) + (z2– 6z+ 9) = 11 + 1 + 4 + 9
or
(x– 1)2+ (y+ 2)2+ (z– 3)2= 25
or
This is a sphere.
() () ()
′+′−′=
xyz
222
113
1
() () ()
′+′−′=
xyz
22
419
1
() () ()
′+′−′=
xyz
222
113
1
282 Exercise Set 9.7

9. The matrix form for the quadric is xTAx+ Kx= –9 where
The eigenvalues of Aare λ1= λ2= –1 and λ3= 2, and the vectors
span the corresponding eigenspaces. Note that u1•u3= u2•u3= 0 but that u1•u2≠0.
Hence, we must apply the Gram-Schmidt process to {u1, u2}. We must also normalize u3.
This gives the orthonormal set
Thus we can let
Note that det(P) = 1,
PAP KP
T=
=− −−
-1 0 0
0-10
002
and 2 2
6
16
3
P=
−
−−
–1
2
1
6
1
3
02
6
1
3
1
2
1
6
1
3
−
−
−
1
2
0
1
2
1
6
5
6
1
6
−
1
3
1
3
1
3
uuuuuu
12 3
1
1
0
1
1
1
=
=
−
=
-1
0
1
and
AK=
=−−−
011
101
110
664and
Exercise Set 9.7 283

Therefore the transformation x= Px′reduces the quadric to
If we complete the squares, this becomes
11. The matrix form for the quadric is xTAx+ Kx– 31 = where
The eigenvalues of Aare λ1= 1, λ2= –1, and λ3= 0, and the corresponding eigenspaces are
spanned by the orthogonal vectors
1
1
0
1
1
0
0
0
1
−
AK=
=−
010
100
000
6101and
Letting and yie
′′ =′+′′ =′+′′ =′−xx yy zz
1
2
1
16
4
3
,, llds
This is the hyperb
()() ()
′′ +′′ −′′ =−xy z
22 2
21
ooloid of two sheets
() () ()
′′ −′′ −′′ =
zxy
222
12 1 1 1
() ()
(
′+′+
+′+′+
−′
xx y y
z
22
21
2
2
6
1
6
2))28
3
16
391
2
1
6
32
3
−′+
=++−z
−′−′+′−′−′′
=−() () () –xy z x y z
22 2
22
2
6
16
39
284 Exercise Set 9.7

Thus, we let x= Px′where
Note that det(P) = 1,
Therefore, the equation of the quadric is reduced to
(x′)2– (y′)2+ 2 2x′+ 8 2y′+ z′– 31 = 0
If we complete the squares, this becomes
[(x′)2+ 2 2x′+ 2]– [(y′)2– 8 2y′+ 32]+ z′= 31 + 2 – 32
Letting x′′ = x′+ 2, y′′ = y′– 4 2, and z′′ = z′– 1 yields
(x
′′
)2– (y′′)2+ z′′ = 0
This is a hyperbolic paraboloid.
13. We know that the equation of a general quadric Qcan be put into the standard matrix form
xTAx+ Kx+ j= 0 where
Since Ais a symmetric matrix, then Ais orthogonally diagonalizable by Theorem 7.3.1.
Thus, by Theorem 7.2.1, Ahas 3 linearly independent eigenvectors. Now let Tbe the matrix
whose column vectors are the 3 linearly independent eigenvectors of A. It follows from the
proof of Theorem 7.2.1 and the discussion immediately following that theorem, that T–1 AT
will be a diagonal matrix whose diagonal entries are the eigenvalues λ1, λ2, and λ3of A.
Theorem 7.3.2 guarantees that these eigenvalues are real.
A
ad e
db f
efc
Kghi=
=
and
PAP KP
T=−
=
100
010
000
22 82 1and
P=
−
1
2
1
20
1
2
1
20
001
Exercise Set 9.7 285

As noted immediately after Theorem 7.3.2, we can, if necessary, transform the matrix T
to a matrix Swhose column vectors form an orthonormal set. To do this, orthonormalize the
basis of each eigenspace before using its elements as column vectors of S.
Furthermore, by Theorem 6.5.1, we know that Sis orthogonal. It follows from Theorem
6.5.2 that det(S) = ±1.
In case det(S) = –1, we interchange two columns in Sto obtain a matrix Psuch that
det(P) = 1. If det(S) = 1, we let P= S. Thus, Prepresents a rotation. Note that Pis
orthogonal, so that P–1 = PT, and also, that Porthogonally diagonalizes A. In fact,
Hence, if we let x= Px′, then the equation of the quadric Qbecomes
(x′)T(PTAP)x′+ KPx′+ j= 0
or
λ1(x′)2+ λ2(y′)2+ λ3(z′)2+ g′x′+ h′y′+ i′z′+ j= 0
where
[g′h′i′] = KP
Thus we have proved Theorem 9.7.1.
PAP
T=
λ
λ
λ
1
2
3
00
00
00
286 Exercise Set 9.7

EXERCISE SET 9.8
1. If AB = Cwhere Ais m×n, Bis n×p, and Cis m×p, then Chas mp entries, each of the
form
cij = ai1b1j+ ai2b2j+ …+ ainbnj
Thus we need nmultiplications and n– 1 additions to compute each of the numbers cij.
Therefore we need mnp multiplications and m(n– 1)padditions to compute C.
5. Following the hint, we have
Sn= 1 + 2 + 3 + …+ n
Sn= n+ (n– 1) + (n– 2) + …+ 1
or
2Sn= (n+ 1) + (n+ 1) + (n+ 1) + …+ (n+ 1)
Thus
7. (a) By direct computation,
(k+ 1)3– k3= k3+ 3k2+ 3k+ 1 – k3= 3k2+ 3k+ 1
(b) The sum “telescopes”. That is,
[23– 13] + [33– 23] + [43– 33] + …+ [(n+ 1)3– n3]
= 23– 13+ 33– 23+ 43– 33+ …+ (n+ 1)3– n3
= (n+ 1)3– 1
Snn
n=+()1
2
287

(c) By Parts (a) and (b), we have
3(1)2+ 3(1) + 1 + 3(2)2+ 3(2) + 1 + 3(3)2+ 3(3) + 1 + …+ 3n2+ 3n+ 1
= 3(12+ 22+ 32+ …+ n2) + 3(1 + 2 + 3 + …+ n) + n
= (n+ 1)3– 1
(d) Thus, by Part (c) and exercise 6, we have
9. Since Ris a row-echelon form of an invertible n×nmatrix, it has ones down the main
diagonal and nothing but zeros below. If, as usual, we let x= [x1x2…xn]Tand b= [b1b2
…bn]T, then we have xn= bnwith no computations. However, since xn–1 = bn–1 – cxnfor
some number c, it will require one multiplication and one addition to find xn–1. In general,
xi= bi– some linear combination of xi+1, xi+2, …, xn
Therefore it will require two multiplications and two additions to find xn–2, three of each to
find xn–3, and finally, n–1 of each to find x1. That is, it will require
multiplications and the same number of additions to solve the system by back substitution.
123 1 1
1
+++⋅⋅⋅+ − = −
()
()
nnn
123 1
3113 1
2
222 2 3
+++⋅⋅⋅+ = + −− +−
nn nn n() ()
== +−− +−
=+−− +−
() ()
() ()
nnnn
nnn
1
3
1
3
1
23
2123 12
3
3nn
nn n
nnnn
6
12 1 3 2
6
12 4 23
2
2
=++−−
=+++−−
()[() ]
()( 22
6
12
6
12 1
6
2
)
()( )
()( )
=++
=++
nnn
nn n
288 Exercise Set 9.8

11. To solve a linear system whose coefficient matrix is an invertible n×nmatrix, A, we form
the n×(n+ 1) matrix [A|b] and reduce Ato In. Thus we first divide Row 1 by a11, using n
multiplications (ignoring the multiplication whose result must be one and assuming that
a11 ≠0 since no row interchanges are required). We then subtract ai1times Row 1 from
Row ifor i= 2,…, nto reduce the first column to that of In. This requires n(n– 1)
multiplications and the same number of additions (again ignoring the operations whose
results we already know). The total number of multiplications so far is n2and the total
number of additions is n(n– 1).
To reduce the second column to that of In, we repeat the procedure, starting with Row
2 and ignoring Column 1. Thus n– 1 multiplications assure us that there is a one on the
main diagonal, and (n– 1)2multiplications and additions will make all n– 1 of the
remaining column entries zero. This requires n(n– 1) new multiplications and (n– 1)2
new additions.
In general, to reduce Column ito the ith column of In, we require n+ 1 – i
multiplications followed by (n+ 1 – i)(n– 1) multiplications and additions, for a total of
n(n+ 1 – i) multiplications and (n+ 1 – i)(n– 1) additions.
If we add up all these numbers, we find that we need
multiplications and
additions to compute the reduction.
nn n n n n n()()()() ()()
(
−+ − + − −+⋅⋅⋅+ − + −
=
11 21211
2
nnnn
nnn
nn
−+−+⋅⋅⋅+ +
=−+
=−
1121
11
2
2
3
)( ( ) )
()()()
22
nnn nn n n nnn
212 21 1+−+−+⋅⋅⋅++=+−+⋅⋅()() ()()(()⋅⋅ + +
=+
=+
21
1
2
22
2
32
)
()nn
nn
Exercise Set 9.8 289


EXERCISE SET 9.9
1. The system in matrix form is
This reduces to two matrix equations
and
The second matrix equation yields the system
3y1= 0
–2y1+ y2= 1
which has y1= 0, y2= 1 as its solution. If we substitute these values into the first matrix
equation, we obtain the system
x1– 2x2= 0
x2= 1
This yields the final solution x1= 2, x2= 1.
30
21
0
1
1
2
−
=
y
y
12
01
1
2
1
2
−
=
x
x
y
y
36
25
30
21
12
01
1
2
−
−−
=−
−
x
x
=
x
x
1
2
0
1
291

3. To reduce the matrix of coefficients to a suitable upper triangular matrix, we carry out the
following operations:
These operations involve multipliers 1/2, 1, and 1/3. Thus the corresponding lower
triangular matrix is
We therefore have the two matrix equations
and
The second matrix equation yields the system
2y1= –2
–y1+ 3y2= –2
which has y1= –1, y2= –1 as its solution. If we substitute these values into the first matrix
equation, we obtain the system
x1+ 4x2=–1
x2=–1
This yields the final solution x1= 3, x2= –1.
20
13
2
2
1
2
−
=−
−
y
y
14
01
1
2
1
2
=
x
x
y
y
L=−
20
13
28
11
14
11
14
03
14
01−−
→−−
→
→
=U
292 Exercise Set 9.9

5. To reduce the matrix of coefficients to a suitable upper triangular matrix, we carry out the
following operations:
These operations involve multipliers of 1/2, 0 (for the 2 row), 1, –1/2, –4, and 1/5. Thus the
corresponding lower triangular matrix is
We therefore have the matrix equations
and
The second matrix equation yields the system
2y1= –4
–2y2= –2
–y1+ 4y2+ 5y3= 6
200
020
145
4
2
6
1
2
3
−
−
=
−
−
y
y
y
111
011
001
1
2
3
1
2
−−
−
=
x
x
x
y
y
yy3
L=−
−
200
020
145
222
022
152
111
022
152
−−
−
−
→
−−
−
−
→
−−
−
→
−−
−
111
022
041
111
011
041
→
−−
−
→
−−
−
111
011
005
111
011
0001
=U
Exercise Set 9.9 293

which has y1= –2, y2= 1 and y3= 0 as its solution. If we substitute these values into the
first matrix equation, we obtain the system
x1– x2– x3=–2
x2– x3=1
x3=0
This yields the final solution x1= –1, x2= 1, x3= 0.
11. (a) To reduce Ato row-echelon form, we carry out the following operations:
This involves multipliers 1/2, 2, –2, 1 (for the 2 diagonal entry), and –1. Where no
multiplier is needed in the second entry of the last row, we use the multiplier 1, thus
obtaining the lower triangular matrix
In fact, if we compute LU, we see that it will equal Ano matter what entry we choose
for the lower right-hand corner of L.
If we stop just before we reach row-echelon form, we obtain the matrices
which will also serve.
UL=
−
=−
112 12
00 1
00 1
200
210
201
L=−
200
210
211
211
212
210
112 12
21 2
21 0
−
−−
→
−
−−
→
−
→
−
112 12
00 1
21 0
112 12
00 1
00 1
→
−
=
112 12
00 1
00 0
U
294 Exercise Set 9.9

(b) We have that A= LU where
If we let
then A= L1DU as desired. (See the matrices at the very end of Section 9.9.)
(c) Let U2= DU and note that this matrix is upper triangular. Then A= L1U2is of the
required form.
13. (a) If Ahas such an LU-decomposition, we can write it as
This yields the system of equations
x= ay= bwx= cyw+ z= d
Since a≠0, this has the unique solution
x= ay= bw= c/az= (ad – bc)/a
The uniqueness of the solution guarantees the uniqueness of the LU-decomposition.
(b) By the above,
ab
cd ca
ab
ad bc a
=
−
()
10
10
ab
cd w
xy
z
xy
wx yw z
=
=+
10
10
LD
1
100
110
111
200
010
011
=−
=
and
LU=−
=
−
200
210
211
112 12
00 1
00 1
Exercise Set 9.9 295

15. We have that L= E1
–1 E2
–1 …Ek
–1 where each of the matrices Eiis an elementary matrix
which does not involve interchanging rows. By Exercise 27 of Section 2.1, we know that if
Eis an invertible lower triangular matrix, then E–1 is also lower triangular. Now the matrices
Eiare all lower triangular and invertible by their construction. Therefore for i= 1, … , kwe
have that Ei
–1 is lower triangular. Hence L, as the product of lower triangular matrices, must
also be lower triangular.
17. Let Abe any n×nmatrix. We know that Acan be reduced to row-echelon form and that
this may require row interchanges. If we perform these interchanges (if any) first, we
reduce Ato the matrix
Ek…E1A= B
where Eiis the elementary matrix corresponding to the ith such interchange. Now we know
that Bhas an LU-decomposition, call it LU where Uis a row-echelon form of A. That is,
Ek…E1A= LU
where each of the matrices Eiis elementary and hence invertible. (In fact, Ei
–1 = Eifor all
Ei. Why?) If we let
P= (Ek…E1)–1 = E1
–1 …Ek
–1 if k> 0
and P= Iif no row interchanges are required, then we have A= PLU as desired.
19. Assume A= PLU, where Pis a permutation matrix. Then note P–1 = P. To solve AX = B,
where A= PLU, set C= P–1B= PB and Y= UX.
First solve LY = Cfor Y.
Then solve UX = Yfor X.
If thenAAPLU=
−
−
=
310
311
021
,,
wwith PL=
=
100
001
010
300
020
301
,
=
−
,U
1130
0112
00 1
296 Exercise Set 9.9

To solve
310
311
021
0
1
0
1
2
3
−
−
=
x
x
x
=
=
,,or
set
AX e
CPe
2
2
100
001
010
=
0
1
0
0
0
1
Solve LLY C
y
y
y
=
,or
300
020
301
1
2
3
=toget =
0
0
1
0
0
1
2
3
,
y
y
y11
1130
0112
00 1
=
−
Solve orUX Y ,
x
x
x
x
x
x
1
2
3
1
2
0
0
1
=
so
33
16
12
1
=
−
−
Exercise Set 9.9 297


EXERCISE SET 10.1
3. (b) Since two complex numbers are equal if and only if both their real and imaginary parts
are equal, we have
x+ y= 3
and
x– y= 1
Thus x= 2 and y= 1.
5. (a) Since complex numbers obey all the usual rules of algebra, we have
z= 3 + 2i– (1 – i) = 2 + 3i
(c) Since (i– z) + (2z– 3i) = –2 + 7i, we have
i+ (–z+ 2z) – 3i= –2 + 7i
or
z= –2 + 7i– i+ 3i= –2 + 9i
299
7. (b) –2z= 6 + 8i
9. (c)
11. Since (4 – 6i)2= 22(2 – 3i)2= 4(–5 – 12i) = –4(5 + 12i), then
(1 + 2i)(4 – 6i)2= –4(1 + 2i)(5 + 12i) = –4(–19 + 22i) = 76 – 88i
13. Since (1 – 3i)2= –8 – 6i= –2(4 + 3i), then
(1 – 3i)3= –2(1 – 3i)(4 + 3i) = –2(13 – 9i)
zz i i ii i
12
1
624 15 2
612 15 1
313=+ −=+ −=−+()()()()( 110 11
3
4
912 4
934
1
415
1
22
2
2
)
()( )
(
=−
=+ =−+
=−
i
zi i
ziiii)( )
21
424 10 6 5
2
=−− =−−
300 Exercise Set 10.1

15.
17. Since i2= –1 and i3= –i, then 1 + i+ i2+ i3= 0. Thus (1 + i+ i2+ i3)100 = 0.
19. (a)
(d)
Hence
21. (a) Let z= x+ iy. Then
Im(iz) = Im[i(x+ iy)] = Im(–y+ ix) = x
= Re(x+ iy) = Re(z)
BA ii
ii
22 9122
18 2 13
−= ++
−+
Ai
iBii
i
224
410
11 12 6
18 6 23
=−
=++
−+
and 2
ii
AiB i
i
ii
ii
i
+=
−
+−+
+
=+
31
3
636
39 12
16 −−+
++
37
38 312
i
ii
Since then() ,
()
21
2
3
4
1
42
21
2
++
=+
++
ii i
i33
4
1
4263
16
22
iii
=+
=− +
Exercise Set 10.1 301

23. (a) We know that i1= i, i2= –1, i3= –i, and i4= 1. We also know that im+ n= imin
and imn = (im)nwhere mand nare positive integers. The proof can be broken into
four cases:
1. n= 1, 5, 9, … or n= 4k+ 1
2. n= 2, 6, 10, … or n= 4k+ 2
3. n= 3, 7, 11, … or n= 4k+ 3
4. n= 4, 8, 12, … or n= 4k+ 4
where k= 0, 1, 2, .... In each case, in= i4k+for some integer between 1 and 4.
Thus
in= i4ki= (i4)ki= 1 ki
= i
This completes the proof.
(b) Since 2509 = 4 ⋅627 + 1, Case 1 of Part (a) applies, and hence i2509 = i.
25. Observe that zz1= zz2⇔zz1– zz2= 0 ⇔z(z1– z2) = 0. Since z≠0 by hypothesis, it
follows from Exercise 24 that z1– z2= 0, i.e., that z1= z2.
27. (a) Let z1= x1+ iy1and z2= x2+ iy2. Then
z1z2= (x1+ iy1)(x2+ iy2)
= (x1x2– y1y2) + i(x1y2+ x2y1)
= (x2x1– y2y1) + i(y2x1+ y1x2)
= (x2+ iy2)(x1+ iy1)
= z2z1
302 Exercise Set 10.1

EXERCISE SET 10.2
3. (a) We have
z–
z= (2 – 4i)(2 + 4i) = 20
On the other hand,
z2= 22+ (–4)2= 20
(b) We have
z–
z= (–3 + 5i)(–3 – 5i) = 34
On the other hand,
z2= (–3)2+ 52= 34
5. (a) Equation (5) with z1= 1 and z2= iyields
(c)
7. Equation (5) with z1= iand z2= 1 + igives
i
i
ii i
1
1
2
1
2
1
2+=−=+
()
177
17
zi
ii=−==
()
11
1i
ii=−=−
()
303

9. Since (3 + 4i)2= –7 + 24i, we have
11. Since
13.We have
and
(1 – 2i)(1 + 2i) = 5
Thus
15. (a) If iz = 2 – i, then
zi
i
ii i=−=−−=− −
22
112
()()
i
iii
ii
()( )( )11212 5
1
10
1
10
1
2
1
2
−− +=−+ =− +
i
i
ii i
1
1
2
1
2
1
2−=+=− +
()
3
3
3
4
223
4
1
2
3
2
3
13
2
+
−=+=+=+
+
−−
i
i
ii
i
i
i
()
()(
then
ii
i
i
ii
)=+
−=+
()
+
()
=−++
1
2
3
2
1
2
3
2
1
1
2
13
4
13
4 i
1
34
724
724
724
6
22 2
()()()+=−−
−+− =−−
i
ii
225
304 Exercise Set 10.2
17. (a) The set of points satisfying the
equation z= 2 is the set of all points
representing vectors of length 2. Thus,
it is a circle of radius 2 and center at the
origin.
Analytically, if z= x+ iy, then
which is the equation of the above circle.
(c) The values of zwhich satisfy the equation z– i= z+ iare just those zwhose
distance from the point iis equal to their distance from the point –i. Geometrically,
then, zcan be any point on the real axis.
We now show this result analytically. Let z= x+ iy. Then
z– i= z+ i⇔z–i2= z+ i2
⇔x+ i(y– 1)2= x+ i(y+ 1)2
⇔x2+ (y– 1)2= x2+ (y+ 1)2
⇔– 2y= 2y
⇔y= 0
19. (a) Re(iz
–) = Re(i
–z
–) = Re[(–i)(x– iy)] = Re(–y– ix) = –y
(c) Re(iz
–) = Re[i(x– iy)] = Re(y+ ix) = y
21. (a) Let z= x+ iy. Then
1
2
1
2
1
22() ( )( ) () Re()zz xiy xiy x x z+= ++−
===
zxy
xy
=⇔ +=
⇔+=
22
4
22
22
Exercise Set 10.2 305

23. (a) Equation (5) gives
Thus
25.
27. (a)
(b) We use mathematical induction. In Part (a), we verified that the result holds when
n= 2. Now, assume that (z
–)n= zn
—. Then
and the result is proved.
35. (a)
It is easy to verify that AA–1 = A–1 A= I.
A
i
i
i
i
i
−=+−
=−
1
2
1
2
2
1
2
1
() ()zzz
zz
z
nn
n
n
+
+
=
=
=
1
1
zzzzzz
22
== =()
zxy xy z=+=+−=
22 2 2
()
Re z
z
xx yy
xy
1
2
12 12
2
2
2
2
=+
+
z
zz
zz
xy
xiy xiy
x
1
22
212
2
2
2
211 22
2
2
1
1
1
=
=++−
=
()( )
++ ++ −
y
xx yy ixy xy
2
212 12 21 12
()()
306 Exercise Set 10.2

39. (a)
Thus
41. (a) We have , which is just the distance between the two
numbers z1and z2when they are considered as points in the complex plane.
zz aa bb
12 12
2
12
2
−= −+−()()
A
iii
i
ii
−=
−−− −+
−
1
22 1
12
1
11 0100
01 010
12 2 0 0 1
11 0 10 0
0
+
−−
+
i
i
ii
i
11010
0201
11 0 10 0
01 010
001 1
i
ii
i
i
ii
−
+
+
−
11 010 0
01012
001 1
1
i
i
ii
000 22 1
010 1 2
001 1
−−− −+
−
iii
i
ii
Exercise Set 10.2 307
RRiR
331
→+
RRiR
332
→+
RRiR
223
→−
RR iR
21 2
1→−+()

(b) Let z1= 12, z2= 6 + 2i, and z3= 8 + 8i. Then
z1– z22= 62+ (–2)2= 40
z1– z32= 42+ (–8)2= 80
z2– z32= (–2)2+ (–6)2= 40
Since the sum of the squares of the lengths of two sides is equal to the square of the
third side, the three points determine a right triangle.
308 Exercise Set 10.2
EXERCISE SET 10.3
1. (a) If z= 1, then arg z= 2kπwhere k= 0, ±1, ±2,...
. Thus, Arg(1) = 0.
(c) If z= –i, then arg z= + 2kπwhere k= 0, ±1, ±2,...
. Thus, Arg(–i) = –π/2.
(e) If then arg z= + 2kπwhere k= 0, ±1, ±2,...
. Thus, Arg
3. (a) Since 2i= 2 and Arg(2i) = π/2, we have
(c) Since and Arg(5 + 5i) = π/4, we have
(e) Since we have
−− = −
+−
33 32 3
4
3
4
iicos sin
ππ
−− = = − − −33 18 32 33 3
4
iiand Arg( ) =
π
,
55 52 44
cos sin+=
+
ii
ππ
55 5052+= =i
22 22
iicos sin=
+
ππ
().−+ =13 2
3
i
π
2
3
π
zi,=− +13
3
2
π
309
5. We have z1= 1, Arg(z1) = , z2= 2, Arg(z2) = – , z3= 2, and Arg(z3) = . So
and
Therefore
= cos(0) + isin(0) = 1
7. We use Formula (10).
(a) We have r= 1,
θ
= – , and n= 2. Thus
Thus, the two square roots of –iare:
cos sin
cos
−
+−
=−
ππ
π
44
1
2
1
2
3
4
ii
+
=− +iisin 3
4
1
2
1
2
π
() cos sin ,−=−+
+−+
=ikikk
12
44
0
ππππ
11
π
2
zz
z
12
3
Arg Arg( Arg Arg
1123
zz
zzzz
2
3
0
=+− =)()()
zz
z
zz
z
12
3
12
3
1==
π
6
π
3
π
2
310 Exercise Set 10.3
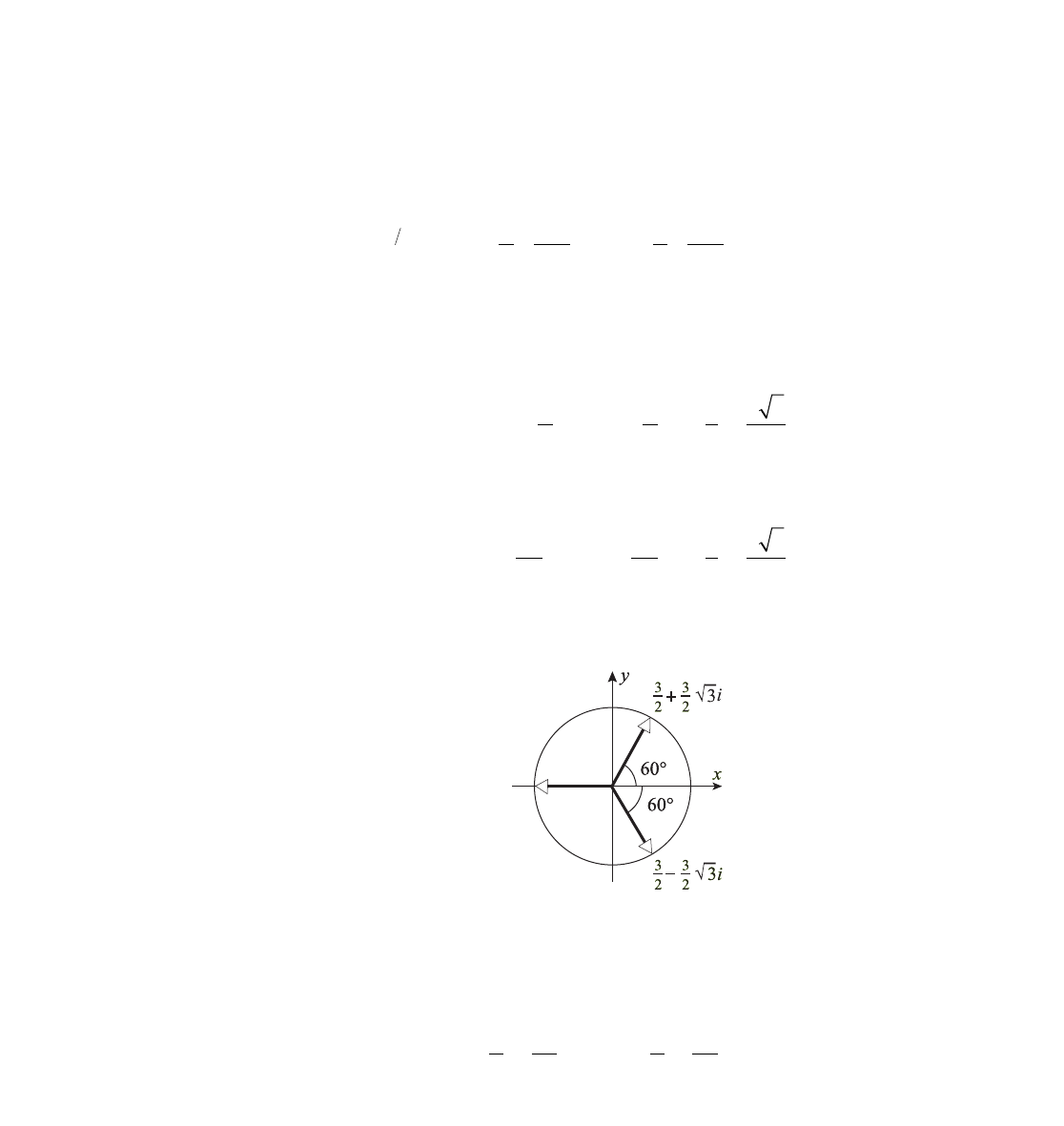
(c) We have r= 27,
θ
= π, and n= 3. Thus
Therefore, the three cube roots of –27 are:
7. (e) Here r= 1,
θ
= π, and n= 4. Thus
() cos sin
/
−= +
++
142 42
14 ππ ππkik
=k0123,,,
333
3
2
33
cos sin
ππ
+
=+i22
33
35
3
i
icos( ) sin( )
cos
ππ
π
+
=−
+iiisin 5
3
3
2
33
2
π
=−
() cos sin−= +
++
27 3 3
2
33
2
3
13
ππ ππ
kik
=k012,,
Exercise Set 10.3 311
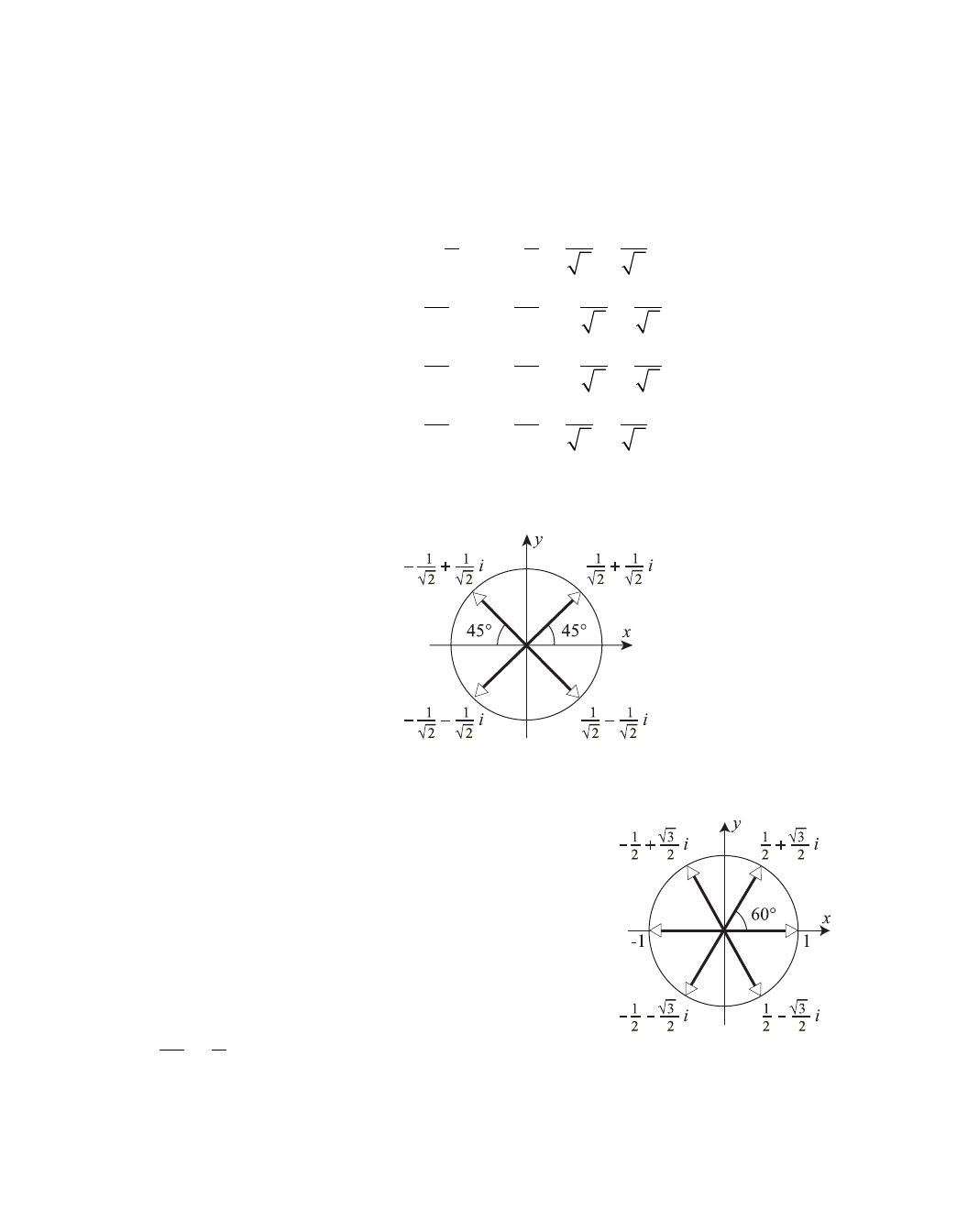
Therefore the four fourth roots of –1 are:
9. We observe that w= 1 is one
sixth root of 1. Since the
remaining 5 must be equally
spaced around the unit circle, any
two roots must be separated
from one another by an angle of
= 60°. We show all six
sixth roots in the diagram.
11. We have z4= 16 ⇔ z= 161/4. The fourth roots of 16 are 2, 2i, –2, and –2i.
2
63
ππ
=
cos sin
cos sin
ππ
ππ
44
1
2
1
2
3
4
3
4
+=+
+=
ii
i
cos sin
cos
−+
+=−−
1
2
1
2
5
4
5
4
1
2
1
2
7
i
ii
ππ
πππ
4
7
4
1
2
1
2
sin+=−ii
312 Exercise Set 10.3
15. (a) Since
z= 3eiπ= 3[cos(π) + isin(π)] = –3
then Re(z) = –3 and Im(z) = 0.
(c) Since
then and hence Re(z) = 0 and .
17. Case 1.Suppose that n= 0. Then
(cos
θ
+ isin
θ
)n= 1 = cos(0) + isin(0)
So Formula (7) is valid if n= 0.
Case 2.In order to verify that Formula (7) holds if nis a negative integer, we first let
n= – 1. Then
Thus, Formula (7) is valid if n= –1.
Now suppose that nis a positive integer (and hence that –nis a negative integer).
Then
This completes the proof.
(cos sin ) cos sin
[cos
θθ θθ
θ
+=+
()
=−
−−
ii
nn
1
(()
+−
()
=−+ −
i
ni n
n
sin ]
cos( ) sin( ) [
θ
θθ
By Formulaa(7)]
(cos sin ) cos sin
cos sin
cos(
θθ θθ
θθ
+=
+
=−
=−
−
ii
i
11
θθθ
)sin()+−i
Im( )z=− 2
zi=− 2
ze i i
i
==
+
=22
22
2
2
πππ
cos sin
Exercise Set 10.3 313

19. We have and . But (see Exercise 17)
If we replace z2by 1/z2in Formula (3), we obtain
which is Formula (5).
21. If
ei
θ
= cos
θ
+ isin
θ
then replacing
θ
with –
θ
yields
e–i
θ
= cos(–
θ
) + isin(–
θ
) = cos
θ
– isin
θ
If we then compute ei
θ
+ e–i
θ
and ei
θ
– e–i
θ
, the results will follow.
23. Let z= r(cos
θ
+ isin
θ
). Formula (5) guarantees that 1/z= r–1 (cos(–
θ
) + isin(–
θ
))
since z≠0. Applying Formula (6) for na positive integer to the above equation yields
which is just Formula (6) for –na negative integer.
zzrnin
n
n
n−−
=
=−
(
)
+−
(
)
(
)
1cos sin
θθ
z
zzz
r
ri
1
2
1
2
1
2
12 1
1
=
=+−
()
()
+cos sin
θθ θ
++−
()
()
=−
()
+−
()
θ
θθ θθ
2
1
2
12 12
r
ricos sin
111
222
2
2
zre re
i
i
==
−
θ
θ
zre
i
22
2
=
θ
zre
i
11
1
=
θ
314 Exercise Set 10.3

EXERCISE SET 10.4
1. (a) u – v= (2i– (–i), 0 – i, –1 – (1 + i), 3 – (–1))
= (3i, –i, –2 – i, 4)
(c) –w+ v= (–(1 + i) – i, i+ i, –(–1 + 2i) + (1 + i), 0 + (–1))
= (–1 – 2i, 2i, 2 – i, –1)
(e) –iv= (–1, 1, 1 – i, i) and 2iw= (–2 + 2i, 2, –4 – 2i, 0). Thus
–iv+ 2iw= (–3 + 2i, 3, –3 – 3i, i)
3. Consider the equation c1u1+ c2u2+ c3u3= (–3 + i, 3 + 2i, 3 – 4i). The augmented matrix
for this system of equations is
The row-echelon form for the above matrix is
Hence, ,cic i i
32
23
2
1
2
1
2
1
2
=− = + − +
==−−cci
31
02,.and
11 0 2
011
2
1
2
3
2
1
2
00 1 1
−+ −−
++
−
ii
ii
i
1203
1232
01234
−−+
++
−−
ii i
iii i
ii
315

5.
9. (a) u •v= (–i)(–3i) + (3i)(–2i) = –3 + 6 = 3.
(c) u •v= (1 – i)(4 – 6i) + (1 + i)(5i) + (2i)(–1 – i) + (3)(–i)
= (–2 – 10i) + (–5 + 5i) + (2 – 2i) + (–3i)
= –5 – 10i
11. Let Vdenote the set and let
We check the axioms listed in the definition of a vector space (see Section 5.1).
(1)
So u+ vbelongs to V.
(2) Since u+ v= v+ uand , it follows that u+ v= v+ u.
(3) Axiom (3) follows by a routine, if tedious, check.
(4) The matrix serves as the zero vector.
(5)
(6) Since ku= , kuwill be in Vif and only if , which is true if and
only if kis real or u= 0. Thus Axiom (6) fails.
ku ku=
ku
ku
0
0
Let = Then−−
−
=−
−
uuuu
u
u
u
u
0
0
0
0.++( )= .−uu00
00
00
uv vu+=+
uuvv+= +
+
=+
+
uv
uv
uv
uv
0
0
0
0
uu= a d
u
u
v
v
0
0
0
0
=
nvv
((aa))vv
((cc))vv
=+=
=++++−=
12
2021 1 4
22
22 2 2
i
ii() ++++=051 10
316 Exercise Set 10.4

(7)–(9) These axioms all hold by virtue of the properties of matrix addition and scalar
multiplication. However, as seen above, the closure property of scalar multiplication
may fail, so the vectors need not be in V.
(10) Clearly 1u= u.
Thus, this set is not a vector space because Axiom (6) fails.
13. Suppose that T(x) = Ax= 0. It is easy to show that the reduced row echelon form for Ais
Hence, x1= (–(1 + 3i)/2)x3and x2= (–(1 + i)/2)x3where x3is an arbitrary complex
number. That is,
spans the kernel of Tand hence Thas nullity one.
Alternatively, the equation Ax= 0 yields the system
ix1– ix2– x3= 0
x1– ix2+ (1 + i)x3= 0
0 + (1 – i)x2+ x3= 0
The third equation implies that x3= –(1 – i)x2. If we substitute this expression for x3
into the first equation, we obtain x1= (2 + i)x2. The second equation will then be valid
for all such x1and x3. That is, x2is arbitrary. Thus the kernel of Tis also spanned by the
vector
If we multiply this vector by –(1 + i)/2, then this answer agrees with the previous one.
x
x
x
i
i
1
2
3
2
1
1
=
+
−+
xx =
−+
()
−+
()
13 2
12
1
i
i
10 13 2
01 1 2
00 0
+
()
+
()
i
i
Exercise Set 10.4 317

15. (a) Since
(f+ g)(1) = f(1) + g(1) = 0 + 0 = 0
and
kf(1) = k(0) = 0
for all functions fand gin the set and for all scalars k, this set forms a subspace.
(c) Since
the set is closed under vector addition. It is closed under scalar multiplication by a real
scalar, but not by a complex scalar. For instance, if f(x) = xi, then f(x) is in the set but
if(x) is not.
17. (a) Consider the equation k1u+ k2v+ k3w= (1, 1, 1). Equating components yields
k1+(1 + i)k2= 1
k2+ ik3= 1
–ik1+ (1 – 2i)k2+ 2k3= 1
Solving the system yields k1= –3 – 2i, k2= 3 – i, and k3= 1 + 2i.
(c) Let Abe the matrix whose first, second and third columns are the components of u, v,
and w, respectively. By Part (a), we know that det(A) ≠0. Hence, k1= k2= k3= 0.
19. (a) Recall that eix = cos x+ isin xand that e–ix = cos(–x) + isin(–x) = cos x– isin x.
Therefore,
and so cos xlies in the space spanned by fand g.
cos xee
ix ix
=+=+
−
2
1
2
1
2
ffgg
()()()() ()()
() () (
fg x f x gxfxgx
fx gx
+−=−+−= +
=+=
ffgx+)( )
318 Exercise Set 10.4

(b) If af+ bg= sin x, then (see Part (a))
(a+ b)cos x+ (a– b)isin x= sin x
Thus, since the sine and cosine functions are linearly independent, we have
a+ b= 0
and
a– b= –i
This yields a= –i/2, b= i/2, so again the vector lies in the space spanned by fand g.
(c) If af+ bg= cos x+ 3isin x, then (see Part (a))
a+ b= 1
and
a– b= 3
Hence a= 2 and b= –1 and thus the given vector does lie in the space spanned by
fand g.
21. Let Adenote the matrix whose first, second, and third columns are the components of u1,
u2, and u3, respectively.
(a) Since the last row of Aconsists entirely of zeros, it follows that det(A) = 0 and hence
u1, u2, and u3, are linearly dependent.
(c) Since det(A) = i≠0, then u1, u2, and u3are linearly independent.
23. Observe that f– 3g– 3h= 0.
25. (a) Since = –4 ≠0, the vectors are linearly independent and hence form a basis
for C2.
(d) Since = 0, the vectors are linearly dependent and hence are not a
basis for C2.
23 32
1
−+
−
ii
i
24
0
ii
i−
Exercise Set 10.4 319
27. The row-echelon form of the matrix of the system is
So x2is arbitrary and x1= –(1 + i)x2. Hence, the dimension of the solution space is one
and is a basis for that space.
29. The reduced row-echelon form of the matrix of the system is
So x3is arbitrary, x2= (–3i)x3, and x1= (3 + 6i)x3. Hence, the dimension of the solution
space is one and is a basis for that space.
31. Let u= (u1, u2,..., un) and v= (v1, v2,..., vn). From the definition of the Euclidean inner
product in Cn, we have
33. Hint: Show that
u+ kv2= u2+–
k(v•u) + k(u•v) + k–
kv2
and apply this result to each term on the right-hand side of the identity.
uuvv•=+ ++
=
() ( ) ( )... ( )
(
kukvukvukv
ukv
nn11 2 2
11
))()... ( )
()( )...
+++
=+++
ukv u kv
kuv kuv
nn22
11 2 2 kkuv
kuv uv u v
k
nn
nn
()
[... ]
()
=+++
=•
11 2 2
uuvv
36
3
1
+
−
i
i
1036
01 3
00 0
−−
i
i
−+
()
1
1
i
11
00
+
i
320 Exercise Set 10.4

EXERCISE SET 10.5
1. Let u= (u1, u2), v= (v1, v2), and w= (w1, w2). We proceed to check the four axioms
(1)
(2) 〈u+ v, w〉= 3(u1+ v1)+ 2(u2+ v2)
= [3u1+ 2u2] + [3v1+ 2v2]
= 〈u, w〉+ 〈v, w〉
(3) 〈ku, v〉= 3(ku1)+ 2(ku2)
= k[3u1+ 2u2] = k〈u, v〉
(4) 〈u, u〉= 3u1+ 2u2
= 3|u1|2+ 2|u2|2(Theorem 10.2.1)
≥0
Indeed, 〈u, u〉= 0
⇔
u1= u2= 0
⇔
u= 0.
Hence, this is an inner product on C2.
3. Let u= (u1, u2) and v= (v1, v2). We check Axioms 1 and 4, leaving 2 and 3 to you.
(1)
vvuu,()()=++ +−+vu i vu i vu vu
11 12 21 2 2
113
==+− +++
=
uv i uv i uv uv
11 21 12 2 2
113() ()
uuvv,
u
2
u
1
v
2
v
1
v
2
v
1
w
2
w
1
w
2
w
1
w
2
w
1
vvuu
uuvv
,=+
=+=
32
32
11 22
11 22
vu vu
uv uv ,
321

(4) Recall that |Re(z)|≤|z|by Problem 37 of Section 10.2. Now
Moreover, 〈u, u〉= 0 if and only if both |u2|and |u1|– |u2|= 0, or u= 0.
5. (a) This is not an inner product on C2. Axioms 1–3 are easily checked. Moreover,
〈u, u〉= u1= |u1|≥0
However, 〈u, u〉= 0
⇔
u1= 0
⇔
/u= 0. For example, 〈i, i〉= 0 although i≠0.
Hence, Axiom 4 fails.
(c) This is not an inner product on C2. Axioms 1 and 4 are easily checked. However, for
w= (w1, w2), we have
〈u+ v, w〉= |u1+ v1|2|w1|2+ |u2+ v2|2|w2|2
≠(|u1|2+ |v1|2)|w1|2+ (|u2|2+ |v2|2)|w2|2
= 〈u, w〉+ 〈v, w〉
For instance, 〈1 + 1, 1〉= 4, but 〈1, 1〉+ 〈1, 1〉= 2. Moreover, 〈ku, v〉= |k|2〈u, v〉, so that
〈ku, v〉≠k〈u, v〉for most values of k, u, and v. Thus both Axioms 2 and 3 fail.
(e) Axiom 1 holds since
vvuu, =+−+
=
22
2
11 12 21 22
11
vu ivu ivu vu
uv −−++
=
iu v iu v u v
21 12 22
2
uuvv,
u
1
2
uuuu,()()=++ +−+
=
uu iuu iuu uu
11 1 2 21 2 2
113
uuiuuiuuu
u
1
2
12 12 2
2
1
2
113
2
() ()
Re
++ ++ +
=+
((( ) )
()
13
21 3
12 2
2
1
2
12 2
2
++
≥−+ +
iuu u
uiuuu
==− +
=−
()
+
uuuu
uuu
1
2
12 2
2
12
2
2
2
22 3
2
322 Exercise Set 10.5

A similar argument serves to verify Axiom 2 and Axiom 3 holds by inspection. Finally,
using the result of Problem 37 of Section 10.2, we have
〈u, u〉= 2u1u
–
1+ iu1u
–
2– iu2u
–
1+ 2u2u
–
2
= 2|u1|2+ 2Re(iu1u
–
2) + 2|u2|2
≥2|u1|2– 2|iu1u
–
2|+ 2|u2|2
= (|u1|– |u2|)2+ |u1|2+ |u2|2
≥0
Moreover, 〈u, u〉= 0
⇔
u1= u2= 0, or u= 0. Thus all four axioms hold.
9. (a) w= [3(–i)(i) + 2(3i)(–3i)]1/2 =
(c) w= [3(0)(0) + 2(2 – i)(2 + i)]1/2 =
11. (a) w= [(1)(1) + (1 + i)(1)(i) + (1 – i)(–i)(1) + 3(–i)(i)]1/2 =
(c) w= [(3 – 4i)(3 + 4i)]1/2 = 5
13. (a) Since u– v= (1 – i, 1 + i), then
d(u, v) = [3(1 – i)(1 + i) + 2(1 + i)(1 – i)]1/2 =
15. (a) Since u– v= (1 – i, 1 + i),
d(u, v)= [(1 – i)(1 + i) + (1 + i)(1 – i)(1 – i)
+ (1 – i)(1 + i)(1 + i) + 3(1 + i)(1 – i)]1/2
=
17. (a) Since u•v= (2i)(–i) + (i)(–6i) + (3i)(k
–), then u•v= 0
⇔
8 + 3ik
–= 0 or
k= –8i/3.
23
10
2
10
21
Exercise Set 10.5 323

19.
Also
and
21. (a) Call the vectors u1, u2, and u3, respectively. Then u1= u2= u3= 1 and
u1•u2= u1•u3= 0. However, u2•u3=. Hence the set is not
orthonormal.
25. (a) We have
and since u2•v1= 0, then u2– (u2•v1)v1= u2. Thus,
uuuuvvvvuuvvvv
31132
−−=
−
()() ,,••
32
66
ii i
33
Also, and anduuvvuuvv
31 32
43 12//••==hhence
vv22 =−
ii
22
0,,
vv11 =
iii
333
,,
ii
22
66
2
60+−
()
=− ≠
xx, 1
3
1
3
(,, ) ,, ,,
•0110ii e i ii
e
i
i
−=
()
−
()
=
θ
θ
(()0
0
−+
=
ii
xx, 1
3
1
3
(,, ) ,, ,,
(
•10 11 10ieii
ei
i
i
=
()()
=
θ
θ
−−+
=
i0
0
)
Since = 1
3we have
1
3
xei
ei
i
i
θ
θ
(,,),
,,
11
11xx =
( ))
=++=
1
31111 1
12
()( )
324 Exercise Set 10.5

Since the norm of the above vector is , we have
27. Let u1= (0, i, 1 –i) and u2= (–i, 0, 1 + i). We shall apply the Gram-Schmidt process
to {u1, u2}. Since , it follows that
and because the norm of the above vector is , we have
Therefore,
and
wwwwww
21
–=
=−
1
4
9
4
19
4
9
4
ii i i,, ,
wwwwvvvvwwvvvv
vvvv
111 22
12
()( )••=+
=+
−
=−
7
6
1
23
5
44
1
4
5
4
9
4
iiii,,,−
vv22 =−
ii ii
23
3
23 23 23
,, ,
vv2=−+
3
15
2
15
1
15
ii
,,
15 3/
uuuuvvvv
2211
−=−+−−+
()(,,),,•ii i01 0 2
3
2
3
2
3
=− +
ii,,
2
3
1
3
1
3
Since thenuuvv
21
23/,•=i
vv1=−
03
1
3
,,
ii
u1=3
vv3=−
ii i
66
2
6
,,
16/
Exercise Set 10.5 325
29. (a) By Axioms (2) and (3) for inner products,
〈u–kv, u– kv〉= 〈u, u–kv〉+ 〈–kv, u– kv〉
= 〈u, u– kv〉– k〈v, u– kv〉
If we use Properties (ii) and (iii) of inner products, then we obtain
〈u– kv, u– kv〉= 〈u, u〉– k
–〈u, v〉– k〈v, u〉+ kk
–〈v, v〉
Finally, Axiom (1) yields
〈u– kv, u– kv〉= 〈u, u〉– k
–〈u, v〉– k+ kk
–〈v, v〉
and the result is proved.
(b) This follows from Part (a) and Axiom (4) for inner products.
33. Hint: Let vbe any nonzero vector, and consider the quantity 〈v, v〉+ 〈0, v〉.
35. (d) Observe that u+ v2= 〈u+ v, u+ v〉. As in Exercise 37,
〈u+ v, u+ v〉= 〈u, u〉+ 2 Re(〈u, v〉) + 〈v, v〉
Since (see Exercise 37 of Section 10.2)
|Re(〈u, v〉)|≤|〈u, v〉|
this yields
〈u+ v, u+ v〉≤〈u, u〉+ 2|〈u, v〉| + 〈v, v〉
By the Cauchy-Schwarz inequality and the definition of norm, this becomes
u+ v2≤u2+ 2uv+ v2= (u+ v)2
which yields the desired result.
(h) Replace uby u– wand vby w– vin Theorem 6.2.2, Part (d).
37. Observe that for any complex number k,
u+ kv2= 〈u+ kv, u+ kv〉
= 〈u, u〉+ k〈v, u〉+ k
–〈u, v〉+ kk
–〈v, v〉
= 〈u, u〉+ 2 Re(k〈v, u〉) + |k|2〈v, v〉
uuvv,
326 Exercise Set 10.5

Therefore,
u+ v2–u –v2+iu +iv2–iu –iv2
= (1–1+i–i)〈u, u〉+2 Re(〈v, u 〉)–2 Re(–〈v, u 〉)+2iRe(i〈v, u 〉)
–2iRe(–i〈v, u 〉)+(1–1+i–i)〈v, v 〉
= 4Re(〈v, u 〉)–4iIm(〈v, u 〉)
=
= 4 〈u, v〉
39. We check Axioms 2 and 4. For Axiom 2, we have
For Axiom 4, we have
Since |f|2≥0 and a< b, then 〈f, f〉≥0. Also, since fis continuous, |f|2dx > 0 unless
f= 0 on [a, b]. [That is, the integral of a nonnegative, real-valued, continuous function (which
represents the area under that curve and above the x-axis from ato b) is positive unless the
function is identically zero.]
a
b
∫
ffffff, ==
=
()
()
+
()
()
∫∫
ffffdx
a
b
a
bdx
fx fx
2
1
2
2
2
∫dx
a
b
ffgghh+,
,
=+
=+
=
∫
∫∫
()ffgghh
ffhhgghh
ff
dx
dx dx
a
b
a
b
a
b
hhhhgghh+,
4vvuu,
Exercise Set 10.5 327

41. Let vm= e2πimx = cos(2πmx) + isin(2πmx). Then if m≠n, we have
Thus the vectors are orthogonal.
vvvv
mn mx i mx nx,cos sincos=
()
+
()
()
∫222
0
1
πππ
−−
()
=
()()
+
inxdx
mx nx
sin
cos cos sin
2
22 2
π
ππ π
mmx nx dx
imx
()()
+
∫sin
sin
2
2
0
1
π
π
(()()
−
()()
=
∫cos cos sin
co
222
0
1
πππ
nx mx nx dx
sssin22
1
0
1
0
1
ππ
mnxdxi mnxdx−
()
+−
()
=
∫∫
22 222
0
1
ππππ
mn mnx i
mn mn
−
()
−
()
−−
()
−sin[ ] cos[
(()
=− −
()
+−
()
=
x
i
mn
i
mn
]0
1
22
0
ππ
328 Exercise Set 10.5

EXERCISE SET 10.6
5. (b) The row vectors of the matrix are
Since r1= r2= 1 and
the matrix is unitary by Theorem 10.6.2. Hence,
(d) The row vectors of the matrix are
and
rr3
3
215
43
215
5
215
=++
iii
,,
rr
rr
1
2
1
2
1
2
1
2
3
1
33
=+−
=−
i
ii
,,
,,
AAA
i
i
T−== =
−+
−
1
1
2
1
2
1
2
1
2
*
rrrr
12
1
2
1
2
1
2
1
20
•=−+
+−
=
ii
rrrr
12
1
2
1
2
1
2
1
2
=
=−++
,,and ii
329

We have r1= r2= r3= 1,
and
Hence, by Theorem 10.6.2, the matrix is unitary and thus
7. The characteristic polynomial of Ais
Therefore, the eigenvalues are λ= 3 and λ= 6. To find the eigenvectors of Acorresponding
to λ= 3, we let
−
−−
=
1
1
0
0
1
2
i
x
x
det ( )( )()(
λ
λλλ λ
−−+
−− −
=− −−=−
41
15
452 6
i
i
λλ
−3)
AAA
ii i
i
ii
T−== =
−− −
−−
−
1
1
23
3
215
1
2
1
3
43
215
1
23
5
2
*
115
rrrr
13
1
2
3
215
1
2
43
2
••=+
−
−−ii i
115
1
2
5
215 0+−=
•i
rrrr
12
1
23
1
2
1
3
1
2
•••=+
−
−+
ii i
33 0
1
3
3
215
1
3
43
23
=
=
−
+−
rrrr
••
i iii i
215 3
5
215 0−−=
•
330 Exercise Set 10.6

This yields x1= –(1 – i)sand x2= swhere sis arbitrary. If we put s=1, we see that
is a basis vector for the eigenspace corresponding to λ= 3. We normalize this
vector to obtain
To find the eigenvectors corresponding to λ= 6, we let
This yields and x2= swhere sis arbitrary. If we put s=1, we have that
is a basis vector for the eigenspace corresponding to λ= 6. We normalize this
vector to obtain
Thus
P
ii
=
−+ −
1
3
1
6
1
3
2
6
PP2
1
6
2
6
=
−
i
12
1
−
()
i
xi
s
1
1
2
=−
21
11
0
0
1
2
−+
−−
=
i
i
x
x
PP
1
1
3
1
3
=
−+
i
−+
1
1
i
Exercise Set 10.6 331

diagonalizes Aand
9. The characteristic polynomial of Ais
Therefore the eigenvalues are λ= 2 and λ= 8. To find the eigenvectors of Acorresponding
to λ= 2, we let
This yields and x2= swhere sis arbitrary. If we put s= 1, we have that
is a basis vector for the eigenspace corresponding to λ= 2. We normalize this
vector to obtain
To find the eigenvectors corresponding to λ= 8, we let
222
22 4
0
0
1
2
−−
−+
=
i
i
x
x
PP
1
1
6
2
6
=
−+
i
−+
()
12
1
i
xis
1
1
2
=− +
−−−
−+ −
=
422
22 2
0
0
1
2
i
i
x
x
det ( )( )
λ
λλλ
−−−
−+ −
=− −
622
22 4 64
i
i−−= − −()()882
λλ
PAP
i
i
i
−=
−−
+
−
1
1
3
1
3
1
6
2
6
41
115
1
3
1
6
1
3
2
6
+
−+ −
i
ii
=
30
06
332 Exercise Set 10.6

This yields x1= (1 + i)sand x2= swhere sis arbitrary. If we set s= 1, we have that
is a basis vector for the eigenspace corresponding to λ= 8. We normalize this
vector to obtain
Thus
diagonalizes Aand
11. The characteristic polynomial of Ais
Therefore, the eigenvalues are λ= 1, λ= 5, and λ= –2. To find the eigenvectors of A
corresponding to λ= 1, we let
−
−
+
=
40 0
021
01 1
0
0
1
2
3
i
i
x
x
x00
det ( )( )(
λ
λ
λ
λλλ
−
+−
+
=− −
50 0
011
01
15i
i
++ 2)
PAP
i
i
i
−=
−+
−
+
1
1
6
2
6
1
3
1
3
622
222 4
1
6
1
3
2
6
1
3
−
−++
i
ii
=
20
08
P
ii
=
−++
1
6
1
6
2
6
1
3
PP2=
+
1
3
1
3
i
1
1
+
i
Exercise Set 10.6 333

This yields x1= 0, x2= – and x3= swhere sis arbitrary. If we set s= 1, we have
that is a basis vector for the eigenspace corresponding to λ= 1. We normalize
this vector to obtain
To find the eigenvectors corresponding to λ= 5, we let
This yields x1= sand x2= x3= 0 where sis arbitrary. If we let s= 1, we have that
is a basis vector for the eigenspace corresponding to λ= 5. Since this vector is already
normal, we let
To find the eigenvectors corresponding to λ= – 2, we let
−
−−
+−
70 0
011
01 2
1
2
3
i
i
x
x
x
=
0
0
0
PP2
1
0
0
=
1
0
0
00 0
061
01 5
1
2
3
−
+
i
i
x
x
x
=
0
0
0
PP
1
2
6
=− −
0
1i
6
0
12
1
−−
()
i
1
2
−is,
334 Exercise Set 10.6

This yields x1= 0, x2= (1 – i)s, and x3= swhere sis arbitrary. If we let s= 1, we have that
is a basis vector for the eigenspace corresponding to λ= –2. We normalize this
vector to obtain
Thus
diagonalizes Aand
13. The eigenvalues of Aare the roots of the equation
det
λ
λλλ
−−
−−
=−+=
14
434190
2
i
i
PAP
i
i
−=
−+
+
1
01
6
2
6
10 0
01
3
1
3
−−+
−−
−−
50 0
011
01 0
010
1
i
i
i
66 01
3
2
601
3
10 0
05 0
00 2
−
=
−
i
Pii
=−−−
010
1
601
3
2
601
3
PP3
0
1
3
1
3
=−
i
0
1
1
−
i
Exercise Set 10.6 335

The roots of this equation, which are λ= are not real. This shows that the
eigenvalues of a symmetric matrix with nonreal entries need not be real. Theorem 10.6.6
applies only to matrices with real entries.
15. We know that det(A) is the sum of all the signed elementary products ,
where aij is the entry from the ith row and jth column of A. Since the ijth element of
,then det is the sum of the signed elementary products or
. That is, det is the sum of the conjugates of the terms in det(A). But
since the sum of the conjugates is the conjugate of the sum, we have
det
19. If Ais invertible, then
A*( A–1)* = ( A–1 A)* (by Exercise 18(d))
=
Thus we have (A–1)* = (A*)–1.
21. Let ridenote the ith row of Aand let cjdenote the jth column of A*. Then, since
we have cj= for j= 1,…, n. Finally, let
Then Ais unitary ⇔A–1 = A*. But
A–1 = A*⇔AA* = I
⇔ricj=
δ
ij for all i, j
⇔
rirj=
δ
ij for all i, j
⇔
{r1,…,rn}is an orthonormal set
δ
ij
ij
ij
=≠
=
0
1
if
if
rrj
AA A
TT
*(),==
II I I
TT
*===
AA
()
=det( )
.
()A
±aa a
jj nj
n
12
12
…
±aa a
jj nj
n
12
12
…
()A
Aa
ij
is
±aa a
jj nj
n
12
12
…
416419
2
±−()
,
336 Exercise Set 10.6

23. (a) We know that A= A*, that Ax= λIx, and that Ay= µIy. Therefore
x* Ay= x*(µIy) = µ(x* Iy) = µx*y
and
x* Ay= [(x* Ay)*]* = [y* A*x]*
= [y* Ax]* = [y* (λIx)]*
= [λy*x]* = λx*y
The last step follows because λ, being the eigenvalue of an Hermitian matrix, is real.
(b) Subtracting the equations in Part (a) yields
(λ–
µ
)(x* y) = 0
Since λ≠
µ
, the above equation implies that x*yis the 1 ×1 zero matrix. Let
x= (x1,…, xn) and y= (y1,…, yn). Then we have just shown that
so that
and hence xand yare orthogonal.
xy x y
nn11 00++ ==
xy x y
nn11 0++ =
Exercise Set 10.6 337


SUPPLEMENTARY EXERCISES 10
3. The system of equations has solution x1= –is + t, x2= s, x3= t. Thus
where sand tare arbitrary. Hence
form a basis for the solution space.
5. The eigenvalues are the solutions,
λ
, of the equation
or
λω ωλω ωλ
32
111110+++
−++
−=
det
λ
λωω
λω ω
01
11
1
01 1
1
−
−−−−
−+++
=00
−
i
1
0
1
0
1
and
x
x
x
i
s
1
2
3
1
0
1
0
1
=
−
+
t
339
But so that . Thus we have
λ
3 – 1 = 0
or
(
λ
– 1)(
λ
2+
λ
+ 1) = 0
Hence
λ
= 1,
ω
, or . Note that =
ω
2.
7. (c) Following the hint, we let z= cos
θ
+ isin
θ
= ei
θ
in Part (a). This yields
If we expand and equate real parts, we obtain
12 1
1
1
++ ++ = −
−
+
cos cos cos Re
()
θθ θ θ
θ
ne
e
ni
i
11
1
21
++ ++ =
−
−
+
ee e e
e
ii ni
ni
i
θθ θ θ
θ
()
ω
ω
ω
ωω
++ = + =11210Re( )
1
ωω
=,
340 Supplementary Exercises 10
But
Observe that because 0 <
θ
<2
π
, we have not divided by zero.
=+ +
1
2122
2
cos sin sin cos
sin
nn
θθθθ
θ
==+
+
1
21
1
2
2
sin
sin
n
θ
θ
Re Re
1
1
11
11
−
−
=−
()
−
+
()
+
()
e
e
ee
ni
i
ni
θ
θ
θ
−−
−
+
()
()
−
()
−
()
=−
i
ii
ni
ee
e
θ
θθ
11
11
Re
θθ θθ
θ
−+
−
=−+
()
−
ee
e
n
ini
i
22
1
2
11
Re( )
cos
θθθθ
θ
θ
−−
()
+
−
=−
cos cos
cos
cos
n
1
1
2
1
11
1
1
1
21
−+−+
()
()
−
=
cos
cos cos
cos
θ
θθ
θ
nn
++ −−
cos cos cos sin sin
sin
nn n
θθθθθ
θ
22
2
=+ −
()
+
1
21
12 22
cos cos sin sin cosnn
θθ θ
θθ
22 2
1
21
222
2
2
sin
cos sin sin
θ
θθ
=+ +nn
θθ θθ
θ
sin cos
sin
22
22
2
Supplementary Exercises 10 341

9. Call the diagonal matrix D. Then
We need only check that (UD)* = (UD)–1. But
and
Hence (UD)* = (UD)–1 and so UD is unitary.
11. Show the eigenvalues of a unitary matrix have modulus one.
Proof:Let Abe unitary. Then A–1 = A*.
Let
λ
be an eigenvalue of A, with corresponding eigenvector .
Then Ax2= (Ax)*(Ax) = (x*A*)(Ax) = x*(A–1A)x= x*x= ,
but also
Ax 2=
λ
x2= (
λ
x)*(
λ
x) = (
λ
)(x*x)
Since λand are scalars ( λ)(x*x) = |λ|
2x2. So, |λ|
2= 1, and hence the eigenvalues
of Ahave modulus one.
λ
λ
λ
x2
x
DD
z
z
z
I
n
=
=
1
2
2
2
2
00
00
00
…
…
…
()*()( )()UD UD DU UD DD==
−1
()*() *
UD UD D U DU DU
TTT
====
−1
342 Supplementary Exercises 10
...
...
...

EXERCISE SET 11.1
1. (a) Substituting the coordinates of the points into Eq. (4) yields
which, upon cofactor expansion along the first row, yields –3x+ y+ 4 = 0; that is,
y= 3x– 4.
(b) As in (a),
yields 2x+ y– 1 = 0 or y= –2x+ 1.
3. Using Eq. (10) we obtain
xxyyxy
22 1
000001
001011
400201
41025251
16 4 1
−
−−
−4411
0
−
=
xy1
011
111
0
−
=
xy1
111
221
0−=
343

which is the same as
by expansion along the second row (taking advantage of the zeros there). Add column five
to column three and take advantage of another row of all but one zero to get
.
Now expand along the first row and get 160x2+ 320xy + 160(y2+ y) – 320x= 0; that is,
x2+ 2xy + y2– 2x+ y= 0, which is the equation of a parabola.
7. Substituting each of the points (x1, y1), (x2, y2), (x3, y3), (x4, y4), and (x5, y5) into the
equation
c1x2+ c2xy + c3y2+ c4x+ c5y+ c6= 0
yields
These together with the original equation form a homogeneous linear system with a non-
trivial solution for c1, c2,…, c6. Thus the determinant of the coefficient matrix is zero,
which is exactly Eq. (10).
9. Substituting the coordinates (xi, yi, zi) of the four points into the equation c1(x2+ y2+ z2)
+ c2x+ c3y+ c4z+ c5= 0 of the sphere yields four equations, which together with the
above sphere equation form a homogeneous linear system for c1,…, c5with a nontrivial
solution. Thus the determinant of this system is zero, which is Eq. (12).
cx cxy cycxcyc
cx
11
2
211 31
2
41 51 6
15
2
0+++++=
+
.
ccxy cy cxcyc
255 35
2
45 55 6 0++++=.
xxyyyx
22
4002
410202
16 4 0 4
0
+
−
−
=.
xxyyxy
22
00101
40020
4102525
16 4 1 4 1
0
−
−−
−−
=
344 Exercise Set 11.1

10. Upon substitution of the coordinates of the three points (x1, y1), (x2, y2) and (x3, y3), we
obtain the equations:
c1y + c2x2+ c3x+ c4= 0.
c1y1+ c2x1
2+ c3x1+ c4= 0.
c1y2+ c2x2
2+ c3x2 + c4= 0.
c1y3+ c2x3
2+ c3x3+ c4 = 0.
This is a homogeneous system with a nontrivial solution for c1, c2, c3, c4, so the determinant
of the coefficient matrix is zero; that is,
yxx
yxx
yxx
yxx
2
11
2
1
22
2
2
33
2
3
1
1
1
1
0=.
Exercise Set 11.1 345

EXERCISE SET 11.2
1.
Applying Kirchhoff’s current law to node Ain the figure yields
I1= I2+ I3.
Applying Kirchhoff’s voltage law and Ohm’s law to Loops 1 and 2 yields
5I1+ 13I2= 8
and
9I3– 13I2+ 5I3= 3.
In matrix form these three equations are
with solution
III
123
255
317
97
317
158
317
===,,.
111
5130
01314
1
2
3
−−
−
I
I
I
=
0
8
3
loop 1
loop 2
node A
5 Ω
5 Ω
13 Ω
9 Ω
3 V
8 V
–
–
+
+
I1
I2
I3
347
3.
Node Agives I1+ I3= I2.
Loop 1 gives –4I1– 6I2= –1.
Loop 2 gives 4I1– 2I3= –2.
In system form we have
with solution
III
123
5
22
7
22
6
11
=− = =,,.
111
460
402
1
2
3
−
−−
−
I
I
I
==−
−
0
1
2
loop 1 loop 2
node A
4 Ω
6 Ω
2 Ω
2 V
1 V
–
–
+
+
I1
I2
I3
348 Exercise Set 11.2
5.
After setting I5= 0 we have that:
node Agives I1= I3
node Bgives I2= I4
loop 1 gives I1R1= I2R2
loop 2 gives I3R3= I4R4.
From these four equations it easily follows that R4= R3R2/R1.
loop 1
loop 2
node AE node B
I1I2
R2
R5
R1
R3R4
I3I4
I5
I0
–
+
Exercise Set 11.2 349

EXERCISE SET 11.3
1.
In the figure, the feasible region is shown and the extreme points are labelled. The values
of the objective function are shown in the following table:
Thus the maximum, 22/3, is attained when x1= 2 and x2= 2/3.
(3/2, 1)
(2, 2/3)
(2, 0)(0, 0)
x1 = 2
x2
x1
x2 = 1
2x1 + 3x2 = 6
(1/2, 1)
351
Extreme point Value of
(x1, x2)z= 3x1+ 2x2
(0, 0) 0
(1/2, 1) 7/2
(3/2, 1) 13/2
(2, 2/3) 22/3
(2, 0) 6
3.
The feasible region for this problem, shown in the figure, is unbounded. The value of
z= –3x1+ 2x2cannot be minimized in this region since it becomes arbitrarily negative
as we travel outward along the line –x1+ x2= 1; i.e., the value of zis –3x1+ 2x2=
–3x1+ 2(x1+ 1) = –x1+ 2 and x1can be arbitrarily large.
5.
The feasible region and its extreme points are shown in the figure. Though the region is
unbounded, x1and x2are always positive, so the objective function z= 7.5x1+ 5.0x2
is also. Thus, it has a minimum, which is attained at the point where x1= 14/9 and
x2= 25/18. The value of zthere is 335/18. In the problem’s terms, if we use 7/9 cups of
milk and 25/18 ounces of corn flakes, a minimum cost of 18.6¢ is realized.
x2
x1
x1 = 3/2 3x1 – 2x1 = 0
x1 – 2x2 = 0
4x1 + 2x2 = 9
(3/2, 9/4)
(14/9, 25/18)
(40/21, 20/21)
x1 +x2 =
1
8
1
10
1
3
(3/2, 3/2)
3x1 – x2 = –5
2x1 + 4x2 = 12
–x1 + x2 = 1
x1
x2
352 Exercise Set 11.3
7. Letting x1be the number of Company A’s containers shipped and x2the number of
Company B’s, the problem is
Maximize z= 2.20x1+ 3.00x2
subject to
40x1+ 50x2≤37,000
2x1+ 3x2≤2,000
x1≥0
x2≥0.
The feasible region is shown in the figure. The vertex at which the maximum is attained
is x1= 550 and x2= 300, where z= 2110.
9. Let x1be the number of pounds of ingredient Aused and x2the number of pounds of
ingredient B. Then the problem is
Minimize z= 8x1+ 9x2
subject to
2x1+ 5x2≥10
2x1+ 3x2≥8
6x1+ 4x2≥12
x1≥0
x2≥0
40x1 + 50x2 = 37,000
(550, 300)
(0, 0) (925, 0)
2x1 + 3x2 = 2000
x2
x1
(0, 666 )
2
3
Exercise Set 11.3 353
Though the feasible region shown in the figure is unbounded, the objective function is
always positive there and hence must have a minimum. This minimum occurs at the vertex
where x1= 2/5 and x2= 12/5. The minimum value of zis 124/5 or 24.8¢.
11.
The level curves of the objective function –5x1+ x2are shown in the figure, and it is readily
seen that the objective function remains bounded in the region.
z decreasing
x2
x1
z increasing
(0,3)
x2
x1
(2/5, 12/5)
(5/2, 1)
6x1 + 4x2 = 12 2x1 + 3x2 = 8 2x1 + 5x2 = 10
(5, 0)
354 Exercise Set 11.3

EXERCISE SET 11.4
1. The number of oxen is 50 per herd, and there are 7 herds, so there are 350 oxen. Hence the
total number of oxen and sheep is 350 + 350 = 700.
3. Note that this is, effectively, Gaussian elimination applied to the augmented matrix
5. (a) From equations 2 through n, xj= aj– n(j= 2, . . ., n). Using these equations in
equation 1 gives
x1+ (a2– x1) + (a3– x1) + . . . + (an– x1) = a1
x1= (a2+ a3+ . . . + an– a1)/(n– 2)
Given xin terms of the known quantities nand the ai. Then we can use
xj= aj– n(j= 2, . . ., n) to find the other xi.
(b) Exercise 7.(b) may be solved using this technique.
7. (a) The system is x+ y= 1000, (1/5)x– (1/4)y= 10, with solution x= 577 and 7/9 staters,
and y= 422 and 2/9 staters.
(b) The system is G+ B= (2/3)60, G+ T= (3/4)60, G+ I= (3/5)60, G+ B+ T+ I= 60,
with solution (in minae) G= 30.5, B= 9.5, T= 14.5, and I= 5.5.
(c) The system is A= B+ (1/3)C, B= C+ (1/3)A, C= (1/3)B+ 10, with solution A= 45,
B= 37.5, and C= 22.5.
1110
114 7
355


EXERCISE SET 11.5
1. We have 2b1= M1, 2b2= M2, …, 2bn–1 = Mn–1 from (14).
Inserting in (13) yields
6a1h+ M1= M2
6a2h+ M2= M3
6an–2h+ Mn–2 = Mn–1,
from which we obtain
Now S′′ (xn)= Mn, or from (14), 6an–1h+ 2bn–1 = Mn.
Also, 2bn–1 = Mn–1 from (14) and so
6an–1h+ Mn–1 = Mn
aMM
h
aMM
h
aMM
h
n
nn
121
2
32
2
12
6
6
6
=−
=−
=−
−−−
.
357

or
Thus we have
for i= 1, 2, … , n– 1. From (9) and (11) we have
aih3+ bih2+ cih+ di= yi+1,i= 1, 2, … , n – 1.
Substituting the expressions for ai, bi, and difrom (14) yields
cih+ yi= yi+1, i= 1, 2, …, n– 1. Solving for cigives
for i= 1, 2, … , n– 1.
3. (a) Given that the points lie on a single cubic curve, the cubic runout spline will agree
exactly with the single cubic curve.
(b) Set h= 1 and
x1= 0 , y1= 1
x2= 1 , y2= 7
x3= 2 , y3= 27
x4= 3 , y4= 79
x5= 4 , y5= 181.
Then
6(y1– 2y2+ y3)/h2= 84
6(y2– 2y3+ y4)/h2= 192
6(y3– 2y4+ y5)/h2= 300
cyy
h
MM
h
i
ii i i
=−−−
++11
2
6
MM
hhMh
ii i+−
++
132
62
aMM
h
i
i
=−
+1
6
aMM
h
n
nn
−−
=−
11
6.
358 Exercise Set 11.5

and the linear system (24) for the cubic runout spline becomes
Solving this system yields
M2= 14.
M3= 32.
M4= 50.
From (22) and (23) we have
M1= 2M2– M3= –4.
M5= 2M4– M3= 68.
Using (14) to solve for the ai’s, bi’s, ci’s, and di’s we have
a1= (M2– M1)/6h= 3
a2= (M3– M2)/6h= 3
a3= (M4– M3)/6h= 3
a4= (M5– M4)/6h= 3
b1= M1 /2 = –21
b2= M2 /2 = 171
b3= M3 /2 = 161
b4= M4 /2 = 251
600
141
006
84
192
2
3
4
=
M
M
M3300
.
Exercise Set 11.5 359

c1= (y2– y1)/h– (M2+ 2M1)h/6 = 55
c2= (y3– y2)/h– (M3+ 2M2)h/6 = 10
c3= (y4– y3)/h– (M4+ 2M3)h/6 = 33
c4= (y5– y4)/h– (M5+ 2M4)h/6 = 74
d1= y1= 1.
d2= y2= 7.
d3= y3= 27.
d4= y4= 79.
For 0 ≤x≤1 we have
S(x) = S1(x) = 3x3– 2x2+ 5x + 1.
For 1 ≤x≤2 we have
S(x) = S2(x) = 3(x– 1)3+ 7(x– 1)2+ 10(x– 1) + 7
= 3x3– 2x2+ 5x+ 1.
For 2 ≤x≤3 we have
S(x) = S3(x) = 3(x– 2)3+ 16(x– 2)2+ 33(x– 2) + 27
= 3x3– 2x2+ 5x+ 1.
For 3 ≤x≤4 we have
S(x) = S4(x) = 3(x– 3)3+ 25(x– 3)2+ 74(x– 3) + 79
= 3x3– 2x2+ 5x+ 1.
Thus S1(x) = S2(x) = S3(x) = S4(x),
or S(x) = 3x3– 2x2+ 5x+ 1 for 0 ≤x≤4.
360 Exercise Set 11.5

5. The linear system (24) for the cubic runout spline becomes
Solving this system yields
M2= –.0000186.
M3= –.0000131.
M4= –.0000106.
From (22) and (23) we have
M1= 2M2– M3= –.0000241.
M5= 2M4– M3= –.0000081.
Solving for the ai’s, bi’s, ci’s and di’s from Eqs. (14) we have
a1= (M2– M1)/6h= .00000009
a2= (M3– M2)/6h= .00000009
a3= (M4– M3)/6h= .00000004
a4= (M5– M4)/6h= .00000004
b1= M1 /2 = –.0000121
b2= M2 /2 = –.0000093
b3= M3 /2 = –.0000066
b4= M4 /2 = –.0000053
600
141
006
000
2
3
4
=
−.
M
M
M
11116
0000816
0000636
−
−
.
.
.
Exercise Set 11.5 361

c1= (y2– y1)/h– (M2+ 2M1)h/6 = .000282
c2= (y3– y2)/h– (M3+ 2M2)h/6 = .000070
c3= (y4– y3)/h– (M4+ 2M3)h/6 = .000087
c4= (y5– y4)/h– (M5+ 2M4)h/6 = .000207
d1= y1= .99815.
d2= y2= .99987.
d3= y3= .99973.
d4= y4= .99823.
The resulting cubic runout spline is
Assuming the maximum is attained in the interval [0, 10], we set S′(x) equal to zero in this
interval:
S′(x) = .00000027x2– .0000186x+ .000070.
To three significant digits the root of this quadratic in the interval [0, 10] is 4.00 and
S(4.00) = 1.00001.
7. (a) Since S(x1)= y1and S(xn)= yn, then from S(x1)= S(xn)we have y1= yn.
By definition S′′(x1)= M1and S′′(xn)= Mn, and so from S′′(x1)= S′′(xn)we have
M1= Mn.
Sx
xx
()
.().().
=
+− + +00000009 10 0000121 10 0
32
000282 10 99815 10 0
00000009 3
().,
.()
xx
x
++ −≤≤
−..() .().,
.
0000093 000070 99987 0 10
0
2
xx x++≤≤
00000004 10 0000066 10 000087
32
(). (). (xxx−− − + −−+ ≤≤
−−
10 99973 10 20
00000004 20 00
3
). ,
.().
x
x000053 20 000207 20 99823 20 30
2
(). ().,xx x−+ −+ ≤≤..
362 Exercise Set 11.5

From (5) we have
S′(x1)= c1
S′(xn)= 3an–1h2+ 2bn–1h+ cn–1.
Substituting for c1, an–1, bn–1, cn–1 from Eqs. (14) yields
S′(x1)= (y2– y1)/h– (M2+ 2M1)h/6
S′(xn)= (Mn– Mn–1)h/2 + Mn–1h
+ (yn– yn–1)/h– (Mn+ 2Mn–1)h/6.
Using Mn= M1and yn= y1, the last equation becomes
S′(xn)= M1h/3 + Mn–1h/6 + (y1– yn–1)/h.
From S′(x1)= S′(xn)we obtain
(y2– y1)/h– (y1– yn–1)/h= M1h/3 + Mn–1h/6 + (M2+ 2M1)h/6
or
4M1+ M2+ Mn–1 = 6(yn–1 – 2y1+ y2)/h2.
(b) Eqs. (15) together with the three equations in part (a) of the exercise statement give
4M1 + 4M2 + Mn–1 = 6(yn–1 – 2y1+ y2)/h2
4M1 + 4M2 + M3= 6(y1– 2y2+ y3)/h2
4M2 +4M3+ M4= 6(y2– 2y3+ y4)/h2
Mn–3 + 4Mn–2+ Mn–1 = 6(yn–3– 2yn–2+ yn–1)/h2
M1+ 4Mn–2 + 4Mn–1 = 6(yn–2 – 2yn–1 + y1)/h2.
Exercise Set 11.5 363

This linear system for M1, M2,…, Mn–1 in matrix form is
4100 0001
1410 0000
0141 0000
00
...
...
...
000 0141
1000 0014
1
2
...
...
M
M
MM
M
M
h
yy
n
n
n
3
2
1
2
1
6
2
−
−
−
=
−112
123
234
321
2
2
2
2
+
−+
−+
−+
−−−
−
y
yyy
yyy
yyy
y
nnn
n
−−+
−
211
yy
n
364 Exercise Set 11.5

EXERCISE SET 11.6
1. (a)
Continuing in this manner yields
(b) Pis regular because all of the entries of Pare positive. Its steady-state vector q
solves (P– I)q= 0; that is,
This yields one independent equation, .6q1– .5q2= 0, or q1= q2.Solutions are thus
of the form q= s
3. (a) Solve (P– I)q= 0, i.e.,
The only independent equation is yielding Setting
yields
qq =
917
817
s=8
17
qq =
98
1.s
2
3qq
12
3
4
=,
−
−
=
23 34
23 34
0
0
1
2
.
q
q
56
1
1
5
61
6
11
51
=
+
==.Set toobtainsqq 11
611
.
5
6
−
−
=
..
.. .
65
65
0
0
1
2
q
q
xxxx
() ()
.
.
.
.
45
4546
5454
45454
54546
=
=
and
.
xx(3) =
.
.,
454
546
xxxxxxxx
() () ( ) ()
.
.,.
.
10 2 1
4
6
46
54
==
==
PP
.
365

(b) As in (a), solve
i.e., .19q1= .26q2. Solutions have the form
Set to get
(c) Again, solve
by reducing the coefficient matrix to row-echelon form:
yielding solutions of the form
Set to get
5. Then since the row sums of
Pare 1. Thus (Pq)i= qi for all i.
Ppq kpkpk
iij j
j
k
ij
j
k
ij
j
k
qq
()
====
== =
∑∑ ∑
11 1
11 1
,
Let qq=
11 1
kk k
T
.
qq =
319
419
12 19
.
s=12
19
qq =
14
13
1
s.
10 14
01 13
00 0
−
−
−
−
−
23 12 0
13 1 0
13 12 14
1
2
3
q
q
q
=
0
0
0
qq =
26 45
19 45 .
s=19
45
qq =
26 19
1s.
−
−
=
..
..
19 26
19 26
0
0
1
2
q
q
366 Exercise Set 11.6

7. Let x= [x1x2]Tbe the state vector, with x1= probability that John is happy and
x2=probability that John is sad. The transition matrix Pwill be
since the columns must sum to one. We find the steady state vector for Pby solving
i.e., Let and get so 10/13 is the
probability that John will be happy on a given day.
qq =
10 13
313 ,
s=3
13
1
5
2
3
10 3
1
12
qq s==
,.so qq
−
−
=
15 23
15 23
0
0
1
2
,
q
q
P=
45 23
15 13
Exercise Set 11.6 367


EXERCISE SET 11.7
1. Note that the matrix has the same number of rows and columns as the graph has vertices,
and that ones in the matrix correspond to arrows in the graph. We obtain
3. (a) As in problem 2, we obtain
P2
P4
P1
P3
((aa))((bb))
0001
1011
1101
0000
011 00
0000
11
10010
00100
00100
01 01 00
1
((cc))
000000
01 0111
000001
000001
001010
369

(b) m12 = 1, so there is one 1-step connection from P1to P2.
So m12
(2) = 2 and m12
(3) = 3 meaning there are two 2-step and three 3-step connections
from P1to P2by Theorem 1. These are:
1-step: P1→P2
2-step: P1→P4→P2and P1→P3→P2
3-step: P1→P2→ P1→P2, P1→P3→P4→P2,
and P1→P4→P3→P2.
(c) Since m14 = 1, m14
(2) = 1 and m14
(3) = 2, there are one 1-step, one 2-step and two 3-step
connections from P1to P4. These are:
1-step: P1→P4
2-step: P1→P3→P4
3-step: P1→P2→P1→P4and P1→P4→P3→P4.
5. (a) Note that to be contained in a clique, a vertex must have “two-way” connections with
at least two other vertices. Thus, P4could not be in a clique, so { P1, P2, P3} is the only
possible clique. Inspection shows that this is indeed a clique.
(b) Not only must a clique vertex have two-way connections to at least two other vertices,
but the vertices to which it is connected must share a two-way connection. This
consideration eliminates P1and P2, leaving { P3, P4, P5} as the only possible clique.
Inspection shows that it is indeed a clique.
(c) The above considerations eliminate P1, P3and P7from being in a clique. Inspection
shows that each of the sets
{P2, P4, P6}, { P4, P6, P8}, { P2, P6, P8},{ P2, P4, P8} and { P4, P5, P6} satisfy conditions
(i) and (ii) in the definition of a clique. But note that P8can be added to the first
set and we still satisfy the conditions. P5may not be added, so { P2, P4, P6, P8} is a
clique, containing all the other possibilities except { P4, P5, P6}, which is also a clique.
MM
23
1211
0111
1110
1101
2322
12
=
=and 111
1212
1221
.
370 Exercise Set 11.7

7.
Then
By summing the rows of M+ M2, we get that the power of P1is 2 + 1 + 2 = 5, the power
of P2is 3, of P3is 4, and of P4is 2.
MMM
22
0201
0011
1100
1000
0212
=
+=and 11011
1201
1100
.
M=
0011
1000
0101
0100
.
Exercise Set 11.7 371


EXERCISE SET 11.8
1. (a) From Eq. (2), the expected payoff of the game is
(b) If player Ruses strategy [p1p2p3] against player C’s strategy
his payoff will be pAq= (–1/4)p1+ (9/4)p2– p3. Since p1, p2and p3are nonnegative
and add up to 1, this is a weighted average of the numbers –1/4, 9/4 and –1. Clearly
this is the largest if p1= p3= 0 and p2= 1; that is, p= [0 1 0].
(c) As in (b), if player Cuses [q1q2q3q4]Tagainst , we get pAq= –6q1+
3q2+ q3– 1
2q4. Clearly this is minimized over all strategies by setting q1= 1 and
q2= q3= q4= 0. That is q= [1 0 0 0]T.
3. (a) Calling the matrix A, we see a22 is a saddle point, so the optimal strategies are pure,
namely: p= [0 1], q= [0 1]T; the value of the game is a22 = 3.
(b) As in (a), a21 is a saddle point, so optimal strategies are p= [0 1 0], q= [1 0]T;
the value of the game is a21 = 2.
(c) Here, a32 is a saddle point, so optimal strategies are p= [0 0 1], q= [0 1 0]T
and v= a32 = 2.
(d) Here, a21 is a saddle point, so p= [0 1 0 0], q= [1 0 0]Tand v= a21 = –2.
1
201
2
1
4
1
4
1
4
1
4
T
,
pqA=
−−
−
−−
1
201
2
4641
5738
8062
=− .
1
4
1
4
1
4
1
4
5
8
373

5. Let a11 = payoff to Rif the black ace and black two are played = 3.
a12 = payoff to Rif the black ace and red three are played = –4.
a21 = payoff to Rif the red four and black two are played = –6.
a22 = payoff to Rif the red four and red three are played = 7.
So, the payoff matrix for the game is
Ahas no saddle points, so from Theorem 2,
that is, player Rshould play the black ace 65 percent of the time, and
player Cshould play the black two 55 percent of the time. The value of the game is ,
that is, player Ccan expect to collect on the average 15 cents per game.
−3
2
0
qq
;
=
11
20
9
20
T
pp,=
13
20
7
20
A.=−
−
34
67
374 Exercise Set 11.8

EXERCISE SET 11.9
1. (a) Calling the given matrix E, we need to solve
This yields , that is, p= s[1 3/2]T. Set s= 2 and get p= [2 3]T.
(b) As in (a), solve
In row-echelon form, this reduces to
Solutions of this system have the form p= s[1 5/6 1]T. Set s= 6 and get p=
[6 5 6]T.
(c) As in (a), solve
()
...
...
...
IE−=
−−
−−
−−
pp
65 50 30
25 80 30
40 30 60
=
p
p
p
1
2
3
0
0
0
,,
10 1
01 56
00 0
1
2
3
−
−
=
p
p
p
00
0
0
.
()
//
//
/
IE−=
−
−−
−−
pp
12 0 12
13 1 12
16 1 1
.
p
p
p
1
2
3
0
0
0
=
1
2
1
3
1
2
pp=
()IE p
p
−= −
−
=
pp 12 13
12 13
0
0
1
2
.
375

which reduces to
Solutions are of the form p= s[78/79 54/79 1]T. Let s= 79 to obtain p=
[78 54 79]T.
3. Theorem 2 says there will be one linearly independent price vector for the matrix Eif some
positive power of Eis positive. Since Eis not positive, try E2:
5. Taking the CE, EE, and ME in that order, we form the consumption matrix C, where
cij = the amount (per consulting dollar) of the i-th engineer’s services purchased by the
j-th engineer. Thus,
We want to solve (I– C)x= d, where dis the demand vector, i.e.
In row-echelon form this reduces to
Back-substitution yields the solution x= [1256.48 1448.12 1556.19]T.
123
01 43877
00 1
1
2
3
−−
−
..
.
x
x
x
=
500
785 31
1556 19
.
.
.
123
11 4
341
1
2
3
−−
−−
−−
..
..
..
x
x
x
=
500
700
600
.
C=
023
10 4
340
..
..
..
.
E2
2341
2546
6123
0=
>
.. .
.. .
.. .
.
134 32
01 5479
00 0
1
2
3
−
−
p
p
p =
.
0
0
0
376 Exercise Set 11.9
7. The i-th column sum of Eis eji, and the elements of the i-th column of I– Eare
the negatives of the elements of E, except for the ii-th, which is 1 – eii. So, the i-th
column sum of I– Eis 1 – eji = 1 – 1 = 0. Now, (I– E)Thas zero row sums, so
the vector x= [1 1 …1]T solves (I– E)Tx= 0. This implies det(I– E)T= 0. But
det(I– E)T= det(I– E), so (I– E)p= 0 must have nontrivial (i.e., nonzero) solutions.
9. (I) Let ybe a strictly positive vector, and x= (I– C)–1y. Since Cis productive
(I– C)–1 ≥0, so x= (I– C)–1y≥0. But then (I– C)x= y> 0, i.e., x– Cx> 0,
i.e., x> Cx.
(II) Step 1:Since both x* and Care ≥0, so is Cx*. Thus x* > Cx* ≥0.
Step 2:Since x* > Cx*, x* – Cx* > 0. Let εbe the smallest element in x* – Cx*, and
Mthe largest element in x*. Then x* – Cx* > 2M
ε
—–x* > 0, i.e., x* – 2M
ε
—–x* > Cx*.
Setting λ= 1– 2M
ε
—– < 1, we get Cx* < λx*.
Step 3:First, we show that if x> y, then Cx> Cy. But this is clear since (Cx)i=
Now we prove Step 3 by induction on n, the case n= 1
having been done in Step 2. Assuming the result for n– 1, then Cn–1x* < λn–1x*.
But then Cnx* = C(Cn–1x*) < C(λn–1x*) = λn–1(Cx*) < λn–1(λx*) = λnx*,
proving Step 3.
Step 4: Clearly, Cnx* ≥0 for all n. So we have
Denote the elements of Then we have for all i. But
–
cij ≥0 and x* < 0 imply –
cij = 0 for all iand j, proving Step 4.
0
1
=
=
∑cx
ij j
j
n*
lim .
n
n
ij
Cc
→∞ by
00≤≤= =
→∞ →∞ →∞
lim * lim * , lim *
n
n
n
n
n
n
CCxxi.e., x
λ
00.
cx cy Cy
ij j
j
n
ij j
j
n
i
==
∑∑
>=
11
()
.
j
n
=
∑
1
j
n
=
∑
1
Exercise Set 11.9 377

Step 5:By induction on n, the case n= 1 is trivial. Assume the result true for n– 1.
Then
(I – C)(I + C + C2+ …+ Cn–1) = (I – C)
(I + C + …+ Cn–2)+ (I – C)Cn–1= (I – Cn–1)+ (I – C)Cn–1
= I – Cn–1+ Cn–1– Cn,
= I – Cn,
proving Step 5.
Step 6:First we show (I– C)–1 exists. If not, then there would be a nonzero
vector zsuch that Cz= z. But then Cnz= zfor all n, so z=lim
n→∞ Cnz= 0, a
contradiction, thus I– Cis invertible. Thus, I+ C+ …+ Cn–1 = (I– C)–1(I– Cn),
so S= lim
n→∞ (I– C)–1(I– Cn) = (I– C)–1 (I– lim
n→∞ Cn) = (I– C)–1, proving
Step 6.
Step 7:Since Sis the (infinite) sum of nonnegative matrices, Sitself must be non-
negative.
Step 8:We have shown in Steps 6 and 7 that (I– C)–1 exists and is nonnegative,
thus Cis productive.
378 Exercise Set 11.9

EXERCISE SET 11.10
1. Using Eq. (18), we calculate
So all the trees in the second class should be harvested for an optimal yield (since
s= 1000) of $15,000.
3. Assume p2= 1, then Yld2== .28s. Thus, for all the yields to be the same we
must have
p3s/(.28–1 + .31–1) = .28s
p4s/(.28–1 + .31–1 + .25–1) = .28s
p5s/(.28–1 + .31–1 + .25–1 + .23–1) = .28s
p6s/(.28–1 + .31–1 + .25–1 + .23–1 + .27–1) = .28s
s
.28 1
(
)
−
Yld ss
Yld ss
2
3
30
215
50
23
2
100
7.
==
=
+
=
379

Solving these sucessively yields p3= 1.90, p4= 3.02, p5= 4.24 and p6= 5.00. Thus the
ratio
p2p3p4p5p6= 1 1.90 3.02 4.24 5.00 .
5. Since yis the harvest vector, N= yiis the number of trees removed from the forest.
Then Eq. (7) and the first of Eqs. (8) yield N= g1x1, and from Eq. (17) we obtain
Ngs
g
g
g
g
s
gg
kk
.
=
++⋅⋅⋅+
=
+⋅⋅⋅+
−−
1
1
2
1
111
111
i
n
=
∑
1
380 Exercise Set 11.10