Introduction To Information Retrieval IR Solution Manual
IR-Solution-Manual
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 119 [warning: Documents this large are best viewed by clicking the View PDF Link!]
Preliminary draft (c)2007 Cambridge UP
An
Introduction
to
Information
Retrieval
Christopher D. Manning
Prabhakar Raghavan
Hinrich Schütze
Cambridge University Press
Cambridge, England
Preliminary draft (c)2007 Cambridge UP
DRAFT!
DO NOT DISTRIBUTE WITHOUT PRIOR PERMISSION
©2007 Cambridge University Press
By Christopher D. Manning, Prabhakar Raghavan & Hinrich Schütze
Printed on December 12, 2007
Website: http://www.informationretrieval.org/
Comments, corrections, and other feedback most welcome at:
informationretrieval@yahoogroups.com
Preliminary draft (c)2007 Cambridge UP
v
Solutions to exercises
This document contains solutions to most exercises in Introduc-
tion to Information Retrieval. The solutions were provided by
a student and many have not been checked by the authors yet.
Please send comments and corrections to informationretrieval
(at) yahoogroups.com .
Requests for this document should be directed to the address
giveninthesection“Problemsets”athttp://informationretrieval.org.
Please do not distribute these solutions without prior permis-
sion.
Preliminary draft (c)2007 Cambridge UP

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. vii
Boolean retrieval
?Exercise 0.1 []
Draw the inverted index that would be built for the following document collection.
(See Figure 1.3 for an example.)
Doc 1 new home sales top forecasts
Doc 2 home sales rise in july
Doc 3 increase in home sales in july
Doc 4 july new home sales rise
SOLUTION. Inverted Index: forecast->1 home->1->2->3->4 in->2->3
increase->3 july->2->3 new->1->4 rise->2->4 sale->1->2->3->4 top->1
Exercise 0.2 []
Consider these documents:
Doc 1 breakthrough drug for schizophrenia
Doc 2 new schizophrenia drug
Doc 3 new approach for treatment of schizophrenia
Doc 4 new hopes for schizophrenia patients
a. Draw the term-document incidence matrix for this document collection.
b. Draw the inverted index representation for this collection, as in Figure 1.3 (page 7).
SOLUTION.
Term-Documentmatrix:d1d2d3d4Approach0010breakthrough1000
drug1100for1011hopes0001new0111of0010patients0001
schizophrenia1111treatment0010
Inverted Index: Approach -> 3 breakthrough ->1 drug ->1->2 for ->1->3-
>4 hopes ->4 new -.>2->3->4 of ->3 patients ->4 schizophrenia ->1->2->3->4
treatment >3
Exercise 0.3 []
For the document collection shown in Exercise 1.2, what are the returned results for
these queries:
a. schizophrenia AND drug

Preliminary draft (c)2007 Cambridge UP
viii Boolean retrieval
b. for AND NOT(drug OR approach)
SOLUTION.
(i) doc1, doc2 (ii) doc4
?Exercise 0.4 []
For the queries below, can we still run through the intersection in time O(x+y),
where xand yare the lengths of the postings lists for Brutus and Caesar?Ifnot,what
can we achieve?
a. Brutus AND NOT Caesar
b. Brutus OR NOT Caesar
SOLUTION. a. Time is O(x+y). Instead of collecting documents that oc-
cur in both postings lists, collect those that occur in the first one and not in
the second. b. Time is O(N) (where N is the total number of documents in the
collection) assuming we need to return a complete list of all documents satis-
fying the query. This is because the length of the results list is only bounded
by N, not by the length of the postings lists.
Exercise 0.5 []
Extend the postings merge algorithm to arbitrary Boolean query formulas. What is
its time complexity? For instance, consider:
c. (Brutus OR Caesar)AND NOT (Anthony OR Cleopatra)
Can we always merge in linear time? Linear in what? Can we do better than this?
SOLUTION. We can always intersect in O(qN)where q is the number
of query terms and N the number of documents, so the intersection time is
linear in the number of documents and query terms. Since the tightest bound
for the size of the results list is N, the number of documents, you cannot do
better than O(N).
Exercise 0.6 []
We can use distributive laws for AND and OR to rewrite queries.
a. Show how to rewrite the above query into disjunctive normal form using the dis-
tributive laws.
b. Would the resulting query be more or less efficiently evaluated than the original
form of this query?
c. Is this result true in general or does it depend on the words and the contents of
the document collection?

Preliminary draft (c)2007 Cambridge UP
ix
SOLUTION. Query in disjunctive normal form: (brutus and not anthony
and not cleopatra) or (caesar and not anthony and not cleopatra). In this case,
disjunctive normal form is more efficient than conjunctive normal form. In
the former case, we compute intersections first and then, in the last step, one
union of two postings lists that (hopefully) are small. In the latter case, we
start with a union of postings lists and have to deal with potentially large
intermediate results.
The above reasoning is probably not true for some words, e.g., (rare-word-1
or rare-word-2) and not (hong or kong), assuming hong and kong are very
frequent and occur in the same documents.
The above is not true if there are only negated query words in the disjunctive
normal form.
Exercise 0.7 []
Recommend a query processing order for
d. (tangerine OR trees)AND (marmalade OR skies)AND (kaleidoscope OR eyes)
given the following postings list sizes:
Term Postings size
eyes 213312
kaleidoscope 87009
marmalade 107913
skies 271658
tangerine 46653
trees 316812
SOLUTION. Using the conservative estimate of the length of unioned
postings lists, the recommended order is: (kaleidoscope OR eyes) (300,321)
AND (tangerine OR trees) (363,465) AND (marmalade OR skies) (379,571)
However, depending on the actual distribution of postings, (tangerine OR
trees) may well be longer than (marmalade OR skies) because the two com-
ponents of the former are more asymmetric. For example, the union of 11 and
9990 is expected to be longer than the union of 5000 and 5000 even though
the conservative estimate predicts otherwise.
S. Singh’s solution
1.7Time for processing : (i) (tangerine OR trees) = O(46653+316812) =
O(363465) (ii) (marmalade OR skies) = O(107913+271658) = O(379571) (iii)
(kaleidoscope OR eyes) = O(46653+87009) = O(300321)
Order of processing: a. Process (i), (ii), (iii) in any order as first 3 steps (total
time for these steps is O(363465+379571+300321) in any case)
b. Merge (i) AND (iii) = (iv): In case of AND operator, the complexity
of merging postings list depends on the length of the shorter postings list.
Therefore, the more short the smaller postings list, the lesser the time spent.
The reason for choosing (i) instead of (ii) is that the output list (iv) is more
probable to be shorter if (i) is chosen.
c. Merge (iv) AND (ii): This is the only merging operation left.

Preliminary draft (c)2007 Cambridge UP
xBoolean retrieval
Exercise 0.8 []
If the query is:
e. friends AND romans AND (NOT countrymen)
how could we use the frequency of countrymen in evaluating the best query evaluation
order? In particular, propose a way of handling negation in determining the order of
query processing.
SOLUTION. For very frequent negated terms, use N-(length of postings
list) instead of (length of postings list). For infrequent negated terms, use
(length of postings list) for ordering. Process the latter group last. (Need to
say what to do with very frequent non-negated terms.)
Exercise 0.9 []
For a conjunctive query, is processing postings lists in order of size guaranteed to be
optimal? Explain why it is, or give an example where it isn’t.
SOLUTION. Theorderisnotguaranteedtobeoptimal. Considerthree
terms with postings list sizes s1 = 100, s2 = 105 and s3 = 110. Suppose the in-
tersection of s1 and s2 has length 100 and the intersection of s1 and s3 length
0. The ordering s1, s2, s3 requires 100+105+100+110=315 steps through the
postings lists. The ordering s1,s3,s2 requires 100+110+0+0=210 steps through
the postings lists.
Exercise 0.10 []
Write out a postings merge algorithm, in the style of Figure 1.6 (page 11), for an xOR y
query.
SOLUTION. UNION(x, y)
1answer<-()
2while x!=NIL and y!=NIL
3do if docID(x)=docID(y)
4 then ADD(answer,docID(x))
5x<-next(x)
6y<-next(y)
7elseifdocID(x)<docID(y)
8 then ADD(answer,docID(x))
9x<-next(x)
10 else ADD(answer,docID(y))
11 y<-next(y)
12 return(answer)
Exercise 0.11 []
How should the Boolean query xAND NOT ybe handled? Why is naive evaluation
of this query normally very expensive? Write out a postings merge algorithm that
evaluates this query efficiently.

Preliminary draft (c)2007 Cambridge UP
xi
SOLUTION.
A naive evaluation of the query x AND (NOT y) would be to calculate (NOT
y) first as a new postings list, which takes O(N) time, and the merge it with
x. Therefore, the overall complexity will be O(N).
An efficient postings merge algorithm to evaluate x AND (NOT y) is:
MERGE(x, y, AND NOT)
1answer<- ( )
2while x!=NIL and y!=NIL
3do if docID(x)=docID(y)
4 then x<- next(x)
5y<-next(y)
6 else if docID(x)<docID(y)
7 then ADD(answer,docID(x))
8x<-next(x)
9elsey<-next(y)
10 return(answer)
?Exercise 0.12 []
Write a query using Westlaw syntax which would find any of the words professor,
teacher,orlecturer inthesamesentenceasaformoftheverbexplain.
SOLUTION. Query = professor teacher lecturer /s explain!
Exercise 0.13 []
Try using the Boolean search features on a couple of major web search engines. For
instance, choose a word, such as burglar,andsubmitthequeries(i)burglar,(ii)burglar
AND burglar, and (iii) burglar OR burglar. Look at the estimated number of results and
top hits. Do they make sense in terms of Boolean logic? Often they haven’t for major
search engines. Can you make sense of what is going on? What about if you try
different words? For example, query for (i) knight,(ii)conquer,andthen(iii)knight OR
conquer. What bound should the number of results from the first two queries place
on the third query? Is this bound observed?
Preliminary draft (c)2007 Cambridge UP
xii Boolean retrieval
SOLUTION.
Following are the observations when certain queries were tried on popular
search engines:
Search Engine/Query(Number of hits in millions)burglarburglar AND bur-
glarburglar OR burglar Google6.52.16.5 Yahoo12.60.312.6 AskJeeves2.42.85
INFERENCES: When the operator AND is used in a query, Google prompts
not to use that because it includes all terms of a query by default which im-
plies it treats AND as a boolean operator. Yahoo and AskJeeves treat the
term AND as a normal term and not as a Boolean operator as shown by
the top results and the total number of hits. AskJeeves unexpectedly gives
higher number of results with AND than just burglar, which I think, is not
a good behavior. In case of Google, the top documents returned with AND
had the term burglar more than once which tells that query processing does
not include redundant terms removal. The term OR is treated as a Boolean
operator by Google and Yahoo. AskJeeves returns almost twice the num-
ber of documents with the term OR than without it. I cant find a reason for
that.(Maybe most documents returned are redundant)
Search Engine/Query(Number of hits in millions)knightconquerknight
AND conquerknight OR conquer Google87322107 Yahoo1294350.9
AskJeeves2390.835
INFERENCES: The number of hits for knight AND conquer should be less
than for knight or conquer separately which is observed in all 3 searches.
The number of hits for knight OR conquer should be more than for knight or
conquer separately which is observed in all 3 searches.

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. xiii
The term vocabulary and postings
lists
?Exercise 0.14 []
Are the following statements true or false?
a. In a Boolean retrieval system, stemming never lowers precision.
b. In a Boolean retrieval system, stemming never lowers recall.
c. Stemming increases the size of the vocabulary.
d. Stemming should be invoked at indexing time but not while processing a query.
SOLUTION. a. False. Stemming can increase the retrieved set without
increasing the number of relevant docuemnts. b. True. Stemming can only
increase the retrieved set, which means increased or unchanged recall. c.
False. Stemming decreases the size of the vocabulary. d. False. The same
processing should be applied to documents and queries to ensure matching
terms.
Exercise 0.15 []
Suggest what normalized form should be used for these words (including the word
itself as a possibility):
a. ’Cos
b. Shi’ite
c. cont’d
d. Hawai’i
e. O’Rourke

Preliminary draft (c)2007 Cambridge UP
xiv The term vocabulary and postings lists
SOLUTION.
a. cos (Reason: Number of Google results for Cos , Cos ,cos and cos are
exactly same. This is true for Yahoo too.)
b. shiite (Reason: On Yahoo and Google, shiite gives more results than shi-
ite. According to Wikipedia and www.dictionary.reference.com , both Shiite,
shiite, Shiite and shiite refer to the same single entity.)
c. contd (Reason: This cannot be normalized to contd or continued as that
would bring unwanted results since they mean different things.)
d. hawaii (Reason: Case folding is not an issue here as Hawaii is a proper
noun. hawaii gives more results than hawaii. Both hawaii and hawaii refer to
the same single entity. (Source: Wikipedia, www.dictionary.reference.com))
e. orourke (Reason: same as d applied to terms ORourke and ORourke)
Exercise 0.16 []
The following pairs of words are stemmed to the same form by the Porter stemmer.
Which pairs would you argue shouldn’t be conflated. Give your reasoning.
a. abandon/abandonment
b. absorbency/absorbent
c. marketing/markets
d. university/universe
e. volume/volumes
SOLUTION. a. conflate: very similar semantics b. conflate: very similar
semantics c. don’t conflate: marketing (subject taught at business schools) is
too different from market (e.g., stock market) d. don’t conflate: university
(higher learning) too different from universe (the world) e. conflate: same
semantics in most contexts (exception: degree of loudness)
Exercise 0.17 []
For the Porter stemmer rule group shown in (2.1):
a. What is the purpose of including an identity rule such as SS →SS?
b. Applying just this rule group, what will the following words be stemmed to?
circus canaries boss
c. What rule should be added to correctly stem pony?
d. The stemming for ponies and pony might seem strange. Does it have a deleterious
effect on retrieval? Why or why not?
SOLUTION.
a. The purpose of including an identity such as SS->SS is to prevent the
wrongstemmingofwordslikecaressusingtherules->nothing.(thelongest
suffix rule comes into play here)i.e. to prevent the longest suffix rule from
harming the stemming process.
b. circus->circu, canaries->canar, boss->boss
c. y->i
d. Note: I can’t get this question clearly.

Preliminary draft (c)2007 Cambridge UP
xv
?Exercise 0.18 []
Why are skip pointers not useful for queries of the form xOR y?
SOLUTION.
IN queries of the form “x OR y”, it is essential to visit every docID in the
posting lists of either terms, thus killing the need for skip pointers.
Exercise 0.19 []
We have a two-word query. For one term the postings list consists of the following 16
entries:
[4,6,10,12,14,16,18,20,22,32,47,81,120,122,157,180]
and for the other it is the one entry postings list:
[47].
Work out how many comparisons would be done to intersect the two postings lists
with the following two strategies. Briefly justify your answers:
a. Using standard postings lists
b. Using postings lists stored with skip pointers, with a skip length of √P,assug-
gested in Section 2.3.
SOLUTION.
Applying MERGE on the standard postings list, comparisons will be made
unless either of the postings list end i.e. till we reach 47 in the upper postings
list, after which the lower list ends and no more processing needs to be done.
Number of comparisons = 11
b. Using skip pointers of length 4 for the longer list and of length 1 for the
shorter list, the following comparisons will be made: 1. 4 & 47 2. 14 & 47 3.
22 & 47 4. 120 & 47 5. 81 & 47 6. 47 & 47 Number of comparisons = 6
Exercise 0.20 []
Consider a postings intersection between this postings list, with skip pointers:
35915
24 39 60 68 75 81 84 89 92 96 97 100 115
and the following intermediate result postings list (which hence has no skip pointers):
3 5 89 95 97 99 100 101
Trace through the postings intersection algorithm in Figure 2.10 (page 37).
a. How often is a skip pointer followed (i.e., p1is advanced to skip(p2))?

Preliminary draft (c)2007 Cambridge UP
xvi The term vocabulary and postings lists
b. How many postings comparisons will be made by this algorithm while intersect-
ing the two lists?
c. How many postings comparisons would be made if the postings lists are inter-
sected without the use of skip pointers?
SOLUTION.
a. The skip pointer is followed once. (from 24 to 75).
b. 19 comparisons are made. (Let (x,y) denote a posting compari-
son. The comparisons are :(3,3),(5,5),(9,89),(15,89),(24,89),(75,89),(75,89),
(92,89),(81,89),(84,89),(89,89),(92,95),(115,95),(96,95),(96,97),(97,9),(100,99),(100,100),(115,101))
c.19
?Exercise 0.21 []
Assume a biword index. Give an example of a document which will be returned
for a query of New York University but is actually a false positive which should not be
returned.
SOLUTION.
Document=”Some alumni had arrived from New York. University faculty
said that Stanford is the best place to study....”.
Exercise 0.22 []
Shown below is a portion of a positional index in the format: term: doc1: position1,
position2, . . . ;doc2:position1, position2, . . . ;etc.
angels:2:36,174,252,651;4:12,22,102,432;7:17;
fools:2:1,17,74,222;4:8,78,108,458;7:3,13,23,193;
fear:2:87,704,722,901;4:13,43,113,433;7:18,328,528;
in:2:3,37,76,444,851;4:10,20,110,470,500;7:5,15,25,195;
rush:2:2,66,194,321,702;4:9,69,149,429,569;7:4,14,404;
to:2:47,86,234,999;4:14,24,774,944;7:199,319,599,709;
tread:2:57,94,333;4:15,35,155;7:20,320;
where:2:67,124,393,1001;4:11,41,101,421,431;7:16,36,736;
Which document(s) if any meet each of the following queries, where each expression
within quotes is a phrase query?
a. “fools rush in”
b. “fools rush in” AND “angels fear to tread”
SOLUTION. Answer (a): All three documents (2, 4, and 7) satisfy the
query. Answer (b): Only document 4.
Exercise 0.23 []
Consider the following fragment of a positional index with the format:
word: document: position, position, . . .;document:position,...
...

Preliminary draft (c)2007 Cambridge UP
xvii
Gates:1:3;2:6;3:2,17;4:1;
IBM:4:3;7:14;
Microsoft:1:1;2:1,21;3:3;5:16,22,51;
The /koperator, word1 /kword2 finds occurrences of word1 within kwords of word2 (on
either side), where kis a positive integer argument. Thus k=1 demands that word1
be adjacent to word2.
a. Describe the set of documents that satisfy the query Gates /2 Microsoft.
b. Describe each set of values for kfor which the query Gates /kMicrosoft returns a
different set of documents as the answer.
SOLUTION. a. 1,3
b. {k=1}gives {3};{2, 3, 4}gives {1, 3};{x:x≥5}gives {1, 2, 3}.
Exercise 0.24 []
Consider the general procedure for merging two positional postings lists for a given
document, to determine the document positions where a document satisfies a /k
clause (in general there can be multiple positions at which each term occurs in a sin-
gle document). We begin with a pointer to the position of occurrence of each term
and move each pointer along the list of occurrences in the document, checking as we
do so whether we have a hit for /k. Each move of either pointer counts as a step. Let
Ldenote the total number of occurrences of the two terms in the document. What is
the big-O complexity of the merge procedure, if we wish to have postings including
positions in the result?
SOLUTION.
O((m+n)L) where m and n are the sizes of the postings lists where sizes are
measured by just the docIDs and not positions.
Exercise 0.25 []
Consider the adaptation of the basic algorithm for intersection of two postings lists
(Figure 1.6, page 11) to the one in Figure 2.12 (page 42), which handles proximity
queries. A naive algorithm for this operation could be O(PLmax2),wherePis the
sum of the lengths of the postings lists (i.e., the sum of document frequencies) and
Lmax is the maximum length of a document (in tokens).
a. Go through this algorithm carefully and explain how it works.
b. What is the complexity of this algorithm? Justify your answer carefully.
c. For certain queries and data distributions, would another algorithm be more effi-
cient? What complexity does it have?

Preliminary draft (c)2007 Cambridge UP
xviii The term vocabulary and postings lists
SOLUTION. It’s an O(PkLmax)algorithm.
Keep a moving window of postings w2for one of the lists. Add next postings
to end of window if there is no match. After adding a posting, check for
all postings in the other window if they meet the proximity constraint. If
yes, add them to the result set. Delete the first posting of the window, if its
proximity to the last posting in the other window is below k.Therecanbe
at most kentries in the window. Each new posting is compared to at most k
entries. Thus, this algorithm is O(k(S1+S2)).Soproximityqueriescanbe
handled in linear time.
c. If cft1<kthen one can simply test the cft1×cft2possible posting pairs to
see if they are within k.
Exercise 0.26 []
Supposewewishtouseapostingsintersectionproceduretodeterminesimplythe
list of documents that satisfy a /kclause, rather than returning the list of positions,
as in Figure 2.12 (page 42). For simplicity, assume k≥2. Let Ldenote the total
number of occurrences of the two terms in the document collection (i.e., the sum of
their collection frequencies). Which of the following is true? Justify your answer.
a. The merge can be accomplished in a number of steps linear in Land independent
of k, and we can ensure that each pointer moves only to the right.
b. The merge can be accomplished in a number of steps linear in Land independent
of k, but a pointer may be forced to move non-monotonically (i.e., to sometimes
back up)
c. The merge can require kL steps in some cases.
SOLUTION. The merge can determine /kin Lmonotonic moves. (If the
pointers’ positions do not satisfy the /kclause, advance the pointer currently
pointing to the smaller position in the document, and repeat.)
Exercise 0.27 []
How could an IR system combine use of a positional index and use of stop words?
What is the potential problem, and how could it be handled?
SOLUTION.
Is the problem referred to in this question is the problem faced in construct-
ing the positional index after removal of stop words as this preprocessing
changes the positions of terms in the original text? As far as the first part
of the question is concerned, can you give a hint of what kind of use is the
question looking for? I am assuming the answer of the question is not the
following: Phrasal queries can handled using both of them. For any query,
remove the stop-words and merge the positional indexes of the remaining
terms looking for exact phrasal match by determining relative positions.
Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. xix
Dictionaries and tolerant
retrieval
?Exercise 0.28
In the permuterm index, each permuterm vocabulary term points to the original vo-
cabulary term(s) from which it was derived. How many original vocabulary terms
can there be in the postings list of a permuterm vocabulary term?
SOLUTION.
One. (If it weren’t for the $ terminal symbol, we could have multiple original
vocabulary terms resulting from rotations of the same permuterm vocabu-
lary term, e.g., leaf and flea.)
Exercise 0.29
Write down the entries in the permuterm index dictionary that are generated by the
term mama.
SOLUTION.
mama$,ama$m,ma$ma,a$mam,$mama.
Exercise 0.30
If you wanted to search for s*ng in a permuterm wildcard index, what key(s) would
one do the lookup on?
SOLUTION. ng$s*
Exercise 0.31
Refer to Figure 3.4; it is pointed out in the caption that the vocabulary terms in the
postings are lexicographically ordered. Why is this ordering useful?
SOLUTION. A lexicographic ordering will make the merging of the two
k-grams lists efficient, i.e. O(x+y)steps where xand yare the sizes of the
lists.
Exercise 0.32
Consider again the query fi*mo*er from Section 3.2.1. What Boolean query on a bigram
index would be generated for this query? Can you think of a term that matches the
permuterm query in Section 3.2.1, but does not satisfy this Boolean query?

Preliminary draft (c)2007 Cambridge UP
xx Dictionaries and tolerant retrieval
SOLUTION. The Boolean query is $f AND fi AND mo AND er AND r$.
The term filibuster will match the permuterm query in Section 3.2.1, but does
not satisfy this Boolean query.
Exercise 0.33
Give an example of a sentence that falsely matches the wildcard query mon*h if the
search were to simply use a conjunction of bigrams.
SOLUTION. His personality is moonish.
?Exercise 0.34
If |S|denotes the length of string S, show that the edit distance between s1and s2is
never more than max{|s1|,|s2|}.
SOLUTION.
Consider two character strings s1 and s2. Without any loss in generality,
let us assume that l1=length(s1)<l2=length(s2).Fortransforming
s1intos2,we can replace each character of s1bythefirstl1charactersof
s2 and insert the remaining characters of s2attheendofs1.The number of
operations incurred is l2=max(l1, l2).
Exercise 0.35
Compute the edit distance between paris and alice. Write down the 5 ×5arrayof
distances between all prefixes as computed by the algorithm in Figure 3.5.
SOLUTION.
a l i c e
0 1 1 2 2 3 3 4 4 5 5
p1
1
12
21
23
2 2
34
3 3
45
4 4
56
5 5
a2
2
12
31
23
2 2
34
3 3
45
4 4
56
5 5
r3
3
32
42
23
32
34
3 3
45
4 4
56
5 5
i4
4
43
53
3 3
43
24
42
4 5
3 3
5 6
4 4
s5
5
54
64
4 4
54
43
53
34
43
45
4 4
Exercise 0.36
Write pseudocode showing the details of computing on the fly the Jaccard coefficient
while scanning the postings of the k-gram index, as mentioned on page 61.

Preliminary draft (c)2007 Cambridge UP
xxi
SOLUTION. Jaccard (query, t) 1. A = set of k-grams of t 2. B = set
of k-grams of query 3. count=0 4. for i = 1 to length(B) 5. list = post-
ingslist of B[i] 6. if (list contains t) 7. count++ 8. Jaccard co-efficient =
count/(length(A)+length(B)-count)
Exercise 0.37
Compute the Jaccard coefficients between the query bord and each of the terms in
Figure 3.7 that contain the bigram or.
SOLUTION.
3.6 Jaccard co-efficients between the following terms:
a. bord and border : 3/5 b. bord and lord : 2/4 c. bord and morbid : 1/7 d.
bord and sordid : 2/6
Exercise 0.38
Consider the four-term query catched in the rye and suppose that each of the query
terms has five alternative terms suggested by isolated-term correction. How many
possible corrected phrases must we consider if we do not trim the space of corrected
phrases, but instead try all six variants for each of the terms?
SOLUTION. 6*6*6*6 = 1296
Exercise 0.39
For each of the prefixes of the query — catched,catched in and catched in the —wehave
a number of substitute prefixes arising from each term and its alternatives. Suppose
that we were to retain only the top 10 of these substitute prefixes, as measured by
its number of occurrences in the collection. We eliminate the rest from consideration
for extension to longer prefixes: thus, if batched in is not one of the 10 most common
2-term queries in the collection, we do not consider any extension of batched in as pos-
sibly leading to a correction of catched in the rye. How many of the possible substitute
prefixes are we eliminating at each phase?
SOLUTION. At catched in, we choose 10 out of 36 possible thus eliminat-
ing 26. At catched in the, out of 60 surviving alternatives, we eliminate 50 of
these, and at catched in the rye, we eliminate 50 of the surviving alternatives.
Exercise 0.40
Are we guaranteed that retaining and extending only the 10 commonest substitute
prefixes of catched in will lead to one of the 10 commonest substitute prefixes of catched
in the?
SOLUTION. No. None of the 10 commonest substitute prefixes of catched
in may lead to a phrase with catchedinthe.
?Exercise 0.41
Find two differently spelled proper nouns whose soundex codes are the same.

Preliminary draft (c)2007 Cambridge UP
xxii Dictionaries and tolerant retrieval
SOLUTION. Mary, Nira (Soundex code = 5600).
Exercise 0.42
Find two phonetically similar proper nouns whose soundex codes are different.
SOLUTION. Chebyshev, Tchebycheff.

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. xxiii
Index construction
?Exercise 0.43
If we need nlog2ncomparisons (where nis the number of termID-docID pairs) and
2 disk seeks for each comparison, how much time would index construction for
Reuters-RCV1 take if we used disk instead of memory for storage and an unopti-
mized sorting algorithm (i.e., not an external sorting algorithm)? Use the system
parameters in Table 4.1.
SOLUTION.
Exercise 0.44 []
How would you create the dictionary in blocked sort-based indexing on the fly to
avoid an extra pass through the data?
SOLUTION.
simply accumulate vocabulary in memory using, for example, a hash
?Exercise 0.45
For n=15 splits, r=10 segments and j=3 term partitions, how long would
distributed index creation take for Reuters-RCV1 in a MapReduce architecture? Base
your assumptions about cluster machines on Table 4.1.

Preliminary draft (c)2007 Cambridge UP
xxiv Index construction
SOLUTION.
?Exercise 0.46
For n=2and1≤T≤30, perform a step-by-step simulation of the algorithm in
Figure 4.7. Create a table that shows, for each point in time at which T=2∗ktokens
have been processed (1 ≤k≤15), which of the three indexes I0,...,I3are in use. The
first three lines of the table are given below.
I3I2I1I0
20000
40001
60010
SOLUTION.
I3I2I1I0
20000
40001
60010
80011
10 0100
12 0101
14 0110
16 0111
18 1000
20 1001
22 1010
24 1011
26 1100

Preliminary draft (c)2007 Cambridge UP
xxv
symbol statistic value
N# documents 1,000,000,000
Lave # tokens per document 1000
M# distinct terms 44,000,000
Tab l e 1 Collection statistics for a large collection.
?Exercise 0.47
Can spelling correction compromise document-level security? Consider the case where
a spelling correction is based on documents the user does not have access to.
SOLUTION.
Suggesting a spelling correction that only occurs in documents the user does
not have access to is a security violation.
?Exercise 0.48
Total index construction time in blocked sort-based indexing is broken down in Ta-
ble 4.4. Fill out the time column of the table for Reuters-RCV1 assuming a system
with the parameters given in Table 4.1.
SOLUTION.

Preliminary draft (c)2007 Cambridge UP
xxvi Index construction
step time
1reading of collection (line 4)
210 initial sorts of 107records each (line 5)
3writing of 10 blocks (line 6)
4total disk transfer time for merging (line 7)
5time of actual merging (line 7)
total
Tab l e 2 The five steps in constructing an index for Reuters-RCV1 in blocked
sort-based indexing. Line numbers refer to Figure 4.2.
Exercise 0.49
Repeat Exercise 4.6 for the larger collection in Table 4.3. Choose a block size that is
realistic for current technology (remember that a block should easily fit into main
memory). How many blocks do you need?
SOLUTION.
Exercise 0.50
Assume that we have a collection of modest size whose index can be constructed with
the simple in-memory indexing algorithm in Figure 1.4 (page 8). For this collection,
compare memory, disk and time requirements of the simple algorithm in Figure 1.4
and blocked sort-based indexing.

Preliminary draft (c)2007 Cambridge UP
xxvii
SOLUTION.
Let there be a collection with the following statistics: Number of documents
= 10000 Average number of tokens per document = 1000 Number of terms
= 100000 Avg. bytes per token = 6 Number of non-positional postings =
10 million Size of collection is approximately 60 MB A simple in-memory
indexing algorithm as the one in Fig. 1.4 would proceed in the following
steps: (Assuming the system parameters from table 4.1) a. Parsing (to create
initial postings):Complexity= O(n) where n = number of postings Time taken
= 10,000,000 * = 1 s b. Sorting the postings created alphabetically : O( ) Time
taken = = 24 s c. Merging the same term postings to form postings lists:O(n)
Time taken = 10,000,000 * = 1 s Total Time = 26 s Disk space required initially
=60MB,Memoryrequired=60MB
Block Sort-based indexing Assuming that we have a memory restriction of
10 MB, Number of blocks = 6 Numbero f postingsperblock =(107)/6 =16 ∗
(105)(i)Reading of collection : (2 disk seeks/block * 6 blocks)+(read/write
transfer time for 6 blocks ) =(2∗5∗)∗6+10 ∗(6∗(106)bytes ∗s/byte)=
0.06 + 0.6 = 0.66 s (ii) Using sorting algorithm of O(n* ): Sort time=2 disk
seek/block reading * 6 blocks + read time for 6 blocks + sorting time =
0.66 +(6blocks ∗16 ∗(105)∗log (16 ∗(105)) ∗(10(−7))) = 21 s app. (iii)With
vocabulary size , the reduction in size of the postings database can be worked
out. Vocabulary size of collection = 100000 (given) Total size of blocks
after indexing = 4*100000 + 4 ∗(107)bytes4∗(107)bytes Timeinwriting =
4∗(107)∗(10(−7)) = 4s(iv) Assuming that number of buffers maintained
at a time of merging various parts of blocks =6 Number of disk seeks =
6*6*2(for read/write)=72 Total disk transfer time for merging = disk seek
time + blocks r/w into buffers =(72 ∗5∗)+(4∗(107)∗(10(−7))s/byte ∗2)
= 0.36 + 8 =8.36 s (v)Time of actual merging for 10 sorted blocks =disk
transfer time + processing time ( O(n) where n= total number of postings)
=0.36s.+(105)∗(10(−7))s/processingop.0.4sTotal time=(i)+(II)+(III)+(v)
= 500 s=1482 hrs. 26 s
Memory required is 6 MB at maximum. Disk space required is 60 MB.
Exercise 0.51
Assume that machines in MapReduce have 100 GB of disk space each. Assume fur-
ther that the postings list of the term the has a size of 200 GB. Then the MapReduce
algorithm as described cannot be run to construct the index. How would you modify
MapReduce so that it can handle this case?
SOLUTION. partition by docid as well as term for very frequent terms
Exercise 0.52
For optimal load balancing, the inverters in MapReduce must get segmented postings
files of similar sizes. For a new collection, the distribution of key-value pairs may not
be known in advance. How would you solve this problem?

Preliminary draft (c)2007 Cambridge UP
xxviii Index construction
SOLUTION.
Before the MapReduce, a few documents from the collection can be scanned
manually or using a machine, to find the distribution of terms starting from
various alphabets, in these documents. This distribution can be assumed to
hold for the entire collection and segments of similar sizes can be made using
this statistic.
Exercise 0.53
Apply MapReduce to the problem of counting how often each term occurs in a set of
files. Specify map and reduce operations for this task. Write down an example along
the lines of Figure 4.6.
SOLUTION.
map: input →list(word,1)
reduce: (word,list(1)) →(word,length(list))
Exercise 0.54
We claimed above (page 80) that an auxiliary index can impair the quality of collec-
tion statistics. An example is the term weighting method idf, which is defined as
log(N/dfi)where Nis the total number of documents and dfiis the number of docu-
ments that term ioccurs in (Section 6.2.1, page 117). Show that even a small auxiliary
index can cause significant error in idf when it is computed on the main index only.
Consider a rare term that suddenly occurs frequently (e.g., Flossie as in Tropical Storm
Flossie).
SOLUTION.

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. xxix
Index compression
?Exercise 0.55 []
Assuming one machine word per posting, what is the size of the uncompressed (non-
positional) index for different tokenizations based on Table 5.1? How do these num-
bers compare with Table 5.6?
SOLUTION.
Size of the uncompressed index(non-positional postings) for Reuters -RCV1:
Assuming 12/3 bytes per posting (as assumed in previous chapters)- Unfil-
tered size=1320/3 MB After excluding numbers, size=1208/3 MB After case
folding, size = 1163/3 MB 30 stop words removed = 1000/3 MB 150 stop
words removed = 8040/3 MB After Stemmimg, size = 7657/3 MB
?Exercise 0.56
Estimate the space usage of the Reuters dictionary with blocks of size k=8and
k=16 in blocked dictionary storage.
SOLUTION. Space usage of the Reuters Dictionary: For k=8, reduction in
space = (400000/8 ) *13=0.65 MB Space used=10.8-0.65=10.15 MB For k=16,
reduction in space = (400000/16 ) *29=0.725 MB Space used=10.8-0.725=10.1
MB
Exercise 0.57
Estimate the time needed for term lookup in the compressed dictionary of Reuters
with block sizes of k=4 (Figure 5.6, b), k=8andk=16. What is the slowdown
compared to k=1 (Figure 5.6, a)?

Preliminary draft (c)2007 Cambridge UP
xxx Index compression
SOLUTION.
Vocabulary size of Reuters=400000. Assuming that a step is counted as mov-
ing from one term pointer to the next one in the table or moving from term
to the next in a block Fork =4, Numbero f blocks =100000Numbero f steps =
(1+2+3+4)forblock1+(2+0+2+1+2+2+2+3)forblock2+(3+
0+3+1+3+2+3+3)forblock3+till100000blocks =4∗(1+2+3+.. +
100000)+6∗100000 =2∗(1010)stepsappr. Similarly for k=8, steps = (50000
blocks in this case) For k=16, steps = approximately. Note: These results do
not go with the inference drawn from calculations on an 8 term dictionary in
the text as the dominating factor in a large dictionary is retrieving the first
terms of blocks rather than searching a term within a block.
S. Singh: Let me be the operation costs involved in performing one iteration
of the Binary search (i.e. changing the search area to half the current list).
Let p be the cost of moving one term in a block. So the time complexity of
Binary search algorithm is O(m∗logn+X)where n is the number of blocks
in this case, logarithm is calculated with base 2 and X varies depending on
the number of blocks. kNumber of blocksTime Complexity 1 400000 18.6m+p
4 100000 16.6m+4p 8 50000 15.6m+8p 16 25000 14.6m+16p
?Exercise 0.58 []
ComputevariablebytecodesforthenumbersinTables5.3and5.5.
SOLUTION.
Variable Byte Codes for numbers in Table 5.3 and Table 5.5 Encoding the
gaps and not docIDs: 283042 = 00010001 00100011 10100010 1 = 10000001
107 = 1111011 5 = 10000101 43 = 10101011 252000 = 00001111 00110000
11100000 248100 = 00001111 00010010 10100100 1025 = 00001000 10000001
511 = 00000011 11111111 24 = 10011000 13 = 10001101 9 = 10001001 4 =
10000100
Exercise 0.59 []
Computevariablebyteandγcodes for the postings list 777, 17743, 294068, 31251336.
Use gaps instead of docIDs where possible. Write binary codes in 8-bit blocks.
SOLUTION.
Gap-encoded postings list: 777, 16,966, 276,325, 30,957,268. Variable
byte encoding (comma-separated for readability): 6 137 , 1 4 198
, 16 110 229 , 14 97 61 212 . Binary: 00000110 1001001 00000001
00000100 11000110 00010000 01101110 11100101 00001110 01100001
00111101 11010100 Gamma encoding (comma-separated for read-
ability): 1111111110100001001 , 11111111111111000001001000110
, 1111111111111111110000011011101100101 ,
1111111111111111111111110110110000101111011010100

Preliminary draft (c)2007 Cambridge UP
xxxi
?Exercise 0.60
Consider the postings list 4, 10, 11, 12, 15, 62, 63, 265, 268, 270, 400with a correspond-
ing list of gaps 4, 6, 1, 1, 3, 47, 1, 202, 3, 2, 130. Assume that the length of the postings
list is stored separately, so the system knows when a postings list is complete. Us-
ing variable byte encoding: (i) What is the largest gap you can encode in 1 byte? (ii)
What is the largest gap you can encode in 2 bytes? (iii) How many bytes will the
above postings list require under this encoding? (Count only space for encoding the
sequence of numbers.)
SOLUTION. (i) 127 =27−1 (ii) 16383 =(214−1)(iii) 13
Exercise 0.61
A little trick is to notice that a gap cannot be of length 0 and that the stuff left to encode
after shifting cannot be 0. Based on these observations: (i) Suggest a modification to
variable byte encoding that allows you to encode slightly larger gaps in the same
amount of space. (ii) What is the largest gap you can encode in 1 byte? (iii) What
is the largest gap you can encode in 2 bytes? (iv) How many bytes will the postings
list in Exercise 5.6 require under this encoding? (Count only space for encoding the
sequence of numbers.)
SOLUTION. (i) Before each byte encoding decision, subtract 1 from the
number still to be encoded. (The most common mistake here was to say to
subtract 1 from the whole number rather than for each by byte) (ii) 128(= 27)
(iii) 16512(= 214+27)(iv) Still 13
Exercise 0.62 []
From the following sequence of γcoded gaps, reconstruct first the gap sequence and
then the postings sequence: 1110001110101011111101101111011.
SOLUTION.
Gaps sequence = 9, 6, 3, 49, 7 Postings sequence = 9, 15, 18, 67, 73
Exercise 0.63
γ-codes are relatively inefficient for large numbers (e.g., 1025 in Table 5.5) as they
encode the length of the offset in inefficient unary code. δ-codes differ from γ-codes
δ-CODES in that they encode the first part of the code (length)inγ-code instead of unary code.
The encoding of offset is the same. For example, the δ-code of 7 is 10,0,11 (again, we
add commas for readability). 10,0 is the γ-code for length (2 in this case) and the
encoding of offset (11) is unchanged. (i) Compute the δ-codes for the other numbers
in Table 5.5. For what range of numbers is the δ-code shorter than the γ-code? (ii) γ
code beats variable byte code in Table 5.6 because the index contains stop words and
thus many small gaps. Show that variable byte code is more compact if larger gaps
dominate. (iii) Compare the compression ratios of δcode and variable byte code for
a distribution of gaps dominated by large gaps.

Preliminary draft (c)2007 Cambridge UP
xxxii Index compression
SOLUTION.
i.. Delta codes for the following numbers are: 1 = 0 2 = 0,0 3 = 0,1 4 = 0,0,00
9 = 0,1,001 13 = 0,1,101 24 = 110,00,1000 511 = 1110,000,11111111 Delta codes
are smaller than the gamma codes for all numbers greater than 1.
Exercise 0.64 []
We have defined unary codes as being “10”: sequences of 1s terminated by a 0. In-
terchanging the roles of 0s and 1s yields an equivalent “01” unary code. When this
01 unary code is used, the construction of a γ-code can be stated as follows: 1. Write
Gdown in binary using b=log2j+1 bits. 2. Prepend (b−1)0s. (i) Encode the
numbersinTable5.5inthisalternativeγ-code. (ii) Show that this method produces
a well-defined alternative γ-code in the sense that it has the same length and can be
uniquely decoded.
SOLUTION. (i) exchange 0s and 1s (ii) the arguments for length and
uniqueness apply to this form of gamma code: just exchange 0s and 1s
Exercise 0.65 []
Unary code is not a universal code in the sense defined above. However, there exists
a distribution over gaps for which unary code is optimal. Which distribution is this?
SOLUTION. Unary code is optimal for P(n)=2−nover N.
Exercise 0.66
Give some examples of terms that violate the assumption that gaps all have the same
size (which we made when estimating the space requirements of a γencoded index).
What are general characteristics of these terms?
SOLUTION.
For a news collection like Reuters RCV-1, examples of such terms could be:
tennis, football, music etc. Since the news collection contains news collected
over a period of time, words like tennis and football would occur a lot in
news documents collected during their sports seasons and very rarely in
documents collected at other times. Although general characteristics of these
terms depend on the type of collection we are dealing with and so its diffi-
cult to formulate a common property, these terms could be the ones which
are rare in the collection

Preliminary draft (c)2007 Cambridge UP
xxxiii
Exercise 0.67
Consider a term whose postings list has size n,say,n=10,000. Compare the size of
the γ-compressed gap-encoded postings list if the distribution of the term is uniform
(i.e., all gaps have the same size) vs. its size when the distribution is not uniform.
Which compressed postings list is smaller?
SOLUTION.
encoding the uniform list 13 13 we need 14 bits (Table 5.5)
encodingthenon-uniformlist224weneed12bits(Table5.5)
in this case non-uniform is shorter because small gaps are encoded efficiently
encoding the uniform list 1000 1000 we need ?? bits
encoding the non-uniform list 200 1800 we need ?? bits
(should be longer)
Exercise 0.68
Work out the sum in Equation (5.7) and show it adds up to about 251 MB. Use the
numbers in Table 4.2, but do not round Lc,cand the number of vocabulary blocks.
SOLUTION.
Exercise 0.69
Go through the above calculation of index size and explicitly state all the approxima-
tions that were made to arrive at Expression 5.6.
SOLUTION.
(i) zipf’s law (ii) uniform gap size (iii) others?

Preliminary draft (c)2007 Cambridge UP
xxxiv Index compression
γencoded gap sequence of run 1 1110110111111001011111111110100011111001
γencoded gap sequence of run 2 11111010000111111000100011111110010000011111010101
Tab l e 3 Two gap sequences to be merged in blocked sort-based indexing.
Exercise 0.70
For a collection of your choosing determine the number of documents and terms and
the average length of a document. (i) How large is the inverted index predicted to
be by Equation (5.6)? (ii) Implement an indexer that creates a γ-compressed inverted
index for the collection. How large is the actual index? (iii) Implement an indexer
that uses variable byte encoding. How large is the variable byte encoded index?
SOLUTION. No solution.
Exercise 0.71
To be able to hold as many postings as possible in main memory, it is a good idea to
compress intermediate index files during index construction. (i) This makes merging
runs in blocked sort-based indexing more complicated. As an example, work out the
γencoded merged sequence of the gaps in Table 5.7. (ii) Index construction is more
space-efficient when using compression. Would you also expect it to be faster?
SOLUTION.
(i). Run 1: gap sequence = 14, 87, 199, 5 Posting list = 14, 101, 300, 305
Run 2: gap sequence = 48, 72, 160, 21 Posting list = 48, 120, 280, 301 Merge
list 1 and 2 : 14, 48, 101, 120, 280, 300, 301, 305 Gap sequence of merged
list = 14, 34, 53, 19, 160, 20, 1, 4 Gamma encoding of final sequence =
1110110111110000101111010101111100011111111100100000111100100011000
(ii). When using compression, decoding would have to be done before we
cammergetheblockswhichwouldrequireextratimebutsincealotofdisk
memory transfer time saving is being done by index blocks compression and
a lot of postings can be held simultaneously in the memory, operations like
decoding which will be done inside memory will not cost more than the sav-
ing. So overall it would be faster.
Exercise 0.72
(i) Show that the size of the vocabulary is finite according to Zipf’s law and infinite
according to Heaps’ law. (ii) Can we derive Heaps’ law from Zipf’s law?

Preliminary draft (c)2007 Cambridge UP
xxxv
SOLUTION.
(i) According to Heaps Law, the vocabulary size M keeps growing with the
number of tokens and hence it is infinite. Vocabulary size is a fixed constant
in Zipf’s law. The law assumes that the vocabulary is fixed and finite.
(ii) No, Zipf’s law states that the vocabulary is finite. Thus, it would follow
that Heaps’ law does not hold.
Note that our definition of Zipf’s law states that the exponent is -1. Some-
times the definition is relaxed to include exponents x<−1. In that case, the
vocabulary is infinite.
See also http://www.cs.ru.nl/~bolke/heapsrapp.pdf A Formal Derivation of Heaps’
Law; by D.C. van Leijenhorst and Th. P. van der Weide; to appear in Informa-
tion Sciences, 2004. Block Addressing Indices for Approximate Text Retrieval
(1997) Ricardo Baeza-Yates, Gonzalo Navarro Journal of the American Soci-
ety of Information Science
Preliminary draft (c)2007 Cambridge UP

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. xxxvii
Scoring, term weighting and the
vector space model
?Exercise 0.73
When using weighted zone scoring, is it necessary for all zones to use the same Boo-
lean match function?
SOLUTION. No. For instance, the Boolean score fromthe Title zone could
be 1 when at least half of the query terms occur in that zone and zero oth-
erwise whereas from the Body zone, the Boolean score is 1 when all query
terms occur in the body and zero otherwise.
Exercise 0.74
In Example 6.1 above with weights g1=0.2, g2=0.31 and g3=0.49, what are all the
distinct score values a document may get?
SOLUTION.
possible values: 0.2, 0.31, 0.49, 0.51, 0.8, 0.69, 1.0
Exercise 0.75
Rewrite the algorithm in Figure 6.4 to the case of more than two query terms.
SOLUTION. ZONESCORE(List(q)) 1 float scores[N]=[0] 2 constant g[l] 3
p <- MERGE(List(q)) 4 // MERGE function merges the postings list of all
query terms using algorithm in 1.6 5 // p is the merged postings list of all
query terms 6 While p (is not) NIL 7 Scores[docID[p]]=WeightedZone(p,g) 8
p<- next(p) 9 return(scores)
Exercise 0.76
Write pseudocode for the function WeightedZone for the case of two postings lists in
Figure 6.4.
SOLUTION. WeightedZone(p1,p2,g) 1 s<-() 2 scores[docID(p1)]=0 3
for i<- 1tol 4 s[i] <- BooleanScore(q, docID(p1)) 5 scores[docID(p1)] =
scores[docID(p1)] + g[i]*s[i]

Preliminary draft (c)2007 Cambridge UP
xxxviii Scoring, term weighting and the vector space model
Exercise 0.77
Apply Equation 6.6 to the sample training set in Figure 6.5 to estimate the best value
of gfor this sample.
SOLUTION. g=0.25.
Exercise 0.78
For the value of gestimated in Exercise 6.5, compute the weighted zone score for each
(query, document) example. How do these scores relate to the relevance judgments
in Figure 6.5 (quantized to 0/1)?
SOLUTION. phi g Relevance judgment
11R
23/4NR
33/4R
40NR
51R
63/4R
71/4NR
Exercise 0.79
Why does the expression for gin (6.6) not involve training examples in which sT(dt,qt)
and sB(dt,qt)have the same value?
SOLUTION. In cases where st(dt,qt) and sb(dt,qt) have same values,
score is independent of g and so these cases do not play a role in optimizing
g.
?Exercise 0.80
Why is the idf of a term always finite?
SOLUTION.
dft≥1⇒id ft≤log N⇒id f alwaysf inite
Exercise 0.81
What is the idf of a term that occurs in every document? Compare this with the use
of stop word lists.
SOLUTION.
It is 0. For a word that occurs in every document, putting it on the stop list
has the same effect as idf weighting: the word is ignored.
Exercise 0.82
Consider the table of term frequencies for 3 documents denoted Doc1, Doc2, Doc3 in
Figure 6.9. Compute the tf-idf weights for the terms car, auto, insurance, best, for each
document, using the idf values from Figure 6.8.

Preliminary draft (c)2007 Cambridge UP
xxxix
Doc1 Doc2 Doc3
car 27 424
auto 333 0
insurance 033 29
best 14 017
Figure 1 Table of tf values for Exercise 6.10.
SOLUTION. terms Doc1 Doc2 Doc3 Car 44.55 6.6 39.6 Auto 6.24 68.64 0
Insurance 0 53.46 46.98 Best 21 0 25.5
Exercise 0.83
Can the tf-idf weight of a term in a document exceed 1?
SOLUTION. Yes(as can be seen in exercise 6.10).
Exercise 0.84
How does the base of the logarithm in (6.7) affect the score calculation in (6.9)? How
does the base of the logarithm affect the relative scores of two documents on a given
query?
SOLUTION.
Exercise 0.85
If the logarithm in (6.7) is computed base 2, suggest a simple approximation to the idf
of a term.
SOLUTION. It is the number of bits in the Boolean representation of the
idf.
?Exercise 0.86
If we were to stem jealous and jealousy to a common stem before setting up the vector
space, detail how the definitions of tf and idf should be modified.
SOLUTION. If jealousy and jealous are stemmed to a common term t,
then their tf’s and their df’s would be added together, in computing the tf-idf
weights.

Preliminary draft (c)2007 Cambridge UP
xl Scoring, term weighting and the vector space model
Exercise 0.87
Recall the tf-idf weights computed in Exercise 6.10. Compute the Euclidean nor-
malized document vectors for each of the documents, where each vector has four
components, one for each of the four terms.
SOLUTION. Doc1=(0.897,0.125,0,0.423), Doc2=(0.076,0.786,0.613,0)
Doc3=(0.595,0,0.706,0.383)
Exercise 0.88
Verify that the sum of the squares of the components of each of the document vectors
in Exercise 6.15 is 1 (to within rounding error). Why is this the case?
SOLUTION. Doc1 =0.8972+0.1252+0.4232=0.999;
Doc2 =0.0762+0.7862+0.613 =0.999;
Doc3 =0.5952+0.7062+0.3832=0.999
Because they’re normalized (unit) vectors.
Exercise 0.89
With term weights as computed in Exercise 6.15, rank the three documents by com-
puted score for the query car insurance, for each of the following cases of term weight-
ing in the query:
1. The weight of a term is 1 if present in the query, 0 otherwise.
2. Euclidean normalized idf.
SOLUTION. (i) Term Weights Term Doc1 Doc2 Doc3 car 0.897 0.076 0.595
Auto 0.125 0.786 0 Insurance 0 0.613 0.706 best 0.423 0 0.383
Term ———QU ERY——– ———PR ODUCT- ———- tf W(t,q) Doc1 Doc2
Doc3Car110.8970.0760.595Auto00000Insurance1100.6130best000
00
Score(q,doc1)=0.897, Score(q,doc2)=0.689, Score(q,doc3)=0.595 Ranking = d1,
d2, d3
(ii) Term —–QU ERY——- Idf W(t,q) Car 1.65 0.478 Auto 2.08 0.602 Insurance
1.62 0.47 best 1.5 0.43
Score(q,doc1)=0.686, Score(q,doc2)=0.797, Score(q,doc3)=0.781 Ranking = d2,
d3, d1
?Exercise 0.90
One measure of the similarity of two vectors is the Euclidean distance (or L2distance)EUCLIDEAN DISTANCE between them:
|x−y|=
M
∑
i=1
(xi−yi)2
Given a query qand documents d1,d2, . . ., we may rank the documents diin order
of increasing Euclidean distance from q. Show that if qand the diare all normalized
to unit vectors, then the rank ordering produced by Euclidean distance is identical to
that produced by cosine similarities.

Preliminary draft (c)2007 Cambridge UP
xli
query document
word tf wf df idf qi=wf-idf tf wf di=normalized wf qi·di
digital 10,000
video 100,000
cameras 50,000
Tab l e 4 Cosine computation for Exercise 6.19.
SOLUTION.
∑(qi−wi)2=∑q2
i−2∑qiwi+∑w2
i=2(1−∑qiwi)
Thus: ∑(qi−vi)2<∑(qi−wi)2⇔2(1−∑qivi)<2(1−∑qiwi)⇔∑qivi>
∑qiwi
Exercise 0.91
Compute the vector space similarity between the query “digital cameras” and the
document “digital cameras and video cameras” by filling out the empty columns in
Table 6.1. Assume N=10,000,000, logarithmic term weighting (wf columns) for
query and document, idf weighting for the query only and cosine normalization for
the document only. Treat and as a stop word. Enter term counts in the tf columns.
What is the final similarity score?
SOLUTION. query document
word tf wf df idf qi=wf-idf tf wf di=normalized wf qi·di
digital 11 10,000 3 3 11 0.52 1.56
video 0 0 100,000 2 0 11 0.52 0
cameras 11 50,000 2.32.3 21.30.68 1.56
Similarity score: 1.56 +1.56 =3.12.
Normalized similarity score is also correct: 3.12/length(query) = 3.12/3.78 =
0.825
Exercise 0.92
Show that for the query affection, the relative ordering of the scores of the three doc-
uments in Figure 6.13 is the reverse of the ordering of the scores for the query jealous
gossip.
SOLUTION.
q=affection,v(q)=(1,0,0) V(SaS)=(0.996,0.087,0.017),v(PaP)=(0.993,0.120.0),v(WH)=(0.847,0.466,0.254)
V(q).v(SaS)=0.996 v(q).v(PaP)=0.993 v(q).v(WH)=0.847 So order of scores in
this case is the reverse as in the query jealous gossip .
Exercise 0.93
In turning a query into a unit vector in Figure 6.13, we assigned equal weights to each
of the query terms. What other principled approaches are plausible?

Preliminary draft (c)2007 Cambridge UP
xlii Scoring, term weighting and the vector space model
SOLUTION. We can assign weights to query terms according to their idf
in the collection, or use other collection statistics.
Exercise 0.94
Consider the case of a query term that is not in the set of Mindexed terms; thus our
standard construction of the query vector results in
V(q)not being in the vector space
created from the collection. How would one adapt the vector space representation to
handle this case?
SOLUTION. Omit this term from the query and proceed; its contribution
to the dot product with any document will be zero.
Exercise 0.95
RefertothetfandidfvaluesforfourtermsandthreedocumentsinExercise6.10.
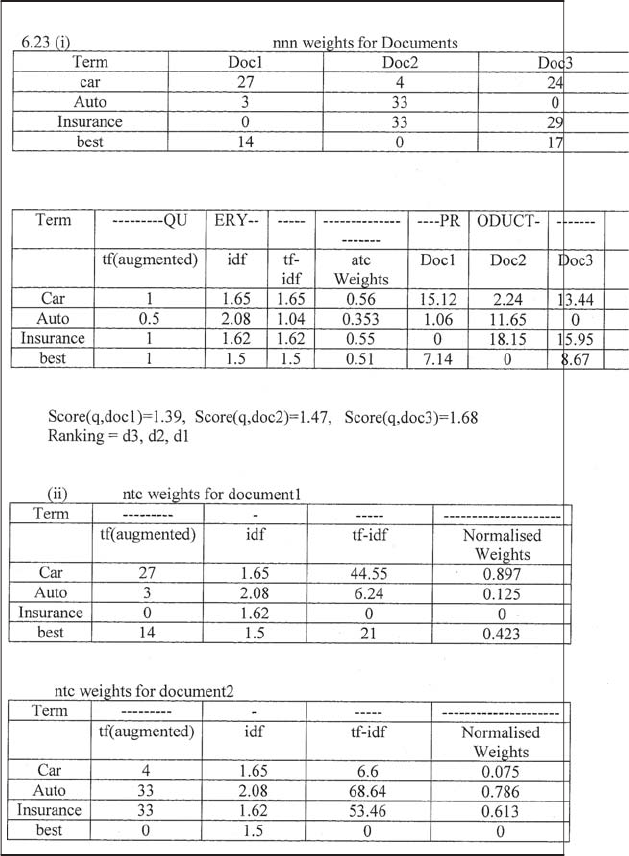
Compute the two top scoring documents on the query best car insurance for each of
the following weighing schemes: (i) nnn.atc;(ii)ntc.atc.
Preliminary draft (c)2007 Cambridge UP
xliii
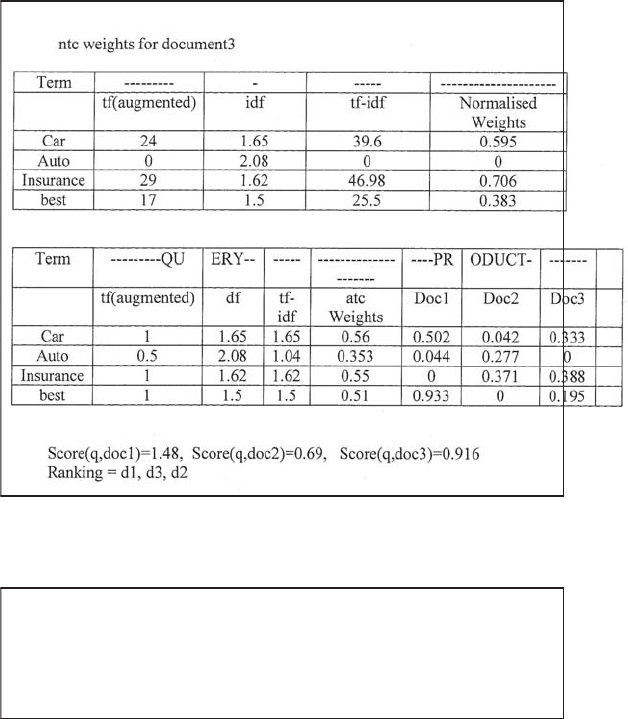
SOLUTION. PART I
Preliminary draft (c)2007 Cambridge UP
xliv Scoring, term weighting and the vector space model
SOLUTION. PART II
Exercise 0.96
Suppose that the word coyote does not occur in the collection used in Exercises 6.10
and 6.23. How would one compute ntc.atc scores for the query coyote insurance?
SOLUTION.
ntc weight contribution by coyote insurance in any document vector =
weight contribution by coyote + weight contribution by insurance = 0 + k(can
be calculated) (since coyote does not occur in any document of the collection)
The atc weight contributed by coyote in the query vector need not be calcu-
lated as the ntc weight for all documents is 0 for coyote.

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. xlv
Computing scores in a complete
search system
?Exercise 0.97
We suggested above (Figure 7.2) that the postings for static quality ordering be in
decreasing order of g(d). Why do we use the decreasing rather than the increasing
order?
SOLUTION. Since documents with higher g(d) have higher scores, a de-
creasing order is good for efficient top-K retrieval.
Exercise 0.98
When discussing champion lists, we simply used the rdocuments with the largest tf
values to create the champion list for t. But when considering global champion lists,
we used idf as well, identifying documents with the largest values of g(d)+tf-idft,d.
Why do we differentiate between these two cases?
SOLUTION. When query = a single term t, union of champion lists for
each term is the same as that of t. Ranking by netscore=g(d)+ tf(d) idf(t,d) is
equivalent to Ranking by netscore=g(d)+ tf(d) So use of global champion list
within m=K suffices for finding K highest scoring documents.
Exercise 0.99
If we were to only have one-term queries, explain why the use of global champion
lists with r=Ksuffices for identifying the Khighest scoring documents. What is a
simple modification to this idea if we were to only have s-term queries for any fixed
integer s>1?
SOLUTION.
For a one-term query, the ordering of documents is independent of the
weight of the term in the query. It only depends on the weight of the term
in the documents. The truncated weight-ordered postings list contains the K
documents with the highest weights. Thus, it is identical to the ranked list
for the one-term query.
Exercise 0.100
Explain how the common global ordering by g(d)values in all high and low lists
helps make the score computation efficient.

Preliminary draft (c)2007 Cambridge UP
xlvi Computing scores in a complete search system
SOLUTION. In the general case, the postings list of query terms are tra-
versed to find the documents which contains all or most of query terms and
then scores are calculated for these documents to find the top K. Thus more
importance is given to v(q) .v(d) in the short listing stage and g(d)is ac-
counted for later. If common global ordering by g(d) is implemented, not
just it increases the efficiency of results but also less documents would have
to undergo score calculation process thereby reducing some work through at
the cost of initial ordering.
Exercise 0.101
Consider again the data of Exercise 6.23 with nnn.atc for the query-dependent scor-
ing. Suppose that we were given static quality scores of 1 for Doc1 and 2 for Doc2.
Determine under Equation (7.2) what ranges of static quality score for Doc3 result in
it being the first, second or third result for the query best car insurance.
SOLUTION.
Let the static quality score of document 3 be x.(x>0)
Document G(d) Score(q,d) Net-score(q,d)
D111.392.39
D221.473.47
D3 x 1.68 x+1.68
a. ForD3torank f irstamongthe3documents,x+1.68 >3.47andx +1.68 >
2.39impliesx +1.68 >3.47impliesx >1.75
b. ForD3toranksecond,x+1.68 <3.47andx +1.68 >2.39implies1.71 <x<
1.75
c. Ford3torankthird,x+1.68 <3.47andx +1.68 <2.39implies0<x<1.71
Exercise 0.102
Sketch the frequency-ordered postings for the data in Figure 6.9.
SOLUTION. car->d1->d3->d2auto->d2->d1->d3insurance-.D2->
d3-> d1 best -> d3 -. D1 ->d2
Exercise 0.103
Let the static quality scores for Doc1, Doc2 and Doc3 in Figure 6.11 be respectively
0.25, 0.5 and 1. Sketch the postings for impact ordering when each postings list is
ordered by the sum of the static quality score and the Euclidean normalized tf values
in Figure 6.11.
SOLUTION. car->d3->d1->d2auto->d2-.D3-.D1insurance->d3
-> d2 -> d1 best -> d3 -> d1 -. D2
Exercise 0.104
The nearest-neighbor problem in the plane is the following: given a set of Ndata
points on the plane, we preprocess them into some data structure such that, given
aquerypointQ, we seek the point in Nthat is closest to Qin Euclidean distance.
Clearly cluster pruning can be used as an approach to the nearest-neighbor problem
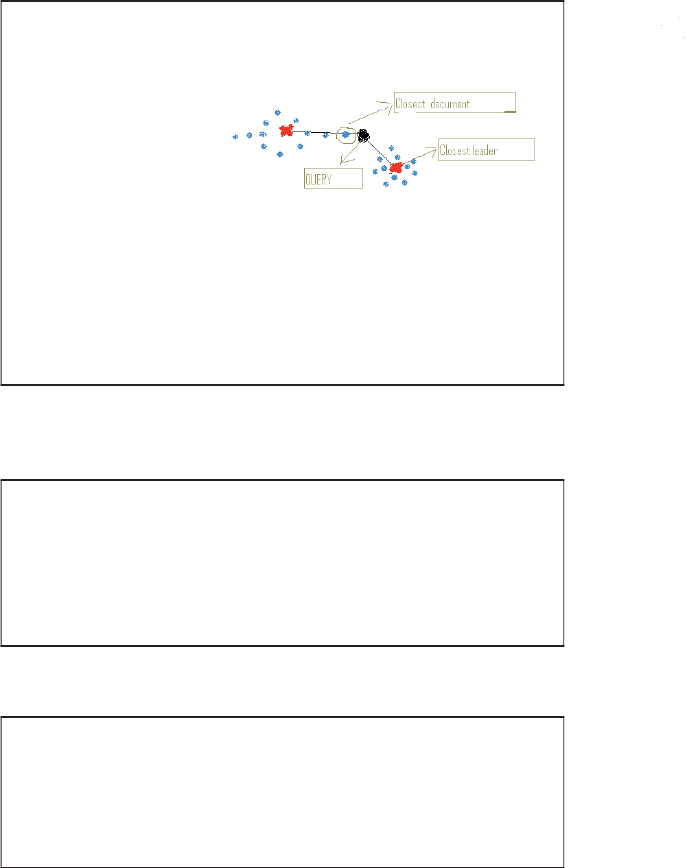
Preliminary draft (c)2007 Cambridge UP
xlvii
in the plane, if we wished to avoid computing the distance from Qto every one of
the query points. Devise a simple example on the plane so that with two leaders, the
answer returned by cluster pruning is incorrect (it is not the data point closest to Q).
SOLUTION.
?Exercise 0.105
Explain how the postings intersection algorithm first introduced in Section 1.3 can be
adapted to find the smallest integer ωthat contains all query terms.
SOLUTION. Move concurrently through the positional postings of all
query terms, until a document D is found that contains all the query terms.
1. Move the cursor on each postings to the first positional occurrence of the
term. 2. Measure the window size to be the distance between the leftmost
and rightmost cursors. 3. Repeat the following until some cursor exits docu-
ment D: 4. Pick the left-most cursor among all postings and move right to the
next occurrence; measure the window size as above. 5. Output the minimum
of all of these measurements.
Exercise 0.106
Adapt this procedure to work when not all query terms are present in a document.
SOLUTION. a. Check whether all k query terms are present in a docu-
ment. If yes, apply algorithm in answer 7.8 b. If k>=2, Make all possible com-
binations of (k-1) query terms and check for a document D which contains
all terms of any of the combinations. If yes, change the query[] to exclude all
query terms not in that combination and recur. If not, repeat step 2 until a
document D is found. If k=1, return all documents containing the remaining
query term.
Preliminary draft (c)2007 Cambridge UP

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. xlix
Evaluation in information
retrieval
?Exercise 0.107 []
An IR system returns 8 relevant documents, and 10 nonrelevant documents. There
are a total of 20 relevant documents in the collection. What is the precision of the
system on this search, and what is its recall?
SOLUTION. Precision = 8/18 = 0.44; Recall = 8/20 =0.4.
Exercise 0.108 []
The balanced F measure (a.k.a. F1) is defined as the harmonic mean of precision and
recall. What is the advantage of using the harmonic mean rather than “averaging”
(using the arithmetic mean)?
SOLUTION.
Since arithmetic mean is more closer to the highest of the two values of pre-
cision and recall, it is not a good representative of both values whereas Har-
monic mean , on the other hand is more closer to min(Precision,Recall).In
case when all documents relevant to a query are returned, Recall is 1 and
Arithmetic mean is more than 0.5 though the precision is very low and the
purpose of the search engine is not served effectively. Since arithmetic mean
is more closer to the highest of the two values of precision and recall, it is not
a good representative of both values whereas Harmonic mean , on the other
hand is more closer to min(Precision,Recall).In case when all documents rel-
evant to a query are returned ,Recall is 1 and Arithmetic mean is more than
0.5 though the precision is very low and the purpose of the search engine is
not served effectively.
Exercise 0.109 []
Derive the equivalence between the two formulas for F measure shown in Equa-
tion (8.5), given that α=1/(β2+1).

Preliminary draft (c)2007 Cambridge UP
lEvaluation in information retrieval
SOLUTION.
?Exercise 0.110 []
What are the possible values for interpolated precision at a recall level of 0?
SOLUTION. 0≤p≤1
Exercise 0.111 []
Must there always be a break-even point between precision and recall? Either show
there must be or give a counter-example.
SOLUTION.
precision = recall iff fp = fn or tp=0. If the highest ranked element is not
relevant, then tp=0 and that is a trivial break-even point.
If the highest ranked element is relevant: The number of false positives in-
creases as you go down the list and the number of false negatives decreases.
As you go down the list, if the item is R, then fn decreases and fp does not
change. If the item is N, then fp increases and fn does not change. At the
beginning of the list fp<fn. At the end of the list fp>fn. Thus, there has to be
abreak-evenpoint.
(One case not covered above: fp=fn=0, tp =1.)
Exercise 0.112 []
What is the relationship between the value of F1and the break-even point?
SOLUTION. At the break-even point: F1=P=R.
Exercise 0.113 []
The Dice coefficient of two sets is a measure of their intersection scaled by their size
DICE COEFFICIENT (giving a value in the range 0 to 1):
Dice(X,Y)= 2|X∩Y|
|X|+|Y|
Show that the balanced F-measure (F1) is equal to the Dice coefficient of the retrieved
and relevant document sets.

Preliminary draft (c)2007 Cambridge UP
li
SOLUTION.
Exercise 0.114 []
Consider an information need for which there are 4 relevant documents in the collec-
tion. Contrast two systems run on this collection. Their top 10 results are judged for
relevance as follows (the leftmost item is the top ranked search result):
System1 RNRNN NNNR R
System 2 N R N N R R R N N N
a. What is the MAP of each system? Which has a higher MAP?
b. Does this result intuitively make sense? What does it say about what is important
in getting a good MAP score?
c. What is the R-precision of each system? (Does it rank the systems the same as
MAP?)
SOLUTION.
a. MAP(System 1) = (1/4)*(1+(2/3)+(3/9)+(4/10)) = 0.6 MAP(System 2) =
(1/4)*(1/2 + 2/5 + 3/6 + 4/7) = 0.493 System 1 has a higher average precision
b. The text says that MAP provides a single figure measure of quality across
recall levels. I am not sure I clearly get what this statement means. For a
good MAP score, it is essential to more relevant documents in the first few
(3-5) retrieved ones
c. R-Precision(system 1) = 1/2 R-Precision(system 2) =1/4 This ranks the
system the same as MAP.
Exercise 0.115 []
The following list of R’s and N’s represents relevant (R) and nonrelevant (N) returned
documents in a ranked list of 20 documents retrieved in response to a query from a
collection of 10,000 documents. The top of the ranked list (the document the system
thinks is most likely to be relevant) is on the left of the list. This list shows 6 relevant
documents. Assume that there are 8 relevant documents in total in the collection.
RRNNN NNNRN RNNNR NNNNR
a. What is the precision of the system on the top 20?
b. What is the F1on the top 20?
c. What is the uninterpolated precision of the system at 25% recall?

Preliminary draft (c)2007 Cambridge UP
lii Evaluation in information retrieval
d. What is the interpolated precision at 33% recall?
e. Assume that these 20 documents are the complete result set of the system. What
is the MAP for the query?
Assume, now, instead, that the system returned the entire 10,000 documents in a
ranked list, and these are the first 20 results returned.
f. What is the largest possible MAP that this system could have?
g. What is the smallest possible MAP that this system could have?
h. In a set of experiments, only the top 20 results are evaluated by hand. The result
in (e) is used to approximate the range (f)–(g). For this example, how large (in
absolute terms) can the error for the MAP be by calculating (e) instead of (f) and
(g) for this query?
SOLUTION.
?Exercise 0.116 []
Below is a table showing how two human judges rated the relevance of a set of 12
documents to a particular information need (0 = nonrelevant, 1 = relevant). Let us as-
sume that you’ve written an IR system that for this query returns the set of documents
{4,5,6,7,8}.
Preliminary draft (c)2007 Cambridge UP
liii
docID Judge 1 Judge 2
10 0
20 0
31 1
41 1
51 0
61 0
71 0
81 0
90 1
10 0 1
11 0 1
12 0 1
a. Calculate the kappa measure between the two judges.
b. Calculate precision, recall, and F1of your system if a document is considered rel-
evant only if the two judges agree.
c. Calculate precision, recall, and F1of your system if a document is considered rel-
evant if either judge thinks it is relevant.
SOLUTION. a.
P(Agree) = 4/12
P(nonrelevant) = 12/24
p(relevant) = 12/24
P(E)=.52+.52=.5
K = (.33 - .5) / .5 = -.34 (unrounded: −1/3)
b.
P=1/5
R=1/2
F=2·1/5 ·1/2/(1/5 +1/2)=2/7
c.
P=1
R=1/2
F=2/3
Preliminary draft (c)2007 Cambridge UP

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. lv
Relevance feedback and query
expansion
?Exercise 0.117
Under what conditions would the modified query qmin Equation 9.3 be the same as
the original query q0? In all other cases, is qmcloser than q0to the centroid of the
relevant documents?
SOLUTION.
Exercise 0.118
Why is positive feedback likely to be more useful than negative feedback to an IR
system? Why might only using one nonrelevant document be more effective than
using several?
SOLUTION.
The idea of feedback system to tell the IR system which documents are rel-
evant to the user and to maximize the return of such documents. Even if
the IR system is not explicitly told that documents d1, d2, etc. are nonrele-
vant, the IR system tries to maximize the precision based upon the relevant
documents feedback which is more important and sufficient in most cases.
If several nonrelevant documents are used for feedback calculation, some of
them might bear some similarity with a few relevant documents (assuming
that the user marks them as nonrelevant based on a few words or sentences
depicted and doesnt process sufficient knowledge about them). In such a
case, some of the properties of relevant documents might not be conveyed
properly to the IR system which results in low precision output. There are
low chances of such a problem if only 1 non- relevant is used.

Preliminary draft (c)2007 Cambridge UP
lvi Relevance feedback and query expansion
Exercise 0.119
Suppose that a user’s initial query is cheap CDs cheap DVDs extremely cheap CDs.The
user examines two documents, d1and d2.Shejudgesd1, with the content CDs cheap
software cheap CDs relevant and d2with content cheap thrills DVDs nonrelevant. As-
sume that we are using direct term frequency (with no scaling and no document
frequency). There is no need to length-normalize vectors. Using Rocchio relevance
feedback as in Equation (9.3) what would the revised query vector be after relevance
feedback? Assume α=1, β=0.75, γ=0.25.
SOLUTION. Term frequencies:
word query qd
1d2
CDs 2 2 0
cheap 3 2 1
DVDs 1 0 1
extremely 1 0 0
software 0 1 0
thrills 0 0 1
For 1.0 ∗q+0.75 ∗
d+1−0.25 ∗
d2,weget:(3.5 4.25 0.75 1 0.75 −0.25)Tor
(7/217/43/413/4 −1/4)T. Negative weights are set to 0. The Rocchio
vector thus is: (3.54.250.7510.750)T.
Exercise 0.120 []
Omar has implemented a relevance feedback web search system, where he is going
to do relevance feedback based only on words in the title text returned for a page (for
efficiency). The user is going to rank 3 results. The first user, Jinxing, queries for:
banana slug
and the top three titles returned are:
banana slug Ariolimax columbianus
Santa Cruz mountains banana slug
Santa Cruz Campus Mascot
Jinxing judges the first two documents Relevant, and the third Not Relevant. Assume
that Omar’s search engine uses term frequency but no length normalization nor IDF.
Assume that he is using the Rocchio relevance feedback mechanism, with α=β=
γ=1. Show the final revised query that would be run. (Please list the vector elements
in alphabetical order.)

Preliminary draft (c)2007 Cambridge UP
lvii
SOLUTION. The vectors are:
qd1d2d3
Ariolimax 0 1 0 0
banana 1 1 1 0
Campus 0 0 0 1
columbianus 0 1 0 0
Cruz 0 0 1 1
Mascot 0 0 0 1
mountains 0 0 1 0
Santa 0 0 1 1
slug 1 1 1 0
Using Rocchio relevance feedback mechanism, with α=β=γ=1, and
after changing negative components back to 0:
qr=[
1
2,2,0,1
2,0,0, 1
2,0,2
]
?Exercise 0.121
In Rocchio’s algorithm, what weight setting for α/β/γdoes a “Find pages like this
one” search correspond to?
SOLUTION. “Find pages like this one” ignores the query and no nega-
tive judgments are used. Hence α=γ=0. This implies β=1.
Exercise 0.122 []
Give three reasons why relevance feedback has been little used in web search.
SOLUTION. i. RF slows down returning results as you need to run two
sequential queries, the second of which is slower to compute than the first.
Web users hate to be kept waiting. ii. RF is mainly used to increase recall,
but web users are mainly concerned about the precision of the top few re-
sults. iii. RF is one way of dealing with alternate ways to express an idea
(synonymy), but indexing anchor text is commonly already a good way to
solve this problem. iv. RF is an HCI failure: it’s too complicated for the great
unwashed to understand.
?Exercise 0.123
If Ais simply a Boolean cooccurrence matrix, then what do you get as the entries in
C?
SOLUTION.
entry cij is the number of times two terms tiand tjcooccur
Preliminary draft (c)2007 Cambridge UP

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. lix
XML retrieval
?Exercise 0.124
Consider computing df for a structural term as the number of times that the structural
term occurs under a particular parent node. Assume the following: the structural
term c,t=author#"Herbert" occurs once as the child of the node squib;thereare
10 squib nodes in the collection; c,toccurs 1000 times as the child of article;thereare
1,000,000 article nodes in the collection. The idf weight of c,tthen is log210/1 ≈3.3
when occurring as the child of squib and log21,000,000/1000 ≈10.0 when occurring
as the child of article. (i) Explain why this is not an appropriate weighting for c,t.
Why should c,tnot receive a weight that is three times higher in squibs than in
articles? (ii) Suggest a better way of computing idf.
SOLUTION.
No solution.
?Exercise 0.125
Write down all the structural terms occurring in the XML document in Figure 10.8.
SOLUTION.
(i) Microsoft (ii) Bill (iii) Gates (iv) title/Microsoft (v) Author/Bill (vi)
Author/Gates (vii) /Book/Title/Microsoft (viii) /Book/Author/Gates (ix)
/Book/Author/Bill
Exercise 0.126
How many structural terms does the document in Figure 10.1 yield?
SOLUTION.
A structural term is a XML path which ends in a single vocabulary term. For
the XML document in fig. 10.1, the vocabulary size for the verse tag is not
known. Assuming it has 6 terms (Will I with wine and wassail), Number
of Structural terms = 3(for Shakespeare) + 3(Macbeth) + 5*2 (macbeth and
castle) + 5*6 (for terms in the verse) = 46
?Exercise 0.127
Find a reasonably sized XML document collection (or a collection using a markup lan-
guage different from XML like HTML) on the web and download it. Jon Bosak’s XML

Preliminary draft (c)2007 Cambridge UP
lx XML retrieval
edition of Shakespeare and of various religious works at http://www.ibiblio.org/bosak/ or
the first 10,000 documents of the Wikipedia are good choices. Create three CAS topics
of the type shown in Figure 10.3 that you would expect to do better than analogous
CO topics. Explain why an XML retrieval system would be able to exploit the XML
structure of the documents to achieve better retrieval results on the topics than an
unstructured retrieval system.
SOLUTION.
(i) //article //content //History [about(., 198! Information re-
trieval)] (ii) //article [about(.,Hendrix)] //content //biography [about(.,
first rays of the rising sun)] (iii)//article // content //community
//fanzine[about(.,fiction)]
Exercise 0.128
For the collection and the topics in Exercise 10.4, (i) are there pairs of elements e1and
e2,withe2a subelement of e1such that both answer one of the topics? Find a case
where (ii) e1(iii) e2is the better answer to the query.
SOLUTION.
(i) e1=//article [about(.,Hendrix)] , e2=//biography [about(., first rays of the
rising sun)] (ii) query = jimi Hendrix (iii) query= first rays
Exercise 0.129
Implement the (i) SIMMERGE (ii) SIMNOMERGE algorithm in Section 10.3 and run it
for the collection and the topics in Exercise 10.4. (iii) Evaluate the results by assigning
binary relevance judgments to the first five documents of the three retrieved lists for
each algorithm. Which algorithm performs better?
SOLUTION.
Pseudocode for searching using No-Merge strategy (a probable answer)
Search Compute structural terms for query S <- ( ) For each structural term
t: S <- all matching structural terms For each matching structural term t (be-
longs to) S For structural term t (belongs to) (S - t) If cr(t,t)> 0 S <- S - t Com-
pute matching weight cr(t, t) Search inverted index with computed terms
and weights Return ranked list
Exercise 0.130
Are all of the elements in Exercise 10.4 appropriate to be returned as hits to a user or
are there elements (as in the example <b>definitely</b> on page 203) that you
would exclude?
SOLUTION.
style attribute in wikipedia
Exercise 0.131
We discussed the tradeoff between accuracy of results and dimensionality of the vec-
tor space on page 207. Give an example of an information need that we can answer

Preliminary draft (c)2007 Cambridge UP
lxi
correctly if we index all lexicalized subtrees, but can’t answer if we only index struc-
tural terms.
SOLUTION.
query= //article [about(., information retrieval)] / history
Exercise 0.132
If we index all structural terms, what is the size of the index as a function of text size?
SOLUTION.
Let T be text size of XML document . By Heaps Law, Vocabulary size
V=k.(Tb)The number of structural terms depends on the structure of the
document. Therefore making the following assumptions, (i) Height of a XML
path leading to a lexicon term = h1 (ii) Number of leaves containing meta-
information (like title, author etc.) is k and height of XML paths leading to
them =h2 Number of structural terms = h1∗V+h2∗k
Exercise 0.133
If we index all lexicalized subtrees, what is the size of the index as a function of text
size?
SOLUTION.
If we view the XML collection as a set of separate documents, then it grows
linear as each new XML document contributes a given number of trees.
If we view the XML collection as one giant XML document, then the number
of index terms has the same order of magnitude as the number of subgraphs
of the tree. That number is exponential in the number of leaves of the tree.
Exercise 0.134
Give an example of a query-document pair for which SIMNOMERGE(q,d)is larger
than 1.0.
SOLUTION.
Take the degenerate case of a query without XML structure consisting of the
single term “gates” and an identical document. There is a single structural
term “gates” we need to consider. weight(q,t,c) of this structural term is
greater than 1 if its idf>1. The normalized weight of the term in the docu-
ment is 1.0. Thus SIMNOMERGE(q,d) is greater than 1.
Preliminary draft (c)2007 Cambridge UP
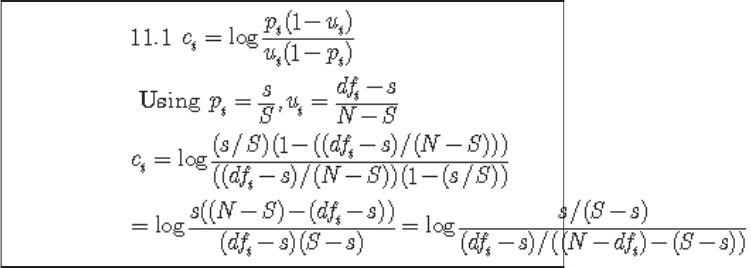
Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. lxiii
Probabilistic information
retrieval
?Exercise 0.135
Work through the derivation of Equation (11.20) from Equations (11.18) and (11.19).
SOLUTION.
Exercise 0.136
What are the differences between standard vector space tf-idf weighting and the BIM
probabilistic retrieval model (in the case where no document relevance information
is available)?
Preliminary draft (c)2007 Cambridge UP
lxiv Probabilistic information retrieval
SOLUTION.
A few differences between standard vector space tf-idf weighting model and
the BIM probabilistic retrieval model on the first iteration are:
a. tf-idf weighting is directly proportional to term frequency of the query
term in the document whereas the BIM just takes into account the absence
or presence of term in the document. Consider the query India Information
Technology on the document set: Document1: Indias Information technol-
ogy sector is booming very fast relative to technology sectors of India. Doc-
ument 2:The Information technology sector of India has grown drastically
over the last few years. Now the tf-idf weighting will give more relevance to
Document 1 whereas the BIM model puts them on the same relevance level.
b. The idf part of the tf-idf weighting keeps the frequently occurring
words(the stop words which cant distinguish between documents) out of
the relevance decision making part as for them idf is approximately is 0. On
the other hand, the BIM treats all terms alike and every word has an equal
say in deciding the relevance.
c. While calculating the relevance of a document, the tf-idf says that the
words occurring in the query but not present in the document have a zero
contribution in the relevance value of the document whereas the BIM counts
their contribution by the fraction of such other documents in the collection
(which are relevant but do not contain this term).
Exercise 0.137 []
Let Xtbe a random variable indicating whether the term tappears in a document.
Suppose we have |R|relevant documents in the document collection and that Xt=1
in sof the documents. Take the observed data to be just these observations of Xtfor
each document in R. Show that the MLE for the parameter pt=P(Xt=1|R=1,q),
that is, the value for ptwhich maximizes the probability of the observed data, is
pt=s/|R|.

Preliminary draft (c)2007 Cambridge UP
lxv
SOLUTION. The probability P(D|μ)will be the product ∏d∈DP(d|μ).
Let θbe pH, the parameter of the model. Then each P(d|μ)is either θ
or 1 −θdepending on whether dis heads or not, respectively. Thus,
P(D|μ)=θNH(1−θ)NT. This is a continuous function of θover [0, 1]and so
it will take its maximum either at 0, 1, or some point in that interval where
∂P(D|μ)
∂θ =0. Note P(D|μ)is zero when θis either 1 or 0, and positive and
non-zero elsewhere in that interval. Thus, we differentiate and get:
∂P(D|μ)
∂θ =∂θNH(1−θ)NT
∂θ
=θNH∂(1−θ)NT
∂θ +(1−θ)NT∂θNH
∂θ
=−θNHNT(1−θ)NT−1+(1−θ)NTNHθNH−1
Setting equal to zero, we get:
θNHNT(1−θ)NT−1=(1−θ)NTNHθNH−1
θNT=(1−θ)NH
NTθ=NH−NHθ
θ=NH
NH+NT
=NH
N
Thus this unique internal solution must be the maximum value over that
interval.
Exercise 0.138
Describe the differences between vector space relevance feedback and probabilistic
relevance feedback.
SOLUTION.
Some differences between vector space (pseudo) relevance feedback and
probabilistic (pseudo) relevance feedback are:
a.In case of the probabilistic (pseudo) relevance feedback, an initial guess is
to be done for the relevant document set under the assumption that all query
terms give same values of document relevance.(i.e. pi is constant) whereas
the vector space feedback system doesnt require any initial assumption or
guess as the relevant document set can be computed over the collection and
the query. b.The vector space feedback system should ideally perform better
by giving improved results in less number of iterations than the probabilistic
feeback system due to the assumptions and guesses
Preliminary draft (c)2007 Cambridge UP

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. lxvii
Language models for information
retrieval
?Exercise 0.139 []
Including stop probabilities in the calculation, what will the sum of the probability
estimates of all strings in the language of length 1 be? Assume that you generate a
word and then decide whether to stop or not (i.e., the null string is not part of the
language).
SOLUTION. No solution.
Exercise 0.140 []
If the stop probability is omitted from calculations, what will the sum of the scores
assigned to strings in the language of length 1 be?
SOLUTION. No solution.
Exercise 0.141 []
What is the likelihood ratio of the document according to M1and M2in Exam-
ple 12.2?
SOLUTION. No solution.
Exercise 0.142 []
No explicit STOP probability appeared in Example 12.2. Assuming that the STOP
probability of each model is 0.1, does this change the likelihood ratio of a document
according to the two models?
SOLUTION. No solution.
Exercise 0.143 []
How might a language model be used in a spelling correction system? In particular,
consider the case of context-sensitive spelling correction, and correcting incorrect us-
ages of words, such as their in Are you their? (See Section 3.5 (page 65) for pointers to
some literature on this topic.)
SOLUTION. No solution.
Preliminary draft (c)2007 Cambridge UP
lxviii Language models for information retrieval
?Exercise 0.144 []
Consider making a language model from the following training text:
the martian has landed on the latin pop sensation ricky martin
a. Under a MLE-estimated unigram probability model, what are P(the)and P(martian)?
b. Under a MLE-estimated bigram model, what are P(sensation|pop)and P(pop|the)?
SOLUTION. No solution.
Exercise 0.145 []
Suppose we have a collection that consists of the 4 documents given in the below
table.
docID Document text
1click go the shears boys click click click
2click click
3metal here
4metal shears click here
Build a query likelihood language model for this document collection. Assume a
mixture model between the documents and the collection, with both weighted at 0.5.
Maximum likelihood estimation (mle) is used to estimate both as unigram models.
Work out the model probabilities of the queries click,shears, and hence click shears for
each document, and use those probabilities to rank the documents returned by each
query. Fill in these probabilities in the below table:
Query Doc 1 Doc 2 Doc 3 Doc 4
click
shears
click shears
What is the final ranking of the documents for the query click shears?
SOLUTION. No solution.
Exercise 0.146 []
Using the calculations in Exercise 12.7 as inspiration or as examples where appro-
priate, write one sentence each describing the treatment that the model in Equa-
tion (12.10) gives to each of the following quantities. Include whether it is present
in the model or not and whether the effect is raw or scaled.
a. Term frequency in a document
b. Collection frequency of a term
c. Document frequency of a term
d. Length normalization of a term

Preliminary draft (c)2007 Cambridge UP
lxix
SOLUTION. No solution.
Exercise 0.147 []
In the mixture model approach to the query likelihood model (Equation (12.12)), the
probability estimate of a term is based on the term frequency of a word in a document,
and the collection frequency of the word. Doing this certainly guarantees that each
term of a query (in the vocabulary) has a non-zero chance of being generated by each
document. But it has a more subtle but important effect of implementing a form of
term weighting, related to what we saw in Chapter 6. Explain how this works. In
particular, include in your answer a concrete numeric example showing this term
weighting at work.
SOLUTION.
The smoothing puts an inverse collection frequency weighting component
into the model.
Suppose we are searching with the query "rare common" where "rare" is a
rare word (its cf is 10 in the 10,000,000 word document collection) and "com-
mon" has cf 10,000. Now suppose we have two documents of length 1000
words: d1 in which "rare" appears once, but not "common", and d2 which
has "common" but not "rare". And assume that the mixture weight between
the two models is 0.5 for simplicity.
Then P("rare common"|d1)=0.5 ∗(0.001 +0.000001)∗0.5 ∗(0+0.001)=
2.5025x10 −7. P("rare common"|d2)=0.5 ∗(0+0.000001)∗0.5 ∗(0.001 +
0.001)=5×10 −10. So, d1 with the rare word ranks much higher than d1
with the common word.
In general, the thing to note is that even though the cf component of the
mixture model is constant over all documents, the effect of it is that for a
high cf word, presence or absence of the word in the document will have
relatively little effect on the probability assigned by the model (e.g., factor of
2 in the example above), whereas for a low cf word, presence or absence of
the word in the document can have a very large effect (factor of almost 1000
in the example)
Preliminary draft (c)2007 Cambridge UP

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. lxxi
Text classification and Naive
Bayes
?Exercise 0.148
Why is |C||V|<|D|Lave in Table 13.2 expected to hold for most text collections?
SOLUTION.
?Exercise 0.149 []
Which of the documents in Table 13.9 have identical and different bag of words rep-
resentations for (a) the Bernoulli model (b) the multinomial model? If there are dif-
ferences, describe them.
SOLUTION. (a) The three documents have identical bag of words repre-
sentations. (b) (1) and (2) are identical, the count of London in the representa-
tion of (3) is 1 instead of 2.
Exercise 0.150
The rationale for the positional independence assumption is that there is no useful
information in the fact that a term occurs in position kof a document. Find exceptions.
Consider formulaic documents with a fixed document structure.
SOLUTION.
Consider the document in Figure 13.9. The term livestock in the topics field
occurs at a fixed position in the document and its semantics is different from
occurrences in other parts of the document.
Preliminary draft (c)2007 Cambridge UP
lxxii Text classification and Naive Bayes
Exercise 0.151
Table 13.3 gives Bernoulli and multinomial estimates for the word the. Explain the
difference.
SOLUTION.
The numerical model calculates P(X=the )by the number of occurrences of
the in the collection which is 5%( large as he is a stop word ). The Bernoulli
model , on the other hand , just calculates the probability by the number of
documents which contain the word the which is 1.0 as all documents will
contain it.
?Exercise 0.152
Consider the following frequencies for the class coffee forfourtermsinthefirst100,000
documents of RCV1:
term N00 N10 N01 N11
brazil 98,012 102 1835 51
council 96,322 133 3525 20
producers 98,524 119 1118 34
roasted 99,824 143 23 10
Select two of these four terms based on (i) χ2(ii) mutual information (iii) frequency.
SOLUTION.
(i) brazil, roasted
(ii) brazil, producer
(iii) brazil, producer
?Exercise 0.153 []
Assume a situation where every document in the test collection has been assigned
exactly one class, and that a classifier also assigns exactly one class to each document.
This setup is called one-of classification (Section 14.5, page 305). Show that in one-of
classification (i) the total number of false positive decisions equals the total number
of false negative decisions and (ii) microaveraged F1and accuracy are identical.
SOLUTION. (i) Each false positive (fp) decision is a false negative (fn)
decision for exactly one other class and vice versa. (ii) Microaveraged preci-
sion, recall and f are the same for fp=fn. Microaveraged precision is tp/N.
(one positive decision for each document) Accuracy is (tp+(c-1)tn)/(cN) =
tp/N, which equals precision.
?Exercise 0.154
The class priors in Figure 13.2 are computed as the fraction of documents in the class
as opposed to the fraction of tokens in the class. Why?
Preliminary draft (c)2007 Cambridge UP
lxxiii
docID words in document in c=China?
training set 1 Taipei Taiwan yes
2 Macao Taiwan Shanghai yes
3 Japan Sapporo no
4 Sapporo Osaka Taiwan no
test set 5 Taiwan Taiwan Sapporo ?
Tab l e 5 Data for parameter estimation exercise.
SOLUTION. We perform document classification, not token classifica-
tion, so we need the prior probability of a document.
Exercise 0.155
The function APPLYMULTINOMIALNB in Figure 13.2 has time complexity Θ(La+
|C|La). How would you modify the function so that its time complexity is Θ(La+
|C|Ma)?
SOLUTION. Preprocess the test document in Θ(La).Theresultingdata
structure has size Θ(Ma)?
Exercise 0.156
Based on the data in Table 13.10, (i) estimate a multinomial Naive Bayes classifier, (ii)
apply the classifier to the test document, (iii) estimate a Bernoulli Naive Bayes classi-
fier, (iv) apply the classifier to the test document. You need not estimate parameters
that you don’t need for classifying the test document.

Preliminary draft (c)2007 Cambridge UP
lxxiv Text classification and Naive Bayes
SOLUTION. (i) ˆ
P(c)= ˆ
P(c)=1/2. The vocabulary has 7 terms:
Japan,Macao,Osaka,Sapporo,Shanghai,Tai p e i ,Ta i w a n.Thereare5tokens
in the concatenation of all cdocuments. There are 5 tokens in the concate-
nation of all cdocuments. Thus, the denominators have the form (5+7).
ˆ
P(Tai wa n |c)=(2+1)/(5+7)=1/4, ˆ
P(Ta i wa n |c)=(1+1)/(5+7)=1/6,
ˆ
P(Sapporo|c)=(0+1)/(5+7)=1/12, ˆ
P(Sapporo|c)=(2+1)/(5+7)=
1/4,
(ii) We then get ˆ
P(c|d)∝1/2 ·(1/4)2·1/12 =1/(27·3)≈0.00260 and
ˆ
P(c|d)∝1/2 ·(1/6)2·(1/4)=1/(25·32)≈0.00347. ˆ
P(c|d)/ˆ
P(c|d)=3/4.
Thus, the classifier assigns the test document to c=not-China.
Exercise 0.157
Your task is to classify words as English or not English. Words are generated by a
source with the following distribution:
event word English? probability
1ozbno 4/9
2uzuno 4/9
3zooyes 1/18
4bunyes 1/18
(i) Compute the parameters (priors and conditionals) of a multinomial Naive Bayes
classifier that uses the letters b, n, o, u, and z as features. Assume a training set that

Preliminary draft (c)2007 Cambridge UP
lxxv
reflects the probability distribution of the source perfectly. Make the same indepen-
dence assumptions that are usually made for a multinomial classifier that uses terms
as features for text classification. Compute parameters using smoothing, in which
computed-zero probabilities are smoothed into probability 0.01, and computed-nonzero
probabilities are untouched. (This simplistic smoothing may cause P(A)+P(A)>1.
Solutions are not required to correct this.) (ii) How does the classifier classify the
word zoo? (iii) Classify the word zoo using a multinomial classifier as in part (i), but
do not make the assumption of positional independence. That is, estimate separate
parameters for each position in a word. You only need to compute the parameters
you need for classifying zoo.

Preliminary draft (c)2007 Cambridge UP
lxxvi Text classification and Naive Bayes
SOLUTION.
(a) Compute the parameters (priors and conditionals) of a multinomial classi-
fier that uses the letters b, n, o, u, and z as features. Assume a training set that
reflects the probability distribution of the source perfectly. Make the same
independence assumptions that are usually made for a multinomial classi-
fier that uses words as features for text classification. Compute parameters
using smoothing, in which computed-zero probabilities are smoothed into
probability 0.01, and computed-nonzero probabilities are untouched. (This
simplistic smoothing may cause P(A) + P(:A) > 1, which can be corrected
if we correspondingly smooth all complementary probability-1 values into
probability 0.99. For this problem, solutions may omit this correction to sim-
plify arithmetic.)
Priors: Class ÒEnglishÓ: 1 9 . Class ÒNot EnglishÓ: 8 9 .
letter o b
Conditionals:
z
n
u
English Not English
11 36
11 66
11 63
10:016
11 63
(b) How does the classifier classify the word ÒzooÓ? 111 1
English: 1/9 1/6 1/3 1/3 = 1/(235)
Not English: 8/9 1/3 1/6 1/6 = 2/(35)
The classifier chooses the class ÒNot English.Ó
(c) Classify the word ÒzooÓ using a multinomial classifier as in part (a), but
do not make the assumption of positional independence. That is, estimate
separate parameters for each position in a word. You only need to compute
the parameters you need for classifying ÒzooÓ. Priors: Class ÒEnglishÓ: 1
9.ClassÒNotEnglishÓ:89.
letter position
z1
Conditionals:
z1:1/20.01
o2:1/20.01
o3:1/20.01
English: 1/9 1/2 1/2 1/2 = 1/72
Not English: 8/9 1/100 1/100 1/100 = 8/9,000,000
The classifier chooses the class ÒEnglish.Ó
Exercise 0.158
What are the values of I(Ut;Cc)and X2(D,t,c)if term and class are completely inde-
pendent? What are the values if they are completely dependent?

Preliminary draft (c)2007 Cambridge UP
lxxvii
SOLUTION.
completely independent: I=0, chisquare close to 0. completely dependent:
I=1.0, chisquare very large
Exercise 0.159
The feature selection method in Equation (13.16) is most appropriate for the Bernoulli
model. Why? How could one modify it for the multinomial model?
SOLUTION.
It is most appropriate for Bernoulli because it is based on binary occurrence
information. A modification for the multinomial would be to estimate the
probabilities for tokens, not for documents
Exercise 0.160
Features can also be selected according to information gain (IG). Information gain is
INFORMATION GAIN defined as:
IG(D,t,c)=H(pD)−∑
x∈{Dt+,Dt−}
|x|
|D|H(px)
where His entropy, Dis the training set, and Dt+,andDt−are the subset of Dwith
term t,andthesubsetofDwithout term t,respectively. pAis the class distribution
in (sub)collection A, e.g., pA(c)=0.25, pA(c)=0.75 if a quarter of the documents in
Aare in class c.
Show that mutual information and information gain are equivalent.

Preliminary draft (c)2007 Cambridge UP
lxxviii Text classification and Naive Bayes
SOLUTION.
Exercise 0.161
Show that the two X2formulas (Equations (13.18) and (13.19)) are equivalent.

Preliminary draft (c)2007 Cambridge UP
lxxix
SOLUTION.
Preliminary draft (c)2007 Cambridge UP
lxxx Text classification and Naive Bayes
Exercise 0.162
In the χ2example on page 276 we have |N11 −E11|=|N10 −E10|=|N01 −E01|=
|N00 −E00|. Show that this holds in general.
SOLUTION.
E00 −N00 =(N00 +N01)(N00 +N10)
N−N00
=N00N00 +N00 N10 +N01N00 +N01N10 −(N00N00 +N00N10 +N00N01 +N00N11)
N
=1
N(N01N10 −N00 N11)
(the other three terms are analogous and need not be written down explicitly)
Exercise 0.163
χ2and mutual information do not distinguish between positively and negatively cor-
related features. Since most good text classification features are positively correlated
(i.e., they occur more often in cthan in c), one may want to explicitly rule out the
selection of negative indicators. How would you do this?
SOLUTION.
(n11n00-n10n01) in the chisquare formula is positive for positive correlation
and negative for negative correlation. remove all terms for which this term
is negative

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. lxxxi
Vector space classification
?Exercise 0.164
For small areas, distances on the surface of the hypersphere are approximated well
by distances on its projection (Figure 14.2) because α≈sin αfor small angles. For
what size angle is the distortion α/sin
(α)(i) 1.01, (ii) 1.05 and (iii) 1.1?
SOLUTION.
For small θ,sinθ(chord or projection distance) is well approximated by θ(arc
distance). This follows from the McLaurin series for sin θ.
(In fact if you look at the next few terms you can bound the error from both
sides because the McLaurin approximation is a bracketing series.)
?Exercise 0.165 []
Show that Rocchio classification can assign a label to a document that is different from
its training set label.
SOLUTION.
Take two classes in the plane, one distributed in a circle of radium 1 an done
distributed in a circle of radius 10, with the two circles touching. Then a large
part of the radius-10 circle will be misclassified.
?Exercise 0.166
Explain why kNN handles multimodal classes better than Rocchio.
SOLUTION.
In case of multimodal class, the continguity hypothesis, which the Rocchio
classification assumes, does not hold. The class is spread in different clusters
and hence the kNN works well as it labels documents by the documents in
the closest proximity anddoes not calculate a global centroid for the clusters.
?Exercise 0.167
Prove that the number of linear separators of two classes is either infinite or zero.
Preliminary draft (c)2007 Cambridge UP
lxxxii Vector space classification
SOLUTION. If there is one linear separator, then there is an epsilon such
that after moving it by in the direction of the closest point, it is still a sepa-
rator
?Exercise 0.168
Create a training set of 300 documents, 100 each from three different languages (e.g.,
English, French, Spanish). Create a test set by the same procedure, but also add 100
documents from a fourth language. Train (i) a one-of classifier (ii) an any-of classi-
fier on this training set and evaluate it on the test set. (iii) Are there any interesting
differences in how the two classifiers behave on this task?
SOLUTION.
(i) The one-of classifier will classify the documents of the fourth language as
belonging to one of the first three classes, the one most similar to it. This may
vary for documents of the fourth language. (take the case when the fourth
language bears nearly same similarity to the two of the first three languages.)
(ii) The any-of classifier will classify the documents of the fourth language
into one or more of the first 3 languages, depending on the similarity it bears
to them.
(iii) In case two of the first 3 languages are very similar (say American En-
glish and UK English), a lot of documents from either of them in the test set
might get classified as belonging to the other one in the one-of case and to
both of them in the any-of case.
?Exercise 0.169
In Figure 14.14, which of the three vectorsa,
b,andcis (i) most similar to xaccording
to dot product similarity, (ii) most similar to xaccording to cosine similarity, (iii)
closest to xaccording to Euclidean distance?
SOLUTION.
(i) c(dot products: 0.05, 0.16, 0.28) (ii)
b(cosines: 0.9805, 1.0, 0.9899) (iii) a
(distances: 0.1118, 0.2828, 0.7211)
Exercise 0.170
Download Reuters-21578 and train and test Rocchio and kNN classifiers for the classes
acquisitions,corn,crude,earn,grain,interest,money-fx,ship,trade,andwheat.Usethe
ModApte split. You may want to use one of a number of software packages that im-
plement Rocchio classification and kNN classification, for example, the Bow toolkit
(McCallum 1996).
SOLUTION. No solution.
Exercise 0.171
Download 20 Newgroups (page 154) and train and test Rocchio and kNN classifiers
for its 20 classes.
SOLUTION. No solution.

Preliminary draft (c)2007 Cambridge UP
lxxxiii
Exercise 0.172
Show that the decision boundaries in Rocchio classification are, as in kNN, given by
the Voronoi tessellation.
SOLUTION.
Rocchio can be viewed as kNN classification with the centroids being the
training points.
Exercise 0.173 []
Computing the distance between a dense centroid and a sparse vector is Θ(M)for
a naive implementation that iterates over all Mdimensions. Based on the equality
∑(xi−μi)2=1.0 +∑μ2
i+2∑xiμiand assuming that ∑μ2
ihas been precomputed,
writedownanalgorithmthatisΘ(Ma)instead, where Mais the number of distinct
terms in the test document.
SOLUTION. No solution.
Exercise 0.174 []
Prove that the region of the plane consisting of all points with the same knearest
neighbors is a convex polygon.
SOLUTION. Assume for contradiction that a tessellation has a non-
convex polygon. Then there exists a line with points A, B, C on it (in that or-
der) such that the nearest neighbor of A and C is d1 and the nearest neighbor
of B is d2: |d2, B|<|d1, B|,|d2, A|>|d1, A|and |d2, C|>|d1, C|.LetZbethe
point on A-B-C with the smallest distance from d1. Without loss of generality,
Z is on the same side of B on line(A-B-C) as A. Case 1: dist(d1,Z)>dist(d2,Z).
Case 2: dist(d1,Z)<dist(d2,Z). (for pic: Let X be the first point on the line
A-B-C that is equidistant from d1 and d2, that is, it is part of the boundary
between the d1 region and the d2 region.)
Case 1 A X Z B C
d1
Case 2
AZXBC
d1
In both cases, C is closer to d2 than to d1. Contradiction.
Exercise 0.175
Design an algorithm that performs an efficient 1NN search in 1 dimension (where
efficiency is with respect to the number of documents N). What is the time complexity
of the algorithm?
SOLUTION. Sort the training set and represent it as a sorted list. Do
a binary search for the test point in the sorted list. Let xbe the training
point you find this way. Let x1and x2be the left and right neighbors of
x. One of these three points must be the nearest neighbor of the test point.
This algorithm requires Θ(Nlog N)“training” (= sorting). Classifying a new
document is Θ(log N).

Preliminary draft (c)2007 Cambridge UP
lxxxiv Vector space classification
Figure 2 A simple non-separable set of points.
Exercise 0.176 []
Design an algorithm that performs an efficient 1NN search in 2 dimensions with at
most polynomial (in N)preprocessingtime.
SOLUTION. Build Voronoi tesselation in O(N2)(N is number of docu-
ments). Do point location in a Voronoi tessellation in the plane in O(log N).
The polygon where the test point is located corresponds to the nearest neigh-
bor.
Exercise 0.177 []
Can one design an exact efficient algorithm for 1NN for very large Malong the ideas
you used to solve the last exercise?
SOLUTION. Precomputing the Voronoi tessellation is Θ(NM)and find-
ing the right polytope is Θ((log N)M)? That’s inefficient for large M
Exercise 0.178
Show that Equation (14.4) defines a hyperplane with w=μ(c1)−μ(c2)and b=
0.5 ∗(|μ(c1)|2−|μ(c2)|2).
SOLUTION.
Exercise 0.179
We can easily construct non-separable data sets in high dimensions by embedding
a non-separable set like the one shown in Figure 14.15. Consider embedding Fig-
ure 14.15 in 3D and then perturbing the 4 points slightly (i.e., moving them a small
distance in a random direction). Why would you expect the resulting configuration

Preliminary draft (c)2007 Cambridge UP
lxxxv
to be linearly separable? How likely is then a non-separable set of mMpoints in
M-dimensional space?
SOLUTION. No solution.
Exercise 0.180
Assuming two classes, show that the percentage of non-separable assignments of the
vertices of a hypercube decreases with dimensionality Mfor M>1. For example,
for M=1 the proportion of non-separable assignments is 0, for M=2, it is 2/16.
One of the two non-separable cases for M=2 is shown in Figure 14.15, the other is
its mirror image. Solve the exercise either analytically or by simulation.
SOLUTION. No solution.
Exercise 0.181
Although we point out the similarities of Naive Bayes with linear vector space classi-
fiers, it does not make sense to represent count vectors (the document representations
in NB) in a continuous vector space. There is however a formalization of NB that is
analogous to Rocchio. Show that NB assigns a document to the class (represented as
a parameter vector) whose Kullback-Leibler (KL) divergence (Section 12.4, page 250)
to the document (represented as a count vector as in Section 13.4.1 (page 270), nor-
malized to sum to 1) is smallest.
SOLUTION. No solution.
Preliminary draft (c)2007 Cambridge UP

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. lxxxvii
Support vector machines and
machine learning on documents
?Exercise 0.182 []
What is the minimum number of support vectors that there can be for a data set
(which contains instances of each class)?
SOLUTION. No solution.
Exercise 0.183 []
The basis of being able to use kernels in SVMs (see Section 15.2.3) is that the classifica-
tion function can be written in the form of Equation (15.9) (where, for large problems,
most αiare 0). Show explicitly how the classification function could be written in this
form for the data set from Example 15.1. That is, write fas a function where the data
points appear and the only variable is x.
SOLUTION. αiwill be 0 for the non-support vector (1, 1).Wewishthe
other two terms to sum to give (2/5, 4/5). It is fairly straightforward to then
see that the solution is:
f(x)=2
5(−1)1
1Tx+2
5(−1)2
3Tx+0(−1)2
0Tx+11
5
Exercise 0.184 []
Install an SVM package such as SVMlight (http://svmlight.joachims.org/), and build an
SVM for the data set discussed in Example 15.1. Confirm that the program gives the
same solution as the text. For SVMlight, or another package that accepts the same
training data format, the training file would be:
+11:22:3
−11:22:0
−11:12:1
The training command for SVMlight is then:
svm_learn -c 1 -a alphas.dat train.dat model.dat
Preliminary draft (c)2007 Cambridge UP
lxxxviii Support vector machines and machine learning on documents
The -c 1 option is needed to turn off use of the slack variables that we discuss in
Section 15.2.1. Check that the norm of the weight vector agrees with what we found
in Example 15.1. Examine the file alphas.dat which contains the αivalues, and check
that they agree with your answers in Exercise 15.2.
SOLUTION. No solution.
?Exercise 0.185 []
Spam email often makes use of various cloaking techniques to try to get through. One
method is to pad or substitute characters so as to defeat word-based text classifiers.
For example, you see terms like the following in spam email:
Rep1icaRolex bonmus Viiiaaaagra pi11z
PHARlbdMACY [LEV]i[IT]l[RA] se∧xual ClAfLlS
Discuss how you could engineer features that would largely defeat this strategy.
SOLUTION. No solution.
Exercise 0.186 []
Another strategy often used by purveyors of email spam is to follow the message
they wish to send (such as buying a cheap stock or whatever) with a paragraph of
text from another innocuous source (such as a news article). Why might this strategy
be effective? How might it be addressed by a text classifier?
SOLUTION. No solution.
Exercise 0.187 []
What other kinds of features appear as if they would be useful in an email spam
classifier?
SOLUTION. No solution.
?Exercise 0.188
Plot the first 7 rows of Figure 15.3 in the α-ωplane to produce a figure like that in
Figure 15.7.
SOLUTION. No solution.
Exercise 0.189
Write down the equation of a line in the α-ωplane separating the Rs from the Ns.
SOLUTION. No solution.

Preliminary draft (c)2007 Cambridge UP
lxxxix
Exercise 0.190
Give a training example (consisting of values for α,ωand the relevance judgment)
that when added to the training set makes it impossible to separate the R’s from the
N’s using a line in the α-ωplane.
SOLUTION. No solution.
Preliminary draft (c)2007 Cambridge UP
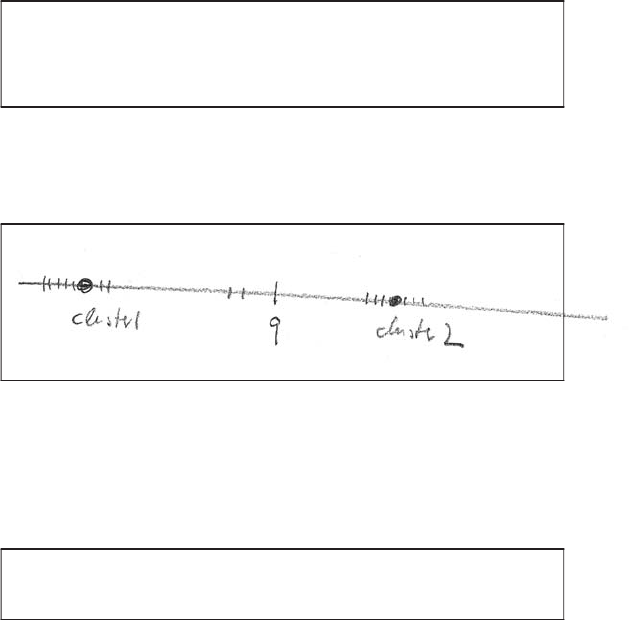
Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. xci
Flat clustering
?Exercise 0.191
Define two documents as similar if they have at least two proper names like Clinton
or Sarkozy in common. Give an example of an information need and two documents,
for which the cluster hypothesis does not hold for this notion of similarity.
SOLUTION.
Document 1 is about Stanford University and Document 2 is about major
search engines. Both documents contain terms Google and Yahoo. For the
information need Search engine technology, document 2 is very relevant
whereas document 1 is not.
?Exercise 0.192
Make up a simple one-dimensional example (i.e. points on a line) with two clusters
where the inexactness of cluster-based retrieval shows up. In your example, retriev-
ing clusters close to the query should do worse than direct nearest neighbor search.
SOLUTION.
?Exercise 0.193
Replace every point din Figure 16.4 with two identical copies of dinthesameclass.
(i) Is it less difficult, equally difficult or more difficult to cluster this set of 34 points
as opposed to the 17 points in Figure 16.4? (ii) Compute purity, NMI, RI, and F5for
the clustering with 34 points. Which measures increase and which stay the same after
doubling the number of points? (iii) Given your assessment in (i) and the results in
(ii), which measures are best suited to compare the quality of the two clusterings?
SOLUTION. purity = 0.71, nmi=0.34, ri=0.906, f5=0.662. purity and nmi
are the same whewas ri and f5 have increased by about 0.2.
python irbookct.py normmutualinfo xxxxxxxxxxoo,xxoooooooodd,xxxxdddddd

Preliminary draft (c)2007 Cambridge UP
xcii Flat clustering
?Exercise 0.194
Why are documents that do not use the same term for the concept car likely to end
up in the same cluster in K-means clustering?
SOLUTION.
Documents which fall into the same cluster are similar, where the similarity
is defined by the dot product of the Euclidean distance in most cases. The
document with the same concept like car but not using the same term(ie car)
are likely to have a lot of other common terms,similar to the term car, which
will put them into the same cluster.
Exercise 0.195
Two of the possible termination conditions for K-means were (1) assignment does not
change, (2) centroids do not change (page 361). Do these two conditions imply each
other?
SOLUTION.
Let each document x(n) be assigned to a particular cluster w(k) for two con-
secutive interations. This implies that the assignment did not change. Also,
each cluster w(k) has a fixed number of same documents belonging to it for
both iterations. This implies that the centroids of clusters did not change. So
termination conditions 1 and 2 imply each other.
?Exercise 0.196
We saw above that the time complexity of K-means is Θ(IKNM). What is the time
complexity of EM?
SOLUTION. EM is also Θ(IKNM)
?Exercise 0.197
Let Ωbe a clustering that exactly reproduces a class structure Cand Ωa clustering
that further subdivides some clusters in Ω. Show that I(Ω;C)=I(Ω;C).
SOLUTION.
Preliminary draft (c)2007 Cambridge UP
xciii
Exercise 0.198
Show that I(Ω;C)≤[H(Ω)+H(C)]/2.
SOLUTION. http://www.lans.ece.utexas.edu/˜strehl/diss/node107.html
I(X;Y)=H(X)+H(Y)+H(X,Y) I(X;Y)<H(X) I(X;Y)<H(Y) I(X;Y)<min(H(X),H(Y))
I(X;Y)<0.5(H(X)+H(Y))
Exercise 0.199
Mutual information is symmetric in the sense that its value does not change if the
roles of clusters and classes are switched: I(Ω;C)=I(C;Ω). Which of the other
three evaluation measures are symmetric in this sense?
SOLUTION. RI is symmtric. F and purity are not symmetric.
Exercise 0.200
Compute RSS for the two clusterings in Figure 16.7.
SOLUTION.
9.68 and 2.5
Exercise 0.201
(i) Give an example of a set of points and three initial centroids (which need not be
members of the set of points) for which 3-means converges to a clustering with an
empty cluster. (ii) Can a clustering with an empty cluster be the global optimum with
respect to RSS?
SOLUTION.
(i) Start with identical cluster centers.
(ii) yes, for example, if all documents are identical
Exercise 0.202
Download Reuters-21578. Discard documents that do not occur in one of the 10
classes acquisitions,corn,crude,earn,grain,interest,money-fx,ship,trade,andwheat.
Discard documents that occur in two of these 10 classes. (i) Compute a K-means
clustering of this subset into 10 clusters. There are a number of software packages
that implement K-means, e.g., WEKA (Witten and Frank 2005) and R (R Develop-
ment Core Team 2005). (ii) Compute purity, normalized mutual information, F1and
RI for the clustering with respect to the 10 classes. (iii) Compile a confusion matrix
(Table 14.5, page 307) for the 10 classes and 10 clusters. Identify classes that give rise
to false positives and false negatives.
SOLUTION. No solution.
Exercise 0.203
Prove that RSSmin(K)is monotonically decreasing in K.

Preliminary draft (c)2007 Cambridge UP
xciv Flat clustering
SOLUTION.
In a clustering with iclusters, take a cluster with non-identical vectors. Split-
ting this cluster in two will lower RSS.
Exercise 0.204
There is a soft version of K-means that computes the fractional membership of a doc-
ument in a cluster as a monotonically decreasing function of the distance Δfrom its
centroid, e.g., as e−Δ. Modify reassignment and recomputation steps of hard K-means
for this soft version.
SOLUTION.
Exercise 0.205
In the last iteration in Table 16.3, document 6 is in cluster 2 even though it was the
initial seed for cluster 1. Why does the document change membership?
SOLUTION.
Initially the document 6 is the centroid of cluster 1 and doc7 of cluster 2.
Slowly documents 1 to 5 which contain words related to Africa, cocoa, but-
ter, beans increase their memberships to cluster 1 and due to their growing
influence, documents 10 and 11 are steadily driven out of cluster 1. Docu-
ments 7,8 and 9 are never are a part of cluster 1. Since document 6 bears
stronger similarity to documents 7 to 11, it is forced to shift to cluster 2.
Exercise 0.206
The values of the parameters qmk in iteration 25 in Table 16.3 are rounded. What are
the exact values that EM will converge to?
SOLUTION.
1/5, 1/6, 3/5, 1/2, 2/3. these are the smoothed estimates for the bernoulli
assuming that the final clustering is the training set.
Preliminary draft (c)2007 Cambridge UP
xcv
Exercise 0.207
Perform a K-means clustering for the documents in Table 16.3. After how many iter-
ations does K-means converge? Compare the result to the EM clustering in Table 16.3
and discuss the differences.
SOLUTION. No solution.
Exercise 0.208 []
Modify the expectation and maximization steps of EM for a Gaussian mixture. As
with Naive Bayes, the maximization step computes the maximum likelihood param-
eter estimates αk,μk,andΣkfor each of the clusters. The expectation step computes
for each vector a soft assignment to clusters (Gaussians) based on their current param-
eters. Write down the equations for Gaussian mixtures corresponding to Equations
(16.16) and (16.17).
SOLUTION. No solution.
Exercise 0.209 []
Show that K-means can be viewed as the limiting case of EM for Gaussian mixtures
if variance is very small and all covariances are 0.
SOLUTION. see ?
Exercise 0.210 []
The within-point scatter of a clustering is defined as ∑k1
2∑xi∈ωk∑xj∈ωk|xi−xj|2.ShowWITHIN-POINT
SCATTER that minimizing RSS and minimizing within-point scatter are equivalent.
SOLUTION.
show that |ωk|RSSk=0.50.5 ∑xi∈ωk∑xj∈ωk|xi−xj|2
Exercise 0.211 []
Derive an AIC criterion for the multivariate Bernoulli mixture model from Equa-
tion (16.12).
SOLUTION. No solution.
Preliminary draft (c)2007 Cambridge UP

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. xcvii
Hierarchical clustering
?Exercise 0.212 []
Describe in a few sentences how you would produce the dendrogram of the hierarchi-
cal clustering from the list A that is returned by the algorithm described in Figure 17.2.
SOLUTION. No solution.
?Exercise 0.213
Show that complete-link clustering creates the two-cluster clustering depicted in Fig-
ure 17.7.
SOLUTION.
?Exercise 0.214
Apply group-average clustering to the points in Figures 17.6 and 17.7. Map them onto
the surface of the unit sphere in a three-dimensional space to get length-normalized
vectors. Is the group-average clustering different from the single-link and complete-
link clusterings?
SOLUTION. No solution.
?Exercise 0.215
For a fixed set of Ndocuments there are up to N2distinct similarities between clusters
in single-link and complete-link clustering. How many distinct cluster similarities are
there in GAAC and centroid clustering?

Preliminary draft (c)2007 Cambridge UP
xcviii Hierarchical clustering
SOLUTION. 2N·2N
?Exercise 0.216
Show the equivalence of the two definitions of combination similarity: the process
definition on page 378 and the static definition on page 393.
SOLUTION.
?Exercise 0.217
A single-link clustering can also be computed from the minimum spanning tree of a
MINIMUM SPANNING
TREE graph. The minimum spanning tree connects the vertices of a graph at the smallest
possible cost, where cost is defined as the sum over all edges of the graph. In our
case the cost of an edge is the distance between two documents. Show that if Δk−1>
Δk>... >Δ1are the costs of the edges of a minimum spanning tree, then these
edges correspond to the k−1 merges in constructing a single-link clustering.
SOLUTION. adapt the proof of optimality of single-link clustering: it is
also a proof that the tree is the minimum spanning tree
Exercise 0.218
Show that single-link clustering is best-merge persistent and that GAAC and centroid
clustering are not best-merge persistent.

Preliminary draft (c)2007 Cambridge UP
xcix
SOLUTION.
3 The Best Merge Persistency means that the Next Best Merge (NBM) for a
cluster ,comprising of just the document d, remains the same as long as any
other document does not merge with this cluster. The single link clustering
uses the maximum similarity criterion. In this case, say we have a cluster
comprising of just the document d and the document most similar to it is
d. Even if d merges with any document (say d) to form a cluster w, the best
merge cluster for w remains d(which was the most similar document to d).
Exercise 0.219
a. Consider running 2-means clustering on a collection with documents from two
different languages. What result would you expect?
b. Would you expect the same result when running an HAC algorithm?
SOLUTION.
a. Two clusters that roughly correspond to the two languages – unless the
initial seed were badly chosen
b. Complete-link clustering is likely to end up with one big cluster containing
both languages and a second small cluster with outliers. Single-link cluster-
ing may intermix the two languages through chaining if there a few docu-
ments(e.g.,tablesofnumbers)thatcanserveasabridgebetweenthetwo
languages. Centroid / GAAC are likely to find two clusters corresponding
roughly to the two languages.
Exercise 0.220
Download Reuters-21578. Keep only documents that are in the classes crude,inter-
est,andgrain. Discard documents that are members of more than one of these three
classes. Compute a (i) single-link, (ii) complete-link, (iii) GAAC, (iv) centroid cluster-
ing of the documents. (v) Cut each dendrogram at the second branch from the top to
obtain K=3 clusters. Compute the Rand index for each of the 4 clusterings. Which
clustering method performs best?
SOLUTION. No solution.
Exercise 0.221
Suppose a run of HAC finds the clustering with K=7 to have the highest value on
some pre-chosen goodness measure of clustering. Have we found the highest-value
clustering among all clusterings with K=7?
SOLUTION. It depends on the HAC algorithms. The answer is yes for
single-link and no for the other three algorithms. See Section 17.5.
Exercise 0.222
Consider the task of producing a single-link clustering of Npoints on a line:

Preliminary draft (c)2007 Cambridge UP
cHierarchical clustering
Show that we only need to compute a total of about Nsimilarities. What is the overall
complexity of single-link clustering for a set of points on a line?
SOLUTION.
Each cluster must be a sequence of adjacent points. Thus, distances between
clusters are distances between adjacent points. So we only need the O(N)
distances between adjacent points. We can order them in O(N log N), so
clustering has time complexity O(N log N)
Exercise 0.223
Prove that single-link, complete-link, and group-average are monotonic in the sense
defined on page 378.
SOLUTION. Proof for intra-cluster by induction induction hypoth-
esis (IH): intra(c1,c2)<=intra(c3) for all clusters let c’ be the merge of
ci and cj assumption: there are (without loss of generality) c1,c2,c3 s.t.
intra(c1,c2)>intra(c3) case 1: c1=c’ from IH: intra(ci,c2)<=intra(c3), in-
tra(cj,c2)<=intra(c3), intra(ci,cj)<=intra(c3) => intra(c1,c2)<=intra(c3), contra-
diction case 2: c3=c’ contradicts prescription to always merge pair with max
similarity intra(c1,c2) [ci and cj would not have been merged, but instead c1
and c2] case 3: c1!=c’,c2!=c’,c3!=c’ contradiction follows directly from IH
Exercise 0.224
For Npoints, there are ≤KNdifferent flat clusterings into Kclusters (Section 16.2,
page 356). What is the number of different hierarchical clusterings (or dendrograms)
of Ndocuments? Are there more flat clusterings or more hierarchical clusterings for
given Kand N?
SOLUTION. N!/2N−1. The denominator is the number of different ways
one can write down a particular tree.

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. ci
Matrix decompositions and latent
semantic indexing
?Exercise 0.225
What is the rank of the 3 ×3diagonalmatrixbelow?
⎛
⎝
110
011
121
⎞
⎠
SOLUTION. The rank is 2, since the first two rows are independent and
the third is the sum of the first two.
Exercise 0.226
Show that λ=2 is an eigenvalue of
C=6−2
40
.
Find the corresponding eigenvector.
SOLUTION.
Exercise 0.227
Compute the unique eigen decomposition of the 2 ×2 matrix in (18.4).

Preliminary draft (c)2007 Cambridge UP
cii Matrix decompositions and latent semantic indexing
SOLUTION.
U=
11
-1 1
lambda =
30
01
?Exercise 0.228
Let
C=⎛
⎝
11
01
10
⎞
⎠
(1)
be the term-document incidence matrix for a collection. Compute the co-occurrence
matrix CCT. What is the interpretation of the diagonal entries of CCTwhen Cis a
term-document incidence matrix?
SOLUTION. 210
110
101
Exercise 0.229
Verify that the SVD of the matrix in Equation (18.12) is
U=⎛
⎝−0.816 0.000
−0.408 −0.707
−0.408 0.707 ⎞
⎠,Σ=1.732 0.000
0.000 1.000 and VT=−0.707 −0.707
0.707 −0.707 ,(2)
by verifying all of the properties in the statement of Theorem 18.3.

Preliminary draft (c)2007 Cambridge UP
ciii
SOLUTION.
Exercise 0.230
Suppose that Cis a term-document incidence matrix. What do the entries of CTC
represent?

Preliminary draft (c)2007 Cambridge UP
civ Matrix decompositions and latent semantic indexing
SOLUTION. The (i,j) entry is the number of terms that documents i and j
have in common.
Exercise 0.231
Let
C=⎛
⎝
021
030
210
⎞
⎠
(3)
be a term-document matrix whose entries are term frequencies; thus term 1 occurs 2
times in document 2 and once in document 3. Compute CCT; observe that its entries
are largest where two terms have their most frequent occurrences together in the same
document.

Preliminary draft (c)2007 Cambridge UP
cv
SOLUTION.
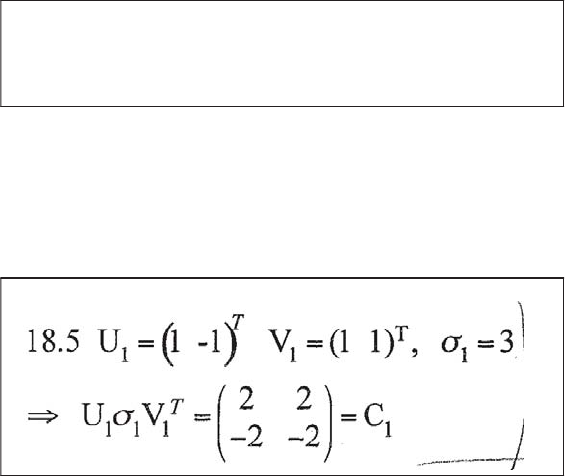
Preliminary draft (c)2007 Cambridge UP
cvi Matrix decompositions and latent semantic indexing
?Exercise 0.232
Compute a rank 1 approximation C1to the matrix Cin Example 18.12, using the SVD
as in Exercise 18.13. What is the Frobenius norm of the error of this approximation?
SOLUTION.
c1 =
22
-2 -2
frobenius norm of X: 26
Exercise 0.233
Consider now the computation in Exercise 18.8. Following the schematic in Fig-
ure 18.2, notice that for a rank 1 approximation we have σ1being a scalar. Denote
by U1the first column of Uand by V1the first column of V. Show that the rank-1
approximation to Ccan then be written as U1σ1VT
1=σ1U1VT
1.
SOLUTION.
Exercise 0.234
Exercise 18.9 can be generalized to rank kapproximations: we let U
kand V
kdenote
the “reduced” matrices formed by retaining only the first kcolumns of Uand V,
respectively. Thus U
kis an M×kmatrix while VT
kis a k×Nmatrix. Then, we have
Ck=U
kΣ
kVT
k,(4)
where Σ
kis the square k×ksubmatrix of Σkwith the singular values σ1,...,σkon
the diagonal. The primary advantage of using (18.20) is to eliminate a lot of redun-
dant columns of zeros in Uand V, thereby explicitly eliminating multiplication by
columns that do not affect the low-rank approximation; this version of the SVD is
sometimes known as the reduced SVD or truncated SVD and is a computationally
simpler representation from which to compute the low rank approximation.
For the matrix Cin Example 18.3, write down both Σ2and Σ
2.
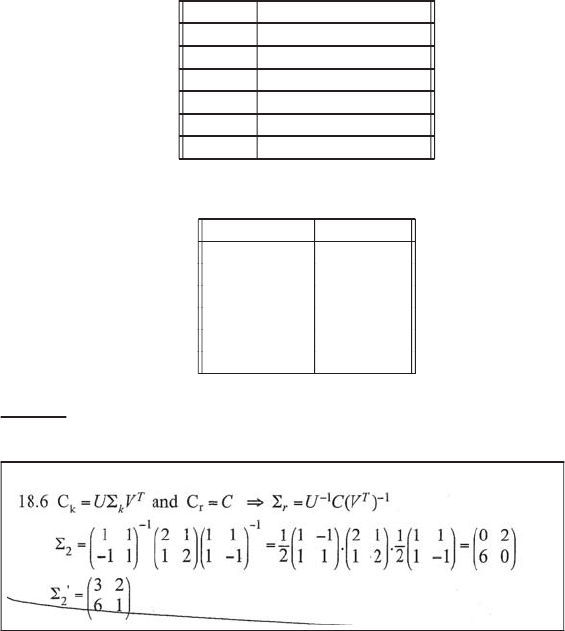
Preliminary draft (c)2007 Cambridge UP
cvii
DocID Document text
1hello
2open house
3mi casa
4hola Profesor
5hola y bienvenido
6hello and welcome
Figure 3 Documents for Exercise 18.11.
Spanish English
mi my
casa house
hola hello
profesor professor
yand
bienvenido welcome
Figure 4 Glossary for Exercise 18.11.
SOLUTION.
?Exercise 0.235
Assume you have a set of documents each of which is in either English or in Spanish.
The collection is given in Figure 18.4.
Figure 18.5 gives a glossary relating the Spanish and English words above for your
own information. This glossary is NOT available to the retrieval system:
1. Construct the appropriate term-document matrix Cto use for a collection con-
sisting of these documents. For simplicity, use raw term frequencies rather than
normalized tf-idf weights. Make sure to clearly label the dimensions of your ma-
trix.
2. Write down the matrices U2,Σ
2and V2and from these derive the rank 2 approxi-
mation C2.
3. State succinctly what the (i,j)entry in the matrix CTCrepresents.

Preliminary draft (c)2007 Cambridge UP
cviii Matrix decompositions and latent semantic indexing
4. State succinctly what the (i,j)entry in the matrix CT
2C2represents, and why it
differs from that in CTC.
SOLUTION.

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. cix
Web search basics
?Exercise 0.236
If the number of pages with in-degree iis proportional to 1/i2.1, what is the probabil-
ity that a randomly chosen web page has in-degree 1?
SOLUTION.
Exercise 0.237
If the number of pages with in-degree iis proportional to 1/i2.1, what is the average
in-degree of a web page?
SOLUTION.
Exercise 0.238
If the number of pages with in-degree iis proportional to 1/i2.1, then as the largest
in-degree goes to infinity, does the fraction of pages with in-degree igrow, stay the
same, or diminish? How would your answer change for values of the exponent other
than 2.1?
SOLUTION.
It will diminish for all values of exponent.

Preliminary draft (c)2007 Cambridge UP
cx Web search basics
Exercise 0.239
The average in-degree of all nodes in a snapshot of the web graph is 9. What can we
say about the average out-degree of all nodes in this snapshot?
SOLUTION. average out-degree =9
?Exercise 0.240
TheGotomethodrankedadvertisementsmatchingaquerybybid: the highest-bidding
advertiser got the top position, the second-highest the next, and so on. What can go
wrong with this when the highest-bidding advertiser places an advertisement that is
irrelevant to the query? Why might an advertiser with an irrelevant advertisement
bid high in this manner?
SOLUTION. The advertisement, being irrelevant, is never clicked on by
any user and therefore generates no revenue to the search engine.
An advertiser may promote such an advertisement because it promotes his
brand to the user, without costing him anything.
Exercise 0.241
Suppose that, in addition to bids, we had for each advertiser their click-through rate:
the ratio of the historical number of times users click on their advertisement to the
number of times the advertisement was shown. Suggest a modification of the Goto
scheme that exploits this data to avoid the problem in Exercise 19.5 above.
SOLUTION. Instead of ranking by bid, the search engine can use a func-
tion of both the bid and the click-through rate to determine the ranking. This
function would ideally grow with both bid and click-through rate, say the
product of these two quantities.
?Exercise 0.242
Two web search engines A and B each generate a large number of pages uniformly at
random from their indexes. 30% of A’s pages are present in B’s index, while 50% of
B’s pages are present in A’s index. What is the number of pages in A’s index relative
to B’s?
SOLUTION.
?Exercise 0.243
Web search engines A and B each crawl a random subset of the same size of the Web.
Some of the pages crawled are duplicates – exact textual copies of each other at dif-
ferent URLs. Assume that duplicates are distributed uniformly amongst the pages

Preliminary draft (c)2007 Cambridge UP
cxi
crawled by A and B. Further, assume that a duplicate is a page that has exactly two
copies – no pages have more than two copies. A indexes pages without duplicate
elimination whereas B indexes only one copy of each duplicate page. The two ran-
dom subsets have the same size before duplicate elimination. If, 45% of A’s indexed
URLs are present in B’s index, while 50% of B’s indexed URLs are present in A’s
index, what fraction of the Web consists of pages that do not have a duplicate?
SOLUTION. Let number of duplicate pages be D. Let S(A) AND S(B) de-
note the sizes of the random subsets to be indexed by A and B respectively.
Given that S(A)=S(B). Both S(A) and S(B) contain (D/2) pages which have
exactly one duplicate. Number of pages indexed by A = S(A) Number of
pages indexed by B = S(B)-(D/2) Given: 0.45 * S(A) = 0.5 * (S(B)-(D/2)) Since
S(A)=S(B), we get D=S(A)/5 Assuming that S(A) is the same as size of the
web, Fraction of web with duplicates = 1/5 Fraction of web without dupli-
cates = 4/5
Exercise 0.244
Instead of using the process depicted in Figure 19.8, consider instead the following
process for estimating the Jaccard coefficient of the overlap between two sets S1and
S2. We pick a random subset of the elements of the universe from which S1and S2
are drawn; this corresponds to picking a random subset of the rows of the matrix Ain
the proof. We exhaustively compute the Jaccard coefficient of these random subsets.
Why is this estimate an unbiased estimator of the Jaccard coefficient for S1and S2?
SOLUTION. We are sampling uniformly each of the four different types
of rows: 00, 01, 10 and 11. Of these, the 00 rows don’t matter in the Jaccard
computation in any case.
Exercise 0.245
Explain why this estimator would be very difficult to use in practice.
SOLUTION. Because almost all rows of Ahave zeros in both columns
(type 00), we are very unlikely to get an estimate unless we use an enormous
number of samples.
Preliminary draft (c)2007 Cambridge UP

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. cxiii
Web crawling and indexes
?Exercise 0.246
Why is it better to partition hosts (rather than individual URLs) between the nodes of
a distributed crawl system?
SOLUTION. Two principal benefits: (1) makes it easier to keep track of
the elapsed time between successive requests to the same host and (2) the
robots.txt file for a host can be cached and re-used at a node of the crawl.
Exercise 0.247
Why should the host splitter precede the Duplicate URL Eliminator?
SOLUTION. Because this allows us to neatly partition DUE set across
web crawlers – the DUE partition on a given crawler contains exactly those
URLs that the crawler is responsible for.
Exercise 0.248 []
In the preceding discussion we encountered two recommended "hard constants" –
the increment on tebeing ten times the last fetch time, and the number back queues
being three times the number of crawl threads. How are these two constants re-
lated?
SOLUTION.
When a number of crawl threads are running, each of them might access
URLs from different non-common hosts and so the number of back queues
needs to be high to accommodate the increased flow of URLs which is why
it is three times the number of crawl threads. This is directly linked to the
increment in t1 being ten times (high) the last fetch. Since URLs from several
hosts are getting appended to the queue at a high rate, the time gap between
accessing successive URLs from the same host also increases largely.
?Exercise 0.249
We noted that expressing a row in terms of one of seven preceding rows allowed us
to use no more than three bits to specify which of the preceding rows we are using
as prototype. Why seven and not eight preceding rows? (Hint: consider the case when
none of the preceding seven rows is a good prototype.)

Preliminary draft (c)2007 Cambridge UP
cxiv Web crawling and indexes
SOLUTION.
The first seven numbers (formed by 3 bits: 0, 1, .7) are used to specify which
of the seven preceding rows we are using as prototype and the eighth num-
ber is used to specify in case none of the preceding seven rows is a good
prototype.
Exercise 0.250
We noted that for the scheme in Section 20.4, decoding the links incident on a URL
could result in many levels of indirection. Construct an example in which the number
of levels of indirection grows linearly with the number of URL’s.
SOLUTION.
There is two things that are not clear to me from the section 20.4. a. Does
the scheme also include cases where a row can be expressed in terms of more
than one of the preceding seven rows? In that case, a row row8 can be ex-
pressed as following: take first 3 integers from row1, then first 3 integers
from row2, then first 3 integers from row3 and so on till row7.If row8 is not
yet complete, again start from row1 and copy the next 3 integers to row8
and continue till row7. Repeat the process until row8 is complete. b. What
do you exactly mean by the term indirection here? Please explain with an
example.

Preliminary draft (c)2007 Cambridge UP
DRAFT! ©December 12, 2007 Cambridge University Press. Feedback welcome. cxv
Link analysis
?Exercise 0.251
Is it always possible to follow directed edges (hyperlinks) in the web graph from any
node (web page) to any other? Why or why not?
SOLUTION.
No. Webpages with no outlinks are the examples of nodes which make the
given statement false. Some of the webpages which fall into this category are
blogs, new webpages and personal pages.
Exercise 0.252
Find an instance of misleading anchor-text on the Web.
SOLUTION. The misleading anchor text, miserable failure brought up
the official George W. Bush biography on Google, Yahoo and MSN and num-
ber two on Ask.com.
Exercise 0.253
Given the collection of anchor-text phrases for a web page x, suggest a heuristic for
choosing one term or phrase from this collection that is most descriptive of x.
SOLUTION.
use any of the feature selection methods from Chapter 13 (e.g., most frequent
non-stop word or phrase)
Exercise 0.254
Does your heuristic in the previous exercise take into account a single domain D
repeating anchor text for xfrom multiple pages in D?
SOLUTION.
No. To account for single-domain effects treat all anchor text from a single
domain as one anchor text.
?Exercise 0.255
Write down the transition probability matrix for the example in Figure 21.2.

Preliminary draft (c)2007 Cambridge UP
cxvi Link analysis
SOLUTION.
Exercise 0.256
Consider a web graph with three nodes 1, 2 and 3. The links are as follows: 1 →
2, 3 →2, 2 →1, 2 →3. Write down the transition probability matrices for the surfer’s
walk with teleporting, for the following three values of the teleport probability: (a)
α=0; (b) α=0.5 and (c) α=1.
SOLUTION.
Exercise 0.257
A user of a browser can, in addition to clicking a hyperlink on the page xhe is cur-
rently browsing, use the back button to go back to the page from which he arrived at
x. Can such a user of back buttons be modeled as a Markov chain? How would we
model repeated invocations of the back button?
SOLUTION.
No, the user can’t be modeled as a Markov chain. This is because the user
may hit the back-button multiply and the semantics should be you unwind
the path up to that point – this is not Markovian.
Exercise 0.258
Consider a Markov chain with three states A, B and C, and transition probabilities as
follows. From state A, the next state is B with probability 1. From B, the next state is
either A with probability pA, or state C with probability 1 −pA. From C the next state
is A with probability 1. For what values of pA∈[0, 1]is this Markov chain ergodic?
SOLUTION. pA∈(0, 1)

Preliminary draft (c)2007 Cambridge UP
cxvii
Exercise 0.259
Show that for any directed graph, the Markov chain induced by a random walk with
the teleport operation is ergodic.
SOLUTION.
Exercise 0.260
Show that the PageRank of every page is at least α/N. What does this imply about
the difference in PageRank values (over the various pages) as αbecomes close to 1?
SOLUTION. The PageRank of every page is at least α/Nbecause of the
teleport operation.
Exercise 0.261
For the data in Example 21.1, write a small routine or use a scientific calculator to
compute the PageRank values stated in Equation (21.6).
SOLUTION.
I calculated the page rank values in example 21.1 and its coming out to be
same as given in equation 21.6.
Exercise 0.262
Suppose that the web graph is stored on disk as an adjacency list, in such a way that
you may only query for the out-neighbors of pages in the order in which they are
stored. You cannot load the graph in main memory but you may do multiple reads
over the full graph. Write the algorithm for computing the PageRank in this setting.

Preliminary draft (c)2007 Cambridge UP
cxviii Link analysis
SOLUTION.
Exercise 0.263
Recall the sets Sand Yintroduced near the beginning of Section 21.2.3. How does the
set Yrelate to S?
SOLUTION.
S is an arbitrary set on a particular topic (sports in case). Y is the superset of
S which contains all webpages on the topic and related topics too.
Exercise 0.264
Is the set Yalways the set of all web pages? Why or why not?
SOLUTION.
No. In Topic specific pagerank calculation, the teleport operation teleports to
a random webpage on that particular topic only and so the entire webgraph
is not connected. Since Y must have a steady-state distribution, Y is not the
set of all webpages.
Exercise 0.265 []
Is the sports PageRank of any page in Sat least as large as its PageRank?
SOLUTION.
What I think is that in case of pagerank the probability would be distributed
overamuchlargercollectionthanstatesthanintopicpageankandsothe
topic pagerank might be greater than the pagerank in some cases.
PR: The answer is YES, but I realize that to prove it requires a careful stochas-
tic domination argument - unless someone can think of an easier way.

Preliminary draft (c)2007 Cambridge UP
cxix
Exercise 0.266 []
Consider a setting where we have two topic-specific PageRank values for each web
page: a sports PageRank
πs, and a politics PageRank
πp.Letαbe the (common)
teleportation probability used in computing both sets of topic-specific PageRanks.
For q∈[0, 1], consider a user whose interest profile is divided between a fraction qin
sports and a fraction 1 −qin politics. Show that the user’s personalized PageRank is
the steady-state distribution of a random walk in which – on a teleport step – the walk
teleports to a sports page with probability qand to a politics page with probability
1−q.
SOLUTION.
see Haveliwala (2002) and Haveliwala (2003)
Exercise 0.267
Show that the Markov chain corresponding to the walk in Exercise 21.16 is ergodic
and hence the user’s personalized PageRank can be obtained by computing the steady-
state distribution of this Markov chain.
SOLUTION.
We know that the Markov chain induced by a random walk with the teleport
operation is an ergodic chain and hence has unique steady-state probability
distribution which will give the users personalized pagerank.
Exercise 0.268
Show that in the steady-state distribution of Exercise 21.17, the steady-state probabil-
ity for any web page iequals qπs(i)+(1−q)πp(i).
SOLUTION.
?Exercise 0.269
If all the hub and authority scores are initialized to 1, what is the hub/authority score
of a node after one iteration?
SOLUTION.
number of outlinks / inlinks
Preliminary draft (c)2007 Cambridge UP
cxx Link analysis
Exercise 0.270
How would you interpret the entries of the matrices AATand ATA? What is the
connection to the co-occurrence matrix CCTin Chapter 18?
SOLUTION.
The number of common out-neighbors/in-neighbors. This is the same as the
co-occurrence matrix from Chapter 18 if one viewed terms as neighbors.
Exercise 0.271
What are the principal eigenvalues of AATand ATA?
SOLUTION. No solution.
q1q2
q3
Figure 5 Web graph for Exercise 21.22.
Exercise 0.272
For the web graph in Figure 21.7, compute PageRank, hub and authority scores for
each of the three pages. Also give the relative ordering of the 3 nodes for each of these
scores, indicating any ties.
PageRank: Assume that at each step of the PageRank random walk, we teleport to a
random page with probability 0.1, with a uniform distribution over which particular
page we teleport to.
Hubs/Authorities: Normalize the hub (authority) scores so that the maximum hub
(authority) score is 1.
Hint 1: Using symmetries to simplify and solving with linear equations might be
easier than using iterative methods.
Hint 2: Provide the relative ordering (indicating any ties) of the three nodes for each
of the three scoring measures.

Preliminary draft (c)2007 Cambridge UP
cxxi
SOLUTION. Sincethein-degreeofAis0,thesteady-visitrate(orrank)
of A is 0.1 ·1/3 =1/30 (from teleport). By symmetry, rank(B) = rank(C).
Thus, rank(B)=rank(C) = 29/60.
Authority: There is no concept of teleport, so authority(A)=0. Again, author-
ity(B)=authority(C). Thus: authority(A)=0, authority(B)=authority(C)=1.
Hub: Use the authority scores above and iterate once to get hub(A)=2,
hub(B)=1, hub(C)=1. Normalized: hub(A)=1, hub(B)=1/2, hub(C)=1/2.