IS 456 2000 PT SL Example 001
User Manual: IS 456-2000 PT-SL Example 001
Open the PDF directly: View PDF ![]() .
.
Page Count: 6
Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
IS 456-2000 PT-SL EXAMPLE 001 - 1
IS 456-2000 PT-SL EXAMPLE 001
Post-Tensioned Slab Design
PROBLEM DESCRIPTION
The purpose of this example is to verify the slab stresses and the required area of
mild steel strength reinforcing for a post-tensioned slab.
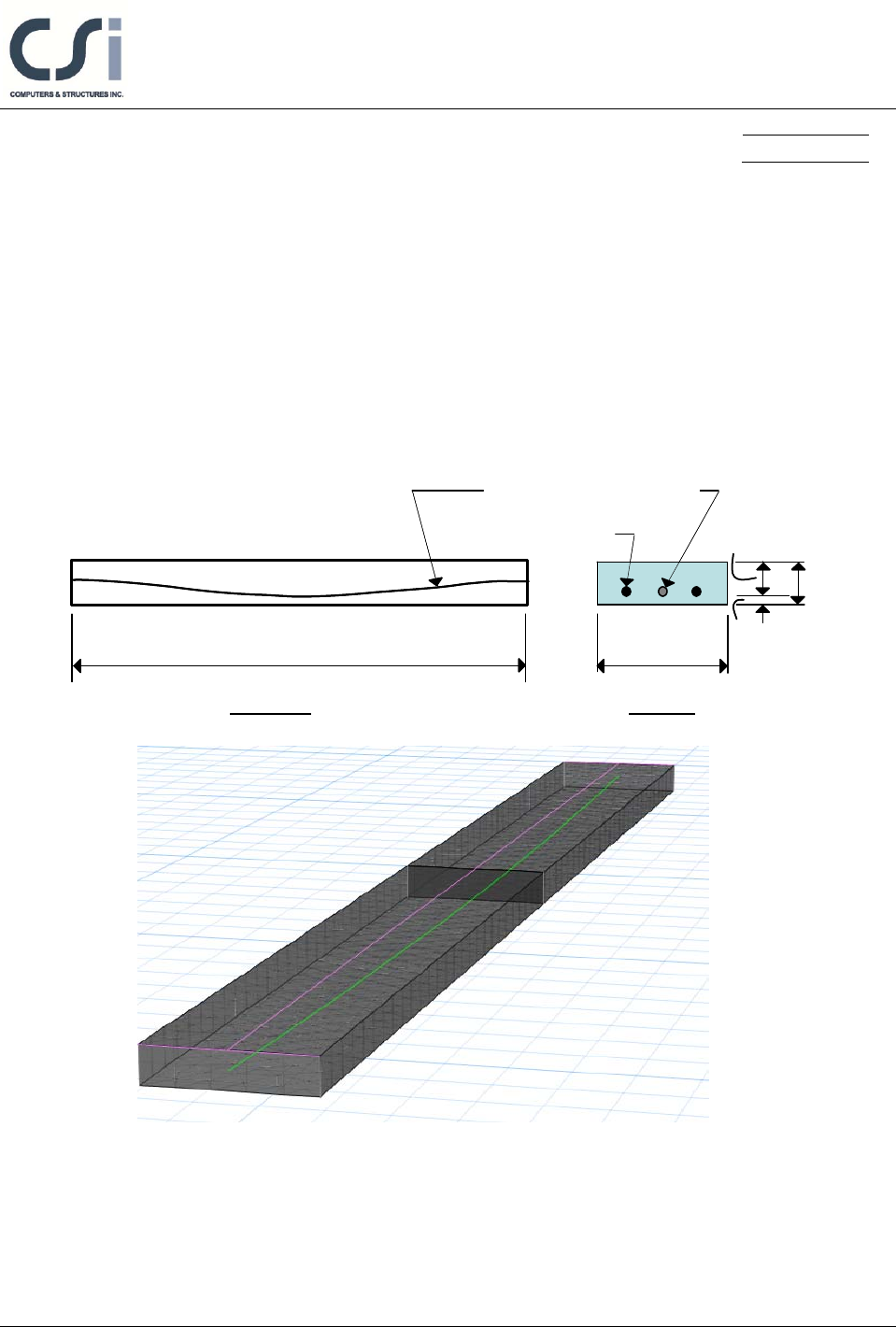
A one-way simply supported slab is modeled in ETABS. The modeled slab is 254
mm thick by 914 mm wide and spans 9754 mm, as shown in shown in Figure 1.
Length, L = 9754 mm
Elevation Section
Prestressing tendon, Ap
Mild Steel, As
914 mm 25 mm
229 mm
254 mm
Length, L = 9754 mm
Elevation Section
Prestressing tendon, Ap
Mild Steel, As
914 mm 25 mm
229 mm
254 mm
Figure 1 One-Way Slab

Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
IS 456-2000 PT-SL EXAMPLE 001 - 2
A 254-mm-wide design strip is centered along the length of the slab and has been
defined as an A-Strip. B-strips have been placed at each end of the span,
perpendicular to Strip-A (the B-Strips are necessary to define the tendon profile).
A tendon with two strands, each having an area of 99 mm2, has been added to the
A-Strip. The self weight and live loads have been added to the slab. The loads and
post-tensioning forces are as follows:
Loads: Dead = self weight, Live = 4.788 kN/m2
The total factored strip moments, required area of mild steel reinforcement, and
slab stresses are reported at the mid-span of the slab. Independent hand
calculations were compared with the ETABS results and summarized for
verification and validation of the ETABS results.
GEOMETRY, PROPERTIES AND LOADING
Thickness T, h = 254 mm
Effective depth d = 229 mm
Clear span L = 9754 mm
Concrete strength f 'c = 30 MPa
Yield strength of steel fy = 400 MPa
Prestressing, ultimate fpu = 1862 MPa
Prestressing, effective fe = 1210 MPa
Area of Prestress (single strand) Ap = 198 mm2
Concrete unit weight wc = 23.56 kN/m3
Modulus of elasticity Ec = 25000 N/mm3
Modulus of elasticity Es = 200,000 N/mm3
Poisson’s ratio = 0
Dead load wd = self kN/m2
Live load wl = 4.788 kN/m2
TECHNICAL FEATURES OF ETABS TESTED
Calculation of the required flexural reinforcement
Check of slab stresses due to the application of dead, live, and post-tensioning
loads
RESULTS COMPARISON
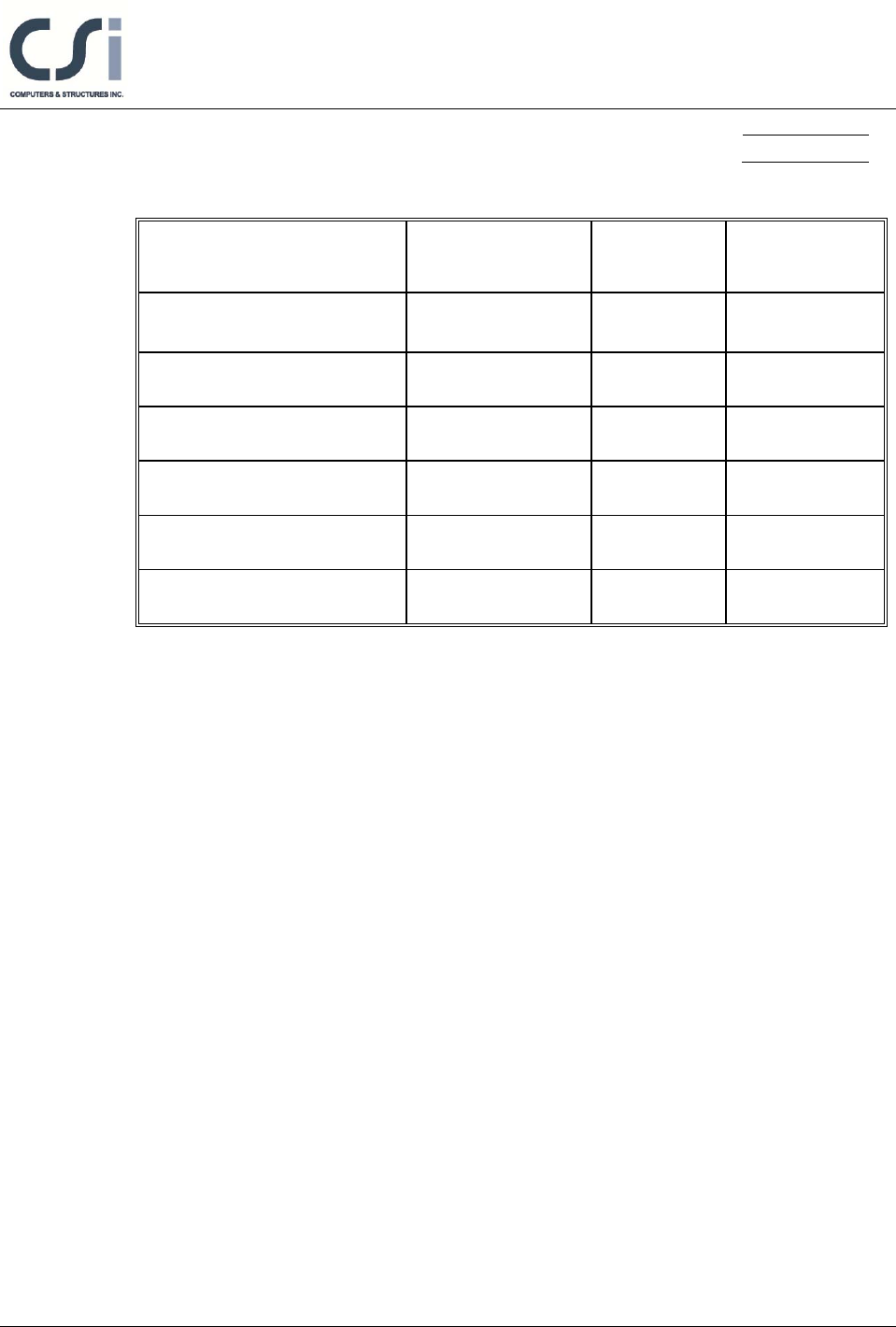
Table 1 shows the comparison of the ETABS total factored moments, required
mild steel reinforcing, and slab stresses with the independent hand calculations.
Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
IS 456-2000 PT-SL EXAMPLE 001 - 3
Table 1 Comparison of Results
FEATURE TESTED INDEPENDENT
RESULTS ETABS
RESULTS DIFFERENCE
Factored moment,
Mu (Ultimate) (kN-m) 175.60 175.69 0.05%
Area of Mild Steel req’d,
As (sq-cm) 19.53 19.775 1.25%
Transfer Conc. Stress, top
(D+PTI), MPa 5.058 5.057 -0.02%
Transfer Conc. Stress, bot
(D+PTI), MPa 2.839 2.839 0.00%
Normal Conc. Stress, top
(D+L+PTF), MPa 10.460 10.467 0.07%
Normal Conc. Stress, bot
(D+L+PTF), MPa 8.402 8.409 0.08%
COMPUTER FILE: IS 456-2000 PT-SL EX001.EDB
CONCLUSION
The ETABS results show an acceptable comparison with the independent results.
Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
IS 456-2000 PT-SL EXAMPLE 001 - 4
HAND CALCULATIONS:
Design Parameters:
Mild Steel Reinforcing Post-Tensioning
fck = 30MPa fpu = 1862 MPa
fy = 400MPa fpy = 1675 MPa
Stressing Loss = 186 MPa
Long-Term Loss = 94 MPa
fi = 1490 MPa
fe =1210 MPa
s = 1.15
c = 1.50
= 0.36
= 0.42 max 250
0 53 0 05 if 250 415 MPa
165
yy
f
x.. f
d
max
u,
x
d0.484
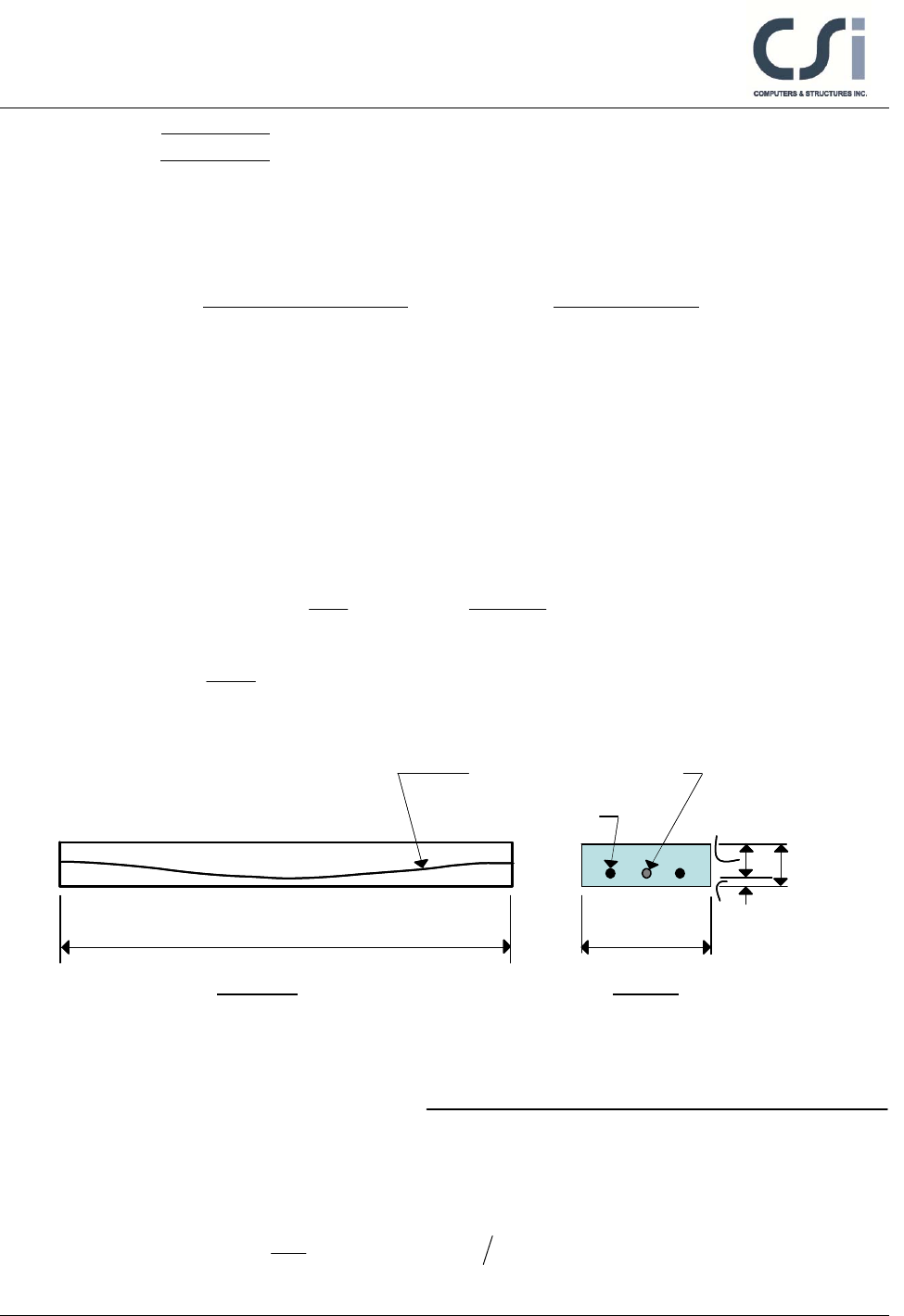
Length, L = 9754 mm
Elevation Section
Prestressing tendon, Ap
Mild Steel, As
914 mm 25 mm
229 mm
254 mm
Length, L = 9754 mm
Elevation Section
Prestressing tendon, Ap
Mild Steel, As
914 mm 25 mm
229 mm
254 mm
Loads:
Dead, self-wt = 0.254 m 23.56 kN/m3 = 5.984 kN/m2 (D) 1.50 = 8.976 kN/m2 (Du)
Live, = 4.788 kN/m2 (L) 1.50 = 7.182 kN/m2 (Lu)
Total = 10.772 kN/m2 (D+L) = 16.158 kN/m2 (D+L)ult
=10.772 kN/m2 0.914 m = 9.846 kN/m, u
= 16.158 kN/m2 0.914 m = 14.768 kN/m
Ultimate Moment, 2
1
8
U
wl
M=
2
14 768 9 754 8.. = 175.6 kN-m

Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
IS 456-2000 PT-SL EXAMPLE 001 - 5
Ultimate Stress in strand, PS
ffrom Table 11: fp = 1435 MPa
Ultimate force in PT,
,( ) 197.4 1435 1000 283.3 kN
ult PT P PS
FAf
Compression block depth ratio: 2ck
M
mbd f
2
175.6 0.3392
0.914 0.229 0.36 30000
Required area of mild steel reinforcing,
114 1140.420.3392 0.4094
2 2 0.42
um
x
d
>
max 0 484
u,
x.
d
The area of tensile steel reinforcement is then given by:
1 229 1 0.42 0.4094 189.6mm
u
x
zd d
2
175.6 1 6 2663 mm
400 1.15 189.6
/
u
NET
ys
M
Ae
fz
As = 2
1435
2663 198 1953 mm
400
P
NET P
y
f
AA
f
Check of Concrete Stresses at Midspan:
Initial Condition (Transfer), load combination (D+PTi) = 1.0D+0.0L+1.0PTI
Tendon stress at transfer = jacking stress stressing losses =1490 186 = 1304 MPa
The force in the tendon at transfer, =
1304 197.4 1000 257.4 kN
Moment due to dead load,
2
5.984 0.914 9.754 8 65.04 kN-m
D
M
Moment due to PT,
(sag) 257.4 102 mm 1000 26.25 kN-m
PT PTI
MF
Stress in concrete,
257.4 65.04 26.23
0.254 0.914 0.00983
PTI D PT
FMM
fAS
where S=0.00983m3
1.109 3.948 MPaf
5.058(Comp)max, 2.839(Tension)maxf

Software Verification
PROGRAM NAME: ETABS
REVISION NO.: 0
IS 456-2000 PT-SL EXAMPLE 001 - 6
Normal Condition, load combinations: (D+L+PTF) = 1.0D+1.0L+1.0PTF
Tendon stress at normal = jacking stressing long-term=1490 186 94 = 1210 MPa
The force in tendon at normal, =
1210 197.4 1000 238.9 kN
Moment due to dead load,
2
5.984 0.914 9.754 8 65.04 kN-m
D
M
Moment due to live load,
2
4.788 0.914 9.754 8 52.04 kN-m
L
M
Moment due to PT,
(sag) 238.9 102 mm 1000 24.37 kN-m
PT PTI
MF
Stress in concrete for (D+L+PTF),
238.8 117.08 24.37
0.254 0.914 0.00983
PTI D L PT
FM M
fAS
1 029 9 431
f
..
10.460(Comp)max, 8.402(Tension)maxf