Instructions
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 2
CSC421/2516 Winter 2019 Homework 1
Homework 1
Deadline: Thursday, Jan. 24, at 11:59pm.
Submission: You must submit your solutions as a PDF file through MarkUs1. You can produce
the file however you like (e.g. LaTeX, Microsoft Word, scanner), as long as it is readable.
Late Submission: MarkUs will remain open until 3 days after the deadline, after which no late
submissions will be accepted.
Weekly homeworks are individual work. See the Course Information handout2for detailed policies.
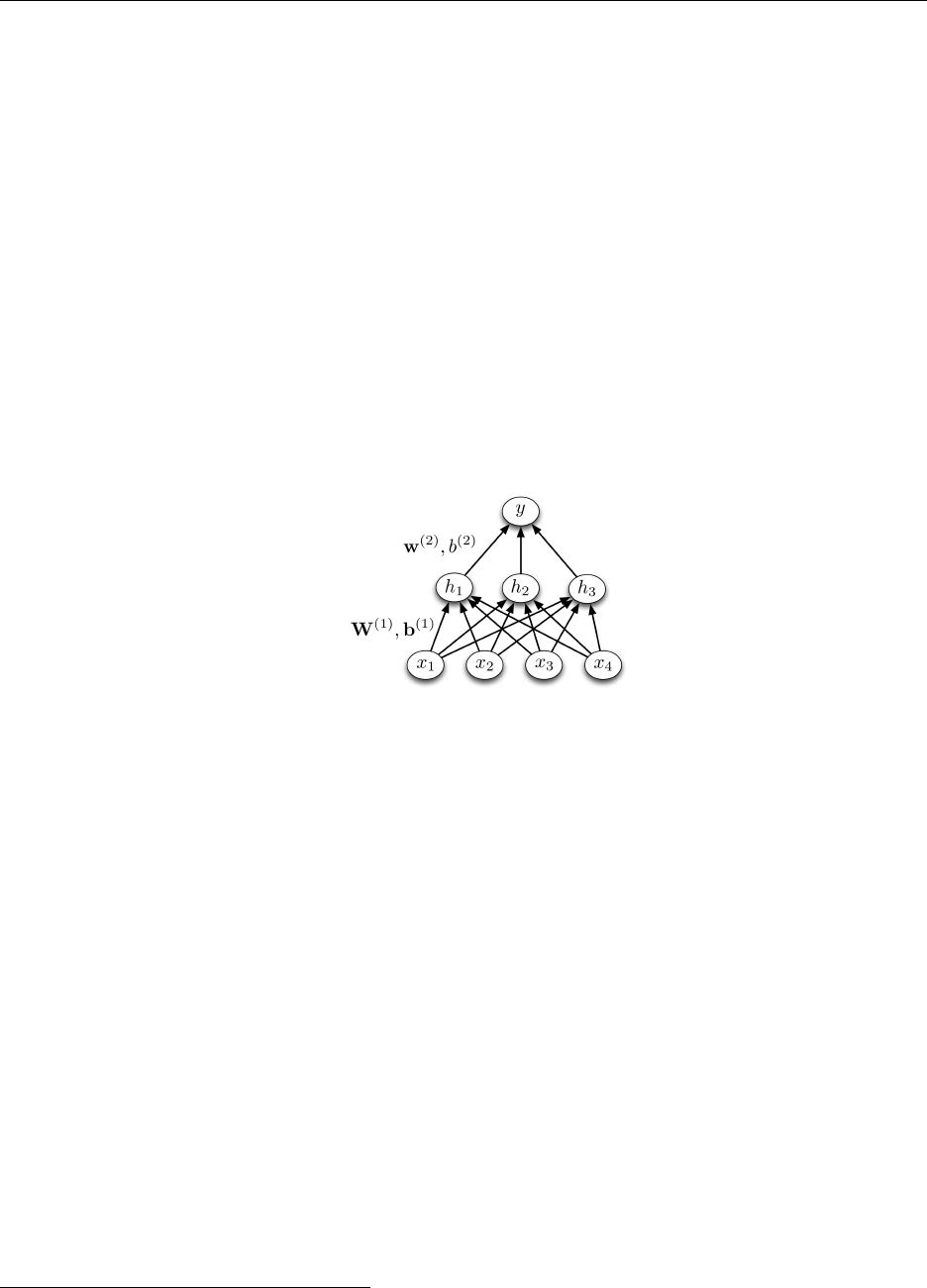
1. Hard-Coding a Network. [2pts] In this problem, you need to find a set of weights and
biases for a multilayer perceptron which determines if a list of length 4 is in sorted order.
More specifically, you receive four inputs x1, . . . , x4, where xi∈R, and the network must
output 1 if x1< x2< x3< x4, and 0 otherwise. You will use the following architecture:
All of the hidden units and the output unit use a hard threshold activation function:
φ(z) = 1 if z≥0
0 if z < 0
Please give a set of weights and biases for the network which correctly implements this function
(including cases where some of the inputs are equal). Your answer should include:
•A 3 ×4 weight matrix W(1) for the hidden layer
•A 3-dimensional vector of biases b(1) for the hidden layer
•A 3-dimensional weight vector w(2) for the output layer
•A scalar bias b(2) for the output layer
You do not need to show your work.
2. Backprop. Consider a neural network with Ninput units, Noutput units, and Khidden
units. The activations are computed as follows:
z=W(1)x+b(1)
h=σ(z)
y=x+W(2)h+b(2),
1https://markus.teach.cs.toronto.edu/csc421-2019-01
2http://www.cs.toronto.edu/~rgrosse/courses/csc421_2019/syllabus.pdf
1
CSC421/2516 Winter 2019 Homework 1
where σdenotes the logistic function, applied elementwise. The cost will involve both hand
y:
J=R+S
R=r>h
S=1
2ky−sk2
for given vectors rand s.
•[1pt] Draw the computation graph relating x,z,h,y,R,S, and J.
•[3pts] Derive the backprop equations for computing x=∂J/∂x. You may use σ0to
denote the derivative of the logistic function (so you don’t need to write it out explicitly).
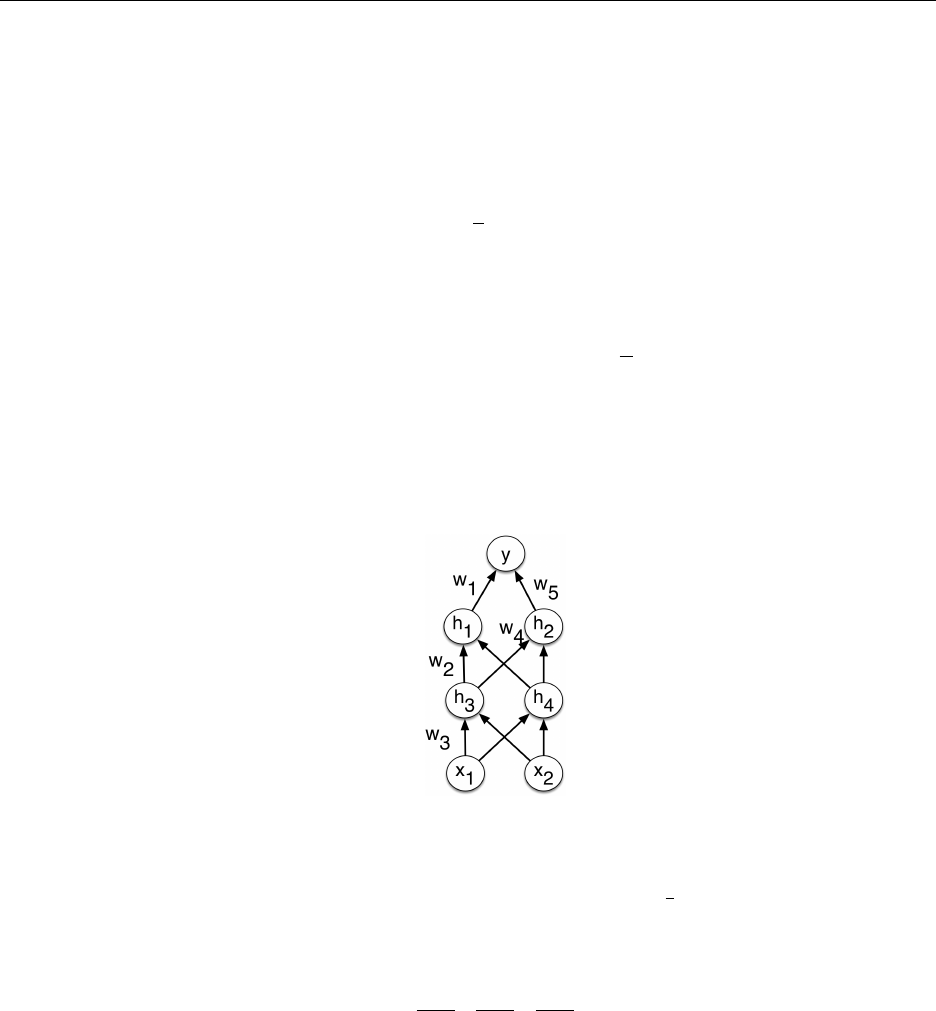
3. Sparsifying Activation Function. [4pts] One of the interesting features of the ReLU
activation function is that it sparsifies the activations and the derivatives, i.e. sets a large
fraction of the values to zero for any given input vector. Consider the following network:
Note that each wirefers to the weight on a single connection, not the whole layer. Suppose
we are trying to minimize a loss function Lwhich depends only on the activation of the
output unit y. (For instance, Lcould be the squared error loss 1
2(y−t)2.) Suppose the unit
h1receives an input of -1 on a particular training case, so the ReLU evaluates to 0. Based
only on this information, which of the weight derivatives
∂L
∂w1
,∂L
∂w2
,∂L
∂w3
are guaranteed to be 0 for this training case? Write YES or NO for each. Justify your
answers.
2