Machine Learning With Python Introduction To A Guide For Data Scientists
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 340 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Cover
- Copyright
- Table of Contents
- Chapter 1. Introduction
- Chapter 2. Supervised Learning
- Classification and Regression
- Generalization, Overfitting and Underfitting
- Supervised Machine Learning Algorithms
- k-Nearest Neighbor
- Linear models
- Naive Bayes Classifiers
- Decision trees
- Ensembles of Decision Trees
- Kernelized Support Vector Machines
- Neural Networks (Deep Learning)
- Uncertainty estimates from classifiers
- Summary and Outlook
- Chapter 3. Unsupervised Learning and Preprocessing
- Chapter 4. Summary of scikit-learn methods and usage
- Chapter 5. Representing Data and Engineering Features
- Chapter 6. Model evaluation and improvement
- Chapter 7. Algorithm Chains and Pipelines
- Chapter 8. Working with Text Data
978-1-491-91721-3
[FILL IN]
Introduction to Machine Learning with Python
by Andreas C. Mueller and Sarah Guido
Copyright © 2016 Sarah Guido, Andreas Mueller. All rights reserved.
Printed in the United States of America.
Published by O’Reilly Media, Inc. , 1005 Gravenstein Highway North, Sebastopol, CA 95472.
O’Reilly books may be purchased for educational, business, or sales promotional use. Online editions are
also available for most titles ( http://safaribooksonline.com ). For more information, contact our corporate/
institutional sales department: 800-998-9938 or corporate@oreilly.com .
Editors: Meghan Blanchette and Rachel Roumelio‐
tis
Production Editor: FILL IN PRODUCTION EDI‐
TOR
Copyeditor: FILL IN COPYEDITOR
Proofreader: FILL IN PROOFREADER
Indexer: FILL IN INDEXER
Interior Designer: David Futato
Cover Designer: Karen Montgomery
Illustrator: Rebecca Demarest
June 2016: First Edition
Revision History for the First Edition
2016-06-09: First Early Release
See http://oreilly.com/catalog/errata.csp?isbn=9781491917213 for release details.
The O’Reilly logo is a registered trademark of O’Reilly Media, Inc. Introduction to Machine Learning with
Python, the cover image, and related trade dress are trademarks of O’Reilly Media, Inc.
While the publisher and the author(s) have used good faith efforts to ensure that the information and
instructions contained in this work are accurate, the publisher and the author(s) disclaim all responsibil‐
ity for errors or omissions, including without limitation responsibility for damages resulting from the use
of or reliance on this work. Use of the information and instructions contained in this work is at your own
risk. If any code samples or other technology this work contains or describes is subject to open source
licenses or the intellectual property rights of others, it is your responsibility to ensure that your use
thereof complies with such licenses and/or rights.
www.it-ebooks.info

Table of Contents
1. Introduction. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Why machine learning? 9
Problems that machine learning can solve 10
Knowing your data 13
Why Python? 13
What this book will cover 13
What this book will not cover 14
Scikit-learn 14
Installing Scikit-learn 15
Essential Libraries and Tools 16
Python2 versus Python3 19
Versions Used in this Book 19
A First Application: Classifying iris species 20
Meet the data 22
Measuring Success: Training and testing data 24
First things first: Look at your data 25
Building your first model: k nearest neighbors 27
Making predictions 28
Evaluating the model 29
Summary 30
2. Supervised Learning. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
Classification and Regression 33
Generalization, Overfitting and Underfitting 35
Supervised Machine Learning Algorithms 37
k-Nearest Neighbor 42
k-Neighbors Classification 42
Analyzing KNeighborsClassifier 45
v
www.it-ebooks.info

k-Neighbors Regression 47
Analyzing k nearest neighbors regression 50
Strengths, weaknesses and parameters 51
Linear models 51
Linear models for regression 51
Linear Regression aka Ordinary Least Squares 53
Ridge regression 55
Lasso 57
Linear models for Classification 60
Linear Models for multiclass classification 66
Strengths, weaknesses and parameters 69
Naive Bayes Classifiers 70
Strengths, weaknesses and parameters 71
Decision trees 71
Building Decision Trees 73
Controlling complexity of Decision Trees 76
Analyzing Decision Trees 77
Feature Importance in trees 78
Strengths, weaknesses and parameters 81
Ensembles of Decision Trees 82
Random Forests 82
Gradient Boosted Regression Trees (Gradient Boosting Machines) 88
Kernelized Support Vector Machines 91
Linear Models and Non-linear Features 92
The Kernel Trick 96
Understanding SVMs 97
Tuning SVM parameters 98
Preprocessing Data for SVMs 101
Strengths, weaknesses and parameters 102
Neural Networks (Deep Learning) 102
The Neural Network Model 103
Tuning Neural Networks 106
Strengths, weaknesses and parameters 115
Uncertainty estimates from classifiers 116
The Decision Function 117
Predicting probabilities 119
Uncertainty in multi-class classification 121
Summary and Outlook 123
3. Unsupervised Learning and Preprocessing. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127
Types of unsupervised learning 127
Challenges in unsupervised learning 128
vi | Table of Contents
www.it-ebooks.info

Preprocessing and Scaling 128
Different kinds of preprocessing 129
Applying data transformations 130
Scaling training and test data the same way 132
The effect of preprocessing on supervised learning 134
Dimensionality Reduction, Feature Extraction and Manifold Learning 135
Principal Component Analysis (PCA) 135
Non-Negative Matrix Factorization (NMF) 152
Manifold learning with t-SNE 157
Clustering 162
k-Means clustering 162
Agglomerative Clustering 173
DBSCAN 178
Summary of Clustering Methods 194
Summary and Outlook 195
4. Summary of scikit-learn methods and usage. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 197
The Estimator Interface 197
Fit resets a model 198
Method chaining 199
Shortcuts and efficient alternatives 200
Important Attributes 200
Summary and outlook 201
5. Representing Data and Engineering Features. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203
Categorical Variables 204
One-Hot-Encoding (Dummy variables) 205
Binning, Discretization, Linear Models and Trees 210
Interactions and Polynomials 215
Univariate Non-linear transformations 222
Automatic Feature Selection 225
Univariate statistics 225
Model-based Feature Selection 227
Iterative feature selection 229
Utilizing Expert Knowledge 230
Summary and outlook 237
6. Model evaluation and improvement. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 239
Cross-validation 240
Cross-validation in scikit-learn 241
Benefits of cross-validation 241
Stratified K-Fold cross-validation and other strategies 242
Table of Contents | vii
www.it-ebooks.info

More control over cross-validation 244
Leave-One-Out cross-validation 245
Shuffle-Split cross-validation 245
Cross-validation with groups 246
Grid Search 247
Simple Grid-Search 248
The danger of overfitting the parameters and the validation set 249
Grid-search with cross-validation 251
Analyzing the result of cross-validation 255
Using different cross-validation strategies with grid-search 259
Nested cross-validation 260
Parallelizing cross-validation and grid-search 261
Evaluation Metrics and scoring 262
Keep the end-goal in mind 262
Metrics for binary classification 263
Multi-class classification 285
Regression metrics 288
Using evaluation metrics in model selection 288
Summary and outlook 290
7. Algorithm Chains and Pipelines. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 293
Parameter Selection with Preprocessing 294
Building Pipelines 295
Using Pipelines in Grid-searches 296
The General Pipeline Interface 299
Convenient Pipeline creation with make_pipeline 300
Grid-searching preprocessing steps and model parameters 304
Summary and Outlook 306
8. Working with Text Data. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 307
Types of data represented as strings 307
Example application: Sentiment analysis of movie reviews 309
Representing text data as Bag of Words 311
Bag-of-word for movie reviews 314
Stop-words 317
Rescaling the data with TFIDF 318
Investigating model coefficients 321
Bag of words with more than one word (n-grams) 322
Advanced tokenization, stemming and lemmatization 326
Topic Modeling and Document Clustering 329
Summary and Outlook 337
viii | Table of Contents
www.it-ebooks.info

CHAPTER 1
Introduction
Machine learning is about extracting knowledge from data. It is a research field at the
intersection of statistics, artificial intelligence and computer science, which is also
known as predictive analytics or statistical learning. The application of machine
learning methods has in recent years become ubiquitous in everyday life. From auto‐
matic recommendations of which movies to watch, to what food to order or which
products to buy, to personalized online radio and recognizing your friends in your
photos, many modern websites and devices have machine learning algorithms at their
core.
When you look at at complex websites like Facebook, Amazon or Netflix, it is very
likely that every part of the website you are looking at contains multiple machine
learning models.
Outside of commercial applications, machine learning has had a tremendous influ‐
ence on the way data driven research is done today. The tools introduced in this book
have been applied to diverse scientific questions such as understanding stars, finding
distant planets, analyzing DNA sequences, and providing personalized cancer treat‐
ments.
Your application doesn’t need to be as large-scale or world-changing as these exam‐
ples in order to benefit from machine learning. In this chapter, we will explain why
machine learning became so popular, and dicuss what kind of problem can be solved
using machine learning. Then, we will show you how to build your first machine
learning model, introducing important concepts on the way.
Why machine learning?
In the early days of “intelligent” applications, many systems used hand-coded rules of
“if” and “else” decisions to process data or adjust to user input. Think of a spam filter
9
www.it-ebooks.info

whose job is to move an email to a spam folder. You could make up a black-list of
words that would result in an email marked as spam. This would be an example of
using an expert designed rule system to design an “intelligent” application. Designing
kind of manual design of decision rules is feasible for some applications, in particular
for those applications in which humans have a good understanding of how a decision
should be made. However, using hand-coded rules to make decisions has two major
disadvantages:
1. The logic required to make a decision is specific to a single domain and task.
Changing the task even slightly might require a rewrite of the whole system.
2. Designing rules requires a deep understanding of how a decision should be made
by a human expert.
One example of where this hand-coded approach will fail is in detecting faces in
images. Today every smart phone can detect a face in an image. However, face detec‐
tion was an unsolved problem until as recent as 2001. The main problem is that the
way in which pixels (which make up an image in a computer) are “perceived by” the
computer is very different from how humans perceive a face. This difference in repre‐
sentation makes it basically impossible for a human to come up with a good set of
rules to describe what constitutes a face in a digital image.
Using machine learning, however, simply presenting a program with a large collec‐
tion of images of faces is enough for an algorithm to determine what characteristics
are needed to identify a face.
Problems that machine learning can solve
The most successful kind of machine learning algorithms are those that automate a
decision making processes by generalizing from known examples. In this setting,
which is known as a supervised learning setting, the user provides the algorithm with
pairs of inputs and desired outputs, and the algorithm finds a way to produce the
desired output given an input.
In particular, the algorithm is able to create an output for an input it has never seen
before without any help from a human.
Going back to our example of spam classification, using machine learning, the user
provides the algorithm a large number of emails (which are the input), together with
the information about whether any of these emails are spam (which is the desired
output). Given a new email, the algorithm will then produce a prediction as to
whether or not the new email is spam.
Machine learning algorithms that learn from input-output pairs are called supervised
learning algorithms because a “teacher” provides supervision to the algorithm in the
form of the desired outputs for each example that they learn from.
10 | Chapter 1: Introduction
www.it-ebooks.info

While creating a dataset of inputs and outputs is often a laborious manual process,
supervised learning algorithms are well-understood and their performance is easy to
measure. If your application can be formulated as a supervised learning problem, and
you are able to create a dataset that includes the desired outcome, machine learning
will likely be able to solve your problem.
Examples of supervised machine learning tasks include:
•Identifying the ZIP code from handwritten digits on an envelope. Here the
input is a scan of the handwriting, and the desired output is the actual digits in
the zip code. To create a data set for building a machine learning model, you need
to collect many envelopes. Then you can read the zip codes yourself and store the
digits as your desired outcomes.
•Determining whether or not a tumor is benign based on a medical image.
Here the input is the image, and the output is whether or not the tumor is
benign. To create a data set for building a model, you need a database of medical
images. You also need an expert opinion, so a doctor needs to look at all of the
images and decide which tumors are benign and which are not.
•Detecting fraudulent activity in credit card transactions. Here the input is a
record of the credit card transaction, and the output is whether it is likely to be
fraudulent or not. Assuming that you are the entity distributing the credit cards,
collecting a dataset means storing all transactions, and recording if a user reports
any transaction as fraudulent.
An interesting thing to note about the three examples above is that although the
inputs and outputs look fairly straight-forward, the data collection process for these
three tasks is vastly different.
While reading envelopes is laborious, it is easy and cheap. Obtaining medical imaging
and expert opinions on the other hand not only requires expensive machinery but
also rare and expensive expert knowledge, not to mention ethical concerns and pri‐
vacy issues. In the example of detecting credit card fraud, data collection is much
simpler. Your customers will provide you with the desired output, as they will report
fraud. All you have to do to obtain the input output pairs of fraudulent and non-
fraudulent activity is wait.
The other type of algorithms that we will cover in this book is unsupervised algo‐
rithms. In unsupervised learning, only the input data is known and there is no known
output data given to the algorithm. While there are many successful applications of
these methods as well, they are usually harder to understand and evaluate.
Examples of unsupervised learning include:
Why machine learning? | 11
www.it-ebooks.info

•Identifying topics in a set of blog posts. If you have a large collection of text
data, you might want to summarize it and find prevalent themes in it. You might
not know beforehand what these topics are, or how many topics there might be.
Therefore, there are no known outputs.
•Segmenting customers into groups with similar preferences. Given a set of cus‐
tomer records, you might want to identify which customers are similar, and
whether there are groups of customers with similar preferences. For a shopping
site these might be “parents”, “bookworms” or “gamers”. Since you don’t know in
advanced what these groups might be, or even how many there are, you have no
known outputs.
•Detecting abnormal access patterns to a website. To identify abuse or bugs, it is
often helpful to find access patterns that are different from the norm. Each
abnormal pattern might be very different, and you might not have any recorded
instances of abnormal behavior. Since in this example you only observe traffic,
and you don’t know what constitutes normal and abnormal behavior, this is an
unsupervised problem.
For both supervised and unsupervised learning tasks, it is important to have a repre‐
sentation of your input data that a computer can understand. Often it is helpful to
think of your data as a table. Each data point that you want to reason about (each
email, each customer, each transaction) is a row, and each property that describes that
data point (say the age of a customer, the amount or location of a transaction) is a
column.
You might describe users by their age, their gender, when they created an account and
how often they bought from your online shop. You might describe the image of a
tumor by the gray-scale values of each pixel, or maybe by using the size, shape and
color of the tumor to describe it.
Each entity or row here is known as data point or sample in machine learning, while
the columns, the properties that describe these entities, are called features.
We will later go into more detail on the topic of building a good representation of
your data, which is called feature extraction or feature engineering. You should keep
in mind however that no machine learning algorithm will be able to make a predic‐
tion on data for which it has no information. For example, if the only feature that you
have for a patient is their last name, no algorithm will be able to predict their gender.
This information is simply not contained in your data. If you add another feature that
contains their first name, you will have much better luck, as it is often possible to tell
the gender by a person’s first name.
12 | Chapter 1: Introduction
www.it-ebooks.info

Knowing your data
Quite possibly the most important part in the machine learning process is under‐
standing the data you are working with. It will not be effective to randomly choose an
algorithm and throw your data at it. It is necessary to understand what is going on in
your dataset before you begin building a model. Each algorithm is different in terms
of what data it works best for, what kinds data it can handle, what kind of data it is
optimized for, and so on. Before you start building a model, it is important to know
the answers to most of, if not all of, the following questions:
• How much data do I have? Do I need more?
•How many features do I have? Do I have too many? Do I have too few?
•Is there missing data? Should I discard the rows with missing data or handle
them differently?
•What question(s) am I trying to answer? Do I think the data collected can answer
that question?
The last bullet point is the most important question, and certainly is not easy to
answer. Thinking about these questions will help drive your analysis.
Keeping these basics in mind as we move through the book will prove helpful,
because while scikit-learn is a fairly easy tool to use, it is geared more towards those
with domain knowledge in machine learning.
Why Python?
Python has become the lingua franca for many data science applications. It combines
the powers of general purpose programming languages with the ease of use of
domain specific scripting languages like matlab or R.
Python has libraries for data loading, visualization, statistics, natural language pro‐
cessing, image processing, and more. This vast toolbox provides data scientists with a
large array of general and special purpose functionality.
As a general purpose programming language, Python also allows for the creation of
complex graphic user interfaces (GUIs), web services and for integration into existing
systems.
What this book will cover
In this book, we will focus on applying machine learning algorithms for the purpose
of solving practical problems. We will focus on how to write applications using the
machine learning library scikit-learn for the Python programming language. Impor‐
Why Python? | 13
www.it-ebooks.info

tant aspects that we will cover include formulating tasks as machine learning prob‐
lems, preprocessing data for use in machine learning algorithms, and choosing
appropriate algorithms and algorithmic parameters.
We will focus mostly on supervised learning techniques and algorithms, as these are
often the most useful ones in practice, and they are easy for beginners to use and
understand.
We will also discuss several common types of input, including text data.
What this book will not cover
This book will not cover the mathematical details of machine learning algorithms,
and we will keep the number of formulas that we include to a minimum. In particu‐
lar, we will not assume any familiarity with linear algebra or probability theory. As
mathematics, in particular probability theory, is the foundation upon which machine
learning is build, we will not be able to go into the analysis of the algorithms in great
detail. If you are interested in the mathematics of machine learning algorithms, we
recommend the text book “Elements of Statistical Learning” by Hastie, Tibshirani and
Friedman, which is available for free at the authors website[footnote: http://stat‐
web.stanford.edu/~tibs/ElemStatLearn/]. We will also not describe how to write
machine learning algorithms from scratch, and will instead focus on how to use the
large array of models already implemented in scikit-learn and other libraries.
We will not discuss reinforcement learning, which is about an agent learning from its
interaction with an environment, and we will only briefly touch upon deep learning.
Some of the algorithms that are implemented in scikit-learn but are outside the scope
of this book include Gaussian Processes, which are complex probabilistic models, and
semi-supervised models, which work with supervised information on only some of
the samples.
We will not also explicitly talk about how to work with time-series data, although
many of techniques we discuss are applicable to this kind of data as well. Finally, we
will not discuss how to do machine learning on natural images, as this is beyond the
scope of this book.
Scikit-learn
Scikit-learn is an open-source project, meaning that scikit-learn is free to use and dis‐
tribute, and anyone can easily obtain the source code to see what is going on behind
the scenes. The scikit-learn project is constantly being developed and improved, and
has a very active user community. It contains a number of state-of-the-art machine
learning algorithms, as well as comprehensive documentation about each algorithm
on the website [footnote http://scikit-learn.org/stable/documentation]. Scikit-learn is
14 | Chapter 1: Introduction
www.it-ebooks.info

a very popular tool, and the most prominent Python library for machine learning. It
is widely used in industry and academia, and there is a wealth of tutorials and code
snippets about scikit-learn available online. Scikit-learn works well with a number of
other scientific Python tools, which we will discuss later in this chapter.
While studying the book, we recommend that you also browse the scikit-learn user
guide and API documentation for additional details, and many more options to each
algorithm. The online documentation is very thorough, and this book will provide
you with all the prerequisites in machine learning to understand it in detail.
Installing Scikit-learn
Scikit-learn depends on two other Python packages, NumPy and SciPy. For plotting
and interactive development, you should also install matplotlib, IPython and the
Jupyter notebook. We recommend using one of the following pre-packaged Python
distributions, which will provide the necessary packages:
•Anaconda (https://store.continuum.io/cshop/anaconda/): a Python distribution
made for large-scale data processing, predictive analytics, and scientific comput‐
ing. Anaconda comes with NumPy, SciPy, matplotlib, IPython, Jupyter note‐
books, and scikit-learn. Anaconda is available on Mac OS X, Windows, and
Linux.
•Enthought Canopy (https://www.enthought.com/products/canopy/): another
Python distribution for scientific computing. This comes with NumPy, SciPy,
matplotlib, and IPython, but the free version does not come with scikit-learn. If
you are part of an academic, degree-granting institution, you can request an aca‐
demic license and get free access to the paid subscription version of Enthought
Canopy. Enthought Canopy is available for Python 2.7.x, and works on Mac,
Windows, and Linux.
•Python(x,y) (https://code.google.com/p/pythonxy/): a free Python distribution for
scientific computing, specifically for Windows. Python(x,y) comes with NumPy,
SciPy, matplotlib, IPython, and scikit-learn.
If you already have a python installation set up, you can use pip to install any of these
packages.
$ pip install numpy scipy matplotlib ipython scikit-learn
We do not recommended using pip to install NumPy and SciPy on Linux, as it
involves compiling the packages from source. See the scikit-learn website for more
detailed installation.
Scikit-learn | 15
www.it-ebooks.info

Essential Libraries and Tools
Understanding what scikit-learn is and how to use it is important, but there are a few
other libraries that will enhance your experience. Scikit-learn is built on top of the
NumPy and SciPy scientific Python libraries. In addition to knowing about NumPy
and SciPy, we will be using Pandas and matplotlib. We will also introduce the Jupyter
Notebook, which is an browser-based interactive programming environment. Briefly,
here is what you should know about these tools in order to get the most out of scikit-
learn.
If you are unfamiliar with numpy or matplotlib, we recommend reading the first
chapter of the scipy lecture notes[footnote: http://www.scipy-lectures.org/].
Jupyter Notebook
The Jupyter Notebook is an interactive environment for running code in the browser.
It is a great tool for exploratory data analysis and is widely used by data scientists.
While Jupyter Notebook supports many programming languages, we only need the
Python support. The Jypyter Notebook makes it easy to incorporate code, text, and
images, and all of this book was in fact written as an IPython notebook.
All of the code examples we include can be downloaded from github [FIXME add git‐
hub footnote].
NumPy
NumPy is one of the fundamental packages for scientific computing in Python. It
contains functionality for multidimensional arrays, high-level mathematical func‐
tions such as linear algebra operations and the Fourier transform, and pseudo ran‐
dom number generators.
The NumPy array is the fundamental data structure in scikit-learn. Scikit-learn takes
in data in the form of NumPy arrays. Any data you’re using will have to be converted
to a NumPy array. The core functionality of NumPy is this “ndarray”, meaning it has
n dimensions, and all elements of the array must be the same type. A NumPy array
looks like this:
import numpy as np
x = np.array([[1, 2, 3], [4, 5, 6]])
x
array([[1, 2, 3],
[4, 5, 6]])
16 | Chapter 1: Introduction
www.it-ebooks.info

SciPy
SciPy is both a collection of functions for scientific computing in python. It provides,
among other functionality, advanced linear algebra routines, mathematical function
optimization, signal processing, special mathematical functions and statistical distri‐
butions. Scikit-learn draws from SciPy’s collection of functions for implementing its
algorithms.
The most important part of scipy for us is scipy.sparse with provides sparse matri‐
ces, which is another representation that is used for data in scikit-learn. Sparse matri‐
ces are used whenever we want to store a 2d array that contains mostly zeros:
from scipy import sparse
# create a 2d numpy array with a diagonal of ones, and zeros everywhere else
eye = np.eye(4)
print("Numpy array:\n%s" % eye)
# convert the numpy array to a scipy sparse matrix in CSR format
# only the non-zero entries are stored
sparse_matrix = sparse.csr_matrix(eye)
print("\nScipy sparse CSR matrix:\n%s" % sparse_matrix)
Numpy array:
[[ 1. 0. 0. 0.]
[ 0. 1. 0. 0.]
[ 0. 0. 1. 0.]
[ 0. 0. 0. 1.]]
Scipy sparse CSR matrix:
(0, 0) 1.0
(1, 1) 1.0
(2, 2) 1.0
(3, 3) 1.0
More details on scipy sparse matrices can be found in the scipy lecture notes.
matplotlib
Matplotlib is the primary scientific plotting library in Python. It provides function for
making publication-quality visualizations such as line charts, histograms, scatter
Scikit-learn | 17
www.it-ebooks.info
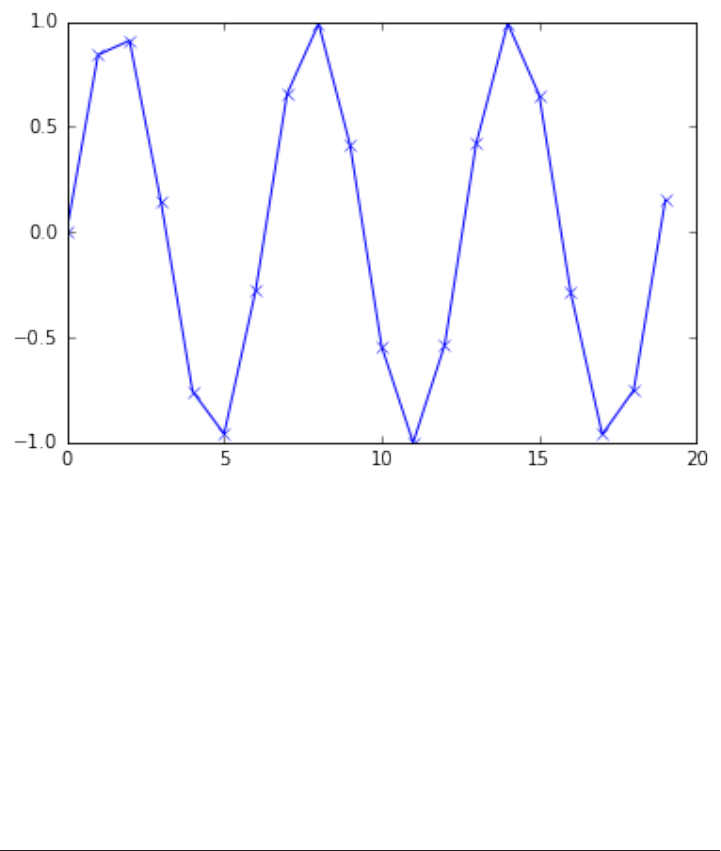
plots, and so on. Visualizing your data and any aspects of your analysis can give you
important insights, and we will be using matplotlib for all our visualizations.
%matplotlib inline
import matplotlib.pyplot as plt
# Generate a sequence of integers
x = np.arange(20)
# create a second array using sinus
y = np.sin(x)
# The plot function makes a line chart of one array against another
plt.plot(x, y, marker="x")
Pandas
Pandas is a Python library for data wrangling and analysis. It is built around a data
structure called DataFrame, that is modeled after the R DataFrame. Simply put, a
Pandas Pandas DataFrame is a table, similar to an Excel Spreadsheet. Pandas provides
a great range of methods to modify and operate on this table, in particular it allows
SQL-like queries and joins of tables. Another valuable tool provided by Pandas is its
ability to ingest from a great variety of file formats and databases, like SQL, Excel files
and comma separated value (CSV) files. Going into details about the functionality of
Pandas is out of the scope of this book. However, “Python for Data Analysis” by Wes
McKinney provides a great guide.
Here is a small example of creating a DataFrame using a dictionary:
18 | Chapter 1: Introduction
www.it-ebooks.info

import pandas as pd
# create a simple dataset of people
data = {'Name': ["John", "Anna", "Peter", "Linda"],
'Location' : ["New York", "Paris", "Berlin", "London"],
'Age' : [24, 13, 53, 33]
}
data_pandas = pd.DataFrame(data)
data_pandas
Age Location Name
024 New York John
113 Paris Anna
253 Berlin Peter
333 London Linda
Python2 versus Python3
There are two major versions of Python that are widely used at the moment: Python2
(more precisely 2.7) and Python3 (with the latest release being 3.5 at the time of writ‐
ing), which sometimes leads to some confusion. Python2 is no longer actively devel‐
oped, but because Python3 contains major changes, Python2 code does usually not
run without changes on Python3. If you are new to Python, or are starting a new
project from scratch, we highly recommend using the latests version of Python3.
If you have a large code-base that you rely on that is written for Python2, you are
excused from upgrading for now. However, you should try to migrate to Python3 as
soon as possible. Writing any new code, it is for the most part quite easy to write code
that runs under Python2 and Python3 [Footnote: The six package can be very handy
for that].
All the code in this book is written in a way that works for both versions. However,
the exact output might differ slightly under Python2.
Versions Used in this Book
We are using the following versions of the above libraries in this book:
import pandas as pd
print("pandas version: %s" % pd.__version__)
import matplotlib
print("matplotlib version: %s" % matplotlib.__version__)
import numpy as np
print("numpy version: %s" % np.__version__)
Scikit-learn | 19
www.it-ebooks.info

import IPython
print("IPython version: %s" % IPython.__version__)
import sklearn
print("scikit-learn version: %s" % sklearn.__version__)
pandas version: 0.17.1
matplotlib version: 1.5.1
numpy version: 1.10.4
IPython version: 4.1.2
scikit-learn version: 0.18.dev0
While it is not important to match these versions exactly, you should have a version
of scikit-learn that is as least as recent as the one we used.
Now that we have everything set up, let’s dive into our first appication of machine
learning.
A First Application: Classifying iris species
In this section, we will go through a simple machine learning application and create
our first model.
In the process, we will introduce some core concepts and nomenclature for machine
learning.
Let’s assume that a hobby botanist is interested in distinguishing what the species is of
some iris flowers that she found. She has collected some measurements associated
with the iris: the length and width of the petals, and the length and width of the sepal,
all measured in centimeters.
20 | Chapter 1: Introduction
www.it-ebooks.info

She also has the measurements of some irises that have been previously identified by
an expert botanist as belonging to the species Setosa, Versicolor or Virginica. For
these measurements, she can be certain of which species each iris belongs to. Let’s
assume that these are the only species our hobby botanist will encounter in the wild.
Our goal is to build a machine learning model that can learn from the measurements
of these irises whose species is known, so that we can predict the species for a new
iris.
Since we have measurements for which we know the correct species of iris, this is a
supervised learning problem. In this problem, we want to predict one of several
options (the species of iris). This is an example of a classication problem. The possi‐
ble outputs (different species of irises) are called classes.
Since every iris in the dataset belongs to one of three classes this problem is a three-
class classification problem.
The desired output for a single data point (an iris) is the species of this flower. For a
particular data point, the species it belongs to is called its label.
A First Application: Classifying iris species | 21
www.it-ebooks.info

Meet the data
The data we will use for this example is the iris dataset, a classical dataset in machine
learning an statistics.
It is included in scikit-learn in the dataset module. We can load it by calling the
load_iris function:
from sklearn.datasets import load_iris
iris = load_iris()
The iris object that is returned by load_iris is a Bunch object, which is very similar
to a dictionary. It contains keys and values:
iris.keys()
dict_keys(['DESCR', 'data', 'target_names', 'feature_names', 'target'])
The value to the key DESCR is a short description of the dataset. We show the begin‐
ning of the description here. Feel free to look up the rest yourself.
print(iris['DESCR'][:193] + "\n...")
Iris Plants Database
====================
Notes
-----
Data Set Characteristics:
:Number of Instances: 150 (50 in each of three classes)
:Number of Attributes: 4 numeric, predictive att
...
The value with key target_names is an array of strings, containing the species of
flower that we want to predict:
iris['target_names']
array(['setosa', 'versicolor', 'virginica'],
dtype='<U10')
The feature_names are a list of strings, giving the description of each feature:
iris['feature_names']
22 | Chapter 1: Introduction
www.it-ebooks.info

['sepal length (cm)',
'sepal width (cm)',
'petal length (cm)',
'petal width (cm)']
The data itself is contained in the target and data fields. The data contains the
numeric measurements of sepal length, sepal width, petal length, and petal width in a
numpy array:
type(iris['data'])
numpy.ndarray
The rows in the data array correspond to flowers, while the columns represent the
four measurements that were taken for each flower:
iris['data'].shape
(150, 4)
We see that the data contains measurements for 150 different flowers.
Remember that the individual items are called samples in machine learning, and their
properties are called features.
The shape of the data array is the number of samples times the number of features.
This is a convention in scikit-learn, and your data will always be assumed to be in this
shape.
Here are the feature values for the first five samples:
iris['data'][:5]
array([[ 5.1, 3.5, 1.4, 0.2],
[ 4.9, 3. , 1.4, 0.2],
[ 4.7, 3.2, 1.3, 0.2],
[ 4.6, 3.1, 1.5, 0.2],
[ 5. , 3.6, 1.4, 0.2]])
The target array contains the species of each of the flowers that were measured, also
as a numpy array:
type(iris['target'])
numpy.ndarray
The target is a one-dimensional array, with one entry per flower:
A First Application: Classifying iris species | 23
www.it-ebooks.info

iris['target'].shape
(150,)
The species are encoded as integers from 0 to 2:
iris['target']
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
The meaning of the numbers are given by the iris['target_names'] array: 0 means
Setosa, 1 means Versicolor and 2 means Virginica.
Measuring Success: Training and testing data
We want to build a machine learning model from this data that can predict the spe‐
cies of iris for a new set of measurements.
Before we can apply our model to new measurements, we need to know whether our
model actually works, that is whether we should trust its predictions.
Unfortunately, we can not use the data we use to build the model to evaluate it. This is
because our model can always simply remember the whole training set, and will
therefore always predict the correct label for any point in the training set. This
“remembering” does not indicate to us whether our model will generalize well, in
other words whether it will also perform well on new data. So before we apply our
model to new measurements, we will want to know whether we can trust its predic‐
tions.
To assess the models’ performance, we show the model new data (that it hasn’t seen
before) for which we have labels. This is usually done by splitting the labeled data we
have collected (here our 150 flower measurements) into two parts.
The part of the data is used to build our machine learning model, and is called the
training data or training set. The rest of the data will be used to access how well the
model works and is called test data, test set or hold-out set.
Scikit-learn contains a function that shuffles the dataset and splits it for you, the
train_test_split function.
24 | Chapter 1: Introduction
www.it-ebooks.info

This function extracts 75% of the rows in the data as the training set, together with
the corresponding labels for this data. The remaining 25% of the data, together with
the remaining labels are declared as the test set.
How much data you want to put into the training and the test set respectively is
somewhat arbitrary, but using a test-set containing 25% of the data is a good rule of
thumb.
In scikit-learn, data is usually denoted with a capital X, while labels are denoted by a
lower-case y.
Let’s call train_test_split on our data and assign the outputs using this nomencla‐
ture:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(iris['data'], iris['target'],
random_state=0)
The train_test_split function shuffles the dataset using a pseudo random number
generator before making the split. If we would take the last 25% of the data as a test
set, all the data point would have the label 2, as the data points are sorted by the label
(see the output for iris['target'] above). Using a tests set containing only one of
the three classes would not tell us much about how well we generalize, so we shuffle
our data, to make sure the test data contains data from all classes.
To make sure that we will get the same output if we run the same function several
times, we provide the pseudo random number generator with a fixed seed using the
random_state parameter. This will make the outcome deterministic, so this line will
always have the same outcome. We will always fix the random_state in this way when
using randomized procedures in this book.
The output of the train_test_split function are X_train, X_test, y_train and
y_test, which are all numpy arrays. X_train contains 75% of the rows of the dataset,
and X_test contains the remaining 25%:
X_train.shape
(112, 4)
X_test.shape
(38, 4)
First things rst: Look at your data
Before building a machine learning model, it is often a good idea to inspect the data,
to see if the task is easily solvable without machine learning, or if the desired infor‐
mation might not be contained in the data.
A First Application: Classifying iris species | 25
www.it-ebooks.info

Additionally, inspecting your data is a good way to find abnormalities and peculiari‐
ties. Maybe some of your irises were measured using inches and not centimeters, for
example. In the real world, inconsistencies in the data and unexpected measurements
are very common.
One of the best ways to inspect data is to visualize it. One way to do this is by using a
scatter plot.
A scatter plot of the data puts one feature along the x-axis, one feature along the y-
axis, and draws a dot for each data point.
Unfortunately, computer screens have only two dimensions, which allows us to only
plot two (or maybe three) features at a time. It is difficult to plot datasets with more
than three features this way.
One way around this problem is to do a pair plot, which looks at all pairs of two fea‐
tures. If you have a small number of features, such as the four we have here, this is
quite reasonable. You should keep in mind that a pair plot does not show the interac‐
tion of all of features at once, so some interesting aspects of the data may not be
revealed when visualizing it this way.
Here is a pair plot of the features in the training set. The data points are colored
according to the species the iris belongs to:
fig, ax = plt.subplots(3, 3, figsize=(15, 15))
plt.suptitle("iris_pairplot")
for i in range(3):
for j in range(3):
ax[i, j].scatter(X_train[:, j], X_train[:, i + 1], c=y_train, s=60)
ax[i, j].set_xticks(())
ax[i, j].set_yticks(())
if i == 2:
ax[i, j].set_xlabel(iris['feature_names'][j])
if j == 0:
ax[i, j].set_ylabel(iris['feature_names'][i + 1])
if j > i:
ax[i, j].set_visible(False)
26 | Chapter 1: Introduction
www.it-ebooks.info
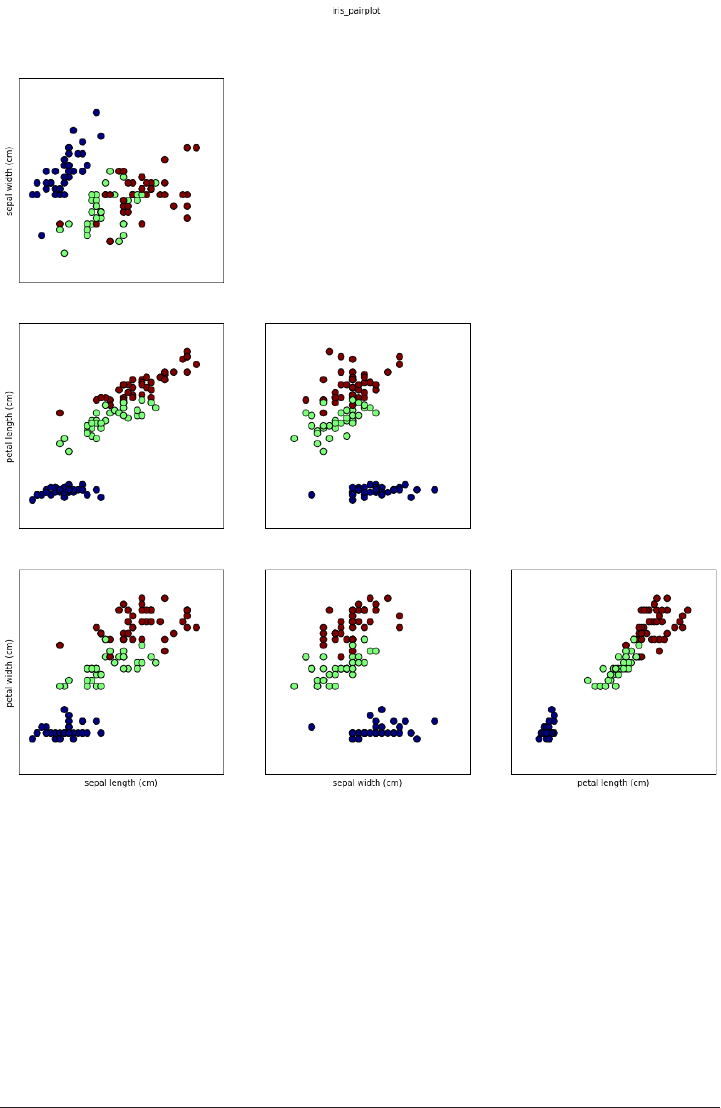
From the plots, we can see that the three classes seem to be relatively well separated
using the sepal and petal measurements. This means that a machine learning model
will likely be able to learn to separate them.
Building your rst model: k nearest neighbors
Now we can start building the actual machine learning model. There are many classi‐
fication algorithms in scikit-learn that we could use. Here we will use a k nearest
neighbors classifier, which is easy to understand.
A First Application: Classifying iris species | 27
www.it-ebooks.info

Building this model only consists of storing the training set. To make a prediction for
a new data point, the algorithm finds the point in the training set that is closest to the
new point. Then, it and assigns the label of this closest data training point to the new
data point.
The k in k nearest neighbors stands for the fact that instead of using only the closest
neighbor to the new data point, we can consider any fixed number k of neighbors in
the training (for example, the closest three or five neighbors). Then, we can make a
prediction using the majority class among these neighbors. We will go into more
details about this later.
Let’s use only a single neighbor for now.
All machine learning models in scikit-learn are implemented in their own class,
which are called Estimator classes. The k nearest neighbors classification algorithm
is implemented in the KNeighborsClassifier class in the neighbors module.
Before we can use the model, we need to instantiate the class into an object. This is
when we will set any parameters of the model. The single parameter of the KNeighbor
sClassifier is the number of neighbors, which we will set to one:
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=1)
The knn object encapsulates the algorithm to build the model from the training data,
as well the algorithm to make predictions on new data points.
It will also hold the information the algorithm has extracted from the training data.
In the case of KNeighborsClassifier, it will just store the training set.
To build the model on the training set, we call the fit method of the knn object,
which takes as arguments the numpy array X_train containing the training data and
the numpy array y_train of the corresponding training labels:
knn.fit(X_train, y_train)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=1, p=2,
weights='uniform')
Making predictions
We can now make predictions using this model on new data, for which we might not
know the correct labels.
28 | Chapter 1: Introduction
www.it-ebooks.info

Imagine we found an iris in the wild with a sepal length of 5cm, a sepal width of
2.9cm, a petal length of 1cm and a petal width of 0.2cm. What species of iris would
this be?
We can put this data into a numpy array, again with the shape number of samples
(one) times number of features (four):
X_new = np.array([[5, 2.9, 1, 0.2]])
X_new.shape
(1, 4)
To make prediction we call the predict method of the knn object:
prediction = knn.predict(X_new)
prediction
array([0])
iris['target_names'][prediction]
array(['setosa'],
dtype='<U10')
Our model predicts that this new iris belongs to the class 0, meaning its species is
Setosa.
But how do we know whether we can trust our model? We don’t know the correct
species of this sample, which is the the whole point of building the model!
Evaluating the model
This is where the test set that we created earlier comes in. This data was not used to
build the model, but we do know what the correct species are for each iris in the test
set.
We can make a prediction for an iris in the test data, and compare it against its label
(the known species). We can measure how well the model works by computing the
accuracy, which is the fraction of flowers for which the right species was predicted:
y_pred = knn.predict(X_test)
np.mean(y_pred == y_test)
0.97368421052631582
We can also use the score method of the knn object, which will compute the test set
accuracy for us:
knn.score(X_test, y_test)
0.97368421052631582
A First Application: Classifying iris species | 29
www.it-ebooks.info

For this model, the test set accuracy is about 0.97, which means we made the right
prediction for 97% of the irises in the test set. Under some mathematical assump‐
tions, this means that we can expect our model to be correct 97% of the time for new
irises.
For our hobby botanist application, this high level of accuracy means that our models
may be trustworthy enough to use. In later chapters we will discuss how we can
improve performance, and what caveats there are in tuning a model.
Summary
Let’s summarize what we learned in this chapter. We started off formulating a task of
predicting which species of iris a particular flower belongs to by using physical meas‐
urements of the flower. We used a dataset of measurements that was annotated by an
expert with the correct species to build our model, making this a supervised learning
task. There were three possible species, Setosa, Versicolor or Virginica, which made
the task a three-class classication problem. The possible species are called classes in
the classification problem, and the species of a single iris is called its label.
The dataset consists of two numpy arrays, one containing the data, which is referred
to as X in scikit-learn, and one containing the correct or desired outputs, which is
called y. The array X is a two-dimensional array of features, with one row per data
point, and one column per feature. The array y is a one-dimensional array, which
here contained one class label from 0 to 2 for each of the samples.
We split our dataset into a training set, to build our model, and a test set, to evaluate
how well our model will generalize to new, unseen data.
We chose the k nearest neighbors classification algorithm, which makes predictions
for a new data point by considering its closest neighbor(s) in the training set.
The algorithm is implemented in the KNeighborsClassifier class, which contains
the algorithm to build the model, as well as the algorithm to make a prediction using
the model. We instantiated the class, setting parameters. Then, we built the model by
calling the fit method, passing the training data X_train and training outputs
y_train as parameters.
We evaluated the model using the score method, that computes the accuracy of the
model. We applied the score method to the test set data and the test set labels, and
found that our model is about 97% accurate, meaning it is correct 97% of the time on
the test set.
This gave us the confidence to apply the model to new data (in our example, new
flower measurements), and trust that the model will be correct about 97% of the time.
30 | Chapter 1: Introduction
www.it-ebooks.info

Here is a summary of the code needed for the whole training and evaluation proce‐
dure:
X_train, X_test, y_train, y_test = train_test_split(iris['data'], iris['target'],
random_state=0)
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)
knn.score(X_test, y_test)
0.97368421052631582
This snippet contains the core code for applying any machine learning algorithms
using scikit-learn. The fit, predict and score methods are the common interface to
supervised models in scikit-learn, and with the concepts introduced in this chapter,
you can apply these models to many machine learning tasks.
In the next chapter, we will go into more depth about the different kinds of super‐
vised models in scikit-learn, and how to apply them successfully.
A First Application: Classifying iris species | 31
www.it-ebooks.info

CHAPTER 2
Supervised Learning
As we mentioned in the introduction, supervised machine learning is one of the most
commonly used and successful types of machine learning. In this chapter, we will
describe supervised learning in more detail, and explain several popular supervised
learning algorithms.
We already saw an application of supervised machine learning in the last chapter:
classifying iris flowers into several species using physical measurements of the flow‐
ers.
Remember that supervised learning is used whenever we want to predict a certain
outcome from a given input, and we have examples of input-output pairs. We build a
machine learning model from these input-output pairs, which comprise our training
set. Our goal is to make accurate predictions to new, never-before seen data.
Supervised learning often requires human effort to build the training set, but after‐
wards automates and often speeds up an otherwise laborious or infeasible task.
Classication and Regression
There are two major types of supervised machine learning algorithms, called classi‐
cation and regression.
In classification, the goal is to predict a class label, which is a choice from a predefined
list of possibilities. In Chapter 1 (Introduction) we used the example of classifying iri‐
ses into one of three possible species. Classification is sometimes separated into
binary classication, which is the special case of distinguishing between exactly two
classes, and multi-class classication which is classificaFItion between more than two
classes. You can think of binary classification as trying to answer a “yes” or “no” ques‐
tion.
33
www.it-ebooks.info

Classifying emails into either spam or not spam is an example of a binary classifica‐
tion problem. In this binary classification task, the yes or no question being asked
would be “Is this email spam?”.
[info box] In binary classification we often speak of one class being the positive class
and the other class being the negative class. Here, positive don’t represent benefit or
value, but rather what the object of study is. So when looking for spam, “positive”
could mean the spam class. Which of the two classes is called positive is often a sub‐
jective manner, and specific to the domain.FI
[/info box]
The iris example on the other hand is an example of a multi-class classification prob‐
lem.
Another example of a multi-class classification problem is predicting what language a
website is in from the text on the website. The classes here would be a pre-defined list
of possible languages.
For regression tasks, the goal is to predict a continuous number, or a oating point
number in programming terms (a real number in mathematical terms). Predicting a
person’s annual income from their education, their age and where they live, is a[n
example of a] regression task. When predicting income, the predicted value is an
amount, and can be any number in a given range. Another example of a regression
task is predicting the yield of a corn farm, given attributes such as previous yields,
weather and number of employees working on the farm. The yield again can be an
arbitrary number.
An easy way to distinguish between classification and regression tasks is to ask
whether there is some kind of ordering or continuity in the output. If there is an
ordering, or a continuity between possible outcomes, then the problem is a regression
problem.
Think about predicting annual income. There is a clear ordering of “making more
money” or “making less money”. There is a natural understanding that 40.000$ per
year is between 50.000$ per year and 30.000$ per year. There is also a continuity in the
output. Whether a person makes 40,000$ or 40,001$ a year does not make a tangible
difference, even though they are different amounts of money. So if our algorithm pre‐
dicts 39,999$ or 40,001$ when it should have predicted 40,000$, we don’t mind that
much.
Contrastively, for the task of recognizing the language of a website (which is a classifi‐
cation problem), there is no matter of degree. A website is in one language, or it is in
another. There is no continuity between languages, and there is no language that is
between English and French [footnote: We ask linguists to excuse the simplified pre‐
sentation of languages as distinct and fixed entities].
34 | Chapter 2: Supervised Learning
www.it-ebooks.info

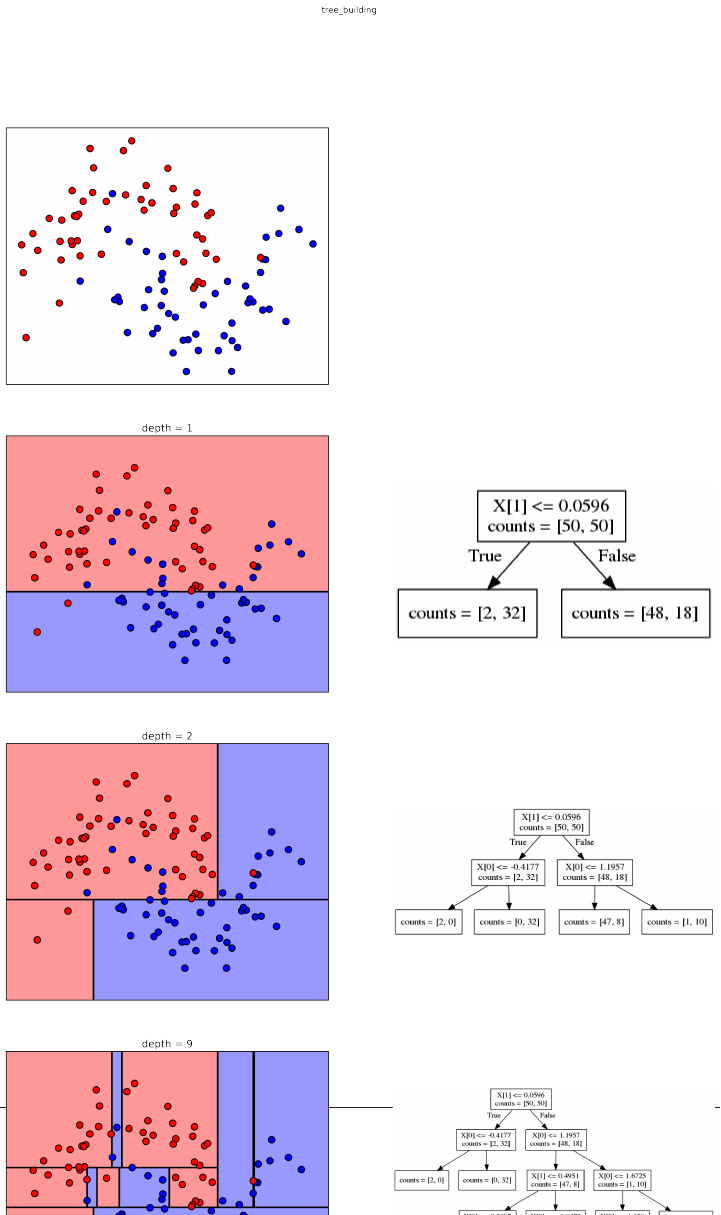
Generalization, Overtting and Undertting
In supervised learning, we want to built a model on the training data, and then be
able to make accurate predictions on new, unseen data, that has the same characteris‐
tics as the training set that we used. If a model is able to make accurate predictions on
unseen data, we say it is able to generalize from the training set to the test set.
We want to build a model that is able to generalize as well as possible.
Usually we build a model in such a way that it can make accurate predictions on the
training set. If the training and test set have enough in common, we expect the model
to also be accurate on the test set.
However, there are some cases where this can go wrong. For example, if we allow our‐
selves to build very complex models, we can always be as accurate as we like on the
training set.
Let’s take a look at a made-up example. Say a novice data scientist wants to predict a
person’s salary, and for each person, the only characteristic he has is the date of birth.
The dataset might look like this:
|Date of Birth|Annual salary ($)|
|-|-|
|30/4/1950|50500|
|05/8/1964|41000|
|09/2/2001|35200|
|17/5/1989|36000|
Because our novice data scientist knows he needs to present a machine learning algo‐
rithm with numbers, he replaces the date of birth with each persons age at the time of
analysis, in 2016. That seems very little to go by, so our novice data scientist also adds
the last four digits of their social security number, their house number, their zip code,
and the number of their children.
Now the data looks like this:
|Age|SSN|House|ZIP|Children|Annual salary ($)|
|-|-|-|-|-|-|
|66|1882|19|10030|2|50500|
|52|1337|2|10028|0|41000|
|22|3467|8|10041|1|35200|
|25|8391|27|10009|4|36000|
Generalization, Overtting and Undertting | 35
www.it-ebooks.info

Now he builds a machine learning model using the first three rows as a training set.
Let’s save how the algorithm works for later. The algorithm produces the following
formula for the annual salary:
salary = 333 * x[0] + 1 * x[1] + 237 * x[2] - 20 * x[3] + 26 * x[4] +
225866
Here x[0] to x[4] contain the age, last digits of the SSN, the house number, ZIP code
and number of children.
The formula works very well on the training set, the first three rows of the dataset.
The predictions for the training set are 53681, 44433 and 37761 which are very close
to the true values.
However, the prediction the formula makes for the fourth point in the dataset, which
was not part of the training set, is 48905, which is quite far from the 36000 which was
the desired output.
So what happened here? The data scientist allowed his machine learning algorithm to
build a relatively complex interaction between the five features and the output (the
annual salary) without a lot of support for this model in the data. The result is a
model that doesn’t reflect a real world relationship. For example, this model predicts
that you would make $237 more if you move to the house next door (237 is the coef‐
ficient for x[2]!
Building a complex model that does well on the training set but does not generalize to
new data is known as overtting, because we are focusing too much on the particular‐
ities of the training data. Avoiding overfitting is a crucial aspect of building a success‐
ful machine learning model. A good way to avoid overfitting is to restrict ourselves to
building very simple models.
A much simpler model for the salary prediction task is to always predict the average
salary of the three people in the training set, which is
Predicting that everybody’s salary is 42233 is clearly too simple, and does not capture
the variation in our training set very well. Using too simple a model is called undert‐
ting, because we don’t explain the target output for the training data well enough.
A middle ground for the salary prediction would be to use age as a single feature,
which restricts us to very simple models, but still allows us to capture some trends in
our data.
A model only including the age feature is:
salary = 323 * age + 27146
This model makes predictions of 48464, 43942, and 34252 for the training set, which
is not as good as our previous model.
36 | Chapter 2: Supervised Learning
www.it-ebooks.info
However, it generalizes much better to the test set when compared to the complex
model we used before. It predicts 35221 for the fourth row in the table.
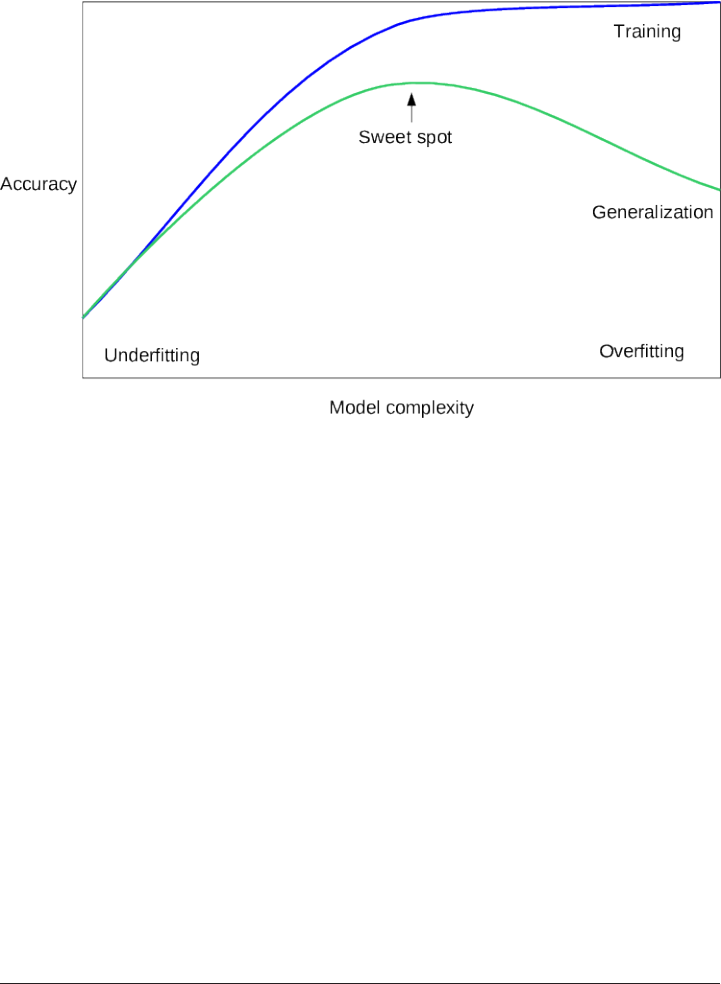
The trade-off between overfitting and underfitting is illustrated in Figure
model_complexity.
If we choose use a model that is too simple, we will do badly on the training set, and
similarly badly on the test set, as we would using only the mean prediction.
The more complex we allow our model to be, the better we will be able to predict on
the training data. However, if our model becomes too complex, we start focusing too
much on the particularities of our training set, and the model will not generalize well
to new data.
There is a sweet spot in between, which will yield the best generalization perfor‐
mance. This is the model we want to find.
Understanding the implications of model complexity is hard, and has different impli‐
cations for each kind of machine learning model.
Supervised Machine Learning Algorithms
We will now go through the most popular machine learning algorithms and explain
how they learn from data and how they make predictions. We will also discuss how
the concept of model complexity plays out for each of these models.
While an in-depth discussion of each algorithm is beyond the scope of this book, we
will try to give some intuition about how each algorithm builds a model.
Supervised Machine Learning Algorithms | 37
www.it-ebooks.info

We will also discuss strength and weaknesses of each algorithm, and what kind of
data they can be best applied to. We will also explain the meaning of the most impor‐
tant parameters and options. Discussing all of them is beyond the scope of the book,
and we refer you to the scikit-learn documentation for more details.
Many algorithms have a classification and a regression variant, and we will describe
both.
It is not necessary to read through the description of each algorithm in detail, but
understanding the models will give you a better feeling for the different ways
machine learning algorithms can work. This chapter can also be used as a reference
guide, and you can come back to it when you are unsure about the workings of any of
the algorithms.
We will use several datasets to illustrate the different algorithms. Some of the datasets
will be small synthetic (meaning made-up) datasets, designed to highlight particular
aspects of the algorithms. Other datasets will be larger, real world examples datasets.
An example of a synthetic two-class classification dataset is the forge dataset, which
has two features. Below is a scatter plot visualizing all of the data points in this data‐
set. The plot has the first feature on the x-axis and the second feature on the y-axis.
As is always the case in in scatter plots, each data point is represented as one dot. The
color of the dot indicates its class, with red meaning class 0 and blue meaning class 1.
X, y = mglearn.datasets.make_forge()
plt.scatter(X[:, 0], X[:, 1], c=y, s=60, cmap=mglearn.cm2)
print("X.shape: %s" % (X.shape,))
38 | Chapter 2: Supervised Learning
www.it-ebooks.info
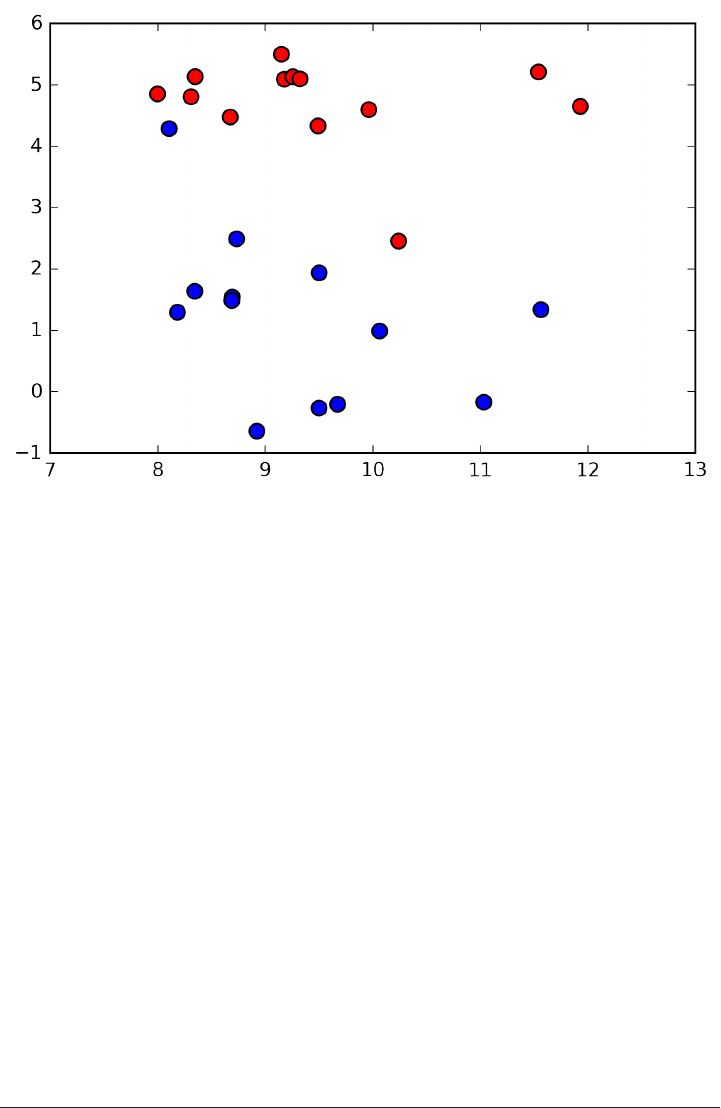
X.shape: (26, 2)
As you can see from X.shape, this dataset consists of 26 data points, with 2 features.
To illustrate regression algorithms, we will use the synthetic wave dataset shown
below. The wave dataset only has a single input feature, and a continuous target
variable (or response) that we want to model.
The plot below is showing the single feature on the x-axis, with the data points as
green dots. For each data point, the target output is plotted in blue on the y-axis.
X, y = mglearn.datasets.make_wave(n_samples=40)
plt.plot(X, y, 'o')
plt.plot(X, -3 * np.ones(len(X)), 'o')
plt.ylim(-3.1, 3.1)
Supervised Machine Learning Algorithms | 39
www.it-ebooks.info
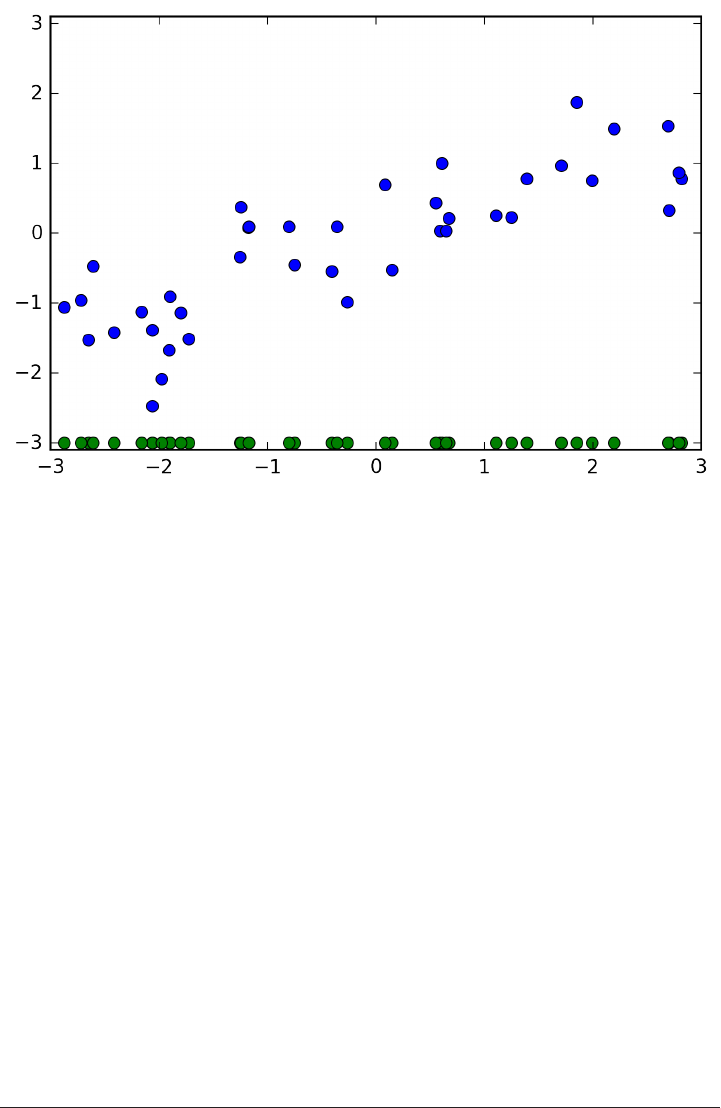
We are using these very simple, low-dimensional datasets as we can easily visualize
them -- a computer monitor has two dimensions, so data with more than two fea‐
tures is hard to show. Any intuition derived from datasets with few features (also
called low-dimensional datasets) might not hold in datasets with many features (high
dimensional datasets). As long as you keep that in mind, inspecting algorithms on
low-dimensional datasets can be very instructive.
We will complement these small synthetic dataset with two real-world datasets that
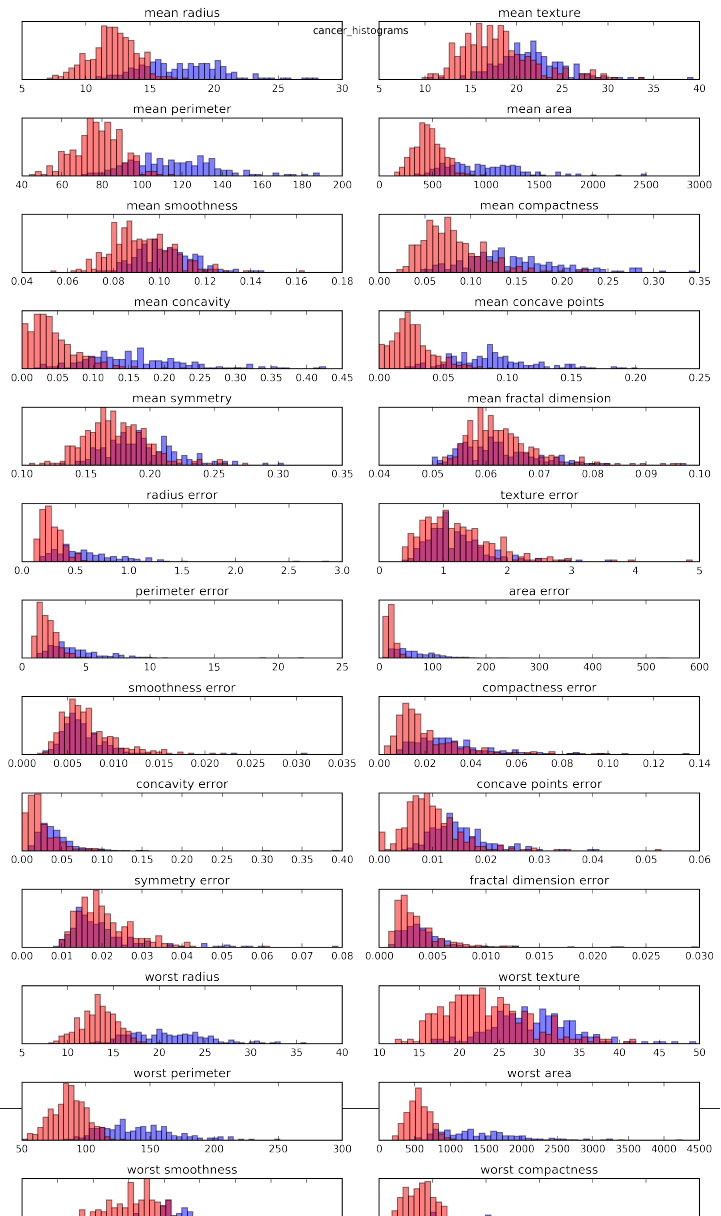
are included in scikit-learn. One is the Wisconsin breast cancer dataset (or cancer for
short), which records clinical measurements of breast cancer tumors. Each tumor is
labeled as “benign” (for harmless tumors) or “malignant” (for cancerous tumors), and
the task is to learn to predict whether a tumor is malignant based on the measure‐
ments of the tissue.
The data can be loaded using the load_breast_cancer from scikit-learn. Datasets
that are included in scikit-learn are usually stored as Bunch objects, which contain
some information about the dataset as well as the actual data.
All you need to know about Bunch objects is that they behave like dictionaries, with
the added benefit that you can access values using a dot (as in bunch.key instead of
bunch['key']).
40 | Chapter 2: Supervised Learning
www.it-ebooks.info

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
cancer.keys()
dict_keys(['DESCR', 'target_names', 'data', 'target', 'feature_names'])
The dataset consists of 569 data points, with 30 features each:
print(cancer.data.shape)
(569, 30)
Of these 569 data points, 212 are labeled as malignant, and 357 as benign:
print(cancer.target_names)
np.bincount(cancer.target)
array([212, 357])
['malignant' 'benign']
To get a description of the semantic meaning of each feature, we can have a look at
the feature_names attribute:
cancer.feature_names
array(['mean radius', 'mean texture', 'mean perimeter', 'mean area',
'mean smoothness', 'mean compactness', 'mean concavity',
'mean concave points', 'mean symmetry', 'mean fractal dimension',
'radius error', 'texture error', 'perimeter error', 'area error',
'smoothness error', 'compactness error', 'concavity error',
'concave points error', 'symmetry error', 'fractal dimension error',
'worst radius', 'worst texture', 'worst perimeter', 'worst area',
'worst smoothness', 'worst compactness', 'worst concavity',
'worst concave points', 'worst symmetry', 'worst fractal dimension'],
dtype='<U23')
You can find out more about the data by reading cancer.DESCR if you are interested.
We will also be using a real-world regression dataset, the Boston Housing dataset.
The task associated with this dataset is to predict the median value of homes in sev‐
eral Boston neighborhoods in the 1970s, using information about the neighborhoods
such as crime rate, proximity to the Charles River, highway accessibility and so on.
The datasets contains 506 data points, described by 13 features:
Supervised Machine Learning Algorithms | 41
www.it-ebooks.info

from sklearn.datasets import load_boston
boston = load_boston()
print(boston.data.shape)
(506, 13)
Again, you can get more information about the dataset by reading the DESCR attribute
of boston.
For our purposes here, we will actually expand this dataset, by not only considering
these 13 measurements as input features, but also looking at all products (also called
interactions) between features.
In other words, we will not only consider crime rate and highway accessibility as a
feature, but also the product of crime rate and highway accessibility. Including
derived feature like these is called feature engineering, which we will discuss in more
detail in Chapter 5 (Representing Data).
This derived dataset can be loaded using the load_extended_boston function:
X, y = mglearn.datasets.load_extended_boston()
print(X.shape)
(506, 105)
The resulting 105 features are the 13 original features, the 13 choose 2 = 91 (Footnote:
the number of ways to pick 2 elements out of 13 elements) features that are product
of two features, and one constant feature.
We will use these datasets to explain and illustrate the properties of the different
machine learning algorithms. But for now, let’s get to the algorithms themselves.
First, we will revisit the k-Nearest Neighbor algorithm, that we already saw in the last
chapter.
k-Nearest Neighbor
The k-Nearest Neighbors (kNN) algorithm is arguably the simplest machine learning
algorithm. Building the model only consists of storing the training dataset. To make a
prediction for a new data point, the algorithm finds the closest data points in the
training dataset, it “nearest neighbors”.
k-Neighbors Classication
In its simplest version, the algorithm only considers exactly one nearest neighbor,
which is the closest training data point to the point we want to make a prediction for.
The prediction is then simply the known output for this training point.
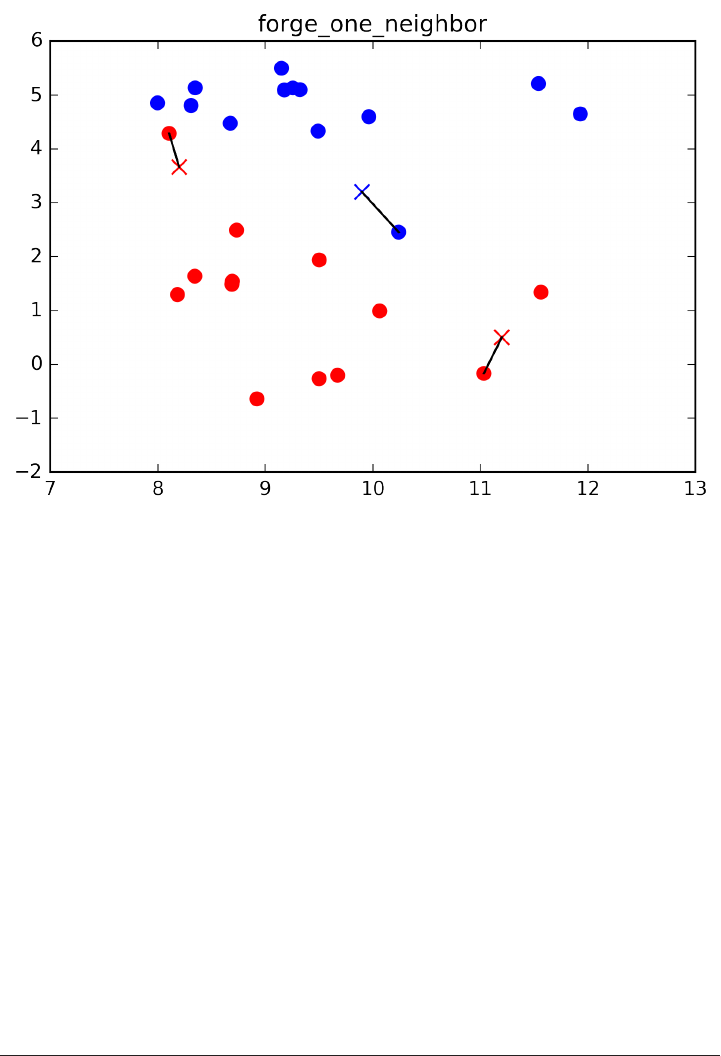
Figure forge_one_neighbor illustrates this for the case of classification on the forge
dataset.
42 | Chapter 2: Supervised Learning
www.it-ebooks.info
mglearn.plots.plot_knn_classification(n_neighbors=1)
plt.title("forge_one_neighbor");
Here, we added three new data points, shown as crosses. For each of them, we
marked the closest point in the training set. The prediction of the one-nearest-
neighbor algorithm is the label of that point (shown by the color of the cross).
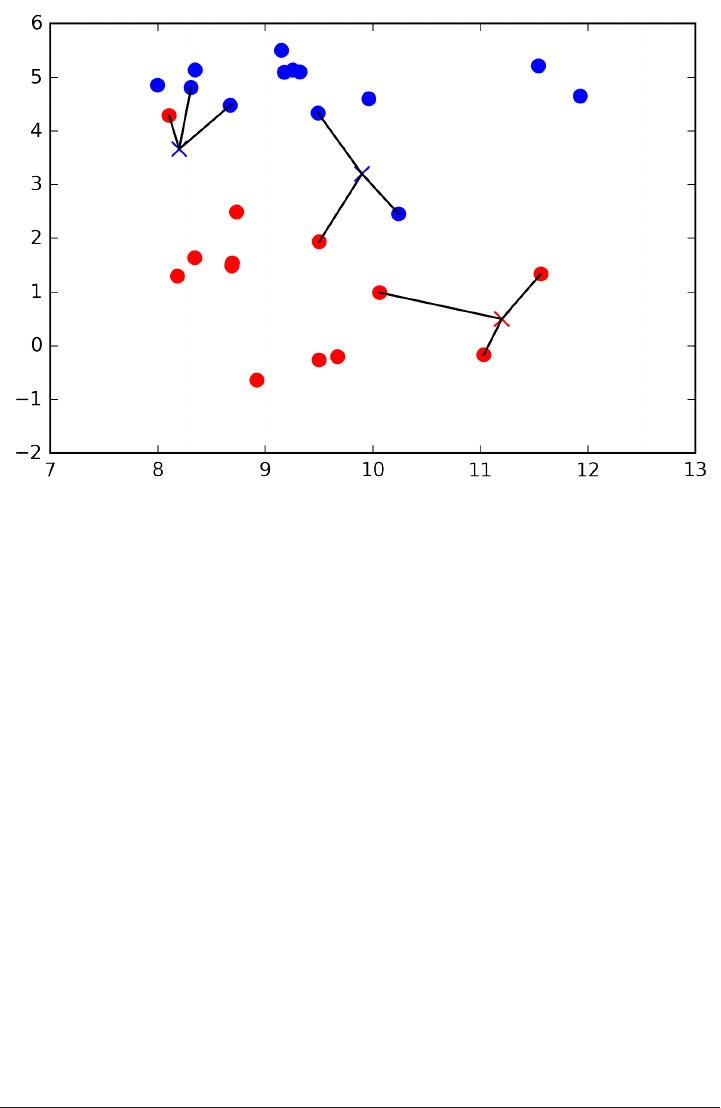
Instead of considering only the closest neighbor, we can also consider an arbitrary
number $k$ of neighbors. This is where the name of the $k$ neighbors algorithm
comes from. When considering more than one neighbor, we use voting to assign a
label. This means, for each test point, we count how many neighbors are red, and
how many neighbors are blue. We then assign the class that is more frequent: in other
words, the majority class among the k neighbors.
Below is an illustration using the three closest neighbors. Again, the prediction is
shown as the color of the cross. You can see that the prediction changed for the point
in the top left from using only one neighbor.
mglearn.plots.plot_knn_classification(n_neighbors=3)
k-Nearest Neighbor | 43
www.it-ebooks.info
While this illustration is for a binary classification problem, you can imagine this
working with any number of classes. For more classes, we count how many neighbors
belong to each class, and again predict the most common class.
Now let’s look at how we can apply the $k$ nearest neighbors algorithm using scikit-
learn.
First, we split our data into a training and a test set, so we can evaluate generalization
performance, as discussed in Chapter 1 (Introduction).
from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.make_forge()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
Next we import and instantiate the class. This is when we can set parameters, like the
number of neighbors to use. Here, we set it to three.
from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=3)
Now, we fit the classifier using the training set. For KNeighborsClassifier this
means storing the dataset, so we can compute neighbors during prediction.
clf.fit(X_train, y_train)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
44 | Chapter 2: Supervised Learning
www.it-ebooks.info
metric_params=None, n_jobs=1, n_neighbors=3, p=2,
weights='uniform')
To make predictions on the test data, we call the predict method. This computes the
nearest neighbors in the training set and finds the most common class among these:
clf.predict(X_test)
array([1, 0, 1, 0, 1, 0, 0])
To evaluate how well our model generalizes, we can call the score method with the
test data together with the test labels:
clf.score(X_test, y_test)
0.8571428571428571
We see that our model is about 86% accurate, meaning the model predicted the class
correctly for 85% of the samples in the test dataset.
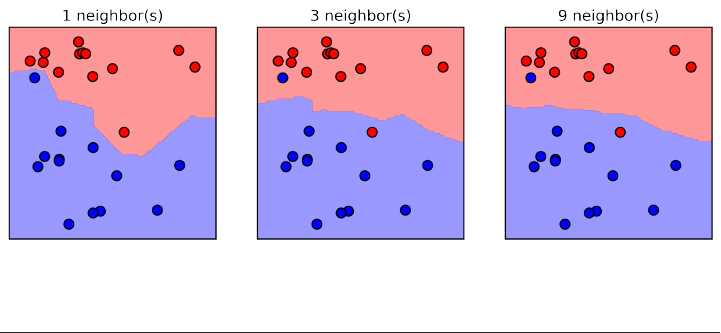
Analyzing KNeighborsClassier
For two-dimensional datasets, we can also illustrate the prediction for all possible test
point in the xy-plane. We color the plane red in regions where points would be
assigned the red class, and blue otherwise. This lets us view the decision boundary,
which is the divide between where the algorithm assigns class red versus where it
assigns class blue.
Here is a visualization of the decision boundary for one, three and five neighbors:
fig, axes = plt.subplots(1, 3, figsize=(10, 3))
for n_neighbors, ax in zip([1, 3, 9], axes):
clf = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y)
mglearn.plots.plot_2d_separator(clf, X, fill=True, eps=0.5, ax=ax, alpha=.4)
ax.scatter(X[:, 0], X[:, 1], c=y, s=60, cmap=mglearn.cm2)
ax.set_title("%d neighbor(s)" % n_neighbors)
k-Nearest Neighbor | 45
www.it-ebooks.info

As you can see in the left figure, using a single neighbor results in a decision bound‐
ary that follows the training data closely. Considering more and more neighbors leads
to a smoother decision boundary. A smoother boundary corresponds to a simple
model. In other words, using few neighbors corresponds to high model complexity
(as shown on the right side of Figure model_complexity), and using many neighbors
corresponds to low model complexity (as shown on the left side of Figure
model_complexity).
Let’s investigate whether we can confirm the connection between model complexity
and generalization that we discussed above.
We will do this on the real world breast cancer dataset.
We begin by splitting the dataset into a training and a test set. Then we will evaluate
training and test set performance with different numbers of neighbors.
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=66)
training_accuracy = []
test_accuracy = []
# try n_neighbors from 1 to 10.
neighbors_settings = range(1, 11)
for n_neighbors in neighbors_settings:
# build the model
clf = KNeighborsClassifier(n_neighbors=n_neighbors)
clf.fit(X_train, y_train)
# record training set accuracy
training_accuracy.append(clf.score(X_train, y_train))
# record generalization accuracy
test_accuracy.append(clf.score(X_test, y_test))
plt.plot(neighbors_settings, training_accuracy, label="training accuracy")
plt.plot(neighbors_settings, test_accuracy, label="test accuracy")
plt.legend()
46 | Chapter 2: Supervised Learning
www.it-ebooks.info
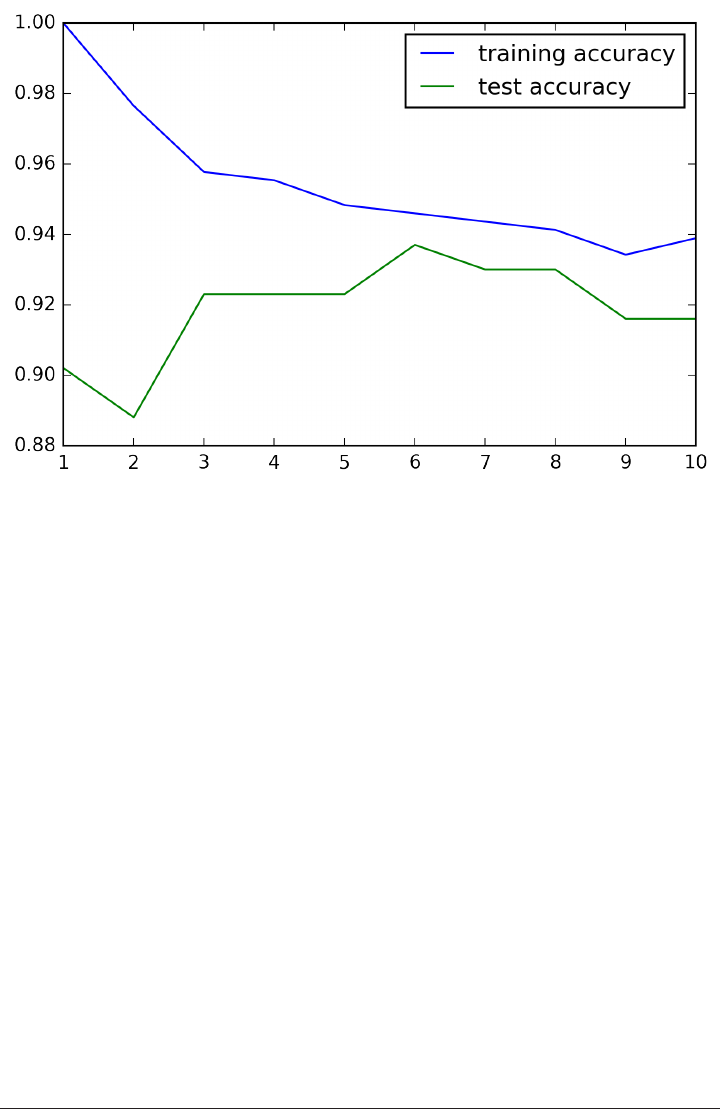
The plot shows the training and test set accuracy on the y axis against the setting of
n_neighbors on the x axis. While the real world plots are rarely very smooth, we can
still recognize some of the characteristics of overfitting and underfitting. As consider‐
ing fewer neighbors corresponds to a more complex model, the plot is horizontally
flipped relative to the illustration in Figure model_complexity.
Considering a single nearest neighbor, the prediction on the training set is perfect.
Considering more neighbors, the model becomes more simple, and the training accu‐
racy drops.
The test set accuracy for using a single neighbor is lower then when using more
neighbors, indicating that using a single nearest neighbor leads to a model that is too
complex. On the other hand, when considering 10 neighbors, the model is too sim‐
ple, and performance is even worse. The best performance is somewhere in the mid‐
dle, around using six neighbors.
Still, it is good to keep the scale of the plot in mind. The worst performance is around
88% accuracy, which might still be acceptable.
k-Neighbors Regression
There is also a regression variant of the k-nearest neighbors algorithm. Again, let’s
start by using a single nearest neighbor, this time using the wave dataset. We added
three test data points as green crosses on the x axis.
k-Nearest Neighbor | 47
www.it-ebooks.info
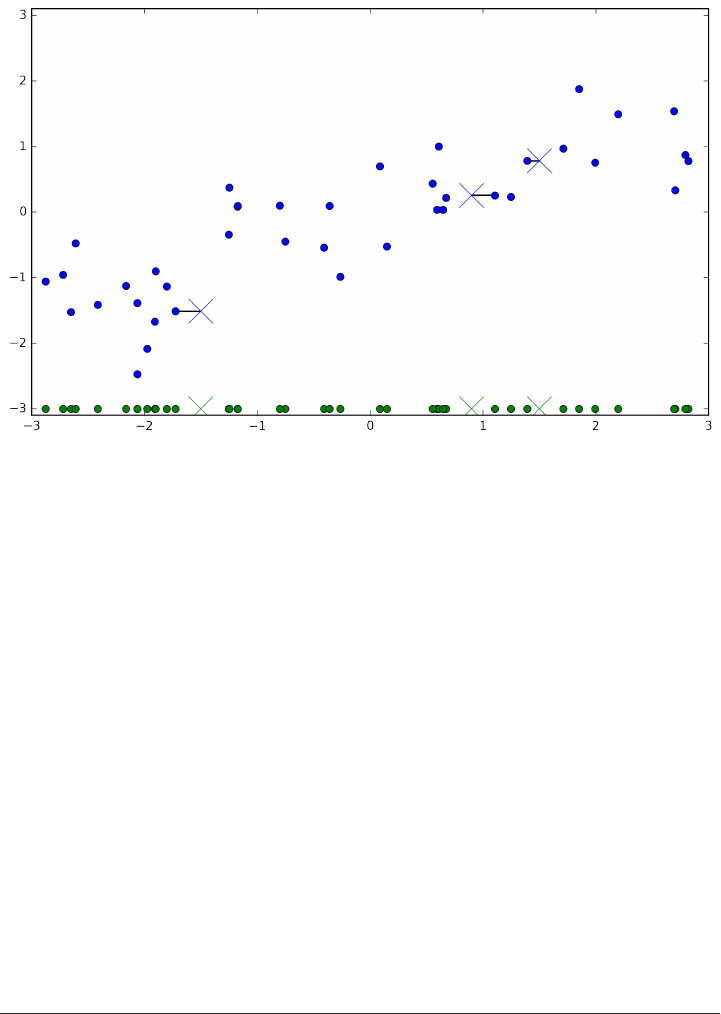
The prediction using a single neighbor is just the target value of the nearest neighbor,
shown as the blue cross:
mglearn.plots.plot_knn_regression(n_neighbors=1)
Again, we can also use more than one nearest neighbor for regression. When using
multiple nearest neighbors for regression, the prediction is the average (or mean) of
the relevant neighbors:
mglearn.plots.plot_knn_regression(n_neighbors=3)
48 | Chapter 2: Supervised Learning
www.it-ebooks.info
The k nearest neighbors algorithm for regression is implemented in the KNeighbors
Regressor class in scikit-learn.
Using it looks much like the KNeighborsClassifier above:
from sklearn.neighbors import KNeighborsRegressor
X, y = mglearn.datasets.make_wave(n_samples=40)
# split the wave dataset into a training and a test set
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# Instantiate the model, set the number of neighbors to consider to 3:
reg = KNeighborsRegressor(n_neighbors=3)
# Fit the model using the training data and training targets:
reg.fit(X_train, y_train)
KNeighborsRegressor(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=3, p=2,
weights='uniform')
Now, we can make predictions on the test set:
reg.predict(X_test)
array([-0.05396539, 0.35686046, 1.13671923, -1.89415682, -1.13881398,
-1.63113382, 0.35686046, 0.91241374, -0.44680446, -1.13881398])
k-Nearest Neighbor | 49
www.it-ebooks.info

We can also evaluate the model using the score method, which for regressors returns
the $R^2$ score.
The $R^2$ score, also known as coefficient of determination, is a measure of good‐
ness of a prediction for a regression model, and yields a score up to 1. A value of 1
corresponds to a perfect prediction, and a value of 0 corresponds to a constant model
that just predicts the mean of the training set responses y_train.
reg.score(X_test, y_test)
0.83441724462496036
Here, the score is 0.83 which indicates a relatively good model fit.
Analyzing k nearest neighbors regression
For our one-dimensional dataset, we can see what the predictions look like for all
possible feature values. To do this, we create a test-dataset consisting of many points
on the line.
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# create 1000 data points, evenly spaced between -3 and 3
line = np.linspace(-3, 3, 1000).reshape(-1, 1)
plt.suptitle("nearest_neighbor_regression")
for n_neighbors, ax in zip([1, 3, 9], axes):
# make predictions using 1, 3 or 9 neighbors
reg = KNeighborsRegressor(n_neighbors=n_neighbors).fit(X, y)
ax.plot(X, y, 'o')
ax.plot(X, -3 * np.ones(len(X)), 'o')
ax.plot(line, reg.predict(line))
ax.set_title("%d neighbor(s)" % n_neighbors)
In the plots above, the blue points are again the responses for the training data, while
the red line is the prediction made by the model for all points on the line.
Using only a single neighbor, each point in the training set has an obvious influence
on the predictions, and the predicted values go through all of the data points. This
leads to a very unsteady prediction. Considering more neighbors leads to smoother
predictions, but these do not fit the training data as well.
50 | Chapter 2: Supervised Learning
www.it-ebooks.info

Strengths, weaknesses and parameters
In principal, there are two important parameters to the KNeighbors classifier: the
number of neighbors and how you measure distance between data points. In practice,
using a small number of neighbors like 3 or 5 often works well, but you should cer‐
tainly adjust this parameter. Choosing the right distance measure is somewhat
beyond the scope of this book. By default, Euclidean distance is used, which works
well in many settings.
One of the strengths of nearest neighbors is that the model is very easy to understand,
and often gives reasonable performance without a lot of adjustments. Using nearest
neighbors is a good baseline method to try before considering more advanced techni‐
ques. Building the nearest neighbors model is usually very fast, but when your train‐
ing set is very large (either in number of features or in number of samples) prediction
can be slow.
When using nearest neighbors, it’s important to preprocess your data (see Chapter 3
Unsupervised Learning). Nearest neighbors often does not perform well on dataset
with very many features, in particular sparse datasets, a common type of data in
which there are many features, but only few of the features are non-zero for any given
data point.
So while the nearest neighbors algorithm is easy to understand, it is not often used in
practice, due to prediction being slow, and its inability to handle many features. The
method we discuss next has neither of these drawbacks.
Linear models
Linear models are a class of models that are widely used in practice, and have been
studied extensively in the last few decades, with roots going back over a hundred
years.
Linear models are models that make a prediction that using a linear function of the
input features, which we will explain below.
Linear models for regression
For regression, the general prediction formula for a linear model looks as follows:
\begin{align*}
&\hat{y} = w[0] x[0] + w[1] x[1] + \dotsc + w[p] x[p] + b \text{ (1) linear regression}
\end{align*}
Linear models | 51
www.it-ebooks.info
Here, $x[0]$ to $x[p]$ denotes the features (here the number of features is $p$) of a
single data point, $w$ and $b$ are parameters of the model that are learned, and $
\hat{y}$ is the prediction the model makes. For a dataset with a single feature, this is
which you might remember as the equation for a line from high school mathematics.
Here, $w[0]$ is the slope, and $b$ is the y-axis offset. For more features, w contains
the slopes along each feature axis. Alternatively, you can think of the predicted
response as being a weighted sum of the input features, with weights (which can be
negative) given by the entries of w.
Trying to learn the parameters $w[0]$ and $b$ on our one-dimensional wave dataset
might lead to the following line:
mglearn.plots.plot_linear_regression_wave()
52 | Chapter 2: Supervised Learning
www.it-ebooks.info

w[0]: 0.393906 b: -0.031804
We added a coordinate cross into the plot to make it easier to understand the line.
Looking at w[0] we see that the slope should be roughly around .4, which we can con‐
firm visually in the plot above. The intercept is where the prediction line should cross
the y-axis, which is slightly below 0, which you can also confirm in the image.
Linear models for regression can be characterized as regression models for which the
prediction is a line for a single feature, a plane when using two features, or a hyper‐
plane in higher dimensions (that is when having more features).
If you compare the predictions made by the red line with those made by the KNeigh‐
borsRegressor in Figure nearest_neighbor_regression, using a straight line to make
predictions seems very restrictive. It looks like all the fine details of the data are lost.
In a sense this is true. It is a strong (and somewhat unrealistic) assumption that our
target $y$ is a linear combination of the features. But looking at one-dimensional
data gives a somewhat skewed perspective. For datasets with many features, linear
models can be very powerful. In particular, if you have more features than training
data points, any target $y$ can be perfectly modeled (on the training set) as a linear
function (FOOTNOTE This is easy to see if you know some linear algebra).
There are many different linear models for regression. The difference between these
models is how the model parameters $w$ and $b$ are learned from the training data,
and how model complexity can be controlled. We will now go through the most pop‐
ular linear models for regression.
Linear Regression aka Ordinary Least Squares
Linear regression or Ordinary Least Squares (OLS) is the simplest and most classic
linear method for regression.
Linear regression finds the parameters $w$ and $b$ that minimize the mean squared
error between predictions and the true regression targets $y$ on the training set. The
mean squared error is the sum of the squared differences between the predictions and
the true values. Linear regression has no parameters, which is a benefit, but it also has
no way to control model complexity.
Here is the code that produces the model you can see in figure XX.
from sklearn.linear_model import LinearRegression
X, y = mglearn.datasets.make_wave(n_samples=60)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
lr = LinearRegression().fit(X_train, y_train)
The “slope” parameters w, also called weights or coecients are stored in the coef_
attribute, while the offset or intercept b is stored in the intercept_ attribute. [Foot‐
note: you might notice the strange-looking trailing underscore. Scikit-learn always
Linear models | 53
www.it-ebooks.info

stores anything that is derived from the training data in attributes that end with a
trailing underscore. That is to separate them from parameters that are set by the
user.]
print("lr.coef_: %s" % lr.coef_)
print("lr.intercept_: %s" % lr.intercept_)
lr.coef_: [ 0.39390555]
lr.intercept_: -0.0318043430268
The intercept_ attribute is always a single float number, while the coef_ attribute is
a numpy array with one entry per input feature. As we only have a single input fea‐
ture in the wave dataset, lr.coef_ only has a single entry.
Let’s look at the training set and test set performance:
print("training set score: %f" % lr.score(X_train, y_train))
print("test set score: %f" % lr.score(X_test, y_test))
training set score: 0.670089
test set score: 0.659337
An $R^2$ of around .66 is not very good, but we can see that the score on training
and test set are very close together. This means we are likely underfitting, not overfit‐
ting. For this one-dimensional dataset, there is little danger of overfitting, as the
model is very simple (or restricted).
However, with higher dimensional datasets (meaning a large number of features), lin‐
ear models become more powerful, and there is a higher chance of overfitting.
Let’s take a look at how LinearRegression performs on a more complex dataset, like
the Boston Housing dataset. Remember that this dataset has 506 samples and 105
derived features.
We load the dataset and split it into a training and a test set. Then we build the linear
regression model as before:
X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
lr = LinearRegression().fit(X_train, y_train)
When comparing training set and test set score, we find that we predict very accu‐
rately on the training set, but the $R^2$ on the test set is much worse:
print("training set score: %f" % lr.score(X_train, y_train))
print("test set score: %f" % lr.score(X_test, y_test))
training set score: 0.952353
test set score: 0.605775
54 | Chapter 2: Supervised Learning
www.it-ebooks.info

This is a clear sign of overfitting, and therefore we should try to find a model that
allows us to control complexity.
One of the most commonly used alternatives to standard linear regression is Ridge
regression, which we will look into next.
Ridge regression
Ridge regression is also a linear model for regression, so the formula it uses to make
predictions is still Formula (1), as for ordinary least squares. In Ridge regression,the
coefficients w are chosen not only so that they predict well on the training data, but
there is an additional constraint. We also want the magnitude of coefficients to be as
small as possible; in other words, all entries of w should be close to 0.
Intuitively, this means each feature should have as little effect on the outcome as pos‐
sible (which translates to having a small slope), while still predicting well.
This constraint is an example of what is called regularization. Regularization means
explicitly restricting a model to avoid overfitting. The particular kind used by Ridge
regression is known as l2 regularization. [footnote: Mathematically, Ridge penalizes
the l2 norm of the coefficients, or the Euclidean length of w.]
Ridge regression is implemented in linear_model.Ridge. Let’s see how well it does
on the extended Boston dataset:
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train, y_train)
print("training set score: %f" % ridge.score(X_train, y_train))
print("test set score: %f" % ridge.score(X_test, y_test))
training set score: 0.886058
test set score: 0.752714
As you can see, the training set score of Ridge is lower than for LinearRegression,
while the test set score is higher. This is consistent with our expectation. With linear
regression, we were overfitting to our data. Ridge is a more restricted model, so we
are less likely to overfit. A less complex model means worse performance on the
training set, but better generalization.
As we are only interested in generalization performance, we should choose the Ridge
model over the LinearRegression model.
The Ridge model makes a trade-off between the simplicity of the model (near zero
coefficients) and its performance on the training set. How much importance the
model places on simplicity versus training set performance can be specified by the
user, using the alpha parameter. Above, we used the default parameter alpha=1.0.
There is no reason why this would give us the best trade-off, though. Increasing alpha
Linear models | 55
www.it-ebooks.info

forces coefficients to move more towards zero, which decreases training set perfor‐
mance, but might help generalization.
ridge10 = Ridge(alpha=10).fit(X_train, y_train)
print("training set score: %f" % ridge10.score(X_train, y_train))
print("test set score: %f" % ridge10.score(X_test, y_test))
training set score: 0.788346
test set score: 0.635897
Decreasing alpha allows the coefficients to be less restricted, meaning we move right
on the figure XXX.
For very small values of alpha, coefficients are barely restricted at all, and we end up
with a model that resembles LinearRegression.
ridge01 = Ridge(alpha=0.1).fit(X_train, y_train)
print("training set score: %f" % ridge01.score(X_train, y_train))
print("test set score: %f" % ridge01.score(X_test, y_test))
training set score: 0.928578
test set score: 0.771793
Here, alpha=0.1 seems to be working well. We could try decreasing alpha even more
to improve generalization. For now, notice how the parameter alpha corresponds to
the model complexity as shown in Figure model_complexity. We will discuss meth‐
ods to properly select parameters in Chapter 6 (Model Selection).
We can also get a more qualitative insight into how the alpha parameter changes the
model by inspecting the coef_ attribute of models with different values of alpha. A
higher alpha means a more restricted model, so we expect that the entries of coef_
have smaller magnitude for a high value of alpha than for a low value of alpha.
This is confirmed in the plot below:
plt.title("ridge_coefficients")
plt.plot(ridge.coef_, 'o', label="Ridge alpha=1")
plt.plot(ridge10.coef_, 'o', label="Ridge alpha=10")
plt.plot(ridge01.coef_, 'o', label="Ridge alpha=0.1")
plt.plot(lr.coef_, 'o', label="LinearRegression")
plt.ylim(-25, 25)
plt.legend()
56 | Chapter 2: Supervised Learning
www.it-ebooks.info
Here, the x-axis enumerates the entries of coef_: x=0 shows the coefficient associated
with the first feature, x=1 the coefficient associated with the second feature, and so on
up to x=100. The y-axis shows the numeric value of the corresponding value of the
coefficient. The main take-away here is that for alpha=10 (as shown by the green
dots), the coefficients are mostly between around -3 and 3. The coefficients for the
ridge model with alpha=1 (as shown by the blue dots), are somewhat larger. The red
dots have larger magnitude still, and many of the teal dots, corresponding to linear
regression without any regularization (which would be alpha=0) are so large they are
even outside of the chart.
Lasso
An alternative to Ridge for regularizing linear regression is the Lasso. The lasso also
restricts coefficients to be close to zero, similarly to Ridge regression, but in a slightly
different way, called “l1” regularization.[footnote: The Lasso penalizes the l1 norm of
the coefficient vector, or in other words the sum of the absolute values of the coeffi‐
cients].
The consequence of l1 regularization is that when using the Lasso, some coefficients
are exactly zero. This means some features are entirely ignored by the model. This can
be seen as a form of automatic feature selection. Having some coefficients be exactly
zero often makes a model easier to interpret, and can reveal the most important fea‐
tures of your model.
Linear models | 57
www.it-ebooks.info

Let’s apply the lasso to the extended Boston housing dataset:
from sklearn.linear_model import Lasso
lasso = Lasso().fit(X_train, y_train)
print("training set score: %f" % lasso.score(X_train, y_train))
print("test set score: %f" % lasso.score(X_test, y_test))
print("number of features used: %d" % np.sum(lasso.coef_ != 0))
training set score: 0.293238
test set score: 0.209375
number of features used: 4
As you can see, the Lasso does quite badly, both on the training and the test set. This
indicates that we are
underfitting. We find that it only used four of the 105 features. Similarly to Ridge, the
Lasso also has a regularization parameter alpha that controls how strongly coeffi‐
cients are pushed towards zero . Above, we used the default of alpha=1.0. To dimin‐
ish underfitting, let’s try decreasing alpha:
lasso001 = Lasso(alpha=0.01).fit(X_train, y_train)
print("training set score: %f" % lasso001.score(X_train, y_train))
print("test set score: %f" % lasso001.score(X_test, y_test))
print("number of features used: %d" % np.sum(lasso001.coef_ != 0))
/home/andy/checkout/scikit-learn/sklearn/linear_model/coordinate_descent.py:474: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations
ConvergenceWarning)
A lower alpha allowed us to fit a more complex model, which worked better on the
training and the test data. The performance is slightly better than using Ridge, and we
are using only 32 of the 105 features. This makes this model potentially easier to
understand.
If we set alpha too low, we again remove the effect of regularization and end up with a
result similar to LinearRegression.
lasso00001 = Lasso(alpha=0.0001).fit(X_train, y_train)
print("training set score: %f" % lasso00001.score(X_train, y_train))
print("test set score: %f" % lasso00001.score(X_test, y_test))
print("number of features used: %d" % np.sum(lasso00001.coef_ != 0))
/home/andy/checkout/scikit-learn/sklearn/linear_model/coordinate_descent.py:474: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations
ConvergenceWarning)
Again, we can plot the coefficients of the different models, similarly to Figure
ridge_coefficients.
58 | Chapter 2: Supervised Learning
www.it-ebooks.info
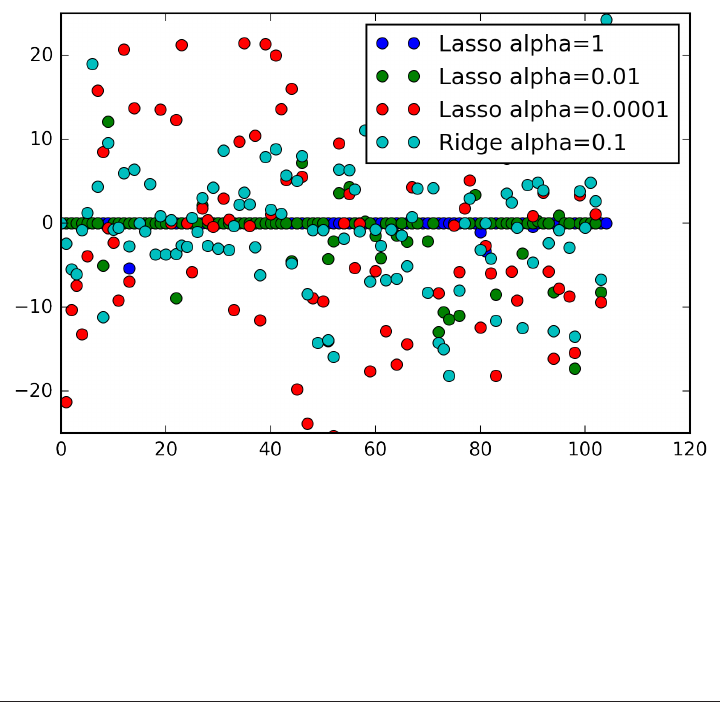
For alpha=1, with coefficients shown as blue dots, we not only see that most of the
coefficients are zero (which we already knew), but that the remaining coefficients are
also small in magnitude. Decreasing alpha to 0.01 we obtain the solution shown as
the green dots, which causes most features be exactly zero. Using alpha=0.00001, we
get a model that is quite unregularized, with most coefficients nonzero and of large
magnitude.
For comparison, the best Ridge solution is shown in teal. The ridge model with
alpha=0.1 has similar predictive performance as the lasso model with alpha=0.01, but
using Ridge, all coefficients are non-zero.
plt.plot(lasso.coef_, 'o', label="Lasso alpha=1")
plt.plot(lasso001.coef_, 'o', label="Lasso alpha=0.01")
plt.plot(lasso00001.coef_, 'o', label="Lasso alpha=0.0001")
plt.plot(ridge01.coef_, 'o', label="Ridge alpha=0.1")
plt.ylim(-25, 25)
plt.legend()
In practice, Ridge regression is usually the first choice between these two models.
However, if you have a large amount of features and expect only a few of them to be
important, Lasso might be a better choice. Similarly, if you would like to have a
model that is easy to interpret, Lasso will provide a model that is easier to under‐
stand, as it will select only a subset of the input features.
Linear models | 59
www.it-ebooks.info

Linear models for Classication
Linear models are also extensively used for classification. Let’s look at binary classifi‐
cation first. In this case, a prediction is made using the following formula:
\begin{align*}
&\hat{y} = w[0] x[0] + w[1] x[1] + \dotsc + w[p] * x[p] + b > 0 &\text{ (2) linear
binary classification}
\end{align*}
The formula looks very similar to the one for linear regression, but instead of just
returning the weighted sum of the features, we threshold the predicted value at zero.
If the function was smaller than zero, we predict the class -1, if it was larger than zero,
we predict the class +1.
This prediction rule is common to all linear models for classification. Again, there are
many different ways to find the coefficients w and the intercept b.
For linear models for regression, the output y was a linear function of the features: a
line, plane, or hyperplane (in higher dimensions). For linear models for classification,
the decision boundary is a linear function of the input. In other words, a (binary) lin‐
ear classifier is a classifier that separates two classes using a line, a plane or a hyper‐
plane. We will see examples of that below.
There are many algorithms for learning linear models. These algorithms all differ in
the following two ways:
1. How they measure how well a particular combination of coefficients and inter‐
cept fits the training data.
1. If and what kind of regularization they use.
Different algorithms choose different ways to measure what “fitting the training set
well” means in 1. For technical mathematical reasons, it is not possible to adjust w and
b to minimize the number of misclassifications the algorithms produce, as one might
hope. For our purposes, and many applications, the different choices for 1. (called loss
function) is of little significance.
The two most common linear classification algorithms are logistic regression, imple‐
mented in linear_model.LogisticRegression and linear support vector machines
(linear SVMs), implemented in svm.LinearSVC (SVC stands for Support Vector Clas‐
sifier). Despite its name, LogisticRegression is a classification algorithm and not a
regression algorithm, and should not be confused with LinearRegression.
We can apply the LogisticRegression and LinearSVC models to the forge dataset,
and visualize the decision boundary as found by the linear models:
60 | Chapter 2: Supervised Learning
www.it-ebooks.info
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
X, y = mglearn.datasets.make_forge()
fig, axes = plt.subplots(1, 2, figsize=(10, 3))
plt.suptitle("linear_classifiers")
for model, ax in zip([LinearSVC(), LogisticRegression()], axes):
clf = model.fit(X, y)
mglearn.plots.plot_2d_separator(clf, X, fill=False, eps=0.5, ax=ax, alpha=.7)
ax.scatter(X[:, 0], X[:, 1], c=y, s=60, cmap=mglearn.cm2)
ax.set_title("%s" % clf.__class__.__name__)
In this figure, we have the first feature of the forge dataset on the x axis and the sec‐
ond feature on the y axis as before. We display the decision boundaries found by Lin‐
earSVC and LogisticRegression respectively as straight lines, separating the area
classified as blue on the top from the area classified as red on the bottom.
In other words, any new data point that lies above the black line will be classified as
blue by the respective classifier, while any point that lies below the black line will be
classified as red.
The two models come up with similar decision boundaries. Note that both misclas‐
sify two of the points. By default, both models apply an l2 regularization, in the same
way that Ridge does for regression.
For LogisticRegression and LinearSVC the trade-off parameter that determines the
strength of the regularization is called C, and higher values of C correspond to less
regularization. In other words, when using a high value of the parameter C, Logisti
cRegression and LinearSVC try to fit the training set as best as possible, while with
low values of the parameter C, the model put more emphasis on finding a coefficient
vector w that is close to zero.
There is another interesting intuition of how the parameter C acts. Using low values
of C will cause the algorithms try to adjust to the “majority” of data points, while
Linear models | 61
www.it-ebooks.info
using a higher value of C stresses the importance that each individual data point be
classified correctly. Here is an illustration using LinearSVC.
mglearn.plots.plot_linear_svc_regularization()
On the left hand side, we have a very small C corresponding to a lot of regularization.
Most of the blue points are at the top, and most of the red points are at the bottom.
The strongly regularized model chooses a relatively horizontal line, misclassifying
two points.
In the center plot, C is slightly higher, and the model focuses more on the two mis‐
classified samples, tilting the decision boundary. Finally, on the right hand side, a very
high value of C in the model tilts the decision boundary a lot, now correctly classify‐
ing all red points. One of the blue points is still misclassified, as it is not possible to
correctly classify all points in this dataset using a straight line. The model illustrated
on the right hand side tries hard to correctly classify all points, but might not capture
the overall layout of the classes well. In other words, this model is likely overfitting.
Similarly to the case of regression, linear models for classification might seem very
restrictive in low dimensional spaces, only allowing for decision boundaries which
are straight lines or planes. Again, in high dimensions, linear models for classification
become very powerful, and guarding against overfitting becomes increasingly impor‐
tant when considering more features.
Let’s analyze LinearLogistic in more detail on the breast_cancer dataset:
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=42)
logisticregression = LogisticRegression().fit(X_train, y_train)
print("training set score: %f" % logisticregression.score(X_train, y_train))
print("test set score: %f" % logisticregression.score(X_test, y_test))
62 | Chapter 2: Supervised Learning
www.it-ebooks.info

training set score: 0.953052
test set score: 0.958042
The default value of C=1 provides quite good performance, with 95% accuracy on
both the training and the test set. As training and test set performance are very close,
it is likely that we are underfitting. Let’s try to increase C to fit a more flexible model.
logisticregression100 = LogisticRegression(C=100).fit(X_train, y_train)
print("training set score: %f" % logisticregression100.score(X_train, y_train))
print("test set score: %f" % logisticregression100.score(X_test, y_test))
training set score: 0.971831
test set score: 0.965035
Using C=100 results in higher training set accuracy, and also a slightly increased test
set accuracy, confirming our intuition that a more complex model should perform
better.
We can also investigate what happens if we use an even more regularized model than
the default of C=1, by setting C=0.01.
logisticregression001 = LogisticRegression(C=0.01).fit(X_train, y_train)
print("training set score: %f" % logisticregression001.score(X_train, y_train))
print("test set score: %f" % logisticregression001.score(X_test, y_test))
training set score: 0.934272
test set score: 0.930070
As expected, when moving more to the left in Figure model_complexity from an
already underfit model, both training and test set accuracy decrease relative to the
default parameters.
Finally, lets look at the coefficients learned by the models with the three different set‐
tings of the regularization parameter C.
plt.plot(logisticregression.coef_.T, 'o', label="C=1")
plt.plot(logisticregression100.coef_.T, 'o', label="C=100")
plt.plot(logisticregression001.coef_.T, 'o', label="C=0.001")
plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)
plt.ylim(-5, 5)
plt.legend()
Linear models | 63
www.it-ebooks.info
As LogisticRegression applies an L2 regularization by default, the result looks simi‐
lar to Ridge in Figure ridge_coefficients. Stronger regularization pushes coefficients
more and more towards zero, though coefficients never become exactly zero.
Inspecting the plot more closely, we can also see an interesting effect in the third coef‐
ficient, for “mean perimeter”. For C=100 and C=1, the coefficient is negative, while
for C=0.001, the coefficient is positive, with a magnitude that is even larger as for
C=1. Interpreting a model like this, one might think the coefficient tells us which
class a feature is associated with. For example, one might think that a high “texture
error” feature is related to a sample being “malignant”. However, the change of sign in
the coefficient for “mean perimeter” means that depending on which model we look
at, high “mean perimeter” could be either taken as being indicative of “benign” or
indicative of “malignant”. This illustrates that interpretations of coefficients of linear
models should always be taken with a grain of salt.
64 | Chapter 2: Supervised Learning
www.it-ebooks.info
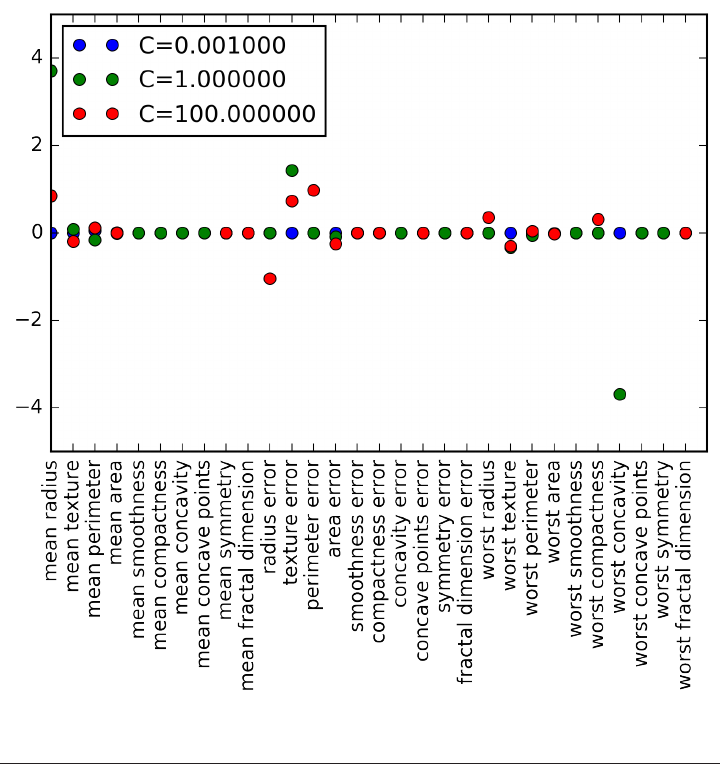
If we desire a more interpretable model, using L1 regularization might help, as it lim‐
its the model to only using a few features. Here is the coefficient plot and classifica‐
tion accuracies for L1 regularization:
for C in [0.001, 1, 100]:
lr_l1 = LogisticRegression(C=C, penalty="l1").fit(X_train, y_train)
print("training accuracy of L1 logreg with C=%f: %f"
% (C, lr_l1.score(X_train, y_train)))
print("test accuracy of L1 logreg with C=%f: %f"
% (C, lr_l1.score(X_test, y_test)))
plt.plot(lr_l1.coef_.T, 'o', label="C=%f" % C)
plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)
plt.ylim(-5, 5)
plt.legend(loc=2)
Linear models | 65
www.it-ebooks.info

training accuracy of L1 logreg with C=0.001000: 0.913146
test accuracy of L1 logreg with C=0.001000: 0.923077
training accuracy of L1 logreg with C=1.000000: 0.960094
test accuracy of L1 logreg with C=1.000000: 0.958042
training accuracy of L1 logreg with C=100.000000: 0.985915
test accuracy of L1 logreg with C=100.000000: 0.979021
Linear Models for multiclass classication
Many linear classification models are binary models, and don’t extend naturally to the
multi-class case (with the exception of Logistic regression). A common technique to
extend a binary classification algorithm to a multi-class classification algorithm is the
one-vs-rest approach. In the one-vs-rest approach, a binary model is learned for each
class, which tries to separate this class from all of the other classes, resulting in as
many binary models as there are classes.
To make a prediction, all binary classifiers are run on a test point. The classifier that
has the highest score on its single class “wins” and this class label is returned as pre‐
diction.
Having one binary classifier per class results in having one vector of coefficients $w$
and one intercept $b$ for each class. The class for which the result of formula
\begin{align*}
& w[0] x[0] + w[1] x[1] + \dotsc + w[p] * x[p] + b & \text{ (3) classification confi‐
dence}
\end{align*}
is highest is the assigned class label.
The mathematics behind logistic regression are somewhat different from the one-vs-
rest approach, but they also result in one coefficient vector and intercept per class,
and the same method of making a prediction is applied.
Let’s apply the one-vs-rest method to a simple three-class classification dataset.
We use a two-dimensional dataset, where each class is given by data sampled from a
Gaussian distribution.
from sklearn.datasets import make_blobs
X, y = make_blobs(random_state=42)
plt.scatter(X[:, 0], X[:, 1], c=y, s=60, cmap=mglearn.cm3)
66 | Chapter 2: Supervised Learning
www.it-ebooks.info
Now, we train a LinearSVC classifier on the dataset.
linear_svm = LinearSVC().fit(X, y)
print(linear_svm.coef_.shape)
print(linear_svm.intercept_.shape)
(3, 2)
(3,)
We see that the shape of the coef_ is (3, 2), meaning that each row of coef_ con‐
tains the coefficient vector for one of the three classes. Each row has two entries, cor‐
responding to the two features in the dataset.
The intercept_ is now a one-dimensional array, storing the intercepts for each class.
Let’s visualize the lines given by the three binary classifiers:
plt.scatter(X[:, 0], X[:, 1], c=y, s=60, cmap=mglearn.cm3)
line = np.linspace(-15, 15)
for coef, intercept in zip(linear_svm.coef_, linear_svm.intercept_):
plt.plot(line, -(line * coef[0] + intercept) / coef[1])
plt.ylim(-10, 15)
plt.xlim(-10, 8)
Linear models | 67
www.it-ebooks.info
The red line shows the decision boundary for the binary classifier for the red class,
and so on.
You can see that all the red points in the training data are below the red line, which
means they are on the “red” side of this binary classifier. The red points are left of the
green line, which means they are classified as “rest” by the binary classifier for the
green class. The red points are below the blue line, which means the binary classifier
for the blue class also classifies them as “rest”. Therefore, any point in this area will be
classified as red by the final classifier (Formula (3) of the red classifier is greater than
zero, while it is smaller than zero for the other two classes).
But what about the triangle in the middle of the plot? All three binary classifiers clas‐
sify points there as “rest”. Which class would a point there be assigned to? The answer
is the one with the highest value in Formula (3): the class of the closest line.
The following figure shows the prediction shown for all regions of the 2d space:
mglearn.plots.plot_2d_classification(linear_svm, X, fill=True, alpha=.7)
plt.scatter(X[:, 0], X[:, 1], c=y, s=60)
line = np.linspace(-15, 15)
for coef, intercept in zip(linear_svm.coef_, linear_svm.intercept_):
plt.plot(line, -(line * coef[0] + intercept) / coef[1])
68 | Chapter 2: Supervised Learning
www.it-ebooks.info
Strengths, weaknesses and parameters
The main parameter of linear models is the regularization parameter, called alpha in
the regression models and C in LinearSVC and LogisticRegression. Large alpha or
small C mean simple models. In particular for the regression models, tuning this
parameter is quite important. Usually C and alpha are searched for on a logarithmic
scale.
The other decision you have to make is whether you want to use L1 regularization or
L2 regularization. If you assume that only few of your features are actually important,
you should use L1. Otherwise, you should default to L2.
L1 can also be useful if interpretability of the model is important. As L1 will use only
a few features, it is easier to explain which features are important to the model, and
what the effect of these features is.
Linear models are very fast to train, and also fast to predict. They scale to very large
datasets and work well with sparse data. If your data consists of hundreds of thou‐
sands or millions of samples, you might want to investigate SGDClassifier and
SGDRegressor, which implement even more scalable versions of the linear models
described above.
Another strength of linear models is that they make i] relatively easy to understand
how a prediction is made, using Formula (1) for regression and Formula (2) for clas‐
Linear models | 69
www.it-ebooks.info

sification. Unfortunately, it is often not entirely clear why coefficients are the way they
are. This is particularly true if your dataset has highly correlated features; in these
cases, the coefficients might be hard to interpret.
Linear models often perform well when the number of features is large compared to
the number of samples. They are also often used on very large datasets, simply
because other models are not feasible to train. However, on smaller dataset, other
models might yield better generalization performance.
Naive Bayes Classiers
Naive Bayes classifiers are a family of classifiers that are quite similar to the linear
models discussed above. However, they tend to be even faster in training. The price
paid for this efficiency is that naive Bayes models often provide generalization perfor‐
mance that is slightly worse than linear classifiers like LogisticRegression and Line
arSVC.
The reason that naive Bayes models are so efficient is that they learn parameters by
looking at each feature individually, and collect simple per-class statistics from each
feature.
There are three kinds of naive Bayes classifiers implemented in scikit-learn, Gaus
sianNB, BernoulliNB and MultinomialNB.
GaussianNB can be applied to any continuous data, while BernoulliNB assumes
binary data and MultinomialNB assumes count data (that is each feature represents an
integer count of something, like how often a word appears in a sentence). Bernoul
liNB and MultinomialNB are mostly used in text data classification, and we will revisit
them in Chapter 7 (Text Data).
The BernoulliNB classifier counts how often every feature of each class is not zero.
This is most easily understood with an example:
X = np.array([[0, 1, 0, 1],
[1, 0, 1, 1],
[0, 0, 0, 1],
[1, 0, 1, 0]])
y = np.array([0, 1, 0, 1])
Here, we have four data points, with four binary features each. There are two classes,
0 and 1.
For class 0 (the first and third data point), the first feature is zero 2 times and non-
zero 0 times, the second features is zero 1 time and non-zero 1 time, and so on.
These same counts are then calculated for the data points in the second class.
Counting the non-zero entries per class in essence looks like this:
70 | Chapter 2: Supervised Learning
www.it-ebooks.info

counts = {}
for label in np.unique(y):
# iterate over each class
# count (sum) entries of 1 per feature
counts[label] = X[y == label].sum(axis=0)
print(counts)
{0: array([0, 1, 0, 2]), 1: array([2, 0, 2, 1])}
The other two naive Bayes models, MultinomialNB and GaussianNB are slightly dif‐
ferent in what kind of statistics they compute. MultinomialNB takes into account the
average value of each feature for each class, while GaussianNB stores the average value
as well as the standard deviation of each feature for each class.
To make a prediction, a data point is compared to the statistics for each of the classes,
and the best matching class is predicted. Interestingly, for MultinomialNB and Ber
noulliNB, this leads to a prediction formula that is of the same form as in the linear
models (Formula (2)). Unfortunately, coef_ for the naive Bayes models has a slightly
different meaning then in the linear models, in that coef_ is not the same as w.
Strengths, weaknesses and parameters
The MultinomialNB and BernoulliNB have a single parameter alpha, which controls
model complexity. The way alpha works is that the algorithm adds alpha many vir‐
tual data points to the data, that have positive values for all the features. This results
in a “smoothing” of the statistics. A large alpha means more smoothing, resulting in
less complex models. The algorithms performance is relatively robust to the setting of
alpha, meaning that setting alpha is not critical for good performance However, tun‐
ing it usually improves accuracy somewhat.
The GaussianNB model seems to be rarely used by practitioners, while the other two
variants of naive Bayes are widely used for sparse count data such as text. Multino‐
mialNB usually performs better than BinaryNB, in particular on datasets with a rela‐
tively large number of non-zero features (i.e. large documents).
The naive Bayes models share many of the strengths and weaknesses of the linear
models. They are very fast to train and to predict, and the training procedure is easy
to understand. The models work very well with high-dimensional sparse data, and
are relatively robust to the parameters. Naive Bayes models are great baseline models,
and are often used on very large datasets, where training even a linear model might
take too long.
Decision trees
Decision trees are a widely used models for classification and regression tasks.
Essentially, they learn a hierarchy of “if-else” questions, leading to a decision.
Decision trees | 71
www.it-ebooks.info

These questions are similar to the questions you might ask in a game of twenty ques‐
tions.
Imagine you want to distinguish between the following four animals: bears, hawks,
penguins and dolphins.
Your goal is to get to the right answer b] asking as few if-else questions as possible.
You might start off by asking whether the animal has feathers, a question that nar‐
rows down your possible animals to just two animals.
If the answer is yes, you can ask another question that could help you distinguish
between hawks and penguins. For example, you could ask whether or not the animal
can fly. If the animal doesn’t have feathers, your possible animal choices are dolphins
and bears, and you will need to ask a question to distinguish between these two ani‐
mals, for example, asking whether the animal has fins.
This series of questions can be expressed as a decision tree, as shown in Figure ani‐
mal_tree.
In this illustration, each node in the tree either represents a question, or a terminal
node (also called a leaf) which contains the answer. The edges connect the answers to
a question with the next question you would ask.
mglearn.plots.plot_animal_tree()
plt.suptitle("animal_tree");
72 | Chapter 2: Supervised Learning
www.it-ebooks.info
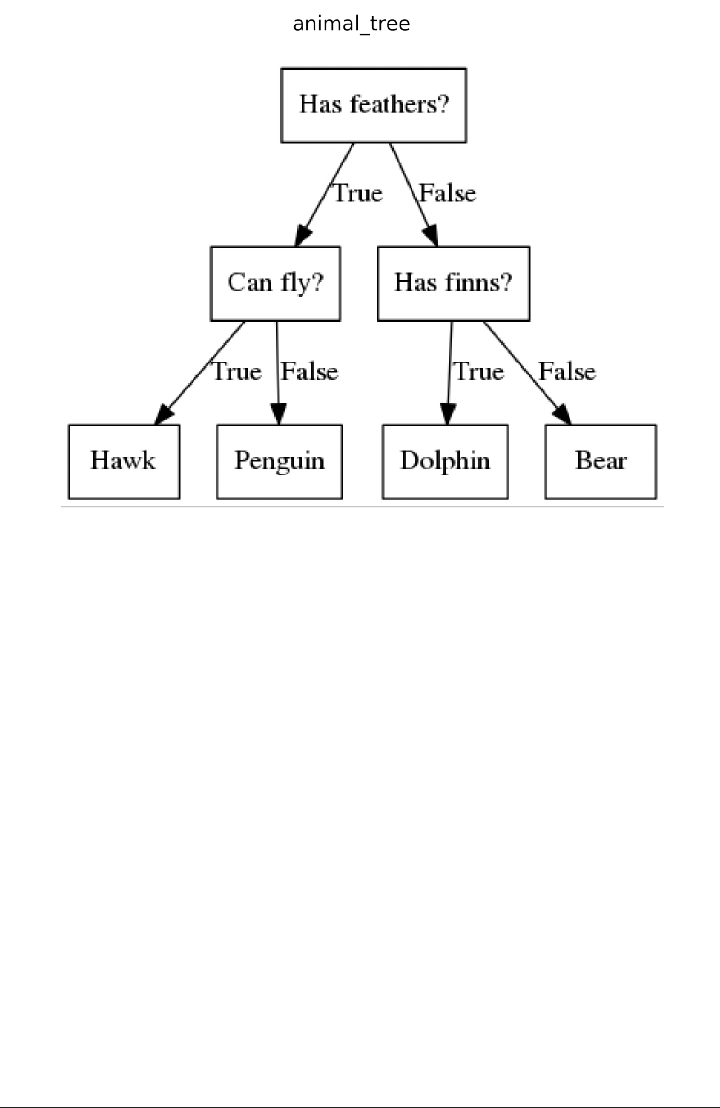
In machine learning parlance, we built a model to distinguish between four classes of
animals (hawks, penguins, dolphins and bears) using the three features “has feathers”,
“can fly” and “has fins”.
Instead of building these models by hand, we can learn them from data using super‐
vised learning.
Building Decision Trees
Let’s go through the process of building a decision tree for the 2d classification dataset
shown at the top of Figure tree_building. The dataset consists of two half-moon
shapes of blue and red points, consisting of 75 data points each. We will refer to this
dataset as two_moons.
mglearn.plots.plot_tree_progressive()
plt.suptitle("tree_building");
Decision trees | 73
www.it-ebooks.info

Learning a decision tree means learning a sequence of if/else questions that gets us to
the true answer most quickly.
In the machine learning setting, these questions are called tests (not to be confused
with the test set, which is the data we use to test to see how generalizable our model
is).
Usually data does not come in the form of binary yes/no features as in the animal
example, but is instead represented as continuous features such as in the 2d dataset
shown in the figure. The tests that are used on continuous data are of the from “is
feature i larger than value a”.
To build a tree, the algorithm searches over all possible tests, and finds the one that is
most informative about the target variable.
The second row in Figure tree_building shows the first test that is picked. Splitting
the dataset vertically at x[1]=0.2372 yields the most information; it best separates the
blue points from the red points. The top node, also called the root, represents the
whole dataset, consisting of 75 red and 75 blue points. The split is done by testing
whether x[1] <= 0.2372, indicated by a black line. If the test is true, a point is
assigned to the left node, which contains 8 blue points and 58 red points. Otherwise
the point is assigned to the right node, which contains 67 red points and 17 blue
points. These two nodes correspond to the top and bottom region shown in Figure
tree_building.
Even though the first split did a good job of separating the blue and red points, the
bottom region still contains blue points, and the top region still contains red points.
We can build a more accurate model by repeating the process of looking for the best
test in both regions.
Figure tree_building shows that the most informative next split for the left and the
right region are based on x[0].
This recursive process yields a binary tree of decisions, with each node containing a
test.
Alternatively, you can think of each test as splitting the part of the data that is cur‐
rently considered along one axis. This yields a view of the algorithm as building a
hierarchical partition. As each test concerns only a single feature, the regions in the
resulting partition always have axis-parallel boundaries.
Figure tree_building illustrates the partitioning of the data in the left hand column,
and the resulting tree in the right hand column.
The recursive partitioning of the data is usually repeated until each region in the par‐
tition (each leaf in the decision tree) only contains a single target value (a single class
Decision trees | 75
www.it-ebooks.info

or a single regression value). A leaf of the tree containing only one target value is
called pure.
A prediction on a new data point is made by checking which region of the partition
of the feature space the point lies in, and then predicting the majority target (or the
single target in the case of pure leaves) in that region. The region can be found by
traversing the tree from the root and going left or right, depending on whether the
test is fulfilled or not.
Controlling complexity of Decision Trees
Typically, building a tree as described above, and continuing until all leaves are pure
leads to models that are very complex and highly overfit to the training data. The
presence of pure leaves mean that a tree is 100% accurate on the training set; each
data point in the training set is in a leaf that has the correct majority class. The over‐
fitting can be seen on the left of Figure tree_building in the bottom column. You can
see the regions determined to be red in the middle of all the blue points. On the other
hand, there is a small strip of blue around the single blue point to the very right. This
is not how one would imagine the decision boundary to look, and the decision
boundary focuses a lot on single outlier points that are far away from the other points
in that class.
There are two common strategies to prevent overfitting: stopping the creation of the
tree early, also called pre-pruning, or building the tree but then removing or collaps‐
ing nodes that contain little information, also called post-pruning or just pruning. Pos‐
sible criteria for pre-pruning include limiting the maximum depth of the tree,
limiting the maximum number of leaves, or requiring a minimum number of points
in a node to keep splitting it.
Decision trees in scikit-learn are implemented in the DecisionTreeRegressor and
DecisionTreeClassifier classes. Scikit-learn only implements pre-pruning, not post-
pruning.
Let’s look at the effect of pre-pruning in more detail on the breast cancer dataset.
As always, we import the dataset and split it into a training and test part.
Then we build a model using the default setting of fully developing the tree (growing
the tree until all leaves are pure). We fix the random_state in the tree, which is used
for tie-breaking internally.
from sklearn.tree import DecisionTreeClassifier
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=42)
tree = DecisionTreeClassifier(random_state=0)
tree.fit(X_train, y_train)
76 | Chapter 2: Supervised Learning
www.it-ebooks.info

print("accuracy on training set: %f" % tree.score(X_train, y_train))
print("accuracy on test set: %f" % tree.score(X_test, y_test))
accuracy on training set: 1.000000
accuracy on test set: 0.937063
As expected, the accuracy on the training set is 100% as the leaves are pure.
The test-set accuracy is slightly worse than the linear models above, which had
around 95% accuracy.
Now let’s apply pre-pruning to the tree, which will stop developing the tree before we
perfectly fit to the training data.
One possible way is to stop building the tree after a certain depth has been reached.
Here we set max_depth=4, meaning only four consecutive questions can be asked (cf.
Figure tree_building).
tree = DecisionTreeClassifier(max_depth=4, random_state=0)
tree.fit(X_train, y_train)
print("accuracy on training set: %f" % tree.score(X_train, y_train))
print("accuracy on test set: %f" % tree.score(X_test, y_test))
accuracy on training set: 0.988263
accuracy on test set: 0.951049
Limiting the depth of the tree decreases overfitting. This leads to a lower accuracy on
the training set, but an improvement on the test set.
Analyzing Decision Trees
We can visualize the tree using the export_graphviz function from the tree module.
This writes a file in the dot file format, which is a text file format for storing graphs.
We set an option to color the nodes to reflect the majority class in each node and pass
the class and features names so the tree can be properly labeled.
from sklearn.tree import export_graphviz
export_graphviz(tree, out_file="mytree.dot", class_names=["malignant", "benign"],
feature_names=cancer.feature_names, impurity=False, filled=True)
We can read this file and visualize it using the graphviz module (or you can use any
program that can read dot files):
import graphviz
with open("mytree.dot") as f:
Decision trees | 77
www.it-ebooks.info
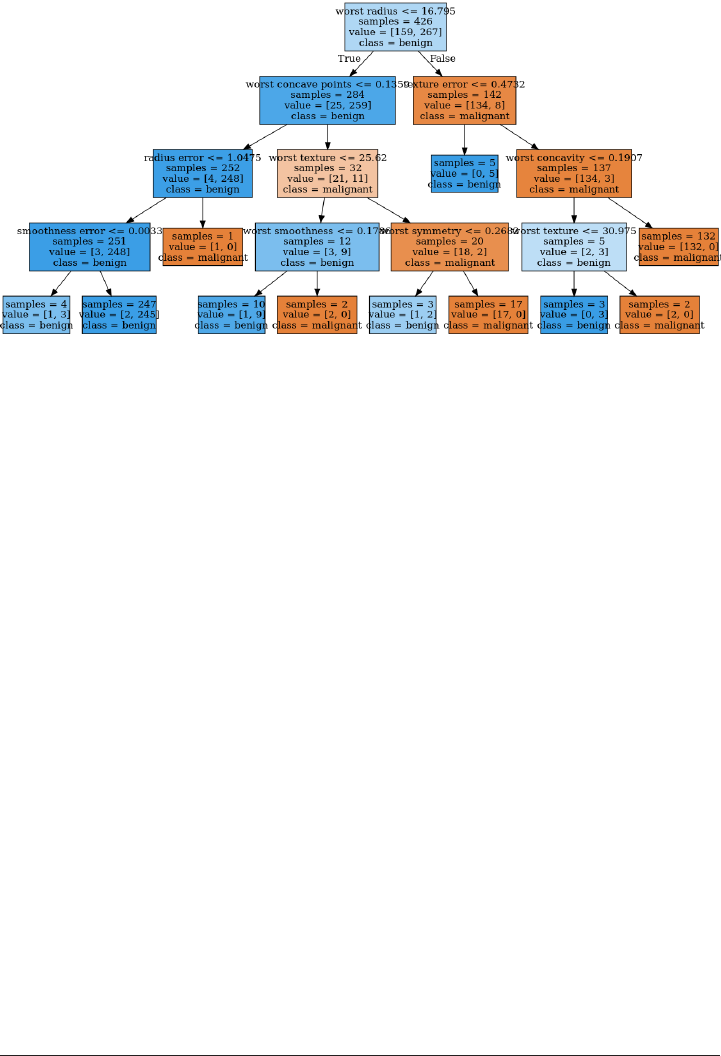
dot_graph = f.read()
graphviz.Source(dot_graph)
The visualization of the tree provides a great in-depth view of how the algorithm
makes predictions, and is a good example of a machine learning algorithm that is
easily explained to non-experts. However, even with a tree of depth four, as seen here,
the tree can become a bit overwhelming. Deeper trees (depth ten is not uncommon)
are even harder to grasp.
One method of inspecting the tree that may be helpful is to find out which path most
of the data actually takes.
The n_samples shown in each node in the figure gives the number of samples in each
node, while value provides the number of samples per class.
Following the branches to the right, we see that texture_error <= 0.4732 creates a
node that only contains 8 benign but 134 malignant samples. The rest of this side of
the tree then uses some finer distinctions to split off these 8 remaining benign sam‐
ples. Of the 142 samples that went to the right in the initial split, nearly all of them
(132) end up in the leaf to the very right.
Taking a left at the root, for texture_error > 0.4732, we end up with 25 malignant
and 259 benign samples.
Nearly all of the benign samples end up in the second leave from the right, with most
of the other leaves only containing very few samples.
Feature Importance in trees
Instead of looking at the whole tree, which can be taxing, there are some useful statis‐
tics that we can derive properties that we can derive to summarize the workings of
the tree. The most commonly used summary is feature importance, which rates how
78 | Chapter 2: Supervised Learning
www.it-ebooks.info

important each feature is for the decision a tree makes. It is a number between 0 and
1 for each feature, where 0 means “not used at all” and 1 means “perfectly predicts the
target”.
The feature importances always sum to one.
tree.feature_importances_
array([ 0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0.01019737, 0.04839825, 0. , 0. , 0.0024156 ,
0. , 0. , 0. , 0. , 0. ,
0.72682851, 0.0458159 , 0. , 0. , 0.0141577 ,
0. , 0.018188 , 0.1221132 , 0.01188548, 0. ])
We can visualize the feature importances in a way that is similar to the way we visual‐
ize the coefficients in the linear model.
plt.plot(tree.feature_importances_, 'o')
plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)
plt.ylim(0, 1)
Decision trees | 79
www.it-ebooks.info
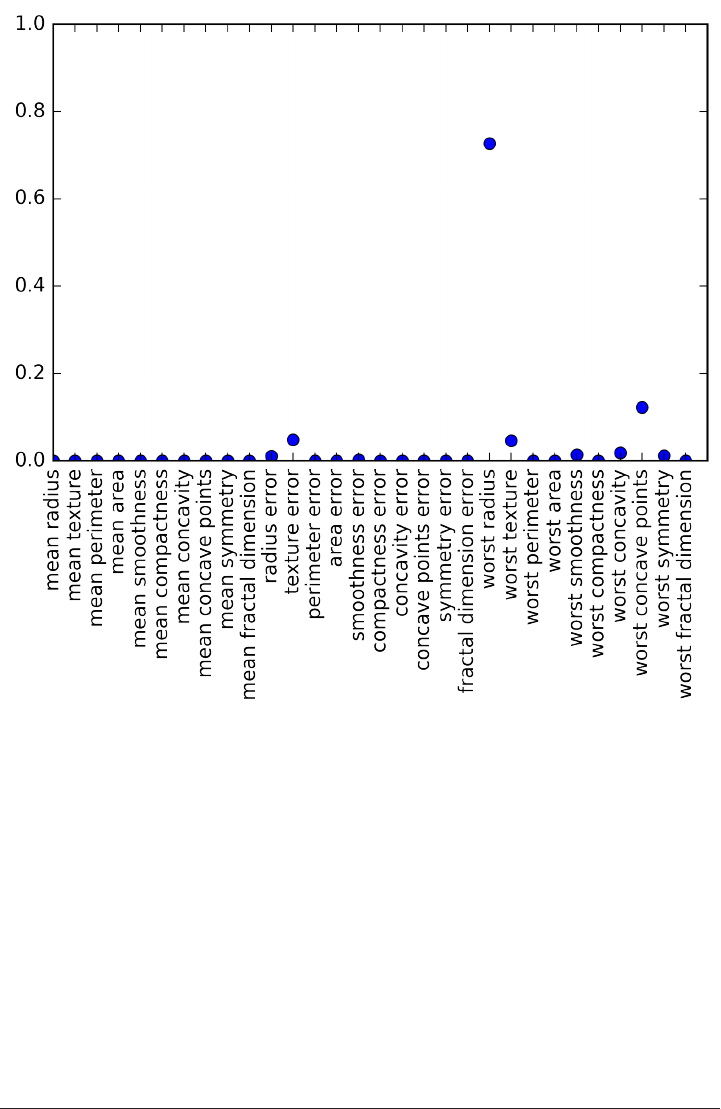
Here, we see that the feature used at the top split (“worst radius”) is by far the most
important feature. This confirms our observation in analyzing the tree, that the first
level already separates the two classes fairly well.
However, if a feature has a low feature_importance, it doesn’t mean that this feature
is uninformative. It only means that this feature was not picked by the tree, likely
because another feature encodes the same information.
In contrast to the coefficients in linear models, feature importances are always posi‐
tive, and don’t encode which class a feature is indicative of. The feature importances
tell us that worst radius is important, but it does not tell us whether a high radius is
indicative of a sample being “benign” or “malignant”. In fact, there might not be such
a simple relationship between features and class, as you can see in the example below:
80 | Chapter 2: Supervised Learning
www.it-ebooks.info
tree = mglearn.plots.plot_tree_not_monotone()
plt.suptitle("tree_not_monotone")
tree
Feature importances: [ 0. 1.]
The plot shows a dataset with two features and two classes. Here, all the information
is contained in X[1], and X[0] is not used at all. But the relation between X[1] and
the output class is not monotonous, meaning we cannot say “a high value of X[0]
means class red, and a low value means class blue” or the other way around.
While we focuses our discussion here on decision trees for classification, all that was
said is similarly true for decision trees for regression, as implemented in Decision
TreeRegressor. Both the usage and the analysis of regression trees are very similar to
classification trees, so we won’t go into any more detail here.
Strengths, weaknesses and parameters
As discussed above, the parameters that control model complexity in decision trees
are the pre-pruning parameters that stop the building of the tree before it is fully
developed. Usually picking one of the pre-pruning strategies, either setting
min_depth, max_leaf_nodes or min_samples_leaf is to prevent overfitting.
Decision trees | 81
www.it-ebooks.info

Decision trees have two advantages over many of the algorithms we discussed so far:
The resulting model can easily be visualized and understood by non-experts (at least
for smaller trees), and the algorithms is completely invariant to scaling of the data: As
each feature is processed separately, and the possible splits of the data don’t depend
on scaling, no preprocessing like normalization or standardization of features is
needed for decision tree algorithms.
In particular, decision trees work well when you have features that are on completely
different scales, or a mix of binary and continuous features.
The main down-side of decision trees is that even with the use of pre-pruning, deci‐
sion trees tend to overfit, and provide poor generalization performance. Therefore, in
most applications, the ensemble methods we discuss below are usually used in place
of a single decision tree.
Ensembles of Decision Trees
Ensembles are methods that combine multiple machine learning models to create
more powerful models.
There are many models in the machine learning literature that belong to this cate‐
gory, but there are two ensemble models that have proven to be effective on a wide
range of datasets for classification and regression, both of which use decision trees as
their building block: Random Forests and Gradient Boosted Decision Trees.
Random Forests
As observed above, a main drawback of decision trees is that they tend to overfit the
training data. Random forests
are one way to address this problem. Random forests are essentially a collection of
decision trees, where each tree is slightly different from the others.
The idea of random forests is that each tree might do a relatively good job of predict‐
ing, but will likely overfit on part of the data.
If we build many trees, all of which work well and overfit in different ways, we can
reduce the amount of overfitting by averaging their results. This reduction in overfit‐
ting, while retaining the predictive power of the trees, can be shown using rigorous
mathematics.
To implement this strategy, we need to build many decision tree. Each tree should do
an acceptable job of predicting the target, and should also be different from the other
trees. Random forests get their name from injecting randomness into the tree build‐
ing to ensure each tree is different. There are two ways in which the trees in a random
82 | Chapter 2: Supervised Learning
www.it-ebooks.info

forest are randomized: by selecting the data points used to build a tree and by select‐
ing the features in each split test. Let’s go into this process in more detail.
Building Random Forests
To build a random forest model, you need to decide on the number of trees to build
(the n_estimator parameter of RandomForestRegressor or RandomForestClassi
fier). Lets say we want to build ten trees. These trees will be built completely inde‐
pendent from each other, and [will?] make random choices to make sure they are
distinct [the trees make random choices?].
To build a tree, we first take what is called a bootstrap sample of our data. A bootstrap
sample means from our n_samples data points, we repeatedly draw an example ran‐
domly with replacement (i.e. the same sample can be picked multiple times), n_sam
ples times. This will create a dataset that is as big as the original dataset, but some
data points will be missing from it, and some will be repeated.
To illustrate, lets say we want to create a bootstrap sample of the list ['a', 'b', 'c',
'd']. A possible bootstrap sample would be ['b', 'd', 'd', 'c']. Another possi‐
ble sample would be ['d', 'a', 'd', 'a'].
Next, a decision tree is built based on this newly created dataset. However, the algo‐
rithm we described for the decision tree is slightly modified. Instead of looking for
the best test for each node, in each node the algorithm randomly selects a subset of
the features, and looks for the best possible test involving one of these features. The
amount of features that is selected is controlled by the max_features parameter.
This selection of a subset of features is repeated separately in each node, so that each
node in a tree can make a decision using a different subset of the features.
The bootstrap sampling leads to each decision tree in the random forest being built
on a slightly different dataset. Because of the selection of features in each node, each
split in each tree operates on a different subset of features. Together these two mecha‐
nisms ensure that all the trees in the random forests are different.
A critical parameter in this process is max_features. If we set max_features to n_fea
tures, that means that each split can look at all features in the dataset, and no ran‐
domness will be injected. If we set max_features to one, that means that the splits
have no choice at all on which feature to test, and can only search over different
thresholds for the feature that was selected randomly.
Therefore, a high max_features means that the trees in the random forest will be
quite similar, and they will be able to fit the data easily, using the most distinctive fea‐
tures. A low max_features means that the trees in the random forest will be quite
different, and that each tree might need to be very deep in order to fit the data well.
Ensembles of Decision Trees | 83
www.it-ebooks.info

To make a prediction using the random forest, the algorithm first makes a prediction
for every tree in the forest. For regression, we can average these results to get our final
prediction. For classification, a “soft voting” strategy is used. This means each algo‐
rithm makes a “soft” prediction, providing a probability for each possible output
label. The probabilities predicted by all the trees are averaged, and the class with the
highest label is predicted.
Analyzing Random Forests
Let’s apply a random forest consisting of five trees to the two_moon data we studied
above.
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
forest = RandomForestClassifier(n_estimators=5, random_state=2)
forest.fit(X_train, y_train)
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=None, max_features='auto', max_leaf_nodes=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=5, n_jobs=1,
oob_score=False, random_state=2, verbose=0, warm_start=False)
The trees that are built as part of the random forest are stored in the estimator_
attribute. Let’s visualize the decision boundaries learned by each tree, together with
their aggregate prediction, as made by the forest.
fig, axes = plt.subplots(2, 3, figsize=(20, 10))
for i, (ax, tree) in enumerate(zip(axes.ravel(), forest.estimators_)):
ax.set_title("tree %d" % i)
mglearn.plots.plot_tree_partition(X_train, y_train, tree, ax=ax)
mglearn.plots.plot_2d_separator(forest, X_train, fill=True, ax=axes[-1, -1], alpha=.4)
axes[-1, -1].set_title("random forest")
plt.scatter(X_train[:, 0], X_train[:, 1], c=np.array(['r', 'b'])[y_train], s=60)
84 | Chapter 2: Supervised Learning
www.it-ebooks.info

You can clearly see that the decisions learned by the five trees are quite different. Each
of them makes some mistakes, as some of the training points that are plotted here
were not actually included in the training set of the tree, due to the bootstrap sam‐
pling.
The random forest overfit less than any of the trees individually, and provides a much
more intuitive decision boundary. In any real application, we would use many more
trees (often hundreds or thousands), leading to even smoother boundaries.
Let’s apply a random forest consisting of 100 trees on the breast cancer dataset:
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=0)
forest = RandomForestClassifier(n_estimators=100, random_state=0)
forest.fit(X_train, y_train)
print("accuracy on training set: %f" % forest.score(X_train, y_train))
print("accuracy on test set: %f" % forest.score(X_test, y_test))
accuracy on training set: 1.000000
accuracy on test set: 0.972028
The random forest gives us an accuracy of 97%, better than the linear models or a
single decision tree, without tuning any parameters. We could adjust the max_fea
tures setting, or apply pre-pruning as we did for the single decision tree.
However, often the default parameters of the random forest already work quite well.
Similarly to the decision tree, the random forest provides feature importances, which
are computed by aggregating the feature importances over the trees in the forest. Typ‐
Ensembles of Decision Trees | 85
www.it-ebooks.info
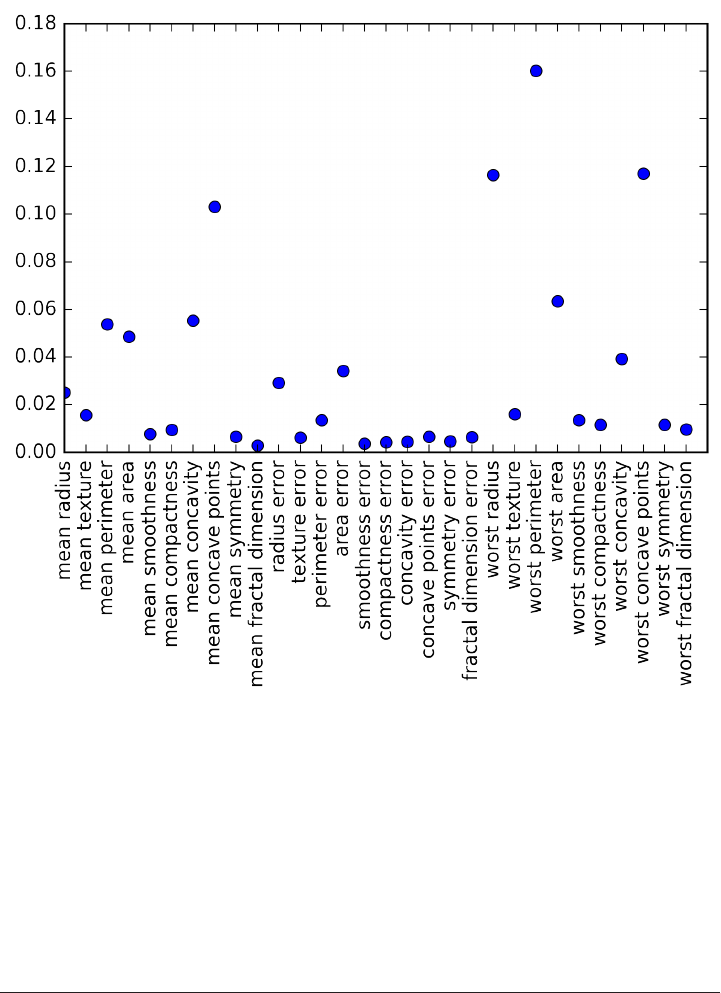
ically the feature importances provided by the random forest are more reliable than
the ones provided by a single tree.
plt.plot(forest.feature_importances_, 'o')
plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90);
As you can see, the random forest gives non-zero importance to many more features
than the single tree.Similarly to the single decision tree, the random forest also gives a
lot of importance to the “worst radius”, but it actually chooses “worst perimeter” to be
the most informative feature overall. The randomness in building the random forest
forces the algorithm to consider many possible explanations, the result of which
being that the random forest captures a much broader picture of the data than a sin‐
gle tree.
86 | Chapter 2: Supervised Learning
www.it-ebooks.info

Strengths, weaknesses and parameters
Random forests for regression and classification are currently among the most widely
used machine learning methods.
They are very powerful, often work well without heavy tuning of the parameters, and
don’t require scaling of the data.
Essentially, random forests share all of the benefits of decision trees, while making up
for some of their deficiencies.
One reason to still use decision trees is if you need a compact representation of the
decision making process. It is basically impossible to interpret tens or hundreds of
trees in detail, and trees in random forests tend to be deeper than decision trees
(because of the use of feature subsets). Therefore, if you need to summarize the pre‐
diction making in a visual way to non-experts, a single decision tree might be a better
choice.
While building random forests on large dataset might be somewhat time-consuming,
it an be parallelized across multiple CPU cores within a computer easily. If you are
using a multi-core processor (as nearly all modern computers do), you can use the
n_jobs parameter to adjust the number of cores to use. Using more CPU cores will
result in linear speed-ups (using two cores, the training of the random forest will be
twice as fast), but specifying n_jobs larger than the number of cores will not help.
You can set n_jobs=-1 to use all the cores in your computer.
You should keep in mind that random forests, by their nature, are random, and set‐
ting different random states (or not setting the random_state at all) can drastically
change the model that is built. The more trees there are in the forest, the more robust
it will be against the choice of random state. If you want to have reproducible results,
it is important to fix the random_state.
Random forests don’t tend to perform well on very high dimensional, sparse data,
such as text data. For this kind of data, linear models might be more appropriate.
Random forests usually work well even on very large datasets, and training can easily
be parallelized over many CPU cores within a powerful computer. However, random
forests require more memory and are slower to train and to predict than linear mod‐
els. If time and memory are important in an application, it might make sense to use a
linear model instead.
The important parameters to adjust are n_estimators, max_features and possibly
pre-pruning options like max_depth. For n_estimators, larger is always better. Aver‐
aging more trees will yield a more robust ensemble. However, there are diminishing
returns, and more trees need more memory and more time to train. A common rule
of thumb is to build “as many as you have time / memory for”.
Ensembles of Decision Trees | 87
www.it-ebooks.info

As described above max_features determines how random each tree is, and a smaller
max_features reduces overfitting. The default values, and a good rule of thumb, are
max_features=sqrt(n_features) for classification and max_features=log2(n_fea
tures) for regression.
Adding max_features or max_leaf_nodes might sometimes improve performance. It
can also drastically reduce space and time requirements for training and prediction.
Gradient Boosted Regression Trees (Gradient Boosting Machines)
Gradient boosted regression trees is another ensemble method that combines multi‐
ple decision trees to a more powerful model. Despite the “regression” in the name,
these models can be used for regression and classification.
In contrast to random forests, gradient boosting works by building trees in a serial
manner, where each tree tries to correct the mistakes of the previous one. There is no
randomization in gradient boosted regression trees; instead, strong pre-pruning is
used. Gradient boosted trees often use very shallow trees, of depth one to five, often
making the model smaller in terms of memory, and making predictions faster.
The main idea behind gradient boosting is to combine many simple models (in this
context known as weak learners), like shallow trees. Each tree can only provide good
predictions on part of the data, and so more and more trees are added to iteratively
improve performance.
Gradient boosted trees are frequently the winning entries in machine learning com‐
petitions, and are widely used in industry. They are generally a bit more sensitive to
parameter settings than random forests, but can provide better accuracy if the param‐
eter are set correctly.
Apart from the pre-pruning and the number of trees in the ensemble, another impor‐
tant parameter of gradient boosting is the learning_rate which controls how
strongly each tree tries to correct the mistakes of the previous trees. A higher learning
rate means each tree can make stronger corrections, allowing for more complex mod‐
els. Similarly, adding more trees to the ensemble, which can be done by increasing
n_estimators, also increases the model complexity, as the model has more chances
to correct mistakes on the training set.
Here is an example of using GradientBoostingClassifier on the breast cancer data‐
set.
By default, 100 trees of maximum depth three are used, with a learning rate of 0.1.
from sklearn.ensemble import GradientBoostingClassifier
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=0)
88 | Chapter 2: Supervised Learning
www.it-ebooks.info

gbrt = GradientBoostingClassifier(random_state=0)
gbrt.fit(X_train, y_train)
print("accuracy on training set: %f" % gbrt.score(X_train, y_train))
print("accuracy on test set: %f" % gbrt.score(X_test, y_test))
accuracy on training set: 1.000000
accuracy on test set: 0.958042
As the training set accuracy is 100%, we are likely to be overfitting. To reduce overfit‐
ting, we could either apply stronger pre-pruning by limiting the maximum depth or
lower the learning rate:
gbrt = GradientBoostingClassifier(random_state=0, max_depth=1)
gbrt.fit(X_train, y_train)
print("accuracy on training set: %f" % gbrt.score(X_train, y_train))
print("accuracy on test set: %f" % gbrt.score(X_test, y_test))
accuracy on training set: 0.990610
accuracy on test set: 0.972028
gbrt = GradientBoostingClassifier(random_state=0, learning_rate=0.01)
gbrt.fit(X_train, y_train)
print("accuracy on training set: %f" % gbrt.score(X_train, y_train))
print("accuracy on test set: %f" % gbrt.score(X_test, y_test))
accuracy on training set: 0.988263
accuracy on test set: 0.965035
Both methods of decreasing the model complexity decreased the training set accuracy
as expected. In this case, lowering the maximum depth of the trees provided a signifi‐
cant improvement of the model, while lowering the learning rate only
increased the generalization performance slightly.
As for the other decision tree based models, we can again visualize the feature impor‐
tances to get more insight into our model. As we used 100 trees, it is impractical to
inspect them all, even if they are all of depth 1.
gbrt = GradientBoostingClassifier(random_state=0, max_depth=1)
gbrt.fit(X_train, y_train)
plt.plot(gbrt.feature_importances_, 'o')
plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90);
Ensembles of Decision Trees | 89
www.it-ebooks.info
We can see that the feature importances of the gradient boosted trees are somewhat
similar to the feature importances of the random forests, though the gradient boost‐
ing completely ignored some of the features.
As gradient boosting and random forest perform well on similar kinds of data, a
common approach is to first try random forests, which work quite robustly. If ran‐
dom forests work well, but prediction time is at a premium, or it is important to
squeeze out the last percentage of accuracy from the machine learning model, mov‐
ing to gradient boosting often helps.
If you want to apply gradient boosting to a large scale problem, it might be worth
looking into the xgboost package and its python interface, which at the time of writ‐
ing is faster (and sometimes easier to tune) than the scikit-learn implementation of
gradient boosting on many datasets.
90 | Chapter 2: Supervised Learning
www.it-ebooks.info

Strengths, weaknesses and parameters
Gradient boosted decision trees are among the most powerful and widely used mod‐
els for supervised learning.
Their main drawback is that they require careful tuning of the parameters, and may
take a long time to train.
Similarly to other tree-based models, the algorithm works well without scaling and
on a mixture of binary and continuous features. As other tree-based models, it also
often does not work well on high-dimensional sparse data.
The main parameters of the gradient boosted tree models are the number of trees
n_estimators, and the learning_rate, which controls how much each tree is
allowed to correct the mistakes of the previous trees.
These two parameters are highly interconnected, as a lower learning_rate means
that more trees are needed to build a model of similar complexity. In contrast to ran‐
dom forests, where higher n_estimators is always better, increasing n_estimators in
gradient boosting leads to a more complex model, which may lead to overfitting.
A common practice is to fit n_estimators depending on the time and memory
budget, and then search over different learning_rates.
Another important parameter is max_depth, which is usually very low for gradient
boosted models, often not deeper than five splits.
Kernelized Support Vector Machines
The next type of supervised model we will discuss is kernelized support vector
machines (SVMs).
We already saw linear support vector machines for classification in the linear model
section. Kernelized support vector machines (often just referred to as SVMs) are an
extension that allows for more complex models which are not defined simply by
hyperplanes in the input space. While there are support vector machines for classifi‐
cation and regression, we will restrict ourself to the classification case, as imple‐
mented in SVC. Similar concepts apply to support vector regression, as implemented
in SVR.
The math behind kernelized support vector machines is a bit involved, and is mostly
beyond the scope of this book.
However, we will try to give you some intuitions about the idea behind the method.
Kernelized Support Vector Machines | 91
www.it-ebooks.info
Linear Models and Non-linear Features
As you saw in Figure linear_classifiers, linear models can be quite limiting in low-
dimensional spaces, as lines or hyperplanes have limited flexibility. One way to make
a linear model more flexible is by adding more features, for example by adding inter‐
actions or polynomials of the input features.
Let’s look at the synthetic dataset we used in Figure tree_not_monotone:
X, y = make_blobs(centers=4, random_state=8)
y = y % 2
plt.scatter(X[:, 0], X[:, 1], c=y, s=60, cmap=mglearn.cm2)
plt.xlabel("feature1")
plt.ylabel("feature2")
A linear model for classification can only separate points using a line, and will not be
able to do a very good job on this dataset:
from sklearn.svm import LinearSVC
linear_svm = LinearSVC().fit(X, y)
mglearn.plots.plot_2d_separator(linear_svm, X)
plt.scatter(X[:, 0], X[:, 1], c=y, s=60, cmap=mglearn.cm2)
plt.xlabel("feature1")
plt.ylabel("feature2")
92 | Chapter 2: Supervised Learning
www.it-ebooks.info
Now, let’s expand the set of input features, say by also adding feature2 ** 2, the
square of the second feature, as a new feature. Instead of representing each data point
as a two-dimensional point (feature1, feature2), we now represent it as a three-
dimensional point (feature1, feature2, feature2 ** 2) (Footnote: We picked
this particular feature to add for illustration purposes. The choice is not particular
important.). This new representation is illustrated below in a three-dimensional scat‐
ter plot:
# add the squared first feature
X_new = np.hstack([X, X[:, 1:] ** 2])
from mpl_toolkits.mplot3d import Axes3D, axes3d
figure = plt.figure()
# visualize in 3D
ax = Axes3D(figure, elev=-152, azim=-26)
ax.scatter(X_new[:, 0], X_new[:, 1], X_new[:, 2], c=y, cmap=mglearn.cm2, s=60)
ax.set_xlabel("feature1")
ax.set_ylabel("feature2")
ax.set_zlabel("feature1 ** 2")
Kernelized Support Vector Machines | 93
www.it-ebooks.info
In the new, three-dimensional representation of the data, it is now indeed possible to
separate the red and the blue points
using a linear model, a plane in three dimensions. We can confirm this by fitting a
linear model to the augmented data:
linear_svm_3d = LinearSVC().fit(X_new, y)
coef, intercept = linear_svm_3d.coef_.ravel(), linear_svm_3d.intercept_
# show linear decision boundary
figure = plt.figure()
ax = Axes3D(figure, elev=-152, azim=-26)
xx = np.linspace(X_new[:, 0].min(), X_new[:, 0].max(), 50)
yy = np.linspace(X_new[:, 1].min(), X_new[:, 1].max(), 50)
XX, YY = np.meshgrid(xx, yy)
ZZ = (coef[0] * XX + coef[1] * YY + intercept) / -coef[2]
ax.scatter(X_new[:, 0], X_new[:, 1], X_new[:, 2], c=y, cmap=mglearn.cm2, s=60)
ax.plot_surface(XX, YY, ZZ, rstride=8, cstride=8, alpha=0.3)
ax.set_xlabel("feature1")
ax.set_ylabel("feature2")
ax.set_zlabel("feature1 ** 2")
94 | Chapter 2: Supervised Learning
www.it-ebooks.info
As a function of the original features, the linear SVM model is not actually linear any‐
more. It is not a line, but more of an ellipse.
ZZ = YY ** 2
dec = linear_svm_3d.decision_function(np.c_[XX.ravel(), YY.ravel(), ZZ.ravel()])
plt.contourf(XX, YY, dec.reshape(XX.shape), levels=[dec.min(), 0, dec.max()],
cmap=mglearn.cm2, alpha=0.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=60, cmap=mglearn.cm2)
plt.xlabel("feature1")
plt.ylabel("feature2")
Kernelized Support Vector Machines | 95
www.it-ebooks.info
The Kernel Trick
The lesson here is that adding non-linear features to the representation of our data
can make linear models much more powerful. However, often we don’t know which
features to add, and adding many features (like all possible interactions in a 100
dimensional feature space) might make computation very expensive.
Luckily, there is a clever mathematical trick that allows us to learn a classifier in a
higher dimensional space without actually computing the new, possibly very large
representation. This trick is known as the kernel trick.
The kernel trick works by directly computing the distance (more precisely, the scalar
products) of the data points for the expanded feature representation, without ever
actually computing the expansion.
There are two ways to map your data into a higher dimensional space that are com‐
monly used with support vector machines: the polynomial kernel, which computes all
possible polynomials up to a certain degree of the original features (like feature1 **
2 * feature2 ** 5), and the radial basis function (rbf) kernel, also known as Gaus‐
sian kernel.
The Gaussian kernel is a bit harder to explain, as it corresponds to an infinite dimen‐
sional feature space. One way to explain the Gaussian kernel is that it considers all
possible polynomials of all degrees, but the importance of the features decreases for
96 | Chapter 2: Supervised Learning
www.it-ebooks.info

higher degrees. [Footnote: this follows from the Taylor expansion of the exponential
map].
If all of this is too much math talk for you, don’t worry. You can still use SVMs
without trying to imagine infinite dimensional feature spaces. In practice, how a
SVM with an rbf kernel makes a decision can be summarized quite easily.
Understanding SVMs
During training, the SVM learns how important each of the training data points is to
represent the decision boundary between the two classes. Typically only a subset of
the training points matter for defining the decision boundary: the ones that lie on the
border between the classes. These are called support vectors and give the support vec‐
tor machine its name.
To make a prediction for a new point, the distance to the support vectors is measured.
A classification decision is made based on the distance to the support vectors, and the
importance of the support vectors that was learned during training (stored in the
dual_coef_ attribute of SVC).
The way distance between data points is measured by the Gaussian kernel:
\begin{align*}
&k_\text{rbf}(x_1, x_2) = \exp(\gamma||x_1 - x_2||^2) &\text{ (4) Gaussian kernel}
\end{align*}
Here, $x_1$ and $x_2$ are data points, $||x_1 - x_2 ||$ denotes Euclidean distance
and $\gamma$ is a parameter that controls the width of the Gaussian kernel.
Below is the result of training an support vector machine on a two-dimensional two-
class dataset.
The decision boundary is shown in black, and the support vectors are the points with
wide black circles.
from sklearn.svm import SVC
X, y = mglearn.tools.make_handcrafted_dataset()
svm = SVC(kernel='rbf', C=10, gamma=0.1).fit(X, y)
mglearn.plots.plot_2d_separator(svm, X, eps=.5)
# plot data
plt.scatter(X[:, 0], X[:, 1], s=60, c=y, cmap=mglearn.cm2)
# plot support vectors
sv = svm.support_vectors_
plt.scatter(sv[:, 0], sv[:, 1], s=200, facecolors='none', zorder=10, linewidth=3)
Kernelized Support Vector Machines | 97
www.it-ebooks.info
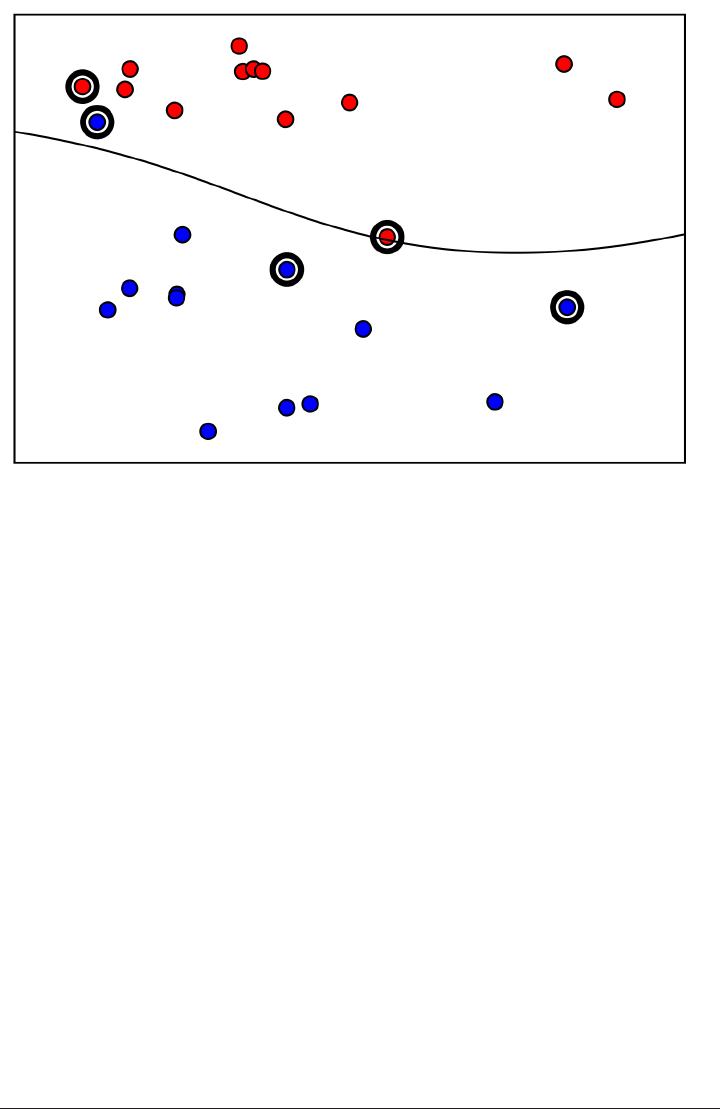
In this case, the SVM yields a very smooth and non-linear (not a straight line)
boundary.
There are two parameters we adjusted here: The C parameter and the gamma parame‐
ter, which we will now discuss in detail.
Tuning SVM parameters
The gamma parameter is the one shown in Formula (4), which controls the width of
the Gaussian kernel. It determines the scale of what it means for points to be close
together.
The C parameter is a regularization parameter similar to the linear models. It limits
the importance of each point (or more precisely, their dual_coef_).
Let’s have a look at what happens when we vary these parameters:
fig, axes = plt.subplots(3, 3, figsize=(15, 10))
for ax, C in zip(axes, [-1, 0, 3]):
for a, gamma in zip(ax, range(-1, 2)):
mglearn.plots.plot_svm(log_C=C, log_gamma=gamma, ax=a)
98 | Chapter 2: Supervised Learning
www.it-ebooks.info
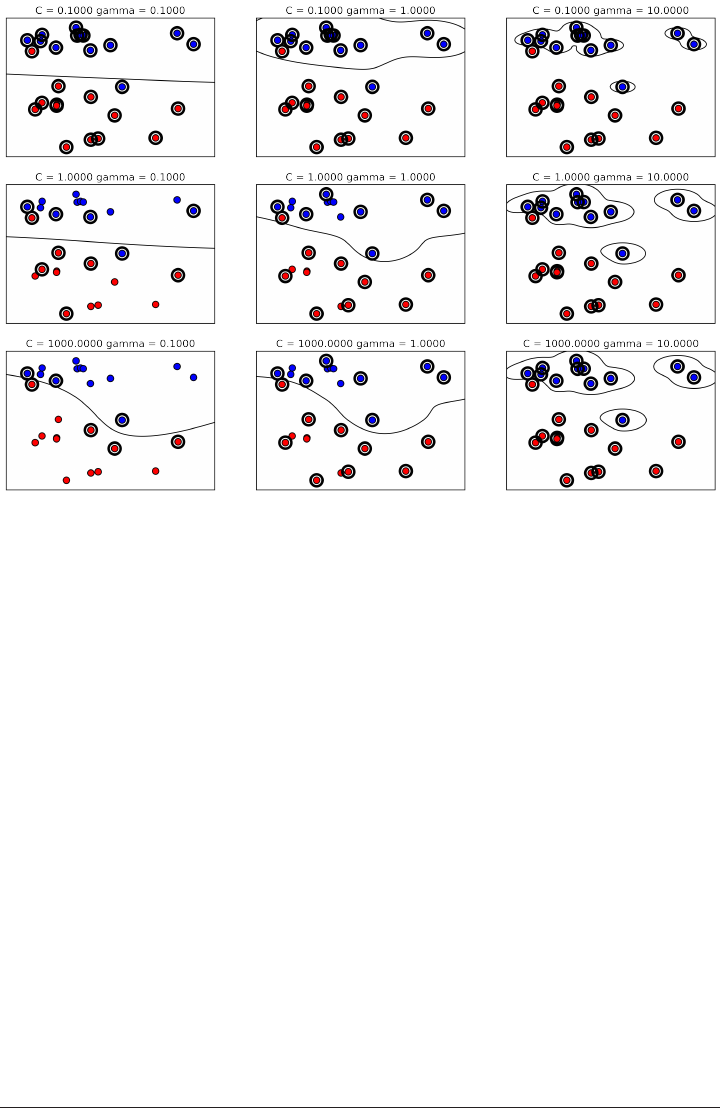
Going from left to right, we increase the parameter gamma from 0.1 to 10. A small
gamma means a large radius for the Gaussian kernel, which means that many points
are considered close-by. This is reflected in very smooth decision boundaries on the
left, and boundaries that focus more on single points further to the right. A low value
of gamma means that the decision boundary will vary slowly, which yields a model of
low complexity, while a high value of gamma yields a more complex model.
Going from top to bottom, we increase the C parameter from 0.1 to 1000. As with the
linear models, a small C means a very restricted model, where each data point can
only have very limited influence. You can see that in the top left, the decision bound‐
ary looks nearly linear, with the red and blue points that are misclassified barely
changing the line.
Increasing C, as shown on the bottom right, allows these points to have a stronger
influence on the model, and makes the decision boundary bend to correctly classify
them.
Let’s apply the rbf kernel SVM to the breast cancer dataset. By default, C=1 and
gamma=1./n_features.
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=0)
svc = SVC()
svc.fit(X_train, y_train)
Kernelized Support Vector Machines | 99
www.it-ebooks.info
print("accuracy on training set: %f" % svc.score(X_train, y_train))
print("accuracy on test set: %f" % svc.score(X_test, y_test))
accuracy on training set: 1.000000
accuracy on test set: 0.629371
The model overfit quite substantially, with a perfect score on the training set and only
62% accuracy on the test set.
While SVMs often perform quite well, they are very sensitive to the settings of the
parameters, and to the scaling of the data. In particular, they require all the features to
vary on a similar scale. Let’s look at the minimum and maximum values for each fea‐
ture, plotted in log-space:
plt.plot(X_train.min(axis=0), 'o', label="min")
plt.plot(X_train.max(axis=0), 'o', label="max")
plt.legend(loc="best")
plt.yscale("log")
From this plot we can determine that features in the breast cancer dataset are of com‐
pletely different orders of magnitude.
This can be somewhat of a problem for other models (like linear models), but it has
devastating effects for the kernel SVM.
100 | Chapter 2: Supervised Learning
www.it-ebooks.info

Preprocessing Data for SVMs
One way to resolve this problem is by rescaling each feature, so that they are approxi‐
mately on the same scale.
A common rescaling methods for kernel SVMs is to scale the data such that all fea‐
tures are between zero and one. We will see how to do this using the MinMaxScaler
preprocessing method in Chapter 3 (Unsupervised Learning), where we’ll give more
details.
For now, let’s do this “by hand”:
# Compute the minimum value per feature on the training set
min_on_training = X_train.min(axis=0)
# Compute the range of each feature (max - min) on the training set
range_on_training = (X_train - min_on_training).max(axis=0)
# subtract the min, divide by range
# afterwards min=0 and max=1 for each feature
X_train_scaled = (X_train - min_on_training) / range_on_training
print("Minimum for each feature\n%s" % X_train_scaled.min(axis=0))
print("Maximum for each feature\n %s" % X_train_scaled.max(axis=0))
Minimum for each feature
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
Maximum for each feature
[ 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
# use THE SAME transformation on the test set,
# using min and range of the training set. See Chapter 3 (unsupervised learning) for details.
X_test_scaled = (X_test - min_on_training) / range_on_training
svc = SVC()
svc.fit(X_train_scaled, y_train)
print("accuracy on training set: %f" % svc.score(X_train_scaled, y_train))
print("accuracy on test set: %f" % svc.score(X_test_scaled, y_test))
accuracy on training set: 0.948357
accuracy on test set: 0.951049
Scaling the data made a huge difference! Now we are actually in an underfitting
regime, where training and test set performance are quite similar. From here, we can
try increasing either C or gamma to fit a more complex model:
Kernelized Support Vector Machines | 101
www.it-ebooks.info

svc = SVC(C=1000)
svc.fit(X_train_scaled, y_train)
print("accuracy on training set: %f" % svc.score(X_train_scaled, y_train))
print("accuracy on test set: %f" % svc.score(X_test_scaled, y_test))
accuracy on training set: 0.988263
accuracy on test set: 0.972028
Here, increasing C allows us to improve the model significantly, resulting in 97.2%
accuracy.
Strengths, weaknesses and parameters
Kernelized support vector machines are very powerful models and perform very well
on a variety of datasets.
SVMs allow for very complex decision boundaries, even if the data has only a few fea‐
tures. SVMs work well on low-dimensional and high-dimensional data (i.e. few and
many features), but don’t scale very well with the number of samples. Running on
data with up to 10000 samples might work well, but working with datasets of size
100000 or more can become challenging in terms of runtime and memory usage.
Another downside of SVMs is that they require careful preprocessing of the data and
tuning of the parameters.
For this reason, SVMs have been replaced by tree-based models such as random for‐
ests (that require little or no preprocessing) in many applications. Furthermore, SVM
models are hard to inspect; it can be difficult to understand why a particular predic‐
tion was made, and it might be tricky to explain the model to a non-expert.
Still it might be worth trying SVMs, particularly if all of your features represent meas‐
urements in similar units (i.e. all are pixel intensities) and are on similar scales.
The important parameters in kernel SVMs are the regularization parameter C, the
choice of the kernel, and the kernel-specific parameters. We only talked about the rbf
kernel in any depth above, but other choices are available in scikit-learn. The rbf ker‐
nel has only one parameter, gamma, which is the inverse of the width of the Gaussian
kernel. gamma and C both control the complexity of the model, with large values in
either resulting in a more complex model. Therefore, good settings for the two
parameters are usually strongly correlated, and C and gamma should be adjusted
together.
Neural Networks (Deep Learning)
A family of algorithms known as neural networks has recently seen a revival under
the name “deep learning”.
102 | Chapter 2: Supervised Learning
www.it-ebooks.info
While deep learning shows great promise in many machine learning applications,
many deep learning algorithms are tailored very carefully to a specific use-case. Here,
we will only discuss some relatively simple methods, namely multilayer perceptrons
for classification and regression, that can serve as a starting point for more involved
deep learning methods. Multilayer perceptrons (MLPs) are also known as (vanilla)
feed-forward neural networks, or sometimes just neural networks.
The Neural Network Model
MLPs can be viewed as generalizations of linear models which perform multiple
stages of processing to come to a decision.
Remember that the prediction by a linear regressor is given as:
In words, y is a weighted sum of the input features x[0] to x[p], weighted by the
learned coefficients w[0] to w[p]. We could visualize this graphically as:
mglearn.plots.plot_logistic_regression_graph()
where each node on the left represents an input feature, the connecting lines repre‐
sent the learned coefficients, and the node on the right represents the output, which is
a weighted sum of the inputs.
Neural Networks (Deep Learning) | 103
www.it-ebooks.info
In an MLP, this process of computing weighted sums is repeated multiple times, first
computing hidden units that represent an intermediate processing step, which are
again combined using weighted sums, to yield the final result:
print("Figure single_hidden_layer")
mglearn.plots.plot_single_hidden_layer_graph()
Figure single_hidden_layer
This model has a lot more coefficients (also called weights) to learn: there is one
between every input and every hidden unit (which make up the hidden layer), and
one between every unit in the hidden layer and the output.
Computing a series of weighted sums is mathematically the same as computing just
one weighted sum, so to make this model truly more powerful than a linear model,
there is one extra trick we need. After computing a weighted sum for each hidden
unit, a non-linear function is applied to the result, usually the rectifying nonlinearity
(also known as rectified linear unit or relu) or the tangens hyperbolicus (tanh). The
result of this function is then used in the weighted sum that computes the output y.
The two functions are visualized in Figure activation_functions. The relu cuts off val‐
ues below zero, while tanh saturates to -1 for low input values and +1 for high input
values. Either non-linear function allows the neural network to learn much more
complicated function than a linear model could.
104 | Chapter 2: Supervised Learning
www.it-ebooks.info
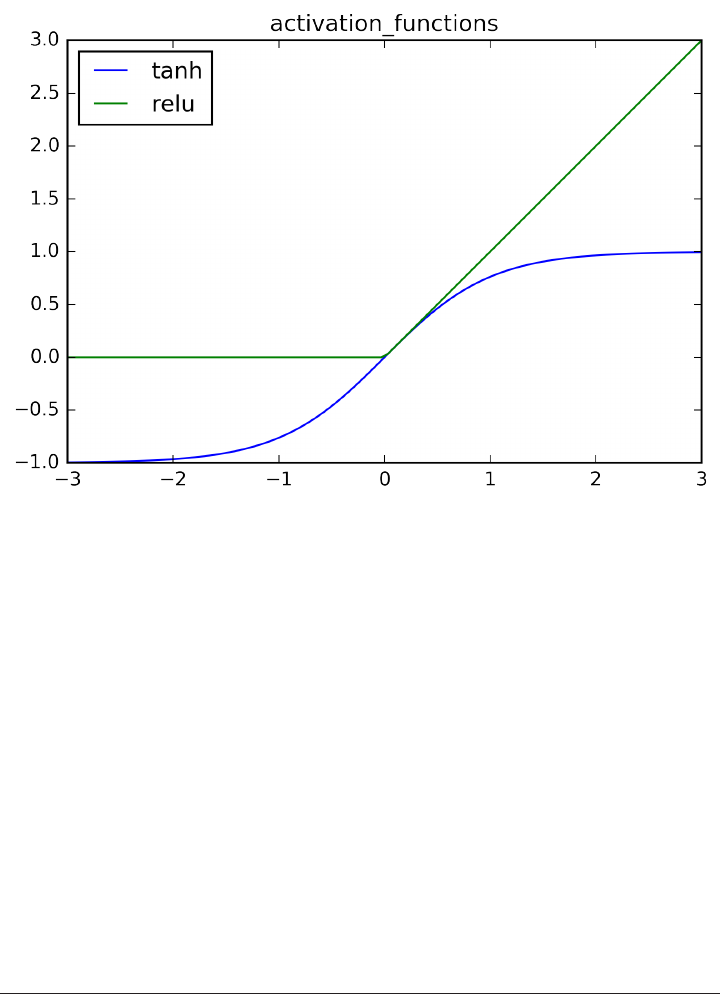
line = np.linspace(-3, 3, 100)
plt.plot(line, np.tanh(line), label="tanh")
plt.plot(line, np.maximum(line, 0), label="relu")
plt.legend(loc="best")
plt.title("activation_functions")
For the small neural network pictures in Figure single_hidden_layer above, the full
formula for computing y in the case of regression would be (when using a tanh non-
linearity):
Here, w are the weights between the input x and the hidden layer h, and v are the
weights between the hidden layer h and the output y. The weights v and w are learned
from data, x are the input features, y is the computed output, and h are intermediate
computations.
An important parameter that needs to be set by the user is the number of nodes in the
hidden layer, and can be as small as 10 for very small or simple datasets, and can be as
big as 10000 for very complex data.
It is also possible add additional hidden layers, as in Figure two_hidden_layers below.
Having large neural networks made up of many of these layers of computation is
what inspired the term “deep learning”.
print("Figure two_hidden_layers")
mglearn.plots.plot_two_hidden_layer_graph()
Neural Networks (Deep Learning) | 105
www.it-ebooks.info
Figure two_hidden_layers
Tuning Neural Networks
Let’s look into the workings of the MLP by applying the MLPClassifier to the
two_moons dataset we saw above.
from sklearn.neural_network import MLPClassifier
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
mlp = MLPClassifier(algorithm='l-bfgs', random_state=0).fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, s=60, cmap=mglearn.cm2)
106 | Chapter 2: Supervised Learning
www.it-ebooks.info
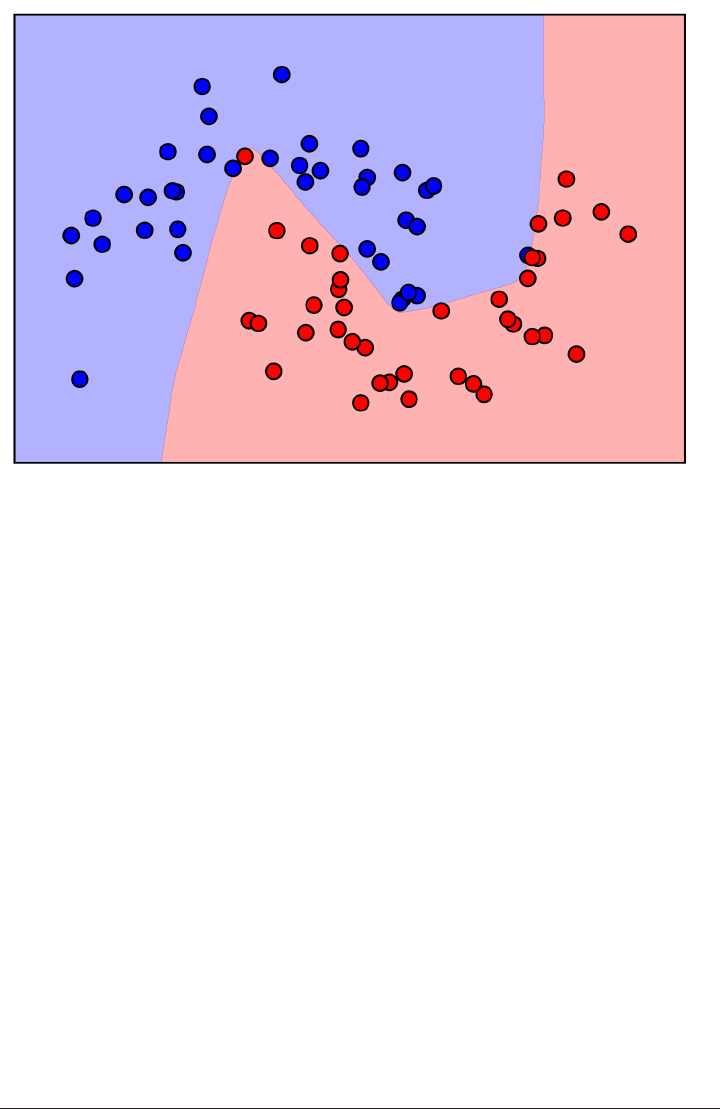
As you can see, the neural network learned a very nonlinear but relatively smooth
decision boundary.
We used algorithm='l-bfgs' which we will discuss later.
By default, the MLP uses 100 hidden nodes, which is quite a lot for this small dataset.
We can reduce the number (which reduces the complexity of the model) and still get
a good result:
mlp = MLPClassifier(algorithm='l-bfgs', random_state=0, hidden_layer_sizes=[10])
mlp.fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, s=60, cmap=mglearn.cm2)
Neural Networks (Deep Learning) | 107
www.it-ebooks.info
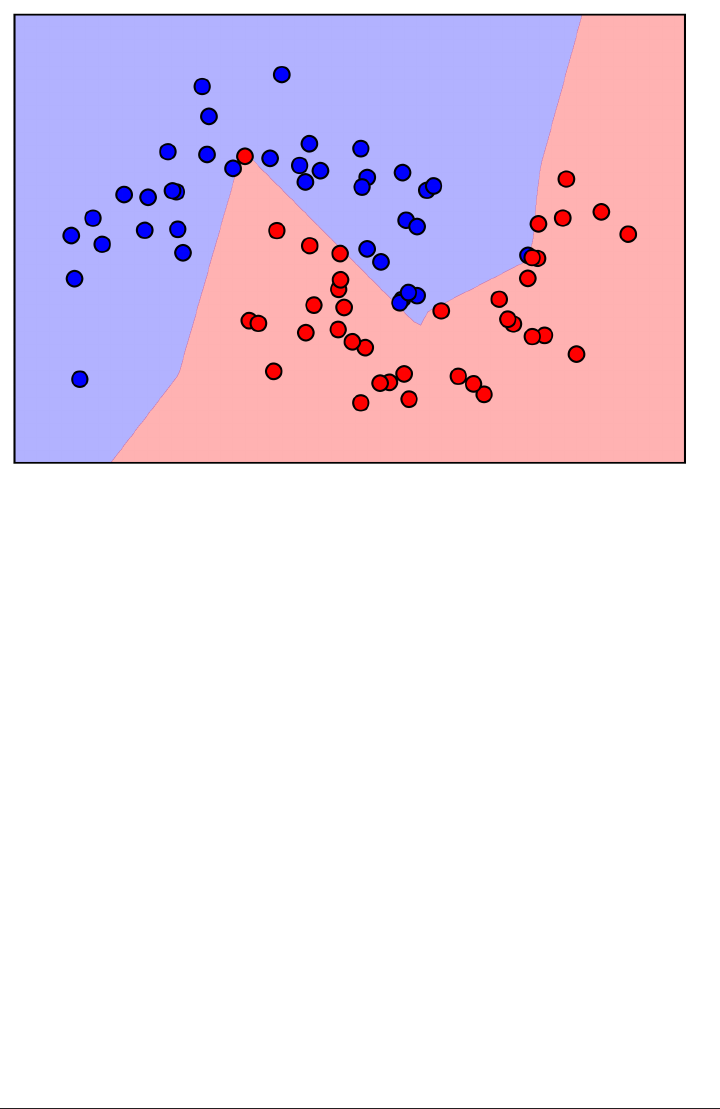
With only 10 hidden units, the decision boundary looks somewhat more ragged. The
default nonlinearity is ‘relu', shown in Figure activation_function. With a single hid‐
den layer, this means the decision function will be made up of 10 straight line seg‐
ments. If we want a smoother decision boundary, we could either add more hidden
units (as in the figure above), add second hidden layer, or use the “tanh” nonlinearity:
# using two hidden layers, with 10 units each
mlp = MLPClassifier(algorithm='l-bfgs', random_state=0, hidden_layer_sizes=[10, 10])
mlp.fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, s=60, cmap=mglearn.cm2)
108 | Chapter 2: Supervised Learning
www.it-ebooks.info
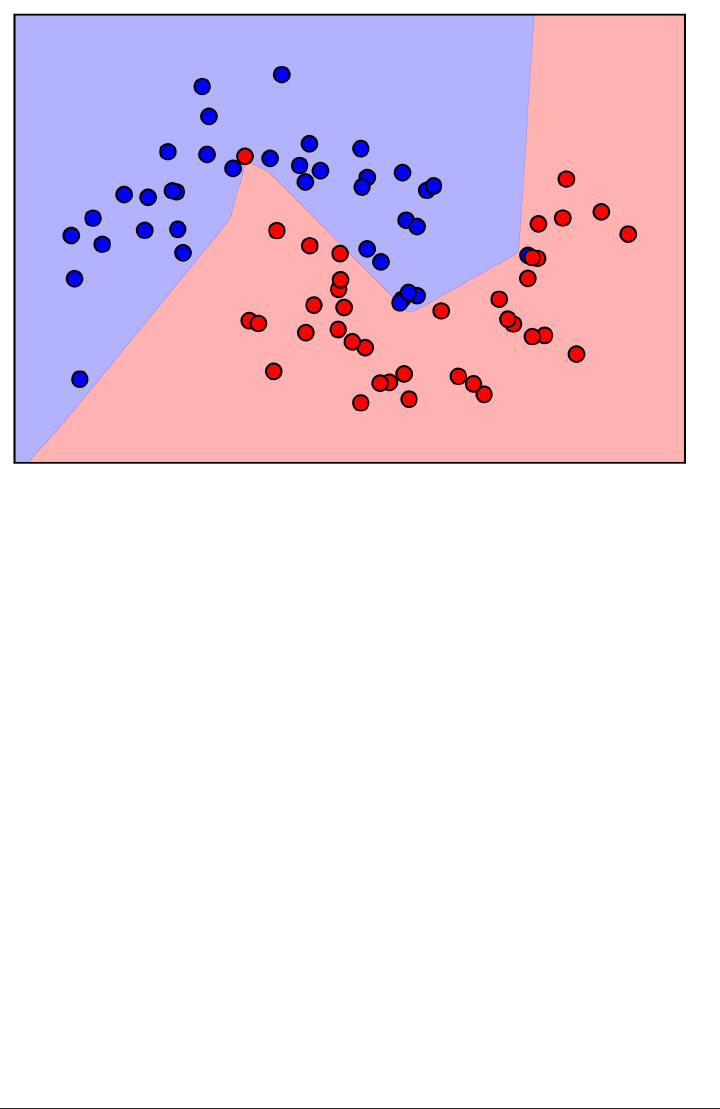
# using two hidden layers, with 10 units each, now with tanh nonlinearity.
mlp = MLPClassifier(algorithm='l-bfgs', activation='tanh',
random_state=0, hidden_layer_sizes=[10, 10])
mlp.fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, s=60, cmap=mglearn.cm2)
Neural Networks (Deep Learning) | 109
www.it-ebooks.info
Finally, we can also control the complexity of a neural network by using an “l2” pen‐
alty to shrink the weights towards zero, as we did in ridge regression and the linear
classifiers. The parameter for this in the MLPClassifier is alpha (as in the linear
regression models), and is set to a very low value (little regularization) by default.
Here is the effect of different values of alpha on the two_moons dataset, using two
hidden layers of 10 or 100 units each:
fig, axes = plt.subplots(2, 4, figsize=(20, 8))
for ax, n_hidden_nodes in zip(axes, [10, 100]):
for axx, alpha in zip(ax, [0.0001, 0.01, 0.1, 1]):
mlp = MLPClassifier(algorithm='l-bfgs', random_state=0,
hidden_layer_sizes=[n_hidden_nodes, n_hidden_nodes],
alpha=alpha)
mlp.fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3, ax=axx)
axx.scatter(X_train[:, 0], X_train[:, 1], c=y_train, s=60, cmap=mglearn.cm2)
axx.set_title("n_hidden=[%d, %d]\nalpha=%.4f"
% (n_hidden_nodes, n_hidden_nodes, alpha))
110 | Chapter 2: Supervised Learning
www.it-ebooks.info
As you probably have realized by now, there are many ways to control the complexity
of a neural network: the number of hidden layers, the number of units in each hidden
layer, and the regularization (alpha). There are actually even more, which we won’t go
into here.
An important property of neural networks is that their weights are set randomly
before learning is started, and this random initialization affects the model that is
learned. That means that even when using exactly the same parameters, we can
obtain very different models when using different random seeds.
If the networks are large, and their complexity is chosen properly, this should not
affect accuracy too much, but it is worth keeping in mind (particularly for smaller
networks).
Here are plots of several models, all learned with the same settings of the parameters:
fig, axes = plt.subplots(2, 4, figsize=(20, 8))
for i, ax in enumerate(axes.ravel()):
mlp = MLPClassifier(algorithm='l-bfgs', random_state=i,
hidden_layer_sizes=[100, 100])
mlp.fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3, ax=ax)
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, s=60, cmap=mglearn.cm2)
Neural Networks (Deep Learning) | 111
www.it-ebooks.info

To get a better understanding of neural networks on real-world data, let’s apply the
MLPClassifier to the breast cancer dataset. We start with the default parameters:
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=0)
mlp = MLPClassifier()
mlp.fit(X_train, y_train)
print("accuracy on training set: %f" % mlp.score(X_train, y_train))
print("accuracy on test set: %f" % mlp.score(X_test, y_test))
accuracy on training set: 0.373239
accuracy on test set: 0.370629
As you can see, the result on both the training and the test set are devastatingly bad
(even worse than random guessing!). As in the SVC example above, this is likely due
to scaling of the data. Neural networks also expect all input features to vary in a simi‐
lar way, and ideally should have a mean of zero, and a variance of one.
We [must] rescale our data so that it fulfills these requirements. Again, we will do this
“by hand” here, but introduce the StandardScaler to do this automatically in Chap‐
ter 3 (Unsupervised Learning).
# compute the mean value per feature on the training set
mean_on_train = X_train.mean(axis=0)
# compute the standard deviation of each feature on the training set
std_on_train = X_train.std(axis=0)
# subtract the mean, scale by inverse standard deviation
# afterwards, mean=0 and std=1
X_train_scaled = (X_train - mean_on_train) / std_on_train
# use THE SAME transformation (using training mean and std) on the test set
X_test_scaled = (X_test - mean_on_train) / std_on_train
mlp = MLPClassifier(random_state=0)
112 | Chapter 2: Supervised Learning
www.it-ebooks.info

mlp.fit(X_train_scaled, y_train)
print("accuracy on training set: %f" % mlp.score(X_train_scaled, y_train))
print("accuracy on test set: %f" % mlp.score(X_test_scaled, y_test))
/home/andy/checkout/scikit-learn/sklearn/neural_network/multilayer_perceptron.py:560: ConvergenceWarning: Stochastic Optimizer: Maximum iterations reached and the optimization hasn't converged yet.
% (), ConvergenceWarning)
The results are much better after scaling, and already quite competative. We got a
warning from the model, though, that tells us that the maximum number of iterations
has been reached. This is part of the adam algorithm for learning the model, and tells
us that we should increase the number of iterations:
mlp = MLPClassifier(max_iter=1000, random_state=0)
mlp.fit(X_train_scaled, y_train)
print("accuracy on training set: %f" % mlp.score(X_train_scaled, y_train))
print("accuracy on test set: %f" % mlp.score(X_test_scaled, y_test))
accuracy on training set: 0.995305
accuracy on test set: 0.965035
Increasing the number of iterations only increased the training set performance, but
not the generalization performance. Still, the model is performing quite well. As there
is some gap between the training
and the test performance, we might try to decrease the model complexity to get better
generalization performance. Here, we choose to increase the alpha parameter (quite
aggressively, from 0.0001 to 1), to add stronger regularization of the weights.
mlp = MLPClassifier(max_iter=1000, alpha=1, random_state=0)
mlp.fit(X_train_scaled, y_train)
print("accuracy on training set: %f" % mlp.score(X_train_scaled, y_train))
print("accuracy on test set: %f" % mlp.score(X_test_scaled, y_test))
accuracy on training set: 0.988263
accuracy on test set: 0.972028
This leads to a performance on par with the best models so far. [Footnote: You might
have noticed at this point that many of the well-performing models achieved exactly
the same accuracy of 0.972. This means that all of the models make exactly the same
number of mistakes, which is four. If you comparing the actual predictions, you can
even see that they make exactly the same mistakes! This might be either a conse‐
quence of data being very small, or may be because these points are really different
from the rest.]
While it is possible to analyze what a neural network learned, this is usually much
trickier than analyzing a linear model or a tree-based model. One way to introspect
Neural Networks (Deep Learning) | 113
www.it-ebooks.info
what was learned is to look at the weights in the model. You can see an example of
this in the scikit-learn example gallery on the website. For the breast cancer dataset,
this might be a bit hard to understand.
The plot below shows the weights that were learned connecting the input to the first
hidden layer.
The rows in this plot correspond to the 30 input features, while the columns corre‐
spond to the 100 hidden units.
Light green represents large positive values, while dark blue represents negative val‐
ues.
plt.figure(figsize=(20, 5))
plt.imshow(mlp.coefs_[0], interpolation='none', cmap='viridis')
plt.yticks(range(30), cancer.feature_names)
plt.colorbar()
One possible inference we can make is that features that have very small weights for
all of the hidden units are “less important” to the model. We can see that “mean
smoothness” and “mean compactness” in addition to the features found between
“smoothness error” and “fractal dimension error” have relatively low weights com‐
pared to other features. This could mean that these are less important features, or,
possibly, that we didn’t represent them in a way that the neural network could use.
We could also visualize the weights connecting the hidden layer to the output layer,
but those are even harder to interpret.
While the MLPClassifier and MLPRegressor provide easy-to-use interfaces for the
most common neural network architectures, they only capture a small subset of what
is possible with neural networks. If you are interested in working with more flexible
or larger models, we encourage you to look beyond scikit-learn into the fantastic deep
learning libraries that are our there. For python users, the most well-established are
keras, lasagna and tensor-flow. Keras and lasagna both build on the theano library.
These libraries provide a much more flexible interface to build neural networks, and
track the rapid process in deep learning research. All of the popular deep learning
libraries also allow the use of high-performance graphic processing units (GPUs),
which scikit-learn does not support.
114 | Chapter 2: Supervised Learning
www.it-ebooks.info

Using GPUs allows to accelerate computations by factors of 10x to 100x, and are
essential for applying deep learning methods to large-scale datasets.
Strengths, weaknesses and parameters
Neural networks have re-emerged as state of the art models in many applications of
machine learning. One of their main advantages is that they are able to capture infor‐
mation contained in large amounts of data and build incredibly complex models.
Given enough computation time, data, and careful tuning of the parameters, neural
networks often beat other machine learning algorithms (for classification and regres‐
sion tasks).
This brings us to the downsides; neural networks, in particular the large and powerful
ones, often take a long time to train. They also require careful preprocessing of the
data, as we saw above. Similarly to SVMs, they work best with “homogeneous” data,
where all the features have similar meanings. For data that has very different kinds of
features, tree-based models might work better.
Tuning neural network parameters is also an art onto itself. In our experiments
above, we barely scratched the surface of possible ways to adjust neural network
models, and how to train them.
Estimating complexity in neural networks
The most important parameters are the number of layers and the number of hidden
units per layer. You should start with one or two hidden layers, and possibly expand
from there. The number of nodes per hidden layer is often around the number of the
input features, but rarely higher than in the low to mid thousands.
A helpful measure when thinking about model complexity of a neural network is the
number of weights or coefficients that are learned. If you have a binary classification
dataset with 100 features, and you have 100 hidden units, then there are 100 * 100 =
10,000 weights between the input and the first hidden layer. There are also 100 * 1
= 100 weights between the hidden layer and the output layer, for a total of around
10,100 weights. If you add a second hidden layer with 100 hidden units, there will be
another 100 * 100 = 10,000 weights from the first hidden layer to the second hid‐
den layer, resulting in a total of 20,100 weights.
If instead, you use one layer with 1000 hidden units, you are learning 100 * 1000 =
100,000 weights from the input to the hidden layer, and 1000 x 1 weights from the
hidden to the output layer, for a total of 101,000.
If you add a second hidden layer, you add 1000 * 1000 = 1,000,000 weights, for a
whopping 1,101,000, which is 50 times larger than the model with two hidden layers
of size 100.
Neural Networks (Deep Learning) | 115
www.it-ebooks.info

A common way to adjust parameters in a neural network is to first create a network
that is large enough to overfit, making sure that the task can actually be learned by
the network. Once you know the training data can be learned, either shrink the net‐
work or increase alpha to add regularization, which will improve generalization per‐
formance.
During our experiments above, we focused mostly on the definition of the model: the
number of layers and nodes per layer, the regularization, and the nonlinearity. These
define the model we want to learn. There is also the question of how to learn the
model, or the algorithm that is used for learning of the parameters, which is set using
the algorithm parameter.
There are two easy-to-use choices for the algorithm. The default is 'adam', which
works well in most situations but is quite sensitive to the scaling of the data (so it is
important to always scale your data to zero mean and unit variance). The other one is
'l-bfgs', which is quite robust, but might take a long time on larger models or larger
datasets.
There is also the more advanced 'sgd' option, which is what many deep learning
researchers use. The 'sgd' option comes with many additional parameters that need
to be tuned for best results. You can find all of these parameters and their definitions
in the user-guide. When starting to work with MLPs, we recommend sticking to adam
and l-bfgs.
Uncertainty estimates from classiers
Another useful part of the scikit-learn interface that we haven’t talked about yet is the
ability of classifiers to provide uncertainty estimates of predictions.
Often, you are not only interested in which class a classifier predicts for a certain test
point, but also how certain it is that this is the right class. In practice, different kinds
of mistakes lead to very different outcomes in real world applications. Imagine a
medical application testing for cancer. Making a false positive prediction might lead
to a patient undergoing additional tests, while a false negative prediction might lead
to a serious disease not being treated.
We will go into this topic in more detail in Chapter 6 (Model Selection).
There are two different functions in scikit-learn that can be used to obtain uncer‐
tainty estimates from classifiers, decision_function and predict_proba. Most (but
not all) classifiers have at least one of them, and many classifiers have both. Let’s look
at what these two functions do on as synthetic two-dimensional dataset, when build‐
ing a GradientBoostingClassifier classifier. GradientBoostingClassifier has
both a decision_function method and a predict_proba.
116 | Chapter 2: Supervised Learning
www.it-ebooks.info

# create and split a synthetic dataset
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.datasets import make_blobs, make_circles
# X, y = make_blobs(centers=2, random_state=59)
X, y = make_circles(noise=0.25, factor=0.5, random_state=1)
# we rename the classes "blue" and "red" for illustration purposes:
y_named = np.array(["blue", "red"])[y]
# we can call train test split with arbitrary many arrays
# all will be split in a consistent manner
X_train, X_test, y_train_named, y_test_named, y_train, y_test = \
train_test_split(X, y_named, y, random_state=0)
# build the gradient boosting model model
gbrt = GradientBoostingClassifier(random_state=0)
gbrt.fit(X_train, y_train_named)
GradientBoostingClassifier(init=None, learning_rate=0.1, loss='deviance',
max_depth=3, max_features=None, max_leaf_nodes=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
presort='auto', random_state=0, subsample=1.0, verbose=0,
warm_start=False)
The Decision Function
In the binary classification case, the return value of decision_function is of shape
(n_samples,), it returns one floating point number for each sample:
print(X_test.shape)
print(gbrt.decision_function(X_test).shape)
(25, 2)
(25,)
This value encodes how strongly the model believes a data point to belong to the
“positive” class, in this case class 1.
Positive values indicate a preference for the positive class, negative values indicate
preference for the “negative”, that is the other class:
# show the first few entries of decision_function
gbrt.decision_function(X_test)[:6]
Uncertainty estimates from classiers | 117
www.it-ebooks.info

array([ 4.13592629, -1.68343075, -3.95106099, -3.6261613 , 4.28986668,
3.66166106])
We can recover the prediction by looking only at the sign of the decision function:
print(gbrt.decision_function(X_test) > 0)
print(gbrt.predict(X_test))
[ True False False False True True False True True True False True
True False True False False False True True True True True False
False]
['red' 'blue' 'blue' 'blue' 'red' 'red' 'blue' 'red' 'red' 'red' 'blue'
'red' 'red' 'blue' 'red' 'blue' 'blue' 'blue' 'red' 'red' 'red' 'red'
'red' 'blue' 'blue']
For binary classification, the “negative” class is always the first entry of the classes_
attribute, and the “positive” class is the second entry of classes_. So if you want to
fully recover the output of predict, you need to make use of the classes_ attribute:
# make the boolean True/False into 0 and 1
greater_zero = (gbrt.decision_function(X_test) > 0).astype(int)
# use 0 and 1 as indices into classes_
pred = gbrt.classes_[greater_zero]
# pred is the same as the output of gbrt.predict
np.all(pred == gbrt.predict(X_test))
True
The range of decision_function can be arbitrary, and depends on the data and the
model parameters:
decision_function = gbrt.decision_function(X_test)
np.min(decision_function), np.max(decision_function)
(-7.6909717730121798, 4.289866676868515)
This arbitrary scaling makes the output of decision_function often hard to inter‐
pret.
Below we plot the decision_function for all points in the 2d plane using a color
coding, next to a visualization of the decision boundary, as we saw it in Chapter 2. We
show training points as circles and test data as triangles.
Encoding not only the predicted outcome, but also how certain the classifier is pro‐
vides additional information. However, in this visualization, it is hard to make out the
boundary between the two classes.
118 | Chapter 2: Supervised Learning
www.it-ebooks.info
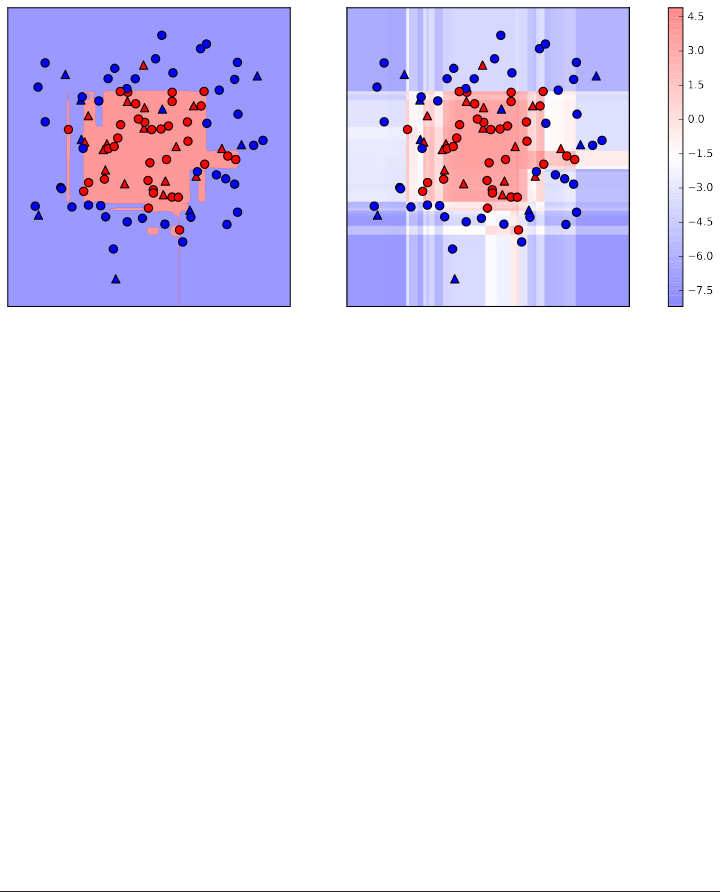
fig, axes = plt.subplots(1, 2, figsize=(13, 5))
mglearn.tools.plot_2d_separator(gbrt, X, ax=axes[0], alpha=.4, fill=True, cm=mglearn.cm2)
scores_image = mglearn.tools.plot_2d_scores(gbrt, X, ax=axes[1], alpha=.4, cm='bwr')
for ax in axes:
# plot training and test points
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=mglearn.cm2, s=60, marker='^')
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=mglearn.cm2, s=60)
plt.colorbar(scores_image, ax=axes.tolist())
Predicting probabilities
The output of predict_proba however is a probability for each class, and is often
more easily understood. It is always of shape (n_samples, 2) for binary classifica‐
tion:
gbrt.predict_proba(X_test).shape
(25, 2)
The first entry in each row is the estimated probability of the first class, the second
entry is the estimated probability of the second class. Because it is a probability, the
output of predict_proba is always between zero and 1, and the sum of the entries for
both classes is always 1:
np.set_printoptions(suppress=True, precision=3)
# show the first few entries of predict_proba
gbrt.predict_proba(X_test[:6])
array([[ 0.016, 0.984],
[ 0.843, 0.157],
[ 0.981, 0.019],
Uncertainty estimates from classiers | 119
www.it-ebooks.info
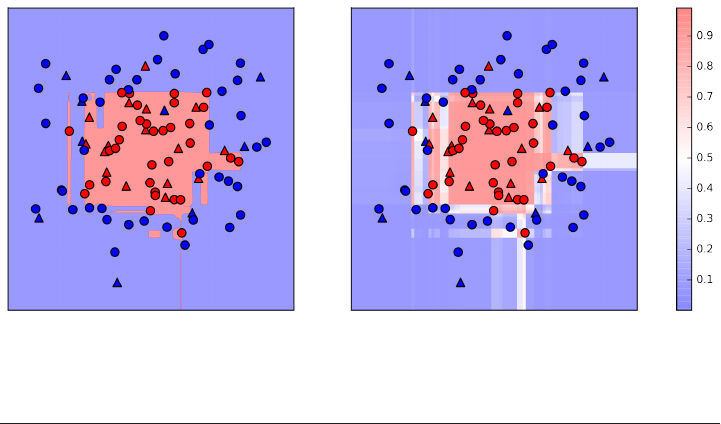
[ 0.974, 0.026],
[ 0.014, 0.986],
[ 0.025, 0.975]])
Because the probabilities for the two classes sum to one, exactly one of the classes is
above 50% certainty. That class is the one that is predicted.
You can see in the output above, that the classifier is relatively certain for most points.
How well the uncertainty actually reflects uncertainty in the data depends on the
model and parameters. A model that is more overfit tends to make more certain pre‐
dictions, even if they might be wrong. A model with less complexity usually has more
uncertainty in predictions. A model is called calibrated if the reported uncertainty
actually matches how correct it is - in a calibrated model, a prediction made with 70%
certainty would be correct 70% of the time.
Below we show again the decision boundary on the dataset, next to the class proba‐
bilities for the blue class:
fig, axes = plt.subplots(1, 2, figsize=(13, 5))
mglearn.tools.plot_2d_separator(gbrt, X, ax=axes[0], alpha=.4,
fill=True, cm=mglearn.cm2)
scores_image = mglearn.tools.plot_2d_scores(gbrt, X, ax=axes[1], alpha=.4,
cm='bwr', function='predict_proba')
for ax in axes:
# plot training and test points
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=mglearn.cm2, s=60, marker='^')
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=mglearn.cm2, s=60)
plt.colorbar(scores_image, ax=axes.tolist())
The boundaries in this this plot are much more well-defined, and the small areas of
uncertainty are clearly visible.
120 | Chapter 2: Supervised Learning
www.it-ebooks.info

The scikit-learn website [Footnote: http://scikit-learn.org/stable/auto_examples/clas‐
sification/plot_classifier_comparison.html] has a great comparison of many models,
and how their uncertainty estimates look like.
We reproduced the figure below, and encourage you to go though the example there.
Uncertainty in multi-class classication
Above we only talked about uncertainty estimates in binary classification. But the
decision_function and predict_proba methods also work in the multi-class setting.
Let’s apply them on the iris dataset, which is a three-class classification dataset:
from sklearn.datasets import load_iris
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(
iris.data, iris.target, random_state=42)
gbrt = GradientBoostingClassifier(learning_rate=0.01, random_state=0)
gbrt.fit(X_train, y_train)
GradientBoostingClassifier(init=None, learning_rate=0.01, loss='deviance',
max_depth=3, max_features=None, max_leaf_nodes=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
presort='auto', random_state=0, subsample=1.0, verbose=0,
warm_start=False)
print(gbrt.decision_function(X_test).shape)
# plot the first few entries of the decision function
print(gbrt.decision_function(X_test)[:6, :])
(38, 3)
Uncertainty estimates from classiers | 121
www.it-ebooks.info

[[-0.529 1.466 -0.504]
[ 1.512 -0.496 -0.503]
[-0.524 -0.468 1.52 ]
[-0.529 1.466 -0.504]
[-0.531 1.282 0.215]
[ 1.512 -0.496 -0.503]]
In the multi-class case, the decision_function has the shape (n_samples,
n_classes), and each column provides a “certainty score” for each class, where a
large score means that a class is more likely, and a small score means the class is less
likely. You can recover the prediction from these scores by finding the maximum
entry for each data point:
print(np.argmax(gbrt.decision_function(X_test), axis=1))
print(gbrt.predict(X_test))
[1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0 0 0 1 0 0 2 1
0]
[1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0 0 0 1 0 0 2 1
0]
The output of predict_proba has the same shape, (n_samples, n_classes). Again,
the probabilities for the possible classes for each data point sum to one:
# show the first few entries of predict_proba
print(gbrt.predict_proba(X_test)[:6])
# show that sums across rows are one
print("sums: %s" % gbrt.predict_proba(X_test)[:6].sum(axis=1))
[[ 0.107 0.784 0.109]
[ 0.789 0.106 0.105]
[ 0.102 0.108 0.789]
[ 0.107 0.784 0.109]
[ 0.108 0.663 0.228]
[ 0.789 0.106 0.105]]
sums: [ 1. 1. 1. 1. 1. 1.]
We can again recover the predictions by computing the argmax of predict_proba:
122 | Chapter 2: Supervised Learning
www.it-ebooks.info

print(np.argmax(gbrt.decision_function(X_test), axis=1))
print(gbrt.predict(X_test))
[1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0 0 0 1 0 0 2 1
0]
[1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0 0 0 1 0 0 2 1
0]
To summarize, predict_proba and decision_function always have shape (n_sam
ples, n_classes) -- apart from the special case of decision_function in the binary
case. In the binary case, decision_function only has one column, corresponding to
the “positive” class classes_[1]. This is mostly for historical reasons.
You can recover the prediction when there are n_classes many columns by simply
computing the argmax across columns.
Be careful, though, if your classes are strings, or you use integers, but they are not
consecutive and starting from 0. If you want to compare results obtained with pre
dict to results obtained via decision_function or predict_proba make sure to use
the classes_ attribute of the classifier to get the actual class names.
Summary and Outlook
We started this chapter with a discussion of model complexity, and discussed general‐
ization, or learning a model that is able to perform well on new, unseen data. This led
us to the concepts of underfitting, which describe a model that can not capture the
variations present in the training data, and overfitting, which describe a model that
focuses too much on the training data, and is not able to generalize to new data very
well.
We then discussed a wide array of machine learning models for classification and
regression, what their advantages and disadvantages are, and how to control model
complexity for each of them.
We saw that for many of the algorithms, setting the right parameters is important for
good performance. Some of the algorithms are also sensitive to how we represent the
input data, in particular to how the features are scaled.
Therefore, blindly applying an algorithm to a dataset without understanding the
assumptions the models makes and the meaning of the parameter settings will rarely
lead to an accurate model.
This chapter contains a lot of information about the algorithms, and it is not neces‐
sary for you to remember all of these details for the following chapters. However,
knowing the models described above, and knowing which to use in a specific situa‐
Summary and Outlook | 123
www.it-ebooks.info

tion, is important for successfully applying machine learning in practice. Here is a
quick summary of when to use which model:
• Nearest neighbors: for small datasets, good as a baseline, easy to explain.
• Linear models: Go-to as a first algorithm to try, good for very large datasets, good
for very high-dimensional data.
•Naive Bayes: Only for classification. Even faster than linear models, good for very
large, high-dimensional data. Often less accurate than linear models.
•Decision trees: Very fast, don’t need scaling of the data, can be visualized and
easily explained.
•Random forests: Nearly always perform better than a single decision tree, very
robust and powerful. Don’t need scaling of data. Not good for very high-
dimensional sparse data.
•Gradient Boosted Decision Trees: Often slightly more accurate than random for‐
est. Slower to train but faster to predict than random forest, and smaller in mem‐
ory. Need more parameter tuning than random forest.
•Support Vector Machines: Powerful for medium-sized datasets of features with
similar meaning. Needs scaling of data, sensitive to parameters.
•Neural Networks: Can build very complex models, in particular for large data‐
sets. Sensitive to scaling of the data, and to the choice of parameters. Large mod‐
els need a long time to train.
When working with a new dataset, it is in general a good idea to start with a simple
model, such as a linear model, naive Bayes or nearest neighbors and see how far you
can get. After understanding more about the data, you can consider moving to an
algorithm that can build more complex models, such as random forests, gradient
boosting, SVMs or neural networks.
You should now be in a position where you have some idea how to apply, tune, and
analyze the models we discussed above.
In this chapter, we focused on the binary classification case, as this is usually easiest to
understand.
Most of the algorithms presented above have classification and regression variants,
however, and all of the classification algorithms support both binary and multi-class
classification.
124 | Chapter 2: Supervised Learning
www.it-ebooks.info

Try to apply any of these algorithms to the build-in datasets in scikit-learn, like the
boston_housing or diabetes datasets for regression, or the digits dataset for multi-
class classification.
Playing around with the algorithms on different datasets will give you a better feel on
how long they need to train, how easy it is to analyze the model, and how sensitive
they are to the representation of the data.
While we analyzed the consequences of different parameter settings for the algo‐
rithms we investigated, building a model that actually generalizes well to new data in
production is a bit trickier than that. We will see how to properly adjust parameters,
and how to find good parameters automatically in Chapter 6 Model Selection.
Before we do this, we will dive in more detail into preprocessing and unsupervised
learning in the next chapter.
Summary and Outlook | 125
www.it-ebooks.info

CHAPTER 3
Unsupervised Learning and Preprocessing
The second family of machine learning algorithms that we will discuss is unsuper‐
vised learning.
Unsupervised learning subsumes all kinds of machine learning where there is no
known output, no teacher to instruct the learning algorithm. In unsupervised learn‐
ing, the learning algorithm is just shown the input data, and asked to extract knowl‐
edge from this data.
Types of unsupervised learning
We will look into two kinds of unsupervised learning in this chapter: transformations
of the dataset, and clustering.
Unsupervised transformations of a dataset are algorithms that create a new representa‐
tion of the data which might be easier for humans or other machine learning algo‐
rithms to understand.
A common application of unsupervised transformations is dimensionality reduction,
which takes a high-dimensional representation of the data, consisting of many fea‐
tures, and finding a new way to represent this data that summarizes the essential
characteristics about the data with fewer features. A common application for dimen‐
sionality reduction is reduction to two dimensions for visualization purposes.
Another application for unsupervised transformations is finding the parts or compo‐
nents that “make up” the data. An example of this is topic extraction on collections of
text documents. Here, the task is to find the unknown topics that are talked about in
each document, and to learn what topics appear in each document.
This can be useful for tracking the discussion of themes like elections, gun control or
talk about pop-stars on social media.
127
www.it-ebooks.info

Clustering algorithms on the other hand partition data into distinct groups of similar
items.
Consider the example of uploading photos to a social media site. To allow you to
organize your pictures, the site might want to group together pictures that show the
same person. However, the site doesn’t know which pictures show whom, and it
doesn’t know how many different people appear in your photo collection. A sensible
approach would be to extract all faces, and divide them into groups of faces that look
similar. Hopefully, these correspond to the same person, and can be grouped together
for you.
Challenges in unsupervised learning
A major challenge in unsupervised learning is evaluating whether the algorithm
learned something useful. Unsupervised learning algorithms are usually applied to
data that does not contain any label information, so we don’t know what the right
output should be. Therefore it is very hard to say whether a model “did well”. For
example, the clustering algorithm could have grouped all face pictures that are shown
in profile together, and all the face pictures that are face-forward together.
This would certainly be a possible way to divide a collection of face pictures, but not
the one we were looking for. However, there is no way for us to “tell” the algorithm
what we are looking for, and often the only way to evaluate the result of an unsuper‐
vised algorithm is to inspect it manually.
As a consequence, unsupervised algorithms are used often in an exploratory setting,
when a data scientist wants to understand the data better, rather than as part of a
larger automatic system. Another common application for unsupervised algorithms
is as a preprocessing step for supervised algorithms. Learning a new representation of
the data can sometimes improve the accuracy of supervised algorithms, or can lead to
reduced memory and time consumption.
Before we start with “real” unsupervised algorithms, we will briefly discuss some sim‐
ple preprocessing methods that often come in handy. Even though preprocessing and
scaling are often used in tandem with supervised learning algorithms, scaling meth‐
ods don’t make use of the supervised information, making them unsupervised.
Preprocessing and Scaling
In the last chapter we saw that some algorithms, like neural networks and SVMs, are
very sensitive to the scaling of the data. Therefore a common practice is to adjust the
features so that the data representation is more suitable for these algorithms. Often,
this is a simple per-feature rescaling and shift of the data. A simple example is shown
in Figure scaling_data.
128 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info
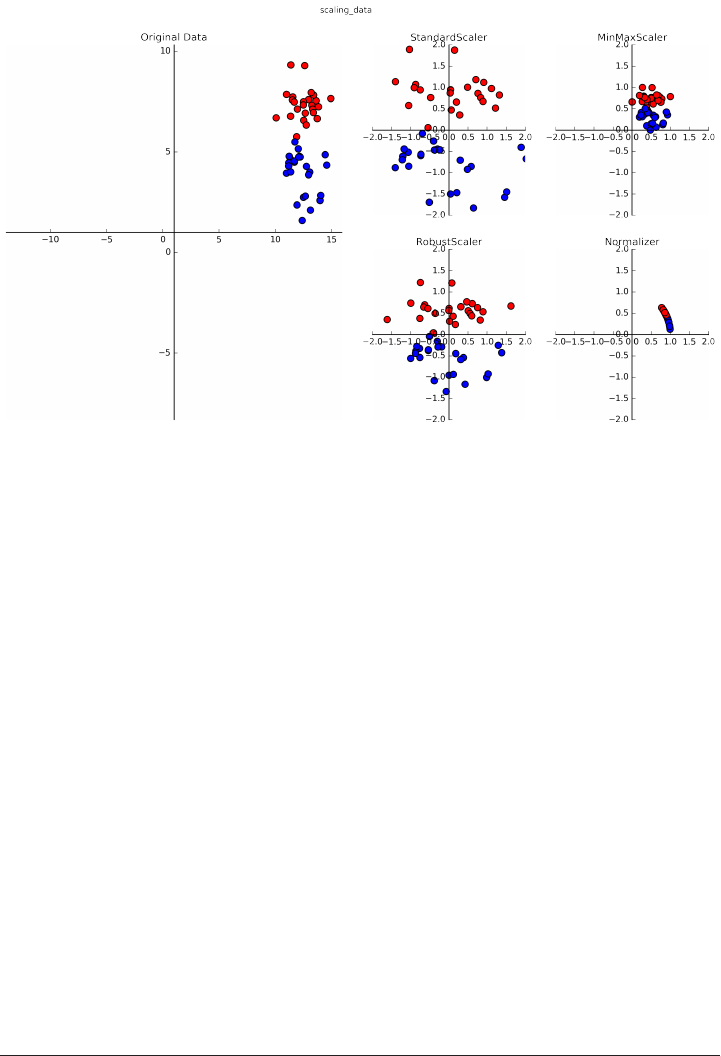
mglearn.plots.plot_scaling()
plt.suptitle("scaling_data");
Dierent kinds of preprocessing
The first plot shows a synthetic two-class classification dataset with two features. The
first feature (the x-axis value) is between 10 and 15. The second feature (the y-axis
value) is between around 1 and 9.
The following four plots show four different ways to transform the data that yield
more standard ranges.
The StandardScaler in scikit-learn ensures that for each feature, the mean is zero,
and the variance is one, bringing all features to the same magnitude. However, this
scaling does not ensure any particular minimum and maximum values for the fea‐
tures.
The RobustScaler works similarly to the StandardScaler in that it ensures statistical
properties for each feature that guarantee that they are on the same scale. However,
the RobustScaler uses the median and quartiles [Footnote: the median of a set of
numbers is the number x such that half of the numbers are smaller than x and half of
the numbers are larger than x. The lower quartile is the number x such that 1/4th of
the numbers are smaller than x, the upper quartile is so that 1/4th of the numbers is
larger than x], instead of mean and variance. This makes the RobustScaler ignore
data points that are very different from the rest (like measurement errors). These odd
data points are also called outliers, and might often lead to trouble for other scaling
techniques.
Preprocessing and Scaling | 129
www.it-ebooks.info

The MinMaxScaler on the other hand shifts the data such that all features are exactly
between 0 and 1. For the two-dimensional dataset this means all of the data is con‐
tained within the rectangle created by the x axis between 0 and 1 and the y axis
between zero and one.
Finally, the Normalizer does a very different kind of rescaling. It scales each data
point such that the feature vector has a euclidean length of one. In other words, it
projects a data point on the circle (or sphere in the case of higher dimensions) with a
radius of 1. This means every data point is scaled by a different number (by the
inverse of it’s length).
This normalization is often used when only the direction (or angle) of the data mat‐
ters, not the length of the feature vector.
Applying data transformations
After seeing what the different kind of transformations do, let’s apply them using
scikit-learn.
We will use the cancer dataset that we saw in chapter 2. Preprocessing methods like
the scalers are usually applied before applying a supervised machine learning algo‐
rithm. As an example, say we want to apply the kernel SVM (SVC) to the cancer data‐
set, and use MinMaxScaler for preprocessing the data. We start by loading and
splitting our dataset into a training set and a test set. We need a separate training and
test set to evaluate the supervised model we will build after the preprocessing:
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target,
random_state=1)
print(X_train.shape)
print(X_test.shape)
(426, 30)
(143, 30)
As a reminder, the data contains 150 data points, each represented by four measure‐
ments. We split the dataset into 112 samples for the training set and 38 samples for
the test set.
As with the supervised models we built earlier, we first import the class implementing
the preprocessing, and then instantiate it:
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
130 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

We then fit the scaler using the fit method, applied to the training data. For the Min
MaxScaler, the fit method computes the minimum and maximum value of each fea‐
ture on the training set. In contrast to the classifiers and regressors of chapter 2, the
scaler is only provided with the data X_train when fit is called, and y_train is not
used:
scaler.fit(X_train)
MinMaxScaler(copy=True, feature_range=(0, 1))
To apply the transformation that we just learned, that is, to actually scale the training
data, we use the transform method of the scaler. The transform method is used in
scikit-learn whenever a model returns a new representation of the data:
# don't print using scientific notation
np.set_printoptions(suppress=True, precision=2)
# transform data
X_train_scaled = scaler.transform(X_train)
# print data set properties before and after scaling
print("transformed shape: %s" % (X_train_scaled.shape,))
print("per-feature minimum before scaling:\n %s" % X_train.min(axis=0))
print("per-feature maximum before scaling:\n %s" % X_train.max(axis=0))
print("per-feature minimum after scaling:\n %s" % X_train_scaled.min(axis=0))
print("per-feature maximum after scaling:\n %s" % X_train_scaled.max(axis=0))
transformed shape: (426, 30)
per-feature minimum before scaling:
[ 6.98 9.71 43.79 143.5 0.05 0.02 0. 0. 0.11
0.05 0.12 0.36 0.76 6.8 0. 0. 0. 0.
0.01 0. 7.93 12.02 50.41 185.2 0.07 0.03 0.
0. 0.16 0.06]
per-feature maximum before scaling:
[ 28.11 39.28 188.5 2501. 0.16 0.29 0.43 0.2
0.3 0.1 2.87 4.88 21.98 542.2 0.03 0.14
0.4 0.05 0.06 0.03 36.04 49.54 251.2 4254.
0.22 0.94 1.17 0.29 0.58 0.15]
per-feature minimum after scaling:
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
Preprocessing and Scaling | 131
www.it-ebooks.info

per-feature maximum after scaling:
[ 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
The transformed data has the same shape as the original data - the features are simply
shifted and scaled.
You can see that all of the feature are now between zero and one, as desired.
To apply the SVM to the scaled data, we also need to transform the test set. This is
done by again calling the transform method, this time on X_test:
# transform test data
X_test_scaled = scaler.transform(X_test)
# print test data properties after scaling
print("per-feature minimum after scaling: %s" % X_test_scaled.min(axis=0))
print("per-feature maximum after scaling: %s" % X_test_scaled.max(axis=0))
per-feature minimum after scaling: [ 0.03 0.02 0.03 0.01 0.14 0.04 0. 0. 0.15 -0.01 -0. 0.01
0. 0. 0.04 0.01 0. 0. -0.03 0.01 0.03 0.06 0.02 0.01
0.11 0.03 0. 0. -0. -0. ]
per-feature maximum after scaling: [ 0.96 0.82 0.96 0.89 0.81 1.22 0.88 0.93 0.93 1.04 0.43 0.5
0.44 0.28 0.49 0.74 0.77 0.63 1.34 0.39 0.9 0.79 0.85 0.74
0.92 1.13 1.07 0.92 1.21 1.63]
Maybe somewhat surprisingly, you can see that for the test set, after scaling, the mini‐
mum and maximum are not zero and one. Some of the features are even outside the
0-1 range!
The explanation is that the MinMaxScaler (and all the other scalers) always applies
exactly the same transformation to the training and the test set. So the transform
method always subtracts the training set minimum, and divides by the training set
range, which might be different than the minimum and range for the test set.
Scaling training and test data the same way
It is important that exactly the same transformation is applied to the training set and
the test set for the supervised model to make sense on the test set. The following fig‐
ure illustrates what would happen if we would use the minimum and range of the test
set instead:
from sklearn.datasets import make_blobs
# make synthetic data
132 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info
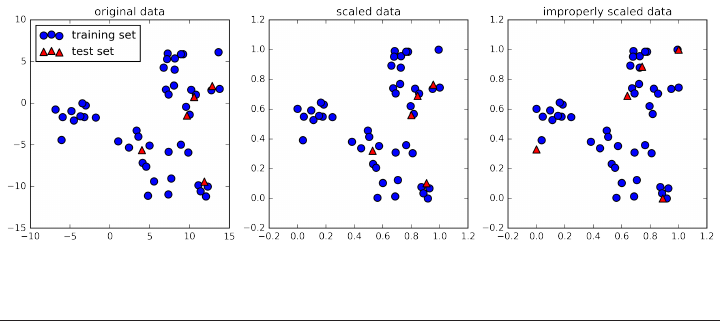
X, _ = make_blobs(n_samples=50, centers=5, random_state=4, cluster_std=2)
# split it into training and test set
X_train, X_test = train_test_split(X, random_state=5, test_size=.1)
# plot the training and test set
fig, axes = plt.subplots(1, 3, figsize=(13, 4))
axes[0].scatter(X_train[:, 0], X_train[:, 1],
c='b', label="training set", s=60)
axes[0].scatter(X_test[:, 0], X_test[:, 1], marker='^',
c='r', label="test set", s=60)
axes[0].legend(loc='upper left')
axes[0].set_title("original data")
# scale the data using MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# visualize the properly scaled data
axes[1].scatter(X_train_scaled[:, 0], X_train_scaled[:, 1],
c='b', label="training set", s=60)
axes[1].scatter(X_test_scaled[:, 0], X_test_scaled[:, 1], marker='^',
c='r', label="test set", s=60)
axes[1].set_title("scaled data")
# rescale the test set separately, so that test set min is 0 and test set max is 1
# DO NOT DO THIS! For illustration purposes only
test_scaler = MinMaxScaler()
test_scaler.fit(X_test)
X_test_scaled_badly = test_scaler.transform(X_test)
# visualize wrongly scaled data
axes[2].scatter(X_train_scaled[:, 0], X_train_scaled[:, 1],
c='b', label="training set", s=60)
axes[2].scatter(X_test_scaled_badly[:, 0], X_test_scaled_badly[:, 1], marker='^',
c='r', label="test set", s=60)
axes[2].set_title("improperly scaled data")
Preprocessing and Scaling | 133
www.it-ebooks.info

The first panel is an unscaled two-dimensional dataset, with the training set shown in
blue and the test set shown in red. The second figure is the same data, but scaled
using the MinMaxScaler. Here, we called fit on the training set, and then transform
on the training and the test set. You can see that the dataset in the second panel looks
identical to the first, only the ticks on the axes changed. Now all the features are
between 0 and 1.
You can also see that the minimum and maximum feature values for the test data (the
red points) are not 0 and 1.
The third panel shows what would happen if we scaled training and test set sepa‐
rately. In this case, the minimum and maximum feature values for both the training
and the test set are 0 and 1. But now the dataset looks different. The test points
moved incongruously to the training set, as they were scaled differently. We changed
the arrangement of the data in an arbitrary way. Clearly this is not what we want to
do.
Another way to reason about this is the following: Imagine your test set was a single
point. There is no way to scale a single point correctly, to fulfill the minimum and
maximum requirements of the MinMaxScaler. But the size of your test set should not
change your processing.
The eect of preprocessing on supervised learning
Now let’s go back to the cancer dataset and see what the effect of using the Min
MaxScaler is on learning the SVC (this is a different way of doing the same scaling we
did in chapter 2).
First, let’s fit the SVC on the original data again for comparison:
from sklearn.svm import SVC
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target,
random_state=0)
svm = SVC(C=100)
svm.fit(X_train, y_train)
print(svm.score(X_test, y_test))
0.629370629371
Now, let’s scale the data using MinMaxScaler before fitting the SVC:
# preprocessing using 0-1 scaling
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# learning an SVM on the scaled training data
134 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

svm.fit(X_train_scaled, y_train)
# scoring on the scaled test set
svm.score(X_test_scaled, y_test)
0.965034965034965
As we saw before, the effect of scaling the data is quite significant. Even though scal‐
ing the data doesn’t involve any complicated math, it is good practice to use the scal‐
ing mechanisms provided by scikit-learn, instead of reimplementing them yourself,
as making mistakes even in these simple computations is easy.
You can also easily replace one preprocessing algorithm by another by changing the
class you use, as all of the preprocessing classes have the same interface, consisting of
the fit and transform methods:
# preprocessing using zero mean and unit variance scaling
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# learning an SVM on the scaled training data
svm.fit(X_train_scaled, y_train)
# scoring on the scaled test set
svm.score(X_test_scaled, y_test)
0.95804195804195802
Now that we’ve seen how simple data transformations for preprocessing work, let’s
move on to more interesting transformations using unsupervised learning.
Dimensionality Reduction, Feature Extraction and
Manifold Learning
As we discussed above, transforming data using unsupervised learning can have
many motivations. The most common motivations are visualization, compressing the
data, and finding a representation that is more informative for further processing.
One of the simplest and most widely used algorithms for all of these is Principal
Component Analysis.
Principal Component Analysis (PCA)
Principal component analysis (PCA) is a method that rotates the dataset in a way
such that the rotated features are statistically uncorrelated. This rotation is often fol‐
lowed by selecting only a subset of the new features, according to how important they
are for explaining the data.
Dimensionality Reduction, Feature Extraction and Manifold Learning | 135
www.it-ebooks.info
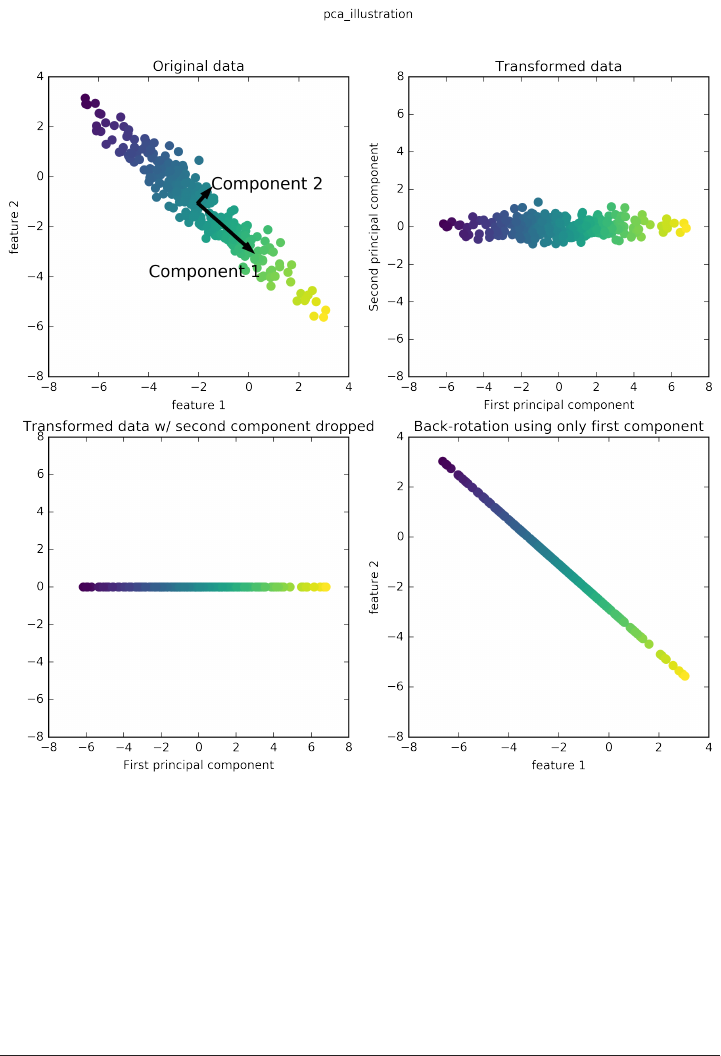
mglearn.plots.plot_pca_illustration()
plt.suptitle("pca_illustration");
The plot above shows a simple example on a synthetic two-dimensional dataset. The
first plot shows the original data points, colored to distinguish the points. The algo‐
rithm proceeds by first finding the direction of maximum variance, labeled as “Com‐
ponent 1”. This is the direction in the data that contains most of the information, or
in other words, the direction along which the features are most correlated with each
other.
Then, the algorithm finds the direction that contains the most information while
being orthogonal (is at a right angle) to the first direction. In two dimensions, there is
136 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

only one possible orientation that is at a right angle, but in higher dimensional spaces
there would be (infinitely) many orthogonal directions.
Although the two components are drawn as arrows, it doesn’t really matter where the
head and the tail is; we could have drawn the first component from the center up to
the top left instead of to the bottom right.The directions found using this process are
called principal components, as they are the main directions of variance in the data. In
general, there are as many principal components as original features.
The second plot shows the same data, but now rotated so that the first principal com‐
ponent aligns with the x axis, and the second principal component aligns with the y
axis. Before the rotation, the mean was subtracted from the data, so that the trans‐
formed data is centered around zero. In the rotated representation found by PCA, the
two axes are uncorrelated, meaning that the correlation matrix of the data in this rep‐
resentation is zero except for the diagonal.
We can use PCA for dimensionality reduction by retaining only some of the principal
components. In this example, we might keep only the first principal component, as
shown in the third panel in Figure X.
This reduced the data from a two-dimensional dataset to a one-dimensional dataset.
But instead of keeping only one of the original features, we found the most interest‐
ing direction (top left to bottom right in the first panel) and kept this direction, the
first principal component.
Finally, we can undo the rotation, and add the mean back to the data. This will result
in the data shown in the last panel. These points are in the original feature space, but
we kept only the information contained in the first principal component. This trans‐
formation is sometimes used to remove noise effects from the data, or visualize what
part of the information is kept in the PCA.
Applying PCA to the cancer dataset for visualization
One of the most common applications of PCA is visualizing high-dimensional data‐
sets. As we already saw in Chapter 1, it is hard to create scatter plots of data that has
more than two features. For the iris dataset, we could create a pair plot (Figure
iris_pairplot in Chapter 1), which gave us us a partial picture of the data by showing
us all combinations of two features. If we want to look at the breast cancer dataset,
even using a pair-plot is tricky. The breast cancer dataset has 30 features, which
would result in 30 * 14 = 420 scatter plots! You’d never be able to look at all these plots
in detail, let alone try to understand them.
We could go for an even simpler visualization, showing histograms of each of the fea‐
tures for the two classes, benign and malignant cancer:
fig, axes = plt.subplots(15, 2, figsize=(10, 20))
malignant = cancer.data[cancer.target == 0]
Dimensionality Reduction, Feature Extraction and Manifold Learning | 137
www.it-ebooks.info

benign = cancer.data[cancer.target == 1]
ax = axes.ravel()
for i in range(30):
_, bins = np.histogram(cancer.data[:, i], bins=50)
ax[i].hist(malignant[:, i], bins=bins, color='b', alpha=.5)
ax[i].hist(benign[:, i], bins=bins, color='r', alpha=.5)
ax[i].set_title(cancer.feature_names[i])
ax[i].set_yticks(())
fig.tight_layout()
plt.suptitle("cancer_histograms")
138 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

Here we create a histogram for each of the features, counting how often a data point
appears with a feature in a certain range (called a bin).
Each plot overlays two histograms, one for all of the points of the benign class (blue)
and one for all the points in the malignant class (red). This gives us some idea of how
each feature is distributed across the two classes, and allows us to venture a guess as
to which features are better at distinguishing malignant and benign samples. For
example, the feature “smoothness error” seems quite uninformative, because the two
histograms mostly overlap, while the feature “worst concave points” seems quite
informative, because the histograms are quite disjoint.
However, this plot doesn’t show us anything about the, which indicate variables that
are varying together . We can find the first two principal components, and visualize
the data in this new, two-dimensional space, with a single scatter-plot.
Before we apply PCA, we scale our data so that each feature has unit variance using
StandardScaler:
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
scaler = StandardScaler()
scaler.fit(cancer.data)
X_scaled = scaler.transform(cancer.data)
Learning the PCA transformation and applying it is as simple as applying a prepro‐
cessing transformation. We instantiate the PCA object, find the principal components
by calling the fit method, and then apply the rotation and dimensionality reduction
by calling transform.
By default, PCA only rotates (and shifts) the data, but keeps all principal components.
To reduce the dimensionality of the data, we need to specify how many components
we want to keep when creating the PCA object:
from sklearn.decomposition import PCA
# keep the first two principal components of the data
pca = PCA(n_components=2)
# fit PCA model to beast cancer data
pca.fit(X_scaled)
# transform data onto the first two principal components
X_pca = pca.transform(X_scaled)
print("Original shape: %s" % str(X_scaled.shape))
print("Reduced shape: %s" % str(X_pca.shape))
Original shape: (569, 30)
Reduced shape: (569, 2)
We can now plot the first two principal components:
140 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info
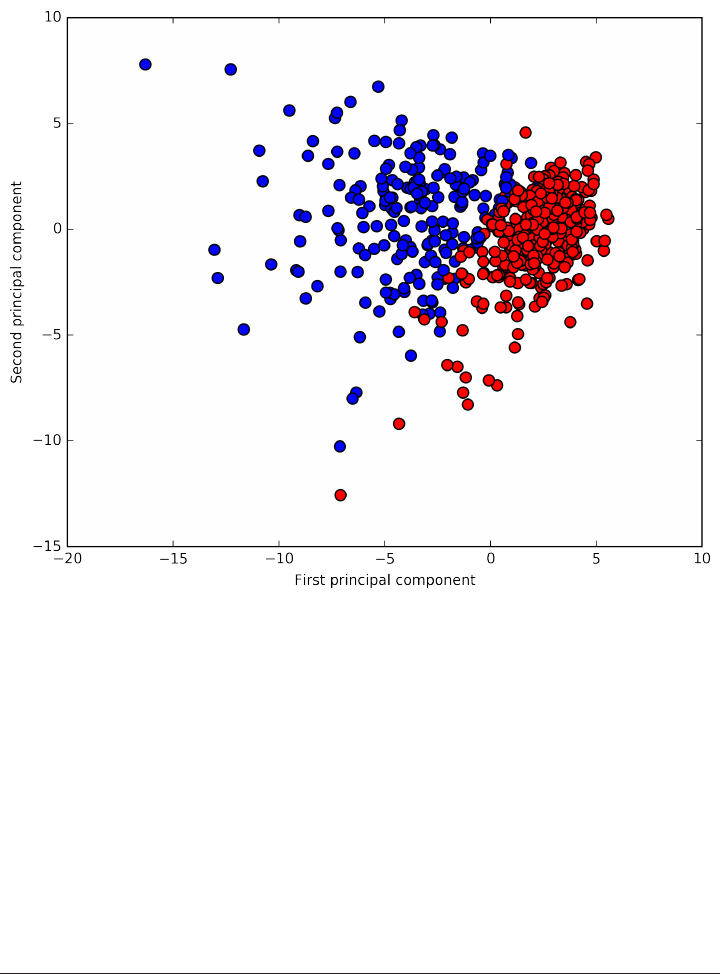
# plot fist vs second principal component, color by class
plt.figure(figsize=(8, 8))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=cancer.target, cmap=mglearn.tools.cm, s=60)
plt.gca().set_aspect("equal")
plt.xlabel("First principal component")
plt.ylabel("Second principal component")
It is important to note is that PCA is an unsupervised method, and does not use any
class information when finding the rotation. It simply looks at the correlations in the
data. For the scatter plot above, we plotted the first principal component against the
second principal component, and then used the class information to color the points.
You can see that the two classes separate quite well in this two-dimensional space.
This can lead us to believe that even a linear classifier (that would learn a line in this
space) could do a reasonably good job at distinguishing the two classes. We can also
see that the malignant (red) points are more spread-out than the benign (blue)
points, something that we could already see a bit from the histograms in Figure can‐
cer_histograms.
Dimensionality Reduction, Feature Extraction and Manifold Learning | 141
www.it-ebooks.info
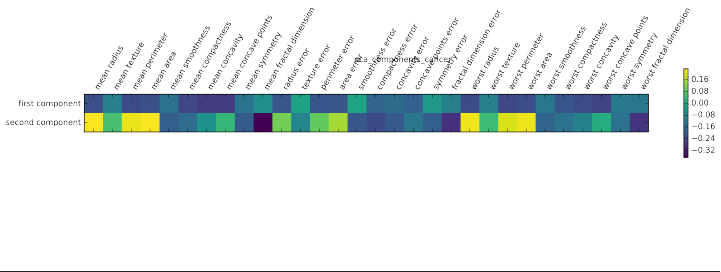
A downside of PCA is that the two axes in the plot above are often not very easy to
interpret. The principal components correspond to directions in the original data, so
they are combinations of the original features. However, these combinations are usu‐
ally very complex, as we’ll see below.
The principal components themselves are stored in the components_ attribute of the
PCA during fitting:
pca.components_.shape
(2, 30)
Each row in components_ corresponds to one principal component, sorted by their
importance (the first principal component comes first, etc). The columns correspond
to the original features, in this example “mean radius”, “mean texture” and so on.
Let’s have a look at the content of components_:
print(pca.components_)
[[-0.22 -0.1 -0.23 -0.22 -0.14 -0.24 -0.26 -0.26 -0.14 -0.06 -0.21 -0.02
-0.21 -0.2 -0.01 -0.17 -0.15 -0.18 -0.04 -0.1 -0.23 -0.1 -0.24 -0.22
-0.13 -0.21 -0.23 -0.25 -0.12 -0.13]
[ 0.23 0.06 0.22 0.23 -0.19 -0.15 -0.06 0.03 -0.19 -0.37 0.11 -0.09
0.09 0.15 -0.2 -0.23 -0.2 -0.13 -0.18 -0.28 0.22 0.05 0.2 0.22
-0.17 -0.14 -0.1 0.01 -0.14 -0.28]]
We can also visualize the coefficients using a heatmap, which might be easier to
understand:
plt.matshow(pca.components_, cmap='viridis')
plt.yticks([0, 1], ["first component", "second component"])
plt.colorbar()
plt.xticks(range(len(cancer.feature_names)),
cancer.feature_names, rotation=60, ha='left');
plt.suptitle("pca_components_cancer")
You can see that in the first component, all feature have the same sign (it’s negative,
but as we mentioned above, it doesn’t matter in which direction you point the arrow).
142 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

That means that there is a general correlation between all features. As one measure‐
ment is high, the others are likely to be high as well.
The second component has mixed signs, and both of the components involve all of
the 30 features. This mixing of all features is what makes explaining the axes in Figure
pca_components_cancer above so tricky.
Eigenfaces for feature extraction
Another application of PCA that we mentioned above is feature extraction. The idea
behind feature extraction is that it is possible to find a representation of your data
that is better suited to analysis than the raw representation you were given. A great
example of an application when feature extraction if helpful is with images. Images
are usually stored as red, green and blue intensities for each pixel. But images are
made up of many pixels, and only together are they meaningful; objects in images are
usually made up of thousands of pixels.
We will give a very simple application of feature extraction on images using PCA,
using face images from the “labeled faces in the wild” dataset. This dataset contains
face images of celebrities downloaded from the internet, and it includes faces of poli‐
ticians, singers, actors and athletes from the early 2000s. We use gray-scale versions of
these images, and scale them down for faster processing. You can see some of the
images below:
from sklearn.datasets import fetch_lfw_people
people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = people.images[0].shape
fix, axes = plt.subplots(2, 5, figsize=(15, 8), subplot_kw={'xticks': (), 'yticks': ()})
for target, image, ax in zip(people.target, people.images, axes.ravel()):
ax.imshow(image)
ax.set_title(people.target_names[target])
plt.suptitle("some_faces")
Dimensionality Reduction, Feature Extraction and Manifold Learning | 143
www.it-ebooks.info

There are 3023 images, each 87 x 65 pixels large, belonging to 62 different people:
print(people.images.shape)
print(len(people.target_names))
(3023, 87, 65)
62
The dataset is a bit skewed, however, containing a lot of images of George W. Bush
and Colin Powell, as you can see here:
# count how often each target appears
counts = np.bincount(people.target)
# print counts next to target names:
for i, (count, name) in enumerate(zip(counts, people.target_names)):
print("{0:25} {1:3}".format(name, count), end=' ')
if (i + 1) % 3 == 0:
print()
Alejandro Toledo 39 Alvaro Uribe 35 Amelie Mauresmo 21
Andre Agassi 36 Angelina Jolie 20 Ariel Sharon 77
Arnold Schwarzenegger 42 Atal Bihari Vajpayee 24 Bill Clinton 29
Carlos Menem 21 Colin Powell 236 David Beckham 31
Donald Rumsfeld 121 George Robertson 22 George W Bush 530
Gerhard Schroeder 109 Gloria Macapagal Arroyo 44 Gray Davis 26
144 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

Guillermo Coria 30 Hamid Karzai 22 Hans Blix 39
Hugo Chavez 71 Igor Ivanov 20 Jack Straw 28
Jacques Chirac 52 Jean Chretien 55 Jennifer Aniston 21
Jennifer Capriati 42 Jennifer Lopez 21 Jeremy Greenstock 24
Jiang Zemin 20 John Ashcroft 53 John Negroponte 31
Jose Maria Aznar 23 Juan Carlos Ferrero 28 Junichiro Koizumi 60
Kofi Annan 32 Laura Bush 41 Lindsay Davenport 22
Lleyton Hewitt 41 Luiz Inacio Lula da Silva 48 Mahmoud Abbas 29
Megawati Sukarnoputri 33 Michael Bloomberg 20 Naomi Watts 22
Nestor Kirchner 37 Paul Bremer 20 Pete Sampras 22
Recep Tayyip Erdogan 30 Ricardo Lagos 27 Roh Moo-hyun 32
Rudolph Giuliani 26 Saddam Hussein 23 Serena Williams 52
Silvio Berlusconi 33 Tiger Woods 23 Tom Daschle 25
Tom Ridge 33 Tony Blair 144 Vicente Fox 32
Vladimir Putin 49 Winona Ryder 24
To make the data less skewed, we will only take up to 50 images of each person.
Otherwise the feature extraction would be overwhelmed by the likelihood of George
W Bush.
mask = np.zeros(people.target.shape, dtype=np.bool)
for target in np.unique(people.target):
mask[np.where(people.target == target)[0][:50]] = 1
X_people = people.data[mask]
y_people = people.target[mask]
# scale the grey-scale values to be between 0 and 1
# instead of 0 and 255 for better numeric stability:
X_people = X_people / 255.
A common task in face recognition is to ask if a previously unseen face belongs to a
known person from a database. This has applications in photo collection, social
media and security. One way to solve this problem would be to build a classifier
where each person is a separate class. However, there are usually many different peo‐
ple in face databases, and very few images of the same person (i.e. very few training
Dimensionality Reduction, Feature Extraction and Manifold Learning | 145
www.it-ebooks.info

examples per class). That makes it hard to train most classifiers. Additionally, you
often want to easily add new people, without retraining a large model.
A simple solution is to use a one-nearest-neighbor classifier which looks for the most
similar face image to the face you are classifying. A one-nearest-neighbor could in
principle work with only a single training example per class. Let’s see how well KNeigh
borsClassifier does here:
from sklearn.neighbors import KNeighborsClassifier
# split the data in training and test set
X_train, X_test, y_train, y_test = train_test_split(
X_people, y_people, stratify=y_people, random_state=0)
# build a KNeighborsClassifier with using one neighbor:
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)
knn.score(X_test, y_test)
0.26615969581749049
We obtain an accuracy of 26.6%, which is not actually that bad for a 62 class classifi‐
cation problem (random guessing would give you around 1/62 = 1.5% accuracy), but
is also not great. We only correctly identify a person a every fourth time.
This is where PCA comes in. Computing distances in the original pixel space is quite
a bad way to measure similarity between faces [add a sentence saying why]. We hope
that using distances along principal components can improve our accuracy. Here we
enable the whitening option of PCA, which rescales the principal components to have
the same scale. This is the same as using StandardScaler after the transformation.
Reusing the data from Figure pca_illustration again, whitening corresponds to not
only rotating the data, but also rescaling it so that the center panel is a circle instead
of an ellipse:
mglearn.plots.plot_pca_whitening()
146 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info
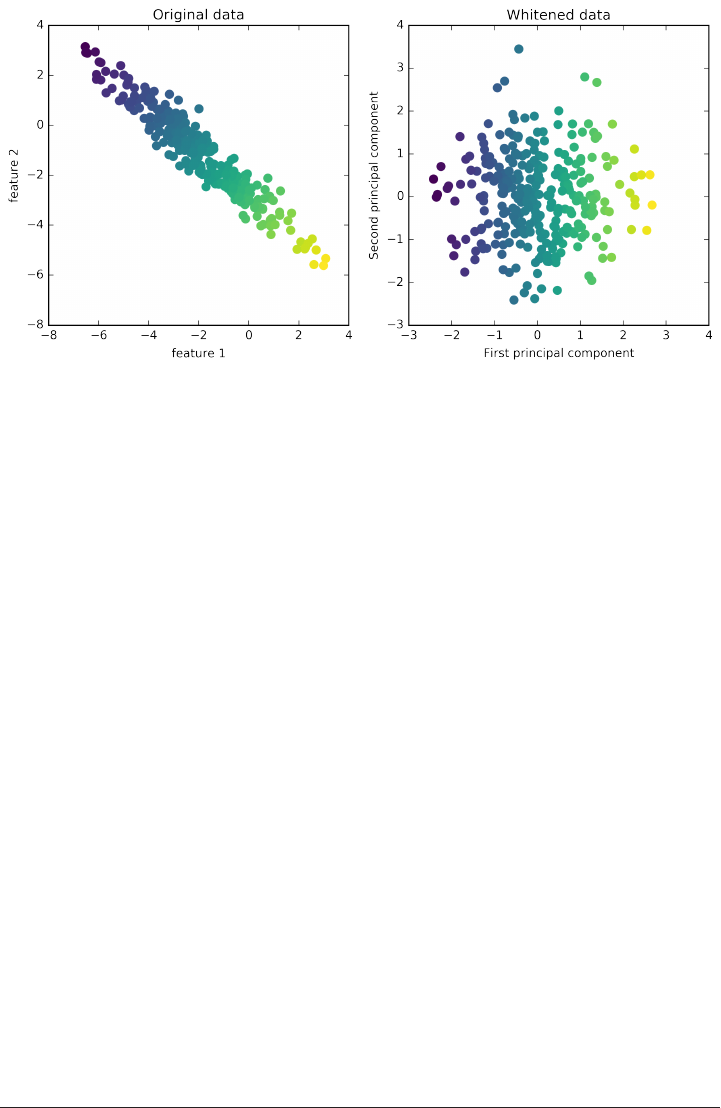
We fit the PCA object to the training data and extract the first 100 principal compo‐
nents. Then we transform the training and test data:
pca = PCA(n_components=100, whiten=True).fit(X_train)
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
print(X_train_pca.shape)
(1537, 100)
The new data has 100 features, the first 100 principal components. Now, we can use
the new representation to classify our images using one-nearest-neighbors:
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train_pca, y_train)
knn.score(X_test_pca, y_test)
0.36882129277566539
Our accuracy improved quite significantly, from 26.6% to 36.8%, confirming our
intuition that the principal components might provide a better representation of the
data.
For image data, we can also easily visualize the principal components that are found.
Remember that components correspond to directions in the input space. The input
space here is 50x37 gray-scale images, and so directions within this space are also
50x37 gray-scale images. Let’s look at the first couple of principal components:
pca.components_.shape
(100, 5655)
fix, axes = plt.subplots(3, 5, figsize=(15, 12),
subplot_kw={'xticks': (), 'yticks': ()})
Dimensionality Reduction, Feature Extraction and Manifold Learning | 147
www.it-ebooks.info
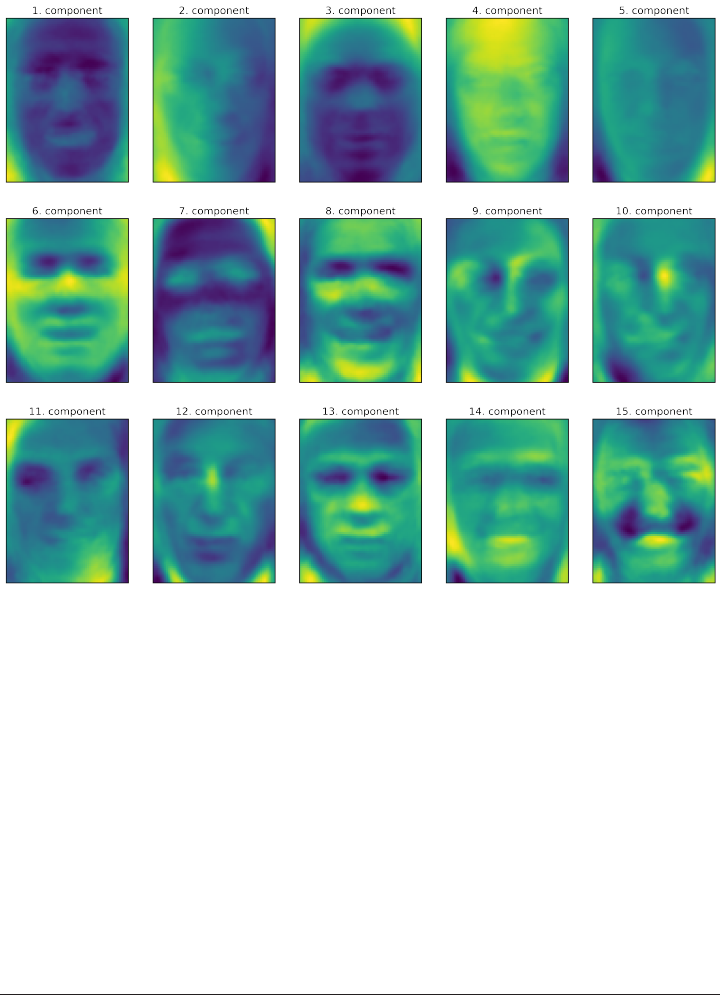
fig.suptitle("pca_face_components")
for i, (component, ax) in enumerate(zip(pca.components_, axes.ravel())):
ax.imshow(component.reshape(image_shape),
cmap='viridis')
ax.set_title("%d. component" % (i + 1))
While we certainly can not understand all aspects of these components, we can guess
which aspects of the face images some of the components are capturing. The first
component seems to mostly encode the contrast between the face and the back‐
ground, the second component encodes differences in lighting between the right and
the left half of the face, and so on. While this representation is slightly more semantic
than the raw pixel values, it is still quite far from how a human might perceive a face.
As the PCA is based on pixels, the alignment of the face (the position of eyes, chin
and nose), as well as the lighting, both have a strong influence on how similar to
images are in their pixel representation. Alignment and lighting are probably not
what a human would perceive first. When asking a person to rate similarity of faces,
they are more likely to use attributes like age, gender, facial expression and hair style,
which are attributes that are hard to infer from the pixel intensities.
148 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info
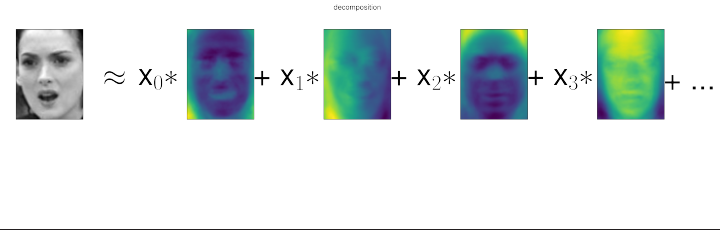
It’s important to keep in mind that algorithms often interpret data, in particular data
that humans are used to understand, like images, quite differently from how a human
would.
Let’s come back to the specific case of PCA, though.
Above we introduced the PCA transformation as rotating the data, and then drop‐
ping the components with low variance.
Another useful interpretation is that we try to find some numbers (the new feature
values after the PCA rotation), so that we can express the test points as a weighted
sum of the principal components:
from matplotlib.offsetbox import OffsetImage, AnnotationBbox
image_shape = people.images[0].shape
plt.figure(figsize=(20, 3))
ax = plt.gca()
imagebox = OffsetImage(people.images[0], zoom=7, cmap="gray")
ab = AnnotationBbox(imagebox, (.05, 0.4), pad=0.0, xycoords='data')
ax.add_artist(ab)
for i in range(4):
imagebox = OffsetImage(pca.components_[i].reshape(image_shape), zoom=7, cmap="viridis")
ab = AnnotationBbox(imagebox, (.3 + .2 * i, 0.4),
pad=0.0,
xycoords='data'
)
ax.add_artist(ab)
if i == 0:
plt.text(.18, .25, 'x_%d *' % i, fontdict={'fontsize': 50})
else:
plt.text(.15 + .2 * i, .25, '+ x_%d *' % i, fontdict={'fontsize': 50})
plt.text(.95, .25, '+ ...', fontdict={'fontsize': 50})
plt.rc('text', usetex=True)
plt.text(.13, .3, r'\approx', fontdict={'fontsize': 50})
plt.axis("off")
plt.title("decomposition")
plt.rc('text', usetex=False) # THIS SHOULD NOT SHOW IN THE BOOK! it's needed for the figure above
Dimensionality Reduction, Feature Extraction and Manifold Learning | 149
www.it-ebooks.info

Here, $x_0$, $x_1$ and so on are the coefficients of the principal components for this
data point; in other words, they are the representation [of what? of the image? this is
not clear] in the rotated space.
Another way we can try to understand what a PCA model is doing is by looking at
the reconstructions of the original data using only some components. In Figure
pca_illustration, after dropping the second component and arriving at the third
panel , we undid the rotation and added the mean back to obtain new points in the
original space with the second component removed, as shown in the last panel.
We can do a similar transformation for the faces by reducing the data to only some
principal components and then rotating back into the original space. This return to
the original feature space can be done using the inverse_transform method. Here
we visualize the reconstruction of some faces using 10, 50, 100, 500 or 2000 compo‐
nents:
mglearn.plots.plot_pca_faces(X_train, X_test, image_shape)
plt.suptitle("pca_reconstructions");
150 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

/home/andy/checkout/scikit-learn/sklearn/externals/joblib/logger.py:77: DeprecationWarning: The 'warn' function is deprecated, use 'warning' instead
logging.warn("[%s]: %s" % (self, msg))
________________________________________________________________________________
[Memory] Calling mglearn.plot_pca.pca_faces...
pca_faces(array([[ 0.036601, ..., 0.742484],
...,
[ 0.105882, ..., 0.393464]], dtype=float32),
array([[ 0.162091, ..., 0.677124],
...,
[ 0.109804, ..., 0.07451 ]], dtype=float32))
_______________________________________________________pca_faces - 12.9s, 0.2min
You can see that with using only the first 10 principal components, only the essence
of the picture, like the face orientation and lighting, is captured. Using more and
more principal components, more and more details in the image are preserved. This
corresponds to extending the sum in Figure decomposition to include more and
more terms. Using as many components as there are pixels would mean that we
would not discard any information after the rotation, and we would reconstruct the
image perfectly.
We can also try to use PCA to visualize all the faces in the dataset in a scatter plot
using the first two principal components, with classes given by who is shown in the
image, similarly to what we did for the cancer dataset:
plt.scatter(X_train_pca[:, 0], X_train_pca[:, 1], c=y_train, cmap='Paired', s=60)
Dimensionality Reduction, Feature Extraction and Manifold Learning | 151
www.it-ebooks.info
As you can see, when using just the first two principal components, the whole data is
just a big blob, with no separation of classes visible. This is not very surprising, given
that even with 10 components, as shown in Figure faces_pca_reconstruction above,
PCA only captures very rough characteristics of the faces.
Non-Negative Matrix Factorization (NMF)
Non-negative matrix factorization is another unsupervised learning algorithm that
aims to extract useful features. It works similarly to PCA and can also be used for
dimensionality reduction. As in PCA we are trying to write each data point as a
weighted sum of some components as illustrated in Figure decomposition. In PCA,
we wanted components that are orthogonal, and that explain as much variance of the
data as possible. In NMF, we want the components and the coefficients to be non-
negative; that is, we want both the components and the coefficients to be greater or
equal then zero.
Consequently, this method can only applied to data where each feature is non-
negative, as a non-negative sum of non-negative components can not become nega‐
tive. The process of decomposing data into a non-negative weighted sum is
particularly helpful for data that is created as the addition of several independent
sources, such as an audio track of multiple speakers, or music with many instruments.
In these situations, NMF can identify the original components that make up the com‐
bined data. Overall, NMF leads to more interpretable components than PCA, as neg‐
152 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info
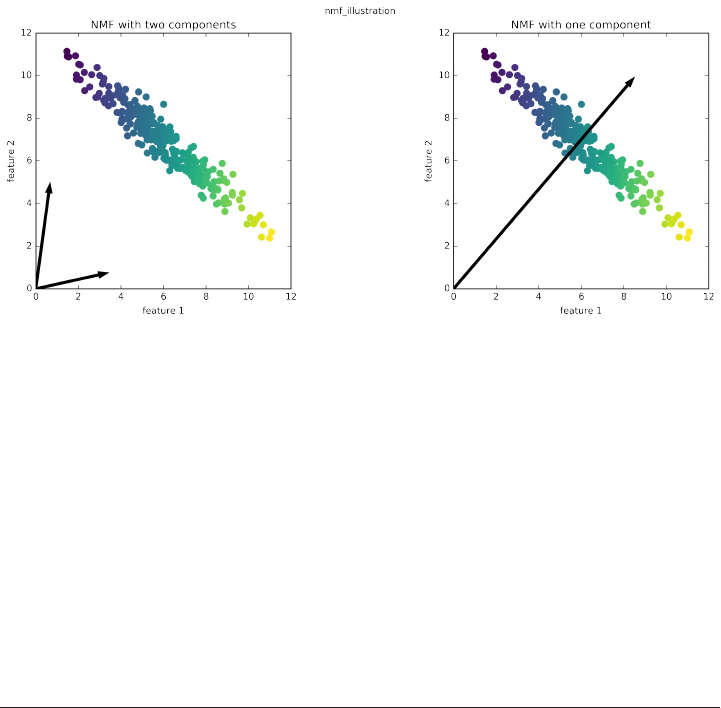
ative components and coefficients can lead to hard-interpret cancellation effects. The
eigenfaces in Figure pca_face_components for example contain both positive and
negative parts, and as we mentioned in the description of PCA, the sign is actually
arbitrary.
Before we apply NMF to the face dataset, let’s briefly revisit the synthetic data.
Applying NMF to synthetic data
In contrast to PCA, we need to ensure that our data is positive for NMF to be able to
operate on the data.
This means where the data lies relative to the origin (0, 0) actually matters for NMF.
Therefore, you can think of the non-negative components that are extracted as direc‐
tions from (0, 0) towards the data.
mglearn.plots.plot_nmf_illustration()
plt.suptitle("nmf_illustration")
The figure above shows the results of NMF on the two-dimensional toy data. For
NMF with two components, as shown on the left, it is clear that all points in the data
can be written as a positive combination of the two components. If there are enough
components to perfectly reconstruct the data (as many components are there are fea‐
tures), the algorithm will choose directions that point towards the extremes of the
data.
If we only use a single component, NMF creates a component that points towards the
mean, as pointing there best explains the data. You see that in contrast to PCA, reduc‐
ing the number of components not only removes directions, it actually changes all
directions! Components in NMF are also not ordered in any specific way, so there is
no “first non-negative component”: all components play an equal part.
Dimensionality Reduction, Feature Extraction and Manifold Learning | 153
www.it-ebooks.info

NMF uses a random initialization, which might lead to different results depending on
the random seed. In relatively easy cases as the synthetic data with two components,
where all the data can be explained perfectly, the randomness has little effect (though
it might change the order or scale of the components). In more complex situations,
there might be more drastic changes.
Applying NMF to face images
Now, let’s apply NMF to the “labeled faces in the wild” dataset we used above.
The main parameter of NMF is how many components we want to extract. Usually
this is lower than the number of input features (otherwise the data could be explained
by making each pixel a separate component).
First, let’s inspect how the number of components impacts how well the data can be
reconstructed using NMF:
mglearn.plots.plot_nmf_faces(X_train, X_test, image_shape)
________________________________________________________________________________
[Memory] Calling mglearn.plot_nmf.nmf_faces...
154 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

nmf_faces(array([[ 0.036601, ..., 0.742484],
...,
[ 0.105882, ..., 0.393464]], dtype=float32),
array([[ 0.162091, ..., 0.677124],
...,
[ 0.109804, ..., 0.07451 ]], dtype=float32))
_____________________________________________________nmf_faces - 763.1s, 12.7min
The quality of the back-transformed data is similar to PCA, but slightly worse. This is
expected, as PCA finds the optimum directions in terms of reconstruction. NMF is
usually not used for the ability to reconstruct or encode data, but rather for finding
interesting patterns within the data.
As a first look into the data, let’s try extracting only a few components, say 15, on the
faced data:
from sklearn.decomposition import NMF
nmf = NMF(n_components=15, random_state=0)
nmf.fit(X_train)
X_train_nmf = nmf.transform(X_train)
X_test_nmf = nmf.transform(X_test)
fix, axes = plt.subplots(3, 5, figsize=(15, 12),
subplot_kw={'xticks': (), 'yticks': ()})
for i, (component, ax) in enumerate(zip(nmf.components_, axes.ravel())):
ax.imshow(component.reshape(image_shape))
ax.set_title("%d. component" % i)
Dimensionality Reduction, Feature Extraction and Manifold Learning | 155
www.it-ebooks.info

These components are all positive, and so resemble prototypes of faces much more so
than the components shown for PCA in Figure Eigenfaces. For example, one can
clearly see that component 3 shows a face rotated somewhat to the right, while com‐
ponent 7 shows a face somewhat rotated to the left. Let’s look at the images for which
these components are particularly strong:
compn = 3
# sort by 3rd component, plot first 10 images
inds = np.argsort(X_train_nmf[:, compn])[::-1]
fig, axes = plt.subplots(2, 5, figsize=(15, 8),
subplot_kw={'xticks': (), 'yticks': ()})
fig.suptitle("Large component 3")
for i, (ind, ax) in enumerate(zip(inds, axes.ravel())):
ax.imshow(X_train[ind].reshape(image_shape))
compn = 7
# sort by 7th component, plot first 10 images
inds = np.argsort(X_train_nmf[:, compn])[::-1]
fig.suptitle("Large component 7")
fig, axes = plt.subplots(2, 5, figsize=(15, 8),
subplot_kw={'xticks': (), 'yticks': ()})
156 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

for i, (ind, ax) in enumerate(zip(inds, axes.ravel())):
ax.imshow(X_train[ind].reshape(image_shape))
As expected, faces that have a high coefficient for component 3 are faces looking to
the right, while faces with a high component 7 are looking to the left. As mentioned
above, extracting patterns like these works best for data with additive structure,
including audio, gene expression data, and text data. We will see applications of NMF
to text data in Chapter 7 (Text Data).
There are many other algorithms that can be used to decompose each data point into
a weighted sum of a fixed set of components, as PCA and NMF do. Discussing all of
them is beyond the scope of this book, and describing the constraints made on the
components and coefficients often involves probability theory. If you are interested in
these kinds of pattern extraction, we recommend to study the user guide of Inde‐
pendent Component Analysis (ICA), Factor Analysis (FA) and Sparse Coding (dictio‐
nary learning), which are widely used decomposition methods.
Manifold learning with t-SNE
While PCA is often a good first approach for transforming your data so that you
might be able to visualize it using a scatter plot, the nature of the method (applying a
rotation and then dropping directions) limits its usefulness, as we saw with the scatter
plot of the labeled faces in the wild. There is a class of algorithms for visualization
called manifold learning algorithms which allows for much more complex mappings,
and often provides better visualizations. A particular useful one is the t-SNE algo‐
rithm.
Manifold learning algorithms are mainly aimed at visualization, and so are rarely
used to to generate more than two new features. Some of them, including t-SNE,
Dimensionality Reduction, Feature Extraction and Manifold Learning | 157
www.it-ebooks.info
compute a new representation of the training data, but don’t allow transformations of
new data. This means these algorithms can not be applied to a test set: rather, they
can only transform the data they were trained for. Manifold learning can be useful for
exploratory data analysis, but is rarely used if the final goal is supervised learning.
The idea behind t-SNE is to find a two-dimensional representation of the data that
preserve the distances between points as best as possible. t-SNE tarts with a random
two-dimensional representation for each data point, and then tries to make points
closer that are close in the original feature space, and points far apart that are far apart
in the original feature space. t-SNE puts more emphasis on points that are close by,
rather than preserving distances between far apart points. In other words, it tries to
preserve the information of which points are neighbors to each other.
We will apply the t-SNE manifold learning algorithm on a dataset of handwritten dig‐
its that is included in scikit-learn [Footnote: not to be confused with the much larger
MNIST dataset].
Each data point in this dataset is a 8x8 grey-scale image of a handwritten digit
between 0 and 1. Here is an example image for each class:
from sklearn.datasets import load_digits
digits = load_digits()
fig, axes = plt.subplots(2, 5, figsize=(10, 5),
subplot_kw={'xticks':(), 'yticks': ()})
for ax, img in zip(axes.ravel(), digits.images):
ax.imshow(img)
Let’s use PCA to visualize the data reduced to two dimensions. We plot the first two
principal components, and color each dot by its class:
# build a PCA model
pca = PCA(n_components=2)
158 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info
pca.fit(digits.data)
# transform the digits data onto the first two principal components
digits_pca = pca.transform(digits.data)
colors = ["#476A2A", "#7851B8", "#BD3430", "#4A2D4E", "#875525",
"#A83683", "#4E655E", "#853541", "#3A3120","#535D8E"]
plt.figure(figsize=(10, 10))
plt.xlim(digits_pca[:, 0].min(), digits_pca[:, 0].max())
plt.ylim(digits_pca[:, 1].min(), digits_pca[:, 1].max())
for i in range(len(digits.data)):
# actually plot the digits as text instead of using scatter
plt.text(digits_pca[i, 0], digits_pca[i, 1], str(digits.target[i]),
color = colors[digits.target[i]],
fontdict={'weight': 'bold', 'size': 9})
plt.xlabel("first principal component")
plt.ylabel("second principal component")
Dimensionality Reduction, Feature Extraction and Manifold Learning | 159
www.it-ebooks.info

Here, we actually used the true digit classes as glyphs, to show which class is where.
The digits zero, six and four are relatively well-separated using the first two principal
components, though they still overlap. Most of the other digits overlap significantly.
Let’s apply t-SNE to the same dataset, and compare results. As t-SNE does not sup‐
port transforming new data, the TSNE class has no transform method. Instead, we can
call the fit_transform method, which will build the model, and immediately return
the transformed data:
from sklearn.manifold import TSNE
tsne = TSNE(random_state=42)
# use fit_transform instead of fit, as TSNE has no transform method:
digits_tsne = tsne.fit_transform(digits.data)
plt.figure(figsize=(10, 10))
plt.xlim(digits_tsne[:, 0].min(), digits_tsne[:, 0].max() + 1)
plt.ylim(digits_tsne[:, 1].min(), digits_tsne[:, 1].max() + 1)
for i in range(len(digits.data)):
# actually plot the digits as text instead of using scatter
plt.text(digits_tsne[i, 0], digits_tsne[i, 1], str(digits.target[i]),
color = colors[digits.target[i]],
fontdict={'weight': 'bold', 'size': 9})
160 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info
The result of t-SNE is quite remarkable. All the classes are quite clearly separated.
The ones and nines are somewhat split up, but most of the classes form a single dense
group. Keep in mind that this method has no knowledge of the class labels: it is com‐
pletely unsupervised. Still, it can find a representation of the data in two dimensions
that clearly separates the classes, based solely on how close points are in the original
space.
t-SNE has some tuning parameters, though it often works well with the default set‐
tings. You can try playing with perplexity and early_exaggeration, though the
effects are usually minor.
Dimensionality Reduction, Feature Extraction and Manifold Learning | 161
www.it-ebooks.info

Clustering
As we described above, clustering is the task of partitioning the dataset into groups,
called clusters. The goal is to split up the data in such a way that points within a single
cluster are very similar and points in different clusters are different. Similarly to clas‐
sification algorithms, clustering algorithms assign (or predict) a number to each data
point, indicating which cluster a particular point belongs to.
k-Means clustering
k-Means clustering is one of the simplest and most commonly used clustering algo‐
rithms. It tries to find cluster centers that are representative of certain regions of the
data.
The algorithm alternates between two steps: assigning each data point to the closest
cluster center, and then setting each cluster center as the mean of the data points that
are assigned to it.
The algorithm is finished when the assignment of instances to clusters no longer
changes.
Figure kmeans_algorithm illustrates the algorithm on a synthetic dataset:
mglearn.plots.plot_kmeans_algorithm()
plt.suptitle("kmeans_algorithm");
We specified that we are looking for three clusters, so the algorithm was initialized by
declaring three data points as cluster centers (see “Initialization”). Then the iterative
algorithm starts: Each data point is assigned to the cluster center it is closest to (see
162 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info
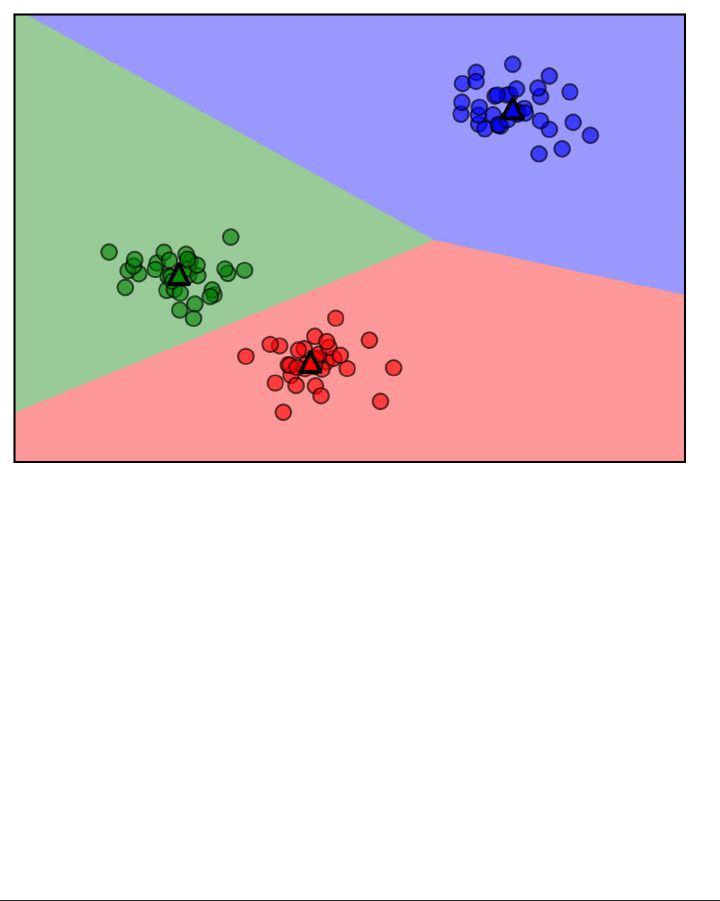
“Assign Points (1)”). Next, the cluster centers are updated to be the mean of the
assigned points (see “Recompute Centers (1)”). Then the process is repeated. After
the second iteration, the assignment of points to cluster centers remained unchanged,
so the algorithm stops.
Given new data points, k-Means will assign them to the closest cluster center. Here
are the boundaries of the cluster centers that were learned in the diagram above:
mglearn.plots.plot_kmeans_boundaries()
Applying k-Means with scikit-learn is quite straight-forward. Here we apply it to the
synthetic data that we used for the plots above. We instantiate the KMeans class, and
set the number of clusters we are looking for [footnote: If you don’t provide n_clus
ters it is set to eight by default. There is no particular reason why you should use
eight.]. Then we call the fit method with the data:
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# generate synthetic two-dimensional data
X, y = make_blobs(random_state=1)
# build the clustering model:
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
Clustering | 163
www.it-ebooks.info

KMeans(copy_x=True, init='k-means++', max_iter=300, n_clusters=3, n_init=10,
n_jobs=1, precompute_distances='auto', random_state=None, tol=0.0001,
verbose=0)
During the algorithm, each training data point in X is assigned a cluster label. You can
find these labels in the kmeans.labels_ attribute:
print(kmeans.labels_)
[1 9 3 6 9 4 1 2 1 2 7 8 9 2 0 1 5 8 5 0 4 2 5 2 7 3 9 4 3 5 1 7 2 3 1 4 8
1 0 3 8 7 5 3 9 7 1 0 3 2 0 8 4 6 2 1 5 2 5 7 8 6 9 1 2 6 7 9 7 6 8 6 8 3
2 6 3 1 5 8 4 7 8 4 3 7 1 7 8 4 5 1 4 0 4 9 9 8 6 3 2 4 7 1 6 3 6 7 9 5 0
7 7 6 1 9 5 4 8 1 1 0 3 7 3 0 1 3 2 4 1 0 6 8 2 9 2 6 4 1 3 3 5 7 7 1 3 2
5 3 8 9 1 5 8 7 2 8 5 5 3 2 5 9 8 9 5 8 9 2 5 6 6 0 3 2 4 0 0 5 9 6 4 9 4
5 7 2 6 0 6 5 1 1 3 0 4 3 5 9]
As we asked for three clusters, the clusters are numbered 0 to 2.
You can also assign cluster labels to new points, using the predict method. Each new
point is assigned to the closest cluster center when predicting, but the existing model
is not changed. Running predict on the training set returns the same as labels_:
print(kmeans.predict(X))
[1 2 2 2 0 0 0 2 1 1 2 2 0 1 0 0 0 1 2 2 0 2 0 1 2 0 0 1 1 0 1 1 0 1 2 0 2
2 2 0 0 2 1 2 2 0 1 1 1 1 2 0 0 0 1 0 2 2 1 1 2 0 0 2 2 0 1 0 1 2 2 2 0 1
1 2 0 0 1 2 1 2 2 0 1 1 1 1 2 1 0 1 1 2 2 0 0 1 0 1]
You can see thgat clustering is somewhat similar to classification, in that each item
gets a label. However, there is no ground truth, and consequently the labels them‐
selves have no a priori meaning. Let’s go back to the example of clustering face images
that we discusse before. It might be that the cluster 3 found by the algorithm contains
only faces of your friend Bela. You can only know that after you looked at the pic‐
tures, though, and the number 3 is arbitrary. The only information the algorithm
gives you is that all faces labeled as 3 are similar.
For the clustering we just computed on the two dimensional toy dataset, that means
that
Here is a plot of this data again. The cluster centers are stored in the cluster_cen
ters_ attribute, and we plot them as triangles:
164 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info
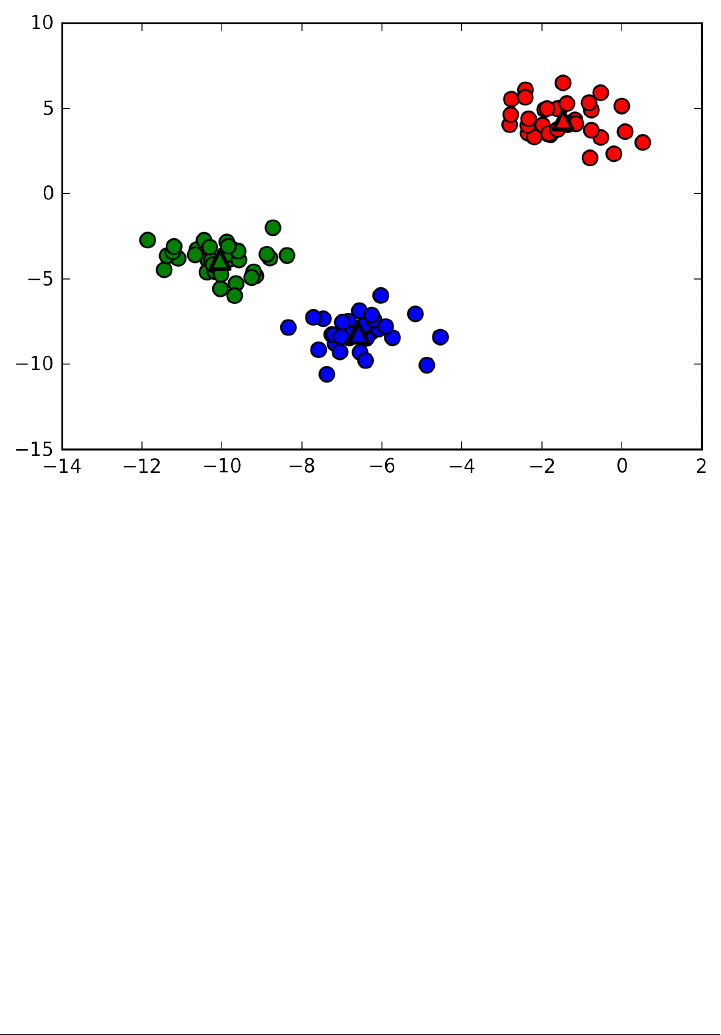
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_, cmap=mglearn.cm3, s=60)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
marker='^', s=100, linewidth=2, c=[0, 1, 2], cmap=mglearn.cm3)
We can also use more or less cluster centers:
fig, axes = plt.subplots(1, 2)
# using two cluster centers:
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)
assignments = kmeans.labels_
axes[0].scatter(X[:, 0], X[:, 1], c=assignments, cmap=mglearn.cm2, s=60)
# using five cluster centers:
kmeans = KMeans(n_clusters=5)
kmeans.fit(X)
assignments = kmeans.labels_
axes[1].scatter(X[:, 0], X[:, 1], c=assignments, cmap='jet', s=60);
Clustering | 165
www.it-ebooks.info
Failure cases of k-Means
Even if you know the “right” number of clusters for a given dataset, k-Means might
not always be able to recover them. Each cluster is defined solely by its center, which
means that each cluster is a convex shape. As a result of this is that k-Means can only
capture relatively simple shapes.
k-Means also assumes that all clusters have the same “diameter” in some sense; it
always draws the boundary between clusters to be exactly in the middle between the
cluster centers. That can sometimes lead to surprising results, as shown below:
X, y = make_blobs(random_state=0)
plt.scatter(X[:, 0], X[:, 1]);
166 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info
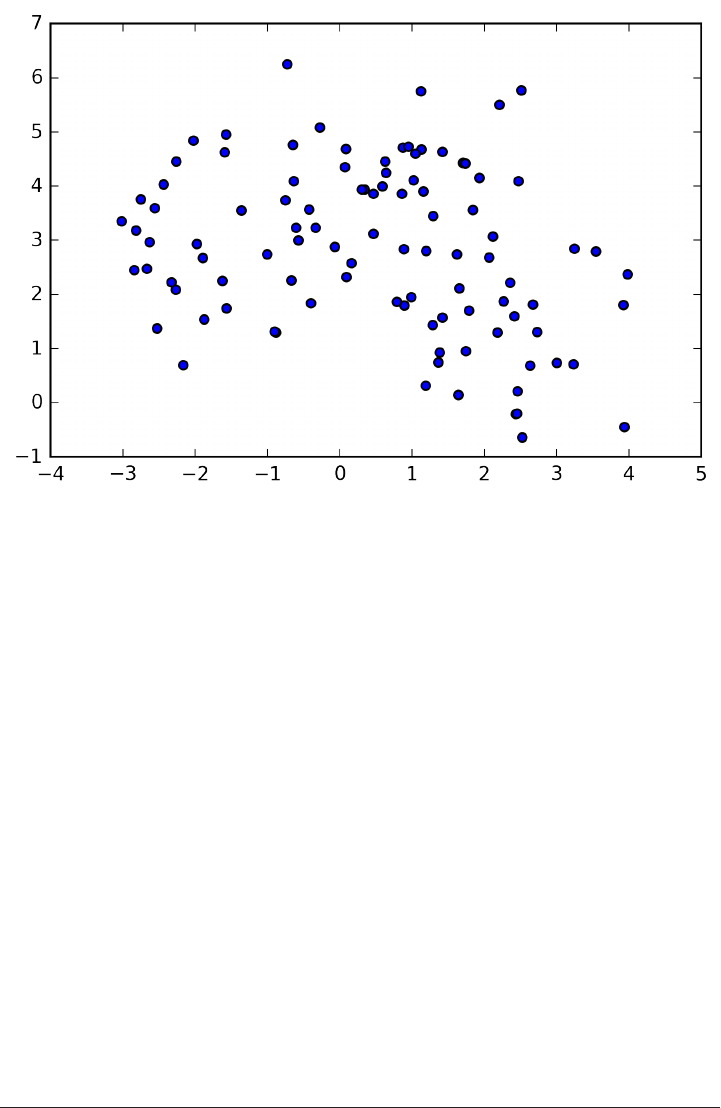
k-Means also assumes that all directions are equally important for each cluster. The
plot below shows a two-dimensional dataset where there are three clearly separated
parts in the data. However, these groups are stretched towards the diagonal. As k-
Means only considers the distance to the nearest cluster center, it can’t handle this
kind of data.
# generate some random cluster data
X, y = make_blobs(random_state=170, n_samples=600)
rng = np.random.RandomState(74)
# transform the data to be streched
transformation = rng.normal(size=(2, 2))
X = np.dot(X, transformation)
# cluster the data into three clusters
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
y_pred = kmeans.predict(X)
# plot the cluster assignments and cluster centers
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap=mglearn.cm3)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
marker='^', c=['b', 'r', 'g'], s=60, linewidth=2);
Clustering | 167
www.it-ebooks.info

k-Means also performs poorly if the clusters have more complex shapes, like the
two_moons data we encountered in Chapter 2:
# generate synthetic two_moons data (with less noise this time)
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# cluster the data into two clusters
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)
y_pred = kmeans.predict(X)
# plot the cluster assignments and cluster centers
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap=mglearn.cm3, s=60)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
marker='^', c=['b', 'g'], s=60, linewidth=2);
168 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info
Here, we would hope that the clustering algorithm can discover the two half-moon
shapes. However, this is not possible using the k-Means algorithm.
Vector Quantization - Or Seeing k-Means as Decomposition
Even though k-Means is a clustering algorithm, there are interesting parallels
between k-Means and decomposition methods like PCA and NMF that we discussed
above. You might remember that PCA tries to find directions of maximum variance
in the data, while NMF tries to find additive components, which often correspond to
“extremes” or “parts” of the data (see Figure nmf_illustration). Both methods tried to
express data points as a sum over some components.
k-Means on the other hand tries to represent each data point using a cluster center.
You can think of that as each point being represented using only a single component,
which is given by the cluster center. This view of k-Means as a decomposition
method, where each point is represented using a single component, is called vector
quantization.
Here is a side-by-side comparison of PCA, NMF and k-Means, showing the compo‐
nents extracted, as well as reconstructions of faces from the test set using 100 compo‐
nents. For k-Means, the reconstruction is the closest cluster center found on the
training set:
X_train, X_test, y_train, y_test = train_test_split(X_people, y_people, stratify=y_people, random_state=0)
nmf = NMF(n_components=100)
Clustering | 169
www.it-ebooks.info

nmf.fit(X_train)
pca = PCA(n_components=100)
pca.fit(X_train)
kmeans = KMeans(n_clusters=100)
kmeans.fit(X_train)
X_reconstructed_pca = pca.inverse_transform(pca.transform(X_test))
X_reconstructed_kmeans = kmeans.cluster_centers_[kmeans.predict(X_test)]
X_reconstructed_nmf = np.dot(nmf.transform(X_test), nmf.components_)
fig, axes = plt.subplots(3, 5, figsize=(8, 8)) #, subplot_kw={'xticks': (), 'yticks': ()}
fig.suptitle("Extracted Components")
for ax, comp_kmeans, comp_pca, comp_nmf in zip(axes.T, kmeans.cluster_centers_, pca.components_, nmf.components_):
ax[0].imshow(comp_kmeans.reshape(image_shape))
ax[1].imshow(comp_pca.reshape(image_shape), cmap='viridis')
ax[2].imshow(comp_nmf.reshape(image_shape))
axes[0, 0].set_ylabel("kmeans")
axes[1, 0].set_ylabel("pca")
axes[2, 0].set_ylabel("nmf")
fig, axes = plt.subplots(4, 5, subplot_kw={'xticks': (), 'yticks': ()}, figsize=(8, 8))
fig.suptitle("Reconstructions")
for ax, orig, rec_kmeans, rec_pca, rec_nmf in zip(axes.T, X_test, X_reconstructed_kmeans,
X_reconstructed_pca, X_reconstructed_nmf):
ax[0].imshow(orig.reshape(image_shape))
ax[1].imshow(rec_kmeans.reshape(image_shape))
ax[2].imshow(rec_pca.reshape(image_shape))
ax[3].imshow(rec_nmf.reshape(image_shape))
axes[0, 0].set_ylabel("original")
axes[1, 0].set_ylabel("kmeans")
axes[2, 0].set_ylabel("pca")
axes[3, 0].set_ylabel("nmf")
170 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

An interesting aspect of vector quantization using k-Means is that we can use many
more clusters than input dimensions to encode our data. Let’s go back to the
two_moons data. Using PCA or NMF, there is nothing much we can do to this data, as
it lives in only two dimensions. Reducing it to one dimension with PCA or NMF
would completely destroy the structure of the data. But we can find a more expressive
representation using k-Means, by using more cluster centers:
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
kmeans = KMeans(n_clusters=10)
kmeans.fit(X)
y_pred = kmeans.predict(X)
Clustering | 171
www.it-ebooks.info
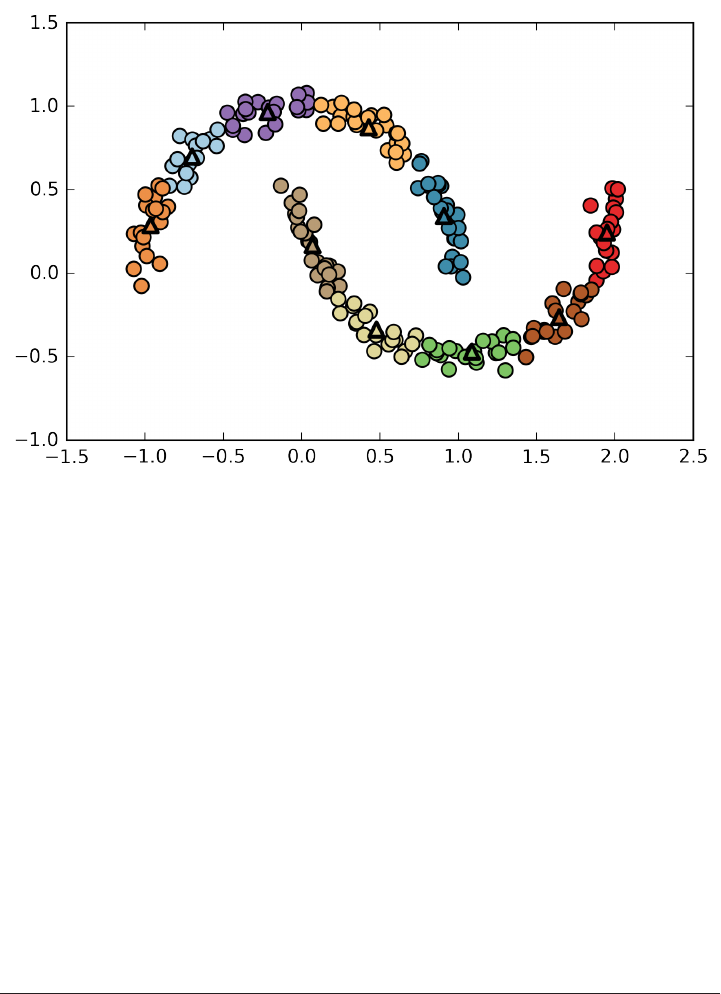
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=60, cmap='Paired')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
marker='^', c=range(kmeans.n_clusters), s=60, linewidth=2, cmap='Paired')
print(y_pred)
[1 9 3 6 9 4 1 2 1 2 7 8 9 2 0 1 5 8 5 0 4 2 5 2 7 3 9 4 3 5 1 7 2 3 1 4 8
1 0 3 8 7 5 3 9 7 1 0 3 2 0 8 4 6 2 1 5 2 5 7 8 6 9 1 2 6 7 9 7 6 8 6 8 3
2 6 3 1 5 8 4 7 8 4 3 7 1 7 8 4 5 1 4 0 4 9 9 8 6 3 2 4 7 1 6 3 6 7 9 5 0
7 7 6 1 9 5 4 8 1 1 0 3 7 3 0 1 3 2 4 1 0 6 8 2 9 2 6 4 1 3 3 5 7 7 1 3 2
5 3 8 9 1 5 8 7 2 8 5 5 3 2 5 9 8 9 5 8 9 2 5 6 6 0 3 2 4 0 0 5 9 6 4 9 4
5 7 2 6 0 6 5 1 1 3 0 4 3 5 9]
We used 10 cluster centers, which means each point is now assigned a number
between 0 and 9. We can see this as the data being represented using 10 components
(that is, we have ten new features), with all features being zero, apart from the one
that represents the cluster center the point is assigned to. Using this 10-dimensional
representation, it would now be possible to separate the two half-moon shapes using
a linear model, which would not have been possible using the original two features.
[really? can you show what that would look like, maybe?]
172 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

It is also possible to get an even more expressive representation of the data by using
the distances to each of the cluster centers as features. This can be done using the
transform method of kmeans:
distance_features = kmeans.transform(X)
print(distance_features.shape)
print(distance_features)
(200, 10)
[[ 1.53 0.2 1.03 ..., 1.12 0.92 1.14]
[ 2.56 1.01 0.54 ..., 2.28 1.14 0.12]
[ 0.8 0.93 1.33 ..., 0.72 0.79 1.75]
...,
[ 1.12 0.81 1.02 ..., 1.05 0.45 1.49]
[ 0.88 1.03 1.76 ..., 0.34 1.39 1.98]
[ 2.5 0.91 0.59 ..., 2.19 1.15 0.05]]
k-Means is a very popular algorithm for clustering, not only because it is relatively
easy to understand and implement, but also because it runs relatively quickly. k-
Means scales easily to large datasets, and scikit-learn even includes a more scalable
variant in the MiniBatchKMeans class, which can handle very large datasets.
One of the drawbacks of k-Means is that it relies on a random initialization, which
means the outcome of the algorithm depends on a random seed. By default, scikit-
learn runs the algorithm 10 times with 10 different random initializations, and
returns the best result [Footnote: best here meaning that the sum of variances of the
clusters is small].
Further downsides of k-Means are the relatively restrictive assumptions made on the
shape of clusters, and the requirement to specify the number of clusters you are look‐
ing for (which might not be known in a real-world application).
Next, we will look at two more clustering algorithms that improve upon these proper‐
ties in some ways.
Agglomerative Clustering
Agglomerative clustering refers to a collection of clustering algorithms that all build
upon the same principles: The algorithm starts by declaring each point its own clus‐
ter, and then merges the two most similar clusters until some stopping criterion is
satisfied.
Clustering | 173
www.it-ebooks.info
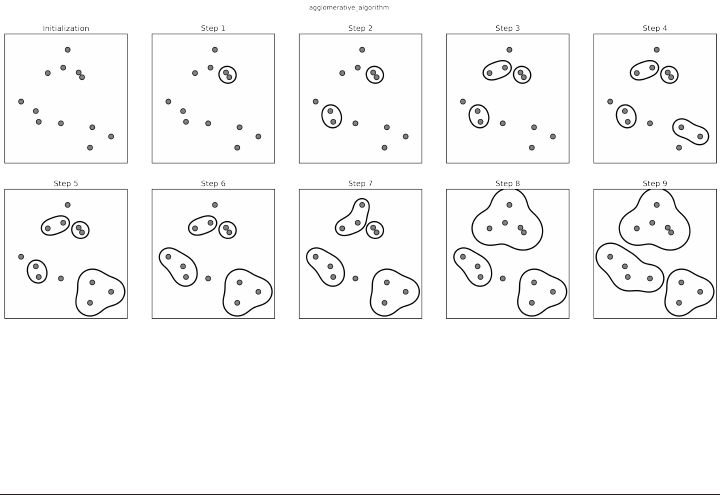
The stopping criterion implemented in scikit-learn is the number of clusters, so simi‐
lar cluster are merged until only the specified number of clusters is left.
There are several linkage criteria that specify how exactly “most similar cluster” is
measured. [this sentence looks a lot like the next sentence - combine into one]
The following three choices are implemented in scikit-learn:
•“ward”, which is the default choice. Ward picks the two clusters to merge such
that the variance within all clusters increases the least. This often leads to clusters
that are relatively equally sized.
•“average” linkage merges the two clusters that have the smallest average distance
between all their points.
•“complete” linkage (also known as maximum linkage) merges the two clusters
that have the smallest maximum distance between their points.
[you keep writing ‘the two clusters', but you did not specify that there would be two
clusters - rahter said that there are a ‘number of clusters']
Ward is generally a good default; all our examples below will use ward.
The plot below illustrates the progression of agglomerative clustering on a two-
dimensional dataset, looking for three clusters.
mglearn.plots.plot_agglomerative_algorithm()
plt.suptitle("agglomerative_algorithm");
In the beginning, each point is its own cluster. Then, in each step, the two clusters
that are closest are merged. In the first four steps, two single point clusters are picked
and these are joined into two-point clusters. In step four, one of the two-point clus‐
ters is extended to a third point, and so on. In step 9, there are only three clusters
174 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

remaining. As we specified that we are looking for three clusters, the algorithm then
stops.
Let’s have a look at how agglomerative clustering performs on the simple three-
cluster data we used above.
Because of the way the algorithm works, agglomerative clustering can not make pre‐
dictions for new data points. Therefore, agglomerative clustering has no predict
method. To build the model, and get the cluster memberships on the training set, use
the fit_predict method instead. [footnote: we could also use the labels_ attribute
as we did for k-Means]
from sklearn.cluster import AgglomerativeClustering
X, y = make_blobs(random_state=1)
agg = AgglomerativeClustering(n_clusters=3)
assignment = agg.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=assignment, cmap=mglearn.cm3, s=60)
As expected, the algorithm recovers the clustering perfectly. While the scikit-learn
implementation of agglomerative clustering requires you to specify a number of clus‐
ters you want the algorithm to find, agglomerative clustering methods provide some
help with choosing the right number, which we will now discuss next.
Clustering | 175
www.it-ebooks.info
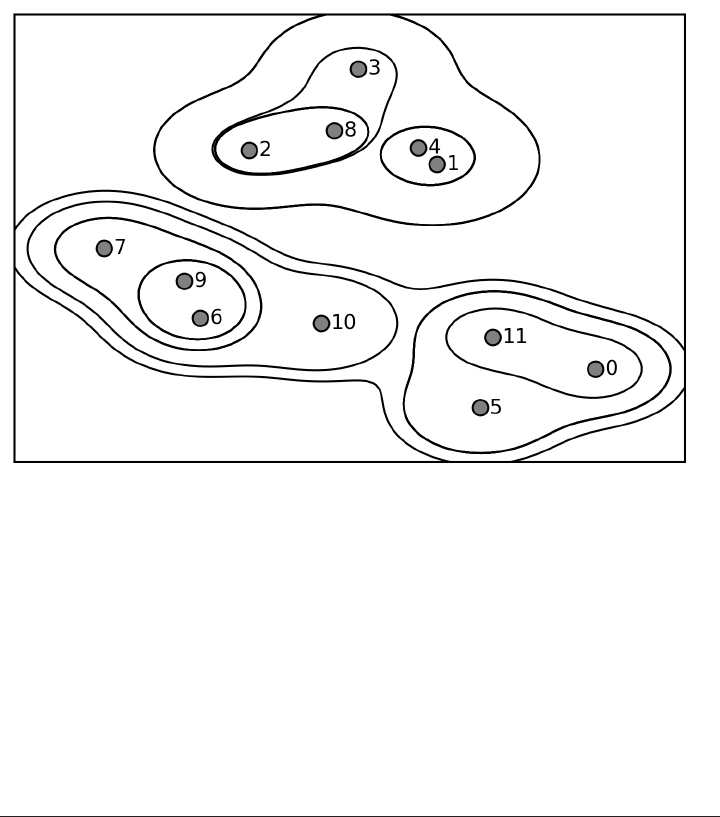
Hierarchical Clustering and Dendrograms
Agglomerative clustering produces what is known as a hierarchical clustering. The
clustering proceeds iteratively, and every point makes a journey from being a single
point cluster to belonging to some final cluster. Each intermediate step provides a
clustering of the data (with a different number of clusters). It is sometimes helpful to
look at all possible clusterings jointly.
The figure below shows an overlay of all possible clusterings shown in Figure agglom‐
erative_algorithm, providing some insight into how each cluster breaks up into
smaller clusters.
mglearn.plots.plot_agglomerative()
While this visualization provides a very detailed view of the hierarchical clustering, it
relies on the two-dimensional nature of the data, and can therefore not be used on
datasets that have more than two features. There is, however, another tool to visualize
hierarchical clustering, called a dendrogram (as shown in Figure dendrogram below).
Unfortunately, scikit-learn currently does not have the functionality to draw dendro‐
grams. However, you can generate them easily using scipy.
The scipy clustering algorithms have a slightly different interface from the scikit-learn
clustering algorithms.
scipy provides function that take data arrays X linkage array encoding cluster similari‐
ties.
176 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info
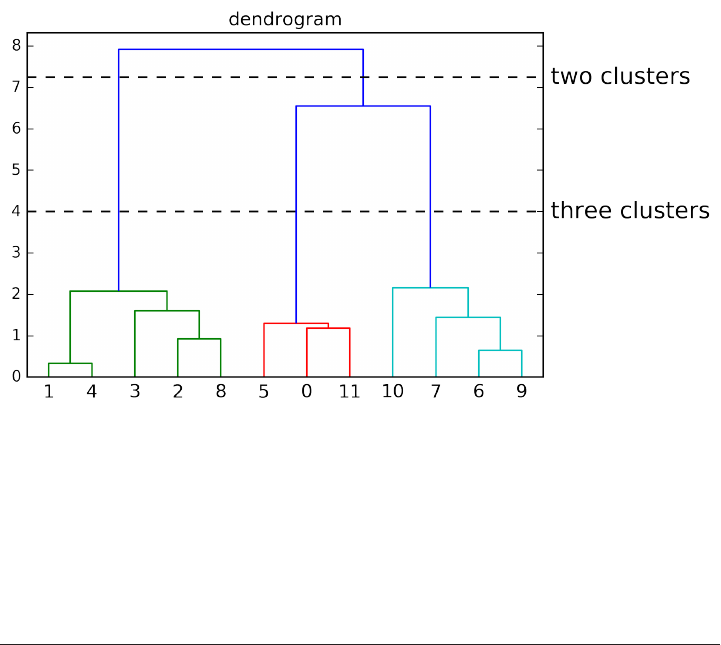
We can then feed this linkage array into the scipy dendrogram function to plot the
dendrogram:
# import the dendrogram function and the ward clustering function from scipy
from scipy.cluster.hierarchy import dendrogram, ward
X, y = make_blobs(random_state=0, n_samples=12)
# apply the ward clustering to the data array X
# The scipy ward function returns an array that specifies the distances bridged when performing agglomerative clustering
linkage_array = ward(X)
# now we plot the dendrogram for the linkage_array containing the distances between clusters
dendrogram(linkage_array);
# mark the cuts in the tree that signify two or three clusters
ax = plt.gca()
bounds = ax.get_xbound()
ax.plot(bounds, [7.25, 7.25], '--', c='k')
ax.plot(bounds, [4, 4], '--', c='k')
ax.text(bounds[1], 7.25, ' two clusters', verticalalignment='center', fontdict={'size': 15})
ax.text(bounds[1], 4, ' three clusters', verticalalignment='center', fontdict={'size': 15})
plt.title("dendrogram")
The dendrogram shows data points as points on the bottom (numbered from zero to
eleven). Then, a tree is plotted with these points (representing single-point clusters)
as the leafs, and a new node parent is added for each two clusters that are joined.
Reading from bottom to top, the data points 1 and 4 are joined first (as you could see
in Figure agglomerative_algorithm). Next, points 6 and 9 are joined into a cluster,
and so on. The top level, there are two branches, one consisting of point 11, 0, 5, 10,
Clustering | 177
www.it-ebooks.info

7, 6 and 9, and the other one consisting of points 1, 4, 3, 2 and 8. These correspond to
the two largest clusters in in the left hand side of the plot.
The y axis in the dendrogram not only specifies when in the agglomerative algorithm
two clusters get merged. The length of each branch also shows how far apart the
merged clusters are. The longest branches in this dendogram are the three lines that
are around the “10” mark on the y-axis. That these are the longest branches indicates
that going from three to two clusters meant merging some very far-apart points. We
see this again at the top of the chart, where merging the two remaining clusters into a
single cluster again bridges a large distance.
Unfortunately, agglomerative clustering still fails at separating complex shapes like
the two_moons dataset. The same is not true for the next algorithm we will look at,
DBSCAN.
DBSCAN
Another very useful clustering algorithm is DBSCAN (which stands for “Density-
based spatial clustering of applications with noise”). The main benefits of DBSCAN
are that a) it does not require the user to set the number of clusters a priori, b) it can
capture clusters of complex shapes, and c) it can identify point that are not part of any
cluster.
DBSCAN is somewhat slower than agglomerative clustering and k-Means, but still
scales to relatively large datasets.
The way DBSCAN works is by identifying points that are in “crowded” regions of the
feature space, where many data points are close together. These regions are referred
to as dense regions in feature space. The idea behind DBSCAN is that clusters form
dense regions of data, separated by regions that are relatively empty.
Points that are within a dense region are called core samples, and they are defined as
follows.
There are two parameters in DBSCAN, min_samples and eps. If there are at least
min_samples many data points within a distance of eps to a given data point, it’s
called a core sample. Core samples that are closer than the distance eps are put into
the same cluster by DBSCAN.
The algorithm works by picking a point to start with.
It then finds all points with distance eps or less. If there are less than min_samples
points within distance eps or less, this point is labeled as noise, meaning that this
point doesn’t belong to any cluster.
If there are more than min_samples points within a distance of eps, the point is
labeled a core sample and assigned a new cluster label. Then, all neighbors (withing
178 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

eps) of the point are visited. If they have not been assigned a cluster yet, they are
assigned the new cluster label we just created. If they are core samples, their neigh‐
bors are visited in turn, and so on.
The cluster grows, until there are no more core-samples within distance eps of the
cluster.
Then another point, which hasn’t yet been visited, is picked, and the same procedure
is repeated.
In the end, there are three kinds of points: core points, points that are within distance
eps of core points (called boundary points), and noise. When running the DBSCAN
algorithm on a particular dataset multiple times, the clustering of the core points is
always the same, and the same points will always be labeled as noise. However, a
boundary point might be neighbor to core samples of more than one cluster. There‐
fore, the cluster membership of boundary points depends on the order in which
points are visited. Usually there are only few boundary points, and this slight depend‐
ence on the order of points is not important.
Let’s apply DBSCAN on the synthetic data from above. As in agglomerative cluster‐
ing, DBSCAN does not allow predictions on new test data, so we will use the fit_pre
dict method to perform clustering and return the cluster labels in one step:
from sklearn.cluster import DBSCAN
X, y = make_blobs(random_state=0, n_samples=12)
dbscan = DBSCAN()
clusters = dbscan.fit_predict(X)
clusters
array([-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1])
As you can see, all data points were assigned the label -1, which stands for noise. This
is a consequence of the default parameter settings for eps and min_samples, which
are not attuned to small toy datasets.
Let’s investigate the effect of changing eps and min_samples.
fig, axes = plt.subplots(3, 4, figsize=(11, 8), subplot_kw={'xticks': (), 'yticks': ()})
# Plot clusters as red, green and blue, and outliers (-1) as white
colors = np.array(['r', 'g', 'b', 'w'])
# iterate over settings of min_samples and eps
for i, min_samples in enumerate([2, 3, 5]):
for j, eps in enumerate([1, 1.5, 2, 3]):
# instantiate DBSCAN with a particular setting
dbscan = DBSCAN(min_samples=min_samples, eps=eps)
# get cluster assignments
clusters = dbscan.fit_predict(X)
print("min_samples: %d eps: %f cluster: %s" % (min_samples, eps, clusters))
Clustering | 179
www.it-ebooks.info
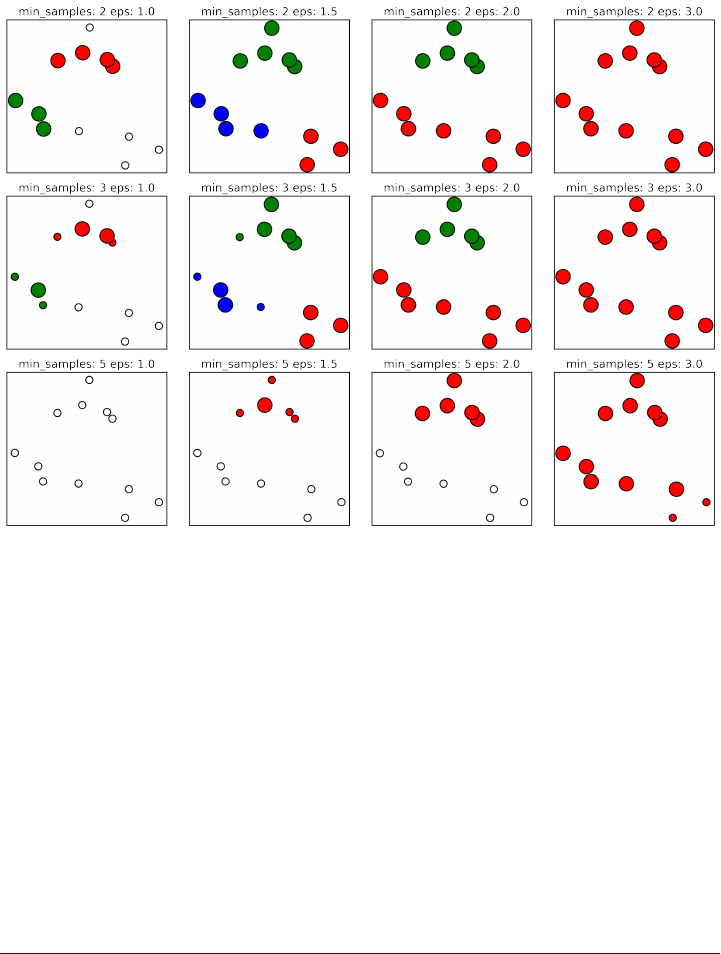
# vizualize core samples and clusters.
sizes = 60 * np.ones(X.shape[0])
# size is given by whether something is a core sample
sizes[dbscan.core_sample_indices_] *= 4
axes[i, j].scatter(X[:, 0], X[:, 1], c=colors[clusters], s=sizes)
axes[i, j].set_title("min_samples: %d eps: %.1f" % (min_samples, eps))
fig.tight_layout()
min_samples: 2 eps: 1.000000 cluster: [-1 0 0 -1 0 -1 1 1 0 1 -1 -1]
min_samples: 2 eps: 1.500000 cluster: [0 1 1 1 1 0 2 2 1 2 2 0]
min_samples: 2 eps: 2.000000 cluster: [0 1 1 1 1 0 0 0 1 0 0 0]
min_samples: 2 eps: 3.000000 cluster: [0 0 0 0 0 0 0 0 0 0 0 0]
min_samples: 3 eps: 1.000000 cluster: [-1 0 0 -1 0 -1 1 1 0 1 -1 -1]
min_samples: 3 eps: 1.500000 cluster: [0 1 1 1 1 0 2 2 1 2 2 0]
min_samples: 3 eps: 2.000000 cluster: [0 1 1 1 1 0 0 0 1 0 0 0]
min_samples: 3 eps: 3.000000 cluster: [0 0 0 0 0 0 0 0 0 0 0 0]
min_samples: 5 eps: 1.000000 cluster: [-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]
180 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

min_samples: 5 eps: 1.500000 cluster: [-1 0 0 0 0 -1 -1 -1 0 -1 -1 -1]
min_samples: 5 eps: 2.000000 cluster: [-1 0 0 0 0 -1 -1 -1 0 -1 -1 -1]
min_samples: 5 eps: 3.000000 cluster: [0 0 0 0 0 0 0 0 0 0 0 0]
In this plot, points that belong to clusters are colored, while the noise points are
shown in white.
Core samples are shown as large points, while border points are displayed as smaller
points.
Increasing eps (going from left to left to right in the figure) means that more points
will be included in a cluster. This makes clusters grow, but might also lead to multiple
clusters joining into one. Increasing min_samples (going from top to bottom in the
figure) means that fewer points will be core points, and more points will be labeled as
noise.
The parameter eps is somewhat more important, as it determines what it means for
points to be “close”.
Setting eps to be very small will mean that no points are core samples, and may lead
to all points being labeled as noise. Setting eps to be very large will result in all points
forming a single cluster.
The setting of min_samples mostly determines whether points in less dense regions
will be labeled as outliers, or as their own cluster. If you decrease min_samples, any‐
thing that would have been a cluster with less than min_samples many samples will
now be labeled as noise. The min_samples therefore determines the minimum cluster
size. You can see this very clearly in the plot above, when going from min_samples=3
to min_samples=5 with eps=1.5. With min_samples=3, there are three clusters: one of
four points, one of five points and one of three points. Using min_samples=5, the two
smaller clusters (with three or four points) are now labeled as noise, and only the
cluster with 5 samples remains.
While DBSCAN doesn’t require setting the number of clusters explicitly, setting eps
implicitly controls how many clusters will be found.
Finding a good setting for eps is sometimes easier after scaling the data using Stand
ardScaler or MinMaxScaler, as using these scaling techniques will ensure that all fea‐
tures have similar ranges.
Below is the result of DBSCAN running on the two_moons dataset. The algorithm
actually finds the two half-circles and separates them using the default settings.
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# Rescale the data to zero mean and unit variance
Clustering | 181
www.it-ebooks.info

scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)
dbscan = DBSCAN()
clusters = dbscan.fit_predict(X_scaled)
# plot the cluster assignments
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=clusters, cmap=mglearn.cm2, s=60)
As the algorithm produced the desired number of clusters (two), the parameter set‐
tings seem to work well.
If we decrease eps to 0.2 (from the default of 0.5), we will get 8 clusters, which are
clearly too many. Increasing eps to 0.7 results in a single cluster.
When using DBSCAN, you need to be careful about handling the returned cluster
assignments. The use of -1 to indicate noise might result in unexpected effects when
using the cluster labels to index another array. [an example here could be useful - sort
of know what you’re talking about, but sort of not]
Comparing and evaluating clustering algorithms
After talking about the algorithms behind k-Means, agglomerative clustering and
DBSCAN, we will now compare them on some real world datasets. One of the chal‐
lenges in applying clustering algorithms is that it is very hard to access how well a
clustering algorithm worked, and to compare outcomes between different algorithms.
182 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info
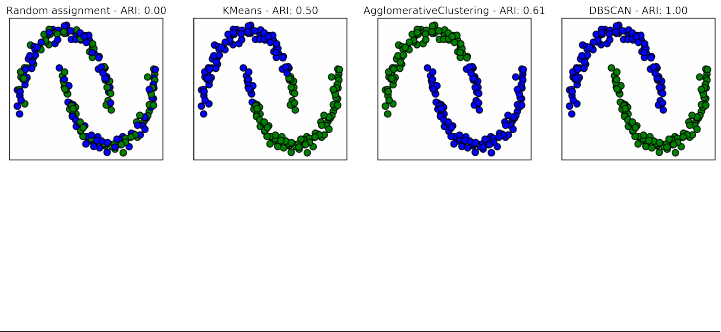
Evaluating clustering with ground truth
There are metrics that can be used to assess the outcome of a clustering algorithm
relative to a ground truth clustering, the most important ones being the adjusted rand
index (ARI) and normalized mutual information (NMI), which both provide a quanti‐
tative measure between 0 and 1.
Below we compare the k-Means, agglomerative clustering and DBSCAN algorithms
using ARI. We also include what it looks like when we randomly assign points to two
clusters for comparison.
from sklearn.metrics.cluster import adjusted_rand_score
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# Rescale the data to zero mean and unit variance
scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)
fig, axes = plt.subplots(1, 4, figsize=(15, 3), subplot_kw={'xticks': (), 'yticks': ()})
# make a list of algorithms to use
algorithms = [KMeans(n_clusters=2), AgglomerativeClustering(n_clusters=2), DBSCAN()]
# create a random cluster assignment for reference:
random_state = np.random.RandomState(seed=0)
random_clusters = random_state.randint(low=0, high=2, size=len(X))
# plot random assignment:
axes[0].scatter(X_scaled[:, 0], X_scaled[:, 1], c=random_clusters, cmap=mglearn.cm3, s=60)
axes[0].set_title("Random assignment - ARI: %.2f" % adjusted_rand_score(y, random_clusters))
for ax, algorithm in zip(axes[1:], algorithms):
# plot the cluster assignments and cluster centers
clusters = algorithm.fit_predict(X_scaled)
ax.scatter(X_scaled[:, 0], X_scaled[:, 1], c=clusters, cmap=mglearn.cm3, s=60)
ax.set_title("%s - ARI: %.2f" % (algorithm.__class__.__name__, adjusted_rand_score(y, clusters)))
The adjusted rand index provides intuitive results, with a random cluster assignment
having a score of 0, and DBSCAN (which recovers the desired clustering perfectly)
having a score of 1. A common mistake when evaluating clustering in this way is to
Clustering | 183
www.it-ebooks.info

use accuracy_score instead of a clustering metric like adjusted_rand_score and
normalized_mutual_info_score.
The problem in using accuracy is that it requires the assigned cluster labels to exactly
match the ground truth. However, the cluster labels themselves are meaningless, and
only which points are in the same cluster matters:
from sklearn.metrics import accuracy_score
# These two labelings of points correspond to the same clustering:
clusters1 = [0, 0, 1, 1, 0]
clusters2 = [1, 1, 0, 0, 1]
# accuracy is zero, as none of the labels are the same:
print("Accuracy: %.2f" % accuracy_score(clusters1, clusters2))
# adjusted rand score is 1, as the clustering is exactly the same:
print("ARI: %.2f" % adjusted_rand_score(clusters1, clusters2))
Accuracy: 0.00
ARI: 1.00
Evaluating clustering without ground truth
Although we have just shown how to evaluate on clustering algorithms, in practice,
there is a big problem with the evaluation using measures like ARI.
When applying clustering algorithms, there is usually no ground truth to which to
compare. If we knew the right clustering of the data, we could use this information to
build a supervised model like a classifier.
Therefore, using metric like ARI and NMI usually only really helps in developing
algorithms, not in assessing success in an application.
There are scoring metrics for clustering that don’t require ground truth, like the sil‐
houette coecient. However, these often don’t work well in practice. The silhouette
score computes the compactness of a cluster, where higher is better, with a perfect
score of 1. While compact clusters are good, compactness doesn’t allow for complex
shapes.
Here is an example comparing the outcome of k-Means, agglomerative clustering and
DBSCAN on the two moons using the silhouette score:
from sklearn.metrics.cluster import silhouette_score
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# Rescale the data to zero mean and unit variance
scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)
184 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

fig, axes = plt.subplots(1, 4, figsize=(15, 3), subplot_kw={'xticks': (), 'yticks': ()})
# create a random cluster assignment for reference:
random_state = np.random.RandomState(seed=0)
random_clusters = random_state.randint(low=0, high=2, size=len(X))
# plot random assignment:
axes[0].scatter(X_scaled[:, 0], X_scaled[:, 1], c=random_clusters, cmap=mglearn.cm3, s=60)
axes[0].set_title("Random assignment: %.2f" % silhouette_score(X_scaled, random_clusters))
algorithms = [KMeans(n_clusters=2), AgglomerativeClustering(n_clusters=2), DBSCAN()]
for ax, algorithm in zip(axes[1:], algorithms):
clusters = algorithm.fit_predict(X_scaled)
# plot the cluster assignments and cluster centers
ax.scatter(X_scaled[:, 0], X_scaled[:, 1], c=clusters, cmap=mglearn.cm3, s=60)
ax.set_title("%s : %.2f" % (algorithm.__class__.__name__, silhouette_score(X_scaled, clusters)))
As you can see, k-Means gets the highest silhouette score, even though we might pre‐
fer the result produced by DBSCAN.
A slightly better strategy for evaluating clusters are robustness-based clustering met‐
rics. These run an algorithm after adding some noise to the data, or using different
parameter settings, and compare the outcomes. The idea is that if many algorithm
parameters and many perturbations of the data return the same result, it is likely to
be trustworthy.
Unfortunately, this strategy is not implemented in scikit-learn at the time of writing.
Even if we get a very robust clustering, or a very high silhouette score, we still don’t
know if there is any semantic meaning in the clustering, or whether the clustering
reflects an aspect of the data that we are interested in.
Let’s go back to the example of face images. We hope to find groups of similar faces,
say men and women, or old people and young people, or people with beards and
without. Let’s say we cluster the data into two clusters, and all algorithms agree about
which points should be clustered together. We still don’t know if the clusters that are
found correspond in any way to the concepts we are interested in. It could be that
they found side-views versus front-views. Or pictures taken at night versus pictures
taken during the day. Or pictures taken with iPhones versus pictures taken with
Android phones.
Clustering | 185
www.it-ebooks.info

Only if we actually analyze the clusters can we know whether the clustering corre‐
sponds to anything we are interested in.
Comparing algorithms on the faces dataset
Let’s apply the k-Means, DBSCAN and agglomerative clustering algorithms to the
labeled faces in the wild dataset, and see if any of them find interesting structure.
We will use the eigenface representation of the data, as produced by
PCA(whiten=True), with 100 components. We saw above that this is a more semantic
representation of the face images than the raw pixels. It will also make computation
faster.
It’s a good exercise for you to run the experiments below on the original data and
compare results.
# extract eigenfaces from lfw data and transform data
from sklearn.decomposition import PCA
pca = PCA(n_components=100, whiten=True)
pca.fit_transform(X_people)
X_pca = pca.transform(X_people)
We will start by applying DBSCAN, which we just discussed.
Analyzing the faces dataset with DBSCAN
# apply DBSCAN with default parameters
dbscan = DBSCAN()
labels = dbscan.fit_predict(X_pca)
np.unique(labels)
array([-1])
We see that all returned labels are -1, so all of the data was labeled as “noise” by
DBSCAN. There are two things we can change to help this: we can make eps higher,
to expand the neighborhood of each point, and min_samples lower, to consider
smaller groups of points as clusters. Let’s try changing min_samples first:
dbscan = DBSCAN(min_samples=3)
labels = dbscan.fit_predict(X_pca)
np.unique(labels)
array([-1])
Even when considering groups of three points, everything is labeled as noise. So we
need to increase eps.
dbscan = DBSCAN(min_samples=3, eps=15)
labels = dbscan.fit_predict(X_pca)
np.unique(labels)
array([-1, 0])
186 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

Using a much larger eps=15 we get only a single clusters and noise points. We can use
this result and find out what the “noise” looks like compared to the rest of the data. To
understand better what’s happening, let’s look at how many points are noise, and how
many points are inside the cluster:
# count number of points in all clusters and noise.
# bincount doesn't allow negative numbers, so we need to add 1.
# the first number in the result corresponds to noise points
np.bincount(labels + 1)
array([ 27, 2036])
There are only very few noise points, 27, so we can look at all of them:
noise = X_people[labels==-1]
fig, axes = plt.subplots(3, 9, subplot_kw={'xticks': (), 'yticks': ()}, figsize=(12, 4))
for image, ax in zip(noise, axes.ravel()):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1)
Comparing these images to the random sample of face images from Figure
some_faces, we can guess why they were labeled as noise: the image in the sixth image
in the first row one has a person drinking from a glass, there are images with hats,
and the second to last image has a hand in front of the face. The other images contain
odd angles or crops that are too close (see the first image in the first row) or too wide
(see the last image in the first row).
This kind of analysis, trying to find “the odd one out”, is called outlier detection. If this
was a real application, we might try to do a better job in cropping images, to get more
homogeneous data. There is little we can do about people sometimes wearing hats or
drinking from a glass, but it’s good to know that these are issues in the data that any
algorithm we might apply needs to handle.
If we want to find more interesting clusters than just one large one, we need to set eps
smaller, somewhere between 15 and 0.5 (the default). Let’s have a look at what differ‐
ent values of eps result in:
Clustering | 187
www.it-ebooks.info

for eps in [1, 3, 5, 7, 9, 11, 13]:
print("\neps=%d" % eps)
dbscan = DBSCAN(eps=eps, min_samples=3)
labels = dbscan.fit_predict(X_pca)
print("Number of clusters: %s" % np.unique(labels))
print("Clusters: %s" % np.bincount(labels + 1))
eps=1
Number of clusters: [-1]
Clusters: [2063]
eps=3
Number of clusters: [-1]
Clusters: [2063]
eps=5
Number of clusters: [-1]
Clusters: [2063]
eps=7
Number of clusters: [-1 0 1 2 3 4 5 6 7 8 9 10 11 12]
Clusters: [2008 4 6 3 6 9 5 3 3 4 3 3 3 3]
eps=9
Number of clusters: [-1 0 1 2]
Clusters: [1273 784 3 3]
eps=11
Number of clusters: [-1 0]
188 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

Clusters: [ 429 1634]
eps=13
Number of clusters: [-1 0]
Clusters: [ 115 1948]
For small numbers of eps, again all points are labeled as noise. For eps=7, we get
many noise points, and many smaller clusters. For eps=9 we still get many noise
points, one big cluster and some smaller clusters. Starting from eps=11 we get only
one large cluster and noise.
What is interesting to note is that there are never more than one large cluster. There
is at most one large cluster containing most of the points, and some smaller clusters.
This indicates that there are not two or three different kinds of face images in the data
that are very distinct, but that all images are more or less equally similar (or dissimi‐
lar) from the rest.
The results for eps=7 look most interesting, with many small clusters. We investigate
this clustering in more detail, by visualizing all of the points in each of the 13 small
clusters:
# dbscan = DBSCAN(min_samples=3, eps=7)
labels = dbscan.fit_predict(X_pca)
for cluster in range(max(labels)):
mask = labels == cluster
n_images = np.sum(mask)
fig, axes = plt.subplots(1, n_images, subplot_kw={'xticks': (), 'yticks': ()}, figsize=(n_images * 1.5, 4))
for image, label, ax in zip(X_people[mask], y_people[mask], axes):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1)
ax.set_title(people.target_names[label].split()[-1])
Clustering | 189
www.it-ebooks.info

Some of the clusters correspond to people with very distinct faces (within this data‐
set), such as Tayyip or Koizumi. Within each cluster, the orientation of the face is also
quite fixed, as well as the facial expression. Some of the clusters contain faces of mul‐
tiple people, but they share a similar orientation of the face and expression.
This concludes our analysis of the DBSCAN algorithm applied to the faces dataset.
As you can see, we are doing a very manual analysis here, different from the much
more automatic search approach we could use for supervised learning, based on
$R^2$ or accuracy.
Let’s move on to applying k-Means and Agglomerative Clustering.
Analyzing the faces dataset with k-Means
We saw that it was not possible to create more than one big cluster using DBSCAN.
Agglomerative clustering and k-Means are much more likely to create clusters of even
size, but we do need to set a number of clusters.
We could set the number of clusters to the known number of people in the dataset,
though it is very unlikely that an unsupervised clustering algorithm will recover
them.
Instead, we can start with a low number of clusters, like 10, which might allow us to
analyze each of the clusters.
n_clusters = 10
# extract clusters with k-Means
km = KMeans(n_clusters=n_clusters, random_state=0)
labels_km = km.fit_predict(X_pca)
print("cluster sizes k-Means: %s" % np.bincount(labels_km))
cluster sizes k-Means: [185 146 168 190 153 284 263 133 223 318]
As you can see, k-Means clustering partitioned the data into relatively similarly sized
clusters from 133 to 318. This is quite different from the result of DBSCAN.
We can further analyze the outcome of k-Means by visualizing the cluster centers. As
we clustered in the representation produced by PCA, we need to rotate the cluster
centers back into the original space to visualize them, using pca.inverse_transform.
fig, axes = plt.subplots(2, 5, subplot_kw={'xticks': (), 'yticks': ()}, figsize=(12, 4))
for center, ax in zip(km.cluster_centers_, axes.ravel()):
ax.imshow(pca.inverse_transform(center).reshape(image_shape), vmin=0, vmax=1)
190 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

The cluster centers found by k-Means are very smooth version of faces. This is not
very surprising, given that each center is an average of 133 to 318 face images. Work‐
ing with a reduced PCA representation adds to the smoothness of the images (com‐
pared to faces reconstructed using 100 PCA dimensions in Figure
pca_reconstructions).
The clustering seems to pick up on different orientations of the face, different expres‐
sion (the third cluster center seems to show a smiling face), and presence of collars
(see the second to last cluster center).
For a more detailed view, we show for each cluster center the five most typical images
in the cluster (the images that are assigned to the cluster and closest to the cluster
center) and the five most atypical images in the cluster (the images that are assigned
to the cluster and furthest to the cluster center):
n_clusters = 10
for cluster in range(n_clusters):
center = km.cluster_centers_[cluster]
mask = km.labels_ == cluster
dists = np.sum((X_pca - center) ** 2, axis=1)
dists[~mask] = np.inf
inds = np.argsort(dists)[:5]
dists[~mask] = -np.inf
inds = np.r_[inds, np.argsort(dists)[-5:]]
fig, axes = plt.subplots(1, 11, subplot_kw={'xticks': (), 'yticks': ()}, figsize=(10, 8))
axes[0].imshow(pca.inverse_transform(center).reshape(image_shape), vmin=0, vmax=1)
for image, label, asdf, ax in zip(X_people[inds], y_people[inds], labels_km[inds], axes[1:]):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1)
ax.set_title("%s" % (people.target_names[label].split()[-1]), fontdict={'fontsize': 9})
print("kmeans_face_clusters")
Clustering | 191
www.it-ebooks.info

kmeans_face_clusters
Figure kmeans_face_clusters confirms our intuition about smiling faces for the third
cluster, and also the importance of orientation for the other clusters. The “atypical”
points are not very similar to the cluster center, though, and the assignment seems
somewhat arbitrary. This can be attributed to the fact that k-Means partitions all the
data points, and doesn’t have a concept of “noise” points, as DBSCAN does.
Using a larger number of clusters, the algorithm could find finer distinctions. How‐
ever, adding more clusters makes manual inspection even harder.
Analyzing the faces dataset with agglomerative clustering
Now, let’s look at the results of agglomerative clustering:
# extract clusters with ward agglomerative clustering
agglomerative = AgglomerativeClustering(n_clusters=10)
labels_agg = agglomerative.fit_predict(X_pca)
print("cluster sizes agglomerative clustering: %s" % np.bincount(labels_agg))
cluster sizes agglomerative clustering: [167 50 252 367 160 80 50 67 521 349]
Agglomerative clustering produces relatively equally sized clusters, with cluster sizes
between 50 and 521. These are more uneven than k-Means, but much more even
than the ones produced by DBSCAN.
We can compute the ARI to measure if the two partitions of the data given by
agglomerative clustering and k-Means are similar:
adjusted_rand_score(labels_agg, labels_km)
0.09733057984938646
An ARI of only 0.1 means that the two clusterings labels_agg and labels_km have
quite little in common. This is not very surprising, given the fact that points further
away from the cluster centers seem to have little in common for k-Means.
Next, we might want to plot the dendrogram. We limit the depth of the tree in the
plot, as branching down to the individual 2063 data points would result in an unread‐
ably dense plot.
# import the dendogram function and the ward clustering function from scipy
from scipy.cluster.hierarchy import dendrogram, ward
# apply the ward clustering to the data array X
# The scipy ward function returns an array that specifies the distances bridged
# when performing agglomerative clustering
linkage_array = ward(X_pca)
# now we plot the dendogram for the linkage_array containing the distances between clusters
plt.figure(figsize=(20, 5))
dendrogram(linkage_array, p=7, truncate_mode='level', no_labels=True);
192 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

Creating ten clusters, we cut across the tree at the very top, where there are 10 vertical
lines. In the dendrogram for the toy data shown in Figure dendrogram, you could see
by the length of the branches that two or three clusters might capture the data appro‐
priately. For the faces data, there doesn’t seem to be a very natural cut-off point. There
are some branches that represent more distinct groups, but there doesn’t seem to be a
particular number of clusters that is a good fit. This is not particularly surprising,
given the results of DBSCAN, which tried to cluster all points together.
Here is a visualization of the ten clusters, similarly to k-Means above.
Note that there is no notion of cluster center in agglomerative clustering (though we
could compute the mean), and we simply show the first couple of points in each clus‐
ter. We show the number of points in each cluster to the left of the first image.
n_clusters = 10
for cluster in range(n_clusters):
mask = labels_agg == cluster
fig, axes = plt.subplots(1, 10, subplot_kw={'xticks': (), 'yticks': ()}, figsize=(15, 8))
axes[0].set_ylabel(np.sum(mask))
for image, label, asdf, ax in zip(X_people[mask], y_people[mask], labels_agg[mask], axes):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1)
ax.set_title("%s" % people.target_names[label].split()[-1], fontdict={'fontsize': 9})
While some of the clusters seem to have a semantic theme, many of them are too
large to be actually homogeneous. To get more homogeneous cluster, we run the
algorithm again, this time with 40 clusters, and pick out some of the clusters that are
particularly interesting:
# extract clusters with ward agglomerative clustering
agglomerative = AgglomerativeClustering(n_clusters=40)
labels_agg = agglomerative.fit_predict(X_pca)
print("cluster sizes agglomerative clustering: %s" % np.bincount(labels_agg))
n_clusters = 40
for cluster in [15, 7, 17, 20, 25, 29]: # hand-picked "interesting" clusters
Clustering | 193
www.it-ebooks.info

mask = labels_agg == cluster
fig, axes = plt.subplots(1, 15, subplot_kw={'xticks': (), 'yticks': ()}, figsize=(15, 8))
cluster_size = np.sum(mask)
axes[0].set_ylabel(cluster_size)
for image, label, asdf, ax in zip(X_people[mask], y_people[mask], labels_agg[mask], axes):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1)
ax.set_title("%s" % (people.target_names[label].split()[-1]), fontdict={'fontsize': 9})
for i in range(cluster_size, 15):
axes[i].set_visible(False)
cluster sizes agglomerative clustering: [ 50 111 103 120 60 169 50 53 10 33 187 30 50 85 53 28 35 6
111 18 3 78 81 36 10 16 22 5 57 27 75 26 92 5 13 35
8 23 20 69]
Here, the clustering seems to have picked up on “dark skinned and smiling”, “serious
eyebrows”, “collared shirt”, “white hat and showing front teeth”, “high forehead” and
“Asian”.
We could also] find these highly similar clusters using the dendrogram, if we did
more a detailed analysis.
Summary of Clustering Methods
We saw above that applying and evaluating clustering is a highly qualitative proce‐
dure, and often most helpful in the exploratory phase of data analysis. We looked at
three clustering algorithms, k-Means, DBSCAN and Agglomerative Clustering. All
three have a way of controlling the granularity of clustering. k-Means and Agglomer‐
ative Clustering allow you to directly specify the number of desired clusters, while
DBSCAN lets you define proximity using the eps parameter, which indirectly influ‐
ences cluster size.
All three methods can be used on large, real-world datasets, are relatively easy to
understand, and allow for clustering into many clusters.
Each of the algorithms has somewhat different strengths. k-Means allows for a char‐
acterization of the clusters using the cluster means. It can also be viewed as a decom‐
position method, where each data point is represented by its cluster center.
DBSCAN allows for the detection of “noise points” that are not assigned any cluster,
and it can help automatically determine the number of clusters. In contrast to the
other two methods, it allow for complex cluster shapes, as we saw in the two_moons
example. DBSCAN sometimes produces clusters of very differing size, which can be a
194 | Chapter 3: Unsupervised Learning and Preprocessing
www.it-ebooks.info

strength or a weakness. Agglomerative clustering can provide a whole hierarchy of
possible partitions of the data, which can be easily inspected via dendrograms.
Summary and Outlook
This chapter introduced a range of unsupervised learning algorithms that can be
applied for exploratory data analysis and preprocessing. Having the right representa‐
tion of the data is often crucial for supervised or unsupervised learning to succeed,
and preprocessing and decomposition methods play an important part in data prepa‐
ration.
Decomposition, manifold learning and clustering are essential tools to further your
understanding of your data, and can be the only way to make sense of your data in
the absence of supervision information. Even in the supervised setting, exploratory
tools are important for a better understanding of the properties of the data.
Often it is hard to quantify the usefulness of an unsupervised algorithm, though this
shouldn’t deter you from using them to create insights from your data.
With these methods under your belt, you are now equipped with all the essential
learning algorithms that machine learning practitioners use every day.
We encourage you to try clustering and decomposition methods both on two-
dimensional toy data, as well as real world datasets included in scikit-learn, like the
digits, iris and cancer data sets.
Summary and Outlook | 195
www.it-ebooks.info

CHAPTER 4
Summary of scikit-learn methods and
usage
In this chapter, we briefly recapitulate the main parts of the scikit-learn API that we
have seen so far, as well as show some ways to simplify your code.
The Estimator Interface
All algorithms in scikit-learn, whether preprocessing, supervised learning or unsu‐
pervised learning algorithms are all implemented as classes. These classes are called
estimators in scikit-learn. To apply an algorithm, you first have to instantiate an object
of the particular class:
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression()
The estimator class contains the algorithm, and also stored the model that is learned
from data using the algorithm.
When constructing the model object, this is also the time when you should set any
parameters of the model. These parameters include regularization, complexity con‐
trol, number of clusters to find, etc, as we discussed in detail in Chapter 2 and Chap‐
ter 3.
All estimators have a fit method, which is used to build the model. The fit method
always requires as first argument the data X, represented as a numpy array or a scipy
sparse matrix, where each row represents a single data point. The data X is always
assumed to be a numpy array or scipy sparse matrix that has continuous (floating
point) entries.
197
www.it-ebooks.info
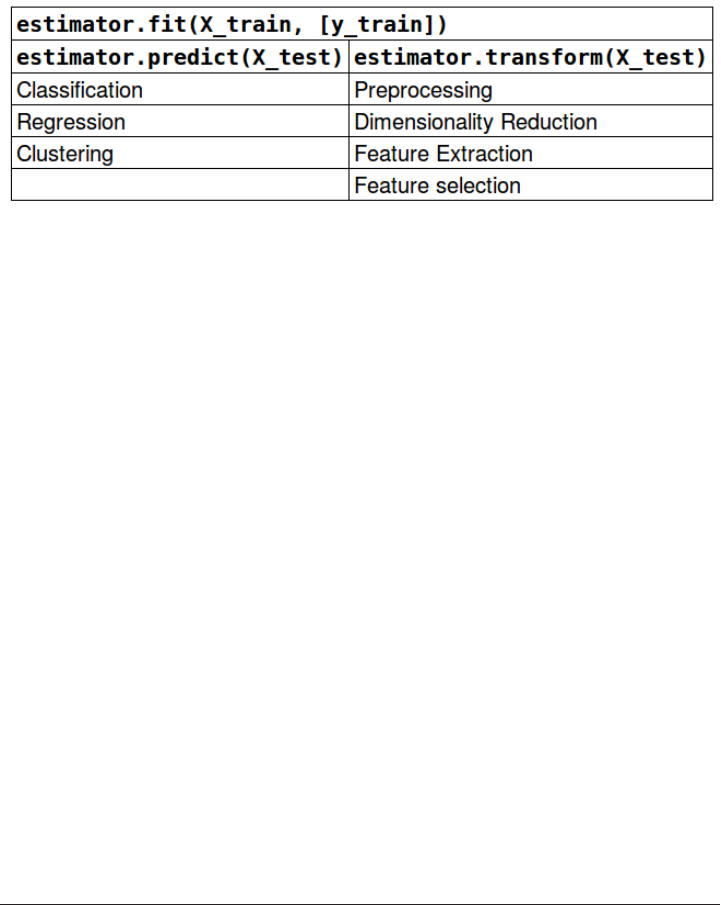
Supervised algorithms also require a y argument, which is a one-dimensional numpy
array, containing target values for regression or classification, i.e. the known output
labels or responses.
There are two main ways to apply a learned model in scikit-learn. To create a predic‐
tion in the form of a new output like y, you use the predict method. To create a new
representation of the input data X, you use the transform method. Table api_sum‐
mary summarizes the use-cases of the predict and transform methods.
Table api_summary
Additionally, all supervised models have a score(X_test, y_test) method, that
allows an evaluation of the model.
Here X_train and y_train refere to the training data and training labels, while
X_test and y_test refer to the test data and test labels (if applicable).
Fit resets a model
An important property of scikit-learn models is that calling fit will always reset
everything a model previously learned. So if you build a model on one dataset, and
then call fit again on a different dataset, the model will “forget” everything it learned
from the first data. You can call fit as often as you like on a model, and the outcome
will be the same as calling fit on a “new” model:
# get some data
from sklearn.datasets import make_blobs, load_iris
from sklearn.model_selection import train_test_split
# load iris
iris = load_iris()
# create some blobs
X, y = make_blobs(random_state=0, centers=4)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# build a model on the iris dataset
logreg = LogisticRegression()
198 | Chapter 4: Summary of scikit-learn methods and usage
www.it-ebooks.info

logreg.fit(iris.data, iris.target)
# fit the model again on the blob dataset
logreg.fit(X_train, y_train)
# the outcome is the same as training a "fresh" model:
new_logreg = LogisticRegression()
new_logreg.fit(X_train, y_train)
# predictions made by the two models are the same
pred_new_logreg = new_logreg.predict(X_test)
pred_logreg = logreg.predict(X_test)
pred_logreg == pred_new_logreg
array([ True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True], dtype=bool)
As you can see, fitting the logreg model first on the iris dataset has no effect. The
iris dataset has a different number of features and classes than the blobs dataset, but
all about the first fit is erased when fit is called again.
Next, we will go into several shortcuts that allow you to write less code for common
tasks, and speed up some computations. The first way to write more compact code is
to make use method chaining.
Method chaining
The fit method of all scikit-learn models returns self. This allows you to write code
like this:
# instantiate model and fit it in one line
logreg = LogisticRegression().fit(X_train, y_train)
Here, we used the return value of fit (which is self) to assign the trained model to
the variable logreg. This concatenation of method calls (here __init__ and then
fit) is known as method chaining. Another common application of method chaining
in scikit-learn is to fit and predict in one line:
logreg = LogisticRegression()
y_pred = logreg.fit(X_train, y_train).predict(X_test)
Finally, you can even do model instantiation, fitting and predicting in one line:
y_pred = LogisticRegression().fit(X_train, y_train).predict(X_test)
This very short variant is not ideal, though. A lot is happening in a single line, which
might make the code hard to read. Additionally, the fitted logistic regression model
isn’t stored in any variable. So we can’t inspect it, or use it to predict on any other
data.
Method chaining | 199
www.it-ebooks.info

Shortcuts and ecient alternatives
Often, you want to fit a model on some dataset, and then immediately predict on
the same data, or transform it. These are very common tasks, which can often be
computed more efficiently than simply calling fit and then predict or fit and then
transform. For this use-case, all models that have a predict method also have a
fit_predict method, and all model that have a transform method also have a
fit_transform method. Here is an example using PCA:
from sklearn.decomposition import PCA
pca = PCA()
# calling fit and transform in sequence (using method chaining)
X_pca = pca.fit(X).transform(X)
# same result, but more efficient computation
X_pca_2 = pca.fit_transform(X)
While fit_transform and fit_predict are not more efficient for all algorithms, it is
still good practice to use them when trying to predict on, or transform the training
set.
For some unsupervised methods that we saw in Chapter 3, like some clustering and
manifold learning methods, using fit_transform and fit_predict are the only
options. For example DBSCAN does not have a predict method, only fit_predict,
and t-SNE does not have a transform method, only fit_transform. T-SNE and
DBSCAN are algorithms that can not be applied to new data, they can only be applied
to the training data.
Important Attributes
scikit-learn has some standard attributes that allow you to inspect what a model
learned. All these attributes are available after the call to fit, and, as we mentioned
before, all attributes learned from the data are marked with a trailing underscore.
We already discussed the following common attributes:
•For clustering algorithms, the labels_ attribute stores the cluster membership
for the training data.
• For manifold learning algorithms, the embedding_ attribute stores the embedding
(transformation) of the training data in the lower-dimensional space.
• For linear models, the coef_ attribute stores the weight or coefficient vector.
200 | Chapter 4: Summary of scikit-learn methods and usage
www.it-ebooks.info

•For linear decomposition and dimensionality reduction methods, components_
stores the array of components (the prototypes in the additive decomposition in
Figure decomposition in Chapter 3).
Additionally, for classifiers, classes_ contains the names of the classes the classifier
was trained on, that is the unique entries of the training labels y_train:
import numpy as np
logreg = LogisticRegression()
# fit model using original data
logreg.fit(iris.data, iris.target)
print("unique entries of iris.target: %s" % np.unique(iris.target))
print("classes using iris.target: %s" % logreg.classes_)
# represent each target by its class name
named_target = iris.target_names[iris.target]
logreg.fit(iris.data, named_target)
print("unique entries of named_target: %s" % np.unique(named_target))
print("classes using named_target: %s" % logreg.classes_)
unique entries of iris.target: [0 1 2]
classes using iris.target: [0 1 2]
unique entries of named_target: ['setosa' 'versicolor' 'virginica']
classes using named_target: ['setosa' 'versicolor' 'virginica']
Summary and outlook
You should now be be intimately familiar with the interfaces of supervised and unsu‐
pervised models in scikit-learn, and how to use them. With a good grasp on how to
use the different models, we will continue with more complex topics, such as evaluat‐
ing and selecting models.
Summary and outlook | 201
www.it-ebooks.info

CHAPTER 5
Representing Data and Engineering
Features
So far, we assumed that our data comes in as a two-dimensional array of floating
point numbers, where each column is a continuous feature that describes the data
points. For many applications, this is not how the data is collected. A particular com‐
mon type of feature is categorical features, also known as discrete features, which are
usually not numeric. The distinction between categorical feature and continuous fea‐
ture is analogous to the distinction between classification and regression - only on the
input side, not the output side.
Examples for continuous features that we saw are pixel brightnesses and size meas‐
urements of plant flowers. Examples for categorical features are the brand of a prod‐
uct, the color of a product, or the department (books, clothing, hardware) it is sold in.
These are all properties that can describe a product, but they don’t vary in a continu‐
ous way. A product belongs either in the clothing department or in the books depart‐
ment. There is no middle ground between books and clothing, and no natural order
for the different categories (books is not greater or smaller than clothing, hardware is
not between books and clothing, etc).
Regardless of the type of features your data consists of, how you represent them can
have an enormous effect on the performance of machine learning models. We saw in
Chapter 2 and Chapter 3 that scaling of the data is important. In other words, if you
don’t rescale your data (say, to unit variance), then it makes a difference whether you
represent a measurement in centimeters or inches. We also saw in Chapter 2 that it
can be helpful to augment your data with additional features, like adding interactions
(products) of features or more general polynomials.
The question of how to represent your data best for a particular application is known
as feature engineering, and it is one of the main tasks of data scientists and machine
203
www.it-ebooks.info

learning practitioners trying to solve real-world problems. Representing your data in
the right way can have a bigger influence on the performance of a supervised model
than the exact parameters you choose.
We will first go over the important and very common case of categorical features, and
then give some examples of helpful transformations for specific combinations of fea‐
tures and models.
Categorical Variables
As an example, we will use the dataset of adult incomes in the United States, derived
from the 1994 census database.
The task of the adult dataset is to predict whether a worker has an income of over
50.000$ or under 50.000$.
The features in this dataset include the workers age, how they are employed (self
employed, private industry employee, goverment employee, ...), their education, their
gender, their working hours per week, occupation and more.
Below is a table showing the first few entries in the data set:
| | age | workclass | education | gender | hours-per-week | occupation | income |
|------|-----|------------------|--------------|--------|----------------|-------------------|----------|
| 0 | 39 | State-gov | Bachelors | Male | 40 | Adm-clerical | <=50K |
| 1 | 50 | Self-emp-not-inc | Bachelors | Male | 13 | Exec-managerial | <=50K |
| 2 | 38 | Private | HS-grad | Male | 40 | Handlers-cleaners | <=50K |
| 3 | 53 | Private | 11th | Male | 40 | Handlers-cleaners | <=50K |
| 4 | 28 | Private | Bachelors | Female | 40 | Prof-specialty | <=50K |
| 5 | 37 | Private | Masters | Female | 40 | Exec-managerial | <=50K |
| 6 | 49 | Private | 9th | Female | 16 | Other-service | <=50K |
| 7 | 52 | Self-emp-not-inc | HS-grad | Male | 45 | Exec-managerial | >50K |
| 8 | 31 | Private | Masters | Female | 50 | Prof-specialty | >50K |
| 9 | 42 | Private | Bachelors | Male | 40 | Exec-managerial | >50K |
| 10 | 37 | Private | Some-college | Male | 80 | Exec-managerial | >50K |
The task is phrased as a classification task with the two classes being income <=50k
and >50k. It would also be possible to predict the exact income, and make this a
regression task. However, that would be much more difficult, and the 50K division is
interesting to understand on its own.
204 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info

In this dataset, age and hours-per-week are continuous features, which we know
how to treat. The workclass, education, sex and ocupation features are categorical,
however. All of them come from a fixed list of possible values, as opposed to a range,
and denote a qualitative property, as opposed to a quantity.
As a starting point, let’s say we want to learn a logistic regression classifier on this
data. We know from Chapter 2 that a logistic regression makes predictions $\hat{y}$
using the formula
\begin{align*}
&\hat{y} = w[0] x[0] + w[1] x[1] + \dotsc + w[p] * x[p] + b > 0 &\text{ (1) linear
binary classification}
\end{align*}
where w[i] and b are coefficients learned from the training set and x[i] are the input
features.
This formula makes sense when x[i] are numbers, but not when x[2] is "Masters"
or "Bachelors".
So clearly we need to represent our data in some different way when applying logistic
regression.
One-Hot-Encoding (Dummy variables)
By far the most common way to represent categorical variables is using the one-hot-
encoding or one-out-of-N encoding, also known as dummy variables.
The idea behind dummy variables is to replace a categorical variable with one or
more new features that can have the values 0 and 1. The values 0 and 1 make sense in
Formula (1) (and for all other models in scikit-learn), and we can represent any num‐
ber of categories by introducing one new feature per category as follows.
Let’s say for the workclass feature we have possible values of "Government
Employee", "Private Employee", "Self Employed" and "Self Employed Incorpora
ted". To encode this four possible values, we create four new features, called "Govern
ment Employee", "Private Employee", "Self Employed" and "Self Employed
Incorporated". The feature is 1 if workclass for this person has the corresponding
value, and 0 otherwise.
So exactly one of the four new features will be 1 for each data point. This is why this is
called one-hot or one-out-of-N encoding.
The principle is illustrated here. A single feature is encoded using four new features.
When using this data in a machine learning algorithm, we would drop the original
workclass feature and only keep the 0-1 features.
Categorical Variables | 205
www.it-ebooks.info

| workclass | Government Employee | Private Employee | Self Employed | Self
Employed Incorporated |
|----------------------------|---------------------|------------------|---------------|----------------------------|
| Government Employee | 1 | 0 | 0 | 0 |
| Private Employee | 0 | 1 | 0 | 0 |
| Self Employed | 0 | 0 | 1 | 0 |
| Self Employed Incorporated | 0 | 0 | 0 | 1 |
There are two ways to convert your data to a one-hot encoding of categorical vari‐
ables, either using pandas or using scikit-learn. At the time of writing, using pan
das for this setting is slightly easier, so let’s go this route. First we load the data using
pandas from a comma seperated values (CSV) file:
import pandas as pd
# The file has no headers naming the columns, so we pass header=None and provide the column names explicitly in "names"
data = pd.read_csv("/home/andy/datasets/adult.data", header=None, index_col=False,
names=['age', 'workclass', 'fnlwgt', 'education', 'education-num',
'marital-status', 'occupation', 'relationship', 'race', 'gender',
'capital-gain', 'capital-loss', 'hours-per-week', 'native-country', 'income'])
# For illustration purposes, we only select some of the columns:
data = data[['age', 'workclass', 'education', 'gender', 'hours-per-week', 'occupation', 'income']]
# print the first 5 rows
data.head()
age workclass education gender hours-per-week occupation income
039 State-gov Bachelors Male 40 Adm-clerical <=50K
150 Self-emp-not-inc Bachelors Male 13 Exec-managerial <=50K
238 Private HS-grad Male 40 Handlers-cleaners <=50K
353 Private 11th Male 40 Handlers-cleaners <=50K
428 Private Bachelors Female 40 Prof-specialty <=50K
Checking string-encoded categorical data
After reading a dataset like this, it is often good to first check if a column actually
contains meaningful categorical data. When working with data that was input by
humans (say users on a website), there might not be a fixed set of categories, and dif‐
ferences in spelling and capitalization might require preprocessing. For example, it
might be that some people specified gender as “male” and some as “man”, and we
might want to represent these two inputs using the same category.
A good way to check the contents of a column is using the value_counts function of
a pandas series (the type of a single column in a dataframe), to show us what the
unique values are, and how often they appear:
206 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info
data.gender.value_counts()
Male 21790
Female 10771
Name: gender, dtype: int64
We can see that there are exactly two values for gender in this datasets, Male and
Female, meaning the data is already in a good format to be represented using one-
hot-encoding. In a real application, you should look at all columns, and check their
values. We will skip this here for brevity’s sake.
There is a very simple way to encode the data in pandas, using the get_dummies func‐
tion:
print("Original features:\n", list(data.columns), "\n")
data_dummies = pd.get_dummies(data)
print("Features after get_dummies:\n", list(data_dummies.columns))
Original features:
['age', 'workclass', 'education', 'gender', 'hours-per-week', 'occupation', 'income']
Features after get_dummies:
['age', 'hours-per-week', 'workclass_ ?', 'workclass_ Federal-gov', 'workclass_ Local-gov', 'workclass_ Never-worked', 'workclass_ Private', 'workclass_ Self-emp-inc', 'workclass_ Self-emp-not-inc', 'workclass_ State-gov', 'workclass_ Without-pay', 'education_ 10th', 'education_ 11th', 'education_ 12th', 'education_ 1st-4th', 'education_ 5th-6th', 'education_ 7th-8th', 'education_ 9th', 'education_ Assoc-acdm', 'education_ Assoc-voc', 'education_ Bachelors', 'education_ Doctorate', 'education_ HS-grad', 'education_ Masters', 'education_ Preschool', 'education_ Prof-school', 'education_ Some-college', 'gender_ Female', 'gender_ Male', 'occupation_ ?', 'occupation_ Adm-clerical', 'occupation_ Armed-Forces', 'occupation_ Craft-repair', 'occupation_ Exec-managerial', 'occupation_ Farming-fishing', 'occupation_ Handlers-cleaners', 'occupation_ Machine-op-inspct', 'occupation_ Other-service', 'occupation_ Priv-house-serv', 'occupation_ Prof-specialty', 'occupation_ Protective-serv', 'occupation_ Sales', 'occupation_ Tech-support', 'occupation_ Transport-moving', 'income_ <=50K', 'income_ >50K']
You can see that the continuous features age and hours-per-week were not touched,
while the categorical features were expanded into one new feature for each possible
value:
data_dummies.head()
age hours-
per-
week
workclass_ ? workclass_
Federal-
gov
workclass_
Local-gov
workclass_
Never-
worked
workclass_
Private
workclass_
Self-emp-
inc
workclass_
Self-emp-
not-inc
workclass_
State-gov
... occupation_
Machine-
op-inspct
occupation_
Other-
service
occupation_
Priv-house-
serv
occupation_
Prof-
specialty
occupation_
Protective-
serv
occupation_
Sales
occupation_
Tech-
support
occupation_
Transport-
moving
income_
<=50K
income_
>50K
039 40 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0
150 13 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0
238 40 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0
353 40 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0
428 40 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0 0.0
5 rows × 46 columns
We can use the ``values`` attribute to convert the ``data_dummies`` dataframe into a
numpy array, and then train a machine learning model on it. Be careful to separate the
Categorical Variables | 207
www.it-ebooks.info

target variable (which is now encoded in two ``income`` columns) from the data before
training a model. Including the output variable, or some derived property of the output
variable, into the feature representation is a very common mistake in building supervised
machine learning models. [Warning box] Careful: column indexing in pandas includes
the end of the range, so ``'age’:'occupation_ Transport-moving'`` is inclusive of ``occupa‐
tion_ Transport-moving``. This is in constrast to slicing a numpy array, where the end of
a range is not included: ``np.arange(11)[0:10]`` does not include the entry with index 10.
[/Warning box] ``` # Get only the columns containing features, that is all columns from
‘age’ to ‘occupation_ Transport-moving’ # This range contains all the features but not the
target features = data_dummies.ix[:, ‘age’:'occupation_ Transport-moving'] # extract
numpy arrays X = features.values y = data_dummies['income_ >50K'].values
print(X.shape, y.shape) ``` ``` (32561, 44) (32561,) ``` Now the data is represented in a
way that scikit-learn can work with, and we can proceed as usual: ``` from sklearn.lin‐
ear_model import LogisticRegression from sklearn.model_selection import
train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
logreg = LogisticRegression() logreg.fit(X_train, y_train) print(logreg.score(X_test,
y_test)) ``` ``` 0.808745854318 ``` [FIXME Warning callout] Above, we called
``get_dummies`` on a dataframe containing both the training and the test data. This is
imporant to ensure categorical values are represented in the same way in the training set
and the test set. Imagine we had the training and the test set in two different dataframes.
If the “Private Employee” value for the ``workclass`` feature does not appear in the test
set, pandas would assume there are only three possible values for this feature, and would
create only three new dummy features. Now our training and test set have different num‐
bers of features, and we can’t apply the model we learned on the training set to the test set
any more. Even worse, imagine the ``workclass`` feature had the values “Government
Employee” and “Private Employee” in the training set, and “Self Employed” and “Self
Employed Incorporated” in the test set. In both cases, pandas would create two new
dummy features, so the encoded dataframes would have the same number of features.
However, the two dummy features have entirely different meanings on the training and
the test set. The column that means “Goverment Employee” for the training set would
encode “Self Employed” for the test set. If we build a machine learning model on this data,
it would work very badly, because it assumes the columns mean the same (because they
are in the same position), when they mean very different things. To fix this, either call
``get_dummies`` on a dataframe that contains the training and the test data points, or
make sure that the column names are the same for training and test set after calling
``get_dummies``, to ensure they have the same semantics. ### Numbers can encode cate‐
goricals In the example of the ``adult`` dataset, the categorical variables were encoded as
strings. On the one hand, that opens up the possibility of spelling errors, but on the other
hand, it clearly marks a variable as categorical. Often, whether for ease of storage or
because of the way the data is collected, categorical variables are actually encoded as inte‐
gers. For example, imagine the census data in the ``adult`` dataset was collected using a
questionaire, and the answers for ``workclass`` were recorded as 0 (first box ticked), 1
(second box ticked), 2 (third box ticked) and so on. Now the column contains number
from 0 to eight, instead of strings like ``Private``, and looking at the table representing
208 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info

the dataset, it is not clear from the numbers whether we should treat this variable as con‐
tinuous or categorical. Knowing that the numbers indicate employment status, it is clear
that these are very distinct states, and should not be modelled by a single continuous vari‐
able. [Warning box] Categorical features are often encoded using integers. That they are
numbers doesn’t mean that they should be treated as continuous features, as we men‐
tioned above. It is not always clear whether an integer feature should be treated as contin‐
uous or discrete (and [one-hot-encoded). If there is no ordering between the semantics
that are encoded (like the ``workclass`` example above), the feature must be treated as
discrete. For other cases like 5-star ratings, the better encoding depends on the the partic‐
ular task and data and which machine learning algorithm is used.[/warning box] The
``get_dummies`` function in pandas treats all numbers as continuous and will not create
dummy variables for them. To get around this, you can either use ``scikit-learn``’s
``OneHotEncoder``, for which you can specify which variables are continuous and which
are discrete, or convert numeric columns in the dataframe to strings. To illustrate, we cre‐
ate a dataframe object with two columns, one containing strings and one containing inte‐
gers. ``` # create a dataframe with an integer feature and a categorical string feature
demo_df = pd.DataFrame({'Integer Feature’: [0, 1, 2, 1], ‘Categorical Feature’: [’socks',
‘fox', ’socks', ‘box']}) demo_df ```
Categorical Feature Integer Feature
0socks 0
1fox 1
2socks 2
3box 1
Using get_dummies will only encode the string feature, and not change “Integer Feature”:
``` pd.get_dummies(demo_df) ```
Integer Feature Categorical Feature_box Categorical Feature_fox Categorical Feature_socks
00 0.0 0.0 1.0
11 0.0 1.0 0.0
22 0.0 0.0 1.0
31 1.0 0.0 0.0
If you want dummy variables to be created for the “Integer Feature” column, one solution
is to convert it to a string. Then, both features will be treated as categorical: ```
demo_df['Integer Feature'] = demo_df['Integer Feature'].astype(str) pd.get_dum‐
mies(demo_df) ```
Categorical Variables | 209
www.it-ebooks.info

Categorical
Feature_box
Categorical
Feature_fox
Categorical
Feature_socks
Integer
Feature_0
Integer
Feature_1
Integer
Feature_2
00.0 0.0 1.0 1.0 0.0 0.0
10.0 1.0 0.0 0.0 1.0 0.0
20.0 0.0 1.0 0.0 0.0 1.0
31.0 0.0 0.0 0.0 1.0 0.0
Binning, Discretization, Linear Models and Trees
The best way to represent data not only depends on the semantics of the data, but also
on the kind of model you are using. Two large and very commonly used families of
models are linear models and tree-based models (such as decision trees, gradient
boosted trees and random forests). Linear models and tree-based models have very
different properties when it comes to how they work with different feature represen‐
tations.
Let’s go back to the wave regression dataset that we used in chapter 2. It only has a
single input feature. Here is a comparison of a linear regression model and a decision
tree regressor on this dataset:
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
X, y = mglearn.datasets.make_wave(n_samples=100)
plt.plot(X[:, 0], y, 'o')
line = np.linspace(-3, 3, 1000)[:-1].reshape(-1, 1)
reg = LinearRegression().fit(X, y)
plt.plot(line, reg.predict(line), label="linear regression")
reg = DecisionTreeRegressor(min_samples_split=3).fit(X, y)
plt.plot(line, reg.predict(line), label="decision tree")
plt.ylabel("regression output")
plt.xlabel("input feature")
plt.legend(loc="best")
210 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info
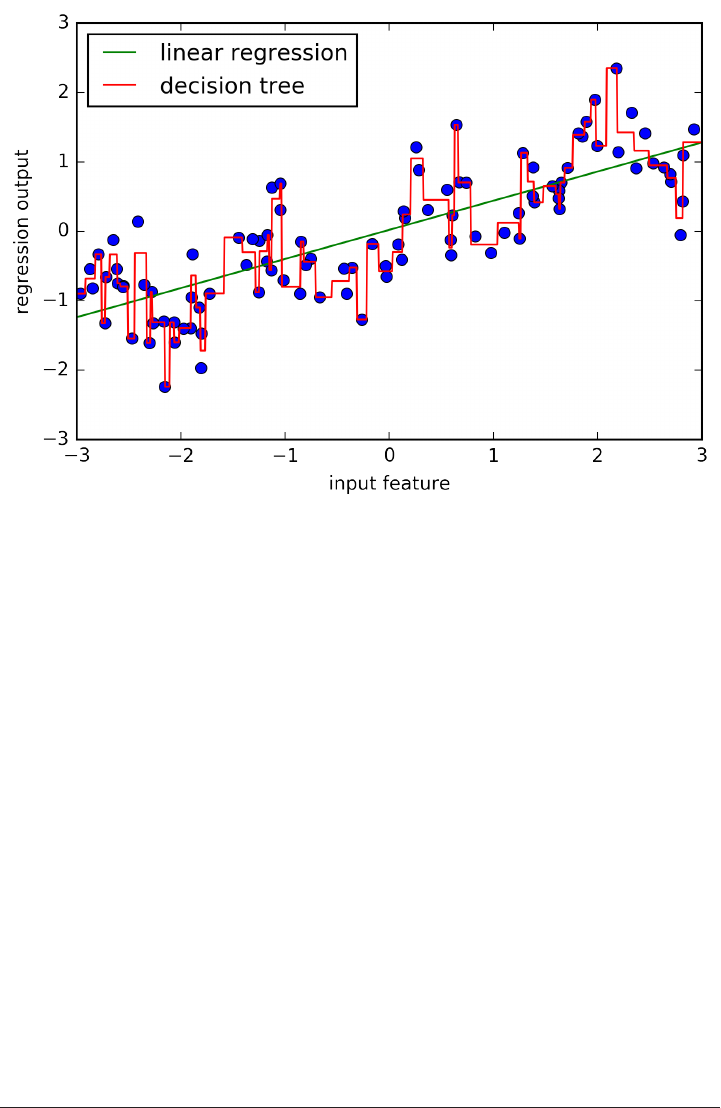
As you know, linear models can only model linear relationships, which are lines in
the case of a single feature. The decision tree an build a much more complex model of
the data.
However, this is strongly dependent on our representation of the data. One way to
make linear models more powerful on continuous data is to using binning (also
known as discretization) of the feature to split it up into multiple features as follows:
We imagine a partition of the input range of -3 to 3 of this feature into a fixed number
of bins. Here, we pass bin boundaries from -3 to 3 with 11 equally sized steps. An
array of 11 bin boundaries will create 10 bins - they are the space in between two con‐
secutive boundaries.
np.set_printoptions(precision=2)
bins = np.linspace(-3, 3, 11)
bins
array([-3. , -2.4, -1.8, -1.2, -0.6, 0. , 0.6, 1.2, 1.8, 2.4, 3. ])
Here, the first bin contains all data points with feature values -3 to -2.68, the second
bin contains all points feature values from -2.68 to -2.37 and so on.
Next, we record for each data point which bin it falls into. This can be easily compu‐
ted using the np.digitize function:
Binning, Discretization, Linear Models and Trees | 211
www.it-ebooks.info

which_bin = np.digitize(X, bins=bins)
print("\nData points:\n", X[:5])
print("\nBin membership for data points:\n", which_bin[:5])
Data points:
[[-0.75]
[ 2.7 ]
[ 1.39]
[ 0.59]
[-2.06]]
Bin membership for data points:
[[ 4]
[10]
[ 8]
[ 6]
[ 2]]
What we did here is transform the single continuous input feature in the wave dataset
into a categorical feature which encodes which bin a data point is in. To use a scikit-
learn model on this data, we transform this discrete feature to a one-hot encoding
using the OneHotEncoder from the preprocessing module. The OneHotEncoder does
the same encoding as pandas.get_dummies, though it currently only works on cate‐
gorical variables that are integers.
from sklearn.preprocessing import OneHotEncoder
# transform using the OneHotEncoder.
encoder = OneHotEncoder(sparse=False)
# encoder.fit finds the unique values that appear in which_bin
encoder.fit(which_bin)
# transform creates the one-hot encoding
X_binned = encoder.transform(which_bin)
print(X_binned[:5])
[[ 0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
212 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info

[ 0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
[ 0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]]
Because we specified 10 bins, the transformed dataset X_binned now is made up of
10 features:
X_binned.shape
(100, 10)
Now we build a new linear regression model and a new decision tree model on the
one-hot encoded data.
The result is visualized below, together with the bin boundaries, shown as dotted
black lines:
line_binned = encoder.transform(np.digitize(line, bins=bins))
plt.plot(X[:, 0], y, 'o')
reg = LinearRegression().fit(X_binned, y)
plt.plot(line, reg.predict(line_binned), label='linear regression binned')
reg = DecisionTreeRegressor(min_samples_split=3).fit(X_binned, y)
plt.plot(line, reg.predict(line_binned), label='decision tree binned')
for bin in bins:
plt.plot([bin, bin], [-3, 3], ':', c='k')
plt.legend(loc="best")
plt.suptitle("linear_binning")
Binning, Discretization, Linear Models and Trees | 213
www.it-ebooks.info
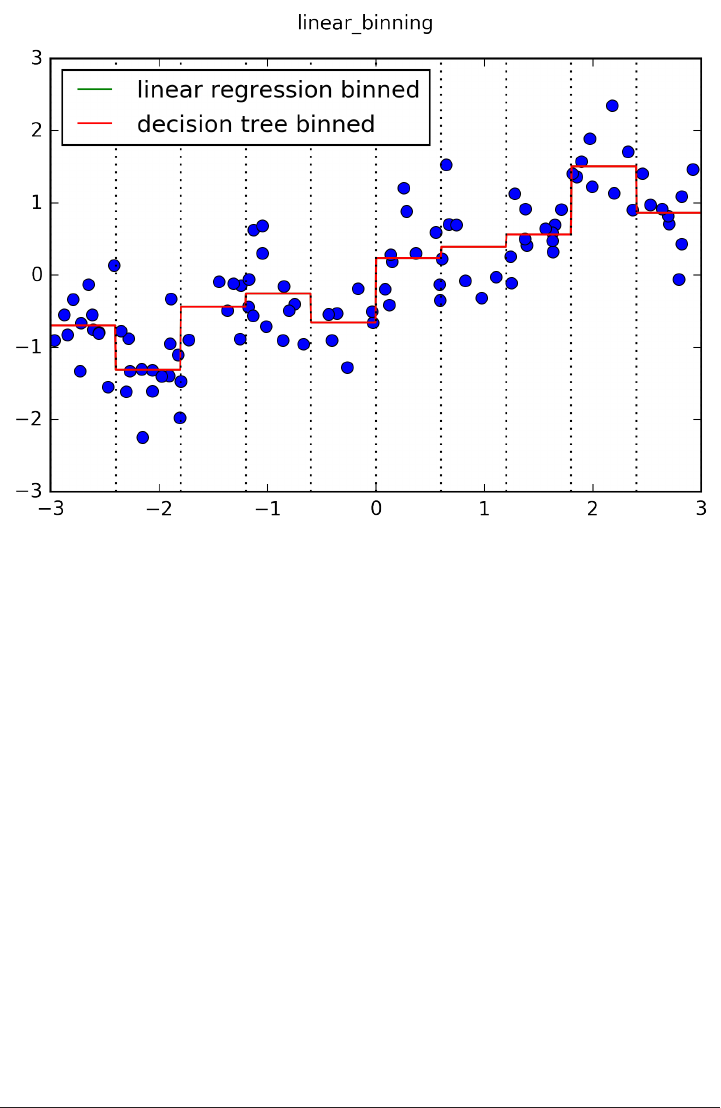
The green line and red line are exactly on top of each other, meaning the linear
regression model and the decision tree make exactly the same predictions. For each
bin, they predict a constant value. As features are constant within each bin, any
model must predict the same value for all points within a bin. Comparing what the
models learned before binning the features and after, we see that the linear model
became much more flexible, because it now has a different value for each bin, while
the decision tree model got much less flexible.
Binning features generally has no beneficial effect for tree-based models, as the model
can learn to split up the data anywhere. In a sense, that means the decision trees can
learn a binning that is particularly beneficial for predicting on this data. Additionally,
decision trees look at multiple features at once, while binning is usually done on a
per-feature basis.
However, the linear model benefited greatly in expressiveness from the transforma‐
tion of the data.
If there are good reasons to use a linear model for a particular data set, say because it
is very large and high-dimensional, but some features have non-linear relations with
the output, binning can be a great way to increase modelling power.
214 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info

Interactions and Polynomials
Another way to enrich a feature representation, in particular for linear models, is
adding interaction features and polynomial features of the original data. This kind of
feature engineering is often used in statistical modelling, but also common in many
practical machine learning applications.
As a first example, look again at Figure linear_binning above. The linear model
learned a constant value for each bin on the wave dataset. We know, however, that lin‐
ear models can not only learn offsets, but also slopes. One way to add a slope to the
linear model on the binned data, is to add the original feature (the x axis in the plot)
back in.
This leads to a 11 dimensional dataset:
X_combined = np.hstack([X, X_binned])
print(X_combined.shape)
(100, 11)
plt.plot(X[:, 0], y, 'o')
reg = LinearRegression().fit(X_combined, y)
line_combined = np.hstack([line, line_binned])
plt.plot(line, reg.predict(line_combined), label='linear regression combined')
for bin in bins:
plt.plot([bin, bin], [-3, 3], ':', c='k')
plt.legend(loc="best")
Interactions and Polynomials | 215
www.it-ebooks.info
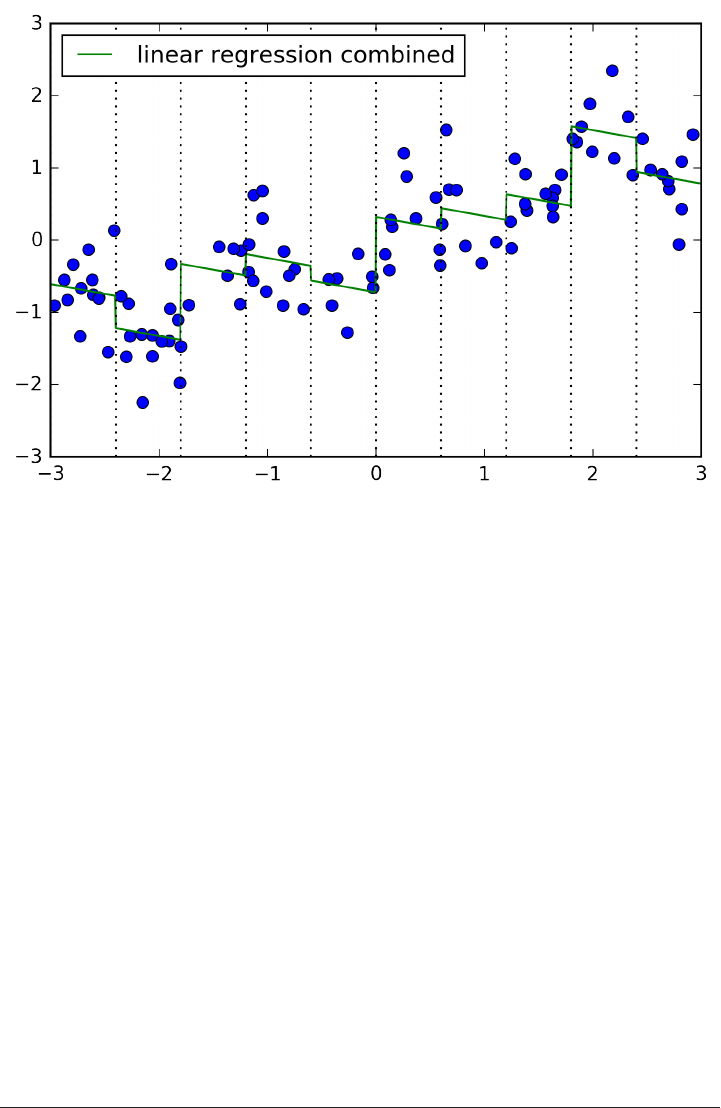
Now, the model learned an offset for each bin, together with a slope. The learned
slope is downward, and shared across all the bins - there is the single x-axis feature
which has a single slope. Because the slope is shared across all bins, it doesn’t seem to
be very helpful. We would rather have a separate slope for each bin! We can achieve
this by adding an interaction or product feature that indicates in which bin a data‐
point is and where it lies on the x-axis.
This feature is a product of the bin-indicator and the original feature. Let’s create this
dataset:
X_product = np.hstack([X_binned, X * X_binned])
print(X_product.shape)
(100, 20)
This dataset not has 20 features: the indicator for which bin a data point is in, and a
product of the original feature and the bin indicator. You can think of the product
feature as a separate copy of the x-axis feature for each bin. It is the original feature
within the bin, and zero everywhere else.
Here is the linear model on this new representation:
plt.plot(X[:, 0], y, 'o')
reg = LinearRegression().fit(X_product, y)
216 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info
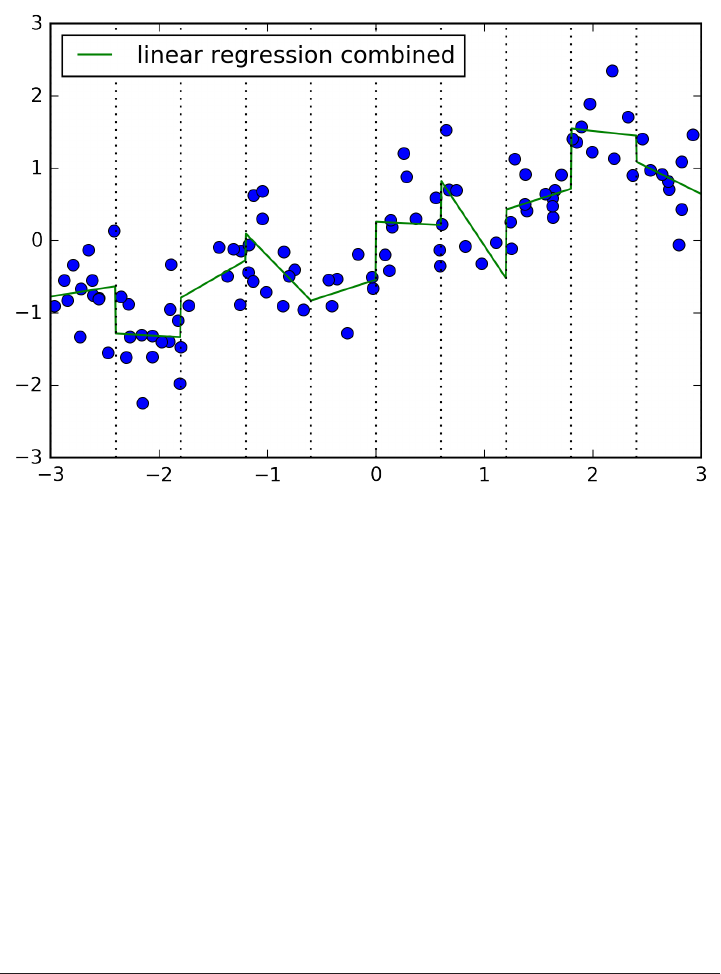
line_product = np.hstack([line_binned, line * line_binned])
plt.plot(line, reg.predict(line_product), label='linear regression combined')
for bin in bins:
plt.plot([bin, bin], [-3, 3], ':', c='k')
plt.legend(loc="best")
As you can see, now each bin has its own offset and slope in this model.
Using binning is one way to expand a continuous feature. Another one is to use poly‐
nomials of the original features.
For a given feature x, we might want to consider x ** 2, x ** 3, x ** 4 and so on.
This is implemented in PolynomialFeatures in the preprocessing module:
from sklearn.preprocessing import PolynomialFeatures
# include polynomials up to x ** 10:
poly = PolynomialFeatures(degree=10)
poly.fit(X)
X_poly = poly.transform(X)
Using a degree of 10 yields 11 features, as by default, a constant feature (x ** 0) is
added, too:
X_poly.shape
Interactions and Polynomials | 217
www.it-ebooks.info

(100, 11)
You can obtain the semantics of the features by looking at the powers_ attribute,
which gives the exponents for each feature:
poly.powers_
array([[ 0],
[ 1],
[ 2],
[ 3],
[ 4],
[ 5],
[ 6],
[ 7],
[ 8],
[ 9],
[10]])
Using polynomial features together with a linear regression model yields the classical
model of polynomial regression:
plt.plot(X[:, 0], y, 'o')
reg = LinearRegression().fit(X_poly, y)
line_poly = poly.transform(line)
plt.plot(line, reg.predict(line_poly), label='polynomial linear regression')
plt.legend(loc="best")
218 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info
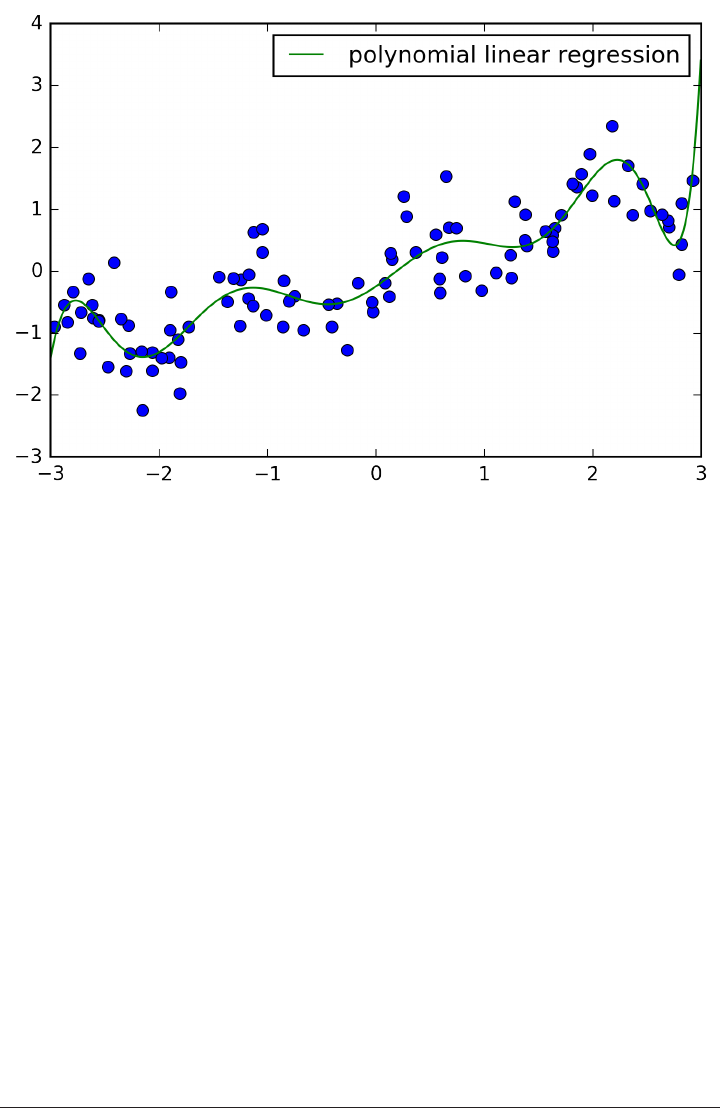
As you can see, polynomial feature yield a very smooth fit on this one-dimensional
data. However, polynomials of high degree tend to behave in extreme ways on the
boundaries or in regions of little data.
As a comparison, here is a kernel SVM model learned on the original data, without
any transformation:
from sklearn.svm import SVR
plt.plot(X[:, 0], y, 'o')
for gamma in [1, 10]:
svr = SVR(gamma=gamma).fit(X, y)
plt.plot(line, svr.predict(line), label='SVR gamma=%d' % gamma)
plt.legend(loc="best")
Interactions and Polynomials | 219
www.it-ebooks.info
Using a more complex model, a kernel SVM, we are able to learn a similarly complex
prediction to the polynomial regression without using any transformations of the fea‐
tures.
As a more realistic application of interactions and polynomials, let’s look again at the
Boston Housing data set. We already used polynomial features on this dataset in
Chapter 2. Now let us have a look at how these features were constructed, and at how
much the polynomial features help. First we load the data, and rescale it to be
between 0 and 1 using MinMaxScaler:
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
boston = load_boston()
X_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=0)
# rescale data:
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
Now, we extract polynomial features and interactions up to a degree of 2:
poly = PolynomialFeatures(degree=2).fit(X_train_scaled)
X_train_poly = poly.transform(X_train_scaled)
220 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info

X_test_poly = poly.transform(X_test_scaled)
print(X_train.shape)
print(X_train_poly.shape)
(379, 13)
(379, 105)
The data originally had 13 features, which were expanded into 105 interaction fea‐
tures. These new features represent all possible interactions between two different
original features, as well as the square of each original feature. degree=2 here means
that we look at all features that are the product of up to two original features. The
exact correspondence between input and output features can be found using the
get_feature_names method:
print(poly.get_feature_names())
['1', 'x0', 'x1', 'x2', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x9', 'x10', 'x11', 'x12', 'x0^2', 'x0 x1', 'x0 x2', 'x0 x3', 'x0 x4', 'x0 x5', 'x0 x6', 'x0 x7', 'x0 x8', 'x0 x9', 'x0 x10', 'x0 x11', 'x0 x12', 'x1^2', 'x1 x2', 'x1 x3', 'x1 x4', 'x1 x5', 'x1 x6', 'x1 x7', 'x1 x8', 'x1 x9', 'x1 x10', 'x1 x11', 'x1 x12', 'x2^2', 'x2 x3', 'x2 x4', 'x2 x5', 'x2 x6', 'x2 x7', 'x2 x8', 'x2 x9', 'x2 x10', 'x2 x11', 'x2 x12', 'x3^2', 'x3 x4', 'x3 x5', 'x3 x6', 'x3 x7', 'x3 x8', 'x3 x9', 'x3 x10', 'x3 x11', 'x3 x12', 'x4^2', 'x4 x5', 'x4 x6', 'x4 x7', 'x4 x8', 'x4 x9', 'x4 x10', 'x4 x11', 'x4 x12', 'x5^2', 'x5 x6', 'x5 x7', 'x5 x8', 'x5 x9', 'x5 x10', 'x5 x11', 'x5 x12', 'x6^2', 'x6 x7', 'x6 x8', 'x6 x9', 'x6 x10', 'x6 x11', 'x6 x12', 'x7^2', 'x7 x8', 'x7 x9', 'x7 x10', 'x7 x11', 'x7 x12', 'x8^2', 'x8 x9', 'x8 x10', 'x8 x11', 'x8 x12', 'x9^2', 'x9 x10', 'x9 x11', 'x9 x12', 'x10^2', 'x10 x11', 'x10 x12', 'x11^2', 'x11 x12', 'x12^2']
The first new feature is a constant feature, called “1” here. The next 13 features are the
original features (called “x0” to “x12”). Then follows the first feature squared
(“x0^2”) and combinations of the first and the other features.
Let’s compare the performance using Ridge on the data with and without interac‐
tions:
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train_scaled, y_train)
print("score without interactions: %f" % ridge.score(X_test_scaled, y_test))
ridge = Ridge().fit(X_train_poly, y_train)
print("score with interactions: %f" % ridge.score(X_test_poly, y_test))
score without interactions: 0.621370
score with interactions: 0.753423
Clearly the interactions and polynomial features gave us a good boost in performance
when using Ridge. When using a more complex model like a random forest, the story
is a bit different, though:
from sklearn.ensemble import RandomForestRegressor
rf = RandomForestRegressor(n_estimators=100).fit(X_train_scaled, y_train)
print("score without interactions: %f" % rf.score(X_test_scaled, y_test))
rf = RandomForestRegressor(n_estimators=100).fit(X_train_poly, y_train)
print("score with interactions: %f" % rf.score(X_test_poly, y_test))
score without interactions: 0.794226
score with interactions: 0.775016
You can see that even without additional features, the random forest beats the perfor‐
mance of Ridge. Adding interactions and polynomials actually decreases performance
slightly.
Interactions and Polynomials | 221
www.it-ebooks.info

Univariate Non-linear transformations
We just saw that adding squared or cubed features can help linear models for regres‐
sion. There are other transformations that often prove useful for transforming certain
features, in particular applying mathematical functions like log, exp or sin. While
tree-based models only care about the ordering of the features, linear models and
neural networks are very tied to the scale and distribution of each feature, and if there
is a non-linear relation between the feature and the target, that becomes hard to
model---in particular in regression. The functions log and exp can help adjusting the
relative scales in the data so that they can be captured better by a linear model or neu‐
ral network.
The sin or cos functions can come in handy when dealing with data that encodes
periodic patterns.
Most models work best when each feature (and in regression also the target) are
loosely Gaussian distributed, that is a histogram of each feature should have some‐
thing resembling the familiar bell-curve shape. Using transformations like log and
exp are a hacky, but simple and efficient way to achieve this. A particular common
case when such a transformation can be helpful is when dealing with integer count
data. By count data, we mean features like “how often did user A log in”. Counts are
never negative, and often follow particular statistical patterns. We are using a syn‐
thetic dataset of counts here, that has properties similar to those you can find in the
wild. The features are all integer, while the response is continuous:
rnd = np.random.RandomState(0)
X_org = rnd.normal(size=(1000, 3))
w = rnd.normal(size=3)
X = np.random.poisson(10 * np.exp(X_org))
y = np.dot(X_org, w)
Let’s look at the first ten entries of the first feature. All are integer and positive, but
apart from that it’s hard to make out a particular pattern:
If we count the appearance of each value, the distribution of values becomes more
clear:
np.bincount(X[:, 0])
array([17, 44, 65, 42, 62, 57, 51, 46, 59, 42, 39, 35, 28, 28, 25, 20, 32,
22, 16, 14, 20, 12, 7, 21, 12, 9, 18, 8, 11, 10, 8, 10, 4, 6,
6, 0, 4, 4, 4, 2, 2, 4, 1, 3, 10, 2, 1, 4, 2, 3, 2,
1, 2, 1, 3, 2, 1, 1, 3, 1, 0, 2, 1, 1, 4, 2, 0, 0,
0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 2, 1, 1, 1, 1, 1,
222 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info
0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0,
0, 2, 1, 2, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 1, 1])
The value 2 seems to be the most common with 62 appearances (bincount always
starts at 0), and the counts for higher values fall quickly. However, there are some
very high values, like 134 appearing twice. We visualized the counts below:
bins = np.bincount(X[:, 0])
plt.bar(range(len(bins)), bins, color='w')
plt.ylabel("number of appearances")
plt.xlabel("value")
Features X[:, 1] and X[:, 2] have similar properties. This kind of distribution of
values (many small ones, and a few very large ones) is very common in practice [foot‐
note: This is a Poisson distribution, which is quite fundamental to count data]. How‐
ever, it is something most linear models can’t handle very well. Let’s try to fit a Ridge
regression to this model:
from sklearn.linear_model import Ridge
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
Ridge().fit(X_train, y_train).score(X_test, y_test)
0.61099786602482975
Univariate Non-linear transformations | 223
www.it-ebooks.info
Applying a logarithmic transformation can help, though. Because the value 0 appears
in the data (and the logarithm is not defined at 0), we can not actually just apply log,
but we have to compute log(X + 1):
X_train_log = np.log(X_train + 1)
X_test_log = np.log(X_test + 1)
After the transformation, the distribution of the data is less asymmetrical and doesn’t
have very large outliers any more:
plt.hist(np.log(X_train_log[:, 0] + 1), bins=25, color='w');
Building a ridge model on the new data provides a much better fit:
Ridge().fit(X_train_log, y_train).score(X_test_log, y_test)
0.85919272057341256
Finding the transformation that works best for each combination of dataset and
model is somewhat of an art. In this example, all the features had the same properties.
This is rarely the case in practice, and usually only a subset of the features should be
transformed, or sometimes each feature needs be transformed in a different way. As
we mentioned above, these kind of transformations are irrelevant for tree-based
models, but might be essential for linear models.
Sometimes it is also a good idea to transform the target variable y in regression. Try‐
ing to predict counts (say, number of orders) is a fairly common task, and using the
224 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info

log(y + 1) transformation often helps [footnote: this is a very crude approximation
of using Poisson regression, which would be the proper solution from a probabilistic
standpoint.]
As you saw in the examples above, binning, polynomials and interactions can have a
huge influence on how models perform on a given dataset. This is in particularly true
for less complex models like linear models and naive Bayes.
Tree-based models on the other hand are often able to discover important interac‐
tions themselves, and don’t require transforming the data explicitly most of the time.
Other models like SVMs, nearest neighbors and neural networks might sometimes
benefit from using binning, interactions or polynomials, but the implications there
are usually much less clear than in the case of linear models.
Automatic Feature Selection
With so many ways to create new features, you might get tempted to increase the
dimensionality of the data way beyond the number of original features. However,
adding more features makes all models more complex, and so increases the chance of
overfitting. When adding new features, or with high-dimensional datasets in general,
it can be a good idea to reduce the number of features to only the most useful ones,
and discard the rest. This can lead to simpler models that generalize better.
But how can you know how good each feature is?
There are three basic strategies: Univariate statistics, model-based selection and itera‐
tive selection. We will discuss all three of them in detail. All three of these methods are
supervised methods, meaning they need the target for fitting the model. This means
we do need to split the data into training and test set
and fit the feature selection only on the training part of the data.
Univariate statistics
In univariate statistics, we compute whether there is a statistically significant relation‐
ship between each feature and the target. Then the features that are related with the
highest confidence are selected. In the case of classification, this is also known as
analysis of variance (ANOVA).
A key property of these tests are that they are univariate meaning that they only con‐
sider each feature individually. Consequently a feature will be discarded if it is only
informative when combined with another feature. Univariate tests are often very fast
to compute, and don’t require building a model. On the other hand, they are com‐
pletely independend of the model that you might want to apply after the feature selec‐
tion.
Automatic Feature Selection | 225
www.it-ebooks.info

To use univariate feature selection in scikit-learn, you need to choose a test, usually
either f_classif (the default) for classification or f_regression for regression, and a
method to discard features based on the p-values determined in the test. All methods
for discarding parameters use a threshold to discard all features with too high a p-
values (which means they are unlikely to be related to the target). The methods differ
in how they compute this threshold, with the simplest ones being SelectKBest which
selects a fixed number k of features, and SelectPercentile, which selectes a fixed
percentage of features.
Let’s apply the feature selection for classification on the cancer dataset. To make the
task a bit harder, we add some non-informative noise features to the data. We expect
the feature selection to be able to identify the features that are non-informative and
remove them.
from sklearn.datasets import load_breast_cancer
from sklearn.feature_selection import SelectPercentile
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
# get deterministic random numbers
rng = np.random.RandomState(42)
noise = rng.normal(size=(len(cancer.data), 50))
# add noise features to the data
# the first 30 features are from the dataset, the next 50 are noise
X_w_noise = np.hstack([cancer.data, noise])
X_train, X_test, y_train, y_test = train_test_split(
X_w_noise, cancer.target, random_state=0, test_size=.5)
# use f_classif (the default) and SelectPercentile to select 10% of features:
select = SelectPercentile(percentile=50)
select.fit(X_train, y_train)
# transform training set:
X_train_selected = select.transform(X_train)
print(X_train.shape)
print(X_train_selected.shape)
(284, 80)
(284, 40)
As you can see, the number of features was reduced from 80 to 40 (50 percent of the
original number of features). We can find out which features have been selected using
the get_support method, which returns a boolean mask of the selected features:
mask = select.get_support()
print(mask)
# visualize the mask. black is True, white is False
plt.matshow(mask.reshape(1, -1), cmap='gray_r')
226 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info

[ True True True True True True True True True False True False
True True True True True True False False True True True True
True True True True True True False False False True False True
False False True False False False False True False False True False
False True False True False False False False False False True False
True False False False False True False True False False False False
True True False True False False False False]
As you can see from the visualization of the mask above, most of the selected features
are the original features, and most of the noise features were removed. However, the
recovery of the original features is not perfect.
Let’s compare the performance of logistic regression on all features against the perfor‐
mance using only the selected features:
from sklearn.linear_model import LogisticRegression
# transform test data:
X_test_selected = select.transform(X_test)
lr = LogisticRegression()
lr.fit(X_train, y_train)
print("Score with all features: %f" % lr.score(X_test, y_test))
lr.fit(X_train_selected, y_train)
print("Score with only selected features: %f" % lr.score(X_test_selected, y_test))
Score with all features: 0.929825
Score with only selected features: 0.940351
In this case, removing the noise features improved performance, even though some
of the original features where lost. This was a very simple synthetic example, though,
and outcomes on real data is usually mixed. Univariate feature selection can still be
very helpful if there is such a large number of features that building a model on them
is infeasible, or if you suspect that many features are completely uninformative.
Model-based Feature Selection
Model based feature selection uses a supervised machine learning model to judge the
importance of each feature, and keeps only the most important ones. The supervised
model that is used for feature selection doesn’t need to be the same model that is used
for the final supervised modeling.
Automatic Feature Selection | 227
www.it-ebooks.info

The model that is used for feature selection needs to provide some measure of impor‐
tance for each feature, so that they can be ranked by this measure. Decision trees and
decision tree based models provide feature importances, which can be used; Linear
models have coefficients which can be used by considering the absolute value. As we
saw in Chapter 2, linear models with L1 penalty learn sparse coefficients, which only
use a small subset of features. This can be viewed as a form of feature selection for the
model itself, but can also be used as a preprocessing step to select features for another
model.
In contrast to univariate selection, model-based selection considers all features at
once, and so can capture interactions (if the model can capture them).
To use model based feature selection, we need to use the SelectFromModel trans‐
former:
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestClassifier
select = SelectFromModel(RandomForestClassifier(n_estimators=100, random_state=42), threshold="median")
The SelectFromModel class selects all features that have an importance measure of
the feature (as provided by the supervised model) greater than the provided thresh‐
old. To get a comparable result to what we got with univariate feature selection, we
used the median as a threshold, so that half of the features will be selected. We use a
random forest classifier with 100 trees to compute the feature importances. This is a
quite complex model and much more powerful than using univariate tests. Now let’s
actually fit the model:
select.fit(X_train, y_train)
X_train_l1 = select.transform(X_train)
print(X_train.shape)
print(X_train_l1.shape)
(284, 80)
(284, 40)
Again, we can have a look at the features that were selected:
mask = select.get_support()
# visualize the mask. black is True, white is False
plt.matshow(mask.reshape(1, -1), cmap='gray_r')
This time, all but two of the original features were selected. Because we specified to
select 40 features, some of the noise features are also selected.
X_test_l1 = select.transform(X_test)
LogisticRegression().fit(X_train_l1, y_train).score(X_test_l1, y_test)
0.9508771929824561
228 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info

With the better feature selection, we also gained some improvements in performance.
Iterative feature selection
In univariate testing, we build used no model, while in model based selection we used
a single model to select features. In iterative feature selection, a series of models is
built, with varying numbers of features. There are two basic methods: starting with
no features and adding features one by one, until some stopping criterion is reached,
or starting with all features and removing features one by one, until some stopping
criterion is reached. Because a series of models is built, these methods are much more
computationally expensive then the methods we discussed above. One particular
method of this kind is recursive feature elimination (RFE) which starts with all fea‐
tures, builds a model, and discards the least important feature according to the
model. Then, a new model is built, using all but the discarded feature, and so on, until
only a pre-specified number of features is left. For this to work, the model used for
selection needs to provide some way to determine feature importance, as was the case
for the model based selction.
We use the same random forest model that we used above:
from sklearn.feature_selection import RFE
select = RFE(RandomForestClassifier(n_estimators=100, random_state=42), n_features_to_select=40)
#select = RFE(LogisticRegression(penalty="l1"), n_features_to_select=40)
select.fit(X_train, y_train)
# visualize the selected features:
mask = select.get_support()
plt.matshow(mask.reshape(1, -1), cmap='gray_r')
The feature selection got better compared to the univariate and model based selec‐
tion, but one feature was still missed. Running the above code takes significantly
longer than the model based selection, because a random forest model is trained 40
times, once for each feature that is dropped.
X_train_rfe= select.transform(X_train)
X_test_rfe= select.transform(X_test)
LogisticRegression().fit(X_train_rfe, y_train).score(X_test_rfe, y_test)
0.9508771929824561
We can also use the model used inside the RFE to make predictions. This uses only
the feature set that was selected:
select.score(X_test, y_test)
0.9508771929824561
Automatic Feature Selection | 229
www.it-ebooks.info

If you are unsure when selecting what to use as input to your machine learning algo‐
rithms, automatic feature selection can be quite helpful. It is also great to reduce the
amount of features needed, for example to speed up prediction, or allow for more
interpretable models. In most real-world cases, applying feature selection is unlikely
to provide large gains in performance. However, it is still a valuable tool in the tool‐
box of the feature engineer.
Utilizing Expert Knowledge
Feature engineering is often an important place to use expert knowledge for a particu‐
lar application. While the purpose of machine learning often is to avoid having to
create a set of expert-designed rules, that doesn’t mean that prior knowledge of the
application or domain should be discarded. Often, domain experts can help in identi‐
fying useful features that are much more informative than the initial representation of
the data.
Imagine you are a travel agency and want to predict flight prices. Let’s say we have a
record of prices together with date, airline, start location and destination. A machine
learning model might be able to build a decent model from that. Some important fac‐
tors in flight prices, however can not be learned. For example, flights are usually more
expensive during school holidays or around public holidays. While some holidays can
potentially be learned from the dates, like Christmas, others might depend on the
phases of the moon (like Hannukah and Easter), or be set by authorities like school
holidays. These events can not be learned from the data if each flight is only recorded
using the (Gregorian) date. It is easy to add a feature that encodes whether a flight
was on, preceding, or following a public or school holiday. In this way, prior knowl‐
edge about the nature of the task can be encoded in the features to aid a machine
learning algorithm. Adding a feature does not force a machine learning algorithm to
use it, and even if the holiday information turns out to be non-informative for flight
prices, augmenting the data with this information doesn’t hurt.
We’ll now go through one particular case of using expert knowledge - though in this
case is might be more rightfully called “common sense”. The task is predicting citibike
rentals in front of Andreas’ house.
In New York, there is a network of bicycle rental stations, with a subscription system.
The stations are all over the city and provide a convenient way to get around. Bike
rental data is made public in an anonymized form [Footnote: at https://www.citibike‐
nyc.com/system-data] and has been analyzed in various ways.
The task we want to solve is to predict for a given time and day how many people will
rent a bike in front of Andreas’ house - so he knows if any bikes will be left for him.
We first load the data for August 2015 of this particular station as a pandas dataframe.
We resampled the data into 3 hour intervals to obtain the main trends for each day.
230 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info
from importlib import reload
reload(mglearn.datasets)
citibike = mglearn.datasets.load_citibike()
/home/andy/checkout/book/notebooks/mglearn/datasets.py:40: FutureWarning: how in .resample() is deprecated
the new syntax is .resample(...).sum()
data_resampled = data_starttime.resample("3h", how="sum").fillna(0)
citibike.head()
starttime
2015-08-01 00:00:00 3.0
2015-08-01 03:00:00 0.0
2015-08-01 06:00:00 9.0
2015-08-01 09:00:00 41.0
2015-08-01 12:00:00 39.0
Freq: 3H, Name: one, dtype: float64
Below is a visualization of the rental frequencies for the whole month:
plt.figure(figsize=(10, 3))
xticks = pd.date_range(start=citibike.index.min(), end=citibike.index.max(), freq='D')
plt.xticks(xticks, xticks.strftime("%a %m-%d"), rotation=90, ha="left")
plt.plot(citibike, linewidth=2)
Looking at the data, we can clearly distinguish day and night for each day. The pat‐
terns for week days and weekends also seem to be quite different.
When evaluating a prediction task on a time series like this, we usually want to learn
from the past and predict for the future. This means when doing a split into a training
Utilizing Expert Knowledge | 231
www.it-ebooks.info

and a test set, we want to use all the data up to a certain date as training set, and all
the data past that date as a test set. This is how we would usually use time series pre‐
diction: given everything that we know about rentals in the past, what do we think
will happen tomorrow?
We will use the first 184 data points, corresponding to the first 23 days, as our train‐
ing set, and the remaining 64 data points corresponding to the remaining 8 days as
our test set.
The only feature that we are using in our prediction task is the date and time when a
particular number of rentals occurred. So the input feature is the time, say
2015-08-01 00:00:00, and the output is the number of rentals in the following three
hours, 3 in this case (according to the dataframe above).
A (surprisingly) common way that dates are stored on computers is using POSIX
time, which is the number of seconds since January 1970 00:00:00 (aka the beginning
of time). As a first try, we can use this single integer feature as our data representa‐
tion:
# extract the target values (number of rentals)
y = citibike.values
# convert the time to posixtime using "%s"
X = citibike.index.strftime("%s").astype("int").reshape(-1, 1)
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
We first define a function to split the data into training and test set, build the model,
and visualize the result:
# use the first 184 data points for training, the rest for testing
n_train = 184
# function to evaluate and plot a regressor on a given feature set
def eval_on_features(features, target, regressor):
# split the given features into a training and test set
X_train, X_test = features[:n_train], features[n_train:]
# split also the
y_train, y_test = target[:n_train], target[n_train:]
regressor.fit(X_train, y_train)
print("Test-set R^2: ", regressor.score(X_test, y_test))
y_pred = regressor.predict(X_test)
y_pred_train = regressor.predict(X_train)
plt.figure(figsize=(10, 3))
plt.xticks(range(0, len(X), 8), xticks.strftime("%a %m-%d"), rotation=90, ha="left");
plt.plot(range(n_train), y_train, label="train", linewidth=2)
plt.plot(range(n_train, len(y_test) + n_train), y_test, label="test", linewidth=2)
plt.plot(range(n_train), y_pred_train, label="prediction train", linewidth=2)
232 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info
plt.plot(range(n_train, len(y_test) + n_train), y_pred, label="prediction test", linewidth=2)
plt.legend(loc=(1.01, 0))
We saw above that random forests need very little preprocessing of the data, which
makes it seem like a good model to start with.
We use the POSIX time feature X and pass a random forest regressor to our
eval_on_features function:
regressor = RandomForestRegressor(n_estimators=100, random_state=0)
plt.figure()
eval_on_features(X, y, regressor);
Test-set R^2: -0.035486463626
The predictions on the training set are quite good, as is usual for random forests.
However, for the test set, a constant line is predicted. The R^2 is -0.03, which means
that we learned nothing. What happened?
The problem lies in the combination of our feature and the random forest. The value
of the POSIX time feature for the test set is outside of the range of the feature values
on the training set: the points in the test set have time stamps that are later than all
the points in the training set.
Trees, and therefore random forests, can not extrapolate to feature ranges outside the
training set.
The result is that the model simply predicts the same as for the closest point in the
training set - which is the last time it observed any data.
Clearly we can do better than this. This is where our “expert knowledge” comes in.
From looking at the rental figures on the training data, two factors seem to be very
important: the time of day, and the day of the week. So let’s add these two features. We
can’t really learn anything from the POSIX time, so we drop that feature.
First, let’s use only the hour of the day:
X_hour = citibike.index.hour.reshape(-1, 1)
eval_on_features(X_hour, y, regressor)
Utilizing Expert Knowledge | 233
www.it-ebooks.info
Test-set R^2: 0.599577599331
Now the predictions have the same pattern for each day of the week. The $R^2$ is
already much better, but the predictions clearly miss the weekly pattern. Now let’s
also add the day of the week:
X_hour_week = np.hstack([citibike.index.dayofweek.reshape(-1, 1), citibike.index.hour.reshape(-1, 1)])
eval_on_features(X_hour_week, y, regressor)
Test-set R^2: 0.841948858797
Now, we have a model that models the periodic behavior considering day of week and
time of day. It has an $R^2$ of 0.84, and show pretty good predictive performance.
What this model likely is learning is the mean number of rentals for each combina‐
tion of weekday and time of day from the first 23 days of August. This would actually
not require a complex model like a random forest.
So let’s try with a simpler model, LinearRegression:
eval_on_features(X_hour_week, y, LinearRegression())
234 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info
Test-set R^2: 0.132041572622
Linear Regression works much worse, and the periodic pattern looks odd. The reason
for this is that we encoded day of the week and time of the day using integers, which
are interpreted as categorical variables. Therefore, the linear model can only learn a
linear function of the time of day - and it learned that later in the day, there are more
rentals. However, the patterns are much more complex that that, which we can cap‐
ture by interpreting the integers as categorical variables, by transforming them using
OneHotEncoder:
enc = OneHotEncoder()
X_hour_week_onehot = enc.fit_transform(X_hour_week).toarray()
eval_on_features(X_hour_week_onehot, y, Ridge())
Test-set R^2: 0.619113916866
This gave us a much better match than the continuous feature encoding. Now, the lin‐
ear model learns one coefficient for each day of the week, and one coefficient for each
time of the day. That means that the “time of day” pattern is shared over all days of
the week, though.
Using interaction features, we can allow the model to learn one coefficient for each
combination of day and time of day:
poly_transformer = PolynomialFeatures(degree=2, interaction_only=True, include_bias=False)
X_hour_week_onehot_poly = poly_transformer.fit_transform(X_hour_week_onehot)
Utilizing Expert Knowledge | 235
www.it-ebooks.info
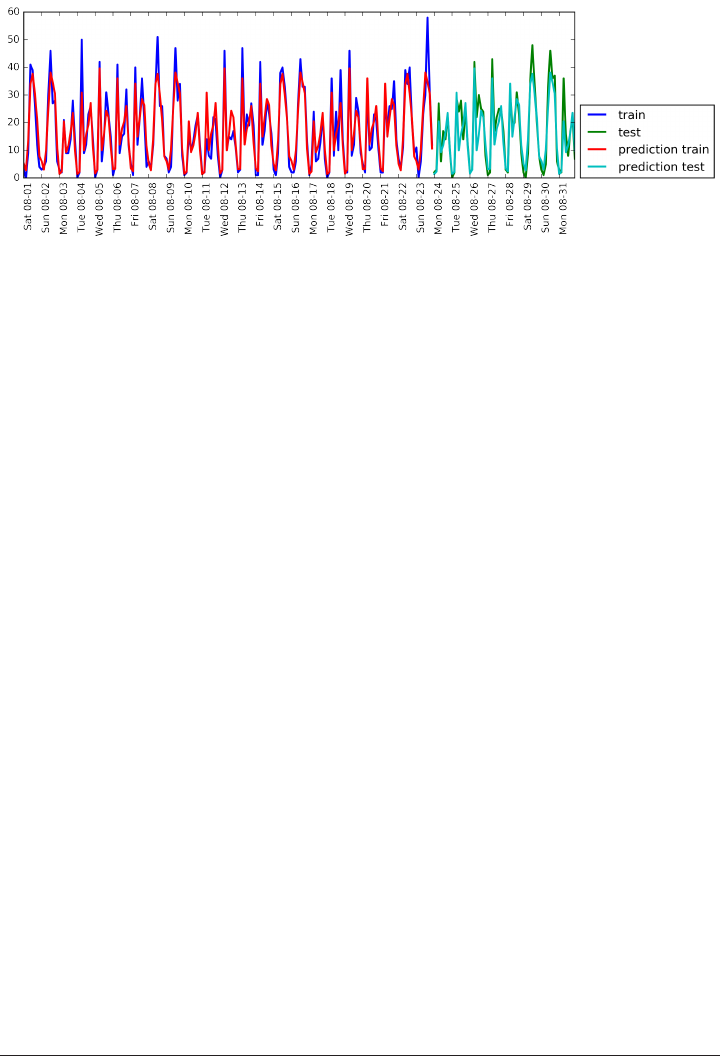
lr = Ridge()
eval_on_features(X_hour_week_onehot_poly, y, lr)
Test-set R^2: 0.845170635797
This transformation finally yields a model that performs similarly well to the random
forest.
A big benefit of this model is that it is very clear what is learned: one coefficient for
each day and time.
We can simply plot the coefficients learned by the model, something that would not
be possible for the random forest.
First, we create feature names for the hour and day features:
hour = ["%02d:00" % i for i in range(0, 24, 3)]
day = ["Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun"]
features = day + hour
Then we name all the interaction feature extracted by the PolynomialFeatures, using
the get_feature_names method, and keep only the feature with non-zero coeffi‐
cients:
features_poly = poly_transformer.get_feature_names(features)
features_nonzero = np.array(features_poly)[lr.coef_ != 0]
coef_nonzero = lr.coef_[lr.coef_ != 0]
Now we can visualize the coefficients learned by the linear model:
plt.figure(figsize=(15, 2))
plt.plot(coef_nonzero, 'o')
plt.xticks(np.arange(len(coef_nonzero)), features_nonzero, rotation=90);
236 | Chapter 5: Representing Data and Engineering Features
www.it-ebooks.info

Summary and outlook
In this chapter, we discussed how to deal with different data types, in particular with
categorical variables.
We emphasized the importance of representing your data in a way that is suitable for
the machine learning algorithm, for example by one-hot-encoding categorical vari‐
ables.
We also discussed the importance of engineering new features, and the possibility of
utilizing expert knowledge in creating derived features from your data.
In particular linear models might benefit greatly from generating new features via
binning and adding polynomials and interactions, while more complex, nonlinear
models like random forests and SVMs might be able to learn more complex tasks
without explicitly expanding the feature space.
In practice, the features that are used, and the match between features and method is
often the most important piece in making a machine learning approach work well.
Having our data represented in an appropriate way, and knowing which algorithm to
use for which task, the next chapter will focus on evaluating performance of machine
learning models and selecting the right parameter settings.
Summary and outlook | 237
www.it-ebooks.info

CHAPTER 6
Model evaluation and improvement
Having discussed the fundamentals of supervised and unsupervised learning, and
having explored a variety of machine learning algorithms, we will now dive more
deeply into evaluating models and selecting parameters.
We will focus on the supervised methods, regression and classification, as evaluating
and selecting models in unsupervised learning is often a very qualitative process (as
we have seen in Chapter 3).
To evaluate our supervised models, so far we have split our data set in to a training set
and a test set using the train_test_split function, built a model on the training set
calling the fit method, and evaluated it on the test set using the score method,
which, for classification, computes the fraction of correctly classified samples:
from sklearn.datasets import make_blobs
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
# create a synthetic dataset
X, y = make_blobs(random_state=0)
# split data and labels into a training and a test set
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# Instantiate a model and fit it to the training set
logreg = LogisticRegression().fit(X_train, y_train)
# evaluate the model on the test set
logreg.score(X_test, y_test)
# we predicted the correct class on 88% of the samples in X_test
0.88
As a reminder, the reason we split our data into training and test sets is that we are
interested in measuring how well our model generalizes to new, unseen data. We are
239
www.it-ebooks.info

not interested in how well our model fit the training set, but rather, how well it can
make predictions for data that was not observed during training.
In this chapter, we will expand on two aspects of this evaluation. We will a) introduce
cross-validation, a more robust way to assess generalization performance than a single
split of the data into a training and a test set and b) discuss methods to evaluate clas‐
sification and regression performance that go beyond the default measures of accu‐
racy and $R^2$ provided by the score method.
We will also discuss grid search, an effective method for adjusting the parameters in
supervised models for the best generalization performance.
Cross-validation
Cross-validation is a statistical method to evaluate generalization performance in a
more stable and thorough way than using a split into training and test set.
In cross-validation, instead of splitting the data set in to a training set and a test set,
the data is split repeatedly and multiple models are trained.
The most commonly used version of cross-validation is k-fold cross-validation, where
k is a user specified number, usually five or ten. When performing five-fold cross-
validation, the data is first partitioned into five parts of (approximately) equal size,
called folds.
Next, a sequence of models is trained. The first model is trained using the first fold as
the test set, and the remaining folds 2-5 as the training set. The model is build using
the data in the folds 2-5, and then the accuracy is evaluated on fold 1.
Then another model is build, this time using fold 2 as the test set, and the data in
folds 1, 3, 4 and 5 as the training set.
This process is repeated using the folds 3, 4 and 5 as test sets. For each of these five
splits of the data into training and test set, we computed the accuracy. In the end, we
have collected five accuracy values.
The process is illustrated in Figure cross_validation.
Usually, the first fifth of the data is the first fold, the second fifth of the data is the
second fold, and so on.
mglearn.plots.plot_cross_validation()
240 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

Cross-validation in scikit-learn
Cross-validation is implemented in scikit-learn using the cross_val_score function
from the model_selection module.
The parameters of the cross_val_score function are the model we want to evaluate,
the training data and the ground-truth labels. Let’s evaluate LogisticRegression on
the iris dataset:
from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
iris = load_iris()
logreg = LogisticRegression()
scores = cross_val_score(logreg, iris.data, iris.target)
print("cross-validation scores: ", scores)
cross-validation scores: [ 0.961 0.922 0.958]
By default, cross_val_score performs three-fold cross-validation, returning three
accuracy values.
We can change the number of folds used by changing the cv parameter:
scores = cross_val_score(logreg, iris.data, iris.target, cv=5)
scores
array([ 1. , 0.967, 0.933, 0.9 , 1. ])
A common way to summarize the cross-validation accuracy is to compute the mean:
scores.mean()
0.96000000000000019
Benets of cross-validation
There are several benefits of using cross-validation instead of a single split into a
training and test set.
First, remember that train_test_split performs a random split of the data. Imagine
that we are “lucky” when randomly splitting the data, and all examples that are hard
Benets of cross-validation | 241
www.it-ebooks.info

to classify are in the training set. Then, the test set will only contain “easy” examples,
and our test set accuracy will be unrealistically high. Conversely, if we are “unlucky”,
we might have randomly put all the hard to classify examples in the test set, and
obtain an unrealistically low score.
However, when using cross-validation, each example will be in the training set exactly
once: each example is in one of the folds, and each fold is the test set once. Therefore
the model needs to generalize well to all of the samples in the data set for all of the
cross-validation scores (and their mean) to be high.
Having multiple splits of the data also provides some information about how sensi‐
tive our model is to the selection of the training dataset. Looking at the scores for the
iris dataset above, we see accuracies between 90% and 100%. This is quite a range,
and provides us with an idea about how the model might perform in the worst case
and the best case scenarios when applied to new data.
Another benefit of cross-validation as compared to using a single split of the data is
that we use our data more effectively. When using train_test_split, we usually use
75% of the data for training and 25% of the data for evaluation, which is a good rule
of thumb. When using five-fold cross-validation, in each iteration we can use 4/5 of
the data (or 80% of our data) to fit the model. When using ten-fold cross-validation,
we can use 9/10 of the data (90%)to fit the model. More data will usually result in
more accurate models.
The main disadvantage of cross-validation is increased computational cost. As we are
now training k models, instead of a single model, cross-validation will be roughly k
times slower than doing a single split of the data.
[info box] It is important to keep in mind that cross-validation is not a way to build a
model that can be applied to new data. Cross-validation does not return a model.
When calling cross_val_score, multiple models are build internally, but the purpose
of cross-validation is only to evaluate how well a given algorithm will generalize when
trained on a specific dataset. [/end infobox]
Stratied K-Fold cross-validation and other strategies
Splitting the dataset into k-folds by starting with the first 1/k-th part of the data as
described above might not always be a good idea. Let’s have a look at the iris dataset
for example:
from sklearn.datasets import load_iris
iris = load_iris()
print(iris.target)
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
242 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
As you can see above, the first third of the data is the class 0, the second third is the
class 1, and the last third is class 2. Imagine doing three-fold cross-validation on this
dataset. The first fold would be only class 0, so in the first split of the data, the test set
would be only class zero, and the training set would be only class 1 and 2.
As the classes in training and test set would be different for all three splits, the three-
fold cross-validation accuracy would be zero on this dataset. That is not very helpful,
as we can do much better than 0% accuracy on iris.
As the simple k-fold strategy fails here, scikit-learn does not use k-fold for classifica‐
tion, but rather stratied k-fold cross-validation. In stratified cross-validation, we split
the data such that the proportions between classes are the same in each fold as they
are in the whole dataset, as illustrated in Figure stratified_kfold.
For example, if 90% of your samples belong to class A, and 10% of your samples
belong to class B, then stratified cross-validation ensures that in each fold, 90% of
samples belong to class A and 10% of samples belong to class B.
It is always a good idea to use stratified k-fold cross-validation instead of k-fold cross-
validation to evaluate a classifier, because it results in more reliable estimates of gen‐
eralization performance. In the case of only 10% of samples belonging to class B,
using standard k-fold cross-validation, it might easily happen that one fold only con‐
tains samples of class A. Using this fold as a test-set would not be very informative of
the overall performance of the classifier.
For regression, scikit-learn uses the standard k-fold cross-validation by default. It
would be possibly to also try to make each fold representative of the different values
the regression target has, but this is not a commonly used strategy and would be sur‐
prising to most users.
mglearn.plots.plot_stratified_cross_validation()
Stratied K-Fold cross-validation and other strategies | 243
www.it-ebooks.info

More control over cross-validation
We saw above that we can adjust the number of folds that are used in
cross_val_score using the cv parameter. However, scikit-learn allows for much finer
control over what happens during the splitting of the data, by providing a cross-
validation splitter as the cv parameter.
For most use cases, the default of k-fold cross validation for regression and stratified
k-fold for classification work well, but there are some cases when you might want to
use a different strategy.
Say for example we want to use the standard k-fold cross-validation on a classifica‐
tion dataset, to reproduce someone else’s results. To do this, we first have to import
the KFold splitter class from the model_selection module, and instantiate it with the
number of folds you want to use:
from sklearn.model_selection import KFold
kfold = KFold(n_folds=5)
Then, we can pass the kfold splitter object as the cv parameter to cross_val_score:
cross_val_score(logreg, iris.data, iris.target, cv=kfold)
array([ 1. , 0.933, 0.433, 0.967, 0.433])
This way, we can verify that it is indeed a really bad idea to use 3-fold (non-stratified)
cross-validation on the iris dataset:
kfold = KFold(n_folds=3)
cross_val_score(logreg, iris.data, iris.target, cv=kfold)
array([ 0., 0., 0.])
Remember: each fold corresponds to one of the classes, and so nothing can be
learned. [specify again that this is on the iris dataset, it’s a little unclear]
Another way to resolve this problem instead of stratifying the folds is to shuffle the
data, to remove the ordering of the samples by label. We can do that setting the shuf
244 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info
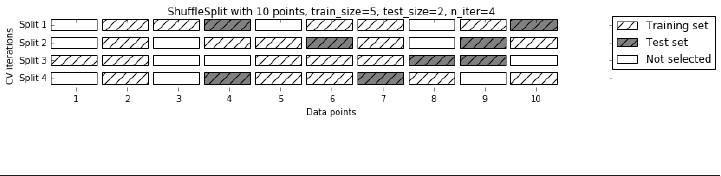
fle parameter of KFold to True. If we shuffle the data, we also need to fix the ran
dom_state to get a reproducible shuffling. Otherwise, each run of cross_val_score
would yield a different result, as each time a different split would be used (this might
not be a problem, but can be surprising).
kfold = KFold(n_folds=3, shuffle=True, random_state=0)
cross_val_score(logreg, iris.data, iris.target, cv=kfold)
array([ 0.9 , 0.96, 0.96])
Leave-One-Out cross-validation
Another frequently used cross-validation method is leave-one-out. You can think of
leave-one-out cross-validation as k-fold cross-validation where each fold is a single
sample. For each split, you pick a single data point to be the test set. This can be very
time-consuming, in particular for large datasets, but sometimes provides better esti‐
mates on small datasets:
from sklearn.model_selection import LeaveOneOut
loo = LeaveOneOut()
scores = cross_val_score(logreg, iris.data, iris.target, cv=loo)
print("number of cv iterations: ", len(scores))
print("mean accuracy: ", scores.mean())
number of cv iterations: 150
mean accuracy: 0.953333333333
Shue-Split cross-validation
Another, very flexible strategy for cross validation is shue-split cross-validation. In
shuffle-split cross-validation, each split samples train_size many points for the
training set, and test_size many (disjoint) point for the test set. This splitting is
repeated n_iter many times. Figure shuffle_split illustrates running four iterations of
splitting a dataset consisting of 10 points, with a training set of 5 points and a test set
of 2 points each.
You can use integers for train_size and test_size to use absolute sizes of these sets,
or floating points numbers, to use fractions of the whole dataset.
mglearn.plots.plot_shuffle_split()
shuffle_split
More control over cross-validation | 245
www.it-ebooks.info

The following code splits the dataset into 50% training set and 50% test set for ten
iterations:
from sklearn.model_selection import ShuffleSplit
shuffle_split = ShuffleSplit(test_size=.5, train_size=.5, n_iter=10)
cross_val_score(logreg, iris.data, iris.target, cv=shuffle_split)
array([ 1. , 0.933, 0.88 , 0.933, 0.853, 0.973, 0.787, 0.947,
0.92 , 0.973])
Shuffle-split cross-validation allows for control over the the number of iterations
independently of the training and test sizes, which can sometimes be helpful. It also
allows for using only part of the data in each iteration, by providing train_size and
test_size settings that don’t add up to one. Subsampling the data in this way can be
useful for experimenting with large datasets.
There is also a stratified variant of ShuffleSplit, aptly named StratifiedShuffleS
plit, which can provide more reliable results for classification tasks.
Cross-validation with groups
Another very common setting for cross-validation is when there are groups in the
data that are highly related.
Say you want to build a system to recognize emotions from pictures of faces, and you
collect a dataset of pictures of 100 people where each person is captured multiple
times, showing various emotions. The goal is to build a classifier that can correctly
identify emotions of people not in the dataset.
You could use the default stratified cross-validation to measure the performance of a
classifier here. However, it is likely that pictures of the same person will be in the
training and the test set. It will be much easier for a classifier to detect emotions in a
face that is part of the training set, compared to a completely new face.
To accurately evaluate the generalization to new faces, we must therefore ensure that
the training and test set contain images of different people.
To achieve this, we can use LabelKFold, which takes a label argument, which we can
use to indicate which person is in the image. So label here indicates groups in the
data that should not be split when creating training and test set, and should not be
confused with the class label.
This example of groups in the data is common in medical applications, where you
might have multiple samples from the same patient, but are interested in generalizing
to new patients. Similarly, in speech recognition, you might have multiple recordings
of the same speaker in you dataset, but are interested in recognizing speech of new
speakers.
246 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

Below is an example of using a synthetic dataset with a grouping given by the labels
list. The dataset consists of 12 data points, and for each of the data points, labels
specifies which group (think patient) the point belongs to. The labels specify there are
four groups, and the first three samples belong to the first group, the next four sam‐
ples belong to the second group, and so on. The samples don’t need to be ordered by
group, we just did this for illustration purposes. The splits that are calculated based
on these labels are visualized in Figure label_kfold.
As you can see, for each split, each group is either entirely in the training set, or
entirely in the test set.
print("label_kfold")
mglearn.plots.plot_label_kfold()
label_kfold
from sklearn.model_selection import LabelKFold
# create synthetic dataset
X, y = make_blobs(n_samples=12, random_state=0)
# assume the first three samples belong to the same group, then the next four etc.
labels = [0, 0, 0, 1, 1, 1, 1, 2, 2, 3, 3, 3]
cross_val_score(logreg, X, y, labels, cv=LabelKFold(n_folds=3))
array([ 0.75 , 0.8 , 0.667])
There are more splitting strategies for cross-validation in scikit-learn, which you can
find in the scikit-learn user guide, which allow for even more different use-cases.
However, the standard KFold, StratifiedKFold and LabelKFold are by far the most
commonly used ones.
Grid Search
Now that we know how to evaluate how well a model generalizes, we can do the next
step and improve the model’s generalization performance by tuning its parameters.
We discussed the parameter settings of many of the algorithms in scikit-learn in
chapters 2 and 3, and it is important to understand what the parameters mean before
trying to adjust them.
Finding the values of the important parameters of a model (the ones that provide the
best generalization performance) is a tricky task, but necessary for almost all models
and datasets.
Grid Search | 247
www.it-ebooks.info

Because it is such a common task, there are standard methods in scikit-learn to help
you with it.
The most commonly used method is grid search, which basically means trying all
possible combinations of the parameters of interest.
Consider the case of a kernel SVM with an RBF (radial basis function) kernel, as
implemented in the SVC class. As we discussed in chapter 2, there are two important
parameters: the kernel bandwidth gamma and the regularization parameter C. Say we
want to try values 0.001, 0.01, 0.1, 1 and 10 for the parameter C, and the same
for gamma. Because we have six different settings for C and gamma that we want to try,
we have 36 combinations of parameters in total.
Looking at all possible combinations creates a table (or grid) of parameter settings for
the SVM as shown below:
| |C = 0.001 | C = 0.01 | C = 0.1 | C = 1 | C = 10 |
|-----------|----------|----------|---------|-------|--------|
|gamma=0.001|SVC(C=0.001, gamma=0.001)|SVC(C=0.01, gamma=0.001)|
SVC(C=0.1, gamma=0.001)|SVC(C=1, gamma=0.001)|SVC(C=10, gamma=0.001)|
|gamma=0.01|SVC(C=0.001, gamma=0.01)|SVC(C=0.01, gamma=0.01)|SVC(C=0.1,
gamma=0.01)|SVC(C=1, gamma=0.001)|SVC(C=10, gamma=0.01)|
|gamma=0.1|SVC(C=0.001, gamma=0.1)|SVC(C=0.01, gamma=0.1)|SVC(C=0.1,
gamma=0.1)|SVC(C=1, gamma=0.1)|SVC(C=10, gamma=0.1)|
|gamma=1|SVC(C=0.001, gamma=1)|SVC(C=0.01, gamma=1)|SVC(C=0.1,
gamma=1)|SVC(C=1, gamma=1)|SVC(C=10, gamma=1)|
|gamma=10|SVC(C=0.001, gamma=10)|SVC(C=0.01, gamma=10)|SVC(C=0.1,
gamma=10)|SVC(C=1, gamma=10)|SVC(C=10, gamma=10)|
Simple Grid-Search
We can implement a simple grid-search just as for-loops over the two parameters,
training and evaluating a classifier for each combination:
# naive grid search implementation
from sklearn.svm import SVC
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=0)
print("Size of training set: %d size of test set: %d" % (X_train.shape[0], X_test.shape[0]))
best_score = 0
for gamma in [0.001, 0.01, 0.1, 1, 10, 100]:
for C in [0.001, 0.01, 0.1, 1, 10, 100]:
# for each combination of parameters
248 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

# train an SVC
svm = SVC(gamma=gamma, C=C)
svm.fit(X_train, y_train)
# evaluate the SVC on the test set
score = svm.score(X_test, y_test)
# if we got a better score, store the score and parameters
if score > best_score:
best_score = score
best_parameters = {'C': C, 'gamma': gamma}
print("best score: ", best_score)
print("best parameters: ", best_parameters)
Size of training set: 112 size of test set: 38
best score: 0.973684210526
best parameters: {'C': 100, 'gamma': 0.001}
best_score
0.97368421052631582
The danger of overtting the parameters and the validation set
Given this result, we might be tempted to report that we found a model that performs
97.3% accurate on our dataset. However, this claim could be overly optimistic (or just
wrong) for the following reason: we tried many different parameters, and selected the
one with best accuracy on the test set. However, that doesn’t mean that this accuracy
carries over to new data.
Because we used the test data to adjust the parameters, we can no longer use it to
assess how good the model is. This is the same reason we needed to split the data into
training and test set in the first place; we need an independent data set to evaluate,
one that was not used to create the model.
One way to resolve this problem is to split the data again, so we have three sets: the
training set to build the model, the validation (or development) set to select the
parameters of the model, and the test set, to evaluate the performance of the selected
parameters, as shown in Figure threefold_split below.
After selecting the best parameters using the validation set, we can rebuild a model
using the parameters settings we found, but now training on both the training data
and the validation data. This way, we can use as much data as possible to build our
model.
print("threefold_split")
mglearn.plots.plot_threefold_split()
Grid Search | 249
www.it-ebooks.info

threefold_split
This leads to the following implementation:
from sklearn.svm import SVC
# split data into train+validation set and test set
X_trainval, X_test, y_trainval, y_test = train_test_split(iris.data, iris.target, random_state=0)
# split train+validation set into training and validation set
X_train, X_valid, y_train, y_valid = train_test_split(X_trainval, y_trainval, random_state=1)
print("Size of training set: %d size of validation set: %d size of test set: %d" % (X_train.shape[0], X_valid.shape[0], X_test.shape[0]))
best_score = 0
for gamma in [0.001, 0.01, 0.1, 1, 10, 100]:
for C in [0.001, 0.01, 0.1, 1, 10, 100]:
# for each combination of parameters
# train an SVC
svm = SVC(gamma=gamma, C=C)
svm.fit(X_train, y_train)
# evaluate the SVC on the test set
score = svm.score(X_valid, y_valid)
# if we got a better score, store the score and parameters
if score > best_score:
best_score = score
best_parameters = {'C': C, 'gamma': gamma}
# rebuild a model on the combined training and validation set, and evaluate it on the test set
svm = SVC(**best_parameters)
svm.fit(X_trainval, y_trainval)
test_score = svm.score(X_test, y_test)
print("best score on validation set: ", best_score)
print("best parameters: ", best_parameters)
print("test set score with best parameters: ", test_score)
Size of training set: 84 size of validation set: 28 size of test set: 38
best score on validation set: 0.964285714286
best parameters: {'C': 10, 'gamma': 0.001}
test set score with best parameters: 0.921052631579
The best score on the validation set is 96.4%: slightly lower than before, probably
because we used less data to train the model (X_train is smaller now because we split
our dataset twice).
250 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

However, the score on the test set - the score that actually tells us how well we gener‐
alize - is even lower, at 92%.
So we can only claim to classify new data 92% correctly, not 97% correctly as we
thought before!
The distinction between the training set, validation set and test set is fundamentally
important to apply machine learning methods in practice. Any choices made based
on the test set accuracy “leak” information from the test set into the model.
Therefore, it is important to keep a separate test set, which is only used for the final
evaluation. It is good practice to do all exploratory analysis and model selection using
the combination of a training and a validation set, and reserve the test set for a final
evaluation---this is even true for exploratory visualization. Strictly speaking, evaluat‐
ing more than one model on the test set and choosing the better of the two will result
in an overly optimistic estimate of how accurate the model is.
Grid-search with cross-validation
While the above method of splitting the data into a training, a validation and a test set
is workable, and relatively commonly used, it is quite sensitive to how exactly the data
is split. From the output of the code [FIXME Reference code above] we can see that
GridSearchCV selects 'C': 10, 'gamma': 0.01 as the best parameters, while the out‐
put of the code in [FIXME Reference code two up] selects 'C': 10, 'gamma': 0.001
as the best parameters. For a better estimate of the generalization performance,
instead of using a single split into a training and a validation set, we can use cross-
validation to evaluate the performance of each parameter combination.
This method can be coded up as follows:
# reference: manual_grid_search_cv
for gamma in [0.001, 0.01, 0.1, 1, 10, 100]:
for C in [0.001, 0.01, 0.1, 1, 10, 100]:
# for each combination of parameters
# train an SVC
svm = SVC(gamma=gamma, C=C)
# perform cross-validation
scores = cross_val_score(svm, X_trainval, y_trainval, cv=5)
# compute mean cross-validation accuracy
score = np.mean(scores)
# if we got a better score, store the score and parameters
if score > best_score:
best_score = score
best_parameters = {'C': C, 'gamma': gamma}
# rebuild a model on the combined training and validation set
svm = SVC(**best_parameters)
svm.fit(X_trainval, y_trainval)
Grid Search | 251
www.it-ebooks.info

SVC(C=100, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=None, degree=3, gamma=0.01, kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
To evaluate the accuracy of the SVM using a particular setting of C and gamma using
five-fold cross-validation we need to train 36 * 5 = 180 models. As you can imagine,
the main down-side of the use of cross-validation is the time it takes to train all these
models.
Figure cross_val_selection illustrates how the best parameter setting is selected in the
code above. For each parameter setting (only a subset is shown), five accuracy values
are computed, one for each split in the cross validation. Then the mean validation
accuracy is computed for each parameter setting. The parameters with the highest
mean validation accuracy are chosen, marked by the circle.
[warning / note box] As we said above, cross-validation is a way to evaluate a given
algorithm on a specific dataset.
However, it is often used in conjunction with parameter search methods like grid
search. For this reason, many people colloquially use the term cross-validation to
refer to grid-search with cross-validation. [/end warning box]
mglearn.plots.plot_cross_val_selection()
mglearn.plots.plot_grid_search_overview()
252 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info
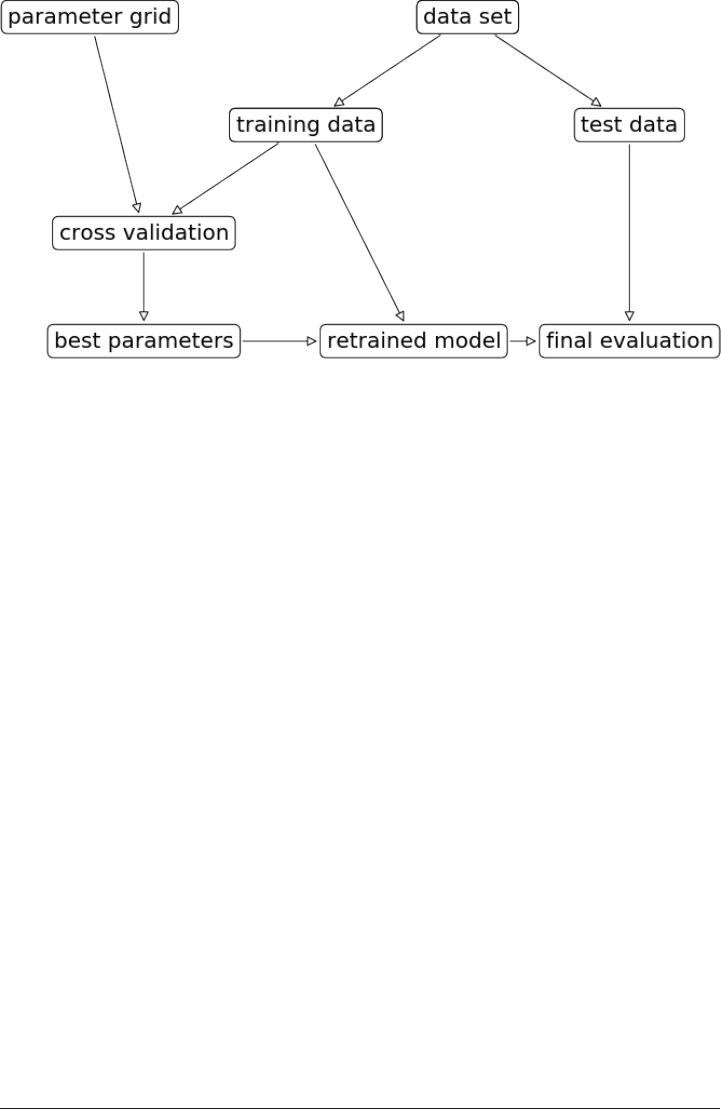
Because grid-search with cross-validation is such a commonly used method to adjust
parameters scikit-learn provides the GridSearchCV class that implements it in the
form of an estimator. To use the GridSearchCV class, you first need to specify the
parameters you want to search over using a dictionary. GridSearchCV will then per‐
form all the necessary model fits. The keys of the dictionary are the names of parame‐
ters we want to adjust (as given when constructing the model), in this case C and
gamma), and the values are the parameter settings we want to try out. Trying the val‐
ues 0.001, 0.01, 0.1, 1, 10 and 100 for C and gamma translates to the following
dictionary:
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100],
'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
param_grid
{'C': [0.001, 0.01, 0.1, 1, 10, 100], 'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
We can now instantiate the GridSearchCV class with the model SVC, the parameter
grid to search param_grid, and the cross-validation strategy we want to use, say 5 fold
(stratified) cross-validation:
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
grid_search = GridSearchCV(SVC(), param_grid, cv=5)
GridSearchCV will use cross-validation in place of the split into a training and valida‐
tion set that we used before. However, we still need to split the data into a training
and a test set, to avoid overfitting the parameters:
Grid Search | 253
www.it-ebooks.info

X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=0)
The grid_search object that we created behaves just like a classifier; we can call the
standard methods fit, predict and score on it [footnote: A scikit-learn estimator
that is created using another estimator is called a a meta-estimator in scikit-learn.
GridSearchCV is the most commonly used meta-estimator, but we will see more
later.]. However, when we call fit, it will run cross-validation for each combination
of parameters we specified in param_grid.
grid_search.fit(X_train, y_train)
GridSearchCV(cv=5, error_score='raise',
estimator=SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=None, degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False),
fit_params={}, iid=True, n_jobs=1,
param_grid={'C': [0.001, 0.01, 0.1, 1, 10, 100], 'gamma': [0.001, 0.01, 0.1, 1, 10, 100]},
pre_dispatch='2*n_jobs', refit=True, scoring=None, verbose=0)
Fitting the GridSearchCV object not only searches for the best parameters, it also
automatically fits a new model on the whole training dataset with the parameters that
yielded the best cross-validation performance. What happens in fit is therefore
equivalent with FIXME reference manual_grid_search_cv. The GridSearchCV class
provides a very convenient interface to access the retrained model using the predict
and score methods. To evaluate how well the best found parameters generalize, we
can call score on the test set:
grid_search.score(X_test, y_test)
0.97368421052631582
Choosing the parameters using cross-validation, we actually found a model that ach‐
ieves 97.3% accuracy on the test set. The important part here is that we did not use the
test set to choose the parameters.
The parameters that were found are scored in the best_params_ attribute, and the
best cross-validation accuracy (the mean accuracy over the different splits for this
parameter setting) is stored in best_score_:
print(grid_search.best_params_)
print(grid_search.best_score_)
254 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

{'C': 100, 'gamma': 0.01}
0.973214285714
[warning box]
Again, be careful not to confuse best_score_ with the generalization performance of
the model as computed by the score method on the test set. Using the score method
(or evaluating the output of the predict method) employs a model trained on the
whole training set. The best_score_ attribute stores the mean validation cross-
validation accuracy, with cross-validation performed on the training set.
[/end warning box]
Sometimes it is helpful to have access to the actual model that was found, for example
to look at coefficients or feature importances. You can access the model with the best
parameters trained on the whole training set using the best_estimator_ attribute:
grid_search.best_estimator_
SVC(C=100, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=None, degree=3, gamma=0.01, kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
Because grid_search itself has predict and score methods, using best_estimator_
is not needed to make predictions or evaluate the model.
Analyzing the result of cross-validation
It is often helpful to visualize the results of cross-validation, to understand how the
model generalization depends on the parameters we are searching. As grid-searches
are quite computationally expensive to run, often it is a good idea to start with a rela‐
tively coarse and small grid.
We can then inspect the results of the cross-validated grid-search, and possibly
expand our search.
The results of a grid search can be found in the grid_scores_ attribute:
grid_search.grid_scores_
[mean: 0.36607, std: 0.01137, params: {'C': 0.001, 'gamma': 0.001},
mean: 0.36607, std: 0.01137, params: {'C': 0.001, 'gamma': 0.01},
mean: 0.36607, std: 0.01137, params: {'C': 0.001, 'gamma': 0.1},
mean: 0.36607, std: 0.01137, params: {'C': 0.001, 'gamma': 1},
Grid Search | 255
www.it-ebooks.info

mean: 0.36607, std: 0.01137, params: {'C': 0.001, 'gamma': 10},
mean: 0.36607, std: 0.01137, params: {'C': 0.001, 'gamma': 100},
mean: 0.36607, std: 0.01137, params: {'C': 0.01, 'gamma': 0.001},
mean: 0.36607, std: 0.01137, params: {'C': 0.01, 'gamma': 0.01},
mean: 0.36607, std: 0.01137, params: {'C': 0.01, 'gamma': 0.1},
mean: 0.36607, std: 0.01137, params: {'C': 0.01, 'gamma': 1},
mean: 0.36607, std: 0.01137, params: {'C': 0.01, 'gamma': 10},
mean: 0.36607, std: 0.01137, params: {'C': 0.01, 'gamma': 100},
mean: 0.36607, std: 0.01137, params: {'C': 0.1, 'gamma': 0.001},
mean: 0.69643, std: 0.01333, params: {'C': 0.1, 'gamma': 0.01},
mean: 0.91964, std: 0.04442, params: {'C': 0.1, 'gamma': 0.1},
mean: 0.95536, std: 0.03981, params: {'C': 0.1, 'gamma': 1},
mean: 0.36607, std: 0.01137, params: {'C': 0.1, 'gamma': 10},
mean: 0.36607, std: 0.01137, params: {'C': 0.1, 'gamma': 100},
mean: 0.69643, std: 0.01333, params: {'C': 1, 'gamma': 0.001},
mean: 0.92857, std: 0.04278, params: {'C': 1, 'gamma': 0.01},
mean: 0.96429, std: 0.03405, params: {'C': 1, 'gamma': 0.1},
mean: 0.94643, std: 0.03251, params: {'C': 1, 'gamma': 1},
mean: 0.91964, std: 0.06507, params: {'C': 1, 'gamma': 10},
mean: 0.50893, std: 0.04666, params: {'C': 1, 'gamma': 100},
mean: 0.92857, std: 0.04278, params: {'C': 10, 'gamma': 0.001},
mean: 0.96429, std: 0.03405, params: {'C': 10, 'gamma': 0.01},
mean: 0.96429, std: 0.01793, params: {'C': 10, 'gamma': 0.1},
mean: 0.93750, std: 0.04556, params: {'C': 10, 'gamma': 1},
mean: 0.91964, std: 0.06507, params: {'C': 10, 'gamma': 10},
mean: 0.56250, std: 0.04966, params: {'C': 10, 'gamma': 100},
256 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info
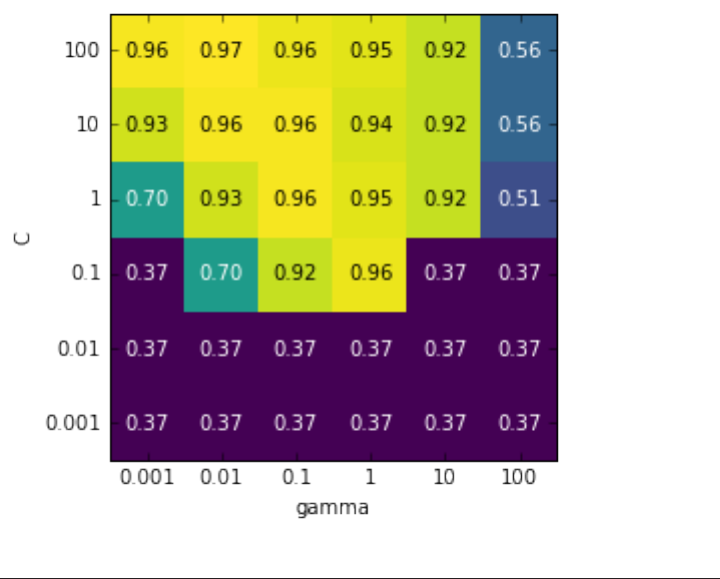
mean: 0.96429, std: 0.03405, params: {'C': 100, 'gamma': 0.001},
mean: 0.97321, std: 0.02234, params: {'C': 100, 'gamma': 0.01},
mean: 0.95536, std: 0.04983, params: {'C': 100, 'gamma': 0.1},
mean: 0.94643, std: 0.05199, params: {'C': 100, 'gamma': 1},
mean: 0.91964, std: 0.06507, params: {'C': 100, 'gamma': 10},
mean: 0.56250, std: 0.04966, params: {'C': 100, 'gamma': 100}]
This attribute contains the mean cross-validation accuracy (and it’s standard devia‐
tion) for all parameter settings that we tried. As we were searching a two-dimensional
grid of parameters ('C’ and ‘gamma'), this is best visualized as a heat map. First, we
extract the mean validation scores, then we reshape the scores so that the axes corre‐
spond to C and gamma:
scores = [score.mean_validation_score for score in grid_search.grid_scores_]
scores = np.array(scores).reshape(6, 6)
# plot the mean cross-validation scores
mglearn.tools.heatmap(scores, xlabel='gamma', ylabel='C', xticklabels=param_grid['gamma'],
yticklabels=param_grid['C'], cmap="viridis")
Grid Search | 257
www.it-ebooks.info

Each point in the heat map corresponds to one run of cross-validation, with a partic‐
ular parameter setting. The color encodes the cross-validation accuracy, with light
colors meaning high accuracy, and dark colors meaning low accuracy.
You can see that SVC is very sensitive to the setting of the parameters. For many of the
parameter settings, the accuracy is around 40%, which is quite bad; for other settings
the accuracy is around 96%.
We can take away from this plot several things. First, the parameters we adjusted are
very important for obtaining good performance. Both parameters C and gamma matter
a lot, as adjusting them can change the accuracy from 40% to 96%. Also, the ranges
we picked for the parameters are ranges in which we see significant changes in the
outcome. It’s also important to note that the ranges for the parameters are large
enough: the optimum values for each parameter is not on the edge of the plot.
Figure gridsearch_failures shows some plots where the result is less ideal, because the
search ranges were not chosen properly.
fig, axes = plt.subplots(1, 3, figsize=(13, 5))
param_grid_linear = {'C': np.linspace(1, 2, 6),
'gamma': np.linspace(1, 2, 6)}
param_grid_one_log = {'C': np.linspace(1, 2, 6),
'gamma': np.logspace(-3, 2, 6)}
param_grid_range = {'C': np.logspace(-3, 2, 6),
'gamma': np.logspace(-7, -2, 6)}
for param_grid, ax in zip([param_grid_linear, param_grid_one_log,
param_grid_range], axes):
grid_search = GridSearchCV(SVC(), param_grid, cv=5)
grid_search.fit(X_train, y_train)
scores = [score.mean_validation_score for score in grid_search.grid_scores_]
scores = np.array(scores).reshape(6, 6)
# plot the mean cross-validation scores
scores_image = mglearn.tools.heatmap(scores, xlabel='gamma', ylabel='C', xticklabels=param_grid['gamma'],
yticklabels=param_grid['C'], cmap="viridis", ax=ax)
plt.colorbar(scores_image, ax=axes.tolist())
print("gridsearch_failures")
258 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info
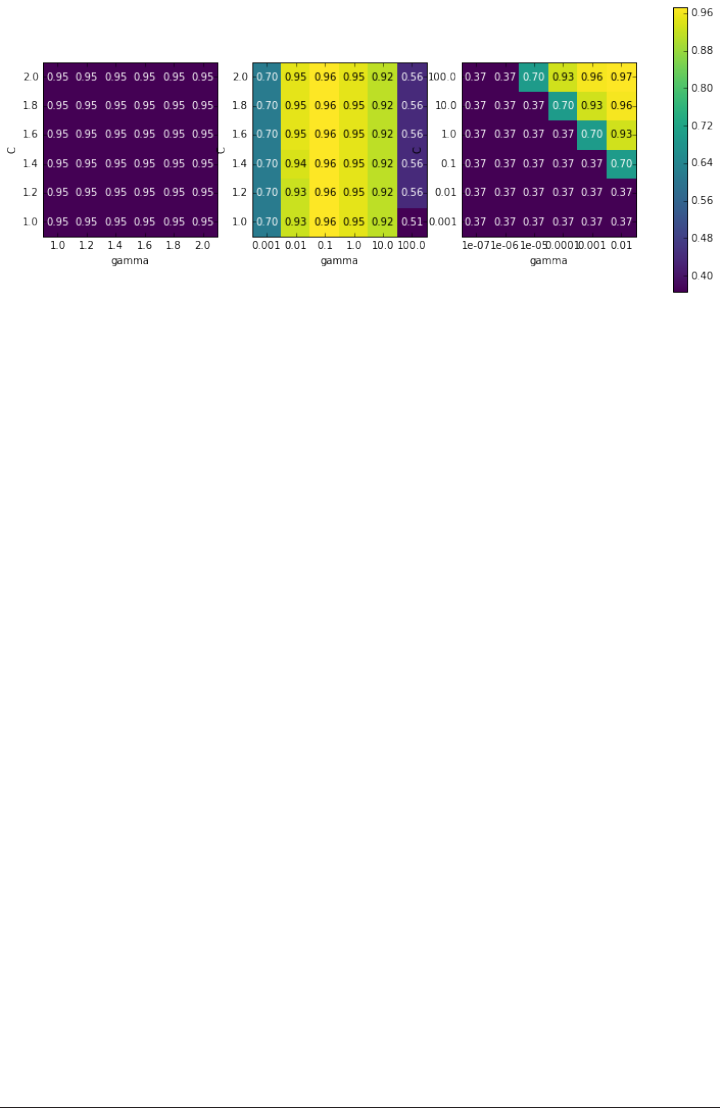
gridsearch_failures
The first panel shows no changes at all, with a constant color over the whole parame‐
ter grid. This is caused by improper scaling and range of the parameters C and gamma.
However, if no change in accuracy is visible over the different parameter settings, it
could also be that a parameter is just not important at all. It is usually good to try very
extreme values first, to see if there are any changes in the accuracy as a result of
changing a parameter.
The second panel shows a vertical stripe pattern. This indicates that only the setting
of the gamma parameter makes any difference. This could mean that the gamma
parameter is searching over interesting values, but the C parameter is not -- or it
could mean the C parameter is not important at all.
The third panel shows changes in both C and gamma. However, we can see that in the
top right of the plot, nothing interesting is happening. We can probably exclude the
very small values from future grid-searches. The optimum parameter setting is on the
bottom right. As the optimum is in the border of the plot, we can expect that there
might be even better values beyond this border, and we might want to change our
search range to include more parameters in this region.
Tuning the parameter grid based on the cross-validation scores is perfectly fine, and a
good way to explore the importance of different parameters. However, you should
not test different parameter ranges on the the final test set---as we discussed above,
evaluation of the test set should happen only once we know exactly what model we
want to use.
Using dierent cross-validation strategies with grid-search
Similarly to cross_val_score, GridSearchCV uses stratified k-fold cross-validation
by default for classification, and k-fold cross-validation for regression. However, you
Grid Search | 259
www.it-ebooks.info

can also pass any cross-validation splitter, as described in section XX as the cv param‐
eter in GridSearchCV.
In particular, to get only a single split into a training and validation set, you can use
ShuffleSplit or StratifiedShuffleSplit with n_iter=1. This might be helpful for
very large datasets, or very slow models.
Nested cross-validation
In the above examples, we went from using single split of the data into a training, val‐
idation and test set to spitting the data into training and test sets, and then perform‐
ing cross-validation on the training set. When using GridSearchCV as above, we still
have a single split of the data in training and test set however, which might still make
our results unstable, and may make us depend too much on this single split of the
data.
We can go a step further, and instead of splitting the original data into training and
test set once, we use multiple splits of cross-validation. This will result in what is
called nested cross-validation. In nested cross-validation, there is an outer loop over
splits of the data into training and test set. For each of them, a grid-search is run
(which might result in different best parameters for each split in the outer loop).
Then, for each outer split, the test set score using the best settings is reported.
The result of this procedure is a list of scores, not a model, and not a parameter set‐
ting. The scores tell us how well a model generalizes, given the best parameters found
by grid-search. As it doesn’t provide a model that can be used on new data, nested
cross-validation is rarely used when looking for a predictive model to apply to future
data.
It can be good to evaluate how good a given model works on a particular dataset,
though.
Implementing nested cross-validation in scikit-learn is straightforward; we call
cross_val_score with an instance of GridSearchCV as the model:
scores = cross_val_score(GridSearchCV(SVC(), param_grid, cv=5), iris.data, iris.target, cv=5)
print("Cross-validation scores: ", scores)
print("Mean cross-validation score: ", scores.mean())
Cross-validation scores: [ 0.967 1. 0.967 0.967 1. ]
Mean cross-validation score: 0.98
The result of our nested cross-validation can be summarized as “SVC can achieve
98% mean cross-validation accuracy on the iris dataset” - nothing more and nothing
less.
260 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

Here, we used stratified five-fold cross validation in both the inner and the outer
loop. As our param_grid contains 36 combinations of parameters, this results in a
whopping 36 * 5 * 5 = 900 models being build, making nested cross-validation a
very expensive procedure. Here, we used the same cross-validation splitter in the
inner and outer loop; however, this is not necessary and you can use any combination
of cross-validation strategies in the inner and outer loop. It can be a bit tricky to
understand what is happening in the single line given above, and it can be helpful to
visualize it as for loops, as done in simplified implementation given below:
def nested_cv(X, y, inner_cv, outer_cv, Classifier, parameter_grid):
outer_scores = []
# for each split of the data in the outer cross-validation
# (split method returns indices)
for training_samples, test_samples in outer_cv.split(X, y):
# find best parameter using inner cross-validation:
best_parms = {}
best_score = -np.inf
# iterate over parameters
for parameters in parameter_grid:
# accumulate score over inner splits
cv_scores = []
# iterate over inner cross-validation
for inner_train, inner_test in inner_cv.split(X[training_samples], y[training_samples]):
# build classifier given parameters and training data
clf = Classifier(**parameters)
clf.fit(X[inner_train], y[inner_train])
# evaluate on inner test set
score = clf.score(X[inner_test], y[inner_test])
cv_scores.append(score)
# compute mean score over inner folds
mean_score = np.mean(cv_scores)
if mean_score > best_score:
# if better than so far, remember parameters
best_score = mean_score
best_params = parameters
# build classifier on best parameters using outer training set
clf = Classifier(**best_params)
clf.fit(X[training_samples], y[training_samples])
# evaluate
outer_scores.append(clf.score(X[test_samples], y[test_samples]))
return outer_scores
from sklearn.model_selection import ParameterGrid, StratifiedKFold
nested_cv(iris.data, iris.target, StratifiedKFold(5), StratifiedKFold(5), SVC, ParameterGrid(param_grid))
[0.96666666666666667, 1.0, 0.96666666666666667, 0.96666666666666667, 1.0]
Parallelizing cross-validation and grid-search
While running grid-search over many parameters and on large datasets can be com‐
putationally challenging, it is also embarassingly parallel. This means that building a
Grid Search | 261
www.it-ebooks.info

model using a particular parameter setting on a particular cross-validation split can
be done completely independently from the other parameter settings and models.
This makes grid-search and cross-validation ideal candidates for parallelization over
multiple CPU cores or over a cluster. You can make use of multiple cores in Grid
SearchCV and cross_val_score by setting the n_jobs parameter to the number of
CPU cores you want to use. You can set n_jobs=-1 to use all available cores.
You should to be aware that scikit-learn does not allow nesting of parallel operations.
So if you are using the n_jobs option on your model (for example a random forest),
you cannot use it in GridSearchCV to search over this model.
If your dataset and model are very large, it might be that using many cores uses up
too much memory, and you should monitor your memory usage when building large
models in parallel.
It is also possible to parallelize grid-search and cross-validation over multiple
machines in a cluster. However, at the time of writing, this is not supported within
scikit-learn. It is, however, possible to use the IPython parallel framework for parallel
grid-searches, if you don’t mind writing the for-loop over parameters as in [reference
“naive implementation"] yourself.
For spark users, there is also the recently developed spark-sklearn package [foot‐
note https://github.com/databricks/spark-sklearn] which allows running grid-search
over an already established spark cluster.
Evaluation Metrics and scoring
So far, we always evaluated classification performance using accuracy (the fraction of
correctly classified samples) and regression performance using $R^2$. However,
these are only two of the many possible ways to summarize how well a supervised
model performs on a given dataset.
In practice, these evaluation metrics might not be appropriate for your application,
and it is important to choose the right metric when selecting between models and
adjusting hyper-parameters.
Keep the end-goal in mind
When selecting a metric, you should always have the end-goal of the machine learn‐
ing application in mind. In practice, we are usually not interested in just making
accurate predictions, but in using these predictions as part of a larger decision mak‐
ing process. Before picking a machine learning metric, you should think about what
the high-level goal of the application is, often called business metric. The conse‐
quences of choosing a particular algorithm for a machine learning application has is
called the business impact. [Footnote: We ask scientific minded readers to excuse the
262 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

commercial language in this section. Not losing track of the end-goal is equally
important in science, though the authors are not aware of a similar phrase as “busi‐
ness impact” being used in the sciences.] Maybe this is avoiding traffic accidents, or
decreasing the number of hospital admissions. It could also be getting more users for
your website, or having users spend more money in your shop. When choosing mod‐
els or adjusting parameters, you should then pick the model that has the most posi‐
tive influence on the business metric.
Often this is hard, as assessing the business impact of a particular model might
require putting it in production in a real-life system. In the early stages of develop‐
ment, and for adjusting parameters, it is often infeasible to put models into produc‐
tion just for testing purposes, because of high business risk or personal risks that can
be involved. Imagine evaluating the pedestrian avoidance capabilities of a self-driving
car by just letting it drive around, without verifying it first; if your model is bad,
pedestrians will be in trouble!
Therefore we often need to find some surrogate evaluation procedure, using an eval‐
uation metric that is easier to compute. For example, we could test classifying images
of pedestrians against non-pedestrians and measure accuracy. Keep in mind that this
is only a surrogate, and it pays off to find the closest metric to the original business
goal that is feasible to evaluate. This closest metric should be used whenever possible
for model evaluations and selection. This evaluation might not be a single number---
he consequence of your algorithm could be that you have 10% more customers, but
each customers will spend 15% less---but it should capture the expected business
impact of choosing one model over another.
We will first discuss metrics for the important special case of binary classification,
then multi-class classification, and finally regression.
Metrics for binary classication
Binary classification is arguably the most common and conceptually simple applica‐
tion of machine learning in practice. However, there are still a number of caveats in
evaluating even this simple task.
Before we dive into alternative metrics, let’s have a look into the ways in which meas‐
uring accuracy might be misleading.
Remember that for binary classification, we often speak of a positive class and a nega‐
tive class, with the understanding that the positive class is the one we are “looking
for”.
Kinds of Errors
Often, accuracy is not a good measure of predictive performance, as the number of
mistakes we make does not contain all the information we are interested in.
Evaluation Metrics and scoring | 263
www.it-ebooks.info

Imagine an application to screen for the early detection of cancer using an automated
test. If the test is negative, the patient will be assumed healthy, while if the test is posi‐
tive, the patient will undergo additional screening.
Here, we would call a positive test (indication of cancer) the positive class, and a neg‐
ative test the negative class.
We can’t assume that our model will always work perfectly, and it will make mistakes.
For any application, we need to ask ourselves what the consequence of these mistakes
are in the real world.
One possible mistake is that a healthy patient will be classified as positive, leading to
additional testing. This leads to some costs and a slight inconvenience for the patient.
Making an incorrect positive prediction is called a false positive.
The other possible mistake is that a sick patient will be classified as negative, and will
not receive further tests and treatment. The undiagnosed cancer might lead to serious
health issues, and could even be fatal. Making a mistake of this kind, an incorrect
negative prediction is called a false negative.
In this particular example, it is clear that we want to avoid false negatives as much as
possible, while false positives just create a minor nuisance.
While this is a particularly drastic example, the consequence of false positives and
false negatives are rarely the same. In commercial applications, it might be possible to
assign dollar values to both kinds of mistakes, which would allow measuring the error
of a particular prediction in dollars, instead of accuracy - which might be much more
meaningful for making business decisions on which model to use.
Imbalanced datasets
Types of errors in particularly play an important role when one of two classes is much
more frequent then the other one. This is very common in practice; a good example
for this is click-through prediction, where each data point represents an “impression”,
an item that was shown to a user. This item might be an add, or a related story, or a
related person to follow on a social media site. The goal is to predict whether, if
shown a particular item, a user will click on it (indicating they are interested).
Most thing users are shown on the internet (in particular, ads) will not result in a
click. You might need to show a user 100 ads or articles before they find something
interesting enough to click on.
This results in a dataset where for each 99 “no click” data points, there is 1 “clicked”
data point; in other words, 99% of the samples belong to the “no click” class. Datasets
in which one class is much more frequent than the other are often called imbalanced
dataset, or datasets with imbalanced classes.
264 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

In reality, imbalanced data is the norm, and it is rare that the events of interest have
equal or even similar frequency in the data.
Now let’s say you build a classifier that is 99% accurate on the click prediction task.
What does that tell you? 99% accuracy sounds impressive, but this doesn’t take the
class imbalance into account. You can achieve 99% accuracy without building a
machine learning model, by always predicting “no click”. On the other hand, even
with imbalanced data, a 99% accurate model could in fact be quite good. However,
accuracy doesn’t allow us to distinguish the constant “no click” model and a poten‐
tially good model.
To illustrate, we create a 9:1 imbalanced dataset from the digits dataset, by classifying
the digit four against the nine other classes:
from sklearn.datasets import load_digits
digits = load_digits()
y = digits.target == 9
X_train, X_test, y_train, y_test = train_test_split(
digits.data, y, random_state=0)
We can use the DummyClassifier to always predict the majority class (here “not
four”) to see how uninformative accuracy can be:
from sklearn.dummy import DummyClassifier
dummy_majority = DummyClassifier(strategy='most_frequent').fit(X_train, y_train)
pred_most_frequent = dummy_majority.predict(X_test)
print("predicted labels: %s" % np.unique(pred_most_frequent))
print("score: %f" % dummy_majority.score(X_test, y_test))
predicted labels: [False]
score: 0.895556
We obtained close to 90% accuracy without learning anything. This might seem strik‐
ing. Imagine someone telling you their model is 90% accurate. You might think they
did a very good job. But depending on the problem, that might be possible by just
predicting one class! Let’s compare this against using an actual classifier:
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(max_depth=2).fit(X_train, y_train)
pred_tree = tree.predict(X_test)
tree.score(X_test, y_test)
0.9177777777777778
According to accuracy, the GaussianNB model is clearly worse than the constant pre‐
dictor! This could either indicate that something is wrong with how we use Gaus
sianNB or that accuracy is in fact not a good measure here.
Evaluation Metrics and scoring | 265
www.it-ebooks.info

For comparison purposes, we evaluate two more classifiers: SVC and the default Dummy
Classifier which makes random predictions, but producing classes with the same
proportions as in the training set:
from sklearn.linear_model import LogisticRegression
dummy = DummyClassifier().fit(X_train, y_train)
pred_dummy = dummy.predict(X_test)
print("dummy score: %f" % dummy.score(X_test, y_test))
logreg = LogisticRegression(C=0.1).fit(X_train, y_train)
pred_logreg = logreg.predict(X_test)
print("logreg score: %f" % logreg.score(X_test, y_test))
dummy score: 0.808889
logreg score: 0.977778
The dummy that produces random output is still better than the GaussianNB, while
LogisticRegression produces very good results.
Clearly accuracy is an inadequate measure to quantify predictive performance in this
imbalanced setting. For the rest of this chapter, we will explore alternative metrics
that provide better guidance in selecting models. In particular, we would like to have
metrics that tell us how much better a model is than making “most frequent” predic‐
tions or random predictions, as they are computed in pred_most_frequent and
pred_dummy. If we use a metric to assess our models, it should definitely be able to
weed out these nonsense predictions.
Confusion matrices
One of the most comprehensive ways to represent the result of evaluating binary clas‐
sification is using confusion matrices. Let’s inspect the predictions of LogisticRegres
sion above using the confusion_matrix function. We already stored the predictions
on the test set in pred_logreg.
from sklearn.metrics import confusion_matrix
confusion = confusion_matrix(y_test, pred_logreg)
print(confusion)
[[401 2]
[ 8 39]]
The output of confusion_matrix is a two by two array, where the rows correspond to
the true classes, and the columns corresponds to the predicted classes. Each entry
counts for how many data points in the class given by the row the prediction was the
class given by the column.
266 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info
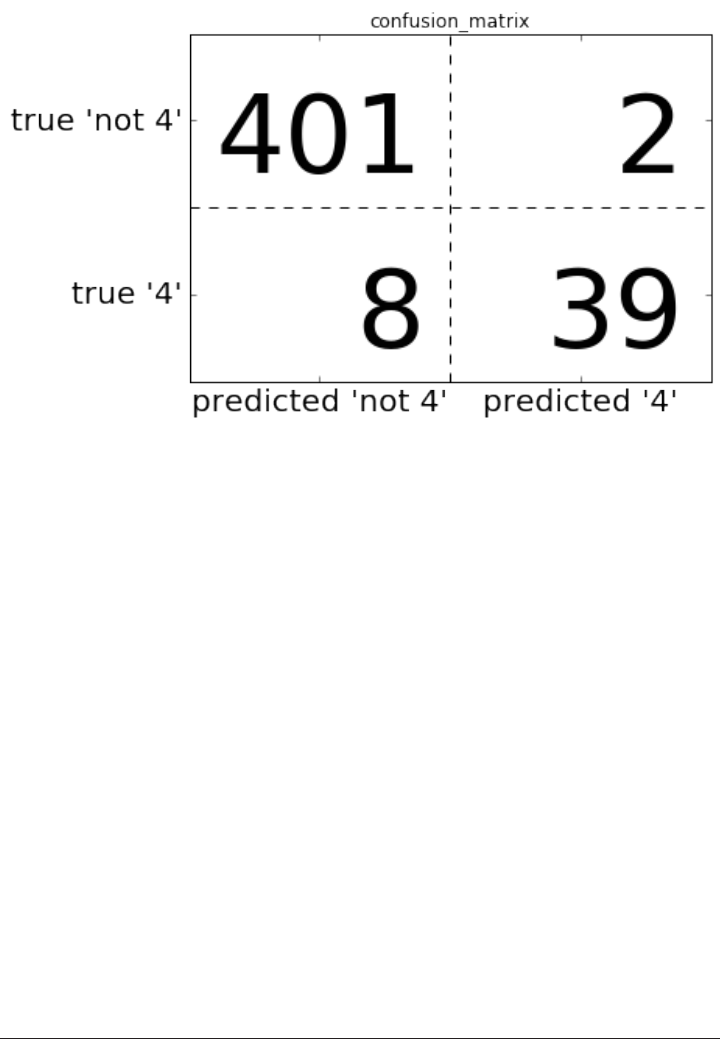
Figure confusion_matrix below illustrates this meaning:
mglearn.plots.plot_confusion_matrix_illustration()
This means of the 403 data points (sum of the first row) that are not a four, 401 got
predicted correctly as such, and two of which were incorrectly predicted as a four.
Similarly there are 47 data points that are fours, 39 of which got correctly classified,
and 8 of which were predicted incorrectly as not a four.
Entries on the main diagonal [footnote: The main diagonal of a two-dimensional
array or matrix A are A[i, i]] of the confusion matrix correspond to correct classifi‐
cations, while other entries tell us how many samples of one class got mistakenly clas‐
sified as another class.
If we declare “being a four” the positive class, we can relate the entries of the confu‐
sion matrix with the terms false positives and false negatives that we introduced earlier.
To complete the picture, we call correctly classified samples belonging to the positive
class true positives and correctly classified samples of the negative class true negatives.
These terms are usually abbreviated FP, FN, TP and TN and lead to the following
interpretation for the confusion matrix:
mglearn.plots.plot_binary_confusion_matrix()
Evaluation Metrics and scoring | 267
www.it-ebooks.info

Now let’s use the confusion matrix to compare the models we fitted above, the two
dummy models, the decision tree and the logistic regression:
print("Most frequent class:")
print(confusion_matrix(y_test, pred_most_frequent))
print("\nDummy model:")
print(confusion_matrix(y_test, pred_dummy))
print("\nDecision tree:")
print(confusion_matrix(y_test, pred_tree))
print("\nLogistic Regression")
print(confusion_matrix(y_test, pred_logreg))
Most frequent class:
[[403 0]
[ 47 0]]
Dummy model:
[[377 26]
[ 42 5]]
Decision tree:
[[390 13]
268 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

[ 24 23]]
Logistic Regression
[[401 2]
[ 8 39]]
Looking at the confusion matrix, it is quite clear that something is wrong with
pred_most_frequent, because it always predicts the same class. pred_dummy on the
other hand has a very small number of true positives (3) in particular compared to
the number of false negatives and false positives - there are many more false positives
than true positives!
The predictions made by the tree make much more sense than the dummy predic‐
tions, even though the accuracy was nearly the same. Finally, we can see that logistic
regression does better than tree in all aspects: it has more true positives and true
negatives while having fewer false positives and false negatives.
From this comparison, it is clear that only the tree and the logistic regression give
reasonable results, and that the logistic regression works better than the tree on all
accounts.
However, inspecting the full confusion matrix is a bit cumbersome, and while we
gained a lot of insight from looking at all aspects of the matrix, the process was very
manual and qualitative.
There are several ways to summarize the information in the confusion matrix, which
we will discuss next.
Relation to accuracy. We already saw one way to summarize the result in the confu‐
sion matrix, by computing accuracy, which can be expressed as
\begin{equation}
\text{Accuracy} = \frac{\text{TP} + \text{TN}}{\text{TP} + \text{TN} + \text{FP} +
\text{FN}}
\end{equation}
In other words: accuracy is the number of correct prediction (TP and TN) divided by
the number of all samples (all entries of the confusion matrix summed up).
Precision, recall and f-score
There are several other ways to summaries the confusion matrix, with the most com‐
mon one being precision and recall.
Evaluation Metrics and scoring | 269
www.it-ebooks.info

Precision measures how many of the samples predicted as positive are actually posi‐
tive:
\begin{equation}
\text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}}
\end{equation}
Precision is used as a performance metric when the goal is to limit the number of
false positives. As an example, imagine a model to predict whether a new drug will be
effective in treating a disease in clinical trials. Clinical trials are notoriously expensive,
and a pharmaceutical company will only want to run an experiment if it is very sure
that the predicted drugs will actually work. Therefore, it is important that the model
does not produce many false positives, in other words, it has a high precision. Preci‐
sion is also know as positive predictive value (PPV).
Recall on the other hand measures how many of the positive samples are captured by
the positive predictions:
\begin{equation}
\text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}}
\end{equation}
Recall is used as performance metric when we need to identify all positive samples,
that is when it is important to avoid false negatives. The cancer diagnosis example
from the Section “Kinds of Errors” is a good example for this: it is important to find
all people that are sick, possible including healthy patients in the prediction. Other
names for recall are sensitivity, hit rate or true positive rate (TPR).
There is a trade-off between optimizing recall and optimizing precision. You can triv‐
ially obtain a perfect recall if you predict all samples to belong to the positive class -
there will be no false negatives, and no true negatives either. However, predicting all
samples as positive will result in many false positives, therefore the precision will be
very low. On the other hand, if you find a model that predicts only the single data
point it is most sure about as positive, and the rest as negative, then precision will be
perfect (assuming this data point is in fact positive), but recall will be very bad.
[info box]Precision and recall are only two of many classification measures derived
from TP, FP, TN and FN. You can find a a great summary of all the measures on wiki‐
pedia: https://en.wikipedia.org/wiki/Sensitivity_and_specificity In the machine learn‐
ing community, precision and recall are arguably the most commonly used measures
for binary classification, but other communities might use other, related metrics.[/
info box]
270 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

So while precision and recall are very important measures, looking at only one of
them will not provide you with the full picture. One way to summarize them is the f-
score or f-measure, which is the harmonic mean of precision and recall:
\begin{equation}
\text{F} = 2 \cdot \frac{\text{precision} \cdot \text{recall}}{\text{precision} +
\text{recall}}
\end{equation}
This particular variant is also known as the $f_1$-score. As it takes precision and
recall into account, it can be a better measure than accuracy on imbalanced binary
classification datasets. Let’s run it on the predictions on the “nine vs rest” dataset that
we computed above. Here, we will assume that the “nine” class is the positive class (it
is labeled as True while the rest is labeled as False, so the positive class is the minor‐
ity class.
from sklearn.metrics import f1_score
print("f1 score most frequent: %.2f" % f1_score(y_test, pred_most_frequent))
print("f1 score dummy: %.2f" % f1_score(y_test, pred_dummy))
print("f1 score tree: %.2f" % f1_score(y_test, pred_tree))
print("f1 score: %.2f" % f1_score(y_test, pred_logreg))
/home/andy/checkout/scikit-learn/sklearn/metrics/classification.py:1117: UndefinedMetricWarning: F-score is ill-defined and being set to 0.0 due to no predicted samples.
'precision', 'predicted', average, warn_for)
We can note two things: we get an error message for the most_frequent prediction,
as there was no predictions of the positive class (which makes the denominator in the
F score zero).
Also, we can see a pretty strong distinction between the dummy predictions and the
tree predictions, which wasn’t clear when looking at accuracy alone.
Using the f-score for evaluation we summarized the predictive performance again in
one number, which reflect our intuition about how well a model predicts much better
than accuracy in the imbalanced class setting. A disadvantage of the f-score however
is that it is harder to interpret and explain than accuracy.
If we want a more comprehensive summary of precision, recall and f1 score, we can
use the classification_report convenience function to compute all three at once,
and print them in a nice format:
from sklearn.metrics import classification_report
print(classification_report(y_test, pred_most_frequent,
target_names=["not nine", "nine"]))
/home/andy/checkout/scikit-learn/sklearn/metrics/classification.py:1117: UndefinedMetricWarning: Precision and F-score are ill-defined and being set to 0.0 in labels with no predicted samples.
'precision', 'predicted', average, warn_for)
Evaluation Metrics and scoring | 271
www.it-ebooks.info

The classification_report function produces one line per class, here True and
False and reports precision, recall and f-score with this class as the positive class.
Before, we assumed the minority “nine” class is the positive class. If we change the
positive class to “not nine”, we can see from the output of classification_report
that we obtain an f-score of .94 with the most_frequent model.
Furthermore, for the not_nine class we have a recall of 1, as we classified all samples
as “not nine”.
The last column next to the f-score provides the support of each class, which simply
means the number of samples in this class according to the ground truth.
The last row in the classification report shows a weighted (by support) average of the
numbers for each class.
Here are two more reports, one for the dummy classifier and one for the logistic
regression:
print(classification_report(y_test, pred_dummy,
target_names=["not nine", "nine"]))
precision recall f1-score support
not nine 0.90 0.94 0.92 403
nine 0.16 0.11 0.13 47
avg / total 0.82 0.85 0.83 450
print(classification_report(y_test, pred_logreg,
target_names=["not nine", "nine"]))
precision recall f1-score support
not nine 0.98 1.00 0.99 403
nine 0.95 0.83 0.89 47
avg / total 0.98 0.98 0.98 450
As you may notice, when looking at the reports, the differences between the dummy
models and a very good model is not as clear any more.
272 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

Picking which class is declared the positive class has a big impact on the metrics.
While the f-score for the dummy classification vs the logistic regression was 0.13 vs
0.89 on the “nine” class, it is 0.90 vs 0.99 on the “not nine” class, which both seem like
reasonable results.
Looking at all numbers together paints a pretty accurate picture, though, and we can
clearly see the superiority of the logistic regression model.
Taking uncertainty into account
The confusion matrix and the classification report provide a very detailed analysis of
a particular set of predictions. However, the predictions themselves already threw
away a lot of information that is contained in the model. As we discusses in Chapter
2, most classifiers provide a decision_function or a predict_proba method to
assess degrees of certainty about predictions.
Making predictions can be seen as thresholding the output of decision_function or
predict_proba at a certain fixed point - in binary classification zero for the decision
function and 0.5 for predict_proba.
Below is an example of an imbalanced binary classification task, with 400 blue points
classified against 50 red points.
The training data is shown on the right of Figure decision_threshold. We train a ker‐
nel SVM model on this data, and the left of Figure decision_threshold illustrates the
values of the decision function as a heat-map. A red background means points there
will be classified as red, blue background means that points there will be classified as
blue.
You can see a black circle, which denotes the threshold of the decision_function
being exactly zero. Points inside this circle will be classified as red, and outside as
blue.
from mglearn.datasets import make_blobs
X, y = make_blobs(n_samples=(400, 50), centers=2, cluster_std=[7.0, 2],
random_state=22)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
svc = SVC(gamma=.05).fit(X_train, y_train)
mglearn.plots.plot_decision_threshold()
Evaluation Metrics and scoring | 273
www.it-ebooks.info
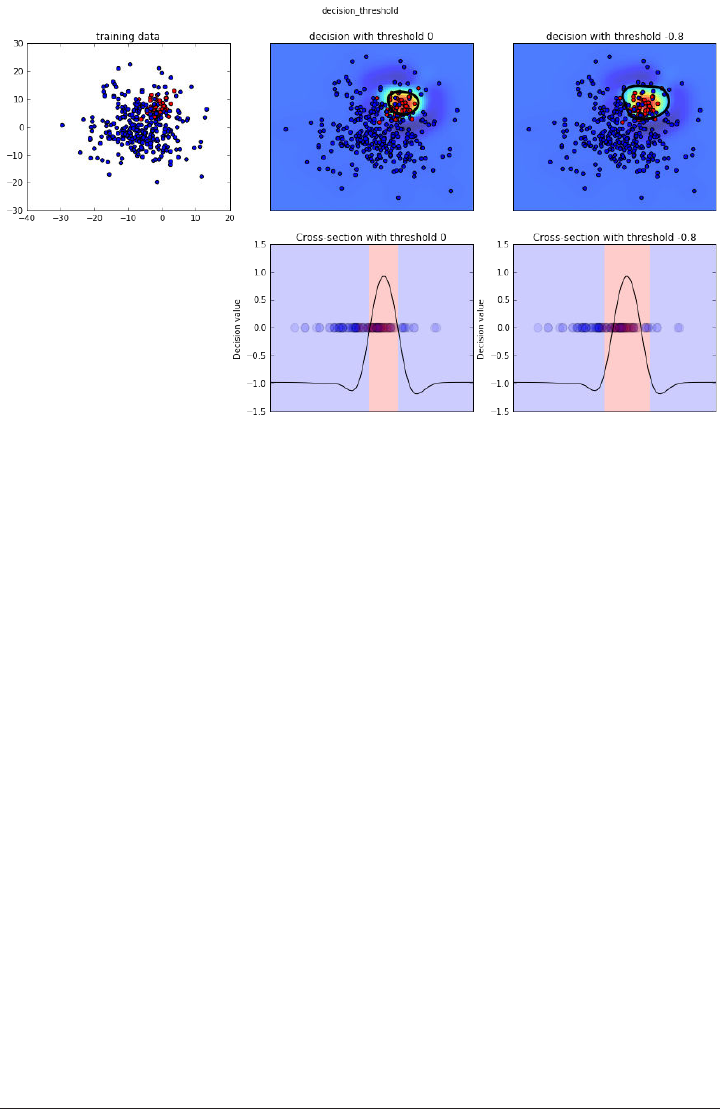
We can use the classification_report to evaluate precision and recall for both
classes:
print(classification_report(y_test, svc.predict(X_test)))
precision recall f1-score support
0 0.97 0.89 0.93 104
1 0.35 0.67 0.46 9
avg / total 0.92 0.88 0.89 113
In Figure decision_threshold, blue is the negative class and red is the positive class.
For class 1, we get a fairly small recall, and precision is mixed. Because class 0 is so
much larger, the classifier focuses on getting class 0 right, and not the smaller class 1.
Let’s assume in our application it is more important to have a high recall for class 1, as
in the cancer screening example above. This means we are willing to risk more false
positives (false class 1) in exchange for true positives (which will increase the recall).
The predictions generated by svc.predict above really do not fulfill this require‐
ment. But we can adjust the predictions to focus on a higher recall of class 1, by
changing the decision threshold away from 0.
274 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

By default, points with a decision_function value greater than 0 will be classified as
class 1. We want more points to be classified as class 1, so we need to decrease the
threshold:
y_pred_lower_threshold = svc.decision_function(X_test) > -.8
Let’s look at the classification report for this prediction:
print(classification_report(y_test, y_pred_lower_threshold))
precision recall f1-score support
0 1.00 0.82 0.90 104
1 0.32 1.00 0.49 9
avg / total 0.95 0.83 0.87 113
As expected, the recall of class 1 went up, and the precision went down. We are now
classifying a larger region of space as class 1, as illustrated in the right panel of Figure
decision_threshold.
If you value precision over recall or the other way around, or you data is heavily
imbalanced, changing the decision threshold is the easiest way to obtain better
results. As the decision_function can have arbitrary ranges, how to pick the right
threshold is hard to say. If you do set a threshold, you need to be careful not to do this
on the test set. As with any other parameter, setting a decision threshold on the test
set is likely to give you too optimistic results. Use a validation set or cross-validation
instead.
Picking a threshold for models that implement the predict_proba method can be
easier, as the output of predict_proba is on a fixed zero to one scale, and models
probabilities. By default, the threshold of 0.5 means that if the model is more than
50% “sure” that a point if of the positive class, it will be classified as such. Increasing
the threshold means that the model needs to be more confident to make a positive
decision (and less confident to make a negative decision). While working with proba‐
bilities may be more intuitive than working with arbitrary thresholds, not all models
provide realistic models of uncertainty (a DecisionTree that is grown to it’s full depth
is always 100% sure on its decisions - even though it might be often wrong). This
relates to the concept of calibration: A calibrated model is a model that provides an
accurate measure of it’s uncertainty. Discussing calibration in detail is beyond the
scope of this book, unfortunately.
Evaluation Metrics and scoring | 275
www.it-ebooks.info

Precision-Recall curves and ROC curves
As we just discussed, changing the threshold that is used to make a classification deci‐
sion in a model is a way to adjust the trade-off of precision and recall for a given clas‐
sifier. Maybe you want miss less than 10% of positive samples - meaning a desired
recall of 90%. This decision is a decision that depends on the application, and is (or
should be) driven by business goals. Once a particular goal is set, say a particular
recall or precision value for a class, a threshold can be set appropriately. It is always
possible to set a threshold to fulfill a particular target like 90% recall. The hard part is
to develop a model that still has reasonable precision with this threshold - if you clas‐
sify everything as positive, you will have 100% recall, but your model is useless.
Setting a requirement on a classifier like 90% recall is often called the operating point.
Fixing an operating point is often helpful in business settings to make performance
guarantees to customer or other groups inside your organization.
Often, when developing a new model, it is not entirely clear what the operating point
will be. For this reason, and to understand a modeling problem better, it is instructive
to look at all possible thresholds, or all possible trade-offs of precision and recall at
once. This is possible using a tool called the precision-recall curve.
You can find the function to compute the precision-recall curve in the sklearn.met
rics module. It needs the ground truth labeling and predicted uncertainties, created
via decision_function or predict_proba:
from sklearn.metrics import precision_recall_curve
precision, recall, thresholds = precision_recall_curve(y_test,
svc.decision_function(X_test))
The precision_recall_curve function returns a list of precision and recall values
for all possible thresholds (all values that appear in the decision function) in sorted
order, so we can plot a curve:
# create a similar dataset as before, but with more samples to get a smoother curve
X, y = make_blobs(n_samples=(4000, 500), centers=2, cluster_std=[7.0, 2], random_state=22)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
svc = SVC(gamma=.05).fit(X_train, y_train)
precision, recall, thresholds = precision_recall_curve(
y_test, svc.decision_function(X_test))
# find threshold closest to zero:
close_zero = np.argmin(np.abs(thresholds))
plt.plot(precision[close_zero], recall[close_zero], 'o', markersize=10,
label="threshold zero", fillstyle="none", c='k', mew=2)
plt.plot(precision, recall, label="precision recall curve")
plt.xlabel("precision")
plt.ylabel("recall")
276 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info
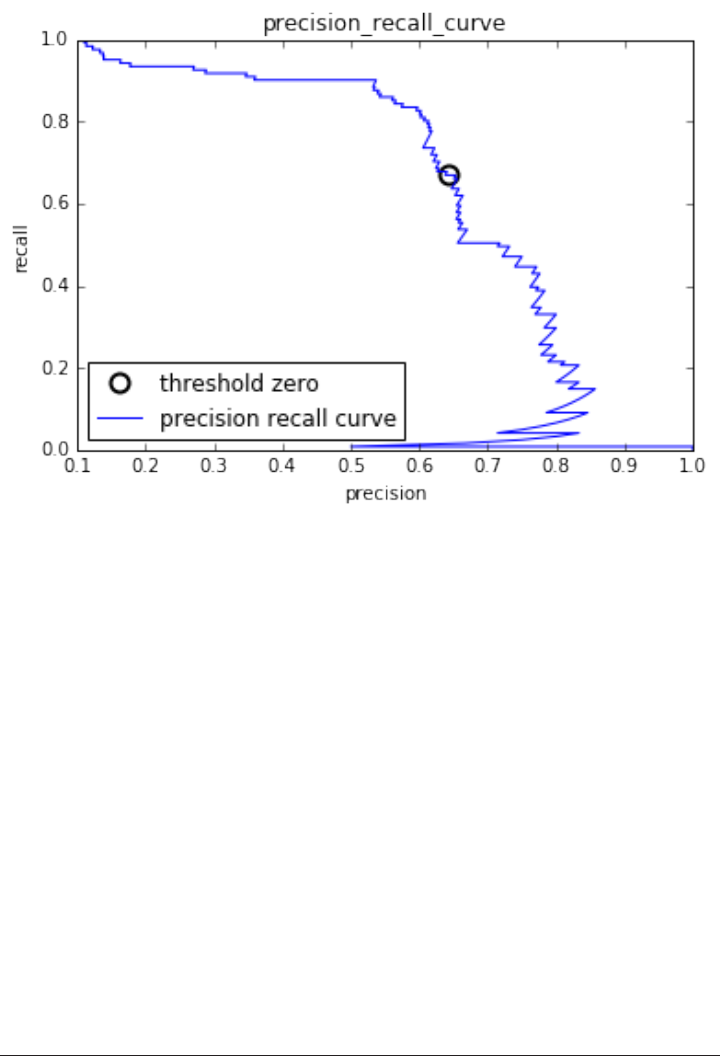
plt.title("precision_recall_curve");
plt.legend(loc="best")
Each point along the curve in “precision_recall_curve” corresponds to a possible
threshold on the decision_function. We can see for example that we can achieve a
recall of 0.4 at a precision of about 0.75. The black circle marks the point that corre‐
sponds to a threshold of zero, the default threshold for decision_function. This
point is the trade-off that is chosen when calling the predict method.
The closer a curve stays to the upper right corner, the better the classifier. A point at
the upper right means high precision and high recall for the same threshold. The
curve starts at the top left corner, corresponding to a very low threshold, classifying
everything as the positive class. Raising the threshold moves the curve towards higher
precision, but also lower recall. Raising the threshold more and more, we get to a sit‐
uation where most of the points classified as being positive are true positives, leading
to a very high precision at lower recall. The more the model keeps recall high as pre‐
cision goes up, the better.
Looking at this particular curve a bit more, we can see that with this model it is possi‐
ble to get a precision up to around 0.5 with very high recall. If we want a much higher
precision, we have to sacrifice a lot of precision. In other words: on the left, the curve
is relatively flat, meaning that recall does not go down a lot when we require
Evaluation Metrics and scoring | 277
www.it-ebooks.info

increased precision. For precision greater than 0.5, reach gain in precision costs us a
lot of recall.
Different classifiers can work well in different parts of the curve, that is at different
operating points. Below we compare the SVC we trained to a random forest trained
on the same dataset.
The RandomForestClassifier doesn’t have a decision_function, only pre
dict_proba. The precision_recall_curve function expects as second argument a
certainty measure for the positive class (class 1), so we pass the probability of a sam‐
ple being class one, that is rf.predict_proba(X_test)[:, 1]. The default threshold
for predict_proba in binary classification is 0.5, so this is the point we marked on
the curve.
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=100, random_state=0, max_features=2)
rf.fit(X_train, y_train)
# RandomForestClassifier has predict_proba, but not decision_function
precision_rf, recall_rf, thresholds_rf = precision_recall_curve(
y_test, rf.predict_proba(X_test)[:, 1])
plt.plot(precision, recall, label="svc")
plt.plot(precision[close_zero], recall[close_zero], 'o', markersize=10,
label="threshold zero svc", fillstyle="none", c='k', mew=2)
plt.plot(precision_rf, recall_rf, label="rf")
close_default_rf = np.argmin(np.abs(thresholds_rf - 0.5))
plt.plot(precision_rf[close_default_rf], recall_rf[close_default_rf], '^', markersize=10,
label="threshold 0.5 rf", fillstyle="none", c='k', mew=2)
plt.xlabel("precision")
plt.ylabel("recall")
plt.legend(loc="best")
plt.title("precision_recall_comparison");
278 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info
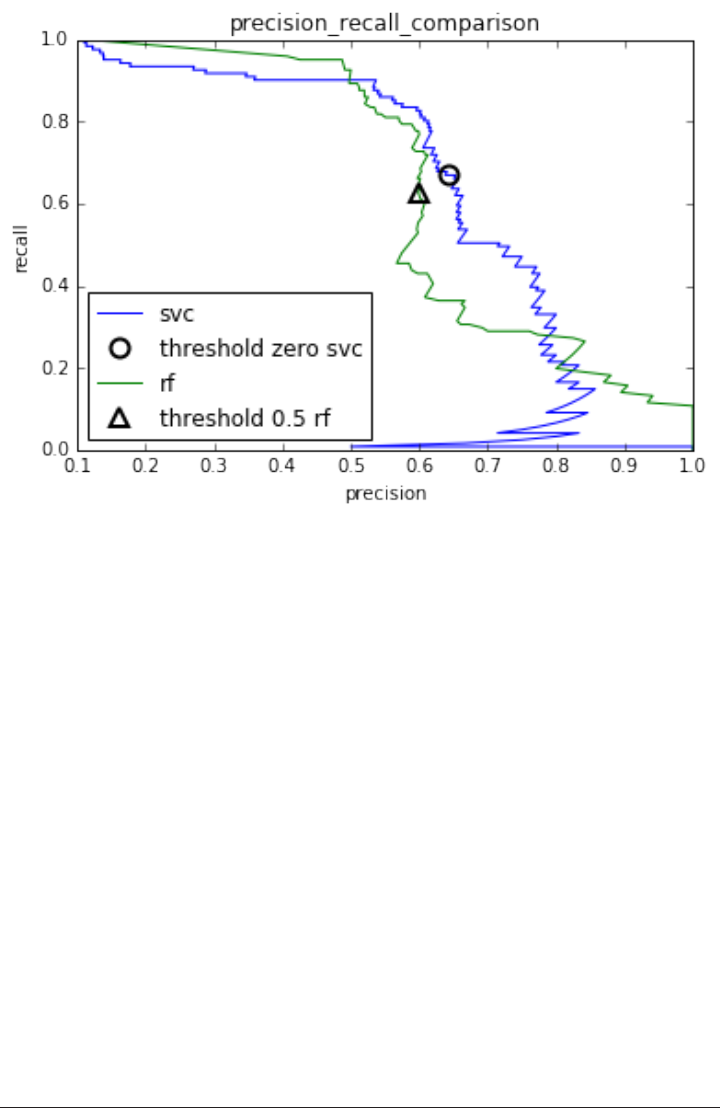
From the comparison plot we can see that the random forest performs better at the
extremes, for very high recall or very high precision requirements. Around the mid‐
dle (around precision=0.7), the SVM performance better. If we only looked at the f1-
score to compare overall performance, we would have missed these subtleties. The f1-
score only captures one point on the precision-recall curve, the one given by the
default threshold:
print("f1_score of random forest: %f" % f1_score(y_test, rf.predict(X_test)))
print("f1_score of svc: %f" % f1_score(y_test, svc.predict(X_test)))
f1_score of random forest: 0.609756
f1_score of svc: 0.655870
Comparing two precision-recall curves provides a lot of detailed insight, but is a fairly
manual process. For automatic model comparison, we might want to summarize the
information contained in the curve, without limiting ourselves to a particular thresh‐
old or operating point.
One particular way to summarize the precision-recall curve by computing the inte‐
gral or area under the curve of the precision-recall curve, also known as average preci‐
sion.
You can compute the average precision using the average_precision_score.
Because we need to compute the ROC curve, and consider multiple thresholds, we
Evaluation Metrics and scoring | 279
www.it-ebooks.info

need to pass the result of decision_function or predict_proba to average_preci
sion_score, not the result of predict:
from sklearn.metrics import average_precision_score
ap_rf = average_precision_score(y_test, rf.predict_proba(X_test)[:, 1])
ap_svc = average_precision_score(y_test, svc.decision_function(X_test))
print("average precision of random forest: %f" % ap_rf)
print("average precision of svc: %f" % ap_svc)
average precision of random forest: 0.665737
average precision of svc: 0.662636
When averaging over all possible thresholds, we see that random forest and SVC per‐
form similarly well, with the random forest even slightly ahead. This is quite different
than the result we got from f1_score above.
Because average precision is the area under a curve that goes from 0 to 1, average pre‐
cision always returns a value between 0 (worst) and 1 (best). The average precision of
a classifier that assigns decision_function at random is the fraction of positive sam‐
ples in the dataset.
Receiver Operating Characteristics (ROC) and AUC
There is another tool commonly used to analyze the behavior of classifiers at different
thresholds: the receiver operating characteristics curve, or ROC curve for short. The
ROC curve similarly considers all possible thresholds for a given classifier, but
instead of reporting precision and recall, it shows the false positive rate FPR against
the true positive rate TPR. Recall that the true positive rate is simply another name for
recall, while the false positive rate is the fraction of false positives out of all negative
samples:
\begin{equation}
\text{FPR} = \frac{\text{FP}}{\text{FP} + \text{TN}}
\end{equation}
The ROC curve can be computed using the roc_curve function:
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_test, svc.decision_function(X_test))
plt.plot(fpr, tpr, label="ROC Curve")
plt.xlabel("FPR")
plt.ylabel("TPR (recall)")
plt.title("roc_curve");
# find threshold closest to zero:
close_zero = np.argmin(np.abs(thresholds))
plt.plot(fpr[close_zero], tpr[close_zero], 'o', markersize=10,
280 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info
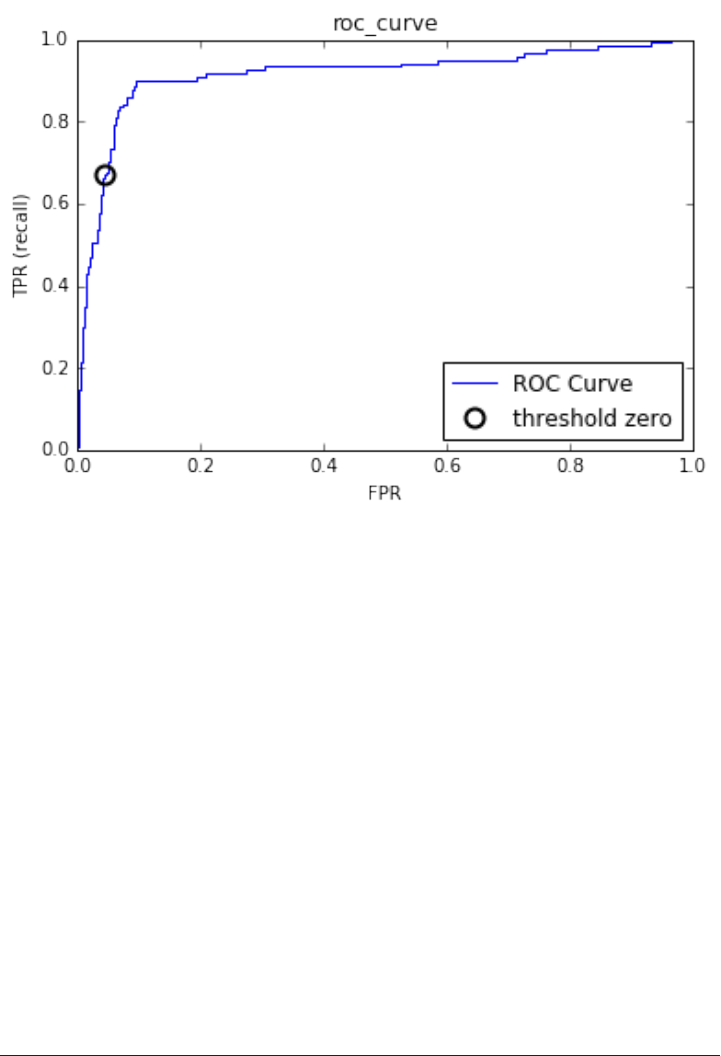
label="threshold zero", fillstyle="none", c='k', mew=2)
plt.legend(loc=4)
For the ROC curve, the ideal curve is close to the top left: you want a classifier that
produces a high recall while keeping a low false positive rate. Compared to the default
threshold of zero, the curve shows that we could achieve a significant higher recall
(around 0.9) while only increasing the FPR slightly. The point closes to the top left
might be a better operating point than the one chosen by default. Again, be aware that
choosing a threshold should not be done on the test set, but on a separate validation
set.
You can find a comparison of the Random Forest and the SVC using ROC curves in
Figure roc_curve_comparison.
from sklearn.metrics import roc_curve
fpr_rf, tpr_rf, thresholds_rf = roc_curve(y_test, rf.predict_proba(X_test)[:, 1])
plt.plot(fpr, tpr, label="ROC Curve SVC")
plt.plot(fpr_rf, tpr_rf, label="ROC Curve RF")
plt.xlabel("FPR")
plt.ylabel("TPR (recall)")
plt.title("roc_curve_comparison");
plt.plot(fpr[close_zero], tpr[close_zero], 'o', markersize=10,
label="threshold zero SVC", fillstyle="none", c='k', mew=2)
Evaluation Metrics and scoring | 281
www.it-ebooks.info
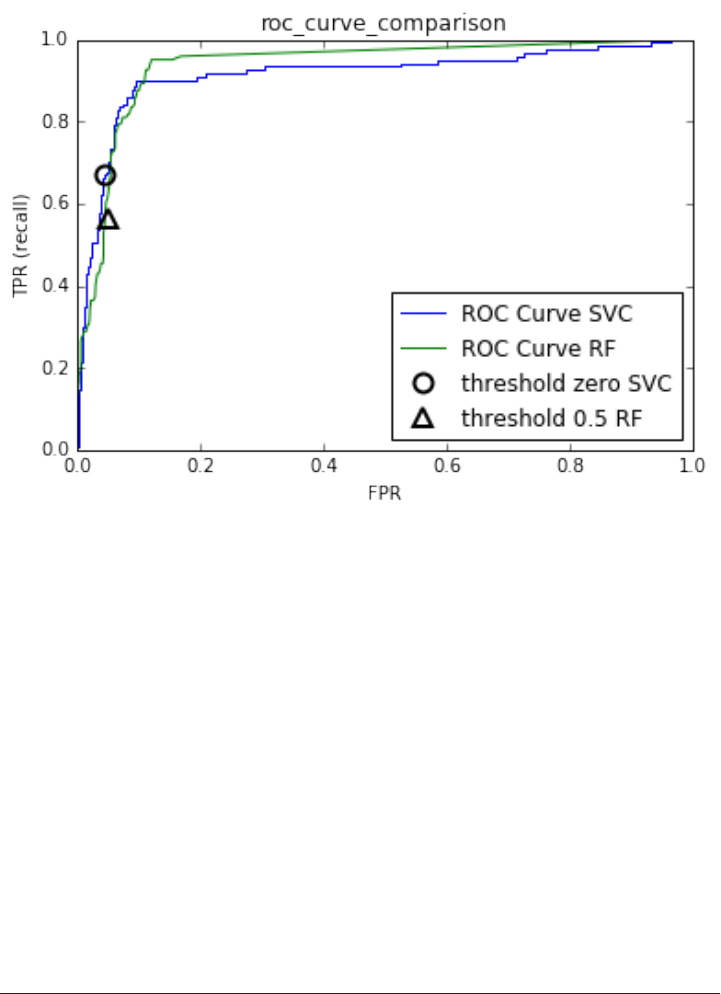
close_default_rf = np.argmin(np.abs(thresholds_rf - 0.5))
plt.plot(fpr_rf[close_default_rf], tpr[close_default_rf], '^', markersize=10,
label="threshold 0.5 RF", fillstyle="none", c='k', mew=2)
plt.legend(loc=4)
As for the precision-recall curve, we often want to summarize the ROC curve using a
single number, the area under the curve. Often the area under the ROC-curve is just
called AUC (area under the curve) and it is understood that the curve in question is
the ROC curve. We can compute the area under the ROC curve using the
roc_auc_score function:
from sklearn.metrics import roc_auc_score
rf_auc = roc_auc_score(y_test, rf.predict_proba(X_test)[:, 1])
svc_auc = roc_auc_score(y_test, svc.decision_function(X_test))
print("AUC for Random Forest: %f" % rf_auc)
print("AUC for SVC: %f" % svc_auc)
AUC for Random Forest: 0.936695
AUC for SVC: 0.916294
Comparing random forest and SVC using the AUC score, we find that Random For‐
est performs quite a bit better than SVC.
282 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

Because average precision is the area under a curve that goes from 0 to 1, average pre‐
cision always returns a value between 0 (worst) and 1 (best). Predicting randomly
always produces an AUC of 0.5, not matter how imbalanced the classes in a dataset
are. This makes it a much better metric for imbalanced classification problems than
accuracy.
The AUC can be interpreted as evaluating the ranking of positive samples. The AUC
is equivalent to the probability that a randomly picked point of the positive class will
have a higher score according to the classifier than a randomly picked point from the
negative class. So an perfect AUC of 1 means that all positive points have a higher
score than all negative points.
For classification problems with imbalanced classes, using AUC for model-selection
is often much more meaningful than using accuracy. Let’s go back to the problem we
studied above of classifying all nines in the digits dataset versus all other digits. We
will classify the dataset with an SVM with three different settings of the kernel band‐
width gamma:
y = digits.target == 9
X_train, X_test, y_train, y_test = train_test_split(
digits.data, y, random_state=0)
plt.figure()
for gamma in [1, 0.05, 0.01]:
svc = SVC(gamma=gamma).fit(X_train, y_train)
accuracy = svc.score(X_test, y_test)
auc = roc_auc_score(y_test, svc.decision_function(X_test))
fpr, tpr, _ = roc_curve(y_test , svc.decision_function(X_test))
print("gamma = %.02f accuracy = %.02f AUC = %.02f" % (gamma, accuracy, auc))
plt.plot(fpr, tpr, label="gamma=%.03f" % gamma, linewidth=4)
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.xlim(-0.01, 1)
plt.ylim(0, 1.02)
plt.legend(loc="best")
Evaluation Metrics and scoring | 283
www.it-ebooks.info
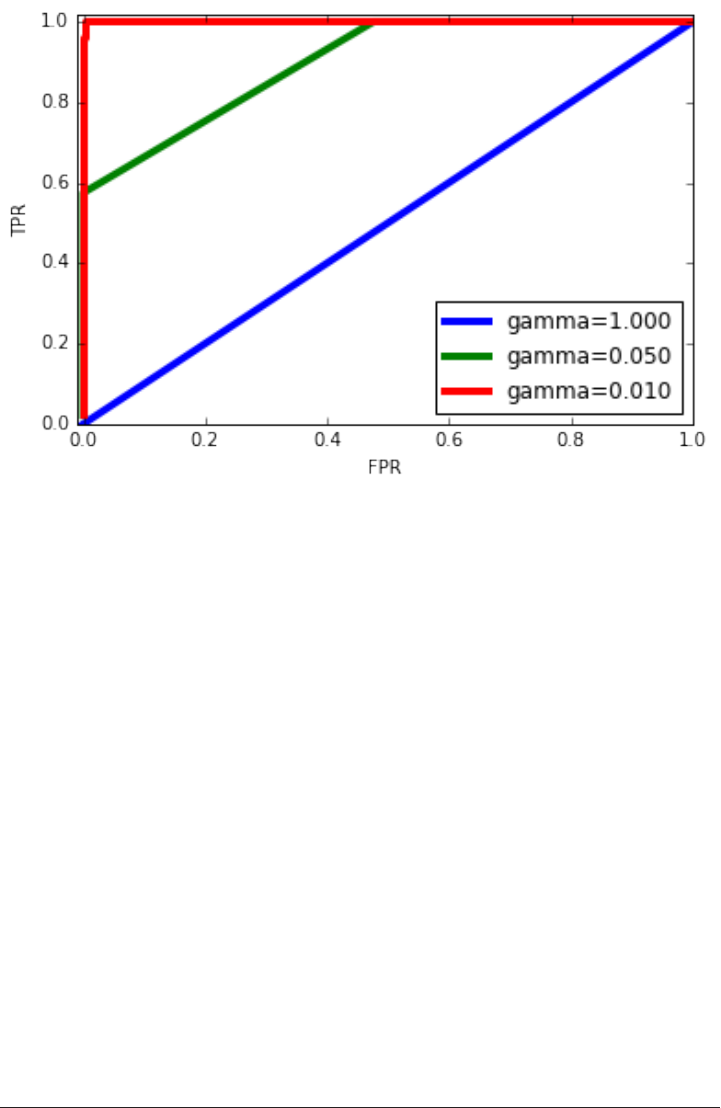
gamma = 1.00 accuracy = 0.90 AUC = 0.50
gamma = 0.05 accuracy = 0.90 AUC = 0.90
gamma = 0.01 accuracy = 0.90 AUC = 1.00
The accuracy of all three settings of gamma is the same, 90%. This could either be
chance performance, or it could be not. Looking at the AUC and the corresponding
curve, however, we see a clear distinction between the three models: With
gamma=1.0, the AUC is actually at chance level, meaning that the output of the deci
sion_function is as good as random. With gamma=0.05, performance drastically
improves to an AUC of 0.5. Finally with gamma=0.01, we get a perfect AUC of 1.0.
That means that all positive points are ranked higher than all negative points accord‐
ing to the decision function. In other words, with the right threshold, this model can
classify the data perfectly! [Footnote: Looking at the curve for gamma=0.01 in detail
you can see a small kink close to the top left. That means that at least one point was
not ranked correctly. The AUC of 1.0 is a consequence of rounding to the second dec‐
imal.] Knowing this, we can adjust the threshold on this model, and obtain great pre‐
dictions.
If we only used accuracy, we would have never discovered this.
For this reason, we highly recommend using AUC when evaluating models on imbal‐
anced data. Keep in mind that AUC does not make use of the default threshold, so
284 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

adjusting the decision threshold might be necessary to obtain useful classification
results from a model with high AUC.
Multi-class classication
Now that we have discussed evaluation of binary classification tasks in-depth, let’s
move on to metrics to evaluate multi-class classification. Basically all metrics for
multi-class classification are derived from binary classification metrics, but averaged
over all classes.
Accuracy for multi-class classification is again defined as the fraction of correctly
classified examples. And again, when classes are imbalanced, accuracy is not a great
evaluation measure. Imagine a three-class classification problem with 85% of points
belonging to class A, 10% belonging to class B and 5% belonging to class C. What
does being 85% accurate mean on this dataset?
In general, multi-class classification results are harder to understand than binary clas‐
sification results.
Apart from accuracy, common tools are the confusion matrix and the classification
report we saw in the binary case above.
Let’s apply these two detailed evaluation methods on the task of classifying the 10 dif‐
ferent hand-written digits in the digits dataset:
from sklearn.metrics import accuracy_score
X_train, X_test, y_train, y_test = train_test_split(
digits.data, digits.target, random_state=0)
lr = LogisticRegression().fit(X_train, y_train)
pred = lr.predict(X_test)
print("accuracy: %0.3f" % accuracy_score(y_test, pred))
print("confusion matrix:")
print(confusion_matrix(y_test, pred))
accuracy: 0.953
confusion matrix:
[[37 0 0 0 0 0 0 0 0 0]
[ 0 39 0 0 0 0 2 0 2 0]
[ 0 0 41 3 0 0 0 0 0 0]
[ 0 0 1 43 0 0 0 0 0 1]
[ 0 0 0 0 38 0 0 0 0 0]
[ 0 1 0 0 0 47 0 0 0 0]
[ 0 0 0 0 0 0 52 0 0 0]
Evaluation Metrics and scoring | 285
www.it-ebooks.info
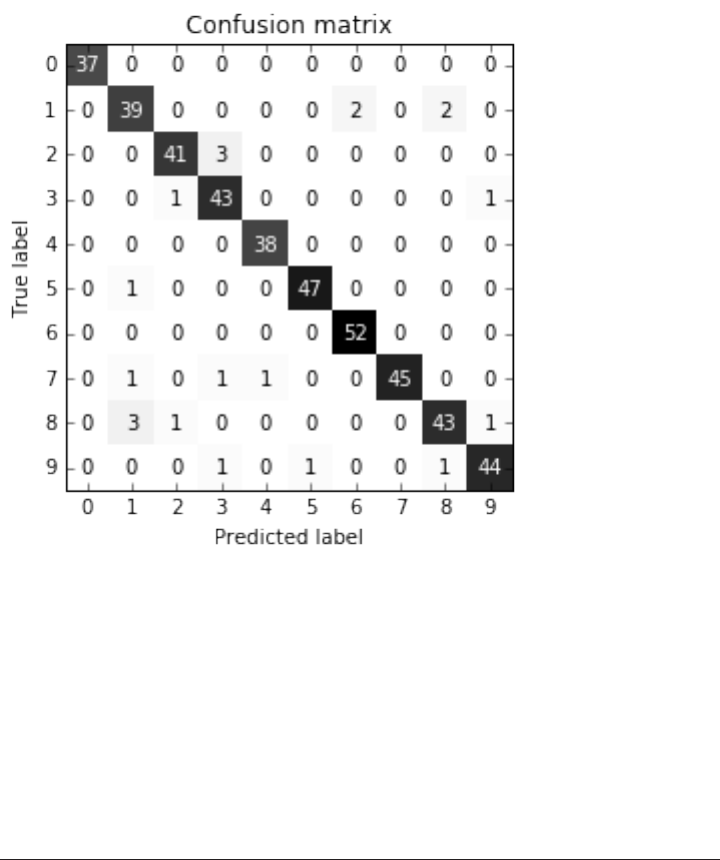
[ 0 1 0 1 1 0 0 45 0 0]
[ 0 3 1 0 0 0 0 0 43 1]
[ 0 0 0 1 0 1 0 0 1 44]]
scores_image = mglearn.tools.heatmap(confusion_matrix(y_test, pred), xlabel='Predicted label', ylabel='True label',
xticklabels=digits.target_names, yticklabels=digits.target_names,
cmap=plt.cm.gray_r, fmt="%d")
plt.title("Confusion matrix")
plt.gca().invert_yaxis()
The model has an accuracy of 95.6%, which already tells us that we are doing pretty
well. The confusion matrix provides us with some more detail. As for the binary case,
each row corresponds to a true label, and each column corresponds to a predicted
label. You can find a visualy more appealing plot in Figure multi_class_confu‐
sion_matrix. For the first class, the digit 0, there are 37 samples in the class, and all of
these samples were classified as class 0 (no false negatives for the zero class). We can
see that because all other entries in the first row of the confusion matrix are zero. We
can also see that no other digits was mistakenly classified as zero, because all other
286 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

entries in the first column of the confusion matrix are zero (no false positives for class
zero).
Some digits that were confused with others are the digit two (third row), three of
which were classified as the digit three (fourth column). There was also one digit
three that was classified as two (third coloumn, fourth row) and one digit eight that
was classified as two (thrid column, fourth row).
With the classification_report function, we can compute the precision, recall and
f-score for each class:
print(classification_report(y_test, pred))
precision recall f1-score support
0 1.00 1.00 1.00 37
1 0.89 0.91 0.90 43
2 0.95 0.93 0.94 44
3 0.90 0.96 0.92 45
4 0.97 1.00 0.99 38
5 0.98 0.98 0.98 48
6 0.96 1.00 0.98 52
7 1.00 0.94 0.97 48
8 0.93 0.90 0.91 48
9 0.96 0.94 0.95 47
avg / total 0.95 0.95 0.95 450
Unsurprisingly, precision and recall are a perfect 1 for class zero, as there are no con‐
fusions with this class. For class seven on the other hand, precision is 1 because no
other class was mistakenly classified as seven, while for class six, there are not false
negatives, so the recall is 1. We can also see that the model has particular difficulties
with classes eight and three.
The most commonly used metric for imbalanced datasets in the multi-class setting is
the multi-class version of the f-score. The idea behind multi-class F-score is to com‐
pute one binary F-score per class, with that class being the positive class, and the
Evaluation Metrics and scoring | 287
www.it-ebooks.info

other classes making up the negative classes. Then, these per-class F-scores are aver‐
aged using one of the following strategies:
•“macro” averaging computes the unweighted the per-class f-scores. This gives
equal weight to all classes, no matter what their size is.
•“weighted” averaging computes the mean of the per-class f-scores, weighted by
their support. This is what is reported in the classification report.
•“micro” averaging computes total number of false positives, false negatives and
true positives over all classes, and then compute precision, recall and f-score
using these counts.
If you care about each sample equally much, it is recommended to use "micro" aver‐
age f1-score, if you care about each class equally much, it is recommended to use the
"macro" average f1-score:
print("micro average f1 score: %f" % f1_score(y_test, pred, average="micro"))
print("macro average f1 score: %f" % f1_score(y_test, pred, average="macro"))
micro average f1 score: 0.953333
macro average f1 score: 0.954000
Regression metrics
Evaluation for regression can be done in similar detail as we did for classification
above, for example by analyzing over-predicting the target versus under-predicting
the target. However, in most application we’ve seen, using the default $R^2$ used in
the score method of all regressors is enough. Sometimes business decisions are made
on the basis of mean squared error or mean absolute error, which might give incen‐
tive to tune models using these metrics. In general, though, we have found $R^2$ to
be a more intuitive metric to evaluate regression models.
Using evaluation metrics in model selection
We now discussed many evaluation methods in detail, and how to apply them given
the ground truth and a model.
However, we often want to use metrics like AUC in model selection using Grid
SearchCV or cross_val_score.
Luckily scikit-learn provides a very simple way to achieve this, via the scoring argu‐
ment that can be used in both GridSearchCV and cross_val_score. You can simply
provide a string describing the desired evaluation metric you want to use. Say, for
example, we want to evaluate the SVC classifier on the “nine vs rest” task on the digits
288 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

dataset, using the AUC score. Changing the score from the default (accuracy) to AUC
can be done by providing "roc_auc" as the scoring parameter:
# default scoring for classification is accuracy
print("default scoring ", cross_val_score(SVC(), digits.data, digits.target == 9))
# providing scoring="accuracy" doesn't change the results
explicit_accuracy = cross_val_score(SVC(), digits.data, digits.target == 9, scoring="accuracy")
print("explicit accuracy scoring ", explicit_accuracy)
roc_auc = cross_val_score(SVC(), digits.data, digits.target == 9, scoring="roc_auc")
print("AUC scoring ", roc_auc)
default scoring [ 0.9 0.9 0.9]
explicit accuracy scoring [ 0.9 0.9 0.9]
AUC scoring [ 0.994 0.99 0.996]
Similarly we can change the metric used to pick the best parameters in GridSearchCV:
X_train, X_test, y_train, y_test = train_test_split(
digits.data, digits.target == 9, random_state=0)
# we provide a somewhat bad grid to illustrate the point:
param_grid = {'gamma': [0.0001, 0.01, 0.1, 1, 10]}
# using the default scoring of accuracy:
grid = GridSearchCV(SVC(), param_grid=param_grid)
grid.fit(X_train, y_train)
print("Grid-Search with accuracy")
print("Best parameters:", grid.best_params_)
print("Best cross-validation score (accuracy)):", grid.best_score_)
print("Test set AUC: %.3f" % roc_auc_score(y_test, grid.decision_function(X_test)))
print("Test set accuracy %.3f: " % grid.score(X_test, y_test))
# using AUC scoring instead:
grid = GridSearchCV(SVC(), param_grid=param_grid, scoring="roc_auc")
grid.fit(X_train, y_train)
print("\nGrid-Search with AUC")
print("Best parameters:", grid.best_params_)
print("Best cross-validation score (AUC):", grid.best_score_)
print("Test set AUC: %.3f" % roc_auc_score(y_test, grid.decision_function(X_test)))
print("Test set accuracy %.3f: " % grid.score(X_test, y_test))
Grid-Search with accuracy
Best parameters: {'gamma': 0.0001}
Best cross-validation score (accuracy)): 0.970304380104
Test set AUC: 0.992
Test set accuracy 0.973:
Using evaluation metrics in model selection | 289
www.it-ebooks.info

Grid-Search with AUC
Best parameters: {'gamma': 0.01}
Best cross-validation score (AUC): 0.997467845028
Test set AUC: 1.000
Test set accuracy 1.000:
When using accuracy, the parameter gamma=0.0001 is selected, while gamma=0.01 is
selected when using AUC. The cross-validation accuracy is consistent with the test set
accuracy in both cases. However, using AUC found a better parameter setting, both in
terms of AUC and even in terms of accuracy [Footnote: Finding a higher accuracy
solution using AUC is likely a consequence of accuracy being a bad measure of model
performance on imbalanced data].
The most important values for the scoring parameter for classification are accuracy
(the default), roc_auc for the area under the ROC curve, average_precision for the
area under the precision-recall curve, f1, f1_macro, f1_micro and f1_weighted for
the binary F1 score and the different weighted variants.
For regression, the most commonly used values are r2 for the $R^2$ score,
mean_squared_error for mean squared error and mean_absolute_error for mean
absolute error.
You can find a full list of supported arguments in the documentation or by looking at
the SCORER dictionary defined in the metrics.scorer module:
from sklearn.metrics.scorer import SCORERS
print(sorted(SCORERS.keys()))
['accuracy', 'adjusted_rand_score', 'average_precision', 'f1', 'f1_macro', 'f1_micro', 'f1_samples', 'f1_weighted', 'log_loss', 'mean_absolute_error', 'mean_squared_error', 'median_absolute_error', 'precision', 'precision_macro', 'precision_micro', 'precision_samples', 'precision_weighted', 'r2', 'recall', 'recall_macro', 'recall_micro', 'recall_samples', 'recall_weighted', 'roc_auc']
Summary and outlook
In this chapter we discussed cross-validation, grid-search and evaluation metrics, the
corner-stones of evaluating and improving machine learning algorithms. The tools
described in this chapter, together with the algorithms described in Chapters 2 and 3
are the bread and butter of every machine learning practitioner. There are two partic‐
ular points that we made in this chapter that warrant repeating, because they are often
overlooked by new practitioners: Cross-validation or the use of a test set allow us to
evaluate a machine learning model as it will perform in the future. However, if we use
the test-set or cross-validation to select a model or select model parameters, we “used
up” the test data, and using the same data to evaluate how well our model will do in
the future will lead to overly optimistic estimates. We therefore need to resort to a
split into training data for model building, validation data for model and parameter
290 | Chapter 6: Model evaluation and improvement
www.it-ebooks.info

selection, and test data for model evaluation. Instead of a simple split, we can replace
each of these splits with cross-validation. The most commonly used form as
described above is a train-test split for evaluation, and using cross-validation on the
training set for model and parameter selection.
The second important point is the importance of the evaluation metric or scoring
function used for model selection and model evaluation. The theory of how to make
business decisions from the predictions of a machine learning model is somewhat
beyond the scope of this book. However, it is rarely the case that the end goal of a
machine learning task is building a model with a high accuracy. Make sure that the
metric you choose to evaluate and select a model is a good stand-in for what the
model will actually be used for. In reality, classification problems rarely have balanced
classes, and often false positives and false negatives have very different consequences.
Make sure you understand what these consequences are, and pick an evaluation met‐
ric accordingly.
The techniques model evaluation and selection techniques we described so far are the
most important tools in a data scientists toolbox. However, grid search and cross vali‐
dation as we described it in this chapter can only be applied to a single supervised
model. We have seen before, however, that many models require preprocessing, and
that in some applications, like the face recognition example in Chapter 3, extracting a
different representation of the data can be useful. In the next chapter, we will intro‐
duce the Pipeline class, which allows us to use grid-search and cross-validation on
these complex chains of algorithms.
Summary and outlook | 291
www.it-ebooks.info

CHAPTER 7
Algorithm Chains and Pipelines
For many machine learning algorithms, the particular representation of the data that
you provide is very important, as we discussed in Chapter 5. This starts with scaling
the data and combining features by hand and goes all the way to learning features
using unsupervised machine learning as we saw in Chapter 3.
Consequently, most machine learning applications require not only the application of
a single algorithm, but the chaining together of many different processing steps and
machine learning models.
For example we noticed that we can greatly improve the performance of a kernel
SVM on the cancer dataset by using the MinMaxScaler for preprocessing. The code
for splitting the data, computing minimum and maximum, scaling the data, and
training the SVM is shown below:
from sklearn.svm import SVC
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
# load and split the data
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=0)
# compute minimum and maximum on the training data
scaler = MinMaxScaler().fit(X_train)
# rescale training data
X_train_scaled = scaler.transform(X_train)
svm = SVC()
# learn an SVM on the scaled training data
svm.fit(X_train_scaled, y_train)
293
www.it-ebooks.info

# scale test data and score the scaled data
X_test_scaled = scaler.transform(X_test)
svm.score(X_test_scaled, y_test)
0.95104895104895104
Parameter Selection with Preprocessing
Now let’s say we want to find better parameters for SVC using GridSearchCV, as dis‐
cussed in Chapter 6.
How should we go about doing this? A naive approach might look like this:
from sklearn.model_selection import GridSearchCV
# illustration purposes only, don't use this code
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100],
'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
grid = GridSearchCV(SVC(), param_grid=param_grid, cv=5)
grid.fit(X_train_scaled, y_train)
print("best cross-validation accuracy:", grid.best_score_)
print("test set score: ", grid.score(X_test_scaled, y_test))
print("best parameters: ", grid.best_params_)
best cross-validation accuracy: 0.981220657277
test set score: 0.972027972028
best parameters: {'gamma': 1, 'C': 1}
Here, we ran the grid-search over the parameters of the SVC using the scaled data.
However, there is a subtle catch in what we just did. When scaling the data, we used
all data in the training set to find out how to train it.
We then use the scaled training data to run our grid-search using cross-validation. For
each split in the cross-validation, some part of the original training set will be
declared the training part of this split, and some the test part of the split. The test part
is used to measure how new data will look like to a model trained on the training
part. However, we already used the information contained in the test part of the split,
when scaling the data. Remember that the test part in each split in the cross-
validation is part of the training set, and we used the information from the whole train‐
ing data to find the right scaling of the data. is is fundamentally dierent to how new
data looks to the model. If we observe new data (say in form of our test set), this data
will not have been used to scale the training data. This data might have a different
minimum and maximum than the training data.
The illustration below shows how the data processing during cross-validation and the
final evaluation differ:
mglearn.plots.plot_improper_processing()
294 | Chapter 7: Algorithm Chains and Pipelines
www.it-ebooks.info
So the splits in the cross-validation no longer correctly mirror how new data will look
to the modeling process. We already leaked information from these parts of the data
into our modeling process. This will lead to overly optimistic results during cross-
validation, and possibly the selection of suboptimal parameters.
To get around this problem, the splitting of the data set during cross-validation
should be done before doing any preprocessing. Any process that extracts knowledge
from the dataset should only ever be applied to the training portion of the data set, so
any cross-validation should be the “outermost loop” in your processing.
To achieve this in scikit-learn with the cross_val_score function and the Grid
SearchCV function, we can use the Pipeline class. The Pipeline class is a class that
allows “gluing” together multiple processing steps into a single scikit-learn estimator.
The Pipeline class itself has fit, predict and score methods and behaves just like
any other model in scikit-learn. The most common use-case of the pipeline class is in
chaining preprocessing steps (like scaling of the data) together with a supervised
model like a classifier.
Building Pipelines
Let’s look at how we can use the Pipeline to express the work-flow for training an
SVM after scaling the data MinMaxScaler (for now without the grid-search). First, we
build a pipeline object, by providing it with a list of steps. Each step is a tuple contain‐
Parameter Selection with Preprocessing | 295
www.it-ebooks.info

ing a name (any string of your choosing [Footnote: With one exception: the name
may not contain a double underscore "__".]) and an instance of an estimator:
from sklearn.pipeline import Pipeline
pipe = Pipeline([("scaler", MinMaxScaler()), ("svm", SVC())])
Here, we created two steps, the first called "scaler" is a MinMaxScaler, the second,
called "svm" is an SVC. Now, we can fit the pipeline, like any other scikit-learn estima‐
tor:
pipe.fit(X_train, y_train)
Pipeline(steps=[('scaler', MinMaxScaler(copy=True, feature_range=(0, 1))), ('svm', SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=None, degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False))])
Here, pipe.fit first calls fit on the first step, the scaler, then transforms the training
data using the scaler, and finally fits the SVM with the scaled data. To evaluate on the
test data, we simply call pipe.score:
pipe.score(X_test, y_test)
0.95104895104895104
Calling the score method on the pipeline first transforms the test data using the
scaler, and then calls the score method on the SVM using the scaled test data. As you
can see, the result is identical to the one we got from the code above, doing the trans‐
formations “by hand”.
Using the pipeline, we reduced the code needed for our “preprocessing + classifica‐
tion” process.
The main benefit of using the pipeline, however, is that we can now use this single
estimator in cross_val_score or GridSearchCV.
Using Pipelines in Grid-searches
Using a pipeline in a grid-search works the same way as using any other estimator.
We define a parameter grid to search over, and construct a GridSearchCV from the
pipeline and the parameter grid. When specifying the parameter grid, there is a slight
change, though. We need to specify for each parameter which step of the pipeline it
belongs to.
Both parameters that we want to adjust, C and gamma are parameters of SVC, the sec‐
ond step. We gave this step the name "svm". The syntax to define the a parameter grid
for a pipeline is to specify for each parameter the step name, followed by "__" (dou‐
296 | Chapter 7: Algorithm Chains and Pipelines
www.it-ebooks.info
ble underscore), followed by the parameter name. To search over the C parameter of
the SVC we therefore have to use "svm__C" as the key in the parameter grid dictionary,
and similarly for gamma:
param_grid = {'svm__C': [0.001, 0.01, 0.1, 1, 10, 100],
'svm__gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
Using this parameter grid we can use GridSearchCV as usual:
grid = GridSearchCV(pipe, param_grid=param_grid, cv=5)
grid.fit(X_train, y_train)
print("best cross-validation accuracy:", grid.best_score_)
print("test set score: ", grid.score(X_test, y_test))
print("best parameters: ", grid.best_params_)
best cross-validation accuracy: 0.981220657277
test set score: 0.972027972028
best parameters: {'svm__C': 1, 'svm__gamma': 1}
In contrast to the grid-search we did before, now for each split in the cross-
validation, the MinMaxScaler is refit with only the training splits, not leaking any
information of the test split into the parameter search, as illustrated below. Compare
this with Figure improper_preprocessing above.
mglearn.plots.plot_proper_processing()
The impact of leaking information in the cross-validation varies depending on the
nature of the preprocessing step. Estimating the scale of the data using the test fold
Parameter Selection with Preprocessing | 297
www.it-ebooks.info

usually doesn’t have a terrible impact, while using the test fold in feature extraction
and feature selection can lead to substantial differences in outcomes.
[FIXME info box] Illustrating information leakage
A great example of leaking information in cross-validation is given in Hastie et al.
(FIXME insert cite) and we reproduce an adapted version here.
Let us consider a synthetic regression task with 100 samples and 1000 features that
are sampled independently from a Gaussian distribution. We also sample the
response from a Gaussian distribution:
rnd = np.random.RandomState(seed=0)
X = rnd.normal(size=(100, 10000))
y = rnd.normal(size=(100,))
Given the way we created the dataset, there is no relation between the data X and the
target y (they are independent), so it should not be possible to learn anything from
this data set.
We will now do the following: First select the most informative of the ten features
using SelectPercentile feature selection, and then evaluate a Ridge regressor using
cross-validation:
from sklearn.feature_selection import SelectPercentile, f_regression
select = SelectPercentile(score_func=f_regression, percentile=5).fit(X, y)
X_selected = select.transform(X)
print(X_selected.shape)
(100, 500)
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import Ridge
np.mean(cross_val_score(Ridge(), X_selected, y, cv=5))
0.90579530652398221
The mean $R^2$ computed by cross-validation is 0.9, indicating a very good model.
This can clearly not be right, as our data is entirely random. What happened here is
that our feature selection picked out some features among the 10000 random features
that are (by chance) very well correlated with the target. Because we fit the feature
selection outside of the cross-validation, it could find features that are correlated both
on the training and the test folds. The information we leaked from the test-folds was
very informative, leading to highly unrealistic results.
Let’s compare this to a proper cross-validation using a pipeline:
pipe = Pipeline([("select", SelectPercentile(score_func=f_regression, percentile=5)), ("ridge", Ridge())])
np.mean(cross_val_score(pipe, X, y, cv=5))
-0.24655422384952805
298 | Chapter 7: Algorithm Chains and Pipelines
www.it-ebooks.info

This time, we get a negative $R^2$ score, indicating a very poor model.
Using the pipeline, the feature selection is now inside the cross-validation loop. This
means features can only be selected using the training folds of the data, not the test
fold. The feature selection finds features that are correlated with the target on the
training set. But because the data is entirely random, these features are not correlated
with the target on the test set.
In this example, rectifying the data leakage issue in the feature selection makes the
difference between concluding that a model works very well and concluding that a
model works not at all.
[end infobox]
The General Pipeline Interface
The Pipeline class is not restricted to preprocessing and classification, but can in
fact join any number of estimators together.
For example, you could build a pipeline containing feature extraction, feature selec‐
tion, scaling and classification, for a total of four steps. Similarly the last step could be
regression or clustering instead of classification.
The only requirement for estimators in a pipeline is that all but the last step need to
have a transform method, so they can produce a new representation of the data that
can be used in the next step.
Internally, during the call to Pipeline.fit, the pipeline calls first fit and then trans
form on each step in turn [Footnote: or just fit_transform], with the input given by
the output of the transform method of the previous step. For the last step in the pipe‐
line, just fit is called. Brushing over some finer details, this is implemented as fol‐
lows. Remember that pipeline.steps is a list of tuples, so pipeline.steps[0][1] is
the first estimator, pipeline.steps[1][1] is the second estimator, and so on.
def fit(self, X, y):
X_transformed = X
for step in self.steps[:-1]:
# iterate over all but the final step
# fit and transform the data
X_transformed = step[1].fit_transform(X_transformed, y)
# fit the last step
self.steps[-1][1].fit(X_transformed, y)
return self
When predicting using Pipeline, similarly we transform the data using all but the
last step, and then call predict on the last step:
def predict(self, X):
X_transformed = X
Parameter Selection with Preprocessing | 299
www.it-ebooks.info
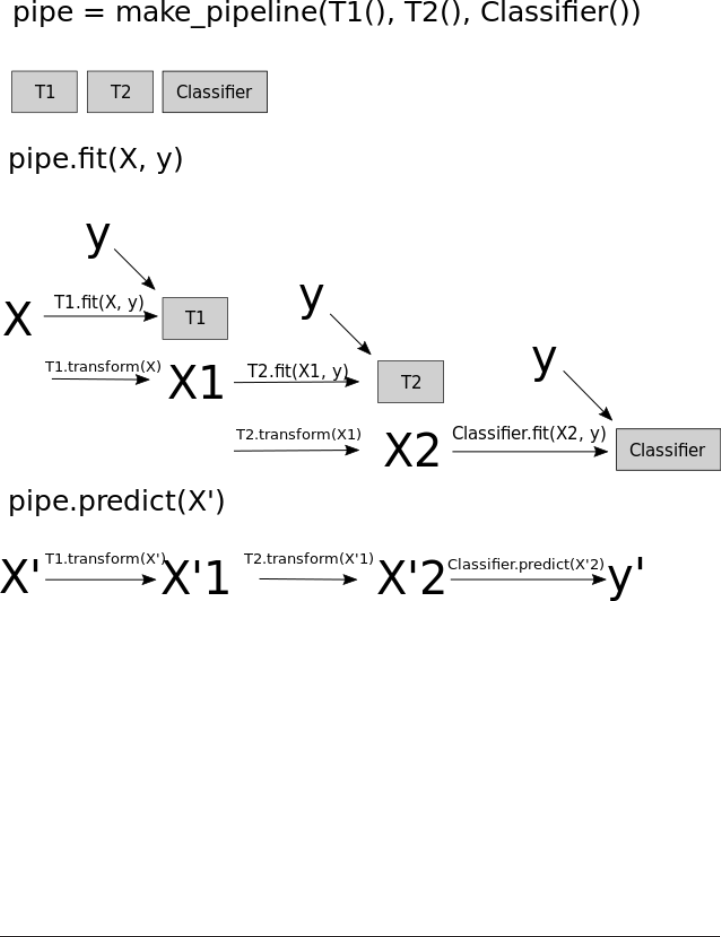
for step in self.steps[:-1]:
# iterate over all but the final step
# transform the data
X_transformed = step[1].transform(X_transformed)
# fit the last step
return self.steps[-1][1].predict(X_transformed)
The process is illustrated below for two transformers T1 and T2 and a classifier Clf:
The pipeline is actually even more general than this. There is no requirement for the
last step in a pipeline to have a predict function, and we could create a pipeline just
containing, for example, a scaler and PCA. Then, because the last step PCA has a trans
form method, we could call transform on the pipeline to get the output of PCA.trans
form applied to the data that was processed by the previous step. The last step of a
pipeline is only required to have a fit method.
Convenient Pipeline creation with make_pipeline
Creating a Pipeline using the syntax described above is sometimes a bit cumbersome,
and we often don’t need user-specified names for each step. There is a convenience
300 | Chapter 7: Algorithm Chains and Pipelines
www.it-ebooks.info

function make_pipeline that will create a pipeline for us and automatically name
each step based on its class. The syntax for make_pipeline is as follows:
from sklearn.pipeline import make_pipeline
# standard syntax
pipe_long = Pipeline([("scaler", MinMaxScaler()), ("svm", SVC(C=100))])
# abbreviated syntax
pipe_short = make_pipeline(MinMaxScaler(), SVC(C=100))
The pipeline objects pipe_long and pipe_short do exactly the same, only that
pipe_short has steps that were automatically named. We can see the name of the
steps by looking at the steps attribute:
pipe_short.steps
[('minmaxscaler', MinMaxScaler(copy=True, feature_range=(0, 1))),
('svc', SVC(C=100, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=None, degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False))]
The steps are named minmaxscaler and svc. In general the step names are just lower-
case version of the class names. If multiple steps have the same class, a number is
appended:
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
pipe = make_pipeline(StandardScaler(), PCA(n_components=2), StandardScaler())
pipe.steps
[('standardscaler-1',
StandardScaler(copy=True, with_mean=True, with_std=True)),
('pca', PCA(copy=True, iterated_power=4, n_components=2, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)),
('standardscaler-2',
StandardScaler(copy=True, with_mean=True, with_std=True))]
As you can see, the first StandardScaler was named "standardscaler-1" and the
second "standardscaler-2". However, in such settings it might be better to use the
Pipeline construction with explicit names, to give more semantic names to each
step.
Parameter Selection with Preprocessing | 301
www.it-ebooks.info

Accessing step attributes
Often you might want to inspect attributes of one of the steps of the pipeline, say the
coefficients of a linear model or the components extracted by PCA. The easiest way to
access the step in a pipeline is the named_steps attribute, which is a dictionary from
step names to the estimators:
# fit the pipeline defined above to the cancer dataset
pipe.fit(cancer.data)
# extract the first two principal components from the "pca" step
components = pipe.named_steps["pca"].components_
print(components.shape)
/home/andy/checkout/scikit-learn/sklearn/utils/extmath.py:368: UserWarning: The number of power iterations is increased to 7 to achieve higher precision.
warnings.warn("The number of power iterations is increased to "
Accessing attributes in grid-searched pipeline.
As we discussed above, one of the main reasons to use pipelines is for doing grid-
searches. A common task then is to access some of the steps of a pipeline inside a
grid-search.
Let’s grid-search a LogisticRegression classifier on the cancer dataset, using Pipe
line and StandardScaler to scale the data before passing it to the LogisticRegres
sion classifier.
First we create a pipeline using the make_pipeline function:
from sklearn.linear_model import LogisticRegression
pipe = make_pipeline(StandardScaler(), LogisticRegression())
Next, we create a parameter grid. The regularization parameter to tune for Logisti
cRegression is the parameter C as explained in Chapter 2. We use a logarithmic grid
for this parameter, searching between 0.01 and 100. Because we used the make_pipe
line function, the name of the LogisticRegression step in the pipeline is the lower-
cased class-name "logisticregression". To tune the parameter C, we therefore
have to specify a parameter grid for "logisticregression__C":
param_grid = {'logisticregression__C': [0.01, 0.1, 1, 10, 100]}
We split the cancer dataset into training and test set, and fit a grid-search as usual:
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=4)
grid = GridSearchCV(pipe, param_grid, cv=5)
grid.fit(X_train, y_train)
GridSearchCV(cv=5, error_score='raise',
estimator=Pipeline(steps=[('standardscaler', StandardScaler(copy=True, with_mean=True, with_std=True)), ('logisticregression', LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
302 | Chapter 7: Algorithm Chains and Pipelines
www.it-ebooks.info

intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False))]),
fit_params={}, iid=True, n_jobs=1,
param_grid={'logisticregression__C': [0.01, 0.1, 1, 10, 100]},
pre_dispatch='2*n_jobs', refit=True, scoring=None, verbose=0)
So how do we access the coefficients of the best LogisticRegression model that was
found by GridSearchCV? From Chapter 6 we know that the best model found by Grid
SearchCV, trained on all the training data, is stored in grid.best_estimator_:
print(grid.best_estimator_)
Pipeline(steps=[('standardscaler', StandardScaler(copy=True, with_mean=True, with_std=True)), ('logisticregression', LogisticRegression(C=0.1, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False))])
This best_estimator_ in our case is a pipeline with two steps, "standardscaler"
and "logisticregression". To access the logisticregression step, we can use the
named_steps attribute of the pipeline that we explained above:
print(grid.best_estimator_.named_steps["logisticregression"])
LogisticRegression(C=0.1, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False)
Now that we have the trained LogisticRegression instance, we can access the coeffi‐
cients (weights) associated with each input feature:
print(grid.best_estimator_.named_steps["logisticregression"].coef_)
[[-0.389 -0.375 -0.376 -0.396 -0.115 0.017 -0.355 -0.39 -0.058 0.209
-0.495 -0.004 -0.371 -0.383 -0.045 0.198 0.004 -0.049 0.21 0.224
-0.547 -0.525 -0.499 -0.515 -0.393 -0.123 -0.388 -0.417 -0.325 -0.139]]
This might be a somewhat lengthy expression, but often comes in handy in under‐
standing your models.
Parameter Selection with Preprocessing | 303
www.it-ebooks.info

Grid-searching preprocessing steps and model parameters
Using pipelines, we can encapsulate all processing steps in our machine learning
work flow in a single scikit-learn estimator. Another benefit of doing this is that we
can now adjust the parameters of the preprocessing using the outcome of a supervised
task like regression or classification.
In previous chapters, we used polynomial features on the boston dataset before
applying the ridge regressor. Let’s model that using a pipeline. The pipeline contains
three steps: scaling the data, computing polynomial features, and ridge regression:
from sklearn.datasets import load_boston
boston = load_boston()
X_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=0)
from sklearn.preprocessing import PolynomialFeatures
pipe = make_pipeline(
StandardScaler(),
PolynomialFeatures(),
Ridge())
But how do we know which degree of polynomials to choose, or whether to choose
any polynomials or interactions at all? Ideally we want to select the degree parameter
based on the outcome of the classification.
Using our pipeline, we can search over the degree parameter together with the
parameter alpha of Ridge. To do this, we define a param_grid that contains both,
appropriately prefixed by the step names:
param_grid = {'polynomialfeatures__degree': [1, 2, 3],
'ridge__alpha': [0.001, 0.01, 0.1, 1, 10, 100]}
Now we can run our grid-search again:
grid = GridSearchCV(pipe, param_grid=param_grid, cv=5, n_jobs=-1)
grid.fit(X_train, y_train)
GridSearchCV(cv=5, error_score='raise',
estimator=Pipeline(steps=[('standardscaler', StandardScaler(copy=True, with_mean=True, with_std=True)), ('polynomialfeatures', PolynomialFeatures(degree=2, include_bias=True, interaction_only=False)), ('ridge', Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None,
normalize=False, random_state=None, solver='auto', tol=0.001))]),
fit_params={}, iid=True, n_jobs=-1,
param_grid={'ridge__alpha': [0.001, 0.01, 0.1, 1, 10, 100], 'polynomialfeatures__degree': [1, 2, 3]},
pre_dispatch='2*n_jobs', refit=True, scoring=None, verbose=0)
We can visualize the outcome of the cross-validation using a heatmap, as we did in
Chapter 6:
304 | Chapter 7: Algorithm Chains and Pipelines
www.it-ebooks.info
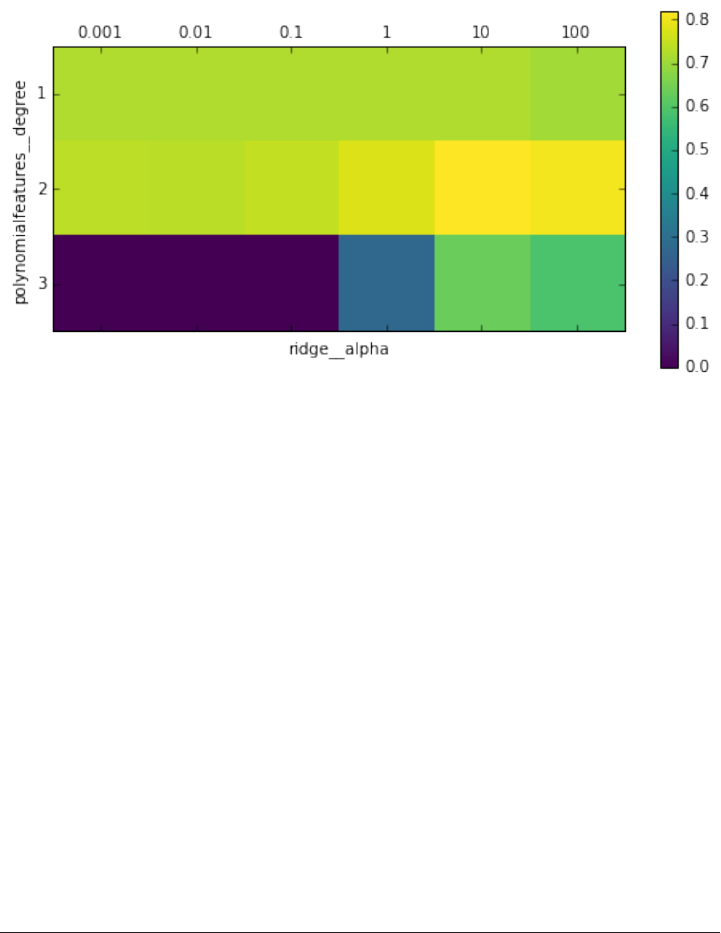
plt.matshow(np.array([s.mean_validation_score for s in grid.grid_scores_]).reshape(3, -1),
vmin=0, cmap="viridis")
plt.xlabel("ridge__alpha")
plt.ylabel("polynomialfeatures__degree")
plt.xticks(range(len(param_grid['ridge__alpha'])), param_grid['ridge__alpha'])
plt.yticks(range(len(param_grid['polynomialfeatures__degree'])), param_grid['polynomialfeatures__degree'])
plt.colorbar()
Looking at the results produced by the cross-validation, we can see that using polyno‐
mials of degree two helps, but that degree three polynomials are much worse than
either degree one or two.
This is reflected in the best parameters that were found:
print(grid.best_params_)
{'ridge__alpha': 10, 'polynomialfeatures__degree': 2}
Which lead to the following score:
grid.score(X_test, y_test)
0.76735803503061784
Let’s run a grid-search without polynomial features for comparison:
param_grid = {'ridge__alpha': [0.001, 0.01, 0.1, 1, 10, 100]}
pipe = make_pipeline(StandardScaler(), Ridge())
grid = GridSearchCV(pipe, param_grid, cv=5)
grid.fit(X_train, y_train)
grid.score(X_test, y_test)
0.62717803817745799
Parameter Selection with Preprocessing | 305
www.it-ebooks.info

As we had expected from the grid-search results visualized above, using no polyno‐
mial features leads to decidedly worse results. Searching over preprocessing parame‐
ters together with model parameters is a very powerful strategy. However, keep in
mind that GridSearchCV tries all possible combinations of the specified parameters.
Adding more parameters to your grid therefore increases the number of models that
need to be built exponentially.
Summary and Outlook
In this chapter we introduced the Pipeline class a general purpose tool to chain
together multiple processing steps in a machine learning work flow. Real-world appli‐
cations of machine learning are rarely an isolated use of a model, and instead a
sequence of processing steps. Using pipelines allows us to encapsulate multiple steps
into a single python object that adheres to the familiar scikit-learn interface of fit,
predict and transform.
In particular when doing model evaluation using cross-validation and parameter
selection using grid-search, using the Pipeline class to capture all processing steps is
essential for proper evaluation.
The Pipeline class also allows writing more succinct code, and reduces the likeli‐
hood of mistakes that can happen when building processing chains without the pipe‐
line class (like forgetting to apply all transformers on the test set, or maybe not
applying them in the right order).
Choosing the right combination of feature extraction, preprocessing and models is
somewhat of an art, that often requires some trial-and-error. However, using pipe‐
lines, this “trying out” of many different processing steps is quite simple. When
experimenting, be careful not to over-complicate your processes, and make sure to
evaluate whether every component your are including in your model is necessary.
With this chapter, we complete our survey of general purpose tools and algorithms
provided by scikit-learn. You now possess all the required skills and know the neces‐
sary mechanisms to apply machine learning in practice. In the next chapter, we will
dive in more detail into one particular type of data that is commonly seen in practice,
and that requires some special expertise to handle correctly: text data.
306 | Chapter 7: Algorithm Chains and Pipelines
www.it-ebooks.info

CHAPTER 8
Working with Text Data
In Chapter 5, we talked about two kinds of features that can represent properties of
the data: continuous features that describe a quantity, and categorical features that are
items from a fixed list. There is a third kind of feature that can be found in many
application, which is text.
For example, if we want to classify in email into whether it is a legitimate email or
spam, the content of the email will certainly contain important information for this
classification task. Or maybe we want to learn about the opinion of a politician on the
topic of immigration. Here, their speeches or tweets might provide useful informa‐
tion.
In customer services, we often want to find out if a message is a complaint or an
inquiry. And depending on the kind of complaint, we might be able to provide auto‐
matic advice or forward it to a specific department. These decisions can all be sup‐
ported by the content of the message that was sent to customer service.
Text data is usually represented as strings, made up of characters. In any of the exam‐
ples above, the length of the text of each text will be different.
This feature is clearly very different from the numeric features that we discussed so
far, and we need to process the text data before we can apply our machine learning
algorithms to the text data.
Types of data represented as strings
Before we dive into the processing steps that go into representing text data for
machine learning, we want to briefly discuss different kinds of text data that you
might encounter. Text is usually just a string in your dataset, but not each string fea‐
ture should be treated as text. A string feature can sometimes represent categorical
307
www.it-ebooks.info

variables, as we discussed in Chapter 5. There is no way to know how to treat a string
feature before looking at the data.
There are four kinds of string data you might see:
• Categorical data
• Free strings that can be semantically mapped to categories
•Structured string data
•Text data
Categorical data is data that comes from a fixed list. Say you collect data via a survey
where you ask people their favorite color, with a drop-down menu that allows them
to select from “red”, “green”, “blue”, “yellow”, “black”, “white”, “purple” and “pink”. This
will result in a dataset with exactly 8 different possible values, which clearly encode a
categorical variable. You can check whether this is the case for your data by eyeballing
it (if you see very many different strings it is unlikely that this is a categorical vari‐
able), and confirming it by computing the unique values over the dataset, and possi‐
bly a histogram over how often each appears. You also might want to check whether
each variable actually corresponds to a category that makes sense for your applica‐
tion. Maybe half-way through the existence of your survey, someone found that
“black” was misspelled as “blak” and subsequently fixed the survey. As a result your
dataset contains both “blak” and “black”, which correspond to the same semantic
meaning, and should be consolidated.
Now imagine instead of providing a drop-down menu, you provide a text field for the
user to provide their own favorite color. Many people might respond with a color
name like “black” or “blue”. Others might have typographic errors, or use aliases, or
different spellings like “gray” and “grey”, use more evocative names like “midnight
blue”, and there will certainly be answers that can not reasonably be related to any
color, say “calmly checkered hissing” or “asdfasdfasdf”.
The responses you can obtain from a text field belong to the second category, free
strings that correspond to a set of categories. It will probably be best to encode this data
as a categorical variable, where you can select the categories either using the most
common entries, or by defining categories that will capture responses in a way that
makes sense for your application.
You might then have some categories for standard colors, maybe a category “multi-
colored” for people that gave answers like “green and red stripes” and an “other” cate‐
gory, for things that can not be encoded otherwise. This kind of preprocessing of
strings can take a lot of manual effort, and is not easily automated.
308 | Chapter 8: Working with Text Data
www.it-ebooks.info

If you are in a position where you can influence data collection, we highly recom‐
mend avoiding manually entered values for concepts that are better captured using
categorical variables.
Often, manually entered values do not correspond to fixed categories, but still have
some underlying structure, like addresses, names of places or people, dates, telephone
numbers or other identifiers. These kind of strings are often very hard to parse, and
their treatment is highly dependent on context and domain. A systematic treatment
of these cases is beyond the scope of this book.
The final category of string data is free form text that consists of phrases or sentences.
Examples of these include tweets, chat logs, hotel reviews, but also the collected
works of Shakespeare, the content of Wikipedia or the project Gutenberg collection
of 50.000 e-books. All of these collections contain information mostly as sentences of
words[footnote: arguably the content of websites linked to in tweets contain more
information than the text of the tweet]. For simplicity’s sake, let’s assume all our
documents are in one language, English [footnote: most of what we will talk about in
the rest of the chapter also applies to other languages that use the Roman alphabet,
and partially also to other alphabets with word boundary delimiters. Chinese for
example does not delimit word boundaries, and has other challenges that make
applying the techniques of this chapter difficult]. In the context of text analysis, the
dataset if often called the corpus, and each data point, represented as a single text, is
called a document.
These terms come from the information retrieval (IR) and natural language processing
(NLP) community, which both deal mostly in text data.
Example application: Sentiment analysis of movie reviews
As a running example in this chapter, we will use a data set of movie reviews collected
from the IMDb (Internet Movie Database) website collected by Standford Researcher
Andrew Maas [footnote: The dataset is available at http://ai.stanford.edu/~amaas/
data/sentiment/]. This dataset contains the text of the reviews, together with a label
that indicates “positive” and “negative” reviews. The IMDb website itself contains rat‐
ings from one to ten. To simplify the modeling, this annotation is summarized as a
two-class classification dataset where reviews with a score of 6 or higher are labeled as
positive, and the rest as negative. We will leave the question of whether this is a good
representation of the data open, and simply use the data as provided by Andrew
Maas.
After unpacking the data, the data set is provided as text files in two separate folders,
one for the training data, and one for the test data. Each of these in turn has two sub-
folders, one called “positive” and one called “negative”:
!tree -L 2 data/aclImdb
Types of data represented as strings | 309
www.it-ebooks.info

data/aclImdb
├── test
│ ├── neg
│ └── pos
└── train
├── neg
└── pos
6 directories, 0 files
The “positive” folder contains all the positive documents, each as a separate text file,
and similarly for the “negative” folder. There is a helper function in scikit-learn to
load files stored in such a folder-structure, where each subfolder corresponds to a
label, called load_files. We apply the load_files function first to the training data:
from sklearn.datasets import load_files
reviews_train = load_files("data/aclImdb/train/")
# load_files returns a bunch, containing training texts and training labels
text_train, y_train = reviews_train.data, reviews_train.target
print("type of text_train: ", type(text_train))
print("length of text_train: ", len(text_train))
print("text_train[1]:")
# print review number 1
print(text_train[1])
type of text_train: <class 'list'>
length of text_train: 25000
text_train[1]:
b'Words can\'t describe how bad this movie is. I can\'t explain it by writing only. You have too see it for yourself to get at grip of how horrible a movie really can be. Not that I recommend you to do that. There are so many clich\xc3\xa9s, mistakes (and all other negative things you can imagine) here that will just make you cry. To start with the technical first, there are a LOT of mistakes regarding the airplane. I won\'t list them here, but just mention the coloring of the plane. They didn\'t even manage to show an airliner in the colors of a fictional airline, but instead used a 747 painted in the original Boeing livery. Very bad. The plot is stupid and has been done many times before, only much, much better. There are so many ridiculous moments here that i lost count of it really early. Also, I was on the bad guys\' side all the time in the movie, because the good guys were so stupid. "Executive Decision" should without a doubt be you\'re choice over this one, even the "Turbulence"-movies are better. In fact, every other movie in the world is better than this one.'
We can see that text_train is a list of length 25.000, where each entry is a string con‐
taining a review. We printed the review with index one. You can see that the review
contains some HTML line breaks ("<br />"). While these are unlikely to have a large
impact on our machine learning models, it is better to clean the data from this for‐
mating before we proceed:
text_train = [doc.replace(b"<br />", b" ") for doc in text_train]
The type of the entries of text_train depends on your Python version. In Python3,
they will be of type “bytes” which represents a binary encoding of the string data. In
310 | Chapter 8: Working with Text Data
www.it-ebooks.info

Python2, text_train contains strings. We won’t go into the details of the different
string types in Python here, but recommend that you read the documentation regard‐
ing strings and unicode in Python [Footnote: https://docs.python.org/3/howto/
unicode.html for Python 3 and https://docs.python.org/2/howto/unicode.html for
Python 2].
The dataset was collected such that the positive class and the negative class balanced,
so that there are as many positive as negative strings:
print(np.bincount(y_train))
[12500 12500]
We load the test dataset in the same manner:
reviews_test = load_files("data/aclImdb/test/")
text_test, y_test = reviews_test.data, reviews_test.target
print("Number of documents in test data: %d" % len(text_test))
print(np.bincount(y_test))
text_test = [doc.replace(b"<br />", b" ") for doc in text_test]
Number of documents in test data: 25000
[12500 12500]
The task we want to solve is given a review, we want to assign the labels “positive” and
“negative” based on the text content of the review. This is a standard binary classifica‐
tion task. However, the text data is not in a format that a machine learning model can
handle. We need to convert the string representation of the text into a numeric repre‐
sentation that we can apply our machine learning algorithms to.
Representing text data as Bag of Words
One of the most simple, but effective and commonly used ways to represent text for
machine learning is using the bag-of-words representation. When using bag-of-
words, we discard most of the structure of the input text, like chapters, paragraphs,
sentences and formatting, and only count how oen each word appears in each text.
Discarding all this structure and counting only occurrence leads to the mental image
of representing text as a “bag”.
Computing the bag-of-word representation for a corpus of documents consists of the
following three steps:
1) Tokenization: Split each document into the words that appear in it (called tokens),
for example by splitting them by whitespace and punctuation.
2) Vocabulary building: Collect a vocabulary of all words that appear in any of the
documents, and number them (say in alphabetical order).
Types of data represented as strings | 311
www.it-ebooks.info

3) Encoding: For each document, count how often each of the words in the vocabu‐
lary appear in this document.
bag_of_words
Figure bag_of_words illustrates the process on the string “This is how you get ants”.
The output of the process is one vector of word-counts for each document. For each
word in the vocabulary, we have a count of how often it appears in each document.
That means our numeric representation has one feature for each unique word in the
whole dataset. Note how the order of the words in the original string is completely
irrelevant to the bag of words feature representation. There are some subtleties
involved in step 1 and step 2 above, which we will discuss in more detail later in this
chapter.
For now, let’s look at how we can apply the bag-of-word processing using scikit-learn.
Applying bag-of-words to a toy dataset
The bag-of-word representation is implemented in the CountVectorizer, which is a
transformer. Let’s first apply it to a toy dataset, consisting of two samples, to see it
working:
bards_words =["The fool doth think he is wise,",
"but the wise man knows himself to be a fool"]
We import and instantiate the CountVecorizer and fit it to our toy data:
from sklearn.feature_extraction.text import CountVectorizer
vect = CountVectorizer()
vect.fit(bards_words)
312 | Chapter 8: Working with Text Data
www.it-ebooks.info

CountVectorizer(analyzer='word', binary=False, decode_error='strict',
dtype=<class 'numpy.int64'>, encoding='utf-8', input='content',
lowercase=True, max_df=1.0, max_features=None, min_df=1,
ngram_range=(1, 1), preprocessor=None, stop_words=None,
strip_accents=None, token_pattern='(?u)\\b\\w\\w+\\b',
tokenizer=None, vocabulary=None)
Fitting the CountVectorizer consists of the tokenization of the training data and
building of the vocabulary, which we can access as the vocabulary_ attribute:
print(len(vect.vocabulary_))
print("vocabulary content:")
vect.vocabulary_
{'be': 0,
'but': 1,
'doth': 2,
'fool': 3,
'he': 4,
'himself': 5,
'is': 6,
'knows': 7,
'man': 8,
'the': 9,
'think': 10,
'to': 11,
'wise': 12}
13
vocabulary content:
The vocabulary consists of 13 words, from “be” to “wise”.
To create the bag-of-words representation for the training data, we call the transform
method:
Types of data represented as strings | 313
www.it-ebooks.info

bag_of_words = vect.transform(bards_words)
bag_of_words
<2x13 sparse matrix of type '<class 'numpy.int64'>'
with 16 stored elements in Compressed Sparse Row format>
The bag of word representation is stored in a SciPy sparse matrix that only stores the
entries that are non-zero (see Chapter 1). The matrix is of shape 2 x 13, one row for
each of the two data points, and one feature for each of the words in the vocabulary.
A sparse matrix is used as most documents only contain a small subset of the words
in the vocabulary, meaning most entries in the feature array are zero. Think about
how many different words might appear in a movie review compared to all the words
in the English language (which is what the vocabulary models). Storing all these zeros
would be prohibitive, and a waste of memory.
To look at the actual content of the sparse matrix, we can convert it to a “dense”
NumPy array (that also stores all the zero entries) using the toarray method. This is
possible because we are using a small toy dataset that contains only 13 words. For any
real dataset, this would result in a MemoryError.
print(bag_of_words.toarray())
[[0 0 1 1 1 0 1 0 0 1 1 0 1]
[1 1 0 1 0 1 0 1 1 1 0 1 1]]
We can see that the word counts for each word are either zero or one, none of the two
strings in bards_words contain a word twice. You can read these feature vectors as
follows: The first string "The fool doth think he is wise," is represented as the
first row in, and it contains the first word in the vocabulary, "be", zero times. It also
contains the second word in the vocabulary, "but", zero times. It does contain the
third word, "doth", once, and so on. Looking at both rows, we can see that the fourth
word, "fool", the tenth word "the" and the thirteenth word "wise" appear in both
strings.
Bag-of-word for movie reviews
Now that we went through the bag-of-word process in detail, let’s apply it to our task
of sentiment analysis for movie reviews. Above, we already loaded our training and
test data from the IMDb reviews into lists of strings (text_train and text_test),
which we will now process:
vect = CountVectorizer().fit(text_train)
X_train = vect.transform(text_train)
print(repr(X_train))
314 | Chapter 8: Working with Text Data
www.it-ebooks.info

<25000x74849 sparse matrix of type '<class 'numpy.int64'>'
with 3431196 stored elements in Compressed Sparse Row format>
The shape of X_train, the bag-of-words representation of the training data, is 25.000
x 74.849, indicating that the vocabulary contains 74.849 entries. Again, the data is
stored as a SciPy sparse matrix. Let’s look in a bit more detail at the vocabulary.
Another way to access the vocabulary is using the get_feature_name method of the
vectorizer, which returns a convenient list where each entry corresponds to one fea‐
ture:
feature_names = vect.get_feature_names()
print(len(feature_names))
# print first fifty features
print(feature_names[:20])
# print feature 20010 to 20030
print(feature_names[20010:20030])
# get every 2000th word to get an overview
print(feature_names[::2000])
74849
['00', '000', '0000000000001', '00001', '00015', '000s', '001', '003830', '006', '007', '0079', '0080', '0083', '0093638', '00am', '00pm', '00s', '01', '01pm', '02']
['dratted', 'draub', 'draught', 'draughts', 'draughtswoman', 'draw', 'drawback', 'drawbacks', 'drawer', 'drawers', 'drawing', 'drawings', 'drawl', 'drawled', 'drawling', 'drawn', 'draws', 'draza', 'dre', 'drea']
['00', 'aesir', 'aquarian', 'barking', 'blustering', 'bête', 'chicanery', 'condensing', 'cunning', 'detox', 'draper', 'enshrined', 'favorit', 'freezer', 'goldman', 'hasan', 'huitieme', 'intelligible', 'kantrowitz', 'lawful', 'maars', 'megalunged', 'mostey', 'norrland', 'padilla', 'pincher', 'promisingly', 'receptionist', 'rivals', 'schnaas', 'shunning', 'sparse', 'subset', 'temptations', 'treatises', 'unproven', 'walkman', 'xylophonist']
As you can see, possibly a bit surprisingly, is that the first ten entries in the vocabu‐
lary are all numbers. All these numbers appear somewhere in the reviews, and are
therefore extracted as words. Most of these numbers don’t have any immediate
semantic meaning---apart from “007”, which, in particular in the context of movies, is
likely to refer to the James Bond character [footnote: A quick analysis of the data con‐
firms that this is indeed the case. Try confirming it yourself.]. Weeding out the mean‐
ingful from the non-meaningful “words” is sometimes tricky. Looking at some words
further along in the vocabulary, we find a collection of English words starting with
“dra”. You might notice that for “draught”, “drawback” and “drawer” both the singular
and plural form are contained in the vocabulary as distinct words. These words have
very closely related semantic meanings, and counting them as different words, corre‐
sponding to different features, might not be ideal.
Before we try to improve our feature extraction, let us obtain a quantitative measure
of performance by actually building a classifier. We have the training labels stored in
y_train and the bag-of-word representation of the training data in X_train, so we
can train a classifier on this data. For high-dimensional, sparse data like this, linear
models, like LogisticRegression often work best. Let’s start by evaluating Logisti
cRegresssion using cross-validation[footnote: The attentive reader might notice that
we violate our lesson from Chapter 7 on cross-validation with preprocessing. Using
Types of data represented as strings | 315
www.it-ebooks.info

the default settings of CountVectorizer, it actually does not collect any statistics, so
our results are valid. Using Pipeline from the start would be a better choice for
applications, but we defer it for ease of exposure.]
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
scores = cross_val_score(LogisticRegression(), X_train, y_train, cv=5)
np.mean(scores)
0.88131999999999999
We obtain a mean cross-validation score of 88.2%, which indicates reasonable perfor‐
mance for a balanced binary classification task. We know that LogisticRegression
has a regularization parameter C which we can tune via cross-validation:
from sklearn.model_selection import GridSearchCV
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10]}
grid = GridSearchCV(LogisticRegression(), param_grid, cv=5)
grid.fit(X_train, y_train)
print("Best cross-validation score: ", grid.best_score_)
print("Best parameters: ", grid.best_params_)
Best cross-validation score: 0.88816
Best parameters: {'C': 0.1}
We obtain a cross-validation score of 88.8% using C=0.1. We can now assess the
generalization-performance of this parameter setting on the test set:
X_test = vect.transform(text_test)
grid.score(X_test, y_test)
0.87895999999999996
Now, let’s see if we can improve the extraction of words. The way the CountVector
izer extracts tokens is using a regular expression. By default, the regular expression
that is used is "\b\w\w+\b". If you are not familiar with regular expressions, this
means it finds all sequences of characters that consist of at least two letters or num‐
bers ("\w") and that are separated by word boundaries ("\b"), in particular it does
not find single-letter words, and it splits up contractions like “doesn’t” or “bit.ly”, but
matches “h8ter” as a single word. The CountVectorizer then converts all words to
lower-case characters, so that “soon”, “Soon” and “sOon” all correspond to the same
token (and therefore feature).
This simple mechanism works quite well in practice, but as we saw above, we get
many uninformative features like the numbers. One way to cut back on these is to
only use tokens that appear in at least 2 documents (or at least 5 documents etc). A
token that appears only in a single document is unlikely to appear in the test set and
is therefore not helpful.
316 | Chapter 8: Working with Text Data
www.it-ebooks.info

We can set the minimum number of documents a token needs to appear in with the
min_df parameter:
vect = CountVectorizer(min_df=5).fit(text_train)
X_train = vect.transform(text_train)
print(repr(X_train))
<25000x27271 sparse matrix of type '<class 'numpy.int64'>'
with 3354014 stored elements in Compressed Sparse Row format>
By requiring at least five appearances of each token, we can bring down the number
of features to 27.272 (see the output above), only about a third of the original fea‐
tures. Let’s look at some tokens again:
feature_names = vect.get_feature_names()
# print first fifty features
print(feature_names[:50])
# print feature 20010 to 20020
print(feature_names[20010:20030])
#
print(feature_names[::700])
['00', '000', '007', '00s', '01', '02', '03', '04', '05', '06', '07', '08', '09', '10', '100', '1000', '100th', '101', '102', '103', '104', '105', '107', '108', '10s', '10th', '11', '110', '112', '116', '117', '11th', '12', '120', '12th', '13', '135', '13th', '14', '140', '14th', '15', '150', '15th', '16', '160', '1600', '16mm', '16s', '16th']
['repentance', 'repercussions', 'repertoire', 'repetition', 'repetitions', 'repetitious', 'repetitive', 'rephrase', 'replace', 'replaced', 'replacement', 'replaces', 'replacing', 'replay', 'replayable', 'replayed', 'replaying', 'replays', 'replete', 'replica']
['00', 'affections', 'appropriately', 'barbra', 'blurbs', 'butchered', 'cheese', 'commitment', 'courts', 'deconstructed', 'disgraceful', 'dvds', 'eschews', 'fell', 'freezer', 'goriest', 'hauser', 'hungary', 'insinuate', 'juggle', 'leering', 'maelstrom', 'messiah', 'music', 'occasional', 'parking', 'pleasantville', 'pronunciation', 'recipient', 'reviews', 'sas', 'shea', 'sneers', 'steiger', 'swastika', 'thrusting', 'tvs', 'vampyre', 'westerns']
There are clearly much fewer numbers, and some of the more obscure words or mis‐
spellings seem to have vanished. Let’s see how well our model performs by doing a
grid-search again:
grid = GridSearchCV(LogisticRegression(), param_grid, cv=5)
grid.fit(X_train, y_train)
print("Best cross-validation score: ", grid.best_score_)
Best cross-validation score: 0.88812
The best validation accuracy of the grid-search is still 88.8%, unchanged from before.
We didn’t improve our model, but having less features to deal with speeds up process‐
ing and throwing away useless features might make the model more interpretable.
Stop-words
Another way that we can get rid of uninformative words is by discarding words that
are too frequent to be informative. There are two main approaches: using a language-
specific list of stop words, or discarding words that appear too frequently. Scikit-learn
had a built-in list of English stop-words in the feature_extraction.text module:
from sklearn.feature_extraction.text import ENGLISH_STOP_WORDS
# print number of stop words
Types of data represented as strings | 317
www.it-ebooks.info

print(len(ENGLISH_STOP_WORDS))
# print some of the stop words
print(list(ENGLISH_STOP_WORDS)[::10])
318
['show', 'however', 'something', 'is', 'of', 'are', 'about', 'least', 'eight', 'thereupon', 'always', 'de', 'enough', 'nothing', 'what', 'un', 'though', 'around', 'go', 'due', 'cry', 'first', 'whereas', 'eg', 'ten', 'whatever', 'seem', 'further', 'therein', 'whom', 'everything', 'because']
Clearly, removing the stop-words in the list can only decrease the number of features
by the lenght of the list, here 318, but it might lead to an improvement in perfor‐
mance. Let’s give it a try:
# specifying "english" uses the build-in list. We could also augment it and pass our own.
vect = CountVectorizer(min_df=5, stop_words="english").fit(text_train)
X_train = vect.transform(text_train)
print(repr(X_train))
<25000x26966 sparse matrix of type '<class 'numpy.int64'>'
with 2149958 stored elements in Compressed Sparse Row format>
There are now 305 (=27272 - 26967) less features in the dataset, which means that
most, but not all of the stop-words appeared. Let’s run the grid-search again:
grid = GridSearchCV(LogisticRegression(), param_grid, cv=5)
grid.fit(X_train, y_train)
print("Best cross-validation score: ", grid.best_score_)
Best cross-validation score: 0.88296
The grid-search performance decreased slightly using the stop words. The change is
very slight, but given that excluding 305 features is unlikely to change performance or
interpretability a lot, it doesn’t seem worth using this list. Fixed lists are mostly help‐
ful for small datasets, that might not contain enough information for the model to
determine which words are stop words from the data itself. As an exercise, you can
try out the other approach, discarding frequently appearing words, by setting the
max_df option of CountVectorizer and see how it influences the number of features
and the performance.
Rescaling the data with TFIDF
Instead of dropping features that are deemed unimportant, another approach is to
rescale features by how informative we expect them to be. One of the most common
ways to do this is using the term frequency–inverse document frequency (tf-idf)
method. The intuition of this method is to give high weight to a term that appears
often in a particular document, but not in many documents in the corpus. If a word
appears often in a particular document, but not in very many documents, it is likely
to be very descriptive of the content of that document.
318 | Chapter 8: Working with Text Data
www.it-ebooks.info

Scikit-learn implements the tf-idf method in two classes, the TfidfTransformer,
which takes in the sparse matrix output produced by CountVectorizer and trans‐
forms it, or TfidfVectorizer, which takes in the text data and does both the bag-of-
words feature extraction and the tf-idf transformation.
There are several variants of the tf-idf rescaling scheme, which you can find on the
wikipedia page [footnote: https://en.wikipedia.org/wiki/Tf-idf]. The tf-idf score for
word $w$ in document $d$ as implemented in both the TfidfTransformer and
TfidfVectorizer is given by:
\begin{equation*}
\text{tfidf}(w, d) = \text{tf} \log\big(\frac{N + 1}{N_w + 1}\big) + 1
\end{equation*}
where $N$ is the number of documents in the training set, $N_w$ is the number of
documents in the training set that the word $d$ appears in, and $\text{tf}$, the term
frequency, is the number of times that the word $w$ appears in the query document
(the document you want to transform or encode). Both classes also apply l2 normal‐
ization after computing the tf-idf representation, in other words they rescale the rep‐
resentation of each document to have euclidean norm 1. Rescaling in this way means
that the length of a document (the number of words) does not change the vectorized
representation. We provide this formula here mostly for completeness, and you don’t
need to remember it to use the tf-idf encoding.
Because tf-idf actually makes use of the statistical properties of the training data, we
will use a pipeline, as described in Chapter 7, to ensure the results of our grid-search
are valid. This leads to the following code:
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.pipeline import make_pipeline
pipe = make_pipeline(TfidfVectorizer(min_df=5, norm=None), LogisticRegression())
param_grid = {'logisticregression__C': [0.001, 0.01, 0.1, 1, 10]}
grid = GridSearchCV(pipe, param_grid, cv=5)
grid.fit(text_train, y_train)
print("Best cross-validation score: ", grid.best_score_)
Best cross-validation score: 0.89392
As you can see, there is some improvement of using tf-idf instead of using just word
counts. We can also inspect which words tf-idf found most important. Keep in mind
that the tf-idf scaling is meant to find words that distinguish documents, but it is a
purely unsupervised technique. So “important” here does not necessarily related to
the “positive review” and “negative review” labels we are interested in. First we extract
the TfidfVectorizer from the pipeline:
Rescaling the data with TFIDF | 319
www.it-ebooks.info

vectorizer = grid.best_estimator_.named_steps["tfidfvectorizer"]
# transform the training dataset:
X_train = vectorizer.transform(text_train)
# find maximum value for each of the features over dataset:
max_value = X_train.max(axis=0).toarray().ravel()
sorted_by_tfidf = max_value.argsort()
# get feature names
feature_names = np.array(vectorizer.get_feature_names())
print("features with lowest tfidf")
print(feature_names[sorted_by_tfidf[:20]])
print("features with highest tfidf")
print(feature_names[sorted_by_tfidf[-20:]])
features with lowest tfidf
['poignant' 'disagree' 'instantly' 'importantly' 'lacked' 'occurred'
'currently' 'altogether' 'nearby' 'undoubtedly' 'directs' 'fond' 'stinker'
'avoided' 'emphasis' 'commented' 'disappoint' 'realizing' 'downhill'
'inane']
features with highest tfidf
['coop' 'homer' 'dillinger' 'hackenstein' 'gadget' 'taker' 'macarthur'
'vargas' 'jesse' 'basket' 'dominick' 'the' 'victor' 'bridget' 'victoria'
'khouri' 'zizek' 'rob' 'timon' 'titanic']
Features with low tf-idf are those that are either very commonly used across docu‐
ments, or are only used sparingly, and only in very long documents. Interestingly,
many of the high tf-idf features actually identify certain shows or movies. These
terms only appear in reviews for this particular show or franchise, but tend to appear
very often in these particular reviews. This is very clear for example for “pokemon”,
“smallville” and “doodlebops”, but “scanners” here actually also refers to a movie title.
These words are unlikely to help us in our sentiment classification task (unless maybe
some franchises are universally reviewed positively or negatively) but certainly con‐
tain a lot of specific information about the review.
We can also find the words that have low inverse document frequency, that is those
that appear frequently and are therefore deemed less important. The inverse docu‐
ment frequency values found on the training set are stored in the idf_ attribute:
sorted_by_idf = np.argsort(vectorizer.idf_)
print("features with lowest idf")
print(feature_names[sorted_by_idf[:100]])
320 | Chapter 8: Working with Text Data
www.it-ebooks.info

features with lowest idf
['the' 'and' 'of' 'to' 'this' 'is' 'it' 'in' 'that' 'but' 'for' 'with'
'was' 'as' 'on' 'movie' 'not' 'have' 'one' 'be' 'film' 'are' 'you' 'all'
'at' 'an' 'by' 'so' 'from' 'like' 'who' 'they' 'there' 'if' 'his' 'out'
'just' 'about' 'he' 'or' 'has' 'what' 'some' 'good' 'can' 'more' 'when'
'time' 'up' 'very' 'even' 'only' 'no' 'would' 'my' 'see' 'really' 'story'
'which' 'well' 'had' 'me' 'than' 'much' 'their' 'get' 'were' 'other'
'been' 'do' 'most' 'don' 'her' 'also' 'into' 'first' 'made' 'how' 'great'
'because' 'will' 'people' 'make' 'way' 'could' 'we' 'bad' 'after' 'any'
'too' 'then' 'them' 'she' 'watch' 'think' 'acting' 'movies' 'seen' 'its'
'him']
As expected, these are mostly English stop words like “the” and “no”. But some are
clearly domain specific to the movie reviews, like “movie”, “film”, “time”, “story” and
so on. Interestingly, “good”, “great” and “bad” are also among the most frequent, and
therefore “least relevant” words, even though we might expect these to be very impor‐
tant for our sentiment analysis task.
Investigating model coecients
Finally, let us look into a bit more detail into what our logistic regression model
actually learned from the data.
Because there are so many features, 27.272 after removing the infrequent ones, we
can clearly not look at all of the coefficients at the same time. However, we can look at
the largest coefficients, and see which words these correspond to.
We will use the last model that we trained, based on the tf-idf features.
mglearn.tools.visualize_coefficients(grid.best_estimator_.named_steps["logisticregression"].coef_,
feature_names, n_top_features=40)
plt.title("tfidf-coefficient")
Rescaling the data with TFIDF | 321
www.it-ebooks.info

The bar-chart in Figure tfidf-coefficient shows the 25 largest and 25 smallest coeffi‐
cients of the logistic regression model, with the bar showing the size of each coeffi‐
cient. The negative coefficients on the left belong to words that according to the
model are indicative of negative reviews, while the positive coefficients on the right
belong to word that according to the model indicate positive reviews. Most of the
terms are quite intuitive, like “worst”, “waste”, “disappointment” and “laughable” indi‐
cating bad movie reviews, while “excellent”, “wonderful”, “enjoyable” and “refreshing”
indicate positive movie reviews. Some words are slightly less clear, like “bit”, “job” and
“today”, but these might be part of phrases like “good job” or “best today”.
Bag of words with more than one word (n-grams)
One of the main disadvantages of using a bag-of-word representation is that word
order is completely discarded. Therefore the two strings “it’s bad, not good at all” and
“it’s good, not bad at all” have exactly the same representation, even though the mean‐
ings are inverted. Putting “not” in front of a word is only one (if extreme) example of
how context matters. There is a way of capturing context when using a bag-of-word
representation, by not only considering the counts of single tokens, but also the
counts of pairs or triples of tokens that appear next to each other.
Pairs of tokens are known as bigrams, triplets of tokens are known as trigrams and
more generally sequences of tokens are known as n-grams. We can change the range
of tokens that are considered as features by changing the ngram_range parameter of
the CountVecorizer or TfidfVectorizer. The ngram_range parameter is a tuple,
consisting of the minimum length and the maximum length of the sequences of
tokens that are considered. Here is an example on the toy data from above:
print(bards_words)
['The fool doth think he is wise,', 'but the wise man knows himself to be a fool']
The default is to create one feature per sequence of tokens that are at least one token
long, and at most one token long, in other words exactly one token long (single
tokens are also called unigrams):
322 | Chapter 8: Working with Text Data
www.it-ebooks.info

cv = CountVectorizer(ngram_range=(1, 1)).fit(bards_words)
print(len(cv.vocabulary_))
print(cv.get_feature_names())
13
['be', 'but', 'doth', 'fool', 'he', 'himself', 'is', 'knows', 'man', 'the', 'think', 'to', 'wise']
To look only at bigrams, that is only at sequences of two tokens following each other,
we can set ngram_range to (2, 2):
cv = CountVectorizer(ngram_range=(2, 2)).fit(bards_words)
print(len(cv.vocabulary_))
print(cv.get_feature_names())
14
['be fool', 'but the', 'doth think', 'fool doth', 'he is', 'himself to', 'is wise', 'knows himself', 'man knows', 'the fool', 'the wise', 'think he', 'to be', 'wise man']
Using longer sequences of tokens usually results in many more features, and in more
specific features. There is no common bigram between the two phrases in
bard_words:
cv.transform(bards_words).toarray()
array([[0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0],
[1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1]])
For most applications, the minimum number of tokens should be one, as single
words often capture a lot of meaning. Adding bigrams helps in most cases, and
adding longer sequences, up to 5-grams, might help, but will lead to an explosion of
the number of features, and might lead to overfitting, as there are many very specific
features.
Here is what using unigrams, bigrams and trigrams on bards_words looks like:
cv = CountVectorizer(ngram_range=(1, 3)).fit(bards_words)
print(len(cv.vocabulary_))
print(cv.get_feature_names())
39
['be', 'be fool', 'but', 'but the', 'but the wise', 'doth', 'doth think', 'doth think he', 'fool', 'fool doth', 'fool doth think', 'he', 'he is', 'he is wise', 'himself', 'himself to', 'himself to be', 'is', 'is wise', 'knows', 'knows himself', 'knows himself to', 'man', 'man knows', 'man knows himself', 'the', 'the fool', 'the fool doth', 'the wise', 'the wise man', 'think', 'think he', 'think he is', 'to', 'to be', 'to be fool', 'wise', 'wise man', 'wise man knows']
Let’s use the TfidfVectorizer on the IMDb movie review data and find the best set‐
ting of n-gram range using grid-search:
pipe = make_pipeline(TfidfVectorizer(min_df=5), LogisticRegression())
param_grid = {'logisticregression__C': [0.001, 0.01, 0.1, 1, 10, 100, 1000],
"tfidfvectorizer__ngram_range": [(1, 1), (1, 2), (1, 3)]}
grid = GridSearchCV(pipe, param_grid, cv=5)
grid.fit(text_train, y_train)
Rescaling the data with TFIDF | 323
www.it-ebooks.info
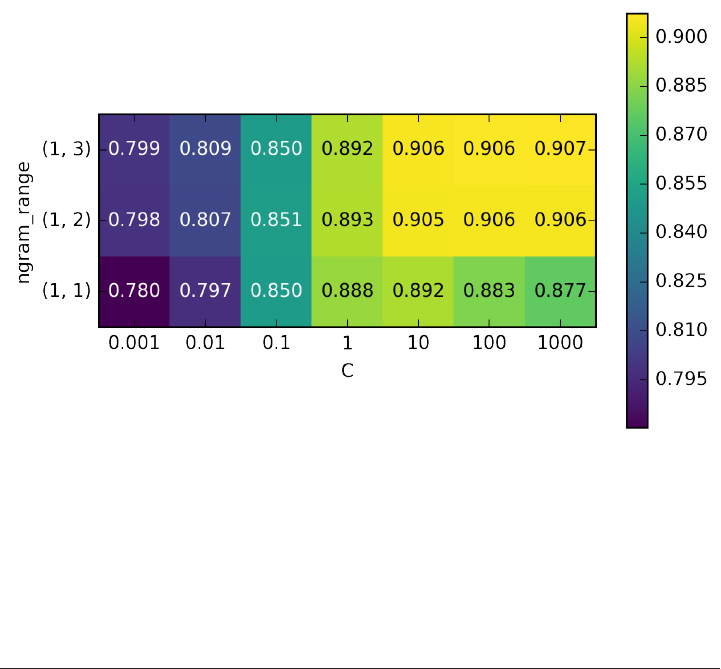
print("Best cross-validation score: ", grid.best_score_)
grid.best_params_
{'logisticregression__C': 1000, 'tfidfvectorizer__ngram_range': (1, 3)}
Best cross-validation score: 0.9074
As you can see from the results, we improved performance a bit more than a percent
by adding bigram and trigram features.
We can visualize the cross-validation accuracy as a function of the ngram_range and C
parameter as a heat map, as we did in Chapter 6:
# extract scores from grid_search
scores = [s.mean_validation_score for s in grid.grid_scores_]
scores = np.array(scores).reshape(-1, 3).T
# visualize heatmap
heatmap = mglearn.tools.heatmap(scores, xlabel="C", ylabel="ngram_range",
xticklabels=param_grid['logisticregression__C'],
yticklabels=param_grid['tfidfvectorizer__ngram_range'],
cmap="viridis", fmt="%.3f")
plt.colorbar(heatmap);
From the heat map we can see that using bigrams increases performance quite a bit,
while adding three-grams only provides a very small benefit in terms of accuracy. To
understand better how the model improved, we visualize the important coefficient for
the best model (which includes unigrams, bigrams and trigrams):
# extract feature names and coefficients
feature_names = np.array(grid.best_estimator_.named_steps['tfidfvectorizer'].get_feature_names())
coef = grid.best_estimator_.named_steps['logisticregression'].coef_
324 | Chapter 8: Working with Text Data
www.it-ebooks.info
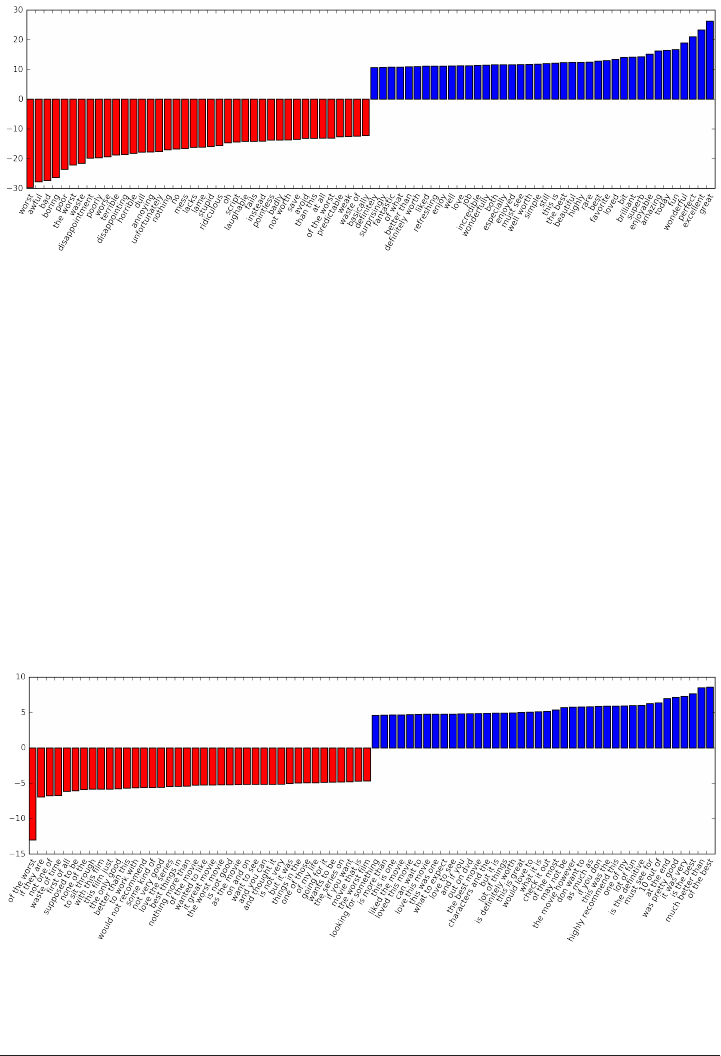
mglearn.tools.visualize_coefficients(coef, feature_names, n_top_features=40)
plt.title("ngram-coefficient")
There are particularly interesting features containing the word “worth” that were not
present in the unigram model: “not worth” is indicative of a negative review, while
“definitely wroth” and “well worth” are indicative of a positive review. This is a prime
example of context influencing the meaning of the word “worth”.
Below, we visualize only bigrams and trigrams, to provide further insight into why
these features are helpful. Many of the useful bigrams and trigrams consist of com‐
mon words that would not be informative on their own, as in the phrases “none of
the”, “the only good”, “on and on”, “this was one of”, “of the most” and so on. However,
the impact of these features is quite limited compared to the importance of the unig‐
ram features.
# find 3-gram features
mask = np.array([len(feature.split(" ")) for feature in feature_names]) == 3
# visualize only 3-gram features:
mglearn.tools.visualize_coefficients(coef.ravel()[mask],
feature_names[mask], n_top_features=40)
Rescaling the data with TFIDF | 325
www.it-ebooks.info

Advanced tokenization, stemming and lemmatization
We mentioned above that the feature extraction in the CountVectorizer and Tfidf
Vectorizer is relatively simple, and much more elaborate methods are possible. One
particular step that is often improved in more sophisticated text processing applica‐
tions is the first step in the bag-of-word model, the tokenization, the step defines
what constitutes a word for the purpose of feature extraction.
We saw above that the vocabulary often contains singular and plural version of words
as in 'drawback', 'drawbacks', 'drawer', 'drawers', 'drawing', 'drawings'.
For the purpose of a bag-of-words model, the semantics of “drawback” and “draw‐
backs” are so close that distinguishing them will only increase overfitting, and not
allow the model to fully exploit the training data. Similarly, we found the vocabulary
includes words like 'replace', 'replaced', 'replacement', 'replaces',
'replacing', which are different verb forms and a nouns relating to the verb “to
replace”.
Similarly to having singular and plural of a noun, treating different verb-forms and
related words as distinct tokens is disadvantageous for building a model that general‐
izes well. This problem can be overcome by representing each word using its word
stem, identifying (or conating) all the words that have the same word stem. If this is
done by using a rule-based heuristic, like dropping common suffixes, this is usually
referred to as stemming. If instead a dictionary of known word forms is used (that is
using an explicit and human-verified system), and the role of the word in the sen‐
tence taken into account, the process is referred to as lemmatization and the standar‐
dized form of the word is referred to as lemma. Both processing methods,
lemmatization and stemming, are forms of normalization that try to extract some
normal form of a word. Another interesting case of normalization is spell correction,
which can be helpful in practice, but is outside of the scope of this book.
To get a better feeling for normalization, let’s compare a method for stemming, the
Porter stemmer, a widely used collection of heuristics (here imported from the nltk
package) to lemmatization as implemented in the SpaCy package. For details of the
interface, consult the nltk and SpaCy documentations. We are more interested in the
general principles here.
import spacy
import nltk
# load spacy's English language models
en_nlp = spacy.load('en')
# instantiate NLTK's Porter stemmer
stemmer = nltk.stem.PorterStemmer()
# define function to compare lemmatization in spacy with stemming in NLKT
def compare_normalization(doc):
326 | Chapter 8: Working with Text Data
www.it-ebooks.info

# tokenize document in spacy:
doc_spacy = en_nlp(doc)
# print lemmas found by spacy
print("Lemmatization:")
print([token.lemma_ for token in doc_spacy])
# print tokens found by Porter stemmer
print("Stemming:")
print([stemmer.stem(token.norm_.lower()) for token in doc_spacy])
We will compare lemmatization and the Porter stemmer on a sentence designed to
show some of the differences:
compare_normalization(u"Our meeting today was worse than yesterday, I'm scared of meeting the clients tomorrow.")
Lemmatization:
['our', 'meeting', 'today', 'be', 'bad', 'than', 'yesterday', ',', 'i', 'be', 'scared', 'of', 'meet', 'the', 'client', 'tomorrow', '.']
Stemming:
['our', 'meet', 'today', 'wa', 'wors', 'than', 'yesterday', ',', 'i', "'m", 'scare', 'of', 'meet', 'the', 'client', 'tomorrow', '.']
Stemming is always restricted to trimming the word to a stem, so “was” becomes
“wa”, while lemmatization can retrieve the correct base verb form, “be”. Similarly, lem‐
matization can normalize “worse” to “bad”, while stemming produces “wors”. Another
major difference is that stemming reduces both occurrences of “meeting” to “meet”.
Using lemmatization, the first occurrence of “meeting” is recognized as a noun, and
left as-is, while the second occurrence is recognized as verb, and reduced to “meet”. In
general, lemmatization is a much more involved process than stemming, but usually
produces better results when used for normalizing tokens for machine learning.
While scikit-learn implements neither form of normalization, CountVectorizer
allows specifying your own tokenizer to convert each document into a list of tokens
using the tokenizer parameter. We can use the lemmatization from SpaCy to create a
callable that will take a string and produce a list of lemmas:
# Technicallity: we want to use the regexp based tokenizer that is used by CountVectorizer
# and only use the lemmatization from SpaCy. To this end, we replace en_nlp.tokenizer (the SpaCy tokenizer)
# with the regexp based tokenization
import re
# regexp used in CountVectorizer:
regexp = re.compile('(?u)\\b\\w\\w+\\b')
# load spacy language model and save old tokenizer
en_nlp = spacy.load('en')
old_tokenizer = en_nlp.tokenizer
# replace the tokenizer with the regexp above
en_nlp.tokenizer = lambda string: old_tokenizer.tokens_from_list(regexp.findall(string))
# create a custom tokenizer using the SpaCy document processing pipeline
# (now using our own tokenizer)
Rescaling the data with TFIDF | 327
www.it-ebooks.info

def custom_tokenizer(document):
doc_spacy = en_nlp(document, entity=False, parse=False)
return [token.lemma_ for token in doc_spacy]
# define a count vectorizer with the custom tokenizer
lemma_vect = CountVectorizer(tokenizer=custom_tokenizer, min_df=5)
Let’s transform the data and inspect the vocabulary size:
# transform text_train using CountVectorizer with lemmatization
X_train_lemma = lemma_vect.fit_transform(text_train)
print("X_train_lemma.shape: ", X_train_lemma.shape)
# Standard CountVectorizer for reference
vect = CountVectorizer(min_df=5).fit(text_train)
X_train = vect.transform(text_train)
print("X_train.shape: ", X_train.shape)
X_train_lemma.shape: (25000, 21596)
X_train.shape: (25000, 27271)
As you can see from the output above, lemmatization reduced the number of features
from 27.272 (with the standard CountVectorizer processing) to 21.596. Lemmatiza‐
tion can be seen as a kind of regularization, as it conflates certain features. Therefore,
we expect lemmatization to improve performance most when the dataset is small. To
illustrate how lemmatization can help, we will use StratifiedShuffleSplit for
cross-validation, using only 1% of the data as training data, and the rest as test data:
# build a grid-search using only 1% of the data as training set:
from sklearn.model_selection import StratifiedShuffleSplit
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10]}
cv = StratifiedShuffleSplit(n_iter=5, test_size=0.99, train_size=0.01, random_state=0)
grid = GridSearchCV(LogisticRegression(),
param_grid, cv=cv)
# Perform grid-search with standard CountVectorizer
grid.fit(X_train, y_train)
print("Best cross-validation score (standard CountVectorizer): {:.3f}".format(grid.best_score_))
# Perform grid-search with Lemmatization
grid.fit(X_train_lemma, y_train)
print("Best cross-validation score (lemmatization): {:.3f}".format(grid.best_score_))
Best cross-validation score (standard CountVectorizer): 0.721
Best cross-validation score (lemmatization): 0.731
In this case, lemmatization provided a modest improvement in performance. As with
many of the different feature extraction techniques, the result varies depending on
the dataset. Lemmatization and stemming can sometimes help in building better, or
at least more compact models, so we suggest you give these techniques a try when
trying to squeeze out the last bit of performance on a particular task.
328 | Chapter 8: Working with Text Data
www.it-ebooks.info

Topic Modeling and Document Clustering
One particular technique that is often applied to text data is topic modeling, which is
an umbrella term, describing the task of assigning each document to one or multiple
topics, usually without supervision. A good example for this is news data, which
might be categorized into topics like “politics”, “sports”, “finance” and so on. If each
document is assigned a single topic, this is the task of clustering the documents, as
discussed in Chapter 3.
If each document can have more than one topic, the task relates to decomposition
methods from Chapter 3. Each of the components we learn then corresponds to one
topic, and the coefficient of the components in the representation of a document tells
us how much each document is about a particular topic.
Often, when people talk about topic modeling, they refer to one particular decompo‐
sition method called Latent Dirichlet Allocation (often LDA for short [footnote:
There is another machine learning model called LDA, which is Linear Discriminant
Analysis, a linear classification model. This leads to quite some confusion. In this
book, LDA refers to Latent Dirichlet Allocation).
Intuitively, the LDA model tries to find groups of words (the topics) that appear
together frequently. LDA also requires that each document can be understood as a
“mixture” of a subset of the topics. It is important to understand that for the machine
learning model a “topic” might not be what we would normally call a topic in every‐
day speech, but that it resembles more the components extracted by PCA or NMF,
which might or might not have a semantic meaning.
Even if there is a semantic meaning for an LDA “topic”, it might not be something
we’d usually call a topic. Going back to the example of news articles, we might have a
collection of articles about sports, politics and finance, written by two specific
authors. In a politics article, we might expect words like “govenor”, “vote”, “party” etc,
while in a sports article we might expect words like “team”, “score” and “season”. Each
of these groups will likely appear together, while it’s less likely that “team” and “gove‐
nor” appear together.
However, these are not the only groups of words we might expect to appear together.
The two reporters might prefer different phrases or different choices of words. Maybe
one of them likes to use he word “demarcate” and one likes the word “polarize”.
Another “topic” would then be “words often used by reporter A” and “words often
used by reporter B”, thought these are not topics in the usual sense of the word.
Let’s apply LDA to our movie review dataset to see how it works in practice. For
unsupervised text document models, it is often good to remove very common words,
as they might otherwise dominate the analysis. We remove words that appear in at
Topic Modeling and Document Clustering | 329
www.it-ebooks.info

least 20 percent of the documents, and we limit the bag-of-words model to the 10.000
that are most common after removing the top 20 percent:
vect = CountVectorizer(max_features=10000, max_df=.15)
X = vect.fit_transform(text_train)
We learn a topic model with 10 topics, which is few enough that we can look at all of
them.
Similarly to the components in NMF, topics don’t have an inherent ordering, and
changing the number of topics will change all of the topics. [footnote: In fact, NMF
and LDA solve quite related problems, and we could also use NMF to extract “top‐
ics”.]
We choose the “batch” learning method, which is somewhat slower than the default,
but usually provides better results, and increase “max_iter”, which can also lead to
better models.
from sklearn.decomposition import LatentDirichletAllocation
lda = LatentDirichletAllocation(n_topics=10, learning_method="batch", max_iter=25, random_state=0)
# be build the model and transform the data in one step
# computing transform takes some time, and we can save time by doing both at once.
document_topics = lda.fit_transform(X)
As in the decomposition methods we saw in Chapter 3, LDA has a components_
attribute, that stores how important each word is for each topic. The size of compo
nents_ is (n_topics, n_words).
lda.components_.shape
(10, 10000)
To understand better what the different topics mean, we will look at the most impor‐
tant word for each of the topics. The print_topics function we use below provides a
nice formatting for these features.
# for each topic (a row in the components_), sort the features (ascending).
# Invert rows with [:, ::-1] to make sorting descending
sorting = np.argsort(lda.components_, axis=1)[:, ::-1]
# get the feature names from the vectorizer:
feature_names = np.array(vect.get_feature_names())
# print out the 10 topics:
mglearn.tools.print_topics(topics=range(10), feature_names=feature_names,
sorting=sorting, topics_per_chunk=5, n_words=10)
topic 0 topic 1 topic 2 topic 3 topic 4
-------- -------- -------- -------- --------
between war funny show didn
young world worst series saw
330 | Chapter 8: Working with Text Data
www.it-ebooks.info

family us comedy episode am
real our thing tv thought
performance american guy episodes years
beautiful documentary re shows book
work history stupid season watched
each new actually new now
both own nothing television dvd
director point want years got
topic 5 topic 6 topic 7 topic 8 topic 9
-------- -------- -------- -------- --------
horror kids cast performance house
action action role role woman
effects animation john john gets
budget game version actor killer
nothing fun novel oscar girl
original disney both cast wife
director children director plays horror
minutes 10 played jack young
pretty kid performance joe goes
doesn old mr performances around
Judging from the important words, topic 1 seems to be about historical and war mov‐
ies, topic 2 might be about bad comedy, topic 3 might be about tv series, topic 4
seems to caputre some very common words, topic 6 seem to capture children’s mov‐
ies, and topic 8 seems to capture award-related reviews. Using only ten topics, each of
the topics needs to be very broad, so that they can together cover all the different
kinds of reviews in our dataset.
Topic Modeling and Document Clustering | 331
www.it-ebooks.info

Next, we will learn another model, this time with 100 topics. Using more topics
makes the analysis much harder, but makes it more likely that topics can specialize to
intesting subsets of the data.
lda100 = LatentDirichletAllocation(n_topics=100, learning_method="batch", max_iter=25, random_state=0)
document_topics100 = lda100.fit_transform(X)
Looking at all 100 topics would be a bit overwhelming, so we selected some interest‐
ing and representative topics.
topics = np.array([7, 16, 24, 25, 28, 36, 37, 45, 51, 53, 54, 63, 89, 97])
sorting = np.argsort(lda100.components_, axis=1)[:, ::-1]
feature_names = np.array(vect.get_feature_names())
mglearn.tools.print_topics(topics=topics, feature_names=feature_names, sorting=sorting,
topics_per_chunk=7, n_words=20)
topic 7 topic 16 topic 24 topic 25 topic 28 topic 36 topic 37
-------- -------- -------- -------- -------- -------- --------
thriller worst german car beautiful performance excellent
suspense awful hitler gets young role highly
horror boring nazi guy old actor amazing
atmosphere horrible midnight around romantic cast wonderful
mystery stupid joe down between play truly
house thing germany kill romance actors superb
director terrible years goes wonderful performances actors
quite script history killed heart played brilliant
bit nothing new going feel supporting recommend
de worse modesty house year director quite
performances waste cowboy away each oscar performance
dark pretty jewish head french roles performances
twist minutes past take sweet actress perfect
hitchcock didn kirk another boy excellent drama
tension actors young getting loved screen without
interesting actually spanish doesn girl plays beautiful
332 | Chapter 8: Working with Text Data
www.it-ebooks.info

mysterious re enterprise now relationship award human
murder supposed von night saw work moving
ending mean nazis right both playing world
creepy want spock woman simple gives recommended
topic 45 topic 51 topic 53 topic 54 topic 63 topic 89 topic 97
-------- -------- -------- -------- -------- -------- --------
music earth scott money funny dead didn
song space gary budget comedy zombie thought
songs planet streisand actors laugh gore wasn
rock superman star low jokes zombies ending
band alien hart worst humor blood minutes
soundtrack world lundgren waste hilarious horror got
singing evil dolph 10 laughs flesh felt
voice humans career give fun minutes part
singer aliens sabrina want re body going
sing human role nothing funniest living seemed
musical creatures temple terrible laughing eating bit
roll miike phantom crap joke flick found
fan monsters judy must few budget though
metal apes melissa reviews moments head nothing
concert clark zorro imdb guy gory lot
playing burton gets director unfunny evil saw
hear tim barbra thing times shot long
fans outer cast believe laughed low interesting
Topic Modeling and Document Clustering | 333
www.it-ebooks.info

prince men short am comedies fulci few
especially moon serial actually isn re half
The topics we extracted this time seem to be more specific, though many are hard to
interpret. Topic 7 seems to be about horror movies and thrillers, topics 16 and 54 see,
to capture bad reviews, while topic 63 mostly seems to be capturing positive reviews
of comedies.
If you want to make further inferences using the topics that were discovered, it is
good to confirm the intuition we gained from looking the highest ranking words for
each topic, by looking at the documents that are assigned to these topics. For exam‐
ple, topic 45 seems to be about music. Let’s check which kind of reviews are assigned
this topic:
# sort by weight of "music" topic 45
music = np.argsort(document_topics100[:, 45])[::-1]
# print the five documents where the topic is most important
for i in music[:10]:
# pshow first two sentences
print(b".".join(text_train[i].split(b".")[:2]) + b".\n")
b'I love this movie and never get tired of watching. The music in it is great.\n'
b"I enjoyed Still Crazy more than any film I have seen in years. A successful band from the 70's decide to give it another try.\n"
b'Hollywood Hotel was the last movie musical that Busby Berkeley directed for Warner Bros. His directing style had changed or evolved to the point that this film does not contain his signature overhead shots or huge production numbers with thousands of extras.\n'
b"What happens to washed up rock-n-roll stars in the late 1990's? They launch a comeback / reunion tour. At least, that's what the members of Strange Fruit, a (fictional) 70's stadium rock group do.\n"
b'As a big-time Prince fan of the last three to four years, I really can\'t believe I\'ve only just got round to watching "Purple Rain". The brand new 2-disc anniversary Special Edition led me to buy it.\n'
b"This film is worth seeing alone for Jared Harris' outstanding portrayal of John Lennon. It doesn't matter that Harris doesn't exactly resemble Lennon; his mannerisms, expressions, posture, accent and attitude are pure Lennon.\n"
b"The funky, yet strictly second-tier British glam-rock band Strange Fruit breaks up at the end of the wild'n'wacky excess-ridden 70's. The individual band members go their separate ways and uncomfortably settle into lackluster middle age in the dull and uneventful 90's: morose keyboardist Stephen Rea winds up penniless and down on his luck, vain, neurotic, pretentious lead singer Bill Nighy tries (and fails) to pursue a floundering solo career, paranoid drummer Timothy Spall resides in obscurity on a remote farm so he can avoid paying a hefty back taxes debt, and surly bass player Jimmy Nail installs roofs for a living.\n"
b"I just finished reading a book on Anita Loos' work and the photo in TCM Magazine of MacDonald in her angel costume looked great (impressive wings), so I thought I'd watch this movie. I'd never heard of the film before, so I had no preconceived notions about it whatsoever.\n"
b'I love this movie!!! Purple Rain came out the year I was born and it has had my heart since I can remember. Prince is so tight in this movie.\n'
b"This movie is sort of a Carrie meets Heavy Metal. It's about a highschool guy who gets picked on alot and he totally gets revenge with the help of a Heavy Metal ghost.\n"
As we can see, this topic covers a wide variety of music-centered reviews, from musi‐
cals, to bigraphic movies, to some hard-to-specify genre in the last review. Another
interesting way to inspect the topics is to see how much weight each topic gets over‐
all, by summing the document_topics over all reviews. We name each topic by the
two most comen words:
plt.figure(figsize=(10, 30))
plt.barh(np.arange(100), np.sum(document_topics100, axis=0))
topic_names = ["{:>2} ".format(i) + " ".join(words) for i, words in enumerate(feature_names[sorting[:, :2]])]
334 | Chapter 8: Working with Text Data
www.it-ebooks.info

The most important topics are 97, which seems to consist mostly of stop-words, pos‐
sibly with a slight negative direction, topic 16, which is clearly about bad reviews, fol‐
lowed by some genre-specific and 36 and 37, both of which seem to contain laudatory
words.
It seems like LDA mostly discovered two kind of topics: genre-specific and rating-
specific, in addition to several more unspecific topics. This seems like an interesting
discovery, as most reviews are made of some movie-specific comments, and some
comments that justify or emphasize the rating.
Topic models like LDA are an interesting methods to understand large text corpora in
the absence of labels --- or, as here, even if labels are available. The LDA algorithms is
randomized, though, and changing the random_state parameter can lead to quite
different outcomes. While identifying topics can be helpful, any conclusions you
draw from an unsupervised model should be taken with a grain of salt, and we rec‐
ommend verifying your intution by looking at the documents in a specific topic.
Summary and Outlook
In this chapter we talked about the basics of processing text, also known as natural
language processing (NLP) with an example application classifying movie reviews. The
tools discussed here should serve as a great starting point when trying to process text
data. In particular for text classification such as spam and fraud detection or senti‐
ment analysis, bag of word representations provide a simple and powerful solution.
As so often in machine learning, the representation of the data is key in NLP applica‐
tions, and inspecting the tokens and n-grams that are extracted can give powerful
insights into the modeling process. In text processing applications, it is often possible
to introspect models in a meaningful way, as we saw above, both for supervised and
unsupervised tasks. You should take full advantage of this ability when using NLP
based methods in practice.
NLP and text processing is a large research field, and discussing the details of
advanced methods is far beyond the scope of this book. If you want to learn more
about text processing and natural language processing, we recommend the O’Reilly
book Natural Language Processing with Python by Bird, Klein and Loper, which pro‐
vides an overview of NLP together with an introduction to the nltk python package
for NLP. Another great and more conceptual book is the standard reference Introduc‐
tion to information retrieval by Manning, Raghavan and Schütze, which
describes fundamental algorithms in information retrieval, NLP and machine learn‐
ing. Both books have online versions that can be accessed free of charge.
As we discussed above, the classes CountVectorizer and TfidfVectorizer only
implement relatively simple text processing methods. For more advanced text pro‐
cessing methods, we recommend the Python packages SpaCy, a relatively new, but
Summary and Outlook | 337
www.it-ebooks.info

very efficient and well-designed package, nltk, a very well-established and complete,
but somewhat dated library, and gensim, an NLP package with an emphasis on topic
modelling.
There have been several very exciting new developments in text processing in recent
years, which are outside of the scope of this book and relate to neural networks. The
first is the use of continuous vector representations, also known as word vectors or
distributed word representations, as implemented in the word2vec library. The origi‐
nal paper “Distributed representations of words and phrases and their compositional‐
ity” by Mikolov, Suskever, Chen, Corrado and Dean is a great introduction to the
subject. Both SpaCy and gensim provide functionality for the techniques discussed in
this paper and its follow-ups.
Another direction in NLP that has picked up momentum in recent years are recurrent
neural networks (RNNs) for text processing. RNNs are a particularly powerful type of
neural network that can produce output that is again text, in contrast to classification
models that can only assign class labels. The ability to produce text as output makes
RNNs well-suited for automatic translation and summarization. An introduction to
the topic can be found in the relatively technical paper “Sequence to Sequence Learn‐
ing
with Neural Networks” by Suskever, Vinyals and Le. A more practical tutorial using
tensorflow framework can found on the tensorflow website [footnote https://
www.tensorflow.org/versions/r0.8/tutorials/seq2seq/index.html].
338 | Chapter 8: Working with Text Data
www.it-ebooks.info