Python James R. Parker An Introduction To Programming

User Manual: James-R.-Parker-Python-An-Introduction-to-Programming

Open the PDF directly: View PDF .
Page Count: 534 [warning: Documents this large are best viewed by clicking the View PDF Link!]

PYTHON

LICENSE,DISCLAIMEROFLIABILITY,ANDLIMITEDWARRANTY

By purchasing or using this book (the “Work”), you agree that this license grants

permission to use the contents contained herein, but does not give you the right of

ownership to any of the textual content in the book or ownership to any of the

informationorproductscontainedinit.Thislicensedoesnotpermituploadingofthe

WorkontotheInternetoronanetwork(ofanykind)withoutthewrittenconsentofthe

Publisher. Duplication or dissemination of any text, code, simulations, images, etc.

contained herein is limited to and subject to licensing terms for the respective

products, and permission must be obtained from the Publisher or the owner of the

content,etc.,inordertoreproduceornetworkanyportionofthetextualmaterial(in

anymedia)thatiscontainedintheWork.

MERCURYLEARNINGANDINFORMATION(“MLI”or“thePublisher”)andanyoneinvolved

in the creation, writing, or production of the companion disc, accompanying

algorithms,code,orcomputerprograms(“thesoftware”),andanyaccompanyingWeb

siteorsoftwareoftheWork,cannotanddonotwarranttheperformanceorresultsthat

mightbeobtainedbyusingthecontentsoftheWork.Theauthor,developers,andthe

Publisherhave usedtheir besteffortstoinsure theaccuracy andfunctionality ofthe

textual material and/or programs contained in this package; we, however, make no

warrantyofanykind,expressorimplied,regardingtheperformanceofthesecontents

orprograms.TheWorkissold“asis”withoutwarranty(exceptfordefectivematerials

usedinmanufacturingthebookorduetofaultyworkmanship).

Theauthor,developers,andthepublisherofany accompanyingcontent,andanyone

involvedinthecomposition,production,andmanufacturingofthisworkwillnotbe

liable for damages of any kind arising out of the use of (or the inability to use) the

algorithms, source code, computer programs, or textual material contained in this

publication. This includes, but is not limited to, loss of revenue or profit, or other

incidental,physical,orconsequentialdamagesarisingoutoftheuseofthisWork.

Thesoleremedyintheeventofaclaimofanykindisexpresslylimitedtoreplacement

ofthebook,andonlyatthediscretionofthePublisher.Theuseof“impliedwarranty”

andcertain“exclusions”varyfromstatetostate,andmightnotapplytothepurchaser

ofthisproduct.

Companion disc files are available for download from the publisher by writing to

info@merclearning.com.

Thispublication,portionsofit,oranyaccompanyingsoftwaremaynotbereproduced

in any way, stored in a retrieval system of any type, or transmitted by any means,

media, electronic display or mechanical display, including, but not limited to,

photocopy,recording,Internet

postings,orscanning,withoutpriorpermissioninwritingfromthepublisher.

Publisher:DavidPallai

MERCURYLEARNINGANDINFORMATION

22841QuicksilverDrive

Dulles,VA20166

info@merclearning.com

www.merclearning.com

(800)232-0223

JamesR.Parker.PYTHON:AnIntroductiontoProgramming.

ISBN:978-1-9445346-5-3

The publisher recognizes and respects all marks used by companies, manufacturers,

and

developers as a means to distinguish their products. All brand names and product

names

mentionedinthisbookaretrademarksorservicemarksoftheirrespectivecompanies.

Anyomissionormisuse(ofanykind)ofservicemarksortrademarks,etc.isnotan

attempttoinfringeonthepropertyofothers.

LibraryofCongressControlNumber:2016915244

161718321PrintedintheUnitedStatesofAmerica

Thisbookisprintedonacid-freepaper.

Our titles are available for adoption, license, or bulk purchase by institutions,

corporations,etc.

For additional information, please contact the Customer Service Dept. at 800-232-

0223 (toll free).Digital versions of our titles are available at:

www.authorcloudware.comandothere-vendors.Allcompanionfilesareavailableby

writingtothepublisheratinfo@merclearning.com.

The sole obligation of MERCURY LEARNINGAND INFORMATION to the purchaser is to

replacethebookand/ordisc,basedondefectivematerialsorfaultyworkmanship,but

notbasedontheoperationorfunctionalityoftheproduct.

Contents
Prefacexv
Chapter0ModernComputers
0.1CalculationsbyMachine
0.2HowComputersWorkandWhyWeMadeThem
0.2.1Numbers
Example:Base
ConvertBinaryNumberstoDecimal
ConvertDecimalNumberstoBinary
ArithmeticinBinary
0.2.2Memory
0.2.3StoredPrograms
0.3ComputerSystemsAreBuiltinLayers
0.3.1AssemblersandCompilers
0.3.2GraphicalUserInterfaces(GUIs)
Widgets
0.4ComputerNetworks
0.4.1Internet
0.4.2WorldWideWeb
0.5Representation
0.6Summary
Chapter1ComputersandProgramming
1.1SolvingaProblemUsingaComputer
1.2ExecutingPython
1.3GuessaNumber
1.4Rock-Paper-Scissors
1.5SolvingtheGuessaNumberProblem
1.6SolvingtheRock-Paper-ScissorsProblem
1.6.1VariablesandValues–ExperimentingwiththeGraphicalUserInterface

6.2ExchangingInformationwiththeComputer
6.3Example1:DrawaCircleUsingCharacters
6.4Strings,Integers,andRealNumbers
6.5NumberBases
6.6Example2:ComputetheCircumferenceofanyCircle
6.7GuessaNumberAgain
7IFStatements
7.1Else
8Documentation
9Rock-Paper-ScissorsAgain
10TypesAreDynamic(Advanced)
11Summary
Chapter2Repetition
1TheWHILEStatement
1.1TheGuess-A-NumberProgramYetAgain
1.2ModifyingtheGame
2Rock-Paper-ScissorsYetAgain
2.1RandomNumbers
3CountingLoops
4PrimeorNon-Prime
4.1ExitingfromaLoop
4.2Else
5LoopsThatareNested
6DrawaHistogram
7LoopsinGeneral
8ExceptionsandErrors
8.1Problem:AFinalLookatGuessaNumber
9Summary
Chapter3Sequences:Strings,Tuples,andLists
1Strings

3.1.1ComparingStrings
Problem:DoesaCityName,EnteredattheConsole,Comebeforeorafterthe
NameDenver?
3.1.2Slicing–ExtractingPartsofStrings
Problem:Identifya“Print”StatementinaString
3.1.3EditingStrings
Problem:CreateaJPEGFileNamefromaBasicString
Problem:ChangetheSuffixofaFileName
Problem:ReversetheOrderofCharactersinaString
Problem:IsaGivenFileNameThatofaPythonProgram?
3.1.4StringMethods
3.1.5SpanningMultipleLines
3.1.6ForLoopsAgain
3.2TheTypeBytes
3.3Tuples
3.3.1TuplesinForLoops
Problem:PrinttheNumberofNeutronsinanAtomicNucleus
3.3.2Membership
Problem:WhatEvenNumbersLessthanorEqualto100areAlsoPerfect
Squares?
3.3.3Delete
Problem:DeletetheElementLithiumfromtheTupleAtoms,alongwithIts
AtomicNumber.
3.3.4Update
Problem:ChangetheEntryforLithiumtoanEntryforOxygen
3.3.5TupleAssignment
3.3.6Built-InFunctionsforTuples
3.4Lists
Problem:ComputetheAverage(Mean)ofaListofNumbers
3.4.1EditingLists
3.4.2Insert
3.4.3Append

4.4Extend
4.5Remove
4.6Index
4.7Pop
4.8Sort
4.9Reverse
4.10Count
4.11ListComprehension
4.12ListsandTuples
4.13Exceptions
Problem:DeletetheElementHeliumfromaList
Problem:DeleteaSpecifiedElementfromaList
5SetTypes
5.1Example:Craps
6Summary
Chapter4Functions
1FunctionDefinition:SyntaxandSemantics
1.1Problem:UsepoundntoDrawaHistogram
1.2Problem:GeneralizetheHistogramCodeforOtherYears
2FunctionExecution
2.1ReturningaValue
Problem:WriteaFunctiontoCalculatetheSquareRootofitsParameter
2.2Parameters
2.3DefaultParameters
2.4None
2.5Example:TheGameofSticks
2.6Scope
2.7VariableParameterLists
2.8VariablesasFunctions
Example:FindtheMaximumValueofaFunction
2.9FunctionsasReturnValues

4.3Recursion
4.3.1AvoidingInfiniteRecursion
4.4CreatingPythonModules
4.5ProgramDesignUsingFunctions–Example:TheGameofNim
4.5.1TheDevelopmentProcessExposed
4.6Summary
Chapter5Files:InputandOutput
5.1WhatIsaFile?ALittle“Theory”
5.1.1HowAreFilesStoredonaDisk?
5.1.2FileAccessisSlow
5.2KeyboardInput
5.2.1Problem:ReadaNumberfromtheKeyboardandDivideItby2
5.3UsingFilesinPython:LessTheory,MorePractice
5.3.1OpenaFile
FileNotFoundExceptions
5.3.2ReadingfromFiles
EndofFile
CommonFileInputOperations
CSVFiles
Problem:PrinttheNamesofPlanetsHavingFewerThanTenMoons
Problem:PlayJeopardyUsingaCSVDataSet
TheWithStatement
5.4WritingToFiles
Example:WriteaTableofSquarestoaFile
5.4.1AppendingDatatoaFile
Example:AppendAnother20SquarestotheTableofSquaresFile
5.5Summary
Chapter6Classes
6.1ClassesandTypes
6.1.1ThePythonClass–SyntaxandSemantics

6.1.2AReallySimpleClass
6.1.3Encapsulation
6.2ClassesandDataTypes
6.2.1Example:ADeckofCards
6.2.2ABouncingBall
6.2.3Cat-A-Pult
BasicDesign
DetailedDesign
6.3SubclassesandInheritance
6.3.1Non-TrivialExample:ObjectsinaVideoGame
6.4DuckTyping
6.5Summary
Chapter7Graphics
7.1IntroductiontoGraphicsProgramming
7.1.1Essentials:TheGraphicsWindowandColors
7.1.2PixelLevelGraphics
Example:CreateaPageofNotepaper
Example:CreatingaColorGradient
7.1.3LinesandCurves
Example:NotepaperAgain
7.1.4Polygons
7.1.5Text
7.1.6Example:AHistogram
7.1.7Example:APieChart
7.1.8Images
Pixels
Example:IdentifyingaGreenCar
Example:Thresholding
Transparency
7.1.9GenerativeArt
7.2Summary

Chapter8ManipulatingData
1Dictionaries
1.1Example:ANaiveLatin–EnglishTranslation
1.2FunctionsforDictionaries
1.3DictionariesandLoops
2Arrays
3FormattedText,FormattedI/O
3.1Example:NASAMeteoriteLandingData
4AdvancedDataFiles
4.1BinaryFile
Example:CreateaFileofIntegers
4.2TheStructModule
Example:AVideoGameHighScoreFile
4.3RandomAccess
Example:MaintainingtheHighScoreFileinOrder
5StandardFileTypes
5.1ImageFiles
5.2GIF
5.3JPEG
5.4TIFF
5.5PNG
5.6SoundFiles
WAV
5.7OtherFiles
HTML
EXE
6Summary
Chapter9Multimedia
1MouseInteraction
Example:DrawaCircleattheMouseCursor

Example:ChangeBackgroundColorUsingtheMouse
9.1.1MouseButtons
Example:DrawLinesUsingtheMouse
Example:AButton
9.2TheKeyboard
Example:Pressinga“+”CreatesaRandomCircle
Example:ReadingaCharacterString
9.3Animation
9.3.1ObjectAnimation
Example:ABallinaBox
Example:ManyBallsinaBox
9.3.2FrameAnimation
Example:ReadFramesandPlayThemBackasanAnimation
Example:SimulationoftheSpaceShuttleControlConsole(AClassThatWill
DrawanAnimationataSpecificLocation)
9.4RGBAColors–Transparency
9.5Sound
Example:PlayaSound
Example:ControlVolumeUsingtheKeyboard.PauseandUnpause
Example:PlayaSoundEffectattheRightMoment:Bounces
9.6Video
Example:Carclub–DisplaytheVideocarclub2.mpg(Annotated)
Exercise:ThresholdaVideo(ProcessingPixels)
9.7Summary
Chapter10BasicAlgorithms
10.1Sorting
10.1.1SelectionSort
10.1.2MergeSort
10.2Searching
10.2.1Timings
10.2.2LinearSearch

2.3BinarySearch
3RandomNumberGeneration
3.1LinearCongruentialMethod
4Cryptography
4.1One-TimePad
4.2PublicKeyEncryption(RSA)
Example:EncrypttheMessage“DepartatDawn”UsingRSA
5Compression
5.1HuffmanEncoding
5.2LZWCompression
6Hashing
djb2
6.1sdbm
7Summary
Chapter11ProgrammingfortheSciences
1FindingRootsofEquations
2Differentiation
3Integration
4Optimization:FindingMaximaandMinima
4.1NewtonAgain
4.2FittingDatatoCurves–Regression
4.3EvolutionaryMethods
5LongestCommonSubsequence(EditDistance)
5.1DeterminingLongestCommonSubsequence(LCS)
6Summary
Chapter12HowtoWriteGoodPrograms
1ProceduralProgramming–WordProcessing
1.1Top-Down
1.2Centering
1.3RightJustification

1.4OtherCommands
2ObjectOrientedProgramming–Breakout
3DescribingtheProblemasaProcess
3.1InitialCodingforaTile
3.2InitialCodingforthePaddle
3.3InitialCodingfortheBall
3.4CollectingtheClasses
3.5DevelopingthePaddle
3.6BallandTileCollisions
3.7BallandPaddleCollisions
3.8FinishingtheGame
4RulesforProgrammers
5Summary
Chapter13CommunicatingwiththeOutsideWorld
1Email
Example:SendanEmail
1.1ReadingEmail
Example:DisplaytheSubjectHeadersforEmailsinInbox
2FTP
Example:DownloadandDisplaytheREADMEFilefromanFTPSite
3CommunicationBetweenProcesses
Example:AServerThatCalculatesSquares
4Twitter
Example:ConnecttotheTwitterStreamandPrintSpecificMessages
5CommunicatingwithOtherLanguages
Example:FindTwoLargeRelativelyPrimeNumbers
6Summary
Chapter14ABriefGlibReference
1Glibtkinter
2Images

14.3DynamicGlib

14.4Video

14.5Audio

14.6Interaction

14.7Other

Index

Preface

This book is intended to teach introductory programming. Material is included for the

introductory computer science course, but also for students and readers in science and

other disciplines. I firmly believe that programming is an essential skill for all

professionalsandespeciallyacademicsinthe21stcenturyandhaveemphasizedthatinthe

contentdiscussedinthebook.

Thebookusesa“just-in-time”approach,meaningthatItrytopresentnewinformation

just before or just after the reader needs it. As a result, there are numerous examples,

carefullyselectedtofitintotheirproperplacesinthetext.Nottoosoon,andnottoolate.

Ibelieveinobject-orientedprogramming.Mymaster’sthesisinthelate1970swason

that subject, cut my teeth on Simula, was there when C++ was created, and knew the

creator of Java. I do not believe that object-oriented programming is the only solution,

though, and realized early that good objects can only be devised by someone who can

alreadyprogram. Iam thereforenot an“objects first”instructor, but a “whateverworks

best”instructor.

Manyoftheexamplesinvolvecomputergamesandgamedevelopment.Asweknow,

themajorityofundergraduatestudentsplaygames.Theyunderstandthembetterthan,say,

accountingorinventorysystems,whichhavebeenthetypicalearlyassignments.Ibelieve

inpresentingstudentsassignmentsthatareinteresting.

Idon’tthinkthatcateringtoanyparticularlanguageforminanintroductorytextserves

thestudentorthelanguage.Thestudent,ifsensible,willlearnotherlanguages.Bringing

Python idioms into play too soon may interfere with the generality of the ideas being

presentedandwillnotassistthestudentwhenlearningJava,C++,orRuby.

This book introduces a multimedia code module Glib that can assist the programmer

withgraphics,animation,sound,interaction,andvideo.Glibisincludedonthecompanion

discorcanbedownloadedfromthebook’swebsite.Thebasiclibrary,staticGlib,needs

nothingbutastandard3.4orbetterinstallationofPython.Itusestkinterasabasis,which

is distributed with the language. The expanded library uses pygame, and that is easily

downloaded and installed. The extended Glib, called dynamic Glib, allows exactly the

same interface as does static Glib, but extends it to also include sound, interface, and

video.Thus,ifstaticGlibcompilesandrunsaprogram,thendynamicGlibshouldtoo.

Thereisawikiconcerningthebookathttps://sites.google.com/site/pythonparker/andI

am happy to receive comments, code fixes, extensions, extra teaching material, and

general suggestions. I see a good textbook as a community, and encourage everyone –

especially first year students, the target audience of this book - to send me their

experiencesandideas.

Software(anycomputerprogram)isubiquitous.Cars,phones,refrigerators,television,

(and almost everything in our society) are computerized. Decisions made about how a

programistobebuilttendtosurvive,andevenaftermanymodifications,theycanaffect

how people use that device or system. Creating efficient software helps in achieving a

productiveandhappycivilization.

Python is a great language for beginning programmers. It is easy to write the first

programs,becausetheconceptualoverheadissmall.Thatis,there’snoneedtounderstand

what“void”or“public”meansattheoutset.Pythondoesmanythingsforaprogrammer.

Do you want something sorted? It’s a part of the language. Lists and hash tables

(dictionaries)areapartofthelanguage.Youcanwriteclasses,butdonothaveto,soitcan

be taught objectsfirst or not. The required indentation means that it is much harder to

placecodeincorrectlyinloopsorifstatements.TherearehundredsofreasonswhyPython

isagreatidea.

Anditisfree.Thisbookwaswrittenusingversion3.4,andwiththePyCharmAPI.The

modulesusedthatrequiredownloadarefew,butincludePyGameandtweepy.Allfree.

OverviewofChapters

Here’s a brief outline of the book. It can be used to teach computer science majors or

sciencestudentswhowishtohaveacompetencyinprogramming.

Chapter 0: Historical and technological material on computers. Binary numbers, the

fetch-excutecycle.Thischaptercanbeskippedinsomesyllabi.

Chapter 1: Problem solving witha computer; breaking a problem down so itcan be

solved. The Python system. Some simple programs involving games that introduce

variables,expressions,print,types,andtheifstatement.

Chapter 2: Repetition in programming: while and for statements. Random numbers.

Countingloops,nestedloops.Drawingahistogram.Exceptions(try-except).

Chapter3:Stringsandstringoperations.Tuples,theirdefinitionanduse.Listsandlist

comprehension. Editing, slices. The bytes type. And set types. Example: the game of

craps.

Chapter4:Functions:modularprogramming.Definingafunction,callingafunction.

Parameters,includingdefaultparameters,andscope.Returnvalues.Recursion.TheGame

ofSticks.Variableparameterlists,assigningafunctiontoavariable.Findthemaximumof

amathematicalfunction.Modules.GameofNim.

Chapter5:Files.Whatisafileandhowarefilesrepresented.Propertiesoffiles.File

exceptions.Input,output,append,open,close.Commaseparatedvalue(CSV)files.Game

ofJeopardy.Thewithstatement.

Chapter6:Classesandobjectorientation.Whatisanobjectandwhatisaclass?Types

andclasses.Pythonclassstructure.Creatinginstances,__init__andself.Encapsulation.

Examples: deck of playing cards; a bouncing ball; Cat-a-pult. Designing with classes.

Subclassesandinheritance.Videogameobjects.Ducktyping.

Chapter7:Graphics.TheGlibmodule.Drawingwindow;colorrepresentation,pixels.

Drawing lines, curves, and polygons. Filling. Drawing text. Example: Histogram, Pie

chart.Imagesandimagedisplay,gettingandsettingpixels.Thresholding.Generativeart.

Chapter 8: Data and information. Python dictionaries. Latin to English translator.

Arrays,formattedtext,formattedinput/output.Meteoritelandingdata.Non-textfilesand

thestructmodule.Highscorefileexample.Randomaccess.Imageandsoundfiletypes.

Chapter9:Digitalmedia:dynamicGlibmodule.Usingthemouseandthekeyboard.

Animation. Space shuttle control console example. Transparent colors. Sound: playing

soundfiles,volume,pause.Video:playandpositionavideo,accessingframesandpixels

inavideo.

Chapter 10: Basic algorithms in computer science. Sorting (selection, merge) and

searching (linear, binary). Timing code execution. Generating random numbers;

cryptography;datacompression(includingHuffmancodesandRLE);hashing.

Chapter 11: Programming for Science. Roots of equations; differentiation and

integration. Optimization (minimum and maximum) and curve fitting (regression).

Evolutionaryalgorithms.Longestcommonsubsequence,oreditdistance.

Chapter12:Writinggoodcode.Awalkthroughtwomajorprojects:awordprocessor

written as procedural code and a breakout game written as object oriented code. A

collectionofeffectiverulesforwritinggoodcode.

Chapter 13: Dealing with real world interfaces, which tend to defined for you.

ExamplesareEmail(sendandreceive),FTP,inter-processcommunication(client-server),

Twitter,callingotherlanguageslikeC++.

Chapter14:AreferenceforbothversionsofGlib.

ChapterCoverageforDifferentMajors

Acomputerscienceintroductioncouldusemostchapters,dependingonthebackground

ofthestudents,butChapters0,7,9,and/or11couldbeomitted.

Anintroductiontoprogrammingforsciencecouldomitchapters0,10,12.

Chapter13isalwaysoptional,butisinterestingasitexplainshowsocial

mediasoftwareworksundertheinterface.

Basicintroductiontoprogrammingfornon-scienceshouldinclude

Chapters0,1,2,3,4,5,and7.

CompanionFiles(Discincludedinphysicalbookorfiles

availablefordownloading)

Thecompanionfilescontainusefulmaterialforeachchapter:

•Selectedexercisesaresolved,includingworkingcodewhenthatisapartofthe

solution.

•AllsignificantprogrammingexamplesareprovidedasPythoncodefiles(over100),

thatcanbecompiledandexecuted,andthatcanbemodifiedasexercisesorclass

projects.Thisincludessampledatafileswhenappropriate.

•AnimportantaspectofthisbookistheuseofagraphicslibrarynamedGlib.Source

codeforthismoduleisprovidedonthediscandonline.Therearetwoversions:one

thatworkswiththebuilt-inmoduletkinterwhichallowsgraphics,andasecondthat

extendsthepreviousmoduleusing

pyGameandallowsvideos,interaction,andsound.

•Allfiguresareavailableasimages,infullcolor.

InstructorAncillaries

•Solutionstoalmostalloftheprogrammingexercisesgiveninthetext.

•MSPowerPointlecturesprovidedforanentiresemester(35files)includingsome

newexamplesandshortvideos.

•Likelythemostimportantaspectofthisbook,asidefromtheverypractical

viewpoint,istheprovisionoftheGlibgraphicsandmultimedialibrary.Thiscomes

intwoversions:auniversalversionthathandlesbasicgraphicsandthatcanexecute

withoutanyextrainstallationstep;andthefullmultimediaextensionthathandles

sound,video,andinteraction,butthatrequiresthatpyGamebeinstalled,whichisa

simpleprocess.

•AllofthePythoncodethatappearsinthebookshasbeenexecuted,andallcomplete

programsareprovidedas.pyfiles.Someofthenumerousprogrammingexamples

(over100)thatareexploredinthebookandforwhichworkingcodeisincluded:

oAninteractivebreakoutgame

oAtextformattingsystem

oPlottinghistogramsandpiecharts

oReadingTwitterfeeds

oPlayJeopardyUsingaCSVDataSet

oSendingandreceivingEmail

oAsimpleLatintoEnglishtranslator

oRock-Paper-Scissors

•HundredsofansweredmultiplechoicequizandexaminationquestionsinMSWord

filesthatcanbeeditedandusedinvariousways.

DedicatedWebSite

An online community has been started at https://sites.google.com/site/pythonparker/ for

comments, new exam questions and exercises, extra code, and as a place to report

problems.

Pleaseconsidercontributingmaterialtotheon-linecommunity,anddohavefun.Ifyou

don’t,thenyou’redoingitwrong.



J.Parker

October2016

CHAPTER0

MODERNCOMPUTERS

0.1CalculationsbyMachine

0.2HowComputersWorkandWhyweMadeThem

0.3ComputerSystemsareBuiltinLayers

0.4ComputerNetworks

0.5Representation

0.6Summary

Inthischapter

Humansaretoolmakersandtoolusers.Thisisnotuniqueintheanimalkingdom,butthe

facilitythathumanshavewithtoolsandthevarietyofapplicationswehaveforthemdoes

make us unique. Starting with mechanical tools (machines) like levers and wheels that

could lighten the physical effort of everyday life, more and more complex and specific

deviceshavebeencreatedtoassistwithallfacetsofourlives.Thiswasextendedinthe

twentiethcenturytoassistingwithmentalefforts,specificallycalculation.

Computers are devices that humans have built in order to facilitate complex

calculations.Earlycomputerswereusedtodosomeofthecomputationsneededtodesign

thefirstnuclearbombs,butnowcomputersseemtobeeverywhere,evenembeddedwithin

carsandkitchenappliances,andevenwithinourownbodies.Thesuccessofthesedevices

insuchawiderangeofapplicationareasisaresultoftheirabilitytobeprogrammed—

thatis,thedeviceitselfisonlyapotentialwhenfirstbuiltandhasnospecificfunction.It

isdesignedtobeconfiguredtodoanytaskthatrequirescalculations,andtheconfiguring

processiswhatwecallprogramming.

Tosomeextentthishastakentheplaceofalotofothertooldevelopmentthatusedto

be done by engineers. When designing a complex machine like an automobile, for

example,there usedto be alot of mechanicalwork involved.The careful timingof the

currenttothesparkplugwasaccomplishedbyrotatingshaftswithsensors,andresultedin

thefiringofeachcylinderatthecorrectmoment.Theairtogasolinemixturefedintothe

enginewascontrolledbytubesandcablesandsprings.Nowallofthesethingsandmany

morearedoneusingcomputersthatsenseelectricand magneticevents,docalculations,

andsendelectricalcontrolsignalstoactuatorsintheengine.Thesamecomputercanbe

usedtocontrolarefrigerator,maketelephonecallsonacellularphone,changechannels

onatelevision,andwakeyouupinthemorning.Itistheflexibilityofthecomputerthat

has led to them becoming a dominant technology in human society, and the flexibility

comeslargelyfromtheirabilitytobeprogrammed.

0.1 CALCULATIONSBYMACHINE

People have been calculating things for thousands of years, and have always had

mechanicalaidstohelp.

Whensomeoneprogramsacomputer,theyarereallycommunicatingwithit.Itisavery

imperativeandprecisecommunicationtobesure.Imperativebecausethecomputerhasno

choice;itisbeingtoldwhattodo,andwilldoexactlythat.Precisebecauseacomputer

doesnotapplyanyinterpretationtowhatitisbeingtold.Humanlanguagesarevagueand

subject to interpretation and ambiguity. There are sentences that are legal in terms of

syntax that have no real meaning: “Which is faster, to Boston or by bus?” is a legal

sentence in English that has no meaning. Such things are not possible in a computer

language. Also, computers do not think and so can’t evaluate a command that would

amount to “expose the patient to a fatal dose of radiation” with any skepticism. As a

result,we,asprogrammers,mustbecarefulandpreciseinwhatweinstructthemachineto

do.

Whenhumanscommunicatewitheachotherweusealanguage.Similarly,humansuse

languagestocommunicatewithcomputers;itiseasyforus.Suchlanguagesareartificial

(humansinventedthemforthispurpose,allatonce),terse(therearefewifanymodifiers,

no way to express emotions or graduations of any feeling), precise (each item in the

language means one thing), and written (we do not speak to the computer in a

programminglanguage.Notyet,perhapsnever).

Computerlanguagesoperateatahighlevel,anddonotrepresentthewaythecomputer

actually works. For the purposes of learning to program there are a few fundamental

thingsthatneedtobeknownaboutcomputers.It’snotrequiredtoknowhowtheyoperate

electronically,buttherearebasicprinciplesthatshouldbeunderstoodinordertoputthe

processofusingcomputersinpracticalcontexts.

0.2 HOWCOMPUTERSWORKANDWHYWEMADE

THEM

Thereasonpeopleusecomputersisdifferentdependingonthepointinhistoryinwhich

one looks, but the military always seems to be involved. There have been many

calculating devices built and used throughout history, but the first one that would have

been programmable was designed by Charles Babbage. The military, as well as the

mathematiciansoftheday,wereinterestedinmoreaccuratemathematicaltables,suchas

those for logarithms. At the time these were calculated by hand, but the idea that a

machine could be built to compute more digits of accuracy was appealing. This would

havebeenamechanicaldeviceofgearsandshafts,butitwasnotcompletedduetobudget

andcontractingissues.

Babbage continued his work in design and created, on paper, a programmable

mechanicaldevicecalledtheanalyticalenginein1837.Whatdoesprogrammablemean?

Acalculationdeviceismanipulatedbytheoperatortoperformasequenceofoperations:

addthistothat,thensubtractthisanddividebysomethingelse.Onamoderncalculator

thiswouldbedoneusingasequenceofkeypresses,butonolderdevicesitmayinvolve

movingbeadsalongwiresorrotatinggearsalongshafts.Nowimaginethatthesequence

ofkeypressescanbeencodedonsomeothermedia:asetofcams,orplugsintosockets,

orholespunchedintocards.Thisisaprogram.

Suchasetofpunchedcardsorcamswouldbesimilartoasetofinstructionswrittenin

English and given to some human to calculate, but would instead be coded in a form

(language)thatthecomputingdevicecoulduseimmediately.Thedirectionsonthecards

could be changed so that something new could be computed as needed. The difference

enginewouldonlyfindlogarithmsandtrigonometricfunctions,butadevicethatcouldbe

programmedin this way could, intheory,calculateanything. The analytical enginewas

programmedbypunchingholesinstiffcards,anideathatwasderivedfromtheJacquard

loom of the day. The location of holes would indicate either an operation (e.g., add,

subtract,etc.)ordata(anumber).Asequenceofsuchcardswouldbeexecutedoneata

timeandyieldavalueattheend.

Althoughtheanalyticalenginewasnevercompleted,aprogramwaswrittenforit,but

notbyhim.Theworld’sfirstprogrammermayhavebeenawoman,AugustaAdaKing,

CountessofLovelace.SheworkedwithBabbageforafewyearsandwroteaprogramto

computeBernoullinumbers.Thisisthefirstalgorithmeverdesignedforacomputerandis

often claimed to be the first computer program ever written, although it was never

executed.

The very concept of programmability is a more important development than is the

developmentofthedifferenceoranalyticalengines.Theideathatamachinecanbemade

tododifferentthingsdependingonauser-definedsetofinstructionsistheverybasisofall

moderncomputers,whiletheuseofmechanicalcalculationhasbecomeobsolete;itistoo

slow,expensive,andcumbersome.Thisiswhereitbegan,though,andtheprogramming

conceptisthesametoday.

During World War II computers made the leap to being electrical. Work on breaking

codesandbuildingtheatomicbombrequiredlargeamountsofcomputing.Initiallysome

ofthiswasprovidedbyroomsfullofhumansoperatingmechanicalcalculators,butthey

couldnotkeepupwiththedemand,soelectroniccomputersweredesignedandbuilt.The

firstwasColossus,designedandbuiltbyTommyFlowersin1943.Itwascreatedtohelp

breakGermanmilitarycodes,andanupdatedversion(MarkII)wasbuiltin1944.

IntheUnitedStatestherewasaneedforcomputationalpowerinLosAlamoswhenthe

firstnuclearweapons werebeing built.Electro-mechanicalcalculators werereplaced by

IBMpunched-cardcalculators,originallydesignedforaccounting,andthesewerealittle

faster than the humans running calculators, but could run twenty-four hours a day and

made fewer errors. This computer was programmed by plugging wires into sockets to

createnewconnectionsbetweencomponents.

0.2.1 Numbers

Theelectroniccomputersdescribedsofar,andthoseofthe1940sgenerally,hadalmost

no storage for numbers. Input was through devices like cards, and they could have

numbersonthem.Theycouldbetransferredtothecomputationunit,thenmovedaheador

back,andperhapsreadagain.Memorywasaprimitivething,andvariousmethodswere

devisedtostorejustafewdigits.Asignificantadvancecamewhenengineersdecidedto

usebinarynumbers.Thiswillrequiresomeexplanation.

Electronicdevicesusecurrentandvoltagetorepresentinformation,suchassoundsor

pictures(radioand television).One ofthe simplestdevices isa switch,which canopen

and close a circuit and turn things like lights on and off. Electricity needs a complete

circuitorroutefromthesourceofelectrons,thenegativepoleofabatteryperhaps,tothe

sink,whichcouldbethepositivepole.Electrons,whichiswhatelectricityis,inasimple

sense,flowfromthenegativetothepositivepolesofabattery.Electricitycanbemadeto

do work by putting devices in the way of the flow of electrons. Putting a lamp in the

circuitcancausethelamptolightup,forexample.

A switch makes a break in the circuit, which stops the electrons from flowing; they

cannotjumpthegap.Thiscausesthelamptogodark.Thisseemsobvioustoanyonewith

electriclightsintheirhouse,butwhatmaynotbesoobviousisthatthiscreatestwostates

of the circuit, on and off. These states can be assigned numbers. Off could be 0, for

example,andoncouldbe1.Thisishowmostcomputersrepresentnumbers:ason/offor

1/0states. Tobe more clearabout this way ofrepresenting numbers, considerthe usual

way,whichiscalledpositionalnumbering.

Mosthumansocietiesnowuseasystemthatusestendigits:0,1,2,3,4,5,6,7,8,and

9.Thenumber123isacombinationofdigitsandpowersoften.Itisashorthandnotation

for100+20+3,or1×102+2*101+3*100.Eachdigitismultipliedbyapoweroften

andsummedtogetthevalueofthenumber.Anyonewhohasbeentoschoolacceptsthis

anddoesnotthinkaboutit,butreallythevalueusedasthebasisofthesystem,ten,isnot

magical.Itsimplyhappenstobethenumberofdigitshumanshaveontheirhands.Any

basewouldworkalmostaswell.

Example:Base

Numbersthatuse4asabasecanonlyhavethedigits0,1,2,and3.Eachpositioninthe

numberrepresentsapowerof4.Thusthenumber123is,inbase4,1×42+2*41+3*40,

whichis1×16+2*4+3=16+8+3=27intraditionalbase10representation.

This could get confusing, what with various bases and such, so numbers will be

considered to be in base 10 unless specific by a suffix. 1234 is 123 in base 4, whereas

1238is123inbase8,andsoon.

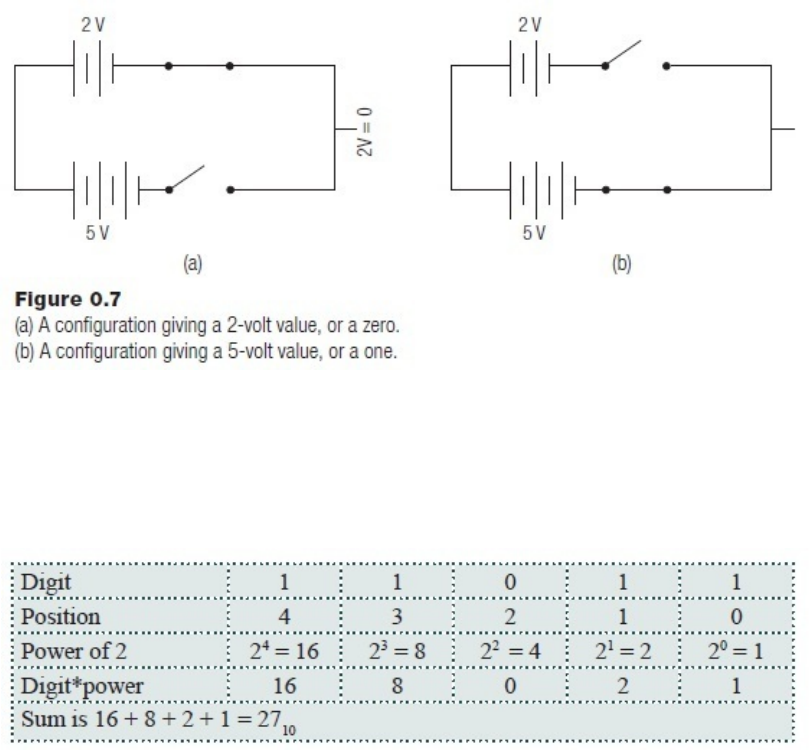
Binary numbers can have digits that are 1 or 0. The numbers are in base 2, and can

thereforeonly have the digits 0 and 1. These numbers can be representedby the on/off

stateofaswitchortransistor,whichisanelectronicswitch,whichiswhytheyareusedin

electroniccomputers.Moderncomputersrepresentalldataasbinarynumbersbecauseitis

easytorepresentthosenumbersinelectronicform;avoltageisarbitrarilyassignedto“0”

and to “1.” When a device detects a particular voltage, it can then be converted into a

digit,andviceversa.If2voltsisassignedtoa0and5voltsisassignedtoa1,thenthe

followingcircuitcouldsignala0or1dependingonwhatswitchwasselected:

ConvertBinaryNumberstoDecimal

Considerthebinarynumber110112.Itcanbeconvertedinbase10bymultiplyingeach

digitbyitscorrespondingpoweroftwoandthensummingtheresults.

Someobservations:

•Terminology:Adigitinabinarynumberiscalledabit(forbinarydigit)

•Anyevennumberhas0asthelowdigit,whichmeansthatoddnumbershave1asthe

lowdigit.

•Anyexactpoweroftwo,suchas16,32,64,andsoon,willhaveexactlyonedigit

thatisa1,andallotherswillbe0.

•Terminology:Abinarydigitorbitthatis1issaidtobeset.Abitthatis0issaidtobe

clear.

ConvertDecimalNumberstoBinary

Going from base 10 to base 2 is more complicated than the reverse. There are a few

waystodothecalculation,buthere’sonethatmanypeoplefindeasytounderstand.Ifthe

lowest digit (rightmost) is 1 then the number is odd, and otherwise it is even. If the

number 7310 is to be converted into binary the rightmost digit will be 1, because the

numberisodd.

Thenextstepistodividethenumberby2,eliminatingtherightmostbinarydigit,the

one that was just identified, from the number. 7310 / 210 = 3610, and there can be no

fractionalpart,soanysuchpartistobediscarded.Nowtheproblemistoconvert3610to

binaryandthenappendthepartalreadyconvertedtothat.Is3610evenorodd?Itiseven,

sothenextdigitis0.Thefinaltwodigitsof7310inbinaryare01.

Theprocessisrepeated:

Divide36by2toget18,whichiseven,sothenextdigitis0.

Divide18by2toget9,whichisodd,sothenextdigitis1.

Divide9by2toget4,whichiseven,sothenextdigitis0.

Divide4by2toget2,whichiseven,sothenextdigitis0.

Divide2by2toget1,whichisodd,sothenextdigitis1.

Divide1by2toget0.Whenthenumberbecomes0,theprocessiscomplete.

Theconversionprocessgivesthebinarynumbersinreverseorder(righttoleft)sothe

resultisthat7310=10010012.

Isthiscorrect?Convertthisbinarynumberintodecimalagain:

10010012=1×20+1*23+1*26=1+8+64=7310.

Asummaryoftheprocessforconvertingxintobinaryis:

Startatdigitn=0(rightmost)

repeat

Ifxiseven,thecurrentdigitnis0,otherwiseitis1

Dividexby2

Add1ton

Ifxiszero,thenendtherepetition

ArithmeticinBinary

Computers do all operations on data as binary numbers, so when two numbers are

added,forexample,thecalculationisperformedinbase2.Itturnsoutthatbase2iseasier

thanbase10forsomethings,andaddingisoneofthosethings.It’sdoneinthesameway

asinbase10butthereareonly2digits,andtwosarecarriedinsteadoftens.Forexample:

add010112to011102:

010112

011102

Startingthesumontherightasusual,thereisa0addedtoa1andthesumis1,justas

inbase10.

010112

011102

–––—

The next column in the sum contains two 1s. 1 + 1 is two, but in binary that is

representedas102.So,theresultof1+1is0withacarryof1:

010112

011102

–––—

012

Thenextcolumnhas1+0,butthereisacarryof1soitis1+0+1.That’s0witha1

carryagain:

010112

011102

–––—

0012

Nowthecolumnis1+1witha1carry,or1+1+1.Thisis1withacarryof1:

010112

011102

–––—

10012

Finally, the leading digits are 0 + 0 with a carry of 1, or 0 + 0 + 1. The answer is

110012.Isthiscorrect?Well,010112is1110and011102is142,and1110+1410=2510.

Theanswer110012is,infact,2510(confirmthis!)soitallworksout.

Binarynumberscanbesubjectedtothesameoperationsasanyotherformofnumber

(i.e.,multiplication,subtraction,division).Inaddition,theseoperationscanbeperformed

byelectroniccircuitsoperatingonvoltagesthatrepresentthedigits1and0.

0.2.2 Memory

Adding memory to computers was another huge step forward. A computer memory

mustholdsteadyacollectionofvoltagesthatrepresentdigits,andthedigitsarecollected

intosets,each ofwhich is anumber.A switchcan hold abinary digit,butswitches are

activated by people. Computer memory must store and recall (retrieve) numbers when

theyarerequiredbyacalculationwithouthumanintervention.

The first memories were rather odd things: acoustic delay lines store numbers as a

soundpassingthroughmercuryinatube.Thespeedofsoundallowsasmallnumberof

digits,around500,tobestoredintransitfromaspeakerononeendtoareceiveronthe

other. A phosphor screen can be built that is activated by an electric pulse and draws a

brightspotonascreenthatneedsnopowertomaintainit.Numberscanbesavedasbright

anddarkspots(1and0)andretrievedusinglightsensitivedevices.

Other devices were used in the early years, such as relays and vacuum tubes, but in

1947 the magnetic core memory was patented, in which bits were stored as magnetic

fieldsinsmalldonut-shapedelements.Thiskindofmemorywasfasterandmorereliable

than anything used before, and even held the data in memory without power being

applied,ahandythinginapowerfailure.Itwasalsoexpensive,ofcourse.

This kind of memory is almost never used anymore, but its legacy remains in

terminology:memoryisstillfrequentlyreferredtoascore,andacoredumpisstillwhat

manypeoplecallalistingofthecontentsofacomputermemory.

Currentcomputers use transistors tostore bitsand solidstate memoriesthat canhold

billionsofbits(Gigabits),butthewaytheyareusedinthecomputerisstillthesameasit

was.Bitsarecollectedintogroupsof8(abyte)andthengroupsofmultiplebytestofora

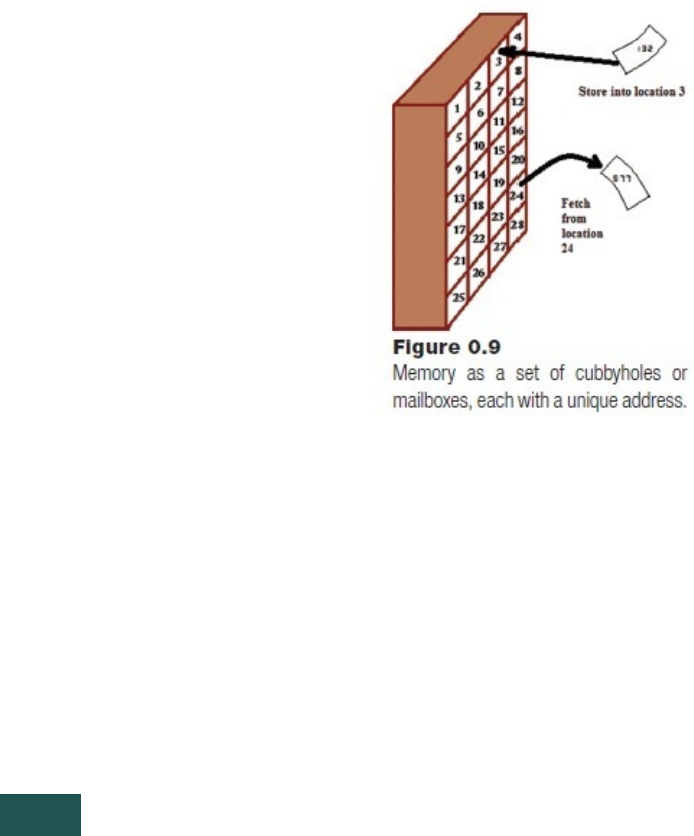
word. Words are collected into a linear sequence, each numbered starting at 0. These

numbersarecalledaddresses,andeachword,andsometimeseachbyte,canbeaccessed

by specifying the address of the data that is wanted. Acquiring the data element at a

particular location is called a fetch, and placing a number into a particular location is a

store.Acomputerprogramtoaddtwonumbersmightbespecifiedas:

Fetchthenumberatlocation21

Fetchthenumberatlocation433

Addthosetwonumbers

Storetheresultinlocation22

Thismayseemlikeaverbosewaytoaddtwonumbers,butrememberthatthiscanbe

accomplishedinatinyfractionofasecond.

Memoryisoftenpresentedtobeginningprogrammersasacollectionofmailboxes.The

addressisanumberidentifyingthemailbox,whichalsocontainsanumber.Thereissome

specialmemoryinthecomputerthathasnospecificaddress,andisreferredtoinvarious

ways.Whenafetchisperformed,thereisaquestionconcerningwherethevaluethatwas

fetchedgoes.Itcangotoanothermemorylocation,whichisamoveoperation,oritcango

intooneofthesespeciallocations,calledregisters.

Acomputercanhavemanyregistersorveryfew,buttheyareveryfastmemoryunits

that are used to keep intermediate results of computations. The simple program above

wouldnormallyhavetobemodifiedtogiveregistersthatareinvolvedintheoperations:

Fetchthenumberatlocation21intoregisterR0

Fetchthenumberatlocation433intoregisterR1

AddR1andR0andputtheresultintoR3

StoreR3(theresult)inlocation22

Thisisstillverbose,butmorecorrect.

0.2.3 StoredPrograms

The final critical step in creating the modern computer occurred in 1936 with Alan

Turing’s theoretical paperon the subject, butan actual computer toemploy the concept

was not built until 1948 when the Manchester Small-Scale Experimental Machine ran

whatisconsideredtobethefirststoredprogram.Ithasbeenthebasicmethodbywhich

computersoperateeversince.

Theideaistostoreacomputerprograminmemorylocationsinsteadofoncardsorin

some other way. Programs and data now coexist in memory, and this also means that

computerprogramshavetobeencodedasnumbers;everythinginacomputerisanumber.

Therearemanydifferentwaystodothis,andmanypossibledifferentinstructionsetsthat

have been implemented and various different configurations of registers, memory, and

instructions.Thecomputerhardwarealwaysdoesthesamebasicthing:firstitfetchesthe

next instruction to be executed, and then it decodes it and executes it. Executing an

instructioncouldinvolvemoreaccessestomemoryorregisters.

This repeated fetch then execute process is called, not surprisingly, the fetch-execute

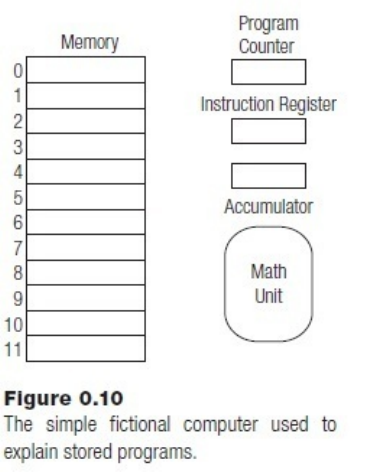
cycle,andisattheheartofallcomputers.Thelocationoraddressofthenextinstruction

resides in a register called the program counter, and this register is incremented every

time an instruction is executed, meaning that instructions will be placed in consecutive

memorylocationsandwillbefetchedandexecutednaturallyinthatorder.Sometimesthe

instructionisfetchedintoaspecialregistertoo,calledtheinstructionregister, so that it

canbeexaminedquicklyforimportantcomponentslikedatavaluesoraddresses.Finally,

acomputerwillneedatleastoneregistertostoredata;thiswillbecalledtheaccumulator,

becausethat’susuallywhatsucharegisteriscalled.

Thestoredprogramconceptisactuallyprettydifficulttograsp,soadetailedexampleis

inorder.Imagineacomputerthathas12bitwordsasmemorylocationsandthatpossesses

theregistersdescribedabove.Thisisafictionalmachine,butitturnsouttohavesomeof

thepropertiesofanoldcomputerfromthe1960scalledthePDP-8.

Todemonstratetheexecutionofaprogramonastoredprogramcomputeraverysimple

program will be used: add 21 and 433, placing the answer in location 11. As an initial

assumption, assume that the value 21 is in location 9 and 433 is in location 10. The

programitselfwillresideinconsecutivememorylocationsbeginningataddress0.

The program should be described in English first. Note that it is very much like the

previous two examples, but in this case there is only one register to put data into, the

accumulator.Theprogramcouldperhapslooklikethis:

Fetchthecontentsofmemorylocation9intotheaccumulator

Addthecontentsofmemorylocation10totheaccumulator

Storethecontentsoftheaccumulatorintomemorylocation11

Theprogramisnowcomplete,andtheresult21+433shouldbefoundinlocation11.

Computerprogramsarenormallyexpressedintermsthatthe computercanimmediately

use,normallyasfairlyterseandprecisecommands.Thenextstageinthedevelopmentof

thisprogram is to use a symbolicform of the actual instructionsthat the computer will

use.

Thefirststepistomovethecontentsoflocation9totheaccumulator.Theinstruction

thatdoesthiskindofthingiscalledLoadAccumulator,shortedasthemnemonicLDA.

Theinstructionwouldbeinlocation0:

0:LDA9#Loadaccumulatorwithlocation9

The text following the “#” character is ignored by the computer, and is really a

commenttoremindtheprogrammerwhatishappening.Thenextinstructionistoaddthe

contents of location 10 to the accumulator; the instruction is ADD and it is placed in

address1:

1:ADD10#Addcontentsofaddress10totheaccumulator

Finally,the result, current in the accumulator register,will be savedinto the memory

locationataddress11.ThisisaStoreinstruction:

2:STO11#Answerintolocation11

Theprogramiscomplete.ThereisaHaltinstruction:

3:HLT#Endofprogram

If this program starts executing at address 0, and if the correct data is in the correct

locations,thentheresult454shouldendupinlocation11.Buttheseinstructionsarenot

yetinaformthecomputercanuse.Theyarecharacters,textthatahumancanread.Ina

stored program computer these instructions must be encoded as numbers, and those

numbersmustagreewiththeonesthecomputerwasbuilttoimplement.

Aninstructionmustbeabinarynumber,soallofthepossibleinstructionshavenumeric

codes.Aninstructioncanalsocontainamemoryaddress;theLDAinstructionspecifiesa

memorylocationfromwhichtoloadtheaccumulator.Boththeinstructioncodeandthe

addresshavetobeplacedintoonecomputerword.Thedesignersofthecomputerdecide

howthatwillbedone,andtheprogrammershavetolivewiththeresult.

This computer has 12 bit words. Imagine that the upper 3 bits indicate what the

instructionis.Thatis,atypicalinstructionisformattedlikethis:

Thereare9bitsatthelower(right)endoftheinstructionforanaddress,and3atthetop

endforthecodethatrepresentstheinstruction.ThecodeforLDAis3;thecodeforADD

is5andthecodeforSTOis6.HLTonmostcomputersthathavesuchaninstructionis

code0.Hereiswhattheprogramlookslikeasnumbers:

Code3Address9

Code5Address10

Code6Address11

Code0Address0

Thesehaveto bemade intobinary numbersto bestored in memory, butthat’spretty

easy.FortheLDAinstructionthecode310is0112andtheaddressis910=0000010012,

so the instruction as a binary number is 011 0000010012, where the space between the

codeandtheaddressisonlypresenttomakeitobvioustoapersonreadingit.

The ADD instruction has code 510, which is 1012, and the address is 10, which in

binaryis00010102.Theinstructionis1010000010102.

The STO instruction has code 6, which is 1102, and the address is 11, which is

0010112.Theinstructionis1100000010112.

TheHLTinstructioniscode0,orin12bitbinary0000000000002.

Thecodes aremade up bythe designersof the computer. Whenmemory is setup to

containthisprogramhere’swhatitlookslike:

Thisishowmemorylookswhentheprogrambegins.Theactofsettingupthememory

likethissothattheprogramcanexecuteiscalledloading.Thebinarynumbersinmemory

locations9and10are21and433respectively(checkthis!),whicharethenumberstobe

summed.

Of course there are more instructions than these in a useful computer. There is not

alwaysasubtractinstruction,butsubtractioncanbedonebymakinganumbernegative

andthenadding,sothereisoftenaNEGateinstruction.Settingtheaccumulatortozerois

acommonthingtodo,sothereisaCLA(ClearAccumulator)instruction;andthereare

manymore.

The fetch-execute cycle involves fetching the memory location addressed by the

programcounterintotheinstructionregister,incrementingtheprogramcounter,andthen

executingtheinstruction.Executioninvolvesfiguringoutwhatinstructionisrepresented

bythecodeandthensendingtheaddressordatathroughthecorrectelectroniccircuits,a

processbeyondanythingthischapterwilladdress.

Averyimportantinstructionthatthisprogramdoesnotuseisabranch.Theinstruction

BRA0willcausethenextinstructiontobeexecutedstartingatmemorylocation0.This

allows a program to skip over some instructions or to repeat some many times. A

conditional branch will change the current instruction if a certain condition is true. An

example would be Branch if Accumulator is Zero (BAZ), which will only perform a

branch if, as the instruction indicates, there is a value of zero in the accumulator. The

combinationofarithmeticandcontrolinstructionsmakesitpossibleforaprogrammerto

describeacalculationtobeperformedveryprecisely.

0.3 COMPUTERSYSTEMSAREBUILTINLAYERS

Enteringaprogramasbinarynumbersusingswitchesisaverytedious,time-consuming

process. Lacking a disk drive, the early computers depended on other kinds of storage:

punched cards again, or paper tape. It should be understood that because there was no

permanent storage, booting one of these machines often meant toggling a small “boot

loader”program,thenreadingapapertape.Nowthecomputerwouldrespondsensiblyto

itsperipheraldevices,likeaprinterorcardreader.Thepapertapecontainedaprimitive

“operating system” that would control the few devices available. That’s what operating

systemsdo:allocateresourcesandcontroldevices.

Thebootloader(bootstrapprogram)isthelowestlayerofsoftware.Itwasprovidedby

thecomputermanufacturer,buthastobeenteredbytheuser.Thepapertapesystemwas

the second layer, and the user did not have to write this program. Gradually more and

morelayerswerewrittensoastoprovidetheuserwithahighlevelofabstractionrather

than having to understand the entire machine. After all, physicists and engineers have

otherthingstodoratherthantendtothecomputer.

Whendiskdrivesbecameavailable,theoperatingsystemwouldbestoredonthem,and

abootstraploaderwouldbesavedinaspecialsectionofmemorythatcouldnotbeerased

(read only memory) so that when the computer was turned on it would run the loader,

which would load the operating system. Very convenient, and it is essentially what

happenstodayonWindows.

Thisoperating systemon the diskdrive is athird layerof software. Itprovides basic

hardwareallocationfunctionalityandalsogivestheuseraccesstosomeprogramstouse

forprintingandsavingthingsondisk—afilesystem.

0.3.1 AssemblersandCompilers

Programming a computer could still be a daunting task if done in binary, so the first

thing that was provided was an assembler. This was a program that would permit a

programmertoentera textprogramthatcould beconvertedinto abinaryexecutable.It

would allow memory locations to be named instead of using an absolute number as an

address,andwouldconverttextoperationcodesandaddressesintobinaryprograms.The

additionprogramfromtheprevioussectioncouldbewritteninassembleras:

LDAData1

ADDData2

STORes

HLT

Data1:21

Data2:433:

Res:0

Usuallyonelineoftextinanassemblercorrespondstoasingleinstructionormemory

location.It’sthesameprogrambutiseasierforaprogrammertounderstand because of

thenamedmemorylocationsandmnemonicinstructionnames.

Itismuchhardertodescribehowacompilerworks,butrelativelyeasytoexplainwhat

itdoes.Acompilertranslateshighlevellanguagestatementsintoassembler,whichinturn

convertsitintobinarycode.Compilerstranslatestatementslike:

A=21

B=433

C=A+B

into executable code. It is a very complex process, but essentially it allows the

programmer to declare that certain names represent integers, that values are to be

assigned,and that arithmeticcan be done. Thereare also more complexstatements like

conditionalexecutionofcodeandfunctioncallswithparameters,aswillbeseeninlater

chapters.

Compilersalsoimplementinputandoutputfromtheuser(readingfromakeyboardand

writing to the video screen), sophisticated data types, and mathematical functions. An

interpreter,whichiswhatthelanguagePythonis,doesapartofthecompilationprocess

but does not produce executable code. Instead, it simulates the execution of the code,

doingmostoftheworkinsoftware.TheJavalanguagedoesasimilarthinginmanycases.

Theprogramsthatsomeonewrites(software)createanotherlayerforsomeonetouse.

An example might be a database management system that gives a user access to a

computer that can query data for certain kinds of values. A graphics system gives a

programmeraccesstoasetofoperationsthatcandrawpictures.

0.3.2 GraphicalUserInterfaces(GUIs)

Mostcomputers now interfacewith their owners througha keyboard, one of thefirst

devicestobeinterfacedtoacomputer;amouse,thefirstdevicetopermit2Dnavigation

on a screen; and windows, a graphical construction that allows many independent

connectionstoacomputertoshareasinglevideoscreen.GUIsarepopularbecausethey

improve the user’s perception of what is happening on a computer. Previous computer

interfaceswerecompletelytextbased,soifsomethingwasgoingwronginaplacewhere

theuserwasnotlooking,thenitwouldprobablynotbenoticed.

Ontheotherhand,GUIsaremoredifficulttoprogram.Justopeninganewwindowina

Microsoft-basedoperatingsystemcanrequirescoresoflinesofC++codethatwouldtake

agreatdealoftimetounderstand.Naturally,itisthejobofaprogrammertobeabletodo

this, but it means that the average user could not create their own software that

manipulated the interface in any reasonable way. So, what is a window, and what’s

involvedinaGUI?

Awindow,intheoperatingsystemsense,isarectangleonthecomputerscreenwithin

which an exchange of information takes place between the user and the system. The

rectangle can generally be resized, removed from the screen temporarily (minimized),

moved,andclosed.Itcanbethoughtofasavirtualcomputerterminalinthateachonecan

dowhattheentirevideoscreenwasneededtodoinearlysystems.Whenthewindowis

active,ausercantypeinformationtobereceivedbytheprogramcontrollingit,andcan

manipulategraphicalobjectswithinthewindowusingamouseor,morerecently,byusing

their fingers on a touch screen. Without a mouse or something like it, a window-based

systemisprettymuchcrippled,sothetwoarealmostalwaysusedtogether.

The mouse is a variation on the tracker ball, and it is agreed that the German

engineeringcompanyTelefunkendevisedaworkingversionandwasthefirsttosellit.A

mouseislinkedthroughsoftwaretoacursoronthescreen,andleft-rightmotionsofthe

mousecauseleft-rightmotionsofthecursor;forwardandbackwardmotionsofthemouse

causethecursortomoveupanddownthescreen.Whenthecursorisinsideofawindow,

thenthatwindowisactive.Amousehasbuttons,andpressingamousebuttonactivates

whatever software object is related to the cursor position on the screen. This describes

thingsthatareobvioustoanyoneusedtocomputersbuiltsincethe1980s.

Widgets

Awidgetisagraphicalobjectdrawninawindoworotherwiseonacomputerscreen

thatcanbeselectedand/oroperatedusingthemouseandmousebuttons.Itisconnectedto

asoftwareelementthatwillbesentacontrolsignalornumericalparameterbyvirtueof

the widget being manipulated. That’s a pretty formal description, but a widget is

exemplifiedby the button, a very commonly used widget on web pages and interfaces.

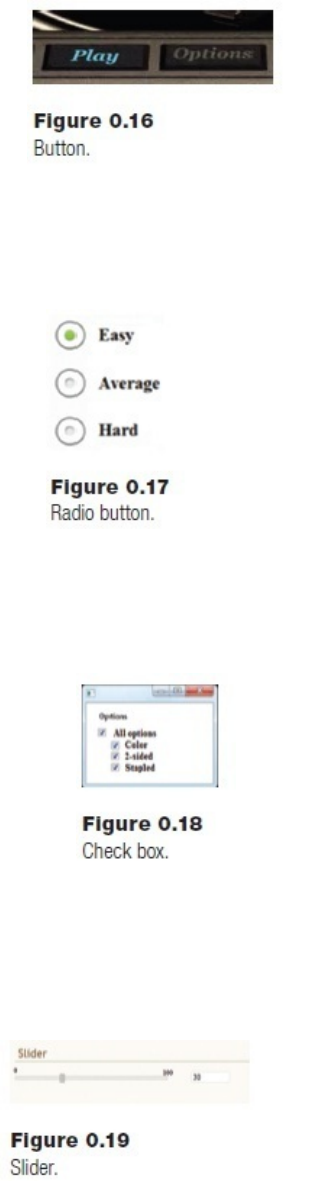
Buttonscanbeusedtodisplayinformationaswellastocontrolaprogram.Somepopular

widgetsare:

Button:Whenthemousecursoriswithintheboundariesofthebuttononthescreen,

thebuttonissaidtobeactivated.Pressingamousebuttonwhenthebuttonwidgetis

activatedwillcausethesoftwareconnectedtothebuttontoperformitsfunction.

Radio Button: A set of two or more buttons used to select from a set of discrete

options.Onlyoneofthebuttonscanbeselectedatatime,meanthattheoptionsare

mutuallyexclusive.

CheckBox:Awaytoselectasetofoptionsfromalargerset.Thiswidgetconsistsof

acollectionofboxesorbuttonsthatcanbechosenbyclickingonthem.Whenchosen,

they indicate that fact by using a graphical change, sometimes a check mark but

sometimesacolororothervisualeffect.

Slider:Ahorizontalorverticalcontrolwithaselectiontoolthatcanbeslidalongthe

control.Therelativepositionofthecontroldictatesthevaluethatthewidgetprovides.

Thisvalueisoftendisplayedinatextbox,andtherangeisalsocommonlydisplayed.

Drop-downList: A box containing text that displays a complete set of options that

can be displayed when the mouse button is clicked within it. Then any one of the

optionscanbeselectedusingthemouseandthemousebutton.

Icon: An icon is a small graphical representation (pictogram) that represents the

functionofaprogramorfile.Whenselected,theprogramwillexecuteorthefilewill

beopened.

There are many other widgets and variations on the ones shown here. There are two

basicprinciplesatplay:

1.Thewidgetrepresentsanactivityusingacommonlyunderstoodsymbol,and

performsthatactivity,oronerelatedtothesymbol,whenselectedusingthemouse.

Thisisagraphicalandtactileoperationthatreplacesthetypingofacommandin

previouscomputersystems.

2.Thesoftwarethatimplementsthewidgetisamodule,apieceofsoftwarethatcan

bereusedandreconfiguredforvariouscircumstances.Abuttoncanbequickly

createdtoperformanynumberoftasksbecausetheprogramthatimplementsitis

designedforthatdegreeofflexibility.

0.4 COMPUTERNETWORKS

Schools, offices, and some homes are equipped with computer networks, which are

wiresthatconnectcomputerstogetherandsoftwareandspecialhardwarethatallowsthe

computers to communicate with each other. This allows people to send information to

eachotherthroughtheircomputers;alotofworkisdoneinacomputerreadableformin

anycase,anditisconvenienttoallowcomputerstoshareinformation.Buthowdoesthis

reallywork?

Computersuseelectricitytoperformcalculationsonbinarynumbers.Arbitraryvoltages

have been selected to represent 0 and 1, and so long as everyone agrees on that

representation, those voltages can be sent along a wire no matter how long and still be

numbersatthereceivingend.Aslongastwocomputersarebeingconnectedthisworks

fine,butiftwowiresareneededtoconnectanytwocomputersthensixareneededtofully

connectthreecomputerstoeachotherandtwelvetoconnectfourcomputers.Aroomwith

thirtynetworkedcomputerswouldbefullofwires(870toeachcomputer)!Theremustbe

abetterway.

Hawaiihasanunusualproblemwhenitcomestocomputernetworkcommunication.It

isacollectionofislands.Linkingthembycablesisanexpensiveproposition.Intheearly

1970sthefolksattheUniversityofHawaiihadagoodidea—tolinkthecomputersusing

radio. Radio transmission is really similar to wire transmission in many practical ways,

andallocating35radiofrequenciestoconnectonecomputeroneachislandtoallofthe

otherswouldhavebeenpossible,buttheirideawasbetter.Theyusedasingleradiolink

for all computers. When a computer wanted to send information along the network, it

wouldlistentoseeifanothercomputerwasalreadydoingso.Ifso,itwouldwait.Ifnot,it

would begin to send data to all of the other computers and would include in the

transmissionacodeforwhichcomputerwassupposedtoreceiveit.Allcouldhearit,but

allwouldknowwhichcomputerwasthecorrectdestinationsotheotherswouldignoreit.

ThissystemwascalledAlohanet.

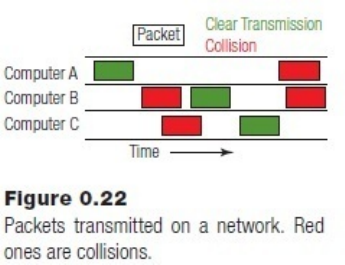
There is a problem with this scheme. Two or more computers could try to send at

almost the same time, having noted that no other computer was sending when they

checked. This is called a collision, and is relatively easy to detect; the data received is

nonsense.Whenthathappenseachcomputerwaitsforarandomtime,checksagain,and

triesagaintosendthedata.Ananalogywouldbeameetingwheremanypeoplearetrying

tospeakatonce.

Obviously the busier the network is the more likely a collision will be, and the

retransmissions will make things worse. Still, this scheme works very well and is

functioningtodayintheformofthemostcommonnetworkingsysteminearth—Ethernet.

Ethernet is essentially Alohanet along a wire. It means that each computer has one

connectiontoit,ratherthanconnectionstoeachofthepossibledestinations,andcollisions

arepossible.Thereisanotherconsiderationthatmakesthisschemeworkbetter,andthatit

isuseofpackets.Informationalongthesenetworksissentinfixed-sizepackagesofafew

thousand bytes. In this way, the time needed to send a packet should be more or less

constant,andit’smoreefficientthansendingabitorabyteatatime.

Eachpacketcontainsasetofdatabytesintendedforanothercomputer,sowithinthat

packetshouldbesomeinformationaboutthedestination,thesender,andotherimportant

stuff.Forinstance,ifadatafileisbiggerthanapacket,thenithastobesplitupintoparts

tobesent.Thus,apartofthepacketisasequencenumberindicatingwhichpacketitis

(e.g.,number3of5).Ifaparticularpacketnevergetsreceivedforsomereason,thenthe

missing one is known, and the receiver can ask the sender for that packet to be resent.

Therearealsocodesthancanbeusedtodeterminewhetheranerrorhasoccurred.

0.4.1 Internet

The Internet is a computer network designed to communicate reliably over long

distances. It was originally created to be a reliable communications system that could

surviveanuclearattack,andwasfundedbythemilitary.Itisdistributed,inthatdatacan

besentfromonecomputertoanotherinachainuntilitreachesitsdestination.

Imagine a collection of a few dozen computers, and that each one is connected to

multiple others, but not directly to all others. Computer A wishes to send a message to

computerB,anddoessousingapacketthatincludesthedestination.ComputerAsends

themessagetoallcomputersthatitisconnectedto.Eachofthosecomputerssendsittoall

ofthecomputersthattheyareconnectedto,andsoonuntilthedestinationisreached.All

of the computers will receive every message, which is pretty inefficient, but so long as

thereexistssomepathfromAtoBthemessagewillbedelivered.

Itwouldbehardtotellwhentostopsendingamessageinthisscheme.Anotherwayto

do it is to have a table in each computer saying which computers in the network are

connectedtowhichothers.Amessagecanbesenttoacomputerknowntobeashortpath

to the destination, one computer at a time, and in this case not all computers see the

message,onlythe onesalong theroute do.Anewcomputer added to the networkmust

sendaspecialmessagetoalloftheotherstellingthemwhichoftheexistingcomputersit

isdirectlyconnectedto,andthismessagewillpropagatetoallmachines,allowingthemto

updatetheirmap.Thisisessentiallytheschemeusedtoday.

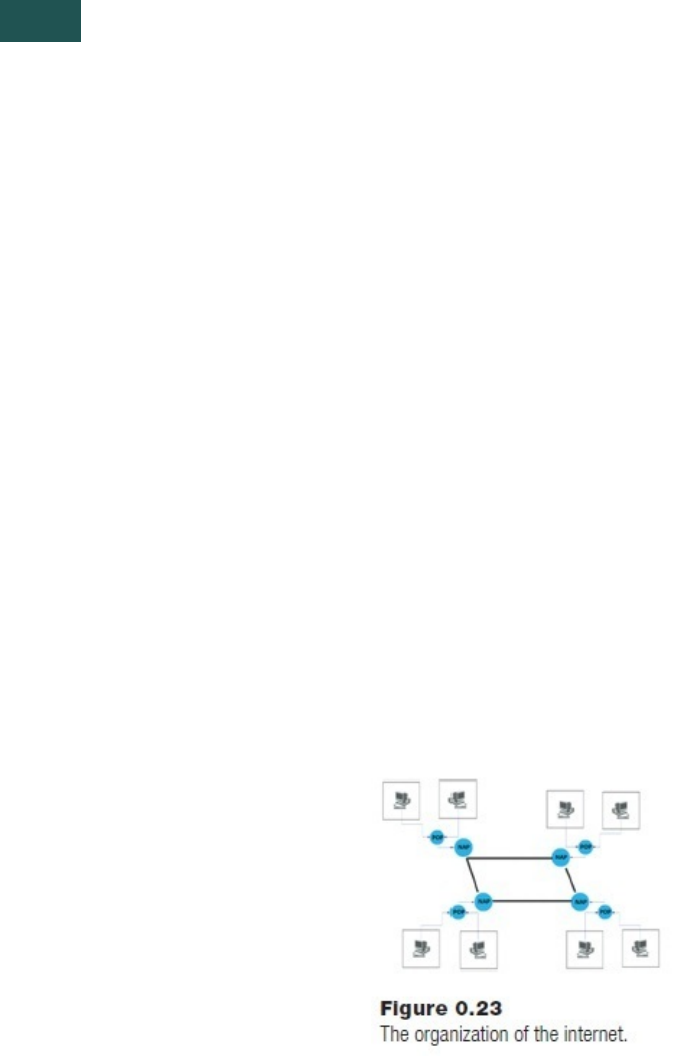
The Internet has a hierarchy of communication links and processors. First, all

computersontheInternethaveauniqueIP(InternetProtocol)addressthroughwhichthey

are reached. Because there are a lot of computers in the world, an IP address is a large

number.Anexamplewouldbe172.16.254.1(obtainedfromWikipedia).Whenacomputer

in,say,Portlandwantstosendamessageto,forexample,London,thePortlandcomputer

composes a packet that contains the message, its address, and the recipient’s address in

London.ThismessageissentalongtheconnectiontoitsInternetserviceprovider,which

isalocalcomputer,atarelativelowspeed,10megabitspersecondperhaps.Theservice

provider operates a collection of computers designed to handle network traffic. This is

calledaPointofPresence(POP)andcollectsmessagesfromalocalareaandconcentrates

themfortransmissionfurtherdowntheline.

Multiple POP sites connect to a Network Access Point (NAP) using much faster

connectionsthanusershavetoconnectwiththePOP.The NAPconcentratesevenmore

users, and provides a layer of addressing that can be used to send the data to the

destination. The NAP for the Portland user would have the message delivered to a

relativelylocalNAP,whichwouldsendittothenextNAPalongapathtothedestination

in London using an exceptionally fast (high bandwidth) data connection. The London

NAPwouldsendthemessagetotheappropriatelocalPOP,whichwouldinturnsenditto

thecorrectuser.

AnimportantconsiderationisthatthemessagecanbereadbyanyPOPnorNAPserver

alongtheroute.DatasentalongtheInternetispublicunlessitisproperlyencryptedbythe

users.

0.4.2 WorldWideWeb

The World Wide Web, or simply the Web, is in fact a layer of software above the

Internetprotocols.Itisawaytoaccessfilesanddataremotelythroughavisualinterface

provided by a program that runs on the user’s computer, a browser. When someone

accesses a web page, a file that describes that page is downloaded to the user and

displayed.Thatfileistextinaparticularformat,andthefilenameusuallyendsin“.html”

or“.htm.”Thefileholds adescriptionofhow todisplaythepage: whattexttodisplay,

whereimagescanbefoundthatarepartofthepage,howthepageisformatted,andwhere

otherconnectedpages(links)arefoundontheInternet.Oncethefileisdownloaded,allof

thehardworkconcernedwiththedisplayofthefile,suchasplayingsoundsandvideos

anddrawinggraphicsandtext,isdonebythelocal(receiving)computer.

TheWebisthebasisformostofthemodernadvancesinsocialnetworkingandpublic

dataaccess.TheInternetprovidestheunderlyingnetworkcommunicationsfacilitywhile

theWebusesthattofetchanddisplayinformationrequestedbytheuserinavisualand

auditory fashion. Podcasts, blogs, and wikis are simple extensions of the basic

functionality.

The Web demands the ability for a user in Portland to request a file from a user in

Londonandtohavethatfiledeliveredandmadeintoagraphicaldisplay,allwithasingle

click of a mouse button. Web pages are files that reside on a computer that has an IP

address, but the IP address is often hidden by a symbolic name called the Universal

Resource Locator (URL). Almost everyone has seen one of these:

“http://www.facebook.com”isoneexample.Webpageseachhaveauniquepathoraddress

basedonaURL.Itisaprettyamazingfactthatanyonecancreateanewwebpagethat

usesitsveryownunambiguousURLatanytime,andthatmostoftheworldwouldbeable

toviewit.

TheWebisanexampleofwhatprogrammerscallaclient-serversystem.Theclientis

where the person requesting the web page lives, and is making a request. The server is

where the web page itself lives, and it satisfies the request. Other examples of such

systemswouldbeonlinecomputergames,Email,Skype,andSecondLife.

0.5 REPRESENTATION

Whenapplyingacomputertoataskorwritingaprogramtodealwithatypeofdata

thatseemstobenon-numeric,theissueofhowtorepresentthedataonthecomputerwill

invariably arise. Everything stored and manipulated on a computer has to be a number.

Whatifthedataisnotnumeric?

A fundamental example of this is character data. When a user types at the computer

keyboard,whatactuallyhappens?Eachkey,and some keycombinations(e.g.,shiftkey

and“1”helddownatthesametime),whenpressedwillresultinelectricalsignalsbeing

sent along a set of wires that connect to an input device on the computer, a USB port

perhaps. While knowing the details of USB and the keyboard hardware is beyond the

scopeofthisbook,itiseasytounderstandthatpressingakeycanresultinanidentifiable

combination of wires being given a voltage. This is in fact a representation of the

character, and one that underlies the one that will be used on the computer itself. As

describedpreviously,voltagescanbeusedtorepresentbinarynumbers.

Therepresentationofcharactersonacomputeramountstoanassignmentofanumber

toeachpossiblecharacter.Thisassignmentcouldbearbitrary,andforsomedataitis.The

valueoftheletter“a”couldbe1,“b”couldbe12,and“c”couldbe6.Thiswouldwork,

butitwouldbeapoorrepresentationbecausecharactersarenotinanarbitraryorder.The

letter“b”shouldbebetween“a”and“c”invaluebecauseitispositionedthereinthedata

set,thesetofcharacters.Inanycase,whencreatinganumericrepresentation,thefirstrule

is:

1.Iftherearearelativelysmallnumberofindividualdataitems,assignthem

consecutivevaluesstartingat0.Ifthereisapracticalreasontostartatsomeother

number,thendoso.

Thesecondruleconsiderstheexistingorderingoftheelements:

2.Incaseswheredataitemsareassignedconsecutivevalues,assigntheminamanner

thatmaintainsanypredefinedorderoftheelements.

Thismeansthatinadefinitionofcharacters,theletters“a,”“b,”and“c”should

appearinthatorder.

3.Incaseswheredataitemsareassignedconsecutivevalues,assigntheminamanner

thatmaintainsanypreexistingdistancebetweentheelements.

Thismeansthattheletters“a,”“b,”and“c”wouldbeadjacenttoeachotherinthe

numericrepresentationbecausetheyarenexttoeachotherinthealphabet.Italso

meansthatcharacterclasseswillstaytogether;theuppercaseletterswillbe

consecutive,thedigitswillalsohaveconsecutivecodessothatthecodefor“0”will

beadjacenttoandsmallerthanthecodefor“1”,andsoon.Thissetofthreerules

actuallycreatesaprettygoodmappingofcharacterstonumbers.However,thereare

morerulesformakingrepresentations.

4.Incaseswheredataitemsareassignedconsecutivevalues,assigntheminamanner

thatsimplifiestheoperationsthatarelikelytobeperformedonthedata.

Inthepresentexampleofcharacterdata,therearerelativelyfewplaceswherethis

rulewouldbeinvoked,butonewouldbewhencomparingcharacterstoeachother.

Acharacter“A”isusuallythoughttocomebefore“a,”sothismeansthatallofthe

uppercaseletterswillcomebeforealllowercaseones,inanumericalsense.

Similarly,“0”comesbefore“A,”soalldigitscomebeforealllettersinthe

representation.Aspacewouldcomebefore(i.e.,haveasmallervaluethan)any

characterthatprints.

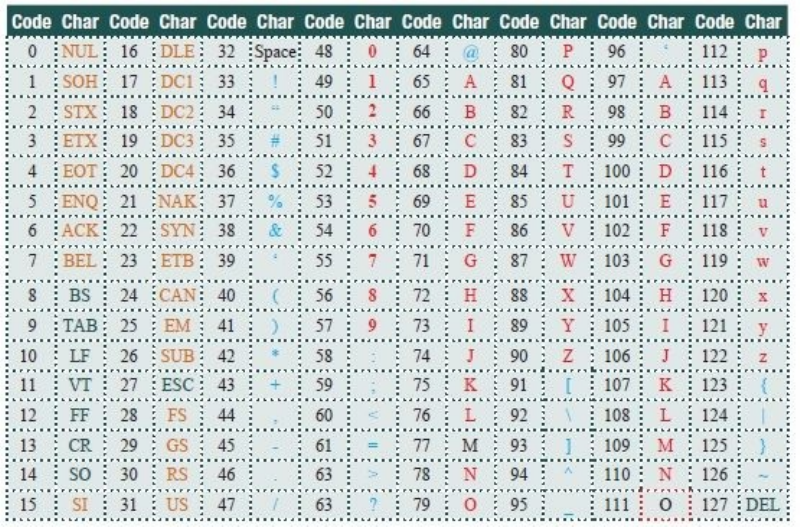
Oneofthemostcommoncharacterrepresentations,namedtheAmericanStandard

CodeforInformationInterchangeorASCII,hasallofthesepropertiesandafew

others.ThestandardASCIIcharactersetlists128characterswithnumericalcodes

from0to127.Inthetablebelow,eachcharacterislistedwiththecodethat

representsit.Theyappearinnumericalorder.Thecharactersinorangeare

telecommunicationscharactersthatareneverusedbyatypicalcomputeruser;green

charactersarenon-printingcharactersthatareusedforformattingtextonapage;

lettersandnumbersforEnglisharered;specialcharacterslikepunctuationareblue.

Thespacecharacterisinsomesenseunique,andisblack.

Furtheronthesubjectofrepresentation,ifthereareaverylargenumberofpossible

datavalues,thenenumeratingthemwouldseemunreasonable.Thereareusually

otherwaystoattackthatsortofproblem.

5.Ifthedatacanbebrokenupintoenumerableparts,thentrytodothat.

Datescanbeanexampleofthiskindofdata.Therearetoomanydatestostoreas

discretevalues,asthereisnoactualday0andthereisnopracticalfinaldayinthe

generalcase.However,acommonwaytostateadateistogiveayear,amonth,and

aday.Thisisawkwardfromacomputerperspectivebecauseofthevariablenumber

ofdaysineachmonth,butworksprettywellforhumans.Eachcomponentis

enumerable,soapossiblerepresentationforadatewouldbeasthreenumbers:year,

month,day;itwouldbeYYYYMMDD,whereYYYYisafour-digityear,MMisa

numberbetween0(January)and11(December),andDDisanumberbetween0

and30,whichisthedayofthemonth.

Thisrepresentationshouldkeepthedatesinthecorrectsequence,soDec9,1957

(19571108)willcomeafterAug24,1955(19550723).However,anothercommon

operationondatesistofindthenumberofdaysbetweentwospecifieddates.Thisis

difficult,andtheonlyrepresentationthatwouldsimplifyitwouldbetostart

countingdaysatazeropoint.IfthatzeropointwereJan1,1900,thenthe

representationforthedateOct31,2017wouldbe43037.Thenumberofdays

betweentwodateswouldbefoundbysubtraction.However,printingthedateina

formforhumanstoreadisdifficult.Whenselectingarepresentation,themost

commonoperationsonthedatashouldbetheeasiestonestoperform.

Anotherexampleofthissortorrepresentationiscolor,whichwillbediscussedin

detailinalaterchapter.

6.Whenthedataispartofacontinuousstreamofrealvalues,thenitmaybepossible

tosamplethemand/orquantizethem.

Samplingmeanstorepresentasequencebyusingasubsetofthevalues.Imagineaset

ofnumberscomingfromaseismometer.Thenumbersequencerepresentsmeasurements

ofthemotionofthegroundcapturedcontinuouslybyamechanicaldevice.Itisnormally

OKtoignoresomeofthesevalues,knowingthatbetweenavalueof5.1(whateverthat

means)andavalueof6.3,thenumberswouldhavetakenonallpossiblevaluesbetween

thosetwo;that’swhatcontinuousmeans.

So instead of capturing an infinite number of values, which is not possible, why not

captureavalueeverysecond,ortenthofasecond,oratwhateverintervalmakessensefor

the data concerned. Some data will be lost. The important thing is not to lose anything

valuable.

The samething can bedone spatially. If someone is building a road, then it must be

surveyed.Aset ofheight values forpoints alongthearea tobe occupiedbythe roadis

collectedsothatamodelofthe3Dregioncanbebuilt.Butbetweenanytwopointsthat

can be sampled there is another point that could be sampled, on to infinity. Again, a

decisionismadetolimitthenumberofsamplessothatthemeasurementsaremadeevery

fewyards.Thislimitstheaccuracy,butnotinapracticalway.Theheightatsomespecific

pointmaynothavebeenmeasured,butitcanbeestimatedfromthenumbersaroundit.

The distance between two sample points is referred to casually as the resolution. In

spatial sampling it will be expressed in distance units and says something about the

smallestthingthatcanbepreciselyknown.Intimesamplingitisexpressedinseconds.

Quantization means how accurately each measurement is known. In high school

science,numbersthataremeasurementsaregiventosomenumberofsignificantfigures.

Measuringaweightas110.9881poundswouldseemimpossiblyaccurate,and111would

be a more reasonable number. Quantization in computer terms would be restricting the

numberofbitsusedtorepresentthevalue.Somethingthatisstoredasan8-bitnumbercan

have256distinctvalues,forexample.Iftheworld’stallestpersonisunder8feettall,then

using8bitstorepresentheightwouldmeanthat8feetwouldbebrokenupinto256parts,

whichis0.375inches;thatis,8feetx12inches/foot=96inches,anddividingthisinto

256parts=0.375.Thesmallestdifferenceinheightthatcouldbeexpressedwouldbethis

value,alittleoverathirdofaninch.

Quantization is reflected in the representation as a possible error in each value. The

greaterthenumberofbitspersamplethemoreaccuratelyeachoneisrepresented.Theuse

of sampling and quantization is very common, and is used when saving sounds (MP3),

images(JPEG),andvideos(AVI).

Thereareotherpossibleoptionsforcreatingarepresentationfordata,butthesixbasic

ideasherewillworkmostofthetime,aloneorincombination.Aprogrammerwillspend

mostofhisorhertimelivingwiththeconsequencesoftherepresentationstheychosefor

theirdata.Apoorchoicewillresultinmorecomplexcode,whichgeneratesmoreerrors

andlessoverallsatisfactionwiththeresult.Spendingalittleextratimeatthebeginning

analyzingthepossibilitiescansavealotofeffortlater.

0.6 SUMMARY

Computersaredevicesthathumanshavebuiltinordertofacilitatecomplexcalculations

and are tools for rapidly and accurately manipulating numbers. When humans

communicate with each other, we use a language. Similarly, humans use languages to

communicate with computers. A computer program can be thought of as a sequence of

operationsthatacomputercanperforminordertoaccomplishacalculation.Thekeyis

thatitmustbeexpressedintermsthatthecomputercando.

Early computers were mechanical, using gears to represent numbers. Electronic

computers usually use two electrical states or voltages to represent numbers, and those

numbersareinbinaryorbase2form.Electroniccomputershavememoriesthatcanstore

numbers, and everything stored in memory must be in numeric form. That includes the

instructionsthatthecomputercanexecute.

Computers have been around long enough to provide many layers of computer

programs that can assist in their effective use: graphical user interfaces, assemblers,

compilers for programming languages, web browsers, and accounting packages each

provideauserwithadifferentviewofacomputerandadifferentwaytouseit.Computers

can exchange data between each other using wires over short distances (computer

network) and long ones (Internet). The World Wide Web sits atop the Internet and

provides an easy and effective way for computers all over the world to exchange

informationinanyform.

Everythingstoredandmanipulatedonacomputerhastobeanumber.Whatifthedata

is not numeric? In that case a numeric representation has to be devised that effectively

characterizestheinformationwhilepermittingitsefficientmanipulation.

Exercises

1.Convertthefollowingbinarynumbersintodecimal:

a)0100000

b)0000100

c)0000111

d)0101010

e)0110100101

f)0111111

g)110110110

2.Convertthefollowingdecimalnumbersintobinary:

a)10

b)100

c)64

d)128

e)254

f)5

g)999

3.Corememorywouldnoteraseitselfwhenitspowersourcewasremoved.Give

reasonswhythisisavaluableproperty.

___________________________________________________

4.Specifyadevicethatisusedfor:

a)Outputonly

b)Inputonly

c)Bothinputandoutput

5.AdaCountessofLovelaceisgenerallyconsideredtobethefirstprogrammer,but

somecontraryinformationhascometolightrecently.Searchtheliteraturefortwo

articlesoneachsideoftheargumentandformulateaconclusion.Wasshe?

6.Whatisthedifferencebetweenacompilerandaninterpreter?Giveanexampleof

each.

7.IdentifyaGUIwidgetthatwasnotdiscussedinthischapter.Sketchitsappearanceand

describeitsoperation.Giveanexampleofasituationwhereitmightbeused.

8.GivetheASCIIcodesforthefollowingcharacters:

a)ꞌPꞌ

b)ꞌ;ꞌ

c)ꞌrꞌ

d)ꞌ,ꞌ

e)ꞌ=ꞌ

9.WhatisthevalueoftheASCIIcodeforthecharacter“1”minusthecodeforthe

character“0”?Whatis“2”-“0”?Whatdoesthissayaboutconvertingfromthe

characterformofanumberintoitsnumericvalueingeneral?

10.Considertheimaginarycomputerdevisedinthischapter.Ithasamemoryinwhich

eachlocationhas12binarydigits(bits)tostoreanumber.Inoneofthememory

locationsthevalue101000000000isseen.Whatisthis?Isitaninstruction,anumber,

acharacter,anaddress,orsomethingelse?Howcanthisbedetermined?

NotesandOtherResources

1.L.Carlitz.(1968).Bernoullinumbers,FibonacciQuarterly,6,71–85.

2.DigitalEquipmentCorporation.(1972).IntroductiontoProgramming,PDP-8

handbookseries,onlineversion

http://www.mirrorservice.org/sites/www.bitsavers.org/pdf/dec/pdp8/handbooks/IntroToProgramming1969.pdf

3.JamesEssinger.(2004).Jacquard’sWeb,OxfordUniversityPress,Oxford,ISBN

978-0-19-280578-2.

4.TonySale.TheColossusComputer1943–1996:HowItHelpedtoBreakthe

GermanLorenzCipherinWWII,M.&M.Baldwin,Kidderminster,2004,ISBN0-

947712-36-4.

5.StephenStephenson.(2013).AncientComputers,PartI-Rediscovery,2nd

Edition,ISBN1-4909-6437-1.

6.A.M.Turing.(1936).OnComputableNumbers,withanApplicationtothe

Entscheidungsproblem.

7.MichaelR.Williams.(1998).The“LastWord”onCharlesBabbage,IEEEAnnals

oftheHistoryofComputing,20(4),10–4,doi:10.1109/85.728225

8.JavierYanes.(2015).AdaLovelace:OriginalandVisionary,butNoProgrammer,

OpenMind,December9,2015,https://www.bbvaopenmind.com/en/ada-lovelace-

original-and-visionary-but-no-programmer/

CHAPTER1

COMPUTERSANDPROGRAMMING

1.1SolvingaProblemUsingaComputer

1.2ExecutingPython

1.3GuessaNumber

1.4Rock-Paper-Scissors

1.5SolvingtheGuessaNumberProblem

1.6SolvingtheRock-Paper-ScissorsProblem

1.7IFStatements

1.8Documentation

1.9Rock-Paper-ScissorsAgain

1.10TypesAreDynamic(Advanced)

1.11Summary

Inthischapter

The vast majority of computers that most people encounter are referred to as digital

computers. This refers to the fact that the computer works on numbers. Other kinds of

computersdoexistbutarenotascommon;analogcomputersoperateinanumberofother

ways, but are usually electrical—they manipulate electrical voltages and currents—or

mechanical—theyusegearsandshaftstocalculateamechanicalresponse.

Thefactthatanyproblemmustbeexpressedinnumericalformhaspresentedaproblem

to some potential programmers. I’m not good at math is a common complaint, and the

beliefthatcomputerprogrammingrequiresaknowledgeof

advancedmathematicsisusedasareasontonotstudyprogramming.Infact,thekindof

mathcommonlyneededwouldmoreproperlybecalledarithmetic,notmath.

Inorderforaproblemtobesolvedusingacomputer,theproblemmustbeexpressedin

a way that manipulates numbers, and the data involved must be numeric. This is often

accomplishedbysomekindofencodingofthedata.Itissocommonthattheprocessis

invisibleonmoderncomputers.Mostdatahaveavarietyofencodingsthathavebeenused

for years and are taken for granted: images in JPEG format or sounds in MP3 are

examplesofcommonlyusedencodingofdataintonumbers.

What can computers do with numbers? Addition, subtraction, multiplication, and

divisionarethebasicoperations,butcomputerscancomparethevalueofnumberstoo.

1.1 SOLVINGAPROBLEMUSINGACOMPUTER

Theprocessbeginswithaproblemtobesolved,andthefirststepistostatetheproblem

asclearlyaspossible.Thisfirststepiscriticallyimportantbecauseunlesstheproblemis

completely understood, its solution on a computer is impossible. Then the problem is

analyzedtodeterminemethodsbywhichitmaybesolved.Ascomputerscanonlydirectly

manipulatenumbers,itiscommonforsolutionsdiscussedatthisstagetobenumericalor

mathematicalandforthemtoinvolvedecidinguponrepresentationsforthedatathatwill

facilitatesolvingtheproblem.Thenasketchofthesolution,perhapsonpaperinahuman

languageandmath,iscreated.Thisistranslatedintocomputerlanguageandthentyped

intocomputerformusingakeyboard.Theresultingtextfileiscalledascript,sourcecode,

or more commonly the computer program. A program called a compiler takes this

programandconvertsitintoaformthatcanbeexecutedonthecomputer.Basically,all

programsareconvertedinto asetof numberscalledmachine code,whichthe computer

canexecute.

WearegoingtolearnalanguagecalledPython.Itwasdevelopedasageneralpurpose

programming language and is a good language for teaching because it makes a lot of

thingseasy.QuiteafewapplicationsarebuiltusingPython;forexample:thegamesEve

OnlineandCivilizationIV,BitTorrent,andDropboxtonameonlyafew.Itisabitlikea

lot of other languages in use these days in terms of structure (syntax) but has some

simplifyingideasthatwillbediscussedinlaterchapters.

Inordertouseaprogramminglanguage,therearesomebasicconceptsandstructures

thatneedtobeunderstoodatabasiclevel.Someoftheseconceptswillbeintroducedin

thischapter,andtherestofthebookwillteachyoutoprogrambyexample;inallcases,

codingexampleswillbeintroducedbystatingaproblemtobesolved.Theproblemstobe

solvedinthischapterinclude:asimpleguess-a-numbergameandthegameofrock-paper-

scissors.TheseproblemswillbethemotivationforlearningmoreabouteitherthePython

language itself or about methods of solving problems. Any computer programs in this

bookwillexecuteonacomputerrunninganymajoroperatingsystemoncethefreePython

languagedownloadhasbeeninstalled.

1.2 EXECUTINGPYTHON

InstallingPythonisnottoodifficult,andinvolvesdownloadingtheinstaller,runningit,

andperhapsconfiguringafewspecificdetails.Thisprocesscanbefoundonthenet.Once

installedthereareafewvariationsthatcanbeusedwithit,thesimplestprobablybeingthe

PythonGraphicalUserInterfaceorGUI.IfrunningPythononaWindowsPC,lookatthe

Start menu for Python and click; a link named “IDLE (Python GUI)” will be seen, as

showninFigure1.1.Clickonthisandtheuserinterfacewillopen.Clickthemouseinthe

GUIwindowsothatyoucanstarttypingcharactersthere.

PythoncanberuninteractivelyintheGUIwindow.Thecharacters“>>>”arecalleda

prompt, and indicate that Python is waiting for something to be typed at the keyboard.

AnythingtypedherewillbepresumedtobeaPythonprogram,oratleastpartofone.Asa

demonstration, type “1” followed by “Enter.” Python responds by printing “1.” Why?

When“1”wastypeditwasaPythonexpression,somethingtobeevaluated.Thevalueof

“1”issimply“1,”sothatwastheanswerPythoncomputed.

Nowtype“1+1.”Pythonrespondswith“2.”Pythoninputswhattheuser/programmer

types,evaluatesitasamathematical(inPythonform)expression,andprintstheanswer.

Thisisnotreallyprogrammingyet,becauseabasictwo-dollarcalculatorcandothis,butit

iscertainlyastart.

IDLEisgoodformanythings,buteventuallyamoresophisticatedenvironmentwillbe

needed,onethatcanindentautomatically,detectsomekindsoferrors,andallowprograms

toberunanddebuggedandsavedasprojects.Thiskindofsystemiscalledanintegrated

development environment, or IDE. There are many of these available for Python, some

costing quite a lot and some freely downloadable. The code in this book has been

compiledandtestedusingonecalledPyCharm,butmostIDEs outtherewouldbe fine,

anditislargelyamatterofpersonalpreference.BasicPyCharmisfree,andithasabigger

brotherthatcostsasmallamount.

AnadvantageofanIDEisthatitiseasytotypeinawholeprogram,runit,findthe

errors, fix them, and run it again. This process is repeated until the program works as

desired. Multiple parts of a large program can be saved as separate files and collected

togetherbytheIDE,andtheycanbeworkedonindividuallyandtestedtogether.Anda

good IDE uses color to indicate syntax features that Python understands and can show

somekindsoferrorwhilethecodeisbeingentered.

Tobeginprogrammingitmustbeunderstoodthatalanguagehasasyntaxorstructure,

andthatforcomputerlanguagesthisstructurecannotbevaried.Thecomputerwillalways

bethearbiterofwhatiscorrect,andifanyprogramhasasyntaxerrorinitorproduces

erroneousresults,thenitistheprogramandnotthecomputerthatisatfault.

Next, one should appreciate that the syntax is arbitrary. It was designed by a human

withattitudesand biasesand newideas, andwhile thesyntax mightsometimes beugly

andhardtorecall,itiswhatitis.Partsofitmightnotbeunderstoodatfirst,butaftera

whileandafterreadingandexecutingthefirstprogramsinthisbook,mostofitwillmake

sense.

A program, just like any sentence or paragraph in English, consists of symbols, and

ordermatters.Somesymbolsarespecialcharacterswithadefinedmeaning.Forexample,

“+”usuallymeansadd,and“-”usuallymeanssubtract.Somesymbolsarewords.Words

definedbythelanguage,likeif,while,andtrue,cannotalsobedefinedbyaprogrammer

—they mean what the language says they mean, and are called reserved words. Some

names have a definition given by the system but can be reused by a programmer as

needed.Thesearecalledpredefinednamesorsystemvariables.However,somewordscan

bedefinedbytheprogrammer,andarethenamesforthingstheprogrammerwantstouse

intheprogram:variablesandfunctionsareexamples.

1.3 GUESSANUMBER

Games that involve guessing are common, and are sometimes used to resolve minor

conflictssuchaswhogetsthenextpieceofcakeorwhogetsthefirstkickatafootball.

It’s also sometimes a way to occupy time, and can simply be fun. How can we write a

programtohavetheuserguessanumberthattheprogramhaschosen?

There are many variations on this simple game. In one the number is to be guessed

precisely.Oneperson(thechooser)hasselectedanumber,aninteger,inaspecifiedrange.

“Pickanumberbetweenoneandten”wouldbeatypicalproblem.Theotherperson,the

guesser,must choose anumberinthatrange.Iftheyselectthecorrectnumber,thenthe

guesserwins.Thisisaboringgameandisbiasedinfavorofthechooser.

Amoreinterestingvariationwouldbetostartwithoneguessandhavethechooserthen

saywhetherthetargetnumberisgreaterthanorlessthantheguessednumber.Theguesser

thenguessesagain,andtheprocesscontinuesuntilthenumberisguessedcorrectly.The

rolesofguesserandchoosercannowswitchandthegamestartsagain.Thebestguesseris

theonewhousesthefewestguesses.

Athirdalternativeisto havemultipleguessers.Allguessersmaketheirselectionand

theonewhohaschosenanumbernearestthecorrectnumberisthewinner.Thisisthebest

game for solving disputes, because it involves one guess from each person. Ties are

possible,inwhichcasethegamecanbeplayedagain.

1.4 ROCK-PAPER-SCISSORS

Althoughthisgameisusedbychildrentosettledisputes and makerandomdecisions

suchas “who goes first,” ithas beentaken moreseriously byadults. There areactually

competitions where money is at stake. A televised contest in Las Vegas had a prize of

$50,000.Thisgameisnotastrivialasitoncewas.

Inthisgameeachoftwoplayersselectsoneitemfromthelist[rock,paper,scissors]in

secret,andthenbothdisplaytheirchoicesimultaneously.Ifbothplayersselectedthesame

item,thentheytryagain.Otherwise,rockbeatsscissors,scissorsbeatspaper,andpaper

beatsrock.Thiscontestcanberepeatedfora“bestoutofN”competition.

Bothofthesegamesformthefirstproblemset,andserveas

themotivationforlearningtheelementsofthePythonlanguage.

1.5 SOLVINGTHEGUESSANUMBERPROBLEM

The simple version of the guessing program has two versions, depending on who is

guessing.Thecomputershouldpickthenumberandthehumanusershouldguess,because

theotherwayaroundcanusesomecomplexprogramming.Inthatcasehere’swhathasto

happen:

1.Thecomputerselectsanumber.

2.Thecomputeraskstheplayertoguess.

3.Theplayertypesanumberonthekeyboardandthecomputerreadsitin.

4.Thecomputercomparestheinputnumberagainsttheonethatitselected,andifthe

twoagree,thentheplayerwins.Otherwisethecomputerwins.

ThePythonfeaturesneededtodothisinclude:printingamessage,readinginanumber,

havingaplacetostoreanumber(avariable),havingawaytoselectanumber,andhaving

awaytocomparethetwonumbersandactdifferentlydependingontheresult.

Thesecondversionrequirestheabove,plusawaytorepeattheprocessincaseswhen

theguessiswronganduntilitiscorrect.Inthiscasethemethodbecomes:

1.Thecomputerselectsanumber.

2.Thecomputeraskstheplayertoguess.

3.Theplayertypesanumberonthekeyboardandthecomputerreadsitin.

4.Thecomputercomparestheinputnumberagainsttheonethatitselected,andifthe

twoagree,thentheplayerhasguessedcorrectly.ExittoStep7.

5.Thecomputerdetermineswhethertheguessishigherorlowerthantheactual

numberandprintsanappropriatemessage.

6.RepeatfromStep2.

7.Gameover.

Therepetitionmechanismistheonlynewaspecttothissolution,butitisanessential

componentofPythonandeveryotherprogramminglanguage.

1.6 SOLVINGTHEROCK-PAPER-SCISSORS

PROBLEM

The solution to this problem has no new requirements, but re-enforces the language

featuresoftheprevioussolutions.Onesolutiontothisproblemis:

1.Selectarandomchoiceformthethreeitemsrock,paper,orscissors.Savethis

choiceinavariablenamedchoice

2.Asktheplayerfortheirchoice.Useanintegervalue,where1=rock,2=paper,and

3=scissors

3.Readtheplayer’sselectionintoavariablenamedplayer

4.Ifplayerisequaltochoice

5.Printthemessage“Tie.We’lltryagain.”

6.RepeatfromStep1

7.Ifplayerisequaltorock

8.Ifchoiceisequaltoscissors,gotoStep17

9.ElsegotoStep18

10.Ifplayerisequaltopaper

11.Ifchoiceisequaltoscissors,gotoStep17

12.ElsegotoStep18

13.Ifplayerisequaltoscissors

14.Ifchoiceisequaltorock,gotoStep17

15.ElsegotoStep18

16.Printerrormessageandterminate

17.Print“Computerwins”andterminate

18.Print“Youwin”andterminate

Foreachplayerselection,oneofthealternateitemswillbeatitandonewilllosetoit.

Eachchoiceischeckedandthewin/losedecisionismadebasedontheknownoutcomes.

The solutions to both problems require similar language elements: a way to store a

value(avariable),awaytoexecutespecificpartsoftheprogramdependingonthevalue

ofavariableorexpression(anifstatement),awaytoreadavaluefromthekeyboard,a

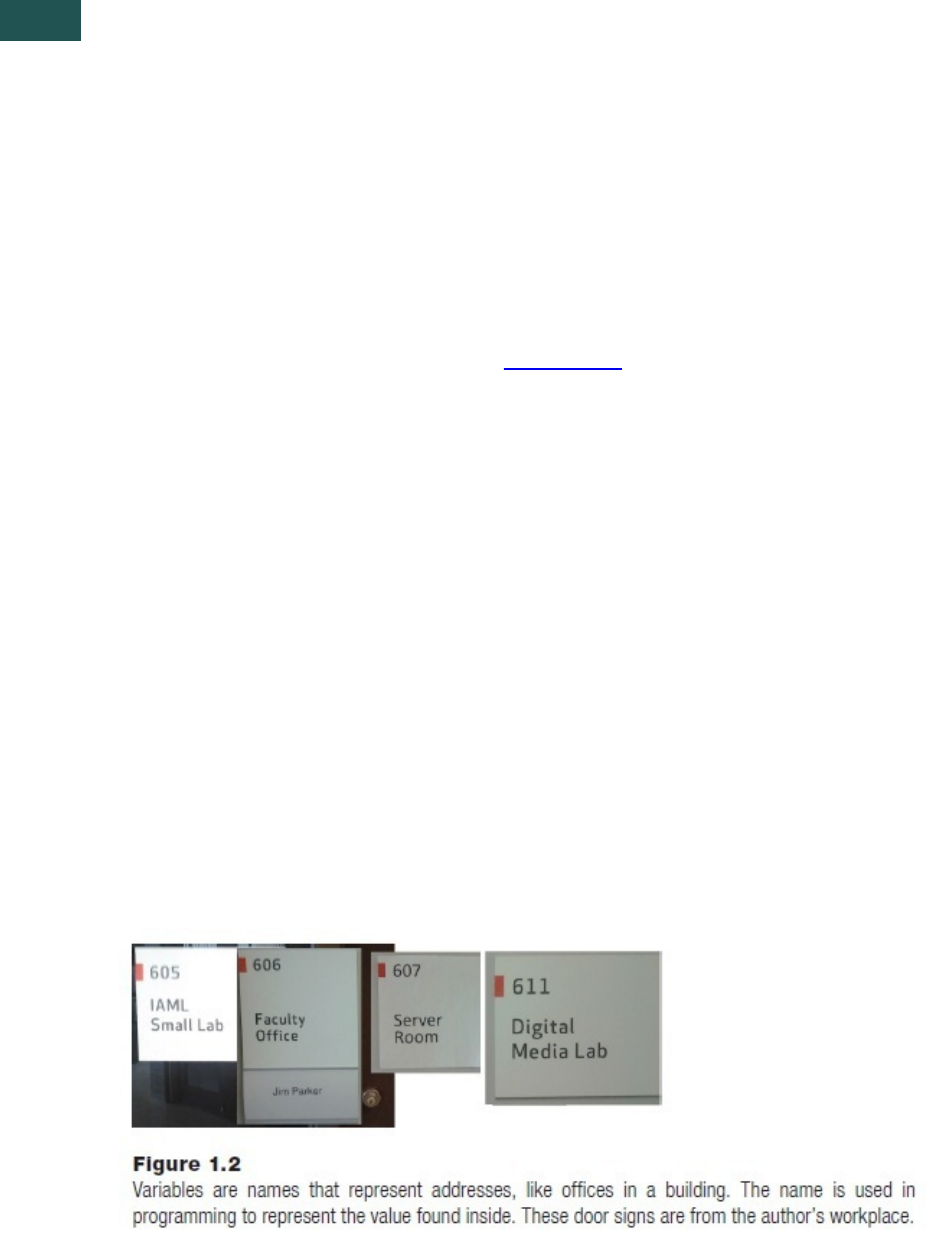
waytoprintamessageonthescreen,andawaytoexecutecoderepeatedly(aloop).

1.6.1 VariablesandValues–ExperimentingwiththeGraphicalUser

Interface

Avariableisanamethattheprogrammercandefinetorepresentsomevalue,anumber

oratextstringgenerally.Itrepresentstheplacewherethecomputerstoresthatvalue;itis

a symbol in text form, something humans like, representing a value. Everything that a

computerdoesisultimatelydonewithnumbers,sothelocationofanythingisanumber

thatrepresentstheplaceincomputermemorywherethatthingisstored.It’slikeofficesin

a building. Each office has a number (its address) and usually has a name too (the

occupantorbusinessfoundthere).Additionally,theofficehascontents,andthosecontents

areoftendescribedbythenamegiven.InFigure1.2acollectionofofficesinaspecific

buildingcanbeseen.Inthismetaphortheofficenumbercorrespondstotheaddress,and

thename(variablename),beingmorehumanfriendly,ishowitisoftenreferredtobya

person(programmer).Inallcases,though,itisthecontentsoftheoffice(location)thatare

important.Thenumberandnamearewaystoaccessit.So,someonemightsay“Bringme

thePythonmanualfromtheServerRoom”or“BringmethePythonmanualfrom607”and

bothwouldbethesamething.Thecontentsoflocation607wouldbethePythonmanual.

Nowsomeonecouldsay“PutthisPythonmanualintheDigitalMediaLab,”whichwould

changethecontentsoflocation611.InactualPythontheactofretrievingavaluefroma

locationdoesnotchangethecontentsofthatlocation,butinsteadmakesacopy,butthe

basicmetaphorissound.

Notallstringsorcharacterscanbevariablenames.Avariablecannotbeginwithadigit,

for example, or with most non-alphabetic characters like “&” or “!,” although in some

casesbeginningwith“_”isacceptable.Avariablenamecancontainupper-orlowercase

letters,digits,and“_”.Uppercaseandlowercasearedistinct,sothevariablesHelloand

helloaredifferent.

Soavariablecanchangevaluesbut,unlikearealoffice,asimplevariablecanholdonly

onevalueatatime.Thenamechosendoesnothavetobesignificant.Programsoftenhave

variablesnamediorx.However,itisagoodideatoselectnamesthatrepresentthekind

of value that the variable it to contain so as to communicate that meaning to another

person,aprogrammerprobably.Forexample,thevalue3.1415926shouldbestoredina

variablenamedpi,becausethat’sthenameeveryoneelsegivestothisvalue.

IntheGUItypepi=3.1415926.Pythonrespondswithaprompt,whichindicatesthatit

is content with this statement, and that it has no value to print. If you now type pi,the

responsewillbe3.1415926;thevariablenamedpithatwasjustcreatednowhasavalue.

InthesyntaxofPython,thenamepiisavariable,thenumber3.1415926isaconstant,

but is also an expression, and the symbol = means assign to. In the precise domain of

computer language, pi = 3.1415926 is an assignment statement and gives the variable

namedpithespecifiedvalue.

Continuingwiththisexample,defineanewvariablenamedradiustobe10.0usingan

assignmentstatementradius=10.0.Ifyoutyperadiusand“enter,”Pythonrespondswith

10.0.Finally,weknowthatthecircumferenceofacircleis2prinmathterms,or2times

pi times the radius in English. Type 2*pi*radius into the Python GUI, and it responds

with62.831852, which is the correct answer. Now type circumference = 2*pi*radius,

andPythonassignsthevalueofthecomputationtothevariablecircumference.

Python defines a variable when it is given a value for the first time. The type of the

variableisdefinedatthatmomenttoo;thatis,ifanumberisassignedtoaname,thenthat

nameisexpectedtorepresentanumberfromthenon.Ifastringisassignedtoaname,

thenthatnamewillbeexpectedtobeastringfromthenon.Tryingtouseavariablebefore

ithasbeengivenavalueandatypeisanerror.Attemptingthecalculation:

area=side*side

is not allowed unless there is a variable named side already defined at this point. The

followingisOKbecauseitdefinessidefirst,andtheninturnisusedto

definearea:

side=12.0

area=side*side

Thetwolinesabovearecalledstatementsinaprogramminglanguage,andinPythona

statementusuallyendsattheendoftheline(the“enter”keywaspressed).Thisisabit

unusualinacomputerlanguage,andpeoplewhoalreadyknowJava orC++havesome

difficultywiththisideaatfirst.Inothercomputerlanguagesstatementsareseparatedby

semicolons,notbytheendoftheline.Infact,inmostlanguagestheindentingoflinesin

theprogramdoesnothaveanymeaningexcepttotheprogrammer.InPythonthat’snotthe

caseeither,aswillbeseenshortly.

Theexpressionsweuseinassignmentscanbepretty complicated,but arereallyonly

thingsthatwelearnedinhighschool.Add,subtract,multiply,anddivide.Multiplication

anddivisionareperformedbeforeadditionandsubtraction,whichiscalledaprecedence

rule,so3*2+1is7,not9;otherwise,evaluationisdonelefttoright,so6/3*2is4(dothe

divisionfirst)asopposedto1(ifthemultiplicationwasdonefirst).Thesearerulesthat

shouldbefamiliarbecauseitishowpeoplearetaughttodoarithmetic.Thesymbol“**”

meansexponentortothepowerof,so2**3is23whichis8,andthisoperatorhasahigher

precedence (i.e., is done before) than the others. Parentheses can be used to specify the

order of things. So, for example, (2+3)**2 is 25, because the expression within the

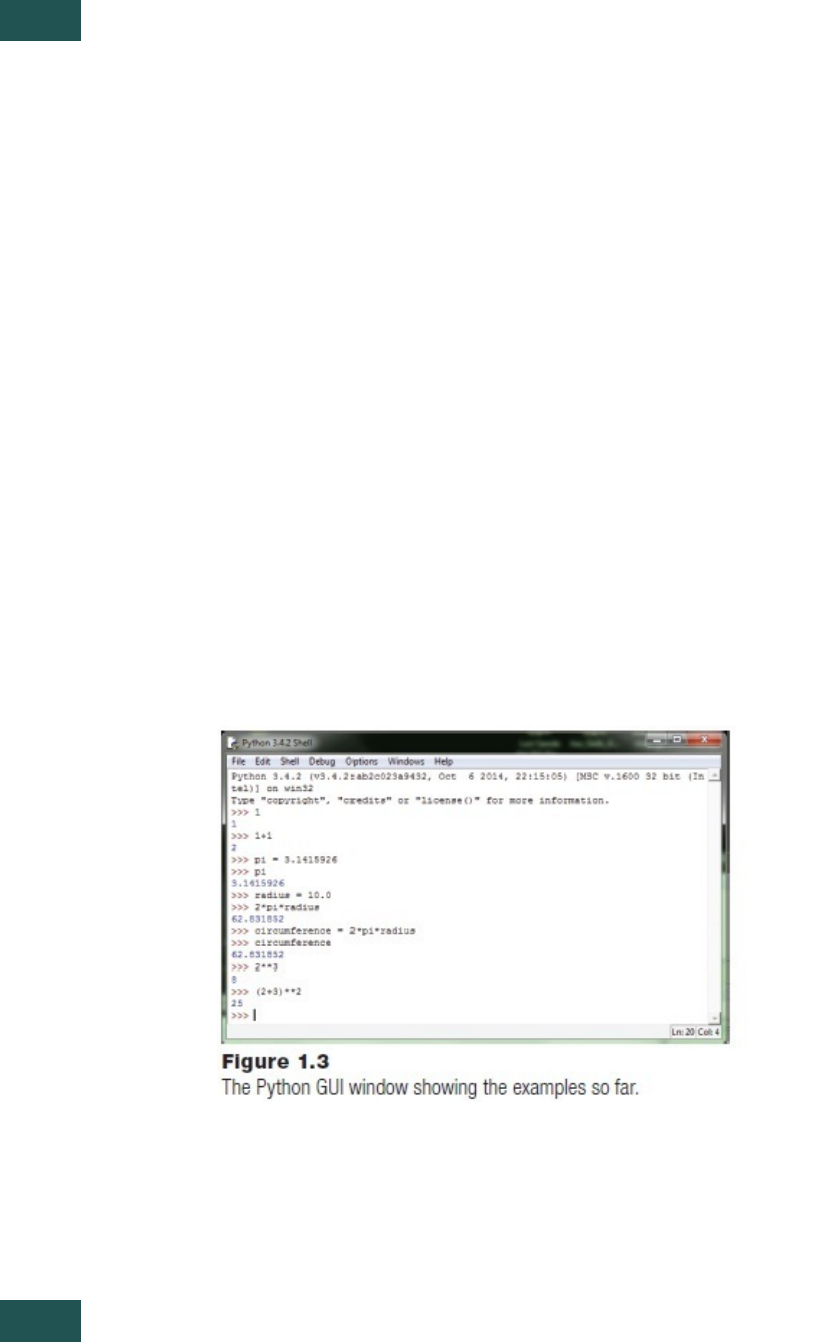
parenthesisisdonefirst,thentheexponent.

1.6.2 ExchangingInformationwiththeComputer

When using most programming languages, it is necessary to design communication

with the computer program. This goes two ways: the program will inform the user of

things,suchasthecircumferenceofacirclegivenaspecificradius,andtheusermaywant

totelltheprogramcertainthings,likethevalueoftheradiuswithwhichtocomputethe

circumference. We communicate with a program using text, which is to say characters

typedintoakeyboard.Whenacomputerispresentingresults,thattextisoftenintheform

ofhuman language, messages as sentences.“The circumference is62.831852” could be

suchamessage.Thesentenceisactuallycomposedbyaprogrammerandhasanumberor

collectionofnumbersembeddedwithinit.

Python allows a programmer to send a message to the screen, and hence to the user,

using a print directive. This is the word print followed by a characterstring, which is

oftenasetofcharactersinquotes.Anexample:

print(“Theanswerisyes.”)

Theparenthesesareusedtoencloseeverythingthatistobeprinted;suchastatement

canprintmanystringsiftheyareseparatedbycommas.Numberswillbeconvertedinto

stringsforprinting.Sothefollowingiscorrect:

print(“Thecircumferenceis“,62.831852)

Ifavariableappearsinthelistfollowingprint,thenthevalueofthatvariablewillbe

printed,notthenameofthevariable.So:

print(“Thecircumferenceis“,circumference)

isalsocorrect.

1.6.3 Example1:DrawaCircleUsingCharacters

Assumingthatitisdesiredtoprintacirclehavingaconstantpredefinedradius,thiscan

bedonewithafewprintstatements.Theplanningofthegraphicitself(thecircle)canbe

doneusinggraphpaper.Assumingthateachcharacterusesthesameamountofspace,a

circlecanbe approximatedusingsome skillfullyplaced“*”characters. Thenprinteach

rowofcharactersusingaprintstatement.Asamplesolutionis:

print(”***“)

print(”*********“)

print(”*************“)

print(”***************“)

print(”*************“)

print(”*********“)

print(”***“)

1.6.4 Strings,Integers,andRealNumbers

Computerprogramsdealmainlywithnumbers.Integers,orwholenumbers,andrealsor

floating point numbers, which represent fractions, are represented differently, and

arithmetic works differently on the two types of numbers. A Python variable can hold

eithertype,butifavariablecontainsanintegerthenitistreatedasaninteger,andifit’s

holdingafloatingpointnumberthenitistreatedasoneofthose.What’sthedifference?

First,there’sadifferenceinhowtheyareprintedout.Ifwemaketheassignmentvar=1

andthenprintthevalueofvar,itprintssimplyas1.Ifwemaketheassignmentvar=1.0

andthenprintvar,itprintsas1.0.Inbothcasesvarisarealorfloatingpointnumberand

willbetreatedassuch.Numericconstantswillbethoughtofasrealnumbers.However,a

variablecanbefirstonethingandthenanother.Itwillbethelastthingitwasassigned.

Arithmeticdiffersbetweenintegersandreals,buttheonlytimethatdifferenceisreally

apparentiswhendoingdivision.Integersarealwayswhole,non-fractionalnumbers.Ifwe

divide3by2,both3and2areintegersandsothedivisionmustresultinaninteger:the

resultis1.Thisisbecausethereisexactlyasingle2in3,orifyoulike,2goesinto3just

once,witharemainderof1.Thereisaspecificoperatorfordoingintegerdivision:“//.”

So,3//2 isequalto1. Theremainderpartcan’tbe handledandis discarded,butcanbe

foundseparatelyusingthe“%”operator.Forexample,8//5is1,and8%5istheremainder,

3.Thisexplanationisanapproximationtothetruth,andonethatcanbecleareduplater,

butitworksperfectlywellforpositivenumbers.

Ofcoursefractionsworkfineforrealnumbers,andwillbeprintedasdecimalfractions:

8.0/5.0 is 1.6, for example. What happens if we mix reals and integers? In those cases

things get converted into real, but now things get more complicated, because order can

mattera greatdeal.Theexpression7//2*2.0doesthedivision7//2first,whichis3, and

thenmultipliesthatby2.0,yieldingtheresult6.0;theresultof8/3*3.0wouldbe5.333.

Mixing integers and reals is not a good idea, but if done, the expressions should use

parenthesestospecifyhowtheexpressionshouldbeevaluated.

Arealcanbeusedinplaceofanintegerinmostplaces,buttheresultwillbereal.Thus,

2.0* 3 =6.0, not 6,and 6.0//2is 3.0, not3. There aresome exceptions. To convert an

integertoareal,thereisaspecialoperationnamedfloat:float(3)yields3.0.Ofcourseit’s

possibletosimplymultiplyby1.0andtheresultwillbefloattoo.Convertingfloatvalues

tointegersismorecomplicated,becauseofthefractionissue:whathappenstothedigits

totherightofthedecimal?Theoperationintwilltakeafloatingpointvalueandthrow

away the fraction. The value of int(3.5) will be 3, as a result. It is normal in human

calculations to round to the nearest integer, and the operation round(3.5) does that,

resultingin4.

1.6.5 NumberBases

In elementary school, perhaps grade 3 or 4, the idea of positional number systems is

taught. The number 216 is a way to write the value of 6 + 1*10 + 2*100. Not all

civilizations use such a scheme; Roman numerals are not positional,for example. Still,

most people are comfortable with the idea. What people are not as comfortable with is

changingthenumberbaseawayfrom10.InChapter0,thebinarysystem,orbase2,was

discussed,butanybasethatisapowerof2isofsomeinterest,especiallybase8andbase

16.

Humansuseabase10schemeprobablybecausewehave10fingers.Whatitmeansis

thatwehaveasymbolforeachofthe10digits,0through9,andeachdigitpositiontothe

leftofthefirstdigitismultipliedbythenextpowerof10.Thenumber216isreally2*102

+1*101+6*100.Thebaseis10,andeachdigitrepresentsapowerofthebasemultiplied

by a digit. What if the base is 8? In that case 216 is really 2*82 + 1*81 + 6. If the

arithmeticiscarriedout,thisnumberturnsouttobe128+8+6=142.

If multiple number bases are used, it is common to give the base as a subscript. The

number216inbase8iswrittenas2168.Thedefaultwouldbebase10.Inbase8thereare

only8digits,0through7.Thedigits8and9cannotappear.Inbaseslargerthan10more

symbolsareneeded.Acommonbasetobeusedoncomputersis16,orhexadecimal(hex

forshort).Inahexnumber16digitsareneeded,sotheregularonesareusedandthen“A”

represents10,“B”is11,“C”is12,“D”is13,“E”is14,and“F”is15.Thehexnumber

1216is1*16+2,or1810.Thenumber1A16is1*16+10=2610.

In Python numbers are given in decimal (base 10) by default. However, if a number

constantbegins with“0o” (zero followedby the letter“o”) Pythonassumes it isbase 8

(octal).Thenumber0o21,forexample,is218=1710.Anumberthatbeginswith“0x”is

hexadecimal.0x21is2116=3310.Thisappliesonlytointegers.

There is a number base that is the most important, because it lies under all of the

numbersonacomputer.Thatwouldbebase2.Allnumbersonamoderndigitalcomputer

arerepresentedinbase2,orbinary,intheirinternalrepresentation.Abinarynumberhas

onlytwodigits,0and1,andeachrepresentsapowerof2.Thus,11012is1*23+1*22+

0*21+1=8+4+1=1310.InPythonabinarynumberbeginswith“0b,”sothenumber

0b10101represents2110.

These number bases are important for many reasons, but base 2 is fundamental, and

bases8and16areimportantbecausetheyarepowersof2andsoconvertveryeasilyto

binarybuthavefewerdigits.Oneexampleoftheuseofhexisforcolors.InPythonthey

can represent a color, and on web pages they are certainly used that way. The number

0xFF0000isthecolorred,forexample,ifusedonawebpage.Butmoreofthatlater.

1.6.6 Example2:ComputetheCircumferenceofanyCircle

When humans send information into a computer program, the text tends to be in the

formofnumbers.ThePythoncodethatwaswrittentocalculatetheradiusofacircleonly

didthecalculationforasingleradius:10.That’snotasusefulasaprogramthatcomputes

thecircumferenceofanycircle,andthatwouldmeanallowingtheusertotelltheprogram

what radius to use. This should be easy to do, because it is something that is needed

frequently. Frequently needed things should always be easy. In the case of sending a

number into a program in Python, the word input can be used within a program. For

example:

radius=input()

willacceptanumberfromthekeyboard,typedbytheuser,andwillreturnitasastringof

characters.Thismakessensebecausetheusertypeditasastringofcharacters,butitcan’t

beusedinacalculationinthisform.Toconvertitintotheinternalformofanumber,we

mustspecificallyaskforthistobedone:

radius=input()

radius=float(radius)

willreadastringintoradius,thenconvertitintoafloatingpoint(real)numberandassign

ittothevariableradiusagain.Thiscanbedoneallinonestatement:

radius=float(input())

Now the variable radius can be used to calculate a circumference. This is a whole

computerprogramthatdoesausefulthing.Ifthevalueofradiuswastobeaninteger,the

codewouldread:

radius=int(input())

If the conversion to a number is not done, then Python will

giveanerrormessagewhenthecalculationisperformed,like:

Traceback(mostrecentcalllast):

File“<pyshell#13>”,line1,in<module>

circumference=2*pi*radius

TypeError:can'tmultiplysequencebynon-intof

type'float'

Thisisprettyuninformativetoabeginningprogrammer.WhatisaTraceback?What’s

pyshell?Therearecluesastowhatthismeans,though.Thelineofcodeatwhichtheerror

occursisgivenandthetermTypeErrorisdescriptive.Thiserrormeansthatsomethingthat

can’tbemultiplied(astring)wasusedinanexpressioninvolvingamultiplication.That

thing is the variable radius in this instance because it was a text string and was not

convertedtoanumber.

Alsonotethatint(input())canpresentproblemswhentheinputstringisnotinfactan

integer. If it is a floating point number, this results in an error. The expression

int(“3.14159”) could be interpreted as an attempt convert pi into an integer, and would

havethevalue3;infact,itisanerror.Thefunctionintwaspassedastringandthestring

containedafloat,notanint.ThisissomethingofaquirkofPython.Itisbettertoconvert

inputnumbersintofloats.

1.6.7 GuessaNumberAgain

The simple version of the guessing program can now nearly be written in Python.

Examiningthemethodofsolution,here’swhatcanbecodedsofar;versionsdependon

whoisguessing.Thecomputershouldpickthenumberandthehumanusershouldguess,

becausetheotherwayaroundcaninvolvesomecomplexprogramming.Inthatcasehere’s

whathastohappen:

1.Thecomputerselectsanumber.

choice=7

2.Thecomputeraskstheplayertoguess.

print(“Pleaseguessanumberbetween1and10:“)

3.Theplayertypesanumberonthekeyboardandthecomputerreadsitin.

playerchoice=input()

4.Thecomputercomparestheinputnumberagainsttheonethatitselected,

andifthetwoagree,thentheplayerwins.Otherwisethecomputerwins.

Itisthe finalstepthat isstillnot possiblewithwhat isknown.It isnecessary in this

program,asit isin mostcomputer programs,to makeadecision andto executecertain

code(i.e.,dospecificthings)conditionallybasedontheoutcomeofthatdecision.People

dothatsortofthingallofthetimeinreallife.Examplesinclude:

“Ifthelightisredthenstop,otherwisecontinuethroughtheintersection.”

“Ifalltellersarebusywhenyouarriveatthebank,thenstandinlineandwaitfor

thenextonetobecomeavailable.”

“Ifyouneedbreadormilk,thenstopatthegrocerystoreonthewayhome.”

“Ifitrains,thepicnicwillbecancelled.”

Notice that all of these examples use the word “if.” This word indicates a standard

conditionalsentenceinEnglish.Theconditioninthefirstcaseisthephrase“ifthelightis

red” (called in English the protaxis or antecedent) and the consequence to that is the

phrase“thenstop”(theapodosisorconsequent).Terminologyaside,theintentisclearto

an English speaker: on the condition that or in the event that the light is red, then the

necessary action is that the driver is to stop their car. The action is conditional on the

antecedent, which in Python will be called an expression or, more precisely, a logical

expression,whichhasthevalueTrueorFalse.

ThestructureorsyntaxofthissortofthinginPythonwouldbe:

ifthelightisred:

stop

ormoreexactly:

iflight==red:

#executewhatevercodemakesthecarstop

Thisiscalledanifstatement,andismoreprofoundwithamorecomplexsyntaxthan

canbeinferredfromthisexample.

1.7 IFSTATEMENTS

In Python an if statement begins with the word if, followed by an expression that

evaluatestoTrueorFalse,followedby acolon (:), then a series of statements that are

executed if the expression is true. The names True and False are constants having the

obvious meaning, and a variable that can take on these values is a logical or Boolean

(namedafterthemanwhoinventedtwostateorlogicalalgebra)variable.Theexpression

istheonlytrickypart.ItcanbeaconstantlikeTrue,oravariablethathasaTrueorFalse

value,orarelationalexpression(onethatcomparestwothings)oralogicalcombination

ofanyofthese—anythingthathasaresultthatistrueorfalse.

ifTrue: #Constant

ifflag: #Logicalvariable

ifa<b: #relationalexpression

ifa<bandc>d: #logicalcombination

Alogicalexpressioncanbeanyarithmeticexpressionsbeingcomparedusinganyofthe

followingoperators:

<Lessthan

>Greaterthan

<=Lessthanorequalto

>=Greaterthanorequalto

==Equalto

!=Notequalto

Logicalcombinationscanbe:

andEG:a==bandb==c

orEG:a==bora==c

notEG:not(a==b)#sameas!=

Thesyntaxissimpleandyetallowsahugenumberofcombinations.Forexample:

ifp==qandnotp==zandnotz==p:

ifpi**2<12:

if(a**b)**(c-d)/3<=z**3:

Theconsequent,ortheactionstobetakenifthelogicalexpressionistrue,followsthe

colon on the following lines. The next statement is indented more than the if, and all

statements that follow immediately that have the same indentation are a part of the

consequentandareexecutedifthecondition istrue, otherwisenone ofthemare. Asan

example,consider:

ifa<b:

a=a+1

b=b–1

c=a–b

Inthiscasethetwostatementsfollowingthe“:”areindentedby4morespacesthanis

theif.ThistellsPythonthattheyarebothapartoftheifstatement,andthatifthevalueof

aissmallerthanthevalueofb,then bothof thosestatements willbe executed.Python

callssuchagroupofstatementsasuite.Theassignmenttothevariablecisindentedtothe

samelevelastheif,soitwillbeexecutedinanycaseandisnotconditional.

The use of indentation to connect statements into groups is unusual in programming

languages. Most languages in use pretty much ignore spaces and line breaks altogether,

anduseastatementseparatorsuchasasemicolontodemarkstatements.So,intheJava

languagetheabovecodewouldlooklikethis:

if(a<b){

a=a+1;

b=b–1;

}

c=a–b;

Thebraces{…}enclosethesuite,whichwouldprobablybecalledablockinJavaor

C++. Notice that this code is also indented, but in Java this means nothing to the

computer.Indentationisusedforclarity,sothatsomeonereadingthecodelatercansee

moreclearlywhatishappening.

SemicolonsareusedinPythontoo,butmuchmorerarely.Ifitisdesiredtoplacemore

thanone statement on a singleline, then semicolons can be used to separate them. The

Pythonifstatementunderconsiderationherecouldbewrittenas:

ifa<b:

a=a+1;

b=b-1

c=a-b

Thisishardertocomprehendquicklyandisthereforelessdesirable.Therearetoomany

symbolsallgroupedtogether.Aprogramthatiseasytoreadisalsoeasiertomodifyand

maintain.Codeiswrittenforcomputerstoexecute,butitisalsoforhumanstoread.

There are some special assignment operators that can be used for incrementing and

decrementingvariables.Intheabovecodethestatementa=a+1couldbewrittenasa+=

1,andb=b–1canbewrittenasb-= 1.Thereisnorealadvantagetodoingthis,but

other languages permit it so Python adopted it too. There is another syntax that can be

used to simplify certain code in languages like Java and C, and that is the increment

operator“++”andthedecrementoperator“—.”Pythondoesnothavethese.However,an

effectofthewaythatPythondealswithvariablesandexpressionsisthat“++x”islegal;so

is“++++x.”Thevalueissimplyx.Theexpression“x++”isnotcorrect.

1.7.1 Else

An if statement is a two-way or binary decision. If the expression is true, then the

indicatedstatementsareexecuted.Ifitisnottrue,thenitispossibletoexecuteadistinct

setofstatements.Thisisneededforthepickanumberprogram.Inonecasethecomputer

wins,andintheotherthehumanwins.Anelseclauseiswhatwillallowthis.

Theelseisnotreallyastatementonitsown,becauseithastobeprecededbyanif,so

it’spartoftheifstatement.Itmarksthepartofthestatementthatisexecutedonlywhen

theconditionintheifstatementisfalse.Itconsistsofthewordelsefollowedbyacolon,

followedbyasuite(sequenceofindentedstatements).Soatrivialexampleis:

ifTrue:

print(“Theconditionwastrue”)

else:

print(“theconditionwasfalse”)

Theelseasaclauseisnotrequiredtoaccomplishanyspecificprogramminggoals,and

itcanbeimplementedusinganotherif.Thecode:

ifa<b:

print(“a<b”)

else:

print(“a>=b”)

couldalsobewrittenas:

ifa<b:

print(“a<b”)

ifnot(a<b):

print(“a>=b”)

Theelseisexpressive,efficient, and syntacticallyconvenient. It is expressive because it

representsawaythathumansactuallycommunicate.Thewordelsemeansprettymuchthe

samethinginPythonasitdoesinEnglish.Itisefficientbecauseitavoidsevaluatingthe

same expression twice, which costs something in terms of execution speed. And it is

syntactically convenient because it expresses an important element of the language in

fewersymbolsthanwhentwoifsareused.

ThefinalPythoncodeforthesimplesolutionoftheguessanumberprogramcannow

bewritten.Itis:

choice=7

print(“Pleaseguessanumberbetween1and10:“)

playerchoice=int(input())

ifchoice==playerchoice:

print(“Youwin!”)

else:

print(“Sorry,Youlose.”)

1.8 DOCUMENTATION

Therearesomeproblemswiththisprogram,butisdoeswork.Alargeproblemisthatit

alwayschoosesthesamenumbereverytimeitisexecuted(thatnumberbeing7).Thiswill

befixedlateron.Alesscriticalproblemisthatitisundocumented;thatis,thereareno

instructionstoaplayerconcerninghowtousetheprogramandthereisnodescriptionof

howtheprogramworksthatanotherprogrammermightuseifmodifyingthiscode.This

canbefixedbyprovidinginternalandexternaldocumentation.

Externaldocumentationislikeamanualfortheuser.Mostprogramshavesuchathing,

andeventhoughthisprogramisquitesimple,somedegreeof

documentation can be provided. In fact, it is brief enough that it could be printed

whenevertheprogramstartstorun.Forexample:

print(“Pick-a-numberisasimpleguessinggame.The”)

print(“computerwillselectanumberbetween1and10”).

print(“andyouareexpectedtoguesswhatitis.”)

print(“Whentheprogramdisplays'Pleaseguess”)

print(“anumberbetween1and10:'youtypein”)

print(“yourguessfollowedbythe<enter>key.Your“)

print(“guessmustbeanintegerintherange1to10.”)

print(“Thecomputerwilltellyouifyouwinorlose.)

For many more sophisticated programs, such as PowerPoint for example, the

documentationismanypagesandformsasmallbook.Itwouldbedistributedasabooklet

alongwiththesoftwareorprovidedasawebsite.

Internaldocumentationisintendedforprogrammerswhohaveaccesstothesourcecode

oftheprogram.Itcantaketheformofwrittendocumentstoo,butiscommonlyasetof

commentsthatappearsalongwiththecodeitself.High-levellanguageslikePythonallow

theprogrammertoaddhumanlanguagetexttothecodethatwillbecompletelyignoredby

the computer but that can be read by anyone looking at the code. These comments

describetheactionoftheprogram,themeaningofthevariables,detailsofcomputational

methodsused,andmanyotheritemsofinterest.

InPythonacommentbeginswiththecharacter“#”andendsattheendoftheline.

There are no rules for what can appear typed in a comment, but there are some

guidelines developed through years of programming practice. A comment should not

simplyrepeatwhatappearsinthecode;acommentshouldshedsomelightonanaspectof

theprogramthatmightnotbecleartoeveryonelookingatit,anditshouldbewrittenin

plain language. As an example, here is the guess-a-number program with comments

included:

#Thisprogramselectsanumberbetween1and

#10andallowsauser(player)toguesswhat

#itis.

choice=7#Thenumberselectedbythecomputer



#Prompttheuser,indicatingwhatisexpected

print(“Pleaseguessanumberbetween1and10:“)



#Readtheplayer'sinputfromthekeyboard

playerchoice=int(input())#convertfromstring



#Printtheoutcomeofthegame.

ifchoice==playerchoice:#Istheplayer'sguess

print(“Youwin!”)#correct?Playerwins!

else:#Otherwisethecomputerwins

print(“Sorry,Youlose.”)

All programsshould be documented, not after the factbut as they are being written.

Why?Becauserelativelyfewprogramsarewrittenallinonesitting.Thecommentsinthe

codeserve as reminders tothe programmer about what the variables representand why

particular code segments read the way they do. It also indicates the current state of

thinking about the design of the code. When the program is looked at again at the

beginningofanewworking(orschool)day,thecommentscanbeessentialinresuming

thework.

There is also something called a docstring that seems to do the same things as a

comment,butcoversmultiplelinesandisnotreallyacomment.Adocstringbeginsand

endswithatriplequote:

print(“Thiscodewillexecute”)

”””

print(“Thiscodeiswithinadocstring”)

”””

Adocstringisactuallyastring,notacomment,butbehaveslikeacommentandcanbe

usedinthatway.Itcanbeespeciallyusefulfortemporarilycommentingoutsmallsections

ofcodewhiletryingtofindoutwhereerrorsare.Therearealsoprogramsthatwillcollect

thedocstringsintoaseparatedocumentthatcanbeusedasadescriptionoftheprogram.

Forthat reasontheir intended useis to allowthe programmerto explain thepurpose of

certainsectionsofcode.

1.9 ROCK-PAPER-SCISSORSAGAIN

With what is now known about Python, it is time to look at the rock-paper-scissors

problem and see if it can be coded. It takes more steps, but it is really no more

complicatedthantheguess-a-numberprogram.Thecodeisthesame.

1.Selectachoicefromthethreeitemsrock,paper,orscissors.Savethischoiceina

variablenamedchoice.

Arepresentationforthethreeitemswaswhenthesolutionwasfirst

described,whereeachchoicewasaninteger.However,inputreadsstrings,soit

shouldbepossibletoavoidtheconversiontonumbersandusethestringsdirectly.

choice=“paper”#Computerchoosespaper.

2.Asktheplayerfortheirchoice.

Printaspromptmessage.

print(“Rock-paper-scissors:typeinyourchoice:“)

3.Readtheplayer’sselectionintoavariablenamedplayer.

Useinputaswedidbefore,butthistimereadastringandkeepitthatway.The

playermusttypeoneof“rock,”“paper,”or“scissors,”orelseanerrorwillbe

reported.

player=input()

4.Ifplayerisequaltochoice:

5.Printthemessage“Tie.We’lltryagain.”

Stringscanbecomparedagainsteachotherforequality,sothisstepisquitesimple:

ifplayer==choice:

print(“Gameisatie.Pleasetryagain.”)

6.Ifplayerisequaltorock

7.Ifchoiceisequaltoscissors,gotoStep17

Thewillbeno“gotoStep17,”butthatstepsimplysaysthattheplayerwins.Just

printthatmessagehere.

ifplayer==“rock”:

ifchoice==“scissors”:

print(“Congratulations.Youwin.”)

else:

print(“Sorry-computerwins.”)

8.Ifplayerisequaltopaper

9.Ifchoiceisequaltoscissors,gotoStep17

ifplayer==“paper”:

ifchoice==“scissors”:

print(“Sorry-computerwins.”)

else:

print(“Congratulations.Youwin.”)

10.Ifplayerisequaltoscissors

11.Ifchoiceisequaltorock,gotoStep17

ifplayer==“scissors”:

ifchoice==“rock”:

print(“Sorry-computerwins.”)

else:

print(“Congratulations.Youwin.”)

Thiscodeillustratesanewconcept,ifnotanewlanguagefeature.Ithasifstatements

thatarenestedonewithintheother.Again,it’snotnecessarytodothisbecausenon-nested

statementscanimplementthesamedecision.Forexample:

NestedIFs Non-nestedIFs

ifplayer==“scissors”: ifplayer==“scissorsand

choice==“rock”

ifchoice==“rock”: print(“Computerwins”)

print(“Computerwins.”) ifplayer==“scissors”and

choice!=“rock”

else: print(“Youwin”)

print(“Youwin.”) 

Nested if statements seem more expressive, and communicate the flow of the program

bettertoahumanprogrammerthandoesthenon-nestedcode.

ThereisanotherPythonlanguageelementthatcanbeusedhere.Lookingatthecode,

there is no indication when the user makes an error. For example, if the user enters

“ROCK”(i.e.,uppercase),thenitwillnotmatchanyofthechoices,andtheprogramwill

notindicatethis.Infact,itwon’tprintanythingatall.Whatisreallywantedisasequence

ofif-else-if-elsestatementssuchas:

ifplayer==“scissors”:

ifchoice==“rock”:

else:

ifplayer==“rock”:

ifchoice==paper:

else:

ifplayer==“scissors”:

##andsoon…

Pythonhasaspecialfeaturethatimplementsthisnestingofifandelse:theelif.Theelif

constructcombinesanelseandanif,andthisreducestheamountofindentingthathasto

bedone.Thefollowingcodesnippetsdothesamething:

ifa<b:ifa<b:

print(“a<b”)print(“a<b”)

elifa>b:else:

print(“a>b”)if(a>b):

else:print(“a>b”)

print(“a=b”)else:

else:print(“a=b”)

If too many nested if-else statements exist, then the indenting gets to be too much,

whereas the elif allows the same indent level and has the same meaning. In some

programs this is essential, and in general is easy to read. Using the elif statement the

programfortherock-paper-scissorsproblemlookslikethis:

choice=“paper”#Computerchoosespaper.

print(“Rock-paper-scissors:typeinyourchoice:“)

player=input()

ifplayer==choice:

print(“Gameisatie.Pleasetryagain.”)

ifplayer==“rock”:

ifchoice==“scissors”:

print(“Congratulations.Youwin.”)

else:

print(“Sorry-computerwins.”)

elifplayer==“paper”:

ifchoice==“scissors”:

print(“Sorry-computerwins.”)

else:

print(“Congratulations.Youwin.”)

elifplayer==“scissors”:

ifchoice==“rock”:

print(“Sorry-computerwins.”)

else:

print(“Congratulations.Youwin.”)

else:

print(“Error:Selectoneof:rock,paper,scissors”)

Nowallofthepossibleoutcomesarehandledbythecode.

1.10 TYPESAREDYNAMIC(ADVANCED)

ToprogrammerswhoonlyprogramusingPython,itwouldseemoddthataparticular

variablecouldhaveonly one typeandthatit wouldhavetobe initiallydefinedtohave

that type, but it is true. In Python the type associated with a variable can change. For

example,considerthestatements:

x=10#Xisaninteger

x=x*0.1#Xisfloatingpointnow

x=(x*10==10)#XisBoolean

Somefindthisperfectlylogical,andothersfinditconfusing.Thefactisthatsolongasthe

variableisusedaccordingtoitscurrenttype,allwillbewell.

ItisalsotruethatevenapparentlysimplePythontypescanbequitecomplexintermsof

their implementation. The point is that the programmer rarely needs to know about the

underlying details of types like integers. In many programming languages an integer is

simplyaoneortwo-wordnumber,andthelanguagesbuildoperationslike“+”fromthe

instructionsetofthecomputer.If,forexample,aone-wordintegerAisaddedtoanother

oneB,itcanbedoneusingasinglecomputerinstructionlikeADDA,B.Thisisveryfast

atexecutiontime.

Python was designed to be convenient for the programmer, not fast. An integer is

actuallyacomplexobjectthathasattributesandoperations.Thiswillbecomecleareras

morePython examples arewritten andunderstood, butas asimple casethink aboutthe

way that C++ represents an integer. It is a 32-bit (4 byte) memory location, which is a

fixedsizespaceinmemory.Thelargestnumberthatcanbestoredthereis232-1.Isthat

trueinPython?

Here’s a program that will answer that question, although it uses more advanced

features:

foriinrange(0,65):

print(i,2**i)

Evenanespeciallylongintegerwouldbelessthan65bits.Thefactisthatthisprogram

runssuccessfully,andevenratherquickly.IntegersinPythonhaveanarbitrarilylargesize.

So calculating 264 * 264 is possible and results in

340282366920938463463374607431768211456. This is very handy indeed from a

programmer’sperspective.

Thetypeofavariablecanbedeterminedbytheprogrammerastheprogramexecutes.

Thefunctiontype()willreturnthetypeofitsparameterasastring,andcanbeprintedor

tested.So,thecode:

z=1

print(type(z))

z=1.0

print(type(z))

willresultin:

<class'int'>

<class'float'>

Ifoneneededtoknowifzwasafloatataparticularmoment,then:

iftype(z)isfloat:

woulddothetrick.Type(z)doesnotreturnastring,itreturnsatype.Theprint()function

recognizesthatandprintsastring,justasitdoesforTrueandFalse.So:

iftype(z)==“<class'float'>”:

wouldbeincorrect.

In future chapters this malleability of types will be further described, and practical

methodsfortakingadvantageofitinPythonwillbeexamined.

1.11 SUMMARY

Acomputerisatoolforrapidlyandaccuratelymanipulatingnumbers.Itcanperform

tediousrepetitivetasksaccuratelyandquickly,butmustbetoldwhattodoandfollowsits

instructions very literally. A computer program is a set of instructions for performing a

task using a computer, and Python is one language that can be used for this purpose.

Pythonallowsaprogrammertodefinevariablesbysimplyusingthem, and associatesa

typewithavariablebasedonwhatitisgiven.Anifstatementallowspartsofaprogramto

be executed when a certain condition becomes true, and it can have an else part that is

executedwhentheconditionisfalse.Ifstatementscanbenested,andsometimestheelif

structureisagoodwaytoexpressasetofnestedconditionalcode.

Inthischapterthemainexamplesweretwoprograms,oneofwhichallowedauserto

guessanumber,whiletheotherwasthewell-knowngameofrock-paper-scissors.

Exercises

Inthefollowingexercisessomeof the expressionsmayresultin anerror.If so,explain

whytheerroroccurs.WhenaskedtowritecodeitshouldbePython3code.

1.Evaluatethefollowingexpressions:

a)3*3/2

b)3*3//2

c)3*3%2

d)(3*3)%2

e)3**3/3

f)(3+2)-(2-4)

g)(3+2)/(2-4)

2.Ifthestatements:

x=3

y=9

z=“2.4”

havebeenexecutedthenevaluatethefollowingexpressions.Ifanerroroccurs,state

why:

a)x/y

b)x//y

d)x%y

e)y/x*z

f)float(x)/float(z)

g)float(x)//float(z)

h)int(x)//int(z)

3.Giventhevariabledefinitionspresented,evaluatethefollowingexpressionsasbeing

TrueorFalse.

x=12

y=14

a)x>3

b)x>=12

c)x<y

d)x<yandy>14

e)x<yory>14

f)not(x==y)

g)not(x<y)andnot(y>14)

4.Whatwillbeprintedbythefollowingstatements?

a)print(int(“23”))

b)if3**2+4**2==5**2:

print(“345”)

elif3**2<4**2:

print(“34”)

else:

print(“5”)

c)if“toast”<“jam”:

print(“toast”)

else:

print(“jam”)

d)if“12”<“5”:

print(“12”)

else:

print(“5”)

e)a=12.3

b=100

c=0

ifa<b:a=a+1;b=b-1

c=c–b

print(a)

print(c)

f)a=100

b=200

c=300

ab=a<b

cd=(c==a+b)

ifabandcd:

print(“ABandCD”)

elifab:

print(“AB”)

else:

print(“Nope”)

5.TheUnitedStatesmeasurestemperatureinFahrenheitdegrees,whereasCanadauses

Celsius.Acompanyisdevelopinganapptoconvertbetweenthetwoforpeople

wantingtoskiinBanfforWhistler.TheformulatoconvertfromCelsiusdegreesCto

FahrenheitdegreesFis:

F=C*9/5+32

Writeaprogramthatwillbethebasisofthisapp:itwillreadatemperatureinCelsius,

convertittoFahrenheit,andprinttheresult.

6.Thenumericalvaluesofcoinshavebeenarrangedsothatthegreedyalgorithmwill

resultinthesmallestnumberofcoinswhenmakingchange.Thismeansthatthe

largestvaluedcoinistriedfirst,andasmanyofthosecoinsareusedaspossible.Then

thenextsmallerdenominationcoinisused,andsoonuntilthepenniesaredealtout.

Sofor84centsinchange,a50-centpiececouldbeused(leaving34cents),thena25-

centpiece(leaving9cents),a5centpiece(leaving4cents),and4pennies.Ifno50-

centpiecewasavailable,then25-centpieceswouldbeusedinitsplace:3quarters,

followedbyanickelandfourpennies.Writeaprogramthatreadsanumberbetween1

and99thatisanamountofchangetobegivenandprintsthecoinvaluesthatwouldbe

used.

7.Threefloatingpointvariablesa,b,andchavebeenreadinfromtheconsole.Writea

setofifstatementsthatprintstheseindescendingorder.

8.Ifthevalueof1.0/7.0isprinted,therearemanynumberstotherightofthedecimal

place.DeviseawaytoprintonlythreeplacesandwritesomePythoncodetotestthe

idea.

9.Calculateanapproximationtopi.ThereisaninfiniteseriescalledtheGregory-Leibniz

seriesthatsumstopi.Ofcourseitcanneverreachtheexactvaluebecausethereisno

suchthing,butitcancomputeasmanydigitsasaredesired.Theseriesis:

Π=4/1–4/3+4/5–4/7+4/9–4/11….

Writeaprogramthatcalculatestheresultofthefirst15termsofthisseries.Howmany

digitsofpiarecorrect?Addsixmoreterms.Howmanydigitsarecorrectnow?

10.AnotherseriesthatcancalculatepiistheNilakanthaseries.Itisalittlemore

complicatedtocalculate,butgetsclosetopimuchfasterthandoestheGregory-

LeibnizseriesofExercise9.TheNilakanthaseriesis:

Π=3+4/(2*3*4)–4/(4*5*6)+4/(6*7*8)–4/(8*9*10)…

Calculatethefirst15termsofthisseries.Howmanydigitsofpiarecorrect?

NotesandOtherResources

ManyteachingresourcesforPythonexist,bothinprintandontheInternet.

Hereisthedevelopmentenvironmentusedtotestthecodeforthisbook.

PyCharm.https://www.jetbrains.com/pycharm/

1.DavidBeazleyandBrianK.Jones.PythonCookbook,3rdEdition:Recipesfor

MasteringPython3,http://www.onlineprogrammingbooks.com/python-cookbook-

third-edition/

2.CodyJackson.LearningtoProgramUsingPython,

http://www.onlineprogrammingbooks.com/learning-program-using-python/

3.BradMiller.ProblemSolvingwithAlgorithmsandDataStructuresUsingPython,

http://www.onlineprogrammingbooks.com/problem-solving-with-algorithms-and-data-

structures/

4.HarryPercival.Test-DrivenDevelopmentwithPython,

http://www.onlineprogrammingbooks.com/test-driven-development-with-python/

5.LennartRegebro.PortingtoPython3:AnIn-DepthGuide,

http://www.onlineprogrammingbooks.com/porting-to-python-3-an-in-depth-guide/

6.ZedA.Shaw.LearnPythontheHardWay,http://learnpythonthehardway.org/book/

CHAPTER2

REPETITION

2.1TheWHILEStatement

2.2Rock-Paper-ScissorsYetAgain

2.3CountingLoops

2.4PrimeorNon-Prime

2.5LoopsThatareNested

2.6DrawaHistogram

2.7LoopsinGeneral

2.8ExceptionsandErrors

2.9Summary

Inthischapter

Oneofthethingsthatmakescomputersattractivetohumansistheirabilitytodotedious,

repetitivetasksaccurately and at high speedwithout gettingbored. Itis somethingthey

were designed to do. Humans have to do things repeatedly, and not all of them can be

doneforusbycomputers.Brushingourteeth,drivingtowork,cleaningthecarpet—allare

repeatedactions,andmanywouldbecalledchores.Inprogrammingtermssomemightbe

referredtoasloops.

Considerafactoryjobonanassemblyline.AccordingtoHenryFord,oneofthepeople

principallyconnectedwithdevisingtheassemblylineconcept,itismoreefficienttohave

eachworkerdoonejobwellandrepeatitmanytimesadaythantoteachworkershowto

buildentirethings,inhiscaseautomobiles.Eachworkerdoesonerelativelyshortjob,and

then the piece they are working on goes to the next station where the next person does

theirrelativelyshortjob.Onesuchjobcouldbetheinstallationoftheelectronicignition

modulebracket:

1.Acquireabracketandplaceoverattachmentholeswithwideendbelowthe

smallerend.

2.Placeatwo-inchboltintheupperleftboltholeandscrewintotwopoundsof

torque.

3.Placeafour-inchboltintheupperrightboltholeandscrewintotwopoundsof

torque.

4.Placeatwo-inchboltinthelowerleftboltholeandscrewintotwopoundsof

torque.

5.Placeaten-millimeternutovertheboltatthelowerrightandtightentotenpounds.

6.Re-tightentheboltstotenpoundsinthefollowingorder:upperleft,

upperright,lowerleft.

BeforeStep1aboveanewworkpiece(anengine,probably)isplacedinfrontofthe

worker, and after Step 6 the piece is moved to the next station. So from the worker’s

perspective,solongasorwhilethereisanengineattheirstationthatneedsabracket,they

repeat the steps. In a form that a computer might be able to understand this might be

writtenas:

whilethereisanengineattheirstationthatneedsabracket:

Acquireabracketandplaceoverattachmentholeswithwideendbelowthesmaller

end.

Place a two-inch bolt in the upper left bolt hole and screw in to two pounds of

torque.

Place a four-inch bolt in the upper right bolt hole and screw in to two pounds of

torque.

Place a two-inch bolt in the lower left bolt hole and screw in to two pounds of

torque.

Placeaten-millimeternutovertheboltatthelowerrightandtightentotenpounds.

Re-tighten the bolts to ten pounds in the following order: upper left, upper right,

lowerleft.

Alloftheactionsthatfollowthewhileareindentedtoindicatethattheyareapartof

theactivitiestoberepeated,justaswasdoneinaPythonifstatementtomarkthethings

thatweretobedoneiftheconditionwastrue.Thisexample

illustratesoneofthePythonrepetitionstructuresquiteaccurately:thewhilestatement.

2.1 THEWHILESTATEMENT

Whenusingthisrepetitionstatement,theconditionistestedatthetoporbeginningof

the loop. If upon that initial test the condition is true, then the body of the loop is

executed;otherwiseitisnot,andthestatementfollowingtheloopisexecuted.Thismeans

thatitispossiblethatthecodeintheloopisnotexecutedatall.Theconditiontestedisthe

samekindofexpressionthatisevaluatedinanifstatement:onethatevaluatestoTrueor

False.Itcouldbe,andoftenis,acomparisonbetweentwonumericorstringvalues,asitis

intheexampleofFigure2.1.

Whenthecodeinthebodyofthewhilestatementhasbeenexecuted,thenthecondition

istestedagain.Ifitisstilltrue,thenthebodyoftheloopisexecutedagain,otherwisethe

loopisexitedandthestatementfollowingtheloopisexecuted.Thereisanimplicationin

this description that the body of the loop must change something that is used in the

evaluationoftheloopcondition,otherwisetheconditionwillalwaysbethesameandthe

loopwillneverterminate.So,hereisanexampleofaloopthatisenteredandterminates:

a=0

b=0

whilea<10:

a=a+1

print(a)

Theconditiona<10istrueattheoutsetbecauseahasthevalue0,sothecodeinthe

loopisexecuted.Thelonestatementinthisloopincrementsa,sothatafterthefirsttime

theloopisexecuted,thevalueofais1.Nowtheconditionistestedand,again,a<10so

theloopexecutesagain.Inthefinaliterationoftheloop,thevalueofastartsoutas9,is

incrementedandbecomes10.Whentheconditionistesteditfails,becauseaisnolonger

lessthan10(itisequal)andsotheloopends.Thestatementfollowingtheloopisprint

(a)andthevalueprintedis10.Thisloopexplicitlymodifiesoneofthevariablesinthe

loopcondition,anditiseasytoseethattheloopwillendandwhatthevalueofawillbe

atthattime.

Hereisanexampleofaloopthatisenteredanddoesnotterminate:

a=0

b=0

whileb<10:

a=a+1

print(a)

Inthiscasethevalueofbislessthan10attheoutset,sotheloopisentered.Thebody

oftheloopincrementsaas before,butdoes notchangeb. The loop condition does not

dependona,onlyonb,sowhentheloopconditionistestedagainthevalueofbisstill0,

andtheloopexecutesagain.Thevalueofbwillalwaysbe0eachtimeitistested,sothe

loopconditionwillalwaysbetrueandtheloopwillneverend.Theprintstatementwill

neverbeexecuted.

When this program is executed, the computer will seem to become unresponsive. As

longastheloopisexecutingtheprogramcandonothingelse,andsotheonlyindication

that something is wrong is that nothing is happening. There are many reasons why a

programcanappeartobedoingnothing:whenwaitingfortheusertotypesomeinput,for

instance, or when performing an especially difficult calculation. However, in this case,

whichiscalledaninfiniteloop,theonlythingtodoistoterminatetheprogramandfixthe

loop.

Hereisanexampleofaloopthatisnotentered:

a=100

b=0

whilea<10:

a=a+1

print(a)

Theconditiona<10isfalseattheoutsetbecauseahasthevalue100,sothecodeinthe

loopisnotexecuted.Thestatementfollowingtheloopisexecutednext,whichistheprint

statement,andthevalueprintedis100.

Theseloopsaremerelyexamplesthatillustratethethreepossibilitiesforawhileloop

and do not calculate anything useful. The two examples from the previous chapter can

makepracticaluseofawhileloop,anditwouldbeusefultolookatthoseagain.

2.1.1 TheGuess-A-NumberProgramYetAgain

TheprogramasitwaswritteninChapter1is:

choice=7

print(“Pleaseguessanumberbetween1and10:“)

playerchoice=int(input())

ifchoice==playerchoice:

print(“Youwin!”)

else:

print(“Sorry,Youlose.”)

Thegamewouldbebetterifitallowedtheplayertoguessagain,perhapsuntilacorrect

guesswasachieved.Awhileloopcouldbeusedtoaccomplishthis.Thinkaboutwhatthe

condition might be. The loop should end when the player guesses the answer. Another

waytosaythisisthattheloopshouldcontinuesolongastheplayerhasnotguessedthe

answer. The condition is one for continuation of the loop, not termination, so the loop

mustbeconstructedinsuchawaythatitcontinueswhentheconditionistrue.Theloop

willbeginwiththis:

whilechoice!=playerchoice:

At the beginning of the loop the variables choice and playerchoice must be defined.

This means that before the while statement, there must be code that does this. The

programnowlookslikethis:

choice=7

print(“Pleaseguessanumberbetween1and10:“)

playerchoice=int(input())

whilechoice!=playerchoice:

If the player has guessed incorrectly, then the body of the loop will execute. What

shouldbedone?Oneofthevariablesintheconditionhastobechanged,firstofall,and

thegoaloftheprogrammustbekeptinmind.Inthiscase,becausetheplayerhasguessed

incorrectly,twothingsshouldhappen.First,theplayermustbetoldthattheyarewrong

and to make another guess. Next, the new guess must be read into the variable

playerchoice,thussatisfyingtherulethattheloopconditionmusthaveanopportunityto

becomeFalse.Theprogramisnow:

choice=7

print(“Pleaseguessanumberbetween1and10:“)

playerchoice=int(input())

whilechoice!=playerchoice:

print(“Sorry,notcorrect.Guessagain:“)

playerchoice=int(input())

When the player finally guesses the number the loop will exit; if the first guess is

correctthentheconditionfailsatthebeginning,andthisamountstothesamethinginthis

case.Thelastthingtodoistoprintamessagetotheplayer:

choice=7

print(“Pleaseguessanumberbetween1and10:“)

playerchoice=int(input())

whilechoice!=playerchoice:

print(“Sorry,notcorrect.Guessagain:“)

playerchoice=int(input())

print(“Youhaveguessedcorrectly.”)

Note that, as was true with the if statement and as is always true in Python, the

indentation indicates which statements are a part of the loop (the suite) and which are

outside.

2.1.2 ModifyingtheGame

Asimplemodificationofthegameinvolvestellingtheplayerwhethertheirguesswas

toolargeortoo small.This will helpthem shrinkthe possiblerange of valuesand thus

guess the right answer more quickly. A modification to the body of the loop will

accomplish this. If the value that the player guessed is smaller than the target, then a

messagetothateffectisprinted,andsimilarlyiftheplayerguessesavaluelargerthanthe

target.Theuseofanifstatementherewouldbeappropriate,andthatifstatementwould

benestedinsideofthewhileloop:

choice=7

print(“Pleaseguessanumberbetween1and10:“)

playerchoice=int(input())

whilechoice!=playerchoice:

if(playerchoice<choice):

print(“Sorry,yourguesswastoosmall.

Guessagain:“)

else:

print(“Sorry,yourguesswastoolarge.

Guessagain.”)

playerchoice=int(input())

print(“Youhaveguessedcorrectly.”)

This program illustrates a second level of indentation. The if-else are indented to

indicatetheyarepartofthewhilestatement.Theprintstatementsareindentedfurther,to

showthattheyarealsopartoftheifstatement.

Doing some printing inside of the loop is useful because an infinite loop will be

obvious.It willprint awhole lotof stuffand never stop.It’snotalways practicalto do

that,soadegreeofcarefulanalysisshouldalwaysbedonetoensurethattheloopcanand

willterminate.

2.2 ROCK-PAPER-SCISSORSYETAGAIN

Thisgamereallyneedsaloop,andthepreviousimplementationwasnotcomplete.If

there is a tie then the game has to be repeated, and a winner must be determined. This

meansthattheloopinthiscasewillbesomethinglike:

whilethereisnowinner:

Thishappensonlywhentheplayerandthecomputerselectthesameobject,andinthe

originalcodewashandledbythestatements:

ifplayer==choice:

print(“Gameisatie.Pleasetryagain.”)

Thecondition“nowinner”becomesplayer==choice.Thecompletesolutioninvolves

the while loop and another input from the user within the loop. Here is one possible

answer:

choice=“paper”#Computerchoosespaper.

print(“Rock-paper-scissors:typeinyourchoice:“)

player=input()



#–––Thenewsectionofcode–––––––

whileplayer==choice:#Repeatinputuntilthereisa

winner

print(“Gameisatie.Pleasetryagain.”)

player=input()

#––––––––––––––––––-

ifplayer==“rock”:

ifchoice==“scissors”:

print(“Congratulations.Youwin.”)

else:

print(“Sorry-computerwins.”)

elifplayer==“paper”:

ifchoice==“scissors”:

print(“Sorry-computerwins.”)

else:

print(“Congratulations.Youwin.”)

elifplayer==“scissors”:

ifchoice==“rock”:

print(“Sorry-computerwins.”)

else:

print(“Congratulations.Youwin.”)

else:

print(“Error:Selectoneof:rock,paper,scissors”)

Theterminationoftheloopdependsontheuser’sinputandthevalueofthecomputer’s

choice,whichcouldalso(andshould)changeinsidetheloop.Theprobabilityoftheloop

continuingafteroneiterationis1in3,andtheprobabilitythatitwillstillbeloopingafter

Niterationsis(1/3)N,sothereisaverysmallchanceofthelooprepeatingmorethan2or

3times.

2.2.1 RandomNumbers

Most games depend on an element of unpredictability or chance. Those that do not

might be more properly called puzzles (or sports—football and hockey ought to have a

certain degree of skill involved). Given that computers do calculations, and that

calculationsshouldhavethesameresulteverytime,howdoesoneproduceanythingthat

israndomusingacomputer?Theanswerispartlyinhowthetermrandomisdefined.The

discussion involves some mathematics or at least some basic ideas in probability and

statistics.

If integers in the range 1 through 10 inclusive are considered, what is the likelihood

(chance,probability)thatthenumber5willbeselectedatrandom?Theansweris1in10,

or 0.1. This is true each time that question is asked. So if the number 5 has just been

chosenandanothernumberistobechosen,whatisthechancethatitwillbea5?Same

answer:1in10.Theprincipleisthatthenextchoicedoesnotdependonthepreviousone;

it’sapartofwhatmakesthemrandom.

Perhapsthewrongquestionwasbeingasked.So,whatisthelikelihoodthatthenumber

5 will be selected twice in a row at random? The answer is 1 in 100, or 0.01. Why?

Becauseitdependsonthequestionasked.Togettwoinarow,thefirstonemustbea5(1

in10)andthesecondonemustalsobea5(also1in10)sotheresultinglikelihoodis1in

10*10or1in100.Buteachtimeanumberischosen,thenumber5hasa1in10chanceof

beingselected.Amathematicaldiscussionofrandomnessdependsontheaskingtheright

question,andonprobabilities.Ifsomeeventiscompletelyrandom,thenitshouldhavethe

sameprobabilityofhappeningastheotherpossibleevents,buteventscanbecollectedto

formmore complex events. Each cardin a deck of playing cardsshould have the same

probabilityofturningup,butifthequestionis“What’sthechanceofaflush,”thenthe

differentwaysthataflushcanbecomprisedhavetobetakenintoaccount.Itcanbeavery

complicatedandinterestingsubject.

Numbers,inparticular,arerandomonlywithrespecttoeachother.Isthenumber“6”

random?That’snotreallyagoodquestion.Isthesequence87394random?Perhapsatest

couldbedevisedtoanswerthat.Isthesequence66666random?Mostwouldsaynot,but

ithasthesameprobabilityofbeinggeneratedatrandomasdoes87354.Tocreategood

gamesandsimulations,itisnecessarytodevisewaystogeneratearandomnumberusing

a computer, and to test numbers to see if they are in fact random. Then it would be

possibletosimulatetheflippingofacoin,ortherollingofadie.

What is the 100th digit of pi? It can be found easily. Are consecutive digits of pi

effectively random? As it happens, the answer is not known, but it is a good question.

Whatis108763dividedby98581?Whatistheremainder?Calltheremainderx:whatis

108763dividedbyx?Arethesenumbersrandom?Thesearchforamethodforgenerating

really good random numbers continues, but there are some pretty good methods (See:

Chapter 10). In Python a random number created by a computer algorithm can be

requestedbyusingabuilt-infunction.

A built-in function is like a mathematical function, and is provided by the language

itself (and so is “built-in”). The language element print that has been used so much is

really a built-in function. So are int() and float(). The functions sine and square root

shouldbewellunderstoodbyanyonewhohasgraduatedfromhighschool,andarealso

built-infunctions.SuchfunctionsbelongtomodulesinPythonandhavetobespecifically

requested by the program so that they can be used. This means that the name of the

module has to be known as well as the names of the built-in functions within it. The

commonmathematicalfunctionsarelocatedwithinthemodulemathandcanbeusedby

requestingthemathmodulewiththestatement:

importmath

Using a function in the math module involves using the name math followed by a

period(“.”)followedbythenameofthefunction.The“.”opensthemodulesothatthe

nameswithincanbeused,becausetheremaybeotherbuilt-infunctionsorevenvariables

thathavethesamename.So,ifthestatements:

x=math.sqrt(64)

print(x)

are executed, the program will print the number 8, which is the square root of 64. The

expressionsqrt(64)iscalledafunctioncall,andexecutesthecodeneededtocalculatethe

squarerootof64.Thenamesqrtisthenameofthefunction,whichiscodeprovidedby

the Python language. This particular call will always return the value 8, because 8 is

alwaysthesquarerootof64.Itisverymuchlikethefunctionsthatarestudiedingrade

school mathematics, such as sine and cosine. A module can be thought of as a bag of

programs. Each bag contains a set of programs that do a particular class of things, like

mathematics or drawing. By specifying the name of the module, access to all of the

functionswithinis granted,and byspecifying thespecific nameof afunction, thecode

thatwewantisspecificallymadeavailable.

Bytheway,theimportstatementshouldbeattheverybeginningoftheprogram.

Nowimaginethatitispossibletohaveafunctionthatproducesarandomnumberasa

value.Itisinthemodulenamedrandom,andthefunctioncouldbecalledrandomtoo.

Forexample:

importrandom

print(random.random())

Everytime(wellalmosteverytime,becauseitisrandom,afterall)thefunctionisused

itwillgiveadifferentvalue,arandomvalue.Thisvaluecanbeusedtomakegamesmore

realistic,becausegameshavearandomaspect.

This code prints the value 0.07229650795715237. Why? Because random.random()

producesarandomnumberbetween0.0and1.0.Thisisthemostcommonexampleofa

randomnumberfunction,anditisreallyverygeneral.Increasingtherangeisdonesimply

by multiplying by the maximum value desired; random.random()*100 gives a random

numberbetween0and100,forinstance.

Whatiftheproblemistosimulatetherollofadie?Thebagofcodethatistherandom

modulecontainsotherfunctionsrelatedtothegenerationofrandomnumbers,andoneof

themisespeciallysuitedtothisproblem.Adierollwouldbeimplementedas:

random.randint(1,6)

Therandint function accepts two numbers, called parameters. The first is the lower

limit of the range of random integers to be produced and the second is the upper limit.

Specifying1asthelowerlimitand6astheupper,asintheexampleabove,meansthatit

willgeneratenumbersbetween1and6inclusive,whichiswhatwouldbeexpectedfrom

rollingadie.Theresultofrollingtwodicewouldbeanumberbetween2and12,foundby

random.randint(2,12).

Flipping a coin is a two-level choice, and could be done with random.randint(1,2).

Morecompletely:

if(random.randint(1,2)==1):

print(“Heads”)

else:

print(“Tails”)

Going back again to the number guessing game, a random choice for the computer’s

numberisnowpossible.Insteadofthefirstlineofcodebeing:

choice=7

itshouldnowbe:

choice=random.randint(1,10)

Every time the program executes, the program will select a new random number, as

opposedtothechoicealwaysbeing7.

The introduction of a random choice is a little more complicated for the rock-paper-

scissors program because the variable holding the player’s choice is a string. There are

threepossiblechoices,sotoselectoneatrandommightlooklikethis:

i=random.randint(1,3)

ifi==1:

choice=“rock”

elifi==2:

choice=“paper”

else:

choice=“scissors”

Many of the examples that will be developed will involvea game or puzzle of some

kind,sotheuseofrandomnumberswillbeaconsistentfeatureofthecodeshown.

2.3 COUNTINGLOOPS

Featuresofprogramminglanguagesareprovidedbecausethedesignersknowtheywill

beuseful.Thewhileloopisobviouslyuseful,andisinfacttheonlykindofloopthatis

required in order to implement any program. However, loops that involve counting a

certainnumberofiterationsareprettycommon,andaddingsyntaxforthiskindofthing

wouldbecertaintobevaluableforaprogrammer.Theideaisthatsometimesaloopthat

executes,forexample,tentimesoraloopthatiteratedNtimesforsomevariableNwould

bewanted.InPythonandmanyotherlanguages,thisiscalledaforloop.

Insomelanguagesaforloopinvolvesaspecialsyntax,butinPythonitinvolvesanew

type(aclassoftypes,really):atuple.Hereisanexampleofaforloop:

foriin(1,2,3,4,5):

printi

Thiswillprintthenumbers12345eachonaseparateline.Thevariableitakeson

eachofthevaluesinthecollectionprovidedinparentheses,andtheloopexecutesoncefor

eachvalue of i. Thecollection (1,2,3,4,5) iscalled a tuple, and can contain any Python

objectsinanyorder.It’sbasicallyjustasetofobjects.Thefollowingarelegaltuples:

(3,6,9,12)

(2.1,3.5,9.1,0,12)

(“green”,“yellow”,“red”)

(“red”,3,4.5,2,“blue”,i)#whereiisavariablewitha

value

Theforloophastheloopcontrolvariable(inthecaseaboveitisi)takeoneachofthe

valuesinthetuple,inlefttorightorder,andthenexecutestheconnectedsuite.Theloop

willthereforeexecutethesamethenumberoftimesasthereareelementsinthetuple.

Sometimesitmaybenecessarytohavetheloopexecuteagreatmanytimes.Iftheloop

wastoexecuteamilliontimes,itwouldbemorethanawkwardtorequireaprogramtolist

a million integers in a tuple. Python provides a function to make this more convenient:

range().Itreturnsatuplethatconsistsofalloftheintegersbetweenthetwoparametersit

isgiven,includingthelowerendpoint.So:

range(1,10)is(1,2,3,4,5,6,7,8,9)

range(-1,2)is(-1,0,1)

range(-1,-3)isnotaproperrange.

range(1,1000000)ifthesetofallintegersfrom1to

9999999

Ranges involving strings are not allowed, although tuples having strings in them are

certainlyallowed.Theoriginalexampleforloopcannowbewritten:

foriinrange(1,6):

printi

andtheloopthatistoexecuteamilliontimescouldbespecifiedas:

foriin(0,1000000):

printi

This would print the integers from 0 to 999999. If range() is passed only a single

argument,thentherangeisassumedtostartat0;thismeansthatrange(0,10)andrange

(10)arethesame.

2.4 PRIMEORNON-PRIME

Here’sagamethatcanillustratetheuseofaforloop,andsomeotherideasaswell.The

computerpresentstheplayerwithlargenumbers,oneatatime.Theplayerhastoguess

whethereachnumberisprimeornon-prime.Aprimenumberdoesnothaveanydivisors

except 1 and itself; 3, 5, 11, and 17 are prime numbers. The game ends either when a

specificnumberofguesseshavebeenmade,orwhentheplayermakesaspecificnumber

ofmistakes.

A key problem to solve in this game is to determine when a number is prime. The

computermust beable to determinewhether theplayer is correct,and so forany given

numbertheremustbeawaytofigureoutwhetheritisprime.

Otherwise,theprogramforthisgameisnotverycomplicated:

whilegameisnotover:

selectarandomintegerk

printkandasktheplayerifitisprime

readtheplayerꞌsanswer

ifplayerꞌsansweriscorrect:

print“Youareright”

else:

print“Youarewrong.”

The mysterious portion of this program is the if statement that asks if the player’s

answeriscorrect.Thisreallymeansthattheprogrammustdeterminewhetherornotthe

number K is prime and then see if the player agrees. How can it be determined that a

numberisprime?Aprimenumberhasnodivisors,soifonecanbefoundthenthenumber

isnotprime.Themodulooperator%canbeusedtotellifadivisionhasaremainder:ifk

%n=0thenthenumberndividesevenlyintok,andkisnotprime.

Sotofindoutwhetheranumberisprime,trydividingitbyallnumberssmallerthanit,

andifanyofthemhaveazeroremainderthenthenumberisnotprime.Thisisajobfora

forloop.Here’safirstdraft:

isprime=True

forninrange(1,K):

ifk%n==0:

isprime=False

Aftertheloophascompleted,thevariableisprimeindicateswhetherKisprimeornot.

Thisseemsprettysimple,iftedious.Itdoesalotofdivisions.Toomany,infact,becauseit

isnotpossibleforanynumberlargerthanK/2todivideevenlyintoK.Soaslightlybetter

programwouldbe:

isprime=True#IsthenumberKprime?

forninrange(1,int(k/2))#DivideKbyallnumbers<K/2

ifk%n==0:#Iftheremainderis0thenn

isprime=False#dividesevenlyintoK:not

#prime

#Ifisprimeisstilltrueherethenthenumberisprime.

Next,thissectionofprogramshouldbeincorporatedintoacompleteprogramthatplays

thegame.Ifthegameissupposedtoallow10guesses,thenthefirststepistorepeatthe

wholething10times:

importrandom

correct=0#Thenumberofcorrectguesses

foriterationinrange(0,10):#10guesses

Now select a number at random. It should be large enough so that it is hard to see

immediatelyifitisprime,althoughevennumbersareagiveaway:

K=random.randint(10000,1000000)#Generateanewnumber

Nextprintamessagetotheuseraskingfortheirguess,andreadit:

print(“PrimeorNot:Isthenumber“,K,”prime?(yesor

no)”)

answer=input()#Readtheuserꞌschoice

Theusertypesinastring,“yes”or“no,”astheirresponse.Thevariableisprimethat

was used in the program that determines whether K is prime is logical, being True or

False.Itcouldbemadeintoastringtoosothatitwasthesameaswhattheusertyped,and

thenitcouldbecompareddirectlyagainsttheuser’sinput:

isprime=“yes”

Nowcomesthecodefordeterminingprimalityascodedabove,exceptwithisprimeas

astring:

isprime=True#IsthenumberKprime?

forninrange(1,int(k/2))#DivideKbyallnumbers<K/2

ifk%n==0:#Iftheremainderis0thenn

isprime=“no”#dividesevenlyintoK:notprime

#Ifisprimeisstilltrueherethenthenumberisprime.

Atthispointthevariableisprimeiseither“yes”or“no,”dependingonwhetherKis

actually prime. The user’s guess is also “yes” or “no.” If they are equal then the user

guessedcorrectly.

ifisprime==answer:

print(“Youarecorrect!”)

correct=correct+1

else:

print(“Youareincorrect.”)

Finally, the outer loop is ended and the result is printed. The value of the variable

correctisthenumberofcorrectguessestheusermade,becauseitwasincrementedevery

timeacorrectanswerwasdetected.Thelaststatementis:

print(“Yougave“,correct,“rightanswersoutof10.”)

ThisprogramcanbefoundontheCDinthedirectory“primegame.”

2.4.1 ExitingfromaLoop

Acleverprogrammerwouldnoticeaprettyseriousinefficiencywiththeprimenumber

program.Whenithasbeendeterminedthatthenumberisnotprime,theloopcontinuesto

divide more numbers into k until k/2 of them have been tried. If k= 999992 then it is

knownafterthefirstiterationthatthenumberifnotprime;itiseven,soitcan’tbeprime.

But the program continues to try nearly another half million numbers anyway. What is

neededisawaytotelltheprogramthattheloopisover.Thereisawaytodothis.

Aloopcanbeexitedusingthebreakstatement.Itissimplythewordbreakbyitself.

Thecorrectwaytousethisintheprogramabovewouldbe:

forninrange(1,int(k/2))#DivideKbyallnumbers<K/2

ifk%n==0:#Iftheremainderis0thenn

isprime=“no”#dividesevenlyintoK:notprime

break

This loop terminates when the number k is known to be not prime. The statement

followingtheloopwillbeexecutednext.Thiscansavealotofcomputercycles,butdoes

notmaketheprogrammorecorrect—justfaster.

Avariationonthisisthecontinuestatement.Thiswillresultinthenextiterationofthe

loop being started without executing any more statements in the current iteration. This

avoids doing a lot of work in a loop after it is known it’s not necessary. For example,

doing some task for a bunch of names except for people named “Smith” could use a

continuestatement:

fornamein(ꞌJonesꞌ,ꞌSmithꞌ,ꞌPetersꞌ,ꞌSinatraꞌ,ꞌBohrꞌ,

ꞌConradꞌ):

print(name);

ifname==ꞌSmithꞌ:

continue

#Nowdoabunchofstuff…

Boththebreakandcontinuedothesamethinginbothwhileandforloops.

Modifying the loop variable will not change the number of iterations the loop will

execute.Infact,ithasnoeffect.Thisloopdemonstratesthat:

foriinrange(0,10):

print(“Before“,i)

i=i+1000

print(“After“,i)

Itprints:

Before0

After1000

Before1

After1001

...

andsoon.Itseemsthatthevalueofichangesaftertheassignmentfortheremainderof

the loop and then is set to what it should be for the next iteration. This makes sense if

Pythonistreatingtherangeasasetofelements(itis),anditassignsthenextonetoiat

thebeginningofeachiteration.Unlikeawhileloop,thereisnotatestforcontinuation.In

anycase,changingiheredoesnotalterthenumberofiterationsandcan’tbeusedinplace

ofabreak.

2.4.2 Else

Theideathattheloopcanbeexitedexplicitlymakesthenormalterminationoftheloop

something that should be detectable too. When a while or for loop exits normally by

exhaustingtheiterationsorhavingtheexpressionbecomeFalse,itissaidtohavefallen

through.Whentheforloopintheprimenumberprogramdetectsafactor,itnowexecutes

abreakstatement,thusexitingtheloop.

What if it never does that? In that case no factor exists, and the number isprime. The

programasitstandshasaflagthatindicatesthis,butitcouldbedonewithanelseclause

ontheloop.

Theelsepartofawhileorforloopisexecutedonlyiftheloopfallsthrough;thatis,

whenitisnotexitedthroughabreak.Thiscanbequiteuseful,especiallywhentheloopis

involvedinasearch,aswillbediscussedlater.Inthecaseoftheprimenumberprogram,

anelsecouldbeusedwhenthenumberisinfactprime,asfollows:

forninrange(1,int(k/2))#DivideKbyallnumbers<K/2

ifk%n==0:#Iftheremainderis0thenn

isprime=“no”#dividesevenlyintoK:not

#prime

break

else:

isprime=“yes”#Loopnotexited:itisprime

Anelseinawhileloopoccurswhentheconditionbecomesfalse.Consideraloopthat

readsfrominputuntiltheusertypes“end”andissearchingforthename“Smith”:

inp=input()

while(inp!=“Smith”):

s=input()

ifs==“end”:

break

else:

print(“Smithwasfound”)

#Whentheprogramreachesthispointitisno

#longerknownwhetherSmithwasfound.

Ofcourse,theelseisnotrequired,andsomeprogrammersbelieveitisevenharmful.

Therearealwaysotherwaystoaccomplishthesamething.

2.5 LOOPSTHATARENESTED

Just as it is possible to have if statements nested within other if statements, it is

possible,andevenlikely,tohavealoopnestedwithinanotherloop.Anexampleofnested

forloopswouldbe:

foriinrange(0,10)

forjinrange(0,10)

print(i,j)

Theprintinthisexamplewouldexecute100times.Eachtimetheouterloopexecutes

oncetheinneroneisexecuted10times,foratotalof10*10or100iterations.Loopscan

be nested to a greater depth if necessary, and while and for loops can be nested

interchangeably.Isiteverusefultodothis?Yes,veryoften.

Sincetherehasbeenarecentdiscussionofprimenumbersandfactoring,considerthe

problemoffindthenumberwithinagivenrangethathasthegreatestnumberofdifferent

factors.Leavingout1andthenumberitself,2hasnofactors,nordoes3;4hasone(=2),5

hasnone,and6hastwo(2and3).Whichnumberbetween0and1000hasthemost?

Fromtheprimenumbergameitisclearthatthefactorscanbefoundusingaloop.Ifthe

loopisnotexitedwhenoneisfound,allofthemcanbeidentifiedand,moreimportantly

forthisproblem,counted.Foragivennumberk,thefactors can beidentifiedusing the

followingloop:

count=0;

forninrange(1,int(k/2)):#DivideKbyallnumbers<K/2

ifk%n==0:#Iftheremainderis0thenn

count=count+1

#Thenumberkhascountnumbersthatdivideevenlyintoit.

Thestatementcount=count+1hasreplacedtheisprime=“no”statementfromthe

prime number game. When the loop ends the value of count will be the number of

divisors it has. If this number is 0, then the number k is prime, by the way. Okay, the

problemhasbeensolvedforanynumberk.Nowsolveitforallnumbersbetween1and

1000andidentifythenumberwiththelargestvalueofcount(i.e.,thelargestnumberof

divisors).Thisinvolvesanotherloopenclosingthisonethatcountsfrom1to1000.

Defineavariablemaxvwhichisatanygivenmomentthenumberthathasthegreatest

numberofdivisors,andanothervariablemaxcountwhichisthenumberofdivisorsthat

maxvhas.Initiallymaxvis1andmaxcountis0(i.e.,thenumber1hasnodivisors).Now

loop between 1 and 1000 and replace maxv and maxcount whenever a new number is

foundforwhichthenumberofdivisorsisgreaterthanmaxcount.Specifically:

maxv=1

maxcount=0

forkinrange(1,1000):#Countthedivisorsforarange

count=0;

forninrange(2,int(k/2)):#DivideKbyallnumbers

#<K/2

ifk%n==0:#Iftheremainderis0

#thenn

count=count+1#Countthisdivisor

ifcount>maxcount:#Anewmaximum

maxcount=count#Savethecount

maxv=k#andthevalueitself

print(“Themostdivisorsis“,maxv,”with“,maxcount)

Theresultfor1to1000is:

Themostdivisorsis840with30

Theresultfor1to10000:

Themostdivisorsis7560with62

Bytheway,thislastversionneeded10secondstoexecute.

2.6 DRAWAHISTOGRAM

A histogram is a kind of graph. It usually represents the frequency of occurrence of

certaindiscretevalues.Commonexamplesincludetemperatureasafunctionofmonthof

theyear,orhistogramsofincomeasafunctionofyear,age,race,orgender.Drawingone

involvesknowing howmany categoriesthere areand whatthe numericalvalues arefor

each category. Then the numbers are scaled so they fit in a particular area, and the

rectanglesaredrawnsothattheheightsreflectthe relative numerical values. Figure 2.3

showssometypicalexamples.

A company wishes to plota histogram oftheir income for each quarterof 2016. The

numerical values are stored in variables Q1,Q2,Q3, and Q4 and range between 0 and 1

million.Usingfancygraphicsisnotpossibleyet,sohowcansimplehistogramsbedrawn?

Byusingtext.Ifthehistogramisdrawnsothatthebarsarehorizontalinsteadofvertical,

thenthenumberofcharactersdrawninarowcanbeusedtorepresentthe“height”ofthe

histogrambar.Usingthe“#”character,avalueof20couldbedrawnas:

Q1:####################20

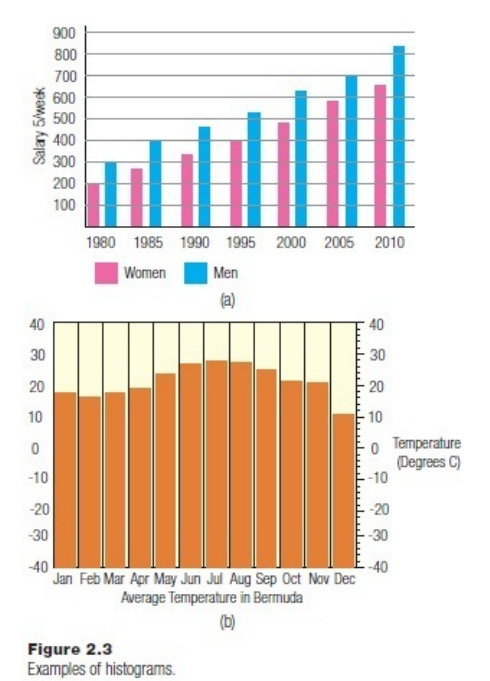
Thisisanothersituationwherealoopisnecessary.

Therearethreepartstothehistogrambarabove:thelabel,thebar,andthedatavalue.

Thelabeliseasytoprint,andintheexampletherearefourpossibilities;thesearesimply

printedatthebeginningofeachlinebeingdrawn.Thedatavalueisnotnecessary,butitis

useful for people looking at the graph to know what the exact number is. Each “#”

character drawn could represent a range of values. The histogram bar is the trick. If

numbersuptoamillionmustberepresented,thenthebarmustbescaledsothatitfitsona

line.If50charactersfitonaline,theneach“#”printedneedstorepresent1000000/50,or

20000dollars.Anotherwaytosaythisisthatevery$20000ofincomeresultsinone“#”

character being printed. How many “#” are printed for the first quarter? Q1/20000 of

them.

Aproblem:theprintfunctionprintsoutalineeverytimeitiscalled.Howcanmultiple

thingsbeprintedonaline?Happily,printhasaspecialparametertoallowthat.Thecall:

print(i,end=ꞌ!′)

willprintthevariableiandthenprintthe“!”stringfollowingthat,everytime.Normally

theprintwillplaceanendoflinecharacter(representedas“\n”)attheendofeveryline,

buttheend= clause allows the programmer to change this to whatever they like. If the

string provided is empty (contains no characters) then the print will not print anything

extra after each call, meaning specifically that no end of line will be printed. Thus, the

statement:

print(“#”,end=””)

printsone“#”characterbutnoendofline.Ifanother“#”isprinted,thenitwillcomeright

aftertheonejustprinted.Thisisexactlywhatisneededforthehistogramprogram.Aloop

thatwouldprintten“#”charactersononelinecannowbewrittenas:

foriinrange(0,10):

print(“#”,end=””)

Given that the value of the variable Q1 is between 0 and 1000000 and each 20000

shouldresultinasingle“#”characterbeingprinted,thefirstquarterhistogrambarcould

bedrawnbythefollowing:

print(“Q1:“,end=””)

forkinrange(0,int(Q1/20000)):

print(ꞌ#ꞌ,end=ꞌꞌ)

print(”“,q1)

Thisincludesallofthelabels,andtheoutputwouldlooklikethis:

Q1:########190000

A complete solution to the problem would draw the histogram for all four quarters

alongwithaheadingforthegraph.Theoutputmightlooklikethis:

EarningsforWidgetCorpfor2016

Dollarsforeachquarter

==============================

Q1:#########190000

Q2:#################340000

Q3:###########################################873000

Q4:#####################439833

Exercise5attheendofthechapterinvolvesfinishingthisprogram.

2.7 LoopsinGeneral

Theconceptofaloopinaprogramminglanguagehasbeendiscussedformanyyears

andhasalargedegreeofboththeoryandpracticeunderlyingit.Theoriginal“loop”wasa

branchorgoto,wherethetopoftheloopwasidentifiedwithanaddressorlabelandatthe

bottom there was a statement that said to “go to” or transfer control to that location.

Examplesofthisare:

label1:add1tox12x=x+1

subtract2fromminmin=min-2

branchtolabel1goto12

Branchesweretypicalofassemblylanguageprogramming,whereeachlineofcodewas

one actual computer instruction. The goto statement was introduced in the first real

programminglanguageFORTRAN,butwas quicklysupplementedbyamorestructured

loopconstruct,thedostatement.Bothbranchandgotostatementscanbeconditional.

Variouskindsofloophavebeendevelopedovertheyears,andthemostcommonlyused

variationisthewhileloop.Theorysaysthattheonlykindthatisneeded,andprobablythe

most general, is the loop statement as defined in the Ada language. It is essentially an

infinite loop that allows escapes at multiple and various pointson specified conditions.

Thebasicsyntaxis:

loop

exitwhencondition1;

Statements…

…

exitwhencondition2;

endloop;

Anexitatthetopoftheloopisawhileloop.Anexitattheendcouldbearepeat…

until as in Pascal or C++, and it is a simple matter to declare and initialize a control

variableandtesttheconditiontoimplementaforloop.Everythingispossiblewiththis

loopsyntax.

When specifically using Python, a while loop is all that is needed. If the range is an

integerone,thentheloop:

foriinrange(a..b):

isthesameastheloop:

i=a

whilei<b:

…

i=i+1

This loop has an initialization, a condition, and an increment. As individual entities

thesearesomewhathiddeninPython,beingmaskedbythesyntax, but theloopcontrol

variabletakesonthefirstvaluethefirsttimetheloopisexecuted(initialization),iterates

throughtheselections(increment),andterminatesafteritselectsthefinalone(condition).

The loop control variable is not really what gets incremented; what is incremented is a

countthatindicateswhichoftheitemsinthetupleiscurrentlybeingused.Intheloop:

foriin(“red”,“yellow”,“green”):

thevariableitakesonthevalues“red,”“yellow,”and“green,”butwhatgetsincremented

eachtimethroughtheloopisanindicationofwhichpositioninthetupleisrepresentedby

i.Thevalue“red”is0,“yellow”is1,and“green”is2andacountimplicitlystartsat0and

stepsuntil2assigningvaluestoi.Thiskindofloopissimilartothatfoundinthelanguage

PHP,andisalevelofabstractionabovethoseinJavaandC++.

2.8 EXCEPTIONSANDERRORS

Computersdonot,asageneralrule,makemistakes.Likeotherhuman-designedand-

constructeddevicessuchascarsandstoves,computerscanbeawkwardtouse,canhave

designfeaturesthatdon’tturnoutasexpected,andcanevenbreakdowntooquickly.But

theydonotmakemistakes.Acomputerprogram,ontheotherhand,almostcertainlyhas

mistakesorbugscodedwithinit.Consumersdon’tusuallymakeadistinctionbetweenthe

computerandthesoftwarethatrunsonit,butprogrammersandengineersmust.Whena

computer program does not work properly, a programmer must exhaust all ways the

programcouldbewrongbeforelookingatanerrorinthecomputeritself.

Creatingacorrectprogramisdifficultformanyreasons.Firstofall,beforeanycodeis

written,theproblemtobesolvedmustbeclearlyunderstood,anditmustbethecorrect

problem.Solvingthe wrongproblem isa prettycommon error,but can’tbe detectedor

correctedbythecomputer.Commonexamplesofthissortoferrorcomefromstatingthe

problem in English (or a human language of any description) where errors in

understanding occur. “Find the average of the first ten integers,” for example, is a little

ambiguous. Is the first integer 0 or 1? What is meant by “average”—the mean or the

median? Computer programmers tend to be quite literal, and so what they think is the

answer will be written into the code, and then they will argue for that answer as being

correct.Itisveryimportanttorealizethat,whatevertheliterallycorrectansweris,thereal

correctanswerisbasedonthecorrectunderstandingoftheproblem.Sometimesitisstated

badly, but no matter whose fault the problem is, the job of fixing it will lie with the

programmer. Sometimes a little time at the beginning clarifying the question can save

moretimelater,andstickingwithanoverlypedanticinterpretationwillcauseproblemsin

thelongrun.

Acorrectprogramalsodependsontheprogrammerbeingabletoidentifyallpossible

circumstances that can occur and knowing how to deal with each of them. Failing to

handleonepossiblesituationisanerror,andtheprogramwillbehaveunpredictablyifthat

situation occurs in practice. Statements that handle errors appear all though real (in the

fieldorcommercial)code.Infact,itiscommonthattherearemorestatementsthatdetect

anddealwitherrorsthancodethatactuallycomputesananswer.Onethingthatshouldbe

remembered:alllinesofthecodeneedtobetested.Inverylargeprogramsthismaybe

impossible,buteverylineofcodethathasneverbeenexecutedisapotentialerror.Testas

manyaspossible,includingtheerrordetectioncode.

User input is a frequent cause of mistakes in programs. It’s not that the user is the

problem; the programmer must anticipate all possible ways that a user can enter data.

Thereisusuallyonecorrectwaybutmanyerroneousones,anditisimpossibletopredict

whatauserwillenterfromakeyboardinresponsetoanyrequest.Similarly,thecontents

of a file may not be what the programmer expects. File formats are standards, but

sometimes there are variations and at other times a user may have entered the data

improperly.Whilethemistakeisonthepartoftheuser,itisalsoaprogrammingmistake

if the error is not detected and is allowed to have an impact on the execution of the

program.

Programmerstendtomakeassumptionsabouttheproblem.Itisacommonmistaketo

think“thissituationcanneverhappen”andthenignoreit,howeverunlikelythesituation

seems. Testing every statement for everything that could possibly go wrong may be

impossible,buttestingforthegeneralsituationmaybepossible.Itwouldbegreattobe

abletosay“ifanystatementinthissectionofcodedividesbyzero,”or“ifanyvariables

inthiscodehavethewrongtype,”thendosomeparticularthing.

Sinceitisimpossibletowriteaprogramofanylengthwithouttherebeingcodingerrors

of some kind included, a step towards a solution may be to check all data before it is

operated on to ensure the pending operation is going to succeed. For instance, before

performingthedivisiona/b,testtomakesurethatbisnotzero.Thisdependsontheerror

being at least in principle predictable. Most modern languages, Python included, have

implemented a way to catch errors and permit the programmer to handle them without

havingtestsbeforeeachstatementorexpression.Thisfacilityiscalledtheexception.

The word exception communicates a way to think about how errors will be handled.

Somecodeislegalandcalculatesadesiredvalueexceptundercertaincircumstances,or

unless some particular thing happens. The way it works is that the program tries to

perform some operation and errors are allowed to occur. If one does, the computer

hardwareoroperatingsystemdetectsitandtellsPython.Theprogramcannotcontinuein

thewaythatwasplanned,whichiswhythisiscalledanexception.Theprogrammercan

tellPython whatto do if specific errorsoccur bywriting some codethat dealswith the

problem.Iftheprogrammerdidnotdothis,thenthedefaultisforPythontoprintanerror

messagethatdescribestheerrorandthenstopexecutingtheprogram.Errormessagescan

beseenasafailureonthepartoftheprogrammertohandleerrorscorrectly.

A simple exampleis the divide byzero error mentioned previously.If the expression

a/bistobeevaluated,thevalueofbcanbecheckedtomakesureitisnotzerobeforethe

divisionisdone:

ifb!=0:

c=a/b

Thiscanbetediousfortheprogrammerifalotofcalculationsarebeingdone,andcan

beerrorprone.Theprogrammermayforgettotestoneortwoexpressions,especiallyif

engagedinmodificationsortesting.Usingexceptionsisamatterofallowingtheerrorto

happenandlettingthesystemtestfortheproblem.Thesyntaxisasfollows:

try:

c=a/b

except:

c=1000000

The try statement begins a section of code within which certain errors are being

handledbytheprogrammer’scode.Afterthatstatement,codeisindentedtoshowthatitis

partof the try region. Nearly any code can appear here, but the try statement must be

endedbeforetheprogramends.

Theexceptstatementconsistsofthekeywordexceptand,optionally,thenameofan

error.TheerrorsarenamedbythePythonsystem,andthecorrectnamehastobeused,but

if no error name is given as in this example, then any error will cause the code in the

exceptstatementtobeexecuted.Notspecifyinganamehereisanimplicitassumptionthat

eitheronlyonekindoferrorcouldpossiblyoccurorthatnomatterwhaterrorhappens,the

samecodewillbeusedtodealwithit.Specifyinganunrecognizednameisitselfanerror.

Thenamecanbeavariable,butthatvariablemusthavebeenassignedarecognizederror

namebeforetheerroroccurs.Thecodefollowingtheexceptkeywordisindentedtoo,to

showthatitispartoftheexceptstatement.Thisisreferredtobyprogrammersasanerror

handler,andisexecutedonlyifthespecifiederroroccurs.

Thisappearstobeevenmoreverbosethantestingb,butanynumberofstatementscan

appearbetweenthetryandtheexcept.Thissectionofcodeisnowprotectedfromdivide

byzeroerrors.Ifanyoccur,thencodefollowingtheexceptstatementwillbeexecuted,

otherwisethatcodewillnotexecute.Ifothererrorsoccur,thenthedefaultactionwilltake

place—anerrormessagewillbeprinted.

Testingspecificallyforthedividebyzeroerrorcanbedonebyspecifyingthecorrect

errornameintheexceptstatement:

try:

c=a/b

exceptZeroDivisionError:

c=1000000

Morethanonespecificerrorcanbecaughtinoneexceptstatement:

try:

c=a/b

except(ValueError,ZeroDivisionError):

c=1000000

Clearly (ValueError, ZeroDivisionError) is a tuple, and could be made longer and

couldbeassignedtoavariable.

Also,therecanbemanyexceptstatementsassociatedwithasingletry:

try:

c=a/b

exceptValueError:

c=0

exceptZeroDivisionError:

c=1000000

And,aswasmentioned,avariablecanholdthevalueoftheerrortobecaught:

k=ZeroDivisionError

try:

c=a/b

exceptk:

c=1000000

Finally,the exceptionnamecan be left outaltogether.Inthat caseany exceptionthat

occurswillbecaughtandtheexceptioncodewillbeexecuted:

try:

c=a/b

except:

c=0

2.8.1 Problem:AFinalLookatGuessaNumber

Thefinalversionoftheprograminvolvingguessinganumberlookslikethis:

choice=7

print(“Pleaseguessanumberbetween1and10:“)

playerchoice=int(input())

ifchoice==playerchoice:

print(“Youwin!”)

else:

print(“Sorry,youlose.”)

Usingexceptionsandwhathasbeendiscussedabouterrorchecking,thisprogramcan

beimproved.First,iftheuserenterssomethingthatisnotaninteger,itisanerror.This

should be caught using an exception. Also, rather than forcing the player to run the

programagain,aloopcanbeusedtoaskforanotherguess.Theinputshouldbewithin

the try statement. The except statement should print an error message, and the entire

collectionshouldbewithinaloopthatcontinuestoasktheusertoguessanumber.Hereis

abetterversion:

choice=7

guessed=False#Hastheuserguessedareasonable

number?

whilenotguessed:#Keeptryinguntiltheyhave

print(“Pleaseguessanumberbetween1and10:“)

try:#Catchpotentialinputerrors

playerchoice=int(input())

guessed=True#Successsofar

except:#Anerroroccurred.

print(“Sorry,yourguessmustbeaninteger.”)

ifchoice==playerchoice:#Correctguess?

print(“Youwin!”)

else:

print(“Sorry,youlose.”)

ThevariableguessedissettoTruewhenasuccessfulguessismade,andthisstopsthe

loopfromrepeating.Iftheuserentersarealnumberorastring,theexceptioniscaught

beforethathappens, theerror messageis printed,and theuser is askedto enteranother

guess.

Whatelseiswrongwiththiscode?Well,theuserisaskedtoenteranumberbetween1

and10,butthatvalueisnevercheckedtoseeifitisOK.True,ifitfallsoutsidetherange,

then it will always be an incorrect guess and the player will lose. It’s a penalty for not

payingattentiontotherules.Aprogramshouldwheneverpossiblegivetheuserasmuch

information as is reasonable, so it would be better to check the value of the variable

playerchoiceandgiveanerrormessageifitisoutofrange.Thebestwaytodothisisto

placethecheckaftertheexceptstatementatthebottomoftheloop,andsetthevariable

guessedtoFalseiftheguessisanimproperone.Thentheloopwillrepeatandtheplayer

willgetanotherguess.

Thisversionoftheprogramis:

choice=7

guessed=False

whilenotguessed:

print(“Pleaseguessanumberbetween1and10:“)

try:

playerchoice=int(input())

guessed=True

except:

print(“Sorry,yourguessmustbeaninteger.”)

ifplayerchoice<10orplayerchoice>10:#Istheguess

#in1..10?

print(“Yourguesswas”,playerchoice,”whichisoutofrange.”)

guessed=False#Nope.Guessagain

ifchoice==playerchoice:

print(“Youwin!”)

else:

print(“Sorry,youlose.”)

2.9 SUMMARY

Theabilitytorepeatacollectionofoperationsisanessentialpartofanyprogramming

language.Thewhileloophasaconditionatthebeginning,andsolongasthatconditionis

true,thestatementscomprisingtheloopwillbeexecutedrepeatedly.Theforloophasan

explicitlistofitemsforwhichtheloopwillbeexecuted,orarangeofnumericalvalues

thatdefinehowmanytimesthecodewillberepeated.

Most problems that are solved using a computer program have some degree of

repetitionimplicitintheimplementation,andsomecomputeralgorithmsarequiteexplicit

abouthowtheiterationsaretobesetupandhowmanyareneededtosolvetheproblem

(See:Exercises3and4).

CertainerrorsthatcanoccurinprogramcanbedetectedautomaticallybyPython.Ifthe

programmerdoesnotspecifyotherwise,thentheseerrorscauseamessageandpremature

program termination. The try-except statement allows the programmerto handle errors

withoutendingtheprogram, andpermitsbetter communicationofthekind oferrorthat

occurred,inthecontextoftheprogram,totheprogrammeroruser.

Exercises

1.Giventhefollowingdefinitions:

var1=12

var2=100

var3=-2

var4=0

Whatisprintedbythefollowingwhileloops:

a.whilevar1<var2:

print(var1)

var1=var1+30

b.whilevar1<var2:

print(var1)

var1=var1*2

c.whilevar1>0:

var4=var4+1

var1=var1–1

print(var1,var2)

d.whilevar1>0:

var4=var4+1

var1=var1–var4

print(var1,var2)

e.whilevar1<var3:

print(”*”,end=””)

var3=var3+2

f.whilevar2>var1*var4:

var1=var1+1

var4=var4+1

print(var1,var2)

2.Whatwouldbeprintedbythefollowingforloops:

a.foriinrange(1,10):

print(i)

b.foriin(1,10):

print(i)

c.foriin(“red”,“green”,“blue”):

print(i)

d.foriinrange(0,10):

forjinrange(1,10):

ifi==j:

print(i)

e.foriinrange(0,10):

forjinrange(0,50):

ifi*i==j:

print(i)

f.foriin(0,10):

i=i*2

print(i)

g.foriinrange(1,10):

forjinrange(1,i):

print(j,end=””)

print()

h.oriinrange(0,10):

i=i+1

forjinrange(1,i):

print(j,end=””)

print()

3.TheGreekmathematicianZeno(c.450BCE)iscreditedwithcreatingtheparadoxof

theTortoiseandAchilles.AtortoisechallengedthegreatheroandathleteAchillestoa

footrace.Allthetortoiseaskedwasaten-yardheadstart.Theideawasthatoncethe

racebegan,Achillescouldruntheten-yardheadstartinasmalltime;however,inthat

sametimethetortoisewouldmoveforwardasmallamount,perhapsayard.When

Achillesmadeupthatyard,thetortoisewouldhavemovedaheadagainasmall

distance;andsoon.ThelogicwasthatAchillescouldnevercatchup.The

misunderstandinghereisthataninfinitelylongseriesofnumberscanadduptoafinite

value.WriteasmallPythonprogramthatsumsthenumbers½,¼,⅛,1/16,andsoon

for20iterationsandsuggestwhatthesumwouldbeifitwerecarriedtoaninfinite

numberofiterations.

4.OnewaytocalculatethesquarerootofanumberistouseNewton’smethod.This

startswithaninitialguess:ifthesquarerootofxisbeingcomputed,thenafairinitial

guessgwouldbex/2.Successiveestimatesaregivenbytheexpression:

newg=(g+x/g)/2

Successiveestimatesarenearerandnearertotheactualsquareroot.Writeaprogramto

computethesquarerootofanumberthatisenteredfromthekeyboard.

5.CompletetheprogramthatdrawsahistogramfortheearningsofWidgetCorpforfour

quartersof2016.Earningsare:

a.190000

b.340000

d.873000

d.439833

6.ModifytheprograminExercise5sothatthedataforthefourquartersisreadfromthe

terminal(i.e.,enteredbytheuserfromthekeyboard).Testitforthevalues:

a.900000

b.874000

d.200000

d.439000

7.ModifythesolutiontoExercise6inChapter1(makingchange)sothatitmakes

effectiveuseofaforloop.Theprogramshouldstillreadanumberbetween1and99,

whichisanamountofchangetobegiven,andprintthecoinvaluesthatwouldbe

used.Modifyittonotuse50-centpieces,becausenobodyhasthoseanymore.

8.Convertthefollowingforloopsintotheequivalentwhileloop:

a.foriinrange(1,10):

print(i,i*i)

b.sum=0

foriin(range(10,0,-1):

sum=sum+i

print(i,sum)

9.AgoodsolutiontoExercise4above(squareroot)woulddetectnegativenumbersand

printamessagetotheeffectthatsquarerootsofnegativenumbersdonotexist(notas

realnumbers,anyway).ModifythesolutiontoExercise4touseanexceptiontodeal

withthatsituation,andhandleotherpotentialerrors.

NotesandOtherResources

Online tutorial on Python loops:

http://www.tutorialspoint.com/python/python_loops.htm

Cornell University summary of if statements and loops:

http://www.cs.cornell.edu/courses/cs1130/2012sp/1130selfpaced/module2/module2part1/ifloop.html

Sthurlow.com,Loops,loops,loops…,http://sthurlow.com/python/lesson04/

1.HenryFordandSamuelCrowther.(1922).MyLifeandWork,GardenCity

Publishing,GardenCity,NY,http://www.gutenberg.org/ebooks/7213

2.DavidBeazleyandBrianK.Jones.PythonCookbook,3rdEdition:Recipesfor

MasteringPython3,http://www.onlineprogrammingbooks.com/python-cookbook-

third-edition/

CHAPTER3

SEQUENCES:STRINGS,TUPLES,AND

LISTS

3.1Strings

3.2TheTypeBytes

3.3Tuples

3.4Lists

3.5SetTypes

3.6Summary

Inthischapter

ItwasmentionedinChapter2thatforloopsinPythonaredifferentfromthosefoundin

manyotherlanguages.InJavaandC++,aforloophas a veryexplicitincrement;a for

statementlookslikethisinJava:

Fromthisitcanbeinferredthatthevariableiwillstartoutas0,andsolongasiisless

than10theloopwillcontinue.Aftereachiterationthevalueofiwillbeincreasedby1,

andthentheconditionistestedagain.

InPythontheiterationismoreimplicit,withtheloopcontrolvariabletakingononeofa

setofvaluesinturn.Thereisanimplicationhere,too,thatthereisakindofthing,atype

thatavariablecanhave,thatamountstoalistorsequenceofother,simplerthings.Thisis

true, and using variables having these types is an essential part of writing useful and

effectivecode. Pythonoffersstrings,tuples, and lists as objects that consist of multiple

parts.Theyarecalledsequencetypes.Anintegerorafloatisasinglenumber,whereasa

sequencetypeconsistsofacollectionofitems,eachofwhichisanumberoracharacter.

Eachmemberofasequenceisgivenanumberbasedonitsposition:thefirstelementin

thesequenceisgiven0,thesecondis1,andsoon.Thisisafundamentaldatastructurein

Pythonandhasinfluencedthesyntaxofthelanguage.

Stringsarefamiliarobjectsandhavebeenusedinprogramsalready,sothediscussion

willbeginthere.

3.1 Strings

Astringis asequenceofcharacters. Thewordsequenceimpliesthattheorderofthe

characterswithinthestringmatters,andthatiscertainlytrue.Stringsmostoftenrepresent

the way that communication between a computer and a human takes place. Human

languageconsistsofwordsandphrases,andeachwordorphrasewouldbeastringwithin

a program. The order of the characters within a word matters a great deal to a human

because some sequences are words and others are not. The string “last” is a word, but

“astl” is not. Also, the strings “salt” and “slat” are words and use exactly the same

charactersas“last”butinadifferentorder.

Becauseordermatters,therepresentationofastringonacomputerwillimposeanorder

onthecharacterswithin,andsotherewillbeafirstcharacter,asecond,andsoon,andit

shouldbepossibletoaccesseachcharacterindividually.Astringwillalsohavealength,

whichisthenumberofcharacterswithinit.

Acomputerlanguagewillprovidespecificthingsthatcanbedonetosomethingthatisa

string:thesearecalledoperations,andatypeisdefinedatleastpartlybywhatoperations

canbedonetosomethingofthattype.Becauseastringrepresentstextinthehumansense,

theoperationsonstringsshouldrepresentthekindsofthingsthatwouldbedonetotext.

This would include printing and reading, accessing any character, linking strings into

longerstrings,searchingastringforaparticularword,andsoon.

The examples of code written so far use only string constants. These are simply

characters enclosed in either single or double quotes. Assigning a string constant to a

variablecausesthatvariabletohavethestringtypeandgivesitavalue.Sothestatements:

name=“JohnDoe”

address='121SecondStreet'

causethevariablesnamednameandaddresstobestringswiththeassignedvalue.Note

thateithertypeofquotecanbeused,butastringthatbeginswithadoublequotemustend

withone.

Astringbehavesasifitscharactersarestoredasconsecutivecharactersinmemory.The

first character in a string is at location or index 0, and can be accessed using square

bracketsafterthestringname.Usingthedefinitionsabove,name[0]is“J”andname[5]=

“D.”Ifanindexisspecifiedthatistoolarge,itresultsinanerror,becauseitamountstoan

attempttolookpasttheendofthestring.

How many characters are there in the string name? The built-in function len() will

returnthelengthofthestring.Thelargestlegalindexisonelessthanthisvalue:thefirst

characterofastringnamehasindex0,andthefinalonehasindex7;thelengthis8.Thus,

any index between 0 and len(name)-1 is legal. The following code prints all of the

charactersofnameandcanbethoughtofasthebasicpatternforcodethatscansthrough

thecharactersinstrings:

foriinrange(0,len(name)):

print(name[i],end=””)

Thismay be a little confusing, but rememberthat the range(0,n)does notinclude n.

Thislooprunsthroughvaluesofifrom0tolen(name)-1.

Somelanguageshaveacharactertype,butPythondoesnot.Astringoflengthoneis

whatPython uses instead.Acomponent ofa string istherefore another string.The first

character of the string name, which is name[0], is “J,” the string containing only one

character.

3.1.1 ComparingStrings

Twostringscanbecomparedinthesamemannerasaretwointegersorrealnumbers,

by using one of the relational operators ==, !=, <, >, <= or >=. What it means for two

stringstobeequalissimpleandreasonable:ifeachcorrespondingcharacterintwostrings

isthesame,thenthestringsareequal. That is,forstringsaandb,ifa[0]==b[0], and

a[1]==b[1]andsoontothefinalcharactern,anda[n]==b[n],thenthetwostringsaand

bareequalanda==b.Otherwise,a!=b.Bytheway,thisimpliesthatequalstringshave

thesamelength.

What about inequalities? Strings in real life are often sorted in alphabetical order.

Namesinatelephonebook,filesinadoctor’soffice,andbooksinastore:thesetendto

appear in a logical order basedon the alphabet. This is also true in Python. The string

“abc” is less than the string “def,” for example. Why? Because the first letter in “abc”

comesbeforethefirstletterin“def”;inotherwords,“abc”[0]<“def”[0].Yes,characters

instringconstantscanbeaccessedusingtheirindex.

Astrings1islessthanstrings2ifallcharactersfrom0throughkinthetwostringsare

equal,ands1[k+1]<s2[k+1].Sothefollowingstatementsaretrue:

“abcd”<“abce”

“123”<“345”

“ab”<“abc”

Inthelastexample,thespacecharacter“.”issmallerthan(i.e.,comesbefore)theletter

“c.”Whatifthestringsarenotthesamelength?Thestring“ab”<“abc”,soiftwostrings

areequaltotheendofoneofthem,thentheshorteroneisconsideredtobesmaller.These

rulesareconsistentsofarwiththosetaughtingradeschoolforalphabetization.Trailing

spaces do not matter. Leading spaces can matter, because a space comes before any

alphabeticcharacter;thatis,

““<“a”.Thus“ab”>“z”.

Digitscomebeforelowercaseletters.“1”<“a”,and“1a”<“a1”.Mostimportantly,

uppercase comes before lowercase, so “John” < “john”. All of these rules are

consistent with those that secretaries understand when filing paper documents. As an

examplethatcomparesstrings,considerthefollowing:

a=“J”

b=“j”

c=“1”

ifb<c:

print(“Lcase<numbers”)

else:

print(“Lcase>numbers”)

ifa<c:

print(“Ucase<numbers”)

else:

print(“Ucase>numbers”)

Thisresultsintheoutput:

Lcase>numbers

Ucase>numbers

Problem:DoesaCityName,EnteredattheConsole,Come

beforeoraftertheNameDenver?

This involves reading a string and comparing it against the constant string “Denver.”

Lettheinputstringbereadintoavariablenamedcity.Thentheansweris:

city=input()

ifcity<“Denver”:

print(“ThenamegivencomesbeforeDenverinan

alphabeticlist”)

elifcity>“Denver”:

print(“ThenamegivencomesafterDenverinan

alphabeticlist”)

else:

print(“ThenamegivenwasDenver”)

If“Chicago”istypedattheconsoleasinput,theresultis:

Chicago

ThenamegivencomesbeforeDenverinanalphabeticlist

However,ifcaseisignoredand“chicago”istypedinstead,thentheresultis:

chicago

ThenamegivencomesafterDenverinanalphabeticlist

because, of course, the lowercase “c” comes (as do all lowercase letters) after the

uppercase“D”atthebeginningof“Denver.”

3.1.2 Slicing–ExtractingPartsofStrings

Toaperson,astringusuallycontainswordsandphrases,whicharesmallerpartsofa

string. Identifying individual words is important. To Python this is true also. A Python

programconsistsofstatementsthatcontainindividualwordsandcharactersequencesthat

each have a particular meaning. The words “if,” “while,” and “for” are good examples.

Individualcharacterscanbereferencedthroughindexing,butcanwordsorcollectionsof

charactersbeaccessed?Yes,ifthe

location(index)ofthewordisknown.

Problem:Identifya“Print”StatementinaString

Thestatement:

print(“Lcase<numbers”)

appearsintheexampleprogramabove.Thiscanbethoughtofasastring,andassignedto

avariable:

statement='print(“Lcase<numbers”)'

Question:isthisaprintstatement?Itisifthefirstfivecharactersaretheword“print.”

Eachofthosecharacterscouldbetestedindividuallyusing:

ifstatement[0]=='p':

ifstatement[1]=='r':

ifstatement[2]=='i':

ifstatement[3]=='n':

ifstatement[4]=='t':

ifstatement[5]=='':

#Thisisaprintstatement.

Thisisprettyugly,andissomethingthatisneededoftenenoughthatPythonoffersa

nicerway to do it. A slice is a set of continuous characters within a string. This means

their indices are consecutive, and they can be accessed as a sequence by specifying the

rangeofindiceswithinbrackets.Thesituationaboveconcerningtheprintstatementcould

bedonelikethis:

ifstatement[0:5]==“print”:

Thesliceheredoesnotincludecharacter5,butis5characterslongincludingcharacters

0through 4 inclusive.Aslice fromitoj(i.e.,x[i:j]) does not include character j.This

meansthatthefollowingstatementsproducethesameresult:

fname[0]

fname[0:1]

Ifthefirstindexisomitted,thenthestartindexisassumed,sothestatement:

ifstatement[0:5]==“print”:

isthesameas:

ifstatement[:5]==“print”:

Ifthesecondindexisomitted,thenthelastlegalindexisassumed,whichistosaythe

indexofthefinalcharacter.Sotheassignment:

str=statement[6:]

results in the value of str being “(“Lcase < numbers”).” Both indices can be omitted,

which does sound silly, but really just means from the first to the last character, or the

entirestring.

3.1.3 EditingStrings

Pythondoesnotallow themodificationofindividual partsofa string.Thatis,things

like:

str[3]=“#”

str[2:3]=“..”

are not allowed. So how can strings be modified? For example, consider the string

variable:

fname=“image”

IfthisissupposedtobethenameofaJPEGimagefile,thenitmustendwiththesuffix

“.jpg.”

Problem:CreateaJPEGFileNamefromaBasicString

Thestringfnamecanbeeditedtoendwith“.jpg”inafewways,buttheeasiestoneto

useistheconcatenationoperator“+’.

Toconcatenatemeans“tolinkorjointogether.”Ifthevariablesaandbarestrings,then

a+b is the string consisting of all characters in a followed by all characters in b; the

operator “+” in this context means to concatenate, rather than to add numerically. The

designers of Python and many other languages that implement this operator think of

concatenationasstringaddition.

Tousethistocreatetheimagefilename,simplyconcatenate“.jpg”tothestringfname:

fname=fname+“.jpg”

Theresultisthatfnamecontains“image.jpg.”

File suffixes are very often the subject of string manipulations and provide a good

example of string editing. For instance, given a file name stored as a string variable

fname,isthesuffix“.jpg”?Basedontheprecedingdiscussion,thequestion

canbeansweredusingasimpleifstatement:

iffname[len(fname)-4:len(fname)]=='.jpg':

Usingasliceitcouldalsotaketheform:

iffname[len(fname)-4:]==“.jpg”

Avaluablethingtoknowisthatnegativeindicesindexfromtheright-handsideofthe

string;thatis,fromtheend.Sofname[-1]isthefinalcharacterinthestring,fname[-2]is

theoneprevioustothat,andsoon.Thelast4characters,thesuffix,wouldbecapturedby

usingfilename[-4:].

Problem:ChangetheSuffixofaFileName

Some individuals use the suffix “.jpeg” instead of “.jpg.” Some programs allow this,

othersdonot.Somecodethatwoulddetectandchangethissuffixwouldbe:

iffname[len(fname)-5:]==“.jpeg”:#identfythejpeg

#suffix

fname=fname[0:len(fname)-5]#removethelastfive

#characters

fname=fname+“.jpg”#appendthecorrect

#suffix

Problem:ReversetheOrderofCharactersinaString

There are things about any programming language that could be considered to be

“idioms.” These are things that a programmer experienced in the use of that language

wouldconsidernormaluse,butthatothersmightconsiderodd. This problemexposesa

Python idiom. Given what is known so far about Python, the logical approach to string

reversalmightbeasfollows:

#cityhasalegalvalueatthispoint

k=len(city)

foriinrange(0,len(city)):

city=city+city[k-i-1]

city=city[len(city)//2:]

Thisreversesthestringnamedcitythatexistspriortotheloopandcreatesthereversed

string.Itdoessointhefollowingway:

1.Letibeanindexintothestringcity,startingat0andrunningtothefinalcharacter.

2.Indexacharacterfromtheendofthestring,startingatthefinalcharacterand

steppingbackwardsto0.Sincethelastcharacterislen(city)andthecurrentindexis

i,thecharactertobeusedinthecurrentiterationwouldbek-i-1wherekisthe

lengthoftheoriginalstring.

3.Appendcity[k-i-1]tothenendofthestring.Alternatively,anewstringrscouldbe

createdandthischaracterappendedtoitduringeachiteration.

4.Afterallcharactershavebeenexamined,thestringcitycontainstheoriginalstring

at the beginning and the reversed string at the end. The first characters can be

removed,leavingthereversedstringonly.

AnexperiencedPythonprogrammerwoulddothisdifferently.Thesyntaxfortakinga

slicehasavariationthathasnotbeendiscussed;athirdparameterexists.Astringslicecan

beexpressedas:

myString[a:b:c]

whereaisthestartingindex,bisthefinalindex+1,andcistheincrement.

Increment?If:

str=“Thisstringhas30characters.”

Thenstr[0:30:2] is“Ti tighs3hrces,” which isevery secondcharacter.The increment

representsthewaythestringissampled,thatis,everyincrementcharacteriscopiedinto

theresult.Mostrelevanttothecurrentexample,theincrementcanbenegative.Theidiom

forreversingastringis:

print(str[::-1])

Ashasbeenexplained,thevalueofstr[:]isthewholestring.Specifyinganincrementof

-1impliesthatthestringisscannedfrom0totheend,butinreverseorder.Thisisfarfrom

intuitive,butisprobablythewaythatanexperiencedPythonprogrammerwouldreversea

string.Anyprogrammershouldusethepartsofanylanguagethattheycomprehendvery

well,andshouldkeepinmindthelikelyskillsetofthepeoplelikelytoreadthecode.

Problem:IsaGivenFileNameThatofaPythonProgram?

APythonprogramterminateswiththesuffix“.py.”Anobvioussolutiontothisproblem

istosimplylookatthelast3charactersinthestringstoseeiftheymatchthatsuffix:

ifs[len(s)-3:len(s)]=='.py':

print(“ThisisaPythonprogram.”)

Perhaps.Butis“PROGRAM.PY”alegalPythonprogram?Ithappensthatitis.Sois

“program.Py”and“program.pY.”Whatcanbedonehere?

3.1.4 StringMethods

A good way to do the test in this case is to convert the suffix to all upper- or all

lowercase before doing the comparison. Comparing against “.py” means converted to

lowercase,whichisdonebyusingabuilt-inmethodnamedlower:

s1=s[len(s)-3:len(s)]

ifs1.lower()=='.py':

print(“ThisisaPythonprogram.”)

Thevariables1isastringthatwillcontainthefinal3charactersofs.Theexpression

s1.lower()createsacopyofs1inwhichallcharactersarelowercase.It’scalledamethod

todistinguishitfromafunction,buttheyareverysimilarthings.Youshouldrecallthata

method is simply a function that belongs to one type or class of objects. In this case

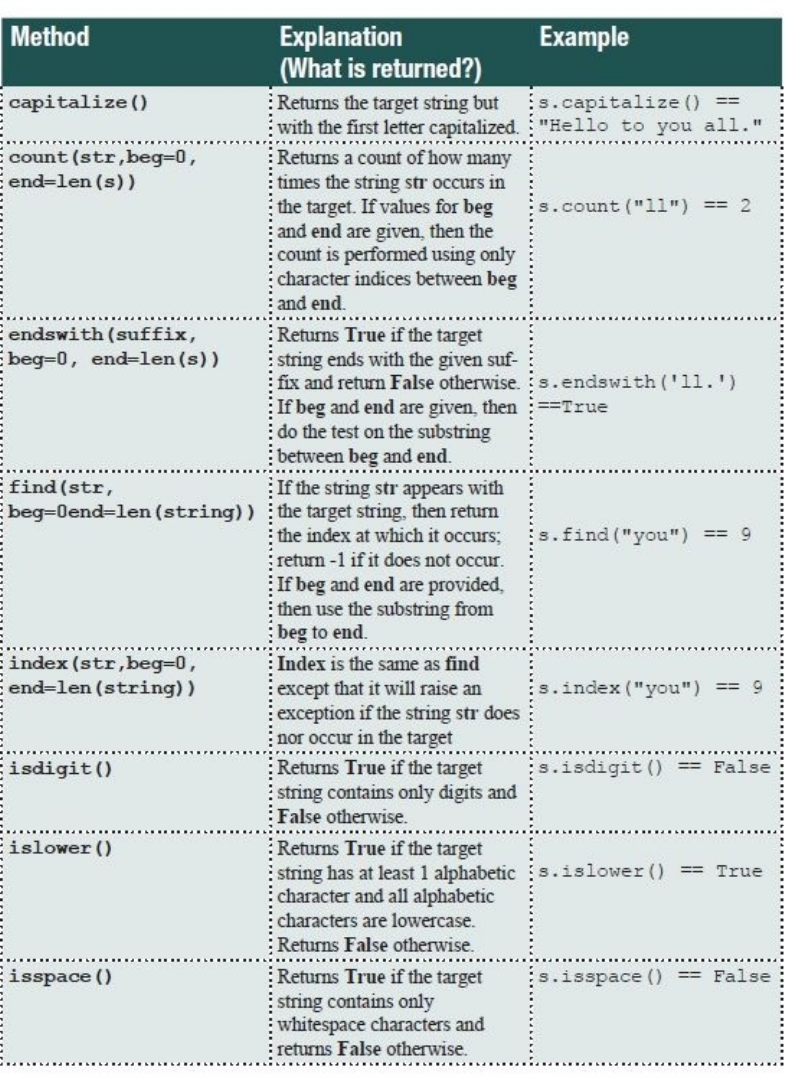
lower() belongs to the type (or class) string. There could be another method named

lower() that belongs to another class and that did a completely different thing. The dot

notationindicatesthatitisamethod,andwhatclassitbelongsto:thesameclassofthings

thatthevariablebelongsto.Inaddition,thevariableitselfisreallythefirstparameter;if

lowerwereafunction,thenitmightbecalledbylower(s1)insteadofs1.lower().Inthe

lattercase,the“.”isprecededbythefirstparameter.

Stringsallhavemanymethods.Inthetablebelowthevariablesisthe

targetstring,theonebeingoperatedupon.Thismeansthatthemethodnamesbelowwill

appearfollowing“s.,”asins.lower().Letthevalueofsbegivenby

s=“hello toyou all.” Thesemethodsareintendedto providetheoperationsneededto

makethestringtypeinPythonfunctionasamajorcommunicationdevicefromhumansto

aprogram.

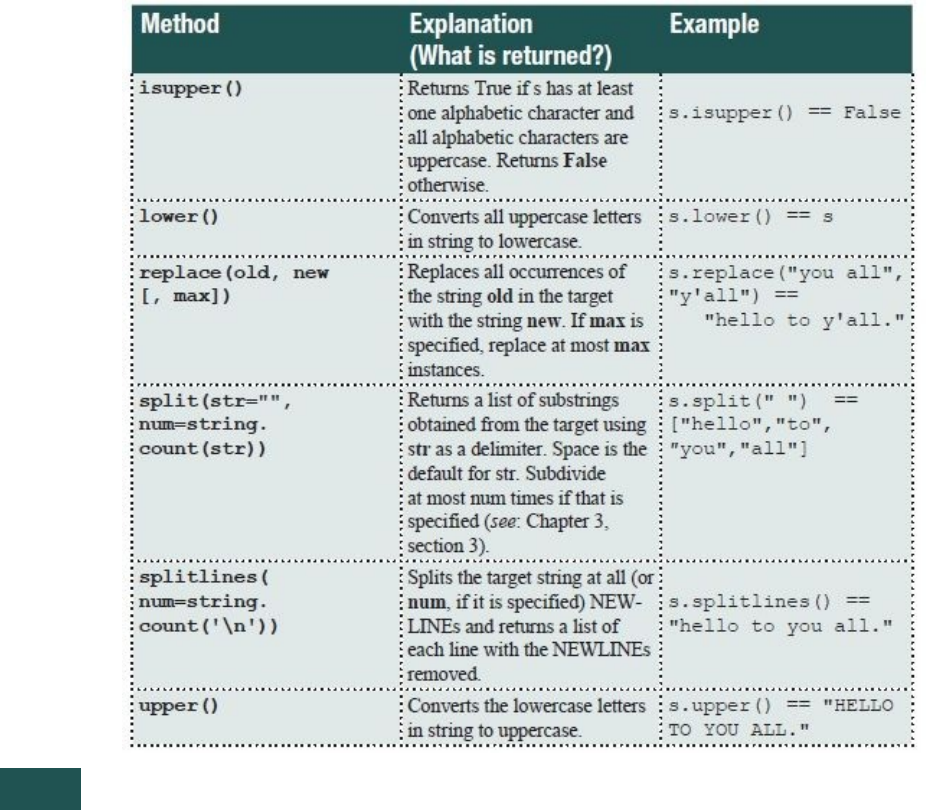
3.1.5 SpanningMultipleLines

Textasseeninhumandocumentsmaycontainmanycharacters,evenmultiplelinesand

paragraphs.Aspecialdelimiter,thetriplequote,isusedwhenastringconstantistospan

manylines.Thishasbeenmentionedpreviouslyinthecontextofmultilinecomments.The

regularstringdelimiterswillterminatethe stringattheend oftheline. The triplequote

consists of either of the two existing delimiters repeated three times. For example, to

assign the first stanza of Byron’s poem “She Walks in Beauty” to the string variable

poem:

poem='''Shewalksinbeautylikethenight

Ofcloudlessclimesandstarryskies,

Andallthat'sbestofdarkandbright

Meetsinheraspectandhereyes;

Thusmellow'dtothattenderlight

WhichHeaventogaudydaydenies.'''

Whenpoemisprintedthelineendingsappearwheretheywereplacedintheconstant.

Thisexampleisaparticularlygoodoneinthatmostpoemsrequirethatlinesendprecisely

wherethepoetintended.

AnotherexampleofastringthatmustbepresentedjustastypedisaPythonprogram.A

programcanbeplacedinastringvariableusingatriplequote:

program=“““list=[1,2,4,7,12,15,21]

foriinlist:

print(i,i*2)”””

When printed this string has the correct form to be executed by Python. In fact, the

followingstatementwillactuallyexecutethecodeinthestring:

exec(program)

3.1.6 ForLoopsAgain

Earlierinthissectionaforloopwaswrittentoprinteachcharacterinthestring.That

loopwas:

foriinrange(0,len(name)):

print(name[i],end=””)

Obviouslythestringcouldhavebeenprintedusing:

print(name)

butitwasbeingusedasanexampleofindexingindividualcomponentswithinthestring.

Thecharacters donot need tobe indexed explicitlyin Python;the loop variablecan be

assignedthevalueofeachcomponent:

foriinname:

print(i,end=””)

Inthiscasethevalueofiisthevalueofthecomponent,notitsindex.Eachcomponent

ofthestringisassignedtoiinturn,andthereisnoneedtotestfortheendofthestringor

toknowitslength.Thisisabetterwaytoaccesscomponentsinastringand,asithappens,

canbeusedwithallsequencetypes.Whetheran

indexisusedorthecomponentsarepulledoutoneatatimedependsontheproblembeing

solved;sometimestheindexisneeded,othertimesitisnot.

3.2 THETYPEBYTES

Astring is a sequence of characters, a sequence being defined as a collection within

whichordermatters.Stringsare commonlyusedfor communicationbetweencomputers

andhumans:toprintheadingsandvaluesonthescreen,andtoreadobjectsincharacter

stringform.Humansdealwithcharactersverywell.Thetypebytesrepresentsasequence

of integers, albeit small ones. A bytes object of length 1 is an 8-bit integer, or a value

between0and255.Abytesobjectoflengthgreaterthan1isasequenceofsmallintegers.

Tobeclear,ifsisastringandbisabytesthen:

s[i]isacharacter

b[i]isasmallinteger

Astringconstant(literal)isasequenceofcharactersenclosedinquotes.Abytesliteral

isasequenceofcharactersenclosedinquotesandprecededbytheletter“b.”Thus:

'thisisastring'

isastring,whereas:

b'thisisastring'

hastypebytes.Anymethodthatappliestoastringalsoappliestoabytesobject,butbytes

objects have some new ones. In particular, to convert a bytes object to a string, the

decode()methodisusedandacharacterencodingshouldbegivenastheparameter.Ifno

parameterisgiven,thenthedecodingmethodistheonecurrentlybeingused.Therearea

fewpossibledecodingmethods(e.g.,“utf-8”).Sotoconvertabytesobjectbtoacharacter

strings,thefollowingwouldwork:

s=b.decode(“utf-8”)

Aquestionremains:“whyisthebytestypeneeded?”Whatisitusedfor?Because(and

this is a little ahead of what is needed) it implements the buffer interface. Certain file

operationsrequireabufferinterfacetoaccomplishtheirtasks.Anythingreadfromsome

specifictypesoffilewillbeofthetypebytes,forexample,asithasthatinterface.This

will be discussed further in Chapters 5 and 8, but for the moment it simply serves to

explainwhythetypeexistsatall.Otherthanthebufferinterface,thebytestypeisvery

muchlikeastring,andcanbeconvertedbackandforth.

3.3 TUPLES

Atupleisalmostidenticaltoastringinbasicstructure,exceptthatitiscomposedof

arbitrary components instead of characters. The quotes can’t be used to delimit a tuple

becauseastringcanbeacomponent,soatupleisgenerallyenclosedinparentheses.The

followingaretuples:

tup1=(2,3,5,7,11,13,17,19)#Primenumbersunder20

tup2=(“Hydrogen”,“Helium”,“Lithium”,”Beryllium”,“Boron”,

“Carbon”)

tup3=“hi”,“ohio”,“salut”

Ifthereisonlyoneelementinatuple,thereshouldbeacommaattheend:

tup4=(“one”,)

tup5=“two”,

That’sbecauseitwouldnotbepossibleotherwisetotellthedifferencebetweenatuple

andastringenclosedinparentheses.Is(1)atuple?Orisitsimplythenumber1?

Atuplecanbeempty:

tup=()

Becausetheyarelikestrings,eachelementinatuplehasanindex,andtheybeginat0.

Tuplescanbeindexedandsliced,justlikestrings.So:

tup1[2:4]is(5,7)

Concatenationislikethatofstringstoo:

tup4=tup4+tup5#yieldstup4=('one','two')

Asisthecasewithstrings,theindex-1givesthelastvalueinthetuple,-2givesthe

secondlast,andsoon.Sointheexampleabove,tup2[-1]is“Carbon.”Also,likestrings,

thetupletypeisimmutable;thismeansthatelementsinthetuplecan’tbealtered.Thus,

statementssuchas:

tup1[2]=6

tup3[1:]“bonjour”

arenotallowedandwillgenerateanerror.

Tuplesareanintermediateformbetweenstrings,whichhavejustbeendiscussed,and

lists, which will be discussed next. They are simpler to implement than list (are

lightweight)andaremoregeneralthanstrings.

Are tuples useful? Yes, it turns out, and part of their use is that they underlie other

aspectsofPython.

3.3.1 TuplesinForLoops

Sequences can be used in a for loop to control the iteration and assign to the loop

controlvariable.Tuplesareinterestinginthiscontextbecausetheycanconsistofstrings,

orintegersorfloats.Theloop:

foriin(“Hydrogen”,“Helium”,“Lithium”,”Beryllium”,“Boron”,

“Carbon”):

will iterate 6 times, and the variable i will take on the values in the tuple in the order

specified.Thevariableiisastringinthiscase.Incaseswherethetypesinthetupleare

mixed,thingsaremorecomplicated.

Problem: Print the Number of Neutrons in an Atomic

Nucleus

Considerthetuple:

atoms=(“Hydrogen”,1,“Helium”,2,“Lithium”,3,“Beryllium”,4,

“Boron”,5,“Carbon”,6)

andtheloop

foriinatoms:

print(i)

Thisprints:

Hydrogen

Helium

Lithium

Beryllium

Boron

Carbon

Thenumberfollowingthenameoftheelementistheatomicnumberofthatelement,

the number of protons in the nucleus. In this case the type of the variable i alternates

betweenstringandinteger.Forelementswithalowatomicnumber(lessthan21),agood

guess for the number of neutrons in the nucleus is twice the number of protons. The

problemisthatsomeofthecomponentsarestringsandsomeareintegers.Theprogram

shouldonly do the calculationwhen it is inan iteration having aninteger value for the

loopvariable,becauseastringcan’tbemultipliedbytwo.

Abuilt-infunctionthatcanbeofassistanceisisinstance.Ittakesavariableandatype

name and returns True if the variable is of that type and False otherwise. Using this

function,hereisafirststabataprogramthatmakestheneutronguess:

atoms=(“Hydrogen”,1,“Helium”,2,“Lithium”,3,“Beryllium”,4,

“Boron”,5,“Carbon”,6)

foriinatoms:

ifisinstance(i,int):

j=i*2

print(“has“,i,“protonsand“,j,”neutrons.”)

else:

print(“Element“,i)

Inotherwords,initerationswhereiisanintegerasdeterminedbyisinstance,thenican

legallybemultipliedby2andtheguessaboutnumberofneutronscanbeprinted.

Anotherwaytosolve thesameproblemwould betoindexthe elementsofthe tuple.

Elements0,2,4,etc.(evenindices)refertoelementnames,whiletheothersrefertoatomic

numbers.Thiscodewouldlookasfollows:

atoms=(“Hydrogen”,1,“Helium”,2,“Lithium”,3,“Beryllium”,4,

“Boron”,5,“Carbon”,6)

foriinrange(0,len(atoms)):

ifi%2==1:

j=atoms[i]*2

print(“has“,atoms[i],“protonsand“,j,

”neutrons.”)

else:

print(“Element“,atoms[i])

Notethatinthiscasetheloopvariableisalwaysaninteger,andisnotanelementofthe

tuplebutisanindexatwhichtofindanelement.That’swhytheexpressionatoms[i]is

usedinsidetheloopinsteadofsimplyiasbefore.

3.3.2 Membership

Tuplesarenotsetsinthemathematicalsense,becauseanelementcanbelongtoatuple

morethanonce,andthereisanordertotheelements.However,somesetoperationscould

beimplementedusingtuplesbylookingatindividualelements.Setunionandintersection,

forexample.TheintersectionoftwosetsAandBisthesetofelementsthataremembers

ofAandalsomembersofB.Themembershipoperatorfortuplesisthekeywordin:

If1intuple1:

The intersection of A and B, where A and B are tuples, could be found using the

followingcode:

foriinA:

ifiinB:

C=C+i

ThetupleCwillbetheintersectionofAandB.Itworksbytakingeachknownelement

ofAandtestingtoseeifitisamemberofB;ifso,itisaddedtoC.

Problem: What Even Numbers Less than or Equal to 100

areAlso

PerfectSquares?

Thiscouldbeexpressedasasetintersectionproblem.Thesetofevennumberslessthan

100couldbeenumerated(thisisnotactualcode):

A=(2,4,6,8,10…andsoon

Orcouldbegeneratedwithinaloop:

A=()#Startwithanemptytuple

foriinrange(0,51):#forappropriateintegers

A=A+(i*2,)#addthenextevennumbertothe

#tuple

#Can'tsimplyuseA+ibecauseiisinteger,notatuple.

Similarly,theperfectsquarescouldbeenumerated:

B=(4,9,16,25,36,49,64,81,100)

Or,again,createdinaloop:

B=()

foriinrange(0,11):

B=B+((i*i),)

NowthesetAcanbeexamined,elementbyelement,toseewhichmembersalsobelong

toB:

C=()

foriinA:

ifiinB:

C=C+(i,)

Theresultis:(0,4,16,36,64,100).

Twoimportantthingsarelearnedfromthis.First,whenconstructinganewtuplefrom

components,onecan beginwithan emptytuple.Second, individualcomponentscan be

addedtoatupleusingtheconcatenationoperator“+,”buttheelementshouldbemadeinto

atuplewithonecomponentbeforedoingtheconcatenation.

3.3.3 Delete

A tuple is immutable, meaning that it cannot be altered. Individual elements can be

indexedbutnot changedor deleted. Whatcan bedoneis tocreate anewtuple thathas

newelements;inparticular,deletinganelementmeanscreatinganewtuplethathasallof

theotherelementsexcepttheonebeingdeleted.

Problem:DeletetheElementLithiumfromtheTupleAtoms,

alongwithItsAtomicNumber.

Goingbacktothetupleatoms,deletingoneofthecomponents—inparticular,Lithium

—beginswithdeterminingwhichcomponentLithiumis;thatis,whatisitsindex?Sostart

atthefirstelementofthetupleandlookforthestring

“Lithium,”stoppingwhenitisfound.

foriinrange(0,len(atoms)):

ifatoms[i]==“Lithium”:#Founditatlocationi

break;

else:

i=-1#notfound

Knowing the index of the element to be deleted, it is also known that all elements

before that one belong to the new tuple and all elements after it do too. The elements

beforeelementi can be written as atoms[0:i]. Each element consists of a string and an

integer, and assuming that both are to be deleted means that the elements following

element i are atoms[i+2:]. In general to delete one element the second half would be

atoms[i+1:].Finishingthecodethatdeletes“Lithium”:

ifi>=0:

atoms=atoms[0:i]+atoms[i+2:]

So the tuple atoms has not been altered so much as it has been replaced completely

withanewtuplethathasnoLithiumcomponent.

3.3.4 Update

Again, because a tuple is immutable, individual elements cannot be changed. A new

tuple can be created that has new elements; in particular, updating an element means

creatinganewtuplethathasalloftheotherelementsexcepttheonebeingupdated,and

thatincludesthenewvalueinthecorrectposition.

Problem: Change the Entry for Lithium to an Entry for

Oxygen

An update is usually a deletion followed by the insertion or addition of a new

component.Adeletionwasdoneintheprevioussection,sowhatremainsistoaddanew

component where the old one was deleted. Inserting the element Oxygen in place of

Lithiumwouldbegininthesamewayasthesimpledeletionalreadyimplemented:

foriinrange(0,len(atoms)):

ifatoms[i]==“Lithium”:#Founditatlocationi

break;

else:

i=-1#notfound

Next,anewtupleforOxygeniscreated:

newtuple=(“Oxygen”,8)

AndfinallythisnewtupleisplacedatlocationiwhileLithiumisremoved:

ifi>=0:

atoms=atoms[0:i]+newtuple+atoms[i+2:]

However,anupdatemaynotalwaysinvolveadeletion.IfLithiumisnotacomponent

ofthetupleatoms,thenperhapsOxygenshouldbeaddedtoatomsanyway.Where?How

aboutattheend?

else:#Ifiis-1thenthenewtuplegoesattheend

atoms=atoms+newtuple

3.3.5 TupleAssignment

One of the unique aspects of Python is so-called tuple assignment. When a tuple is

assignedtoavariable,thecomponentsareconvertedintoaninternalformthatistheone

tuplesalwaysuse.Thisiscalledtuplepacking,andishasalreadybeenencountered:

atoms=(“Hydrogen”,1,”Helium”,2,“Lithium”,3,“Beryllium”,4,

“Boron”,5,“Carbon”,6)

Whatisreallyinterestingisthattupleunpackingcanalsobeused.Considerthetuple:

srec=('Parker','Jim',1980,'Math550','C+','Cpsc302','A+')

whichisatuplepackingofastudentrecord.Itcanbeunpackedintoindividualvariables

inthefollowingway:

(fname,lname,year,cmin,gmin,cmax,gmax)=srec

Whichisthesameas:

fname=srec[0]

lname=srec[1]

year=srec[2]

cmin=srec[4]

gmin=srec[5]

cmax=srec[6]

gmax=srec[7]

Ofcourse,theimplicationisthatNvariablescanbeassignedthevalueofNexpressions

orvariables“simultaneously”ifbotharewrittenastuples.Exampleswouldbe:

(a,b,c,d,e)=(1,2,3,4,5)

(f,g,h,i,j)=(a,b,c,d,e)

Theexpression

(f,g,h,i,j)=2**(a,b,c,d,e)

isinvalidbecausetheleftsideof“**”isnotatuple,andPythonwon’tconvert2intoa

tuple.Also:

(f,g,h,i,j)=(2,2,2,2,2)**(a,b,c,d,e)

isalsoinvalidbecause“**”isnotdefinedontuples,norareotherarithmeticoperations.

Aswithstrings,“+”meansconcatenation,though,so(1,2,3)+(4,5,6)yields(1,2,3,4,5,6).

Exchangingvaluesbetweentwovariablesisacommonthingtodo.It’sanessentialpart

of a sorting program, for example. The exchange in many languages requires three

statements:atemporarycopyofoneofthevariableshastobemadeduringtheswap:

temp=a

a=b

b=temp

Because of the way that tuples are implemented, this can be performed in one tuple

assignment:

(a,b)=(b,a)

This is a little obscure, not to an experienced Python programmer but certainly to a

beginner,andoftentoexperiencedprogrammersinotherlanguages.AJavaprogrammer

couldseewhatwasmeant,butinitiallytherationalewouldnotbeobvious.Thisstatement

deservesacommentsuchas“performanexchangeofvaluesusingatupleassignment.’

3.3.6 Built-InFunctionsforTuples

Asexamplesforthetablebelow,usethefollowing:

T1=(1,2,3,4,5)

T2=(-1,2,4,5,7)

Inaddition,tuplescanbecomparedusingthesameoperatorsasforintegersandstrings.

Comparison is done on an element-by-element basis, just as it is with strings. In the

exampleabove,T1>T2becauseatthefirstlocationwherethetwotuplesdiffer(theinitial

component), the element in T1 is greater than the corresponding element in T2. It is

necessaryforthecorrespondingelementsofthetupletobecomparable;thatis,theyneed

tobeofthesametype.Soifthetuplest1andt2aredefinedas:

t1=(1,2,3,“4”,“5”)

t2=(-1,2,4,5,7)

thentheexpressiont1>t2isnot allowed.A stringcan’tbecomparedagainstaninteger,

andtheelementindexedby3oft1isastring,whereastheelementindexedby3oft2is

anint.

3.4 Lists

OnewaytothinkofaPythonlististhatitisatupleinwhichthecomponentscanbe

modified.TheyhavemanypropertiesofanarrayofthesortonemightfindinJavaorC,

inthattheycanbeusedasaplacetostorethingsandhaverandomaccesstothem;any

elementcanbereadorwritten.Theyareoftenusedasonemightuseanarray,buthavea

greaternaturalfunctionality.

Initiallyalistlookslikeatuple,butusessquarebracketstodelimitit.

list1=[2,3,5,7,11,13,17,19]#Primenumbersunder20

list2=[“Hydrogen”,“Helium”,“Lithium”,”Beryllium”,“Boron”,

“Carbon”]

list3=[“hi”,“ohio”,“salut”]

Alistcanbeempty:

list4=[]

andbecausetheyareliketuplesandstrings,eachelementinalisthasanindex,andthey

begin(asusual)at0.Listscanbeindexedandsliced,asbefore:

list1[2:4]is[5,7]

Concatenationislikethatofstringstoo:

list6=list1+[23,31]

yields[2,3,5,7,11,13,17,19,23,31]

Negativevaluesindexfrom theendof thestring.However, unlikestringsand tuples,

individualelementscanbemodified.So:

list1[2]=6

resultsinlist1being[2,3,6,7,11,13,17,19].Also:

list3[1:]=“bonjour”

resultsinlist3takingthevalue—oops,itbecomes:

[‘hi’,“b’,“o’,“n’,“j’,“o’,“u’,“r’].

That’sbecauseastringisasequencetoo,andthisstringconsistsofsevencomponents.

Eachcomponentofthestringbecomesacomponentofthelist.Ifthestring“bonjour”is

supposedtobecomeasinglecomponentofthelist,thenitneedstobedonethisway:

list3[1:]=[“bonjour”]

The other components of list3 are sequences, and now so is the new one. However,

integersarenotsequences,andtheassignment:

list1[2]=[6,8,9]

resultsinthevalueoflist2being:

[2,3,[6,8,9],7,11,13,17,19]

Thereisalistwithinthislist;thatis,thethirdcomponentoflist1isnotaninteger,butis

alistofintegers.That’slegitimate,andworksfortuplesaswell,butmaynotbewhatis

intended.

Problem:ComputetheAverage(Mean)ofaListofNumbers

Themeanisthesumofallnumbersinacollectiondividedbythenumberofnumbers.

Ifasetofnumbersalreadyexistsasalist,calculatingthemeanmightinvolvealoopthat

sumsthemfollowedbyadivision.Forexample,assumingthatlist1=[2,3,5,7,11,13,

17,19]:

mean=0.0

foriinlist1:

mean=mean+i

mean=mean/len(list1)

Itcanbeseenthatalistcanbeusedinalooptodefinethevaluesthattheloopvariablei

will take on, a similar situation to that of a tuple. A second way to do the same thing

wouldbe:

mean=0.0

foriinrange(0,len(list1)):

mean=mean+list1[i]

mean=mean/len(list1)

Inthiscasetheloopvariableiisanindexintothe list andnotalistelement,butthe

result is the same. Python lists are more powerful than this, and making use of the

extensivepowerofthelistsimplifiesthecalculationgreatly:

mean=sum(list1)/len(list1)

Thebuilt-infunctionsumwillcalculateandreturnthesumofalloftheelementsinthe

list.Thatwasthepurposeoftheloop,sotheloopisnotneededatall.Thefunctionsthat

workfortuplesalsoworkforlists(min,max,len),butsomeofthepoweroflistsisinthe

methodsitprovides.

3.4.1 EditingLists

Editingalistmeanstochangethevalueswithinit,usuallytoreflectanewsituationto

behandledbytheprogram.Themostobviouswaytoeditalististosimplyassignanew

valuetooneofthecomponents.Forexample:

list2=[“Hydrogen”,“Helium”,“Lithium”,”Beryllium”,“Boron”,

“Carbon”]

list2[0]=“Nitrogen”

print(list2)

resultsinthefollowingoutput:

[‘Nitrogen’,“Helium’,“Lithium’,“Beryllium’,“Boron’,“Carbon’]

Thissubstitutionofacomponentisnotpossiblewithstringsortuples.Itispossibleto

replaceasinglecomponentwithanotherlist:

list2=[“Hydrogen”,“Helium”,“Lithium”,”Beryllium”,“Boron”

“Carbon”]

list2[0]=[“Hydrogen”,“Nitrogen”]

resultsin:

list2=[['Hydrogen','Nitrogen'],'Helium','Lithium',

'Beryllium','Boron','Carbon']

3.4.2 Insert

This is not normally what is thought of as an insertion, though. To place new

componentswithinalist,theinsertmethodisprovided.Thismethodplacesacomponent

ataspecifiedindex;thatis,theindexofthenewelementwillbetheonegiven.Toplace

“Nitrogen”atthebeginningoflist2,whichisindex0:

list2.insert(0,“Nitrogen”)

The first value given to insert, 0 in this case, is the index at which to place the

component,andthesecond valueisthe thingtobe inserted. Inserting“Nitrogen”atthe

endofthelistwouldbeaccomplishedby:

list2.insert(len(list2),“Nitrogen)

However,considerthis:

list2.insert(-1,“Nitrogen)

Willthisinsert“Nitrogen”attheend?No.Atthebeginningofthestatement,thevalue

oflist2[-1]is“Carbon.”Thisisthevalueatindex5.Therefore,the

insertof“Nitrogen”willbeatindex5,resultingin:

[ꞌHydrogenꞌ,ꞌHeliumꞌ,ꞌLithiumꞌ,ꞌBerylliumꞌ,ꞌBoronꞌ,

ꞌNitrogenꞌ,ꞌCarbonꞌ]

3.4.3 Append

Anotherwaytoaddsomethingtotheendofalististousetheappendmethod:

list2.append(“Nitrogen”)

Resultsin:

[ꞌHydrogenꞌ,ꞌHeliumꞌ,ꞌLithiumꞌ,ꞌBerylliumꞌ,ꞌBoronꞌ,

ꞌCarbon’,ꞌNitrogen’]

Remember, the “+” operation will only concatenate a list to a list, so the equivalent

expressioninvolving“+”wouldbe:

list2=list2+[“Nitrogen”]

3.4.4 Extend

The extend method does pretty much the same things as the “+” operator. With the

definitions:

a=[1,2,3,4,5]

b=[6,7,8,9,10]

print(a+b)

a.extend(b)

print(a)

theoutputis:

[1,2,3,4,5,6,7,8,9,10]

However,ifappendhasbeenusedinsteadofextendabove:

a=[1,2,3,4,5]

b=[6,7,8,9,10]

print(a+b)

a.append(b)

print(a)

theresultwouldhavebeen:

[1,2,3,4,5,6,7,8,9,10]

[1,2,3,4,5,[6,7,8,9,10]]

3.4.5 Remove

The remove method does what is expected: it removes an element from the list. But

unlike insert, for example, it does not do it using an index; the value to be removed is

specified.So:

list1=[“Hydrogen”,“Helium”,“Lithium”,“Beryllium”,“Boron”,

“Carbon”]

list1.remove(“Helium”)

results in the list1 being [‘Hydrogen’, “Lithium’, “Beryllium’, “Boron’, “Carbon’].

Unfortunately,ifthecomponent being deletedisnota memberofthe list,thenanerror

occurs.Therearewaystodealwiththat,oratestcanbemadefortryingtodeleteanitem:

if“Nitrogen”inlist1:

list1.remove(“Nitrogen”)

Ifthereismorethanasingleinstanceoftheitembeingremoved,thenonlythefirstone

willberemoved.

3.4.6 Index

Whendiscussingtuplesitwaslearnedthattheindexmethodlookedthroughthetuple

andfoundtheindexatwhichaspecifieditemoccurred.Theindexmethodforlistsworks

inthesameway.So:

list1=[“Hydrogen”,“Helium”,“Lithium”,“Beryllium”,“Boron”,

“Carbon”]

print(list1.index(“Boron”))

prints“4,”becausethestring“Boron”appearsatindex4inthislist(startingfrom0,of

course).Ifthereismorethanoneoccurrenceof“Boron”inthelist,thentheindexofthe

firstone(i.e.,smallestindex)isreturned.Ifthevalueisnotfoundinthestring,thenan

erroroccurs.Again,itmightbeappropriatetocheck:

if“Boron”inlist1:

print(list1.index(“Boron”))

3.4.7 Pop

Thepopmethodiseffectivelythereverseorinverseofappend.Itremovesthelastitem

(i.e., the one having the largest index) from the list. If the list is empty, then an error

occurs.Foranexample:

list1=[“Hydrogen”,“Helium”,“Lithium”,“Beryllium”,“Boron”,

“Carbon”]

list1.pop()

print(list1)

printstheresult:

[ꞌHydrogenꞌ,ꞌHeliumꞌ,ꞌLithiumꞌ,ꞌBerylliumꞌ,ꞌBoronꞌ]

Toavoidtheerrorthatcanoccurifthelistisempty,simplychecktoseethatthelength

ofthelistisgreaterthanzerobeforeusingpop:

iflen(list1)>0:

list1.pop()

Themethodiscalledpopbecauseitrepresentsawaytoimplementtheoperationofthe

samenameonadatastructurecalledastack.

3.4.8 Sort

This method places the components of a list into ascending order. Using the list1

variablethathasbeenusedsooften:

list1=[“Hydrogen”,“Helium”,“Lithium”,“Beryllium”,“Boron”,

“Carbon”]

list1.sort()

print(list1)

theresultis:

[ꞌBerylliumꞌ,ꞌBoronꞌ,ꞌCarbonꞌ,ꞌHeliumꞌ,ꞌHydrogenꞌ,

ꞌLithiumꞌ]

whichisinalphabeticorder.Themethodwillsortintegersandfloatingpointnumbersas

well.Stringsandnumberscannotbemixed,though,becausetheycan’tbecompared.So:

list2=[“Hydrogen”,1,“Helium”,2,“Lithium”,3,“Beryllium”,4,

“Boron”,5]

list2.sort()

resultsinanerrorthatwillbesomethinglike:

list2.sort()

TypeError:unorderabletypes:int()<str()

The meaning of this error should be clear. Things of type int(integer) and things of

typestr(string)can’tbecomparedagainsteachotherandsocan’tbeplacedinasensible

order if mixed. For sort to work properly, all of the elements of the list must be of the

sametype.Itisalwayspossibletoconvertonetypeofthingintoanother,andinPython

convertinganintegertoastringisaccomplishedwiththestr()function;stringtointegeris

convertedusingint(). So str(3) would result in “3,” and int(“12”)is 12. An error will

occurifitisnotpossible,soint(12.2)willfail.

Ifeachelementofalistisitselfalist,itcanstillbesorted.Considerthelist:

z=[[“Hydrogen”,3],[“Hydrogen”,2],[“Lithium”,3],

[“Beryllium”,4],[“Boron”,5]]

Whensortedthisbecomes:

[['Beryllium',4],['Boron',5],['Hydrogen',2],['Hydrogen',3],

['Lithium',3]]

Eachcomponentofthislistiscompatiblewiththeothers,consistingofastringandan

integer.Thustheycanbecomparedagainsteachother.Noticethattherearetwoentriesfor

hydrogen:onewithanumber2andonewithanumber3.Thesortmethodarrangesthem

correctly.Alistissortedbyindividualelementsinsequenceorder,sothefirstthingtested

would be the string. If those are the same, then the next element is checked. That’s an

integer,sothecomponentwiththesmallestintegercomponentwillcomefirst.

3.4.9 Reverse

Inanysequencetheorderofthecomponentswithinitisimportant.Reversingthatorder

isalogicaloperationtoprovide,butmaynotbeusedveryoften.Oneinstancewhereit

canbeimportantisafterasort.Thesortmethodalwaysplacescomponentsintoascending

order.Iftheyaresupposedtobeindescendingorder,thenthereversemethodbecomes

valuable.Asanexampleconsidersortingthelistq:

q=[5,6,1,5,4,9,9,1,6,3]

q.sort()

Thevalueofqatthispointis

[1,1,3,4,5,5,6,6,9,9]

Toplacethislistisdescendingorderthereversemethodisused:

q.reverse()

andtheresultis

[9,9,6,6,5,5,4,3,1,1]

Itishardtosaywhetherascendingorderisneededmoreoftenthandescendingorder.

Namesareoftensortedsmallestfirst(ascending),butdatesaremorelikelytorequiremore

recentdatesbeforelaterones(descending).

3.4.10 Count

This method is used to determine how many times a potential component of a list

actuallyoccurs.Itdoesnotreturnthenumberofelementsinthelist—thatjobisdoneby

thelenfunction.Usingthelistqasanexample:

q=[5,6,1,5,4,9,9,1,6,3]

print(1,q.count(1),2,q.count(2),3,q.count(3),99,

q.count(99))

willresultintheoutput:

122031990

where the spacing is enhanced for emphasis. This says that there are 2 instances of the

number1(1,2)inthelist,zeroinstancesof2(2,0),oneinstanceofthenumber3(3,1)and

noneof99(99,0).

3.4.11 ListComprehension

Whencreatingalistofitems,twomechanismshavebeendiscussed.Thefirstistouse

constants,asinthelistqintheprevioussection.Thesecondappendsitemstoalist,and

thiscouldbedonewithinaloop.Makingalistofperfectsquarescouldbedonelikethis:

t=[]

foriinrange(0,10):

t=t+[i*i]

whichcreates thelist [0, 1,4, 9, 16,25, 36, 49,64, 81]. Thiskind of thingis common

enoughthataspecialsyntaxhasbeencreatedforitinPython—thelistcomprehension.

Thebasicideaissimpleenough,althoughsomespecificcasesarecomplicated.Inthe

situationaboveinvolvingperfectsquares,theelementsinthelistaresomefunctionofthe

index. When that is true the loop, index, and function can be given within the square

bracketsasadefinitionofthelist.Sothelisttcouldbedefinedas:

tt=[i**2foriinrange(10)]

The for loop is within the square brackets, indicating that the purpose is to define

componentsofthelist.Thevariableihereistheloopvariable,andi**2 is thefunction

thatcreatestheelementsfromtheindex.Thisisasimpleexampleofalistcomprehension.

Creatingrandomintegervalues?Noproblem:

tt=[random.randint(0,100)foriinrange(10)]

Thefirstsixelementsinalluppercase?

list1=[“Hydrogen”,“Helium”,“Lithium”,“Beryllium”,

“Boron”,“Carbon”]

ss=[i.upper()foriinlist1]

This is a very effective way to create lists, but it does depend on having a known

connectionbetweentheindexandtheelement.

3.4.12 ListsandTuples

Atuplecanbeconvertedintoalist.Listshaveagreaterfunctionalitythantuples;that

is,theyprovidemoreoperationsandgreaterabilitytorepresentdata.Ontheotherhand,

they are more complicated and require more computer resources. If something can be

representedasatuple,thenitislikelybesttodoso.Atupleisdesignedtobeacollection

ofelementsthatasawholerepresentsomemorecomplicatedobject,butthatindividually

areperhapsofdifferenttypes.ThisisratherlikeaCstructorPascalrecord.Alistismore

oftenusedtoholdasetofelementsthatallhavethesametype,morelikeanarray.Thisis

a good way to think of the two types when deciding what to use to solve a specific

problem.

Python provides tools for conversion. The built-in function list takes a tuple and

convertsitintoalist;thefunctiontupledoesthereverse,takingalistandturningitintoa

tuple.Forexample,convertinglist1intoatuple:

tuple1=tuple(list1)

print(tuple1)

yields

(ꞌHydrogenꞌ,ꞌHeliumꞌ,ꞌLithiumꞌ,ꞌBerylliumꞌ,ꞌBoronꞌ,

ꞌCarbonꞌ)

Thisisseentobeatuplebecauseofthe“(‘and’)”delimiters.Thereverse:

v=list(tuple1)

print(v)

printsthetextline:

[ꞌHydrogenꞌ,ꞌHeliumꞌ,ꞌLithiumꞌ,ꞌBerylliumꞌ,ꞌBoronꞌ,

ꞌCarbonꞌ]

andthesquarebracketsindicatethisisalist.

3.4.13 Exceptions

Exceptionsaretheusualwaytocheckforerrorsofindexingandmembershipinlists.

Theerrorisallowedtooccur,buranexceptionistestedandhandledinthecasewhere,for

example,anitembeingdeletedisnotinthelist.

Problem:DeletetheElementHeliumfromaList

Earlier,asanexampleoftheremovemethod,aprogramsnippetwaswrittentodelete

theelementHeliumfromalistofelements:

list1=[“Hydrogen”,“Helium”,“Lithium”,“Beryllium”,“Boron”,

“Carbon”]

if“Helium”inlist1:

list1.remove(“Helium”)

Becauselist1maynothaveHeliumasoneofthecomponents,acheckwasmadebefore

anattempttodeleteit.Anattempttodeleteanelementfromalistwheretheelementdoes

notappearinthatlistresultsinanAttributeError.Ratherthanperformanexplicittest,a

Pythonprogrammerwouldmorelikelyuseanexceptionhere.Theerrorcanbecaughtas

follows:

list1=[“Hydrogen”,“Helium”,“Lithium”,“Beryllium”,“Boron”,

“Carbon”]

try:

list1.remove(“Helium”)

except:

print('Can'tfindHelium')

Theadvantageofthisoverallowingtheerrortooccuristhattheprogramcancontinue

toexecute.

Problem:DeleteaSpecifiedElementfromaList

Giventhesamelist,readanelementfromthekeyboardanddeletethatelementfromthe

list.Thebasiccodeisthesame,butnowthestringisenteredandcouldbeanythingatall.

It’seasiertotestaprogramwhenitcanbemadetofailonpurpose.Thenameisentered

usingtheinputfunctionandisusedastheparametertoremove.Nowitispossibletotest

allofthecodeinthisprogramwithoutchangingit.First,hereistheprogram:

list1=[“Hydrogen”,“Helium”,“Lithium”,“Beryllium”,“Boron”,

“Carbon”]

s=input(“Enter:”)

try:

list1.remove(s)

except:

print('Can'tfind',s)

print(list1)

Properlytestingaprogrammeansexecutingallofthestatementsthatcompriseitand

ensuringthattheanswergiveniscorrect.Sointhiscase,firstdeleteanelementthatisa

partofthelist.TryLithium.Hereistheoutput:

Enter:Lithium

[“Hydrogen”,“Helium”,“Beryllium”,“Boron”,“Carbon”]

Thisiscorrect.Thesearethestatementsthatwereexecutedinthisinstance:

list1=[“Hydrogen”,“Helium”,“Lithium”,“Beryllium”,“Boron”,

“Carbon”]

s=input(“Enter:”)

try:

list1.remove(s)#Thiswassuccessful

print(list1)

NowtrytodeleteOxygen.Outputis:

Enter:Oxygen

Can’tfindOxygen

[‘Hydrogen’,“Helium’,“Lithium’,“Beryllium’,“Boron’,“Carbon’]

Thisiscorrect.Thesestatementswereexecuted:

list1=[“Hydrogen”,“Helium”,“Lithium”,“Beryllium”,“Boron”,

“Carbon”]

s=input(“Enter:”)

try:

list1.remove(s)#thiswasnotsuccessful

except:

print('Can'tfind',s)

print(list1)

Allofthecodeintheprogramhasbeenexecutedandtheresultscheckedforbothmajor

situations. For any major piece of software this kind of testing is exhausting, but it is

reallytheonlywaytominimizetheerrorsthatremaininthefinalprogram.

3.5 SETTYPES

Somethingoftypesetisanunorderedcollectionofobjects.Anelementcanonlybea

memberofagivensetonce,sointhatsenseitismuchlikeamathematicalset.Infact,

that’sthepoint.Becauseasetisunordered,operationssuchasindexingandslicingarenot

provided.Itdoessupportmembership(is),size(len()),andloopingonmembership(fori

inset).

Anyone (probably an older person) who knows the Pascal language has some

familiaritywiththesettypeinPython.

Mathematicalsetshavecertainspecific,well-definedoperations,andthoseareavailable

onaPythonsetalso.

Subsetset1<set2meansset1isatruesubsetofs2.

Intersectionset1 & set2 creates a new set containing members in common with

both.

Unionset1|set2createsanewsetwithallelementsofboth.

Differenceset1-set2createsanewsetwithmembersthatarenotinboth.

Equalityset1==set2istrueifbothsetscontainonlythesameelements.

Creatinganewobjectoftypesetisamatterofspecifyingeitherthatitisasetorwhat

theelementsare.So,onewayistousethe{}syntax:

set1={1,3,5,7,9}

ortousetheconstructor:

set2=set(range(1,10))

whichgivestheset{1,2,3,4,5,6,7,8,9}.So:

set1<set2isTrue

set1&set2is{9,1,3,5,7}Note:orderdoesnotmattertoaset.

set1|set2is{1,2,3,4,5,6,7,8,9}

set2–set1is{8,2,4,6}

Anewelementcanbeaddedtoasetusingadd():

set1.add(11)

andremovedusingremove():

set1.remove(11)

ordiscard():

set1.discard(11)

Iftheelementbeingremovedisnotintheset,thenanerrorwilloccur(KeyError)when

remove()iscalled,butnotwithdiscard().Thisshouldbetestedfirstorbeplacedinan

exceptstatement.

All of the examples so far involve integers belonging to a set, but other types can

belongaswell:floatingpointnumbers,strings,andeventuples(notlists).Forexample,

thefollowingarelegalsets:

{“a”,“e”,“i”,“o”,“u”}

{“cyan”,“yellow”,“magenta”}

{(2,4),(3,9),(4,16),(5,25),(6,36),(7,49)}

3.5.1 Example:Craps

Crapsisadicegame,forthoseunfamiliarwithit,andcommonlyinvolvesbettingon

theoutcome.Theplayer(shooter)rollstwodice.If,onthefirstroll(pass),atotalof7or

11isobtained,thentheshooterwins.Ontheotherhand,aninitialrollof2,3,or12loses

immediately.Anyotherrolliscalledthepoint.Inthatcasetheshootercontinuestoroll

thedice.Ifa7isobtainedthentheshooterloses,andifthepointnumberisrolledthenthe

shooter wins. The shooter continues to roll until one or the other occurs. One way to

implementthisgameinPythonistousesets.

Elementsofthesetswillbevaluesoneachdie,whichistosayoneroll.Therearetwo

dice so a total of 36 combinations exist. A single roll is a tuple, such as (1,1) or (3,4).

There are only 12 distinct sums of two dice, and multiple ways to achieve them. A

sequencenamedrollwillbecreatedthatcontainsasetforeachpossiblevalue,andthatset

containsallofthewaysthatthevaluecanbeobtained.Forinstance,therearetwowaysto

rolla3,so:

roll[3]={(1,2),(2,1)}

Initiallyasetiscreatedforeachpossiblerollofapairofdiceandthenisinitializedas

described:

fromrandomimport*



roll=list(range(0,13))#Createtheemptylist

foriinrange(1,13):#andfillwithemptysets.

roll[i]=set()

foriinrange(1,7):#Nowforeachpossibleroll

forjinrange(1,7):#oftwodice,addthatroll

k=i+j#totheelementofrollfor

roll[k].add((i,j))#thatvalue(sumofthe

#dice)

Nowroll[i]containsallofthewaystorollavalueofi,Inparticular,roll[7]containsall

waystorolla7androll[11]containsallwaystorollan11.Thus,alloftherollsthatwill

winonthefirstpasscanbeplacedinasingleset,theunionofroll[7]androll[11]:

winner=roll[7]|roll[11]

Similarly,therollsthatwilllosefortheshooteronthefirstpassare:

loser=roll[2]|roll[3]|roll[12]

Ifanyotherrollisthrown,thenthatbecomesthepoint.Rollingadieamountstogetting

arandomnumberbetween1and6inclusive,or:

die1=randrange(1,7)

die2=randrange(1,7)

Rememberthatrandrange()producesanumberlessthanthesecondparameter.

Giventhisroll,thepointisthesetroll[die1+die2].Continuingtheprogramfromthedie

rolls:

val=(die1,die2)#Atuple,thecurrentroll

print(“Shooterrolls“,val)

ifvalinwinner:#Isthistupleawinner?

print(“Theshooterwins!”)

elifvalinloser:#Isitaloser?

print(“Theshooterloses”)

else:

point=roll[die1+die2]#Definethepointset

print(die1+die2,”isyourpoint.”)

Nowthedicearerolledrepeatedly.Iftherollisinthepointset,thentheshooterwins.If

therollisa7(inthesetroll[7])thentheplayerloses.Otherwisetheshooterrollsagain.

whileTrue:#Repeatuntilawinor

#losshappens

die1=randrange(1,7)#Rollthedice

die2=randrange(1,7)

val=(die1,die2)#valisatuple

print(“Rolls“,val)

ifvalinroll[7]:#Any7rollloses

print(“Theshooterloses!”)

break

ifvalinpoint:#Rollingthe'point'wins.

print(“Theshootermakesthepoint.Awinner!”)

break

Andthat’sthegame.Inarealcrapsgamethisentireprocessisrepeated,andbetsare

placedoneachindividualgameastowhethertheplayerwillwinorlose.

3.6 SUMMARY

Thereisakindtypethatavariablecanhavethatamountstoalistorsequenceofother,

simpler,things.Thisistrue,andusingvariableshavingthesetypesisanessentialpartof

writing useful and effective code. Python offers strings,tuples, and lists as objects that

consistofmultipleparts.Theyarecalledsequencetypes.

Astringis asequenceofcharacters. Thewordsequenceimpliesthattheorderofthe

characters within the string matters, and that is true of a string. Strings most often

represent the way that communication between a computer and a human takes place.

Stringscanbeindexedtoseewhatcharacterisinanyposition(e.g.,s[i]),canbesearched

for a string that occurs with it, can have characters concatenated to it, and many other

usefuloperations.Ifastringscontainsaninteger,thenint(s)willyieldthatintegerand

str(i)willcreateastringfromanintegeri.

Atupleisalmostidenticaltoastringinbasicstructure,exceptthatitiscomposedof

arbitrary components instead of characters. Examples are tup1 = (2, 3, 5) and tup2 =

(“Hydrogen”,“Helium”,“Carbon”). A tuple can contain mixed type, such as integers

andstrings:tup3=(“star”,1,“planet”,2).Anelementofatuplecannotbealtered,soit

issaidtobeimmutable,althoughconcatenationispossible.

Alistislikeatuplebutisnotimmutable,soindividualelementscanbemodified.Alist

usessquarebracketsasadelimiter,insteadofparenthesesasusedforatuple.Changingan

elementinvolvesindexingit,soiflist1isalistthenlist1[2]=

6modifieselement2ofthatlist.

Asetisanunorderedcollectionofobjects.Anelementcanbealmostanytype,butcan

only occur in a set once. This mimics a mathematical set. Elements can be added and

removed,andthesetoperationsunion,intersection,anddifferencecanbeperformed.

Exercises

Fortheexercisesbelow,assumethefollowingdefinitions:

str1=“okraistheclosestthingtonyloni'veevereaten.”

str2=“pullthestring,anditwillfollowwhereveryou

wish.”

str3=“letoutalittlemorestringonyourkite.”

str4=“everystringisadifferentcolor,adifferentvoice.”

vowels='aeiou'

atoms=(“Hydrogen”,1,“Helium”,2,“Lithium”,3,“Boron”,5,“Carbon”,6,

“Oxygen”,8)

1.Whatisprintedbythefollowingcodesnippets:

a)foriinrange(0,len(str3)):

print(str3[i],end=ꞌꞌ)

b)foriinrange(0,len(str3)):

print(i,end='')

c)foriinrange(0,len(str3)):

print(str2[i],end='')

d)foriinstr3:

print(i,end=ꞌꞌ)

e)foriinstr3:

ifiinvowels:

print(i,end=ꞌꞌ)

f)foriinstr1:

ifnot(iinvowels):

print(i,end=ꞌꞌ)

2.Constructaloopthatprintsoutallcharactersofstr4thatcorrespondtoavowelin

str3.Note:thetwostringsaredifferentlengths.

3.ACaesarcypherisawaytotransmitasecretmessage.Whenencodingamessage

eachcharacterisreplacedbyonethatisafixeddistancefurtheralongthealphabet.If

thatdistanceis6,forexample,theletter“a”wouldbereplacedby“g,”whichis6

positionsfurtheralong.Thecharactersattheendwillwraparoundtothebeginning,so

“z”willbecome“f.”WritesomePythoncodethatwillencodestr1inthisway.Ensure

thatitworksbydecryptingthefollowingstring:

“varrznkyzxotm,gtjozcorrlurruccnkxkbkxeuacoyn.”

Ans:uqxgoyznkiruykyzznotmzuteruto’bkkbkxkgzkt.

4.WriteaPythonsnippetthatwillcreatetwotuplesfromthesingletupleatoms:one

namedelementsthatcontainsonlythenames,andonecallednumbersthatcontains

theatomicnumbersoftheelementsinthetupleatoms.

5.WriteaPythonprogramthatreadsnumbersfromthekeyboardandappendsthemtoa

tuple.Stoptheprocesswhenanegativenumberisenteredandthenprintthetuplethat

wascreated.

6.Adeckofplayingcardsconsistsof52items:eachonehasoneoffoursuits(clubs,

diamonds,hearts,andspades)andwithineachsuitarevaluesfrom1–10and“Jack,”

“Queen,”and“King.”WriteaPythonprogramthatcreatesadeckofcards,shuffles

them,andprintsouttheresult.

7.WriteaPythonprogramthatreadsnames(singlewords)oneatatimefroma

keyboardanddeletesthemfromalistnamednamesiftheyarealreadyelementsof

thatlist.Ifthenameisnotalreadyamemberofthelist,thenitwillbeadded.Typing

thename“quit”terminatestheprogram.

8.Assumethatastringnamedtempexistsandhasavalue.WritePythoncodethatwill

printtempbackwards.

9.Apalindromeisaphrase(astring)thatreadsthesameforwardsandbackwards.The

name“hannah”isapalindrome;sois“Ogopogo,”thenameofamonsterwholivesin

lakeOkanogan,andtheword“redivider.”WriteaPythonprogramthatdetermines

whetheragivenstringisapalindrome.

10.Mostexamplesofpalindromescontainspacesandpunctuation,andthesecharacters

areignoredwhendecidingwhetherornotthephraseispalindromic.Soiscase.Thus,

thephrase“Ipreferpi”isapalindrome.Withtheseconsiderationsinmind,writea

Pythonprogramthatdetermineswhetherastringisapalindromeornot.

NotesandOtherResources

Built-intypes:https://docs.python.org/3.4/library/stdtypes.html?highlight=set#set

Pythonstrings:https://docs.python.org/3/library/string.html

RulesofCraps:http://www.bigmcasino.com/learn-more/learn-to-play-craps/what-are-

the-basic-rules-of-craps/

1.DavidMertz.(2003).TextProcessinginPython,AddisonWesleyProfessional,

ISBN-13:978-0321112545.

2.DavidMakinson.(2012).Sets,Logic,andMathsforComputing,2ndedition,

Springer,ISBN-13:978-1447124993.

3.J.D.Oldham.(2005).WhathappensafterPythoninCS1?JournalofComputing

SciencesinColleges,20(6),7–13.

CHAPTER4

FUNCTIONS

4.1FunctionDefinition:SyntaxandSemantics

4.2FunctionExecution

4.3Recursion

4.4CreatingPythonModules

4.5ProgramDesignUsingFunctions–Example:TheGameofNim

4.6Summary

Inthischapter

ThereisalargeandusefulsetoffunctionsbuiltintoPython.Thesearesometimessimply

therefortheusing,likeprintandinput,andsometimesarepartofamodulethatmustbe

imported, like random. However, as large as this collection of functions is, it is

impossible that it will include everything that every programmer needs. At some point

there will be a need to create a function that does something new, and Python should

permitthis.

Why would a programmer want to create a function of their own? It is partly out of

convenience; if some section of code can be invoked as a function instead of being

repeated many times, then there will be less typing involved. It is also to support more

correct programs: a small code unit like a function can be very thoroughly tested and

nearlyguaranteedtobecorrect.Anditisalsotosupportreuseofworkingcode:oncea

functionis tested,it canbe placed ina collectionof code (module)and usedagain and

againinsteadofbeingrewrittenmanytimes.

A function is really just some code that has a name, and can be executed simply by

invokingthatname.Itusuallyrepresentssometaskthathastobedonefairlyfrequently,

but that’s not a requirement. Some functions are invoked (or called) only once. In this

context a function is a way to break up a long piece of code into many shorter pieces

which,ashasbeenpointedout,areeasiertotestandmaintain.

Afunctionshouldalsohaveonesingletask,oratleastonemaintask.Thattaskshould

berepresentedinthefunctionname.Afunctionnamedmaximumshouldhavethetaskof

locatingthemaximumofsomething;afunctionnamedcosineshouldcalculatethecosine

ofanangle.Ifafunctionisnamedwilmaittellsanotherprogrammerwhoisreadingthe

code nothing about the what the program is doing, and if a function named cosine

computes the square root of a number then it is not just uninformative but misleading.

NevermindthatthePythonlanguagedoesnotinsistthatnamesbeinformative;thereisa

social compact between programmers that says that you should be as clear as possible

aboutwhatyourcodeisdoing.

Thefactthatmanyfunctionsreturnavaluehasbeenskippedover,butitisakeypartof

thefunctionconstruct.Thecodewithinthefunctionhasapurpose,andoftenthatpurpose

isconcentratedinthereturnvalue.Howeveritworks,andwhateverthecodelookslike,

the purpose of the cosine function is to return a single value that is the mathematical

cosineofagivenangle.Thenatureofthefunctionisencapsulatedinthatvalue.Thereare

some functions that do not explicitly return a value; such a function might be called to

printanerrormessageordrawagraphicalobjectinawindow.Evenifitisnotspecifically

declaredinthedefinition,allfunctionsreturnsomething.Ifnotdefined,thenitreturnsa

valuecalledNone.

Enoughexposition—howcanfunctionsbedeclaredandusedinPython?

4.1 FUNCTIONDEFINITION:SYNTAXAND

SEMANTICS

Unlike in the cases of if statements or for statements, a function definition does not

involvetheword“function.”AsanexampleofasimpledefinitioninPython,imaginea

programthatneedsafunctiontoprinttwenty“#”charactersonaline.Itcouldbedefined

as:

defpound20():

foriinrange(0,20):

print(“#”,end=””)

TheworddefisknowntoPythonandalwaysbeginsthedefinitionofafunction.Thisis

followedbythenameofthefunction,inthiscasepound20becausethefunctionprints20

poundcharacters(alsoknownasahashcharactersoroctothorpe).Thencomesthelistof

parameters,whichcanbethoughtofasatupleofvariablenames.Inthiscasethetupleis

empty,meaningthatnothingispassedtothefunction.Finallycomesthe“:”characterthat

definesanewsuitethatcomprisesthecodebelongingtothefunction.Fromhereonthe

codeisindentedonemorelevel,andwhentheindentationrevertstotheoriginallevelthe

functiondefinitioniscomplete.

Callingthis functionisamatterofusingitsnameasastatementorinanexpression,

beingcarefultoalwaysincludethetupleofparameters.Evenwhenthetupleisempty,it

helpsdistinguishafunctionfromavariable.Acalltothisfunctionwouldbe:

pound20()

andtheresultwouldbethat20“#”characterswouldbeprintedononelineoftheoutput

console.

Afunctioncanbegivenorpassedoneormorevaluesthatwilldeterminetheresultof

the function. A function cosine, for example, would be passed an angle, and that angle

would be used to compute the cosine. Each call to cosine passing a different value can

yieldadifferentresult.Inthecaseofthefunctionthatprintspoundcharacters,itmightbe

usefultopassitthenumberofpoundcharacterstoprint.Itshouldnotbecalledpound20

anymorebecauseitdoesnotalwaysprint20characters.Itwillbecalledpoundnthistime:

defpoundn(ncharacters):

foriinrange(0,ncharacters):

print(“#”,end=””)

Thevariablencharactersthatisgiveninparenthesesafterthefunctionnameiscalleda

parameteroranargument,andindicatesthenamebywhichthefunctionwillrefertothe

value passed to it. This name is known only inside of the function, and while it can be

modified within the function, this modification will not have any bearing on anything

outside.Thecalltopoundnmustnowincludeavaluetobepassedtothefunction:

poundn(3)

Whenthiscallisperformed,thecodewithinpoundnbeginsexecuting,andthevalueof

ncharacters is 3, the value that was passed. It prints 3 characters and returns. A

subsequent call to poundn could be passed a different number, perhaps 8, and then

ncharacterswouldtakeonthevalue8andthefunctionwouldprint8characters.Itwill

printasmanycharactersasrequestedthroughtheparameter.

4.1.1 Problem:UsepoundntoDrawaHistogram

InChapter2, a simple histogram was created from some print statements and loops.

Thesamecodewasrepeatedmanytimes,oneforeachhistogrambar.Asithappensthe

character used to draw the histogram bars was the pound character, so the function

poundn could be used as a basis for a histogram program. As a reminder, here is the

outputthatisdesired:

EarningsforWidgetCorpfor2016

Dollarsforeachquarter

==============================

Q1:########190000

Q2:################340000

Q3:##########################################873000

Q4:####################439833

Each pound character represents $20000, and there are four variables that hold the

profitforeachofthefourquarters:q1,q2,q3,andq4.Giventhese

criteria, a solution using poundn would call the function four times, once for each

quarter:

print(“EarningsforWidgetCorpfor2016”)

print(”Dollarsforeachquarter“)

print(”===============================”)

q1=190000#Thedollaramountsforprofits

q2=340000#ineachofthefourquartersof2016

q3=873000

q4=439833



print(”Q1:“,end=””)

poundn(int(q1/20000))#Rawdollaramountisdividedby

#20000

#toyieldthenumberofcharacters.

print(”“,q1)



print(“Q2:“,end=””)

poundn(int(q2/20000))

print(”“,q2)



print(“Q3:“,end=””)

poundn(int(q3/20000))

print(”“,q3)



print(“Q4:“,end=””)

poundn(int(q4/20000))

print(”“,q4)

Eachprofitvaluemustbescaledbydividingby20000,justashappenedbefore.Inthis

casetheresultingvalueispassedtopoundnindicatingthenumberof“#”’stodraw.

4.1.2 Problem:GeneralizetheHistogramCodeforOtherYears

Anycompanywillneedtodofinancialreportseveryyearatleast.Hiringaprogrammer

todothistaskonacomputerisnotareasonablethingtodo,becausecomputerscanbe

madeto dothis jobin a very general way.For example,given thateach year will have

fourquartersandeachquarterwillhaveaprofit,whynotstorethesedataasalist?Each

yearwillhaveonelistcontainingfouritems,andthenameofthevariablecouldinitially

berelatedtotheyear:

profit2016=[190000,340000,873000,439833]

Theprofitforthefirstquarterisprofit2016[0],thesecondquarterisprofit2016[1],and

soon.Usingthisvariablemeanspassingoneoftheelementsofthelisttopoundninstead

ofasimplevariable,butthatisfine,it’salegalexpression.Sodrawingthecharactersfor

thefirstquarterwouldbedonewiththefollowingcode:

poundn(int(profit2016[0]/20000))

Nowconsiderwhatelsegetsprinted.Toprinteverythingforthefirstquarterthecode

was:

print(“Q1:“,end=””)

poundn(int(profit2016[0]/20000))

print(”“,q1)

Thismeansthatthelabelontheleft,“Q1,”theparameterstopoundn,andtheactual

value of the profit are needed. All of these are available, and can be provided within a

simpleloop.Assumingthattheloopvariableirunsfrom0to3,thecodewithinthatloop

that duplicates the previous example can be constructed one line at a time. In each

iterationthequarterisi+1becauseistartsat0;convertthattoastringandbuildthelabel

“Q1:”fromit:

print(Q1:“,end=””)

print(“Q”+str(i+1)+”:“,end=””)

Thisisprobablythetrickiestpart.Thelabelstringisconstructedfromtheletter“Q,”a

numberbetween1and4indicatingthequarter,and“:”fortheterminalstring.Theyare

simplyconcatenatedtogetherintheprintstatement.

Nowcallpoundnasbefore:

poundn(int(profit2016[i]/20000))

finally,printtherawdollarvalueontheright:

print(”“,q1)

print(”“,profit2016[i])

So,usingthisplantheentirehistogramcanbedrawnusingonlyfourstatements:

foriinrange(0,4):

print(“Q”+str(i+1)+”:“,end=””)

poundn(int(profit2016[i]/20000))

print(”“,profit2016[i])

That’sprettybrief,readable,andgeneral.Still,there’sanotherstep.Sincethiswillbe

doneeveryyear,whynotcreateafunctionthattakesthedataandtheyearasparameters,

anddothewholejob?Itshallbecalledpqhistogram:

defpqhistogram(profit,year):

print(“EarningsforWidgetCorpfor“+str(year))

print(”Dollarsforeachquarter“)

print(”==============================”)

foriinrange(0,4):

print(“Q”+str(i+1)+“:“,end=””)

poundn(int(profit[i]/20000))

print(”“,profit[i])

Thefunctionpqhistogramproducesthesameoutputasdidtheoriginalprogram,and

does so more generally and concisely. This function also brings to light two new ideas.

Oneisthatitispossibletopassmorethanoneparametertoafunction.Thesecondisthat

itispossibletocallafunctionfromwithinanotherfunction;inthiscasepoundniscalled

frominsideofpqhistogram.Thecallismadeafterdefiningthelistthatcontainstheprofit

values:

profit2016=[190000,340000,873000,439833]

pqhistogram(profit2016,2016)

Itisimportanttonotethattheparametersarepositional;thatis,thefirstvaluepassed

willcorrespondtothefirstnameintheparameterlist,andthesecondtothesecond.This

isthedefaultforfunctionswithanynumberofparameters.

NOTEA def statement is not a declaration. Such things are foreign to Python. A def

statementexecutes,andit“creates”anewfunctioneachtimeitisexecuted.This

isanadvancedtopic,andwillbehandledlater.

4.2 FUNCTIONEXECUTION

Whenafunctionis called,thefirststatementof thatfunctionstartsto execute,andit

continuesstatementbystatementthroughthecodeuntilthelaststatementofthatfunction

or until it returns prematurely. When that last statement executes, then execution will

continue from the place where it was called. As a function can be called from many

places, Python has to remember where the function was called so that it can return.

Parameterscanbeexpressionsorvariables,andnormallydiffereachtimethefunctionis

called.Functionscanalsoaccessvariablesdefinedelsewhere.

Mostimportantly,andafactorthathasnotbeendealtwithyet,isthatfunctionsreturn

values.

4.2.1 ReturningaValue

All functions return a value, and as such can be treated within expressionsas if they

werevariableshavingthatvalue.So,assumingtheexistenceofacosinefunction,itcould

beusedinanexpressionintheusualways.Forexample:

x=cosine(x)*r

ifcosine(x)<0.5:

print(cosine(x)*cosine(x))

In these cases the value returned by the function is used by the code to calculate a

furthervalueortocreateoutput.Theexpression“cosine(x)”resolvestoavalueofsome

Pythontype.Themostcommonpurposeofafunctionistocalculateavalue,whichisthen

returned to the calling part of the program and can possibly be used in a further

calculation.Buthowdoesafunctiongetitsvalue?Inareturnstatement.

Thereturnstatementassignsavalueandatypetotheobjectreturnedbythefunction.It

alsostopsexecutingthefunctionandresumesexecutionatthelocationwherethefunction

was called. A simple example would be to return a single value, such as an integer or

floatingpointnumber:

return0

returnsthevalue0fromafunction.Thereturnvaluecouldbeanexpression:

returnx*x+y*y

Afunctionhasonlyonereturnvalue,butitcanbeofanytype,soitcouldbealistor

tuplethatcontainsmultiplecomponents:

return(2,3,5,7,11)

return[“fluorine”,“chlorine”,“bromine”,“iodine”,“astatine”]

Expressionscanincludefunctioncalls,soareturnvaluecanbedefinedinthiswayas

well;forexample:

returncosine(x)

Oneofthesimplestfunctionsthatcanbeusedasanexampleisonethatcalculatesthe

squareofitsparameter.Itnonethelessillustratessomeinterestingthings:

defsquare(x):

returnx*x

Theprintstatement:

print(square(12))

willprint:

144

Interestingly,thestatement:

print(square(12.0))

resultsin:

144.0

Thesamefunctionreturnsanintegerinonecaseandafloatintheother.Why?Because

thefunctionreturnstheresultofanexpressioninvolvingitsparameter,whichinonecase

wasanintegerandintheotherwasreal.Thisimpliesthatafunctionhasnofixedtype,

andcanreturnanytypeatall.Indeed,thesamefunctioncanhavereturnstatementsthat

returnaninteger,afloat,astring,andalistindependentoftypeoftheparameterpassed:

deftest(x):#Returnoneoffourtypesdependingonx

ifx<1:

return1

ifx<2:

return2.0

ifx<3:

return“3”

return[1,2,3,4]



print(test(0))

print(test(1))

print(test(2))

print(test(3))

Theoutput:

2.0

[1,2,3,4]

Problem:WriteaFunctiontoCalculatetheSquareRootof

its

Parameter

Two thousand years ago the Babylonians had a way to calculate the square root of a

number. They understood the definition of a square root: that if y*y = x then y is the

squarerootofx.Theyfiguredoutthatifywasanoverestimatetothetruevalueofthe

squarerootofx,thenx/ywouldbeanunderestimate.Inthatcase,abetterguesswouldbe

toaveragethosetwovalues:thenextguesswouldbey1=(y+x/y)/2.Theguessafterthat

wouldbey2=(y1+x/y1)/2,andsoon.Atanypointinthecalculationtheerror(difference

betweenthecorrectanswerandtheestimate)canbefoundbysquaringtheguessyiand

subtractingxfromit,knowingthatyi*yiissupposedtoequalx.

Thefunctionwillthereforestartbyguessingwhatthesquarerootmightbe.Itcannotbe

0becausethenx/ywouldbeundefined.xisagoodguess.Thenconstructaloopbasedon

theexpressiony2=(y1+x/y1)/2,ormoregenerallyyi+1=(yi+x/yi)/2foriterationi.At

first,runthisloopafixednumberoftimes,perhaps20.Hereisthefunctionthatresults:

defroot(x):#Computethesquarerootofx

y=x#Firstguess:toobig,probably

foriinrange(1,20):#Iterate20times

y=(y+x/y)/2.0#Averagethepriorguessand

#x/y

returny#Returnthelastguess

This correctly computes the square root of 2 to 15 decimal places. This is probably

morethanisnecessary,meaningthattheloopisexecutingmoretimesthanitneedsto.In

fact,changingthe20iterationstoonly6stillgives15correctplaces.Thisisexceptional

accuracy: if the distance between the Earth and the Sun were known this accurately it

wouldbe within 0.006inches of thecorrect value. TheBabylonians seem tohave been

veryclever.

What’s the square root of 10000? If the number of iterations is kept at 6, then the

answer is avery poor one indeed:323.1. Why? Some numbers (large ones) need more

iterationsthanothers.Toguaranteethatagoodestimateofthesquarerootisreturned,an

estimateoftheerrorshouldbeused.Whentheerrorissmallenough,thenthevaluewill

begoodenough.Theerrorwillbex-yi*yi.Thefunctionshouldnotloopafixednumberof

times,butinsteadshouldrepeatuntiltheerrorislessthan,say,0.0000001.Thisfunction

willbenamedroote,wherethe“e”isfor“error.”

#ComputerthesquarerootofXto7decimalplaces

defroote(x):

y=x#yissupposedtobethesquareroot

#ofx,so

e=abs(x-y*y)#theerrorisx–y*y

whilee>0.0000001:#repeatwhiletheerrorisbigger

#than0.0000001

y=(y+x/y)/2.0#Newestimateforsquareroot

e=abs(x-y*y)Newerrorvalue

returny

Thisfunctionwillreturnthesquarerootofanypositivevalueofxtowithin7decimal

places.Itshouldcheckfornegativevalues,though.

4.2.2 Parameters

Aparametercanbeeitheraname,meaningthatitisaPythonvariable(object)ofsome

kind, or an expression, meaning it has a value but no permanence in that it can’t be

accessedlateron—ithasnoname.Botharepassedtoafunctionasanobjectreference.

The expression is evaluated before being given to the function, and its type does not

matterinsofarasPythonwillalwaysknowwhatitis;itsvalueisassignedanamewhenit

ispassed.Consider,forexample,thefunctionsquareinthefollowingcontext:

…

pi=3.14159

r=2.54

c=square(2*pi*r)

print(“Circumferenceis“,c)

Theassignmentstopiandrareperformed,andwhenthecalltosquare

occurs,theexpression2*pi*risevaluatedfirst.Itsvalueisassignedtoatemporary

variable,whichispassedastheparametertosquare.Insidethefunctionthisparameter

isnamedx,andthefunctioncalculatesxsquaredandreturnsitasavalue.Itisasifthe

followingcodeexecutes:

pi=3.14159

r=2.54

#callsquare(2*pi*r)

parameter1=2*pi*r#settheparametervalue

x=parameter1#Firstparameterisnamedxinside

#SQUARE

returnvalue=x*x#CodewithinSQUARE,returnx*x

c=returnvalue#assignresultoffunction

#calltoc

print(“Circumferenceis“,c)

Thisisnothowafunctionisimplemented,butitshowshowtheparameteriseffectively

passed;acopyismadeoftheparametersandthosearepassed.Iftheexpression2*pi*r

was changed to a simple variable, then the internal location of that variable would be

passed.

Passingmorestructuredobjectsworksthesamewaybutcanbehavedifferently.Ifalist

ispassedtoafunctionthenthelistitselfcannotbemodified,butthecontentsofthelist

canbe.Thelistisassignedanothername,butitisthesamelist.Tobeclear,considera

simplefunctionthateditsalistbyaddinganew

elementtotheend:

defaddend(arg):

arg.append(“End”)



z=[“Start”,“Add”,“Multiply”]

print(1,z)

addend(z)

print(1,z)

Thelistassociatedwiththevariablezischangedbythisfunctioncall.Itnowendswith

thestring“End.”Outputfromthisis:

1[ꞌStartꞌ,ꞌAddꞌ,ꞌMultiplyꞌ]

2[ꞌStartꞌ,ꞌAddꞌ,ꞌMultiplyꞌ,ꞌEndꞌ]

Whyisthis?Becausethenamezreferstoathingthatconsistsofmanyotherparts.The

namezisusedtoaccessthem,andthefunctioncan’tmodifythevalueofzitself.Itcan

modifywhatzindicates;thatis,thecomponents.Thinkofit,ifitmakesitsimpler,asa

levelofindirection.Abookcanbeexchangedbetweentwopeople.Thereceiverwritesa

noteinitandgivesitback.It’sthesamebook,butthecontentsarenowdifferent.

Asmallmodificationtoaddend()illustratessomeconfusingbehavior.Insteadofusing

appendtoadd“End”tothelist,usetheconcatenationoperator“+”:

defaddend(arg):

arg=arg+[“End”]



z=[“Start”,“Add”,“Multiply”]

print(1,z)

addend(z)

print(2,z)

Nowtheoutputis:

1[ꞌStartꞌ,ꞌAddꞌ,ꞌMultiplyꞌ]

2[ꞌStartꞌ,ꞌAddꞌ,ꞌMultiplyꞌ]

The component “End” is not a part of the list zanymore. It was made a component

insideofthe function,but it’s notpresent afterthe functionreturns.This isbecause the

statement:

arg=arg+[“End”]

actuallycreatesanewlistwith“End”asthefinalcomponent,andthenassignsthatnew

list as a value to arg. This represents an attempt to change the value that was passed,

which can’t happen: changing the value of arg will not change the value of the passed

variablez.So,withinthefunctionargis anew listwith“End” asthe finalcomponent.

Outside,thelistzhasnotchanged.

ThewaythatPythonpassesparametersisthesubjectofalotofdiscussiononInternet

blogsandlists.Therearemanynamesgivenforthemethodused,andwhilethetechnique

isunderstood,itdoesdifferfromthewayparametersarepassedinotherlanguagesandis

confusingtopeoplewholearnedanotherlanguagelikeJavaorCbeforePython.Thething

torememberisthattheactualvalueofthething(anobjectreference)beingpassedcan’t

beassignedanewvalueinsidethefunction,butthethingsthatitreferencesorpointsto

canbemodified.

Multipleparameters are passedby position; the firstparameter passed is given to the

firstonelistedinthefunctiondeclaration,thesecondonepassedisgivento the second

onelistedinthedeclaration,andsoon.Theyareallpassedinthesamemanner,though,as

objectreferences.

4.2.3 DefaultParameters

Itispossibletospecifyavalueforaparameterintheinstancethatitisnotgivenoneby

thecaller.Thatmaynotseemtomakesense,buttheimplicationisthatitwillsometimes

be passed explicitly and sometimes not. When debugging code it is common to embed

print statements in specific places to show that the program has reached that point.

Sometimes it is important to print out a variable orvalue there, other times it is just to

showthattheprogramgottothatstatementsafely.Considerafunctionnamedgothere:

defgothere(count,value):

print(“GotHere:“,count,”valueis“,value)

thenthroughouttheprogram,callstogotherewouldbe sprinkledwithadifferentvalue

forcount every time; the value of count indicates the statement that has been reached.

Thisisawayofinstrumentingtheprogram,andcanbeveryusefulforfindingerrors.So

thecodebeingdebuggedmaylooklike:

year=2015#Thecodebelowisnotespecially

#meaningful

a=year%19#andisanexampleonly.

gothere(1,0)

b=year//100

c=year%100

gothere(2,0)

d=(19*a+b-b//4-((b-(b+8)//25+1)

//3)+15)%30

e=(32+2*(b%4)+2*(c//4)-d-(c%4))%7

f=d+e-7*((a+11*d+22*e)//451)+114

gothere(3,f)

month=f//31

day=f%31+1

gothere(4,day)

returndate(year,month,day)

Outputis:

GotHere:1valueis0

GotHere:2valueis0

GotHere:3valueis128

GotHere:4valueis5

201545

Theprogramreacheseachofthefourcheckpointsandprintsapropermessage.Thefirst

two calls to gothere did not need to print a value, only the count number. The second

parametercouldbegivenadefaultvalue,perhapsNone,andthenitwouldnothavetobe

passed.Thedefinitionofthefunctionwouldnowbe:

defgothere(count,value=None):

ifvalue:

print(“GotHere:“,count,”valueis“,value)

else:

print(GotHere:“,count)

andtheoutputthistimeis:

GotHere:1

GotHere:2

GotHere:3valueis128

GotHere:4valueis5

201545

Theassignmentwithintheparameterlistgivesthenamevalueaspecialproperty.Ithas

a default value. If the parameter is not passed, then it takes that value; otherwise, it

behavesnormally.Thisalsomeansthatgotherecanbecalledwithoneortwoparameters,

which can be very handy. It is important to note that the parameters that are given a

defaultvaluemustbedefinedaftertheonesthatarenot.That’sbecauseotherwiseitwould

notbeclearwhatwasbeingpassed.Considerthe(illegal)definition:

defwrong(a=1,b,c=12):

…

Nowcallwrongwithtwoparameters:

wrong(2,5)

Whatparametersarebeingpassed?Isitaandb?Isitaandc?Itisimpossibletotell.A

legaldefinitionwouldbe:

defright(b,a=1,c=12)

Thisfunctioncanbecalledas:

right(19)

inwhichcaseb=19,a=1,andc=12.Itcanbecalledas:

right(19,20)

inwhichcaseb=19,a=19,andc=12.Itcanbecalledas:

right(19,19,19)

inwhichcaseb=19,a=19,andc=19.Buthowcanitbecalledpassingbandcbutnota?

Likethis:

right(19,c=19)

Inthiscaseahasbeenallowedtodefault.Theonlywaytopasscwithoutalsopassinga

istogiveitsnameexplicitlysothatthecallisnotambiguous.

4.2.4 None

Mistakes happen when writing code. They are unavoidable, and much time is spent

gettingridofthem.Onecommonkindofmistakeistoforgettoassignareturnvaluewhen

one is needed. This is especially likely when there are multiple points in the function

whereareturncanoccur.Inmanyprogramminglanguagesthiswillbecaughtasanerror,

butinPythonitisnot.Instead,afunctionthatisnotexplicitlyassignedareturnvaluewill

returnaspecialvaluecalledNone.

None has its own type (NoneType), and is used to indicate something that has no

definedvalueortheabsenceofavalue.Itcanbeexplicitlyassignedtovariables,printed,

returnedfromafunction,andtested.Testingforthisvaluecanbedoneusing:

ifx==None:

orby:

ifxisNone:

4.2.5 Example:TheGameofSticks

Thisis arelatively simplecombinatorial gamethat involvesremoving sticks or chips

fromapile.Therearetwoplayers,andthegamebeginswithapileof

21sticks.Thefirstplayerbeginsbyremoving1,2,or3sticksfromthepile.

Thenthenextplayerremovessomesticks,again1,2,or3ofthem.Playersalternatein

this way. The player who removes the last stick wins the game; in other words, if you

can’tmove,youlose.

Functionsareusefulintheimplementationofthisgamebecausebothplayersdosimilar

things.Theactionconnectedwithmakingamove,displayingthecurrentposition,andso

onarethesameforthehumanplayerandthecomputeropponent. The currentstatusor

stateofthegameissimplyanumber,thenumberofsticksremaininginthepile.When

thatnumberiszero,thenthegameisover,andtheloseriswhateverplayerissupposedto

movenext.Thecodeforapairofmoves,onefromthehumanandonefromthecomputer,

mightbecodedinPythonasfollows:

displayState(val)#Showthegameboard

userMove=getMove()#Askuserfortheirmove

val=val–userMove#Makethemove

print(“Youtook“,userMove,”sticksleaving“,val)

ifgameOver(val):

print(“Youwin!”)

else:

move=makeComputerMove(val)#Calculatethe

#computerꞌsmove

print(“Computertook“,move,”sticksleaving“,val)

ifgameOver(val):

print(“Computerwins!”)

Thecurrentstateofthegameisdisplayedfirst,andthenthehumanplayerisaskedfor

theirmove.Themoveissimplythenumberofstickstoremove.Whenthemovehasbeen

made,iftherearenosticksleftthenthehumanwins.Otherwise,thecomputercalculates

and makes a move; again, if no sticks remain then the game is over, in this case the

computerbeingthewinner.Thisentiresectionofcodeneedstoberepeateduntilthegame

isover,ofcourse.

There are four functions that must be written for this version: displayState(),

getMove(),gameOver(),andmakeComputerMove().

The function displayState() prints the current situation in the game. Specifically, it

printsone“O”characterforeachstickstillinthepile,anddoessoinrowsof6.Atthe

beginningofthegamethisfunctionwouldprint:

OOOOOO

OOO

whichis21sticks.Thecodeis:

defdisplayState(val):

k=val#Krepresentsthenumberofsticksnot

#printed

whilek>0:#Solongassomearenotprinted…

ifk>=6:#Ifthereisawholerow,printit.

print(“OOOOOO“,end=””)

k=k–6#Sixfewersticksareunprinted

else:

forjinrange(0,k):#Printtheremainder

print(“O“,end=””)

k=0#Noneremain

print(””)

Thisshouldbeobvious.Alsonotethatthefunctionisnamedforwhatitdoes.Itdoes

onlyonething;itmodifiesnovaluesoutsideofthefunction,anditservesapurposethatis

neededmultipletimes.Theseareallgoodpropertiesofafunction.

ThefunctiongetMove()willprintaprompttotheuser/playeraskingforthenumberof

sticks they wish to remove and reads that value from the keyboard, returning it as the

function value. Again, this function is named for what it does and performs a single,

simpletask.Onepossibilityforthecodeis:

defgetMove():

n=int(input(“Yourmove:Takeawayhowmany?“))

whilen<=0orn>3:

print(“Sorry,youmusttake1,2,or3sticks.”)

n=int(input(“Yourmove:Takeawayhowmany?“))

returnn

ThefunctiongameOver()istrivial,butlendsstructuretotheprogram.Allitdoesistest

toseewhetherthevalueofval,thegamestatevariable,iszero.Itleavesopentheideathat

theremaybeotherendofgameindicatorsthatcouldbetestedhere.

defgameOver(state):

ifstate==0:

returnTrue

returnFalse

Finally, the most complicated function, getComputerMove(), can be attempted.

Naturallyagoodgamepresentsachallengetotheplayer,andsothecomputershouldwin

the game it if can. It should not play randomly if that is possible. In the case of this

particulargame,thewinningstrategyiseasytocode.Theplayertomakethefinalmove

wins,soifthereare1,2,or3sticksleftattheend,thecomputerwouldtakethemalland

win.Forcingthehumanplayertohave4sticksmakesthishappen.Thesameistrueifthe

computercangivethehumanplayer(i.e.,leavethegameinthestateofhaving)8,12,or

16 sticks. This can be demonstrated by playing the game with actual sticks. So, if the

humanmovesfirst(asitdoesinthisimplementation)thecomputertriestoleavethegame

inastatewherethereare16,12,8,or4sticksleftafteritsmove.Thecodecouldbe:

defgetComputerMove(val):

n=val%4

ifn<=0:

return1

else:

returnn

There are a couple of details needed to finish this game properly that are left as an

exercise.

4.2.6 Scope

Avariablethatisdefined(firstused)inthemainprogramiscalledaglobalvariable,

andcanbeaccessedbyallfunctionsiftheyaskforit.Avariablethatisusedinafunction

canbeaccessedby thatfunction,andis notavailableinthemain program.It’s calleda

localvariable.Thisschemeiscalledscoping:thelocationsinaprogramwhereavariable

can be accessed is called its scope. It’s all pretty clear unless a global variable has the

samenameasalocalone,inwhichcasethequestionis:“whatvalueisrepresentedbythis

name?”Ifavariablenamed“x”isglobalandafunctionalsodeclaresavariablehavingthe

samename,thisiscalledaliasing,anditcanbeaproblem.

InPython,avariableisassumedtobelocalunlesstheprogrammerspecificallysaysitis

global.Thisisdoneinastatement;forexample:

globala,b,c

tells Python that the variables named a, b, and c are global variables, and are defined

outsideofthefunction.Thismeansthatafterthefunctionhascompletedexecution,those

variablescanstillbeaccessedbythemainprogramandbyanyotherfunctionsthatdeclare

themtobeglobal.

Globalvariablesarethoughtbysomeprogrammerstobeabadthing,butinfactthey

canbequiteusefulandcanassistinthegeneralityofthefunctionsthatareapartofthe

program.Aglobalvariableshouldrepresentsomethingthatis,infact,global,something

thatshouldbeknowntothewholeprogram.Forinstance,iftheprogramisonethatplays

checkersorchess,thentheboardcanbeglobal.Thereisonlyoneboard,anditisessential

tothewholeprogram.Thesameappliestoanyprogramthathasacentralsetofdatathat

manyofthefunctionsneedtomodify.

Anexampleofcentraldataisgamestateinavideogame.IntheSticksgameprogram

forexample,thefunctiongetComputerMove()takesaparameter—thegamestate.There

isonlyonegamestate,andalthoughforsomegamesitcaninvolvemanyvalues,inthis

casethereisonlyonevalue:thenumberofsticksremaining.Thefunctioncanberewritten

tousethegamestatevariablevalasaglobalinthefollowingway:

defgetComputerMove():

globalval

n=val%4

ifn<=0:

return1

else:

returnn

Similarly, the function that determines whether the game is over could use val as a

globalvariable.OntheotherhanditwouldbepoorstylisticformtohavegetMove()usea

globalfortheuser’smove.Thenamedoesimplythatthefunctionwillgetamove,andso

thatvalueshouldbereturnedasanexplicitfunctionreturnvalue.

Ifavariableisnamedasglobal,thenthatnamecannotbeusedinthefunctionasalocal

variable as well. It would be impossible to access it, and it would be confusing. It is a

commonprogrammingerrortoforgettodeclareavariableasglobal.Whenthishappens

thevariableisanewonelocaltothefunction,andstartsoutwithavalueof0.Thusno

syntaxerrorisdetected,butthecalculationwillalmostcertainlybeincorrect.Itmightbea

goodideatoidentifyglobalvariablesintheirname.Forexample,placethestring“_g”at

the end of the names of all globals. The game state above would be named val_g, for

example.Thiswouldbearemindertodeclarethemproperlywithinfunctions.

Other kinds of data that could be kept globally would include lists of names,

environment or configuration variables, complex data structures that represent a single

underlying process, and other programming objects that are referred to as singletons in

software engineering. In Python, because they have to be explicitly named in a

declaration,thereisaconstantreminderofthevariable’sscope.

4.2.7 VariableParameterLists

Theprint()functionisinterestingbecauseitseemstobeabletoacceptanynumberof

parametersanddealwiththem.Thestatement:

print(i)

printsthevalueofthevariablei,and

print(i,j,k)

prints the value of all three variables i, j, and k. Is this some sort of special thing

reserved for print() because Python knows about it? Nope. Any function can do this.

Considerafunction:

fprint(“formatstring”,variablelist)

where the format string can contain the characters “f” or “i” in any combination. Each

instanceofalettershouldcorrespondtoavariablepassedtothefunctioninthevariable

list,anditwillbeprintedasafloatingpointifthecorrespondingcharacterintheformat

stringis“f”andasanintegerifitis“i.”Thecall:

fprint(“fi”,12,13)

will print the values 12 and 13 as a float and an integer respectively. How can this be

writtenasaPythonfunction?

Thefunctionwouldstartoutwiththefollowingdefinition:

deffprint(fstring,*vlist)

The expression *vlist represents a set of positional parameters, any number of them.

Thisisprecededbyaspecificparameterfstring,whichwillbethe

formatstring.Asimpletestofthiswouldbetojustprintthevariablesinthelisttoseeifit

works:

deffprint(fstring,*vlist)

forvinvlist:

printv

Whencalledasfprint(“”,12,13,14,15)thisprints:

It removes some of the magic to point out that what is going on is that the list of

variablesafterthe*characteristurnedintoatuple,whichispassedastheparameter,so

the*vlistactuallycountsasasingleparameterwithmanycomponents.Nomagic.

Tofinishtheoriginalfunction,whathastobedoneistopeelcharactersoffofthefront

of the format string, match them against a variable, and print the result as the format

characterdictates.Soitisthesameloopasabove,butalsoanindexintotheformatstring

increaseseachtimethroughandisusedtoindicatetheformat.Itisalsoimportantthatthe

numberofformatitemsequalsthenumberofvariables:

deffprint(s,*vlist):

i=0

iflen(s)!=len(vlist):#Formatstringand

#variablelistagree?

print(“Theremustbethesamenumberofvariablesasformatitems.”)

return

forvinvlist:#Foreachvariable

ifs[i]==“f”:#Isthecorresponding

#formatꞌfꞌ?

fv=float(v)#Yes.Makeitafloat

print(fv,”“,end=””)#…andprintit

elifs[i]==“i”:#Isthecorresponding

#formatꞌiꞌ?

iv=int(v)#Yes.Makeitan

#integer

print(iv,““,end=””)#…andprintit

else:

print(“?”,end=””)#Donꞌtknowwhatthis

#is.Printit

i=i+1

Alloftheknownpositionalparametersmustcomebeforethevariablelist;otherwisethe

endofthevariablelistcan’tbedetermined.Thereisasecondcomplication,thatbeingthe

existenceofnamedparameters.Thoseareindicatedbyaparametersuchas**nlist.The

two“*” characters indicatea list of named variables. Thisis properly amore advanced

topic.

4.2.8 VariablesasFunctions

BecausePythoniseffectivelyuntypedandvariablescanrepresentanykindofthingat

all, a variable can be made to refer to a function; not the function name itself, which

always refers to a specific function, but a variable that can be made to refer to any

function.Considerthefollowingfunctions,eachofwhichdoesonetrivialthing:

defprint0():

print(“Zero”)

defprint1():

print(“One”)

defprint2():

print(“Two”)

defprint3():

print(“Three”)

Nowmakeavariablereferenceoneofthesefunctionsbymeansofan

assignmentstatement:

printNum=print1#Notethatthereisnoparameterlist

#given

ThevariableprintNum nowrepresentsa function,and wheninvoked, thefunction it

representswillbeinvoked.So:

printNum()

willresultintheoutput:

One

Why did the statement printNum = print1 not result in the function print1 being

called?Becausetheparameterlistwasabsent.Thestatement:

printNum=print1()

resultsinacalltoprint1atthatmoment,andthevalueofthevariableprintNumwillbe

the return value of the function. This is the essential syntactic difference: print1 is a

functionvalue,andprint1()isacalltothefunction.Toemphasizethispoint,hereissome

codethatwouldallowtheEnglishnameofanumberbetween1and3tobeprinted:

ifa==1:

printNum=print1#Assignthefunctionprint1to

#printNum

elifa==2:

printNum=print2#Assignthefunctionprint2to

#printNum

else:

printNum=print3#Assignthefunctionprint3to

#printNum

…

printNum()#Callthefunctionrepresentedby

#printNum

Therearemoresubtleusesinthiscase.Considerthisuseofalist:

a=1

printList=[print0,print1,print2,print3]

printNum=printList[a]

printNum()

willresultintheoutput:

One

Thefinaliterationofthisistocallthefunctiondirectlyfromthelist:

printList[1]()

ThisworksbecauseprintList[1]isafunction,andafunctioncallisafunctionfollowed

by().Seemsoverlycomplicated,doesn’tit?Itisrarelyused.

Forthosewithaninterestorneedformathematics,considerafunctionthatcomputes

thederivativeorintegralofanotherfunction.Passingthefunctiontobedifferentiatedor

integratedasaparametermaybethebestwaytoproceedinthesecases.

Example:FindtheMaximumValueofaFunction

Maximizingafunctioncanhaveimportantconsequencesinreallife.Thefunctionmay

represent how much money will be made by manufacturing various objects, how many

patientscangetthroughanemergencywardinanhour,orhowmuchfoodwillbegrown

withparticularcrops.Ifthefunctioniswellbehavedthentherearemanymathematically

soundwaystofindamaximumorminimumvalue,butifafunctionishardertodealwith,

thenlessanalyticalmethodsmayhavetobeused.Thisproblemproposesasearchforthe

best pair of parameters to a problem that could be solved using a method called linear

programming.

Theproblemgoeslikethis:

A calculator company produces a scientific calculator and a graphing calculator.

Long-term projections indicate an expected demand of at least 100 scientific

and80graphingcalculatorseachday.Becauseoflimitationsonproductioncapacity,

no more than 200 scientific and 170 graphing calculators can be made daily. To

satisfyashippingcontract, atotalofat least200calculators much beshippedeach

day.

If each scientific calculator sold results in a $2 loss, but each graphing calculator

producesa$5profit,howmanyofeachtypeshouldbemadedailytomaximizenet

profits?

Let s be the number of scientific calculators manufactured and g be the number of

graphingcalculators.Fromtheproblemstatement:

100<=s<=200

80<=g<=170

Also:

s+g>200,org>200-s

Finally,theprofit,whichistobemaximized,is:

P=–2s+5g

First,codetheprofitasafunction:

defprofit(s,g):

return-2*s+5*g

Asearchthroughtherangeofpossibilitieswillrunthroughallpossiblevaluesofsand

allpossiblevaluesofg;thatis,sfrom100to200andgfrom80to170.Thefunctionwill

beevaluatedateachpointandthemaximumwillberemembered:

#Rangeforsisx0..x1

#Rangeforgisy0..y1

#s+gmustbe>=sum

defsearchmax(f,x0,y0,x1,y1,sum):

pmax=-1.0e12

ps=-100

pg=-100

forsinrange(x0,x1+1):#Forallpossibles

forginrange(y0,y1+1):#Forallpossibleg

ifs+g>=sum:#Conditionisok?

p=f(s,g)#Calculatetheprofit.

ifp>=pmax:#Bestsofar?

pmax=p#Yes.

ps=s#Saveitand

pg=g#theparameters

return((ps,pg))

Finally,thecallthat doestheoptimization callsthesearch function passingtheprofit

functionasaparameter:

c=searchmax(profit,100,80,200,170,200)

print(c)

Theanswerfoundisthetuple(100,170),ors=100andg=170,whichagreeswiththe

correctanswerasfoundbyothermethods.Thisisonlyoneexampleofthevalueofbeing

abletopassfunctionsasparameters.Mostofthecodethatdoesthisismathematical,but

mayaccomplishpracticaltaskslikeoptimizingperformance,drawinggraphsandcharts,

andsimulatingreal-worldevents.

4.2.9 FunctionsasReturnValues

Justasanyvalue,includingafunction,canbestoredinavariable,anyvalue,including

afunction,canbereturnedbyafunction.IfafunctionthatprintsanEnglishnameofa

numberisdesired,itcouldbereturnedbyafunction:

defprint0():

print(“Zero”)

defprint1():

print(“One”)

defprint2():

print(“Two”)

defprint3():

print(“Three”)



defgetPrintFun(a):#Returnafunctiontoprinta

#numericvalue0..3

ifa==0:

returnprint0#Returnthefunctionprint0as

#theresult

elifa==1:

returnprint1#Returnthefunctionprint1as

#theresult

elifa==2:

returnprint2#Returnthefunctionprint2as

#theresult

else:

returnprint3#Returnthefunctionprint3as

#theresult

Callingthisfunctionandassigningittoavariablemeansreturningafunctionthatcan

printanumericalvalue:

printNum=getPrintFun(2)#AssignafunctiontoprintNum

andthen:

printNum()#CallthefunctionrepresentedbyprintNum

resultsintheoutput:

Two

The function printFun returns, as a value, the function to be called to print that

particular number. Returning the name of the function returns something that can be

called.

Why would any of these seemingly odd aspects of Python be useful? Allowing a

general case, permitting the most liberal interpretation of the language, would permit

unanticipatedapplications,ofcourse.Andtheabilitytouseafunctionasavariablevalue

andareturnresultareanaturalconsequenceofPythonhavingnospecifictypeconnected

withavariableatcompilationtime.Therearemanyspecificreasonstousefunctionsin

thisway,ontheotherhand.Imagineafunctionthatplotsagraph.Beingabletopassthis

functionanotherfunctionto beplottedissurely themostgeneral waytoaccomplishits

task.

4.3 RECURSION

Recursion refers to a way of defining things and a programming technique, not a

languagefeature.Somethingthatisrecursiveisdefinedatleastpartlyintermsofitself.

Thisseemsimpossibleatfirst,butconsiderthecaseofagrocerylist(notaPythonlist)of

itemssuchas:

milk,bread,coffee,sugar,peanutbutter,cheese,jam

Eachelementinthelistcanbecalledanitem,andrepresentssomethingtobepurchased

atagrocerystore.Thesmallestlistisonehavingonlyasingleelement:

milk

Thus,alistcanbesimplyanitem.Whatelsecanitbe?Itappearstobeabunchofitems

separatedbycommas.Onewaytodescribethisistosayitcanbeanitemfollowedbya

commafollowedbyalist.Thecompletedefinitionis,presumingthatthesymbol->means

“canbedefinedas”:

list->item#listcanbedefinedasanitem

list->item,list#listcanbedefinedasanitem,acomma,andalist

Inthiswaythelistmilkisdefinedasalistbythefirstrule.Thelistmilk,breadisalist

becauseitisanitem(milk)followedbyacommafollowedbyalist(bread).Itisplain

that a list is defined here in terms of itself, or at least in terms of a previous partial

definitionofitself.

When talking about functions, a function is recursive if it contains within it a call to

itself.Thisisnormallydoneonlywhenthethingthatitisattemptingtoaccomplishhasa

definitionthatisrecursive.Recursionasaprogrammingtechniqueisanattempttomake

the solution simpler. If it does not, then it is inappropriate to use recursion. A problem

somebeginningprogrammershavewiththeideasofarecursivefunctionisthatitappears

that it does not terminate. Of course, it is essential that a function does return, and a

program that never ends is almost always in error. The problem really is how to make

certainthatachainoffunctioncallsterminateseventually.

Thefollowingfunctionwillneverreturnoncecalled:

defrecur1(i):

recur1(i+1)

print(i)

Itwillnotresultinanyoutput,either.Whynot?Becausethefirstthingitdoesiscall

itself,andalwaysdoesso.Whenitdoes,thenextthingisdoesiscallitselfagain,andthen

again,andsoon.Thefollowingfunction,ontheotherhand,willterminate:

defrecur2(i):

ifi>0:

recur2(i-1)

print(i)

Whencalleditchecksitsparameteri.Ifthatparameterisgreaterthanzero,thenitcalls

itselfwithasmallervalueofi,meaningthateventuallyiwillbecomesmallerthan0and

thechainofcallswillstop.Whatwillbeprinted?Thefirstcalltorecur2thatdoesnotend

upcallingitselfiswheni==0,sothefirstthingprintedwillbe0.Thenthefunctionreturns

tothepreviousrecursivecall,whichhadtobewherei==1.Thesecondthingprintedwill

be1.Andsoonuntilitreturnstotheoriginalcalltothefunctionwiththeoriginalvalueof

i,atwhichpointitprintsi.Thisisatrivialexampleofarecursivefunction,butillustrates

howtoexitfromthechainofcalls:theremustbeaconditionthatdefinestherecursion.

Whenthatconditionfails,therecursionceases.

Eachcalltothefunctioncanbethoughtofasaninstanceofthatfunction,anditwill

createallofthelocalvariablesthataredeclaredwithinit.Eachinstancehasitsowncopy

ofthese, includingits parameters, andeach callreturns to thecaller as occurswith any

otherfunction call. So, when the recursivecallto recur2()returns, thenext thing to be

done will be (in this case) to print the parameter value. A call to recur2() passing the

parameter4willresultinthefollowinginstancesofthatfunctionbeingcreated:

Bytracingthroughthestatementsthatareexecutedinthisway,itcanbeseenthatthe

recursiondoesend,andtheoutputorresultcanbeverified.

One important use of recursion is in reducing a problem into smaller parts, each of

which has a simpler solution than does the whole problem. An example of this is

searchingalistforanitem.Ifnames=[Adams,Alira,Attenbourough,…]isaPython

listofnamesinalphabeticalorder,answerthequestion:“DoesthenameParkerappearin

this list?” Of course there is a built-in function that will do this, but this example is a

pedagogicalmoment,andanywayperhapsthebuilt-infunctionisslowerthanthesolution

thatwillbedevisedhere.

ThefunctionwillreturnTrueorFalsewhenpassedalistandaname.Theobviousway

tosolvetheproblemistoiteratethroughthelist,lookingatalloftheelementsuntilthe

namebeingsearchedforiseitherfoundoritisnotpossibletofinditanymore(i.e.,the

current name in the list is larger than the target name). Another, less obvious way to

conductthesearchistodividethelistinhalf,andonlysearchthehalfthathasthetarget

nameinit.Considerthefollowingnamesinthelist:

…BroadbentButterworthCaitCaraCarlingDeversDillanEberlyFoxworthy…

The name in the middle of this list is Carling. If the name being searched for is

lexicographicallysmallerthanCarling,thenitmustappear inthefirsthalf;otherwiseit

must appear in the second half. That is, if it is there at all. A recursive example of an

implementationofthisis:

#Searchthelistforthegivenname,recursively.

defsearchr(name,nameList):

n=len(nameList)#Howmanyelementsinthis

#list?

m=n/2

ifname<nameList[m]:#targetnameisinthefirst

#half

returnsearchr(name,nameList[0:m])#Searchthe

#firsthalf

elifname>nameList[m]:#targetmustbeinthe

#secondhalf

returnsearchr(name,nameList[m:n]#Searchthe

#secondhalf

else:

returnTrue

Ifthenameisinthelist,thisworksfine.Onewaytothinkofthisisthatthefunction

searchr()will take a string and a list as parameters and find the name in the list if it’s

there.Thewayitworksisnotclearfromoutsidethefunction(withoutbeingabletosee

thesource)andshouldnotmatter.SO:ifthetargetistobefoundinthefirsthalfofthelist,

forexample,thencallsearchr()withthefirsthalfofthelist.

searchr(name,nameList[0:m])

Thefactthatthecallisrecursiveisnotreallytheconcernoftheprogrammer,butisthe

concern of the person who created the Python system. Now, how can the problem of a

namenotbeinginthelistbesolved?

Whenthenameisnotinthelist,theprogramwillcontinueuntilthereisbutoneitemin

thelist.Ifthatitemisnotthetarget,thenitisnottobefound.So,ifn=1(onlyoneitemin

thelist)andnameList[0]isnotequaltothetarget,thenthetargetisnottobefoundinthe

listandthereturnvalueshouldbeFalse.Thefinalprogramwillthereforebe:

defsearchr(name,nameList):

n=len(nameList)#Howmanyelementsinthislist?

m=int(n/2)

ifn==1andnameList[0]!=name:#Endoftherecursive

#calls

returnFalse#Itꞌsnotinthis

#list.

ifname<nameList[m]:#targetnameisinthefirst

#half

returnsearchr(name,nameList[0:m])#Searchthe

#firsthalf

elifname>nameList[m]:#targetmustbeinthe

#secondhalf

returnsearchr(name,nameList[m:n])#Searchthe

#secondhalf

else:

returnTrue

Many algorithms have fundamentally recursive implementations, meaning that the

effectivesolutionincodeinvolvesarecursivefunctioncall.Manystandardexamplesin

beginning programming are not properly implemented recursively. Commonly

encounteredsampleswitharecursivesolutionincludethefactorial,whichhasarecursive

definition but is not best implemented in that manner, and any other basically linear

technique (linear search, counting, min/max finding) that does not do a reasonable

subdivision.Testingthefirstcomponent,forexample,andthenrecursivelylookingatthe

remainingelementsisapoorwaytouserecursion.Itwouldbemuchbettertousealoop.

Here’sanexample:findthemaximumvalueinagivenlist.Thenon-recursivemethod

(reasonable)wouldbe:

defmax(myList):

max=myList[0]

foriinrange(1,len(myList)):

ifmyList[i]>max:

max=myList[i]

returnmax

Thisisaneffectivewaytofindthelargestvalueinalist,andisprettyeasilyunderstood

byaprogrammerreadingthecode.Nowhereisarecursivesolution:

defmaxr(myList):

m1=myList[0]

iflen(myList)>1:

m2=maxr(myList[1:])

else:

returnm1

ifm1>m2:

returnm1

else:

returnm2

This function works by subdividing the list into two parts, as is often done with a

recursivesolution.Theideaistocomparethefirstelementinthelistwiththemaximumof

theremainderofthelisttoseewhichisbigger.Forthisparticularproblemthisisnotan

obvious approach. It is less efficient and less obvious than the iterative version that

preceded it. The use of recursion simplifies some problems, but it is not a universally

applicable technique and should never be used to show off. Examples of very useful

recursivefunctionswillbeexaminedinlaterchapters.

4.3.1 AvoidingInfiniteRecursion

Thereisalimittohowmanytimesafunctioncancallitselfwithoutreturning,because

eachcallusesupsomeamountofmemory,andmemoryisafiniteresource.Usuallywhen

this happens a programming error has occurred and the function has slipped into an

infiniterecursion, in which it will continue to call itself without end. Recursion can be

confusingtovisualizeandthissortofproblemoccursfrequently.Howcanitbeavoided?

Programming the function correctly eliminates the problem, of course, but there are

some basic rules that will avoid the problem at early stages. Assuming that global

variablesarenotbeingreferenced:

1.Afunctionthatbeginswithacalltoitselfisalwaysinfinitelyrecursive.Thefirst

thingthefunctiondoesiscallitself,andnomatterwhattheparametersareitcan

neverend.

2.Everyrecursivecallwithinafunctionmusthaveaconditionuponwhichthatcall

willbeavoided.Thefunctionmayreturnsometimebeforethecallismade,or

perhapsthecallhappenswithinanifstatement,buttheremustbesuchacondition.

IfitexistsitisexpressibleasaBooleanexpression,andthisshouldbeplacedina

commentneartherecursivecall.Thecallissuspectuntilthishappens.

3.Avoidpassingafunctiontoitself.Thecalltoaparameterhidesthefactthat

recursionistakingplace.

4.Itispossibletohaveaglobalvariablethatisacountofthedepthofrecursion.The

functionwillincrementthiscountwheneverarecursivecallismadeanddecreaseit

justbeforereturning.Ifthecountevergetslargerthanareasonableestimateofthe

maximumdepth,thenthefunctioncouldstopanymorecallsandbackout,oran

errormessagecouldbeprinted.

4.4 CREATINGPYTHONMODULES

Insomeoftheexamplesgivensofarthereisastatementatthebeginningthatlookslike

“import name.” The implication is that there are some functions that are needed by the

programthatareprovidedelsewhere,possiblybythePythonsystemitselforperhapsby

some other software developer. The idea of writing functions that can be reused in a

straightforwardwayisveryimportanttothesoftwaredevelopmentprocess.Itmeansthat

no programmer is really alone; that code is available for doing things like generating

randomnumbersorinterfacingwiththeoperatingsystemortheInternet,andthatitdoes

not to be created each time. In addition, there is an assumption that a module works

correctly.Whenaprogrammerbuildsacollectionofcodefortheirownuse,itneedstobe

testedasthoroughlyaspossible,andfromthattimeonitcanbeusedinapackagewith

confidence.Ifaprogramhaserrorsinit,thenlookinthecodeforthatprogramfirstand

notinthemodules.Thismakesdebuggingcodefaster.

Whatisamodule?Itissimplyafunctionorcollectionoffunctionsthatresideinafile

whose name ends in “.py.” Technically, all of the code developed so far qualifies as

modules. Consider as an example the function from the previous section that finds the

maximumvalueinalist.Savethefunctionsmax()andmaxr()inafilenamedmax.py.

NowcreateanewPythonprogramnamedusemax.pyandplaceitinthesamedirectoryas

max.py.Ifthetwofilesareinthesamedirectory,theycan“see”eachotherinsomesense.

Hereissomecodetoplaceinthefileusemax.py:

importmax

d=[12,32,76,45,9,26,84,25,61,66,1,2]

print(“MAXis“,max.max(d),“MAXRis“,max.maxr(d))

ifmax.maxr(d)!=max.max(d):

print(“***NOTEQUAL****”)

Thisprogramisjustatestofthetwofunctionstomakecertainthattheyreturnthesame

valueforthesamelist,thevariabled.Notetwothings:

1.Thestatementimportmaxoccursatthebeginningoftheprogram,meaningthat

thecodeinsidethisfileisavailabletothisprogram.Pythonwilllookinsideofthis

fileforfunctionandvariablenames.

2.Whenthefunctionmax()ormaxr()iscalled,thefunctionnameisprecededbythe

modulename(max)andaperiod.ThissyntaxinformsthePythonsystemthatthe

namemaxr()(forexample)isfoundinthe

modulemaxandnotelsewhere.

ThefirsttimethatthemoduleisloadedintothePythonprogramthecodeinthemodule

isexecuted.Thisallowsanyvariableinitializationstobeperformed.Henceforththatcode

is not executed again, and functions within the module can be called knowing that the

initializationshavebeenperformed.

Themodulecouldresideinthesamedirectoryastheprogramthatusesit,butdoesnot

haveto.ThePythonsystemrecognizesasetofdirectoriesandpathsandmodulescanbe

placedinsomeofthoselocationsaswell,makingiteasierforotherprogramsonthesame

computertotakeadvantageofthem.Onthecomputerusedtocreatetheexamplesinthis

book, the directory C:\Python34\Lib can be used to store modules, and they will be

recognizedbyimportstatements.

Finally, if the syntax max.maxr(list) seems a bit cumbersome, then it is possible to

importspecificnamesfromthemoduleintotheprogram.Considerthefollowingrewrite

ofusemax.py:

frommaximportmax,maxr

d=[12,32,76,45,9,26,84,25,61,66,1,2]

print(“MAXis“,max(d),”MAXRis“,maxr(d))

ifmaxr(d)!=max(d):

print(“***NOTEQUAL****”)

Thestatementfrommaximportmax,maxrinstructsPythontorecognizethenames

maxandmaxrasbelongingtothemodulenamedmax(i.e.,asresidinginthefilenamed

max.py).Inthatcasethefunctioncanbecalledbysimplyreferencingitsname.

There would appear to be a name conflict with the package named max and the

functionnamedmax,butinfactthereisnot.Indeed,it’snotuncommontofindthissortof

namingrelationship(example:random.random()).Themodulenamemaxreferstoafile

name,max.py.Thefunctionnamemaxreferstoafunctionwithinthatfile.

4.5 PROGRAMDESIGNUSINGFUNCTIONS–

EXAMPLE:THEGAMEOFNIM

Nimisagamesooldthatitsoriginshavebeenlost.ItwaslikelyinventedinChina,and

isoneoftheoldestgamesknown.Itwasalsooneofthefirstgamestohaveacomputeror

electronicimplementationandhasbeenthefrequentsubjectofassignmentsincomputer

programming classes. This program will implement the game and will play one side. It

will serve as an example of how to design a computer program using functions and

modularity—itisanexampleofa

top-downdesign.

The game starts with three rows of objects, such as sticks or coins, and there are a

different number of objects in each row. In this version there are 9, 7, and 5 “sticks,”

whicharerepresentedby“|”characters.Aplayermayremoveasmanyobjectsfromone

rowastheychoose,buttheymustremoveatleastoneandmusttakethemonlyfromone

row.Playerstaketurnsremovingobjects,andtheplayertakingthatfinaloneisthewinner.

Playing this game involves asking the user for two numbers: the row from which to

removesticks,andhowmanytoremove.Thehumanplayerwillbepromptedfortherow,

thenthenumber.Thenthecomputerwillremovesomesticks(takeitsturn)andprintthe

newstate.

Alistnamedvalcontainsthenumberofsticksineachrow.Initially:

val=[5,7,9]

Thisisthegamestate,andiscriticaltothegameasitdefineswhatmovesarepossible.

Also,whenthestateis[0,0,0]thenthegameisover.

WhentheuserchosestoremoveNsticksfromrowMtheactionis:

val[M]=val[M]-N

OfcourseNandMmustbetestedtomakecertainthatMisbetween0and2,andMis

aslargeasval[M].Mdefinestherowchosentoremovesticksfrom,andNisthenumber

ofstickstoremove.Amovecanthereforebedefinedasalist[row,sticks].

A program that uses functions should be built from the highest level of abstraction

downwards.Thatis,themainprogramshouldbedevelopedfirst,andshouldbeexpressed

intermsoffunctionsthatdologicalthings,butthatmaynotbedesignedorcodedyet.So,

themainprogramcouldlooksomethinglikethis:

val=[5,7,9]#thegamestate:5,7,and9sticks

done=False#Isthegameover?

userMove=[-1,-1]#Amoveisarowandanumberof

#sticks.

print(“ThegameofNim.”)

rules()#Printtherulesforthegame

whilenotdone:#Rununtilthegameisover

displayState(val)#Showthegameboard

prompt(userMove)#Askuserfortheirmove

ok=legalMove(userMove,val)#Wastheplayerꞌsmove

#OK?

whilenotok:

print(“Thismoveisnotlegal.”)

displayState(val)

prompt(userMove)#Askuserfortheirmove

ok=legalMove(userMove,val)

makeMove(userMove)#Makeit

ifgameOver(val):

print(“Youwin!”)

break;

print(“Stateafteryourmoveis“)#displayit.

displayState(val)

Thisprogramisbuiltusingcomponents(modules)thatarenotwrittenyet,butthathave

apurposethatisdefinedbywhattheprogramneeds.Thosemodules/functionsare:

rules()-Printouttherulesofthegame

displayState(v)-Printthegamestate(howmanysticksineachrow)

prompt()-Asktheuserfortheirmove

legalMove(r,n)-isthemovelegal?

makeMove(r,n)-makethismove

Usingfunctions,thefirstthingthatisneededistodisplaythegamestate.Itprintsthe

numberofsticksineachofthethreerows,anddoessoinagraphicalway(i.e.,ratherthan

justdisplayingthenumbers).Giventhesituationasdescribedsofar,thenon-trivialsuch

functionisdisplayState(),whichprintsthecurrentstateofthegame—howmanysticksin

eachrow.Itwillbepassedalistrepresentingthecurrentstate.

defdisplayState(val):#valisthelistwith

#thestate

forjinrange(0,3):#thereare3rows;

#printeachone

print(j+1,“:“,end=””)#Printtherownumber

foriinrange(0,val[j]):#val[j]isthecurrent

#row

print(“|“,end=””)#printaꞌ|ꞌforeach

#stick

print(””)#printanendofline

When called at the beginning of the game, here’s what the result of a call to this

functionwouldbe:

1:|||||

2:|||||||

3:|||||||||

Thisfunctiondoesasingletask,usesaparametertoguideitandmakeitmoregeneral,

andisnamedforwhatitdoes.Thesearesignsofagoodfunction.Notethatthefirstrowis

labeled“1,”butisinfactelement0ofthelist.Itiscommoninuserinterfacestoadaptto

the standard human numbering scheme that begins with 1 instead of 0. When the user

entersarownumbercaremustbetakentosubtract1fromitbeforeusingitasanindex.

There is no required order for writing these functions, but the next one used in the

programisprompt().Thiswillasktheusertoinputarowandthenreadarownumber,

thenprompttheusertoenteranumberofstickstoremoveandthenreadthatvaluetoo.

The two numbers will be placed into a list that was passed so that the values can be

returnedtothecaller.

defprompt(move):

row=input(“Yourmove:whichrow?“)#Promptforrow&

#readit

sticks=input(”howmanysticks?”)#Promptfor

#sticks&read



#Convertrowtointegeranddecrementtobefrom0to2.

move[0]=int(row)-1#Assigntothelist[0]

move[1]=int(sticks)#Assignvaluetolist[1]

This function again does a simple task, uses a parameter, and is named pretty

appropriately.

Nextisthequestion“Isthismovelegal”?Amoveislegaliftherowisbetween0and2

inclusive,andifthenumberofsticksinthatrowisgreaterthanorequaltothenumberof

stickstoberemoved.ThefunctionreturnsTrueorFalse.

deflegalMove(move,state):

row=move[0]#Whichrowwasrequested?

sticks=move[1]#Howmanysticks

ifrow<0orrow>2:#Legalnumberofrows?

returnFalse#No

ifsticks<=0orsticks>val[row]:#Legalnumberof

#sticks?

returnFalse#No

returnTrue#Bothwereok,sothemoveisOK.

Makingamoveinvolvesdecreasingthespecifiedrowbythespecifiednumberofsticks.

This could have been done in legalMove() if it were thought to be OK to do multiple

thingsinafunction.Eventuallythatwillbenecessary,butfornowanewfunctionwillbe

written,namedmakeMove(),thatwillactuallyimplementaspecifiedplayinthegame.

defmakeMove(move,state):

row=move[0]#Subtractmove[1]sticksfrom

sticks=move[1]#thosethatareinrowmove[0].

#Placethenewnumberofsticksinthestatelist

state[row]=state[row]-sticks

Thereisastrategythatwillpermitaplayertoalwayswin.Itinvolvescomputingwhat

amountstoaparityvalueandmakingamovetoensurethatparityismaintained.Consider

theinitialstateandthestateaftertakingtwosticksfromrow1:

Row1=5=0101row1=3=0011

Row2=7=0111row2=7=0111

Row3=9=1001row3=9=1001

Parity10111101

The parity is determined by looking at each digit in the binary representation of the

values.Ineachcolumn(digitposition)theparitybitforthatcolumnis1ifthenumberof1

bitsinthecolumnisoddand0ifitiseven.Thiscanbecalculatedusingtheexclusive-OR

operator,whichis“^”inprocessing.ThestrategyinNimistomakeamovethatmakesthe

parityvalue0. Itturnsout thatthisis alwayspossibleif parityisnot 0;in thesituation

above,thecomputermightremove5sticksfromrow3givingthestate:

row1=3=0011

row2=7=0111

row3=4=0100

Parity0000

Thisiswhatthesketchdoesaftereverymovetheplayermakes:itmakesallpossible

moves, computing the parity after each one. When the one with zero parity is found it

makes that move. The function eval() calculates the current parity value as

val[0]^val[1]^val[2].

NOTEThe computer always wins because the user always makes the first move.

Alternatingwhomovesfirstwouldmakethegameplayfairer.

4.5.1 TheDevelopmentProcessExposed

IntheintroductiontotheNimprogramitwassaidthatthiswasanexampleoftop-down

design. This means that the larger program, or the main program, is designed first. The

questionshouldbewhatarethestepsinvolvedinsolvingthisproblem?Theanswertothat

questioniswrittendownintermsoffunctionsthathavenotbeenwrittenyet,butthathave

aknownandrequiredpurposewithinthesolution.IntheNimgameitisknownthatthe

user’smovewillhavetobereadfromthekeyboardandthatthecurrentstateofthegame

willhavetobedisplayed,sothosetwofunctionscanbepresumedtobeimportanttothe

solutionwhensketchingthemainprogram.

Oncethehigh-levelpartoftheprogramhasbeendevised,itcanbetypedinandtested.

Thefunctionsthatareneededbutarenotyetwrittencanbecodedasstubs:functionsthat

donotimplementtheirtaskbutthatarepresentandpreventsyntaxerrors.Thefirsttryata

solutionofthissortdoesnot,ofcourse,solvetheproblem,butissimplyasteptowardsthe

solution.InthecaseofNim,theveryfirststepcouldbesomethinglike:

Repeat

Displaythegame

Askuserfortheirmove

Makeuserꞌsmove

Generatecomputerꞌsmove

Makecomputer'smove

Untilsomeonewins

Displaythewinner

Noneofthesesteps arewrittenasproper Python code,andthat’sOK forafirststep.

TranslatingthisintoPythonwouldbeagoodidea:

Done=false

whilenotdone:#Rununtilthegameisover

displayState()#Showthegameboard

prompt()#Askuserfortheirmove

makeMove()#Makeit

ifnotgameOver():#Computermove?

makeComputerMove()#Determinecomputer'smove

done=gameOver()#Isthegameover?

printWinner()

Atthispointinthedesignthedatastructurestobeusedinthesolutionhavenotbeen

devised, nor have the algorithms needed. This is merely a sequence of steps that could

leadtoaprogramthatworks.Thefunctionscannowbewrittenasstubs:

defdisplayState():defprompt():

print(“Displaystate”)print(“Entermove”)

defmakeMove():defgameOver():

print(“Makemove”)ifrandom.random()<0.2:

returnFalse

returnTrue

defmakeComputerMove():defprintWinner():

print(“computeamove”)print(“Thewinneris:”)

Theoutputfromthisprogrammightbe:

Displaystate

Entermove

Makemove

Displaystate

Entermove

Makemove

computeamove

Thewinneris:

Theexactoutputwillberandom,dependingonwhatthereturnvalueofgameOver()is.

Thiscodecanbethoughtofasoneiterationofthesolution,orasaprototype.Thenext

step will be to refine the solution by implementing one of the stubs. Each time that

happensasetofdecisionswilllikelybemadeconcerningthenatureofthedatastructures

used to implement the solution: the use of a list for the game state, for instance. Three

integerscouldhavebeenusedinstead,butoncethedecisionismadeonewayortheother

itshouldbestuckwithunlessitbecomesinfeasible.

Repeatedly implementing the stubs creates new prototypes, each one more functional

than the one before. Some of the functions may require an application of this same

process.Complexfunctionscanbecodedintermsofotherstubs,andsoon.Thesimpler

functions,suchasthosethatcalculatebasedonlyontheirparameter,shouldbecompleted

firstandshouldnotinvolvepermanentdesignchoices.

A programming process of this kind can be thought of as iterativerefinement. At all

times after the first step, a complete program that compiles and runs will exist to be

demonstratedandrefined.Thiscanbeveryuseful,especiallywhendealingwithgraphical

user interfaces and games. The interface might well be complete before any real

functionality is present, and this permits a demonstration of the concept before the

programisdone.

4.6 Summary

Pythonallowsaprogrammertocreateafunctionthatdoessomethingnew.Afunctionis

reallyjustsomecodethathasaname,andcanbeexecutedsimplybyinvokingthatname.

Itusuallyrepresentssometaskthathastobedonefairlyfrequently.Afunctionshouldalso

haveonemaintask,andthattaskshouldberepresentedinthefunctionname:maximum,

square, search, and so on. Many functions return a value, and finding that value is

frequentlythepurposeofthefunction(e.g.,sine,cosine).

Thenameofafunctioncanbeusedtocallthatfunction,butitcanalsobeassignedtoa

variable,passedasaparametertoanotherfunction,orreturnedasavalue.Afunctioncan

have variables that belong to it; they are called local variables and vanish after the

functionreturns.Theycanalsousevariablesdefinedoutsideofthefunctioniftheyappear

inaglobalstatement.

AspecialvaluenamedNoneisusedtorepresentnovalue,andisreturnedbyafunction

thatdoesnotexplicitlyreturnsome othervalue.Amoduleisafunctionorcollectionof

functionsthatresideinafilewhosenameendsin“.py.”

Theuseoffunctionscanorganizeacomputerprograminalogicalway.Aprogramcan

be defined in terms of functions that are desired but not yet written, and then those

functionscanbedefinedascodeorintermsofotherfunctions.Functionsareoftennamed

butareincomplete,andarecalledstubs—theypermittheprogramtobecompiledwhile

stillunderdevelopment.

Afunctionthatcallsitselfissaidtoberecursive.Suchfunctionscanbeveryvaluablein

simplifyingthecodeforsomealgorithms,especiallyonesinwhichsomethingisactually

defined in terms of itself, but care must be taken when programming to ensure that a

recursivefunctionalwaysultimatelyreturns.

Exercises

1.WriteaPythonfunctionthattakesatupleofnumbersasaparameterandreturnsthe

location(index)ofthemaximumvaluefoundinthattuple.

2.Awordprocessingsystemsometimesneedstoshortenawordtomakeitfitonaline.

Writeafunctionthattakesastringcontainingasinglewordanddecideswhereto

hyphenateit.Ahyphencanoccurbeforetheendings:“ing,”“ed,”“ate,”“tion,”or

“ment.”Itcouldalsooccurafteraprefix:“pre,”“post,”“para,”“pro,”“con,”or

“com.”Otherwise,placeahyphensomewhereinthemiddleoftheword.Thefunction

shouldreturnatuplecontainingthefirstandsecondhalfofthewordsplitatthe

hyphen.

3.Pascal’striangleisanarrangementofnumbersinrowsandcolumnssuchthateach

numberinarowisthesumofthetwonumbersaboveit.Anexampleis:

11

121

1331

Write a function triangle(n) that prints the first n rows of such a triangle. Useextra

marksforproperindentationsoitlookslikeatriangle.

4.Writeafunctionthatreturnsthevalueofaquadraticfunctionataparticularxvalue.A

quadraticisapolynomialoftheform:

ax2+bx+c

The function quad() is passed values for a, b, c, and x and returns the value of the

polynomial.

5.Aquadraticpolynomialhasarootatanyvaluexforwhichthevalueofthe

polynomialiszero;thatis,anyxsuchthat

ax2+bx+c=0

Therecanonlybeatmosttwosuchvalues(atuple),andtheexpressionforfindingthese

valuesofxis:

Writeafunction(root(a,b,c))thatreturnsthetworootsofaquadraticequationhaving

beenpasseda,b,andc.Theresultisatuple,orifthereisnosolution(i.e.,squareroot

ofanegativenumber,ora=0)thenitreturnsNone.

6.Writeafunction(inputfloat(s))thattakesasingleparameter,astringtobeusedasa

prompt,andreturnsanumberreadfromtheconsole.Thefunctionmustpromptthe

userforthenumberusingthegivenstring,readtheinput,andreturntheresultasa

floatingpointnumber.IfanerroroccursreturnNone.

7.Thegameoftabletennisissometimescalledping-pong.Writefunctionsping()and

pong()thateachtake,asaparameter,aprobabilityofhittingtheball.Aprobabilityis

between0.0and1.0.ThefunctionreturnsTrueiftheballisreturnsandFalse

otherwise.Therearetwosidestothegame,andeachsideserves(playsfirst)twice,

thentheothersideservestwice.Itwillbeassumedherethattheserveralways

succeeds.Ifpingisservingthenpong()getscalledfirst,thenifpongsucceededthen

ping()getscalled,andsoon.Thesidethatmadethelastsuccessfulhitwinsapoint.

Thegamegoesto11points,butmustbewonbya2-pointmargin.Writeaprogram

thatsimulatesping-pongusingtwofunctionsnamedping()andpong().

8.Inmutualrecursiontwofunctionscalleachother,usuallyrepeatedlytosomedepth.

So:AcallsB,whichcallsAagain,whichcallsBagain,andsoon.Recodetheping-

pongexercise(Number7above)sothatping()callspong()andpong()callsping().

Thefunctionsreturnastring,thatofthewinneroftheexchange.

9.Writeafunctionprime(n)thatreturnsTrueifthenumbernisprime,andFalse

otherwise.Howmanyprimenumbersaretherebetween1and1000?

NotesandOtherResources

Tutorial on Python Functions:

http://www.tutorialspoint.com/python/python_functions.htm

Also:http://anh.cs.luc.edu/python/hands-on/3.1/handsonHtml/functions.html

1.ThomasS.Ferguson.GameTheory,

https://www.math.ucla.edu/~tom/Game_Theory/comb.pdf

2.D.G.Luenberger.(1973).IntroductiontoLinearandNonlinearProgramming

(Vol.28),Reading,MA:Addison-Wesley.

3.MitchellWand.(1980).Induction,Recursion,andProgramming,NorthHolland,

NY,http://tocs.ulb.tu-darmstadt.de/82570701.pdf

CHAPTER5

FILES:INPUTANDOUTPUT

5.1WhatIsaFile?ALittle“Theory”

5.2KeyboardInput

5.3UsingFilesinPython:LessTheory,MorePractice

5.4WritingToFiles

5.5Summary

Inthischapter

Intheearlydaysofcomputing,whenarespectablemachinewouldfillaroom,thefilewas

invented.Itwasanobvious thing,really:apackagein whichtoplacedata onatapeor

disk drive. Storage that was not memory, which was pretty fast, was called secondary

storage,andwasterriblyslowcomparedtohowfastacomputercouldexecuteinstructions

(which is terribly slow compared to how fast a modern computer can execute

instructions).

Filesstillexist,andatypicalPChashundredsofthousandsofthem.Thedetailsofhow

filesareimplementedisinteresting,butunimportanttothediscussionofhowtousethem

inPython.Thefocuswillbeonhowandwhytousethemeffectively.

Thefirstthingtoknowaboutafileisthatitisacollectionofbytesstoredonadiskor

similardevice.Onesetofbytescanlookverymuchlikeanother,andunlesstheformatof

thefile(i.e.,thewaythebytesareordered)anditsbasiccontents(i.e.,whatkindofthing

the bytes represent) is known ahead of time, the information stored there is unusable.

Computer programs are written assuming that the files they will read have a particular

nature; if given a file that does not have that nature, the program will not function

properly.

Whatkindsoffilesarethere?Hereisashortlist:

1.Textfiles.Thesecontaincharactersthatapersoncanread,andcanbethoughtofas

documents.

2.Executablefiles.Theseholdinstructionsthatacomputercanexecute.Suchafileis

aprogramoran“app.”

3.Datafiles.Itcouldalsobeatextfileifitisstoredascharacters,butitcouldbeaset

ofbytesthatrepresentintegersorrealnumbers.

4.Imagefiles.Therearemanytypesofimagefiles,andtheycontainpicturesin

digitalformat.ManydigitalcamerasuseaformatcalledJPEG,butGIForPNGare

twoofmanyothers.Notonlyareimagesstoredinsuchafile,butalsodataabout

howlargetheimageis,whenitwastaken,andotherdetails.

5.Soundfiles.ThemorecommonsoundfileistheMP3,buttherearemanyothers.

6.Video.MPEGandAVIarestandardformatsforvideo,andthereareagreatmany

filesofthissortavailableontheInternet.

7.  Web pages. These are a special kind of text file. They can be examined and

modifiedusingbasictexteditors,butcan’tbeviewedproperly(i.e.,asawebpage)

exceptthroughabrowser,whichisreallyaspecialkindofdisplayutilitythatcan

bothdrawimagesandconnecttotheInternettodownloadmoreinformation.

Allofthese files,and indeedall files,have certain thingsin common.Some ofthese

thingscanbeignoredwhenwritingPythonprograms,butotherscannot.

Fileshavenames.Thefirstwaytoaccessafileisusuallybyspecifyingitsname.In

human folklore, knowledge of a true name allows one to affect another person or

being;knowingsomething’struenamegivesthepersonpoweroverthatthing.Soit

iswithfiles.Knowingthenameofafileisthewaytoaccesstheinformationwithin.

Fileshaveasize.Itisusuallyexpressedinbytes,whichistosaysimplecharacters.

One byte is one traditional alphabetic character, although there are now many

standards for characters in German and Swedish and Chinese that break that rule.

Knowinghowlargeafileishelpswhenusingitasinput,andwhenwritingafileits

sizegrows.

Basicoperationsonafilearereadandwrite.Toreadfromafilemeanstoexamine

a byte (at least); usually bytes are read in large blocks for efficiency. This means

movingacopyofthebytesfromthediskintomemory,becauseaprogramcanonly

examinedatathatisinmemory.Writingisthereverseprocess:abyteorbytesare

copiedfrommemoryontodisk.

Filesmustbeopenbeforetheycanbeused.Toopenafileaprogrammustknow

itsname,andtheninvoketheopenfunctionorprogram.Ifthetruenameofthefile

givesyoupoweroverit,thenopenisthespellusedtowieldthatpower.Whethera

filewillbe reador writtenisnormally decidedat the timethe fileis opened. The

openfunctionandmanyotherfile-relatedoperationsbelongtotheoperatingsystem

of the computer, and not normally to the language. It’s one reason why so much

softwareisnotportable.

Onlyone programata timecan writeto afile.Many programscan read afile

simultaneously,butonlyonecanwritetoit,andnotwhileanyoneelseisreadingit.

Many computers can have more than one user accessing a file at a time, and the

Internetcertainlyallows manyusers toaccess a web page atone time,and aweb

pageisafile.However,chaosensuesifmorethanoneusercanchangeafileatthe

samemoment.

Anotherthingtoconsideristhattext,andthereforetextfiles,areaprincipalmeansfor

communicationbetweenhumansandcomputers.Itiscriticalthatanyschemeforwriting

text to a file takes into account the human aspects of text: sentences, lines, paragraphs,

special characters, numbers, and so on. This chapter will be concerned with the way in

whichPythoncanusefiles,withfilesasaconceptingeneral,andwithhowhumansthink

ofdataandfiles.

5.1 WHATISAFILE?ALITTLE“THEORY”

Theclaimintheprevioussectionwasthatafileis“acollectionofbytesstoredonadisk

or similar device.” This is correct, but it does not have enough detail to enable a

programmertotakeadvantageofthewayafileisimplementedtocreateagoodprogram.

Whatisneededisanunderstandingofthedevicesthatcontainfilesandtheiradvantages

and limitations. This information will begin to explain the traditional mechanisms that

have evolved for using files from programming languages generally and Python in

particular.

The file as a data structure was devised for storing information on tapes and disks.

Togetherwithsomeotherdevicesthatareusedrarely(e.g.,cramfiles)thesearereferred

toassecondarystorage,whereprimarystoragewouldbecomputermemory.Memorywas

(andstillis)tooexpensivetostoreeverythingthatisneededonacomputer,sosecondary

storagehastheadvantagesofbeingcheaperthanmemoryandcancontainamuchlarger

amountofdata.ModerndiskscancontainTerabytesofdata,whereoneTerabyte(Tb)is

1012bytes.Ithasbeenestimatedthatahumanbeing’sfunctionalmemoryisabout1.25

Tb.ATerabyteisalotofstorage.

Most secondary storage devices store data magnetically. Since tapes are rarely seen

anymore, the example presented here will be that of a disk. A disk is a circular platter

madeofglassorceramicmaterialandcoatedwithathinlayerofmagneticmaterial,often

acompoundofiron.That’swhytheylookbrown:ironoxideorrustisthatcolor.Thedisk

ismountedonaspindlethatisconnectedtoamotor,whichspinsitatahighrateofspeed.

Adevicecalledaread/writeheadismadetositabovethemovingdiskbutverynearto

it.Thisdeviceisbasicallyasmallpieceofmagnetizablemetalwrappedinafinewire,not

unliketheread/writeheadsinanoldvideotaperecorder(VCR)orcassettemachine.Itisa

propertyofmagnetsandcoilsthatamovingmagnetwillcreate(induce)anelectriccurrent

inanearbycoil,andacoilwithacurrentflowingthroughitcancreateamagneticfield.

So, to write data to the moving disk, a current is sent to the read/write head, which

createsasmallmagneticmarkonthediskbelowthehead.Magnetshavetwoorientations;

theyhaveaNorthPoleandaSouthPole.Currentflowingonewaywillcreateamagnetin

thediskthathasaNorthPoleappearingbeforetheSouthPole,oranN-Smark.Current

flowingtheotherdirectionthroughtheheadwillcreateamagnetonthediskthathasthe

SouthPoleappearingbefore theNorthPole,or anS-Nmark. Oneorientation,say N-S,

willrepresentabinarynumber“1,”andtheother(S-N)willrepresenta“0.”Inthisway,

binarynumberscanbewrittentothesurfaceofthemovingdisk.

Reading numbers involved the magnetic regions of the disk passing quickly past the

read/writeheadandinducingsmallcurrentsinthecoil.Theseareamplifiedandclassified

by a simple electronic circuit that will detect current flow one way as N-S and another

wayasS-N,thusallowingbinarynumberstobereadfromthedisk.

Therearesomeverycomplicatedphysicsinvolvedinadiskdrive.Theread/writehead

mustbeveryclosetothesurfaceofarapidlyrotatingdisk,ascloseas3nanometers.To

accomplishthis,theheadisactuallyaerodynamically

flyingabovethedisk.Ifiteveractuallytouchesthedisksurfacetheresultiscatastrophic.

Atthespeedsinvolvedalargesectionofthemagneticmaterialonthedisk’ssurfacewill

bescrapedaway,andalldatatherewillbelost.Inaddition,theread/writeheadwillalmost

certainlybedamaged.Thiseventiscalledaheadcrash,andnormallyresultsintheentire

diskdrivebeingruined.It’sonereasonthatfrequentbackupcopiesofalldatashouldbe

made.

Thepicturethatisdevelopingisthatofadevicethatreturnsdataasastreamofbits.To

makebestuseoftheareaofthedisk,theread/writeheadcanmovefromtheouteredgeof

thedisktonearlythecenter.Imagineasetofconcentriccirclesonthedisk’ssurface:the

moving read head can position itself over any of them and read the data that had been

writtenthere.

The disk is divided into a set of concentric circles called tracks, each of which

corresponds to one position of the read/write head (Figure 5.2a). The head can move

across the disk surface, but for obvious reasons the positions are quantized: position 0-

Ntrackscanbereachedthroughcommandstoacontrollerthatchangetheheadposition.

Theoutermosttrackisnumbered0,andnumbersincreaseastheheadmovesinwardtothe

center.Thediskisalsodividedintosectors,eachofwhichisawedge-shapedportionof

thedisk(Figure5.2b).Theseareagainnumbered0toNsectors,andcreateanaddressfora

setofbits.Datacanbereadfromsector3track12bypositioningthereadheadovertrack

12andwaitingforsector3torotateintopositionunderthehead.Thedatatakesaslongto

readasthesectortakestopassunderthereadhead.

Thisdescriptionanswerstwoimportantquestions.First,datacanbeaccessedbyusing

the<track,sector>address.Thedatainasingletrackandsectorisablock,andallblocks

are the same size in terms of bits for the sake of convenience, traditionally 512 bytes

(4096bytesforAFdrives).Second,itexplainswhy

accessingdatatakessolongwhenreadingfromadisk.Disksrotateat7200RPMor120

revolutionspersecond;thisisonerotationevery8.3milliseconds.

5.1.1 HowAreFilesStoredonaDisk?

Afilecanbethoughtofasasetofblocks.Ifblocksare512bytesinsizeandsomedata

tobestoredin afileconsistsof Nbytes,then that filewillneed blocks,thenextlarger

integerthanN/512;it’snotpossibletohavetwofilesshareasingleblock.

Itgetsmorecomplicated,though,becauseitwillnotalwaysbepossibletohaveallof

theblocksthatbelongtoafilelienexttoeachother.Afilemightconsistofmanyblocks,

allofwhicharesomedistanceapartintermsoftheirtrackandsector.Thereisaneedfora

datastructuretoconnecttheseblocksinthecorrectordertomakeafile.It’snotveryhard

todobutisanotherstep.Thisdatastructureiswrittentothediskalso.Theresultisthat

readingafilemeansfindingthelocationofthisdatastructureonthedisk,gettingthetrack

andsectorvalues,andthenreadingthedatafromthoseandcopyingitintomemory.The

datastructurecontainingthesectorsisusuallyfoundthroughafilenamethattheuserhas

provided.Thereisalistoffilenamesandthetrack/sectoraddressoftheirindexsectorsin

aspecialfilesomeplaceonthedrive,orinmanyplaces.Filesystemstendtobeorganized

hierarchically,sothatonemainnameisaccessedtofindthefileswithinthatpartofthe

disk(directory),andwithinthatdirectoryarenamesofmorefilesanddirectories.Itisa

significantpartofthefunctionofanoperatingsystemlikeLinuxorWindowstoprovidea

convenientwaytoaccessfiles.

5.1.2 FileAccessisSlow

Howlongdoesittaketoaccessablockofdataonthedisk?Itdependsonwherethe

diskheadisandwherethediskrotationhasplacedthetargetblockatthetimetherequest

ismade.Therewillbeonlyastatisticalanswer,butforarandomblockitcouldtakean

averageof10mStomovetheheadtothecorrecttrack(seektime),andwilltakehalfofa

rotation(4.15mS).Addtothisthetimeneededtoreadtheblock,whichis8.3*1/Nsectors

mS,orabout0.008mSforadiskwith1024sectors.Thiscanbeignored,andthetimeto

accessarandomblockcanbeestimatedas14.15milliseconds.

As a comparison, fast computer memory can access data within 8 nanoseconds. If a

person could write the word “Gigabyte” on a whiteboard in 8 nanoseconds, then what

couldtheydoin14milliseconds?TheycouldcopytheentireBibleontotheboardover16

times.Diskisvastlyslowerthanmemory,andinordertousethedataitmustbecopied

intomemory.Thisisabottleneckinmanycomputersystems.

5.2 KEYBOARDINPUT

Readingdatafrom thekeyboard isvery differentfrom readingdata froma file.Files

exist before being read, and normally have a fixed size that is known in advance. It is

commontoknowtheformatofafile,sothatthefactthatthenextdatumisanintegerand

theonefollowingthatisafloatisoftenknown.Whenauserisenteringdataatakeyboard

thereisnosuchinformationavailable.

Infact,theusermaybemakingupthedataastheygoalong.Beforegettingtoofarinto

fileinputitisimportanttounderstandthekindoferrorsthatcanhappeninteractively.

Theseare usingtype errors, where the userenters data that is thewrong typefor the

programmertouse:astringinsteadofaninteger,forexample.Thiskindoferrorcanarise

infileinputalsoiftheformatisnotknowninadvance.

5.2.1 Problem:ReadaNumberfromtheKeyboardandDivideItby2

Inthisinstancetheproblemisoneoftype:howtotreatintegerslikeintegersandfloats

likefloats.Whenthestringsisreadinit’sjustastring,anditissupposedtocontainan

integer. However, users will be users, and some may type in a float by mistake. The

program should not crash just because of a simple input mistake. How is this situation

handled?

Theproblemisthatwhenthestringisconvertedintoaninteger,ifthereisadecimal

pointorothernon-digitcharacterthatdoesnotbelong,thenanerrorwilloccur.Itseems

thatananswerwouldbetoputtheconversionintoatrystatementblockandifthestring

hasadecimalpointthenconvertthestringtofloatwithintheexceptpart.Somethinglike

this:

s=input(“Inputaninteger:“)

try:

k=int(s)

ks=k//2

except:

z=float(s)

k=int(z/2)

print(k)

Iftheusertypes“12”inresponsetotheprompt“Inputan integer:”thentheprogram

prints“6.”Iftheusertypes“12.5”thentheprogramcatchesaValueError,because12.5

isnotalegalinteger.Theexceptpartisexecuted,convertingthenumbertofloatingpoint,

dividingby2,thenfinallyconvertingtoaninteger.

Oneproblemisthattheexceptpartisnotpartofthetry, soerrors thathappen there

willnotbecaught.Imaginethattheusertypes“one”inresponsetotheprompt.Thecallto

int(s)resultsinaValueError,andtheexceptpartisexecuted.Thestatement:

z=float(s)

willresultinanotherValueError.Thisonewillnotbecaughtandtheprogramwillstop

executing,givingamessagelike:

ValueError:couldnotconvertstringtofloat:'one'

s=input(“Inputaninteger:“)

try:

k=int(s)

k=k//2

exceptValueError:

try:

z=float(s)

k=int(z/2)

exceptValueError:

k=0

print(s,k)

5.3 USINGFILESINPYTHON:LESSTHEORY,MORE

PRACTICE

ThegeneralparadigmforreadingandwritingfilesisthesameinPythonasitisinmost

otherlanguages.Thestepsforreadingorwritingafilearethese:

1.Openthefile.Thisinvolvescallingafunction,usuallynamedopen,andpassing

thenameofthefiletobeused.Sometimesthemodeforopeningispassed;thatis,a

filecanbeopenedforinput,output,update(bothinputandoutput)andinbinary

modes.Thefunctionlocatesthefileusingthenameandreturnsavariablethatkeeps

trackofthecurrentstateofinputfromthefile.Aspecialcaseexistsifthereisno

filehavingthegivenname.

2.Readdatafromthefile.Usingthevariablereturnedbyopen,afunctioniscalled

to read data. The function might read a character, or a number, or a line, or the

wholefile.Thefunctionisoftencalledread,andcanbecalledmultipletimes.The

nextcalltoreadwillreadfromwherethelastcallended.Aspecialcaseexistswhen

allofthedatahasbeenreadfromthefile(calledtheendoffilecondition).

3.Writedatatothefile.Usingthevariablereturnedbyopen,afunctioniscalledto

writedatatothefile.Thefunctionmightwriteacharacter,oranumber,oraline,or

manylines.Thefunctionisoftencalledwrite,andcanbecalledmultipletimes.The

nextcalltowritewillcontinuewritingdatafromwherethelastcallended.Writing

datamostfrequentlyappendsdatatotheendofthefile.

4.Closethefile.Closingafileisalsoaccomplishedusingacalltoafunction(yes,it

isusuallynamedclose).Thisfunctionfreesstorageassociatedwiththeinput

processandinsomecasesunlocksthefilesoitcanbeusedbyotherprograms.A

variablereturnedbyopenispassedtoclose,andafterwardsthatvariablecan’tbe

usedforinputanymore.Thefileisnolongeropen.

5.3.1 OpenaFile

Pythonprovidesafunctionnamedopenthatwillopenafileandreturnavaluethatcan

beusedtoreadfromorwritetothefile.Thatvalueactuallyreferstoacomplexcollection

of values that refers to the file status and is called a handle or a file descriptor in the

computingliterature,althoughknowledgeofthedetailsisnotneededtouseit.Itcanbe

thoughtofassomethingoftypefile,andmustbeassignedtoavariableorthefilecan’tbe

accessed. The open function is given the name of the file to be opened and a flag that

indicates whether the file is to be read from or written to. Both of these are strings. A

simpleexampleofacalltoopenis:

infile=open(“datafile.txt”,“r”)

Thiswillopenafilenamed“datafile.txt”thatresidesinthesamedirectoryasdoesthe

Pythonprogram,andopensitforinput:the“r”flagmeansread.Itreturnsthehandleto

thevariableinfile,whichcannowbeusedtoreaddatafromthefile.

Therearesomedetailsthatarecrucial.Thenameofthefileonmostcomputer

systemscanbeapathname,whichistosaythenameincludingalldirectorynamesthat

are used to find it on your computer. For example, on some computers the name

“datafile.txt” might have the complete path name

“C:/parker/introProgramming/chapter05/datafile.txt.”Ifpathnamesareused,thefilecan

beopenedfromanydirectoryonthecomputer.Thisishandyforlargedatasetsthatare

usedbymultipleprograms,suchasnamesofcustomersorsuppliers.

The read flag “r” that is the second parameter is what was called the mode in the

previousdiscussion. The “r” flag meansthat the file will beopen for reading only, and

startsreadingatthebeginningofthefile.Thedefaultistoreadcharactersfromthefile,

whichispresumedtobeatextfile.Openingwiththemode“rb”opensthefileinbinary

format,andallowsreadingnon-textfiles,suchasMP3andvideofiles.

Passingthemode“w”meansthatthefileistobewrittento.Ifthefileexists,thenitwill

beoverwritten;ifnot,thefilewillbecreated.Using“wb”meansthatabinaryfileistobe

written.

Appendmodeisindicatedbythemodeparameter“a,”anditmeansthatthefilewillbe

openedforwriting;ifthefileexists,thenwritingwillbeginattheendoftheexistingfile.

Inotherwords,thefilewillnotstartoverasbeingemptybutwillbeaddedto,attheend

ofthefile.Themode“ab”appendsdatatoabinaryfile.Thereareafewothermodesthat

willbediscussedwhentheyareneeded.

Ifthefiledoesnotexistanditisbeingopenedforinput,thereisaproblem.It’sanerror,

of course; a nonexistent file can’t be read from. There are ways to tell whether a file

exists,andtheerrorcausedbyanonexistentfilecanbecaughtandhandledfromwithin

Python. This involves an exception. It is always a bad idea to assume that everything

works properly, and when dealing with files it is especially important to check for all

likelyproblems.

FileNotFoundExceptions

Theproperwaytoopenafileiswithinatry-exceptpairofstatements.Thiswillensure

thatnonexistentfilesorpermissionerrorsarecaughtratherthancausing

theprogramtoterminate.Thebasicschemeissimple:

try:

infile=open(“datafile.txt”,“r”)

exceptFileNotFoundError:

print(“Thereisnofilenamedꞌdatafile.txt'.Pleasetryagain”)

return#endprogramorabortthis

#sectionofcode

The exception FileNotFoundError will be thrown if the file name can’t be found.

Whattodointhatcasedependsontheprogram:ifthefilenamewastypedinbytheuser,

thenperhapstheyshouldgetanotherchance.Inanycasethefileisnotopenanddatacan’t

beread.

There are multiple versions of Python on computers around the world, and some

versionshavedifferentnamesforthings.TheexampleshereallusePython3.4.Inother

versionstheFileNotFoundErrorexceptionhasanothername;itmaybeIOErrororeven

OSError. The documentation for the version being used should be consulted if a

compilationerroroccurswhenusingexceptionsandsomebuilt-infunctions.Forthe3.4

compilerversion,allthreeseemtoworkwithamissingfile.

All attempts to open a file should take place while catching the FileNotFoundError

exception.

5.3.2 ReadingfromFiles

Afterafileisopenedwithareadmode,thefiledescriptorreturnedcanbeusedtoread

datafromthefile.Usingthevariableinfilereturnedfromthecalltoopen()above,acall

tothemethodread()cangetacharacterfromthefile:

s=infile.read(1)

Readingonecharacteratatimeisalwaysgoodenough,butisinefficient.Ifablockon

diskis512characters(bytes)thenthatshouldbeagoodnumberofbytestoreadatone

time, or a multiple of that. Reading more data than you need and saving it is called

buffering,andbuffersareusedinmanyinstances:livevideoandaudiostreaming,audio

players,andeveninprogramminglanguagecompilers.Theideaistoreadalargerblock

ofdatathanisneededatthemomentandtohanditoutasneeded.Readingabuffercould

bedoneas:

s=infile.read(512)

and then dealing characters from the strings one at a time as needed. A buffer is a

collection of memory locations that is temporary storage for data that was recently on

secondarystore.

Text files, those that contain printable characters that humans can read, are normally

arrangedaslinesseparatedbyacarriagereturnoralinefeedcharacter,somethingusually

calledanewline.Anentirelinecanbereadusingthereadline()function:

s=infile.readline()

Alineisnotusuallyasentence,somanylinesmightbeneededtoreadonesentence,or

perhaps only half of a line. Computer text files are structured so that humans can read

them, but the structure of human language and convention is not understood by the

computer,noritisbuiltintothefilestructure.However,itisnormalforpeopletomake

datafilesthatcontaindataforaparticularitemoreventononeline,followedbydatafor

thenextitem.Ifthisistruethenonecalltoreadline()willreturnalloftheinformationfor

aparticularthing.

EndofFile

Whentherearenomorecharactersinthefile,read()willreturntheemptystring:“”.

Thisiscalledtheendoffilecondition,and it isimportant thatit bedetected.There are

manywaystoopenandreadfiles,butforreadingcharactersinthiswaytheendoffileis

checkedasfollows:

infile=open(“data.txt”,“r”)

whileTrue:

c=infile.read(1)

ifc=='':

print(“Endoffile”)

exit()

else:

c=infile.read(1)

Whenreadingafileinaforstatement,theendoffileishandledautomatically.Inthis

casethelooprunsfromthefirstlinetothefinallineandthenstops.

forcinf:

print(“'”,c,“'”)

Oddlyanexceptioncan’tbeusedinanobviouswayforhandlingtheendoffileonfile

input.However,whenreadingfromtheconsoleusingtheinput()functiontheexception

EOFErrorcanbecaught:

whileTrue:

try:

c=input()

print(c)

exceptEOFError:

print(“Endfile”)

break

There are many errors that could occur for any set of statements. It is possible to

determinewhatspecificexceptionhasbeenthrowninthefollowingmanner:

whileTrue:

try:

c=input()

print(c)

exceptExceptionasx:

print(x)

break

Thiscodeprints“EOFwhenreadingaline”whentheendoffileisencountered.

CommonFileInputOperations

There are a few common ways to use files that should be mentioned as patterns.

Althoughoneshouldneveruseapatternifitisnotunderstood,it’ssometimeshandyto

haveafewsimplesnippetsofcodethatareknowntoperformbasictaskscorrectly.For

example, one common operation to use with files is to read each line from a file,

followedbysomeprocessingstep.Thislookslike:

f=open(“data.txt”,“r”)

forcinf:

print(“'”,c,“'”)

f.close()

Theexpressioncinfresultsinconsecutivelinesbeingreadfromthefilesintoastring

variablec,andthisstopswhennomoredatacanbereadfromthefile.

Anotherwaytodothesamethingwouldbetousethereadline()function:

f=open(“data.txt”,“r”)

c=f.readline()

whilec!='':

print(“'”,c,“'”)

c=f.readline()

f.close()

Inthiscasetheendoffilehastobedeterminedexplicitly,bycheckingthestringvalue

thatwasreadtoseeifitisnull.

Anothercommonfileoperationistocopyafiletoanother,characterbycharacter.A

fileisopenedforinputandanotherforoutput.Thebasic“readafile”patternisused,with

theadditionofafileoutputaftereachcharacterisread:

f=open(“data.txt”,“r”)

g=open(“copy.txt”,“w”)

c=f.read(1)

whilec!='':

g.write(c)

c=f.readline(1)

f.close()

g.close()

Afilterisaprogramthatreadsdatafromafileandconvertsittosomeotherform,then

writesit out. Thisis often done from standard input andoutput, but can be done in the

middleofafilecopy.Forexample,toconvertatextfiletoalllowercase,thepatternabove

isusedwithasmallmodification:

f=open(“data.txt”,“r”)

g=open(“copy.txt”,“w”)

c=f.read(1)

whilec!='':

g.write(c.lower())

c=f.readline(1)

f.close()

g.close()

Thisfiltercanbedoneinlesscodeiftheentirefilecanbereadinatonce.Theread()

functioncanreadalldataintoastring.

f=open(“data.txt”,“r”)

g=open(“copy.txt”,“w”)

c=f.read()

g.write(c.lower())

f.close()

g.close()

Twofilescanbemergedintoasinglefileinmanyways:onefileafteranother,aline

fromonefilefollowedbyalinefromanother,characterbycharacter,andsoon.Asimple

mergingoftwofileswhereoneiscopiedfirstfollowedbytheotheris:

f=open(“data1.txt”,“r”)

outfile=open(“copy.txt”,“w”)

c=f.read()

outfile.write(c)

f.close()

g=open(“data2.txt”,“r”)

c=g.read()

outfile.write(c)

g.close()

outfile.close()

Amorecomplexproblemoccurswhenbothfilesaresortedandaretoremainsorted

afterthemerge.Ifeachlineisinalphabeticalorderineachfilethenmergingthemmeans

readingalinefromeachandwritingtheonethatissmallest.Whenonefileiscomplete,

theremainderofthesecondfileiswrittenandallfilesareclosed.

f=open(“data1.txt”,“r”)

g=open(“data2.txt”,“r”)

outfile=open(“copy.txt”,“w”)

cf=f.readline()

cg=g.readline()

whilecf!=””andcg!=””:

ifcf<cg:

outfile.write(cf)

cf=f.readline()

else:

outfile.write(cg)

cg=g.readline()

ifcf==””:

outfile.write(cg)

cg=g.read()

outfile.write(cg)

else:

outfile.write(cf)

cf=f.read()

outfile.write(cf)

f.close()

g.close()

outfile.close()

Copying the input from console to a file means reading each line using input() and

writingittothefile.Thiscodeassumesthatanemptyinputlineimpliesthatthecopyingis

complete.

outfile=open(“copy.txt”,“w”)

line=input(“!“)

whilelen(line)>1orline[0]!=”!”:

outfile.write(line)

outfile.write(“\n”)

line=input(“!“)

outfile.close()

Theendofthelineisindicatedbyacharacter,whichisrepresentedbythestring“\n.”

Readingcharactersfromafilewillreadtheendoflinecharacteralso,anddetectingitcan

beveryimportant.

f=open(“data.txt”,“r”)

c=f.read(1)

whilec!='':

print(“'”,c,“'”)

c=f.read(1)

ifc=='\n':

print(“Newline”)

CSVFiles

A very common format for storing data is called Comma Separated Variable (CSV)

format,namedforthefactthateachpairofdataitemshaveacommabetweenthem.CSV

filescanbeuseddirectlybyspreadsheetssuchasExcelandbyalargecollectionofdata

analysistools,soitisimportanttobeabletoreadthemcorrectly.

AsimpleCSVfilenamedplanets.txtisprovidedforexperimentingwithreadingCSV

files.ItcontainssomebasicdatafortheplanetsinEarth’ssolarsystem,andwhilethereis

noactualstandardforhowCSVfilesmustlook,thisoneistypicalofwhatisusuallyseen.

Thefirstlineinthefilecontainsheadingsforeachofthevariablesorcolumns,separated

bycommas.Thisisfollowedbyninelinesofdata,oneforeachplanet.It’sasmalldata

fileasthesethingsarecounted,butillustrativeforthepurpose.Hereitis:

Problem: Print the Names of Planets Having Fewer Than

TenMoons

Thisisnotaveryprofoundproblem,andusestherawdataasitappearsonthefile.The

filemustbeopenedandtheneachlineofdataisread,thevalueofthe11thdataelement

(i.e.,index10)retrievedandcomparedagainst10.Iflarger,thenameoftheplanet(index

0)isprinted.Theplanis:

Openthefile

Read(skipover)theheaderline

Foreachplanet

Readalineasstrings

BreaksintocomponentsbasedoncommasgivinglistP

IfP[10]<10printtheplanetname,whichisP[0]

Itisall somethingthat hasbeen donebefore exceptforbreaking thestring intoparts

basedonthecomma.Fortunately,thedesignersofPythonanticipatedthiskindofproblem

and have provided a very useful function: split(). This function breaks up a string into

parts using a specified delimiter character or string and returns a list in which each

componentisonesectionofthefracturedstring.Forexample:

s=“Thisisastring”

z=s.split(”“)

yieldsthelistz=[“This”,“is”,“a”,“string”].Itsplitsthestringsintosubstringsateach

space character. A call like s.split(“,”) should give substrings that are separated by a

comma.Giventheabovesketchandthesplit()function,thecodenowprettymuchwrites

itself.

try:

#Openthefile

infile=open(“planets.txt”,“r”)

#Read(skipover)theheaderline

s=infile.readline()

#Foreachplanet

foriinrange(0,8):

#Readalineasstrings

s=infile.readline()

#BreaksintocomponentsbasedoncommasgivinglistP

P=s.split(“,”)

#IfP[10]<10printtheplanetname,whichisP[0]

ifint(P[10])<10:

print(P[0],”hasfewerthan10moons.”)

exceptFileNotFoundError:

print(“Thereisnofilenamed'planets.txt'.Pleasetryagain”)

Thingstonotice:almosttheentireprogramresideswithinatrystatement,sothatifthe

filedoesnotexist,thenamessagewillbeprintedandtheprogramwillendnormally.Also

notethatP[10]hastobeconvertedintoaninteger,becauseallcomponentsofthelistPare

strings.Stringsarewhathasbeenreadfromthefile.

CSV files are common enough so that Python provides a module for manipulating

them.Themodulecontainsquitealargecollectionofmaterial,andforthepurposesofthe

planets.pyprogramonlythebasicsareneeded.Toavoidthedetailsofageneralpackage,a

simplerversionisincluded withthisbook:simpleCSV has the essentials neededto read

mostCSVfileswhilebeingwritteninsuchawaythatabeginningprogrammershouldbe

abletoreadandunderstandit.

Touseit,thesimpleCSVmoduleisfirstimported.Thismakestwoimportantfunctions

available:nextRecord()andgetData().ThenextRecord()functionreadsoneentireline

ofCSVdata.Itallowsskippinglineswithoutexaminingthemindetail(likeheaders).The

functiongetData()willparseonelineofdata,thelastoneread,intoatuple,eachelement

ofwhichisoneofthecomma-separatedfields.

ThesimpleCSVlibraryneedstobeinthesamedirectoryastheprogramthatusesit,or

beinthestandardPythondirectoryforinstalledmodules.Thesourcecoderesidesonthe

accompanyingdisc

andiscalledsimpleCSV.py.TheprogramabovecanberewrittentousethesimpleCSV

moduleasfollows:

importsimpleCSV

try:#Read(skipover)theheaderline

infile=open(“planets.txt”,“r”)#Openthefile

simpleCSV.nextRecord(infile)#Readtheheader

foriinrange(0,8):#Foreachplanet

simpleCSV.nextRecord(infile)#Readalineand

#collectsubstrings

#inalist

p=simpleCSV.getData(infile)

ifint(P[10])<10:#Ifnumberofmoonsless

#than10

print(P[0],”hasfewerthan10moons.”)

#printtheplanetname

exceptFileNotFoundError:

print(“Thereisnofilenamed'planets.txt'.Pleasetryagain”)

Problem:PlayJeopardyUsingaCSVDataSet

ThetelevisiongameshowJeopardyhasbeenontheairfor35yearsinoneofitstwo

incarnations,andisperhapsthebestknownsuchprogramontelevision.Playersselecta

topicandapointvalueandareaskedatriviaquestionthattheymustanswerintheformof

a question. There are sets of questions that have been used in Jeopardy over the years,

someinCSVform,soitshouldbepossibletostageasimulatedgameusingPythonasthe

moderator.

A simple version of the game could work like this: read a bunch of questions and

answers, and select questions at random to ask. Questions that have single word

unambiguous answers would be best. The player types in an answer and wins if they

answertencorrectlybeforegettingthreewrong.

Asinglelineofdatafromthefilemightlooklikethis:

5957,2010-07-06,Jeopardy!,”LETꞌSBOUNCE”,”$600”,”Inthiskid’sgame,youbounce

asmallrubberballwhilepickingup6-prongedmetalobjects”,”jacks”

Thereare7differentdatafieldshereseparatedbycommas.They are:ShowNumber,

Air Date, Round, Category, Value, Question, and Answer; all are strings, but some

questionsmaycontaincommas.TheCSVmodulecandealwiththat.

Therearemanywaysthatarandomquestioncanbechosen.Onewouldbetoreadallof

thedataintoalist,butthatwouldrequirealotofmemory.Onewaywouldbetorandomly

readaquestionfromthefile,butthatwouldbehardtodobecauseeachlinehasadifferent

length. What could be done relatively easily would be to pick a random number of

questionstoskipoverbeforereadingonetouse.So,selectarandomnumberKbetweenN

andM,readKquestions,andthereadthenextoneandasktheuserthatquestion.When

theendofthefileisreached,itcanbereadagainfromthebeginning.Ifthefileislarge

enoughitwouldbeunlikelytoaskthesamequestiontwiceinashorttimeperiod.

Hereisasketchofhowthismightwork:

Openinfileasthefileofquestionstobeused

Whilegamecontinues:

SelectarandomnumberKbetweenNandM

ForI=NtoM:

Readalinefromthefile

Ifnomorelines:

Closeinfileandreopen

Readaquestionandprintit,asktheuserforananswer

Readtheuser’sanswerfromthekeyboard

Iftheuser’sansweriscorrect:

Countrightanswers

Else:

Countwronganswers

IftheCSVmoduleisused,theparsingoftheinputfileisdealtwith.Whatisnewabout

this? When all of the data in the file has been used, the program may not be complete.

Whatisdonethenisnew:closethefile,reopenit,andstartagainfromthebeginning.This

isanunusualactionforaPythonprogram,butillustratestheflexibilityofthefilesystem.

There is a nested try-except pair, the outer one that checks the existence of the file of

questionsandtheinneronethatchecksfortheendofthefile.Whenthefileisreopeneda

newreaderhastobecreated,becausetheoldoneisconnectedtoaclosedfile.Thefileon

thediskisthesame,butwhenitisopenedagainanewhandleisbuilt;theoldCSVreader

islinkedtotheoldhandle.

The program counts the number of right answers (CORRECT) and the number of

wrongones(INCORRECT).Whenthereare10correctanswersor3incorrectones,the

game is over; a variable again is set to False and the main while loop exits. A break

could have been used, but having the condition become False is the polite way to exit

fromawhileloop.

Theentireprogramlookslikethis:

#Jeopardy!

importsimpleCSV,random



try:

infile=open(“q.txt”,“r”)#Openthefile

simpleCSV.nextRecord(infile)#Read(skipover)the

#headerline



CORRECT=0

INCORRECT=0

again=True

whileagain:

k=random.randint(5,10)#Howmanyquestionsto

#skip?

foriinrange(0,k):

ifnotsimpleCSV.nextRecord(infile):

#Skipthisquestion

infile.close()

print(“Reopening”)

infile=open(“JEOPARDY_small.txt”,“r”)

simpleCSV.nextRecord(infile)

s=simpleCSV.getData(infile)#Readthequestion

#tobeasked.

print(s[5])#Printthequestion

a=input()#Readtheanswer

ifa.lower()==s[6].lower():#Doesplayeranswer

#agree?

CORRECT=CORRECT+1#Yes.countto10.

ifCORRECT>=10:

print(“Youwin!”)

again=False

else:

INCORRECT=INCORRECT+1#No.Countto3

print(“Sorry.Theansweris“,s[6])

ifINCORRECT>12:

print(“Youlose.”)

again=False

exceptFileNotFoundError:

print(“Thereisnoquestionfile.Wecan'tplay.”)

TheWithStatement

Adifficultywiththecodepresentedsofaristhatitdoesnotcleanupafteritself.Afile

shouldbeclosedafterinputfromitoroutputtoitisfinished;noneoftheprogramswritten

so far do that, at least not after the file operations are complete. There has been no

significant discussion of the close() operation, but what it does has been described.

Normallywhenaprogramterminates,itsresourcesarereturnedtothesystem,including

the closing of any open files. Intentionally closing a file is important for three reasons:

first,iftheprogramabortsforsomereason,openfilesshouldbeclosedbythesystembut

may not be, and file problems can be the result. Second, as in the Jeopardy program,

closingafilecanbeusedasastepinre-usingit.Openingitagainstartsreadingitatthe

beginning. Third, closing a file frees its resources. Programs that use many files and/or

manyresourceswillprofitfromfreeingthemwhentheyarenolongerneeded.

The Python with statement, in its simplest form, takes care of many of the details

surroundingfileaccess.Anexampleofitsuseis:

try:

withopen(“planets.txt”)asinfile:#Openthefile

simpleCSV.nextRecord(infile)#Readtheheader

foriinrange(0,9):#Foreachplanet

simpleCSV.nextRecord(infile)#Readaline,

#makealist

P=simpleCSV.getData(infile)

ifint(P[10])<10:#Ifnumberofmoons

#lessthan10

print(P[0],”hasfewerthan10moons.”)

#printthename

exceptFileNotFoundError:

print(“Thereisnofilenamed'planets.txt'.Pleasetryagain”)

Oncethefileisopen,thewithstatementguaranteesthatcertainerrorswillbedealtwith

and the file will be closed. The problem is that the file has to be open first, so the

FileNotFounderrorshouldstillbecaughtasanexception.

5.4 WRITINGTOFILES

Thefirststepinwritingtoafileisopeningit,butthistimeforoutput:

outfile=open(“out.txt”,“w”)

The“w”asthesecondparametertoopen()meanstoopen thefileforwriting. When

writingtoafileitisimportanttonotethatopeningitwillcreateanewfilebydefault.Ifa

filewiththegivennamealreadyexistsitwillberewritten,andthepreviouscontentswill

begone.

Thebasicfileoutputfunctioniswrite();ittakesaparameter,astringtobewrittento

thefile.Itonlywritesstrings,sonumbersandothertypeshavetobeconvertedintostrings

before being written. Also, there is no concept of a line. This function simply moves

characterstoafile,oneatatime,intheordergiven.Inordertowritealine,anendofline

character has to be written. This is usually specified in a string as “\n,” spoken as

“backslashn.”The“n”standsfornewline.

Example:WriteaTableofSquarestoaFile

This will illustrate the typical code involved in writing to a file. The file must be

opened,thenaloopfrom0to25isconstructed.Eachnumberinthatrangeiswrittento

thefile,asisthatnumbermultipliedbyitself.Eachoutputstringrepresentsaline,andso

musthaveanewlinecharacteraddedtotheend.

outfile=open(“out.txt”,“w”)

outfile.write(”XXsquared\n”)

foriinrange(0,25):

sout=”“+str(i)+”“+str(i*i)+”\n”

outfile.write(sout)

outfile.close()

Notethattheintegersareexplicitlyconvertedintostringsandconcatenatedintoaline

tobewritten.Theelementsofthelinecouldbewritteninseparatecallstowrite:

outfile=open(“out.txt”,“w”)

outfile.write(”XXsquared\n”)

foriinrange(0,25):

outfile.write(”“)

outfile.write(str(i))

outfile.write(”“)

outfile.write(str(i*i))

outfile.write(“\n”)

outfile.close()

Theoutputfileisclosedafteralldatahasbeenwritten.

5.4.1 AppendingDatatoaFile

Openingthefilein“w”modestartswritingatthebeginningofthefile,andwillresult

inexistingdatabeinglost.Thisisnotalwaysdesirable.Forexample,whatifalogfileis

beingcreated?Thelogshouldcontainarecordofeverythingthathashappened,notjust

themostrecentthing.

Opening the file in append mode, signified by the parameter “a,” opens the file for

outputandstartswritingattheendofthefileifitalreadyexists.Thismeansthatdatacan

beaddedtotheendofanexistingfile.

Example: Append Another 20 Squares to the Table of

SquaresFile

Thepreviousexamplecreatedafilenamed“out.txt”andwrote26linestoit.Itwasa

tableofsquares,andthefinalonewas24.Thisexamplewillthereforebeginat25andadd

20morevaluestothetable.

Themaindifferenceistheopeningoftheoutputfileinappendmode,andstartingthe

loopat25insteadofat0:

outfile=open(“out.txt”,“a”)

foriinrange(25,45):

sout=”“+str(i)+”“+str(i*i)+”\n”

outfile.write(sout)

outfile.close()

The file “out.txt” will contain the squares of the integer between 0 and 44 inclusive

afterthisprogramruns.

5.5 SUMMARY

Filesarecomputerstructureswithinwhichdataarestored,andalmostalwaysresideon

disk devices, tape devices, or other secondary storage. Files have some common

properties: files have names; files have a size; basic operations on a file are read and

write;filesmustbeopenbeforetheycanbeused;onlyoneprogramatatimecanwriteto

afile.Accesstodataonafileismuchslowerthanaccesstodatainmemory,butfiledata

hastobemovedintomemorybeforeitcanbemanipulated.

Exceptionsareeventsthatoccurwhileaprogramisexecuting,suchasdividingbyzero.

Ratherthancheckforallpossibleexceptionseverytimeastatementisexecuted,Python

providesatry-exceptstatementthatallowstheprogrammertoprovidecodetorunwhen

anerroroccurs.SpecificnamedexceptionsexistinPythonthatcanbespecificallycaught,

likeValueError,orallexceptionscanbecaughtbynotspecifyingaparticularone.

Filesareopenedusingacalltoopenpassingafilenameandamode.Ifthemodeis“r”

then the file will be read from; if it is “w” it will be written to. Example: x =

open(“input.txt”,“r”).Readingfromafilexisaccomplishedbyareadcall:x.read(n)

willreturnastringofncharacters;x.readline()willreturnonelinefromthefilex.When

there are no more characters in the file read() will return the empty string: “”. This is

calledtheendoffilecondition,anditisimportantthatitbedetected.

A CSV (comma separated values) file is a specific format that is common for some

kinds of data, including spreadsheets. The simpleCSV package provided on the

accompanyingdisccanbehelpfulinreadingthesefiles.

Outputtoafilexisdonewithacalltowrite:x.write(s)writesthestringstothefile

representedbyx.Thestring“\n”representstheendofaline.

NOTE ThischapterwillbeextendedinChapter8toexpandthekindoffileoperations

anddatathatcanbereadfromandwrittentoafile.

Exercises

1.Writeaprogramthatreadsafilenamefromtheuser(console)andprintsouthow

manycharactersbelongtothatfile.

2.Writeaprogramthatopensafilecontainingalistoffilenames.Foreachoneprintthe

filenamefollowedbyYESifthatfileexistsinthecurrentdirectoryandNOifitdoes

not.

3.Createafilecopyfacility.Theprogramtobewrittenreadsthenameofafilefromthe

userconsoleandcreatesanotherfilewiththesamecontents.Iftheoriginalfileis

named“xx.txt”thenthenewfilewillbenamed“xx-copy.txt.”Theoriginalfilewill

alwayshaveanameendingin“.txt,”andsowillthecopy.

4.TheCSVfile“avatardata.csv”containssavedinformationconcerningthepreferred

avatarsforplayersofavideogame.Thefieldsare:playercode(integer),avatartype

(string,noquotes),numberoftimesthisavatarwasplayedatthislevel(integer),a

gamelevelreached(integer,outof12),andthehighestscoreachievedonthislevel

(integer);thereisnoheader.Readthisfileanddetermineandprintwhichplayer/avatar

hasthehighestscoreoneachlevel.

5.UsingaPythonprogram,createaCSVfilefrom“avatardata.csv”thatcontainsonly

informationforlevel10.

6.InanHTMLfile(i.e.,awebpage)animagetobedisplayedisusuallyidentifiedina

sourcetagoftheform:src=“name.jpg.”Thequotesareapartofthetag,andthetext

betweenthemisanimagefilename.WriteaprogramthatreadsanHTMLfileand

printsthenamesofalloftheimagefilesthatitreferences.

7.Auserwillspecifythenameofanimagefile(i.e.,afilenamethatendsin“.jpg,”

“.gif,”or“.png”)fromtheconsole.Yourprogramwillreadthisnameandcreate

“disp.html,”anhtmlfilethat,whenopenedbyabrowser,willdisplaythisimage

(requiresaknowledgeofbasicHTML).

8.Twofiles,namedsorted1.txtandsorted2.txt,containnumericdatathatappearinthe

fileinsortedascendingorder(whenlookedatasastring).Mergethesetwofilesto

createasinglefilehavingthedataofboth,alsoinsortedorder.

NotesandOtherResources

PythonCSVLibrary:https://docs.python.org/3/library/csv.html

1.RemziArpaci-DusseauandAndreaArpaci-Dusseau.(2015).OperatingSystems:

ThreeEasyPieces,AmazonDigitalServices,Inc.

2.DanielP.BovetandMarcoCesati.(2005).UnderstandingtheLinuxKernel,

O’ReillyMedia.

3.DominicGiampaolo.(1999).PracticalFilesystemDesign,MorganKaufmann

Publishers,Inc.,http://www.nobius.org/~dbg/practical-file-system-design.pdf,

www.nobius.org/~dbg/practical-file-system-design.pdf

4.RobertStetson.(2013).HowDiskDrivesWork,CreateSpaceIndependentPublishing

Platform.

5.Jeopardyquestionsmaybefoundathttps://docs.google.com/uc?

id=0BwT5wj_P7BKXUl9tOUJWYzVvUjA&export=download

CHAPTER6

CLASSES

6.1ClassesandTypes

6.2ClassesandDataTypes

6.3SubclassesandInheritance

6.4DuckTyping

6.5Summary

Inthischapter

Howmanyjokesbeginwithaphraselike“Amanwalksintoabar”?Somanythatwhen

someonehearsthatphrase,itislikelythattheywillassumeitisajoke.So,toruinthejoke

andspeak philosophically, what is a man,what isa bar, andwhat does walking entail?

Walkingseemstobesomethingthatamancando,anactiontheycanperform.Andabar

isaplacewhereamancanwalk.Canamandoanythingelsebutwalk?Isabartheonly

placeamancanwalkto?

It seems silly to examine a sentence in that way, but in the context of a computer

program it may be more meaningful. Imagine that this discussion involves a computer

game or simulation. A man now represents some kind of thing or object that is

manipulatedbytheprogram.Amanhaspropertiesandthingsitcando,whichistosay

operationsitcanperform.Whatpropertiesdoesamanhave?Well,asasmallsubsetofthe

possibilities:

Property Type

Name String

Sex Boolean

Phonenumber Integer

Height Float

Weight Float

Job String?

Home(location,address) String?

Interests ArrayofString

Income Float

Possessions(otherobjects) Arrayofobject

Spouse person

Children Arrayofperson

Soamanwouldappeartobeacomplexdatatypehavinganumberofproperties.Note

especially that a man can have a property or characteristic called spouse. A spouse is

somethingcalledaperson;soisaman,really.Thisisprettyabstract,butstaywithit:a

manisaperson,andperhapssomeofthecharacteristicsofamanarereallythoseof(i.e.,

inheritedfrom)aperson.Infact, it wouldappearthatmostofthemare.Theonly thing

that distinguishes a man from other persons would (from the list above) be sex, which

wouldbe(perhaps)falseforamanandtrueforawoman,anotherkindofperson.

Imagine that there is a whole class of things called person that have most of these

properties.Amancouldbederivedfromthis,sincemanhasmanyofthesepropertiesin

common.Awomancouldbeanotherclass,perhapshavingafewdifferentproperties.A

mancouldhave,forexample,a“dateoflastprostateexam”asaproperty,butawoman

couldnot.Awomancouldhavea“dateoflastpapsmear,”butamancouldnot.Atsome

point,personhasmanycommon

characteristics,butmanhassomethatwomandoesnotandviceversa.

So,consideringtheoriginalproposition:whatisabar?Itisclearlysomething(object)

thatcanhold(contain)aman.Perhapsitcancontainmanymen.Women?Whynot?Ifa

personhastobeeitheramanorawoman,thenabarcancontainsomenumberofpersons.

Abarisaclassofobjectsthatcanholdorcontainsomenumberofpersons.Itwouldbea

containerclass,onesupposes,oraholderofsomekind.

So,thephrase“Amanwalksintoabar”mightbeexpressedas:

aMan.walksInto(aBar)

whereaManisaparticularman(aspecificinstanceofamanclass)andaBarisaspecific

instanceofaclassofobjectsknownasbar.ThismanhasaName,whichistosaythatone

ofthepropertiesthatamanhasisaName,andthisisreallyjustavariable.Sinceeach

individualmanhasaName,therehastobeawayofgettingat(accessing)eachone.Itis

donethrougheachinstance,likeso:

print(aMan.Name)#Accessing/printingthename.

aMan.Name=“TedSmith”#Assigningtothename.

Using this syntax, the dot (“.”) is placed after the name of the instance. The syntax

“aMan.Name” means “look at the variable aMan, which is an instance of man, for a

propertycalledName.”

Okay, so what is walksInto in the above expression aMan.walksInto(aBar)?

Consideringthesyntaxjustdescribed,itwouldappeartobeafunctionthatwasapartof

thedefinitionofman.Ittakesoneparameter,whichissomethinghavingthetypebar.

Thismayallseemveryabstractstill,butthiswayoflookingatthingsseemssensiblein

thatitappearstoorganizeinformationandprovideaclearandformalwaytoaccessitand

manipulateit.Thisdiscussionhasbeenametaphorfortheconceptofaclassandtheideas

behindobjectorientation, two key elements of modern programming structures. Python

permitstheprogrammertodefineclasseslikethemanorbarobjectspreviouslydescribed

and to use them to encapsulate variables and functions and create convenient modular

constructions.

6.1 CLASSESANDTYPES

A class, in the general sense, is a template for something that involves data and

operations(functions).Anobjectisaninstanceofaclass,aspecificinstantiationofthe

template.DefiningaclassinPythoninvolvesspecifyingaclassnameandacollectionof

variablesandfunctionsthatwillbelongtothatclass.Themanclassthathasbeenreferred

to so far has only a few characteristics that we know about for certain. It does have a

functioncalledwalksInto,asone

example.Afirstdraftofthemanclasscouldbeasfollows:

classman:

defwalksInto(aBar):

#codegoeshere

Afunctionthatbelongstoaclassisgenerallyreferredtoasamethod.Thisterminology

likelyrefersbacktoalanguagedevisedinthe1970snamedSmalltalk.Accordingtothe

standardforthatlanguage,“Amethodconsistsofa

sequence of expressions. Program execution proceeds by sequentially evaluating the

expressions in one or more methods.”In the above example, walksInto is a method;

essentially,amethodisanyfunctionthatispartofaclass.

Classescanhavetheirowndatatoo,whichwouldbevariablesthat‘belong’totheclass

inthattheyexistinsideit.Suchvariablescanbeusedinsidetheclassbutcan’tbeseen

fromoutside.

Lookingcloselyat thesimpleclass manabove, notice that it isactually still a rather

abstractthing.Inthenarrativeaboutamanwalkingintoabaritwasaspecificman,as

indicated by a variable aMan. So it would seem that a class is really a description of

something,andthatexamplesorinstancesshouldbecreatedinordertomakeuseofthat

description.Thisiscorrect.Infact,manyindividualinstancesofanyclasscanbecreated

(instantiated) and assigned to variables. To create a new instance of the class man,the

followingsyntaxcouldbeused:

aMan=man()

Whenthisisdoneallofthevariablesusedinthedefinitionofmanareallocated.Infact,

whenevera new manclass is created, aspecial method thatis local toman is called to

initializevariables.Thismethodistheconstructor,andcantakeparametersthathelpin

the initialization. Creating a man might involve giving him a name, so the instantiation

maybe:

aMan=man(“JimParker”)

Inthiscase theconstructor acceptsa parameter,astring, andprobably assignsit toa

variablelocaltotheclass(Name,mostlikely).Theconstructorisalwaysnamed__init__:

def__init__(self,parameter1,parameter2,…):

Theinitialparameternamedselfisareferencetotheclassbeingdefined.Anyvariable

thatisapartofthisclassisreferredtobyprefixingthevariablenamewith“self.”Tomake

aconstructorformanthatacceptedaname,itwouldlooklikethis:

def__init__(self,name):

self.Name=name

Whenamaniscreated,thestatementwouldbe:

aMan=man(“JimParker”)

This metaphor has fulfilled its purpose for the moment. There are some exercises

concerningitattheendofthechapter,butanothermorepracticalexamplemightbebetter

now.

6.1.1 ThePythonClass–SyntaxandSemantics

ThemanwalksintoabarexampleillustratesmanyaspectsofthePythonclassstructure

but obviously omits many details, especially formal ones that can be so important to a

programmer.Aclasslookslikea function inthatthereisakeyword, class,andaname

andacolon,followedbyanindentedregionofcode.Everythinginthatindentedregion

“belongs”totheclass,andcannotbeusedfromoutsidewithoutusingtheclassnameor

thenameofavariablethatisaninstanceoftheclass.

The method __init__ is used to initialize any variables that belong to the class. Java

wouldcallthismethodaconstructor,andthat’showitwillbereferencedheretoo.Any

variables that belong to the class must be accessed through either an instance (from

outside of the class) or by using the name self (from within the class). So, self.name

wouldrefertoavariablethatwasdefinedinsideoftheclass,whereassimplyusingname

wouldrefertoavariablelocaltoamethod.When__init__iscalled,asetofparameters

canbepassedandusedtoinitializevariablesintheclass.Ifthefirstparameterisself,it

meansthatthemethodcanaccessclass-localvariables;otherwiseitcannot.Normallyself

ispassedto__init__oritcan’tinitializethings.Anyvariableinitializedwithin__init__

andprefixedbyselfisaclass-localvariable.Anymethodthatispassedselfasaparameter

candefinea newclass-local variable,butit makessense toinitializeall ofthemin one

placeifthat’spossible.

Asimpleexampleofaclass,initialization,andmethodis:

classperson:

def__init__(self,name):

self.name=name



defintroduce(self):

print(“Hi,mynameis“,self.name)



me=person(“Jim”)

me.introduce()

This class has two methods, __init__()andintroduce(). After the class is defined, a

variablenamedmeisdefinedandisgivenanewinstanceofthepersonclasshavingthe

name“Jim.”Thenthisvariableisusedtoaccesstheintroducemethod,whichprintsthe

introduction message “Hi, my name is Jim.” A second instance could be created and

assignedtoasecondvariablenamedyouusing:

you=person(“Mike”)

andthemethodcall

you.introduce()

would result in the message “Hi, my name is Mike.” Any number of instances can be

created,andsomehavethesamenameasothers—theyarestilldistinctinstances.

Anewclass-localvariablecanbecreatedbyanymethod.Inintroduce(),forexample,a

newlocalnamedintroductionscanbecreatedsimplybyassigningavaluetoit.

defintroduce(self):

print(“Hi,mynameis“,self.name)

self.introductions=True

ThisvariableisTrue if the method introductions has been called. The main program

canaccessthisvariabledirectly.Ifthemainprogrambecomes:

me=person(“Jim”)

me.introduce()

print(me.introductions)

thentheprogramwillgeneratetheoutput:

Hi,mynameisJim

True

This is the essential information needed to define and use a class in Python. A more

complexexamplewouldbeusefulinseeinghowthesefeaturescanbeusedinpractice.

6.1.2 AReallySimpleClass

Acommonexampleofabasicclassisapoint,aplaceonaplanespecifiedbyxandy

coordinates.Thebeginningofthisclassis:

classpoint:

def__init__(self,x,y):

self.x=x

self.y=y

Thissimplyrepresentsthedataassociatedwithamathematicalpoint.Whatmoredoesit

need?Well,twopointshaveadistancebetweenthem.Adistancemethodcouldbeadded

tothepoint:

defdistance(self,p):

d=(self.x-p.x)*(self.x-p.x)+(self.y-p.y)*

(self.y-p.y)

returnsqrt(d)

If a traditional function were to be used to compute distance, it would be written

similarlybutnotidentically.Itwouldtaketwopointsasparameters:

defdistance(p1,p2):

d=(p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y)

returnsqrt(d)

Thedistance method uses one of the points as a preferred parameter,in a sense. The

distancebetweenpointsp1andp2wouldbecalculatedas:

d=p1.distance(p2)ord=p2.distance(p1)

usingthedistancemethod,butas:

d=distance(p1,p2)

if the function was used. To a degree the difference is a philosophical one. Is distance

somepropertythatapointhasfromanotherpoint(themethod),orisitsomethingthatisa

thingthatiscalculatedfortwothings(thefunction)?Aprogrammerbegins,afterawhile,

toseethemethodsanddataofaclassasbelongingtotheobject,andassomehowbeing

propertiesofit.That’swhatmakesaclassatypedefinition.

Many object-oriented languages offer the concept of accessor methods. Some

languages do not allow variables that belong to a class to be used directly, or allow

specificcontrolsonaccesstothem.Thetruthisthathavingtheabilitytofindthevalueof

variablesandtomodifythemisgenerallyabadidea.Iftheonlyplacethataclasslocal

variable can be modified is within the class, then that limits the places where that can

occur, and allows more control over what is possible. Preventing errors in programs is

partlyamatterofrestrictingactionstoasmallregion,ofknowingexactlywhatisgoingon

atalltimes.

Similarly,ifsomeobjectoutsideofaclasshasaccesstothelocalvariablesofthatclass,

thenitpromotesadependencyonaspecificimplementation,andoneoftheadvantagesof

an object-oriented implementation is that the interface to the class is fixed and

independentofthewaythatclassisimplemented.Itmayseemobviousthatapointobject

has an x, y position and that those would be real numbers, but the point class is the

simplestclass,andtakingadvantageofhowaclassiscodeditnotalwayshealthy.

Allthatanaccessormethoddoesisreturnavalueimportanttoauserofaclass.Thex

and y positions are variables local to the class, and many would agree that they should

haveanaccessormethod:

defgetx(self):

returnself.x

defgety(self):

returnself.y

Rewritingthedistance()methodtouseaccessormethodschangesitonlyslightly:

defdistance(self,p):

d=(self.x-p.getx())*(self.x-p.getx())+

(self.y-p.gety())*(self.y-p.gety())

returnsqrt(d)

Methodscalledmutatorsorsettersareusedtomodifythevalueofavariableinaclass.

They may do more than that, such as checking ranges and types, and tracking

modifications.

defsetx(self,x):

self.x=x

defsety(self,y):

self.y=y

Thereareothermethodsthatcouldbeaddedtoeventhissimpleclassjustincasethey

wereneeded,suchastodrawthepoint,toreturnastringthatdescribestheobject,torotate

abouttheoriginorsomeotherpoint,touseadestructormethodthatiscalledwhenthe

objectisnolongerneeded,andsoon.Untilitisknownwhattheclasswillbeusedfor,

there may not be any value for this effort, but if a class is being provided for general

utility, like the Python string, as much functionality would be provided as the

programmer’s imagination could invent. A draw method could simply print the

coordinates,andcouldbeusefulfor

debugging:

defdraw(self):

print(“(“,self.x,“,”,self.y,“)“)

Usingthisclass involvescreatinginstances and usingthe providedmethods,and that

shouldbeall.Atriangleconsistsofthreepoints.Atriangleclasscouldbedefinedas:

classtriangle:

def__init__(self,p0,p1,p2):

self.v0=p0

self.v1=p1

self.v2=p2

self.x=(p0.getx()+p1.getx()+p2.getx())/3

self.y=(p0.gety()+p1.gety()+p2.gety())/3



defset_vertices(self,p0,p1,p2):

self.v0=p0

self.v1=p1

self.v2=p2



defget_vertices(self):

return((self.v0,self.v1,self.v2))



defgetx(self):

returnself.x



defgety(self):

returnself.y



The (x, y) value of a triangle is its center, or the average value of the x and the y

coordinatesofthevertices.Thesearethebasicmethods.Atriangleislikelytobedrawn

somehow,andthenextchapterwillexplainhowtodothatspecifically.However,without

knowingthedetails,atriangleisasetoflinesdrawnbetweentheverticesandsomightbe

donethatway.Asitis,usingtextonly,itwillprintitsvertices:

defdraw(self):

print(”Triangle:”)

self.v0.draw()

self.v1.draw()

self.v2.draw()

Thetrianglecanbemovedtoanewposition.Achangeinthexandylocationspecifies

thechange,anditisdonebychangingthecoordinatesofeachofthevertices:

defmove(self,dx,dy)

coord=p0.getx()

p0.setx(coord+dx)

coord=p0.gety()

p0.sety(coord+dy)

coord=p1.getx()

p1.setx(coord+dx)

coord=p0.gety()

p1.sety(coord+dy)

coord=p2.getx()

p2.setx(coord+dx)

coord=p2.gety()

p2.sety(coord+dy)

self.x=self.x+dx

self.y=self.y+dy

In this way of expressing things, it is clear that moving the triangle is a matter of

changingthecoordinatesofthevertices.Ifeachpointhadamove()method,thenitwould

beclearer:movingatriangleisamatterofmovingeachofthevertices:

defmove(self,dx,dy):

p0.move(dx,dy)

p1.move(dx,dy)

p2.move(dx,dy)

self.x=self.x+dx

self.y=self.y+dy

Whichofthesetwomove()methodsseemsthebestdescriptionofwhatishappening?

Themorecomplexaretheclasses,themorevaluethereisinmakinganefforttodesign

themtoeffectivelycommunicatetheirbehaviorsandtomakethingseasiertoexpandand

modify. It is also plain that the move() method for a point is simpler than that for a

triangle.Thatfactisinvisiblefromoutsidetheclass,anditactuallynotrelevant.

6.1.3 Encapsulation

Intheexampleofthepointclassthereisnoactualneedforanaccessormethod,because

thevariablescanbeaccessedfromoutsidetheclass,inspiteoftheargumentsthathave

beengivenformorecontrolleduseofthesevariables.

A careful programmer would want to ensure the integrity of classes by forcing the

variablestoremainprotectedinsomeway,andPythonallowsthiswhilenotrequiringit.

Thevariablesxandyareaccessibleandmodifiablefromoutsidebecauseofhowthey

arenamed.Anyvariable nameina classthatbeginswith anunderscorecharacter (“_”)

cannotbemodifiedbycodethatdoesnotbelongtotheclass.Suchavariableissaidtobe

protected.Avariablenamethatbeginswithtwounderscorecharacterscan’tbemodified

orevenexaminedfromoutsideoftheclass,andissaidtobeprivate.Allothervariables

arepublic.Thisappliestomethodnamestoo,sothemethod__init__()thatistheusually

constructorisprivate.

Rewritingthepointclasstomaketheinternalvariablesprivatewouldbedonelikethis:

classpoint:

def__init__(self,x,y):

self.__x=x

self.__y=y



defgetx(self):

returnself.__x



defgety(self):

returnself.__y



detsetx(self,x):

self.__x=x



defsety(self,y):

self.__yy=y



defdistance(self,p):

d=(self.__x-p.getx())*(self.__x-p.getx())+

(self.__y-p.gety())*(self.__y-p.gety())

returnsqrt(d)



defmove(self,dx,dy):

self.__x=self.__x+dx

self.__y=self.__y+dy



defdraw(self):

print(“(“,self.__x,“,”,self.__y,“)“)

Now the internal variables x and y can’t be modified or even have their values

examinedunlessexplicitlyallowedbyamethod.

6.2 CLASSESANDDATATYPES

Consideraninteger. How can it be described so that a person who has not used one

beforecanimplementsomethingthatlooksandactslikeaninteger?Thisisaspecificcase

of the general problem faced when using computers—to describe a problem in enough

detailsothatamachinecansolveit.Thedefinitioncouldstartwiththeideathatintegers

canbeusedforcountingthings.Theyarenumbersthathavenofractionalpart,andthat

havebeenextendedsothattheycanbepositiveornegative.

What can be done with them? Integers can be added and subtracted, multiplied and

divided.Whendividingtwointegerstherecanbeanintegerremainderleftover.Theycan

bedisplayedinmanyforms:asbase10numbers,inanyotherbase,asRomannumerals,

andsoon.Thereareotheroperationsonintegers,butthesearethemostcommonlyused

ones.

What has been done here is to define a type. Python types, the ones built into the

language,includetheintegertype,aswellasfloatingpointnumbers,strings,andsoon.

Each is characterized by an underlying implementation, which is often hidden from the

programmer,andasetofoperationsthataredefinedonthingsofthattype.Thisisafair

definitionofatypeingeneral.Aclasscanbeusedtoimplementatype—notoneofthe

typesthatthelanguagealreadyefficientlyprovides,butnewtypesthatprogrammersfind

usefulfortheirpurposes.Themanandpersonclassesdescribedearliercanbethoughtof

astypes.

Whendesigningprogramsthatuseclasses,itislikelythattheclassesrepresenttypes,

althoughtheymaynotbecompletelyimplemented.Thedesignschemewouldbetosketch

ahigh-levelsolutionandobservewhatcomponentsofthatsolutionlookandbehavelike

types.Those components can be implementedas classes. The remainder ofthe solution

willhavestructureimposedonitbyvirtueofthefactthattheseothertypesexistandare

defined to be used in specific ways. Types can hide their implementation, for example.

Theunderlyingnatureofanintegerprobablydoesnotmattermuchtoaprogrammermost

times,andsocanbehiddenbehindtheclassboundary.Thishastheaddedfeaturethatit

encourages portability: if the implementation has to change, the class can be rewritten

whileprovidingthesameinterfacetotheprogrammer.

Theoperationson the typeareimplemented asmethods.The methodscanaccess the

internal structure of the class while providing the desired view ofthe data and ways of

manipulatingit.Ifaclassnamedintegerexisted,forexample,thenadd(),subtract(),and

soonwouldbemethods.Theninstancesofthisclasscouldbeimplemented:

a=integer(5)

b=integer(21)

andcomputingasumwouldbe:

c=a.add(b)

Theunderlyingrepresentationofanintegerisunknowntoauserofthisclass.Allthatis

known is the interface, described as methods. If the interface is well-documented, then

that’s all a programmer needs to know. In fact, exposing too much of the class to a

programmercancompromiseit.

6.2.1 Example:ADeckofCards

Traditionalplayingcardsthesedayshaveredandblackcolors,foursuits,andatotalof

52cards,13ineachsuit.Individualcardsarecomponentsofadeck,andcanbesorted:a2

islessthana3,aJacklessthanaKing,andsoon.TheAceisaproblem:sometimesitis

thehighcard,sometimesthelowcard.Acardwouldpossessthecharacteristicsofsuitand

value.Whenplayingcardgames,cardsaredealtfromthedeckintohandsofsomenumber

ofcards:13cardsforbridge,

5formostpokergames,andsoon.Thevalueofacardusuallymatters.Sometimes

cards are compared against each other (poker), sometimes the sum of values is key

(blackjack,cribbage),andsometimesthesuitmatters.Theseusesofadeckofcardscanbe

usedtodefinehowclasseswillbecreatedtoimplementcardgamesonacomputer.

Operationsonacardcouldincludetoviewit(itcouldbefaceuporfacedown)andto

compare it against another card. Comparison operations could include a set of complex

specificationstoallowforacesbeinghighorlowandforsomecardshavingspecialvalues

(spades,baccarat)soadefinitionstepmightbeveryimportant.

Adeckisacollectionofcards.Thereareusuallyoneofeachcardinadeck,butinsome

places(e.g.,LasVegas) therecouldbe fourormore complete decksusedwhen playing

blackjack.Operationsonadeckwouldincludetoshuffle,toreplacetheentiredeck,andto

deal a card or a hand. With these things in mind, a draft of some Python classes for

implementingacarddeckcanbecreated:

Thewaythatthemethodsareimplementeddependsontheunderlyingrepresentation.

Whentheprogrammercallsdeal()theyexpectthemethodtoreturnacard,whichisan

instanceofthecardclass.Howthathappensisnotrelevanttothem,butitisrelevantto

the person who implements the class. In addition, how it happens may be different on

differentcomputers,andaslongastheresultisthesameitdoesnotmatter.

Forexample,acardcouldbeaconstantvaluerthatrepresentedoneofthe52cardsin

the deck. The class could contain a set of values for these cards and provide them to

programmersasareference:

classcard:

CLUBS_1=1

DIAMONDS_1=2

…

HEARTS_ACE=51

SPADES_ACE=52



Def__init__(self,face,suit):

…

ThevariablesCLUBS_1,DIAMONDS_1,andsoonareaccessibleinallinstancesof

the card class and have the appropriate value. Variables defined in this way have one

instanceonly,andaresharedbyallinstances.

Asecondimplementationcouldbeasatuple.Theaceofclubswouldbe(Clubs,1),for

instance.Eachhasadvantages,butthesewillnotbeapparenttotheuseroftheclass.For

example, the tuple implementation makes it easier todetermine the suit of a card. This

matterstogamesthathavetrumpsuits.Theintegervalueimplementationmakesiteasier

todeterminevaluesanddospecificcomparisons.Thevalueofacardcouldbestoredina

tuplenamedranks,forexample,andranks[r]wouldbeanumericalvalueassociatedwith

thespecificcard.

6.2.2 ABouncingBall

Animations and computer simulations see the world as a set of samples captured at

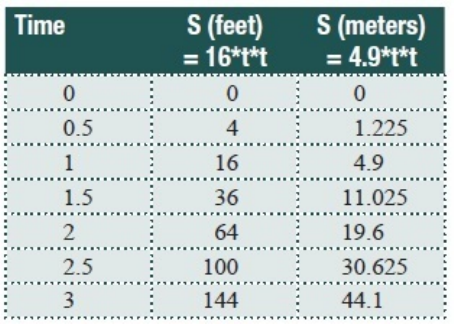
discretetimes.Ananimation,forexample,isasetofimagesofsomescenetakenatfixed

timeintervals,generally1/24thofasecondor1/30thofasecond. Simulationsuse time

intervalsthatare appropriate to the thingbeing simulated.This exampleis asimulation

andanimationofabouncingball,firstinonedimensionandthenintwodimensions.

Aballdroppedfromaheighthfallstothegroundwhenreleased.Itsspeedincreasesas

itfalls,becauseitisbeingpulleddownwardsbygravity.Thebasicequationgoverningits

movementis:

s=1/2at2+v0t(6.1)

wheresisthedistancefallenattimet,v0isthevelocitytheobjecthadattimet=0,anda

isthevalueoftheacceleration.Foranobjectattheearth’ssurface,thevalueofais32

feet/second2=9.8meters/second2.Foraballbeingdropped,v0is0,sinceitisstationary

initially.So,thedistancesatsuccessivetimeintervalsof0.5secondswouldbe:

Aclasscouldbemadethatwouldrepresentaball.Itwouldhaveapositionandaspeed

at any given time, and could even be drawn on a computer screen. Making it bounce

wouldbeamatterofgivingtheballavaluethatindicatedhowmuchofitsenergywould

belosteachtimeitbounced,meaningthatitwouldeventuallystopmoving.Writingthe

codefortheclassBallcouldbeginwiththeinitialization(theconstructor):

classBall:

def__init__(self,height,elasticity):

self.height=height

self.e=e

self.speed=0.0

self.a=32.0

Thiscreatesandinitializesfourvariablesnamedheight,e,a,andspeedthatarelocalto

the class. Remember, the parameter selfrefers to the classitself, and any variable that

beginswith‘self.’isapartoftheclass.Avariablewithinthefunction__init__thatdidnot

beginwith‘self.’andwasnotglobalwouldbelongtothefunction,andwouldbecreated

anddestroyedeachtimethatfunctionwascalled.

Amethod(function)thatcalculatestheheightoftheballataspecifictimeissomething

elsethattheBallclassshouldprovide.Thisissimplythevalueoftheclasslocalvariable

height,so:

defheight(self):

returnself.height

The self parameter has to be passed, otherwise the function can’t access the local

variableheight.Thesimulationwillneedvaluesofheightasafunctionoftime,andtime

willincreaseindiscretechunks.Thiscouldbeimplementedinacoupleofways:theclass

couldkeeptrackofthetimesinceitwasdropped,oritcouldusethetimeincrementto

determine the next speed and position. If the former then a new class variable must be

usedtostorethetime;ifthelatterthenameanshastobefoundtoincrementthespeed

ratherthanusingtotalduration.Thissecondideaissimplerthanitsounds.Theequationof

motion s = 1/2at2 + v0t can use a time increment in place of t, and v0 would be the

velocityatthestartofthetimeinterval;thisyieldsthenewposition.Thenewvelocitycan

befoundfromarelatedequationofmotion,whichis:

v=at+v0(6.2)

wheretisagainthetimeincrementandv0isthespeedatthebeginningoftheinterval.

Thefunctionthatupdatesthespeedandpositioninthismannerwillbecalleddelta:

defdelta(self,dt):

s=0.5*self.a*dt*dt+self.speed*dt

height=height-s

self.speed=self.speed+self.a*dt

Heretheparameterdtisthetimeinterval,andsothatcanbevariedbytheprogrammer

togetpositionvaluesatvariousresolutions.

FornowthiswillbetheBallclass.Somecodeisneededtotestthisclassandshowhow

well(orwhether)itworks,andthiswillbethemainpartoftheprogram.Aninstanceof

Ball has to be created and then the delta method will be called repeatedly at time

incrementsof,foranexample,0.1seconds.Atableofheightandtimecanbeconstructed

inthis way, and itis a simplematter to see whether the numbers arecorrect. The main

programis:

b=Ball(12.0,0.5)

foriinrange(0,20):

b.delta(0.1)

print(“Attime“,i*0.1,”theballhasfallento”,b.height(),”Feet”)

Theresultsarewhatshouldbeexpected,showingthatthisclassfunctionscorrectly:

Attime0.0theballhasfallento12.0Feet

…

Attime0.5theballhasfallento7.999999999999997Feet

…

Attime1.0theballhasfallento-4.0000000000000036Feet

…

Attime1.5theballhasfallento-24.000000000000004Feet

…

Attime2.0theballhasfallento-52.000000000000014Feet

…

Attime2.5theballhasfallento-88.00000000000003Feet

…

Becausetheinitialheightwas12feet,thedistancefallenis12minusthevaluegiven

above,so:4,16,36,64,and100feet,whichisinagreementwiththeinitialtableforthe

timeslisted.Itappearstoworkcorrectly.

Thiscodedoesnotyetdothebounce,though.Whentheheightreaches0theballisat

groundlevel.Itshouldthenbounce,whichistosaybeginmovinginthereversedirection,

withaspeedequaltoitsformerdownwardspeedmultipliedbytheelasticityvalue.This

doesnotseemhardtodountilitisrealizedthattheballisnotlikelytoreachaheightof0

exactlyatatimeincrementboundary.Atonepointtheballwillbeabove0andthenafter

the next time unit the ball will be below 0. When does it actually hit the ground, and

where will be the ball actually be at the end of the time increment? This is not a

programmingissuesomuchasanalgorithmicormathematicalone,butisadetailthatis

importanttothecorrectnessoftheresults.

Itseemsclearthatthebouncecomputationshouldbeperformedinthemethoddelta().

Theheightvalueintheclassbeginsatapositivevalueanddecreasestowards0astheball

falls. During some specific call to delta(), the ball will have a positive height at the

beginningofthecallandanegativeoneattheend;thismeansabounceshouldhappen.At

thattimetheheightoftheballwillbenegative.Theheightofthebouncedballattheend

of the time interval will be the negated value of the height (i.e., so it is positive again)

multipliedbytheelasticity.

Thespeedthatshouldbeusedinthebounceisbasednotthefinalspeedbutthespeed

theballwastravelingatthetimewhentheheightwas0.Thishappenswhenself.height-s

iszero,orwhen:

self.height=s=0.5*self.a*dt*dt+self.speed*dt

Solve this for the time xt that makes the equation work out, which would be the

standardsolutiontoaquadraticequationthatistaughtinhighschool:

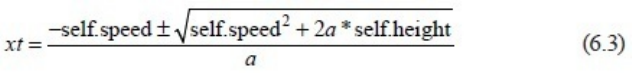
Thevalueofxtwillbebetween0anddt,andisthetimewithintheincrementatwhich

theballstrucktheground.Atthistimetheballwillbemovingwithspeed(self.speed+

self.a*xt) instead of (self.speed + self.a*dt) for a normal time interval. The ball will

reverse direction and reduce speed by the value of elasticity. Now the ball is moving

upwards.

The ball will be slowed by gravity until it stops on its upward path and drops down

again.Atthetopofthepathitsspeedwillbe0;atthebeginningofthetimeintervalthe

speed will be negative and at the end it will be positive, and that’s how the peak is

detected.Thissituationismuchsimplerthanthebounce.

Theannotatedprogramisasfollows:

#Ball.py

importmath

classBall:

#Constructor/initializer

def__init__(self,height,elasticity):

self.height=height#Currentheightoftheball

self.e=elasticity#Howmuchenergyisretainedeachbounce

self.speed=0.0#Currentspeedoftheball,

#initially0,down+

self.a=32.0#Acceleration:G=32ft/sec^2



#WhatJavawouldcallanaccessor:notreallyneeded.

defgetHeight(self):

returnself.height



#Calculatethenewheightandspeedforachangeintimeofdtseconds.

defdelta(self,dt):

startHeight=self.height#Rememberthestate

#beforedt

startSpeed=self.speed

s=0.5*self.a*dt*dt+self.speed*dt#Equation1:

#positionupdate

self.height=self.height-s

self.speed=self.speed+self.a*dt#Equation2:Speed

#update

ifself.height<0:#Thesignchanged;bounce,when?



#Equation3:Solvethequadraticequationtofindthetime

#ofbounce

xt=(-startSpeed-math.sqrt(startSpeed*startSpeed+2*self.a*startHeight))/self.a

ifxt<0:

xt=(-startSpeed+math.sqrt(startSpeed*startSpeed+2*self.a*startHeight))/self.a

print(“Bouncesattime“,xt)



#Equation2withelasticity

self.speed=-(self.speed+self.a*xt)*self.e

self.height=-self.height*self.e#Correctthe

#height

ifself.e<0.03:self.e=0.0

else:self.e=self.e-0.03



#Peakoftheupwardbounce,velocitychangessignfrom+to-

elifstartSpeed*self.speed<0:#Ifsigndiffersthen

#theproductis-ve

self.speed=0#Speedis0atthetop

#ofthebounce

print(“Peak”)

print(”Newspeedis“,self.speed,”andheightstarts

at“,self.height)

ifself.height<0.:

self.height=0.



b=Ball(12.0,0.5)#Initialheight12feet,elasticityis0.5

s=Screen(20,40)



foriinrange(0,50):

b.delta(0.1)#Timeincrementis0.1seconds

Howcanthisprogrambeeffectivelytested?Thecomputedvaluescouldbecompared

againsthandcalculations,butthisistime-consuming.Itwasdoneforafewcasesandthe

simulation was accurate. For this example, another program was written in a different

programminglanguagetocalculatethesamevalues,andtheresultfromthetwoprograms

wascompared—theywerenearlyexactlythesame.Thisisnotdefinitive,butiscertainlya

good indication that this simulation is working properly. In both programs similar

approximationsweremade,andthenumbersagreedtosevendecimalplaces.

Thisclasswillbeexpandedlatertoincludeananimationofthebouncingball.

6.2.3 Cat-A-Pult

Early in the development of personal computers, a simple game was created that

involved shooting cannons. The player would set an angle and a power level and a

cannonballwouldbefiredtowardstheopposingcannon.Iftheballstruckthecannonthen

it would be destroyed, but if not then the opposing player (or the computer) would fire

back at the player’s cannon. This process would continue until one or the other cannon

was destroyed. This game evolved with time, having more complex graphics,

mountainous terrain, and more complex aspects. Its influence can be seen in modern

gameslikeAngryBirds.

A variation of this game is proposed asan example of how classes can be used. The

basicideaistoeliminateamousethatiseatingyourgardenbyfiringcatsatit;hencethe

namecat-a-pult.Thegamewillusetextasinputandoutput,becausenographicsfacility

isavailableyet.Aplayertypestheangleandthepowerlevelandthecomputerwillfirea

catatthemouse.Thelocationwherethecatlandswillbemarkedonasimplecharacter

display, and the player can try again. The goal is to hit the mouse with as few tries as

possible.

BasicDesign

Beforewritinganycode,oneneedstoconsidertheitemsinthisgameandtheactions

theycantake.Theitemswillbeclasses,theactionswillbemethods.Thereseemtobetwo

items:acannonball(acat)andacannon.Thetarget(themouse)couldbeaclasstoo.The

cannonhasalocation,anangle,andapowerorforcewithwhichthecannonballwillbe

ejected. Both of the last two factors affect the distance the ball travels. The cannon is

givenatargetasaparameter—inthisexamplethetargetwillbeanothercannon,basically

toavoidmakingyetanotherclassdefinition.

The action a cannon can perform is to be fired. This involves releasing a cannonball

with a particular speed and direction from the location of the cannon. In this

implementation an instance of the cannonball class will be created when the cannon is

firedandwillbegiventheangleandvelocityasinitialparameters;theballwill,fromthen

on, be independent. As a class, the ball has a position (x, y) and a speed (dx, dy). The

actionthatitcanperformistomove,whichwillbeaccomplishedusingamethodnamed

step(),andtocollidewithsomething,

accomplishedbythemethodtestCollision().

DetailedDesign

Inthemetaphorofthisgame,thecannonballisactuallyacatandthetargetisamouse,

buttotheprogramthesedetailsarenotimportant.Here’swhatisimportant:

ClassCannonClassBall

Has:positionx,ypositionx,y

angle(whenfired)speeddx,dy

power(whenfired)name(text)

target(anothercannon)target(aCannonclassinstance)

ballgravity(forcechangingtheheight)



Does:firestep

steptestforcollision

AlloftheHasaspectsareclasslocalvariables,andinthisdesigntheywillbeinitialized

withinthe__init__methodofeachclass.Thiswouldentailthefollowing:

self.x=xself.x=x

self.y=yself.y=y

self.power=0self.dx=dx

self.angle=0self.dy=dy

self.target=targetself.target=target

self.ball=Noneself.gravity=1.0

self.name=””

The game is essentially one-dimensional. The cannonball will land at a specific x

coordinate,andifthatisnearenoughtothexcoordinateofthetarget,thenthetargetis

destroyed and the game is over. Without a way to draw proper graphics, this can be

imaginedasasimpletextdisplaywiththecannonononesideofthescreenandthetarget

ontheother,somethinglikethatseeninFigure6.1.

Theslashcharacter(“/”)ontheleftrepresentsthecannon,andthe“Y”representsthe

mouse,whichisthetarget.Thecannonisathorizontalcoordinate12,andthemouseisat

60;bothverticalcoordinatesare0.

AlloftheDoesaspectsrepresentactions,orthingstheclassobjectcando.Whenthe

cannonisfiredtheballiscreatedatthecannoncoordinates(12,0)andisgivenaspeed

that is related to the angle and power level using the usual trigonometric calculations

learnedinhighschool(Figure6.2):

dy=sin(angle*3.1415/180.0)

dx=cos(angle*3.1415/180.0)

The angles passed to sin and cos must be in radians, so the value PI/180 is used to

convert degrees into radians. The coordinates in this case have y increasing as the ball

moves upwards. So, when the cannon is fired a ball is created that has the x and y

coordinates of the cannon and the dx and dy values determined as above. This is

accomplishedbyamethodnamedfire():

Fire:takesanangleandapower.

Angleisindegrees,between0and360

Powerisbetween0and100(apercentage)

1.Computevaluesfordxanddyfromangleandpower,wheremaxpoweris0.1

2.Createaninstanceof Ballgivingitx,y, dx,dy,a name(“cat”),andatarget(the

mouse)

Thesimulationmakestimestepsofafixeddurationandcalculatespositionsofobjects

at the end of that step. Each object should have a method that updates the time by one

interval, and it will be named step(). The cannon does not move, but sometimes has a

cannonballthatithasfired,soupdatingthestatusofthecannonshouldupdatethestatus

oftheballaswell:

Step:makeone-timestepforthisobjectinthesimulation.Noparameter.

1.Ifaballhasbeenfired,thenupdateitsposition.Thisisdonebycallingthestep()

methodoftheball.

Thisdefinesthecannon.

Theballmustalsopossessastep()method,anditwillupdatetheball’spositionbased

onitscurrentspeedandlocation.Thexpositionisincreasedbydx,andtheyisincreased

bydy.Gravitypullsdownontheball,effectivelydecreasingtheverticalspeedoftheball

duringeachinterval.After sometrialsit wasdeterminedthatthe valueofdy should be

decreasedbythe valueof gravity during each interval. If the ball strikes the ground, it

shouldstopmoving.Whendoesthishappen?Whenybecomessmallerthan0.Whenthis

occurs,setdxanddyto0,andchecktoseeiftheimpactlocationisneartothetarget.

Step:makeaone-timestepforthisobjectinthesimulation.Noparameter.

1.Letx=x+dx,changingthexposition

2.Lety=y+dy,changingtheyposition

3.Decreasedybygravity(dy=dy-gravity)

4.Iftheballhasstrucktheground

5.Letdx=dy=gravity=0

6.Checkforcollisionwithtarget

Checkingtoseeiftheballhitthetargetisamatteroflookingatthexvalueoftheball

andthexvalueofthetarget.Ifthedifferenceissmallerthansomepredefinedvalue,say

1.0, then the target was hit. This is determined by a method that will be called

testCollision().Ifthecollisionoccurredthensuccesshasbeenachievedbytheplayer,so

setaflagthatwillendthegame.

testCollision:checktoseeiftheballhashitthetargetand,ifso,setaflag:

1.Subtractthexpositionoftheballfromthexpositionofthetarget.Callthisd.

2.Ifd<=1.0thensetaflagdonetoTrue.

ThisdefinestheclassBallandcompletesthetwomajorclasses.

Themainprogramthatusestheseclassescouldlooksomethinglikethis:

mouse=Cannon(60,0,None)#Createthetarget

player=Cannon(12,0,mouse)#createthecannon

player.fire(42,65)#Example:firecannonat

#42degrees65%power

done=False#initializevariable

#ꞌdoneꞌ

whilenotdone:#solongasthesimulation

#isnotover

player.step()#Updatethepositionof

#theball.

ActualcodeformostofthisexampleisshowninFigure6.4,andtheentireprogramis

ontheaccompanyingdisc.Includedinthediscversionisanextraclassthatdrawseach

stateofthegameascharactergraphicsthatcanbedisplayedinthePythonoutputwindow;

theexampleinthefiguredoesnotincludeanyoutput,andisunsatisfyingtoexecute.The

program on the disc will generate a numeric and graphical representation of the state,

showingtheaxes,thecannon,theball,andthetargetaftereachstep.Thesecanbemade

into distinct text files and can be made into an animation using MovieMaker on a

WindowscomputerorFinalCutonaMac.Suchananimationisalsoincludedonthedisc,

andisnamedcatapult.mp4.

The process by which Cat-a-pult was designed and coded loosely defines a way to

designandcodealmostanyprogramthatusesclasses.

6.3 SUBCLASSESANDINHERITANCE

Classesaredesignedaslanguagefeaturesthatcanrepresentahierarchyofinformation

orstructure.Aclasscanbeusedtodefineanother,andpropertiesfromthefirstclasswill

bepassedon(inherited)bytheother.Aclassthatisbasedonanotherinthiswayiscalled

asubclass,andexplanatoryexamplessuffusetheInternet:apetclasswithdogsandcatsas

special cases; a polygon having triangles and rectangles as subclasses; a dessert class,

havingsubclassespie,cake,andcookie;eventheinitialexampleinthischapterofaman

and a woman class and the person class that they can be derived from. A subclass is a

morespecificcaseofthesuperclass(orparentclass)onwhichitisbased.

The examples above are for explanation, and are not really useful as software

components, which begs a question about whether subclasses are really useful things.

Theyare,butitrequiresnon-trivialexamplestoreallydemonstratethis.

6.3.1 Non-TrivialExample:ObjectsinaVideoGame

Tosomedegreeallobjectsinagamehavesomethingsincommon.Theyarethingsthat

can interact with other game objects; they have a position within the volume of space

definedbythegame,andtheyhaveavisualappearance.Thus,adescriptionofaclassthat

couldimplementagameobjectwouldinclude:

classgobject:

position=(0,0,0)#Objectpositionin3D

visual=None#Graphicsthatrepresent

#theobject

def__init__(self,pos,vis)

defgetPosition(self):

defsetPosition(self,p):

defsetVisual(self,v):

defdraw(self):

Anyonewhohasplayedavideogameknowsthatsomeoftheobjectscanmovewhile

otherscannot.Objectsthatmovecanhavetheirpositionchange,andthepositionhastobe

updatedregularly.Anobjectthatcanmovecanhaveaspeedandamethodthatupdates

theirposition;otherwiseitislikeagobject.Thisisagoodcaseforasubclass:

classmobject(gobject):

speed=(0,0,0)#Speedinpixelsperframethe

#x,y,zdirections

def__init__(self,s)

defgetSpeed(self):

defsetSpeed(self,s):

defmove(self):

defcollision(self,gobject):

Thesyntaxofthishasthesuperclassgobjectasaparameter(apparently)ofthesubclass

mobjectbeingdefined.Ifaninstanceofagobjectiscreated,its__init__methodiscalled

andtheresultingreferencehasaccesstoallofthemethodsinthegobjectdefinition,just

asonewouldexpect.Ifaninstanceofmobjectiscreated,the__init__methodofmobject

iscalled,butnotthatofgobject.Nonetheless,allpropertiesandmethodsofbothclasses

areavailablethroughthemobjectreference;thatis,thefollowingislegal:

m=mobject((12,0,0))#Creatembojectwithspeed

#(12,0,0)

m.draw()#Drawthisobject

eventhoughanmobjectdoesnotpossessamethoddraw();themethoddefinedinthe

parent class is accessible and will be used. When the mobject is created it is also a

gobject, and all of the variables and methods belonging to a gobject are defined also.

However,the__init__()methodforgobjectisnot calledunlessthe mobject__init__()

methoddoesso.Thismeansthat,forthemobject,thevaluesofpositionandvisualare

not specified by the constructor and will take the default values they were given in the

gobjectclass.Ifnosuchvaluewasgiven,theywillbeundefinedandanerrorwilloccurif

theyarereferenced.

Callingthe__init__()methodoftheparentclasscanbedoneasfollows:

super().__init__((10,10,10),None)

In this instance the constructor for gobject is called, passing a position and a visual.

Thiswouldnormallybedoneonlyinthe__init__()ofthesubclass.

Nowconsiderthefollowingcode.Themethodsaremainlystubsthatprintamessage,

buttheoutputoftheprogramisinstructive:

Outputfromthisis:

gobjectinitfromthecreationofthegobjectinstanceg

gobjectinitwhenmiscreateditcallstheparent__init__

mobjectinitfromthemobject__init__whenmiscreated

(10,10,10)m.getPosition,showingaccesstoparent

methods

Movem.movecall

Drawm.drawcall,againshowingaccesstoparentmethod

Attemptingtocallg.move()wouldfailbecausethereisnomove()methodwithinthe

gobjectclass.Hence,ifanobjectwaspassedtoafunctionthatwouldattempttomoveit,

itwouldbecriticaltoknowwhethertheparameterpassedwasagobjectoranmobject.

Consideramethodthatmovesanobjectxoutofthepathofanmobjectinstanceifitcan,

orchangesthepathofthemobjectifitcannot.Thismethod,nameddodge(),mightdothe

following:

defdodgeself,(x):

c=x.getPosition()

c=c+(dx,dy,0)

x.setPosition(c)

However,iftheparameterisaninstanceofagobject,thenitshouldnotbemoved.The

functionisinstance()canbeusedtodeterminethis.Theresultof:

isinstance(x,gobject)

willbeTrueifxisagobjectandFalseotherwise.IfFalse,thenitcan’tbemovedandthe

dodge()methodwillhavetomovethecurrentmobjectoutofthewayinstead:

defdodgeself,(x):

ifisinstance(x,gobject):

self.position=self.position+(dx,dy,0)

else:

c=x.getPosition()

c=c+(dx,dy,0)

x.setPosition(c)

6.4 DUCKTYPING

In many programming languages, types are immutable and compatibility is enforced.

ThisisnotgenerallytrueinPython,butstillthereareoperationsthat

requirespecifictypes.Indexingintoastringortuplemustbedoneusingsomething

muchlikeaninteger,andnotbyusingafloat.Nowthatclassescanbeusedtobuildwhat

amountstonewtypes,moreattentionshouldbepaidtothethingsatypeshouldofferand

therequirementsthisputsonaprogrammer.APythonphilosophycouldbethatthefewer

restrictionsthebetter,andthisisaprincipleofducktypingaswell.

Itshouldnotreallymatterwhattheexacttypeoftheobjectisthatisbeingmanipulated,

onlythatitpossesses thepropertiesthatare needed.Inavery simplecase,considerthe

classes point and triangle that were discussed at the beginning of this chapter. It was

proposed that both could have a draw() method that would create a graphical

representationoftheseonthescreen,andbothhaveamove()methodaswell.Afunction

couldbewrittenthatwouldmoveatriangleawayfromapointanddrawthemboth:

defmoveaway(a,b)

dx=a.getx()-b.getx()

dy=a.gety()-d.gety()

a.move(dx/10,dy/10)

b.move(-dx/10,-dy/10)

Question: which of the parameters, a or b, is the triangle, and which is the point?

Answer:itdoesnotmatter.Bothclasseshavethemethodsneededbythisfunction,namely

getx(),gety(),andmove().Becauseofthisthecallsaresymmetrical,

andbothofthefollowingarethesame:

moveaway(a,b)

moveaway(b,a)

Infact,aclassthatpossessesthesethreemethodscanbepassedtomoveaway()anda

resultwillbecalculatedwithouterror.Theessenceofducktypingisthat,solongasan

objectofferstheserviceneeded(i.e.,amethodofthecorrectnameandparameterset)to

anotherfunctionormethod,thenthecallisacceptable.Thereisawaytotellwhetherthe

classinstanceahasagetx()method.Thebuilt-infunctionhasattr():

ifhasattr(v1,“getx”):

x=v1.getx()

Thefirstargumentisaclassinstance,andthesecondisthenameofthemethodthatis

needed,asastring.ItreturnsTrueifthemethodexists.

Thenamecomesfromtheoldsayingthat“ifsomethingwalkslikeaduckandquacks

likeaduck,thenitisaduck.”Aslongasaclassoffersthethingsaskedfor,thenitcanbe

usedinthatcontext.

6.5 SUMMARY

A class, in the general sense, is a template for something that involves data and

operations(functions).Anobjectisaninstanceofaclass,aspecificinstantiationofthe

template.DefiningaclassinPythoninvolvesspecifyingaclassnameandacollectionof

variablesandfunctionsthatwillbelongtothatclass.Amethodisafunctionthatbelongs

toaclass,andsocanhaveeasyaccesstoitsinternaldata.Asafirstparameter,amethod

canbepassedtheselfvariablebydefault,whichcanbethoughtofasareferencetothe

objectcurrentlyexecuting.Thus,withinamethod,theexpressionself.xreferstoavariable

xdefinedintheclass.Anobjectiscreatedusingthenameoftheclass:foraclassnamed

thing,aninstancexiscreatedusingx=thing().Whenthisoccurs,ifthereisamethodin

thingnamed__init__,thenthatmethodiscalled.Thisisreferredtoasaninitializerora

constructor.

Accessingmethodsinanobjectisdoneusinga“dot”notation:obj.method().Variables

canbeaccessedinthiswaytoo.

Asubclassisaclassthatpossessesallofthepropertiesofsomeotherclass,theparent

classorsuperclass,plussomenewones.Thedataandmethodsoftheparentclasscanbe

accessedfromthesubclass(orchildclass).Asubclassofthingnamedsomethingwould

bedefinedusingthesyntax:

classsomething(thing):

Aclasscanrepresentanewtype,wheremethodsrepresentoperations.

Public variables can be accessed and modified from outside of a class; protected

variablescanbeaccessedbutnotmodifiedfromoutsideofaclass,andmustbeginwithan

underscore character (e.g., “_variable”); private variables can neither be accessed nor

modifiedfromoutsideoftheclass,andmustbeginwithtwounderscorecharacters(e.g.,

“__variable”).

Theprincipleofducktypingisthatitshouldnotreallymatterwhattheexacttypeofthe

objectisthatisbeingmanipulated,onlythatitpossessestheproperties

thatareneeded.

Exercises

1.Defineaclassnamedsquareinwhichtheconstructtakesthelengthofthesideasa

parameter.Thisclassshouldhaveamethodarea()thatcomputesandreturnsthearea

ofthesquare.

2.Defineasubclassofsquarenamedbuttonthatalsohasalocation,passedasXandY

parameterstotheconstructor.Abuttonalwayshasawidthof10.Thebuttonclasshas

thefollowingmethods:

center()Returnthecoordinatesofthecenterofthebutton

label(s)Setthevalueofatextlabeltobedrawntos

3.Createaclassclient.Aclientisadata-onlyclassthathasnomethodsotherthan

__init__(),butthatholdsdata.Inthiscasetheclientclassholdsaname,acategory

(retailorcommercial),atimevalue(integer),andaservicevalue(integer).Allvalues

areestablishedwhentheinstanceiscreatedbypassingparametersto__init__().Now

createtwosubclassesofclient,oneforeachcategory,retailandcommercial.

4.Defineaclassnamedfractionthatimplementsfractionalnumbers.Theconstructor

takesthenumeratoranddenominatorasparameters,andtheclassprovidesmethodsto

add,multiply,negate(makenegative),print,andfindthereciprocalofafraction.Test

thisclassbycalculating:

14/16*3/4

1/2–1/4

Bonus:resultsarereducedtosmallestpossibledenominator.

5.Giventhefollowingclass:

classvalue:

def__init__(self)

self.val=randrange(0,100)

andtheinitialization:

t=()

foriinrange(0,100):

v=value()

t=t+(v,)

writethecodethatscansthetupletandlocatesthesmallestintegersavedinanyofthe

classinstances.

6.CreateaclassthatsimulatesaNANDlogicgatewiththreeinputs.Theoutputwillbe

1unlessallthreeinputsare1,inwhichcasetheoutputis0.Everytimeaninputis

changed,theoutputischangedtoreflectthenewstate;thus,methodstoseteachinput

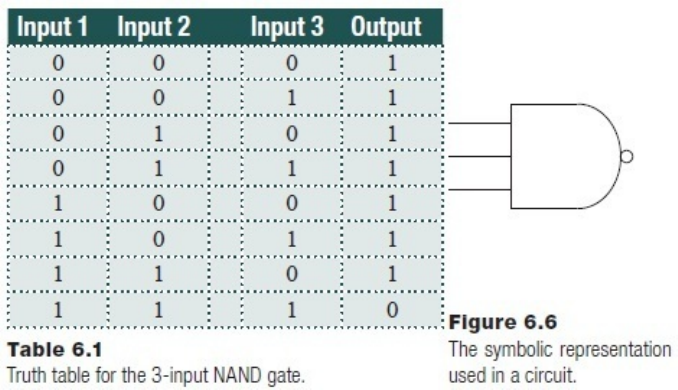
andtocalculatetheresultwillbeneeded,inadditiontoamethodthatreturnsthe

output.

7.Aqueueisadatastructurethatacceptsnew(incoming)dataatoneend(theback)and

storesitintheorderofarrival,givingthedataatthefrontofthequeuewhen

requested.It’slikealineatacashierinastore:customerswaitforthecashierinorder

ofarrival.Implementaqueueasaclass;ithasoperationsinto()andout()toadd

thingsandremovethingsfromthequeue,andempty(),whichreturnsTrueifthe

queuehasnodatainit.Whatisaddedtothequeueareobjectsofaclassclient,asseen

inExercise6.3above.

8.Simulation:Thegestationperiodforarabbitis28–32days,andtheywillbreeda

weekafterhavingalitter.Afemalerabbit(adoe)willbreedforthefirsttimeatabout

100daysold.Createaclassthatrepresentsarabbitandsimulatethegrowthofarabbit

populationthatstartswiththreedoesatday0.Assumealittersizeofbetween3and8,

andthathalfoftheoffspringwillbemale.Increasetimeby1dayatatimeandanswer

thequestion:“Howmanyrabbitswilltherebeafter1year?”iftheinitialpopulationis

threedoesandonemale(buck).

NotesandOtherResources

NotesonPythonClasses:

http://www.jesshamrick.com/2011/05/18/an-introduction-to-classes-and-inheritance-

in-python/

August12,2015.http://componentsprogramming.com/using-the-right-terms-method/

Duck typing in Python:

http://www.voidspace.org.uk/python/articles/duck_typing.shtml

1.R.Chugh,P.Rondon,andR.Jhala.(2012,January).Nestedrefinements:

Alogicforducktyping,ACMSIGPLANNotices,47(1),231–244.

2.Ole-JohanDahl.(2002).Thebirthofobjectorientation:

TheSimulalanguages,inSoftwarePioneers:ContributionstoSoftwareEngineering,

editedbyManfredBroyandErnstDenert,Programming,SoftwareEngineering,and

OperatingSystemsSeries,Springer,79–80.

3.O.-J.DahlandK.Nygaard.(1968).Classandsubclassdeclarations,inSimulation

ProgrammingLanguages,editedbyJ.Buxton,ProceedingsfromtheIFIPWorking

ConferenceinOslo,May1967,NorthHolland.

4.AdeleGoldbergandAlanKay.Smalltalk-72InstructionManual,44.

5.ANSISmalltalkStandardv1.9199712NCITSX3J20draft,Section3.1,9.

6.B.Liskov,ASnyder,R.Atkinson,andC.Schaffert.(1977).Abstractionmechanisms

inCLU,CommunicationsoftheACM,20(8),564–576.

CHAPTER7

GRAPHICS

7.1IntroductiontoGraphicsProgramming

7.2Summary

Inthischapter

Since the advent of Windows, computer graphics has been assumed as a feature of a

computer.Beforethatitwasarelativelyrarething,relegatedtosomeresearch,toafew

expensive Hollywood movies, and to science fiction. Believe it or not, the first use of

computergraphicsinacommercialmotionpicturewasinthefilmTheAndromedaStrain

(1971) in which it was used to show a rotating 3D map (they called it an electronic

diagram)oftheundergroundinstallationwheretheactionmainlytakesplace.Afewyears

laterthefilmWestworld(1973)used2½minutesofdigitallyprocessedvideotoshowthe

visualperspectiveofanandroid.Itwasaverytime-consumingandexpensivetaskatthat

time;ittookabout8hourstoprocess10secondsoffilm,orabout120hoursinall.

Modern computers all possess very fast graphics cards that perform most of the

renderingtasks,andaddedtothebuilt-insoftwareoncurrentoperatingsystems,itallows

for a very sophisticated yet simple-to-use graphical/windows interface to desktop

computers. The graphics software is hierarchical; the screen itself is merely an array of

pictureelements(pixels)thatcanbesettoanycolor,anditisdifficulttoseehowthatcan

bemadetodisplaycomplexpictures.

Ithasreachedthepointwhereeverythingseenonacomputerscreenisactuallydrawn—

icons,windows,backgrounds,andeventext.

What this means is that interacting with a computer is now done with graphics, not

characters and text. Since that is the situation, it makes sense to permit a beginning

programmertoexperimentwithprogramminggraphicsapplications.

7.1 INTRODUCTIONTOGRAPHICSPROGRAMMING

Atthemostprimitivelevelofgraphicssoftwareistheabilitytosetindividualpixels.It

is,aswasmentioned,quitedifficulttousethiscapabilitytocreatecomplexpictures.How

isadogdrawn,orabuilding,orevenjustastraightline?Thosethingshavebeenfigured

out,fortunately.

Soatthebottomlayerofsoftwarearefunctionsthatmanipulatepixels.Atthenextlevel

arelinesandcurves;thesearethebasiccomponentsofdrawingsandsketches.Anartist

with a pencil uses lines and curves to represent scenes. At the level above lines are

functions that use lines to create other objects, such as rectangles, circles, and ellipses.

These can be line drawings or can be filled with colors. The next higher levels can be

arguedabout,buttextisprobablyinthenextsoftwarelayerandthenshadingandimages

followedby3Dobjects,whichincludesperspectivetransformationandtextures.

Pythondoesnotitselfhavegraphicstools,butvariousmodulesthatareassociatedwith

Python do. The standard graphical user interface library for use with Python is tkinter.

Therearemanyfeaturesofthismodule,includingthecreationofwindows,drawing,user

interface widgets like buttons, and a host of other features. It is free and is normally

included in the Python distribution but it can easily be downloaded and used with any

Pythonversion.BecausetherearemanywaysthatPythoncanbeconfiguredonvarious

differentsystems,theinstallationprocesswillnotbedescribedindetailhere.Agraphics

modulewillbedescribedandisincludedontheDVDthataccompaniesthisbook,andit

requiresthattkinterbeavailable.Thisisalmostalwaystrue(rememberthatthisbookuses

Python3).

ThelibrarythatallowsgraphicsprogrammingiscalledGlib.IftheGlib.pyfileisinthe

samedirectoryasthesourcecodeforthePythonprogramthatusesit,thenitshouldwork

fine. Glib consists of a collection of functions that implement the first few levels of a

graphicssystemandthatcreateawindowwithinwhichdrawingcantakeplace.Itdoesnot

allowforinteraction,animation,sound,orvideo,allofwhicharethesubjectofthenext

chapter.

7.1.1 Essentials:TheGraphicsWindowandColors

To start creating computer graphics, it is necessary to understand how colors and

images are represented. When using a computer everything must be represented as

numbers.Apixelisthecolorofapictureataparticularlocation,andsotheremustbea

way to describe a color at that place. In physics frequency is used: each color has a

specific frequency of electromagnetic radiation. Unfortunately, this does not map very

wellontoacomputerdisplay,becauseitisbasedontelevisiontechnology.OnaTV,there

are three colors, red, green, and blue, that are used in various proportions to represent

everycolor.Therearered,green,andbluedotsontheTVscreenthatarelituptovarious

degreestocreatethecolorsthatareseen.Thisisbasedonthewayahumaneyeseescolor;

there are red, green, and blue sensors in the eye that in combination create our color

perception.Anotherreasonthatfrequencyisnotusedisthattherearecolorsthatarenot

accuratelyrepresentedasfrequencies;theydonotappearintherainbow.Thecolorspink

andbrownaretwoexamples.

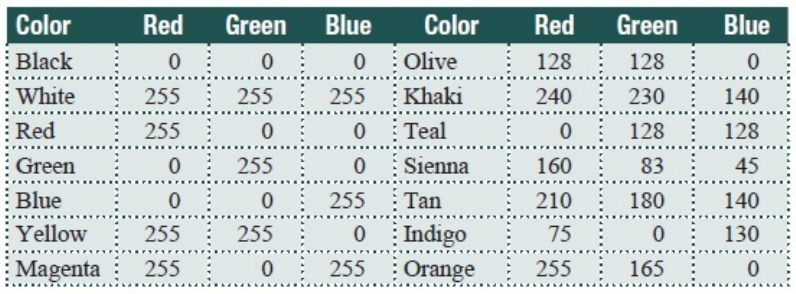
So,eachcolorinthegraphicssystemisrepresentedasthedegreeofred,green,andblue

thatcombinetocreatethatcolor.Inthatsenseitisabitlikemixingpaint.Yellow,ona

computer,isamixtureofredandgreen.Eachpixelthereforehasthreecomponents:ared,

green,andblue component.Thesecouldbe expressedas percentages, butwhenusing a

computeritisbettertoselectnumbersbetween0and255(8bits,or1byte)foreachcolor.

Each pixel requires 3 bytes of storage; actually 4 bytes in some cases, as will be seen

shortly. If an image contains 100 rows of 100 pixels, then it has 10,000 pixels and is

10000*3=30000bytesinsize.

To humans, colors have names. Here’s a list of some named colors and their RGB

equivalents:

Thereare,ofcourse,agreatmanymorenamedcolors,andevenmorecolorsthatcanbe

represented with RGB values in this way—16,777,202 of them in fact. Each pixel is a

colorvalue.AllgreyvalueshavethespecialsituationR=G=B,sothereare256 distinct

valuesofgreyrangingfromblacktowhite.

The graphics library provides functions for creating colors. The functions are

cvtColor()andcvtColor3():

cvtColor(g)  - Return a color value that has R=G=B = g, which is to say it

specifiesagreylevel=g.

cvtColor3(r,g,b)-ReturnacolorvaluethathasthespecifiedR,G,B

values.

When using Glib the program must initialize the system before drawing anything. All

graphics must take place between a call to startdraw() and a call to enddraw(). If

startdraw() is not called then important items will not be initialized, most especially a

drawing window will not be created and an error will occur at some time during

execution.Ifenddraw()isnotcalledthennothingwillbedrawn.Foranabstractexample,

ahypotheticalmainprogramcouldbe:

#startofprogram

Manycalculations

…

startdraw(width,height)

#Graphicscalls

…

enddraw()

The function startdraw() accepts two parameters: the width and the height of the

drawingregiontobecreated.Thesevaluescanberetrievedbyaprogramusingcallstothe

functions Width() and Height() if they are needed. Startdraw() creates the needed

windowanddrawingarea,initializesstartingcolors,fonts,andmodes,butdoesnotopen

thewindow.Nothingthatisdrawnwillbevisibleuntilenddraw()iscalled.

7.1.2 PixelLevelGraphics

Theonlypixelleveloperationdrawsapixelataspecifiedlocation;so,forexample,the

call:

point(x,y)

willsetapixelatcolumn(horizontalposition)xandrow(verticalposition)ytoacolor.

Whatcolor?Glibhastwodefaultcolorsthatcanbeset:thefillcolor,whichisthecolor

withwhichpixelswillbedrawn,polygonsandellipseswillbefilled,andcharacterswill

bedrawn;andthestrokecolor,thecolorwithwhichlineswillbedrawn.Settingthefill

colorisdoneusingacalltothefill()function:

fill(200)#Setthefillcolorto(200,200,200)

fill(100,200,100)#Setthefillcolorto(100,200,100)

Usingoneparametersetsthefillcolortoagreyvalue,whereaspassingthreeparameters

specifies the red, green, and blue values (respectively) of the fill color. Similarly the

functionstroke()canacceptoneorthreeparameters:

stroke(200)#Setthestrokecolorto(200,200,200)

stroke(255,0,0)#Setthestrokecolorto

#(255,0,0)=red

Thereisonemorefunctionthatcouldbethoughttobeinthepixellevelcategory.The

functionbackground()isusedtosetthebackgroundcolorofthegraphicswindow.Again,

itcanaccepteitheroneparameter(grey)orthree

(color).Thisleadstothefirstexample.

Example:CreateaPageofNotepaper

Notepaperhasbluelinesseparatedbyenoughspacetowriteorprinttextbetweenthem.

It often has a red vertical line indicating an indentation level, a place to begin writing.

Drawingthisisamatterofdrawingasetofconnectedbluepixelsinasetofrows,and

thenmakingaverticalcolumnofredpixels.Hereisonewaytocodethis:

fromGlibimport*

y=60#Heightatwhichtostart

startdraw(400,600)#Begindrawingthings

background(255)#Papershouldbewhite

fill(0,0,200)#Fillcolor=pixel

#color=blue

forninrange(0,27):#Draw30horizontalblue

#lines

forxinrange(0,Width()):#Drawallpixelsinone

#line

point(x,y)#Drawabluepixel

y=y+20#Thenextlineis20

#pixelsdown

fill(200,0,0)#Pixelcolorred

foryinrange(0,Height()):#Drawconnectedvertical

#pixels

point(25,y)#toformthemarginline

enddraw()

The output of this program is shown in Figure 7.2a. When pixels are drawn

immediatelynexttoeachothertheyappeartobeconnected,andsointhiscasetheyform

horizontal and vertical lines. This is not easy to do for arbitrary lines; it is not obvious

exactlywhichpixelstofillforalinebetween,say,(10,20)and(99,17).That’swhythe

linedrawingfunctionsexist.

Example:CreatingaColorGradient

Whencreatingavisualonacomputer,thefirststepistohaveaclearpictureofwhatit

will look like. For this example, imagine the sky on a clear day. The horizon shows a

lighterbluethantheskydirectlyabove,andthecolorchangescontinuouslyalloftheway

from horizon to zenith. If a realistic sky background were needed, then it would be

necessarytodrawthisusingthetoolsavailable.Whatwouldthemethodbe?

First,decideonwhatthecolorisatthehorizon(y=ymax)andatthehighestpointinthe

scene(y=ymin).Nowask:“howmanypixelsbetweenthosepoints?”Thechangeinpixel

color will be the color difference from ymax to ymin divided by the number of pixels.

Nowsimplydrawrowsofpixelsbeginningwiththe

horizon and moving up the image (i.e., decreasing Y value), changing the color by this

amounteachtime.

Asanimplementation,assumethatthecoloratthehorizonwillbeblue=(40,40,255)

andthetopoftheimagewillbe(40,40,128),adarkerblue.Theheightoftheimagewill

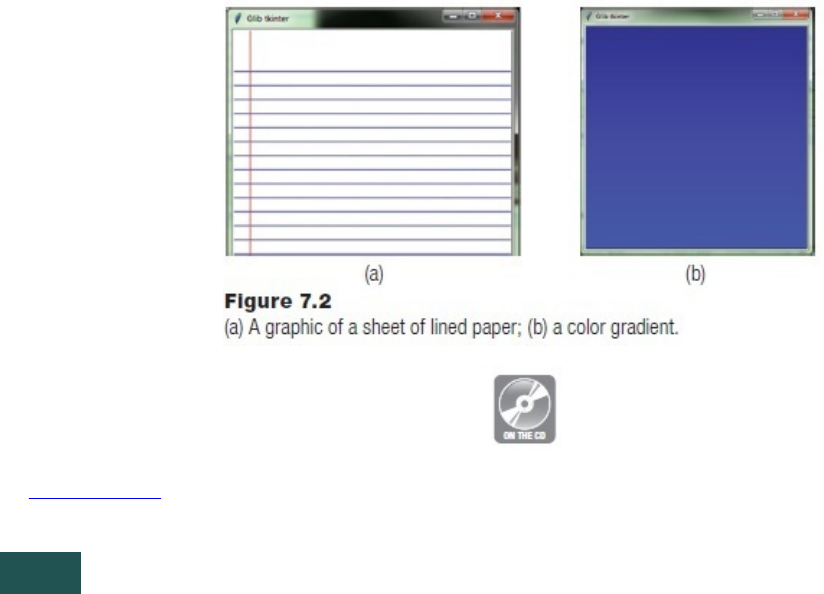
be400pixels;thechangeinblueoverthatrangeis127units.Thus,thecolorchangeover

each pixel is going to be 127.0/400, or about 0.32. A color can’t change a fractional

amount,ofcourse,butwhatthismeansisthatthebluevaluewilldecreaseby1unitfor

every 3-pixel increase in height. Do not forget that the horizon is at the bottom of the

image, which has the greatest Y coordinate value, so that an increase in Y means a

decreaseinheightandviceversa.

Theexampleprogramthatimplementsthisis:

fromGlibimport*

blue=128

startdraw(400,400)

delta=127.0/Height()

foryinrange(0,Height()):

yy=Height()-y

fill(40,40,blue)

forxinrange(0,Width()):

point(x,y)

blue=blue+delta

enddraw()

Figure7.2bshowswhatthegradientimagelookslike(afull-colorversionofthisand

allimagesisontheaccompanyingdisc).

7.1.3 LinesandCurves

Straight lines and curves are more complex objects than pixels, consisting of many

pixelsinanorganizedarrangement.Alineisactuallydrawnbysettingpixels,though.The

factthataline() functionexists meansthat the programmerdoes nothave to figure out

whatpixelstodrawandcanfocusonthehigherlevelconstruct,thelineorcurve.

Alineisdrawnbyspecifyingtheendpointsoftheline.UsingGlibthecallis:

line(x0,y0,x1,y1)

whereoneendofthelineisat(x0,y0)andtheotherisat(x1,y1).Thecolorofthelineis

specified by the stroke color. If any part of the line extends past the boundary of the

window,that’sOK;thelinewillbeclippedtofit.

Example:NotepaperAgain

Theexampleofdrawingapieceofnotepapercanbedoneusinglinesinsteadofpixels,

andwillbealittlefaster.Setthestrokecolortoblueanddrawacollectionofhorizontal

lines (i.e., that have the same Y coordinate at the endpoints) separated by 20 pixels, as

before. Then draw a vertical red line for the margin. The program is a variation on the

previousversion:

fromGlibimport*

y=60#Heightatwhichtostart

startdraw(400,600)#Begindrawingthings

background(255)#Papershouldbewhite

stroke(0,0,200)#Fillcolor=pixel

#color=blue

forninrange(0,27):#Draw30horizontalbluelines

line(0,y,Width(),y)#Drawabluehorizontalline

y=y+20#Thenextlineis20pixels

#down

stroke(200,0,0)#Pixelcolorred

line(25,0,25,Height())#Drawaverticalredline

enddraw()

Theoutputfromthisprogramisthesameasthatfortheversionthatdrewpixels,which

isshowninFigure7.2a.

Acurveistrickierthanaline,inthatitishardertospecify.ThemethodusedinGlibis

basedonthatintkinter:acurve(arc)isdefinedasaportionofanellipsefromastarting

angleforaspecifiednumberofdegrees,asreferencedfromthecenteroftheellipse.The

angle0degreesishorizontalandtotheright;90degreesisupwards(decreasingYvalue).

Theellipseisdefinedbyaboundingrectangle,specifyingtheupperleftandlowerright

coordinates of a box that just holds the ellipse. So, looking at Figure7.3, the rectangle

definedbytheupperleftcornerat(100,50)andthelowerrightat(300,200)hasacenter

at (200, 125) and contains an ellipse slightly longer than it is high (upper left of the

figure).Thefunctionthatdrawsacurveisnamedarc(),andtakestheupperleftandlower

rightcoordinates,astartingangle,andthesizeofthearcalsoexpressedasanangle.

Intheupperrightofthefigureisthearcdrawnbythecallarc(100,50,300,200,0,90),

whichmeansthatthepartoftheellipsefromthe0degreepointcounterclockwisefor90

degreeswillbedrawn.Theexampleatthelowerleftofthefiguredrawsthecurvefrom

the 45-degree point for 90 degrees, resulting in the upper section of the ellipse being

drawn. The final arc shown, at the lower right, uses a negative angle. The call

arc(100,50,300,200,45,-60) starts at the 45-degree point and draws the arc clockwise,

becausetheanglespecifiedwasnegative.

Thiswayofspecifyingarcsisfineforsimpleexamplesandsingle curves, butmakes

combiningmanyarcsintoamorecomplexcurveratherdifficult.Joiningtheendstogether

smoothlyisthetrick.

Thearc()functionhasanotherparameterthatcanbespecified.Theseventhparameter

tells the system what kind of arc to draw; the possibilities are ARC, CHORD, and

PIESLICE,andthedefaultvalueARCisillustratedinthefigure.Thecall:

arc(100,50,300,200,45,-60,CHORD)

givestheresultshowninFigure7.3a.Theresultofthecall:

arc(100,50,300,200,45,-60,PIESLICE)

isshowninFigure7.34b.Iffillingisturnedon,thentheseshapeswouldbefilledwiththe

defaultfillcolor.Amajorexampleinvolvingcurves/arcsisthepiechartprogramlaterin

thischapter.

7.1.4 Polygons

For the purposes of discussion, a polygon will include all closed regions, including

ellipses and circles. In that context, the arc() function can be used to draw circles and

ellipsesbyspecifyinganangleverynearto360degrees.Thecall:

arc(100,100,300,300,0,359.9,ARC)

willdrawanearlycompletecircle,onethatlookscomplete.However,thereisafunction

thatdrawsrealcirclesandrealellipses:itisnamedellipse().Inthedefaultdrawingmode

theellipse()functionispassedthecoordinatesofthecenteroftheellipseanditswidthand

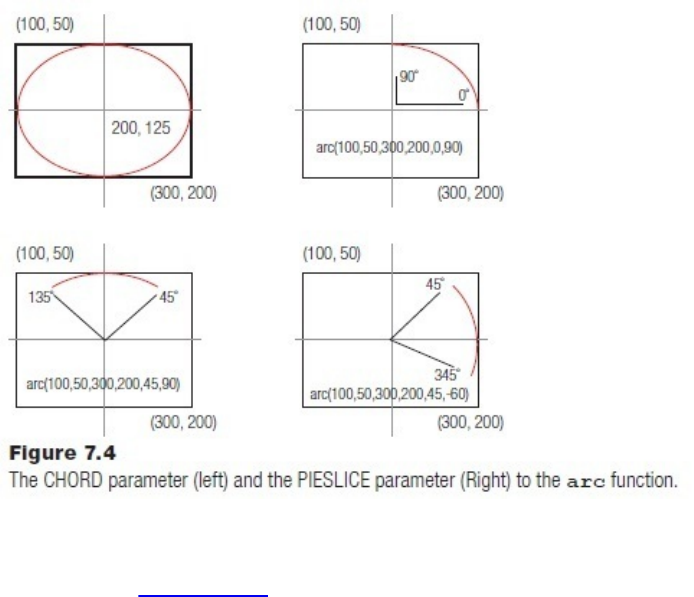
heightinpixels.Ifthewidthandheightareequal,thentheresultisacircle.Thecall:

ellipse(100,100,30,40)

drawstheellipseshowninFigure7.4a.Thecolorwithwhichtheellipseisfilledisthefill

color.Ifnofillingisdesiredthenacalltonofill()turnsofffilling.

The default mode for drawing ellipses is referred to as CENTER mode, where the

centeroftheellipseisgiven.Therearethreeothers:RADIUSmode,inwhichthewidth

and height parameters represent semi-major and semi-minor axes; CORNER mode in

which the upper left corner is specified instead of the center; andCORNERS mode, in

which the upper left and the lower right corner of the bounding box are specified. The

mode is changed using a call to the function ellipsemode(), passing one of the four

constantsastheparameter:CENTER,RADIUS,CORNER,orCORNERS.

A rectangle is drawn using the rect() function. Again, there are four drawing modes.

Considerthecallrect(x,y,w,h):

CENTER mode:  x, y are the coordinates of the center; w andh are the width and

height.

RADIUSmode:x,yarethecoordinatesofthecenter;wandrarethehorizontaland

verticaldistancestoanedge.

CORNERmode:x,yarethecoordinatesoftheupperleftcorner;

wandharethewidthandtheheight.

CORNERSmode:x,yarethecoordinatesoftheupperleftcorner;

wandharethecoordinatesofthelowerrightcorner.

Aswiththeellipse,therectangledrawingmodeischangedbycallafunction,thistime

rectmode().

Thefunctiontriangle()draws—yes,atriangle.Itispassedthreepoints,whichistosay

sixparameters:triangle(10,10,20,20,30,30)drawsatrianglebetweenthethreepoints

(10,10),(20,20),and(30,30).

7.1.5 Text

Drawingtextisnotcomplicated,butchangingfontsismoreofaproblem.

Afontissavedonafileandhastobeinstalled.Ifafontisspecifiedbyaprogrambutdoes

notexist,theneitherthefinishedimagewilllookdifferentfromwhatwasanticipatedor

anerrorwilloccur.Drawingtextisperformedbyacalltotext():

text(”Hellothere.”,x,y)

Thisdrawsthetextstring“Hellothere!”inthegraphicswindowsothatthelowerleftof

thetextisatlocationx,y.Thedefaulttextsizeis12pixels,butcanbechangedbyacallto

textsize()passingthesizedesired.

7.1.6 Example:AHistogram

Ahistogramisawaytovisualizenumericaldata.Itisespeciallyusefulfordiscretedata

likecolorsorpoliticalpartiesorchoicesofsomekind,butcanalsobeusedforcontinuous

data.Itdisplayscountsofsomethingagainstsomeothervalue,acategory;percentageof

peoplevotingforspecificparties,ortheheightsofgradesixgirls.Itdrawsbarsofvarious

heightseachrepresentingthenumberofentriesineachcategory.Inthisexampletheonly

problem is the plotting of the histogram, but the more general programming problem

wouldincludecollectingandorganizingthedata.Inthiscasetheprogramwillreadadata

filenamed “histogram.txt” that containsa few key values. The programvariable names

andthecorrespondingdatafilevaluesare:

Whencreatingagraph,itpaystodesignitcarefully.Inthiscasethehistogramwillhave

thegeneralappearanceshowninFigure7.5a.Thisvisuallayouthelpswiththedetailsof

thecode,especiallyifthedesignhasbeendrawnongraphpapersothatthecoordinates

caneasilybedetermined.

Assumethatthevariablesneededhavebeenreadfromthefile(See:Exercise2).Here’s

whattheprogrammustdo:

Createawindowabout600x600pixelsinsize.

Drawthehorizontalandverticalaxes(120,80)

Drawthetitleandaxislabels.

Determinethewidthandheightofeachrectangle.

Foriinrange(0,ncategories)

Drawrectanglei

Drawlabeli

Development can now proceed according to the plan. Create a window, set the

background,andchangethefonttoHelvetica(afavorite):

startdraw(600,600)

background(180)

setfont(“Helvetica”)

Nowdrawtheaxes.Y-axis(vertical)from100,100to100,500;X-axis(horizontal)from

100,500to500,500.Useathickerlinebysettingthestrokeweightto3pixels.

strokeweight(3)

line(100,100,100,500)#Yaxis

line(100,500,500,500)#Xaxis

Thetitleisinalargefont(24pixels)atthetoppartofthecanvas(y=80)

textsize(24)#Titleusesabigfont

text(title,120,80)#It’satthetopofthedrawing

Thehorizontalaxislabelisinasmallerfont(14pixels)atthebottomofthecanvas(y-

580). It looks nicer if the text is basically centered. It’s hard to do this exactly because

thereisnoeasywaytofindouthowlongastringwillbewhendrawn.However,astring

that is 14 pixels in size and N characters long will be approximately N*14 pixels long

when drawn. The axis is 400 pixels wide, so the amount of leftover space will be 400-

N*14. Divide this in half to get the indentation of the left to approximately center the

string!

textsize(14)#Labelsuseamediumsizedfont

cx=(400-len(hlabel)*14)/2#Howmanypixelstoindent

text(hlabel,100+cx,580)#Centeredatthebottom

Drawing the vertical label is more difficult, and so it will be done later. Make it a

functionandmoveon

verticalLabel(vlabel)

It is time to draw the rectangles. The width of each one will be the same, and is the

width of the drawing area divided by the number of categories. The height will be the

heightofthedrawingareadividedbythemaximumvaluetobedrawn,maxsize.Compute

those values and set the line thickness to one pixel, then set a fill color. Using the

CORNER rectangle drawing mode is easiest for this application, as all that needs to be

figuredoutistheupperleftcoordinate—thewidthandheightarealreadyknown.

wid=(400-10)/ncategories#Widthofaboxinpixels

ht=390.0/maxsize#Eachvalueisthismanypixelshigh

strokeweight(1)#Rectangleoutline1pixelthick

fill(200,50,200)#Purplefill

rectmode(CORNER)#Cornermodeiseasiest

Nowmakealoopthatdrawseachrectangle.TheXpositionofarectangleisitsindex

timesthewidthofarectangle—that’seasy.Theheightoftherectangleisthevalueofthat

data element multiplied by the variable ht that was determined before. It’s also a good

ideatodrawthevaluebeingrepresentedatthetopofthebar,whichisjustaboveandto

therightoftherectangle’supperleft.

foriinrange(0,ncategories):

ulx=100+i*wid+2#UpperleftX

uly=500-val[i]*ht#UpperleftY

rect(ulx,uly,wid,val[i]*ht-2)#Heightisval[i]*ht

text(val[i],ulx+5,uly-2)#Drawthevalueatthetop

Finally,drawthelabelsforeachrectangle.ThesearebelowtheXaxis,centeredmore

orlesswithinthehorizontalregionforeachbin.ThelabelsstartattheYaxis(X=100or

so)andtheirlocationincreasesbythewidthofthebinduringeachiterationofthedrawing

loop.TheYlocationisfixed,at520—theXaxisis500.Finally,anattempttocenterthese

labelsisdoneinthesamewaythatitwasdoneforthehorizontallabel,buttheparameters

aredifferent.

x=100+2#StartatX=100withextraforthethinckline

textsize(10)#Useasmallsizefont

fill(255,255,255)#Textwillbewhite

foriinrange(0,ncategories):#foreachrectangle

cx=(wid-len(lab[i]*9))#Indexnttocenterthetext

ifcx<0:cx=0#Indentcan’tbenegative

text(lab[i],x+cx/2,520)#Drawthelabel

x=x+widNextlabelisonerectangleright

enddraw()

Drawingtheverticallabelinvolvespullingouttheindividualwordsanddrawingeach

oneonitsownpixelrow.Wordsareseparatedbyspaces(blanks),soonewayofdrawing

theverticaltextistolookforaspaceinthetext,drawthatword,thenmovedownafew

pixels,extractthenextword,drawit,andsoonuntilallwordshavebeendrawn.Thetext

willbedrawnstartingatX=12,andtheinitialverticalpositionwillbe200,movingdown

(increasingY)by40pixelsforeachword.ThisisdonebythefunctionverticalLabel(),

whichispassedthestringtobedrawn:

defverticalLabel(v):

lasti=0#Indexofthenextwordinthestring

x=12#StartdrawingatX=12

y=200#andY=200

foriinrange(0,len(v)):#Lookatallcharactersin

#thelabel

if(v[i]==”“):#Ablackindicatetheendofa

#word

text(v[lasti:i],x,y)#Drawtheword

y=y+40#Movedown40pxiels

lasti=i#endofthiswordisthe

#startofthenext

text(v[lasti:],x,y)#Drawthelastword

#afterexitingtheloop

This program is available on the disk as two examples: “viperHisto.py” and

“gradesHisto.py,”which drawhistograms of twodifferentsetsof data.The output from

thesetwoprogramsisshowninFigure7.6.

Thisisaminimalprogram,andwon’talwayscreateaniceimage.Labelsthataretoo

longandusetoomanycategoriescancausebadlyformattedgraphics.

7.1.7 Example:APieChart

A pie chart is really just a histogram where the relative size of the categories is

illustratedbyanangleinsteadoftheheightofarectangle.Eachclassisshownasapie-

shapedsliceofacirclewhoseareaisrelatedtoitsproportionofthewholesample.Pie-

shapedregionsare easy, becausearc()will drawthem. So, using the same examples as

before,lookspecificallyatthegradesdata:thereare38studentswhosegradesarebeing

displayed,andthereare360degreesinacircle.Acategoryof10 students,forexample

(suchasthosereceivinga“B”grade),willrepresentapieslicethatis10/38ofthewhole

circle,orabout95degrees.Theprocessseemstobetodeterminehowmanydegreeseach

categoryrepresentsanddrawapiesliceofthatsizeuntilthewholepie(circle)isusedup.

Createawindowabout600x600pixelsinsize

Drawthetitlelabel

Establishafillcolor

Foriinrange(0,ncategories)

DeterminetheangleAusedforthiscategoryi

DrawarcfrompreviousangleforAdegrees

Drawlabeliforthisslice

Changethefillcolor

Thelabelsmaypresentaproblem,astheymaynotfitinsidethepieslice.Itisprobably

besttodisplaythelabeloutsideofthesliceanddrawalinetotheslicethatrepresentsit.

Theprogramissimilartothatforthehistogram.So,beginningafterthelabelisdrawn:

Findthetotalnumberofelementsinallcategories—inthiscase,thenumberofstudents

intheclass.Thisisthesumofallelementsinval.

totalSize=0

r=255

fill(r,200,200)

foriinrange(0,ncategories):

totalSize=totalSize+val[i]

Eachcountval[i]inacategoryrepresentsval[i]/totalSizeoftheentiredataset,orthe

angle360.0*val[i]/totalSize.Theconstant360/totalSizewillbenamedanglePerCount.

Nowstartingatangle0degrees,createapie-shapedarcthesizeofeachcategory:

angle=0

foriinrange(0,ncategories):

span=val[i]*anglePerCount

arc(150,150,450,450,angle,span,PIESLICE)

Drawthelabel—thishasbeenleftforlater,socallafunction.

label(300,300,150,lab[i],angle,span)

Theangletostartdrawingmustbeincreasedsothatthenextarcstartswherethisone

leftoff:

angle=angle+span

Changethefillcolorsothateachpiepieceisadifferentcolor.Thecode

belowchangestheredcomponentjustalittle.

r=r-20

fill(r,200,200)

Figure7.7bshowsawaytodeterminewherealabelcouldgo;alinefromthecenterof

thecirclethroughtheouteredgepointsinthedirectionofthelabel.Simplyfindthexand

ycoordinates.Theycoordinateisthesineoftheangle*thedistancefromthecenter,and

the x coordinate is the cosine of the angle * the same distance. For a distance, use the

radius*1.5.Thefunctionlabel()cannowbewritten:

deflabel(xx,yy,r,s,a1,ap):

angle=a1+ap/2#Bisector=startangle+halfof

#span

d=r*1.25#Distance

x=cos(angle*3.1415/180.)*d+xx#Angleisradians

y=-sin(angle*3.1415/180.)*d+yy#Yisinverted

text(s,x,y)

TheresultisillustratedinFigure7.8.

There’sonemorethingthatcouldbeaddedtothepiechartprogram.Sometimes,oneof

thepiecesismovedoutofthecircletoemphasizeit.Itturnsoutthatthisusefulfeature

canbeimplementedinamannerverysimilartothewaythelabelsweredrawn.Findthe

bisectoroftheangleforthatsectionandbeforeitisdrawnidentifyanewcenterpointfor

that piece a few pixels down that bisector. This pulls the piece away from the original

circlecenter.

Thecodeisbrief,andisincludedbelowtobecomplete:

defpull(x,y,a1,ap):

angle=a1+ap/2#a1istheangle,apisthespan

d=12#Pulloutonlyasmallamount

#(12pixels)

y=-sin(angle*3.1415/180.)*d+y#Newcenter

#coordinates

x=cos(angle*3.1415/180.)*d+x

arc(x-150,y-150,x+150,y+150,a1,ap,PIESLICE)

Thisfunctioniscalledinsteadofthecalltoarc()forthepiecethatistobepulledout.A

sampleoutputisshowninFigure7.8b.

7.1.8 Images

Unlike the graphical components displayed so far, an image is fundamentally a

collectionofpixels.Acameracapturesanimageandstoresitdigitallyaspixels,andsoit

wasneveranythingelse.Displayinganimagemeansdrawingeachpixelintheappropriate

color,ascaptured.

Glibcanloadanddisplayimagesinalimitedfashion.Imagesresideinfilesofvarious

formats: JPEG, GIF, BMP, PNG. The same image in each format is stored in a quite

distinctway,anditcanrequirealotofcodejusttogetthepixelsfromtheimage.Python,

through tkinter, allows GIF image files to be read directly. Any image file can be

convertedinto a GIF by using one of a hundred conversion tools, includingPhotoshop,

Paint,andGimptonameafew.

ThefunctionloadImage()willreadaGIFimagefileandreturnanimageofasortthat

canbedisplayedinthegraphicswindow.Thefile“charlie.gif”isaphotoofcheckpoint

CharlieinBerlin,andhasbeenincludedontheaccompanyingdisc.Itcouldbereadintoa

Pythonprogramwiththecall:

im=loadImage(“charlie.gif”)

Thevariableimnowholdstheimage,andwhilethedetailsarenotcompletelyrelevant,

itisgoodtoknowthatim.widthandim.heightgivethewidthandheightoftheimagein

pixels.Displaying the image is a matterof calling the function image()and passing the

imageandthecoordinateswheretheupperleftcorneroftheimageistobeplaced.Acall

suchas:

image(im,0,0)

woulddisplaythecheckpointCharlieimage.

ThesmallestPythonprogram(usingGlib)thatcanloadanddisplayanimageisthus5

lines:

fromGlibimport*

startdraw(600,600)

im=loadImage(“charlie.gif”)

image(im,0,0)

enddraw()

However,thisdisplaystheimageinawindowthatisbiggerthanitis.ThatmaybeOK,

butoftenanimageistobeusedasabackgroundimage,andthesizeofthewindowshould

bethesameastheimagesize.Ifthatiswhatisneededthereisaspecialfunctiontocall:

imageSize().Itmustbecalledbeforestartdraw(),ofcourse,becauseitreturnsthesizeof

theimage,andhencethesizetobepassedtostartdraw().Itreturnsatuplethathasthe

widthasthefirstcomponentandtheheightasthesecond.

Openingawindowthatisthesamesizeasanimageisaccomplishedasfollows:

fromGlibimport*

s=imageSize(“charlie.gif”)

startdraw(s[0],s[1])

im=loadImage(“charlie.gif”)

image(im,0,0)

enddraw()

TheoutputofthisprogramisshowninFigure7.9.

Pixels

AnimageasreturnedbyloadImage()isabuilt-intypenamedPhotoImage.Itisreally

not designed to be used for much except displaying in the window, but some more

advanced operations are possible, if slow. For example, individual pixel values can be

extracted and modified. Glib offers a handful of low-level functions to make pixel

operationseasier.

Animageconsistsofrowsandcolumnsofpixels,andapixelisacolor.Thecolorofthe

pixelathorizontalpositionxandverticalpositionyofimagepiccanbeaccessedusing

thecall:

c=getpixel(pic,x,y)

The value of c is a color, and the components of this can be accessed using the

functions:

r=red(c)

g=green(c)

b=blue(c)

Settingthevalueofthepixelatlocation(x,y)isaccomplishedbycallingsetpixel().It

requiresthattheimage,thecoordinates,andthecolorbepassedasparameters:

setpixel(pic,x,y,c)

Thesefunctionsoperateonanimage,notdirectlyonthescreendisplay.Changestoan

imagewillonlybevisibleiftheyaredonebeforetheimageisdisplayed.

Example:IdentifyingaGreenCar

Thereisapatternherethatisimportanttorecognizewhenworkingwithimagesatthe

pixellevel—therasterscan.Allofthepixelsintheimageareusuallyexaminedoneata

timeusinganestedloop.Itwilllooklikethis:

foriinrange(0,Width()):

forjinrange(0,Height()):

#Dosomethingtopixel(i,j)

Thisexampleusescolortoidentifythepixelsthatbelongtoacarinanimage,asseen

in Figure 7.10. The problem requires identifying pixels that are “green” and somehow

makingthemstandoutintheimage.Whatisgreen?Allpixelshaveagreencomponent.

Whensomethingisgreen,thegreencomponentisthemostsignificantone;itislargerthan

theredandbluecomponentsbysomemargin.Inthiscasethatmarginwillbearbitrarily

setat20,andifitdoesnotworkthenitcanbemodified.Ifapixelisgreenitwillbesetto

black,otherwiseitwillbecomewhite;thiswillmakethepixelsthatbelongtothecarstand

out.

Theprogrambeginsbycreatingawindowandreadingintheimage:

startdraw(640,480)

im=loadImage(”eclipse.gif”)

Nowlookatallofthepixels,searchingforagreenone:

foriinrange(0,Width()):

forjinrange(0,Height()):

c=getpixel(im,i,j)#Getthecolorofthepixel

#(i,j)

Ifthepixelisgreen,thenchangeittoblack.Otherwise,changeittowhite:

ifgreen(c)>(red(c)+20)andgreen(c)>(blue(c)+20):#Green?

setpixel(im,i,j,cvtColor3(0,0,0))#Black

else:

setpixel(im,i,j,cvtColor3(255,255,255))#White

AnimagecanbesavedintoafilebycallingtheGlibfunctionsave():

save(im,“out.gif”)

TheoutputofthisprogramisshowninFigure7.10b.Therearesome“green”pixelsthat

donotbelongtothecar,butmostofthecarpixelshavebeenidentified.

Example:Thresholding

Imageprocessingisalargesubjectallbyitself,andthisparticularlibraryisnotthebest

choice for exploring it in detail. There are some basic things that can be done, and

commononesincludethresholding,edgeenhancement,noisereduction,andcount,allof

whichcanbedoneusingGlib.Thresholdinginparticularisanearlystepinmanyimage-

analysis processes. It is the creation of a bi-level image, having just black and white

pixels,fromagreyorcolorimage.Thepreviousexampleisdifferentfromthresholdingin

thataparticularcolorwasbeingsearchedfor.InthresholdingasimplegreyvalueT,the

threshold,isusedtoseparatepixelsintoblackandwhite:allpixelshavingavaluesmaller

thanTwillbeblack,andtheotherswillbewhite.

Glibhasonemorefunctionthatisuseful,especiallyinthiscontext.Thefunctiongrey()

willconvertacolorintoasimplegreylevel,whichisanintegerintherange0to255.It

finds the mean of the three color components. The thresholding program begins in the

samewayasdidthepreviousexample.Lookatthecolorofallofthepixelsintheimage,

oneatatime:

startdraw(640,480)

im=loadImage(”eclipse.gif”)

foriinrange(0,Width()):

forjinrange(0,Height()):

c=getpixel(im,i,j)

This is the standard scan of all pixels. Now convert the color c to a grey level and

comparethatagainstthethresholdT=128.Pixelshavingagreylevelbelow128willbeset

toblack,theremainderwillbewhite:

ifg<T:

setpixel(im,i,j,cvtColor3(0,0,0))

else:

setpixel(im,i,j,cvtColor3(255,255,255))

image(im,0,0)

save(im,“out.gif”)

enddraw()

Theresult,theimagedisplayedbythisprogram,isshowninFigure7.11.

Transparency

AGIFimagecanhaveonecolorchosentobetransparent,meaningthatitwillnotshow

upandanypixeldrawnpreviouslyatthesamelocationwillbevisible.Thisisveryhandy

ingamesandanimations.Imagesarerectangular,whereasmostobjectsarenot.Considera

smallimageofadoughnut;thepixelssurroundingitandintheholecanhavethepixelsset

tobetransparent,andthenwhentheimageisdrawnoveranotheronethebackgroundwill

beseenthroughthehole.

The transparency value must be set within the image by a program. Photoshop, for

example,candothis.ThenwhenPythondisplaystheimages,thebackgroundimagemust

bedisplayedfirst,followedbytheimageswithtransparency.Asanexample,Figure7.12a

shows a photo of the view through the rear and side windows of a Volvo. The window

glassarea,theplaceswheretransparencyisdesired,havebeencoloredyellow.Thecolor

yellowwasthenselectedinPhotoshopastransparent,andtheimagewassavedagainasa

GIF. A short Python program using Glib will display a background image and the car

imageoverit,andthebackgroundwillbeseenthroughthewindowregionsasinFigure

7.12b.Theprogramis:

fromGlibimport*

s=imageSize(“car.gif”)#Getsizeofimage

startdraw(s[0],s[1])#Openwindowoftheright

#size

s=loadImage(“perseus.gif”)#Backgroundimage

t=loadImage(“car.gif”)#Carimagewithtransparency

image(s,0,0)#Displaybackgroundfirst

image(t,0,0)#thendisplaythecarimage

enddraw()

7.1.9 GenerativeArt

Ingenerativeartanartworkisgeneratedbyacomputerprogramthatusesanalgorithm

createdbytheartist.Theartististhecreativeforce,thedesignerofthevisualdisplay,and

thecomputerimplementsit.TherearemanygenerativeartiststobefoundontheInternet:

onelistcanbefoundhere:

http://blog.hvidtfeldts.net/index.php/generative-art-links/

Muchgenerativeartisdynamic,whichistosayitinvolvesmotionand/orinteraction,

butmanyworksareequivalenttopaintingsanddrawings(static).Glibcouldbeatoolfor

helping create these sorts of generative art works. Unlike other sorts of computer

programs, those associated with art do not have a known predictable result that can be

affirmedascorrectornot.Itistruethatanartistbeginswithanideaofwhattheirwork

should look like and what the message underlying it is, but paintings, sculptures, and

generativeworksrarelyfinishthewaytheybegan.

So,eitherbeginwithanideaofwhattheimagewilllooklikeoradmitthatthewhole

thingisanexperimentandcouchtheideaintermsofasentenceortwo.Here’sonesuch

sentence:“Imagineacollectionofstraightlinesradiatingfromasetofrandomlyplaced

points within the drawing window, with each set of lines drawn in a saturated strong

color.”

NowanattemptwouldbemadetocreatesuchanimageusingthefunctionsthatGlib

offers. It is often the case that the first few tries are in error, but that one of them is

interesting.Anartistwouldpursuetheinterestingcourseinsteadofstickingtotheoriginal

idea,ofcourse.Hereisanexample:thecodebelowwaswrittenwiththeideathatitwould

produceacollectionoflinesradiatingfromthepoint(400,600)from0degrees(horizontal

right)to180degrees(horizontalleft)withthecolorvaryingslightly:

r=255

foriinrange(1,180,2):

stroke(r,128,128)

line(400,600,cos(i*conv)*500,sin(i*conv)*500)

r=r-0.5

Thecalltoline()shouldhavebeen:

line(400,600,400+cos(i*conv)*500,600-sin(i*conv)*500)

soas toinvert theY coordinate.Instead,this createda muchmore interestingimage.

Thecodeforoneofthefourloopsinthefinalcodeis:

x=randrange(100,Width())

y=randrange(100,Height()-100)

r=255

foriinrange(1,180,2):

stroke(128,r,128)

line(x,y,sin(i*conv)*500,cos(i*conv)*500)

r=r-0.5

Sometimesasmallerrorcanresultinamoreinterestingresult.Thisisrarelythecase

whenwritingscientificorcommercialsoftware.

Generativeartshouldbeunderthecontroloftheartist,butdoesuserandomelementsto

addinteresttotheimage.InthepieceSnowBoxesbyNoahLarsenasetofrectanglesis

drawn,butthespecificsizeandlocationoftheserectanglesisrandomwithinconstrained

parameters.Theoverallcolorisalsorandomwithinspecifiedboundaries.Eachrectangle

isdrawnasacollectionofwhitepixelswithadensitythathasbeendefinedspecifically

for that rectangle so that the image consists of spatters of white pixels that can be

identified as rectangular regions (Figure 7.14). Each time the program is executed a

different image is created. The program for Snow Boxes was originally written in a

languagecalledProcessing,butaPythonversionthatusesGlibis:

#Snowboxes

#OriginalbyNoahLarsen,@earlatron

fromGlibimport*

fromrandomimport*



startdraw(640,480)

background(randrange(0,75),randrange(150,255),

randrange(0,75))



fill(255,255,255)

foriinrange(0,10000):

point(randrange(0,Width()),randrange(0,Height()))

foriinrange(0,20):

xs=randrange(0,Width())

ys=randrange(0,Height())

xe=randrange(xs,xs+randrange(30,300))

ye=randrange(ys,ys+randrange(30,300))

forjinrange(0,10000):

point(randrange(xs,xe+1),randrange(ys,ye+1))

enddraw()

7.2 SUMMARY

Since the advent of Windows, computer graphics has been assumed as a feature of a

computer, but this has not always been true. Python does not have built-in features for

doing graphics, but the standard user interface library tkinter does, and the library that

accompanies this book, Glib, expands this and makes it more accessible. Drawing is

accomplished by setting pixels within a drawing window to a desired color. Colors are

specifiedbygivingtheamountofred,green,andbluethatcomprisethecolor.

Gliband most graphics libraries allow the userto draw lines, polygons,text, images,

andtosetpixels.Thesebasicfunctionsarecombinedbytheprogrammertocreatedesired

visualizations,suchashistogramsandpiecharts.

Exercises

1.WriteaPythonprogramtocreatetheimageshowninFigure7.15a.Theimageisgrey,

butthecolorsthataretobeusedtofillthecirclesaregivenastext.Youneednot

includethetextinyouroutput.

2.Drawasetof10linesseparatedhorizontallyby20pixels,eachparalleltotheline

specifiedbytheendpoints(10,20)and(200,421).Theselinesmaybeginanywhere

inthewindow.

3.Drawapyramidusingdarkgreybricks(rectangles)ascomponents.Thebaseofthe

pyramidistobe15brickshorizontally,andeachsuccessivelevelisonebricksmaller.

(Figure7.15b)

4.Drawacheckerboard.Eachsquareshouldbe20x20pixels,andthesquaresareredor

yellow,alternating.Acheckerboardis8x8squares.

5.Drawatriangle,asquare,aregularpentagon,andaregularhexagon.Labelthesewith

theirnamesastextabovetheshapes.

6.WriteaprogramtodrawavisualworkinthevisualstyleofPietMondrian’sfamous

rectangularcompositions,anexampleofwhichisshowninFigure7.15d.Could

triangularshapesbeusedinsteadofrectangles?

7.Modifythepiechartprogramsothatthedataisreadfromafilename

“piein.dat.”

8.Writeaprogramthatreadsthefilenameofanimageanddisplaystheimageina

windowthatiscorrectlysized.

9.Theprovidedimagenamed“digit.gif”containssomepixelsthatarepurered;thatis,

theyhaveapixelvalueof(255,0,0).Writeaprogramthatlocatesthesepixels,drawsa

circlearoundtheminadisplayoftheimage,andprintstheirxandycoordinates.

10.Anedgeinanimagehasthepropertythatthepixelvaluesononesideoftheedgeare

significantlydifferent(i.e.,morethan40levels)fromthoseontheotherside.Writea

pythonprogramthatreadsanimageandsetspixelsatverticaledgelocationstoblack

andallotherpixelstowhite;itthendisplaystheresultinawindow.Hints:convertthe

imagetogreyorselectonecolorvaluefortheedges;makeaworkingcopyofthe

image.

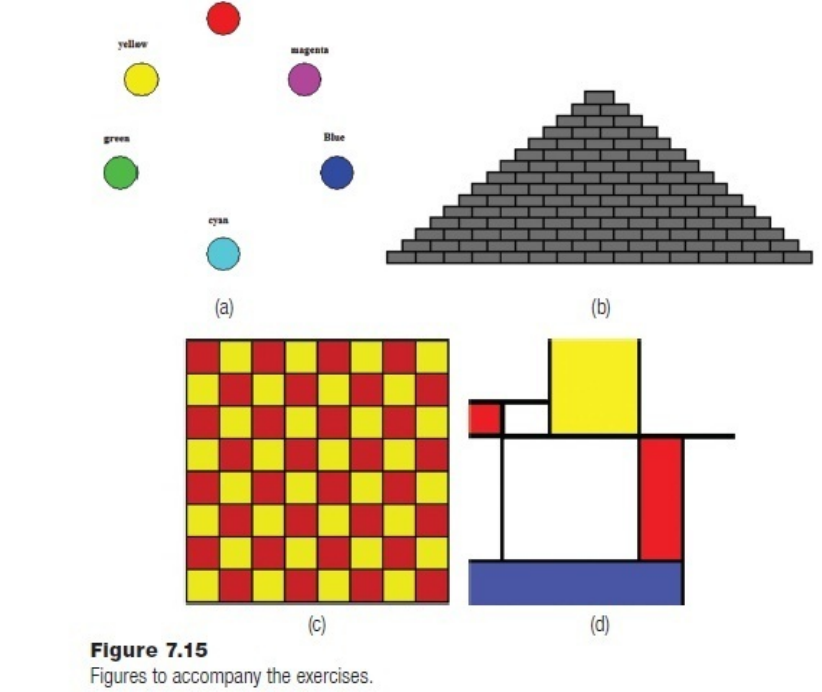
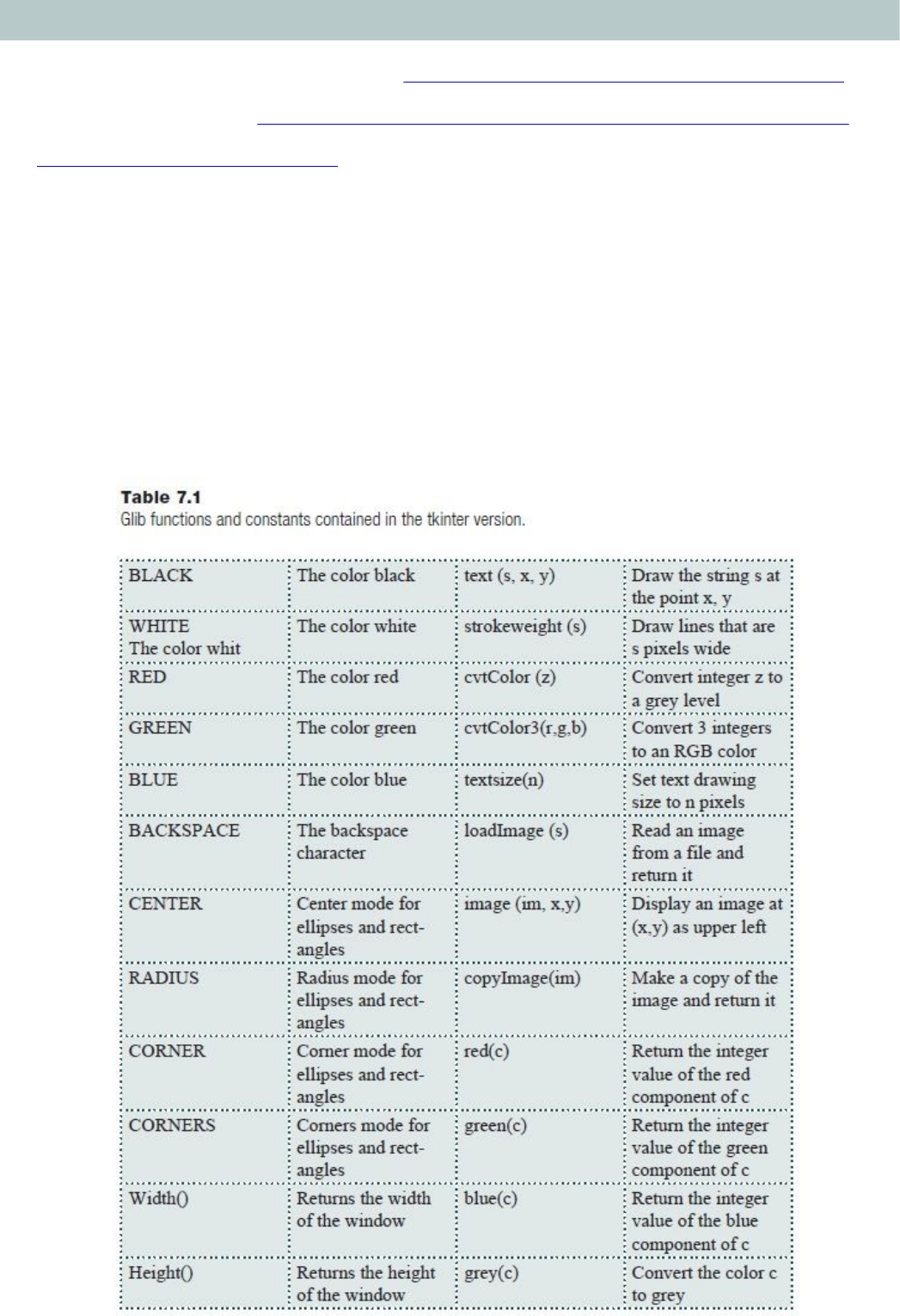
NotesandOtherResources

Tkinter-PythoninterfacetoTcl/Tk,https://docs.python.org/3/library/tkinter.html

Tkinter8.5reference.http://infohost.nmt.edu/tcc/help/pubs/tkinter/web/index.html

http://www.generativeart.com/

1.JohnF.Hughes,AndriesvanDam,MorganMcGuire,DavidF.Sklar,JamesD.Foley,

StevenK.Feiner,andKurtAkeley.(2013).ComputerGraphics:Principlesand

Practice,3rdEdition,Addison-WesleyProfessional.

2.RobinLanda,RoseGonnella,andStevenBrower.(2006).2DVisualBasicsfor

Designers,DelmarCengageLearning.

3.JeffreyMcConnell.(2005).ComputerGraphics:TheoryintoPractice,Jones&

BartlettLearning.

4.MattPearson.(2011).GenerativeArt,ManningPublications,ISBN-10:1935182625.

CHAPTER8

MANIPULATINGDATA

8.1Dictionaries

8.2Arrays

8.3FormattedText,FormattedI/O

8.4AdvancedDataFiles

8.5StandardFileTypes

8.6Summary

Inthischapter

A fair definition of Computer Science would be the discipline that concerns itself with

information.Computersareanenablingtechnology,butcomputerscienceislargelyabout

how to store, retrieve, represent, compress, display, transmit, and otherwise handle

information. Python happens to be pretty good at offering facilities for manipulating

information or, at a lower level, data. Data becomes information when a person can

interpretit,andinformationbecomesknowledgeonceunderstood.

Repeatingathemeofthisbook,dataonacomputerisstoredasnumbersnomatterwhat

itsoriginalformwas.Computerscanonlyoperateonnumbers,soanimportantaspectof

usingdata is therepresentation of complexthings as numbers.Based on manyyears of

experience, it seems to be possible in all cases, and the manner in which the data is

representedasnumbersisreflectedinthemethodsusedtooperateonthem.

Thischapterwillbeanexaminationofhowcertainkindsofdataarerepresentedandthe

consequencesinsofarascomputerprogramscanusethesedata.Pythoninparticularwill

beusedforthisexamination,althoughsomeofthediscussionismoregeneral.Ofcourse,

thediscussionwillbedrivenbypracticalthingsandbyhowthingscanbeaccomplished

usingPython.

Most data consist of measurements of something, and as such are fundamentally

numeric.Astronomersmeasurethebrightnessofstars,asanexample,andnotehowthey

vary or not as a function of time. The data consists of a collection of numbers that

represent brightness on some arbitrary scale; the units of measurements are always in

some sense arbitrary. However, units can be converted from one kind to another quite

simply,sothisisnotaproblem.Biologistsfrequentlycountthings,soagaintheirdatais

fundamentally numeric. Social scientists ask questions and collect answers into groups,

againanumericresult.Whatthingsarenot?

Photographsarecommonenoughinscienceandarenotnumericvaluesbutare,instead,

visual;theyrelatetoahumansensethatcanbeunderstoodbyotherhumanseasily,rather

thantoananalyticalapproach.Ofcoursemostphotographsareultimatelyanalyzedbya

computerthesedays,sotheremustbeawaytorepresentthemdigitally.Anotherhuman

sensethatisusedtoexaminedataishearing.Birdsmakesongsthatindicatemanythings,

includingwhattheyobserveandtheirwillingnesstomate.Soundsarevibrations,andcan

indicateproblemswithmachinery,theapproachofavehicle,thepresenceofapredator,or

thecurrentstateoftheweather.Touchislessoftenused,butisessentialinthecontrolof

objectsbyhumans.Apersoncontrollingadeviceatagreatdistancecanprofitfromthe

abilitytofeelthetouchofatoolacrossacomputernetwork.

Then there are search engines, which can be thought of as an extension of human

memoryandreasoning.Theabilityofhumanstoaccessinformationhasimprovedhugely

over the past twenty years. If the phrase “python data manipulation” is entered into the

Google search engine, over half a million results are returned. True, many may not

directly relate to the query as it was intended, but part of the problem will be in the

phrasingoftherequest.Bytheway,thefirstresponsetothequeryconcernsthepandas

modulefordataanalysis,whichmayinfacthavebeentherightanswer.

Howisallof thisdone?It doestakesome cleveralgorithmsandgood programming,

butitalsorequiresalanguagethatofferstherightfacilities.

8.1 DICTIONARIES

A Python dictionary is an important structure for dealing with data, and is the only

important language feature that has not been discussed until now. One reason is that a

dictionaryis more properly anadvanced structurethat isimplemented interms ofmore

basic ones. A list, for example, is a collection of things (integers, reals, strings) that is

accessed by using an index, where the index is an integer. If the integer is given, the

contentsofthelistatthatlocationcanberetrievedormodified.

A dictionary allows a more complex, expensive, and useful indexing scheme: it is

accessedbycontent.Well,byadescriptionofcontentatleast.Adictionarycanbeindexed

by a string, which in general would be referred to as a key, and the information at that

locationinthedictionaryissaidtobeassociatedwiththatkey.Anexample:adictionary

that returns the value of a color given the name. A color, as described in Chapter 7, is

specifiedbyared,green,andbluecomponent.Atuplesuchas(100,200,100)canbeused

torepresentacolor.Soinadictionarynamedcolorsthevalueofcolors[“red”]mightbe

(255,0,0)andcolors[“blue”]is(0,0,255).Naturally,itisimportanttoknowwhatnames

are possible or the index used will not be legal and will cause an error. So

colors[“copper”]mayresultinanindexerror,whichiscalledaKeyErrorforadictionary.

ThePythonsyntaxforsettingupadictionarydiffersfromanythingthathasbeenseen

before.Thedictionarycolorscouldbecreatedinthisway:

colors={'red':(255,0,0),'blue':(0,0,255),'green':(0,255,0)}

Thebraces{…}encloseallofthethingsbeingdefinedaspartofthedictionary.Each

entryisapair,withakeyfollowedbya“:”followedbyadataelement.Thepair“red”:

(255,0,0) means that the key “red” will be associated with the value (255,0,0) in this

dictionary.

Nowthenamecolorslookslikealist,butisindexedbyastring:

print(colors['blue'])

Theindexiscalledakeywhenreferringtoadictionary.That’sbecauseitisnotreally

anindex,inthatthestringcan’tdirectlyaddressalocation.Insteadthekeyissearchedfor,

andifitisalegalkey(i.e.,hasbeendefined)thecorresponding

dataelementisselected.Thedefinitionofcolorscreatesalistofkeysandalistofdata:

Whentheexpressioncolors[“blue”]isseen,thekey“blue”issearchedforinthelistof

allkeys.Itisfoundatlocation1,sotheresultoftheexpressionisthedataelementat1,

which is (0,0,255). Python does all of this work each time a dictionary is accessed, so

whileitlookssimpleitreallyinvolvesquiteabitofwork.

Newassociationscanbemadeinassignmentstatements:

colors['khaki']=(240,230,140)

Indeed,adictionarycanbecreatedwithanemptypairofbracesandthenhavevalues

givenusingassignments:

colors={}

colors['red']=(255,0,0)

...

Aswithothervariables,thevalueofanelementinadictionarycanbechanged.This

wouldchangetheassociationwiththekey;therecanonlybeonethingassociatedwitha

key.Theassignment:

colors['red']=(200.,0,0)

reassigns the value associated with the key “red.” To delete it altogether use the del()

function:

del(colors['blue'])

Other types can be used as keys in a dictionary. In fact, any immutable type can be

used.Henceitispossibletocreateadictionarythatreversestheassociationofnametoits

RGB color, allowing the color to be used as the key and the name to be retrieved. For

example:

names={}

names[(255,0,0)]='red'

names[(0,255,0)]='green'

Thisdictionaryusestuplesaskeys.Listscan’tbeusedbecausetheyarenotimmutable.

8.1.1 Example:ANaiveLatin–EnglishTranslation

Asuccessfullanguagetranslationprogramisdifficulttoimplement.Humanlanguages

are unlike computer languages in that they have nuances. Words have more than one

meaning,andmanywordsmeanessentiallythesamething.Somewordsmeanonething

inaparticularcontextandadifferentthinginanothercontext.Sometimesawordcanbea

noun and a verb. It is very confusing. What this program will do is substitute English

wordsforLatinones,usingaPythondictionaryasthebasis.

From various sites on the Internet a collection of Latin words with their English

counterpartshasbeencollected.Thisisatextfilenamed“latin.txt.”IthastheLatinword,

aspace,andtheEnglishequivalentonsinglelinesinthefile.Theprogramwillaccepttext

fromthekeyboardandtranslateitintoEnglish,wordbyword,assumingthatitoriginally

consisted of Latin words. The file of Latin words has 3129 items, but it should be

understoodthatonewordinanylanguagehasmanyformsdependingonhowitisused.

Manywordsaremissinginoneformoranother.

Thewaytheprogramworksisprettysimple.Thefileofwordsisreadinandconverted

intoadictionary.ThefilehasaLatinword,acomma,andanEnglishword,soalineis

read,convertedtoatupleusingsplit(),andtheLatinwordisusedasakeytostorethe

Englishwordintothedictionary.

Next, the program asks the user for a phrase in Latin, and the user types it in. The

phraseissplitintoindividualwordsandeachoneislookedupinthedictionaryandthe

Englishversionisprinted.This will notworkverywell ingeneral,butisa firststepin

creatingatranslationprogram.Thecodelookslikethis:

defload_words(name,dict): #Readthefileofwords

f=open(name,“r”)

s=f.readline() #Readonewordpair

whiles!=””: #exitwhenthefilehasbeen

#read

c=s.split(“,”) #Splitatthecomma

iflen(c)<2: #Possibleerror:nowords?

s=f.readline() #Readnextandcontinue

continue

sw=c[0].strip() #GetthelatinandEnglish

#words.

ew=c[1].strip()

iflen(ew)<=0: #OK?

s=f.readline() #Nope.Justskipit.

continue

ifew[-1]==“\n”: #Getrideoftheendline

ew=ew[0:-2]

dict[sw]=ew #Placeindictionary

s=f.readline() #Nextwordpairfromthefile

f.close() #Alwaysclosewhendone



dict={}

load_words(“latin.txt”,dict) #Readallofthewordpairs



inp=input(“Enteralatinphrase“) #GettheLatintext

whileinp!=””: #Done?

book=inp.split(”“) #Splitatwords

foriinrange(0,len(book)): #Foreachwordthisline

sword=book[i].lower() #Lowercase

try:

enword=dict[sword] #LookupLatinword

print(enword,end=””) #PrintEnglishversion

except:

print(sword,end=””) #Latinnotin

#dictionary

print(”“,end=””) #PrinttheLatin

print(“.”)

inp=input(“Enteralatinphrase“) #Doitagain

Of course translation is more complex than just changing words, and that’s all this

programdoes.Still,sometimesitdoesnotdotoobadly.AfavoriteLatinphrasefromthe

TVprogramTheWestWingis“Posthocergopropterhoc.”Giventhisphrasetheprogram

produced:

afterthisthereforebecauseofthis.

whichisaprettyfairtranslation.Tryinganother,“Alldogsgotoheaven”wassentto

anonlinetranslationprogramanditgave

omnescanesadcaelumireconspexerit

ThisprogramheretranslatesitbackintoEnglishas:

“alldogstoskygoconspexerit.”

Theword ‘conspexerit’ wasnot successfullytranslated,so itwas leftas itwas (the

onlineprogramtranslatesthatwordas“glance”).Thisisstillnotterrible.

Sadly,itmakesacompletehashoftheLord’sPrayer:

Paternosterquiesincaelissanctificeturnomentuum.

Adveniatregnumtuum.

Fiatvoluntastuasicutincaeloetinterra.

Panemnostrumquotidianumdanobishodieetdimittenobisdebitanostrasicutetnos

dimittimusdebitoribus.

Fiatvoluntastuasicutincaeloetinterra.

Amen



Isturnedinto:

fatherourthatyouareagainstheavensholynameyour.

downruleyour.

becomeslastyourasagainstheavenandagainstearth.

breadourdailydausdayanddimitteusdebitaourasandusforgivedebtors.

becomeslastyourasinheavenandinearth.

amen

A useful addition to the code would be to permit the user to add new words into the

dictionary. In particular, it could prompt the user for words that it could not find, and

perhaps even ask whether similar words were related to the unknown one, such as

“dimittimus”and“dimitte.”Ofcourse,beingabletohavesomebasicunderstandingofthe

grammarwouldbebetterstill.

8.1.2 FunctionsforDictionaries

The power of the store-fetch scheme in the dictionary is impressive. There are some

methods that apply mainly to dictionaries and that can be useful in more complex

programs.Themethodkeys()returnsthecollectionofallofthekeysthatcanbeusedwith

adictionary.So:

list(dict.keys())

isalistofallofthekeys,andthiscanbesearchedbeforedoinganycomplex

operationsonthedictionary.Thelistofkeysisnotinanyspecificorder,andiftheyneed

tobesortedthen:

sorted(dict.keys())

willdothejob.Thedel()methodhasbeenusedtoremovespecifickeysbutdict.clear()

willremoveallofthem.

The method setdefault() can establish a default value for a key that has not been

defined.Whenanattemptismadetoaccessadictionaryusingakey,anerroroccursifthe

keyhasnotbeendefinedforthatdictionary.Thismethodmakesthekeyknownsothatno

errorwilloccurandavaluecanbereturnedforit;None,perhaps.

dict.setdefault(key,default=None)

Otherusefulfunctionsinclude:

dict.copy() returnsa(shallow)copyofdictionary

dict.fromkeys() createsanewdictionarysettingkeysandvalues;e.g.,dict.fromkeys(

(“one”,“two”),3)creates{(“one”,3),(“two”,3)}

dict.items() returnsalistofdict’s(key,value)tuplepairs.

dict.values() returnslistofdictionarydict’svalues

dict.update(dict2) addsthekey-valuepairsfromdictionarydict2todict

TheexpressionkeyindictisTrueifthekeyspecifiedexistsinthedictionarydict.

8.1.3 DictionariesandLoops

Dictionaries are intended for random access, but on occasion it is necessary to scan

throughpartsorallofone.Thetrickistocreatealistfromthepairsinthedictionaryand

thenloopthroughthelist.Forexample:

for(key,value)indict.items():

print(key,”hasthevalue“,value)

Thekeysaregiveninaninternalorderwhichisnotalphabetical.Itisasimplematterto

sortthem,though:

for(key,value)insorted(dict.items()):

print(key,”hasthevalue“,value)

Byconvertingthedictionarypairsinalist,anyoftheoperationsonlistscanbeapplied

toadictionaryaswell.Itisevenpossibletousecomprehensionstoinitializeadictionary.

Forexample

d={angle:sin(radians(angle))foranglein(0,45.,90.,135.,180.)}

createsadictionaryofthesinesofsomeanglesindexedbytheangle.

8.2 ARRAYS

For programmers who have used other languages, Python lists have many of the

properties of an array, which in C++ or Java is a collection of consecutive memory

locationsthatcontainthesametypeofvalue.Listsmaybedesignedtomakeoperations

suchasconcatenationefficient,whichmeansthatalistmaynotbethemostefficientway

tostorethings.APythonarrayisaclassthatmimicsthearraytypeofotherlanguagesand

offersefficiencyinstorage,exchangingthatforflexibility.

Onlycertaintypescanbestoredinanarray,andthetypeofthearrayisspecifiedwhen

itiscreated.Forexample:

data=array('f',[12.8,5.4,8.0,8.0,9.21,3.14])

createsanarrayof6floatingpointnumbers;thetypeisindicatedbythe“f”asthefirst

parameter to the constructor. This concept is unlike the Python norm of types being

dynamicandmalleable.Anarrayisanarrayofonekindofthing,andanarraycanonly

holdarestrictedsetoftypes.

Thetypecode,thefirstparametertotheconstructor,canhaveoneof13values,butthe

mostcommonlyusedoneswillbe:

“b”AC++chartype

“B”AC++unsignedchartype

“i”:AC++inttype

“l”:AC++longtype

“f”:AC++floattype

“d”:AC++doubletype

Arraysareclassobjectsandareprovidedinthebuilt-inmodulearray,whichmustbe

imported:

fromarrayimportarray

Anarray is a sequence type, and has the basic properties and operations that Python

provides all sequence types. Array elements can be assigned to and can be used in

expressions, and arrays can be searched and extended like other sequences. There are

somefeaturesofarraysthatareunique:

frombytes

(s)

Thestringargumentsisconvertedintobytesequencesandappendedtothe

array.

fromfile(f,

num)

Readnumitemsfromthefileobjectfandappendthem.Aninteger,for

example,isoneitem.

fromlist(x) Appendtheelementsfromthelistxtothearray.

tobytes() Convertthearrayintoasequenceofbytesinmachinerepresentation.

tofile(f) Writethearrayasasequenceofbytestothefilef.

In most cases arrays are used to speed up numerical operations, but they can also be

used(andwillbeinthenextsection)toaccesstheunderlying

representationsofnumbers.

8.3 FormattedText,FormattedI/O

There is a generally believed theory among many users of data, including some

engineersandfinancialanalysts,thatifnumberslineupinnicecolumnsthentheymustbe

correct.Thisisobviouslynottrue,butappearancescanmatteragreatdeal,andnumbers

thatdonotlineupproperlyforeasyreadinglooksloppyandgivepeopletheimpression

thattheymaynotbeascarefullypreparedastheyshouldhavebeen.ThePythonprint()

functionasusedsofarsimplyprintsacollectionofvariablesandconstantswithnoreal

attentiontoaformat.Eachoneisprintedintheorderspecifiedwithaspacebetweenthem.

Sometimesthat’sgoodenough.

ThePythonversionssince2.7haveincorporatedastringformat()methodthatallowsa

programmertospecifyhowvaluesshouldbeplacedwithinastring.Theideaistocreatea

stringthatcontainstheformattedoutput,andthenprintthestring.Asimpleexampleis:

s=“x={}y={}”

fs=s.format(121.2,6)

Thestringfsnowcontains“x=121.2y=6.”Thebraceswithintheformatstringshold

theplaceforavalue.Theformat()methodlistsvaluestobeplacedintothestring,and

with no other information given it does so in order of appearance, in this case 121.2

followedby6.Thefirstpairofbracesisreplacedbythefirstvalue,121.2,andthesecond

pairofbracesisreplacedbythesecondvalue,whichis6.Nowthestringfscanbeprinted.

This is not how it is usually done, though. Because this is usually part of the output

process,itisoftenplacedwithintheprint()call:

print(“x={}y={}”.format(121.2,6))

wheretheformat()methodisreferencedfromthestringconstant.Noactualformattingis

donebythisparticularcall,merelyaconversiontostringandasubstitutionofvalues.The

way formatting is done depends on the type of the value being formatted, the most

commontypesbeingstrings,integers,andfloats.Anexamplewillbeilluminating.

8.3.1 Example:NASAMeteoriteLandingData

NASApublishesahugeamountofdataonitswebsites,andoneoftheseisacollection

ofmeteoritelandings.Itcoversmanyyearsandhasover4800entries.Thetaskassigned

hereistoprintanicelyformattedreportonselectedpartsofthedata.Thedataonthefile

has its fields separated by commas, and there are ten of them: name, id, nametype,

recclass,mass, Fall, year, reclat,reclong, and GeoLocation. The reportrequires that the

name,recclass,mass,reclatandreclongbearrangedinanicelyformattedsetofcolumns.

Readingthedataisamatterofopeningthefile,whichisnamed“met.txt,”andcalling

readline(),thencreatingalistofthefieldsusingsplit(“,”).Ifthisisdoneandthefields

aresimplyprintedusingprint(),theresultismessy.Anabbreviatedexampleis(simulated

data):

infile=open(“met.txt”,“r”)

inline=infile.readline()



whileinline!=””:

inlist=inline.split(“,”)

mass=float(inlist[4])

lat=float(inlist[7])

long=float(inlist[8])

print(inlist[0],inlist[3],inlist[4],inlist[7],

inlist[8])

inline=infile.readline()

infile.close()

Theresultis,aspredicted,messy:

AshdonH5121.1351998525487489.85924301385958-126.27404435776049

ArbolSoloH666.9477713434351625.567048824444797160.58088365396014

BaldwynL647.6388587105465-7.708508536783924-81.22266156597777

AnkoberL615.265523451122064-32.01862330869428102.31244557598723

AnkoberLL657.584802700693885-84.85880091616322106.31130649523368

AshCreekL662.13008952551615576.02832670618457-140.03422105516938

AlmahataSittaLL530.476879105555653-12.90674540458647.411816322674

Nothinglinesupincolumns,andthenumbersshowanimpossibledegreeofprecision.

Alsothereshouldbeheadings.

Thefirstfieldtobeprintediscalledname,andisastring;itisthenameofthelocation

wheretheobservationwasmade.Theprintstatementsimplyaddsaspaceafterprintingit,

and so the next thing is printed immediately following it. Things do not line up.

Formattingastringforoutputinvolvesspecifyinghowmuchspacetoallowandwhether

thestringshouldbecenteredoralignedtotheleftorrightsideoftheareawhereitwillbe

printed.Applyingaleftalignmenttothestringvariablenamedplacenameinafieldof16

characterswouldbedoneasfollows:

ꞌ{:16s}ꞌ.format(placename)

The braces, which have previously been empty, contain formatting directives. Empty

braces mean noformatting, and simply hold the place for a value. A full format could

containaname,aconversionpart,andaspecification:

{[name][‘!’conversion][‘:’specification]}

where optional parts are in square brackets. Thus, the minimal format specification is

‘“{}.” In the example “{:16s}” there is no name and no conversion parts, only a

specification.Afterthe“:”is‘16s,’meaningthatthedatatobeplacedhereisastring,and

that 16 characters should be allowed for it. It will be left aligned by default, so if

placenamewas“Atlanta,”theresultoftheformattingwouldbethestring“Atlanta,”left

aligned in a 16-character string. Unfortunately, if the original string is longer than 16

charactersitwillnotbetruncated,andallofthecharacterswillbeplacedintheresulting

stringevenifitmakesittoolong.

Torightalignastring,simplyplacea“>”characterimmediatelyfollowingthe“:”.So:

“{:>16s}”.format(“Atlanta”)

wouldbe“Atlanta.”Placinga“<”charactertheredoesaleftalignment(thedefault)and

“^” means to center it in the available space. The alignment specifications apply to

numbersaswellasstrings.

Thefirsttwovaluestobeprintedintheexamplearethecityname,whichisininlist[0]

andthemeteoriteclasswhichisinlist[3].Formattingtheseisdoneasfollows:

s='{:16s}{:10s}'.format(inlist[0],inlist[3])

Bothstringswillbeleftaligned.

Numericformats are morecomplicated. For integersthere is the totalspace to allow,

andalsohowtoalignitandwhattodowiththesignandleadingzeros.Theformatting

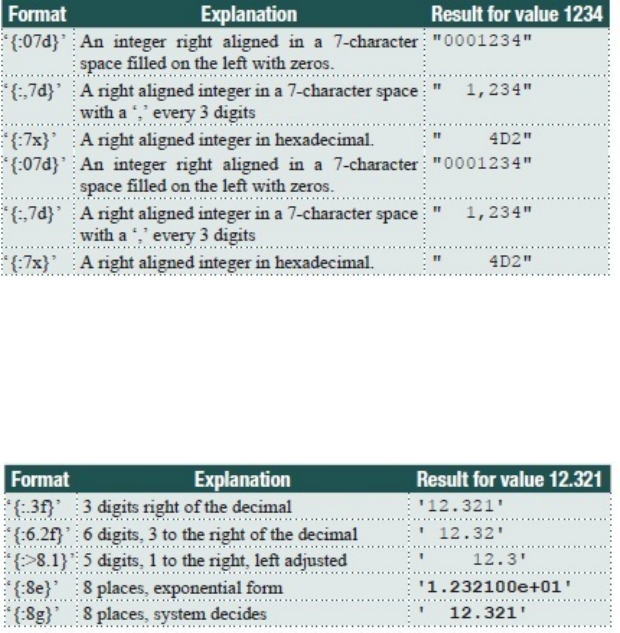
letterforanintegeris“d”,sothefollowingarelegaldirectivesandtheirmeaning:

Floatingpointnumbershavetheextraissueofthedecimalplace.Theformatcharacter

isoften“f,”butitcanbe“e”forexponentialformator“g”forgeneralformat,meaningthe

systemdecideswhethertouse“f”or“e.”Otherwise,theformattingofafloatingpointis

likethatofpreviousversionsofPythonandlikethatofCandC++:

Thenextthreevaluestobeprintedarefloatingpoint:themassofthemeteoriteandthe

location,aslatitudeandlongitude.Printingeachoftheseas7places,2totherightofthe

decimal,wouldseemtowork.Or,asaformat:“{:7.2f}.”

Thesolutiontotheproblemisnowathand.Thedataisreadlinebyline,convertedinto

alist,andthenthefieldsareformattedandprintedintwosteps:

infile=open(“met.txt”,“r”)

inline=infile.readline()

print(”PlaceClassMassLatitude

Longitude”)

whileinline!=””:

inlist=inline.split(“,”)

mass=float(inlist[4])

lat=float(inlist[7])

long=float(inlist[8])

print('{:16s}{:14s}{:7.2f}'.format(inlist[0],

inlist[3],mass),end=””)

print('{:7.2f}{:7.2f}'.format(lat,long))

inline=infile.readline()

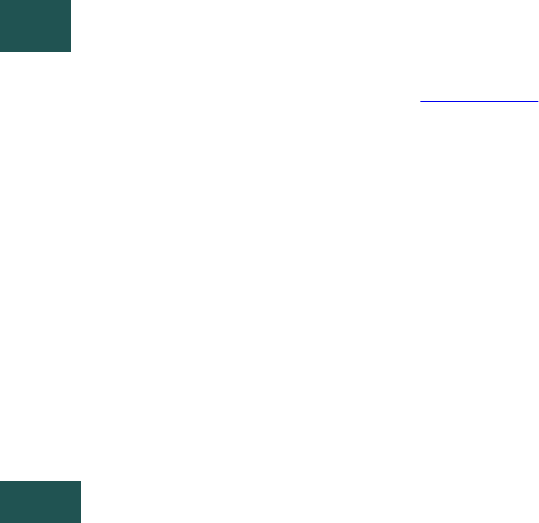
infile.close()

Theresultis:

Place Class Mass Latitude Longitude

Bloomington L5 13.58 9.53 -150.85

Bogou LL6 121.09 -66.28 -53.08

Alessandria L4 106.11 63.68 10.96

BoXian L5 85.92 0.33 -50.28

Ashdon Eucrite-mmict 6.59 -88.22 -178.84

Berduc L6 111.76 -64.20 107.10

…

Therearemanymoreformattingdirectives,andahugenumberoftheircombinations.

8.4 ADVANCEDDATAFILES

File operations were discussed Chapter 5, but the discussion was limited to files

containingtext.Textiscrucialbecauseitishowhumanscommunicatewiththecomputer;

peopleare unhappy abouthaving to enterbinary numbers. On the other hand, textfiles

takeupmorespacethanneededtoholdtheinformationtheydo.Eachcharacterrequiresat

least one byte. The number 3.1415926535 thus takes up 12 bytes, but if stored as a

floatingpointnumberitneedsonly4or8dependingonprecision.

Thefilesystem onmost computersalso permitsa varietyof operationsthat havenot

beendiscussed.Thisincludesreadingfromanypointinafile,appendingdatatofiles,and

modifyingdata.Theneedforprocessingdataeffectivelyisamainreasonforcomputersto

exist at all, so it is important to know as much as possible about how to program a

computerforthesepurposes.

8.4.1 BinaryFiles

A binary file is one that does not contain text, but instead holds the raw, internal

representationofitsdata.Of course,allfileson acomputerdiskare binaryinthestrict

sense,becausetheyallcontainnumbersinbinaryform,butabinaryfileinthisdiscussion

does not contain information that can be read by a human. Binary files can be more

efficientthatotherkinds,bothinfilesize(smaller)andthetimeittakestoreadandwrite

them(less).Manystandardfilestypes,suchasMP3,existasbinaryfiles,soitisimportant

tounderstandhowtomanipulatethem.

Example:CreateaFileofIntegers

Thearraytypeholdsdatainaformthatismorenaturalformostcomputersthanalist,

andalsohasthetofile() methodbuilt in. If a collection of integers is to bewritten as a

binaryfile,afirststepistoplacethemintoanarray.Ifasetof10000consecutiveintegers

aretobewrittentoafilenamed“ints,”thefirststepistoimportthearrayclassandopen

theoutputfile.Noticethatthefileisopenin“wb”mode,whichmeans“writebinary”:

fromarrayimportarray

output_file=open('ints','wb')

Now create an array to hold the elements and fill the array with the consecutive

integers:

arr=array('i')

forkinrange(10000,20000):

arr.append(k)

Finally,writethedatainthearraytothefile:

arr.tofile(out)

out.close()

Thisfilehasasizelistedas40kbonaWindowsPC.Afilehavingthesameintegers

writtenastextis49kb.Thisisnotexactlyahugesavingofspace,butitdoesaddup.

Readingthesevaluesbackisjustassimple:

inf=open('ints','rb')

arrin=array('i')

forkinrange(0,10001):

try:

arrin.fromfile(inf,1)

except:

break

print(arrin[k])

inf.close()

Thetryisusedtocatchanendoffileerrorincaseswherethenumberofitemsonthe

fileisnotknowninadvance.Orjustbecausealwaysdoingsoisagoodidea.

Sometimesabinaryfilewillcontaindatathatisallofthesametype,butthatsituationis

not very common. It is more likely that the file will have strings, integers, and floats

intermixed. Imagine a file of data for bank accounts or magazine subscriptions; the

information included will be names and addresses, dates, financial values, and optional

data, depending on the specific situation. Some customers have multiple accounts, for

example.Howcanbinaryfilesbecreatedthatcontainmorethanonekindofinformation?

Byusingstructs.

8.4.2 TheStructModule

Thestructmodulepermitsvariablesandobjectsofvarioustypestobeconvertedinto

whatamountstoasequenceofbytes.Itisacommonclaimthatthisisinordertoconvert

between Python forms and C forms, because C has a struct type (short for structure).

However, many files exist that consist of mixed-type data in raw (i.e., machine

compatible) form that have been created by many programs in many languages. It is

possiblethatCissingledoutbecausethenamestructwasused.

Example:AVideoGameHighScoreFile

Videogameplayersneedlittleincentivetotryhardtowinagame,butformanyyearsa

specialrewardhasbeengiventothebetterplayers.Thegame

“remembers”thebestplayersandliststhematthebeginningandendofthegame.This

kindofegoboostisapartoftherewardsystemofthegame.Thegameprogramstoresthe

informationon afile indescending order ofscore. Thedata that issaved isusually the

player’snameorinitials,thescore,andthedate.Thismixesstringwithnumericdata.

Considerthattheplayer’snameisheldinavariablename,thescoreisanintegerscore,

andthe dateis aset ofthree stringsyear,month,andday. In this situation the size of

eachvalueneedstobefixed,soallow32charactersforthename,4foryear,2formonth,

and 2 for day. The file was created with the name first, then the score, then the year,

month,and day.The order matters because it will be read inthe sameorder thatit was

written.Onthefilethedatawilllooklikethis:

cccccccccccccccccccccccccccccccc iiii cccc cc cc

Player’sname Score Year Month Day

Each letter in the first string represents a byte in the data for this entry. The ‘c’s

representcharacters;the‘i’srepresentbytesthatarepartofaninteger.Thereare44bytes

in all, which is the size of one data record,which is what one set of related data is

generallycalled.Afilecontainstherecordsforalloftheelementsinthedataset,andin

thiscasearecordisthedataforoneplayer,oratleastonetimethattheplayerplayedthe

game.Therecanbemultipleentriesforaplayer.

Oneway to convert mixed data like thisinto a struct is to use the pack() method. It

takesaformatparameterfirst,whichindicateswhatthestructwillconsistofintermsof

bytes. Then the values are passed that will be converted into components of the final

struct.Fortheexampleherethecalltopack()wouldbe:

s=pack(“32si4s2s2s”,name,score,year,month,day)

Theformatstringis“32si4s2s2s”;thereare5partstothis,oneforeachofthevaluesto

bepacked:

32sisa32-characterlongstring.Itshouldbeoftypebytes.

iisoneinteger.However,2iwouldbetwointegers,and12iis12integers.

4sisa4-characterlongstring.

2sisa2-characterlongstring.

Otherimportantformatitemsare:

cisacharacter

fisafloat

disadoubleprecisionfloat

Thevaluereturnedfrompack()hastypebytes,andinthiscaseis44byteslong.The

highscorefileconsistsofmanyoftheserecords,allofwhicharethesamesize.Arecord

canbewrittentoafileusingwrite().So,aprogramthatwritesjustonesuchrecordwould

be:

fromstructimport*



f=open(“hiscores”,“wb”)

name=bytes(“JimParker”,'UTF-8')

score=109800

year=b”2015”

month=b”12”

day=b”26”

s=pack(“32si4s2s2s”,name,score,year,month,day)

f.write(s)

Readingthisfileinvolvesfirstreadingthestringofbytesthatrepresentedadatarecord.

Thenitisunpacked,whichisthereverseofwhatpack()does,andthevariablesarepassed

totheunpack()functiontobefilledwithdata.Theunpack()methodtakesaformatstring

asthefirstparameter,thesamekindofformatstringaspack()uses.Itwillreturnatuple.

Anexamplethatreadstherecordintheabovecodewouldbe:

fromstructimport*



f=open(“hiscores”,“rb”)

s=f.read(44)

name,score,year,month,day=unpack(“32si4s2s2s”,s)

name=name.decode(“UTF-8”)

year=year.decode(“UTF-8”)

month=month.decode(“UTF-8”)

day=day.decode(“UTF-8”)

The data returned by unpack are bytes, and need to be converted into strings before

beingusedinmostcases.Notetheinputmodeontheopen()callis“rb,”readbinary.

Afileinthisformathasbeenprovided,andisnamedsimply‘hiscore.’Whenaplayer

playsthegametheywillentertheirname;thecomputerknowstheirscoreandthedate.A

newentrymustbemadeinthe‘hiscore’filewiththisnewscoreinit.Howisthatdone?

StartwiththenewplayerdataforKarlHolter,withascoreof100000.Toupdatethe

fileitisopenedandrecordsarereadandwrittentoanewtemporaryfile(named“tmp”)

untiloneisfoundthathasasmallerscorethanthe100000thatKarlachieved.ThenKarl’s

recordiswrittentothetemporaryfile,andtheremainderof‘hiscores’iscopiedthere.This

createsanewfilenamed“tmp”thathasKarl’sdataaddedtoit,andinthecorrectplace.

Nowthatfilecanbecopiedto“hiscores”replacingtheoldfile,orthefilenamed“tmp”

canberenamedas“hiscores.”Thisiscalledasequentialfileupdate.

Renaming the file requires access to some of the operating system functions in the

moduleos;inparticular:

os.rename(“tmp”,“hiscores”)

8.4.3 RandomAccess

It seems natural to begin reading a file from the beginning, but that is not always

necessary. If the data that is desired is located at a known place in the file, then the

locationbeingreadfromcanbesettothatpoint.Thisisanaturalconsequenceofthefact

thatdiskdevicescanbepositionedatanylocationatanytime.Whynotfilestoo?

Thefunctionthatpositionsthefileataspecificbytelocationisseek():

f.seek(44)#Positionthefileatbyte44,

#whichisthesecondrecordinthehiscores

#file.

It’salsopossibletopositionthefilerelativetothecurrentlocation:

f.seek(44,1)#Positionthefile44bytesfromthis

#location,

#whichskipsoverthenextrecordin

#hiscores.

Afilecanberewoundsothatitcanbereadoveragainbycallingf.seek(0),positioning

the file at the beginning. It is otherwise difficult to make use of this feature unless the

recordsonthefileareofafixedsize,astheyareinthefile‘hiscores,’ortheinformation

onrecordsizesissavedinthefile.Somefilesareintendedfromtheoutsettobeusedas

randomaccessfiles.Thosefileshaveanindexthatallowsspecificrecordstobereadon

demand.This is verymuch like adictionary, buton afile. Assumingthat thescore for

playerArlenFranksisneeded,thenameissearchedforintheindex.Theresultisthebyte

offsetforArlen’shighscoreentryinthefile.

Arlen’srecordstartsatbyte352(8threcord*44bytes).Hejustplayedthegameagain

andimprovedhisscore.Whynotupdatehisrecordonthefile?Thefileneedstobeopen

for input and output, so mode “rb+,” meaning open a binary file for input and output,

wouldworkinthiscase.ThenpositionthefiletoArlen’srecord,createanewrecord,and

writethatonerecord.Thisisnew—beingabletobothreadandwritethesamefileseems

odd,butifthedatabeingwrittenisexactlythesamesizeastherecordonthefilethenno

harmshouldcomefromit.Theprogramis:

#readandprinthiscorefile

fromstructimport*



f=open(“hiscores”,“r+b”)#Openbinaryfile,inputand

#output

pos=44*8#Desiredrecordis8,44

#bytesper

f.seek(pos)#Seektothatpositionone

#thefile

s=f.read(44)#Readthetargetrecord

name=bꞌArlenFranksꞌ#Makeanewonewithanew

#score

score=100300

year=bꞌ2015ꞌ

month=bꞌ12ꞌ

day=bꞌ26ꞌ#Packthenewdata

ss=pack(“32si4s2s2s”,name,score,year,month,day)

f.seek(44*8)#Seektheoriginalposition

#again!

f.write(ss)#Writethenewdataover

#theold

f.close()#Closethefile

Thisworksfine,providedthatthepositionofArlen’sdatainthefileisknown.Itdoes

notmaintainthefileindescendingorder,though.

Example:MaintainingtheHighScoreFileinOrder

Thecircumstancesofthenewproblemarethataplayeronlyappearsinthehighscore

fileonceandthefileismaintainedindescendingorderofscore.Ifaplayerimprovestheir

score, then their entry should move closer to the beginning of the file. This is a more

difficultproblemthanbefore,butonethatisstillpractical.So,presumethataplayerhas

achievedanewscore.Theentireprocessshouldbe:

Gettheplayer’sold

score.

Readthefile,gettheplayer’srecord,unpackit.

Isthenewscorelarger? Ifnot,closethefile.Done.

Yes,sofindoutwhere

thescore

belongs,inthefile.

Lookatsuccessivelyprecedingrecordsuntiloneisfoundthathas

alargerscore.

Placethenewrecord

whereitbelongs.

Copytherecordsfromthenewpositionfortherecordaheadone

positionuntiltheoldpositionisreached.

Theprocessislikemovingaplayingcardclosertothetopofthedeckwhileleavingthe

other cards in the same order. It’s probably more efficient to move the record while

searchingforthecorrectposition,though.Eachtimethepreviousrecordisexamined,ifit

does not have a larger score then the record being placed is copied ahead one position.

Thisresultsinaprettycompactprogram,giventhenatureoftheproblem,butitisabit

trickytogetright.Forexample,whatifthenewscoreisthehighest?Whatifthecurrent

highscoregetsahigherscore?(See:Exercise11)

8.5 STANDARDFILETYPES

Everyone’s computer has files on it that the owner did not create. Some have been

downloaded; some merely came with the machine. It is common practice to associate

specific kinds of files, as indicated initially by some letters at the end of the file name,

withcertainapplications.Afilethatendsin“.doc,”forexample,isusuallyafilecreated

byMicrosoftWord,andafileendingin“.mp3”isusuallyasoundfile,oftenmusic.Such

fileshave a formatthat is understoodby existing softwarepackages, and someof them

(“.gif”)havebeenaroundforthirtyyears.

Eachfiletype hasbeen designedto makecertain operationseasy, andto pass certain

informationtotheapplication.Overtheyearsasetofdefactostandardshaveevolvedfor

howthesefilesarelaidout,andforwhatdataareprovidedforwhatkindsoffile.Andyet

most users and many programmers do not understand how these files are structured or

why.Manyusersdonotcare,ofcourse,andsomeprogrammerstoo,butopeningupthese

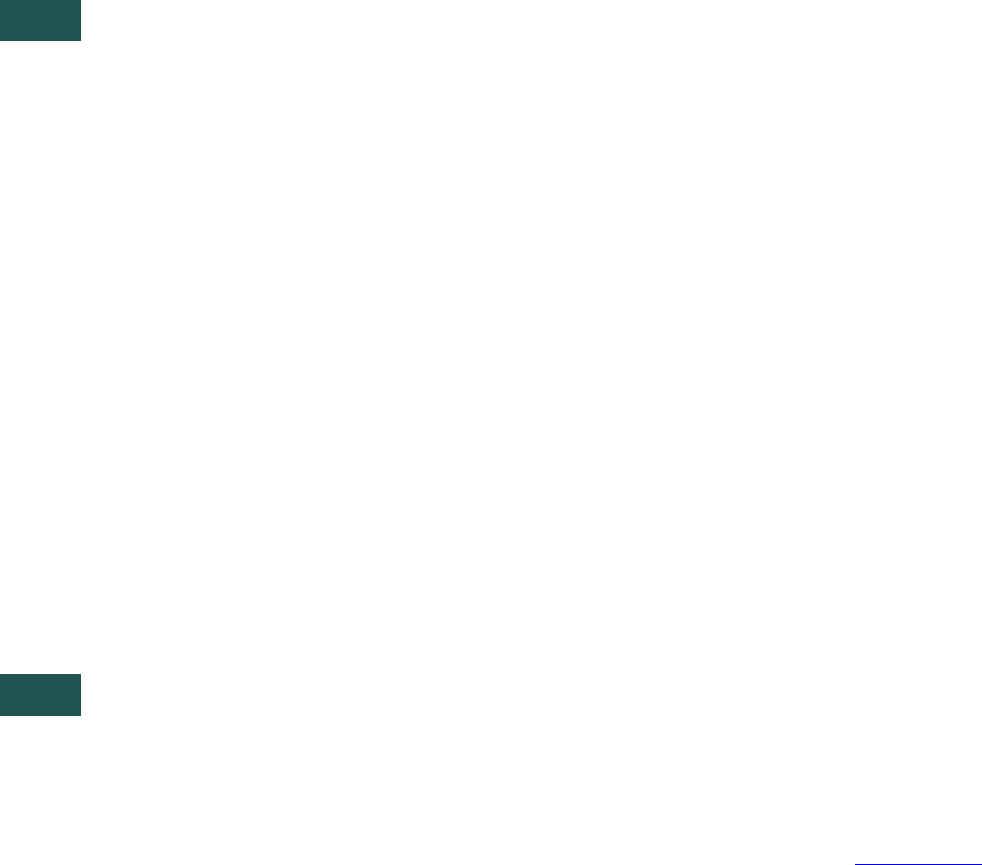
filestosomescrutinyisaneducationalexperience.

8.5.1 ImageFiles

Images have been processed using computers since the 1960s when NASA started

processingimagesat theJet Propulsion Laboratory.After someyearspeople (scientists,

mainly) decided that having standards for computer images would be useful. The first

formatswereadhoc,andbasedessentiallyonrawpixeldata.Rawdatameansknowing

what the image size is in advance, so headers were introduced providing at least that

information,leadingtotheTARGAformat(.tga)andtiff(TaggedImageFileFormat)in

themid-1980s.WhentheInternetandtheWorldWideWebbecamepopular,theGIFwas

invented, which compressed the image data. This was followed by JPEG and other

formatsthat couldbeused bywebdesignersand renderedbybrowsers, andeachhad a

specificadvantage.Afterall,reducingsizemeantreducingthetimeittooktodownloadan

image.

Onceafileformathasbeenaroundforafewyearsandhasbecomesuccessfulittends

tostickaround,somanyoftheimagefileformatscreatedinthe1980sarestillhereinone

formoranother.Therearenewonestoo,likePNG(PortableNetworkGraphics),which

have been specifically designed for the Internet. Older ones (like JPEG) have found

commonusesinnewtechnologies,likedigitalcameras.Aprogrammer/computerscientist

needstoknowaboutthenatureofthevariousformats,theirprosandconsasitwere.

8.5.2 GIF

TheGraphicsInterchange Formatisinteresting frommanyperspectives. First,it uses

compression to reduce the size of the file, but the compression method is not lossy,

meaningthattheimagedoesnotchangeafterbeingcompressedandthendecompressed.

ThecompressionalgorithmusediscalledLZW,andwillbediscussedinChapter10.GIF

usesacolormaprepresentation,soanelementintheimageisnotacolor,butinsteadisan

indexintoanarraythatholdsthecolor.Thatis,ifv=image[row][column]thenthecolor

ofthatpixelis(red[v],green[v],blue[v]).Thecoloritselfcouldbeafull24bits,butthe

valuevisabyte,andsoinaGIFtherecanonlybe256distinctcolors.GIFusesalittle-

endianrepresentation,meaningthattheleastsignificantbyteofmulti-byteobjectscomes

firstonthefile.

OneadvantageoftheGIFisthatoneofthecolorscanbemadetransparent.Thismeans

thatwhenthiscolorisdrawnoveranother,thecolorbelowshowsthrough.Itisessentially

a“donotdrawthispixel”value.Itisimportantforthingslikespritesincomputergames.

AnotheradvantageofGIFisthatmultipleimagescanbestoredinasinglefile,allowing

an animation to be saved in a single file. GIF animations have been common on the

Internetformanyyears,andwhiletheyusuallyrepresentsmall,briefanimationssuchas

Christmas trees with flashing lights, they can be as long and complex as television

programs.Still,thefactthattherecanonlybe256differentcolorscanbeaproblem.

AGIFisabinaryfile,butthefirstsixcharactersareaheaderblockcontainingwhatis

called a magic number, or an identifying label. For a GIF file the three characters are

always“GIF”andthenextthreerepresenttheversion;forthe1989standardthefirstsix

characters are “GIF89a.” Magic numbers are common in binary files, and are used to

identifythefiletype.Thefilenamesuffixdoesnotalwaystellthetruth.

Followingtheheaderisthelogicalscreendescriptor,whichexplainshowmuchscreen

spacetheimagerequires.Thisissevenbytes:

Canvaswidth 2bytes

Canvasheight 2bytes

Packedbyte 1byte

Asetofflagsandsmallvalues

Bit 8 765 4 321

Global color sort sizeof

Color resolution flag globalcolor

Table? table

Backgroundcolorindex 1byte

Pixelaspectratio 1byte

Thisis followed by the global colortable, other descriptors,and the imagedata. The

details can be found in manuals and online. The information in the first few bytes is

critical,though,andtheknowledgethatLZWcompressionisusedmeansthatthepixels

arenotimmediatelyavailable.Decompressionisdonetotheimageasawhole.

fromstructimport*

f=open(“test.gif”,“rb”)

s=f.read(13)#Readtheheader

id,ht,wd,flags,bci,par=unpack('6shhBBB',s)

#6shhBBB

f.close()

id=id.decode(“utf-8”)

print(id)

print(“Height”,ht,“Width”,wd)

print(“Flags:”,flags)

print(“Backgroundcolorindex:“,bci)

print(“Pixelaspectratio:”,par)

8.5.3 JPEG

AJPEGimageusesalossycompressionscheme,andsotheimageisnotthesameafter

compression as it was before compression. For this reason it should never be used for

scientific or forensic purposes when measurements will be made using the image. It

shouldneverbeusedforastronomy,forexample,

althoughitisperfectlyfineforportraitsandlandscapephotographs.

ThenameJPEGisanacronymfortheJointPhotographicExpertsGroup,andactually

refers to the nature of the compression algorithm. The file format is an envelope that

contains the image, and is referred to as JFIF (JPEG File Interchange Format). The file

headercontains20bytes:themagicnumberisthefirst4andbytes6–10.Thefirst4bytes

are hex FF, D8, FF, and E0. Bytes 6–10 should be “JFIF\0,” and this is followed by a

revisionnumber.Ashortprogramthatdecodestheheaderis:

fromstructimport*



f=open(“test.jpg”,“rb”)

s=f.read(20)#Readtheheader

b1,b2,a1,a2,sz,id,v1,v2,unit,xd,yd,xt,yt=unpack('BBBBh5sBBBhhBB',s)

#BBBBh5sBBBhhBB

f.close()

id=id.decode(“utf-8”)

print(id,“revision”,v1,v2)

ifb1==0xffandb2==0xd8:

print(“SOIchecks.”)

else:

print(“SOIfails.”)

ifa1==0xffanda2==0xe0:

print(“Applicationmarkerchecks.”)

else:

print(“Applicationmarkerfails.”)

print(“App0segmentis”,sz,“byteslong.”)

ifunit==0:

print(“Nounitsgiven.”)

elifunit==1:

print(“Unitsaredotsperinch.”)

elifunit==2:

print(“Unitsaredotspercentimeter.”)

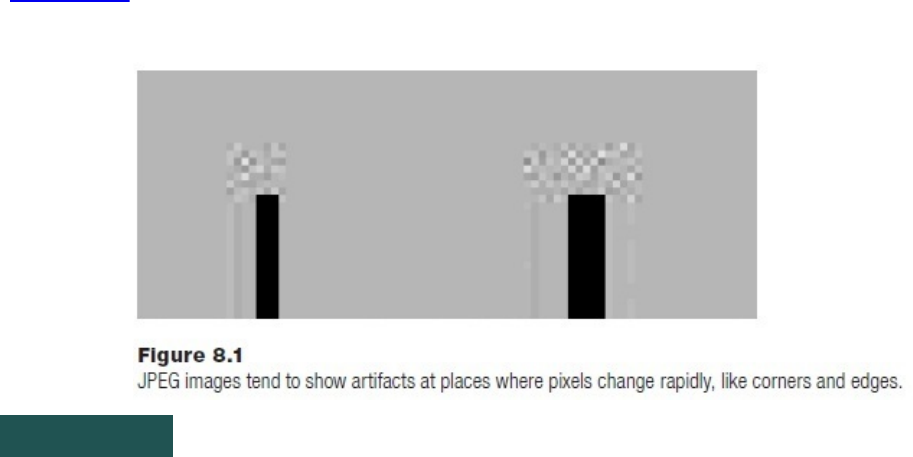
ifunit==0:

print(“Aspectratiois“,xd,“:”,yd)

else:

print(“Xdensity:“,xd,”Ydensity:“,yd)

ifxt==0andyt==0:

print(“Nothumbnail”)

else:

print(“Thumbnailimageis“,xt,“x”,yt)

The compression scheme used in JPEG is very involved, but is does cause certain

identifiable artifacts in an image. In particular, pixels near edges and boundaries are

smeared,essentiallyaveragingvaluesacrosssmallregions

(Figure8.1). This can cause problems if a JPEG image is to be edited, for example in

PhotoshoporPaint.

8.5.4TIFF

TheTaggedImageFileFormathasapotentiallyhugeamountofmetadataassociated

withit,andthatisallintextforminthefile.It’safavoriteamongscientistsbecauseof

that:thedeviceusedtocapturetheimage,thefocallengthofthelens,time,subject,and

scoresofotherinformationcanaccompanytheimage.Infact,theTIFFhasbeenseconded

forusewithnumericnon-imagedataaswell.Theotherreasonitispopularisthatiscan

beusedwithuncompressed(raw)data.

ThewordTaggedcomesfromthefactthatinformationisstoredinthefileusingtags,

suchasmightbefoundinanHTMLfile—exceptthatthetagsinaTIFFarenotintext

form.Ataghasfourcomponents:anID(2bytes,whattagisthis?),adatatype(2bytes,

whattypearetheitemsinthistag?),adatacount

(4bytes,howmanyitems?),andabyteoffset(4bytes,wherearetheseitems?).Tagsare

identifiedbynumber,andeachtaghasaspecificmeaning.Tag257meansImageHeight

and256isImageWidth;315isthecodemeaningArtist,306meansDate/Time,and270is

the Image Description. They can be in any order. In fact, the whole file structure is

flexiblebecauseallcomponentsarereferencedusingabyteoffsetintothefile.

ATIFFbeginswithan8-byteImageFileHeader(IFH):

Byteorder:Thisis2bytes,andis“II”ifdataisinlittle-endianformand“MM”ifitis

big-endian.

VersionNumber:Always42.

FirstImageFileDirectoryoffset:4bytes,theoffsetinthefileofthefirst

image.

TheotherimportantpartofaTIFFistheImageFileDirectory(IFD),whichcontains

informationaboutthespecificimage,includingthedescriptivetagsanddata.TheIFHis

always8byteslongandisatthebeginningofthefile.AnIFDcanbealmostanysizeand

canbeanywhereinthefile;therecanbemorethanone,aswell.ThefirstIFDisfoundby

positioningthe file to the offsetfound in the IFH. Subsequentones are indicated in the

IFD.TheIFDstrictureis:

Numberoftags:2bytes

Tags:Arrayoftags,sizeunknown

NextIFDoffset:4bytes.FileoffsetofthenextIFD.Iftherearenomore,

then=0.

Thestructureofatagwasgivenpreviously,soaTIFisnowdefined.Theimagedata

canbe,andfrequentlyis,rawpixels,butcanalsobecompressedinmanywaysasdefined

bythetags.

The program below reads the IFH and the first IFD, dumping the information to the

screen:

#TIFF

fromstructimport*



f=open(“test.tif”,“rb”)

s=f.read(8)#ReadtheIFH

id,ver,off=unpack('2shL',s)

#2shL



id=id.decode(“utf-8”)

print(“TIFFIDis“,id,end=””)

ifid==“II”:

print(“whichmeanslittle-endian.”)

elifid==“mm”:

print(“whichmeansbig-endian”)

else:

print(“whichmeansthisisnotaTIFF.”)

print(“Version”,ver)

print(“Offset”,off)



f.seek(off)#GetthefirstIFD

n=0

b=f.read(2)#Numberoftags

n=b[0]+b[1]*256

#n=int(s.decode(“utf-8”))

foriinrange(0,n):

s=f.read(12)#Readatag

id,dt,dc,do=unpack(“hhLL”,s)

print(“Tag“,id,“type”,dt,“count”,dc,“Offset”,do)

f.close()

Whenthisprogramexecutes using “test.tif”as the input file, the firsttwo tags in the

IFDare256and257(widthandheight)whicharecorrect.

8.5.5 PNG

A PNG (Portable Network Graphics) file consists of a magic number, which in this

context is called a signature and consists of 8 bytes, and a collection of chunks,which

resembleTIFFtags.Thereare18differentkindsofchunk,thefirstofwhichisanimage

header.TheSignatureisalways:13780787113102610.Thebytes807871arethe

letters“PNG.”

Achunk haseither3or 4fields:alength field, achunktype,an optionalchunkdata

field, and a check code based on all previous bytes in the chunk that is used to detect

errors(calledacyclicredundancycheck,orCRC).

Theimageheaderchink(IHDR)hasthefollowingstructure:

Imagewidth: 4bytes

Imageheight: 4bytes

Bitdepth: 1byte.Numberofbitspersample(1,2,4,8,or16).

Colortype: 1byte.0(grey),2(RGB),3(colormap),4(greyscalewithtransparency)

or6(RGBwithtransparency)

Compression

method:

1byte.Always0.

Filtermethod: 1byte.Always0.

Interlace

method:

1byte.0=nointerlace.1=Adam7interlace

(See:references)

Thisfilehascompression,butitisnon-lossy.Italso,likeGIF,allowstransparency,but

allows full RGB color. It does not have an option for animations, though. Reading the

signatureandthefirst(IHDR)chunkisdoneinthefollowingway:

#PNG

fromstructimport*

b2=(137,80,78,71,13,10,26,10)#Correctheader

types=(“Grey”,””,“RGB”,“Colormap”,

“Greywithalpha”,””,“RGBA”)#Colortypes

f=open(“test.png”,“rb”)

s=f.read(8)#Readtheheader

b1=unpack('8B',s)

ifb1==b2:

print(“HeaderOK”)

else:

print(“Badheader”)



s=f.read(8)#ThenextchunkmustbetheIHDR

length,type=unpack(“>I4s”,s)#Unpackthefirst

8bytesprint(“Firstchunk:Lengthis”,length,“Type:”,type)



s=f.read(length)#Weknowthelength,readthechunk

wd,ht,dep,ctype,compress,filter,interlace=unpack(“>ii5B”,s)

#IIBBBBB

print(“PNGImagewidth=”,wd,“Height=”,ht)

print(“Imagehas“,dep,“bytespersample.”)

print(“Colortypeis“,types[ctype])

ifcompress==0:

print(“CompressionOK”)

else:

print(“Compressionshouldbe0butis”,compress)

iffilter==0:

print(“FilterisOK”)

else:

print(“Filtershouldbe0butis”,filter)

ifinterlace==0:

print(“Nointerlace”)

elifinterlace==1:

print(“Adam7interlace”)

else:

print(“Badinterlacespecified:“,interlace)

f.close()

8.5.6 SoundFiles

Asoundfilecanbealotmorecomplexthananimagefile,andsubstantiallylarger.To

properlyplaybackasound,itiscriticaltoknowhowitwassampled:howmanybitsper

sample,howmanychannels,howmanysamplespersecond,compressionschemes,andso

on.Thefilemustbereadableinrealtimeorthesoundcan’tbeplayedwithoutaseparate

decoding step. All that is really needed to display an image is its size pixel format and

compression.

There are, once again, many existing audio file formats. MP3 is quite complex, too

muchsotodiscusshere.TheusualoptiononaPCwouldbe“.wav”and,asithappens,

thatformatisnotespeciallycomplicated.

WAV

AWAVfilehasthreeparts:theinitialheader,usedtoidentifythefiletype;theformat

sub-chunk, which specifies the parameters of the sound file; and the data sub-chunk,

whichholdsthesounddata.

The initial header should contain the string “RIFF” followed by the size of the file

minus8bytes(i.e.,thesizefromthispointforward),andthestring“WAVE.”Thisis12

bytesinsize.

Thenext“sub-chunk”hasthefollowingform:

ID: =“fmt”

Size1: Sizeoftherestofthesub-chunk

Format: 1ifPCM,anothernumberifcompressed

No.ofChannels: mono=1,stereo=2,etc.

Samplerate: Soundsamplespersecond.CDrateis44100

Alignment: ShouldbeNo.ofchannels*samplerate*bitsper

sample/8

Bitspersample: AKAquantization.Bitsineachsample:8,12are

usual.

Thefinalsectioncontainsthe

following:

ID: =“data”

Size: Numberofbytesinthedata

Data: Theactualsounddata,asalargeblockofSizebytes.

Aprogramthatreadsthefirsttwosub-chunksis:

#WAV

fromstructimport*



f=open(“test.wav”,“rb”)

s=f.read(12)

riff,sz,fmt=unpack(“4si4s”,s)

riff=riff.decode(“utf-8”)

fmt=fmt.decode(“utf-8”)

print(riff,sz,“bytes“,fmt)



s=f.read(24)

id,sz1,fmt,nchan,rate,bytes,algn,bps=unpack

(“4sihhiihh”,s)

#4sihhiihh

id=id.decode(“utf-8)”)

print(“IDis”,id,“Channels“,nchan,“Samplerateis“,rate)

print(“Bitspersampleis“,bps)

iffmt==1:

print(“FileisPCM”)

else:

print(“Fileiscompressed“,fmt)

print(“Byteratewas“,bytes,“shouldbe“,rate*nchan*bps/8)

8.5.7 OtherFiles

Every type of file has a specific purpose and a format that is appropriate for that

purpose.Forthatreasonthenatureoftheheadersandthefilecontentsdiffer,butthefact

thattheheadersandotherspecificfieldsexistshouldbynowmakesomesense.Whena

programisaskedtoopenafilethereshouldbesomewaytoconfirmthatthecontentsof

the file can be read by the program. The code that has been presented so far is only

sufficienttodeterminethefiletypeandsomeofitsbasicparameters.Thecodeneededto

readanddisplayaGIF,forexample,wouldlikelybeover1000lineslong.Itisimportant,

forsomeonewhowishestobeaprogrammer,toseehowtoconstructafilesothatitcan

be used effectively by others and so that other programmers can create code that can

identifythatfileanduseit.

With that in mind, some other file types will be described briefly and considered as

examplesofhowtoorganizedataintoafile.

HTML

AnHTML(HyperTextMarkupLanguage) file is one that is recognizedby a browser

and can be displayed as a web page. It is a text file, and can be edited, saved, and

redisplayedusingsimpletools;thefancywebeditorsareuseful,butnotnecessary.

ThefirstlineoftextinanHTMLfileshouldbeeitheravariationon:

<!DOCTYPEhtml>

oravariationon:

<html>

The problem is that these are text files, so spaces and tabs and newlines can appear

without affecting the meaning. Browsers are also supposed to be somewhat forgiving

abouterrors,displayingthepageifatallpossible.Asimpleexamplethatshowssomeof

theproblemswhilebeinglargelycorrectis:

importwebbrowser

f=open(“other.html”)

html=False

whileTrue:#Lookatmanylines

s=f.readline()#Read

s=s.strip()#Removewhitespace

#(blanks,tabs)

s=s.lower()#Converttolowercasefor

#compare

k=(s.find(“doctype”))#doctypefound?

ifk>0:#Yes

kk=s.find(“html”)#Lookalsofor'html'

ifkk>=k+7:#Foundit,afterDOCTYPE

html=True#Closeenough

break

else:

k=s.find(“html”)#No'doctype'.'html'?

ifk>0ands[k-1]==“<”:#Yes.Precededby'<'?

html=True#Yes,Closeenough.

break

iflen(s)>0:#isthestringnon-blank?

html=False#Yes.SoitisnotHTML

#probably

break



ifhtml:

webbrowser.open_new_tab('other.html')

else:

print(“ThisisnotanHTMLfile.”)

Thisprogram usesthe webbrowsermodule of Pythonto display theweb page ifit is

one.Thecallwebbrowser.open_new_tab('other.html')opensthepageinanewtab,ifthe

browserisopen.Thismoduleisnotabrowseritself.Itsimplyopensanexistinginstalled

browsertodotheworkofdisplayingthepage.

EXE

ThisisaMicrosoftexecutablefile.Thedetailsoftheformatareinvolved,andrequirea

knowledge of computers and formats beyond a first-year level, but detecting one is

relativelysimple.ThefirsttwobytesthatidentifyanEXEfileare:

Byte0:0x4D

Byte1:0x5a

Itisalwayspossiblethatthefirsttwobytesofafilewillbethesetwoby

accident,butitisunlikely.Ifthefilebeingexaminedis,infact,anEXEfile,thenaPython

programcanexecuteit.Thisusestheoperatingsysteminterfacemoduleos:

importos

os.system(“program.exe”)

8.6 SUMMARY

AfairdefinitionofComputerSciencewouldbethedisciplinethatconcernsitselfwith

information.Computerscanonlyoperateonnumbers,soanimportantaspectofusingdata

istherepresentationofcomplexthingsasnumbers.Mostdataconsistofmeasurementsof

something,andassucharefundamentally

numeric.

A dictionary allows a more complex indexing scheme: it is accessed by content. A

dictionarycanbeindexedbyastringortuple,whichingeneralwouldbereferredtoasa

key,andtheinformationatthatlocationinthedictionaryissaidtobeassociatedwiththat

key.

A Python array is a class that mimics the array type of other languages and offers

efficiencyinstorage,exchangingthatforflexibility.Thestructmodulepermitsvariables

andobjectsofvarioustypestobeconvertedintowhatamountstoasequenceofbytes.It

hasapack()andanunpack()methodforconvertingPythonvariablesintosequencesof

bytes.

The string format() method allows a programmer to specify how values should be

placedwithinastring.Theideaistocreateastringthatcontainstheformattedoutput,and

thenprintthestring.

Pythondatacanbewrittentofilesinraw,binaryform.Itisalsopossibletopositionthe

fileatanybyteinabinaryfile,allowingthefiletobereadorwrittenatanylocation.

Exercises

1.Asktheuserforafilename.Extractthesuffixanduseittolookupthetypeofthefile

inadictionaryandprintashortdescriptionofit.Recognizedtypesincludeimagefiles

(jpg,gif,tiff,png),soundfiles(wav),andothers(dll,exe).

2.ModifytheLatintranslationprogramsothatitaskstheuserforatranslationofany

worditcannotfindandaddsthatwordtothedictionary.

3.Writeaprogramthatreadskeysandvalues(strings)fromtheconsoleandcreatesa

dictionaryfromthosedata.Whentheusertypestheword“done”thentheinputis

complete.Citynamesaregoodexamplesofvalues,andcouldrepresentthecitywhere

thepersonnamedinthekeylives.

4.ModifytheanswertoExercise3sothatafterthedataentryiscomplete,theusercan

enteravalueandtheprogramwillprintallofthekeysassociatedwiththatvalue.

5.Givenadictionary,writeafunctionwritedict()thatwritesthatdictionarytoafile,and

anotherfunctionreaddict()thatwillreadthatfileandrecreatethedictionary.For

simplicityassumethatthekeysaresimplenumbersorstrings.

6.ThePNMfileformatforimageshasthreetypesofimageintwoforms:monochrome,

grey,andcolor,savedastextorinbinaryform.Abinarygreylevelimageiscalleda

PGM(PixelGreyMap)andhasashortheaderfollowedbypixels.Theheaderistext

andconsistsoftheidentifyingcode“P5”followedbythewidthoftheimageinpixels

(NC),followedbytheheight(NR),followedbythemaximumvalueforagreylevel

(NGL)followedbyanendofline.NowthedatafollowsasrowsofNCbytes:

ncnrngl

<imagepixels,1byteeach>

Writeaprogramthatwillreadanimagefileinthisformatanddisplayitonthescreen

asanimageusingGlib.

http://netpbm.sourceforge.net/doc/pgm.html

7.Assumethatthefollowingvariablesexistandhavetheobviousmeanings:year,

month,day,hour,minute,second.Allareintegerexceptsecond,whichisafloat.

TheISO8601standardfordisplayingdatesusestheformat:

YYYY-MM-DDThh:mm:ss.s

wheretheletter“T”endsthedateportionandbeginsthetime.Anexamplewouldbe

2015-12-27T10:38:12.3

Writeafunctionthattakesthegivenvariablesasparametersandprintsthedateinthis

format.

http://www.w3.org/TR/NOTE-datetime

8.WriteaPythonprogramthatopensafilenamedbytheuserfromthekeyboard;the

filehasthesuffix“.jpg,”“.gif,”or“.png.”Determinewhetherthefilecontentsagree

withthesuffix,andprintamessageindicatingtheresult.

9.Aconcordanceisalistofwordsfoundinatext.Buildaconcordanceusinga

dictionarythatkeepstrackofthenumberoftimesthatawordisused,inadditiontoits

merepresence.Printtheresultinglistinalphabeticalorder.

10.Writeaprogramthatprintsoutchecks.Thedateandthepayeeareenteredasstrings

andtheamountisenteredasafloatingpointnumber,themaximumamountbeing

1000dollars.TheFORfieldisalways“Books.”Theprogramformatsthecheck

accordingtothefollowingimage(Figure8.2),where:

Thedateisline3startingatcharacter58

Thepaytofieldisline6startingatcharacter20

Thenumericamountisline6startingatcharacter57

Thetextamountisline8character10

TheFORfieldisline12character15

NotesandOtherResources
Listoffreedatasetstodownload:https://r-dir.com/reference/datasets.html
NASAMeteoriteLandingDatabase:https://data.nasa.gov/view/ak9y-cwf9
String Formatting: https://infohost.nmt.edu/tcc/help/pubs/python/web/format-
spec.html
TheArraytype:https://docs.python.org/3/library/array.html
Image file formats:
https://www.library.cornell.edu/preservation/tutorial/presentation/table7-1.html
http://www.scantips.com/basics09.html
HomepageforMPEG:http://mpeg.chiariglione.org/
GIF1989specification:http://www.w3.org/Graphics/GIF/spec-gif89a.txt
Byte by byte GIF:
http://www.matthewflickinger.com/lab/whatsinagif/bits_and_bytes.asp
TIFFDescription:http://www.fileformat.info/format/tiff/egff.htm#TIFF.FO
PNGSpecification:http://www.w3.org/TR/PNG/
Adam7Interlacing:http://www.libpng.org/pub/png/pngpics.html
EXEfileformat:http://www.delorie.com/djgpp/doc/exe/
FileSignatures:http://www.garykessler.net/library/file_sigs.html
SamplePGMImages:http://people.sc.fsu.edu/~jburkardt/data/pgmb/pgmb.html
1.GunterBorn.(1995).TheFileFormatsHandbook,CengageLearningEMEA,
ISBN-13:978-1850321170.
2.DavidKay.(1994).GraphicsFileFormats,Windcrest,ISBN-13:978-0070340251.
3.Dr.CharlesR.Severance.(2013).PythonforInformatics:ExploringInformation,
CreateSpaceIndependentPublishingPlatform,ISBN-13:978-1492339243.
4.AlanTharp.(1988).FileOrganizationandProcessing,1stedition,JohnWiley&
Sons,ISBN-13:978-0471605218.
5.JohnWatkinson.(2001).MPEGHandbook,FocalPress,ISBN-13:978-0240516561.

CHAPTER9

MULTIMEDIA

9.1MouseInteraction

9.2TheKeyboard

9.3Animation

9.4RGBAColors–Transparency

9.5Sound

9.6Video

9.7Summary

Inthischapter

Foragreatmanypeoplecomputershavebecometheplatformofchoiceforthedeliveryof

entertainment,education,andinformation.Partofthereasonforthisistheubiquityand

speedoftheInternet,butthemainreasonisthatcomputerscandelivermediainalmost

any form: text and images, sound, video, animation, and mixtures of all of these. If

someonehassomethingtosay,thecomputercanpresentittotheworldinfullcolorand

5.1 channel sound. Moreover, the availability of free and inexpensive tools for content

creationallowsalmostanyonetobeamusicproducerorfilmdirector.

Pythoncanbeusedtoprocessanddisplaymostformsofmediathroughpackagesthat

can be downloaded and installed. There are many of these and multiple versions in a

bewilderingarrayofcombinations.ItisnotpossibletodiscussallofthewaysthatPython

canbeusedtodomultimediaandallofthepackagesandlibrariesthathelpprogrammers

implementthesethings.Afacilityhasalreadybeendescribedfordisplayingimagesand

graphics:Glib.WhynotsimplyaddmoremediacapabilitytoGlib,thusbuildingonwhat

has already been discussed? At the same time, of course, yet another module is being

addedtotheglobalmixture.

This extended version of Glib is built using an easily available module that must be

installed first—that module is Pygame. For the new version of Glib to work properly,

Pygamemustbeinstalledonthehostcomputerfirst.Thisshouldnotbedifficult,butthe

processvariesdependingontheoperatingsystemandthenatureofthecomputer(e.g.,32

bitor64bit)sotheprocesswillnotbedescribedhere.TheResourcessectionattheendof

thechapterprovideslinksand

referencesthatwillbehelpful.

ItisessentialtoinstallaversionofPygamethatworkswithPython3.

TherearetwoversionsofGlib.TheversionthatwasusedinChapter7usestkinterasa

basisandshouldnotrequireanythingextratobeinstalled.ItisreferredtoasStaticGlib,

whereasthenew,extendedversionisDynamicGlib.DynamicGlibisupwardscompatible

from Static Glib in that all programs that run using Static Glib should also run using

DynamicGlib,andproduceaverysimilaroutput.Therearesomedifferencesbetweenthe

two,such as font styles and such.There are also new programming idioms that will be

neededwhenusingDynamicGlibonaccountofthedynamicnatureofsomeofthemedia

forms.Infact,onewaytolookatitistothinkofStaticGlibandDynamicGlibasbeing

twodifferentoperatingmodesofthesamelibrary.DynamicGlibisusedindynamicmode,

whereinteractionwiththeusercanoccur,thegraphicsscreencanchange,andsoundcan

beplayed.

Dynamic mode will be explained using the example of mouse positions and button

clicks, which represent a form of dynamic interaction that most people would have

experienced.Followingthat,animation,video,andsoundcanbe

discussedandcombinedintointerestingprojects.

9.1 MOUSEINTERACTION

Using mouse position and button presses is a basic form of communication with a

computer.Theuseofthemousepositiontoactivatesomevisualdeviceonthescreenlike

a button is familiar to everyone who uses a computer, although it is being gradually

replacedbytouchscreens.Theideaisthatwhentheusermovesthemouse,acursoror

indicator moves correspondingly. The position of this cursor indicates a point on the

screen that is active in some way, and if a graphical device is there then it can be

manipulatedusingthemousebuttons.Theproblemisthatamousebuttonpresscanoccur

atanytime; itisunpredictable.This iswhat programmers callan event: something that

happensat an unpredictable moment that must be dealt with. Somesoftware someplace

mustbewatchingthemouseatalltimes,determiningthex,ycoordinatesofthecursoron

thescreenanddrawingthecursorinthecorrectplace.

TheGlibmodulekeepstrackofthemouseusingPygameandcontinuallyupdatesthe

position,whichcanbeaccessedusingfunctions:mouseX()andmouseY(),whichreturn

themost recent xand y coordinates.However, if auser’sPythonprogram is executing,

howcantheGlibsystemalsorunandupdatethemouseposition?Itcannot.So,adynamic

modeprogramgivesupcontrolandletsGlibcontrolmostofthework.

AdynamicGlibprogramconsistsoftwoparts:aninitializationpartandadrawingpart.

Initializationtakesplaceonlyonce,whentheprogramstartsexecuting;itcantakeplacein

afunctioncalledinitialize(),orit can beinthemain program.Glibwill calla function

namedinitialize()once,ifitexists.

Thepart of the computer thatdraws willbe codedas afunction nameddraw(). Glib

willcallthisfunctionmanytimeseachsecond,andtheprogrammerisexpectedtoredraw

the graphics window each time. This scheme allows the mouse position to update very

frequentlyandallowstheprogrammertoaccessthemostrecentmousecoordinatesfrom

within the draw() function, which can take the place of the main program. A simple

example of the dynamic mode and use of the mouse is a program that moves a circle

around the screen. The scheme described here is something that will be familiar to

programmersoftheProcessinglanguage.

Example:DrawaCircleattheMouseCursor

UsingGlibrequirestheuseofthefunctionstartdraw()toinitializethings,inparticular

toestablishthesizeofthedrawingwindow.InDynamicGlibthecalltostartdraw()will

also call the user’s initialize() function if one exists. Other code can appear between

startdraw()andenddraw(),usuallycalculations

andinitializations.Onceenddraw()iscalledcontrolpassestotheuser’sdraw()function.

Itwillbecalled30timespersecondbydefault,althoughthisratecanbechanged.

Drawing a circle at the current mouse position involves repeatedly determining the

mousepositionandthendrawingacircleatthatsetofcoordinates.Thisshouldbedone

withindraw().Initializationinthisprogramistrivialsono

initialize()functionisneeded.

ImportGlib



defdraw():

Glib.background(200)

Glib.fill(255,0,0)

Glib.ellipse(Glib.mouseX(),Glib.mouseY(),30,30)



Glib.startdraw(400,400)

Glib.enddraw()

The result is a red circle that follows the mouse! The draw() function sets the

backgroundcolortoagreylevelof255,thensetsthefillcolortored,thendrawsthecircle

(ellipse).Itdoesthis30timesper second,everytimedraw()iscalled.Themostrecent

mousepositionisalwaysfoundusingthefunctionsGlib.mouseX()andGlib.mouseY().It

seemslikeitshouldnotbenecessarytosetthefillcoloreachtime,sothatcanbeputin

themainprogrambetweenstartdraw()andenddraw()orintheinitialize()function:

Inmain: Ininitialize():

importGlib



importGlib



defdraw():

Glib.background(200)

Glib.ellipse (Glib.mouseX(),

Glib.mouseY(),30,30)



Glib.startdraw(400,400)

Glib.fill(255,0,0)

Glib.enddraw()

definitialize():

Glib.fill(255,0,0)

defdraw():

Glib.background(200)

Glib.ellipse (Glib.mouseX,

Glib.mouseY,30,30)



Glib.startdraw(400,400)

Glib.enddraw()

Isitnecessary tocallthe background()function eachtimedrawis called?Yes. This

functionnotonlysetsthebackgroundcolorbutfillsthescreenwithit,thuserasingwhat

hasbeendrawnsofar.Unlessacalltobackground()occursindraw(),allofthecircles

drawntothatpointwillbevisible(Figure9.1).

Ifthestatement:

fromGlibimport*

appearsatthebeginningoftheprogramthentheGlibfunctionswon’thavetobeprefixed

withthenameGlib.VariablesthatbelongtoGlibstilldo.Theimport*allowsallofthe

namesfromGlib to be used in the program, but is not always recommended because it

complicates the collection of names to be remembered. Still, for the purposes of this

chapter,itwillbeused.

Example:ChangeBackgroundColorUsingtheMouse

Theideahereistochangethebackgroundcolorbasedonthemouseposition.Thereare

only two directions to move, horizontally or vertically, so one of the three colors will

remainconstant;letthatcolorbeblue.Thehorizontalmousepositionwillcontrolthered

value,with the leftmost positionrepresenting no red and the rightmostrepresenting full

red(255).Similarly,themousebeingatthebottomoftheimagerepresentsnogreen,and

at the top it represents full green. The background color will be changed in draw()

accordingly.

GiventhatthepositionofthemouseonthescreenisgivenbymouseX(),thevalueof

theredcoordinatewillbe(mouseX()/width*255).Itmayrequireachangeinxcoordinate

ofmultiplepixelstoshiftthecolorbyoneunit.Asimilarexpressionisusedtochangethe

greenvalue.

Theprogramis:

fromGlibimport*

importGlib



defdraw():

r=int((Glib.mouseX/width)*255.0)

g=int((Glib.mouseY/height)*255.0)

background(r,g,128)



startdraw(400,400)

enddraw()

9.1.1 MouseButtons

Mouse button clicks, as they are called, can be retrieved by writing a function that

handles them. Each time a mouse button is pressed, Glibtries to calla function named

mousePressed().Ifthereisnosuchfunction,that’sOK,andnothingelsehappens.Ifthe

userwritesafunctionnamedmousePressed(),thenitwillbeexecuted.Similarly,whena

mousebuttonisreleased,ittriestocallmouseReleased().Ifthemousebuttonispressed,

then the mouse is moved, and then it is released, the coordinates of the press and the

releasepointwillbedifferent,andbothcanberetrieved.Forexample,when the mouse

buttonis pressed,the mouse coordinatescould be savedas the beginningof a line,and

whenreleasedthecoordinatescouldbetheendoftheline.Multiplelinescouldbedrawn

inthisway.

Example:DrawLinesUsingtheMouse

Usingtheschemedescribedabove,thefunctionmousePressed()willstorethemouse

position in global variables x0 and y0, and mouseReleased() will store the release

coordinatesatx1andy1.mouseReleased() will also draw the line from (x0,y0)to (x1,

y1):

fromGlibimport*

importGlib

x0=x1=y1=y0=0



defmousePressed(b):

globalx0,y0

x0=Glib.mouseX()

y0=Glib.mouseY()



defmouseReleased(b):

globalx1,y1

x1=Glib.mouseX()

y1=Glib.mouseY()

line(x0,y0,x1,y1)



startdraw(400,400)

enddraw()

Notethatthereisnodraw()functionandnoinitialize()function.Drawingisperformed

insideofmouseReleased(),andnoinitializationisneeded.Thisisararesituation.These

functionsacceptoneparameter,whichisthenumberofthebuttonthatwaspressed:leftis

0, middle is 1, and right is 2. Note that all buttons could be pressed before any are

released.Inthisexampleitdoesnotmatterwhatbuttonispressed;theresultisthesame.

These functions are traditionally called callback functions. The occurrence of some

eventcausesthefunctiontobecalled.

Example:AButton

This example will change the background color of the drawing window when a

graphicalbuttonispressed.Abutton,intheuserinterfacesense,isarectangularregionon

thecomputerscreenthatrespondstoamouseclickwithaspecificaction.Itisatwo-part

process: when the mouse cursor enters the rectangular region, the button is said to be

activated.Sometimesitwillbecausedtochangecoloratthispoint,orsomeotheraction

will be performed that indicates that it is ready to function. When a mouse button is

pressed while the button is activated, then some action occurs, usually as defined by a

function being called. The basic idea is simple enough to implement, although some

buttonscanhavecomplexactionssuchassounds,images,andirregularshapes.

Thecursoriswithinarectangularregionwhenitscoordinatesaregreaterthantheupper

left coordinate of the rectangle and smaller than the lower right coordinates. When that

occursthebuttonisreadytobepressed,andshouldchangecolor.Thisdoesnotrequire

anythingbutknowledgeofthemousecoordinates.Ittheleftbuttonispressedinthisstate

(activated), then the action defined by the button will occur; the background color will

change,inthiscase.Theprogrambeginsasnormal,withimportsandinitialization.Here

isaprogramthatdoesthisforabuttonat(100,100)thatis60x20pixelsinsize:

fromGlibimport*

fromrandomimport*



x0=100#upperleftbuttonposition

y0=100

w=60#Buttonsize

h=20

bc=cvtColor(200)#Initialcolor

active=False#Isthebuttoncurrentlyactive?



defdraw():

globalbc,w,h,x0,x1,y0,y1,active

background(red(bc),green(bc),blue(bc))

#Setbackgroundcolortobc

x=mouseX()#Isthemouseintherectangle?

y=mouseY()

ifx>x0andx<x0+wandy>y0andy<y0+h:

fill(50,200,50)#YES.Buttonisactive.Green

active=True

else:

fill(200,50,50)#NO.Buttonisinactive.Red

active=False

rect(x0,y0,w,h)#Drawthebutton



defmouseReleased(b):

globalactive,bc

ifactiveandb==0:#Buttonactive?Leftbutton

#released?

#Ifsogeneratearandom

#backgroundcolor.

bc=(randrange(100,200),randrange(100,200),randrange(100,200))



startdraw(400,400)

enddraw()

Allofthesoftwarebuttonseverywhereworkinbasicallythisway.

9.2 THEKEYBOARD

Like mouse motions and button presses, pressing a key on the keyboard is an event.

Likebuttonpresses,akeypressisasingleeventwithmultipleoptions.Thefactthatakey

hasbeenpressedisanevent,andexactlywhichkeyitwasisa

detail,justasitwaswhenamousebuttonwaspressed.Itisimportanttounderstandthat

using a function such as input() will not be successful when trying to read from the

keyboardwithanevent-drivensystem,althoughknowingabouteventscanbevaluablein

understanding how input() could be implemented. When input() is called it does not

returnuntilalinehasbeenread;keyPressed()capturesthekeypressevent.Itappearsthat

acalltoinput()mayinvolvemanykeypressevents.Whatsoftwarereceivesthem?That

istheimportantquestion.Thesituationisreallytooconfusingtoberesolvedsensibly,so

theruleis:neveruseinput()andrelatedfunctionswhenhandlingkeypresses.ItisOKto

callprint()becauseitisprintingtoaconsoledeviceforwhichnoconflictexists.

Everykeypresswilleventuallycorrespondtoakeyrelease,sotherearetwocallback

functionsagain:

keyPressed(k): Calledwhenakeyispressed.Parameterkisthekeythatwaspressed.

keyReleased(k): Calledwhenakeyisreleased.Parameterkisthekeythatwasreleased.

Theparametersarenotcharactersinthenormalsense,butarenumericcodesthatcan

identify the character. These are based on the Pygame character constants, but extends

them slightly. Table 9.1 gives a list of all of the constants provided by Glib. As an

example,ifaprogrammustrecognizewhentheuparrowkeyispressed,thekeyPressed

()functionthatwoulddothisis:

defkeyPressed(k):

ifk==K_UP:

print(“Uparrowkeypressed.”)

Inanevent-drivenprogramitisunusualforkeypressestobeconvertedintostrings,as

theynormallywouldbeinatypicalconsole-styleprogram.That’sbecauseitisexpected

thattheinterfacetotheevent-drivenprogramwillbethroughmousegesturesandusing

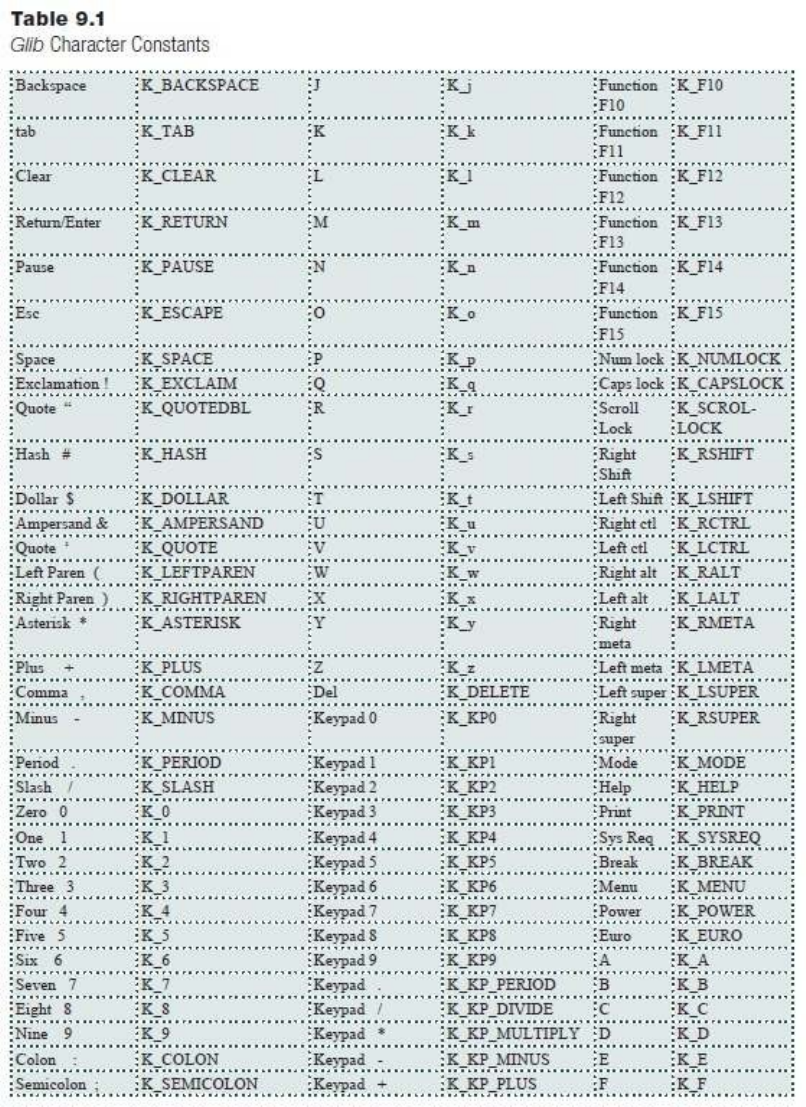
singlekeycommandsfromthekeyboard,like“up

arrow”meaning“moveforward.”

Example:Pressinga“+”CreatesaRandomCircle

Thisprogramwilldrawacircleatarandomlocationwhenthe“+”keyispressed.Old

circles will remain. This illustrates the use of the keyboard in an obvious way. The

initialization is to clear the screen and set the background color and fill color. The

keyPressed()functiongeneratesrandomx,ycoordinatesanddrawsacirclethere:

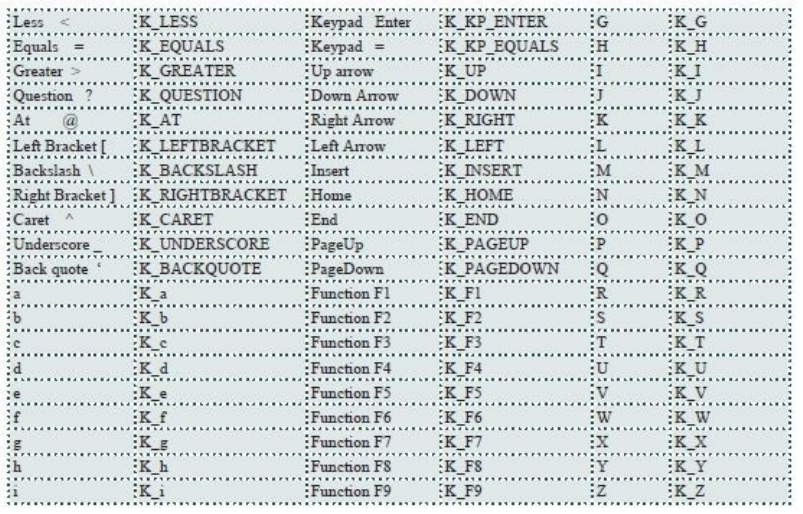
fromGlibimport*

fromrandomimport*



defkeyPressed(k):

ifk==K_PLUS:

ellipse(randrange(0,width),randrange(0,height),30,30)



startdraw(400,400)

fill(200,0,0)

background(200)

enddraw()

Thekeyvalueispassedasaninteger,butthebuilt-infunctionchr()willconvertthatto

thepropercharacterinmanycases.WhatispossiblytheshortestfunctionalGlibprogram

simplyreadsthekeysandprintsthemontheconsole:

fromGlibimport*



defkeyPressed(k):

print(chr(k))

startdraw()

enddraw()

Thestartdraw()functionhasdefaultparameters,andcreatesa50x50pixelwindowif

nosizeisspecified.Thisprogramdoesnotdrawanything,sodraw()isnotneeded.

Example:ReadingaCharacterString

Therearesomereasonswhyanevent-drivenprogrammightwishtoreaddatafromthe

user as a string. Perhaps a name is required, or a key value to access a database, or a

password.Whateverthereason,itshouldbepossibletoreadastringusingkeyPressed().

The way it would normally be done is to read one character at a time, normal for

keyPressed(),andconstructastringbyconcatenation.That’showthisprogramworks:

fromGlibimport*



s=””

t=””



defkeyPressed(k):#kisthevalueofthekeythat

#waspressed

globals,t

ifk==K_RETURN:#TypingRETURNendsthestring

#construction

t=s

s=””

return

ifk==K_BACKSPACEandlen(s)>0:#Deletethe

#previouscharacter

s=s[0:len(s)-1]#Shortenthestringbyone

#character

else:

s=s+chr(k)#Appendthenewcharacterto

#thestring



defdraw():

globals,t

background(200)

text(“Enterastring:“,10,100)

text(s,20,130)

if(t!=””):

text(“Completedstringis“+t,20,150)



startdraw(200,200)

enddraw()

Theglobalvariablesholdsthestringbeingbuilt,andthestringtholdsthefinalstring.

Characters are captured from the keyboard by keyPressed() and fall into one of three

categories:

1.Mostcharactersareaddedtotheglobalstringsthroughconcatenation.The

characterpassedtokeyPressed()isaninteger.Thechr()functionconvertsittoa

characterwhichisaddedtotheendofs.

2.ABACKSPACEwilldeletethelastcharactertypedfromthestring.Thisisdone

usingasubstringfrom0tothesecondlastcharacter.

3.ARETURNwillendthestring.Thecurrentstringinswillbeassignedtot,ands

willberesettoanemptystring.

Thiskindofstringdataentryisespeciallyusefulwhenenteringfilenamesandnumeric

parameters. There are frequently special interface objects (widgets) that perform these

tasks,suchastextboxes.Glibcouldbeusedtoimplementsuchawidget(see:Exercise6).

9.3 ANIMATION

Makinggraphicalobjectschangepositionissimple,butmakingthemseemtomoveis

more difficult. Animation is something of an optical illusion; images are drawn in

succession,andsoquicklythatthehumaneyecan’tdetectthattheyaredistinctimages.

Smallchangesinpositioninasequenceoftheseimageswillbeseenasmotionratherthan

asasetofstillpictures.Atypicalanimationdrawsanewimage(frame)between24and

30timespersecondtomaketheillusionwork.

TherearetwokindsofanimationthatcanbedoneusingGlib.Thefirstinvolvesobjects

thatconsistofprimitivesthataredrawnbythelibrary.Acirclecanrepresentaball,for

instance,orasetofrectanglesandcurvescouldbeacar.Thesecondkindofanimation

usesimages,whereeachimageisoneframeinthesequence.Theseimagesaredisplayed

entirelyinrapidsuccessiontocreatetheanimation.Inthefirstcasetheanimationisbeing

createdastheprogram

executes,whereasinthesecondtheanimationiscompletebeforetheprogramruns,and

theprogramreallyjustputsitonthescreen.

9.3.1 ObjectAnimation

Animatinganobjectinvolvesupdatingitsposition,speed,andorientationatsmalltime

intervals,soalloftheseaspectsoftheobjectmustbekeptinvariables.Iftherearemany

objects being animated, then all of these variables must exist for each object, and are

updated at the end of each time interval. If the animation is displaying 30 frames per

second, then a new frame is drawn every 0.03 seconds. In Glib the function named

framerate() can be called passing the number of times that draw() will be called each

second,andthendraw()candotheworkneededtoupdatetheobjectsanddrawtheframe.

Example:ABallinaBox

Imagineaballbouncinginasquarebox.Aboxhasthreedimensions,ofcourse,butfor

thisexampleitwillberestrictedtotwo,soitwilllooklikeacirclewithinasquare.The

ball is moving, and when it strikes one of the sides of the square it will bounce, thus

changingdirection.Thereisonemovingobject:theball.Graphicallyitissimplyacircle,

withpositionx,yandspeeddxinthexdirectionanddyintheydirection.Itwillhavesize

30pixels.Theboxwillsimplybethewindowthecircleisdrawnin.

Duringeachframetheballwillmovedxpixelsinthexanddypixelsintheydirection,

sowithinthedraw()functionthepositionisupdatedas:

x=x+dx

y=y+dy

Thisnewpositioniswheretodrawthecircle.However,iftheballisoutsideofthebox

afteritismoved,thenabouncehastobeperformed.Thatis,ifthenewpositionofxis,

for instance, less than 0, then it would have struck the left side of the square and then

changed x direction (bounced). In this case, and also if x>width, the bounce is

implementedby:

dx=-dx

Similarly,iftheycoordinateoftheballbecomeslessthan0orgreaterthantheheight,

thenitbouncesvertically:

dy=-dy

Thiswouldallbetrueiftheballwereverytiny,asinglepoint,butithasasizeof30

pixels,andthecoordinatesofthecirclearethecoordinatesofitscenter.Thismeansthat

themethoddescribedabovewillbouncethecircleonlyafterthecentercoordinatepasses

theboundary,meaningthathalfofthecircleisalreadyontheotherside.It’seasytofix:

the ball is 30 pixels in size, so it should bounce when it gets within 15 pixels of any

boundary. For example, the x bounce should occur when x<=15 or x>=width-15. The

entiresolutionis:

#Bouncingballanimation.

fromGlibimport*



defdraw():

globaldx,dy,x,y

background(200)#Erasethepriorframe

x=x+dx#Changeballposition

y=y+dy

ifx<=15orx>=width-15:#BounceinXdirection?

dx=-dx

ify<=15ory>=height-15:#BounceinYdirection?

dy=-dy

ellipse(x,y,30,30)#Drawtheball

startdraw(200,200)

x=100#Initialxpositionofthe

#ball

y=100#Initialyposition

dx=3#Speedinx

dy=2#Speediny

fill(30,200,20)#Fillwithgreen

enddraw()

Eightframesfromthisanimationshowingtheballbouncinginacorneroftheboxare

shown in Figure 9.2. An entire second’s worth of frames (30) are given on the

accompanyingdisc.

Iftherearemanyobjectsthenallofthepositionsandspeeds,andperhapsevenshape,

size,andcolorwouldhavetobekeptandupdatedduringeachframe.Therearetwousual

waystodothis.Inthefirstcasetheparametersarekeptinarrays(lists).Therewouldbe

an array of x coordinates, an array of y coordinates, of speeds, and so on. Each frame

couldinvolveanupdatetoallelementsofthearrays.Updatingthepositioncanbedone

likethis:

foriinrange(0,Nobjects):

x[i]=x[i]+dx[i]

y[i]=y[i]+dy[i]

Theotherusualmethod forhandlingmultipleobjects is to create anobject classthat

containsalloftheparametersneededtodisplaytheobject.Thereisstillanarray,butitis

anarrayofobjectinstances,andifitiscleverlyprogrammedtheclasscanbeupdatedby

callinganupdate()method:

foriinrange(0,Nobjects):

ball[i].update()

Example:ManyBallsinaBox

Thisexampleusesthesamepremiseasthepreviousone,butwilldrawmanyballsin

thewindow,allofthembouncing.Bothmethodsforkeepingtrackofobjects,arrays,and

classeswillbeillustrated.Themanyarrayssolutionhaslistsforxandy,fordxanddy,for

colorandforsize.Allparametersareinitializedatrandomwhentheprogrambegins.

The solution that uses classes defines a class ball within which the position, speed,

color,andsizearedefined.Theconstructorinitializesthevalues,andtheupdatemethod

changestheball’spositionandperformsanyneededbounces.Thetwosolutionsare:

These two solutions illustrate how classes work very neatly. The class contains

individualpropertiesofaballandmanyarecreated;thearrayscontainmanyinstancesof

eachproperty.Sox[i]andball[i].xrepresentthesamething.Inthiscasethetwoprograms

areaboutthesamesize,buttheclass-basedimplementationencapsulatesthedetailsofthe

ballandwhatcanbedonewithit.Theclass-baseddraw()functiononlysays“draweach

ball,”butinthearrayimplementationthedraw()functionlooksatallofthedetailsofall

ballstodrawthem.Oneoftheimplicationsisthatitwouldbepossibletodividethelabor

betweentwopersons,onewhowrotetheclassandanotherwhowrotetherestofthecode.

Forlargeprogramsthiscanmatterquitealot.

9.3.2 FrameAnimation

Thehardworkinframeanimationisdonebeforethecomputerprogramiswritten.An

animator has created drawings of an object in various stages of movement. All the

program does is display frames one after the other, often looping them to create the

desiredeffect.Acommonexampleofthisistheanimationofgait,walkingorrunning.An

artistdrawsmultiplestagesofasinglestep,beingcarefultoensurethattimingiscorrect:

howlongdoesittakeforanormalpersontostakeapairofsteps(left,right)?Thistime

shouldagreewiththeframestheartistcreates.Ifittakesonesecondtomakethestep,then

itshouldbedrawnas30frames.

Other kinds of animation are performed too. A fire can be animated as a very few

frames,as can smoke and water. The programthat draws theanimation readsall of the

image files into a collection. When the animation is played, the program displays one

image after another within the draw function. This can be complicated by the fact that

theremaybemultipleanimationsplayingatthesametime,possiblyofdifferentlengths

andframesizes.

Example: Read Frames and Play Them Back as an

Animation

In this example there are 10 drawn animation frames of a cartoon character walking.

Theseframesareintendedtorepresentasinglegaitcycle,andsoshouldberepeated.The

program will do the following: when the up arrow key is pressed and held down, the

characterdrawninthewindowwill“walk”;otherwiseastillimagewillbedisplayed.

Firsttheimagesshouldbereadinandstoredinanarray(list)sothattheycanbeplayed

repeatedly.ThenthekeyPressed()functionshouldbewrittensothatwhentheuparrow

keyispressedtheframeswillbedrawn.AflagcanbesetTruewhenthekeyispressed,

andFalsewhenthekeyisreleasedsothatdraw()cantellwhentodrawframesandwhen

not.

defkeyPressed(k):

globalkeydown

keydown=True



defkeyReleased(k):

globalkeydown

keydown=False

A list named frames is initialized with all of the images in the sequence. All that

draw()doesisplaythenextone,usingaglobalvariableftoidentifythecurrentframe.

defdraw():

globalkeydown,f

ifkeydown:

image(frames[f],0,0)

f=f+1

if(f>10):

f=1

Itcyclesthroughtheframesandrepeatswhenallhavebeendisplayed.

The initialization can be a simple matter of reading ten images into variables and

creatingalist.Thiscodedoesitinaloop,usinganumberinthenameandincrementingit:

startdraw(320,240)

keydown=False

frames=[]

foriinrange(1,10):

s=“images/a00”+str(i)+”.bmp”

x=loadImage(s)

frames=frames+[x,]

x=loadImage(“images/a010.bmp”)

frames=frames+[x,]

x=loadImage(“images/a011.bmp”)

frames=frames+[x,]

f=1

image(frames[0],0,0)

enddraw()

Thevariableframesisalistholdingalloftheimages,andframes[i]istheithimagein

thesequence.

Thebuildingofthefilenameisinteresting.Itiscommontousenumberednamesfor

animationframes; thingslike frame01,frame02,and so on. In this case the sequence is

a***.bmpwhere the *** represents a three-digit number. If the variable i is an integer,

thenstr(i)isastringcontainingthatinteger,butleadingzerosarenotpresent.Thus,for

valuesofibetween0and9(onedigit),thestringwillbe“a00”+str(i)+“.bmp”;forvalues

ofibetween10and99(twodigits),thestringwillbe“a0”+str(i)++“.bmp”;finally,for

numbersbetween100and999,thestringwillbe“a”+str(i)+“.bmp”(three digits). The

leadingzerosaremanuallyinsertedintothestring.

Theanimationframesforthegaitsequenceareonthediskalongwiththiscode.

Example: Simulation of the Space Shuttle Control Console

(A Class That Will Draw an Animation at a Specific

Location)

Animationscan sometimesbeusedtodecorateascenein interestingways. Acontrol

panel showing video screens and data displays could use animations to fill the screens,

givingtheillusionofrealthingsbeingmonitored.Aclassthatcanplayaframe-by-frame

animationatanylocationonthescreencouldbeinstantiatedmanytimes,onceforeach

display.

Theclasswouldhavetoreadtheframesitwastoplayandstorethem,playbackthe

framesinaloopwhenrequested,andplacethemwithinthewindowatanylocation.None

ofthesetasksisespeciallyhard.Codeforreadingframesfromafilewaswrittenforthe

previousexample,aswascodefordisplayingtheframes.Eachclassinstancewouldneed

aframecountsothattheloopcouldstartoverattherightplace,andeachclassinstance

couldhaveananimation withadifferentnumber offrames.Finally, placingattheright

locationisamatterofpassingthecorrectparameterstotheimage() function. The class

wouldbeinstantiatedgiventhepositionasxandycoordinatesoftheupperleftcorner.

Sometimes, especially when multiple animations are playing, it will be necessary to

slowdownsomeanimationssothattheylookright.TheGlibcodecallsdraw()afixed

number of times each second, but that may not always be the correct speed for an

animation.Acountcanbeintroducedsothattheframeadvancestothenextonlywhena

countexceedsafixeddelayvalue.Ifthecountis2,forexample,then2callstodraw()are

requiredbeforeanewframeischosen,meaningthattheframeratehasbeendecreasedby

50%.

Thespecificexampleissupposedtoimplementa“simulation”ofaspaceshuttlecontrol

console.Thisisavisualsimulation,notonethatallowsinteractionatanylevel,andthe

idea is to insert animations into a still photo of a real shuttle console and make it look

moreactive.Figure9.4ashowsthestaticimagethatwillbeused.Therearemanyvideo

screensvisible,andtheprogrambeingdevelopedwillreplacethestillimageonsomeof

thosescreenswithmoving,animatedimages.

Threeofthescreensareselectedforanimation.TheimagewasdisplayedusingPaint

andthecoordinatesoftheupperleftcornerofeachofthesescreenswasdetermined,as

werethesizes.Figure9.4bshowsthelocationoftheseregionsontheimage.

Thecodefortheclassstartslikethis:

classAnim:

def__init__(self,x,y):#Constructor––––-

self.frames=[]#Theactualimages

self.xpos=x#Positionofupperleft

self.ypos=y

self.n=0#Howmanyframesarethere?

self.f=0#Whichframeiscurrently

#beingshown?

self.active=False#Isthisanimationbeing

#played?

self.delay=1#Usedtoslowtheframe

#rate

self.count=100000#Whencount>delayaframe

#isdrawn



defdraw(self):

ifself.active:#Drawthecurrentframeatthe

#correctlocation

image(self.frames[self.f],self.xpos,self.ypos)

self.count=self.count+1#Incrementcount.

ifself.count>=self.delay:#Changetheframe

#yet?

self.f=self.f+1#Yes.Andalso

#resetthecount

self.count=0

if(self.f>=self.n):#Looptheframes;

#startoverat0

self.f=0

Thepartoftheclassthatreadstheframesasimagesisbasicallytakenfromtheprevious

example:

defgetframes(self,s1,s2):

self.frames=[]#Thelistvariable

#'frames'containsall

#images

foriinrange(0,100):#Upto100imagescanbe

#read.

ifi<10:

s=s1+“0”+str(i)+s2

print(“Reading“,s)

elifi<100:

s=s1+str(i)+s2

x=loadImage(s)

ifx==None:

self.n=i

print(“Saw“,self.n,”frames.”)

break

self.frames=self.frames+[x,]

There is a flag named active that determines whether the animations are currently

runningornot.Themethodsstart()andstop()turntheanimationonandoffbytoggling

thisvariable.

defstart(self):

self.active=True



defstop(self):

self.active=False

Finally,forthisclass,thedelaycanbesetusingacalltothesetdelay()method,which

simplychangesthevalueofaclasslocalvariabledelay.

defsetdelay(self,d):

self.delay=d

Thedraw()methodoftheprogramsimplydrawsthe

animationsbycallingtheirrespectivedraw()methods:



defdraw():

a.draw()

b.draw()

c.draw()

Themainprogramopensthewindowandloadsanddrawsthebackgroundimage:

startdraw(800,531)#Thesizeofthebackgroundimage

background=loadImage(“images/800px-STSCPanel.jpg”)

image(background,0,0)

Thefirstanimation,atx=239andy=284,willshowsometelevisionstatic,sevenframes

ofwhichwerecreatedforthispurposeusinganotherprogram.

A class instance is created to draw at (239,284) and getFrames() is called to load the

images(thefilenamesare“g100.gif”through“g106.gif”):

a=Anim(239,284)

a.getframes(“images/g1”,“.gif”)

Thesecondanimationisatx=319andy=258andwilldisplaysomeexteriorshotsofthe

spaceshuttle.Theprocessisthesameasbefore,butthefilenamesare“g200.jpg”through

“g204.jpg.”Inaddition,adelayof100isset,becausetheseimagesaretobedisplayedfor

multiplesecondseachtosimulateadisplayscanningasetofcameras:

b=Anim(319,258)

b.getframes(“images/g2”,“.jpg”)

b.setdelay(100)

Finally the third animation, at x=319 and y=322, consists of a computer display

showingPythoncode(thisclass,infact).Itwascreatedbyanotherprogramandconsists

ofnineframesnamed“g300.gif”through“g308.gif.”Thisanimationisdelayedalittleas

wellsothatitappearsasifthetextisscrollingproperly:

c=Anim(319,322)

c.getframes(“images/g3”,“.gif”)

c.setdelay(10)

Thelaststepintheprogramistostartalloftheanimationsplaying:

a.start()

b.start()

c.start()

enddraw()

The example is complete on the disk, and needs to be executed with the images

directory,whichcontainstheanimationframes.

https://commons.wikimedia.org/wiki/File:STSCPanel.jpg

9.4 RGBACOLORS–TRANSPARENCY

InChapter7,itwasseenhowitwaspossibletousetransparencyinanimagetoallow

thevisualizationto‘seethrough’toanimageinthebackground.Asithappens,anypixel

canbeassignedadegreeoftransparencythatpermitsthesamevisualcharacter.Acolor

can be assigned a value that dictates how opaque or transparent it is, allowing colors

behindittoinfluencehowthatpixelisseen.Onecanthinkofthisasafourthcolorvalue,

inadditiontored,green,andblue.Itisreferredtoasalpha,andacolorwithfourcolor

parametersissaidtobeintheRGBAcolorspace,forRed,Green,Blue,andAlpha.

If the value of Alpha is 255, then the color is opaque; as it decreases in value the

transparency increases until at Alpha=0 pixel or object cannot be seen. A program that

drawsthreeoverlappingcirclesusingcolorswithanAlphavalueof60showsthevisual

effect of using transparency (Figure 9.5a). Transparency is specified in this case by

providingtheAlphavalueasafourthparametertofill():

fromGlibimport*



startdraw(300,300)

fill(255,0,0,60)

ellipse(100,100,150,150)

fill(0,255,0,60)

ellipse(200,100,150,150)

fill(0,0,255,60)

ellipse(150,200,150,150)

enddraw()

Transparencycanbeaddedtostrokecolorsalso,andinthesameway(Figure9.5b).For

example:

stroke(255,0,0,65)

9.5 SOUND

Soundisanessentialcomponentofdigitalmedia.Proof?Almostnobodywatchessilent

filmsanymore, and nobody makesthem. Video games are rarelyplayed with the sound

turnedoff.Thereareafewimportantreasonsforthis.

1.Muchhumancommunicationisthroughsound.Speechisthebestexample,but

non-speechsounds,clapping,stampingoffeet,andsoon,arewaysthatpeople

maketheirfeelingsandintentionsknown.

2.Soundsareassociatedwithevents.Whenanobjectfallstothefloorasoundoccurs

withtheimpact.Abuttonispressedandadoorbellrings.Thesesoundsare

importantindicators.

3.  Sounds cause emotional reactions in people. Music can do this; it can convey a

moodbetterthanalmostanythingelse.Butsoundcanalsoindicatethingsunseen.A

growling in the dark; a screech in the sky; the sound of an approaching vehicle

aroundacurveintheroad.

InGlibasoundismuchlikeanimageintermsofhowitisused.Asoundfileisloaded

and assigned to a variable, then that variable can be used to play, stop, rewind, and

perform all audio operations on that sound. Each sound must be loaded into a distinct

variableandhasitsowncontrols.TheGlibinterfacetosoundsfilesshouldthereforelook

familiar.

Oneproblemisthatthesoundsystemdoesnothavealargevarietyofsoundfilesthatit

canhandle:“.wav”and“.ogg”areaboutit.Thisleavesthemorepopularformat,“mp3,”

outofcontentionforPythonmediasoftware,atleastfornow.

Thefirststepinplayingasoundistoloadthefile.ThefunctionloadSound()isused

forthis,passingthenameofthesoundfile:

s=loadSound(“song.wav”)

PlayingthesoundisdoneusingtheplaySound()functionofGlib:

playSound(s)

StoppingasoundfromplayingisamatterofcallingstopSound().Settingthevolume

meanscallingvolumeSound()passingaparameterbetween0.0and1.0,where0.0isno

soundand1.0ismaximumvolume.That’sprettymuchitforthebasics.

Example:PlayaSound

The act of reading and playing a sound file will illustrate the essential operations for

usingsound.Thefileinputisdoneasaninitialization.Startingtoplaythefilecouldbe

donethatwaytoo.CallingplaySound()repeatedlyfromdraw()willcausethefiletostart

playing over and over again. A solution is to start some sounds in the main program;

anotheristosetaflagwhenasoundstartsplayingandchecktheflag.Thebestwaywould

betorecordthetimewhenthesoundstartedplayingandseeifthecurrenttimeexceeds

thelengthofthesound.

IfplaySound() is called with a second parameter, an integer, then the sound will be

replayed or repeated that many times. The call playsound(s,3) plays the sound s three

times.Iftherequestedfiledoesnotexist,thenloadSound()returnsNone.

Example: Control Volume Using the Keyboard. Pause and

Unpause

This example adds volume control. The function volumeSound() accepts a single

parameter, and it is a number between 0.0 (lowest volume) and 1.0 (highest volume).

AddingavolumecontrolisassimpleascodingakeyPressed()functionthatchangesthe

volumelevelbyanincrementeachtimeakeyispressed.Use“+”foravolumeincrease

and“-”foradecrease.Thenewprogramis:

fromGlibimport*



defkeyPressed(k):

globalvolume,s

ifk==K_PLUS:

volume=volume+.1

elifk==K_MINUS:

volume=volume-.1

ifvolume<0:volume=0

ifvolume>1:volume=1

volumeSound(s,volume)



startdraw()

s=loadSound(“sun.wav”)

volume=1.0

volumeSound(s,volume)

ifs==None:

print(“Nosuchsoundfile.”)

else:

playSound(s)

enddraw()

Example: Play a Sound Effect at the Right Moment:

Bounces

Asoundeffectrepresentssomeevent,andneedstobeplayedatthemomenttheevent

happens.Synchronizingthetwothingsisassimpleasplayingasoundwhentheeventis

detected. This example program will play a sound representing a ball hitting something

when a simulated ball hits the side of the window and bounces. The bouncing ball

animation program will provide the impact event: when the ball hits the side of the

window,thesoundofanimpactwillbeplayed.

The sound effect is a file, and was recorded using an inexpensive microphone, a

computerwithasoundcard,andtheAudacitysoftware,whichisfreeanddownloadable

(see the end-of-chapter resources). The sound of a glass hitting a desk was recorded,

edited, and saved as a “.wav” file named “bounce.wav.” The program was modified to

readthatfile,andthenplayitbackwheneveracollisionwiththewindowwasdetected.

Theprogramhasthreenewlinesofcode:

#Bouncingballanimation.

fromGlibimport*



defdraw():

globaldx,dy,x,y

background(200)#Erasethepriorframe

x=x+dx#Changeballposition

y=y+dy

ifx<=15orx>=width-15:#BounceinXdirection?

playSound(s)

dx=-dx

ify<=15ory>=height-15:#BounceinYdirection?

dy=-dy

playSound(s)

ellipse(x,y,30,30)#Drawtheball



startdraw(200,200)

x=100#Initialxpositionofthe

#ball

y=100#Initialyposition

dx=3#Speedinx

dy=2#Speediny

s=loadSound(“bounce.wav”)

fill(30,200,20)#Fillwithgreen

enddraw()

Inmanysituationsthere can beasmall delaybetweentheevent andthesound being

played.Asoundcanrarelybeplayedinstantaneously.

9.6 VIDEO

The video facilities provided by Glib are limited, but the library increases the

functionalityoftheunderlyingPygamemodule. It isimportant tounderstand thatvideo

playsataparticularrateand,unlikeaudio,mustacquireaportionofthedisplaywindow

withinwhichtobedrawn.Thismeansthatplayingavideointhenormalwaytakescontrol

awayfromtheprogrammerandallowsthevideosoftwareautonomy.Thiscancausesome

trouble,asprogrammersoftenwanttodrawintothedisplaywindowaswell.

UsingthebasicfunctionalityitispossibletoplayanMPEG-formattedvideowithsound

anywhereinthewindow,andthewindowcanbesizedtosuitthepurpose.Onlyasingle

videocanbeplayedinthiswayatonetime,though.Avideohascharacteristicsofboth

sounds and images: the video resides in a file; it is placed in a specific location in the

window, and has a two-dimensional size (a width and height), but the image displayed

changes as a function of time. Also, a video can have sound as one of its properties.

However,becausemultiplevideosmayhavemultiplesoundchannels,onlyoneofthemis

giventhesoundoutputchannel,meaningthatonlyonecanplaysound.

A video is read into a variable in the same way as an image or sound: a function

loadVideo()returnsavariablethatreferencesthedataonanMPEGfilewhichisspecified

byfilenameastheparameter.AvideoisplayedbycallingthefunctionplayVideo()and

passingthevaluereturnedbyloadVideo().Thesmallestprogram thatplaysavideo file

wouldbesomethinglikethis:

fromGlibimport*



startdraw(400,400)

s=loadVideo(“ellipsis.mpg”)

ifs!=None:

playVideo(s)

enddraw()

Thefilebeingopenedandplayedisoneprovidedontheaccompanying

disc, “ellipsis.mpg,” and it has no sound. The variable s represents the video in the

program,andisreturnedbyloadVideo().Itis,infact,areferencetoaGlibclassnamed

Gvideo.IfithasthevalueNone,thennovideofilewasloadedforsomereason:perhaps

the file does not exist or is in a format that can’t be processed. Glib only recognizes

MPEG video files, and even then only MPEG I. The playVideo() function places the

imageintheupperleftcornerofthewindowandbeginsplayingit,soundincluded.

ThereareasmallcollectionofusefulfunctionsinGlibfordealingwithvideos.They

are:

pauseVideo(m):Parametermisavideo.Pausesthevideoifitisplayingorresumesit

ifitispaused

stopVideo(m):Parametermisavideo.Stopsplayingthevideom

rewindVideo(m):Parametermisavideo.Returnsthevideotothebeginning

isVideoPlaying(m):Parametermisavideo.ReturnsTrueifthevideoisplaying

setVideoVolume(m, v): Parameter m is a video. Adjusts the audio volume on the

videomtobethevaluev,wherev=0istheminimumandv=1.0isthemaximum

lengthVideo(m):Parametermisavideo.Returnsthelengthofthevideoinseconds

whereVideo(m):Parametermisavideo.Returnsthecurrentlocationinthevideo,in

secondsfromthestart

getVideoFrame(m):Parametermisavideo.Returnsthecurrentvideoframeplaying

setVideoFrame(m, f): Parameter m is a video. Changes the playback so the next

frameinthevideotoplayisframef

getVideoPixel(m, x, y): Parameter m is a video. Returns the value of the pixel at

location(x,y)intheframecurrentlybeingdisplayed

sizeVideo(m):Parametermisavideo.Returnsthedimensionsofavideoframe.The

videomustbeloaded

videoSize(s):Parametersisastring.Returnsthedimensionsaframeinthevideofile

s,wheresisastring.Usethisforfindingthesizebeforeloadingthefile

locVideo (m, x, y, w, h): Position the video m at position (x,y) in the window, and

makeitwxhpixelsinsize.Doesnotstartitplaying

Example: Carclub – Display the Video carclub2.mpg

(Annotated)

Whenthepkeyispressedthevideowillpause,andwhenpressedagainitwillresume.

Displaythevideoatlocation100,100inthewindowandmakeit200x200pixels.Display

thenumberofthecurrentframeandthecurrenttimeoftheframebeingplayed.

Thisprogramuseseightofthefifteenvideofunctions.Firstthefileisloadedandthe

locationandsizearesetusinglocVideo().Thenthemainprogramstartsthevideoplaying.

Thedraw()functionisresponsibleforupdatingthenumericvaluesdisplayed.Itresets

thebackgroundandthencheckstoseeifthevideoisplaying;itdisplays“Playing”ifso,

or“Notplaying”otherwise.Thecurrentposition,currenttime,andtotaltimeareextracted

anddisplayedusingcallstotext().

Finally the pause feature is implemented. In the function keyPressed() the function

checksthatthekeypressedwas“p,”andifsoitcallspauseVideo().Thisfunctionkeeps

track of whether or not the function is playing and knows whether to start or stop the

video.Hereistheprogram:

fromGlibimport*



defdraw():

globalvid

background(0,200,190)#Clearthebackground,

#settoaqua.

ifisVideoPlaying(vid):#Playing?Printan

#indicator

text(“playing”,10,40)

else:

text(“Notplaying”,10,40)

whr=whereVideo(vid)#Currenttimeofplay

text(“Frame“+str(getVideoFrame(vid)),10,60)

#Currentframe

text(“Length“+str(whr)+”of“+str(lengthVideo(vid)),

40,370)



defkeyPressed(k):

globalvid

ifk==K_p:#Keypressedwasa'p'

pauseVideo(vid)#Pause



startdraw(500,500)

vid=loadVideo(“carclub2.mpg”)#Loadthecarclubvideo

locVideo(vid,100,100,200,200)#Positionitat

#(100,100)

playVideo(vid)#Playit.

enddraw()

A screen shot of this program in action is shown in Figure9.5. Note that the current

time is displayed to 16 or so digits. This can be changed to display something more

reasonable(see:Exercise8).

Therearefourdifferentwaysto“play”avideousingGlib,andeachhasadistinctsetof

prosand cons and a processfor how to manage the video. After loading the video into

variablem:

1.UsingtheGlibfunctions–loadVideo(),locVideo(),play()andsoonisolatethe

programmerfromtheactualvideoclassGvideo.Thesearetypicallyusedwhen

thereareoneortwovideosandthereisnocomplicatedprocessinggoingon.Only

onevideowithsoundcanbeplayed;theotherswillplaymuted.

2.AutoPlay(m)–Thevideomwillplayautomaticallyinthecurrentdisplaywindow.

Theuserhassomecontrol:thevideocanbepausedandcanbelocatedataspecific

locationandsize.Itwillplayattheinternallydesignatedrate(framespersecond)

withsound.Onlyonevideowithsoundcanbeplayedinthisway;theotherswill

nothavethesoundplayed.

3.PlayVideo(m)–Thevideowillplayatitsinternalframerate,butaframewillnot

bedisplayeduntilthedrawVid()functioniscalled.IfdrawVid()iscalledinsideof

theuser’sdraw()functionthentheframeswillbedisplayedattheGlib-specified

framerate,butsomevideoframesmightbemissed.

4.DrawFrame(m,f)–Theframenumberedfofthevideomwillbedrawn.Sound

willnotplay.Thispermitsthebestcontrolofthevideo,becauseeachframecanbe

played at any speed without missing any; or, every second or third frame can be

played;orrandomframescanbeplayed.Thevideocanevenbeplayedbackwards–

simplystartfatthelargestframevalueanddecreaseby1eachtime.

Threeofthesedifferentstylesareillustratedinthetablebelow:

Exercise:ThresholdaVideo(ProcessingPixels)

InChapter7,aprogramwaswrittenthatthresholdedanimage.Itconvertedeachpixel

toagreyvalueandifthatvaluewassmallerthanaspecifiedthresholditwouldbesetto

black;otherwiseitwouldbesettowhite.Eachframeofavideoisanimage,anditshould

bepossibletothresholdeachframeandthendisplayit.GlibprovidesthegetVideoPixel()

functionthatreturnsthevalueofaspecifiedpixelinthecurrentframeofavideo.

Thisexamplewillusedraw_frame()todisplaythevideo,anddraw_frame()willbe

calledfromtheuser’sdraw()function.Aftertheframeisdisplayedeachpixelintheframe

isexamined(getVideoPixel()),convertedtoagreyvalue(grey(p)),andtestedagainsta

threshold;if smallerthan the threshold,it will be drawn as black bycalling fill(0)and

drawingthepixelwithpoint().Otherwise,thepixelwillbedrawnaswhite.Theoriginal

imageisdisplayedatthetopofthewindow,thethresholdedonebelow.Thusthewindow

has to be created initially with double the height of the image to make room for two

copies.

fromGlibimport*



defdraw():

globalframe,v,wid,ht,x

background(200)

draw_frame(v,frame)

foriinrange(0,wid):

forjinrange(0,ht):

p=getVideoPixel(v,i,j)

g=grey(p)

ifg<t:

fill(0)

else:

fill(255)

point(i,j+ht)

frame=frame+1

fill(0)

text(“Original:Frame”+str(frame),10,30)

text(“Thresholded:Frame“+str(frame),10,ht+30)



s=videoSize(“carclub2.mpg”)

startdraw(s[0],s[1]*2)

v=loadVideo(“carclub2.mpg”)

frame=1

wid=s[0]

ht=s[1]

t=100

locVideo(v,0,0,wid,ht)

enddraw()

9.7 SUMMARY

Afacilityhasalreadybeendescribedfordisplayingimagesandgraphics:Glib,andhere

moremediacapabilityisaddedtoGlib,thusbuildingonwhathasalreadybeendiscussed,

sothatsoundandvideocanbedisplayed.Thenew

library is dynamic Glib and offers the same functionality as previously plus sound,

animation,andvideo.

Using mouse position and button presses is a basic form of communication with a

computer. The Glib module keeps track of the mouse using Pygame and continually

updatesthepositionastwovariables:mouseXandmouseYholdthemostrecentxandy

coordinates.IftheuserwritesafunctionnamedmousePressed(),thenitwillbeexecuted

whenamousebuttonispressed.Similarly,whenamousebuttonisreleasedittriestocall

mousereleased().A software graphical button is a rectangle or other area which, if the

mousebuttonisclickedwhilethemousecursoriswithinthatarea,willperformatask;in

otherwords,theclickwhilethecursorisinthatareacallsafunction.

Thekeyboardissimilarlydealtwithbyhavingauser-codedfunctionkeyPressed()and

anothernamedkeyReleased().Theyarepassedthevalueofthekeythatwaspressedas

theparameter.

Animationis performedby rapidlydisplaying drawn images, or frames,one afterthe

other,orbycreatinganddrawinggraphicalobjectsandthenchangingtheirpositions.A

functionnameddraw()canbewrittenbytheprogrammertodrawtheframesmanytimes

eachsecond.

Soundsaredisplayedbyreadingthemfromafileandcallingaplay()functionwhenthe

soundisneeded.Soundscanbemusic,voice,ambiance,orsoundeffects.

Video is the most resource-consuming of the media types. Glib allows videos to be

recalledandplacedinthewindow,andtobeplayedautomaticallyorframebyframe.

Exercises

1.Writeaprogramthatfiguresouthowfastthemouseismoving(pixelspersecond

assuming30framespersecond)anddisplaysthatvalue.

2.Considertheexamplethatprintsacircleatarandompositionwhena“+”keyis

pressed.Modifyitsothatwhenthe“-”keyispressed,thepreviouscircleisdeleted

(nolongerappearsonthescreen).

3.Writeaprogramthatreadslinesfromafileaspairsofx,ycoordinatesonasingleline

anddrawthemall.Eachlinewouldhavefourintegers:

100100200200

whicharethe(x,y)coordinatesofthestartandendpointsoftheline.Intheexample

above,thelinewouldbedrawnbetween(100,100)and(200,200).

4.Implementacircularbutton.Itisrepresentedonthescreenasacircleat(100,100)of

size30pixels.Normallyitisred,butitturnsgreenwhenactivated.Whenamouse

buttonispressedwhilethebuttonisactivated,arectangleisdrawnsomewhere

(random)inthewindow.

5.Implementabuttonthatnormallyhasthetext“Yes”drawnwithinit,butthatchanges

thattextto“No”whenthebuttonisactivated.Pressingitdoesnothing.

6.UseGlibtoimplementatextboxthatpermitsafilenameorothertexttobeentered

whenthemousecursoriswithinthatregiondefinedbythebox.Usethistocreatea

programthatallowstheusertoenterafilenameofanimageandhavetheprogram

displaythisimageinthewindow.

7.ModifytheprogramfromExercise5abovesothatasoundismadewhenthebuttonis

pressed.Aclickingsoundwouldbemostappropriate,butwhateveritisitmustbeof

shortduration.

8.Floatingpointvalues,suchasthecurrenttimeofthevideoinseconds,areoften

convertedintostringsandrequiretenormoredigitstobedisplayed.Writeafunction

thatchangesafloatingpointnumbersothatitwilldisplayinfivedigits,andmodify

thevideodisplayprogramnamedcarclubsothatallfloatsaredisplayedwithonlytwo

digitstotherightofthedecimal.

9.Modifythesimulationofthespaceshuttleconsolesothatvideosareplayedinthe

simulatedscreensinsteadofframe-by-frameanimations.

NotesandOtherResources

ThankstotheestateofcomposerandmusicianandfriendMichaelBeckerforthe

useofthesong‘HoldingOn,’andfortheuseofthe.wavfile.

DownloadforthePygamemodule.http://www.pygame.org/download.shtml

Anexcellentsoundeditorfor.wavand.mp3files.http://www.goldwave.ca/

Anotherexcellentsoundfileeditor.http://sourceforge.net/projects/audacity/

Complete Pygame documentation.

https://media.readthedocs.org/pdf/pygame/latest/pygame.pdf

Convert video files into MPEG-I format. http://video.online-convert.com/convert-to-

mpeg-1

A good tutorial on video formats. http://www.videomaker.com/article/c10/15362-

video-formats-explained

Free software that converts between video formats. http://www.any-video-

converter.com/products/for_video_free/

1.AlSweigart.(2012).MakingGameswithPython&Pygame,CreateSpace

IndependentPublishingPlatform,ISBN-13:978-1469901732.

2.SeanRiley.(2003).GameProgrammingwithPython,CharlesRiverMedia.

3.VicCostello.(2016).MultimediaFoundations,2ndedition,FocalPress,ISBN-

13:978-0415740036.

4.RichardBoulangerandVictorLazzarini(Eds.).(2010).TheAudioProgramming

Book,TheMITPress,Har/DVDedition,ISBN-13:978-0262014465.

5.Sendpoints.(2015).GUI:GraphicalUserInterfaceDesign,ISBN-13:978-

9881383495.

6.MaheshVenkitachalam.(2015).PythonPlayground:GeekyProjectsforthe

CuriousProgrammer,NoStarchPress,ISBN-13:978-1593276041.

CHAPTER10

BASICALGORITHMS

10.1Sorting

10.2Searching

10.3RandomNumberGeneration

10.4Cryptography

10.5Compression

10.6Hashing

10.7Summary

Inthischapter

Analgorithm,asdiscussedinpreviouschapters,isastep-by-stepdescriptionofameans

tosolveaproblem.Assomeonewhoislearningtoprogram,whatarethemostimportant

algorithms? That rather depends on how “important” is defined. Does it reflect

commercialvalue?Numberoftimesitisused?Pedagogicaluses?Sincetherearemany

waysanalgorithmcanbeimportant,thischapterdealswiththemostcommonalgorithms

discussedonprogrammingwebpagesandinintroductorycomputingtexts.Noneofthese

methodsrequireaknowledgeofadvancedmathematicsordatastructures.

10.1 SORTING

Mostpeopleknowwhatsortingisandcansortasmallsequenceofnumbersinafew

seconds.Eachmayhaveadistinctstrategyfordoingit,butfewcan

explaintosomeoneelsehowtosortanarbitrarysetofnumbers.Theythemselvesmaynot

know how they do it; they can simply tell when something is sorted, and have some

processforsortinginmind.Inshort,theprocessofsortingisoneofthesimplestthings

thatishardtodescribe.

Becausesortingissoimportantincomputerscience,ithasbeenstudiedatgreatlength.

Butwhatisit?Sortinginvolvesplacingthingsinanorderdefinedbyafunctionthatranks

themsomehow.Fornumbers,rankingmeansusingthenumericalvalue.So:thesequence

1,3,2isnotinproperorder,but1,2,3isinascending(gettinglarger)orderand3,2,1is

indescending(gettingsmaller)order.Formally,asequencesisinascendingorderifsi<=

si-1foralli.Theactofsortingmeansarrangingthevaluesinasequencesothatthisis

true.Itisclearthatitcanbedecidedwhenasequenceissorted.

So how can a sequence be placed in sorted order? By using a sorting algorithm, of

course.Forallofthefollowingdiscussiononsorting,assumethattheproblemistosort

intoascendingorder.

10.1.1 SelectionSort

Smallsequencesareeasiertosortthanlongerones,andmayprovidesomeinsightinto

theprocess.Thesequence:

84

isnotsortedinascendingorder,buttestingthisiseasyandfixingitistrivial:simplyswap

thetwovalues.Thelongersequence:

849

is also not sorted but is more difficult to sort because it is longer and there are more

combinationsofthenumbersthatareunsorted.Howcanthissequencebeplacedinorder?

Here’soneidea:

1.Findthesmallestelementinthelist.

2.Swapthatelementfortheelementatthebeginningofthelist.

3.Findthesmallestelementintherestofthelist.

4.Swapthatelementforthesecondelementinthelist.

…andsoonuntilthelistissorted.

Thisiscalledtheselectionsortalgorithm,becauseateachstageitselectsthesmallest

oftheunsorteditemsinthelistandplacesitwhereitbelongs.Considerthefollowinglist:

[12,18,5,21,9]

01234-index

Thesmallestelementinthislistis5,atindex2.Swapelement2forelement0:

[5,18,12,21,9]

Theboldelementsaboveareinsortedorder,whichhereisonlytheoneatlocation0.

Fortheremainderoftheelements,repeattheprocessoffindingthesmallestelementand

placingitatthebeginningoftheunsortedlist(element1).Thatmeansswapping9for18,

element4forelement1:

[5,9,12,21,18]

Repeating,itturnsoutthatelement2,value12,isnowthesmallest,andisinthecorrect

place.

[5,9,12,21,18]

Nowthevalue18issmallestandshouldbeplacedatlocation3.

[5,9,12,18,21]

Nowthesortiscomplete.Whenonlyoneremainsitmustbeinthecorrectplace.

Findingthesmallestelementinalistinvolvesthreethings.First,beginwiththeinitial

elementandassumethatisitthesmallest.Identifyitusingitsindeximin.Next,checkthe

valueofallsuccessiveelementsinthelist(fromimin to theendof thelist)againstthe

valueatimin.Finally,inthecasewhereoneofthesuccessivevaluesatindexkissmaller

than the one at index imin, set imin to k to indicate where a new smallest value was

found.Insimple,impreciseEnglish,scanallof theelementsaboveiminandremember

thelocation ofthe smallest one.Presuming thatthe list tobe sorted isnamed data,the

codeforfindingthesmallestelementfromimintotheendofthelistis:

foriinrange(imin,len(data)):

ifdata[i]<data[imin]:

imin=i

Thiscodedoeswork,butitmodifiesimin,whichisusedtodeterminetheloopbounds,

withintheloopitself.Thiscanbeconfusingtosome,andisbadformgenerally.Itisbetter

tocodethisloopas:

imin=istart

foriinrange(iend,len(data)):

ifdata[i]<data[imin]:

imin=i

What happens after this is to swap the smallest value found for the one at location

istart. In most programming languages this would take three statements, which would

looksomethinglikethis:

temp=data[imin]

data[imin]=data[istart]

data[istart]=temp

Oneofthejoys ofPythonisthat thisswapcanbe performedusingadifferent,some

wouldsayprettier,syntax:

(data[istart],data[imin])=(data[imin],data[istart])

Thisisthecore of thealgorithm,andneeds tobedone for allvaluesof imin; that is

from0tolen(data)-1.Thisisanotherforloop,ofcourse,withinwhichthiscodeisplaced.

Thatouterloopwouldbe:

foristartinrange(0,len(data)-1):

Thisisallthatisneededforthesort.Writingitasafunction,itlookslikethis:

defselection(data):

foristartinrange(0,len(data)-1):

imin=istart

foriinrange(istart,len(data)):

ifdata[i]<data[imin]:

imin=i

(data[istart],data[imin])=(data[imin],data[istart])

Thissortingmethodappearstobenaturaltohumans.Itistheonemostoftendescribed

by students when asked how they sort numbers. It is not the fastest in many cases, but

does a small number of swaps. If the data is already sorted it does no swaps; if it is in

reverseorderitdoeslen(data)-1swaps,thesmallestthatcanbedoneandstillsortthelist.

Whenlookingatalgorithmsitiscommontodefineaworstcaseandabestcase,andto

defineperformancenotinsecondsbutintermsofoneoftheoperationsperformed.Inthat

waythenatureofthecomputer,whetheritisfastorslow,doesnotaffecttheanalysis.For

sortingitiscommontoselecttheoperationtobeusedasabasisforcomparisontobethe

compareoperation:data[i]<data[imin].Howmanyofthesearedone?

Thebestcasefortheselectionsortoccurswhenthelistisalreadysorted.Inthatcaseit

willperformclosetoN2comparisons,whereN=len(data).Thisisthesamenumberof

comparisonsneededfortheworstcase,inwhichthelistisinreverseorder.Atleastitis

consistent. However, it minimizes the number of times swaps occur, and if swapping is

expensivethenthiscouldbethesortingmethodtochoose.

Selection sort is unstable. If there are repeated values in the data, then they will of

courseenduptogetherinthefinal,sortedlist.However,ifasortisstabletheywillremain

inthesameordertheywereoriginally.Selectionsort,likemanyothers,doesnotguarantee

this.Itseemsasifthisisaminorthing,butitdoesmatterinsomecases.Consideralistof

namesinalistthataregiven,inorderofsomesortofscore,onawebpage.Namesfortie

scoresshouldalwaysbeinthesameorderonthepage,sothatifthepageisrefreshedora

linkisfollowedthepagelooksthesame.

Itshouldbesaidherethatgenerallythereisnobestsortingmethod.Thepropertiesof

suchamethodwouldbe:

1.Fast.SelectionsortisN2intermsofcomparisons.Thebestonecannormally

expectfromanysortwouldbeN*log(N)intheworstcase.

2.Doesnotneedextraspace.Thismeansthatthearraycanbesortedinplace,with

perhapsatemporaryvariableforperformingswaps.

3.PerformsnomorethanNswapsintheworstcase.

4.Adaptive.Themethoddetectswhenitisfinishedinsteadofloopingthrough

unproductiveiterations.If,forexample,suchamethodisgivenanalreadysorted

list,itwillfinishinasinglepassthroughthedata.

5.Stable.

Nomethodhasallofthesecharacteristics.

10.1.2 MergeSort

Iftherewerea“best”sortingalgorithmthenthiswouldbetheplaceto

describeit.Asthereisnot,perhapsthebestthingtodowouldbetolookatanalgorithm

thatisquitedifferentfromtheselectionsort,andthathaspropertiesthatitdoesnothave.

Themethodnamedmergesortfitsthatdescriptionnicely:itisanN*log(N)sort,itdoes

needextraspace,anditusesmorethanNswapsbutitisstable.

Merge sort is an example of a divide and conquer style of algorithm, in which a

problemisrepeatedlybrokenupintosub-problems,oftenusingrecursion,untiltheyare

smallenoughtosolve;thesolutionsarecombinedtosolvethelargerproblem.Theidea

behindmergesortistobreakthedataintopartsthatcanbesortedtrivially,thencombine

those parts knowing that they are sorted. Using the sample data from the selection sort

example, the first step in the merge sort is to split the data into two parts. There are 5

elementsinthislist,andthemiddle

elementwouldbeat5//2,or2,sothetwopartsare:

[12,18][5,21,9]

Splittingagain,thefirstsethas2elements,themiddlebeingat0;thesecondsethas3

elements,sosplitat1:

[12][18][5][21,1]

Thefinalsplitbreaksthedataintoindividualcomponents:

[12][18][5][21][1]

The splitting is done in such a way that the original locations are remembered. This

happensintherecursivesolution,butcouldbedoneinotherways.Onewaytovisualize

thisisasatreestructure:

Thiscompletesthedivide portionof thedivideandconquer. Now that the individual

elementsareavailable,itiseasytosortthem,aspairs.Onthelowerrightthepair[21]and

[9]isoutoforder,sotheymustbeswappedwitheachother.Nowtheyaresorted.Onthe

nextlevelupwards,lookingfromlefttoright,theelementsaresorted,althoughmostare

singleelements:

Moving up again, [12] and [18] are combined to make [12,18], a sorted pair. On the

right,thesingleton[5]ismergedwiththepair[9,21]bylookingatthebeginningofeach

listandcopyingthesmallestelementofthepairintoanewlist:

Theresultis:

Ateach stage,the listscontain moreelements andthey aresorted internally,smallest

elementatthebeginning.Combiningapairoftheseissimplyamatteroflookingatthe

elementatthebeginningofeachandcopyingthesmallestonetotheresultuntilthelists

areempty.Thenext,andfinal,mergeinthissetofdatawouldbe:

Step List1 List2  Mergedlist 

1 [12,18] [5,9,21] [5] 5issmallerthan12,copy5

2 [12,18] [9,21] [5,9] 9issmallerthan12,copy9

3 [12,18] [21] [5,9,12] 12issmallerthan21,copy12

4 [18] [21] [5,9,12,18] 18issmallerthan21,copy18

5 [] [21] [5,9,12,18,21] Firstlistisempty,copy21

Thefinallistis[5,9,12,18,21]whichissorted,aspromised.

Oncethedatahasbeensplitintoindividualcomponents,themergestagecreatessorted

pairs,thenextmergecreatessetsof4sortednumbers,thenext8,andsoon,doublingeach

timeuntiltheyareallsorted.Alogicalwaytowritetheprogramistouserecursion,where

eachrecursivecallsplitsthedataintwomorepartsuntilthereisonlyoneelement.The

lowestlevelofrecursioncombinestheindividualsintosortedpairs,andreturnstothenext

levelwherethepairsarecombinedintofours,theneights,andsoonuntilatthehighest

levelthelistiscompletelysorted.Writtenasarecursivefunctionthisis:

data=[12,18,5,21,9]

defmergesort(data):

n=len(data)#Forthiscalltherearenelements

#tobesorted

ifn<=1:#Dividethedataintotwoparts

return#unlessn-1,whichmeanssortingis

#complete

middle=n//2#Indexoftheelementinthemiddle

lower=data[:middle]#Lowerindexes,ortheleft

#sublist

upper=data[middle:]#Largerindices,ortheright

#sublist

mergesort(upper)#Sorttheleftsublist

mergesort(lower)#Sorttherightsublist



#TherearenowtwosortedsublistsoflengthN//2.

#MergethemintoonelistoflengthN

(i,j,k)=(0,0,0)

whilei<len(lower)andj<len(upper):#Onesublist

#maybeshorter…

iflower[i]<=upper[j]:#Iftheelementatindexi

#ofthe

data[k]=lower[i]#leftlistissmaller,

#copyittotheresult

i=i+1

else:

data[k]=upper[j]#Otherwisecopytheelement

#atindexj

j=j+1#oftherightsublistto

#theresult

k=k+1#Resultgetslongerby1element



foriinrange(i,len(lower)):#Iftheleftlistwas

#longer,copy

data[k]=lower[i]#theremainingitemsto

#theresult

k=k+1

forjinrange(j,len(upper)):#Iftherightlistwas

#longer,copy

data[k]=upper[j]#theremainingitems

#totheresult

k=k+1

Themergesortisnotasobviousaswasselectionsort,butisfasterinmostcases.Ithas

anotherinterestingapplication:itcanbeusedtosortfiles.Ifafilecontains,forexample,a

billiondatasamplesthatneedtobesorteditisunlikelythattheycanbereadintomemory

andsortedwithaselectionsort.Howthentosortthem?

10.2 SEARCHING

Searching is the act of determining whether some specific data item appears in a list

and,ifso,atwhichindex.Itseemslikeanoddthingtodo;whatcanbedoneknowingthis

information?Itisespeciallyusefulwhenmultiplelistsholddifferentdataconcerningthe

sameitems.Anemployee,asoneexample,mighthavetheirvariousdatasavedasaname

list, an employee ID list, phone number, office number, home address, and so on. The

same index gives information of the same individual for each list. Thus, search the

employeeIDlistfor18762;ifthatindexis32,thentheemployee’snamecanbefoundat

name[32].

OfcoursePythonhasbuilt-inoperationsonalistthatwilldothis:

if18762inemployeeID:#IsthisIDamemberofthelist?

k=employeeID.index(18762)#Whatistheindexof

#18762?

A reason to examine searching algorithms is that not all languages possess these

specificfeaturesandnotallprogramsarewritteninPython.Anotheristhatsomeonehad

toimplementtheoperationsforthePythonsystemitself,andtheyhadtoknowhow.Did

theydoagoodjob?Arethebuilt-inoperationsasfastasonesthataprogrammercould

codeforthemselves?Thiswillbediscoveredusinganexperiment.

10.2.1 Timings

AnysectionofcodeinPythonrequiressomeamountoftimetoexecute.Thespecific

amountdependsonmanythings:thecomputerbeingused,the

Pythoncompiler,thespecificstatements,thedata,andrandomeventssuchaswhatother

programsareexecutingonthatcomputeratthesametime.However,ifitisimportantto

knowwhetherasectionofcodeisfasterthananother,therearetimingfunctionsthatcan

provide a pretty good idea. The time module includes a function named clock() that

returns(onWindows)theelapsedtimeexpressedinsecondselapsedsincethefirstcallto

thisfunction.OnLinuxitbehavesdifferently,andtime.time()maybeabetterchoice.Be

suretolookitup.

Timing a section of code is done by calling time.clock() before and after the code

executesandsubtractingthetwotimes.Forexample,timingasearchofalistusingthein

operatorcouldbedonethisway:

importtime



list=[19872,87656,10982,18756,56344,29765,12856,12534,

88768,90012]

t0=time.clock()

if90012inlist:

found=True

t1=time.clock()

print(“Timewas“,t1-t0)

Thisprintsthemessage:

Timewas2.062843880463903e-05

That’s a pretty small time, as is to be expected. When run again the result was

3.07232e-06; running again gets 2.194514766e-06 and again 7.9002531e-06. These

numbers are all small but very different. Since that is true it is better to time many

executionsofthecodeanddividebythenumberoftimesitran:

t0=time.clock()

foriinrange(0,10000):

if90012inlist:

found=True

t1=time.clock()

print(“Timewas“,(t1-t0)/10000)

This yields more consistent results: 5.5284e-07, 5.5951e-07, and 5.415e-07 in three

different trials. Averaging the result of multiple trials gives even better results, because

spurioustimesonanyonerunwillbeaveragedout.

10.2.2 LinearSearch

Considerthelistthatwasusedinthetimingexample:

list=[19872,87656,10982,18756,56344,29765,12856,12534,

88768,90012]

Findingwhetherthetargetnumber90012appearsinthislistisamatteroflookingat

eachelementtoseeifitisequaltothetarget.Ifsotheansweris“yes”and,bytheway,the

indexatwhichitwasfoundisalsoknown.Thiscanbedoneinabasicforstatement:

index=-1

foriinrange(0,len(list)):

iflist[i]==target:

index=i

break

#Ifthevalueofindexis>=0thenitwasfound.

Thisalgorithmlooksateachelementasking“Isthisequaltothetarget?”When/ifthe

targetislocated,theloopendsandtheanswerisknown.Ifthetargetisnotamemberof

thelist,thenthealgorithmhastoexamineallmembersofthelisttodeterminethatfact.

Thus,theworstcaseiswhentheelementisnotinthelist,anditrequiresNcomparisonsto

findthatout.Iftheelementisapartofthelistthen,ontheaverage,itwillrequireN/2

comparisonstofindit.Itcouldbethefirstelement,orthelast,oranyoftheothers,which

averagesouttoN/2.

Ifthelistisinsortedorderthentheloopcanbeexitedassoonasitisknownwhether

theelementisinthelistornot.Thatis,assoonasthetargetissmallerthantheelementit

isbeingcomparedagainstinthelist,itisclearthatitcan’tbeamemberofthelist,andthe

loopcanbeexited.Thisnormallyspeedsuptheexecution,butthepenaltyisthatthelist

hastobesorted,andthetimeneededtodothis(onlyonce,ofcourse)hastobetakeninto

account.

10.2.3 BinarySearch

Ifthelisthasbeensortedthenthereisafasterwaytosearchforanelement.Thelistcan

bedividedintotwopartsbylookingatthevalueinthemiddleofthelistandcomparingit

tothetarget.Ifthetargetissmallerthanthemiddleelement,thenitwouldhavetobein

thelowerindices(left),otherwiseitwouldhavetoexistinahighervaluedindex(tothe

right).Whatthismeansforperformanceisthatthesearchareaiscutinhalfeachtimea

comparisonisdone.

Thisidea seems simple,but is actuallydifficulttoget right in an implementation. At

conferences where many PhDs in computer science are presenting papers, it has been

foundthatfewerthan10%oftheparticipantscancodeabinarysearchthatworksthefirst

time.Theterminalconditionsaretricky:inparticular,howcanitbedeterminedthatthe

targetisnotinthelist?OK,sothedetailsarecrucial.Atthebeginningthereisalist,and

itslengthisknown.Theindexofthemiddleelementisknowntoo,andthelistissorted.

So:findtheindexofthemiddleelement:

istart=0

iend=len(list)

m=(iend+istart)//2

Ifthetargetisinthelist,isitatasmallerindexthanm(i.e.,islist[m]>target):

iflist[m]>target:

Ifso,don’tbotherlookingatanyindexbiggerthanm.Inotherwords,thelargestindex

tolookatwouldbem-1:

iend=m-1

Ifthetargetisinthelist,isitatalargerindex(i.e.,islist[m]<target)?Ifso,don’tlook

atanylocationswithanindexlessthanm;inotherwords:

eliflist[m]<target:

istart=m+1

Iftarget=list[m]thenithasbeenfoundandthealgorithmterminates.

else:

returnm

Thiscodehastoberepeateduntilthetargethasbeenfound,orithasbeendetermined

thatitisnotinthelist.Theloopconditioniscritical.Theloopcontinuessolongasistart

<=iendsothatifthefinalstepfindsthetargetinthelist,thenitwillreturntheindex.If

theloopexitswithoutfindingtheelement,thentheindexvalueis-1.Thefinalcode,asa

function,is:

defsearch(list,target):

istart=0

iend=len(list)

whileistart<=iend:

m=(iend+istart)//2

iflist[m]>target:

iend=m-1

eliflist[m]<target:

istart=m+1

else:

returnm

returnNone

The speed of the binary search depends on the fact that it is searching a randomly

accessibledatasetlikeaPythonlistoraJavaarray,andnotafile.Itwilltakeontheorder

of log(n) probes into the list to find what it is looking for or to determine that it is not

there.

Timingthebinarysearchgaveanexecutiontimeof3.305e-06seconds,stillslowerthan

thebuilt-inoperation.

10.3 RANDOMNUMBERGENERATION

Pythonoffersarandomnumbermodulenamedrandomthatoffersabroadcollectionof

random number generation facilities. How is it possible to generate a random number

usingsoftware?Shouldn’tacomputerprogramexecuteconsistentlyandalwaysproduce

thesameanswereachtime?Yes,itshould.Theresolutionofthisapparentproblemliesis

thedefinitionofrandom.

First,randomnessisdefinedonlyforcollectionsofeventsornumbers.Onenumber,or

even a small collection, can’t be said to be random. Randomness reflects the lack of a

pattern,andonlyoneortwoeventsdon’treallydisplayapattern.Randomnessismoreof

a statistical property of a sequence, and is not necessarily related strictly to

unpredictability. After all, if a computer program can generate random numbers, then it

shouldbepossibletopredictthenextoneitwillgenerate.

Arandomnumbergenerator(RNG)onacomputerisreferredtoaspseudo-random;itis

not truly random, but exhibits properties of randomness. These properties can be tested

statistically. A typical RNG returns a floating point number between 0.0 and 1.0. This

value can easily be transformed into a random number, either real or integer, in any

desiredrange.Adierollisanintegerbetween1and6inclusive.AnRNGfunctionnamed

rand01()canbeconvertedintoadierollas:

int(rand01()*6+1)

Ifthenumbersgeneratedbyrand01()arerandom,thenitshouldproducedierollsthat

eachhaveaprobabilityof1/6.Ifnotthenthereisabias.

If a coin is flipped many times and the sequence HTHTHTHTHTHTHT results, the

probabilityofHorT(headsortails)is0.5,or50%,whichiswhatwouldbeexpected.Ifa

sequencehasthecorrectpercentagesforeachoutcome,thenitpassesthefrequencytest.

Yetthissequenceisprobablynotrandombecauseoftheobviouspatternintheresults.The

frequencytestisnotenough.

A second test would consider pairs in the sequence and compare the probability of

occurrence of each pair against the theoretical. In the coin toss there are four possible

pairs:HH,HT,TH,andTT.Eachpairshouldappearwithequalprobability,andyetthe

stringaboveshowsonlyHTinstances.Itisnotrandom.Astandardsuiteofrandomness

testscalledDiehardincludesamorecomplexversionofthistest,involvinggroupsoffive

elementsinthesequence,eachonehavingatheoreticalprobabilityof1in120.Thiskind

oftestcanbecalledtheserialtestoroverlappingpermutations.

AthirdtestinvolvesusingtheRNGtogeneratepokerhands.Theprobabilityofspecific

handsiswell-known,andanyconsistentvariationfromtheseprobabilitieswouldimplya

flawintheRNG.Thisisthepokertest.Anycomplexrandomgamecouldbeused,andthe

Diehardsuiteusesthegameofcraps.

There are many other tests that could be applied, and all are based on generating

complex situations and comparing the theoretical distribution of properties generated

againstwhattheRNGcreates.So,nowthattherearewaysoftestinganRNG,canonebe

writteninPythonandtested?

10.3.1 LinearCongruentialMethod

Pseudo-random number generators basically shuffle the bits around in a number in

complexandnon-repeatingways;atleast,theydon’trepeatforalargenumberoftrials.A

historicallycommonmethodfordoingthisistocalculateavaluethatisboundtobelarger

thantheplacewhereitistobestoredandkeeponlytheremaindereachtime.Thevalueof

thisremainderispseudo-randomundercertainconditions.Alinearequationcanbeused

andisfasttocalculate:

Xi+1=(aXi+b)modm(10.1)

whereXiisthepreviousrandomnumberinthesequenceandXi+1isthenextone.The

valueofmshouldbequitelargeanditshouldbeaprimenumber.Manycomputershave

used a 32-bit integer size, and as it happens 232 – 1 is a good value for m ( =

2147483647).Pythonintegerscanbeaslargeasdesired,solargervaluescouldbeused.

Keepingthen to 32 bits is accomplished using an and operation and masking the result

witha32-bitconstant:0xFFFFFFFF.

Valuesforaandb aremore flexible,but largevalues area good idea,and toomany

factors can cause problems. One good set of values is a=69069 and b=362437. This

methodusesapreviousvaluetocalculatethenextone,soaninitialvalueisrequired.This

iscalledtheseed,anditmustbepossibleforauser/programmertobeabletosetthisseed

valuetowhatevertheychoose.IfnotthentheRNGwillgeneratethesamesetofvalues

eachtimeitis used.That’s actuallyagood thingfordebugging, becausewhentracking

downaproblem,itisimportantthattheprogrambehaveconsistently.

ThebasicRNGdescribedabovewouldbe:

_xseed=76951



defirand01():

global_xseed

_xseed=(69069*_xseed+362437)&0xFFFFFFFF

return_xseed

Thisfunctionreturnsanumberbetween0and2147483647,andresetstheseed(_xseed,

aglobal)eachtime.It’sagoodstart,butwhatiswantedisafunctionthatreturnsanumber

between0and1;so,asecondfunctiondoesthissimplybydividingtheaboveresultby

2147483647:

defrand01():

returnirand01()/0xFFFFFFFF

Afunctionthatcansettheseedisneededtoo:

defsetseed(x):

global_xseed

_xseed=x

AcommonlyusedfunctioninthePythonrandompackageisrandrange(a,b),which

returnsarandomintegerbetweenaandb.Thecodeforadiehasalreadybeenwritten,and

sothemathisknown.Usingthetoolsjustwritten,thisiscodedas:

defrandrange(n1,n2):

x=(int)(rand01()*(n2-n1+1))+n1

returnx

How can a random number generator be made to generate a different set of numbers

everytimeaprogramstartsusingit?Simplybysettingtheseedtoanumberthatishardto

predict. Such a number is found in the low bits (milliseconds and microseconds) ofthe

systemclock.Itisimpossibletopredictwhatthesewillbe.SorandomizingtheRNGcan

beaccomplishedlikethis:

defrandomize():

global_xseed

_xseed=int(time.time())&0xFF

Thetime.time()functionreturnsthenumberofsecondssinceafixeddateinthepast,

calledtheepoch.ThisdateisusuallyJanuary1st,1970,midnight.

Othermethodsforgeneratingrandomnumbersexistandarecommonlyused.Python’s

random class uses the Mersenne Twister algorithm, which is often seen as a default in

programming languages but is a trifle slow. Blum-Blum-Shub resembles the linear

congruentialbutusestherelationxi+1=xi2modmwheremistheproductoftwoprime

numbers.Dozensmoremethodsexist.Therearealsopracticalmethodsforgeneratingtrue

randomnumbers,andthesearebasedonspecifichardwarethatcapturesatrulyrandom

process such as radioactive decay, the photoelectric effect, or random electromagnetic

noise.

Finally,therearewebsitesthatwillofferrandomnumbersandsequencesonrequest.

Random.org will serve up true random numbers, for example, and there are dozens of

othersuchsites.Thetimeneededtoconnecttoaserveranduploadarandomnumberis

considerable, so they should be used knowing the tradeoff of time for random number

quality.

10.4 CRYPTOGRAPHY

Cryptographyinvolvessendingmessagesthatonlycertainintendedpeoplecanreceive

andunderstand.Thisinvolvescodesandciphers.Acodesubstitutesonestringforalonger

message;thereisacodebookinwhichthecodestringsareassociatedwiththeirrelevant

message. So, the string “A76” could mean “retreat 100 meters.” Code books had to be

changedregularlybecauseeventuallyonewouldfallintothehandsofsomeonewhowas

notsupposedtohaveone.

A cipher is an algorithm that converts one string of characters into another one of

generallythesamelength.Itcanoperateonbits,oncharacters,oronblocksofcharacters.

Acipherdoesnothaveacodebookbutdoeshaveakey,whichisastringofnumbersor

characters, that the algorithm uses to transform the original string (called the plaintext)

intotheencryptedstring(calledtheciphertext).Theciphertextcanbetransmittedsafely

becauseitcannotbeunderstoodwithoutthekey.

Cryptographyhasbecomemuchmoreimportantinthelast30yearsorso.It’snotjust

that the world is an uncertain place. It is more that people wish to share private

information across the Internet. If a purchase is made with a credit card, then the card

number should be encrypted before sending it to the seller. Access to certain sites that

have valuable services or information requires a password. Installing new software

requiresanaccesskey.Theseareallexampleswhereencryptionisrequired.

Itshouldbementionedthatthesecuretransferofinformationdependsonoperational

securityaswellasonencryption.Someonewithapasswordcan access allservicesand

dataassociatedwiththatpassword,sokeysandpasswordsmustbeprotected.Thisaspect

isbeyondtheabilityofaprogrammertocontrol,andisoftenthewaysecuritysystemsare

broken.

Thereissometerminologythatneedstobeunderstood.Asymmetrickeysystemuses

one key to encode and the same key to decode. Asymmetric systems like public key

systemsuseonekeytoencryptthemessage,akeythatanyonecanknow,andasecond,

privatekeythatonlytherecipientknowsandisusedtodecrypt.Ablockcipherappliesa

keytoacollection(block)ofdata,oftenasizeof64,128,or256bitsatatime.Astream

cipher is usually a symmetric key cipher that encrypts a plain text character with a

characterfromthekey.It’salsocalledastatecipherbecausethe encryptionofthe next

characterdependsonwhathashappenedbefore.

Knowing a little about encryption is important, but it is also important to understand

that it is a very complex and highly mathematical subject, and requires a significant

amountofstudytobecomeanexpert.

10.4.1 One-TimePad

Having just said how complex the field of cryptography is, the first algorithm to be

examinedis,infact,ratheroldandperfectlysecure,ifdifficulttouseinpractice.Suppose

personAwishestosendpersonBthemessage“Meetyouatninepmatlocationalpha.”

Encodingthisrequiresasequenceofrandomcharactersatleastaslongasthemessage.In

actual use, this cipher often used pages from books as keys, books that were easily

accessiblebybothparties.Inthiscasethefollowingtextisusedasthekey:“itwasthe

bestoftimesitwastheworstoftimes.”Theencryptionprocess,knowntoboth, and in

factnotreallyasecret,istoapplytheexclusiveORoperationtocorrespondingcharacters

inthemessageandthekeytoproducetheciphertext:

TheexclusiveORoperationisabit-by-bitlogicaloperatorthatis0ifthetwobitsare

equalandis1otherwise.Itisappliedtothenumericalrepresentationsofthecharacters.

Thisisquite handybecause itis veryfast andcan easilybeaccomplished usingsimple

hardware.Considerthefirstcharacterinthemessage“m.”Thefirstcharacterinthekeyis

“i.”TheASCIIcodesarethenumbers109and105respectively,orinbinary:

01101101109“m”

01101001105“i”

000001004ExclusiveOR

One interesting observation here is that different characters can be encrypted to the

same cipher text byte, as in the above string where “s” and “t” both encrypt to 26.

Anyway,nowthisciphertextistransmittedtoBandisdecodedinexactlythesameway

that it was encoded: apply the exclusive OR between the ciphertext and the same key

(symmetrickey):

ThePythoncodethatcandothebasicencryptionis:

pt=“meetyouatninepmatlocationalpha”

key=“itwasthebestoftimesitwastheworstoftimes”

ct=””

xt=””



foriinrange(0,len(pt)):

v=ord(pt[i])^ord(key[i])

print(v)

ct=ct+chr(v)

print(ct)

Theexclusive-ORoperatoris“^”,andtheexpressionord(pt[i])^ord(key[i])performs

theXORonthemessageandthekeybytes,asnumbers.Doingitagainwiththesamekey

getsthemessageback.

The reason that this is called a one-time pad is that the key can only be used once,

otherwise the cipher is not secure. The security lies in the randomness of the key, and

reusing it reduces the randomness. Eventually if the same key is used often enough, an

observer, someone who can intercept all of the messages, can extract the pattern and

determinethekey.Soinpracticethekeyswerewrittenonpadsofpaperand,onceused,

weredestroyed.Keepingthepadssynchronizedbetweenthesenderandreceivercanbea

problem,especiallyiftherearemanyofeach.Hence,althoughthesystemissecure,itis

notusedveryoften.

10.4.2 PublicKeyEncryption(RSA)

A public key system is commonly used for secure communication across computer

networks,andinvolvesonekeyforencryptionandanotherfordecryption.Therearemany

variationsonthebasicidea,somebeingmuchtoocomplextodiscussinafewpages,but

theRSAalgorithmisrelativelysimple,quitepopular,andverysecure.Itisnamedforits

inventorsRivest,Shamir,andAdleman.

ThemathematicalideathatunderliesRSAisthatonecanfindthreeverylargeintegers

e,d,andn

for any m, and that even knowing e and n or even m, it can be extremely difficult to

findd.Thevaluesdandearethekeys,andmisthemessage.

So,encryptingamessagewouldworkasfollows:AsendsmessagemtoBusingB’s

publiclyknownencryptionkeye:

The value of c is the ciphertext and can be transmitted to B. When B receives the

message,itisdecryptedusingtheirprivatekeyd:

wheren> m.Thisworks becauseof the originalassertionthat (me)d mod n =m.The

successofthismethoddependsonafewotherthings:cancdmodnbecalculatedquickly

enough for large numbers (i.e., 500 bits), and can the numbers d,e, and n be found to

makethiswork?

Thefirststepindeterminingthekeysistoselecttwoverylargeprimenumberspandq.

Let n = p*q. A large number in this context has hundreds of bits, but that creates a

cumbersomeexample,sosmallernumberswillbeusedinthisdiscussion.

Nowcalculateφ(n)=(p-1)*(q-1)andfindanintegeresothateandn are co-prime;

thatisthegreatestcommondivisorbetweeneandnis1.

Letd=(e-1)modφ(n)sothatd*emodn=1.Thiscanbefoundusingasearch,which

maybeinfeasibleduetothesizeofthenumbers:

foriinrange(e,n):

if(i*e)%j==1:

d=i

break

oramathematicalprocessthatusesEuler’stheoremcangivetheanswerfaster,andcode

hasbeenprovidedforthisontheaccompanyingdisc.

Example: Encrypt the Message “Depart at Dawn” Using

RSA

Thefirststepistodeterminesomekeystouseandtodistributethepublickey.Using

theprimenumbers73and83(fartoosmallforarealsituation)thedeterminationofthe

keysis:

nis6059andϕ(n)is5904

eis17,chosenbecauseitisprime.Nowfinddsuchthatd*emodn=1.Searchingforitis

practicalfornumbersthissizeandonegets:

d=3473

Sothepublickeyis(17,6059)andtheprivatekeyis(3473).

Themessageis14characterslong,andwouldbe112bits;nisonly10bitslong,andthe

messagehastobeshorterthanthis.Inthisinstancethemessagecanbesentonecharacter

atatime,butthisisgenerallypoorpractice.Normallylargerblocksofdataareencrypted

at one time. The plaintext string is converted into integers using ord(),and each oneis

encryptedusingtheformula:

Anexamplewouldbe:

message=“Departatdawn”

imessage=()

cmessage=()

foriinrange(0,len(message)):

m=ord(message[i])

imessage=imessage+(ord(message[i]),)

c=(m**e)%n

cmessage=cmessage+(c,)

Nowthemessageconsistsof14blocksof1charactereach.Itcanbetransmittedtothe

recipient,whoisnormallynamedBorBob,inthisform.Thesender,namedAorAlice,

hadaccessto thepublickey only,which isall thatisneeded toencryptthe message.It

cannotbedecryptedusingthepublickey.

dgivend⋅e≡1(modφ(n))

Bobreceivestheciphertextmessage,whichinthiscaseis:

(4652,3518,4274,5770,1663,344,2498,5770,344,2498,2144,5770,1725,4601)

Hetakeseachblockanddecryptsitusing:

ThePythoncodeforthiscouldbe:

dmessage=()

foriinrange(0,len(cmessage)):

c=cmessage[i]

m=(c**d)%n

dmessage=dmessage+(m,)

Theresultingdecryptedmessageis:

(68,101,112,97,114,116,32,97,116,32,100,97,119,110)

Whichis the original message. Noticethat because only oneblock per characterwas

encrypted,theeffectisthatofasubstitutioncipher,inwhicheachletterhasbeenreplaced

byanother.This is very easy to decrypt by noting patterns of letters and frequencies of

letters in the language; the letter “e” is usually the most commonly used letter in an

Englishmessage.Thatiswhythemessageisencryptedasblocksofcharacters.Itishighly

unlikelythatalargeblockwouldberepeatedexactly,andifitwereitwouldbedifficultto

guesswhatitwasanyway.

10.5 COMPRESSION

A little arithmetic will start this discussion. The song “Blackbird” by The Beatles is

almostexactly 4 minutes long. This is 240 seconds, and if itwas converted into digital

form,itwouldbesampledatarateof44,100sampleseachsecond.Thismeansthatthe

songhas240*44100=10.6millionsamples.Butwait—it’sstereo,sodoublethatto21.2

millionsamples.Atypicalsampleis16bits,sothisworksoutto42.4millionbytes;42

megabytes!TheMP3fileforthissongistypically1.9megabytes.Howisthatpossible?

Byusingacompressionalgorithm.

Datacompressionisallaboutwaystotake,forexample,100bytesofinformationand

turnit into 10bytes while losingnone of theessential message. Ofcourse, compressed

datais incomprehensible justto look at and mustbe decompressed in orderfor it to be

used. Data is often compressed before storing it in a file to reduce its footprint on the

storage device, or before transmitting it along a communications channel to take better

advantageoflimitedbandwidth.

The question of how a string of data bytes can be made shorter while losing no

importantinformationremains,andasimpleexamplemaybeinorder.Consideracartoon

image.Thesehavearelativelysmallnumberofdistinctbutvividcolors,usuallylessthan

10colorsandthecolorvariationwithinanyregionissmall.TheexampleimageinFigure

10.1isinPNGformandis23.2Kbytesinsizeat400x456(=182400)pixels.Asrawdata

itwouldbealittleover182Kbytesinsize,547KbytesifRGBcolorwasused.

A simple compression technique that will work in this case is called run-length

encoding. In its simplest form data bytes are preceded by a count indicating how many

repetitionsofthatvaluewereencounteredinthedata.Soiftherewasasectionofdata:

11000000222121200000022222

Thiswouldbeencodedas

21 60 32 11 12 11 12 50 52

Twoones six

zeros

threetwos a

one

a

two

a

one

a

two

fivezeros fivetwos

In this case the original data required 26 bytes and the compressed data required 17

bytes. The new data takes 65% of the space that the original does. This is not a huge

saving,butisprobablyworththeeffort.Itdoesdependheavilyonthenatureofthedata.

ConsidertheimageofFigure10.1.Thecolorareasareuniformandratherlarge,sothis

imagewouldbeanidealcandidateforrun-lengthencoding.Whenwritingtheprogram,it

isimportanttouseabinaryfileandconvertthevalueandcountintounsignedbytesbefore

writing them to the file. This is a new data type called an unsigned byte that was not

discussedinChapter8, and hasthe code“B.”So, writingthecountand valuecouldbe

donelikethis:

s=pack(“BB”,n,v[1])

f.write(s)

Theentireprogramthatwillrun-lengthencodetheimagewillreadtheimagefileand

collectidenticalpixels,countingthemastheyarecollected,untilachangeinpixelvalue

occurs.Thenthe(count,value)pairiswrittentothefile.Alsothepairwillbewrittenif

255pixelshavebeencollected,sincethatisthebiggestnumberthatcanbecountedin8

bits.Theresultisabinaryfileofpairsofnumbers(count,value)thatrepresentthepixels

intheimage.Asthereareonlytwocolors,valuecanbe0or1,0beingwhiteand1being

green;ingeneraltherecanbe256distinctvalues.Theencodingprogramlookslikethis:

fromstructimport*

importGlib

defemit(v,n,f):#Writeapairofbytes(count,value)

s=pack(“BB”,n,v[1])#”'B'isunsignedbyte.

f.write(s)



Green=(123,210,0)#Theobjectcolor

White=(255,255,255)#Thebackgroundcolor



Glib.startdraw(400,456)

b1=Glib.loadImage(“b1.png”)#Readtheimage

outf=open(“b1.txt”,“wb”)#Opentheoutputfile

Glib.image(b1,0,0)#Displaytheimage

count=0

value=Glib.getpixel(b1,0,0)#Readapixelvalue

#initially

forjinrange(0,456):

foriinrange(0,400):#Foreveryimagepixel

ifcount==255:#Largestpossiblecount.

emit(value,count,outf)#Write(255,value)

count=0#Resetthecount

c=Glib.getpixel(b1,i,j)#Getthenextpixelvalue

ifc==value:#Sameasbefore?

count=count+1#Yes.Incrementthecount

else:#No,different

emit(value,count,outf)#Writethecountand

#value

count=1#Resetthecount

value=c#andthevalue

ifcount>0:#Aftertheloopendsaretherepixelsto

#write?

emit(value,count,outf)#Yes,sodoit.

outf.close()

Glib.enddraw()

Thedecodingprogramreadspairsofunsignedbytesfrom the binaryfile,andcreates

pixels.Apair(12,0)wouldbe12whitepixels,forinstance.Apair(12,1)couldbe12

pixelsofsomeothercolor,andthisprogramwritesthepixelssoitdecideswhatcolorthat

willbe.Itwillreadpairsanddrawpixels,intoanimageof400columnsand456rows,

untilallareaccountedfor.Aprogramthatdoesthis(nottheonlyonepossible)is:

fromstructimport*

importGlib



Glib.startdraw(400,456)

inf=open(“b1.txt”,“rb”)#Opentherunlengthencoded

#file

i=0

j=0

cols=400#Thesizeisknown,butcouldbea

rows=456#partofthedatafile.



whileTrue:

s=inf.read(2)#Reada(count,value)pair(bytes)

iflen(s)<=0:#Endoffile?

break#Yes.Exitloop,stopdrawing.



c,v=unpack(“BB”,s)#Converttointegers

ifv==255:#Backgroundpixel?(White)

Glib.fill(255,255,255)

else:#Objectpixel?(Green)

Glib.fill(123,210,0)



forkinrange(0,c):#Drawthepixelstothe

#screen.

ifi>=cols:#Atendofcolumn,add1torow

i=0

j=j+1

Glib.point(i,j)#Drawasa'point'

i=i+1#Nextpixel(increaseX)

ifj>=456:#Lastrow

break

Glib.enddraw()

Themorecomplexthedatais,inthiscasemeaningthemoredistinctvaluesthedatacan

take,thelessusefulthisencodingmethodwillbe.Insomecasesitcanmakethefilesize

larger that the raw data would have been. In the case of this particular image, the run-

lengthencodedfileisabout6Kbytes,asopposedtohalfamillionbytesthatwouldhave

beenneededfortherawimage,savedaspixels.Still,thisservesasabasicproofthatitis

possible to compress a data file without losing any information. There are, of course,

many more algorithms that will compress data to a greater extent and with fewer

constraints.

10.5.1 HuffmanEncoding

Ifatypicaltextfileisexaminedcarefully,itcanbefoundthatthevastmajorityofthe

fileconsistsofrelativelyfewcharacters.Asageneralestimate,over95%ofthecharacters

canbe accounted forby between 25–30 distinctvalues. Acoding scheme thattook this

intoaccountwouldreducethesizeofatextfile,andperhapsitwouldgeneralizetoother

kindsoffile.Forexample,inmanyfilesthevalue0isthemostcommon,andgivingita

smallerrepresentationthan,say,9mayreducetheoverallfilesize.

Thisisnotreallyanovelidea.TheinternationalMorsecodeisbasedonthisideaand

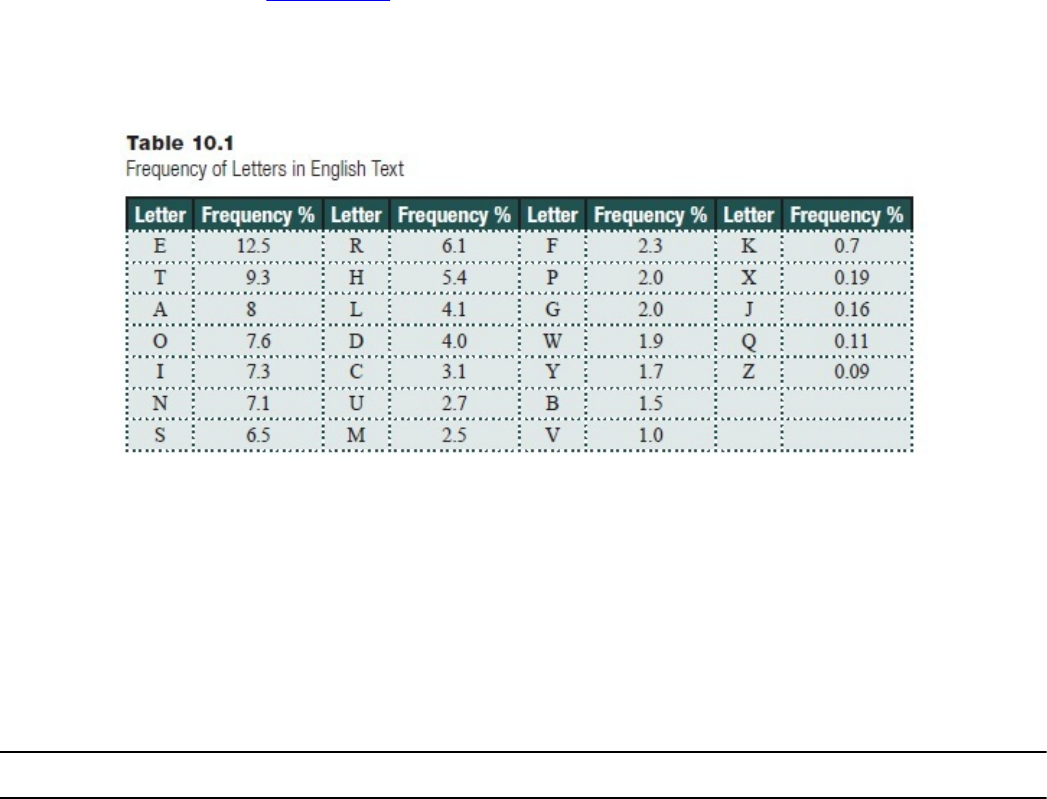
hasbeenaroundforalongtime,beginningin1836.Themostcommonlyusedlettersin

English are shown in Table 10.1. In the Morse code the letter “E” is represented by a

singledot,theletter“T”isasingledash,and“A”isadotfollowedbyadash.Inother

wordsthemostcommonlettershavethesmallestcoderepresentation,asageneralrule.

ThisishowtheHuffmancodeisorganizedtoo.

AHuffmancodeisconstructedfromthegroundup,likeawall.Thelowerlevelsofthe

wallrepresenttheleastfrequentlyusedsymbols,andhavethegreatestnumberofbricks

abovethem.Thefinalcodewillbebinarynumbers,andthelengthofthecodeinbitsfora

symbol is related to the number of bricks above it. The wall is actually shaped like a

pyramid,andiscalledabinarytreebycomputersciencefolks.It’saveryusefulstructure

ingeneral,butthedescriptionwillberestrictedheretoitsuseinHuffmancodes.

Asanexample,considertheEnglishtext:

IthinkthatatthattimenoneofusquitebelievedintheTimeMachine11

Thecharactersoccurinthisparticulartextwiththefollowingfrequencies:

t10 a4 q1 k1

e9 m3 c1 s1

i8 o2 d1 l1

n5 u2 v1 

h5 b1 f1 

The‘leaves’(ornodes)atthebottomofthetree(itisdrawnupside-down)containthe

lowestfrequencyitems,andsoareplacedfirst.Eachtwonodesinthetreewillhaveone

node above them, straddling them, containing the sum of the frequencies of all nodes

below. All characters are turned into nodes, and each also contains the number of

occurrencesofthatletter.Thiscollectionofnodeswillbecalledaheap.Initiallyallhave

onlyonecharacter,butthiswillchange.

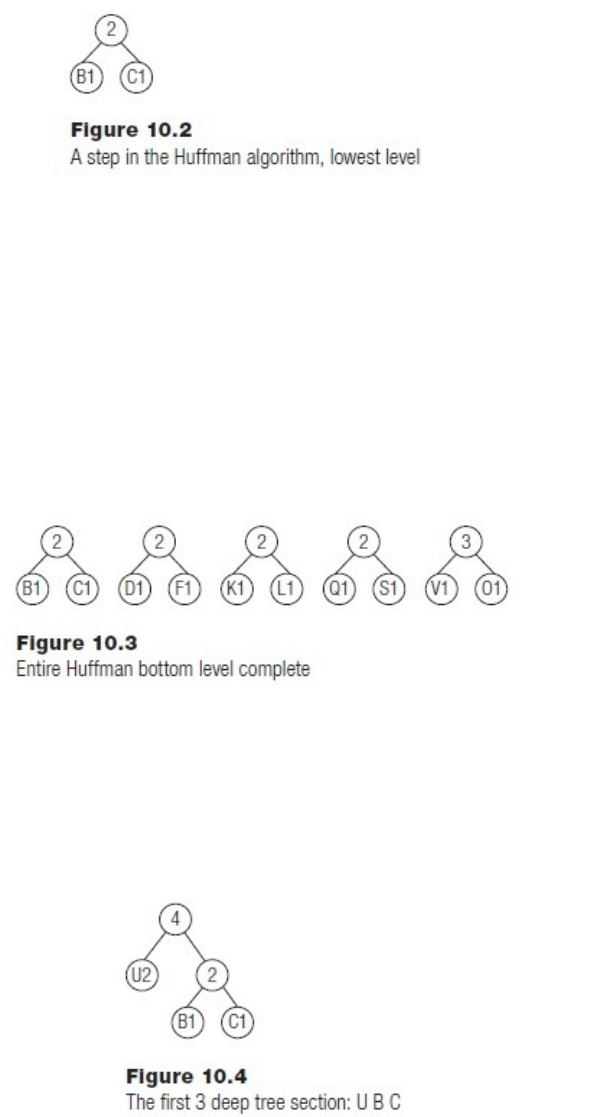
Theruleinbuildingthetreeistopickthepairofnodes(initiallycharacters)thatsumto

thesmallestnumberandconnectthemusinganothernode,oneabovethemthathasaleft

and right node. The first bricks, alphabetically, would be “b” and “c” both with a

frequencyof1.Thefirsttwowouldlooklikethis:

Thebottomnodeshavecharactersandcounts.Theoneabovehasonlyacount,anditis

thesumofthecountsofthetwonodesitisconnectedto.Thisnewnode,withacountof

2,isplacedbackintheheapandthenodesforBandCareremoved.Theheapwillalways

getsmaller.

Repeatingthisprocesswiththeothers,thesmallestpairwecanmakeiswith“d”and

“f,”then“k”and“l,”andthen“q”and“s.”Atthatpointthesmallestnodeis“v”witha

countof1,buttherearenomorenodeswithacountof1.Thesmallest

sumis2,whichuses“v”and‘o’:

Alloftheseare intheheap, andasearch isdonefor the smallestsum of nodes.The

character “u” has a count of 2 and so do any of the nodes above that link to twoother

characters.Thesearenodestoo,solink“u”withtheleftmostnodeabovetogetabigger

grouping—thisiscalledasubtree,becauseitisatree,butitisalsopartofabiggertree.

The‘u’nodeandtheothergivesasumof4:

The tree that is being built has the least commonly used characters placed at a greater

distancefromthetopofthetreethanarethefrequentlyusedcharacters.Thisdistancewill

beusedtoconstructthecodes,smallerforcommoncharacters.Nowthesmallestsumsof

twonodesinthetreeis4,thenodesconnecting“d,”“f,”“k,”and“l”:

Themethodheretakesthesmallesttwonodes,whicharegoingtocreatethesmallest

sum, and connects them, removing the original nodes and replacing them with the new

one.Thesmallestnodesnowarethenodeconnecting“q”and“2”(value2),thenodewith

“m”(value3)andthenodeconnecting“v”and“o”(value3).Thenodewith“m”willbe

selectedtolinktothe2-valuednode.Thetreeisadisconnectedcollectionofnodes,but

rightnowlookslikethis:

plus all of the unconnected nodes for individual letters. So, what’s next? The smallest

valued character remaining is ‘a’ at 4. That would make the smallest sum 7 after

connectingitwiththesubtreeontheright(‘v’and‘o’).Nextintheheaparethetwo4-

nodesabovetocreatean8,andlinking‘h’(5)and‘n’(also5)togeta10:

The pattern should be clear by now. Notice that the nodes with nothing below them

always consist of characters, and the nodes above have only numbers. But oops—the

spacecharacterswerenotcounted,andtheymustbeforthemessagetomakeanysense.

Thereare14spacesinthemessage.Thefinalsumwillbe14+9forthespace.Anodefora

spacehastobeaddedtotheheap.

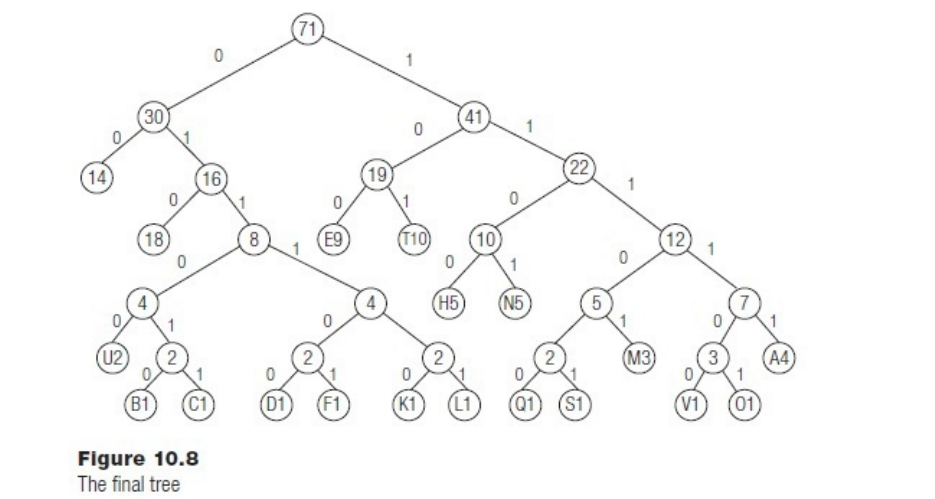
Thelasttwostepsdon’tinvolveanynewcharacters,buttheywilllinkallofthenodes

togetherandmakethemaccessiblefromonesinglenodeatthetop.Thefinal(top)node

shouldhaveavaluethatisthelengthoftheoriginalstring.

Now comes the bottom line: what was the point of all this? The tree that has been

constructedwillbeusedtoconstructthecodesforeachletter,andthelengthofeachcode

willbethenumberofnodesbetweenthecharactersandthetop(root)ofthetree.Thepath

toeachleftnodeislabeledwithadigit,inthiscasea0,andthepathtotherightnodesis

labelledwitha1,asinthetreeabove.Thecodeforanycharacterisreadoffofthelinks

thatwerefollowedtogetfromthetopofthetreetothenodecontainingthecharacter.So

thespace character, the mostcommon one, is reached by goingleft two times; its code

willbe“00.”The“t”isthesecondmostfrequentcharacter,andisreachedfromthetop

nodebygoingright,thenleft,thenright;thecodeis“101.”Thecompletesetofcodesis:

‘‘ 00 A 11111 D 011100 V 111100

T 101 M 11101 F 011101  

E 100 U 01100 K 011110  

I 010 O 111101 L 011111  

H 1100 B 011010 Q 111000  

N 1101 C 011011 S 111001  

The coded message is the concatenation of all of the codes for the characters in the

ordertheyappearinthemessage.Theencodedmessagewouldread:

This amounts to 259 bits = 33 bytes. The original string is 71 bytes long, so the

compressed data is 46% of the size of the original data. The Huffman coded string is

brokeninto8-bitbytesandtransmittedthatway:

010001011100010110101111000101110011111101001111

110100101110011111101001010101110110000110111110

111011000011110101110100011001110010011100001100

010101100000110101000111110101001111001000111000

001011010010111001000010101011101100001110111111

0110111000101101100

Decoding requires the table or the tree. If a known table is used, such as the natural

frequencies of English letters, then it would not have to be transmitted along with the

message. The use of a Python dictionary type makes the program for decoding very

elegantindeed.Giventhetableandthemessage,bitsareremovedfromthebeginningof

themessageandplacedintocodestringuntiltheymatchoneofthecodesinthetable.The

Huffmancodehasthepropertythatthebitsequencesareuniquewhenappendedasalong

message.Thefirstbitsequencethatmatchesacodewillbethecodeforthefirstletterin

themessage.

#Huffmandecode

#Thisisthecodedmessage:

bitstring=“01000101110001011010111100010111001111110100111111”+\

“0100101110011111101001010101110110000110111110111011000011110”+\

“1011101000110011100100111000011000101011000001101010001111101”+\

“0100111100100011100000101101001011100100001010101110110000111”+\

“011111101101111000101101100”

table={}#Thisisthetableofcodes

table['00']=”“

table[“11111”]=“A”

table[“011100”]=“D”

table[“111100”]=“V”

table[“101”]=“T”

table[“11101”]=“M”

table[“011101”]=“F”

table[“100”]=“E”

table[“01100”]=“U”

table[“011110”]=“K”

table[“010”]=“I”

table[“111101”]=“O”

table[“011111”]=“L”

table[“1100”]=“H”

table[“011010”]=“B”

table[“111000”]=“Q”

table[“1101”]=“N”

table[“011011”]=“C”

table[“111001”]=“S”



#Pullbitsfromthestringmakingasubstringuntilthe

#substringisfoundinthedictionary.Thenemitthe

#characterindexed.



#Loopuntilallbitsareused

whilelen(bitstring)>0:

code=””#Clearthecurrentcode

#WhilecodeNOTinthedictionary…

whilenot(codeintable):

#Addthenextbitfromthemessage

code=code+bitstring[0]

#Removethatbitfromthemessage

bitstring=bitstring[1:]

#Whenthecodematches,printthecharactercorresponding

#tothecode

print(table[code],end=””)

10.5.2 LZWCompression

Likemanyalgorithms,LZWcompressionisnamedafterthepeoplewhodevisedit:A.

Lempel,J.Ziv,andTerryWelch.Ithasbeenthestandardfordatacompressionformany

years,itwasthemethodusedintheGIFfileformat,andwasusedinmanyversionsof

PDF. It is notthe most effectivemethod ofcompression, but itis lossless andefficient.

LiketheHuffmancode,LZWcreatesatablefromtheoriginaltextandusesthecodesin

thetabletoperformthecompression.UnliketheHuffmancode,thedecompressionstage

doesnotrequirethatthetablebeknowninadvance;itbuildsthetableasitdecompresses

the file. The LZW algorithm also replaces multiple characters with single codes, thus

increasingthecompressionrate.

LZWcompressionusuallybeginswithaknowncodetable,mostoftenthe256ASCII

characters, but any table known by the compressor and decompressor will work. As an

example,anothershortsectionoftextfromTheTimeMachinewillbecompressed:

The Time Traveller for so it will be convenient to speak of him was expounding a

reconditemattertousHisgreyeyesshoneandtwinkledandhisusuallypalefacewas

flushed and animated The fire burned brightly and the soft radiance of the

incandescentlightsintheliliesofsilvercaughtthebubblesthatflashedandpassedin

ourglasses.

Punctuation has been removed for simplicity. The algorithm begins with a table of

characters,inthisinstancetheonesthatappearinthequote,butingeneralthetablecan

contain any starting set of symbols. This is called the code table, and associates a

numerical code with a string. The code table in this case will consist of the letters

(uppercase)andtheirvaluesstartingwith0:“A”=0,“B”=1,andsoon.Thespacehastobe

includedaswell.Thecodesequence024wouldbethestring“ACE”usingthisscheme.

Naturallytherehastobemoretothisifitistobeaviablecompressionmethod.When

encoding,thecharactersareexaminedoneatatimeandappendedtoaninputstring,and

lookedupinthetable.Ifthestringisfoundinthetable,thenthenextcharacterisreadand

appendedtothestringanditislookedupagain.Thisrepeatsuntilthestringisnotfound,

atwhichpointafewthingshappen:thecodeforthelaststringthatwasfoundiswrittento

theoutput,thenewstringthatwasencounteredinthestringbutnotfoundinthetableis

addedtothetables,andtheprocesscontinuesusingthelastcharacterreadin.Thismeans

that not only characters but also short strings that occur in the text will have numeric

codes,andthatthetablewillbecreatedfromthetextthatwasgiven.

Considerthetextintheexample:Thefirstcharacterseenis“T”:

1.“T”existsinthetablealready,soanewcharacterisreadinandappendedtothe“T”

tocreatethepair“TH.”

2.“TH”isnotinthetable.Thecharacter“T”hasthecode19,so19iswrittentothe

outputfile.

3.Thestring“TH”isaddedtothetable.Itwillbecode27.

4.Theinputstringisnow“H.”

5.Thecharacter“H”isinthetableandhascode7.Thenextcharacterisreadinand

appendedto“H”creating“HE.”

6.“HE”isnotinthetable,sothecodeforcharacter“H,”whichis7,iswrittentothe

outputfile.

7.Thestring“HE”isaddedtothetable,code28.

8.Theinputstringisnow“E.”

Theprocessrepeats.Ifamultiple-characterstringisfoundinthetable,thenthesteps

arebasicallythesame.Hypothetically:

1.Thecharacter“T”isnextandisinthetable.Readthenextcharacter“H”and

appendto“T”toget“TH.”

2.“TH”isinthetable.Readthenextcharacter“E”andappendto“T”toget“THE.”

3.“THE’isnotinthetabletoemitthecodefor“TH,”whichis27.

4.Inputstringisnow“E.”

Step1repeatsuntilastringisobtainedthathasnotbeenseenbefore.Intheexample

herethefirst27codesarelettersandthespacecharacter.Thenextfewcodesare:

TH27 HE28 E29

T30 TI31 IM32

ME33 ET34 TR35

Thefirst3-characterstring(trigram)inthetableis“ET.”

Python’s dictionary type is especially valuable for coding the LZW algorithm. The

facilityforlookingupastringinatableisexactlywhatisrequiredhere.Thecriticalpart

oftheprogramcouldbewrittenasfollows:

#countisthenextunassignedsymbol

#chisthelastcharacterreadin

#sisthecurrentcharacterstring

#infistheinputfile(text)

s=””#Initialstringisempty.

ch=inf.read(1).upper()#Readthefirstcharacter,upper

#case.

whilelen(ch)>0:#Whilethefilestillhasdata…

ifs+chindict:#Isstringconcatenatedwithch

#inthetable?

s=s+ch#Yes.Concatenateandrepeat

else:#No.

print(dict[s],”“,end=””)#Printthecodefor

#thestrings

dict[s+ch]=count#Putthenewstringinto

#thedictionary

count=count+1#Newcodeisnextinteger.

s=ch#Stringisnowthelast

#characterread.

ch=inf.read(1).upper()#Readanewcharacter

When decoding the LZW file, the initial table is known. Again, this is often just the

ASCIIcharactersbutcanbesomethingelse,andinthiscaseisthelettersplusthespace.

Thefilecontainscodes,notcharacters,butthecodesareinthetable,right?No,onlythe

startingcodesareinthetable.Sodecodingthemessageintheexamplestartseasily.The

firstfewcodesinthemessageare:

19742619812291917021…

Thefirstcodeisreadinandisthecodefortheletter“T.”Thisisfollowedby7(“H”)

and4(“E”)andsoonuntilthecode29isreached.Thereisnoentryforthecode29inthe

table.ThisiswherethereallycleverpartoftheLZWalgorithmhappens.

Whendecoding,theprogrambuildsthetableagain.Afterall,thecharactersareinthe

sameorderintheencodeddata,soitshouldbepossibletoreproducetheprocessthatwas

usedtobuildthecodetableinthefirstplace.Whenthefirstcodeisreadin,thecodeis

expectedtobeinthetable,andthecorrespondingletter“T”iswrittenandplacedintoa

string.Thenextcodeisreadandcorrespondsto‘H.’Now“TH”isaddedtothedictionary,

and“H”iswrittenandbecomesthecurrentstring.Now“E”isseen,“HE”isaddedtothe

table,and“E”iswritten,andsoon.Againadictionarycanbeusedtostorethecodes,but

alistismoreefficient.Theindicesarecodes,whicharenumbers,soalistisfinehere.The

centralpartoftheprocessis:

code1=int(inf.readline())#CODE1isthefirstcode

#onthefile

print(dict[code1],end=””)#Outputthestringfor

#CODE1

whileTrue:#Whilemodecodesonthe

#file…

code0=int(inf.readline())#CODE0isthenextcode

#onthefile

ifcode0<len(dict):#IsCODE0inthetable?

s=dict[code0]#YES.Sisthestring

#forCODE0

else:

s=dict[code1]#NO.Sisthestringfor

#CODE1

s=s+ch#AppendCHtoS.

print(s,end=””)#INEITHERCASEemitS

ch=s[0]#CHbecomesthefirst

#characterofS

dict=dict+[dict[code1]+ch,]#Addnewstringtothe

#table

count=count+1

code1=code0

A pseudo-code summary of both the encoding and decoding processes is given in

Figure10.9,andworkingprogramsareprovidedonthedisc

(lzwe.py and lzwd.py). If punctuation is to be added, then a different conversion to

uppercasewouldhavetobedone.Forpracticalapplications,theentireASCIIcharacterset

wouldbeusedattheoutset.

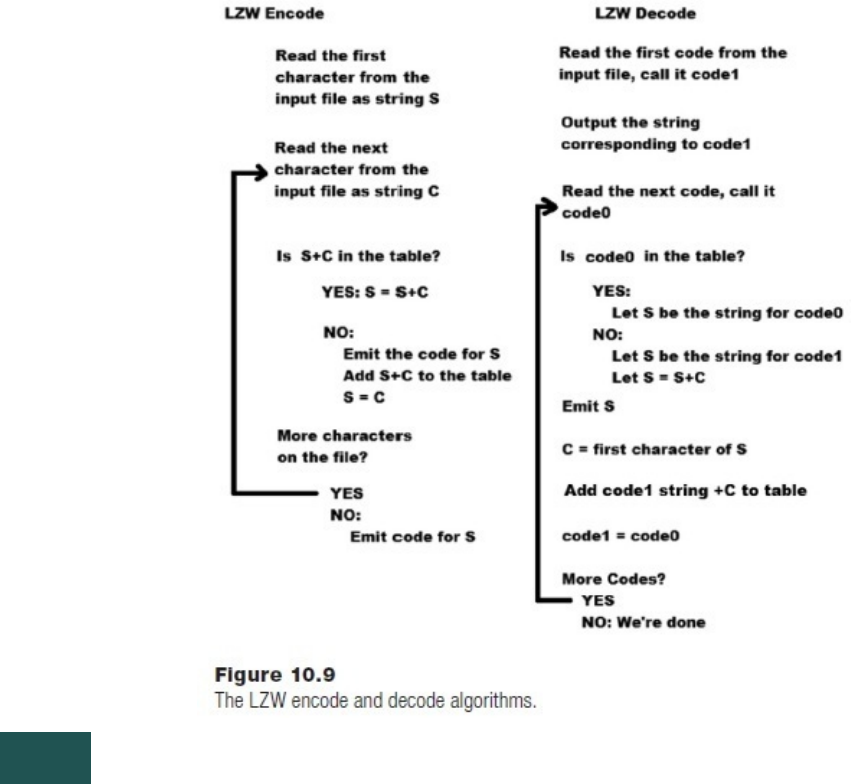
10.6 HASHING

Ahashing algorithmattempts to characterizeacomplexpieceofdatawithsomething

simpler, and preferably unique. The most common example would be to find a number

thatcouldrepresentacharacterstring.Ahashingalgorithmhastobefast,becausetheidea

veryoftenistoconvertastringintoanindextoalistortuple.Considerthestring“while.”

There are five characters (bytes) here. How can this string be used as an index into a

tuple?

Anynumericaloperationonthecodesusedtorepresentthecharactermightwork,but

some result in codes that are too large. Simply adding the codes would give a value of

537,whichcouldworkbutalsomightbetoolarge.Imaginetheapplicationistolookup

Pythonkeywords;thereare33ofthem.Thevalueresultingfromthehashshouldbean

indexbetween0and32,sotakethehashmod33.Ifthatistriedtheresultisthathalfof

the33entries willbeempty, andhalf willhavetwo ormore stringsthathave thesame

index.Theresultis:

4:“None” 12:“return” 21:“try” 31:“global”

6:“class” 13:“global” 22:“is” 

7:“from” 14:“as” 25:“finally” 

9:“while” 15:“lambda” 27:“or” 

10:“and” 17:“in” 29:“False” 

11:“continue” 20:“True” 30:“for” 

When two things hash to the same value it is said to be a collision. In this case the

collisionsare:

(class,def) (False,nonlocal) (return,del) (from,not) (lambda,with)

(True,elif) (while,if) (from,yield) (global,assert) (False,else)

(from,import) (and,pass) (is,break) (is,except) (None,raise)

Twovaluescan’toccupythesamelocationinatuple,sosomethingmustbedone.The

simplestwaytodealwithcollisionsistohaveextraspaceinthelistortuple.Ifthesizeof

thetupleisspecifiedas145,thenallstringshashtodistinctvalues.Ofcourse,now112

tupleentriesareempty,butdoesthatreallymatter?Thealternativetoatableindexedby

hashing(ahashtable)wouldbealistthathastobesearched,andhashingisverymuch

faster.

Asithappens,simplyaddingthecharacterstogetherisnotaverygood

hashingmethod.Thereareafewwell-knownones.

djb2

Thisalgorithm startswith apredefined seed for a hashvalue, multipliesit by 33 and

addsthenextcharacterfromthestring,multipliesthatby33,addsthenextcharacter,and

soon.Thecodeis:

defdjb2(s,size):

sum=5381

foriinrange(0,len(s)):

sum=sum*33+ord(s[i])

sum=sum%size

returnsum

Whymultiplyby33?Itworkswell,andnobodyknowswhy.Theseedof5381canbe

changedtosee howdifferentvalueswork. Withtheconfigurationgiven here,therewill

needtobe112elementsinthetupletoavoidcollisions.Iftheprogramischangedslightly

sothatanexclusiveORreplacesthesum,thesizedecreasesto105.Thatis:

sum=sum*33^ord(s[i])

10.6.1 sdbm

Thisisamethoddevisedforscramblingbits,butmakesfora goodhashingfunction.

Theiterationishash(i)=hash(i-1)*65599+str[i].Thenumber65599isarbitrary,but

happenstobeprime.Afunctiontoimplementthisis:

defsdbm(s,size):

hash=0

foriinrange(0,len(s)):

hash=ord(s[i])*65599+hash

returnhash%size.

Therearemanyotherhashingmethods(see:Knuth).Theideaisanimportantone.Itis,

forexample,awaytoimplementPythondictionaries:hashthekeytoanintegeranduse

thattoaccessthevalue.

10.7 SUMMARY

The goal of this chapter was to introduce important algorithms or general techniques

used in computer science. Sorting is a traditional programming problem for

undergraduatesandisessentialinmanydata-handlingapplications.Theselectionsortand

themergesortwerediscussedatlength.

Searching involves finding some piece of data within a larger collection. A linear

searchstartsatthebeginningandlooksatconsecutiveelementsuntilthetargetisfound.A

binarysearchsplitsthedataintotwohalveseachtimeanelementinthesetisexamined

andsoisfaster,butitdependsonthedatabeingsorted.

Randomnumbergenerationcreatesasequenceofnumbersthatsatisfiesastatisticaltest

for randomness. Such numbers are crucial in computer simulations and games, and in

somenumericalalgorithms.

Cryptographyinvolvessendingmessagesthatonlycertainintendedpeoplecanreceive

andunderstand.Acipherisanalgorithmthatconvertsonestringofcharactersintoanother

oneofgenerallythesamelength.Theone-timepadmethodwasexamined,followedby

theverypopularRSAalgorithm.

Datacompressionisaboutwaystotakemanybytesofinformationandturntheminto

fewer bytes while losing none of the essential message. Of course, compressed data is

incomprehensiblejusttolookatandmustbedecompressedinorderforittobeused.This

sectiondemonstratedrunlengthencoding,Huffmancodes,andtheLZWalgorithm.

Thefinalsectionwasa briefdiscussionofhashing, awayto convertstringsor other

complexdatatypesandreducethemtosimplerformssuchasintegers.Thedjb2andthe

sdbmmethodsweresingledoutasbeingtypicalofthewaythatsuchalgorithmswork.

Exercises

1.Hashingalgorithmsmustbefast.Usethetimingschemesdiscussedinthischapterto

determinewhichofthethreehashingalgorithmspresentedisthefastest.

2.Whenasequenceofnumbersissortedintoascendingorderthenelementi-1isalways

smallerthanorequaltoelementi.Hereisadescriptionofasortingalgorithm:scanthe

datasetStofindanypairsofadjacentlocationswhereS[i-1]>S[i],andwhenanyare

foundswapthetwovalues.Repeattheprocessuntilthearrayissorted.Doesitever

getsorted?Whatisthebestcaseandwhatistheworstcase?Implementthemethodin

Python.

3.Comparethelinearcongruentialrandomnumbergeneratordescribedinthischapter

againsttherandom()functioninPython.Implementadierollusingeachmethod,and

rolladie1000times.Whichmethodisnearesttotheexpectedfrequencydistribution

(equalforallvalues)?Repeattheprocess1000timesandscorePythononepointwhen

itsrandomnumbergeneratorwinsbythismeasure,andscorethebook’sgeneratorone

pointwhenitwins.Whichistheoverallwinner?

4.Thequalityofahashingalgorithmismeasuredbyhowrandomthehashcodesare

whengivenasamplesetofstrings.Oneestimateofrandomnessisthenumberofcells

withmorethanonevaluehashedtoit(thebestherewouldbe0),andtheaverage

numberofvalueshashedtooccupiedcells—thisshouldbecloseto1.Measurethese

forthethreehashingmethodspresentedforasizeof60cells.

5.Dataforregistrantsinaswimmingcompetitionconsistsoftheswimmersname,

number,nationalranking,andtimeinthe200-meterfreestylecompetition.Thesedata

arelocatedinfourlists:name,number,rank,t200.Inallcasesthesameindexis

usedtoaccessallofthedataforthesameperson.Sortthesedataindescendingorder

ontimeandidentifythepersonsinthetopthreespotsandtheirtimes.

6.Steganographyworksbyconcealingamessageratherthanmakingitunreadable,asis

donewhenusingencryption.Intheidealsituationnobodywillevensuspectthatthere

isasecondmessagehiddenwithinthefirst.Consideraschemethatusesthespacesin

amessage:asinglespaceisa‘0’andadoublespaceisa“1.”Thelettersarecodedas

5-bitcodesstartingwith“A”=00000,“B”=00001,andsoon.Writeprogramsthat

encodeanddecodesuchmessages.

NotesandOtherResources

Random.orgrandomnumberserver.https://www.random.org/

A pretty good description of RSA:

https://en.wikipedia.org/wiki/RSA_%28cryptosystem%29

Encode/decodestenographicmessagesdisguisedasspam.http://www.spammimic.com/

1.DonaldKnuth.(1997).TheArtofComputerProgramming,Volume3:Sorting

andSearching,3rdEdition,Addison-Wesley,138–141,ISBN0-201-89685-0.

2.AnanyLevitin.IntroductiontotheDesign&AnalysisofAlgorithms,2ndEdition,

98–100,ISBN0-321-35828-7.

3.RobertSedgewick.(1998).AlgorithmsinC++,Parts1–4:Fundamentals,Data

Structure,Sorting,Searching,2ndEdition,Addison-WesleyLongman,273–274,

ISBN0-201-35088-2.

4.G.Marsaglia.(2003).http://www.csis.hku.hk/~diehard

5.MakatoMatsumotoandTakujiNishimura.(January1998).Mersennetwister:A623-

dimensionallyequidistributeduniformpseudo-randomnumbergenerator,ACM

Trans.Model.Comput.Simul.8(1),3–30,DOI=

http://dx.doi.org/10.1145/272991.272995

6.LenoreBlum,ManuelBlum,andMikeShub.(1982).Comparisonoftwopseudo-

randomnumbergenerators,AdvancesinCryptology:ProceedingsofCRYPTO’82,

Plenum,61–78.

7.ClaudeE.Shannon.(October1949).Communicationtheoryofsecrecysystems

(PDF),BellSystemTechnicalJournal,28(4),656–715,retrieved2011-12-21,

doi:10.1002/j.1538-7305.1949.tb00928.x

8.TheOnlyUnbreakableCryptosystemKnown—TheVernamCipher,retrieved

2014-03-17,Pro-technix.com

9.B.Schneier.(1994).Descriptionofanewvariable-lengthkey,64-bitblockcipher

(Blowfish),inFastSoftwareEncryption,editedbyRossAnderson,Cambridge

SecurityWorkshopProceedings(December1993),Springer-Verlag,191–204.

10.StevenW.Smith.(2007).DataCompressionTutorial:Part1,

http://www.eetimes.com/document.asp?doc_id=1275417&page_number=2

11.H.G.Wells.(1895).TheTimeMachine,WilliamHeinemann,

http://www.gutenberg.org/cache/epub/35/pg35.txt

CHAPTER11

PROGRAMMINGFORTHESCIENCES

11.1FindingRootsofEquations

11.2Differentiation

11.3Integration

11.4Optimization:FindingMaximaandMinima

11.5LongestCommonSubsequence(EditDistance)

11.6Summary

Inthischapter

It is true that the earliest calculating devices were created to help with commercial

concerns, like payments, credit, and inventory. The abacus is an excellent example—it

doesbasicarithmeticandwaslikelyanearly“cashregister.”Mucholderdevicesdoexist,

such as the Lebombo bone that helped ancient African bushmen do simple calculations

andkeeptrackoftime.Theelectroniccomputer,ontheotherhand,wasdesignedtocarry

outscientificcalculations,inparticularthoserelatedtodecryptingmilitarymessagesand

buildingtheatombomb.Computersare,ofcourse,usedforthosethingsstill,butthereis

now a vast array of computations in the scientific domain that could not be carried out

withoutthehelpofacomputer.

Scientists from different disciplines would disagree about what the most important

algorithmsandtechniquesforsciencewere.That’sbecauseofthewidelydisparatethings

thatphysicistsandbiologists,astwoexamples,study.Thereareafewrecurringproblems

thatpopupinalmostallsciencedomains,andsomeimportanttechniquesthatgeneralize

tomanyscienceandsomenon-scienceareas.

11.1 FINDINGROOTSOFEQUATIONS

Therootofanequationisthexcoordinatecorrespondingtoitszerovalue.Thismaynot

be the smallest or the largest value, but the place where a function equals zero is often

important. For example, if a function for the error in a calculation can be found, then

finding the place where the error is zero would be important. In one dimension the

problembeingsolvedis:

x:f(x)=0(11.1)

Orinotherwords,findthevalueofxthatresultsinf(x)beingequaltozero.Thefunction

couldbequitecomplicated,butforthetechniquetoworkitshouldhaveaderivative.

ThebasisofmanyrootfindingproceduresisNewton’smethod.Theprocedurebegins

with a guess at the right answer. The guess in many cases does not have to be very

accurate,butissimplyastartingpoint.Ifarangeofvaluesisgivenwithinwhichtofind

thesolution,thecenterofthatrangemaybeagoodstartingguess.So,hereisaproblemto

startwith:

f(x)=(x-1)3betweenx=-2andx=12(11.2)

Thecenteroftherangeisx=5.

Theinitialguessiscalledx0,andherex0=5.Thefunctionvaluethere,f(x0), is 64.

Thealgorithmnowsaysthatthenextguessforx,x1,willbe:

x0–f(x0)/f’(x0)(11.3)

wheref’(x0)isthederivativeoffatthepointx=x0.Thisisawrinkle—thederivativeoff

has to be calculated. It’s easy to do for many functions, hard for others. A numerical

methodwillbeexaminedalittlelaterinthischapter,sointhemeantimeitispossibleto

simplycode a functionthat givesthe derivative,having donethe calculuson paperand

thenwrittenthefunctionbasedonthat.Thederivativeof(x-1)3is3x2-6x+3.

#Rootsofafunction

defobjective(x):

return(x-1)*(x-1)*(x-1)



defderiv(x):

return3*x*x-6*x+3



#Rangeis-2to+12

x=5.

fx=1000.

delta=0.000001

print(“Step0:x=”,x,”obj=“,objective(x))

i=1

whileabs(fx)>delta:

f=objective(x)

ff=f/deriv(x)

x=x-ff

fx=objective(x)

print(“Step“,i,”:x=”,x,“obj=“,fx)

i=i+1



Step0:x=5.0obj=64.0

Step1:x=3.666666666666667obj=18.96296296296297

Step2:x=2.7777777777777777obj=5.618655692729766

Step3:x=2.185185185185185obj=1.6647868719199308

...

Step14:x=1.0137019495631274obj=2.5724508967303e-06

Step15:x=1.0091346330420865obj=7.622076731056633e-07

The correct answer in this case is x=1.0, so the method gets to within 0.009 of the

correct root in 15 steps. Depending on the application, this could be fine. What if the

initialguesswasterrible?Iftheprocessstartsatx=500thenittakes27steps,butgets

justalittleclosertotherightanswer(x=1.0087).Startingat-500alsotakes27steps.

It’s possible that there is no root. What happens in that case? The program keeps

looking.Itovershoots,andthengoesback,andforth,andbackagain.Topresentthisfrom

happeningitiscommontoplacealimitofthenumberoftimestheprogramwilltry.When

thislimitisexceededanerroroccursindicatingthatthereisnosolution.

This first example has illustrated some common concepts that are used in numerical

analysis, which is the mathematical discipline encompassing the computation of

mathematicalfunctionsandoperations.Thecommonconceptsinclude:

Theinitialguess: It isrelativelycommon tohave a numericalalgorithmbegin ata

guessedvalue.

Thedelta:Itisalsocommontohaveanalgorithmstepwhenthechangeintheresult

or some mathematical feature becomes smaller than a specified threshold, called

delta.

Iteration:Numericalmethodsfrequentlyrepeatacalculationexpectingittoconverge

onthecorrectresult,usingthepreviouslycalculatedvalueasthenewstartingpoint.

Maximumiterations:Auserofanumericalmethodcanassumethatthemethodwill

notconverge(getcloseenoughtotherightanswer)ifaspecifiednumberofattempts

havebeenmade.

11.2 DIFFERENTIATION

Determining the derivative of a function is something that is often thought of as a

symbolic operation, and the result is valid for any value of the function. This may not

alwaysbe true, and it may not be easy to do in thegeneral case. Think about what the

previousalgorithmdoes—itneedsthederivativeofafunctionatonespecificpoint.Can

thatbedeterminedifthealgebraicformofthefunctionisnotknown?Yes,itcan,towithin

somedegreeofaccuracy.

The derivative of a function at a point x is the slope of the curve defined by that

functionatthatpoint.Thedefinitionofthederivativeoffatthepointxis:

f’(x)=(f(x+h)–f(x-h))/(2h)(11.4)

ashgetssmallerandsmaller,whatiscalledalimitincalculus.Thisformulaisessentially

themathematicaldefinitionofaderivative.Onacomputerhcanbemadequitesmall,but

canneverbezero.Iftheexpressionaboveisusedasanestimateofthederivative,itwill

work in many cases. It is based on sampling two points of the function each time. An

improvementcanbemadebyusingmorepoints;forexample:

usesfourpointsandoftenproducesbetterresults.

Codingthisusesafunctionpassedasaparameter.Itmakessensethatthefunctiontobe

differentiatedwouldbeaparametertothefunctionthatdifferentiatesit;otherparameters

willbex,thepointatwhichitwillbeevaluated,delta,theaccuracydesired,andniter,the

maximumnumberofiterations.Thecalculationshouldtakeplaceinatry-exceptblockso

that numerical errors will be caught. The two-point and the four-point versions of the

functionthatperformsnumericaldifferentiationare:

Testing these functions is an excellent demonstration. First a function to be

differentiatediswritten.Thepreviousexampleonfindingrootshasasimpleone(renamed

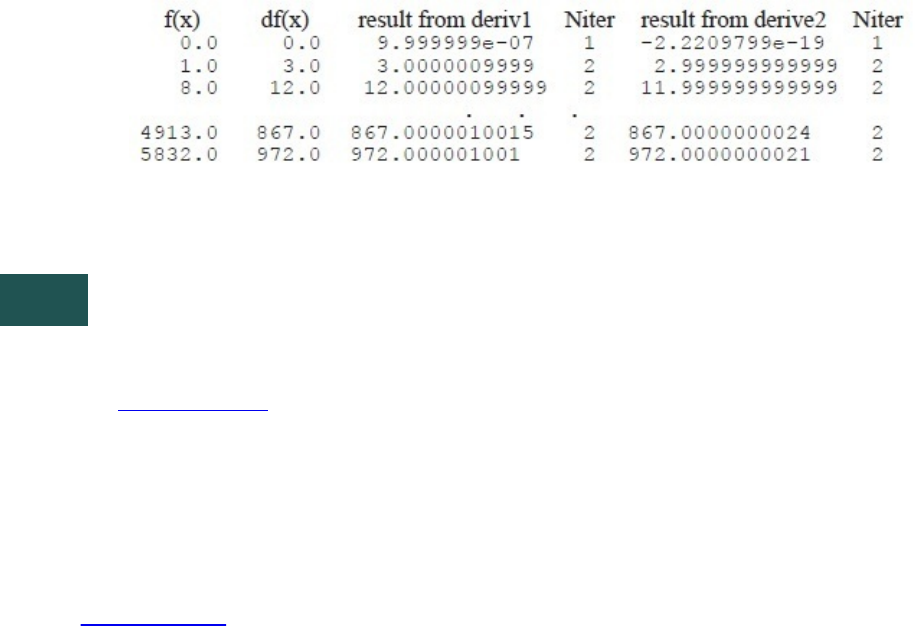
asf1):

deff1(x):

return(x-1)*(x-1)*(x-1)

That example also has a function that represents the derivative of f1 at the point x

(renameddf1):

defdf1(x):

return3*x*x-6*x+3

Thefunctiondf1()shouldreturntheexactderivativeoff1(),andcanbeusedtocheck

thevaluereturnedbyderiv1()orderiv2().Createaloopthatrunsoverarangeofxvalues

andcomparethevaluereturnedfromdf1()tothatreturnedbyderiv1()and/orderiv2():

foriinrange(1,20):

x=i*1.0

f=f1(x)

df=df1(x)

mydf=deriv1(f1,x)

mydf2=deriv2(f1,x)

print(f,df,mydf,n0,”“,mydf2,n1)

Theresultlookssomethinglikethis:

Both functions give excellent results in a very few iterations in this case. Of course,

somefunctionspresentmoredifficultiesthandosimplepolynomials.[2]

11.3 INTEGRATION

An integral is most often thought of as the area under a curve, where the curve is a

function (Figure 11.1a). Numerical integration amounts calculating that area using an

algorithm.Theareaofarectangleiseasytocalculate,soiftheregionunderacurvecould

bereasonablyapproximatedbyabunchofrectangles,thentheproblemwouldbesolved.

Thisistheideabehindthetrapezoidalrule.Theintegralfromx0tox1ofafunctionf(x)

canbeapproximatedbythewidth(x1-x0)multipliedbytheheight(theaveragevalueof

thefunctioninthatrange),whichisjustarectanglethatapproximatestheareaunderthe

curve(Figure11.1b).Inmathematicalnotation:

This would generally be a pretty poor approximation of a curve, and would yield

correspondinglybadapproximationsoftheintegral.However,thesmallerthewidthx1-

x0 the more accurate the approximation can be, and so using a great many small

trapezoidswouldbemuchbetterthanusingonlyone(Figure11.1c).Howmany?Thatis

not known at the outset, but could be increased from an initial guess until a desired

accuracywasachieved.

A function that performs integration using this method would accept a function, the

starting x0 and the ending x1 for the integral. The function would break the interval

betweenx0andx1intonparts,whennisaninitialguess.Thefunctionisevaluatedforall

n parts, the area of each trapezoid is computed, and they are summed to get the final

result.Nowincreasenanddoitagain.Ifthetwovaluesarecloseenough(delta)thenthe

processiscomplete.

Thiswillbedoneintwosteps.Firstafunctiontrap0()thatcomputesandreturnsthe

sumofNtrapezoids.Theobviousbutslowwaytodothisis:

ftrap0(f,x0,x1,n):#Slowmethod

dx=(x1-x0)/n#DividerangeintoNparts

xa=x0#Startatx0

xb=x0+dx#Currenttrapezoidisxatoxb

sum=0#Sumofareasstartsat0.0

foriinrange(0,n):#AddupNtrapezoids

f0=f(xa)#Computefunctionatxaandxb

f1=f(xb)

sum=sum+dx*(f1+f0)/2#Areaofthetrapezoid

xa=xa+dx#Nextxaandxbaredxfrom

xb=xb+dx#thecurrentones

returnsum#Thesumistheintegral.

Theintegrationfunctiontrapezoid()willcallthisfunctionwithincreasingvaluesofn

untiltwoconsecutiveresultsshowasmallenoughdifference(i.e.,smallerthanaprovided

deltavalue):

deftrapezoid(f,x0,x1,delta=0.0001,niter=1024):

n=4

resold=trap0(f,x0,x1,2)

resnew=trap0(f,x0,x1,4)

whileabs(resnew-resold)>delta:

ifn>niter:break

resold=resnew

n=n*2

resnew=trap0(f,x0,x1,n)

returnresnew

The function trap0() can be sped up significantly by not re-computing the function

twiceeachtimethroughtheloop,butrememberingthepreviousvalueinstead(Exercise

2).A morepopularalgorithmfor integrationisSimpson’sRule,which tries to minimize

the error even more by using a quadratic approximation to the curve at the top of the

trapezoid,insteadofastraightline.

11.4 OPTIMIZATION:FINDINGMAXIMAAND

MINIMA

Findingextremevalues,eitherthemaximumorminimum,isaverycommonproblem

incomputing, notjust in sciencebut in manydisciplines. Itis sometimes referredto as

optimization.Naturallyfindingabest(insomesense)valuewouldbeappealing.Whatis

theleastamountof fuelneededto travel fromChicagoto Atlanta?Whatroutebetween

thosetwocitiesrequirestheleastamountofdrivingtime?Whatrouteisshortestinterms

ofdistance?Therearemanyreasonstowantanoptimumandmanywaystodefinewhat

anoptimumis.

Inthefollowingdiscussionthefunctiontobeoptimizedwillbeprovided,sotherewill

no guesswork on that subject. The question concerns how to find location (parameters)

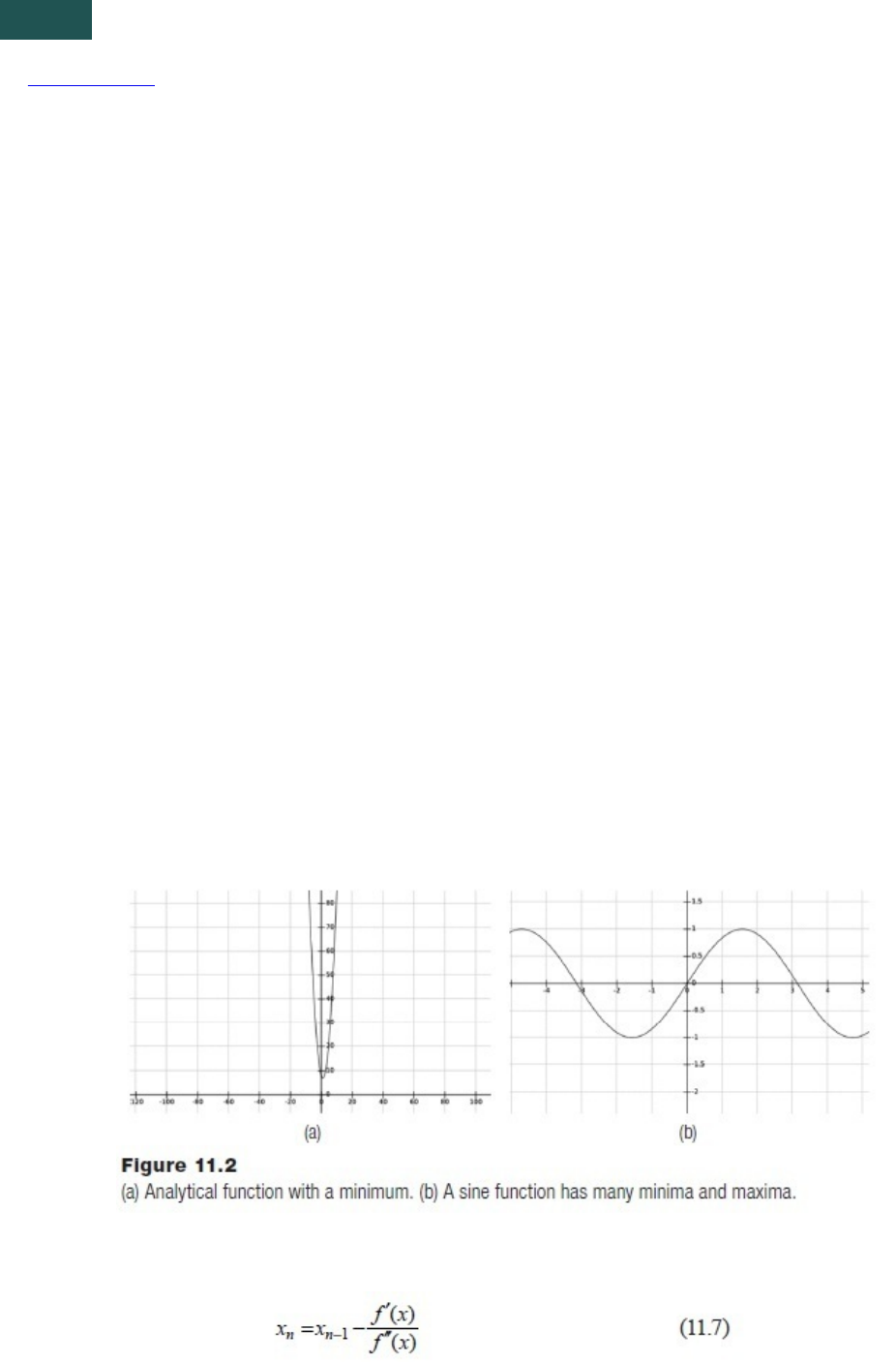
wheretheminimumormaximumoccurs.

11.4.1 NewtonAgain

Figure11.2showsanexampleofafunctiontobeoptimized.Thereisaminimumof7

at the point x= 1. How can this be found? If the nature of the function is known, for

instancethatitisaquadraticpolynomial,thentheoptimumcanbefoundimmediately.It

willbeatthepointwherethederivativeiszero.Theproblemofoptimizationisthatone

doesnotknowmuch,ifanything,aboutthefunction.Itcanonlybeevaluated,andperhaps

thederivativescanbefoundnumerically.Giventhat,howcantheminormaxbefound?

Ifthederivativecanbefound,thenitmaybepossibletosearchforanoptimumpoint.

Atavaluex,ifthederivativeisnegative,thentheslopeofthecurveisnegativeatthat

point; if the derivative is positive then the slope is positive. If an x value can be found

wheretheslopeisnegative(callthispointx0)andanotherwhereitispositive(callthis

x1),thentheoptimum(slope=0)mustbebetweenthesetwopoints.Findingthatpoint

canbedoneasfollows:

1.Selectthepointbetweenthesetwo(x=(x0+x1)/2).

2.Ifthederivativeisnegativeatthispoint,letx0=x.Ifpositiveletx1=x.

3.Repeatfromstep1untilthederivativeiscloseenoughto0.

This process is pretty much random. Finding the two starting points is a matter of

guessinguntiltheyarefound.Thesearchrangegetssmallerbyafactorof2eachiteration.

Thefactthatthefunctioncanbeevaluatedatanypointmeansthatitispossibletomake

better guesses. In particular, it’s possible to assume that the function is approximately

quadratic at each step. Quadratics have an optimum at a predictable place. The method

calledNewton’sMethodfitsaquadraticateachpointandmovestowardsitsoptimalpoint.

Themethodisiterative,andwithoutdoingthemaththeiterationis:

A functiontocalculate the firstand secondderivative is needed.The formulafor the

secondderivativeisbasedonthedefinitionofdifferentiation,aswastheformulaforthe

first.Itis:

The program should therefore be straightforward. Repeat the calculation of xn-1 -

f’(x)/f’’(x)untilitconvergestotheanswer.Thiswillbethelocationoftheoptimum.An

examplefunctionwouldbe:

defnewtonopt(f,x0,x1,delta=0.0001,niter=20):

x=(x0+x1)/2

fa=1000.0

fb=f(x)

i=0

print(“Iteration0:x=”,x,”f=”,fb)

while(abs(fa-fb)>delta):

fa=fb

x=x-deriv(f,x)/derivsecond(f,x)

fb=f(x)

i=i+1

print(“Iteration“,i,“:x=”,x,”f=”,fb)

ifi>niter:

return0

Thisfindsalocaloptimumbetweenthevaluesofx0andx1.Alocaloptimummaynot

be the largest or smallest function value that the function can produce, but may be the

optimuminalocalrangeofvalues.

Figure 11.2a shows a typical quadratic function. It is f(x) = x2-2x+8, and has an

optimumatx=1.BecauseitisquadratictheNewtonoptimizationfunctionabovefinds

theresultinasinglestep.Figure11.2bisasinefunction,andcanbeseentohavemany

minimaandmaxima.AnyoneofthemmightbefoundbytheNewtonmethod,whichis

whyarangeofvaluesisprovidedtothefunction.

Thenewtonopt()functionsuccessfullyfindstheoptimuminFigure11.2aatx=1,and

finds one in Figure 11.2b at x = 90 degrees (π/2 radians). If there is no optimum the

iterationlimitwillbe reached.Ifeitherderivativedoesnotexist,thenanexceptionwill

occur.

11.4.2 FittingDatatoCurves–Regression

Scientists collect data on nearly everything. Data are really numerical values that

representsomeprocess,whetheritbephysical,chemical,biological,orsociological.The

numbersaremeasurements,andscientistsmodelprocesses using thesemeasurementsin

ordertofurtherunderstandthem.Oneofthefirstthingsthatisusuallydoneistotryto

findapatterninthedatathatmaygivesomeinsightintotheunderlyingprocess,oratleast

allow predictions for situations not measured. One of the common methods in data

analysisistofitacurvetothedata;thatis,todeterminewhetherastrongmathematical

relationshipexistsbetweenthemeasurements.

Asanexample,asetofmeasurementsoftreeheightswillbeused.Theheightofaset

ofaspecificvarietyoftreesismadeoveraperiodoftenyearsandthedataresidesinafile

named “treedata.txt.” The question: is there a linear relationship (i.e., does a tree grow

generally the same amount each year)? Specifically, what is that relationship (i.e., how

muchcanweexpectatreetogrow)?Figurezshowsavisualizationofthesedatainthe

formof a scattergramorscatterplot, in which the data are displayed as points in their

(x,y)positiononagrid.

The“curve”tobefitinthiscasewillbealine.Whatistheequationofthelinethatbest

representsthedatainthefigure?Ifthatwereknownthenitwouldbepossibletopredict

theheightofatreewithsomedegreeofconfidence,ortoestimateatree’sagefromits

height.

Oneformoftheequationofalineisthepoint-slopeform:

y=mx+b

wheremistheslope (angle) of theline and b is the intercept, the place where the line

crossestheYaxis.Thegoaloftheregressionprocess,inwhichthebestlineisfound,isto

identifythevaluesofmandb.Asimpleobservationisneededfirst:theequationofaline

canbewrittenas:

mx+b-y=0

Ifapointactuallysitsonthisline,thenpluggingitsxandyvaluesintotheequationwill

resultina0value.Ifapointisnotontheline,thenmx+b-ywillresultinanumberthat

amounts to an error; its magnitude indicates how far away the point is from the line.

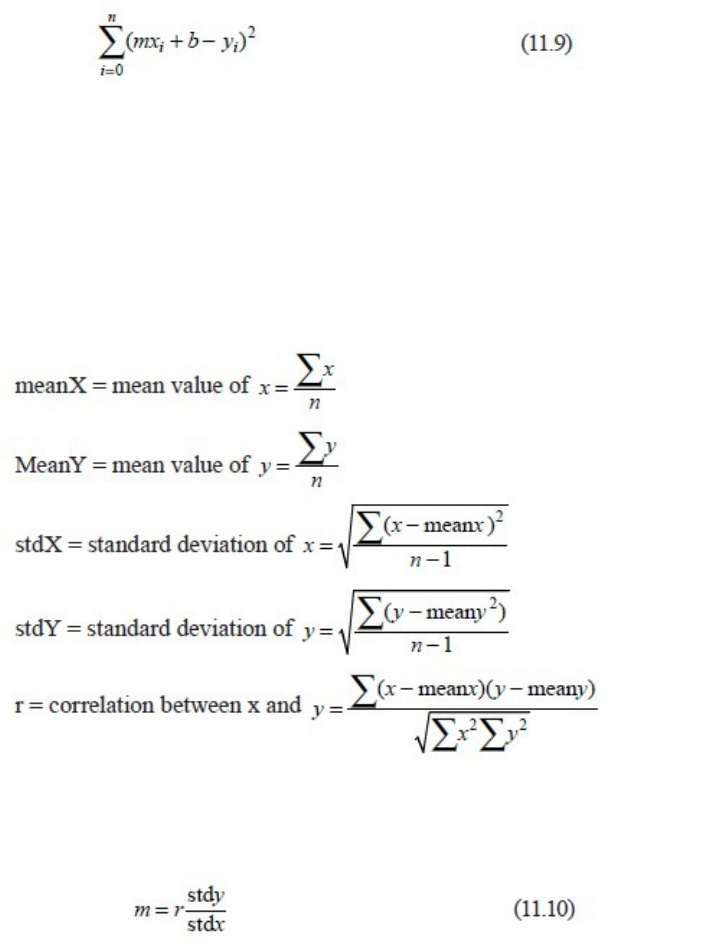
Fitting a line to the data can be expressed as an optimization problem: find a line that

minimizesthetotalerroroverallsampledatapoints.If(xi,yi)isdatapointithenthegoal

istominimize:

byfindingthebestvaluesofmandb.Theexpressionissquaredsothatitwillalwaysbe

positive, which simplifies the math. It may be possible to do this optimization using a

generaloptimizationprocesssuchasNewton’s,butfortunatelyforastraightlinethemath

has been done in advance. Other situations are more complicated, depending on the

functionbeingfitandthenumberofdimensions.

Asimplelinearregressionisdonebylookingatthedataandcalculatingthefollowing:

Eachofthesecanbecalculatedusingaseparatefunction.Thentheslopeofthebestline

throughthedatawouldbe:

Andtheinterceptis:

b=meany–m*meanx(11.11)

The function regress() that does the regression accepts a tuple of X values and a

correspondingtupleofYvalues,andreturnsatuple(m,b)containingtheparametersof

the line that fits the data. It depends on other functions to calculate the mean, standard

deviation, and correlation; these functions could generally be more useful in other

applications.Theentirecollectionofcodeis:

11.4.3 EvolutionaryMethods

A genetic algorithm (GA) or an evolutionary algorithm (EA) is an optimization

techniquethatusesnaturalselectionasametaphortooptimizeafunctionorprocess.The

ideaistocreateacollectionofmanypossiblesolutions(apopulation),whicharereally

just sets of parameters to the objective function. These are evaluated (by calling the

function)andthebestofthemarekeptinthepopulation;theremainderarediscarded.The

population is refilled by combining the remaining parameter sets with each other in

various ways in a process that mimics reproduction, and then this new population is

evaluatedandtheprocessrepeats.

Theideais thatthe populationcontains the bestsolutions thathave beenseen sofar,

andthatbyrecombiningthemanew,bettersetofsolutionscanbecreated,justasnature

selects plants and animals to suit their environment. This method does not require the

calculationofaderivative,soitcanbeusedtooptimize“functions”thatcan’tbehandled

inotherways.Itcanalsodealwithlargedimensions;thatis,functionsthattakealarge

numberofparameters.

Thisideamaybenew,andsodevelopingitwithanexamplemaybethe best wayto

illustrateit.Considertheproblemoffindingtheminimumofafunctionoftwovariables.

This is really an attempt to find values for x and y that result in the smallest function

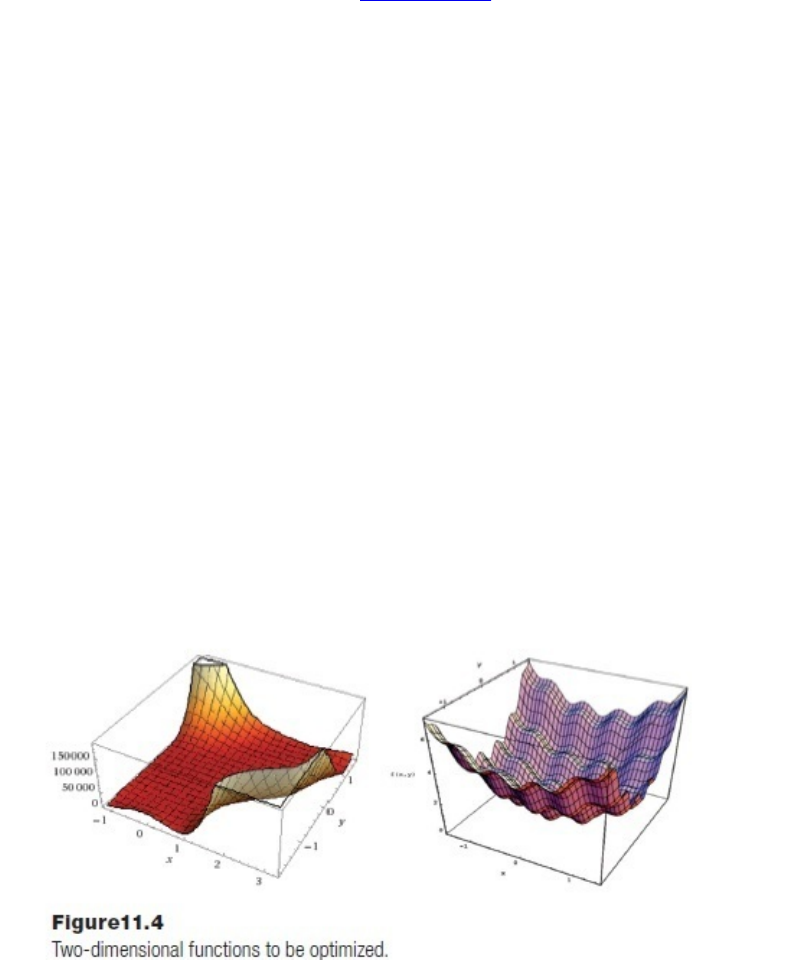
result. Evolutionary algorithms are often tested on quite nasty functions, having lots of

localminimaorlargeflatregions.Twosuchfunctionswillbeusedhere:theGoldstein-

Pricefunction:

(1+(x+y+1)2(19-14x+3x2-14y+6xy+3y2)(30+(2x+3y)2(18-32x+12x2+48y-

36xy+27y2))(11.12)

andBohachevsky’sfunction:

x2+y2–0.3cos(3px)–0.4cos(4py)+0.7(11.13)

GraphsofthesefunctionsareshowninFigure11.4.

The first step in the evolutionary algorithm is to create a population of potential

solutions. This is just a collection of parameter pairs (x,y) created at random. The

populationsizeforthisexamplewillbe100,andisaparameteroftheEAprocess.Thisis

doneintheobviousway:

defgenpop(population_size):

pop=()

foriinrange(0,population_size):

p=(randrange(-10,10),randrange(-100,100))

pop=pop+(p,)

returnpop

The population is a tuple of a hundred (x,y) parameter pairs. Now these need to be

evaluated, and so the objective function must be written. This will differ for each

optimizationproblem,ofcourse.Inthiscaseitisthesumoftheerrorsbetweenagiven

line(oneoftheparameters)andthedatapoints.Onewaytocalculatethisis:

defobjective(x,y):#Oneofmanypossiblkeobjective

#functions

returngoldsteinprice(x,y)

#returnboha(x,y)

defgoldsteinprice(x,y):#Goldstein-Pricefunction

#f(0,-1)=3

return(1+(x+y+1)**2*(19-14*x+3*x*x-14*y+6*x*y+

3*y*y))*\(30+(2*x-3*y)**2*(18-32*x+12*x*x+

48*y-36*x*y+27*y*y))



defboha(x,y):

z=x*x+y*y-0.3*cos(3*pi*x)-0.4*cos(4*pi*y)+0.7

returnz

Allmembersofthepopulationareevaluated,andthebestones—inthiscasetheones

havingthesmallestobjectivefunctionvalue—arekept.Agoodwaytodothisistohave

thevaluesinatupleEwhereE[i]istheresultofevaluatingparametersP[i],andsorting

thecollectionisdescendingorderonE.Sincethereare100entriesinEthiswillmeanthat

E[0:n]willcontainthebestn%ofthepopulation.Thefunctioneval()willcreateatuple

of function evaluations for the whole population, and sort() will sort these and the

correspondingparameters. These contain nothingnew,and willnot be shown here. The

program here will select the best 10% and discard the remainder, replacing them with

copiesofthegoodones.

Thekeyissueisoneofintroducingvarietyinthepopulation.Thismeanschangingthe

valuesoftheparameterswhile,onewouldhope,improvingtheoverallperformanceofthe

group. Using the metaphor of natural selection and genetics, there are two ways to

introducechangeintothepopulation:mutationandcrossover.Mutationinvolvesmakinga

smallchangeinaparameter.InrealDNA,amutationwouldchangeoneofthebasepairs

inthesequencewhichwouldusuallyamounttoarathersmallchange,butwhichwillbe

fatalinsomecases.IntheEAbeingwritten,amutationwillbearandomamountaddedto

orsubtractedfromaparameter.Mutationsoccurrandomlyandwithasmallprobability,

whichwillbenamedpmutintheprogram.Valuesbetween0.015and0.2aretypicalfor

pmut,butabestvaluecan’tbedetermined,andisproblemspecified.Avalueof0.02will

beusedhere.

The function mutate() will examine all elements in the global population, mutating

thematrandom(i.e.,addingrandomvalues):

defmutate(m):

globalpmut,population

foriinrange(int(m),len(population)):

c=population[i]

ifrandom()<pmut:#Mutatethexparameter

c[0]=c[0]+random()*10.0-5

ifrandom()<pmut:#Mutatetheyparameter

c[1]=c[1]+random()*10.0-5

population[i]=c

A crossoveris morecomplex, involvingtwo setsof parameters.It involves swapping

parts of the parameters sets from two “parents.” Some parameters could be swapped

entirely,inthiscasemeaningthat(x0,y0)and(x1,y1)wouldbecome(x0,y1)and(x1,

y0).Othertimespartsofoneparameterwouldbecombinedwithpartsofanother.There

are implementations involving bit strings that make this easier, but when using floating

pointvaluesasisbeingdonehere,agoodwaytodoacrossoveristoselecttwo“parents”

and replace one of the parameters in each with a random value that lies between the

originaltwo.

defcrossover(m):

globalpopulation,pcross

foriinrange(m,len(population)):#Keepthebestones

#unchanged

ifrandom()<pcross:#Crossoveratthe

#givenrate

k=randrange(m,len(population))#Pickarandom

#mate

w=randrange(0,1)#ChangeXorY?

c=population[i]#Getindividual1

g1=c[w]#GetXorYforthisguy

cc=population[k]#getindividual2

g2=cc[w]#GetXorY

if(g1>g2):t=g1;g1=g2;g2=t

#swapsog1issmallest

c[w]=random()*(g2-g1)+g1#Generatenew

#parameterfor1

cc[w]=random()*(g2g1)+g1#Generatenew

#parameterfor2

SampleoutputfromthreeattemptstofindtheoptimalvalueofBohachevsky’sfunction

is:

Iterations x y Result

5 [0.002528698, 0.0] at9.158793881192118e-05

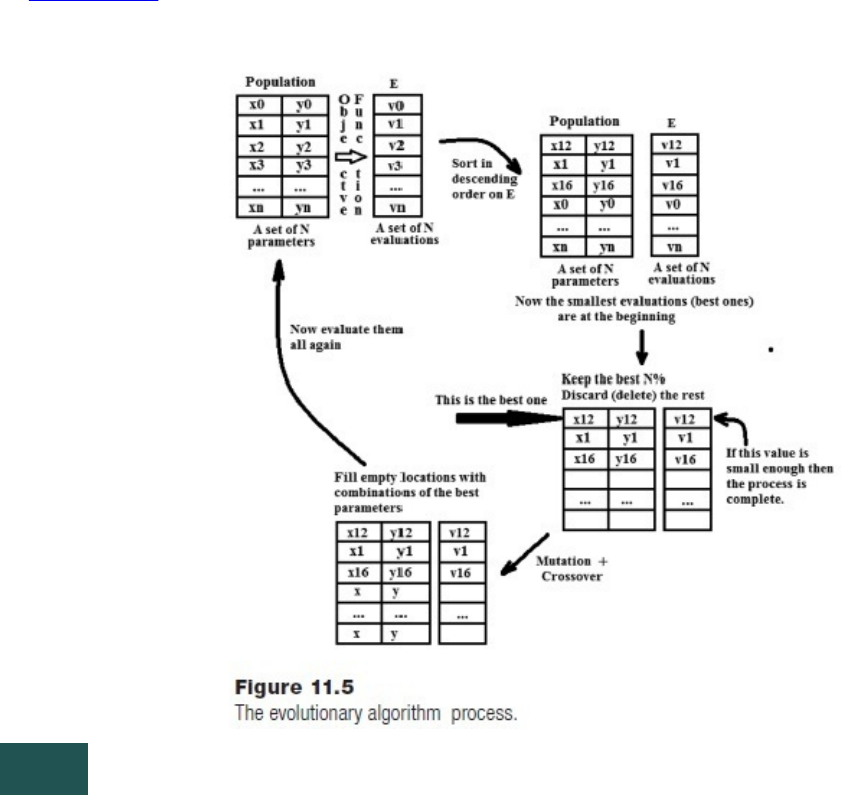
173 [5.38185770e-10, -0.0006229] at1.2643415301605287e-05

4 [-0.0007491, 0.0] at8.0394329584621e-06

Thisshowsthatsometimestheprocesstakesmuchmoretimetoarriveatasolutionthan

others.Itdependsontheinitialpopulation,aswellasontheparametersoftheprogram:

themutation and crossover probabilities,the percentage of the top individualsto retain,

andthenatureofthemutationandcrossover

operatorsthemselves.

Figure11.5outlinestheoverallprocessinvolvedintheoptimization.Detailsonspecific

techniquescanbefoundinthereferences.

11.5 LONGESTCOMMONSUBSEQUENCE(EDIT

DISTANCE)

So far in this chapter the methods being discussed are numerical ones, and given the

topic being discussed that makes some sense. There are, on the other hand, many

algorithms that are not numeric in nature, but may be more symbolic, involve patterns,

pictures, sounds, or other more complex data forms. It is true that at some level all

problems to be solved on a computer must be formulated using numbers, but in the

examplessofarthenumbersarereallythesubjectoftheproblem,andtheproblemwould

besolvednumericallyevenifdonewithapencilandpaper.Inothercasesthisisnotso.

As a major example, consider the problem of comparing two sequences of DNA. A

sequenceinthisinstanceconsistsofastringofletters,eachonereferredtoasabaseinthe

sequence. DNA consists of a long sequence of base pairs involving four molecules:

Adenine (A), Guanine (G), Thymine (T), and Cytosine (C) linked together chemically.

Theseultimatelydefinethestructureofaprotein,anditisthesequencethatisimportant.

Acommonproblemincomputationalbiologyistofindthelongestsequenceincommon

betweentwoDNAstrands,wherethesamplesmaybefromdifferentindividualsoreven

differentspecies.MethodsfordoingthistendtoinvolvetheeditdistanceorLevenshtein

distance.

Theeditdistanceisawayofspecifyinghowsimilarordissimilartwostringsaretoone

anotherbyfindingtheminimumnumberofeditingoperationsrequiredtotransformone

stringintotheother.Aneditingoperationcanbeachangeinacharacter,adeletion,oran

insertion.Forexample,whatistheeditdistance

betweentheword“planning”andtheword“pruning”?Itis3:

planning

pranningchange“l”to“r”

prunningchange“a”to“u”

pruningdelete“n”

Howis this used when looking at DNA?ADNAsequence is a set ofthe codes read

fromapieceofDNA,andisastringcontainingonlythelettersG,A,T,andC.Comparing

two pieces of DNA is a matter of comparing the two strings. So, the two strings

AGGACAT and ATTACGAT are distance 3 from each other. The longest common

subsequencehas5charactersinit:

AGGACAT

ATTACGAT

11.5.1 DeterminingLongestCommonSubsequence(LCS)

Exhaustive searching of two S1 and S2 strings for the longest common subsequence

wouldsimplybetooslowforanypracticalpurpose.Fortunately,alotofworkhasbeen

doneoverthepast50yearsonthisproblem,andthemethodofchoiceappearstobethe

Smith-Watermanmethod.Itbuildsamatrix(two-dimensionalarray)whereeachcharacter

ofthefirststringrepresentsacolumnofthematrix,andeachcharacterintheotherstring

formsarow,inorderofappearance.Thematrixisfilledwithnumbersusingthefollowing

relation:

Thefunctionσ(a,b)givesapenaltyforamatch/mismatchbetweentwocharactersaand

b.Hereitwillbe2foramatchand-2foramiss.Thegappenaltyisthevalueassignedto

havingtoleaveagapinthesequencetoperformabettermatch.Usuallythiswouldbe-1.

Theschemeoffersadegreeofflexibility,sothatdifferentpenalties(andrewards)canbe

appliedindifferentcircumstances.

ThefirststepintheSmith-Watermanmethodistocreateamatrix(atable)Tinwhich

there are len(S1+1) columns and len(S2+1) rows. The first index in T(i,j) refers to the

columnandthesecondindexistherow.Thevaluesinthecurrentrowareafunctionof

thoseinthepreviousone.Placea0ineachelementofthefirstrowandthefirstcolumn.

Forthetwostringsusedpreviouslythiswouldlooklikethetablebelow.

Now,foranyelementT(i,j)theneighboringelementsare:

T(i-1,j-1)T(i,j-1)T(i+1,j-1)

T(i-1,j)T(i,j)T(i+1,j)

ThefirstcelltofillinthetableTisT(1,1),markedwitha“*”characterintheexample

totheleft.Therelationusedtofillthiscellhasfourparts:

1.T(i–1,j–1)+σ(S1(i),S2(j))Thecharactersintherowandcolumnmatch,

soσ(S1(i),S2(j))=σ(A,A)=1+T(0,0)=2

2.Gappenaltyis-1,T(i-1,j)=0,T(0,1)=0.Resultis-1

3.Gappenaltyis-1,T(i,j-1)=T(1,1)=0.Resultis-1

4.Resultis0

Themaximumvalueofthesefourcalculationsis1,soT(1,1)=2.

ThenextcelltocomputeisT(2,1).Thistimethetwocharactersarenotthesame,so:

1.T(i−1,j−1)+σ(S1(i),S2(j))whereσ(S1(i),S2(j))=σ(G,A)=−1+T(1,0)

2.Gappenaltyis-1,T(i-1,j)=T(1,1)=2.

Resultis2-1=1

3.Gappenaltyis-1,T(i,j-1)=T(2,1)=0.Resultis-1

Resultis0

andsoT(2,1)=1

ForT(3,1):

1.GandAarenotthesame,s(G,T)=-2:

2.T(i-1.j)=T(2,1)=1so1-1=0

3.T(i,j-1)=T(3,0)=0so0–1=-1

4.0

Resultis0

ForT(4,1):

1.σ(A,A)=2,

2.T(i-1,j)=T(3,1)=0,0-gap=-1

3.T(i,j-1)=T(4,0)=0,0-gap=-1

4.0

Resultis2

ForT(5,1):

1.σ(C,A)=-2,

2.T(i-1,j)=T(4,1)=2,2-gap=1

3.T(i,j-1)=T(5,0)=0,0-gap=-1

4.0

Resultis1

ForT(6,1):

1.σ(A,A)=2,

2.T(i-1,j)=T(5,1)=1,1-gap=0

3.T(i,j-1)=T(60)=0,0-gap=-1

4.0

Resultis2

FinallyforT(7,1):

1. σ(T,A)=-2,

2. T(i-1,j)=T(6,1)=2,2-gap=1

3. T(i,j-1)=T(70)=0,0-gap=-1

4. 0

Resultis1

Theresultafterrow2iscompleteis:

Nowmovetothenextrow.Theprocessrepeatsuntilallcellshavebeenexaminedand

assignedvalues.Forthisexamplethefinalmatrixis:

Thelowerrightentryiscolumn7row8,or(7,8).

Thismatrixindicatesthedegreeofmatchatpointsinthestring.Todeterminetheactual

matchbetweenthestrings,beginwiththelargestvalueinthematrix.Inthiscaseitisin

thelowerrightcorner,butthat’snotalwaystrue.Whereverthemaximumis,startatthat

pointinthematrixandtraceleftandupwards;thisisessentiallymovingfromtheendof

eachstringbacktothebeginning.Ateachstepthemoveisleft,up,ordiagonally.

Theprocesswillbuildtwowaystomatchthestring.Oneindicateshowtochanges1

intos2(callthisM1),andtheotherindicateshowtoturns2intos1(callthisM2).Both

stringsareconstructedfrom,inthiscase,(7,9)back

to(0,0).

IfthereismorethanonecellinTwithamaximumvalue,thenarouteshouldbetraced

backfromeachmaximum.

Fortheexamplestringtheresultis:

M1=AGGACCAT

M2=ATTAC_AT

ThereisamismatchattheGG/TTpairandaninsertedgapinM2.

11.6 SUMMARY

A discussion of some of the more important problem types studied by scientists was

presentedalongwithsomemethodfortheirsolution.Therootofanequationistheplace

whereitsvalueiszero,andNewton’smethodwasdescribedasameansoffindingaroot.

Newton’s method requires that the derivative of the function be known, so means of

numericallydeterminingthederivativewerealsodiscussed.

Since derivatives could be calculated, methods for performing integration were

describedandfunctionsfordoingthecalculationusingthetrapezoidalrulewerewritten.

One of the more common calculations in science is to find an optimumvalue for a

function.AnothermethodofNewton’swasusedtofindmaximaorminimaofafunction.

The modeling of data is important in scientific (and other) disciplines. A method for

finding the best straight line that passes through a set of data was illustrated (linear

regression)andcodewasdesignedandtestedforthisproblem.

Evolutionaryalgorithmscanbeusedtofindtheoptimumofafunction,andisespecially

useful when dealing with multidimensional functions or functions that have many local

optima,andwhennoderivativeofthefunctionexists.

BiologistssometimesneedtomatchsequencesofDNA.Amethodthatdoesthisusing

bases as characters and sequences as strings was presented; this is the Smith-Waterman

algorithmforlocalsequencematching,andiscommonlyusedfortheseproblems.

Exercises

1.Modifytherootfindingexamplesothatanumericalderivativeisusedinsteadofan

analyticalone(i.e.,usederive1()orderive2()).Thisisamorepracticalsituation.What

istheeffect?

2.Modifythetrap0()functioninthetrapezoidruleexamplesothatitnevercallsthe

functionbeingevaluatedmorethanonceforanypoint.

3.LookupSimpson’sRuleandcodeyourownversion.Compareitwiththetrapezoid

rulefortwofunctionsofyourchoice.Whichoneismoreaccurateaftereachiteration?

4.Writeafunctionerror()thatacceptsXandYdatatuples,andvaluesaandb.Itreturns

thetotalerrorbetweenthedatapointsandthecurveax2+bx.

5.The(natural)logarithmofavaluevisdefinedtobetheintegralof1/xfrom1tov.

Createafunctionthatcalculatesthenaturallogusingtheexistingintegrationfunction.

6.RuntheevolutionaryalgorithmtooptimizetheGoldstein-Pricetwentytimes.Doesit

everfailtoapproachtheminimum?Howoften?WhatcanbedoneifanEAdoesnot

arriveatanoptimum,andhowcanitbedetermined?

7.Usingsoftwaredevelopedinthischapter,findtwopositivenumberswhosesumis9

andsothattheproductofonenumberandthesquareoftheothernumberisa

maximum.

NotesandOtherResources

Onlineeditdistancecalculator:http://planetcalc.com/1721/

Smith-Waterman algorithm: http://www.slideshare.net/avrilcoghlan/the-smith-

waterman-algorithm

https://www.youtube.com/watch?v=jrJ23aaByE8

1.D.Levy.LectureNotes,(Ch5)NumericalDifferentiation,

http://www2.math.umd.edu/~dlevy/classes/amsc466/lecture-notes/differentiation-

chap.pdf

2.WilliamPress,SaulTeukolsky,WilliamVetterling,andBrianFlannery.(2007).

NumericalRecipes:TheArtofScientificComputation,3rdedition,Cambridge

UniversityPress.

3.RichardHamming.(1987).NumericalMethodsforScientistsandEngineers,Dover

Publications.

4.J.R.Parker.(2002).GeneticAlgorithmsforContinuousProblems,15thCanadian

ConferenceonArtificialIntelligence,Calgary,Alberta,

May27–29.

5.D.E.Goldberg.(1989).GeneticAlgorithms,Optimization,andMachine

Learning,Addison-Wesley,Reading,MA.

6.vlab.amrita.edu.(2012).GlobalAlignmentofTwoSequences-Needleman-

WunschAlgorithm,Retrieved9December2015,vlab.amrita.edu/?

sub=3&brch=274&sim=1431&cnt=1

7.S.B.NeedlemanandC.D.Wunsch.(1970).Ageneralmethodapplicabletothe

searchforsimilaritiesintheaminoacidsequenceoftwoproteins,

J.Mol.Biol.,48,443–453.

8.T.F.SmithandM.S.Waterman.(1981).Identificationofcommonmolecular

subsequences,J.Mol.Biol.,147(1),195-197.

CHAPTER12

HOWTOWRITEGOODPROGRAMS

12.1ProceduralProgramming–WordProcessing

12.2ObjectOrientedProgramming–Breakout

12.3DescribingtheProblemasaProcess

12.4RulesforProgrammers

12.5Summary

Inthischapter

Thereisnogeneralagreementonhowbesttoputtogetheragoodprogram.Good,bythe

way,meansfunctionallycorrect,readable,modifiable,reasonablyefficient,andthatsolves

aproblemthatsomeoneneedssolved.Thischapterwillbedistinctfromtheothersinthis

book:we’llmoveintosecondpersonnarrative,partlybecauseofthemorepersonalnature

ofthesubjectmaterial.Writingcodeforsomepeopleisliketellingastoryormakinga

painting:it’snotthatitisart,butthatitispersonal.Ifyouwishtoinsultaprogrammer,

saythattheircodeispoorlystructured,ornaïve,orinsomewaylessthanadequate.

Therearemanyprocessesthathavebeendescribedforprogramming,andthetruthis

thatnotonlyistherenotonebestone,butitisrarelycertainthananyofthemisbetter

than any of the others. When someone writes a program, they are trying to solve a

problem.Whattheyaredoingistranslatingaloosecollectionofideasintoaformthatcan

berepresentedonacomputer,whichistosayas

numbers.Theideasareassociatedwithalgorithms,thingsthatcanbeshowntoworkforat

leastarangeofsituations.Thenthatneedstobeconvertedintoasequenceofstepsthat

leadstoasolutiontotheoriginalproblem.

Thisisinpartaprobleminsynthesis,thecombiningofseparatecomponents,elements,

and ideas into a coherent whole. There is something called synthesis programming, but

that’snotwhatisbeingdiscussed.Thepartsofaprogramincludedecisionconstructs(IF

statements), looping (FOR and WHILE), expressions, assignment statements, and data

structures(tuples,dictionaries,strings,etc.).Thereisadegreeofskillinvolvedinusing

theseunitstobuildasensiblelargerprogram.Thisskillissomewhatindividual.Notwo

programmerswillcreateexactlythesameprogramforanon-trivialproblem.

Whatwe’regoingtodointhischapterisshowthedevelopmentofanentirecomputer

program,withallof theintermediatesteps,flaws, errors,andflashes of genius(ifany).

Why?Theansweris“becausethatisrarelydoneinlecturesorinabook.”Whenteaching

mathematics the professor often shows the proof of a theorem on the blackboard (or as

PowerPointslides)andexplainsthesteps.Whattheyneverdoisshowhowthetheorem

wasactuallyprovedwhentheoriginalpersonprovedit—deadends,daysofnoprogress,

goodideas,badideas:thewholemessyprocess.

Thisiscrucial.Notheoremandnocomputerprogramflows fully formedandcorrect

fromsomeone’shead.Observingthefullprocessmaybeavaluablestageintheeducation

of a programmer. They will see that the process is prone to error, even for good

programmers. They’ll see that not all ideas that seem good are actually good; that the

processisnotalinearone,butthatitappearsinsomesensetospiral,gainingfunctionality

ateachloop.Andtheywillseethattherecanbeasimpleandobviousmethodthatcould

beagreeduponbymanydifferentprogrammersandyet adapted foreachnewsituation.

Themethod that we’ll use is callediterativerefinement, and it is nearly independent of

languageorphilosophy.Ofcourse,noteveryonewillagree.

Oneexampleprogramwillbeacomputergame,andonethatcan’tbeplayedwithouta

computer.Itwillbeabreakoutstylegamethatusescirclesinsteadofrectangles.Theother

willbeasystemthatformatstypedtext.

12.1 PROCEDURALPROGRAMMING–WORD

PROCESSING

Intheearlydaysofdesktoppublishing,theprogramsthatwritersuseddidnotdisplay

theresultsonthescreenin“what-you-see-is-what-you-get”form.Formattingcommands

were embedded within the text and were implemented by the program, which would

createaprintableversionthatwasproperlyformatted.Programslikeroff,nroff,tex,and

variationsthereofarestillused,butmostwritingtoolsnowlooklikeWordorPageMaker

withcommandsbeinggiventhroughagraphicaluserinterface.

Thereisalimittowhatkindoftextprocessingcanbedoneusingsimpletextfiles,but

when you think about it that’s really what a typewriter produces—simple text on paper

withfixed size fonts. Thatworked for a verylong time. It was good enough for Ernest

HemingwayandRaymondChandler.

The program that will be developed here will accept text from a file and format it

according to a set of commands that have a specific format and are predefined by the

system.Theinputwillresemblethatacceptedbynroff,anoldUnixutility,butwillbea

subsetforsimplicity.Sinceitusesstandardtextinputandoutputanymeasurementswill

bemadeincharacters,notinchesorpoints.Commandswillbeginonanewlinewitha“.”

character and will be alphabetic. A line beginning with “.br”, for instance, results in a

forcedlinebreak.Somecommandstakeaparameter:thecommand“.ll55”setstheline

lengthto55characters.

Hereisalistofallofthecommandsthatthesystemwillrecognize:

.pln Setsthepagelengthtonlines

.bpn Beginpagen

.br Break

.fi Filloutputlines(e.g.,justify)

.nf Don’tfilloutputlines

.na Nojustificaton

.cen Centerthenextninputlines

.lsn Outputn-1linespacesaftereachline

.lln Linelengthisncharacters

.inn Indentncharacters

.tin Temporarilyindentncharacters

.nh Donothyphenate

.hy Hyphenationon

.spn Generatenlines

Theprogramwillreadatextfileandidentifythewordsandthecommands.Thewords

willbewrittentoanoutputfileformattedasdescribedbythecommands.Thedefaultwill

betorightjustifythetext,andtouseemptylinesasparagraphbreaks.Thequestionstobe

answeredhereare:

1.Howdoesonebegincreatingsuchaprogram?

2.Cantheprocessofprogramcreationbedescribed?

a.Istheprocesssystematicorcasual?

b.Isthereonlyoneprocess?

Beginningwiththelastquestionfirst,thereisnosingleprocess.Whatispresentedhere

is only one, but it should be understood that there are others, and that some processes

probablyworkbetterthanothersforsomekindsofprogram.Theprogramtobecreated

herewillnotuseclasses,andwillinvolveaclassicalortraditionalmethodologygenerally

referredtoastop-down.Somepeopleonlyuseobject-orientedcode,butaproblemwith

teachingthatwayisthataclasscontainstraditional,procedure-orientedcode.Tomakea

class,onemustfirstknowhowtowriteaprogram.

12.1.1 Top-Down

The idea behind top-down programming is that the higher levels of abstraction are

describedfirst.Adescriptionof what theentire programis to dois writtenin akind-of

English/computer hybrid language (pseudocode), and this description involves making

callstofunctionsthathavenotyetbeenwrittenbutwhosefunctionisknown.Whenthe

highestleveldescriptionisacceptable,thenthefunctionsusedaredescribed.Inthisway

thehigh-leveldecisionsaredescribedintermsofthelowerlevel,whoseimplementationis

postponeduntilthedetailsareappropriate.Theprocessrepeatsuntilallpartshave been

described, at which time the translation of the pseudocode into a real programming

language can proceed, and should be straightforward. This can result in many distinct

programs,butallshoulddobasicallythesamething,simplyinsomewhatdifferentways.

Forthetaskathand,thefirststepistosketchtheactionsoftheprogramasawhole.The

programbeginsbyopeningthetextfileandopeninganoutputfile.Thebasicactionisto

copyfrominputtooutput,withcertainadditionstotheoutputtext.Thedatafileisreadin

ascharactersorwords,butoutputaslinesandpages.Soperhapsthefollowing:

Openinputfileinf

Openoutputfileoutf

Readawordwfrominf

Whilethereismoretextoninf:

Ifwisacommand:

Processthecommandw

Else:

Thenextwordisw.Processit

Readawordfrominf

Closeinf

Closeoutf

Thisrepresentstheentireprogram,althoughlackingadegreeofdetail.AsPythonthis

wouldlookalmostthesame:

filename=input(“PYROFF:Enterthenameiftheinput

file:“)

inf=open(filename,“r”)

outf=open(“pyroff.txt.“w”)

w=getword(inf)

whilew!=””:

ifiscommand(w):

process_command(w)

else:

process_word(w)

w=getword(inf)

inf.close()

outf.close()

Inorderfortheprogramtocompilethefunctions,theymustexist.Theyshouldinitially

bestubs,relativelynon-functionalbutresultinginoutput:

fromrandomimport*



defgetword(f):

print(“Getword“)



defiscommand(w):

print(“ISCOMMANDgiven“,w)

ifrandom()<0.5:

returnFalse

returnTrue



defprocess_command(w):

print(“Processingcommand“,w)



defprocess_word(w):

print(“Processingtheword“,w)

Thisprogramwillrun,butneverendsbecauseitneverreadsthefile.Still,wehavea

structure.

Nowthefunctionsneedtobedefined,andintheprocessfurtherdesigndecisionsare

made. Consider getword(): what comprises a word and how does it differ from a

command?Acommandstartsatthebeginningofalinewitha“.”character.Itisfollowed

bytwoalphabeticcharactersthataredefinedbythesystem.Ifthetwocharactersdonot

matchanycombinationsinthelistofcommands,thenitisnotacommand.Aword,onthe

otherhand,beginsorendswithawhitespace(blank,tab,orendofline)andcontainsall

ofthecharactersbetweenthosewhitespaces.Itmaynotbeawordinthetraditionalsense,

in that it may not be an English word; it could be a number or other sequence of

characters.Thosemay causeproblems,but itwillbe leftup totheuser tofigure itout.

Example:alongURLmayextendoveraline.Theprogramhastodosomething,andso

will probably put an end of line when the count of characters exceeds a maximum and

leavetheproblemtotheusertofix.

So,let’sfigureoutthegetword()function.Itwillconstructawordasacharacterstring

fromindividualcharactersthathavebeenreadfromtheinputfile.Afirsttrycouldbe:

defgetword(f):

w=””

whilewhitespace(ch(f)):

nextch(f)

whilenotwhitespace(ch(f)):

w=w+ch(f)

nextch(f)

print(“Getwordis“,w)

returnw

Thefunctionwhitespace()returnsTrueifitsparameterisawhitespacecharacter.The

functionnextch() reads the next characterfrom the specified file, andthe function ch()

returns the value of the current character. To effectively test getword(), we need to

implementthesethreefunctions.Here’safirstattempt:

defwhitespace(c):

ifc==”“:returnTrue

ifc==“\t”:returnTrue

ifc==“\n”:returnTrue

returnFalse



defch(f):

globalc

return(c)



defnextch(f):

globalc

c=f.read(1)

This way of handling input is a bit unusual, but there is a reason for it. We are

anticipating a need to buffer characters or to place them back on the input stream. It is

similartotheinputschemeusedinPascal,orthesystemfoundinearlyformsofUNIX

whichusedgetchar–putchar-ungetc.Thenecessityofextractingcommandsfromthe

input stream, and that commands must begin a new line, might make this particular

schemeuseful.Theinitialimplementationofnextch()simplyreadsanewcharacterfrom

thefile,butitcouldeasilybemodifiedtoextractacharacterfromabuffer,andrefilethe

bufferifitisempty.Bothwouldlookthesametotheprogrammerusingthem.

Theprogramruns,buthasaproblem:itneverterminates.Afterthetextfilehasbeen

read,theprogramseemstocallnextch()repeatedly.Aftersomethoughtthereasonisclear

—whentheinputrequestresultsinanemptystring(“”)thecurrentcharacterisnotawhite

space,andtheloopingetword()thatisbuildingawordrunsforever.Thisisatraditional

end-of-fileproblemandcanbesolvedinafewdifferentways:aspecialcharactercanbe

usedforEOF,aflagcanbeset,ortheemptystringcanbetestedforintheloopexplicitly.

Thelattersolutionwaschosen,andfixestheinfiniteloop.Thewordconstructionloopin

getword()becomes:

whilenotwhitespace(ch(f))andch(f)!=””:

A possible next step is to distinguish between commands and words. Because a

commandstartsalineandbeginswitha“.”therearetwothingstodo:markthebeginning

ofanewline,andlookuptheinputstringinatableofcommands.Thecommandcouldbe

searchedfirst,thenifitmatchesacommandnamewecouldbackuptheinputtoseeifit

was preceded by a newline character (“\n”). A newline counts as a white space, and

anotheroptionwouldbetosetaflagwhenanewlinecharacterisseen,clearingitwhen

anothercharacterisreadin.Nowastringisacommandiftheflagsetbeforeitwasreadin

anditmatchesoneofthecommands.Timingiseverythinginthismethod,butwhitespace

separates words, so it could work by simply remembering (saving) the last white space

characterseenbeforeanyword.Thatsoundslikeagoodidea.

Oops.Whenimplemented,noneofthecommandsarerecognized.Atableofnameswas

implementedasatuple:

table = (“.pl”,”.bp”,”.br”,”.fi”,”.nf”,”.na”,”.ce”,

“.ls”,”.ll”,”.in”,”.ti”,”.nh”,”.hy”,”.sp”)

Thenextch()functionwasmodifiedso:

defnextch(f):

globalc,lastws

c=f.read(1)

ifwhitespace(c):

lastws=c

and the function iscommand() is implemented by checking for the newline and the

matchofthestringinthetable:

defiscommand(w):

globaltable,lastws

iflastws==“\n”:

ifwintable:

returnTrue

returnFalse

To discover the problem some print statements were inserted that show the previous

white space character and the match in the table for all calls to iscommand(). The

problem,whichshouldhavebeenobvious,isthatwhenthecommandisreadin,thelast

whitespaceseenwillbetheonethatterminatedit,nottheoneinfrontofit.

A solution: keeping the same theme of remembering white space characters, how about

savetheprevioustwowhitespacecharactersseen.Themostrecentwhitespacewillbethe

one that terminated the word string, and the second most recent will always be the one

before it. All of the others, if any, would have been skipped within getword(). The

solution,ascodedinthenextch()function,wouldbe:

defnextch(f):

globalc,clast,c2last

c=f.read(1)

ifwhitespace(c):

c2last=clast

clast=c

Therearetwovariablesneeded,clastbeingthepreviouswhitespaceandc2lastbeing

the one encountered before clast. Now iscommand() is modified slightly to look for

c2last:

defiscommand(w):

globaltable,c2last

ifc2last==“\n”:

ifwintable:

returnTrue

returnFalse

Yes,thisnowidentifiesthecommandsinthesourcefile,eventhetextthatlookslikea

commandbutisnot:“.xx.”

Noticethatthedevelopmentoftheprogramconsistsofaninitialsketchandthenfilling

inthecodeasstubsandcodingthestubstobefunctionalcode,oneatatime.Sometimesa

stub requires further undefined functions to be used, and those could be coded as stubs

too,orcompletediftheyaresmallsoastoallowtestingtoproceed.It’sajudgmentcallas

towhethertocompletethestubsdownthechainforonepartoftheprogramortoproceed

tothenextoneatthecurrentlevel.Forexample,shouldwehavecompletedthenextch()

andch()functionsbeforetryingtodesignprocess_command()?Itdoesdependonhow

testingcanproceedandwhat“level”we’reat.Thenextch()functionlookslikeitwon’t

call other functions that have not been implemented, and it is tough to test getword()

withoutfinishingnextch().

Thisdiscussionspeakstowhatthenextstepwillbefromhere,andtheansweris“there

couldbemany.”Let’s lookatcommandsnext,becausetheywilldictatetheoutput,and

then deal with formatting last. It is known that a string represents a command, and the

function called as a consequence is process_command(). This function must determine

whichcommandstringwasseenandwhattodoaboutit.Thewaycommandsarehandled

andthewaytheoutputdocumentisspecifiedhastobesortedoutbeforethisfunctioncan

befinished,butasetofstubscanholdtheplaceoffuturedecisionsasbefore.

Thestringthatwasseentobeacommandisstoredinatuple.Theindexofthestring

withinthetupletellsuswhichcommandwasseen,althoughastringmatchcouldbedone

directly.Usingatupleisbetterbecausenewcommandscanalwaysbeaddedtotheendof

the tuple during future modifications and it is easier to modify command names. The

function,whichusedtobeastub,isnow:

defprocess_command(w):

globaltable,inf,page_length,fill,center,center_

count,globalspacing,line_length,adjust,hyphenate

k=table.index(w)

ifk==0:#.PL

s=getword(inf)

page_length=int(s)

elifk==1:#.BP

genpage()

elifk==2:#.BR

genline()

elifk==3:#.FI

fill=True

elifk==4:#.NF

fill==False

elifk==5:#.NA

adjust=False

elifk==6:#.CE

center=True

s=getword(inf)

center_count=int(s)

elifk==7:#.LS

s=getword(inf)

spacing=int(s)

elifk==8:#.LL

s=getword(inf)

line_length=int(s)

print(“Linelength“,line_length,“characters”)

elifk==9:#.IN

s=getword(inf)

indent(int(s))

elifk==10:#.TI

s=getword(inf)

temp_indent(int(s))

elifk==11:#.NF

hyphenate=False

elifk==12:#.HY

hyphenate=True

elifk==13:#.TL

dotl()

elifk==14:#.SP

s=getword(inf)

space(int(k))

This completes iteration 5 of the system and generates quite a few new stubs and

defineshowsomeoftheoutputfunctionswilloperate.Therearesomeflags(hyphenate,

center,fill, adjust) and some parameters for the output process (line_length, spacing,

etc.)thatareset,andsowillbeusedinsendingoutputtexttothefile.Theseparameters

beingknown,itistimetodefinetheoutputprocess,whichwillbeimplementedstarting

withthefunctionprocess_word().

Aswasmentionedearlier,theprogramreadsdataonecharacteratatimeandemitsitas

words.Thereisaspecifiedlinelength,andwordscanbereadandstoreduntilthatlength

isnearedorexceeded.Wordscouldbestoredinastring.Whenthelinelengthisreached,

thestringcouldbewrittentothefile.Ifrightjustificationisbeingdone,spacescouldbe

addedtosomeotherspacesinthestringuntilthelinelengthwasmetexactly,orthefinal

wordcouldbehyphenatedtomeetthelinelength.Ifrightjustificationisnotbeingdone,

thenthelinelengthonlyhastobeapproached,butnotexceeded.

Fortextcenteringinputlinesarepaddedwithequalnumbersofspacesonbothsides.

Thepagesizeismetbycountinglines,andthenbycreatinganewpagewhenthepage

sizeis met, possibly byentering a form feedor perhaps by printing emptylines until a

specifiedcountisreached.Indentingissimple:theincommandresultsinafixednumber

ofspacesbeingplacedatthebeginningofeachoutputline;theticommandresultsina

specifiednumberofspacesbeingplacedatthebeginningofthecurrentline.Hyphenation

isdonebytablelookup.Certainsuffixesandprefixesandlettercombinationsarepossible

locationsforahyphen.Thefinalwordonalinecanbehyphenatedifalocationwithinitis

subjecttoahyphenasindicatedbythetable.

Theprocessistoreadandbuildwordsandcopythemtoastring,thenextoutputline.

Noactionistakenuntilthestringnearsthelinelength,atwhichpointinsertionofspaces,

hyphenation,orotheractionsmaybetakentomakethestringfittheline,eithercloselyor

precisely.Afteralinemeetsthesizeneededitiswritten,perhapsfollowedbyothersifthe

linespacingislargerthanone.So,thebasicactionoftheprocess_word()functionwillbe

tocopythewordtoastring,theoutputbuffer,underthecontrolofasetofvariablesthat

aredefinedbytheuserthroughcommands:

page_length 55 Numberoflinesoftextonasinglepage

fill True Controlswhetherthetextisbeingformatted

adjust True Controlswhetherthetextisrightjustified

center False Controlswhethertextisbeingcentered

center_count 0 Numberoflinesstilltobecentered

spacing 1 Numberoflinesoutputperlineoftext

nindent 0 Numberofspacesontheleft

line_length 66 Numberofcharactersononeline

hyphenate True Arewordshyphenatedbythesystem?

Thesimplestversionofprocess_word()wouldcopywordstothebufferuntiltheline

wasfullandthensimplywritethatlinetotheoutputfile.

defprocess_word(w):

globalbuffer,line_length

iflen(buffer)+len(w)+1<=line_length:

buffer=buffer+””+w

else:

emit(buffer)

buffer=w

The code above adds the given word plus a space to the buffer if there is room.

Otherwiseitcallstheemit()functiontowritethebuffertotheoutputfileandplacesthe

word at the beginning of a new line. This is nearly correct. Some of the output for the

samplesourceis:

ThisissampletextfortestingPyroff.Thedefaultistoright

adjustcontinuously,butembeddedcommandscanchangethis.

Nowthelinewidthshouldbe

30characters,andsotheleft

marginwillpulledback.This

lineiscentered.xxnota

command.Indented4

Notethatthecommand“.ll30”wascorrectlyhandled,butthatthereisanextraspaceat

the beginning of the first line. That’s due to the fact that process_word() adds a space

between words, and if the buffer is empty that space gets placed at the beginning. The

solutionistocheckforanemptybuffer:

iflen(buffer)+len(w)+1<=line_length:

iflen(buffer)>0:

buffer=buffer+””+w

else:

buffer=w

Thiswasasuccessful fix,andcompletesiteration6 ofthesystem, whichisnow150

lineslong.

Withinprocess_word()therearemultipleoptionsforhowwordswillbewrittentothe

output. What has been done so far amounts to filling but no rightjustification. Other

optionsare:nofilling,centering,andjustification.Whenthefillingisturnedoff,aninput

linebecomesanoutputline.Thisistrueforcenteringaswell.Whenjustificationistaking

place the program will make the output lines exactly line_length characters long by

insertingspacesinthelinetoextenditandbyhyphenation,wherepermitted,toshortenit.

Theruleisthatthelinemustbethecorrectlengthandmustnotbeginorendwithaspace.

Theimplementationofthispartoftheprogramisattheheartoftheoverallsystem,but

wouldnotbepossiblewithoutasensibledesignuptothispoint.

12.1.2 Centering

First,acenteredlineistobewrittentooutputwhenanendoflineisseenoninput.This

meansthattheclastvariablewillbeusedtoidentifytheendoflineandtoemitthetext.

Next, the line will have spaces added to the beginning and end to center it. The buffer

holdsthe lineto be writtenand haslen(buffer) characters.The number of spacesto be

addedtotalsline_length–len(buffer),andhalfwillbeaddedtothebeginningoftheline

andhalftotheend.Afunctionthatcentersagivenstringwouldbe:

defdo_center(s):

globalline_length

k=len(s)#Howlongisthestring?

b1=line_length-k#Howmuchshorterthantheline?

b2=b1//2#Splitthatamountintwo

b1=line_length-k-b2

s=”“*b1+s+”“*b2#Addspacestocenterthetext

emit(s)#Writetofile

In the process_word() function some code must be added to handle centering. This

codehas todetect theend ofline andpass the bufferto do_center().It alsocounts the

lines,becausethe“.ce”commandspecifiesanumberoflinestobecentered.

ifcenter:#Textisbeingcentered,nofill

iflen(buffer)>0:#Addthiswordtotheline

buffer=buffer+””+w

else:

buffer=w

ifclast==“\n”:#Aninputline=anoutputline

do_center(buffer)#Emitthetext

center_count=center_count-1#Countlines

ifcenter_count<=0:#Done?

center=False#Yes.Stopcentering.

Thiscodeisnotquiteenough.Therearetwoproblemsobserved.Oneproblemisthat

thebuffercouldbepartlyfullwhenthe“.ce”commandisseen,andmustbeemptied.This

problem is serious, because filling may be taking place and the line might have to be

justified.Forthemomentacalltoemit()willhappenwhenthe“.ce”commandisseen,

butthiswillhavetobeexpanded.

Theotherproblemissimpler:thedo_center()functiondoesnotemptythebuffersothe

linebeingcenteredoccurstwiceintheoutput.Forexample:

marginwillpulledback.

Thislineiscentered←Thisiscorrect

Thislineiscentered.xxnot←Thisiswrong.Textisrepeated.

acommand.Indented4

Thesolutionistoclearthebufferafterdo_center()iscalled:

do_center(buffer)#Emitthetext

buffer=””#Clearthebuffer

12.1.3 RightJustification

Centeringtextisafirststeptounderstandinghowtojustifyit.Rightjustifiedtexthas

the sentences arranged so that the right margin is aligned to the line. When centering,

spaces are added to the left and right ends of the string so as to place any text in the

middle of the line. When justifying, any space in the line can be made into multiple

spaces,thusextendingthetextuntilitreachestherightmargin.Naturallyitwouldnotbe

acceptabletoplacealloftheneededspacesinonespot.Itlooksbestiftheyaredistributed

asevenlyaspossible.However,nomatterwhatisdonetherewillbesomesituationsthat

causeuglyspacing.We’llhavetolivewiththat.

Thenumberofspacesneededtofillupalineisline_length–len(buffer),justasitwas

whencentering.Aswordsareaddedtothelinethisvaluebecomessmaller,andwhenitis

smallerthanthelengthofthenextwordtobeadded,thentheextraspacesmustbeadded

andanewlinestarted.Thatis,when

k=line_length-len(buffer)

ifk<len(word):

thenadjustingisperformed.First,countthespacesinthebufferandcallthisnspaces.If

k>nspaces then change each single space into k//nspaces space characters and set k =

k%nspaces.Thiswillrarelyhappen.Nowweneedtochangesomeofthespacesinthe

bufferintodoublespaces.Whichones?Inanattempttospreadthemaround,setxk=k+

k//2. This will be used as an increment to find consecutive spots to put spaces. So for

example,letk=5,inwhichcasexk=7.Thefirstspacecouldbeplacedinthemiddle,or

atspacenumber2.Nowcountxkpositionsfrom2,startingoveratzerowhenyouhitthe

end.Thiswillgive4asthenextposition,followedby1,then3,andthen0.Thisprocess

seemstospreadthemout.Nowthebufferiswrittenoutandthenewwordisplacedinan

emptybuffer.

Thissoundstricky,solet’swalkthroughit.Neverentercodethatisnotlikelytowork!

Insideoftheprocess_word()function,checktoseeifadjustingisgoingon.Ifso,check

toseeifthecurrentwordfitsinthecurrentline.Ifso,putitthereandmoveon.

elifadjust:

k=line_length-len(buffer)#Numberofspaces

#remaining

ifk>len(w):#Doesthewordwfit?

iflen(buffer)==0:#Yes.Emptybuffer?

buffer=w#Yes.Buffer=word.

else:#No.Addwordtothe

#buffer

buffer=buffer+””+w

print(“Buffernow“,buffer,k,len(w))

else:#Notenoughspaceremains

print(buffer,k,w,len(w))

nspaces=buffer.count(”“)#Howmanyspacesin

#buffer?

xk=k+k//2+1#Spaceinsertincrement

whilek>0:

i=nth_space(buffer,xk)

buffer=buffer[0:i]+””+buffer[i:]

k=k-1

xk=xk+1

emit(buffer)

buffer=w

The function nth_space (buffer, xk) locates the nth space character in the string s

modulo the string length. The spaces were not well distributed with this code in some

cases.Therewasasuspicionthatitdependedonwhetherthenumberofremainingspaces

wasevenorodd,sothecodewasmodifiedtoread:

...

xk=k+(k+1)//2#Spaceinsertincrement

ifk%2==0:

xk=xk+1

...

whichworkedbetter.Theoutputforthefirstpartofthetestdatawas:

This is sample textfor testing Pyroff. The default is to right adjust continuously, but

embeddedcommandscanchangethis.

Nowthelinewidthshouldbe

30characters,andsotheleft

marginwillpulledback.

Thislineiscentered

.xxnotacommand.Indented4

characters.Theideabehind

top-downprogrammingisthat

thehigherlevelsof

abstractionaredescribed

...

Theshortlinesarerightjustified,butthedistributionofthespacescouldstillbebetter.

Thefunctionnth_space()isimportant,andlookslikethis:

defnth_space(s,n):

globalnindent

nn=0#nnisacountofspacesseensofar

i=0#iistheindexofthecharacterbeingexamined

whileTrue:

ifs[i]==”“:#Ischaracteriaspace?

nn=nn+1#Yes.Countit

ifnn>=n:#Isthisenoughspaces?

returni#Yes,returnthelocation

i=(i+1)%len(s)#Nexti,wrappingaroundtheend

12.1.4 OtherCommands

The rest of the commands have to do with hyphenation, pagination, and indentation,

exceptforthe“.br”command.Dealingwithindentationfirst,thecommand“.in”specifies

anumberofcharacterstoindent,asdoes“.ti.”The“.in”commandbeginsindentinglines

from the current point on, whereas “.ti” only indents the next line. Since the “.ti”

commandonlyindentsthenextlineoftext,perhapsinitializingthebuffertothecorrect

numberofspaceswilldothetrick.Therestofthetextforthelinewillbeconcatenatedto

thespaces,resultinginanindentedline.

The“.in”commandcurrentlyresultsinthesettingofavariablenamednindenttothe

numberofspacestobeindented.Followingthesuggestionfor atemporaryindent,why

notreplaceallinitializationsofthebufferwithindentedones?Therearemultiplelocations

withintheprocess_word()functionwherethe

bufferissettothenextword:

buffer=w

Thesecouldbechangedto:

buffer=”“*nindent+w

Thissoundscleanandsimple,butitfailsmiserably.Hereiswhatitlookslike.Forthe

inputtext:

Indented4characters.

.in2

The idea behind top-down programming is that the higher levels of abstraction are

described first. A description of what he entire program is to do is written in a kind-of

English/computer hybrid language (pseudocode), and this description involves making

callstofunctionsthathavenotyetbeenwrittenbutwhosefunctionisknown.

Weget:

Indented4characters.The

ideabehindtop-down

programmingisthatthe

higherlevelsofabstraction

aredescribedfirst.A

descriptionofwhathe

entireprogramistodois

writteninakind-of

English/computerhybrid

language(pseudocode),and

thisdescriptioninvolves

makingcallstofunctions

thathavenotyetbeen

Canyoufigureoutwheretheproblemisbylookingattheoutput?Thisisaskillthat

developsasyoureadmorecode,writemorecode,anddesignmorecode.Thereisaplace

intheprogramthatwilladdspacestothetext,andclearlythathasbeendonehere.Itis,in

fact,howthetextisrightadjusted.Thespacesarecountedandsometimesreplacedwith

doublespaces.Thishappenedheretosomeofthespacesusedtoimplementtheindent.

Possiblesolutionsincludetheuseofspecialcharactersinsteadofleadingblanks,tobe

replacedwhenprinted; findinganotherway toimplementindenting; modifyingthe way

right adjusting is done. Because the number of spaces at the beginning of the line is

known,thelattershouldbepossible:whencountingspacesintheadjustmentprocess,skip

thenspacescharactersatthebeginningoftheline.Thisisamodificationtothefunction

nth_character()topositionthecountaftertheindent:

defnth_space(s,n):

globalnindent

nn=0

i=0

whileTrue:

print(“nn=”,nn)

ifs[i]==”“:

nn=nn+1

print(ꞌ”“ꞌ)

ifnn>=n:

returni

i=(i+1)%len(s)

ifi<nindent+tempindent:←

i=nindent+tempindent←

Asecondproblemintheindentationcodeisthatthereshouldbealinebreakwhenthe

commandisseen.Thisisamatterofwritingthebufferandthenclearingit.Thisshould

also occur when a temporary indent occurs, but before it inserts the spaces. Say, the

temporaryindentwillhavethesameproblemasindentwithrespecttorightadjustment,

andwehavenotdealtwiththat.

Thelinebreakcanbehandledwithanewfunction:

deflbreak():

globalbuffer,tempindent,nindent

iflen(buffer)>0:

emit(buffer)

buffer=”“*(nindent+tempindent)

tempindent=0

Thebreakinvolveswritingthebufferandclearingit.Clearingitalsomeanssettingthe

indentation.Becausethissequenceofoperationshappenselsewhereintheprogram,those

sequencescanbereplacedbyacalltolbreak().Notethatanewvariabletempindenthas

beenadded;itholdsthenumberofspacesforatemporaryindentation,andisaddedtothe

regularnindentvalueeverywherethatvariableisusedtoobtainthetotalindentationfora

line.Nowrightadjustmentofatemporarilyindentedlineshouldwork.

The lbreak() function is used directly to implement the “.br” command. A stub

previouslynamedgenline()canberemovedandreplacedbyacalltolbreak().

Linespacingcanbehandledinemit(),whichiswhere linesarewrittentothe output

file.Afterthecurrentbufferiswritten,anumberofnewlinecharactersarewrittentoequal

thecorrectlinespacing.Thenewemit()functionis:

defemit(s):

globaloutf,lines,tempindent,spacing,page_length

outf.write(s+”\n”)

lines=(lines+1)%page_length

foriinrange(1,spacing):

outf.write(“\n”)

lines=(lines+1)%page_length

tempindent=0

Whataboutpages?Thereisacommandthatdealswithpagesdirectly,andthatis“.bp,”

whichstartsanewpage.Thepagelengthisknownintermsofthenumberoflines,and

emit counts the lines as it writes them. Implementing the “.bp” command should be a

matter of emitting the number of lines needed to complete the current page. Something

likethis:

defgenpage():

globalpage_length,lines

lbreak()

foriinrange(lines,page_length):

emit(””)

Atthispointallthatismissingistheabilitytohyphenate,whichwillbeleftasoneof

theexercises.Thesystemappearstodowhatisneededusingthe

smalltestfile,sothetimehascometoconstructmorethoroughtests.Afile“preface.txt”

holdsthetextfortheprefaceofabooknamed“PracticalComputerVisionUsingC.”This

book was written using Nroff, and the commands not available in pyroff were removed

fromthesourcetextsothatitcouldbeusedastestdata.Itconsistsofover500linesof

text.Theresultofthefirsttrywasinteresting.

Pyroff appeared to run using this input file but never terminated. No output file was

created.Thefirststepwastotrytoseewhereitwashavingtrouble,soaprintstatement

wasadded toshow whatword had been processed last.That wordwas “spectrograms,”

anditappearsinthefirstparagraphoftext,after

headingsandsuch.Nowthedatathatcausedtheproblemisknown.Whatistheprogram

doing? There must be an unterminated loop someplace. Putting prints in likely spots

identifies the culprit as the loop in the nth_space() function. Tracing through that loop

findsanoddthing:thevalueofnindentbecomesnegative,andthatcausestheloopnever

toterminate.Thetestdatacontainedasituationthatcausedtheprogramtofail,andthat

situationresultedfromadifferencebetweenNroffandpyroff:inNroffthecommand“.in

-4”subtracts4fromthecurrentindentation,whereasinpyroffitsetsthecurrentindentto

-4.

Thiskindoferrorisverycommon.Allvaluesenteredbyausermustbetestedagainst

thelegalboundsforthatvariable.Thiswasnotdonehere,andthefixissimple.However,

itremindsustodothatforallotheruserinputvalues.Theseareprocessedinthefunction

process_command(),solocatingthosevaluesiseasy.Oncethiswasdonethingsworked

prettywell.Therewasoneproblemobserved,andthatwasanindentationerror.Consider

theinputtext:

.nf

1.Introduction

.in3

1.1Imagesasdigitalobjects

1.2Imagestorageanddisplay

1.3Imageacquisition

1.4Imagetypesandapplications

Theprogramformatsthisas:

1.Introduction

1.1Imagesasdigitalobjects

1.2Imagestorageanddisplay

1.3Imageacquisition

1.4Imagetypesandapplications

Thereisanextraspaceinthefirstlineaftertheindent.Thisseemslikeitshouldbeeasy

to find where the problem is, but the function that implements the command, indent(),

looksprettyclean.However,oncarefulexamination(andprintingsomebuffervalues)it

can be seen that it should not call lbreak() because that function sets the buffer to the

properlyindentednumberofspacecharacters.Thismeansthatwhenthelatertestsforan

emptybufferoccur, thebufferis not empty and text is appended toit rather than being

simplyassignedtoit.Thatis,foranemptybufferthefirstwordisplacedintoit:

buffer=word

Whereasiftextispresentthewordisappendedafteraddingaspace:

buffer=buffer+””+word

Theindentfunctionnowlookslikethis:

defindent(n):

globalnindent,buffer

nindent=n

emit(buffer)

buffer=””

Theprefacenowformatsprettywell,ifnotuptoWordstandards.Otherproblemsmay

well exist, and should be reported to the author and publisher when discovered. The

book’swikiistheplaceforsuchdiscussions.

12.2 OBJECTORIENTEDPROGRAMMING–

BREAKOUT

TheoriginalgamenamedBreakoutwasbuiltin1976,conceivedbyNolanBushnelland

SteveBristowandbuiltbySteveWozniak(somesayaidedbySteveJobs).Inthisgame

there are layers of colored rectangles in the upper part of the screen. A simulated ball

moves around the game window, and if it hits a rectangle it accumulates points and

bounces. The ball also bounces off of the top and sides of the window, but will pass

throughthebottomandbelostunlesstheplayermovesapaddleintoitspath.Ifsotheball

will bounce back up and perhaps score more points; if not the ball moves out of play.

Afterafixednumberofballsarelostthegameisover.

The game being developed here will use circles, that we’ll call tiles, rather than

rectangles.Therewillbe5rowsoftiles,eachofadifferentcolorandpointvalue:5,10,

15,10,and5pointsforeachrowrespectively.Thatwaythemostconcealedrowhasthe

mostpoints.Theplayerwillgetthreeballstotrytoclearallofthetilesaway.Thepaddle

willmove leftwhentheleftarrowkeyispressedandrightwhentherightarrowkeyis

pressed. The speed of the ball and of the paddle will be determined when the game is

tested.Asoundwillplaywhenatileisremoved,whentheballhitsthesideortopofthe

window,whentheballhitsthepaddle,andwhentheballislost.Thecurrentscoreandthe

numberofballsremainingwillbedisplayedonthescreensomeplaceatalltimes.

Figure12.1 showsanexampleof a breakoutgamecloneontheleft,withrectangular

bricks. On the right is a possible example of how the game that we’re developing here

mightlook.

12.3 DESCRIBINGTHEPROBLEMASAPROCESS

The first step is to write down a step-by-step description of how the program might

operate. This may be changed as it is expanded, but we have to start someplace. A

problemoccursalmostimmediately:istheprogramtobeaclass?Functions?Doesituse

Glib?

Thisdecisioncanbepostponedalittlewhile,butinmostcasesaprogramisnotaclass.

It is more likely to be a collection of classes operated by a mail program. However, if

objectorientationisalogicalstructure,anditoftenis,itshouldevolvenaturallyfromthe

waytheproblemisorganizedandnotimposeitselfonthesolution.

Thegameconsistsofmultiplethingsthatinteract.Playisaconsequenceofthebehavior

ofthosethings.Forexample,theballwillcollidewithatileresultinginsomepoints,the

tiledisappearing,andabounce.Thenexteventmaybethattheballcollideswithawall,

orbouncesoffofthepaddle.Thegameisasetofmanagedeventsandconsequences.This

makesitappearasifanobjectorienteddesignandimplementationwouldbesuitable.The

ball,eachtime,andthepaddlecouldbeobjects(classinstances)andcouldinteractwith

eachotherunderthesupervisionofamainprogramwhichkepttrackofallobjects,time,

scores,andotherdetails.

Let’sjustfocusonthegameplaypartofthegame,andignoreintroductorywindowsand

highscorelistsandotherpartsofarealgame.Thegamewillstartwithaninitialsetupof

the objects. Tiles will be placed in their start locations, the paddle will be placed, the

locationsofthewallsdefined;thenitwillbedrawn.Theinitialsetupwasoriginallydrawn

on paper and then a sample rendering was made, shown in Figure 12.1. The code that

drawsthisis:

#Ver0-Renderinitialplayarea

importGlib



Glib.startdraw(400,800)

Glib.fill(100,100,240)

foriinrange(0,12):

Glib.ellipse(i*30+15,30,30,30)

Glib.fill(220,220,90)

foriinrange(0,12):

Glib.ellipse(i*30+15,60,30,30)

Glib.fill(220,0,0)

foriinrange(0,12):

Glib.ellipse(i*30+15,90,30,30)

Glib.fill(180,120,30)

foriinrange(0,12):

Glib.ellipse(i*30+15,120,30,30)

Glib.fill(90,220,80)

foriinrange(0,12):

Glib.ellipse(i*30+15,150,30,30)

Glib.fill(0)

Glib.rect(180,350,90,10)

Glib.enddraw()

This code is just for a visual examination of the potential play area. The first one is

alwayswrong,andthisoneistoo,butitallowsustoseewhyitiswrongandtodefinea

morereasonablesetofparameters.Inthiscasethetilesdon’tfullyoccupythehorizontal

region,thetilegroupsaretooclosetothetop,becausewewanttoallowaballtobounce

betweenthetoprowandthetopoftheplayarea,andtheplayareaistoolargevertically.

Fixing these problems is a simple matter of modifying the coordinates of some of the

objects. This code will not be a part of the final result. It’s common, especially in

programs involving a lot of graphics, to test the visual results periodically, and to write

sometestingprogramstohelpwiththis.

This program already has some obvious objects: a tile will be an object. So will the

paddle,andsowill theball.Theseobjects havesomeobviousproperties too:atilewill

haveapositioninx,ycoordinates,anditwillhaveacolorandasize.Itwillhaveamethod

todrawitonthescreen,andawaytotellifithasbeenremovedorifitstillactive.The

paddlehasapositionandsize,andsodoestheball,althoughtheballhasnotbeenseen

yet.

Whatwillthemainprogramlooklikeifthesearetheprincipalobjectsinthedesign?

Thefirstsketchisveryabstractanddependsonmanyfunctionsthathavenotbeenwritten.

Thisfleshesoutthewaytheclassesandtheremainderofthecodewillinteractandpartly

definesthemethodstheywillimplement.Theinitializationstepwillinvolvecreatingrows

oftilesthatwillappearmuchlikethoseintheinitialrenderingabovebutactuallyconsist

offiverowsoftileobjects.Thiswillbedonefromafunctioninitialize(), buteach row

wouldbecreatedinaforloop:

foriinrange(0,12):

tiles=tiles+tile(i*30+15,y,thiscolor,npoints)

wherethetilewillbecreatedandispasseditsx,yposition,color,andnumberofpoints.

Theentirecollectionoftilesisplacedintoatuplenamedtiles.Theballwillbecreatedata

random location and with a random speed within the space between the paddle and the

tiles, and the paddle will be created so that is initially is drawn in the horizontal center

nearthebottomofthewindow.

definitialize():

score=0

nballs=2

b=ball()#Createtheball

p=paddle()#createthepaddle

thiscolor=(100,100,240)#Blue

npoints=5#Toprowis5pointseach

foriinrange(0,12):

tiles=tiles+tile(i*30+15,y,thiscolor,npoints)

#andsoonfor4morerows

Themaindraw()functionwillcallthedraw()methodsofeachoftheclassinstances,

andtheywilldrawthemselves:

defdraw():

background(200)

b.move()#Movetheball

b.draw()#Drawtheball

p.draw()#Drawthepaddle

forkintiles:

k.draw()#Draweachtile

text(“Scoreis:”+score,scorex,scorey)

text(“Ballsremaining:“+nballs,remainx,remainy)

When this function is called (many times each second) the ball is placed in its new

position,possiblyfollowingabounce,andthenisdrawn.Thepaddleisdrawn,andifitis

to be moved it will be done through the user pressing a key. Then the active tiles are

drawn,andthemessages aredrawnonthe screen.Thestructureof the mainpartof the

programisdefinedbytheorganizationoftheclasses.

12.3.1 InitialCodingforaTile

Atilehasagraphicalrepresentationonthescreen,butitismorecomplexthanthat.It

cancollidewithaballandhasacolorandapointvalue.Alloftheseaspectsofthetile

have to be coded as a part of its class. In addition, a tile can be active,meaningthat it

appearsonthescreenandcancollidewiththeball,orinactive,meaningthattheballhas

hititanditisoutofplayforallintentsandpurposes.Here’saninitialversion:

classtile:

def__init__(self,x,y,color,points):

self.x=x

self.y=y

self.color=color

self.points=points

self.active=True

self.size=30



defdraw(self):

ifself.active:

Glib.fill(self.color)

Glib.ellipse(self.x,self.y,self.size,self.size)

Atthebeginningofthegameeverytilemustbecreatedandinitializedwithitsproper

position,color,andpointvalue.Thenthedraw()functionforthemainprogramwillcall

thedraw()methodofeverytileduringeverysmalltimeinterval,orframe.Accordingto

thecodeaboveifthetileisnotactive,thenitwillnotbedrawn.Let’stestthis.

Rule: Never write more than 20-30 lines of code without testing at least part of it.

Thatwayyouhaveaclearerideawhereanyproblemsyouintroducemaybe.

Asuitabletestprogramtostartwithcouldbe:

defdraw():

globaltiles

forkintiles:

k.draw()



Glib.startdraw(360,350)

red=(250,0,0)

print(red)

tiles=()

foriinrange(0,12):

tiles=tiles+(tile(i*30,90,red,15),)

Glib.enddraw()

whichsimplyplacessometilesonthescreeninarow,passingacolorandpointvalue.

Thisalmostworks,butthefirsttileiscutinhalfbytheleftboundary.Iftheinitialization

becomes:

tiles=tiles+(tile(i*30+15,90,red,15),)

thenaproperrowof12redcirclesisdrawn.Modificationswillbemadetothisclassonce

weseemoreclearlyhowitwillbeused.

12.3.2 InitialCodingforthePaddle

Thepaddleisrepresentedasarectangleonthescreen,butitsroleinthegameismuch

moreprofound:itistheonlywaytheplayerhastoparticipateinthegame.Theplayerwill

typekeystocontrolthepositionofthepaddlesoastokeeptheballfromfallingoutofthe

area.Sotheballhastobedrawn,asthetilesdo,butalsomustbemoved(i.e.,changethe

Xposition)inaccordancewiththe player’swishes. Thepaddleclass initiallyhas a few

basicoperations:

classpaddle:

def__init__(self,x,y):

self.x=x

self.y=y

self.speed=3

self.width=90

self.height=10



defdraw(self):

Glib.fill(0)

Glib.rect(self.x,self.y,self.width,self.height)



defmoveleft(self):

ifself.x<=self.speed:

self.x=0

else:

self.x=self.x–self.speed



defmoveright(self):

ifself.x>width-self.width-self.speed:

self.x=width-self.width

else:

self.x=self.x+self.speed

WhentherightarrowkeyispressedaflagissettoTrue,andthepaddlemovestothe

right (i.e., its x coordinate increases) each time interval, or frame. When the key is

released the flag is set to False and the movement stops as a result. Movement is

accomplishedbycallingmoveleft()andmoveright(),andthesefunctionsenforcealimit

onmotion:thepaddlecannotleavetheplayarea.Thisisdonewithintheclasssothatthe

outsidecodedoesnotneedtoknowanythingabouthowthepaddleisimplemented.Itis

important to isolate details of the class implementation to the class only, so that

modificationsanddebuggingcanbelimitedtotheclassitself.

Thepaddleis simplya rectangle,as faras thegeometryis concerned,and presentsa

horizontal surface from which the ball will bounce. It is the only means by which the

playercanmanipulatethegame,soitisimportanttogetthepaddleoperationsandmotion

correct.Fortunately,movingarectangleleftandrightisaneasythingtodo.

Testingthisinitialpaddleclassusedadraw()functionthatrandomlymovedthepaddle

leftandright,andamainprogram,thatcreatesthepaddle:

defdraw():

globalp,f

Glib.background(200)

p.draw()

iff:

p.moveright()

else:

p.moveleft()

ifrandom()<.01:

f=notf



Glib.startdraw(360,350)

f=True

p=paddle(130)

Glib.enddraw()

Thiscodeworks,andsumsupthefunctionalityofthepaddle.

12.3.3 InitialCodingfortheBall

The ball really does much of the actual work in the game. Yes, the bounces are

controlledbytheuserthroughthepaddle,butoncetheballbouncesoffofthepaddleithas

to behave properly and do the works of the game: destroying tiles. According to the

standardclassmodelofthisprogram,theballshouldhaveadraw()methodthatplacesit

into its proper position on the screen. But the ball is moving, so its position has to be

updatedeachframe.Italsohastobounceoffofthesidesandtopoftheplayingarea,and

thedraw()methodcanmakethishappen.Theessentialcodefordoingthisis:

classball():

def__init__(self,x,y):

self.x=x

self.y=y

self.dx=3

self.dy=-4

self.active=True

self.color=(230,0,230)

self.size=9



defdraw(self):

ifnotself.active:

return

Glib.fill(self.color[0],self.color[1],

self.color[2])

Glib.ellipse(self.x,self.y,self.size,self.size)

self.x=self.x+self.dx

self.y=self.y+self.dy

if(self.x<=self.size/2)or\

(self.x>=Glib.width-self.size/4):

self.dx=-self.dx

ifself.y<=self.size/2:

self.dy=-self.dy

elifself.dy>=Glib.height:

self.active=False

This version only bounces off of the sides and top, and passes through the bottom.

Testingitrequiresamainprogramthatcreatestheballandadraw()functionthatsimply

callstheball’sdraw()method:

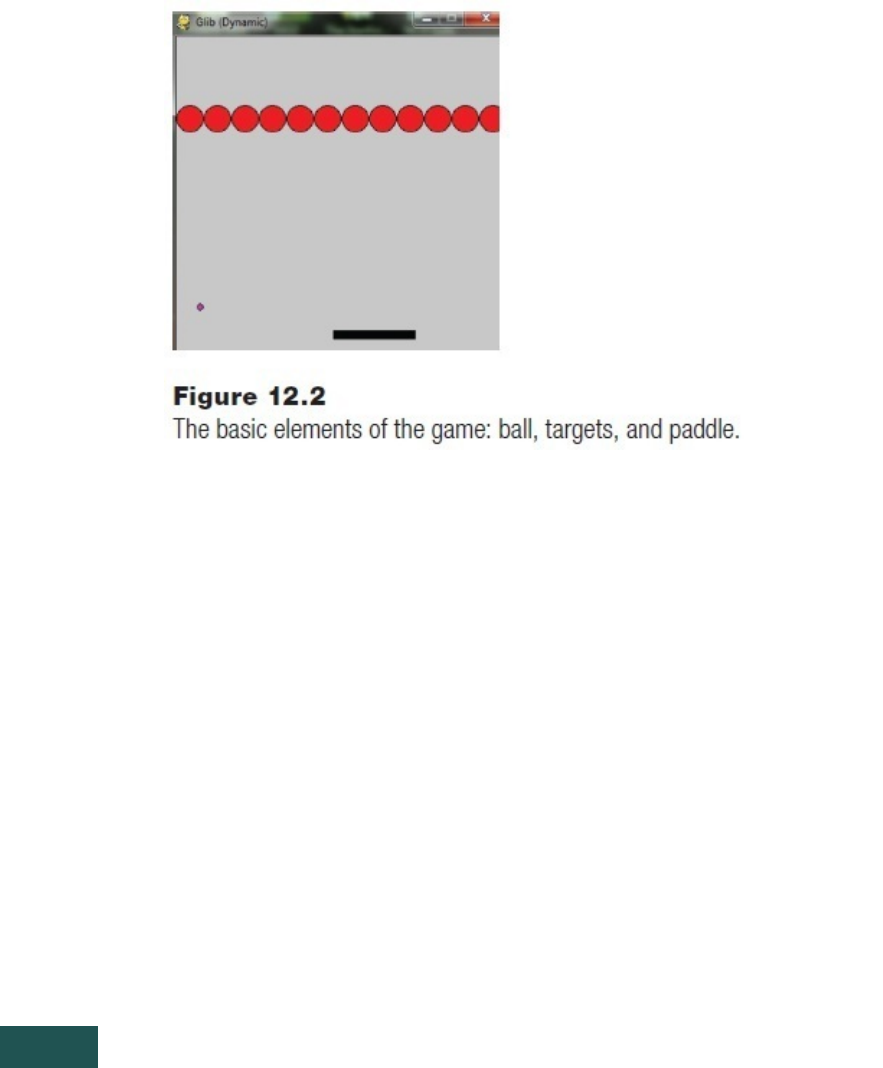
defdraw():

globalb

Glib.background(200)

b.draw()



Glib.startdraw(360,350)

b=ball(300,300)

Glib.enddraw()

The ball is created at coordinates (300,300) and does three bounces, disappearing

throughthebottomafterthat.Abouncingballhasbeencodedbefore,sothereisnothing

newhereyet.

12.3.4 CollectingtheClasses

Anextstepistotestallthreeclassesrunningtogether.Thiswillensurethatthereareno

problems with variable, method, and function names and that interactions between the

classes are in fact isolated. All three should work together, creating the correct visual

impressiononthescreen.Thecodeforthethreeclasses

was copied to one file for this test. The main program simply creates instances of each

classasappropriate,reallydoingwhattheoriginaltestprogramdidineachcase:

Glib.startdraw(360,350)

red=(250,0,0)

print(red)

tiles=()

foriinrange(0,12):

tiles=tiles+(tile(i*30+15,90,red,15),)

f=True

p=paddle(130)

b=ball(300,300)

Glib.enddraw()

Thedraw() function callsthe draw() methods for each class instance and moves the

paddlerandomlyasbefore:

defdraw():

globaltiles,p,f,b

Glib.background(200)

forkintiles:

k.draw()

p.draw()

iff:

p.moveright()

else:

p.moveleft()

ifrandom()<.01:

f=notf

b.draw()

Theresultwasthatallthreeclassesfunctionedtogetherthefirsttimeitwasattempted.

The game itself depends on collision, which will be implemented next, but at the very

leasttheclassesneedtocooperate,oratleastnotinterferewitheachother.That’strueat

thispointinthedevelopment.

12.3.5 DevelopingthePaddle

Placingthepaddleundercontroloftheuseristhenextstep.Whenakeyispressedthen

thepaddlestatewillchange,fromstilltomoving,andviceversawhenreleased.Thisis

accomplishedusingthekeypressed()andkeyreleased()functions.Theywillsetorcleara

flag, respectively, that causes the paddle to move by calling the moveleft() and

moveright() methods. The flag movingleft will result in a decrease in the paddle’s x

coordinateeachtimedraw()iscalled;movingrightdoesthesameforthe+xdirection:

defkeyPressed(k):

globalmovingleft,movingright

ifk==Glib.K_LEFT:

movingleft=True

elifk==Glib.K_RIGHT:

movingright=True



defkeyReleased(k):

globalmovingleft,movingright

ifk==Glib.K_LEFT:

movingleft=False

elifk==Glib.K_RIGHT:

movingright=False

Fromtheuserperspectivethepaddlemovesaslongasthekeyisdepressed.Insideof

theglobaldraw()function,theflagsaretestedateachiterationandthepaddleismovedif

necessary:

defdraw():#07-classes-01-20.py

global…movingleft,movingright

...

ifmovingleft:

p.moveleft()

elifmovingright:

p.moveright()

p.draw()

...

The other thing the paddle has to do is serve as a bounce platform for the ball. A

question surrounds the location of collision detection; is this the job of the ball or the

paddle?Itdoesmakesensetoperformmostofthistaskintheballclass,becausetheball

isalwaysinmotionandisthethingthatbounces.However,thepaddleclasscanassistby

providing necessary information. Of course, the paddle class can allow other classes to

examine and modify its position and velocity and thus perform collision testing, but if

thosedataare tobe hidden, theoption istohave amethod thattestswhether amoving

objectmighthavecollidedwith thepaddle.Theypositionof thepaddleis fixedandis

storedinaglobalvariablepaddle,sothatisnotanissue.Amethodinpaddlethatreturns

Trueifthex

coordinatepassedtoitliesbetweenthestartandendofthepaddleis:

definpaddle(self,x):

ifx<self.x:

returnFalse

ifx>self.x+self.width:

returnFalse

returnTrue

Theball classcan now determinewhether it collides with the paddle by checkingits

own y coordinate against the paddle and by calling inpaddle() to see if the ball’s x

position lies within the paddle. If so, it should bounce. The method hitspaddle() in the

ballclassreturnsTrueiftheballhitsthepaddle:

defhitspaddle(self):#08classes-01-21.py

ifself.y<=paddleY+2andself.y>=paddleY-2:

ifp.inpaddle(self.x):

returnTrue

returnFalse

Themostbasicreactiontohittingthepaddleistochangethedirectionofdyfromdown

toup(dy=-dy).

12.3.6 BallandTileCollisions

Thecollisionbetweenaballandatileismoredifficulttodocorrectlythananyofthe

othercollisions.Yes,determiningwhetheracollisionoccursisasimilarprocess,andthen

pointsarecollectedandthetileisdeactivated.Itisthebounceoftheballthatishardto

figureout.Theballmaystrikethetileatnearlyanyangleandatnearlyanylocationonthe

circumference. This is not a problem in the original game, where the tiles were

rectangular,becausetheballwasalwaysbouncingoffofahorizontalorverticalsurface.

Nowthere’ssomethinkingtodo.

Thecorrectcollisioncouldbecalculated,butwouldinvolveacertainamountofmath.

The specification of the problem does not say that mathematically correct bounces are

required.Thisisagamedesignchoice,perhapsnotaprogrammingchoice.Whatdoesthe

gamelooklikeifasimplebounceisimplemented?Thatcouldinvolvesimplychanging

dyto–dy.

Thisversionofthegameturnsouttobeplayable,evenfun;buttheballalwayskeeps

thesamexdirectionwhenitbounces.Whatwoulditlooklikeifitbouncedinroughlythe

right direction, and how difficult would that be? The direction of the bounce would be

dictated by the impact location on the tile, as seen in Figure12.3. This was figured out

afterafewminuteswithapencilandpaper,andisintuitiveratherthanprecise.

We’llhavetofigureoutwheretheballhitsthetile,determinewhichofthefourpartsof

thetilethisliesin,andthencreatethenewdxanddyvaluesfortheball.Akeyaspectof

the solution being developed is to avoid too much math that has to be done by the

program.Isthispossible?

Thefirststepistofindtheimpactpoint.Wecouldusealittlebitofanalyticgeometry,

orwecouldapproximate.Thefactisthattheballisnotmovingveryfast,andtheexact

coordinatesoftheimpactpointarenotrequired.Atthebeginningofthecurrentframethe

ball was at (x,y) and at the beginning of the next is will be at (x+dx, y+dy). A good

estimateofthepointofimpactwouldbethemeanvalueofthesetwopoints,or(x+dx/2,

y+dy/2).Closeenoughforacomputergame.

Now the question is: within which of the four regions defined in Figure 12.3 is the

impactpoint?Theregionsaredefinedbylinesat45degreesand-45degrees.Theatan()

functionwill, when using screencoordinates, havethe –dxpoints between-45 and +45

degrees.The–dypoints,wherethedirectionofYmotionchanges,involvetheremaining

collisions.Whatneedstobedoneistofindtheangleofthelinefromthecenterofthetile

totheballandthencomparethatto-45…+45.

Hereisanexamplemethodnamedbounce()thatdoesexactlythis.

#Returnthedistancesquaredbetweenthetwopoints

defdistance2(self,x0,y0,x1,y1):

return(x0-x1)*(x0-x1)+(y0-y1)*(y0-y1)



defbounce(self,t):

dd=t.size/2+self.size/2#Bounceoccurswhenthe

#distance

dd=dd*dd#Betweenballandtile<

#radiisquared

collide=False

ifself.distance2(self.x,self.y,t.x,t.y)>=ddand\

self.distance2(self.x+self.dx,self.y+self.dy,t.x,

t.y)<dd:

self.x=self.x+self.dx/2#Estimatedimpact

#pointoncircle

self.y=self.y+self.dy/2

collide=True

elifself.distance2(self.x,self.y,t.x,t.y)<dd:

collide=True#Balliscompletelyinside

#thetime

ifnotcollide:

return



#Iftheballisinsidethetile,backitout.

whileself.distance2(self.x,self.y,t.x,t.y)<dd:

self.x=self.x-self.dx*0.5

self.y=self.y-self.dy*0.5

ifself.x!=t.x:#Computetheball-tileangle

a=atan((self.y-t.x)/(self.x-t.y))

a=a*180./3.1415

else:#Ifdx=0thetangentisinfinite

a=90.0

ifa>=-45.0anda<=45.0:#Thexspeedchange

self.dx=-self.dx

else:

self.dy=-self.dy#Theyspeedchanges

Aftersometestingthecode:

#Iftheballisinsidethetile,backitout.

whileself.distance2(self.x,self.y,t.x,t.y)<dd:

self.x=self.x-self.dx*0.5

self.y=self.y-self.dy*0.5

wasadded.Itwasfoundthatiftheballwastoofarinsidethetilethenitsmotionwasvery

odd; as it moved through the tile it constantly changed direction because the program

determinedthatitwasalwayscolliding.

12.3.7 BallandPaddleCollisions

Now we return to examine the collision between the ball and the paddle. Thepaddle

seems to be flat, and colliding with any location on the paddle should have the same

result.Perhaps.Whatiftheballhitsthepaddleveryneartooneend?Thereisacorner,

andmaybehittingtooneartothecornershouldyieldadifferentbounce.Thiswasthecase

intheoriginalgames.Iftheballstruckthenearedgeofthepaddleonthecorneritcould

actuallybouncebackintheoriginaldirectiontoagreaterorlesserdegree.Thisgivesthe

playeragreaterdegreeofcontrol,oncetheyunderstandthesituation.Otherwisethegame

isreallypredeterminediftheplayermerelyplacesthepaddleinthewayoftheball.Itwill

alwaysbounceinexactlythesamemanner.

Theproposedideaistobounceatadifferentangledependingonwheretheballstrikes

thepaddle.Weneedtodecidehownearandhowintensetheeffectwillbe.Iftheballhits

thepaddlenearthecenter,thenitwillbouncesothattheincomingangleisthesameasthe

outgoingangle.Whenithitsthenearendofthepaddleitwillbouncesomewhatbackin

theincomingdirection,andwhenitstrikesthefarendthebounceanglewillbeshallower

abouncefromthecenter.

Let’s say that if the ball hits the first pixel on the paddle it will bounce back in the

originaldirection,meaningthatdx=-dxanddy=-dy.Abouncefromthecenterdoesnot

change dx but does set dy = -dy. If the relationship is linear across the paddle, the

implication would be that striking the final pixel would set dx = 2*dx and dy = -dy.

Strikinganypixelinbetweenwoulddividethechangeindxbythenumberofpixelsinthe

paddle,initially90.Iftheballhitspixelntheresultwillbe:

delta=2*dx/90.0

dx=-dx+n*delta

Aproblemhereisthatthedxvaluewilldecreasecontinuouslyuntiltheballisbouncing

upanddown.Perhapstheincomingangleshouldnotbeconsidered.Thebounceangleof

theballcouldbecompletelydependentonwhereithitsthepaddleandnothingelse.Ifdx

is-5onthenearendofthepaddleand+5onthefarend,then:

dx=-5+n*10.0/90.0

Thecodeinthedraw()methodoftheballclassismodifiedtoread:

ifself.hitspaddle():

self.dy=-self.dy

self.dx=-5+(1./9.)*(self.x-p.x)

Theusernowhasalotmorecontrol.Thegamedoesappearslow,though.Andthereis

onlyoneball.Oncethatislost,thegameisover.

12.3.8 FinishingtheGame

What remains to be done is to implement multiple balls. Multiple balls are tricky

becausetherearetimingissues.Whentheballdisappearsthroughthebottomoftheplay

area it should reappear someplace, and at a random place. It should not appear

immediately, though, because the player needs some time to respond; let’s say three

seconds.Meanwhilethescreenmustcontinuetobe

displayed.It’stimetointroducestates.

Astateisasituationthatcanbedescribedbyacharacteristicsetofparameters.Astate

canbelabeledwithasimplenumberbutrepresentssomethingcomplex.Inthisinstance

specificallytherewillbeaplaystate,inwhichthepaddlecanbemovedandtheballcan

scorepoints,andapausestate,whichhappensafteraballislost.Thedraw()functionis

the place where each step of the program is performed at a high level, and so will be

responsibleforthemanagementofstates.

Thecurrentstageoftheimplementationhasonlytheplaystate,andallofthecodethat

managesthatisinthedraw()functionalready.Changethenameofdraw()tostate0()and

createa statevariable statethat can havevalues 0or 1: playis 0, pause is1. The new

draw()functionisnowcreated:

defdraw():

globalplaystate,pausestate

ifstate==playstate:

state0()

elifstate==pausestate:

state1()

where:

playstate=0

pausestate=1

The program should still be playable as it was before as long as state == playstate.

Whathappensinthepausestate?Thecontrolsofthepaddleshouldbedisabled,andno

ballisdrawn.Thegoalofthepausestateistoallowsometimefortheusertogetready

forthenextball,sosometimeisallowedtopass.Perhapstheplayershouldbepermitted

tostartthegameagainwithanewballwhenakeyispressed.Thiseliminatestheneedfor

atimer, which are generally to beavoided. So, the pause state is entered when the ball

departsthefieldofplay. The gameremainsinthepause stateuntilthe playerpressesa

key,atwhichpointanewballiscreatedandthegameenterstheplaystate.

Enteringthepausestatemeansmodifyingthecodeintheballclassalittle.Thereisa

lineofcodeattheendofthedraw()methodoftheballclassthatlookslikethis:

elifself.dy>=Glib.height:

self.active=False

Thisiswheretheclassdetectstheballleavingtheplayarea.Weneedtoaddtothis:

elifself.dy>=Glib.height:

self.active=False

while,ofcourse,makingcertainthatthevariablesneededarelistedasglobal.Thisdidnot

do as was expected until it was noted that the condition should have been if self.y >=

Glib.height.Thecomparisonwithdywasanerrorintheinitialcodingthathadnotbeen

noticed.Also,itseemsliketheactivevariableintheballclasswasnotuseful,soitwas

removed.

NowinthekeyPressed()functionallow akey press tochange from the pause tothe

playstate.Anykeywilldo:

ifstate=pausestate:

resume()

Theresume()functionmustdotwothings.First,itmustchangestatebacktoplay.Next

itmustrepositiontheballtoanewlocation.Easy:

defresume():

globalstate,playstate

b.x=randrange(30,Glib.width-30)

b.y=250

state=playstate

Thisworksfine.Thegameistoonlyhaveaspecifiednumberofballs,though,andthis

numberwastobedisplayedonthescreen.So,whenintheplaystateandaballislost,the

count of remaining balls (balls_remaining) will be decreased by one. If there are any

ballsremaining,thenthepausestateisentered.Otherwisethegameisover.Perhapsthat

shouldbeathirdstate:gameover?Yes,probably.

Thegameoverstateisenteredwhentheballleavestheplayareaandnoballsareleft

(intheballclassdraw()method.Intheglobaldraw()functionthethirdstatedetermines

ifthegameiswonorlostandrendersanappropriatescreen:

…

Glib.text(“Score:“+str(score),10,30)

ifscore>=maxscore:

Glib.background(0,230,0)

Glib.text(“YouWin”,200,200)

else:

Glib.background(100,10,10);

Glib.text(“YouLose”,200,200)

Glib.text(“Score:“+str(score),10,30)

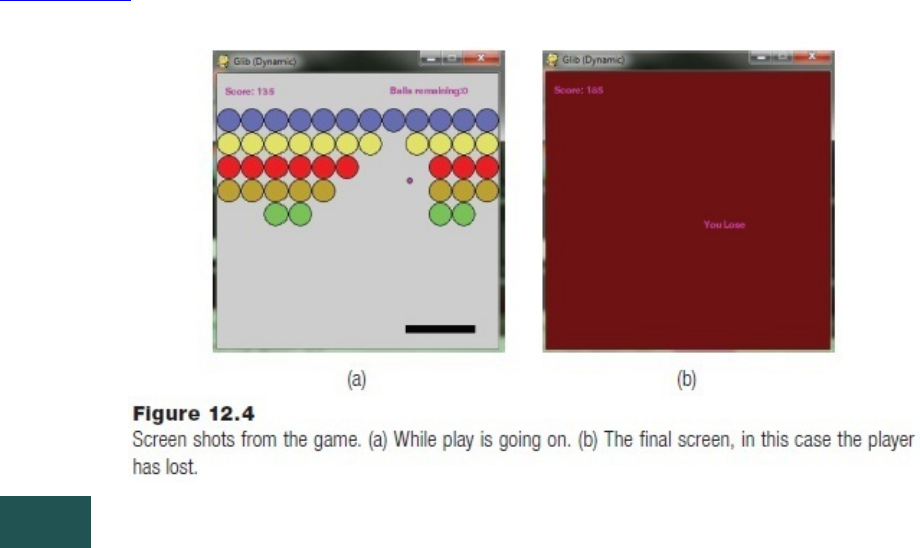
Andthat’sit!Screenshotsfromthegameinvariousstatesareshownin

Figure12.4.(14playble3.py)

12.4 RULESFORPROGRAMMERS

Theauthorofthisbookhascollectedasetofrulesandlawsthatapplytowritingcode,

andontensofthousandsoflineswrittenand45yearsasaprogrammer(hestartedvery

young). There are over 250 of them, but not all apply to Python. For example, Python

enforcesindentingandhasnobegin-endsymbols.Theonesthatdoapplyareasfollows:

2.Usefour-spaceindentsandnottabs.

5.Placeacommentinlieuofadeclarationforallvariablesinlanguageswhere

declarationsarenotpermitted.

6.Declarenumericconstantsandprovideacommentexplainingthem.

7.Rarelyuseanumericconstantinanexpression;nameanddeclarethem.

8.Usevariablenamesthatrefertotheuseormeaningofthevariable.

9.Makeyourcodecleanfromthebeginning,notafteritworks.

10.Anon-workingprogramisuseless,nomatterhowwellstructured.

11.Writecodethatisasgeneralaspossible,evenifthatmakesitlonger.

12.Ifthecodeyouwriteisgeneral,thenkeepitandreuseitwhenappropriate.

13.Functionslongerthan12(notincludingdeclarations)linesaresuspect.

15.Avoidrecursionwhereverpossible.

16.Everyprocedureandfunctionmusthavecommentsexplainingfunctionanduse.

17.Writeexternaldocumentationasyoucode—everyprocedureandfunctionmust

haveadescriptioninthatdocument.

18.Somedocumentationisforprogrammers,andsomeisforusers.Distinguish.

19.Documentationforusersmustneverbeinthecode.

20.Avoidusingoperatingsystemcalls.

21.Avoidusingmachinedependenttechniques.

22.Dousetheprogramminglanguagelibraryfunctions.

23.Documentationforaprocedureincludeswhatotherproceduresarecalled.

24.Documentationforaprocedureincludeswhatproceduresmightcallit.

26.Whendoinginput:assumethattheinputfileiswrong.

27.YourprogramshouldacceptANYinputwithoutcrashing.Feeditanexecutableas

atest.

28.Sideeffectsareverybad.Aproperfunctionshouldreturnavaluethatdependsonly

onitsparameters.Exceptionsdoexistandshouldbedocumented.

29.Everythingnotdefinedisundefined.

33.Buffersandstringshavefixedsizes.Knowwhattheyareandbeconstrainedby

them.

34.Ahandleisapointertoastructureforanobject;makecertainthathandlesusedare

stillvalid.

35.Stringsandbuffersshouldnotoverlapinstorage.

36.Contentsofstringsandbuffersareundefineduntilwrittento.

40.Everyvariablethatisdeclaredistobegivenavaluebeforeitisused.

41.Putsomeblanklinesbetweenmethoddefinitions.

42.Explaineachdeclaredvariableinacomment.

44.Solvetheproblemrequested,notthegeneralcaseorsubsets.

45.Whitespaceisoneofthemosteffectivecomments.

48.Avoidglobalsymbolswherepossible;usethemproperlywhereuseful.

49.Avoidcasts(typecasting).

50.Roundexplicitlywhenroundingisneeded.

51.Alwayschecktheerrorreturncodes.

52.Leavespacesaroundoperatorssuchas=,==,!=,andsoon.

53.Amethodshouldhaveaclear,single,identifiabletask.

54.Aclassshouldrepresentaclear,single,identifiableconcept.

57.Dothecommentsfirst.

58.Afunctionshouldhaveonlyoneexitpoint.

59.Readcode.

60.Commentsshouldbesentences.

61.Acommentshouldn’trestatetheobvious.

62.Commentsshouldalign,somehow.

65.Don’tconfusefamiliaritywithreadability.

67.Afunctionshouldbecalledmorethanonce.

68.Codeusedmorethanonceshouldbeputintoafunction.

69.Allcodeshouldbeprintable.

70.Don’twriteverylonglines.80Characters.

71.Thefunctionnamemustagreewithwhatthefunctiondoes.

72.Formatprogramsinaconsistentmanner.

75.Havealog.

76.Documentalltheprincipaldatastructures.

77.Don’tprintamessageforarecoverableerror—logit.

78.Don’tusesystem-dependentfunctionsforerrormessages.

79.Youmustalwayscorrectlyattributeallcodeinthemoduleheader.

80.Providecrossreferencesinthecodetoanydocumentsrelevanttotheunderstanding

ofthecode.

81.AllerrorsshouldbelistedtogetherwithanEnglishdescriptionofwhattheymean.

82.Anerrormessageshouldtelltheuserthecorrectwaytodoit.

83.Commentsshouldbeclearandconciseandavoidunnecessarywordiness.

84.Spellingcounts.

85.Runyourcodethroughaspellingchecker.

87.Functiondocumentationincludesthedomainofvalidinputstothefunction.

88.Functiondocumentationincludestherangeofvalidoutputsfromthefunction.

91.Eachfilemuststartwithashortdescriptionofthemodulecontainedinthefileand

abriefdescriptionofallexportedfunctions.

92.Donotcommentoutoldcode—removeit.

93.Useasourcecodecontrolsystem.

95.Commentsshouldneverbeusedtoexplainthelanguage.

96.Don’tputmorethanonestatementonaline.

97.Neverblindlymakechangestocodetryingtoremoveanerror.

98.Printingvariablevaluesinkeyplacescanhelpyoufindthelocationofabug.

99.Onecompilationerrorcanhidescoresofothers.

100.Ifyoucan’tseemtosolveaproblem,thendosomethingelse.

101.Explainittotheduck.Getaninanimateobjectandexplainyourproblemtoit.This

oftensolvesit.(Wyvill)

102.Don’tconfuseeaseoflearningwitheaseofuse.

103.Aprogramshouldbewrittenatleasttwice—throwawaythefirstone.

104.Hasteisnotspeed.

105.Youcan’tmeasureproductivitybyvolume.

106.Expecttospendmoretimeindesignandlessindevelopment

107.Youcan’tprograminisolation.

108.Ifanifendsinreturn,don’tuseelse.

109.Avoidoperatoroverloading.

110.Scoresofcompilationerrorscansometimesbefixedwithonecharacter—startat

thefirstone.

111.Programsthatcompilemostlystilldonotwork.

112.Incrementallyrefineyourcode.StartwithBEGIN-SOLVE-END,thenrefine

SOLVE.

113.Drawdiagramsofdataandalgorithms.

114.Useasymbolicdebuggerwhereverpossible.

115.Makecertainthatfileshavethecorrectname(andsuffix!)whenopening.

116.Neverassignavalueinaconditionalexpression.

117.Ifyoucan’tsayitinEnglish,youcan’tsayitinanyprogramminglanguage.

118.Don’tmovelanguageidiomsfromonelanguagetoanother.

119.First,donoharm.

120.Ifobjectoriented,designtheobjectsfirst.

121.Don’twritedeeplynestedcode.

122.Multipleinheritanceisevil.Avoidsin.

123.Productivitycanbemeasuredinthenumberofkeystrokes(sometimes).

125.Yourcodeisnotperfect.Notevenclose.Havenoegoaboutit.

126.Variablesaretobedeclaredwiththesmallestpossiblescope.

127.Thenamesofvariablesandfunctionsaretobeginwithalowercaseletter.

133.Collectyourbestworkingmodulesintoacodelibrary.

134.Isolatedirtycode(e.g.,codethataccessesmachinedependencies)intodistinctand

carefullyannotatedmodules.

135.Anythingyouassumeabouttheuserwilleventuallybewrong.

136.Everytimearuleisbroken,thismustbeclearlydocumented.

137.Writecodeforthenextprogrammer,notforthecomputer.

138.Yourprogramshouldalwaysdegradegracefully.

139.Don’tsurpriseyouruser.

140.Involveusersinthedevelopmentprocess.

142.Mostprogramsshouldrunthesamewayandgivethesameresultseachtimethey

areexecuted.

143.Mostofyourcodewillbecheckingforerrorsandpotentialerrors.

144.Normalcodeanderrorhandlingcodeshouldbedistinct.

145.Don’twriteverylargemodules.

146.Puttheshortestclauseofanif/elseontop.

149.Havealibraryoferror-reportingcodeanduseit(beconsistent).

150.Reporterrorsinawaythattheymakesense.

151.Reporterrorsinawaythatallowsthemtobecorrected.

152.Onlyfoolsthinktheycanoptimizecodebetterthanagoodcompiler.

153.Changethealgorithm,notthecode,tomakethingsfaster.Polynomialis

polynomial.

154.Copyandpasteisonlyforprototypes.

155.It’salwaysyourfault.

156.Knowwhattheproblemisbeforeyoustartcoding.

157.Don’tre-inventthewheel.

158.Keepthingsassimpleaspossible.

159.Datastructures,notalgorithms,arecentraltoprogramming.(Pike)

160.Learnfromyourmistakes.

161.Learnfromthemistakesofothers.

162.Firstmakeitwork;THENmakeitworkfaster.

163.Wealmostneverneedtomakeitfaster.

164.Firstmakeitwork;thenmakeitworkbetter.

165.Programmersdon’tgettomakebigdesigndecisions—dowhatisasked,effectively.

166.Learnnewlanguagesandtechniqueswhenyoucan.

167.Neverstartanewprojectinalanguageyoudon’talreadyknow.

168.Youcanlearnanewlanguageeffectivelybycodingsomethingsignificantinit,just

don’texpecttoselltheresult.

169.Youwillalwaysknowonlyasubsetofanygivenlanguage.

170.Thesubsetyouknowwillnotbethesameasthesubsetyourcoworkersknow.

171.Objectorientationisnottheonlywaytodothings.

172.Objectorientationisnotalwaysthebestwaytodothings.

173.Tocreateadecentobject,onefirstneedstobeaprogrammer.

174.Youmaybesmarterthanthepreviousprogrammer,butleavetheircodealone

unlessitisbroken.

175.Youprobablyarenotsmarterthanthepreviousprogrammer,soleavetheircode

aloneunlessitisbroken.

176.Yourprogramwillneveractuallybecomplete.Livewithit.

177.Allfunctionshavepreconditionsfortheircorrectuse.

178.Sometimesafunctioncannottellwhetheritspreconditionsaretrue.

180.Computershavegigabytesofmemory,mostly.Optimizingitisthelastthingtodo.

181.Computeimportantvaluesintwodifferentwaysandcomparethem.

182.0.1*10isnotequalto1.

183.Addingmanpowertoalatesoftwareprojectmakesitlater.

184.Italwaystakeslongerthanyouexpect.

185.Ifitcanbenull,itwillbenull.

186.Donotusecatchandthrowunlessyouknowexactlywhatyouaredoing.

187.Beclearaboutyourintention.i=1-iisnotthesameasif(i==0)theni=1elsei=0.

188.Fancyalgorithmsarebuggierthansimpleones,andthey’remuchharderto

implement.(Pike)

189.Thefirst90%ofthecodetakes10%ofthetime.Theremaining10%takesthe

other90%ofthetime.

190.Allmessagesshouldbetagged.

191.DonotuseFORloopsastimedelays.

192.Auserinterfaceshouldnotlooklikeacomputerprogram.

193.Decomposecomplexproblemsintosmallertasks.

194.Usetheappropriatelanguageforthejob,whengivenachoice.

195.Knowthesizeofthestandarddatatypes.

198.Ifyousimultaneouslyhittwokeysonthekeyboard,theonethatyoudonotwant

willappearonthescreen.

199.Patternsarefortheweak—itassumesyoudon’tknowwhatyouaredoing.

200.Don’tassumeprecedencerules,especiallywhendebugging—parenthesize.

202.++and—areevil.What’swrongwithi=i+1??

204.It’shardtoseewhereaprogramspendsmostofitstime.

205.Fancyalgorithmsareslowwhennissmall,andnisusuallysmall.(Pike)

206.Assumethatthingswillgowrong.

207.Computersdon’tknowanymath.

208.Expecttheimpossible.

209.Testeverything.Testoften.

210.Dothesimplebitsfirst.

211.Don’tfixwhatisnotbroken.

212.Ifitisnotbroken,thentrytobreakit.

213.Don’tdrawconclusionsbasedonnames.

214.Acarelesslyplannedprojecttakesthreetimeslongertocompletethanexpected;a

carefullyplannedprojecttakesonlytwiceaslong.

215.Anysystemwhichdependsonhumanreliabilityisunreliable.

216.Theeffortrequiredtocorrectcourseincreasesgeometricallywithtime.

217.Complexproblemshavesimple,easytounderstand,andwronganswers.

218.Anexpertisthatpersonmostsurprisedbythelatestevidencetothecontrary.

219.Oneman’serrorisanotherman’sdata.

220.Noiseissomethingindatathatyoudon’twant.Someonedoeswantit.

12.5 SUMMARY

There is no general agreement on how best to put together a good program. A good

programisonethatisfunctionallycorrect,readable,modifiable,reasonablyefficient,and

that solves a problem that someone needs solved. No two programmers will create the

sameprogramforanon-trivialproblem.Theprogramdevelopmentstrategydiscussedin

this chapter is called iterative refinement, and is nearly independent of language or

philosophy.

There is no single process that is best for writing programs. Some people only use

object-oriented code, but a problem with teaching that way is that a class contains

traditional,procedure-orientedcode.Tomakeaclass,onemustfirstknowhowtowritea

program.

The idea behind top-down programming is that the higher levels of abstraction are

described first. A description of what he entire program is to do is written in a kind-of

English/computer hybrid language (pseudocode), and this description involves making

calls to functions that have not yet been written but whose function is known—these

functionsarecalledstubs.Thefirststepistosketchtheactionsoftheprogramasawhole,

then to expand each step that is not well-defined into a detailed method that has no

ambiguity.Compile and testthe program asfrequently as possibleso that errorscan be

identifiedwhileitisstilleasytoseewheretheyare.

Thekeytoobject-orienteddesignisidentifyingthebestobjectstobeimplemented.The

restoftheprogramwilltakealogicalshapedependingontheclassesthatituses.Tryto

isolatethedetailsoftheclassfromtheoutside.Alwaysbewillingtorethinkachoiceand

rewritecodeasaconsequence.

Exercises

1.Addsoundtothegame.Whentheballcollideswithanobjectasoundeffectshould

play.

2.ConsiderhowhyphenationmightbeaddedtoPyroff.Howwoulditbedecidedto

hyphenateaword,andwherewouldthenewcodebeplaced?Inotherwords,sketcha

solution.

3.InsomeversionsofBreakout-stylegames,certainofthetilesortargetshavespecial

properties.Forexample,sometimeshittingaspecialtargetwillresultintheball

speedinguporslowingdown,willhaveanextrapointvalue,orwillchangethesizeof

thepaddle.Modifythegamesothatsomeofthetargetsspeeduptheballandsome

othersslowitdown.

4.ThePyroffsystemcanturnrightadjustingoff,butnoton.Thisseemslikeaflaw.Add

anewcommand,“.ra,”thatwillturnrightadjustingon.

5.Mostwordprocessorsallowforaheaderandafooter,somespaceandpossiblysome

textatthebeginningandend,respectively,ofeverypage.Designacommand“.he”

thatattheleastallowsforemptyspaceatthebeginningofapage,andacorresponding

command“.fo”thatallowsforsomelinesattheendofapage.

6.WhichthreeoftheRulesforProgrammersdoyouthinkmakethegreatestdifference

inthecode?Whichthreeaffectcodetheleast?Arethereanythatyoudon’t

understand?

NotesandOtherResources

Bouncing a ball off of a wall: https://sinepost.wordpress.com/2012/08/19/bouncing-

off-the-walls/

1.JonBentley.(1999).ProgrammingPearls,2nded.,Addison-WesleyProfessional,

ISBN-13:978-0201657883.

2.AdrianBowyerandJohnWoodwark.(1983).AProgrammer’sGeometry,

Butterworth-HeinemannLtd.,ISBN-13:978-0408012423.

3.FrederickBrooks.(1995).TheMythicalMan-Month:EssaysonSoftware

Engineering,AnniversaryEdition,Addison-WesleyProfessional.

4.JimParker.(2015).100CoolProcessingSketches,eBook,

https://leanpub.com/100coolprocessingsketches

5.JimParker.(2015).GameDevelopmentUsingProcessing,MercuryLearningand

Publishing.

6.R.Rhoad,G.Milauskas,andR.Whipple.(1984).GeometryforEnjoymentand

Challenge,rev.ed.,Evanston,IL,McDougal,Littell&Company.

7.GeraldM.Weinberg.(1998).ThePsychologyofComputerProgramming,AnlSub

ed.,DorsetHouse,ISBN-13:978-0932633422.

CHAPTER13

COMMUNICATINGWITHTHEOUTSIDE

WORLD

13.1Email

13.2FTP

13.3CommunicationBetweenProcesses

13.4Twitter

13.5CommunicatingwithOtherLanguages

13.6Summary

Inthischapter

Pythoncanreaddatafromthekeyboardandprintonthescreen,itcandisplaygraphics,

audio, and video, allow mouse (and touch) interactions, and read and writedata to and

fromfiles.That’salotofcommunication,butitallhappensononecomputer—theoneon

whichtheprogramisrunning.Intheageofhigh-speedInternet,socialmedia,podcasts,

blogs,andwikis,thisisnotenough.Thewideworldoutsideofthedesktopbeckons,anda

programmerwithaknowledgeofPythonandtherelevantmodulescanrespond.

Canacomputercommunicatewithanotherone?Ofcourse.Canaprogramsendemail?

Yes, that’s what a mail program like Thunderbird or Outlook does. Can a program be

writtenthatreadstweetsastheyaresent?Sure,butthereisaprice.Thatis:thesethings

aredoneaccordingtosomeoneelse’srules.Thefirstemailwassentin1971onaprivate

network named Arpanet. It sent mail between distinct computers, rather than sending

messagesbetweenusersonaspecificmachine.In1972UnixEmailwasmadeavailable,

andwasnetworkedin1978;thatwasthestartofsomethingbig.

Thesenderandreceiverhadtoagreeonhowtoencodeanddecodeamessage,andhow

toaccessitfromthenetwork.Tosendmailbetweendifferentcomputersalwaysrequiresa

standard,aschemethatisagreeduponbyimplementersofthesystem.Otherwisemailcan

onlybesentbetweenUNIXsystems,orWindows,oriOS.Email,tobepractical,needsto

bemoreflexible.Itneedstobeubiquitous,andsoallneedtoagreeonastandardforhow

Emailcanbesentandreceived.Astandardwaseventuallyagreedon,anditwascalledthe

SimpleMailTransferProtocol(SMTP)andwasestablishedin1982.

ThiswassevenyearsbeforetheWorldWideWeb,soEmailreallyrepresentsthefirst

practicalwaytocommunicatebetweencomputersoveralongdistance.FTPhappenedat

about the same time. The enabling technology for the Web, TCP/IP, came next. All of

these developments in networking and software combined to create the modern

interconnectedsociety,butallarebasedonacollectionofrulesthatsoftwaremustagree

to(protocols)iftheyaretomakeuseofthenetworkinfrastructure.Thisisanexampleof

design by contract, in which designers create formal specifications for components and

using those involves a kind-of contract or agreement between programmers developing

clientsoftwareandthosewhobuiltthemodulesanddesignedtheprotocols.

Therearehigh-levelprogramsthatprovideagooduserinterfacetotheInternetandthat

implement these protocols beneath their visual presentation. When using Python a

collectionofmodulesareusedthathandletheverylow-leveldetails,buttheinterfaceto

theprogrammerexposestheprotocol.Someofthesemodulesareprovidedinastandard

Pythoninstallation(smtplib,email),andsomearenot(MPI,Tweepy),andwillhavetobe

installedbeforethecodeinthischapterwillrun.

When communicating with another machine a key issue is that of authentication.

Almost all protocols require that a connection be formed between the two computers,

usingsomekindofidentificationofthosemachinessuchastheirIPaddress.Thentheone

initializingtheconnectionmustprovethatithaspermissiontodowhatitisabouttodo.

Thisresemblesloggingin,andinvolvesauseridentificationandapasswordofsometype.

Oncethe user has been identified there is an exchange of messages that tell the remote

computerwhatisdesiredofit,andthatallowinformationtobereturnedtothecaller.This

processisnearlyuniversal,buttakessomewhatdifferentformsondifferentsystems.

13.1 EMAIL

Emailisagoodexampleofaclient-serversystem,andonethatgetsusedmillionsof

timeseachminute.TheEmailprogramonaPCistheclient,andallowsausertoentertext

messages,specifydestinations,attachimages,andallofthefeaturesexpectedbysucha

program.ThisclientpackagestheEmailmessage(data)accordingtotheSimpleMessage

TransferProtocol(SMTP)andsendsthattoanothercomputerontheInternet,theEmail

server.AnEmailusermusthaveanaccountontheserverforthistoworksotheycanbe

identified and the user can receive replies; so, the process is: log into the Email server,

thensendtheSMTPmessagetotheEmailserverprogramonthatserver.Thustheclient

side of the contract is to create a properly formatted message, to log into the server

properly,andpassthemessagetoit.

Nowtheserverdoesthework.Giventhedestinationofthemessage,itsearchesforthe

server that is connected to that destination. For example, given the address

xyz@gmail.com, the server for gmail.com is located. Then the email message is sent

acrossthenetworktothatserver.Theserversoftwareatthatendreadsthemessageand

placesitintothemailbox,whichisreallyjustadirectoryonadiskdriveconnectedtothe

server,forthespecifiedusexyz.Themail

messageisessentiallyatextfileatthispoint.

This description is simplified but essentially accurate, and describes what has to be

donebyaprogramthatissupposedtosendanEmailmessage.ThePythonmodulethat

permitsthesendingofEmailimplementstheprotocolandofferstheprogrammerwaysto

specifytheparameters,likethedestinationandthemessage.Theinterfaceisimplemented

asasetoffunctions.Thelibraryneededforthisissmtplib,apartofthestandardPython

system.

Example:SendanEmail

Sending an Email message starts with establishing a connection between the client

computerandtheuser’smailserver,theoneonwhichtheyhaveanaccount(username

and password). For the purposes here a Gmail (Google) server will be used, which

complicatestheissueatinybit.TheEmailaccountsintheexamplearealsoGmailones,

andthesecanbehadforfreefromGoogle.

Theprogrammustdeclaresmtplibasanimportedmodule.Thesendingaddressandthe

receivingaddresswillbethesameinthisexample,butthisisjustatest.Normallythiswill

not be the situation. The Email address is the user ID for Gmail authentication and the

passwordisdefinedbytheuser.Thesearealljuststrings.

importsmtplib



#LoginpasswordforGmail,string

sndr=pythontextbook@gmail.com#Senderꞌsemailaddress

rcvr=pythontextbook@gmail.com#Receiverꞌsemailaddress

Part of the SMTP scheme is a syntax for Email messages. There is a header at the

beginningthatspecifiesthesender,receiver,andsubjectofthemessage.Theseareusedto

formatthemessage,nottorouteit—thereceiveraddressisspecifiedlater.Asimplesuch

messagelookslikethis:

From:user_me@gmail.com

To:user_you@gmail.com

Subject:Justamessage

Astringmustbeconstructedthatcontainsthisinformation:

msgt=“From:user_me@gmail.com\n”

msgt=msgt+“To:user_you@gmail.com\n”

msgt=msgt+“Subject:Justamessage\n”

msgt=msgt+“\n”

Nowthebodyofthemessageisattachedtothisstring.ThisisthepartoftheEmailthat

isimportanttothesender:

msgt=msgt+“Attention:ThismessagewassentbyPython!\n”

Thestringvariablemsgtnowholdsthewholemessage.Thismessageisintheformat

definedbytheMultipurposeInternetMailExtensions(MIME)standard.Thenextstepfor

theprogramistotrytoestablishaconnectionwiththesender’semailserver.Forthisthe

smtpmoduleisneeded,specificallytheSMTP()function.Itiscalledpassingthenameof

theuser’sEmailserverasaparameter,anditreturnsavariablethatreferencesthatserver.

Inthisexamplethatvariableisnamedserver:

server=smtplib.SMTP(ꞌsmtp.gmail.comꞌ)

Ifitisnotpossibletoconnecttotheserverforsomereason,thenanerrorwilloccur.It

isthereforeagoodideatoplacethisinatry-exceptblock:

try:

server=smtplib.SMTP(ꞌsmtp.gmail.comꞌ)

except:

print(“Erroroccurred.Canꞌtconnect”)

else:

Now comes the complexity that Gmail and some other servers introduce. What has

happened after the call to smtplib.SMTP() is that a communications session has been

openedup.Thereisnowanactiveconnectionbetweentheclientcomputerandtheserver

at smtp.gmail.com. Some servers demand a level of security that, among other things,

ensures that other parties can’t modify or even read the message. This is accomplished

using a protocol named Transport Layer Security (TLS), the details of which are not

completely relevant because the modules take care of it. However, to send data to

smtp.gmail.comtheservermustbetoldtobeginusingTLS:

server.starttls()

NowtheusermustbeauthenticatedusingtheirIDandpassword:

server.login(LOGIN,PASSWD)

Onlynowcanamessagebesent,andonlyiftheloginIDandpasswordarecorrect.The

senderisthestringsndr,therecipientisrcvr,andthemessageismsgt:

server.sendmail(sndr,rcvr,msgt)

Nowthatthemessagehasbeensent,itispolitetoclosethesession.Loggingoffofthe

serverisdoneasfollows:

server.quit()

Thisprogramwillsendoneemail,butitcanbeeasilymodifiedtosendmany emails

oneaftertheother.Itcanbemodifiedtoreadthemessagefromthekeyboard,orperform

anyofthefunctionsofatypicalEmail-sendingprogram

(Exercise1).

ThemoduleemailcanbeinvokedtoformatthemessageinMIMEform.Thefunction

MIMEText(s) converts the message string s into an internal form, which is a MIME

message.Fieldslikethesubjectandsendercanbeaddedtothemessage,andthenitissent

aswasdonebefore.Forexample:

importsmtplib

fromemail.mime.textimportMIMEText



PASSWD=yourpassword



fp=open(“message.txt”,“r”)#Readthemessagefroma

#file

mtest=fp.read()

#Or:simplyuseastring

#mtest=“AmessagefromPython:MerryChristmas.”

fp.close()



msg=MIMEText(mtest)#CreateaMIMEstring

sndr=pythontextbook@gmail.com#SenderꞌsEmail

rcvr=pythontextbook@gmail.com#RecipientꞌsEmail

msg[ꞌSubjectꞌ]=ꞌMailfromPythonꞌ#AddSubjecttothe

#message

msg[ꞌFromꞌ]=sndr#Addsendertothe

#message

msg[ꞌToꞌ]=rcvr#Addrecipenttothe

#message



#SendthemessageusingGoogleꞌsSMTPserver,asbefore

s=smtplib.SMTP(ꞌsmtp.gmail.comꞌ)#localhostcouldwork

s.starttls()

s.login(LOGIN,PASSWD)

s.send_message(msg)

s.quit()

UsingMIMEText() to create the message avoids having to format it correctly using

basicstringoperations.

13.1.1 ReadingEmail

ReadingEmailismorecomplicatedthanwritingit.ThecontentofanEmailisoftena

surprise,andsoareadermustbepreparedtoparseanythingthatmightbesent.Therecan

be multiple mailboxes: which mailbox will be looked at? There are usually many

messages in a mailbox: how can they be distinguished? In addition, the protocol for

retrievingmailfromaserverisdifferentfromthatusedtosendit;infact,therearetwo

competingprotocols:POPandIMAP.

ThePostOfficeProtocol(POP)istheolderofthetwoschemes,althoughithasbeen

updatedafewtimes.Itcertainlyallowsthebasicrequirementsofamailreader,whichis

todownloadanddeleteamessageinaremotemailbox(i.e.,ontheserver).TheInternet

Message Access Protocol (IMAP) is intended for use by many Email clients, and so

messagestendnottobedeleteduntilthatisrequested.WhensettingupanEmailclient

oneoftheseprotocolsusuallyhastobespecified,andthenitwillbeusedfromthenon.

TheexampleherewilluseIMAP.

Example:DisplaytheSubjectHeadersforEmailsinInbox

AnoutlinefortheprocessofreadingEmailissketchedontheright-handsideofFigure

13.1. Reading Email uses a different module that was used to send Email: imaplib, for

readingfromanIMAPserver.Thefunctionnamesaredifferentfromthoseinsmtplib,but

thepurposeofsomeofthemisthesame.ThefirstthreestepsinreadingEmailare:

importimaplib

server=ꞌimap.gmail.comꞌ#GmailꞌsIMAPserver

USER=pythontextbook@gmail.com#UserID

PASSWORD=“password”#Maskthispassword

EMAIL_FOLDER=“Inbox”



mbox=imaplib.IMAP4_SSL(server)#Connecttotheserver

mbox.login(USER,PASSWORD)#Authenticate(login)

The next step is to select a mailbox to read. Each has a name, and is really just a

directory someplace. The variable mbox is a class instance of a class named

imaplib.IMAP4_SSL, the details of which can be found in many places, including the

Internet.Ithasamethodnamedselect()thatallowstheexaminationofamailbox,given

its name (a string). The string is a variable named EMAIL_FOLDER which contains

“Inbox,”andthecalltoselect()thatessentiallyopenstheinboxis:

z=mbox.select(EMAIL_FOLDER)

The return value is a tuple. The first element indicates success or failure, and if z[0]

contains the string “OK” then the mailbox is open. The usual alternative is “NO.” The

secondelement of the tupleindicates how many messagesthere are, but itis in an odd

format. If there are 2 messages, as in the example, this string is b’2’; if there were 3

messagesitwouldbeb’3’;andsoon.Thesearecalledmessagesequencenumbers.

Havingopened the mailbox, the nextstep is to read it andextract the messages. The

protocol requires that the mailbox be searched for the messages that are wanted. The

imaplib.IMAP4_SSLclassoffersthesearch()methodforthis,thesimplestformbeing:

mbox.search(None,“ALL”)

whichreturnsallofthemessagesinthemailbox.IMAPprovidessearchfunctionality,and

all this method does is connect to it, which is why it seems awkward to use. The first

parameterspecifiesacharacterset,andNoneallowsittodefaulttoageneralvalue.The

secondparameterspecifiesasearchcriterionasastring.Therearedozensofparameters

thatcanbeusedhereandthedocumentationforIMAPshouldbeexaminedindetailfor

solutionstospecificproblems.However,someofthemoreusefultagsinclude:

ANSWERED:Messagesthathavebeenanswered.

BCC<string>:MessageswithaspecificstringintheBCCfield.

BEFORE<date>:Messageswhosedate(nottime)isearlierthanthespecifiedone.

HEADER<field-name><string>:Aspecifiedfieldintheheadercontainsthestring.

SUBJECT<string>:MessagesthatcontainthespecifiedstringintheSUBJECTfield.

TO<string>:MessagesthatcontainthespecifiedstringintheTOfield.

UNSEEN:Messagesthatdonothavethe\Seenflagset.

So,acalltosearch()thatlooksforthetext“Python”inthesubjectlinewouldbe:

mbox.search(None,“SUBJECTPython”)

Thesearch()functionreturnsatupleagain,wherethefirstcomponentisastatusstring

(i.e., “OK,” “NO,” “BAD”) and the second is a list of messages satisfying the search

criteriainthesameformatasbefore.Ifthesecondmessageiftheonlymatch,thisstring

willbeb’2.’Ifthefirstthreematchitwillbeb’123.’

Finally,themessagesareread,orfetched.Theimaplib.IMAP4_SSLclasshasafetch()

methodtodothis,anditagaintakessomeoddparameters.Whataprogrammerthinksof

theinterfaceortheAPIor,inotherwords,thecontract,isnotimportant.Whatmustbe

doneistosatisfytherequirementsandacceptthedataasitisoffered.Thefetch()method

acceptstwoparameters:thefirstistheindicationofwhichmessageisdesired.Thefirst

messageisb’1’, the secondis b’2’, and so on. The second parameter is an indicator of

whatitisthat shouldbereturned. Theheader?Ifso, pass“(RFC822.HEADER)”as the

parameter.Why?Becausetheyaskforit.RFC822isthenameofaprotocol.IftheEmail

bodyiswanted,thenpass“(RFC822.TEXT)”.Ashortlistofpossibilitiesis:

RFC822-Everything

RFC822.HEADER-Nobody,headeronly

RFC822.TEXT-Bodyonly

RFC822.SIZE-Messagesize

UID-Messageidentifier

Multipleofthesespecifierscanbepassed;forexample:

mbox.fetch(num,ꞌ(UIDRFC822.TEXTRFC822.HEADER)ꞌ)

returnsatuplehavingthreeparts:theID,thebody,andtheheader.Bytheway,theheader

tends to be exceptionally long, 40 lines or so, and is mostly uninteresting to a specific

application.Forthisexample,theonlypartoftheheaderthatisinterestingisthe“Subject”

part.Fieldsintheheaderareseparatedbythecharacters“\r\n”sotheyareeasytoextract

inacalltosplit().Eliminatingtheheaderdataforamoment,thecall:

(env,data)=mbox.fetch(num,ꞌ(UIDRFC822.TEXT)ꞌ)

resultsinatuplethathasan“envelope”thatshouldindicate“OK”(theenvvariable).The

datapartisastringthatcontainstheUIDandthetextbodyofthemessage.Forexample:

[(bꞌ2(UID22RFC822.TEXT{718}ꞌ,b”Gota collectionof old45ꞌs for sale. Contact

me.\r\n\r\n—\r\n”),bꞌ)ꞌ]

Thissaysthatthisismessage2andshowsthetextofthatmessage.

Thisexampleissupposedtoprintallofthesubjectheadersinthismailbox.Thecallto

fetch()shouldextracttheheaderonly:

(env,data)=mbox.fetch(num,ꞌ(RFC822.HEADER)ꞌ)

ThedetailsofIMAParecomplexenoughthatitiseasytoforgetwhattheoriginaltask

was, which was to print the subject lines from the messages in the mailbox. All of the

relevantmethodshavebeendescribedandcompletingtheprogramispossible.Theentire

programis:

importimaplib



server=ꞌimap.gmail.comꞌ#IMAPServer

USER=“pythontextbook@gmail.com”#USERID

PASSWORD=””#Maskthispassword

EMAIL_FOLDER=“Inbox”#Whichmailbox?



mbox=imaplib.IMAP4_SSL(server)#Connect

mbox.login(USER,PASSWORD)#Authenticate



env,data=mbox.select(EMAIL_FOLDER)#Selectthemailbox

ifenv==ꞌOKꞌ:#Diditwork?

print(”Printingsubjectheaders:“,EMAIL_FOLDER)



env,data=mbox.search(None,“ALL”)#Selectthe

#messageswanted.

ifenv!=ꞌOKꞌ:#Arethereany?

print(“Nomessages.”,env)#Nope.

exit()



fornumindata[0].split():#Foreachselected

#messagebꞌ123…ꞌ

(env,data)=mbox.fetch(num,ꞌ(RFC822.HEADER)ꞌ)

#Readit

ifenv!=ꞌOKꞌ:

print(“ERRORgettingmessage”,num,“,“,env)

break

s=str(data[0][1])#Lookforthestring

#“Subject”intheheader

k=s.find(“Subject”)

if(k>=0):#Foundit?

s=s[k:]#Extractthestringtothe

#nextꞌ\rꞌ

k=s.find(ꞌ\rꞌ)

s=s[:k]

print(s)#Andprintit.

mbox.close()

else:

print(“Nosuchmailboxas“,EMAIL_FOLDER)

mbox.logout()

Typicaloutputwouldbe:

Printingsubjectheaders:Inbox

Subject:ContentsofChapter13

Subject:45RPM

Subject:anotherEmail

ThepointofthissectionwastodemonstratehowaPythonprogram,oranyprogramfor

thatmatter,mustcomplywithexternalspecificationswheninterfacingwithsophisticated

software systems, and to introduce the concept of a protocol, a contract between

developers.OfcourseaprogramthatcansendEmailisusefulbyitself.

13.2 FTP

TheFileTransferProtocolisusedtoexchangefilesbetweencomputersonanetwork,

inparticularacrosstheInternet.Itprovidesthesamesortofinterfacetodataonadistance

computeraswouldbeexpectedfromafilesystemonadesktop.Itcancopyafileineither

direction, but can also change directories, list the directory contents, and perform other

useful operations. This again presumes that the rules set up by the FTP interface are

followed.

Havingjustseenthecommunicationrequirementsforsendingand receivingEmail,it

shouldbepossibletopredictthewaythatFTPwilloperate.Aconnectionwillhavetobe

madetoaremotecomputer,andsomeformofauthenticationwilltakeplace.Theclient

(the program that established the connection) will now send a set of commands to the

server, which will read and process them. Then, finally, the client will terminate the

connection.Thisisalltrue.

The commands that can be processed by an FTP server include things like LIST the

contents of this directory, change the working directory (CWD), retrieve a file (RETR)

andsendorstoreafile(STOR).Thesearesentacrossthenetworkasstringsandrepresent

raw FTP commands, those that take place at a low level of abstraction in the system.

HigherlevelcommandsareimplementedasspecificmethodsintheFTPclassofftplib.

Forexample,thereisacommandnamedPWDthatwilldisplaythenameofthecurrent

remotedirectory.FTPoffersafunctionthatwillsendthiscommand:

FTP.pwd()

Doing the same thing by sending the command directly would use the sendcmd()

methodofFTP,andwouldpassthecommandasastring:

ftp.sendcmd(“PWD”)

There is a difference to the programmer. The pwd() method returns the string that

representsthedirectory,whereaswhenthetextcommandissent,the return valueisthe

stringthattheFTPsystemreturned,whichissomethinglike:

257“/”isthecurrentdirectory

AnexamplewillbeusedtoillustratetheuseofFTP.

Example:DownloadandDisplaytheREADMEFilefroman

FTPSite

The site chosen for the example belongs to NASA, but any ftp site will work. The

connectionandauthenticationstepsare:

fromftplibimportFTP



ftp=FTP(“ftp.hq.nasa.gov”)#PleasedonꞌtalwaysuseNASA

ftp.login()#Selectadifferentsite.

The login step is interesting because there are no parameters given. This is an

anonymous FTP connection, which is common for sites that offer things for download.

The default login when using the login() method is a user ID of “anonymous” and a

password, if one is requested, of “anonymous.” It is also possible to specify an ID and

passwordiftheuserhasthem:

ftp.login(“myuserid”,“mypassword”)

Thelogin()functionreturnsthesite’swelcomemessage,whichisastringthatcanbe

ignored.

The example is supposed to download the file named README and display it. The

methodretrlines()candothis,becauseitisatextfile.Ifitwereabinaryfile,likeanMP3

orJPGfile,thentheretrbinary()methodwouldbeusedinstead.Thefirstparameterto

retrlines()isacommand.ToretrieveafilethecommandisthekeywordRETRfollowed

bythefilename.Thesimplestversionis:

ftp.retrlines(ꞌRETRREADMEꞌ)

whichwilldisplaythetextfromthefileonthescreen.That’swhatwaswanted,butthe

method can do more. If a function name is passed as the second parameter, then that

functionwillbecalledforeverylineoftext,andwillbepassedthatlineasaparameter.To

illustratethisconsiderasimplefunctionthattakesastringandprintseachline,lookingfor

“\n”characters.Thefunctionis:

defmyprint(ss):

s=str(ss)#Sometimestheparameterssistypebyte.

x=s.split(“\n”)

foriinrange(0,len(x)):

print(x[i])

Nowacalltoretrlines()couldbeasfollows:

ftp.retrlines(ꞌRETRREADMEꞌ,myprint)

oreven:

ftp.retrlines(ꞌRETRREADMEꞌ,print)

tousethestandardprint()function.Ofcourseanyfunctionthattakesastringparameter

couldbepassed.TosavetheREADMEfileasalocalfile,forexample:

ftp.retrlines(ꞌRETRREADMEꞌ,open(ꞌREADMEꞌ,ꞌwꞌ).write)

willwritethefiletoalocalonenamedREADME,butlackingtheend-of-linecharacters.

Binary files use retrbinary(), and it has the same form as retrlines(). However, the

secondparameter,thefunction,mustbepassed,becausebinaryfilescannotbesenttothe

screen.Downloadingandsavinganimagefilemightbedoneasfollows:

ftp.retrbinary(ꞌRETRorion.jpg,open(ꞌorion.jpg,ꞌwbꞌ).write)

Thesessionwouldendbyloggingout:

ftp.quit()

Uploadingafile,thatismovingafilefromadesktoptoasiteontheInternet,usedthe

methodstorlines()fortextandstorbinary()forbinaryfiles.Examples:

f=open(“message.txt”,“rb”)

ftp.storlines(“STORmessage.txt”,f)

Themethodcopieslinesfromthelocalfiletotheremoteone.Thefiletobecopiedis

openin“rb”mode.Forabinaryexampleassumeanimage:

f=open(“image.jpg”,“rb”)

ftp.storbinary(“STORimage.jpg”,f)

session.storbinary(“STORkitten.jpg,”file)#sendthefile

13.3 COMMUNICATIONBETWEENPROCESSES

UnderneaththeFTPandEmailprotocols,whichallowinterfacestoapplications,liesa

communications layer, the programs that actually send bytes between computers or

betweenprogramsonthesamecomputer.Itisconductedverymuchlikeaconversation.

One person, the client, initiates the conversation (“Hi there!”). The other (the server)

responds (“Hello. Nice to see you.”). Now it is the client’s turn again. They take turns

sendingandacceptingmessagesuntilonesays“goodbye.”Thesemessagesmightcontain

Email,orFTPdata,orTVprograms.Thislayerdoesnotcarewhatthedatais;noneofits

business,really.Itsjobistodeliverit.

Dataaredeliveredinpackets,eachcontainingacertainamount.Inorderfortheclient

todeliverthedatatheremustbeaserverwillingtoconnecttoit.Theclientneedstoknow

theaddressofaserver,justasanFTPaddressorEmaildestinationwasrequiredbefore,

butnowallthatisneededisthehostnameandaportnumber.Aportisreallyalogical

construction,somethingakintoanelementofalist.Iftwoprogramsagreetosharedata

byhavingoneofthemplaceitinlocation50001ofalistandtheotheronereaditfrom

there,itgivesanapproximateideaofwhataportis.Someportnumbersareassignedand

should not be used for anything else; FTP and Email have assigned ports. Others are

availableforuse,andanytwoprocessescanagreetouseone.

Amodulenamedsocket,basedontheinterprocesscommunicationschemeonUNIXof

the same name, is used with Python to send messages back and forth. To create an

exampletwocomputersshouldbeused,onebeingtheclientandonetheserver,andtheIP

addressoftheserverisrequiredtoo.

Example:AServerThatCalculatesSquares

Theclientwillopenacommunicationslink(socket)totheserver,whichhasaknownIP

address.Theserverwillengageinashorthandshake(exchangeofstrings)andthenexpect

toreceiveanumberfortheclient.Theclientwillsendaninteger,theserverwillreceiveit,

square it, and send back the answer. This simple exchange is really the basis for all

communicationsbetweencomputers:onemachinesendsinformation,theotherreceivesit,

processesit,andreturnsareplybasedonthedataitreceived.

Theclient:willbegintheconversation.Itcreatesaconnection,asocket,totheserver

using the socket() function of the socket module. Protocols must be specified, and the

mostcommononeswillbeused:

importsocket



HOST=ꞌ19*.***.*.***ꞌ#Theremotehost

PORT=50007#Thesameportasusedbytheserver

s=socket.socket(socket.AF_INET,socket.SOCK_STREAM)

s.connect((HOST,PORT))

Port 50007 is used because nothing else is using it. Now the client starts the

conversation,justasitappearsatthebeginningofthissection:

s.send(bꞌHithere!ꞌ)

Thesend()functionsendsthemessagepassedasaparameter.Thestring(asbytes)is

transmitted to the server through the variable s, which represents the server. The client

nowwaitsfortheconfirmationstringfromtheserver,whichshouldbe“Hello.Nicetosee

you.”Theclientcalls:

data=s.recv(1024)

whichwaits for a response from the server.This response will be 1024 bytes long at

most,anditwillwaitonlyforashorttime,atwhichpointitwillgiveupandanerrorwill

bereported.Whenthisclientgetstheresponse,itproceedstosendnumberstotheserver.

Theyareconvertedintothebytestypebeforetransmission.Inthisexampleitsimplyloops

through100consecutiveintegers:

foriinrange(0,100):

data=str(i).encode()

s.send(data)

Aftersendingtotheserveritwaitsfortheanswer.Actuallythat’sapartofthereceive

function:

data=s.recv(1024)

after100integerstheloopendsandtheconnectionisclosed:

s.close()

The Server: is always listening. It creates a socket on a particular port so that the

operatingsystemknowssomethingispossiblethere,butbecausetheservercannotpredict

whenaclientwillconnectorwhatclientitwillbeitsimplylistensforaconnection,by

callingafunctionnamedlisten():

importsocket

fromrandomimport*



HOST=ꞌꞌ#Anullstringiscorrecthere.

PORT=50007

s=socket.socket(socket.AF_INET,socket.SOCK_STREAM)

s.bind((HOST,PORT))

s.listen()

AF_INETandSOCK_STREAMareconstantsthattellthesystemwhichprotocolsare

beingused.Thesearethemostcommon,butseethedocumentationforothers.Thebind()

andthelisten()functionsarenew.Associatingthisconnectionwithaspecificportisdone

usingbind().Thetuple(HOST,PORT)saystoconnectthishosttothisport.Theempty

stringforHOSTimpliesthiscomputer.

Thelisten()callstartstheserverprocess,thisprogram,acceptingconnectionswhenasked.

A process connecting on the port that was specified in bind() will now result in this

process, the server, being notified. When a connection request occurs, the server must

acceptitbeforedoinganyinputoroutput:

conn,addr=s.accept()

Inthe tuple (conn, addr) that isreturned, conn represents the connection, like a file

descriptorreturnedfromopen(),andisusedtosendandreceivedata;addristheaddress

ofthesender,theclient,andisastring.Iftheaddrwereprinted:

print(“Connectedto“,addr)

ItwouldlooklikeanIPaddress:

Connectedto423.121.12.211

Nowtheservercanreceivedataacrosstheconnection,anddoessobycallingrecv():

data=conn.recv(1024)

print(“Serverheardꞌ“,data,“ꞌ“)

Theparameter1024specifiesthesizeofthebuffer,orthemaximumnumberofbytes

thatcanbereceivedinonecall.Thevariabledataisoftypebytes,justastheparameterto

send() was in the client. The client was the first to send, and it sent the message “Hi

there!” That should be the value of data now, if it has been received properly. The

responsefromtheservershouldbe“Hello,nicetoseeyou.”

conn.send(bꞌHello.Nicetoseeyou.ꞌ)

Thesameconnectionisusedforsendingandreceiving.

Nowtherealdatagetsexchanged.Theserverwillacceptintegers,sentasbytes.Itwill

squarethemandtransmittheanswerback.

whileTrue:

data=conn.recv(1024)#Readtheincomingdata

ifdata:

i=int(data)#Convertittointeger

print(“Received“,i)

data=str(i*i).encode()#Squareitandconverttobytes

conn.send(data)#Sendtotheclient

Theservercantellwhentheconnectionisclosedbytheclient,butitisalsopolitetosay

“Goodbye”somehow, perhaps by sending aparticular code.If the loopever terminates,

theservershouldclosetheconnection:

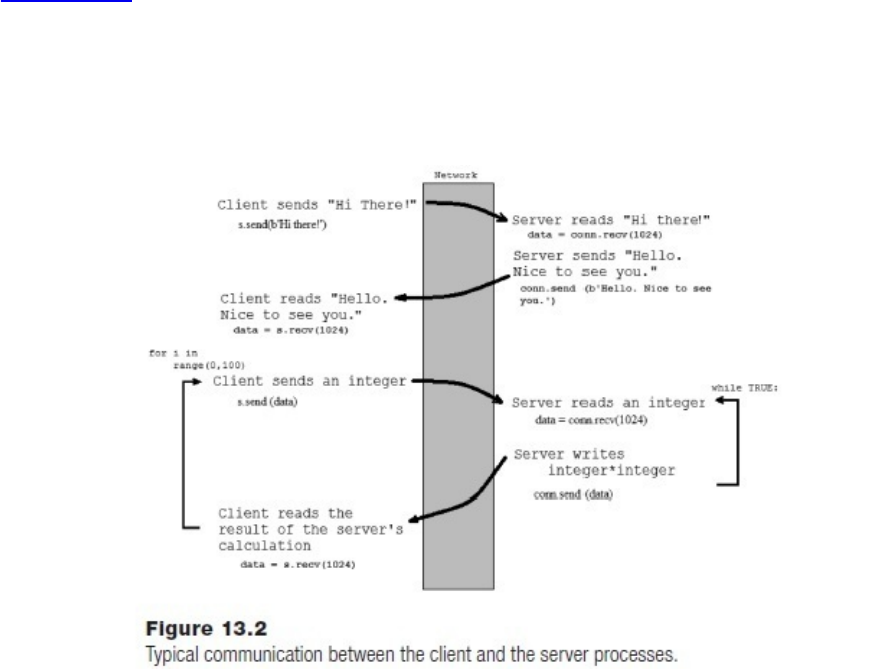
conn.close()

This is a pretty good example of a data exchange and a contract, because there are

specified requirements for each side of this conversation which will result in success if

done correctly and failure if messed up. Failure is sometimes indicated by an error

message,oftenatimeout where theclient or server was expecting something thatnever

arrived.Inothercasesfailureisnotformallyindicatedatall;theprogramsimply“hangs”

thereanddoesnothing.Ifatanytimebothprocessesaretryingtoreceivedata,thenthe

programwillfail.

Figure13.2showsthecommunicationbetweentheclientandtheserverasadiagram.If

theclientandtheserverareatanytimebothtryingtoacceptdatafromtheconnection,

thentheprogramwillfail.Inthediagramalldatatransferscanbeseenastransmit-accept

pairsbetweenthetwoprocesses,andasread-writepairswithintheserverandwrite-read

pairswithintheclient.

The FTP protocol can now be seen as a socket connection, wherein the client sends

strings (commands) to the server, which parses them, carries out the request, and then

sendsanacknowledgementback.

13.4 TWITTER

ForthefewpeoplewhomaybeunfamiliarwithTwitter,itisasocialmediaservicethat

allowsitsuserstosendshort(140character)messagesouttotheworld,orreallytotheir

subscribedlisteners.Fromitsbeginningin2006,Twitterhasgrowntothepointwhereit

handleshundredsofmillionsofmessages(tweets)perdayfromtheir302millionactive

users. It differs from Email in that it broadcasts messages, and the recipients are self-

selected.

ThemessagesareenteredbyTwitterusers,eachofwhomhasanaccount.Allmessages

becomepartofastream,andtheonesthataparticularuserwantstoseearepulledfrom

that stream and placed on the user’s feed. It is, however, possible to see the feed and

examinemessagesastheyaresent,collectingdataoridentifyingpatterns.Twitterallows

accesstothestream,butwhenusingPythonitrequirestheuseofamodulethatmustbe

downloadedandinstalled.That

moduleiscalledtweepy.

Awarning:settinguptheauthenticationsothattheTwitterstreamcanbeaccessedis

notsimple.Atwitteraccountisneeded,anapplicationhastoberegistered,andtheapp

mustbespecifiedasbeingabletoread,write,anddirectmessages.Twitterwillcreatea

unique set of keys that must be used for the authentication: the consumer key and

consumersecretkey,thentheaccesstokenandaccesssecrettoken.Again,itdoesnotpay

toaskwhybecauseitsimplymustbedone.Howisabetterquestion.

Atweetislimitedto140characters,butthatonlyconsiderscontent.Theamountofdata

sentinatweetissubstantiallylargerthanthat,6000bytesormore.That’sduetothelarge

amountofmetadata,ordescriptiveinformation,inatweet.Mostpeopleneverseethat,but

aprogramthatreadstweetsandsiftsthemforinformationwillhavetodealwithit.The

twitterinterfacereturnstweetdatainJSONformat(JavaScriptObjectNotation)whichisa

standardforexchangingdata,similarinpurposetoXML.Thisformathasto beparsed,

butasecondPythonmodulenamedjsonwilldothatsonofurtherdiscussionofJSONwill

benecessary.

Example:ConnecttotheTwitterStreamandPrintSpecific

Messages

This program will examine the twitter feed and print messages that have the term

“startrek” in them. It is useful to see that once again, authentication is one of the first

thingstodo.InthecaseofTweepyanobjectiscreated,passingtheauthenticationstrings.

First:

importtweepy

importjson



#Authenticationdetailsfromdev.twitter.com

consumer_key=ꞌgetyourownꞌ

consumer_secret=ꞌgetyourownꞌ

access_token=ꞌgetyourownꞌ

access_token_secret=ꞌꞌgetyourownꞌ



authentication=tweepy.OAuthHandler(consumer_key,

consumer_secret)

authentication.set_access_token(access_token,

access_token_secret)

Nowsomethingdifferentisneeded.Tweepywantstohaveanobjectpassedtoitthatis

asubclassofonethatitdefines,StreamListener.Asapartofthedealthatismadewith

Tweepy,theclassmusthaveamethodnamedon_data()andanothernamedon_error().

Theon_data()methodiscalledbyTweepywhenthereisdatainthestreamtoberead,and

thedatais passedas astringin JSONformat; theon-error()method iscalled whenan

erroroccurs,andispassedastringwiththeerrormessage.Creatingthissubclasswillbe

describedalittlelater.However,assumethatitiscalledtweet_listener.Thenextstepin

theprocessistocreateaninstanceofthisclass:

listener=tweet_listener()

Through this class instance the stream will be accessed. Now tell Tweepy what this

instanceissoitcanuseit.Alsodotheauthentication:

stream=tweepy.Stream(authentication,listener)

FinallytellTweepywhattoextractfromtheTwitterstream.Forthisexample,thecallis:

stream.filter(track=[ꞌStarTrekꞌ])

butotherpartsofthestreamcanbeaccessedandsenttothisprogram:timesand dates,

locations, etc. In this case the track argument looks into the message text for the “Star

Trek”string,caseinsensitive.Multiplesearchstringscanbeplacedinthelist:[“startrek”,

“casablanca”].

OK,whataboutthetweet_listenerclass?ItisasubclassofStreamListener,aswassaid

earlier.Theon_data()methodneedstoparsetheJSON-formattedstringitispassedand

printthepartsofthemessagethataredesired.Sincethefilter()callrestrictsthemessages

tothosecontainingthestring“startrek,”allthathastobedoneinthismethodistoprint

thebodyofthemessage.Hereistheclassshowingthemethod;theexplanationfollows:

classtweet_listener(tweepy.StreamListener):



defon_data(self,data):

#TwitterreturnsdatainJSONformat-decodeitfirst

dict=json.loads(data)

print(dict[ꞌuserꞌ][ꞌlocationꞌ])

print(dict[ꞌuserꞌ][ꞌscreen_nameꞌ],dict[ꞌtextꞌ])

returnTrue



defon_error(self,status):

print(status)

TheparameterdataisinJSONformat.Toconvertitintosomethinguseable,passitto

thejson.loads()method.ItreturnsaPythondictionarywiththedataavailable,indexedby

fieldname.ThedatastructureusedbyTwitteriscomplex,andisshowninsmallpartin

Table13.1.Theleftsideofthetableshowsthemessagefieldnames,therightlistssome

oftheuserfields;userisafieldwithinthemessagethatdescribesthesender.Thevariable

dictistheresultingdictionary.

To simply solve the problem posed, all that would have to be done is to print

dict[‘text’],whichisthemessagebody.Thevalueofdict[‘user’]isthedataforthesender

ofthemessage.Thereisalotofthat,mostlynotusefultoanyonebutanappdeveloper

(e.g., background color of the user’s window), but dict[‘user’]’[‘screen_name’] is the

Twitteridentityofthesender,anddict[‘user’][‘location’]oftenindicateswheretheyare.

Itwouldbepossibletocollectdataonwherethelargestnumberoftweetsarebeingsent

from, what kind of information is being conveyed, and in this way perhaps develop an

earlywarningsystemforeventshappeningintheworld.

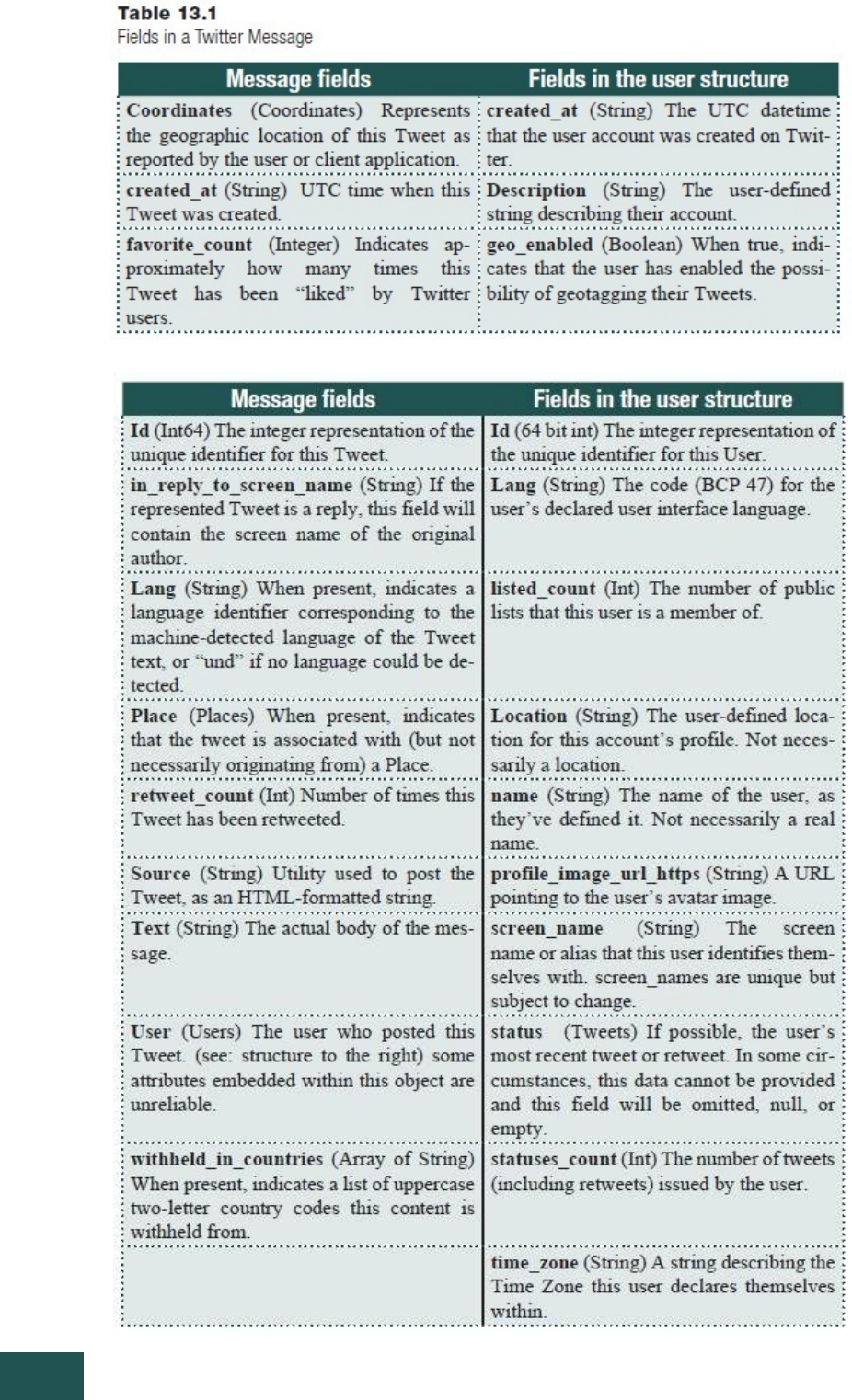
13.5 COMMUNICATINGWITHOTHERLANGUAGES

Pythonisterrificformanythings,butitcanbequiteslow.Itisinterpretedandhasalot

ofoverheadformanyofitsfeatures;dynamictypingdoesnotcomecheap.Also,itmaybe

hard to easily access operating system functions from Python. C, C++, and other

languagesdonothavetheseproblems.It’spossibletowriteaprograminPythonthatcalls,

forexample,aCprogramtodocomplexcalculationsofsystemcalls.

Consider the problem of finding the greatest common divisor (GCD) between two

integers; that is, the largest number that divides evenly into both of them. If the GCD

betweenNandMis1,thenthesenumbersarerelativelyprime,andtheycouldfindusein

arandomnumbergenerator.

Example:FindTwoLargeRelativelyPrimeNumbers

ThisproblemwillbesolvedusingaCprogramtodotheGCDcalculationandaPython

programtopassitlargenumbersuntilarelativelyprimeparisfound.TherearemanyC

versionsoftheGCDprogram.Thisisacommonfirst-yearprogrammingassignment.One

suchisgcd.c,providedontheaccompanyingdisc

#include“stdafx.h”

#include<stdio.h>



int_tmain(intargc,_TCHAR*argv[])

{

longn,m;

scanf(“%ld%ld”,&n,&m);

while(n!=m)

{

if(n>m)

n-=m;

else

m-=n;

}

printf(“%d”,n);

return0;

This is written for Visual C++ 2010 Express, but very similar code will compile for

othercompilersandsystems.Thebasicideaisthatitreadstwolargenumbers,namedn

and m, determines their largest common divisor, and prints that number to standard

output. The way that Python will communicate with this C program is through the I/O

system.Creadsfromstandardinput,andwritestostandardoutput.ThePythonprogram

will co-opt input and output, pushing text data containing the values of n and m to the

input,andcapturingstandardoutputandcopyingittoastring.

Thisrequirestheuseofamodulenamedsubprocessthatpermitstheprogramtoexecute

thegcd.exeprogramandconnecttothestandardI/O.AfunctionnamedPopen()takesthe

nameofthefiletobeexecutedasaparameterandrunsit.Italsoallowsthecreationof

pipes,which are data connections thatcan take the place of files. The Popen() call that

runsthegcdprogramis:

p=subprocess.Popen(ꞌgcd.exeꞌ,

stdin=subprocess.PIPE,

stdout=subprocess.PIPE)

ConnectingstdinandstdouttosubprocessPIPEsmeansthatnowPythoncanperform

I/Owiththem.WhenGCDstartstoexecuteitexpectstwointegersoninput.Thesecan

nowbesentfromthePythonprogramlikethis:

p.stdin.write(data)

Theexpressionp.stdinrepresentsthefileconnectiontotheprogram,andwritingtoit

does the obvious thing. The Python program writes data to the C program, and the C

programreadsitfromstdin.Datashouldbeoftypebytes,andshouldcontainbothlarge

numbersincharacterform.Correspondingly,whentheCprogramhasfoundthegreatest

commondivisor,itwritestostandardoutput.CapturingthisinPython:

s=str(p.stdout.readline())

TheCprogramwrites;thePythonprogramreads.Thevaluereturnedisoftypebytes

again,soitisconvertedintoastring.

ThefinalPythonsolutioncallstheCprogramrepeatedlyuntiltheGCDis1:

importsubprocess



n=11111122

m=121

data=bytes(str(n)+ꞌꞌ+str(m),ꞌutf-8ꞌ)

whileTrue:

p=subprocess.Popen(ꞌgcd.exeꞌ,

stdin=subprocess.PIPE,

stdout=subprocess.PIPE)

p.stdin.write(data)

p.stdin.close()

s=str(p.stdout.readline())

print(s)

ifs==“bꞌ1ꞌ“:

print(“Numbersare“,n,m)

break

m=m+1

data=bytes(str(n)+ꞌꞌ+str(m),ꞌutf-8ꞌ)

Thismethodofcommunicatingwithotherlanguagesisquiteuniversal,butslowerthan

passing parameters to functions and methods directly. There are a lot of problems with

calling functions in other languages, not the least of which concerns typing. Python,

dynamically typed interpreted language that it is, would have to have the programmer

performsomesignificantgymnasticstoconvertlistsordictionariesintoaformthatCor

Javacoulduse.

13.6 SUMMARY

Design by contract has designers create formal specifications for components, and

using those involves a kind-of contract or agreement between programmers developing

clientsoftwareandthosewhobuiltthemodulesanddesignedtheprotocols.ForEmail,as

anexample,senderandreceiverhavetoagreeonhowtoencodeanddecodeamessage,

andhowtoaccessitfromthenetwork.Tosendmailbetweendifferentcomputersalways

requires a standard, a scheme that is agreed upon by implementers of the system, a

protocol.

TheSimpleMessageTransferProtocolisaspecificationoftheprocessanddataneeded

tosend anEmail message.The Python modulesmtplibprovides the methods needed to

interfacewiththissystem,whichistosaythatsmtplibimplementsSMTPandprovidesa

programmeraccessatvariousplaces.ForreadingEmailtherearetwoschemesinplay:the

Post Office Protocol (POP) and the more modern Internet Message Access Protocol

(IMAP). An Email client must agree to satisfy one of these. They Python module for

IMAPisimaplib.

The File Transfer Protocol (FTP) is used to move entire files and directories across

networks.Itprovidesthesamesortofinterfacetodataonadistancecomputer

aswouldbeexpectedfromafilesystemonadesktop.Theftplibmoduleoffersmethods

for handling this protocol. After authentication, commands are sent as character strings,

andfilescanbesentorreceivedusinganalogsofreadandwriteoperations.

FTP is built on top of lower level communication primitives such as sockets, which

createbidirectionaldataconnectionsbetweentwoprogramsondifferentcomputers.

Twitter sends out a stream of data containing all of the tweets sent by users, and the

client can scan these for tweets that are of interest (subscribed). This stream can be

capturedusingPythonandtheTweepymodule,andautomaticscanningofthefeedcanbe

doneaccordingtotheuser’sprogram.

It is also possible for Python to communicate with other programs written in other

languagesbyco-optingtheinputandoutputfilesforthoseprogramsandfeedingdatainto

andextractingresultsfromtheI/Ochannels.

Exercises

1.WriteasimpleEmailsendingprogramsendmail.Itwillaskforthedestinationfrom

thekeyboardandacceptthemessagethatwaytoo.Multipledestinationaddressescan

bespecifiedbyseparatingthemwithcommas.Thesender’sEmailaddressandthe

servernameshouldbebuiltintotheprogram.

2.Writeanapplicationthatallowsausertospecifyawordorwordsandwillexamine

theirmailboxforanyEmailthatcontainsthem.ThecorrespondingEmailmessages

willbewrittentoatextfilenamed“search.txt.”

3.WriteaPythonprogramthatwilldownloadthefilesnamed“one.txt,”“two.txt,”and

“three.txt”fromanftpsitespecifiedbyyourinstructorintofilesofthesamenameona

desktopcomputer.

4.Designandcodeaserverprogramthatwilldealpokerhandsusingthesocket

protocol.Whentheserverisconnectedtobyaclient,theclientsendsastring“deal.”

Theserverwillgeneratearandompokerhandandsenditastext:Thespadessuitin

thisschemeis:s1s2s3s4s5s6s7s8s9s10sjsqsk;heartsare“h,”diamondsare“d,”

andclubsare“c.”Writeatestprogramthatreadsandprintstheresultinghands.

5.DIFFICULT.Writeatwo-playerponggameusingsockets.Thegamewilldisplaya

graphicalversionofthestandardPongscreenonthelocalandremotescreens.The

localplayercanmoveonlythelocalpaddle,andmotionsbytheremoteplayerare

reflectedonthelocalscreen.Theballispositionedatthesameplace,asnearlyas

possible,onbothscreenssimultaneously.

6.Therearewordsandphrasesthatmanygovernmentsusetoindicateapotential

securityproblem.Theycanexamineemailsandvarioussocialmediaoutlets.Examine

theTwitterstreamfortweetscontainingthewords“assassination,”“security,”

“weapon,”or“hostage.”Printthetweetandlocationfromwhichitclaimstobesent.

7.HowcantheIPaddressofadistantsitebedetermined?SearchtheInternetforthat

informationasitcanbeimplementedinaPythonprogram,andimplementaprogram

thataskstheuserforaURLandreturnsanIPaddressforthatURL.

NotesandOtherResources

Pythonftplibdocumentation:https://docs.python.org/3/library/ftplib.html

SearchcriteriainIMAP:http://tools.ietf.org/html/rfc3501#section-6.4.4

Tweepdownload:https://pypi.python.org/pypi/tweepy/3.4.0

Tweepyintro:http://docs.tweepy.org/en/latest/streaming_how_to.html

How to use the Twitter API to stream tweets. https://www.youtube.com/watch?

v=pUUxmvvl2FE

Twittermessagefields:https://dev.twitter.com/overview/api/tweets

Twitteruserfields:

JSONTutorial:http://www.w3schools.com/json/

1.ToddCampbell.(2002).TheFirstEmailMessage,

https://www.cs.umd.edu/class/spring2002/cmsc434-

0101/MUIseum/applications/firstemail.html

2.TimBerners-Lee,RobertCailliau,AriLuotonen,HendrykNielsen,andArthurSecret.

(1994).TheWorld-WideWeb,CommunicationsoftheACM,37(8),76–82.

3.TakeshiSakaki,MakotoOkazaki,andYutakaMatsuo.(2010).Earthquakeshakes

Twitterusers:Real-timeeventdetectionbysocialsensors,inProceedingsofthe

19thInternationalConferenceontheWorldWideWeb(WWW’10),ACM,NewYork,

NY,USA,851–860.

CHAPTER14

ABRIEFGLIBREFERENCE

14.1Glibtkinter

14.2Images

14.3DynamicGlib

14.4Video

14.5Audio

14.6Interaction

14.7Other

Inthischapter

The reason that there are two “versions” of Glib is that not all schools and other

institutions will permit installing new modules. The module tkinter is standard with

Python3,butdoesnotbyitselfofferthetoolsformultimedia.Thebasicsystemconsists

ofgraphicsoperations,includingimageinput,output,anddisplay.

Forplaceswhereitispossibletoinstallthepygamemodule,thedynamicGlibmodule

canbeused.Thisoffersthesametoolsasdoesthetkinterversionplushassound,mouse

andkeyboardinteraction,andvideo.

Whatfollowsisdocumentationforbothsystems.

14.1 GLIBTKINTER

BLACK=“#000000”

WHITE=“#ffffff”

RED=“#ff0000”

GREEN=“#00ff00”

BLUE=“#0000ff”

BACKSPACE='\b'

Width()

Returnthewidthofthegraphicswindowinpixels.

Height()

Returntheheightofthegraphicswindowinpixels.

fill(r,g=1000,b=1000)

Turnonfilling.Setthefillcolorforpolygons,textcolortoo,to(r,g,b)orjustrifone

parameterisgiven.

nofill()

Turnfillingoff.

stroke(r,g=1000,b=1000)

Set the line and outline color to (r,g,b). If one parameter is given, then it is a grey

level.

nostroke()

Turnoffoutlinedrawing.

ellipsemode(z)

Setthemodefordrawingellipses.Thedefaultmodefordrawingellipsesisreferredto

as CENTER mode, where the center of the ellipse is given. There are three others:

RADIUSmode,inwhichthewidthandheightparametersrepresentsemi-majorandsemi-

minor axes; CORNER mode in which the upper left corner is specified instead of the

center; and CORNERS mode, in which the upper left and the lower right corner of the

boundingboxarespecified.

rectmode(z)

Setthemodefordrawingrectangles.Thedefaultmodefordrawingellipsesisreferred

to as CENTER mode, in which x, y are the coordinates of the center; w and h are the

widthandheight.InRADIUSmodex,yarethecoordinatesofthecenter;wandrarethe

horizontalandverticaldistancestoanedge.InCORNERmodex,yarethecoordinatesof

theupperleftcorner;wandharethewidthandtheheight.InCORNERSmodex,yare

the coordinates of the upper left corner; w and h are the coordinates of the lower right

corner.

ellipse(xpos,ypos,width,height)

Drawanellipse.Alsousedforcircles.Fourmodesasdescribedinellipsemode.

line(x0,y0,x1,y1)

Draw a line using the current stroke color between screen coordinates (x0, y0) and

(x1,y1).

point(x,y)

Drawapoint(pixel)atlocation(x,y)inthecurrentfillcolor.

rect(xpos,ypos,x2,y2)

Drawarectangle.Same4modesasellipse.Fillwiththecurrentfillcolor.

triangle(x0,y0,x1,y1,x2,y2)

Drawatrianglespecifiedbythreepoints.

bold()

Setfonttobold.

italic()

Setfonttoitalic.

normal()

Setthefontweightandslanttonormal(notbold)androman(notitalic).

setfont(s)

Setthefontfamilytothenamegiveninthestringparameters.Defaultis“Helvetica.”

text(s,x,y)

Drawthetextstringsstartingatscreencoordinate(x,y).

quad(x0,y0,x1,y1,x2,y2,x3,y3)

Drawaquadrilateralhavingthefourcornersbeing(x0,y0),(x1,y1),(x2,y2)and(x3,y3).

strokeweight(n)

Setthethicknessofdrawnlinesandstrokestonpixels.

arc(x0,y0,x1,y1,start,angle,s=ARC)

Draw anarc.An arc is defined as a portion of an ellipse from a starting angle for a

specified number of degrees, as referenced from the center of the ellipse. The angle 0

degrees is horizontal and to the right; 90 degrees is upwards (decreasing Y value). The

ellipse is defined by a bounding rectangle, specifying the upper left and lower right

coordinatesofaboxthatjustholdstheellipse.ThefinalparameterbeingARCmeansto

draw only the curve; if it is CHORD then it will draw the curve and a line joining the

endpoints.PIESLICEdrawsthearcandlinesfromtheendpointsofthearctothecenterof

theellipse.

cvtColor(z)

Takethegreyvaluezandreturnacolorobjectthathasred=z,green=z,andblue=z.

cvtColor3(r,g,b)

Take thecolor componentvaluesr, g,and b(red, green, andblue) andreturn acolor

objecthavingthosevalues.

background(r,g=1000,b=1000)

Set the background color to the color given by components (r,g,b). This effectively

clearsthegraphicswindowaswell.

textsize(n)

Changethesizeoftexttonpixelshigh.

14.2 IMAGES

loadImage(s)

Readtheimagefromthefilewhosenameisstoredintheparametersandreturnitas

thevalue.

image(im,x,y)

Displaytheimageimatwindowcoordinate(x,y).

copyImage(x)

Returnacopyoftheimageparameterx.

getpixel(im,i,j)

Returnthecolorofthepixelatlocation(i,j)oftheimageim.

setpixel(im,i,j,c)

Setthepixelvalue(color)oftheimageimatcoordinates(i,j)tothecolorc.

grey(c)

Returnthegreylevelequivalentofthecolorc.Itaveragesthethreecolorcomponents.

red(c)

Extractandreturntheredcomponentofthecolorpassedasc.

green(c)

Extractandreturnthegreencomponentofthecolorpassedasc.

blue(c)

Extractandreturnthebluecomponentofthecolorpassedasc.

save(im,s)

Savetheimageiminafilenamedbythestrings.

imageSize(s)

Acquire the size (width, height in pixels) of an image that exists as a file named s.

Return a tuple with the (width,height). This can be executed outside of the startdraw–

enddrawblocksothatstartdraw()canopenawindowofasizeappropriatetoanimage.

startdraw(xs=width,ys=height)

Thisindicatesthebeginningofasectionofcodewithinwhichdrawingoperationswill

beperformed.Itopensawindowonthescreenwithawidthofxspixelsandaheightofys

pixels.Itsetsupatitleonthewindowanddoessomeinitializations,suchassettingupa

font,settingdrawingmodes,andestablishingabackgroundcolor.

enddraw()

Forusersoftkinter,allthisfunctiondoesistocallmainloop().Foreveryoneelse,this

functionmustbecalledinorderthatcontrolcanbepassedtothedrawingfunctionsand

thattheuser’sdrawingcanbedisplayedinthegraphicswindow.Itistheclosetotheblock

ofcodebegunwiththecalltostartdraw().

14.3 DYNAMICGLIB

Symbolicnamesforspecialcharacters(LEFT,etc.)Theseareglobalvariablesthatare

usedbytheuser.

K_BACKSPACE =pygame.K_BACKSPACE

K_TAB =pygame.K_TAB

K_CLEAR =pygame.K_CLEAR

K_RETURN =pygame.K_RETURN

K_PAUSE =pygame.K_PAUSE

K_ESCAPE =pygame.K_ESCAPE

K_SPACE =pygame.K_SPACE

K_EXCLAIM =pygame.K_EXCLAIM

K_QUOTEDBL =pygame.K_QUOTEDBL

K_HASH =pygame.K_HASH

K_DOLLAR =pygame.K_DOLLAR

K_AMPERSAND =pygame.K_AMPERSAND

K_QUOTE =pygame.K_QUOTE

K_LEFTPAREN =pygame.K_LEFTPAREN

K_RIGHTPAREN =pygame.K_RIGHTPAREN

K_ASTERISK =pygame.K_ASTERISK

K_PLUS =pygame.K_PLUS

K_COMMA =pygame.K_COMMA

K_MINUS =pygame.K_MINUS

K_PERIOD =pygame.K_PERIOD

K_SLASH =pygame.K_SLASH

K_0 =pygame.K_0

K_1 =pygame.K_1

K_2 =pygame.K_2

K_3 =pygame.K_3

K_4 =pygame.K_4

K_5 =pygame.K_5

K_6 =pygame.K_6

K_7 =pygame.K_7

K_8 =pygame.K_8

K_9 =pygame.K_9

K_COLON =pygame.K_COLON

K_SEMICOLON =pygame.K_SEMICOLON

K_LESS =pygame.K_LESS

K_EQUALS =pygame.K_EQUALS

K_GREATER =pygame.K_GREATER

K_QUESTION =pygame.K_QUESTION

K_AT =pygame.K_AT

K_LEFTBRACKET =pygame.K_LEFTBRACKET

K_BACKSLASH =pygame.K_BACKSLASH

K_RIGHTBRACKET =pygame.K_RIGHTBRACKET

K_CARET =pygame.K_CARET

K_UNDERSCORE =pygame.K_UNDERSCORE

K_BACKQUOTE =pygame.K_BACKQUOTE

#K_a =pygame.K_a

K_b =pygame.K_b

K_c =pygame.K_c

K_d =pygame.K_d

K_e =pygame.K_e

K_f =pygame.K_f

K_g =pygame.K_g

K_h =pygame.K_h

K_i =pygame.K_i

K_j =pygame.K_j

K_k =pygame.K_k

K_l =pygame.K_l

K_m =pygame.K_m

K_n =pygame.K_n

K_o =pygame.K_o

K_p =pygame.K_p

K_q =pygame.K_q

K_r =pygame.K_r

K_s =pygame.K_s

K_t =pygame.K_t

K_u =pygame.K_u

K_v =pygame.K_v

K_w =pygame.K_w

K_x =pygame.K_x

K_y =pygame.K_y

K_z =pygame.K_z

K_DELETE =pygame.K_DELETE

K_KP0 =pygame.K_KP0

K_KP1 =pygame.K_KP1

K_KP2 =pygame.K_KP2

K_KP3 =pygame.K_KP3

K_KP4 =pygame.K_KP4

K_KP5 =pygame.K_KP5

K_KP6 =pygame.K_KP6

K_KP7 =pygame.K_KP7

K_KP8 =pygame.K_KP8

K_KP9 =pygame.K_KP9

K_KP_PERIOD =pygame.K_KP_PERIOD

K_KP_DIVIDE =pygame.K_KP_DIVIDE

K_KP_MULTIPLY =pygame.K_KP_MULTIPLY

K_KP_MINUS =pygame.K_KP_MINUS

K_KP_PLUS =pygame.K_KP_PLUS

K_KP_ENTER =pygame.K_KP_ENTER

K_KP_EQUALS =pygame.K_KP_EQUALS

K_UP =pygame.K_UP

K_DOWN =pygame.K_DOWN

K_RIGHT =pygame.K_RIGHT

K_LEFT =pygame.K_LEFT

K_INSERT =pygame.K_INSERT

K_HOME =pygame.K_HOME

K_END =pygame.K_END

K_PAGEUP =pygame.K_PAGEUP

K_PAGEDOWN =pygame.K_PAGEDOWN

K_F1 =pygame.K_F1

K_F2 =pygame.K_F2

K_F3 =pygame.K_F3

K_F4 =pygame.K_F4

K_F5 =pygame.K_F5

K_F6 =pygame.K_F6

K_F7 =pygame.K_F7

K_F8 =pygame.K_F8

K_F9 =pygame.K_F9

K_F10 =pygame.K_F10

K_F11 =pygame.K_F11

K_F12 =pygame.K_F12

K_F13 =pygame.K_F13

K_F14 =pygame.K_F14

K_F15 =pygame.K_F15

K_NUMLOCK =pygame.K_NUMLOCK

K_CAPSLOCK =pygame.K_CAPSLOCK

K_SCROLLOCK =pygame.K_SCROLLOCK

K_RSHIFT =pygame.K_RSHIFT

K_LSHIFT =pygame.K_LSHIFT

K_RCTRL =pygame.K_RCTRL

K_LCTRL =pygame.K_LCTRL

K_RALT =pygame.K_RALT

K_LALT =pygame.K_LALT

K_RMETA =pygame.K_RMETA

K_LMETA =pygame.K_LMETA

K_LSUPER =pygame.K_LSUPER

K_RSUPER =pygame.K_RSUPER

K_MODE =pygame.K_MODE

K_HELP =pygame.K_HELP

K_PRINT =pygame.K_PRINT

K_SYSREQ =pygame.K_SYSREQ

K_BREAK =pygame.K_BREAK

K_MENU =pygame.K_MENU

K_POWER =pygame.K_POWER

K_EURO =pygame.K_EURO

K_A =65

K_B =66

K_C =67

K_D =68

K_E =69

K_F =70

K_G =71

K_H =72

K_I =73

K_J =74

K_K =75

K_L =76

K_M =77

K_N =78

K_O =79

K_P =80

K_Q =81

K_R =82

K_S =83

K_T =84

K_U =85

K_V =86

K_W =87

K_X =88

K_Y =89

K_Z =90

noloop()

Stopcallingthedrawfunctionrepeatedly.Thishastheeffectofceasinganydynamic

activity.

defsize(xs,ys):

globalwidth,height,canvas

width=xs

height=ys

canvas=pygame.display.set_mode((xs,ys),

pygame.DOUBLEBUF,32)#Makethesketchwindow

pygame.display.set_caption('Drawing')

14.4 VIDEO

loadVideo(s)

Loadsavideofromthefilenamedbythestringsandreturnsareferencetothatvideo

asaGvideoclassinstance.Thisinstanceneedsneverbemanipulatedbytheprogrammer,

onlypassedtootherfunctions.

playVideo(m)

Playthevideorepresentedbythevariablem.

pauseVideo(m)

Pause(orunpauseifpaused)thevideorepresentedbythevariablem.

stopVideo(m)

Stopplayingthevideorepresentedbythevariablem.

rewindVideo(m)

Placethevideombackatthebeginningframe.

isVideoPlaying(m)

ReturnsTrueifthevideomiscurrentlyplayingandFalseifnot.

setVideoVolume(m,v)

Settheaudiovolumeofthevideomtoalevelbetween0(off)and1

(maximum).

lengthVideo(m)

Returnthelengthofthecurrentvideo,inseconds.

whereVideo(m)

For the video m, return the number of seconds that the video has been playing (i.e.,

currentposition)

getVideoFrame(m)

Returnthenumberofthecurrentframeplayinginthevideom.

setVideoFrame(m,f)

Setthepositionofthevideomsothatthenextframetoplaywillbenumberf.

getVideoPixel(m,x,y)

Returnthepixelatlocation(x,y)inthevideoframefrommcurrentlybeingdisplayed.

sizeVideo(m)

Returnthesizeofaframe(widthxheightinpixels)ofthevideom.

locVideo(m,x,y,w,h)

Placethevideomatposition(x,y)onthegraphicswindow,andgiveitsize(w,h).

videoSize(s)

Return the size (width, height) of the video in the file s without loading it. For

specifyingthesizeofthegraphicswindow.

14.5 AUDIO

loadSound(s)

Loadasoundfilewherethefilenameisinstrings.Returnanobjectreference(handle)

tothatfile.

playSound(a,loop=0)

Playthesoundindicatedbya.

defstopSound(a):

Stopplayingthesoundindicatedbya.

volumeSound(a,v)

Setthevolumeofsoundatoavaluebetween0(off)and1(maximum).

durationSound(a)

Returnthelengthofthesoundsinseconds.

14.6 INTERACTION

mouse()

Returnthecoordinatesofthemousecursorasatuple(x,y).

14.7 OTHER

capture(s)

Savetheimageinthecurrentgraphicswindowastheimagefiles.

TheGlibmodulecontainstwoclassesforinternaluse,animageclassandavideoclass.

Theyaredescribedhereonlyforcompleteness,butifyouplantousetheirinternalcodein

anywaypleasereaditcarefullyfromthesourcefileandbecertainthatyouunderstandit.

Animageclass:

classGimage:

im=None#Image

pixels=None#Pixelsdata

w=h=0



defsetIm(self,x):

defget(self,x,y):

defset(self,x,y,c):

defsave(self,s):

defdraw(self,canvas,x,y):

Avideoclass:

classGvideo:

def__init__(self,name):

defloadVideo(self,s):

defplay(self):

deflocVideo(self,x,y,w,h):

defdraw(self):

defcopy(self,x,y,w,h):

defstop(self):

defrewind(self):

defis_playing(self):

deflength(self):

defwhere(self):

defget_frame(self):

defpause(self):

defget_frame_number(self):

defdraw_frame(self,f,iplay=0):

defget_pixel(self,x,y):

defauto_play(self):

defset_volume(self,v):

INDEX
A
A
Accessor,224
Accumulator,14
LoadAccumulator,14
Acousticdelaylines,11
Addresses,12
Advanceddatafiles,299–317
Binaryfiles,299–301
EXE,317
HyperTextMarkupLanguage(HTML),316–317
Randomaccess,304–306
Maintainingthehighscorefileinorder,305–306
Standardfiletypes,306–315
GIF,307–308
Imagefiles,306–307
JPEG,309–310
PNG,312–314
Soundfiles,314–315
TaggedImageFileFormat(TIFF),310–312
WAVfile,314
Structmodule,301–303
Aliasing,161
Alohanet,23
AmericanStandardCodeforInformationInterchange(ASCII),27
Analyticalengine,3
Assignmentstatements,432
B
Babbage,Charles,3

Basicalgorithms,361–398
Bernoullinumbers,4
Binarynumbers,6
Arithmeticin,9–11
Converttodecimal,8
Bit,8
Bootloader,18
BranchifAccumulatorisZero(BAZ),17
Bristow,Steve,452
Buffering,200
Bushnell,Nolan,452
Button,21
C
Calculationsbymachine,2–3
Changetheworkingdirectory(CWD),490
Checkbox,21
Cipher,399
Class,217–248
Datatypesand,228–243
Abouncingball,231–237
Adeckofcards,229–231
Basicdesign,237–238
Cat-a-pult,237–243
Detaileddesign,238–243
Ducktyping,246–248
Subandinheritance,243–246
Objectsinavideogame,243–246
Typesand,219–228
Areallysimple,223–227
Encapsulation,227–228
ClearAccumulator(CLA),17

Client-serversystem,26
Codetable,393
Collision,23
Compression,382–396
Huffmanencoding,385–392
Huffmanalgorithm,388
LZW,392–396
Runlengthencoding,383
Computernetworks,22–26
Internet,24–25
WorldWideWeb,25–26
Computersystemlayers,17–22
Assemblersandcompilers,18–19
Graphicaluserinterfaces(GUIs),19–22
Concatenate,107
Constructor,221
Core,12
Coredump,12
Crossover,418
Cryptography,376–382
One-timepad,378–379
Plaintextandciphertext,377
PublicKeyEncryption(RSA),379–382
Statecipher,377
Streamcipher,377
Symmetrickey,377
D
Datastructures,432
Decimalnumbers,8
Converttobinary,8–9
Delta,406

Designbycontract,504
Dictionary(Python),287–293,304,391
AnaiveLatin–Englishtranslation,289–291
Functionsfor,291–292
Loopsand,292–293
Differentiation,406–407
2and4-pointfunctionversions,407
Documentation,55–57
Docstring,57
Drop–downlist,21
E
Email,481–497
Communicationbetweenprocesses,492–497
Communicationbetweentheclientandtheserverprocesses,497
Packetsandportnumber,493
FileTransferProtocol(FTP),490
Ftplib,490
Reading,484–490
Procedureforsending,485
Usefultags,486–487
READMEFile,491
Sendan,481
Smtplib,482
Endoffilecondition,201
Epoch,376
Equationroots,404–406
Commonconcepts,406
Event,325
Exception,92,199
F
Fetch,12

Fetch-executecycle,13,17
File(s),189–213
Alittletheory,191–195
Filestorageondisk,194–195
Slowfileaccess,195
Commonthingsin,190–191
Keyboardandinput,195–197
Listof,190
Writingto,211–213
Appendingdatatoa,212–213
Filedescriptororhandle,198
FormattedtextandI/O,294–299
NASAmeteoritelandingdata,295–299
Function(s),144–184
Definition,144–149
Generalizethehistogramcodeforotheryears,147–149
Parameterorargument,146
Syntaxofa,145
Usepoundntodrawahistogram,146–147
Execution,149–170
Defaultparameters,156–158
Functionsasreturnvalues,168–170
Gameofsticks,158–161
None,158
Parameters,153–156
Returningavalue,150–153
Scope,161–163
Variableparameterlists,163–165
Variablesasfunctions,165–168
Recursion,170–176
Avoidinginfinite,175–176

Programdesign(Nimgame),178–184
Developmentprocessexposed,182–184
G
Glib,255,283,507–519
Audio,518
Dynamic,512–516
Functionsandconstants,283–284
Images,510–512
Interaction,518–519
Playavideo,353–355
Staticanddynamic,324
tkinter,507–510
Ellipsemode,509
Usefulfunctionsin,351–353
Video,516–517
Graphics,254–280
Graphicprogramming,254–280
Generativeart,277–280
Histogramexample,264–268
Images,271–277
Identifyingacar,274–275
Pixels,273–274
Thresoldingexample,275–276
Transparency,276–277
Linesandcurves,260–262
Piechartexample,268–271
Poixellevelgraphics,257–260
Polygons,262–263
Text,263–264
Windowandcolors,255–257
Guessanumber,37,39–40,50–51,71–72,

Solvingproblem,40–41,94–96
H
Hashing,396–398
djb2,397–398
sdbm,398
Headcrash,193
I
Icon,21
IfStatements,52–55,432
Else,54–55
Infiniteloop,70
Infiniterecursion,175
Initialguess,406
Interpreter,19
Integration,408–410
Instructionregister,14
InternetMessageAccessProtocol(IMAP),485
InternetProtocol(IP),24
Iteration,184,406
Maximum,406
Iterativerefinement,184,432
L
Linearprogramming,167
List(s),123–135
Append,126–127
Count,131
Editing,125–126
Exceptions,133–135
Extend,127
Index,128
Insert,126

Listcomprehension,131–132
Pop,128–129
Remove,127–128
Reverse,130–131
Sort,129–130
Tuplesand,132–133
Loading,17
Longestcommonsequence(editdistance),421–427
DeterminingLongestCommonSubsequence(LCS),422–427
EditdistanceorLevenshteindistance,421
Smith–Watermanmethod,422
Loops,67,432
Counting,78–79
Forloop,78
Nested,84–86
M
Memory,11–13
MersenneTwisteralgorithm,376
Method,220
Multimedia,323–356
Animation,335–346
Aballinabox,336–338
ChangeBackgroundColorUsingtheMouse,327–328
DrawaCircleattheMouseCursor,325–327
Framewithtwoexamples,340–346
Manyballsinabox,338–340
Object,336–340
Keyboard,330–335
Pressinga“+”CreatesaRandomCircle,331–334
ReadingaCharacterString,334–335
Mouseinteraction,324–330

Button,329–330
DrawLinesUsingtheMouse,328–329
Mousebuttons,328–330
RGBAcolors,346–347
Sound,347–350
Controllingvolume,349
Playasound,348
Playasoundeffect,349–350
Video,350–355
PlayvideousingGlib,353–355
Processingpixels,355–356
UsefulfunctionsinGlib,351–353
MultipurposeInternetMailExtensions(MIME)standard,482
Mutation,418
Mutatorsorsetters,224
N
NetworkAccessPoint(NAP),25
Newline,200
Newton’smethod,404
O
Objectorientedprogramming–breakout,452–453
Optimization:maximaandminima,410–420
Evolutionaryorgeneticalgorithm,416–420
Goldstein–Pricefunction,417
Fittingdatatocurves-regression,413–416
Newton’smethod,411–413
P
Parameterorargument,146
PDP–8,14
Predefinednamesorsystemvariables,39
Point,136

PointofPresence(POP),25
PostOfficeProtocol(POP),485
Primeornon–primenumber,79–84
Else,83–84
Exitingfromaloop,82–83
Problemasprocess,453–470
Ballandpaddlecollusions,466–467
Ballandtilecollusions,463–466
Collectingtheclasses,461–462
Developingthepaddle,462–463
Finishingthegame,467–470
Initialcodingforatile,456–457
Initialcodingfortheball,459–461
Initialcodingforthepaddle,457–459
Proceduralprogramming,433–452
Centering,443–445
Commands,442
Filling,443
Listofsystemcommands,433–434
Othercommands,447–452
Pseudocode,434
Rightjustification,445–447
Top–down,434–443
Program,4
Programcounter,13
Programmability,4
Programminglanguagecommunication,502–504
Greatestcommondivisor(GCD),502
Prompt,38
Publicvariables,248
Puzzles,74

PyCharm,38
Pygame,324
Python,19,36–62,69,75,78,90,92,101,107,109,121,123,135,144,153,163,
177,191,219,228,230,272,286,293,318,323,369,373,394,470,479,485,498,
502,504,507
Arrays,293
Class-SyntaxandSemantics,221–223
Creatingmodules,176–178
Dictionaries,287–293
Executing,37–39
List,123–135
PythonGUI,38
Usingfilesin,197–211
CommaSeparatedVariable(CSV),205
Commonfileinputoperations,202–205
Endoffile,201
Filenotfoundexceptions,199
Openafile,198–200
Playjeopardy,208–210
Printtheplanetname,205–207
Readingfromfiles,200–211
Thewidthstatement,210–211
Q
Quantization,30
R
Randomnumber(s),74–78
Built–infunction,75
Functioncall,76
Generation,373–376
Linearcongruentialmethod,374–376
Registers,12
Repetition,67–96

Drawingahistogram,86–89
Exceptionsanderrors,90–96
Loopsingeneral,89–90
Representation,26–31
Reservedwords,39
Retrieveafile(RETR),490
Rock–paper–scissors,37,40,57–62,73–78
Solvingproblem,41–42
Exchanginginformationwithcomputers,45–46
Numberbases,48–50
Strings,integers,andrealnumbers,47–48
VariablesandvaleswithGUI,42–45
Typesaredynamic(advanced),60–62
Rulesforprogrammers,470–477
S
Sampling,29
Script,sourcecodeorcomputerprogram,36
Searching,369–373
Binarysearch,371–373
Linearsearch,371
Timings,370–371
Secondarystorage,192
Swendorstoreafile(STOR),490
Sequence,102
Settypes,135–138
Crap,136–138
SimpleMailTransferProtocol(SMTP),480
Simpson’sRule,410
Slice,106
Slider,21
Sorting,361–369

Mergesort,365–369
Propertiesof,365
Selectionsort,362–365
Squareroot,76
Statements,44
Storedprograms,13–17
String(s),102–114
Comparing,103–105
Editing,107–110
Forloops,113
Methods,110–112
Slicing,105–107
Spanningmultiplelines,112–113
Stubs,477
Synthesisprogramming,432
T
TheWhileStatements,69–73
Modifyingthegame,72–73
Tracks,194
TransportLayerSecurity(TLS),483
Transistor,7
Tuple(s),78,115–123
Assignment,121–122
Built–infunctionsfor,122–123
Delete,119–120
Inforloops,116–118
Membership,118–119
Update,120–121
Turing,Alan,13
Twitter,497–501
Fieldsinamessage,500

StreamListener,499

Tweepy,498

Typebytes,114–115

UniversalResourceLocator(URL),26

Variable,42

Widget,20

Wozniak,Steve,452

Python James R. Parker An Introduction To Programming

Navigation menu

Versions of this User Manual:

Views

Navigation