Krijnen Intro Bio Inf Statistics
User Manual: Krijnen-IntroBioInfStatistics
Open the PDF directly: View PDF ![]() .
.
Page Count: 278 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Preface
- Brief Introduction into Using R
- Data Display and Descriptive Statistics
- Important Distributions
- Estimation and Inference
- Linear Models
- Micro Array Analysis
- Probe data
- Preprocessing methods
- Gene filtering
- Applications of linear models
- Searching an annotation package
- Using annotation to search literature
- Searching GO numbers and evidence
- GO parents and children
- Gene filtering by a biological term
- Significance per chromosome
- Overview and concluding remarks
- Exercises
- Cluster Analysis and Trees
- Classification Methods
- Analyzing Sequences
- Markov Models
- Answers to exercises
- References
Applied Statistics for Bioinformatics using R
Wim P. Krijnen
November 10, 2009
ii
Preface
The purpose of this book is to give an introduction into statistics in order
to solve some problems of bioinformatics. Statistics provides procedures to
explore and visualize data as well as to test biological hypotheses. The book
intends to be introductory in explaining and programming elementary statis-
tical concepts, thereby bridging the gap between high school levels and the
specialized statistical literature. After studying this book readers have a suf-
ficient background for Bioconductor Case Studies (Hahne et al., 2008) and
Bioinformatics and Computational Biology Solutions Using R and Biocon-
ductor (Genteman et al., 2005). The theory is kept minimal and is always
illustrated by several examples with data from research in bioinformatics.
Prerequisites to follow the stream of reasoning is limited to basic high-school
knowledge about functions. It may, however, help to have some knowledge
of gene expressions values (Pevsner, 2003) or statistics (Bain & Engelhardt,
1992; Ewens & Grant, 2005; Rosner, 2000; Samuels & Witmer, 2003), and
elementary programming. To support self-study a sufficient amount of chal-
lenging exercises are given together with an appendix with answers.
The programming language R is becoming increasingly important because
it is not only very flexible in reading, manipulating, and writing data, but
all its outcomes are directly available as objects for further programming.
R is a rapidly growing language making basic as well as advanced statisti-
cal programming easy. From an educational point of view, R provides the
possibility to combine the learning of statistical concepts by mathematics,
programming, and visualization. The plots and tables produced by R can
readily be used in typewriting systems such as Emacs, L
A
T
EX, or Word.
Chapter 1 gives a brief introduction into basic functionalities of R. Chap-
ter 2 starts with univariate data visualization and the most important de-
scriptive statistics. Chapter 3 gives commonly used discrete and continuous
distributions to model events and the probability by which these occur. These
distributions are applied in Chapter 4 to statistically test hypotheses from
bioinformatics. For each test the statistics involved are briefly explained and
its application is illustrated by examples. In Chapter 5 linear models are ex-
plained and applied to testing for differences between groups. It gives a basic
approach. In Chapter 6 the three phases of analysis of microarray data (pre-
processing, analysis, post processing) are briefly introduced and illustrated
by many examples bringing ideas together with R scrips and interpretation of
results. Chapter 7 starts with an intuitive approach into Euclidian distance

iii
and explains how it can be used in two well-known types of cluster analysis to
find groups of genes. It also explains how principal components analysis can
be used to explore a large data matrix for the direction of largest variation.
Chapter 8 shows how gene expressions can be used to predict the diagnosis
of patients. Three such prediction methods are illustrated and compared.
Chapter 9 introduces a query language to download sequences efficiently and
gives various examples of computing important quantities such as alignment
scores. Chapter 10 introduces the concept of a probability transition matrix
which is applied to the estimation of phylogenetic trees and (Hidden) Markov
Models.
R commands come after its prompt >, except when commands are part
of the ongoing text. Input and output of R will be given in verbatim
typewriting style. To save space sometimes not all of the original output
from R is printed. The end of an example is indicated by the box . In
its Portable Document Format (PDF)1there are many links to the Index,
Table of Contents, Equations, Tables, and Figures. Readers are encouraged
to copy and paste scripts from the PDF into the R system in order to study
its outcome. Apart from using the book to study application of statistics in
bioinformatics, it can also be useful for statistical programming.
I would like to thank my colleges Joop Bouman, Sven Warris and Jan
Peter Nap for their useful remarks on parts of an earlier draft. Many thanks
also go to my students for asking questions that gave hints to improve clarity.
Remarks to further improve the text are appreciated.
Wim P. Krijnen
Hanze University
Institute for Life Science and Technology
Zernikeplein 11
9747 AS Groningen
The Netherlands
w.p.krijnen@pl.hanze.nl
Groningen
October 2009
1c
°This document falls under the GNU Free Document Licence and may be used freely
for educational purposes.
iv
Contents
Preface ............................... iii
1 Brief Introduction into Using R 1
1.1 Getting R Started on your PC .................. 1
1.2 Getting help ............................ 3
1.3 Calculating with R ........................ 4
1.4 Generating a sequence and a factor ............... 4
1.5 Computing on a data vector ................... 5
1.6 Constructing a data matrix ................... 6
1.7 Computing on a data matrix ................... 8
1.8 Application to the Golub (1999) data .............. 10
1.9 Running scripts .......................... 12
1.10 Overview and concluding remarks ................ 13
1.11 Exercises .............................. 14
2 Data Display and Descriptive Statistics 17
2.1 Univariate data display ...................... 17
2.1.1 Pie and Frequency table ................. 17
2.1.2 Plotting data ....................... 18
2.1.3 Histogram ......................... 19
2.1.4 Boxplot .......................... 20
2.1.5 Quantile-Quantile plot .................. 22
2.2 Descriptive statistics ....................... 24
2.2.1 Measures of central tendency .............. 24
2.2.2 Measures of spread .................... 25
2.3 Overview and concluding remarks ................ 26
2.4 Exercises .............................. 26
v
vi CONTENTS
3 Important Distributions 31
3.1 Discrete distributions ....................... 31
3.1.1 Binomial distribution ................... 31
3.2 Continuous distributions ..................... 34
3.2.1 Normal distribution .................... 35
3.2.2 Chi-squared distribution ................. 37
3.2.3 T-Distribution ....................... 39
3.2.4 F-Distribution ....................... 40
3.2.5 Plotting a density function ................ 41
3.3 Overview and concluding remarks ................ 42
3.4 Exercises .............................. 43
4 Estimation and Inference 47
4.1 Statistical hypothesis testing ................... 47
4.1.1 The Z-test ......................... 48
4.1.2 One Sample t-Test .................... 51
4.1.3 Two-sample t-test with unequal variances ....... 54
4.1.4 Two sample t-test with equal variances ......... 56
4.1.5 F-test on equal variances ................. 57
4.1.6 Binomial test ....................... 58
4.1.7 Chi-squared test ..................... 59
4.1.8 Normality tests ...................... 63
4.1.9 Outliers test ........................ 64
4.1.10 Wilcoxon rank test .................... 65
4.2 Application of tests to a whole set gene expression data . . . . 66
4.3 Overview and concluding remarks ................ 68
4.4 Exercises .............................. 69
5 Linear Models 73
5.1 Definition of linear models .................... 74
5.2 One-way analysis of variance ................... 77
5.3 Two-way analysis of variance .................. 83
5.4 Checking assumptions ...................... 85
5.5 Robust tests ............................ 86
5.6 Overview and concluding remarks ................ 88
5.7 Exercises .............................. 88
CONTENTS vii
6 Micro Array Analysis 91
6.1 Probe data ............................ 91
6.2 Preprocessing methods ...................... 94
6.3 Gene filtering ........................... 97
6.4 Applications of linear models ..................100
6.5 Searching an annotation package ................104
6.6 Using annotation to search literature ..............106
6.7 Searching GO numbers and evidence ..............107
6.8 GO parents and children .....................108
6.9 Gene filtering by a biological term ................109
6.10 Significance per chromosome ...................110
6.11 Overview and concluding remarks ................112
6.12 Exercises ..............................112
7 Cluster Analysis and Trees 117
7.1 Distance .............................118
7.2 Two types of Cluster Analysis ..................121
7.2.1 Single Linkage .......................121
7.2.2 k-means ..........................125
7.3 The correlation coefficient ....................130
7.4 Principal Components Analysis .................133
7.5 Overview and concluding remarks ................141
7.6 Exercises ..............................142
8 Classification Methods 145
8.1 Classification of microRNA ....................146
8.2 ROC types of curves .......................147
8.3 Classification trees ........................150
8.4 Support Vector Machine .....................160
8.5 Neural Networks .........................162
8.6 Generalized Linear Models ....................164
8.7 Overview and concluding remarks ................167
8.8 Exercises ..............................167
9 Analyzing Sequences 173
9.1 Using a query language ......................173
9.2 Getting information on downloaded sequences .........174
9.3 Computations on sequences ...................176
viii CONTENTS
9.4 Matching patterns ........................181
9.5 Pairwise alignments ........................182
9.6 Overview and concluding remarks ................189
9.7 Exercises ..............................189
10 Markov Models 193
10.1 Random sampling .........................193
10.2 Probability transition matrix ...................194
10.3 Properties of the transition matrix ...............199
10.4 Stationary distribution ......................201
10.5 Phylogenetic distance .......................203
10.6 Hidden Markov Models ......................209
10.7 Appendix .............................213
10.8 Overview and concluding remarks ................214
10.9 Exercises ..............................214
A Answers to exercises 219
B References 257
List of Figures
2.1 Plot of gene expression values of CCND3 Cyclin D3. ...... 20
2.2 Stripchart of gene expression values of CCND3 Cyclin D3 for
ALL and AML patients. ..................... 20
2.3 Histogram of ALL expression values of gene CCND3 Cyclin D3. 21
2.4 Boxplot of ALL and AML expression values of gene CCND3
Cyclin D3. ............................. 21
2.5 Q-Q plot of ALL gene expression values of CCND3 Cyclin D3. 23
2.6 Boxplot with arrows and explaining text. ........... 29
3.1 Binomial probabilities with n= 22 and p= 0.7........ 34
3.2 Binomial cumulative probabilities with n= 22 and p= 0.7. . . 34
3.3 Graph of normal density with mean 1.9 and standard deviation
0.5. ................................. 36
3.4 Graph of normal distribution with mean 1.9 and standard de-
viation 0.5. ............................ 36
3.5 χ2
5-density. ............................. 38
3.6 χ2
5distribution. .......................... 38
3.7 Density of T10 distribution. .................... 39
3.8 Distribution function of T10.................... 39
3.9 Density of F26,10.......................... 41
3.10 Distribution of F26,10........................ 41
4.1 Acceptance and rejection regions of the Z-test. ......... 50
4.2 Acceptance and rejection regions of the T5-test. ........ 52
4.3 Rejection region of χ2
3-test. .................... 59
5.1 Plot of SKI-like oncogene expressions for three patient groups. 81
5.2 Plot of Ets2 expression values for three patient groups. . . . . 81
ix
xLIST OF FIGURES
6.1 Mat plot of intensity values for a probe of MLL.B........ 93
6.2 Density of MLL.B data. ...................... 93
6.3 Boxplot of the ALL1/AF4 patients. ............... 97
6.4 Boxplot of the ALL1/AF4 patients after median subtraction
and MAD division. ........................ 97
6.5 Venn diagram of seleced ALL genes. ...............100
6.6 Boxplot of the ALL1/AF4 patients after median subtraction
and MAD division. ........................100
7.1 Plot of five points to be clustered. ................122
7.2 Tree of single linkage cluster analysis. ..............122
7.3 Example of three without clusters. ...............123
7.4 Three clusters with different standard deviations. .......123
7.5 Plot of gene ”CCND3 Cyclin D3” and ”Zyxin” expressions for
ALL and AML patients. .....................124
7.6 Single linkage cluster diagram from gene ”CCND3 Cyclin D3”
and ”Zyxin” expressions values. ................124
7.7 K-means cluster analysis. .....................126
7.8 Tree of single linkage cluster analysis. ..............126
7.9 Plot of kmeans (stars) cluster analysis on CCND3 Cyclin D3
and Zyxin discriminating between ALL (red) and AML (black)
patients. .............................130
7.10 Vectors of linear combinations. ..................135
7.11 First principal component with projections of data. ......135
7.12 Scatter plot of selected genes with row labels on the first two
principal components. ......................138
7.13 Single linkage cluster diagram of selected gene expression values.138
7.14 Biplot of selected genes from the golub data. ..........144
8.1 ROC plot for expression values of CCND3 Cyclin D3. .....149
8.2 ROC plot for expression values of gene Gdf5. .........149
8.3 Boxplot of expression values of gene a for each leukemia class. 151
8.4 Classification tree for gene for three classes of leukemia. . . . . 151
8.5 Boxplot of expression values of gene a for each leukemia class. 154
8.6 Classification tree of expression values from gene A, B, and C
for the classification of ALL1, ALL2, and AML patients. ...154
8.7 Boxplot of expression values from gene CCND3 Cyclin D3 for
ALL and AML patients .....................156
LIST OF FIGURES xi
8.8 Classification tree of expression values from gene CCND3 Cy-
clin D3 for classification of ALL and AML patients. .....156
8.9 rpart on ALL B-cel 123 data. ..................159
8.10 Variable importance plot on ALL B-cell 123 data. ......159
8.11 Logit fit to the CCND3 Cyclin D3 expression values. .....171
9.1 G + C fraction of sequence ”AF517525.CCND3” along a win-
dow of length 50 nt. .......................178
9.2 Frequency plot of amino acids from accession number AF517525.CCND3.179
9.3 Frequency plot of amino acids from accession number AL160163.CCND3.179
10.1 Graph of probability transition matrix .............196
10.2 Evaluation of models by AIC . ..................216
10.3 Tree according to GTR model. ..................217
xii LIST OF FIGURES
List of Tables
2.1 A frequency table and its pie of Zyxin gene. .......... 18
3.1 Discrete density and distribution function values of S3, with
p= 0.6. .............................. 33
3.2 Built-in-functions for random variables used in this chapter. .42
3.3 Density, mean, and variance of distributions used in this chapter. 43
7.1 Data set for principal components analysis. ..........134
8.1 Frequencies empirical p-values lower than or equal to 0.01. . . 146
8.2 Ordered expression values of gene CCND3 Cyclin D3, index
2 indicates ALL, 1 indicates AML, cutoff points, number of
false positives, false positive rate, number of true positives,
true positive rate. ........................170
9.1 BLOSUM50 matrix. .......................186
xiii
xiv LIST OF TABLES
Chapter 1
Brief Introduction into Using R
To get started a gentle introduction to the statistical programming language
R will be given (R Development Core Team, 2009), specific for our purposes.
This will solve the practical issues to follow the stream of reasoning. In
particular, it is briefly explained how to install R and Bioconductor, how to
obtain help, and how to perform simple calculations.
Since many computations are essentially performed on data vectors, sev-
eral basic illustrations of this are given. With respect to gene expressions the
data vectors are placed one beneath the other to form a data matrix with
the genes as rows and the patients as columns. The idea of a data matrix is
extensively explained and illustrated by several examples. A larger example
consists of the classical Golub et al. (1999) data, which will be analyzed
frequently to illustrate statistical procedures.
1.1 Getting R Started on your PC
You can downloaded R freely from http://cran.r-project.org. Click on
your favorite operating system (Windows,Linux or MacOS) and simply follow
the instructions. After a little patience you should be able to start R (Ihaka
& Gentleman, 1996) after which a screen is opened with the prompt >. The
input and output of R will be displayed in verbatim typewriting style.
All useful functions of R are contained in libraries which are called ”pack-
ages”. The standard installation of R makes basic packages available such
as base and stats. From the button Packages at cran.r-project.org it
can be seen that R has a huge number of packages available for a wide scale
1

2CHAPTER 1. BRIEF INTRODUCTION INTO USING R
of statistical procedures. To download a specific package you can use the
following.
> install.packages(c("TeachingDemos"),repo="http://cran.r-project.org",
+ dep=TRUE)
This installs the package TeachingDemos developed by Greg Snow from the
repository http://cran.r-project.org. By setting the option dep to TRUE
the packages on which the TeachingDemos depend are also installed. This is
strongly recommended! Alternatively, in the Windows application of R you
can simply click on the Packages button at the top of your screen and follow
the instructions. After installing you have to load the package in order to use
its functions. For instance, to produce a nice plot of the outcome of throwing
twelve times with a die, you can use the following.
> library(TeachingDemos)
> plot(dice(12,1))
In the sequel we shall often use packages from Bioconductor, a very useful
open source software project for the analysis and comprehension of genomic
data. To follow the book it is essential to install Bioconductor on your PC
or network. Bioconductor is primarily based on R and can be installed, as
follows.
> source("http://www.bioconductor.org/biocLite.R")
> biocLite()
Then to download the ALL package from a repository to your system, to load
it, and to make the ALL data (Chiaretti, et. al, 2004) available for usage, you
can use the following.
> biocLite("ALL")
> library(ALL)
> data(ALL)
These data will be analyzed extensively later-on in Chapter 5 and 6. General
help on loaded Bioconductor packages becomes available by openVignette().
For further information the reader is referred to www.bioconductor.org or
to several other URL’s1.
1http://mccammon.ucsd.edu/~bgrant/bio3d/user_guide/user_guide.html
http://rafalab.jhsph.edu/software.html
http://dir.gmane.org/gmane.science.biology.informatics.conductor

1.2. GETTING HELP 3
In this and the following chapters we will illustrate many statistical ideas
by the Golub et al. (1999) data, see also Section 1.8. The golub data become
available by the following.2
> library(multtest)
> data(golub)
R is object-oriented in the sense that everything consists of objects belonging
to certain classes. Type class(golub) to obtain the class of the object golub
and str(golub) to obtain its structure or content. Type objects() or ls()
to view the currently loaded objects, a list probably growing soon to be large.
To prevent conflicting definitions, it is wise to remove them all at the end of
a session by rm(list=ls()). To quit a session, type q(), or simply click on
the cross in the upper right corner of your screen.
1.2 Getting help
All functionalities of R are well-organized in so-called packages. Use the func-
tion library() to see which packages are currently installed on your oper-
ating system. The packages stats and base are automatically installed, be-
cause these contain many basic functionalities. To obtain an overview of the
content of a package use ls(package:stats) or library(help="stats").
Help on the purpose of specific functions can be obtained from the (package)
manual by typing a question mark in front of a function. For instance, ?sum
gives details on summation. In case you are seeking help on a function which
uses if, simply type apropos("if"). When you are starting with a new con-
cept such as ”boxplot”, it is convenient to have an example showing output
(a plot) and programming code. Such is given by example(boxplot). The
function history can be useful for collecting previously given commands.
Type help.start() to launch an HTML page linking to several well-
written R manuals such as: ”An Introduction to R”, ”The R Language Defi-
nition”, ”R Installation and Administration”, and ”R Data Import/Export”.
Further help can be obtained from http://cran.r-project.org. Its ”con-
tributed” page contains well-written freely available on-line books3and use-
ful reference charts4. At http://www.r-project.org you can use R site
2Functions to read data into R are read.table or read.csv, see also the ”The R Data
Import/Export manual”.
3”R for Beginners” by Emmanuel Paradis or the ”The R Guide” by Jason Owen
4”R reference card” by Tom Short or by Jonathan Baron

4CHAPTER 1. BRIEF INTRODUCTION INTO USING R
search,Rseek, or other useful search engines. There are a number of useful
URL’s with information on R.5
1.3 Calculating with R
R can be used as a simple calculator. For instance, to add 2 and 3 we simply
insert the following.
> 2+3
[1] 5
In many calculations the natural base e= 2.718282 of exponential functions
is used. Such type of functions can be called as follows.
> exp(1)
[1] 2.718282
To compute e2=e·ewe use exp(2).6So, indeed, we have ex=exp(x), for
any value of x.
The sum 1 + 2 + 3 + 4 + 5 can be computed by
> sum(1:5)
[1] 15
and the product 5! = 5 ·4·3·2·1 by
> prod(1:5)
[1] 120
1.4 Generating a sequence and a factor
In order to compute so-called quantiles of distributions (see e.g. Section
2.1.4) or plots of functions, we need to generate sequences of numbers. The
easiest way to construct a sequence of numbers is by
> 1:5
[1] 1 2 3 4 5
5We mention in particular:
http://faculty.ucr.edu/~tgirke/Documents/R_BioCond/R_BioCondManual.html
6The argument of functions is always placed between parenthesis ().

1.5. COMPUTING ON A DATA VECTOR 5
This sequence can also be produced by the function seq, which allows for
various sizes of steps to be chosen. For instance, in order to compute per-
centiles of a distribution we may want to generate numbers between zero and
one with step size equal to 0.1.
> seq(0,1,0.1)
[1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
For plotting and testing of hypotheses we need to generate yet another
type of sequence, called a “factor”. It is designed to indicate an experimen-
tal condition of a measurement or the group to which a patient belongs.7
When, for instance, for each of three experimental conditions there are mea-
surements from five patients, the corresponding factor can be generated as
follows.
> factor <- gl(3,5)
> factor
[1] 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3
Levels: 1 2 3
The three conditions are often called “levels” of a factor. Each of these
levels has five repeats corresponding to the number of observations (patients)
within each level (type of disease). We shall further illustrate the idea of a
factor soon because it is very useful for purposes of visualization.
1.5 Computing on a data vector
A data vector is simply a collection of numbers obtained as outcomes from
measurements. This can be illustrated by a simple example on expression
values of a gene. Suppose that gene expression values 1,1.5,and 1.25 from
the persons ”Eric”, ”Peter”, and ”Anna” are available. To store these in a
vector we use the concatenate command c(), as follows.
> gene1 <- c(1.00,1.50,1.25)
> gene1
[1] 1.00 1.50 1.25
7See e.g. Samuals & Witmer (2003, Chap. 8) for a full explanation of experiments
and statistical principles of design.

6CHAPTER 1. BRIEF INTRODUCTION INTO USING R
Now we have created the object gene1 containing three gene expression val-
ues. To compute the sum, mean, and standard deviation of the gene expres-
sion values we use the corresponding built-in-functions.
> sum(gene1)
[1] 3.75
> mean(gene1)
[1] 1.25
> sum(gene1)/3
[1] 1.25
> sd(gene1)
[1] 0.25
> sqrt(sum((gene1-mean(gene1))^2)/2)
[1] 0.25
By defining x1= 1.00, x2= 1.50, and x3= 1.25, the sum of the weights can
be expressed as Pn
i=1 xi= 3.75. The mathematical summation symbol Pis
in R language simply sum. The mean is denoted by x=P3
i=1 xi/3=1.25
and the sample standard deviation as
s=v
u
u
t3
X
i=1
(xi−x)2/(3 −1) = 0.25.
1.6 Constructing a data matrix
In various types of spreadsheets it is custom to store data values in the
form of a matrix consisting of rows and columns. In bioinformatics gene
expression values (from several groups of patients) are stored as rows such
that each row contains the expressions values of the patients corresponding
to a particular gene and each column contains all gene expression values for
a particular person. To illustrate this by a small example suppose that we
have the following expression values on three genes from Eric, Peter, and
Anna.8
> gene2 <- c(1.35,1.55,1.00)
> gene3 <- c(-1.10,-1.50,-1.25)
> gene4 <- c(-1.20,-1.30,-1.00)
8By the function data.entry you can open and edit a screen with the values of a
matrix.

1.6. CONSTRUCTING A DATA MATRIX 7
Before constructing the matrix it is convenient to add the names of the rows
and the columns. To do so we construct the following list.
> rowcolnames <- list(c("gene1","gene2","gene3","gene4"),
+ c("Eric","Peter","Anna"))
After the last comma in the first line we give a carriage return for R to come
up with a new line starting with +in order to complete a command. Now we
can construct a matrix containing the expression values from our four genes,
as follows.
> gendat <- matrix(c(gene1,gene2,gene3,gene4), nrow=4, ncol=3,
+ byrow=TRUE, dimnames = rowcolnames)
Here, nrow indicates the number of rows and ncol the number of columns.
The gene vectors are placed in the matrix as rows. The names of the rows
and columns are attached by the dimnames parameter. To see the content of
the just created object gendat, we print it to the screen.
> gendat
Eric Peter Anna
gene1 1.00 1.50 1.25
gene2 1.35 1.55 1.30
gene3 -1.10 -1.50 -1.25
gene4 -1.20 -1.30 -1.00
A matrix such as gendat has two indices [i,j], the first of which refers to
rows and the second to columns9. Thus, if you want to print the second
element of the first row to the screen, then type gendat[1,2]. If you want
to print the first row, then use gendat[1,]. For the second column, use
gendat[,2].
It may be desirable to write the data to a file for using these in a later
stage or to send these to a college of yours. Consider the following script.
> write.table(gendat,file="D:/data/gendat.Rdata")
> gendatread <- read.table("D:/data/gendat.Rdata")
> gendatread
Eric Peter Anna
gene1 1.00 1.50 1.25
9Indices referring to rows, columns, or elements are always between square brackets [].

8CHAPTER 1. BRIEF INTRODUCTION INTO USING R
gene2 1.35 1.55 1.30
gene3 -1.10 -1.50 -1.25
gene4 -1.20 -1.30 -1.00
An alternative is to use write.csv.10
1.7 Computing on a data matrix
Means or standard deviations of rows or columns are often important for
drawing biologically relevant conclusions. Such type of computations on a
data matrix can be accomplished by “for loops”. However, it is much more
convenient to use the apply functionality on a matrix. To do so we specify
the name of the matrix, indicate rows or columns (1 for rows and 2 for
columns), and the name of the function. To illustrate this we compute the
mean of each person (column).
> apply(gendat,2,mean)
Eric Peter Anna
0.0125 0.0625 0.0750
Similarly, the mean of each gene (row) can be computed.
> apply(gendat,1,mean)
gene1 gene2 gene3 gene4
1.250000 1.400000 -1.283333 -1.166667
It frequently happens that we want to re-order the rows of a matrix according
to a certain criterion, or, more specifically, the values in a certain column
vector. For instance, to re-order the matrix gendat according to the row
means, it is convenient to store these in a vector and to use the function
order.
> meanexprsval <- apply(gendat,1,mean)
> o <- order(meanexprsval,decreasing=TRUE)
> o
[1] 2 1 4 3
10For more see the ”R Data import/Export” manual, Chapter 3 of the book ”R for
Beginners”, or search the internet by the key ”r wiki matrix”.

1.7. COMPUTING ON A DATA MATRIX 9
Thus gene2 appears first because it has the largest mean 1.4, then gene1
with 1.25, followed by gene4 with -1.16 and, finally, gene3 with -1.28. Now
that we have collected the order numbers in the vector o, we can re-order
the whole matrix by specifying oas the row index.11
> gendat[o,]
Eric Peter Anna
gene2 1.35 1.55 1.30
gene1 1.00 1.50 1.25
gene4 -1.20 -1.30 -1.00
gene3 -1.10 -1.50 -1.25
Another frequently occurring problem is that of selecting genes with a certain
property. We illustrate this by several methods to select genes with positive
mean expression values. A first method starts with the observation that the
first two rows have positive means and to use c(1,2) as a row index.
> gendat[c(1,2),]
Eric Peter Anna
gene1 1.00 1.50 1.25
gene2 1.35 1.55 1.30
A second way is to use the row names as an index.
> gendat[c("gene1","gene2"),]
Eric Peter Anna
gene1 1.00 1.50 1.25
gene2 1.35 1.55 1.30
A third and more advanced way is to use an evaluation in terms of TRUE
or FALSE of logical elements of a vector. For instance, we may evaluate
whether the row mean is positive.
> meanexprsval > 0
gene1 gene2 gene3 gene4
TRUE TRUE FALSE FALSE
Now we can use the evaluation of meanexprsval > 0 in terms of the values
TRUE or FALSE as a row index.
11You can also use functions like sort or rank.

10 CHAPTER 1. BRIEF INTRODUCTION INTO USING R
> gendat[meanexprsval > 0,]
Eric Peter Anna
gene1 1.00 1.50 1.25
gene2 1.35 1.55 1.30
Observe that this selects genes for which the evaluation equals TRUE. This
illustrates that genes can be selected by their row index, row name or value
on a logical variable.
1.8 Application to the Golub (1999) data
The gene expression data collected by Golub et al. (1999) are among the clas-
sical in bioinformatics. A selection of the set is called golub and is contained
in the multtest package, which is part of Bioconductor. The data consist
of gene expression values of 3051 genes (rows) from 38 leukemia patients12.
Twenty seven patients are diagnosed as acute lymphoblastic leukemia (ALL)
and eleven as acute myeloid leukemia (AML). The tumor class is given by
the numeric vector golub.cl, where ALL is indicated by 0 and AML by
1. The gene names are collected in the matrix golub.gnames of which the
columns correspond to the gene index, ID, and Name, respectively. We shall
first concentrate on expression values of a gene with manufacturer name
"M92287_at", which is known in biology as "CCND3 Cyclin D3". The ex-
pression values of this gene are collected in row 1042 of golub. To load the
data and to obtain relevant information from row 1042 of golub.gnames, use
the following.
> library(multtest); data(golub)
> golub.gnames[1042,]
[1] "2354" "CCND3 Cyclin D3" "M92287_at"
The data are stored in a matrix called golub. The number of rows and
columns can be obtained by the functions nrow and ncol, respectively.
> nrow(golub)
[1] 3051
> ncol(golub)
[1] 38
12The data are pre-processed by procedures described in Dudoit et al. (2002).
1.8. APPLICATION TO THE GOLUB (1999) DATA 11
So the matrix has 3051 rows and 38 columns, see also dim(golub). Each
data element has a row and a column index. Recall that the first index refers
to rows and the second to columns. Hence, the second value from row 1042
can be printed to the screen as follows.
> golub[1042,2]
[1] 1.52405
So 1.52405 is the expression value of gene CCND3 Cyclin D3 from patient
number 2. The values of the first column can be printed to the screen by the
following.
> golub[,1]
To save space the output is not shown. We may now print the expression
values of gene CCND3 Cyclin D3 (row 1042) to the screen.
> golub[1042,]
[1] 2.10892 1.52405 1.96403 2.33597 1.85111 1.99391 2.06597 1.81649
[9] 2.17622 1.80861 2.44562 1.90496 2.76610 1.32551 2.59385 1.92776
[17] 1.10546 1.27645 1.83051 1.78352 0.45827 2.18119 2.31428 1.99927
[25] 1.36844 2.37351 1.83485 0.88941 1.45014 0.42904 0.82667 0.63637
[33] 1.02250 0.12758 -0.74333 0.73784 0.49470 1.12058
To print the expression values of gene CCND3 Cyclin D3 to the screen only
for the ALL patients, we have to refer to the first twenty seven elements of
row 1042. A possibility to do so is by the following.
> golub[1042,1:27]
However, for the work ahead it is much more convenient to construct a factor
indicating the tumor class of the patients. This will turn out useful e.g.
for separating the tumor groups in various visualization procedures. The
factor will be called gol.fac and is constructed from the vector golub.cl,
as follows.
> gol.fac <- factor(golub.cl, levels=0:1, labels = c("ALL","AML"))
In the sequel this factor will be used frequently. Obviously, the labels corre-
spond to the two tumor classes. The evaluation of gol.fac=="ALL" returns
TRUE for the first twenty seven values and FALSE for the remaining eleven.
This is useful as a column index for selecting the expression values of the
ALL patients. The expression values of gene CCND3 Cyclin D3 from the
ALL patients can now be printed to the screen, as follows.

12 CHAPTER 1. BRIEF INTRODUCTION INTO USING R
> golub[1042,gol.fac=="ALL"]
For many types of computations it is very useful to combine a factor with
the apply functionality. For instance, to compute the mean gene expression
over the ALL patients for each of the genes, we may use the following.
> meanALL <- apply(golub[,gol.fac=="ALL"], 1, mean)
The specification golub[,gol.fac=="ALL"] selects the matrix with gene ex-
pressions corresponding to the ALL patients. The 3051 means are assigned
to the vector meanALL.
After reading the classical article by Golub et al. (1999), which is strongly
recommended, one becomes easily interested in the properties of certain
genes. For instance, gene CD33 plays an important role in distinguishing
lymphoid from myeloid lineage cells. To perform computations on the ex-
pressions of this gene we need to know its row index. This can obtained by
the grep function.13
> grep("CD33",golub.gnames[,2])
[1] 808
Hence, the expression values of antigen CD33 are available at golub[808,]
and further information on it by golub.gnames[808,].
1.9 Running scripts
It is very convenient to use a plain text writer like Notepad, Kate, Emacs, or
WinEdt for the formulation of several consecutive R commands as separated
lines (scripts). Such command lines can be executed by simply using copy
and paste into the command line editor of R. Another possibility is to execute
a script from a file. To illustrate the latter consider the following.
> library(multtest); data(golub)
> gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
> mall <- apply(golub[,gol.fac=="ALL"], 1, mean)
> maml <- apply(golub[,gol.fac=="AML"], 1, mean)
> o <- order(abs(mall-maml), decreasing=TRUE)
> print(golub.gnames[o[1:5],2])
13Indeed, several functions of R are inspired by the Linux operating system.
1.10. OVERVIEW AND CONCLUDING REMARKS 13
[1] "CST3 Cystatin C (amyloid angiopathy and cerebral hemorrhage)"
[2] "INTERLEUKIN-8 PRECURSOR"
[3] "Interleukin 8 (IL8) gene"
[4] "DF D component of complement (adipsin)"
[5] "MPO Myeloperoxidase"
The row means of the expression values per patient group are computed and
stored in the object mall and maml, respectively. The absolute values of the
differences in means are computed and their order numbers (from large to
small) are stored in the vector o. Next, the names of the five genes with the
largest differences in mean are printed to the screen.
After saving the script under e.g. the name meandif.R in the directory
D:\\Rscripts\\meandif.R, it can be executed by using source("D:\\Rscripts\\meandif.R").
Once the script is available for a typewriter it is easy to adapt it and to re-run
it.
Readers are strongly recommended to trial-and-error with respect to writ-
ing programming scripts. To run these it is very convenient to have your
favorite word processor available and to use, for instance, the copy-and-paste
functionality.
1.10 Overview and concluding remarks
It is easy to install R and Bioconductor. R has many convenient built-in-
functions for statistical programming. Help and illustrations on many topics
are available from various sources. With the reference charts, R manuals,
(on-line) books and R Wiki at hand you have various sources of information
to help you along with practical issues. Although there recently became
several GUI’s available, we shall concentrate on the command line editor
because its range of possibilities is much larger.
The above introduction is of course very brief. A more extensive in-
troduction into R, assuming some background on biomedical statistics, is
given by Dalgaard (2002). There are book length treatments combining R
with statistics (Venables, & Ripley, 2002; Everitt & Hothorn, 2006). Other
treatments go much deeper into programming aspects (Becker, Chambers, &
Wilks, 1988; Venables & Ripley, 2000; Gentleman, 2008).
For the sake of illustration we shall work frequently with the data kindly
provided by Golub et al. (1999) and Chiaretti et al. (2004). The corre-

14 CHAPTER 1. BRIEF INTRODUCTION INTO USING R
sponding scientific articles are freely available from the web. Having these
available may further motivate readers for the computations ahead.
1.11 Exercises
1. Some questions to orientate yourself.
(a) Use the function class to find the class to which the follow-
ing objects belong: golub,golub[1,1],golub.cl,golub.gnames,
apply,exp,gol.fac,plot,ALL.
(b) What is the meaning of the following abbreviations: rm,sum,prod,
seq,sd,nrow.
(c) For what purpose are the following functions useful: grep,apply,
gl,library,source,setwd,history,str.
2. gendat Consider the data in the matrix gendat, constructed in Sec-
tion 1.6. Its small size has the advantage that you can check your
computations even by a pocket calculator. 14
(a) Use apply to compute the standard deviation of the persons.
(b) Use apply to compute the standard deviation of the genes.
(c) Order the matrix according to the gene standard deviations.
(d) Which gene has the largest standard deviation?
3. Computations on gene means of the Golub data.
(a) Use apply to compute the mean gene expression value.
(b) Order the data matrix according to the gene means.
(c) Give the names of the three genes with the largest mean expression
value.
(d) Give the biological names of these genes.
4. Computations on gene standard deviations of the Golub data.
(a) Use apply to compute the standard deviation per gene.
14Obtaining some routine with the apply functionality is quite helpful for what follows.
1.11. EXERCISES 15
(b) Select the expression values of the genes with standard deviation
larger than two.
(c) How many genes have this property?
5. Oncogenes in Golub data.
(a) How many oncogenes are there in the dataset? Hint: Use grep.
(b) Find the biological names of the three oncogenes with the largest
mean expression value for the ALL patients.
(c) Do the same for the AML patients.
(d) Write the gene probe ID and the gene names of the ten genes with
largest mean gene expression value to a csv file.
6. Constructing a factor. Construct factors that correspond to the follow-
ing setting.
(a) An experiment with two conditions each with four measurements.
(b) Five conditions each with three measurements.
(c) Three conditions each with five measurements.
7. Gene means for B1 patients. Load the ALL data from the ALL library
and use str and openVignette() for a further orientation.
(a) Use exprs(ALL[,ALL$BT=="B1"] to extract the gene expressions
from the patients in disease stage B1. Compute the mean gene
expressions over these patients.
(b) Give the gene identifiers of the three genes with the largest mean.
16 CHAPTER 1. BRIEF INTRODUCTION INTO USING R
Chapter 2
Data Display and Descriptive
Statistics
A few essential methods are given to display and visualize data. It quickly
answers questions like: How are my data distributed? How can the frequen-
cies of nucleotides from a gene be visualized? Are there outliers in my data?
Does the distribution of my data resemble that of a bell-shaped curve? Are
there differences between gene expression values taken from two groups of
patients?
The most important central tendencies (mean, median) are defined and
illustrated together with the most important measures of spread (standard
deviation, variance, inter quartile range, and median absolute deviation).
2.1 Univariate data display
To observe the distribution of data various visualization methods are made
available. These are frequently used by practitioners as well as by experts.
2.1.1 Frequency table
Discrete data occur when the values naturally fall into categories. A fre-
quency table simply gives the number of occurrences within a category.
Example 1. A gene consists of a sequence of nucleotides {A, C, G, T }.
The number of each nucleotide can be displayed in a frequency table. This
17
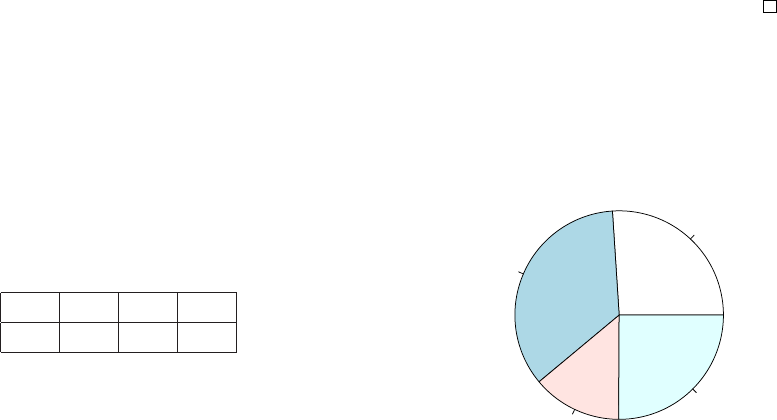
18 CHAPTER 2. DATA DISPLAY AND DESCRIPTIVE STATISTICS
will be illustrated by the Zyxin gene which plays an important role in cell
adhesion (Golub et al., 1999). The accession number (X94991.1) of one of
its variants can be found in a data base like NCBI (UniGene). The code
below illustrates how to read the sequence ”X94991.1” of the species homo
sapiens from GenBank, , to construct a pie from a frequency table of the four
nucleotides.
install.packages(c("ape"),repo="http://cran.r-project.org",dep=TRUE)
library(ape)
table(read.GenBank(c("X94991.1"),as.character=TRUE))
pie(table(read.GenBank(c("X94991.1"))))
From the resulting frequencies in Table 2.1 it seems that the nucleotides are
not equally likely. A nice way to visualize a frequency table is by plotting a
pie.
Table 2.1: A frequency table and its pie of Zyxin gene.
A C G T
410 789 573 394
a
c
g
t
2.1.2 Plotting data
An elementary method to visualize data is by using a so-called stripchart,
by which the values of the data are represented as e.g. small boxes. Often,

2.1. UNIVARIATE DATA DISPLAY 19
it is useful in combination with a factor that distinguishes members from
different experimental conditions or patients groups.
Example 1. Many visualization methods will be illustrated by the Golub
et al. (1999) data. We shall concentrate on the expression values of gene
"CCND3 Cyclin D3", which are collected in row 1042 of the data matrix
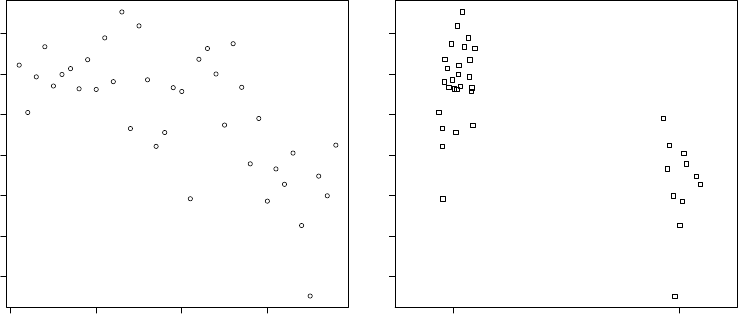
golub. To plot the data values one can simply use plot(golub[1042,]). In
the resulting plot in Figure 2.1 the vertical axis gives the size of the expression
values and the horizontal axis the index of the patients. It can be observed
that the values for patient 28 to 38 are somewhat lower, but, indeed, the
picture is not very clear because the groups are not plotted separately.
To produce two adjacent stripcharts one for the ALL and one for the
AML patients, we use the factor called gol.fac from the previous chapter.
data(golub, package = "multtest")
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
stripchart(golub[1042,] ~ gol.fac, method="jitter")
From the resulting Figure 2.2 it can be observed that the CCND3 Cyclin D3
expression values of the ALL patients tend to have larger expression values
than those of the AML patients.
2.1.3 Histogram
Another method to visualize data is by dividing the range of data values into
a number of intervals and to plot the frequency per interval as a bar. Such
a plot is called a histogram.
Example 1. A histogram of the expression values of gene "CCND3 Cyclin
D3" of the acute lymphoblastic leukemia patients can be produced as follows.
> hist(golub[1042, gol.fac=="ALL"])
The function hist divides the data into 5 intervals having width equal to
0.5, see Figure 2.3. Observe from the latter that one value is small and the
other are more or less symmetrically distributed around the mean.
20 CHAPTER 2. DATA DISPLAY AND DESCRIPTIVE STATISTICS
0 10 20 30
−0.5 0.0 0.5 1.0 1.5 2.0 2.5
Index
golub[1042, ]
Figure 2.1: Plot of gene ex-
pression values of CCND3
Cyclin D3.
ALL AML
−0.5 0.0 0.5 1.0 1.5 2.0 2.5
Figure 2.2: Stripchart of
gene expression values of
CCND3 Cyclin D3 for ALL
and AML patients.
2.1.4 Boxplot
It is always possible to sort ndata values to have increasing order x1≤x2≤
··· ≤ xn, where x1is the smallest, x2is the first-to-the smallest, etc. Let
x0.25 be a number for which it holds that 25% of the data values x1,··· , xn
is smaller. That is, 25% of the data values lay on the left side of the number
x0.25, reason for which it is called the first quartile or the 25th percentile.
The second quartile is the value x0.50 such that 50% of the data values are
smaller. Similarly, the third quartile or 75th percentile is the value x0.75 such
that 75% of the data is smaller. A popular method to display data is by
drawing a box around the first and the third quartile (a bold line segment
for the median), and the smaller line segments (whiskers) for the smallest and
the largest data values. Such a data display is known as a box-and-whisker
plot.
Example 1. A vector with gene expression values can be put into in-
creasing order by the function sort. We shall illustrate this by the ALL
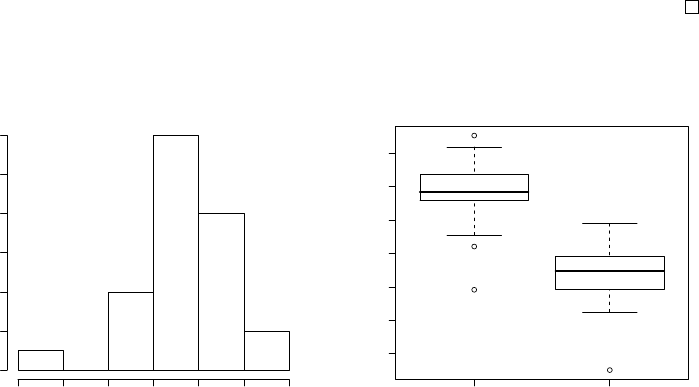
2.1. UNIVARIATE DATA DISPLAY 21
expression values of gene "CCND3 Cyclin D3" in row 1042 of golub.
> x <- sort(golub[1042, gol.fac=="ALL"], decreasing = FALSE)
> x[1:5]
[1] 0.458 1.105 1.276 1.326 1.368
The second command prints the first five values of the sorted data values
to the screen, so that we have x1= 0.458, x2= 1.105, etc. Note that the
mathematical notation xicorresponds exactly to the R notation x[i]
Histogram of golub[1042, gol.fac == "ALL"]
golub[1042, gol.fac == "ALL"]
Frequency
0.0 0.5 1.0 1.5 2.0 2.5 3.0
0 2 4 6 8 10 12
Figure 2.3: Histogram of ALL ex-
pression values of gene CCND3
Cyclin D3.
ALL AML
−0.5 0.0 0.5 1.0 1.5 2.0 2.5
Figure 2.4: Boxplot of ALL and
AML expression values of gene
CCND3 Cyclin D3.
Example 2. A view on the distribution of the expression values of the
ALL and the AML patients on gene CCND3 Cyclin D3 can be obtained by
constructing two separate boxplots adjacent to one another. To produce such
a plot the factor gol.fac is again very useful.
> boxplot(golub[1042,] ~ gol.fac)
From the position of the boxes in Figure 2.4 it can be observed that the gene
expression values for ALL are larger than those for AML. Furthermore, since
the two sub-boxes around the median are more or less equally wide, the data
are quite symmetrically distributed around the median.

22 CHAPTER 2. DATA DISPLAY AND DESCRIPTIVE STATISTICS
To compute exact values for the quartiles we need a sequence running
from 0.00 to 1.00 with steps equal to 0.25. To construct such a sequence the
function seq is useful.
> pvec <- seq(0,1,0.25)
> quantile(golub[1042, gol.fac=="ALL"],pvec)
0% 25% 50% 75% 100%
0.458 1.796 1.928 2.179 2.766
The first quartile x0.25 = 1.796, the second x0.50 = 1.928, and the third
x0.75 = 2.179. The smallest observed expression value equals x0.00 = 0.458
and the largest x1.00 = 2.77. The latter can also be obtained by the function
min(golub[1042, gol.fac=="ALL"]) and max(golub[1042, gol.fac=="ALL"]),
or more briefly by range(golub[1042, gol.fac=="ALL"]).
Outliers are data values laying far apart from the pattern set by the
majority of the data values. The implementation in R of the (modified)
boxplot draws such outlier points separately as small circles. A data point
xis defined as an outlier point if
x < x0.25 −1.5·(x0.75 −x0.25) or x > x0.75 + 1.5·(x0.75 −x0.25).
From Figure 2.4 it can be observed that there are outliers among the gene
expression values of ALL patients. These are the smaller values 0.45827 and
1.10546, and the largest value 2.76610. The AML expression values have one
outlier with value -0.74333.
To define extreme outliers, the factor 1.5 is raised to 3.0. Note that this
is a descriptive way of defining outliers instead of statistically testing for the
existence of an outlier.
2.1.5 Quantile-Quantile plot
A method to visualize the distribution of gene expression values is by the
so-called quantile-quantile (Q-Q) plot. In such a plot the quantiles of the
gene expression values are displayed against the corresponding quantiles of
the normal (bell-shaped). A straight line is added representing points which
correspond exactly to the quantiles of the normal distribution. By observing
the extent in which the points appear on the line, it can be evaluated to
what degree the data are normally distributed. That is, the closer the gene
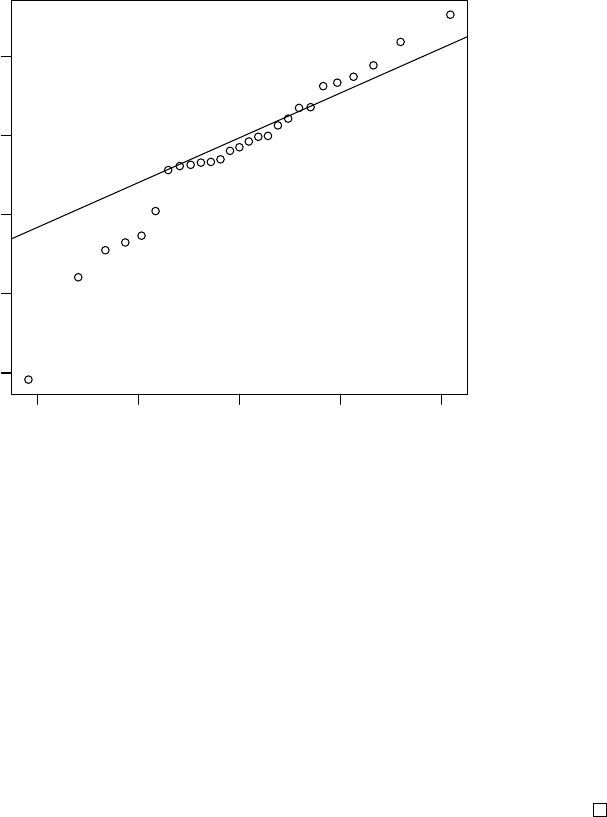
2.1. UNIVARIATE DATA DISPLAY 23
expression values appear to the line, the more likely it is that the data are
normally distributed.
−2 −1 0 1 2
0.5 1.0 1.5 2.0 2.5
Normal Q−Q Plot
Theoretical Quantiles
Sample Quantiles
Figure 2.5: Q-Q plot of ALL gene expression values of CCND3 Cyclin D3.
Example 1. To produce a Q-Q plot of the ALL gene expression values
of CCND3 Cyclin D3 one may use the following.
qqnorm(golub[1042, gol.fac=="ALL"])
qqline(golub[1042, gol.fac=="ALL"])
From the resulting Figure 2.5 it can be observed that most of the data points
are on or near the straight line, while a few others are further away.
The above example illustrates a case where the degree of non-normality
is moderate so that a clear conclusion cannot be drawn. By making the

24 CHAPTER 2. DATA DISPLAY AND DESCRIPTIVE STATISTICS
exercises below, the reader will gather more experience with the degree in
which gene expression values are normally distributed.
2.2 Descriptive statistics
There exist various ways to describe the central tendency as well as the spread
of data. In particular, the central tendency can be described by the mean or
the median, and the spread by the variance, standard deviation, interquartile
range, or median absolute deviation. These will be defined and illustrated.
2.2.1 Measures of central tendency
The most important descriptive statistics for central tendency are the mean
and the median. The sample mean of the data values x1,··· , xnis defined
as
x=1
n
n
X
i=1
xi=1
n(x1+··· +xn).
Thus the sample mean is simply the average of the ndata values. Since it
is the sum of all data values divided by the sample size, a few extreme data
values may largely influence its size. In other words, the mean is not robust
against outliers.
The median is defined as the second quartile or the 50th percentile, and
is denoted by x0.50. When the data are symmetrically distributed around the
mean, then the mean and the median are equal. Since extreme data values
do not influence the size of the median, it is very robust against outliers.
Robustness is important in bioinformatics because data are frequently con-
taminated by extreme or otherwise influential data values.
Example 1. To compute the mean and median of the ALL expression
values of gene CCND3 Cyclin D3 consider the following.
> mean(golub[1042, gol.fac=="ALL"])
[1] 1.89
> median(golub[1042, gol.fac=="ALL"])
[1] 1.93

2.2. DESCRIPTIVE STATISTICS 25
Note that the mean and the median do not differ much so that the distribu-
tion seems quite symmetric.
2.2.2 Measures of spread
The most important measures of spread are the standard deviation, the in-
terquartile range, and the median absolute deviation. The standard deviation
is the square root of the sample variance, which is defined as
s2=1
n−1
n
X
i=1
(xi−x)2=1
n−1¡(x1−x)2+··· + (xn−x)2¢.
Hence, it is the average of the squared differences between the data values
and the sample mean. The sample standard deviation sis the square root
of the sample variance and may be interpreted as the distance of the data
values to the mean. The variance and the standard deviation are not robust
against outliers.
The interquartile range is defined as the difference between the third and
the first quartile, that is x0.75 −x0.25. It can be computed by the function
IQR(x). More specifically, the value IQR(x)/1.349 is a robust estimator of
the standard deviation. The median absolute deviation (MAD) is defined as
a constant times the median of the absolute deviations of the data from the
median (e.g. Jureˇckov´a & Picek, 2006, p. 63). In R it is computed by the
function mad defined as the median of the sequence |x1−x0.50|,··· ,|xn−x0.50|
multiplied by the constant 1.4826. It equals the standard deviation in case
the data come from a bell-shaped (normal) distribution (see Section 3.2.1).
Because the interquartile range and the median absolute deviation are based
on quantiles, these are robust against outliers.
Example 1. These measures of spread for the ALL expression values of
gene CCND3 Cyclin D3 can be computed as follows.
> sd(golub[1042, gol.fac=="ALL"])
[1] 0.491
> IQR(golub[1042, gol.fac=="ALL"]) / 1.349
[1] 0.284
> mad(golub[1042, gol.fac=="ALL"])
[1] 0.368

26 CHAPTER 2. DATA DISPLAY AND DESCRIPTIVE STATISTICS
Due to the three outliers (cf. Figure 2.4) the standard deviation is larger
than the interquartile range and the mean absolute deviation. That is, the
absolute differences with respect to the median are somewhat smaller, than
the root of the squared differences.
2.3 Overview and concluding remarks
Data can be stored as a vector or a data matrix on which various useful
functions are defined. In particular, it is easy to produce a pie, histogram,
boxplot, or Q-Q plot of a vector of data. These plots give a useful first
impression of the degree of (non)normality of gene expression values.
To construct the histogram used the default method to compute the num-
ber of bars or breaks. If the data are distributed according to a bell-shaped
curve, then this is often a good strategy. The number of bars can be chosen
by the breaks option of the function hist. Optimal choices for this are dis-
cussed by e.g. Venables and Ripley (2002).
2.4 Exercises
Since the majority of the exercises are based on the Golub et al. (1999)
data, it is essential to make these available and to learn to work with it. To
stimulate self-study the answers are given at the end of the book.
1. Illustration of mean and standard deviation.
(a) Compute the mean and the standard deviation for 1,1.5,2,2.5,3.
(b) Compute the mean and the standard deviation for 1,1.5,2,2.5,30.
(c) Comment on the differences.
2. Comparing normality for two genes. Consider the gene expression val-
ues in row 790 and 66 of the Golub et al. (1999) data.
(a) Produce a boxplot for the expression values of the ALL patients
and comment on the differences. Are there outliers?

2.4. EXERCISES 27
(b) Produce a QQ-plot and formulate a hypothesis about the normal-
ity of the genes.
(c) Compute the mean and the median for the expression values of
the ALL patients and compare these. Do this for both genes.
3. Effect size. An important statistic to measure the effect size which
is defined for a sample as x/s. It measures the mean relative to the
standard deviation, so that is value is large when the mean is large and
the standard deviation small.
(a) Determine the five genes with the largest effect size of the ALL
patients from the Golub et al. (1999) data. Comment on their
size.
(b) Invent a robust variant of the effect size and use it to answer the
previous question.
4. Plotting gene expressions "CCND3 Cyclin D3". Use the gene expres-
sions from "CCND3 Cyclin D3" of Golub et al. (1999) collected in row
1042 of the object golub from the multtest library. After using the
function plot you produce an object on which you can program.
(a) Produce a so-called stripchart for the gene expressions separately
for the ALL as well as for the AML patients. Hint: Use a factor
for appropriate separation.
(b) Rotate the plot to a vertical position and keep it that way for the
questions to come.
(c) Color the ALL expressions red and AML blue. Hint: Use the col
parameter.
(d) Add a title to the plot. Hint: Use title.
(e) Change the boxes into stars. Hint: Use the pch parameter.
Hint: Store the final script you like the most in your typewriter
in order to be able to use it efficiently later on.
5. Box-and-Whiskers plot of "CCND3 Cyclin D3". Use the gene expres-
sions "CCND3 Cyclin D3" of Golub et al. (1999) from row 1042 of the
object golub of the multtest library.
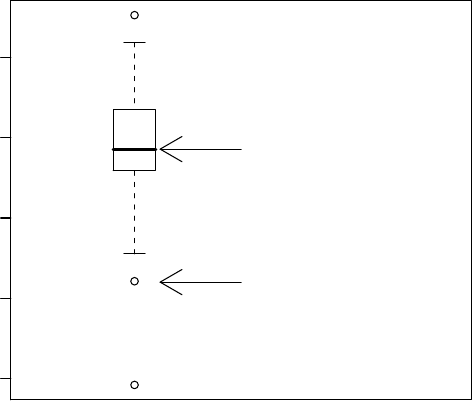
(a) Construct the boxplot in Figure 2.6.
28 CHAPTER 2. DATA DISPLAY AND DESCRIPTIVE STATISTICS
(b) Add text to the plot to explain the meaning of the upper and
lower part of the box.
(c) Do the same for the wiskers.
(d) Export your plot to eps format.
Hint 1: Use locator() to find coordinates of the position of the plot.
Hint 2: Use xlim to make the plot somewhat wider.
Hint 3: Use arrows to add an arrow.
Hint 4: Use text to add information at a certain position.
6. Box-and-wiskers plot of persons of Golub et al. (1999) data.
(a) Use boxplot(data.frame(golub)) to produce a box-and-wiskers
plot for each column (person). Make a screen shot to save it in
a word processor. Describe what you see. Are the medians of
similar size? Is the inter quartile range more or less equal. Are
there outliers?
(b) Compute the mean and medians of the persons. What do you
observe?
(c) Compute the range (minimal and maximum value) of the standard
deviations, the IQR and MAD of the persons. Comment of what
you observe.
7. Oncogenes of Golub et al. (1999) data.
(a) Select the oncogens by the grep facility and produce a box-and-
wiskers plot of the gene expressions of the ALL patients.
(b) Do the same for the AML patients and use par(mfrow=c(2,1))
to combine the two plots such that the second is beneath the first.
Are there genes with clear differences between the groups?
8. Descriptive statistics for the ALL gene expression values of the Golub
et al. (1999) data.
(a) Compute the mean and median for gene expression values of the
ALL patients, report their range and comment on it.
(b) Compute the SD, IQR, and MAD for gene expression values of
the ALL patients, report their range and comment on it.
2.4. EXERCISES 29
0.5 1.0 1.5 2.0 2.5
Median
Outlier
Figure 2.6: Boxplot with arrows and explaining text.
30 CHAPTER 2. DATA DISPLAY AND DESCRIPTIVE STATISTICS
Chapter 3
Important Distributions
Questions that concern us in this chapter are: What is the probability to
find fourteen purines in a microRNA of length twenty two? If expressions
from ALL patients of gene CCND3 Cyclin D3 are normally distributed with
mean 1.90 and standard deviation 0.5, what is the probability to observe
expression values larger than 2.4?
To answer such type of questions we need to know more about statis-
tical distributions (e.g. Samuels & Witmer, 2003). In this chapter several
important distributions will be defined, explained, and illustrated. In par-
ticular, the discrete distribution binomial and the continuous distributions
normal, T, F, and chi-squared will be elaborated. These distributions have
a wealth of applications to statistically testing biological hypotheses. Only
when deemed relevant, the density function, the distribution function, the
mean µ(mu), and the standard deviation σ(sigma), are explicitly defined.
3.1 Discrete distributions
The binomial distribution is fundamental and has many applications in medicine
and bioinformatics.
3.1.1 Binomial distribution
The binomial distribution fits to repeated trials each with a dichotomous out-
come such as succes-failure, healthy-disease, heads-tails, purine-pyrimidine,
etc. When there are ntrials, then the number of ways to obtain ksuccesses
31
32 CHAPTER 3. IMPORTANT DISTRIBUTIONS
out of nis given by the binomial coefficient
n!
k!(n−k)!,
where n! = n·(n−1) ···1 and 0! = 1 (Samuels & Witmer, 2003). The
binomial probability of ksuccesses out of nconsists of the product of this
coefficient with the probability of ksuccesses and the probability of n−
kfailures. Let pbe the probability of succes in a single trial and Xthe
(random) variable denoting the number of successes. Then the probability P
of the event (X=k) that ksuccesses occur out of ntrails can be expressed
as
P(X=k) = n!
k!(n−k)!pk(1 −p)n−k,for k= 0,···, n. (3.1)
The collection of these probabilities is called the probability density function.
1
Example 1. To visualize the Binomial distribution, load the TeachingDemos
package and use the command vis.binom(). Click on ”Show Normal Ap-
proximation” and observe that the approximation improves as nincreases,
taking pfor instance near 0.5.
Example 2. If two carriers of the gen for albinism marry, then each of the
children has probability of 1/4 of being albino. What is the probability for
one child out of three to be albino? To answer this question we take n= 3,
k= 1, and p= 0.25 into Equation (3.1) and obtain
P(X= 1) = 3!
1!(3 −1)!0.2510.752= 3 ·0.140625 = 0.421875.
An elementary manner to compute this in R is by
> choose(3,1)* 0.25^1* 0.75^2
where choose(3,1) computes the binomial coefficient. It is more efficient to
compute this by the built-in-density-function dbinom(k,n,p), for instance
to print the values of the probabilities.
1For a binomially distributed variable np is the mean, np(1 −p) the variance, and
pnp(1 −p) the standard deviation.
3.1. DISCRETE DISTRIBUTIONS 33
> for (k in 0:3) print(dbinom(k,3,0.25))
Changing dinto pyields the so-called distribution function with the cumula-
tive probabilities. That is, the probability that the number of Heads is lower
than or equal to two P(X≤2) is computed by pbinom(2,3,0.25). The
values of the density and distribution function are summarized in Table 3.1.
From the table we read that the probability of no albino child is 0.4218 and
the probability that all three children are albino equals 0.0156.
Table 3.1: Discrete density and distribution function values of S3, with p=
0.6. number of Heads k= 0 k= 1 k= 2 k= 3
density P(X=k) 0.4218 0.4218 0.1406 0.0156
distribution P(X≤k) 0.4218 0.843 0.9843 1
Example 3. RNA consists of a sequence of nucleotides A, G, U, and C,
where the first two are purines and the last two are pyrimidines. Suppose, for
the purpose of illustration, that the length of a certain micro RNA is 22, that
the probability of a purine equals 0.7, and that the process of placing purines
and pyrimidines is binomially distributed. The event that our microRNA
contains 14 purines can be represented by X= 14. The probability of this
event can be computed by
P(X= 14) = 22!
14!(22 −14)!0.7140.38=dbinom(14,22,0.7) = 0.1423.
This is the value of the density function at 14. The probability of the event of
less than or equal to 13 purines equals the value of the distribution function
at value 13, that is
P(X≤13) = pbinom(13,22,0.7) = 0.1865.
The probability of strictly more than 10 purines is
P(X≥11) =
22
X
k=11
P(S22 =k) = sum(dbinom(11 :22,22,0.7)) = 0.9860.
The binomial density function can be plotted by:
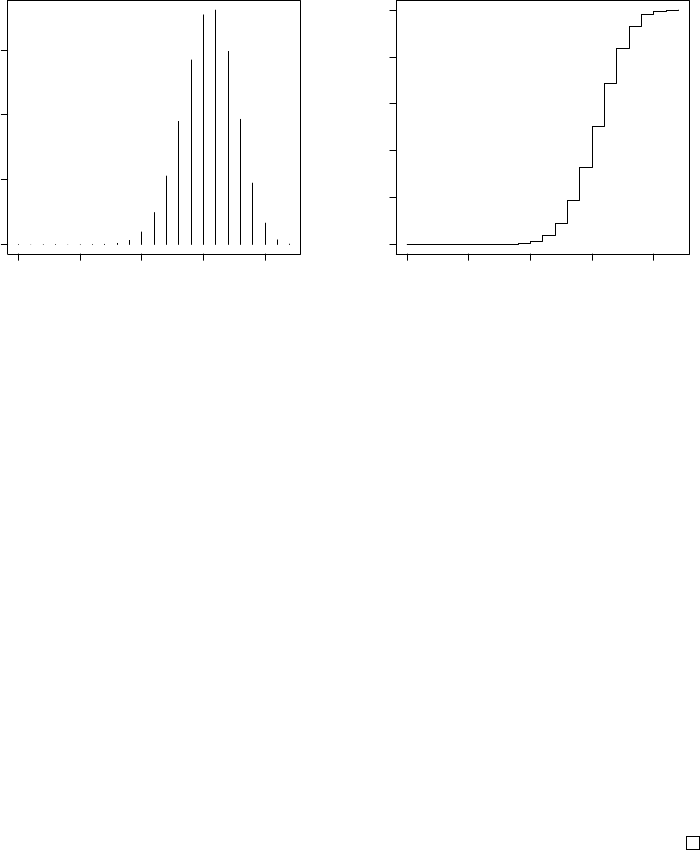
34 CHAPTER 3. IMPORTANT DISTRIBUTIONS
0 5 10 15 20
0.00 0.05 0.10 0.15
x
f(x)
Figure 3.1: Binomial probabilities
with n= 22 and p= 0.7
0 5 10 15 20
0.0 0.2 0.4 0.6 0.8 1.0
x
F(x)
Figure 3.2: Binomial cumulative
probabilities with n= 22 and p=
0.7.
> x <- 0:22
> plot(x,dbinom(x,size=22,prob=.7),type="h")
By the first line the sequence of integers {1,2,···,22}is constructed and by
the second the density function is plotted, where the argument hspecifies
pins. From Figure 3.1 it can be observed that the largest probabilities oc-
cur near the expectation 15.4. The graph in Figure 3.2 illustrates that the
distribution is an increasing step function, with xon the horizontal axis and
P(X≤x) on the vertical.
A random sample of size 1000 from the binomial distribution with n= 22
and p= 0.7 can be drawn by the command rbinom(1000,22,0.7). This
simulates the number of purines in 1000 microRNA’s each with purine prob-
ability equal to 0.7 and length 22.
3.2 Continuous distributions
The continuous distributions normal, T, F, and chi-squared will be defined,
explained and illustrated.

3.2. CONTINUOUS DISTRIBUTIONS 35
3.2.1 Normal distribution
The normal distribution is of key importance because it is assumed for many
(preprocessed) gene expression values. That is, the data values x1,··· , xn
are seen as realizations of a random variable Xhaving a normal distribution.
Equivalently one says that the data values are members of a normally dis-
tributed population with mean µ(mu) and variance σ2(sigma squared). It
is good custom to use Greek letters for population properties and N(µ, σ2)
for the normal distribution. The value of the distribution function is given
by P(X≤x), the probability of the population to have values smaller than
or equal to x. Various properties of the normal distribution are illustrated
by the examples below.
Example 1. To view members of the normal distribution load the
TeachingDemos package and give the command vis.normal() to launch an
interactive display of bell-shaped curves. These bell-shaped curves are also
called normal densities. The curves are symmetric around µand attain a
unique maximum at x=µ. If xmoves further away from the mean µ, then
the curves moves to zero so that extreme values occur with small probability.
Move the Mean and the Standard Deviation from the left to the right to
explore their effect on the shape of the normal distribution. In particular,
when the mean µincreases, then the distribution moves to the right. If σis
small/large, then the distribution is steep/flat.
Example 2. Suppose that the expression values of gene CCND3 Cyclin
D3 can be represented by Xwhich is distributed as N(1.90,0.52). From
the graph of its density function in Figure 3.3, it can be observed that it
is symmetric and bell-shaped around µ= 1.90. A density function may
very well be seen as a histogram with arbitrarily small bars (intervals). The
probability that the expression values are less then 1.4 is
P(X < 1.4) = pnorm(1.4,1.9,0.5) = 0.1586.
Figure 3.4 illustrates the value 0.16 of the distribution function at x= 1.4.
It corresponds to the area of the blue colored surface below the graph of the
density function in Figure 3.3. The probability that the expression values
are larger than 2.4 is
P(X≥2.4) = 1−pnorm(2.4,1.9,0.5) = 0.1586.
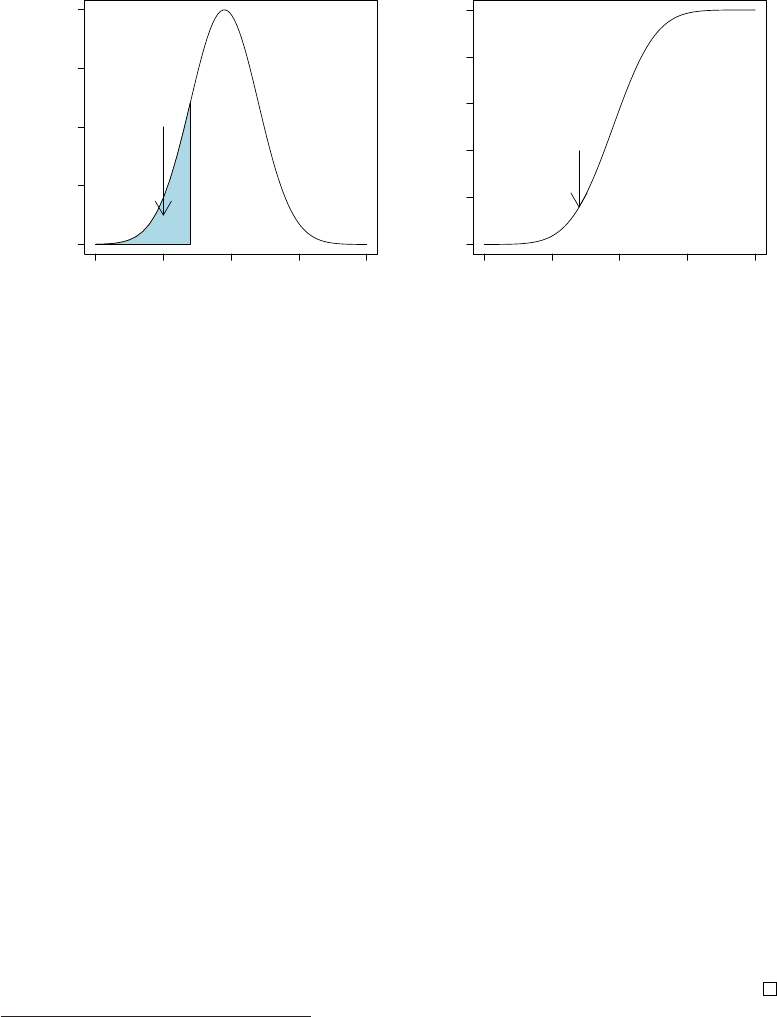
36 CHAPTER 3. IMPORTANT DISTRIBUTIONS
0 1 2 3 4
0.0 0.2 0.4 0.6 0.8
x
density f(x)
1.4
P(X<=1.4)
= 0.16
Figure 3.3: Graph of normal den-
sity with mean 1.9 and standard
deviation 0.5.
0 1 2 3 4
0.0 0.2 0.4 0.6 0.8 1.0
x
normal distribution F(x)
1.4
0.16
Figure 3.4: Graph of normal dis-
tribution with mean 1.9 and stan-
dard deviation 0.5.
The probability that Xis between 1.4 and 2.4 equals
P(1.4≤X≤2.4) = pnorm(2.4,1.9,0.5)−pnorm(1.4,1.9,0.5) = 0.9545.
The graph of the distribution function in Figure 3.4 illustrates that it is
strictly increasing. The exact value for the quantile x0.025 can be computed
by
> qnorm(0.025,1.9,0.5)
[1] 0.920018
That is, the quantile x0.025 = 0.920018. Hence, it holds that the probability of
values smaller than 0.920018 equals 0.025, that is P(X≤0.920018) = 0.025,
as can be verified by pnorm(0.920018,1.9,0.5). When Xis distributed as
N(1.90,0.52), then the population mean is 1.9 and the population standard
deviation 0.5. To verify this we draw a random sample of size 1000 from this
population by
> x <- rnorm(1000,1.9,0.5)
The estimate mean(x)=1.8862 and sd(x)=0.5071 are close to their popula-
tion values µ= 1.9 and σ= 0.5. 2
2Use the function round to print the mean in a desired number a decimal places.

3.2. CONTINUOUS DISTRIBUTIONS 37
For Xdistributed as N(µ, σ2), it holds that (X−µ)/σ =Zis distributed
as N(0,1). Thus by subtracting µand dividing the result with σany normally
distributed variable can be standardized into a standard normally distributed
Zhaving mean zero and standard deviation one.
3.2.2 Chi-squared distribution
The chi-squared distribution plays an important role in testing hypotheses
about frequencies, see Chapter 4. To define it, let {Z1,··· , Zm}be indepen-
dent and standard normally distributed random variables. Then the sum of
squares
χ2
m=Z2
1+···+Z2
m=
m
X
i=1
Z2
i,
is the so-called chi-squared distributed (random) variable with mdegrees of
freedom.
Example 1. To view various members of the χ2distribution load the
TeachingDemos package. Use the command vis.gamma() to open an inter-
active display of various distributions. Click on ”Visualizing the gamma”,
”Visualizing the Chi-squared”, and adapt ”Xmax”. Move the ”Shape” but-
ton to the right to increase the degrees of freedom. Observe that the graphs
of chi-squared densities change from heavily skew to the right into more bell-
shaped normal as the degrees of freedom increases.
Example 2. Let’s consider the chi-squared variable with 5 degrees of
freedom; χ2
5=Z2
1+··· +Z2
5. To compute the probability of values smaller
than eight we use the function pchisq, as follows.
P¡χ2
5≤8¢=pchisq(8,5) = 0.8437644.
This yields the value of the distribution function at x= 8 (see Figure 3.6).
This value corresponds to the area of the blue colored surface below the graph
of the density function in Figure 3.5. Often we are interested in the value for
the quantile x0.025, where P(χ2
5≤x0.025)=0.025. 3Such can be computed
by
3If the distribution function is strictly increasing, then there exists an exact and unique
solution for the quantiles.
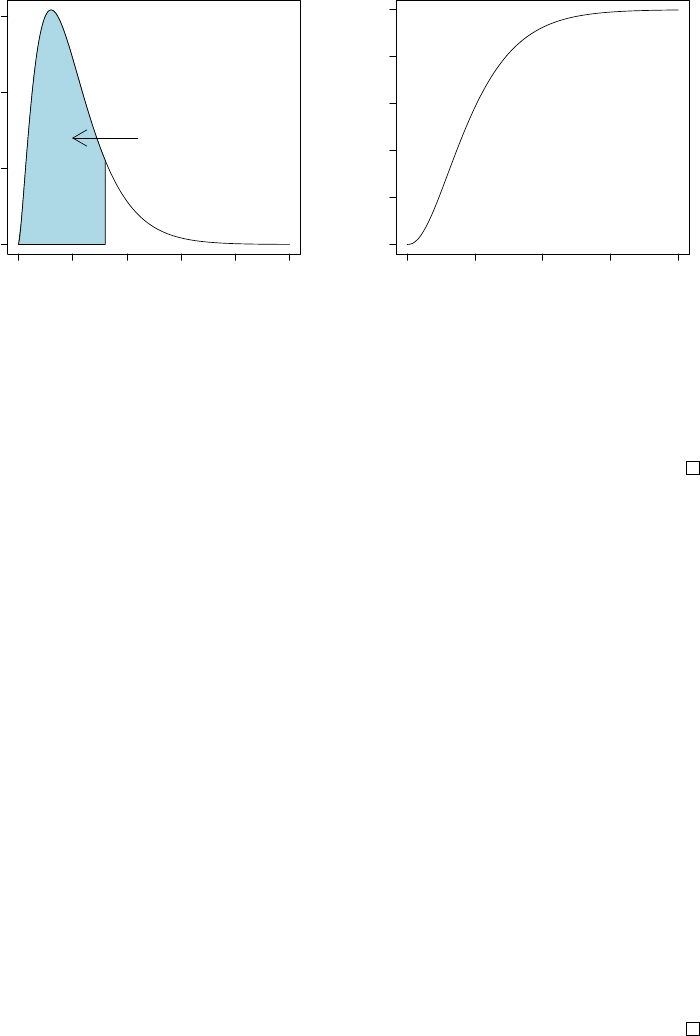
38 CHAPTER 3. IMPORTANT DISTRIBUTIONS
0 5 10 15 20 25
0.00 0.05 0.10 0.15
Chi−Squared Density f(x)
8
area=0.84
Figure 3.5: χ2
5-density.
0 5 10 15 20
0.0 0.2 0.4 0.6 0.8 1.0
Chi−Squared Distribution F(x)
8
0.84
x
Figure 3.6: χ2
5distribution.
> qchisq(0.025, 5, lower.tail=TRUE)
[1] 0.8312
Example 3. The chi-squared distribution is frequently used as a so-called
goodness of fit measure. With respect to the Golub et. al. (1999) data we
may hypothesize that the expression values of gene CCND3 Cyclin D3 for
the ALL patients are distributed as N(1.90,0.502). If this indeed holds,
then the sum of squared standardized values equals their number and the
probability of larger values is about 1/2. In particular, let x1,··· , x27 be the
gene expression values. Then the standardized values are zi= (xi−1.90)/0.50
and their sum of squares P27
1z2
i= 25.03312. The probability of larger values
is P(χ2
27 ≥25.03312) = 0.5726, which indicates that this normal distribution
fits the data well. Hence, it is likely that the specified normal distribution is
indeed correct. Using R the computations are as follows.
library(multtest); data(golub)
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
x <- golub[1042,gol.fac=="ALL"]
z <- (x-1.90)/0.50
sum(z^2)
pchisq(sum(z^2),27, lower.tail=FALSE)
3.2. CONTINUOUS DISTRIBUTIONS 39
3.2.3 T-Distribution
The T-distribution has many useful applications for testing hypotheses about
means of gene expression values, in particular when the sample size is lower
than thirty. If the data are normally distributed, then the values of √n(x−
µ)/s follow a T-distribution with n−1 degrees of freedom. The T-distribution
is approximately equal to the normal distribution when the sample size is
thirty.
−4 −2 0 2 4
0.0 0.1 0.2 0.3 0.4
x−axis
Density f(x)
Figure 3.7: Density of T10 distri-
bution.
−4 −2 0 2 4
0.0 0.2 0.4 0.6 0.8 1.0
x−axis
Distribution F(x)
Figure 3.8: Distribution function
of T10.
Example 1. Load the TeachingDemos and give vis.t() to explore a vi-
sualization of the T-distribution. Click on ”Show Normal Distribution” and
increase the number of degrees of freedom to verify that df equal to thirty is
sufficient for the normal approximation to be quite precise.
Example 2. A quick NCBI scan makes it reasonable to assume that
the gene Gdf5 has no direct relation with leukemia. For this reason we take
µ= 0. The expression values of this gene are collected in row 2058 of the
golub data. To compute the sample t-value √n(x−µ)/s use
n <- 11
x <- golub[2058, gol.fac=="AML"]

40 CHAPTER 3. IMPORTANT DISTRIBUTIONS
t.value <- sqrt(n)*(mean(x)-0)/sd(x)
t.value
[1] 1.236324
From the above we know that this has a T10 distribution. The probability
that T10 is greater than 1.236324 can be computed, as follows.
P(T10 ≥1.236324) = 1 −P(T10 ≤1.236324) = 1 −pt(1.236324,10) = 0.12.
This probability corresponds to the area of the blue colored surface below of
the graph of the density function in Figure 3.7. The Tdistribution function
with ten degrees of freedom is illustrated in Figure 3.8. The probability that
the random variable T10 is between -2 and 2 equals
P(−2≤T11 ≤2) = pt(2,10)−pt(−2,10) = 0.926612.
The 2.5% quantile can be computed by qt(0.025,n-1)=-2.228139.
3.2.4 F-Distribution
The F-distribution is important for testing the equality of two variances. It
can be shown that the ratio of variances from two independent sets of nor-
mally distributed random variables follows an F-distribution. More specifi-
cally, if the two population variances are equal (σ2
1=σ2
2), then s2
1/s2
2follows
an F-distribution with n1−1, n2−1 degrees of freedom, where s2
1is the
variance of the first set, s2
2that of the second, and n1is the number of ob-
servations in the first and n2in the second.4
Example 1. For equal population variances the probability is large that
that the ratio of sample variances is near one. With respect to the Golub
et. al. (1999) data it is easy to compute the ratio of the variances of the
expression values of gene CCND3 Cyclin D3 for the ALL patients and the
AML patients.
> var(golub[1042,gol.fac=="ALL"])/var(golub[1042,gol.fac=="AML"])
[1] 0.7116441
4It is more correct to define S2
1/S2
2for certain random variables S2
1and S2
2, we shall ,
however, not border.
3.2. CONTINUOUS DISTRIBUTIONS 41
0 2 4 6 8 10
0.0 0.2 0.4 0.6 0.8
F density f(x)
x0.71
0.23
Figure 3.9: Density of F26,10.
0 2 4 6 8 10
0.0 0.2 0.4 0.6 0.8 1.0
F Distribution F(x)
0.23
0.71
Figure 3.10: Distribution of F26,10.
Since n1= 27 and n2= 11 this ratio is a realization of the F26,10 distribution.
Then, the probability that the ratio attains values smaller than 0.7116441 is
P(X≤0.7116441) = pf(0.7116441,26,10) = 0.2326147.
Figure 3.9 illustrates that this value corresponds to the area of the blue col-
ored surface below the graph of the density function. Figure 3.10 gives the
distribution function. To find the quantile x0.025 use qf(.025,26,10)=0.3861673.
This subject is taken further in Section 4.1.5.
3.2.5 Plotting a density function
5A convenient manner to plot a density function in by using the correspond-
ing built-in-function. For instance to plot the bell-shaped density from the
normally distributed variable use the function dnorm, as follows.
> f<-function(x){dnorm(x,1.9,0.5)}
> plot(f,0,4,xlab="x-axis",ylab="density f(x)")
5This subsection is solemly on plotting and can be skipped without loss of continuity.
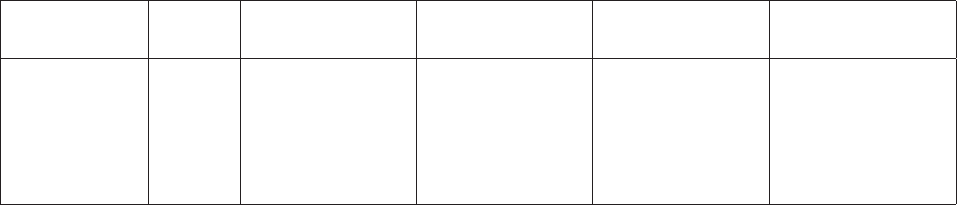
42 CHAPTER 3. IMPORTANT DISTRIBUTIONS
This produces the graph of the density function in Figure 3.3. The specifica-
tion 0,4 defines the interval on the horizontal axis over which fis plotted.
The vertical axis is adapted automatically. We can give the surface under f
running xfrom 0 to 1.4 a nice blue color by using the following.
plot(f,0,4,xlab="x-axis",ylab="density f(x)")
x<-seq(0,1.4,0.01)
polygon(c(0,x,1.4), c(0,f(x),0), col="lightblue")
The basic idea of plotting is to start with a plot and next to add colors, text,
arrows, etc. In particular, the command polygon is used to give the surface
below the graph the color "lightblue". The polygon (surface enclosed by
many angles) is defined by the sequence of points defined as xand f(x).
3.3 Overview and concluding remarks
For practical computations R has built-in-functions for the binomial, normal,
t, F, χ2-distributions, where dstands for density, pfor (cumulative) prob-
ability distribution, qfor quantiles, and rfor drawing random samples, see
Table 3.2. The density, expectation, and variance of most the distributions
in this chapter are summarized in Table 3.3.
Table 3.2: Built-in-functions for random variables used in this chapter.
para- random
Distribution meters density distribution quantiles sampling
Bin n, p dbinom(x, n, p)pbinom(x, n, p)qbinom(α, n, p)rbinom(10, n, p)
Normal µ, σ dnorm(x, µ, σ)pnorm(x, µ, σ)qnorm (α, µ, σ)rnorm(10, µ, σ)
Chi-squared m dchisq(x, m)pchisq(x, m)qchisq(α, m)rchisq(10, m)
T m dt(x, m)pt(x, m)qt(α, m)rt(10, m)
F m,n df(x, m, n)pf(x, m, n)qf(α, m, n)rf(10, m, n)
Although for a first introduction the above distributions are without
doubt among the most important, there are several additional distributions
available such as the Poisson, Gamma, beta, or Dirichlet. Obviously, these
can also be programmed by yourself. The freeware encyclopedia wikipedia of-
ten gives a useful first, though technical, orientation. Note that a distribution
acts as a population from which a sample can be drawn. Hence, distributions

3.4. EXERCISES 43
can be seen as models of data generating procedures. For a more thorough
treatment of distribution we refer the reader to Bain & Engelhardt (1992),
Johnson et al. (1992), and Miller & Miller (1999).
Table 3.3: Density, mean, and variance of distributions used in this chapter.
Distribution parameters density expectation variance
Binomial n, p n!
k!(n−k)! pk(1 −p)n−knp np(1 −p)
Normal µ, σ 1
σ√2πexp(−1
2(x−µ
σ)2)µ σ2
Chi-squared df=m m 2m
3.4 Exercises
It is importance to obtain some routine with the computation of probabilities
and quantiles.
1. Binomial Let Xbe binomially distributed with n= 60 and p= 0.4.
Compute the following.
(a) P(X= 24), P(X≤24), and P(X≥30).
(b) P(20 ≤X≤30), P(20 ≤X).
(c) P(20 ≤Xor X≥40), and P(20 ≤Xand X≥10).
(d) Compute the mean and standard deviation of X.
(e) The quantiles x0.025,x0.5, and x0.975.
2. Standard Normal. Compute the following probabilities and quantiles.
(a) P(1.6< Z < 2.3).
(b) P(Z < 1.64).
(c) P(−1.64 < Z < −1.02).
(d) P(0 < Z < 1.96).
(e) P(−1.96 < Z < 1.96).
(f) The quantiles z0.025,z0.05,z0.5,z0.95, and z0.975.
3. Normal. Compute for Xdistributed as N(10,2) the following proba-
bilities and quantiles.
44 CHAPTER 3. IMPORTANT DISTRIBUTIONS
(a) P(X < 12).
(b) P(X > 8).
(c) P(9 < X < 10,5).
(d) The quantiles x0.025,x0.5, and x0.975.
4. T-distribution. Verify the following computations for the T6distribu-
tion.
(a) P(T6<1).
(b) P(T6>2).
(c) P(−1< T6<1).
(d) P(−2< T6<−2).
(e) The quantiles t0.025,t0.5, and t0.975.
5. Fdistribution. Compute the following probabilities and quantiles for
the F8,5distribution.
(a) P(F8,5<3).
(b) P(F8,5>4).
(c) P(1 < F8,5<6).
(d) The quantiles f0.025,f0.5, and f0.975.
6. Chi-squared distribution. Compute the following for the chi-squared
distribution with 10 degrees of freedom.
(a) P(χ2
10 <3).
(b) P(χ2
10 >4).
(c) P(1 < χ2
10 <6).
(d) The quantiles g0.025,g0.5, and g0.975.
7. MicroRNA. Suppose that for certain microRNA of size 20 the proba-
bility of a purine is binomially distributed with probability 0.7.
(a) What is the probability of 14 purines?
(b) What is the probability of less than or equal to 14 purines?
3.4. EXERCISES 45
(c) What is the probability of strictly more than 10 purines?
(d) By what probability is of the number of purines between 10 and
15?
(e) How many purines do you expect? In other words: What is the
mean of the distribution?
(f) What is the standard deviation of the distribution?
8. Zyxin. The distribution of the expression values of the ALL patients
on the Zyxin gene are distributed according to N(1.6,0.42).
(a) Compute the probability that the expression values are smaller
than 1.2?
(b) What is the probability that the expression values are between 1.2
and 2.0?
(c) What is the probability that the expression values are between 0.8
and 2.4?
(d) Compute the exact values for the quantiles x0.025 and x0.975.
(e) Use rnorm to draw a sample of size 1000 from the population and
compare the sample mean and standard deviation with that of the
population.
9. Some computations on Golub et al. (1999) data.
(a) Take µ= 0 and compute the t-values for the ALL gene expression
values. Find the three genes with largest absolute t-values.
(b) Compute per gene the ratio of the variances for the ALL and the
AML patients. How many are between 0.5 and 1.5?
10. Extreme value investigation. This (difficult!) question aims to teach
the essence of an extreme value distribution! An interesting extreme
value distribution is given by Pevsner (2003, p.103). Take the maximum
of a sample (with size 1000) from the standard normal distribution and
repeat this 1000 times. So that you sampled 1000 maxima. Next,
subtract from these maxima an and divide by bn, where
an <- sqrt(2*log(n)) - 0.5*(log(log(n))+log(4*pi))*(2*log(n))^(-1/2)
bn <- (2*log(n))^(-1/2)
46 CHAPTER 3. IMPORTANT DISTRIBUTIONS
Now plot the density from the normalized maxima and add the extreme
value function f(x) from Pevsner his book, and add the density (dnorm)
from the normal distribution. What do you observe?
Chapter 4
Estimation and Inference
Questions that we deal with in this chapter are related to statistically testing
biological hypothesis. Does the mean gene expression over ALL patients
differ from that over AML patients? That is, does the mean gene expression
level differ between experimental conditions? Is the mean gene expression
different from zero? To what extent are gene expression values normally
distributed? Are there outliers among a sample of gene expression values?
How can an experimental effect be defined? How can genes be selected with
respect to an experimental effect? Other important questions are: How can
it be tested whether the frequencies of nucleotide sequences of two genes are
different? How can it be tested whether outliers are present in the data?
What is the probability of a certain micro RNA to have more than a certain
number of purines?
In the foregoing chapters many population parameters were used to define
families of theoretical distributions. In any research (empirical) setting the
specific values of such parameters are unknown so that these must be esti-
mated. Once estimates are available it becomes possible to statistically test
biologically important hypotheses. The current chapter gives several basic
examples of statistical testing and some of its background. Robust type of
testing is briefly introduced as well as an outlier test.
4.1 Statistical hypothesis testing
Let µ0be a number representing the hypothesized population mean by a
researcher on the basis of experience and knowledge from the field. With
47

48 CHAPTER 4. ESTIMATION AND INFERENCE
respect to the population mean the null hypothesis can be formulated as
H0:µ=µ0and the alternative hypothesis as H1:µ6=µ0. These are two
statements of which the latter is the opposite of the first: Either H0or H1
is true. The alternative hypothesis is true if H1:µ<µ0or H1:µ>µ0
holds true. This type of alternative hypothesis is called “two-sided”. In case
H1:µ > µ0, it is called “one-sided”.
Such a null hypothesis will be statistically tested against the alternative
using a suitable distribution of a statistic (e.g. standardized mean). After
conducting the experiment, the value of the statistic can be computed from
the data. By comparing the value of the statistic with its distribution, the
researcher draws a conclusion with respect to the null hypothesis: H0is
rejected or it is not. The probability to reject H0, given the truth of H0, is
called the significance level which is generally denoted by α. We shall follow
the habit in statistics to use α= 0.05, but it will be completely clear how to
adapt the procedure in case other significance levels are desired.
4.1.1 The Z-test
The Z-test applies to the situation where we want to test H0:µ=µ0against
H1:µ6=µ0and the standard deviation σis known. Assuming that the gene
expression values (x1,··· , xn) are from a normal distribution we compute
the standardized value z=√n(x−µ0)/σ. Next we define the so-called p-
value as the standard normal probability of Zattaining values being more
extreme than |z|, that is occurring to the left of −|z|or to the right of |z|.1
Accordingly, the p-value equals
P(Z≤ −|z|) + P(Z≥ |z|) = 2 ·P(Z≤ −|z|).
The conclusion from the test is now as follows: If the p-value is larger than
the significance level α, then H0is not rejected and if it is smaller than the
significance level, then H0is rejected.
Example 1. To illustrate the Z-test we shall concentrate on the Gdf5
gene from the Golub et al. (1999) data2. The corresponding expression
values are contained in row 2058. A quick search through the NCBI site
1Recall from a calculus course that | − 2|= 2 and |2|= 2.
2We will work with golub throughout this chapter, so it is essential to load these data
and to define the factor gol.fac.

4.1. STATISTICAL HYPOTHESIS TESTING 49
makes it likely that this gene is not directly related to leukemia. Hence,
we may hypothesize that the population mean of the ALL expression values
equals zero. Accordingly, we test H0:µ= 0 against H1:µ6= 0. For the sake
of illustration we shall pretend that the standard deviation σis known to be
equal to 0.25. The z-value (=0.001116211) can be computed as follows.
data(golub, package = "multtest")
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
sigma <- 0.25; n <- 27; mu0 <- 0
x <- golub[2058,gol.fac=="ALL"]
z.value <- sqrt(n)*(mean(x) - mu0)/sigma
The p-value can now be computed as follows.
> 2*pnorm(-abs(z.value),0,1)
[1] 0.9991094
Since it is clearly larger than 0.05, we conclude that the null hypothesis of
mean equal to zero is not rejected (accepted).
Note that the above procedure implies rejection of the null hypothesis
when zis highly negative or highly positive. More precisely, if zfalls in the
region (−∞, z0.025] or [z0.975,∞), then H0is rejected. For this reason these
intervals are called “rejection regions”. If zfalls in the interval (z0.025, z0.975),
then H0is not rejected and consequently this region is called ”acceptance
region”. The situation is illustrated in Figure 4.1.
The interval (z0.025, z0.975) is often named “confidence interval”, because
if the null hypothesis is true, then we are 95% confident that the observed
z-value falls in it. It is custom to rework the confidence interval into an
interval with respect to µ(Samuels & Witmer, 2003, p. 186). In particular,
the 95% confidence interval for the population mean µis
µx+z0.025
σ
√n, x +z0.975
σ
√n¶.(4.1)
That is, we are 95% certain3that the true mean falls in the confidence inter-
val. Such an interval is standard output of statistical software.
3If we would repeat the procedure sufficiently often
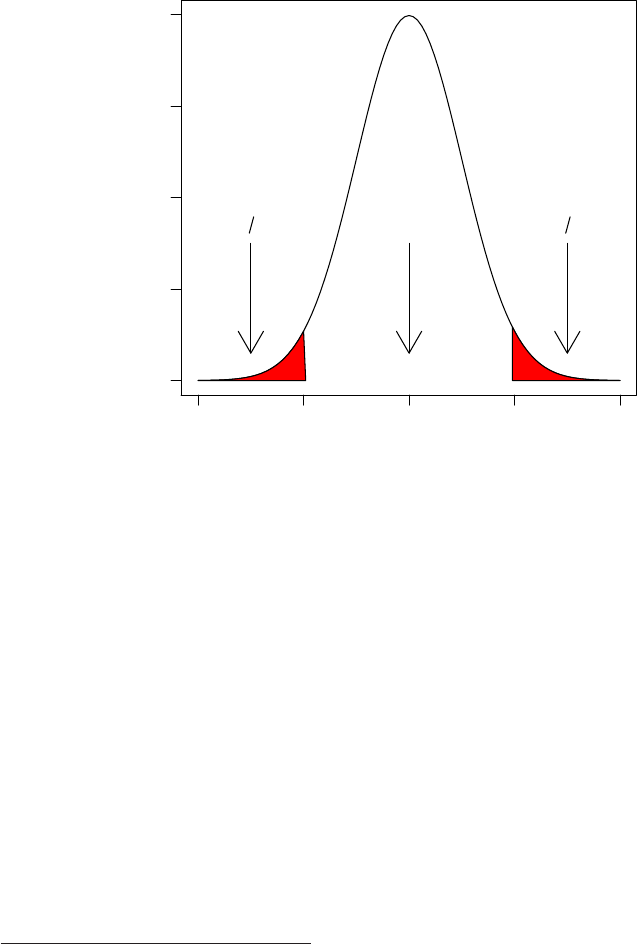
50 CHAPTER 4. ESTIMATION AND INFERENCE
−4 −2 0 2 4
0.0 0.1 0.2 0.3 0.4
normal density
z
rejection
area
α2
rejection
area
α2
acceptance
area
1−α
Figure 4.1: Acceptance and rejection regions of the Z-test.
Example 2. Using the data from Example 1, the 95% confidence interval
given by Equation 4.1 can be computed as follows.4
> mean(x)+qnorm(c(0.025),0,1)*sigma/sqrt(n)
[1] -0.0942451
> mean(x)+qnorm(c(0.975),0,1)*sigma/sqrt(n)
[1] 0.09435251
Hence, the rounded estimated 95% confidence interval is (−0.094,0.094).
Since µ0= 0 falls within this interval, H0is not rejected. It is instructive and
convenient to run the Z-test from the TeachingDemos package, as follows.
4These computations only work together with those of Example 1, especially the defi-
nition of x.

4.1. STATISTICAL HYPOTHESIS TESTING 51
> library(TeachingDemos)
> z.test(x,mu=0,sd=0.25)
One Sample z-test
data: x
z = 0.0011, n = 27.000, Std. Dev. = 0.250, Std. Dev. of the sample mean
= 0.048, p-value = 0.9991
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
-0.09424511 0.09435251
sample estimates:
mean of x
5.37037e-05
From the z-value, the p-value, and the confidence interval, the conclusion is
not to reject the null-hypothesis of mean equal to zero. This illustrates that
testing by either of these procedures yields equivalent conclusions.
Example 3. To develop intuition with respect to confidence intervals
load the package TeachingDemos and give the following command.
> ci.examp(mean.sim =0, sd = 1, n = 25, reps = 100,
+ method = "z", lower.conf=0.025, upper.conf=0.975)
Then 100 samples of size 25 from the N(0,1) distribution are drawn and for
each of these the confidence interval for the population mean is computed
and represented as a line segment. Apart from sampling fluctuations, the
confidence level corresponds to the percentage of intervals containing the
true mean (colored in black) and that the significance level corresponds to
intervals not containing it (colored in red or blue).
4.1.2 One Sample t-Test
Indeed, in almost all research situations with respect to gene expression val-
ues, the population standard deviation σis unknown so that the above test
is not applicable. In such cases t-tests are very useful for testing H0:µ=µ0
against H1:µ6=µ0. The test is based on the t-value defined by t=
52 CHAPTER 4. ESTIMATION AND INFERENCE
√n(x−µ0)/s. The corresponding p-value is defined by 2 ·P(Tn−1≤ −|t|).
Similar to the above, H0is not rejected if the p-value is larger than the signif-
icance level and H0is rejected if the p-value is smaller than the significance
level. Equivalently, if tfalls in the acceptance region (t0.025,n−1, t0.975,n−1),
then H0is not rejected and otherwise it is. For n= 6 the acceptance and
rejection regions are illustrated in Figure 4.2. The 95% confidence interval
for the population mean is given by (x+t0.025 ·s/√n, x +t0.975 ·s/√n), where
the expression s/√ngives the so-called “standard error of the mean”.
−4 −2 0 2 4
0.0 0.1 0.2 0.3
x−axis
T density
rejection
region
α2
rejection
region
α2
acceptance
region
t0.025 t0.975
Figure 4.2: Acceptance and rejection regions of the T5-test.
Example 1. Let’s test H0:µ= 0 against H1:µ6= 0 for the ALL
population mean of the Gdf5 gene expressions. The latter are collected in
row 2058 of the golub data. The t-value is computed as follows.
4.1. STATISTICAL HYPOTHESIS TESTING 53
> x <- golub[2058,gol.fac=="ALL"]; mu0 <- 0; n <- 27
> t.value<-sqrt(n)*(mean(x) - mu0)/sd(x)
> t.value
[1] 0.001076867
The corresponding p-value can be computed by
2·P(T26 ≤ −0.0010) = 2∗pt(−0.0010,26) = 0.9991 > α,
so that the conclusion is not to reject the null hypothesis of mean equal to
zero.
To see whether the observed t-value belongs to the 95% confidence inter-
val, we compute
(t0.025,26, t0.975,26) = (qt(0.025,n−1),qt(0.975,n−1)) = (−2.055,2.055).
Since this interval does contain the t-value, we do not reject the hypothesis
that µequals zero. The left boundary of the 95% confidence interval for the
population mean can be computed, as follows.
> mean(x)+qt(0.025,26)*sd(x)/sqrt(n)
[1] -0.1024562
The 95% confidence interval equals (−0.1025,0.1025). Since it contains zero,
we do not reject the null-hypothesis.
In daily practice it is much more convenient to use the built-in-function
t.test. We illustrate it with the current testing problem.
> t.test(x,mu=0)
One Sample t-test
data: x
t = 0.0011, df = 26, p-value = 0.9991
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
-0.1024562 0.1025636
sample estimates:
mean of x
5.37037e-05

54 CHAPTER 4. ESTIMATION AND INFERENCE
This yields by one command line the observed t-value, the p-value, and the
95% confidence interval for µ0.
In the previous example the test is two-sided because H1holds true if
µ<µ0or µ > µ0. If, however, the researcher desires to test H0:µ=µ0
against H1:µ>µ0, then the alternative hypothesis is one-sided and this
makes the procedure slightly different: H0is accepted if P(Tn≥t)> α and
it is rejected if P(Tn≥t)< α. We shall illustrate this by a variant of the
previous example.
Example 2. In Chapter 2 a box-and-whiskers plot revealed that the
ALL gene expression values of CCND3 Cyclin D3 are positive. Hence, we
test H0:µ= 0 against H1:µ > 0 by the built-in-function t-test. Recall
that the corresponding gene expression values are collected in row 1042 of
the golub data matrix (load it if necessary).
> t.test(golub[1042,gol.fac=="ALL"],mu=0, alternative = c("greater"))
One Sample t-test
data: golub[1042, gol.fac == "ALL"]
t = 20.0599, df = 26, p-value < 2.2e-16
alternative hypothesis: true mean is greater than 0
95 percent confidence interval:
1.732853 Inf
sample estimates:
mean of x
1.893883
The large t-value indicates that, relative to its standard error, the mean dif-
fers largely from zero. Accordingly, the p-value is very close to zero, so that
the conclusion is to reject H0.
4.1.3 Two-sample t-test with unequal variances
Suppose that gene expression data from two groups of patients (experimen-
tal conditions) are available and that the hypothesis is about the difference
between the population means µ1and µ2. In particular, H0:µ1=µ2is to
4.1. STATISTICAL HYPOTHESIS TESTING 55
be tested against H1:µ16=µ2. These hypotheses can also be formulated
as H0:µ1−µ2= 0 and H1:µ1−µ26= 0. Suppose that gene expression
data from the first group are given by {x1,···xn}and that of the second by
{y1,··· , ym}. Let xbe the mean of the first and ythat of the second, and s2
1
the variance of the first and s2
2that of the second. Then the t-statistic can
be formulated as
t=(x−y)−(µ1−µ2)
ps2
1/n +s2
2/m .(4.2)
The decision procedure with respect to the null-hypothesis is completely sim-
ilar to the above tests. Note that the t-value is large if the difference between
xand yis large5, the standard deviations s1and s2are small, and the sample
sizes are large. This test is known as the Welch two-sample t-test (Lehmann,
1999).
Example 1. Golub et al. (1999) argue that gene CCND3 Cyclin D3 plays
an important role with respect to discriminating ALL from AML patients.
The boxplot in Figure 2.4 suggests that the ALL population mean differs from
that of AML. The null hypothesis of equal means can be tested by the func-
tion t.test and the appropriate factor and specification var.equal=FALSE.
> t.test(golub[1042,] ~ gol.fac, var.equal=FALSE)
Welch Two Sample t-test
data: golub[1042, ] by gol.fac
t = 6.3186, df = 16.118, p-value = 9.87e-06
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.8363826 1.6802008
sample estimates:
mean in group ALL mean in group AML
1.8938826 0.6355909
The t-value is quite large, indicating that the two means xand ydiffer largely
from zero relative to the corresponding standard error (denominator in Equa-
tion 4.2). Since the p-value is extremely small, the conclusion is to reject the
null-hypothesis of equal means. The data provide strong evidence that the
5Assuming µ1−µ2= 0.

56 CHAPTER 4. ESTIMATION AND INFERENCE
population means do differ.
When the first group is an experimental group and the second a control
group, then µ1−µ2is the experimental effect in the population and x−ythat
in the sample. The t-value is the experimental effect in the sample relative
to the standard error. The size of the effect is measured by the p-value in
the sense that it is smaller for larger effects.
If the two population variances are equal, then the testing procedure
simplifies considerably. This is the subject of the next paragraph.
4.1.4 Two sample t-test with equal variances
Suppose exactly the same setting as in the previous paragraph, but now
the variances σ2
1and σ2
2for the two groups are known to be equal. To test
H0:µ1=µ2against H1:µ16=µ2, there is a t-test which is based on the
so-called pooled sample variance s2
p. The latter is defined by the following
weighted sum of the sample variances s2
1and s2
2, namely
s2
p=(n−1)s2
1+ (m−1)s2
2
n+m−2.
Then the t-value can be formulated as
t=x−y−(µ1−µ2)
spq1
n+1
m
.
Example 1. The null hypothesis for gene CCND3 Cyclin D3 that the
mean of the ALL differs from that of AML patients can be tested by the
two-sample t-test using the specification var.equal=TRUE.
> t.test(golub[1042,] ~ gol.fac, var.equal = TRUE)
Two Sample t-test
data: golub[1042, ] by gol.fac
t = 6.7983, df = 36, p-value = 6.046e-08
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.8829143 1.6336690

4.1. STATISTICAL HYPOTHESIS TESTING 57
sample estimates:
mean in group ALL mean in group AML
1.8938826 0.6355909
From the p-value 6.046 ·10−8, the conclusion is to reject the null hypothesis
of equal population means. Note that the p-value is slightly smaller than
that of the previous test.
In case of any uncertainty about the validity of the assumption of equal
population variances, one may want to test this.
4.1.5 F-test on equal variances
The assumption of the above t-test it that the two population variances are
equal. Such an assumption can serve as a null hypothesis. That is, we desire
to test H0:σ2
1=σ2
2against H0:σ2
16=σ2
2. This can be accomplished by
the so-called F-test, as follows. From the sample variances s2
1and s2
2, the
f-value f=s2
1/s2
2can be computed, which is Fn1−1,n2−1distributed with
n1−1 and n2−1 degrees of freedom. If P(Fn1−1,n2−1< f)≥α/2 for f < 1
or P(Fn1−1,n2−1> f)≥α/2 for f > 1, then H0is not rejected and otherwise
it is rejected.
Example 1. The null hypothesis for gene CCND3 Cyclin D3 that the
variance of the ALL patients equals that of the AML patients can be tested
by the built-in-function var.test, as follows.
> var.test(golub[1042,] ~ gol.fac)
F test to compare two variances
data: golub[1042, ] by gol.fac
F = 0.7116, num df = 26, denom df = 10, p-value = 0.4652
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.2127735 1.8428387
sample estimates:
ratio of variances
0.7116441

58 CHAPTER 4. ESTIMATION AND INFERENCE
From the p-value 0.4652, the null-hypothesis of equal variances is not re-
jected.
4.1.6 Binomial test
Suppose that for a certain micro RNA a researcher wants to test the hy-
pothesis that the probability of a purine equals a certain value p0. However,
another researcher has reason to believe that this probability is larger. In
such a setting we want to test the null-hypothesis H0:p=p0against the
one-sided alternative hypothesis H1:p > p0. Suppose that sequencing re-
veals that the micro RNA has kpurines out of a total n. Assuming that the
binomial distribution holds, the null-hypothesis can be tested by computing
the p-value P(X≥k). If it is larger than the significance level α= 0.05,
then H0is not rejected and otherwise it is.
Example 1. A micro RNA of length 22 contains 18 purines. The null
hypothesis H0:p= 0.7 is to be tested against the one-sided H1:p > 0.7.
From
P(X≥18) = 1 −pbinom(17,22,0.7) = 0.1645 ≥0.05 = α,
the conclusion follows not to reject the null-hypothesis. This test can also
be conducted by the function binom.test as follows.
> binom.test(18, 22, p = 0.7, alternative = c("greater"),
+ conf.level = 0.95)
Exact binomial test
data: 18 and 22
number of successes = 18, number of trials = 22, p-value = 0.1645
alternative hypothesis: true probability of success is greater than 0.7
95 percent confidence interval:
0.6309089 1.0000000
sample estimates:
probability of success
0.8181818
The p-value 0.1645 is larger than the significance level 0.05, so that the null
hypothesis is not rejected.
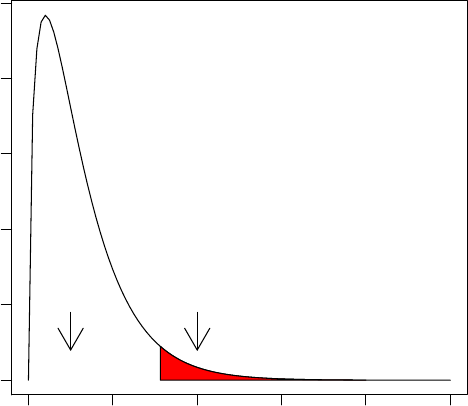
4.1. STATISTICAL HYPOTHESIS TESTING 59
4.1.7 Chi-squared test
It often happens that we want to test a hypothesis with respect to more than
one probability. That is, the H0: (π1,··· , πm) = (p1,··· , pm) against H1:
(π1,···, πm)6= (p1,··· , pm), where p1to pmare given numbers corresponding
to the hypothesis of a researcher. By multiplying the probabilities with the
total number of observations we obtain the expected number of observations
(ei=n·pi). Now we can compute the statistic q=Pm
i=1(oi−ei)2/ei, where
oiis the i-th observed and eithe i-th expected frequency. This statistic is
chi-squared (χ2
m−1) distributed with m−1 degrees of freedom. The p-value
of the chi-squared test is defined as P(χ2
m−1≥q). If it is larger than the
significance level, then the null hypothesis is not rejected, and otherwise it is.
0 5 10 15 20 25
0.00 0.05 0.10 0.15 0.20 0.25
Chi−Squared Density f(x)
rejection
region
acceptance
region
q7.8
Figure 4.3: Rejection region of χ2
3-test.

60 CHAPTER 4. ESTIMATION AND INFERENCE
Example 1. Suppose we want to test the hypothesis that the nucleotides
of Zyxin have equal probability. Let the probability of {A, C, G, T }to occur
in the sequence be given by (π1, π2, π3, π4). Then the null hypothesis to be
tested is (π1, π2, π3, π4) = (1/4,1/4,1/4,1/4). In particular, for the sequence
”X94991.1” from Table 1.1 the total number of nucleotides is n= 2166, so
that the expected frequencies eiare equal to 2166/4 = 541.5. Then, the
q-value equals P4
i=1(oi−ei)2/ei=
(410 −541.5)2
541.5+(789 −541.5)2
541.5+(573 −541.5)2
541.5+(394 −541.5)2
541.5= 187.0674
Since, P(χ2[3] ≥187.0674) is close to zero, the null hypothesis is clearly
rejected. The nucleotides of Zyxin do not occur with equal probability.
A more direct manner to perform the test is by using the built-in-function
chisq.test, as follows.
> library(ape)
> zyxinfreq <- table(read.GenBank(c("X94991.1"),as.character=TRUE))
> chisq.test(zyxinfreq)
Chi-squared test for given probabilities
data: zyxinfreq
X-squared = 187.0674, df = 3, p-value < 2.2e-16
The package ape is loaded, the Zyxin sequence "X94991.1" is downloaded,
and the frequency table is constructed. The observed frequencies are given
as input to chisq.test which has equal probabilities as the default option.
The q-value equals X-squared and the degrees of freedom df = 3. From the
corresponding p-value, the conclusion is to reject the null hypothesis of equal
probabilities. The testing situation is illustrated in Figure 4.3, where the
red colored surface corresponds to the rejection region (7.81,∞). Remember
from the previous chapter that the left bound of this rejection interval can
by found by qchisq(0.95, 3). The observed q= 187.0674 obviously falls
far into the right hand side of the rejection region, so that the corresponding
p-value is very close to zero.
Example 2. In the year 1866 Mendel observed in large number of exper-
iments frequencies of characteristics of different kinds of seed and their off-
spring. In particular, this yielded the frequencies 5474, 1850 the seed shape

4.1. STATISTICAL HYPOTHESIS TESTING 61
of ornamental sweet peas. A crossing of B and b yields off spring BB, Bb and
bb with probability 0.25, 0.50, 0.25. Since Mendel could not distinguish Bb
from BB, his observations theoretically occur with probability 0.75 (BB and
Bb) and 0.25 (bb). To test the null hypothesis H0: (π1, π2) = (0.75,0.25)
against H1: (π1, π2)6= (0.75,0.25), we use the chi-squared test6, as follows.
> pi <- c(0.75,0.25)
> x <-c(5474, 1850)
> chisq.test(x, p=pi)
Chi-squared test for given probabilities
data: x
X-squared = 0.2629, df = 1, p-value = 0.6081
From the p-value 0.6081, we do not reject the null hypothesis.
To further illustrate the great flexibility of the chi-squared test another
example is given.
Example 3. Given certain expression values for a healthy control group
and an experimental group with a disease, we may define a certain cut off
value and classify e.g. smaller values to be healthy and larger ones to be
infected. In such a manner cut-off values can serve as a diagnostic instru-
ment. The classification yields true positives (correctly predicted disease),
false positives (incorrectly predicted disease), true negatives (correctly pre-
dicted healthy) and false negatives (incorrectly predicted healty). For the
sake of illustration suppose that among twenty patients there are 5 true pos-
itives (tp), 5 false positives (fp), 5 true negatives (tn), and 5 false negatives
(fn). These frequencies can be put is a two-by-two table giving the frequen-
cies on two random variables: the true state of the persons and the predicted
state of the persons (by the cut off value). In the worst case the prediction by
the cut-off value is independent of the disease state of the patient. The null
hypothesis of independence, can be tested by a chi-square test, as follows.
> dat <- matrix(c(5,5,5,5),2,byrow=TRUE)
> chisq.test(dat)
6For the sake of clarity the code is somewhat unelegant in using the symbol pi, the
constant representing the ratio of a circle’s circumference to its diameter.
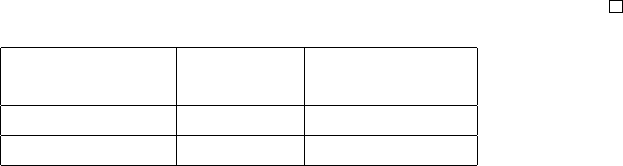
62 CHAPTER 4. ESTIMATION AND INFERENCE
Pearson’s Chi-squared test with Yates’ continuity correction
data: dat
X-squared = 0.2, df = 1, p-value = 0.6547
Since the p-value is larger than the significance level, the null hypothesis of
independence is not rejected.
Suppose that for another cutoff value we obtain 8 true positives (tp), 2
false positives (fp), 8 true negatives (tn), and 2 false negatives (fn). Then
testing independence yields the following.
> dat <- matrix(c(8,2,2,8),2,byrow=TRUE)
> chisq.test(dat)
Pearson’s Chi-squared test with Yates’ continuity correction
data: dat
X-squared = 5, df = 1, p-value = 0.02535
Since the p-value is smaller than the significance level, the null hypothesis of
independence is rejected.
significant non-significant
genes genes
Chromosome 1 100 2000
genome 300 6000
Example 4. A related and frequently applied test in Bioinformatics
is the Fisher exact test. In a two by two table with frequencies f11,f22,
(f12, and f21), this test is based on the so-called odds ratio f11f22/(f12f21).
Suppose that the number of significant onco type of genes in Chromosome 1
is f11 = 100 out of a total of f12 = 2000 and the number of significant genes
in the whole genome is f21 = 300 out of a total of f22 = 6000. Then the
odds ratio equals 100 ·6000/(2000 ·300) = 1 and the number of significant
oncogenes in Chromosome 1 is exactly proportional to that in the genome.
The null-hypothesis of the Fisher test is that the odds ratio equals 1 and
the alternative hypothesis that it differs from 1. Suppose that the frequencies

4.1. STATISTICAL HYPOTHESIS TESTING 63
of significant oncogenes for Chromosome 1 equals f11 = 300 out of a total of
f12 = 500 and for the genome f21 = 3000 out of f22 = 6000. The hypothesis
that the odd ratio equals one can now be tested as follows.
> dat <- matrix(c(300,500,3000,6000),2,byrow=TRUE)
> fisher.test(dat)
Fisher’s Exact Test for Count Data
data: dat
p-value = 0.01912
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
1.029519 1.396922
sample estimates:
odds ratio
1.199960
Since the p-value is smaller than the significance level, the null hypothesis
of odds ratio equal to one is rejected. There are more significant oncogenes
in Chromosome 1 compared to that in the genome. Other examples of the
Fisher test will be given in Chapter 6.
4.1.8 Normality tests
Various procedures are available to test the hypothesis that a data set is
normally distributed. The Shapiro-Wilk test is based on the degree of lin-
earity in a Q-Q plot (Lehmann, 1999, p.347) and the Anderson-Darling test
is based on the distribution of the data (Stephens, 1986, p.372).
Example 1. To test the hypothesis that the ALL gene expression values
of CCND3 Cyclin D3 from Golub et al. (1999) are normally distributed, the
Shapiro-Wilk test can be used as follows.
> shapiro.test(golub[1042, gol.fac=="ALL"])
Shapiro-Wilk normality test

64 CHAPTER 4. ESTIMATION AND INFERENCE
data: golub[1042, gol.fac == "ALL"]
W = 0.947, p-value = 0.1774
Since the p-value is greater than 0.05, the conclusion is not to reject the null
hypothesis that CCND3 Cyclin D3 expression values follow from a normal
distribution. The Anderson-Darling test is part of the nortest package which
probably needs to be installed and loaded first. Running the test on our
CCND3 Cyclin D3 gene expression values comes down to the following.
> library(nortest)
> ad.test(golub[1042,gol.fac=="ALL"])
Anderson-Darling normality test
data: scale(golub[1042, gol.fac == "ALL"])
A = 0.5215, p-value = 0.1683
Hence, the same conclusion is drawn as from the Shapiro-Wilk test. Note
that the p-values from both tests are somewhat low. This confirms our obser-
vation in Section 2.1.5 based on the Q-Q plot that the distribution resembles
the normal. From the normality tests the conclusion is that the differences
in the left tail are not large enough to reject the null-hypothesis that the
CCND3 Cyclin D3 expression values are normally distributed.
4.1.9 Outliers test
When gene expression values are not normally distributed, then outliers may
appear with large probability. The appearance of outliers in gene expression
data may influence the value of a (non-robust) statistic to a large extent.
For this reason it is useful to be able to test whether a certain set of gene
expression values is contaminated by an outlier or not. Accordingly, the
null-hypothesis to be tested is that a set of gene expression values does not
contain an outlier and the alternative is that it is contaminated with at least
one outlier. Under the assumption that the data are realizations of one and
the same distribution, such a hypothesis can be tested by the Grubbs (1950)
test. This test is based on the statistic g=|suspect value −x|/s, where the
suspect value is included for the computation of the mean xand the standard

4.1. STATISTICAL HYPOTHESIS TESTING 65
deviation s.
Example 1. From Figure 2.4 we have observed that expression values
of gene CCND3 Cyclin D3 may contain outliers with respect to the left tail.
This can actually be tested by the function grubbs.test of the outliers
package, as follows.
> library(outliers)
> grubbs.test(golub[1042, gol.fac=="ALL"])
Grubbs test for one outlier
data: golub[1042, gol.fac == "ALL"]
G = 2.9264, U = 0.6580, p-value = 0.0183
alternative hypothesis: lowest value 0.45827 is an outlier
Since the p-value is smaller than 0.05, the conclusion is to reject the null-
hypothesis of no outliers.
In case the data are normally distributed, the probability of outliers is
small. Hence, extreme outliers indicate that the data are non-normally dis-
tributed with large probability. Outliers may lead to such an increase of
the standard error that a true experimental effect remains uncovered (false
negatives). In such cases a robust test based on ranks may be preferred as a
useful alternative.
4.1.10 Wilcoxon rank test
In case the data are normally distributed with equal variance, the t-test is
an optimal test for testing H0:µ1=µ2against H1:µ16=µ2(Lehmann,
1999). If, however, the data are not normally distributed due to skewness or
otherwise heavy tails, then this optimality does not hold anymore and there
is no guarantee that the significance level of the test equals the intended
level α(Lehmann, 1999). For this reason rank type of tests are developed for
which on beforehand no specific distributional assumptions need to be made.
In the below we shall concentrate on the two-sample Wilcoxon test because
of its relevance to bioinformatics. We sustain with a brief description of the
basic idea and refer the interested reader to the literature on non-parametric

66 CHAPTER 4. ESTIMATION AND INFERENCE
testing (e.g. Lehmann, 2006). To broaden our view we switch from hypothe-
ses about means to those about distributions. An alternative hypothesis
may then be formulated as that the distribution of a first group lays to the
left of a second. To set the scene let the gene expression values of the first
group (x1to xm) have distribution Fand those of the second group (y1to
yn) distribution G. The null hypothesis is that both distributions are equal
(H0:F=G) and the alternative that these are not. For example that the
x’s are smaller (or larger) than the y’s. By the two-sample Wilcoxon test the
data x1,··· , xm, y1,···, ynare ranked and the rank numbers of the x’s are
summed to form the statistic Wafter a certain correction (Lehmann, 2006).
The idea is that if the ranks of x’s are smaller than those of the y’s, then the
sum is small. The distribution of the sum of ranks is known so that a p-value
can be computed on the basis of which the null hypothesis is rejected if it is
smaller than the significance level α.
Example 1. The null hypothesis that the expression values for gene
CCND3 Cyclin D3 are equally distributed for the ALL patients and the AML
patients can be tested by the built-in-function wilcox.test, as follows.
> wilcox.test(golub[1042,] ~ gol.fac)
Wilcoxon rank sum test
data: golub[1042, ] by gol.fac
W = 284, p-value = 6.15e-07
alternative hypothesis: true location shift is not equal to 0
Since the p-value is much smaller than α= 0.05, the conclusion is to reject
the null-hypothesis of equal distributions.
4.2 Application of tests to a whole set gene
expression data
Various tests are applied in the above to a single vector of gene expressions.
In daily practice, however, we want to analyze a set of thousands of (row)
vectors with gene expression values which are collected in a matrix. Such

4.2. APPLICATION OF TESTS TO A WHOLE SET GENE EXPRESSION DATA67
can conveniently be accomplished by taking advantage of the fact that R
stores the output of a test as an object in such a manner that we can extract
information such as p-values. Recall that the smaller the p-value the larger
the experimental effect. Hence, by collecting p-values in a vector we can
select genes with large differences between patient groups. This and testing
for normality will be illustrated by two examples.
Example 1. Having a data matrix with gene expression values, a ques-
tion one might ask is: What is the percentage of genes that passes a normality
test? Such can be computed as follows.
> data(golub,package="multtest")
> gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
> sh <- apply(golub[,gol.fac=="ALL"], 1, function(x) shapiro.test(x)$p.value)
> sum(sh > 0.05)/nrow(golub) * 100
[1] 58.27598
Hence, according to the Shapiro-Wilk test, 58.27% of the ALL gene ex-
pression values is normally distributed (in the sense of non-rejection). For
the AML expression values this is 60.73%. It can be concluded that about
forty percent of the genes do not pass the normality test.
Example 2. In case the gene expression data are non-normally dis-
tributed the t-test may indicate conclusions different from those of the Wilcoxon
test. Differences between these can be investigated by collecting the p-values
from both tests and seeking for the largest differences.
> data(golub, package = "multtest");
> gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
> pt <- apply(golub, 1, function(x) t.test(x ~ gol.fac)$p.value)
> pw <- apply(golub, 1, function(x) wilcox.test(x ~ gol.fac)$p.value)
> resul <- data.frame(cbind(pw,pt))
> resul[pw<0.05 & abs(pt-pw)>0.2,]
pw pt
456 0.04480288 0.2636088
1509 0.03215830 0.4427477
The p-value is extracted from the output of the t.test function and stored
in the vector pt. The logical operator &is used to select genes for which the

68 CHAPTER 4. ESTIMATION AND INFERENCE
Wilcoxon p-value is smaller than 0.05 and the absolute difference with the
p-value from the t-test is larger than 0.2. Since there are only two such genes
we can draw the reassuring conclusion that the tests give similar results.
4.3 Overview and concluding remarks
Statistical hypothesis testing consists of hypotheses, distributional assump-
tions, and decisions (conclusions). The hypotheses pertain to the outcome
of a biological experiment and are always formulated in terms of population
values of parameters. Statistically, the outcomes of experiments are seen as
realizations of random variables. The latter are assumed to have a certain
suitable distribution which is seen as a statistical model for outcomes of an
experiment. Then a statistic is formulated (e.g. a t-value) which is treated
both as a function of the random variables and as a function of the data
values. By comparing the distribution of the statistic with the value of the
statistic, the p-value is computed and compared to the level of significance.
A large p-value indicates that the model fits the data well and that the as-
sumptions as well as the null-hypothesis are correct with large probability.
However, a low p-value indicates, under the validity of the distributional as-
sumptions, that the outcome of the experiment is so unlikely that this causes
a sufficient amount of doubt to the researcher to reject the null hypothesis.
The quality of a test is often expressed in terms of efficiency, which is
usually directly related to the (asymptotic) variance of an estimator. The
relative efficiency is the ratio of the asymptotic variances. For Wilcoxon’s test
versus the t-test this equals .955, which means that in the optimal situation
where the (gene expression) data are normally distributed, Wilcoxon’s test
is only a little worse than the t-test. In case, however, of a few outliers or
a slightly heavier tail, the Wicoxon test can be far more efficient than the
t-test (Lehmann, 1999, p.176). Efficiency is directly related to power; the
probability to reject a false hypothesis. The probability of drawing correct
conclusions can always be improved by increasing the sample size.
These considerations set the scene for making some recommendations,
which obviously should not be followed blindly. If gene expression data pass
a normality test, then the Welch type of t-test provides a general test with
good power properties (Ramsey, 1980; Wang, 1971). In case normality does
not hold and the sample size per group is at least least four, the Wilcoxon
4.4. EXERCISES 69
test is recommended.
Because the Wilcoxon p-values are based on ranks many of these are
equal for different genes, so that it is less suitable for ordering in case of
small sample size. On the other hand, it is obviously questionable whether
extremely small differences in p-values produced by the t-test contribute to
biologically relevant gene discrimination. That is, extremely small differences
should not be over-interpreted.
4.4 Exercises
1. Gene CD33. Use grep to find the index of the important gene CD33
among the list of characters golub.gnames. For each test below for-
mulate the null hypothesis, the p-value and your conclusion.
(a) Test the normality of the ALL and AML expression values.
(b) Test for the equality of variances.
(c) Test for the equality of the means by an appropriate t-test.
(d) Is the experimental effect strong?
2. Gene ”MYBL2 V-myb avian myeloblastosis viral oncogene homolog-
like 2” has its expression values in row 1788.
(a) Use a boxplot to construct a hypothesis about the experimental
effect.
(b) Test for the equality of means by an appropriate t-test.
3. HOXA9. Gene ”HOXA9 Homeo box A9” with expression values in row
1391, can cause leukemia (Golub et al., 1999).
(a) Test the normality of the expression values of the ALL patients.
(b) Test for the equality of means by an appropriate t-test.
4. Zyxin. On NCBI there are various cDNA clones of zyxin.
(a) Find the accession number of cDNA clone with IMAGE:3504464.
(b) Test whether the frequencies of the nucleotides are equal for each
nucleic acid.
70 CHAPTER 4. ESTIMATION AND INFERENCE
(c) Test whether the frequencies of ”X94991.1” can be predicted by
the probabilities of the cDNA sequence ”BC002323.2”.
5. Gene selection. Select the genes from the golub data with smallest
two-sample t-test values for which the ALL mean is greater than the
AML mean. Report the names of the best ten. Scan the Golub (1999)
article for genes among the ten you found and discuss their biological
function briefly.
6. Antigenes. Antigenes play an important role in the development of
cancer. Order the antigenes according to their p-values from the Welch
two-sample t-test with respect to gene expression values from the ALL
and AML patients of the Golub et al. (1999) data.
7. Genetic Model. A certain genetic model predicts that four phenotypes
occur in ration 9:3:3:1. In a certain experiment the offspring is observed
with frequencies 930, 330, 290, 90. Do the data confirm the model?
8. Comparing two genes. Consider the gene expression values in row 790
and 66 of the Golub et al. (1999) data.
(a) Produce a boxplot for the ALL expression values and comment on
the differences. Are there outliers?
(b) Compute the mean and the median for the ALL gene expression
values for both genes. Do you observed difference between genes?
(c) Compute three measures of spread for the ALL expression values
for both genes. Do you observe difference between genes?
(d) Test by Shapiro-Wilk and Anderson-Darling the normality for the
ALL gene expression values for both genes.
9. Normality tests for gene expression values of the Golub et al. (1999)
data. Perform the Shapiro-Wilk normality test separately for the ALL
and AML gene expression values. What percentage passed the normal-
ity test separately for the ALL and the AML gene expression values?
What percentage passes both testes?
10. Two-sample tests on gene expression values of the Golub et al. (1999)
data.
4.4. EXERCISES 71
(a) Perform the two-sample Welch t-test and report the names of the
ten genes with the smallest p-values.
(b) Perform the Wilcoxon rank test and report the names of the ten
genes with the smallest p-values.
11. Biological hypotheses. Suppose that the probability to reject a biolog-
ical hypothesis by the results of a certain experiment is 0.05. Suppose
that the experiment is repeated 1000 times.
(a) How many rejections do you expect.
(b) What is the probability of less than 10 rejections?
(c) What is the probability of more than 5 rejections?
(d) What is the probability that the number of rejections is between
two and eight?
12. Programming some tests.
(a) Program the two-sample t-test with equal variances and illustrate
it with the expression values of row 1024 the of Golub et al. (1999)
data.
(b) The value of W in the two-sample Wilxoxon test equals the sum
of the ranks of Group 1 minus n(n+ 1)/2, where nis the number
of gene expression values in Group 1. Program this and illustrate
it with the expression values of row 1024 of Golub et al. (1999)
data.
(c) The value of W in the two-sample Wilxoxon test equals the num-
ber of values xi> yj, where xi, yjare values from Group 1 and
2, respectively. Program this and illustrate it with the expression
values of row 1024 of Golub et al. (1999) data.
72 CHAPTER 4. ESTIMATION AND INFERENCE
Chapter 5
Linear Models
We have seen that the t-test can be used to discover genes with different
means in the population with respect to two groups of patients. In case,
however, there are three groups of patients the question arises how genes can
be selected having the largest differential expressions between group means
(experimental effect)? A technique making this possible is an application of
the linear model and is called analysis of variance. It is frequently applied
bioinformatics.
The validity of the technique is based on the assumption that the gene
expression values are normally distributed and have equal variance across
groups of patients. It is of importance to investigate these assumptions be-
cause it either reassures our confidence in the conclusions or it indicates that
alternative tests should be used.
In this chapter the linear model will briefly be explained. The main focus,
however, is on application of the linear model for testing the hypothesis that
three or more group means are equal. Several illustrations of analyzing gene
expression data will be given. It will be explained how the assumptions about
normality and equal variances (homogeneity) can be investigated and what
alternatives can be used in case either of these does not hold. The somewhat
technical concepts of “model matrix” and “contrast matrix” are explained
because these are useful for several applications in the next chapter.
73

74 CHAPTER 5. LINEAR MODELS
5.1 Definition of linear models
Given a gene expression Yi, a basic form of the linear model is
Yi=xiβ+εi,for i= 1,··· , n,
where Yiis an observable variable, xia fixed number, βan unknown weight,
εia unobservable error variable. The fixed number xifollows from a sta-
tistical “design”, as we shall see. The xivalue is part of the predictor, Yi
the criterion, and εithe error of the model. The systematical part of the
model xiβequals the mean of the gene expression Yi. The model is called
”linear” because the degree of the coefficient βis one. For a linear model
to be a statistical model there must be some assumption with respect to
the distribution of the error variables. Frequently, it is assumed that the er-
ror variables ε1,··· , εnare independent and normally distributed with zero
mean, that is, according to N(0, σ2). Then the mean of Yiequals xiβand its
variance σ2.
Example 1. A common manner to introduce the linear model is by writing
Yi=β1+xiβ2+εi,for i= 1,··· , n,
so that the model part represents a straight line with intercept β1and
slope β2. Given data points y1,···, ynand x1,··· , xn, a best fitting line
through the data can easily be computed by least squares estimation of the
intercept and slope. A nice application to explore this is by the function
put.points.demo() from the TeachingDemos package. It allows points to
be added and deleted to a plot which interactively computes estimates for
the slope and the intercept given the data. By choosing the points more or
less on a horizontal line, the slope will be near zero. By choosing the points
nearly vertical, the slope will be large. By choosing a few gross errors in the
data it can be observed that the estimates are not robust against outliers.
In order to handle gene expression data for three or more groups of pa-
tients we need to extend the model. The idea simply is to increase the
number of weights to the number of groups k, so that, we obtain the weights
β1,··· , βkand the corresponding design values xi1,···, xik . The system-
atic part of the model consists of a weighted sum of these design values:
5.1. DEFINITION OF LINEAR MODELS 75
xi1β1+···+xikβk. By adding measurement error to this systematic part we
obtain the linear model
Yi=
k
X
j=1
xij βj+εi.
The design values xij for Patient iin Group jare collected in the so-called
”design” matrix denoted by X. In particular, the design value xij is chosen
to be equal to 1 if Patient ibelongs to Group jand zero if (s)he does not.
By this choice it becomes possible to use linear model estimation for testing
hypotheses about group means. This will be illustrated by an example.
Example 2. Suppose we have the following artificial gene expressing values
2,3,1,2, of Group 1, 8,7,9,8 of Group 2, and 11,12,13,12 of Group 3. We may
assign these to a vector y, as follows.
> y <- c(2,3,1,2, 8,7,9,8, 11,12,13,12)
Next, we construct a factor indicating to which group each expression value
belongs. In particular, the first four belong to Group 1, the second four to
Group 2, and the third four to Group 3. We conveniently use the function
gl to define the corresponding factor.
> a <- gl(3,4)
> a
[1] 1 1 1 1 2 2 2 2 3 3 3 3
Levels: 1 2 3
The design matrix Xis also called “model matrix”. It is illuminating to
print it to the screen.
> model.matrix(y ~ a - 1)
a1 a2 a3
1 1 0 0
2 1 0 0
3 1 0 0
4 1 0 0
5 0 1 0
6 0 1 0
7 0 1 0
8 0 1 0

76 CHAPTER 5. LINEAR MODELS
9 0 0 1
10001
11001
12001
The notation y~a-1 represents a model equation, where -1 means to skip
the intercept or general constant.1In this situation, the weights (β1, β2, β3)
of the model specialize to the population means (µ1, µ2, µ3). The model for
the first gene expression value of Group 1 is Y1=µ1+ε1, for the second
expression value of Group 1 it is Y2=µ1+ε2, for the first member of Group
2 it is Y5=µ2+ε5, and for the first member of Group 3 it is Y9=µ3+ε9.
Recall that population means are generally estimated by sample means.
Similarly, in the current setting, estimation of the linear model comes down
to estimation of group means for which there are one-sample t-type of tests
available (see e.g. Rao & Toutenburg, 1995; Samuels & Witmer, 2003). To
illustrate this we employ the estimation function lm and ask for a summary.
> summary(lm(y ~ a - 1))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
a1 2.0000 0.4082 4.899 0.000849 ***
a2 8.0000 0.4082 19.596 1.09e-08 ***
a3 12.0000 0.4082 29.394 2.98e-10 ***
The output in the first column gives the estimated mean per group. The sec-
ond gives the standard error of each mean, the third the t-value (the estimate
divided by the standard error), and the last the corresponding p-values. From
the p-values the conclusion follows to reject the null hypotheses H0:µj= 0
for Group index jrunning from 1 to 3.
Using the above design matrix, the model for the gene expression values
from different groups can be written as
Yij =µj+εij ,where εij is distributed as N(0, σ2),
and Yij is the expression of Person iin Group j,µjthe mean of Group j, and
the εij the error of Person iin Group j. The error is assumed to be normally
distributed with zero mean and variance equal for different persons.
1See also Chapter 11 of the manual ”An Introduction to R”.
5.2. ONE-WAY ANALYSIS OF VARIANCE 77
The above illustrates that the linear model is useful for testing hypotheses
about group means. In bioinformatics the linear model is applied to many
sets of gene expressions, so that it is of great importance to have an overall
test for the equality of means.
5.2 One-way analysis of variance
A frequent problem is that of testing the null hypothesis that three or more
population means are equal. By comparing two types of variances, this is
made possible by a technique called analysis of variance (ANOVA). To set
the scene, let three groups of patients be available with measurements in the
form of gene expression values. The null-hypothesis to be tested is H0:µ1=
µ2=µ3. In statistical language such groups are called levels of a factor.
Let the data for Group 1 be represented by y11, y21,···, yn1those of Group
2 by y12, y22,··· , yn2and those of Group 3 by y13, y23,··· , yn3, where nis
the number of expression values in each group. The three sample means per
patient group can be expressed by
y1=1
n
n
X
i=1
yi1, y2=1
n
n
X
i=1
yi2,and y3=1
n
n
X
i=1
yi3.
The total number of measurements N= 3n, so that the overall mean yis
equal to
y=1
NÃn
X
i=1
yi1+
n
X
i=1
yi2+
n
X
i=1
yi3!.
For the definition of the overall test on the equality of means there are two
sums of squares of importance. The sum of squares within (SSW) is the sum
of the squared deviation of the measurements to their group mean, that is
SSW =
g
X
j=1
n
X
i=1
(yij −yj)2,
where gis the number of groups. The sum of squares between (SSB) is the
sum of squares of the deviances of the group mean with respect to the total
mean, that is
SSB =
g
X
j=1
n
X
i=1
(yj−y)2=n
g
X
j=1
(yj−y)2.

78 CHAPTER 5. LINEAR MODELS
Now the f-value is defined by
f=SSB/(g−1)
SSW/(N−g).
If the data are normally distributed, then this f-value follows the Fg−1,N−g
distribution, where g−1 and N−gare the degrees of freedom (Rao, 1973,
p.245). If P(Fg−1,N −g> f)≥α, then H0:µ1=µ2=µ3is not rejected, and,
otherwise it is. The idea behind the test is that, under the null-hypothesis
of equal group means, the value for SSB will tend to be small, so that the
observed f-value will be small and H0is accepted.
Example 1. Let’s continue with the data from the previous example.
Recall that the data of Group 1 are 2, 3, 1, 2, those of Group 2 are 8, 7, 9,
8, and of Group 3 are 11, 12, 13, 12. The number of expression values per
group n= 4, the total number of data values N= 12, and the number of
groups g= 3.
To load the data, to construct the corresponding factor, and to compute
the group means one may use the following.
> y <- c(2,3,1,2, 8,7,9,8, 11,12,13,12)
> a <- gl(3,4)
> gm <- as.numeric(tapply(y, a, mean))
> gm
[1] 2 8 12
Thus we find that y1= 2, y2= 8, and y3= 12. These group means are
now collected in the vector gm. The grand mean ycan be computed by
mean(y)=7.333333. An elementary manner to compute the sums of squares
between SSB is by
gm <- as.numeric(tapply(y, a, mean))
g <- 3; n <- 4; N <-12; ssb <- 0
for (j in 1:g) {ssb <- ssb + (gm[j]- mean(y))^2}
SSB <- n*ssb
This results in SSB = 202.6667. In a similar manner the sums of squares
within (SSW) and the f-value can be computed, as follows.
> SSW <- 0
> for (j in 1:g) {SSW <- SSW + sum((y[a==j]-gm[j])^2)}
> f <- (SSB/(g-1))/(SSW/(N-g))

5.2. ONE-WAY ANALYSIS OF VARIANCE 79
This results in SSW = 6 and an observed f-value equal to 152. Hence, the
overall p-value is
P(F2,9>152) = 1 −P(F2,9<152) = 1−pf(152,2,9) = 1.159156 ·10−7.
Since this is smaller than the significance level 0.05, the conclusion is to reject
the null hypothesis of equal means.
The built-in-function anova can be used to extract the so-called analysis
of variance table from an lm object.
> anova(lm(y ~ a))
Analysis of Variance Table
Response: x
Df Sum Sq Mean Sq F value Pr(>F)
fact 2 202.667 101.333 152 1.159e-07 ***
Residuals 9 6.000 0.667
This gives the degrees of freedom g−1 = 2 and N−g= 9, the sums of
squares between (202.667), the sums of squares within (6.0), the f-value 152
and the overall p-value 1.159 ·10−7.
Example 2. By the previous analysis of variance it is concluded that
there are differences in population means. It is, however, not clear which of
the means differ. A way to clarify this is by estimating the mean of Group 1
(Level 1) and then computing the difference between Group 2 and Group 1,
and the difference between Group 3 and Group 1. Such corresponds to the
following contrast matrix
C=
1 1 1
0−1 0
0 0 −1
.
This contrast matrix is by default implemented by the model specification
y~a, as follows.
> summary(lm(y ~ a))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.0000 0.4082 4.899 0.000849 ***

80 CHAPTER 5. LINEAR MODELS
factLevel 2 6.0000 0.5774 10.392 2.60e-06 ***
factLevel 3 10.0000 0.5774 17.321 3.22e-08 ***
Residual standard error: 0.8165 on 9 degrees of freedom
Multiple R-Squared: 0.9712, Adjusted R-squared: 0.9649
F-statistic: 152 on 2 and 9 DF, p-value: 1.159e-07
The estimated intercept is the mean of Group 1 (Level 1). The factLevel
2is the difference in means between Group 2 (Level 2) and Group 1 and
factLevel 3 is the difference in means between Group 3 and Group 1. By
t-tests the null-hypothesis is tested that the mean of Group 1 is zero, the
difference in means between Group 2 and Group 1 is zero and the difference
in means between Group 3 and Group 1 is zero. That is, the null-hypotheses
are H0:µ1= 0, H0:µ2−µ1= 0, and H0:µ3−µ2= 0. Since the p-values
that correspond to the t-values are smaller than the significance level 0.05, all
null-hypotheses are rejected. The last line of the output gives the f-value,
the degrees of freedom, and the corresponding overall p-value. The latter
equals that of ANOVA.
Before we analyze real gene expression data it seems well to give an ex-
ample where the means do not differ.
Example 3. Let’s sample data from the normal distribution with mean
1.9 and standard deviation 0.5 corresponding to three groups of patients that
do not possess any type of differences between groups.
> y <- rnorm(12,1.9,0.5)
> round(x,2)
[1] 1.75 1.82 1.35 1.61 2.08 1.27 2.50 2.40 2.13 0.71 2.80 2.00
> a <- gl(3,4)
> anova(lm(y ~ a))$Pr[1]
[1] 0.6154917
Note that by the $Pr[1] operator extracts the p-value from the list generated
by the anova function. The p-value implies the conclusion not to reject the
null-hypotheseis of equal means, which is consistent with the data generation
process.
5.2. ONE-WAY ANALYSIS OF VARIANCE 81
B1 B2 B3
3.5 4.0 4.5 5.0 5.5
Figure 5.1: Plot of SKI-like onco-
gene expressions for three patient
groups.
B1 B2 B3
6.0 6.2 6.4 6.6 6.8 7.0 7.2
Figure 5.2: Plot of Ets2 expression
values for three patient groups.
Example 4. B-cell ALL: 1866_g_at. To illustrate analysis of variance
by real data we shall use the ALL data from the ALL package, see Section
1.1. Specifically, expression levels from B-cell ALL patients in stage B1, B2,
and B3 are selected with row name 1866_g_at, which refers to an SKI-like
oncogene related to oncoproteins. From the plot of the data in Figure 5.1 it
can be observed that the expression levels differ between the disease stages.
The null hypothesis is tested that the expression means in each stage are
equal or in other words that there are no experimental effects. It is briefly
indicated how the data are loaded.
> library(ALL);data(ALL)
> ALLB123 <- ALL[,ALL$BT %in% c("B1","B2","B3")]
> y <- exprs(ALLB123)["1866_g_at",]
> summary(lm(y ~ ALLB123$BT))
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.58222 0.08506 53.873 < 2e-16 ***

82 CHAPTER 5. LINEAR MODELS
ALLB123$BTB2 -0.43689 0.10513 -4.156 8.52e-05 ***
ALLB123$BTB3 -0.72193 0.11494 -6.281 2.00e-08 ***
Residual standard error: 0.3707 on 75 degrees of freedom
Multiple R-squared: 0.3461, Adjusted R-squared: 0.3287
F-statistic: 19.85 on 2 and 75 DF, p-value: 1.207e-07
From the overall p-value 1.207 ·10−7of the f-test the conclusion follows to
reject the hypothesis of equal means. From the t-tests we conclude that the
mean of B1 differs from zero and the differences between B2 and B1 as well
as between B3 and B2 are unequal to zero. That is, the population means
of Group B1, B2, and B3 do differ.
Example 5. B-cell ALL: 1242_at. To illustrate a case where the means
do not differ we selected the expression values for probe 1242_at of the B-
cell ALL patients in stage B1, B2, and B3 from the ALL data. This probe
corresponds to the Ets2 repressor factor which plays a role in telomerase
regulation in human cancer cells. From the plot of the data in Figure 5.2,
however, it can be observed that the expression values hardly differ between
disease stages. The data are extracted from the ALL object and collected in
the vector y. The corresponding factor is given by ALLB123$BT.
> library(ALL); data(ALL)
> ALLB123 <- ALL[,ALL$BT %in% c("B1","B2","B3")]
> y <- exprs(ALLB123)["1242_at",]
> summary(lm(y ~ ALLB123$BT))
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.55083 0.05673 115.483 <2e-16 ***
ALLB123$BTB2 0.03331 0.07011 0.475 0.636
ALLB123$BTB3 -0.04675 0.07665 -0.610 0.544
Residual standard error: 0.2473 on 75 degrees of freedom
Multiple R-squared: 0.01925, Adjusted R-squared: -0.006898
F-statistic: 0.7362 on 2 and 75 DF, p-value: 0.4823
From the overall p-value 0.4823, the conclusion is not to reject the null hy-
pothesis of equal means. More specifically, the null-hypotheses H0:µ1= 0
is rejected, but from the p-value 0.636 the H0:µ2−µ1= 0 is not rejected,

5.3. TWO-WAY ANALYSIS OF VARIANCE 83
and from p-value 0.544 the H0:µ3−µ2= 0 is not rejected either.
Example 6. An interesting question is of course for how many genes of
the ALL data the hypothesis of equal means is rejected by the overall ANOVA
p-value? Such can be answered by collecting the p-values in a vector.
> pano <- apply(exprs(ALLB123),1,function(x) anova(lm(x~ALLB123$BT))$Pr[1])
> sum(pano<0.05)
[1] 2526
Thus the hypothesis of equal means is rejected for 2526 out of a total of
12625 genes (probes).
5.3 Two-way analysis of variance
Having some experience with one way analysis of variance, the question may
arise whether the model for means of groups can be extended from one factor
to more factors. This is indeed possible. The model would then be equal to
Yijk =αi+βj+ (αβ)ij +εijk,
where αiis the mean of Group iindicated by the first factor, βjthe mean
of Group jindicated by the second factor, (αβ)ij the interaction effect and
εijk the error which is distributed according to N(0, σ2). If the means of
the igroups differ, then there is a main effect of the first factor which is
expressed in a p-value smaller than 0.05. Similarly, in case the means of the
jgroups differ, there is a main effect of the second factor, expressed in a
p-value smaller than 0.05. Two-way analysis of variance will briefly be illus-
trated.
Example 5. A two-way approach. It case of the ALL data from Chiaretty
et al. (2004) we may aggregate the B cell patients into two groups: B, B1 and
B2 in the first and B3 and B4 in the second. For the second group we select
from the molecular biology of the patients assigned to BCR/ABL and NEG.
We shall perform the analysis on the expression values of NEDD4 binding
protein 1 with probe id 32069_at. This can be computed as follows.
library("ALL"); data(ALL)
ALLBm <- ALL[,which(ALL$BT %in% c("B","B1","B2","B3","B4") & ALL$mol.biol %in% c("BCR/ABL","NEG"))]
84 CHAPTER 5. LINEAR MODELS
facmolb <- factor(ALLBm$mol.biol)
facB <- factor(ceiling(as.integer(ALLBm$BT)/3),levels=1:2,labels=c("B012","B34"))
> anova(lm(exprs(ALLBm)["32069_at",] ~ facB * facmolb))
Analysis of Variance Table
Response: exprs(ALLBm)["32069_at", ]
Df Sum Sq Mean Sq F value Pr(>F)
facB 1 1.1659 1.1659 4.5999 0.0352127 *
facmolb 1 3.2162 3.2162 12.6891 0.0006433 ***
facB:facmolb 1 1.1809 1.1809 4.6592 0.0340869 *
Residuals 75 19.0094 0.2535
First the patients are selected with B-cell ALL and assigned molecular biology
of the cancer to BCR/ABL or NEG. Next the factors are constructed to group
the patients. From the p-values in the analysis of variance table it can be
concluded that there two main effects as well as an interaction effect.
One may also ask for a summary of the individual effects.
> summary(lm(exprs(ALLBm)["32069_at",] ~ facB * facmolb))
Call:
lm(formula = exprs(ALLBm)["32069_at", ] ~ facB * facmolb)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.7649 0.1073 63.026 < 2e-16 ***
facBB34 -0.5231 0.1686 -3.103 0.0027 **
facmolbNEG -0.6020 0.1458 -4.128 9.4e-05 ***
facBB34:facmolbNEG 0.5016 0.2324 2.159 0.0341 *
Residual standard error: 0.5034 on 75 degrees of freedom
Multiple R-squared: 0.2264, Adjusted R-squared: 0.1954
F-statistic: 7.316 on 3 and 75 DF, p-value: 0.0002285
In bioinformatics the question often arises how many probes there are with
have significant effects. In this case we may compute the number of probes
with significant main as well as interaction effects.
> pval <- apply(exprs(ALLBm), 1, function(x) anova(lm(x ~ facB * facmolb))$Pr[1:3])

5.4. CHECKING ASSUMPTIONS 85
> pvalt <- data.frame(t(pval))
> colnames(pvalt) <- c("maineffectB","maineffectmolbiol","interaction")
> sum(pvalt$maineffectB < 0.05 & pvalt$maineffectmolbiol < 0.05 & pvalt$interaction < 0.05)
[1] 47
The three p-values per probe are collected in a matrix. This matrix is trans-
posed so that the columns correspond to the p-values and the rows to the
probes. Using the logical AND (&) operator and summing the TRUE values
yield 47 probes with significant main and interaction effects.
5.4 Checking assumptions
When the linear model is applied for analysis of variance there are in fact
two assumptions made. First, the errors are assumed to be independent and
normally distributed, and, second, the error variances are assumed to be
equal for each level (patient group). The latter is generally known as the
homoscedasticity assumption. The normality assumption can be tested as
a null hypothesis by applying the Shapiro-Wilk test on the residuals. The
homoscedasticity assumption can be tested as a hypothesis by the Breusch
and Pagan (1979) test on the residuals. This latter test may very well be
seen as a generalization of the F-test for equal variances.
Example 1. Testing normality of the residuals. From Figure 5.1 it can
be observed that there are outliers being far apart from the bulk of the other
expression values. This raises the question whether the normality assumption
holds. The normality of the residuals from the estimated linear model on the
B-cell ALL data from 1866_g_at, can be tested as follows.
> data(ALL,package="ALL");library(ALL)
> ALLB123 <- ALL[,ALL$BT %in% c("B1","B2","B3")]
> y <- exprs(ALLB123)["1866_g_at",]
> shapiro.test(residuals(lm(y ~ ALLB123$BT)))
Shapiro-Wilk normality test
data: residuals(lm(y ~ ALLB123$BT))
W = 0.9346, p-value = 0.0005989

86 CHAPTER 5. LINEAR MODELS
From the p-value 0.0005989, the conclusion is to reject the null-hypothesis of
normally distributed residuals.
Example 2. Testing homoscedasticity of the residuals. From Figure
5.1 it can be observed that the spread of the expression values around their
mean differs between groups of patients. In order to test the homoscedasticity
assumption we use the function bptest from the lmtest package.
> library(ALL); data(ALL); library(lmtest)
> ALLB123 <- ALL[,ALL$BT %in% c("B1","B2","B3")]
> y <- exprs(ALLB123)["1866_g_at",]
> bptest(lm(y ~ ALLB123$BT),studentize = FALSE)
Breusch-Pagan test
data: lm(y ~ ALLB123$BT)
BP = 8.7311, df = 2, p-value = 0.01271
From the p-value 0.01271, the conclusion follows to reject the null hypothesis
of equal variances (homoscedasticity).
5.5 Robust tests
In case departures from normality or homoscedasticity are large enough to
cause concern with respect to the actual significance level or to the power
of the test, an alternative testing procedure is called for. In case only ho-
moscedasticity is violated, we are in a situation quite similar to that of t-
testing with unequal variances. That is, the null hypothesis H0:µ1=µ2=
µ3of equal means can be tested without assuming equal variances by a test
proposed by Welch (1951).
Example 1. In Example 2 of the previous section the hypothesis of
equal variances was rejected. To apply analysis of variance without assuming
equal variances (homoscedasticity) one may use the function oneway.test,
as follows.
> data(ALL,package="ALL");library(ALL)

5.5. ROBUST TESTS 87
> ALLB123 <- ALL[,ALL$BT %in% c("B1","B2","B3")]
> y <- exprs(ALLB123)["1866_g_at",]
> oneway.test(y ~ ALLB123$BT)
One-way analysis of means (not assuming equal variances)
data: y and ALLB123$BT
F = 14.1573, num df = 2.000, denom df = 36.998, p-value = 2.717e-05
From the p-value 2.717 ·10−5, the conclusion follows to reject the hypothesis
of equal means.
In case normality is violated a rank type of test is more appropriate. In
particular, to test the null-hypothesis of equal distributions of groups of gene
expression values, the Kruskal-Wallis rank sum test is recommended. This
test can very well be seen as a generalization of the Wilcoxon test for testing
the equality of two distributions. Because it is based on ranking the data,
it is highly robust against non-normality, it, however, does not estimate the
size of experimental effects.
Example 2. In Example 1 of the previous section we rejected the hypoth-
esis of normally distributed residuals. We use the function kruskal.test to
perform a non-parametric test.
> data(ALL,package="ALL");library(ALL)
> ALLB123 <- ALL[,ALL$BT %in% c("B1","B2","B3")]
> y <- exprs(ALLB123)["1866_g_at",]
> kruskal.test(y ~ ALLB123$BT)
Kruskal-Wallis rank sum test
data: y by ALLB123$BT
Kruskal-Wallis chi-squared = 30.6666, df = 2, p-value = 2.192e-07
From the p-value 2.192 ·10−7, the null-hypothesis of equal distributions of
expression values between patient groups is rejected.
By the apply functionality the p-values can easily be computed for all
12625 gene expression values of the ALL data.
88 CHAPTER 5. LINEAR MODELS
5.6 Overview and concluding remarks
By applying the above normality and homogeneity tests to complete sets of
gene expression values it can quickly be seen to what extent the assumptions
for the classical analysis of variance test are violated. Based on these it can
be decided to add rank type of testing in order to reduce the amount of false
positives and false negatives. Here, false positives are significant p-values for
equal populations means and false negatives are non-significant p-values for
unequal populations means.
In the next chapter it will briefly be indicated how to combine two factors
into a single analysis of variance. For instance, one may want to combine
B-cell stage with age groups of persons. The interested reader is referred to
Faraway (2004) and Venables & Ripley (2002) for more information on using
linear models in R and for a general treatment of linear models to Rao &
Toutenburg (1995).
The p-values from overall tests of equality of means or distributions are
important tools to order genes according to their experimental effect with
respect to different patient groups. More examples are given in the next
chapter where several functionalities of Bioconductor will be used for the
analysis of microarray data.
5.7 Exercises
1. Analysis of gene expressions of B-cell ALL patients.
(a) Construct a data frame containing the expression values for the
B-cell ALL patients in stage B, B1, B2, B3, B4 from the ALL data.
(b) How many patients are in each group.
(c) Test the normality of the residuals from the linear model used
for analysis of variance for all gene expression values. Collect the
p-values in a vector.
(d) Do the same for the homoscedasticity assumption.
(e) How many gene expressions are normally distributed and how
many homoscedastic? For how many do both hold?
2. Further analysis of gene expressions of B-cell ALL patients. Continue
with the previous data frame containing the expression values for the
5.7. EXERCISES 89
B-cell ALL patients in stage B, B1, B2, B3, B4 from the ALL data.
(a) Collect the overall p-values from ANOVA in a vector.
(b) Use featureNames() to report the affymetrix id’s of the genes
with smaller p-values than 0.000001.
(c) Collect the overall p-values from the Kruskal-Walles test in a vec-
tor.
(d) Use featureNames() to report the affymetrix id’s of the genes
with smaller p-values than 0.000001.
(e) Briefly comment on the differences you observe. That is, how
many genes have p-values smaller than 0.001 from both ANOVA
and Krusal-Wallis? How many only from one type of test? Hint:
Collect TRUE/FALSES in logical vectors and use table.
3. Finding the ten best best genes among gene expressions of B-cell ALL
patients. Continue with the previous data frame containing the expres-
sion values for the B-cell ALL patients in stage B, B1, B2, B3, B4 from
the ALL data.
(a) Print the p-values and the corresponding (affimetrix) gene identi-
fiers of the ten best from ANOVA.
(b) Do the same for the p-values from the Kruskal-Wallis test.
(c) Use the function intersect to find identifiers in both sets.
4. A simulation study on gene expression values.
(a) Construct a data matrix with 10000 rows and 9 columns with data
from the normal distribution with mean zero and variance equal to
one. Such a matrix simulates gene expressions without differences
between groups (sometimes called negatives).
(b) Construct a factor for three groups each with three values.
(c) How many p-values are smaller than the significance level α=
0.05?
(d) If the p-value is smaller than the significance level, then the con-
clusion is that there an experimental effect (a positive). How many
false positives do you expect and how many did you observe?
90 CHAPTER 5. LINEAR MODELS
(e) Construct a matrix with 10000 rows and 9 columns with normally
distributed data with mean zero, one and two and variance equal
to one. Assume again that there three groups each with three data
values. This data matrix simulates gene expressions with differ-
ences between groups (sometimes called positives). Use ANOVA
and kruskal-Wallis to find the number of significant genes (true
positives). report the number of true positives and false nega-
tives.

Chapter 6
Micro Array Analysis
The analysis of gene expression values is of key importance in bioinformatics.
The technique makes it possible to give an initial answer to many important
genetic type of questions. In this chapter you learn how to preprocess probe
data, filter genes, to program various visualizations, to use gene ontology
identifiers, to load public available gene expression data, as well as how to
summarize results in html output. 1
6.1 Probe data
The microarray technique takes advantage of hybridization properties of nu-
cleic acids. That is, to give a rough idea, complementary molecules are
attached and labeled on a solid surface in order for a specialized scanner
measure the intensity of target molecules. Per gene there are about twenty
such measures obtained for each probe (gene). Per probe these measures
come in pairs. The intensity of the perfect match (PM) intends to measure
the amount of transcripts from the gene. The intensity of the mismatch
(MM) is related to non-specific binding and is often seen as a background
type of noise.
The raw data from the Affymetrix scanner is stored in so-called DAT
files, which are processed to so-called CEL files, where we will work with.
The package affy has facilities to read data from a vector specifying several
CEL files produced by the Affymetrix scanner.
1It may be convenient to explore the possibilities of the limmaGUI. Our approach,
however, will be to concentrate on the programming aspects using the commandline.
91
92 CHAPTER 6. MICRO ARRAY ANALYSIS
Example 1. We will start with a built-in data set called MLL.B from the
ALLMLL package. To load it and to retrieve basic information use
> library(affy)
> data(MLL.B, package = "ALLMLL")
> MLL.B
It is very useful to print the structure of the object str(MLL.B) and its slot
names.
> slotNames(MLL.B)
[1] "cdfName" "nrow" "ncol"
[4] "assayData" "phenoData" "featureData"
[7] "experimentData" "annotation" ".__classVersion__"
Additional information become available from str(MLL.B). The raw probe
intensities are available from exprs(MLL.B), which extracts the probe in-
tensities from the MLL.B object. The number of rows and columns of the
expression values of MLL.B can be obtained by the dim function.
> dim(exprs(MLL.B))
[1] 506944 20
The annotation can be extracted as follows.
> annotation(MLL.B)
[1] "hgu133b"
To print the first 10 names of the probes use
> probeNames(MLL.B)[1:10]
[1] "200000_s_at" "200000_s_at" "200000_s_at" "200000_s_at" "200000_s_at"
[6] "200000_s_at" "200000_s_at" "200000_s_at" "200000_s_at" "200000_s_at"
Note that the probe names are the same as those obtained by geneNames.
The PM and MM values are collected by the functions pm and mm. To print
the PM values of the first four out of the sixteen rows of the probe with
identifier 200000_s_at we may use the following.
6.1. PROBE DATA 93
> pm(MLL.B,"200000_s_at")[1:4,1:3]
JD-ALD009-v5-U133B.CEL JD-ALD051-v5-U133B.CEL JD-ALD052-v5-U133B.CEL
200000_s_at1 661.5 321.5 312.5
200000_s_at2 838.8 409.3 395.3
200000_s_at3 865.3 275.5 341.3
200000_s_at4 425.8 253.5 196.8
By function matplot a quick view on the variability of the data within and
between probes can be obtained.
> matplot(pm(MLL.B,"200000_s_at"),type="l", xlab="Probe No.",
+ ylab="PM Probe intensity")
From the resulting plot in Figure 6.1 it can be observed that the variability
is substantial.
Density plots of the log of the probe values can be obtained by hist(MLL.B).
From the density plot of the log of the intensity data in Figure 6.2 it can be
seen that these are quite skew to the right. The script to program such plots
2 4 6 8 10
500 1000 1500 2000
Probe No.
PM Probe intensity
Figure 6.1: Mat plot of intensity
values for a probe of MLL.B.
6 8 10 12 14
0.0 0.2 0.4 0.6 0.8 1.0 1.2
log intensity
density
Figure 6.2: Density of MLL.B data.
is quite brief.
> MAplot(MLL.B,pairs=TRUE, plot.method= "smoothScatter")
> image(MLL.B)
94 CHAPTER 6. MICRO ARRAY ANALYSIS
6.2 Preprocessing methods
From various visualization methods it is clear that preprocessing of probe
intensities is necessary for making biologically relevant conclusions. Biocon-
ductor gives facilities for various preprocessing methods. Here we will only
sketch what the main methods are and how these can be implemented. It
should be noted that the topic of optimal preprocessing currently is a field
of intense research (probably for the coming years), so that definitive recom-
mendations are not mandatory. Preprocessing consists of three major steps:
Background correction, normalization, and summarization. To obtain the
available background and pm correction methods use the following.
> bgcorrect.methods
[1] "mas" "none" "rma" "rma2"
The mas background is part of the MAS Affymetrix software and is based
on the 2% lowest probe values. RMA uses only the PM values, neglects the
MM values totally, and is based on conditional expectation and the normality
assumption of probes values. There are also a number of correction methods
available for the PM values:
> pmcorrect.methods
[1] "mas" "pmonly" "subtractmm"
The following normalization methods are available:
> normalize.methods(MLL.B)
[1] "constant" "contrasts" "invariantset" "loess"
[5] "qspline" "quantiles" "quantiles.robust"
Constant is a scaling method equivalent to linear regression on a reference
array although without intercept term. More general are the non-linear nor-
malization methods such as loess, qspline, quantiles, and robust quantiles.
Loess is a nonlinear method based on local regression of MA plots. The
methods of contrasts is based on loess regression. Quantile normalization
is an inverse transformation of the empirical distribution with respect to an
averaged sample quantile in order to impose one and the same distribution to
each array. The method qspline uses quantiles from each array and a target
array to fit a system of cubic splines. The target should be the mean (geo-
metric) or median of each probe, but could also be the name of a particular
group.

6.2. PREPROCESSING METHODS 95
The final step of preprocessing is to aggregate multiple probe intensities
into a gene expression value. The available methods are:
> express.summary.stat.methods
[1] "avgdiff" "liwong" "mas" "medianpolish" "playerout"
The first is the simplest as it is based on averaging.
There is no single best method for all preprocessing problems. It seems,
however, wise to use methods robust against outliers together with non-linear
normalization methods.
Example 1. The three pre-processing steps can be employed one after
the other by the function expresso. To combine the background correction
RMA with constant normalization and to use average differences for the
computation of gene expression values, we may use the following.
eset <- expresso(MLL.B,bgcorrect.method="rma",
normalize.method="constant",pmcorrect.method="pmonly",
summary.method="avgdiff")
Example 2. Another frequently applied preprocessing method is RMA.
It combines convolution background correction, quantile normalization, and
summarization based on multi-array model fit in a robust manner by a so-
called median polish algorithm.
> library(affy)
> data(MLL.B, package = "ALLMLL")
> eset3 <- rma(MLL.B)
Background correcting
Normalizing
Calculating Expression
> boxplot(data.frame(exprs(eset3)))
The three stages of preprocessing by rma are part of the output. Before a
box-and-whiskers plot can be constructed the expression values need to be
extracted from the object eset3.
After the foregoing it is often desirable to further preprocess the data in
order to remove patient specific means or medians. When the patient me-
dian is zero, for instance, testing for a gene to have mean expression value
96 CHAPTER 6. MICRO ARRAY ANALYSIS
different from zero becomes meaningful.
Example 3. In the sequel we shall frequently work with the ALL data
from the ALL package of Bioconductor. Here the data set is briefly introduced
(see also Section 1.1) and further processing steps are illustrated. The raw
data have been jointly normalized by RMA and are available in the form of an
exprSet object. 12625 gene expression values are available from microarrays
of 128 different persons suffering from acute lymphoblastic leukemia (ALL).
A number of interesting phenotypical co-variates are available. For instance,
the ALL$mol variable has TRUE/FALSE values for each of the 128 patients
depending on whether a reciprocal translocation occurred between the long
arms of Chromosome 9 and 22. This is casually related to chronic and acute
leukemia. One can also ask for table(ALL$BT) to obtain an overview of
the numbers of patients which are in certain phases of a disease. See also
the general help ?ALL for further information on the data or the article by
Chiaretti et al. (2004).
> data(ALL, package = "ALL")
> slotNames(ALL)
[1] "assayData" "phenoData" "featureData"
[4] "experimentData" "annotation" ".__classVersion__"
> row.names(exprs(ALL))[1:10]
[1] "1000_at" "1001_at" "1002_f_at" "1003_s_at" "1004_at" "1005_at"
[7] "1006_at" "1007_s_at" "1008_f_at" "1009_at"
By feno <- pData(ALL) phenotypical information from the patients is stored
in a data frame, which is useful for further analysis. In case the gene expres-
sion values over the patients are non-normally distributed one may want to
subtract the median and divide by the MAD. An efficient manner to do so
is to use an apply function to compute the column mad and median, and
sweep to subtract the median from each column entry and, next, to divide
each column entry by the MAD.
ALL1pp <- ALL1 <- ALL[,ALL$mol == "ALL1/AF4"]
mads <- apply(exprs(ALL1), 2, mad)
meds <- apply(exprs(ALL1), 2, median)
dat <- sweep(exprs(ALL1), 2, meds)
exprs(ALL1pp) <- sweep(dat, 2, mads, FUN="/")
6.3. GENE FILTERING 97
By this script the patients are selected with assigned molecular biology
equal to ALL1/AF4. Then ALL1 is copied in order to overwrite the expression
values in a later stage. The median and the MAD are computed per column
by the specification 2 (column index) in the apply function. Then the first
sweep function subtracts the medians from the expression values and second
divides these by the corresponding MAD. By comparing the box plots in
Figure 6.3 and 6.4 the effect of preprocessing can be observed. The medians
of the preprocessed data are equal to zero and the variation is smaller due
to the division by their MAD. Note that by box plotting a data frame a fast
overview of the distributions of columns in a data frame is obtained.
X04006 X16004 X24005 X28028 X31007
2 4 6 8 10 12 14
Figure 6.3: Boxplot of the
ALL1/AF4 patients.
X04006 X16004 X24005 X28028 X31007
−1 0 1 2 3 4
Figure 6.4: Boxplot of the
ALL1/AF4 patients after median
subtraction and MAD division.
6.3 Gene filtering
A few important methods to filter genes are illustrated here. It is wise to
keep in mind that there are statistical as well as and biological criteria for
filtering genes and that a combination of these often gives the most satisfac-
tory results. The examples stress the importance of careful thinking.

98 CHAPTER 6. MICRO ARRAY ANALYSIS
Example 1. Filtering by the coefficient of variation. A manner to filter
genes is by the coefficient of variation, which is defined as the standard
deviation divided by the absolute value of the mean: cv =σ/|µ|. If cv = 1,
then the standard deviation equals the mean, so that the experimental effect
is small relative to the precision of measurement. If, however, cv < 0.2, then
the mean is five times larger than the standard deviation, so that both the
experimental effect and the measurement precision are large. Let’s compute
the coefficient of variation per gene for the ALL1pp data of the previous
section.
> cvval <- apply(exprs(ALL1pp),1,function(x){sd(x)/abs(mean(x))})
Now using sum(cvval<0.2) yields 4751 genes with a coefficient of variation
smaller than 0.2. These genes can be selected by ALL1pp[cvval<0.2,].
Example 2. Combining several filters. It is often desired to combine
several filters. Of course it is possible to program filters completely on your
own, however, we may conveniently use the function filterfun to combine
several filters. The script in this example is useful when several functions are
to be applied to a single data set.
library("genefilter")
f1 <- function(x)(IQR(x)>0.5)
f2 <- pOverA(.25, log2(100))
f3 <- function(x) (median(2^x) > 300)
f4 <- function(x) (shapiro.test(x)$p.value > 0.05)
f5 <- function(x) (sd(x)/abs(mean(x))<0.1)
f6 <- function(x) (sqrt(10)* abs(mean(x))/sd(x) > qt(0.975,9))
ff <- filterfun(f1,f2,f3,f4,f5,f6)
library("ALL"); data(ALL)
selected <- genefilter(exprs(All[,ALL$BT=="B"]), ff)
After running this script and using sum(selected) one obtains 317 genes
that pass the combined filter. The first function returns TRUE if the in-
terquartile range is larger than 0.5, the second if 25% of the gene expression
values is larger than 6.643856, the third if the median of the expression values
taken as powers to the base two is larger than 300, the fourth if it passes the
Shapiro-Wilk normality test, the fifth if the coefficient of variation is smaller
than 0.1, and the sixth if the one-sample t-value is significant. The filter

6.3. GENE FILTERING 99
functions are combined by filterfun and the function genefilter returns
a logical vector indicating whether the gene passed all the filters or failed
at least one of them. In order to use these filter steps properly it is well to
think them through because several filters focus on similar properties. In
particular, since the IQR divided by 1.349 is a robust estimator of the stan-
dard deviation, the first filter selects genes with a certain minimal standard
deviation. With respect to the third filter note that 2x>300 is equivalent
to x > 2log(300) ≈8.228819, which is highly similar to the second filter.
Furthermore, s/|x|<0.1 is equivalent to √10|x|/s > 1/√10, so that the last
two filters are highly similar.
Example 3. Filtering by t-test and normality. One may also want to
select genes with respect to p-values of a two-sample t-test over B-cell ALL
versus T-cell ALL. This can be combined with a normality test in the sense
that only those genes are filtered which pass the Shapiro-Wilk normality test.
The latter will be applied separately for the B-cell ALL patients and for the
T-cell ALL patients. For this we write a function that will be used twice.
First, however, we create a logical factor patientB indicating patients with
B-cell ALL (TRUE) and with T-cell ALL (FALSE). The filter defined selects
genes that have their p-value from the Welch two-sample t-test smaller than
the significance level 0.05. A logical variable named selected is defined
which attains TRUE only if sel1,sel2, as well as sel3 have the value
TRUE.
library("genefilter");library("ALL"); data(ALL)
patientB <- factor(ALL$BT %in% c("B","B1","B2","B3","B4"))
f1 <- function(x) (shapiro.test(x)$p.value > 0.05)
f2 <- function(x) (t.test(x ~ patientB)$p.value < 0.05)
sel1 <- genefilter(exprs(ALL[,patientB==TRUE]), filterfun(f1))
sel2 <- genefilter(exprs(ALL[,patientB==FALSE]), filterfun(f1))
sel3 <- genefilter(exprs(ALL), filterfun(f2))
selected <- sel1 & sel2 & sel3
ALLs <- ALL[selected,]
This gives 1817 genes which pass the three filters. For these genes it
holds that the expression values for B-cell ALL patients as well as for T-cell
ALL patients are normally distributed (in the sense of non-rejection). A
fundamental manner to visualize how the genes are divided among filters is
100 CHAPTER 6. MICRO ARRAY ANALYSIS
by construction of a Venn diagram. This can conveniently be done by using
functions from the limma package (Smyth, 2005).
library(limma)
x <- matrix(as.integer(c(sel1,sel2,sel3)),ncol = 3,byrow=FALSE)
colnames(x) <- c("sel1","sel2","sel3")
vc <- vennCounts(x, include="both")
vennDiagram(vc)
From the resulting Venn diagram in Figure 6.5 it can be seen that 1817 genes
pass all three filters, 1780 genes pass none, 3406 genes pass the normality
tests but not the t-test filter, etc.
sel1 sel2
sel3 1780
920
2151
1366
826
359
3406
1817
Figure 6.5: Venn diagram of se-
leced ALL genes.
X04006 X16004 X24005 X28028 X31007
−1 0 1 2 3 4
Figure 6.6: Boxplot of the
ALL1/AF4 patients after median
subtraction and MAD division.
6.4 Applications of linear models
The limma package is frequently used for analyzing microarray data by linear
models, such as ANOVA.

6.4. APPLICATIONS OF LINEAR MODELS 101
Example 1. Analysis of variance. We select patients with B-cell leukemia in
a beginning stage B and in more progressive stages B1 and B2. The type of
analysis is specified by using a factor that defines the model (design) matrix.
Then the linear model is fitted to the data and an empirical Bayes procedure
is used to adapt the gene specific variances with a global variance estimator
(Smyth, 2004)2.
library("ALL"); library("limma");
data(ALL, package = "ALL")
allB <- ALL[,which(ALL$BT %in% c("B","B1","B2"))]
design.ma <- model.matrix(~ 0 + factor(allB$BT))
colnames(design.ma) <- c("B","B1","B2")
fit <- lmFit(allB, design.ma)
fit <- eBayes(fit)
> toptab <- topTable(fit, coef=2,5,adjust.method="fdr")
> print(toptab[,1:5],digits=4)
ID logFC AveExpr t P.Value
12586 AFFX-hum_alu_at 13.42 13.50 326.0 3.165e-99
2488 32466_at 12.68 12.70 306.3 1.333e-97
2773 32748_at 12.08 12.11 296.3 9.771e-97
5328 35278_at 12.44 12.45 295.5 1.146e-96
4636 34593_g_at 12.64 12.58 278.0 4.431e-95
By topTable the five genes are selected with the smallest p-values adjusted
for the false discovery rate. Let’s call the mean of the Bpatients µ, that of
B1 µ1, and that of B2 µ2. In the current case we are not so much interested
in the hypothesis H0:µ−µ2, because this is the difference between Stage
0 and Stage 3. Rather, we are interested in the hypothesis H0:µ−µ1and
H0:µ1−µ2. Such a specific hypothesis can be tested by using a contrast
matrix, which can be specified as follows.
> cont.ma <- makeContrasts(B-B1,B1-B2, levels=factor(allB$BT))
> cont.ma
Contrasts
Levels B - B1 B1 - B2
B10
B1 -1 1
B2 0 -1
2To obtain the appropriate number of levels we make a factor of ALLB$BT.

102 CHAPTER 6. MICRO ARRAY ANALYSIS
Observe that the contrast matrix specifies the difference between the levels
B and B1 as well as between B1 and B2. It can be implemented as follows.
fit1 <- contrasts.fit(fit, cont.ma)
fit1 <- eBayes(fit1)
toptabcon <- topTable(fit, coef=2,5,adjust.method="fdr")
print(toptabcon[,1:5],digits=4)
> toptabcon <- topTable(fit1, coef=2,5,adjust.method="fdr")
> print(toptabcon[,1:5],digits=4)
ID logFC AveExpr t P.Value
3389 33358_at 1.4890 5.260 7.374 5.737e-10
419 1389_at -1.7852 9.262 -7.081 1.816e-09
1016 1914_at 2.0976 4.939 7.019 2.315e-09
6939 36873_at 1.8646 4.303 6.426 2.361e-08
7542 37471_at 0.8701 6.551 6.106 8.161e-08
Here, we have applied a method called “false discovery rate” (fdr) which in-
creases the p-values somewhat in order to reduce the number false positives.
The number of genes requested equals 5.
A very convenient manner to summarize, collect, and communicate vari-
ous types of results is in the form of an HTML file.
Example 2. Summarizing output in HTML format. It is often desired to
combine the typical output from a function like topTable with that of an
HTML output page containing various types of information. To illustrate
this we proceed with the object toptabcon of the previous example.
library("annaffy");library("hgu95av2.db")
anntable <- aafTableAnn(as.character(toptabcon$ID), "hgu95av2.db", aaf.handler())
saveHTML(anntable, "ALLB123.html", title = "B-cell 012 ALL")
By the function aafTableAnn various types of information are gathered from
the output topTable of the estimated linear model, the annotation package,
and the aaf.handler functionality. The information collected contains the
following: Probe, Symbol, Description, Function, Chromosome, Chromo-
some Location, GenBank, LocusLink, Cytoband, UniGene, PubMed, Gene
Ontology, and Pathway. The resulting anntable is saved in HTML format
in the working directory or the Desktop. It contains a wealth of information

6.4. APPLICATIONS OF LINEAR MODELS 103
on e.g. Chromosome location, KEGG mappings, summaries from Pubmed
articles, etc.
Example 3. Using basic R functions. It is also possible to summarize
results in an HTML table on the basis of p-values from e.g. analysis of
variance (ANOVA). That is, the selected genes can directly be used as input
for aafTableAnn.
library("multtest"); library("annaffy"); library("hgu95av2.db")
library("ALL"); data(ALL, package = "ALL")
ALLB <- ALL[,which(ALL$BT %in% c("B","B1","B2"))]
panova <- apply(exprs(ALLB), 1, function(x) anova(lm(x ~ ALLB$BT))$Pr[1])
genenames <- featureNames(ALLB)[panova<0.000001]
atab <- aafTableAnn(genenames, "hgu95av2.db", aaf.handler()[c(1:3,8:9,11:13)])
saveHTML(atab, file="ANOVAonB-cellGroups.html")
hgu95av2.db is a meta data annotation package connecting the requested
information by the call to aaf.handler. The meaning of the columns can
be obtained from the help page of the function. The resulting table is saved
as an HTML file in the working directory (getwd()) or desktop. In a similar
manner the p-values from the Kruskal-Wallis test can be used to select genes.
Bioconductor has a useful facility to download publicly available microar-
ray data sets from NCBI.
Example 4. Analyzing public available data. The GDS1365 data con-
tain primed macrophage response to IFN-gamma restimulation after different
time periods. The purpose is to gain insight into the influence of IFN-gamma
priming on IFN-gamma induced transcriptional responses. Among the phe-
notypical covariates of the data there is a factor time with levels 0, 3 and 24
hours and a factor protocol with the levels ”IFN-gamma primed” and ”un-
primed”, which can be extracted by the function pData. Since researchers
are often interested in the interaction between factors, we shall select genes
with a significant interaction effect.
library(GEOquery); library(limma); library(hgu95av2.db);library(annaffy)
gds <- getGEO("GDS1365")
eset <- GDS2eSet(gds,do.log2=T)

104 CHAPTER 6. MICRO ARRAY ANALYSIS
prot <- pData(eset)$protocol
time <- pData(eset)$time
pval <- apply(exprs(eset)[1:12625,], 1,
function(x) anova(lm(x ~ prot * time))$Pr[1:3])
pvalt <- data.frame(t(pval))
colnames(pvalt) <- c("meffprot","mefftime","interaction")
genenames <- featureNames(eset)[pvalt$meffprot< 0.01 &
pvalt$mefftime < 0.01 & pvalt$interaction < 0.01]
atab <- aafTableAnn(genenames,"hgu95av2.db",aaf.handler()[c(1:3,8:9,11:13)])
saveHTML(atab, file="Two-way ANOVA protocol by time.html")
By getGEO the data are downloaded to the disk and next these can be loaded
into the R system. By GDS2eSet these are transformed to an expression set
so that these can be analyzed statistically. The function pData extracts the
factors from the expression set eset. The function anova extracts the p-
value of the interaction effect from the estimated linear model. We restrict
the analysis to the first 12625 rows because the additional ones contain not
available values. The resulting html file seems to contain may interesting
genes.
6.5 Searching an annotation package
Detailed information on microarray experiments is stored in an annotation
package.
> library("ALL"); data(ALL)
> annotation(ALL)
[1] "hgu95av2"
Hence, the annotation package we need is hgu95av2.db. Let’s load it and
obtain an overview of its functionality.
> library(hgu95av2.db)
> ls("package:hgu95av2.db")
[1] "hgu95av2" "hgu95av2_dbconn" "hgu95av2_dbfile"
[4] "hgu95av2_dbInfo" "hgu95av2_dbschema" "hgu95av2ACCNUM"
[7] "hgu95av2ALIAS2PROBE" "hgu95av2CHR" "hgu95av2CHRLENGTHS"
[10] "hgu95av2CHRLOC" "hgu95av2CHRLOCEND" "hgu95av2ENSEMBL"
6.5. SEARCHING AN ANNOTATION PACKAGE 105
[13] "hgu95av2ENSEMBL2PROBE" "hgu95av2ENTREZID" "hgu95av2ENZYME"
[16] "hgu95av2ENZYME2PROBE" "hgu95av2GENENAME" "hgu95av2GO"
[19] "hgu95av2GO2ALLPROBES" "hgu95av2GO2PROBE" "hgu95av2MAP"
[22] "hgu95av2MAPCOUNTS" "hgu95av2OMIM" "hgu95av2ORGANISM"
[25] "hgu95av2PATH" "hgu95av2PATH2PROBE" "hgu95av2PFAM"
[28] "hgu95av2PMID" "hgu95av2PMID2PROBE" "hgu95av2PROSITE"
[31] "hgu95av2REFSEQ" "hgu95av2SYMBOL" "hgu95av2UNIGENE"
[34] "hgu95av2UNIPROT"
The annotation package contains environments with different types of infor-
mation. An easy manner to make the content of an environment available is
by converting it into a list and to print part of it to the screen.
> ChrNrOfProbe <- as.list(hgu95av2CHR)
> ChrNrOfProbe[1]
$‘1000_at‘
[1] "16"
We recognize the manufacturers identifier of genes and the corresponding
chromosome. Asking information by ?hgu95av2CHR reveals that it is an
environment (hash table) which provides mappings between identifiers and
chromosomes. From these we obtain various types of information on the
basis of the manufacturer’s identifier such as "1389_at". Below we obtain,
respectively, the GenBank accession number, the Entrez Gene identifier, the
gene abbreviation, gene name, brief summaries of functions of the gene prod-
ucts, and the UniGene identifier. For this we use the get function in order
to search an environment for a name.
> get("1389_at", env = hgu95av2ACCNUM)
[1] "J03779"
> get("1389_at", env = hgu95av2ENTREZID)
[1] 4311
> get("1389_at", env = hgu95av2SYMBOL)
[1] "MME"
> get("1389_at", env = hgu95av2GENENAME)
[1] "membrane metallo-endopeptidase (neutral endopeptidase,
enkephalinase, CALLA, CD10)"
> get("1389_at", env = hgu95av2SUMFUNC)
[1] NA
106 CHAPTER 6. MICRO ARRAY ANALYSIS
> get("1389_at", env = hgu95av2UNIGENE)
[1] "Hs.307734"
Let’s use the GenBank accession number to search its nucleotide data base.
> library(annotate)
> genbank("J03779",disp="browser")
From this we obtain the corresponding GI:179833 number, which can be used
to obtain a complete XML document.
> genbank(1430782,disp="data",type="uid")
Obviously, probes correspond to genes and frequently we are interested in
their chromosome location, and, specifically, in starting position(s).
> get("1389_at", env = hgu95av2CHRLOC)
333
156280152 156280327 156280748
Its cytoband location can also be obtained.
> get("1389_at", env = hgu95av2MAP)
[1] "3q25.1-q25.2"
Hence, we see that the gene is on Chromosome 3 at q arm band 25 sub-
band 1 and 2. In case we have a LocusLink ID, e.g. 4121, available the
corresponding GO terms can be obtained and stored in a list.
ll1<-GOENTREZID2GO[["4121"]]
6.6 Using annotation to search literature
Given the manufactures probe identifier it is possible to search literature by
collecting Pubmed ID’s and to use these to collect relevant articles.
> library(hgu95av2.db);library(annotate); library(ALL); data(ALL)
> pmid <- get("1389_at",env=hgu95av2PMID)
> pubmed(pmid,disp="browser")
Another possibility is to collect a list containing PubMed ID, authors, ab-
stract text, title, journal, and publication date.
6.7. SEARCHING GO NUMBERS AND EVIDENCE 107
> absts <- pm.getabst("1389_at", "hgu95av2")
> pm.titles(absts)
The list can obviously be searched for regular expressions.
ne <- pm.abstGrep("neutral endopeptidase",absts[[1]])
Another possibility is to construct an HTML table with the titles.
> pmAbst2HTML(absts[[1]],filename="pmon1389_at.html")
6.7 Searching GO numbers and evidence
By the phrase “ontology” we mean a structured language about some con-
ceptual domain. The gene ontology consortium defines three ontologies: A
Molecular Function (MF) describes a phenomenon at the biochemical level
such as “enzyme”, “transporter”, or “ligand”. A Biological Process (BP)
may coordinate various related molecular functions such as “DNA replica-
tion” or “signal transduction”. A Cellular Component (CC) is a unit within
a part of the cell such as “chromosome”, “nucleus”, or “ribosome”.
Each term is identified by a unique GO number. To find GO numbers
and their dependencies we use get to extract a list from the annotation files
hgu95av2GO for example. From the latter we extract a list and use an apply
type of function to extract another list containing GO identification numbers.
> go1389 <- get("1389_at", env = hgu95av2GO)
> idl <- lapply(go1389,function(x) x$GOID)
> idl[[1]]
[1] "GO:0006508"
The list idl contains 8 members of which only the first is printed to the
screen. By changing GOID into Ontology more specific information pertaining
to ontology is extracted. From the annotate package we may now select the
GO numbers which are related to a biological process.
> library(annotate)
> getOntology(go1389,"BP")
[1] "GO:0006508" "GO:0007267"
108 CHAPTER 6. MICRO ARRAY ANALYSIS
There are various types of evidence such as: inferred from genetic interaction
(IGI), inferred from electronic annotation (IEA), traceable author statement
(TAS), etc. Per GO identifier the type of evidence can be obtained.
> getEvidence(go1389)
GO:0004245 GO:0005886 GO:0005887 GO:0006508 GO:0007267 GO:0008237 GO:0008270
"IEA" "TAS" "TAS" "TAS" "TAS" "TAS" "IEA"
GO:0046872
"IEA"
When we now want to select the GO numbers with evidence of a traceable
author statement we can use the subset function to create a list.
go1389TAS <- subset(go1389,getEvidence(go1389)=="TAS")
A manner to extract information from this list is by using an apply type of
function.
> sapply(go1389TAS,function(x) x$GOID)
> sapply(go1389TAS,function(x) x$Evidence)
> sapply(go1389TAS,function(x) x$Ontology)
We shall use this list in the below.
6.8 GO parents and children
The term “transmembrane receptor protein-tyrosine kinase” is more specific
and therefore a ’child’ of the more general term parent term “transmembrane
receptor” (Gentleman, et. al, 2005).
Example 1. Collecting GO information. There are functions to obtain
parents and children from a GO identifier.
> GOMFPARENTS$"GO:0003700"
isa isa
"GO:0003677" "GO:0030528"
> GOMFCHILDREN$"GO:0003700"
isa
"GO:0003705"

6.9. GENE FILTERING BY A BIOLOGICAL TERM 109
In case of a list of GO identifiers you may want to collect the ontology,
parents, and children identifiers in a vector.
go1389 <- get("1389_at", env = hgu95av2GO)
gonr <- getOntology(go1389, "BP")
gP <- getGOParents(gonr)
gC <- getGOChildren(gonr)
gPC <- c(gonr,gP,gC)
pa <- sapply(gP,function(x) x$Parents)
ch <- sapply(gC,function(x) x$Children)
gonrc <- c(gonr,unlist(pa),unlist(ch))
Example 2. Probe selection by GO. A research strategy may be to start
with a probe number, to find the GO identifiers of the biological process, to
obtains its parents, and next to transform these to probes.
library(GO); library(annotate); library("ALL"); data(ALL)
go1389 <- get("1389_at", env = hgu95av2GO)
gonr <- getOntology(go1389, "BP")
gP <- getGOParents(gonr)
pa <- sapply(gP,function(x) x$Parents)
probes <- mget(pa,hgu95av2GO2ALLPROBES)
probeNames <- unlist(probes)
ALLpr <- ALL[probeNames,]
> dim(exprs(ALLpr))
[1] 7745 128
Indeed, you may end up with many genes, useful for further analysis.
6.9 Gene filtering by a biological term
An application of working with GO numbers is to filter for genes which are
related to a biological term.
Example 1. Filter gene by a term. From a biological point of view
it is most interesting to select genes which are related to a certain biolog-
ical process to be specified by a term such as ”transcriptional repression”.

110 CHAPTER 6. MICRO ARRAY ANALYSIS
We combine this with the previous filter. For this we need the annota-
tion package used in the stage of data collection. This can be obtained by
annotation(ALL). First we define a function (Gentleman, et al., 2005, p.
123) to collect appropriate GO numbers from the environment GOTERM.
library("GO"); library("annotate"); library("hgu95av2.db")
GOTerm2Tag <- function(term) {
GTL <- eapply(GOTERM, function(x) {grep(term, x@Term, value=TRUE)})
Gl <- sapply(GTL, length)
names(GTL[Gl>0])
}
> GOTerm2Tag("transcriptional repressor")
[1] "GO:0016564" "GO:0016565" "GO:0016566" "GO:0017053"
The functions eapply and sapply search an environment like GOTERM by
grep for matches of a specified term. A precaution is taken to select only
those names which are not empty. This gives the GO terms which can now
be translated to probe of the ALLs data.
tran1 <- hgu95av2GO2ALLPROBES$"GO:0016564"
tran2 <- hgu95av2GO2ALLPROBES$"GO:0016566"
tran3 <- hgu95av2GO2ALLPROBES$"GO:0017053"
tran <- c(tran1,tran2,tran3)
inboth <- tran %in% row.names(exprs(ALLs))
ALLtran <- ALLs[tran[inboth],]
The GO translated probe names are intersected with the row names of the
data giving the logical variable inboth. The variable tran[inboth] gives
the ids by which genes can be selected. Next, gene ids for which inboth
equals TRUE are selected and the corresponding data are collected in the data
frame ALLtran. More information can be obtained by GOTERM$"GO:0016564.
By dim(exprs(ALLtran)) it can be observed that 26 genes which passed the
normality filter are related to ”transcriptional repression”.
6.10 Significance per chromosome
After a statistical analysis to filter and order genes it is often quite useful to
do post analysis on the results. In particular, after collecting p-values from
6.10. SIGNIFICANCE PER CHROMOSOME 111
at-test one may wonder whether genes with significant p-values occur more
often within a certain chromosome. To test for such over or under represen-
tation the Fisher test is very useful (see Section 4.1.7).
Example 1. On the expression values of the ALL data we perform a two
sample t-test using the patient group for which remission was achieved and
for which it was not achieved. Per chromosome it can be tested whether the
odds ratio differs from 1 or, equivalently, whether there is independence. The
data for the test consist of the number of significant probes on Chromosome
19, the number of non-significant probes on Chromosome 19, the number of
remaining significant probes, and the number of remaining non-significant
probes.
> library("ALL"); data(ALL); library("hgu95av2.db")
> rawp <- apply(exprs(ALL), 1, function(x) t.test(x ~ ALL$remission)$p.value)
> xx <- as.list(hgu95av2CHR)
> AffimIDChr <- names(xx[xx=="19"])
> names(rawp) <- featureNames(ALL)
> f <- matrix(NA,2,2)
> f[1,1] <- sum(rawp[AffimIDChr]<0.05); f[1,2] <- sum(rawp[AffimIDChr]>0.05)
> f[2,1] <- sum(rawp<0.05) - f[1,1] ; f[2,2] <- sum(rawp>0.05) - f[1,2]
> print(f)
[,1] [,2]
[1,] 106 638
[2,] 832 11049
> fisher.test(f)
Fisher’s Exact Test for Count Data
data: f
p-value = 4.332e-11
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
1.757949 2.748559
sample estimates:
odds ratio
2.206211

112 CHAPTER 6. MICRO ARRAY ANALYSIS
> chisq.test(f)
Pearson’s Chi-squared test with Yates’ continuity correction
data: f
X-squared = 52.3803, df = 1, p-value = 4.573e-13
The number of significant probes is larger for Chromosome 19 resulting in an
odds ratio of 2.2. The hypothesis of independence is rejected by both tests.
6.11 Overview and concluding remarks
Many examples are given on using analysis of variance or T-tests for select-
ing genes with large experimental effects on different patient groups. The
above statistical methods seem to cover the majority of problems occurring
in practice.
6.12 Exercises
1. Gene filtering on normality per group of B-cell ALL patients.
(a) Use genefilter to program the Shapiro normality test separately
for each gene of the groups ”B1”,”B2”,”B3”,”B4”.
(b) How many pass the filter?
(c) Compute a Venn diagram for group ”B2”, ”B3”, and ”B4”, plot
it, and give a correct interpretation for each number.
2. Analysis of gene expressions of B-cell ALL patients using Limma.
(a) Construct a data frame containing the expression values for the
B-cell ALL patients in stage B, B1, B2, B3, B4 from the ALL data.
(b) Construct the design matrix and an appropriate contrast matrix.
(c) Compute the twenty best genes by topTable.
(d) Collect information on the twenty best gene s in an HTML page.
6.12. EXERCISES 113
3. Finding a row number. Use grep to find the row number of gene
1389_at. Hint: Use row.names or featureNames.
4. Remission (genezing) from acute lymphocytic leukemia (ALL). With
respect to the ALL data from the ALL library there is a phenotypical vari-
able called remission indicating complete remission CR or refractory
REF meaning improvement from disease and less or no improvement,
respectively.
(a) How many persons are classified as CR and REF, respectively?
Hint: Use pData to extract a data frame with phenotypical data.
(b) Program the two-sample t-test not assuming equal variances to
select genes with p-values smaller than 0.001. Hint: You may
have to select the persons with values on remission, excluding not
available data.
(c) Collect and give the manufactures probe names of the genes with
p-values smaller than 0.001.
(d) Use the probe names to find the corresponding gene names. Give
the code.
(e) Is the famous protein p53 is among them?
(f) How many unique gene names are there?
5. Remission achieved. For the ALL data from its ALL library the patients
are checked for achieving remission. The variable ALL$CR has values CR
(became healthy) and REF (did not respond to therapy; remain ill).
(a) Construct a separate data frame consisting of only those gene
expression values from patients that have values CR or REF.
(b) How many genes have a p-value smaller than 0.0001 from the two-
sample T-test not assuming equal variances? Hint: Use the apply
functionality to program the test.
(c) Give the affymetrix names (symbols) of the genes the pass the
selection criterion of p-value smaller than 0.0001.
(d) Use the latter to find the biological names.
(e) How many oncogenes are there is total?
114 CHAPTER 6. MICRO ARRAY ANALYSIS
(f) Do the Fisher test on the number of oncogenes out of the total
versus the number of significant oncogenes out of the selected.
6. Gene filtering of ALL data. The data are in the library called ”ALL”.
The persons with T-cell leukemia which are in stage T2 and T3 can
be selected by the variable ALL$BT. You may use the function ”table”
to find the frequencies of the patient types and leukemia stages. To
answer the questions below functions from the library ”genefilter” are
helpful.
(a) Program a gene filter step separately for T2 and T3 patients such
that only those genes pass which are normally distributed.
(b) Program a second filter step which passes only those genes with a
significant p-value from the two sample T-test.
(c) How many genes pass all filter steps?
(d) How many genes pass normality?
7. Stages of B-cell ALL in the ALL data. Use the limma package to answer
the questions below.
(a) Select the persons with T-cell leukemia which are in stage B1, B2,
B3, and B4.
(b) What type of contrast matrix would you like to suggest in this
situation? Give its code.
(c) Perform analysis of variance to test the hypothesis of equal pop-
ulation means. Use the Benjamini & Hochberg (1995) (”BH”)
adjustment method for the false discovery rate and topTable to
report the five best genes.
(d) For how many genes is the null-hypothesis to be rejected?
8. Analysis of public micro array data on rheumatoid arthritis.
(a) Download GDS486 and transform it into eset form. Here we meet
a missing data problem. A manner to solve it is as follows. Use
the function function(x) sum(is.na(x)) in apply on the rows
to count the number of missing values per row. Select the rows
without missing value to perform a two-sample t-test with the
6.12. EXERCISES 115
groups in cell.line. Overwrite the vector with the number of
missing values with the p-values in a suitable manner.
(b) Download GDS711 and repeat the above using ANOVA p-values
with the covariate disease.state to indicate the groups.
(c) Download GDS2126 and repeat the above using ANOVA p-values
with the covariate disease.state to indicate the groups.
(d) Compute the symbols of the twenty best genes in the sense of
having smallest summed p-values.
(e) Summarize information of the twenty best genes in an HTML
table. Does p53 play a role in the path way of the best gene?
9. Analysis of genes from a GO search.
(a) Select the patients on the covariate mol.biol with values ALL1/AF4,
BCR/ABL, and NEG.
(b) Collect the ANOVA p-values with contrast between NEG and ALL1/AF4,
and between NEG and BCR/ABL. Report the number of significant
affy ID’s and the total. Hint: Re-order the columns into ”NEG”,
”ALL1/AF4”, and ”BCR/ABL”.
(c) Find the GO ID’s refereing to the term ”protein-tyrosine kinase”
since it mediates many steps due to BCR/ABL translocation.
(d) Select the affy ID’s corresponding to the GO ID’s and report its
number and the number of significant genes.
(e) Perform Fisher exact to test the odds ratio equal to one hypoth-
esis.
116 CHAPTER 6. MICRO ARRAY ANALYSIS
Chapter 7
Cluster Analysis and Trees
Given the expression values of several genes, a problem which often arises
is to find genes which are similar or close. Genes with expressions in small
distance may have similar functions and may be potentially interesting for
further research. In order to discover genes which form a group there are sev-
eral methods developed called cluster analysis. These methods are based on
adistance function and an algorithm to join data points to clusters. The so-
called single linkage cluster analysis is intuitively appealing and often applied
in bioinformatics. By this method several clusters of genes can be discov-
ered without specifying the number of clusters on beforehand. The latter is
necessary for another method called k-means cluster analysis. Each analysis
produces a tree which represents similar genes as close leaves and dissimilar
ones on different edges.
An other measure to investigate similarity or dependency of pairs of gene
expressions is the correlation coefficient. Various examples of applications
will be given. It prepares the way to searching a data set for directions of
large variance. That is, since gene expression data sets tend to be large,
it is of importance to have a method available which discovers important
“directions” in the data. A frequently used method to find such directions is
that by principal components analysis. Its basic properties will be explained
as well as how it can be applied in combination with cluster analysis.
In applications where it is difficult to formulate distributional assumptions
of the statistic it may still be of importance to construct a confidence interval.
It will be illustrated by several examples how the bootstrap can be applied to
construct 95% confidence intervals. Many examples are given to clarify the
application of cluster analysis and principal components analysis.
117
118 CHAPTER 7. CLUSTER ANALYSIS AND TREES
7.1 Distance
The concept of distance plays a crucial role in all types of cluster analysis.
For real numbers aand badistance function dis defined as the absolute
value of their difference
d(a, b) = |a−b|=p(a−b)2.
The properties of a distance function should be in line with our intuition.
That is, if a=b, then d(a, a) = 0 and if a6=b, then d(a, b)>0. Hence,
the distance measure should be definitive in the sense that d(a, b) = 0 if and
only if a=b. Since the square is symmetric, it follows that
d(a, b) = |a−b|=p(a−b)2=p(b−a)2=|b−a|=d(b, a).
In other words, d(a, b) = d(b, a), the distance between aand bequals that
between band a. Furthermore, it holds for all points cbetween aand bthat
d(a, b) = d(a, c) + d(c, b). For all points cnot between aand b, it follows that
d(a, b)< d(a, c) + d(c, b). The latter two notions can be summarized by the
so-called triangle inequality. That is, for all real cit holds that
d(a, b)≤d(a, c) + d(c, b).
Directly going from ato bis shorter than via c. Finally, the distance between
two points aand bshould increase as these move further apart.
Example 1. Let a= 1 and b= 3. Then, obviously, the distance d(1,3) = 2.
The number c= 2 is between aand b, so that d(1,3) = 2 = 1 + 1 =
d(1,2) + d(2,3) and the triangle inequality becomes an equality.
For the situation where gene expression values for several patients are
available, it is of importance to define a distance for vectors of gene expres-
sions such as a= (a1,··· , an) and b= (b1,··· , bn). We shall concentrate
mainly on the Euclidian distance, which is defined as the root of the sum of
the squared differences
d(a,b) = v
u
u
t
n
X
i=1
(ai−bi)2.
7.1. DISTANCE 119
The distance measure satisfies the above properties of definiteness, symme-
try, and triangle inequality. Although many other, but often highly similar,
distance functions are available we shall mainly concentrate on Euclidian dis-
tance because it is applied most frequently in bioinformatics.
Example 2. Suppose that a= (a1, a2) = (1,1) and b= (b1, b2) = (4,5).
Then
d(a,b) = p(a1−b1)2+ (a2−b2)2=p(1 −4)2+ (1 −5)2=√9 + 16 = 5.
Since the differences are squared it is immediate that d(a,b) = d(b,a), the
distance from ato bequals that from bto a. For c= (c1, c2) = (2,2) we
have that d(a,c) = √2, d(b,c) = √22+ 32=√13. Hence,
d(a,b) = 5 <√2 + √13 = d(a,c) + d(b,c),
so that the triangle inequality is strict. This is in line with our intuitive idea
that the road directly from ato bis shorter than from ato bvia c.
Example 3. To compute the Euclidian distance between two vectors one
may use the following.
> a <- c(1,1); b <- c(4,5)
> sqrt(sum((a-b)^2))
[1] 5
Example 4. Distances between Cyclin gene expressions. By the build-in-
function dist the Euclidian distance between two vectors of gene expression
values can be computed. To select genes related to the biological term ”Cy-
clin” and to compute the Euclidian distance between the gene expression
values of the Golub et al. (1999) data, we may use the following.
> library(multtest); data(golub)
> index <- grep("Cyclin",golub.gnames[,2])
> golub.gnames[index,2]
[1] "CCND2 Cyclin D2"
[2] "CDK2 Cyclin-dependent kinase 2"
[3] "CCND3 Cyclin D3"
[4] "CDKN1A Cyclin-dependent kinase inhibitor 1A (p21, Cip1)"
[5] "CCNH Cyclin H"

120 CHAPTER 7. CLUSTER ANALYSIS AND TREES
[6] "Cyclin-dependent kinase 4 (CDK4) gene"
[7] "Cyclin G2 mRNA"
[8] "Cyclin A1 mRNA"
[9] "Cyclin-selective ubiquitin carrier protein mRNA"
[10] "CDK6 Cyclin-dependent kinase 6"
[11] "Cyclin G1 mRNA"
[12] "CCNF Cyclin F"
> dist.cyclin <- dist(golub[index,],method="euclidian")
> diam <- as.matrix(dist.cyclin)
> rownames(diam) <- colnames(diam) <- golub.gnames[index,3]
> diam[1:5,1:5]
D13639_at M68520_at M92287_at U09579_at U11791_at
D13639_at 0.000000 8.821806 11.55349 10.056814 8.669112
M68520_at 8.821806 0.000000 11.70156 5.931260 2.934802
M92287_at 11.553494 11.701562 0.00000 11.991333 11.900558
U09579_at 10.056814 5.931260 11.99133 0.000000 5.698232
U11791_at 8.669112 2.934802 11.90056 5.698232 0.000000
By the grep function the order numbers of the genes with the phrase ”Cy-
clin” in their names are assigned to the vector called index. The euclidian
distances are assigned to the matrix called diam. Its diagonal has distances
between identical genes which are, of course, zero. The distance between
the first (CCND2 Cyclin D2) and the third (CCND3 Cyclin D3) is relatively
small, which is in line with the fact the these genes have related functions.
Note, however, that there are genes with in smaller distance.
Example 5. Finding the ten closest genes to a given one. After selecting
certain genes it often happens that one wants to find genes which are close
to the selected ones. This can be done with the genefinder functionality
by specifying either an index or a name (consistent with the geneNames of
the exprSet). To find genes from the ALL data (Chiaretti et al., 2004) close
to the MME expression values of the probe with identifier 1389_at, we may
use the following.
library("genefilter"); library("ALL"); data(ALL)
closeto1389_at <- genefinder(ALL, "1389_at", 10, method = "euc")
closeto1389_at[[1]]$indices
round(closeto1389_at[[1]]$dists,1)
featureNames(ALL)[closeto1389_at[[1]]$indices]

7.2. TWO TYPES OF CLUSTER ANALYSIS 121
The function genefilter produces a list from which the selected row num-
bers can be extracted as well as the probe names can be found.1If desired,
these can be used for further analysis. From the output it can be observed
that the gene expressions of row 2653 with probe identifier 32629_f_at has
the smallest distance (12.6) to those of 1389_at.
7.2 Two types of Cluster Analysis
Some important types of cluster analysis are defined and illustrated here.
7.2.1 Single Linkage
A cluster Iis simply a set of data points I={xi}, where xiis the i-th vector
with gene expressions. In single linkage cluster analysis the distance between
clusters Iand Jis defined as the smallest distance over all pairs of points of
the two clusters:
d(I, J) = min
i,j {d(xi,xj,) : xiin Iand xjin J}.
Hence, the distance between the two clusters is the same as that of the nearest
neighbors. The algorithm of single linkage cluster analysis starts with creat-
ing as many clusters as data points. Next, the nearest two are determined
and these are merged into one cluster. Then the next two nearest clusters
are determined and merged into one cluster. This process continuous until
all points belong to one cluster.
Example 1. An explanatory example. To illustrate single linkage cluster
analysis suppose we the following five gene expressions g1= (1,1), g2=
(1,1.2), g3= (3,2), g4= (3,2.2), and g5= (5,5), from two persons. The
expressions for each gene can be seen as coordinates on two perpendicular
axis p1and p2. The script below produces Figure 7.1 which illustrates the
idea. It computes the the distances between the genes and performs a single
linkage cluster analysis.
names <- list(c("g1","g2","g3","g4","g5"),c("p1","p2"))
1For information on lists, see Chapter 6 of the manual ”An Introduction to R”.
122 CHAPTER 7. CLUSTER ANALYSIS AND TREES
1 2 3 4 5
1 2 3 4 5
a1
a2
x1
x2
x3
x4
x5
Figure 7.1: Plot of five points to
be clustered.
x5
x1
x2
x3
x4
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5
Cluster Dendrogram
hclust (*, "single")
dist(sl.clus.dat, method = "euclidian")
Height
Figure 7.2: Tree of single linkage
cluster analysis.
sl.clus.dat <- matrix(c(1,1,1,1.1,3,2,3,2.3,5,5),ncol = 2,
byrow = TRUE,dimnames = names)
plot(sl.clus.dat,type="n", xlim=c(0,6), ylim=c(0,6))
text(sl.clus.dat,labels=row.names(sl.clus.dat))
> print(dist(sl.clus.dat,method="euclidian"),digits=3)
x1 x2 x3 x4
x2 0.10
x3 2.24 2.19
x4 2.39 2.33 0.30
x5 5.66 5.59 3.61 3.36
> sl.out<-hclust(dist(sl.clus.dat,method="euclidian"),method="single")
> plot(sl.out)
At the start each data point is seen as a separate cluster. Then the nearest
two points (genes) from the Euclidian distance matrix are g1and g2, having
d(g1,g2)=0.10. These two data points are merged into one cluster, say
I={g1,g2}. In Figure 7.2 this is illustrated by the horizontal line at height
0.10 in the tree. The other three data points g3,g4,g5are seen as three
different clusters. Next, the minimal distance between clusters can be read
from the Euclidian distance matrix. Since the smallest is d(g3,g4)=0.30,
the new cluster J={g3,g4}, corresponding to the horizontal line at height
7.2. TWO TYPES OF CLUSTER ANALYSIS 123
0.30. Now there are three clusters, I,J, and K={x5}. From the Euclidian
distance matrix, it can be observed that the distance between cluster Iand
Jis 2.19, see the corresponding horizontal line at this height. Hence, the
cluster Iand Jare merged into one. Finally, the distance between cluster
{g1,g2,g3,g4}, and the data point g5equals d(g4,g5) = 3.36, see the corre-
sponding horizontal line at this height.
9
2
1
15
3
5
4
18
8
14
20
10
17
11
16
19
7
13
6
12
0.0 0.2 0.4 0.6 0.8 1.0
Cluster Dendrogram
hclust (*, "single")
dist(rnorm(20, 0, 1), method = "euclidian")
Height
Figure 7.3: Example of three with-
out clusters.
22
25
28
30
24
21
29 23
26
27
2
1
9
7
10
5
6
4
3
8
16
19
20
17
15
13
18
12
11
14
0 1 2 3 4 5
Cluster Dendrogram
hclust (*, "single")
dist(x, method = "euclidian")
Height
Figure 7.4: Three clusters with dif-
ferent standard deviations.
Example 2. Relating data generation processes to cluster trees. It is of
importance to have some experience with data that does and does not con-
tain clusters. To illustrate this we perform single linkage cluster analysis on
twenty data points from the standard normal population.
sl.out<-hclust(dist(rnorm(20,0,1),method="euclidian"),method="single")
plot(sl.out)
From the resulting tree in Figure 7.3 one might get the impression that
there are five separate clusters in the data. Note, however, that there is no
underlying data generation process which produces separate clusters from
different populations.
If, however, the data are generated by different normal distributions,
then there are different processes producing separate clusters. To illustrate
124 CHAPTER 7. CLUSTER ANALYSIS AND TREES
this, ten data points were sampled from the N(0,0.1) population, ten from
N(3,0.5), and ten from N(10,1).
x <- c(rnorm(10,0,0.1),rnorm(10,3,0.5),rnorm(10,10,1.0))
plot(hclust(dist(x,method="euclidian"),method="single"))
plot(sl.out)
From the tree in Figure 7.4, it can be observed that there clearly exist three
clusters.
These examples illustrate that results from cluster analysis may very well
reveal population properties, but that some caution is indeed in order.
−0.5 0.0 0.5 1.0 1.5 2.0 2.5
−1 0 1 2
CCND3 Cyclin D3
Zyxin
ALL
AML
Figure 7.5: Plot of gene ”CCND3
Cyclin D3” and ”Zyxin” expres-
sions for ALL and AML patients.
21
35
29
16
20
10
19
5
12 26
4
13
15
22
24
1
3
6
11
23
8
27
7
925
17
18
2
14 34
30
37
32
36 38
33
28
31
0.0 0.2 0.4 0.6 0.8 1.0 1.2
Cluster Dendrogram
hclust (*, "single")
dist(clusdata, method = "euclidian")
Height
Figure 7.6: Single linkage cluster
diagram from gene ”CCND3 Cy-
clin D3” and ”Zyxin” expressions
values.
Example 3. Application to the Golub (1999) data. Recall that the first
twenty seven patients belong to ALL and the remaining eleven to AML and
that we found earlier that the expression values of the genes ”CCND3 Cyclin
D3” and ”Zyxin” differ between the patient groups ALL and AML. Figure
7.5 illustrates that the patient groups differ with respect to gene expression
values. How to produce this plot and a single linkage cluster analysis is shown
by the script below.

7.2. TWO TYPES OF CLUSTER ANALYSIS 125
data(golub, package="multtest")
clusdata <- data.frame(golub[1042,],golub[2124,])
colnames(clusdata)<-c("CCND3 Cyclin D3","Zyxin")
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
plot(clusdata, pch=as.numeric(gol.fac))
legend("topright",legend=c("ALL","AML"),pch=1:2)
plot(hclust(dist(clusdata,method="euclidian"),method="single"))
Figure 7.6 gives the tree from single linkage cluster analysis. Apart from
three expressions the tree shows two clusters corresponding to the two pa-
tient groups.
7.2.2 k-means
K-means cluster analysis is a popular method in bioinfomatics. It is defined
by minimizing the within cluster sum of squares over Kclusters. That is,
given the data points x1,··· ,xnthe method seeks to minimize the function
K
X
k=1
nk
X
i∈Ik
d2(xi,ak)
over all possible points a1,···aK. This is accomplished by an algorithm
(Hartigan & Wong, 1979) which starts by partitioning the data points into
Kinitial clusters, either at random or using some heuristic device. It then
computes the cluster means (step 1) and constructs a new partition by asso-
ciating each point with the closest cluster mean (step 2). The latter yields
new clusters of which the means are calculated (step 1). Then it constructs
a new partition by associating each point with the closest cluster mean (step
2). These two steps are repeated until convergence. The latter occurs when
the data points no longer change clusters. The iterative algorithm is fast
in the sense that it often converges in less iterations than the number of
points n, but it need not to attain the global minimum. For the optimal
points a1,···aK, it holds that these are equal to the mean per cluster, that
is ak=xkfor each cluster k. When the data points are independent and
identically distributed, then the cluster means converge in probability to the
corresponding population means (Pollard, 1981).
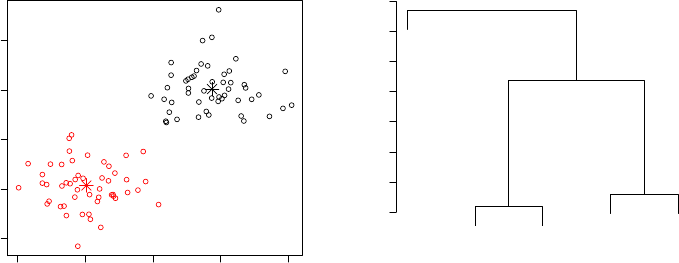
126 CHAPTER 7. CLUSTER ANALYSIS AND TREES
−1 0 1 2 3
−1 0 1 2 3
data[,1]
data[,2]
Figure 7.7: K-means cluster anal-
ysis.
x5
x1
x2
x3
x4
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5
Cluster Dendrogram
hclust (*, "single")
dist(sl.clus.dat, method = "euclidian")
Height
Figure 7.8: Tree of single linkage
cluster analysis.
Example 1. Relating a data generation process to k-means cluster analysis.
To illustrate k-means cluster analysis we shall simulate gene expressions from
two different normal populations. That is, we randomly take fifty gene ex-
pressions for two persons from the N(0,0.5) population and fifty expressions
for two persons from the N(2,0.5) population. The data points are collected
in two matrices of order fifty by two which are placed one above the other.
On the total of one hundred data points a (k=)2-means cluster analysis is
performed.
> data <- rbind(matrix(rnorm(100,0,0.5), ncol = 2),
+ matrix(rnorm(100,2,0.5), ncol = 2))
> cl <- kmeans(data, 2)
K-means clustering with 2 clusters of sizes 50, 50
Cluster means:
[,1] [,2]
1 1.87304978 2.01940342
2 0.01720177 0.07320413
Clustering vector:
[1]2222222222222222222222222222222222222
7.2. TWO TYPES OF CLUSTER ANALYSIS 127
[38]2222222222222111111111111111111111111
[75] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Within cluster sum of squares by cluster:
[1] 22.60733 20.54411
Available components:
[1] "cluster" "centers" "withinss" "size"
The output of k-means cluster analysis is assigned to a list called cl. Observe
that the cluster means are fairly close to the population means (0,0) and
(2,2). The Clustering vector indicates to which cluster each data point
(gene) belongs and that these correspond exactly to the two populations
from which the data are sampled. The variable cl$cluster contains cluster
membership and can be used to specify the color of each data point a plot,
as follows.
> plot(data, col = cl$cluster)
> points(cl$centers, col = 1:2, pch = 8, cex=2)
The data points are plotted in red and black circles and the cluster means by
a star, see Figure 7.7. The sum of the within cluster sum of squares equals
the minimal function value obtained by the algorithm.
Before performing a k-means cluster analysis a plot from a single linkage
cluster analysis may reveal the number of clusters. If the number of clusters is
not at all clear, then it becomes questionable whether k-means is appropriate.
For cases where the number of clusters is only moderately clear, the algorithm
is more sensible to get stuck into a solution which is only locally optimal.
Such solutions are of limited scientific value. To cope with the danger of
suboptimal solutions one may simply run the algorithm repeatedly by using
the nstart option. Another possibility is to use rational initial starting
values for the cluster means. In particular, the sample means of potential
clusters or the hypothesized population means can be used.
> initial <- matrix(c(0,0,2,2), nrow = 2, ncol=2, byrow=TRUE)
> cl<- kmeans(data, initial, nstart = 10)
The so-called bootstrap (Efron, 1979) can be used to estimate 95% confidence
intervals around cluster means. The idea is to re-sample with replacement
from the given sample one thousand times with replacement and to compute
quantiles for the corresponding confidence intervals.

128 CHAPTER 7. CLUSTER ANALYSIS AND TREES
n <- 100; nboot<-1000
boot.cl <- matrix(0,nrow=nboot,ncol = 4)
for (i in 1:nboot){
dat.star <- data[sample(1:n,replace=TRUE),]
cl <- kmeans(dat.star, initial, nstart = 10)
boot.cl[i,] <- c(cl$centers[1,],cl$centers[2,])
}
> quantile(boot.cl[,1],c(0.025,0.975))
2.5% 97.5%
-0.1098886 0.1627979
> quantile(boot.cl[,2],c(0.025,0.975))
2.5% 97.5%
-0.04830563 0.19721732
> quantile(boot.cl[,3],c(0.025,0.975))
2.5% 97.5%
1.730495 2.009014
> quantile(boot.cl[,4],c(0.025,0.975))
2.5% 97.5%
1.898407 2.162019
From the bootstrap confidence intervals the null hypothesis that the cluster
population means are equal to (0,0) and (2,2) are accepted.
Example 2. Application to the Golub (1999) data. In the above we found
that the expression values of the genes ”CCND3 Cyclin D3” and ”Zyxin” are
closely related to the distinction between ALL and AML. Hence, a 2-means
cluster analysis of these gene expression values is appropriate here.
> data <- data.frame(golub[1042,],golub[2124,])
> colnames(data)<-c("CCND3 Cyclin D3","Zyxin")
> cl <- kmeans(data, 2,nstart = 10)
> cl
K-means clustering with 2 clusters of sizes 11, 27
Cluster means:
CCND3 Cyclin D3 Zyxin
1 0.6355909 1.5866682
2 1.8938826 -0.2947926

7.2. TWO TYPES OF CLUSTER ANALYSIS 129
Clustering vector:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
22222222222222222222222222
27 28 29 30 31 32 33 34 35 36 37 38
211111111111
Within cluster sum of squares by cluster:
[1] 4.733248 19.842225
The two clusters discriminate exactly the ALL patients from the AML pa-
tients. This can also be seen from Figure 7.9, where expression values of
CCND3 Cyclin D3 are depicted on the horizontal axis and those of Zyxin
on the vertical, and the ALL patients are in red and the AML patients in
black. By the bootstrap the cluster means and their confidence intervals can
be estimated.
> mean(data.frame(boot.cl))
X1 X2 X3 X4
0.6381860 1.5707477 1.8945878 -0.2989426
> quantile(boot.cl[,1],c(0.025,0.975))
2.5% 97.5%
0.2548907 0.9835898
> quantile(boot.cl[,2],c(0.025,0.975))
2.5% 97.5%
1.259608 1.800581
> quantile(boot.cl[,3],c(0.025,0.975))
2.5% 97.5%
1.692813 2.092361
> quantile(boot.cl[,4],c(0.025,0.975))
2.5% 97.5%
-0.60802142 -0.02420802
The difference between the bootstrap means and the k-means from the orig-
inal data gives an estimate of the estimation bias. It can be observed that
the bias is small. The estimation is quite precise because the 95% bootstrap
confidence intervals are fairly small.
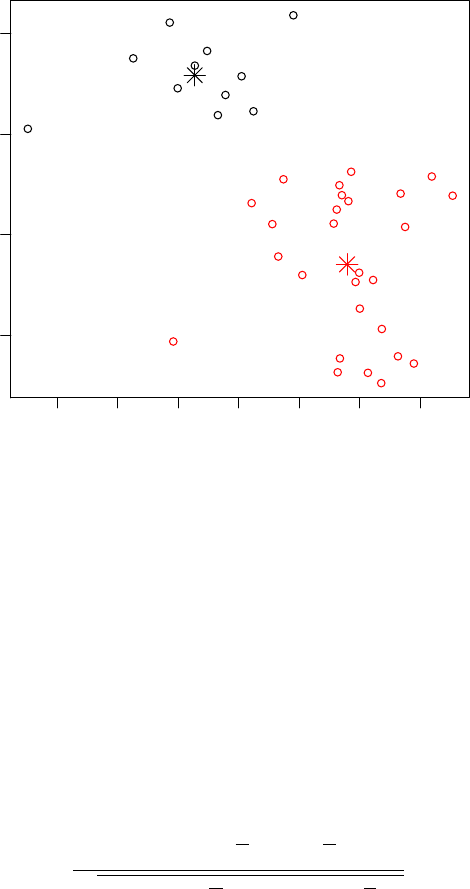
130 CHAPTER 7. CLUSTER ANALYSIS AND TREES
−0.5 0.0 0.5 1.0 1.5 2.0 2.5
−1 0 1 2
CCND3 Cyclin D3
Zyxin
Figure 7.9: Plot of kmeans (stars) cluster analysis on CCND3 Cyclin D3 and
Zyxin discriminating between ALL (red) and AML (black) patients.
7.3 The correlation coefficient
A frequently used coefficient to express the degree of linear relationship
between two sets of gene expression values is the correlation coefficient ρ.
For two sequences of gene expressions such as x= (x1,··· , xn) and y=
(y1,··· , yn), the correlation coefficient ρis estimated by
bρ=Pn
i=1(xi−xi)(yj−yj)
qPn
i=1(xi−xi)2Pn
i=1(yj−yj)2
.
The value of the correlation coefficient is always between minus one and plus
one. If the value is close to either of these values, then the variables are

7.3. THE CORRELATION COEFFICIENT 131
linearly related in the sense that the first is a linear transformation of the
second. That is, there are constants aand bsuch that axi+b=yifor all
i. By the function cor.test, the null hypothesis H0:ρ= 0 can be tested
against the alternative H0:ρ6= 0.
Example 1. Teaching demonstration. To develop intuition with respect to
the correlation coefficient the function run.cor.examp(1000) of the TeachingDemos
package is quite useful. It launches an interactive plot with 1000 data points
on two random variables Xand Y. When the correlation is near zero, then
the data points are distributed along contours of circles. By moving the
slider slowly from the left to the right it can be observed that all points are
approximately on a straight line. If the sign of the correlation coefficient is
positive, then small/large values of Xtend to go together with small/large
values of Y.
Example 2. Another teaching demonstration. By the function put.points.demo()
it is possible to add and delete points to a plot which interactively re-
computes the value for the correlation coefficient. By first creating a few
points that lie together on a circle the corresponding correlation coefficient
will be near zero. By next adding one outlier, it can be observed that the
correlation coefficient changes to nearly ±1. This illustrates that the corre-
lation coefficient is not robust against outliers.
Example 3. Application to the Golub (1999) data. We shall illustrate the
correlation coefficient by two sets of expression values of the MCM3 gene
of the Golub et al. (1999) data. This gene encodes for highly conserved
mini-chromosome maintenance proteins (MCM) which are involved in the
initiation of eukaryotic genome replication. Here, we find its row numbers,
collect the gene expression value in vectors xand y, and compute the value
of the correlation coefficient by the function cor(x,y).
> library(multtest); data(golub)
> x <- golub[2289,]; y <- golub[2430,]
> cor(x,y)
[1] 0.6376217
The value is positive which means that larger values of xoccur together with
larger values of yand vice versa. This can also be observed by plot(x,y). By

132 CHAPTER 7. CLUSTER ANALYSIS AND TREES
the function cor.test, the null hypothesis H0:ρ= 0 can be tested against
the alternative H0:ρ6= 0. It also estimates a 95% confidence interval for ρ.
> cor.test(x,y)
Pearson’s product-moment correlation
data: x and y
t = 4.9662, df = 36, p-value = 1.666e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.3993383 0.7952115
sample estimates:
cor
0.6376217
The test is based on the normality assumption and prints therefore a t-value.
Since the corresponding p-value is very small, we reject the null hypothesis
of zero correlation. The left bound of the confidence interval falls far to the
right hand side of zero.
Example 4. Confidence interval by the bootstrap. Another method to con-
struct a 95% confidence interval is by the bootstrap. The idea (Efron, 1979)
is to obtain thousand samples from the original sample with replacement and
to compute the correlation coefficient for each of these. This yields thousand
coefficients from which the quantiles for the 95% confidence interval can be
computed.
> nboot <- 1000; boot.cor <- matrix(0,nrow=nboot,ncol = 1)
> data <- matrix(c(x,y),ncol=2,byrow=FALSE)
> for (i in 1:nboot){
+ dat.star <- data[sample(1:nrow(data),replace=TRUE),]
+ boot.cor[i,] <- cor(dat.star)[2,1]}
> mean(boot.cor)
[1] 0.6534167
> quantile(boot.cor[,1],c(0.025,0.975))
2.5% 97.5%
0.2207915 0.9204865

7.4. PRINCIPAL COMPONENTS ANALYSIS 133
Observe that the 95% confidence interval is larger than that found by cor.test.
This indicates that the assumption of normality may not be completely valid
here. Since the confidence interval does not contain zero, we reject the null-
hypothesis of zero correlation.
Example 5. Application to the Golub (1999) data. The ALL and AML
patients of the Golub et al. (1999) data are indicated by zero and ones of
the binary vector golub.cl. A manner to select genes it by the correlation
of the expression values with this binary vector. Such can be computed by
using the apply functionality.
> library(multtest); data(golub)
> corgol<- apply(golub, 1, function(x) cor(x,golub.cl))
> o <- order(corgol)
By golub.gnames[o[3041:3051],2] it can be seen that various of these
genes seem indeed to have important cell functions referred to by Golub et
al. (1999). In particular, Interleukin 8 is recently related to inflammatory
cytokine production in myeloid cells (Tessarz et al., 2007).
7.4 Principal Components Analysis
To make the basic ideas behind principal components analysis explicit, it is
wise to start with a small artificial example. Suppose that for six genes the
standardized expression values on two patients (variables) became available
as these are given in Table 7.1. The data are collected in a 6 by 2 data
matrix Z, where e.g. element z21 is expression value -0.40 which belongs to
the second gene of the first patient.
The whole idea of principal components analysis is to find new directions
in the data along which there is maximal variation. A direction is defined as
a linear combination Zk of the data Zby a vector kwith weights. The i-th
element of the linear combination is the weighted sum P2
j=1 zij kj. The direc-
tion of maximal variation is defined as the linear combination with maximal
variance. To find this direction the correlation matrix plays an important
role. The latter contains the correlations between each pair of patients (vari-
ables). In our case correlations between the columns (patients) in Table 7.1

134 CHAPTER 7. CLUSTER ANALYSIS AND TREES
Table 7.1: Data set for principal components analysis.
Var 1 Var 2
gene 1 1.63 1.22
gene 2 −0.40 0.79
gene 3 0.93 0.97
gene 4 −1.38 −1.08
gene 5 −0.17 −0.96
gene 6 −0.61 −0.93
can be placed in a matrix R, which has ones on the diagonal and the value
0.8 elsewhere.
To illustrate a direction let’s try the linear combination k= (2,1)2of the
sample correlation matrix R. This gives
Rk =·1 0.8
0.8 1 ¸·2
1¸=·2.8
2.6¸.
Both vectors kand Rk can be plotted in the xy-plane. The vector (2,1)
is plotted by drawing an arrow from (0,0) to the point with x= 2 and
y= 1. This is done completely similar for (2.8,2.6) in Figure 7.10. It can
be observed that the two vectors (arrows) do not fall on the same line and
therefore have different directions. The crux of principal components analysis
is that a linear combination with the same direction as the weights represent
the direction of maximum variation. Such is the case if Rk differs from k
only by a constant of multiplication, that is there exists a constant dsuch
that Rk =dk. We shall determine such a constant by finding the weights
vector first. To do so observe from our correlations matrix that the sum of
both rows equals 1.8. Taking k= (1,1) yields
Rk =·1 0.8
0.8 1 ¸·1
1¸=·1.8
1.8¸= 1.8·1
1¸= 1.8k.
So that we obtain d= 1.8. A similar result follows by observing that the
differences per row are equal in absolute value. That is, taking k= (1,−1)
2For the sake of simple notation we shall not use the transposition operator Tto indicate
rows.
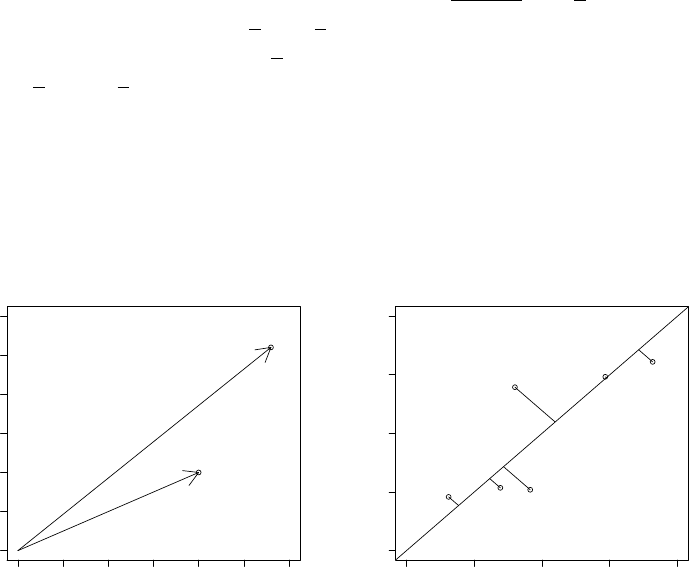
7.4. PRINCIPAL COMPONENTS ANALYSIS 135
yields
Rk =·1 0.8
0.8 1 ¸· 1
−1¸=·0.2
−0.2¸= 0.2·1
−1¸= 0.2k.
A vector kfor which Rk =dkholds is called an eigenvector corresponding to
the eigenvalue d. Eigenvectors are often re-scaled by dividing by their Euclid-
ian length. Since the Euclidian length of (1,1) is √12+ 12=√2, we obtain
the new eigenvector k1= (1/√2,1/√2) ≈(0.71,0.71). Since the length of
eigenvector (1,−1) also equals √2 the re-scaled second eigenvector equals
k2= (1/√2,−1/√2) ≈(0.71,−0.71). Now the first principal component is
defined as Zk1and the second as Zk2. In practical applications the actual
computation of eigenvectors and eigenvalues is performed by well-designed
numerical methods (Golub & Van Loan, 1983).
0.0 0.5 1.0 1.5 2.0 2.5 3.0
0.0 0.5 1.0 1.5 2.0 2.5 3.0
V[,1]
V[,2]
Figure 7.10: Vectors of linear com-
binations.
−2 −1 0 1 2
−2 −1 0 1 2
Z[,1]
Z[,2]
Figure 7.11: First principal com-
ponent with projections of data.
Example 1. Using R on the above data. It is convenient to store the data of
the first two columns of Table 7.1 as a matrix object called Z. The correlations
matrix can be computed by the built-in-function cor and the eigenvectors
and eigenvalues by the built-in-function eigen, as follows.
Z <- matrix(c( 1.63, 1.22, -0.40, 0.79, 0.93, 0.97, -1.38,
136 CHAPTER 7. CLUSTER ANALYSIS AND TREES
-1.08, -0.17, -0.96, -0.61, -0.93), nrow=6, byrow=TRUE)
K <- eigen(cor(Z))
The output is stored as an object called Kwhich can be printed to the screen
in two digits.
> print(K,digits=2)
$values
[1] 1.8 0.2
$vectors
[,1] [,2]
[1,] 0.71 0.71
[2,] 0.71 -0.71
The eigenvalues are assigned to K$values and the eigenvectors are the columns
of K$vectors. To compute the principal components we use the matrix mul-
tiplication operator %*%. Then the first principal component is defined as the
linear combination of the data with the first eigenvector, Z%*%K$vec[,1]. To
print the scores on the first and the second principal component one can use
the following.
> print(Z %*% K$vec, digits=2)
[,1] [,2]
[1,] 2.02 0.290
[2,] 0.28 -0.841
[3,] 1.34 -0.028
[4,] -1.74 -0.212
[5,] -0.80 0.559
[6,] -1.09 0.226
To illustrate the first principal component the six data points from the Z
matrix are plotted as small circles in Figure 7.11. Gene 1, for instance, has
xcoordinate 1.63 and ycoordinate 1.22 and appears therefore in the right
upper corner.
A convenient manner to perform principal components analysis is by using
the built-in-function princomp, as follows.
pca <- princomp(Z, center = TRUE, cor=TRUE, scores=TRUE)
pca$scores

7.4. PRINCIPAL COMPONENTS ANALYSIS 137
The scores are the component scores and the loadings from princomp are
the eigenvectors.
The eigenvalues represent an amount of variance related to the compo-
nent. In the previous example the first component has variance 1.8 and the
second 0.2, so that the first represents 1.8/2 = 0.9 or 90% of the variance. On
the basis of the eigenvalues the number of interesting directions in the data
can be evaluated by two rules of thumb. The first is that each eigenvalue
should represent more variance than that of any of the observed variables.
The second is the so-called elbow rule saying that when the first few eigen-
values are large and the remaining considerably smaller, then the first few
are the most interesting.
Principal components analysis is a descriptive method to analyze depen-
dencies (correlations) between variables. If there are a few large eigenvalues,
then there are equally many directions in the data which summarize the
most important variation among the gene expressions. Then it may be use-
ful to explore simultaneously a two dimensional visualization of the genes
and the patients. Furthermore, it can be rewarding to study the weights of
the eigenvectors because these may reveal a structure in the data otherwise
gone unnoticed. Finally, the principal components contain less (measure-
ment) error than the individual variables. For this reason, cluster analysis
on the values on the principal components may be useful.
Example 2. Application to the Golub (1999) data. The first five eigenvalues
from the correlation matrix of golub can be printed by the following.
> eigen(cor(golub))$values[1:5]
[1] 25.4382629 2.0757158 1.2484411 1.0713373 0.7365232
Because the eigenvalues are arranged in decreasing order the sixth to the 38th
are smaller than one. Reason for which these will be neglected. The first
eigenvalue is by far the largest, indicating that the persons are dependent to
a large extent. Applying the previous bootstrap methods to estimate 95%
confidence intervals for the eigenvalues we obtain the following intervals.
data <- golub; p <- ncol(data); n <- nrow(data) ; nboot<-1000
eigenvalues <- array(dim=c(nboot,p))
for (i in 1:nboot){dat.star <- data[sample(1:n,replace=TRUE),]
eigenvalues[i,] <- eigen(cor(dat.star))$values}
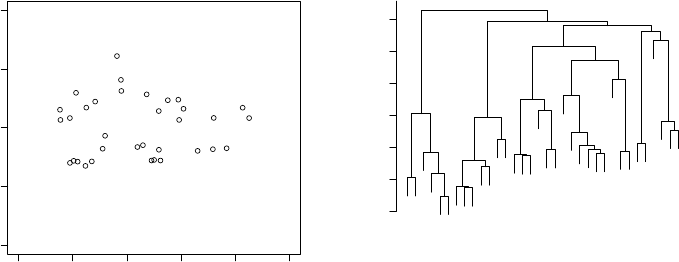
138 CHAPTER 7. CLUSTER ANALYSIS AND TREES
> for (j in 1:p) print(quantile(eigenvalues[,j],c(0.025,0.975)))
2.5% 97.5%
for (j in 1:5) cat(j,as.numeric(quantile(eigenvalues[,j],
+ c(0.025,0.975))),"\n" )
1 24.83581 26.00646
2 1.920871 2.258030
3 1.145990 1.386252
4 0.9917813 1.154291
5 0.6853702 0.7995948
The cat function allows for much control in printing. The null hypothesis
of eigenvalue being equal to one is accepted for the fourth component and
rejected for the first three and the fifth. Thus the fourth represents less
variance than an individual variable, reason for which it is neglected.
The percentages of variance explained by the first two components can be
computed by sum(eigen(cor(golub))$values[1:2])/38*100, which yields
the amount 72.4052%. Thus the first two components represent more than
72% of the variance in the data. Hence, the data allow for a reduction in
dimensions from thirthy eight to two.
−10 −5 0 5 10 15
−10 −5 0 5 10
X1
X2
68
182
313
504
792
808
885
892
893
1101
1616
1737 1754
1756
1798
1882
1910
1911 2233
2321 2350
2397
2459
2611
2653 2673
2749
2761
2874
450
849
316
2289
2430
Figure 7.12: Scatter plot of se-
lected genes with row labels on the
first two principal components.
1910
28742350
1737
1911
2749
2761
792
2321 68
808 2611
450
504
313
1756 893
182
2653 2289
2430
316
1616
1101
2673 2459
892
1882
885
849 2397
1754
1798
2233
0.0 0.5 1.0 1.5 2.0 2.5 3.0
Cluster Dendrogram
hclust (*, "single")
dist(leu, method = "euclidian")
Height
Figure 7.13: Single linkage cluster
diagram of selected gene expres-
sion values.
It can be checked that all correlations between the patients are positive.

7.4. PRINCIPAL COMPONENTS ANALYSIS 139
This implies that large expression values on gene ico-vary positively with
large deviations of gene j. The positivity of the correlations also implies that
the weights of the first eigenvector have the same sign, so that these can be
taken to be positive for all patients (Horn & Johnson, 1985). Unfortunately,
this is not automatic in R so that caution is in order with respect to inter-
pretation of the components. By using -eigen(cor(golub))$vec[,1:2] to
print the weights to the screen it can be observed that those that correspond
to the first component are positive. All weights of the first eigenvector are
positive and have very similar size (all are between 0.13 and 0.17). Thus the
first component is almost equal to the sum of the variables (the correlation
equals 0.9999). The weights of the second component have a very interesting
pattern. Namely, almost all of the first 27 weights are positive and the last 11
weights are negative. Thus the second component contrasts the ALL patients
with the AML patients. By contrasting ALL patients with AML patients a
second to the largest amount of variance is explained in the data. Hence,
the AML-ALL distinction is discovered by the second component, which is
in line with findings of Golub et al. (1999).
Obviously the genes with the largest expression values from the first com-
ponent can be printed. We shall, however, concentrate on the second compo-
nent because it appears to be more directly related to the research intentions
of Golub et. al. (1999). The first and the last ten gene names with respect
to the values on the second component can be printed by the following.
> pca <- princomp(golub, center = TRUE, cor=TRUE, scores=TRUE)
> o <- order(pca$scores[,2])
> golub.gnames[o[1:10],2]
> golub.gnames[o[3041:3051],2]
Many of these genes are related to leukemia (Golub, et al., 1999).
Example 3. Biplot. A useful manner to plot both genes (cases) and patients
(variables) is the biplot, which is based on a two-dimensional approximation
of the data very similar to principal components analysis. Here, we illustrate
how it can be combined with principal components analysis.
> biplot(princomp(data,cor=TRUE),pc.biplot=TRUE,cex=0.5,expand=0.8)
The resulting plot is given by Figure 7.14. The left and bottom axis refer
to the component scores and the top and right to the patient scores, which
140 CHAPTER 7. CLUSTER ANALYSIS AND TREES
are scaled to unit length by the specification cor. It can be seen that the
patients are clearly divided in two groups corresponding to ALL and AML.
Example 4. Critical for S-phase. Golub et al. (1999) mention that among
genes which are useful for tumor class prediction there are genes that encode
for proteins critical for S-phase cell cycle progression such as Cyclin D3,
Op18, and MCM3. We select genes which carry ”CD”, ”Op”, or ”MCM” in
their names and collect the corresponding row numbers.
data(golub, package = "multtest")
factor <- factor(golub.cl)
o1 <- grep("CD",golub.gnames[,2])
o2 <- grep("Op",golub.gnames[,2])
o3 <- grep("MCM",golub.gnames[,2])
o <- c(o1,o2,o3)
This yields 110 genes. In order to select those that do have an experimental
effect, we use a two-sample t-test.
pt <- apply(golub, 1, function(x) t.test(x ~ gol.fac)$p.value)
oo <- o[pt[o]<0.01]
This yields 34 genes, of which the row numbers are selected in the vector
oo. In order to identify genes in directions of large variation we use the scores
on the first two principal components.
Z <- as.matrix(scale(golub, center = TRUE, scale = TRUE))
K <- eigen(cor(Z))
P <- Z %*% -K$vec[,1:2]
leu <- data.frame(P[oo,], row.names= oo)
attach(leu)
The scores on the first two principal components of the selected genes are
stored in the data frame leu. From the plotted component scores in Figure
7.12, it seems that there are several sub-clusters of genes. The genes that
belong to these clusters can be identified by hiearchical cluster analysis.
cl <- hclust(dist(leu,method="euclidian"),method="single")
plot(cl)

7.5. OVERVIEW AND CONCLUDING REMARKS 141
From the tree (dendrogram) in Figure 7.13 various clusters of genes are
apparent that also appear in Figure 7.12.3The ordered genes can be
obtained from the object cl as follows.
> a <- as.integer(rownames(leu)[cl$order])
> for (i in 1:length(a)) cat(a[i],golub.gnames[a[i],2],"\n")
1910 FCGR2B Fc fragment of IgG, low affinity IIb, receptor for (CD32)
2874 GB DEF = Fas (Apo-1, CD95)
The cluster with rows 504, 313, 1756, and 893 consists of antigenes. The
genes MCM3 Minichromosome maintenance deficient (S. cerevisiae) 3 with
row numbers 2289 and 2430 appear adjacent to each other. This illustrates
that genes with similar functions may indeed be close with respect to their
gene expression values.
7.5 Overview and concluding remarks
Single linkage cluster analysis can be applied to explore for groups in a set of
gene expressions. When groups are present a k-means cluster analysis can be
applied in combination with the bootstrap to estimate confidence intervals
for the cluster means.
The correlation coefficient measures the degree of dependency between
pairs of gene expression values. It can also be used to find gene expressions
which are highly dependent with a phenotypical variable. It is reassuring to
find in applications that the confidence interval for a correlation coefficient
is small.
Principal components analysis is very useful for finding directions in the
data where the gene expression values vary maximally, see Jolliffe (2002) for
a complete treatment of the principal component analysis. When these di-
rections can be represented well by the first two components a biplot helps to
simultaneously visualize genes and patients. Principal components analysis
can be useful in identifying clusters of genes in a lower dimensional space.
3Unfortunately, some row numbers of genes are less readable because the points are
very close.
142 CHAPTER 7. CLUSTER ANALYSIS AND TREES
7.6 Exercises
1. Cluster analysis on the ”Zyxin” expression values of the Golub et al.
(1999) data.
(a) Produce a chatter plot of the gene expression values using showing
different symbols for the two groups.
(b) Use single linkage cluster analysis to see whether the three indi-
cates two different groups.
(c) Use k-means cluster analysis. Are the two clusters according to
the diagnosis of the patient groups?
(d) Perform a bootstrap on the cluster means. You will have to modify
the code here and there. Do the confidence intervals for the cluster
means overlap?
2. Close to CCND3 Cyclin D3. Recall that we did various analysis on
the expression data of the CCND3 Cyclin D3 gene of the Golub (1999)
data.
(a) Use genefilter to find the ten closed genes to the expression
values of CCND3 Cyclin D3. Give their probe as well as their
biological names.
(b) Produce of combined boxplot separately for the ALL and the AML
expression values. Compare it with that on the basis of CCND3
Cyclin D3 and comment of the similarities.
(c) Compare the smallest distances with those among the Cyclin genes
computed above. What is your conclusion?
3. MCM3. In the example on MCM3 a plot shows that there is an outlier.
(a) Plot the data and invent a manner to find the row number of the
outlier.
(b) Remove the outlier, test the correlation coefficient. Compare the
results to those above.
(c) Perform the bootstrap to construct a confidence interval.
4. Cluster analysis on part of Golub data.
7.6. EXERCISES 143
(a) Select the oncogenes from the Golub data and plot the tree from
a single linkage cluster analysis.
(b) Do you observe meaningful clusters.
(c) Select the antigenes and answer the same questions.
(d) select the receptor genes and answer the same questions.
5. Principal Components Analysis on part of the ALL data.
(a) Construct an expression set with the patients with B-cell in stage
B1, B2, and B3. Compute the corresponding ANOVA p-values
of all gene expressions. Construct the expression set with the p-
values smaller than 0.001. Report the dimensionality of the data
matrix with gene expressions.
(b) Are the correlations between the patients positive?
(c) Compute the eigenvalues of the correlation matrix. Report the
largest five. Are the first three larger than one?
(d) Program a bootstrap of the largest five eigenvalues. Report the
bootstrap 95% confidence intervals and draw relevant conclusions.
(e) Plot the genes in a plot of the first two principal components.
6. Some correlation matrices.
·1−0.8
−0.8 1 ¸,
1 0.8 0.8
0.810.8
0.8 0.8 1
,
1−0.5−0.5
−0.5 1 −0.5
−0.5−0.5 1
,
(a) Verify that the eigenvalues of the matrices are 1.8, 0.2,2.6,
0.2, 0.2, and 1.500000e+00, 1.500000e+00, -7.644529e-17.
(b) How much variance represents the first component corresponding
to the second matrix?
(c) Verify that the first eigen vector of the second correlation matrix
has identical signs.
144 CHAPTER 7. CLUSTER ANALYSIS AND TREES
−3 −2 −1 0 1 2
−3 −2 −1 0 1 2
Comp.1
Comp.2
23
68
96
108
126
182
202
244
246
259
313
323
329
345
357376
377
378
394 422 462
494
522
523
546
561
563
566
571
621 648
703
704
713
717
725
735
738
746
766
786
801
803 808
829
838
839
866
888
896
922
932
937
938
968
984
1006
1030
1037
1042
1045
1060
1066
1069
1081
1086
1109
1110
1145
1162
1206
1245
1271
1334
1348
1368
1396
1413
1445
1448
1455
1524
1542
1556
1585 1598
1638
1640
1642
1652
1653
1665
1732
1754
1774
1778
1817
1829
1834
1856
1869
1882
1887
1901
1909
1911
1916
1920
1939 1959
1978
1995
2002
2020
2065
2122
2124
2172
2179
2198
2265
2266
2289
2307 2343
2347
2356
2386
2410
2418
2459
2466
2489
2553
2589
2593
2600
2616
2627
2645
2656
2663
2664
2673
2702
2734
2749
2786
2794
2801
2813
2821
2829
2851
2889
2920
2921
2922
2937
2939
2950
2955
3046
−1.0 −0.5 0.0 0.5
−1.0 −0.5 0.0 0.5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
Figure 7.14: Biplot of selected genes from the golub data.
Chapter 8
Classification Methods
In medical settings groups of patients are often diagnosed into classes corre-
sponding to types of diseases. In bioinformatics the question arises whether
the diagnosis of a patient can be predicted by gene expression values? Re-
lated is the question which genes play an important role in the prediction of
class membership. A similar question is the prediction of micro RNA’s from
values of folding energy. More generally, for objects like proteins, mRNA’s,
or microRNA’s it may be of importance to classify these on the basis of
certain measurements.
Many classification methods have been developed for various scientific
purposes. In bioinformatics, methods such as recursive partitioning, support
vector machine and neural network are frequently applied to solve classifica-
tion problems.
In this chapter you learn what recursive partitioning is and how to use it.
To evaluate the quality of prediction the fundamental concepts of sensitivity
and specificity are frequently used. The specificity can be summarized in a
single number by the area under the curve of a receiver operator curve. This
will be explained and illustrated. Two other methods to predict disease class
from gene expression data are the support vector machine and the neural
network. It will briefly be explained what these methods are about and how
these can be applied. A validation set will be used to evaluate the predictive
accuracy.
145

146 CHAPTER 8. CLASSIFICATION METHODS
8.1 Classification of microRNA
The subject of making a correct medical diagnosis is highly similar to that
of correctly classifying microRNA.
Example 1. Classification of Micro RNA. MicroRNA are small RNA molecules
with important functions in cell growth and disease development. In order
to identify microRNA’s from arbitrary sequences its characterizing proper-
ties are used to distinguish non-microRNA from microRNA molecules. One
of these properties is that microRNA’s have the capacity to fold in a cer-
tain hairpin type of structure. Such a structure typically exhibits a small
minimum folding energy (Zuker, 2003; Zuker & Stiegler, 1981). This prop-
erty can be used as a test to discriminate microRNA’s from non-microRNA’s
(Bonnet, et al., 2004), as follows. Given a set of 3424 different microRNA’s
the minimum folding energy was computed for each of these. Next, for each
microRNA the order of the nucleotides was shuffled with replacement 1000
times. This yielded per microRNA 1000 differently shuffled sequences of nu-
cleotides for which the minimum folding energy is computed.1Per microRNA
the 1001 energy values were arranged to have increasing order, similar as for
empirical distributions in the previous chapter. Then the number of mini-
mum folding energies below that of the original microRNA is counted and
divided by 1001 as the p-value. If the minimum folding energie of the original
microRNA is the smallest, then the empirical p-value is zero. This proce-
dure yielded a total of 3424 p-values. The number of sequences with p-values
below the threshold value 0.01 is given in Table 8.1. The same procedure is
conducted for non-microRNA molecules which were taken as sequences with
similar length and nucleotide percentages.
Table 8.1: Frequencies empirical p-values lower than or equal to 0.01.
test positive test negative total
p≤0.01 p > 0.01
microRNA 2973 451 3424
non microRNA 33 3391 3424
total 3006 3842 6848
1I am obliged to Sven Warris for computing the minimum energy values.
8.2. ROC TYPES OF CURVES 147
From the frequency Table 8.1, the sensitivity, the specificity, and the
predictive power can be computed in order to evaluate the quality of the
test. The sensitivity is the probability that the test is positive given that the
sequence is a microRNA (true positive). Thus
sensitivity = P(true positive) = P(test positive|microRNA) = 2973
3424 = 0.8682.
The specificity is the probability that the test is negative given that the
sequence is not a microRNA (true negative). Thus
specificity = P(true negative) = P(test negative|no microRNA) = 3391
3424 = 0.9903.
For practical applications of a test the predictive power is of crucial impor-
tance. In particular, the predictive value positive is the probability that the
sequence is a microRNA given that the test is positive. That is,
Predictive value positive = P V +=P(microRNA|test positive) = 2973
3006 = 0.9890
Thus when the test is positive we are 98.90% certain that the sequence is
indeed a microRNA. The predictive value negative is the probability that the
sequence is not a microRNA given that the test is negative.
Predictive value negative = P V −=P(no microRNA|test negative) = 3391
3842 = 0.8826.
Thus when the test is negative we are 88.26% certain that the sequence
is not a microRNA. From the estimated conditional probabilities it can be
concluded that the test performs quite well in discriminating between mi-
croRNA’s from non-microRNA’s.
8.2 ROC types of curves
In Chapter 2 we have observed with respect to the Golub et al. (1999) data
that the expression values of gene CCND3 Cyclin D3 tend to be greater for
ALL patients. We may therefore use these as a test for predicting ALL using
a certain cutoff value. In particular, for gene expression values larger than a
cutoff we declare the test “positive” in the sense of indicating ALL. By doing

148 CHAPTER 8. CLASSIFICATION METHODS
so the corresponding true and false positives can be computed for each cutoff
value. To briefly indicate the origin of the terminology, imagine that the test
results are a characteristic received by an operator. The receiver operator
characteristic (ROC) is a curve where the false positive rates are depicted
horizontally and the true positive rates vertically. The larger the area under
the ROC curve, the better the test is because then low false positive rates
go together with large true positive rates.2These ideas are illustrated by
several examples.
Example 1. For the sake of illustration we consider the prediction of ALL
from the expression values for gene CCND3 Cyclin D3 from Golub et al.
(1999) in row 1042 of the matrix golub. Now consider cutoff point 1.27. For
such a cutoff point we can produce a table with TRUE/FALSE frequencies
of predicting ALL/not ALL.
> data(golub, package = "multtest")
> gol.true <- factor(golub.cl,levels=0:1,labels= c(" ALL","not ALL"))
> gol.pred <- factor(golub[1042,]>1.27,levels=c("TRUE","FALSE"),
labels=c("ALL","notALL"))
> table(gol.pred,gol.true)
gol.true
gol.pred ALL not ALL
ALL 25 1
notALL 2 10
There are 25 ALL patients with expression values greater than or equal to
1.27, so that the true positive rate is 25/27=0.93. For this cutoff value there
is one false positive because one patient without ALL has a score larger than
1.27. Hence, the false positive rate is 1/11 = 0.09.
Example 2. The expression values for gene CCND3 Cyclin D3 from the
Golub et al. (1999) data are sorted in decreasing order, see Table 8.2. The
procedure to draw the ROC curve starts with cutoff point infinity. Obviously,
there are no expression values equal to infinity, so there is no patient tested
positive. Next, the cut off point 2.77 is taken and values greater than or
equal to 2.77 are tested as positive. This yields one true positive implying a
2More detailed information can be obtained from a wikipedia search using ”ROC
curve”.
8.2. ROC TYPES OF CURVES 149
true positive rate of 1/27, see second row of Table 8.2. For this cutoff value
there are no negatives so that the false positive rate is zero.
Now consider cutoff point 1.52. There are 22 ALL patients with expres-
sion values greater than or equal to 1.52, so that the true positive rate is
22/27=0.81. For this cutoff value there are no false positives because all pa-
tients without ALL have expression values lower than 1.51. Hence, the false
positive rate is 0 and the true positive rate is 0.81. To indicate this there is
a vertical line drawn in the ROC curve from point (0,0) to point (0,0.81)
in Figure 8.1. Now consider the next cutoff point 1.45. There are 22 ALL
patients with expression values greater than or equal to 1.45, so that the
true positive rate is again 22/27=0.81. However, there is one patient with-
out ALL having expression value 1.45, whom receives therefore a positive
test. Hence, the number of false positives increases from zero to one, which
implies a false positive rate of 1/11=0.09. In the ROC curve this is indicated
by point (0.09,0.81) and the horizontal line from (0,0.81) to (0.09,0.81), see
Figure 8.1.
This process goes on (see Table 8.2) until the smallest data point -0.74 is
taken as cutoff point. For this point all patients are tested positive, so that
the false positive rate is 11/11 and the true positive rate is 27/27. This is
indicated by the end point (1,1) in the plot at the top on the right hand side.
False positive rate
True positive rate
0.0 0.2 0.4 0.6 0.8 1.0
0.0 0.2 0.4 0.6 0.8 1.0
Figure 8.1: ROC plot for expres-
sion values of CCND3 Cyclin D3.
False positive rate
True positive rate
0.0 0.2 0.4 0.6 0.8 1.0
0.0 0.2 0.4 0.6 0.8 1.0
Figure 8.2: ROC plot for expres-
sion values of gene Gdf5.

150 CHAPTER 8. CLASSIFICATION METHODS
It is obviously helpful to use a computer for producing an ROC such as
in Figure 8.1. To do so we construct an appropriate factor with the value
TRUE for ALL and FALSE for not ALL gol.true and use functions from
the ROCR package.
library(ROCR)
gol.true <- factor(golub.cl,levels=0:1,labels= c("TRUE","FALSE"))
pred <- prediction(golub[1042,], gol.true)
perf <- performance(pred, "tpr", "fpr" )
plot(perf)
It seems clear that the expression values are better in testing for ALL when
the curve is very steep in the beginning and attains its maximum value soon.
In such a case the true positive rate is large for a small false positive rate. A
manner to express the predictive accuracy of a test in a single number is by
the area under the curve. Using the function performance(pred,"auc") we
obtain that the area under the curve is 0.96, which is large. Hence, the ex-
pression values of CCND3 Cyclin D3 are suitable for discrimination between
ALL and not ALL (AML). The ROC curve for the expression values of gene
Gdf5 is given by Figure 8.2. It can be observed that the true positive rate
is much lower as one moves on the horizontal axis from the left to the right.
This corresponds to the area under the curve of 0.35, which is small. This
illustrates that genes may express large differences with respect to prediction
of the disease status of patients.
In practical applications one is often interested in a single optimal cut-off
value and in combining several predictors in a decision scheme.
8.3 Classification trees
The purpose of classification is to allocate organisms into classes on the ba-
sis of measurements on attributes. For instance, in case of the Golub et al.
(1999) data the organisms are 38 patients which have measurements on 3051
genes. The classes consist of diagnosis of patients into the ALL class (27
patients) and the AML class (11 patients). A tree model resembles that of
a linear model, where the criterion is the factor indicating class membership
and the predictor variables are the gene expression values. In case of, for in-
stance, the Golub et al. (1999) data the gene expression values {x1,···, x38}
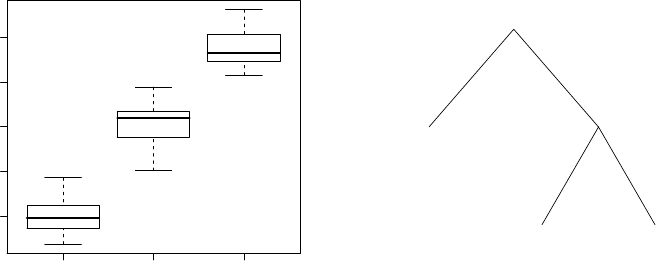
8.3. CLASSIFICATION TREES 151
can serve as predictors to form a decision tree. For instance, if xj< t, then
patient jis AML, and otherwise if xj≥t, then patient jis ALL. Obvi-
ously, the threshold value ton which the decision is based should be optimal
given the predictor. Such can be estimated by a regression tree (Breiman
et al., 1984; Chambers & Hastie, 1992; Venables, & Ripley, 2000), which is
implemented in the rpart package (Therneau & Atkinson, 1997).
A training set is used to estimate the threshold values that construct the
tree. When many predictor variables are involved, 3051 for instance, then we
have a tremendous gene (variable) selection problem. The rpart package au-
tomatically selects genes which are important for classification and neglects
others. A further problem is that of overfitting where additional nodes of a
tree are added to increase prediction accuracy. When such nodes are specific
for the training sample set, these can not be generalized to other samples
so that these are of limited scientific value. Prevention of such overfitting is
called pruning and is automatically done by the rpart function. Many basic
ideas are illustrated by an elementary example.
ALL1 ALL2 AML
01234
Figure 8.3: Boxplot of expression
values of gene a for each leukemia
class.
genea< 0.9371
genea< 3.025
ALL1
10/0/0
ALL2
0/10/0 AML
0/0/10
Figure 8.4: Classification tree for
gene for three classes of leukemia.
Example 1. Optimal gene expressions. Suppose microarray expres-
sion data are available with respect to patients suffering from three types of

152 CHAPTER 8. CLASSIFICATION METHODS
leukemia abbreviated as ALL1, ALL2, and AML. Gene A has expression val-
ues from the populations (patient groups) N(0,0.52) for ALL1, N(2,0.52) for
ALL2, and N(4,0.52) for AML. The script below generates thirty expression
values for gene A, the patients of the three disease classes, and the estimates
of the classification tree.
set.seed(123); n<-10 ; sigma <- 0.5
fac <- factor(c(rep(1,n),rep(2,n),rep(3,n)))
levels(fac) <- c("ALL1","ALL2","AML")
geneA <- c(rnorm(10,0,sigma),rnorm(10,2,sigma),rnorm(10,4,sigma))
dat <- data.frame(fac,geneA)
library(rpart)
rp <- rpart(fac ~ geneA, method="class",data=dat)
plot(rp, branch=0,margin=0.1); text(rp, digits=3, use.n=TRUE)
From the boxplot in Figure 8.3 it can be observed that there is no overlap of
gene expressions between classes. This makes gene A an ideal predictor for
separating patients into classes. By the construction of the gene expression
values x1,··· , x30 we expect the following partition. If xi<1, then ALL1,
if xiis in interval [1,3], then ALL2, and if xi>3, then AML. From the
estimated tree in Figure 8.4 it can be observed that the estimated splits are
close to our expectations: If xi<0.971, then ALL1, if xiis in [0.9371,3.025],
then ALL2, and if xi>3.025, then AML. The tree consists of three leaves
(nodes) and two splits. The prediction of patients into the three classes per-
fectly matches the true disease status.
Obviously, such an ideal gene need not exist because the expression values
overlap between the disease classes. In such a case more genes may be used
to build the classification tree.
Example 2. Gene selection. Another situation is where Gene A discrim-
inates between ALL and AML and Gene B between ALL1 patients and ALL2
or AML patients and Gene C does not discriminate at all. To simulate this
setting we generate expression values for Gene A from N(0,0.52) for both
ALL1 and ALL2, and from N(2,0.52) for AML patients. Next, we generate
expression values for Gene B from N(0,0.52) for ALL1 and from N(2,0.52)
for ALL2 and AML. Finally, we generate for Gene C from N(1,0.52) for
ALL1, ALL2, and AML. For this and for estimating the tree, we use the
following script.

8.3. CLASSIFICATION TREES 153
set.seed(123)
n<-10 ; sigma <- 0.5
fac <- factor(c(rep(1,n),rep(2,n),rep(3,n)))
levels(fac) <- c("ALL1","ALL2","AML")
geneA <- c(rnorm(20,0,sigma),rnorm(10,2,sigma))
geneB <- c(rnorm(10,0,sigma),rnorm(20,2,sigma))
geneC <- c(rnorm(30,1,sigma))
dat <- data.frame(fac,geneA,geneB,geneC)
library(rpart)
rp <- rpart(fac ~ geneA + geneB + geneC, method="class",data=dat)
Note the addition in the model notation for the rpart function.3It is con-
venient to collect the data in the form of a data frame.4
From the boxplot in Figure 8.5 it can be seen that Gene A discriminates
well between ALL and AML, but not between ALL1 and ALL2. The expres-
sion values for Gene B discriminate well between ALL1 and ALL2, whereas
those of Gene C do not discriminate at all. The latter can also be seen from
the estimated tree in Figure 8.6, where Gene C plays no role at all. This il-
lustrates that rpart automatically selects the genes (variables) which play a
role in the classification tree. Expression values on Gene A larger than 1.025
are predicted as AML and smaller ones as ALL. Expression values on Gene
B smaller than 0.9074 are predicted as ALL1 and larger as ALL2. Hence,
Gene A separates well within the ALL class.
Example 3. Prediction by CCND3 Cyclin D3 gene expression values.
From various visualizations and statistical testing in the previous chapters,
it can be conjectured that CCND3 Cyclin D3 gene expression values form a
suitable predictor for discriminating between ALL and AML patients. Note,
however, from Figures 2.2 and 8.7 that there is some overlap between the
expression values from the ALL and the AML patients, so that a perfect
classification is not possible. By the function rpart the regression partition-
ing can be computed as follows.
> library(rpart);data(golub); library(multtest)
> gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
> gol.rp <- rpart(gol.fac ~ golub[1042,] , method="class")
3See Chapter 11 of the manual ”An Introduction to R” for more on model notation.
4See Chapter 6 of the manual ”An Introduction to R” for more on data frames.
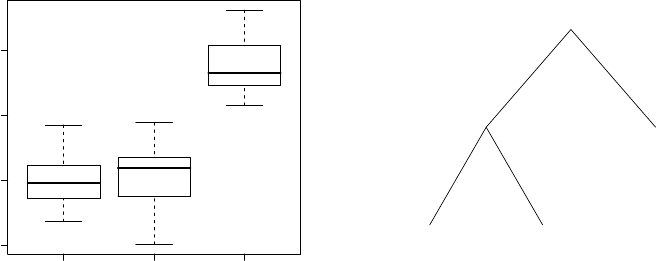
154 CHAPTER 8. CLASSIFICATION METHODS
ALL1 ALL2 AML
−1 0 1 2
Figure 8.5: Boxplot of expression
values of gene a for each leukemia
class.
genea< 1.025
geneb< 0.9074
ALL1
10/0/0 ALL2
0/10/0
AML
0/0/10
Figure 8.6: Classification tree of
expression values from gene A,
B, and C for the classification of
ALL1, ALL2, and AML patients.
> predictedclass <- predict(gol.rp, type="class")
> table(predictedclass, gol.fac)
gol.fac
predictedclass ALL AML
ALL 25 1
AML 2 10
Note that (25 + 10)/38 ·100% = 92.10% of the ALL/AML patients are cor-
rectly classified by gene CCND3 Cyclin D3. By the function predict(gol.rp,type="class")
the predictions from the regression tree of the patients in the two classes can
be obtained. The factor gol.fac contains the levels ALL and AML corre-
sponding to the diagnosis to be predicted. The predictor variable consists
of the expression values of gene CCND3 Cyclin D3. The output of recursive
partitioning is assigned to an object called gol.rp, a list from which fur-
ther information can be extracted by suitable functions. A summary can be
obtained as follows.
> summary(gol.rp)
Call:
8.3. CLASSIFICATION TREES 155
rpart(formula = gol.fac ~ golub[1042, ], method = "class")
n= 38
CP nsplit rel error xerror xstd
1 0.7272727 0 1.0000000 1.0000000 0.2541521
2 0.0100000 1 0.2727273 0.5454545 0.2043460
Node number 1: 38 observations, complexity param=0.7272727
predicted class=ALL expected loss=0.2894737
class counts: 27 11
probabilities: 0.711 0.289
left son=2 (26 obs) right son=3 (12 obs)
Primary splits:
golub[1042, ] < 1.198515 to the right, improve=10.37517, (0 missing)
Node number 2: 26 observations
predicted class=ALL expected loss=0.03846154
class counts: 25 1
probabilities: 0.962 0.038
Node number 3: 12 observations
predicted class=AML expected loss=0.1666667
class counts: 2 10
probabilities: 0.167 0.833
26
[1] 0.03846154
The expected loss in prediction accuracy of Node number 2 is 1/26 and that
of Node number 3 is 2/12. This equals the probabilities from the class counts.
The primary splits gives the estimated threshold value. To predict the class
of the individual patients one may use the function predict, as follows.
> predict(gol.rp,type="class")
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
ALL ALL ALL ALL ALL ALL ALL ALL ALL ALL ALL ALL ALL ALL ALL ALL AML ALL ALL ALL
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38
AML ALL ALL ALL ALL ALL ALL AML ALL AML AML AML AML AML AML AML AML AML
Levels: ALL AML
156 CHAPTER 8. CLASSIFICATION METHODS
Hence, Patient 17 and 21 are erroneously predicted as AML and Patient 29
is erroneously predicted in the ALL class. A more precise output is obtained
by asking for the probability of class membership.
> predict(gol.rp, type="prob")
ALL AML
1 0.9615385 0.03846154
2 0.9615385 0.03846154
etc.
Based on this the probability of patient 21 to have ALL is 0.16 and that to
have AML is 0.83.
ALL AML
−0.5 0.0 0.5 1.0 1.5 2.0 2.5
Figure 8.7: Boxplot of expression
values from gene CCND3 Cyclin
D3 for ALL and AML patients
golub[1042, ]>=1.199
ALL
25/1 AML
2/10
Figure 8.8: Classification tree
of expression values from gene
CCND3 Cyclin D3 for classifica-
tion of ALL and AML patients.
Example 4. Gene selection of the Golub (1999) data. By recursive
partitioning it is possible to select among the genes of Golub et al. (1999)
those which give the best partitioning. For the latter to work we have to
specify the gene expressions as the variables (columns). For this we use the
transposition operator t. To facilitate reading the output we add gene 1 to
gene 3051 as column names.

8.3. CLASSIFICATION TREES 157
library(rpart);data(golub); library(multtest)
row.names(golub)<- paste("gene", 1:3051, sep = "")
goldata <- data.frame(t(golub[1:3051,]))
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
gol.rp <- rpart(gol.fac~., data=goldata, method="class", cp=0.001)
plot(gol.rp, branch=0,margin=0.1); text(gol.rp, digits=3, use.n=TRUE)
golub.gnames[896,]
Inspection of the plot yields gene ”FAH Fumarylacetoacetate” as the predic-
tor by which the two classes of patients can be predicted perfectly.
In order to further illustrate possibilities of classification methods we use
the ALL data collected by Chiaretti, et al. (2004), see also Chapter 6.
Example 5. Application to the Chiaretti (2004) data. With respect to
the ALL data we want to predict from the gene expressions the diagnosis of B-
cell State B1, B2, and B3. Since the complete set of 12625 gene expressions is
too large, we select the genes with different means over the patients groups. It
is obvious that only these gene can contribute to the prediction of the disease
states. In particular we select the gene with ANOVA p-value is smaller than
0.000001.
library("hgu95av2.db");library(ALL);data(ALL)
ALLB123 <- ALL[,ALL$BT %in% c("B1","B2","B3")]
pano <- apply(exprs(ALLB123), 1, function(x) anova(lm(x ~ ALLB123$BT))$Pr[1])
names <- featureNames(ALL)[pano<0.000001]
symb <- mget(names, env = hgu95av2SYMBOL)
ALLBTnames <- ALLB123[names, ]
probedat <- as.matrix(exprs(ALLBTnames))
row.names(probedat)<-unlist(symb)
The probe symbols are extracted from the hgu95av2SYMBOL environment and
used as row names to facilitate readability of the resulting tree. There are 78
patients selected and 29 probes. The recursive partitioning to find the tree
can be performed by the following script.
> diagnosed <- factor(ALLBTnames$BT)
> tr <- rpart(factor(ALLBTnames$BT) ~ ., data = data.frame(t(probedat)))
> plot(tr, branch=0,margin=0.1); text(tr, digits=3, use.n=TRUE)
158 CHAPTER 8. CLASSIFICATION METHODS
> rpartpred <- predict(tr, type="class")
> table(rpartpred,diagnosed)
diagnosed
rpartpred B1 B2 B3
B1 17 2 0
B2 1 33 5
B3 1 1 18
The rows to the left of the table give the frequencies of the predicted B cell
stages and the columns on top the diagnosed B cell stages from the factor.
The matrix with frequencies of the predicted and true patient status is often
called a “confusion table”. The resulting tree in Figure 8.9 should be read
as follows. If gene expression MME is strictly smaller than the cutoff value
8.395, then the patient is predicted to be in state (class) B1. If the expression
of LSM6 smaller than 4.192, then the predicted state is B2, and if it is larger
than the predicted state it is B3.
The misclassification rate is 10/78=0.1282051, which is low, but not zero.
It may happen that the probability of the predicted class is close to that of
the diagnosed. An overview of the latter can be obtained as follows.
predicted.class <- predict(tr, type="class")
predicted.probabilities <- predict(tr, type="prob")
out <- data.frame(predicted.probabilities,predicted.class,
diagnosis=factor(ALLBTnames$BT))
> print(out,digits=2)
B1 B2 B3 predicted.class diagnosis
01005 0.026 0.85 0.13 B2 B2
01010 0.026 0.85 0.13 B2 B2
04006 0.895 0.11 0.00 B1 B1
04007 0.026 0.85 0.13 B2 B2
04008 0.895 0.11 0.00 B1 B1
04010 0.050 0.05 0.90 B3 B1
04016 0.895 0.11 0.00 B1 B1
06002 0.026 0.85 0.13 B2 B2
08001 0.026 0.85 0.13 B2 B2
08011 0.026 0.85 0.13 B2 B3
08012 0.026 0.85 0.13 B2 B3
08018 0.050 0.05 0.90 B3 B3
08024 0.895 0.11 0.00 B1 B2
8.3. CLASSIFICATION TREES 159
09008 0.026 0.85 0.13 B2 B3
...
For instance, the sixth patient is with probability .90 in class B3 and with
probability .05 in class B1, which is the diagnosed disease state.
MME< 8.395
LSM6< 4.192
B1
17/2/0
B2
1/33/5 B3
1/1/18
Figure 8.9: rpart on ALL B-cel 123
data.
40480_s_at
1173_g_at
37320_at
40729_s_at
36829_at
32716_at
32116_at
32977_at
34378_at
36711_at
37544_at
307_at
40440_at
38032_at
1389_at
0.35 0.45 0.55 0.65
MeanDecreaseAccuracy
32977_at
32716_at
307_at
34333_at
34347_at
35769_at
37043_at
37544_at
34891_at
36829_at
40493_at
40440_at
38032_at
36711_at
1389_at
0.0 0.2 0.4 0.6
MeanDecreaseGini
rf1
Figure 8.10: Variable importance
plot on ALL B-cell 123 data.
Note the reduction in variables from twenty nine to two in the actual
construction of the tree. In a construction like this the gene expressions
(variables) are linearly dependent in the sense that once the first gene is
selected for the first split, then highly similar ones are not selected anymore.
It can be instructive to leave out the variables selected from the data and to
redo the analysis.
A generally applied manner to evaluate an estimated model is by its pre-
dictive accuracy with respect to a future data set. When such a future data
set is not available, it is common practice to split the available data in two
parts: A training set and a validation set. Then the model is estimated from
the training set and this is used to predict the class of the patients in the
validation set. Then a confusion matrix is constructed with the frequencies
of true classes against predicted classes. Next, the misclassification rate can
be computed to evaluate the predictive accuracy. This can very well be seen

160 CHAPTER 8. CLASSIFICATION METHODS
as a method to detect for over fitting where the model estimates are so data
specific that generalization to future data sets is in danger.
Example 6. Training and validation. In the setting of B-cell ALL data
with State 1, 2, and 3 the manner to split the data centers around randomly
splitting the patients in two halves. The 78 patients in State 1, 2 or 3 can
be split in two halves, as follows.
i <- sample(1:78, 39, replace = FALSE)
noti <- setdiff(1:78,i)
df <- data.frame(Y = factor(ALLBTnames$BT), X =t(probedat))
rpart.est <- rpart(Y ~ ., data = df, subset=i)
rpart.pred.t <- predict(rpart.est, df[i,], type="class")
> table(rpart.pred.t,factor(ALLBTnames$BT[i]))
rpart.pred.t B1 B2 B3
B1 11 1 0
B2 0 12 0
B3 0 1 14
> rpart.pred.v <- predict(rpart.est,df[noti,], type="class")
> table(rpart.pred.v,factor(ALLBTnames$BT[noti]))
rpart.pred.v B1 B2 B3
B1610
B2 1 19 3
B3126
The misclassification rate in the training set is 2/39 = 0.05 and in the val-
idation set is 7/39 = 0.18. Note that the differences mainly occur between
State 2 and 3. Generally the prediction of disease state from the training set
is better because the model is estimated from these data.
The same split of the data into training and validation set will be used
for other methods as well.
8.4 Support Vector Machine
A support vector machine finds separating lines (hyper planes) between
groups of points. This works like a classification problem where the classes

8.4. SUPPORT VECTOR MACHINE 161
of patients are to be predicted from gene expression values. If such sepa-
rating lines do exist in the data, then a linear support vector machine will
find these. This is because the optimization method behind it is based on
quadratic programming by iterative algorithms which find the globally opti-
mal solution with certainty. Support vector machines do not automatically
select variables and are designed for continuous predictor variables. Since
the mathematical details are beyond the current scope, we shall confine with
illustrating applications to gene expression data.
Example 1. Application to the Chiaretti (2004) data. The parameters
for the support vector machine can be determined by the function svm from
the e1071 package, as follows.
library(e1071)
df <- data.frame(Y = factor(ALLBTnames$BT), X =t(probedat))
Y <- factor(ALLBTnames$BT);X <- t(probedat)
svmest <- svm(X, Y, data=df, type = "C-classification", kernel = "linear")
svmpred <- predict(svmest, X, probability=TRUE)
> table(svmpred, factor(ALLBTnames$BT))
svmpred B1 B2 B3
B1 19 0 0
B2 0 36 1
B3 0 0 22
The confusion matrix shows that the misclassification rate of the three classes
of B-cell ALL is 1/78=0.0128 is very small, so that the prediction is almost
perfect. Note, however, from summary(svmest) that the number of support
vectors per class equals 20, 9, and 11, for class B1, B2, and B3, respectively.
These have values for all input variables (genes) as can be obtained from
dim(svmest$SV) and the coefficient vectors dim(svmest$coefs). Hence,
the excellent prediction properties are obtained by a very large number of
estimated parameters.
Example 2. Training and validation. A generally applied manner to
evaluate the predictive quality of an estimated model is by splitting the data
into a training and a validation set. The model is estimated by the training
set and then the class of the patients in the validation set is predicted. We
shall use the same split as in Example 6 of the previous section.

162 CHAPTER 8. CLASSIFICATION METHODS
> Yt <- factor(ALLBTnames$BT)[i]; Yv <- factor(ALLBTnames$BT)[noti]
> X <- t(probedat); Xt <- X[i,]; Xv <- X[noti,]
> svmest <- svm(Xt, Yt, type = "C-classification", kernel = "linear")
> svmpredt <- predict(svmest, Xt, probability=TRUE)
> table(svmpredt, Yt)
Yt
svmpredt B1 B2 B3
B1 11 0 0
B2 0 14 0
B3 0 0 14
> svmpredv <- predict(svmest, Xv, probability=TRUE)
> table(svmpredv, Yv)
Yv
svmpredv B1 B2 B3
B1500
B2 1 19 4
B3235
The predictions of the disease states of the patients from the training set per-
fectly match the diagnosed states. The predictions, however, of the classes
of the patients from the validation set have misclassification rate 10/39=0.25
and are therefore less accurate. Hence, the parameter estimates from the
training set are sample specific and do not generalize with the same accuracy
to the validation set.
8.5 Neural Networks
Neural networks are nonlinear models consisting of nonlinear hyperplanes
around classes of objects given a set of prediction variables (Ripley, 1996).
We confine with illustrating the method by two examples.
Example 1. Application to the Chiaretti (2004) data. The models can
be estimated by the function nnet from the package that goes under the
same name. To avoid having to many variables we randomly select a subset
of 20 genes.
> Y <- factor(ALLBTnames$BT);X <- t(probedat)

8.5. NEURAL NETWORKS 163
> library(nnet)
> df <- data.frame(Y = Y, X = X[, sample(ncol(X), 20)])
> nnest <- nnet(Y ~ .,data = df, size = 5, maxit = 500, decay = 0.01,
+ MaxNWts = 5000)
> pred <- predict(nnest, type = "class")
> table(pred, Y) # prints confusion ma
Y
pred B1 B2 B3
B1 19 0 0
B2 0 36 0
B3 0 0 23
The confusion matrix shows that zero out of 78 patients are mis-classified.
Example 2. Training and validation. The results from cross validation
on the neural networks are as follows.
> nnest.t <- nnet(Y ~ ., data = df,subset=i, size = 5,decay = 0.01,
+ maxit=500)
> prednnt <- predict(nnest.t, df[i,], type = "class")
> table(prednnt,Ytrain=Y[i])
Ytrain
prednnt B1 B2 B3
B1 11 0 0
B2 0 14 0
B3 0 0 14
> prednnv <- predict(nnest.t, df[noti,], type = "class")
> table(prednnv, Yval= Y[noti])
Yval
prednnv B1 B2 B3
B1410
B2 4 17 4
B3045
The predictions on the training set have misclassification rate zero and that
on the validation set 13/39=0.33.

164 CHAPTER 8. CLASSIFICATION METHODS
8.6 Generalized Linear Models
Within the framework of generalized linear models the diagnosis of a patient
is seen as a response. In case the response has the values healthy or disease
for which it may be assumed that the binomial distribution holds with a
succes probability pi. Recall from Chapter 3 that for a binomially distributed
variable with yisuccesses out of niit holds that the probability of yisuccesses
out of ni equals
P(Yi=yi) = ni!
yi!(ni−yi)!pyi
i(1 −pi)ni−yi,for k= 0,··· , ni.
The value of piis closely related to one or more predictor variables x1and
x2via a linear combination. That is, the linear model holds such that ηi=
β0+β1xi1+β2xi2. The predictors are linked to the succes probability via the
so-called logit link
pi=eηi
eηi+ 1 =exp(β0+β1xi1+β2xi2)
1 + exp(β0+β1xi1+β2xi2).
Rather than going deeper into the details, the usefulness of generalized linear
models will be illustrated with two examples.
Example 1. CCND3 Cyclin D3. In the Golub et al. (1999) data we
may model Yi= 1 if the patient is diagnosed as ALL and Yi= 0 if (s)he is
diagnosed as AML. We use the CCND3 Cyclin D3 gene expression values as
predictor. To will be convenient to compute the response by -golub.cl +
1. This yield 1 for ALL and 0 for not ALL5.
library(faraway)
logitmod <- glm((-golub.cl + 1) ~ golub[1042,],
family=binomial(link = "logit"))
pchisq(deviance(logitmod),df.residual(logitmod),lower=FALSE)
plot((-golub.cl + 1) ~ golub[1042,], xlim=c(-2,5), ylim = c(0,1),
xlab="CCND3 expression values ", ylab="Probability of ALL")
x <- seq(-2,5,.1)
lines(x,ilogit(-4.844124 + 4.439953*x))
pchisq(deviance(logitmod),df.residual(logitmod),lower=FALSE)
5One may also conveniently use a factor as response variable

8.6. GENERALIZED LINEAR MODELS 165
> summary(logitmod)
Call:
glm(formula = (-golub.cl + 1) ~ golub[1042, ], family = binomial(link = "logit"))
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -4.844 1.849 -2.620 0.00880 **
golub[1042, ] 4.440 1.488 2.984 0.00284 **
Null deviance: 45.728 on 37 degrees of freedom
Residual deviance: 18.270 on 36 degrees of freedom
AIC: 22.270
From Figure 8.11 it can be seen that the logit curve fits the data fairly well.
From the summary of the output it can be seen that the estimated intercept
is -4.844 and the estimated slope is 4.440. Both coefficients are significantly
different from zero. The goodness-of-fit value of the model is computed from
the chi-square distribution and equals .99. The model fits the data well. The
predictive accuracy of the model may be obtained as follows.
> pred <- predict(logitmod,type="response") > 0.5
> pred.fac <- factor(pred,levels=c(TRUE,FALSE),labels=c("ALL","not ALL"))
> table(pred.fac,gol.fac)
gol.fac
pred.fac ALL AML
ALL 26 2
not ALL 1 9
The diagnosis of the majority of patients is predicted correctly.
Example 2. Application to the Chiaretti (2004) data. With respect to
the ALL data we want model the diagnosis of B-cell State B1, B2, and B3 as
a response. The factor representing these levels can be used as input for the
response. Here we use the gene expressions with greatest importance from
the classification tree in Section 8.3. We assign the biological name to the
predictor variables and estimate the generalized linear model.
library(nnet);library("hgu95av2.db");library(ALL);data(ALL)

166 CHAPTER 8. CLASSIFICATION METHODS
probe.names <- c("1389_at","35991_at","40440_at")
ALLB123 <- ALL[,ALL$BT %in% c("B1","B2","B3")]
probedat <- exprs(ALLB123)[probe.names,]
row.names(probedat) <- unlist(mget(probe.names, env = hgu95av2SYMBOL))
fac <- factor(ALLB123$BT,levels=c("B1","B2","B3"))
dat <- data.frame(fac,t(probedat))
mnmod <- multinom(fac ~ ., family=binomial(link = "logit"),data=dat)
> summary(mnmod)
Call:
multinom(formula = fac ~ ., data = dat, family = binomial(link = "logit"))
Coefficients:
(Intercept) MME LSM6 SERBP1
B2 14.36158 4.14002 -0.8494635 -5.104337
B3 -12.90584 4.94908 4.7415802 -5.655420
Std. Errors:
(Intercept) MME LSM6 SERBP1
B2 16.36959 1.367058 1.716513 2.222486
B3 17.97896 1.424526 1.744425 2.313700
Residual Deviance: 59.88298
AIC: 75.88298
Apart from the intercepts, the estimated coefficients are significantly different
from zero.
> predmn <- predict(mnmod,type="class")
> table(predmn,fac)
fac
predmn B1 B2 B3
B1 17 2 1
B2 1 31 5
B3 1 3 17
The model predict the diagnosed classes quite well.
Generalized linear models are statistical models which have to be esti-
mated by an iterative process which may need some computation time. It

8.7. OVERVIEW AND CONCLUDING REMARKS 167
has the advantage that confidence intervals or the significance of the param-
eters can be estimated. On the other hand, using statistical model building
procedures may not designed to handle large amounts of predictor variables.
Hence, the researcher does need to have some idea on which gene expressions
(s)he want to use as predictors. Indeed, better models than those estimated
in the above example may certainly exist.
8.7 Overview and concluding remarks
Central themes in prediction methods are the face validity (clarity) of the
model, the size of the model, and predictive accuracy on a validation set.
For many researchers it is of crucial importance to have a clear idea on what
a method is essentially doing. Some models and their estimation procedures
are mathematically intricate and seem to be recollected in the mind of many
researchers as black boxes. Even from a more pragmatic point of view such
need not be devastating if the predictive accuracy is excellent. However,
support vector machines and neural networks typically use a large number
of parameters to predict well on a test set, but less well on validation sets.
It is, furthermore, questionable whether a zero misclassification rate is ra-
tional since patients may be misclassified by the diagnosis or very close to
transferring from one state to the other.
Recursive partitioning to estimate a classification tree performs very well
on variable selection and pruning in order to discover as few variables (gene
expressions) as possible for maximum predictive accuracy. In addition, it
seems obvious that classification trees have great clarity, see e.g. the CART
package (Breiman et al., 1984) for further types of recursive trees. Note
that several methods have different misclassification rates with respect to
the whole sample, but comparable rates on the validation sets. It should,
however, be clear that when there are non-linear relationships between pre-
dictor variables and classes, then nonlinear models should outperform linear
ones6.
8.8 Exercises
1. Classification tree of Golub data. Use recursive partitioning in rpart
6Some people may want to use the ade4TkGUI()
168 CHAPTER 8. CLASSIFICATION METHODS
(a) Find a manner to identify an optimal gene with respect the Golub
data to prediction of the ALL AML patients.
(b) Explain what the code does.
(c) Use rpart to construct the classification tree with the genes that
you found. Does it have perfect predictions?
(d) Find the row number of gene Gdf5, which is supposed not to have
any relationship with leukemia. Estimate a classification tree and
report the probability of misclassification. Give explanations of
the results.
2. Sensitivity versus specificity.
(a) Produce a sensitivity versus specificity plot for the gene expression
values of CCND3 Cyclin D3.
(b) In what sense does it resemble Figure 8.2.
(c) Compute the area under the curve for sensitivity versus specificity
curve.
3. Comparing Classification Methods. To obtain an idea on the misclas-
sification rate when there is no relation between the predictors and the
factor indicating groups, we perform a small simulation study.
(a) Construct a factor with 100 values one and two and a matrix
with predictor variables of 500 by 4 with values from the normal
distribution. Use the first four letters of the alphabet for the
column names.
(b) Use rpart to construct a recursive tree and report the misclassi-
fication rate. Comment on the results.
(c) Do the same for support vector machines.
(d) Do the same for neural networks.
(e) Think through your results and comment on these.
4. Prediction of achieved remission. For the ALL data from its ALL library
the patients are checked for achieving remission. The variable ALL$CR
has values CR (became healthy) and REF (did not respond to therapy;
remain ill).
8.8. EXERCISES 169
(a) Construct an expression set containing the patients with values
on the phenotypical variable remission and the gene expressions
with a significant p-value on the t-test with the patient groups CR
or REF.
(b) Use recursive partitioning to predict the remission. Report the
misclassification rate and the names of the genes that play a role
in the tree.
5. Gene selection by area under the curve. A strategy of selecting genes
is to compute the auc for each gene and to use the best 10 for further
investigation. Compute the auc for each row with gene expressions of
the Golub at al. (1999) data. Collect these in a vector and select the
ten best. Is ”CCND3 Cyclin D3” among these?
6. Classification Tree for Ecoli. The ecoli data can be download by the
following: (Hint: Copy two separated lines into one before running it.)
ecoli <- read.table(
"http://www.grappa.univ-lille3.fr/~torre/Recherche/Datasets/
downloads/ecoli/ecoli.data",sep=",",header = TRUE)
colnames(ecoli) <- c("SequenceName","mcg","gvh","lip","chg",
"aac","alm1","alm2","ecclass")
(a) Use ecclass to construct a factor containing the ”cp”,”im”,and
”pp”.
(b) Construct a classification tree using the variables ”mcg”,”gvh”,”lip”,”aac”,”alm1”,”alm2”.
Give the code. Hint: Use the addition notation.
(c) Plot the tree and report the variables that play a role in the con-
structed tree.
(d) Predict the class by the tree. Report the code and the miss-
classification rate.
(e) Leaf out the upper variable in the classification tree and re-estimate
the tree. Report the miss-classification rate. Is it much worse?

170 CHAPTER 8. CLASSIFICATION METHODS
Table 8.2: Ordered expression values of gene CCND3 Cyclin D3, index 2
indicates ALL, 1 indicates AML, cutoff points, number of false positives,
false positive rate, number of true positives, true positive rate.
data index cutoff fp fpr tp tpr
1 Inf 0 0.00 0 0.00
2 2.77 2 2.77 0 0.00 1 0.04
3 2.59 2 2.59 0 0.00 2 0.07
4 2.45 2 2.45 0 0.00 3 0.11
.
.
.
22 1.78 2 1.78 0 0.00 21 0.78
23 1.52 2 1.52 0 0.00 22 0.81
24 1.37 2 1.45 1 0.09 22 0.81
25 1.33 2 1.37 1 0.09 23 0.85
26 1.28 2 1.33 1 0.09 24 0.89
27 1.11 2 1.28 1 0.09 25 0.93
28 0.46 2 1.12 2 0.18 25 0.93
29 1.45 1 1.11 2 0.18 26 0.96
30 1.12 1 1.02 3 0.27 26 0.96
31 1.02 1 0.89 4 0.36 26 0.96
32 0.89 1 0.83 5 0.45 26 0.96
33 0.83 1 0.74 6 0.55 26 0.96
34 0.74 1 0.64 7 0.64 26 0.96
35 0.64 1 0.49 8 0.73 26 0.96
36 0.49 1 0.46 8 0.73 27 1.00
37 0.43 1 0.43 9 0.82 27 1.00
38 0.13 1 0.13 10 0.91 27 1.00
39 −0.74 1 −0.74 11 1.00 27 1.00
8.8. EXERCISES 171
−2 −1 0 1 2 3 4 5
0.0 0.2 0.4 0.6 0.8 1.0
CCND3 expression values
Probability of ALL
Figure 8.11: Logit fit to the CCND3 Cyclin D3 expression values.
172 CHAPTER 8. CLASSIFICATION METHODS
Chapter 9
Analyzing Sequences
For many purposes in bioinformatics nucleotide or amino acid sequences are
analyzed. The idea is that highly similar sequences may have identical bi-
ological functions. For expressing the similarity of sequences it is necessary
to compute first their optimal alignment. It will be explained and illustrated
how optimal pairwise alignment can be obtained. Furthermore, it is of im-
portance to compute quantities for DNA sequences such as the CG fraction,
or, for amino acid sequences, the isoelectric point or the hydropathy score.
It will be explained and illustrated how such quantities can be computed.
In this chapter you learn how to query online data bases, to translate RNA
into protein sequences, to match patterns, and to program pairwise align-
ments. We will start, however, with a query language in order to download
sequences.
9.1 Using a query language
It will be illustrated how the query language from the seqinr package can be
used for various types of searches. However, before we download anything,
it is important to know which banks can be chosen.
> library(seqinr)
> choosebank()
[1] "genbank" "embl" "emblwgs" "swissprot" "ensembl"
[6] "refseq" "nrsub" "hobacnucl" "hobacprot" "hovergendna"
[11] "hovergen" "hogenom" "hogenomdna" "hogennucl" "hogenprot"
[16] "hoverclnu" "hoverclpr" "homolens" "homolensdna" "greview"
173

174 CHAPTER 9. ANALYZING SEQUENCES
[21] "polymorphix" "emglib" "HAMAPnucl" "HAMAPprot" "hoppsigen"
[26] "nurebnucl" "nurebprot" "taxobacgen"
There are many possibilities to use the query language e.g. for answering
questions about sequences from online data bases (Gouy, et al. 1984). We
give a few examples to illustrate some of its possibilities. For this we shall
temporary use the option virtual=TRUE to save time by preventing actual
downloading.1We may ask: How many ccnd sequences has genbank?
> choosebank("genbank")
> query("ccnd","k=ccnd",virtual=TRUE)$nelem
[1] 147
More specific: How many sequences ccnd sequences has genbank for the
species homo sapiens.
> query("ccnd3hs","sp=homo sapiens AND k=ccnd3",virtual=TRUE)$nelem
[1] 9
For many other combinations of search options we refer to the manual of
the seqinr package and for a book length treatment with many examples to
Charif et al. (2008).
9.2 Getting information on downloaded se-
quences
After sequences are downloaded in binary format it is essential to obtain
information with respect to their accession number, length, actual elements,
translation to amino acids, and annotation. How to do this will briefly be
illustrated by an example.
Example 1. Let’s download sequences related to the species homo sapi-
ens and a gene name like ”CCND3”.
> choosebank("genbank")
> query("ccnd3hs","sp=homo sapiens AND k=ccnd3@")
> ccnd3hs$nelem
[1] 9
1The results below are obviously time dependent.

9.2. GETTING INFORMATION ON DOWNLOADED SEQUENCES 175
The sequences are downloaded in binary format. The symbol @acts as a
wildcard for any zero or other characters. There are a number of useful
functions available to obtain further information. Some of these are getName,
getLength,getSequence,getTrans, and getAnnot. To use these on a list
containing sets of sequences the functionality sapply is very convenient. This
is illustrated by extracting the NCBI accession numbers.
> sapply(ccnd3hs$req, getName)
[1] "AF517525.CCND3" "AL160163.CCND3" "AL160163.PE5" "AL161651"
[5] "BC011616.CCND3" "CR542246" "HUMCCND3A.CCND3" "HUMCCND3PS.PE1"
[9] "HUMCCNDB04.CCND3" "HUMCYCD3A.CCND3"
The length of the sequences can be obtained by the getLength function.
> sapply(ccnd3hs$req, getLength)
[1] "879" "879" "729" "211627" "879" "879" "879" "537" "559" "879"
Let’s obtain the first sequence and print its first fifteen nucleotides to the
screen. 2
> getSequence(ccnd3hs$req[[1]])[1:15]
[1] "a" "t" "g" "g" "a" "g" "c" "t" "g" "c" "t" "g" "t" "g" "t"
Its translation into amino acids can be obtained
> getTrans(ccnd3hs$req[[1]])[1:15]
[1] "M" "E" "L" "L" "C" "C" "E" "G" "T" "R" "H" "A" "P" "R" "A"
as well as its annotation from the corresponding web page:
> getAnnot(ccnd3hs$req[[1]])
[1] " CDS join(1051..1248,2115..2330,5306..5465,6005..6141,"
[2] " 6593..6760)"
[3] " /gene=\"CCND3\""
[4] " /codon_start=1"
[5] " /product=\"cyclin D3\""
[6] " /protein_id=\"AAM51826.1\""
[7] " /db_xref=\"GI:21397158\""
[8] " /translation=\"MELLCCEGTRHAPRAGPDPRLLGDQRVLQSLLRLEERYVPRASY"
2Use double brackets to extract a sequence from a list.

176 CHAPTER 9. ANALYZING SEQUENCES
[9] " FQCVQREIKPHMRKMLAYWMLEVCEEQRCEEEVFPLAMNYLDRYLSCVPTRKAQLQLL"
[10] " GAVCMLLASKLRETTPLTIEKLCIYTDHAVSPRQLRDWEVLVLGKLKWDLAAVIAHDF"
[11] " LAFILHRLSLPRDRQALVKKHAQTFLALCATDYTFAMYPPSMIATGSIGAAVQGLGAC"
[12] " SMSGDELTELLAGITGTEVDCLRACQEQIEAALRESLREAAQTSSSPAPKAPRGSSSQ"
[13] " GPSQTSTPTDVTAIHL\""
9.3 Computations on sequences
A basic quantity to compute are the nucleotide and the dinucleotide frequen-
cies.
Example 1. Frequencies of (di)nucleotides. We shall continue with
the first result from the CCND3 (Cyclin D3) search with accession num-
ber ”AF517525.CCND3”. To compute the frequencies we may extract the
sequence from a list in order to use the basic function table, as follows.
> table(getSequence(ccnd3hs$req[[1]]))
a c g t
162 288 267 162
This table can also be computed by the seqinr function count, which is
more general in the sense that frequencies of dinucleotides can be computed.
> count(getSequence(ccnd3hs$req[[1]]),2)
aa ac ag at ca cc cg ct ga gc gg gt ta tc tg tt
25 44 64 29 68 97 45 78 52 104 76 34 16 43 82 21
This will be quite useful in the next chapter. Indeed, changing 2 into 3 makes
it possible to count trinucleotides.
Example 2. G + C percentage. We are often interested in the fraction
G plus C in general (GC), or starting from the first position of the codon
bases (GC1), the second (GC2), or third (GC3).
> GC(getSequence(ccnd3hs$req[[1]]))
[1] 0.6313993

9.3. COMPUTATIONS ON SEQUENCES 177
> GC1(getSequence(ccnd3hs$req[[1]]))
[1] 0.6484642
> GC2(getSequence(ccnd3hs$req[[1]]))
[1] 0.4641638
> GC3(getSequence(ccnd3hs$req[[1]]))
[1] 0.78157
Hence, the G + C percentage is largest when started at position three. It
is also possible to compute the G + C fraction in a window of length 50 nt,
say, and to plot it along the sequence.
GCperc <- double()
n <- length(ccnd3[[1]])
for (i in 1:(n - 50)) GCperc[i] <- GC(ccnd3[[1]][i:(i+50)])
plot(GCperc,type="l")
By double() we first create a vector. From Figure 9.1 it can be seen that
the G + C fraction changes drastically along a window of 50 nucleotides.
With respect to over or under representation of dinucleotides there is a func-
tion ρ(rho) available, which is defined as
ρ(xy) = fxy
fx·fy
,
where fxy,fx, and fyare the frequencies of the (di)nucleotide xy,x, and y,
respectively. The z-score is computed by subtracting the mean and dividing
by the standard deviation (Palmeira, et al., 2006). The latter is somewhat
more sensitive for over and under representation.
Example 3. Rho and z-scores. The coefficient rho and the corresponding
z-scores will be computed from the sequence with NCBI accession number
”AF517525.CCND3”.
> round(rho(getSequence(ccnd3hs$req[[1]])),2)
aa ac ag at ca cc cg ct ga gc gg gt ta tc tg tt
0.84 0.83 1.30 0.97 1.28 1.03 0.51 1.47 1.06 1.19 0.94 0.69 0.54 0.81 1.67 0.70
> round(zscore(getSequence(ccnd3hs$req[[1]]),modele=’base’),2)
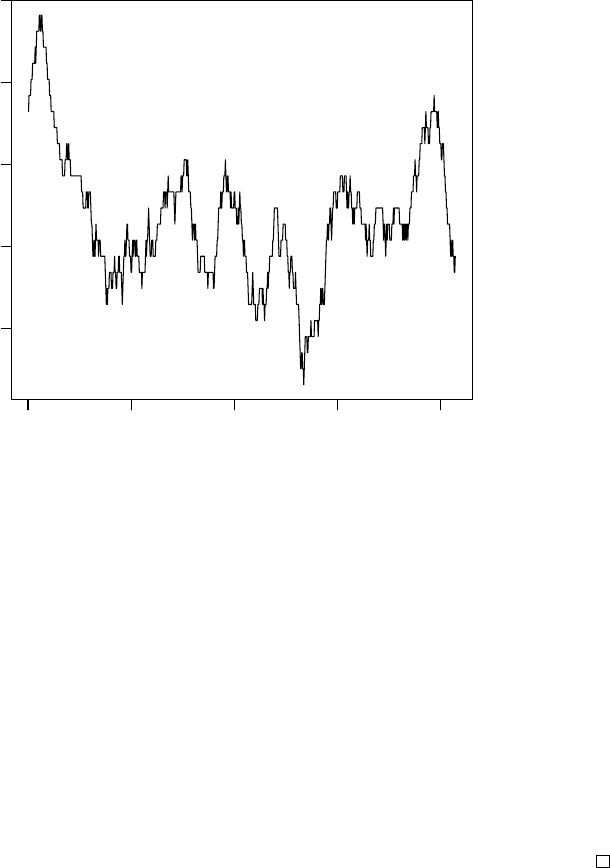
178 CHAPTER 9. ANALYZING SEQUENCES
0 200 400 600 800
0.5 0.6 0.7 0.8 0.9
Index
GCperc
Figure 9.1: G + C fraction of sequence ”AF517525.CCND3” along a window
of length 50 nt.
aa ac ag at ca cc cg ct ga gc gg gt ta
-1.08 -1.67 2.81 -0.18 2.78 0.42 -6.63 4.64 0.54 2.60 -0.80 -2.87 -3.10
tc tg tt
-1.86 6.22 -1.98
The rho value for CG is not extreme, but its z-score certainly is.
In case we have an amino acid sequence it may be useful to obtain a
plot of the amino acid frequencies. When we have translated the nucleotide
sequence into an amino acid sequence, it may be interesting to construct a
9.3. COMPUTATIONS ON SEQUENCES 179
plot expressing their frequencies. Such can be useful for a first impression on
sequence similarity.
Example 4. Comparing Amino acid frequencies. We continue with the
first result from the CCND3 (Cyclin D3) search, translate and order it, and,
next, produce a dotchart with amino acid frequencies.
tab <- table(getTrans(ccnd3hs$req[[1]]))
taborder <- tab[order(tab)]
names(taborder) <- aaa(names(taborder))
dotchart(taborder,pch=19,xlab="Stop and amino-acid-counts")
abline(v=1,lty=2)
The script was run on both sequences AF517525.CCND3 and AL160163.CCND3
resulting in Figure 9.2 and 9.3, respectively. The two sequences are highly
similar with respect to amino acid frequencies.
Stp
Asn
Trp
Phe
His
Tyr
Met
Ile
Lys
Cys
Asp
Gly
Val
Gln
Pro
Thr
Ser
Glu
Arg
Ala
Leu
0 10 20 30 40
Stop and amino−acid−counts
Figure 9.2: Frequency plot of
amino acids from accession num-
ber AF517525.CCND3.
Stp
Asn
Trp
Phe
His
Tyr
Met
Ile
Lys
Cys
Asp
Gly
Val
Gln
Pro
Thr
Ser
Glu
Arg
Ala
Leu
0 10 20 30 40
Stop and amino−acid−counts
Figure 9.3: Frequency plot of
amino acids from accession num-
ber AL160163.CCND3.
For amino acid sequences it may be of importance to compute the the-
oretical isoelectric point or the molecular weight of the corresponding protein.

180 CHAPTER 9. ANALYZING SEQUENCES
Example 5. Isoelectric point. The function computePI computes the
theoretical isoelectric point of a protein, which is the pH at which the protein
has a neutral charge (Gasteiger, et al. 2005).
> computePI(getTrans(ccnd3hs$req[[1]]))
[1] 6.657579
The protein molecular weight can be computed as follows.
> pmw(getTrans(getSequence(ccnd3hs$req[[1]])))
[1] 32503.38
Note that it is easy to compute these for all downloaded proteins and to
compare these.
Another important quantity is hydropathy score (Kyte & Doolittle, 1982)
of proteins, which is defined as a weighted sum P20
i=1 αifiof amino acid co-
efficients αiand the relative frequencies fi. An example will illustrate how
it can be computed.
Example 6. Hydropathy score. The coefficients α1,··· , α20 are available
as KD data from the EXP list of the seqinr package. The unique names are
lexicographically ordered and stored in the object kdc. The scale is changed
by the minus sign below so that hydrophilic proteins are positive, but smaller
than one. A function is defined to compute the hydropathy score for a set of
amino acid sequences.
ccnd3 <- sapply(ccnd3hs$req, getSequence)
ccnd3transl <- sapply(ccnd3, getTrans)
data(EXP)
names(EXP$KD) <- sapply(words(), function(x) translate(s2c(x)))
kdc <- EXP$KD[unique(names(EXP$KD))]
kdc <- -kdc[order(names(kdc))]
linform <- function(data, coef) { #data are sequences
f <- function(x) {
freq <- table(factor(x, levels = names(coef)))/length(x)
return(coef %*% freq) }
res <- sapply(data, f)
names(res) <- NULL

9.4. MATCHING PATTERNS 181
return(res)
}
kdath <- linform(ccnd3transl, kdc)
> print(kdath,digits=3)
[1] 0.0874 0.0962 0.0189 0.1496 0.0962 0.0874 0.0874 0.2659 0.2220
Indeed, the largest score is still much smaller than one, so the conclusion is
that there are no hydrophilic proteins among our sequences.
The data set aaindex of the seqinr library contains more than five hun-
dred sets of coefficients for computing specific quantities with respect to
proteins.
9.4 Matching patterns
A manner to investigate a long sequence is to search for identical patterns,
eventually allowing for a specified number of mismatches. There are many
relevant examples such as seeking for one of the stop codons UAG,UGA UAA in
RNA, or recognition sequences of enzymes (e.g. Roberts, et al., 2007). We
sustain with a brief example.
Example 1. Pattern match. In the sequence with NCBI accession number
”AF517525.CCND3”, we seek the pattern ”cccggg” with zero mismatches as
well as those with a single mismatch. By the function c2s a sequence of
characters is converted into a single string.
library(seqinr)
choosebank("genbank")
query("ccnd3hs","sp=homo sapiens AND k=ccnd3@")
ccnd3 <- sapply(ccnd3hs$req, getSequence)
ccnd3nr1 <- c2s(ccnd3[[1]])
> ccnd3nr1
[1] "atggagctgctgtgttgcgaaggcacccggcacgcgccccgggccgggccggacccgcgg"...
> subseq <- "cccggg"
> countPattern(subseq, ccnd3nr1, mismatch = 0)
[1] 2
> matchPattern(subseq, ccnd3nr1, mismatch = 0)
Views on a 879-letter BString subject

182 CHAPTER 9. ANALYZING SEQUENCES
Subject: atggagctgctgtgttgcgaaggcacccggcacg...actcctacagatgtcacag
Views:
start end width
[1] 38 43 6 [cccggg]
[2] 809 814 6 [cccggg]
> matchPattern(subseq, ccnd3nr1, mismatch = 1)
Views on a 879-letter BString subject
Subject: atggagctgctgtgttgcgaaggcacccggcacg...actcctacagatgtcacag
Views:
start end width
[1] 26 31 6 [cccggc]
[2] 37 42 6 [ccccgg]
[3] 38 43 6 [cccggg]
[4] 43 48 6 [gccggg]
[5] 54 59 6 [cccgcg]
[6] 119 124 6 [cccgcg]
[7] 236 241 6 [ccctgg]
[8] 303 308 6 [cctggg]
[9] 512 517 6 [cccgtg]
[10] 612 617 6 [cacggg]
[11] 642 647 6 [cctggg]
[12] 661 666 6 [tccggg]
[13] 662 667 6 [ccgggg]
[14] 808 813 6 [ccccgg]
[15] 809 814 6 [cccggg]
[16] 810 815 6 [ccgggg]
The number of counted patterns allowing two mismatches is much larger.
9.5 Pairwise alignments
Among the basic questions about genes or proteins is to what extent a pair
of sequences are similar. To find this out these are aligned in a certain man-
ner after which a similarity score can be computed. In order to understand
sequence alignment it is fundamental to have some idea about recursion.

9.5. PAIRWISE ALIGNMENTS 183
Example 1. Basic recursion. The idea of recursion is to generate a sequence
by defining the current value as a function of the previous. Suppose that the
first element is one, x1= 1, and that the sequence is defined by
xi=xi−1+ 1.
Then we obtain x1= 1, x2= 2, x3= 3, etc, so that the sequence becomes
1,2,3,···. Indeed, this is as fundamental as counting.
Another manner to define a sequence is by multiplying the previous value
by a constant. For example, let xi= 2xi−1with x1= 1. Then the values of
the sequence are x1= 1, x2= 2, x3= 4, x3= 8, etc. Also we see that in fact
xn= 2n, so that a value of the sequence can be computed without actually
computing all previous elements.
Another example would be xi= 2xi−1−10, with x1= 1. In order to
compute the value x10 we may use R, as follows.
> x<-double();x[1]<-1
> for (i in 2:10) {x[i]<- 2*x[i-1]-10}
> x[10]
[1] -4598
This illustrates basic ideas about recursively defined sequences.
Suppose we want to compute an alignment score for two small DNA
sequences GAATTC and GATTA (Durbin et. al., 1998, p.18). We agree
that a match between two letters should have the score +2 and a mismatch
the score -1. A gap at a certain position of the sequences should be punished
by subtracting a score by d= 2. A possible alignment is G
G
A
A
A
T
T
T
T
−
C
A, where
the minus sign indicates a gap. Then the alignment consists of a match,
match, mismatch, match, gap, mismatch, respectively, so that the score is
2+2−1+2−2−1 = 2. Now the question is whether this alignment is
optimal in the sense that the score is maximal? The answer is: No! To see
this, consider the alignment G
G
A
A
A
−
T
T
T
T
C
A. Then we have a match, match, gap,
match, match, mismatch, respectively, so that the score is 2+2−2+2+2−1 =
5. This is better, but still we do not know whether this alignment is optimal.
In order to ascertain that the alignment is optimal we have to build an
alignment score matrix F(i, j). To do so it is convenient to start with building
the (mis)match score matrix s(i, j). Its (i, j)th element s(i, j) has the value
2 in case of a match and the value -1 is case of a mismatch. Note that for
184 CHAPTER 9. ANALYZING SEQUENCES
each step we can choose between a gap, a match, or a mismatch. Building
up the matrix F(i, j) recursively, means that we define its elements on the
basis of the values of its preceding elements. That is, given the values of
the previous elements F(i−1, j −1), F(i−1, j), and F(i, j −1), we will be
able to find the best consecutive value for F(i, j). In particular, in case of
a match or a mismatch, we take F(i, j) = F(i−1, j −1) + s(xi, yj) and in
case of a gap we take F(i, j) = F(i−1, j)−dor F(i, j) = F(i, j −1) −d.
The famous Needleman-Wunsch alignment algorithm consists of taking the
maximum out of these possibilities at each step (e.g, Durbin et. al., 1998,
p.21). Their algorithm can be summarized, as follows.
F(i, j) = max
F(i−1, j −1) + s(i, j)
F(i−1, j)−d
F(i, j −1) −d
Note, however, that this will not yet work because we have not defined any
initial values. In fact we will agree to start with F(0,0) = 0 and due to the
gap penalties we take F(i, 0) = −id for the first column and F(0, j) = −jd
for the first row. Then, the final score F(n, m) is the optimal score and the
values of the matrix F(i, j) indicates the optimal path. By informaticians
this recursive scheme is often called a “dynamic programming algorithm”.
Example 2. Dynamic programming of DNA sequences. Consider again
the DNA sequences GAATTC, GATTA, the score +2 for a match, -1 for a
mismatch, and the gap penalty d= 2. It is clarifying to first construct the
score matrix s(i, j). For this we use the string-to-character function s2c, a
for loop, and an if else statement.
library(seqinr)
x <- s2c("GAATTC"); y <- s2c("GATTA"); d <- 2
s <- matrix(data=NA,nrow=length(y),ncol=length(x))
for (i in 1:(nrow(s))) for (j in 1:(ncol(s)))
{if (y[i]==x[j]) s[i,j]<- 2 else s[i,j]<- -1 }
rownames(s) <- c(y); colnames(s) <- c(x)
> s
GAATTC
G 2 -1 -1 -1 -1 -1
A -1 2 2 -1 -1 -1
T -1 -1 -1 2 2 -1

9.5. PAIRWISE ALIGNMENTS 185
T -1 -1 -1 2 2 -1
A -1 2 2 -1 -1 -1
To initialize the first row and column of the matrix F(i, j), it is convenient
to use the function seq. The purpose of the max function seems obvious.
F <- matrix(data=NA,nrow=(length(y)+1),ncol=(length(x)+1))
rownames(F) <- c("",y); colnames(F) <- c("",x)
F[,1] <- -seq(0,length(y)*d,d); F[1,] <- -seq(0,length(x)*d,d)
for (i in 2:(nrow(F)))
for (j in 2:(ncol(F)))
{F[i,j] <- max(c(F[i-1,j-1]+s[i-1,j-1],F[i-1,j]-d,F[i,j-1]-d))}
> F
G A A T T C
0 -2 -4 -6 -8 -10 -12
G -2 2 0 -2 -4 -6 -8
A-40420-2-4
T -6 -2 2 3 4 2 0
T -8 -4 0 1 5 6 4
A -10 -6 -2 2 3 4 5
From the lower corner to the right hand side we see that the optimal score
is indeed 5.
Optimal alignment for pairs of amino acid sequences are often considered
to be more relevant because these are more closely related to biological func-
tions. For this purpose we may modify the previous scheme by changing the
gap penalty dand the (mis)match scores s(i, j). In particular, we shall use
the gap penalty d= 8 and for the (mis)match the scores from the so-called
BLOSUM50 matrix.
Example 3. Programming Needleman-Wunsch. For the two sequences
”PAWHEAE” and ”HEAGAWGHEE” (see, Durbin et. al., 1998, p.21) we
seek the Needleman-Wunsch optimal alignment score, using the BLOSUM50
(mis)match score matrix and gap penalty d= 8. You can either directly read
a BLOSUM matrix from NCBI
> file <- "ftp://ftp.ncbi.nih.gov/blast/matrices/BLOSUM50"
> BLOSUM50 <- as.matrix(read.table(file, check.names=FALSE))

186 CHAPTER 9. ANALYZING SEQUENCES
Table 9.1: BLOSUM50 matrix.
A R N D C Q E G H I L K M F P S T W Y V
A 5 -2 -1 -2 -1 -1 -1 0 -2 -1 -2 -1 -1 -3 -1 1 0 -3 -2 0
R -2 7 -1 -2 -4 1 0 -3 0 -4 -3 3 -2 -3 -3 -1 -1 -3 -1 -3
N -1 -1 7 2 -2 0 0 0 1 -3 -4 0 -2 -4 -2 1 0 -4 -2 -3
D -2 -2 2 8 -4 0 2 -1 -1 -4 -4 -1 -4 -5 -1 0 -1 -5 -3 -4
C -1 -4 -2 -4 13 -3 -3 -3 -3 -2 -2 -3 -2 -2 -4 -1 -1 -5 -3 -1
Q -1 1 0 0 -3 7 2 -2 1 -3 -2 2 0 -4 -1 0 -1 -1 -1 -3
E -1 0 0 2 -3 2 6 -3 0 -4 -3 1 -2 -3 -1 -1 -1 -3 -2 -3
G 0 -3 0 -1 -3 -2 -3 8 -2 -4 -4 -2 -3 -4 -2 0 -2 -3 -3 -4
H -2 0 1 -1 -3 1 0 -2 10 -4 -3 0 -1 -1 -2 -1 -2 -3 2 -4
I -1 -4 -3 -4 -2 -3 -4 -4 -4 5 2 -3 2 0 -3 -3 -1 -3 -1 4
L -2 -3 -4 -4 -2 -2 -3 -4 -3 2 5 -3 3 1 -4 -3 -1 -2 -1 1
K -1 3 0 -1 -3 2 1 -2 0 -3 -3 6 -2 -4 -1 0 -1 -3 -2 -3
M -1 -2 -2 -4 -2 0 -2 -3 -1 2 3 -2 7 0 -3 -2 -1 -1 0 1
F -3 -3 -4 -5 -2 -4 -3 -4 -1 0 1 -4 0 8 -4 -3 -2 1 4 -1
P -1 -3 -2 -1 -4 -1 -1 -2 -2 -3 -4 -1 -3 -4 10 -1 -1 -4 -3 -3
S 1 -1 1 0 -1 0 -1 0 -1 -3 -3 0 -2 -3 -1 5 2 -4 -2 -2
T 0 -1 0 -1 -1 -1 -1 -2 -2 -1 -1 -1 -1 -2 -1 2 5 -3 -2 0
W -3 -3 -4 -5 -5 -1 -3 -3 -3 -3 -2 -3 -1 1 -4 -4 -3 15 2 -3
Y -2 -1 -2 -3 -3 -1 -2 -3 2 -1 -1 -2 0 4 -3 -2 -2 2 8 -1
V 0 -3 -3 -4 -1 -3 -3 -4 -4 4 1 -3 1 -1 -3 -2 0 -3 -1 5
or load a BLOSUM matrix from the Biostrings package. For the sake of
clarity we shall conveniently construct the matrix s(i, j) without any concern
about computer memory.
library(seqinr);library(Biostrings);data(BLOSUM50)
x <- s2c("HEAGAWGHEE"); y <- s2c("PAWHEAE"); s <- BLOSUM50[y,x]; d <- 8
F <- matrix(data=NA,nrow=(length(y)+1),ncol=(length(x)+1))
F[1,] <- -seq(0,80,8); F[,1] <- -seq(0,56,8)
rownames(F) <- c("",y); colnames(F) <- c("",x)
for (i in 2:(nrow(F)))
for (j in 2:(ncol(F)))
{F[i,j] <- max(c(F[i-1,j-1]+s[i-1,j-1],F[i-1,j]-d,F[i,j-1]-d))}

9.5. PAIRWISE ALIGNMENTS 187
> F
HEAGAWGHEE
0 -8 -16 -24 -32 -40 -48 -56 -64 -72 -80
P -8 -2 -9 -17 -25 -33 -41 -49 -57 -65 -73
A -16 -10 -3 -4 -12 -20 -28 -36 -44 -52 -60
W -24 -18 -11 -6 -7 -15 -5 -13 -21 -29 -37
H -32 -14 -18 -13 -8 -9 -13 -7 -3 -11 -19
E -40 -22 -8 -16 -16 -9 -12 -15 -7 3 -5
A -48 -30 -16 -3 -11 -11 -12 -12 -15 -5 2
E -56 -38 -24 -11 -6 -12 -14 -15 -12 -9 1
Hence, from the lower-right corner we observe that the optimal score equals
one.
Example 4. Needleman-Wunsch. We may also conveniently use the pairwiseAlignment
function from the Biostrings package to find the optimal Needleman-Wunsch
aligment score for the sequences PAWHEAE” and ”HEAGAWGHEE” (see,
Durbin et. al., 1998, p.21).
library(Biostrings);data(BLOSUM50)
> pairwiseAlignment(AAString("PAWHEAE"), AAString("HEAGAWGHEE"),
+ substitutionMatrix = "BLOSUM50",gapOpening = 0, gapExtension = -8,
+ scoreOnly = FALSE)
Global Pairwise Alignment
1: --P-AW-HEAE
2: HEAGAWGHE-E
Score: 1
Hence, we obtain the optimal score 1 as well as a representation of the opti-
mal alignment.
An obvious question is whether in the previous example the obtained
score 1 is to be evaluated as being “large” or not. A manner to answer this
question is by comparing it with the alignment score of random sequences.
That is, we may compute the probability of alignment scores larger than 1.
Example 5. Comparing with random sequences. To illustrate how the
probability of alignment scores larger than 1 can be computed we sample
randomly from the names of the amino acids, seven for y and 10 for x and

188 CHAPTER 9. ANALYZING SEQUENCES
compute the maximum alignment score. This is repeated 1000 times and the
probability of optimal alignment scores greater than 1 is estimated by the
corresponding proportion.
library(seqinr);library(Biostrings);data(BLOSUM50)
randallscore <- double()
for (i in 1:1000) {
x <- c2s(sample(rownames(BLOSUM50),7, replace=TRUE))
y <- c2s(sample(rownames(BLOSUM50),10, replace=TRUE))
randallscore[i] <- pairwiseAlignment(AAString(x), AAString(y),
substitutionMatrix = "BLOSUM50",gapOpening = 0, gapExtension = -8,
scoreOnly = TRUE)
}
> sum(randallscore>1)/1000
[1] 0.003
By the option scoreOnly = TRUE the optimal score is written to the vector
randallscore. The probability of scores larger than 1 equals 0.003 and is
therefore small and the alignment is stronger than expected from randomly
constructed sequences.
Example 6. Sliding window on Needleman-Wunsch scores. We may also
program a sliding window such that for each the Needleman-Wunsch align-
ment score is computed. Then the maximum can be found and localized.
choosebank("genbank"); library(seqinr)
query("ccnd3hs","sp=homo sapiens AND k=ccnd3@")
ccnd3 <- sapply(ccnd3hs$req, getSequence)
ccnd3transl <- sapply(ccnd3, getTrans)
x <- c2s(ccnd3transl[[1]])
y <- c2s(ccnd3transl[[1]][50:70])
nwscore <- double() ; n <- length(ccnd3transl[[1]])
for (i in 1:(n-21))
nwscore[i] <-
pairwiseAlignment(AAString(c2s(ccnd3transl[[1]][i:(i+20)])),
AAString(y),substitutionMatrix = "BLOSUM50",gapOpening = 0,
gapExtension = -8, scoreOnly = TRUE)
> pairwiseAlignment(AAString(y), AAString(y),
substitutionMatrix = "BLOSUM50", gapOpening = 0, gapExtension = -8,

9.6. OVERVIEW AND CONCLUDING REMARKS 189
+ scoreOnly = TRUE)
[1] 152
> max(nwscore)
[1] 152
> which.max(nwscore)
[1] 50
Note that the maximum occurs when the subsequences are identical. The
value of the maximum is 152 which occurs at position 50.
9.6 Overview and concluding remarks
It was illustrated how the query language of the seqinr library can be used
to download sequences, to translate these and to compute relevant quanti-
ties such as the isoelectric point or the hydropathy score. Furthermore, it
was illustated how patterns can be matched and how algorithms for optimal
pairwise alignment can be programmed. Further applications are given by
the exercises below.
The package Biostrings contains the various PAM matrices for optimal
alignment, as well as facilities to find palindromes, and to read and write
data in FASTA format (readFASTA).
9.7 Exercises
1. Writing to a FASTA file. Read, similar to the above, the ccnd3 se-
quences using the query language and write the first sequence to a files
in FASTA format. Also try to write them all to FASTA format.
2. Dotplot of sequences. Use the function dotPlot of the seqinr package
and par(mfrow=c(1,2)) to produce two adjacent plots.
(a) Construct two random sequence of size 100 and plot the first
against second and the first against the first.
(b) Construct a plot of the first against the first and the first against
the first in reverse order.
190 CHAPTER 9. ANALYZING SEQUENCES
(c) Download the sequences related to the species homo sapiens and
a gene name like ”CCND3 Cyclin D3”. Construct a dotplot of
the most similar and the least similar sequences. Report your
observations.
3. Local alignment. The Smith-Waterman algorithm seeks maximum lo-
cal alignment between subsequences of sequences. Their algorithm can
be summarized (Durbin et al., 2005, p.22), as follows.
F(i, j) = max
F(i−1, j −1) + s(i, j)
F(i−1, j)−d
F(i, j −1) −d
The algorithm allows the score zero if the others have negative values.
The idea is that the maximum alignment can occur anywhere in the
matrix, optimal alignment is defines as the maximum over the whole
matrix. Program the Smith-Waterman algorithm and find the optimal
local alignment of the sequences PAWHEAE” and ”HEAGAWGHEE”.
4. Probability of more extreme alignment score. Sample x and y randomly
from the names of the amino acids, seven for y and 10 for x. repeat
this 1000 times and compute the optimal alignment score and use it to
evaluate the significance of the previously obtained score.
5. Prochlorococcus marinus. Each of three strains of P. marinus is ex-
posed to different intensities of UV radiation because these live in dif-
ferent depths in water. The MIT 9313 strain lives at depth 135 m,
SS120 at 120 m, and MED4 at 5 m. The latter strain is considered
to be high-light-adapted. The residual intensities of 260-nm UVb ir-
radiation corresponding to the given depths is 0.00007%, 0.0002% and
70%, respectively. It is hypothesized that the G + C content depends
on the amount of radiation. The accession numbers of Gen bank are
AE017126, BX548174, and BX548175, respectively.
(a) Use the operator OR together with the accession numbers to
download the sequences of the bacteria strains.
(b) Compte the GC fraction of each of the sequences.
(c) Is there a relation between UVb radiation and GC fraction?
(d) Formulate a relevant hypothesis and test it.
9.7. EXERCISES 191
6. Sequence equality. Download the sequences ”AF517525.CCND3” and
”AL160163.CCND3”. Hint: These are the first two from the query
”ccnd3” within homo sapiens.
(a) Compute the length of the sequences.
(b) Translate the sequences into amino acids and compare their fre-
quencies.
(c) Are they equal or, if not, in what position do they differ?
7. Conserved region. At http://blocks.fhcrc.org there are blocks of
highly conserved regions for proteins in PROSITE. Find PR00851A
which contains blocks of protein related to a human gene responsible
for DNA-repair defect xeroderma pigmentosum (sensitivity to ultravi-
olet light) Perform a pairwise alignment with these subsequences and
report the ones most and least similar. Use BLOSUM50.
8. Plot of CG proportion from Celegans.
(a) Produce a plot of the CG proportion of the chromosome I of Cel-
egans (Celegans.UCSC.ce2) along a window of 100 nucleotides.
Take the first 10,000 nucleotides.
(b) A binding sequence of the enzyme EcoRV is the subsequence
GATATC. How many exact matches has Chromosome I of Cel-
egans. How many do you expect by chance?
9. Plot of codon usage. Go to the seqinr help page on dotchart.uco.
(a) Redo the example and briefly describe its usage.
(b) Use the query language to find
192 CHAPTER 9. ANALYZING SEQUENCES

Chapter 10
Markov Models
The idea of a Markov process forms the basis of many important models in
bioinformatics such as (Hidden) Markov Models, models for sequence align-
ment, and models for phylogenetic trees. By the latter it is possible to
estimate distances between several sequences and to visualize these in a tree.
Classical matrices for sequence alignment such as BLOSUM and PAM are
constructed on the basis of a Markov process. By (Hidden) Markov Mod-
els the specific repetitive order of DNA sequences can be modeled so that
predictions of families becomes possible.
In this chapter you learn what a probability transition matrix is and which
role it plays in a Markov process to construct specific sequences. Various
models for phylogenetic trees are explained in terms of the rate matrix as
well as the probability transition matrix. The basic ideas of the Hidden
Markov Model are briefly explained and illustrated by an example1.
10.1 Random sampling
Models to predict and classify DNA type of sequences make it possible to
draw a sample from a population. The latter is the same as a distribution
with certain properties. Recall from Chapter 3 that a discrete distribution
is a set of values with certain probabilities that add up to one. Two basic
examples illustrate this point.
1This chapter is somewhat more technical in its notation with respect to e.g. conditional
probability. This is, however, inevitable for the understanding of Markov processes.
193

194 CHAPTER 10. MARKOV MODELS
Example 1. Throwing a coin. A fair coin Xattains Head and Tail with
probability 1/2. Thus we may write P(X=H)=0.5 and P(X=T)=0.5.
With such a random variable there always correspond a population as well
as a sampling scheme which can be simulated on a computer (e.g. Press, et
al., 1992).
> sample(c("H","T"),30,rep=TRUE,prob=c(0.5,0.5))
[1] "H" "H" "T" "T" "T" "H" "H" "T" "T" "H" "H" "H" "T" "T" "H" "T"
[20] "H" "T" "T" "T" "H" "T" "H" "T" "T" "T" "T"
Thus the sampled values Head and Tail correspond to the process of actu-
ally throwing with a fair coin. The function sample randomly draws thirty
times one of the values c("H","T") with replacement (rep=TRUE) and equal
probabilities (prob=c(0.5,0.5)).
Example 2. Generating a sequence of nucleotides. Another example is
that of a random variable Xwhich has the letters of the nucleotides as its
values. So the events are X=A,X=C,X=G, and X=T. These events
may occur in a certain DNA sequence with probabilities P(X=A) = 0.1,
P(X=G) = 0.4, P(X=C) = 0.4, and P(X=T) = 0.1, respectively. Then
the actual placement of the nucleotides along a sequence can be simulated.
> sample(c("A","G","C","T"),30,rep=TRUE,prob=c(0.1,0.4,0.4,0.1))
[1] "G" "C" "T" "G" "C" "G" "G" "G" "T" "C" "T" "T" "C" "C" "C"
[20] "G" "G" "C" "G" "G" "G" "C" "C" "C" "G" "C"
Of course, if you do this again, then the resulting sequence will differ due to
the random nature of its generation.
For these sampling schemes it holds that the events occur independently
from the previous.
10.2 Probability transition matrix
In order to build a model that produces specific sequences we will consider
a certain type of random variable. In particular, we will consider a sequence
{X1, X2,···} with values from a certain state space E. The latter is simply
a set containing the possible values or states of a process. If, for instance,
Xn=i, then the process is in state iat time n. Similarly, the expression

10.2. PROBABILITY TRANSITION MATRIX 195
P(X1=i) denotes the probability that the process is in state iat time
point 1. The event that the process changes its state from ito j(transition)
between time point one and two corresponds to the event (X2=j|X1=i),
where the bar means ”given that”. The probability for this event to happen
is denoted by P(X2=j|X1=i). In general, the probability of the transition
from ito jbetween time point nand n+ 1 is given by P(Xn+1 =j|Xn=i).
These probabilities can be collected in a probability transition matrix Pwith
elements
pij =P(Xn+1 =j|Xn=i).
We will assume that the transition probabilities are the same for all time
points so that there is no time index needed on the left hand side. Given
that the process Xnis in a certain state, the corresponding row of the tran-
sition matrix contains the distribution of Xn+1, implying that the sum of the
probabilities over all possible states equals one. The probability transition
matrix contains a (conditional) discrete probability distribution on each of
its rows. For a Markov process it holds that the state at time point n+ 1 de-
pends upon the state at time point n, but not on states at earlier time points.
Example 1. Using the probability transition matrix to generate a Markov
sequence. Suppose Xnhas two states: 1 for a pyrimidine and 2 for a purine.
A sequence can now be generated, as follows. If Xn= 1, then we throw
with a fair die: If the outcome is lower than or equal to 5, then Xn+1 = 1
and, otherwise, (outcome equals 6) Xn+1 = 2. If Xn= 2, then we throw
with a fair coin: If the outcome equals Tail, then Xn+1 = 1, and otherwise
Xn+1 = 2. For this process the two by two probability transition matrix
equals
from
to
1 2
1p11 p12
2p21 p22
,
where p21 is the probability that the process changes from 2 to 1. This
transition matrix can also be written as
P=µp11 p12
p21 p22 ¶=µP(X1= 1|X0= 1) P(X1= 2|X0= 1)
P(X1= 1|X0= 2) P(X1= 2|X0= 2) ¶=µ5
6
1
6
1
2
1
2¶.
Any matrix probability transition matrix Pcan be visualized by a transi-
tion graph, where the transition probabilities are visualized by an arrow from

196 CHAPTER 10. MARKOV MODELS
state ito state jand the value of pij . For the current example the transition
graph is given by Figure 10.12. The values 1 and 2 of the process are written
within the circles and the transition probabilities are written near the arrows.
To actually generate a sequences with values equal to 1 and 2 according the
5/6
1/6
1/2
1/2
01
Figure 10.1: Graph of probability transition matrix
transition matrix we may use the following.
markov1 <- function(x,P,n){ seq <- x
for(k in 1:(n-1)){
seq[k+1] <- sample(x, 1, replace=TRUE, P[seq[k],])}
return(seq)
}
P <- matrix(c(1/6,5/6,0.5,0.5), 2, 2, byrow=TRUE)
rownames(P) <- colnames(P) <- StateSpace <- x <- c(1,2)
> markov1(x,P,30)
[1]121212212122121221212121222222
In the function markov1 the actual sampling is conducted by sample. We
sample one element from the set containing 1 and 2 according to the prob-
abilities in row seq[k] of the matrix P. This makes the probabilities of the
states dependent on the corresponding row of the transition matrix. We con-
veniently use the fact that R adds an element to the sequence; we do not
have to declare its length on beforehand (although we could!). The sequence
has a fixed start at State 1 and thereafter the first row in the probability
transition matrix. Note that without the return command the function does
2The values 1 and 2 are erroneously depicted as 0 and 1, respectively

10.2. PROBABILITY TRANSITION MATRIX 197
not give any output.
Example 2. A sequence with a large frequency of C and G. To illustrate
that certain probability transition matrices imply a large frequency of C and
G residues, we use the following.
markov2 <- function(StateSpace,P,pi0,n){
seq <- character(n)
seq[1] <- sample(StateSpace, 1, replace=TRUE, pi0)
for(k in 1:(n-1)){
seq[k+1] <- sample(StateSpace, 1, replace=TRUE, P[seq[k],])}
return(seq)
}
P <- matrix(c(
1/6,5/6,0,0,
1/8,2/4,1/4,1/8,
0,2/6,3/6,1/6,
0,1/6,3/6,2/6),4,4,byrow=TRUE)
rownames(P) <- colnames(P) <- StateSpace <- c("a","c","g","t")
pi0 <- c(1/4,1/4,1/4,1/4)
x <- markov2(StateSpace,P,pi0,1000)
> table(x)
x
a c g t
72 409 378 141
The function starts with sampling just once from the distribution with equal
probabilities pi0. It conveniently uses the the column and row names of the
probability transition matrix for the sampling. The probabilities to go from
”a” or ”t” to ”c” or ”g” are large and as well as that to stay within ”c”
or ”g”. From the frequency table it can be observed that the majority of
residues are ”c” or ”g”.
Example 3. A sequence with high phenylalanine frequency. Now it is
possible to construct a sequence which produces the amino acid phenylalanine
(F) with high probability. Recall that it is coded by the triple TTT or TTC.
We use the function getTrans of the seqinr package to translate nucleotide
triplets into amino acids.

198 CHAPTER 10. MARKOV MODELS
pi0 <- c(1/4,1/4,1/4,1/4)
P <- matrix(c(.01,.01,.01,.97,
.01,.01,.01,.97,
.01,.01,.01,.97,
.01,.28,.01,0.70),4,4,byrow=T)
rownames(P) <- colnames(P) <- StateSpace <- c("a","c","g","t")
x <- markov2(StateSpace,P,pi0,30000)
> table(getTrans(x))
*ACDFHILMNPRSTVW
2 1 75 2 5205 24 76 2260 1 2 19 26 2154 1 91 1
Y
60
From the table it is clear that the F frequency is the largest among the gen-
erated amino acids.
Example 4. To illustrate estimation of the probability transition matrix
we proceed with the sequence produced by the previous example.
nr <- count(x,2)
names(nr)
A <- matrix(NA,4,4)
A[1,1]<-nr["aa"]; A[1,2]<-nr["ag"]; A[1,3]<-nr["ac"]; A[1,4]<-nr["at"]
A[2,1]<-nr["ga"]; A[2,2]<-nr["gg"]; A[2,3]<-nr["gc"]; A[2,4]<-nr["gt"]
A[3,1]<-nr["ca"]; A[3,2]<-nr["cg"]; A[3,3]<-nr["cc"]; A[3,4]<-nr["ct"]
A[4,1]<-nr["ta"]; A[4,2]<-nr["tg"]; A[4,3]<-nr["tc"]; A[4,4]<-nr["tt"]
rowsumA <- apply(A, 1, sum)
Phat <- sweep(A, 1, rowsumA, FUN="/")
rownames(Phat) <- colnames(Phat) <- c("a","g","c","t")
> round(Phat,3)
a g c t
a 0.011 0.000 0.007 0.982
g 0.017 0.003 0.010 0.969
c 0.010 0.011 0.012 0.967
t 0.009 0.009 0.279 0.703
The number of transitions are counted and divided by the row totals. The
estimated transition probabilities are quite close to the true transition proba-
bilities. The zero transition probabilities are exactly equal to the true because

10.3. PROPERTIES OF THE TRANSITION MATRIX 199
these do not occur. This estimation procedure can easily be applied to DNA
sequences.
10.3 Properties of the transition matrix
In the above, the sequence was started at a certain state. Often, however,
the probabilities of the initial states are available. That is, we have a vec-
tor π0with initial probabilities π10 =P(X0= 1) and π20 =P(X0= 2).
Furthermore, if the transition matrix
P=µp11 p12
p21 p22 ¶=µP(X1= 1|X0= 1) P(X1= 2|X0= 1)
P(X1= 1|X0= 2) P(X1= 2|X0= 2) ¶,
then the probability that the process is in State 1 at time point 1 can be
written as
P(X1= 1) = π10p11 +π20p21 =πT
0p1,(10.1)
where p1is the first column of P, see Section 10.7. Note that the last
equality holds by definition of matrix multiplication. In a similar manner,
it can be shown that P(X1= 2) = πT
0p2, where p2is column 2 of the
transition matrix P= (p1,p2). It can be concluded that πT
0P=πT
1, where
πT
1= (P(X1= 1), P (X1= 2)); the probability at time point 1 that the
process is in State 1, State 2, respectively. This holds in general for all time
points n, that is
πT
nP=πT
n+1.(10.2)
Thus to obtain the probabilities of the states at time point n+ 1, we can
simply use matrix multiplication 3.
Example 1. Matrix multiplication to compute probabilities. Suppose
the following initial distribution and probability matrix
π0=¡2
3
1
3¢,P=µ5
6
1
6
1
2
1
2¶,
for State 1 and 2, respectively. Then P(X1= 1) and P(X1= 2) collected in
πT
1= (P(X1= 1), P (X1= 2)) can be computed as follows.
πT
1=πT
0P=¡2
3
1
3¢µ5
6
1
6
1
2
1
2¶=¡2
3·5
6+1
3·1
2
2
3·1
6+1
3·1
2¢=¡13
18
5
18 ¢
3The transposition sign Tsimply transforms a column into a row.
200 CHAPTER 10. MARKOV MODELS
Using R its operator %*% for matrix multiplication, the product πT
0Pcan be
computed as follows.
> P <- matrix(c(5/6,1/6,0.5,0.5),2,2,byrow=T)
> pi0 <- c(2/3,1/3)
> pi0 %*% P
[,1] [,2]
[1,] 0.7222222 0.2777778
Yet, another important property of the probability transition matrix deals
with the probability of being in state 1 given that the process is in state 1
two time points before. In particular, it holds (see Section 10.7) that
P(X2= 1|X0= 1) = p2
11,(10.3)
where the latter is element (1,1) of the matrix4P2. In general, we have that
P(Xn=j|X0=i) = pn
ij ,
which is element i, j of Pn.
Example 3. Given the probability matrix of the previous example, the
values P(X2=j|X0=i) for all of i, j can be computed by matrix multipli-
cation.
P2=µ5
6
1
6
1
2
1
2¶·µ5
6
1
6
1
2
1
2¶=µ(5
6)2+1
6
1
2
5
6
1
6+1
6
1
2
1
2
5
6+ (1
2)21
2
1
6+ (1
2)2¶=µ28
36
8
36
24
36
12
36 ¶.
Obviously, such matrix multiplications can be accomplished much more con-
venient on a personal computer.
> P %*% P
[,1] [,2]
[1,] 0.7777778 0.2222222
[2,] 0.6666667 0.3333333
Larger powers of Pcan be computed more efficiently by methods given be-
low.
4For a brief definition of matrix multiplication, see Pevsner (2003, p.56) or wikipedia
using the search string ”wiki matrix multiplication”.
10.4. STATIONARY DISTRIBUTION 201
10.4 Stationary distribution
A probability distribution πsatisfying
πT=πTP
is stationary because the transition matrix does not change the probabilities
of the states of the process. Such a distribution usually exists, is unique,
and plays an essential role in the long term behavior of the process. It sheds
light on the question: What is the probability P(Xn= 1|X0= 1) = pn
11, as n
increases without bound. That is: What is the probability that the process is
in State 1, given that it started in State 1, as time increases without bound?
To answer such a question we need large powers of the probability transition
matrix. To compute these we need the eigen-decomposition of the probability
transition matrix
P=VΛV−1,
where Vis the eigenvector matrix and Λthe diagonal matrix with eigen-
values. The latter are usually sorted in decreasing order so that the first
(left upper) is the largest. Now the third power of the probability transition
matrix can be computed, as follows
P3=VΛV−1VΛV−1VΛV−1=VΛΛΛV−1=VΛ3V−1.
So that, indeed, in general
Pn=VΛnV−1.
The latter is a computationally convenient expression because we only have
to take the power of the eigenvalues in Λand to multiply by the left and
right eigenvector matrices. This will be illustrated below.
In the long term the Markov process tends to a certain value (Br´emaud,
1999, p.197) because a probability transition matrix has a unique largest
eigenvalue equal to 1 with corresponding eigenvectors 1and π(or rather
normalized versions of these). It follows that, as nincreases without bound,
then Pntends to 1πT. In other words, P(Xn=j|X0=i) = pn
ij tends to
element (i, j) of 1πT, which is equal to element jof π. For any initial dis-
tribution π0, it follows that π0
0Pntends to πT.
Example 1. Stationary distribution. To compute the eigen-decomposition
of the probability transition matrix Pas well as powers of it, we may use
the function eigen.

202 CHAPTER 10. MARKOV MODELS
> P <- matrix(c(1/6,5/6,0.5,0.5),2,2,byrow=T)
> V <- eigen(P,symmetric = FALSE)
> V$values
[1] 1.0000000 -0.3333333
> V$vectors
[,1] [,2]
[1,] -0.7071068 -0.8574929
[2,] -0.7071068 0.5144958
The output of the function eigen is assigned to the list Vfrom which the
eigenvalues and eigenvectors can be extracted and printed to the screen.
Now we can compute P16; the probability transition matrix raised to the
power sixteen.
> V$vec %*% diag(V$va)^(16) %*% solve(V$vec)
[,1] [,2]
[1,] 0.375 0.625
[2,] 0.375 0.625
So that the stationary distribution πTequals (0.375,0.625).
Example 2. Diploid. Suppose Ais a dominant gene, aa recessive
and that we start with a heterozygote aA. From the latter we obtain the
initial state probability πT= (0,1,0) for the events (AA, aA, aa). When
we consider pure self-fertilization, then the offspring from AA is AA with
probability (1,0,0), that of aa is aa with probability (0,0,1), and that of
aA is (AA, aA, aa) with probability 1/4,1/2,1/4, respectively. Hence, the
probability transition matrix becomes
P=
100
1/4 1/2 1/4
001
We can now compute the transition probability matrix after five generations.
P <- matrix(c(1,0,0, 1/4,1/2,1/4,0,0,1),3,3,byrow=T)
V <- eigen(P,symmetric = FALSE)
> V$vec %*% diag(V$va)^(5) %*% solve(V$vec)
[,1] [,2] [,3]
[1,] 1.000000 0.00000 0.000000

10.5. PHYLOGENETIC DISTANCE 203
[2,] 0.484375 0.03125 0.484375
[3,] 0.000000 0.00000 1.000000
Hence, the distribution we obtain can be read from the second row which
is highly homozygotic. A little more precise, using Equation 10.2, it can be
shown that
πT
n+1 =µ1
2−µ1
2¶n
,µ1
2¶n
,1
2−µ1
2¶n¶,
so that the distribution converges to (1/2,0,1/2).
Note that this method of raising the transition probability matrix to a
large power can easily be applied to determine the stationary distribution.
The idea of taking a transition matrix to a certain power is also used to
construct the PAM250 matrix given the PAM1 matrix (Pevsner, 2003, p.53)
and for the construction of various BLOSUM matrices (Pevsner, 2003, p.50-
59; Deonier, et al. 2005, 187-190).
10.5 Phylogenetic distance
Phylogenetic trees are constructed on the basis of distances between DNA
sequences. These distances are computed from substitution models which
are defined by a matrix representing the rate of substitutions of one state
to the other. The latter is usually expressed as a matrix Q. The rates of
staying in a state are given by a negative number on the diagonal of the
substitution matrix. The probability transition matrix Pcan be computed
by matrix exponentiation P= exp(Q). How to do this in practice will be
illustrated by an example.
Example 1. From a rate matrix to a probability transition matrix.
Suppose the rate matrix
Q=
A
G
C
T
A G C T
−0.60 0.20 0.20 0.20
0.20 −0.60 0.20 0.20
0.20 0.20 −0.60 0.20
0.20 0.20 0.20 −0.60
.
Thus within a certain time period a proportion of 0.20 Achanges into G,
0.20 Ainto C, and 0.20 Ainto T. Consequently, a proportion of 0.60 of the

204 CHAPTER 10. MARKOV MODELS
residues goes back to A. Given this rate matrix, we can find the probabil-
ity transition matrix P= exp(Q) by using the function expm(Q) from the
package Matrix.
library(Matrix)
Q <- 0.2 * Matrix(c(-3,1,1,1,1,-3,1,1,1,1,-3,1,1,1,1,-3),4)
rownames(Q) <- colnames(Q) <- c("A","G","C","T")
P <- as.matrix(expm(Q))
> round(P,2)
A G C T
A 0.59 0.14 0.14 0.14
G 0.14 0.59 0.14 0.14
C 0.14 0.14 0.59 0.14
T 0.14 0.14 0.14 0.59
Thus the probability that the state changes from Ato Ais 0.59, from Ato
Gis 0.14, etc.
Because all phylogenetic models are defined in terms of rate matrices, we
shall concentrate on these. For instance, the rate matrix for the Jukes and
Cantor (1969) (JC69) model can be written as
QJC69 =
A
G
C
T
A G C T
·α α α
α·α α
α α ·α
α α α ·
.
The sum of each row of a rate matrix equals zero, so that from this require-
ment the diagonal elements of the JC69 model are equal to −3α. Further-
more, the non-diagonal substitution rates of the JC69 model all have the
same value α. That is, the change from ito jequals that from jto i, so
that the rate matrix is symmetric. Also the probability that the sequence
equals one of the nucleotides is 1/4. This assumption, however, is unrealistic
is many cases.
Transitions are substitutions of nucleotides within types of nucleotides,
thus purine to purine or pyrmidine to pyrmidine (A↔Gor C↔T).
Transversions are substitutions between nucleotide type (A↔T,G↔
T,A↔C, and C↔G). In the JC69 model a transition is assumed to
10.5. PHYLOGENETIC DISTANCE 205
happen with equal probability as a transversion. That is, it does not account
for the fact that transitions are more common that transversions. To cover
this for more general type of models are proposed by Kimura (1980, 1981),
which are commonly abbreviated by K80 and K81. In terms of the rate
matrix these models can we written as
QK80 =
·α β β
α·β β
β β ·α
β β α ·
,QK81 =
·α β γ
α·γ β
β γ ·α
γ β α ·
.
In the K80 model a change within type (transition) occurs at rate αand
between type (transversion) at rate β. In the K81 model all changes occur
at a different though symmetric rate; the rate of change A→Gis αand
equals that of A←G. If αis large, then the amount of transitions is large;
if both βand γare very small, then the number of transversions is small.
A model is called “nested” if it is a special case of a more general model.
For instance, the K80 model is nested in the K81 model because when we
take γ=β, then we obtain the K80 model. Similarly, the JC69 model is
nested in the K80 model because if we take β=α, then we obtain the JC69
model.
Some examples of models with even more parameters are the Hasegawa,
Kishino, and Yano (1985) (HKY85) model and the General Time-Reversable
Model (GTR) model
QHKY 85 =
·απGβπCβπT
απA·βπCβπT
βπAβπG·απT
βπAβπGαπC·
,QGT R =
·απGβπCγπT
απA·δπC²πT
βπAδπG·ζπT
γπA²πGζπC·
.
The distance between DNA sequences is defined on the basis of these models.
From these distances the phylogenetic tree is computed by a neighbor-joining
algorithm such that it has the smallest total branch length.
Example 2. The K81 model. To compute the rate matrix of the K81
model with α= 3/6, β= 2/6, γ= 1/6 we may use the following.
alpha <- 3/6; beta <- 2/6; gamma<- 1/6; Q <- matrix(data=NA,4,4)
Q[1,2] <- Q[2,1] <- Q[3,4] <- Q[4,3] <- alpha

206 CHAPTER 10. MARKOV MODELS
Q[1,3] <- Q[3,1] <- Q[2,4] <- Q[4,2] <- beta
Q[1,4] <- Q[4,1] <- Q[2,3] <- Q[3,2] <- gamma
> diag(Q) <- -(alpha + beta + gamma)
> Q
[,1] [,2] [,3] [,4]
[1,] -1.0000000 0.5000000 0.3333333 0.1666667
[2,] 0.5000000 -1.0000000 0.1666667 0.3333333
[3,] 0.3333333 0.1666667 -1.0000000 0.5000000
[4,] 0.1666667 0.3333333 0.5000000 -1.0000000
> Q <- Matrix(Q)
> P <- as.matrix(expm(Q))
> P
[,1] [,2] [,3] [,4]
[1,] 0.4550880 0.2288517 0.1767105 0.1393498
[2,] 0.2288517 0.4550880 0.1393498 0.1767105
[3,] 0.1767105 0.1393498 0.4550880 0.2288517
[4,] 0.1393498 0.1767105 0.2288517 0.4550880
By raising the power of the probability transition matrix to a sufficiently
large number, it can be observed that the stationary distribution πT=
(0.25,0.25,0.25,0.25).
Example 3. Stationarity for the JC69 model. Let’s take α= 1/5
as in Example 1 and compute the rate matrix Qof the JC69 model, the
corresponding probability transitionmatrix P, and raise it to the power 50.
library(Matrix)
alpha <- 1/5; Q <- matrix(rep(alpha,16),4,4)
diag(Q) <- -3 * alpha
Q <- Matrix(Q)
P <- as.matrix(expm(Q))
V <- eigen(P,symmetric = FALSE)
> V$vec %*% diag(V$va)^(50) %*% solve(V$vec)
[,1] [,2] [,3] [,4]
[1,] 0.25 0.25 0.25 0.25
[2,] 0.25 0.25 0.25 0.25
[3,] 0.25 0.25 0.25 0.25
[4,] 0.25 0.25 0.25 0.25

10.5. PHYLOGENETIC DISTANCE 207
Hence, the stationary distribution is πT= (0.25,0.25,0.25,0.25) (cf. Ewens
& Grant, 2005, p. 477).
Example 4. Distance between two sequences according to the JC69
model. In case of the JC69 model, the distance between sequences is a
function of the proportion of different nucleotides. Namely,
d=−3
4log(1 −4p/3),
where pis the proportion of different nucleotides of the two sequences. The
pairwise distances between DNA sequences can be computed by the function
dist.dna from the ape package.
> library(ape);library(seqinr)
> accnr <- paste("AJ5345",26:27,sep="")
> seqbin <- read.GenBank(accnr, species.names = TRUE, as.character = FALSE)
> dist.dna(seqbin, model = "JC69")
AJ534526
AJ534527 0.1326839
Hence, the distance is 0.133. Over a total of 1143 nucleotides there are 139
differences, som that the proportion of different nucleotides 139/1143 = p.
Inserting this into the previous distance formula gives the distance. This can
be verified as follows.
> seq <- read.GenBank(accnr, species.names = TRUE, as.character = TRUE)
> p <- sum(seq$AJ534526==seq$AJ534527)/1143
> d <- -log(1-4*p/3)*3/4
> d
[1] 0.1326839
Example 5. Phylogenetic tree of a series of downloaded sequences. To
further illustrate distances between DNA sequences we shall download the
Chamaea fasciata mitochondrial cytb gene for cytochrome b for 10 species of
warblers of the genus sylvia (Paradis, 2006). The function paste is used to
quickly define the accession numbers and read.GenBank to actually down-
load the sequences. The species names are extracted and attached to the
sequences. We shall use the dist.dna function with the K80 model.

208 CHAPTER 10. MARKOV MODELS
library(ape);library(seqinr)
accnr <- paste("AJ5345",26:35,sep="")
seq <- read.GenBank(accnr)
names(seq) <- attr(seq, "species")
dist <- dist.dna(seq, model = "K80")
plot(nj(dist))
Obviously, in this manner various trees can be computed and their plots
compared.
When various different models are defined the question becomes appar-
ent which of these fits best to the data relative to the number of parameters
(symbols) of the model. When the models are estimated by maximum likeli-
hood, then the Akaike information criterion (AIC = -2 ·loglik + 2 ·number
of free parameters) can be used to select models. The best model is the one
with the smallest AIC value.
Example 6. A program called PHYML (Guindon & Gascuel, 2003)
can be downloaded from http://atgc.lirmm.fr/phyml/ and run by the R
function phymltest, if the executable is available at the same directory. We
first write the sequences to the appropriate directory. The output from the
program is written to the object called out for which the functions plot(out)
and summary(out) can be used to extract more detailed information.
> setwd("/share/home/wim/bin")
> write.dna(seq,"seq.txt", format ="interleaved")
> out <-phymltest("seq.txt",format = "interleaved", execname ="phyml_linux")
> print(out)
nb.free.para loglik AIC
JC69 1 -4605.966 9213.931
JC69+I 2 -4425.602 8855.203
JC69+G 2 -4421.304 8846.608
JC69+I+G 3 -4421.000 8848.001
K80 2 -4423.727 8851.455
K80+I 3 -4230.539 8467.079
K80+G 3 -4224.457 8454.915
K80+I+G 4 -4223.136 8454.272
F81 4 -4514.331 9036.662

10.6. HIDDEN MARKOV MODELS 209
F81+I 5 -4309.600 8629.199
F81+G 5 -4304.530 8619.060
F81+I+G 6 -4303.760 8619.519
F84 5 -4351.164 8712.328
F84+I 6 -4112.006 8236.012
F84+G 6 -4106.568 8225.135
F84+I+G 7 -4105.500 8225.001
HKY85 5 -4333.086 8676.171
HKY85+I 6 -4102.262 8216.524
HKY85+G 6 -4097.401 8206.802
HKY85+I+G 7 -4096.624 8207.248
TN93 6 -4323.291 8658.581
TN93+I 7 -4097.099 8208.198
TN93+G 7 -4091.461 8196.922
TN93+I+G 8 -4090.790 8197.580
GTR 9 -4293.398 8604.795
GTR+I 10 -4084.522 8189.043
GTR+G 10 -4079.010 8178.020
GTR+I+G 11 -4078.149 8178.299
The notation ”+I” and ”+G” indicates the presence of invariant sites and/or
a gamma distribution of substitution rates. It can be seen that the smallest
AIC corresponds to model 27 called GTR+G. To plot it, we have to read the
trees, and, next, to extract the 27th, see Figure 10.3.
tr <- read.tree("seq.txt_phyml_tree.txt")
plot(tr[[27]])
add.scale.bar(length=0.01)
In case similar sequences have slightly different lengths, these have to be
aligned by programs such as clustalx or clustalw before these can be
used.
10.6 Hidden Markov Models
In a Hidden Markov Model (HMM) there are two probability transition ma-
trices. There is an emission matrix Eand a transition matrix A. The
210 CHAPTER 10. MARKOV MODELS
generation of an observable sequence goes in two steps. First, there is a tran-
sition from a Markov process of a hidden state and given this value there
is an emission of an observable value. We shall illustrate this by the clas-
sical example of the occasionally dishonest casino (Durbin et. al., 1998, p.18).
Example 1. Occasionally dishonest casino. A casino uses a fair die most
of the time, however, occasionally it switches to an unfair die. The state with
respect to fairness is hidden for the observer. The observer can only observe
the values of the die and not its hidden state with respect to its fairness. It
is convenient to denote fair by 1 and unfair by 2. The transition probabilities
of the hidden states are by the emission matrix
E=·P(Di= 1|Di−1= 1) P(Di= 2|Di−1= 1)
P(Di= 1|Di−1= 2) P(Di= 2|Di−1= 2) ¸=·0.95 0.05
0.10 0.90 ¸.
Thus the probability is 0.95 that the die is fair at time point i, given that
it is fair at time point i−1. The probability that it will switch from fair to
unfair is 0.05. The probability that it will switch from loaded to fair is 0.10
and that it stays loaded is 0.90. With this emission matrix we can generate a
sequence of hidden states, where the values 1 and 2 indicate whether the die
is fair (1) or loaded (2). Given the fairness of the die we define the probability
transition matrix.
A=·P(Oi= 1|Di= 1) P(Oi= 2|Di= 1) P(Oi= 3|Di= 1) ···
P(Oi= 1|Di= 2) P(Oi= 2|Di= 2) P(Oi= 3|Di= 2) ··· ¸
=·1/6 1/6 1/6 1/6 1/6 1/6
1/10 1/10 1/10 1/10 1/10 1/2¸.(10.4)
Thus given that the die is fair, the probability of any outcome equals 1/6.
However, given that the die is unfair (loaded), the probability of outcome 6
equals 1/2 and that of any other outcome equals 1/10.
The HMM with this transition and emission matrix can be programmed.
After sampling the hidden states from a Markov chain and the outcomes of
the die are sampled according to the value of the hidden state (die type).
hmmdat <- function(A,E,n){
observationset <- c(1:6)
hiddenset <- c(1,2)
x <- h <- matrix(NA,nr=n,nc=1)

10.6. HIDDEN MARKOV MODELS 211
h[1]<-1; x[1]<-sample(observationset,1,replace=T,E[h[1],])
h <- markov(hiddenset,A,n)
for(k in 1:(n-1)){x[k+1] <- sample(observationset,1,replace=T,E[h[k],])}
out <- matrix(c(x,h),nrow=n,ncol=2,byrow=FALSE)
return(out)
}
E <- matrix(c(rep(1/6,6),rep(1/10,5),1/2),2,6,byrow=T) #emission matrix
A <- matrix(c(0.95,0.05,0.1,0.9),2,2,byrow=TRUE) #transition matrix
dat <- hmmdat(A,E,100)
colnames(dat) <- c("observation","hidden_state")
rownames(dat) <- 1:100
> t(dat)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
observations 5 2 3 1 6 1 3 1 1 5 6 6 2 2 3 5 4 6 1 2 4 4 3 2 3
hidden_states 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
observations 4 3 2 4 1 6 6 6 6 6 5 5 3 6 1 6 5 2 4 1 4 2
hidden_states1112222221111111111111
48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69
observations 5 6 5 2 3 3 1 3 3 5 6 6 2 4 5 4 6 1 6 5 2 6
hidden_states1111111111111111111111
70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91
observations 1 1 4 4 1 5 6 4 3 5 4 2 6 1 3 6 5 2 2 6 6 1
hidden_states1111111112222222222211
92 93 94 95 96 97 98 99 100
observations 4 1 6 5 5 6 5 3 4
hidden_states 1 1 1 1 1 1 1 1 1
In certain applications to bioinformatics, it is of most importance to es-
timate the value of the hidden state given the data. The Viterbi algorithm
is developed to predict the hidden state given the data and the (estimated)
transition and emission matrix. The algorithm builds up a matrix v(i, l),
where iruns from one to the number of observations and lfrom one to the
number of states. The initial values are v(1,1) = 1, and v(1, l) = 0 for all l.
Then the values for v(i, l) are recursively defined by
v(i, l) = e(l, x(i)) ·max
k{v(i−1, k)a(k, l)}.
212 CHAPTER 10. MARKOV MODELS
For each row of the matrix the maximum is taken as the best predictor of
the hidden state.
Example 2. The viterbi algorithm can be programmed and applied
to the hidden states of the data generated with respect to the occasionally
dishonest casino.
viterbi <- function(A,E,x) {
v <- matrix(NA, nr=length(x), nc=dim(A)[1])
v[1,] <- 0; v[1,1] <- 1
for(i in 2:length(x)) {
for (l in 1:dim(A)[1]) {v[i,l] <- E[l,x[i]] * max(v[(i-1),] * A[l,])}
}
return(v)
}
vit <- viterbi(A,E,dat[,1])
vitrowmax <- apply(vit, 1, function(x) which.max(x))
hiddenstate <- dat[,2]
> table(hiddenstate, vitrowmax)
vitrowmax
hiddenstate 1 2
1 72 11
2 15 2
datt <- cbind(dat,vitrowmax)
colnames(datt) <- c("observation","hidden_state","predicted state")
> t(datt)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
observation 5 2 3 1 6 1 3 1 1 5 6 6 2 2 3 5 4 6 1 2 4 4 3 2
hidden_state 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
predicted state 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
observation 343241666665536165241
hidden_state 111122222211111111111
predicted state 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2
46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66
observation 425652331335662454616
hidden_state 111111111111111111111

10.7. APPENDIX 213
predicted state 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87
observation 5 2 6 1 1 4 4 1 5 6 4 3 5 4 2 6 1 3 6 5 2
hidden_state 111111111111222222222
predicted state 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
88 89 90 91 92 93 94 95 96 97 98 99 100
observation 2 6 6 1 4 1 6 5 5 6 5 3 4
hidden_state 2 2 1 1 1 1 1 1 1 1 1 1 1
predicted state 1 1 1 1 1 1 1 1 1 1 1 1 1
The misclassification rate is 0.27 which is quite large given the fact that we
used the true transition and emission matrix. An important observation is
that after a transition of a hidden state, it takes a few values for the predic-
tion to change. This is caused by the recursive nature of the algorithm.
10.7 Appendix
The probability that the process is in State 1 at time point 1 can be computed
as follows.
P(X1= 1) = P(X1= 1, X0= 1) + P(X1= 1, X0= 2)
=P(X1= 1|X0= 1) ·P(X0= 1) + P(X1= 1|X0= 2) ·P(X0= 2)
=π10p11 +π20p21
=πT
0p1,
where p1is the first column of P.

214 CHAPTER 10. MARKOV MODELS
In particular, it holds that
P(X2= 1|X0= 1) = P(X2= 1, X1= 1|X0= 1) + P(X2= 1, X1= 2|X0= 1)
=
2
X
k=1
P(X2= 1, X1=k|X0= 1)
=
2
X
k=1
P(X2= 1|X1=k, X0= 1) ·P(X1=k|X0= 1)
=
2
X
k=1
P(X2= 1|X1=k)·P(X1=k|X0= 1)
=p11p11 +p21p12
= row 1 of Ptimes column 1 of P=P2
11,
where the latter is element (1,1) of the matrix P2=P·P.
10.8 Overview and concluding remarks
The probability transition matrix is extensively explained and illustrated
because it is a cornerstone to many ideas in bioinformatics. A thorough
treatment of phylogenetics is given by Paradis (2006) and of Hidden Markov
Models by Durbin et. al (2005).
10.9 Exercises
1. Visualize by a transition graph the following transition matrices. For
the process with four states take the names of the nucleotides in the
order A, G, T, and C.
µ1
3
2
3
3
4
1
4¶,µ1 0
0 1 ¶,µ0 1
1 0 ¶,
1
4
2
401
4
1
6
2
6
2
6
1
6
02
7
5
70
1
8
1
8
2
8
4
8
,
1
4
3
40 0
1
6
5
60 0
0 0 5
7
2
7
0 0 3
8
5
8
.
2. Computing probabilities. Given the states 0 and 1 and the following
initial distribution and probability matrix
π0=¡1
2
1
2¢,P=µ3
4
1
4
1
2
1
2¶.
10.9. EXERCISES 215
(a) Compute P(X1= 0).
(b) Compute P(X1= 1).
(c) Compute P(X2= 0|X0= 0).
(d) Compute P(X2= 1|X0= 0).
3. Programming GTR. Use πA= 0.15, πG= 0.35, πC= 0.35, πT= 0.15,
α= 4, β= 0.5, γ= 0.4, δ= 0.3, ²= 0.2, and ζ= 4.
(a) Program the rate matrix in such a manner that it is simple to
adapt for other values of the parameters.
(b) Is the transversion rate larger or smaller then the transition rate?
(c) Compute the corresponding the probability transition matrix.
(d) Try to argue whether you expect a large frequency of transversions
or translations.
(e) Generate a sequence of 99 nucleotide residues according to the
markov model.
4. Distance according to JC69.
(a) Down load the sequences AJ534526 and AJ534527. Hint: Use
as.character = TRUE in the read.GenBank function.
(b) Compute the proportion of different nucleotides.
(c) Use this proportion to verify the distances between these sequences
according to the JC69 model.
216 CHAPTER 10. MARKOV MODELS
Akaike information criterion for phymlout
8200
8400
8600
8800
9000
9200
GTR +Γ
GTR +I+Γ
GTR +I
TN93 +Γ
TN93 +I+Γ
HKY85 +Γ
HKY85 +I+Γ
TN93 +I
HKY85 +I
F84 +I+Γ
F84 +Γ
F84 +I
K80 +I+Γ
K80 +Γ
K80 +I
GTR
F81 +Γ
F81 +I+Γ
F81 +I
TN93
HKY85
F84
JC69 +Γ
JC69 +I+Γ
K80
JC69 +I
F81
JC69
Figure 10.2: Evaluation of models by AIC .

10.9. EXERCISES 217
Chamaea fasciata
Sylvia nisoria
Sylvia layardi
Sylvia subcaeruleum
Sylvia boehmi
Sylvia buryi
Sylvia lugens
Sylvia leucomelaena
Sylvia hortensis
Sylvia crassirostris
0.01
Figure 10.3: Tree according to GTR model.
218 CHAPTER 10. MARKOV MODELS
Appendix A
Answers to exercises
Answers to exercises of Chapter 1: Brief Introduction to R
1. Some questions to orientate yourself.
(a) matrix, numeric, numeric, matrix, function, function, factor, stan-
dardGeneric, ExpressionSet.
(b) remove, summation, product, sequence, standard deviation, num-
ber of rows,
(c) Use R its help or use the internet search key ”r wiki grep” to
find the following answers: searching regular expressions, return
a vector from a function on the rows or columns of a matrix,
generate a factor by specifying the pattern of levels, load add-
on packages, make R reading input from a file or URL, set the
working directory to a certain map, print the last ·commands
given from the command line, give the structure of an object.
2. gendat
(a) apply(gendat,2,sd).
(b) apply(gendat,1,sd).
(c) To order the data frame according to the gene standard deviations.
sdexprsval <- apply(gendat,1,sd)
o <- order(sdexprsval,decreasing=TRUE)
gendat[o,]
219
220 APPENDIX A. ANSWERS TO EXERCISES
(d) gene1
3. Computations on gene means of the Golub data.
(a) Computation of mean gene expression values.
data(golub, package = "multtest")
meangol <- apply(golub,1,mean)
(b) To order the data frame use o <- order(meangol,decreasing=TRUE)
and golub[o,]
(c) Give the names of the three genes with the largest mean expression
value.
> golub.gnames[o[1:3],3]
[1] "U43901_rna1_s_at" "M13934_cds2_at" "X01677_f_at"
(d) Give their biological names.
> golub.gnames[o[1:3],2]
[1] "37 kD laminin receptor precursor/p40 ribosome associated protein gene"
[2] "RPS14 gene (ribosomal protein S14) extracted from Human ribosomal protein S14 gene"
[3] "GAPD Glyceraldehyde-3-phosphate dehydrogenase"
4. Computations on gene standard deviations of the Golub data.
(a) The standard deviation per gene can be computed by sdgol <-
apply(golub,1,sd).
(b) The gene with standard deviation larger than 0.5 can be selected
by golubsd <- golub[sdgol>0.5,].
(c) sum(sdgol>0.5) gives that the number of genes having sd larger
than 0.5 is 1498.
5. Oncogenes in Golub data.
(a) length(agrep("^oncogene",golub.gnames[,2])) gives 42.
(b) By the script below the "Cellular oncogene c-fos is found.
data(golub, package="multtest")
rowindex <- agrep("^oncogene",golub.gnames[,2])
oncogol <- golub[rowindex,]
221
oncogolub.gnames <- golub.gnames[rowindex,]
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
meangol <- apply(oncogol[,gol.fac=="ALL"],1,mean)
o <- order(meangol,decreasing=TRUE)
> oncogolub.gnames[o[1:3],2]
[1] "PIM1 Pim-1 oncogene" "JUNB Jun B proto-oncogene"
[3] "Proto-oncogene BCL3 gene"
(c) meangol <- apply(oncogol[,gol.fac=="AML"],1,mean)
o <- order(meangol,decreasing=TRUE)
> oncogolub.gnames[o[1:3],2]
[1] "PIM1 Pim-1 oncogene" "JUNB Jun B proto-oncogene"
[3] "Proto-oncogene BCL3 gene"
(d) Writing results to a csv file. Be aware of the correct column
separation.
x <- oncogolub.gnames[o[1:10],c(3,2)]
colnames(x) <- c("probe ID","gene name")
write.csv(x,file="goluboutcsv")
write.table(x,file="goluboutnorowname",row.names=FALSE)
6. Constructing a factor.
(a) gl(2,4).
(b) gl(5,3).
(c) gl(3,5).
7. Gene means for B1 patients.
library(ALL); data(ALL)
meanB1 <- apply(exprs(ALL[,ALL$BT=="B1"]),1, mean)
o <- order(meanB1,decreasing=TRUE)
> meanB1[o[1:3]]
AFFX-hum_alu_at 31962_at 31957_r_at
13.41648 13.16671 13.15995
Answers to exercises of Chapter 2: Descriptive Statistics and Data Dis-
play
222 APPENDIX A. ANSWERS TO EXERCISES
1. Illustration of mean and standard deviation.
(a) Use x<- c(1,1.5,2,2.5,3) and mean(x) and sd(x) to obtain
the mean is 2 and the standard deviation is 0.7905694.
(b) Now the mean is 7.4 and dramatically increased the standard de-
viation 12.64615.
(c) The outlier increased the mean as well as the standard deviation.
2. Comparing two genes. Take i <- 66 or i <- 790.
(a) Use boxplot(golub[i,]~gol.fac) to observe that 790 has three
outliers and 66 has no.
(b) Use qqnorm(golub[i,gol.fac=="ALL") and qqline(golub[i,gol.fac=="ALL"])
to observe that nearly all values of 66 are on the line, where as for
790 the three outliers are way of the normality line. Hypothesis:
The expression values of 66 are normally distributed, but those of
row 790 are not.
(c) Use mean(golub[i,gol.fac=="ALL"]) and median(golub[i,gol.fac=="ALL"]).
The mean (-1.174024) is larger than the median (-1.28137) due to
outliers on the right hand side. For the gen in row 66 the mean is
1.182503 and the median 1.23023. The differences are smaller.
3. Effect size.
(a) The size 11 is large, because the mean is eleven times larger than
the standard deviation.
data(golub, package="multtest")
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
efs <- apply(golub[,gol.fac=="ALL"],1,function(x) mean(x)/sd(x))
o <- order(efs,decreasing=TRUE)
> efs[o[1:5]]
[1] 11.138128 10.638308 9.155108 8.954115 8.695353
> golub.gnames[o[1:5],2]
[1] "YWHAZ Tyrosine 3-monooxygenase/tryptophan 5-monooxygenase activation protein, zeta polypeptide"
[2] "ZNF91 Zinc finger protein 91 (HPF7, HTF10)"
[3] "HnRNP-E2 mRNA"
[4] "54 kDa protein mRNA"
[5] "Immunophilin homolog ARA9 mRNA"
223
(b) The robust variant can be defined by dividing the median by the
MAD. An alternative would be to divide the median by the IQR.
This gives other best genes indicating that the some genes may
have outliers that influence the outcome.
refs <- apply(golub[,gol.fac=="ALL"],1,function(x) median(x)/mad(x))
o <- order(refs,decreasing=TRUE)
> refs[o[1:5]]
[1] 14.51217 13.57425 13.27698 13.14419 12.91608
> golub.gnames[o[1:5],2]
[1] "COX6B gene (COXG) extracted from Human DNA from overlapping chromosome 19 cosmids R31396,
F25451, and R31076 containing COX6B and UPKA, genomic sequence"
[2] "AFFX-HSAC07/X00351_M_at (endogenous control)"
[3] "ATP5A1 ATP synthase, H+ transporting, mitochondrial F1 complex, alpha subunit,
isoform 1, cardiac muscle"
[4] "ATP SYNTHASE GAMMA CHAIN, MITOCHONDRIAL PRECURSOR"
[5] "YWHAZ Tyrosine 3-monooxygenase/tryptophan 5-monooxygenase activation protein,
zeta polypeptide"
4. Plotting gene expressions "CCND3 Cyclin D3". The answers in the
script below.
data(golub, package = "multtest")
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
stripchart(golub[1042,] ~ gol.fac,method="jitter")
stripchart(golub[1042,] ~ gol.fac,method="jitter",vertical = TRUE)
stripchart(golub[1042,] ~ gol.fac,method="jitter",col=c("red", "blue"),
vertical = TRUE)
stripchart(golub[1042,] ~ gol.fac,method="jitter",col=c("red", "blue"),
pch="*",vertical = TRUE)
title("CCND3 Cyclin D3 expression value for ALL and AMl patients")
5. Box-and-Whiskers plot of "CCND3 Cyclin D3"..
locator()
x11()
x <- data(golub, package = "multtest")
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
boxplot(x,xlim=c(0,4))
224 APPENDIX A. ANSWERS TO EXERCISES
arrows(2.0,1.93,1.24,1.93);text(2.5,1.93,"Median")
arrows(2.0,1.1,1.24,1.1) ;text(2.5,1.1,"Outlier")
arrows(2.0,1.79,1.24,1.79);text(2.5,1.79,"first quartile")
arrows(2.0,2.17,1.24,2.17);text(2.5,2.17,"third quartile")
arrows(2.0,1.27,1.24,1.27);text(2.5,1.27,"lower wisker")
arrows(2.0,2.59,1.24,2.59);text(2.5,2.59,"upper wisker")
dev.copy2eps(device=x11,file="BoxplotWithExplanation.eps")
boxplot.stats(x, coef = 1.5, do.conf = TRUE, do.out = TRUE) #finds values
6. Box-and-wiskers plot of persons of Golub et al. (1999) data..
(a) The medians are all around zero, the inter quartile range differ
only slightly, the minimal values are all around minus 1.5. All
persons have outliers near three.
(b) The means are very close to zero. The medians are all between
(−0.15383,0.06922), so these are also close to zero.
personmean <- apply(golub,2,mean)
personmedian <- apply(golub,2,median)
(c) The data seem preprocessed to have standard deviation equal to
one. The re-scaled IQR and MAD have slightly larger range.
> range(apply(golub,2,sd))
[1] 0.9999988 1.0000011
> range(apply(golub,2,function(x) IQR(x)/1.349))
[1] 0.9599036 1.3361527
> range(apply(golub,2,mad))
[1] 0.9590346 1.2420185
7. Oncogenes of Golub et al. (1999) data.
(a) Note that we need the transpose operator tto change rows into
columns. The script below will do.
data(golub, package="multtest")
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
rowindex <- agrep("^oncogene",golub.gnames[,2])
oncogol <- golub[rowindex,]
oncogolub.gnames <- golub.gnames[rowindex,]
225
row.names(oncogol) <- oncogolub.gnames[,3]
boxplot(data.frame(t(oncogol[,gol.fac=="ALL"])))
(b) The plot gives a nice overview of the distributions of the gene
expressions values of the onco gene separately for the ALL and
the AML patients. Several genes behave similarly for ALL and
AML. Some are clearly distributed around zero, but others not.
Also, some have a small inter quartile ranges, while for others
this is large. A similar statement holds for outliers, some do not
have outliers, but others certainly have. Some gene show distinct
distributions between patient groups. For instance, the sixth has
ALL expressions around zero, but those for AML are larger than
zero.
par(mfrow=c(2,1))
boxplot(data.frame(t(oncogol[,gol.fac=="ALL"])))
title("Box and wiskers plot for oncogenes of ALL patients ")
boxplot(data.frame(t(oncogol[,gol.fac=="AML"])))
title("Box and wiskers plot for oncogenes of AML patients ")
par(mfrow=c(1,1))
8. Descriptive statistics for the ALL gene expression values of the Golub
et al. (1999) data.
(a) The ranges indicate strong difference in means. The range of the
mean and of the median are similar. The bulk of the data seems
symmetric.
> range(apply(golub[,gol.fac=="ALL"],1,mean))
[1] -1.330984 3.278551
> range(apply(golub[,gol.fac=="ALL"],1,median))
[1] -1.36832 3.35455
(b) The range of the standard deviation is somewhat smaller than of
the re-scaled IQR and MAD.
> range(apply(golub[,gol.fac=="ALL"],1,sd))
[1] 0.1336206 2.0381309
> range(apply(golub[,gol.fac=="ALL"],1,function(x) IQR(x)/1.349))
[1] 0.1153113 2.7769867
> range(apply(golub[,gol.fac=="ALL"],1,mad))
226 APPENDIX A. ANSWERS TO EXERCISES
[1] 0.1056649 2.9656744
Answers to exercises of Chapter 3: Important Distributions
1. Binomial
(a) P(X= 24) = 0.1046692, P(X≤24) = 0.5557756, and P(X≥
30) = 0.0746237.
(b) P(20 ≤X≤30) = 0.83856, P(20 ≤X) = 0.8830403.
(c) P(20 ≤XorX ≥40) = 0.8830403, and P(20 ≤XandX ≥10) =
0.999975.
(d) E(X) = 24, var(X) = 3.794733 Use: sqrt(60 * 0.4 *0.6)
(e) x0.025 = 17, x0.5= 24, and x0.975 = 32.
2. Standard Normal.
(a) P(1.6< Z < 2.3) = 0.04408.
(b) P(Z < 1.64) = 0.9495.
(c) P(−1.64 < Z < −1.02) = 0.1034.
(d) P(0 < Z < 1.96) = 0.4750.
(e) P(−1.96 < Z < 1.96) = 0.9500.
(f) z0.025 =−1.959964, z0.05 =−1.644854, z0.5= 0, z0.95 = 1.644854,
and z0.975 = 1.959964.
3. Normal.
(a) P(X < 12) = 0.8413.
(b) P(X > 8) = 0.8413.
(c) P(9 < X < 10,5) = 0.2917.
(d) The quantiles x0.025 = 6.080072, x0.5= 10, and x0.975 = 13.91993.
4. T-distribution.
(a) P(T6<1) = 0.8220412.
(b) P(T6>2) = 0.04621316.
(c) P(−1< T6<1) = 0.6440823.
227
(d) P(−2< T6<−2) = 0.9075737.
(e) t0.025 =−2.446912, t0.5= 0, and t0.975 = 2.446912.
5. Fdistribution.
(a) P(F8,5<3) = 0.8792198.
(b) P(F8,5>4) = 0.07169537.
(c) P(1 < F8,5<6) = 0.4931282.
(d) The quantiles f0.025 = 0.2075862, f0.5= 1.054510, and f0.975 =
6.757172.
6. Chi-squared distribution.
(a) P(χ2
10 <3) = 0.01857594.
(b) P(χ2
10 >4) = 0.947347.
(c) P(1 < χ2
10 <6) = 0.1845646.
(d) The quantiles g0.025 = 3.246973, g0.5= 9.341818, and g0.975 =
20.48318.
7. MicroRNA.
(a) P(X= 14) = dbinom(14,20,0.7) = 0.191639.
(b) P(X≤14) = pbinom(14,20,0.7) = 0.5836292.
(c) P(X > 10) = 1 −P(X≤10) = 1−pbinom(10,20,0.7) =
0.9520381.
(d) P(10 ≤X≤15) = P(X≤15)−P(X≤9) = pbinom(15,20,0.7)−pbinom(9,20,0.7) =
0.7453474.
(e) 20 ·0.7 = 14.
(f) sqrt(20* 0.7 * 0.3)=2.04939.
8. Zyxin.
(a) P(X≤1.2) =pnorm(1.2,1.6,0.4)=0.1586553.
(b) P(1.2≤X≤2.0) =pnorm(2.0,1.6,0.4) - pnorm(1.2,1.6,0.4)=0.6826895.
(c) P(2.4≤X≤0.8) =pnorm(2.4,1.6,0.4) - pnorm(0.8,1.6,0.4)=0.9544997.
228 APPENDIX A. ANSWERS TO EXERCISES
(d) x0.025 =qnorm(0.025,1.6,0.4)=0.8160144. Similarly, x0.975 =
2.383986.
(e) x <- rnorm(1000,1.6,0.4) gives mean(x) = 1.608401 and sd(x)=0.4022082.
Both are close to the values in the population.
9. Some computations on Golub et al. (1999) data.
(a) The tree larges t-value 57.8, 55.2, and 47.5 are extremely large.
data(golub, package="multtest")
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
tval <- apply(golub[,gol.fac=="ALL"],1,function(x) sqrt(27) * mean(x)/sd(x))
o <- order(tval,decreasing=TRUE)
tval[o[1:3]]
golub.gnames[o[1:3],2]
(b) The scrip below gives 2185 ratios between 0.5 and 1.5.
sdall <- apply(golub[,gol.fac=="ALL"],1, sd)
sdaml <- apply(golub[,gol.fac=="AML"],1, sd)
sdratio <- sdall/sdaml
sum( sdratio > 0.5 & sdratio < 1.5)
10. Extreme value investigation. The blue line (extreme value) fits to the
black line (density of generated extreme data) much better than the
red line (normal distribution).
an <- sqrt(2*log(n)) - 0.5*(log(log(n))+log(4*pi))*(2*log(n))^(-1/2)
bn <- (2*log(n))^(-1/2)
e <- double(); n <- 10000 # Serfling p.90
for (i in 1:1000) e[i] <- (max(rnorm(n))-an)/bn
plot(density(e),ylim=c(0,0.5))
f<-function(x){exp(-x)*exp(-exp(-x))}
curve(f,range(density(e)$x),add=TRUE,col = "blue")
curve(dnorm,add=TRUE,col = "red")
Answers exercise chapter 4: Estimation and Inference
1. Gene CD33. Use agrep("^CD33",golub.gnames[,2]) to find 808.
(a) The code
229
library(multtest);data(golub)
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
shapiro.test(golub[i,gol.fac=="ALL"])
gives p-value = 0.592 and changing ALL into AML gives p-value
= 0.2583. Hence, for normality is accepted.
(b) var.test(golub[i,] ~ gol.fac) gives p-value = 0.1095 so equal-
ity of variances is accepted.
(c) t.test(golub[i,] ~ gol.fac, var.equal = TRUE) gives p-value = 1.773e-09,
so equality of means is rejected.
(d) Yes, t = -7.9813 is quite extreme.
2. Gene MYBL2 V-myb avian myeloblastosis viral oncogene homolog-like
2. Take i <- 1788.
(a) Use boxplot(golub[i,] ~ gol.fac) to observe from the box-
plot that one is quite certain that the null-hypothesis of no exper-
imental effect holds.
(b) t.test(golub[i,] ~ gol.fac, var.equal = TRUE) gives p-value = 0.8597,
so that the null hypothesis of equal means is accepted.
3. HOXA9. Use i <- 1391.
(a) shapiro.test(golub[i,gol.fac=="ALL"]) gives p-value = 1.318e-07,
so that normality is rejected.
(b) wilcox.test(golub[i,] ~ gol.fac) gives p-value = 7.923e-05,
so that equality of means is rejected. Note that the p-value from
Grubbs test of the ALL expression values is 0.00519, so the null
hypothesis of no outliers is rejected. Nevertheless the Welch two-
sample T-test is also rejects the null-hypothesis of equal means.
Its t-value equals -4.3026 and is quite large.
4. Zyxin.
(a) Searching NCBI UniGene on zyxin gives BC002323.2.
(b) Use chisq.test(as.data.frame(table(read.GenBank(c("BC002323.2"))))$Freq)
to find p-value < 2.2e-16, so that the null-hypothesis of equal
frequencies is rejected.
230 APPENDIX A. ANSWERS TO EXERCISES
(c) We download and store the frequencies of the sequences in xand
y. Next the empirical probabilities from yare use to predict the
frequencies from y.
x <- as.data.frame(table(read.GenBank(c("X94991.1"))))$Freq
y <- as.data.frame(table(read.GenBank(c("BC002323.2"))))$Freq
>chisq.test(x, p=y/sum(y))
Chi-squared test for given probabilities
data: x
X-squared = 0.0277, df = 3, p-value = 0.9988
5. Gene selection.
ptg <- apply(golub, 1, function(x) t.test(x ~ gol.fac,
alternative = c("greater"))$p.value)
golub.gnames[order(ptg)[1:10],2]
6. Antigenes.
library(multtest); data(golub)
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
pt <- apply(golub, 1, function(x) t.test(x ~ gol.fac)$p.value)
index <-agrep("^antigen",golub.gnames[,2])
golub.index<-golub[index,]
pt.index<-pt[index]
golub.gnames.index<-golub.gnames[index,]
golub.gnames.index[order(pt.index)[1:length(index)],2]
7. Genetic Model. From the output below the null hypothesis that the
probabilities are as specified is accepted.
> chisq.test(x=c(930,330,290,90),p=c(9/16,3/16,3/16,1/16))
Chi-squared test for given probabilities
data: c(930, 330, 290, 90)
X-squared = 4.2276, df = 3, p-value = 0.2379
8. Comparing two genes.
231
all66 <- golub[66,gol.fac=="ALL"]
all790 <- golub[790,gol.fac=="ALL"]
boxplot(all66,all790)
mean(all66);mean(all790)
median(all66);median(all790)
sd(all66);sd(all790)
IQR(all66)/1.349 ;IQR(all790)/1.349
mean(all66);mean(all790)
mad(all66);mad(all790)
shapiro.test(all66);shapiro.test(all790)
9. Normality tests.
library(multtest);data(golub)
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
allsh <- apply(golub[,gol.fac=="ALL"], 1, function(x) shapiro.test(x)$p.value)
amlsh <- apply(golub[,gol.fac=="AML"], 1, function(x) shapiro.test(x)$p.value)
> 100 * sum(allsh>0.05)/length(allsh)
[1] 58.27598
> 100 * sum(amlsh>0.05)/length(amlsh)
[1] 78.5644
> 100 * sum(allsh>0.05 & allsh>0.05)/length(allsh)
[1] 58.27598
10. Two-sample tests on gene expression values of the Golub et al. (1999)
data.
(a) data(golub, package = "multtest");
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
pt <- apply(golub, 1, function(x) t.test(x ~ gol.fac)$p.value)
pw <- apply(golub, 1, function(x) wilcox.test(x ~ gol.fac)$p.value)
o <- order(pt,decreasing=FALSE)
> golub.gnames[o[1:10],2]
[1] "Zyxin"
[2] "FAH Fumarylacetoacetate"
[3] "APLP2 Amyloid beta (A4) precursor-like protein 2"
[4] "LYN V-yes-1 Yamaguchi sarcoma viral related oncogene homolog"
[5] "CST3 Cystatin C (amyloid angiopathy and cerebral hemorrhage)"
232 APPENDIX A. ANSWERS TO EXERCISES
[6] "X-LINKED HELICASE II"
[7] "RB1 Retinoblastoma 1 (including osteosarcoma)"
[8] "TOP2B Topoisomerase (DNA) II beta (180kD)"
[9] "TCRA T cell receptor alpha-chain"
[10] "T-COMPLEX PROTEIN 1, GAMMA SUBUNIT"
(b) > o <- order(pw,decreasing=FALSE)
> golub.gnames[o[1:10],2]
[1] "FAH Fumarylacetoacetate"
[2] "Zyxin"
[3] "CST3 Cystatin C (amyloid angiopathy and cerebral hemorrhage)"
[4] "ELA2 Elastatse 2, neutrophil"
[5] "TCF3 Transcription factor 3 (E2A immunoglobulin enhancer binding factors E12/E47)"
[6] "Macmarcks"
[7] "LYN V-yes-1 Yamaguchi sarcoma viral related oncogene homolog"
[8] "CD33 CD33 antigen (differentiation antigen)"
[9] "VIL2 Villin 2 (ezrin)"
[10] "APLP2 Amyloid beta (A4) precursor-like protein 2"
11. Biological hypotheses.
(a) n= 1000, p= 0.05 so np = 50
(b) pbinom(9,1000,.05)=5.24 ·10−13.
(c) sum(dbinom(6:1000,1000,.05))=1.
(d) sum(dbinom(2:8,1000,.05))= 8.8·10−14.
12. Programming some tests.
(a) data(golub,package="multtest")
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
x <- golub[1042,gol.fac=="ALL"]
n <- length(x)
y <- golub[1042,gol.fac=="AML"]
m <- length(y)
t <- (mean(x)-mean(y))/sqrt(var(x)/n + var(y)/m)
v <- (var(x)/n + var(y)/m)^2/( (var(x)/n)^2/(n-1) + (var(y)/m)^2/(m-1) )
2*pt(-abs(t),v)
mean(x) - mean(y) + qt(0.025,v)* sqrt(var(x)/n + var(y)/m)
mean(x) - mean(y) + qt(0.975,v)* sqrt(var(x)/n + var(y)/m)
233
(b) z <- golub[1042,]
> sum(rank(z)[1:27]) - 0.5*27*(27+1)
[1] 284
(c) x <- golub[1042,gol.fac=="ALL"]
y <- golub[1042,gol.fac=="AML"]
w <- 0
for (i in 1:27) w <- w + sum(x[i]>y)
> w
[1] 284
Answers to exercises of Chapter 5Linear Models
1. Analysis of gene expressions of B-cell ALL patients.
library(ALL); data(ALL)
ALLB <- ALL[,ALL$BT %in% c("B","B1","B2","B3","B4")]
> table(ALLB$BT)
B B1 B2 B3 B4 T T1 T2 T3 T4
5 19 36 23 12 0 0 0 0 0
psw <- apply(exprs(ALLB), 1, function(x) shapiro.test(residuals(lm(x ~ ALLB$BT)))$p.value)
library(lmtest)
pbp <-apply(exprs(ALLB), 1, function(x)
as.numeric(bptest(lm(x ~ ALLB$BT),studentize = FALSE)$p.value))
> sum(psw > 0.05)
[1] 6847
> sum(pbp > 0.05)
[1] 10057
> sum(psw > 0.05 & pbp > 0.05)
[1] 6262
2. Further analysis of gene expressions of B-cell ALL patients.
> panova <- apply(exprs(ALLB), 1, function(x) anova(lm(x ~ ALLB$BT))$Pr[1])
> featureNames(ALLB)[panova<0.000001]
[1] "1125_s_at" "1126_s_at" "1134_at" "1389_at" "1500_at"
234 APPENDIX A. ANSWERS TO EXERCISES
[6] "1866_g_at" "1914_at" "205_g_at" "31472_s_at" "31615_i_at"
[11] "31616_r_at" "33358_at" "35614_at" "35991_at" "36873_at"
[16] "37809_at" "37902_at" "38032_at" "38555_at" "39716_at"
[21] "40155_at" "40268_at" "40493_at" "40661_at" "40763_at"
[26] "41071_at" "41139_at" "41448_at" "873_at"
> pkw <- apply(exprs(ALLB), 1, function(x) kruskal.test(x ~ ALLB$BT)$p.value)
> featureNames(ALLB)[pkw<0.000001]
[1] "1389_at" "1866_g_at" "38555_at" "40155_at" "40268_at"
> panovasmall <- panova < 0.001
> pkwsmall <- pkw < 0.001
> table(panovasmall,pkwsmall)
pkwsmall
panovasmall FALSE TRUE
FALSE 12172 38
TRUE 124 291
There are 124 significant gene expressions from ANOVA which are not
significant on Kruskal-Wallis. There are only 38 significant gene ex-
pressions from Kruskal-Wallis which are non-significant according to
ANOVA. The tests agree on the majority of gene expressions.
3. Finding the ten best best genes among gene expressions of B-cell ALL
patients.
> sort(panova)[1:10]
1914_at 1389_at 38555_at 33358_at 40268_at 39716_at
1.466523e-14 5.891702e-14 4.873245e-10 1.117406e-09 1.145502e-09 4.748615e-09
40763_at 37809_at 36873_at 1866_g_at
5.256410e-09 2.155457e-08 2.402379e-08 3.997065e-08
> sort(pkw)[1:10]
1389_at 40268_at 38555_at 1866_g_at 40155_at 1914_at
2.348192e-09 7.764046e-08 1.123068e-07 2.335279e-07 6.595926e-07 1.074525e-06
1125_s_at 40662_g_at 38032_at 40661_at
1.346907e-06 1.384281e-06 1.475170e-06 1.719456e-06
npanova <- names(sort(panova)[1:10])
npkw <- names(sort(pkw)[1:10])
235
> intersect(npanova,npkw)
[1] "1914_at" "1389_at" "38555_at" "40268_at" "1866_g_at"
4. A simulation study for ANOVA.
> x <- matrix(rnorm(90000),nrow = 10000, ncol = 9)
> a <- gl(3,3)
> panova <- apply(x, 1, function(x) anova(lm(x ~ a))$Pr[1])
> sum(panova<0.05)
[1] 514
The number of false positives is 514. The expected number is α·n=
0.05 ·10,000 = 500, which is quite close to the observed.
A matrix with differences between three groups of gene expression val-
ues.
sigma <- 1; n <- 10000
data <- cbind(matrix(rnorm(n*3,0,sigma),ncol=3),
matrix(rnorm(n*3,1,sigma), ncol = 3),matrix(rnorm(n*3,2,sigma), ncol = 3))
a <- gl(3,3)
panova <- apply(data, 1, function(x) anova(lm(x ~ a))$Pr[1])
> sum(panova<0.05)
[1] 3757
> pkw <- apply(data, 1, function(x) kruskal.test(x ~ a)$p.value)
> sum(pkw<0.05)
[1] 1143
Thus the number of true positives from ANOVA is 3757 and the num-
ber of false negatives is 6243. For the Kruskal-Wallis test there are
1143 true positives and 8857 false negatives. This can be impoved by
increasing the number of gene expressions per group.
Answers to exercises of Chapter 6: Micro Array Analysis.
1. Gene filtering on normality per group of B-cell ALL patients.
236 APPENDIX A. ANSWERS TO EXERCISES
library("genefilter")
data(ALL, package = "ALL")
ALLB <- ALL[,ALL$BT %in% c("B1","B2","B3","B4")]
f1 <- function(x) (shapiro.test(x)$p.value > 0.05)
sel1 <- genefilter(exprs(ALL[,ALLB$BT=="B1"]), filterfun(f1))
sel2 <- genefilter(exprs(ALL[,ALLB$BT=="B2"]), filterfun(f1))
sel3 <- genefilter(exprs(ALL[,ALLB$BT=="B3"]), filterfun(f1))
sel4 <- genefilter(exprs(ALL[,ALLB$BT=="B4"]), filterfun(f1))
selected <- sel1 & sel2 & sel3 & sel4
library(limma)
x <- matrix(as.integer(c(sel2,sel3,sel4)),ncol = 3,byrow=FALSE)
colnames(x) <- c("sel2","sel3","sel4")
vc <- vennCounts(x, include="both")
vennDiagram(vc)
137 pass filter 2 but not the other
510 pass filter 2 and 3 but not 4
1019 pas filter 2 and 4 but not 3
5598 pass filter 2, 3 and 4. etc.
2. Analysis of gene expressions of B-cell ALL patients using Limma.
library("ALL"); library("limma");library("annaffy");library(hgu95av2.db)
data(ALL)
ALLB <- ALL[,ALL$BT %in% c("B1","B2","B3","B4")]
design.ma <- model.matrix(~0 + factor(ALLB$BT))
colnames(design.ma) <- c("B1","B2","B3","B4")
cont.ma <- makeContrasts(B2-B1,B3-B2,B4-B3,levels=factor(ALLB$BT))
fit <- lmFit(ALLB, design.ma)
fit1 <- contrasts.fit(fit, cont.ma)
fit1 <- eBayes(fit1)
topTable(fit1, coef=2,5,adjust.method="fdr")
tab <- topTable(fit1, coef=2, number=20, adjust.method="fdr")
anntable <- aafTableAnn(as.character(tab$ID), "hgu95av2", aaf.handler())
saveHTML(anntable, "ALLB1234.html", title = "B-cell ALL of stage 1,2,3,4")
3. Finding a row number: grep("1389_at",row.names(exprs(ALL))).
4. Remission (genezing) from acute lymphocytic leukemia (ALL).
237
library(ALL); data(ALL)
table(pData(ALL)$remission)
remis <- which(pData(ALL)$remission %in% c("CR","REF"))
ALLrem <- ALL[,remis]
remfac <-factor(pData(ALLrem)$remission)
pano <- apply(exprs(ALLrem),1,function(x) t.test(x ~ remfac)$p.value)
sum(pano<0.001)
> sum(pano<0.001)
[1] 45
library(hgu95av2.db)
names <- featureNames(ALLrem)[pano<.001]
ALLremsel<- ALLrem[names,]
symb <- mget(names, env = hgu95av2SYMBOL)
genenames <- mget(names,hgu95av2GENENAME)
listofgenenames <- as.list(hgu95av2GENENAME)
unlistednames <- unlist(listofgenenames[names],use.names=F)
> grep("p53",unlistednames)
[1] 12 21
> length(unique(unlistednames))
[1] 36
5. Remission achieved.
library(ALL); data(ALL)
ALLCRREF <- ALL[,which(ALL$CR %in% c("CR","REF"))]
pano <- apply(exprs(ALLCRREF),1,function(x) t.test(x ~ ALLCRREF$CR)$p.value)
> sum(pano<0.0001)
[1] 11
> featureNames(ALLCRREF)[pano<.0001]
[1] "1472_g_at" "1473_s_at" "1475_s_at" "1863_s_at" "34098_f_at" "36574_at" "38124_at" "38279_at" "41337_at" "577_at" "953_g_at"
library("hgu95av2.db")
affynames <- featureNames(ALLCRREF)[pano<.0001]
genenames <- mget(affynames, env = hgu95av2GENENAME)
238 APPENDIX A. ANSWERS TO EXERCISES
> grep("oncogene",genenames)
[1] 1 2 3
affytot <- unique(featureNames(ALLCRREF))
genenamestot <- mget(affytot, env = hgu95av2GENENAME)
> length(grep("oncogene",genenamestot))
[1] 239
> length(genenamestot)
[1] 12625
> dat <- matrix(c(12625,239,11,3),2,byrow=TRUE)
> fisher.test(dat)
Fisher’s Exact Test for Count Data
data: dat
p-value = 0.002047
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
2.562237 54.915642
sample estimates:
odds ratio
14.39959
6. Gene filtering of ALL data.
library("ALL")
data("ALL")
table(ALL$BT)
ALLT23 <- ALL[,which(ALL$BT %in% c("T2","T3"))]
library(genefilter)
f1 <- function(x) (shapiro.test(x)$p.value > 0.05)
f2 <- function(x) (t.test(x ~ ALLT23$BT)$p.value < 0.05)
sel1 <- genefilter(exprs(ALLT23[,ALLT23$BT=="T2"]), filterfun(f1))
sel2 <- genefilter(exprs(ALLT23[,ALLT23$BT=="T3"]), filterfun(f1))
sel3 <- genefilter(exprs(ALLT23), filterfun(f2))
> sum(sel1 & sel2 & sel3)
239
[1] 905
> sum(sel1 & sel2)
[1] 9388
> sum(sel3)
[1] 1204
7. Stages of B-cell ALL in the ALL data.
library("ALL")
library("limma");
allB <- ALL[,which(ALL$BT %in% c("B1","B2","B3","B4"))]
facB123 <- factor(allB$BT)
cont.ma <- makeContrasts(B2-B1,B3-B2,B4-B3, levels=facB123)
design.ma <- model.matrix(~ 0 + facB123)
colnames(design.ma) <- c("B1","B2","B3","B4")
fit <- lmFit(allB, design.ma)
fit1 <- contrasts.fit(fit, cont.ma)
fit1 <- eBayes(fit1)
> topTable(fit1, coef=2,5,adjust.method="BH")
ID logFC AveExpr t P.Value adj.P.Val B
6048 35991_at 0.5964481 4.144598 6.624128 2.578836e-09 0.0000325578 10.842989
3909 33873_at 0.5707770 7.217570 6.083524 2.891823e-08 0.0001825464 8.625253
5668 35614_at 1.7248509 5.663477 5.961231 4.946078e-08 0.0002081474 8.132884
6776 36711_at -2.3664712 7.576108 -5.759565 1.187487e-07 0.0003054110 7.329631
7978 37902_at 0.8470235 4.258491 5.742783 1.276579e-07 0.0003054110 7.263298
> sum(fit1$p.value<0.05)
[1] 4328
8. Analysis of public micro array data.
library(GEOquery); library(limma); library(hgu95av2.db);library(annaffy)
gds486 <- getGEO("GDS486"); eset486 <- GDS2eSet(gds486,do.log2=T)
nrmissing <- apply(exprs(eset486), 1, function(x) sum(is.na(x)) )
eset486sel <- eset486[nrmissing<1,]
pval486sel <- apply(exprs(eset486sel), 1, function(x) t.test(x ~ eset486sel$cell.line)$p.value)
pval486 <- nrmissing
pval486[pval486==0]<-pval486sel
240 APPENDIX A. ANSWERS TO EXERCISES
pval486[pval486>1]<-1
gds711 <- getGEO("GDS711"); eset711 <- GDS2eSet(gds711,do.log2=T)
nrmissing <- apply(exprs(eset711), 1, function(x) sum(is.na(x)) )
eset711sel <- eset711[nrmissing<1,]
panova711sel <- apply(exprs(eset711sel), 1, function(x) anova(lm(x ~ eset711sel$disease.state))$Pr[1])
pval711sel <- panova711sel
pval711 <- nrmissing
pval711[pval711==0]<-pval711sel
pval711[pval711>1]<-1
gds2126 <- getGEO("GDS2126"); eset2126 <- GDS2eSet(gds2126,do.log2=T)
nrmissing <- apply(exprs(eset2126), 1, function(x) sum(is.na(x)) )
eset2126sel <- eset2126[nrmissing<1,]
pval2126sel <- apply(exprs(eset2126sel), 1, function(x) anova(lm(x ~ eset2126sel$disease.state))$Pr[1])
pval2126 <- nrmissing
pval2126[pval2126==0]<-pval2126sel
pval2126[pval2126>1]<-1
sumpval <- pval486 + pval711 + pval2126
o <- order(sumpval,decreasing=FALSE)
genenames <- names(sumpval[o[1:20]])
symb <- "aap"
for (i in 1:20) symb[i] <- get(genenames[i], env = hgu95av2SYMBOL)
> symb
[1] "GADD45A" "DUSP4" "OAS1" "STAT1" "STAT1" "AKR1C3" "PSMB9" "OAS2" "STAT1" "BUB1B" "UBE2L6" "STAT1" "ZFP36L2" "IL1R1" "IL8"
[16] "TKT" "NFKB1" "SLC7A5" "CXCL2" "DLG5"
library("KEGG");library("GO");library("annaffy")
atab <- aafTableAnn(genenames, "hgu95av2", aaf.handler() )
saveHTML(atab, file="ThreeExperiments.html")
# p53 plays a role.
9. Analysis of genes from a GO search.
library(ALL)
data(ALL,package="ALL")
241
ALLP <- ALL[,ALL$mol.biol %in% c("ALL1/AF4","BCR/ABL","NEG")]
neg <- which(ALLP$mol.biol=="NEG")
aal1 <- which(ALLP$mol.biol=="ALL1/AF4")
bcr <- which(ALLP$mol.biol=="BCR/ABL")
orderpat <- c(neg,aal1,bcr)
ALLP <- ALL[,ALL$mol.biol %in% c("ALL1/AF4","BCR/ABL","NEG")]
ALLPo <- ALLP[,c(neg,aal1,bcr)]
facnr <- c(rep(1,74),rep(2,10),rep(3,37))
nab.fac <- factor(facnr,levels=1:3, labels= c("NEG","ALL1/AF4","BCR/ABL"))
panova <- apply(exprs(ALLPo), 1, function(x) anova(lm(x ~ nab.fac))$Pr[1])
library("GO"); library("annotate"); library("hgu95av2")
GOTerm2Tag <- function(term) {
GTL <- eapply(GOTERM, function(x) {grep(term, x@Term, value=TRUE)})
Gl <- sapply(GTL, length)
names(GTL[Gl>0])
}
> GOTerm2Tag("protein-tyrosine kinase")
[1] "GO:0004713"
probes <- hgu95av2GO2ALLPROBES$"GO:0004713"
> sum(panova[probes]<0.05)
[1] 86
> sum(panova[probes]<1)
[1] 320
> sum(panova<0.05)
[1] 2581
> sum(panova<1)
[1] 12625
> fisher.test(matrix(c(12625, 2581,320,86),2,byrow=TRUE))
Fisher’s Exact Test for Count Data
242 APPENDIX A. ANSWERS TO EXERCISES
data: matrix(c(12625, 2581, 320, 86), 2, byrow = TRUE)
p-value = 0.03222
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
1.019848 1.679625
sample estimates:
odds ratio
1.314569
the odds ratio differs significantly from zero; there are more significant results among the probes related to protein-tyrosine kinase.
Answers to exercises of Chapter 7: Cluster Analysis and Trees.
1. Cluster analysis on the ”Zyxin” expression values of the Golub et al.
(1999) data.
data(golub, package="multtest")
data <- data.frame(golub[2124,])
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
stripchart(golub[2124,]~gol.fac, pch=as.numeric(gol.fac))
plot(hclust(dist(clusdata,method="euclidian"),method="single"))
initial <- as.matrix(tapply(golub[2124,],gol.fac,mean), nrow = 2, ncol=1, byrow=TRUE)
cl<- kmeans(data, initial, nstart = 10)
table(cl$cluster,gol.fac)
n <- length(data); nboot<-1000
boot.cl <- matrix(0,nrow=nboot,ncol = 2)
for (i in 1:nboot){
dat.star <- data[sample(1:n,replace=TRUE)]
cl <- kmeans(dat.star, initial, nstart = 10)
boot.cl[i,] <- c(cl$centers[1,],cl$centers[2,])
}
> quantile(boot.cl[,1],c(0.025,0.975))
2.5% 97.5%
-1.07569310 -0.03344292
243
> quantile(boot.cl[,2],c(0.025,0.975))
2.5% 97.5%
0.731493 1.784468
2. Close to CCND3 Cyclin D3.
library("genefilter"); data(golub, package = "multtest")
closeg <- genefinder(golub, 1042, 10, method = "euc", scale = "none")
golub.gnames[closeg[[1]][[1]],2]
boxplot(golub[394,] ~gol.fac)
3. MCM3.
data(golub, package = "multtest")
x <- golub[2289,]; y <- golub[2430,]
plot(x,y)
which.min(y) # the plot suggests the smallest y as the outlier
> cor.test(x[-21],y[-21])
Pearson’s product-moment correlation
data: x[-21] and y[-21]
t = 10.6949, df = 35, p-value = 1.42e-12
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.7690824 0.9341905 # much smaller
sample estimates:
cor
0.875043 # much larger than 0.6376217
nboot <- 1000; boot.cor <- matrix(0,nrow=nboot,ncol = 1)
data <- matrix(c(x[-21],y[-21]),ncol=2,byrow=FALSE)
for (i in 1:nboot){
dat.star <- data[sample(1:nrow(data),replace=TRUE),]
boot.cor[i,] <- cor(dat.star)[2,1]}
> mean(boot.cor)
[1] 0.8725835 # very similar to cor.test
> quantile(boot.cor[,1],c(0.025,0.975))
2.5% 97.5%
0.7755743 0.9324625 # very similar to cor.test
244 APPENDIX A. ANSWERS TO EXERCISES
4. Cluster analysis on part of Golub data.
library(multtest);data(golub);
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
o1 <- grep("oncogene",golub.gnames[,2])
plot(hclust(dist(golub[o1,],method="euclidian"),method="single"))
o2 <- grep("antigene",golub.gnames[,2])
plot(hclust(dist(golub[o2,],method="euclidian"),method="single"))
o3 <- grep("receptor",golub.gnames[,2])
plot(hclust(dist(golub[o3,],method="euclidian"),method="single"))
5. Principal Components Analysis on part of the ALL data.
library(ALL); data(ALL)
ALLB <- ALL[,ALL$BT %in% c("B1","B2","B3")]
panova <- apply(exprs(ALLB), 1, function(x) anova(lm(x ~ ALLB$BT))$Pr[1])
ALLBsp <- ALLB[panova<0.001,]
> dim(exprs(ALLBsp))
[1] 499 78
> min(cor(exprs(ALLBsp)))
[1] 0.5805595
> eigen(cor(exprs(ALLBsp)))$values[1:5]
[1] 65.2016203 2.9652965 2.4781567 0.7556439 0.6040647
data <- exprs(ALLBsp); p <- ncol(data); n <- nrow(data) ; nboot<-1000
eigenvalues <- array(dim=c(nboot,p))
for (i in 1:nboot){dat.star <- data[sample(1:n,replace=TRUE),]
eigenvalues[i,] <- eigen(cor(dat.star))$values}
> for (j in 1:p) print(quantile(eigenvalues[,j],c(0.025,0.975)))
2.5% 97.5%
63.43550 66.77785
2.5% 97.5%
2.575413 3.530350
2.5% 97.5%
2.081573 2.889933
2.5% 97.5%
245
0.6475809 0.9942871 #Hence, the first three are significant!
2.5% 97.5%
0.5067404 0.7482680
2.5% 97.5%
biplot(princomp(data,cor=TRUE),pc.biplot=T,cex=0.5,expand=0.8)
6. Some correlation matrices.
eigen(matrix(c(1,-0.8,-0.8,1),nrow=2))
eigen(matrix(c(1,0.8,0.8,0.8,1,0.8,0.8,0.8,1),nrow=3))
eigen(matrix(c(1,-0.5,-0.5,-0.5,1,-0.5,-0.5,-0.5,1),nrow=3))
> 2.6/3 * 100
[1] 86.66667
> eigen(matrix(c(1,0.8,0.8,0.8,1,0.8,0.8,0.8,1),nrow=3))$vectors
[,1] [,2] [,3]
[1,] -0.5773503 0.8164966 0.0000000
[2,] -0.5773503 -0.4082483 -0.7071068
[3,] -0.5773503 -0.4082483 0.7071068
Answers to exercises of Chapter 8: Classification Methods.
1. Classification tree of Golub data. Use recursive partitioning in rpart
library(multtest);data(golub);
gol.fac <- factor(golub.cl,levels=0:1, labels= c("ALL","AML"))
maxgol <- apply(golub[,gol.fac=="ALL"], 1, function(x) max(x))
mingol <- apply(golub[,gol.fac=="AML"], 1, function(x) min(x))
sum(maxgol < mingol)
> which.min(maxgol - mingol)
[1] 2124
> golub.gnames[2124,]
[1] "4847" "Zyxin" "X95735_at"
> boxplot(golub[2124,] ~gol.fac)
gol.rp <- rpart(gol.fac ~ golub[2124,], method="class", cp=0.001)
plot(gol.rp, branch=0,margin=0.1); text(gol.rp, digits=3, use.n=TRUE)
246 APPENDIX A. ANSWERS TO EXERCISES
grep("Gdf5",golub.gnames[,2])
> grep("Gdf5",golub.gnames[,2])
[1] 2058
gol.rp <- rpart(gol.fac ~ golub[2058,], method="class", cp=0.001)
plot(gol.rp, branch=0,margin=0.1); text(gol.rp, digits=3, use.n=TRUE)
gol.rp <- rpart(gol.fac ~., data.frame(t(golub)), method="class", cp=0.001)
plot(gol.rp, branch=0,margin=0.1); text(gol.rp, digits=3, use.n=TRUE)
2. Sensitivity versus specificity.
(a) library(multtest);library(ROCR);data(golub)
golub.clchanged <- -golub.cl +1
pred <- prediction(golub[1042,], golub.clchanged)
perf <- performance(pred, "sens", "spec")
plot(perf)
(b) The function is essentially the same.
(c) Use auc as before.
3. Comparing Classification Methods.
library(rpart)
predictors <- matrix(rnorm(100*4,0,1),100,4)
colnames(predictors) <- letters[1:4]
groups <- gl(2,50)
simdata <- data.frame(groups,predictors)
rp<-rpart(groups ~ a + b + c + d,method="class",data=simdata)
predicted <- predict(rp,type="class")
table(predicted,groups)
plot(rp, branch=0,margin=0.1); text(rp, digits=3, use.n=TRUE)
> table(predicted,groups)
groups
predicted 1 2
1 41 12
247
2 9 38
library(e1071)
svmest <- svm(predictors, groups, data=df, type = "C-classification", kernel = "linear")
svmpred <- predict(svmest, predictors, probability=TRUE)
> table(svmpred, groups)
groups
svmpred 1 2
1 31 25
2 19 25
library(nnet)
nnest <- nnet(groups ~ ., data = simdata, size = 5,maxit = 500, decay = 0.01, MaxNWts = 5000)
pred <- predict(nnest, type = "class")
> table(pred, groups) # prints confusion ma
groups
pred 1 2
1 45 10
2 5 40
The misclassification rate of rpart, svm, and nnet is, respectively, 21/100,
44/100, and 15/100. If we increase the number of predictors, then the
misclassification rate decreases.
4. Prediction of achieved remission.
library(ALL); library(hgu95av2.db); library(rpart); data(ALL)
ALLrem <- ALL[,which(pData(ALL)$remission %in% c("CR","REF"))]
remfac <-factor(pData(ALLrem)$remission)
pano <- apply(exprs(ALLrem),1,function(x) t.test(x ~ remfac)$p.value)
names <- featureNames(ALLrem)[pano<.001]
ALLremsel<- ALLrem[names,]
data <- data.frame(t(exprs(ALLremsel)))
all.rp <- rpart(remfac ~., data, method="class", cp=0.001)
plot(all.rp, branch=0,margin=0.1); text(all.rp, digits=3, use.n=TRUE)
rpart.pred <- predict(all.rp, type="class")
> table(rpart.pred,remfac)
remfac
248 APPENDIX A. ANSWERS TO EXERCISES
rpart.pred CR REF
CR 93 1
REF 6 14
> 7/(93+1+6+14)
[1] 0.06140351
> mget(c("1840_g_at","36769_at","1472_g_at","854_at"), env = hgu95av2GENENAME)
$‘1840_g_at‘
[1] NA
$‘36769_at‘
[1] "retinoblastoma binding protein 5"
$‘1472_g_at‘
[1] "v-myb myeloblastosis viral oncogene homolog (avian)"
$‘854_at‘
[1] "B lymphoid tyrosine kinase"
5. Gene selection by area under the curve.
library(ROCR); data(golub, package = "multtest")
gol.true <- factor(golub.cl,levels=0:1,labels= c("TRUE","FALSE"))
auc.values <- apply(golub,1,
function(x) performance(prediction(x, gol.true),"auc")@y.values[[1]])
o <- order(auc.values,decreasing=TRUE)
golub.gnames[o[1:25],2]
6. Classification Tree for Ecoli.
ecoli <- read.table("http://www.grappa.univ-lille3.fr/~torre/Recherche/Datasets/
downloads/ecoli/ecoli.data",sep=",",header = TRUE)
colnames(ecoli) <- c("SequenceName","mcg","gvh","lip","chg","aac","alm1","alm2","ecclass")
ecolisel<- ecoli[which(ecoli$ecclass %in% c("cp","im","pp")),]
ecolisel$ecclass <- factor(ecolisel$ecclass, levels=c("cp","im","pp"))
library(rpart)
rpfit <- rpart(ecolisel$ecclass ~ mcg + gvh + lip + aac + alm1 + alm2,data=ecolisel, method="class")
plot(rpfit, branch=1,margin=0.1); text(rpfit, digits=3, use.n=TRUE)
title(main = "rpartfit ecoli classes cp im and pp")
249
predictedclass <- predict(rpfit, type="class")
table(predictedclass,ecolisel$ecclass) #predictors are alm1, gvh and im
> (1+2+7+4)/length(ecolisel$ecclass)
[1] 0.05166052
Answers to exercises of Chapter 9: Analyzing Sequences
1. Writing to a FASTA file.
choosebank("genbank"); library(seqinr)
query("ccnd3hs","sp=homo sapiens AND k=ccnd3@")
ccnd3 <- sapply(ccnd3hs$req, getSequence)
x1 <- DNAStringSet(c2s(ccnd3[[1]]))
write.XStringSet(x1, file="ccnd3.fa", format="fasta", width=80)
ccnd3c2sn <- sapply(ccnd3, c2s)
x1 <- DNAStringSet(ccnd3c2sn)
write.XStringSet(x1, file="ccnd3n.fa", format="fasta", width=80)
An alternative would be to use the write.dna function of the ape
package.
2. Dotplot of sequences.
seq1 <- sample(c("A","G","C","T"),100,rep=TRUE,prob=c(0.1,0.4,0.4,0.1))
seq2 <- sample(c("A","G","C","T"),100,rep=TRUE,prob=c(0.1,0.4,0.4,0.1))
par(mfrow=c(1,2))
dotPlot(seq1, seq2, main = "Dot plot of different random sequences\nwsize = 1, wstep = 1, nmatch = 1")
dotPlot(seq1, seq1, main = "Dot plot of equal random sequnces\nwsize = 1, wstep = 1, nmatch = 1")
par(mfrow=c(1,1))
par(mfrow=c(1,2))
dotPlot(seq1, seq2, main = "Dot plot of different random sequences\nwsize = 3, wstep = 3, nmatch = 3")
dotPlot(seq1, seq1, main = "Dot plot of equal random sequnces\nwsize = 3, wstep = 3, nmatch = 3")
par(mfrow=c(1,1))
par(mfrow=c(1,2))
dotPlot(seq1, seq1, main = "Dot plot of different random sequences\nwsize = 3, wstep = 3, nmatch = 3")
250 APPENDIX A. ANSWERS TO EXERCISES
dotPlot(seq1, seq1[100:1], main = "Dot plot of equal random sequnces\nwsize = 3, wstep = 3, nmatch = 3")
par(mfrow=c(1,1))
x <- c("RPLWVAPDGHIFLEAFSPVYK")
y <- c("RPLWVAPDGHIFLEAFSPVYK")
z <- c("PLWISPSDGRIILESFSPLAE")
choosebank("genbank"); library(seqinr)
query("ccnd3hs","sp=homo sapiens AND k=ccnd3@")
ccnd3 <- sapply(ccnd3hs$req, getSequence)
sapply(ccnd3hs$req, getName)
ccnd3prot <- sapply(ccnd3hs$req, getTrans)
dotPlot(ccnd3prot[[1]], s2c("EEEVFPLAMN"), main = "Dot plot of two protein\nwsize = 1, wstep = 1, nmatch = 1")
dotPlot(ccnd3prot[[7]], ccnd3prot[[8]], main = "Dot plot of two protein\nwsize = 1, wstep = 1, nmatch = 1")
dotPlot(s2c(x), s2c(z), main = "Dot plot of two protein\nwsize = 1, wstep = 1, nmatch = 1")
3. Local alignment.
library(seqinr);library(Biostrings);data(BLOSUM50)
x <- s2c("HEAGAWGHEE"); y <- s2c("PAWHEAE")
s <- BLOSUM50[y,x]; d <- 8
F <- matrix(data=NA,nrow=(length(y)+1),ncol=(length(x)+1))
F[1,] <- 0 ; F[,1] <- 0
rownames(F) <- c("",y); colnames(F) <- c("",x)
for (i in 2:(nrow(F)))
for (j in 2:(ncol(F)))
{F[i,j] <- max(c(0,F[i-1,j-1]+s[i-1,j-1],F[i-1,j]-d,F[i,j-1]-d))}
> max(F)
[1] 28
4. Probability of more extreme alignment score.
library(seqinr);library(Biostrings);data(BLOSUM50)
randallscore <- c(1,1)
for (i in 1:1000) {
x <- c2s(sample(rownames(BLOSUM50),7, replace=TRUE))
y <- c2s(sample(rownames(BLOSUM50),10, replace=TRUE))
randallscore[i] <- pairwiseAlignment(AAString(x), AAString(y), substitutionMatrix = "BLOSUM50",
251
gapOpening = 0, gapExtension = -8, scoreOnly = TRUE)
}
> sum(randallscore>1)/1000
[1] 0.003
> plot(density(randallscore))
5. Prochlorococcus marinus.
library(seqinr)
choosebank("genbank")
query("ccmp","AC=AE017126 OR AC=BX548174 OR AC=BX548175")
ccmpseq <- sapply(ccmp$req,getSequence)
gc <- sapply(ccmpseq, GC)
> wilcox.test(gc[1:2],gc[3:9])
Wilcoxon rank sum test
data: gc[1:2] and gc[3:9] W = 0, p-value = 0.05556 alternative
hypothesis: true location shift is not equal to 0
> t.test(gc[1:2],gc[3:9])
Welch Two Sample t-test
data: gc[1:2] and gc[3:9] t = -5.8793, df = 1.138, p-value =
0.08649 alternative hypothesis: true difference in means is not
equal to 0 95 percent confidence interval:
-0.4507417 0.1079848
sample estimates: mean of x mean of y 0.3362065 0.5075849
gc in the left group is lower, the tests are not significant.
6. Sequence equality.
\begin{verbatim}
library(seqinr)
choosebank("genbank")
query("ccnd3hs","sp=homo sapiens AND k=ccnd3@")
252 APPENDIX A. ANSWERS TO EXERCISES
sapply(ccnd3hs$req,getLength)
> ccnd3prot <- sapply(ccnd3hs$req, getTrans)
> table(ccnd3prot[[1]])
*ACDEFGHIKLMNPQRSTVWY
1 31 12 12 21 6 14 7 10 10 41 9 1 17 16 22 19 18 15 3 8
> table(ccnd3prot[[2]])
*ACDEFGHIKLMNPQRSTVWY
1 30 12 12 21 6 14 7 10 10 41 9 1 17 16 22 20 18 15 3 8
# Hence, there is only one difference!
> which(!ccnd3prot[[1]]==ccnd3prot[[2]])
[1] 259
7. Conserved region.
ID XRODRMPGMNTB; BLOCK
AC PR00851A; distance from previous block=(52,131)
DE Xeroderma pigmentosum group B protein signature
BL adapted; width=21; seqs=8; 99.5%=985; strength=1287
XPB_HUMAN|P19447 ( 74) RPLWVAPDGHIFLEAFSPVYK 54
XPB_MOUSE|P49135 ( 74) RPLWVAPDGHIFLEAFSPVYK 54
P91579 ( 80) RPLYLAPDGHIFLESFSPVYK 67
XPB_DROME|Q02870 ( 84) RPLWVAPNGHVFLESFSPVYK 79
RA25_YEAST|Q00578 ( 131) PLWISPSDGRIILESFSPLAE 100
Q38861 ( 52) RPLWACADGRIFLETFSPLYK 71
O13768 ( 90) PLWINPIDGRIILEAFSPLAE 100
O00835 ( 79) RPIWVCPDGHIFLETFSAIYK 86
library(Biostrings);data(BLOSUM50)
x <- c("RPLWVAPDGHIFLEAFSPVYK")
y <- c("RPLWVAPDGHIFLEAFSPVYK")
z <- c("PLWISPSDGRIILESFSPLAE")
x == y
pairwiseAlignment(AAString(x), AAString(z), substitutionMatrix = "BLOSUM50",gapOpening = 0, gapExtension = -8, scoreOnly = FALSE)
> pairwiseAlignment(AAString(x), AAString(y), substitutionMatrix = "BLOSUM50",gapOpening = 0, gapExtension = -8, scoreOnly = FALSE)
Global Pairwise Alignment
253
1: RPLWVAPDGHIFLEAFSPVYK
2: RPLWVAPDGHIFLEAFSPVYK
Score: 154
>
> z <- c("PLWISPSDGRIILESFSPLAE")
>
> x == y
[1] TRUE
> pairwiseAlignment(AAString(x), AAString(z), substitutionMatrix = "BLOSUM50",gapOpening = 0, gapExtension = -8, scoreOnly = FALSE)
Global Pairwise Alignment
1: RPLWVAP-DGHIFLEAFSPVYK
2: -PLWISPSDGRIILESFSPLAE
Score: 85
8. Plot of CG proportion from Celegans.
(a) Produce a plot of the CG proportion of the chromosome I of Cel-
egans (Celegans.UCSC.ce2) along a window of 100 nucleotides.
Take the first 10,000 nucleotides.
library(seqinr)
source("http://bioconductor.org/biocLite.R")
biocLite("BSgenome.Celegans.UCSC.ce2")
library(BSgenome.Celegans.UCSC.ce2)
GCperc <- double()
for (i in 1:10000) GCperc[i] <- GC(s2c(as.character(Celegans$chrI[i:(i+100)])))
plot(GCperc,type="l")
(b) A binding sequence of the enzyme EcoRV is the subsequence
GATATC. How many exact matches has Chromosome I of Cel-
egans.
> subseq <- "gatatc"
> countPattern(subseq, Celegans$chrI, max.mismatch = 0)
[1] 3276
> length(s2c(as.character(Celegans$chrI))) * (1/4)^6
[1] 3681.759
9. Plot of codon usage.
254 APPENDIX A. ANSWERS TO EXERCISES
data(ec999)
ec999.uco <- lapply(ec999, uco, index="eff")
df <- as.data.frame(lapply(ec999.uco, as.vector))
row.names(df) <- names(ec999.uco[[1]])
global <- rowSums(df)
title <- "Codon usage in 999 E. coli coding sequences"
dotchart.uco(global, main = title)
choosebank("genbank"); library(seqinr)
query("ccndhs","sp=homo sapiens AND k=ccnd@")
ccnd <- sapply(ccndhs$req, getSequence)
ccnd.uco <- lapply(ccnd3, uco, index="eff")
df <- as.data.frame(lapply(ccnd.uco, as.vector))
row.names(df) <- names(ccnd.uco[[1]])
global <- rowSums(df)
title <- "Codon usage in ccnd3 homo sapiens coding sequences"
dotchart.uco(global, main = title)
Answers to exercises of Chapter 10: Markov Models.
1. Visualize by a transition graph the following transition matrices. Con-
sult your teacher.
2. Computing probabilities. The answers are provided by the following.
> P <- matrix(c(3/4,1/4,1/2,1/2),2,2,byrow=T)
> pi0 <- c(1/2,1/2)
> pi0 %*% P
[,1] [,2]
[1,] 0.625 0.375
> P %*% P
[,1] [,2]
[1,] 0.6875 0.3125
[2,] 0.6250 0.3750
> P
[,1] [,2]
[1,] 0.75 0.25
[2,] 0.50 0.50
255
3. Programming GTR. Use πA= 0.15, πG= 0.35, πC= 0.35, πT= 0.15,
α= 4, β= 0.5, γ= 0.4, δ= 0.3, ²= 0.2, and ζ= 4.
(a) Program the rate matrix in such a manner that it is simple to
adapt for other values of the parameters.
library(Matrix)
piA <- 0.15; piG <- 0.35; piC <- 0.35; piT <- 0.15
alpha <- 4; beta <- 0.5; gamma <- 0.4; delta <- 0.3
epsilon <- 0.2; zeta <- 4
Q <- matrix(data=NA,4,4)
Q[1,2] <- alpha * piG; Q[1,3] <- beta * piC;
Q[1,4] <- gamma * piT
Q[2,1] <- alpha * piA; Q[2,3] <- delta * piC;
Q[2,4] <- epsilon * piT
Q[3,1] <- beta * piA; Q[3,2] <- delta * piG;
Q[3,4] <- delta* piT
Q[4,1] <- gamma * piA; Q[4,2] <- epsilon* piG; Q[4,3] <- zeta * piC
diag(Q) <- 0
diag(Q) <- -apply(Q,1,sum)
Q <- Matrix(Q)
> Q
4 x 4 Matrix of class "dgeMatrix"
[,1] [,2] [,3] [,4]
[1,] -1.635 1.400 0.175 0.060
[2,] 0.600 -0.735 0.105 0.030
[3,] 0.075 0.105 -0.225 0.045
[4,] 0.060 0.070 1.400 -1.530
(b) The transversion rate is larger then the transition rate because
the blocks outside the main diagonal have lower values.
(c) The probability transition matrix is
> P <- as.matrix(expm(Q))
> P
[,1] [,2] [,3] [,4]
[1,] 0.32199057 0.51569256 0.1392058 0.02311107
[2,] 0.22097363 0.64908639 0.1115233 0.01841667
256 APPENDIX A. ANSWERS TO EXERCISES
[3,] 0.05203969 0.09913633 0.8263804 0.02244359
[4,] 0.04621015 0.08457814 0.6397090 0.22950271
rownames(P) <- colnames(P) <- StateSpace <- c("a","g","c","t")
pi0 <- c(1/4,1/4,1/4,1/4)
markov2 <- function(StateSpace,P,n){
seq <- matrix(0,nr=n,nc=1)
seq[1] <- sample(StateSpace,1,replace=T,pi0)
for(k in 1:(n-1)){ seq[k+1] <- sample(StateSpace,1,replace=T,P[seq[k],])}
return(seq) }
seq <- markov2(StateSpace,P,99)
4. Distance according to JC69.
(a) accnr <- paste("AJ5345",26:27,sep="")
seqbin <- read.GenBank(accnr, species.names = TRUE, as.character = FALSE)
Down load the sequences AJ534526 and AJ534527. Hint: Use
as.character = TRUE in the read.GenBank function.
(b) Two solution of computing the proportion of different nucleotides
are
dist.dna(seqbin, model = "raw")
p <- sum(seq$AJ534526 != seq$AJ534527)/1143
(c) Simply insert the obtained pin the formula d <- -log(1-4*p/3)*3/4.
Appendix B
References
Dalgaard, P. (2002). Introductory statistics with R. New York: Springer.
Bain, L.J. & Engelhardt, M. (1992). Introduction to probability and mathe-
matical statistics. Pacific Grove: Duxbury.
Becker, R.A., Chambers, J.M. & Wilks, A.R. (1988). The new S language.
New Jersey: Bell Telephone Laboratories.
Beran, B. & Srivastava, M.S. (1985). Bootstrap tests and confidence regions
for functions of a covariance matrix. The Annals of Statistics, 13, 95-
115.
Beran, R. & Ducharme, G.R. (1991). Asymptotic theory for bootstrap meth-
ods in statistics. Montreal: Centre de recherche math´ematique.
Breiman, L., J. H. Friedman, R. A. Olshen, and C. J. Stone. (1984) Classi-
fication and Regression Trees. Monterey: Wadsworth.
Breusch, T.S. & Pagan A.R. (1979). A Simple Test for Heteroscedasticity
and Random Coefficient Variation. Econometrica 47, 12871294.
Bonnet, E. Wuyts, J., & Rouze, P. and Van de Peer, Y. (2004). Evidence that
microRNA precursors, unlike other non-coding RNAs, have lower fold-
ing free energies than random sequences Bioinformatics, 20, 29112917.
Charif, D. Humblot, L. Lobry, J.R. Necxsulea, A. Palmeira, L. Penel, S.
(2008). SeqinR 2.0-1: a contributed package to the project for statistical
computing devoted to biological sequences retrieval and analysis. URL:
http://seqinr.r-forge.r-project.org/.
Chambers, J.M. & Hastie, T.J. eds. (1992) Statistical Models in S. Pacific
Grove: Wadsworth and Brooks/Cole.
Chiaretti, S., Xiaochun Li, Gentleman, R., Vitale, A., Vignetti, M., Mandelli,
F., Ritz, J. and Foa R., (2004) Gene expression profile of adult T-cell
257
258 APPENDIX B. REFERENCES
acute lymphocytic leukemia identifies distinct subsets of patients with
different response to therapy and survival. Blood. Vol. 103, No. 7.
Cleveland, W.S. & Devlin, S.J. 1988). Locally weighted regression: An ap-
proach to regression analysis by local fitting. Journal of the American
statistical association. 83, 596-610.
Clopper, C. J. & Pearson, E. S. (1934). The use of confidence or fiducial
limits illustrated in the case of the binomial. Biometrika, 26, 404413.
Dalgaard, P. (2002). Introductory Statistics with R. New York: Springer.
DeRisi, J.L., Iyer, V.R. & Brown, P.O. (1997). Exploring the metabolic and
genetic control of gene expression on a genomic scale. Science, 278,
680-686.
Deonier, R.C. Tavere, S. Waterman, M.S. (2005). Computational genome
Analysis. New York: Springer.
Dudoit, J. Fridlyand, & T. P. Speed (2002). Comparison of discrimination
methods for the classification of tumors using gene expression data.
Journal of the American Statistical Association, Vol. 97, 7787.
Durbin, R., Eddy, S., Krogh, A. & Mitchison, G. (2005). Biological sequence
analysis. Cambridge: Cambridge University Press.
Efron, B. (1979). Bootstrap methods: Another look at the Jackknive. The
Annals of Statistics, 7, 1-26.
Efron, B. & Tibshirani, R.F. (1993). An introduction to the bootstrap. New
York: Chapman & Hall
Everitt, B.S. & Hothorn, T. (2006) A Handbook of Statistical Analyses Using
R. New York : Chapman & Hall.
Ewens, W.J. & Grant, G.R. (2005). Statistical methods in bioinformatics.
New York: Springer.
Faraway, J. (2004). Linear Models with R. Boca Raton, FL: Chapman &
Hall/CRC.
Feller, W. (1967). An Introduction to Probability Theory and its Applications.
(3rd ed.). New York: Wiley.
Gasteiger E., Hoogland C., Gattiker A., Duvaud S., Wilkins M.R., Appel
R.D., Bairoch A. (2005) Protein Identification and Analysis Tools on
the ExPASy Server; (In) John M. Walker (ed): The Proteomics Proto-
cols Handbook, Humana Press (2005). pp. 571-607
Gentleman, R., Huber, W., Carey , V., Irizarry, R.A., & Irizarry, R. (2005).
Bioinformatics and Computational Biology Solutions Using R and Bio-
conductor, New York: Springer.
259
Golub, G.H. & Van Loan, C.F. (1983). Matrix Computations. Baltimore:
The John Hopkins University Press.
Golub et al. (1999). Molecular classification of cancer: class discovery and
class prediction by gene expression monitoring, Science, Vol. 286:531-
537.
Gouy, M., Milleret, F., Mugnier, C., Jacobzone, M., Gautier,C. (1984). AC-
NUC: a nucleic acid sequence data base and analysis system. Nucl.
Acids Res., 12:121-127.
Grubbs, F.E. (1950). Sample criteria for testing outlying observations. An-
nals of Mathematical Statistics, 21, 1, 27-58.
Hahne, F. Huber, W., Gentleman, R. & Falcon, S. (2008) Bioconductor Case
Studies. New York: Springer.
Hartigan, J.A. & Wong, M.A. (1975). A k-means clustering algorithm. Ap-
plied Statistics, 28, 100-108.
Horn, R.A. & Johnson, C.R. (1985). Matrix Analysis. Cambridge: Cam-
bridge University Press.
Huber, P.J. (1964). Robust estimation of a location parameter. The Annals
of Mathematical Statistics, 35, 73-101.
Huber, P. J. (1981) Robust Statistics. Wiley.
Ihaka,R. and Gentleman,R. (1996) R: a language for data analysis and graph-
ics. J. Comput. Graphic Statist., 5, 299314.
Johnson, N.L. & Kotz, S. & Kemp, A. (1992). Univariate discrete distribu-
tions. New York: John Wiley & Sons.
Jolliffe, I.T. (2002). Principal Components Analysis. New York: Springer.
Jureˇckov´a, J. & Picek, J. (2006). Robust Statistical Methods with R. New
York: Chapman & Hall.
Kyte J. & Doolittle R.F. (1982). A simple method for displaying the hydro-
pathic character of a protein. Journal of Molecular Biology, 157:105132.
Laub, M.T., McAdams, H.H., Feldblyum, Fraser, C.M., and Shapiro, L.
(2000). Global analysis of the genetic network controlling a bacterial
cell cycle. Science, 290, 21441248.
Lehmann, E.L. (1999). Elements of large sample theory . New York: Springer.
Little, R. J. A., and Rubin, D. B. (1987) Statistical Analysis with Missing
Data. New York: Wiley.
Luenberger, D.G. (1969). Optimization by vector space methods. New York:
Wiley.
Maindonald J. & Braun, J. (2003). Data analysis and Graphics Using R.
Cambridge: Cambridge University Press.
260 APPENDIX B. REFERENCES
Miller, I. & Miller, M. (1999). John E. Freund’s Mathematical Statistics.
New Jersey: Prentice Hall.
Marazzi, A. (1993). Algorithms, routines, and S functions for robust statis-
tics. Wadsworth & Brooks/Cole, Pacific Grove, CA.
Palmeira, L., Guguen, L. and Lobry, J.R. (2006) UV-targeted dinucleotides
are not depleted in light-exposed Prokaryotic genomes. Molecular Bi-
ology and Evolution, 23:2214-2219.
Paradis, E. (2006). Analysis of Phylogenetics and Evolution with R. New
York: Springer.
Pevsner, J. (2003). Bioinformatics and functional genomics. New York:
Wiley-Liss.
Pollard, D. (1981). Strong consistency of K-means clustering. Annals of
statistics, 9, 135-140.
Press, W.H., Flannery, B.P., Teukolsky, S.A. & Vettering W.T. (1992). Nu-
merical recipes in Pascal. New York: Cambridge University press.
R Development Core Team (2009). R: A language and environment for
statistical computing. R Foundation for Statistical Computing, Vienna,
Austria. ISBN 3-900051-07-0, URL http://www.R-project.org.
Rao, C.R. & Toutenburg (1995). Linear Models. New York: Springer.
Ramsey, P.H. (1980). Exact type 1 error rates for robustness of Student’s
t=testwith unequal variances. Journal of educational statistics, 5, 337-
349.
Ripley, B.D. (1996). Pattern Recognition and Neural Networks. Cambridge:
Cambridge University Press.
Roberts, R.J., Vincze, T., Posfai, J., Macelis, D. (2007). REBASE–enzymes
and genes for DNA restriction and modification. Nucleic Acids Res,
35.
Rogner, U.C., Wilke, K., Steck, E., Korn, B., Poustka, A. (1995). The
melanoma antigen gene (MAGE) family is clustered in the chromosomal
band Xq28. Genomics, 10;29(3):725-31.
Rosner, B. (2000) Fundamentals of Biostatistics. Pacific Grove: Duxbury.
Royston. P. (1995) A Remark on Algorithm AS 181: The W Test for Nor-
mality. Applied Statistics, 44, 547551.
Samuels, M.L. & Witmer, J.A. (2003) Statistics for the Life Sciences, New
Jersey: Pearson Education.
Stephens, M.A. (1986): Tests based on EDF statistics. In: D’Agostino, R.B.
and Stephens, M.A., eds.: Goodness-of-Fit Techniques. Marcel Dekker,
New York.
261
Tessarz, A.S., Weiler, S., Zanzinger, K., Angelisova, P., Horejsi, V., Cer-
wenka, A. (2007). Non-T cell activation linker (NTAL) negatively reg-
ulates TREM-1/DAP12-induced inflammatory cytokine production in
myeloid cells. Journal of Immunolgy. 178(4) 1991-1999.
Therneau, T.M. & Atkinson, E.J. (1997). An introduction to recursive par-
titioning using RPART routines. Technical report, Mayo Foundation.
Smyth, G. K. (2004). Linear models and empirical Bayes methods for as-
sessing differential expression in microarray experiments. Statistical
Applications in Genetics and Molecular Biology, 3, No. 1, Article 3.
Smyth, G. K. (2005). Limma: linear models for microarray data. In: ’Bioin-
formatics and Computational Biology Solutions using R and Biocon-
ductor’. R. Gentleman, V. Carey, S. Dudoit, R. Irizarry, W. Huber
(eds), Springer, New York, pages 397–420.
Venables W.N. & Ripley B.D. (2000). S programming. New York: Springer.
Venables, W. N. & Ripley, B. D. (2002) Modern Applied Statistics with S.
Fourth edition. Springer.
Wang, Y.Y. (1971). Probabilities of the type I errors of the Welch tests
for the Behrens-Fisher problem. Journal of the American Statistical
Association, 66, 605-608.
Wichert, S., Fokianos, K., and Strimmer, K. (2004). Identifying periodically
expressed transcripts in microarray time series data. Bioinformatics,
20:5-20.
Zuker, M. & Stiegler,P. (1981) Optimal computer folding of large RNA
sequences using thermodynamics and auxiliary information. Nucleic
Acids Res., 9, 133148.
Zuker, M. (2003). Mfold web server for nucleic acid folding and hybridization
prediction. Nucleic Acids Research, 31, 3406-3415.
Guindon, S. and Gascuel, O. (2003) A simple, fast, and accurate algorithm to
estimate large phylogenies by maximum likelihood. Systematic Biology,
52, 696704.
Saitou, N. and Nei, M. (1987). The neighbor-joining method: a new method
for reconstructing phylogenetic trees. Molecular Biology and Evolu-
tion,4, 406425.
262 APPENDIX B. REFERENCES
Index
aggregation, 95
Anderson-Darling test, 64
annotation, 104
background correction, 94
Binomial test, 58
BLOSUM50, 185
bootstrap, 127,132
box-and-wiskers-plot, 20
calculator, 4
chi-squared distribution, 37
chi-squared test, 59
classification tree, 150
confusion table, 158
construct a sequence, 4
correlation coefficient, 130
data matrix, 6
data vector, 5
density, 41
design matrix, 101
dinucleotide, 176
distance, 118
downloading sequences, 174
F-distribution, 40
F-test, 57
Fisher test, 62
frequency table, 17
genBank, 18
gene filtering, 97
gene ontology, 107
GO, 107
gol.fac, 11
Golub et al. (1999) data, 10
grep, 12
help, 3
histogram, 19
homoscedasticity, 85
install R, 1
installing Bioconductor, 2
installing R, 2
interquartile range, 25
k-means cluster analysis, 125
Kruskal-Wallis test, 87
linear model, 74
matrix computations, 8
mean, 24
median, 24
median absolute deviation, 25
misclassification rate, 158
mismatch, 91
model matrix, 101
Needleman-Wunsch, 184
neural network, 162
normal distribution, 35
263
264 INDEX
normality of residuals, 85
normality test, 63
normalization, 94
one sample t-test, 51
one sided hypothesis, 48
one-way analysis of variance, 77
packages, 2
perfect match, 91
Phylogenetic tree, 203
predictive power, 147
principal components analysis, 133
Quantile-Quantile plot, 22
quartile, 20
query language, 173
receiver operator curve, 148
rma, 95
running scripts, 13
sample variance, 25
sensitivity, 147
Shapiro-Wilk test, 63
significance level, 48
single linkage cluster analysis, 121
specificity, 147
standard deviation, 25
stripchart, 19
support vector machine, 161
T-distribution, 39
training set, 159
triangle inequality, 118
two sided hypothesis, 48
two-sample t-test, 54
validation set, 159
Wilcoxon rank test, 65
Z-test, 48