LANL2018 NJOY Nuclear Data Processing System Manual
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 800 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Contents
- List of Figures
- List of Tables
- INTRODUCTION
- NJOY
- RECONR
- BROADR
- UNRESR
- HEATR
- THERMR
- GROUPR
- Multigroup Constants
- Group Ordering
- Basic ENDF Cross Sections
- Weighting Flux
- Flux Calculator
- Fission Source
- Diffusion Cross Sections
- Cross Sections for Transport Theory
- Photon Production and Coupled Sets
- Thermal Data
- Generalized Group Integrals
- Two-Body Scattering
- Charged-Particle Elastic Scattering
- Continuum Scattering and Fission
- File 6 Energy-Angle Distributions
- Smoothing
- GENDF Output
- Running GROUPR
- Coding Details
- Error Messages
- GAMINR
- ERRORR
- Introduction
- Definitions of Covariance-Related Quantities
- Structure of ENDF Files 31, 33, and 40: Energy-Dependent Data
- Resonance-Parameter Formats—File 32
- Secondary Particle Angular Distribution Covariances—File 34
- Secondary Particle Energy Distribution Covariances—File 35
- Radioactive Nuclide Production Covariances–File 40
- Calculation of Multigroup Fluxes, Cross Sections, and Covariances on the Union Grid
- Basic Strategy for Collapse to the User Grid
- Group-Collapse Strategy for Data Derived by Summation
- Processing of Data Derived from Ratio Measurements
- Multigroup Processing of Resonance-Parameter Uncertainties
- Processing of Lumped-Partial Covariances
- Input Instructions and Sample Input for ERRORR
- ERRORR Output File Specification
- Error Messages
- Input/Output Units
- COVR
- MODER
- DTFR
- CCCCR
- MATXSR
- RESXSR
- ACER
- ACER and ACE Data Classes
- Continuous-Energy Neutron Data
- Energy Grids and Cross Sections
- Two-Body Scattering Distributions
- Secondary-Energy Distributions
- Energy-Angle Distributions
- Photon Production
- Probability Tables for the Unresolved Region
- Charged-Particle Production
- Gas Production
- Consistency Checks and Plotting
- Thermal Cross Sections
- Dosimetry Cross Sections
- Photoatomic Data
- Photonuclear Data
- Type 1 and Type 2
- Running ACER
- Coding Details
- Error Messages
- POWR
- WIMSR
- PLOTR
- VIEWR
- MIXR
- PURR
- LEAPR
- GASPR
- NJOY Maintenance and Testing
- Code Maintenance with GIT
- Standard Test Problems
- Test Problem 1
- Test Problem 2
- Test Problem 3
- Test Problem 4
- Test Problem 5
- Test Problem 6
- Test Problem 7
- Test Problem 8
- Test Problem 9
- Test Problem 10
- Test Problem 11
- Test Problem 12
- Test Problem 13
- Test Problem 14
- Test Problem 15
- Test Problem 16
- Test Problem 17
- Test Problem 18
- Test Problem 19
- Test Problem 20
- Application of the NJOY System
- References
LA-UR-17-20093
The NJOY Nuclear Data Processing System,
Version 2016
Original Author: R. E. MacFarlane
Theoretical Division
Los Alamos National Laboratory
Contributing Authors
D. W. Muir
R. M Boicourt
A. C. Kahler
J. L. Conlin
W. Haeck
Current Editor: A. C. Kahler
Original Issue: December 19, 2016
Updated for NJOY2016.39
July 3, 2018
Abstract
The NJOY Nuclear Data Processing System, version 2016, is a comprehensive com-
puter code package for producing pointwise and multigroup cross sections and related
quantities from evaluated nuclear data in the ENDF-4 through ENDF-6 legacy cardim-
age formats. NJOY works with evaluated files for incident neutrons, photons, and
charged particles, producing libraries for a wide variety of particle transport and reac-
tor analysis codes.
Disclaimer of Liability:
Neither the United States Government nor the Los Alamos National Security, LLC., nor
any of their employees, makes any warranty, express or implied, including the warranties
of merchantability and fitness for a particular purpose, or assumes any legal liability or
responsibility for the accuracy, completeness, or usefulness of any information, appara-
tus, product, or process disclosed, or represents that its use would not infringe privately
owned rights.
Disclaimer of Endorsement:
Reference herein to any specific commercial products, process, or service by trade name,
trademark, manufacturer, or otherwise, does not necessarily constitute or imply its
endorsement, recommendation, or favoring by the United States Government or the Los
Alamos National Security, LLC. The views and opinions of authors expressed herein do
not necessarily state or reflect those of the United States Government or the Los Alamos
National Security, LLC., and shall not be used for advertising or product endorsement
purposes.
Copyright Notice:
Copyright 2016. Los Alamos National Security, LLC. This software was produced under
U.S. Government contract DE-AC52-06NA25396 for Los Alamos National Laboratory
(LANL), which is operated by Los Alamos National Security, LLC for the U.S. Depart-
ment of Energy. The U.S. Government has rights to use, reproduce, and distribute this
software. NEITHER THE GOVERNMENT NOR LOS ALAMOS NATIONAL SECU-
RITY, LLC MAKES ANY WARRANTY, EXPRESS OR IMPLIED, OR ASSUMES
ANY LIABILITY FOR THE USE OF THIS SOFTWARE. If software is modified to
produce derivative works, such modified software should be clearly marked, so as not
to confuse it with the version available from LANL.
Additionally, redistribution and use in source and binary forms, with or without
modification, are permitted provided that the following conditions are met:
1. Redistributions of source code must retain the above copyright notice, this list of
conditions and the following disclaimer.
2. Redistributions in binary form must reproduce the above copyright notice, this
list of conditions and the following disclaimer in the documentation and/or other
materials provided with the distribution.
3. Neither the name of Los Alamos National Security, LLC, Los Alamos National
Laboratory, LANL, the U.S. Government, nor the names of its contributors may
be used to endorse or promote products derived from this software without specific
prior written permission.
THIS SOFTWARE IS PROVIDED BY LOS ALAMOS NATIONAL SECURITY, LLC
AND CONTRIBUTORS ”AS IS” AND ANY EXPRESS OR IMPLIED WARRANTIES,
INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MER-
CHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED.
IN NO EVENT SHALL LOS ALAMOS NATIONAL SECURITY, LLC OR CONTRIB-
UTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL,
EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIM-
ITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF
USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED
AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LI-
ABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN
ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE
POSSIBILITY OF SUCH DAMAGE.
c
Copyright 2016 Los Alamos National Security, LLC All Rights Reserved

LA-UR-17-20093 CONTENTS
Contents
Contents iv
List of Figures x
List of Tables xiii
1 INTRODUCTION 1
1.1 The Modules of NJOY ........................... 1
1.2 Data Flow in NJOY ............................ 3
1.3 Computer Implementation ......................... 7
1.4 History and Acknowledgments ....................... 8
2 NJOY 19
2.1 The NJOY Program ............................ 19
2.2 Interface Files ................................ 21
2.3 Free Format Input ............................. 22
2.4 ENDF Input-Output ............................ 23
2.5 Buffered Binary Scratch Storage ...................... 27
2.6 Dynamic Storage Allocation ........................ 28
2.7 ENDF/B Utility Routines ......................... 28
2.8 Math Routines ............................... 29
2.9 System-Related Utility Routines ...................... 29
2.10 Error and Warning Messages ........................ 30
2.11 Coding Details for the NJOY Main Program ............... 33
3 RECONR 43
3.1 ENDF/B Cross Section Representations ................. 43
3.2 Unionization and Linearization Strategy ................. 45
3.3 Linearization and Reconstruction Methods ................ 46
3.4 Resonance Representations ......................... 51
3.5 Code Description .............................. 65
3.6 Input Instructions .............................. 71
3.7 Error Messages ............................... 72
3.8 Input-Output Units ............................. 75
3.9 Storage Allocation ............................. 75
4 BROADR 77
4.1 Doppler-Broadening Theory ........................ 77
4.2 Thermal Quantities ............................. 83
4.3 Data-Paging Methodology ......................... 84
4.4 Coding Details ............................... 85
4.5 User Input .................................. 88
4.6 Error Messages ............................... 91
4.7 Input/Output Units ............................ 92
4.8 Storage Allocation ............................. 92
iv NJOY2016

CONTENTS LA-UR-17-20093
5 UNRESR 93
5.1 Theory .................................... 93
5.2 Implementation ............................... 106
5.3 User Input .................................. 109
5.4 Output Example .............................. 110
5.5 Coding Details ............................... 111
5.6 Error Messages ............................... 114
6 HEATR 115
6.1 Theory of Nuclear Heating ......................... 115
6.2 Theory of Damage Energy ......................... 119
6.3 Computation of KERMA Factors By Energy Balance .......... 120
6.3.1 The general case ........................... 120
6.3.2 The special case of fission ...................... 122
6.4 Kinematic Limits .............................. 124
6.5 Computation of Damage Energy ...................... 127
6.6 Heating and Damage from File 6 ..................... 130
6.7 User Input .................................. 133
6.8 Reading HEATR Output .......................... 137
6.9 Diagnosing Energy-Balance Problems ................... 147
6.10 Coding Details ............................... 151
6.11 Error Messages ............................... 161
6.12 Storage Allocation ............................. 164
7 THERMR 165
7.1 Coherent Elastic Scattering ........................ 166
7.2 Incoherent Inelastic Scattering ....................... 168
7.3 Incoherent Elastic Scattering ........................ 174
7.4 Coding Details ............................... 174
7.5 Using the ENDF/B Thermal Data Files ................. 179
7.6 Input Instructions .............................. 181
7.7 Error Messages ............................... 184
7.8 Input/Output Units ............................ 186
7.9 Storage Allocation ............................. 186
8 GROUPR 187
8.1 Multigroup Constants ........................... 187
8.2 Group Ordering ............................... 190
8.3 Basic ENDF Cross Sections ........................ 190
8.4 Weighting Flux ............................... 191
8.5 Flux Calculator ............................... 197
8.6 Fission Source ................................ 201
8.7 Diffusion Cross Sections .......................... 203
8.8 Cross Sections for Transport Theory ................... 205
8.9 Photon Production and Coupled Sets ................... 207
8.10 Thermal Data ................................ 208
8.11 Generalized Group Integrals ........................ 211
8.12 Two-Body Scattering ............................ 214
8.13 Charged-Particle Elastic Scattering .................... 217
8.14 Continuum Scattering and Fission ..................... 218
8.15 File 6 Energy-Angle Distributions ..................... 224
NJOY2016 v

LA-UR-17-20093 CONTENTS
8.16 Smoothing .................................. 227
8.17 GENDF Output ............................... 228
8.18 Running GROUPR ............................. 230
8.19 Coding Details ............................... 252
8.20 Error Messages ............................... 266
9 GAMINR 273
9.1 Description of ENDF/B Photon Interaction Files ............ 273
9.2 Calculational Method ............................ 275
9.3 Integrals Involving Form Factors ..................... 276
9.4 Coding Details ............................... 277
9.5 User Input .................................. 278
9.6 I/O Units .................................. 281
9.7 Error Messages ............................... 281
10 ERRORR 285
10.1 Introduction ................................. 285
10.2 Definitions of Covariance-Related Quantities ............... 287
10.3 Structure of ENDF Files 31, 33, and 40: Energy-Dependent Data . . . 289
10.4 Resonance-Parameter Formats—File 32 .................. 294
10.5 Secondary Particle Angular Distribution Covariances—File 34 . . . . . 296
10.6 Secondary Particle Energy Distribution Covariances—File 35 . . . . . 296
10.7 Radioactive Nuclide Production Covariances–File 40 .......... 299
10.8 Calculation of Multigroup Fluxes, Cross Sections, and Covariances on
the Union Grid ............................... 302
10.9 Basic Strategy for Collapse to the User Grid ............... 306
10.10 Group-Collapse Strategy for Data Derived by Summation . . . . . . . 307
10.11 Processing of Data Derived from Ratio Measurements ......... 310
10.12 Multigroup Processing of Resonance-Parameter Uncertainties . . . . . 314
10.13 Processing of Lumped-Partial Covariances ................ 315
10.14 Input Instructions and Sample Input for ERRORR ........... 315
10.15 ERRORR Output File Specification .................... 336
10.16 Error Messages ............................... 344
10.17 Input/Output Units ............................ 354
11 COVR 357
11.1 Introduction ................................. 357
11.2 Production of Boxer-Format Libraries .................. 357
11.3 Generation of Plots ............................. 359
11.4 Input Instructions for COVR ....................... 361
11.5 COVR Example Problem .......................... 368
11.6 Error Messages ............................... 370
11.7 Input/Output Units ............................ 371
11.8 Retrieval Program for COVR Output Libraries ............. 372
12 MODER 377
12.1 Code Description .............................. 377
12.2 Input Instructions .............................. 377
12.3 Sample Input ................................ 379
12.4 Error Messages ............................... 380
vi NJOY2016

CONTENTS LA-UR-17-20093
13 DTFR 383
13.1 Transport Tables .............................. 383
13.2 Data Representations ............................ 386
13.3 Plotting ................................... 392
13.4 User Input .................................. 395
13.5 Coding Details ............................... 400
13.6 Error Messages ............................... 402
14 CCCCR 403
14.1 Introduction ................................. 403
14.2 CCCC Procedures and Programming Standards ............. 404
14.3 The Standard Interface Files ........................ 407
14.4 ISOTXS ................................... 408
14.5 BRKOXS .................................. 423
14.6 DLAYXS ................................... 431
14.7 Coding Details ............................... 435
14.8 User Input .................................. 444
14.9 Error Messages ............................... 450
15 MATXSR 453
15.1 Background ................................. 453
15.2 The MATXS Format ............................ 454
15.3 Historical Notes ............................... 474
15.4 MATXS Libraries .............................. 475
15.5 User Input .................................. 481
15.6 Coding Details ............................... 484
15.7 Error Messages ............................... 490
16 RESXSR 493
16.1 Method ................................... 493
16.2 RESXS Format Specification ........................ 494
16.3 User Input .................................. 497
17 ACER 499
17.1 ACER and ACE Data Classes ....................... 499
17.2 Continuous-Energy Neutron Data ..................... 500
17.3 Energy Grids and Cross Sections ..................... 500
17.4 Two-Body Scattering Distributions .................... 504
17.5 Secondary-Energy Distributions ...................... 504
17.6 Energy-Angle Distributions ........................ 505
17.7 Photon Production ............................. 510
17.8 Probability Tables for the Unresolved Region .............. 512
17.9 Charged-Particle Production ........................ 512
17.10 Gas Production ............................... 513
17.11 Consistency Checks and Plotting ..................... 513
17.12 Thermal Cross Sections ........................... 514
17.13 Dosimetry Cross Sections .......................... 519
17.14 Photoatomic Data ............................. 520
17.15 Photonuclear Data ............................. 521
17.16 Type 1 and Type 2 ............................. 522
17.17 Running ACER ............................... 522
NJOY2016 vii

LA-UR-17-20093 CONTENTS
17.18 Coding Details ............................... 531
17.19 Error Messages ............................... 546
18 POWR 551
18.1 Input Instructions .............................. 551
19 WIMSR 557
19.1 Resonance Integrals ............................. 557
19.2 Cross Sections ................................ 561
19.3 Burn Data .................................. 564
19.4 User Input .................................. 564
19.5 Coding Details ............................... 569
19.6 WIMS Data File Format .......................... 572
19.7 WIMSR Auxiliary Codes .......................... 576
19.8 Error Messages ............................... 576
20 PLOTR 579
20.1 Simple 2-D Plots .............................. 580
20.2 Multicurve and Multigroup Plots ..................... 583
20.3 Right-Hand Axes .............................. 588
20.4 Plotting Input Data ............................. 590
20.5 Three-D Plots of Angular Distributions .................. 591
20.6 Three-D Plots of Energy Distributions .................. 592
20.7 Two-D Spectra Plots from Files 5 and 6 ................. 594
20.8 Input Instructions .............................. 596
20.9 Coding Details ............................... 603
20.10 Storage Allocation ............................. 605
20.11 Input and Output Units .......................... 605
20.12 Error Messages ............................... 606
21 VIEWR 607
21.1 Modular Structure ............................. 607
21.2 Using VIEWR ................................ 608
21.3 Input Instructions .............................. 608
21.4 Coding Details ............................... 619
21.5 The Graphics Module ............................ 621
21.6 VIEWR Messages .............................. 625
22 MIXR 627
22.1 User Input .................................. 627
22.2 Coding Details ............................... 632
22.3 Error Messages ............................... 632
23 PURR 635
23.1 Sampling from Ladders ........................... 635
23.2 Temperature Correlations ......................... 641
23.3 Self-Shielded Heating Values ........................ 641
23.4 Random Numbers .............................. 642
23.5 User Input .................................. 642
23.6 Coding Details ............................... 643
23.7 Error Messages ............................... 650
viii NJOY2016

CONTENTS LA-UR-17-20093
24 LEAPR 653
24.1 Theory .................................... 654
24.2 Input Instructions .............................. 670
24.3 LEAPR Examples .............................. 676
24.4 Coding Details ............................... 717
24.5 Error Messages ............................... 721
25 GASPR 723
25.1 Gas Production ............................... 723
25.2 User Input .................................. 724
25.3 Coding Details ............................... 725
25.4 Error Messages ............................... 725
26 NJOY Maintenance and Testing 727
26.1 Code Maintenance with GIT ........................ 727
26.2 Standard Test Problems .......................... 727
26.3 Test Problem 1 ............................... 729
26.4 Test Problem 2 ............................... 733
26.5 Test Problem 3 ............................... 736
26.6 Test Problem 4 ............................... 738
26.7 Test Problem 5 ............................... 739
26.8 Test Problem 6 ............................... 740
26.9 Test Problem 7 ............................... 743
26.10 Test Problem 8 ............................... 745
26.11 Test Problem 9 ............................... 746
26.12 Test Problem 10 ............................... 749
26.13 Test Problem 11 ............................... 750
26.14 Test Problem 12 ............................... 753
26.15 Test Problem 13 ............................... 754
26.16 Test Problem 14 ............................... 756
26.17 Test Problem 15 ............................... 757
26.18 Test Problem 16 ............................... 760
26.19 Test Problem 17 ............................... 763
26.20 Test Problem 18 ............................... 766
26.21 Test Problem 19 ............................... 769
26.22 Test Problem 20 ............................... 771
26.23 Application of the NJOY System ..................... 772
References 777
NJOY2016 ix

LA-UR-17-20093 LIST OF FIGURES
List of Figures
1 RECONR reconstructed xs with smooth, RR and URR regions ..... 44
2 Inverted stack mesh generation description ................. 47
319F elastic scattering Legendre coefficients from RML data ....... 63
4 The 10B (n,α) cross section versus Doppler broadening temperature . . 81
5 The natC elastic scattering cross section versus Doppler broadening tem-
perature .................................... 82
6 The 240Pu low energy (n,γ) cross section versus Doppler broadening tem-
perature .................................... 82
7 Energy grid variation with Doppler broadening .............. 83
8 Components of nuclear heating ....................... 116
9 Sample recoil energy and lattice displacement data ............ 120
10 Components of radiation damage energy production for 27Al ...... 130
11 Total photon energy production and kinematic limits for 55 Mn . . . . . 145
12 MT301 and MT443 for 59Co ......................... 148
13 Example of File 3 and File 13 energy grid mis-match ........... 149
14 Example of energy-balance problems .................... 149
15 Computed photon energy production and kinematic values ........ 150
16 Example of coherent elastic cross section for a crystalline material (graphite)167
17 Adaptive reconstruction of emission spectra (graphite) .......... 171
18 Neutron distribution for incoherent inelastic scattering from graphite (T
= 293.6K) ................................... 172
19 Neutron distribution for incoherent inelastic scattering from graphite (T
= 293.6K), expanded view .......................... 172
20 Distributions for H in H2O with E-µ-E0ordering ............. 173
21 Incoherent inelastic distribution for H-H2O (expanded view) ....... 183
22 Pointwise and multigroup cross section comparison ............ 192
23 The self-shielding effect on the first three 238U capture resonances. . . . 196
24 238U capture resonance integral versus temperature and background cross
section ..................................... 197
25 Flux model predictions for 238UO2in water in the region near the 6.7 eV
238U resonance ................................ 200
26 Coupled Neutron/Photon Tables ...................... 208
27 Bragg edges seen in the BeO coherent elastic scattering cross section . . 210
28 Interpolation along lines of constant energy transfer ........... 211
29 Sample two-body scattering feed function ................. 216
30 Coordinate mapping between CM and LAB reference frames for A=2 . 226
31 GROUPR weight functions on a logarithmic flux/unit lethargy scale . . 236
32 GROUPR weight functions on a linear energy scale ............ 237
33 Coupled neutron-proton-photon table ................... 251
34 Photon coherent scattering angular distributions ............. 277
35 Photon interaction cross sections for uranium ............... 282
36 Photon interaction cross sections for hydrogen ............... 282
37 ENDF/B-VII.0 Uranium photoelectric subshell cross sections . . . . . . 283
38 ENDF/B-VII.0 10B(n,α) covariance data .................. 286
39 Example of elastic scattering and (n,n1) covariance data ......... 297
40 Example of angular distribution covariance data ............. 298
41 252Cf(n,f) spontaneous fission spectrum covariance data ......... 300
42 Radioactive nuclide production covariance example ............ 301
43 Illustration of energy grid relations. ..................... 302
x NJOY2016

LIST OF FIGURES LA-UR-17-20093
44 Ratioed covariance data for 239Pu(n,f) and 241Am(n,f) cross sections . . 313
45 7Li “Lumped” covariance data ....................... 316
46 Illustration of Boxer format ......................... 360
47 Pattern-search logic in used in COVR’s subroutine matshd . . . . . . . 362
48 DTFR cross section plot example ...................... 392
49 DTFR cross section plot example, expanded energy range ........ 393
50 DTFR scattering matrix plot example ................... 393
51 DTFR photon production matrix plot example .............. 394
52 DTFR plot example, multiple plots per frame ............... 394
53 DTFR plot example, compound edit .................... 398
54 Principal cross sections for ENDF/B-VII.0 27Al .............. 515
55 Neutron energy distributions from 27Al(n,n’α) reaction .......... 516
56 Neutron scattering distribution from H in H2O.............. 519
57 Sample 2-D plot with default axes ..................... 581
58 Sample 2-D plot with modified axes .................... 582
59 Sample 2-D plot with linear axes ...................... 583
60 Sample plot with pointwise and multigroup data ............. 585
61 Sample plot displaying self-shielded cross sections ............. 586
62 Sample plot with left- and right-hand axes defined ............ 588
63 Sample plot with user data ......................... 591
64 Sample 3-D plot of angular distribution data ............... 593
65 Sample 3-D plot of neutron secondary-energy distribution data . . . . . 594
66 Sample 2-D plot of neutron secondary-energy distribution data . . . . . 596
67 Sample region fill options in VIEWR .................... 618
68 Sample 3-D plot with default axis and perspective ............ 619
69 Sample total cross section probability distributions ............ 638
70 Bondarenko-style self-shielding ....................... 639
71 Self-shielding variation with temperature and dilution .......... 640
72 Graphite phonon frequency spectrum .................... 680
73 Coherent elastic scattering cross section for graphite ........... 680
74 Incoherent elastic scattering cross section for graphite .......... 681
75 Frequency spectra for BeO .......................... 684
76 The frequency spectrum for H in H22O .................. 685
77 S(α, −β) for H in H2O at room temperature ............... 694
78 S-hat vs beta ................................. 695
79 Incoherent inelastic spectra for H in H2O................. 695
80 Incoherent inelastic spectra for H in H2O, detailed view ......... 696
81 The incoherent inelastic cross section for H in H2O at two temperatures 696
82 The incoherent inelastic cross section for H in H2O for higher incident
energies .................................... 697
83 The average scattering cosine for H in H2O compared to the static value
for scattering from atoms at rest ...................... 698
84 A perspective view of an angle-energy distribution for H in H2O. . . . . 699
85 A perspective view of the isotropic part of the incoherent inelastic scat-
tering from H in H2O. ............................ 699
86 Comparison of the ENDF/B-VII.0 thermal cross section for water at
lower incident energies with experimental results ............. 700
87 Comparison of the ENDF/B-VII.0 thermal cross section for water at
higher incident energies with experimental results ............. 701
88 Harker-Brugger frequency spectrum used for solid methane . . . . . . . 702
89 S(α, −β) for solid methane ......................... 705
NJOY2016 xi

LA-UR-17-20093 LIST OF FIGURES
90 Inelastic and incoherent elastic cross sections for solid methane . . . . . 705
91 Outgoing neutron spectra for solid methane ................ 706
92 Agrawal-Yip frequency spectrum for liquid methane ........... 708
93 Frequency spectrum for liquid methane with translational and rotational
modes ..................................... 708
94 S(α, β) for Liquid Methane ......................... 710
95 Cross section for liquid methane at 100K .................. 711
96 Neutron Spectra for liquid methane ..................... 711
97 Keinert-Sax frequency spectrum ...................... 712
98 The static structure factor, S(κ), for liquid hydrogen ........... 713
99 script-S vs beta for para-hydrogen ..................... 713
100 script-S vs alpha for para-hydrogen ..................... 714
101 script-S vs beta for ortho-hydrogen ..................... 714
102 script-S vs alpha for ortho-hydrogen .................... 715
103 Para-hydrogen neutron spectra ....................... 715
104 Ortho-hydrogen neutron spectra ...................... 716
105 Liquid hydrogen cross sections ....................... 716
xii NJOY2016

LIST OF TABLES LA-UR-17-20093
List of Tables
1 Energy Parameter for Effective Doppler-Broadening ........... 79
2 Atomic Displacement Energy Data for DPA ................ 120
3 ENDF/B-III Thermal Data Files ...................... 180
4 ENDF/B-VII Thermal Data Files ...................... 180
5 Covariance Matrices Affected by Ratio Measurements In ENDF/B-V . . 312
6 Reaction pairs in the ENDF/B-V 238U evaluation ............. 326
7 Organization of Data for One Group in a Transport Table ........ 383
8 Example of a Transport Table with Internal Edits ............ 385
9 Predefined Edits for DTFR ......................... 387
10 Example of DTFR Transport Tables Using Separate Edits ........ 388
11 Thermal Reactions Available to DTFR ................... 391
12 Standard MATXSR particle names ..................... 455
13 Standard MATXSR data-type names .................... 456
14 MATXSR neutron emitting reaction names ................ 457
15 MATXSR breadkup reaction (LR flag) names ............... 457
16 MATXSR neutron absorption reaction names ............... 458
17 MATXSR fission reaction names ...................... 458
18 Special MATXSR NJOY names ....................... 459
19 MATXSR gas production names ...................... 459
20 MATXSR incident proton reaction names ................. 460
21 MATXSR thermal material names (ENDF/B-VII) ............ 460
22 MATXSR photoatomic cross section names ................ 461
23 ACE Data Classes and ZAID suffixes .................... 499
24 Example of union grid size variation in ACER .c files ........... 501
25 ENDF/B-VII thermal MT numbers used in ACER and THERMR . . . 529
26 ACE particle codes for photonuclear files .................. 545
27 Sample Intermediate Resonance λValues ................. 560
28 Conventional thermal material MT numbers used in WIMSR, GROUPR
and THERMR ................................ 568
29 Oscillator beta values for α= 1 for H in H2O............... 694
30 H in H2O SCT effective temperatures ................... 698
31 Criticality benchmark results from MCNP5 with NJOY processed
ENDF/B-VII.0 data ............................. 774
32 “FAST” criticality benchmark results from TRANSX/PARTISN with
NJOY processed ENDF/B-VII.0 data ................... 774
33 “THERMAL” criticality benchmark results from TRANSX/PARTISN
and NJOY processed ENDF/B-VII.0 data ................. 774
NJOY2016 xiii

LA-UR-17-20093 LIST OF TABLES
xiv NJOY2016

1 INTRODUCTION LA-UR-17-20093
1 INTRODUCTION
The NJOY nuclear data processing system[1, 2, 3, 4, 5, 6] is a comprehensive
computer code package for producing pointwise and multigroup nuclear cross
sections and related quantities from evaluated nuclear data in the ENDF format.
The U.S. Evaluated Nuclear Data Files (ENDF) have progressed through a
number of versions, notably ENDF/B-III, ENDF/B-IV, ENDF/B-V, ENDF/B-
VI, and ENDF/B-VII[7, 8]. The ENDF format has also evolved through many
versions. Variations of the format called “ENDF-6” were used for ENDF/B-VI
and ENDF/B-VII, and will be used in ENDF/B-VIII. The latest version of the
format is described in the ENDF-102 document[9, 10]. The ENDF format
is also used in other nuclear data libraries such as the JEFF libraries in Europe
and the JENDL libraries in Japan, or in specialized libraries distributed through
the Nuclear Data Section of the International Atomic Energy Agency (IAEA).
These libraries represent the underlying nuclear data from a physics viewpoint,
but practical calculations usually require special libraries for particle transport
codes or reactor core physics codes. This is the mission of NJOY — to take the
basic data from the nuclear data library and convert it into the forms needed
for applications.
1.1 The Modules of NJOY
The NJOY code consists of a set of main modules, each performing a well-defined
processing task. Each of these main modules is essentially a separate computer
program. They are linked to one another by input and output files. The main
modules are supported by a number of subsidiary modules providing things like
physics constants, utility routines, and mathematics subroutines that can be
“used” by the main modules. The NJOY modules are grouped as follows:
NJOY directs the flow of data through the other modules. Subsidiary modules
for locale, ENDF formats, physics constants, utility routines, and math
routines are grouped with the NJOY module for descriptive purposes.
RECONR reconstructs pointwise (energy-dependent) cross sections from ENDF
resonance parameters and interpolation schemes.
BROADR Doppler-broadens and thins pointwise cross sections.
UNRESR computes effective self-shielded pointwise cross sections in the un-
resolved energy range.
HEATR generates pointwise heat production cross sections (neutron KERMA
factors) and radiation damage production cross sections.
NJOY2016 1

LA-UR-17-20093 1 INTRODUCTION
THERMR produces cross sections and energy-to-energy matrices for free or
bound scatterers in the thermal energy range.
GROUPR generates self-shielded multigroup cross sections, group-to-group
scattering matrices, photon production matrices, and charged-particle multi-
group cross sections from pointwise input.
GAMINR calculates multigroup photoatomic cross sections, photon KERMA
factors, and group-to-group photon scattering matrices.
ERRORR computes multigroup covariance matrices from pointwise covariance
data.
COVR reads the output of ERRORR and performs covariance plotting and
output formatting operations.
MODER converts ENDF “tapes” back and forth between formatted (that is,
ASCII) and blocked binary modes.
DTFR formats multigroup data for transport codes that use formats based on
the DTF-IV code.
CCCCR formats multigroup data for the CCCC standard files ISOTXS, BRKOXS,
and DLAYXS.
MATXSR formats multigroup data for the newer MATXS cross-section inter-
face file, which works with the TRANSX code to make libraries for many
particle transport codes.
RESXSR prepares pointwise cross sections in a CCCC-like format for thermal
flux calculators.
ACER prepares libraries in ACE format for the Los Alamos continuous-energy
Monte Carlo MCNP and MCNPX codes. The ACER module is supported
by subsidiary modules for the different classes of the ACE format.
POWR prepares libraries for the EPRI-CELL and EPRI-CPM codes.
WIMSR prepares libraries for the thermal reactor assembly codes WIMS-D
and WIMS-E.
PLOTR makes plots of cross sections and perspective plots of distributions for
both pointwise and multigroup data by generating input for the VIEWR
module.
VIEWR converts plotting files produced by the other modules into high-quality
color Postscript plots.
MIXR is used to combine cross sections into elements or mixtures, mainly for
plotting.
PURR is used to prepare unresolved-region probability tables for the MCNP
continuous-energy Monte Carlo code.
LEAPR produces thermal scattering data in ENDF-6 File 7 format that can
be processed using the THERMR module.
GASPR generates gas-production cross sections in the pointwise PENDF for-
mat from basic ENDF cross sections.
2 NJOY2016

1 INTRODUCTION LA-UR-17-20093
The methods used in these modules and instructions on how to use them are
given in subsequent sections of this report. The sections on the modules are
followed by an additional section on NJOY maintenance and testing.
1.2 Data Flow in NJOY
The modules of NJOY can be linked in a number of different ways to prepare
libraries for various nuclear applications. The following brief summary illustrates
the general flow of data in the code.
RECONR reads an ENDF file and produces a common energy grid for all
reactions (the union grid) such that all cross sections can be obtained to within
a specified tolerance by linear interpolation. Resonance cross sections are recon-
structed using a method of choosing the energy grid that incorporates control
over the number of significant figures generated and a resonance integral crite-
rion to reduce the number of grid points generated for some materials. Sum-
mation cross sections (for example, total, inelastic) are reconstructed from their
parts. The resulting pointwise cross sections are written onto a “point-ENDF”
(PENDF) file for future use. BROADR reads a PENDF file and Doppler-
broadens the data using the accurate point-kernel method. The union grid
allows all resonance reactions to be broadened simultaneously, resulting in a
saving of processing time. After broadening and thinning, the summation cross
sections are again reconstructed from their parts. The results are written out
on a new PENDF file for future use. UNRESR produces effective self-shielded
pointwise cross sections, versus energy and background cross section, in the un-
resolved range. This is done for each temperature produced by BROADR, using
the average resonance parameters from the ENDF evaluation. The results are
added to the PENDF file using a special format.
If desired, additional special kinds of data can be added to the PENDF file.
HEATR computes energy-balance heating, KERMA, and damage energy using
reaction kinematics or by applying conservation of energy. The ENDF pho-
ton production files can be used in this step, when available. Comparisons of
momentum and energy calculations with the photon files can be used to find
energy-balance errors in the evaluations. For ENDF-6 formatted data, charged-
particle distributions in File 6 are used directly to compute accurate heating
and damage parameters. The energy-balance heating results are added to the
PENDF file using ENDF reaction numbers in the 300 series; kinematic KERMA
uses the special identifier 443, and damage results use the special identifier 444.
THERMR produces pointwise cross sections in the thermal range. Energy-to-
NJOY2016 3

LA-UR-17-20093 1 INTRODUCTION
energy incoherent inelastic scattering matrices can be computed for free-gas
scattering or for bound scattering using a precomputed scattering law S(α,β)
in ENDF format. The secondary angle and energy grids are determined adap-
tively so as to represent the function to a desired precision by linear interpo-
lation; the angular representation is then converted to one based on equally
probable angles. See the chapter on THERMR for another possible represen-
tation. Coherent-elastic scattering from crystalline materials can be computed
using internal lattice information, or for ENDF-6 formatted files, using data
from the evaluation directly. The scheme used provides a detailed representa-
tion of the delta functions in energy and angle. Incoherent-elastic scattering for
hydrogenous materials is represented using equally probable angles computed
analytically or using ENDF-6 parameters. The results for all the processes are
added to the PENDF file using special formats and special reaction numbers
between 221 and 250. Additional reactions describing the production of the
gases 1H, 2H, 3H, 3He, and 4He can be added to the PENDF file with MT=203
– 207 using the GASPR module.
GROUPR processes the pointwise cross sections produced by the modules
described above into multigroup form. The weighting function for group aver-
aging can be taken to be the Bondarenko form, or it can be computed from the
slowing-down equation for a heavy absorber in a light moderator. Self-shielded
cross sections, scattering matrices, photon production matrices, charged-particle
matrices, and photonuclear matrices are all averaged in a unified way, the only
difference being in the function that describes the “feed” into a secondary group
g0with Legendre order `from initial energy E. The feed function for two-
body scattering is computed using a center-of-mass (CM) Gaussian integration
scheme, which provides high accuracy even for small Legendre components of the
scattering matrix. Special features are included for delayed neutrons, coupled
energy-angle distributions (either from THERMR or from ENDF-6 evaluations
using File 6), discrete scattering angles arising from thermal coherent reactions,
and charged-particle elastic scattering. Prompt fission is treated with a full
group-to-group matrix. The results are written in a special “groupwise-ENDF”
format (GENDF) for use by the output formatting modules. GAMINR uses
a specialized version of GROUPR to compute photoatomic cross sections and
group-to-group matrices. Coherent and incoherent atomic form factors are pro-
cessed in order to extend the useful range of the results to lower energies. Photon
heat production cross sections are also generated. The results are saved on a
GENDF file.
4 NJOY2016

1 INTRODUCTION LA-UR-17-20093
The covariance module, ERRORR, can either produce its own multigroup
cross sections using the methods of GROUPR or start from a precomputed
set. The cross sections and ENDF covariance data are combined in a way that
includes the effects of deriving one cross section from several others. Special
features are included to process covariances for data given as resonance param-
eters or ratios (for example, fission ¯ν). It is also possible to process covariances
for the P1component of an angular distribution, a secondary-energy distribu-
tion, and radionuclide production. The COVR module uses the output from
ERRORR together with the VIEWR module to make publication-quality plots
of covariance data; it also provides output in the efficient BOXER format, and
it provides a site for user-supplied routines to prepare covariance libraries for
various sensitivity systems.
MODER is often used at the beginning of an NJOY job to convert ENDF
library files into binary mode for calculational efficiency, or at the end of a job to
obtain a printable version of a result from ENDF, PENDF, GENDF or ERRORR
input. It can also be used to extract desired materials from a multimaterial
library, or to combine several materials into new ENDF, PENDF, GENDF or
ERRORR files. DTFR is a simple reformatting code that produces cross-section
tables acceptable to many discrete-ordinates transport codes. It also converts
the GROUPR fission matrix to χand ¯νσfand prepares a photon-production
matrix, if desired. The user can define edit cross sections that are any linear
combination of the cross sections on the GENDF file. This makes complex edits
such as gas production possible. DTFR also produces plotting files for VIEWR
to use in making routine plots for the cross sections, P0scattering matrix, and
photon production matrix. This module has become somewhat obsolete with
the advent of the MATXS/TRANSX system.
A number of other interface file formats are available from NJOY. The CC-
CCR module is a straightforward reformatting code that supports all the options
of the CCCC-IV[11] file specification. In the cross-section file (ISOTXS), the
user can choose either isotope χmatrices or isotope χvectors collapsed using any
specified flux. The BRKOXS file includes the normal self-shielding factors plus
self-shielding factors for elastic removal. The DLAYXS provides delayed-neutron
data for reactor kinetics codes. Note that some of the cross sections producible
with NJOY are not defined in the CCCC files. For that reason, we have intro-
duced the new CCCC-type material cross section file MATXS. The MATXSR
module reformats GENDF data for neutrons, photons, and charged particles
into the MATXS format, which is suitable for input to the TRANSX (trans-
NJOY2016 5

LA-UR-17-20093 1 INTRODUCTION
port cross section) code[12]. TRANSX can produce libraries for a variety of
particle transport codes that have been used over the years, such as ANISN[13],
ONEDANT[14], TWODANT[15], and DIF3D[16]. TRANSX has special fea-
tures to support the latest SNtransport code from Los Alamos, PARTISN[17].
The MATXS format uses efficient packing techniques and flexible naming con-
ventions that allow it to store all NJOY data types. A companion module,
RESXSR, formats pointwise data into a CCCC-like format for use in thermal
flux calculators.
Pointwise data can also be fed directly into the ACER module. This module
prepares cross sections and scattering laws in ACE format (A Compact ENDF)
for the MCNP code[18]. All the cross sections are represented on a union grid for
linear interpolation by taking advantage of the representation used in RECONR
and BROADR. “Laws” for describing scattering and photon production are very
detailed, providing a faithful representation of the ENDF-format evaluation with
few approximations. The data are organized for random access for purposes of
efficiency. MCNP handles self-shielding in the unresolved-energy range using
probability tables. The PURR module of NJOY can be used to prepare these
tables and add them to a PENDF file for reading by the ACER module.
Another alternate path for multigroup data is to use the POWR module
to produce libraries for the power reactor codes EPRI-CELL or EPRI-CPM 1.
Similarly, the WIMSR module can be used to prepare libraries for the thermal
reactor assembly codes WIMS-D and WIMS-E[19].
At the end of any NJOY run, the PLOTR and VIEWR modules can be used
to view the results or the original ENDF data. PLOTR can prepare 2-D plots
with the normal combinations of linear and log axes, including legend blocks
or curve tags, titles, and so on. Several curves can be compared on one plot
(for example, pointwise data can be compared with multigroup results), and
experimental data points with error bars can be superimposed, if desired. Plots
can be prepared showing the ratio or percent difference of two cross sections.
PLOTR can also produce 3-D perspective plots of ENDF and GENDF angle
or energy distributions or thermal S(α, β) tables. The output of PLOTR is
passed to VIEWR, which renders the plotting commands into high-quality color
Postscript graphics for printing or for viewing. The HEATR,COVR,DTFR,
and ACER modules also produce plotting files in VIEWR format that are useful
for quality reviews of data-processing results. The MIXR module can be used
1EPRI-CELL and EPRI-CPM are proprietary products of the Electric Power Research Institute (EPRI),
3420 Hillview Avenue, Palo Alto, CA 94304.
6 NJOY2016

1 INTRODUCTION LA-UR-17-20093
to combine isotopes into elements for plotting and other purposes. It only works
for simple cross sections at the present time.
1.3 Computer Implementation
NJOY2016 is written in a modern subset of Fortran-90 and later, stressing the
use of modules. The modules help to enforce information hiding. Thus, for
example, the RECONR module only makes the single subroutine reconr public;
all the internal routines and data structures of the module are protected. The
modules also help to promote logical structuring. For example, all of the routines
and data structures for working with the ENDF formats, such as subroutine
contio and the math,mfh,mth values are made public by the endf module, and
they can be easily accessed wherever they are need by the use endf statement.
As another example, what could be a very large ACER module is made more
structured by providing subsidiary modules for handling each of the different
“classes” of the ACE format (e.g. acefc for continuous class “c” data, or acepn
for “u” class photonuclear data).
The advanced capabilities that modern Fortran provides for typing variables
(the “kind” property) have enabled us to remove all of the complex short-
word/long-word controls from NJOY. Almost all of the internal data in NJOY
are handled using 8-byte kinds for real and integer words. These properties are
set up in the locale module, and they can be changed, if necessary, without
touching the balance of the code. An exception is made for the CCCC modules
CCCCR,MATXSR, and RESXSR, where 4-byte variables and equivalencing are
still used to construct records with mixed real, integer, and Hollerith values.
Modern Fortran also provides a capability for the dynamic allocation of mem-
ory for data structures. In the past, NJOY used its own storag system for this
purpose; this system has now been abandoned for the readability, consistency,
and exportability provided by the new Fortran standard. We have limited our-
selves to the use of “allocatable arrays”. This relieves us of some storage limi-
tations in NJOY, and introduces others.
The earliest versions of NJOY used their own free-form input routine, FREE,
which was developed long before Fortran supported equivalent capabilities. More
recently we have abandoned FREE in favor of the standard Fortran READ*
method. In doing this, we have lost some capabilities (such as the repeat field),
but we have gained in transportability. Test fields that were previously delimited
with the star character now must be delimited with the single-quote character.
For consistency and convenience, the NJOY modules in previous versions
NJOY2016 7

LA-UR-17-20093 1 INTRODUCTION
of the code made use of a set of common functions and subroutines located
in the NJOY module. Beginning with NJOY2012, these utility routines have
been repackaged into Fortran-90 modules. They include locale for localization
variables, physics for physics constants, mainio for input, output, and scratch
units, util for utility routines like time and date, endf for ENDF processing
routines and variables, and math for mathematics routines. Each of these mod-
ules only makes public the minimum set of routines and variables needed by the
other modules that “use” them. These modules are described in detail in the
NJOY chapter of this report.
NJOY is heavily commented. Each module starts with a long block of com-
ment cards that gives a brief description of the module and then gives the current
user input instructions. Users should always check the input instructions in the
current version of the NJOY source code rather than the instructions summa-
rized in this manual — changes may have been made. For the convenience of
users, the input instructions are also available on the web[20]. Furthermore,
each function or subroutine starts with a block of comment cards that describes
its function and special requirements. Additional lines of comment cards are
used inside each procedure to block off its major components.
Typography conventions for Fortran differ from place to place. On most
machines at Los Alamos National Laboratory (LANL), Fortran text is given in
lowercase. In order to avoid translation problems, previous versions of NJOY
avoided using mixed-case text for comments or for labels on graphs. We are
gradually moving away from this limiting convention. In this report, Fortran
text and variable names are printed using a lowercase typewriter font. ENDF-
related formats and variables are given using an uppercase TYPEWRITER FONT.
CCCC formats were traditionally given using uppercase characters, but the
usage in this report is mixed.
1.4 History and Acknowledgments
NJOY was started as a successor to MINX[21] (A Multigroup Interpretation
of Nuclear X-sections) late in 1973 (it was called MINX-II then). The current
name was chosen in late 1974 to be evocative of “MINX plus” and to eliminate
the reference to “multigroup.” The first goals were to add a photon production
capability like that in LAPHAN0[22], to add a photon interaction capability like
GAMLEG[23], to provide an easy link to the Los Alamos 30-group libraries of
the day using DTF[24] format, and to merge in the capabilities of ETOPL[25] to
produce libraries for the MCN Monte Carlo code (the ancestor of MCNP). Most
8 NJOY2016

1 INTRODUCTION LA-UR-17-20093
of the work was done by MacFarlane; Rosemary Boicourt joined the project in
1975. First, the RESEND[26] and SIGMA1[27] modules of MINX were con-
verted to use union grids, and a new method of resonance reconstruction was
developed. These steps led to RECONR and BROADR.UNRESR, which was
based on methods from ETOX[28], was moved over from MINX with only a few
changes. Next, a completely new multigroup averaging program, GROUPR, was
developed around the unifying concept of the “feed function,” which handled
neutron- and photon-production cross sections in a parallel manner. The CM
Gaussian integration for discrete two-body scattering was developed. DTFR was
developed as the first NJOY output module. The first versions of the NJOY
utility codes were introduced; the new concepts of “structured programming”
inspired some of the features of the new NJOY code.
Major influences during this period included Don Harris, Raphe LaBauve,
Bob Seamon, and Pat Soran at Los Alamos, and Chuck Weisbin at the Oak Ridge
National Laboratory (ORNL). Odelli Ozer at the Brookhaven National Labo-
ratory (and later EPRI) helped with RESEND, and Red Cullen at Lawrence
Livermore National Laboratory and John Hancock at Los Alamos helped with
the Doppler broadening module. In those days, the development of NJOY was
supported by the U.S. Fast Breeder Reactor and Weapons Programs.
Code development continued during 1975. The ERRORR module was added
for calculating covariances from ENDF/B files. The ACER module was created
by borrowing heavily from ETOPL and Chuck Forrest’s MCPOINT code. Rich
Barrett joined the project, and he did most of the work in creating a new CCCCR
module for NJOY that had several advances over the MINX version and met
the CCCC-III standards[29]. By the end of the year, HEATR had also been
added to the code (with ideas from Doug Muir). HEATR gave NJOY most of
the capabilities of the original KERMA factor code, MACK [30].
During 1976, free-form input and dynamic data storage were added to NJOY.
GAMINR was written to complete the original NJOY goal of processing photon
interaction cross sections, and the MATXSR module was designed and written,
primarily by Rich Barrett. This completed the capability to construct fully cou-
pled cross sections for neutron-photon heating problems. A major new effort was
writing the THERMR module to improve upon the thermal moderator scatter-
ing cross sections then produced using the FLANGE-II[31] and HEXSCAT[32]
codes, and starting the POWR module to produce cross sections for the EPRI-
CELL and EPRI-CPM codes used by the U.S. electric utility companies. This
work was funded by the Electric Power Research Institute (EPRI).
NJOY2016 9

LA-UR-17-20093 1 INTRODUCTION
The first release of NJOY to what was then called the Radiation Shielding
Information Center (RSIC) at Oak Ridge and to the National Energy Software
Center (NESC) at Argonne was NJOY77 in the summer of 1977. This ver-
sion was tested and converted for IBM machines by R. Q. Wright (ORNL).
Also, TRANSX was developed during 1977, the MATXS1 30x12 library was
produced based on ENDF/B-IV, the flux calculator was added to NJOY to sup-
port the EPRI library work, and the first version of the EPRI-CELL library was
generated and used.
A second release of NJOY called NJOY78 was made in 1978[33]. In addi-
tion, further improvements were made for preparing EPRI cross sections, the
MATXS/TRANSX system was improved, and a thermal capability was added to
the MCNP Monte Carlo code using cross sections from THERMR as processed
by ACER.
In 1979, the radiation damage calculation was added to HEATR, and the
GROUPR flux calculator was further improved. In 1980, a plotting option
was added to ERRORR. During this period, NJOY had become more stable.
Changes usually consisted of small improvements or bug fixes instead of major
new capabilities. Starting in this period, NJOY received some support from
the U.S. Magnetic Fusion Energy Program, mostly for covariance work and
TRANSX related library support.
In 1981 and 1982, improvements included the momentum-conservation method
for radiative capture in HEATR . Analytic ψχ broadening was added to RE-
CONR for some cases, and the integral criteria for resonance reconstruction
with significant-figure control were installed in RECONR. Several new capabil-
ities were added to ERRORR, and the COVR module was added to NJOY to
handle both ERRORR plotting and covariance library output. Much of this
covariance-related work was done by Doug Muir. Wiley Davidson (LANL) and
B.H. Broadhead and R. W. Peele at ORNL were helpful. Some support for the
documentation work came from the Paul Scherer Institute (PSI) in Switzerland
and OECD Nuclear Energy agency during visits to those institutions. In addi-
tion, CCCCR was updated to the CCCC-IV standards. A new release, NJOY
(10/81), was made to the code centers, and the first two volumes of a new NJOY
report were written and published. European users began to make important
contributions about this time. Enrico Sartori of the NEA Data Bank, then at
Saclay in France, Margarete Mattes of the University of Stuttgart in Germany,
and Sandro Pelloni of the Paul Scherer Institute in Switzerland deserve mention.
Another major release, NJOY 6/83, was made in 1983. By this time, NJOY
10 NJOY2016

1 INTRODUCTION LA-UR-17-20093
was in use in at least 20 laboratories in the United States and around the world.
Small improvements continued, such as the kinematic KERMA calculation in
HEATR. The temperature dependence of the BROADR energy grid was intro-
duced early in 1984 based on an observation by Ganesan (India). Volume IV of
the NJOY report was published in 1985, and Volume III appeared in 1987.
The next big set of improvements in NJOY was associated with the intro-
duction of the ENDF-6 format. This required significant changes in RECONR
to support new resonance formats like Reich-Moore and Hybrid R-Function
(implemented with help from Charlie Dunford of Brookhaven), in HEATR to
implement direct calculations of KERMA and damage from charged-particle and
recoil distributions in File 6, in THERMR to support new formats for File 7,
and in GROUPR to support the group-to-group transfer matrices using energy-
angle data from File 6. The PLOTR module was also developed during this
period. The result was the release of NJOY89[34] in time for processing the new
ENDF/B-VI library and the JEF-2 library (which was also in ENDF-6 format).
During 1989 and 1990, initial processing of ENDF/B-VI and JEF-2 exposed a
number of small problems that had to be fixed. In addition, the ACER module
was rewritten to clean it up, to add capabilities to produce ACE dosimetry
and photoatomic libraries, and to provide for convenient generation of files in
several different formats for users away from LANL. A MIXR module was added
to NJOY, mostly to allow elemental cross sections to be reconstructed from
ENDF/B-VI isotopes for plotting purposes. A new technique was introduced
into GROUPR and all the output modules for multigroup data that provided for
more efficient processing of fission and photon production matrices with lots of
low-energy groups. Major revisions were made to the MATXS format to allow for
charged-particle cross sections, to pack matrices with lots of low-energy groups
more efficiently, and to make inserting and extracting new materials easier. The
WIMSR module, which had been under development for a number of years
in cooperation with WIMS users in Canada and Mexico, was introduced into
NJOY. Finally, the PURR module for generating unresolved-region probability
tables for use with MCNP, which had also been under development for many
years, was formally added to the code. The result of this year-and-a-half of work
was NJOY91.
During the balance of 1991 and 1992, a number of changes were made in
response to problems identified by users as ENDF-6 evaluations began to be
used in earnest. The first of a number of attempts to handle laboratory-frame
Legendre data in File 6 in MCNP was made — namely, the attempt to convert
NJOY2016 11

LA-UR-17-20093 1 INTRODUCTION
such sections to use Kalbach systematics. Treatments for phase-space and angle-
energy versions of File 6 were added in 1993, as well as improvements in WIMSR
(with contributions of Fortunato Aguilar, ININ, Mexico). Plotting was added
for S(α, β) curves from ENDF-6 File 7 and for 2-D and 3-D plots from GENDF
data. HEATR was modified to include incident-energy effects on the fission
Q values in 1993. In 1994, we made another attempt to handle the cases of
File 6 using laboratory-frame Legendre expansions for MCNP by converting
them into the LAW=7 angle-energy format. A fix to the Kalbach option for
energy-angle distributions was made based on work by Bob Seamon (LANL).
Also, work was done in HEATR to properly handle the damage energy cutoff
at low energies. Quite a bit of work was done during this period to improve the
portability of the code by installing it on a variety of systems and using codes like
cflint. Other people providing suggestions during this period included Margarete
Mattes (Stuttgart), Piet De Leege (Delft), John White (RSIC), and the Petten
users. The final version of the NJOY91 series was 91.118 in November 1994, and
it was able to process all of the ENDF/B-VI evaluations that had been tried
up to that date. A new user manual for NJOY91[3] was released in 1994. This
document was the primary reference for NJOY until the release of NJOY2012
manual[5].
NJOY94 was issued at the end of 1994 to clean up 91.118 after 3 years of
changes. It also provided a new direct-to-Postscript plotting system by splitting
the old PLOTR module into PLOTR and VIEWR, an updated version of the
PURR module, and a new LEAPR module for computing thermal scattering
functions. In 1995, a new capability was added to handle nuclide production
based on a proposed extension to the ENDF-6 File 8, and the new GASPR
module was added to handle gas production. Early in 1996, a capability to
pass damage cross sections into MCNP was added. A number of changes were
made based on suggestions from users, and based on processing experience with
the new 150-MeV evaluations becoming available during this period. A change
in the erfc function was made to improve the consistency of 1/v cross sections
(problem observed by Cecil Lubitz, KAPL). Late in the year, the plotting sys-
tem was upgraded to promote color Postscript plotting. In mid 1997, a large
update to the WIMSR module was made based on the work of Andrej Trkov
(Slovenia). Problems with calculational accuracy (especially for BROADR) led
to a major upgrade of the math routines. Routines from the SLATEC library
were adopted and converted to NJOY style. A new capability was added to
BROADR to compute and display some standard thermal quantities, such as
12 NJOY2016

1 INTRODUCTION LA-UR-17-20093
thermal cross sections, g factors, and ratio integrals (α, K1). After some addi-
tional bug patches and portability improvements, the NJOY94 series was con-
cluded with the issuance of 94.105 in July of 1997.
NJOY 97.0 was released in October of 1997. The major change was to move
to using 8-byte words throughout the code. Modern resonance evaluations push
the limit of 6 significant figures available using 32-bit words, and obtaining
consistency between people using 32-bit machines and people on 64-bit machines
was becoming more and more desirable. Many changes were associated with
this, including taking great care with all literal constants in the code, removing
Hollerith constants, changing from the FREE input routine to a more standard
READ* method, and developing the techniques to use either 7-digits or 9-digits
in resonance grids, as needed. SAVE statements were added to support stack-
based compilers. The code now automatically determined the version of ENDF
data on the input files, which changed the input a little. Finally, some steps
were made to remove statement numbers and move part way to Fortran-90 style
without abandoning Fortran-77 compatibility.
A number of changes were made during 1998 to cement the features of the
new version. The first new capability added was new conditional probabilities
in PURR for heating. This feature requires running HEATR with partial cross
sections for elastic, fission, and capture. Corresponding changes were also made
in ACER. The tolerances in RECONR and BROADR were modified to use a
tighter tolerance in the thermal range to help preserve the 0.0253-eV cross sec-
tion and other thermal parameters better (Lubitz). Piet DeLeege (Delft), Sandro
Pelloni (PSI), and Andrej Trkov (IJS/Slovenia) were helpful in finding problems
during this period. A large number of changes were made based on issues raised
by testing the code with the ftnchek program. These help for portability be-
tween different computer systems. This work was motivated after Giancarlo
Panini (Italy) questioned small differences seen using different compilers. Early
in 1999, the method for setting the damage threshold in HEATR was revised.
An internal table of default values was provided, and a new option to allows the
user to enter a value for Edwas added. This change affects the damage near the
threshold for elastic displacements. John White (RSIC) helped with this. Based
on some code comparisons, Nancy Larson (ORNL) promoted updating the basic
constants in the various codes to enhance compatibility, and we followed suit in
NJOY. More work was done to enhance activation processing and to provide an
automatic loop over all the production reactions for GROUPR. Finally, a new
option to properly handle channel spin in Reich-Moore resonance evaluations
NJOY2016 13

LA-UR-17-20093 1 INTRODUCTION
was added using code contributed by ORNL. The NJOY97 series was frozen in
September of 2000.
During the last part of the life of NJOY97, we also had NJOY99 available
(dated 31 December 1999). It is a cleaned up version of NJOY97 that moves
further toward using block constructs and eliminating statement numbers (but
lots of statement numbers are still left). It is compatible with both Fortran-77
and Fortran-90 compilers. Physical constants were moved into a few common
blocks and standardized on the 1987 CODATA values from NIST. The NJOY
Y2K problem was fixed. The bulk of the changes are in the ACER module
to support new MCNP features, including high-energy data, incident charged
particles, and photonuclear data. Before release, this version was tested for
a large number of different machine/compiler combinations, including tests on
X86 PCs. Compatibility has improved to the point where the unix diff function
can be used to compare files and only a small number of very small differences
are found. This version was able to process all the materials from ENDF/B-
VI Release 5 into a library using the new ACE formats (cumulative elastic
distributions, LAW=61, and charged-particle production sections) that were
planned to come out with MCNP4c.
We began making patches to NJOY99 in the spring of 2000, starting with
fixing a problem with the cold hydrogen and deuterium calculations in LEAPR.
This was followed by a number of other small patches. A capability was added
for processing anisotropic charged particle emission in ACER. In 2001 the series
of MT numbers from 875 – 891 was installed to represent levels in the (n,2n)
reaction (needed for a new European 9Be evaluation). We added a capability
to include delayed neutron data in the ACE files to feed a new capability in
MCNP. A photonuclear capability was added to MATXSR — this enables the
TRANSX code to generate fully coupled sets for n-γtransport. Some coding
was added to generate fluorescence data for MCNP using the existing format
with new numbers coming from the ENDF/B-VI atomic data. This work does
not completely support all the atomic data now available in ENDF/B-VI. The
ACER consistency checks were upgraded to include delayed neutrons, and plots
for ¯νand the delayed neutron spectra were added. In addition, delayed neu-
tron processing was generalized to allow for 8 time bins as used by the JEFF
evaluations.
PLOTR was modified to allow ratio and difference plots using the right-hand
scale. The default tolerances used in RECONR and BROADR were tightened
up a bit. Some changes to the heating for photoatomic data were provided by
14 NJOY2016

1 INTRODUCTION LA-UR-17-20093
Morgan White (LANL). A change was made to HEATR to provide the photon
contribution to heating using a special MT number (442). When passed to
MCNP, it allows the code to get good answers for heating even when photons are
not being transported. Late in 2002, LEAPR was updated to include coherent
elastic scattering for FCC and BCC crystalline lattices. In 2004, some extensions
to the energy grid used for incoherent inelastic scattering were made. A few
additional smaller patches were also made during this period.
In 2005, changes proposed for THERMR and LEAPR by Margarete Mattes
(IKE/ Stuttgart) to support the new IAEA-sponsored evaluations for thermal
scattering in water, heavy water, and ZrH were installed. Some additional group
structures used in Europe were added. Through this period, we were always in-
creasing the storage space allowed as we adapted to newer and larger evaluations
coming out for ENDF/B-VII. During the summer, a number of changes to co-
variance processing were provided by Andrej Trkov (working at IAEA). Early in
2006, a new sampling scheme for thermal scattering was developed for MCNP
that uses continuous distributions for secondary energy instead of the previous
discrete values. This removed unsightly artifacts in computed fluxes at low en-
ergies, and it alleviated some problems that the cold-neutron-source people were
having. More code improvements were made based on detailed compiler check-
ing. Some errors in the treatment of energy-dependent fission Q were fixed based
on a review of the work of Dave Madland (LANL). An approximate treatment
for the relativistic gamma in the ENDF/B-VII evaluation for n+1H was added
in HEATR and GROUPR based on theoretical work from Gerry Hale (LANL).
We added a new plot to the ACER set that shows the recoil part of the heating.
This is a sensitive test of energy-balance.
In the summer of 2007, we added some smoothing options to make the
low-energy shape of neutron distributions look more like the theoretical shape,
namely sqrt(E0). Similar changes were provided for delayed neutron spectra.
Additional smoothing was provided for some of the fission spectra at energies
above 10 MeV using an exponential shape. A change was made in GROUPR to
override Cartesian interpolation in favor of unit-base interpolation for scattering
distributions. This gives smoother scattering source functions and is consistent
with what MCNP does.
In 2007, a big change was made to covariance processing by replacing the
original NJOY ERRORR module with ERRORJ[35] as contributed to the NJOY
project by Japan (Go Chiba). This new module added covariance capabilities
for the more modern resolved-resonance representations, angular distributions,
NJOY2016 15

LA-UR-17-20093 1 INTRODUCTION
and secondary-energy distributions. A series of additional changes to the new
ERRORR were made over the next couple of years. Go Chiba, Andrej Trkov
(IAEA and IJS Slovenia), and Ramon Arcilla (BNL) were involved in this. A
capability to handle energy-dependent scattering radius data in the unresolved
range was added. In 2008, ERRORJ work continued. Some work was done in
PLOTR to implement graphs of GROUPR emission spectra. In 2009, changes
were made for unresolved resonance cross sections to force log-log interpolation
to better represent 1/v cross sections. The parameter that looked for steps
in the unresolved-range energy grids that were too large was changed from its
former value of 3 to 1.26. Some of the steps in ENDF/B-VII are unreasonably
large when representing 1/v cross sections. The default energy grid used in
the unresolved range was upgraded to one using about 13 points per decade.
Additional pages were added to the ACER plots to display the unresolved-range
self-shielded cross sections. This work was influenced by Red Cullen (LLNL).
In a related effort, some changes were made in the binning logic for PURR to
improve unresolved-range results. In 2010, changes were made to support the
processing of the IRDF international dosimetry file, including the addition of
many new reaction MT numbers. Some work was done on the photonuclear
options to support the TENDL-2009 library. More ERRORR changes from
Trkov were implemented, and a capability to process the uncertainty in the
scattering radius was added. Finally, several updates were submitted by the
Japan Atomic Energy Agency (JAEA) related to processing discrete photon
data from file 6 into ACE files. NJOY 99.364 was released in February of 2011.
Concurrent with the maintenance of NJOY99, we worked on a new Fortran-
90 version of NJOY that took advantage of the module system, the numerical
precision system, and the dynamic storage system of modern Fortran. This
enabled us to get rid of COMMON statements (always problematic in Fortran)
and to obtain a more readable scheme for allocated storage. Additional work was
done to upgrade to block structures, but some statement numbers still remain.
That new version was called NJOY2010, but was only released to a few in-house
(LANL) users, selected external users at Brookhaven, Oak Ridge and Argonne
National Laboratories plus the Naval Reactors laboratories, Bettis and KAPL
in the United States and to the Atomic Weapons Establishment in the UK.
Further code revisions lead to NJOY2012[5]. For most applications NJOY2012
is compatible with NJOY99. However, there were some new capabilities in
NJOY2012 that are not supported by NJOY99. We borrowed coding from
the SAMMY[36] code (thanks are due to Nancy Larson, ORNL) to handle the
16 NJOY2016

1 INTRODUCTION LA-UR-17-20093
new Reich-Moore-Limited resonance parameter representation now included in
the ENDF-6 format. This coding is used in RECONR to generate pointwise
resonance cross sections and angular distributions. It is used in ERRORR to
generate the sensitivity of resonance cross sections to the resonance parameters
for use in calculating cross section uncertainties and covariances in the resonance
range. In THERMR, we added an option to construct thermal cross sections
using (E, µ, E0) ordering in addition to the normal (E, E0, µ) ordering. This
ordering is convenient for comparing to experiment, and it is used for thermal
sampling in some Monte Carlo codes.
With NJOY2016 we now have an “open source” code release. The current
version of the source code is now freely available, and can be downloaded from
http://njoy.lanl.gov.
NJOY2016 17

LA-UR-17-20093 1 INTRODUCTION
18 NJOY2016

2 NJOY LA-UR-17-20093
2 NJOY
The NJOY module of the NJOY system contains the main program for the
system, which directs the sequence of other modules that makes up the desired
calculational path. This section of the report also describes a number of sub-
sidiary modules containing common data structures, subroutines, and functions
for use in the other modules. This manual describes NJOY version 2016 (or
NJOY2016 for short).
2.1 The NJOY Program
The njoy program starts by initializing the page size for blocked-binary ENDF
files, opening the output listing file, and writing the NJOY banner on the output
listing. It then sets up a loop that simply reads a module name and calls the
requested module. The loop continues until the “stop” name is read, and then
NJOY exits. The first card read by any module contains the unit numbers for
the various input and output files. In this way, the output of one module can
be assigned to be the input of another module, thereby linking the modules to
perform the desired processing task. An example of the linking procedure is
given below:
[mount an ENDF file as tape20]
-- Optional comment card (signified by "dash" "dash" "space")
reconr
20 21
[input lines for RECONR]
groupr
20 21 0 22
[input lines for GROUPR]
dtfr
22 23 21
[input lines for DTFR]
stop
Optional comment cards may only appear at the point in an input deck
where a module name is expected. Multiple comment cards are allowed and
each must start with the three character string “dash” “dash” “space”. An
important feature of a good modular system is that there be a minimum of
NJOY2016 19

LA-UR-17-20093 2 NJOY
interactions between the modules in order to reduce side effects. In the NJOY
system, modules communicate only by means of the input and output units
specified as shown above, and through a limited number of common constants
provided by the subsidiary modules. The common constants used in the NJOY
main program are in the following modules:
version provides the version number string vers, initially “2016.0,” and the
corresponding date vday, initially “ddmmm16,”
locale provides localization information, including the laboratory and machine
strings, initially “our-lab” and “our-mx,”
mainio provides the system unit numbers, nsysi,nsyso, and nsyse,
endf provides the page size for blocked-binary ENDF files, npage. We recom-
mend users not change this value as there may still be some legacy fixed
array definitions sprinkled in the code that were sized based upon the cur-
rent value.
The input instructions for the NJOY module are given as comment cards at the
beginning of the module. They are reproduced here for the convenience of the
user.
!---input specifications (free format)----------------------------------
!
! card 1 module option
!
! module six character module name, e.g., reconr.
! it is not necessary to use quotes.
!
! repeat card 1 for each module desired, and
! use the name "stop" to terminate the program.
!
! See the comments at the start of each module for its specific input
! instructions.
!
!-----------------------------------------------------------------------
NJOY is usually invoked from a terminal or command window, or from a
script. The standard I/O redirection syntax is used to control the choice of an
input file:
20 NJOY2016

2 NJOY LA-UR-17-20093
njoy < test1
Of course, the system messages that normally appear in the terminal or com-
mand window could be redirected to a file by appending something like “ > out1”
to this execution line.
2.2 Interface Files
Another requirement of a good modular system is that the input and output
files be in a common format so that modules can work with each other’s output
in a flexible way. Since NJOY is basically an ENDF processing code, ENDF-
compatible formats were chosen for linking modules together. “Input” and “out-
put” modules can be specified to communicate with other formats (the “outside
world”). In the example above, tape23 is an example of such an external file.
The other tapes2in the example are ENDF-type files, and the sequence shown
is fairly typical. If the user in the example needs data at a higher tempera-
ture, the RECONR point-ENDF, or PENDF, file (tape21) can be run through
BROADR to produce a Doppler-broadened PENDF file for GROUPR. Many
other combinations are possible simply by rearranging the sequence of module
names and changing the unit numbers that link them. These common-format
files also provide for convenient restarts at many points in the calculational se-
quence. For example, if a user is trying to produce pointwise cross sections at
300K, 600K, and 900K and runs out of time while working on 900K, he or she
can save the partially completed PENDF file and restart from 600K. Multigroup
modules use specially constructed groupwise-ENDF formats (GENDF) that are
compatible with the multigroup output modules. A GENDF file from GROUPR
can be saved in the NJOY data library, run through CCCCR to produce one
output format, and then run through MATXSR for another output format.
In NJOY, unit numbers from 20 through 99 are used for storing results or
linking modules, units 10 through 19 are reserved for scratch files, which will be
destroyed after a module has completed its job, and units below 10 are reserved
for the system. Negative unit numbers indicate binary mode.
2The word “tape” will often be used in this report as a synonym for “file”; an actual physical tape is not
implied. This is consistent with ENDF custom, where the phrase “ENDF tape” is traditional. Furthermore,
in most NJOY installations, the actual files on the machine will have names like “tape23.”
NJOY2016 21

LA-UR-17-20093 2 NJOY
There are special utility routines to open, close, and reposition files. These
routines automatically handle the NJOY conventions on positive or negative unit
numbers, scratch files, and so on. These routines are available as the following
public calls in module util:
openz(lun,new)
Open the unit=abs(lun). If lun≥0, use coded (formatted) mode, and if
lun≤0, use binary mode. Destroy on close or job termination if 10≤lun≤20.
If new=1, destroy the file on this unit (if it exists) and open a new file.
closz(lun)
Close the file with unit=abs(lun). Do nothing if lun=0 or if lun refers to
a scratch file.
repoz(ntape)
Rewind the file with unit=abs(ntape). Do nothing if ntape=0.
skiprz(lun,nrec)
Skip nrec records forward or backwards. Caution: Some systems have a
call for this option; others can use loops of backspace and dummy reads as
given in the NJOY code. Both these operations work well for systems that
use “linked-list” data structures for I/O files. On some systems, however,
backspace is implemented as a rewind followed by forward dummy reads
to the desired location. In such cases (for example, VAX), skiprz must be
recoded to avoid calling backspace repeatedly. This caution is somewhat
moot for current operating systems.
2.3 Free Format Input
Free-form input is handled by the standard Fortran-90 READ(* method. Pre-
vious versions of NJOY used a special routine FREE for free-form input. This
routine was developed before free-form input was routinely available in Fortran,
but it has now been retired. Some capabilities that were provided by FREE, such
as repeat fields, are no longer supported using READ(*. Basically, users can
type in their input quantities separated by spaces. Lines can be terminated early
with the slash (/) symbol, leaving any variables not provided at their default
values. Whether all input variables are defined in a users input record or not we
recommend that every input record be terminated with a slash (/). This assures
that all variables have been read, or assigned their default values, and provides
a more robust input file if future code changes specify additional input variables.
In the absence of a slash, fortran i/o rules may cause the next input record to be
read; an action that is certain to cause the job to crash. Text values consisting
of single words can be entered without delimiters, but more complex strings
22 NJOY2016

2 NJOY LA-UR-17-20093
containing spaces must be delimited using the single-quote character (’). Real
numbers can be entered in a variety of forms; 1,1.,1.e0, and 1e0 should all
be equivalent. Examples of NJOY input will be found throughout this report.
2.4 ENDF Input-Output
The ENDF format for evaluated nuclear data is well documented elsewhere,[9]
but for the convenience of the reader, some features of the format will be de-
scribed here.
ENDF “tapes” are subdivided internally into “materials” (MAT), “files”
(MF), and “sections” (MT). A MAT contains all data for a particular evalu-
ation for an element or isotope (for example, MAT=825 is an evaluation for 16O
in ENDF/B-VII). A file contains a particular type of data for that MAT: MF=3
is cross-section versus energy data; MF=15 contains secondary photon energy
distributions. A section refers to a particular reaction [for example, MT=2 is
elastic scattering and MT=107 is the (n, α) reaction]. Every record contains
the current MAT, MF and MT values. Two materials are separated by a record
with MAT=0 (the material-end or MEND record). Two files are separated by a
record with MF=0 (the file-end or FEND record). Two sections are separated
by a record with MT=0 (the section-end or SEND record). Finally, the tape is
terminated with a record with MAT = −1 (tape-end or TEND record).
NJOY has a set of utility subroutines for locating desired positions on an
ENDF tape. They are located in module endf, and they can be made available
to any other module with the statement “use endf.”
findf(mat,mf,mt,nin)
Search nin backward or forward for the first record with this MAT, MF,
MT. Issue a fatal error message if the record is not found.
tosend(nin,nout,nscr,a)
tofend(nin,nout,nscr,a)
tomend(nin,nout,nscr,a)
totend(nin,nout,nscr,a)
Skip forward past the next SEND, FEND, MEND, or TEND card on NIN.
If nout and/or nscr are nonzero, copy the records. Input and output files
must be in the same mode.
The data on an ENDF tape are written in eight different kinds of “struc-
tures”, each of which has a binary and a formatted form. In modern systems,
formatted data is normally coded in ASCII. The words “coded,” “formatted”,
NJOY2016 23

LA-UR-17-20093 2 NJOY
and “ASCII” will often be used interchangeably here). The structures are:
(1) TAPEID, a character-string title for the tape; (2) CONT, a control record
(includes SEND, FEND, MEND, and TEND); (3) LIST, a list of data items;
(4) HOLL, a list of character-string words (what used to be called Hollerith
data); (5) TAB1, a one-dimensional tabulation of data pairs; (6) TAB2, a two-
dimensional tabulation control record; (7) INTG, a special structure of integer
fields used for encoding correlation data, and (8) DICT, a directory or index (it
used to be called the “dictionary”) to the sections found in the MAT. It should
be noted that HOLL is a special case of LIST and DICT is a special case of
CONT.
In binary mode, each structure is written as a single logical record as follows:
TAPEID[MAT,MF,MT/A(I),I=1,17] 3
where MAT=tape number, MF=MT=0, and the character data are 16A4,A2;
CONT[MAT,MF,MT/C1,C2,L1,L2,N1,N2]
LIST[MAT,MF,MT/C1,C2,L1,L2,N1,N2/A(I),I=1,N1]
HOLL[MAT,MF,MT/C1,C2,L1,L2,N1,N2/A(I),I=1,N1]
where MF=1, MT=451, and each line of Hollerith characters is stored in Aas
16A4,A2;
TAB1[MAT,MF,MT/C1,C2,L1,L2,N1,N2/NBT(I),JNT(I),I=1,N1
/X(I),Y(I),I=1,N2] where NBT and JNT are the interpolation table and
Y(X) is the one-dimensional tabulation;
TAB2[MAT,MF,MT/C1,C2,L1,L2,N1,N2/NBT(I),JNT(I),I=1,N1]
where the interpolation table is to be used to control a series of N2 LIST
or TAB1 structures that follow;
INTGIO[MAT,MF,MT/A(I),I=1,NW]
where each line of the array can contain 18 I3 integers, 13 I4 integers, 11
I5 integers, 9 I6 integers, or 8 I7 integers. The specific format is governed
by the value of L1 from the CONT record immediately preceding this data
structure.
DICT[MAT MF,MT/0.,0.,MFS,MTS,NCS,MODS]
where there is a record for each section in the material (MFS,MTS) giving
the card count (NCS) for that section. For ENDF/B-V, MODS indicates the
revision number for that section.
The ENDF format manual[9] explains how these structures are combined to
represent various physical quantities.
3In ENDF/B manuals, the slash is used as a logical divider. Replace it with a comma and add parentheses
when constructing a FORTRAN I/O list.
24 NJOY2016

2 NJOY LA-UR-17-20093
In formatted mode, each structure is broken up into many card images, each
containing 6 data words, followed by MAT, MF, MT, and a line sequence num-
ber. There is no intrinsic limit to the length of a data structure written in
coded form because a program reading the data can normally be coded to use
the data in “pages” of reasonable size. The MINX code[21] (the predecessor of
NJOY) was forced to use coded formats to handle the large tabulations found on
PENDF tapes. Analysis showed that this code used large amounts of its running
time coding and decoding number formats. In order to eliminate this waste, a
blocked binary format was developed for the ENDF data structures. A structure
is divided up into several logical records of intermediate length (typically about
300 words), each having the following form:
[MAT,MF,MT,NB,NW/A(I),I=1,NW]
where NB is the number of words remaining in the data structure (the last record
has NB=0). This type of record is compatible with the official ENDF binary
record, but is also adaptable to paging methods. The page size can be chosen
to optimize input/output rates for a particular computer system.
A set of utility subroutines has been devised to handle both blocked-binary
and paged-BCD input and output. They are also provided by module endf.
contio(nin,nout,nscr,a,nb,nw)
Read/write a control record from/to a(nb=0, nw=6). contio uses asend,
amend,etc. for END cards.
listio(nin,nout,nscr,a,nb,nw)
Read/write the first record or page of a list record from/to a. If nb is not
zero, continue with moreio, as shown in Examples 1 and 2 that follow.
tab1io(nin,nout,nscr,a,nb,nw)
Read/write the first record or page of a TAB1 structure. If nb is not zero,
use moreio.
tab2io(nin,nout,nscr,a,nb,nw)
Read/write a TAB2 structure (nb=0).
moreio(nin,nout,nscr,a,nb,nw)
Read/write continuation records or pages from/to the array a. Returns
nb=0 after processing the last record or page.
tpidio(nin,nout,nscr,a,nb,nw)
Read/write the character-string tape identification record from/to array a
(nb=0, nw=17).
NJOY2016 25

LA-UR-17-20093 2 NJOY
hdatio(nin,nout,nscr,a,nb,nw)
Read/write the first record or page of the character descriptive data (MF=1,
MT=451) from/to a, taking account of the 16A4,A2 format needed in
ASCII mode. If nb is not zero, use moreio.
intgio(nin,nout,nscr,a,nb,nw)
Read/write an INTG record.
dictio(nin,nout,nscr,a,nb,nw)
Read/write the entire material directory from/to a. On entry, nw is the
number of entries in the dictionary. moreio is not used.
asend(nout,ncr)
afend(nout,nscr)
amend(nout,nscr)
atend(nout,nscr)
Write a section (MT=0), file (MF=MT=0), material (MAT=MF=MT=0)
or tape (MAT=-1, MF=MT=0) “end” record on the desired units.
In these calling sequences, the unit numbers can be positive, negative, or
zero. Positive numbers mean ASCII mode, negative numbers mean blocked-
binary mode, and zero means the file corresponding to this position in the calling
sequence is not used. All of these routines use the following variables made public
by module endf:
c1h,c2h,l1h,l2h,n1h,n2h,math,mfh,mth,nsh,nsp,nsc
where c1h corresponds to the ENDF C1 field, and so on. The variable nsh is
the sequence number for nin,nsp is the sequence number for nout, and nsc is
the sequence number for nscr. Two examples may help to make clear the use
of these routines.
Example 1. Read All Data
loc=1
call tab1io(nin,0,0,a(loc),nb,nw)
loc=loc+nw
do while (nb.ne.0)
call moreio(nin,0,0,a(loc),nb,nw)
loc=loc+nw
enddo
(process data in A)
26 NJOY2016

2 NJOY LA-UR-17-20093
Example 2. Paging
call tab1io(nin,0,0,a(1),nb,nw)
110 (process this page of data in A)
if (nb.eq.0) go to 120
call moreio(nin,0,0,a(1),nb,nw)
go to 110
120 continue
When nin is BCD, paging is automatic. Positive and negative unit numbers can
be mixed in tpidio,contio,listio,etc., when mode conversion is desired.
2.5 Buffered Binary Scratch Storage
During the execution of a program, large amounts of data often need to be
stored in mass storage temporarily. In order to make such scratch storage as
efficient as possible, NJOY includes a pair of utility subroutines in module util
that automatically buffer such data through fast memory to disk.
loada(i,a,na,ntape,buf,nbuf)
finda(i,a,na,ntape,buf,nbuf)
Load or find data in a buffered binary scratch file. Here iis the data point
number (imust increase, except i=1 causes a rewind and i<0 flushes the
fast memory buffer to mass storage), The array acontains data to be stored
or provides a destination for data to be read, na is the number of words
to be transmitted (must be the same for all i), ntape is the logical unit
number of the disk file, buf is the fast memory buffer array, and nbuf is
the length of the buffer array.
When a point is to be saved, loada stores it in buf. When buf becomes
full, it is automatically dumped to disk. When a point is to be retrieved, finda
checks to see whether the desired point is in buf. If not, it reads through the
disk until the desired point is in memory. It then returns the desired point.
When na is small with respect to nbuf, using loada/finda reduces the number
of I/O operations dramatically. Sometimes it is necessary to find a particular
part of the buffered data. In such cases, use
scana(e,ip,np,na,ntape,buf,nbuf)
NJOY2016 27

LA-UR-17-20093 2 NJOY
where eis a value for the first of the na words, and ip points to part of the data
whose first word is either equal to eor is the first value less than e.
2.6 Dynamic Storage Allocation
Previous versions of NJOY used an internal package called storag for dynamic
memory allocation. Beginning with NJOY2012 we use the standard Fortran-90
storage allocation mechanism. The only feature used is the “allocatable array.”
When needed, an array is allocated that will contain a defined number of values.
The array can be deallocated when no longer needed, and it will disappear
automatically when the scope within which it is defined is exited. This method
produces more transparent code than the old storag package, because pointers
into a single container array are not needed.
2.7 ENDF/B Utility Routines
There are several operations performed on ENDF/B data that are needed in so
many other modules that it is practical to put them into the endf module.
terp1(x1,y1,x2,y2,x,y,i)
Interpolate for y(x) between y1(x1) and y2(x2) using the ENDF interpo-
lation law i(i=1 means y=y1,i=2 means yis linear in x,i=3 means
yis linear in ln(x), i=4 means ln(y) is linear in x,i=5 means ln(y) is
linear in ln(x)), and i=6 means to interpolate using the charged-particle
penetrability with a kinematic threshold of thr6.
terpa(y,x,xnext,idis,a,ip,ir)
Interpolate for y(x) in the TAB1 structure in array a. The routine searches
for the correct interpolation range starting from ip and ir (initialize to 2
and 1 for first call). It returns xnext, the next xvalue in the tabulation.
idis is set to 1 if there is a discontinuity at xnext; it is zero otherwise).
gety1(x,xnext,idis,y1,itape,a)
gety2(x,xnext,idis,y1,itape,a)
Find y(x) in a TAB1 structure starting at the current location on itape
by paging the data through array a.gety1 and gety2 are identical for
occasions when two different tapes are being searched at the same time.
xnext and idis behave as in terpa. The array amust be at least npage+50
words in length. These routines are normally used to retrieve cross sections
from MF=3.
gral(xl,yl,xh,yh,x1,x2,i)
28 NJOY2016

2 NJOY LA-UR-17-20093
This function returns the integral from x1to x2of an ENDF function with
interpolation law i(see terp1). xl,yl,xh, and yh are the low and high
limits of the interpolation panel.
intega(f,x1,x2,a,ip,ir)
Integrate the TAB1 function stored in afrom x1to x2. The routine auto-
matically determines the correct interpolation law for each panel or fraction
of a panel and uses gral to compute each part of the integral. Set ip=2
and ir=1 on the first call to intega. In subsequent calls, the previous
values of ip and ir will usually provide a good starting point for searching
in the TAB1 structure.
2.8 Math Routines
Several mathematics routines are included in the mathm module for use by other
modules. Most of these routines are based on routines from the SLATEC library
converted to NJOY style and Fortran-90.
legndr(x,p,np)
Generate Legendre polynomials P`(x). The `= 0 value is in p(1), the
`= 1 value in p(2), etc. np is the maximum Legendre order produced, so
the largest index for pis np+1.
e1(x)
Compute the first-order exponential integral function E1(x).
gami(a,x)
Compute the incomplete gamma function γ(a, x).
erfc(x)
Compute the complementary error function erfc(x).
2.9 System-Related Utility Routines
As much as possible, actions that related to system functions have been put into
subroutines or functions in the util module. The I/O routines have already
been discussed. Sometimes these routines might have to be altered for unusual
system environments.
timer(time)
Returns the run time in seconds. The meaning of this number may vary
from system to system. It might be central-processor (CP) time, or at
some installations, it may include other factors, such as I/O time or memory
charges. This makes it difficult to compare NJOY runs on different systems.
NJOY2016 29

LA-UR-17-20093 2 NJOY
This routine may have to be revised for some systems, because there is no
standard Fortran-90 call.
dater(hdate)
Returns the date as an 8-character string in one of the forms mm/dd/yy
or ddmmyy; for example, 11/15/90 or 03jun91. For the Fortran-90 version
of NJOY, this is handled using the standard date and time call.
wclock(htime)
Returns the “wall clock” time. This is the time of day that the NJOY run
started, and it shouldn’t be confused with the elapsed CP time for the run
as returned by timer. The time is represented as an 8-character string in
the form hh:mm:ss; for example, 12:13:47. The user is free to use a 24-hour
convention for time. The standard date and time call is used to retrieve
the information from the system.
sigfig(x,ndig,idig)
Because of the many comparisons and searches that it makes, NJOY often
has to match two numbers that are different only in the few least significant
bits. This routine is intended to make such numbers exactly equal to each
other by truncating the numbers to a given number of digits and removing
any low-significance junk resulting from nonterminating binary fractions.
The idig parameter can be used to move the result up or down by idig in
the last significant figure. Although this routine was sometimes machine
dependent in previous versions of NJOY, the subroutine now used seems
to work on all systems tried so far.
a10(x,hx)
Converts x to a 10-column format as a string in hx to provide more digits
in some NJOY listings without taking too much space. This allows 4, 5,
or 6 significant figures to be printed where we previously had four. hx has
the forms +1.23456+6, +1.2345-38, or -1.234+308.
2.10 Error and Warning Messages
NJOY has a pair of standard routines for printing fatal error messages and
warning messages. This helps to enforce consistency in the messages, insulates
other subroutines from the complexities of the system (for example, I/O units,
“console”, “standard error file”), and provides a site for machine-dependent error
handling, including such things as saving “drop files” and generating trace-back
listings. These routines are in module util.
error(from,mess1,mess2)
This subroutine should result in a fatal error exit and must be adjusted to
reflect the local system. Special features such as traceback information or
30 NJOY2016

2 NJOY LA-UR-17-20093
saving files for later analysis can be performed here. from is a character
string containing the name of the procedure that called error, and mess1
and mess2 are two 60-character strings containing messages describing the
error. mess2 is not printed if it is empty.
mess(from,mess1,mess2)
This routine is for nonfatal warning messages. from is the routine that
called it. It prints from,mess1, and mess2 (if not empty), and returns to
the calling routine.
The actual error messages produced by functions and subroutines in the NJOY
module and the subsidiary modules util,endf, and mathm are listed below, in-
cluding explanations of the meaning of the errors and suggested steps to alleviate
them.
error in njoy***illegal module name
Check spelling, and check for missing (/) or incorrect item counts in the
preceding module. This error message is generated directly by NJOY in-
stead of using error.
error in openz***illegal unit number
error in closz***illegal unit number
Units less than 10 are reserved for the system.
error in tomend***mode conversion not allowed
error in tofend***mode conversion not allowed
error in tosend***mode conversion not allowed
Input and output units must both be binary or both be BCD. Check the
signs of the unit numbers in the input file.
error in findf***mat---mf---mt---not on tape
Desired section cannot be found. Either the wrong tape was mounted, or
there is a mistake in the input deck.
error in scana***initial ip ne 0
Must be called with ip=0.
error in scana***did not find energy ---
Energy requested is greater than the highest energy in the LOADA/FINDA
file.
error in gral***x2 lt x1
The integration interval is bad.
error in e1***x is 0
Result is not defined.
error in gami***a must be gt zero
NJOY2016 31

LA-UR-17-20093 2 NJOY
error in gami***x must be gt zero
Illegal parameter values.
error in dlngam***abs(x) so big dlngam overflows
error in dlngam***x is a negative integer
Illegal parameter values.
message from dlngam---answer lt half precision...
Just a warning.
error in csevl***number if terms le 0
error in csevl***number if terms gt 1000
Won’t happen in NJOY.
error in csevl***x outside the interval (-1,1)
Bad parameter value.
error in d9lgit***x should be gt 0 and le a
error in d9lgit***no convergence in 200 terms...
Problems computing Tricomi’s incomplete gamma function. This error
should not occur.
message from d9lgit---result less than half precision...
Just a warning.
error in d9lgmc***x must be ge 10
Bad parameter value.
error in dgamit***x is negative
Bad parameter value.
message from dgamit---result less than half precision...
Just a warning.
error in dgamlm***unable to find xmin
error in dgamlm***unable to find xmax
Having trouble finding the minimum and maximum bounds for the argu-
ment in the gamma function.
error in dgamma***x is 0
error in dgamma***x is a negative integer
error in dgamma***x so big gamma overflows
Bad parameters for the gamma function.
message from dgamma---answer lt half precision...
Just a warning.
error in d9gmit***x should be gt 0
error in d9gmit***no convergence in 200 terms...
Problem’s with Tricomi’s gamma function at small arguments.
error in d9lgic***no convergence in 300 terms...
Problems with the log complementary incomplete gamma function.
32 NJOY2016

2 NJOY LA-UR-17-20093
2.11 Coding Details for the NJOY Main Program
The njoy main program of the NJOY code starts with a with a block of comment
cards that gives a short description of the NJOY module and specifications for
the user’s input lines. (The term “card” is used out of respect for the past;
this usage should not be taken to imply that a real card that can be “folded,
spindled, or mutilated” has to be used.) These blocks of comments cards occur
at the beginning of every NJOY module. It is a good idea to check the input
instructions in the comment cards for the current version in order to see whether
there have been any changes from the input instructions reproduced in this
manual.
The first step in the body of the code is to give “use module” statements for
each module that provides a variable or subroutine call to be used here. There
are several common variables used in this module. The vers string and its
associated date string vday from the version module are important parts of the
NJOY Quality Assurance (QA) scheme. They are updated each time a change
is made to the code, and they are always printed on the output listing. They are
also available to other modules to be written in libraries generated by NJOY or
on plots, if desired. The lab and mx strings are normally used to localize NJOY
to a particular institution and to tell what machine was used for an NJOY run
when several are available. They are carried in the locale module. The quantity
npage in the endf module must be a multiple of 6 (because ENDF records have
6 fields on a line) and 17 (since Hollerith lines use the format “16a4,a2”);
therefore, a value of 306 was chosen. We do not recommend changing this value.
Next, NJOY writes an “banner” on the output listing file giving the date,
time, version, and so on, for this NJOY run. The program now starts an infinite
loop, reading in module names, and executing the requested module, until the
name “stop” is read.
Module “locale” This purpose for this module is to provide localization in-
formation for NJOY. Users may find it necessary to change things in this module
for their site, machines, or compilers. The public variables provided are
lab – a string identifying the user’s institution.
mx – a string identifying the machine used, the system, the compiler, or what-
ever.
kr – the kind value for normal real numbers.
NJOY2016 33
LA-UR-17-20093 2 NJOY
k4 – the kind value for 4-byte real numbers and 4-byte integers (mostly for
CCCC records).
k8 – the kind value for 8-byte Hollerith variables in the CCCC formats.
The default value for lab is “our-lab,” and it can be changed to reflect the
users site. Up to 8 characters are allowed. The default value for mx is “our-mx.”
At one time, LANL had a system call that would tell which machine out of a
cluster was being used, and this field was used for that. It can also be used to
identify the type of machine (e.g., sun, vax, x86, linux) or the compiler used.
NJOY2016 uses the built-in features of Fortran-90 to control the precision of
the numbers used internally. This allows us to remove the complex short-word
and long-word controls used for the Fortran-77 versions, a great simplification.
The normal internal representation used in NJOY2016 is a high-precision one,
normally implemented using 64-bit reals and the system default for integers
(either 4 or 8 bytes should be OK). The “kind” value to obtain these high-
precision reals is returned using the Fortran-90 selected real kind function,
and it should be portable. However, k4 and k8 are simply set to the values 4
and 8, respectively. These choices are not standardized by Fortran-90, and the
values given here may have to be adjusted for some systems. Anyway, once a
proper value of kr has been provided, variables, arrays, and constants can be
typed using statements like
real(kr)::za
real(kr)::elast(20)
real(kr),dimension(:),allocatable::enode
real(kr),parameter::therm=.0253e0_kr
Module “version” This module provides public version and date strings to
any of the other NJOY modules. The initial values are vers=’2016.0’ and
vday=’xxdec16’. It is an important part of the NJOY QA procedure to keep
these values up to date as changes are made to the code.
Module “mainio” This module provides public values for the system I/O
units, namely, nsysi,nsyso, and nsyse. In the past we assigned fixed numeric
values to these variables based upon legacy fortran definitions. We now use
the iso fortran env package to define these units, thereby providing greater
portability over multiple computing platforms. Specifically, nsysi, used in
34 NJOY2016
2 NJOY LA-UR-17-20093
“READ(nsysi,...” statements was set equal to 5 in the past and is now set
to INPUT UNIT.nsyso, used in “WRITE(nsyso,...” statements was set equal
to 7 previously and is now given by ERROR UNIT. Finally, nsyse, used in
“WRITE(nsyse,...” statements directed to the terminal, was set equal to 6 previ-
ously and is now given by OUTPUT UNIT. As used by NJOY the “ERROR UNIT”
and “OUTPUT UNIT” names are counter-intuitive since write(nsyse, ...)
goes to the terminal while write(nsyso, ...) goes to a file called “output”, a
file that is opened in the main NJOY program. As noted elsewhere, NJOY uses
unit numbers between 10 and 19 for scratch files, and allows users to specify
unit numbers from 20 and above for file i/o between NJOY modules. If users
encounter conflicts on their local platforms with the values in iso fortran env
we recommend they revert to the legacy definitions noted above.
Module “physics” Because NJOY is divided into a number of separate mod-
ules, it is important to provide a common set of physical constants to ensure
consistency. These constants are as follows:
pi – a high precision of 15 digits is provided.
bk – Boltzmann’s constant.
amassn – the mass of the neutron in AMU.
amu – the value of the AMU.
hbar – Planck’s constant divided by 2π.
ev – the value of the electron volt.
clight – the velocity of light.
These numbers were obtained from the CODATA’89 set as published by the
National Institute of Standards and Technology (NIST). Other NJOY modules
can access these values by including the statement “use physics.” We have
taken pains in NJOY to compute values that can be derived from these standards
from these values rather than multiplying the number of physical constants used
in the program.
Module “util” As outlined above, module util makes the following routines
public:
error – fatal error routine
mess – warning message routine
NJOY2016 35

LA-UR-17-20093 2 NJOY
timer – CPU elapsed time routine
dater – returns a date string
wclock – returns a wall-clock time string
repoz – repositions a file to the beginning
skiprz – skips records in a file forward and back
openz – opens a new or exiting file
closz – closes a file
loada/finda – a buffered storage system
scana – search in a loada/finda system
sigfig – truncate numbers to a given significance
a10 – print real numbers compactly
There are no private subroutines or variables in this module.
The default versions of error and mess simply write the one or two lines of
message characters to the appropriate units. The Fortran-90 len trim function
is used to measure the real length of a character string by removing trailing
blanks. By changing nsyse, messages can be directed to the user’s terminal, to
a standard error unit, or left to appear on the output file only. The default fatal
error exit “stop 77” can be sometimes be changed to cause a “traceback” to the
subroutine that called error, and backward through the stack of subroutines
that called it. Also, some systems can cause a drop file or “core” file to be
generated for post-mortem analysis with a debugging program.
Subroutines timer,dater, and wclock provide standard interfaces to system
routines that sometimes have different names and return different kinds of an-
swers on different computer systems. This is less of a problem with Fortran-90
than it was with previous compilers. The date and wall-clock strings are easy to
construct using the standard date and time call, which is portable to all sys-
tems. Some system have an analogous cpu time call, but it is not standard. For
other systems, it is necessary to use machine-dependent calls. Some examples of
implementing this function on various computer systems are included as UPD
machine-dependent idents in the NJOY distribution.
The next four routines in NJOY provide a uniform way of handling input and
output files. The unit numbers obey the following convention: zero means do
nothing, negative means a binary unit, and positive means a coded unit (ASCII
for modern systems.). Unit numbers between 10 and 19 are scratch files, which
will be automatically destroyed at the end of the job. Therefore, repoz simply
takes the absolute value of the unit number and calls rewind if it is nonzero.
36 NJOY2016

2 NJOY LA-UR-17-20093
Similarly, closz takes the absolute value of the unit number and closes it if
nonzero and not a scratch file. Subroutine skiprz skips forward with dummy
reads of the correct type for the sign of the unit, and it skips backward with
backspace. Note that this can be very inefficient for some systems. For example,
the VAX executes backspace by first rewinding and then skipping forward by
n−1 records. Making successive calls to backspace, as done in this routine,
would be very expensive. It is better to rewind before calling skiprz; then only
forward skips would be required to get to the desired record. Finally, subroutine
openz is used to open files with the desired characteristics (that is, binary or
formatted, new or old, scratch or permanent). Standard Fortran-90 statements
are used. Note that the file names are constructed to have the forms tape20,
tape21,etc. Scratch files will have whatever names are standard for the system
being used.
The loada/finda system was discussed in Section2.5. The data represen-
tation consists of a fairly large buffer array buf of length nbuf. This buffer
contains a number of component blocks, each of length na. Therefore, it is easy
to compute the location of any block using modular arithmetic on the block
index i. If the location is currently in the buffer array, the block can be read
or written. Otherwise, the associated scratch file ntape must be repositioned
before being read or written. The files ntape have to be written sequentially,
but they can be searched in any order. Subroutine scana takes advantage of
this to locate the block whose first element is closest to the input parameter e.
Subroutine sigfig is used to control the precision of numbers in several
NJOY modules. This is a difficult problem because the true representation of
numbers in the machine is as non-terminating binary fractions. In addition, dif-
ferent representations for floating-point numbers are used in different computer
systems, and significant-figure truncation can be machine-dependent. The ver-
sion of sigfig used in NJOY2016 seems to be very portable.
Subroutine a10 is used to make the printing of real numbers on NJOY output
listings more compact by stripping off excess characters in the exponent field.
It converts the input real number into a 10-character string with the following
forms: +1.23456+6, +1.2345-38 and -1.234+308. This subroutine is closely
related to the private subroutine a11 in the endf module, except for forcing a
10-character field rather than an 11-character field.
Module “endf” As discussed in Section 2.4 of this chapter, NJOY uses files
in ENDF-like formats for most communications between modules. Subroutines
NJOY2016 37

LA-UR-17-20093 2 NJOY
are provided in module endf to work with the various ENDF record types. The
routines that are public for this module are as follows:
contio – to read or write CONT records
listio – to read or write LIST records
tab1io – to read or write TAB1 records
moreio – to read or write continuation records
tab2io – to read or write TAB2 records
tpidio – to read or write TAPEID records
hdatio – to read or write character-string records
intgio – to read or write INTG reconrds
dictio – to read or write “dictionary” records
tosend – to read or write to the next SEND record
tofend – to read or write to the next FEND record
tomend – to read or write to the next MEND record
totend – to read or write to the next TEND record
asend – to write SEND record
afend – to write FEND record
amend – to write MEND record
atend – to write TEND record
In addition, the following data words are public for this module:
c1h – ENDF C1 field
c2h – ENDF C2 field
l1h – ENDF L1 field
l2h – ENDF L2 field
n1h – ENDF N1 field
n2h – ENDF N2 field
math – ENDF MAT field
mf – ENDF MF field
mt – ENDF MT field
nsh – NS card number (input file)
nsp – NS card number (output file)
nsc – NS card number (scratch file)
thr6 – threshold energy for interpolation law 6
38 NJOY2016

2 NJOY LA-UR-17-20093
There are additional private routines and global variables used inside the mod-
ule.
Subroutines contio,listio,tab1io,tab2io,moreio,tpidio,hdatio,
intgio, and dictio are used to read, write, copy, or convert the mode of binary
or formatted records on these interface files. They all have similar structures.
First, records are read using binary or coded commands, depending on the sign
of the unit number. Then the records are written back out, once again using a
mode that depends on the sign of the unit number. Unit numbers can be zero,
in which case that unit is not used. When these numbers are read, they are
converted into integers for the l1h,l2h,n1h, and n2h fields using the Fortran
nearest-integer function, nint. If programmers choose to use a number in the
array adirectly, they should be careful to make the same conversion. Private
subroutine lineio is used by several of these routines to read or write a line of
floating-point numbers. It has two special features. First, any empty fields at the
end of a line are filled in with blanks. The second feature is the construction of
floating-point numbers without the normal Fortran “E” using subroutine a11.
Private subroutine tablio is used by tab1io and tab2io to read and write
ENDF-style interpolation tables. Subroutine hollio is used to read or write
lines of Hollerith information. Note that Hollerith data are represented using
17 fields per card, but all other ENDF data uses 6 fields per card.
Subroutine a11 simply breaks up the real-number xinto a fraction part f, a
sign part S, and an exponent part n. The number of digits in the fraction part
depends on the number of digits in the exponent part in order to maximize the
precision of the formatted representation of x. It then constructs a string con-
taining the real number without the normal Fortran “E” and omitting leading
zeros in the exponent. If the number being represented has more significant dig-
its than can be represented with the “E” formats, the subroutine automatically
shifts to an appropriate “F” format (e.g., F11.8, F11.7, —it etc.) depending on
the size of the number. This feature is sometimes needed for the fine texture of
resonance data.
As discussed above, ENDF tapes are divided into materials, files, and sections
by special end cards with names like MEND, FEND, SEND, and TEND. The
subroutines tosend,tofend,tomend, and totend can be used to move from
the current location to one of these end cards, optionally copying the records as
they go. Since these routines do not know the actual structure of the records,
they cannot change the mode of the data while copying. They simply read in a
record, write it out again if desired, and watch for the specified end card.
NJOY2016 39

LA-UR-17-20093 2 NJOY
The parallel set of routines asend,afend,amend, and atend write one of the
requested end cards to one or two different output files using the mode defined
by the sign of the unit number. The NJOY convention is to use blanks for the
first 66 columns of formatted end cards in order to make them easy to see on
ENDF listings. The tapes as received from the National Nuclear Data Center
(NNDC) of the Brookhaven National Laboratory may have these fields filled
in with numerical values of zero. The MODER module automatically changes
ENDF tapes from the BNL convention to the NJOY one.
Subroutine findf is used very frequently in NJOY modules to search through
an ENDF-type tape for a desired section (mat,mf,mt). Since the three numbers
that describe sections are always arranged in order, it is possible to search both
up and down. On entry, the routine reads the first card and decides if it has
to read up or down to find the desired section. It then continues by reading
records in the proper direction until it comes to the desired section. It then
backs up by one record so that the next read after the call to findf will read
the first record of the desired section. If the desired section is not found, a fatal
error message will be issued. Subroutine findf can go into an infinite loop if
the MAT number requested is smaller than the number for the first material on
the tape (thus findf is moving backwards) and the number in the MAT field
on the tape identification record is larger than the material number for the first
material. Some systems have an “IF (BOI)” function that can be used to detect
when the tape is at the “beginning of information.”
Subroutine terp1 is used to interpolate between two points x1,y1 and x2,y2
using ENDF interpolation law i. The results for yat xare given by simple for-
mulas. No tests are made for values that give illegal arguments for the Fortran
log and exponent functions. Therefore, fatal arithmetic errors from terp1 are
fairly common. Going slightly out of order, gral is a routine that computes
integrals inside the endpoints of a segment represented using the ENDF inter-
polation laws. Once again, simple formulas are used, and it is also possible to
get arithmetic errors from the log and exponent functions with this routine.
It is usually necessary to interpolate or integrate functions that involve more
than one panel of ENDF interpolated data. Most commonly, this occurs for
data in TAB1 format. If the TAB1 record is small enough so that it can fit into
an array ain memory, subroutine terpa can be used to search for the panel
that contains x, and to interpolate for yat x. Similarly, intega can be used to
compute the integral from x1 to x2 by integrating over all the panels and parts
of panels within these limits. Subroutine terpa uses terp1, and subroutine
40 NJOY2016

2 NJOY LA-UR-17-20093
intega uses gral.
NJOY works with some very large TAB1 records that cannot fit into memory.
For these cases, gety1 and gety2 can be used to interpolate for yat x. Array
aonly has to be big enough for one page of data (plus a little extra space for
parameters like c1h,n2h, and TAB1 interpolation tables). If the desired xis
not in memory, new pages of data are read from itape until the desired value is
found. The subroutine then uses terp1 to compute y. Note that zero is returned
if xis outside the range of the table, and xnext=1.e12 when the last point is
returned. Subroutines gety1 and gety2 are almost identical so that numbers
can be retrieved independently from two different input tapes at the same time.
Module “mathm” There are several math routines that are needed in various
NJOY modules that are provided in this module:
legndr – provides Legendre polynomials
e1 – provides the first-order exponential integral function.
gami – provides the incomplete gamma function.
erfc – provides the complementary error function.
The last three of these were taken from the SLATEC library, which was devel-
oped by the Los Alamos National Laboratory, the Sandia National Laboratory,
and the Stanford Linear Accelerator Laboratory. These routines produce very
high-precision results as compared to other publicly available routines. They
were converted to NJOY conventions and Fortran-90 style for NJOY. This mod-
ule also contains a large number of private routines that are used in the course
of computing the numbers returned by the public routines. Subroutine legndr
is used to compute Legendre polynomials by recursion. The formulas are as
follows:
P0(x)=1. , (1)
P1(x) = x , (2)
P`+1)(x) = (2`−1)xP`(x)−(`−1)P`−2
`,(3)
where P0is stored in p(1),P1is stored in p(2), and so on.
NJOY2016 41

LA-UR-17-20093 2 NJOY
42 NJOY2016

3 RECONR LA-UR-17-20093
3 RECONR
The RECONR module is used to reconstruct resonance cross sections from res-
onance parameters and to reconstruct cross sections from ENDF nonlinear in-
terpolation schemes. The output is written as a pointwise-ENDF (PENDF) file
with all cross sections on a unionized energy grid suitable for linear interpo-
lation to within a specified tolerance. Redundant reactions (for example, total
inelastic, charged-particle reactions) are reconstructed to be exactly equal to the
sum of their reconstructed and linearized parts at all energies. The resonance
parameters are removed from File 2, and the material directory is corrected to
reflect all changes. RECONR has the following features:
•Efficient use of dynamic storage allocation and a special stack structure
allow very large problems to be run.
•The unionized grid improves the accuracy, usefulness, and ENDF compat-
ibility of the output. All summation cross sections are preserved on the
union grid. Up to nine significant figures are allowed.
•A correct directory of the output tape is provided.
•Approximate ψχ Doppler broadening may be used in some cases to speed
up reconstruction.
•A resonance-integral criterion is added to the normal linearization criterion
in order to reduce the number of points added to the tabulation to represent
“unimportant” resonances.
•All ENDF-6 resonance formats currently active are handled, including the
calculation of angular distributions from resonance parameters in some
cases.
This chapter describes the RECONR module in NJOY2016.0.
3.1 ENDF/B Cross Section Representations
A typical cross section derived from an ENDF/B evaluation is shown in Fig. 1.
The low-energy cross sections are “smooth”. They are described in File 3 (see
Section 2.4 for a review of ENDF/B nomenclature) using cross-section values
given on an energy grid with a specified law for interpolation between the points.
In the resolved resonance range, resonance parameters are given in File 2, and
the cross sections for resonance reactions have to be obtained by adding the
contributions of all the resonances to “backgrounds” from File 3. At still higher
energies comes the unresolved region where explicit resonances are no longer
defined. Instead, the cross section is computed from statistical distributions
NJOY2016 43
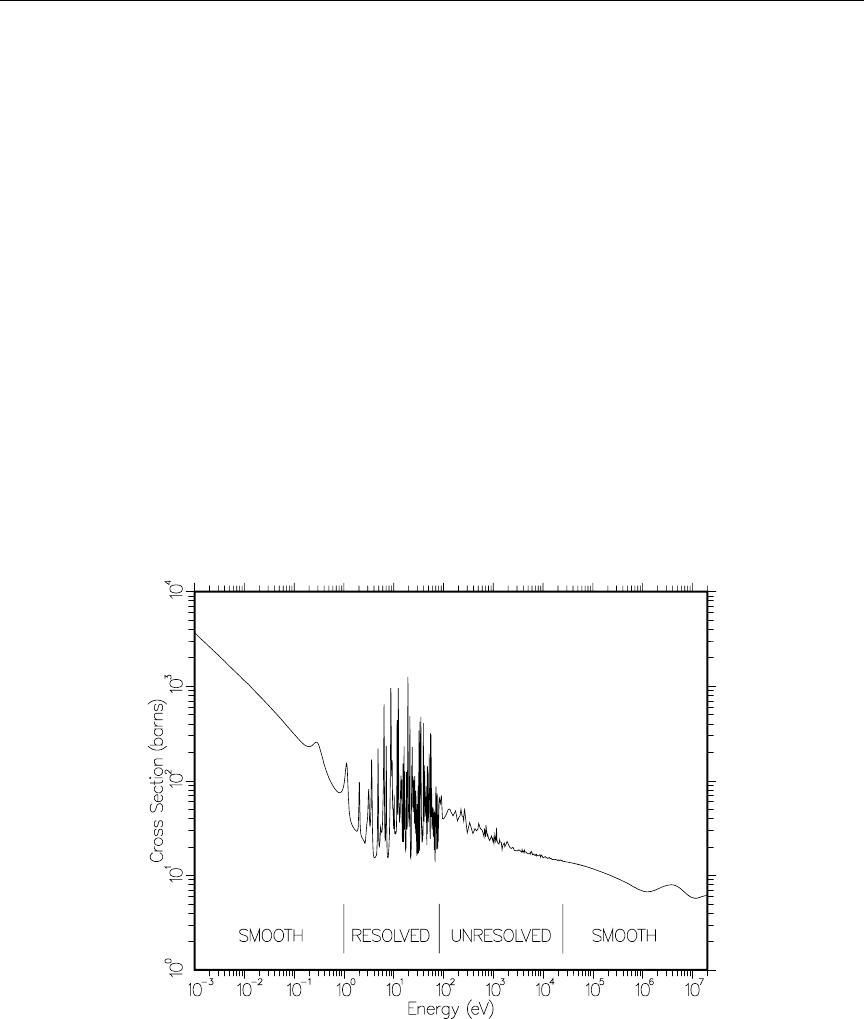
LA-UR-17-20093 3 RECONR
of the resonance parameters given in File 2 and backgrounds from File 3 (or
optionally taken directly from File 3 as for smooth cross sections). Finally, at
the highest energies, the smooth File 3 representation is used again.
For light and medium-mass isotopes, the unresolved range is usually omit-
ted. For the lightest isotopes, the resolved range is also omitted, the resonance
cross sections being given directly in the “smooth” format. In addition, several
different resonance representations are supported (Single-Level Breit-Wigner
(SLBW), Multilevel Breit-Wigner (MLBW), Adler-Adler, Hybrid R-Function
(HRF), Reich-Moore (RM), Reich-Moore-Limited (RML), energy-independent
unresolved, and energy-dependent unresolved). The Adler-Adler and Hybrid
formats are not being used in modern evaluations. For an increasing number of
modern evaluations, the low energy “smooth” region is omitted, and the resolved
resonance region is extended to the low energy limit.
RECONR takes these separate representations and produces a simple cross
section versus energy representation like the one shown in Fig. 1.
Figure 1: A typical cross section reconstructed from an ENDF/B evaluation using RE-
CONR. The smooth, resolved, and unresolved energy regions use different rep-
resentations of the cross sections. This is the total cross section for 235U from
ENDF/B-V.
44 NJOY2016

3 RECONR LA-UR-17-20093
3.2 Unionization and Linearization Strategy
Several of the cross sections found in ENDF/B evaluations are summation cross
sections (for example, total, inelastic, sometimes (n,2n) or fission, and sometimes
charged-particle reactions), and it is important that each summation cross sec-
tion be equal to the sum of its parts. However, if the partial cross sections
are represented with nonlinear interpolation schemes, the sum cannot be rep-
resented by any simple interpolation law. A typical case is the sum of elastic
scattering (MT=2 interpolated linearly to represent a constant) and radiative
capture (MT=102 interpolated log-log to represent 1/v). The total cross sec-
tion cannot be represented accurately by either scheme unless the grid points
are very close together. This effect leads to significant balance errors in multi-
group transport codes and to splitting problems in continuous-energy Monte
Carlo codes.
The use of linear-linear interpolation (i.e., σlinear in E) can be advanta-
geous in several ways. The data can be plotted easily, they can be integrated
easily, cross sections can be Doppler broadened efficiently (see BROADR), and,
linear data can be retrieved efficiently in continuous-energy Monte Carlo codes.
Therefore, RECONR puts all cross sections on a single unionized grid suitable
for linear interpolation. As described in more detail below, RECONR makes
one pass through the ENDF/B material to select the energy grid, and then a
second pass to compute cross sections on this grid. Each cross section on the
PENDF file (except for the summation cross sections) is exactly equal to its
ENDF/B value. The summation cross sections are then obtained by adding up
the partial cross sections at each grid point.
While RECONR is going through the reactions given in the ENDF/B eval-
uation, it also checks the reaction thresholds against the Qvalue and atomic
weight ratio to the neutron A(AWR in the file) given for the reaction. If
threshold ≥A+ 1
AQ(4)
is not true, the threshold energy is moved up to satisfy the condition. This
is usually a small change, often only in the least significant digit, and is a
consequence of comparing two REAL numbers of finite precision.
If desired, the unionized grid developed from the ENDF/B file can be supple-
mented with “user grid points” given in the input data. The code automatically
adds the conventional thermal point of 0.0253 eV and the 1, 2, and 5 points in
each decade to the grid if they are not already present. These simple energy grid
NJOY2016 45

LA-UR-17-20093 3 RECONR
points help when comparing materials, and they provide well-controlled starting
points for further subdivision of the energy grid.
There are special problems with choosing the energy grid in the unresolved
range. In some cases, the unresolved cross section is represented using resonance
parameters that are independent of energy. The cross sections are not constant,
however, but have a shape determined by the energy variation of neutron wave
number, penetrability factors, and so on. RECONR handles this case by choos-
ing a set of energies (about 13 per decade) to be used to calculate the cross
sections; the set of energies gives a reasonable approximation to the result in-
tended. For evaluations that use energy-dependent resonance parameters, it is
supposed to be sufficient to compute the unresolved cross sections at the given
energies and to use interpolation on the cross sections to obtain the appropriate
values at other energies. However, some evaluations carried over from earlier
versions of ENDF/B were not evaluated using this convention, and cross sec-
tions computed using cross-section interpolation are not sufficiently accurate.
Even some modern evaluations use inadequate energy grids for the unresolved
range. RECONR detects such cases by looking for large steps between the points
of the given energy grid. It then adds additional energy grid points using the
same 13-per-decade rule used for energy-independent parameters. “Large” is
currently defined by wide to be a factor of 1.26.
3.3 Linearization and Reconstruction Methods
Linearization (lunion) and resonance reconstruction (resxs) both function by
inserting new energy grid points between the points of an original grid using an
“inverted stack”. The general concepts involved are illustrated with a simple
example shown in Fig. 2.
The stack is first primed with two starting values. For linearization, they
will be two adjacent points on the original union grid. For reconstruction, they
will usually be the peaks and half-height energies of resonances. The stack is
said to be inverted because the lower energy is at the “top” (I=2).
This interval or panel is now divided into two parts, and the cross section
computed at the intermediate point is compared to the result of linear inter-
polation between the adjacent points. If the two values do not agree within
various criteria, the top of the stack is moved up one notch (I=3), and the new
value is inserted (I=2). The code then repeats the checking process for the new
(smaller) interval at the top of the stack. The top of the stack rises until con-
vergence is achieved for the top interval. The top energy and cross section are
46 NJOY2016
3 RECONR LA-UR-17-20093
12
1
1
2
2
3
34
12354
1234
123
123
12
energy
cross
section
1.
2.
3.
4.
5.
6.
7.
8.
4
3
12
9.
Figure 2: Inverted -stack method used in RECONR and several other places in NJOY. Line
1 shows the two initial points (the lower energy is higher in the stack). In line 2, a
new point has been calculated at the midpoint, but the result was not converged,
and the new point has been inserted in the stack. In line 3, the midpoint of the
top panel has been checked again, found to be not converged, and inserted into
the stack. The same thing happens in line 4. In line 5, the top panel is found to be
converged, and the top point (5) has been written out. The same thing happens
in line 6. In line 7, the top panel is tested and found to be not converged. The
midpoint is added to the stack. Finally, in line 8, the top panel is found to be
converged, and the top point is written out. This leaves two points in the stack
(see line 9). Note that the energy points come off the stack in the desired order
of increasing energy, and that only one point has to be moved up in the stack as
each new result is inserted.
NJOY2016 47

LA-UR-17-20093 3 RECONR
then saved on a scratch file, the stack index is decremented, and the checks are
repeated. This process is continued with the top of the stack rising and falling
in response to the complexity of the cross section until the entire panel ∆Ehas
been converged (I=1). The stack is then reprimed with the bounds of the next
panel. The process continues until the entire energy range for linearization or
reconstruction has been processed.
This stack logic enables a panel to be subdivided into parts as small as ∆E/2n
where nis the stack size, and several different cross sections (elastic, capture,
fission) can easily be stored in arrays of this size.
The convergence criterion used for linearization is that the linearized cross
section at the intermediate point is within the fractional tolerance err (or a
small absolute value errlim) of the actual cross section specified by the ENDF
law. More complicated criteria are used for resonance reconstruction.
There are two basic problems that arise if a simple fractional tolerance test
is used to control resonance reconstruction. First, as points are added to the en-
ergy grid, adjacent energy values may become so close that they will be rounded
to the same number when a formatted output file is produced. There can be
serious problems if the code continues to add grid points after this limit is
reached. Through the use of dynamic format reconstruction, the energy res-
olution available for formatted NJOY output (which use ENDF 11-character
fields) is 7 significant figures (that is, ±1.234567 ±n) rather than the usual 5
or 6 (see Section 2.4). For NJOY2016, the Fortran-90 “kind” parameter is used
to assure sufficient precision for this. Even this seven significant figure format
is sometimes insufficient for very narrow resonances. If necessary, NJOY can go
to nine significant figures by using a Fortran “F” format, e.g., ±1234.56789.
Significant-figure control is implemented as follows: each intermediate energy
is first truncated to 7 significant figures before the corresponding cross sections
are computed. If the resulting number is equal to either of the adjacent values
and convergence has not been obtained, subdivision continues using energies
truncated to 9 significant figures. If an energy on this finer grid is equal to
either of the adjacent values, the interval is declared to be converged even though
convergence has not been achieved. Thus, no identical energies are produced,
but an unpredictable but very small loss in accuracy results.
The second basic problem alluded to above is that a very large number of
resonance grid points arise from straightforward linear reconstruction of the res-
onance cross section of some isotopes. Many of these points come from narrow,
weak, high-energy resonances, which do not need to be treated accurately in
48 NJOY2016

3 RECONR LA-UR-17-20093
many applications. As an example, the capture and fission resonance integrals
important for thermal reactors must be computed with a 1/E flux weighting. If
the resonance reconstruction tolerance is set high (say 1%) to reduce the cost
of processing, the resonance integrals will be computed to only 1% accuracy.
However, if the reconstruction tolerance were set to a smaller value, like 0.1%,
and if the high-energy resonances (whose importance is reduced by the 1/E
weight and the 1/v trend of the capture and fission cross sections) were treated
with less accuracy than the low-energy resonances, then it is likely that one
could achieve an accuracy much better than 1% with an overall reduction in the
number of points (hence computing cost). Since 1/E weighting is not realistic
in all applications (for example, in fast reactors), user control of this “thinning”
operation must be provided.
Based on these arguments, the following approach was chosen to control the
problem of very large files. First, panels are subdivided until the elastic, capture,
and fission cross sections are converged to within errmax, where errmax ≥err.
These two tolerances are normally chosen to form a reasonable band, such as 1%
and 0.1%, to ensure that all resonances are treated at least roughly (for example,
for plotting). If the resonance integral (1/E weight) in some panel is large, the
panel is further subdivided to achieve an accuracy of err (say 0.1%). However,
if the contribution to the resonance integral from any one interval gets small,
the interval will be declared converged, and the local value of the cross section
will end up with some intermediate accuracy. The contribution to the error in
the resonance integral should be less than 0.5×∆σ×∆E. This value is added
into an accumulating estimate of the error, and a count of panels truncated by
the resonance integral check is incremented.
The problem with this test is that RECONR does not know the value of the
resonance integral in advance, so the tolerance parameter errint is not the ac-
tual allowed fractional error in the integral. Instead, it is more like the resonance
integral error per grid point (barns/point). Thus, a choice of errint=err/10000
with err=0.001 would limit the integral error to about 0.001 barn if 10000 points
resulted from reconstruction. Since important resonance integrals vary from a
few barns to a few hundred barns, this is a reasonable choice. The integral check
can be suppressed by setting errint very small or errmax=err.
When resonance reconstruction is complete, RECONR provides a summary
of the possible resonance integral error due to the integral check over several
coarse energy bands. An example from ENDF/B-VII.0 235U follows:
NJOY2016 49

LA-UR-17-20093 3 RECONR
estimated maximum error due to
resonance integral check (errmax,errint)
upper elastic percent capture percent fission percent
energy integral error integral error integral error
1.00E-05
1.00E-04 3.50E+01 0.000 8.15E+03 0.000 4.29E+04 0.000
1.00E-03 3.50E+01 0.000 2.57E+03 0.000 1.36E+04 0.000
1.00E-02 3.50E+01 0.000 8.02E+02 0.000 4.24E+03 0.000
1.00E-01 3.46E+01 0.000 2.15E+02 0.000 1.26E+03 0.000
1.00E+00 3.25E+01 0.000 6.03E+01 0.000 3.26E+02 0.000
2.00E+00 8.95E+00 0.000 7.31E+00 0.000 2.62E+01 0.000
5.00E+00 1.08E+01 0.000 1.25E+01 0.000 1.56E+01 0.000
1.00E+01 7.75E+00 0.000 2.40E+01 0.000 3.52E+01 0.000
2.00E+01 8.18E+00 0.000 2.92E+01 0.000 3.31E+01 0.000
5.00E+01 1.07E+01 0.000 2.57E+01 0.000 3.83E+01 0.000
1.00E+02 8.30E+00 0.000 1.07E+01 0.000 2.34E+01 0.000
2.00E+02 8.04E+00 0.000 8.17E+00 0.000 1.42E+01 0.000
5.00E+02 1.10E+01 0.001 6.81E+00 0.008 1.51E+01 0.004
1.00E+03 8.28E+00 0.008 3.44E+00 0.080 7.62E+00 0.038
2.00E+03 8.27E+00 0.033 2.54E+00 0.261 5.06E+00 0.185
points added by resonance reconstruction = 232418
points affected by resonance integral check = 80445
final number of resonance points = 242170
number of points in final unionized grid = 242600
The parameters errmax and errint, taken together, should be considered as
adjustment “knobs” that can increase or decrease the errors in the “res-int”
columns to get an appropriate balance between accuracy and economy for a
particular application. The error from significant figure reduction provided by
earlier versions of NJOY is no longer needed.
For energies in the thermal range (energies less than trange=0.5 eV), the
user’s reconstruction tolerance is divided by a factor of 5 in order to give better
results for several important thermal integrals, especially after Doppler broad-
ening, and to make the 0.0253 eV cross section behave well under Doppler
broadening.
50 NJOY2016

3 RECONR LA-UR-17-20093
3.4 Resonance Representations
RECONR uses the resonance formulas as implemented in the original RESEND
code[26] with several changes: a more efficient calculation of MLBW cross sec-
tions developed by C. R. Lubitz of the Knolls Atomic Power Laboratory (KAPL)
and coded by P. Rose of the National Nuclear Data Center (NNDC) at the
Brookhaven National Laboratory (BNL), the addition of competitive widths
introduced for ENDF/B-V, a ψχ Doppler-broadening calculation for SLBW
and Adler-Adler resonance shapes, and a capability to process either the multi-
level multi-channel R-matrix Reich-Moore parameters or the multi-level single-
channel Hybrid R-Function parameters based on the work of M. Bhat and C.
Dunford of the NNDC, an implementation of the GH method for MLBW res-
onances, which allows psi-chi broadening, and a capability to process the new
RML parameters, including resolved resonance energy region angular distribu-
tions.
Expanded discussions of the following formulas can be found in the ENDF-6
format manual[9].
Single-Level Breit-Wigner Representation (SLBW) The subroutine that
computes Single-Level Breit-Wigner cross sections (csslbw) uses
σn=σp
+X
`X
r
σmrnhcos 2φ`−(1 −Γnr
Γr
)iψ(θ, x)
+ sin 2φ`χ(θ, x)o,(5)
σf=X
`X
r
σmr
Γfr
Γr
ψ(θ, x),(6)
σγ=X
`X
r
σmr
Γγr
Γr
ψ(θ, x),and (7)
σp=X
`
4π
k2(2`+ 1) sin2θ`,(8)
where σn,σf,σγ, and σpare the neutron (elastic), fission, radiative capture,
and potential scattering components of the cross section arising from the given
resonances. There can be “background” cross sections in File 3 that must be
added to these values to account for competitive reactions such as inelastic
scattering or to correct for the inadequacies of the single-level representation
with regard to multilevel effects or missed resonances. The sums extend over
NJOY2016 51
LA-UR-17-20093 3 RECONR
all the `values and all the resolved resonances rwith a particular value of
`. Each resonance is characterized by its total, neutron, fission, and capture
widths (Γ,Γn,Γf,Γγ), by its Jvalue (AJ in the file), and by its maximum value
(smax=σmr/Γrin the code)
σmr =4π
k2gJ
Γnr
Γr
,(9)
where gJis the spin statistical factor
gJ=2J+ 1
4I+ 2 ,(10)
and Iis the total spin (SPI) given in File 2, and kis the neutron wave number,
which depends on incident energy Eand the atomic weight ratio to the neutron
for the isotope A(AWRI in the file), as follows:
k= (2.196771×10−3)A
A+ 1√E . (11)
There are two different characteristic lengths that appear in the ENDF resonance
formulas: first, there is the “scattering radius” ˆa, which is given directly in File
2 as AP; and second, there is the “channel radius” a, which is given by
a= 0.123 A1/3+ 0.08 .(12)
If the File 2 parameter NAPS is equal to one, ais set equal to ˆain calculat-
ing penetrabilities and shift factors (see below). The ENDF-6 option to enter
an energy-dependent scattering radius is not supported. The neutron width
in the equations for the SLBW cross sections is energy dependent due to the
penetration factors P`; that is,
Γnr(E) = P`(E) Γnr
P`(|Er|),(13)
52 NJOY2016

3 RECONR LA-UR-17-20093
where
P0=ρ , (14)
P1=ρ3
1 + ρ2,(15)
P2=ρ5
9+3ρ2+ρ4,(16)
P3=ρ7
225 + 45ρ2+ 6ρ4+ρ6,and (17)
P4=ρ9
11025 + 1575ρ2+ 135ρ4+ 10ρ6+ρ8,(18)
where Eris the resonance energy and ρ=ka depends on the channel radius or
the scattering radius as specified by NAPS. The phase shifts are given by
φ0= ˆρ , (19)
φ1= ˆρ−tan−1ˆρ , (20)
φ2= ˆρ−tan−13ˆρ
3−ˆρ2,(21)
φ3= ˆρ−tan−115ˆρ−ˆρ3
15 −6ˆρ2,and (22)
φ4= ˆρ−tan−1105ˆρ−10ˆρ3
105 −45ˆρ2+ ˆρ4,(23)
where ˆρ=kˆadepends on the scattering radius. The final components of the cross
section are the actual line shape functions ψand χ. At zero temperature,
ψ=1
1 + x2,(24)
χ=x
1 + x2,(25)
x=2(E−E0
r)
Γr
,(26)
and
E0
r=Er+S`(|Er|)−S`(E)
2(P`(|Er|)Γnr(|Er|),(27)
NJOY2016 53

LA-UR-17-20093 3 RECONR
in terms of the shift factors
S0= 0 ,(28)
S1=−1
1 + ρ2,(29)
S2=−18 + 3ρ2
9+3ρ2+ρ4,(30)
S3=−675 + 90ρ2+ 6ρ4
225 + 45ρ2+ 6ρ4+ρ6,and (31)
S4=−44100 + 4725ρ2+ 270ρ4+ 10ρ6
11025 + 1575ρ2+ 135ρ4+ 10ρ6+ρ8.(32)
To go to higher temperatures, define
θ=Γr
r4kT E
A
,(33)
where kis the Boltzmann constant and Tis the absolute temperature. The line
shapes ψand χare now given by
ψ=√π
2θReWθx
2,θ
2,(34)
and
χ=√π
2θImWθx
2,θ
2,(35)
in terms of the complex probability function (see quickw,wtab, and w, which
came from the MC2code[37])
W(x, y)=e−z2erfc(−iz) = i
πZ∞
−∞
e−t2
z−tdt , (36)
where z=x+iy. The ψχ method is not as accurate as kernel broadening (see
BROADR) because the backgrounds (which are sometimes quite complex) are
not broadened, and terms important for energies less than about 16kT/A are
neglected; however, the ψχ method is less expensive than BROADR. Previous
versions of RECONR included ψχ broadening for the SLBW and Adler-Adler
representations only. This version also allows the method to be used for MLBW
cases. The SLBW approach can produce negative elastic cross sections. If found,
they are set to a small positive value, and a count is accumulated for a diagnostic
in the listing file.
54 NJOY2016

3 RECONR LA-UR-17-20093
Multilevel Breit-Wigner Representation (MLBW) The Lubitz-Rose method
used for calculating Multi-Level Breit-Wigner cross sections (csmlbw) is formu-
lated as follows:
σn(E) = π
k2X
`
I+1
2
X
s=|I−1
2|
l+s
X
J=|l−s|
gJ|1−U`sJ
nn (E)|2,(37)
with
U`J
nn(E)=e2iφ`−X
r
iΓnr
E0
r−E−iΓr/2,(38)
where the other symbols are the same as those used above. Expanding the
complex operations gives
σn(E) = π
k2X
`
I+1
2
X
s=|I−1
2|
l+s
X
J=|l−s|
gJ1−cos 2φ`−X
r
Γnr
Γr
2
1 + x2
r2
+sin 2φ`+X
r
Γnr
Γr
2xr
1 + x2
r2,(39)
where the sums over rare limited to resonances in spin sequence `that have
the specified value of sand J. Unfortunately, the sdependence of Γ is not
known. The file contains only ΓJ=Γs1J+Γs2J. It is assumed that the ΓJcan be
used for one of the two values of s, and zero is used for the other. Of course,
it is important to include both channel-spin terms in the potential scattering.
Therefore, the equation is written in the following form:
σn(E) = π
k2X
`X
J
gJ1−cos 2φ`−X
r
Γnr
Γr
2
1 + x2
r2
+sin 2φ`+X
r
Γnr
Γr
2xr
1 + x2
r2+ 2D`(1 −cos 2φ`),(40)
where the summation over Jnow runs from
||I−`| − 1
2| → I+`+1
2,(41)
and D`gives the additional contribution to the statistical weight resulting from
duplicate Jvalues not included in the new Jsum; namely,
NJOY2016 55

LA-UR-17-20093 3 RECONR
D`=
I+1
2
X
s=|I−1
2|
l+s
X
J=|l−s|
gJ−
I+`+1
2
X
J=||I−`|− 1
2|
gJ(42)
= (2`+ 1) −
I+`+1
2
X
J=||I−`|− 1
2|
gJ.(43)
A case where this correction would appear is the `=1 term for a spin-1 nuclide.
There will be 5 Jvalues: 1/2, 3/2, and 5/2 for channel spin 3/2; and 1/2 and
3/2 for channel spin 1/2. All five contribute to the potential scattering, but the
file will only include resonances for the first three.
The fission and capture cross sections are the same as for the single-level
option. The ψχ Doppler-broadening cannot be used with this formulation of
the MLBW representation.
However, there is an alternate representation available that does support ψχ
broadening:
σn=σp
+X
`X
r
σmrnhcos 2φ`−(1 −Γnr
Γr
) + Gr`
Γnr iψ(θ, x)
+(sin 2φ`+Hr`
Γnr
)χ(θ, x)o,(44)
where
Gr` =1
2X
r06=r
Jr06=Jr
ΓnrΓnr0Γr+ Γr0
(Er−Er0)2+ (Γr+ Γr0)2/4,(45)
and
Hr` =X
r06=r
Jr06=Jr
ΓnrΓnr0Er−Er0
(Er−Er0)2+ (Γr+ Γr0)2/4.(46)
Nominally, this method is slower than the previous one because it contains a
double sum over resonances at each energy. However, it turns out that G and H
are slowly varying functions of energy, and the calculation can be accelerated by
computing them at just a subset of the energies and getting intermediate values
by interpolation. It is important to use a large number of r0values on each side
of r. The GH MLBW method is implemented in csmlbw2.
56 NJOY2016

3 RECONR LA-UR-17-20093
Adler-Adler Representation (Adler-Adler) The multilevel Adler-Adler
representation (csaa) is defined for `=0 only. It is useful for fissionable materials.
The total cross sections are given by
σt(E) = 4π
k2sin2φ0
+π√E
k2X
r
1
νr(Grcos 2φ0+Hrsin 2φ0)ψ(θ, x)
+ (Hrcos 2φ0−Grsin 2φ0)χ(θ, x)
+A1+A2
E+A3
E2+A4
E3+B1E+B2E2,(47)
where
x=µr−E
νr
,(48)
and where νris the resonance half-width (corresponds to Γ/2 in the Breit-Wigner
notation), µris the resonance energy, Gris the symmetric total parameter, Hr
is the asymmetric total parameter, and the Aiand Biare coefficients of the
total background correction.
The fission and capture cross section both use the form
σx(E) = π√E
k2X
r
1
νr
[Grψ(θ, x) + Hrχ(θ, x)]
+A1+A2
E+A3
E2+A4
E4+B1E+B2E2,(49)
where the values of G,H,Ai, and Biappropriate for the desired reaction are
used.
Doppler-broadening can be applied as for the SLBW case, except note that
Γrin Eq. 27 must be replaced with 2νr. Doppler-broadened Adler-Adler cross
sections are more accurate than SLBW cross sections because the background is
smoother. However, cross sections below about 16kT/A will still be inaccurate.
The Adler-Adler method is not used in modern evaluations.
NJOY2016 57
LA-UR-17-20093 3 RECONR
Reich-Moore Representation (RM) The Reich-Moore representation as
implemented in subroutine csrmat is a multi-level formulation with two fission
channels; hence, it is useful for both structural and fissionable materials. The
cross sections are given by
σt=2π
k2X
`X
J
gJn1−Re U`J
nm+ 2d`J 1−cos(2φ`)o,(50)
σn=π
k2X
`X
J
gJn|1−U`J
nn|2+ 2d`J 1−cos(2φ`)i,(51)
σf=4π
k2X
`X
J
gJX
c|I`J
nc |2,and (52)
σγ=σt−σn−σf,(53)
where Inc is an element of the inverse of the complex R-matrix and
U`J
nn = e2iφ`h2Inn −1i.(54)
The elements of the R-matrix are given by
R`J
nc =δnc −i
2X
r
Γ1/2
nr Γ1/2
cr
Er−E−i
2Γγr
.(55)
In these equations, “c” stands for the fission channel, “r” indexes the resonances
belonging to spin sequence (`, J), and the other symbols have the same meanings
as for SLBW or MLBW. Of course, when fission is not present, σfcan be
ignored. The R-matrix reduces to an R-function, and the matrix inversion
normally required to get Inn reduces to a simple inversion of a complex number.
As in the MLBW case, the summation over Jruns from
||I−`| − 1
2| → I+`+1
2.(56)
The term d`J in the expressions for the total and elastic cross sections is used
to account for the possibility of an additional contribution to the potential scat-
tering cross section from the second channel spin. It is unity if there is a second
Jvalue equal to J, and zero otherwise. This is just a slightly different approach
for making the correction discussed in connection with Eq. (43). Returning to
the I=1, `=1 example given above, dwill be one for J=1/2 and J=3/2, and it
will be zero for J=5/2.
58 NJOY2016

3 RECONR LA-UR-17-20093
ENDF-6 format RM evaluations can contain a parameter LAD that indicates
that these parameters can be used to compute an angular distribution for elastic
scattering if desired (an approximate angular distribution is still given in File 4
for these cases). The current version of RECONR has such a capability, and it
can be used with RM evaluations. Because of channel-spin issues, it works best
with RML evaluations. See below for a discusion of angular distributions.
Hybrid R-Function Representation (HRF) The Hybrid R-Function rep-
resentation treats elastic scattering as a multi-level cross section using formulas
similar to those given above for the Reich-Moore format in the case where fis-
sion is absent. The other reactions are treated with formulas similar to those of
the SLBW method. The main use for this format is to provide a better repre-
sentation of competitive reactions than is provided by any of the other formats
described above. This treatment can include a background R-function, tabu-
lated charged-particle penetrabilities, and optical model phase shifts. Following
the RM notation, the elastic cross section is given by
σn=π
k2X
`
I+1
2
X
s=|I−1
2|
l+s
X
J=|l−s|
gJ|1−U`sJ
nn |2,(57)
where the Ufunction is given by the scalar version of Eq. (54):
U`sJ
nn = e2iφ`h2
R`sJ
nn −1i.(58)
The R-function itself is given by
R`sJ
nn = 1 −i
2X
r
Γnr
Er−E−i
2Γγr −i P`sJ R0
`sJ ,(59)
where R0
`sJ is a (complex) background R function and P`sJ is a penetrability
factor. The background R function can either be read in or set to zero. The pen-
etrability and shift factors are computed from the scattering radius or channel
radius as for SLBW. The phase shifts φ`sJ can be computed from the scattering
radius as before, or the (complex) phase shifts can be read in from an optical
model calculation.
Note that resonance parameters are given explicitly for all three quantum
numbers `,s, and J. No correction to the potential scattering cross section
from repeated Jvalues is needed.
NJOY2016 59

LA-UR-17-20093 3 RECONR
Elastic angular distributions can also be computed from HRF parameters if
the LAD parameter is set; however, RECONR does not support that.
Reich-Moore-Limited Representaton (RML) The Reich-Moore-Limited
representation is a more general multilevel and multichannel formulation. In ad-
dition to the normal elastic, fission, and capture reactions, it allows for inelastic
scattering and Coulomb reactions. Furthermore, it allows resonance angular
distributions to be calculated. It is also capable of computing derivatives of
cross sections with respect to resonance parameters. See ERRORR. The RML
processing in NJOY is based on the SAMMY code[36]. The calculation in RE-
CONR makes use of several subroutines exported by the samm module; namely,
s2sammy,ppsammy,rdsammy,cssammy, and desammy.
The quantities that are conserved during neutron scattering and reactions
are the total angular momentum Jand its associated parity π, and the RML
format lumps all the channels with a given Jπinto a “spin group.” In each spin
group, the reaction channels are defined by c= (α, `, s, J), where αstands for
the particle pair (masses, charges, spins, parities, and Q-value), `is the orbital
angular momentum with associated parity (−1)`, and sis the channel spin (the
vector sum of the spins of the two particles of the pair). The `and svalues
must vector sum to Jπfor the spin group. The channels are divided into incident
channels and exit channels. Here, the important input channel is defined by the
particle pair neutron+target. There can be several such incident channels in
a given spin group. The exit channel particle pair defines the reaction taking
place. If the exit channel is the same as the incident channel, the reaction is
elastic scattering. There can be several exit channels that contribute to a given
reaction.
The R-matrix in the Reich-Moore “eliminated width” approximation for a
given spin group is given by
Rcc0=X
λ
γλcγλc0
Eλ−E−iΓλγ/2+Rb
cδcc0,(60)
where cand c0are incident and exit channel indexes, λis the resonance index
for resonances in this spin group, Eλis a resonance energy, γλc is a resonance
amplitude, and Γλγ is the “eliminated width,” which normally includes all of the
radiation width (capture). The channel indexes runs over the “particle channels”
only, which doesn’t include capture. The quantity Rb
cis the “background R-
matrix.”
60 NJOY2016
3 RECONR LA-UR-17-20093
In order to calculate the contribution of this spin group to the cross sections,
we first compute the following quantity:
Xcc0=P1/2
cL−1
cX
c00
Y−1
cc00 Rc00c0P1/2
c0,(61)
where
Ycc00 =L−1
cδcc00 −Rcc00 ,(62)
and
Lc=Sc−Bc+iPc.(63)
Here, the Pcand Scare penetrability and shift factors, and the Bcare boundary
constants. The cross sections can now be written down in terms of the Xcc0. For
elastic scattering
σelastic =4π
k2
αX
Jπhsin2φc(1 −2Xi
cc)−Xr
cc sin(2φc) + X
c0|Xcc0|2i,
where Xr
cc0is the real part of Xcc0,Xi
cc0is the imaginary part, φcis the phase
shift, the sum over Jπis a sum over spin groups, the sum over cis limited to
incident channels in the spin group with particle pair αequal to neutron+target,
and the sum over c0is limited to exit channels in the spin group with particle
pair α. Similarly, the capture cross section becomes
σcapture =4π
k2
αX
JπX
c
gJα X
chXi
cc −X
c0|Xcc0|2i,(64)
where the sum over Jπis a sum over spin groups, the sum over cis a sum over
incident channels in the spin group with particle pair αequal to neutron+target,
and the sum over c0includes all channels in the spin group. The cross sections
for other reactions (if present) are given by
σreaction =4π
k2
αX
Jπ
gJα X
chXi
cc −X
c0|Xcc0|2i,(65)
where the sum over cis limited to channels in the spin group Jπwith particle
pair αequal to neutron+target, and the sum over c0is limited to channels in
the spin group with particle pair α0. The reaction is defined by α→α0. This
is one of the strengths of the RML representation. The reaction cross sections
can include multiple inelastic levels with full resonance behavior. They can
also include cross sections for outgoing charged particles, such as (n,α) cross
NJOY2016 61
LA-UR-17-20093 3 RECONR
sections, with full resonance behavior. The total cross section can be computed
by summing up its parts.
For non-Coulomb channels, the penetrabilities P, shift factors S, and phase
shift φare the same as those given for the SLBW representation, except if a Q
value is present, ρmust be modified as follows:
ρ= (2.196771×10−3)A
A+ 1r|E+A+ 1
AQ|.(66)
These factors are a little more complicated for Coulomb channels. See the
SAMMY reference for more details.
The RML representation is new to the ENDF format, and it isn’t represented
by any cases in ENDF/B-VII.0. There are experimental evaluations for 19F
and 35Cl from ORNL available. However, the RML approach provides a very
faithful representation of resonance physics, and it should see increasing use in
the future.
RML Angular Distributions. One of the physics advances available when
using the RML format is the calculation of angular distributions from the reso-
nance parameters. A Legendre representation is used:
dσαα0
dΩCM
=X
L
BLαα0(E)PL(cos β),(67)
where the subscript αα0indicates the cross section as defined by the two particle
pairs, PLis the Legendre polynomial of order L, and βis the angle of the
outgoing particle with respect to the incoming neutron in the CM system. The
coefficients BLαα0(E) are given by a complicated six level summation over the
elements of the scattering matrix U, where
Ucc0= ΩcWcc0Ωc0,(68)
where
Ωc= ei(wc−φc),(69)
and
W=I+ 2iX , (70)
62 NJOY2016
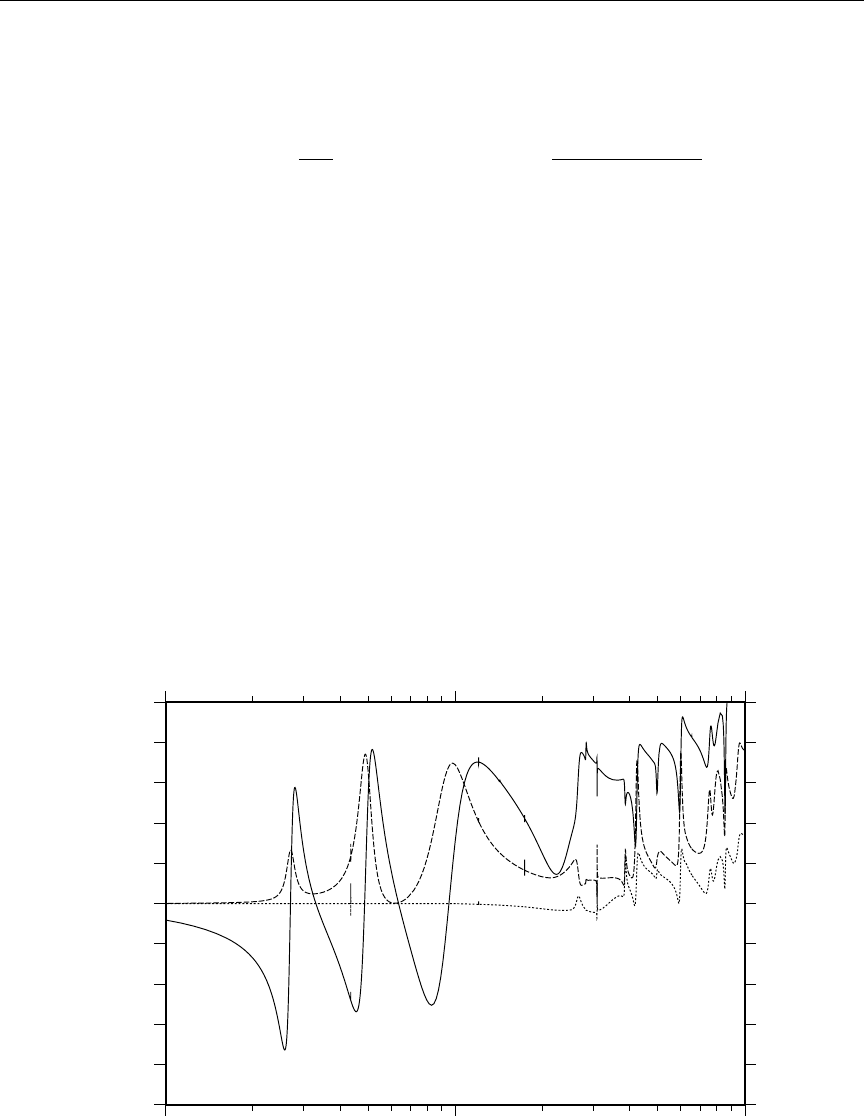
3 RECONR LA-UR-17-20093
with Ibeing the identity matrix and Xhaving been already given in Eq. 61.
The coefficients Bbecome
BLαα0(E) = 1
4k2
αX
AX
BX
CX
DX
EX
F
1
(2i+ 1)(2I+ 1)
×Gc1c0
1;c2c0
2;LRe[(δc1c0
1−Uc1c0
1)(δc2c0
2−U∗
c2c0
2)] .(71)
The spins Iand iare for the target and projectile for particle pair α. The
complex expressions for the geometric coefficient Gare given in the SAMMY
documentation. The six summations are as follows:
A sum over spin groups defined by Jπ
1
B sum over spin groups defined by Jπ
2
C sum over entrance channels c1belonging to group Jπ
1with particle pair α
D sum over exit channels c0
1belonging to group Jπ
1with particle pair α0
E sum over entrance channels c2belonging to group Jπ
2with particle pair α
F sum over exit channels c0
2belonging to group Jπ
2with particle pair α0
Fig. 3shows the first few Legendre coefficients for the elastic scattering cross
sections as computed by NJOY from the experimental evaluation for 19F.
104105106
Energy (eV)
-0.5
-0.4
-0.3
-0.2
-0.1
-0.0
0.1
0.2
0.3
0.4
0.5
Coefficient
Figure 3: Legendre coefficients of the angular distribution for elastic scattering in 19F using
the RML resonance representation (P1solid, P2dashed, P3dotted).
NJOY2016 63

LA-UR-17-20093 3 RECONR
Although first introduced in NJOY2012, computing resonance angular dis-
tributions is a new, little used feature, and so it is not enabled by default. To
activate it, change Want Angular Dist to true. The Legendre coefficients are
written into a section of File 4 on the RECONR PENDF file. Because the nor-
mal ENDF File 4 sections are not copied to the PENDF File 4, the presence of
File 4 on a PENDF file can be detected by subsequent modules, such a ACER or
GROUPR, and the resonance angular distributions can be used to replace the
ENDF File 4 values over the resonance energy range. The default in NJOY2016
is to use the conventional RM processing path for RM parameters. However,
there is an option to convert the RM parameters into RML format and process
them with the RML methods. If this is done, resonance angular distributions
can be computed for an RM evaluation. Change Want SAMRML RM to true.
Infinitely-Dilute Unresolved Range Parameters Infinitely dilute cross
sections in the unresolved-energy range are computed in csunr1 or csunr2 using
average resonance parameters and probability distributions from File 2. With
the approximations used, these cross sections are not temperature dependent;
therefore, the results are a good match to resolved resonance data generated
using tempr>0. The formulas used are based on the SLBW approximation with
interference.
σn(E) = σp+2π2
k2X
`,J
gJ
DΓ2
nRn−2Γnsin2φ`,(72)
σx(E) = 2π2
k2X
`,J
gJ
DΓnΓxRx,and (73)
σp=4π
k2X
`
(2`+ 1) sin2φ`,(74)
where xstands for either fission or capture, Γiand Dare the appropriate average
widths and spacing for the `,J spin sequence, and Riis the fluctuation integral
for the reaction and sequence (see gnrl). These integrals are simply the averages
taken over the chi-square distributions specified in the file; for example,
ΓnΓfRi=ΓnΓf
Γ
=ZdxnPµ(xn)ZdxfPν(xf)ZdxcPλ(xc) (75)
×Γn(xn) Γf(xf)
Γn(xn)+Γf(xf)+Γγ+ Γc(xc),(76)
64 NJOY2016

3 RECONR LA-UR-17-20093
where Pµ(x) is the chi-square distribution for µdegrees of freedom. The integrals
are evaluated with the quadrature scheme developed by R. Hwang for the MC2-2
code[38] giving
Rf=X
i
Wµ
iX
j
Wν
jX
k
Wλ
k
Qµ
iQν
j
ΓnQµ
i+ ΓfQν
j+ Γγ+ ΓcQλ
k
.(77)
The Wµ
iand Qµ
iare the appropriate quadrature weights and values for µdegrees
of freedom, and Γγis assumed to be constant (many degrees of freedom). The
competitive width Γcis assumed to affect the fluctuations, but a corresponding
cross section is not computed. The entire competitive cross section is supposed
to be in the File 3 total cross section as a smooth background.
It should be noted that the reduced average neutron width Γ0
n(AMUN) is
given in the file, and
Γn= Γ0
n√E V`(E),(78)
where the penetrabilities for the unresolved region are defined as
V0= 1 ,(79)
V1=ρ2
1 + ρ2,and (80)
V2=ρ4
ρ+ 3ρ2+ρ4.(81)
Other parameters are defined as for SLBW.
Unresolved resonance parameters can be given as independent of energy, with
only fission widths dependent on energy, or as fully energy dependent. The first
two options are processed in csunr1, and the last one is processed in csunr2.
3.5 Code Description
RECONR is implemented as a public subroutine reconr exported by the Fortran-
90 module reconm defined by reconr.f90.
The first step is to read cards 1, 2, and 3 of the user’s input. The TAPEID
record of the input file (nendf) is read and printed, then the new TAPEID record
is written to the output file (npend). RECONR is now ready to enter the loop
over the desired materials.
For each material, space is allocated for the energy nodes (enode), and ruin
is called to read cards 4 through 7 of the user’s input. If the reconstruction tem-
perature (tempr) is greater than zero, a table of ψand χfunctions is generated
NJOY2016 65

LA-UR-17-20093 3 RECONR
(the W table is used; see wtab and quickw). The findf utility routine from
module endf is then used to find the first card of File 1 (MF=1, MT=451) for
the desired material.
File 1 on the input ENDF file is examined to obtain certain constants and
flags and to analyze the directory (anlyzd). Subroutine anlyzd determines
which reactions should be considered “redundant”; that is, the reactions that
are sums of other reactions and will be included on the output PENDF file.
The total cross section (MT=1 for neutrons, MT=501 for photons) will always
be included; the nonelastic cross section (MT=3) will be included if it is needed
for photon production (that is, MF=12, MT=3 is found); the inelastic cross
section (MT=4) will be included if sections with MT in the range 51 – 91 occur
in the file, and the total fission reaction (MT=18) will be called redundant if
the partial fission representation (MT=19, 20, 21, 38) is found. MT103 (n,p)
can be a summation reaction if its partials MT600, MT601, ..., are present, and
the same for the other charged-particle absorption reactions. Space for the new
material directory is then allocated (mfs,mts,ncs). Section identification and
card counts will be entered into these arrays as they are determined.
File 2 on the ENDF file is now checked using s2sammy (which was imported
from the samm module) to see whether the sammy method is needed. This
depends on whether RML resonance parameters are found, and whether con-
version to RML format has been requested for Reich-Moore or Breit-Wigner
data (see Want SAMRML RM and Want SAMRML BW). The variable nmtres flags the
use of SAMMY processing. Because RML evaluations can include more than
the normal elastic, fission, and capture reactions, a list of reactions identified is
printed. Here is an example from an experimental 19F evaluation.
resonance range information
----------------------------------
ier energy-range lru lrf method
1 1.000E-05 1.000E+06 1 7 sammy
samm resonance reactions: 2 102 51 52
samm max legendre order: 7
generating File 4 for resonance angular distributions
The next step is to read File 2, which contains resolved and unresolved res-
onance parameters (if any). The array res is allocated to contain the File 2
66 NJOY2016

3 RECONR LA-UR-17-20093
data and rdfil2 is called to read them. This routine uses the additional rou-
tines rdf2bw,rdf2aa,rdf2hy,rdsammy,rdf2u0,rdf2u1, and rdf2u2 to read
the different types of resonance parameters. The subroutine rdsammy is im-
ported from the samm module. In addition, another imported routine ppsammy
is used to prepare for the SAMMY calculation. While the resonance parame-
ters are being stored, RECONR adds each resonance energy to its list of energy
nodes (enode). In the unresolved energy range, RECONR uses the energies
of tabulated parameters or fission widths if available. If the evaluation uses
energy-independent parameters, or if the energy steps between the nodes are
too large (see wide), rdfil2 creates additional node energies at a density of
approximately 13 points per decade (see egridu). Note that regions where the
unresolved representation for an element overlaps the resolved or smooth ranges
are found and marked by negative energy values. The energy nodes are sorted
into order and duplications are removed.
If the SAMMY method is active, and if angular distributions have been
requested (see Want Angular Dist), the maximum Legendre order defined by
the resonance data is printed out.
If unresolved data are present, subroutine genunr is called to compute the
infinitely-dilute unresolved average cross sections on the unresolved energy grid
using csunr1 or csunr2. Any backgrounds on File 3 are included, except in
regions of resolved-unresolved or unresolved-smooth overlap. The computed
cross sections are arranged in the order required by the special section with
MF=2 and MT=152, which is written onto the PENDF tape by recout. Using
the normal ENDF style, this format is defined by the following:
[MAT,2,152/ZA,AWR,LSSF,0,0,INTUNR]HEAD
[MAT,2,152/0.,0.,5,1,NW,NUNR/
E1,STOT1,SELAS1,SFIS1,SCAP1,STRN1,
E2,STOT2,SELAS2,SFIS2,SCAP2,STRN2,
...
ENUNR,STOTNUNR,....]LIST
where NW = 6 + 6*NUNR. The definitions of the energy and cross section en-
tries are fairly obvious, except STRN stands for the current-weighted total cross
section. This format is specialized to “infinite dilution.” The more general form
used for self-shielded effective cross sections will be described in the UNRESR,
PURR, and GROUPR chapters of this manual.
NJOY2016 67

LA-UR-17-20093 3 RECONR
The subroutine lunion is used to linearize and unionize the ENDF data.
Space is reserved for two buffers to be used by loada/finda, for the lineariza-
tion stack (xand y), and for the ENDF scratch area (scr). The length of
the stack (ndim) determines the smallest possible subdivision of each panel (en-
ergy points as close as 2−ndim times the panel width can be generated). Since
the number of energies in the union grid may soon exceed the capacity of any
reasonable memory array, the existing list of energy nodes is copied to binary
scratch storage (the loada/finda system). This storage system consists of the
buffers bold and bnew and the scratch units iold and inew. The energy grid
points will “ping-pong” back and forth between units 14 and 15 as the union grid
is built up. Subroutine lunion now starts with MT=2 and checks each reaction
in sequence to determine whether the current grid (on iold) is sufficient to rep-
resent the reaction to within the desired tolerance using linear interpolation. If
not, RECONR adds additional points by adaptively halving the intervals. The
new grid is stored on inew. The units inew and iold are swapped, and the next
MT is processed. When all nonredundant reactions have been examined, the
list of energies in loada/finda storage is the desired linearized and unionized
grid. The storage used is deallocated.
This grid is used as the starting point for resonance reconstruction in resxs.
Subroutine resxs first reserves space for the loada/finda buffers bufr and
bufg, the linearization stack (xand y), and the partial cross sections (sig).
The length of the stack (ndim) determines the smallest possible subdivision of
a panel between two nodes (energy points as close a 2−ndim times the panel
width can be generated). Subroutine resxs then examines the grid on ngrid
(iold from lunion) panel by panel. Grid points are added and cross sections
computed until the convergence criteria discussed in Section 3.3 are satisfied.
The cross sections are copied to nout using loada, and resxs continues to the
next panel. This procedure is continued until all panels are converged. The
result is a tape (nout) containing the energy grid in the resonance region and
the total, elastic, fission, capture, and possibly additional cross sections at each
energy point.
Unionization is obtained automatically in the resonance region since all of
the partials are computed simultaneously in sigma, using csslbw for SLBW
parameters, csmlbw for MLBW parameters, csaa for multi-level Adler-Adler
parameters, csrmat for Reich-Moore parameters, cshyb for Hybrid R-Function
parameters, cssammy for Reich-Moore-Limited parameters, and sigunr for unre-
solved resonance parameters. This last routine retrieves the cross sections from
68 NJOY2016

3 RECONR LA-UR-17-20093
the table prepared by genunr. Subroutine cssammy is imported from the samm
module. A special feature of RECONR is the ability to reconstruct the cross
sections at tempr by ψχ broadening if SLBW or Adler-Adler parameters are
given. This can also be done for MLBW using the GH method implemented by
csmlbw2. The Doppler-broadened resonance shapes are obtained using quickw
(see description in the UNRESR chapter), and the linearization procedure pro-
ceeds as before.
The resonance cross sections on ngrid are merged with the ENDF cross
sections in emerge. First, the background grid from lunion is merged with the
resonance grid from resxs and written onto the loada/finda file, which will
accumulate the total cross section and any other redundant reactions required
(iold/inew). A loop is then set up over all nonredundant reactions. For each
grid point, the ENDF background cross section is obtained by interpolation. If
this grid point has a resonance contribution on nres, it is added. The resulting
net cross section at this point is added into the appropriate redundant cross
sections on iold/inew and also saved on ngrid. When all the energies for this
reaction have been processed, the cross sections on ngrid are converted into a
TAB1 record and written on nscr. This loop is continued until all reactions
have been processed. When emerge is finished, nscr contains cross sections for
all the nonredundant reactions, and iold contains the redundant summation
reactions.
Control now passes to recout, which writes the new File 1 comments and dic-
tionary. It also writes a default version of the section with MF=2 and MT=151
that gives no resonance parameters. The upper limit of the resolved energy
range, eresh, is added to the “C2” field of the third card so that BROADR
knows not to broaden into the unresolved energy range. For materials with un-
resolved data, a specially formatted section (MF=2, MT=152) is written con-
taining the infinitely-dilute unresolved cross sections. This section can be used
by BROADR and GROUPR to correct for resolved-unresolved overlap effects,
if necessary. Subroutine recout then steps through the reactions on nscr and
iold. Redundant summation reactions are converted to TAB1 records and in-
serted in the correct order. Nonredundant reactions are simply copied. Finally,
a MEND record is added and control is returned to reconr.
Now reconr either directs that this process be repeated for another isotope
or writes a TEND record and terminates. The result is a new file in ENDF
format containing the desired pointwise cross sections. Normally, only Files 1,
2, 3, 10, and 13 are included for neutron files. However, if angular distribution
NJOY2016 69

LA-UR-17-20093 3 RECONR
processing has been requested, a File 4 containing the Legendre coefficients will
also be written. Because the original ENDF File 4 was not copied to the PENDF
file, the presence of sections of File 4 on the PENDF file provides a flag to
subsequent modules that resonance angular distributions have been calculated.
Only Files 1 and 23 are included for a photon file.
The SAMMY method is implemented in a separate Fortran-90 module samm
defined by sammy.f90. It exports the subroutines cssammy (computes cross sec-
tions, angular distributions, and derivatives), s2sammy (scans File 2 to see if
SAMMY method is needed and measure some sizes), ppsammy (sets up SAMMY
calculation), rdsammy (reads in File 2 data with optional conversion of BW or
RM data to RML form), and desammy (cleans up after the SAMMY calcula-
tion). It also exports some logical parameters, namely, Want Partial Derivs,
Want Angular Dist,Want SAMRML RM and Want SAMRML BW. See ERRORR for
the use of derivatives. If conversion from BW and/or RM was requested, it is
possible to get the resulting File 2 values printed out for checking. Just set imf2
in sammy.f90 to 1.
The cssammy subroutine uses abpart to compute some energy-independent
pieces of the cross sections and derivatives. The main work for cross sections,
angular distributions, and derivatives in done in cross. The results for cross
sections are returned in sigp to be consistent with the other “cs” routines in RE-
CONR. Angular distributions are returned in siga, and sensitivities are returned
in sigd (derivatives of cross sections with respect to parameters). Subroutine
cross starts by initializing the quantities being calculated (cross sections, maybe
angular distributions, maybe derivatives), and then it sets up a loop over the
spin-parity groups. It initializes the results for this spin group and then calls
setr to compute the elements of the R-matrix (see Eq. 60 and other quantities,
such as the Y matrix, penetrabilities (rootp), and phase shifts. It then inverts
the Y matrix and calculates the X matrix of Eq. 61. See setxqx. It can then
use the X matrix to compute the contributions to the cross sections (sectio),
maybe angular distributions (setleg), and maybe derivatives from this spin
group and add them into the sum over groups. When the loop over spin groups
is complete, it normalizes things properly and returns its results.
Going back to subroutine setr, it computes the R-matrix first. It then
computes the phase shift, penetrabilities, and shift factors. For non-Coulomb
cases, the phase shifts come from sinsix, and the penetrability Pand boundry
condition (S−B+iP )−1come from pgh. For Coulomb cases, subroutine pghcou
computes all of these quantities. The penetrability Pis converted to rootp for
70 NJOY2016

3 RECONR LA-UR-17-20093
use in Eq. 61.
3.6 Input Instructions
The input instructions for each module are given in the code as comment cards
at the beginning of the source code for each module. The RECONR instructions
are reproduced here for the convenience of the reader.
!---input specifications (free format)---------------------------
!
! card 1
! nendf unit for endf tape
! npend unit for pendf tape
! card 2
! tlabel 66 character label for new pendf tape
! delimited with quotes, ended with /.
! card 3
! mat material to be reconstructed
! ncards number of cards of descriptive data for new mf1
! (default=0)
! ngrid number of user energy grid points to be added.
! (default=0)
! card 4
! err fractional reconstruction tolerance used when
! resonance-integral error criterion (see errint)
! is not satisfied.
! tempr reconstruction temperature (deg kelvin)
! (default=0)
! errmax fractional reconstruction tolerance used when
! resonance-integral error criterion is satisfied
! (errmax.ge.err, default=10*err)
! errint maximum resonance-integral error (in barns)
! per grid point (default=err/20000)
! (note: the max cross section difference for
! linearization, errlim, and for reconstruction,
! errmin, are also tied to errint. to get maximum
! accuracy, set errint to a very small number.
! for economical production, use the defaults.)
! card 5
! cards ncards of descriptive comments for mt451
! each card delimited with quotes, ended with /.
NJOY2016 71

LA-UR-17-20093 3 RECONR
! card 6
! enode users energy grid points
!
! cards 3, 4, 5, 6 must be input for each material desired
! mat=0/ terminates execution of reconr.
!
!-------------------------------------------------------------------
A sample input for processing an isotope from ENDF/B-VII follows (the line
numbers are for reference only and are not part of the input). First, mount the
ENDF/B-VII file for 235U on unit 20.
1. reconr
2. 20 21/
3. ’pendf tape for U-235 from ENDF/B-VII’/
4. 9228 2/
5. .001/
6. ’92-U-235 from ENDF/B-VII’/
7. ’processed with NJOY’/
8. 0/
Card 2 tells RECONR that the input ENDF tape will be on unit 20, and that
the output PENDF tape will be on unit 21. Card 3 is a “TAPEID” label for the
output PENDF file. Card 4 gives the MAT number for U-235 and says that two
additional comment cards will be given. Card 5 sets the reconstruction tolerance
to 0.1% (.001 as a fraction) with all its other parameters defaulted. Cards 6 and
7 are the two comment cards to be inserted into the PENDF files MF1/MT451
section. Finally, the “0/” terminates the RECONR input. The capability to
loop over multiple isotopes in RECONR is rarely used for neutron files, but it is
useful for photon interaction processing (see GAMINR). The resulting PENDF
tape will contain the desired TAPEID card, followed by 235U data, a MEND
card and a TEND card.
3.7 Error Messages
error in reconr***illegal nsub for reconr
72 NJOY2016

3 RECONR LA-UR-17-20093
RECONR only processes sublibraries that contain cross section data. Check
whether the right input ENDF input tape was mounted.
error in anlyzd***too many redundant reactions
Increase the global parameter nmtmax=10.
error in xxxxxx***storage in enode exceeded
Too many energy nodes including the user’s nodes and the energies from
MF=2. Increase the global parameter nodmax=800000. This message can
come from rdf2bw,rdf2aa,rdf2hy,rdf2u0,rdf2u1, or rdf2u2.
error in xxxxxx***res storage exceeded
Too much resonance data. This should not occur for a conforming ENDF-
format file, because maxres is computed from the MF=2 line count in
the MF=1/MT=451 index. This message can come from rdfil2,rdf2bw,
rdf2aa,rdf2hy,rdf2u0,rdf2u1, or rdf2u2.
error in xxxxxx***storage in eunr exceeded.
Increase the global parameter maxunr=500. This message can come from
rdfil2,rdf2u1, or rdf2u2.
error in rdfil2***illegal resonance mode.
A resonance mode has been requested that RECONR does not understand.
error in rdf2bw***energy-dep scattering radius ...
This option is only used in MLBW for current evaluations.
message from rdf2bw***calc... of angular distribution not...
This option is only partially available in RECONR. This message can come
from rdf2bw (for Reich-Moore cases) or from rdf2hy (Hybrid R function).
error in rdf2hy***hybrid competing reactions not yet added
This option is not yet available in RECONR.
error in lunion***ill behaved threshold
The routine is having trouble adjusting the threshold to agree with the Q
value. Check the points near the threshold for this evaluation.
error in lunion***exceeded stack
Increase length of linearization stack ndim (currently 50).
error in resxs***stack exceeded
Increase length of reconstruction stack ndim (currently 50).
error in sigma***general r-matrix not installed.
This option is not yet available in RECONR.
error in sigma***illegal option.
There is a problem with the ENDF tape.
error in csmlbw***not coded for temperature gt 0 deg k
The ψχ Doppler-broadening doesn’t work for normal MLBW. This message
shouldn’t occur, because temperatures greater than zero will cause csmlbw2
to be called.
NJOY2016 73

LA-UR-17-20093 3 RECONR
error in csrmat***not coded for temperature gt 0 deg k
The ψχ Doppler-broadening doesn’t work for RM. Use tempr=0. only.
error in cshybr***doppler broad’g not provided for hybrid
The ψχ Doppler-broadening doesn’t work for hybrid parameters. Use
tempr=0. only.
error in csaa***bad li value
There is an error in the evaluation format.
message from emerge---negative elastic cross sects found
Negative elastic cross sections can occur for SLBW evaluations.
error in recout***for mf --- mt ---
Indexing and pair count for this section do not make sense.
calculation of angular distribution not installed -
Message comes from several resonance types that do not support the calcu-
lation of angular distributions. Some of them can be used if Want SAMRL RM
or Want SAMRML BW are true.
message from s2sammy***multiple isotopes... -
Multiple isotopes for RM sections don’t work with the SAMMY method.
The code automatically reverts to normal RM processing.
error in s2sammy***res storage exceeded. -
Storage limited to maxres. Shouldn’t occur.
error in s2sammy***energy-dep scattering length... -
This only works for MLBW parameters.
error in rearrange***nres fault -
Trouble while rearranging resonances into spin-group order.
errorr in findsp***quantum numbers in file 2 do not... -
Problems with the quantum numbers for the evaluation.
error in checkqn***error in quantum numbers -
Problems with the quantum numbers for the evaluation.
error in lmaxxx***lllmax limit to 51 -
Problems with the Clebsch-Gordan coefficients for the angular distribu-
tions.
error in clbsch***did not count correctly -
Problems with the Clebsch-Gordan coefficients for the angular distribu-
tions.
error in pspcou***llmax larger than 100 -
Problem computing the Coulomb phase shifts.
error in bigeta***I0 sum failed -
Problem for the Coulomb routine.
74 NJOY2016

3 RECONR LA-UR-17-20093
error in bigeta***K0 sum failed -
Problem for the Coulomb routine.
error in bigeta***L1 sum failed -
Problem for the Coulomb routine.
error in bigeta***K1 sum failed -
Problem for the Coulomb routine.
error in setleg***nppx too large -
Problem generating Legendre polynomials.
3.8 Input-Output Units
The following logical units are used:
10 nscr1 in reconr,nout in lunion, and nin in emerge. Contains copy
of nonredundant sections from original ENDF tape.
11 nscr2 in reconr;ngrid in lunion,resxs, and emerge. Contains
union grid for ENDF tape (not counting resonances).
12 nscr3 in reconr,nout in resxs, and nres in emerge. Contains
resonance grid and cross sections.
13 nscr4 in reconr is used for two separate purposes. In resxs it is
a binary scratch file nscr used for the unthinned resonance data.
In emerge and recout, it is nmerge and contains the nonredundant
reactions on the union grid.
14/15 iold/inew in lunion. Are used locally only to accumulate union
grid for ENDF cross sections. Destroy after use.
14/15 iold/inew in emerge. Are used locally only to accumulate summa-
tion cross sections on union grid.
20-99 User’s choice for ENDF (nendf) and PENDF (npend) tape numbers
to link RECONR with other NJOY modules.
5,6,7 See the NJOY chapter for a description of the I/O units.
Note that 11, 12, 14, and 15 are always binary. Unit 10 has the same mode as
nendf. Unit 13 is binary when used in RESXS, and it has the same mode as
npend elsewhere. npend can have a different mode than nendf.
3.9 Storage Allocation
Storage allocation in RECONR is sensitive to (1) the amount of resonance pa-
rameter data, (2) the number of energy-grid node values, (3) the size of the
NJOY2016 75

LA-UR-17-20093 3 RECONR
resonance reconstruction stack, (4) the use of ψχ broadening, and (5) the sizes
of the loada/finda buffers. Other storage requirements are minor.
Buffer sizes can be reduced or increased at will. The result is a storage/speed
tradeoff with no change in capability or accuracy. See the global parameters
nbufg=2000, nbufr=2000, and nbuf=2000 at the beginning of the reconm mod-
ule.
The ψχ broadening option requires 7688 words of additional storage. There-
fore, memory use can be reduced if ψχ is not required. No code changes are
needed — just avoid tempr greater than zero.
Resonance reconstruction in resxs uses 5×ndim words. The parameter ndim
determines the smallest subdivision of a panel that can be obtained. Using
ndim=30 allows points to be generated with spacing as small as one-billionth of
the panel size (230).
The code currently allows for nodmax=800000 energy nodes and maxunr=500
unresolved points. These values tend to increase as additional very detailed
resonance evaluations appear, but the current values seem to be sufficient for
the evaluations existing as of this writing.
76 NJOY2016

4 BROADR LA-UR-17-20093
4 BROADR
BROADR module generates Doppler-broadened cross sections in PENDF for-
mat starting from piecewise linear cross sections in PENDF format. The input
cross sections can be from RECONR or from a previous BROADR run. The
code is based on SIGMA1[27] by D. E. Cullen. The method is often called “ker-
nel broadening” because it uses a detailed integration of the integral equation
defining the effective cross section. It is a fully accurate method, treating all res-
onance and non-resonance cross sections including multilevel effects. BROADR
has the following features:
•An alternate calculation is used for low energies and high temperatures
that corrects a numerical problem of the original SIGMA1. (This problem
has been corrected in another way in later versions of SIGMA1.)
•Dynamic storage allocation is used, which allows the code to be run on
large or small machines with full use of whatever storage is made available.
•Reactions are broadened in parallel on a union grid, with the top of the
resolved resonance range being the typical upper limit for Doppler broad-
ening.
•The union grid is constructed adaptively to give a linearized representation
of the broadened cross section with tolerances consistent with those used
in RECONR. Energy points may be added to or removed from the input
grid as required for the best possible representation. Precision up to 9
significant figures is allowed for energies.
•The summation cross sections such as total, nonelastic, and sometimes
fission or (n,2n) are reconstructed to equal the sum of their parts.
•Standard thermal cross sections, integrals, and ratios are computed when
the temperature is 293.6K (0.0253 eV).
•The file directory (actually an index to the reactions present) is updated.
This chapter describes the BROADR module in NJOY2016.0.
4.1 Doppler-Broadening Theory
The effective cross section for a material at temperature Tis defined to be that
cross section that gives the same reaction rate for stationary target nuclei as the
real cross section gives for moving nuclei. Therefore,
ρvσ(v, T ) = Zdv0ρ|v−v0|σ(|v−v0|)P(v0, T ),(82)
NJOY2016 77
LA-UR-17-20093 4 BROADR
where vis the velocity of the incident particles, v0is the velocity of the target,
ρis the density of target nuclei, σis the cross section for stationary nuclei, and
P(v0, T ) is the distribution of target velocities in the laboratory system. For
many cases of interest, the target motion is isotropic and the distribution of
velocities can be described by the Maxwell-Boltzmann function
P(v0, T )dv0=α3/2
π3/2exp(−αv02)dv0,(83)
where α=M/(2kT ), kis Boltzmann’s constant, and Mis the target mass.
Eq. 82 can be partially integrated in terms of the relative speed V=|v−v0|
to give the standard form of the Doppler-broadened cross section:
σ(v) = α1/2
φ1/2v2Z∞
0
dV σ(V)V2ne−α(V−v)2−e−α(V+v)2o.(84)
It is instructive to break this up into two parts:
σ(v) = σ∗(v)−σ∗(−v),(85)
where
σ∗(v) = α1/2
π1/2v2Z∞
0
dV σ(V)V2e−α(V−v)2.(86)
The exponential function in Eq. (86) limits the significant part of the integral
to the range
v−4
√α< V < v +4
√α.
For σ∗(−v), the integral depends only on velocities satisfying
0≤V < 4
√α.
These results can be converted to energy units using
Em=1
2m4
√α2=16kT
A.
Some examples are given in Table 1. Doppler-broadening effects will be impor-
tant below this energy and for any features such as resonances, thresholds, or
artificial discontinuities in evaluations that are not slowly varying with respect
to 2√EmE. As an example, for 235U at 100 eV, Doppler effects are important
for features smaller than about 0.8 eV.
78 NJOY2016

4 BROADR LA-UR-17-20093
Table 1: Energy Parameter for Effective Doppler-Broadening
Target Temperature Energy Parameter (Em)
2H 300K 0.2 eV
235U 300K 0.0017 eV
235U 1.0 keV 69 eV
The numerical evaluation of Eq. (86) developed for SIGMA1 assumes that
the cross section can be represented by a piecewise linear function of energy
to acceptable accuracy. This is just the form of the NJOY PENDF files (see
RECONR). Defining the reduced variables y=√αx and x=√αV , the cross
section becomes
σ(x) = σi+si(x2−x2
i),(87)
with slope si= (σi+1 −σi)/(x2
i+1 −x2
i). Eq. (86) can now be written as
σ∗(y) = 1
π1/2y2
N
X
i=0 Zxi+1
xi
σ(x)x2e−(x−y)2dx =X
iAi[σi−six2
i]+Bisi,(88)
where
x0= 0 ,
xN+1 =∞,
Ai=1
y2H2+2
yH1+H0,and
Bi=1
y2H4+4
yH3+ 6H2+ 4yH1+y2H0,
and where Hnis shorthand for Hn(xi−y, xi+1−y). The extrapolations to zero
and infinity assume a constant cross section (s0=sN=0). The Hfunctions are
the incomplete probability integrals defined by
Hn(a, b) = 1
√πZb
a
zne−z2dz . (89)
These functions can be computed in two ways. First,
Hn(a, b) = Fn(a)−Fn(b),(90)
NJOY2016 79
LA-UR-17-20093 4 BROADR
where
Fn(a) = 1
√πZ∞
a
zne−z2dz . (91)
These functions satisfy a recursion relation that can be used to obtain
F0(a) = 1
2erfc(a),(92)
F1(a) = 1
2√πexp(−a2),and (93)
Fn(a) = n−1
2Fn−2(a) + an−1F1(a),(94)
where erfc(a) denotes the complementary error function
erfc(a) = 2
√πZ∞
a
e−z2dz . (95)
However, when Fn(a)≈Fn(b), the difference in Eq. (90) may lose significance.
In such cases, Hn(a, b) can be computed by a second method based on a direct
Taylor expansion of the defining integral. Write
Hn(a, b) = 1
√πZb
0
zne−zdz −1
√πZa
0
zne−z2dz =Gn(b)−Gn(a).(96)
But by Taylor’s Theorem,
Gn(b)−Gn(a) = b−a
1! G0
n(a) + ... +(b−a)m
m!G(m)
n(a) + ... . (97)
Also,
G(m)
n(x) = dm−1
dxm−1xne−x2= e−x2Pm
n(x),(98)
where Pm
n(x) is a polynomial with recursion relation
Pm
n(x) = d
dxPm−1
n(x)−2xP m−1
n(x),(99)
with P1
n=xn. From this point, it is straightforward to generate terms until the
desired number of significant figures is obtained.
When interpreting BROADR output, it is useful to remember several impor-
tant features of the Doppler-broadening process. A 1/v cross section remains
unchanged. Contrary to “popular knowledge”, the area under a resonance does
not remain unchanged unless EkT/A. In fact, each resonance develops a
new 1/v tail. Finally, a constant cross section (for example, elastic scattering)
80 NJOY2016
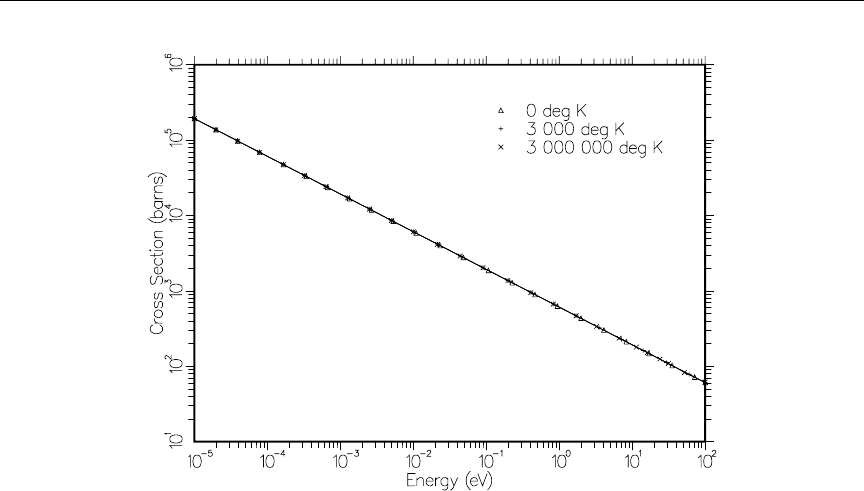
4 BROADR LA-UR-17-20093
Figure 4: The (n,α) cross section for 10B from ENDF/B-V for three different temperatures
showing that a 1/v cross section is invariant under Doppler-broadening.
develops a 1/v tail at low energies after Doppler-broadening. These effects are
shown in Figs. 4,5, and 6; they can be best understood by noting that the
Doppler process preserves reaction rate vσ(v) according to Eq. (82), and a finite
reaction rate is expected for T > 0K even as v→0.
Very early (1980s) versions of BROADR and SIGMA1 assumed that the
input energy grid from RECONR could also be used to represent the Doppler-
broadened cross section before thinning. The grid was then thinned to take
advantage of the smoothing effect of Doppler broadening. Unfortunately, this
assumption is inadequate. The reconstruction process in RECONR places many
points near the center of a resonance to represent its sharp sides. After broad-
ening, the cross section in this energy region becomes rather smooth; the sharp
sides are moved out to energies where RECONR provides few points. At still
higher energies, the resonance line shape returns to its asymptotic value, and the
RECONR grid is adequate once more. The more recent versions of BROADR
check the cross section between points of the incoming energy grid, and add ad-
ditional grid points if they are necessary to represent the broadened line shape
to the desired accuracy. This effect is illustrated in Fig. 7.
NJOY2016 81
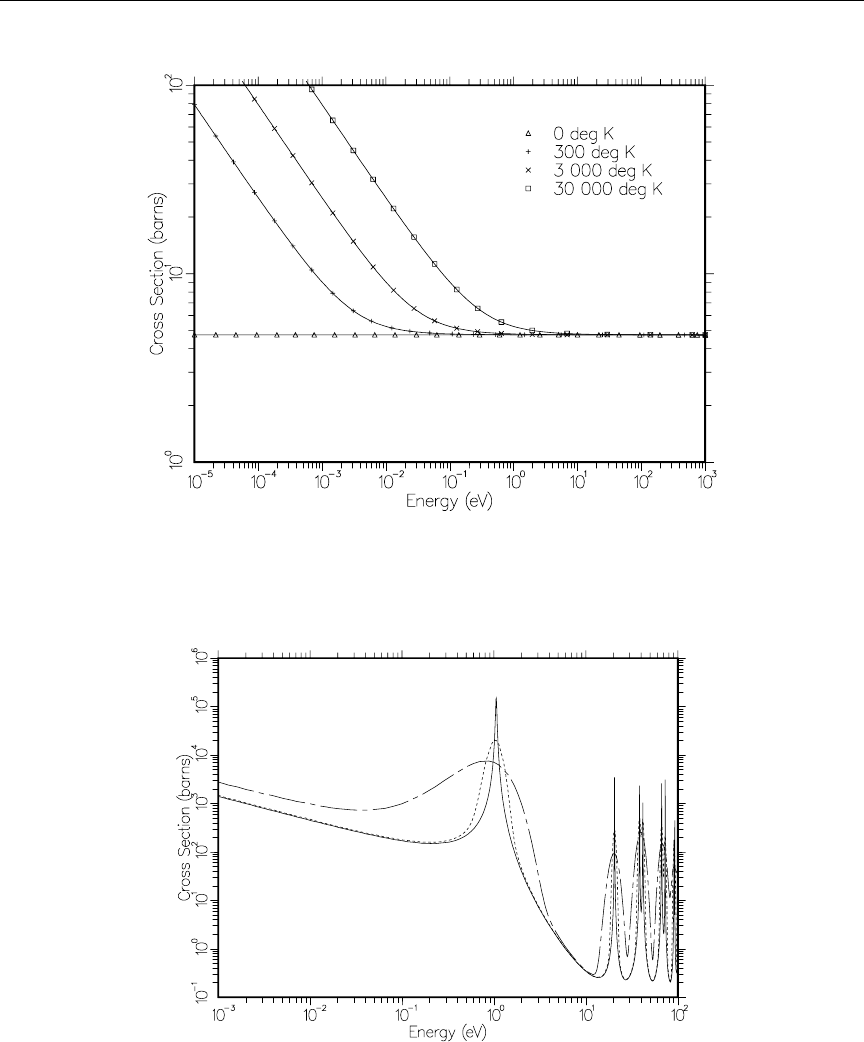
LA-UR-17-20093 4 BROADR
Figure 5: The elastic cross section for carbon from ENDF/B-V showing that Doppler-
broadening a constant cross section adds a 1/v tail.
Figure 6: The (n,γ) cross section for 240Pu for several temperatures showing the effects of
Doppler broadening on resonances. The temperatures are 0K (solid), 30 000K
(dotted), and 300 000K (dash-dot). The higher resonances behave in the classical
manner even at 30 000K; note that the line shape returns to the asymptotic value
in the wings of the resonance. All resonances at 300 000K (and to a lesser extent
the first resonance for 30 000K) show the additional 1/v component that appears
when kT/A is large with respect to the resonance energy.
82 NJOY2016
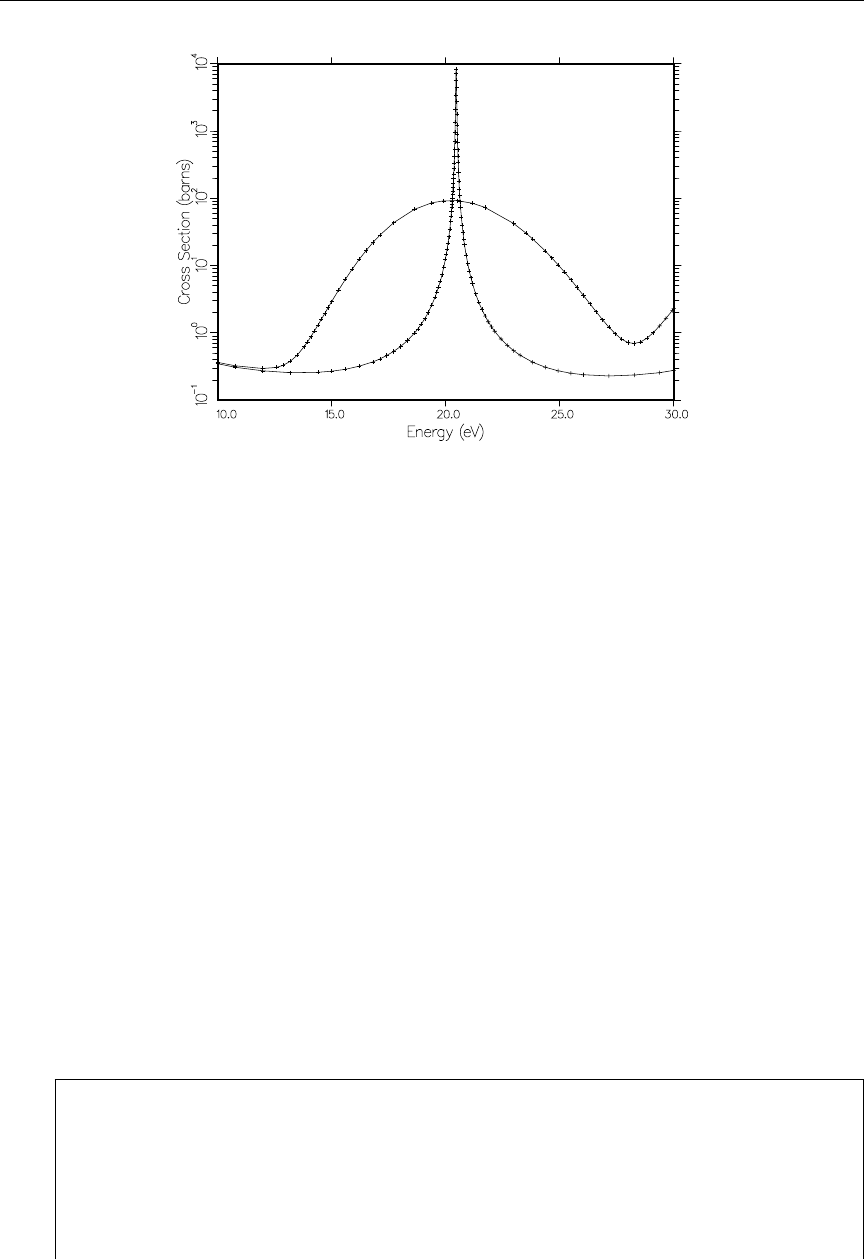
4 BROADR LA-UR-17-20093
Figure 7: An expanded plot of the 20 eV resonance from Fig. 6showing both thinning
and “thickening” of the energy grid produced adaptively by BROADR. The two
curves show the capture cross section at 0K and 300 000K. Note that the high-
temperature curve has fewer points than the 0K curve near the peak at 20 eV
and more points in the wings near 15 eV and 25 eV. Clearly, using the 0K grid to
represent the broadened cross section in the wings of this resonance would give
poor results.
4.2 Thermal Quantities
In thermal-reactor work, people make very effective use of a few standard ther-
mal constants to characterize nuclear systems. These parameters include the
cross sections at the standard thermal value of 0.0253 eV (2200 m/s), the in-
tegrals of the cross sections against a Maxwellian distribution for 0.0253 eV,
the g-factors (which express the ratio between a Maxwellian integral and the
corresponding thermal cross section), η,α, and K1. Here, ηis the Maxwellian-
weighted average of ( ¯
ν)σf)/(σf+σc), αis the average of σc/σf, and K1 is the
average of (¯ν−1)σf−σc. If BROADR is run for a temperature close to 293.6K
(which is equivalent to 0.0253 eV), these thermal quantities are automatically
calculated and displayed. Here is a sample output for 235U from ENDF/B-VII:
thermal quantities at 293.6 K = 0.0253 eV
-----------------------------------------
thermal fission xsec: 5.8490E+02
thermal fission nubar: 2.4367E+00
thermal capture xsec: 9.8665E+01
NJOY2016 83
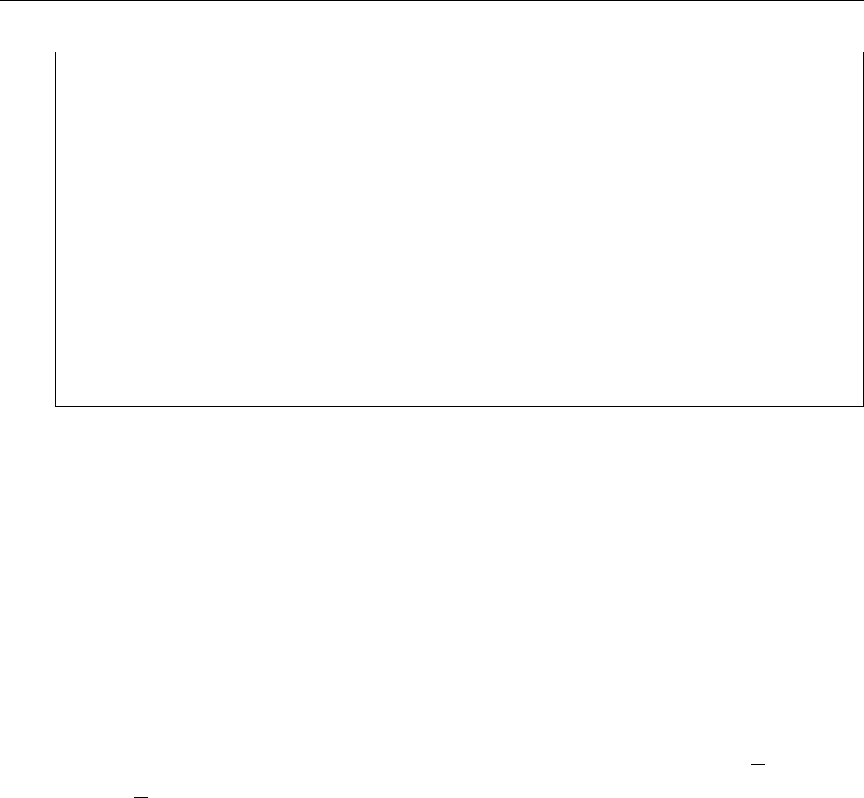
LA-UR-17-20093 4 BROADR
thermal capture g-factor: 9.9086E-01
thermal capture integral: 8.6639E+01
capture resonance integral: 1.4043E+02
thermal fission integral: 5.0605E+02
thermal fission g-factor: 9.7628E-01
thermal alpha integral: 1.6828E-01
thermal eta integral: 2.0859E+00
thermal k1 integral: 6.4040E+02
equivalent k1: 7.2262E+02
fission resonance integral: 2.7596E+02
-----------------------------------------
4.3 Data-Paging Methodology
A piecewise linear representation of a reaction cross section of a resonance mate-
rial may require a very large number of energy points. For example, ENDF/B-
VII 238U (MAT9237) requires 167 000 points for the total cross section for 0.1%
precision (errmax=err). It is impractical to load all these points into memory
simultaneously. However, the discussion following Eq. (86) in the theory section
shows that only a limited energy range around the point of interest is required.
The strategy used is to stage the cross-section data into three “pages” of
npage points each. Points in the center page can then be broadened using the
npage or more points on each side of the point of interest. If v−4/√αand
v+ 4/√αare both included in the three-page range, accurate broadening can
be performed. If not, a diagnostic warning is printed; the user should repeat
the calculation with a smaller temperature step or a larger page size.
There are many different reaction cross sections for each material. However,
the cross sections for high velocities are normally smooth with respect to 32kT/A
for any temperatures outside of stellar photospheres; therefore, they do not show
significant Doppler effects. Until recently the upper energy limit for Doppler
broadening was the smallest of (i) the input value thnmax, (ii) the upper limit
of the resolved-resonance energy range, (iii) the lowest threshold, or (iv) 1.0
MeV (the default input value for thnmax). No Doppler broadening or energy-
grid reconstruction is performed above that energy. In the past, and what users
typically expect as the default action, the second condition often set the Doppler
broadening upper limit.
However recent evaluated files have increasingly included threshold reactions
at energies within the resolved resonance energy range. For example, recent
84 NJOY2016

4 BROADR LA-UR-17-20093
JENDL evaluations for 235U include a resolved-resonance range upper limit of
2.25 keV, but also include non-zero cross sections for an inelastic level with a
77 eV threshold. Under the rules itemized above, Doppler broadening of these
data stops at 77 eV. Other evaluations (e.g., ENDF/B-VI, ENDF/B-VII and
JEFF-3.1) share the same resolved-resonance range data but have zeroed out
this inelastic cross section from 77 eV to 2.25 keV and so Doppler broadening of
these files occurs throughout the resolved-resonance range, as most users expect.
Zeroing out non-zero data is a cludge from the past and so we have changed
the Doppler upper energy limit logic so that the top of the resolved resonance
range is now the default condition. This means that non-threshold reactions
are also Doppler broadened. The mathematics of this operation can produce
non-zero cross sections at energies below the reaction threshold. If this occurs
those cross sections are zeroed.
As noted in the BROADR module source code comments, users may specify
a negative value for thnmax to override these selection rules and force Doppler
broadening to an upper energy of abs(thnmax) eV. This has been a long-term
NJOY feature that remains unchanged in NJOY2016.
Finally, we note that the Aiand Bifactors in Eq. (88) depend only on the
energy (or velocity) values and not on the cross sections. Since the Aiand Bi
are expensive to compute, the code computes them only once for the points
of a unionized energy grid. The sum of Eq. (88) is accumulated for all the
non-threshold reactions simultaneously. This feature helps make BROADR run
faster.
4.4 Coding Details
The main subroutine for BROADR is broadr from module broadm. The code
begins by reading the user’s input (see Section 4.5). Storage is then allocated for
the loada/finda buffers (ibufo and ibufn) and for the scratch storage (iscr).
The buffer length nbuf can be changed at will (currently nbuf is 1000).
The input PENDF tape is searched for the desired material (mat1). If the
restart option is set (istart=1), the temperatures less than or equal to temp1
for mat1 are assumed to have been broadened previously, and they are copied
to the output file. In either case, the files for temp1 are copied to a scratch file
on unit nscr1.
Next, nscr1 is rewound and examined reaction by reaction. The energy grid
from the total cross section (MT1) is saved on scratch storage using loada. If
the input tape has not been through RECONR, the BROADR module will still
NJOY2016 85

LA-UR-17-20093 4 BROADR
run, but at possibly reduced accuracy. The next low-threshold reaction (that
is, the next reaction with a threshold less than emin, which is currently 1 eV) is
located on nscr1. The energy points are retrieved from scratch file iold (12 or
13) using finda, the cross sections for this reaction are computed on this grid,
and the results are stored on scratch file inew (13 or 12) using loada. The units
for iold and inew are then exchanged, and the entire process is repeated for
the next low-threshold reaction.
The final result of this process is a list of nreac low-threshold-reaction types
in mtr (usually MT2, MT18, and MT102), the threshold value for the first
high-threshold reaction (or the input value) in thnmax, and scratch file iold
containing the energy grid and all the low-threshold reactions (there are n2in
points).
Now that the number of reactions to be broadened simultaneously is known
(nreac), storage for data paging can be assigned. The total amount of storage
available is namax. The value of namax should be as large as possible (current
value is 15 000 000). This space is divided up into the largest possible page size,
npage. An overflow region nstack is also allocated. Now that the page size
is known, the code allocates three pages for energies (e), three pages for each
reaction cross section (s), one extended page for the broadened energy grid (eb),
and three extended pages for the broadened cross section (sb). This system is
designed to use the available storage with maximum efficiency.
The cross sections on iold are now broadened by bfile3 (see below) and
the results are written on scratch unit inew using loada.
The directory from nscr1 is revised to reflect any thinning or thickening and
written on the output PENDF tape (nout). Note that the new temperature is
written into the first word of the Hollerith data record to simplify later searching.
The broadened cross sections are now converted into ENDF TAB1 records
and merged with the unbroadened cross sections on nscr1. The total cross
section (and sometimes nonelastic, inelastic, fission, (n,2n), or charged-particle
reactions) is reconstructed to equal the sum of its parts. The new Doppler-
broadened “MAT” on NOUT is a legal PENDF file with the same MAT number
as the original data but with a new temperature.
The process is now repeated for each of the ntemp2 final temperatures temp2
requested. Note that after each step inew contains the new data and iold
contains the previous data. If the “bootstrap” option is set (istrap=1), these
units are interchanged. For this option, stemp2(it) is always obtained from
temp2(it-1). Because of the thinning effect of Doppler-broadening, the broad-
86 NJOY2016

4 BROADR LA-UR-17-20093
ening runs faster at each step. The accumulation of error is usually not a
problem. For istrap=0, temp1 is used for the starting temperature every time.
The broadening and energy-grid reconstruction are directed by bfile3 . The
routine loads data into the appropriate memory pages from scratch file iold and
then either calls broadn to broaden it (with thinning or thickening of the grid as
necessary) or calls thinb to thin it without broadening. The results are written
onto scratch file inew.
In broadn, the energy grid points just loaded into eby bfile3 are converted
to the dimensionless variables x and y [see Eq. (87)]. An adaptive reconstruction
of the Doppler broadened cross section is then performed for the energy range
in the center page using an inverted stack algorithm like the one described for
RECONR. The upper limit of each panel is taken to be a point from the input
grid, but in order to allow for thinning, up to nmax=10 of the input grid points
can be skipped before the actual upper limit is selected. In addition, the energy
of the upper limit cannot be more than step=2.01 times the energy of the
preceding point. The cross sections are now computed at the midpoint of the
top panel in the stack using bsigma. If the results differ from the values obtained
by interpolation by more than the specified tolerance, the new point is added to
the stack, and the tests are repeated. Otherwise, the top point in the stack is
converged. A backward check is made to see if some of the previous points can
be removed based on the new value, the new value is stored in the output array,
and the height of the stack is reduced by one. The routine now tries to subdivide
the new panel at the top of the stack in the same way. When the stack has been
reduced to one element, a new upper limit is chosen from the input energy grid
as described above, and the entire process is repeated. The reconstruction logic
in BROADR uses the same integral tests as RECONR. Refer to the RECONR
chapter for more details.
Subroutine bsigma is used to calculate the actual broadened cross section at
an energy point using the data in the three pages. First, the routine locates the
energy panel containing the desired energy en. It then loops over intervals below
the current point adding in contributions to ¯σfrom the V−vterm of Eq. (84)
until the contributions to the cross section become small. If the lower limit of
the bottom page is reached before convergence, a warning message is issued.
The routine then loops over intervals above the current point until convergence.
Once again, a warning is issued if necessary. Finally, the low-energy term [the
one involving V+vin Eq. (84)] is added, if applicable.
Subroutine thinb is provided for cases where the input cross section set is
NJOY2016 87
LA-UR-17-20093 4 BROADR
to be thinned only. This routine uses the original SIGMA1 method. The first
input point is always kept. The routine then loops over higher energy values.
For each grid point, all the points from there back to the last accepted point
are checked for their deviation from a straight line. If they all can be removed
without violating the specified tolerance, the interval is extended to the next
higher point and the tests are repeated. If any point in the range is too far
from the linear approximation, the last point in the range is accepted as an
output point, and the testing process is repeated starting from this new lower
limit. The procedure terminates when all of the points in the middle page
have been thinned, and control is returned to bfile3 to get the next page of
data. Thinning may have been a necessary feature in the past when computing
resources were limited but is a rarely used feature today.
Subroutine hunky has been modified from the original SIGMA1 version to
implement the alternate Hn(a, b) calculation when necessary (see hnabb). When
using the direct method, Fnvalues from the previous step are used in the dif-
ference of Eq. (90), and funky is called to get the new values. The Aiand Bi
of Eq. (88) are related to the s1 and s2 here.
Subroutine funky evaluates Fn(a) by the recursion formula of Eq. (94) using
the very accurate SLATEC version of the reduced complementary error function
from the NJOY2016 math module.
Function hnabb implements the alternate calculation described by Eqs. (96)-
(99). The series expansion is continued until about six significant figures are
guaranteed (see eps and hnabb). Currently, hnabb is called when only four
significant figures are reliable in hunky (see toler in hunky).
4.5 User Input
The following input instructions have been copied from the comment cards at
the start of BROADR.
!---input specifications (free format)---------------------------
!
! card 1
! nendf input endf tape (for thermal nubar only)
! nin input pendf tape
! nout output pendf tape
!
! card 2
! mat1 material to broadened and thinned
88 NJOY2016

4 BROADR LA-UR-17-20093
! ntemp2 number of final temperatures (default=1)
! istart restart (0 no, 1 yes, default 0)
! istrap bootstrap (0 no, 1 yes, default 0
! temp1 starting temperature from nin (default=0K)
!
! card 3
! errthn fractional tolerance for thinning
! thnmax max. energy for broadening and thinning
! (default=1 MeV)
! errmax fractional tolerance used when integral criterion
! is satisfied (same usage as in reconr)
! (errmax.ge.errthn, default=10*errthn)
! errint parameter to control integral thinning
! (usage as in reconr) (default=errthn/20000)
! set very small to turn off integral thinning.
! (A good choice for the convergence parameters
! errthn, errmax, and errint is the same set of
! values used in reconr)
!
! card 4
! temp2 final temperatures (deg Kelvin)
!
! card 5
! mat1 next MAT number to be processed with these
! parameters. Terminate with mat1=0.
!
!---input options------------------------------------------------
!
! The output tape will contain the ntemp2 final temperatures
! specified. It is necessary to have temp1.le.temp2(1).
! if temp2.eq.temp1, the data will be thinned only.
!
! restart Continue broadening an existing pendf tape. All
! temperatures are copied through temp1. Additional
! final temperatures are added by starting with the
! data at temp1.
!
! bootstrap If bootstrap is not requested, each final tempera-
! ture is generated by broadening directly from temp1
! to temp2. If bootstrap is requested, each final temp-
! erature is broadened from the preceding temperature.
! Bootstrapping is faster due to the thinning in the
NJOY2016 89

LA-UR-17-20093 4 BROADR
! previous step. However, errors accumulate.
!
! thnmax A possible upper limit for broadening and thinning.
! The actual upper limit is the lowest of (i) this input
! value; (ii) the end of the resolved resonance range;
! (iii) the lowest reaction threshold; or (iv) 1.0 MeV.
!
! A negative value for thnmax forces the Doppler
! broadening upper limit to be abs(thnmax) irrespective
! of the other conditions.
!
! Caution: this may cause one or more threshold
! reactions to be broadened. The magnitude of
! thnmax must be chosen to keep the number of
! broadenable reactions less than or equal to the
! maximum of ntt (160).
!
! Caution: for use in transport codes, it is recommended
! to use the program default. We don’t know how
! to compute the spectrum of scattered neutrons from
! a broadened inelastic level in the current generation
! of codes. Broadened cross sections for threshold
! reactions may be useful for other purposes.
!
!-------------------------------------------------------------------
Note that temp1 need not occur on nout if istart=0. The restart option
(istart=1) enables the user to add new temperatures to the end of an existing
PENDF tape. This option is also useful if a job runs out of time while processing,
for example, the fifth temperature in a job requesting six or more final temper-
atures. The job can be restarted from the nout. The first four temperatures
will be copied to the new nout and broadening will continue for temperature
five. The bootstrap option speeds up the code by using the broadened result for
temp2(i-1) as the starting point to obtain temp2(i). The thnmax parameters
can be used to speed up a calculation or to prevent the broadening of inappro-
priate data such as sharp steps or triangles in an evaluated cross section (for
example, ENDF/B-V lead).
The following example prepares a broadened PENDF file for 235U from
ENDF/B-VII at two temperatures. The line numbers are for reference only;
they are not part of the input.
90 NJOY2016

4 BROADR LA-UR-17-20093
1. broadr
2. 20 21 22/
3. 9228 2/
4. .001/
5. 300. 1200./
6. 0/
On line 2, unit 20 should contain the ENDF file and unit 21 should a RECONR-
generated ASCII PENDF file of 0K cross sections for the isotope. Two materials
will be generated on unit 21 with 0.1% accuracy. First will be the 300K data,
followed by a MEND record, followed by the 1200K data, followed by MEND
and and TEND records. Best results are obtained when the error tolerance
errthn and the optional integral-thinning controls errmax and errint are the
same as those used for the RECONR run.
4.6 Error Messages
error in broadr***nin and nout must be same mode
Use coded to coded, or blocked binary to blocked binary. The latter is
faster due to the several tape copies performed in BROADR.
error in broadr***max. energy too large ...
The user requested Doppler broadening to an energy beyond the maximum
energy in the ENDF file.
error in broadr***too many low threshold reactions
The current limit is set by the global parameter ntt=180. Check tt,mtr,
and ntt in broadr,tt in bfile3, and sbt in broadn.
message from broadr---desired mat and temp not on tape
Check the input PENDF file and the user input.
message from broadr---no broadenable reactions
No low threshold reactions were found.
error in broadr***storage exceeded
Insufficient storage to update directory. Increase nwscr=1000 in broadr.
message from stounx---sigma zero data removed ...
The input PENDF tape already contained a special unresolved section in
File 2. It has been removed. Rerun UNRESR if necessary.
NJOY2016 91

LA-UR-17-20093 4 BROADR
message from bsigma---broadening truncated at a=----
The page is too small for the temperature difference requested. Increase
total storage available (namax) or repeat the calculation with smaller tem-
perature steps and istrap=1. The normal maximum size of ais 4.0 and a
is inversely proportional to Ti−Ti−1.
4.7 Input/Output Units
The following units are used for input and output by BROADR.
10 nscr1 in BROADR. Contains the ENDF/B data at the initial tem-
perature.
12/13 iold/inew in BROADR. Contains union grid and low threshold re-
actions.
20-99 User’s choice for nin and nout to link with other modules.
Units 12 and 13 will always be binary. Unit 10 will have the same mode as nin
and nout.
4.8 Storage Allocation
All storage is divided in the most efficient way possible. The container array size
namax should be made as large as possible. The value of nbuf can be increased or
decreased at will — larger values will give faster execution. The value for nwscr
depends on the size of the ENDF/B dictionary, and 1000 words is sufficient for
all current evaluations.
92 NJOY2016

5 UNRESR LA-UR-17-20093
5 UNRESR
The UNRESR module is used to produce effective self-shielded cross sections
for resonance reactions in the unresolved energy range. In ENDF-format evalu-
ations, the unresolved range begins at an energy where it is difficult to measure
individual resonances and extends to an energy where the effects of fluctuations
in the resonance cross sections become unimportant for practical calculations.
As described in the ENDF format manual,[9] resonance information for this en-
ergy range is given as average values for resonance widths and spacings together
with distribution functions for the widths and spacings. This representation can
be converted into effective cross sections suitable for codes that use the back-
ground cross section method, often called the Bondarenko method,[39] using a
method originally developed for the MC2 code[37] and extended for the ETOX
code[28]. This unresolved-resonance method has the following features:
•Flux-weighted cross sections are produced for the total, elastic, fission, and
capture cross sections, including competition with inelastic scattering.
•A current-weighted total cross section is produced for calculating the effec-
tive self-shielded transport cross section.
•The energy grid used is consistent with the grid used by RECONR.
•The computed effective cross sections are written on the PENDF tape in
a specially defined section (MF2, MT152) for use by other modules.
•The accurate quadrature scheme from the MC2-2 code[38] is used for com-
puting averages over the ENDF statistical distribution functions.
This chapter describes the UNRESR module in NJOY2016.0.
5.1 Theory
In the unresolved energy range, it is not possible to define precise values for the
cross sections of the resonance reactions σx(E), where xstands for the reaction
type (total, elastic, fission, or capture). It is only possible to define average
values. Of course, these average values should try to preserve the reaction rate:
σ0x(E∗) = ZE2
E1
σx(E)φ0(E)dE
ZE2
E1
φ0(E)dE
,(100)
where φ0(E) is the scalar flux, E∗is an effective energy in the range [E1, E2],
and the range [E1, E2] is large enough to hold many resonances but small with
NJOY2016 93

LA-UR-17-20093 5 UNRESR
respect to slowly varying functions of E. In order to calculate effective values
for the transport cross section, it is necessary to compute the current-weighted
total cross section also. It is given by
σ1t(E∗) = ZE2
E1
σx(E)φ1(E)dE
ZE2
E1
φ1(E)dE
,(101)
where the P1component of the neutron flux, φ1(E), is proportional to the
neutron current. To proceed farther, it is necessary to choose a model for the
shape of φ`(E) in the vicinity of E∗. The model used in UNRESR is based on
the B0approximation for large homogeneous systems and narrow resonances:
φ`(E) = C(E)
[ Σt(E) ]`,(102)
where C(E) is a slowly varying function of E, and Σt(E) is the macroscopic total
cross section for the system. In order to use this result in Eq. 100, it is further
assumed that the effects of other isotopes in the mixture can be approximated
by a constant called σ0in the range [E1, E2], or
φ`(E) = C(E)
[σ0+σt(E) ]`.(103)
Therefore, the effective cross sections in the unresolved range are represented by
σ0x(E∗) = ZE2
E1
σx(E)
σ0+σt(E)C(E)dE
ZE2
E1
1
σ0+σt(E)C(E)dE
,(104)
with xbeing tfor total, efor elastic, ffor fission, and γfor capture, and
σ1t(E∗) = ZE2
E1
σx(E)
[σ0+σt(E) ]2C(E)dE
ZE2
E1
1
[σ0+σt(E) ]2C(E)dE
.(105)
94 NJOY2016

5 UNRESR LA-UR-17-20093
This equation can also be written in the equivalent form
σ1t(E∗) = ZE2
E1
1
σ0+σt(E)C(E)dE
ZE2
E1
1
[σ0+σt(E) ]2C(E)dE −σ0.(106)
The parameter σ0in Eq. 103 deserves more discussion. It can be looked at
as a parameter that controls the depth of resonance dips in the flux. When
σ0is large with respect to the peak cross sections of resonances in σt(E), the
shape of the flux is essentially C(E). For smaller values of σ0, dips will develop
in the flux that correspond to peaks in σt. These dips will cancel out part of
the reaction rate in the region of the peaks, thus leading to self-shielding of the
cross section. Analysis shows that it is possible to use this single parameter to
represent the effects of admixed materials or the effects of neutron escape from
an absorbing region. See the GROUPR chapter of this manual for additional
details.
The cross sections that appear in the above integrals can be written as the
sum of a resonant part and a smooth part as follows:
σx(E) = bx+σRx(E) = bx+X
sX
r
σxsr(E−Esr),(107)
where sis an index to a spin sequence, ris an index to a particular resonance
in that spin sequence, and Esr is the center energy for that resonance. The
smooth part bxcan come from a smooth background given in the ENDF file,
and it also includes the potential scattering cross section σpfor the elastic and
total cross sections (x=tand x=e). In terms of the smooth and resonant parts,
the effective cross sections become
σ0x(E∗) = bx+ZE2
E1
σRx(E)
σ+σRt(E)C(E)dE
ZE2
E1
1
σ+σRt(E)C(E)dE
,(108)
and
σ1t(E∗) = ZE2
E1
1
σ+σRt(E)C(E)dE
ZE2
E1
1
[σ+σRt(E) ]2C(E)dE −σ0,(109)
NJOY2016 95
LA-UR-17-20093 5 UNRESR
where σ=bt+σ0. It is convenient to transform the denominators of Eqs. 108
and 109 into
Z1
σ+σt
C dE =1
σZC dE −Zσt
σ+σt
C dE,(110)
and
Z1
[σ+σt]2C dE =1
σ2ZC dE −Zσt
σ+σt
C dE −Zσσt
[σ+σt]2C dE.
(111)
Furthermore, since C(E) is assumed to be a slowly-varying function of E, it
can be pulled out through all integrals and dropped. The average cross sections
become
σ0x=bx+σI0x
1−I0t
,(112)
and
σ1t=bt+σI1t
1−I0t−I1t
.(113)
The last equation can also be written in the form
σ1t=σ1−I0t
1−I0t−I1t−σ0.(114)
The average cross sections are thereby seen to depend on two types of “fluctu-
ation integrals:”
I0x=1
E2−E1ZE2
E1
σRx(E)
σ+σRt(E)dE , (115)
and
I1t=1
E2−E1ZE2
E1
σσRt(E)
[σ+σRt(E) ]2dE , (116)
where xcan take on the values t,n,f, or γ. Note that I1t≤I0t, the difference
increasing as σ0decreases from infinity.
Inserting the actual sums over resonances into the formula for I0xgives
I0x=1
E2−E1ZE2
E1Psr σxsr(E−Esr)
σ+Psr σtsr(E−Esr)dE . (117)
96 NJOY2016

5 UNRESR LA-UR-17-20093
If the resonances were widely separated, only the “self” term would be impor-
tant, and one would obtain
I0x=X
sr
1
E2−E1ZE2
E1
σxsr(E−Esr)
σ+σtsr(E−Esr)dE . (118)
Since the range of integration is large with respect to the width of any one
resonance, the variable of integration can be changed to ξ=E−Esr, and the
limits on ξcan be extended to infinity. For any one sequence, the interval
E2−E1is equal to the average spacing of resonances in that sequence times the
number of resonances in the interval. Therefore,
II
0x=X
s
1
Ds
1
NsX
rZ∞
−∞
σxsr(ξ)
σ+σtsr(ξ)dξ (119)
where Dsis the average spacing, and the “I” superscript indicates that this is the
“isolated resonance” result. Because there are assumed to be many resonances
in the interval, the sum over resonances can be changed to a multiple integration
over some characteristic set of parameters (such as widths) times the probability
of finding a resonance with some particular values of the parameters:
1
NX
r∈s
fr=<f>s=ZdαPs(α)ZdβPs(β)···f(α, β, ···).(120)
In the following text, this multiple integral (up to four fold) will be abbreviated
by writing the αintegral only. The final results for isolated resonances are as
follows:
II
0x=X
s
1
DsZP(α)Z∞
−∞
σxsα(ξ)
σ+σtsα(ξ)dξ dα , (121)
and
II
1t=X
s
1
DsZP(α)Z∞
−∞
σσtsα(ξ)
[σ+σtsα(ξ) ]2dξ dα . (122)
If the effects of overlap are too large to be neglected, overlap corrections to
the isolated resonance result can be constructed using the continued-fraction
generator
1
a+b=1
a1−b
a+b.(123)
NJOY2016 97
LA-UR-17-20093 5 UNRESR
Starting with the I0integrals,
Psr σxsr
σ+Psr σtsr
=X
sr
σxsr
σ+σtsr n1
−X
r06=r
σtsr0
σ+Pσtsr −X
s06=sX
r0
σts0r0
σ+Pσtsr o.(124)
Expand the second term in the braces to get
Psr σxsr
σ+Psr σtsr
=X
sr
σxsr
σ+σtsr n1
−X
r06=r
σtsr0
σ+σtsr +σtsr0
n1−X
r006=r
r006=r0
σtsr00
σ+Pσtsr −X
s06=sX
r0
σts0r0
σ+Pσtsr o
−X
s06=sX
r0
σts0r0
σ+Pσtsr o.(125)
Neglecting the products of three different resonances in sequence sgives
Psr σxsr
σ+Psr σtsr
=X
sr
σxsr
σ+σtsr
×n1−X
r06=r
σtsr0
σ+σtsr +σtsr0o
×h1−X
s06=sX
r0
σts0r0
σ+Pσtsr i.(126)
The factor before the opening brace is the isolated resonance result, the factor
in braces is the in-sequence overlap correction, and the factor in brackets is
the sequence-sequence overlap correction. Note that recursion can be used to
refine the sequence-sequence correction to any desired accuracy. Similarly, the
I1integral requires
Psr σσxsr
[σ+Psr σtsr ]2=X
sr
σσxsr
[σ+σtsr ]2h1
−X
r06=r
σtsr0
σ+Pσtsr −X
s06=sX
r0
σts0r0
σ+Pσtsr i2.(127)
98 NJOY2016
5 UNRESR LA-UR-17-20093
Once more, we expand the fraction and neglect terms that will result in products
of three or more different resonances in the same sequence. The result is
Psr σσxsr
[σ+Psr σtsr ]2=X
sr
σσxsr
[σ+σtsr ]2
×n1−2X
r06=r
σtsr0
σ+σtsr +σtsr0
+X
r06=rσtsr0
σ+σtsr +σtsr02o
×h1−X
s06=sX
r0
σts0r0
σ+Pσtsr i,(128)
where in-sequence and sequence-sequence overlap terms have been factored out.
The next step is to substitute these results back into the fluctuation integrals
I0and I1. The integrals over energy and the sums over different resonances in
each sequence can be handled as described above for isolated resonances. This
procedure will result in three different kinds of integrals. The first kind includes
the isolated resonance integrals already considered above
Bxs =1
E2−E1ZE2
E1X
r
σxsr
σ+σtsr
dE
=1
DsZP(α)Z∞
−∞
σxsα(ξ)
σ+σtsα(ξ)
dξ dα , (129)
and
Dts =1
E2−E1ZE2
E1X
r
σσtsr
[σ+σtsr ]2dE
=1
DsZP(α)Z∞
−∞
σσxsα(ξ)
[σ+σtsα(ξ) ]2dξ dα . (130)
Note that Dt≤Bt, the difference increasing as σ0decreases from infinity.
The next kind are the in-sequence overlap integrals. The sum over r0is
replaced by integrals over the probabilities of finding each partial width and the
probability of finding a resonance r0at a distance ηfrom resonance r.
NJOY2016 99

LA-UR-17-20093 5 UNRESR
V0xs =1
E2−E1ZE2
E1X
rX
r06=r
σxsr
σ+σtsr
σtsr0
σ+σtsr +σtsr0
dE
=1
D2
sZP(α)ZP(β)Z Z Ω(η)σxsα(ξ)
σ+σtsα(ξ)
σtsβ(ξ−η)
σ+σtsα(ξ) + σtsβ (ξ−η)dη dξ dβ dα , (131)
where ξ=E−Esr and η=Esr0−Esr. Similarly,
V1ts =1
E2−E1ZE2
E1X
rX
r06=r
σσtsr
[σ+σtsr ]2n2σtsr0
σ+σtsr +σtsr0
−σtsr0
σ+σtsr +σtsr02odE
=1
D2
sZP(α)ZP(β)Z Z Ω(η)σσtsα(ξ)
[σ+σtsα(ξ) ]2
n2σtsβ(ξ−η)
σ+σtsα(ξ) + σtsβ (ξ−η)
−hσtsβ(ξ−η)
σ+σtsα(ξ) + σtsβ (ξ−η)i2odη dξ dβ dα . (132)
The final class of integrals includes the sequence-sequence overlap corrections.
They are simplified by noting that the positions of resonances in different spin
sequences are uncorrelated. Therefore, Ω(η)=1, and the integral of the product
reduces to the product of the integrals.
Using the results and definitions from above, the fluctuation integrals become
I0x=X
s
Axs ,(133)
Axs = (Bxs −V0xs)h1−X
s06=s
Ats0i,(134)
and
I1t=X
s
(Dts −V1ts)h1−X
s06=s
Ats0i2,(135)
where Eq. 134 provides a recursive definition of the Ats for the sequence-sequence
corrections as well as the normal value of Axs.
100 NJOY2016

5 UNRESR LA-UR-17-20093
These equations are formally exact for the sequence-sequence overlaps, but
in-sequence overlaps only include the interactions between pairs of resonances.
Three different approximations to this result are currently in use.
The MC2/ETOX Approximation The MC2 and ETOX codes use similar
approximations to the results above, except that MC2 does not include a calcu-
lation of the current-weighted total cross section. Both codes explicitly neglect
the in-sequence overlap corrections. This approximation was based on the as-
sumption that resonance repulsion would reduce the overlap between resonances
in a particular spin sequence, leaving the accidental close spacing of resonances
in different sequences as the dominant overlap effect. In addition, both codes
stop the recursion of Eq. 134 at At=Bt. Thus,
I0x=X
s
Bxs1−X
s06=s
Bts0,(136)
and
I1t=X
s
Dts1−X
s06=s
Bts02.(137)
The equations for the effective cross sections in the MC2/ETOX approximation
become
σ0x=bx+
σX
s
Bxs1−X
s06=s
Bts0
1−X
s
Bts1−X
s06=s
Bts0,(138)
and
σ1t=bt+
σX
s
Dts1−X
s06=s
Bts02
1−X
s
Bts1−X
s06=s
Bts0−X
s
Dts1−X
s06=s
Bts02,(139)
NJOY2016 101
LA-UR-17-20093 5 UNRESR
or
σ1t=σ
1−X
s
Bts1−X
s06=s
Bts0
1−X
s
Bts1−X
s06=s
Bts0−X
s
Dts1−X
s06=s
Bts02
−σ0.(140)
These are the equations that are used in the UNRESR module of NJOY. Note
that the equation in the ETOX code and report corresponding to Eq. 140 is
incorrect. The following equation was used in the ETOX code:
σ1t=σ
1−X
s
Bts1−X
s06=s
Bts0
1−X
s
Cts1−X
s06=s
Cts0
−σ0,(141)
with Cts =Bts +Dts.
The MC2-2 Approximation The MC2-2 code includes the in-sequence over-
lap corrections, which the authors found to be more important than previously
thought. It uses additional approximations to obtain the equivalent of
σ0x=bx+σX
s
Bxs −V0xs
1−Bts +V0ts
.(142)
The additional approximations used are
1. Set Ats =Bts −V0ts (first-order sequence-sequence overlap),
2. Neglect the factor (1 −Ps06=sAts0) in the denominator, and
3. Use the approximation 1 −Pifi≈Qi(1 −fi) on the numerator and de-
nominator.
These simplifications result in a loss of accuracy for the sequence-sequence
overlap correction at relatively low values of σ0. The σ1tterm is not calculated.
The UXSR Approximation The experimental UXSR module was devel-
oped at Oak Ridge (with some contributions from LANL) based on coding from
the Argonne National Laboratory (ANL) in an attempt to include the sophis-
ticated in-sequence overlap corrections from MC2-2 without approximating the
sequence-sequence corrections so badly. It also implemented a calculation of the
102 NJOY2016
5 UNRESR LA-UR-17-20093
current-weighted total cross section, which was omitted in MC2-2. The addi-
tional cost of using the full expressions for Eqs. 133 and 135 is minimal, and
effective cross sections can be computed for lower values of σ0when in-sequence
overlap is small (e.g., 238U).
Now that expressions have been chosen for computing the cross sections in
terms of the isolated-resonance integrals, it is necessary to select an efficient
numerical method for computing them. The resonant parts of the cross sections
are given by
σxsr(E−Esr) = σm
Γx
Γψ(θ, X)sr
,(143)
and
σtsr(E−Esr) = [ σm{cos 2φ`ψ(θ, X) + sin 2φ`χ(θ, X)}]sr ,(144)
where xtakes on the values γ,f, or cfor capture, fission, or competition, and
σm=4πgJ
k2
Γn
Γ,(145)
θ=rA
4kT E0
Γ,(146)
X=2(E−E0)
Γ,(147)
gJ=2J+ 1
2(2I+ 1) ,and (148)
k= 2.196771 ×10−3A
1 + A√E . (149)
The functions ψand χare the symmetric and antisymmetric components of the
broadened resonance line shape:
ψ(θ, X) = θ√π
2ReWθX
2,θ
2,(150)
and
χ(θ, X) = θ√πImWθX
2,θ
2,(151)
NJOY2016 103

LA-UR-17-20093 5 UNRESR
where
W(x, y) = exp[−(x+iy)2] erfc[−i(x+iy)] (152)
is the complex probability integral. The methods for computing ψand χare
well known (see quikw).
The first integral needed is
Bxs =1
DsZP(α)Zσxsα(ξ)
σ+σtsα(ξ)dξ dα
=1
DsZP(α)Zσm(Γx/Γ)ψ(θ, X)
σ+σm{cos 2φ`ψ(θ, X) + sin 2φ`χ(θ, X)}dξ dα
=1
DsZP(α)Γx
2 cos 2φ`Zψ(θ, X)
β+ψ(θ, X) + tan 2φ`χ(θ, X)dX dα ,(153)
where
β=σ
σmcos 2φ`
.(154)
The second integral needed is
Bts =1
DsZP(α)Zσtsα(ξ)
σ+σtsαξ)dξ dα
=1
DsZP(α)Γ
2Zψ(θ, X) + tan 2φ`χ(θ, X)
β+ψ(θ, X) + tan 2φ`χ(θ, X)dX dα . (155)
Both of these integrals can be expressed in terms of the basic Jintegral:
Bxs =1
DsZP(α)Γ
cos 2φ`
J(β, θ, tan 2φ`,0) dα , and
Bts =1
DsZP(α) Γ J(β, θ, tan 2φ`,tan 2φ`)dα , (156)
where
J(β, θ, a, b) = 1
2Z∞
−∞
ψ(θ, X) + b χ(θ, X)
β+ψ(θ, X) + a χ(θ, X)dX . (157)
The Dintegral can be handled in the same way, but only total reaction is
required.
104 NJOY2016
5 UNRESR LA-UR-17-20093
Dts =1
DsZP(α)Zσσtsα(ξ)
[σ+σtsα(ξ) ]2dξ dα
=1
DsZP(α)Γ
2Zβψ(θ, X) + tan 2φ`χ(θ, X)
[β+ψ(θ, X) + tan 2φ`χ(θ, X) ]2dX dα
=1
DsZP(α) Γ K(β, θ, tan 2φ`,tan 2φ`)dα , (158)
where
K(β, θ, a, b) = 1
2Z∞
−∞
β[ψ(θ, X) + b χ(θ, X) ]
[β+ψ(θ, X) + a χ(θ, X) ]2dX . (159)
A method for computing J, including the interference effects, has been de-
veloped by Hwang for MC2-2[38]. However, this method was not available in
the days when MC2 and ETOX were developed. Therefore, UNRESR uses only
J(β, θ, 0,0) and K(β, θ, 0,0) in computing the isolated-resonance fluctuation in-
tegrals. A direct integration is used over most of the Xrange, but the part of
the integral arising from large Xis handled using analytic integrations of the
asymptotic forms of the arguments (see ajku).
The final step is to do the n-fold integration over the probability distributions
for the resonance widths. This integration has been abbreviated as a single inte-
gration over αin the above equations. The method used was originally developed
for MC2-2 and is based on Gauss-Jacobi quadratures. A set of 10 quadrature
points and weights is provided for each of the χ2probability distributions with
1 through 4 degrees of freedom. These quadratures convert the n-fold integral
into an n-fold summation. The value of ncan be as large as 4 when Γn, Γf, Γγ,
and Γc(competitive width) are all present.
Although UNRESR neglects the effects of overlap between resonances in
the same spin sequence and the effects of interference in the elastic and total
cross sections, it still gives reasonable results for the background cross section
values needed for most practical problems. Modern evaluations are steadily
reducing the need for accurate unresolved calculations by extending the resolved
resonance range to higher and higher energies. Ultimately, UNRESR should be
upgraded to use the UXSR approach. Another alternative is to generate self-
shielded effective cross sections from ladders of resonances chosen statistically
(see PURR). This avoids many of the approximtions in the overlap corrections.
In NJOY2016, running the PURR module after UNRESR overwrites the
UNRESR output with the PURR results. In fact, UNRESR can be omitted
NJOY2016 105

LA-UR-17-20093 5 UNRESR
from the processing stream. To use UNRESR results, either omit PURR from
the processing stream or run it before running UNRESR.
5.2 Implementation
In implementing this theory in UNRESR, there are special considerations in-
volving the choice of an incident energy grid, what to do if the unresolved range
overlaps the resolved range or the range of smooth cross sections, the choice of
the σ0grid, how to interpolate on σ0, and how to communicate the results to
other modules.
Choice of Energy Grid. The same logic is used to choose the incident energy
grid in UNRESR and RECONR. It is complicated, because of the several differ-
ent representations available for unresolved data, and because of the existence
of evaluations that have been carried over from previous versions of ENDF/B
or ENDF/B-VII evaluations with inadequate energy grids. Even many modern
evaluations have inadequate energy grids.
For evaluations that give energy-independent unresolved-resonance param-
eters, there is still an energy dependence to the cross sections. Because this
dependence is normally somewhere between constant and a 1/v law, a fairly
coarse grid with about 13 points per decade should be sufficient to allow the
cross sections to be computed reliably using linear-linear interpolation.
If the evaluation uses energy-dependent parameters, the normal rule would
be to use the energies that were provided by the evaluator and to obtain inter-
mediate cross sections by interpolation. Unfortunately, some of the evaluations
carried over from earlier days contain some energy intervals that are quite large
(for example, steps by factors of 10). The evaluators for these isotopes assumed
that the user would use parameter interpolation and compute the cross sections
at a number of intermediate energies in these long steps. Even some newer
evaluations contain large jumps in the energy grid. UNRESR will detect such
evaluations and add additional energy points in the large energy steps using an
algorithm similar to the one used for the cases with energy-independent param-
eters. For NJOY2016, large jumps in the energy grid are any with step ratios
greater than wide, which is currently set to 1.26.
The final energy grid can be observed by scanning the printed output from
UNRESR.
106 NJOY2016

5 UNRESR LA-UR-17-20093
Resolved-Unresolved Overlap. Elemental evaluations include separate en-
ergy ranges in MF2/MT151 for each of the isotopes of the element, and these
energy ranges do not have to be the same for each isotope. This means that the
lower end of an unresolved range may overlap the resolved range from another
isotope, and the upper end of the unresolved range for an isotope can overlap
the smooth range of another isotope. These overlap regions are detected by
UNRESR as the resonance data are read in, and they are marked by making
the sign of the incident energy value negative.
Choosing a σ0Grid. There are two factors to consider, namely, choosing
values that will represent the shape adequately, and limiting the range of σ0to
the region where the theory is valid. The σx(σ0) curves start out decreasing
from the infinite dilution value as 1/σ0as σ0decreases from infinity (1 ×1010
in the code). The curve eventually goes through an inflection point at some
characteristic value of σ0, becomes concave upward, and approaches a limiting
value at small σ0that is smaller than the infinite-dilution value. Decade steps
are often used, but the user should try to select values that include the inflection
point and not waste values on the 1/σ0region. Half-decade values are useful
near the inflection point (e.g., 100, 300, 1000 for 235U). The grid interval chosen
should be consistent with the interpolation method used (see below).
Choosing the lower limit for σ0is a more difficult problem. As shown in
the theory section (5.1), resonance overlap effects are developed as a series in
1/σ0, and the series is truncated after only one step of recursion in Eq. 134.
This means that the overlap correction should be most accurate for large σ0
and gradually get worse as σ0decreases. Experience shows that the correction
can actually get large enough to produce negative cross sections for small σ0.
(This problem can also show up as a failure in interpolation when a log scheme
has been selected.) For isotopes that have relatively narrow resonances spaced
relatively widely, such as 238U, UNRESR gives reasonable results to σ0values
as low as 0.1. For materials with stronger overlap, such as 235U, a lower limit
around 100 is more reasonable. A few of the heavy actinide evaluations have
been seen to break down for σ0values lower than 1000. This problem is not too
serious in practice. The fertile materials, which appear in large concentrations
in reactors, allow the necessary small values of σ0. The fissile materials have to
be more dilute, and the larger σ0limit needed for them is not usually a problem.
The UXSR approximation discussed above allows one to reach somewhat
smaller σ0values.
NJOY2016 107

LA-UR-17-20093 5 UNRESR
Interpolating on σ0.It turns out that these functions are difficult to interpo-
late because they have a limited radius of convergence. Although approximate
schemes have been developed based on using functions of similar shape such as
the tanh function[40], better results can be obtained by using different interpo-
lation schemes for the low- and high-σ0ranges. The TRANSX-CTR code[12]
used interpolation in 1/σ0for high σ0, Lagrangian interpolation of lnσxvs lnσ0,
for intermediate values, and a σ2
0extrapolation for very low σ0. Unfortunately,
schemes like this sometimes give ridiculous interpolation excursions when the
polynomials are not suitable. Therefore, TRANSX-2[41] has had to revert to
using simple linear interpolation, which is always bounded and predictable, but
which requires relatively fine σ0grids.
Communicating Results to Other Modules. NJOY tries to use ENDF-
like files for all communications between the different calculational modules.
Because the unresolved effective cross sections were originally derived from the
resonance parameters in File 2, it seemed reasonable to create a new section in
File 2 to carry the unresolved cross sections onto other modules, and a special
MT number of 152 was selected for this purpose. RECONR creates an MT152
that contains only the infinitely-dilute unresolved cross sections. UNRESR over-
writes it with self-shielded unresolved cross sections. GROUPR can then use
these cross sections in its calculation of the multigroup constants. The format
used for MT152 is given below using the conventional ENDF style.
[MAT,2,152/ ZA, AWR, LSSF, 0, 0, INTUNR ] HEAD
[MAT,2,152/ TEMZ, 0, NREAC, NSIGZ, NW, NUNR/
SIGZ(1), SIGZ(2),...,SIGZ(NSIGZ),
EUNR(1),
SIGU(1,1,1), SIGU(1,2,1),...,SIGU(1,NSIGZ,1),
SIGU(2,1,1),...
...
SIGU(NREAC,1,1),...,SIGU(NREAC,NSIGZ,1),
EUNR(2),...
<continue for energies through EUNR(NUNR)>
...SIGU(NREAC,NSIGZ,NUNR) ] LIST
where NREAC is always 5 (for the total, elastic, fission, capture, and current-
weighted total reactions, in that order), NSIGZ is the number of σ0values, NUNR
is the number of unresolved energy grid points, and NW is given by
108 NJOY2016

5 UNRESR LA-UR-17-20093
NW=NSIGZ+NUNR*(1+5*NSIGZ)
5.3 User Input
The following summary of the user input instructions was copied from the com-
ment cards at the beginning of the UNRESR module in the NJOY2016 source
file.
!---input specifications (free format)---------------------------
!
! card 1
! nendf unit for endf tape
! nin unit for input pendf tape
! nout unit for output pendf tape
! card 2
! matd material to be processed
! ntemp no. of temperatures (default=1)
! nsigz no. of sigma zeroes (default=1)
! iprint print option (0=min, 1=max) (default=0)
! card 3
! temp temperatures in Kelvin (including zero)
! card 4
! sigz sigma zero values (including infinity)
! cards 2, 3, 4 must be input for each material desired
! matd=0/ terminates execution of unresr.
!
!--------------------------------------------------------------------
Card 1, as usual, specifies the input and output units for the module. The
input PENDF file on nin must have been processed through RECONR and
BROADR. It will contain default versions of the special unresolved section with
MF=2 and MT=152 that gives the infinitely-dilute unresolved cross sections for
each temperature. The output PENDF file nout will contain revised sections
MF2, MT152 that give effective cross sections vs σ0for all temperatures.
Card 2 is used to specify the material desired (matd), the number of temper-
atures and background cross sections desired (ntemp and nsigz), and the print
NJOY2016 109

LA-UR-17-20093 5 UNRESR
option (iprint). The actual temperature and σ0values are given on Cards 3
and 4. Temperatures should be chosen to be adequate for the planned appli-
cations. The temperature dependence of the effective cross sections is usually
monotonic and fairly smooth. Polynomial interpolation schemes using Tare
often used, and roughly uniform spacing for the temperature grid (or spacing
that increases modestly as Tincreases) is usually suitable.
The choice of a grid for σ0is more difficult. The curves of cross section
versus σ0have an inflection point, and it is important to choose the grid to
represent the inflection point fairly well. A log spacing for σ0is recommended.
Very small values of σ0should not be used. These considerations are discussed
in more detail in the “Implementation” section (5.2) above. Unfortunately, the
best choice for a grid can only be found by trial and error.
5.4 Output Example
The following portion of UNRESR output is for 238U from ENDF/B-VII.0.
unresr...calculation of unresolved resonance cross sections 494.4s
storage 8/ 20000
unit for input endf/b tape ........... -21
unit for input pendf tape ............ -23
unit for output pendf tape ........... -24
temperatures ......................... 2.936E+02
4.000E+02
...
sigma zero values .................... 1.000E+10
1.000E+03
1.000E+02
5.000E+01
2.000E+01
1.000E+01
5.000E+00
2.000E+00
1.000E+00
5.000E-01
print option (0 min., 1 max.) ........ 1
110 NJOY2016

5 UNRESR LA-UR-17-20093
mat = 9237 temp = 2.936E+02 494.4s
energy = 2.0000E+04
1.433E+01 1.428E+01 ... 1.311E+01 1.297E+01 1.291E+01 1.288E+01
1.380E+01 1.375E+01 ... 1.264E+01 1.252E+01 1.247E+01 1.244E+01
0.000E+00 0.000E+00 ... 0.000E+00 0.000E+00 0.000E+00 0.000E+00
5.294E-01 5.280E-01 ... 4.654E-01 4.540E-01 4.491E-01 4.464E-01
1.433E+01 1.424E+01 ... 1.246E+01 1.230E+01 1.223E+01 1.220E+01
energy = 2.3000E+04
1.414E+01 1.411E+01 ... 1.307E+01 1.293E+01 1.288E+01 1.285E+01
1.364E+01 1.361E+01 ... 1.262E+01 1.250E+01 1.245E+01 1.242E+01
0.000E+00 0.000E+00 ... 0.000E+00 0.000E+00 0.000E+00 0.000E+00
4.962E-01 4.951E-01 ... 4.426E-01 4.325E-01 4.281E-01 4.257E-01
1.414E+01 1.407E+01 ... 1.246E+01 1.229E+01 1.223E+01 1.219E+01
...
energy = 1.4903E+05
1.140E+01 1.140E+01 ... 1.124E+01 1.118E+01 1.115E+01 1.113E+01
1.126E+01 1.126E+01 ... 1.110E+01 1.104E+01 1.101E+01 1.099E+01
0.000E+00 0.000E+00 ... 0.000E+00 0.000E+00 0.000E+00 0.000E+00
1.427E-01 1.427E-01 ... 1.406E-01 1.386E-01 1.374E-01 1.367E-01
1.213E+01 1.212E+01 ... 1.174E+01 1.156E+01 1.147E+01 1.141E+01
generated cross sections at 18 points 494.9s
The display of the cross section table for each energy has σ0reading across (in
decreasing order) and reaction type reading down (in the order of total, elastic,
fission, capture, and current-weighted total). Four σ0values were removed from
the table to make it narrower for this report.
5.5 Coding Details
The main entry point for UNRESR is subroutine unresr, which is exported by
module unresm. The subroutine starts by reading in the user’s input and output
unit numbers and opening the files that will be needed during the UNRESR run.
After printing the introductory timer line, storage is allocated for an array scr,
which will be used for reading in ENDF records. The default size of this array
is maxscr=1000, which has proved sufficient for all evaluations tried so far.
UNRESR now prints out the user’s unit numbers on the output listing and calls
uwtab to prepare internal tables used by uw to compute the real and imaginary
parts of the complex probability integral.
The next step is to read in the tapeid records of the ENDF and PENDF
NJOY2016 111

LA-UR-17-20093 5 UNRESR
tapes. The loop over materials starts at statement number 110 by reading in
the user’s values for the ENDF MAT number, number of temperatures ntemp,
number of σ0values nsigz, and print flag iprint. If this is not the end of the
material loop (mat=0), the actual values of the temperatures and background
cross sections are read into the arrays temp and sigz. The input quantities are
echoed to the output listing to help detect input errors.
The code then begins a loop over the requested temperatures. It writes the
current values of material ID, temperature, and time on the output listing. It
then reads the resonance parameters from the section with MT=151 in File 2
of the ENDF tape using rdunf2. The arrays eunr with length maxeunr=150
and arry with length with length maxarry=10000 are used to store these data.
Next, it reads the background cross sections from File 3 for each of the reso-
nance reactions using rdunf3. Here, sb is used to store the data. The array
bis allocated with sufficient length to build the output record to be written in
MT=152 on the new PENDF file.
The next loop is over all the energy grid points at this temperature. The
grid points were determined in rdunf2, and the nunr points are stored in the
array eunr. The background cross sections are stored in an array sb(ie,ix).
The energy index takes on nunr values, and the reaction index ix takes on
four values. The calculation of the actual effective cross sections takes place in
unresl. The results for each energy appear in the array sigu(ix,is), where
is takes on nsigz values. Each unresl array is stored into the accumulating
output array band printed on the output listing.
At this point, UNRESR checks to see if there is a previous version of MT152
on the PENDF tape. If so, these new data will replace it. If not, a new section
with MT=152 will be created. In either case, a new section MT451 in File 1
is generated containing the current temperature and the correct entry in the
directory for the PENDF tape. Finally, the new MT152 for this temperature is
copied onto the output file from the barray, and the rest of the contents of this
temperature on the old PENDF file are copied to the new PENDF file. After
writing a report on the number of resonance points generated and the amount
of computer time used, UNRESR branches back to continue the temperature
loop. When the last temperature has been processed, the code closes the files,
writes a final report on the output listing, and terminates.
Note that UNRESR takes special branches for materials with no resonance
parameters or materials with no unresolved parameters. Therefore, the user can
freely request an UNRESR run even when there are no unresolved resonance
112 NJOY2016

5 UNRESR LA-UR-17-20093
data present on the ENDF tape. UNRESR simply copies nin to nout in this
case.
The subroutine rdunf2 is used to read in the unresolved resonance parame-
ters from File 2 of the input ENDF tape. It is very similar to the corresponding
coding in RECONR. The array scr is used to read in the ENDF record, the
resonance parameter data are stored in the array arry, and the final grid of en-
ergy values is stored in eunr. Note that rdunf2 will add extra energy nodes for
evaluations with energy-independent parameters or for energy-dependent evalu-
ations that have energy steps larger than the factor wide, which is currently set
to 1.26. The subroutine also discovers resolved-unresolved or unresolved-smooth
overlap, flags those energy values, and prints messages to the user on the output
listing.
Subroutine ilist is used to insert a new energy into a list of energies in
ascending order. It is used to manage the accumulation of the grid of energy
nodes.
Subroutine rdunf3 is used to read in the background cross sections in the
unresolved range from File 3. The unresolved energy grid determined by rdunf2
is used for the background cross sections.
The main calculation of the effective cross sections for the unresolved range
is performed in subroutine unresl. The calculation is done in two passes: first,
the potential scattering cross section is computed; second, the unresolved cross
sections are computed. The passes are controlled by the parameter ispot. In
both cases, resonance parameter data stored in arry by rdunf2 are used. The
coding is similar to that used in RECONR down to the point where the ETOX
statistical averages are computed. The three loops over kf,kn, and kl carry
out the n-fold quadrature represented as integrals over αin the text. They ac-
count for variations in the fission width, neutron width, and competitive width.
The capture width is assumed to be constant. Note that ajku is called in the
innermost loop to compute the Jand Kintegrals in xj and xk, respectively.
The Kintegral returned by this routine is actually J+Kin our notation. The
final quantities are computed in the loops over itp and is0. Note that tk is
equivalent to Bts +Dts in our notation. Similarly, tl is equivalent to Bxs, and tj
is equivalent to Bts. The last step in this subroutine is to compute the average
cross sections by summing over spin sequences. The loop over ks computes xj
as PsBts and xk as PsCts. With these quantities available, it is easy to finish
the calculation of the effective cross sections as given by Eq. 138 and Eq. 140.
The subroutines uunfac,intrf, and intr are similar to corresponding rou-
NJOY2016 113

LA-UR-17-20093 5 UNRESR
tines from RECONR and don’t require further discussion here. Subroutine ajku
is used to compute the Jand Kintegrals without interference corrections. The
subroutines quikw,uwtab, and uw implement a package for computing the com-
plex probability integral efficiently. It was originally developed at ANL for the
MC2 code. When it is used, a pair of 62 ×62 tables for the real and imaginary
parts of the complex probability integral are precomputed using uwtab and uw.
Values of W for small arguments are obtained by interpolating in these pre-
computed tables. Values of W for larger arguments are obtained using various
asymptotic formulas.
5.6 Error Messages
error in unresr***mode conversion between nin and nout
Input and output files must both be in ASCII mode (positive unit numbers),
or they must both be in binary mode (negative unit numbers).
error in unresr***storage exceeded
There is not enough room in the barray. Increase nb, which currently is
5000.
error in rdunf2***energy dependent data undefined
When using unresolved resonance formalisms with energy dependent pa-
rameters (e.g. the fission width, etc.), these data need to be defined over
the entire unresolved resonance region. In rare cases, such as ENDF/B-
VII.0 Pu239, this is not the case, leading to NaN cross section values. This
is an evaluation error.
error in rdunf2***storage exceeded
There is not enough room in arry. Increase the value of maxarry, which
currently is 10000.
error in unresl***storage exceeded
The code is currently limited to 50 spin sequences. For more spin sequences,
it will be necessary to increase the dimensions of several arrays in this
subroutine.
114 NJOY2016

6 HEATR LA-UR-17-20093
6 HEATR
The HEATR module generates pointwise heat production cross sections and
radiation damage energy production for specified reactions and adds them to
an existing PENDF file. The heating and damage numbers can then be easily
group averaged, plotted, or reformatted for other purposes. An option of use to
evaluators checks ENDF/B files for neutron/photon energy-balance consistency.
The advantages of HEATR include
•Heating and damage are computed in a consistent way.
•All ENDF/B neutron and photon data are used.
•ENDF/B-6 charged-particle distributions are used when available.
•Kinematic checks are available to improve future evaluations.
•Both energy-balance and kinematic KERMA factors can be produced.
This chapter describes the HEATR module in NJOY2016.0.
6.1 Theory of Nuclear Heating
Heating is an important parameter of any nuclear system. It may represent
the product being sold – as in a power reactor – or it may affect the design of
peripheral systems such as shields and structural components.
Nuclear heating can be conveniently divided into neutron heating and photon
heating (see Fig. 8). Neutron heating at a given location is proportional to the
local neutron flux and arises from the kinetic energy of the charged products
of a neutron induced reaction (including both charged secondary particles and
the recoil nucleus itself). Similarly, photon heating is proportional to the flux of
secondary photons transported from the site of previous neutron reactions. It is
also traceable to the kinetic energy of charged particles (for example, electron-
positron pairs and recoil induced by photoelectric capture).
Heating, therefore, is often described by KERMA[30] (Kinetic Energy Release
in Materials) coefficients kij(E) defined such that the heating rate in a mixture
is given by
H(E) = X
iX
j
ρikij(E)φ(E),(160)
where ρiis the number density of material i,kij(E) is the KERMA coefficient
for material iand reaction jat incident energy E, and φ(E) is the neutron or
NJOY2016 115
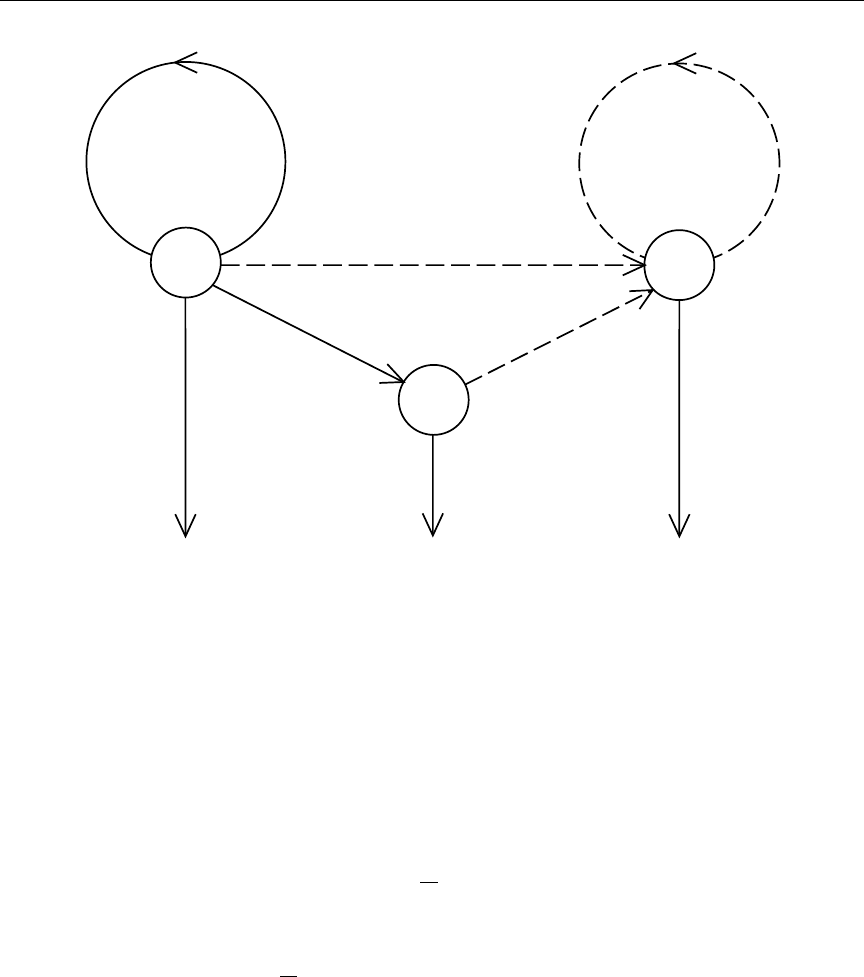
LA-UR-17-20093 6 HEATR
A Z
A'
GAMMA
FLUX
prompt
gammas
delayed
gammas
production
and burnup
prompt local
heating delayed local
heating
prompt and
delayed
non-local
heating
NEUTRON
FLUX
Figure 8: Components of nuclear heating. HEATR treats the prompt local neutron heating
only. Gamma heating is computed in GAMINR. Delayed local heating and photon
production are not treated by NJOY, and they must be added at a later stage.
photon scalar flux at E. KERMA is used just like a microscopic reaction cross
section except that its units are energy ×cross section (eV-barns for HEATR).
When multiplied by a flux and number density, the result would give heating in
eV/s.
The “direct method” for computing the KERMA coefficient is
kij(E) = X
`
Eij`(E)σij (E),(161)
where the sum is carried out over all charged products of the reaction including
the recoil nucleus, and Eij` is the total kinetic energy carried away by the `th
species of secondary particle. These kinds of data are now becoming available for
some materials with the advent of ENDF/B-VI and later, but earlier ENDF/B
versions did not include the detailed spectral information needed to evaluate
Eq. 161.
For this reason, NJOY computes KERMA factors for many materials by the
“energy-balance method”[42]. The energy allocated to neutrons and photons is
simply subtracted from the available energy to obtain the energy carried away
116 NJOY2016

6 HEATR LA-UR-17-20093
by charged particles:
kij(E) = E+Qij −Eijn −Eijγ σij (E),(162)
where Qij is the mass-difference Q-value for material iand reaction j,Enis the
total energy of secondary neutrons including multiplicity, and Eγis the energy
of secondary photons including photon yields.
This method was well suited for use with ENDF/B-V, or any other evalua-
tion containing neutron and photon spectral data, but not the particle spectra
required by the direct method. The disadvantage of this method is that the
KERMA factor sometimes depends on a difference between large numbers. In
order to obtain accurate results, care must be taken by the evaluator to ensure
that photon and neutron yields and average energies are consistent. In fact,
the lack of consistency in ENDF/B-V often revealed itself as negative KERMA
coefficients[43].
However, a negative KERMA coefficient is not always the defect it seems to
be. It must be remembered that heating has both neutron and photon com-
ponents. A negative KERMA might indicate that too much energy has been
included with the photon production in the evaluation. This will result in ex-
cessive photon heating if most of the photons stay in the system. However,
the negative KERMA will have just the right magnitude to cancel this excess
heating. The energy-balance method guarantees conservation of total energy in
large homogeneous systems.
In this context, large and homogeneous means that most neutrons and pho-
tons stay in their source regions. It is clear that energy-balance errors in the
evaluation affect the spatial distribution of heat and not the total system heating
when the energy-balance method is employed.
A final problem with the energy-balance method occurs for the elemental
evaluations common in earlier versions of ENDF/B. Isotopic Q-values and cross
sections are not available in the files. It will usually be possible to define ad-
equate cross sections, yields, and spectra for the element. However, it is clear
that the available energy should be computed with an effective Q given by
Q=X
i
ρiσiQi
X
i
ρiσi
,(163)
NJOY2016 117

LA-UR-17-20093 6 HEATR
where ρiis the atomic fraction of isotope iin the element. This number is energy
dependent and can be represented only approximately by the single constant
Q allowed in ENDF/B. HEATR allows the user to input an auxiliary energy-
dependent Q for elements.
For elastic and discrete-level inelastic scattering, the neutron KERMA coef-
ficient can be evaluated directly without reference to photon data. For other
reactions, conservation of momentum and energy can be used to estimate the
KERMA or to compute minimum and maximum limits for the heating. HEATR
includes an option that tests the energy-balance KERMA factors against these
kinematic limits, thereby providing a valuable test of the neutron-photon consis-
tency of the evaluation. If the energy-balance heating numbers for a particular
isotope should fail these tests, and if the isotope is important for a “small” sys-
tem, an improved evaluation is probably required. The alternative of making ad
hoc fixes to improve the local heat production is dangerous because the faults
in the neutron and/or photon data revealed by the tests may lead to significant
errors in neutron transport and/or photon dose and nonlocal energy deposition.
In practice, an exception to this conclusion must be made for the radiative
capture reaction (n,γ). The difference between the available energy E+Qand
the total energy of the emitted photons is such a small fraction of E+Qthat it
is difficult to hold enough precision to get reasonable recoil energies. Moreover,
the emitted photons cause a component of recoil whose effect is not normally
included in evaluated capture spectra. Finally, the “element problem” cited
above is especially troublesome for capture because the available energy may
change by several MeV between energies dominated by resonances in different
isotopes of the element, giving rise to many negative or absurdly large heating
numbers. These problems are more important for damage calculations (see
below) where the entire effect comes from recoil and the compensation provided
by later deposition of the photon energy is absent.
For these reasons, HEATR estimates the recoil due to radiative capture using
conservation of momentum. The recoil is the vector sum of the “kick” caused
by the incident neutron and the kicks due to the emission of all subsequent
photons. Assuming that all photon emission is isotropic and that the directions
of photon emission are uncorrelated, the photon component of recoil depends
on the average of E2
γover the entire photon spectrum
ER=E
A+ 1 +E2
γ
2(A+ 1)mc2,(164)
118 NJOY2016

6 HEATR LA-UR-17-20093
where mc2is the neutron mass energy. The second term is important below
25 – 100 keV. This formula gives an estimate that works for both isotopes and
elements and has no precision problems. However, it does not explicitly conserve
energy, and isotopes with bad capture photon data can still cause problems.
6.2 Theory of Damage Energy
Damage to materials caused by neutron irradiation is an important design con-
sideration in fission reactors and is expected to be an even more important
problem in fusion power systems. There are many radiation effects that may
cause damage, for example, direct heating, gas production (e.g., helium embrit-
tlement), and the production of lattice defects.
A large cluster of lattice defects can be produced by the primary recoil nucleus
of a nuclear reaction as it slows down in a lattice. It has been shown that
there is an empirical correlation between the number of displaced atoms (DPA,
displacements per atom) and various properties of metals, such as elasticity.
The number of displaced atoms depends on the total available energy Eaand
the energy required to displace an atom from its lattice position Ed. Since the
available energy is used up by producing pairs,
DPA = Ea
2Ed
.(165)
The values of Edused in practice are chosen to represent the empirical correla-
tions, and a wide range of values is found in the literature[44, 45, 46]. Table 2
gives the default values used in NJOY2016. The energy available to cause dis-
placements is what HEATR calculates. It depends on the recoil spectrum and
the partition of recoil energy between electronic excitations and atomic motion.
The partition function used is given by Robinson[47] based on the electronic
screening theory of Lindhard[48] (see Fig. 9).
The damage output from HEATR is the damage energy production cross
section (eV-barns). As in Eq. 160, multiplying by the density and flux gives
eV/s. Dividing by 2Edgives displacements/s. This result is often reduced by
an efficiency factor (say 80%) to improve the fit to the empirical correlations.
NJOY2016 119
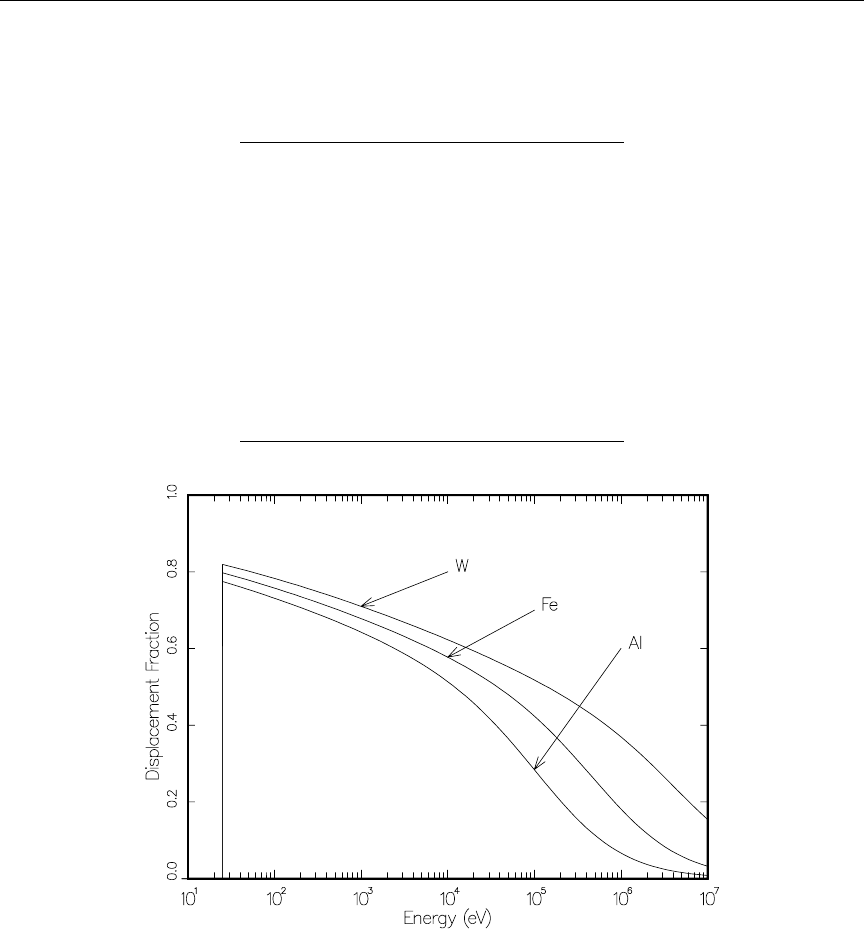
LA-UR-17-20093 6 HEATR
Table 2: Typical Values for the Atomic Displacement Energy Needed to Compute DPA[46].
Element Ed, eV Element Ed, eV
Be 31 Co 40
C 31 Ni 40
Mg 25 Cu 40
Al 27 Zr 40
Si 25 Nb 40
Ca 40 Mo 60
Ti 40 Ag 60
V 40 Ta 90
Cr 40 W 90
Mn 40 Au 30
Fe 40 Pb 25
Figure 9: Examples of the portion of the primary recoil energy that is available to cause
lattice displacements in metallic lattices. The remaining energy leads to electronic
excitation. The quantity plotted is P(E) from Eq. 200 divided by E. The 25 eV
cutoff is also discussed in connection with Eq. 200.
6.3 Computation of KERMA Factors By Energy Balance
6.3.1 The general case
The older ENDF/B files do not usually give photon production data for all
partial reactions. Summation reactions such as nonelastic (MT=3) and inelastic
120 NJOY2016

6 HEATR LA-UR-17-20093
(MT=4) are often used. It is still possible to compute partial KERMA factors
for those summation reactions by reordering Eq. 162 as follows:
kij =X
j∈J
kn
ij(E)−X
`∈J
Ei`γσi`(E),(166)
where jruns over all neutron partials contained in J, and `runs over all photon
partials in J. The total KERMA is well defined, but partial KERMAS should
be used only with caution.
HEATR loops through all the neutron reactions on the ENDF/B tape. If
energy balance is to be used, it computes the neutron contributions needed for
the first term. These are
kn
ij(E) = hE+Qij −Eijn(E)iσij (E).(167)
The Q-value is zero for elastic and inelastic scattering. For (n,n0) particle
reactions represented by scattering with an LR flag set, Q is the ENDF “C1”
field from MF=3. For most other reactions, Q is the “C2” field from MF=3.
HEATR allows users to override any Q-value with their own numbers.
The Envalue as used in Eq. 167 is defined to include multiplicity. The
multiplicity is either implicit — for example, 2 for (n,2n) — or is retrieved from
the ENDF/B file (e.g. for the mt5 reaction). The average energy per neutron is
computed differently for discrete two-body reactions and continuum reactions.
For elastic and discrete inelastic scattering (MT=2, 51-90),
En=E
(A+ 1)21+2Rf1+R2,(168)
where f1is the center-of-mass (CM) average scattering cosine from MF=4 and
Ris the effective mass ratio. For elastic scattering, R=A, but for threshold
scattering,
R=Ar1−(A+ 1)S
AE ,(169)
where Sis the negative of the C2 field from MF=3.
For continuum scattering, the average energy per neutron is computed from
NJOY2016 121

LA-UR-17-20093 6 HEATR
the secondary neutron spectrum, g, in MF=5 using
En(E) = ZU
0
E0g(E, E0)dE0,(170)
where Uis defined in MF=5. If gis tabulated (LAW=1 or LAW=5), the in-
tegral is carried out analytically for each panel by making use of the ENDF/B
interpolation laws. For the simple analytic representations (LAW=7, 9, or 11),
the average energies are known[9].
The neutron cross sections required by Eq. 167 are obtained from an existing
PENDF file (see RECONR, and BROADR).
When the neutron sum in Eq. 166 is complete, the code processes the photon
production files. If the evaluation does not include photon data, HEATR returns
only the first sum. This is equivalent to assuming that all photon energy is
deposited locally, consistent with the fact that there will be no contribution to
the photon transport source from this material. The same result can be forced
by using the local parameter (see “User Input”, Section 6.7, below).
Discrete photon yields and energies are obtained from MF=12 or 13. Con-
tinuum photon data are obtained from MF=15, and the average photon energy
and E2
γare computed. For radiative capture, the photon term becomes
Eγσγ= E+Q−E
A+ 1 +E2
γ
2(A+ 1)mc2Yγ!σγ,(171)
[9] where Yγis the capture photon yield from MF=12. This corrects the capture
contribution from Eq. 167 by conservation of momentum. For other reactions,
Eq. 167 is sufficient, and the product of Eγ,Yγ, and σγis subtracted from the
neutron contribution.
6.3.2 The special case of fission
The partial KERMA for fission is a special case due to the particular problems
with obtaining the Q-value for fission. First, the fission Q-value given in the C1
field of MF=3 includes delayed neutron and gamma contributions that we need
to exclude, and second, the Q-value for fission is energy dependent.
As a result, the KERMA for fission will be calculated differently when com-
pared to the other reactions which use Eq. 167 as is. Theoretically speaking,
there is no difference with Eq. 167 as we will show here.
Energy dependent fission energy release and its components are given in the
MT=458 section of MF=1 on the ENDF file. This section of the ENDF file
122 NJOY2016

6 HEATR LA-UR-17-20093
defines the following components to the fission energy release:
•Qk: the kinetic energy of the fission fragments
•Qn,p and Qn,d : the kinetic energy of the prompt and delayed fission neu-
trons
•Qγ,p and Qγ,d : the energy of the prompt and delayed gamma rays
•Qβ: the energy of the delayed beta radiation
•Qν: the energy carried away by the neutrinos
With these components, we can now define the total energy release from
fission Qt, the total energy release from fission excluding neutrinos Qrand the
total prompt energy release from fission Qpas as follows:
Qt(E) = Qk(E) + Qn,p +Qn,d +Qγ,p +Qγ,d +Qβ+Qν,(172)
Qr(E) = Qt(E)−Qν,(173)
Qp(E) = Qr(E)−Qn,d −Qγ,d −Qβ=Qk(E) + Qn,p +Qγ,p .(174)
Using these fission energy release components, we can define the fission reac-
tion Q-value (i.e. the energy released through the fission reaction) as the prompt
fission energy release minus the incident neutron energy:
Q(E) = Qp(E)−E=Qk(E) + Qn,p +Qγ,p −E . (175)
It should be noted that we have chosen to ignore the energy dependence of
delayed beta and gamma emission because we don’t yet treat it in subsequent
codes. However, the impact of such an approximation is somewhat limited due
to the amount of energy involved. For example, for U235 the value of Qkis
roughly 169 MeV at 1e-5 eV while the sum of Qn,d,Qγ,d and Qβis roughly 12
MeV at 1e-5 eV.
For the calculation of the fission KERMA factor, we also need to know the
energy of the outgoing neutrons (i.e. Efrom Eq. 167). Because we are consider-
ing the prompt energy release only, this is simply equal to the prompt neutron
energy release Qn,p.
As a result, the partial fission KERMA factor kn
fwill be given by:
kn
f(E) = hE+Q(E)−E(E)iσf(E) = hQk(E) + Qγ,p(E)iσf(E).(176)
NJOY2016 123

LA-UR-17-20093 6 HEATR
The fission KERMA is thus equal to the fission cross section times the sum of
the kinetic energy of the fission products and the prompt gamma energy release.
This value will then be used in Eq. 166 to calculate the total KERMA.
In some cases it is possible that a fissile nuclide does not have an MT458
section. In this case, Eq. 167 will be used directly as follows:
kn
f(E) = hE+Q(E)−ν(E)E(E)iσf(E) (177)
where the fission Q-value is approximated using the thermal point energy de-
pendencies defined for MT458:
Q(E) = QENDF −8070000 (ν(E)−ν(0)) + 0.307E(178)
In this equation, QENDF is the reaction Q-value for fission as given in MF3.
6.4 Kinematic Limits
As an option provided mainly as an aid to evaluators, HEATR will compute the
kinematic maximum and minimum KERMA coefficients and compare them with
the energy-balance results. The formulas are as follows. For elastic scattering
(MT=2), the expected recoil energy is
ER=2AE
(A+ 1)2(1 −f1).(179)
For discrete-inelastic scattering (MT=51-90), the photon momentum is ne-
glected to obtain
ER=2AE
(A+ 1)2"1−f1r1−(A+ 1)Eγ
AE #−Eγ
A+ 1 ,(180)
where Eγ=−C2 from MF=3. For continuum inelastic scattering (MT=91), sec-
ondary neutrons are assumed to be isotropic in the laboratory system (LAB)
giving
ER=E−En
A,(181)
and
Eγ=(A−1)E−(A+ 1)En
A,(182)
124 NJOY2016

6 HEATR LA-UR-17-20093
where Eγis the average photon energy expected for this representation. For
radiative capture (MT=102),
ER=E
A+ 1 +EK(183)
and
Eγ=Q+AE
A+ 1 −EK,(184)
where
EK=1
2MRc2AE
A+ 1 +Q21−1
MRc2AE
A+ 1 +Q ,(185)
with
MRc2= (939.565 ×106)(A+ 1) −Q(186)
being the mass energy in eV. The value of this constant is actually computed
from fundamental constants in NJOY2016.
For two-body scattering followed by particle emission (MT=51-91, LR flag
set), a minimum and maximum can be defined:
(E0
R+Ex)min =ER,and (187)
(E0
R+Ex)max =ER+Q+ (Eγ)max ,(188)
where ERis the value from Eq. 180 or (181), Qis the C2 field from File 3, and
(Eγ)max is the negative of the C2 field from File 3. In these equations, E0
Ris
the recoil energy and Exis the energy of the charged product. For absorption
followed by particle emission (MT=103-120),
(ER+Ex)min =E
A+ 1 −x,(189)
(Eγ)max =Q+A−x
A+ 1 −xE , and (190)
(ER+Ex)max =E+Q , (191)
where Qis the C2 field from MF=3 and xis the particle mass ratio (x=1 gives
a minimum for all reactions). For (n,2n) reactions,
NJOY2016 125

LA-UR-17-20093 6 HEATR
(ER)min = 0 ,and (192)
(ER)max =E+En
A−1,(193)
and for (n,3n) reactions,
(ER)min = 0 ,and (194)
(ER)max =E+ 2En
A−2.(195)
For both (n,2n) and (n,3n), if (ER)max is greater than ER, it is set equal to ER.
In addition, these formulas are not used for A<10; (ER)max is set to ER. For
other neutron continuum scattering reactions (MT=22-45),
(ER+Ex)min = 0 ,and (196)
(ER+Ex)max =E+Q−En,(197)
where Qis the C2 field from File 3. Finally, for fission (MT=18-21, 38), the
limits are
(ER)min =E+Q−1
2En−15×106eV ,and (198)
(ER)max =E+Q−En,(199)
where Qis the prompt fission Q-value less neutrinos. It is determined by taking
the total (less neutrinos) value from File 3 and subtracting the delayed energy
obtained from MF=1/MT=458.
These values are intended to be very conservative. Note that EKis only
significant at very low neutron energy. In order to reduce unimportant error
messages, a tolerance band is applied to the above limits. If all checks are
satisfied, the resulting KERMA coefficients should give good local heating results
even when 99.8% of the photons escape the local region. More information on
using the kinematic checks to diagnose energy-balance problems in evaluations
will be found in “Diagnosing Energy-Balance Problems”, Section 6.9.
The upper kinematic limit can also be written out to the output tape as
126 NJOY2016

6 HEATR LA-UR-17-20093
MT=443 if desired. It is similar to the KERMA factors generated by the MACK
code[30], and it is sometimes preferable to the energy-balance KERMA for cal-
culating local heating for evaluations with severe energy-balance problems. The
kinematic value in MT=443 is useful for plots (see the examples in this report).
6.5 Computation of Damage Energy
The formulas used for calculating damage energy are derived from the same
sources as the heating formulas given above, except in this case, the effects of
scattering angle do not result in simple factors like f1because the Robinson
partition function is not linear. Instead, it is calculated as follows:
P(E) = ER
1 + FL(3.40081/6+ 0.402443/4+),(200)
if ER≥25.0 eV, and zero otherwise. In Eq. 200,ERis the primary recoil energy,
=ER
EL
,(201)
EL= 30.724ZRZLZ2/3
R+Z2/3
L1/2(AR+AL)/AL,and (202)
FL=0.0793Z2/3
RZ1/2
L(AR+AL)3/2
Z2/3
R+Z2/3
L3/4A3/2
RA1/2
L
,(203)
and Ziand Airefer to the charge and atomic number of the lattice nuclei (L)
and the recoil nuclei (R). The function behaves like ERat low recoil energies
and then levels out at higher energies. Therefore, the damage-energy production
cross section is always less than the heat production cross section. See Fig. 9
for examples.
For elastic and two-body discrete-level inelastic scattering,
ER(E, µ) = AE
(A+ 1)21−2Rµ +R2,(204)
where the “effective mass” is given by
R=r1−(A+ 1)(−Q)
AE ,(205)
and µis the CM scattering cosine. The damage energy production cross section
NJOY2016 127

LA-UR-17-20093 6 HEATR
is then obtained from
D(E) = σ(E)Z1
−1
f(E, µ)P(ER[E, µ]) dµ , (206)
where fis the angular distribution from the ENDF/B File 4. This integration is
performed with a 20-point Gauss-Legendre quadrature. Discrete-level reactions
with LR flags to indicate, for example, (n,n0)αreactions, are treated in the same
way at present. The additional emitted particles are ignored.
Continuum reactions like (n,n0) give a recoil spectrum
ER(E, E0, µ) = 1
AE−2√EE0µ+E0,(207)
where E0is the secondary neutron energy, µis the laboratory cosine, and the
photon momentum has been neglected. The damage becomes
D(E) = σ(E)Z∞
0
dE0Z1
−1
dµ f(E, µ)g(E, E0)P(ER[E, E0, µ]) ,(208)
where gis the secondary energy distribution from File 5. In the code, the
angular distribution is defaulted to isotropic, and a 4-point Gaussian quadrature
is used for the angular integration. For analytic representations of g, an adaptive
integration to 5% accuracy is used for E0; for tabulated File 5 data, a trapezoidal
integration is performed using the energy grid of the file. The same procedure
is used for (n,2n), (n,3n), etc., but it is not realistic for reactions like (n,n0p)
or (n,n0α). The neutron in these types of reactions can get out of the nucleus
quite easily; thus, much of the energy available to secondary particles is typically
carried away by the charged particles[49]. HEATR treats these reactions in the
same way as (n,p) or (n,α).
The recoil for radiative capture must include the momentum of the emitted
photons below 25 – 100 keV giving
ER=E
A+ 1 −2rE
A+ 1sE2
γ
2(A+ 1)mc2cos φ+E2
γ
2(A+ 1)mc2,(209)
where φis the angle between the incident neutron direction and emitted photon
direction. If subsequent photons are emitted in a cascade, each one will add
an additional term of E2
γand an additional angle. A complete averaging of
Eq. 209 with respect to P(ER) would be very difficult and would require angular
128 NJOY2016

6 HEATR LA-UR-17-20093
correlations not present in ENDF/B evaluations. However, damage calculations
are still fairly crude, and an estimate for the damage obtained by treating the
neutron “kick” and all the photon kicks independently should give a reasonable
upper limit because
Z1
−1
D(ER)dcos φ≤DE
A+ 1+X
γ
D E2
γ
2MRc2!.(210)
The actual formula used in the code is
D(E) = DE
A+ 1+D 1
2MRc2AE
A+ 1 +Q2!
+X
γ
D E2
γ
2MRc2!−D 1
2MRc2AE
A+ 1 +Q2!,(211)
where the first line is computed in the neutron section, and the second line is
computed in the photon section. This form also provides a reasonable default
when no photons are given.
Finally, for the (n,particle) reactions, the primary recoil is given by
ER=1
A+ 1E∗−2paE∗Eacos φ+aEa,(212)
where ais the mass ratio of the emitted particle to the neutron, E∗is given by
E∗=A+ 1 −a
A+ 1 E , (213)
and the particle energy Eais approximated as being equal to the smaller of the
available energy
Q+AE
A+ 1 ,(214)
or the Coulomb barrier energy
1.029 ×106zZ
a1/3+A1/3in eV ,(215)
NJOY2016 129
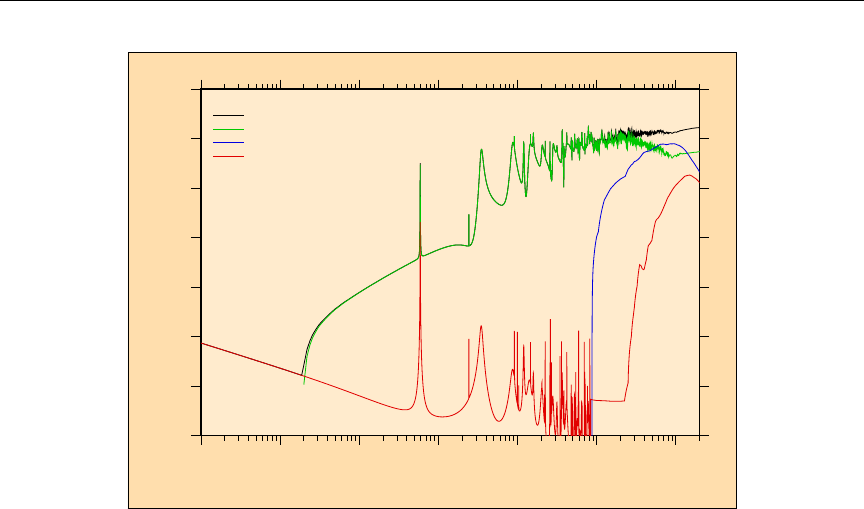
LA-UR-17-20093 6 HEATR
101102103104105106107
Energy (eV)
10-1
100
101
102
103
104
105
106
Damage (eV-barns)
total
elastic
inelastic
absorption
Figure 10: Components of radiation damage energy production for 27Al from ENDF/B-
VII.0. Note that capture dominates at very low energies, then elastic dominates,
and finally inelastic begins to contribute at very high energies.
where zis the charge of the emitted particle and Zis the charge of the target.
A more reasonable distribution would be desirable[49], but this one has the
advantage of eliminating an integration, and most results are dominated by the
kick imparted by the incident neutron anyway. The angular distribution for
the emitted particle is taken as isotropic in the lab. At high incident energies,
direct interaction processes would be expected to give rise to a forward-peaked
distribution, thereby reducing the damage. However, the importance of this
effect is also reduced by the dominance of the neutron kick.
Fig. 10 gives a typical result for a damage energy production calculation,
showing the separate contributions of elastic, inelastic, and absorption processes.
6.6 Heating and Damage from File 6
A number of the evaluations in ENDF/B-VI and later include complete energy-
angle distributions for all of the particles produced by a reaction, including
the residual nucleus. In these cases, HEATR can compute the contributions to
KERMA by calculating the average energy in the spectrum of each outgoing
charged particle or residual nucleus and using Eq. 161.
A fully-populated section of File 6 contains subsections for all of the particles
130 NJOY2016

6 HEATR LA-UR-17-20093
and photons produced by the reaction, including the recoil nucleus. There are
a number of different schemes used to represent the energy-angle distributions
for these outgoing particles. The most important ones for HEATR follow:
•No distribution. In this case, the subsection is inadequate for use in heating
and damage calculations. A warning message is issued.
•Two-body angular distribution. These are basically the same as distribu-
tions in File 4.
•Recoil distribution. This particle is a recoil nucleus from a two-body re-
action. Its angular distribution is assumed to be the complement of the
angular distribution for the first subsection in this section.
•CM Kalbach distribution. This format is often used by LANL evaluations,
and transformation to the laboratory frame is required. The looping order
for the data is E,E0,µ.
•LAB Legendre distribution. This format is used in most of the ORNL
evaluations for ENDF/B-VI. It is already in the laboratory frame, and the
angular information can be simply ignored.
•LAB angle-energy distribution. This format is used for the 9Be evaluation
of ENDF/B-VI by LLNL. The looping order is E,µ,E0.
The normal procedure is to loop through all of these subsections. The subsec-
tions producing neutrons are processed to be used in a total energy check, but
they contribute nothing to the heating or to the damage. Subsections describ-
ing charged particles and residual nuclei are processed into heating and damage
contributions. Finally, the photon subsection is processed for the photon energy
check and the total energy check, even though it does not affect either heating
or damage. Any remaining difference between the eV-barns available for the
reaction and the eV-barns carried away by the neutrons, photons, particles, and
recoil is added into the heating to help preserve the total energy deposition in
the spirit of the energy-balance method.
For “two-body” sections, the emitted particle energy is given by
E0=A0E
A+ 11+2Rµ +R2,(216)
where
R=rA(A+ 1 −A0)
A0,(217)
and A0is the ratio of the mass of the outgoing particle to that of the incident
NJOY2016 131

LA-UR-17-20093 6 HEATR
particle. The heating is obtained by doing a simple integral over µ, and the
damage is computed using the integral over µgiven in Eq. 206. In both cases,
the integrals are performed using either a 20-point Gauss-Legendre quadrature
(for Legendre representations) or a trapezoidal integration (for tabulated data).
For “recoil” sections, the code backs up to the particle distribution and cal-
culates the recoil using the same method described above with the sign of µ
changed.
For laboratory distributions that use the E,E0,µordering, the angular part
can be ignored, and the heating and damage become
K(E) = Zg(E→E0)E0dE0,(218)
and
D(E) = Zg(E→E0)P(E0)dE0,(219)
where g(E→E0) is the angle-integrated energy distribution from File 6, and
P(E0) is the damage partition function. Trapezoidal integration is used for
the continuum, and the integrand is simply added into the sum for the delta
functions (if any).
Heating for subsections that use the ordering E,µ,E0is computed using the
formula
K(E) = ZZg(E→E0, µ)E0dE0dµ , (220)
where an inner integral is performed using trapezoidal integration for each value
in the µgrid. The results are then used in a second trapezoidal integration over
µ. The damage integral is performed at the same time in a parallel manner.
The problem is somewhat more difficult for subsections represented in the
center-of-mass frame. The definitions for K(E) and D(E) are the same as those
given above, except that the quantity g(E→E0) has to be generated in the lab
system. The methods used to do the transformation are basically the same in
HEATR and GROUPR. The first step is to set up an adaptive integration over
E0. The first value needed to prime the stack is obtained by calling h6cm with
E0=0. It returns the corresponding value of gin the lab system and a value for
epnext. The second value for the stack is computed for E=epnext. The routine
then subdivides this interval until 2% convergence is achieved, accumulating the
contributions to the heating and damage integrals as it goes. It then moves up
132 NJOY2016
6 HEATR LA-UR-17-20093
to a new panel. This process continues until the entire range of E0has been
covered.
The key to this process is h6cm. As described in more detail in the GROUPR
chapter of this manual, it performs integrals of the form
gL(E→E0
L) = Z+1
µmin
gC(E→E0
C, µC)J dµL,(221)
where Land Cdenote the laboratory and center-of-mass systems, respectively,
and Jis the Jacobian for the transformation. The contours in the E0
C,µCframe
that are used for these integrals have constant E0
L. The limiting cosine, µmin,
depends on kinematic factors and the maximum possible value for E0
Cin the
File 6 tabulation.
The ENDF/B-VII library contains a few abbreviated versions of File 6 that
contain an energy-angle distribution for neutron emission, but no recoil or pho-
ton data. In order to get semi-reasonable results for both heating and damage
for such cases, HEATR applies a “one-particle recoil approximation,” where
the first particle emitted is assumed to induce all the recoil. There are also
some cases where capture photons are described in MF=6/MT=102 with no
corresponding recoil data. Here, the recoil can be added using the same logic
described above for capture represented using File 15. The difference between
the eV-barns available for the reaction and the energy accounted for by the emit-
ted neutrons, photons, particles, and the approximated recoil is added into the
heating in order to preserve the total heating in the spirit of the energy-balance
method.
6.7 User Input
The input instructions that follow were reproduced from the comment cards in
the current version of HEATR.
!---input specifications (free format)------------------------
!
! card 1
! nendf unit for endf tape
! nin unit for input pendf tape
! nout unit for output pendf tape
! nplot unit for graphical check output
! card 2
! matd material to be processed
NJOY2016 133

LA-UR-17-20093 6 HEATR
! npk number of partial kermas desired (default=0)
! nqa number of user q values (default=0)
! ntemp number of temperatures to process
! (default=0, meaning all on pendf)
! local 0/1=gamma rays transported/deposited locally
! (default=0)
! iprint print (0 min, 1 max, 2 check) (default=0)
! ed displacement energy for damage
! (default from built-in table)
! card 3 for npk gt 0 only
! mtk mt numbers for partial kermas desired
! total (mt301) will be provided automatically.
! partial kerma for reaction mt is mt+300
! and may not be properly defined unless
! a gamma file for mt is on endf tape.
! special values allowed--
! 303 non-elastic (all but mt2)
! 304 inelastic (mt51 thru 91)
! 318 fission (mt18 or mt19, 20, 21, 38)
! 401 disappearance (mt102 thru 120)
! 442 total ev-barns
! 443 total kinematic kerma (high limit)
! damage energy production values--
! 444 total
! 445 elastic (mt2)
! 446 inelastic (mt51 thru 91)
! 447 disappearance (mt102 thru 120)
! cards 4 and 5 for nqa gt 0 only
! card 4
! mta mt numbers for users q values
! card 5
! qa user specified q values (ev)
! (if qa.ge.99.e6, read in variable qbar
! for this reaction)
! card 5a variable qbar (for reactions with qa flag only)
! qbar tab1 record giving qbar versus e (1000 words max)
!
!----------------------------------------------------------------
Card 1 specifies the input and output units for HEATR. They are all ENDF-
type files. The input PENDF file has normally been through RECONR and
134 NJOY2016

6 HEATR LA-UR-17-20093
BROADR, but it is possible to run HEATR directly on an ENDF file in order
to do kinematic checks. In this case, the results in the resonance range should
be ignored. Defining nplot will produce a file of input for the VIEWR module
containing detailed energy-balance test results. This option should only be used
together with iprint=2.
On Card 2, the default value for npk is zero, which instructs the code to
process the energy-balance total KERMA (MT=301) only. Most often, the
user will also want to include MT=443 and MT=444 (npk=2). The kinematic
KERMA computed when MT=443 is requested is very useful for judging the
energy-balance consistency of an evaluation (see the subsection on “Diagnosing
Energy-Balance Problems”, Section 6.9, below). It can also be used instead of
the energy-balance value in MT=301 when local heating effects are important
and the evaluation scores poorly in an energy-balance check. Damage energy
production cross sections (MT=444) should be computed for important struc-
tural materials; this expensive calculation can be omitted for other materials.
When kinematic checks are desired, a number of additional npk values can
be included. They can be determined by checking the evaluation to see what
partial KERMA factors are well defined. For old-style evaluations that do not
use File 6, look for the MT values used in Files 12 and 13. Many evaluations use
only MT=3 and MT=102 (or 3, 18, and 102 for fissionable materials); in these
cases, the only mtk values that make sense are 302, 303, and 402 (or 302, 303,
318, and 402 for fissionable materials). Caution: in many evaluations, MT=102
is used at low energies and taken to zero at some breakpoint. MT=3 is used
at higher energies. In these evaluations, the partial KERMA MT=402 does not
make sense above the breakpoint, and MT=3 does not make sense below it.
More complicated photon-production evaluations may include MT=4 and/or
discrete-photon data in MT=51-90. In these cases, the user can request mtk=304.
The same kind of energy-range restriction discussed for MT=102 can occur for
the inelastic contributions. Other evaluations give additional partial reactions
that can be used to check the photon production and energy-balance consistency
of an evaluation in detail. HEATR can handle 6 additional reactions at a time.
Multiple runs may be necessary in complex cases.
Note that several special mtk values are provided for the components of the
damage-energy production cross section. They were used to prepare Fig. 10,
and may be of interest to specialists, but they are not needed for most libraries.
In a few cases in the past, it has been necessary to change the Q-values that
are normally retrieved from the ENDF tape. In addition, it is sometimes neces-
NJOY2016 135
LA-UR-17-20093 6 HEATR
sary to replace the single Q-value supplied in MF=3 with an energy-dependent
Q function for an element. One example of the former occurred for 16O for
ENDF/B-V. The first inelastic level (MT=51) decays by pair production rather
than the more normal mode of photon emission. In order to get the correct
heating, it was necessary to change the Q-value by giving Card 4 and Card 5 as
follows:
51
-5.0294e6
That is, the Q-value is increased by twice the electron energy of 0.511 MeV.
Another example is the sequential (n,2n) reaction for 9Be in ENDF/B-V. It is
necessary to include 4 changes to the Q-values:
46 47 48 49/
-1.6651e6 -1.6651e6 -1.6651e6 -1.6651e6/
The next example illustrates using energy-dependent Q-values for elemental
titanium. Set nqa equal to 3 and give the following values on Cards 4, 5, and
5a:
16 103 107/
99e6 99e6 99e6/
0.0.0018
8 2
8.0e6 -8.14e6 9.0e6 -8.14e6 1.1e7 -8.38e6
1.2e7 -8.74e6 1.3e7 -1.03e7 1.4e7 -1.091e7
1.5e7 -1.11e7 2.0e7 -1.125e7/
0.0.0019
9 2
1.0e-5 1.82e5 4.0e6 1.82e5 5.0e6 -1.19e6
6.0e6 -2.01e6 7.0e6 -2.20e6 8.0e6 -2.27e6
1.4e7 -2.35e6 1.7e6 -2.43e6 2.0e7 -2.37e6/
0.0.0019
9 2
1.0e-5 2.182e6 6.0e6 2.182e6 7.0e6 2.10e6
8.0e6 -3.11e5 9.0e6 -9.90e5 1.0e7 -1.20e6
136 NJOY2016

6 HEATR LA-UR-17-20093
1.1e7 -1.27e6 1.4e6 -1.32e6 2.0e7 -1.48e6/
The next parameter on Card 2 is ntemp. For normal runs, use zero, and all
the temperatures on the input PENDF tape will be processed. For kinematic
check runs, use ntemp=1. The local parameter suppresses the processing of
the photon-production files, if any. The photon energy appears in the KERMA
factors as if the photons had very short range. A useful way to use the iprint
parameter is to set it to zero for normal runs, which produce heating and damage
values at all temperatures, and to use iprint=2 for the energy-balance check
run, which is performed for the first temperature on nin only.
Card 3 gives the partial KERMA and damage selection MT numbers. Note
that the user does not include MT=301 in this list. It is always inserted as the
first value automatically. Giving MT=301 in this list will cause an informative
message to be issued.
Cards 4, 5, and 5a give the user’s changes to the ENDF Q values. The way
in which to use these cards was described in connection with nqa on Card 2.
6.8 Reading HEATR Output
When full output and/or kinematic checks have been requested, HEATR loops
through the reactions found in Files 3, 12, and 13. For each reaction, it prints
out information about the energies, yields, cross sections, and contributions to
heating. The energy grid used is a subset of the PENDF grid. At present,
decade steps are used below 1 eV, factor-of-two steps are used from 1 eV to 100
keV, quarter-lethargy steps are used above 100 keV, and approximately 1 MeV
steps are used above 2 MeV. An example of this printout for elastic scattering
in ENDF/B-VII.0 27Al is shown below:
neutron heating for mt 2 q0 = 0.0000E+00 q = 0.0000E+00
e ebar ... xsec heating damage
1.0000E-05 9.3052E-06 ... 1.5694E+01 1.0903E-05 0.0000E+00
1.0000E-04 9.3052E-05 ... 5.1179E+00 3.5557E-05 0.0000E+00
1.0000E-03 9.3052E-04 ... 2.0644E+00 1.4342E-04 0.0000E+00
1.0000E-02 9.3052E-03 ... 1.4925E+00 1.0369E-03 0.0000E+00
1.0000E-01 9.3052E-02 ... 1.4318E+00 9.9474E-03 0.0000E+00
...
1.0000E+03 9.3052E+02 ... 1.3662E+00 9.4914E+01 7.7171E+01
2.0000E+03 1.8610E+03 ... 1.3196E+00 1.8337E+02 1.5115E+02
NJOY2016 137

LA-UR-17-20093 6 HEATR
5.0000E+03 4.6526E+03 ... 1.2130E+00 4.2136E+02 3.3998E+02
1.0000E+04 9.3052E+03 ... 1.0367E+00 7.2028E+02 5.6725E+02
2.0000E+04 1.8610E+04 ... 6.6204E-01 9.1991E+02 7.0347E+02
5.0000E+04 4.6526E+04 ... 2.3220E+00 8.0660E+03 5.8732E+03
1.0000E+05 9.3052E+04 ... 5.2976E+00 3.6805E+04 2.5521E+04
...
1.0000E+07 9.7233E+06 ... 7.4942E-01 2.0738E+05 4.5689E+04
1.1000E+07 1.0699E+07 ... 7.4953E-01 2.2576E+05 4.7347E+04
1.2000E+07 1.1682E+07 ... 7.6363E-01 2.4286E+05 4.9202E+04
1.3000E+07 1.2673E+07 ... 7.6329E-01 2.4980E+05 4.9559E+04
1.4000E+07 1.3670E+07 ... 7.7918E-01 2.5737E+05 5.0566E+04
1.5000E+07 1.4671E+07 ... 7.9297E-01 2.6088E+05 5.1189E+04
1.6000E+07 1.5676E+07 ... 8.1414E-01 2.6347E+05 5.1973E+04
1.7000E+07 1.6681E+07 ... 8.3429E-01 2.6577E+05 5.2680E+04
1.8000E+07 1.7689E+07 ... 8.4524E-01 2.6246E+05 5.2747E+04
1.9000E+07 1.8695E+07 ... 8.7093E-01 2.6568E+05 5.3787E+04
2.0000E+07 1.9703E+07 ... 8.9326E-01 2.6547E+05 5.4573E+04
...
1.4000E+08 1.3985E+08 ... 2.9730E-01 4.3523E+04 1.4994E+04
1.4600E+08 1.4585E+08 ... 2.7580E-01 4.1851E+04 1.3890E+04
1.5000E+08 1.4984E+08 ... 2.6510E-01 4.1161E+04 1.3339E+04
Note the identification and Q information printed on the first line; qis the ENDF
Q-value from File 3, and q0 is the corresponding mass-difference Q-value needed
for Eq. 162. The ebar,yield (which was replaced by “...” to make this listing
fit better), and xsec columns contain En,Y, and σ, respectively. The heating
column is just (E+Q−Y En)σ. The results are similar for discrete inelastic
levels represented using File 4. The heating due to the associated photons will
be subtracted later while MF=12 or MF=13 is being processed. However, if
an LR flag is set, the residual nucleus from the (n,n0) reaction breaks up by
emitting additional particles. This extra breakup energy changes the q0 value.
An example of such a section for 27Al(n,n25)p from ENDF/B-V follows:
neutron heating for mt 75 q0 = -8.2710e+06 q = -1.0750e+07
e ebar yield xsec heating
1.2000e+07 7.8653e+05 1.0000e+00 8.2242e-02 2.4199e+05
1.3000e+07 1.7116e+06 1.0000e+00 8.0121e-02 2.4176e+05
1.4000e+07 2.6427e+06 1.0000e+00 5.9282e-02 1.8296e+05
1.5000e+07 3.5864e+06 1.0000e+00 4.1834e-02 1.3147e+05
138 NJOY2016
6 HEATR LA-UR-17-20093
1.6000e+07 4.5096e+06 1.0000e+00 2.8880e-02 9.2977e+04
1.7000e+07 5.4335e+06 1.0000e+00 1.9867e-02 6.5472e+04
1.8000e+07 6.3848e+06 1.0000e+00 1.3677e-02 4.5739e+04
1.9000e+07 7.2944e+06 1.0000e+00 9.4771e-03 3.2550e+04
2.0000e+07 8.2479e+06 1.0000e+00 6.6142e-03 2.3025e+04
Starting with ENDF/B-VI, discrete-inelastic sections may also be given in File
6. Such sections contain their own photon production data, and the heating
column will represent the entire recoil energy as in Eq. 180. (See below for
detailed discussion of ENDF/B-VI output.)
For continuum reactions that use MF=4 and MF=5, such as (n,n0) or (n,2n),
the neutron part of the display looks like this:
neutron heating for mt 16 q0 = -1.3057e+07 q = -1.3057e+07
e ebar yield xsec heating
1.4000e+07 1.9960e+05 2.0000e+00 2.4000e-02 1.3051e+04
1.5000e+07 6.6850e+05 2.0000e+00 1.2320e-01 7.4659e+04
1.6000e+07 1.0855e+06 2.0000e+00 2.0710e-01 1.5987e+05
1.7000e+07 1.4308e+06 2.0000e+00 2.6510e-01 2.8667e+05
1.8000e+07 1.6379e+06 2.0000e+00 3.0300e-01 5.0518e+05
1.9000e+07 1.7659e+06 2.0000e+00 3.3000e-01 7.9567e+05
2.0000e+07 1.8755e+06 2.0000e+00 3.5000e-01 1.1172e+06
Once again, the photon effects will be subtracted later.
Absorption reactions such as (n,γ) or (n,p), lead to similar displays, but the
particle ebar columns will always be set to zero (no emitted neutrons). An
example follows:
neutron heating for mt103 q0 = -1.8278e+06 q = -1.8278e+06
e ebar yield xsec heating
2.5000E+06 0.0000E+00 1.0000E+00 3.2800E-05 2.2048E+01
3.0000E+06 0.0000E+00 1.0000E+00 1.3300E-03 1.5590E+03
3.5000E+06 0.0000E+00 1.0000E+00 1.0100E-02 1.6889E+04
4.0000E+06 0.0000E+00 1.0000E+00 6.9667E-03 1.5133E+04
4.5000E+06 0.0000E+00 1.0000E+00 1.7000E-02 4.5427E+04
5.0000E+06 0.0000E+00 1.0000E+00 2.3300E-02 7.3912E+04
...
1.7000E+07 0.0000E+00 1.0000E+00 5.5200E-02 8.3751E+05
NJOY2016 139
LA-UR-17-20093 6 HEATR
1.8000E+07 0.0000E+00 1.0000E+00 4.7800E-02 7.7303E+05
1.9000E+07 0.0000E+00 1.0000E+00 4.0200E-02 6.9032E+05
2.0000E+07 0.0000E+00 1.0000E+00 3.2200E-02 5.8514E+05
If File 6 is present (which happens for evaluations in ENDF-6 format only,
such as the evaluations in ENDFB-VII), each reaction will be divided into sub-
sections, one for each emitted particle. The neutron subsections are displayed
as part of the energy-balance checks, but they do not contribute to KERMA
or damage. The subsection for each charged particle or residual nucleus will
give the incident energy, average energy for the emitted particle, cross section,
heating contribution, and (optionally) damage contribution as follows:
file six heating for mt 28, particle = 1 q = -8.2721E+06
e ebar yield xsec heating
9.0000E+06 1.2303E+05 1.0000E+00 1.0385E-03 0.0000E+00
1.0000E+07 4.6746E+05 1.0000E+00 1.3526E-02 0.0000E+00
...
1.8000E+07 3.1862E+06 1.0000E+00 3.7721E-01 0.0000E+00
1.9000E+07 3.4535E+06 1.0000E+00 3.7577E-01 0.0000E+00
2.0000E+07 3.7207E+06 1.0000E+00 3.7434E-01 0.0000E+00
file six heating for mt 28, particle = 1001 q = -8.2721E+06
e ebar yield xsec heating
9.0000E+06 4.5909E+05 1.0000E+00 1.0385E-03 4.7677E+02
1.0000E+07 8.9616E+05 1.0000E+00 1.3526E-02 1.2121E+04
...
1.8000E+07 3.5193E+06 1.0000E+00 3.7721E-01 1.3275E+06
1.9000E+07 3.8257E+06 1.0000E+00 3.7577E-01 1.4376E+06
2.0000E+07 4.1321E+06 1.0000E+00 3.7434E-01 1.5468E+06
file six heating for mt 28, particle = 12026 q = -8.2721E+06
e ebar yield xsec heating
9.0000E+06 3.2104E+05 1.0000E+00 1.0385E-03 3.3340E+02
1.0000E+07 3.8540E+05 1.0000E+00 1.3526E-02 5.2128E+03
...
1.8000E+07 8.0820E+05 1.0000E+00 3.7721E-01 3.0486E+05
1.9000E+07 8.6147E+05 1.0000E+00 3.7577E-01 3.2372E+05
2.0000E+07 9.1475E+05 1.0000E+00 3.7434E-01 3.4243E+05
file six heating for mt 28, particle = 0 q = -8.2721E+06
140 NJOY2016

6 HEATR LA-UR-17-20093
e ebar yield xsec heating
9.0000E+06 1.8347E+05 2.8104E-06 1.0385E-03 0.0000E+00
ebal -1.8204E+02
1.0000E+07 4.4913E+05 3.0441E-05 1.3526E-02 0.0000E+00
ebal -2.8626E+02
...
1.8000E+07 1.8309E+06 1.2028E+00 3.7721E-01 0.0000E+00
ebal 4.5397E+03
1.9000E+07 1.8856E+06 1.3695E+00 3.7577E-01 0.0000E+00
ebal 1.8336E+03
2.0000E+07 1.9403E+06 1.5363E+00 3.7434E-01 0.0000E+00
ebal -7.6798E+03
Note that the last subsection in this example was for emitted photons. Pho-
tons do not contribute to the KERMA or damage, but this information is used
to check the total energy conservation for this reaction. The ebal lines show
the difference between the available energy and the sum over all the outgoing
particles. The values should be a small percentage of the total heating. If the
ebal values are too large, there may be an error in the evaluation, or it may
be necessary to refine the energy grids in the distributions. In addition, this
photon production information is needed later for the photon energy check.
After all the sections corresponding to MT numbers in File 3 have been
processed (using the File 4, File 4/5, or File 6 method as appropriate), the
photon production sections in Files 12 and 13 are processed, if present. File
12 data are usually present for radiative capture (MT=102), at least at low
energies. Simple files normally give a tabulated photon spectrum. The display
gives the average energy for this spectrum in the ebar column and the negative
contribution to the heating computed with Eq. 171 in the heating column. The
edam column contains the E2
γterm needed to compute the photon contribution
to the damage, which is given in the damage column. See Eq. 211. The display
also has an extra line for each incident energy containing the percent error
“--- pc” between the total photon energy as computed from File 12 and the
value E+Q−E/(A+1) computed from File 3. As discussed above, HEATR does
not guarantee energy balance in large systems if this error occurs. The following
example shows some large errors due to mistakes in the ENDF/B-V evaluation
for 55Mn. Two columns labeled edam and xsec have been removed to show the
heating and damage columns. The text has also been shifted to the left of its
normal position to fit better on the printed page.
NJOY2016 141

LA-UR-17-20093 6 HEATR
photon energy (from yields) mf12, mt102
e ebar/err egam ... yield heating damage
1 continuum gammas
1.0000e-05 4.5088e+06 2.4237e+02 ... 2.4791e+00 -4.8477e+09 5.4975e+04
1.0000e-05 53.7 pc
1.0703e-04 4.5088e+06 2.4237e+02 ... 2.4791e+00 -1.4819e+09 1.6806e+04
1.0703e-04 53.7 pc
1.2520e-03 4.5088e+06 2.4237e+02 ... 2.4791e+00 -4.3347e+08 4.9159e+03
1.2520e-03 53.7 pc
...
1.3571e+04 4.4522e+06 2.3887e+02 ... 2.4836e+00 -7.3869e+03 -1.2406e-01
1.3571e+04 51.8 pc
2.7142e+04 4.3957e+06 2.3536e+02 ... 2.4881e+00 -3.7037e+05 -1.6487e+01
2.7142e+04 49.9 pc
5.4287e+04 4.2826e+06 2.2834e+02 ... 2.4972e+00 -2.5604e+04 -2.5340e+00
5.4287e+04 46.0 pc
1.0858e+05 4.0563e+06 2.1430e+02 ... 2.5154e+00 -1.3327e+04 -2.7289e+00
1.0858e+05 38.3 pc
Many MF=12, MT=102 sections give multiplicities for the production of
discrete photons. In these cases, HEATR prints out data for all of the parts,
and it provides a sum at the end. The balance error is printed with the sum.
The following example shows a case with discrete photons. The last two columns
have been removed (heating,damage), and the text has been compacted and
shifted to the left to fit on the printed page.
photon energy (from yields) mf12, mt102
e ebar/err egam edam xsec yield
1 7.7260E+06 ev gamma
1.0000e-05 7.7260e+06 1.1448e+03 8.9780e+02 1.1677e+01 3.0000e-01
1.1406e-04 7.7260e+06 1.1448e+03 8.9780e+02 3.4574e+00 3.0000e-01
1.1406e-03 7.7260e+06 1.1448e+03 8.9780e+02 1.0934e+00 3.0000e-01
...
2.0000e+07 2.7005e+07 1.1448e+03 8.9780e+02 1.0000e-03 3.0000e-01
2 7.6950e+06 ev gamma
1.0000e-05 7.6950e+06 1.1356e+03 8.9091e+02 1.1677e+01 5.0000e-02
1.1406e-04 7.6950e+06 1.1356e+03 8.9091e+02 3.4574e+00 5.0000e-02
...
142 NJOY2016

6 HEATR LA-UR-17-20093
2.0000e+07 2.6974e+07 1.1356e+03 8.9091e+02 1.0000e-03 5.0000e-02
3 6.8630e+06 ev gamma
1.0000e-05 6.8630e+06 9.0330e+02 7.1515e+02 1.1677e+01 1.2000e-03
1.1406e-04 6.8630e+06 9.0330e+02 7.1515e+02 3.4574e+00 1.2000e-03
1.1406e-03 6.8630e+06 9.0330e+02 7.1515e+02 1.0934e+00 1.2000e-03
...
89 3.1000e+04 eV gamma
1.0000e-05 3.1000e+04 1.8430e-02 0.0000e+00 1.1677e+01 2.8884e-01
1.0000e-05 0.0 pc
1.1406e-04 3.1000e+04 1.8430e-02 0.0000e+00 3.4574e+00 2.8884e-01
1.1406e-04 0.0 pc
1.1406e-03 3.1000e+04 1.8430e-02 0.0000e+00 1.0934e+00 2.8884e-01
1.1406e-03 0.0 pc
1.1912e-02 3.1000e+04 1.8430e-02 0.0000e+00 3.3832e-01 2.8884e-01
1.1912e-02 0.0 pc
...
2.0000e+07 3.1000e+04 1.8430e-02 0.0000e+00 1.0000e-03 2.8884e-01
2.0000e+07 0.0 pc
In this case (27Al), the capture energy production checks out perfectly for the
sum of all 89 discrete photons.
Other sections using either File 12 or File 13 generate displays similar to the
following:
photon energy (from xsecs) mf13, mt 3
e ebar xsec energy heating
1 continuum gammas
2.0000e+05 3.6753e+06 4.2076e-03 1.5464e+04 -1.5464e+04
4.0500e+05 3.3863e+06 5.2873e-03 1.7904e+04 -1.7904e+04
6.0031e+05 3.1097e+06 6.4478e-03 2.0051e+04 -2.0051e+04
8.0182e+05 2.0089e+06 9.3236e-02 1.8730e+05 -1.8730e+05
1.0000e+06 9.2622e+05 1.7859e-01 1.6541e+05 -1.6541e+05
1.2000e+06 9.6151e+05 2.8329e-01 2.7239e+05 -2.7239e+05
...
Note that the photon Eσ is simply subtracted from the heating column for
each incident energy.
If the partial KERMA mtk=443 was requested in the user’s input, HEATR
will print out a special section that tests the total photon energy production
NJOY2016 143
LA-UR-17-20093 6 HEATR
against the kinematic limits (see Section 6.4 above for the formulas used). An
example follows:
photon energy production check
e ev-barns min max
1.0000e-05 9.0215e+07 9.0187e+07 9.0200e+07
1.1406e-04 2.6712e+07 2.6704e+07 2.6708e+07
1.1406e-03 8.4479e+06 8.4453e+06 8.4466e+06
1.1912e-02 2.6138e+06 2.6130e+06 2.6134e+06
1.2812e-01 7.9895e+05 7.9871e+05 7.9883e+05
1.2812e+00 2.5211e+05 2.5203e+05 2.5207e+05
2.6875e+00 1.7420e+05 1.7415e+05 1.7417e+05
5.5000e+00 1.2186e+05 1.2182e+05 1.2184e+05
1.1406e+01 8.4662e+04 8.4636e+04 8.4648e+04
2.4062e+01 5.8231e+04 5.8213e+04 5.8222e+04
4.9375e+01 4.0614e+04 4.0601e+04 4.0607e+04
1.0000e+02 2.8522e+04 2.8514e+04 2.8518e+04
...
8.0000e+06 3.8972e+06 3.7964e+06 4.4880e+06
9.0000e+06 4.4782e+06 4.4401e+06 5.4986e+06
1.0000e+07 4.9645e+06 5.2078e+06 6.6176e+06
1.1000e+07 5.3712e+06 6.1302e+06 7.8374e+06 ----
1.2000e+07 5.3212e+06 5.8699e+06 8.0618e+06
1.3000e+07 5.0984e+06 5.9333e+06 8.5312e+06 ----
1.4000e+07 4.7415e+06 5.7172e+06 8.6605e+06 ----
1.5000e+07 4.0795e+06 4.7419e+06 8.0409e+06 ----
1.6000e+07 3.2521e+06 3.6806e+06 7.2734e+06 ----
1.7000e+07 2.8079e+06 2.8418e+06 6.6927e+06
1.8000e+07 2.7492e+06 2.2915e+06 6.2850e+06
1.9000e+07 2.9626e+06 1.9674e+06 6.2330e+06
2.0000e+07 3.4419e+06 1.7938e+06 6.1994e+06
The low and high kinematic limits will be the same at low energies where only
kinematics affect the calculations. They may be the same for all energies for
ENDF/B-VII evaluations that provide complete distributions for all outgoing
charged particles and recoil nuclei. Normally, the limits diverge above the
threshold for continuum reactions. Note that HEATR marks lines where the
computed value goes more than a little way outside the limits with the symbols
++++ or ----. It is often convenient to extract these numbers from the output
144 NJOY2016
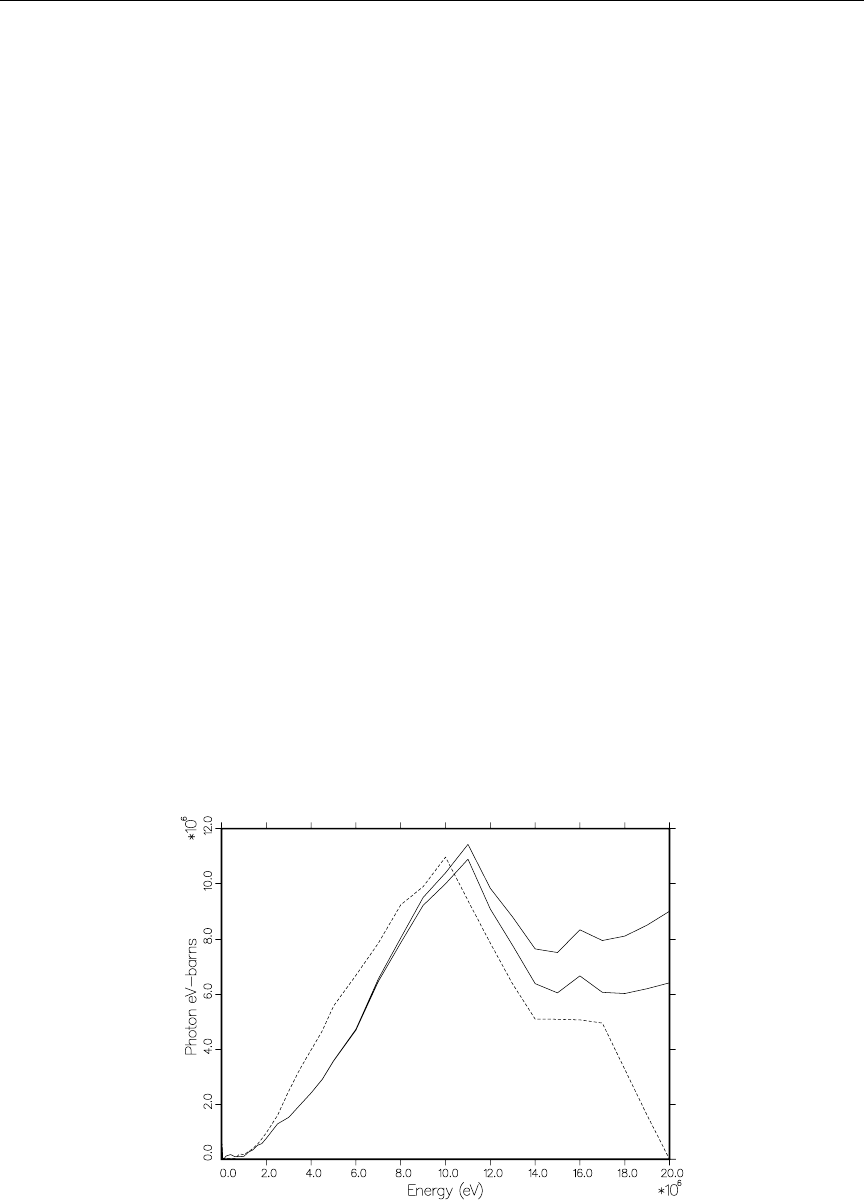
6 HEATR LA-UR-17-20093
listing and plot them (see Fig. 11). Although the energy grid is a little coarse,
such plots can often be useful (see below).
The last part of a full HEATR output listing is a tabulation of the computed
KERMA and damage coefficients on the normal coarse energy grid. Columns
are provided for the total KERMA and for each of the partial KERMA results
requested with mtk values in the user’s input. If kinematic checks were requested,
the check values are written just above and below the corresponding partial
KERMA values. In addition, low and high messages are written just above or
just below the kinematic limits in every column where a significant violation of
the limits occurs. Caution: if summation reactions (MT=3, MT=4) were used
to define the photon production over some parts of the energy range, the partial
KERMA results may not make sense at some energies. For example, consider
the common pattern in ENDF/B-V where MT=102 is used for capture at low
energies, but at higher energies, it is set to zero, and the capture contribution is
included in MT=3 (nonelastic). Clearly, the partial KERMA MT=402 doesn’t
make sense above this breakpoint. The following example shows part of the final
KERMA listing for ENDF/B-V.1 55Mn. The damage column was removed and
the columns compressed to fit on the printed page.
Figure 11: Example of a plot comparing the total photon energy production for 55Mn from
ENDF/B-V.1 (dashed) with the kinematic limits (solid).
NJOY2016 145

LA-UR-17-20093 6 HEATR
final kerma factors
e 301 302 303 402 443
min 1.2400e-04 3.7775e-06 1.2022e-04 1.2022e-04
1.0000e-05 4.0068e+05 3.7775e-06 4.0068e+05 4.0068e+05 4.0068e+05
max 3.3820e+05 3.7775e-06 3.3820e+05 3.3820e+05
high high high
...
min 3.2373e+04 2.3497e+04 8.8759e+03 4.1114e+01
6.0031e+05 1.0017e+05 2.3497e+04 7.6673e+04 2.9899e+04 3.2375e+04
max 3.2375e+04 2.3497e+04 8.8781e+03 4.3366e+01
high high high
low low
min 7.3041e+04 5.9403e+04 1.3638e+04 4.4748e+01
8.0182e+05 -2.4355e+04 5.9403e+04 -8.3758e+04 2.4987e+04 7.3043e+04
max 7.3043e+04 5.9403e+04 1.3640e+04 4.6676e+01
high
low low
min 9.8973e+04 7.7075e+04 2.1898e+04 4.7777e+01
1.0000e+06 3.7682e+04 7.7075e+04 -3.9393e+04 2.1917e+04 9.8974e+04
max 9.8974e+04 7.7075e+04 2.1900e+04 4.9509e+01
high
low low
min 1.1397e+05 7.7800e+04 3.6168e+04 4.9760e+01
1.2000e+06 9.5321e+04 7.7800e+04 1.7521e+04 1.9482e+04 1.1397e+05
max 1.1397e+05 7.7800e+04 3.6169e+04 5.1335e+01
high
low low
min 1.4632e+05 1.0192e+05 4.4402e+04 5.3005e+01
1.4000e+06 9.8251e+04 1.0192e+05 -3.6667e+03 1.8208e+04 1.4632e+05
max 1.4632e+05 1.0192e+05 4.4403e+04 5.4511e+01
high
...
146 NJOY2016
6 HEATR LA-UR-17-20093
min 2.3650e+05 1.6907e+05 6.7426e+04 1.7607e+02
1.9000e+07 7.1384e+06 1.6907e+05 6.9693e+06 1.3503e+04 2.5435e+06
max 2.5435e+06 1.6907e+05 2.3744e+06 1.7939e+02
high high high
min 2.4001e+05 1.8261e+05 5.7406e+04 1.4423e+02
2.0000e+07 9.2369e+06 1.8261e+05 9.0543e+06 1.0908e+04 2.8385e+06
max 2.8385e+06 1.8261e+05 2.6559e+06 1.4701e+02
high high high
The following subsection discusses how to analyze the “check” output of
HEATR in order to diagnose energy-balance errors in ENDF-format evaluations.
The examples are drawn from ENDF/B-V testing[43]. In general, results like
these are less likely to occur in modern evaluations.
6.9 Diagnosing Energy-Balance Problems
The analysis should start with MT=102, because if it is wrong, the guarantee of
energy conservation for large systems breaks down. If the display for MF=12,
MT=102 shows messages of the form “--- pc”, there may be a problem. If these
messages only show up at the higher energies, and if the size of the error increases
with energy, it is probable that the evaluator has used a thermal spectrum over
the entire energy range (this is very common). Of course, the total photon
energy production from radiative capture should equal
A
A+ 1E+Q , (222)
where the rest of the total energy E+Qis carried away by recoil. If only a ther-
mal spectrum is given, the Eterm is being neglected, and errors will normally
appear above about 1 MeV. The Eterm can be included in evaluations that use
tabulated data by giving E-dependent spectra in File 15; and it can be included
for evaluations that use discrete photons by setting the “primary photon” flags
in File 12 properly. In practice, the capture cross sections above 1 MeV are
often comparatively small due to the 1/v tendency of capture, and the errors
introduced by neglecting the Eterm can be ignored.
If the MT=102 errors show up at low energies, there is probably an error
in the average photon yield from File 12, in the average energy computed from
File 15, or both. In the 55Mn case shown above, the yield had been incorrectly
NJOY2016 147
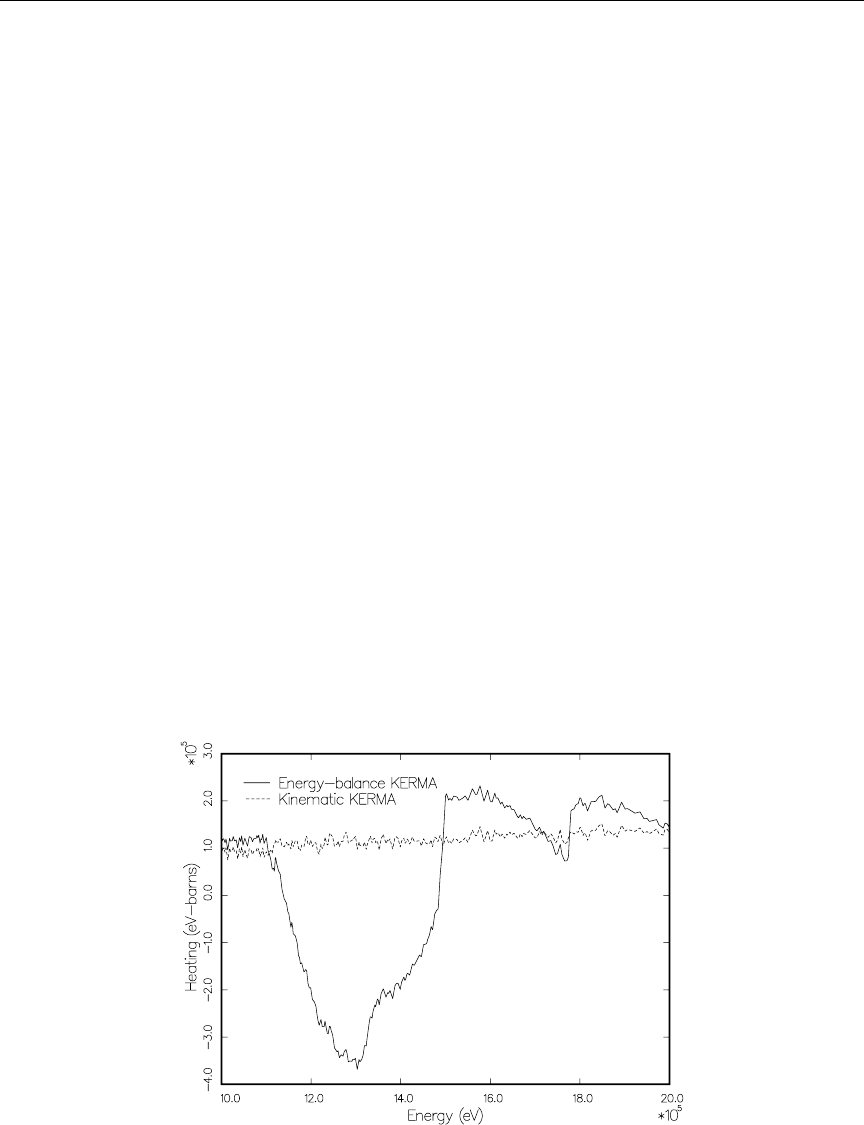
LA-UR-17-20093 6 HEATR
entered. In addition, the spectrum didn’t agree with the experimental data
because the bin boundaries were shifted. Each case must be inspected in detail
to find the problems.
The next common source of energy-balance errors in ENDF files arises from
the representation used for inelastic scattering. Typically, the neutron scattering
is described in detail using up to 40 levels for the (n,n0) reaction. However, the
photon production is often described using MF=13/MT=3 or MF=13/MT=4
and rather coarse energy resolution. As a result, it is possible to find photons for
(n,n1) being produced for incident neutron energies slightly below the MT=51
threshold! These photons would lead to a spike of negative KERMA factors. A
more common effect of the coarse grid used for photon production is to lead to
an underestimate or overestimate of the photon production by not following the
detailed shape of the inelastic cross section. The HEATR “kinematic KERMA”
is correct in this range since only two-body reactions are active. Therefore, a
plot of MT=301 and MT=443 on the same frame normally shows these effects
in detail. Fig. 12 is an example of such a plot.
Fig. 13 shows both the inelastic cross section from File 3 and the photon pro-
duction cross section from File 13 to demonstrate the mismatch in the energy
grids that contributes to the energy-balance errors. These kinds of errors are
best removed by changing to a representation that uses File 12 to give photon
Figure 12: Comparison of MT=301 with MT=443 for the region of the discrete-inelastic
thresholds for 59Co from ENDF/B-V.2. Note the large region of negative
KERMA. The best way to remove this kind of problem is by using yields in
File 12, MT=51, 52, 53, . . . to represent the photon production.
148 NJOY2016
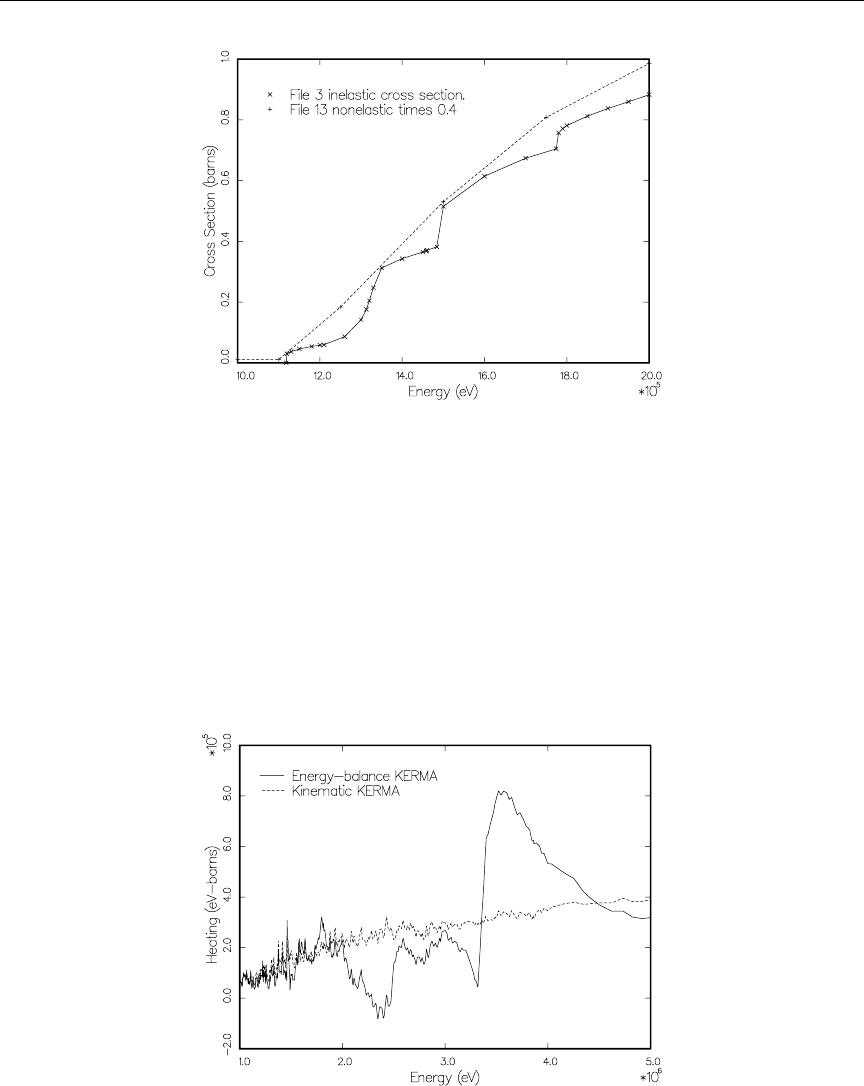
6 HEATR LA-UR-17-20093
Figure 13: Plot showing the mismatch between the energy grids used for File 3 and File 13
in the region of the thresholds for discrete-inelastic scattering levels for the case
shown in Fig. 12. The cross and ex symbols show the actual grid energies in the
evaluation.
production yields for the separate reactions MT=51, MT=52, etc. This repre-
sentation makes full use of the File 3 cross sections, and as long as each section
of File 12 conserves energy, the total inelastic reaction is guaranteed to conserve
energy, even at the finest energy resolution.
Figure 14: Typical energy-balance problems between points where balance is satisfied. Dis-
crete photons were used below about 2 MeV, and energy balance is reasonably
good there. The energy points in MF=13 for the continuum part are at 2, 3, and
5 MeV, and the balance is also good at those energies. Clearly, a grid in File 13
that used steps of about 0.25 MeV between 2 and 4 MeV would reduce the size
of the deviations substantially and remove the negative KERMA factors.
NJOY2016 149
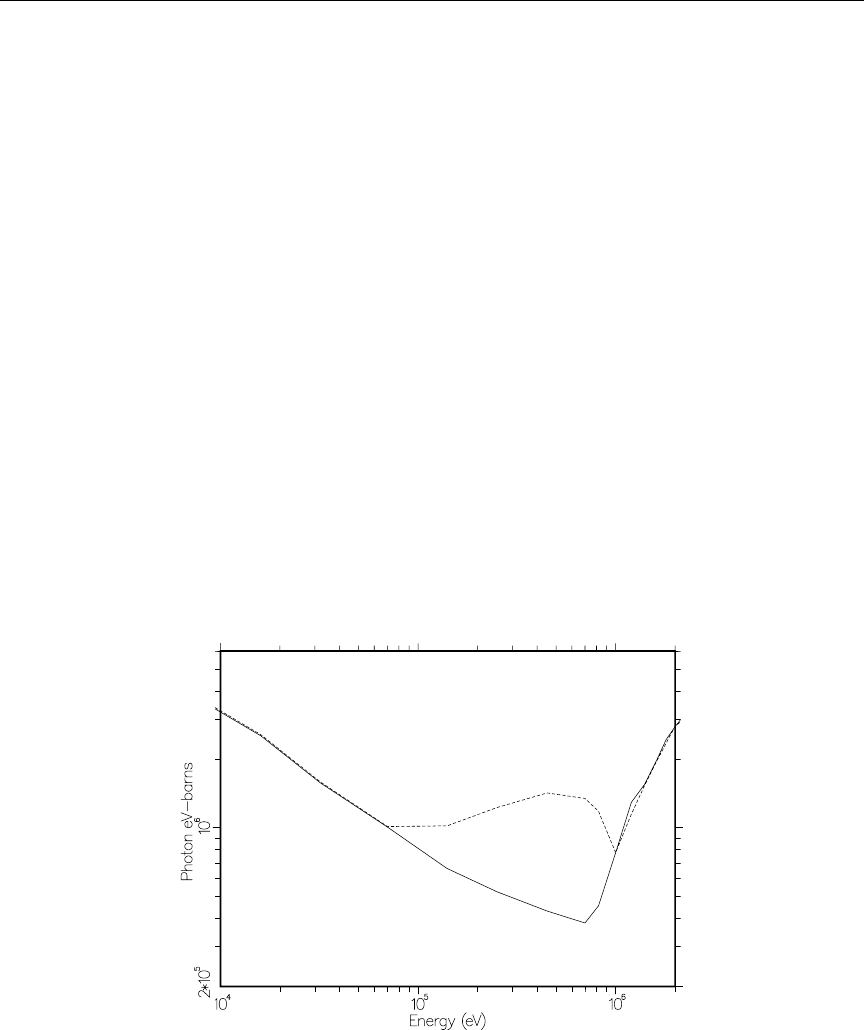
LA-UR-17-20093 6 HEATR
A method that is frequently used by evaluators of photon production files
is to select a number of nonelastic photon spectra on a fairly coarse incident-
energy grid using theory or experiment, and then to readjust the photon yield
on this energy grid so as to conserve energy at each grid point. However, the
results do not, in general, conserve energy at intermediate points. If a very
coarse energy grid is used for File 13, quite large deviations between MT=301
and MT=443 can result. Fig. 14 shows such a case. The solution to this kind
of violation of energy balance is to add intermediate points in Files 13 and 15
until the magnitude of the deviations is small enough for practical calculations.
Especially large energy-balance errors of this type are caused by interpolating
across the minimum formed by the decreasing capture heating and the increasing
inelastic heating. Fig. 15 shows a dramatic example using a photon energy
production comparison.
For energies above the threshold for continuum reactions like (n,n0) or (n,2n),
it is difficult to use the results of the kinematic checks to fix evaluations. The
representation of Eqs. 181 and 182 for continuum inelastic scattering is very
rough. Comparison to other more accurate methods suggests that a CM formula
Figure 15: Computed photon energy production (dashed) compared with the kinematic
value (solid) for 93Nb from ENDF/B-V. The original File 13 has grid points at
100 keV and 1 MeV. Interpolating across that wide bin gives a photon production
rate that is much too large for energies in the vicinity of a few hundred keV.
This will result in a large region of negative heating heating numbers. Since this
is just the region of the peak flux in a fast reactor, niobium-clad regions could
be cooled instead of heated!
150 NJOY2016

6 HEATR LA-UR-17-20093
would be better here[50], even though the ENDF file says “lab.” Most other
reactions give very wide low and high limits. Two exceptions are (n,2n) and
(n,3n). If they dominate the cross section, the kinematic limits will be fairly
close together. In the 14 MeV range, energy errors could be in the photon
data, the neutron data, or both. The best way to eliminate balance errors is to
construct a new evaluation based on up-to-date nuclear model codes.
6.10 Coding Details
The main subroutine is heatr, which is exported by module heatm. It starts by
reading the user’s input and locating the desired material on the PENDF file.
The main loop is over temperature. For each temperature, a check is made to
see if the user provided a value for the damage displacement energy. If not, a
default value is provided. Next, hinit is called to examine the directory. Flags
are set if MF=12 or 13 is present, if MT=18 or 19 is used, and if MT=458 is
present (see mgam,mt19, and mt458). The flags mt103,mt104,mt105,mt106
and mt107 are set if the corresponding particle production levels are present.
The MT numbers used for the levels depend on whether the input file used
version 6 format or one of the earlier formats. For example, mt103 is set if
MT=600-649 is found for ENDF-6 data, or if MT=700-719 is found for earlier
versions. The code also checks to see if the corresponding angular distribution
data are present (see nmiss4). If any are not present, the code will assume they
are isotropic. Note that hinit also collects a list of the File 6 MT numbers in
mt6(i6). For fissionable materials, the delayed fission energy values are retrieved
from MF=1/MT=458, and the correction, qdel, is computed for later use when
calculating the heating from prompt fission.
The next step in hinit is to make a copy of File 6 on a scratch file (if
any sections of File 6 were found). While doing this, it searches through the
subsections for each reaction accumulating the ZA residual remaining after each
particle is given. If it comes to the photons (zap=0), which should be last, and
there is still a ZA residual left, then it concludes that there is no subsection
describing the residual. It loads a value into mt6no(ii6) that is the index to
the subsection that the recoil should have followed had it been present. If it
comes to the end of the subsection list without finding photons and still has
a ZA residual, it sets mt6no(ii6) to nk; that is, the residual missing should
follow the last subsection. In either case, the routine prints out messages about
“photon recoil correction” or “one-particle recoil approximation.”
Finally, hinit makes a standardized copy of the ENDF tape using hconvr,
NJOY2016 151

LA-UR-17-20093 6 HEATR
and it also saves the grid of the total cross section (MT=1) on the loada/finda
scratch file that will be used to accumulate the KERMA factors, damage, and
kinematic checks (if requested). Note also mt303, which tells which of the re-
quested edits is for nonelastic heating, MT=303. This is used later for writing
out the photon energy production check.
Now nheat is called. Its basic function is to loop over the “nonredundant”
reactions in File 3, and to accumulate the corresponding contributions to the
partial heating and partial damage values into the appropriate elements of the c
array on the loada/finda file. Redundant reactions are reactions that duplicate
or include effects that can be obtained from another MT number. They are
determined using a set of if statements just after the entry to the reaction loop
at statement number 105. The structure of the carray depends on whether
kinematic checks are being accumulated or not and whether photon production
files are present. If neither occurs, the structure has npk+1 elements as follows:
Element Contents
1energy
2total heating
3value for first partial
···
npk+1 value for last partial
where npk is the number of partial KERMA or damage values being accumu-
lated, including the total. If checks are being accumulated, the carray has the
following 3*npk+1 elements:
Element Contents
1energy
2total heating
3value for first partial
···
2+npk lower kinematic limit for total
3+npk lower kinematic limit for first partial
···
2+2*npk upper kinematic limit for total
3+2*npk upper kinematic limit for first partial
···
3*npk+1 upper kinematic limit for last partial
If photon production files are present in the evaluation, the total length of the
152 NJOY2016

6 HEATR LA-UR-17-20093
carray increases by the following three words (len is the old length from above
plus three):
Element Contents
len-2 photon capture correction
len-1 total photon eV-barns
len total energy yield for “subtot”
Back inside the loop over nonredundant reactions, subroutine gety1 is ini-
tialized for this reaction. The code checks to see if this section uses File 6 for its
distributions; if so, it arranges to make multiple passes through the reaction’s
energy grid, one pass for each subsection of the MF=6 section, and perhaps one
additional pass to synthesize the missing recoil subsection. It is now possible to
select the appropriate Q-value and particle yield, and to initialize the appropri-
ate calculational routine. This routine will be sixbar for all reactions described
in File 6, disbar for two-body reactions using File 4 (including charged-particle
reactions in the 600 or 700 series of MT numbers), conbar for continuum re-
actions represented using File 5, and capdam for the neutron disappearance
reactions (MT=102, 103, etc.) and the charged-particle continuum reactions
from the 600 or 700 series of MT numbers. The last step before beginning the
energy loop for this reaction is to call indx, which determines which element of
the carray is to receive the heating or damage contribution from this reaction
(see below).
The energy loop in nheat goes through statement number 190. For each
energy, finda is called to retrieve the current values for the energy [see c(1)] and
the partial heating and damage values as accumulated so far. On the first pass
through the scratch file, the list of energies to be used for printing information
on the listing is established in elist using a few if statements based on the
range of the energy variable e. For each energy, the corresponding cross section is
retrieved using gety1 and the appropriate Eand damage numbers are computed
by calling getsix,disbar,conbar, or capdam. The heating contribution is
computed from the appropriate formula, and the heating and damage numbers
are summed into the carray at location index. If requested, the kinematic limits
on the heating are computed and summed into the carray at index+npk and
index+2*npk. The completed results for this energy and reaction are written
out onto the loada/finda scratch file, and the energy loop is continued.
When the energy loop is complete, the subroutine jumps to the next section
(or subsection in the case of File 6) and repeats the entire energy loop for that
reaction (or particle from File 6).
NJOY2016 153

LA-UR-17-20093 6 HEATR
Subroutine indx is used to select what element of the carray is to receive
the heating or damage contribution for a section with a particular MT num-
ber. The meaning of each element of the carray is obtained from the mtp
array. Normally, a reaction MT contributes to the partial heating element with
mtp(i)=MT+300. But it can also contribute to several other elements of c,
such as nonelastic (MT=303), inelastic (MT=304), etc. Therefore, indx returns
the count of reactions contributed to by mt in nmt and the indexes for the c
array in imt(nmt).
Subroutine capdam is used to compute the damage energy for neutron capture
(or disappearance) reactions; that is, for MT=102, 103, etc. On the initialization
entry (ee=0.0), the routine sets up various kinematics parameters, such as zx
and ax to describe the outgoing particle, and initializes df. In order to save
time, the routine only calculates the damage on a grid that increases by steps of
10%. Intermediate values are obtained by interpolation (see el,daml,en, and
damn). The values at the grid points are computed using
DE
A+ 1+D 1
2MRc2AE
A+ 1 +Q2!(223)
for radiative capture (the corrections for multiple photon emission will be made
later), or using Eq. 206 with ERfrom Eq. 212 and a 4-point Gauss-Legendre
quadrature. The angular distribution for particle emission is taken to be isotropic.
Subroutine disbar is used by nheat to compute the average secondary energy
and damage energy for elastic scattering (MT=2), discrete-inelastic scattering
(MT=51-90), or discrete-level particle production (MT=600-648, 650-698, etc.
for ENDF/B-VI or ENDF/B-VII, or MT=700-717, 720-737, etc. for earlier
versions). It starts by initializing hgtfle (which is very similar to getfle in the
GROUPR module), determining kinematic parameters like awp (the mass ratio
to the neutron for the emitted particle), and initializing df. In order to save time,
it only computes the heating and damage on a grid based on steps by a factor
of 1.1 and the enext values from hgtfle. On a normal entry, it interpolates
between these values (see el,cl,daml,en,cn, and damn). When the desired
ee exceeds en, the old high values are moved down to the low positions, and
new high values are calculated. The calculation of cn follows Eq. 168. The
calculation of damn uses Eq. 206 with a 20-point Gauss-Legendre quadrature
(see nq,qp, and qw).
Function df is used to compute the damage partition function given in
Eq. 200. The constants that depend on the recoil atom or particle type and
154 NJOY2016

6 HEATR LA-UR-17-20093
lattice type (see zr,ar,zl,al) are computed in an initialization call with
e=0.0. Thereafter, it can be called with any other value of e.
Similarly, conbar computes the average secondary energy and damage en-
ergy for continuous distributions described in File 5. Analytic representations
use simple formulas coded into anabar or a combination of adaptive and Gaus-
sian quadrature in anadam. Tabulated data are interpolated from the File 5
table using tabbar or integrated using trapezoidal and Gaussian quadratures
in tabdam. As usual, the routine is initialized by calling it with e=0.0. The
secondary-particle yield is either chosen from the MT number, or hgtyld is ini-
tialized. The desired section of File 5 is located on the input ENDF tape, and the
kinematic constants are computed. The reactions with MT=22, 28, 32, 33, and
34 will be treated using the capdam method; if mtd has one of these values (see
mtt), capdam is initialized. As is the case for getsed in the GROUPR module,
this routine can handle some sections of File 5 that contain multiple subsec-
tions, but the analytic subsections must come first. As each analytic subsection
is read, appropriate data are stored in in the external array cusing pointers
saved in the array loc. Only the first energy is read and stored for a tabulated
subsection (lf=1). The idea is to have only two energy values in memory at a
time in order to save storage; the second subsection will be read during the first
normal entry to the subroutine. The final step in the initialization pass is to
initialize df. For a normal entry into conbar, the energy-dependent fission yield
is retrieved, if needed, and the loop over subsections is entered. Each subsection
in File 5 starts with a fractional-probability record. The desired value for energy
eis computed by interpolation using the standard NJOY utility routine terpa.
For analytic subsections, the routine uses anabar to compute En, and anadam or
capdam to compute the damage energy. Note that in order to save time, anadam
is only calculated on a fairly coarse grid based on steps by a factor of 1.5. The
intermediate values are obtained by interpolation using terp1. For tabulated
subsections, ebar and dame values are normally obtained by interpolation (see
elo,flo,dlo,ehi,fhi, and dhi). However, for the first entry, or whenever
ereaches ehi, the high data are moved into the low positions, new high data
are read from the File 5 subsection, and the values for heating and damage are
computed at ehi using tabbar and either tabdam or capdam.
Subroutine hgtyld is similar to getyld in the GROUPR module. It finds
the required section on the ENDF tape and reads the entire LIST or TAB1
record into memory. On normal entries, it either computes the yield using the
polynomial formula with constants from the LIST record, or it uses terpa to
NJOY2016 155

LA-UR-17-20093 6 HEATR
interpolate for the yield in the TAB1 data.
Subroutine anabar is used to compute the average energy for a neutron
described by an analytic subsection of File 5. The simple formulas used are
tabulated in the ENDF format manual[9]. Similarly, anadam is used to compute
the damage energy for an analytic subsection of File 5. Only LF=9 (the Simple
Maxwellian Distribution) is supported; the routine returns zero for other laws.
Note that a statement function is defined to compute the secondary energy
distribution for this law (see sed). For each incident energy, the spectrum
temperature theta is retrieved using terpa, and an adaptive integration stack
is initialized with points at four secondary energies, namely, 1., .5(E−U), θ, and
E−U, where Uis a parameter that sets the maximum possible value of E0. The
adaptive procedure proceeds to solve Eq. 208 by subdividing this starting grid
until trapezoidal integration can be used on each panel. The inner integral over
emission cosine µis performed using a 4-point Gauss-Legendre quadrature for
each point on the adaptive grid. The function sed is used to compute g(E0),
and df is used to compute the partition function.
Subroutine tabbar is used to compute the average energy of the emitted
neutron for a tabulated subsection of File 5. It can also be used for a tabulated
subsection of File 6. This option is flagged by law negative. The trick is to
set the “stride” or “cycle” through the file to be larger than 2 (see ncyc). The
angular part of the g(E→E0) table is skipped, and only the E0and gvalues are
retrieved. For File 5, this routine only works for laws 1 and 5; others cause a
fatal error message to be issued. In both of these cases, the integral over E0
needed to compute the average energy is done analytically for each panel in the
input data using a different formula for each interpolation scheme int.
Subroutine tabdam is used to compute the damage energy for a tabulated
subsection of File 5. The integration that is needed is given in Eq. 208. The
energy grid of the tabulation is assumed to be good enough to allow trapezoidal
integration to be used for E0, and a 4-point Gauss-Legendre quadrature is used
for µ.
Subroutine sixbar is used to compute charged-particle average energy and
damage energy represented by using a subsection of File 6. As is common with
NJOY subroutines, sixbar is initialized by calling it with e=0.0. The initial-
ization path is controlled by j6, which is the index to the current subsection in
File 6; by irec, which is 1 when a recoil response is to be calculated, and by
jrec, which tells the routine how to get back to the next subsection after a recoil
calculation. If this is not a recoil subsection, the routine jumps to statement
156 NJOY2016

6 HEATR LA-UR-17-20093
110 and starts reading in the data for the desired subsection. If it is flagged
as a recoil (see irec), the routine backs up to the subsection describing the
particle that induced the recoil and then continues by reading in the data for
that particle.
The first step is to read in the TAB1 record that contains the particle yield,
identity (zap and awp), and representation law. If this law describes a two-
body recoil distribution, the routine sets jrec for a proper return, sets irec to
back up to the corresponding direct emission subsection, and jumps back to the
beginning of the routine to do the recoil calculation.
When the code finally arrives at statement number 210, it is ready to start
processing the current subsection. It reads in the parameters for laws 3 and 6,
or the TAB2 record and the data for the first energy point for the other laws.
With the data in place, it computes the corresponding values for mean energy
and damage energy using getsix or tabsq6 and returns.
In the special case where the section contains only a single subsection that
describes a neutron, the data stored in memory will be the data for that sub-
section, and the subroutine tabbar with a negative value for the law is used to
produce the low values.
On a normal entry (e>0), sixbar checks to see whether eis in the current
interpolation range. If it is, the code jumps to statement number 400. For the
analytic laws (law=3 and law=6), it uses a direct call to getsix to compute
the mean energy and damage energy. For the tabulated laws, it interpolates for
the results using the low and high data (see elo,flo,dlo,ehi,fhi, and dhi).
On the first entry, or whenever eincreases to ehi, the code moves the high
data to the low positions, and then it reads in the data for the next energy and
computes a new set of high values for mean energy and damage using getsix
or tabsq6.
Subroutine getsix is used to compute the mean energy and damage energy
for one particular incident energy in a subsection of File 6. The method used
depends on the value of law and the reference frame for the subsection. The
first case in the coding is for law=1 with data in the CM system.
This case uses Eqs. 218 and 219 with an adaptive integration over E0. The
integration stack is contained in the arrays xand y. It is primed with x(2)=0,
and h6cm is called to compute y(2) and the next grid point epnext. The first
panel is completed by calculating y(1) and x(1)=epnext. The panel is then
divided in half, and the midpoint is tested to see if it is within tol=0.02 (i.e.,
2%) of the linearly interpolated value. If not, the midpoint is inserted in xand
NJOY2016 157

LA-UR-17-20093 6 HEATR
y, and the new top panel [that is x(2)−x(3)] is tested. This continues until
convergence is achieved in the top panel. The contributions to the heating and
damage are added into the accumulating integrals at statement number 190, and
iis decremented so that the process can be repeated for the next panel down.
When idecreases to one, the current value of epnext is used to start the next
higher E0panel. This loop over panels continues until the entire E0range has
been integrated.
The next special case is for tabulated distributions that use E,E0,µordering
in the lab system. The angular part is ignored. A simple loop over the NEP points
in g(E→E0) is carried out. Trapezoidal integration is used for each panel for
both heating and damage (hand d). If nd>0, the first nd entries are discrete
energies, and the values of the integrand at those energies are added into hand
d. Finally, hand dare copied into ebar and dame.
The block of coding starting at statement number 450 is used to compute
particle mean energies for the emitted particles from two-body reactions, or to
compute the mean recoil energy for a two-body reaction (see irec>0). The
calculation follows Eq. 216. Note that the kinematic factors include awp, the
mass ratio of the emitted particle to the incident particle. The parameter beta
here is the same as Rin Eq. 217. If the angular distribution in File 6 is in
Legendre form, the heating and damage integrals are performed using a 20-point
Gauss-Legendre quadrature (see nq,qp, and qw). If the angular distribution is
tabulated as f(µ)versus µ, a trapezoidal integration is used for both heating
and damage.
The final option in getsix is for lab distributions that use E,µ,E0ordering.
See Eq. 220. The inner integrals are computed using trapezoidal integration.
The outer integral over µalso uses trapezoidal integration on the results of the
inner integrals for each µgrid point.
Note that getsix has an irec parameter in its calling list. When this pa-
rameter is greater than zero, the angular distribution is complemented and the
charge and mass of the particle are modified to represent the recoil species. The
value of irec is controlled by sixbar.
Subroutine h6cm is used by getsix to compute the lab distribution g(E→E0
L)
of Eq. 221 using the CM data in File 6. This subroutine uses h6dis,h6ddx and
h6psp to retrieve the CM discrete, tabulated or phase-space data from the file.
These routines are basically the same as f6cm,f6dis,f6ddx and f6psp. See
GROUPR for more details.
Subroutine gheat is used to correct the heating and damage values accumu-
158 NJOY2016

6 HEATR LA-UR-17-20093
lated during the pass through the neutron sections. It loops through all of the
reactions in File 12 and File 13 using two ENDF-type tapes. One is the input
PENDF tape, which is used to retrieve cross sections for use with the photon
multiplicities in File 12. The other is a version of the input ENDF tape that
has been passed through hconvr to put the photon data in a standard form (see
Chapter 8(GROUPR) of this manual for a more detailed discussion of conver).
This scratch tape is used to retrieve the File 12 and File 13 data. It is very
common to find reaction MT=3 (nonelastic) in File 12, but this reaction has
been removed from the PENDF tape because it is redundant; that is, it is equal
to MT1−MT2. Therefore, two passes are made through the File 12 data for
MT=3, an addition pass with MT=1 from the PENDF tape, and a subtrac-
tion pass with MT=2 from the PENDF tape. Once the desired sections on the
two tapes have been found, the subroutines gambar,capdam, and disgam are
initialized.
The energy loop for gheat goes through statement number 190. For each
energy, finda is used to retrieve the partial KERMA factors as computed from
the pass through the neutron files. The yield or cross section is retrieved using
gety1 into the variable y. If necessary, the corresponding cross section xis
retrieved using gety2. For cases where an energy-dependent Q is available, it is
retrieved using terp1 on the data stored at lqx. The next two lines correct the
energy of “primary” photons (lp=2).
For radiative capture represented in File 12 (MT=102), gambar,disgam,
and/or capdam are called to return Eγand E2
γ/(2mRc2) for this photon spectrum
or discrete photon and to correct the heating and values in the carray using
Eq. 171 and the second line of Eq. 211. The capture contribution to the total
photon eV-barns is added into c(npkk-1) and the photon energy yield is loaded
into c(npkk) for each subsection. When the last subsection is reached, the
capture energy check is made using this subtotal. Note that the capture error
is loaded into c(npkk-2) for later use in calculating the kinematic limits for
photon energy production.
For other photon-production reactions, the photon eV-barns contribution is
subtracted from the energy-balance heating position, added into the total photon
energy value in c(npkk-1), and added into c(npkk) for the subtotal for a section
with multiple subsections. After all the corrections have been completed for this
energy, the revised values are written out using loada. The code then moves on
to the next reaction and repeats the entire process.
When the reaction loop has been finished, gheat checks to see if it can
NJOY2016 159

LA-UR-17-20093 6 HEATR
print out a photon energy production check. It can do this if kinematic checks
have been requested and if MT=303 was requested in the user’s list of partial
KERMA calculations. The code reads through the loada/finda file one more
time. For each energy in elist, it prints out the total photon eV-barns from
c(npkk-1) and the kinematic limits elo and ehi. If the limits are violated by
more than 10%, alarms consisting of the strings ++++ or ---- are printed after
the eV-barns values.
Subroutine gambar is used to compute the mean energy for continuous photon
spectra and the photon recoil correction for capture. When called with e=0.0,
it locates the desired section of File 15 on the ENDF tape and reads in the first
incident energy. On a normal entry, it checks to see if eis in the range of the
data already computed (elo,ehi, etc.), and if so, it interpolates for the desired
results. If not (or on the first real entry), it moves the high data down to the
low positions, reads in the next energy from File 15, prepares new values at
the new ehi, and checks the energy range again. The photon ebar is returned
by tabbar, and the corrections to the heating value (esqb) and damage value
(esqd) from photon production are generated using tabsqr.
Subroutine tabsqr is used to compute the average recoil energy
E2
γ
2MRc2(224)
for radiative capture for a tabulated subsection of File 15. The corresponding
damage energy is computed at the same time. The basic secondary-energy
integral is over the panels defined by the grid points given in File 15. Inside
each panel, the integral is computed using a 4-point Gauss-Legendre quadrature.
Subroutine disgam is used to compute the E2
γand corresponding damage
energy for a discrete capture photon. The rest-mass constant is computed by
calling disgam once with e=0.
Subroutine hout writes the new PENDF tape with the desired heating and
damage MT numbers added. It also corrects the directory in MF=1/MT=451,
and it prepares the output listing for printing. The first step is to loop through
the partial KERMA factors requested and to write the data on the loada/finda
file onto a scratch tape in ENDF File 3 format. While the first partial is being
prepared, the code matches energies in c(1) against the energy list for printing
in elist. When a match is found, the partial KERMA factors are checked
against the kinematic limits, and the variables klo or khi are set if any of the
comparisons are out of bounds. The KERMA factors, kinematic limits, and error
160 NJOY2016

6 HEATR LA-UR-17-20093
flags are then printed on the output listing. When all of the new sections for
File 3 have been prepared, the code updates the contents of the File 1 directory.
It then loops through the rest of the input PENDF tapes copying sections to
the output and inserting the new sections in the appropriate places. When the
new PENDF file has been completed, hout makes VIEWR input for a set of
plots showing the total heating and the photon production compared to their
kinematic limits in both lin-lin and log-log forms. The lin-lin plots show the
high-energy range better, and the log-log plots expand the low-energy range.
6.11 Error Messages
error in heatr***requested too many kerma mts
6 values in addition to MT=301 are allowed with kinematic checks; oth-
erwise, 25 can be requested. See npkmax=28. When checks are requested,
the number of words needed is 3*npk+7; otherwise, npk+3 are needed.
error in heatr***requested too many q values
Limited to 30 by the global parameter nqamax=30.
error in heatr***too much energy-dependent q data
Limited to maxqbar=10000.
error in heatr***mode conversion not allowed...
Both units must be BCD (positive) or blocked binary (negative).
error in hinit***too many mf6 reactions
A maximum of 320 reactions are allowed. See the global parameter maxmf6=320.
message from heatr---mt301 always calculated
MT=301 was given in the input list of partial KERMA factors. This is not
necessary; it is always inserted automatically.
message from hinit---mf4 and 6 missing, isotropy...
Cross sections were found for charged-particle levels in the 600 or 700 series
of MT numbers, but no corresponding angular distributions were found.
Isotropy is assumed to enable the calculation to proceed, but this evaluation
should be upgraded to include the proper sections of File 4 or 6.
message from hinit---mt18 is redundant...
If MT=19 is present, MT=18 will be ignored.
message from hinit---mt19 has no spectrum...
In some evaluations, the partial fission reactions MT=19, 20, 21, and 38
are given in File 3, but no corresponding distributions are given. In these
cases, it is assumed that MT=18 should be used for the fission neutron
distributions.
NJOY2016 161

LA-UR-17-20093 6 HEATR
error in hinit***upper energy mismatch for ifc=... in mt=458
When using tabulated fission energy release components in mf1/mt458,
NJOY detected different values for the upper energy limit of some of the
components. This is an evaluation error.
error in hinit***no tabulated fission q components found
mf1/mt458 contains no tabulated fission energy release components even
thought the LFC value was set to 1. This is an evaluation error.
error in hinit***bad LFC in mt=458
The LFC value in mf1/mt458 can only be equal to 0 or 1. This is an
evaluation error.
message from hinit---mt458 is missing for this mat
The fission Q-value cannot be adjusted for delayed effects.
message from hinit---photon momentum recoil used
message from hinit---one-particle recoil approx. used
message from nheat---changed Q from --- to ---
The fission Q-value is adjusted from the total (non-neutrino) value given in
File 3 to a prompt value using the delayed neutron energy from MF=1/MT=458.
error in nheat***binding energy for sequential n,2n needed
The user must enter special Q-values for the ENDF/B evaluation for 9Be.
See the discussion in Section 6.7.
error in nheat***storage exceeded
Insufficient storage for diagnostic energy grid. See the global parameter
ilmax=100 at the start of the module.
error in nheat***upper energy tabulated fission q components ...
The tabulated fission energy components are tabulated up to an upper
energy value that is inconsistent with the upper energy value of the fission
cross section. This is an evaluation error.
error in conbar***nktot gt nkmax
More than 12 subsections found. See the parameter nkmax=12.
error in conbar***insufficient storage for raw endf data
The allocatable array ain nheat is too small. Increase na=10000.
error in hgtyld***illegal lnd, must be 6 or 8
The LND value in the ENDF file is not correct, only 6 or 8 are allowed.
error in hgtyld***storage exceeded
Increase nwmax in nheat. Currently 7000.
error in tabbar***coded for lf=1 and lf=5 only
Self-explanatory. Should not occur.
162 NJOY2016

6 HEATR LA-UR-17-20093
message from sixbar---no distribution for mt --- ...
The ENDF-6 format allows the evaluator to describe a subsection of File 6
with “law=0”; that is, no distribution is given. Such sections are fine for
giving particle yields for gas production and similar applications, but they
are not adequate for computing heating and damage.
error in h6ddx***too many legendre terms
See nlmax=65 in h6ddx.
error in h6ddx***illegal lang
The allowed values for the angular law flag are 1, 2, and 11–15.
error in h6dis***illegal lang
The allowed values for the angular law flag are 1, 2, and 11–15.
error in bacha***dominant isotope not known for...
The Kalbach-systematics approach to computing angular distributions for
particle emission requires the separation energy as computed by the liquid
drop model. If the target for an evaluation is an element, it is necessary
to choose a dominant isotope that adequately represents the effect for this
element. Dominant isotopes for materials often evaluated as elements are
given in if statements in this routine. If the desired value is missing, it must
be added, and NJOY will have to be recompiled. See the corresponding
routines in GROUPR and ACER as well.
error in h6psp***3, 4, or 5 particles only
The phase-space law is defined for 3, 4, or 5 particles only.
message from hgtfle---lab distribution changed to cm...
ENDF procedures require that two-body reactions be described in the CM
system. Some earlier evaluations claim to be in the lab system. However,
they are for relatively heavy targets, and changing to the CM frame will
cause only a small change in the results.
error in hgtfle***desired energy above highest energy...
Fault in the evaluation.
error in getco***limited to 64 legendre coefficients
The upgraded ENDF limit.
error in getco***lab to cm conversion not coded
Discrete scattering data should be in the CM system already.
message from hconvr---mf3, mt... is missing
message from hconvr---mf12, mt... is missing
error in hconvr---missing mf3 mt’s, probable endf error
All these messages indicate missing sections in either mf3 or mf6. This is
an evaluation error.
message from hconvr---gamma prod patch made for mt ---
This reflects some problems in the old ENDF-III evaluations for Cl and K,
which were also carried over to later ENDF versions.
NJOY2016 163

LA-UR-17-20093 6 HEATR
error in hconvr***too many lo=2 gammas
See lmax=500.
error in hconvr***exceeded storage for nubar
See nnu=6000.
error in gheat***lo=2 not coded
Will not occur since lo=2 data have been transformed to lo=1 format by
hconvr.
message from gheat---no file 12 for this material
Information only.
message from gheat---skipping mf.../mt... processed in mf6
NJOY has found photon data for a given mt in both mf6 and mf12 - mf15.
Only the mf6 data are used.
error in gambar***storage exceeded in a
Increase nd=10000 in gheat.
error in gambar***requested energy gt highest given
Probably reflects an error in the evaluation.
error in hout***nin out of order. read mfh,mth = ...
error in hout***nscr out of order. read mfh,mth = ...
These errors indicate that the various sections in the ENDF file are not
sequentially ordered. Check the ENDF file and correct it if possible.
6.12 Storage Allocation
Allocatable arrays are used for most large data blocks. Storage requirements are
dominated by the length of File 5 or File 15 for the evaluation. The loada/finda
buffer size nbuf may be decreased or increased at will. The code is currently
dimensioned as follows:
100 coarse grid points
30 auxiliary Q-values
25 partial KERMAS (7 when kinematic limits are requested)
10000 words of energy-dependent Q data
10000 maximum for File 5 or 15 raw data
7000 maximum for fission yield data
320 File 6 reactions
164 NJOY2016

7 THERMR LA-UR-17-20093
7 THERMR
The THERMR module generates pointwise neutron scattering cross sections
in the thermal energy range and adds them to an existing PENDF file. The
cross sections can then be group-averaged, plotted, or reformatted in subse-
quent modules. THERMR works with either the original ENDF/B-III thermal
format[51] and data files[52] (which were also used for ENDF/B-IV and -V),
or the newer ENDF-6 format[9]. Coherent elastic cross sections are generated
for crystalline materials using either parameters given in an ENDF-6 format
evaluation or an extended version of the method of HEXSCAT[32]. Incoherent
elastic cross sections for non-crystalline materials such as polyethylene and ZrH
can be generated either from parameters in an ENDF-6 format file or by direct
evaluation using parameters included in the THERMR coding. Inelastic cross
sections and energy-to-energy transfer matrices can be produced for a gas of
free atoms, or for bound scatterers when ENDF S(α, β) scattering functions are
available. This function has previously been performed using FLANGE-II[31].
THERMR has the following features:
•The energy grid for coherent elastic scattering is produced adaptively so as
to represent the cross section between the sharp Bragg edges to a specified
tolerance using linear interpolation.
•The secondary energy grid for inelastic incoherent scattering when using
E-E0-µordering is produced adaptively so as to represent all structure with
linear interpolation. Discrete-angle representations are used to avoid the
limitations of Legendre expansions.
•An option to use E-µ-E0ordering is available. Dependences on µand E0
are constructed adaptively.
•Incoherent cross sections are computed by integrating the incoherent dis-
tributions for consistency.
•Free-atom incoherent scattering is normalized to the Doppler broadened
elastic scattering cross section in order to provide an approximate repre-
sentation of resonance scattering and to preserve the correct total cross
section.
•Hard-to-find parameters for the ENDF/B-III evaluations are included in
the code for the user’s convenience.
•ENDF-6 format files can be processed. This gives the evaluator more con-
trol over the final results, because all parameters needed to compute the
cross sections are contained in the file.
This chapter describes the THERMR module in NJOY2016.0.
NJOY2016 165
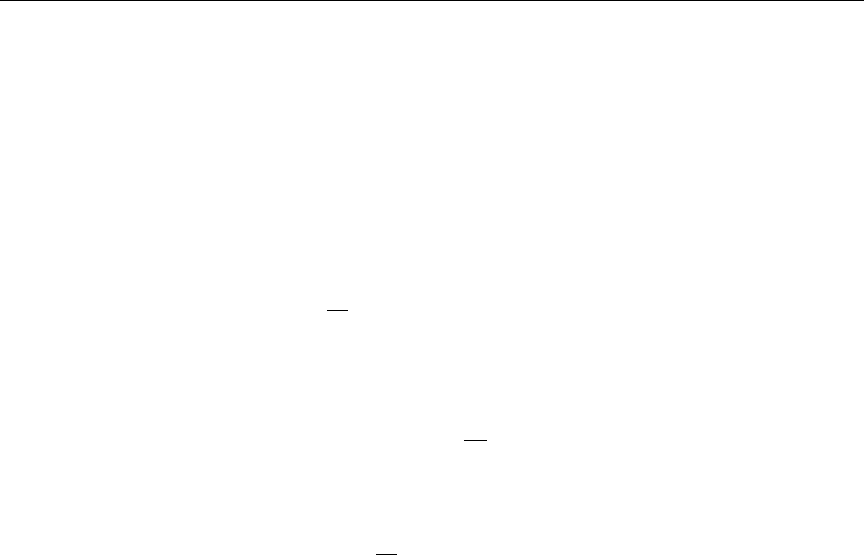
LA-UR-17-20093 7 THERMR
7.1 Coherent Elastic Scattering
In crystalline solids consisting of coherent scatters — for example, graphite
— the so-called “zero-phonon term” leads to interference scattering from the
various planes of atoms of the crystals making up the solid. There is no energy
loss in such scattering, and the ENDF term for the reaction is coherent elastic
scattering. The cross section may be represented as follows:
σcoh(E, E0, µ) = σc
EX
Ei>E
fie−2W Eiδ(µ−µ0)δ(E−E0),(225)
where
µ0= 1 −2Ei
E,(226)
and the integrated cross section is given by
σcoh =σc
EX
Ei>E
fie−2W Ei.(227)
In these equations, Eis the incident neutron energy, E0is the secondary neutron
energy, µis the scattering cosine in the laboratory (LAB) reference system, σc
is the characteristic coherent cross section for the material, Wis the effective
Debye-Waller coefficient (which is a function of temperature), the Eiare the
so-called “Bragg edges”, and the fiare related to the crystallographic structure
factors.
It can be seen from Eq. 227 and the example in Fig. 16 that the coherent
elastic cross section is zero before the first Bragg edge, E1(typically about 2 to 5
meV). It then jumps sharply to a value determined by f1and the Debye-Waller
term. At higher energies, the cross section drops off as 1/E until E=E2. It then
takes another jump and resumes its 1/E drop-off. The sizes of the steps in the
cross section gradually get smaller, and at high energies there is nothing left but
an asymptotic 1/E decrease (typically above 1 to 2 eV).
For evaluations in the ENDF-6 format, the section MF=7/MT=2 contains
the quantity Eσcoh(E) as a function of energy and temperature. The energy
dependence is given as a histogram with breaks at the Bragg energies. The
cross section is easily recovered from this representation by dividing by E. The
Eiare easily found as the tabulation points of the function, and the fifor a
point can be obtained by subtracting the value at the previous point.
For evaluations using the older ENDF/B-III thermal format, it is necessary to
166 NJOY2016
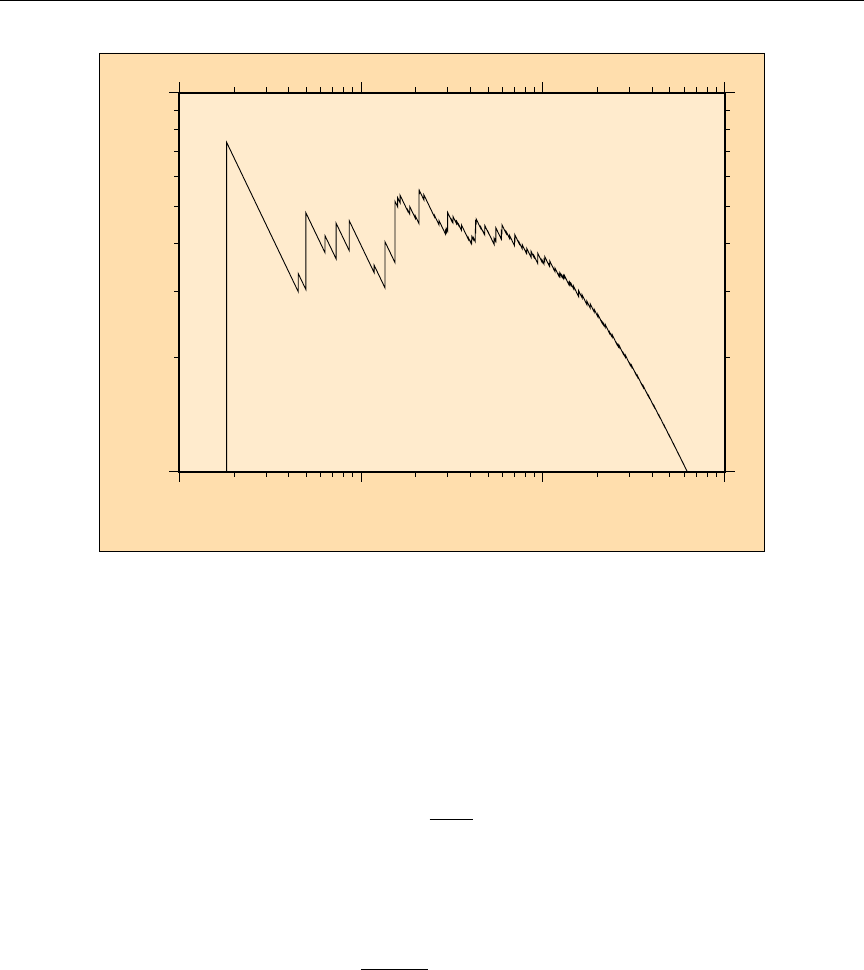
7 THERMR LA-UR-17-20093
10-3 10-2 10-1 100
Neutron Energy (eV)
100
101
Cross section (barns)
Figure 16: Typical behavior of the coherent elastic scattering cross section for a crystalline
material as computed by THERMR. This cross section is for graphite at 293.6K.
compute the Eiand fiin THERMR. The methods used are based on HEXSCAT
and work only for the hexagonal materials graphite, Be, and BeO. The Bragg
edges are given by
Ei=¯h2τ2
i
8m,(228)
where τiis the length of the vectors of one particular “shell” of the reciprocal
lattice, and mis the neutron mass. The fifactors are given by
fi=π2¯h2
2mNV X
shell |F(τ)|2,(229)
where the shell sum extends over all reciprocal lattice vectors of the given length,
Nis the number of atoms in the unit cell, and Fis the crystallographic structure
factor. The calculation works by preparing a sorted list of precomputed τiand
fivalues. As τigets large, the values of τiget more and more closely spaced. In
order to save storage and run time, a range of τvalues can be lumped together
to give a single effective τiand fi. This device washes out the Bragg edges
at high energies while preserving the proper average cross section and angular
dependence. The current grouping factor is 5% (see eps in sigcoh).
NJOY2016 167
LA-UR-17-20093 7 THERMR
Lattice constants (given in sigcoh for graphite, Be, and BeO), form fac-
tor formulas (see form), Debye-Waller coefficients, and methods for computing
reciprocal lattice vectors were borrowed directly from HEXSCAT.
The energy grid for Eis obtained adaptively (see coh). A panel extending
from just above one Bragg edge to just below the next higher edge is subdivided
by successive halving until linear interpolation is within a specified fractional
tolerance (tol) of the exact cross section at every point. This procedure is
repeated for every panel from the first Bragg edge to the specified maximum
energy for the thermal treatment (emax).
The code usually computes and writes out the cross section of Eq. 227, the
average over µof Eq. 225, which is sometimes called the P0cross section. Sub-
sequent modules can deduce the correct discrete scattering angles µ0from the
location of the Bragg edges Eiand the factors fifrom the cross section steps at
the Bragg edges (see GROUPR). Legendre cross sections can also be computed
by making a small change to the code. It is not necessary to give the P1, P2,
and P3cross sections explicitly as was done in some earlier codes or in File 4 of
the ENDF thermal tapes.
7.2 Incoherent Inelastic Scattering
In ENDF/B notation, the thermal incoherent scattering cross section is given
by
σinc(E, E0, µ) = σb
2kT rE0
Ee−β/2S(α, β),(230)
where Eis the initial neutron energy, E0is the energy of the scattered neutron,
µis the scattering cosine in the laboratory system, σbis the characteristic bound
incoherent cross section for the nuclide, Tis the Kelvin temperature, βis the
dimensionless energy transfer,
β=E0−E
kT ,(231)
αis the dimensionless momentum transfer,
α=E0+E−2µ√EE0
AkT ,(232)
kis Boltzmann’s constant, and Ais the ratio of the scatter mass to the neu-
tron mass. The bound scattering cross section is usually given in terms of the
168 NJOY2016

7 THERMR LA-UR-17-20093
characteristic free cross section, σf,
σb=σf
(A+ 1)2
A2.(233)
The scattering law S(α, β) describes the binding of the scattering atom in a
material. For a free gas of scatterers with no internal structure
S(α, β) = 1
√4πα exp −α2+β2
4α.(234)
For binding in solids and liquids, S(α, β) for a number of important moderator
materials is available in ENDF/B File 7 format. The scattering law is given
as tables of Sversus αfor various values of β. Values of Sfor other values
of αand βcan be obtained by interpolation. The scattering law is normally
symmetric in βand only has to be tabulated for positive values, but for materials
like orthohydrogen and parahydrogen of interest for cold moderators at neutron
scattering facilities, this is not true. These kinds of materials are identified by
the ENDF-6 LASYM option, and THERMR assumes that the scattering law is
given explicitly for both positive and negative values of β.
If the αor βrequired is outside the range of the table in File 7, the differential
scattering cross section can be computed using the short collision time (SCT)
approximation
σSCT(E, E0, µ) = σb
2kT pE0/E
p4π α Teff /T exp −(α− |β|)2
4α
T
Teff −β+|β|
2,(235)
where Teff is the effective temperature for the SCT approximation. These tem-
peratures are available[52] for the older ENDF/B-III evaluations; they are usu-
ally somewhat larger than the corresponding Maxwellian temperature T. For
the convenience of the user, the values of Teff for the common moderators are
included as defaults (see input instructions). For the newer ENDF-6 format,
the effective temperatures are included in the data file. However, there is a
complication. Some evaluations give S(α, β) for a molecule or compound (in
the ENDF/B-III files, these cases are BeO and C6H6). The corresponding SCT
approximation must contain terms for both atoms. The two sets of bound
cross sections and effective temperatures are included in the data statements in
THERMR, and they can be given in the new ENDF-6 format if desired.
THERMR expects the requested temperature Tto be one of the temper-
atures included on the ENDF/B thermal file, or within a few degrees of that
NJOY2016 169

LA-UR-17-20093 7 THERMR
value (296K is used if 300K is requested). Intermediate temperatures should
be obtained by interpolating between the resulting cross sections and not by
interpolating S(α, β).
The cross sections for incoherent inelastic scattering are computed in the
calcem subroutine. There are two possible orderings of the basic variables al-
lowed (see iform). For E-E0-µordering, the secondary energy grid for incoherent
scattering is obtained adaptively. A stack is first primed with the point at zero
and the first point above zero that can be derived from the positive and negative
values of βfrom the evaluator’s βgrid using Eq. 231. (For free-gas scattering,
the βgrid is taken to have 45 entries between 0.0 and 3500). This interval is
then subdivided by successive halving until the cross section obtained by linear
interpolation is within the specified tolerance of the correct cross section (from
sigl). The next highest energy derived from the βgrid is then calculated,
and the subdivision process is repeated for this new interval. This process is
continued until the βgrid has been exhausted. Excess points with zero cross
section are removed before writing the spectrum into File 6. This procedure is
sure to pick up all the structure in the evaluation; giving points related to the β
grid avoids excessive work in trying to fit sharp corners introduced by breaks in
the interpolation of S(α, β). Fig. 17 shows how the procedure picks up features
resulting from the sharp excitation features in the graphite phonon frequency
distribution.
The result of this adaptive reconstruction is easily integrated by the trapezoid
rule to find the incoherent cross section at energy E.
The cross section for one particular E→E0is the integral over the angular
variable of Eq. 230. The angular dependence is obtained by adaptively subdi-
viding the cosine range until the actual angular function (see sig) is represented
by linear interpolation to within a specified tolerance. The integral under this
curve is used in calculating the secondary-energy dependence as described above.
Rather than providing the traditional Legendre coefficients, THERMR divides
the angular range into equally probable cosine bins and then selects the single
cosine in each bin that preserves the average cosine in the bin. These equally
probable cosines can be converted to Legendre coefficients easily when produc-
ing group constants, and they are suitable for direct use in Monte Carlo codes.
For strongly peaked functions, such as scattering for EkT when the result
begins to look “elastic”, all the discrete angles will be bunched together near
the scattering angle defined by ordinary kinematics. This behavior cannot be
obtained with ordinary P3Legendre coefficients. Conversely, if such angles are
170 NJOY2016
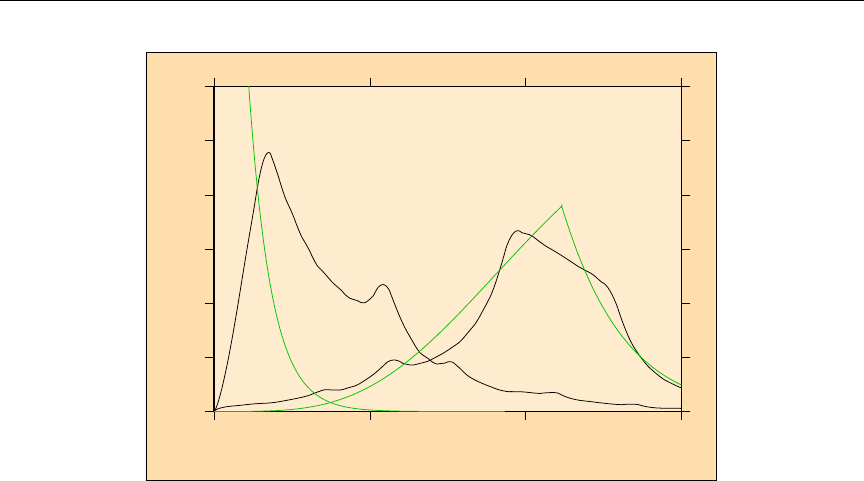
7 THERMR LA-UR-17-20093
0 50 100 150
*10-3
Neutron Energy (eV)
0
5
10
15
20
25
30
Probability
Figure 17: Adaptive reconstruction of two of the emission curves for graphite at 293.6K
(E=.00016 eV to the left, and E=.1116 eV to the right). Note the presence of
excitation features from the phonon frequency spectrum for both upscatter and
downscatter. The breaks in the curves are due to βinterpolation in S(α, β) and
not to the tolerances in the reconstruction process. The green curves are the
corresponding free gas results.
converted to Legendre form, very high orders can be used. If a direct calculation
of Legendre components is desired, reverse the sign of nnl in calcem.
The incident energy grid is currently stored directly in the code (see egrid
in calcem). The choice of grid for σinc(E) is not critical since the cross section
is a slowly varying function of E. However, the energy grid would seem to be
important for the emission spectra. In order to demonstrate the problem, two
perspective plots of the full energy distribution of incoherent inelastic scattering
from graphite at 293.6K are shown in Figs. 18 and 19. The second plot is simply
an expansion of the high-energy region of the distribution.
It is clear that σinc(E, E0) for one value of E0is a very strongly energy-
dependent function for the higher incident energies. However, as shown in
Fig. 19, the shape of the secondary energy distribution changes more slowly,
with the peak tending to follow the line E0=E. This behavior implies that a
relatively coarse incident energy grid might prove adequate if a suitable method
is used to interpolate between the shapes at adjacent Evalues. One such in-
terpolation scheme is implemented in GROUPR. The use of discrete angles is
especially suitable for this interpolation scheme.
NJOY2016 171
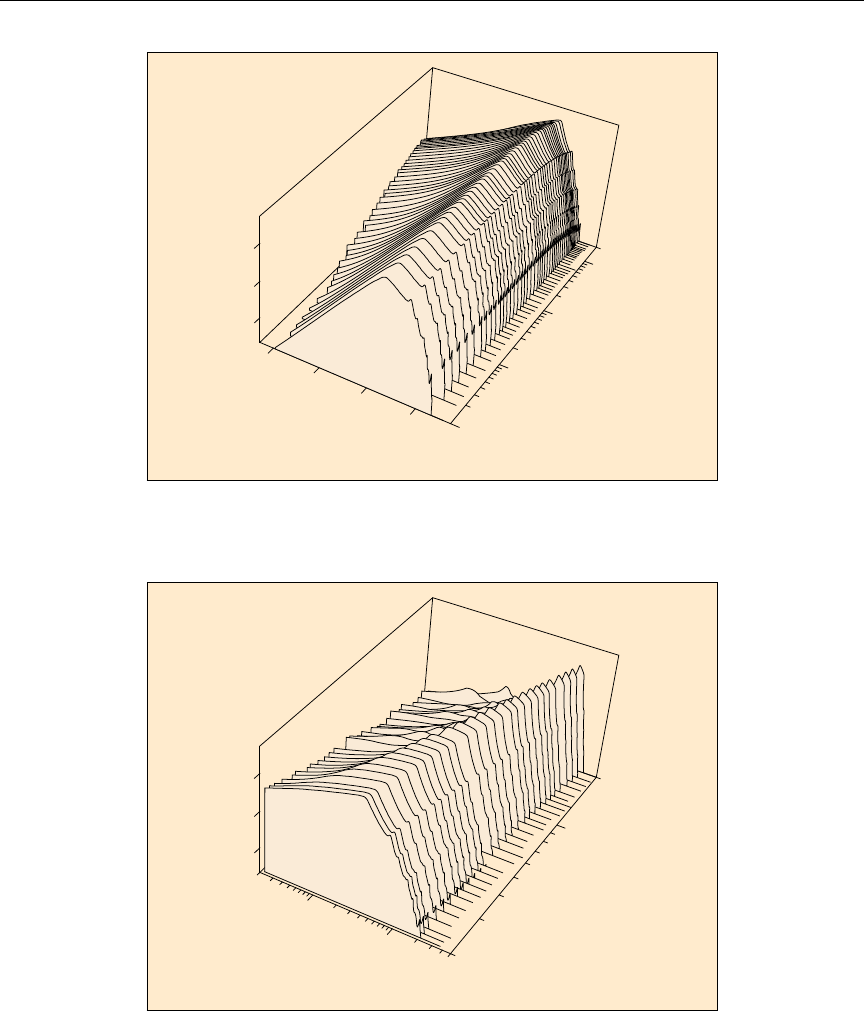
LA-UR-17-20093 7 THERMR
GRAPHITE AT 293.6K FROM ENDF/B-VII
thermal inelastic
1
0
5
1
0
6
1
0
7
P
r
o
b
/
M
e
V
1
0
-
1
0
1
0
-
9
1
0
-
8
1
0
-
7
S
e
c
.
E
n
e
r
g
y
1
0
-
1
1
1
0
-
1
0
1
0
-
9
1
0
-
8
E
n
e
r
g
y
(
M
e
V
)
Figure 18: Neutron distribution for incoherent inelastic scattering from graphite (T =
293.6K).
GRAPHITE AT 293.6K FROM ENDF/B-VII
thermal inelastic
1
0
5
1
0
6
1
0
7
P
r
o
b
/
M
e
V
1
0
-
8
1
0
-
7
S
e
c
.
E
n
e
r
g
y
1
0
-
7
E
n
e
r
g
y
(
M
e
V
)
Figure 19: Expanded view of the high-energy region of the graphite incoherent inelastic
distribution.
Strictly speaking, the scattering law for free-gas scattering given in Eq. 234
is only applicable to scatterers with no internal structure. However, many ma-
terials of interest in reactor physics have strong scattering resonances in the
thermal range (for example, 240Pu and 135Xe). The Doppler broadened elastic
172 NJOY2016
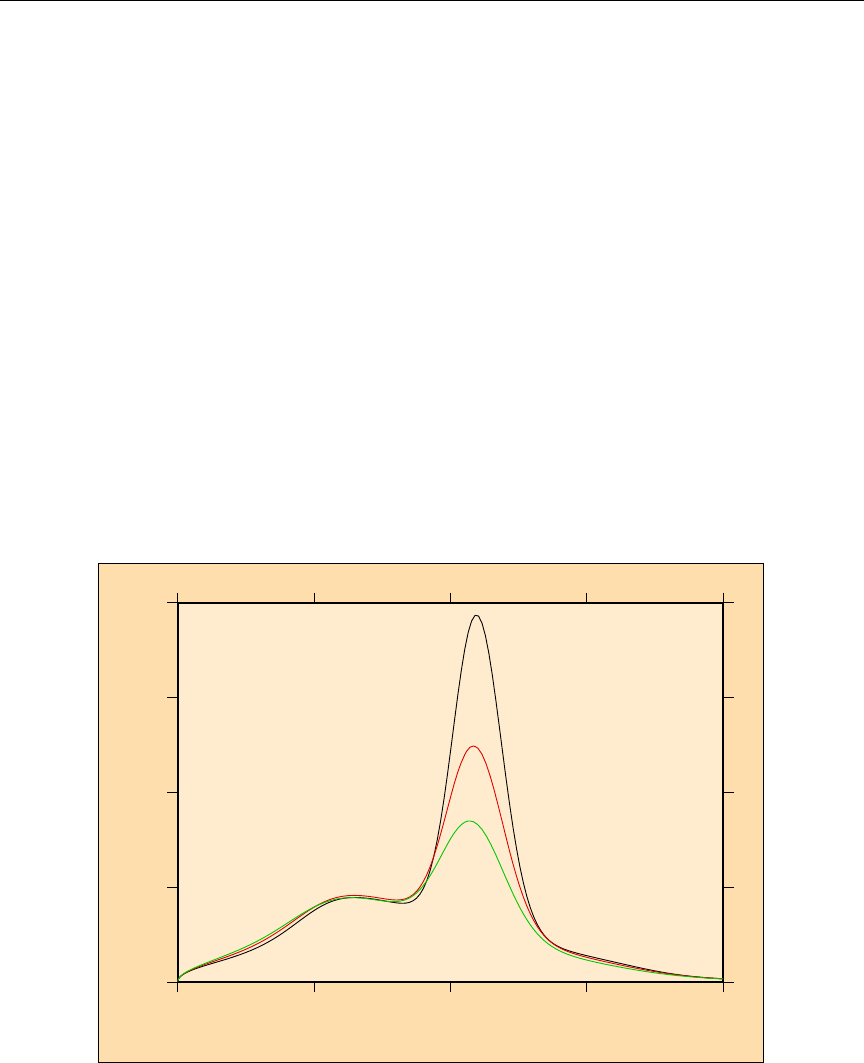
7 THERMR LA-UR-17-20093
cross section produced by BROADR is formally correct for a gas of resonant
scatterers, but the cross section resulting from Eq. 234 is not. In order to al-
low for resonance scattering in a way that at least provides the correct total
cross section, THERMR renormalizes the free-atom scattering to the broadened
elastic cross section. The secondary energy distribution will still be incorrect.
The built-in grid for incident neutron energies is suitable for normal temper-
atures found in reactors. For higher temperatures (higher than break=3000),
the grid values are scaled up to span the kinds of energies expected.
If the E-µ-E0option is selected (iform=1), an adaptive reconstruction of
the angular cross section σ(E, µ) is performed. For each µvalue, the secondary
energy spectrum is generated adaptively, and the integral over that spectrum
is saved as σ(E, µ). The results are written out using the ENDF-6 format File
6/law 7 option. This ordering is more like the results of experiments, and the
THERMR results can be used to compare to experiment. See Fig. 20 for a figure
based on this kind of ordering.
0 50 100 150 200
*10-3
Neutron Energy (eV)
0
5
10
15
20
Probability
Figure 20: Example of distributions for H in H2O with E-µ-E0ordering. The incident
energy is 0.115 eV. The black curve is at 51.3 deg, the red curve is at 60 deg,
and the green curve is at 68 deg.
NJOY2016 173
LA-UR-17-20093 7 THERMR
7.3 Incoherent Elastic Scattering
In hydrogenous solids, there is an elastic (no energy loss) component of scat-
tering arising from the zero-phonon term that can be treated in the incoherent
approximation because of the large incoherent cross section of hydrogen. The
ENDF term for this process is incoherent elastic scattering, and it is found in the
materials polyethylene and zirconium hydride. The differential cross section is
given by
σiel(E, E0, µ) = σb
2e−2W E(1−µ)δ(E−E0),(236)
where σbis the characteristic bound cross section and Wis the Debye-Waller
coefficient. The energy grid of the elastic cross section is used for E, and the
average cross section and equally probable angles are computed using
σiel(E) = σb
21−e−4W E
2W E ,(237)
and
¯µi=N
2W E he−2W E(1−µi)(2W Eµi−1)
−e−2W E(1−µi−1)(2W Eµi−1−1)i/(1 −e−4W E),(238)
where
µi= 1 + 1
2W E ln 1−e−4W E
N+ e−2W E(1−µi−1)(239)
is the upper limit of one equal probability bin and ¯µiis the selected discrete
cosine in this bin. Here Nis the number of bins and µ0is −1.
The characteristic bound cross sections and the Debye-Waller coefficients
can be read from MF=7/MT=2 of an ENDF-6 format evaluation, or obtained
directly from data statements in the code for the older format.
7.4 Coding Details
The thermr routine comes from module thrmm. The procedure begins with the
reading of the user’s input. The required ENDF tape (nendf) is only used for
MF=7 data; it can be set to zero if only free-gas scattering is needed. Similarly,
matde is the material number for the File 7 tape and can be set to zero for
174 NJOY2016
7 THERMR LA-UR-17-20093
free-atom problems. The ENDF File 7 format only gives “M0σf0”, the product
of the free scattering cross section for the principal scatterer and the number of
principal scatterer atoms in the molecule. As a result, THERMR needs the pa-
rameter natom to obtain the effective microscopic cross section (for example, for
H in H2O, use natom=2). For ENDF/B-III format files, default parameters are
supplied for mixed moderators (BeO and benzine) and effective temperatures,
if needed.
Continuing, thermr finds the desired material on the input PENDF and
ENDF tapes. It will automatically loop over ntemp materials on nin. The input
tape must have been through BROADR. The elastic cross section at the current
temperature is saved on a loada/finda scratch file to be used for normalizing
free-atom scattering if necessary. For ENDF-6 format materials, the parameters
for the elastic calculation are read in using rdelas. Next, thermr computes
elastic and/or inelastic cross sections by calls to coh,iel, and calcem. Finally,
the results are written onto the output PENDF tape by tpend.
Some alteration of ENDF/B formats and conventions was required to ac-
commodate thermal cross sections. The incoherent inelastic cross sections fit
well into MF=3 using MT=mtref (see user input). The coherent or incoher-
ent elastic cross section (if present) uses mtref+1. Other modules of NJOY
expect that thermal MT numbers will be between 221 and 250. The incoherent
energy-to-energy matrix is stored in MF=6 (coupled angle-energy distributions).
Before the introduction of the ENDF-6 format, the ENDF File 6 formats were
not well-suited to this application because secondary angle and energy were not
tightly coupled as required by the physics of the problem. Therefore, three new
formats were defined for File 6: LTT=5 for discrete-angle inelastic transfer cross
sections, LTT=6 for discrete-angle elastic data, and LTT=7 for coherent elastic
reactions. The format for LTT=5 follows in the notation of ENDF-102[51]:
MAT,6,MT [ ZA, AWR, 0, LTT, 0, 0 ] CONT LTT=5
MAT,6,MT [ T, 0., 0, 1, NNE / NNE, 2 ] TAB2
MAT,6,MT [ 0., EN, 0, 0, NEP*(NL+1), NL+1 /
EP(1), PP(1), EPM(1,1), ...
EP(2), PP(2), ... ] LIST
... repeat the LIST for the NNE values of EN ...
MAT,6,0 [ 0., 0., 0, 0, 0, 0 ] SEND
There is a list record for each of the NNE values of incident energy. Each list
NJOY2016 175

LA-UR-17-20093 7 THERMR
record gives the normalized secondary energy distribution as NEP values of PP
vs. E0, and for each value of E0, the record gives NL equally probable cosines,
EPM. Similarly, the format for LTT=6 is:
MAT,6,MT [ ZA, AWR, 0, LTT, 0, 0 ] CONT LTT=6
MAT,6,MT [ T, 0., 0, 1, NNE / NNE, 2 ] TAB2
MAT,6,MT [ 0., EN, 0, 0, NU+2, NU+2 /
EN, 1., U(1), U(2), ... ] LIST
... repeat the LIST for the NNE values of EN ...
MAT,6,0 [ 0., 0., 0, 0, 0, 0 ] SEND
Here, there is just a set of NU equally probable cosines given for each incident
energy. Note that this format was designed to look like that for LTT=5 with
NEP=1. Finally, the format for LTT=7 is:
MAT,6,MT [ ZA, AWR, 0, LTT, 0, 0 ] CONT LTT=7
MAT,6,MT [ 0,, 0., 0, 0, 0, NBRAGG ] CONT
MAT,6,0 [ 0., 0., 0, 0, 0, 0 ] SEND
In this case, all the important information is in File 3 under MT=mtref+1. For
convenience, the number of Bragg edges used is given here in File 6 as NBRAGG.
In subroutine coh, the energy grid is determined adaptively and stored into
the same loada/finda scratch file used for the elastic cross section. The elastic
cross section is converted to the coherent grid using Lagrangian interpolation
(see terp). The structure of the record stored on the scratch file is [energy /
static elastic / incoherent inelastic / coherent elastic].
Coherent cross sections at a given energy Eare computed by sigcoh. If
this is the first entry (E=0) for an ENDF-III type material, the appropriate
lattice constants are selected and the Debye-Waller coefficient is obtained for the
desired temperature by interpolation. Then the reciprocal lattice wave vectors
and structure factors are computed, sorted into shells, and stored for later use.
On a normal entry (E>0), the stored list is used to compute the cross section.
For ENDF-6 format materials, the initialization step is used to organize the data
already read from MF=7/MT=2 by rdelas, and subsequent entries are used to
compute the cross section.
176 NJOY2016

7 THERMR LA-UR-17-20093
Incoherent elastic cross sections are computed in subroutine iel. The appro-
priate bound cross sections and Debye-Waller coefficients are either extracted
from the data already read from an ENDF-6 format MF=7/MT=2 by rdelas,
or they are extracted from data statements in iel and then adjusted to the
specified temperature using terp or terpa. The angle-integrated cross section
is computed analytically on the grid of the static elastic cross section and written
back onto the loada/finda scratch file in the same slot used for coherent elastic
as described above (both never occur simultaneously in the same material). The
discrete equally probable cosines are cast into LTT=7 format and written onto
a scratch tape for use by tpend.
Incoherent cross sections and distributions are generated in calcem. On the
first entry, the ENDF/B scattering law is read in or parameters are set for
free-atom scattering. For ENDF-6 files, the effective temperatures for the SCT
approximation are read in. For the older formats, these numbers were either
read in or set to default values during the user input process. The calculation
for E-E0-µordering (iform=0) goes through statement 300. An adaptive loop
to determine the secondary energy grid is carried out. The required cross sec-
tions and discrete cosines are returned by sigl, which uses sig to compute the
differential cross sections. Because the spectrum curve will have discontinuities
in slope at energies corresponding to the break points of the βgrid, it is impor-
tant to use these energies as the starting points for the adaptive reconstruction.
The first panel starts at E0= 0 and ends at the first energy greater than zero
that can be derived from the βgrid. This will normally be a negative βvalue
corresponding to E0<E. These two energies and their corresponding cross sec-
tions are loaded into an inverted stack like the one used in RECONR. Next, the
top interval in the stack is divided in half, and new cross sections are computed
at this midpoint. If the new cross section is not within the desired tolerance
of the value obtained by linear interpolation between the adjacent points, the
new value is inserted into the stack. Otherwise, the top value in the stack is
converged and can be saved to the location where the spectrum is accumulating.
Each time the stack gets down to a single element, a new point is calculated
from the next βvalue in the evaluator’s βgrid, and the subdivision process is
continued. During this reconstruction process, the integrated cross section is
computed by adding in each trapezoid. In addition, note is taken of the last
nonzero cross section value in order to remove excess zero values from the end of
the record. The σvs. E0curve is complete when the βgrid has been exhausted
(the highest positive value). The result is put directly into the modified MF=6
NJOY2016 177

LA-UR-17-20093 7 THERMR
format and written onto a scratch file.
When all the desired incident energies have been processed, the incoherent
cross section is calculated on the File 3 energy grid by interpolating in the table
of values computed by the reconstruction process. The results are stored on the
loada/finda tape. If free-atom scattering has been selected, the elastic cross
section is stored in the incoherent slot.
Incoherent inelastic scattering cross sections and discrete cosines are com-
puted in sigl. The stack for the adaptive reconstruction of the angular distri-
bution for a given E→E0is primed with µ=−1, µ=+1, and the angle for static
scattering. The top interval on the stack is subdivided by halving until the
actual cross section computed by sig is within a specified tolerance of a linear
interpolate. As each panel is converged, its area is added to the accumulating
cross section. On convergence, the fraction of the cross section corresponding to
each equally probable bin is computed, and the linearization process is repeated
to find the bin boundaries and discrete cosines. Note that Legendre coefficients
can be computed in this routine from the discrete cosines.
Subroutine sig is used to compute the actual double-differential cross section
for a given value of E,E0, and µ. This is done using S(α, β) (with the possible
use of the SCT approximation for large values of αor β), or using the free-gas
scattering law. Normally, s(α, β) is symmetrical in βand results are extracted
from the table at isab using |β|. However, this is not true for materials like
orthohydrogen and parahydrogen. In these cases, the LASYM parameter is
set, and explicit S(α, β) values are given for both negative and positive β. For
liquids, the presence of diffusion leads to a singularity for β= 0 and small α
(the quasi-elastic scattering peak). The normal ENDF interpolation laws do not
represent S(α, β) well in this region. Therefore, THERMR tries to determine if
the material is a liquid by looking at the small-αbehavior of the β= 0 curve
(see cliq). It then extrapolates low-βcurves to low-αvalues using a β2/α law.
The calculation for E-µ-E0ordering starts at statement number 510. In
a loop over incident energies, subroutine sigu is called to reconstruct σ(E, µ)
adaptively. The method used is the same as that described above for the energy
distribution, and the result represents the angular cross section to within a
desired tolerance. The inelastic cross section is obtained as the integral over the
angular cross section. Subroutine sigu obtains the secondary energy spectrum
corresponding to E and µadaptively. It uses the beta values from the evaluation
as starting points for subdivision, just as described above for E-E0-µordering.
It uses sig to obtain the cross section for a given E,E0, and µ. The results of
178 NJOY2016

7 THERMR LA-UR-17-20093
this calculation are written onto nscr using the ENDF-6 File 6/Law 7 format
and passed to tpend.
Finally, tpend is called to prepare the output tape. The File 1 directory is
updated to account for the new sections that are being added. File 3 is located
and the cross sections stored on the loada/finda scratch file are retrieved,
formatted, and written to the output tape. Note that the elastic cross section
in MT=2 and the total cross section in MT=1 are not changed from their static
values, nor is the union grid updated. As a result, MT=221 – 250 must be
considered supplemental. Subsequent modules could ignore them or use them in
place of the static values. Also note that it is possible to run THERMR several
times with different values of mtref. The result would be one PENDF tape
containing static cross sections and cross sections for several different binding
states that can be selected at will (for example, MT=2 for static hydrogen,
MT=221 for free hydrogen, MT=222 for hydrogen in water, and MT=223 and
MT=224 for hydrogen in polyethylene, all on one PENDF tape).
File 6 distributions are read from a scratch file (nscr) in ENDF format,
normalized, and written back onto the final tape. Since free incoherent scat-
tering was set equal to elastic scattering in calcem, the approximate resonance
correction of the matrix is now complete.
7.5 Using the ENDF/B Thermal Data Files
The thermal data files originally prepared for ENDF/B-III were also used for
ENDF/B-IV and ENDF/B-V.4Table 3summarizes the contents of these data
tapes.
For most of these evaluations, THERMR will produce cross sections appro-
priate for the major scattering atom bound in a particular material, for example,
hydrogen bound in water, or Zr bound in ZrH. In these cases, the cross sections
are combined later (for example, hydrogen bound in water would be combined
with free-gas oxygen, and Zr bound in ZrH would be combined with H bound
in ZrH). The treatment to be used for the secondary scattering atoms for each
evaluation is indicated in the table.
In two cases – BeO and Benzine – the scattering laws S(α, β) for the two
component atoms have been combined into a single scattering law normalized to
be used with the cross section of the primary scattering atom. For these cases,
THERMR produces a cross section for the molecule or compound directly. In
4The data files and the reference manual[52] are available from the National Nuclear Data Center,
Brookhaven National Laboratory, Upton, NY 11973. Request Tapes 320 through 325 and report ENDF-269.
NJOY2016 179

LA-UR-17-20093 7 THERMR
Table 3: Moderator Materials on ENDF/B-III Thermal Data Tapes Showing Their MAT
Numbers and Distribution Tape Numbers
Material MAT Tape MTs elastic secondary
Be 1064 321 231,232 coh
BeO 1099 321 233,234 coh none
C (graphite) 1065 322 229,230 coh
H(CH2) 1114 322 223 iel free C
C6H61095 325 227 none
D(D2O) 1004 320 228 free O
H(H2O) 1002 320 222 free O
Zr(ZrHn) 1096 323 235,236 iel 1097
H(ZrHn) 1097 323 225,226 iel 1096
making a macroscopic cross section for BeO, the user would multiply the thermal
BeO cross section from THERMR by the atomic density of Be, taking care not
to add any additional thermal contribution for the oxygen.
Table 4: ENDF/B-VII Moderator Materials with Their MAT and MT Numbers
Material MAT MTs elastic secondary
Al 45 243,244 coh
Be 26 231,232 coh
Be(BeO) 27 233,234 coh
O(BeO) 28 237,238 coh
C(graphite) 31 229,230 coh
Fe 56 245,246 coh
H(CH2) 37 223 iel free C
H(liquidCH4) 33
H(solidCH4) 34
C6H640 227 none
D(D2O) 11 228 free O
D(paraD2) 12
D(orthoD2) 13
H(H2O) 1 222
H(paraH2) 2
H(orthoH2) 3
Zr(ZrHn) 58 235,236 iel
H(ZrHn) 7 225,226 iel
U(UO2) 76 241,242 coh
O(UO2) 75 239,240 coh
180 NJOY2016
7 THERMR LA-UR-17-20093
THERMR labels the thermal cross sections that it generates with specially
defined MT numbers. The particular numbers shown in the table are recognized
by the reaction naming logic in MATXSR. Note that two numbers are defined
for materials that have both inelastic and elastic components; the first number
is for inelastic, and the second for elastic.
For ENDF/B-VII, there are additional thermal materials available, and the
numbering has changed. See Table 4. Other thermal moderators are expected
in future ENDF/B generations as well as in other regional libraries (e.g., JEFF,
JENDL, etc.).
7.6 Input Instructions
The following input instructions have been copied from the comment cards in
THERMR:
!---input specifications (free format)-------------------
!
! card 1
! nendf endf tape for mf7 data
! nin old pendf tape
! nout new pendf tape
! card 2
! matde material desired on endf tape
! matdp material desired on pendf tape
! nbin number of equi-probable angles
! ntemp number of temperatures (default=1)
! iin inelastic options
! 0 none
! 1 compute as free gas
! 2 read s(a,b) and compute matrix
! icoh elastic options
! 0 none
! 1 compute using ENDF6 format data
! --------or for earlier formats
! 1 graphite
! 2 beryllium
! 3 beryllium oxide
! 11 polyethylene
! 12 h(zrh)
! 13 zr(zrh)
NJOY2016 181

LA-UR-17-20093 7 THERMR
! iform output format for inelastic distributions
! 0 E-E’-mu ordering (MF6 special)
! 1 E-mu-E’ ordering (MF6/Law7)
! natom number of principal atoms
! mtref mt for inelastic reaction (221-250 only)
! iprint print option (0=minimum, 1=maximum,
! 2=max. normal + intermediate results)
! (default=0)
! card 3
! tempr temperatures (kelvin)
! card 4
! tol tolerance
! emax maximum energy for thermal treatment
! (for temperatures greater than 3000,
! emax and the energy grid are scaled by
! temp/3000. free gas only.)
!
! nendf can be endf-6 format (e.g., from leapr) while
! nin and nout are endf-4 or 5 format, if desired.
!
!-----------------------------------------------------------
The following sample problem illustrates the production of thermal cross
sections for hydrogen in water.
thermr
20 21 22/
11258220022220/
293.6 500/
.01 4.6/
stop
It is assumed that ENDF/B-VII evaluation for H in H2O is mounted on unit
20, and that a previously prepared PENDF file for 1H (MAT125) is mounted
on unit 21. The thermal cross sections for hydrogen in water will be written on
unit 22 using mtref=222. Note that the parameter natom is set to 2 because
the water molecule H2O contains two hydrogen atoms. In addition, icoh=0 for
hydrogen in water, and iform=0 for E-E0-µordering. The higher-energy parts
182 NJOY2016
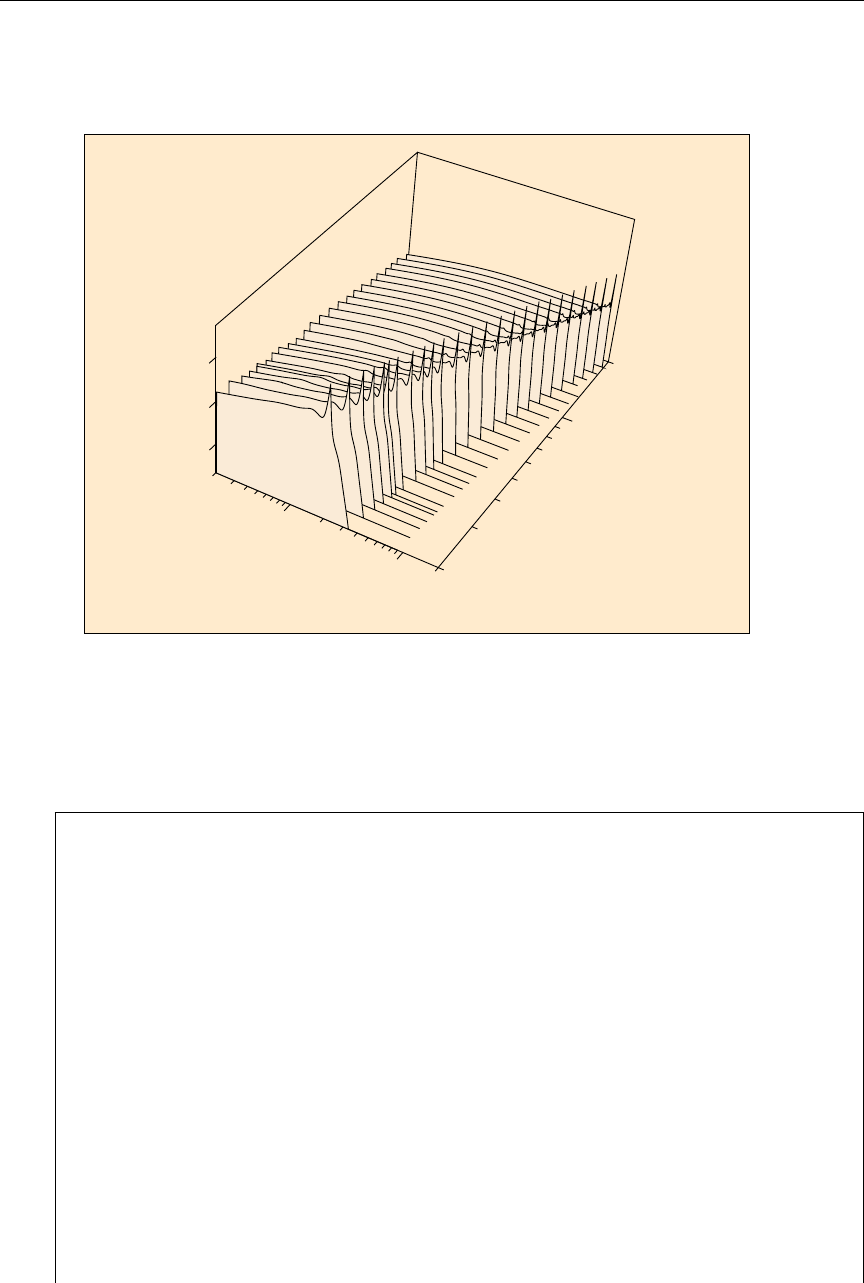
7 THERMR LA-UR-17-20093
of the neutron emission curves for this example are shown in Fig. 21. The sharp
peak at E=E0is quasi-elastic scattering broadened by diffusion.
1-H-1 IN H2O AT 293.6K FROM ENDF/B-VII USING CONTINUOUS
thermal inelastic
1
0
5
1
0
6
1
0
7
P
r
o
b
/
M
e
V
1
0
-
7
1
0
-
6
S
e
c
.
E
n
e
r
g
y
1
0
-
6
E
n
e
r
g
y
(
M
e
V
)
Figure 21: Expanded view of the high-energy region for the incoherent inelastic distribution
of hydrogen bound in water. Note the sharp quasi-elastic peak at E=E0.
A calculation of both free and graphite cross sections for ENDF/B-VII carbon
would go as follows:
reconr
20 22 / tape20 is carbon
/
600 1/
.001/
’6-C-nat from ENDF/B-VII’/
0/
broadr
20 22 23/
600 1/
.001/
293.6/
0/
thermr
0 23 24/
NJOY2016 183
LA-UR-17-20093 7 THERMR
06008120012210/
293.6/
.005 5/
thermr
26 24 25 / tape 26 is ENDF/B-VII graphite
316008121012290/
293.6/
.005 5/
stop
First, ENDF/B-VII carbon must be mounted on unit 20. At LANL this is done
by copying it to a file named tape20 in the user’s local file space. Similarly,
ENDF/B-VII graphite must be copied to tape26. Next, RECONR is run to
linearize the evaluation, and BROADR is run to prepare 293.6K cross sections.
The first THERMR run is for free-gas scattering (mtref=221), and the second
run is for carbon bound in graphite (mtref=229). Note that natom is now 1, and
that 8 discrete angles were requested in both cases. For graphite, icoh is set to 1
in order to request the calculation of coherent elastic scattering like that shown
in Fig. 16. The coherent results will use MF=3 and MT=230. Distributions will
be calculated to 0.5% accuracy for energies up to 5 eV. The final PENDF file
will be tape25.
7.7 Error Messages
error in thermr***nin=0
An input PENDF tape is required.
error in thermr***mode conversion not allowed
nin and nout must both be binary or both be coded.
error in thermr***illegal reference mt
Restricted to MT=221–250. User’s should note that Card 2 has an ad-
ditional input parameter, iform, beginning with NJOY2012. Unmodified
NJOY99 input decks will produce this error message.
error in thermr***desired material not on pendf tape
Check input instructions against contents of thermal tape.
error in thermr***desired temperature not on tape
Check input instructions against contents of thermal tape.
error in rdelas***too much elastic data
There is not enough space in the allocatable array a. See na=10000.
184 NJOY2016

7 THERMR LA-UR-17-20093
error in rdelas***desired temp not found
The temperatures requested in THERMR must be the same as the tem-
peratures on the input PENDF tape.
error in coh***too many legendre orders
The code currently computes only P0, but nl=1 in coh can be changed
if desired. Code is currently limited to 6 (P5). If more coefficients are
desired, increase nlmax and the dimensions of the variables s,ej, and ex
in coh,calcem, and tpend.
error in sigcoh***storage exceeded
Not enough room for lattice factors. Increase nw which is currently 10000.
error in sigcoh***illegal lat
Only three lattices are coded so far. To add others, insert the constants in
sigcoh and form factor formulas in form.
error in iel***bad temperature for debye-waller factor
Shouldn’t occur unless new materials are added incorrectly.
error in iel***unknown material identifier
Only three options are coded so far. To add others, insert data statements
for the Debye-Waller integrals and values for the bound cross sections.
error in calcem***nl too large for binning
Increase the value of the parameter nlmax which is currently 33.
error in calcem***storage exceeded
There is not enough space in the global scratch array. Increase nwscr,
which is currently 99000, in thermr.
error in calcem***desired temperature not found
Any temperature requested in THERMR must be on the input PENDF
tape.
error in calcem***bad temperature for teff
error in calcem***bad temperature for teff2
Data for effective temperatures use a temperature grid that is not consistent
with the S(α, β) data.
error in calcem***isabt=1 pendf tape found
THERMR cannot process this format.
error in calcem***only 2 sct atoms allowed
For mixed moderators, such as BeO and Benzine, the SCT contribution
from each atom must be included. The code only allows for 2.
error in calcem***too many angles
For E-µ-E0ordering, there are more than mumax=300 angles being gener-
ated.
error in sig***illegal option
Only tabulated S(α, β) and free gas are coded at this time.
NJOY2016 185

LA-UR-17-20093 7 THERMR
error in sigl***no legal solution
message from sigl---disc=-ffff, set to abs value....
error in sigl***no legal solution (quadratic path)
The code has trouble solving the equation for the boundary of a bin.
error in tpend***storage exceeded
Increase nwscr in thermr.
error in tpend***cross section = 0
Thermal cross section of zero cannot be used to normalize the distribution.
7.8 Input/Output Units
The following logical units are used.
10/11 iold/inew in thermr. Also used in coh,calcem, and tpend. Used
for the loada/finda scratch file that saves the energy grid and re-
action cross sections.
12 nscr in thermr. Also used in calcem and tpend. Contains the
scattering matrix before normalization.
13 nscr2 in thermr and tpend. Contains data from nin that are to be
simply copied to nout.
20-99 User’s choice for nendf,nin,nout, and nread (iinc=2 only) to link
with other modules. No mode conversion between nin and nout
allowed.
Units 10 and 11 are always binary. Units 12 and 13 have the same mode as
nin and nout. The user can choose the modes for nendf,nin,nout, except nin
and nout must have the same mode.
7.9 Storage Allocation
The storage allocated in THERMR is for the loada/finda buffers and a scratch
array. The value of nbuf my be changed at will; larger values increase I/O
efficiency. The variable nwscr controls the maximum size of the TAB1 records
of σ(E→E0) versus E0for incoherent scattering. Hence it interacts with tol.
The linearization stack (stk) in coh is controlled by imax and the number of
Legendre components requested (always 1 in the standard version). The current
value of imax (20) is sufficient to divide each panel into parts as small as one-
millionth of the panel size. The length of the list of lattice factors (fl) in
sigcoh is controlled by the size of the ENDF/B File 7, and nw=10000 must be
big enough for the problem.
186 NJOY2016

8 GROUPR LA-UR-17-20093
8 GROUPR
GROUPR computes group-to-group scattering matrices, and anisotropic photon
production matrices for neutrons from ENDF/B-IV and later evaluated nuclear
data. With ENDF-6 format files, photonuclear data and incoming and outgoing
charged particles can also be handled. Special features are provided for ratio
quantities (for example, µ,ν, or photon yield), inverse velocity, delayed neutron
spectra by time group, and anisotropic thermal neutron scattering. Fission is
represented as a group-to-group matrix for full generality. Scattering matrices
and photon production matrices may be self-shielded if desired.
The Bondarenko narrow-resonance weighting scheme[39] is normally used.
Optionally, a weighting flux can be computed for various mixtures of heavy
absorbers with light moderators. An accurate pointwise solution of the integral
slowing down equation is used. This option is normally called on to account for
intermediate resonance effects in the epithermal range.
Neutron data and photon-production data are processed in a parallel manner
using the same weight function and quadrature scheme. This assures consistent
cross sections for coupled neutron-photon problems. Two-body scattering is
computed with a center-of-mass (CM) Gaussian quadrature, which gives accu-
rate results even for small Legendre components of the group-to-group matrix.
User conveniences include free-form input and complete control over which
reactions are processed. The neutron group structure, photon group structure,
and weight function can each be read in or set to one of the internal options. Out-
put can be printed and/or written to an output “groupwise-ENDF” (GENDF)
file for further processing by a formatting module (DTFR,CCCCR,MATXSR,
WIMSR), by the covariance module (ERRORR), or by the MCNP continuous-
energy Monte Carlo module (ACER).
This chapter describes the GROUPR module in NJOY2016.0.
8.1 Multigroup Constants
Multigroup constants are normally used by computer codes that calculate the
distributions of neutrons and/or photons in space and energy, and that compute
various responses to these distributions, such as criticality, dose to personnel, or
activation of materials. These distributions are solutions of the neutral particle
transport equation.5
5The following development uses a notation based on Bell and Glasstone[53], where the lower-case sigma
is used for both macroscopic and microscopic cross sections, depending on the context. One-dimensional
NJOY2016 187

LA-UR-17-20093 8 GROUPR
µ∂
∂xφ(x, µ, E) + σt(x, E)φ(x, µ, E)
=ZdΩ0ZdE0σX(x, E0→E, Ω0→Ω)φ(x, µ0, E0)
+Q(x, µ, E),(240)
where the flux φis allowed to vary with position x, direction Ωwith polar cosine
µ, and energy E. Similarly, the macroscopic total cross section σtvaries with
position and energy. The right-hand side of the equation contains the source
due to transfers from other directions Ω0and energies E0(as described by the
macroscopic transfer cross section σX), and a fixed or external source Q.
The macroscopic cross sections (in units of cm−1) in Eq. 240 can be calculated
from microscopic cross sections for the component isotopes or elements (in barns)
using
σt(x, E) = X
i
ρi(x)σi
t(T[x], E),(241)
where ρiis the number density for a constituent (in barns−1cm−1), which may
vary with position, and T is the temperature, which may also vary with position.
A similar formula holds for σX.
The transfer cross section σX(which includes both scattering and fission
processes) is normally assumed to depend only on the cosine of the scattering
angle, µ0=Ω·Ω0. This allows σXto be expanded using Legendre polynomials
σX(x, E0→E, Ω0→Ω) =
∞
X
`=0
2`+ 1
4πσX`(x, E0→E)P`(µ0).(242)
Application of the addition theorem and integration over azimuthal angle then
gives
µ∂
∂xφ(x, µ, E) + σt(x, E)φ(x, µ, E)
=
∞
X
`=0
2`+ 1
2P`(µ)ZσX`(x, E0→E)φ`(x, E0)dE0
+Q(x, µ, E),(243)
slab geometry is used throughout for simplicity.
188 NJOY2016

8 GROUPR LA-UR-17-20093
where
φ`(x, E) = ZP`(µ)φ(x, µ, E)dµ . (244)
The desired responses are then given by
R(x) = Zσr(x, E)φ0(x, E)dE , (245)
where σris the reaction cross section for the response. The next step is to
integrate Eqs. 243 and 245 over a range of energies chosen to lie in group g. The
results are
µ∂
∂xφg(x, µ) +
∞
X
`=0
P`(µ)σt`g(x)φ`g (x)
=
∞
X
`=0
2`+ 1
2P`(µ)X
g0
σX`g0→g(x)φ`g0(x) + Qg(x, µ),(246)
and
R(x) = X
g
σrg (x)φ0g(x),(247)
where
φ`g(x) = Zg
φ`(x, E)dE , (248)
σt`g(x) = Zg
σt(x, E)φ`(x, E)dE
Zg
φ`(x, E)dE
,(249)
σr(x) = Zg
σr(x, E)φ0(x, E)dE
Zg
φ0(x, E)dE
,(250)
and
σX`g0→g=Zg
dE Zg0
dE0σX`(x, E0→E)φ`(x, E)
Zg
φ`(x, E)dE
.(251)
NJOY2016 189

LA-UR-17-20093 8 GROUPR
The last three equations provide the fundamental definitions for the multi-
group cross sections and the group-to-group matrix. Note that the values of
the group constants depend upon the basic energy-dependent cross sections ob-
tained from an ENDF-format evaluation by way of the RECONR,BROADR,
UNRESR,HEATR,THERMR, and PURR modules of NJOY, and the shape of
φwithin the group.
8.2 Group Ordering
Since neutrons normally lose energy in scattering, the scattering source into
group gdepends on the flux at higher-energy groups g0and the cross section for
transferring neutrons from g0to g. For this reason, Eq. 246 is usually solved by
sweeping from high energies to low energies. (Any thermal upscatter or fission
is handled by iteration.) Data libraries for use with transport codes normally
number the groups such that group 1 is the highest-energy group, and all the
scattering matrix elements that transfer neutrons into group 1 are given first,
followed by those for scattering into group 2, and so on.
However, in ENDF files the evaluated nuclear data are always given in order
of increasing incident energy, and secondary neutron distributions are described
by giving emission spectra for given incident energies. Therefore, GROUPR
numbers its groups such that group 1 is the lowest-energy group, and it calculates
that scattering out of group 1, followed by the scattering out of group 2, and so
on.
The “backward” energy-group numbering convention used by GROUPR is
a possible source of confusion in interpreting output produced by the various
modules of NJOY. All group indices printed by GROUPR or written to the
GROUPR output file use the increasing-energy order. The covariance modules
and photon interaction module follow the GROUPR ordering convention. Out-
put modules such as DTFR,CCCCR,MATXSR, and WIMSR invert the group
order and rearrange the scattering matrices from the GROUPR outscatter orga-
nization to the “transport” inscatter form. Any group indices printed by these
three output modules will be in the conventional transport decreasing-energy
order.
8.3 Basic ENDF Cross Sections
The basic energy-dependent cross sections and energy-angle distributions needed
for Eqs. 249,250, and 251 are obtained from evaluated nuclear data in ENDF
190 NJOY2016

8 GROUPR LA-UR-17-20093
format[9]. These data are indexed by material (MAT), type of information (MF),
and reaction (MT). Materials can be single isotopes, elements, or compounds.
Type of information includes energy-dependent cross section (MF=3), angu-
lar distributions (MF=4), secondary energy distributions (MF=5), and energy-
angle distributions (MF=6). Reactions include the total (MT=1) required for
Eq. 249, the partial scattering reactions that must be summed for Eq. 251 [that
is, elastic (MT=2), discrete-level inelastic (MT=51 – 90), (n,2n) (MT=16), etc.],
and the many partial reactions that can be used to calculate responses [for exam-
ple, (n,2n) or (n,α) for activation, gas production, heat production (KERMA),
radiation damage (DPA), etc.].
Before using GROUPR, the basic ENDF/B cross sections should have been
converted into energy- and temperature-dependent pointwise cross sections in
PENDF (pointwise ENDF) format using RECONR and BROADR. For heavy
isotopes, unresolved self-shielding data should have been added to the PENDF
tape6using UNRESR or PURR. If requested, heat production cross sections
(KERMA), radiation damage production (or DPA), and thermal upscatter data
can also have been added to the PENDF tape using HEATR and THERMR.
See the chapters on these other modules for more information.
The detailed methods used for evaluating Eqs. 249,250, and 251 from ENDF
and PENDF tapes are given below (see Sections 8.11 through 8.15). An example
of an ENDF pointwise cross section compared with group-averaged cross sections
from GROUPR is given in Fig. 22.
8.4 Weighting Flux
In general, the weighting flux φis not known; it is, after all, the particle distri-
bution being sought in the transport calculation. However, it is often possible to
obtain fairly accurate group constants for a particular application if the shape
of the flux is reasonably well known over the broad energy ranges of a particular
few-group structure (for example, a fission spectrum, thermal Maxwellian, or
1/E slowing-down spectrum). Alternatively, one can use many small groups so
that mistakes in guessing the shape inside the group are not very important.
The key to using the multigroup method effectively is balancing the tradeoffs
between the choice of weight function and the number of groups used for each
different class of problem being solved.
In many cases of practical interest, the flux φwill contain dips correspond-
6The term “tape” is used loosely in this report to refer to any input or output file. Of course, such files
would be on disk storage in a modern system.
NJOY2016 191
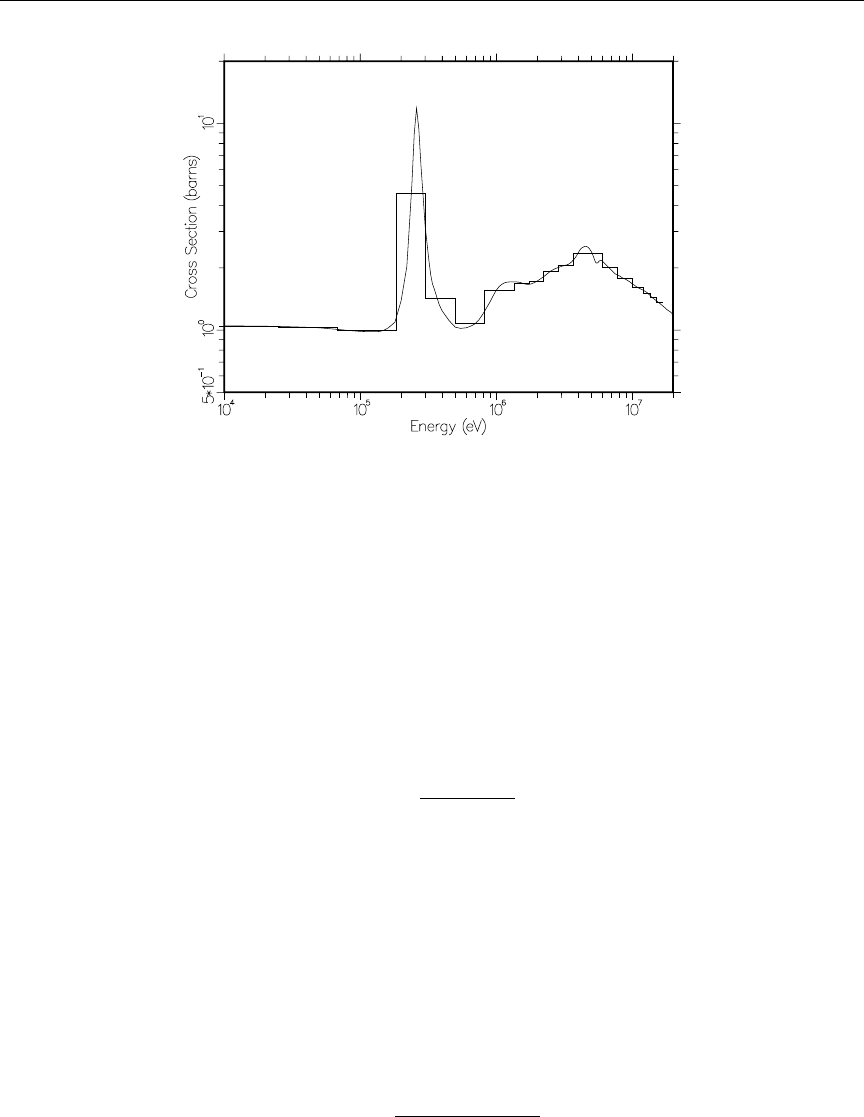
LA-UR-17-20093 8 GROUPR
Figure 22: A comparison of the pointwise and multigroup representations for the total cross
section of 7Li. The Los Alamos 30-group structure is shown.
ing to the absorption resonances of the various materials. In the reaction rate
σ(E)×φ(E), these dips clearly reduce (self-shield) the effect of the correspond-
ing resonance. GROUPR provides two methods to estimate the effect of this
self-shielding: the Bondarenko model and the flux calculator.
In the Bondarenko model[39], the narrow resonance (NR) approximation,
and the BNapproximation for large systems[53] are invoked to obtain
φ`(E) = W`(E)
[σt(E)]`+1 ,(252)
where φ`is the `-th Legendre component of the angular flux, the W`(E) are
smooth functions of energy (such as 1/E+fission), and σt(E) is the total macro-
scopic cross section for the material. GROUPR takes all of the W`to be equal to
the single function C(E), where C(E) can be read in or set to one of several inter-
nally defined functions. It is further assumed that the important self-shielding
effect of the flux can be obtained for isotope iby representing all the other
isotopes with a constant “background cross section”, σ0. Therefore,
φi
`(E) = C(E)
[σi
t(E) + σi
0]`+1 ,(253)
where σi
tis the microscopic total cross section for isotope i. The qualitative
behavior of Eq. 253 is easy to understand. If σ0is larger than the tallest peaks
in σt, the weighting flux φis approximately proportional to the smooth weighting
192 NJOY2016

8 GROUPR LA-UR-17-20093
function C(E). This is called infinite dilution; the cross section in the material
of interest has little or no effect on the flux. On the other hand, if σ0is small
with respect to σt, the weighting flux will have large dips at the locations of the
peaks in σt, and a large self-shielding effect will be expected.
Each component material of a mixture has a different weight function. The
macroscopic total cross sections are given by
σt`g =X
i
ρiσi
t`g(σi
0, T ),(254)
where
σi
t`g(σ0, T ) = Zg
σi
t(E, T )
[σ0+σi
t]`+1 C(E)dE
Zg
1
[σ0+σi
t]`+1 C(E)dE
.(255)
Similar equations are used for σRand σX`g→g0. On the GROUPR level, σ0and T
are simply parameters. Subsequent codes, such as 1DX[54] or TRANSX[12, 41],
can compute an appropriate value for σ0, and then interpolate in tables of cross
section versus σ0and Tto get the desired self-shielded group constants.
The appropriate value for σi
0is obvious when a single resonance material is
mixed with a moderator material (for example, 238UO2), because the admixed
materials typically have a constant cross section in the energy range where
the heavy isotopes have resonances. For a mixture of resonance materials, the
normal procedure is to preserve the average of Eq. 253 in each group by using
σi
0g=1
ρiX
j6=i
ρjσj
t0g(σj
0g, T ),(256)
where the ρiare atomic densities or atomic fractions. Eq. 256 is solved by
iteration. Interference between resonances in different materials is handled in
an average sense only.
In the unresolved energy range (see UNRESR and PURR), the explicit de-
pendence of cross section on energy is not known. The integrands are replaced
by their expected values
σx`g(σ0) = Zgσx
[σ0+σt]`+1 W`dE
Zg1
[σ0+σt]`+1 W`dE
,(257)
NJOY2016 193
LA-UR-17-20093 8 GROUPR
where the expected values are averages over the distributions of resonance posi-
tion and width expected in the vicinity of energy E. The UNRESR and PURR
modules produce effective self-shielded point cross sections defined by
σx`=σx
[σ0+σt]`+1
1
[σ0+σt]`+1 .(258)
Substituting Eq. 258 into Eq. 257 gives an equation of the form of Eqs. 249 and
250, except that σis replaced by σ, and the flux is replaced by an average
effective flux. This effective flux can be obtained by manipulating the effective
total cross section as follows:
σt`=σ0+σt−σ0
[σ0+σt]`+1
1
[σ0+σt]`+1 =1
[σ0+σt]`
1
[σ0+σt]`+1 −σ0,(259)
from which
1
[σ0+σt]`+1 =1
[σ0+σt]`
σ0+σtk
.(260)
Eq. 260 defines a recursion relation which can be used to compute the effective
flux to any order
1
[σ0+σt]`+1 =
`
Y
k=0
1
σ0+σtk
,(261)
This equation reduces to Eq. 253 in the resolved range. It is the formula used
in genflx to compute φ`(E) for the Bondarenko option.
When heterogeneity effects are important, the background cross section method
can be extended as follows. In an infinite system of two regions (fuel and mod-
erator), the neutron balance equations are
Vfσfφf= (1 −Pf)VfSf+PmVmSm,(262)
and
Vmσmφm=PfVfSf+ (1 −Pm)VmSm,(263)
194 NJOY2016

8 GROUPR LA-UR-17-20093
where Vfand Vmare the region volumes, σfand σmare the corresponding total
macroscopic cross sections, Sfand Smare the sources per unit volume in each
region, Pfis the probability that a neutron born in the fuel will suffer its next
collision in the moderator, and Pmis the probability that a neutron born in the
moderator will suffer its next collision in the fuel. As usual, use is made of the
reciprocity theorem,
VfσfPf=VmσmPm,(264)
and the Wigner rational approximation to the fuel escape probability,
Pf=σe
σe+σf
,(265)
where σeis a slowly varying function of energy called the escape cross section,
to obtain an equation for the fuel flux in the form
(σf+σe)φf=σeSm
σm
+Sf.(266)
In the limit where the resonances are narrow with respect to both fuel and
moderator scattering, the source terms Sfand Smtake on their asymptotic
forms of σp/E and σm/E respectively, and this equation becomes equivalent to
the Bondarenko model quoted above with
σf
0=σe
ρf
,(267)
and
C(E) = σe+σp
ρfE.(268)
Note that a large escape cross section (a sample that is small relative to the
average distance to collision), corresponds to infinite dilution as discussed above.
To illustrate the general case, consider a neutron traveling through a lump of
uranium oxide with an energy close to a resonance energy. If the neutron scatters
from an oxygen nucleus, it will lose enough energy so that it can no longer react
with the uranium resonance. Similarly, if the neutron escapes from the lump,
it can no longer react with the uranium resonance. The processes of moderator
scattering and escape are equivalent in some way. Comparing Eq. 267 with
Eq. 256 gives an “equivalence principle” that says that a lump of particular
dimensions and a mixture of particular composition will have the same self-
NJOY2016 195
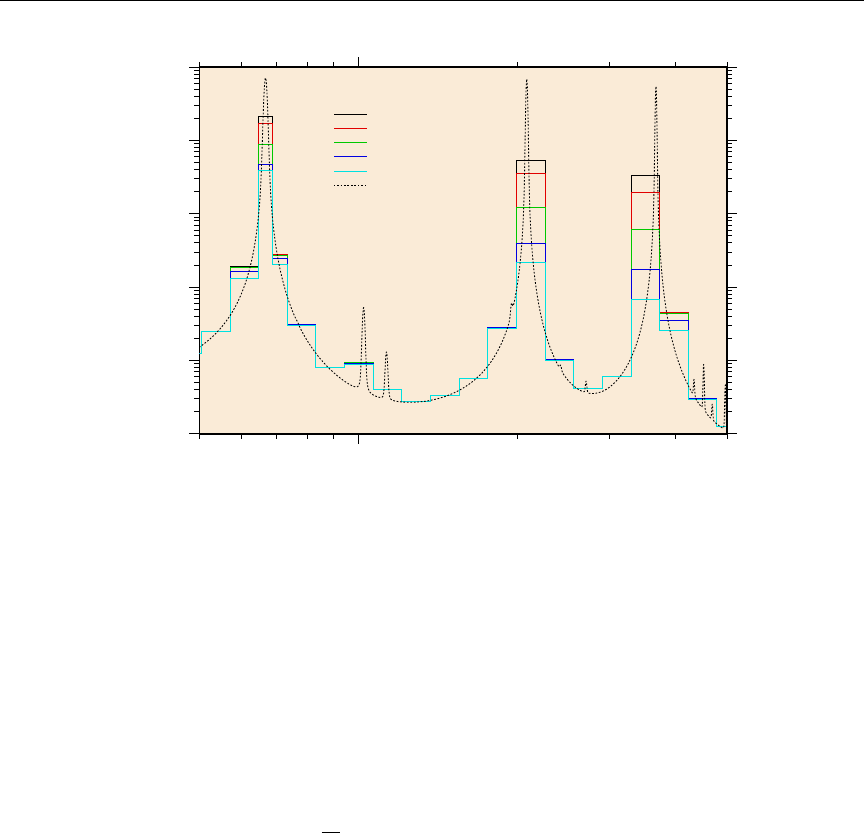
LA-UR-17-20093 8 GROUPR
101
Energy (eV)
10-1
100
101
102
103
104
Cross section (barns)
Infinite
10000 barns
1000 barns
100 barns
10 barns
Pointwise
Figure 23: The self-shielding effect on the first three 238U capture resonances at room tem-
perature in the 5 to 50 eV range. The multigroup boundaries are from the Los
Alamos 187-group structure.
shielded cross sections when the narrow resonance approximation is valid. The
effects of material mixing and escape can simply be added to obtain the effective
σ0for a lump containing admixed moderator material. Therefore, Eq. 256 is
extended to read
σi
0g=1
ρiσe+X
j6=i
ρjσj
t0g(σj
0g, T ),(269)
where the escape cross section for simple convex objects (such as plates, spheres,
or cylinders) is given by (4V/S)−1, where Vand Sare the volume and surface
area of the object, respectively. Many codes that use the background cross
section method modify the escape cross section as defined above to correct for
errors in the Wigner rational approximation (“Bell factor”, “Levine factor” ), or
to correct for the interaction between different lumps in the moderating region
(“Dancoff corrections”). These enhancements will not be discussed here.
As an example of self-shielded cross sections and how they vary with the
background cross section, Fig. 23 shows the first three capture resonances of 238U
(which are very important for thermal power reactors) at room temperature for
σ0values ranging from infinity down to 10 barns. Background cross sections
that range between 20 and 50 barns are typical for uranium-oxide pin cells.
196 NJOY2016

8 GROUPR LA-UR-17-20093
The BROADR chapter of this report showed its capability to compute stan-
dard resonance integrals. However, when self shielding and material temperature
come into play, the effective resonance integral changes. GROUPR can calculate
these quantities by doing one-group calculations with 1/E weighting over a stan-
dard energy range. Using the range 0.5 eV to the upper limit of the evaluation
will match what BROADR does. Fig. 24 shows the temperature dependence of
the capture resonance integral for 238U from ENDF/B-VII at several different
background cross sections. The range between 20 and 50 barns is typical for
reactor pin cells.
8.5 Flux Calculator
This narrow-resonance approach is quite useful for practical fast reactor prob-
lems. However, for nuclear systems sensitive to energies from 1 to 500 eV,
there are many broad- and intermediate-width resonances which cannot be
self-shielded with sufficient accuracy using the Bondarenko approach. The
GROUPR flux calculator is designed for just such problems.
Consider an infinite homogeneous mixture of two materials and assume isotropic
200 400 600 800 1000 1200 1400 1600 1800
Temperature (K)
101
102
Capture Resonance Integral
1000 barns
100 barns
50 barns
20 barns
1 barn
Figure 24: The capture resonance integral for 238U showing its variation with temperature
and background cross section σ0. The resonance integral at infinite dilution
is 275.58 barns. Note the slope with temperature, which helps to produce a
negative temperature coefficient for uranium systems.
NJOY2016 197

LA-UR-17-20093 8 GROUPR
scattering in the center-of-mass system. The integral slowing-down equation be-
comes
σ(E)φ(E) = ZE/α1
E
σs1(E0)
(1 −α1)E0φ(E0)dE0
+ZE/α2
E
σs2(E0)
(1 −α2)E0φ(E0)dE0.(270)
Furthermore, assume that material 1 is a pure scatterer with constant cross
section and transform to the σ0representation. The integral equation becomes
[σ0+σt2(E)] φ(E) = ZE/α1
E
σ0
(1 −α1)E0φ(E0)dE0
+ZE/α2
E
σs2(E0)
(1 −α2)E0φ(E0)dE0.(271)
Finally, assume that the moderator (material 1) is light enough so that all the
resonances of material 2 are narrow with respect to scattering from material 1.
This allows the first integral to be approximated by its asymptotic form, 1/E.
More generally, the integral is assumed to be a smooth function of Egiven by
C(E). In this way, material 1 can represent a mixture of other materials just
as in the Bondarenko method. Fission source and thermal upscatter effects can
also be lumped in C(E). The integral equation has now been reduced to
[σ0+σt(E)] φ(E) = C(E)σ0+ZE/α
E
σs(E0)
(1 −α)E0φ(E0)dE0.(272)
This is the simplest problem that can be solved using the flux calculator. The
results still depend on the single parameter σ0, and they can be used easily by
codes that accept Bondarenko cross sections.
For heterogeneous problems, when the narrow-resonance approximation fails,
both Sfand Smin Eq. 266 will show resonance features. To proceed further
with the solution of this equation, it is necessary to eliminate the moderator
flux that is implicit in Sm. As a sample case, consider a fuel pin immersed in a
large region of water. The fission neutrons appear at high energies, escape from
the pin, slow down in the moderator (giving a 1/E flux), and are absorbed by
the resonances in the pin. In this limit, any dips in the moderator flux caused
198 NJOY2016

8 GROUPR LA-UR-17-20093
by resonances in the fuel are small. On the other hand, in a closely packed
lattice, the flux in the moderator is very similar to the flux in the fuel, and
resonance dips in the moderator flux become very evident. Intermediate cases
can be approximated[55] by assuming
φm= (1 −β)C(E) + βφf,(273)
where βis a heterogeneity parameter given by
β=Vfσe
Vmσm
.(274)
Note that β→0 gives the isolated rod limit and β→1 gives the close-packed
lattice limit. This substitution reduces the calculation of the fuel flux to
(σf+σe)φf= (1 −β)C(E)σe+Sβ,(275)
where Sβis the source term corresponding to a homogeneous mixture of the
fuel isotopes with the isotopes from the moderator region changed by the factor
βσe/σm. If the fuel and moderator each consisted of a single isotope and for
isotropic scattering in the center-of-mass system, the integral equation would
become
[σ0+σt(E)] φf(E) = (1 −β)C(E)σ0
+ZE/αm
E
βσ0
(1 −αm)E0φf(E0)dE0
+ZE/αf
E
σsf (E0)
(1 −αf)E0φf(E0)dE0,(276)
where σ0is σedivided by the fuel density (units are barns/atom), αmand αf
are the maximum fractional energy change in scattering for the two isotopes,
and σsf (E0) is the fuel scattering cross section.
This result has a form parallel to that of Eq. 272, but the solution depends
on the two parameters βand σ0. For any given data set, βmust be chosen in
advance. This might not be difficult if the data are to be used for one particular
system, such as pressurized water reactors. The routine also has the capability
to include one more moderator integral with a different αvalue and a constant
cross section. The full equation is
NJOY2016 199
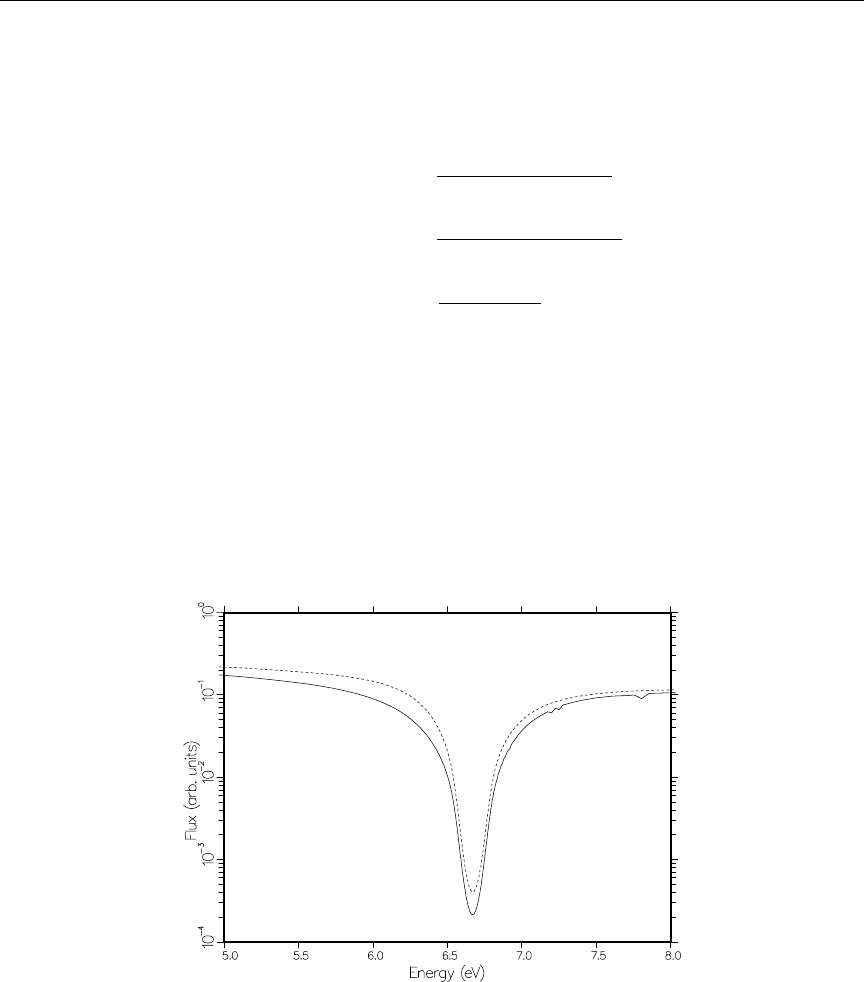
LA-UR-17-20093 8 GROUPR
[σ0+σt(E)] φf(E) = (1 −β)C(E)σ0
+ZE/α3
E
β(1 −γ)(σ0−σam
(1 −α3)E0φf(E0)dE0
+ZE/α2
E
σam +βγ(σ0−σam
(1 −α2)E0φf(E0)dE0
+ZE/αf
E
σsf (E0)
(1 −αf)E0φf(E0)dE0,(277)
where σam is the cross section of the admixed moderator (with energy loss α2),
and γis the fraction of the admixed moderator that is mixed with the external
moderator (which has energy loss α3). This allows calculations with H2O as
the moderator and an oxide as the fuel. The flux calculator can thus obtain
quite realistic flux shapes for a variety of fuel, admixed moderator and external
moderator combinations. An example comparing the Bondarenko flux with a
more realistic computed flux is given in Fig. 25.
Figure 25: A comparison of the Bondarenko flux model (dashed) with a realistic computed
flux (solid) for a 238U oxide pin in water in the region of the 6.7 eV resonance.
In practice, a fuel rod rarely contains only one resonance isotope. As an
example, consider a mixture of a few percent of 239Pu with 238U as the major
component. There will be a strong dip in the flux associated with the 6.7 eV 238U
resonance that will affect the flux in the region of the 7.8 eV 239Pu resonance
(the interference effect), and there will also be a dip in the flux corresponding
to the 7.8 eV resonance (the self-shielding effect). This additional complication
200 NJOY2016

8 GROUPR LA-UR-17-20093
in the flux shape would be expected to change the group constants for 239Pu
since both features lie in the same group for typical group structures. However,
the effect of the 239Pu on the 238U group constants should be minimal. This
argument suggests that the full flux calculation be used for 238U as a single
resonance material. The resulting flux would then be used to estimate the flux
to be used in averaging the 239Pu cross sections as follows:
φ239(E, σ0) = φ238(E, 50)
σ0+σ239(E)
1 + σ238(E)
50
,(278)
where the 238U flux is characteristic of a background of 50 barns/atom, which is
representative of many thermal reactor systems. This formula assumes that the
effect of 239Pu on the scattering source for the mixture is small, but it retains the
absorption effects. The self-shielding of 239Pu is treated in the narrow resonance
approximation only. The GROUPR flux calculator includes an option to write
out a file containing the calculated flux and cross section needed for this formula
(e.g., for 238U) and another option to skip the flux calculation and use the
formula above to obtain the weighting flux (e.g., for 239Pu).
The slowing-down integral equation of Eq. 272 or 276 is solved point by point
(see subroutine genflx) using the total and elastic cross sections on the PENDF
tape produced by RECONR. In order to keep this task within bounds, the flux
is computed from the lower limit of the first group to a specified energy fehi or
until nfmax values have been computed. The flux at higher energies is continued
using the Bondarenko model described above.
8.6 Fission Source
The fission source was included in the transfer cross section σXin the develop-
ment above. It is usually convenient to separate fission from scattering. Assum-
ing isotropy, the source of fission neutrons into group gis given by
Sg=X
g0
σfg0→gφ0g0,(279)
where the group-to-group matrix for fission is defined as in Eq. 251, but with
`equal to zero. Most existing transport codes do not use this matrix form
directly because the upscatter is expensive to handle and a reasonably accurate
alternative exists. Except for relatively high neutron energies, the spectrum
NJOY2016 201

LA-UR-17-20093 8 GROUPR
of fission neutrons is only weakly dependent on initial energy. Therefore, the
fission source can be written
Sg=χgX
g0
νg0σfg0φ0g0,(280)
where νgis the fission neutron yield, σfg is the fission cross section, and χgis
the average fission spectrum (the familiar “chi” vector), which can be defined
by
χg=X
g0
σfg0→gφ0g0
X
gX
g0
σfg0→gφ0g0
.(281)
The fission neutron yield is given by
νg=X
g0
σfg→g0/ σf g .(282)
Clearly, χgas given by Eq. 281 depends on the flux in the system of interest.
The dependence is weak except for high incident energies, and a rough guess for
φ0gusually gives an accurate spectrum. When this is not the case, the problem
can be iterated, or the full matrix representation can be used.
It is possible to take advantage of the weak energy dependence of the shape of
the fission spectrum at low energies to reduce the time required to process fission
data, and to reduce the size of the fission data on the output file. GROUPR
determines a break energy from File 5 such that the fission spectrum is constant
below this energy. It only has to make a single calculation of this spectrum χLE
g.
Then it computes a fission neutron production cross section σHE
fP g for groups
below the break energy using the normal cross section processing methods. A
full matrix σHE
fg0→gis computed for groups above the break point. As an example,
consider using the GROUPR 187-group structure and finding that there are
130 constant groups. The 187×187 matrix is reduced to a 57×187 matrix, a
187-element spectrum vector, and a 130-group production vector, for a total
reduction in size of 68%. The effective fission matrix is given by
σfg0→g=σHE
fg0→g+χLE
gσLE
fP g0.(283)
The fission matrix computed by GROUPR represents the prompt part of
202 NJOY2016

8 GROUPR LA-UR-17-20093
fission only. The delayed component of fission is represented by a delayed-
neutron yield νD
g, decay constants for six (or sometimes 8) time groups, λD
i, and
emission probability spectra for six (or 8) time groups, χD
ig. Steady-state fission
can be obtained using
νSS
g=νg+νD
g,(284)
and
χSS
g=X
g0
σfg0→gφ0g0+χD
gX
g0
νD
g0σfg0φ0g0
X
gX
g0
σfg0→gφ0g0+X
g0
νD
g0σfg0φ0g0
,(285)
where
χD
g=X
i
χD
ig .(286)
Note that χD
gsums to unity, but the χfor each time group sums to the fraction
of the delayed neutron yield that appears in that time group.
In ENDF-format files, the total fission reaction is represented by MT=18.
Important isotopes also give the partial fission reactions (n,f), (n,n0f), (n,2nf),
and sometimes (n,3nf) using MT=19, 20, 21, and 38 respectively. The MT=18
representation is adequate for most fission reactor applications, but the partial
reactions should be processed for applications with significant flux above 6 MeV.
Caution: although the cross section for MT=18 equals the sum of its parts,
the group-to-group fission matrix σfg→g0computed from MT=18 will not, in
general, equal the sum of the partial matrices for MT=19, 20, 21, and 38 above
the 6-MeV threshold for second-chance fission. The breakup into partial fission
matrices has not been used in recent ENDF/B-VII evaluations. The delayed
neutron data are given in MT=455. Sample input instructions for processing
the various combinations of fission reactions used in ENDF/B will be found in
Section 8.14. GROUPR outputs all the components of fission separately in order
to give succeeding modules or codes complete flexibility.
8.7 Diffusion Cross Sections
The diffusion equation is often used in reactor physics calculations. Starting with
Eq. 246, use the Legendre expansion for φgin the derivative term, and make
use of the recursion relation for µP`(µ) and the orthogonality relation for the
NJOY2016 203

LA-UR-17-20093 8 GROUPR
Legendre polynomials to obtain the transport equation in spherical-harmonic
form
n+ 1
2n+ 1
∂φn+1,g
∂x +n
2n+ 1
∂φn−1,g
∂x σtng φng
=X
g0
σsng0→gφng0+Sfg +Qng ,(287)
where the transfer term has been separated into a scattering term with cross
section σs, and a fission source term Sf. When this set of equations is truncated
at n= N, the results are usually called the “PNequations”. For now, all terms
with n > 1 are dropped, and Qis assumed to be isotropic. Thus,
∂φ1g
∂x +σt0gφ0g=X
g0
σs0g0→gφ0g0+Sfg +Q0g,(288)
and
1
3
∂φ0g
∂x +σt1gφ1g=X
g0
σs1g0→gφ1g0.(289)
The second equation can be written in the form of Fick’s Law as follows:
φ1g=−Dg
∂φ0g
∂x ,(290)
Dg=1
3
1
σt1g−X
g0
σs1g0→gφ1g0/ φ1g
,(291)
where Dgis the diffusion constant. The term in the denominator of the second
factor is the transport cross section for diffusion, σtrD. Unfortunately, it depends
on a fairly complete knowledge of the neutron current in the system, perhaps
from a previous calculation. However, for many problems, σtrD can be simplified
by assuming that
X
g0
σs1g0→gφ1g0≈X
g0
σs1g→g0φ1g,(292)
204 NJOY2016

8 GROUPR LA-UR-17-20093
with the result that
σtrD,g =σt1g−X
g0
σs1g→g0,(293)
or
σtrD,g =σt1g−µgσs0g,(294)
where µgis the average scattering cosine for neutrons in group g. These forms
depend only on the shape of the weighting flux within the group, as usual.
Substituting for φ1gin Eq. 288 gives
∂
∂x−Dg
∂φ0g
∂x +σ0tg φ0g=X
g0
σs0g0→gφ0g0+Sfg +Q0g,(295)
which is the standard diffusion equation in slab geometry. Neither the diffusion
coefficient nor the transport cross section for diffusion is produced directly by
GROUPR. However, the components such a σt` and σs0g0→gare made available
to subsequent modules.
8.8 Cross Sections for Transport Theory
The SN(discrete ordinates) transport codes solve the equation
µ∂
∂xφg(µ, x) + σSN
gφg(µ, x)
=
N
X
`=0
2`+ 1
2P`(µ)X
g0
σSN
s`g0→g(x)φ`g0
+Sfg +Qg(µ, x),(296)
where once again one-dimensional slab geometry has been used for simplicity.7
By comparing Eq. 296 with Eq. 246, it is seen that the SNequations require the
following cross sections:
σSN
s`g0→g=σs`g0→g, g06=g , (297)
and
σSN
s`g→g=σs`g→g−σt`g +σSN
g,(298)
7The following development is based on the work of Bell, Hansen, and Sandmeier[56].
NJOY2016 205

LA-UR-17-20093 8 GROUPR
where σSN
gis not determined and can be chosen to improve the convergence
of the SNcalculation. A particular choice of σSN
ggives rise to a “transport
approximation”, and various recipes are in use, such as:
Consistent-P approximation:
σSN
g=σt0g.(299)
Inconsistent-P approximation:
σSN
g=σt,N+1,g .(300)
Diagonal transport approximation:
σSN
g=σt,N+1,g −σs,N+1,g→g.(301)
Bell-Hansen-Sandmeier (BHS) or extended transport approximation:
σSN
g=σt,N+1,g −X
g0
σs,N+1,g→g0.(302)
Inflow transport approximation:
σSN
g=σt,N+1,g −X
g0
σs,N+1,g0→gφN+1,g0
φN+1,g
.(303)
The first two approximations are most appropriate when the scattering orders
above N are small. The inconsistent option removes most of the delta function
of forward scattering introduced by the correction for the anisotropy of the total
scattering rate, and should normally be more convergent than the consistent op-
tion. The diagonal and BHS recipes make an attempt to correct for anisotropy in
the scattering matrix and are especially effective for forward-peaked scattering.
The BHS form is more often used, but the diagonal option can be substituted
when BHS produces negative values. The inflow recipe makes the N+1 term
of the PNexpansion vanish, but it requires a good knowledge of the N+1 flux
moment from some previous calculation. Inflow reduces to BHS for systems
in equilibrium by detail balance (i.e., the thermal region). In the absence of
self-shielding (that is, σ0→∞), the distinction between σt1and σt0disappears,
and so does the distinction between the inconsistent-P and consistent-P options.
Also note that the inflow and BHS versions of σgare equivalent to the definitions
of σtrD,g given in Eqs. 291 and 293, respectively, when N=0.
206 NJOY2016

8 GROUPR LA-UR-17-20093
The transport-corrected cross sections are not computed directly by GROUPR,
but the components needed are written to the GROUPR output file for use by
subsequent modules.
8.9 Photon Production and Coupled Sets
Photon transport is treated with an equation similar to Eq. 246, except that
the flux, cross sections, and groups are all referred to photon interactions and
photon energies instead of to the corresponding neutron quantities. Methods
of producing the photon interaction cross sections are described in GAMINR.
The external photon source Qgdepends on the neutron flux and the photon
production cross sections through
Qg(x, µ) =
∞
X
`=0
2`+ 1
2P`(µ)X
g0
σγ`g0→g(x)φ`g0(x),(304)
where σγ`g0→gis defined by Eq. 251 with X replaced by γ. The ENDF files
define σγusing a combination of photon production cross sections (MF=13),
photon yields (MF=12) with respect to neutron cross sections (MF=3), discrete
lines (MF=12 and 13), and continuous γdistributions (MF=15). Methods for
working with these representations will be discussed in more detail below.
The low-energy groups for fission and capture normally have photon emission
spectra whose shapes do not change with energy. The same method used for
reducing the size of the fission matrix (see Section 8.6) can be used for these
photon production matrices. In mathematical form,
σγg0→g=σHE
γg0→g+sLE
γgσLE
γP g0,(305)
where sLE
γgis the normalized emission spectrum, and σLE
γP g is the associated
production cross section.
For many practical problems, it is convenient to combine the neutron and
photon transport calculations into a single application of Eq. 246 where the
photons are treated as additional groups of low-energy neutrons. Since (γ,n)
events are not usually very important, the downscattering structure (see Sec-
tion 8.2) of the transport calculation is preserved for both n→γand n→n events.
Cross sections for this application are called “coupled sets”. Coupled sets are
not produced directly by GROUPR, but the n→n and n→γcomponents are
NJOY2016 207
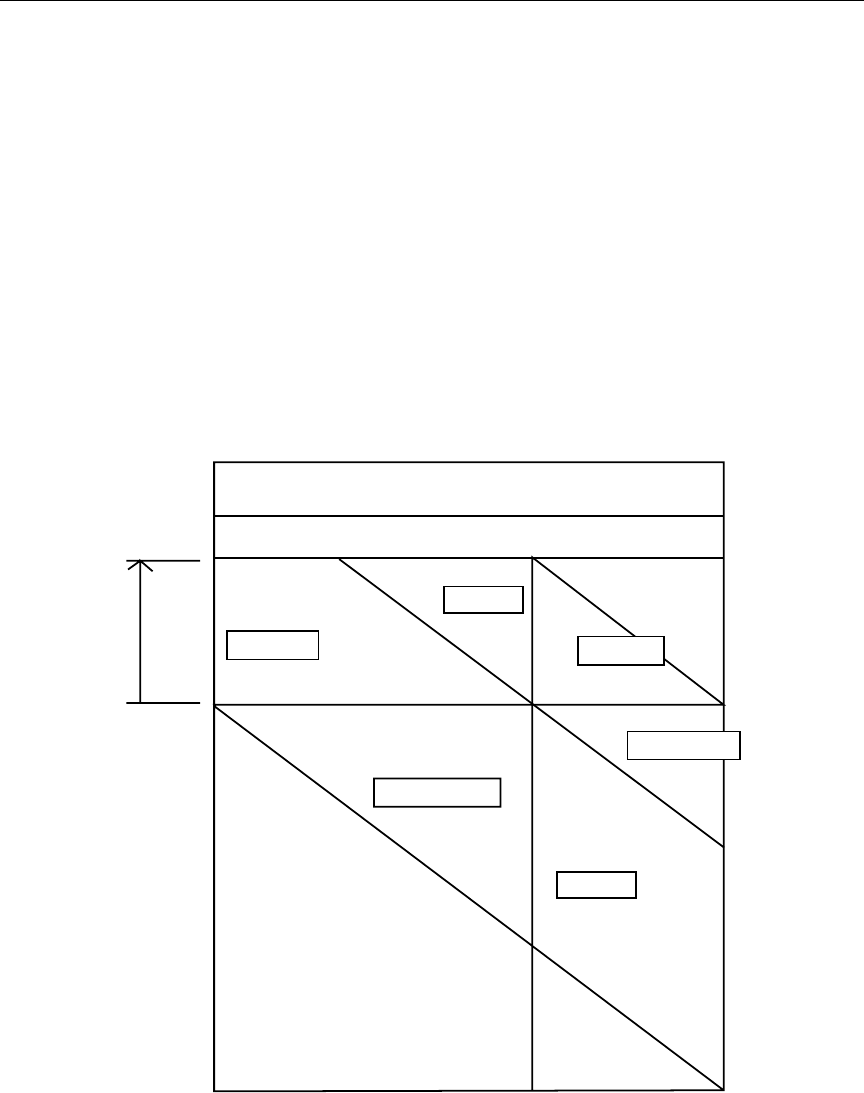
LA-UR-17-20093 8 GROUPR
made available to the other modules where they can be combined with γ→γ
cross sections from GAMINR. As an example, the MATXSR module can for-
mat data for the TRANSX code, which can, in turn, prepare coupled sets for
use by standard transport codes such as ONEDANT[14] or PARTISN[17]. The
normal arrangement of data in a coupled set is shown schematically in Fig. 26.
8.10 Thermal Data
GROUPR uses the thermal data written onto the PENDF tape by the THERMR
module. It does not process ENDF File-7 data directly. Three different repre-
sentations of thermal scattering are used in ENDF.
For crystalline materials like graphite, coherent elastic (with zero energy
n
0
0
γ
typical
truncated
upscatter
n→ γ
n→ n, down
γ→ γ, down
γ→ γ, up
n→n, up
γ→ n
edits
σa,νσf,σt
0
Figure 26: Arrangement of neutron (n) and photon (γ) cross sections in a coupled transport
table. The group index increases from left to right, and the position index
increases from top to bottom. The γ→n and γ→γupscatter blocks are normally
empty.
208 NJOY2016

8 GROUPR LA-UR-17-20093
change) scattering can take place. The cross section for this process shows
well-defined Bragg edges at energies that correspond to the various lattice-plane
spacings in the crystalline powder. As shown in THERMR, the angular depen-
dence of the coherent elastic cross section can be written as
σcoh(E, µ) = X
i
bi
Eδ(µ−µi),(306)
where
µi= 1 −2Ei
E,(307)
and where the Eiare the energies of the Bragg edges. THERMR integrates
Eq. 306 over all angles, and writes the result to the PENDF tape. Clearly, the
bican be recovered from
E σcoh(E) = X0
i
bi,(308)
where the primed sum is over all isuch that Ei< E. It is only necessary to
locate the steps in E σcoh(E). The size of the step gives bi, and the Efor the
step gives Ei. The Legendre cross sections become
σcoh
`(E) = X0
i
bi
EP`(µi),(309)
where any terms with µi<−1 are omitted from the primed sum. An example
of a pointwise cross section for coherent elastic scattering is given in Fig. 27.
For hydrogenous solids like polyethylene and zirconium hydride, the process
of incoherent elastic scattering is important. Here the angular cross section is
given by
σiel(E, µ) = σb
2exp−2EW
A(1 −µ).(310)
THERMR converts this into an integrated cross section, σiel(E), and a set of N
equally probable emission cosines, µi. These angles are present in File 6 on the
PENDF tape. GROUPR can easily determine the Legendre components of the
NJOY2016 209
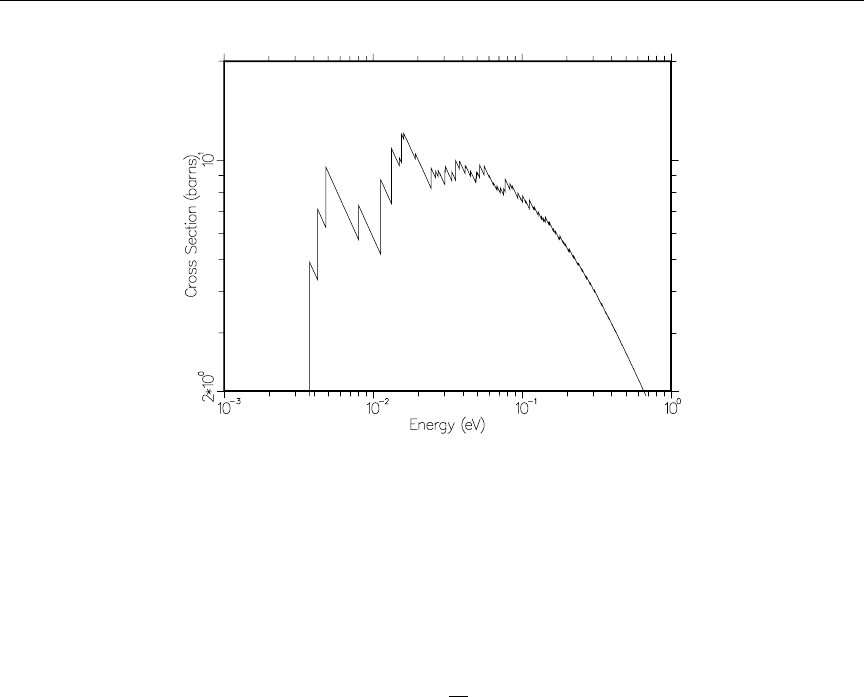
LA-UR-17-20093 8 GROUPR
Figure 27: The coherent elastic scattering cross section for BeO showing the Bragg edges.
The shape of σ(E) between edges is 1/E. Therefore, the function Eσ(E) is a
stair-step function, where the height of each step depends on the structure factor
for scattering from that set of lattice planes (see Eq. 308).
scattering cross section using
σiel
`(E) = σiel(E)1
N
N
X
i=1
P`(µi).(311)
The third thermal process is incoherent inelastic scattering. Here the neutron
energy can either increase or decrease. The data from THERMR are given as
a cross section in File 3 and an energy-angle distribution using a special form
of File 6. The distribution is represented by sets of secondary-energy values
E0for particular incident energies E. For each E→E0, a scattering probability
finc(E→E0) and a set of equally probable cosines µi(E→E0) are given. The
scattering probabilities for each value of Eintegrate to unity. Although the
thermal scattering cross section is a smooth function of incident neutron energy,
this is not true for the scattering from Eto one particular final energy group
g0, since the differential cross section tends to peak along the line E0=Eand at
energy-transfer values corresponding to well-defined excitations in the molecule
or lattice. If interpolation between adjacent values of Ewere to be performed
along lines of constant E0, the excitation peaks and the E=E0feature would
produce double features in the intermediate spectrum, as shown in Fig. 28.
To avoid this problem, while still using a relatively sparse incident energy grid,
GROUPR interpolates between Eand E0along lines of constant energy transfer.
210 NJOY2016
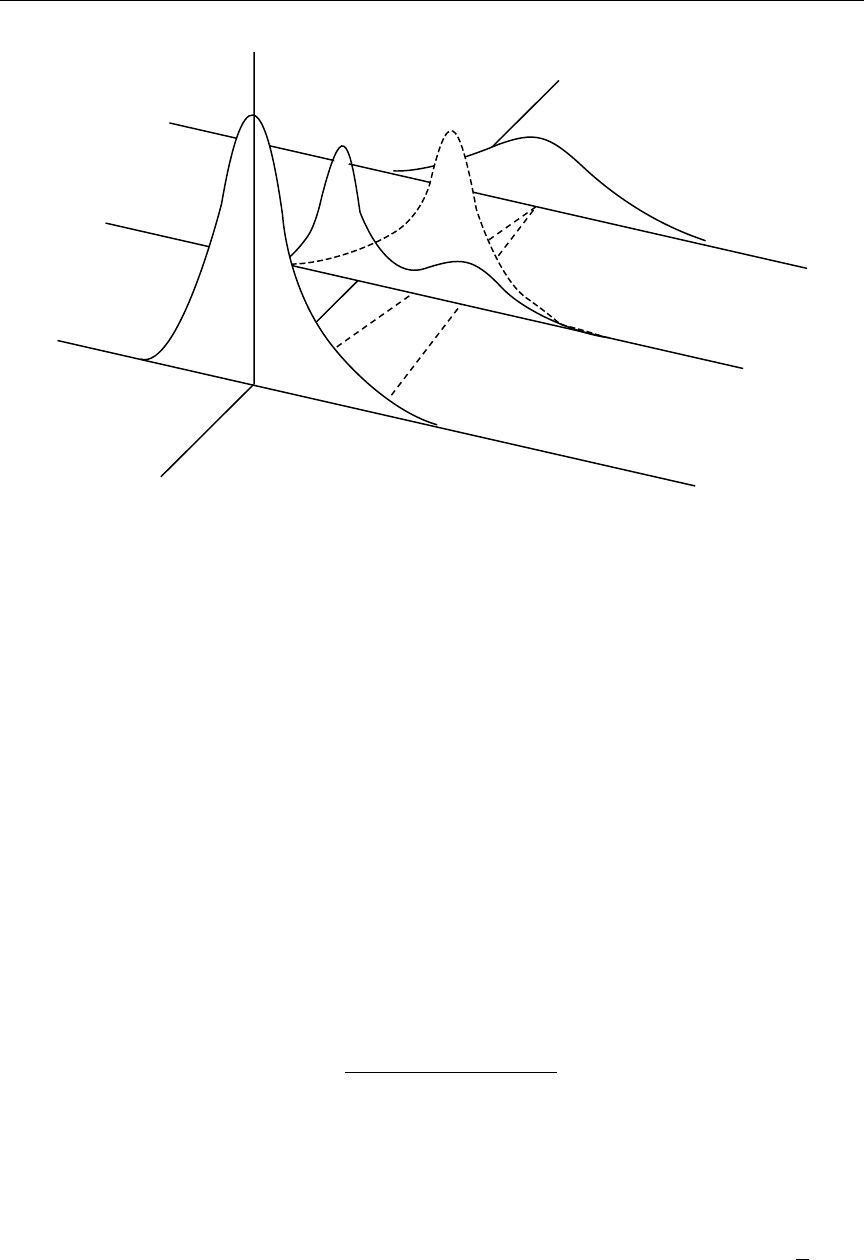
8 GROUPR LA-UR-17-20093
E
E'
Elo
Emid
Ehi
Figure 28: Illustration of thermal interpolation showing the double-humped curve resulting
from simple Cartesian interpolation for a discrete excitation (solid) and the more
realistic curve obtained by interpolating along lines of constant energy transfer
(dashed).
Of course, this breaks down at low values of E0, because one of the spectra will go
to zero before the other one does. In this range, GROUPR transforms the low-
energy parts of the two spectra onto a “unit base,” combines them in fractions
that depend on E, and scales the result back out to the interpolated value of E0
corresponding to E.
8.11 Generalized Group Integrals
In order to unify many formerly different processing tasks, GROUPR uses the
concept of a generalized group integral
σg=ZgF(E)σ(E)φ(E)dE
Zg
φ(E)dE
,(312)
where the integrals are over all initial neutron energies in group g,σ(E) is a
cross section at E, and φ(E) is an estimate of the flux at E. The function
F(E) is called the “feed function”. It alone changes for different data types. To
average a neutron cross section, Fis set to 1. To average a ratio quantity like µ
NJOY2016 211
LA-UR-17-20093 8 GROUPR
with respect to elastic scattering, Fis set to µ. For photon production, Fis the
photon yield. For matrices, Fis the `-th Legendre component of the normalized
probability of scattering into secondary energy group g0from initial energy E.
This definition is clearly independent of whether the secondary particle is a
neutron or a photon.
The question of integration grid or quadrature scheme is important for the
evaluation of Eq. 312. Each factor in the integrands has its own characteristic
features, and it is important to account for them all. First, a grid must be
established for each factor. As an example, the grid of σ(E) is generated in
RECONR such that sigma can be obtained to within a given tolerance by linear
interpolation. GROUPR contains a subroutine getsig which carries out this
interpolation at Eand also returns the next grid energy in enext. Subroutines
getflx and getff perform similar functions for the flux and feed function. It
is now easy to generate a union grid for the three-factor integrand using the
following Fortran:
...
call getsig(e,enext,...)
call getflx(e,en,...)
if (en.lt.enext) enext=en
call getff(e,en,...)
if (en.lt.enext) enext=en
...
On occasion, there will be a discontinuity at enext for one of the factors. In
order to flag such a case, each “get” routine also sets a discontinuity flag idisc.
The grid logic actually used throughout NJOY is as follows:
...
call getsig(e,enext,idisc,...)
call getflx(e,en,idis,...)
if (en.eq.enext.and.idis.gt.idisc) idisc=idis
if (en.lt.enext) idisc=idis
if (en.lt.enext) enext=en
call getff(e,en,idis,...)
if (en.eq.enext.and.idis.gt.idisc) idisc=idis
if (en.lt.enext) idisc=idis
if (en.lt.enext) enext=en
...
This union grid for the integrand in the numerator is used to subdivide the gen-
212 NJOY2016

8 GROUPR LA-UR-17-20093
eralized group integral of Eq. 312 into “panels”. The main program of GROUPR
carries out the integrals with the following logic:
...
elo=egn(ig)
ehi=egn(ig+1)
enext=ehi
230 call panel(elo,enext,...)
if (enext.eq.ehi) go to 240
elo=enext
enext=ehi
go to 230
240 continue
...
A panel is first defined by the energy bounds of group g. Subroutine panel is
called to sum in the contributions from this panel. However, panel discovers
that the integrand has a grid point at enext less than ehi. It adds in the
contributions for the smaller panel elo to enext and returns. GROUPR now
sees that enext is less than ehi, so it tries a new panel from the top of the last
panel (elo=enext) to ehi. This loop continues until a panel with ehi as its
upper bound is summed in. The integral for this group is then complete.
In this simple way, the algorithm accounts for the user’s group structure and
for all structure in the integrand. The method used for establishing the RE-
CONR grid makes this integration algorithm equivalent to adaptive integration
as used in MINX[21]. It has the great advantage that no “stack” of intermedi-
ate results is carried along. This single-pass feature of the quadrature scheme
allows many different integrals to be accumulated simultaneously within reason-
able storage limits. In this way, GROUPR accumulates cross sections for all
values of σ0simultaneously. Similarly, group-to-group cross sections are com-
puted for all secondary energy groups and all Legendre orders simultaneously.
Any degree of complexity can be used for the integral over each subpanel.
Because σ(E) has been linearized, panel is based on trapezoidal integration.
Both φ(E) and R(E) = σ(E)×φ(E) are assumed to vary linearly across each
panel. In some cases, the feed function is oscillatory over a certain energy range
(see Two-Body Scattering, Section 8.12). It is then convenient to integrate
inside the panel using Lobatto quadrature[57] (note the variable nq in panel).
As discussed in more detail later, this method can obtain accurate results for
an oscillatory function whose integral is small with respect to its magnitude.
NJOY2016 213

LA-UR-17-20093 8 GROUPR
This behavior is characteristic of the higher Legendre components of two-body
scattering cross sections.
The generalized integration scheme discussed here is also used by the GAM-
INR and ERRORR modules.
8.12 Two-Body Scattering
Elastic scattering (ENDF/B MT=2) and discrete inelastic neutron scattering
(with MT=51 – 90) are both examples of two-body kinematics and are treated
together by GROUPR. Some other cases that occur for charged particles or in
File 6 will be discussed later. The feed function required for the group-to-group
matrix calculation may be written
F`g0(E) = Zg0
dE0Z+1
−1
dω f(E→E0, ω)P`(µ[ω]) ,(313)
where f(E→E0, ω) is the probability of scattering from Eto E0through a center-
of-mass cosine ωand P`is a Legendre polynomial for laboratory cosine µ. The
laboratory cosine corresponding to ωis given by
µ=1 + Rω
√1 + R2+ 2Rω ,(314)
and the cosine ωis related to secondary energy E0by
ω=E0(1 + A)2/A0−E(1 + R2)
2RE ,(315)
where A0is the ratio of the emitted particle mass to the incident particle mass
(A0=1 for neutron scattering). In Eqs. 314 and 315,Ris the effective mass ratio
R=rA(A+ 1 −A0)
A0r1−(A+ 1)(−Q)
AE ,(316)
where Ais the ratio of target mass to neutron mass, and −Qis the energy level
of the excited nucleus (Q=0 for elastic scattering). Integrating Eq. 313 over
secondary energy gives
F`g0(E) = Zω2
ω1
f(E, ω)P`(µ[ω]) dω , (317)
where ω1and ω2are evaluated using Eq. 315 for E0equal to the upper and lower
214 NJOY2016

8 GROUPR LA-UR-17-20093
bounds of g0, respectively. The scattering probability is given by
f(E, ω) =
L
X
`=0
f`(E)P`(ω),(318)
where the Legendre coefficients are either retrieved directly from the ENDF
File 4 or computed from File 4 tabulated angular distributions (see subroutines
getfle and getco).
The integration in Eq. 317 is performed (see subroutine getdis) simultane-
ously for all Legendre components using Gaussian quadrature[57]. The quadra-
ture order is selected based on the estimated polynomial order of the integrand.
A reasonable estimate is given by
ND + NL + log(300/A),(319)
where ND is the number of Legendre components desired for the feed function,
and NL is the number of components required to represent f(E, ω). The log
term approximates the number of additional components required to represent
the center-of-mass to lab transformation.
The two-body feed function for higher Legendre orders is a strongly oscil-
latory function in some energy ranges. An example is shown in Fig. 29. Fur-
thermore, the integral of the oscillatory part is often small with respect to the
magnitude of the function. Such functions are very difficult to integrate with
adaptive techniques, which converge to some fraction of the integral of the ab-
solute value. This is the reason that MINX[21] gave poor answers for small
Legendre components of the scattering matrix. Gaussian methods, on the other
hand, are capable of integrating such oscillatory functions exactly if they are
polynomials. Since a polynomial representation of the feed function is fairly ac-
curate, a Gaussian quadrature scheme was chosen. The scheme used is also well
adapted to performing many integrals in parallel. In GROUPR, all Legendre
components and all final groups are accumulated simultaneously (see panel).
The boundaries of the various regions of the feed function are called “critical
points.” Between critical points, the feed function is a smooth analytic function
of approximately known polynomial order. It is only necessary to add these crit-
ical points to the incident energy grid of the feed function (the enext variable)
and to tell panel what quadrature order (nq) to use. The critical points are
determined in getff by solving Eq. 315 for the values of Efor which ω= +1
and ω=−1 when E0is equal to the various group boundaries. This can be
NJOY2016 215
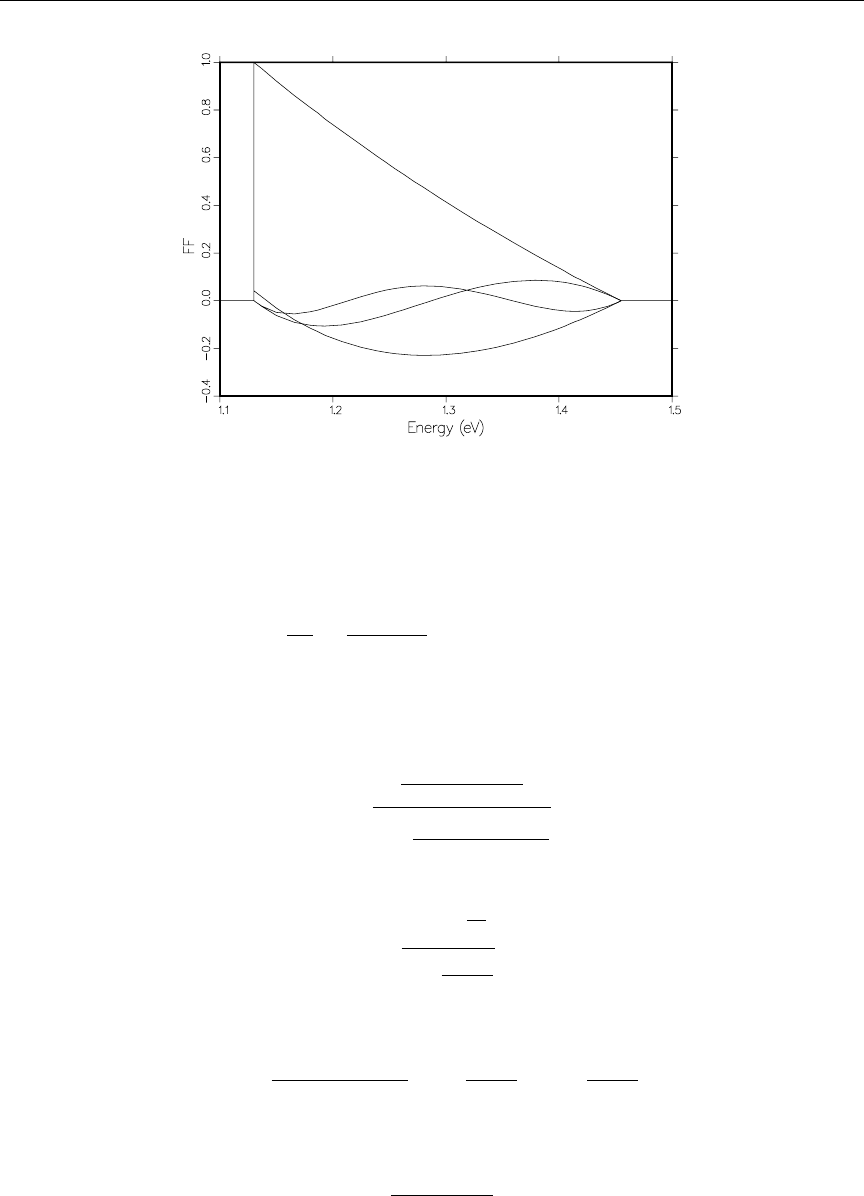
LA-UR-17-20093 8 GROUPR
Figure 29: A typical feed function for two-body scattering showing the oscillations that
must be treated correctly by the integration over incident energy.
done by writing
Eg
E=1
(1 + A)2R2±2R+ 1,(320)
substituting for Eusing Eq. 316, and then solving for R. The result is
Ecrit =
(A+ 1)(−Q)
A
1−A0F2
A(A+ 1 −A0)
,(321)
where
F=1±√D
1 + EF
(−Q)
,(322)
D=A(A+ 1 −A0)
A01 + EF
(−Q)−1EF
(−Q),(323)
and
EF=1 + A
A+ 1 −A0Eg.(324)
File 4 can also contain angular distributions for charged-particle emission
216 NJOY2016

8 GROUPR LA-UR-17-20093
through discrete levels (for ENDF/B-VI and later see MT=600 – 648 for protons,
MT=650 – 698 for deuterons, and so on; the elastic case, MT=2, is discussed
in the next section). Moreover, File 6 can contain angular distributions for
discrete two-body scattering (see Law 3). It can also declare that a particular
particle is the recoil particle from a two-body reaction (Law 4), in which case
the appropriate angular distribution is obtained from the corresponding Law
3 subsection by complementing the angle. The representation of the angular
distribution for these laws is almost identical to that in File 4, and the calculation
is done in getdis using much of the File 4 coding. The effects on the kinematics
of the difference in the mass of the emitted and incident particles are handled
by the variable A0in the above equations.
8.13 Charged-Particle Elastic Scattering
Coulomb scattering only occurs in the elastic channel, and this calculation also
uses the getdis subroutine. The problem with Coulomb scattering is that the
basic Rutherford formula becomes singular at small angles. In practice, this
singularity is removed by the screening effects of the atomic electrons. The
forward transport of charged particles in this screening regime is usually han-
dled by continuous-slowing-down theory by using a “stopping power”. The new
ENDF-6 format allows for three different ways to handle the large-angle scat-
tering regime. First and most general is the nuclear amplitude expansion:
σ=|nucl + coul|2
=σnucl +σcoul + interference (325)
The Coulomb term is given by the Rutherford formula, a Legendre expansion is
defined for the nuclear term, and a complex Legendre expansion is defined for
the interference term. This representation cannot be generated directly from
experimental data; an R-matrix or phase-shift analysis is necessary.
A method very closely related to experiment (σexp) is the nuclear plus inter-
ference (NI) formula:
σNI(µ, E) = σexp(µ, E)−σcoul(µ, E),(326)
where the function is only defined for angles with cosines µ<µmax. The mini-
mum angle is usually taken to be somewhere around 20 degrees (GROUPR uses
NJOY2016 217

LA-UR-17-20093 8 GROUPR
µmax=0.96). This function is still ill-behaved near the cutoff, and it must be
tabulated. The third option is the residual cross section expansion:
σR(µ, E) = (1 −µ)σexp(µ, E)−σcoul(µ, E).(327)
The (1 −µ) term removes the pole at the origin. The residual is uncertain,
but it is usually small enough that the entire curve can be fitted with Legendre
polynomials without worrying about what happens at small angles. In practice,
both the nuclear amplitude expansion and the nuclear plus interference repre-
sentation are converted to the residual cross section representation in subroutine
conver. As a result, getdis only has to cope with the one representation.
8.14 Continuum Scattering and Fission
In ENDF evaluations, scattering from many closely-spaced levels or multibody
scattering such as (n,2n), (n,n0α) or fission is often represented using a separable
function of scattering cosine and secondary neutron energy
f(E→E0, µ) = F(E, µ)g(E→E0),(328)
where Fis the probability that a neutron will scatter through a laboratory
angle with cosine µirrespective of final energy E0. It is obtained from MF=4.
Similarly, gis the probability that a neutron’s energy will change from Eto
E0irrespective of the scattering angle, and it is given in MF=5. Continuum
reactions are mostly identified by MT numbers of 6 – 49 and 91. Recently,
previously unused MT numbers, 152 through 200, were assigned to additional
continuum reactions that are beginning to appear in specialized evaluated files
that extend beyond 20 MeV (e.g., the International Reactor Dosimetry and
Fusion File). Secondary-energy distributions, whether found in MF=5 or MF=6
are represented by “Laws” as follows:
Law Description
1 Arbitrary tabulated function
5 General evaporation spectrum
(Used for delayed neutrons only.)
7 Simple Maxwellian fission spectrum
9 Evaporation spectrum
11 Energy-dependent Watt fission spectrum
12 Energy-dependent spectrum of Madland and Nix
218 NJOY2016

8 GROUPR LA-UR-17-20093
The feed functions for continuum scattering are simply
F`g0(E0) = Z+1
−1
P`(µ)f(E, µ)dµ Zg0
g(E, E0)dE0.(329)
The first integral is returned by getfle [“fle” for f`(E)] as described above, and
the second integral is returned by getsed (“sed” for secondary-energy distribu-
tion).
For Law 1, gis given as a tabulated function of E0for various values of
E. When E1≤E < E2, the term Rg0g(E, E0)dE0is obtained by interpolating
between precomputed values of Rg0g(E1, E0)dE0and Rg0g(E2, E0)dE0in subrou-
tine getsed. Except in the case of fission, any apparent upscatter produced by
the “stairstep” treatment near E=E0is added to the in-group scattering term
(g0=g).
For Law 5, g(x) is given versus x=E0/θ(E) and θ(E) is given vs. E in File
5. This secondary neutron distribution leads to the following group integral:
Zg0
g(E, E0)dE0=θ(E)ZE2/θ
E1/θ
g(x)dx , (330)
with E1and E2being the lower and upper boundary energies for group g0.
For Law 7, the secondary-energy distribution is given by
g(E, E0) = √E0
Iexp−E0
θ(E),(331)
where the effective temperature θ(E) is tabulated in File 5 and the normalization
factor is given by
I=θ3/2rπ
4erf(x)−xe−x,(332)
where
x=E−U
θ.(333)
Here Uis a constant used to define the upper limit of secondary neutron energy
θ≤E0≤E−U. The desired group integral is given by
NJOY2016 219

LA-UR-17-20093 8 GROUPR
Zg0
g(E, E0)dE0=ZE2
E1
g(E, E0)dE0
=X1−X2−Y1+Y2
pπ/4−Y−X,(334)
where
X=√x e−x,(335)
Y=rπ
4rerfc(√x),(336)
and where X1,Y1,X2, and Y2refer to Xand Yevaluated at E1/θ and E2/θ. The
integral of Eq. 334 is computed in anased (“ana” for analytic). The function
“rerfc” is the reduced complementary error function[57].
For Law 9, the secondary-energy distribution is given by
g(E, E0) = E0
Iexp−E0
θ(E),(337)
where
I=θ21−e−x(1 + x).(338)
Here xhas the same meaning as above – see Eq. 333. The group integral is
Zg0
g(E, E0)dE0=(1 + x1)e−x1−(1 + x2)e−x2
1−(1 + x)e−x,(339)
where x1and x2refer to E1/θ and E2/θ, respectively. This result is also com-
puted in anased.
For Law 11, the secondary-energy distribution is given by
g(E, E0) = e−E0/a
Isinh√bE0,(340)
where
I=1
2rπa3b
4ex0erf(√x−√x0) + erf(√x+√x0)−ae−xsinh(abx).(341)
220 NJOY2016
8 GROUPR LA-UR-17-20093
In this case, a(E) and b(E) are given in File 5,
x=E−U
a,(342)
and
x0=ab
4.(343)
The group integrals are given by
Zg0
g(E, E0) = H(x1, x2, x0)
H(0, x, x0),(344)
where
H(x1, x2, x0) = H2(√x1−√x0,√x2−√x0)
+√x0H1(√x1−√x0,√x2−√x0)
−H2(√x1+√x0,√x2+√x0)
+√x0H1(√x1+√x0,√x2+√x0),(345)
and where
Hn(a, b) = 1
πZb
a
zne−z2dz . (346)
The methods for computing Hnare described in BROADR. When √x2< .01,
a short-cut calculation can be used for the numerator of Eq. 344
4√x0e−x0
3pπ/4x3/2
2−x3/2
1.(347)
For Law 12, the Madland-Nix option, the secondary-energy distribution is
given by
g(E, E0) = 1
2G(E0, Efl) + G(E0, Ef h),(348)
where
NJOY2016 221
LA-UR-17-20093 8 GROUPR
G(E0, Ef)
=1
3pEfTmu3/2
2E1(u2)−u3/2
1E1(u1) + γ(3/2, u2)−γ(3/2, u1),
(349)
u1= (√E0−pEf)2/Tm,and (350)
u2= (√E0+pEf)2/Tm,(351)
and where Efl,Ef h, and Tm(E) are given in File 5. The special functions
used are the first-order exponential integral, E1(x), and the incomplete gamma
function, γ(n, x). The group integrals of this function are very complex[58]. Let
α=pTm,(352)
β=pEf,(353)
A=(√E1+β)2
α2,(354)
B=(√E2+β)2
α2,(355)
A0=(√E1−β)2
α2,and (356)
B0=(√E2−β)2
α2.(357)
Then the integral over the range (E1, E2) of Gis given by one of the following
three expression, depending on the region of integration in which E1and E2lie.
222 NJOY2016
8 GROUPR LA-UR-17-20093
Region I (E1≥Ef, E2> Ef)
3pEfTmZE2
E1
G(E0, Ef)dE0
=(2
5α2B5/2−1
2αβB2)E1(B)−(2
5α2A5/2−1
2αβA2)E1(A)
−(2
5α2B05/2+1
2αβB02)E1(B0)−(2
5α2A05/2+1
2αβA02)E1(A0)
+(α2B−2αβB1/2)γ(3/2, B)−(α2A−2αβA1/2)γ(3/2, A)
−(α2B0+ 2αβB01/2γ(3/2, B0)−(α2A0+ 2αβA01/2)γ(3/2, A0)
−3
5α2γ(5/2, B)−γ(5/2, A)−γ(5/2, B0) + γ(5/2, A0)
−3
2αβ e−B(1 + B)−e−A(1 + A) + e−B0
(1 + B0)−e−A0
(1 + A0).
(358)
Region II (E1< Ef, E2≤Ef)
3p(EfTm)ZE2
E1
G(E0, Ef)dE0
=(2
5α2B5/2−1
2αβB2)E1(B)−(2
5α2A5/2−1
2αβA2)E1(A)
−(2
5α2B02)E1(B0)−(2
5α2A05/2−1
2αβA02)E1(A0)
+(α2B−2αβB1/2)γ(3/2, B)−(α2A−2αβA1/2)γ(3/2, A)
−(α2B0−2αβB01/2γ(3,2, B0)−(α2A0−2αβA01/2)γ(3/2, A0)
−3
5αβγ(5/2, B)−γ(5/2, A)−γ(5/2, B0) + γ(5/2, A0)
−3
2αβ e−B(1 + B)−e−A(1 + A)−e−B0
(1 + B0) + e−A0
(1 + A0).
(359)
Region III (E1< Ef, E2> Ef)
3pEfTmZE2
E1
G(E0, Ef)dE0
=(2
5α2B5/2−1
2αβB2)E1(B)−(2
5α2A5/2−1
2αβA2)E1(A)
−(2
5α2B05/2+1
2αβB02)E1(B0)−(2
5α2A05/2−1
2αβA02)E1(A0)
+(α2B−2αβB1/2)γ(3/2, B)−(α2A−2αβA1/2)γ(3,2, A)
−(α2B0+ 2αβB01/2)γ(3/2, B0)−(α2A0−2αβA01/2)γ(3/2, A0
)
−3
5α2γ(5/2, B)−γ(5/2, A)−γ(5/2, B0) + γ(5/2, A0)
−3
2αβ e−B(1 + B)−e−A(1 + A) + e−B0
(1 + B0) + e−A0
(1 + A0)−2.
(360)
NJOY2016 223

LA-UR-17-20093 8 GROUPR
8.15 File 6 Energy-Angle Distributions
If the File 6 data are expressed as a continuous energy-angle distribution (Law 1)
in the laboratory system, it is fairly easy to generate the multigroup transfer
matrix. As usual for GROUPR, the task is to calculate the “feed function”
(the Legendre moments for transferring to all possible secondary-energy groups
starting with incident energy E). The E0integration is controlled by the getmf6
subroutine, which calls f6lab to generate the integrands. This routine expects
data in Law-1 format, where the looping order is E,E0,µ. The only problems
here are handling the new ENDF-6 interpolation laws for two-dimensional tab-
ulations (for example, unit base) and converting tabulated angle functions for
E→E0into Legendre coefficients (which is done with a Gauss-Legendre quadra-
ture of order ∼8).
If the File 6 data are given in the energy-angle form of Law 7 (where the
looping order is E,µ,E0), GROUPR converts it to the Law 1 form using sub-
routine ll2lab. It does this by stepping through an E0grid that is the union of
the E0grids for all the different angles given. At each of these union E0values, it
calculates the Legendre coefficients using a Gauss-Legendre quadrature of order
8, and it checks back to see if the preceding point is still needed to represent the
distribution to the desired degree of accuracy. Now getmf6 and f6lab can be
used to complete the calculation as above.
If the File 6 data are expressed in the CM system, or if the phase-space
option is used, more processing is necessary to convert to the LAB system.
This conversion is done for each incident energy Egiven in the file. The grid for
laboratory secondary energy E0
Lis obtained by doing an adaptive reconstruction
of the emission probability pL`(E, E0
L) such that each Legendre order can be
expressed as a linear-linear function of E0
L. This part is done in subroutine
cm2lab. The values for pL`(E, E0
L) are obtained in subroutine f6cm by doing an
adaptive integration along the contour E0
L=const in the E0
C, µCplane using µL
as the variable of integration:
pL`(E, E0
L) = Z+1
µmin
pC(E, E0
C, µC)P`(µL)J dµL,(361)
where µis a scattering cosine and Land Cdenote the laboratory and center-
of-mass (CM) systems, respectively. The Jacobian is given by
J=sE0
L
E0
C
=1
p1 + c2−2cµL
,(362)
224 NJOY2016

8 GROUPR LA-UR-17-20093
and the cosine transformation is given by
µC=J(µL−c).(363)
The constant cis given by
c=sA0
(A+ 1)2sE
E0
L
,(364)
where Ais the ratio of the atomic weight of the target to the atomic weight of
the projectile, and A0is the ratio of the atomic weight of the emitted particle
to the atomic weight of the projectile. The lower limit of the integral depends
on the maximum possible value for the center-of-mass (CM) secondary energy
as follows:
µmin =1
2c1 + c2−E0
Cmax
E0
L,(365)
where
E0
Lmax =ErE0
Cmax
E+sA0
(A+ 1)22.(366)
An example of the integration contours for this coordinate transformation is
given in Fig. 30.
The CM energy-angle distribution can be given as a set of Legendre co-
efficients or a tabulated angular distribution for each possible energy transfer
E→E0, as a “precompound fraction” r(E, E0) for use with the Kalbach-Mann[59]
or Kalbach[60] angular distributions, or as parameters for a phase-space distri-
bution. The first three options are processed using f6ddx, and the last using
f6psp. The Kalbach option leads to a very compact representation. Kalbach and
Mann examined large number of experimental angular distributions for neutrons
and charged particles. They noticed that each distribution could be divided into
two parts: an equilibrium part symmetric in µ, and a forward-peaked preequi-
librium part. The relative amount of the two parts depended on a parameter r,
the preequilibrium fraction, that varies from zero for low E0to 1.0 for large E0.
The shapes of the two parts of the distributions depended most directly on E0.
This representation is very useful for preequilibrium statistical-model codes like
GNASH[61], because they can compute the parameter r, and all the rest of the
NJOY2016 225
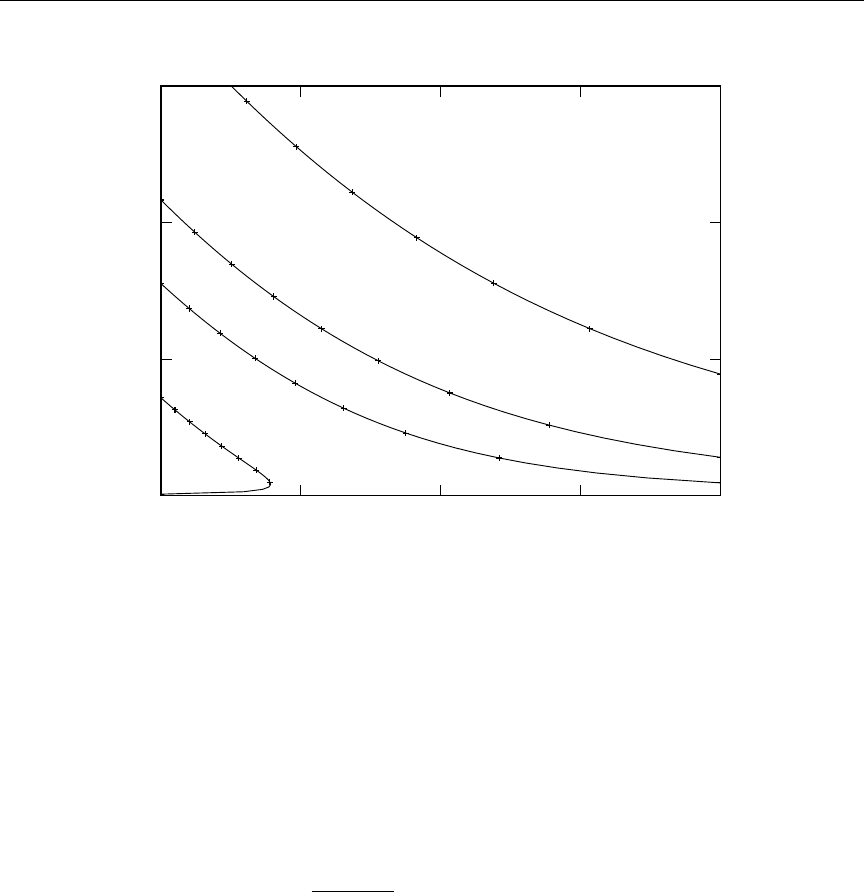
LA-UR-17-20093 8 GROUPR
µC
-1.0 -0.5 0.0 0.5 1.0
EC/E
0.0 0.5 1.0 1.5
EL/E=.07
EL/E=0.3
EL/E=0.5
EL/E=1.0
Figure 30: Coordinate mapping between CM and laboratory reference frames for A=2. The
parameters ELand ECare the secondary energies in the Lab and CM frames.
The crosses on the curves are at µLvalues of -1.0, -.75, -.50, . . . , .75, and 1.0.
This figure also illustrates the advantage of integrating over µLfor the contour
in the lower-left corner. The values of ECand µCare single-values functions of
µL.
angular information comes from simple universal functions. More specifically,
Kalbach’s latest work says that
f(µ) = a
2 sinh(a)hcosh(aµ) + rsinh(aµ)i,(367)
where ais a simple function of E,E0, and Bb, the separation energy of the
emitted particle from the liquid-drop model without pairing and shell terms. The
separation energies are computed by formulas in bach. There is a problem for
elemental evaluations, because the calculations needs an A value for the element,
and it is difficult to guess which A value is most characteristic of the element.
A short table is included in the routine, and an “error in bach” will result if
the function is called for an element that doesn’t appear in the table. Similar
routines appear in HEATR and ACER. A better long-range solution would
be desirable. Fortunately, elemental evaluations are rare in modern evaluated
libraries.
226 NJOY2016

8 GROUPR LA-UR-17-20093
The File 6 processing methods in GROUPR apply equally well to neutrons,
photonuclear photons, and charged particles. The effects on the kinematics due
to the difference in mass between the incident particle and the emitted particle
are handled by the variable A0in the above equations.
8.16 Smoothing
For continuum CM distributions in File 6, the low-energy shape should go like
pE0
C. From Eq. 362, we see that the low-energy shape for the Lab distribution
would then go like pE0
L. However, ENDF/B-VII evaluations for File 6 were
normally prepared using advanced nuclear model codes, such as GNASH from
LANL. These codes naturally produce spectra represented with histogram bins,
and these bins normally give a constant probability from zero energy to the
next bin boundary. This is certainly not a √Eshape! The histogram shape
can cause trouble with the CM-Lab transformation if some care is not taken.
Clearly, the histogram grossly overestimates the probability of scattering to very
low energies. This apparent problem is somewhat alleviated by the fact that the
total probability of that lowest histogram bin is usually quite small. However,
in order to get better looking shapes, GROUPR has coding that replaces the
coarse histogram with a finer histogram chosen to represent a √Eshape more
closely. This smoothing coding scans up through the histogram distribution
from the evaluation to find the region that behaves like √E. It then uses a
recursive procedure to subdivide the region using a given factor until it reaches
a fairly low energy (currently 40 eV).
A similar procedure is used to provide a √Eshape at low energies for delayed
neutron spectra.
For a few of the ENDF/B-VII actinides, the energy grid used to represent the
fission spectrum becomes too coarse above 10 MeV. If that situtation is found,
GROUPR changes the interpolation law from the given lin-lin option to lin-log
— that is, an exponential tail is assumed for the high energies. This assumption
is consistent with the orginal evaluations. This modification can be important
for reaction rates of high-threshold reactions.
These smoothing options are controlled by the global parameter ismooth,
which is turned on by default (in constrast to NJOY99 where it is turned off by
default).
NJOY2016 227

LA-UR-17-20093 8 GROUPR
8.17 GENDF Output
The group constants produced by GROUPR are normally written to an output
file in GENDF (groupwise ENDF) format for use by other modules of NJOY.
For example, DTFR can be used to convert a GENDF material to DTF (or
“transport”) format; CCCCR produces the standard interface files[11] ISOTXS,
BRKOXS, and DLAYXS; MATXSR produces a file in MATXS format[12]; and
POWR produces libraries for the Electric Power Research Institute (EPRI)
codes EPRI-CELL and EPRI-CPM. Other formats can easily be produced by
new modules, and some functions such as group collapse, are conveniently per-
formed directly in GENDF format. The GENDF format is also used for GAM-
INR output, and both ACER and ERRORR use GENDF input for some pur-
poses.
Depending on the sign of ngout2 (see below), the GENDF file will be written
in either coded mode (e.g., ASCII) or in the special NJOY blocked-binary mode.
Conversion between these modes can be performed subsequently by the MODER
module.
The GENDF material begins with a header record (MF=1, MT=451), but
the format of this first section is different from MT=451 on an ENDF or PENDF
tape. The section consists of a “CONT” record, containing
ZA Standard 1000*Z+A value
AWR Atomic weight ratio to neutron
0Zero
NZ Number of σ0values
-1 Identifies a GENDF-type data file
NTW Number of words in title
and a single “LIST” record, containing
TEMPIN Material temperature (Kelvin)
0. Zero
NGN Number of neutron groups
NGG Number of photon groups
NW Number of words in LIST
0Zero
TITLE Title from GROUPR input (NTW words)
SIGZ Sigma-zero values (NZ words)
EGN Neutron group boundaries, low to high (NGN+1 words)
EGG Photon group boundaries, low to high (NGG+1 words).
228 NJOY2016

8 GROUPR LA-UR-17-20093
For photoatomic GENDF files produced by the GAMINR module, the photon
group structure is stored in ngn and egn, and the number of photon groups is
given as ngg=0. The word count is NW=NTW+NZ+NGN+1+NGG+1. The
LIST record is followed by a standard ENDF file-end record (FEND). The nor-
mal ENDF section-end (SEND) is omitted.
This header is followed by a series of records for reactions. The ENDF
ordering requirements are relaxed, and MF and MT values can occur in any
order. Each section starts with a “CONT” record.
ZA Standard 1000*Z+A value
AWR Standard atomic weight ratio
NL Number of Legendre components
NZ Number of sigma-zero values
LRFLAG Break-up identifier flag
NGN Number of groups
It is followed by a series of LIST records, one for every incident-energy group
with nonzero result,
TEMP Material temperature (Kelvin)
0. Zero
NG2 Number of secondary positions
IG2LO Index to lowest nonzero group
NW Number of words in LIST
IG Group index for this record
A(NW) Data for LIST (NW words),
where NW=NL*NZ*NG2. The last LIST record in the sequence is the one with
IG=NGN. It must be given even if its contents are zero. The last LIST record is
followed by a SEND record.
The contents of A(NW) change for various types of data. For simple cross
section “vectors” (MF=3), NG2 is 2, and A contains the two Fortran arrays
FLUX(NL,NZ), SIGMA(NL,NZ)
in that order. For ratio quantities like fission ν,NG2 is 3, and Acontains
FLUX(NL,NZ), RATIO(NL,NZ), SIGMA(NL,NZ).
For transfer matrices (MF=6, 16, 21, etc.), Acontains
FLUX(NL,NZ), MATRIX(NL,NZ,NG2-1).
The actual secondary group indices for the last index of MATRIX are usually
IG2LO,IG2LO+1, etc., using the GROUPR convention of labeling groups in
order of increasing energy. If the low-energy part of the fission matrix (or the
NJOY2016 229

LA-UR-17-20093 8 GROUPR
fission or capture photon production matrices) uses the special format described
in Section 8.6, the spectrum will be found in a LIST record with IG=0 and the
production cross section will be found in a series of records with IG2LO=0. The
group range for the spectrum ranges from IG2LO to IG2LO+NG2-1. For IG2LO=0,
NG2 will be 2 as for a normal cross section, and the two values will be the flux
for group IG and the corresponding production cross section.
Finally, for delayed neutron spectra (MF=5), NL is used to index the time
groups, NZ is 1, and there is only one incident energy record (IG=IGN). The
array Acontains
LAMBDA(NL), CHID(NL,NG2-1),
where LAMBDA contains the delayed-neutron time constants and CHID contains
the spectra.
The GENDF material ends with a material-end (MEND) record, and the
GENDF tape ends with a tape-end (TEND) record.
8.18 Running GROUPR
GROUPR’s input instructions follow. They are reproduced from the comment
cards at the beginning of the 2016.0 version of the GROUPR module. Because
the code changes from time to time, it is a good idea to check these comment
cards in the current version to obtain up-to-date input instructions.
!---input specifications (free format)---------------------------
!
! card1
! nendf unit for endf tape
! npend unit for pendf tape
! ngout1 unit for input gout tape (default=0)
! ngout2 unit for output gout tape (default=0)
! card2
! matb material to be processed
! if ngout=0, matb<0 is an option to automatically
! process all the mats on the endf input tape.
! otherwise, matb<0 is a flag to add mts to and/or
! replace individual mts on gout1.
! ign neutron group structure option
! igg gamma group structure option
! iwt weight function option
! lord legendre order
! ntemp number of temperatures (default=1)
230 NJOY2016

8 GROUPR LA-UR-17-20093
! nsigz number of sigma zeroes (default=1)
! iprint long print option (0/1=minimum/maximum)
! (default=1)
! ismooth switch on/off smoothing operation (1/0, default=1=on)
! set ismooth to 1 to enable sqrt(e) smoothing for
! mf6 cm emission spectra at low energies and for
! histogram delayed neutron spectra at low energies.
! card3
! title run label (up to 80 characters delimited by quotes,
! ended with /) (default=blank)
! card4
! temp temperatures in kelvin
! card5
! sigz sigma zero values (including infinity)
!
! if ign=1, read neutron group structure (6a and 6b)
! card6a
! ngn number of groups
! card6b
! egn ngn+1 group breaks (ev)
!
! if igg=1, read gamma group structure (7a and 7b)
! card7a
! ngg number of groups
! card7b
! egg ngg+1 group breaks (ev)
!
! weight function options (8a,8b,8c,8d)
! card8a flux calculator parameters (iwt.lt.0 only)
! fehi break between computed flux and bondarenko flux
! (must be in the resolved resonance range)
! sigpot estimate of potential scattering cross section
! nflmax maximum number of computed flux points
! ninwt tape unit for new flux parameters (default=0)
! note: weighting flux file is always written binary
! jsigz index of reference sigma zero in sigz array
! (default=0)
! alpha2 alpha for admixed moderator (def=o=none)
! sam admixed moderator xsec in barns per absorber
! atom (def=0=none)
! beta heterogeneity parameter (def=0=none)
! alpha3 alpha for external moderator (def=0=none)
NJOY2016 231

LA-UR-17-20093 8 GROUPR
! gamma fraction of admixed moderator cross section in
! external moderator cross section (def=0)
! card8b tabulated (iwt=1 or -1 only)
! wght read weight function as tab1 record,
! this may span multiple lines and ends with a /.
! card8c analytic flux parameters (iwt=4 or -4 only)
! eb thermal break (ev)
! tb thermal temperature (ev)
! ec fission break (ev)
! tc fission temperature (ev)
! card8d input resonance flux (iwt=0 only)
! ninwt tape unit for flux parameters (binary)
!
! card9
! mfd file to be processed
! mtd section to be processed
! mtname description of section to be processed
! repeat for all reactions desired
! mfd=0/ terminates this temperature/material.
! card10
! matd next mat number to be processed
! matd=0/ terminates groupr run.
!
!---options for input variables----------------------------------
!
! ign meaning
! --- -------
! 1 arbitrary structure (read in)
! 2 csewg 239-group structure
! 3 lanl 30-group structure
! 4 anl 27-group structure
! 5 rrd 50-group structure
! 6 gam-i 68-group structure
! 7 gam-ii 100-group structure
! 8 laser-thermos 35-group structure
! 9 epri-cpm 69-group structure
! 10 lanl 187-group structure
! 11 lanl 70-group structure
! 12 sand-ii 620-group structure
! 13 lanl 80-group structure
! 14 eurlib 100-group structure
! 15 sand-iia 640-group structure
232 NJOY2016

8 GROUPR LA-UR-17-20093
! 16 vitamin-e 174-group structure
! 17 vitamin-j 175-group structure
! 18 xmas nea-lanl
! all new additional group structure with 7 significant
! decimal digits compatible with calendf
! 19 ecco 33-group structure
! 20 ecco 1968-group structure
! 21 tripoli 315-group structure
! 22 xmas lwpc 172-group structure
! 23 vit-j lwpc 175-group structure
!
! igg meaning
! --- -------
! 0 none
! 1 arbitrary structure (read in)
! 2 csewg 94-group structure
! 3 lanl 12-group structure
! 4 steiner 21-group gamma-ray structure
! 5 straker 22-group structure
! 6 lanl 48-group structure
! 7 lanl 24-group structure
! 8 vitamin-c 36-group structure
! 9 vitamin-e 38-group structure
! 10 vitamin-j 42-group structure
!
! iwt meaning
! --- -------
! 1 read in smooth weight function
! 2 constant
! 3 1/e
! 4 1/e + fission spectrum + thermal maxwellian
! 5 epri-cell lwr
! 6 (thermal) -- (1/e) -- (fission + fusion)
! 7 same with t-dep thermal part
! 8 thermal--1/e--fast reactor--fission + fusion
! 9 claw weight function
! 10 claw with t-dependent thermal part
! 11 vitamin-e weight function (ornl-5505)
! 12 vit-e with t-dep thermal part
! -n compute flux with weight n
! 0 read in resonance flux from ninwt
!
NJOY2016 233

LA-UR-17-20093 8 GROUPR
! mfd meaning
! --- -------
! 3 cross section or yield vector
! 5 fission chi by short-cut method
! 6 neutron-neutron matrix (mf4/5)
! 8 neutron-neutron matrix (mf6)
! 12 photon prod. xsec (photon yields given, mf12)
! 13 photon prod. xsec (photon xsecs given, mf13)
! 16 neutron-gamma matrix (photon yields given)
! 17 neutron-gamma matrix (photon xsecs given)
! 18 neutron-gamma matrix (mf6)
! note: if necessary, mfd=13 will automatically change
! to 12 and mfd=16 will automatically change to 17 or 18.
! 21 proton production matrix (mf6)
! 22 deuteron production (mf6)
! 23 triton production (mf6)
! 24 he-3 production (mf6)
! 25 alpha production (mf6)
! 26 residual nucleus (a>4) production (mf6)
! 31 proton production matrix (mf4)
! 32 deuteron production (mf4)
! 33 triton production (mf4)
! 34 he-3 production (mf4)
! 35 alpha production (mf4)
! 36 residual nucleus (a>4) production (mf4)
! note: if necessary, mfd=21-26 will
! automatically change to 31-36.
! 1zzzaaam nuclide production for zzzaaam
! subsection from file 3
! 2zzzaaam nuclide production for zzzaaam
! subsection from file 6
! 3zzzaaam nuclide production for zzzaaam
! subsection from file 9
! 4zzzaaam nuclide production for zzzaaam
! subsection from file 10
! 40000000 fission product production (mtd=18 only)
! subsection from file 10
!
! mtd meaning
! --- -------
! -n process all mt numbers from the previous
! entry to n inclusive
234 NJOY2016

8 GROUPR LA-UR-17-20093
! 221-250 reserved for thermal scattering
! 257 average energy
! 258 average lethargy
! 259 average inverse velocity (m/sec)
!
! automatic reaction processing options
! -------------------------------------
! 3/ do all reactions in file3 on input pendf
! 6/ do all matrix reactions in endf dictionary
! 10/ do all isotope productions using mf8
! 13/ do all photon production cross sections
! 16/ do all photon production matrices
! 21/ do all proton production matrices
! 22/ do all deuteron production matrices
! 23/ do all triton production matrices
! 24/ do all he-3 production matrices
! 25/ do all alpha production matrices
! 26/ do all a>4 production matrices
!
!-------------------------------------------------------------------
In these instructions, card1 defines the input and output units for GROUPR.
The module requires both ENDF and PENDF input tapes, because the PENDF
tapes produced by RECONR,BROADR etc., do not contain angle (MF=4),
energy (MF=5), or photon (MF=12, 15) distributions. For materials that do
not use resonance parameters to represent part of the cross section, it is possible
to use a copy of the ENDF tape in place of the PENDF tape. The normal mode
for GROUPR is to use ngout1=0; however, sometimes it is convenient to add a
new material or reaction to an existing GENDF tape. The old GENDF tape is
then mounted on unit ngout1, and the revised GENDF tape will be written to
ngout2.
Card 2 selects the first material to be processed (matb) and sets up the group
structures, weighting option, Legendre order, and self-shielding parameters for
all the materials to be processed in this run.
The names of the available group structures are given in the input instruc-
tions. Energy bounds or lethargy bounds can be found in the source code. Of
course, it is always possible to read in an arbitrary group structure (see card6a
through card7b). The energies must be given in increasing order (note that this
is opposite from the usual convention). Here is an example of the input cards
NJOY2016 235
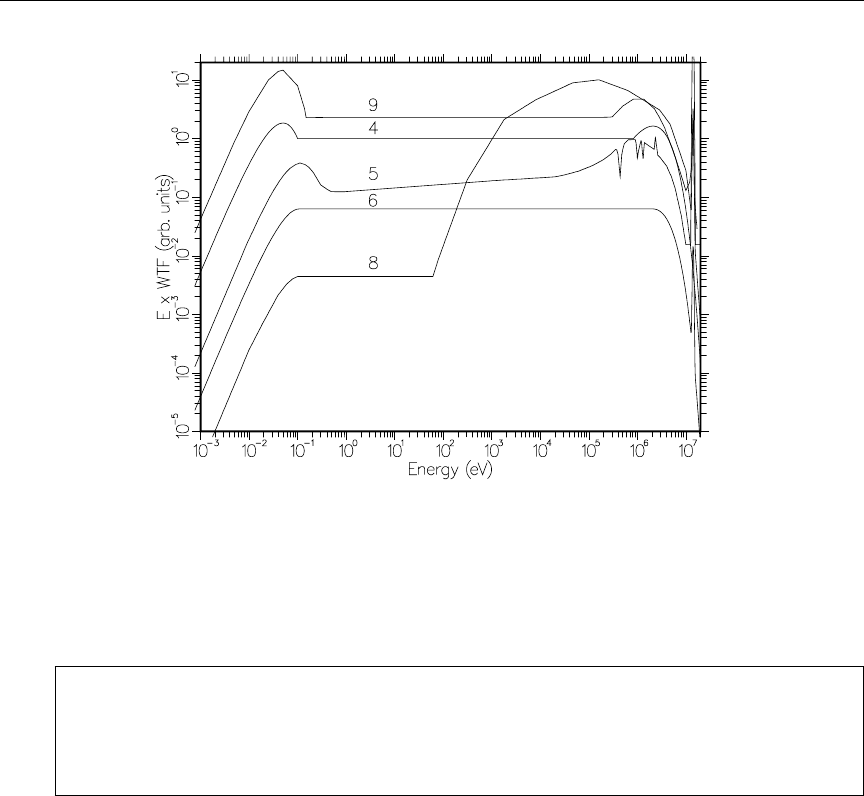
LA-UR-17-20093 8 GROUPR
Figure 31: Built-in neutron weight functions of GROUPR on a logarithmic flux-per-unit-
lethargy plot that emphasizes the low energy range.
for the conventional 4-group structure historically used in some thermal reactor
codes:
4/ card6a
1e-5 .625 5530 .821e6 10e6 / card6b
These cards are read by the standard Fortran READ* method. Fields are delim-
ited by space, and “/” terminates the processing of input on a card. Anything
after the slash is a comment.
The available weight function options are listed in the input instructions
under iwt. See Fig. 31 and Fig. 32. Here are brief descriptions of the options:
IWT=2 The weight function is constant (not shown in the Figures). This
option is usually chosen for very fine group structures such as the 620-
group or 640-group dosimetry structures.
IWT=3 The weight function is proportional to 1/E. The slowing-down of
neutrons in water gives a 1/E flux from about 1 eV up to 100 keV, or
so. This weight function is traditionally used for calculating resonance
integrals, but it is not useful at the lower and higher energies needed for
a full set of transport constants. Although not shown, the graph of this
236 NJOY2016
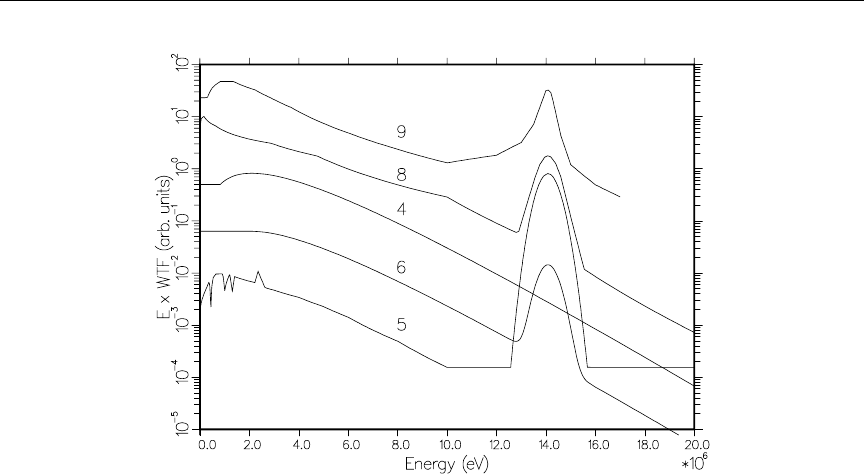
8 GROUPR LA-UR-17-20093
Figure 32: Built-in neutron weight functions on a linear plot that emphasizes the high-
energy range.
function is a flat line on a flux-per-unit-lethargy plot, such as the one in
Fig. 31.
IWT=4 This weight function combines a thermal Maxwellian at low energies,
a 1/E function at intermediate energies, and a fission spectrum at high
energies to obtain a function appropriate for several different applications.
The temperatures of the Maxwellian and fission parts and the energies
where the components join can be chosen by the user. Therefore, option 4
can be used to produce typical thermal reactor weight functions like those
shown in Figures 31 and 32, a pure fission spectrum for calculating some
kinds of dosimetry cross sections, or a pure thermal spectrum for getting
effective thermal average cross sections. The function for IWT=4 shown
in the figure was produced using a thermal temperature of 0.025 eV joined
to 1/E at 0.1 eV, and a fission temperature of 1.40 MeV joined to 1/E at
820.3 keV.
IWT=5 This is a mid-life PWR (pressurized water reactor) flux spectrum with
a fusion peak added (see below for a discussion of the fusion peak used).
Note the peaks and dips resulting from oxygen resonances and windows
at high energies, and the hardening apparent in the epithermal region.
The thermal part of the function is also hardened with respect to a simple
Maxwellian shape. The dips that should show up in the eV range due to
resonances and 238U have been removed to allow the self-shielding method
to work without risk of counting the shielding effects twice. This weight
function has been used for several libraries[62] prepared for the Electric
Power Research Institute (EPRI), and for the MATXS7 library used with
the TRANSX code.
NJOY2016 237

LA-UR-17-20093 8 GROUPR
IWT=6 This function is similar to option 4, but the breakpoints were chosen
to keep the curves continuous. The thermal Maxwellian is calculated for
300K. In this case, the fusion peak (see below) was added to the high-energy
tail of the fission spectrum for smoothness.
IWT=7 This option is reserved for future use.
IWT=8 This function is intended for cross sections libraries used for fast re-
actor analysis (typically, fast breeder designs), but is also useful for fusion-
blanket problems. It has a fusion peak at high energies, followed by a fission
spectrum, a slowing-down spectrum typical of a fast reactor, and a thermal
tail. The tail is provided to help give reasonable results in shields far from
the core; its characteristic temperature is 300K. Note the sharp drop in
the flux as energy decreases from 19 keV. This region is important for 238U
absorption, and this drop-off helps to give good group constants for fast
reactors. Of course, it would be entirely wrong for a thermal reactor.
IWT=9 This is another typical thermal+1/E+fission+fusion function that
has been used for many libraries at LANL in the 30-group structure. The
CLAW-3 and CLAW-4 libraries are available from the Radiation Shielding
Information Computational Center at ORNL.
IWT=10 This is the same as the CLAW weight function (IWT=9), but
the shape of the thermal part is automatically recalculated to follow a
Maxwellian law for temperature T.
IWT=11 This is the weight function used in the VITAMIN-E library. It has
the following segments: a .0253-eV thermal Maxwellian below 0.414 eV,
a 1/E law from .414 eV to 2.12 MeV, a 1.415-MeV fission spectrum from
2.12 to 10 MeV, another 1/E section from 10 to 12.52 MeV, a fusion peak
(25 keV width) between 12.52 and 15.68 MeV, and a final 1/E section for
all higher energies. The shape of the fusion peak is almost identical to
IWT=5 (see Fig. 32). The low-energy part of this weight function is not
shown.
Just as in the case of group structures, an arbitrary weight function can be
read in (see card8b). This function is presented to GROUPR as an ENDF/B
“TAB1” record. This means that a count of E, C(E) pairs and one or more
interpolation schemes are given.
An ENDF/B “TAB1” record consists of three distinct parts:
•two double values and four integer values of which only the last two integers
(the number of interpolation ranges NR and the number of E, C(E) pairs
NP) are needed to read the remainder of the record
•the interpolation scheme data which is a sequence of NR pairs of NBT (index
of the E, C(E) pair corresponding to the end of interpolation range) and
INT (the interpolation type)
238 NJOY2016
8 GROUPR LA-UR-17-20093
•the tabulated data which is a sequence of NP E, C(E) pairs
The interpolation type INT specifies the interpolation law to be used in the
interpolation range. It can take the following values:
INT Meaning
1 histogram
2 linear-linear
3 linear-log
4 log-linear
5 log-log
For example, INT=5 specifies that lnCis a linear function of lnE. Similarly,
INT=4 specifies that lnCis a linear function of E.
In its most general form, these input cards would be
0. 0. 0 0 NR NP
NBT(1) INT(1) ... NBT(NR) INT(NR)
E(1) C(1) ... E(NP) C(NP) / card8b
For example, a function using two interpolation ranges: the first one between
1e-5 eV and 100 eV using a histogram and the second one between 100 eV and
20 MeV using lin-lin interpolation)
0. 0. 0 0 2 6
3162
1e-5 0.5 1. 0.75 100. 0.8
1e+6 0.85 1.5e+6 0.9 2.0e+7 1.0 / card8b
For the special case of a single interpolation scheme, the input cards are simpli-
fied as follows
0. 0. 0 0 1 NP
NP INT
E(1) C(1) ... E(NP) C(NP) / card8b
NJOY2016 239

LA-UR-17-20093 8 GROUPR
As many physical lines as are needed can be used for “card8b”, as long as the
terminating slash is included.
One of the weighting options, IWT=4, is a generalized “1/E+fission+thermal”
function where the thermal temperature, fission temperature, and breakpoint en-
ergies (all in eV) are given on card8c. The weight function for the Los Alamos
LIB-IV cross section library[63] used
.10 .025 820.3e3 1.4e6 / card8c
See Figures 31 and 32 for a plot of this function.
Several of these weight functions include a fusion peak. Because of the finite
width of the distribution of ion energies in a D-T fusion plasma, the emitted
14-MeV neutrons clearly will not have a delta-function energy spectrum. In fact,
owing to the presence of a cross-product term in the kinematic relations, the
typical ion-energy spread of a few tens of kilovolts is magnified into a neutron-
energy spread of around 1 MeV. For an assumed isotropic Maxwellian plasma,
the neutron peak shape (for example, see the review article by Lehner[64]) is
S(E) = CZ∞
0
exp{−bv2+v0(g)2−cg2}sinh(2bvv0)g3σ(g)
v0(g)dg . (368)
Here S(E) is the number of neutrons emitted with laboratory energy between
Eand E+dE,Cis a normalization factor, vis the laboratory velocity corre-
sponding to energy E, and v0is the velocity of the neutron in the CM system.
Both v0and the fusion cross section σare determined by the relative velocity
gof the reacting ions, the integration variable in Eq. 368. The coefficient b
is equal to M/2kT , where Mis the total mass of the reacting ions and kT is
the plasma temperature. Similarly, cis µ/2kT , where µis the reduced mass
of the ion system. The only approximation involved in Lehner’s derivation of
Eq. 368 is that all particles may be treated nonrelativistically. At 14 MeV, the
relativistic factor
γ=1
p1−v2/c2,(369)
is very close to unity (1.015), and it varies negligibly over the range of interest
(say, 13 to 17 MeV). It is sufficient then to invoke relativistic mechanics in
defining the location of the 14-MeV peak but not in discussing the shape. This
240 NJOY2016

8 GROUPR LA-UR-17-20093
effect moves the peak toward lower neutron energies, but only by about 20 keV.
Although the expression for S(E) in Eq. 368 is accurate, it has the disadvantage
of requiring a numerical integration at each point Ein the energy spectrum. For
this reason, we consider what simplifications can be made without serious loss
of accuracy. In the energy range around the 14-MeV peak, the product 2bvv0
in Eq. 368 has a numerical value of about 6000. Thus, the hyperbolic sine can
obviously be replaced by just the positive exponential term. If we make this
change in Eq. 368, we can write the following, still nearly exact, expression for
the neutron spectrum:
S1(E) = C1Z∞
0
exp[−b(v−v0)2]P(v0)dv0.(370)
Here we also have inverted the function v0(g) and changed the integration vari-
able. The spectrum then is a linear superposition of velocity exponentials with
slightly different peak locations. For normal plasma temperatures, the velocity
distribution P(v0) is very narrow, since the expression for v0is dominated by the
nuclear Q-value (17.586 MeV) rather than the contribution from the ion kinetic
energy (typically around 50 keV). Thus, it seems reasonable to approximate
P(v0) as delta function
P(v0)≈δ(v0−vp).(371)
This gives a second approximate form,
S2(E) = C2exp[−b(v−vp)2],(372)
where vphas the obvious meaning of the laboratory neutron velocity at the
center of the peak. We shall refer to this as the velocity exponential form of
the neutron energy spectrum. An expression essentially identical to Eq. 372
was given in an early paper by Nagle and coworkers[65]. In order to examine
the accuracy of the velocity exponential form, we have calculated S(E) from
Eq. 368 and S2(E) from Eq. 372 at 20 keV, a typical plasma temperature in
current fusion-reactor concepts. In performing the numerical integration over g
in Eq. 368, we used numerical values for the D-T fusion cross section taken from
the compilation by Jarmie and Seagrave[66]. In evaluating S2(E) using Eq. 372,
a value of vpwas chosen so as to force agreement between S2(E) and S(E) at 17
MeV. As discussed by Muir[67], the overall agreement is remarkably good, the
maximum error over the range from 13.5 to 17 MeV being about 2%. The value
NJOY2016 241

LA-UR-17-20093 8 GROUPR
of vpthus derived corresponds to a peak-center energy Epof 14.07 MeV. This
value includes the small (∼20 keV) relativistic correction mentioned above. If
we approximate the mass of the D+T system as 5 times the neutron mass, then
we obtain the recommended peak shape
Srec(E) = exp−5
kT (√E−pEp)2,(373)
where Ep=14.07 MeV. The functional form in Eq. 373 was used to calculate the
fusion peak shapes appearing in two of the data statements in genwtf (namely,
those utilized for IWT=5 and 8) and is also used explicitly in getwtf to calculate
analytically the weight function for IWT=6. In all three cases, kT =25 keV is
used as an average or typical fusion-reactor plasma temperature. See Fig. 32 for
a graphical display of the resulting weight functions in the 14-MeV region.
The GROUPR flux calculator is selected by a negative sign on iwt. The
additional card8a is then read. The calculator option used is determined by
the number of parameters given and their values. The parameters fehi and
nflmax are used to select the energy range for the flux calculation, and they
also determine the cost in time and storage. The actual value for sigpot is not
very critical – a number near 10 barns is typical for fissionable materials.
Nonzero values for ninwt and jsigz will cause the computed flux for a given
fissionable isotope (such as 238U) to be written out onto a file. This saved
flux can be used as input for a subsequent run for a fissile material (such as
239Pu) with iwt=0 to get an approximate correction for resonance-resonance
interference. See Eq. 278.
Nonzero values for some of the last five parameters on card8a select the
extended flux calculation of Eq. 276. The simplest such calculation is for an iso-
lated pin containing a heavy absorber with an admixed moderator. For 238UO2,
the card might be
400 10.6 5000 0 0 .7768 7.5 / card8a
where 7.5 barns is twice the oxygen cross section and αis computed from (A−
1)/(A+ 1)2with A= 15.858. A more general case would be a PWR-like lattice
of 238UO2fuel rods in water:
400 10.6 5000 0 0 .7768 7.5 .40 1.7e-7 0.086 / card8a
242 NJOY2016

8 GROUPR LA-UR-17-20093
where 0.086 is computed using 3.75 barns for O and 40 barns for the two H
atoms bound in water; that is,
γ=3.75
2∗20 + 3.75 = 0.086 .(374)
A third example would compute the flux for a homogeneous mixture of 238U
and hydrogen
400 10.6 5000 0 0 0 0 1. 1.7e-7 / card8a
As a final example, consider a homogeneous mixture of uranium and water. This
requires beta=1 and sam=0. Thus,
400 10.6 5000 0 0 .7768 0. 1. 1.7e-7 .086 / card8a
The maximum Legendre expansion order used for scattering matrices is set
by lord. The number of tables produced is lord+1; that is, `= 0, 1, ... lord.
When more than 1 value of σ0is requested, both the `=0 and `=1 components
of the total cross section are produced.
Card 3 contains a short descriptive title that is printed on the listing and
added to the output GENDF tape. Card 4 gives the ntemp values of temperature
for the run. They must be in ascending order, and if unresolved data are included
on the PENDF tape, the temperatures in this list must match the first ntemp
values in MF=2, MT=152 from UNRESR or PURR (see stounr and getunr).
Card 5 gives the σ0values for the run in descending order, starting with infinity
(represented by 1010 barns).
This completes the description of the global input parameters for GROUPR.
The rest of the input cards request reactions to be processed for the various
temperatures and materials desired. Because of the many types of data that it
can process, GROUPR does not have a completely automatic mode for choosing
reactions to be processed. On the basic level, it asks the user to request each
separate cross section or group-to-group matrix using the parameters mfd,mtd,
NJOY2016 243

LA-UR-17-20093 8 GROUPR
and mtname. However, simplified input modes are also available. For example,
the one “card9” containing
3/
will process the cross section “vectors” for all of the reaction MT numbers found
on the PENDF tape.
For completeness, the full input for matd,mfd, and mtname will be described
first. Most readers can skip to the description of automated processing below.
The value of mfd depends on the output desired (vector, matrix) and the form
of the data on the ENDF evaluation. Simple cross section “vectors” σxg are
requested using mfd=3 and the mtd numbers desired from the list of reactions
available in the evaluation (check the directory in MF=1,MT=451 of the ENDF
and PENDF tapes for the reactions available). A typical example would be
3 1 ’total’/
3 2 ’elastic’/
3 16 ’(n,2n)’/
3 51 ’(n,nprime)first’/
3 -66 ’(n,nprime)next’/
3 91 ’(n,nprime)continuum’/
3 102 ’radiative capture’/
The combinations of “3 51” followed by “3 −66” means process all the reac-
tions from 51 through 66; that is, (n,n0
1), (n,n0
2), . . . , (n,n0
16). If self-shielding is
requested, the following reactions will be processed using nsigz values of back-
ground cross section: total (MT=1), elastic (MT=2), fission (MT=18 and 19),
radiative capture (MT=102), heat production (MT=301), kinematic KERMA
(MT=443), and damage energy production (MT=444). The other File-3 reac-
tions will be computed at σ0=∞only. This list of reactions can be altered by
small changes in init if desired.
There are several special options for mtd available when processing cross
section vectors:
mtd Option
259 Average inverse neutron velocity for group in s/m.
244 NJOY2016

8 GROUPR LA-UR-17-20093
258 Average lethargy for group.
251 Average elastic scattering cosine µcomputed from File 4.
252 Continuous-slowing-down parameter ξ(average logarithmic en-
ergy decrement for elastic scattering) computed from File 4.
253 Continuous-slowing-down parameter γ(the average of the square
of the logarithmic energy decrement for elastic scattering, divided
by twice the average logarithmic energy decrement for elastic
scattering) computed from File 4.
452 ν: the average total fission yield computed from MF=1 and
MF=3.
455 νD: the average delayed neutron yield computed from MF=1
and MF=3.
456 νP: the average prompt fission neutron yield computed from
MF=1 and MF=3.
There are also some special options for mfd that can be used when processing
cross sections:
mfd Option
12 Photon production cross section computed from File 12 and File
3.
13 Photon production cross section computed from File 13. Recent
versions of GROUPR will automatically shift between 12 and 13,
if necessary.
1zzzaaam nuclide production for zzzaaam from a subsection of MF=3
2zzzaaam nuclide production for zzzaaam from a subsection of MF=6
3zzzaaam nuclide production for zzzaaam from a subsection of MF=9
4zzzaaam nuclide production for zzzaaam from a subsection of MF=10
40000000 fission product production from the MT=18 subsection of MF=10
An example of the isomer production capability would be the radiative capture
reaction of ENDF/B-V 109Ag(n,γ) from Tape 532:
30471090 102 ’(n,g) TO g.s.’/
30471091 102 ’(n,n) to isomer’/
Starting with ENDF/B-VIII.0, some non-fissile nuclides can have an MT=18
section (fission) in MF=10 (radioactive isotope production) to represent breakup
NJOY2016 245
LA-UR-17-20093 8 GROUPR
due to high energy particles. In these cases, it is often not possible to designate
a specific nuclide, which is why the mfd value is set to 40000000. In such a case,
the following input will make GROUPR process this part of the ENDF file:
40000000 18 ’HE breakup’ /
The next class of reactions usually processed is the group-to-group neutron
scattering matrices. The complete list of mtd values is most easily found under
File 4 in the MF=1,MT=451 “dictionary” section of the evaluation. An example
follows:
6 2 ’elastic matrix’/
6 16 ’(n,2n) matrix’/
6 51 ’(n,nprime)first matrix’/
6 -66 ’(n,nprime)next matrix’/
6 91 ’(n,nprime)continuum matrix’/ .
Using mfd=6 implies that File 4, or File 4 and File 5, will be used to generate the
group-to-group matrix. The elastic matrix will be computed for nsigz values of
background cross section, but the other reactions will be computed for σ0=∞
only. The list of matrices to be self-shielded can be altered by changing init.
Fission is more complex. For the minor isotopes, only the total fission reac-
tion is used, and the following input is appropriate for the prompt component:
3 18 ’fission xsec’/
6 18 ’prompt fission matrix’/
For the important isotopes, partial fission reactions are given. They are really
not needed for most fission reactor problems, and the input above is adequate.
However, for problems where high-energy neutrons are important, the following
input should be used:
3 18 ’total fission’/
3 19 ’(n,f)’/
3 20 ’(n,nf)’/
246 NJOY2016

8 GROUPR LA-UR-17-20093
3 21 ’(n,2nf)’/
3 38 ’(n,3nf)’/
6 19 ’(n,f)’/
6 20 ’(n,nf)’/
6 21 ’(n,2nf)’/
6 38 ’(n,3nf)’/
Note that “6 18” is omitted because it will, in general, be different from the
sum of the partial matrices (see Section 8.6). Some materials don’t have data
for (n,3nf); in these cases, omit the two lines with mtd=38 from the input. The
fission matrix is not self-shielded. Since resonance-to-resonance fission-spectrum
variations are not described in the ENDF format, it is sufficient to self-shield
the cross section and then to use the self-shielding factor for the cross section
to self-shield the fission neutron production.
Delayed fission data are available for the important actinide isotopes, and
the following input to GROUPR is used to process them:
3 455 ’delayed nubar’/
5 455 ’delayed spectra’/
The line for mfd=5 automatically requests spectra for all time groups of de-
layed neutrons. The time constants are also extracted from the evaluation. As
discussed in Section 8.6, formatting modules such as DTFR and CCCCR must
combine the prompt and delayed fission data written onto the GENDF tape in
order to obtain steady-state fission parameters for use in transport codes.
Starting with the ENDF-6 format, neutron production data may also be
found in File 6, and mfd=8 is used to tell the code to use MF6 for this mtd.
When using full input, the user will have to check the File 1 directory and
determine what subsections occur in File 6.
Photon production reactions can be found in the ENDF dictionary under
MF=12 and 13. To request a neutron-to-photon matrix, add 4 to this number.8
For example,
17 3 ’nonelastic photons’/
8In recent versions of NJOY, GROUPR will automatically shift between 16 and 17 using data read from
the ENDF dictionary by the conver subroutine. Thus, use of mfd=17 is no longer necessary.
NJOY2016 247

LA-UR-17-20093 8 GROUPR
16 4 ’inelastic photons’/
16 18 ’fission photons’/
16 102 ’capture photons’/
Yields (MF=12) are normally used with resonance reactions (MT=18 or MT=102),
or for low-lying inelastic levels (MT=51, 52, ....). MT=3 is often used by eval-
uators as a catch-all reaction at high energies where it is difficult to separate
the source reactions in total photon emission measurements. In these cases,
photon production cross sections from other reactions like MT=102 are nor-
mally set equal to zero at high energies. The general rule for photon emission
is that the total production is equal to the sum of all the partial production
reactions given in the evaluation. Starting with the ENDF-6 format, photon
production may also appear in File 6. Use mfd=18 to process these contribu-
tions. Since resonance-to-resonance variations in photon spectra are not given
in ENDF evaluations, GROUPR does not normally self-shield the photon pro-
duction matrices (although this can be done if desired by making a small change
in init); instead, it is assumed that only the corresponding cross section needs
to be shielded. Subsequent codes can use the cross section self-shielding fac-
tor with the infinite-dilution photon production matrix to obtain self-shielded
photon production numbers.
This version of GROUPR can also generate group-to-group matrices for
charged-particle production from neutron reactions and for all kinds of matrices
for incident charged particles. The incident particle is determined by the input
tape mounted. The identity of the secondary particle is chosen by using one of
the following special mfd values:
For distributions given in File 6 (energy-angle):
mfd Meaning
21 proton production
22 deuteron production
23 triton production
24 3He production
25 alpha production
26 residual nucleus (A>4) production
For distributions given in File 4 (angle only):
248 NJOY2016
8 GROUPR LA-UR-17-20093
mfd Meaning
31 proton production
32 deuteron production
33 triton production
34 3He production
35 alpha production
36 residual nucleus (A>4) production
If necessary, mfd=21-26 will automatically change to 31-36.
The user will normally process all reactions of interest at the first temperature
(for example, 300K). At higher temperatures, the threshold reactions should be
omitted, because their cross sections do not change significantly with tempera-
ture except at the most extreme conditions. This means that only the following
reactions should be included for the higher temperatures (if present): total
(MT=1), elastic (MT=2), fission (MT=18), radiative capture (MT=102), heat-
ing (MT=301), kinematic KERMA (MT=443), damage (MT=444), and any
thermal cross sections (MT=221-250). Only the elastic and thermal matrices
should be included at the higher temperatures.
Warning: when using the explicit-input option, it is a fatal error to request
a reaction that does not appear in the evaluation, cannot be computed from
the evaluation, or was not added to the PENDF tape by a previous module.
Reactions with thresholds above the upper boundary of the highest energy group
will be skipped after printing a message on the output file.
Automated processing of essentially all reactions included in an ENDF/B
evaluation is also available. As mentioned previously, the single card
3/
will process all the reactions found in File 3 of the input PENDF tape. How-
ever, this list excludes thermal data (MT=221-250) and special options such as
mtd=251-253, 258-259, and 452-456. If any of these reactions are needed, they
should be given explicitly (see example below). Similarly, the single card
6/
NJOY2016 249
LA-UR-17-20093 8 GROUPR
will process the group-to-group matrices for all reactions appearing in File 4
of the ENDF/B tape, except for MT=103-107 and thermal scattering matrices
(MT=221-250). If MT=18 and 19 are both present, only MT=19 will be pro-
cessed into a fission matrix. For ENDF-6 evaluations, the “8/” option will also
process every neutron-producing subsection in File 6. Photon production cross
sections are requested using
13/
and photon-production matrices are requested with the single card
16/
In both cases, all reactions in both File 12 and File 13 will be processed without
the need for using mfd=12 or mfd=17. For ENDF-6 libraries, this option will
also process all photon-production subsections in File 6. There is no automatic
option for delayed neutron data. An example of a processing run for a fissionable
isotope with thermal cross sections follows:
3/
3 221/ thermal xsec
3 229/ average inverse velocity
3 455/ delayed nubar
5 455/ delayed spectra
6/
6 221/ thermal matrix
16/ photon production matrix
An example of charged-particle processing for the incident-neutron part of a
coupled n-p-γlibrary follows:
3/ cross sections
6/ neutron production matrix
16/ photon production matrix
250 NJOY2016
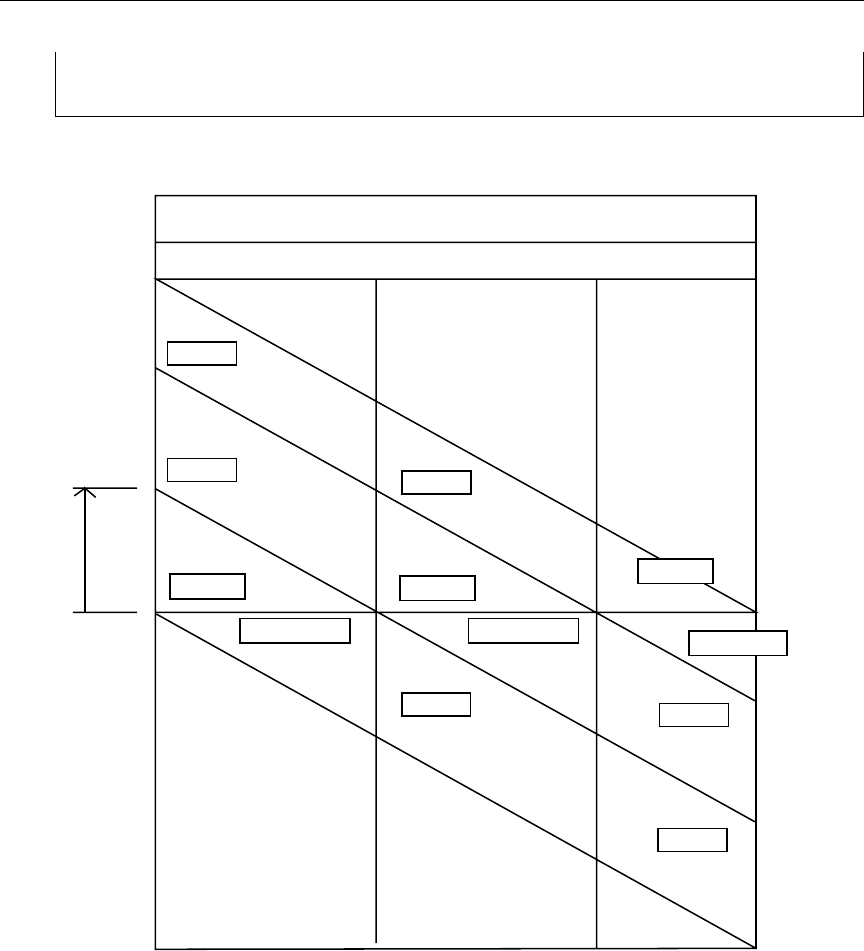
8 GROUPR LA-UR-17-20093
21/ proton production matrix
The layout of data in a n-p-γcoupled set is shown in Figure 33.
n (52)
0
0
0
p (52) γ (22)
max likely
upscatter
n→ γ
n→ p p→ γ
52
n→ n, down p→ p, down γ→ γ, down
γ→ γ, up
p→p, up
n→n, up
p→ n γ→ p
γ→ n
0
0
0
edits
σa,νσf,σt
3
22
52
Figure 33: Layout of a coupled table for the simultaneous transport of neutrons, protons,
and gamma rays. Normally, only the lower triangle of the “p to n” block would
contain values for the upscatter portion of the table (the part above the line in
the middle). The “group” index increases from left to right, and the “position”
index increases from top to bottom.
There is a new ENDF format now becoming available that helps to describe
the production of all isotopes and isomers in a given system. It uses a directory
in File 8 to direct the code to productions represented by MF=3, by MF=9
NJOY2016 251

LA-UR-17-20093 8 GROUPR
times MF=3, by MF=10, or by sections of MF=6 times MF=3. When this
format is used, it is possible to give the simple command
10/
to have production cross sections generated for every nuclide that is produced.
These production sections are labeled with the ZA and isomeric state of the
products for use by subsequent NJOY modules.
8.19 Coding Details
The groupr subroutine is exported by the groupm module. GROUPR begins by
reading most of the user’s input (see ruinb). It then locates the desired material
and temperature on the input ENDF, PENDF, and GENDF tapes, and reads in
the self-shielded unresolved cross sections (if any) from the PENDF tape using
stounr. If self-shielding was requested, genflx is used to compute the weighting
flux as described in Section 8.4. The next step is to write the header record for
this material on the output GENDF tape.
The code is now ready to begin the loop over reactions for this material and
temperature. Either an input card is read to get mfd,mtd and mtname (the
reaction name), or the next reaction in an automatic sequence is selected. First,
the default Legendre order, secondary group count, and σ0count are selected
for the reaction in init, and the retrieval routines are initialized. groupr then
processes the reaction using the panel logic described in Section 8.11. If a
“shortcut” fission spectrum was requested (mfd=5), for delayed fission, and for
the low-energy “constant” spectra, the spectrum is calculated directly using
getff. As the cross sections for each group are obtained, they are printed out
(see displa) and written to the GENDF tape. When the last group has been
processed, groupr loops back to read a new input card for a new reaction.
This loop over reactions continues until a terminating “0/” card is read.
groupr then proceeds to the next temperature, if any, and repeats the loop over
reactions. After the last temperature has been processed for the first material,
an opportunity is provided to change to a new material, keeping all the other
input parameters unchanged. A “0/” card at this point causes all the files to be
closed, prints out the final messages, and terminates the groupr run.
Automatic choice of the next reaction to be processed is done in one of two
ways. For a simple range of MT numbers, such as the example 51 - 66 used above,
252 NJOY2016

8 GROUPR LA-UR-17-20093
the negative value is stored in the variable mtdp in the groupr subroutine. When
mtdp is negative, mtd is incremented after each reaction until it is greater than
the absolute value of mtdp.mtdp is then reset to one, and the code proceeds to
the next input card. When processing photon data, mfd=16 will automatically
change to 17, if necessary. Similarly, mfd=21, 22, . . . will automatically change
to mfd=31, 32, . . . . A more automatic method is triggered by mtd=0. In this
case, a subroutine called nextr is called to return the next value of mtd to be
used, and a subroutine called namer is called to generate the reaction name.
For mfd=3, nextr finds the next reaction in File 3 on the input PENDF tape.
MT=251-253 and thermal data (MT=221-250) are excluded. The MT values
for the special options (258, 259, etc.) do not appear on the PENDF tape, and
they must be requested explicitly. For matrices, GROUPR works with a set of
lists loaded into global arrays by conver. The list mf4 contains all the neutron-
scattering MT numbers that appear in the File 4 part of the directory on the
ENDF tape, and the list mf6 contains all the MT numbers of sections of File
6 that contain subsections that produce neutrons. Therefore, reading through
these two lists returns all the neutron-producing matrix reactions. Similarly, the
list mf12 contains all the File 12 entries from the directory, mf13 contains the
File 13 entries, and mf18 contains all the MT values for sections in File 6 that
contain subsections for photon production. Scanning through these three lists
produces all the photon production matrix reactions. Two arrays are used for
charged-particle producing reactions; the first index runs through the charged
particles in the order p, d, t, 3He, α, recoil. Taking proton production as an
example, the list elements mf6p(1,i) contain the MT numbers of sections in File
6 that contain subsections that produce protons. The list elements mf4r(1,i)
contain MT numbers from File 4 for two-body reactions that produce protons;
namely, MT600 - MT648. nextr scans through both of these lists to return
indexes to all the reactions that produce protons. The same procedure is used
for the other charged particles. The arrays mf10s and mf10i are used in a similar
way for nuclide production.
Subroutine namer generates name strings with up to 15 Hollerith words with 4
characters each (60 characters). The names depend on the “ZA” of the projectile
and the MT number for the reaction. The parameter mfd is used to choose
between the suffixes “cross section” and “matrix”. Some examples of the names
produced follow:
NJOY2016 253

LA-UR-17-20093 8 GROUPR
Name Name Name
(n,total) (n,heat) (p,p02)
(n,elastic) (n,p02) (p,n00)
(n,2n) (p,elastic) (g,total)
(n,n01) (p,2n) (g,pair)
Subroutines mfchk and mfchk2 are used with the full input for reaction se-
lection in GROUPR to check whether mfd=17 is needed when mfd=16 was
requested, or whether one of the charged-particle File 4 values mfd=31-36 is
needed when mfd=21-26 were requested. The lists in global variables like mf12
are used, just as for nextr.
Subroutine gengpn generates the group bounds in the global array egn for
the neutron group structure from input cards, from data statements, or by
calculation. Some of the data statements use energies in eV and some use
lethargy. Similarly, gengpg generates the photon group structure in global array
egg from input cards or data statements; in this case, all bounds are in eV.
Subroutine genwtf sets up the weight function option requested with iwt
by reading the input cards into weights, transferring numbers from data state-
ments to weights, or simply reporting the analytic weight option requested.
Subroutine getwtf returns the values of the weight function at energy Eby
calculation or by interpolation in the table established by genwtf. The current
version returns the same value for all Legendre orders. Choosing enext is dif-
ficult for getwtf because the functions have not been explicitly linearized. It
is important to generate extra grid points in energy regions where the weight
function may vary faster than the cross section (for example, in the fusion peak).
Subroutine genflx computes the self-shielded weighting flux using either the
Bondarenko model or the flux calculator, and it writes the result on a scratch
tape using the loada utility routine. When fluxes are needed for the generalized
group integrals, they are read from this scratch file using finda (see getflx).
Subroutine genflx starts by checking for the weighting option. If the Bon-
darenko model was selected, it initializes gety1 and getwtf to read the total
cross section from the PENDF tape and the smooth weighting function C(E)
set up by genwtf. It then steps through the union grid of σt(E) and C(E)
computing the flux vs. σ0and Legendre order by means of Eq. 253. In the un-
resolved energy range, getunr is used to retrieve the unresolved cross sections
as a function of σ0, and Eq. 261 is used to compute the weighting flux. In both
cases, the data at each energy are stored as the 1+(lord+1)*nsigz components
254 NJOY2016

8 GROUPR LA-UR-17-20093
e, phi(il,iz),
where il runs from 1 to lord+1 and iz runs from 1 to nsigz.
If the flux calculator option was requested, genflx sets up the parameters
for the calculation and requests needed storage space. Next, the cross section
retrieval routines gety1 and gety2 are set up to return total and elastic cross
sections from the PENDF tape. A lower energy limit, felo, is chosen, and
the cross sections are read into storage until a maximum energy, fehi, or a
maximum number of points, nemax, is reached.
The slowing-down equation, either Eq. 272 or Eq. 276, is then solved from
the break energy down to felo. The scattering source from energies above the
break is based on the NR approximation. When the calculation is finished,
fluxes from 10−5eV to felo are written to the scratch file using loada in the
same format used for the Bondarenko option. From felo to the energy break
point, fluxes are transferred from memory to the loada file. Finally, above the
break point, fluxes are computed and saved using the Bondarenko model.
Subroutine init is used to set up the number of σ0values, secondary en-
ergy groups, and Legendre components for each combination of mfd and mtd. If
mfd=8, a special copy of File 6 is made for use in getaed. The list of reactions
to be self-shielded can be changed if desired. The number of secondary groups
ng helps determine the storage required for the accumulating group integrals
(see allocatable array ans) in groupr. For simple cross section vectors, ng=2.
The nz*nl flux components are stored first, followed by the nz*nl cross section
components. When all the panels for one group have been processed, dividing
position 2 by position 1 gives the group-averaged cross section. For ratio quan-
tities like νand µ(mtd=251-253, 452, 455, 456), ng is 3. Once again, the flux
components are stored first, followed by the nl*nz components of ratio*sigma,
followed by the components of the cross section. This arrangement allows for
the calculation of group-averaged values of ratio*sigma,ratio, or cross sec-
tion by dividing position 2 by 1, position 2 by 3, or position 3 by 1, respectively.
For matrices, ng is set to one more than the number of secondary groups (ngn
or ngg). The nl*nz flux components are stored first, followed by the nl*nz
integrals for each secondary-energy group in turn.
Subroutine panel performs the generalized group integrals using the logic
described in Section 8.11. For most calls to panel, the lower point of each
“panel” was computed as the upper point of the previous panel. Therefore,
panel is careful to save these previous values. However, if the bottom of the
panel is just above a discontinuity, new values of cross section and flux are
NJOY2016 255

LA-UR-17-20093 8 GROUPR
retrieved. Once the values at the lower boundary of the panel are in place,
new values for the top of the panel are retrieved (see flux,sig). If the top
of the panel is at a discontinuity in σor at a group boundary, the energy used
is just below the nominal top of the panel. “Just below” and “just above”
are determined by rndoff and delta. For maximum accuracy, these numbers
should be chosen such that rndoff>1, delta<1, and rndoff*delta<1 for the
precision of the machine being used.
For simple average cross sections, the integrals of σ×φand φare computed for
the panel using trapezoids. This is justified by the linearization of σ; the value
of σ×φat the midpoint is too uncertain to justify a more complex treatment.
For two-body scattering, the feed function is far from linear over the panel. In
fact, it can show oscillations as described in Section 8.12. The integral of the
triple product F×σ×φis obtained by Lobatto quadrature of order 6 or 10 using
the quadrature points and weights given in the parameter statements (see qp6,
qw6,qp10,qw10). The cross section and reaction rate are determined at each
quadrature point by interpolation, and the feed function is obtained by getff.
For many reactions, ff will be nonzero for only a certain range of secondary
groups. The value ig1 is the index to the first nonzero result, and ng1 is the
number of nonzero values of ff in the range. Subroutine panel maintains the two
corresponding values iglo and ng to specify the nonzero range of values in array
ans. Finally, the flux and cross section at the top of the panel are transferred
to flst and slst, and control is returned to the panel loop in groupr.
Subroutine displa is used to print cross sections and group-to-group matrices
on the output listing (nsyso). Small values are removed for efficiency. Note
that different formats are used in different circumstances. Infinitely dilute data
are printed without σ0labels. Isotropic matrices are printed with several final
groups on each line. Delayed neutron spectra are printed using the Legendre
order variable for time groups and with the time constants given on a heading
line.
Subroutine getflx returns nl*nz components of the weighting flux. If nsigz
is 1, the flux is computed using getwtf, and all Legendre orders are taken to be
equal. When self-shielding has been requested, the flux components are obtained
by interpolating between adjacent values retrieved with finda from the scratch
tape written by genflx. The grid energies found on the scratch tape are used
to get enext. The flux is taken to be continuous, so idis is always set to zero.
Subroutine getyld returns the yield needed by getff for fission (MT=452,
455, or 456 from File 1) or radionuclide production yields from File 9 (using
256 NJOY2016

8 GROUPR LA-UR-17-20093
mfd=3zzzaaam). This routine also retrieves the delayed neutron time constants
when mtd=455. Tabulated yields are obtained by interpolation using the utility
routine terpa. Polynomial data are expanded by direct computation.
Subroutine getsig returns nl*nz components of the cross section using point
data from the PENDF tape and self-shielded unresolved data, if present, from
getunr. The routine starts by adjusting MF and MT for the special options
(mtd=258-259, mfd=3zzzaaam, etc.) and locating the desired section on the
PENDF tape. Subroutine getsig is then called for each desired energy value
Ein increasing order. For mtd=258 or 259, the appropriate velocity or lethargy
is computed from Eand returned. In the more general cases, gety1 is used to
retrieve the pointwise cross section from the PENDF tape, and getunr is called
to replace this value with self-shielded unresolved cross sections if necessary.
The unresolved cross sections are handled using stounr and getunr. Subrou-
tine stounr locates the desired material and temperature in MF=2, MT=152 of
the PENDF tape, and then it copies the data into the global allocatable storage
array unr. The σ0grid on the PENDF tape does not have to agree with the
list requested for groupr, but a diagnostic message will be printed if they are
different. However, the ntemp values of temperature requested by groupr must
agree with the first ntemp temperatures on the PENDF tape, or a fatal error
will result. Subroutine getunr checks whether Eis in the unresolved energy
range and whether MT is one of the resonance reactions. If so, it locates the de-
sired interpolation range in the unr array, and interpolates for the self-shielded
cross sections. If this is an energy range where resolved and unresolved ranges
overlap, the resolved part is added to the background σ0before interpolation.
The subroutine terpu is used for interpolating in the unresolved cross section
tables. The special value MT=261 is used to select the `=1 component of the
total cross section. Note that getsig also uses this `=1 value for `=2,3, . . . .
Subroutine getff returns the feed function ff using different portions of the
coding for different options. The first section is used for cross sections and ratio
quantities. The same yield yld is returned for every `-component in ff.
The second section of getff is for neutron continuum transfer matrices.
The yield is either determined from MT [for example, yld=2 for MT=16, the
(n,2n) reaction], or it is obtained using getyld for fission. Next, the angular
distribution is obtained using getfle (see Fin Eq. 328), and the secondary
energy distribution is obtained using getsed (see gin Eq. 328). Finally, the
product of the three factors is loaded in ff. Note that the range of groups
returned extends from iglo=1 to the highest nonzero result, for a total of ng
NJOY2016 257

LA-UR-17-20093 8 GROUPR
groups. Since ff for these reactions is a smooth function of incident energy, nq
is set to zero, and no additional quadrature points will be used in panel.
The third section of getff is for gamma production matrices. The photon
yields are obtained using getyld. In general, there are nyl different yields, each
one corresponding to a different discrete gamma ray, or to the continuum. The
angular distributions for these gamma rays are obtained using getgfl (most
ENDF/B photons are given as isotropic). The energy distribution for the con-
tinuum (if any) is obtained by getsed. Now, the code loops through the pho-
ton group structure placing each discrete photon in the appropriate group and
adding in the continuum part. During this loop, the range of nonzero values
(iglo,ighi) is determined. Finally, the nonzero values are packed into ff, and
iglo and ng are returned to describe the distribution. Again, nq=0 is used.
The fourth section of getff handles two-body scattering, either elastic or
discrete-level inelastic, and both neutrons and charged particles. First, subrou-
tine parts is called to set up the particle type, A0value, and the scattering law
for reactions that use File 4. Then getdis is called to finish the processing.
The fifth section handles thermal-neutron scattering. The bulk of the work
is done by getaed, which is discussed below. Subroutine getff takes the output
of getaed and packs it into the final result, ff.
The last two sections of getff are used to process energy-angle distributions
from ENDF-6 format sections of File 6. The subroutine simply calls getmf6.
Subroutine parts is used to set up particles for reactions that use File 4.
Different branches are used for ENDF-6 and earlier ENDF versions because the
MT numbers used for charged-particle discrete levels have been changed. For
example, proton levels use MT=600-649 in ENDF-6 libraries, but MT=700-719
in earlier libraries. If mfd=3, no action is taken. For other mfd values, the
routine determines zap,aprime, and law. The result depends on whether File
4 or File 6 data are to be used.
Subroutine getmf6 is used to compute the feed function for reactions repre-
sented in File 6. As is common with NJOY subroutines, it is called with ed=0 to
initialize the subroutine. The first step is to locate the desired section of File 6
on the input ENDF tape. It then sets the parameter zad (for ZA desired) based
on the input value mfd and searches through the section for the desired subsec-
tion. If this subsection has law=4, it defines a recoil particle; the code backs
up to the first subsection in the section, which is assumed to be the subsection
describing the emitted particle. The subroutine has now arrived at statement
number 140, where it decides whether to branch to special coding for two-body
258 NJOY2016

8 GROUPR LA-UR-17-20093
reactions (statement number 500) or phase-space reactions (statement number
150). All the other options have a TAB2 record at this point that defines the
incident energy grid. For law=1, the data for the first incident energy are read
in and converted to the Lab frame by cm2lab. Similarly, for law=7, the data
are read in and converted to a law=1 format by ll2lab.
For a normal entry, getmf6 interpolates for the particle yield for the current
particle. For all of the laws except 2-5 (discrete two-body laws), it then checks
to see whether the energy ed is in the current panel (or if this is the first time
in the first panel). If not, it moves the high data to the low position and
reads in new high data. Of course, it also converts the new high data to the
correct form with cm2lab or ll2lab. Once ed is in the current panel, the code
reaches statement number 300, which sets up the loop over secondary energy
by initializing f6lab. This loop uses a grid that consists of the epnext values
returned by f6lab and the group bounds eg(i). The actual integral over E0
L
inside each group uses trapezoidal integration. The last step for laws 1, 6, and
7 is to add in the contributions to the feed function from discrete energies in
File 6. For the discrete two-body laws (2-5), the routine goes through statement
number 500, which simply calls getdis. For all laws, the last step is to check
the normalization of the feed function. If the error is large, a message is printed
out. In any case, the results are adjusted to preserve exact normalization.
Subroutine cm2lab is used to convert a CM distribution starting at inow in
cnow into a Lab distribution, which will be stored starting at jnow. This routine
generates a grid for the Lab secondary energy E0
Lby adaptive reconstruction.
The reconstruction stack is first primed with pL`(E, 0) as computed by f6cm
and pL`(E, E0
next) (also from f6cm), where the value E0
next is the value epnext
returned by the first call to f6cm. This panel is then divided in half, and the
value returned by f6cm is compared with the linear interpolate. If they agree
within 0.5% (see tol), this panel is converged. Otherwise, it is subdivided
further. When convergence has been achieved for this panel, a new panel is
chosen, and it is subdivided to convergence. When the entire range for E0
Lhas
been processed, the final parameters are loaded into the new File 6 record for
pL`(E, E0
L) (which starts at jnow in cnow), and the routine returns to getmf6.
Subroutine f6cm is used to compute the Legendre coefficients of the double-
differential scattering function p`(E→E0) in the Lab system from data given in
File 6 in the CM frame. The memory area cnow contains the raw data. It is
necessary to call the routine ep=0 for each new value of E. Thereafter, values
of ep can be requested in any order. This is required by the adaptive scheme
NJOY2016 259

LA-UR-17-20093 8 GROUPR
used to generate the Lab E0grid in cm2lab. The conversion uses Eqs. 361 -366.
On a normal entry with E0
L>0, the code computes the lower limit of the integral
µmin. It then sets up an adaptive integration over a panel starting at µ=1. The
value for E0
Cis computed using
E0
C= (1 + c2−2cµL)E0
L,(375)
which is based on Eq. 362, and either f6ddx or f6psp is called to compute
pC(E, E0
C, µC) and epnext. The lower limit of the integration panel is then
computed by setting E0
Cequal to epnext and solving for the CM cosine using
µC=µL−c
p1 + c2−2cµL
.(376)
Of course, the larger of this result and µmin is used as the lower bound of
the panel. Therefore, the adaptive integration operates on a nice continuous
function. It continues subdividing the µCgrid in this panel until convergence
is achieved within 0.5% for all Legendre orders. The lower bound of this panel
becomes the upper bound of a new panel, and a new lower bound is selected as
above. The integration is carried out over successive panels until µmin is reached.
When the calculation of the continuum part of pL` is finished for these values
of Eand E0
L, the routine checks for possible contributions from delta functions.
Next, the routine scans through the computed coefficients and zeros out any
small ones that may just be noise. Finally, it chooses a value for epnext and
returns.
Function f6ddx is used to compute the double-differential scattering function
f(E→E0, ω), where secondary energy E0and scattering cosine ωare in the CM
system. On entry, cnow contains the File 6 data for a particular value of E, and
f6ddx must be called once with ep=0 for each new value of E. Thereafter, ep
values can be requested in any order (this is required by the adaptive scheme
used to convert to the Lab system in f6cm). For a normal entry with ep>0, the
code searches for the panel in the data that contain the requested value of E0. If
lang=1 for this subsection of File 6, the data are already given as Legendre coef-
ficients, and the code simply interpolates for the desired results. If lang=2, the
data use the Kalbach-Mann scheme for representing the energy-angle distribu-
tion. This routine includes both the original Kalbach-Mann representation[59]
and the newer Kalbach representation[60]. It has been set to use the latter by
the parameter statement k86=1. The code interpolates for the model param-
eters at E0and computes the desired answer with the model’s formulas. The
260 NJOY2016

8 GROUPR LA-UR-17-20093
ENDF-6 format also allows CM distributions given as values tabulated versus
scattering cosine (see lang=11-15). Note that there is a “stub” to take special
action at low energies. It is currently disabled by the statement efirst=0.0,
but it may be used sometime in the future to account for the fact that the
low-energy dependence of the scattering function must vary as f(E0) = c∗√E0.
Function bach computes the Kalbach-86 aparameter, which depends on
the neutron separation energy for the target izat using the liquid-drop model
without pairing and shell terms. The formula used describes the reaction a+B→
C+d:
Esep = 15.68AC−AB
−28.07(NC−ZC)2
AC−(NB−ZB)2
AB
−18.56A2/3
C−A2/3
B
+ 33.22(NC−ZC)2
A4/3
C−(NB−ZB)2
A4/3
B
−0.717Z2
C
A1/3
C−Z2
B
A1/3
B
+ 1.211Z2
C
AC−Z2
B
AB,(377)
where Astands for atomic weight, Zfor charge number, and Nfor neutron
number. Note that, even for reactions like (n,2n), Cis the residual nucleus
resulting from the removal of one particle, d; it is not necessarily the real physical
residual nucleus for the reaction. If the target izat is an element, Esep has to
be computed for some dominant isotope in the element. Dominant isotopes
are assigned in this routine for some materials that often appear as elements
in ENDF evaluations; if the particular target required does not appear, a fatal
error message is issued. The user will have to add a line to the routine for the
material and reassemble the code.
Subroutine ll2lab converts File 6 from Law-7 format to Law-1 format using
the laboratory Legendre representation. Law 7 represents the double-differential
scattering distribution f(E→E0, µ) by giving a series of tables of f(E→E0) for
series of µvalues. On entry, the entire Law-7 section is stored in cstarting at
inow. The code loops through a set of E0values chosen to be the union of all
the E0grids for all the different µvalues. For each point on this union grid,
the code interpolates for all the corresponding f(µ) values, and it uses them to
NJOY2016 261

LA-UR-17-20093 8 GROUPR
compute nl Legendre coefficients f`(E0). After completing the calculation for
a new value of E0, it checks the normalization of the result, and then it checks
back to see whether the previous value is still needed to represent the curves
f`(E0) within a tolerance of 0.5%. The results are written in cstarting at jnow.
They have the Law-1 Legendre form, namely, sets of values E0,f0(E0), f1(E0),
. . . , fNL−1(E0), given for a series of E0values starting with zero.
Subroutine f6lab is used to return the Legendre coefficients of the double-
differential scattering function f`(E→E0) for particular values of Eand E0in
the Lab system (see eand ep) from a part of File 6 in Law-1 format. Since Law-
7 sections have been converted to Law-1 format using ll2lab, and since CM
sections in Law-1 format have been converted to the Lab frame using cm2lab,
the only two roles left for this subroutine are interpolation to the desired values
of Eand E0and preparation of Legendre coefficients for sections that use the
File-6 variant with law=1 and lang=11-15 (laboratory distributions tabulated)
vs. µ. Only the continuum portion of the distribution is processed here; any
delta functions given in File 6 must be handled separately. The routine is ini-
tialized by calling it with ep=0. Data for the two incident energy values that
bracket Eare already present in clo and chi. Then the routine extracts various
parameters from the carray and prepares the variables used to control inter-
polation. These variables are complicated, because this routine handles three
different interpolation schemes: “cartesian”, “unit base”, and “corresponding
point” (see the ENDF-6 manual[9] for more details). For a normal entry, the
code searches the data in clo and chi for the intervals containing E0. If lang=1,
it performs a two-dimensional interpolation for the nl coefficients at Eand E0.
For lang>1, it computes the Legendre coefficients from the File 6 data, and
then does the two-dimensional interpolation. Finally, it computes epnext and
returns.
Subroutine getdis is used to compute the feed function for elastic or discrete
inelastic scattering of neutrons or charged particles using either File 4 or File
6 data. First, the angular distribution is retrieved with getfle, and an appro-
priate quadrature order is selected using Eq. 319. Then, a group loop from low
energy to high energy is used to compute the ω1and ω2limits of Eq. 317, and
the range (ω1, ω2) is subdivided using the appropriate Gauss-Legendre quadra-
ture points (see qp4,qp8,qp12, and qp20). The function f(E, ω) is computed
at each of these quadrature points using Eq. 318 and the angular distribution
previously returned by getfle. The laboratory cosine at the quadrature point,
µω, is computed using Eq. 314. Finally, the integrand of Eq. 317 is multiplied
262 NJOY2016

8 GROUPR LA-UR-17-20093
by the appropriate quadrature weight (qw4,qw8,qw12, or qw20) and added into
the accumulating integral. This continues until ω2= 1. The nonzero values of
ff and the parameters iglo and ng are then complete for this value of E.
The next step is to determine enext based on the next critical point as given
by Eqs. 321 -324. Special cases are used for elastic scattering to avoid numerical
problems. Note that the discontinuity flag idisc is set for critical points. The
nq variable is also set to force panel to subdivide the initial-energy integration.
Subroutine getfle retrieves or computes the Legendre coefficients for the
angular distribution of a reaction at incident energy E. When called with e=0,
getfle requests storage for the raw data, reads in the File 4 information for
the first two incident energies on the file, and then uses getco to retrieve the
corresponding coefficients. On subsequent entries with e>0, getfle simply in-
terpolates for the desired coefficients. When eexceeds the upper energy in stor-
age, the values for the upper energy are moved to the lower positions, and new
upper values are read and converted to coefficients. An isotropic distribution is
returned if eis outside the range of the angular data from File 4.
Subroutine getaed retrieves angle-energy data for thermal scattering reac-
tions. For coherent elastic scattering, the routine reads through the cross section
on the PENDF tape using gety1 and locates the Bragg edges. On each subse-
quent call to getaed, the Legendre components of the cross section are computed
using Eq. 309. For incoherent elastic scattering, the routine is first initialized
by reading in the raw data for the first energy. On subsequent entries, a test is
made to see whether eis in the range elo to ehi. If not, the high data are moved
to the low positions, and new high data are read. The Legendre components
are then computed using Eq. 311. For incoherent inelastic scattering, getaed
is initialized by reading in the raw data for the first two incident energies. On
subsequent entries, the subroutine checks to see whether eis between elo and
ehi. If not, the data for ehi are moved to the low positions, and new raw data
are read from File 6 and binned. Once the correct data are in place, the desired
energy-angle distribution is computed by using a combination of interpolation
along lines of constant energy transfer and unit-base interpolation.
Subroutine getgfl returns the Legendre coefficients for the angular distri-
butions for all discrete and continuum photons for a reaction simultaneously.
When called with ed=0, the routine reads File 14 into scratch storage and finds
the starting location for the subsection describing each photon. On subsequent
entries with ed>0, getgfl sets up a loop over the ng photons on this section
of File 14. For each photon, it searches for the energy panel that contains ed,
NJOY2016 263

LA-UR-17-20093 8 GROUPR
uses getco to retrieve or compute the Legendre coefficients at the upper and
lower File 14 energies, and interpolates for the desired coefficients at ed using
terp1. Since most ENDF photons are represented as isotropic, a special short-
cut calculation is provided for that case. Isotropic results are also returned if
ed is outside the range of the data in File 14.
Subroutine getco is used by both getfle and getgfl to retrieve or compute
Legendre coefficients from data in File 4 or File 14 format. The user can request
output in either the Lab or CM system, and the raw data can be either Legendre
coefficients or tabulated probability versus emission cosine. However, if the raw
data are in the laboratory system, CM coefficients cannot be produced. If the
raw data are already in the form of coefficients in the desired system, getco
simply checks for the maximum Legendre order needed using a tolerance of
toler=1e-6 and returns the coefficients in fl and the order in nl. If coordinate
conversion is required, or if the raw data are tabulated, getco sets up the integral
over cosine using Gauss-Legendre quadrature of order 20 (see qp and qw). The
scattering probability for the quadrature point is computed from the coefficients
or obtained by interpolating in the tabulation. The Legendre polynomials in
the desired reference system are then computed. If the raw data are in the CM
system (ω) and the result is to be in the Lab system (µ), the desired polynomials
are P`(µω); otherwise, the quadrature angle is used directly to compute the
polynomials. Once the coefficients have been computed, they are checked using
toler to determine the maximum order, nl, and the results are returned in fl.
Subroutine getgyl is used to retrieve the yields for all photons emitted in a
specified reaction simultaneously. The raw data are obtained from the ENDF/B
tape as either yields (MF=12) or production cross section (MF=13). In the lat-
ter case, getgyl actually returns the fraction of the total yield assigned to each
photon. The cross section returned by getsig is the total photon production
cross section from MF=13 on the PENDF tape, which makes the resulting in-
tegral correct. Using the normal GROUPR procedure, getgyl is initialized by
calling it with ed=0. The entire File 12 or File 13 is read into scratch storage,
and the starting location for each subsection is determined. On subsequent en-
tries (ed>0), the routine loops over the nyl photons found, and uses terpa to
compute the yield at ed. If this is a primary photon, a discontinuity is set up at
the energy where the photon will change groups. For MF=12, the calculation is
finished. For MF=13, the numbers calculated above are converted to fractions
of the total yield by dividing by the total production subsection from File 13.
This routine does not handle ENDF/B transition probability arrays directly,
264 NJOY2016

8 GROUPR LA-UR-17-20093
because they will have been converted to File 12 yields by conver.
Subroutine conver converts ENDF/B evaluations to a standard form. If
transition probability arrays were used in File 12, they are converted to yields
and written back into File 12. If a section with MF=1 and MT=456 is missing
from the evaluation, a copy of MT=452 is added to the tape as MT=456. In
addition, a second copy of the modified tape is made on unit nscr. While conver
is reading through the tape, lists of the reactions in File 4, File 12, and File 13
are written to to global arrays for use by the automatic reaction selection logic in
nextr. For ENDF-6 evaluations containing File 6, the routine scans through File
6 looking for sections that produce neutrons, photons, or charged particles. The
MT numbers for these sections are stored into mf6,mf18, and mf6p. The routine
also checks for sections of File 4 containing charged-particle angular distributions
and records their MT numbers in mf4r. Finally, if the section MF=6/MT=2
contains charged-particle elastic scattering information given using the nuclear-
plus-interference format, it is converted into the residual-cross-section format
for getdis.
Subroutine getsed returns the secondary-energy distribution for neutrons or
continuum photons for all groups simultaneously. Both tabulated and analytic
functions are handled. getsed is initialized for a particular reaction by calling it
with ed=0. First, scratch storage is allocated, and all the subsections are read in.
Analytic subsections are left in their raw form, but tabulated subsections are
averaged over outgoing energy groups for each of the given incident energies.
The array loc contains pointers for each subsection. On subsequent entries
(ed>0), getsed loops over the subsections for this reaction. It first retrieves
the fractional probability for the subsection using terpa. If an analytic law
is specified, anased is used to compute the group integral for each secondary-
energy group. Each integral is multiplied by the fractional probability for the law
and accumulated into sed. For tabulated data, the routine simply interpolates
between the two values for the group integrals using terp1, and accumulates
them into sed. Note that various restrictions on the ordering of subsections
and prohibition of multiple tabulated subsections needed for earlier versions of
GROUPR are no longer required. Upscatter is not allowed in secondary-energy
distributions except for fission or photon production. If found, it is put into the
“in-group” (g0=g).
Subroutine anased is used to calculate the integral from e1 to e2 for one of
the analytic laws (see Eqs. 331 -360). The routine uses the SLATEC version of
the reduced complementary error function from the NJOY2016 math module.
NJOY2016 265

LA-UR-17-20093 8 GROUPR
The resulting integral is returned in g.
Subroutine hnab is used to compute the special functions required for analytic
law 11, the energy-dependent Watt spectrum. The method used is described in
the BROADR chapter of this manual.
8.20 Error Messages
The fatal error messages and warning messages from GROUPR are listed below,
along with recommended actions to recover from the problem.
error in groupr***unable to find mat=---, t=---.
Check for input error or wrong PENDF tape mounted.
error in groupr***photons not allowed with igg=0.
In order to produce photon data, a photon group structure must be re-
quested. Check the input on card 2.
error in groupr***illegal mfd.
Check input mfd; legal values are 3, 5, 6, 8, 12, 13, 16, 17, 18, 21-26, 31-36,
and the isotope production values like Xzzzaaam for X = 1, 2, 3 or 4.
message from groupr---auto finds no reactions for mf=--.
An automatic reaction selection card of the form “mfd” was given in the
input, but the ENDF and PENDF tapes do not contain any sections that
would produce the desired cross sections or matrices.
error in groupr***unable to find next temp.
The current material ended before the requested temperature was found.
error in ruinb***illegal ismooth.
Check the input, the value for the smoothing option must be either 0 or 1.
error in gengpn***read-in group structure is out of order.
Group structures must be given in ascending energy order.
error in gengpn***illegal group structure.
Check input; current legal values are 1 through 23.
error in gengpg***illegal group structure.
Check input; current legal values are 1 through 10.
error in genwtf***exceeded storage reading user weight function
See the allocatable array tmp with length ntmp=10000.
error in genwtf***illegal weight function.
Check input; current legal values are −12 through +12.
error in genflx***total not defined over energy range.
A complete total cross section is needed for self-shielding. This means that
“dosimetry” and “activation” tapes, which normally give only a few key
reactions, can only be processed using nsigz=1 (infinite dilution).
266 NJOY2016

8 GROUPR LA-UR-17-20093
error in getfwt***temperature ...
The requested temperature could not be found while searching the tape.
NJOY uses a tolerance of 1e-6 for this purpose.
error in getfwt***e outside range of data.
A premature end-of-file was found on the input flux tape when using the
iwt=0 option. Check to be sure the tape was the output from a legal flux
calculator run.
error in getfwt***requested e is out of order.
The cause could be an improper input tape. Check as above.
error in panel***elo.gt.ehi.
This indicates some error in the energy grid for panel. It usually oc-
curs if rndoff and delta are incorrect for your machine. Make sure that
rndoff>1, that delta<1, and that the product rndoff*delta<1 when
evaluated on your machine (for example, 1.00000001 is not greater than
unity on a 32-bit machine).
error in panel***bad nq in panel
The nq parameter can be 2, 6, or 10 with the currently installed quadra-
tures.
message from panel---thermal range problem at ...
NJOY expected scattering to a specific group but found another instead.
error in getyld***illegal lnd.
The maximum number of time groups is 8. See global array dntc(8).
error in getyld***unable to find nuclide for iza=... lfs=...
Unable to find requested nuclide production yield.
error in getsig***illegal mt.
Check input for mtd.
error in getsig***can’t find mf,mt,lfs ...
Check input for mfd greater than 10000000.
message from stounr---no unresolved sigma zero data....
This message probably means that UNRESR or PURR was never run for
this material. Infinitely dilute values will be used.
message from stounr---sigma zero grids do not match....
The unresolved calculations will probably work best if the σ0grid in GROUPR
matches the one in UNRESR or PURR. However, this is not necessary.
getunr will interpolate to get values on the GROUPR grid from the UN-
RESR or PURR grid. A message is issued in case this isn’t what the user
really intended.
error in stounr***storage exceeded.
There is not enough storage for unresolved cross section data on PENDF
tape. The allocatable array tmp has length ntmp=10000.
NJOY2016 267

LA-UR-17-20093 8 GROUPR
error in stounr***cannot find temp=---
The list of temperatures requested for the GROUPR run must agree with
the first ntemp temperatures on the PENDF tape. Check your BROADR
and UNRESR or PURR runs.
message from getunr---Warning, negative URR cross sections found
NJOY found negative cross sections for the unresolved energy range from
UNRESR.
error in getff***do not know how to handle mf,mt ...
The getff routine branches to different blocks of coding for different com-
binations of mfd and mtd, but if no appropriate branch is found for the
current values, this error message is issued. It probably indicates an error
in the evaluation.
error in getmf6***desired particle not found.
The outgoing particle for a group-to-group matrix is implied by the value
of mfd (for example, protons for mfd=21). This message means that the
section of File 6 requested with mfd and mtd does not contain a subsection
that produces that particle. Check the user input. This message should
not occur with automatic reaction selection.
error in getmf6***illegal law.
The value of the law parameter is greater than 7. This implies an error in
the evaluation.
error in getmf6***too many subsection energy points.
Limited by the parameter maxss=500.
error in getmf6***storage exceeded.
See the allocatable array temp with length ntmp=990000.
message from getmf6---bad grids for corresponding point ...
Corresponding-point interpolation won’t work correctly unless the two grids
above and below the point of interest have the same number of points. This
message means that there is an error in the evaluation.
error in getmf6***too many subsections for one particle.
We currently allow for no more than three. See iyss(3),izss(3), and
jss(3).
message from getmf6---there are multiple subsections in mf6
This warning message is issued when a specific particle has multiple sub-
sections in an mf6 section.
error in cm2lab***storage exceeded.
This means that the allocatable array tmp with length ntmp=990000 in
subroutine getmf6 has run out of space.
message from cm2lab---lab normalization problem mt=... e=...
This warning message is issued when the integral after normalisation to
the lab system is different from 1 by more than 1%.
268 NJOY2016

8 GROUPR LA-UR-17-20093
error in f6ddx***illegal lang.
The value of lang for tabulated angular distributions must be in the range
11-15.
message from cm2lab---vertical segment(s) in distribution
There appears to be a jump in the energy dependent multiplicity for the
outgoing particle at a given incident energy. This message is only given
when Kalbach-Mann systematics are used. This is most likely an evaluation
problem.
error in bach***dominant isotope not known.
The calculation of the neutron separation energy needed for the Kalbach
model for particle energy-angle distributions needs a value for the dominant
isotope in an element. It will have to be added to the code. The same
problem will occur with the parallel routines in HEATR and ACER.
error in ll2lab***storage exceeded.
This means that the allocatable array tmp with length ntmp=990000 in
subroutine getmf6 has run out of space.
error in f6cm***nl>mxlg
The current limit is mxlg=65.
error in f6ddx***nl>mxlg
The current limit is mxlg=65.
error in f6lab***illegal lang.
The value of lang must be equal to 1 or be in the range 11–15 for tabulated
angular distributions.
error in f6dis***illegal lang.
The value of lang must be equal to 1 or 2, or be in the range 11–15 for
tabulated angular distributions.
error in getdis***illegal nqp
The allowed quadrature orders are 4, 8, 12, and 20.
error in getfle***desired energy above highest energy given
Should not occur for well-constructed ENDF files. Check the evaluation to
be sure File 3 and File 4 are consistent.
message from getfle---lab distribution changed to cm for mt=...
Angular distributions for two-body reactions are supposed to be given in
the CM frame by ENDF conventions. Some old evaluations for heavy
materials violate this rule; changing to the CM frame has little effect on
the answers.
error in getaed***thermal mf6/law7 not coded
This subroutine can’t handle the E-µ-E0ordering option provided by THERMR.
error in getaed***storage exceeded.
This refers to the allocatable array aes with length maxaes=200000.
NJOY2016 269

LA-UR-17-20093 8 GROUPR
error in getgfl***too many gammas.
See the parameter maxgfl=500.
error in getgfl***storage exceeded.
See the parameter ntmp=10000.
error in getgfl***desired energy at highest given energy.
This problem should not occur in a well-constructed ENDF file. Check
Files 3, 12, 13, and 14 for consistency.
error in getco***limited to 64 legendre coefficients.
See nlmax=65 and P(65).
error in getco***lab to cm conversion not coded.
The need for this type of conversion rarely occurs on the current ENDF
evaluations, because CM is consistently used for two-body reactions, and
the laboratory frame is consistently used for continuum reactions. There
are a few exceptions for the heavy isotopes, where CM and lab are essen-
tially equivalent, but they were errors when the files were generated.
error in getgyl***lo=2 not coded.
This message should not occur, because any transition probability arrays
on the ENDF tape should have been converted to yields by conver.
error in getgyl***too many gammas.
The current limit is 550 photons. See the parameter nylmax=550.
error in getgyl***storage exceeded.
This refers to the allocatable array tmp with length ntmp=15000.
message from conver---cannot do complete particle production...
With the advent of the ENDF-6 format, it is possible to make evaluations
that fully describe all the products of a nuclear reaction. Some carry-over
evaluations from earlier ENDF/B versions also have this capability, but
many do not. This message is intended to goad evaluators to improve
things!
message from conver---gamma production patch made for ...
This patch is used to correct the old ENDF/B-III evaluations for MAT=1149
and MAT=1150 (chlorine and potassium).
message from conver---mf12, mt ... may be missing
This message indicates that the discrete photon data in mf12 for this mt
number may be missing or be incomplete.
error in conver***nnth too large
See mxnnth=350.
message from conver---skipping new mf6/mt18 multiplicity section
Starting with ENDF/B-VIII.0, fission neutrons and photons can now be
described using probability functions for emitting 0, 1, 2, ... particles per
fission. This data can currently not be included in any multigroup or
continuous energy format so the data is simply skipped.
270 NJOY2016

8 GROUPR LA-UR-17-20093
error in conver***too many lo=2 gammas.
The LO=2 processing uses a set of allocatable arrays that are sized using
lmax=500. That number can be increased freely, if necessary.
error in conver***storage for fission nu exceeded.
The storage in the allocatable array nu is sized using nnu=6000, which can
be increased freely.
error in conver***xxxx to big.
The automatic processing of reactions is controlled by lists stored in global
arrays like mf4 or mf6p. This error occurs when one of the particular
indexes, indicated by “xxx” exceeds maxr1=500. The arrays for MF=10
(see imf10) have a limit of maxr2=500.
error in getsed***too many subsections.
The current limit is 20. See the parameter nkmax=20.
error in getsed***storage tmp exceeded.
The input ENDF data are stored in the allocatable array tmp with length
ntmp=50000. An integer will be included in this message to indicate where
exactly in the source code this message was issued.
message from getsed---corresponding point interpolation ...
The interpolation schemes corresponding to the range 11–15 are not sup-
ported.
message from getsed---upscatter correction....
This reaction should not have upscatter. The error is placed into the in-
group element.
error in anased***illegal lf.
Legal values are 5, 7, 9, 11, and 12.
error in f6psp***3, 4, or 5 particles only.
Phase-space formulas for 3, 4, or 5 particles are provided in this routine.
Check for an error in the evaluation.
NJOY2016 271

LA-UR-17-20093 8 GROUPR
272 NJOY2016

9 GAMINR LA-UR-17-20093
9 GAMINR
The GAMINR module of NJOY is designed to produce complete and accurate
multigroup photoatomic (but not photonuclear) cross sections from ENDF/B-IV
and later data[68], including the newer formats developed for ENDF/B-VII. To-
tal, coherent, incoherent, pair-production, and photoelectric cross sections can
be averaged using a variety of group structures and weighting functions. The
Legendre components of the group-to-group coherent and incoherent scattering
cross sections are calculated using the form factors[69] now available in ENDF/B.
These form factors account for the binding of the electron in its atom. Conse-
quently, the cross sections are accurate for energies as low as 1 keV. GAMINR
also computes partial heating cross sections or kinetic energy release in materials
(KERMA) factors for each reaction and sums them to obtain the total heating
factor. The resulting multigroup constants are written on an intermediate in-
terface file for later conversion to any desired format. Photonuclear reactions
such as (γ,n) are not computed by this module.
GAMINR differs from the previously used GAMLEG code[23] in the following
ways:
•Coherent form factors are processed thereby allowing higher Legendre com-
ponents of the coherent scattering cross section to be produced. GAMLEG
processed the P0cross section only.
•Incoherent structure factors are processed giving accurate results at low
energies where the Klein-Nishina formula fails.
•Heat-production cross sections (KERMA factors) are generated.
•Variable dimensioning and dynamic storage allocation allow arbitrarily
complex problems to be run.
•GAMINR is much slower than GAMLEG since charge scaling of the inco-
herent matrix can no longer be used at all energies.
This chapter describes the GAMINR module in NJOY2016.0.
9.1 Description of ENDF/B Photon Interaction Files
In the ENDF/B-IV and later photon interaction files, the coherent scattering of
photons by electrons is represented by
σC(E, E0, µ)dE0dµ =3σT
8(1 + µ2)|F(q, Z)|2δ(E−E0)dE0dµ , (378)
where Eis the energy of the incident photon, E0is the energy of the scattered
NJOY2016 273

LA-UR-17-20093 9 GAMINR
photon, µis the scattering cosine, σTis the classical Thomson cross section
(0.66524486 b), Zis the atomic number of the scattering atom, and Fis the
atomic form factor. The coherent form factor is a function of momentum transfer
qgiven by
q= 2kr1−µ
2,(379)
where kis the energy in free-electron units (k=E/511003.4 eV), but Fis
actually tabulated versus the quantity x= 20.60744q. The coherent form factor
is given as MT=502 in File 27.
Incoherent scattering is represented by the expression
σI(E, E0, µ)dE0dµ =S(q, Z)σKN (E, E0, µ)dE0dµ , (380)
where Sis the incoherent scattering function and σKN is the free-electron Klein-
Nishina cross section
σKN (E, E0, µ) = 3σT
8k2k
k0+k0
k+ 21
k−1
k0+1
k−1
k02.(381)
The scattering angle and momentum transfer for incoherent scattering are given
by
µ= 1 + 1
k−1
k0,(382)
and
q= 2kr1−µ
2p1+(k2+ 2k)(1 −µ)/2
1 + k(1 −µ).(383)
As was the case for coherent scattering, S(q, Z) is actually tabulated vs. x=
20.60744q. It is important to note that Sis essentially equal to Zfor xgreater
than Z. The incoherent scattering function is given as MT=504 in File 27.
The ENDF/B-IV and later photon interaction files also contain tabulated
cross sections for total, coherent, incoherent, pair production, and photoelectric
reactions. They are given in File 23 as MT=501, 502, 504, 516, and 602 respec-
tively (note however, starting with the ENDF/B-VI files, MT=602 data appear
274 NJOY2016

9 GAMINR LA-UR-17-20093
in MT=522). The coherent and incoherent cross sections were obtained by the
evaluator by integrating Eqs. 378 and 380 and are therefore redundant. Due care
must be taken to avoid introducing inconsistencies. Starting with ENDF/B-VI,
there are additional cross sections given for the partial photoelectric reactions
starting with MT=534.
9.2 Calculational Method
The multigroup cross sections produced by GAMINR are defined as follows:
σxg =Rgσxφ0(E)dE
Rgφ0(E)dE ,(384)
σT `g =RgσT(E)φ`(E)dE
Rgφ`(E)dE ,and (385)
σx`g→g0=RgFx`g0(E)σx(E)φ`(E)dE
Rgφ`(E)dE .(386)
In these expressions, grepresents an energy group for the initial energy E,g0is
a group of final energies E0,xstands for one of the reaction types, Tdenotes
the total, and φ`is a Legendre component of a guess for the photon flux. In the
last equation, Fis the “feed function”; that is, the total normalized probability
of scattering from Einto group g0. The feed function for coherent scattering is
FC`g0(E) = R+1
−1σC(E, E0, µ)P`(µ)dµ
σC(E)
=R+1
−1(1 −µ2)|F(x)|2P`(µ)dµ
R+1
−1(1 −µ2)|F(x)|2dµ ,(387)
for Ein g0and zero elsewhere.
Here P`(µ) is a Legendre polynomial. Note that FC0g0= 1; this form as-
sures that the coherent scattering cross sections are consistent with the values
tabulated in File 23.
For incoherent scattering,
FI`g0=Rg0S(q, Z)σKN (E, E0, µ)P`(µ)dE0
Rg0S(q, Z)σKN (E, E0, µ)dE0.(388)
NJOY2016 275
LA-UR-17-20093 9 GAMINR
Because Sis simply equal to Zfor high values of q, it is not necessary to com-
pletely recompute the incoherent matrix when processing a series of elements in
the order of increasing Z. GAMINR automatically determines that some groups
for element Znow can be obtained from element Zlast by scaling by Znow/Zlast.
Finally, pair-production is represented as a (γ, 2γ) scattering event, where
FP P `g0(E) = (2,if g0includes 511003.4 eV;
0,otherwise . (389)
In addition, GAMINR computes multigroup heating cross sections or KERMA
factors as follows:
σHxg =Rg[E−Ex(E)] σx(E)φ0(E)dE
Rgφo(E)dE ,(390)
where Ex(E) is the average energy of photons scattered from Eby reaction type
x. The average energies are computed using
EC=E , (391)
EP P = 1.022007 ∗106eV ,(392)
EP E = 0,and (393)
EI(E) = Z∞
0
E0σI(E, E0, µ)dE0/ σI(E).(394)
These separate contributions to the heating cross section are summed to get a
quantity that can be combined with a calculated flux to obtain the total heating
rate.
9.3 Integrals Involving Form Factors
The integrals of Eqs. 387 and 388 that involve the form factors are very difficult
to perform because of the extreme forward peaking of the scattering at high
energies. Fig. 34 illustrates the problem for coherent scattering.
For coherent scattering, the integral of Eq. 387 is broken up into panels by the
tabulation values of x. Each panel is integrated in the xdomain using Lobatto
quadrature of order 6 for `= 3 or less and order 10 for larger Legendre orders.
Eq. 379 is used to compute the µvalue for each xand to obtain the Jacobian
required.
Since µis quadratic in x, the polynomial order of the integrand in the nu-
merator of Eq. 387 is 2`+ 2 plus twice the polynomial order of Fin the panel.
276 NJOY2016
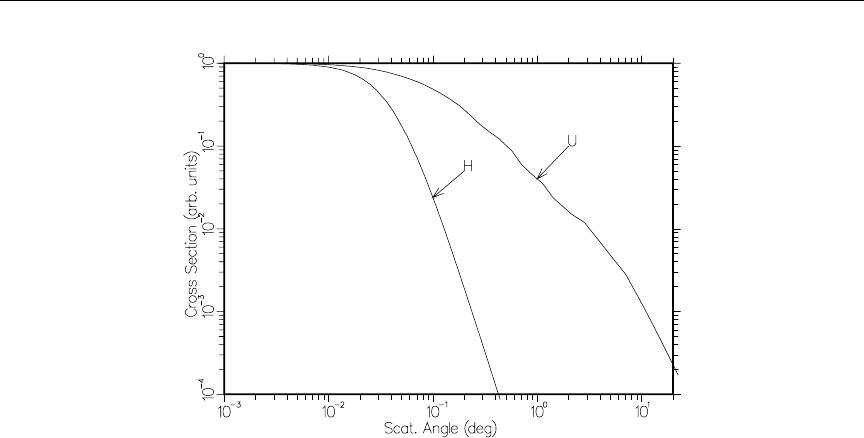
9 GAMINR LA-UR-17-20093
Figure 34: Angular distribution for coherent scattering from hydrogen and uranium at high
photon energy.
For `= 3, the theory of Gaussian quadrature implies that the integral will be
exact if Fcan be represented as a quadratic function over the panel.
The incoherent integral of Eq. 388 is also broken up into panels, but here the
panels are defined by the union of the tabulation values of xand the momenta
corresponding to the secondary-energy group bounds. The relationship between
x,µ, and secondary energy is given in Eqs. 382 and 383. This time, the integral
is performed vs. E0using Lobatto quadrature of order 6 for `less than or equal
to 5 and order 10 for larger `values.
All form factors and structure factors are interpolated using ENDF/B log-log
interpolation as specified by the format. However, the cross sections in the file
were evaluated using a special log-log-quadratic scheme. Ignoring this compli-
cation may lead to a 5% error in the incoherent cross section at 0.1 keV with a
negligible error at the higher energies that are of most practical concern[69].
9.4 Coding Details
The main entry point is subroutine gaminr exported by module gaminm. The
code begins by reading the user’s input. It then locates the position for the new
material on the old GENDF tape (if any) and copies the earlier results to the
new output tape. The desired material is also located on the input PENDF tape
prepared previously using RECONR. A new material header is then written onto
the output tape leaving the code ready to begin the loop over reaction types.
NJOY2016 277

LA-UR-17-20093 9 GAMINR
For each of the preset reaction types, GAMINR uses the panel logic of
GROUPR to average the cross sections (see the “panel” discussion in Sec-
tion 8.11). If this is the first material in a series of elements, the incoherent
matrix is saved to a scratch area. For subsequent materials, the higher energy
matrix elements are obtained by scaling these saved values by the appropriate
Zratio. The resulting cross sections and group-to-group matrix elements are
then printed out and written to the output tape. The heat production contri-
bution from each reaction is summed into a storage area. After all reactions
have been processed for this material, a special pass through the output logic is
used to create a heating section using MT=525 for ENDF/B-VI and later files
or MT=525 for earlier ENDF/B files. Finally, the rest of the old output tape is
copied to the new output tape. A description of the format of the multigroup
output tape will be found in the GROUPR chapter (see Section 8.17).
As with panel in GROUPR,gpanel integrates the triple product F∗σ∗φ.
The feed into secondary group g0for Legendre order `from initial energy Eis
computed in gtff as described in Section 9.3 above. Cross sections are read
from the PENDF tape (see gtsig). Flux can be read in, constant, or 1/E with
high and low energy roll-offs (see gnwtf and gtflx).
9.5 User Input
The following description of the user input is reproduced from the comment
cards at the beginning of the GAMINR module.
!---input specifications (free format)---------------------------
!
! card1
! nendf unit for endf tape
! npend unit for pendf tape
! ngam1 unit for input ngam tape (default=0)
! ngam2 unit for output ngam tape (default=0)
! card2
! matb material to be processed
! input materials in ascending order
! igg gamma group structure option
! iwt weight function option
! lord legendre order
! iprint print option (0/1=minimum/maximum) (default=1)
! card3
278 NJOY2016

9 GAMINR LA-UR-17-20093
! title run label up to 80 characters (delimited by ’,
! ended with /)
! card4 (igg=1 only)
! ngg number of groups
! egg ngg+1 group bounds (ev)
! card5 (iwt=1 only)
! wght read weight function as tab1 record,
! this may span multiple lines and ends with a /.
! card6
! mfd file to be processed
! mtd section to be processed
! mtname description of section to be processed
! repeat for all reactions desired
! mfd=0/ terminates this material
! mfd=-1/ is a flag to process all sections present
! for this material (termination is automatic)
! card7
! matd next mat number to be processed
! terminate gaminr run with matd=0.
!
!---options for input variables----------------------------------
!
! igg meaning
! --- -------
! 0 none
! 1 arbitrary structure (read in)
! 2 csewg 94-group structure
! 3 lanl 12-group structure
! 4 steiner 21-group gamma-ray structure
! 5 straker 22-group structure
! 6 lanl 48-group structure
! 7 lanl 24-group structure
! 8 vitamin-c 36-group structure
! 9 vitamin-e 38-group structure
! 10 vitamin-j 42-group structure
!
! iwt meaning
! --- -------
! 1 read in smooth weight function
! 2 constant
! 3 1/e + rolloffs
!
NJOY2016 279

LA-UR-17-20093 9 GAMINR
!------------------------------------------------------------------
The weight options allowed by GAMINR are a user defined function, a con-
stant weight option and a 1/E option with high and low energy roll-offs. For
more information, see the weight options in the GROUPR module.
Note that both an ENDF/B tape and a PENDF tape from RECONR are re-
quired. Older, pre-ENDF/B-VI, photon interaction tapes are available from the
Radiation Shielding Information Computational Center (RSICC) at ORNL as
DLC7E (for ENDF/B-IV) or DLC-99/HUGO (for ENDF/B-V). A photoatomic
library in ENDF-6 format based on DLC-99 is available from the National Nu-
clear Data Center (NNDC) at the Brookhaven National Laboratory. The latest
photoatomic library is also available from the NNDC. Material numbers (matb)
are simply the element Znumber for versions IV and V; they are equal to 100∗Z
for ENDF-6 formatted files. The values of matd on card 7 should be given in
increasing order for maximum economy. The normal mode of operation uses
mfd=−1. This automatically processes MT=501, 502, 504, 516, 522, and 525.
For pre-ENDF-6 formatted files, the photoelectric cross section is changed from
522 to 602, and the heating cross section is changed from 525 to 621.
The following sample run prepares a GENDF tape for two elements. The
numbers on the left are for reference; they are not part of the input.
1. reconr
2. 20 21/
3. ’pendf tape for 2 elements from ENDF/B-VII’/
4. 100 1 0/
5. .001 0./
6. ’1-hydrogen’/
7. 9200 1 0/
8. .001 0./
9. ’92-uranium’/
10. 0/
11. gaminr
12. 20 21 0 22/
13. 100 7 3 4 0/
14. ’24-group photon interaction library’/
15. -1/
16. 9200/
17. -1/
280 NJOY2016

9 GAMINR LA-UR-17-20093
18. 0/
19. stop
On line 2, an ENDF/B tape containing File 23 has been mounted on logical
unit 20. The title on line 3 will appear on the PENDF tape. Material 100
is hydrogen (lines 4-6) and material 9200 is uranium (lines 7-9). The element
names on lines 8 and 11 will appear on the PENDF tape in MF=1,MT=451.
Linearization is accurate to better than 0.1%. A more complete description of
RECONR’s input may be found in Section 3.6.
GAMINR uses the same ENDF tape as RECONR (actually only MF=27 is
read by GAMINR), but GAMINR also reads the RECONR output tape on unit
21. The GAMINR GENDF tape will be on unit 22. Card 13 specifies hydrogen
as the first material, 24 groups, 1/E weight with roll-offs, Legendre components
through P3, and the full printed output. Cards 16 and 17 select the default
list of reaction types. Card 16 specifies uranium as the second material to be
processed, and line 18 terminates the element loop and the GAMINR run.
Figs. 35 and 36 illustrate plots of the results of this sample run. These graphs
were made using the DTFR and VIEWR modules.
Starting with ENDF/B-VI, the photon interaction (or photoatomic) files con-
tain detailed photoelectric cross sections, not just the MT=522 total photoelec-
tric cross section. These photoelectric cross sections have MT numbers starting
with 534. As an example, Fig. 37 shows the first 9 partial cross sections for
uranium — the K, L, and M subshells — taken from ENDF/B-VII. GAMINR
input is somewhat more complicated when these reactions are included because
they are different for every element.
9.6 I/O Units
There are no scratch files used in GAMINR. The only restriction on the files
assigned on line 1 of the user input is that ngam1 and ngam2 must be in the
same mode (that is, both binary or both formatted).
9.7 Error Messages
error in genggp***illegal group structure
Values of IGG must lie between 1 and 10.
error in genggp***too many groups.
NJOY2016 281
LA-UR-17-20093 9 GAMINR
U PHEAT
104105106107108
Energy (eV)
106
107
108
109
1010
Cross Section (barns)
M.G.
U ABSORP
104105106107108
Energy (eV)
100
101
102
103
104
105
Cross Section (barns)
M.G.
U TOTAL
104105106107108
Energy (eV)
100
101
102
103
104
105
Cross Section (barns)
M.G.
MT501
MT502
MT504
MT516
MT522
U L=0 PHOT-PHOT TABLE
1
0
0
1
0
1
1
0
2
1
0
3
X
s
e
c
1
0
4
1
0
5
1
0
6
1
0
7
1
0
8
S
e
c
.
E
n
e
r
g
y
1
0
4
1
0
5
1
0
6
1
0
7
1
0
8
E
n
e
r
g
y
(
e
V
)
Figure 35: Plots of the photon interaction cross sections and the photon scattering distri-
bution for uranium showing both 24-group and continuous cross sections. Note
the prominent photoelectric absorption edge near 100 keV.
H PHEAT
104105106107108
Energy (eV)
101
102
103
104
105
106
107
Cross Section (barns)
M.G.
H ABSORP
104105106107108
Energy (eV)
10-6
10-5
10-4
10-3
10-2
10-1
100
Cross Section (barns)
M.G.
H TOTAL
104105106107108
Energy (eV)
10-2
10-1
100
101
Cross Section (barns)
M.G.
MT501
MT502
MT504
MT516
MT522
H L=0 PHOT-PHOT TABLE
1
0
-
3
1
0
-
2
1
0
-
1
1
0
0
X
s
e
c
1
0
4
1
0
5
1
0
6
1
0
7
1
0
8
S
e
c
.
E
n
e
r
g
y
1
0
4
1
0
5
1
0
6
1
0
7
1
0
8
E
n
e
r
g
y
(
e
V
)
Figure 36: Plots of the photon interaction cross sections and the photon scattering distri-
bution for hydrogen showing both 24-group and continuous cross sections. The
cross sections are simpler for this case.
282 NJOY2016
9 GAMINR LA-UR-17-20093
Photoatomic cross sections
Uranium photoelectric subshells
103104105106107108
Photon Energy (eV)
10-2
10-1
100
101
102
103
104
105
106
Cross section (barns)
Figure 37: The first nine photoelectric subshell cross sections for uranium from ENDF/B-
VII.0. Black is the S subshell (1s1/2), red is the L1, L2, and L3 subshells (2s1/2,
2p1/2, 2p3/2), and green is the M1 through M5 subshells (3s1/2, 3p1/2, 3p3/2,
3d3/2, 3d5/2).
Increase the size of the global array egg by changing the parameter ngmax=400
located at the start of the module.
error in gnwtf***illegal iwt
Values of iwt must lie between 1 and 3.
error in gpanel***elo gt ehi.
There is something wrong with the energy grids during integration over
incident energy. This usually means there is a problem with the choice of
rndoff and/or delta. Be sure that rndoff<1, delta>1, and rndoff*delta<1
as represented on your machine.
ERROR IN GTFF***ILLEGAL FILE TYPE.
Only files 23 and 26 can be requested.
error in gtff***illegal reaction for cross section=---
Only reactions 501, 502, 504, 516, 602, and 621 (heat) can be requested for
ENDF/B-IV or -V, or only 501, 502, 504, 516, 522, and 525 for ENDF/B-VI
or VII.
error in gtff***insufficient storage for form factor.
This refers to the allocatable array pff with size nwpff=5000 defined in
the main gaminr routine.
NJOY2016 283

LA-UR-17-20093 9 GAMINR
284 NJOY2016

10 ERRORR LA-UR-17-20093
10 ERRORR
The ERRORR module is used to produce cross section and distribution covari-
ances from error files in ENDF format.
This chapter describes the ERRORR module in NJOY2016.0.
10.1 Introduction
After evaluators have completed their review of the available measurements of
various nuclear data (having true values σ1, σ2, σ3,···) and the theoretical anal-
ysis, they will have formed at least a subjective opinion of the joint probability
distribution of the data examined; that is, the probability
P(σ1, σ2,···)dσ1dσ2···
that the true value of σ1lies in the range (σ1, σ1+dσ1), and that σ2lies in
the range (σ2, σ2+dσ2), etc. In the early versions of the ENDF format, only
the first moments (expectation values) of this probability distribution could be
included in the numerical data files. However, beginning with ENDF/B-IV and
expanding significantly in ENDF/B-V and later, the second moments of the data
probability distributions have been included in many of the files. As discussed in
Section 10.2, these second moments (or “data covariances”) contain information
on the uncertainty of individual data, as well as correlations that may exist.
Fig. 38 shows an example of this for 10B from ENDF/B-VII.0. The top plot
shows the first moment (the percent standard deviation) of the uncertainty in
the (n,α) cross section. The right-hand plot shows the cross section. The center
plot shows the correlations between the (n,α) cross section at one energy to itself
at other energies.
Data covariances have many applications. For example, they can be com-
bined with sensitivity coefficients to obtain the uncertainty, due to the data, in
calculated quantities of applied interest[70]. This information can be used in
turn to judge the adequacy of the data for that application.
The availability of data covariances also makes it possible to use the general-
ized method of least squares to improve the data evaluation after new integral or
differential measurements have been performed[71]. The least-squares method
requires only data covariances (not the full probability distribution), and the
improved, or adjusted, data are guaranteed[72] to have the smallest possible
uncertainties, regardless of the actual shape of the underlying probability dis-
NJOY2016 285
LA-UR-17-20093 10 ERRORR
σ vs. E for 10B(n,α)
102103104105106107
10-2
10-1
100
101
102
∆σ/σ vs. E for 10B(n,α)
102103104105106107
10-1
100
101
Ordinate scales are % relative
standard deviation and barns.
Abscissa scales are energy (eV).
Warning: some uncertainty
data were suppressed.
Correlation Matrix
0.0
0.2
0.4
0.6
0.8
1.0
0.0
-0.2
-0.4
-0.6
-0.8
-1.0
Figure 38: Covariance plot for 10B(n,α) from ENDF/B-VII.0. This reaction is used as a
standard in the ENDF system.
tribution function, P(σ1, σ2,···). Thus, the ENDF-formatted covariance files
contain, in about as compact a form as possible, a statement about the quality
of the data, as well as sufficient information (in principle) to carry out future
improvements on an objective basis.
In many of these applications, it is necessary to begin by converting energy-
286 NJOY2016

10 ERRORR LA-UR-17-20093
dependent covariance information in ENDF format[9] into multigroup form.
This task can be performed conveniently in the NJOY environment, using the
ERRORR module. In particular, ERRORR calculates the uncertainty in in-
finitely dilute multigroup cross sections (or multigroup ¯νvalues), as well as the
associated correlation coefficients. These data are obtained by combining ab-
solute or relative covariances from ENDF Files 31, 32, 33, 34, 35 and 40 with
multigroup ¯νdata, cross section data, angular disbribution data, fission spectra
data or radionuclide production data. These multigroup data are obtained from
GROUPR processing, or in some instances are calculated within ERRORR.
ERRORR is coded to treat all approved ENDF-4, -5, and -6 covariance formats
for these files. ERRORR can also treat resolved-resonance covariances given
in File 32 using the old Breit-Wigner resolved-resonance parameter uncertain-
ties (LRF=1 and 2) in Version-5 format, the “Version-5 compatible” option of
Version 6 (LCOMP=0) using the new formats that include resonance-resonance
covariances, and the newest format based on Reich-Moore-Limited parameters
that include resonance-resonance correlations between different reactions.
The methodology of ERRORR assumes that the weighting flux used to con-
vert energy-dependent cross sections into multigroup averages is free of uncer-
tainty. In cases in which the cross-section information is obtained from an ex-
isting multigroup library, it is usually necessary to make assumptions about the
shape of the cross section and the weight function within certain input energy
groups.
10.2 Definitions of Covariance-Related Quantities
For convenient reference in discussing the methodology and input requirements
of the ERRORR module, we next review the basic definitions of covariance-
related quantities. Let x0and y0be the evaluated values of xand y, respectively:
x0≡E[x],(395)
and
y0≡E[y].(396)
Here E is the expectation operator, which performs an average over the joint
probability distribution of xand y. The second moment of this distribution is
NJOY2016 287

LA-UR-17-20093 10 ERRORR
called the covariance of xwith y:
cov(x, y)≡E[(x−x0) (y−y0)] .(397)
Covariance is a measure of the degree to which xand yare both affected by the
same sources of error. The covariance of xwith itself is called the variance of x:
var(x)≡cov(x, x) = E[(x−x0)2].(398)
The more familiar standard deviation ∆x(also called the “uncertainty”) is sim-
ply
∆x≡[var(x)]1/2= [cov(x, x)]1/2.(399)
The correlation between xand y(also called the correlation coefficient) is defined
as
corr(x, y)≡cov(x, y)
∆x∆y.(400)
The absolute value of a correlation coefficient is guaranteed to be less than or
equal to unity. Another useful quantity is the relative covariance of xwith y,
rcov(x, y)≡cov(x, y)
x0y0
.(401)
Unlike cov(x, y), the relative covariance rcov(x, y) is a dimensionless quantity.
Closely related to the relative covariance is the relative standard deviation,
∆x
x0
=[cov(x, x)]1/2
x0
,(402)
which, from Eq. 401, can be written as
∆x
x0
= [rcov(x, x)]1/2.(403)
Combining Eqs. 400 and 401, we have another useful result,
corr(x, y) = rcov(x, y)
(∆x/x0)(∆y/y0).(404)
While it is customary to speak of uncertainties and correlations as separate
entities, these are actually just two different aspects of the covariance. If one has
a set of absolute covariances for various reactions, including the self-covariance,
then Eqs. 399 and 400 can be used to calculate ∆xand corr(x, y). Similarly, if
288 NJOY2016

10 ERRORR LA-UR-17-20093
one has a set of relative covariances, one can use Eqs. 403 and 404 to calculate
∆x/x0and corr(x, y).
Consider now a set of nuclear data σiwith uncertainties characterized by the
covariances cov(σi, σj). Let Aand Bbe two linear functions of the σi,
A=X
i
aiσi(405)
and
B=X
j
bjσj,(406)
where the aiand bjare sets of known constants. The above definitions can
be used to calculate the covariances of the functions Aand Binduced by the
covariances of the data. From Eq. 397,
cov(A, B)=E
X
i
aiσi−X
i
aiE(σi)
X
j
bjσj−X
j
(σj)
=X
i, j
aibjEnσi−E(σi) σj−E(σj)o ,(407)
so that
cov(A, B) = X
i, j
aibjcov(σi, σj) (408)
This result, called the “propagation of errors” formula, is fundamental to the
subject of multigroup processing of ENDF covariance data and will be referenced
frequently in later sections of this chapter.
10.3 Structure of ENDF Files 31, 33, and 40: Energy-Dependent
Data
Data in ENDF format are stored in various numbered “files,” where the file
number depends on the type of information contained. For example, the covari-
ances of ¯ν(E) (the average number of neutrons per fission, which is a function of
the incident neutron energy) are stored in File 31, where the possible “reaction”
types are prompt ¯ν, delayed ¯ν, and total ¯ν. File 33 contains the covariances
of energy-dependent cross sections. In general, for data given in File N, covari-
NJOY2016 289

LA-UR-17-20093 10 ERRORR
ance data are given in File (N+30). The structures of Files 31, 33, and 40 are
identical and will be described first.
Files 31, 33, and 40 describe the covariances of energy-dependent data. To ex-
pand on this point, we recall that the full energy dependence of a cross section
σ(E), for example, is described in the ENDF File 3 by specifying the cross-
section values at a relatively small number of energy points and then providing
a set of interpolation laws to be used in reconstructing the actual cross section
at any intermediate energy. Somewhat the same philosophy is used to describe
the two-dimensional energy dependence of data covariances in Files 31, 33, and
40. That is, one specifies a set of numerical data and a set of formulae, which
together can be used to compute cov(x, y) for any desired pair of energies, Ex
and Ey. Although the interpolation laws are presently restricted to the simple
forms described below, it is not true (as sometimes stated) that ENDF contains
multigroup covariances. The expression “multigroup covariance” refers to the
covariance of one multigroup-averaged quantity with another averaged quantity,
whereas ENDF contains the covariances between point-energy data. It is pre-
cisely the task of ERRORR to compute multigroup covariances, starting from
point covariances.
Files 31, 33, and 40 of an evaluation for material MAT are divided into “sec-
tions,” indexed by the reaction type MT. A section (MAT,MT) is further subdi-
vided into “subsections.” As described in the ENDF formats manual, a sub-
section is the repository for all explicit statements of the two-dimensional en-
ergy dependence of the covariances of reaction (MAT,MT) with another reaction
(MAT1,MT1). Because covariances are symmetric, a subsection with MAT1=MAT
and MT1<MT would be redundant with a subsection in an earlier section, and
such data are, by convention, omitted from the ENDF files.
Subsections are further divided into “sub-subsections.” Two different types
of sub-subsections are used in the ENDF-5 and ENDF-6 formats. ERRORR
also treats data covariances in the earlier ENDF-4 format, but this is of little
practical interest since only three covariance evaluations were released in the
Version-4 format. “NI-type” sub-subsections are used to express covariances
explicitly, while “NC-type” sub-subsections are used to indicate the existence of
connections between various data that result in “implicit” covariance contribu-
tions for various reaction pairs. We shall return to this point when discussing
NC-Type Sub-Subsections.
290 NJOY2016

10 ERRORR LA-UR-17-20093
NI-Type Sub-Subsections. Multiple NI-type sub-subsections are used to
describe multiple, statistically independent sources of uncertainty for a given
reaction pair. If cov(x, y)nis the covariance computed from the data in one
sub-subsection, then, because the uncertainties in different sub-subsections are
uncorrelated,
cov(x, y) =
NI
X
n=1
cov(x, y)n,
where NI is the number of NI-type sub-subsections in the current subsection.
The numerical content of one NI-type sub-subsection consists of either one or
two energy grids, a collection of constants, and a parameter LB. The parameter
LB governs how the energies and constants are to be used in constructing the
covariance in various rectangular regions of Ex−Eyspace. For LB=0, 1, 2 and
8, a single table containing pairs (Ei, Fi) is given. For LB=3 and LB=4, two such
tables are given. For LB=5, a single set of energies Eiis given, along with an
associated square matrix of constants Gij. Finally, for LB=6, two energy grids
are given, along with an associated rectangular matrix of constants G0
ij.
The first of these tables (Ei, Fi) defines a function f(E) that is constant
except for discrete steps at energies Ei,
f(E) = Fi,if Ei≤E<Ei+1 .(409)
Similarly, if there is a second table,
f0(E) = F0
j,if E0
j≤E<E0
j+1 .(410)
The LB=5 matrix data Gij also define a function,
g(Ex, Ey) = Gij,if Ei≤Ex<Ei+1 and Ej,(411)
and similarly for LB=6
g0(Ex, Ey) = G0
ij,if Ei≤Ex<Ei+1 and≤Ey<E0
j+1 .(412)
These functions are simply histograms in either one or two dimensions. Using
the functions f,f0,g, and g0thus defined, we can list the formulae in Eq. 413,
which are used to specify energy-dependent covariances for the different allowed
NJOY2016 291

LA-UR-17-20093 10 ERRORR
values of LB. Thus, if xis the value of the cross section or of the ¯νvalue for the
reaction (MAT,MT) that determines the ENDF/B section, and if yis the value
for the reaction (MAT1,MT1) that determines the subsection, then for
LB = 0,cov(x, y)n=f(Ex)δ(Ex, Ey)
LB = 1,rcov(x, y)n=f(Ex)δ(Ex, Ey)
LB = 2,rcov(x, y)n=f(Ex)f(Ey)
LB = 3,rcov(x, y)n=f(Ex)f0(Ey)
LB = 4,rcov(x, y)n=f(Ex)δ(Ex, Ey)f0(Ex)f0(Ey)
LB = 5,rcov(x, y)n=g(Ex, Ey)
LB = 6,rcov(x, y)n=g0(Ex, Ey).
(413)
The symbol δ(Ex, Ey) has the following meaning: δ(Ex, Ey)=1 if Exand Eyfall
in the same energy interval of the first table (Ei,Fi), and δ(Ex, Ey)=0 otherwise.
The final covariance law, LB=8, is an exceptional case that cannot be ex-
pressed in terms of point covariances. LB=8 is used primarily to represent un-
certainty effects due to suspected, but unresolved, energy-dependent structure
in a given cross section. If ∆Ejis the energy width of the j-th “union” energy
group (see the discussion of union groups in Section 10.8), and if this group lies
within the k-th range (Ek, Ek+1) of an ENDF LB=8 energy grid, then the effect
of the LB=8 subsection is to trigger the addition of an uncorrelated contribution
of Fk(Ek+1 −Ek)/∆Ejto the (absolute) variance of the j-th union-group cross
section. No contributions to off-diagonal elements of the multigroup covariance
matrix are generated by an LB=8 sub-subsection.
NC-Type Sub-Subsections. NC-type sub-subsections, which describe co-
variances indirectly, are used in several evaluation situations, which are flagged
by different values of the parameter LTY. The first situation, LTY=0, occurs when
the following two conditions are met: (a) the covariances of a given reaction MT,
both with itself and with other reactions, can be deduced in an energy range
(E1, E2) solely from the application of a cross-section “derivation relation,”
x(MAT,MT;E) = X
i
Cix(MAT,MTi;E),(414)
and (b) the covariances of all of the reaction cross sections on the right-hand side
of Eq. 414 have been given directly (that is, using only NI-type sub-subsections)
throughout the range (E1, E2). The energy boundaries E1 and E2, the constants
292 NJOY2016

10 ERRORR LA-UR-17-20093
Ci, and the reaction identifiers MTiare specified in an NC-type sub-subsection
with LTY=0. This format is widely used in the ENDF/B library, and it makes
possible the elimination of large volumes of otherwise redundant data. It also
introduces considerable complexity in the multigroup processing, as discussed in
Section 10.8, and adds to the computer running times. The presence of this one
short sub-subsection affects the calculation of the covariances for many different
reaction pairs, such as x(MAT,MT) with x(MAT,MTi). Less widely used are NC-
type sub-subsections with LTY=1. These are employed when a reaction MT in
material MAT is evaluated in some energy range (E1, E2) as a ratio to a standard
reaction MTS in some other material MATS. That is,
x(MAT,MT;E) = R(E)x(MATS,MTS;E).(415)
In practical evaluation situations, the uncertainty of Ris almost never corre-
lated with that of x(MATS,MTS). Because of this, the relative uncertainty in R
is treated simply as one independent component of the relative uncertainty in
x(MAT,MT), and it is described using normal NI-type sub-subsections. On the
other hand, the contribution from uncertainty in x(MATS,MTS) is represented
with an NC-type sub-subsection with LTY=1, which contains, in ENDF/B-V,
only E1,E2,MATS, and MTS. The actual numerical covariance information must
be read from the evaluation for the standard material MATS, which usually resides
on an entirely different ENDF tape. An NC-type sub-subsection with LTY=1,
which occurs in a given subsection (MAT,MT; MAT,MT), affects the calculation of
the covariances only for the current reaction pair (reaction MT with itself) and,
in this respect, is more like an NI-type sub-subsection than, for example, an NC-
type sub-subsection with LTY=0. This similarity is exploited in the processing
of ratio covariances, as discussed in Section 10.11.
An NC-type sub-subsection with LTY=2 is used, in a similar way, to describe
the covariances of x(MAT,MT) with x(MATS,MTS). As in the LTY=1 case, an
LTY=2 sub-subsection contains only E1,E2,MATS, and MTS.
An NC-type sub-subsection with LTY=3 is included in material MATS to de-
scribe the (redundant) covariances of x(MATS,MTS) with x(MAT,MT). The nu-
merical information contained here is the same as for LTY=1 and LTY=2. As
discussed in Section 10.11, an important function of LTY=3 data is to help lo-
cate reactions other than (MAT,MT) that have been measured relative to the
same standard (MATS,MTS).
NJOY2016 293

LA-UR-17-20093 10 ERRORR
10.4 Resonance-Parameter Formats—File 32
File 32 contains covariances of resonance parameters from File 2. Older versions
of ERRORR could only handle the ENDF-5 format (now called the “Version-5
compatible” format. Current versions can handle the newer ENDF-6 formats
that include resonance-resonance correlations.
ENDF-5 Type Resonance Formats. With these formats (LCOMP=0), ER-
RORR processes File 32 in the following limited sense: when infinite-dilution
cross-section covariances are processed (see previous section) from File 33, the
diagonal elements of the resulting (self-reaction) multigroup covariance matrices
are augmented by contributions based on the parameter covariances in File 32.
These methods were sufficient for processing the covariance files in ENDF/B-VI.
For either of the permitted resolved resonance formalisms (LRF=1 or LRF=2),
the parameters considered in File 32 are the resonance energy Er, the neutron
width Γn, the radiative capture width Γγ, the fission width Γf, and (in Version 5
only) the total angular momentum J. All cross-parameter relative covariances,
such as rcov(Γn,Γγ), are included, with the exception of the covariances of Er
with the remaining parameters, which are assumed to be negligible. Cross-
resonance covariances, such as cov(Ei
r, Ej
r), where iand jrefer to different
resonances, are omitted in the LCOMP=0 option.
ENDF/B-VII Resonance Covariances. For ENDF/B-VII, a number of
evaluations include covariance formats that represent the correlations between
resonance parameters for a given resonance and between different resonances.
In later versions of NJOY99, these cases are handled by the ERRORJ[35] mod-
ule, which was developed in Japan and contributed to the NJOY project. The
ERRORJ coding was integrated into NJOY2012’s ERRORR module, and it
remains in NJOY2016. The ERRORJ approach is based on computing the sen-
sitivity of a cross section to a given resonance by numerical differencing and then
combining these sensitivities with parameter covariances from the evaluation.
There are three basic covariance format options, governed by the LCOMP
and/or LRU flags. The LRU flag distinguishes between resolved resonance (LRU=1)
and unresolved resonance (LRU=2) data. For LCOMP=1/LRU=1, there may be
two classes of data, designated as NSRS or NLRS sub-subsections. NSRS sub-
subsections provide covariance data among parameters of specified resolved res-
onances. Covariances may be given for all ENDF recognized resolved resonance
formats (as specified via the LRF flag). NLRS sub-subsections provide long-range
294 NJOY2016

10 ERRORR LA-UR-17-20093
parameter covariances. These data are allowed for all resolved resonance for-
mats. At present there are no NLRS sub-subsection data in ENDF/B-VII, and
NJOY does not process these data.
The LCOMP=2/LRU=1 format provides a combination of resolved resonance
parameters and their uncertainties plus a correlation matrix. The correlation
matrix is given in a special packed form using the ENDF INTG record format
with matrix elements consisting of as few as 2 to as many as 6 digits. Covariance
matrix elements, Vij can be reconstructed as
Vij =DiCijDj(416)
where Diis the uncertainty on parameter iand Cij is the correlation matrix
element relating parameters iand j. Since the correlation matrix is symmetric,
and its diagonal terms are unity, only the upper triangle of matrix elements is
given in the ENDF file. This more compact representation of the covariances
helps for materials with large numbers of resonances.
Finally, the LRU=2 (LCOMP is not defined and its location in the ENDF file
is typically set to zero) format is used to define covariances for unresolved reso-
nance parameters. The data represent an energy independent relative covariance
matrix even if the underlying unresolved resonance parameters are energy de-
pendent. This is a symmetric matrix and so only the upper triangular portion
of the matrix is provided in the ENDF file.
The original covariance data formats did not allow the evaluator to define
an uncertainty in the scattering radius (only for resonance energy and the total
or partial resonance widths). This deficiency was eliminated in 2009, but until
new evaluations are released there are no scattering radius uncertainty data in
current evaluated library files. NJOY can include scattering radius uncertainty
effects if such data are given in the evaluated file. In addition, users can specify
an uncertainty in the ERRORR input so that this important component to the
cross section uncertainty is considered when processing existing files that lack
these data (see the description for dap on Card 7 in Section 10.14 below).
Reich-Moore-Limited Covariance Representations. The current ENDF-
6 format also allows resonances using the LRF=7 Reich-Moore-Limited (RML)
representation. In addition to the covariances described above, the RML ap-
proach can define channel-channel covariances properly. There are two exper-
imental evaluations currently available that use this approach. A sample 19F
evaluation from the ORNL represents the four reactions elastic, capture, (n,n1),
NJOY2016 295

LA-UR-17-20093 10 ERRORR
and (n,n2). Fig. 39 shows that ERRORR can generate the covariances between
elastic and (n,n1). The ENDF/B-VII.1 35Cl evaluation from ORNL uses the
LRF=7 formalism to represent the elastic, capture, and (n,p) reactions. The
coding in NJOY2016 to handle these cases uses analytic calculations for the
parameter sensitivities borrowed from SAMMY[36].
10.5 Secondary Particle Angular Distribution Covariances—File
34
File 34 contains covariances for angular distributions of secondary particles.
While the underlying angular distribution data in File 4 may be given as tab-
ulated distributions or as Legendre polynomial coefficients, File 34’s covariance
data are only given for Legendre coefficients. At present there is no provision to
specify covariances between cross sections from File 3 and angular distributions
from File 4, nor to specify angular distribution covariances between different
materials. The data format is governed by the LB flag discussed above in Sec-
tion 10.3 with LB values of 0, 1, 2, 5 and 6 allowed.
File 34 in the ENDF file may include covariance data for any MT reaction
defined in File 4, but currently NJOY only processes the P1component of MT=2
(elastic scattering).
Fig. 40 shows an example of the covariances computed from File 34 for 238U
from JENDL-3.3. As usual, there are three components to this plot. On the
right side, we illustrate ¯µvs energy, which dislays the expected forward-peaked
characteristic with increasing energy; on the top is the uncertainty in ¯µvs energy;
and in the center is the correlation matrix. The ERRORR input for this case
will be presented below.
10.6 Secondary Particle Energy Distribution Covariances—File
35
File 35 contains covariance matrices for the energy distributions of secondary
particles given in File 5. If the spectral distributions are correlated with angular
distributions and given in File 6, the covariance information still appears in
File 35 (the MT section identifier is the common datum relating these data)
and refers to the angle-integrated distributions only. The secondary energy
distribution is usually defined on a relatively fine energy grid, and multiple
distributions are given as a function of increasing incident particle energy. Since
the uncertainties in secondary distributions are usually highly correlated as a
296 NJOY2016
10 ERRORR LA-UR-17-20093
∆σ/σ vs. E for 19F(n,el.)
105106107
0
1
2
3
4
5
∆σ/σ vs. E for 19F(n,n1)
105106107
10-1
100
101
102
Ordinate scale is %
relative standard deviation.
Abscissa scales are energy (eV).
Correlation Matrix
0.0
0.2
0.4
0.6
0.8
1.0
0.0
-0.2
-0.4
-0.6
-0.8
-1.0
Figure 39: Covariance plot for the elastic and (n,n1) reactions from a sample ORNL evalua-
tion for 19F, demonstrating the channel-channel covariances possible when using
the Reich-Moore-Limited resonance representation.
function of incident particle energy, it is generally sufficient to only define a few
covariance matrices over relatively broad incident energy groups. There is no
provision to specify covariances between these groups nor with data from other
files such as File 3 cross sections or File 1 prompt, delayed or total ¯ν.
NJOY2016 297
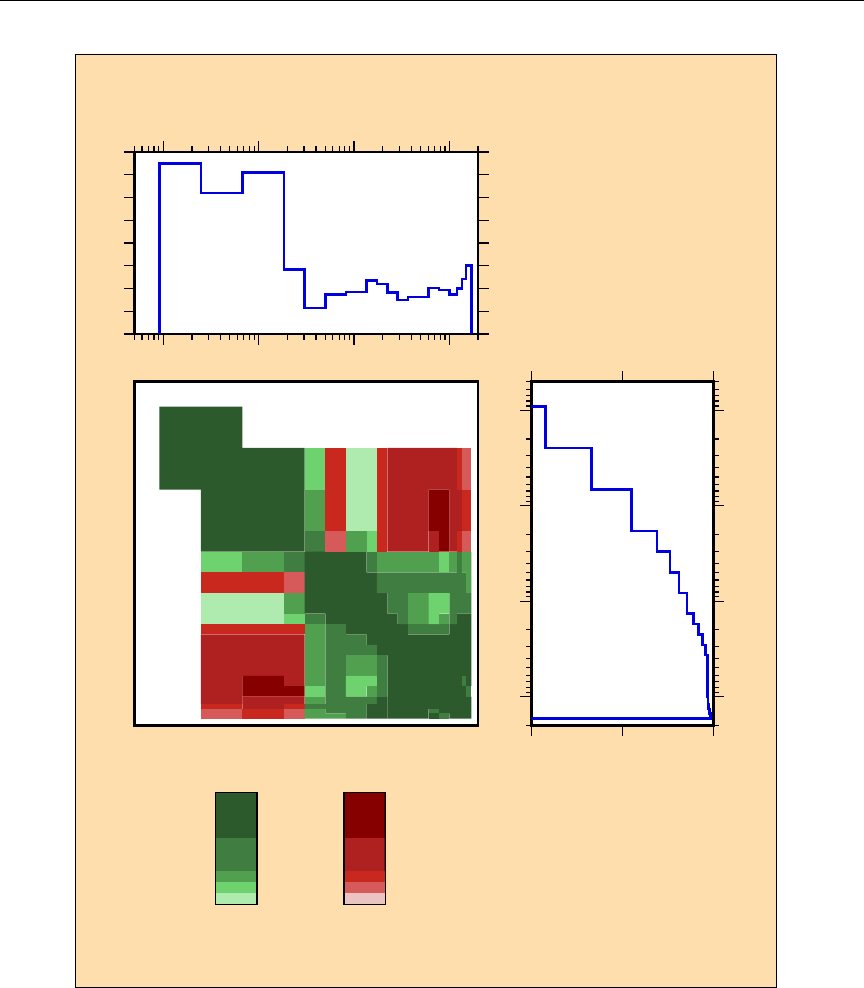
LA-UR-17-20093 10 ERRORR
µ vs. E for 238U(mt251)
104105106107
10-2
10-1
100
∆µ/µ vs. E for 238U(mt251)
104105106107
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0 Ordinate scales are % relative
standard deviation and mu-bar.
Abscissa scales are energy (eV).
Correlation Matrix
0.0
0.2
0.4
0.6
0.8
1.0
0.0
-0.2
-0.4
-0.6
-0.8
-1.0
Figure 40: Example of angular distribution covariance data.
File 35 covariance data are given in a series of NK subsections, with each
subsection covering a unique incident particle energy range. The lowest energy
of the first subsection and the highest energy of the last subsection must cover
the entire incident particle energy range from File 5 (or File 6). When processing
MF35 data, the user can specify the incident particle energy of interest (efmean
on Card 7). NJOY will process the NKth subsection whose energy is closest to,
298 NJOY2016

10 ERRORR LA-UR-17-20093
but less than, efmean. The data tabulated in the ENDF file are normalized
probabilities of absolute covariances identified as an LB=7 subsection. LB=7 is
identical to LB=5 defined in Section 10.3 except that these data are now absolute
rather than relative covariances.
The ENDF format manual notes these matrices are probability distributions
that must remain normalized to unity and therefore the elements in these sym-
metric matrices are constrained such that the sum of the elements in any row
(or column) must be zero. This is sometimes referred to as the “zero sum” rule.
Of course, when dealing with real numbers of finite precision whose values can
vary by orders of magnitude it is virtually impossible to rigorously conform to
this rule. Therefore, if the sum is sufficiently small, the rule is judged to be
satisfied. If not, the ENDF manual provides a correction formula to apply to all
matrix elements. When processing File 35 data NJOY, checks this summation
requirement and, if necessary, applies the required correction. NJOY uses the
“sufficiently small” criteria specified in the Format manual for this check.
At present there are no File 35 data in ENDF/B-VII.0 neutron files, but the
252Cf decay file does contain such data. Also, these data are becoming available
in preliminary ENDF/B-VII.1 files available from the National Nuclear Data
Center (NNDC) at Brookhaven National Laboratory (BNL). These files follow
the “zero sum’ rule discussed above, but users are cautioned that other interna-
tionally distributed files, particularly those from JENDL-3.3, may provide File
35 data in an alternate format. The matrix elements in the JENDL-3.3 files have
been divided by the group energy width to yield energy-group averaged proba-
bility distributions, as this is the data representation expected by the Japanese
ERRORJ code[35]. A conversion code, chmf35, has been developed and is avail-
able from the Nuclear Energy Agency 9to reformat these files so that they are
suitable for processing by NJOY.
Fig. 41 shows the results of processing the ficticious 252Cf evaluation. The
ERRORR input for this job will be presented below.
10.7 Radioactive Nuclide Production Covariances–File 40
There is only one file in ENDF/B-VII.0 that includes File 40 covariance data
–93Nb. The input for calculating the 93mNb production uncertainty will be
shown below, but the resulting covariances are shown here in Fig. 42. The form
of the graphical output obtained when processing File 40 is identical to that
produced when processing File 33; with the cross section shown to the right, the
9chmf35 may be downloaded from http://www.nea.fr/dbprog/Njoy/chmf35.for
NJOY2016 299
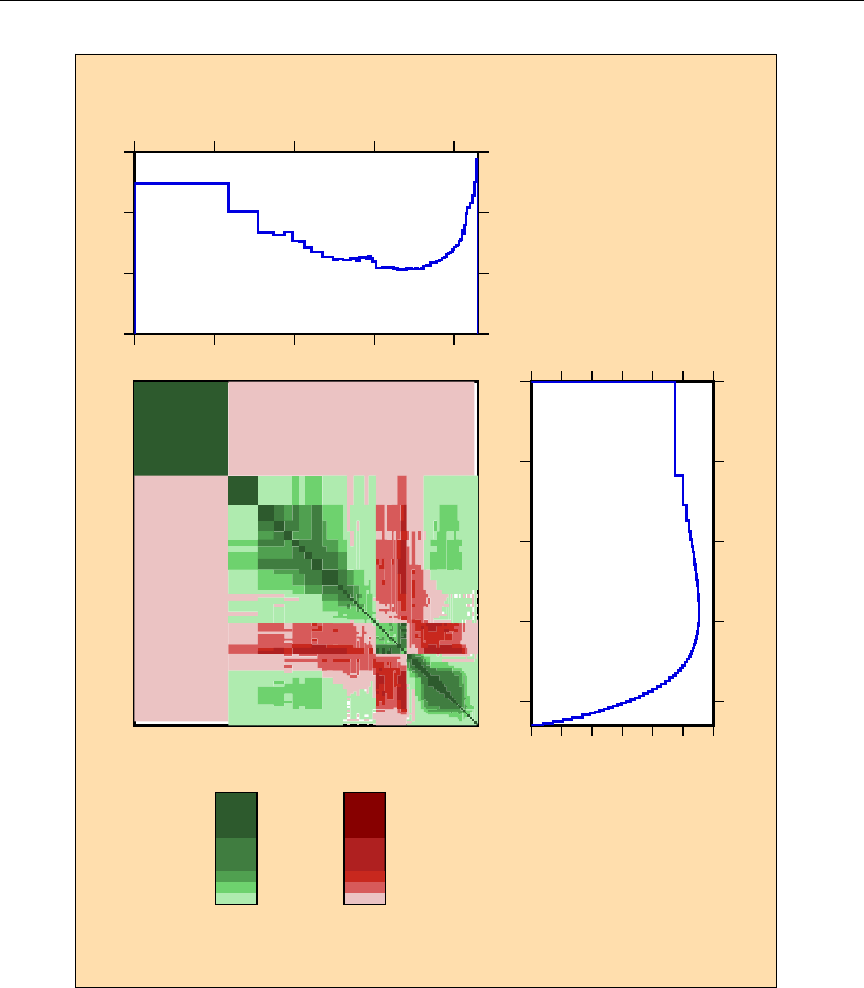
LA-UR-17-20093 10 ERRORR
Grp-average φ(Ein= 1.23 MeV), 252Cf(n,f)
103104105106107
10-12
10-10
10-8
10-6
∆φ/φ vs. E for 252Cf(n,f)
103104105106107
10-1
100
101
102
Ordinate scales are % standard
deviation and spectrum/eV.
Abscissa scales are energy (eV).
Correlation Matrix
0.0
0.2
0.4
0.6
0.8
1.0
0.0
-0.2
-0.4
-0.6
-0.8
-1.0
Figure 41: Example of energy distribution covariances. The appearance of negative corre-
lations results from the requirement for preserving normalization.
uncertainty shown to the top and the correlation matrix shown in the center.
That these are File 40 data can be determined from the label on the uncertainty
portion of the plot. In 2009, the File 40 format was modified to include the IZAP
parameter that identifies the daughter product. We include this IZAP value in
the plot label so that the user can more fully identify these data. If an older File
300 NJOY2016
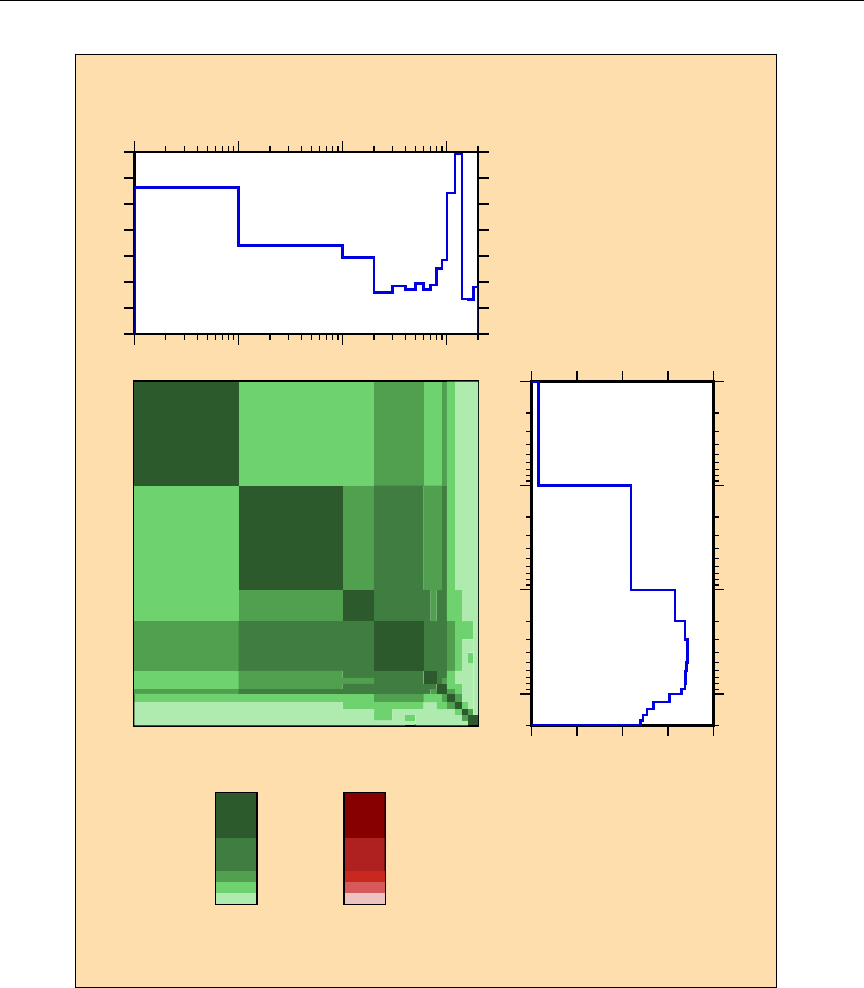
10 ERRORR LA-UR-17-20093
σ vs. E for 93Nb(n,inel.), izap = 410931
104105106107
10-4
10-3
10-2
10-1
100
∆σ/σ vs. E for 93Nb(n,inel.), izap = 410931
104105106107
0
2
4
6
8
10
12
14 Ordinate scales are % relative
standard deviation and barns.
Abscissa scales are energy (eV).
Correlation Matrix
0.0
0.2
0.4
0.6
0.8
1.0
0.0
-0.2
-0.4
-0.6
-0.8
-1.0
Figure 42: Example of radioactive nuclide production covariances.
40 file is processed that does not define IZAP, then the text string “MF40” will
appear in the title. In the example shown here we have modified the original
ENDF/B-VII.0 93Nb file to include the proper IZAP value in File 40, which then
appears in the plot title.
NJOY2016 301

LA-UR-17-20093 10 ERRORR
10.8 Calculation of Multigroup Fluxes, Cross Sections, and Co-
variances on the Union Grid
As mentioned before, the main function of the ERRORR module is to calcu-
late the uncertainty in group-averaged cross sections at infinite dilution due to
uncertainty in the ENDF point data. In this and the following sections, we
describe the procedures used in performing this task.
In order to proceed, it is necessary to introduce into the discussion three
different energy grids, namely, the user grid, the ENDF grid, and the union
grid. The relationship of these three grids is shown in Fig. 43. The user grid is
the multigroup structure in which the output multigroup covariances are to be
produced. The ENDF grid is the collection of energies obtained (in subroutines
gridd and grist) by forming the union of (a) all energy “lists” appearing in any
NI-type sub-subsection of any subsection to be processed in the current ENDF
material, and (b) all energy pairs used to define the range of effectiveness of
any NC-type sub-subsection of any subsection to be processed. The union grid,
on the other hand, is simply the union of the user grid and ENDF grid. The
utility of the union grid is that (a) the covariances are particularly simple to
calculate in this grid, as discussed below, and (b) the multigroup covariances
needed by the user are then easily obtained by a straightforward collapse from
this to the user grid. In fact, the design of the current ENDF covariance format
was strongly influenced by the desire to employ this particular procedure for
multigroup processing[73, 74].
After the union grid is formed in subroutine uniong, the cross sections x(E)
and weighting flux φ(E) are integrated to produce xIand φI, multigrouped on
this grid. If point cross sections are supplied, an exact integration is done in
subroutine grpav. If, on the other hand, a multigroup cross-section library is
supplied, then subroutine colaps is used. If a library group is subdivided by a
union-group boundary, then over the span of that library group, the unknown
energy dependencies of x(E) and φ(E), which are needed to calculate xIand
φI, are approximated in subroutine colaps by constants. Normally, the effect
User Grid |φ1, X1|φ2, X2|
ENDF Grid |F1|F2|F3|
Union Grid |φ1, x1|φ2, x1|φ3, x3|φ4, x4|
Figure 43: Illustration of energy grid relations.
302 NJOY2016

10 ERRORR LA-UR-17-20093
of this approximation is not large and, in any case, can be reduced or eliminated
by increasing the number of groups in the input library.
We next consider the theoretical basis for the calculation of union-grid multi-
group covariances, as performed in subroutine covcal. By definition, xIis just
the average of x(E) over union group I,
xI≡ZI
φ(E)x(E)dE
ZI
φ(E)dE
,(417)
where φ(E) is the flux “model” assumed for the multigroup calculations. Let
yJdenote similarly the average of y(E) over union group J.
Let us imagine that these groups are subdivided into many subintervals of
infinitesimal width, so that in the ith subinterval of group I, for example, x(E)
can be well approximated by the constant xi. By this device, the integrals that
define xIand yJcan be converted to discrete sums:
xI=X
i∈I
φixi
φI
=X
i∈I
αIi xi,(418)
where
φi=Zi
φ(E)dE , (419)
φI=X
i∈I
φi=ZI
φ(E)dE , (420)
and
αIi ≡φi
φI
.(421)
From these definitions, clearly
X
i∈I
αIi = 1 .(422)
NJOY2016 303

LA-UR-17-20093 10 ERRORR
Similarly for y,
yJ=X
j∈J
αJj yj,(423)
and
X
j∈J
αJj = 1 .(424)
The methodology of ERRORR assumes that φ(E) in Eq. 417 is free of un-
certainty. Under this assumption, the terms αIi and αJj are simply known
constants. The covariance of xIwith yJcan then be calculated using the
propagation-of-errors formula, Eq. 408, together with Eqs. 418 and 423.
cov(xI, yJ) = X
i∈I
j∈J
αIi αJj cov(xi, yj)
=X
i∈I
j∈J
αIi αJj X
n
cov(xi, yj)n,(425)
where the summation over nresults from the different independent contribu-
tions to the ENDF point covariances coming from the different NI-type sub-
subsections. Changing the order of summation, we obtain
cov(xI, yJ) = X
n
cov(xI, yJ)n,(426)
where
cov(xI, yJ)n=X
i∈I
j∈J
αIi αJj cov(xi, yj)n.(427)
To evaluate the sum in Eq. 427, we make use of the fact that union groups
Iand Jdo not cross any ENDF grid boundaries. Recalling the discussion of
NI-type sub-subsections (and excluding for the moment the case where sub-
subsections with LB=8 are present), there are only two possibilities for the energy
dependence of the covariance between ENDF grid points; thus, over the limits of
the sum, either cov(xi, yj)nis independent of iand j(if LB=0) or rcov(xi, yj)nis
independent of iand j(if 1 ≤LB ≤6). We consider first the constant-absolute-
304 NJOY2016

10 ERRORR LA-UR-17-20093
covariance case, LB=0. Eq. 427 can then be rewritten as follows:
cov(xI, yJ)n= cov(x, y)nX
i∈I
j∈J
αIi αJj = cov(x, y)n X
i∈I
αIi!
X
j∈J
αJj
.
(428)
Invoking Eqs. 422 and 424, we obtain
cov(xI, yJ)n= cov(x, y)n(LB = 0) .(429)
For LB-values ranging from 1 to 6, the relative covariance is constant over each
union group, so we rewrite Eq. 427 in the form
cov(xI, yJ)n=X
i∈I
j∈J
αIi αJj xixjrcov(xi, xj)n
= rcov(x, y)nX
i∈I
j∈J
(αIi xi) (αJj yj)
= rcov(x, y)n X
i∈I
αIi xi!
X
j∈J
αJj yj
.(430)
Substituting here from Eqs. 418 and 423, we obtain
cov(xI, yJ)n=xIyJrcov(x, y)n(1 ≤LB ≤6) .(431)
The final union-group multigroup covariance is obtained by inserting these re-
sults, Eqs. 429 and 431, back into Eq. 426
cov(xI, yJ) = X
n(LB=0)
cov(x, y)n+X
n(LB=1,6)
xIyJrcov(x, y)n,(432)
where the first sum runs over all sub-subsections with LB=0 and the second
runs over all sub-subsections with LB=1 through 6. The quantities cov(x, y)n
and rcov(x, y)nhere are simply the point-energy covariances from the ENDF
covariance file, as described in Eqs. 409 through 413. Equation 432 then is the
basic equation used in subroutine covcal to calculate the desired union-group
covariances.
NJOY2016 305

LA-UR-17-20093 10 ERRORR
The final step, if sub-subsections with LB=8 are present, is to increment the
diagonal elements (variances) as follows:
cov(xI, xI) = cov(xI, xI) + Fk(Ek+1 −Ek)/∆EI,(433)
where k indexes the range of the LB=8 energy grid that includes union group I.
10.9 Basic Strategy for Collapse to the User Grid
The union-group fluxes φIare used, in subroutine sigc, to collapse the union-
group cross sections to the coarser user grid. Changing notation slightly, let us
denote by xI(a) the cross section in union group Ifor reaction a, and similarly
let XK(a) be the cross section in user group Kfor the same reaction. In complete
analogy with Eq. 418,
XK(a) = X
I∈K
φIxI(a)
φK
=X
I∈K
AKI xI(a),(434)
where
φK=X
I∈K
φI,(435)
and
AKI =φI
φK
.(436)
Applying the propagation-of-errors formula again gives
cov [XK(a), XL(b)] = X
I∈K
J∈L
AKI ALJ cov[xI(a), xJ(b)] .(437)
An alternative expression, obtained by simply rearranging coefficients, is
cov [XK(a), XL(b)] = 1
φKφLX
I∈K
J∈L
TIJ (a, b),(438)
where
TIJ (a, b) = φIφJcov[xI(a), xJ(b)] .(439)
306 NJOY2016
10 ERRORR LA-UR-17-20093
Eqs. 438 and 439 provide the basic framework in the ERRORR module for the
production of multigroup covariances in the coarse user-group structure. Finally,
if requested, the Eq. 438 absolute covariances are converted to relative form,
rcov[XK(a), XL(b)] = cov[XK(a), XL(b)]
XK(a)XL(b).(440)
10.10 Group-Collapse Strategy for Data Derived by Summation
The procedure described in the previous section must be modified if, in some
energy range, either reaction aor bis a “derived” quantity in the sense of Eq. 414
or Eq. 415. In such a case, one cannot apply Eq. 432 directly to the calculation
of cov[xI(a), xJ(b)], because the covariances on the right-hand side of Eq. 432
will be missing from the ENDF file in the affected energy region.
We consider first the case in which some cross sections are evaluated (“de-
rived”) by simply summing other evaluated cross sections, as in Eq. 414. Equa-
tion 433 can then be rewritten as
XK(a) = X
I∈K
AKI (X
all c
CI(a, c)xI(c)),(441)
where the quantity in curly brackets is the value of the derived cross section
“a” in union group I, as reconstructed from the directly evaluated cross sections
xI(c). The derivation coefficients CI(a, c) depend on the union-group index I,
because the evaluator is permitted to employ different derivation strategies in
different energy ranges in order to simplify and shorten the covariance files.
To expand on this last point, suppose there are only three reactions, and
suppose that the cross sections x(1) and x(2) rigorously sum to x(3) at all
energies. Further suppose that within the energy range covered by the first
union group, the cross-section evaluator has used this logical connection in order
to “derive” x(3), that is to evaluate x(3), by summing the existing evaluations
for x(1) and x(2),
x1(3) = x1(1) + x1(2) .(442)
Further suppose that in the range of union group 2, x(1) is derived by employing
the same logical connection, but in a different way,
x2(1) = x2(3) −x2(2) ,(443)
and in union group 3, all three reactions are directly evaluated.
NJOY2016 307

LA-UR-17-20093 10 ERRORR
In this example CI(a, c) has the following values:
C1(1,1) = 1
C1(2,1) = 0
C1(3,1) = 1
C1(1,2) = 0
C1(2,2) = 1
C1(3,2) = 1
C1(1,3) = 0
C1(2,3) = 0
C1(3,3) = 0
C2(1,1) = 0
C2(2,1) = 0
C2(3,1) = 0
C2(1,2) = −1
C2(2,2) = 1
C2(3,2) = 0
C2(1,3) = 1
C2(2,3) = 0
C3(3,3) = 1
C3(1,1) = 1
C3(2,1) = 0
C3(3,1) = 0
C3(1,2) = 0
C3(2,2) = 1
C3(3,2) = 0
C3(1,3) = 0
C3(2,3) = 0
C3(3,3) = 1
Note that in all cases we have formally considered the evaluated cross sections
to be derived from themselves, CI(a, c)|eval=δac. This device allows us to use
Eq. 440 for all reactions, regardless of whether they are derived or evaluated.
Note that, in every case where reaction cis derived in group I, CI(a, c)=0. (See
boxed submatrices.) This null “sensitivity coefficient” is important, because it
means that Eq. 440 remains a linear relation involving only dependent quantities
with known covariances (the evaluated subset of the union-group cross sections)
on the right. This allows us once again to use the propagation-of-errors formula
to obtain the desired user-group covariances.
cov[XK,(a), XL(b)] = X
all c
all d X
I∈K
J∈L
AKI CI(a, c)ALJ CJ(b, d) cov[xI(c), xJ(d)] ,
(444)
or, alternatively,
cov[XK,(a), XL(b)] = 1
φKφLX
all c
all d X
I∈K
J∈L
CI(a, c)CJ(b, d)TIJ (c, d),(445)
where
TIJ (c, d) = φIφJcov[xI(c), xJ(d)] .(446)
In subroutine covcal, the flux-covariance product TIJ is calculated for all
evaluated reaction pairs and written to a “scratch” binary disk file, unit 11.
(For diagnostic purposes, it is possible to change this to a formatted scratch
308 NJOY2016

10 ERRORR LA-UR-17-20093
file by manually resetting the variable imode to +1 in the main program.) In
the subsequent collapse to the user’s group structure in subroutine covout, the
user-group covariances cov[XK(a), XL(b)] for one specific a-b reaction pair, for
all “MT1” energy groups L, and for as large a range of “MT” energy groups K as
possible, are calculated simultaneously in memory.
In covout, the disk file (unit 11) is rewound and read completely through,
once in each range of MT groups for each a-b reaction pair, to access the union-
group covariances for the evaluated reactions. As the union-group data pass
through memory, contributions to the user-group covariances are accumulated
using Eq. 444.
In the fairly common situation where cross sections x(a) and x(b) are directly
evaluated over the whole energy range of the data file,
CI(a, c) = δac,for all I, (447)
and
CJ(b, d) = δbd,for all J. (448)
In this case, Eq. 444 can be greatly simplified.
cov[XK(a), XL(b)] = 1
φKφLX
all c
all d X
I∈K
J∈L
δac δbd TIJ (c, d)
=1
φKφLX
I∈K
J∈L
TIJ (a, b).(449)
This result, which is identical to Eq. 437, suggests a shortcut calculational
path, which is followed in subroutine covout whenever both reactions are di-
rectly evaluated. In preparation for this situation, a second copy of the covcal
binary output file is generated when covout is first called. The second copy,
on unit 12, is read only in the trivial derivation cases just described (flagged
in the code by setting isd=1). Unit 12 is not rewound before processing a
given reaction pair a-b, since earlier reaction pairs on the file do not contribute
to the sum in Eq. 444 in these cases. Reading of the second copy stops after
the union-group covariances for reaction pair a-b are found, because the later
reaction pairs do not contribute either.
NJOY2016 309

LA-UR-17-20093 10 ERRORR
10.11 Processing of Data Derived from Ratio Measurements
The treatment of implicit covariances that arise from ratio measurements, as in
Eq. 415, is totally different from the treatment of data derived by summation,
Eq. 414, discussed in the previous section. Before discussing the processing
details, it is helpful first to review the subject of ratio evaluations generally.
Returning to the “x-y” notation of Section 10.2, let x(Ex) be the value of the
cross section for reaction xat energy Ex, and y(Ey) the cross section for reaction
yat energy Ey. In some energy region (Lx, Hx), suppose that the best knowledge
of x(Ex) is obtained through the application of a measured ratio, u(Ex):
x(Ex) = u(Ex)z(Ex),if Lx≤Ex≤Hx,(450)
where reaction zis some well-known cross section, possibly one of the official
ENDF/B standard cross sections. Similarly, suppose yis derived from the same
standard, over a possibly different energy range:
y(Ey) = v(Ey)z(Ey),if Ly≤Ey≤Hy.(451)
By performing a first-order Taylor-series expansion and then applying the for-
mula for propagation of errors, one can obtain an expression for the contribution
to the relative covariance, rcov[x(Ex), y(Ey)],that is attributable to these ratio
measurements. In the usual case, where the ratios uand vare only weakly
correlated with the standard cross section z, the result is quite simple:
rcov[x(Ex), y(Ey)]ratio = rcov[u(Ex), v(Ey)] + rcov[z(Ex), z(Ey)] (452)
if Lx≤Ex≤Hxand Ly≤Ey≤Hy, and
rcov[x(Ex), y(Ey)]ratio = 0 otherwise.(453)
Thus, in this fairly common evaluation situation, the covariance separates nat-
urally into a part involving only the measured ratios and a part involving only
the standard. Because the second contribution, cov(MTz, MTz), can be read di-
rectly from the NI-type sub-subsections in evaluation for the standard, it is not
included explicitly in the ENDF subsections for the derived quantities, cov(MTx,
MTx) or cov(MTy, MTy). Instead, the existence of this additional contribution
to the covariance is signalled by the presence of an NC-type sub-subsection.
The strategy adopted for processing this information in subroutine stand is
310 NJOY2016

10 ERRORR LA-UR-17-20093
to load the NI-type sub-subsections from the evaluation of the standard into the
same storage array that is used to store NI-type covariances from the evaluation
for reaction x. From that point on, the data from the standard are handled
just as if they had come from the evaluation for x, but with one exception.
As indicated by Eq. 453, the covariance contribution cov[z(Ex), z(Ey)] is not
added into the total covariance matrix for the current reaction pair if either
Exor Eylies outside the corresponding energy “window” (Lx, Hx) or (Ly, Hy),
respectively.
As discussed in Section 10.3, in addition to identifying the standard reaction,
the NC-type sub-subsection contains a control parameter LTY and two energies
EL and EH whose significance depends on LTY.LTY is used to identify particular
evaluation scenarios: reaction xis the same as reaction y(or at least they
are derived from zover the same energy range) (LTY=1); yis identical to the
standard (LTY=2); or xis identical to the standard (LTY=3). A fourth possibility,
namely, that x,y, and zare entirely distinct, cannot presently be treated with
a single NC-type sub-subsection; that is, there is no LTY value defined for this
case. However, as discussed later, it is still possible to process covariances for
this situation by combining information from sub-subsections in two different
evaluations. For convenience, we shall refer to this fourth case as LTY=4.
The interrelationship of LTY,EL,EH, and the windows (Lx, Hx) and (Ly, Hy)
used in ERRORR for the “zeroing-out” operation of Eq. 453, is summarized
below:
LTY =1
(Lx, Hx) = (Ly, Hy) = (EL,EH)
LTY =2
(Lx, Hx) = (EL,EH)
(Ly, Hy) = (10−5eV,20 MeV)
LTY =3
(Lx, Hx) = (10−5eV,20 MeV)
(Ly, Hy)=(EL,EH)
LTY =4
(Lx, Hx) = (EL,EH)
(Ly, Hy)=(EL0,EH0).(454)
If the user requests covariance data, cov(x, y), where xand yare different and
NJOY2016 311
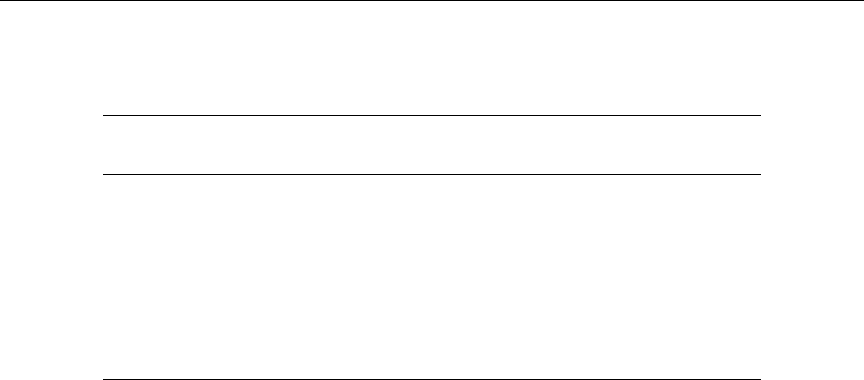
LA-UR-17-20093 10 ERRORR
Table 5: Covariance Matrices Affected by Ratio Measurements In ENDF/B-V
10B238U235U239Pu 239Pu 241Am 242Pu
(n,α) (n,γ) (n,f) (n,f) (n,γ) (n,f) (n,f)
10B(n,α)∗3
238U(n,γ) 2 1
235U(n,f) ∗3 3 3 3
239Pu(n,f) 2 1 1 4 4
239Pu(n,γ) 2 1 1 4 4
241Am(n,f) 2 4 4 1 4
242Pu(n,f) 2 4 4 4 1
∗= standard
Integer = LTY value (see text)
both are distinct from the standard (LTY=4), the ERRORR module obtains
(EL,EH) from the LTY=2 subsection in the evaluation for xthat “points” to z.
Then, the covariance file for zis read to obtain both (a) the explicit covariances
cov(z, z) and (b) the second energy window (EL0,EH0), the latter being found in
the LTY=3 sub-subsection that points back to y.
We will illustrate ratio covariance processing using data from ENDF/B-V.
Table 5lists all ENDF/B-V reactions that contain ratio-to-standard covariance
data. The symbols entered in the reaction-by-reaction matrix indicate which
reactions are referenced as standards (∗), and which reaction pairs have implicit
nonzero covariances (LTY). ERRORR will produce multigroup covariances for
any of the reaction pairs in Table 5that are marked with (∗) or (LTY). The cross-
material covariances (LTY=2, 3, or 4) must be requested individually using the
IREAD=2 option (see Section 10.14, especially the discussion of Cards 10 and
11). An attempt to process covariances for any of the cases LTY=1 through 4
without supplying a separate ENDF tape containing the needed standard will
result in an error stop in subroutine gridd. The error diagnostic, however, will
supply the details of the corrective action required. (See general discussion of
diagnostic messages in Section 10.16.)
As an example of the ratio-data capabilities of ERRORR, Fig. 44 shows
the covariances between the fission cross sections of 239Pu (reaction x) and
those of the important actinide 241Am (reaction y). This is an LTY=4 case
where (Lx, Hx)= (0.2 MeV,15 MeV) and (Ly, Hy)=(0.2 MeV,20 MeV). The
effect of using two different windows is apparent in the lower right corner of the
correlation matrix. The plot itself was produced with NJOY’s COVR module.
312 NJOY2016
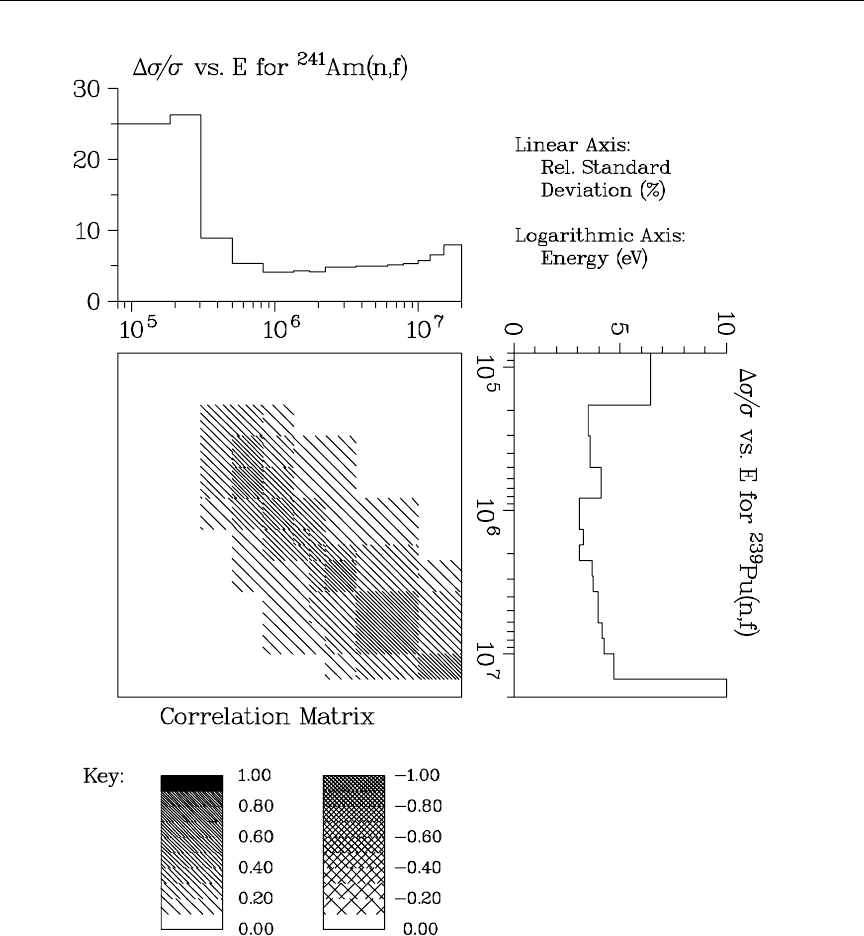
10 ERRORR LA-UR-17-20093
Figure 44: Covariance data for 239Pu(n,f) with 241Am(n,f). This older figure illustrates the
black & white option for covariance plots using hatching to represent levels of
correlation.
The complete input needed to compute and plot these data is given below (see
the fourth input example in Section 10.14).
NJOY2016 313

LA-UR-17-20093 10 ERRORR
10.12 Multigroup Processing of Resonance-Parameter Uncer-
tainties
In some materials, and in certain energy regions, the cross-section uncertainty
is dominated by the uncertainty in resolved resonance parameters. As described
above, there are several formats available in the ENDF-6 format for describ-
ing resonance covariances. When using the early ENDF-5 format (which is
available in the ENDF-6 format as LCOMP=0) the resonance-parameter contri-
bution to the uncertainty in infinite-dilution fission and capture cross sections is
included automatically when cross-section covariances are processed. The con-
tribution is obtained from the Breit-Wigner formulae for the fission and capture
areas of a resonance, Afand Aγ. By differentiating these formulae with re-
spect to the resonance parameters, one obtains a set of sensitivities. With these
sensitivities and the covariance matrix of the parameters from MF32, one can
apply the propagation-of-errors formula to obtain the covariances cov(Aγ, Aγ),
cov(Aγ, Af), and cov(Af, Af).
The resonance contribution is properly weighted with the isotopic abundance
and the ratio of the weight function at the resonance to the average weight
in the group. It is assumed, however, that the area of a resonance lies en-
tirely within the group that contains the resonance energy Er. Because of this
assumption, and because ENDF-5 and the LCOMP=0 option of ENDF-6 pro-
vide no correlations between parameters of different resonances, the calculated
resonance-parameter contribution affects only the diagonal elements of the af-
fected matrices, cov[XK(a), XK(b)].
When one of the more advanced options (LCOMP=1 or LCOMP=2) is found in
MF32, and for Single-Level Breit-Wigner, Multi-Level Breit-Wigner, or Reich-
Moore resonance parameters, the ERRORR code branches to the ERRORJ
logic. The resonance cross sections are computed on a special grid and group
averaged. Then each parameter is changed in turn to generate new cross sections.
Sensitivity parameters are computed from the differences. These sensitivity co-
efficients are then combined with the covariances of the parameters to obtain
covariances on the multigroup cross sections. The matrices are very large in
many cases, and the folding is time consuming. There are two formats in use for
the parameter covariances. One gives each value in a full computer word. With
many resonances, this can become very bulky. The other uses a more compact
representation based on the correlations. Just a few digits are used for each cor-
relation, thus reducing the size of the evaluation. The coding must reconstruct
the actual covariance values before folding them with the sensitivities, so this
314 NJOY2016

10 ERRORR LA-UR-17-20093
economization doesn’t help with the time required to fold the data in the final
cross section covariances.
If Reich-Moore-Limited resonances are found (LRF=7, a different branch is
taken. In this case, it is possible to use analytic formulas to compute the cross
section sensitivities to the parameters. These formulas are given in detail in
the SAMMY reference[36]. These sensitivities are computed on a special energy
grid and group averaged. They are then folded with the parameter covariances
as described above to obtain the cross section covariances.
10.13 Processing of Lumped-Partial Covariances
The lumped-partial covariance format, allows the evaluator to specify a group of
nuclear reactions and to give the uncertainty only in the sum of the cross sections
for that group of reactions. One can, for example, replace 30 or 40 discrete-level
inelastic cross sections with 5 or 6 lumped cross sections when constructing the
covariance files. Because the volume of the covariance data varies, in general, as
the square of the number of reactions, this lumping can greatly reduce the size
of the files.
The first ENDF evaluation to employ the lumped-partial format was Young’s
evaluation[75, 76] for 7Li (ENDF/B-V, Rev. 2). All covariance data for this eval-
uation have been successfully processed into multigroup form using ERRORR.
The covariances for MT854 (a single real level with an excitation energy of 4.63
MeV) with MT855 (6 lumped pseudo-levels, with excitation energies ranging from
4.75 MeV to 6.75 MeV) have been plotted in Fig. 45. The large negative correla-
tions along the diagonal result from the fact that, below 10 MeV, these inelastic
reactions are the major contributors to the relatively well-known tritium produc-
tion cross section. An upward variation in one reaction at a given energy must
be accompanied by a downward change in the other reaction. As shown in the
plot, the magnitude of this negative correlation diminishes at higher energies, as
other reactions begin to contribute significantly to the tritium-production cross
section. Plots of this type, prepared using ERRORR and COVR, have proved
to be useful tools in the validation of the covariance files of new evaluations[77].
10.14 Input Instructions and Sample Input for ERRORR
As an aid to discussions of the user input to ERRORR, we list below the in-
put instructions that appear as comment cards at the beginning of the current
version of this module. Since the code and, hence, the instructions change from
NJOY2016 315
LA-UR-17-20093 10 ERRORR
Figure 45: Covariance data for 7Li (MT854) with 7Li (MT855).
time to time, it is always advisable to consult the comment-card instructions
contained in the version of the code actually being used and not to rely on the
instructions published in any document, including this one. Note that the word
“tape” is used in the instructions to refer to an input or output file, regardless
of the actual storage medium.
316 NJOY2016

10 ERRORR LA-UR-17-20093
!---input specifications (free format)---------------------------
!
! card 1
! nendf unit for endf tape
! npend unit for pendf tape
! ngout unit for input group xsec (gendf) tape
! (if zero, group xsecs will be calculated)
! (if iread eq 2 or if mfcov eq 31, 35 or 40 (see
! card 7), then ngout cannot be zero)
! (if mfcov eq 35 (see card 7),
! ngout cannot be zero)
! (default=0)
! nout unit for output covariance tape (default=0)
! nin unit for input covariance tape (default=0)
! (nin and nout must be both coded or both binary)
! nstan unit for ratio-to-standard tape (default=0)
! card 2
! matd material to be processed
! ign neutron group option
! (ign definition same as groupr, except ign=19,
! which means read in an energy grid, as in ign=1,
! and supplement this with the endf covariance grid
! within the range of the user-specified energies)
! (default=1)
! iwt weight function option (default=6)
! iprint print option (0/1=minimum/maximum) (default=1)
! irelco covariance form (0/1=absolute/relative) (default=1)
! card 3 (*** REQUIRED for njoy2012 and later ***)
! mprint print option for group averaging (0/1=min (default)/max)
! tempin temperature (default=300)
!
!---for endf/b version 4 (iverf=4) only--------------------------
!
! card 4
! nek number of derived xsec energy ranges
! (if zero, all xsecs are independent)
! card 5 (omit if nek=0)
! ek nek+1 derived xsec energy bounds
! card 6 (omit if nek=0)
! akxy derived cross section coefficients, one row/line
NJOY2016 317

LA-UR-17-20093 10 ERRORR
!
!---for endf/b version 5 or 6 (iverf=5 or 6) only------------------------
!
! card 7
! iread 0/1/2=program calculated mts/input mts and eks/
! calculated mts plus extra mat1-mt1 pairs from input
! (default=0)
! mfcov endf covariance file (31, 33, 34, 35 or 40) to be
! processed (default=33).
! note--contribution to group cross section
! covariances from resonance-parameter uncertainties
! (mf=32) is included when mfcov=33 is specified.
! (mf=-33) high speed calc for test case
! (mf=333) hight speed calc for test case (faster)
! irespr processing for resonance parameter covariances
! (mf=32) (default=1)
! 0 = area sensitivity method
! 1 = 1\% sensitivity method
! legord legendre order for calculating covariances (default=1)
! (if mfcov is not 34, legord is ignored)
! ifissp subsection of the fission spectrum covariance
! matrix to process (default=-1 which means process
! the subsection that includes efmean). The value
! for ifissp that appears in njoy’s standard output
! will equal the subsection containing efmean.
! (if mfcov is not 35, ifissp is ignored)
! efmean incident neutron energy (eV). Process the covar-
! iance matrix subsection whose energy interval in-
! cludes efmean. if ifissp=-1 and efmean is not
! specified, set efmean=2.e6_kr. But if there is only
! one subsection, process it and if the input efmean
! was not within this subsection’s energy range then
! redefine efmean to equal the average energy for
! this subsection.
! (if mfcov is not 35, efmean is ignored)
! dap user specified scattering radius uncertainty, given
! as a fraction (i.e., dap=0.1 means 10\% uncertainty
! in the scattering radius). The default value is
! zero. This variable is only defined for mfcov=33
! and if non-zero will be used in lieu of any data
! that might have been read from the nendf tape.
!
318 NJOY2016

10 ERRORR LA-UR-17-20093
! following cards only if iread eq 1
! card 8
! nmt no. mts to be processed
! nek no. derived cross section energy ranges
! (if zero, all xsecs are independent)
! card 8a
! mts nmt mts
! card 8b (omit if nek=0)
! ek nek+1 derived cross section energy bounds
! card 9 (omit if nek=0)
! akxy derived cross section coefficients, one row/line
!
! following card only if iread eq 2
! card 10
! mat1 cross-material reaction to be added to
! mt1 covariance reaction list.
! repeat for all mat1-mt1 pairs desired
! terminate with mat1=0.
!
! following card only if nstan ne 0
! card 11
! matb standards reaction referenced
! mtb in matd.
! matc standards reaction to be
! mtc used instead.
! repeat for all standard reactions to be redefined.
! terminate with matb=0.
! note. if matb(1) and mtb(1) are negative, then matc(1) and
! mtc(1) identify a third reaction, correlated with matd thru
! the use of the same standard. covariances of all reactions
! in matd (which reference the standard) with the reaction
! matc(1)-mtc(1) will be produced. the standard reaction
! must be identified on card 10 and repeated as the negative
! entries on card 11. the group xsec tape ngout must include
! all covariance reactions in matd, plus matc(1)-mtc(1).
!
! card 12a (for ign eq 1 or ign eq 19)
! ngn number of groups
! card 12b
! egn ngn+1 group bounds (ev)
! card 13 (for iwt eq 1 only)
! wght weight function as a tab1 record
NJOY2016 319

LA-UR-17-20093 10 ERRORR
! card 13b analytic flux parameters (iwt=4 only)
! eb thermal break (ev)
! tb thermal temperature (ev)
! ec fission break (ev)
! tc fission temperature (ev)
!
! ---options for input variables------------------------------------
!
! ign meaning
! --- -------
! 1 arbitrary structure (read in)
! 2 csewg 239-group structure
! 3 lanl 30-group structure
! 4 anl 27-group structure
! 5 rrd 50-group structure
! 6 gam-i 68-group structure
! 7 gam-ii 100-group structure
! 8 laser-thermos 35-group structure
! 9 epri-cpm 69-group structure
! 10 lanl 187-group structure
! 11 lanl 70-group structure
! 12 sand-ii 620-group structure
! 13 lanl 80-group structure
! 14 eurlib 100-group structure
! 15 sand-iia 640-group structure
! 16 vitamin-e 174-group structure
! 17 vitamin-j 175-group structure
! 18 xmas 172-group structure
! 19 read in, supplemented with endf covariance grid
!
! iwt meaning
! --- -------
! 1 read in smooth weight function
! 2 constant
! 3 1/e
! 4 1/e + fission spectrum + thermal maxwellian
! 5 epri-cell lwr
! 6 (thermal) -- (1/e) -- (fission + fusion)
! 7 same with t-dep thermal part
! 8 thermal--1/e--fast reactor--fission + fusion
! 9 claw weight function
! 10 claw with t-dependent thermal part
320 NJOY2016

10 ERRORR LA-UR-17-20093
! 11 vitamin-e weight function (ornl-5505)
! 12 vit-e with t-dep thermal part
!
!--------------------------------------------------------------------
As an example of the use of these commands, here is the input used to
produce Fig. 38, the covariance plot for 10B from ENDF/B-VII.0.
1. errorr
2. 31 32 0 33/
3. 525 3 9 1 1/
4. 0 0./
5. 0 33/
6. covr
7. 33 0 34/
8. 1/
9. /
10. /
11. 525/
12. viewr
13. 34 35/
14. stop
The line numbers are for reference and are not part of the input. Identical
versions of the ENDF/B-VII.0 file for 10B can be copied to tape31 and tape32.
The ERRORR output will appear on tape33. In this sample input deck, that
file is the input file to COVR which generates the plot instructions that are
subsequently written to tape34. Line 3 defines the material to be processed
(525, or 10B), the group structure, the weight function, the listing option, and
requests relative covariances. Line 4 turns off printing for the group averaging
and requests zero temperature. Users are cautioned that line 4 is now required
in all ERRORR input decks whereas in njoy99 it is only required when ngout
is zero. Line 5 asks the program to calculate the MT numbers to be processed
and to work with File 33. The COVR and VIEWR input in lines 6 through 13
act to prepare the graph as seen in Fig. 38.
The follwing paragraphs give more detail on how the various input parameters
are used.
NJOY2016 321

LA-UR-17-20093 10 ERRORR
npend, ngout . . . The user must supply either a PENDF tape on unit
npend or a GENDF tape on unit ngout. If present, the npend tape should
contain pointwise (resonance-reconstructed, but not multigrouped) data and is
normally produced with the RECONR module. If the resonance region is of
no interest, a simple copy of the ENDF tape will suffice for this purpose. The
GENDF tape, if present, should contain multigroup cross sections and/or νval-
ues, produced by the GROUPR module, for all reactions for which multigroup
covariances are needed. Group cross sections need not be in the same group
structure as the requested output covariances, although if the input group struc-
ture is much coarser than the output structure, rather crude approximations will
be made in deriving an effective set of fine-group cross sections and fluxes from
the coarse input data. Certain types of covariance calculations related to fission
data or the computation of cross-material covariances require the user to supply
a GENDF tape on ngout (that is, npend must be zero).
nin, nout . . . Input and output covariance tapes in the user’s group struc-
ture may either be both formatted or both binary. Although ERRORR lacks
an explicit multimaterial loop, the same effect can be achieved by executing a
series of ERRORR runs, with the output of one run becoming the input of the
next. Only two unit numbers need be employed, with the data going back and
forth between them until the multimaterial library is complete. To save time,
binary files should be used for this purpose. MODER can be used to convert
the final output tape from binary to formatted form, if desired.
nstan . . . This tape is needed if covariances are requested for a reaction
pair that is related by ratio measurements, as discussed in Section 10.11. The
ENDF subsection for such a pair will contain an NC-type sub-subsection with
LTY=1, 2, or 3. The specific pairs in ENDF/B-V that require a standards tape
are tabulated in Table 5(Section 10.11). For other evaluations, one can assume
nstan is not needed. The code will stop with a clear error message if this
assumption proves incorrect.
iread . . . For ENDF/B versions 5 and 6, the list of reactions for which
covariances are produced is constructed in one of several ways, depending on
the value of iread. If iread=0, which is the generally recommended choice,
the reaction list is assumed to be identical to the list of sections contained in
the ENDF/B covariance file (see mfcov below). Although iread=0 is the most
convenient option for constructing the list of covariance reactions, it leads to a
problem if some covariance reactions have thresholds above the highest group
boundary of the user’s structure. These reactions will have zero cross sections
322 NJOY2016

10 ERRORR LA-UR-17-20093
in all groups and thus will be omitted from ngout. To avoid this difficulty,
ERRORR automatically resets the user’s highest group boundary to 20 MeV
whenever iread=0. By judicious choice of weighting functions, one can minimize
the effect of this resetting on the other cross sections and their covariances.
If iread=1, only the covariance reactions specifically named by the user will
be included in the reaction list. For certain applications, this option can save
considerable execution time. However, to take advantage of this option, the user
must examine the ENDF evaluation visually to determine which reactions are
derived from other reactions in each energy region. As discussed in Section 10.3,
this information is contained in NC-type sub-subsections with LTY=0. Incorrect
results will be obtained if one requests processing for a given reaction without
processing all of the reactions from which the given reaction is derived in the
energy region spanned by the output group structure. The inclusion of those
reactions may require, in turn, additional inclusions as well. In addition, the user
must extract from the file (and enter into the input) the appropriate derivation
coefficients and the energy ranges over which they apply. An example of the
required input is presented below in the discussion of the parameters nmt,nek,
mts,ek, and akxy.
If iread=0 or 1, a complete set of covariance matrices is written. That
is, covariance matrices are produced for every reaction-pair combination that
can be formed from the given reaction list. For those reaction pairs where the
evaluator has not specified the covariances, the output matrix contains only
zeros.
In the evaluation containing cross-material covariances, subsections involv-
ing the other materials will be ignored if iread=0 or 1. These subsections can
be selectively processed by specifying iread=2. If iread=2, the reaction list
is initially constructed in the same way as for iread=0. This list is then sup-
plemented with a list of extra reactions (MAT1k, MT1k) (where (MAT1k6=
MATD), specified by the user. The output in this case contains matrices for all
of the (MATD, MTi; MATD,,MTj) combinations, as before, plus matrices for
all (MATD, MTi; MAT1k, MT1k) combinations. However, covariances among
the extra reactions, for example (MAT1k, MT1k; MAT1m,,MT1m), are not com-
puted. Input for an example problem that illustrates the use of iread=2 is given
below, in the discussion of mfcov. That discussion also includes an illustration
of the set of MAT/MT combinations that are processed when iread=2.
mfcov . . . is used to specify whether covariances of ν(mfcov=31), cross
sections (mfcov=33), angular distributions (mfcov=34), secondary energy distri-
NJOY2016 323

LA-UR-17-20093 10 ERRORR
butions (mfcov=35), or radioactive nuclide production (mfcov=40) are needed.
If mfcov=31, 35, or 40, it is necessary to supply multigrouped cross sections and
νvalues on a GENDF tape that is, npend must be 0); the sample problem below
shows the calculational sequence required. The parameter mfcov=32 is reserved
for a planned future capability to compute uncertainties in self-shielded cross sec-
tions. If mfcov=33, the contribution of the uncertainty in individual resonance
parameters (File 32) is included in the calculated uncertainty in infinite-dilution
group cross sections. Given below is the complete NJOY input for a calcula-
tion of a multigroup νcovariance library for 238U, including five cross-material
reactions.
moder / mount ENDF tapes 515, 516, and 555 on units 20, 21, and 22.
1 -23/
’ENDF/B-V NUBAR COVARIANCE MATERIALS’/
20 1380/
20 1381/
21 1390/
22 1395/
22 1398/
20 1399/
0/
moder / copy ENDF for use as a PENDF.
-23 -24/
groupr / prepare GENDF with multigrouped nubars.
-23 -24 0 25/
13803030110/
’BIG3 + 2 NUBAR’/
0./
1.e10/
3 452 ’TOTAL NUBAR’/
0/
1381/
3 452 ’TOTAL NUBAR’/
0/
1390/
3 452 ’TOTAL NUBAR’/
0/
1395/
3 452 ’TOTAL NUBAR’/
0/
324 NJOY2016

10 ERRORR LA-UR-17-20093
1398/
3 452 ’TOTAL NUBAR’/
3 455 ’DELAYED NUBAR’/
3 456 ’PROMPT NUBAR’/
0/
1399/
3 452 ’TOTAL NUBAR’/
0/
0/
errorr / prepare multigroup nubar covariance library.
-23 0 25 26/
1398 19 1 1/
0 0. /
2 31/
1380 452/
1381 452/
1390 452/
1395 452/
1399 452/
0/
1/
1.e7 1.7e7/
stop
Note the use of the MODER module to prepare a special ENDF tape contain-
ing selected evaluations from other ENDF tapes. Because only high-energy ν
data are requested (10 – 17 MeV), it is unnecessary to use RECONR to prepare
a PENDF tape for GROUPR. A copy of the ENDF tape is used instead.
Following the prescription given in the discussion of the iread=2 option, with
this particular input, covariance matrices will be produced for those reaction
pairs marked with an X in Table 6. The remaining non-redundant possibilities
(dashes) can be filled in with successive ERRORR runs with MATD=1380, 1381,
etc.
nwt,nek,mts,ek,akxy . . . For ENDF/B version 5, if iread=1, the user
specifies a subset of the evaluator’s covariance reactions (that is, a subset of
the sections of mfcov), as the particular set of reactions for which processing
is requested. These nmt desired reactions are entered in the array mts. As
mentioned in the discussion of iread above, one must also include in the mts
array all reactions from which the desired reactions are derived.
NJOY2016 325
LA-UR-17-20093 10 ERRORR
Table 6: Reaction pairs in the ENDF/B-V 238U evaluation
a b c d e f g h i
a = (1398,452) X X X X X X X X X
b = (1398,455) X X X X X X X X
c = (1398,456) X X X X X X X
d = (1380,452) – – – – – –
e = (1381,452) – – – – –
f = (1390,452) – – – –
g = (1395,452) – – –
h = (1398,452) – –
i = (1399,452) –
Another requirement of the iread=1 option is that the actual derivation
coefficients, called akxy in the code, but called CI(a, c) in the discussion in
Section 10.10, must be entered in the ERRORR input for nek energy ranges
spanning the output group structure. Adjacent ENDF derivation ranges may
be merged into a single range if the derivation-coefficient matrix for the nmt
explicitly requested reactions is the same in each of the adjacent ranges. The
ordering of the CI(a, c) data is as follows: on one line of input the coefficients are
specified for a fixed a-value and for all c-values ranging from 1 to nmt. One such
line is given for each a-value. Finally, there is an outer loop over the nek energy
ranges. An example of the input that is required for iread=1 is given below for
the case of ENDF/B-V carbon MAT=1306. It will be necessary to examine File
33 of the evaluation (which is available on the ENDF/B-V standards file, Tape
511), in order to understand the details of this example.
moder
20- 21/
moder / copy ENDF for use as a PENDF.
-21 -22/
errorr
-21 -22 0 -23/
1306 3 1/
2 0 0/
1 33/
7 3/
1 2 4 102 103 104 107/
1.e-5 2e6 4.812e6 2e7/
326 NJOY2016

10 ERRORR LA-UR-17-20093
0101000/
0100000/
0010000/
0001000/
0000100/
0000010/
0000001/
1000000/
0100000/
0010000/
0001000/
0000100/
0000010/
0000001/
1000000/
0100000/
1 -1 0 -1 -1 -1 -1/
0001000/
0000100/
0000010/
0000001/
stop
Note that here, even if the user wanted to process only M=2 and MT=4,
for example, it is nevertheless necessary to include MT=1, MT=102, MT=103,
MT=104, and MT=107, because the ign=3 group structure extends to 17.0
MeV, and above 4.812 MeV, MT=4 is derived from the relation
σ4=σ1−σ2−σ102 −σ103 −σ104 −σ107 .(455)
See the corresponding CI(a, c) matrix in the input above (the last 7 lines before
stop).
matb,mtb,matc,mtc . . . Card 11 provides a capability to remap all ref-
erences to a given standards reaction (matb, mtb) appearing in NC-type sub-
subsections with lty=1, 2, or 3 into references to a different reaction (matc, mtc).
(See the discussion of ratio measurements in Section 10.11.) This facility is use-
ful if the evaluation (matb, mtb) is for some reason unavailable. Up to 5 such
standards can be redefined. As explained in the note on the input instructions
at the beginning of this section, Card 11 is also used, if matb(1) and mtb(1) are
NJOY2016 327

LA-UR-17-20093 10 ERRORR
negative, to process covariances between two distinct reactions, both measured
relative to a common standards reaction. This was referred to as the lty=4
case in Section 10.11. A separate ERRORR run is required for each requested
lty=4 reaction pair.
This second use of Card 11 is illustrated in the sample NJOY input listed
below, which is the input used to generate and plot the data shown in Fig. 44.
The input to the COVR module contained in the sample is explained in the
following chapter.
mount T562 on tape30
mount T563 on tape40
mount T560 on tape50
moder
1 -31/
’U235 FROM T562’/
30 1395/
0/
moder
1 -21/
’AM241 FROM T560 AND PU239 FROM T563’/
50 1361/ AM241
40 1399/ PU239
0/
reconr
-21 -22/
’10 PERCENT PENDF FOR AM241 AND PU239’/
1361/
.1/
1399/
.1/
0/
GROUPR
-21 -22 0 -24/
13613020110/
’30 GROUP XSECS FOR AM241 AND PU239’/
0/
1e10/
3 1/
3 2/
3 4/
328 NJOY2016

10 ERRORR LA-UR-17-20093
3 16/
3 17/
3 18/
3 102/
0/
1399
3 18/
3 102/
0/
0/
errorr
-21 0 -24 -25 0 -31/
1361 3 1 1/
0 0. /
0 33/
0/
errorr
-21 0 -24 -28 -25 -31/
1399 3 1 1/
0 0. /
2 33/
1395 18/
0/
-1395 -18 1361 18/
0/
covr
-28/
0 0 0 8e4/
11002/
1399 18 1361 18/
stop
The input for a File 34 case preparing covariances for an angular distribu-
tion is shown below. This is the input that produced Fig. 40 shown above. This
deck runs a job sequence that includes MODER (ASCII-to-binary conversion),
RECONR and BROADR (cross section reconstruction to 300K), GROUPR (un-
weighted, infinitely dilute multigroup cross sections plus average ¯µ), ERRORR
(specifying mfcov=34 for ¯µcovariance processing), and COVR and VIEWR (for
plot generation and conversion to Postscript format). The input on tape20 was
the JENDL-3.3 evaluation for 238U.
NJOY2016 329

LA-UR-17-20093 10 ERRORR
moder
20 -21 /
reconr
-21 -22 /
’processing jendl-3.3 u-238.’/
9237 0 0 /
0.001 /
0 /
broadr
-21 -22 -23 /
92371000/
0.001 /
300. /
0 /
groupr
-21 -23 0 91 /
92373021110/
’test’/
300. /
1.0e10 /
3 /
3 251 ’mubar’ /
0 /
0 /
--
-- process mf34
errorr
-210912700/
92373211/
0 300. /
03411-1/
--
-- make mf34 plot file.
covr
27 0 37 /
1 /
/
/
9237 /
--
330 NJOY2016

10 ERRORR LA-UR-17-20093
-- make mf34 postscript file.
viewr
37 47 /
stop
The input for the File 35 case that produced the plot of secondary energy
covariances seen in Fig. 41 is given below. This is a problem taken from the
NJOY test suite that uses a fictitious input file for 252Cf. The GROUPR and
ERRORR inputs specify a user-defined group structure that corresponds to the
energies listed in File 1 of the evaluation with the uncertainties provided by the
evaluator. This makes it easy to verify that the results agree with the evaluator’s
intent.
--
-- Copy ascii input to binary.
moder
20 -21 /
--
-- Resonance reconstruction, to 0.1\%.
reconr
-21 -22 /
’processing e70 252Cf with decay mf5/mt18 & mf35/mt18’/
9999 0 0 /
0.001 /
0 /
--
-- Doppler broaden to 300K.
broadr
-21 -22 -23 /
99991000/
0.001 /
300. /
0 /
--
-- Group average, 300K with mf35 group structure.
-- - All file 3 cross sections plus fission spectrum.
groupr
-21 -23 0 91 /
99991021111/
’test’/
NJOY2016 331

LA-UR-17-20093 10 ERRORR
300. /
1.0e10 /
71 / # of groups, energy boundaries follow:
1.000000-5 1.500000+4 3.500000+4 5.500000+4 7.500000+4
9.500000+4 1.150000+5 1.350000+5 1.650000+5 1.950000+5
2.250000+5 2.550000+5 3.050000+5 3.550000+5 4.050000+5
4.550000+5 5.050000+5 5.550000+5 6.050000+5 6.550000+5
7.050000+5 7.550000+5 8.050000+5 8.550000+5 9.050000+5
9.550000+5 1.050000+6 1.150000+6 1.250000+6 1.350000+6
1.450000+6 1.550000+6 1.650000+6 1.750000+6 1.850000+6
1.950000+6 2.150000+6 2.350000+6 2.550000+6 2.750000+6
2.950000+6 3.250000+6 3.550000+6 3.850000+6 4.150000+6
4.450000+6 4.750000+6 5.050000+6 5.550000+6 6.050000+6
6.550000+6 7.050000+6 7.550000+6 8.050000+6 8.550000+6
9.050000+6 9.550000+6 1.005000+7 1.055000+7 1.105000+7
1.155000+7 1.205000+7 1.255000+7 1.305000+7 1.355000+7
1.405000+7 1.460000+7 1.590000+7 1.690000+7 1.790000+7
1.910000+7 2.000000+7/
3 /
5 18 ’chi’ /
0 /
0 /
--
-- ERRORJ, mf35
errorr
200912800/
99991211/
0 300. /
0 35 1 1 -1 1.23e6 /
71 / # of groups, energy boundaries follow:
1.000000-5 1.500000+4 3.500000+4 5.500000+4 7.500000+4
9.500000+4 1.150000+5 1.350000+5 1.650000+5 1.950000+5
2.250000+5 2.550000+5 3.050000+5 3.550000+5 4.050000+5
4.550000+5 5.050000+5 5.550000+5 6.050000+5 6.550000+5
7.050000+5 7.550000+5 8.050000+5 8.550000+5 9.050000+5
9.550000+5 1.050000+6 1.150000+6 1.250000+6 1.350000+6
1.450000+6 1.550000+6 1.650000+6 1.750000+6 1.850000+6
1.950000+6 2.150000+6 2.350000+6 2.550000+6 2.750000+6
2.950000+6 3.250000+6 3.550000+6 3.850000+6 4.150000+6
4.450000+6 4.750000+6 5.050000+6 5.550000+6 6.050000+6
6.550000+6 7.050000+6 7.550000+6 8.050000+6 8.550000+6
9.050000+6 9.550000+6 1.005000+7 1.055000+7 1.105000+7
332 NJOY2016

10 ERRORR LA-UR-17-20093
1.155000+7 1.205000+7 1.255000+7 1.305000+7 1.355000+7
1.405000+7 1.460000+7 1.590000+7 1.690000+7 1.790000+7
1.910000+7 2.000000+7/
--
-- make plot file.
covr
28 0 38 /
1 /
1.e3 /
/
9999 /
--
-- make postscript file.
viewr
38 39 /
stop
The final example gives the input used to prepare Fig. 42 showing the un-
certainties in radionuclide production for 93Nb. This is a fairly elaborate input
deck, as it includes GROUPR/ERRORR/ COVR/VIEWR processing for both
File 3 and File 10.
-- Extract/convert neutron evaluated data
moder
1 -21/
’41-Nb-93 from e70’/
20 4125/
0/
--
-- Make an ASCII copy
moder
-21 41 /
--
-- Reconstruct xs
reconr
41 42/
’pendf for 41-Nb-93’/
4125 2/
0.001 0. 0.003/
’41-Nb-93 from e70’/
’Processed with NJOY’/
NJOY2016 333

LA-UR-17-20093 10 ERRORR
0/
--
-- Doppler broaden xs
broadr
41 42 43/
4125 1 0 0 0./
0.001 2.0e6 0.003/
300./
0/
--
-- groupr, process all file 3 reactions:
groupr
41 43 0 44 /
41251060111/
’41-Nb-93 from e70 with NJOY’/
300. /
1.e10 /
21 /
1.e-5 0.625 10.7 100.0 1.e3 1.e4 1.e5 1.e6
2.e6 3.e6 4.e6 5.e6 6.e6 7.e6 8.e6 9.e6 10.e6
12.e6 14.e6 16.e6 18.e6 20.e6 /
3 /
0/
0/
--
-- errorj, process all file 3 reaction uncertainties:
errorr
41 43 44 45/
41251611/
0 300. /
0 33 /
21 /
1.e-5 0.625 10.7 100.0 1.e3 1.e4 1.e5 1.e6
2.e6 3.e6 4.e6 5.e6 6.e6 7.e6 8.e6 9.e6 10.e6
12.e6 14.e6 16.e6 18.e6 20.e6 /
--
-- create plot of mf33 uncertainty data
covr
45 0 55 /
1 /
1.e-1 /
/
334 NJOY2016

10 ERRORR LA-UR-17-20093
4125 /
viewr
55 65 /
--
-- groupr, process all file 10 reactions:
groupr
41 43 0 46 /
41251060111/
’41-Nb-93 from e70 with NJOY’/
300. /
1.e10 /
21 /
1.e-5 0.625 10.7 100.0 1.e3 1.e4 1.e5 1.e6
2.e6 3.e6 4.e6 5.e6 6.e6 7.e6 8.e6 9.e6 10.e6
12.e6 14.e6 16.e6 18.e6 20.e6 /
10 /
0/
0/
--
-- errorj, process all file 10 reaction uncertainties:
errorr
41 43 46 47/
41251611/
0 300. /
0 40 /
21 /
1.e-5 0.625 10.7 100.0 1.e3 1.e4 1.e5 1.e6
2.e6 3.e6 4.e6 5.e6 6.e6 7.e6 8.e6 9.e6 10.e6
12.e6 14.e6 16.e6 18.e6 20.e6 /
--
-- create plot of mf40 uncertainty data
covr
47 0 57 /
1 /
1.e3 /
/
4125 /
viewr
57 67 /
stop
NJOY2016 335

LA-UR-17-20093 10 ERRORR
10.15 ERRORR Output File Specification
The results from ERRORR are written to an output file on unit nout, provided
that the input parameter nout is nonzero. This file contains the user’s group
structure, the multigroup cross sections, and either absolute (irelco=0) or
relative (irelco=1) covariances. If nout is positive, then a formatted (card-
image) file is written, and, if negative, a binary file is written. In either case,
the output is written with the standard NJOY I/O utilities, and the result has
an ENDF-like structure. As is the case for ENDF, PENDF, and GENDF files,
ERRORR output files can be converted from binary to formatted form (and
vice versa) by using the MODER module. The energy-group ordering of the
data written to nout follows the ENDF convention, that is, low-energy groups
precede high-energy groups.
It is occasionally of interest to examine a formatted ERRORR output file
visually. For this and other reasons, we describe below the detailed form of the
formatted output file. To assist in the description, we give below an example
listing of such a file, which was produced during the processing of COVFILS-
2[78].
The data in the listing are written in the form of standard, 80-column card-
images consisting of 10 data fields. As in ENDF, the first 6 fields are 11 char-
acters wide and are used for either floating-point numbers or integers. The
seventh, eighth, ninth, and tenth fields are 4, 2, 3, and 5 characters wide, re-
spectively, and are used for integers only. The four digits in Field 7 are the
MAT, or material number, of the isotope or element; the two digits in Field 8 are
the MF, or file number, which indicates the general type of data (for example,
cross-section data vs. covariance data); the three digits in Field 9 are the MT, or
section number, which indicates the particular nuclear reaction; and finally, the
five digits in Field 10 are NSEQ, the card sequence number. As usual, sections are
terminated by zeros in the MT field, files by zeros in the MF field, and materials
by zeros in the MAT field.
Following an initial tape header record, the second card shown in the listing
is the first data card for the material MAT=1326, which is ENDF/B-V elemental
iron. Note that on this card the number 2.6×104appears in the first field and
55.365 in the second field. These are the “ZA” (1000 ×Z−A) and “AWR”
(atomic weight relative to the neutron) numbers taken directly from the ENDF
file. The fact that ZA is 26 000 (suggesting that A= 0) is a convention that
means that the data are for the natural element, Fe, rather than for a single
isotope. The value of −11 appearing in Field 5 is a flag (read by the MODER
336 NJOY2016

10 ERRORR LA-UR-17-20093
module, for example) that identifies the present file format as the ERRORR
output format.
Also note that MF=1 and MT=451 on cards NSEQ=1 - 15. This MF, MT combi-
nation is used in the ENDF format for descriptive Hollerith information, but it
is used here to specify the boundaries of the multigroup structure used for the
processed data to follow. On Card 2, note the number 74 in Field 3 and the
number 75 in Field 5, which indicate, respectively, the number of energy groups
and the number of energy-group boundaries in the multigroup set. The values
of the group boundaries, given in eV from low to high energy, follow in Cards 3
through 15. Cards 16 and 17 are section and file terminators, respectively.
Multigroup cross-section data are given in barns on Cards 18 through 631.
This file, denoted by MF=3, corresponds to the smooth cross-section file in
ENDF. The MT-numbers (Field 9) can be identified with particular nuclear
reactions by consulting Appendix B of the ENDF format manual [9]. Note that
cross sections for the lumped-partial reaction MT=851 have been constructed by
ERRORR according to the directions given in the ENDF file.
Example of ERRORR Output Data File
1 0 0 0
2.600000+4 5.536500+1 0 0 -11 01326 1451 1
0.000000+0 0.000000+0 74 0 75 01326 1451 2
1.000000-5 7.602200-4 1.239500-2 4.275500-2 8.196800-2 1.523000-11326 1451 3
4.139900-1 8.764200-1 1.125400+0 1.855400+0 3.927900+0 5.043500+01326 1451 4
8.315300+0 1.760300+1 3.726700+1 7.889300+1 1.013000+2 1.670200+21326 1451 5
3.535800+2 7.485200+2 1.584600+3 3.354600+3 7.101700+3 9.118800+31326 1451 6
1.503400+4 2.478800+4 2.605800+4 2.808800+4 3.182800+4 4.086800+41326 1451 7
5.247500+4 6.737900+4 8.651700+4 1.110900+5 1.426400+5 1.831600+51326 1451 8
2.351800+5 3.019700+5 3.877400+5 4.393700+5 4.978700+5 5.641600+51326 1451 9
6.392800+5 7.244000+5 8.208500+5 1.054000+6 1.194300+6 1.353400+61326 1451 10
1.737700+6 1.969100+6 2.231300+6 2.528400+6 2.865000+6 3.246500+61326 1451 11
3.678800+6 4.168600+6 4.723700+6 5.352600+6 6.065300+6 6.872900+61326 1451 12
7.788000+6 8.825000+6 1.000000+7 1.100000+7 1.200000+7 1.300000+71326 1451 13
1.350000+7 1.375000+7 1.394000+7 1.420000+7 1.442000+7 1.464000+71326 1451 14
1.500000+7 1.600000+7 2.000000+7 1326 1451 15
1326 1 0 16
1326 0 0 17
0.000000+0 0.000000+0 0 0 74 01326 3 1 18
3.242538+1 1.638221+1 1.395614+1 1.310400+1 1.266828+1 1.222209+11326 3 1 19
1.192867+1 1.180887+1 1.173992+1 1.164882+1 1.159180+1 1.155850+11326 3 1 20
1.151292+1 1.146973+1 1.143331+1 1.140845+1 1.137811+1 1.103735+11326 3 1 21
NJOY2016 337

LA-UR-17-20093 10 ERRORR
1.031032+1 9.276154+0 7.382612+0 7.137478+0 1.602539+1 4.178159+01326 3 1 22
1.482726+0 1.406100+0 3.875233+1 3.832471+1 8.517735+0 5.325881+01326 3 1 23
4.200487+0 6.723474+0 4.481126+0 3.610952+0 3.923129+0 4.868550+01326 3 1 24
2.836503+0 3.245566+0 4.853495+0 3.640536+0 3.205600+0 2.250606+01326 3 1 25
2.732808+0 3.895072+0 2.571093+0 2.501068+0 2.958182+0 2.985432+01326 3 1 26
2.899251+0 3.213480+0 3.189247+0 3.477117+0 3.389077+0 3.403654+01326 3 1 27
3.625322+0 3.668095+0 3.697471+0 3.674937+0 3.632669+0 3.545578+01326 3 1 28
3.383465+0 3.214864+0 3.053930+0 2.905813+0 2.743816+0 2.674006+01326 3 1 29
2.635890+0 2.613351+0 2.590513+0 2.567519+0 2.547020+0 2.517568+01326 3 1 30
2.457292+0 2.307503+0 1326 3 1 31
1326 3 0 32
0.000000+0 0.000000+0 0 0 74 01326 3 2 33
1.140000+1 1.140000+1 1.139999+1 1.139998+1 1.139996+1 1.139991+11326 3 2 34
1.139978+1 1.139964+1 1.139947+1 1.139900+1 1.139839+1 1.139764+11326 3 2 35
1.139553+1 1.139053+1 1.137995+1 1.136763+1 1.134459+1 1.101228+11326 3 2 36
1.029462+1 9.055728+0 7.376526+0 7.127705+0 1.599799+1 4.168132+01326 3 2 37
1.450895+0 1.368534+0 3.867417+1 3.827977+1 8.473823+0 5.294164+01326 3 2 38
4.169383+0 6.691388+0 4.451224+0 3.586689+0 3.901454+0 4.844768+01326 3 2 39
2.815969+0 3.225118+0 4.830640+0 3.616074+0 3.180014+0 2.223638+01326 3 2 40
2.703083+0 3.863693+0 2.346491+0 2.057345+0 2.535809+0 2.262868+01326 3 2 41
2.127090+0 2.261804+0 2.256791+0 2.533315+0 2.231035+0 2.144008+01326 3 2 42
2.151420+0 2.170908+0 2.095557+0 2.088164+0 2.073116+0 2.006202+01326 3 2 43
1.857245+0 1.711327+0 1.565212+0 1.419054+0 1.283900+0 1.274210+01326 3 2 44
1.266290+0 1.253001+0 1.238749+0 1.224132+0 1.210283+0 1.196914+01326 3 2 45
1.165341+0 1.042323+0 1326 3 2 46
1326 3 0 47
.
.
0.000000+0 0.000000+0 0 0 74 01326 3107 603
0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+01326 3107 604
0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+01326 3107 605
0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+01326 3107 606
0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+01326 3107 607
0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+01326 3107 608
0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+01326 3107 609
0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+01326 3107 610
0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+01326 3107 611
0.000000+0 0.000000+0 0.000000+0 0.000000+0 5.054213-6 3.154394-51326 3107 612
6.536392-5 1.636755-4 4.937945-4 1.599742-3 4.467725-3 9.026301-31326 3107 613
1.492042-2 2.174807-2 2.912657-2 3.467999-2 3.849531-2 3.982821-21326 3107 614
3.986411-2 3.988542-2 3.971171-2 3.918684-2 3.866013-2 3.800829-21326 3107 615
3.513214-2 1.922833-2 1326 3107 616
338 NJOY2016

10 ERRORR LA-UR-17-20093
1326 3 0 617
0.000000+0 0.000000+0 0 0 74 01326 3851 618
0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+01326 3851 619
0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+01326 3851 620
0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+01326 3851 621
0.000000+0 0.000000+0 0.000000+0 0.000000+0 0.000000+0 1.713016-41326 3851 622
2.605423-2 2.747897-2 2.715636-2 2.656936-2 2.500170-2 2.240780-21326 3851 623
2.044663-2 1.866612-2 1.650006-2 1.483479-2 1.452751-2 1.445474-21326 3851 624
1.484054-2 1.514701-2 1.823890-2 1.948106-2 2.054081-2 2.151007-21326 3851 625
2.239315-2 2.355651-2 2.568895-2 2.711755-2 2.775385-2 2.831557-21326 3851 626
2.892825-2 2.891470-2 2.891944-2 2.909114-2 2.816820-2 2.648783-21326 3851 627
2.379156-2 2.036489-2 1.658885-2 1.236790-2 8.719756-3 5.515926-31326 3851 628
2.789373-3 1.967219-3 1.199289-3 5.263406-4 1.809961-4 1.629883-41326 3851 629
1.542762-4 1.491088-4 1.438805-4 1.385182-4 1.332255-4 1.265700-41326 3851 630
1.111753-4 5.198675-5 1326 3851 631
1326 3 0 632
1326 0 0 633
2.600000+4 5.536500+1 0 0 0 41132633 1 634
0.000000+0 0.000000+0 0 1 0 74132633 1 635
0.000000+0 0.000000+0 17 1 17 1132633 1 636
4.771962-4 6.905149-4 7.654629-4 7.983731-4 8.169108-4 8.372624-4132633 1 637
8.514704-4 8.574701-4 8.609741-4 8.656539-4 8.686033-4 8.703185-4132633 1 638
8.707277-4 8.728724-4 8.748390-4 8.757964-4 7.461125-4 132633 1 639
0.000000+0 0.000000+0 17 1 17 2132633 1 640
6.905149-4 1.247608-3 1.443338-3 1.529285-3 1.577697-3 1.630846-3132633 1 641
1.667951-3 1.683619-3 1.692770-3 1.704992-3 1.712694-3 1.717174-3132633 1 642
1.722305-3 1.727680-3 1.731573-3 1.733468-3 1.476784-3 132633 1 643
0.000000+0 0.000000+0 17 1 17 3132633 1 644
7.654629-4 1.443338-3 1.681504-3 1.786085-3 1.844993-3 1.909666-3132633 1 645
1.954815-3 1.973881-3 1.985016-3 1.999887-3 2.009259-3 2.014710-3132633 1 646
2.021500-3 2.028010-3 2.032580-3 2.034804-3 1.733500-3 132633 1 647
0.000000+0 0.000000+0 17 1 17 4132633 1 648
7.983731-4 1.529285-3 1.786085-3 1.898848-3 1.962365-3 2.032098-3132633 1 649
2.080780-3 2.101337-3 2.113343-3 2.129378-3 2.139484-3 2.145360-3132633 1 650
2.152879-3 2.159888-3 2.164754-3 2.167123-3 1.846226-3 132633 1 651
.
.
0.000000+0 0.000000+0 0 102 0 74132633 1 1738
0.000000+0 0.000000+0 13 1 13 1132633 1 1739
2.593694-4 2.593694-4 2.593694-4 2.593694-4 2.593694-4 2.593694-4132633 1 1740
2.593694-4 2.593694-4 2.593694-4 2.593694-4 2.593694-4 2.593694-4132633 1 1741
7.341822-5 132633 1 1742
NJOY2016 339

LA-UR-17-20093 10 ERRORR
0.000000+0 0.000000+0 13 1 13 2132633 1 1743
1.216493-4 1.216493-4 1.216493-4 1.216493-4 1.216493-4 1.216493-4132633 1 1744
1.216493-4 1.216493-4 1.216493-4 1.216493-4 1.216493-4 1.216493-4132633 1 1745
3.443457-5 132633 1 1746
0.000000+0 0.000000+0 13 1 13 3132633 1 1747
7.326236-5 7.326236-5 7.326236-5 7.326236-5 7.326236-5 7.326236-5132633 1 1748
7.326236-5 7.326236-5 7.326236-5 7.326236-5 7.326236-5 7.326236-5132633 1 1749
2.073796-5 132633 1 1750
0.000000+0 0.000000+0 13 1 13 4132633 1 1751
5.201525-5 5.201525-5 5.201525-5 5.201525-5 5.201525-5 5.201525-5132633 1 1752
5.201525-5 5.201525-5 5.201525-5 5.201525-5 5.201525-5 5.201525-5132633 1 1753
1.472366-5 132633 1 1754
0.000000+0 0.000000+0 13 1 13 5132633 1 1755
4.004717-5 4.004717-5 4.004717-5 4.004717-5 4.004717-5 4.004717-5132633 1 1756
4.004717-5 4.004717-5 4.004717-5 4.004717-5 4.004717-5 4.004717-5132633 1 1757
1.133592-5 132633 1 1758
0.000000+0 0.000000+0 13 1 13 6132633 1 1759
2.690806-5 2.690806-5 2.690806-5 2.690806-5 2.690806-5 2.690806-5132633 1 1760
2.690806-5 2.690806-5 2.690806-5 2.690806-5 2.690806-5 2.690806-5132633 1 1761
7.616711-6 132633 1 1762
0.000000+0 0.000000+0 13 1 13 7132633 1 1763
1.773523-5 1.773523-5 1.773523-5 1.773523-5 1.773523-5 1.773523-5132633 1 1764
1.773523-5 1.773523-5 1.773523-5 1.773523-5 1.773523-5 1.773523-5132633 1 1765
5.020211-6 132633 1 1766
0.000000+0 0.000000+0 13 1 13 8132633 1 1767
1.386183-5 1.386183-5 1.386183-5 1.386183-5 1.386183-5 1.386183-5132633 1 1768
1.386183-5 1.386183-5 1.386183-5 1.386183-5 1.386183-5 1.386183-5132633 1 1769
3.923789-6 132633 1 1770
0.000000+0 0.000000+0 13 1 13 9132633 1 1771
1.159959-5 1.159959-5 1.159959-5 1.159959-5 1.159959-5 1.159959-5132633 1 1772
1.159959-5 1.159959-5 1.159959-5 1.159959-5 1.159959-5 1.159959-5132633 1 1773
3.283431-6 132633 1 1774
0.000000+0 0.000000+0 13 1 13 10132633 1 1775
8.578299-6 8.578299-6 8.578299-6 8.578299-6 8.578299-6 8.578299-6132633 1 1776
8.578299-6 8.578299-6 8.578299-6 8.578299-6 8.578299-6 8.578299-6132633 1 1777
2.428210-6 132633 1 1778
0.000000+0 0.000000+0 13 1 13 11132633 1 1779
6.674139-6 6.674139-6 6.674139-6 6.674139-6 6.674139-6 6.674139-6132633 1 1780
6.674139-6 6.674139-6 6.674139-6 6.674139-6 6.674139-6 6.674139-6132633 1 1781
1.889210-6 132633 1 1782
0.000000+0 0.000000+0 13 1 13 12132633 1 1783
5.566800-6 5.566800-6 5.566800-6 5.566800-6 5.566800-6 5.566800-6132633 1 1784
340 NJOY2016

10 ERRORR LA-UR-17-20093
5.566800-6 5.566800-6 5.566800-6 5.566800-6 5.566800-6 5.566800-6132633 1 1785
1.575762-6 132633 1 1786
0.000000+0 0.000000+0 17 1 17 13132633 1 1787
1.154480-6 1.154480-6 1.154480-6 1.154480-6 1.154480-6 1.154480-6132633 1 1788
1.154480-6 1.154480-6 1.154480-6 1.154480-6 1.154480-6 1.154480-6132633 1 1789
1.342892-5 1.827518-5 1.827518-5 1.827518-5 1.584766-5 132633 1 1790
0.000000+0 0.000000+0 5 13 5 14132633 1 1791
1.237530-5 1.726138-5 1.726138-5 1.726138-5 1.496853-5 132633 1 1792
0.000000+0 0.000000+0 5 13 5 15132633 1 1793
8.364854-6 1.166751-5 1.166751-5 1.166751-5 1.011770-5 132633 1 1794
0.000000+0 0.000000+0 5 13 5 16132633 1 1795
6.412509-6 8.944329-6 8.944329-6 8.944329-6 7.756243-6 132633 1 1796
0.000000+0 0.000000+0 27 13 27 17132633 1 1797
4.578647-6 6.386412-6 6.386412-6 6.386412-6 6.057870-6 3.913034-6132633 1 1798
3.913034-6 3.913034-6 3.913034-6 3.913034-6 3.913034-6 3.913034-6132633 1 1799
3.913034-6 3.913034-6 3.913034-6 3.913034-6 3.913034-6 3.913034-6132633 1 1800
3.913034-6 3.913034-6 3.913034-6 3.913034-6 3.913034-6 3.913034-6132633 1 1801
3.913034-6 3.913034-6 7.376951-7 132633 1 1802
0.000000+0 0.000000+0 23 17 23 18132633 1 1803
3.017049-6 2.271340-5 2.271340-5 2.271340-5 2.271340-5 2.271340-5132633 1 1804
2.271340-5 2.271340-5 2.271340-5 2.271340-5 2.271340-5 2.271340-5132633 1 1805
2.271340-5 2.271340-5 2.271340-5 2.271340-5 2.271340-5 2.271340-5132633 1 1806
2.271340-5 2.271340-5 2.271340-5 2.271340-5 4.281989-6 132633 1 1807
0.000000+0 0.000000+0 23 17 23 19132633 1 1808
2.023187-6 1.523126-5 1.523126-5 1.523126-5 1.523126-5 1.523126-5132633 1 1809
1.523126-5 1.523126-5 1.523126-5 1.523126-5 1.523126-5 1.523126-5132633 1 1810
1.523126-5 1.523126-5 1.523126-5 1.523126-5 1.523126-5 1.523126-5132633 1 1811
1.523126-5 1.523126-5 1.523126-5 1.523126-5 2.871437-6 132633 1 1812
0.000000+0 0.000000+0 23 17 23 20132633 1 1813
3.156422-5 2.376265-4 2.376265-4 2.376265-4 2.376265-4 2.376265-4132633 1 1814
2.376265-4 2.376265-4 2.376265-4 2.376265-4 2.376265-4 2.376265-4132633 1 1815
2.376265-4 2.376265-4 2.376265-4 2.376265-4 2.376265-4 2.376265-4132633 1 1816
2.376265-4 2.376265-4 2.376265-4 2.376265-4 4.479796-5 132633 1 1817
.
.
2.666295-6 2.007280-5 2.007280-5 2.007280-5 2.007280-5 2.007280-5132633 1 1899
2.007280-5 2.007280-5 2.007280-5 2.007280-5 2.007280-5 2.007280-5132633 1 1900
2.007280-5 2.007280-5 2.007280-5 2.007280-5 2.007280-5 2.007280-5132633 1 1901
2.007280-5 2.007280-5 2.007280-5 2.007280-5 3.784176-6 132633 1 1902
0.000000+0 0.000000+0 23 17 23 38132633 1 1903
2.169670-6 1.633404-5 1.633404-5 1.633404-5 1.633404-5 1.633404-5132633 1 1904
1.633404-5 1.633404-5 1.633404-5 1.633404-5 1.633404-5 1.633404-5132633 1 1905
NJOY2016 341

LA-UR-17-20093 10 ERRORR
1.633404-5 1.633404-5 1.633404-5 1.633404-5 1.633404-5 1.633404-5132633 1 1906
1.633404-5 1.633404-5 1.633404-5 1.633404-5 3.079335-6 132633 1 1907
0.000000+0 0.000000+0 23 17 23 39132633 1 1908
2.382007-7 1.793258-6 1.793258-6 1.793258-6 1.793258-6 1.793258-6132633 1 1909
1.793258-6 1.793258-6 1.793258-6 1.793258-6 1.793258-6 1.793258-6132633 1 1910
1.793258-6 1.793258-6 1.793258-6 1.793258-6 1.793258-6 1.793258-6132633 1 1911
1.793258-6 1.793258-6 1.793258-6 1.793258-6 3.380696-7 132633 1 1912
0.000000+0 0.000000+0 1 74 1 74132633 1 1913
0.000000+0 132633 1 1914
0.000000+0 0.000000+0 0 103 0 74132633 1 1915
0.000000+0 0.000000+0 1 74 1 74132633 1 1916
0.000000+0 132633 1 1917
0.000000+0 0.000000+0 0 104 0 74132633 1 1918
0.000000+0 0.000000+0 1 74 1 74132633 1 1919
0.000000+0 132633 1 1920
0.000000+0 0.000000+0 0 105 0 74132633 1 1921
0.000000+0 0.000000+0 1 74 1 74132633 1 1922
0.000000+0 132633 1 1923
0.000000+0 0.000000+0 0 106 0 74132633 1 1924
0.000000+0 0.000000+0 1 74 1 74132633 1 1925
0.000000+0 132633 1 1926
0.000000+0 0.000000+0 0 107 0 74132633 1 1927
0.000000+0 0.000000+0 1 74 1 74132633 1 1928
0.000000+0 132633 1 1929
0.000000+0 0.000000+0 0 851 0 74132633 1 1930
0.000000+0 0.000000+0 1 74 1 74132633 1 1931
0.000000+0 132633 1 1932
132633 0 1933
2.600000+4 5.536500+1 0 0 0 40132633 2 1934
0.000000+0 0.000000+0 0 2 0 74132633 2 1935
0.000000+0 0.000000+0 17 1 17 1132633 2 1936
2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3132633 2 1937
2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3132633 2 1938
2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.128462-3 132633 2 1939
0.000000+0 0.000000+0 17 1 17 2132633 2 1940
2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3132633 2 1941
2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3132633 2 1942
2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.128462-3 132633 2 1943
0.000000+0 0.000000+0 17 1 17 3132633 2 1944
2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3132633 2 1945
2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3132633 2 1946
2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.128462-3 132633 2 1947
342 NJOY2016

10 ERRORR LA-UR-17-20093
0.000000+0 0.000000+0 17 1 17 4132633 2 1948
2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3132633 2 1949
2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.500000-3132633 2 1950
2.500000-3 2.500000-3 2.500000-3 2.500000-3 2.128462-3 132633 2 1951
.
.
The processed multigroup covariance data for MAT=1326 begin with Card
634. The designation of MF=33 in Field 8 is the value of mfcov, as discussed
in Section 10.14. Card 634 repeats the ZA and AWR numbers in Fields 1 and
2, and the number 41 in Field 6 indicates that covariance matrices follow for
41 reaction pairs. The number 1 in the MT field (Field 9) indicates that all 41
reaction-pairs have MT=1 as the first reaction.
The data for one such reaction pair begin at Card 1738. Field 4 of Card
1738 (a CONT record) contains the number 102, so the second reaction here
is MT1=102. In other words, the data to follow refer to the covariance matrix
of the iron total cross section (MT=1) with the iron radiative capture reaction
(MT1=102). This is followed by 74 LIST records, one for each group. The
occurence of the number 14 in Field 6 of Card 1791 indicates that the block
of data starting there refers to Group 14 of MT=1, i.e., the fourteenth row of
the covariance matrix. The number 5 in Field 3 of Card 1791 indicates that
there are 5 consecutive groups of MT1=102 for which covariances will be given
explicitly. The first covariance applies to group 13 of MT1=102, as indicated by
the number 13 in Field 4. Then, in referring to the entry in the fifth field of Card
1792, for example, one would say that the relative covariance of the iron total
cross section in Group 14 (17.603 – 37.267 eV) with the iron radiative capture
cross section in Group 17 (101.3 – 167.02 eV) is 1.496853 ×10−5.
Any row of a covariance matrix, or any part of a row, that contains only
zeros is omitted from the ERRORR output file. The only exception is that the
last row (Group 74 here) is always given explicitly, even if it does contain only
zeros. The occurrence of the last row terminates a given covariance matrix and
signals that the next card will name a new reaction pair. These two conventions
are applied simultaneously in Cards 1915 – 1917 to compactly represent the
covariance matrix for a reaction pair (1, 103) having only zero covariances; a
judgement made by the evalutor.
Although the output file in this example contained no cross-material covari-
ances, the only difference in the file structure in the cross-material case is that
MAT1 is specified in the integer field just preceding MT1, for example, in Field
NJOY2016 343

LA-UR-17-20093 10 ERRORR
3 on Card 1738. The entry MAT1=0 in that position is a flag to indicate that
MAT1=MAT=1326.
10.16 Error Messages
error in errorr***error in 999 option
If an input tape contains MF=32 data but no MF=33 data, the user must
create a new tape with MF=33 placeholder data. This is done by specifying
the input and output tapes and up to five cards with individual MT numbers.
If the user attempts to specify more than 5 MT values, this error message
occurs.
error in errorr***nstan should be different from nendf
Check the input files.
message from errorr---input weighting function not supported
The iwt option is not recognized and ERRORR will set it to 6, which is
the default value.
message from errorr---reset legord from ... to 1
Only a legendre order of 1 is accepted at this time.
error in errorr***illegal iread=---
Currently defined values are 0, 1, and 2.
error in errorr***ngout must be nonzero when mfcov =...
The ngout unit must be used when mfcov=31, 35, or 40.
error in errorr***mfcov=35 requested but no spectra present
The ENDF data doesn’t support a request for mfcov=35. GROUPR should
be run prior to ERRORR to include this data on the ngout unit.
message from errorr---mf35 processing with mf5 spectrum vector
message from errorr---mf35 processing with mf6 spectrum matrix
ERRORR can either use data from mf5 or mf6 when processing covariances
from mf35.
error in errorr***User ifissp -- not found.
When processing MF=35 data, the original tape shall contain information
for a number of energy intervals. “ifissp” is the user specified energy
interval to process and, if greater than zero, must be less than or equal to
the number of intervals on the tape.
error in errorj***storage exceeded.
Can occur in a number of ERRORR’s routines, not just errorj. The
source code should be examined to see what array needs to be increased.
error in errorr***no covariance data found for user ifissp/efmean
344 NJOY2016

10 ERRORR LA-UR-17-20093
When processing MF=35 data, the original tape shall contain information
for a number of energy intervals. The user may specify an energy interval
with ifissp or define ifissp=-1 and then specify a specific mean energy
efmean. If the specified energy is outside the range of the energy intervals
on the input tape, this message results.
message from errorr---only one subsection
The MF=35 data contains only one covariance energy interval. The value
of efmean is reset to the average value of the energy interval.
error in errorr***nendf-to-nendf2 copy for matd failed.
This error should not occur. It means that an attempt to create a scratch
tape for the required MATD from the original input tape has failed. Check
that the input tape is not corrupted.
error in errorr***not coded for mfcov=---.
Allowed values are 31, 33, 34, 35, and 40.
error in errorr***not enough space for endf dictionary.
The allocatable array dict has length nwi=4000. It needs to be increased.
message from errorr---ignoring unknown mt = ...
The covariance data contains one of the following mt numbers: 850, 871 to
874 or is larger than 891. None of these numbers are legal mt numbers.
error in errorr***too many reactions for mf34.
This only occurs for MF=34 when there is no GENDF input on unit ngout.
error in errorr***too many lumped reaction types.
This only occurs when too many sections with mt numbers between 851
to 870 appear in the ENDF file. Normally, ERRORR should be able to
handle it.
error in errorr***too many reaction types.
error in gridd***too many reaction types.
This error occurs in runs with iverf=4 if the number of requested covari-
ance reactions is more than 60. A possible solution is to use the iread=1
option to select only the most needed reactions. This error also occurs in
runs where internal group averaging is requested (ngout=0) if there are
more than 200 sections in MF=33. An alternative is to run GROUPR first,
then ERRORR with ngout.gt.0.
error in errorr***only --- ek energies allowed.
The number of derived-cross-section energy-range boundaries is limited to
nkmax=50.
error in errorr***too many standards redefined.
Limit is 5. See input for nstan.ne.0.
error in errorr***no data on file for mfcov= ....
The ENDF tape does not appear to contain any section of the requested
type. Check the ENDF file or check the mfcov value in the input file.
NJOY2016 345

LA-UR-17-20093 10 ERRORR
error in errorr***ngout input tape is required.
ERRORR cannot continue without the multigroup data from GROUPR.
A GROUPR run should be included prior to calling ERRORR.
error in gridd***not coded for nmt1>1 of mf34
When processing angular distribution uncertainty data (MF=34), ERRORR
can only handle Legendre coefficient uncertainty data (LTT=1).
error in gridd***illegal mt1=0.
There is fault in the evaluation. Evaluator may have meant to indicate
MT1=MT. If so, change the data value for MT1 on nendf from 0 to MT and
resubmit.
error in gridd***mt --- referenced in derivation ....
There is a fault in the evaluation or input.
error in gridd***too many formulas in nc-type sub-sub ....
Limit is irmax=80.
error in gridd***too many mt-numbers in nc-type sub-sub ....
Limit is nmtmax=150.
error in gridd***cannot calculate covariance of reaction....
This message is self-explanatory.
error in gridd***covariances of reaction....
There is a fault in the evaluation.
error in gridd***... subsection too big, see nwscr
Increase nwscr in this subroutine.
error in gridd***nx is too large, increase nxmax
Increase nxmax in this subroutine.
error in gridd***too many reaction types.
This error occurs if iverf=5 and if the requested number of covariance
reactions is greater than 60. If cross-material covariances are not needed,
then a possible solution is to use the iread=1 option to select only the
most needed reactions.
error in merge***... storage exceeded.
Either the number of points in the x grid exceeds nxmax=5000 or the num-
ber in the y grid exceeds nenimx=5000.
error in merge***y(---)=--- lt y(---)=---.
This problem should not occur.
error in grist***standards tape bad.
There is a fault in the evaluation. Standards reactions must have at least
one subsection; that is, they may not be components of a lumped reaction.
error in grist***illegal lb=0.
There is a fault in the evaluation. Absolute covariances are not permitted
in the standards.
346 NJOY2016

10 ERRORR LA-UR-17-20093
error in grist***illegal ni=0 in the standard,...
There is a fault in the evaluation. Standards reactions may not be derived
from other reactions.
error in lumpmt***storage exceeded.
The number of component reactions of a lumped reaction is limited to
nlmt=50.
error in covcal***storage exceeded in loc.
The number of NI-type sub-subsections in any subsection is limited to
locm=30.
error in covcal***lb=--- when lt=---.
There is a fault in the evaluation. The (lb, lt) combination is not defined.
error in covcal***not coded for lb=---.
Currently defined values are 0 through 6 and 8.
error in covcal***storage exceeded in egt.
Should not occur, these arrays are now allocated based upon known storage
requirements for this job.
error in covcal***mfcov mt found not equal to input mt.
There is a conflict between internal list of covariance reactions and the
reactions encountered in the ENDF file. This problem should not occur.
message from covcall---WARNING! izap=0 for mf40 ...
Because of this, the title of the covariance plot may be ambiguous.
error in covcal***storage exceeded in scr.
There is insufficient space to store the information from NI-type sub-sub-
sections. Increase the size of namx=2000000.
error in covcal***illegal mt1=0.
See similar diagnostic in subroutine gridd above.
error in covcal***data in scr(loci) are illegal.
There is a fault in the evaluation. The ratio-to-standard data are bad.
Either LTY is outside the legal ENDF range of 1 – 3 or the energies (EL, EH)
are negative or out of order.
error in covcal***must request mat1=--- and mt1=--- on ....
There is an input error in requesting covariances of X with Y when both
are measured relative to Z. The standard Z must be specified on Card 10
and must appear as negative entries on Card 11.
error in covcal***unpermitted for lb=--.
When processing MF34 data, LB values less than 0, or 3, 4, 7, and 8 are not
supported.
error in sumchk***endf file error....
The MF=35 matrix must be symmetric and the lb flag must be 7.
NJOY2016 347

LA-UR-17-20093 10 ERRORR
message from sumchk---zero-sum test passed
message from sumchk---zero-sum test failed
These messages inform the user whether or not the covariance matrix passes
the zero sum test.
error in sumchk***ne, ncove mismatch.
This error should not occur. It means that the number of elements NE that
define the covariance matrix and that was saved in a working array does
not match the number of elements now being processed to verify the “zero
sum rule.” The LOC(LI) array may be corrupted.
error in spcint***no mf5 or mf6, mt=--- spectrum on nendf2.
This error should not occur. When processing MF=35 data, it means that
the underlying spectrum data for this MT value (normally found in File 5 or
File 6) is not present. The scratch copy nendf2 of the original input tape
has been corrupted.
error in spcint***not ready for lf = --.
We can only calculate the spectrum integral for lf=1 at this time.
error in spcint***array overflow.
nnw, currently 10000, needs to be increased.
error in spcint***looking for mf=6,mt=--.
Spectrum data from File 6 are ordered by increasing IZAP value, with the
IZAP=1=neutron spectrum expected to occur first. For this MT, the initial
spectrum was not for neutrons.
error in spcint***not ready for mf=6, mt=---, law=--.
We can only calculate the spectrum integral for LAW=1 at this time.
message from covbin---converting mf35 data to errorj format
The coding in ERRORR assumes absolute covariances of the probability
distribution function while ENDF-6 formatted files use covariances of the
bin probabilities. This message informs the user of this fact.
error in rdgout***mat --- not found.
Cannot find MAT on multigroup library.
message from rdgout---mf---, mt--- not found.
error in rdgout***mf---, mt--- not found.
Cannot find requested group structure or cross sections on multigroup li-
brary.
error in rdgout***bad index for b equivalent to sig(ig).
This problem should not occur.
error in resprx***illegal or no coding data structure ...
Only certain combinations of lru and lrf are supported. For lru=1,
lrf=1, 2, 3, and 7 work. For lru=2, lrf=1 and 2 work.
348 NJOY2016

10 ERRORR LA-UR-17-20093
error in resprx***illegal or unrecognized data struct ....
nro .ne. 0 is not supported.
error in resprx***cannot handle lrf=7 RML resonance rep....
You must set isammy=1 to enable the calculation of the derivatives using
the SAMMY method to process RML resonances.
error in resprx***not ready for isr=1, lrf=--.
Option not yet coded.
error in resprx***mf2/mf32 l-state mismatch ...
The nls value for mf32 URR data is larger than that specified in mf2. This
is likely an evaluation file error.
message from resprx---mf2 nls=I, but mf32 nls=J ...
The nls value for mf32 URR data is smaller than that specified in mf2.
Processing will continue but covariance data for the complete set of mf2
URR parameters is incomplete.
message from resprx---mls=..., nls=... are inconsistent
The nls value for mf32 URR data and the mls value for the scattering ra-
dius uncertainty are inconsistent. The uncertainty of the scattering radius
will be ignored by ERRORR.
message from resprx---user override for scattering radius unc.
A message to inform the user that a user provided uncertainty is used for
the scattering radius.
message from resprx---scat. radius unc not ready for lrf=7
When LRF=7 is used for the resolved resonances in MF=2, the uncertainty
for the scattering radius cannot be used for the moment.
error in resprx***illegal isr.
Only isr=0 allowed.
error in rpxsamm***storage exceeded.
Increase nwds, currently 1500000, in covout.
message from rpxsamm---convergence issue for e=...
When calculating the cross section and derivatives, ERRORR has not been
able to converge the values due to a very steep increase or decrease of the
cross section. The user should check the reconstructed cross section at the
energy indicated by the message.
message from rpxlc0---lcomp=0 scattering radius unc not included
When using the LCOMP=0 option in the MF32 covariance data, ERRORR
cannot account for scattering radius uncertainty.
error in rpxlc0***storage exceeded.
See maxnls=10.
error in rpxlc0***scr storage exceeded.
See nwscr=1400000.
NJOY2016 349

LA-UR-17-20093 10 ERRORR
error in rpxlc0***not allowed lrf.
Only lrf=1 or 2 allowed here.
error in rpxlc0***number of pointwise xsec ... exceeded....
See maxe=600000.
error in rpxlc0***bad covariance data for....
Wrong number of resonance parameters, negative diagonal elements, etc.
error in rpxlc12***cannot handle RML with isammy=0.
You must set isammy=1 to get the derivatives for RML parameters.
error in rpxlc12***different type of resonance for....
Much of the resonance parameter data found in MF=2 and MF=32 are re-
dundant, but in this instance, the expected redundant data were not found.
This indicates an error in the original evaluated file.
error in rpxlc12***b array storage exceeded....
See maxb=30000.
error in rpxlc12***a array storage exceeded....
Increase nwds, currently 1500000, in covout.
error in rpxlc12***storage exceeded....
See mxnpar=7000.
error in rpxlc12***mpar.gt.4.and.lrf.le.2 not coded.
Format not supported.
error in rpxlc12***lcomp=1 general form.
This value of lrf is not coded.
message from rpxlc12---no scattering radius uncertainty
message from rpxlc12---include scattering radius uncertainty
Informative message to indicate whether or not scattering radius uncer-
tainty is present in the data.
error in rpxlc12***problem.
Resonance parameter data were read frm MF=32, but no corresponding res-
onance is defined in MF=2. This indicates an error in the orginal evaluated
file.
error in rpxlc12***a array for nlrs stroage exceeded.
Increase nwds, currently 1500000, in covout.
error in rpxlc12***nlrs>0 not coded.
Option not supported.
error in rpxlc2***a array storage exceeded.
Increase nwds, currently 1500000, in covout.
message from rpxlc12---ndigit from file is zero ...
350 NJOY2016

10 ERRORR LA-UR-17-20093
error in rpxlc2***illegal value of ndigit.
The ndigit value given in the ENDF file for an INTG record can vary
from 2 through 6. If it is 0, this defaults to 2 while other values are illegal.
error in rpxlc2***not ready for lrf= ...
Coding for this lrf/lcomp=2 combination has not yet been implemented.
error in rpxunr***storage exceeded (lru=2)
See mxnpar=100. Note, perhaps not the best coding practice but mxnpar
can be assigned different values in different subroutines; currently its 7000
elsewhere but 100 here.
error in rpxunr***number of pointwise xsec of res exceede...
See maxe=600000.
error in rpendf***number of pointwise xsec of res exceede...
See maxe=600000.
error in dumrd2***lru=---, lrf=-- no coding.
Option not supported.
error in dumrd2***nlru2 exceeeded mxlru2
See mxlru2=100.
error in rxgrpg***i0>ipoint not coded.
This is a poorly worded message that essentially means that the previ-
ously calculated pointwise cross sections do not span the energy interval
for this multigroup, and therefore it is not possible to internally calculate
the necessary group average data needed for covariance processing.
error in skiprp***no coding type lrf=--.
The lrf value is limited to 1 through 3.
message from grpav4---skipping over mf=3, mt=...
ERRORR does not need the data and skips over it.
message from grpav4---collapsing NGOUT mf=3, mt=...
The GROUPR tape uses a group structure different from the one used by
ERRORR. ERRORR will take the GORUPR data and collapse it to the
grid it needs.
message from grpav4---mf --- mt --- has thresh gt highest ...
Though not a fatal error, this message often precedes an abort in covcal
caused by the absence of this reaction on ngout. If iread=1, then delete
this reaction from the requested list of covariance reactions.
error in grpav4***not coded for multimaterial group av’g.
Single material mfcov=34 data only.
error in alsigc***no coded for lump xsec.
Cannot handle lumped cross sections for mfcov=34 data.
error in egtlgc***no coded for ltt=2.
Option not supported.
NJOY2016 351

LA-UR-17-20093 10 ERRORR
error in covout***illegal condition for sad.
Bad combination of options.
error in covout***unable to find iy or iyp from mts array.
There is a conflict between the internal list of covariance reactions and
the reactions encountered on the union-group covariance file produced in
covcal. This problem should not occur.
error in covout***unexpectedly, ix ne iy or ixp ne iyp.
This problem should not occur.
error in covout***please check isd=1.
Covariances between different MT values are not supported for MF=34.
This is likely a fault in the evaluation.
error in sigc***covariance reaction missing from lumping ...
A covariance reaction in the mt 851 to 870 range cannot be found in the
lumped reaction definition tables. This problem should not occur.
error in resprp***illegal or unrecognized ... in mf=32...
There is a fault in the evaluation. Allowed values of lrf are 1 and 2 (single-
and multi-level Breit-Wigner representations).
error in resprp***bad covariance data for res params....
There is a fault in the evaluation. Covariance matrix of the parameters
has negative variances, infinite correlation coefficients, or correlation coef-
ficients greater than 2.0. Data may be out of order.
error in resprp***unresolved energy range was illegal.
Check evaluation.
error in resprp***storage exceeded.
Increase nwds, currently 1500000, in covout.
error in resprp***storage exceeded (lru=2).
Increase nwds, currently 1500000, in covout.
error in resprp***mpar=-- was not coded.
Option not supported.
error in resprp***storage exceeded for rel. covariance.
See nparmx=60.
error in resprp***bad rel. covariance data for ....
Negative diagonal element.
error in resprp***storage exceeded for sensitivities.
See igumax=20.
message from grpav---mf --- mt --- has thresh gt highest ...
Though not a fatal error, this message often precedes an abort in covcal
caused by the absence of this reaction on ngout. If iread=1, then delete
this reaction from the requested list of covariance reactions.
352 NJOY2016

10 ERRORR LA-UR-17-20093
error in grpav***unable to find temp=---.
The program cannot locate requested material and temperature on npend.
error in grpav***cannot group-average mt=---. use groupr....
The mfcov=31 and ngout=0 options are not compatible.
error in grpav***not coded for multimat group averaging....
The iread=2 and ngout=0 options are not compatible.
message from grpav---mt3 cross sections are constructed ...
The ENDF tape contains mt3, which is defined as the total cross section
minus the elastic scattering cross section. ERRORR will not calculate the
multigroup cross section from the data on the ENDF tape.
error in colaps***ngout is not a groupr output tape.
Check your input.
error in colaps***did not find expected mf1, mt451.
The GROUPR tape should start with an mf1/mt451 section. Check the
file on ngout.
error in colaps***storage exceeded.
Check nwscr. This error should not occur as the array allocation is made
based upon known storage requirements.
error in colaps***did not find expected mf1 mt451.
Multigroup libraries produced with the GROUPR module always contain
the group structure in MF=1, MT=451.
error in colaps***ngout group structure does not span ....
The supplied library must cover the entire energy range of the union grid,
which is the same as the energy range of the user’s grid.
error in colaps***not coded for multiple sigma zeroes ...
Should not occur in njoy2016 which automatically converts general format-
ted gendf files to the more restricted format expected by ERRORR.
error in colaps***not ready for file 6.
We can only handle spectra in file 5 currently.
error in uniong***exceeded storage in mfcov energy grid.
Applies only if iverf=4. See nenimx=5000.
error in uniong***energies out of order. --- lt ---.
Applies only if iverf=4.
error in uniong***exceeded storage in union grid.
Insufficient space to store the union grid. Increase nunmax=5000.
error in egngpn***read-in group structure is out of order.
With the ign=1 option, the supplied group structure must be in increasing
order.
NJOY2016 353

LA-UR-17-20093 10 ERRORR
error in egngpn***illegal group structure requested.
Allowed values of ign are 1-17 and 19.
error in egnwtf***illegal weight function requested.
Allowed values of iwt are 1-12.
error in egtsig***mt=0
In the ngout=0 option, a point cross section has been requested by grpav
for an illegal MT number. In this context, the allowed values of MT are 1-200,
251-253, and 600-799. MT numbers 600-699 are not defined in ENDF-5, but
may be used on ENDF and PENDF files specially prepared as input to
ERRORR, to allow processing of nonstandard reaction types.
message from egtwtf---xs energy range exceeds ...
The cross section multigroup energy range extends beyond the energy range
defined for the weight function. Cross section values in the undefined region
will be wrong or nan.
10.17 Input/Output Units
The following logical units are used:
10 ngout in grpav and ntp in colaps. Contains the union group cross sections
for all reactions with covariances. If the user input value of ngout is zero,
point data are read from npend and written to ngout=-10 in grpav. If
the input value ngout is not zero, coarse group multigroup data are read
from the user’s ngout in colaps and written to ntp=-10. When colaps is
finished, ngout is reset to -10.
11 nscr in covcal and covout. Contains the union-group multigroup covari-
ances for the directly evaluated reactions.
12 nscr2 in covout. This is a second copy of nscr, which is read only for the
“trivial” derivation case, isd=1. Saves execution time by eliminating the
calculation of many zero contributions.
13 nscrg in the covcal and rdgout. This unit is used to extract a single MAT
from a multimaterial ngout.
15 nscr in lumpmt and lumpxs. This unit is used if MT numbers in the 851-870
range (lumped reactions) are found in ENDF covariance file to keep a copy
of the covariance file.
20–99 Users can choose any of these numbers for nendf,npend,ngout,nout,
nin, and nstan.
Units 11 and 12 are normally binary, although they can be switched to formatted
mode by changing the value of the variable imode in the main program to +1.
Unit 13 has the same mode as ngout. The user can choose the modes for nendf,
354 NJOY2016

10 ERRORR LA-UR-17-20093
npend,ngout,nout,nin, and nstan, except that nout and nin must have the
same mode.
NJOY2016 355

LA-UR-17-20093 10 ERRORR
356 NJOY2016

11 COVR LA-UR-17-20093
11 COVR
11.1 Introduction
The COVR module of NJOY is an editing module that post processes the output
of ERRORR in a manner analogous to the way MATXSR and DTFR post
process the output of GROUPR. COVR performs two quite separate functions
using the multigroup covariance file from ERRORR as input. First, it can
prepare a new covariance library in a highly compressed card-image format,
which is suitable for use as input to sensitivity analysis programs[79, 80]. Data
in this form can also be copied to the system output file to obtain a compact
printed summary of an ERRORR run without using the sometimes bulky long-
print option in ERRORR. Such a summary can also provide information on
standard deviations and correlation coefficients, neither of which are printed by
ERRORR. The second main function of COVR is to produce publication-quality
plots[77] of the multigroup covariance information.
This chapter describes the COVR module in NJOY2016.0.
11.2 Production of Boxer-Format Libraries
As discussed in the ERRORR section of this manual, the output file of that mod-
ule contains the group structure, cross sections, and either absolute (irelco=0)
or relative (irelco=1) covariances for one or more materials, in either card-
image or NJOY blocked-binary form. If the COVR user-input parameter nout
is greater than zero, COVR reads an ERRORR output file from unit nin and
produces a new multigroup covariance library on unit nout. COVR performs
only sorting and reformatting operations on the ERRORR data.
In COVR, as well as ERRORR, the ENDF energy ordering is followed. That
is, low group indices correspond to low energies, high indices to high energies.
Regarding group structures, in the library mode of operation COVR (like ER-
RORR) makes extensive use of external (disk) storage so that even on machines
that have a relatively small central memory very large group structures (up to
640 groups) can be handled successfully. (See, however, the comments at the
end of Section 11.3 regarding group-number limitations in the plot mode.)
The material and reaction coverage of COVR post-processing is determined
by a set of reaction pairs (mat,mt;mat1,mt1) supplied by the user (see input
Card 4 in the input instructions and the corresponding discussion that follows
in Section 11.4). At the beginning of the output library, the group structure is
given. Then, for each specified reaction pair, the output library contains either
NJOY2016 357

LA-UR-17-20093 11 COVR
a covariance matrix or a correlation matrix, depending on the output option
(matype) selected. In the case that covariances are requested (matype=3), the
type of data on nout (absolute vs. relative) is governed by the covariance type
present on nin. In addition, whenever mat1=mat and mt1=mt, the group-cross-
section vector and the (absolute/relative) standard-deviation vector for that
particular reaction are written to nout just before the matrix itself. All data
(group structure, cross sections, standard deviations, and matrices) are written
to nout using a highly compressed, card-image format.
The design of this format, called the BOXER format, proceeds from a simple
fact: as discussed in the ERRORR section of this manual, most of the ENDF
covariance formats define certain rectangular regions (boxes) in energy “space,”
over which the relative covariance is constant. (The ENDF format allowing a
constant absolute covariance is only rarely used.) The coordinate axes of the
two-dimensional energy space in question are Exand Ey, where xand yindicate
the particular reaction pair to which the ENDF covariances apply. Because of
this feature of the basic evaluations, one expects that an element of a multigroup
relative covariance matrix, derived from the ENDF data for a given reaction
pair, frequently will be identical either to the element before it in the same
row (Exconstant, Eyvarying) or to the element above it in the same column
(Eyconstant, Exvarying). Thus, the Boxer format allows a combination of
horizontal and vertical repeat operations.
Even though the ERRORR output format already suppresses zero covari-
ances, very large data compression factors can be achieved in transforming data
from the ERRORR format to the Boxer format. As one example, the ERRORR
output file for a particular 137-group reactor-dosimetry library[81] contained 38
000 card images, while the corresponding COVR output file contained fewer
than 1000 card images.
In the BOXER format, data are stored as a list of numerical data values (e.g.,
relative covariances), together with a list of integers that control the loading of
these data into the reconstructed array C(i, j). A negative control integer, −n,
indicates that the next value in the data list is to be loaded into the next n
columns (j-locations) of the current row of C(i, j). A positive integer m, on the
other hand, means that, for the next m j-values, the value to be loaded is to be
carried down from the row above,
C(i, j) = C(i−1, j).(456)
358 NJOY2016

11 COVR LA-UR-17-20093
For the first row (i= 1), the row above is defined to contain all zeros.
In constructing the compressed data set in subroutine press, the choice
between using the “repeat-new-value” method or the “carry-down” method is
made dynamically on the basis of taking the longest possible step. If m=n, the
carry-down method is chosen, as it does not require an entry in the data list.
As an additional compression feature of the format, one may indicate by
a “flag” that the matrix C(i, j) is symmetric; hence, explicit instructions are
provided in the compressed data library for the reconstruction of only the upper
right triangle of C(i, j). These various aspects of the Boxer format are illustrated
by a simple example in Fig. 46. Here a, b, c and dare arbitrary, nonzero, unequal
data values.
Before the data values are tested in press to see if they are indeed equal,
the NJOY utility sigfig is called to round off the trailing digits that would
not appear on the formatted output anyway. Relative covariances, for example,
are written to nout in 1P8E10.3 format, which has only four significant figures.
Thus, the three data values 0.036126, 0.036130, and 0.036134 would all be judged
to be equal by this logic.
11.3 Generation of Plots
The COVR plot mode, which is requested by specifying nout=0, is used to gen-
erate publication-quality plots of multigroup covariance data from a card-image
or binary ERRORR output file. Examples of plots produced by COVR can be
seen in the ERRORR section of this manual. In addition to their usefulness in
preparing publications, the plots have proved to be a useful tool for checking the
reasonableness and mechanical correctness of new covariance evaluations. One
can, for example, execute ERRORR and COVR in tandem, using the evaluator’s
energy grid as the user group structure (ERRORR input option ign=19). The
output of such a run is a series of plots showing all important features of the
covariance evaluation.
As can be seen in the examples mentioned above, each plot contains a shaded
contour map of the correlation matrix. If black & white plots are needed,
positive-correlation regions are shaded with parallel straight lines (hatching),
while negative correlations are indicated by cross-hatching. When color is re-
quested (see the second card in the input instructions, the positive correlations
are represented by shades of green, and the negative correlations are represented
by shades of red. The plots also contain two additional inset graphs giving the
energy dependence of the associated standard deviation vectors. One of the vec-
NJOY2016 359
LA-UR-17-20093 11 COVR
Original Data Set
j→
i
↓
a a b b 0 0
a a b b 0 0
b b b b 0 0
b b b b 0 0
0000c c
0000c d
Boxer Format, Symmetry Flag Off
a b b 0c d
−2−2 8 −4 8 −4−2 5 −1
Boxer Format, Symmetry Flag On
a b c d
−2−2 14 −2−1
Figure 46: Illustration of Boxer format
tor plots is rotated by 90 degrees, so that the logarithmic energy scales for the
vector plots can be aligned with the corresponding scales for the matrix plot.
When MAT=MAT1 and MT=MT1, we plot the cross section rather than repeating
the standard deviation plot.
This type of plot presents the covariance data in a more lucid manner than
most alternative plotting packages. However, use of this option does require the
sophisticated capabilities of the VIEWR module to create rotated subplots and
to fill regions with colors or hatching patterns. See the VIEWR section of this
360 NJOY2016

11 COVR LA-UR-17-20093
report for more details.
Just as in the library mode, the material and reaction coverage of the se-
quence of plots generated in the plot mode is determined by the reaction pairs
specified by the user on input Card 4. Other input, specific to the generation
of plots, is described in Section 11.4. We next discuss some aspects of the
plot-generation coding.
After a covariance matrix is read in subroutine covard, it is converted to a
correlation matrix in subroutine corr. The correlation matrix is then scanned
in subroutine matshd to find a set of boundary curves that divide Ex−Eyenergy
space into a small number of connected regions of nearly constant correlation
strength. Here the phrase “nearly constant” refers to the subdivision of the
range of possible correlation values (−1.0 to +1.0) into a number of equal-
width bands, the fineness of the subdivision being controlled by the user-input
parameter ndiv. Two regions have nearly equal correlations if the correlations
fall into the same band. As each boundary curve is located, the enclosed region
is shaded (with a line density proportional to the band correlation magnitude)
with direct writes to the VIEWR file.
The algorithm used to find the maximum extent of a region of nearly constant
correlation is best described by referring to the simple example in Fig. 47. After
locating the upper left corner of a new correlation region, for example at point
ain the figure, the search proceeds as far as possible down the first column (Ey
held constant) to point b. New columns are scanned in the same way: c−d,e−f,
g−h. Having found that the pattern does continue into column e−f, for the
sake of simplicity, the algorithm ignores the possibility of additional, disjoint,
continuations of the pattern elsewhere in the same column (such as at e0−f0),
and region I is ended at h. (Region II will be found and correctly shaded at a
later stage of the calculation.)
As the plot option is presently coded, the entire correlation matrix must
reside in memory during the pattern-search operation just described.
11.4 Input Instructions for COVR
As an aid to discussions of the user input to COVR, we list below the input in-
structions that appear as comment cards at the beginning of the current version
of this module. It is always advisable to consult the comment-card instructions
embedded in the version of the code actually being used and not to rely on the
instructions published in any document, including this one. Following the listing
are further remarks on several of the input items; the remarks supplement the
NJOY2016 361
LA-UR-17-20093 11 COVR
ac
eg
hf
e'
f'
db
I
II
Figure 47: Pattern-search logic in subroutine matshd.
comment cards below. See especially the lengthy discussion of the parameters
on Card 4.
!---input specifications (free format)---------------------------
!
! card 1
! nin input tape unit
! nout output tape unit
! (default=0=none)
! nplot viewr output unit
! (default=0=none)
!
! ---cards 2, 2a, and 3a for nout.ne.0 only (plot option)
!
! card 2
! icolor select color or monochrome style
! 0=monochrome (uses cross hatching)
! 1=color background and contours
! 2=color background and contours plus
362 NJOY2016

11 COVR LA-UR-17-20093
! card 2’ follows.
! (default=0)
! card 2’ (only when icolor=2)
! nlev,(tlev(i),i=1,nlev)
! defines the number of correlation matrix
! intervals and their boundaries. Zero is
! assumed as the lower limit of the first
! boundary, but the User must specify unity
! as the upper limit of the last boundary.
! nlev is a positive integer .le. 9.
! default values (when icolor=1) are:
! 6,0.001,0.1,0.2,0.3,0.6,1.0
! card 2a
! epmin lowest energy of interest (default=0.)
! card 3a
! irelco type of covariances present on nin
! 0/1=absolute/relative covariances
! (default=1)
! ncase no. cases to be run (maximum=40)
! (default=1)
! noleg plot legend option
! -1/0/1=legend for first subcase only/
! legend for all plots/no legends
! (default=0)
! nstart sequential figure number
! 0/n=not needed/first figure is figure n.
! (default=1)
! ndiv no. of subdivisions of each of the
! gray shades (default=1)
!
! ---cards 2b, 3b, and 3c for nout gt 0 (library option) only--
!
! card 2b
! matype output library matrix option
! 3/4=covariances/correlations
! (default=3)
! ncase no. cases to be run (maximum=40)
! (default=1)
! card 3b
! hlibid up to 6 characters for identification
! card 3c
! hdescr up to 21 characters of descriptive
NJOY2016 363

LA-UR-17-20093 11 COVR
! information
!
! ---cards 4 for both options---
!
! card 4
! mat desired mat number
! mt desired mt number
! mat1 desired mat1 number
! mt1 desired mt1 number
! (default for mt, mat1 and mt1 are 0,0,0
! meaning process all mts for this mat
! with mat1=mat)
! (neg. values for mt, mat1, and mt1 mean
! process all mts for this mat, except for
! the mt-numbers -mt, -mat1, and -mt1. in
! general, -n will strip both mt=1 and mt=n.
! -4 will strip mt=1, mt=3, and mt=4, and
! -62, for example, will strip mt=1, mt=62,
! mt=63, ... up to and incl. mt=90.)
! repeat card 4 ncase times
!
! note---if more than one material appears on the input tape,
! the mat numbers must be in ascending order.
!
!--------------------------------------------------------------------
icolor . . . This parameter is used to specify creation of monochrome (cross-
hatched) or color correlation matrix plots. Although the default setting is
icolor=0 (to produce monochrome plots) the capabilities of modern printers
and display terminals makes creation of color plots the more common option. If
icolor=1 a default six-interval color pattern is used when creating the correla-
tion matrix; if icolor=2 then input card 2’ is required where the user specfies
the number of color intervals (an integer, nlev, where nlev is a positive non-zero
integer <10) plus nlev real numbers that define the color boundaries, tlev(i),
i=1, nlev.tlev(nlev) must be unity. Users are cautioned that use of too many
intervals may require an increase in the value of ipat in subroutine matshd.
epmin . . . This parameter is used to eliminate uninteresting energy regions
from the correlation and standard deviation plots, or to display high-energy
regions with greater resolution.
364 NJOY2016

11 COVR LA-UR-17-20093
irelco . . . This parameter must match the value used in the ERRORR
run that produced the covariances to be plotted.
ncase . . . This is the number of cases, or occurrences of Card 4. See the
discussion of input parameters mat,mt,mat1, and mt1 below. Presently, ncase
is limited to 60. Problems larger than this can be run as a series of COVR jobs,
each processing a batch of up to 60 cases. See also the parameter nstart below.
noleg . . . “Legend” here refers to the gray-shading scale (key) as well as
the figure caption. noleg=1 is used as a rough-draft mode to display plots
quickly.
nstart . . . Unless nstart=0, the plots are assigned a sequential figure
number, beginning at nstart, and a list of figures is drawn on the final plot
frame.
ndiv . . . One gray-shade step equals 0.20 in correlation magnitude if ndiv=1.
Finer gradations are possible with ndiv greater than 1. The plots appearing in
the ERRORR section of this manual were generated with ndiv=2.
hlibid . . . This is a 6-character string, normally containing the name of
the output covariance library. It is written on the header records present at the
beginning of each output data block.
hdescr . . . This contains additional information, for example, on where
and when the library was produced; it is also written on the data header records.
mat, mt, mat1, mt1 . . . The information contained in the output library
or plot file is controlled by means of these parameters on input Card 4. If mt
is positive, then a single covariance matrix for reaction (mat,mt) with reaction
(mat1,mt1) will be read from nin and processed. On unit nin (and, in the
library option, on unit nout), the rapidly varying, or column, index is the group
index of (mat1,mt1), and the slowly varying, or row, index is the group index
of (mat,mt). If mat1 is different from mat, COVR will expect to find separate
materials (produced by separate ERRORR runs) for both mat and mat1 on nin.
The mat numbers must occur on nin in ascending order. In the case of positive
mt, the entries mat1=0 and mt1=0 are shorthand for mat1=mat and mt1=mt,
respectively. If, on the other hand, mt is zero, negative, or defaulted, Card 4
becomes a kind of macro-instruction that is expanded by subroutine expndo into
a request for many (mt, mt1) pairs, all with mat1=mat. If, for example, Card
4 contains the entry
MAT/
NJOY2016 365
LA-UR-17-20093 11 COVR
or, equivalently,
MAT 0 0 0/
first the cross-section file, MF=3, for material MAT is read from the input covari-
ance tape on unit nin to obtain the list of reactions present. Then, all possible
reaction combinations (mt, mt1) are formed in ENDF order. Thus, for example,
if the reactions present are MT=1, 2, 3, and 16, then the behavior of the code
is the same as if the following input were specified:
MAT 1 0 1/
MAT 1 0 2/
MAT 1 0 3/
MAT 1 0 16/
MAT 2 0 2/
MAT 2 0 3/
MAT 2 0 16/
MAT 3 0 3/
MAT 3 0 16/
MAT 16 0 16/
Because of the clear labor-saving advantage of this feature, especially if there
are many reactions, enhancements have been added to permit its use in the
additional situation in which many, but not all, combinations are desired. As
discussed in some detail in the input instructions, it is possible to strip selected
reactions out of the list before the (mt, mt1) combinations are formed. For
example, if the reactions present are once again 1, 2, 3, and 16, then a Card 4
containing
MAT -3/
would produce the same output as the following three cards:
MAT 2 0 2/
MAT 2 0 16/
366 NJOY2016

11 COVR LA-UR-17-20093
MAT 16 0 16/
The stripping of the higher inelastic levels, mentioned in the input instructions,
is useful because ERRORR automatically resets the highest user-group energy
to 20 MeV whenever IREAD=0, and this can result in the inclusion of unwanted
high-threshold reactions on the ERRORR output file.
For one of several reasons, a requested reaction pair (mat,mt; mat1,mt1)
may be absent from the COVR output. The usual reason that this occurs is
that the normal iread option for the ERRORR module is iread=0, and this
results in the generation of an output matrix for every possible reaction-pair
combination. For those combinations that do not occur in the ENDF evaluation,
the ERRORR output matrix contains only zeroes. These null matrices are
omitted at the COVR output stage, in both the library and plot modes.
Additionally, in the plot mode, the correlations may be nonzero, but ev-
erywhere less than 0.2/ndiv in absolute magnitude. In this case, the entire
correlation plot would consist of a single blank region. These rather uninterest-
ing plots having small correlations are also omitted from the plot file. A final,
similar category is the class of “empty” plots. Because parallel lines to achieve
a gray effect when color is not used have limited resolution, there is clearly some
lower limit, for a given value of the correlation magnitude, on the physical size
of a region that can be sensibly shaded. COVR does not attempt to shade re-
gions that are smaller than this limit. If a correlation matrix does contain some
plottable data (magnitudes exceeding 0.2/ndiv), but all plottable regions are
smaller than the size limit discussed above, then an empty plot will be generated
on the plot file. As a convenience in discarding these empty plots at the time a
report is produced, no caption is written on such plots and the figure number is
not advanced. Also, these plots are omitted from the list of figures prepared at
the end of a plot run. (See the discussion of user-input parameter nstart.)
In the library mode, each omission of a requested, but null, matrix is noted
on the output file with an informative diagnostic. In the plot mode, a summary
table is printed at the end of the run to identify all requested matrices that were
omitted because they were null or small, as well as those that were plotted, but
empty.
NJOY2016 367

LA-UR-17-20093 11 COVR
11.5 COVR Example Problem
In this section we discuss the production of a particular COVR output library,
both to illustrate the input and as a supplement to the general discussion of
BOXER format libraries in Section 11.2. In the ERRORR chapter of this report
(the second input set in Section 10.14), we gave the complete NJOY input
for producing a 7-reaction, 30-group covariance library in ERRORR output
format for 12C. By appending the following lines to that input (just before the
stop card), one can produce, in addition, a 2-reaction COVR output library in
BOXER format.
covr
-23 24/
3 3/
’ LIB’/
’MAT1306 COVR EXAMPLE’/
1306 2 0 2/
1306 2 0 4/
1306 4 0 4/
The resulting library occupies only 49 lines and is listed below.
0 LIB-A- 30 MAT1306 COVR EXAMPLE 1306 2 1306 2 31 10 31 3 0 31 1
1.390E-04 1.520E-01 4.140E-01 1.130E+00 3.060E+00 8.320E+00 2.260E+01 6.140E+01
1.670E+02 4.540E+02 1.235E+03 3.350E+03 9.120E+03 2.480E+04 6.760E+04 1.840E+05
3.030E+05 5.000E+05 8.230E+05 1.353E+06 1.738E+06 2.232E+06 2.865E+06 3.680E+06
6.070E+06 7.790E+06 1.000E+07 1.200E+07 1.350E+07 1.500E+07 1.700E+07
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1
1 LIB-A- 30 MAT1306 COVR EXAMPLE 1306 2 1306 2 23 10 23 3 0 30 1
4.739E+00 4.738E+00 4.735E+00 4.729E+00 4.712E+00 4.676E+00 4.579E+00 4.332E+00
4.002E+00 3.619E+00 3.103E+00 2.477E+00 1.998E+00 1.820E+00 1.710E+00 2.256E+00
1.447E+00 9.921E-01 8.223E-01 7.627E-01 8.631E-01 8.228E-01 8.845E-01
-8 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
2 LIB-A- 30 MAT1306 COVR EXAMPLE 1306 2 1306 2 18 10 18 3 0 30 1
2.000E-03 1.964E-03 4.583E-03 3.822E-03 4.583E-03 4.288E-03 3.730E-03 4.141E-03
6.501E-03 1.011E-02 9.558E-03 9.981E-03 1.806E-02 1.854E-02 3.296E-02 3.760E-02
4.255E-02 7.632E-02
-9 -1 -5 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
3 LIB-A- 30 MAT1306 COVR EXAMPLE 1306 2 1306 2 43 10 58 4 0 30 0
368 NJOY2016

11 COVR LA-UR-17-20093
4.000E-06 2.797E-06 3.856E-06 6.317E-06 4.613E-06 2.407E-06 1.229E-06 2.100E-05
1.534E-05 8.000E-06 4.087E-06 1.461E-05 1.366E-05 2.100E-05 1.838E-05 9.004E-06
1.391E-05 8.934E-06 1.715E-05 4.447E-06 4.227E-05 4.373E-05 2.446E-05 1.980E-05
1.223E-05 1.022E-04 6.116E-05 4.048E-05 2.500E-05 9.136E-05 4.572E-05 9.962E-05
6.641E-05 6.308E-05 3.260E-04 1.614E-04 3.437E-04 1.086E-03 4.250E-04 1.413E-03
7.052E-04 1.811E-03 5.825E-03
-9 -1 224 -1 -5 -1 -4 -1 9 -5 -1 -4 -1 79 -1 -1 13 -1 13 -1
-1 11 -1 -1 10 -1 -1 9 -1 -1 -1 -1 -6 -1 -1 -1 -6 -1 -1 6
-1 -1 -1 4 -1 -1 4 -1 4 -1 -2 1 -1 -1 1 -1 1 -1
3 LIB-A- 30 MAT1306 COVR EXAMPLE 1306 2 1306 4 38 10 47 4 0 30 30
-1.106E-04-4.897E-05-3.047E-05-2.164E-05-2.630E-05-2.337E-05-2.192E-05-2.261E-04
-1.001E-04-6.228E-05-4.423E-05-5.376E-05-4.777E-05-4.481E-05-1.441E-03-2.659E-04
-1.571E-04-1.210E-03-1.305E-03-4.021E-04-1.131E-03-6.462E-04-8.562E-04-2.261E-04
-1.001E-04-6.228E-05-1.922E-03-9.140E-04-8.121E-04-7.520E-04-3.040E-03-1.348E-03
-1.517E-03-3.460E-03-4.423E-05-5.376E-05-4.777E-05-1.044E-02
623 -1 -1 -1 -1 -1 -1 -1 23 -1 -1 -1 -1 -1 -1 -1 53 -1 -1 -1
27 -1 -1 -1 27 -1 -1 -1 27 -1 -1 -1 -1 -1 -1 27 -1 -1 -1 28
-1 -1 27 -1 -1 -1 -1
1 LIB-A- 30 MAT1306 COVR EXAMPLE 1306 4 1306 4 7 10 8 3 0 30 1
6.091E-02 2.478E-01 3.301E-01 4.310E-01 4.013E-01 4.306E-01 4.935E-01
23 -1 -1 -1 -1 -1 -1 -1
2 LIB-A- 30 MAT1306 COVR EXAMPLE 1306 4 1306 4 7 10 8 3 0 30 1
2.499E-01 1.085E-01 9.724E-02 9.806E-02 1.358E-01 1.263E-01 2.177E-01
23 -1 -1 -1 -1 -1 -1 -1
3 LIB-A- 30 MAT1306 COVR EXAMPLE 1306 4 1306 4 28 10 29 4 0 30 0
6.245E-02 7.530E-03 3.823E-03 1.154E-03 1.338E-03 1.211E-03 1.155E-03 1.176E-02
2.311E-03 5.938E-04 6.451E-04 5.843E-04 5.578E-04 9.455E-03 1.887E-03 4.735E-04
4.295E-04 4.106E-04 9.617E-03 1.872E-03 1.670E-03 3.033E-04 1.844E-02 5.214E-03
3.493E-04 1.596E-02 5.253E-03 4.741E-02
437 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1
Note that the header card at the start of each data block contains an integer
itype, specifying the type of data contained in the current block, a 12-character
library name (“LIB-A- 30” in this case), 21 characters of user-supplied descrip-
tive information, mat, mt, mat1, mt1, and a set of 7 integers. The meaning
of the various values of itype is as follows: 0 = group boundaries, 1 = cross
sections, 2 = standard deviations, 3 = covariances, and 4 = correlations. The
library name is generated within COVR by adding either “-A-” (for a covariance
library) or “-B-” (for a correlation library), together with the number of energy
groups, to the user-supplied library name hlibid. (The ERRORR input option
NJOY2016 369

LA-UR-17-20093 11 COVR
ign=3 used in this example specifies a built-in 30-group structure). The final
seven integers on the header card indicate the number and format of the data
values, the number and format of the control integers (called “m” and “-n” in
the discussion in Section 11.2), a data paging flag, and the dimensions of the
reconstructed data array, C(i, j).
In order to clarify the process of reconstructing a full matrix from data in
BOXER format, we list in Section 11.8 a short retrieval program, BOXR. With
very few modifications, this program could be incorporated into a sensitivity
analysis program, for example, to allow direct access to covariance libraries[78]
in this compact format. Alternatively, it could be used to translate COVR
libraries into other desired forms. In any case, an examination of the retrieval
program should clarify the meaning of the various integer parameters on the
header cards in a COVR output library.
11.6 Error Messages
error in covr***requested too many cases.
ncase is limited to 40. Note that a case refers to one input Card 4, which
may request processing of either a single reaction pair or a whole series of
reaction pairs. See input instructions for Card 4 and the comments that
follow.
error in expndo***storage exceeded.
Should not occur since array space is allocated based upon known storage
needs.
error in corr***group structures do not agree.
This problem should not occur.
error in covard***storage exceeded.
Should not occur since array space is allocated based upon known storage
needs.
error in covard***did not find file 77 subsection...
Requested reaction y of the current x-y pair is not found on nin.
error in trunc***bad data.
Either all cross sections are very small (less than xslim = 10−4barn) or
epmin is larger than the highest group boundary.
error in matshd***ipat gt 99999.
Maximum number of correlation patterns is 99999. Reduce ndiv to 1 or
raise epmin in order to reduce the complexity of the correlation plot.
error in matshd***storage exceeded.
370 NJOY2016

11 COVR LA-UR-17-20093
nwig=2*(ixmax+1)+600 words are available for storing the boundary curve
of a constant-correlation region. This will not be exceeded for any practical
number of groups ixmax.
error in level***coefficient = --- out of range.
The absolute magnitude of a computed correlation coefficient is greater
than 2. The input covariance file may be faulty.
error in finds***mat --- mf --- mt --- not on tape.
Requested reaction x of the current x-y pair is not found on nin.
error in press***storage exceeded.
This problem should not occur.
error in press***matrix not symmetric....
Symmetric-matrix format is requested for a matrix that is asymmetric.
This problem should not occur.
error in setfor***nvf (= ---) or ncf (= ---) is illegal.
This problem should not occur.
11.7 Input/Output Units
The following logical units are used:
10 nin in corr and covard, nscr in other routines. These units are used to
extract either one or two (if mat16=mat) materials from the input covariance
tape.
11 nscr1 in the plot mode. These units are used to document null and small
covariance matrices and empty plots.
11/12 nscr1/nscr2 in the library mode. In covard, the input covariances for
the current reaction pair are read from unit 10 and written to nscr2 (= 12).
If the output library is to contain correlation coefficients (matype = 4), then
in corr the covariances are read from nscr2, and the calculated correlations
are written to nscr1 (= 11). If output covariances are requested (matype
= 3), the value of nscr1 is simply reset to nscr2 (= 12). In either case,
press reads the data from unit nscr1 and writes the compressed data to
nout.
20-99 User’s choice for nin and nout.
Unit 10 has the same mode as nin. Unit nout, if used, is always formatted.
Unit 11 is formatted in the plot option and it is binary in the library option.
Unit 12, if used, is always binary.
NJOY2016 371

LA-UR-17-20093 11 COVR
11.8 Retrieval Program for COVR Output Libraries
PROGRAM BOXR
C ******************************************************************
C FUNCTION OF PROGRAM. READ DATA FROM UNIT NIN IN THE COMPRESSED
C *BOXER* FORMAT PRODUCED BY THE COVR MODULE OF NJOY, AND LOAD THE
C FULL, RECONSTRUCTED MATRIX INTO C(I,J). THEN WRITE THE RESULT ON
C UNIT NOUT IN HIGH-TO-LOW ENERGY ORDER. FAILURE TO FIND A
C REQUESTED DATA SET RESULTS IN AN ERROR STOP.
C
C ITYPE DATA TYPE REQUESTED,
C = -1, TO WRITE A TABLE OF CONTENTS OF NIN, IN THE
C FORMAT OF BOXR INPUT INSTRUCTIONS, ON UNIT NTAB.
C = 0, FOR GROUP BOUNDARIES,
C = 1, FOR CROSS SECTIONS,
C = 2, FOR STANDARD DEVIATIONS,
C = 3, FOR COVARIANCE MATRIX,
C = 4, FOR CORRELATION MATRIX, OR (IF MT1 IS ZERO)
C TRANSFER MATRIX FROM COVFILS2.
C ITYPEH VALUE OF ITYPE ON CURRENT DATA HEADER CARD.
C
C (MAT,MT,MAT1,MT1) REQUESTED REACTION PAIR.
C (MATH,MTH,MAT1H,MT1H) CURRENT REACTION PAIR.
C (XVAL(IV),IV=1,NVAL) DATA VALUE ARRAY IN THE *BOXER* FORMAT.
C NVMAX MAXIMUM ALLOWABLE VALUE OF NVAL.
C (ICON(IC),IC=1,NCON) CONTROL-PARAMETER ARRAY IN *BOXER* FORMAT.
C NCMAX MAXIMUM ALLOWABLE VALUE OF NCON.
C
C I ROW INDEX OF MATRIX C(I,J), NORMALLY THE ENERGY GROUP
C OF THE REACTION (MAT,MT).
C NROW NUMBER OF ROWS IN C(I,J).
C NROWH VALUE OF NROW ON DATA HEADER CARD.
C NROWM CONTINUATION FLAG, = 0 FOR FINAL DATA BLOCK OF CURRENT
C REACTION PAIR.
C J COLUMN INDEX OF C(I,J), FOR MATRIX DATA THE ENERGY GROUP
C OF THE REACTION (MAT1,MT1), = 1 FOR VECTORS.
C NCOL NUMBER OF COLUMNS IN C(I,J).
C NCOLH VALUE OF NCOL ON DATA HEADER CARD, = 0 IF C(I,J) IS A
C SYMMETRIC MATRIX REPRESENTED IN THE *BOXER* FORMAT BY
C JUST THE UPPER RIGHT TRIANGLE (J.GE.I).
C NGMAX MAXIMUM ALLOWABLE VALUE OF NROW AND NCOL.
372 NJOY2016

11 COVR LA-UR-17-20093
C ******************************************************************
DIMENSION IVFT(3), ICFT(3), IA(9), IB(9)
DIMENSION C(200,200), CR(200), XVAL(880), ICON(900)
DATA NGMAX /200/, NVMAX /880/, NCMAX /900/, IDASH /4H----/
DATA NINPUT /5/, NIN /20/, NOUT /21/, NTAB /22/, IZERO /0/
C
C ***READ USER-SUPPLIED REACTION-TYPE AND MAT-MT INFORMATION.
10 READ (NINPUT,190) ITYPE,MAT,MT,MAT1,MT1
C INPUT IS TERMINATED BY ENTERING (0,0).
IF (ITYPE.GE.0.AND.MAT.EQ.0) STOP
C
C ***RETRIEVE REQUESTED DATA FROM UNIT NIN.
20 READ (NIN,210,END=900) ITYPEH,(IA(K),K=1,9),MATH,MTH,MAT1H,MT1H
1 ,NVAL,NVF,NCON,NCF,NROWM,NROWH,NCOLH
C
C ***IN COVFILS2, ITYPEH=9 IS USED AS A TERMINATOR.
30 IF (ITYPEH.EQ.9) GO TO 900
IF (ITYPE.EQ.-1.AND.MATH.EQ.0) MATH=1
IF (ITYPE.EQ.-1.AND.IA(2).NE.IDASH)
1 WRITE (NTAB,190) ITYPEH,MATH,MTH,MAT1H,MT1H
IF (NVAL.GT.NVMAX) STOP 3
IF (NCON.GT.NCMAX) STOP 4
C SET FORMATS, THEN READ BOXER DATA.
CALL SETFOR (NVF,NCF,NOUT,IVFT,ICFT)
IF (NVAL.GT.0) READ (NIN,IVFT) (XVAL(K),K=1,NVAL)
IF (NCON.GT.0) READ (NIN,ICFT) (ICON(K),K=1,NCON)
C TEST IF THESE ARE THE DESIRED DATA. FOR THE GROUP BOUNDARIES
C ONLY, THE VALUES MATH, MTH, MAT1H, AND MT1H ON THE HEADER CARD
C ARE IGNORED. FOR ITYPE=1 OR 2, MAT1H AND MT1H ARE IGNORED.
C FOR MATRIX DATA, ITYPE=3 OR 4, A COMPLETE MATCH IS REQUIRED.
IF (ITYPEH.NE.ITYPE) GO TO 20
IF (ITYPE.EQ.0) GO TO 40
IF (MATH.NE.MAT.OR.MTH.NE.MT) GO TO 20
IF (ITYPE.EQ.1.OR.ITYPE.EQ.2) GO TO 40
IF (MAT1H.NE.MAT1.OR.MT1H.NE.MT1) GO TO 20
C INITIALIZE
40 NX=0
I=1
ISTART=1
J=0
50 NROW=NROWH
NCOL=NCOLH
NJOY2016 373

LA-UR-17-20093 11 COVR
IV=0
NSYM=0
IF (NCOL.EQ.0) NSYM=1
IF (NCOL.EQ.0) NCOL=NROW
IF (NROW.GT.NGMAX.OR.NCOL.GT.NGMAX) GO TO 910
C
C ***LOAD DATA FROM XVAL INTO C(I,J) AS DIRECTED BY ICON.
DO 110 IC=1,NCON
IF (ICON(IC).LT.0) GO TO 60
IF (ICON(IC).EQ.0) STOP 6
NLOAD=ICON(IC)
GO TO 70
60 NLOAD=-ICON(IC)
IV=IV+1
IF (IV.GT.NVAL) STOP 7
CLOAD=XVAL(IV)
70 CONTINUE
DO 100 N=1,NLOAD
J=J+1
IF (J.LE.NCOL) GO TO 80
C START NEW ROW
I=I+1
IF (I.GT.NROW) STOP 10
J=1
IF (NSYM.EQ.1) J=I
80 IF (ICON(IC).LE.0) GO TO 90
CLOAD=0.
IF (I.GT.ISTART) CLOAD=C(I-1,J)
90 C(I,J)=CLOAD
NX=NX+1
IF (NSYM.EQ.0.OR.I.EQ.J) GO TO 100
C(J,I)=CLOAD
NX=NX+1
100 CONTINUE
110 CONTINUE
IF (NROWM.EQ.0) GO TO 120
C READ IN NEW PAGE OF DATA FROM NIN
IF (J.NE.NCOL) STOP 11
READ (NIN,210) ITYPEH,(IB(K),K=1,9),MATH,MTH,MAT1H,MT1H,NVAL,NVF
1 ,NCON,NCF,NROWM,NROWH,NCOLH
CALL SETFOR (NVF,NCF,NOUT,IVFT,ICFT)
IF (NVAL.GT.0) READ (NIN,IVFT) (XVAL(K),K=1,NVAL)
374 NJOY2016

11 COVR LA-UR-17-20093
IF (NCON.GT.0) READ (NIN,ICFT) (ICON(K),K=1,NCON)
ISTART=I+1
GO TO 50
120 CONTINUE
C FINISHED LOADING C(I,J)
IF (NX.NE.NROW*NCOL) STOP 12
C
C ***WRITE C(I,J) TO NOUT IN HIGH-TO-LOW ENERGY ORDER.
WRITE (NOUT,220)
WRITE (NOUT,210) ITYPEH,(IA(K),K=1,9),MATH,MTH,MAT1H,MT1H,NVAL,NVF
1 ,NCON,NCF,NROWM,NROWH,NCOLH
IF (NCOL.EQ.1) GO TO 150
DO 140 I=1,NROW
IR=NROW+1-I
C IN COVFILS2, TRANSFER MATRICES ARE ALREADY IN HIGH-TO-LOW ORDER
IF (ITYPE.EQ.4.AND.MT1.EQ.0) IR=I
DO 130 J=1,NCOL
JR=NCOL+1-J
IF (ITYPE.EQ.4.AND.MT1.EQ.0) JR=J
130 CR(J)=C(IR,JR)
140 WRITE (NOUT,200) (CR(L),L=1,NCOL)
GO TO 10
150 DO 160 I=1,NROW
IR=NROW+1-I
160 CR(I)=C(IR,1)
WRITE (NOUT,200) (CR(K),K=1,NROW)
GO TO 10
C
C ***PRINT ERROR MESSAGES.
900 IF (ITYPE.NE.-1) WRITE (NOUT,901) ITYPE,MAT,MT,MAT1,MT1
901 FORMAT (/50H ***ERROR IN BOXR***CANNOT FIND ITYPE,MAT,MT,MAT1,
1 ,5HMT1 =,5I5)
IF (ITYPE.EQ.-1) WRITE(NTAB,190) IZERO,IZERO
STOP
910 WRITE (NOUT,911) NGMAX
911 FORMAT (/45H ***ERROR IN BOXR*** NUMBER OF GROUPS EXCEEDS,I4)
STOP
C
190 FORMAT (5I6)
200 FORMAT (1P8E10.3)
210 FORMAT (I1,A3,8A4,2(I5,I4),2(I4,I3),3I4)
220 FORMAT (///)
NJOY2016 375
LA-UR-17-20093 11 COVR
END
SUBROUTINE SETFOR (NVF,NCF,NOUT,IVFT,ICFT)
C ******************************************************************
C SET *BOXER* INPUT/OUTPUT FORMATS.
C ******************************************************************
DIMENSION IFT(3,14), IVFT(3), ICFT(3)
DATA IFT /4H(80I,4H1) ,4H ,4H(40I,4H2) ,4H ,4H(26I,4H3) ,
1 4H ,4H(20I,4H4) ,4H ,4H(16I,4H5) ,4H ,4H(13I,4H6) ,4H
2 ,4H(11F,4H7.4),4H ,4H(10F,4H8.5),4H ,4H(1P8,4HE9.2,4H)
3 ,4H(1P8,4HE10.,4H3) ,4H(1P7,4HE11.,4H4) ,4H(1P6,4HE12.,4H5) ,4
4 H(1P6,4HE13.,4H6) ,4H(1P5,4HE14.,4H7) /
C
IF (NVF.LT.7.OR.NVF.GT.14) GO TO 900
IF (NCF.LT.1.OR.NCF.GT.6) GO TO 900
C
C ***SET FORMATS
DO 10 I=1,3
IVFT(I)=IFT(I,NVF)
10 ICFT(I)=IFT(I,NCF)
RETURN
C
C ERROR MESSAGE
900 WRITE (NOUT,901) NVF,NCF
901 FORMAT (/28H ***ERROR IN SETFOR***NVF (=,I3,11H) OR NCF (=,I3,13H)
1 IS ILLEGAL.)
STOP
END
376 NJOY2016

12 MODER LA-UR-17-20093
12 MODER
The MODER module is used to convert ENDF, PENDF, and GENDF tapes
from the NJOY blocked-binary mode to formatted mode (ASCII on modern
computers), and vice versa. It can also be used to copy data from one logical unit
to another without change of mode, or to make a new tape containing selected
materials from one or more ENDF, PENDF, or GENDF tapes. MODER handles
ENDF-4 through ENDF-6 formats, plus special-purpose formats developed for
NJOY, such as the GROUPR and ERRORR output formats.
This chapter describes the MODER module in NJOY2016.0.
12.1 Code Description
The main subroutine moder is exported by the module modem. At the beginning
of execution, MODER rewinds the output tape nout. Additionally, each time a
new input tape nin is specified, that unit is rewound. MODER then processes
nin one file at a time, either for all materials on nin, or optionally (see follow-
ing section) for a single specified material. As each file is identified, the main
program calls a subroutine dedicated to that file. Each subroutine makes the
series of calls to contio,listio, etc., that is appropriate to that file.
If nin and nout are of opposite sign, then mode conversion is performed
automatically by the utility I/O subroutines. If nin and nout have the same
sign, then no mode conversion is performed; runs of this type can be used simply
to make an extra copy of the input tape or to retrieve selected materials without
mode change. Only a little more than one page of scratch storage is needed, so
there are no limitations on which tapes can be processed.
12.2 Input Instructions
As an aid to discussions of the user input to MODER, the input instructions
that appear as comment cards at the beginning of the current version of this
module are listed below. Since code changes are possible, it is always advisable
to consult the comment-card instructions contained in the version of the code
actually being used before proceeding with an actual calculation.
NJOY2016 377

LA-UR-17-20093 12 MODER
!---input specifications (free format)---------------------------
!
! card 1 unit numbers
! nin input unit
! nout output unit
!
! a positive unit is coded (mode 3).
! a negative unit is blocked binary (njoy mode).
!
! note: abs(nin) ge 1 and le 19 is a flag to select various
! materials from one or more input tapes, with or
! without mode conversion. the kind of data to be
! processed is keyed to nin as follows:
! nin=1, for endf or pendf input and output,
! 2, for gendf input and output,
! 3, for errorr-format input and output.
!
! cards 2 and 3 for abs (nin) ge 1 and le 19 only.
!
! card 2
! tpid tapeid for nout. 66 characters allowed
! (delimited with ’, ended with /)
! card 3
! nin input unit
! terminate moder by setting nin=0
! matd material on this tape to add to nout
!-------------------------------------------------------------------
The contents of nin and nout are positive or negative logical unit numbers,
with absolute magnitudes normally in the range 20-99, inclusive. Positive unit
numbers refer to formatted tapes, and negative unit numbers refer to blocked-
binary tapes. No other input is required to copy or convert the entire contents
of the data file on unit nin, writing the results to unit nout.
A positive value of nin in the range 1-3 is used as a trigger to specify that
the data to be copied or converted are not the contents of a single tape, but,
instead, they are selected materials from one or more input tapes. The type
of data to be processed (ENDF/PENDF vs. GENDF vs. ERRORR-format) is
keyed to the value of nin, as detailed in the instructions above. If nin is in the
378 NJOY2016
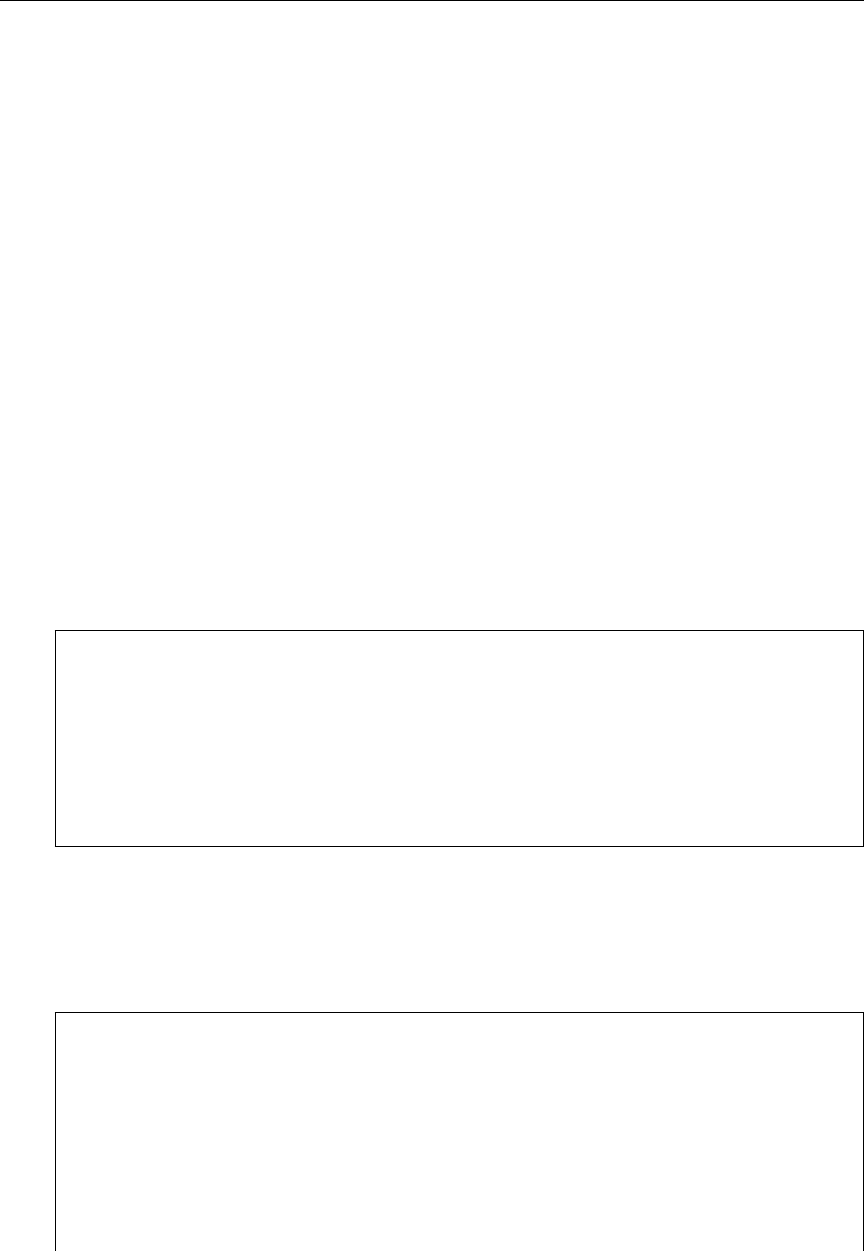
12 MODER LA-UR-17-20093
range 1-3, and only in this case, additional input is supplied to specify (on card
2) the tape-identification information to be written on the first record of the
output tape and to specify (on card 3) both the mat-numbers of the materials
to be included and the logical units where each of the desired materials are to
be found. Note that the slash terminating the Hollerith information on card 2 is
required. In the case of GENDF processing of a material matd, which is present
on the specified input tape at a series of temperatures, a single card 3 causes
the retrieval of all temperatures. Card 3 is repeated as many times as needed,
and input is terminated with a card containing 0/.
12.3 Sample Input
It is good practice to convert the mode of the ENDF/B tape before proceding
with any NJOY run. The time spent in MODER is normally much less than the
time saved by the subsequent modules. The required input for this is extremely
simple. In this first example, an ENDF-formatted file, designated “tape20” is
copied to a binary-formatted file designated “tape21”. This file is subsequently
used as input to RECONR.
moder
20 -21/
reconr
-21 -22/
...
For older versions of ENDF/B, the released “tapes” usually contained mul-
tiple materials. In the following example we specify that a single material,
1305, be extracted from “tape20” and written to “tape21”. Subsequent use of
“tape21” will be more efficient since only the material of interest is on that tape.
moder
1 -21/
’B-10’/
20 1305/
0/
reconr
-21 -22/
NJOY2016 379

LA-UR-17-20093 12 MODER
...
The final example (taken from one of the standard sample problems) shows
the use of MODER to prepare a special multimaterial ENDF tape for a co-
variance calculation involving the 5 primary fissionable isotopes. Since, in this
particular example problem, the resonance region is of no interest, a copy of the
ENDF serves as the PENDF for later modules. Mount ENDF Tape 515, 516,
and 555 on units 20, 21, and 22.
moder
1 -23/
’endf/b-v nubar covariance materials’/
20 1380/
20 1381/
21 1390/
22 1395/
22 1398/
20 1399/
0/
moder
-23 -24/
group
-23 -24 0 25/
...
The second moder run copies the ENDF file to use as a PENDF file for GROUPR.
12.4 Error Messages
error in moder***endf materials must be in ascending order
This is a problem with the material ordering for the input tape.
message from moder---mat nnnn not found on gendf tape
Check the matd value on input card 3 and make sure that the correct input
tape was mounted.
error in moder***this material is not a gendf material
Input file contains an illegal mixture of data, namely, an initial GENDF
material, followed by the indicated non-GENDF mat.
380 NJOY2016

12 MODER LA-UR-17-20093
error in moder***input is not an errorr output tape
User has requested ERRORR-format processing, but input data file is not
aERRORR-format tape.
error in moder***input is not an endf or pendf tape
User has specified nin=1 on card 1, thereby requesting selective multitape
ENDF or PENDF processing, but input data file on the unit nin specified
on card 3 is not an ENDF/PENDF file.
error in moder***input is not an endf tape
See comments above.
error in moder***input is not a gendf tape
User has requested GENDF processing, but input data file is not a GENDF
tape.
error in moder***conversion not coded for mf=nn
There is an illegal or unrecognizable mf value on nin.
error in moder***should have found send card
MODER expected the end of a section but found actual data. The listed
data display the contents of the last card read. Input data file may be bad
or may use a format not yet implemented.
error in moder***illegal covariance mf=nn
ERRORR-format file is missing the required mf=3. ENDF and PENDF
tapes must be mat ordered.
error in file1***bad LFC in mt=458.
There is a bad value for the LFC value in mf=1 mt=458. Only 0 or 1 are
allowed.
error in file1***bad LO in mt=460.
There is a bad value for the LO value in mf=1 mt=460. Only 0 or 1 are
allowed.
error in file1***illegal mt
Only the standard mt=451 to 458 and 460 are allowed in File 1.
error in file2***illegal mt
Only the standard mt=151 and the NJOY special values of mt=152 and
153 are allowed in File 2.
error in file5***illegal lf
The File 5 lf value is outside the legal range 1-12.
error in file6***illegal ltt
This message comes from the branch used for ENDF-5 format or for thermal
data generated by the THERMR module. Check the format of the File 6
sections.
NJOY2016 381

LA-UR-17-20093 12 MODER
error in file6***illegal endf6 law
This message comes from the branch used for ENDF-6 tapes. Check the
values for the law parameter in the sections of File 6. Only law values 0 to
7 are allowed. In the case of fission, negative law values are also allowed.
error in file6***illegal endf6 law for mt=nnn
This message comes from the branch used for ENDF-6 tapes. Check the
values for the law parameter in the corresponding section of File 6. Negative
law values are only allowed for fission (mt=18).
error in file7***bad NS in mt4.
The number of non-principal scattering atom types NS cannot be larger
than 3.
error in file7***illegal mt=nnn
Only mt=2 and mt=4 are allowed in File 7 for the ENDF-6 format.
error in file7***illegal value of lthr=n
Only values of 1 or 2 are allowed for lthr in ENDF-6.
error in file12***bad LO in mt=460.
There is a bad value for the LO value in mf=1 mt=460. Only 0, 1 or 2 are
allowed.
error in file15***illegal lf
Only lf=1 and the special lanl format lf=2 are allowed
error in file32***illegal value of ndigit
There is a bad value for the NDIGIT value in mf=32. Only 0 or 2 to 6 are
allowed.
error in file32***illegal value of lcomp
There is a bad value for the LCOMP value in mf=32. Only 0, 1 or 2 are
allowed.
382 NJOY2016

13 DTFR LA-UR-17-20093
13 DTFR
This module is used to prepare libraries for discrete-ordinates transport codes
that accept the format designed for the SNcode DTF-IV[24]. As this was
one of the early discrete-ordinats codes, many newer SNand diffusion codes
allow DTF format as an input option. DTFR also contains a simple plotting
capability for providing a quick look at its output. DTFR was the first output
module written for the NJOY system, and it has been largely superseded by the
MATXS/TRANSX system. But DTFR is still useful for some purposes because
of its simplicity.
This chapter describes the DTFR module in NJOY2016.0.
13.1 Transport Tables
Transport tables in DTF format are organized to mirror the structure of the data
inside a discrete-ordinates transport code. These codes start with the highest
energy group and work downward. (The conventional order for group indices is
to increase as energy decreases.) Therefore, for each group g, the data required
are the reaction cross sections for group gand the scattering cross sections to g
from other groups g0. Each data element is said to occupy a “position” in the
table for group g. The organization is shown in Table 7.
Table 7: Organization of Data for One Group in a Transport Table
Position Meaning
1 edit cross sections
··· (if any)
iptotl-3 last special edit
iptotl-2 particle-balance absorption
iptotl-1 fission neutron production
iptotl total cross section
iptotl+1 upscatter g←g0(g0>g)
··· (if any)
ipingp ingroup scattering g←g
··· downscatter g←g0(g0< g)
itabl end of table
The basic table consists of the three standard edits, namely, particle balance
absorption (σa), fission neutron production cross section (¯νσf), and total cross
section (σt). These standard edits are followed by the group-to-group scattering
NJOY2016 383

LA-UR-17-20093 13 DTFR
cross sections. If desired, the standard edits can be preceded by iptotl-3 special
edits, which can be used in the transport code to calculate various responses of
the system (for example, heating, activation, or gas production). If iptotl is
the position of the total cross section, the positions of the three standard edits
will be iptotl-2,ipingp-1, and iptotl, respectively. The positions of the
special edits (if iptotl>3) will be 1, 2, . . . iptotl-3.
Most transport tables describe only downscatter. In such cases, the posi-
tion of the ingroup element is ipingp=iptotl+1. Position iptotl+1 would
contain σg←(g−1), and so on. If thermal upscatter is present, the nup upscatter
cross sections are between the total cross section element and the ingroup ele-
ment. Therefore, position iptotl-1 contains σg←(g+1), and so on. The position
parameters must satisfy the following conditions:
iptotl ≥3 , and
ipingp =iptotl +nup + 1 .
The number of positions for a group is called the table length. A full table will
have the table length given by
itabl =iptotl-3 + 3 + nup +ng ,
where ng is the total number of groups in the set. Table lengths can be truncated
in some cases. If this is done correctly, the important cross sections will be
conserved, and valid results can still be obtained.
An example of a transport table is given in Table 8. This table was generated
with DTFR for ENDF/B-VI 235U (mat=9228). It contains three special edits:
the (n,2n) cross section, the fission cross section, and the radiative capture
cross section. These are followed by the three standard edits, and then by the
ingroup scattering for group 1. Since this is the highest energy group, there is no
downscatter to this group from groups above, and the rest of the positions are
filled with zeros. Group 2 starts on line 8 with the six edit cross sections. The
seventh number is the ingroup cross section, and the eighth is the scattering
from group 1 to group 2. Continuing to lines 14 and 15, there are now two
downscatter elements: two to three and one to three. Note that there is an
entire table for each Legendre order, and that each table has a header card that
describes its contents. The ellipses were added to mark removed lines.
384 NJOY2016

13 DTFR LA-UR-17-20093
Table 8: Example of a Transport Table with Internal Edits
IL= 1 TABLE 30 GP 36 POS, MAT= 9228 IZ= 1 TEMP= 3.00000E+02
3.2597E-01 2.0823E+00 6.1629E-04 1.3965E+00 9.7755E+00 5.9989E+00
3.1734E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
4.9950E-01 2.0532E+00 1.1756E-03 1.4681E+00 9.1321E+00 5.8659E+00
3.0495E+00 1.1523E-01 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
6.8192E-01 1.8830E+00 1.5668E-03 1.1928E+00 8.0521E+00 5.7877E+00
2.9838E+00 8.2484E-02 3.1214E-02 0.0000E+00 0.0000E+00 0.0000E+00
...
IL= 2 TABLE 30 GP 36 POS, MAT= 9228 IZ= 1 TEMP= 3.00000E+02
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
2.8003E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
2.5972E+00 3.8535E-02 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
2.4730E+00 2.3851E-02 7.4855E-03 0.0000E+00 0.0000E+00 0.0000E+00
...
IP= 1 TABLE 30 GP 12 POS, MAT= 9228 IZ= 1 TEMP= 3.00000E+02
0.0000E+00 0.0000E+00 1.1808E-02 2.0992E-02 2.4928E-02 5.7726E-02
6.0219E-01 1.8328E+00 5.5365E+00 7.5176E+00 1.0018E+01 2.0404E+00
0.0000E+00 0.0000E+00 1.0938E-02 1.9445E-02 2.4306E-02 5.8998E-02
5.7158E-01 1.7441E+00 5.2857E+00 7.2063E+00 9.5514E+00 1.9537E+00
0.0000E+00 0.0000E+00 8.6352E-03 1.5352E-02 2.6314E-02 7.8974E-02
5.3190E-01 1.6485E+00 5.0937E+00 7.1114E+00 9.1307E+00 1.9158E+00
0.0000E+00 0.0000E+00 5.0549E-03 8.9865E-03 2.9371E-02 1.0974E-01
4.6950E-01 1.4973E+00 4.7871E+00 6.9512E+00 8.4624E+00 1.8534E+00
....
The last table in this example describes the photon production matrix. There
are 30 neutron groups and 12 photon groups. The photon group index replaces
NJOY2016 385

LA-UR-17-20093 13 DTFR
the position index used in the neutron tables. Therefore, the first 12 numbers in
this table correspond to photon production from neutron group 1. The photon
groups are arranged in order of decreasing energy.
The header lines at the start of each table in this example give the Legendre
order, number of groups, number of positions, MAT number, σ0number, and
temperature.
DTFR will also produce a variant of the transport tables that was used
for Los Alamos libraries in years past. These are sometimes called “CLAW
Libraries” after the CLAW-III and CLAW-IV libraries available from the Ra-
diation Safety Information Computational Center (RSICC) at the Oak Ridge
National Laboratory. Although CLAW-IV uses a version of this format, it was
actually generated using MATXS cross sections and the TRANSX code[82, 12].
The key feature of the CLAW tables is that the edits are removed from their
normal position at the beginning of each group in the transport table and writ-
ten out on separate lines. The format specified a particular list of reactions (see
Table 9) that is defined using data statements in DTFR. In addition, thermal
upscatter is not allowed in this format. An example of this style of transport
table is given in Table 10. Note that eye-readable identifiers were added to the
right-hand edge of each card by DTFR. The card labels contain the first two
letters of the material name, the reaction name or the Legendre order, and a
sequence number. The format of the header lines at the start of each table
is different from the last example. The quantity in parentheses on the “EDIT
XSEC” card is groups by number of edit reactions. For the neutron tables, it is
table length by groups. For the gamma table, it is gamma groups by neutron
groups.
13.2 Data Representations
The data stored into the transport tables are obtained from GROUPR. Since all
the scattering matrix reactions are kept separate in the multigroup processing,
it is necessary to add them up to compute the DTF scattering matrix. They are
obtained from the sections with mf=6 on the input GENDF tape. Similarly, all
the photon production matrices have to be added up to obtain the final DTF
photon production table. These sections have mf=16.
386 NJOY2016

13 DTFR LA-UR-17-20093
Table 9: Predefined Edits for DTFR
Reaction Name Position Reaction Multiplicity
els 1 2 1
ins 2 4 1
n2n 3 16 1
3 6 1
3 7 1
3 8 1
3 9 1
n3n 4 17 1
ngm 5 102 1
nal 6 107 1
np 7 103 1
fdir 8 19 1
nnf 9 20 1
n2nf 10 21 1
ftot 11 18 1
nd 12 104 1
nt 13 105 1
nhe3 14 106 1
n2p 15 111 1
npa 16 112 1
nt2a 17 113 1
nd2a 18 114 1
n2a 19 108 1
n3a 20 109 1
nnd 21 32 1
nnd2a 22 35 1
nnhe3 23 34 1
nna 24 22 1
n2na 25 24 1
nn3a 26 23 1
n3na 27 25 1
nnp 28 28 1
nn2a 29 29 1
n2n2a 30 30 1
nnt 31 33 1
nnt2a 32 36 1
n4n 33 37 1
n3nf 34 38 1
chi 35 470 1
chid 36 471 1
nud 37 455 1
phi 38 300 1
theat 39 301 1
39 443 0
kerma 40 443 1
tdame 41 444 1
nusf 42 1 1
totl 43 452 1
NJOY2016 387

LA-UR-17-20093 13 DTFR
Table 10: Example of DTFR Transport Tables Using Separate Edits
U235 EDIT XSEC ( 30X 48) PROC BY NJOY1 ON 05/03/90
3.03110E+00 2.85141E+00 2.75464E+00 2.66464E+00 2.87622E+00 3.56158E+00U2 ELS
4.43195E+00 4.38571E+00 3.94779E+00 3.53864E+00 3.34261E+00 3.61868E+00U2 ELS
4.74566E+00 6.13164E+00 7.65700E+00 9.34710E+00 1.08466E+01 1.16438E+01U2 ELS
1.19400E+01 1.28024E+01 1.32190E+01 1.31520E+01 1.29202E+01 1.30545E+01U2 ELS
1.27990E+01 1.19229E+01 1.32489E+01 1.41192E+01 1.47783E+01 1.54225E+01U2 ELS
3.78514E-01 4.17166E-01 4.61638E-01 5.44816E-01 8.11127E-01 1.37822E+00U2 INS
2.20958E+00 2.30405E+00 2.34199E+00 2.28404E+00 2.14540E+00 1.90879E+00U2 INS
1.60448E+00 1.29695E+00 9.63151E-01 4.00064E-01 4.54497E-02 3.03043E-03U2 INS
1.87467E-06 7.26072E-08 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 INS
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 INS
3.25966E-01 4.99502E-01 6.81925E-01 8.22064E-01 6.05949E-01 3.47278E-01U2 N2N
8.86188E-03 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 N2N
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 N2N
...
U235 L=0 N-N TABLE ( 33X 30)
1.39646E+00 9.77549E+00 5.99892E+00 3.17345E+00 0.00000E+00 0.00000E+00U2 0
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 0
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 0
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 0
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 0
0.00000E+00 0.00000E+00 0.00000E+00 1.46808E+00 9.13206E+00 5.86594E+00U2 0
3.04950E+00 1.15234E-01 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 0
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 0
...
U235 L=1 N-N TABLE ( 33X 30)
0.00000E+00 0.00000E+00 0.00000E+00 2.80033E+00 0.00000E+00 0.00000E+00U2 1
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 1
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 1
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 1
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 1
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 1
2.59724E+00 3.85346E-02 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 1
0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00 0.00000E+00U2 1
...
U235 L=0 N-P TABLE ( 12X 30)
0.00000E+00 0.00000E+00 1.18077E-02 2.09916E-02 2.49277E-02 5.77264E-02U2 0
6.02189E-01 1.83282E+00 5.53653E+00 7.51757E+00 1.00182E+01 2.04037E+00U2 0
0.00000E+00 0.00000E+00 1.09379E-02 1.94453E-02 2.43062E-02 5.89981E-02U2 0
5.71583E-01 1.74411E+00 5.28569E+00 7.20630E+00 9.55138E+00 1.95373E+00U2 0
0.00000E+00 0.00000E+00 8.63521E-03 1.53515E-02 2.63136E-02 7.89737E-02U2 0
5.31904E-01 1.64847E+00 5.09371E+00 7.11139E+00 9.13067E+00 1.91577E+00U2 0
0.00000E+00 0.00000E+00 5.05490E-03 8.98652E-03 2.93715E-02 1.09745E-01U2 0
....
388 NJOY2016

13 DTFR LA-UR-17-20093
The standard edit called particle-balance absorption is used in discrete-
ordinates transport codes to calculate the balance table. The most fundamental
definition for this quantity is
σa,g =σt,g −X
g0
σs,g0←g.(457)
The total cross section is obtained from mf=3, mt=1 on the input GENDF tape.
The scattering matrix is obtained by adding all the matrix reactions found in
File 6 on the input tape. The absorption edit is often written in the form
σa,g =σγ,g +σf,g −σn2n,g ,(458)
which is good up to the threshold for other multiparticle reactions. Because
of the presence of the (n,2n) term, the σaparameter is not equal to the real
neutron absorption for high-energy groups. In fact, it is often negative.
The next standard edit is used to compute the fission neutron production rate
when constructing a fission source. It is used together with a fission spectrum,
which can be included in the specials edits (see below). The fission contribu-
tions from the GENDF tape are complicated. First, the prompt fission matrix
may be given in mt=18 (total fission), or in the partial fission reactions mt=19,
mt=20, mt=21, and mt=38, which stand for (n,f), (n,n0f), (n,2nf), and (n,3nf).
Second, each of these matrices may take advantage of the fact that the shape
of the fission spectrum is constant at low energies. Thus, fission can be repre-
sented using single fission χLE
gvector with this shape at low energies, with an
accompanying fission neutron production cross section σLE
P fg at low energies, and
with a rectangular fission matrix σHE
g,g→g0at high energies. The third complica-
tion is the presence of delayed fission neutron emission. The delayed neutron
yield ¯νD
gis retrieved from mf=3, mt=455, and the delayed neutron spectrum
χD
gis obtained by adding up the spectra for the time groups in mf=5, mt=455.
The following equation shows how these separate terms are combined into the
steady-state fission neutron production edit:
¯νSS
gσfg =X
g0
σHE
fg→g0+σLE
P fg + ¯νD
gσfg .(459)
NJOY2016 389

LA-UR-17-20093 13 DTFR
The associated steady-state fission spectrum is given by
χSS
g0=X
g
σHE
fg→g0φg+χLE
g0X
g
σLE
P fgφg+χD
g0X
g
¯νD
gσfgφg
NORM ,(460)
where NORM is the quantity that will normalize the spectrum, namely, the sum
of the numerator over all g0.
The total cross section is read directly from mf=3, mt=1. No transport
corrections are made. The normal convention for libraries made with DTFR in
the past was to supply P4tables and let the application code construct transport-
corrected P3tables if it wanted them.
A flexible scheme is provided for constructing special edit cross sections. Each
position can contain any of the cross sections available in File 3 of the GENDF
tape, or a position can contain a combination of several cross sections weighted
by multiplicities. For example, the ENDF/B-IV evaluation for 12C contains
the two reactions (n,α) (in mf=3, mt=107) and (n,n0)3α(in mf=3, mt=91). To
obtain the helium production cross section, it is only necessary to request an
edit made up as follows:
1×MT107 + 3 ×MT91 .
Most of the reactions for these special edits are requested by giving their ENDF
MT numbers. The following special MT values are used to request some special
quantities:
Special MT Meaning
300 weighting flux (from mf=3, mt=1)
455 delayed neutron yield (mf=3, mt=455)
470 steady-state spectrum (see Eq. 460)
471 delayed neutron spectrum (mf=5, mt=455)
See Section 13.4 on user input for more details.
DTFR can also construct transport tables suitable for calculations in the
thermal range. These tables allow for upscatter, and the user can specify that
bound scattering cross sections be used in the thermal range instead of the
normal static elastic scattering reaction. The NJOY thermal capabilities are
described in more detail in the THERMR and GROUPR sections of this report.
In brief, NJOY can provide thermal scattering cross sections and matrices for
any material treated as a free gas in thermal equilibrium (a Maxwell-Boltzmann
390 NJOY2016

13 DTFR LA-UR-17-20093
Table 11: Thermal Reactions Available to DTFR when using the ENDF/B-VII.0 Thermal
Evaluations
MTI MTC Thermal Binding Condition
221 free gas
222 H in H2O
223 224 H in polyethylene (CH2)
225 226 H in ZrH
227 Benzene
228 D in D2O
229 230 C in graphite
231 232 Be metal
233 234 Be in BeO
235 236 Zr in ZrH
237 238 O in BeO
239 240 O in UO2
241 242 U in UO2
243 244 Al metal
245 246 Fe metal
distribution), or it can provide data for a number of important moderator ma-
terials whose scattering laws S(α, β) are available in the ENDF/B-VII libraries.
These thermal “materials” look like different reactions for the dominant scat-
tering isotope after being processed by GROUPR. Table 11 lists the different
binding states that are available for ENDF/B-VII and the MT numbers used to
request them. Materials like “H in H2O” give the scattering for the principal
scattering isotope only; the other isotope should be treated using free-gas scat-
tering. There is an exception: benzene was evaluated as a complete molecule,
and the results were renormalized to be used with the cross section for the
dominant isotope 1H. Therefore, this material should be used with the density
corresponding to the dominant isotope, and no thermal contribution from the
other isotope should be included at all (set both mti and mtc to zero).
As described in more detail in the subsection on user input, DTFR has
an input parameter called ntherm that specifies the number of incident-energy
groups to be treated using thermal cross sections; this parameter determines
the breakpoint between the thermal treatment and the normal static treatment.
DTFR subtracts the static elastic cross section (mt=2) from both the total and
absorption edits in this group range, and it adds the mti and mtc cross sections
to these positions. Similarly, it omits the contributions from the mt=2 matrix
for these final-energy groups, and it adds in the contributions from mti and mtc.
The user is free to use a number of upscatter positions less than ntherm. The
NJOY2016 391
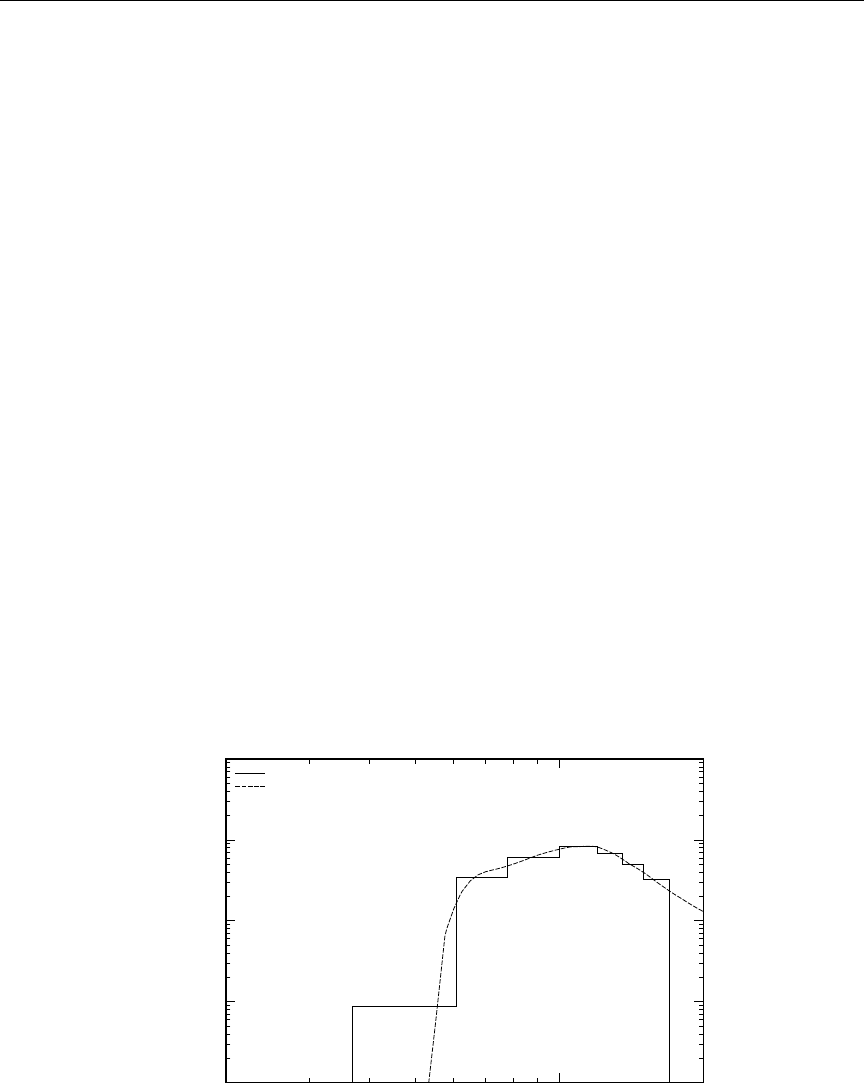
LA-UR-17-20093 13 DTFR
code will truncate the table in a way that preserves the total thermal scattering
cross section.
13.3 Plotting
Plots of the output data from a formatting program like DTFR are useful in
two ways: first, they provide a nice summary of the library and help its users to
understand the trends in the data easily, and second, they are helpful in quality
control as an aid to finding errors in processing. This versions replaces the old-
style plotting from the original version of DTFR with a nicer system making
use of the NJOY VIEWR module to produce attractive Postscript plots.
DTFR automatically makes two-dimensional log-log graphs for all the special
edit positions and the three standard edit positions. If available (see npend),
pointwise cross sections are plotted on the same frame as the group cross sec-
tions. If the multigroup cross section is a combination of several reactions, the
pointwise cross sections for all of the components are plotted. An example of
this will be found below. DTFR also prepares three-dimensional isometric pro-
jections of the P0scattering matrix and the P0photon-production table. The
user can request that one reaction be plotted per page, or that four reactions be
drawn on the same page. Examples of these plots are given in Figures 48–52.
U235 N2N
107
Energy (eV)
10-3
10-2
10-1
100
101
Cross Section (barns)
M.G.
MT 16
Figure 48: An example of DTFR plotting for the (n,2n) reaction of ENDF/B-VI 235U. This
plot was prepared using ifilm=1 and in-table edits. All the threshold reactions
are shown using the same energy range to make comparisons easy.
392 NJOY2016
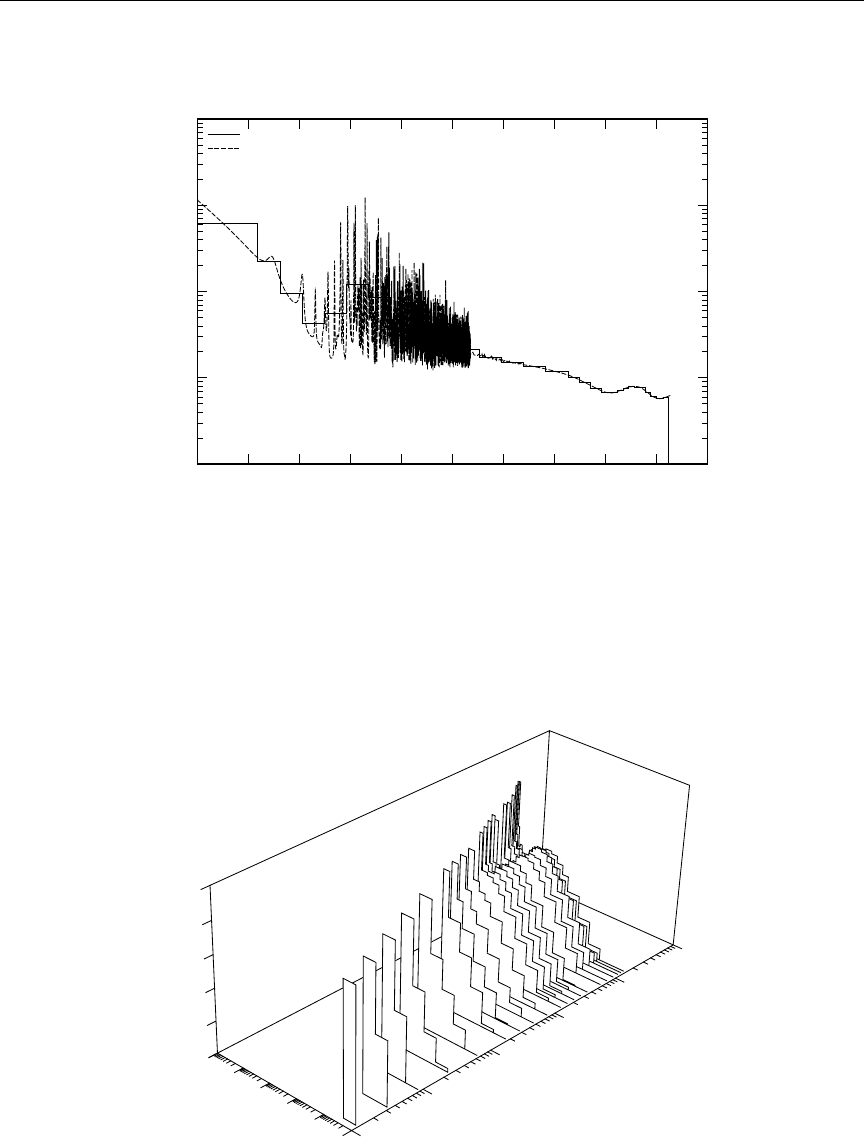
13 DTFR LA-UR-17-20093
U235 TOTAL
10-2 10-1 100101102103104105106107108
Energy (eV)
100
101
102
103
104
Cross Section (barns)
M.G.
MT 1
Figure 49: This is the total cross section for ENDF/B-VI 235U from the same run as the
previous plot. The energy range from 1×10−5eV to 1×10−2eV was removed to
expand the rest of the energy scale.
U235 L=0 NEUT-NEUT TABLE
1
0
-
1
1
0
1
X
s
e
c
/
l
e
t
h
1
0
3
1
0
5
1
0
7
S
e
c
.
E
n
e
r
g
y
1
0
3
1
0
4
1
0
5
1
0
6
1
0
7
1
0
8
E
n
e
r
g
y
(
e
V
)
Figure 50: This plot shows the P0scattering matrix for ENDF/B-VI 235U by incident and
secondary energy.
NJOY2016 393
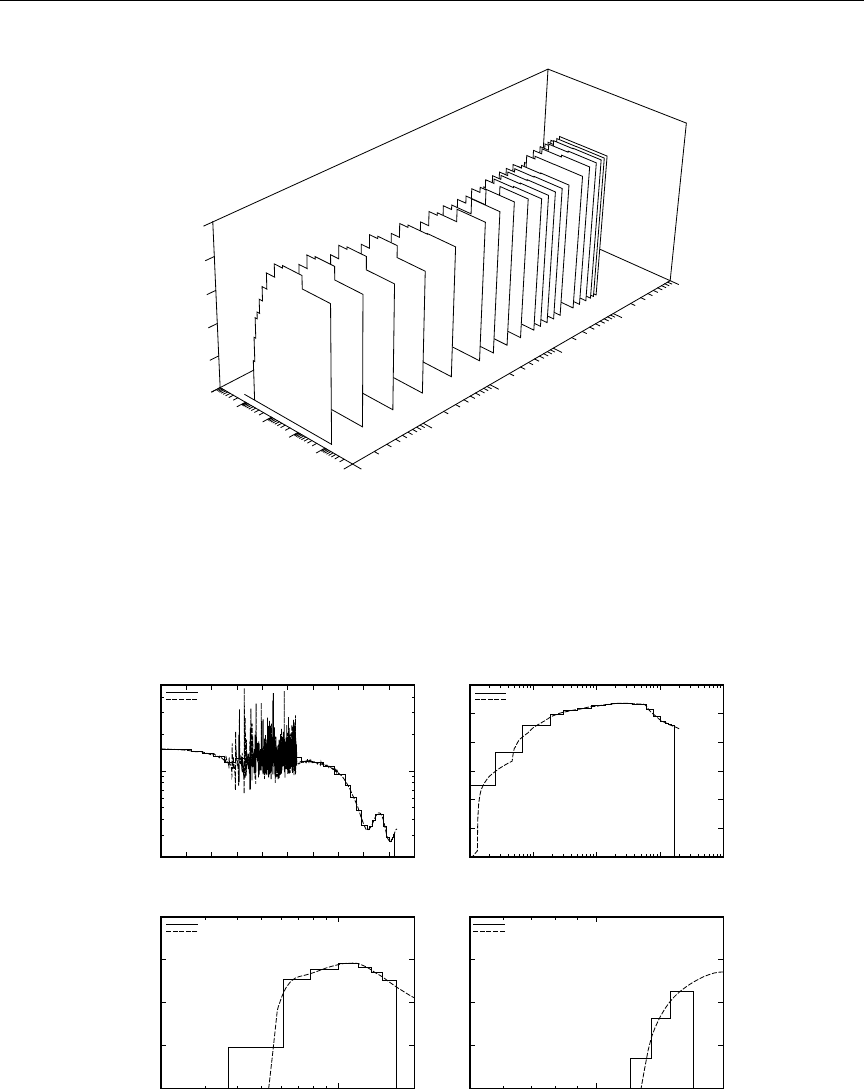
LA-UR-17-20093 13 DTFR
U235 L=0 NEUT-PHOT TABLE
1
0
-
7
1
0
-
5
X
s
e
c
/
e
V
1
0
3
1
0
5
1
0
7
G
a
m
m
a
E
n
e
r
g
y
1
0
3
1
0
4
1
0
5
1
0
6
1
0
7
1
0
8
E
n
e
r
g
y
(
e
V
)
Figure 51: The 30×12 P0photon production matrix for 235U is plotted versus neutron
energy and photon energy.
U235 ELS
10-2 10-1 100101102103104105106107108
Energy (eV)
101
Cross Section (barns)
M.G.
MT 2
U235 INS
104105106107108
Energy (eV)
10-5
10-4
10-3
10-2
10-1
100
101
Cross Section (barns)
M.G.
MT 4
U235 N2N
107
Energy (eV)
10-3
10-2
10-1
100
101
Cross Section (barns)
M.G.
MT 16
U235 N3N
107
Energy (eV)
10-3
10-2
10-1
100
101
Cross Section (barns)
M.G.
MT 17
Figure 52: An example of DTFR plotting using ifilm=2 for ENDF/B-VI 235U for some of
the standard edits with iedit=1.
394 NJOY2016

13 DTFR LA-UR-17-20093
13.4 User Input
The following user input specifications were copied from the comment cards at
the beginning of the DTFR module source code.
!---input specifications (free format)---------------------------
!
! card 1 units
! nin input unit with data from groupr.
! nout output unit containing dtf tables (coded).
! (default=0=none)
! npend input unit with pendf tape for point plots.
! (default=0=none)
! nplot output plot info for plotr module
! (default=0=none)
! card 2 options
! iprint print control (0 minimum, 1 maximum)
! ifilm film control (0/1/2=no/yes with 1 plot per frame/
! yes with 4 plots per frame (default=0)
! iedit edit control (0/1=in table/separate) (default=0)
!
! cards 3 through 5 only for iedit=0
!
! card 3 neutron tables
! nlmax number of neutron tables desired.
! ng number of neutron groups
! iptotl position of total cross section
! ipingp position of in-group scattering cross section.
! itabl neutron table length desired.
! ned number of entries in edit table (default=0).
! ntherm number of thermal groups (default=0).
! card 3a only for ntherm ne 0
! card 3a thermal incoherent and coherent mts
! mti mt for thermal incoherent data
! mtc mt for thermal coherent data (default=0)
! nlc no. coherent legendre orders (default=0)
! card 4 edit names
! six character hollerith names for edits for as many
! cards as needed. there will be iptotl-3 names read.
! each name is delimited with ’.
! card 5 edit specifications
! ned triplets of numbers on as many cards as needed.
NJOY2016 395

LA-UR-17-20093 13 DTFR
! positions can appear more than once.
! reaction types can appear more than once.
! jpos position of edit quantity.
! mt endf reaction number.
! mult multiplicity to be used when adding this mt.
!
! card 6 for iedit=1
!
! card 6 claw-format tables
! nlmax number of neutron tables (def=5)
! ng number of neutron groups (def=30)
! (number of thermal groups is zero)
!
! card 7 gamma ray tables
! nptabl number of gamma tables desired (default=0)
! ngp number of gamma groups (default=0)
! card 8 material description
! one card for each table set desired.
! empty card (/) terminates execution of dtfr.
! hisnam 6-character isotope name
! mat material number as in endf (default=0)
! jsigz index number of sigma-zero desired (default=1)
! dtemp temperature desired (default=300)
!
!-------------------------------------------------------------------
As usual, card 1 is used to assign the input and output units for the module.
nin must be an output tape from GROUPR, and it can be in either binary or
coded mode. The output file nout must be in coded mode. It will contain the
DTF-format card images. File npend should be the same PENDF tape that was
used in GROUPR when nin was made. It is only needed if plots are requested.
The nplot file will contain the input lines that VIEWR will use to prepare
the Postscript plots of the DTFR resilts. Card 2 starts out with the print flag
iprint, which is usually set to 1. The parameter ifilm can be used to suppress
plotting, or to request plots with either 1 or 4 graphs per frame. Examples of
the DTFR plotting capability were given above. The value of iprint is used to
control the output format. If it is equal to zero, a conventional DTF-type table is
produced. If any edits were requested, they are given in the table using the first
few positions in the table. The separate-edits option is used to produce cross
396 NJOY2016

13 DTFR LA-UR-17-20093
sections in the “CLAW” format. In this format, the edits are extracted from
the table and written out separately with identification information appended to
the right side of each card image. The scattering tables have only the standard
3 edits, and they also have standard identification fields added to the right side
of each card. Examples of both styles were given above.
Cards 3 through 5 are used for iedit=0 only. The first parameter is ilmax.
It is the number of Legendre tables desired; that is, it would be 4 for a P3
set. The number of groups ng must agree with the number on the input tape
from GROUPR. The value of iptotl is used to determine both the position of
the total cross section in the table and the number of special edit positions at
the front of the table (iptotl-3, which can be zero). Note that ned is not the
number of edit positions; it is the number of edit specification triplets to be read.
Therefore, ned≥iptotl-3. Also ipingp=iptotl+1 if there is no upscatter,
and ipingp=iptotl+nup+1 when the total number of upscatter groups is nup.
(The parameter nup is not actually given in the input; it is always equal to
ipingp-iptotl-1.) The length of a full table is given by
iptotl-3
+3
+nup
+ng
itable
However, smaller table lengths can be requested; truncation will be performed
in a way that preserves the production cross sections. The parameter ntherm
can be set to zero if no thermal upscatter cross sections are desired. If nonzero,
it refers to the number of incident thermal groups, and it is used to define the
breakpoint between the thermal and epithermal treatments. It is not necessarily
equal to nup.
Card 3a is only given if ntherm>0. It gives the mt numbers for the thermal
incoherent and coherent cross sections to be extracted from the GENDF tape.
Examples might include 221 and zero for free-gas scattering, or 229 and 230 for
graphite. NLC can be used to truncate the anisotropy of the coherent term, if
desired. For thermal cases, DTFR subtracts the static elastic scattering from
both the total and absorption positions for the lowest ntherm groups, and then
it adds in the cross sections corresponding to mti and mtc for these thermal
groups. When reading through the matrices, it omits all the contributions from
the static elastic matrix for the thermal groups, and adds in the mti and mtc
contributions for these groups instead.
NJOY2016 397
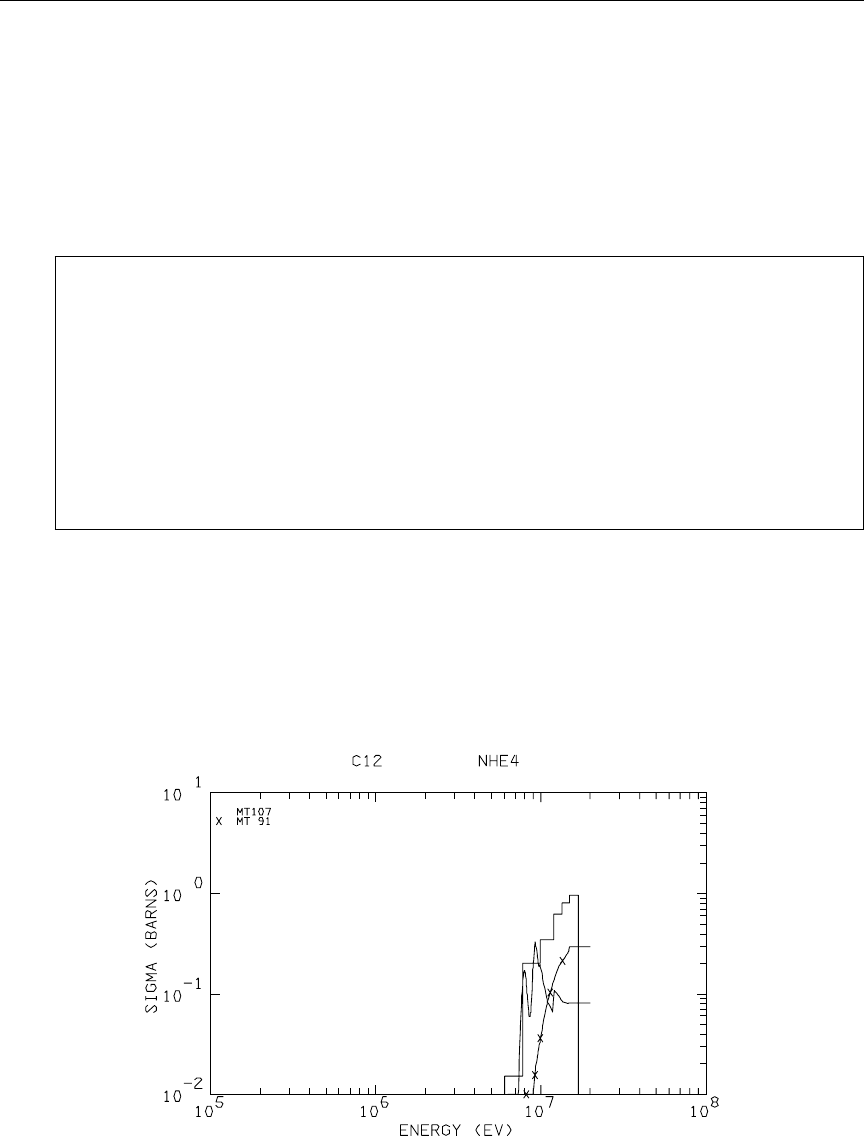
LA-UR-17-20093 13 DTFR
Card 4 gives Hollerith names for the edit cross sections. These ned names
will appear on the output listing, but they are not passed on to the output file.
Card 5 specifies the contents of each of the special edit fields. Note that each
edit can be any linear combination of the cross sections on the input GENDF
tape. This feature can be used to produce complex edits like gas production.
An example follows:
1. ...
2. n.he4 kerma fiss
3. 1 107/
4. 1 91 3/
5. 2 301/
6. 3 444/
7. ....
The line numbers are not part of the input. Line 1 represents all the input cards
before card 4, and line 7 represents all the cards after card 5. This input is
for ENDF/B-IV 12C. Lines 3 and 4 construct a helium-production cross section
as the sum of (n,α) and three times (n,n0)3α. Lines 5 and 6 assign two more
edit positions for heating and damage, respectively. The MT numbers used for
Figure 53: An example of a DTFR edit plot showing multiple pointwise curves that are
the components of a compound edit. This graph is for ENDF/B-IV 12C helium
production. The histogram gives the sum of the (n,α) cross section and three
times the (n,n0)3αcross section.
398 NJOY2016

13 DTFR LA-UR-17-20093
the mt field on card 5 are usually just the ENDF MT numbers for the reaction.
However, there are special values available to request the weighting flux, the
steady-state and delayed components of the fission neutron spectrum, or the
delayed fission neutron yield. Remember that the steady-state fission neutron
production cross section will be found in position iptotl-1 of the transport
table.
When a multigroup edit is a combination of several cross sections as in this
example, the plot of the edit includes the pointwise cross sections for all of the
component reactions. Figure 53 illustrates this for the 12C helium-production
reaction. Another useful technique is to build up a compound edit out of two
reactions using a multiplicity of zero for the second reaction. This causes the
second reaction to be plotted but not included in the edit cross section. This
method can be used to compare the energy-balance (mt=301) and kinematic
(mt=443) versions of the KERMA factor. The appropriate input lines are
...
heat/
1 301 1 1 443 0/
...
Note that this method is used in the predefined edits associated with iedit=1
(see Table 9).
Card 6 is used instead if iedit=1. As described above, the list of special edit
cross sections is fixed for the CLAW format. Therefore, it is only necessary to
give nlmax and ng. The number of thermal groups is automatically set to zero.
The next card read for either choice of output format is card 6, which controls
the generation of a photon production matrix. The number of photon production
tables is usually zero (none), or one. Only a few materials in the ENDF/B
libraries have anisotropic photon production data. Of course, ngp must agree
with the photon group structure used in GROUPR.
The input deck ends with a material description card for each material to be
processed. These materials must all be on the input GENDF tape. (Multi-MAT
GENDF tapes can be prepared using MODER from single-material GROUPR
output files, but since it is easy to combine materials at the DTF-format stage,
DTFR is usually run for one MAT at a time.) The Hollerith material names
given will appear in the comment cards before tables and in the special labels
added to the right-hand edge of each card. The material numbers mat are the
NJOY2016 399

LA-UR-17-20093 13 DTFR
same ENDF MAT numbers used when preparing the multigroup cross sections.
DTFR has only a limited capability for handling self-shielded cross sections.
The user can specify that a given set of tables be prepared using one particular
temperature dtemp and one particular background cross section, the jsigzth
value in the set.
13.5 Coding Details
The main entry point for DTFR is dtfr from module dtfm, which starts by
calling ruin to read the user’s input. Note that the special set of edits used
when iedit=1 is specified using parameter arrays in ruin (see kmted,kjped,
kmultd, and kmtid). The next steps are to open a scratch file nscr and to
initialize the plotting output.
The main loop over materials, dilution values, and temperatures goes through
statement number 105. This is where input card number 8 is read (see input
instructions) to identify the material to be processed. The input GENDF tape
is then rewound, and nin is searched for the material and temperature. If a
PENDF input tape has been mounted, the corresponding material and temper-
ature are located on npend. Note that the materials in the input file do not have
to be in the same order as the materials on either nin or npend. If a requested
material or temperature is not found, a fatal error message is issued.
When the input files have been properly positioned, dtfr checks to see if
there is enough storage for the tables. The limit nwsmax=500000 is large enough
for any reasonable multigroup set. If larger sets are desired, increase the value of
this variable which will automatically increase the dimension of the global array
sig(nwsmax). The loop over reactions and groups in a reaction goes through
statement number 150. Once the cross sections have been read off the input
tape, the code branches to different sections to process different kinds of data.
The first of these processes the File 3 neutron cross sections. Note that the total
cross section is stored in both iptotl and iptotl-2. In addition, the GROUPR
weighting flux can be extracted from the section mf=3, mt=1 and stored into
a special edit requested using mt=300. Special edit cross sections are weighted
with the specified multiplicities and summed into the specified edit positions in
the “do ied=1,ned” loop. Thermal corrections to static scattering are made at
statement number 260. The method used is to subtract mt=2 and add mti and
mtc to both the total and absorption positions.
The block of coding starting with statement number 300 is used to accumu-
late the total scattering matrix. Most numbers are simply added into the correct
400 NJOY2016

13 DTFR LA-UR-17-20093
position in the transport table. The operation specified by Eq. 457 is performed
by subtracting all matrix elements from the absorption position. In addition, in
the thermal range, the mti and mtc data are used instead of the mt=2 data.
The prompt part of fission is handled starting at statement number 340. Note
that a check is made to see if MT=18 was already processed if mt=19 is found.
This results in a fatal error, so the user must be careful to process only one
of these representations in GROUPR. The special cases ig=0 and ig2lo=0 flag
the presence of the low-energy constant spectrum or production cross section,
respectively. Delayed fission contributions are handled by the next block of cod-
ing. The method used for combining the fission matrix, the constant-spectrum
part, and the delayed parts are defined by Eqs. 459 and 460. The normalization
parameter needed to fix up χis accumulated in the variable cnorm.
The photon-production matrix is accumulated starting at statement number
600. It is a very simple process of adding all the partial matrices with mf=16 on
the input GENDF file. When all the reactions and groups for this material and
temperature have been processed, dtfr calls the subroutine dtfout to prepare
the tables and plots, and then it loops back to statement number 105 for the next
requested material. After all the materials, temperatures, and background cross
sections have been written out, the plotting system is terminated (see below),
files are closed, a final message is printed, and control is returned to njoy.
Subroutine dtfout controls the preparation of the output DTF tables on
nout, the printing of the tables on the user’s output device, and the preparation
of plots. This is a simple routine with separate paths for in-table edits and
separate edits. Plotting is handled using different subroutines for the edits, the
neutron table, and the photon-production table.
Subroutine ploted is used to prepare plots of all the special and standard edit
positions, including overlay plots of PENDF cross sections if npend is available.
Subroutine histod is used to convert the multigroup values into a pointwise
cross section with steps at each of the group boundary energies; that is, into
histogram form. Subroutine dpend prepares the PENDF part of the plot by
thinning the original PENDF grid down to a new grid with xspacing something
like the resolution of a typical screen. In addition, it “thickens” reactions, if
necessary, so that there are enough points to properly follow the curve on the
final log-log plot. Both the histogram and PENDF data arrays are written on
the the nplot unit as simple text commands in VIEWR format.
Subroutine plotnn is used to plot an isometric view of the neutron table.
This is done by removing the edits from the table and then writing lines to
NJOY2016 401

LA-UR-17-20093 13 DTFR
nplot. Note that the energies corresponding to the groups are used in the
VIEWR commands, thus producing more realistic pictures than the older DTFR
methods was able to make. A similar process is performed in plotnp for the
photon-production matrix.
13.6 Error Messages
error in dtfr***number of neutron groups disagrees with...
The value of ng in the input must be consistent with the number of groups
on the input GENDF tape. Check the input, and check whether the correct
tape was mounted.
error in dtfr***number of gamma groups disagrees with...
Same as above, except check the number of gamma groups ngp.
error in dtfr***desired temperature not on pendf
Code is unable to find mat and dtemp on the input PENDF tape npend.
Check the input information and check whether the correct PENDF tape
was mounted.
error in dtfr***not enough storage for table
There is not enough space in the sig array to construct a table with so
many positions and groups. See the global parameter nwsmax=500000.
error in dtfr***not enough storage for record
There is not enough space in the aarray to read in the data on the GENDF
tape. See the global parameter nwamax=40000.
error in dtfr***mt18 already processed//mt19 not allowed
Make sure that GROUPR processes the fission matrix using either mt=18
only, or mt=19, 20, 21, and 38, but not both.
error in dtfr***delayed nubar required to add delayed ....
The delayed neutron yield must have been processed in GROUPR (mfd=3,
mtd=455), or DTFR will be unable to construct the steady-state fission
vectors.
error in ruin***iping.le.iptotl
The ingroup position iping is normally iptotl+1, and it will be larger
still if thermal upscatter is to be included. Check input card number 3.
error in ruin***not enough storage for edits
See the global parameter nedmax=50.
error in dpend***npts exceeds ndim
The thinning/thickening process has produced too many points for the
arrays xand y. These are global arrays dimensioned at by the global
parameter ndim=7000.
402 NJOY2016

14 CCCCR LA-UR-17-20093
14 CCCCR
This module is used to produce the standard CCCC interface files ISOTXS,
BRKOXS, and DLAYXS from GROUPR output.
This chapter describes the CCCCR module in NJOY2016.0.
14.1 Introduction
The CCCC interface files (commonly pronounced “four cees”) were developed
by the Committee for Computer Code Coordination for the US Fast Breeder
Reactor Program. When the members of this committee started work in 1970,
they noted that because of the large variety of computers and computer sys-
tems, computer codes developed at one laboratory were often incompatible with
computers at other laboratories. Major rewrites of codes or wasteful duplicate
efforts were common. They hoped to create a system that would allow differ-
ent laboratories to create codes that could be moved to other sites more easily.
Moreover, they hoped that the codes developed at different laboratories could
easily work together, thereby achieving larger and more capable calculational
systems than any one laboratory could hope to develop by itself.
Much of the following discussion was developed long ago, and so some of
the code examples conform to FORTRAN-77. We assume the reader can easily
convert this into modern Fortran.
They approached this problem in two ways. First, they tried to establish
general programming standards that would make computer codes more portable.
And second, they tried to establish standard interface files for reactor physics
codes that would make it easier for computer codes to communicate with each
other. The results of this work appeared in fullest form as the CCCC-III and
CCCC-IV standards[29, 11].
The MINX code[21], which was the predecessor of NJOY, was able to pro-
duce libraries [63] that used the CCCC-III interface formats. The LINX and
BINX library management codes[83] and the CINX group collapse code[84] were
also released during this period. Major codes that used data in CCCC-format
included SPHINX[85] from Westinghouse, TDOWN[86] from General Electric,
DIF3D[16] from Argonne National Laboratory, and ONEDANT[14] from LANL.
It was indeed found that codes could be moved more easily than before. Ana-
lysts could use ONEDANT and DIF3D on similar problems; they could even use
one code to generate utility files (for example, mixture and geometry files) that
would work with the other code! When NJOY was developed, it first produced
NJOY2016 403

LA-UR-17-20093 14 CCCCR
version III formats and was later upgraded to the CCCC-IV standard.
With the demise of the breeder reactor program, development of the CCCC
system has stopped. However, many good programs are still available that
make use of CCCC files and programming standards. The LANL DANDE
system[87] was an example of how the use of standard interface files can be
used to couple several reactor physics programs together into an easy-to-use and
powerful product. In areas where the CCCC standards were not very successful,
such as gamma ray cross sections and cross sections for the fusion energy range,
the MATXS format is available as an alternative. This generalized material
cross section library format uses CCCC-type techniques. The modern SNcode
PARTISN[17] makes very heavy use of both standard and non-standard CCCC
files Thus, the CCCC spirit is not dead.
14.2 CCCC Procedures and Programming Standards
Although the CCCC programming standards went so far as to give advice on
program structure, documentation, and good coding practice, their main pur-
pose was to make it easier to move computer codes from one machine to another.
The main problems in those days were the slightly different implementations of
input/output on CDC and IBM machines, the different word size on CDC and
IBM machines, and the relatively small size of the main memory on the CDC
7600. The last of these problems was attacked by limiting the maximum mem-
ory requirements for CCCC-compliant codes. This problem has disappeared for
modern computers.
The word-size problem has three components. First, it is often necessary to
change the statements that allocate space for variables and arrays [for example,
“DIMENSION A(10)” might have to be changed to “REAL*8 A(10)” when moving
from a long-word machine (CDC, Cray) to a short-word machine (IBM, VAX,
Sun)]. Second, the names of functions that work with double-precision variables
normally must be changed (for example, ALOG10 to DLOG10). And third, the
word boundaries of double-precision variables must be properly aligned in com-
mon blocks and equivalenced arrays. The standard CCCC method for handling
name changes has been based on using standard control cards. As an example,
a code for a long-word machine might contain the following code fragment:
404 NJOY2016
14 CCCCR LA-UR-17-20093
CSW
C REAL*8 HA(10)
CSW
CLW
INTEGER HA(10)
CLW
The variable HA is intended to hold 10 words of Hollerith information using
the standard CCCC 6-character word length. Such a variable must be declared
as double precision on short-word machines, which typically allow four Hol-
lerith characters per word. To change this code to its short-word version, a
special utility code reads through each line removing the comment “C” from
lines bracketed by the “SW” comments and inserting a “C” in column 1 for all
lines bracketed by “LW” comments. Early versions of NJOY used this scheme;
later versions used UPD[88] conditional statements instead. For example, the
source file contained
*IF SW
REAL*8 HA(10)
*ELSE
INTEGER HA(10)
*ENDIF
and the compile file produced by UPD had only one of the two alternatives
activated, depending on whether SW has been set or not. NJOY2016 uses built-
in features of Fortran-90 to handle this problem. The locale module defines a
special ”kind” for the Hollerith data that is packed into CCCC records.
The word-alignment problem requires that some care be used in allocating
arrays and common blocks. For example,
REAL*8 HA
COMMON/BAD/IA(3),HA(10)
should be avoided; it would be OK with IA(4). Most CCCC records contain
NJOY2016 405
LA-UR-17-20093 14 CCCCR
mixtures of Hollerith, floating-point, and integer variables. The desired data is
normally extracted by making use of equivalenced arrays. For example, a code
could contain the following declarations:
REAL*8 HA(10)
DIMENSION A(20),IA(20)
EQUIVALENCE (HA(1),A(1)),(IA(1),A(1))
Assume that a record containing 2 Hollerith variables (which require two single-
precision variables each), 2 floating-point numbers (at single precision), and 2
integers has been read into array A. How do you extract the first of the integers?
The solution depends on defining a CCCC-standard quantity called mult, which
is 1 for long-word machines and 2 for short-word machines. Now, the desired
value can be obtained with an expression of the form
I1=IA(2*MULT+3)
The second Hollerith variable would be extracted using the simple expression
H2=HA(2)
Changing the value of mult when transporting a code to a different machine
is easily handled using control-card brackets or UPD conditionals as described
above.
In NJOY2012 and later, common blocks are no longer used, but equivalencing
is still used to pack Hollerith (or character), integer, and real data into the CCCC
records. While such coding techniques may bring tears to the eyes of modern
programmers, it remains a valid coding mechanism and we continue to exploit
this capability.
The remaining feature of the CCCC programming standards that is used in
codes like PARTISN is the concept of standardized input/output subroutines.
The CCCC interface files are sequential binary files (binary for efficiency and
sequential for simplicity). The interface formats are arranged so that the length
of any record can be calculated using parameters already read from previous
406 NJOY2016

14 CCCCR LA-UR-17-20093
records. It is convenient to insulate CCCC input/output from system variations
by defining two standard routines:
REED(NREF,IREC,ARRAY,NWDS,MODE)
Read record IREC from unit NREF into ARRAY. The record has length NWDS
in single-precision words. The MODE parameter is used to control I/O buffer-
ing, and it is not used in NJOY. Records can be read out of sequence; the
routine does any record skipping (forward or backward) needed to arrive
at record number IREC.
RITE(NREF,IREC,ARRAY,NWDS,MODE)
Write record IREC onto unit NREF using the data in ARRAY. The first NWDS
single-precision words will be written. The MODE parameter is ignored.
The records NREF must be written in sequence. The unit will be rewound
if IREC=1.
When transporting a code between different computer systems, it is only neces-
sary to have (or prepare) operational versions of REED and RITE for the target
machine.
In the conversion to Fortran-90 style, we tried to avoid all these tricks. The
reading and writing of CCCC records was coded in directly to avoid word-length
problems (no more REED or RITE). All internal variable and data read from
the GENDF file use 8-byte words. It is only at the last stage when the data
are stored into the CCCC records that the 8-byte data are converted to 4-byte
words. Thus, mult is always equal to 2. In general, the accuracy obtained with
4-byte words is sufficient for multigroup data.
14.3 The Standard Interface Files
The CCCCR module produces data libraries that use three of the CCCC-IV
standard interface files, namely:
ISOTXS for nuclide (isotope)-ordered multigroup neutron cross sections in-
cluding cross section versus energy functions for the principal cross sec-
tions, group-to-group scattering matrices, and fission neutron production
and spectra tables;
BRKOXS for Bondarenko-type self-shielding factors versus energy group, tem-
perature, and background cross section for the reactions with major reso-
nance contributions; and
DLAYXS for delayed-neutron precursor yields, emission spectra, and decay
constants for the major fissionable isotopes.
NJOY2016 407

LA-UR-17-20093 14 CCCCR
The format of each of these files, the definition of the types of data included,
and the uses and weaknesses of these three standard file formats are discussed
in the following three sections.
As mentioned in the preceding section, the normal form of the CCCC files
is binary and sequential. CCCCR writes its output in this binary mode. Of
course, coded versions (ASCII for modern systems) are needed to move library
files between different machines, and the formats used for the coded versions
are given in the file descriptions below. A separate program, BINX[83], is used
to convert back and forth between coded and binary modes. BINX can also be
used to prepare an interpreted listing of a library. CCCCR can prepare an entire
multimaterial library in one run if a multimaterial GENDF file is available. It
can also be used to prepare an interface file containing only one material. These
one-material files can be merged into multimaterial libraries using the LINX
code[83].
14.4 ISOTXS
The format for the ISOTXS material (isotope)-ordered cross section file is given
below. This computer-text format is standard for the CCCC interface files. Of
course, if these lines were to be inserted into a modern Fortran (say .f90 or later)
code, the initial ”C” will have to be changed to “!”.
C***********************************************************************
C REVISED 11/30/76 -
C -
CF ISOTXS-IV -
CE MICROSCOPIC GROUP NEUTRON CROSS SECTIONS -
C -
CN THIS FILE PROVIDES A BASIC BROAD GROUP -
CN LIBRARY, ORDERED BY ISOTOPE -
CN FORMATS GIVEN ARE FOR FILE EXCHANGE PURPOSES -
CN ONLY. -
C -
C***********************************************************************
C-----------------------------------------------------------------------
CS FILE STRUCTURE -
CS -
CS RECORD TYPE PRESENT IF -
CS =============================== =============== -
408 NJOY2016

14 CCCCR LA-UR-17-20093
CS FILE IDENTIFICATION ALWAYS -
CS FILE CONTROL ALWAYS -
CS FILE DATA ALWAYS -
CS FILE-WIDE CHI DATA ICHIST.GT.1 -
CS **************(REPEAT FOR ALL ISOTOPES) -
CS * ISOTOPE CONTROL AND GROUP -
CS * INDEPENDENT DATA ALWAYS -
CS * PRINCIPAL CROSS SECTIONS ALWAYS -
CS * ISOTOPE CHI DATA ICHI.GT.1 -
CS * **********(REPEAT TO NSCMAX SCATTERING BLOCKS) -
CS * * *******(REPEAT FROM 1 TO NSBLOK) -
CS * * * SCATTERING SUB-BLOCK LORD(N).GT.0 -
CS ************* -
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR FILE IDENTIFICATION -
C -
CL HNAME,(HUSE(I),I=1,2),IVERS -
C -
CW 1+3*MULT=NUMBER OF WORDS -
C -
CB FORMAT(11H 0V ISOTXS ,1H*,2A6,1H*,I6) -
C -
CD HNAME HOLLERITH FILE NAME - ISOTXS - -
CD HUSE(I) HOLLERITH USER IDENTIFICATION (A6) -
CD IVERS FILE VERSION NUMBER -
CD MULT DOUBLE PRECISION PARAMETER -
CD 1- A6 WORD IS SINGLE WORD -
CD 2- A6 WORD IS DOUBLE PRECISION WORD -
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR FILE CONTROL (1D RECORD) -
C -
CL NGROUP,NISO,MAXUP,MAXDN,MAXORD,ICHIST,NSCMAX,NSBLOK -
C -
CW 8=NUMBER OF WORDS -
C -
CB FORMAT(4H 1D ,8I6) -
NJOY2016 409

LA-UR-17-20093 14 CCCCR
C -
CD NGROUP NUMBER OF ENERGY GROUPS IN FILE -
CD NISO NUMBER OF ISOTOPES IN FILE -
CD MAXUP MAXIMUM NUMBER OF UPSCATTER GROUPS -
CD MAXDN MAXIMUM NUMBER OF DOWNSCATTER GROUPS -
CD MAXORD MAXIMUM SCATTERING ORDER (MAXIMUM VALUE OF -
CD LEGENDRE EXPANSION INDEX USED IN FILE). -
CD ICHIST FILE-WIDE FISSION SPECTRUM FLAG -
CD ICHIST.EQ.0, NO FILE-WIDE SPECTRUM -
CD ICHIST.EQ.1, FILE-WIDE CHI VECTOR -
CD ICHIST.GT.1, FILE-WIDE CHI MATRIX -
CD NSCMAX MAXIMUM NUMBER OF BLOCKS OF SCATTERING DATA -
CD NSBLOK SUBBLOCKING CONTROL FOR SCATTER MATRICES. THE -
CD SCATTERING DATA ARE SUBBLOCKED INTO NSBLOK -
CD RECORDS (SUBBLOCKS) PER SCATTERING BLOCK. -
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR FILE DATA (2D RECORD) -
C -
CL (HSETID(I),I=1,12),(HISONM(I),I=1,NISO), -
CL 1(CHI(J),J=1,NGROUP),(VEL(J),J=1,NGROUP), -
CL 2(EMAX(J),J=1,NGROUP),EMIN,(LOCA(I),I=1,NISO) -
C -
CW (NISO+12)*MULT+1+NISO -
CW +NGROUP*(2+ICHIST*(2/ICHIST+1)))=NUMBER OF WORDS -
C -
CB FORMAT(4H 2D ,1H*,11A6,1H*/ HSETID,HISONM -
CB 11H*,A6,1H*,9(1X,A6)/(10(1X,A6))) -
CB FORMAT(6E12.5) CHI (PRESENT IF ICHIST.EQ.1) -
CD FORMAT(6E12.5) VEL,EMAX,EMIN -
CD FORMAT(12I6) LOCA -
C -
CD HSETID(I) HOLLERITH IDENTIFICATION OF FILE (A6) -
CD HISONM(I) HOLLERITH ISOTOPE LABEL FOR ISOTOPE I (A6) -
CD CHI(J) FILE-WIDE FISSION SPECTRUM(PRESENT IF ICHIST.EQ.1) -
CD VEL(J) MEAN NEUTRON VELOCITY IN GROUP J (CM/SEC) -
CD EMAX(J) MAXIMUM ENERGY BOUND OF GROUP J (EV) -
CD EMIN MINIMUM ENERGY BOUND OF SET (EV) -
CD LOCA(I) NUMBER OF RECORDS TO BE SKIPPED TO READ DATA FOR -
CD ISOTOPE I. LOCA(1)=0 -
410 NJOY2016

14 CCCCR LA-UR-17-20093
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR FILE-WIDE CHI DATA (3D RECORD) -
C -
CC PRESENT IF ICHIST.GT.1 -
C -
CL ((CHI(K,J),K=1,ICHIST),J=1,NGROUP),(ISSPEC(I),I=1,NGROUP) -
C -
CW NGROUP*(ICHIST+1)=NUMBER OF WORDS -
C -
CB FORMAT(4H 3D ,5E12.5/(6E12.5)) CHI -
CB FORMAT(12I6) ISSPEC -
C -
CD CHI(K,J) FRACTION OF NEUTRONS EMITTED INTO GROUP J AS A -
CD RESULT OF FISSION IN ANY GROUP,USING SPECTRUM K -
CD ISSPEC(I) ISSPEC(I)=K IMPLIES THAT SPECTRUM K IS USED -
CD TO CALCULATE EMISSION SPECTRUM FROM FISSION -
CD IN GROUP I -
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR ISOTOPE CONTROL AND GROUP INDEPENDENT DATA (4D RECORD) -
C -
CL HABSID,HIDENT,HMAT,AMASS,EFISS,ECAPT,TEMP,SIGPOT,ADENS,KBR,ICHI, -
CL 1IFIS,IALF,INP,IN2N,IND,INT,LTOT,LTRN,ISTRPD, -
CL 2(IDSCT(N),N=1,NSCMAX),(LORD(N),N=1,NSCMAX), -
CL 3((JBAND(J,N),J=1,NGROUP),N=1,NSCMAX), -
CL 4((IJJ(J,N),J=1,NGROUP),N=1,NSCMAX) -
C -
CW 3*MULT+17+NSCMAX*(2*NGROUP+2)=NUMBER OF WORDS -
C -
CB FORMAT(4H 4D ,3(1X,A6)/6E12.5/ -
CB 1(12I6)) -
C -
CD HABSID HOLLERITH ABSOLUTE ISOTOPE LABEL - SAME FOR ALL -
CD VERSIONS OF THE SAME ISOTOPE IN FILE (A6)-
CD HIDENT IDENTIFIER OF LIBRARY FROM WHICH BASIC DATA -
CD CAME (E.G. ENDF/B) (A6) -
CD HMAT ISOTOPE IDENTIFICATION (E.G. ENDF/B MAT NO.) (A6) -
NJOY2016 411

LA-UR-17-20093 14 CCCCR
CD AMASS GRAM ATOMIC WEIGHT -
CD EFISS TOTAL THERMAL ENERGY YIELD/FISSION (W.SEC/FISS) -
CD ECAPT TOTAL THERMAL ENERGY YIELD/CAPTURE (W.SEC/CAPT) -
CD TEMP ISOTOPE TEMPERATURE (DEGREES KELVIN) -
CD SIGPOT AVERAGE EFFECTIVE POTENTIAL SCATTERING IN -
CD RESONANCE RANGE (BARNS/ATOM) -
CD ADENS DENSITY OF ISOTOPE IN MIXTURE IN WHICH ISOTOPE -
CD CROSS SECTIONS WERE GENERATED (A/BARN-CM)-
CD KBR ISOTOPE CLASSIFICATION -
CD 0=UNDEFINED -
CD 1=FISSILE -
CD 2=FERTILE -
CD 3=OTHER ACTINIDE -
CD 4=FISSION PRODUCT -
CD 5=STRUCTURE -
CD 6=COOLANT -
CD 7=CONTROL -
CD ICHI ISOTOPE FISSION SPECTRUM FLAG -
CD ICHI.EQ.0, USE FILE-WIDE CHI -
CD ICHI.EQ.1, ISOTOPE CHI VECTOR -
CD ICHI.GT.1, ISOTOPE CHI MATRIX -
CD IFIS (N,F) CROSS SECTION FLAG -
CD IFIS=0, NO FISSION DATA IN PRINCIPAL CROSS -
CD SECTION RECORD -
CD =1, FISSION DATA PRESENT IN PRINCIPAL -
CD CROSS SECTION RECORD -
CD IALF (N,ALPHA) CROSS SECTION FLAG -
CD SAME OPTIONS AS IFIS -
CD INP (N,P) CROSS SECTION FLAG -
CD SAME OPTIONS AS IFIS -
CD IN2N (N,2N) CROSS SECTION FLAG -
CD SAME OPTIONS AS IFIS -
CD IND (N,D) CROSS SECTION FLAG -
CD SAME OPTIONS AS IFIS -
CD INT (N,T) CROSS SECTION FLAG -
CD SAME OPTIONS AS IFIS -
CD LTOT NUMBER OF MOMENTS OF TOTAL CROSS SECTION PROVIDED -
CD IN PRINCIPAL CROSS SECTIONS RECORD -
CD LTRN NUMBER OF MOMENTS OF TRANSPORT CROSS SECTION -
CD PROVIDED IN PRINCIPAL CROSS SECTION RECORD -
CD ISTRPD NUMBER OF COORDINATE DIRECTIONS FOR WHICH -
CD COORDINATE DEPENDENT TRANSPORT CROSS SECTIONS -
412 NJOY2016

14 CCCCR LA-UR-17-20093
CD ARE GIVEN, IS ISTRPD=0, NO COORDINATE DEPENDENT -
CD TRANSPORT CROSS SECTIONS ARE GIVEN. -
CD IDSCT(N) SCATTERING MATRIX TYPE IDENTIFICATION FOR -
CD SCATTERING BLOCK N, SIGNIFICANT ONLY IF -
CD LORD(N).GT.0 -
CD IDSCT(N)=000 + NN, TOTAL SCATTERING, (SUM OF -
CD ELASTIC, INELASTIC, AND N2N SCATTERING -
CD MATRIX TERMS), -
CD =100 + NN, ELASTIC SCATTERING -
CD =200 + NN, INELASTIC SCATTERING -
CD =300 + NN, (N,2N) SCATTERING,----SEE -
CD NOTE BELOW---- -
CD WHERE NN IS THE LEGENDRE EXPANSION INDEX OF THE -
CD FIRST MATRIX IN BLOCK N -
CD LORD(N) NUMBER OF SCATTERING ORDERS IN BLOCK N. IF -
CD LORD(N)=0, THIS BLOCK IS NOT PRESENT FOR THIS -
CD ISOTOPE. IF NN IS THE VALUE TAKEN FROM -
CD IDSCT(N), THEN THE MATRICES IN THIS BLOCK -
CD HAVE LEGENDRE EXPANSION INDICES OF NN,NN+1, -
CD NN+2,...,NN+LORD(N)-1 -
CD JBAND(J,N) NUMBER OF GROUPS THAT SCATTER INTO GROUP J, -
CD INCLUDING SELF-SCATTER, IN SCATTERING BLOCK N. -
CD IF JBAND(J,N)=0, NO SCATTER DATA IS PRESENT IN -
CD BLOCK N -
CD IJJ(J,N) POSITION OF IN-GROUP SCATTERING CROSS SECTION IN -
CD SCATTERING DATA FOR GROUP J, SCATTERING BLOCK -
CD N, COUNTED FROM THE FIRST WORD OF GROUP J DATA. -
CD IF JBAND(J,N).NE.0 THEN IJJ(J,N) MUST SATISFY -
CD THE RELATION 1.LE.IJJ(J,N).LE.JBAND(J,N) -
C -
CD NOTE- FOR N,2N SCATTER, THE MATRIX CONTAINS TERMS -
CD SCAT(J TO G), WHICH ARE EMISSION (PRODUCTION)- -
CD BASED, I.E., ARE DEFINED SUCH THAT MACROSCOPIC -
CD SCAT(J TO G) TIMES THE FLUX IN GROUP J GIVES -
CD THE RATE OF EMISSION (PRODUCTION) OF NEUTRONS -
CD INTO GROUP G. -
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR PRINCIPAL CROSS SECTIONS (5D RECORD) -
C -
NJOY2016 413

LA-UR-17-20093 14 CCCCR
CL ((STRPL(J,L),J=1,NGROUP),L=1,LTRN), -
CL 1((STOTPL(J,L),J=1,NGROUP),L=1,LTOT),(SNGAM(J),J=1,NGROUP). -
CL 2(SFIS(J),J=1,NGROUP),(SNUTOT(J),J=1,NGROUP), -
CL 3(CHISO(J),J=1,NGROUP),(SNALF(J),J=1,NGROUP), -
CL 4(SNP(J),J=1,NGROUP),(SN2N(J),J=1,NGROUP), -
CL 5(SND(J),J=1,NGROUP),(SNT(J),J=1,NGROUP), -
CL 6((STRPD(J,I),J=1,NGROUP),I=1,ISTRPD) -
C -
CW (1+LTRN+LTOT+IALF+INP+IN2N+IND+ISTRPD+2*IFIS+ -
CW ICHI*(2/(ICHI+1)))*NGROUP=NUMBER OF WORDS -
C -
CB FORMAT(4H 5D ,5E12.5/(6E12.5)) LENGTH OF LIST AS ABOVE -
C -
CD STRPL(J,L) PL WEIGHTED TRANSPORT CROSS SECTION -
CD THE FIRST ELEMENT OF ARRAY STRPL IS THE -
CD CURRENT (P1) WEIGHTED TRANSPORT CROSS SECTION -
CD THE LEGENDRE EXPANSION COEFFICIENT FACTOR (2L+1) -
CD IS NOT INCLUDED IN STRPL(J,L). -
CD STOTPL(J,L) PL WEIGHTED TOTAL CROSS SECTION -
CD THE FIRST ELEMENT OF ARRAY STOTPL IS THE -
CD FLUX (P0) WEIGHTED TOTAL CROSS SECTION -
CD THE LEGENDRE EXPANSION COEFFICIENT FACTOR (2L+1) -
CD IS NOT INCLUDED IN STOTPL(J,L). -
CD SNGAM(J) (N,GAMMA) -
CD SFIS(J) (N,F) (PRESENT IF IFIS.GT.0) -
CD SNUTOT(J) TOTAL NEUTRON YIELD/FISSION (PRESENT IF IFIS.GT.0) -
CD CHISO(J)I ISOTOPE CHI (PRESENT IF ICHI.EQ.1) -
CD SNALF(J) (N,ALPHA) (PRESENT IF IALF.GT.0) -
CD SNP(J) (N,P) (PRESENT IF INP.GT.0) -
CD SN2N(J) (N,2N) (PRESENT IF IN2N.GT.0) ----SEE -
CD NOTE---- -
CD SND(J) (N,D) (PRESENT IF IND.GT.0) -
CD SNT(J) (N,T) (PRESENT IF INT.GT.0) -
CD STRPD(J,I) COORDINATE DIRECTION I TRANSPORT CROSS SECTION -
CD (PRESENT IF ISTRPD.GT.0) -
C -
CN NOTE - THE PRINCIPAL N,2N CROSS SECTION SN2N(J) -
CN IS DEFINED AS THE N,2N REACTION CROSS SECTION, -
CN I.E., SUCH THAT MACROSCOPIC SN2N(J) TIMES THE -
CN FLUX IN GROUP J GIVES THE RATE AT WHICH N,2N -
CN REACTIONS OCCUR IN GROUP J. THUS, FOR N,2N -
CN SCATTERING, SN2N(J) = 0.5*(SUM OF SCAT(J TO G) -
414 NJOY2016

14 CCCCR LA-UR-17-20093
CN SUMMED OVER ALL G). -
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR ISOTOPE CHI DATA (6D RECORD) -
C -
CC PRESENT IF ICHI.GT.1 -
C -
CL ((CHIISO(K,J),K=1,ICHI),J=1,NGROUP),(ISOPEC(I),I=1,NGROUP) -
C -
CW NGROUP*(ICHI+1)=NUMBER OF WORDS -
C -
CB FORMAT(4H 6D ,5E12.5/(6E12.5)) CHIISO -
CB FORMAT(12I6) ISOPEC -
C -
CD CHIISO(K,J) FRACTION OF NEUTRONS EMITTED INTO GROUP J AS -
CD RESULT OF FISSION IN ANY GROUP,USING SPECTRUM K -
CD ISOPEC(I) ISOPEC(I)=K IMPLIES THAT SPECTRUM K IS USED -
CD TO CALCULATE EMISSION SPECTRUM FROM FISSION -
CD IN GROUP I -
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR SCATTERING SUB-BLOCK (7D RECORD) -
C -
CC PRESENT IF LORD(N).GT.0 -
C -
CL ((SCAT(K,L),K=1,KMAX),L=1,LORDN) -
C -
CC KMAX=SUM OVER J OF JBAND(J,N) WITHIN THE J-GROUP RANGE OF THIS -
CC SUB-BLOCK. IF M IS THE INDEX OF THE SUB-BLOCK, THE J-GROUP -
CC RANGE CONTAINED WITHIN THIS SUB-BLOCK IS -
CC JL=(M-1)*((NGROUP-1)/NSBLOK+1 TO JU=MIN0(NGROUP,JUP), -
CC WHERE JUP=M*((NGROUP-1)/NSBLOK+1). -
C -
CC LORDN=LORD(N) -
CC N IS THE INDEX FOR THE LOOP OVER NSCMAX (SEE FILE STRUCTURE) -
C -
CW KMAX*LORDN=NUMBER OF WORDS -
C -
NJOY2016 415

LA-UR-17-20093 14 CCCCR
CB FORMAT(4H 7D ,5E12.5/(6E12.5)) -
C -
CD SCAT(K,L) SCATTERING MATRIX OF SCATTERING ORDER L, FOR -
CD REACTION TYPE IDENTIFIED BY IDSCT(N) FOR THIS -
CD BLOCK, JBAND(J,N) VALUES FOR SCATTERING INTO -
CD GROUP J ARE STORED AT LOCATIONS K=SUM FROM 1 -
CD TO (J-1) OF JBAND(J,N) PLUS 1 TO K-1+JBAND(J,N).-
CD THE SUM IS ZERO WHEN J=1, J-TO-J SCATTER IS -
CD THE IJJ(J,N)-TH ENTRY IN THE RANGE JBAND(J,N), -
CD VALUES ARE STORED IN THE ORDER (J+JUP), -
CD (J+JUP-1),...,(J+1),J,(J-1),...,(J-JDN), -
CD WHERE JUP=IJJ(J,N)-1 AND JDN=JBAND(J,N)-IJJ(J,N)-
C -
C-----------------------------------------------------------------------
Most of the variables in the “File Identification and File Control” record are
taken from the user’s input. Note that MAXUP is always set to zero. CCCCR does
not process the NJOY thermal data at the present time. The ICHIST parameter
will always be zero. CCCCR does not produce a file-wide fission spectrum or
matrix. The old practice of using a single fission spectrum for all calculations
is inaccurate and obsolete. Actually, the effective fission spectrum depends on
the mixture of isotopes and the flux. Any file-wide spectrum would have to
be at least problem dependent, and it should also be region dependent. The
parameters NSCMAX and NSBLOK in the “File Control” record will be discussed in
connection with the scattering matrix format.
In the “File Data” record, the Hollerith set identification and the isotope
names are taken from the user’s input. As mentioned above, the file-wide fission
spectrum CHI never appears. The mean neutron velocities by group (VEL) are
obtained from the inverse velocities computed by GROUPR:
D1
vEg=Zg
1
vφ(E)dE
Zg
φ(E)dE
,(461)
where gis the group index, φ(E) is the GROUPR weighting spectrum, and v
is the neutron velocity, which is computed from the neutron mass and energy
using v=p2E/m. The units of these quantities are s/m; they are converted to
cm/s for ISOTXS by inverting and multiplying by 100. The group structure
416 NJOY2016

14 CCCCR LA-UR-17-20093
[see EMAX(J) and EMIN] is obtained directly from mf=1, mt=451 on the GENDF
tape. Note that GROUPR energy groups are given in order of increasing energy
and ISOTXS energy groups are given in order of decreasing energy. CCCCR
handles the conversion.
The “File-Wide Chi Data” record never appears; see the discussion above for
the reasons.
In the “Isotope Control and Group Independent Data” record, the first ten
parameters are taken from the user’s input. The gram atomic weight for the
material (AMASS) can be computed from the ENDF AWR parameter available
on the GENDF file using the gram atomic weight of the neutron as a multiplier.
The energy-release parameters EFISS and ECAPT must also be computed by the
user. The ECAPT values are normally based on the ENDF Q values given in File
3, but, in some cases, it is also necessary to add additional decay energy coming
from short-lived activation steps. For example, the ECAPT value for 238U should
include the energy for the 239Uβ-decay step, and perhaps even the energy from
the 239Np βdecay. The values for EFISS should be based on the total non-
neutrino energy release, which can be obtained from mf=3, mt=18 or mf=1,
mt=458 on the ENDF tape. The TEMP parameter is normally set to 300K. The
value of SIGPOT can be computed from the scattering-radius parameter AP in
File 2 of the ENDF tape using σp=4πa2. The parameter ADENS is usually set to
zero to imply infinite dilution. KBR can be chosen based on the normal use of
the material by the community for which the library is being produced.
The ICHI parameter is related to the ichix parameter in the user’s input.
As discussed above, the option ICHI=0 is never used by CCCCR. Beyond that,
the NJOY user has the option of producing a fission χvector using the de-
fault GROUPR flux (which is available on the GENDF tape) or a user-supplied
weighting flux SPEC. This enables the user to produce an ISOTXS library ap-
propriate to a class of problems with a flux similar to SPEC. In general, the
incident-energy dependence of the fission spectrum is weak, so the choice of this
weighting spectrum is not critical. Noticeable differences might be expected be-
tween a thermal spectrum on the one hand and a fast-reactor or fusion-blanket
spectrum on the other. The χvector is defined as follows:
χg0=X
g
σfg→g0φg
X
g0X
g
σfg→g0φg
,(462)
NJOY2016 417

LA-UR-17-20093 14 CCCCR
where σfis the fission group-to-group matrix from GROUPR,φgis either the
model flux or SPEC, and the denominator assures that χg0will be normalized.
Actually, the calculation is more complicated than that because of the necessity
to include delayed-neutron production. A “steady-state” value for the fission
spectrum can be obtained as follows:
χSS
g0=X
g
σfg→g0φg+χD
g0X
g
¯νD
gσfg φg
X
g0X
g
σfg→g0φg+X
g
¯νD
gσfg φg
,(463)
where ¯νD
gis the delayed-neutron yield obtained from mf=3, mt=455 on the
GENDF tape, χD
gis the total delayed-neutron spectrum obtained by summing
over the time groups in mf=5, mt=455, and σfg is the fission cross section for
group gobtained from mf=3, mt=18.
This is still not the end of the complications of fission. If the partial fission
reactions MT=19, 20, 21, and 38 are present, the fission matrix term in the above
equations is obtained by adding the contributions from all the partial reactions
found. In these cases, a matrix for MT=18 will normally not be present on
the GENDF tape. If it is, it will be ignored. Beginning with NJOY 91.0, a
new and more efficient representation is used for the fission matrix computed in
GROUPR. It is well known that the shape of the fission spectrum is independent
of energy up to energies of several hundred keV. GROUPR takes advantage of
this by computing this low-energy spectrum only once. It then computes a
fission neutron production cross section for all the groups up to the energy at
which significant energy dependence starts. At higher energies, the full group-
to-group fission matrix is computed as in earlier versions of NJOY. Therefore, it
is now necessary to compute the values of σfg→g0as used in the above equations
using
σfg→g0=χLE
g0(¯νσf)LE
g+σHE
fg→g0,(464)
where LE stands for low energy, HE stands for high energy; the low-energy
production cross sections written as νσfwill be found on the GENDF tape using
the special flag IG2LO=0, and the low-energy χwill be found on the GENDF
tape with IG=0.
418 NJOY2016

14 CCCCR LA-UR-17-20093
In order to obtain still better accuracy, CCCCR can produce a fission χ
matrix instead of the vector. Using the above notation, the full χmatrix becomes
χSS
g→g0=χLE
g0(¯νσf)LE
g+σHE
fg→g0+χD
g0¯νD
gσfg
NORM ,(465)
where NORM is just the value that normalizes the χmatrix; that is, the sum
of the numerator over all g0. Note that the “Isotope Chi Data” record allows
for a rectangular fission matrix similar to the one produced by GROUPR. It is
obtained by using the input SPEC array to define the range of groups that will
be averaged into each of the final ICHIX spectra. For example, to collapse a
ten-group χmatrix into a five-group matrix, SPEC might contain the ten values
1, 2, 3, 4, 5, 5, 5, 5, 5, 5. More formally,
χSS
k→g0=X
s(g)=kχLE
g0(¯νσf)LE
g+σHE
fg→g0+χD
g0¯νD
gσfgφg
NORM ,(466)
where φgis the default weighting function from the GENDF tape, s(g) is the
SPEC array provided by the user, and the summation is over all groups gsatisfy-
ing the condition that s(g)=k. Future versions of CCCCR could construct the
SPEC array automatically using the information in the new GENDF format.
Continuing with the description of the “Isotope Control and Group Indepen-
dent Data” record, the next 9 parameters are flags that tell what reactions will
be described in the “Principal Cross Sections” record. They will be described
below. Similarly, the parameters IDSCT,LORDN,JBAND, and IJJ will be described
later in connection with the “Scattering Sub-Block” records.
The ISOTXS format allows for a fixed set of principal cross sections that was
chosen based on the needs of fission reactor calculations. This is one of its main
defects; the list does not allow for other reactions that become important above
6–10 MeV, and it does not allow for other quantities of interest, such as gas
production, KERMA factors, and radiation damage production cross sections.
Most of the reactions are simply copied from mf=3 on the GENDF tape with the
group order inverted — this is true for SNGAM, the (n,γ) cross section, which is
taken from mt=102; for SFIS, the (n,f) cross section, which is taken from mt=18;
for SNALF, the (n,α) cross section, which is taken from mt=107; for SNP, the
(n,p) cross section, which is taken from mt=103; for SND, the (n,d) cross section,
which is taken from mt=104; and for SNT, the (n,t) cross section, which is taken
from mt=105. The (n,2n) cross section, SN2N, is normally taken from mt=16.
However, earlier versions of ENDF represented the sequential (n,2n) reaction
NJOY2016 419

LA-UR-17-20093 14 CCCCR
in 9Be using mt=6, 7, 8, and 9. If present, these partial (n,2n) reactions are
added into SN2N. The flags IFIS,IALF,INP,IN2N,IND, and INT in the “Isotope
Control and Group Independent Data” record are set to indicate which of these
reactions have been found for this material.
In going from version III of the CCCC specifications to version IV, there was
some controversy over the appropriate definition for the (n,2n) cross section and
matrix. It was decided that the quantity in SN2N would be the (n,2n) reaction
cross section; that is, it would define the probability that an (n,2n) reaction
takes place. The (n,2n) matrix would be defined such that the sum over all
secondary groups would produce the (n,2n) production cross section, which is
two times larger than the reaction cross section.
The CHISO vector, which contains the fission spectrum vector (if any), was
discussed above. A complete calculation of the fission source also requires the
fission yield, SNUTOT, which can be used together with the fission cross section
to calculated the fission neutron production cross section, ¯νσf. The fission yield
can be calculated from the GROUPR fission matrix using
¯νg=X
g0
σfg→g0
σfg
.(467)
Adding delayed neutron contributions and accounting for the partition of the
fission matrix into low-energy and high-energy parts (see the discussion of χ
above) gives the equation actually used by CCCCR:
¯νSS
g=X
g0
σHE
fg→g0+ (¯νσf)LE
g+ ¯νD
gσfg
σfg
.(468)
The total cross section produced by GROUPR contains two components:
the flux-weighted or P0total cross section, and the current-weighted or P1total
cross section. The P0part is stored into STOTPL, and the LTOT flag is set to 1.
STRPL contains the transport cross section used by diffusion codes; this is,
σtr,g =σt1,g −X
g0
σe1,g→g0,(469)
where σt1,g is the P1total cross section and σe1,g→g0is the P1component of the
elastic scattering matrix, which is obtained from mf=6, mt=2 on the GENDF
420 NJOY2016

14 CCCCR LA-UR-17-20093
tape from GROUPR. The flag LTRN is set to 1; that is, no higher-order transport
corrections are provided. Direction-dependent transport cross sections are not
computed by CCCCR; therefore, ISTRPD is always zero, and the STRPD vectors
are missing.
As discussed above, the “Isotope Chi Data” record may be present if the user
set ICHIX>1 and supplied a SPEC vector to define how the full χmatrix is to be
collapsed into a rectangular χmatrix.
The treatment of scattering matrices in the ISOTXS format is complex and
has lots of possible variations. Only the variations supported by CCCCR will
be described here. First of all, the scattering data are divided into blocks and
subblocks. A block is either one of the designated scattering reactions [that is,
total, elastic, inelastic, or (n,2n)] and contains all the group-to-group elements
and Legendre orders for that reaction (IFOPT=1), or it is one particular Legendre
order for one of the designated reactions and contains all the group-to-group ele-
ments for that order and reaction (IFOPT=2). Its actual content is determined by
IDSCT and LORDN. If IFOPT=1 has been selected, IDSCT(1)=100 and LORDN(1)=4
would designate a block for the elastic scattering matrix of order P3that con-
tains all 4 Legendre orders and all group-to-group elements. If IFOPT=2 has
been selected, IDSCT(1)=100 with LORDN(1)=1 would designate a block con-
taining all group-to-group elements for the P0elastic matrix, IDSCT(2)=101
with LORDN(2)=1 would designate a block containing the P1elastic matrix, and
so on. In CCCCR, LORDN is always equal to 1 for IFOPT=2.
The ISOTXS format attempts to pack scattering matrices efficiently. First,
all the scattering matrices treated here are triangular because only downscatter
is present. And second, because of the limited range of elastic downscatter,
only a limited range of groups above the inscatter group will contribute to the
scattering into a given secondary-energy group. Therefore, ISOTXS removes
zero cross sections by defining bands of incident energy groups that contribute
to each final energy group. The bands are defined by JBAND, the number of
initial energy groups in the band, and IJJ, an index to identify the position of
the ingroup element in the band. The following table illustrates banding for a
hypothetical elastic scattering reaction:
NJOY2016 421

LA-UR-17-20093 14 CCCCR
Band Element JBAND IJJ
1 1→1 1 1
2 2→2 2 1
1→2
3 3→3 2 1
2→3
4 4→4 2 1
3→4
Note that IJJ is always 1 in the absence of upscatter. This scheme is efficient
for elastic scattering, but it is not efficient for threshold reactions because the
ingroup element must always be included in the band. This means that lots
of zeros must be given for final energy groups below the threshold group. An
improved and simplified scheme is used in the MATXS format.
For IFOPT=2, the elements in the table above would be stored in the sequence
shown, top to bottom. Each Legendre order would have its own block arranged
in the same order. For IFOPT=1, the Legendre order data are intermixed with
the group-to-group data. In each band, the elements for all initial groups for
P0are given, then all initial groups for P1, and so on through LORDN Legendre
orders.
Scattering matrices can be very large. For example, an 80-group elastic
matrix can have as many as 80 ×79/2 = 3160 elements per Legendre order.
That would be 12 640 words for a P3block using IFOPT=1, or four blocks of
3160 words each for IFOPT=2. The latter is practical; the former is not 10. The
corresponding numbers for 200 groups would be 79 600 and 19 900. Both of
these numbers are clearly impractical as record sizes. This is where subblocking
comes in. If each block is divided up so that there is one subblock for each
energy group, the maximum record size is reduced substantially. For IFOPT=1,
the maximum record size is equal to the number of groups times the number of
Legendre orders, or 800 for the 200-group P3case. For IFOPT=2, the maximum
record size is just equal to the number of groups. Although the ISOTXS formats
allows subblocks to contain several groups, CCCCR does not. The possible
values of NSBLOK are limited to 1 and NGROUP. In summary, the CCCCR user
has four matrix blocking options:
10At least it was not practical many years ago. However we see no benefit in revising the existing algorithm,
and so keep this description
422 NJOY2016
14 CCCCR LA-UR-17-20093
1. IFOPT=1 and NSBLOK=1. This produces a single block and a single
subblock for each reaction. It is probably the best choice for small group
structures (up to about 30 groups). The maximum record size is n`×
ng(ng−1)/2.
2. IFOPT=1 and NSBLOK=NGROUP. This produces a block for each reac-
tion, and each block contains ngsubblocks. The maximum record size is
n`×ng. This is a good choice for larger group structures because it keeps
the record size up as compared with option 4 below.
3. IFOPT=2 and NSBLOK=1. This produces n`blocks and subblocks for
each reaction. The maximum record size is ng(ng−1)/2. It has only a
modest advantage in the maximum number of groups over option 1. Un-
less the application that uses the library finds it convenient to read one
Legendre order at a time, the user might just as well choose option 2 if
option 1 produces records that are too large.
4. IFOPT=2 and NSBLOK=NGROUP. This produces n`blocks for each re-
action, each with ngsubblocks. The maximum record size is ng. The
number of groups would have to be on the order of 1000 before this option
would be preferred to option 2.
If CCCCR does not have enough memory to process option 1 or 3, the code
automatically sets NSBLOK to NGROUP, thereby activating option 2 or 4, respec-
tively.
Note that the ISOTXS format specifies that the total scattering matrix is the
sum of the elastic, inelastic, and (n,2n) matrices [see the definition of IDSCT(N)].
This implies that the inelastic matrix must contain the normal (n,n0) reactions
from mt=51-91, and also any other neutron-producing reactions that might be
present. Examples are (n,n0α), (n,n0p), and (n,3n).
14.5 BRKOXS
The format for the BRKOXS Bondarenko-type self-shielding factor file is given
below in the standard format.
C***********************************************************************
C REVISED 11/30/76 -
C -
CF BRKOXS-IV -
CE MICROSCOPIC GROUP DELAYED NEUTRON PRECURSOR DATA -
C -
CN THIS FILE PROVIDES DATA NECESSARY FOR -
CN BONDARENKO TREATMENT IN ADDITION TO -
CN THOSE DATA IN FILE ISOTXS -
NJOY2016 423

LA-UR-17-20093 14 CCCCR
CN FORMATS GIVEN ARE FOR FILE EXCHANGE PURPOSES -
CN ONLY. -
C -
C***********************************************************************
C-----------------------------------------------------------------------
CS FILE STRUCTURE -
CS -
CS RECORD TYPE PRESENT IF -
CS =============================== =============== -
CS FILE IDENTIFICATION ALWAYS -
CS FILE CONTROL ALWAYS -
CS FILE DATA ALWAYS -
CS **************(REPEAT FROM 1 TO NISOSH) -
CS * SELF-SHIELDING FACTORS ALWAYS -
CS * CROSS SECTIONS ALWAYS -
CS ************** -
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR FILE IDENTIFICATION -
C -
CL HNAME,(HUSE(I),I=1,2),IVERS -
C -
CW 1+3*MULT=NUMBER OF WORDS -
C -
CB FORMAT(11H 0V BRKOXS ,1H*,2A6,1H*,I6) -
C -
CD HNAME HOLLERITH FILE NAME - BRKOXS - -
CD HUSE(I) HOLLERITH USER IDENTIFICATION (A6) -
CD IVERS FILE VERSION NUMBER -
CD MULT DOUBLE PRECISION PARAMETER -
CD 1- A6 WORD IS SINGLE WORD -
CD 2- A6 WORD IS DOUBLE PRECISION WORD -
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR FILE CONTROL (1D RECORD) -
C -
CL NGROUP,NISOSH,NSIGPT,NTEMPT,NREACT,IBLK -
424 NJOY2016

14 CCCCR LA-UR-17-20093
C -
CW 6 = NUMBER OF WORDS -
C -
CB FORMAT(4H 1D ,6I6) -
C -
CD NGROUP NUMBER OF ENERGY GROUPS IN SET -
CD NISOSH NUMBER OF ISOTOPES WITH SELF-SHIELDING FACTORS -
CD NSIGPT TOTAL NUMBER OF VALUES OF VARIABLE X (SEE FILE DATA-
CD RECORD) WHICH ARE GIVEN. NSIGPT IS EQUAL TO -
CD THE SUM FROM 1 TO NISOSH OF NTABP(I) -
CD NTEMPT TOTAL NUMBER OF VALUES OF VARIABLE TB (SEE FILE -
CD DATA RECORD) WHICH ARE GIVEN. NTEMPT IS EQUAL -
CD TO THE SUM FROM 1 TO NISOSH OF NTABT(I) -
CD NREACT NUMBER OF REACTION TYPES FOR WHICH SELF-SHIELDING -
CD FACTORS ARE GIVEN (IN PREVIOUS VERSIONS OF THIS -
CD FILES NREACT HAS BEEN IMPLICITLY SET TO 5). -
CD IBLK BLOCKING OPTION FLAG FOR SELF-SHIELDING FACTORS, -
CD IBLK=0, FACTORS NOT BLOCKED BY REACTION TYPE, -
CD IBLK=1, FACTORS ARE BLOCKED BY REACTION TYPE. -
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR FILE DATA (2D RECORD) -
C -
CL (HISONM(I),I=NISOSH),(X(K),K=1,NSIGPT),(TB(K),K=1,NTEMPT), -
CL 1(EMAX(J),J=1,NGROUP),EMIN,(JBFL(I),I=1,NISOSH), -
CL 2(JBFH(I),I=NISOSH),(NTABP(I),I=1,NISOSH),(NTABT(I),I=1,NISOSH) -
C -
CW (4+MULT)*NISOSH+NSIGPT+NTEMPT+NGROUP+1=NUMBER OF WORDS -
C -
CB FORMAT(4H 2D ,9(1X,A6)/ HISONM -
CB 1(10(1X,A6))) -
CB FORMAT(6E12.5) X,TB,EMAX,EMIN -
CB FORMAT(12I6) JBFL,JBFH,NTABP,NTABT -
C -
CD HISONM(I) HOLLERITH ISOTOPE LABEL FOR ISOTOPE I (A6). THESE -
CD LABELS MUST BE A SUBSET OF THOSE IN FILE ISOTXS -
CD OR GRUPXS, IN THE CORRESPONDING ARRAY. -
CD X(K) ARRAY OF LN(SIGP0)/LN(10) VALUES FOR ALL ISOTOPES, -
CD WHERE SIGP0 IS THE TOTAL CROSS SECTION OF THE -
CD OTHER ISOTOPES IN THE MIXTURE IN BARNS PER ATOM -
NJOY2016 425

LA-UR-17-20093 14 CCCCR
CD OF THIS ISOTOPE. FOR ISOTOPE I, THE NTABP(I) -
CD VALUES OF X FOR WHICH SELF-SHIELDING FACTORS -
CD ARE GIVEN ARE STORED STARTING AT LOCATION L=1+ -
CD SUM FROM 1 TO I-1 OF NTABP(K). -
CD TB(K) ARRAY OF TEMPERATURES (DEGREES C) FOR ALL ISOTOPES.-
CD FOR ISOTOPE I, THE NTBT(I) VALUES OF TB FOR -
CD WHICH SELF-SHIELDING FACTORS ARE GIVEN ARE -
CD STORED AT LOCATION L=1+SUM FROM 1 TO I-1 OF -
CD NTABT(K). -
CD EMAX(J) MAXIMUM ENERGY BOUND OF GROUP J (EV) -
CD EMIN MINIMUM ENERGY BOUND OF SET (EV) -
CD JBFL(I) LOWEST NUMBERED OF HIGHEST ENERGY GROUP FOR WHICH -
CD SELF-SHIELDING FACTORS ARE GIVEN -
CD JBFH(I) HIGHEST NUMBERED OR LOWEST ENERGY GROUP FOR WHICH -
CD SELF-SHIELDING FACTORS ARE GIVEN -
CD NTABP(I) NUMBER OF SIGP0 VALUES FOR WHICH SELF-SHIELDING -
CD FACTORS ARE GIVEN FOR ISOTOPE I. -
CD NTABT(I) NUMBER OF TEMPERATURE VALUES FOR WHICH SELF- -
CD SHIELDING FACTORS ARE GIVEN FOR ISOTOPE I. -
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR SELF-SHIELDING FACTORS (3D RECORD) -
C -
CL ((((FFACT(N,K,J,M),N=1,NBINT),K=1,NBTEM),J=JBFLI,JBFHI),M=ML,MU) -
CL ------ SEE DESCRIPTION BELOW ------ -
C -
CC NBINT=NTABP(I) -
CC NBTEM=NTABT(I) -
CC JBFLI=JBFL(I) -
CC JBFHI=JBFH(I) -
CC FOR ML, MU SEE STRUCTURE BELOW -
C -
CW NBINT*NBTEM*(JBFHI-JBFLI+1)*(MU-ML+1) = NUMBER OF WORDS -
C -
CB FORMAT(4H 3D ,5E12.5/(6E12.5)) -
C -
CC DO 1 L=1,NBLOK -
CC 1 READ(N) *LIST AS ABOVE* -
C -
CC IF IBLK=0, NBLOK=1, ML=1, MU=NREACT -
426 NJOY2016

14 CCCCR LA-UR-17-20093
CC IF IBLK=1, NBLOK=NREACT, ML=MU=L, WHERE L IS THE BLOCK -
C -
CD FFACT(N,K,J,M) SELF-SHIELDING FACTOR EVALUATED AT X(N) AND -
CD TB(K) FOR ENERGY GROUP J, THE M INDEX IS -
CD A DUMMY INDEX TO DENOTE THE REACTION TYPE, -
CD THE FIRST FIVE REACTION TYPES ARE, IN -
CD ORDER, TOTAL, CAPTURE, FISSION, TRANSPORT, -
CD AND ELASTIC. -
C -
CB NOTE THAT IS IBLK=1, EACH REACTION TYPE WILL CONSTITUTE -
CB A SEPARATE DATA BLOCK. -
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR CROSS SECTIONS (4D RECORD) -
C -
CL (XSPO(J),J=1,NGROUP),(XSIN(J),J=1,NGROUP),(XSE(J),J=1,NGROUP), -
CL 1(XSMU(J),J=1,NGROUP),(XSED(J),J=1,NGROUP),(XSX(J),J=1,NGROUP) -
C -
CW 6*NGROUP=NUMBER OF WORDS -
C -
CB FORMAT(4H 4D ,5E12.5/(6E12.5)) -
C -
CD XSPO(J) POTENTIAL SCATTERING CROSS SECTION (BARNS) -
CD XSIN(J) INELASTIC CROSS SECTION (BARNS) -
CD XSE(J) ELASTIC CROSS SECTION (BARNS) -
CD XSMU(J) AVERAGE COSINE OF ELASTIC SCATTERING ANGLE -
CD XSED(J) ELASTIC DOWN-SCATTERING TO ADJACENT GROUP -
CD XSXI(J) AVERAGE ELASTIC SCATTERING LETHARGY INCREMENT -
C -
C-----------------------------------------------------------------------
The BRKOXS file is used to supply self-shielding factors for use with the
Bondarenko method[39] for calculating effective macroscopic cross sections for
the components of nuclear systems. As discussed in detail in the GROUPR
chapter of this manual, this system is based on using a model flux for isotope i
of the form
φi
`(E, T ) = C(E)
[σi
0+σi
t(E, T )]`+1 ,(470)
NJOY2016 427

LA-UR-17-20093 14 CCCCR
where C(E) is a smooth weighting flux, σi
t(E, T ) is the total cross section for
material iat temperature T,`is the Legendre order, and σi
0is a parameter that
can be used to account for the presence of other materials and the possibility of
escape from the absorbing region (heterogeneity). GROUPR uses this model flux
to calculate effective multigroup cross sections for the resonance-region reactions
(total, elastic, fission, capture) for user specified values of σ0and T.
When σ0is large with respect to the highest peaks in σt, the flux is essentially
proportional to C(E). This is called infinite dilution, and the corresponding
cross sections are appropriate for an absorber in a dilute mixture or for a very
thin sample of the absorber. As σ0decreases, the flux φ(E) develops dips where
σthas peaks. These dips cancel out part of the effect of the corresponding peaks
in the resonance cross sections, thereby reducing, or self-shielding, the reaction
rate. It is convenient to represent this effect as a self-shielding factor; that is,
σxg(T, σ0) = fxg(T, σ0)×σxg(300◦K, ∞).(471)
In the CCCC system, the f-factors are stored in the BRKOXS file and the in-
finitely dilute cross sections are stored in the ISOTXS file. A code that prepares
effective cross sections, such as SPHINX[85] or 1DX[54], determines the appro-
priate Tand σ0values for each region and group in a reactor problem, using
equivalence theory together with the user’s specifications for composition and
geometry. It then reads in the cross sections and f-factors from the ISOTXS
and BRKOXS files, interpolates in the Tand σ0tables to obtain the desired
f-factors, and multiplies to obtain the effective cross sections.
In the BRKOXS file specification given above, the components of the “File
Identification” record are the same as for ISOTXS. The parameters in the “File
Control” record are used to calculate the sizes and locations of data in the
records to follow. The “File Data” record contains all the isotope names, all
the σ0values for every isotope, all the Tvalues for every isotope, the group
structure, and several arrays used for unpacking the other data. The Hollerith
material names in HISONM are the same as those used in ISOTXS, and they
are obtained from the user’s input. The σ0values are packed into X(K) using
NTABP(I). Note that the base-10 logarithm of σ0is stored. Therefore, a typical
library might contain the following:
428 NJOY2016

14 CCCCR LA-UR-17-20093
material I NTABP(I) X(K)
1 3 3.0 2.0 1.0
2 7 4.0 3.0 2.0 1.477 1. 0. -1.
3 5 4.0 3.0 2.0 1.0 0.0
··· ··· ···
Similarly, the Tvalues are stored in TB(K) using NTABT(I). The absolute tem-
peratures used by GROUPR must be changed to ◦C before being stored. The
energy bounds for the group structure found on the GENDF tape are stored in
EMAX(J) and EMIN. As discussed in connection with the ISOTXS format, group
boundaries are stored in order of decreasing energy in the BRKOXS file.
The self-shielding factor approach is designed to account for resonance self-
shielding. It is not necessarily appropriate for low energies if only broad res-
onance features are apparent, or for high energies where only small residual
fluctuations in the cross section are seen. For this reason, the BRKOXS format
provides the JBFL(I) and JBFH(I) arrays in the “File Data” record. They are
used to limit the range of the numbers given in the “Self-Shielding Factors”
record. The reactions that are active in the resonance energy range usually
include only the total, elastic, fission, and capture channels. The total cross sec-
tion is usually computed for the two Legendre orders `=0 and `=1. This second
value is often called the current-weighted total cross section, and it is needed
to compute the self-shielded diffusion coefficient. GROUPR also computes a
self-shielded elastic scattering matrix. It can be used to provide two quantities
for the BRKOXS file. First, the diffusion coefficient requires the calculation of
a transport cross section for diffusion. The relationships are as follows:
Dg=1
3σtr,g
,(472)
and
σtr,g =σt1,g −X
g0
σe1,g→g0.(473)
Therefore, the current-weighted P1elastic cross section contributes to the trans-
port self-shielding factor. The second use for the self-shielded elastic scattering
matrix is to compute a self-shielding factor for elastic removal. For heavy iso-
topes, the energy lost in elastic scattering is small, and all the removal is nor-
mally to one group. The format requires that at least the five standard reactions
be given in a specified order. NJOY is able to add one more as follows:
NJOY2016 429

LA-UR-17-20093 14 CCCCR
1. total (P0weighted),
2. capture (P0),
3. fission (P0),
4. transport (P1),
5. elastic (P0), and
6. elastic removal (P0)
The normal pattern for the BRKOXS file expects that there will be one record
of self-shielding factors for each material. Such a record could get quite large.
For example, with 6 reactions, 6 temperatures, 6 σ0values, and 100 resonance
groups, a “Self-Shielding Factors” record could have over 20 000 words. This
number can be made more manageable by setting the IBLK flag in the “File
Control” record to 1. Then there will be a separate record of self-shielding
factors for each reaction; this would reduce the record size for the example to a
more reasonable 3600 words.
The actual self-shielding factors are computed from the cross sections given
on the GENDF tape and stored into the FFACT(N,K,J,M) array of the “Self-
Shielding Factors” record with group order converted to the standard decreasing-
energy convention. Following the FORTRAN convention, Nis the fastest varying
index in this array, Kis the next fastest varying index, and so on. The identities
of these indices are
Nσ0,
Ktemperature T,
Jgroup, and
Mreaction
The “Cross Sections” record contains some additional cross sections and spe-
cial parameters that are often used in self-shielding codes and are not included
in the ISOTXS file. The XSPO cross section is taken to be constant and equal
to the CCCCR input parameter XSPO, which is computed as 4πa2. The XSIN
cross section is obtained by summing over the final group index for every group-
to-group matrix in File 6 except elastic, (n,2n), and fission. Therefore, it may
contain effects of multiplicities greater than 1 if reactions like (n,3n) or (n,2nα)
are active for the material. It may be slightly larger in high-energy groups than
the cross section that would be obtained using the same sum over reactions in
File 3. The XSE cross section is obtained from mf=6, mt=2 on the GENDF tape
430 NJOY2016
14 CCCCR LA-UR-17-20093
by summing over final groups. The parameters for continuous slowing down the-
ory, XSMU and XSXI, are obtained from mt=251 and mt=252, respectively. The
methods used for calculating these quantities are described in the GROUPR sec-
tion of this report. Finally, the elastic downscattering cross section is obtained
from the elastic matrix on the GENDF tape (mf=6, mt=2).
14.6 DLAYXS
The format for the DLAYXS delayed-neutron data file is given below in the
standard format.
C***********************************************************************
C REVISED 11/30/76 -
C -
CF DLAYXS-IV -
CE MICROSCOPIC GROUP DELAYED NEUTRON PRECURSOR DATA -
C -
CN THIS FILE PROVIDES PRECURSOR YIELDS, -
CN EMISSION SPECTRA, AND DECAY CONSTANTS -
CN ORDERED BY ISOTOPE. ISOTOPES ARE IDENTIFIED -
CN BY ABSOLUTE ISOTOPE LABELS FOR RELATION TO -
CN ISOTOPES IN EITHER FILE ISOTXS OR GRUPXS. -
CN FORMATS GIVEN ARE FOR FILE EXCHANGE PURPOSES -
CN ONLY. -
C -
C***********************************************************************
C-----------------------------------------------------------------------
CS FILE STRUCTURE -
CS -
CS RECORD TYPE PRESENT IF -
CS =============================== =============== -
CS FILE IDENTIFICATION ALWAYS -
CS FILE CONTROL ALWAYS -
CS FILE DATA, DECAY CONSTANTS, AND -
CS EMISSION SPECTRA ALWAYS -
CS *************(REPEAT TO NISOD) -
CS * DELAYED NEUTRON PRECURSOR -
CS * YIELD DATA ALWAYS -
CS ************* -
C -
NJOY2016 431

LA-UR-17-20093 14 CCCCR
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR FILE IDENTIFICATION -
C -
CL HNAME,(HUSE(I),I=1,2),IVERS -
C -
CW 1+3*MULT=NUMBER OF WORDS -
C -
CB FORMAT(11H 0V DLAYXS ,1H*,2A6,1H*,I6) -
C -
CD HNAME HOLLERITH FILE NAME - DLAYXS - -
CD HUSE(I) HOLLERITH USER IDENTIFICATION (A6) -
CD IVERS FILE VERSION NUMBER -
CD MULT DOUBLE PRECISION PARAMETER -
CD 1- A6 WORD IS SINGLE WORD -
CD 2- A6 WORD IS DOUBLE PRECISION WORD -
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR FILE CONTROL (1D RECORD) -
C -
CL NGROUP,NISOD,NFAM,IDUM -
C -
CW 4=NUMBER OF WORDS -
C -
CB FORMAT(4H 1D ,4I6) -
C -
CD NGROUP NUMBER OF NEUTRON ENERGY GROUPS IN SET -
CD NISOD NUMBER OF ISOTOPES IN DELAYED NEUTRON SET -
CD NFAM NUMBER OF DELAYED NEUTRON FAMILIES IN SET -
CD IDUM DUMMY TO MAKE UP FOUR-WORD RECORD -
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR FILE DATA, DECAY CONSTANTS, AND EMISSION SPECTRA -
C (2D RECORD) -
C -
CL (HABSID(I),I=1,NISOD),(FLAM(N),N=1,FAM),((CHID(J,N),J=1,NGROUP), -
CL N=1,NFAM),(EMAX(J),J=1,NGROUP),EMIN,(NKFAM(I),I=1,NISOD), -
432 NJOY2016

14 CCCCR LA-UR-17-20093
CL (LOCA(I),I=1,NISOD) -
C -
CW (2+MULT)*NISOD+(NGROUP+1)*(NFAM+1)=NUMBER OF WORDS -
C -
CB FORMAT(4H 2D ,9(1X,A6)) HABSID -
CB 1(10(1X,A6))) -
CB FORMAT(6E12.5) FLAM,CHID,EMAX,EMIN -
CB FORMAT(12I6) NKFAM,LOCA -
C -
CD HABSID(I) HOLLERITH ABSOLUTE ISOTOPE LABEL FOR ISOTOPE I (A6)-
CD FLAM(N) DELAYED NEUTRON PRECURSOR DECAY CONSTANT -
CD FOR FAMILY N -
CD CHID(J,N) FRACTION OF DELAYED NEUTRONS EMITTED INTO NEUTRON -
CD ENERGY GROUP J FROM PRECURSOR FAMILY N -
CD EMAX(J) MAXIMUM ENERGY BOUND OF GROUP J (EV) -
CD EMIN MINIMUM ENERGY BOUND OF SET (EV) -
CD NKFAM(I) NUMBER OF FAMILIES TO WHICH FISSION IN ISOTOPE I -
CD CONTRIBUTES DELAYED NEUTRON PRECURSORS -
CD LOCA(I) NUMBER OF RECORDS TO BE SKIPPED TO READ DATA FOR -
CD ISOTOPE I, LOCA(1)=0 -
C -
C-----------------------------------------------------------------------
C-----------------------------------------------------------------------
CR DELAYED NEUTRON PRECURSOR YIELD DATA (3D RECORD) -
C -
CL (SNUDEL(J,K),J=1,NGROUP),K=1,NKFAMI),(NUMFAM(K),K=1,NKFAMI) -
C -
CC NKFAMI=NKFAM(I) -
C -
CW (NGROUP+1)*NKFAMI=NUMBER OF WORDS -
C -
CB FORMAT(4H 3D ,5E12.5/(6E12.5)) SNUDEL -
CB FORMAT(12I6) NUMFAM -
C -
CD SNUDEL(J,K) NUMBER OF DELAYED NEUTRON PRECURSORS PRODUCED IN -
CD FAMILY NUMBER NUMFAM(K) PER FISSION IN -
CD GROUP J -
CD NUMFAM(K) FAMILY NUMBER OF THE K-TH YIELD VECTOR IN -
CD ARRAY SNUDEL(J,K) -
C -
C-----------------------------------------------------------------------
NJOY2016 433

LA-UR-17-20093 14 CCCCR
This file is used to communicate delayed-neutron data to reactor kinetics
codes. The ENDF files give a total delayed-neutron yield ¯νdin the section
labeled mf=1, mt=455. GROUPR averages this yield for each neutron group g
using
¯νD
g=Zg
νd(E)σf(E)φ(E)dE
Zg
σf(E)φ(E)dE
.(474)
This same section of the ENDF tape contains the decay constants for the
delayed-neutron time groups. These numbers are passed on to the GROUPR
routine that averages the delayed-neutron spectra, and they end up in the mf=5
record on the GENDF tape. The ENDF evaluations give the delayed-neutron
spectra for the time groups in mf=5, mt=455. These spectra are not separately
normalized. Rather, the sum over all time groups is normalized, but the inte-
gral of any one of the spectra gives the “delayed fraction” for that time group.
GROUPR simply averages these spectra using the specified neutron group struc-
ture. The resulting group spectra (and the decay constants from File 1) are
written onto the GENDF tape.
Returning to the DLAYXS format description, the parameters in the “File
Identification” record are obtained from the user’s input, just as for ISOTXS
and BRKOXS. The parameter NGROUP is also a user input quantity. NISOD is
determined after the entire GENDF tape has been searched for isotopes that
are on the user’s list of NISO materials and that have delayed-neutron data.
The NFAM parameter needs some additional explanation. A “family” for the
DLAYXS file is actually an index that selects one particular spectrum from
the CHID array. It could correspond to an actual delayed-neutron precursor
isotope left after a fission event. In such a case, there would be many “families”
corresponding to the many possible fission fragment isotopes. The SNUDEL yields
would be analogous to fission product yields. The ENDF evaluations take a
more macroscopic approach. Spectra are chosen to include all the emissions
from a group of delayed-neutron precursors for a particular fissioning nucleus
with similar decay constants. In this representation, the DLAYXS “family”
corresponds to a particular decay constant and spectrum for a particular target
isotope. Therefore, the number of families is simply six or eight times the number
of isotopes, e.g.,NFAM=6*NISOD.
434 NJOY2016

14 CCCCR LA-UR-17-20093
In the “File Data, Decay Constants, and Emission Spectra” record, the Hol-
lerith isotope names HABSID are obtained from the names in the user’s input.
The FLAM values come directly from the decay constant values originally ex-
tracted from File 1 of the ENDF tape. The family index for isotope ISO and time
group Iis simply computed as 6*(ISO-1)+Ior 8*(ISO-1)+I. The CHID array
is loaded from the mf=5, mt=455 section on the GENDF tape using the family
index and the group index. As usual, the order of groups has to be changed from
the GROUPR convention with increasing-energy order to the CCCC convention
with decreasing-energy order. The group structure itself is obtained from the
GENDF header record and stored into EMAX and EMIN in the conventional order.
The value of NKFAM is simply 6 or 8 for every isotope. The LOCA values are also
easy to compute; they are just ISO minus 1.
The delayed-neutron yields versus incident neutron energy group and family
index are given in the “Delayed Neutron Precursor Yield Data” record. As
mentioned above, the total yield is given in mf=3 of the GENDF tape, and the
delayed fractions can be computed by summing the spectrum for each time group
over the energy group index. The array SNUDEL in this DLAYXS record contains
the product of these values. Note that there is one of these yield records for
each delayed-neutron isotope, and each record contains six or eight families. The
NKFAM vector is used to establish the correspondence between these families and
the entire list of families used in the file data record. As an example, NUMFAM(1)
would contain 1, 2, 3, 4, 5, 6; NUMFAM(2) would contain 7, 8, 9, 10, 11, 12, and
so on.
14.7 Coding Details
Subroutine ccccr is the only public call for module ccccm. The module has
a number of global variables and arrays defined. One key set of variables and
arrays provides the area for accumulating the CCCC data. It provides a set
of equivalenced arrays so that integers, reals, and Hollerith strings can all be
stored in the same binary records. It sets up both integers and reals to be 4-byte
quantities. Hollerith words (with up to 8 characters each) are 8-byte quantities.
The CCCC mult value is set to 2. See a(50000),ia(50000), and ha(25000).
The parameter isiza=50000 defines the size of these equivalenced arrays in
4-byte units.
The main subroutine of CCCCR starts by allocating an array maxe for read-
ing in data from the input ENDF-format files. Note that this array uses 8-byte
words. The values read in will be converted to the 4-byte words used in the
NJOY2016 435

LA-UR-17-20093 14 CCCCR
CCCC a,ia,ha set as necessary. Note the variable next. It will keep track of
the next available location in the a,ia,ha area.
Next, the unit numbers for input and output are read. The signs given
for CCCC units are ignored; they are opened as binary files. The subroutine
continues by reading input cards 2 through 5. At this point, CCCCR branches
to different subroutines for each of the three interface file types that have been
requested (see cisotx,cbrkxs, and cdlyxs). Each of these routines is paired
with a print routine that is called if the iprint flag has been set to 1 (see pisotx,
pbrkxs, and pdlyxs). When the last of these routines returns, CCCCR closes
its active I/O units, writes a report, and terminates.
ISOTXS File Preparation. The cisotx routine starts by calling ruinis to
read in the portion of the user’s input specific to the ISOTXS file. It then calls
isxdat to read through the input GENDF file and extract the ISOTXS data.
Subroutine ISXDAT starts by setting up pointers in the a,ia,ha area for
the different types of data to be read in. These pointers are identified in the
comments at the start of the subroutine. The routine then reads the GENDF
header record for the first material and extracts the group boundary energies. If
the group structure found does not match the one requested in the user’s input,
an error message is issued. Otherwise, the order of the groups is changed from
the GROUPR/ENDF convention of increasing energy to the CCCC convention
of decreasing energy (which is the normal ordering for application programs)
as the 8-byte GENDF data are copied into the 4-byte words of the aarray.
The routine then begins a loop over all the materials (isotopes) requested (see
do 300 i=1,niso). It searches through the input GENDF tape for the first
material with the requested MAT number (that is, the first temperature for the
MAT) and copies it to a scratch file. Note that materials are written in the
order requested by the user’s input material list, not in the order that they are
found on the GENDF tape.
This scratch tape is scanned for the ISOTXS principal cross section data
in prinxs. This process is fairly simple for most of the ENDF File 3 cross
sections. Each MT number in File 3 is compared to the list of desired principal
cross sections in nstx; if a match is found, the corresponding element of iflag
is set, and the cross section table is copied into memory using a pointer from
the iptr array. The (n,2n) reaction is a special case. In addition to mt=16, the
routine watches for the partial (n,2n) representation used in the ENDF/B-IV
and -V evaluations for 9Be (namely, mt=6, 7, 8, and 9), and adds them into
436 NJOY2016

14 CCCCR LA-UR-17-20093
the appropriate memory locations. Fission is obtained from mt=18, but if the
partial fission reactions are present (mt=19, 20, 21, 38), the flag mt=19 is set.
Average neutron velocities are obtained from the special GROUPR-produced
section labeled by mt=259. These are inverse velocities in s/m, and prinxs
inverts them and multiplies by 100 to get velocities in cm/s. In addition to
the normal flux-weighted total cross section, the routine also stores the current-
weighted, or P1, cross section for use in calculating the transport cross section
(see below). Finally, File 3 may also contain mt=455, the delayed-neutron ¯ν
parameter. The GENDF record for this parameter also contains σfand the
flux for each group. The delayed-neutron production rate ¯νdσfis stored for use
in calculating the total ¯νparameter, and ¯νdσfφis added into the dnorm array
for later use in normalizing the total fission spectrum, χ. Note that there are
two options for the flux used in this normalization: it can be the default library
flux found on each record of the GENDF file, or it can be a flux spectrum spec
provided by the user.
While reading through the scratch tape, prinxs also watches for the elastic
scattering matrix (mf=6, mt=2). The total P1elastic cross section is calculated
by summing over all secondary neutron groups, and the result is subtracted from
the current-weighted total cross section to obtain the transport cross section.
The processing of the fission matrix (mf=6, mt=18) and the delayed-fission
spectra (mf=5, mt=455) depend on the ichix option. The ¯νparameter SNUTOT is
always calculated for fissionable isotopes. CHISO is only calculated if the vector
representation was requested; in addition, it can be calculated using the flux
from GENDF or using the input flux in SPECT. Starting with NJOY 91.0, the
fission matrix is represented by a real group-to-group matrix at high energies,
and by a single spectrum (with IG=0) and an associated production cross section
(with IG2LO=0) at low energies. This representation can lead to great savings for
libraries with many low-energy groups. The contributions to SNUTOT from the
low-energy range are easily obtained by adding in the production cross section.
At high energies, the sum of the group-to-group matrix over all secondary-energy
groups is added in. After mf=3, mt=455 and mf=6, mt=18 have been processed,
it is only necessary to divide the total production rate in memory by the fission
cross section to obtain the required total ¯νvalues.
The prompt part of the fission χvector or matrix is obtained from mf=6,
mt=18, or if the MT=19 flag was set while reading File 3, from mt=19, 20, 21,
and 38. The code starts at statement number 207, and it is fairly complicated
because it has to cope with the following options:
NJOY2016 437

LA-UR-17-20093 14 CCCCR
1. χvector versus χmatrix,
2. default weighting for the vector versus input weighting,
3. square matrix versus collapsed rectangular matrix, and
4. constant and matrix parts of mf=6 GENDF record.
Note that separate normalization sums are accumulated in cnorm(ispec) for
the chi vector or for each column of the matrix while the χelements are being
stored. The delayed contributions to the fission χvector or matrix are taken
from mf=5, mt=455 (see statement number 230). The time group spectra are
added and multiplied by the delayed neutron production rate dnorm (which
can be incident energy dependent through the ispec index if a matrix is being
constructed). The delayed contributions to the normalization sum for the χ
vector or for each column of the χmatrix are added into cnorm during this
step. After all the components of the fission spectrum have been read from the
GENDF file, the χvector or the columns of the χmatrix are normalized using
this quantity.
When all sections of the scratch tape have been processed, prinxs goes
through the principal cross section block, removing any parts that have zero
cross sections. The resulting block is written to scratch file nscrt2. Finally, it
writes the chi matrix data, if any, to the same scratch file and returns to isxdat.
Subroutine isomtx is then called to read through the scratch tape and process
the group-to-group matrices into CCCC format. In order to allow large matrices
to be processed on machines with limited memory, one or more passes can
be made through the scratch tape (see do 400 nj=1,npass). The number of
passes used depends upon the amount of space available in scratch array band
on the subblocking option requested by the user. The four options supported
by CCCCR were discussed in connection with the ISOTXS format description.
Only one pass is required for the first option. In the other cases, the length
of one subblock is divided into the length of the scratch array to determine
the number of subblocks that can be accumulated on one pass (nrec) and the
number of passes required (npass).
Four matrix reactions are extracted from the scratch tape (see do 500 i=1,4).
The total matrix is obtained by adding all matrices found on the GENDF tape
except the fission matrices. The elastic matrix is obtained from mt=2 only. The
(n,2n) matrix is normally obtained from MT=16, but the sum of mt=6, 7, 8,
9, 46, 47, 48, and 49 will be used for the old 9Be representation, if found. The
inelastic matrix is the sum of everything else; that is, it includes the normal
inelastic reactions mt=51-91, and it also includes other neutron-producing reac-
438 NJOY2016

14 CCCCR LA-UR-17-20093
tions like (n,3n), (n,n0p), and (n,n0α). Each GENDF section found is passed to
shuffl, which rearranges the input data into the CCCC order in scratch array
b, and then to wrtmtx, which repacks the data into banded form and writes the
results to nscrt2.
Subroutine shuffl reads each of the group-to-group cross sections for a given
reaction (MT) and calculates a location for each cross section in the scratch
array (noloc). Different formulas are used for the location of the two allowed
values of IFOPT. For IFOPT=1, the data are stored with incident group index
jg1 changing fastest, then Legendre index il, and with final group index jg2
changing slowest. Note that the indexing scheme only stores the triangle of the
matrix corresponding to ingroup scattering and downscatter (that is, jg2≥jg1).
In addition, the first group in a subblocking range ng2z is used. This means that
values of jg2 less than ng2z will result in storage locations less than irsize,
and they will not be stored (see statement 200). Groups with jg2 above the
subblock might be stored in memory, or they might end up above the upper limit
of the memory area and be suppressed by statement number 200. Similarly, the
data for IFOPT=2 are stored with jg1 as the fastest varying index, then jg2, and
finally with il as the slowest varying index. Here also, the storage pointer noloc
is calculated so that only elements with jg2≥jg1 are stored, and elements that
are outside of a given subblock are removed if they fall outside the bounds of
the memory array.
Subroutine wrtmtx searches through the memory area loaded in shuffl to
find the bands of group-to-group elements that will be written on the final
ISOTXS file. The calculation of locations in the memory array depends on
the blocking and subblocking options selected. In general, the routine calcu-
lates locations NOLOCA and tests the cross section found there against the value
eps=1.E-10. The highest index that violates this test for a given final energy
group determines the bandwidth for that group. (Remember that the inscat-
tering group is always kept, even if it has zero cross section.) Once the band
limits have been found, the subroutine loops back through the memory area and
squeezes out the locations that are not included in the bands. At this point, all
the elements of the “Scattering Sub-Block” are in their final locations, and the
record is written out to scratch tape nscrt2.
When isomtx returns to isxdat, the “Isotope Control and Group Indepen-
dent Data” record is completed by filling in the values of IDSCT and IJJ, and the
record is written to scratch tape nscrt3. The LOCA values for the “File Date”
record are also calculated at this point. They remain in memory at l19. Once
NJOY2016 439

LA-UR-17-20093 14 CCCCR
the “do 300” loop over the requested isotopes has finished, the isxdat routine
returns.
Back in cisotx, all the data needed for the ISOTXS file are now in memory
or on one of the CCCC-style scratch files nscrt2 or nscrt3. The routine simply
steps through the ISOTXS records and either constructs them or copies them
from a scratch file. When the file has been written, the routine returns to ccccr,
which checks the print flag, and calls pisotx, if requested.
Subroutine pisotx is a fairly simple routine. It reads through the ISOTXS
file produced by CCCCR and prepares an interpreted listing of the data.
BRKOXS File Preparation. Subroutine cbrkxs is used to prepare the
BRKOXS file, if requested. Following the same pattern as cisotx, it calls
ruinbr to read the user’s input, then it calls brkdat to extract the desired data
from the GENDF file, and finally it writes the output BRKOXS file using data
stored in memory and on a scratch tape by brkdat.
The storage locations used by brkdat are outlined in the comment cards at
the beginning of the subroutine. The subroutine now opens the input GENDF
file and reads in the header record. After checking for possibly incompatible
group structures, it reverses the order of the group bounds and loads them into
the emax and emin arrays. The data block starting at l19 is sized to hold
13 infinitely dilute cross section vectors that will either be needed during the
processing (vectors 1 through 7) or will be written into the “Cross Sections”
record. These 13 quantities are
1. P0total cross section,
2. capture cross section,
3. fission cross section,
4. P1total - P1elastic,
5. elastic cross section,
6. P1total cross section,
7. P1flux,
8. XSPO,
9. inelastic cross section,
10. elastic cross section,
11. average elastic scattering cosine ¯µ,
12. elastic downscatter to adjacent group, and
13. average elastic lethargy increment ξ.
440 NJOY2016

14 CCCCR LA-UR-17-20093
Pointer l20 defines the balance of the available memory.
The next step is to determine whether it is necessary to subblock the self-
shielding factor record. The amount of space available in the memory area is
compared with the maximum amount of memory required for the f-factors. If
there is not enough space, nsblk is increased to nreact; otherwise, it is left at 1.
The value of nsblk is stored into the IBLK field of the BRKOXS “File Control”
record.
The isotope loop is complicated because CCCCR allows the materials on the
GENDF tape to be in any order, but it arranges things so that the materials on
the BRKOXS files are in the order that the materials are named in the user’s
input. The main loop is controlled by do 370 i=1,niso. For each pass, the in-
put GENDF tape is rewound and searched for isotope I(see do 170 j=1,niso).
Once a desired material has been found, the σ0list in the header record is ex-
amined. Either the first abs(nzi) values are extracted (for nzi negative), or
the particular values that occur on the input asig list are extracted (for nzi
positive). In either case, nzj is the number of σ0values found, isig contains
the pointers to the values selected, and csig contains the actual values of σ0.
GENDF tapes contain one or more temperatures for each material recorded
as consecutive MATs. Starting at statement number 190, brkdat reads through
all the materials with the current MAT number selecting the desired tempera-
tures and copying them to a scratch file nscrt1. The procedure used to select
temperatures is similar to the one used to select σ0values. If nti is negative, the
first abs(nti) temperatures are extracted. If nti is positive, only temperatures
on the list in atem are extracted. In either case, ntj is the number of tempera-
tures found for this material, item contains indices to those temperatures, and
ctem contains the actual temperature values.
In the loop beginning at do 340 nsb=1,nsblk, a pass through the scratch
tape is made for each subblock (1 or nreact). Each section of the GENDF
format is located, and either xsproc (for mf=3) or mxproc (for mf=6) is called
to process the data in the section.
Subroutine xsproc is called once for each reaction in File 3 of the GENDF
tape. It reads in all the data, checks which reaction is present, and stores the
data in one of the 13 cross section locations (see l19), or in one of the f-factor
locations (see l20). If the denominator for the f-factor calculation is zero, the
division is skipped, and a warning message is issued.
Subroutine mxproc is called once for each reaction in File 6 of the GENDF
tape. It loops through statement number 120 to read all of the incident groups,
NJOY2016 441

LA-UR-17-20093 14 CCCCR
and then it uses different sections of coding to fill in or fix up the rest of the
13 elements in the infinitely dilute cross section block at l19. These quantities
include the elastic and inelastic cross sections, the transport cross section, and
the removal cross section. This routine also computes the elastic removal self-
shielding factors from mf=6, mt=2, and stores the results in the f-factor area at
l20.
Back in brkdat, the self-shielded transport cross sections are converted into
f-factors. A check is then made to see if the transport values were properly
computed. This requires that a self-shielded elastic matrix was available for
all the higher temperatures. A warning message is issued if the required data
were not present. The last 6 of the 13 vectors stored starting at l19 are the
data needed for the “Cross Sections” record; that block is written to scratch file
nscrt2. Next, the accumulated f-factor data at l20 are written to nscrt2, and
the NTABP and NTABT arrays are stored at l14 and l15, respectively.
The last step inside the isotope loop is to call thnwrt to thin out the f-factor
data and write the results onto scratch file nscrt3. It starts by reading the
cross section data from nscrt2 into memory. Then it reads the f-factor data
into memory and repacks it to take account of the group range for interesting
self-shielding factors, namely, JBFL to JBFH. When this is finished, it writes the
f-factor array out to nscrt3, and then it writes the unchanged cross section
block out to nscrt3. Note that these two records are now in the correct order
to be copied to the BRKOXS file.
Subroutine thnwrt now returns control to brkdat. When the “do 370” loop
has finished, the routine cleans up the “File Data” information in memory and
returns to the main BRKOXS routine. At this point, all the information required
to construct the output file is present in memory or on scratch tape nscrt3. The
routine steps through the records of the BRKOXS format constructing them or
copying them from the CCCC-style scratch file. It then returns to ccccr, which
checks to see whether pbrkxs should be called.
Subroutine pbrkxs is a fairly simple routine. It reads through the BRKOXS
file produced by ccccr and prepares an interpreted listing of the data.
DLAYXS File Preparation. Subroutine cdlyxs is used to prepare a DLAYXS
file, if requested. It starts by calling dldata to extract the delayed-neutron
data from the input GENDF file. Since all the data are stored into memory,
cdlyxs continues by simply writing out the required “File Identification”, “File
Control”, “File Data, Decay Constants, and Emission Spectra”, and “Delayed
442 NJOY2016

14 CCCCR LA-UR-17-20093
Neutron Precursor Yield Data” records. If no delayed-neutron data are found,
cdlyxs issues a fatal error message. The coding can handle either the tra-
ditional 6 time groups of ENDF/B or the 8 time groups used in some other
evaluation systems. For convenience, the following discussion will just use the 6
time groups.
Subroutine dldata starts by reserving space for the dynamic arrays used to
store the delayed-neutron data; the purpose for each of these arrays is summa-
rized in the comment block at the beginning of the subroutine. ENDF delayed-
neutron files are based on the traditional 6 time groups; therefore, CCCCR
makes each time group for each isotope correspond to one DLAYXS “delayed-
neutron family” (see NFAM=6*NISOD). Next, dldata starts reading through the
materials on the GENDF tape and looking at each material requested in the
user’s input (the material loop goes through statement 110). For the first ma-
terial, it reads the header record, checks that the group structure is compatible
with the user’s input value ngroup, and stores the structure in EMAX and EMIN
in the conventional decreasing-energy order. For all materials, it watches for
sections with mf=3, mt=455 or mf=5, mt=455.
When mf=3/mt=455 is found (see statement 310), dldata stores the total
delayed-neutron yield from GROUPR in the snudel array (pointer l8) using
an offset computed from the time group index (which varies from 1 to 6), the
group index, and the isotope index. (The group index goes through statement
130). For the present, the same value is stored for every time group.
When mf=5/mt=455 is found (see statement 410), the rest of the data for this
isotope are stored into memory. The HABSID field is obtained from the isotope
name in the user’s input. The LOCA field is easy to calculate from the isotope
index. The decay constants for each of the time groups are copied into FLAM from
the GENDF record. The number of families for this isotope is simply 6; this
number is loaded into the location corresponding to NKFAM. Finally, the actual
delayed-neutron spectra for each time group are loaded into the CHID area using
energy group and family number as indexes. At this point, the spectrum for each
time group is summed over group index to determine the delayed fraction for
that time group [see FRACT(I)]. Then this fraction is used to change the total
delayed-neutron yield for each time group in the SNUDEL area into the fractional
delayed-neutron yield for that time group (family).
When all the isotopes containing delayed-neutron data have been processed,
dldata returns to cdlyxs. When cdlyxs returns to the main subroutine of
CCCCR after writing the DLAYXS file, the print routine pdlyxs may be called.
NJOY2016 443

LA-UR-17-20093 14 CCCCR
This is a fairly simple routine that reads through a file in DLAYXS format and
prepares an interpreted listing.
14.8 User Input
The user input instructions copied from the comment cards at the beginning of
the CCCCR source code are given below. It is always a good idea to check the
comments cards in the current version of the code in case there have been any
changes.
!---input specifications (free format)---------------------------
!
!-ccccr-
! card 1 units
! nin input unit for data from groupr
! nisot output unit for isotxs (0 if isotxs not wanted)
! nbrks output unit for brkoxs (0 if brkoxs not wanted)
! ndlay output unit for dlayxs (0 if dlayxs not wanted)
! card 2 identification
! lprint print flag (0/1=not print/printed)
! ivers file version number (default=0)
! huse user identification (12 characters)
! delimited by *, ended by /.
! (default=blank)
! card 3
! hsetid hollerith identification of set (12 characters)
! delimited by *, ended by /.
! (default=blank)
! card 4 file control
! ngroup number of neutron energy groups
! nggrup number of gamma energy groups
! niso number of isotopes desire
! maxord maximum legendre order
! ifopt matrix blocking option (1/2=blocking by
! reaction/legendre order)
! card 5 isotope parameters (one card per isotope)
! (first four words are hollerith, up to six characters
! each, delimited by *)
! hisnm hollerith isotope label
! habsid hollerith absolute isotope label
! hident identifier of data source library (endf)
444 NJOY2016

14 CCCCR LA-UR-17-20093
! hmat isotope identification
! imat numerical isotope identifier (endf mat number)
! xspo average potential scattering cross sect. (brkoxs)
!-cisotx- (only if nisot.gt.0)
! card 1 file control
! nsblok subblocking option for scattering matrix
! (1 or ngrup sub-blocks allowed)
! maxup maximum number of upscatter groups (always zero)
! maxdn maximum number of downscatter groups
! ichix fission chi representation
! -1 vector (using groupr flux)
! 0 none
! +1 vector (using input flux)
! .gt.1 matrix
! card 2 chi vector control (ichix=1 only)
! spec ngroup flux values used to collapse the groupr
! fission matrix into a chi vector
! card 3 chi matrix control (ichix.gt.1 only)
! spec ngroup values of spec(i)=k define the range of
! groups i to be averaged to obtain spectrum k.
! index k ranges from 1 to ichi.
! the model flux is used to weight each group i.
! card 4 isotope control (one card per isotope)
! kbr isotope classification
! amass gram atomic weight
! efiss total thermal energy/fission
! ecapt total thermal energy/capture
! temp isotope temperature
! sigpot average effective potential scattering
! adens density of isotope in mixture
!
!-cbrkxs- (only if nbrks.gt.0)
! card 1 (2i6) file data
! nti number of temperatures desired
! (-n means accept first n temperatures)
! nzi number of sigpo values desire
! (-n means accept first n dilution factors)
! card 2 (not needed if nti.lt.0)
! atem(nti) values of desired temperatures
! card 3 (not needed if nzi.lt.0)
! asig(nzi) values of desired sigpo
!
NJOY2016 445

LA-UR-17-20093 14 CCCCR
!-cdlayx-- no input required
!--------------------------------------------------------------------
These instructions are divided into four parts. First, there is a general section
that applies to all three interface files following -ccccr-. Second, there is a
section of special parameters for ISOTXS following -cisotx-. Third, there is
a section of special parameters for BRKOXS following -cbrkxs-. And fourth,
there is a comment following -cdlaxs- noting that no special input is required
for the DLAYXS file.
In the -ccccr- section, Card 1 is used to read in the unit numbers for input
and output. nin must be a GENDF tape prepared using GROUPR, and it can
have either binary (nin<0) or ASCII (nin>0) mode. The units for the output
ISOTXS, BRKOXS, and DLAYXS files are all binary, but either sign can be used
on the unit numbers. If any unit number is given as zero, the corresponding
CCCC interface file will not be generated. On Card 2, the lprint=1 is used to
request a full printout of all the CCCC files generated. The file version number
ivers can be used to distinguish between different libraries generated using
NJOY. The user identification field huse can contain any desired 12-character
string. An example of Card 2 might be
0 7 ’T2 LANL NJOY’/
Card 3 contains a description of the library using up to 72 characters (12 stan-
dard CCCC words of 6 characters each). For example,
’LIB-IV 50-GROUP LMFBR LIBRARY FROM ENDF/B-IV (1976)’/
On Card 4, the values given for ngroup must agree with the number of groups
on the input GENDF tape or a fatal error message will be issued. nggrup is
not used. niso is the total number of materials or isotopes to be searched
for on the GENDF tape. The value of maxord should be less than or equal
to the maximum Legendre order used in the GROUPR run. The use of the
matrix blocking parameter ifopt was discussed in detail in connection with the
description of the ISOTXS format above. A value of 1 has been normally used
for Los Alamos libraries.
446 NJOY2016

14 CCCCR LA-UR-17-20093
A line using the Card 5 format is given for each of the niso isotopes or
materials to be processed. The Hollerith isotope label and the Hollerith absolute
isotope label have normally been set to the conventional isotope name at Los
Alamos; for example, u235 or cnat. The library name in habsid can vary quite
a lot now that many other libraries are available in ENDF format. The values
of hmat and imat will normally be derived from the MAT number characteristic
of all libraries in ENDF format. Unfortunately, xspo, the average potential
scattering cross section, must be entered by hand. It can be obtained from
mf=2, mt=151 on the ENDF file for the material by determining the scattering
radius afrom the AP field and computing σp=4πa2. The following fragment of
an ENDF/B evaluation shows the vicinity of AP:
...
9.223500+4 2.330248+2 0 0 1 09228 2151
9.223500+4 1.000000+0 0 1 2 09228 2151
1.000000-5 2.250000+3 1 3 0 19228 2151
3.500000+0 9.602000-1 0 0 1 39228 2151
2.330200+2 9.602000-1 0 0 19158 31939228 2151
-2.038300+3 3.000000+0 1.970300-2 3.379200-2-4.665200-2-1.008800-19228 2151
...
The scattering radius is the second number on the fourth card in the section
mf=2, mt=151. Using it as agives 4π(0.96020)2= 11.582 barns for the value of
xspo. An example of Card 5 follows:
U235 U235 ENDF6 ’9228’ 9228 11.582
Note that the Hollerith string “9228” had to be delimited by quotes because it
does not begin with a letter. The delimiters are optional for the other Hollerith
variables.
The next block of input cards is specific to ISOTXS and only appears if
ISOTXS processing was requested with a nonzero value for nisot. The first
parameter on Card 1 is nsblok, which was discussed in connection with matrix
blocking and subblocking. nsblok and ifopt work together to control how
a large scattering matrix is broken up into smaller records on the ISOTXS
interface file. The important factor is the maximum size of the binary records.
NJOY2016 447

LA-UR-17-20093 14 CCCCR
They should be small enough to fit into a reasonable amount of memory in any
application codes that use ISOTXS files, but they should be large enough to
keep the number of I/O operations to a minimum. The maximum record size
for each option is repeated below for the convenience of the reader:
1. ifopt=1 and nsblok=1:n`×ng(ng−1)/2,
2. ifopt=1 and nsblok=ngroup:n`×ng,
3. ifopt=2 and nsblok=1:ng(ng−1)/2.,
4. ifopt=2 and nsblok=ngroup:ng,
where n`is the number of Legendre orders and ngis the number of groups. If
the user specifies nsblok=1 and the resulting output record is too large for the
available memory, nsblok will be changed to ngroup automatically.
Card 1 of the ISOTXS section continues with maxup. This parameter is
always zero for CCCCR; thermal upscatter matrices are not processed. The
normal value of maxdn is ngroup, but it can be made smaller to reduce the
size of the matrices. The cross section for any removed downscatter groups
will be lumped into the last group in order to preserve the production cross
section. The ichix is used to control the generation of fission χvectors and
matrices. The representations allowed were discussed above in connection with
the description of the ISOTXS format (see Section 14.4). The most commonly
used option has been ichix=-1 because most application codes cannot handle
fission χmatrices. The GROUPR flux is normally chosen to be characteristic of
the class of problems a given library is intended to treat; therefore, it is rarely
necessary to supply an input weighting spectrum (see ichix=+1 and spec). The
following scenario illustrates a case where this option might be useful. Assume
that an 80-group library is made using the GROUPR fast reactor weight function
(iwt=8), which contains a shape in the fission range typical of both fast reactors
and fusion blankets plus a fusion peak at 14 MeV. This GENDF library could
be used to generate two different ISOTXS libraries, one using the default flux
and useful for fusion problems, and one using a spectrum spec from which
the fusion peak has been removed. The latter would be better for fast reactor
analysis because the χvectors would not contain the component of high-energy
fission from the 14 MeV range. Card 2 is used to input the user’s choice for
spec.
CCCCR can also produce fission χmatrices for codes that can use them.
These matrices can be rectangular to take advantage of the fact that the χg→g0
function is basically independent of gat low energies (large values of g). Taking
448 NJOY2016
14 CCCCR LA-UR-17-20093
the GROUPR 30-group structure as an example, if the energy at which sig-
nificant incident-energy dependence begins is taken to be about 100 keV, then
groups 16 through 30 will have identical χvectors. The value of ichix should
be set to 16, and the spec vector of Card 3 should be set to
123456789101112131415
16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16/
The resulting χmatrix will be rectangular with 16 ×30 elements.
Card 4 completes the input specific to ISOTXS. The value of kbr can be set
to reflect the normal use of this material in the applications that this library is
intended to treat. The amass parameter has units of gram atomic weight. It
can be calculated from the normal ENDF AWR parameter (the atomic weight
ratio to the neutron) by multiplying by the gram atomic weight of the neutron.
temp was historically 300K for NJOY CCCC libraries. The same value can be
used for sigpot and xspo (see above). The adens parameter has no meaning
for CCCCR; it can be set to zero to imply infinite dilution.
The choice of values for efiss and ecapt is more complicated. As discussed
in Section 14.4,efiss is basically the total non-neutrino energy released by a
fission reaction. It is available in eV as the pseudo Q value in mf=3, mt=18
(the energy release from fission is given in more detail in mf=1, mt=458). The
following fragment of the ENDF/B-VI evaluation for 235U shows how to find
the Q value:
...
9228 3 0 4413
9.223500+4 2.330250+2 0 0 0 09228 3 18 4414
1.937200+8 1.937200+8 0 0 1 3339228 3 18 4415
333 2 9228 3 18 4416
1.000000-5 0.000000+0 7.712960+1 0.000000+0 2.250000+3 0.000000+09228 3 18 4417
2.250000+3 5.362770+0 2.300000+3 5.396710+0 2.500000+3 5.957280+09228 3 18 4418
...
The Q value is the second number on the second card of the section mf=3,
mt=18. Converting to CCCC units gives
193.72×106eV ×1.602×10−19 watt-s/eV = .31034×10−10 watt-s/fission
NJOY2016 449

LA-UR-17-20093 14 CCCCR
The value for ecapt is determined from the Q value for mf=3, mt=102, the
radiative capture reaction. However, if the isotope remaining after capture has
a relatively short half-life, the energy of the decays leading to the final stable
daughter should be added onto the capture Q value. (The meaning of “stable”
may vary from application to application). As an example, consider aluminum.
The 28Al capture product decays with a half-life of 2.24 minutes producing 9.31
MeV of β−energy and a 1.779 MeV photon. Therefore, the actual value of
ecapt should be calculated as follows:
7.724 MeV mt=102 prompt Q value
9.310 MeV β−energy
1.779 MeV delayed-γenergy
18.813 MeV
×1.602 ×10−13
.3014 ×10−11 in watt-s/capture
The next section of the input file is specific to BRKOXS. Card 1 enables the
user to just accept all or part of the temperatures and sigma-zero values on the
input GENDF tape. If the value of nti is negative, the first abs(nti)Tvalues
for each material will be used. If fewer values are available, only those will be
used. If nti is positive, input Card 2 will be read for a list of Tvalues, and only
data with temperatures on that list will be extracted from the GENDF tape.
The parameter nzi and the list of σ0values on Card 3 work in the same way.
No additional input is required for DLAYXS files.
14.9 Error Messages
error in isxdat***incompatible group structures
The number of groups on the input GENDF tape must match the number
of groups specified in the CCCCR input. Check whether the correct input
file was mounted.
error in isomtx***input record too large
There is not enough space in the scratch array bto read in the input
records from the GENDF tape. The only solution is to increase the size of
the main CCCC equivalanced array set. See a,ia,ha with isiza=50000
at the beginning of the ccccm module.
error in isomtx***output record too large
There is not enough space in the scratch array bfor the output subblock
record, even with nsblok changed to ngroup. The only solution is to
450 NJOY2016

14 CCCCR LA-UR-17-20093
increase the size of the main CCCC equivalanced array set. See a,ia,ha
with isiza=50000 at the beginning of the ccccm module.
error in shuffl***sigze of endf input array exceeded
See the global parameter maxe=8000 at the start of the module.
error in pisotx***input record too large
One of the binary records on the ISOTXS file is too large for the memory
available to prinxs. This should not occur because there was enough
memory to create the record in the first place.
error in brkdat***incompatible group structures
The number of groups on the input GENDF tape must match the number
of groups specified in the CCCCR input. Check whether the correct input
file was mounted.
error in brkdat***max size of endf record exceeded.
See the global parameter maxe=8000 at the start of the module.
message from brkdat---all available mats have been processed
This message is issued when all the materials on the GENDF file have been
processed, but one or more of the materials requested in the user’s input
were not found. Check the input material list, and check which materials
were written onto the input GENDF file.
message from brkdat---no temperatures for mat=nnnn
This means that none of the requested temperatures were found for this
MAT. This makes it impossible to include the material in the BRKOXS
file. The warning message is issued, and all references to this material are
thinned out of the BRKOXS records.
message from brkdat---need elastic matrices at higher temps
The self-shielded transport cross section requires self-shielded P1elastic
scattering matrices for accurate results. This means that mf=6, mt=2
should be available on the GENDF tape for all temperatures. If this scat-
tering matrix is missing for the higher temperatures, this warning message
is issued.
error in xsproc***max size of endf record exceeded.
See the global parameter maxe=8000 at the start of the module.
message from xsproc---infinite f-factor mt jg jz temp
The calculation of an f-factor requires division by the infinitely dilute cross
section. This message means that the divisor was zero for reaction mt, group
jg, background cross section jz, and temperature temp. The division is
skipped, and the numerator is used unchanged.
error in mxproc***max size of endf record exceeded.
See the global parameter maxe=8000 at the start of the module.
error in pbrkxs***input record too large
NJOY2016 451

LA-UR-17-20093 14 CCCCR
One of the binary records on the BRKOXS file is too large for the memory
available to pbrkxs. This should not occur because there was enough
memory to create the record in the first place.
message from cdlyxs---no delayed neutron data found
There was no delayed-neutron data found by DLDATA. Make sure that mf=3,
mt=455 and mf=5, mt=455 were requested during the GROUPR run and
that the delayed-neutron isotopes were included in the material list given
in the CCCCR input.
error in dldata***max size of endf record exceeded.
See the global parameter maxe=8000 at the start of the module.
error in dldata***incompatible group structures
The number of groups on the input GENDF tape must match the number
of groups specified in the CCCCR input. Check whether the correct input
file was mounted.
error in pdlyxs***input record too large
One of the binary records on the DLAYXS file is too large for the memory
available to pdlyxs. This should not occur because there was enough
memory to create the record in the first place.
452 NJOY2016

15 MATXSR LA-UR-17-20093
15 MATXSR
The MATXS material cross section format is a generalized CCCC-type inter-
face format for neutron, photon, and charged-particle data, including cross sec-
tions, group-to-group matrices, temperature variations, self-shielding, and time-
dependence. The CCCC standards are discussed in more detail in the CCCCR
chapter of this manual and in the CCCC-III and CCCC-IV reports[29, 11].
MATXS libraries can be used with the TRANSX code[12, 41] to produce effec-
tive cross sections for a wide variety of application codes.
This chapter describes the MATXSR module in NJOY2016.0.
15.1 Background
Even the very best nuclear cross section processing code would be useless if it
were unable to deliver its products to users. This is the role of the interface file.
There have been interface files since the beginning of calculational neutronics;
examples include the DTF format (see the DTFR chapter of this manual) that
was devised for the early discrete-ordinates transport code DTF-IV[24], and the
CCCC ISOTXS format[11] (see the CCCCR section of this manual). Both of
these interface formats are still in use today, but both of them have problems
and show their age. Some of these problems result from the increase in the
capabilities of computer systems (capabilities that allow us to consider much
more complex problems), some arise from the many new kinds of nuclear systems
that are being studied today, and some come from 20/20 hindsight, which makes
it easy to see the design flaws in earlier formats.
Based on the problems seen with existing interface files, an ideal interface
file should be
extendable, so that new cross section types, new incident or secondary particle
types, or new energy ranges are easy to add without changing the basic
format;
comprehensive, in order to be able to handle as many of the kinds of data
produced by the processing code as possible (results should not be lost just
because there are no places for them);
generalizable, to allow common methods to be used for similar kinds of data
(for example, nn matrices and γγ matrices) in order to transfer the expe-
rience gained in one field to another, and in order to simplify coding by
allowing components to be reused;
NJOY2016 453

LA-UR-17-20093 15 MATXSR
self-contained, because it should not be necessary to provide additional infor-
mation that is not in the file in order to use or interpret the file;
compact, because nuclear data often have many zeros or very small numbers
in tables (for example, threshold reactions, scattering matrices), and these
zeros must be removed effectively for economic storage and fast transfer of
libraries; and
efficient, thus implying that binary mode should be used, that the records
have a well-defined maximum size, and that there is a minimum number
of records to reduce the number of I/O operations.
Comparing the DTF format to these principles gives the following results: it
is fairly extendable because it has no fixed particles, energy limits, or reaction
types; it is not very comprehensive because it can only transmit the total scat-
tering matrix; it is fairly generalizable because of the lack of fixed types; it is
not at all self-contained in that it requires outside definitions like table length,
position of the total, group structure, and identity of edit cross sections; it is
not very compact because most zeros must be given explicitly in the tables; and
it is not very efficient because it uses coded card-image records.
Similarly, studying the ISOTXS format gives the following results: it is not
extendable because it works for neutrons only and allows only very limited types
of reactions to be included; it is not comprehensive because it works for neutrons
only and allows only very limited types of reactions to be included; it is not
generalizable because of its specialization to fast-reactor problems (as proof,
note that the CCCC files for γcross sections use completely different formats);
it is reasonably self-contained because all the parameters are internal, the group
structure is given, and all names needed for labeling an interpreted listing are
well determined; it is fairly compact because many zeros are removed (but too
many still remain); it is fairly efficient because it uses binary mode, but record
sizes are poorly predictable and very nonuniform, thereby needlessly increasing
the size of application codes and the number of I/O operations.
15.2 The MATXS Format
Following these general principles, the MATXS material cross section file was
designed to extend and generalize the existing interface formats while still using
the CCCC approach for efficiency and familiarity (see the CCCCR section of
this report for more details). The first design principle was that all information
would be identified using lists of Hollerith names. As an example, if the list
of reactions included in the file contains entries such as nf,ng, and n2n, it
454 NJOY2016

15 MATXSR LA-UR-17-20093
Table 12: Standard Particle Names
Name Particle
nneutron
ggamma
pproton
ddeuteron
ttriton
h3He nucleus
aalpha
bbeta
rresidual or recoil (heavier than α)
is trivial to add additional reactions such as kerma or dpa. This approach is
much more extendable than the fixed set of reaction flags used in ISOTXS.
The second design principle was that the file would be designed to hold sets
of vectors and rectangular matrices and that the same format would be used
regardless of the contents of the vectors and matrices. As a consequence, once
a code can handle n→n, it can also handle γ→γ; once a code can handle n→γ,
it can also handle γ→n,n→β, or even d→p. This approach is an example of
generalization. Each material is now divided into data types identified by input
and output particle. As an example, n→γis a data type characterized by input
particle equals neutron, and output particle equals photon. The matrices for
this data type contain cross sections for producing photons in photon group γ
due to reactions of neutrons in group n. The vectors, if any, would contain
photon production cross sections versus neutron group. The use of completely
general data types helps make the format comprehensive.
The names for materials are written in the forms u235,fe56,tinat, or
h2a. Note that “nat” is used explicitly for elements; names like be or cshould
be avoided. Suffixes “a”, “b”, or “c” are used to label different versions of a
material in a library. In order to keep names to six characters, isomers should
be identified by incrementing the “thousands” digit in the atomic number field;
for example, nb193a would be the second version of the first isomer of 93Nb.
The standard names for MATXS particles are given in Table 12.
The standard names for the data types (htype) are mostly based on these
particle names; the use of the terms scat,dk,therm are exceptions. Table 13
illustrates the scheme used.
Reactions names are constructed in MATXSR from the ENDF MT number,
NJOY2016 455

LA-UR-17-20093 15 MATXSR
the LR flag (if present), and the incident particle name. Examples of the stan-
dard names are given in Tables 14–22. Note that the first nis omitted from
the last three reactions in Table 14. It is implicit in the data-type name. This
convention saves space in the name for possible breakup products (see Table 15).
The first nis also implicit in the reactions of Table 15. No multiplicity is used
in the breakup product strings in order to avoid possible confusions with the
discrete-level number; just count the like letters to get the multiplicity. The
names used for the most common neutron absorption reactions are given in
Table 16, and the names used for the fission reactions are given in Table 17.
MATXS libraries typically give the total fission cross section and all the partial
cross sections (when available) in the vector blocks, but they do not give the
total fission matrix when the partial matrices are available.
Table 18 gives some additional reaction names, some of which are special
NJOY names. As discussed in the GROUPR chapter of this report, the total
cross section can be averaged with the `th order of the flux to obtain the multi-
group total cross section components σt`,g. These total cross section components
and the corresponding Legendre fluxes are given names like the first four shown
in Table 18. Related names with first letters g,p,d,etc., will also be found
in MATXS libraries. The average inverse velocities are defined to preserve the
Table 13: Standard Data-Type Names
Name Data Type
nscat neutron scattering
ng neutron-induced gamma production
np neutron-induced proton production
nr neutron-to-recoil matrix
gscat gamma scattering
pscat proton scattering
pn proton-induced neutron production
··· ···
ntherm thermal scattering data
dkn delayed-neutron data
dkhg decay heat and gamma data
dkb decay beta data
456 NJOY2016

15 MATXSR LA-UR-17-20093
Table 14: Simple Neutron-Emitting Reactions
Name MT Description
nelas 2 neutron elastic scattering
nnonel 3 neutron nonelastic (MT=1–MT=2)
ninel 4 neutron inelastic sum (MT=51–91)
n2n 16 (n,2n)
n3n 17 (n,3n)
nna 22 (n,n0α)
nnp 28 (n,n0p)
n01 51 (n,n1)
n02 52 (n,n2)
ncn 91 (n,n0) to continuum
time term of the time-dependent Boltzmann equation:
D1
vE=Zg
(1/v)φ(E)dE
Zg
φ(E)dE
.(475)
The meaning of the terms energy-balance heat production and kinematic KERMA
factor are discussed in more detail in the HEATR chapter of this manual. Briefly,
the energy-balance heating (mt=301) is computed by subtracting the energy car-
ried away by neutrons and photons from the energy available for a reaction. The
result should be the energy deposited by charged particles and the recoil nucleus,
that is, the local heating. Unfortunately, problems with the energy-balance con-
sistency of evaluations, the difficulty of determining the available energy for
elements, and the inaccuracy in the difference between relatively large numbers
sometimes cause this value to have unphysical values (for example, negative
Table 15: Breakup Reactions (LR flags)
Name MT LR Description
n07a 57 22 (n,n7)α
n51p 65 28 (n,n15)p
n02aa 52 29 (n,n2)2α
ncnaaa 91 23 (n,n0)3α
n06na 56 24 (n,n5)nα
n01ee 51 40 (n,n1)ee
NJOY2016 457

LA-UR-17-20093 15 MATXSR
Table 16: Neutron-Absorption Reactions
Name MT Description
nabs 101 total absorption
ng 102 radiative capture
np 103 (n,p)
na 107 (n,α)
heating). These values do have the property of always conserving energy for
large systems. The kinematic value (mt=443) is computed from reaction kine-
matics alone. It is very accurate at low energies, but when three or more particles
are involved in the reaction, it begins to fail. The results in kerma are always
larger than the correct heating value. Comparing the two estimates for the local
heating can reveal problems in the evaluations[43, 89]. The MATXS user is free
to choose whichever number is more appropriate for the problem. The reaction
dame is also generated using data from HEATR. As discussed in the HEATR
section of this report, this “damage-energy production” cross section can be
used to obtain the DPA (displacements per atom) parameter used in radiation
damage studies.
The gas-production reaction names given in Table 19 can also appear with
other particle names before the decimal point. The names for reactions induced
by incident charged particles follow the neutron names in most cases, except
that the first letter is changed to indicate the incident particle type. Discrete-
level scattering reactions are exceptions; n01 is used for both (n,n1) and (p,n1).
Also note the n00 cannot be used for incident neutrons; the name nelas is used
instead. Similarly, p00 is not used for incident protons.
As discussed in more detail below, scattering from thermal moderators is
Table 17: Fission Reactions
Name MT Description
nftot 18 total fission
nf 19 (n,f) first-chance fission
nnf 20 (n,n0f) second-chance fission
n2nf 21 (n,n2f) third-chance fission
n3nf 38 (n,n3f) fourth-chance fission
nudel 455 delayed-neutron yield (MF=3)
chid 455 delayed-neutron spectrum (MF=5)
458 NJOY2016

15 MATXSR LA-UR-17-20093
Table 18: Special NJOY Names
Name MT Description
ntot0 1 P0total cross section
ntot1 1 P1total cross section
nwt0 1 P0weight function (flux)
nwt1 1 P1weight function (flux)
mubar 251 scattering ¯µ
xi 252 scattering ξ
invel 259 inverse velocity (sec/m)
heat 301 energy-balance heat production
kerma 443 kinematic KERMA factor
dame 444 damage-energy production
treated like materials in ENDF/B libraries, but it is treated like reactions on the
GENDF files. The free-gas scattering reaction can appear in any material, but
the other thermal MT numbers can only appear in the material corresponding
to the dominant scattering isotope. For example, hh2o only appears in 1H.
There are two versions of zrhyd; one appears in 1H and the other in Zr. The
coherent and incoherent terms in the thermal cross section are kept separate
for the convenience of applications; all the coherent names end with $. Note
that MATXS files contain two different representations for the scattering cross
sections at low energies:
static, where the cross section and group-to-group matrix are obtained from
nscat, which is derived from mt=2 on the ENDF evaluation. (This is
scattering for “static” nuclei; energy loss from recoil is included.); and
thermal, where the cross section and group-to-group matrix are obtained from
one of the thermal reactions in the ntherm data type. (The scattering nuclei
are in motion with a distribution described by the Maxwell-Boltzmann law;
Table 19: Gas-Production Reactions
Name MT Description
n.neut 201 total neutron production
n.gam 202 total γproduction
n.h1 203 hydrogen production
n.h3 205 tritium production
n.HE4 207 helium production
NJOY2016 459

LA-UR-17-20093 15 MATXSR
Table 20: Incident-Proton Reactions
Name MT Description
pelas 2 proton elastic scattering
p01 601 discrete-level (p,p1) scattering
n00 50 discrete-level (p,n0)
n01 51 discrete-level (p,n1)
p2n 16 (p,2n)
pg 102 (p,γ)
pt 104 (p,t)
both energy loss and energy gain events are possible.)
The TRANSX code gives the user the choice of static or thermal scattering, and
it also allows the user to choose which binding state is desired for a particular
moderator material.
Table 21: Thermal Material Names for ENDF/B-VII
Name MT Description
free 221 free-gas scattering
hh2o 222 H in H2O
poly 223 H in polyethylene (CH2) incoherent
poly$ 224 H in polyethylene (CH2) coherent
hzrh 225 H in ZrH incoherent
hzrh$ 226 H in ZrH coherent
benz 227 Benzene incoherent
dd2o 228 D in D2O
graph 229 C in graphite incoherent
graph$ 230 C in graphite coherent
be 231 Be metal incoherent
be$ 232 Be metal coherent
bebeo 233 Be in BeO incoherent
bebeo$ 234 Be in BeO coherent
zrzrh 235 Zr in ZrH incoherent
zrzrh$ 236 Zr in ZrH coherent
obeo 237 O in BeO incoherent
obeo$ 238 O in BeO coherent
ouo2 239 O in UO2incoherent
ouo2$ 240 O in UO2coherent
uuo2 241 U in UO2incoherent
uuo2$ 242 U in UO2coherent
al 243 Al metal incoherent
al 244 Al metal coherent
fe 245 Fe metal incoherent
fe 246 Fe metal coherent
460 NJOY2016

15 MATXSR LA-UR-17-20093
Table 22: Photoatomic Cross Sections
Name MT Description
gtot0 501 P0total
gwt0 501 P0weight function (flux)
gcoh 502 coherent scattering
ginch 504 incoherent scattering
gpair 516 pair production (γ, 2γ)
gabs 522 photoelectric absorption
gheat 525 heating
The ENDF representation of photoatomic reactions was described in the
GAMINR chapter. The gheat reaction, constructed in GAMINR, represents
the local heating from atomic recoil and photo-electric electron production. Flu-
orescence photons from photoelectric interactions are assumed to deposit their
energy locally.
GROUPR and MATXSR are capable of supporting a new experimental ca-
pability for generating nuclide production cross sections. This capability is most
useful for radionuclides and isomers, but it is general enough to handle all the
possible heavy products of a nuclear reaction. The input GENDF file may con-
tain several different sections that produce a given nuclide. MATXSR adds
them up into a single named reaction. The naming convention used for capture
reactions is cZZAAA, where Z and A are the charge and mass numbers for the
nuclide. Isomers are handled by incrementing the first postion of the “AAA”
field. Products of other reactions are named using the pattern rZZAAA, with
the same convention used for isomers. The reason that capture products are
distinguished from those from other reactions is that the former may have to be
self shielded.
The CCCC standards have always used 6-character Hollerith strings for
names. These kinds of names are represented as “REAL*8” double precision
variables on 32-bit machines (IBM, VAX, Sun, etc.) and as single-precision
variables on 60- to 64-bit machines (CDC, Cray). However, a double-precision
variable on a short-word machine can hold 8 characters. So can single-precision
variables on CDC and Cray machines. There do not seem to be any computer
systems currently in use that require 6-character words. Therefore, the latest
versions of the MATXS format and the MATXSR module have been written to
handle 8-character names.
The formal format specification for the MATXS material cross section file
NJOY2016 461

LA-UR-17-20093 15 MATXSR
follows, using the standard CCCC presentation (except for the ! before the c):
! Standardized CCCC format listing for MATXS file
!c
!c**********************************************************************
!c proposed 09/09/77
!c (modified 09/80)
!c (nomenclature changed 06/88)
!c (modified for const sub-blocks 06/90)
!c (ordering changed 10/90)
!c c (bcd format changed 12/21/91)
!c
!cf matxs
!ce material cross section file
!c
!cn this file contains cross section
!cn vectors and matrices for all
!cn particles, materials, and reactions;
!cn delayed neutron spectra by time group;
!cn and decay heat and photon spectra.
!c
!cn formats given are for file exchange only
!c
!c**********************************************************************
!c
!c
!c----------------------------------------------------------------------
!cs file structure
!cs
!cs record type present if
!cs ============================== ===============
!cs file identification always
!cs file control always
!cs set hollerith identification always
!cs file data always
!cs
!cs *************(repeat for all particles)
!cs * group structures always
!cs *************
!cs
!cs *************(repeat for all materials)
462 NJOY2016

15 MATXSR LA-UR-17-20093
!cs * material control always
!cs *
!cs * ***********(repeat for all submaterials)
!cs * * vector control n1db.gt.0
!cs * *
!cs * * *********(repeat for all vector blocks)
!cs * * * vector block n1db.gt.0
!cs * * *********
!cs * *
!cs * * *********(repeat for all matrix blocks)
!cs * * * matrix control n2d.gt.0
!cs * * *
!cs * * * *******(repeat for all sub-blocks)
!cs * * * * matrix sub-block n2d.gt.0
!cs * * * *******
!cs * * *
!cs * * * constant sub-block jconst.gt.0
!cs * * *
!cs *************
!c
!c----------------------------------------------------------------------
!c
!c
!c----------------------------------------------------------------------
!cr file identification
!c
!cl hname,(huse(i),i=1,2),ivers
!c
!cw 1+3*mult
!c
!cb format(4h 0v ,a8,1h*,2a8,1h*,i6)
!c
!cd hname hollerith file name - matxs - (a8)
!cd huse hollerith user identifiation (a8)
!cd ivers file version number
!cd mult double precision parameter
!cd 1- a8 word is single word
!cd 2- a8 word is double precision word
!c
!c----------------------------------------------------------------------
!c
!c
NJOY2016 463

LA-UR-17-20093 15 MATXSR
!c----------------------------------------------------------------------
!cr file control
!c
!cl npart,ntype,nholl,nmat,maxw,length
!c
!cw 6
!c
!cb format(6h 1d ,6i6)
!c
!cd npart number of particles for which group
!cd structures are given
!cd ntype number of data types present in set
!cd nholl number of words in set hollerith
!cd identification record
!cd nmat number of materials on file
!cd maxw maximum record size for sub-blocking
!cd length length of file
!c
!c----------------------------------------------------------------------
!c
!c
!c----------------------------------------------------------------------
!cr set hollerith identification
!c
!cl (hsetid(i),i=1,nholl)
!c
!cw nholl*mult
!c
!cb format(4h 2d /(9a8))
!c
!cd hsetid hollerith identification of set (a8)
!cd (to be edited out 72 characters per line)
!c
!c----------------------------------------------------------------------
!c
!c
!c----------------------------------------------------------------------
!cr file data
!c
!cl (hprt(j),j=1,npart),(htype(k),k=1,ntype),(hmatn(i),i=1,nmat),
!cl 1(ngrp(j),j=1,npart),(jinp(k),k=1,ntype,(joutp(k),k=1,ntype),
!cl 2(nsubm(i)i=1,nmat),(locm(i),i=1,nmat)
464 NJOY2016

15 MATXSR LA-UR-17-20093
!c
!cw (npart+ntype+nmat)*mult+2*ntype+npart+2*nmat
!c
!cb format(4h 3d ,4x,8a8/(9a8)) hprt,htype,hmatn
!cb format(12i6) ngrp,jinp,joutp,nsubm,locm
!c
!cd hprt(j) hollerith identification for particle j
!cd n neutron
!cd g gamma
!cd p proton
!cd d deuteron
!cd t triton
!cd h he-3 nucleus
!cd a alpha (he-4 nucleus)
!cd b beta
!cd r residual or recoil
!cd (heavier than alpha)
!cd htype(k) hollerith identification for data type k
!cd nscat neutron scattering
!cd ng neutron induced gamma production
!cd gscat gamma scattering
!cd pn proton induced neutron production
!cd . .
!cd . .
!cd . .
!cd dkn delayed neutron data
!cd dkhg decay heat and gamma data
!cd dkb decay beta data
!cd hmatn(i) hollerith identification for material i
!cd ngrp(j) number of energy groups for particle j
!cd jinp(k) type of incident particle associated with
!cd data type k. for dk data types, jinp is 0.
!cd joutp(k) type of outgoing particle associated with
!cd data type k
!cd nsubm(i) number of submaterials for material i
!cd locm(i) location of material i
!c
!c----------------------------------------------------------------------
!c
!c
!c----------------------------------------------------------------------
!cr group structure
NJOY2016 465

LA-UR-17-20093 15 MATXSR
!c
!cl (gpb(i),i=1,ngr),emin
!c
!cc ngr=ngrp(j)
!c
!cw ngrp(j)+1
!c
!cb format(4h 4d ,8x,1p,5e12.5/(6e12.5))
!c
!cd gpb(i) maximum energy bound for group i for particle j
!cd emin minimum energy bound for particle j
!c
!c----------------------------------------------------------------------
!c
!c
!c----------------------------------------------------------------------
!cr material control
!c
!cl hmat,amass,(temp(i),sigz(i),itype(i),n1d(i),n2d(i),
!cl 1locs(i),i=1,nsubm)
!c
!cw mult+1+6*nsubm
!c
!cb format(4h 5d ,a8,1p,2e12.5/(2e12.5,5i6))
!c
!cd hmat hollerith material identifier
!cd amass atomic weight ratio
!cd temp ambient temperature or other parameters for
!cd submaterial i
!cd sigz dilution factor or other parameters for
!cd submaterial i
!cd itype data type for submaterial i
!cd n1d number of vectors for submaterial i
!cd n2d number of matrix blocks for submaterial i
!cd locs location of submaterial i
!c
!c----------------------------------------------------------------------
!c
!c
!c----------------------------------------------------------------------
!cr vector control
!c
466 NJOY2016

15 MATXSR LA-UR-17-20093
!cl (hvps(i),i=1,n1d),(nfg(i),i=1,n1d),(nlg(i),i=1,n1d)
!c
!cw (mult+2)*n1d
!c
!cb format(4h 6d ,4x,8a8/(9a8)) hvps
!cb format(12i6) iblk,nfg,nlg
!c
!cd hvps(i) hollerith identifier of vector
!cd nelas neutron elastic scattering
!cd n2n (n,2n)
!cd nnf second chance fission
!cd gabs gamma absorption
!cd p2n protons in, 2 neutrons out
!cd . .
!cd . .
!cd . .
!cd nfg(i) number of first group in band for vector i
!cd nlg(i) number of last group in band for vector i
!c
!c----------------------------------------------------------------------
!c
!c
!c----------------------------------------------------------------------
!cr vector block
!c
!cl (vps(i),i=1,kmax)
!c
!cc kmax=sum over group band for each vector in block j
!c
!cw kmax
!c
!cb format(4h 7d ,8x,1p,5e12.5/(6e12.5))
!c
!cd vps(i) data for group bands for vectors in block j.
!cd block size is determined by taking all the group
!cd bands that have a total length less than or equal
!cd to maxw.
!c
!c----------------------------------------------------------------------
!c
!c
!c----------------------------------------------------------------------
NJOY2016 467

LA-UR-17-20093 15 MATXSR
!cr scattering matrix control
!c
!cl hmtx,lord,jconst,
!cl 1(jband(l),l=1,noutg(k)),(ijj(l),l=1,noutg(k))
!c
!cw mult+2+2*noutg(k)
!c
!cb format(4h 8d ,4x,a8/(12i6)) hmtx,lord,jconst,
!cb jband,ijj
!c
!cd hmtx hollerith identification of block
!cd lord number of orders present
!cd jconst number of groups with constant spectrum
!cd jband(l) bandwidth for group l
!cd ijj(l) lowest group in band for group l
!c
!c----------------------------------------------------------------------
!c
!c
!c----------------------------------------------------------------------
!cr scattering sub-block
!c
!cl (scat(k),k=1,kmax)
!c
!cc kmax=lord times the sum over all jband in the group range of
!cc this sub-block
!c
!cb format(4h 9d ,8x,1p,5e12.5/(6e12.5))
!c
!cw kmax
!c
!cd scat(k) matrix data given as bands of elements for initial
!cd groups that lead to each final group. the order
!cd of the elements is as follows: band for p0 of
!cd group i, band for p1 of group i, ... , band for p0
!cd of group i+1, band for p1 of group i+1, etc. the
!cd groups in each band are given in descending order.
!cd the size of each sub-block is determined by the
!cd total length of a group of bands that is less than
!cd or equal to maxw.
!cd
!cd if jconst.gt.0, the contributions from the jconst
468 NJOY2016
15 MATXSR LA-UR-17-20093
!cd low-energy groups are given separately.
!c
!c----------------------------------------------------------------------
!c
!c
!c
!c----------------------------------------------------------------------
!cr constant sub-block
!c
!cl (spec(l),l=1,noutg(k)),(prod(l),l=l1,ning(k))
!c
!cc l1=ning(k)-jconst+1
!c
!cw noutg(k)+jconst
!c
!cb format(4h10d ,8x,1p,5e12.5/(6e12.5))
!c
!cd spec normalized spectrum of final particles for initial
!cd particles in groups l1 to ning(k)
!cd prod production cross section (e.g., nu*sigf) for
!cd initial groups l1 through ning(k)
!cd
!cd this option is normally used for the energy-independent
!cd neutron and photon spectra from fission and radiative
!cd capture usually seen at low energies.
!c
!c----------------------------------------------------------------------
The MATXS format is intended to communicate multigroup cross sections
and matrices for all reaction types, incident particles, and outgoing particles
from a nuclear data processing code to applications. It also includes temperature
and self-shielding effects, delayed-neutron data, and a limited format for decay
heat and delayed photon or particle emission. As shown in the “File Structure”
presentation above, the main loop is over material. Materials are subdivided into
submaterials, which usually correspond to different data types, temperatures,
and background cross section (σ0) values. Each submaterial can contain a series
of “Vector Blocks” giving cross section versus energy for one of the allowed group
structures and incident particles, and it can contain a series of matrix blocks
and subblocks giving the cross sections for group-to-group transfers.
NJOY2016 469

LA-UR-17-20093 15 MATXSR
The “File Identification” record is the same for all CCCC files. It gives the
Hollerith name for the file (which is always matxs), a version number ivers,
which can be used to distinguish between different libraries in this format,
and a Hollerith identification string huse, which can be used for entries like
“T2 LANL NJOY”.
The “File Control” record contains parameters that are needed to compute
the lengths of the following records. The meaning of the various names is well
explained in the format specification, and the values of the parameters are ob-
tained from the user’s input. The purpose of maxw is to tell application codes
how much memory they will need to read through the records on these MATXS
files. It is used for both vector blocks and matrix subblocks when deciding how
to break them up. The MATXSR value is 5000 words. The code tries to make
as many records as possible that have nearly this size in order to minimize the
number of I/O operations. The parameter length is used to help find the end of
the file when appending a new material to an existing file. Its units are left un-
specified in the format. It is usually the length in records, in which case record
skipping can be used to find the end. Or it could be the length in words on
computer systems that allow direct word-addressed I/O operations (this used
to be possible using CTSS on Cray computers).
The “Set Hollerith Identification” record comes next. It contains an arbitrary
amount of Hollerith text to describe the contents of the library. The description
comes from the user’s input.
The “File Data” record contains a number of important arrays that define
the structure of data types and the location of materials. The parameter hprt
contains the standard names for the npart particles. The standard names for
particles were discussed above. The standard names for the data types and ma-
terials (htype and hmatn) were also discussed above. The next three parameters
are used to complete the specification of the data types included in this MATXS
library. ngrp just gives the number of groups used for each particle type; for
example, the traditional Los Alamos 30×12 library (with 30 neutron groups and
12 photon groups) would have ngrp(1)=30 and ngrp(2)=12. Using the same
example, the nscat data type would have jinp(1)=1 and joutp(1)=1; the ng
data type would have jinp(2)=1 and joutp(2)=2; and the gscat data type
would have jinp(3)=2 and joutp(3)=2. The information for these 6 arrays is
given in the user’s input.
The final two parameters in the “File Data” record are nsubm and locm. The
value of nsubm depends on the number of data types, the number of tempera-
470 NJOY2016

15 MATXSR LA-UR-17-20093
tures, and the number of background cross sections found on the input GENDF
tapes. The value for locm(i) is usually the record index for material i. A code
can then jump directly to a desired material using record skipping (forward or
backward). However, the units for locm have been left unspecified to allow di-
rect random access for systems that use word-addressable random-access I/O
operations.
The “Group Structure” records give the energy bounds for npart group struc-
tures. Following the normal convention for application codes, the energy bounds
are given in the order of decreasing energy. The numbers are obtained from
mf=1, mt=451 on the GENDF tape. The GROUPR module currently uses one
group structure for all particles (n, p, α,etc.), and another for photons (γ).
Inside the material loop, there is a “Material Control” record for each mate-
rial. The choice of names for hmat was discussed above. The amass parameter
is the same as the ENDF AWR parameter; that is, it is the ratio of the tar-
get mass to the neutron mass. Temperatures temp are given in degrees Kelvin,
and background cross sections for self-shielding codes (sigz, or σ0) are given in
barns. The parameter itype tells which data-type each submaterial belongs to
using the data type codes defined by htype. Although it is not specified in the
format description, the order that MATXSR loops through submaterials is as
follows: the outer loop is over data type, the next loop is over temperature, and
the innermost loop is over background cross section. The number of cross sec-
tion vector reactions and matrix reactions for each submaterial are given in n1d
and n2d. Finally, locs(i) normally gives the record index for submaterial i. A
code can search the arrays temp,sigz, and itype for a desired submaterial, and
then jump right to the desired submaterial using record skipping. Alternatively,
a version that uses word addresses in locs could use random-access methods to
jump to the desired submaterial.
Each submaterial that contains vectors (n1d>0) starts with a “Vector Con-
trol” record. This record gives a list of reaction names in hvps. MATXSR con-
structs these reaction names automatically based on the MT number, ENDF
“LR flag” (if any), and the incident particle type. Examples of these names
were given above. The parameters nfg and nlg are used to remove unnecessary
leading or trailing zeros in reaction cross section vectors. The zeroes are usually
due to thresholds. For example, an (n,2n) reaction might only have nonzero
cross sections for groups 1 through 5 out of an 80-group structure. Storing only
the 5-element band will save 75 words on the MATXS file. Even with the zeros
removed, the number of words of vector cross section data for a submaterial can
NJOY2016 471

LA-UR-17-20093 15 MATXSR
be quite large. Therefore, the MATXS format provides a way to break the vector
data into a number of vector blocks. The idea is to sum up the bandwidths for
each reaction (that is, nlg(i)-nfg(i)+1) in order to find the largest number of
reactions that will fit within a block of length less than or equal to maxw. The
data for this block are written to the output file, and then the next group of
reactions is found. This continues until all the vector data have been written out
as a series of “Vector Block” records with lengths less than maxw (5000 words
in MATXSR). This method minimizes the number of records on the file while
allowing the application codes that read MATXS libraries to allocate space for
reading the records economically.
Most submaterials will contain n2b “Scattering Matrix Control” records. The
convention for the reaction names used in hmtx were discussed above. lord gives
the number of Legendre orders present for this reaction; that is, lord=4 for a
P3matrix. Matrices are compacted for efficient storage and data transfer using
two techniques. First, unnecessary leading and trailing zeros for group-to-group
transfers into a particular final group are removed by banding. jband(i) gives
the number of incident groups in the band for final group i, and ijj(i) gives
the group index for the lowest-energy group (highest group index) in the band
for group i. For example, consider an isotropic (n,2n) reaction with a threshold
in group 3 of a 30-group structure. The values for jband and ijj for group 20
might well be 3 and 3, respectively. That is, groups 1 through 3 scatter into
group 20. The order of storage for this matrix would be as follows:
Band Element jband ijj
1 1→1 1 1
2 2→2 2 2
1→2
3 3→3 3 3
2→3
1→3
4 3→4 3 3
2→4
1→4
··· ···
Note that this scheme is more efficient than the similar one used for the CCCC
ISOTXS file, because that method required that the ingroup element had to be
included in the band. For anisotropic matrices, the lord Legendre components
are stored with the source-group elements. Thus, there are lord(i)*jband(i)
472 NJOY2016

15 MATXSR LA-UR-17-20093
elements in each band, and they are stored in the following order (assuming a
P1matrix):
Band Element Order jband ijj
1 1→1 0 1 1
1→1 1
2 2→2 0 2 2
1→2 0
2→2 1
1→2 1
3 3→3 0 3 3
2→3 0
1→3 0
3→3 1
··· ···
This kind of matrix block can be subdivided into subblocks using a method
similar to the one described above for vector cross sections. The code starts sum-
ming the product of jband and lord for the final energy groups until the data
for the next band will cause the sum to exceed maxw (5000 words in MATXSR).
These data are then written out as a matrix subblock. The code then repeats
the process for the rest of the group ranges. The result is a minimal number of
“Scattering Sub-Blocks,” none of which has a size larger than the file limit.
The second method used to compact scattering matrices is based on the
observation that the shape of the outgoing neutron or photon spectrum from
fission and radiative capture reactions tends to be independent of energy at
low neutron energies. GROUPR determines the group where significant energy
dependence begins. Below this point, it computes a single spectrum to describe
the outgoing neutron or photon distribution and a production cross section
to go with it. At high energies, it produces a group-to-group matrix. This
method can lead to appreciable reductions in storage requirements. For example,
consider the 187-group structure, which has many low-energy groups. The fission
spectrum for 235U doesn’t begin to show significant energy dependence until an
energy of about 9 keV. This means that there are 118 constant groups. A
187×187 matrix is thereby reduced to a 187×69 matrix, and 187-group vector,
and a 118-group vector — a 62 % reduction in storage requirements. Even
larger reductions in size are obtained in more favorable cases. The parameter
jconst gives the number of low-energy groups having a constant spectrum. If
jconst>0, a single “Constant Sub-Block” record will be given after the regular
NJOY2016 473

LA-UR-17-20093 15 MATXSR
“Scattering Sub-Block” records. This record will contain the spectrum spec and
the production cross section prod needed to reconstruct the low-energy part of
the full matrix. In mathematical form,
σx,g→g0=χLE
g0σLE
P x,g +σHE
x,g→g0,(476)
where LE stands for low energy, HE stands for high energy, χLE is the constant
spectrum, σLE
P x is the production cross section for reaction x, and σHE is the
normal group-to-group matrix.
15.3 Historical Notes
The original version of the MATXS specification was constructed in September,
1977. The “Matrix Control” record in this original version contained the names
and banding parameters for every group of every reaction. As a result, the record
could become very large for libraries with many groups. The MATXS format
was modified in September of 1980 to have a different “Matrix Control” record
for each reaction. For several years following this date, NJOY contained both
MATXSR and NMATXS modules, and two different versions of TRANSX were
in use. All traces of the original version of the format have now disappeared.
Changes beginning in the late 1980’s were introduced to make MATXSR
able to handle data types with either incoming or outgoing charged particles.
Actually, the format wasn’t changed. The particle, data type, and reaction name
conventions described in Tables 12 –22 were chosen, and these new names
required some corresponding changes in the code. The TRANSX code also
had to be modified to recognize the new names and to work with multiparticle
coupled sets.
The concept of using constant subblocks to reduce the size of GENDF and
MATXS files is actually quite old. Various versions of updates to install the
scheme were written over about a 5-year period. It was finally decided to per-
manently install the scheme in June of 1990. The changes required to GROUPR
were the easier part of the job; corresponding changes were required in DTFR,
CCCCR,MATXSR,POWR, and WIMSR. In addition, TRANSX had to be
changed to accept the new constant subblocks. Unfortunately, this change was
large enough to impact all MATXS users.
If many users were to be impacted, other nagging problems with the code
could also be corrected at that time. With the original format, it was always
474 NJOY2016

15 MATXSR LA-UR-17-20093
very difficult to add, replace, or extract a material. The data type loop was
outside the material loop, and the pieces for a given material were scattered
throughout the file. Therefore, the ordering of the file was changed to put
the data type loop inside the material loop along with the other submaterials.
With this change, it was easy to rewrite the BBC library maintenance code
from the TRANSX package to be able to insert a new material at any point
in the library. It was also easy to give BBC the capability of extracting a
short library containing only selected materials from a large MATXS library.
Using the short library can significantly speed up TRANSX runs to prepare
data for reactor design problems. The only disadvantage of the new ordering is
that identical photoatomic data blocks have to be given for each isotope of an
element. However, these data are not too bulky, and the additional overhead is
manageable. This arrangement might make it easier to add photonuclear data
in the future.
Finally, the current scheme of dividing the vector and matrix data into sub-
blocks was added. The goal was to keep the record size below some fairly large
maximum value (5000 words is currently being used). This kind of limit makes
it easier to design application codes that make efficient use of memory. In ad-
dition, using as few records as possible reduces the number of I/O operations
needed for a trip through the library, thereby improving execution time. The
new subblocking scheme is also very simple.
15.4 MATXS Libraries
The normal process for preparing a MATXS library using NJOY starts with
a series of runs to prepare PENDF tapes for each of the materials of inter-
est. For incident neutrons, these PENDF runs normally involve running the
modules RECONR,BROADR,UNRESR,HEATR, and THERMR. For inci-
dent photons and charged particles, only RECONR is needed. The next step is
to run GROUPR for each material and incident particle. Each GROUPR run
can produce data for all outgoing particles and for photons. As an example,
consider the problem of producing data for a coupled neutron-photon-proton
library. GROUPR would be run using the ENDF-6 incident-neutron data and
requesting mfd values of 3 (cross sections), 6 (neutron matrices, nn), 16 (photon
production matrices, nγ), and 21 (proton production matrices, np). GAM-
INR would be run to produce the photoatomic cross sections and γγ matrices.
GROUPR can be used to produce γn and γp matrices. GROUPR would be
run again for the ENDF-6 format proton sublibrary, requesting mfd values of 3
NJOY2016 475

LA-UR-17-20093 15 MATXSR
(cross sections), 6 (neutron production, pn), 16 (photon production, pγ), and
21 (proton scattering and production, pp).
Once all the GENDF fragments from all these GROUPR and GAMINR
runs are available, they can be merged into multimaterial GENDF tapes using
MODER. For the example above, three multimaterial GENDF tapes should
be prepared: one for incident neutrons, one for incident photons, and one for
incident protons. The input description in the following section shows how the
unit numbers for these three GENDF files are given to MATXSR.
When the MATXSR run is made, the code scans through all the input
GENDF tapes searching for the specified materials. For each material, it ex-
tracts all the data types requested in the MATXSR input and appearing on the
input tapes. In addition, it extracts every temperature, σ0value, reaction, and
Legendre order found on the input tapes. The following paragraphs describe
various special features of the formatting process.
Normal Neutron and Photon Data. Normal, infinitely dilute cross sec-
tions and group-to-group matrices for neutron reactions, photon production,
and photonuclear reactions are read from the input tapes and stored in the
MATXS file using the formats described above. Almost all partial reactions
are kept. Reaction names are constructed automatically; a number of examples
were given above in Tables 14 –22. The total cross section and weighting flux
from GROUPR are given in the section mf=3, mt=1 with both P0and P1com-
ponents. All four vectors are written to the MATXS file. A similar treatment is
used for mt=501 in the photoatomic case, except that only P0terms are saved.
The treatment of fission is also special. ENDF libraries sometimes use only
mt=18, the total fission reaction, for both cross section and emission spectrum
data; sometimes the partial fission cross sections (n,f), (n,n0f), (n,2nf), and
(n,3nf) are also given in File 3 (mt=19, 20, 21, and 38); and sometimes the partial
reactions are also used to describe the neutron emission matrix. If the last case
is found, the mt=18 matrix may not be complete above the threshold for second-
chance fission, and it should be ignored. Normally, it would not be processed in
GROUPR, but just in case, MATXSR will ignore it. Delayed-neutron spectra
processed in GROUPR are written into the section labeled mf=5, mt=455 on
the GENDF tape, and this section includes data for all time groups. MATXSR
adds up these separate time-group spectra to produce a single delayed-neutron
spectrum for the MATXS vector data blocks. Application codes can use the
fission data in the MATXS library to construct steady-state fission vectors as
476 NJOY2016

15 MATXSR LA-UR-17-20093
follows:
¯νSS
g=X
g0
σHE
fg→g0+σLE
P fg + ¯νD
gσfg
σfg
,(477)
where σHE is the matrix part of the prompt fission reaction, σLE
P fg is the low-
energy production cross section for fission neutrons, ¯νDis the total delayed-
neutron yield, and σf g is the fission cross section. If partial fission matrices are
available, the first two terms in the denominator would also have to be summed
over the reactions present. Continuing,
χSS
g0=X
g
σHE
fg→g0φg+χLE
g0X
g
σLE
P fgφg+χD
g0X
g
¯νD
gσfgφg
NORM ,(478)
where χLE is the constant-spectrum part of the fission reaction, χDis the total
delayed-neutron spectrum, and NORM is the quantity that normalizes χSS,
namely, the sum of the numerator over all g0. The weighting flux φgwould
normally be problem- and region-dependent in the application code.
Self-Shielding Data. If higher temperatures and σ0values are found on the
input GENDF file, MATXSR automatically prepares submaterials for them.
This self-shielding information can be used by application codes to prepare ef-
fective cross sections for mixtures of materials in various geometrical arrange-
ments using equivalence theory. This approach is often called the Bondarenko
method[39].
As discussed in more detail in the GROUPR section of this report, this
system is based on using a model flux for isotope iof the form
φi
`(E, T ) = C(E)
[σi
0+σi
t(E, T )]`+1 ,(479)
where C(E) is a smooth weighting flux, σi
t(E, T ) is the total cross section for
material iat temperature T,`is the Legendre order, and σi
0is a parameter that
can be used to account for the presence of other materials and the possibility of
escape from the absorbing region (heterogeneity). GROUPR uses this model flux
to calculate effective multigroup cross sections for the resonance-region reactions
(total, elastic, fission, capture) for several values of σ0and several values of T.
NJOY2016 477

LA-UR-17-20093 15 MATXSR
When σ0is large with respect to the highest peaks in σt, the flux is essentially
proportional to C(E). This is called infinite dilution, and the corresponding
cross sections are appropriate for an absorber in a dilute mixture or for a very
thin sample of the absorber. As σ0decreases, the flux φ(E) develops dips where
σthas peaks. These dips cancel out part of the effect of the corresponding peaks
in the resonance cross sections, thereby reducing, or self-shielding the reaction
rate. In the MATXS format, these effects are represented by differences instead
of the f-factors used in earlier formats (see the description of the BRKOXS file in
the CCCCR section of this report). That is, the submaterial corresponding to
temperature Tand background cross section σ0contains the differences between
the cross sections found on the GENDF tape for those parameters and the
infinitely dilute values found in the first submaterial (normally, T=300K and
σ0=1×1010barns).
This approach has two advantages. First, data for groups with no self-
shielding are automatically removed from MATXS vectors and matrices by the
banding process without having to violate the principle of generalization and
define a special format for neglecting values of “1.0” instead of values of “0.0.”
Second, effective cross sections can be accumulated by simply adding the self-
shielding effects multiplied by appropriate interpolation weights to an accumu-
lating sum that starts out equal to the infinitely dilute cross section. With
f-factors, it is necessary to save the infinitely dilute cross sections during each
step so that they can be multiplied by the f-factors. Thus, using differences is
more economical in coding and in storage space requirements. The TRANSX
code makes good use of this feature.
Thermal Data. ENDF-6 thermal data comes from a thermal sublibrary. In
this sublibrary, the various material configurations are handled as separate ma-
terials. However, after the ENDF data have been processed by the THERMR
module, the different thermal materials are handled as reactions. Table 21 gives
the correspondence between the special NJOY thermal MT numbers and the
actual thermal materials. These are the names that work for ENDF/B-VII[7].
If MATXSR is used for ENDF/B-VII (or earlier) materials, the name for BeO
will be slightly wrong, but it could be fixed by hand editing of the MATXS file.
Each of these thermal reactions corresponds to a particular dominant mate-
rial. For example, mt=222 gives the thermal cross section for hydrogen bound
in water. It will only appear in the material H1 in a MATXS library. Similarly,
478 NJOY2016

15 MATXSR LA-UR-17-20093
mt=223-227 will only appear in 1H, mt=228 will only appear in 2H, mt=229-230
will only appear in natC, mt=231-234 will only appear in 9Be, and mt=235-
236 will only appear in natZr. Free-gas scattering (mt=221) will appear in all
materials.
Many of these materials describe the scattering from one atom of a compound
bound in that compound; for example, H in H2O, D in D2O, or Zr in ZrH. The
application code using this data is expected to add on the effects of scattering
from the other atoms of the compound. For water, the scattering from free
oxygen is added to the “H in H2O” scattering. For zirconium, the scattering for
“H in ZrH” is added to the scattering from “Zr in ZrH”. There are two exceptions
in the existing ENDF/B evaluations. The benzene data set contains the entire
scattering from the C6H6molecule normalized to the hydrogen cross section.
Therefore, if an application code specifies H1 with the benzene scattering option
and the correct density for H1 in the system, the result will contain all of the
benzene scattering effect. No additional scattering is to be added for the carbon
atoms. Similarly, BeO contains all the scattering from the compound normalized
to the beryllium cross section. Check the THERMR section of this report for
more information.
Six of these materials have names ending with $. These reactions represent
coherent elastic scattering from crystalline powdered materials (C, Be, BeO)
or incoherent elastic scattering from solids containing hydrogen (polyethylene,
ZrH). These reactions contain ingroup elements only in the scattering matrices;
that is, they cause angular redistribution without energy loss in scattering. Each
$ reaction should be added to the corresponding inelastic reaction by the appli-
cation code. This part of the scattering can lead to difficulties with transport
corrections in discrete-ordinates transport codes.
The final unique aspects of the thermal data are that the matrices show
upscatter, and they are only defined below some maximum energy. The energy
range aspect is easily handled by the banding method used to reduce the size
of the vector blocks. The upscatter aspect is handled by jband and ijj. The
order of storage for a simple thermal case with only 2 upscatter groups would
be as follows:
NJOY2016 479
LA-UR-17-20093 15 MATXSR
Band Element jband ijj
··· ···
27 27→27 2 27
26→27
28 29→28 3 29
28→28
27→28
29 30→29 3 30
29→29
28→29
30 30→30 2 30
29→30
Charged-Particle Data. The treatment of data for incident charged parti-
cles is very similar to that used for neutron data, except for charged-particle
elastic scattering. The elastic channel has contributions from Coulomb scat-
tering that become infinite as the scattering angle goes to zero. In nature,
this singularity is removed by electronic screening, but some other approach
is needed for a data set that concentrates on isolated nuclear reactions. The
approach selected is used in some existing applications. The elastic scattering
distribution is broken up into two parts: (1) a normal angular distribution for
angles from some low cutoff, say 20◦, back to 180◦, and (2) a straight-ahead
continuous slowing-down contribution to represent the effects of angles below
the cutoff. The continuous slowing-down part is closely related to the normal
“stopping power” for charged particles. The large-angle part can be converted
into a normal scattering matrix (see the discussion of charged-particle elastic
scattering in the GROUPR chapter of this manual for more details).
Discrete-ordinates transport codes can often be modified to handle charged-
particle data in this form, but they require an effective total cross section. The
ENDF-6 format for charged-particle data does not define a total cross section
because of the singularity in the elastic contribution. However, for application
purposes, a reasonable definition of an effective total cross section is that it is the
sum of all the partial reaction cross sections including the cross section obtained
for the truncated elastic scattering reaction. This is the method that MATXSR
uses to compute the quantities ptot0,dtot0,ttot0,etc.
480 NJOY2016

15 MATXSR LA-UR-17-20093
Delayed-Neutron Data. Delayed-neutron yields, spectra, and decay con-
stants by time group are required by reactor kinetics codes. The previous CCCC
format for these data was DLAYXS (see the CCCCR chapter of this manual).
Because of the generalization inherent in the MATXS format, these data can
be added without any changes in the structure of the file. This option has not
yet been added to MATXSR, and the procedures used will be described in a
future version of this report.
Decay-Photon and Decay-Heat Data. Many nuclear reactions leave ra-
dioactive products. These products may be simple daughter isotopes that decay
in a few steps to a stable final state with the emission of a few photons and elec-
trons (or heat), or they may be a complex array of fission product isotopes that
emit a complex spectrum of photons and electrons (or heat) showing many time
constants. Procedures to store these data in MATXS libraries will be included
in a future version of this report.
15.5 User Input
The user input specifications below were copied from the comment cards at
the beginning of the MATXSR module. It is always a good idea to check the
comment cards in the current version of the code for possible changes.
!---input specifications (free format)---------------------------
!
! card 1 units
! ngen1 input unit for data from groupr
! ngen2 input unit for data from gaminr
! nmatx output unit for matxs
! ngen3 incident proton data from groupr (default=0)
! ngen4 incident deuteron data from groupr (default=0)
! ngen5 incident triton data from groupr (default=0)
! ngen6 incident he3 data from groupr (default=0)
! ngen7 incident alpha data from groupr (default=0)
! card 2 user identification
! ivers file version number (default=0)
! huse user id (up to 16 characters, delimited by ’,
! ended by /) (default=blank)
! card 3 file control
! npart number of particles for which group
! structures are given
NJOY2016 481

LA-UR-17-20093 15 MATXSR
! ntype number of data types in set
! nholl number of cards to be read for hollerith
! identification record.
! nmat number of materials desired
! card 4 set hollerith identification
! hsetid hollerith identification of set
! (each line can be up to 72 characters,
! delimited with ’, ended by /)
! card 5 particle identifiers
! hpart hollerith identifiers for particles
! (up to 8 characters each)
! card 6 energy groups
! ngrp number of groups for each particle
! card 7 data type identifiers
! htype hollerith identifiers for data types
! (up to 8 characters each)
! card 8 input particle ids
! jinp input particle id for each data type
! card 9 output particle ids
! joutp output particle id for each data type
! card 10 material data (one card per material)
! hmat hollerith material identifier
! (up to 8 characters each)
! matno integer material identifier
! (endf mat number)
! matgg mat number for photoatomic data
! (default=100*(matno/100) as in endf-6)
!
!-------------------------------------------------------------------
Card 1 is used to specify the units for the input GENDF tapes and the
output MATXS library. As usual, the sign of a GENDF unit number is used
to determine its mode; negative numbers mean binary, and positive numbers
mean coded (i.e., ASCII). The output file is always binary, and its sign is ig-
nored. The most common MATXSR runs are for neutron and photon data only.
In these cases, card 1 can be truncated after the nmatx. If incident charged-
particle GENDF files are available, any of the units ngen3 through ngen7 can
be assigned.
Card 2 is used to control the MATXSR print option iprint and to provide
the information for the MATXS “User Identification” record. An example for
482 NJOY2016
15 MATXSR LA-UR-17-20093
Card 2 follows:
0 17 ’T2 LANL NJOY’/
Card 3 is used to input the counts for the “File Control” record and to tell the
user input routine how many quantities to read in subsequent input cards. Card
4 is repeated nholl times to give the Hollerith description for the library. Each
line must be delimited by quote characters and terminated by /. For example,
’ MATXS17 27 FEB 91 ’/
’ 69-GROUP THERMAL LIBRARY FROM ENDF/B-VI ’/
’ THIS LIBRARY INCLUDES NEUTRON, PHOTON, AND ’/
’ THERMAL SCATTERING DATA FOR 133 MATERIALS. ’/
The lines are written out on the MATXS file as given, except that the maximum
length for each line is 72 characters.
Card 5 is used to read in the Hollerith names for the npart particles for this
library. The standard names for the particles were given above in Table 12. The
number of groups desired for each particle are given on card 6. The data-type
names (see Table 13) are given on Card 7. Cards 8 and 9 are used to specify
the input and output particles for each data type. The user should take care
that the number of groups given for each particle is consistent with the input
data, and that the particle assignments to data type names (jinp and joutp)
are consistent with the names. The code does not check.
Card 10 is repeated nmat times to specify the materials to be written out
on the library. The rules for constructing the material names hmat were given
in Section 15.2. The matno parameter is the ENDF MAT number for this
material as used on the input GENDF files. For ENDF/B-VI, the MAT number
is the same for all sublibraries (that is, for incident neutrons, photons, protons,
etc.), and only one value is needed to specify the desired material. However,
photoatomic data are atomic in character, and the MAT numbers always refer
to the element. For example, MAT=2600 for the photoatomic data of iron.
MATXSR reads a second MAT number field, matgg, for the photoatomic data.
Its default value is given by
NJOY2016 483
LA-UR-17-20093 15 MATXSR
100*(MATNO/100)
and it is, therefore, not usually needed. The normal form for card 10 would be
as follows:
FE56 2631/
However, the photoatomic libraries for earlier versions of the ENDF/B files
used MAT numbers like 26 for elements. The matgg parameter can be used to
process data from these older libraries. Note that delimiting quote characters
are not required for Hollerith names that are single words and start with a letter.
MATXSR always processes all submaterials found on all the nonzero GENDF
units ngen1 through ngen7. It processes every temperature and σ0value found.
It processes (almost) every reaction cross section and matrix found, and it pro-
cesses every Legendre order given. The only way to control the contents of
the MATXS library is through the input to GROUPR or GAMINR and by the
materials included when building the input GENDF files. A convenient way
to handle this task is to assemble the results of a number of single-material
GROUPR runs into composite GENDF tapes using MODER.
15.6 Coding Details
Subroutine matxsr is the only public call for module matxsm. The module has
a number of global variables and arrays defined. One key set of variables and
arrays provides the area for accumulating the MATXS data. It provides a set
of equivalenced arrays so that integers, reals, and Hollerith strings can all be
stored in the same binary records. It sets up both integers and reals to be 4-byte
quantities. Hollerith words (with up to 8 characters each) are 8-byte quantities.
The CCCC mult value is set to 2. See a(200000), ia(200000), and ha(100000).
The parameter isiza=200000 defines the size of these equivalenced arrays in
4-byte units.
The internal representation for all the elements of the MATXS file and for
GENDF data uses 8-byte quantities.
The next step in subroutine matxsr is to read in the unit numbers for the
input and output files and to open the files. Note that the sign for nmatx is
484 NJOY2016

15 MATXSR LA-UR-17-20093
ignored. It will always be binary. Several binary scratch files are also opened.
Next, the user input for the “File Identification” record is read (see card 2 in
the user input description), and the cmatxs routine is called to read the input
GENDF files and construct the output MATXS file. When cmatxs returns, the
main routine closes the units, prints its final timer line, and returns to the NJOY
program.
Subroutine cmatxs starts by defining three constants:
nsubmx=100 is the maximum number of submaterials allowed for a material,
including data types, temperatures, and background cross sections;
maxord=5 is the maximum Legendre order (that is, P5allowed for group-to-
group matrices; and
maxw=5000 is the maximum size for vector block and matrix subblock records
on the MATXS file.
It continues by calling ruinm to read the user’s input. Some of the quantities
read by ruinm are stored directly into ia,a, and ha using pointers like icont
and iholl. Note the use of mult=2 to compute the jump in the index when
Hollerith items or stored, and note the the variable next keeps track of the
current location in the MATXS equivalenced arrays. Subroutine ruinm returns
to cmatxs after loading the “File Data” record.
The next step is to call subroutine mtxdat to read the input GENDF data
and write it to the scratch tapes used later in this subroutine. The first step is to
set up an area at pointer igrup for the npart group structures and to calculate
its length. Note that the number of words reserved is forced to be even in order
to avoid possible word-alignment problems for these 4-byte words. With the
current version of GROUPR, all particles are assumed to use the same group
structure. Photons have a different one. It is only necessary to look through the
unit numbers from input card 1 and find the first one that contains data. The
group structures are then read in from mf=1,mt=451 and reversed to have the
conventional decreasing-energy order. The subroutine now reserves space for the
“Material Control” record starting at imatc with length nwmc and begins the
material loop (see do 700 im=1,nmat). Note how the Hollerith material name
is loaded into the “Material Control” record storage area by making use of the
mult parameter and the equivalence between the arrays aand ha.
The first loop inside the material loop is the data-type loop (see do 600 i=1,
ntype). The same MAT number is used for all particles, but a different one is
used for photoatomic data. The input unit to be used depends on the identity
NJOY2016 485

LA-UR-17-20093 15 MATXSR
of the incident particle. Since these comparisons use constants like hprot with
values like “6hp ,” it is important to use the standard names in the user input
(see Table 12). The identity of the outgoing particle for the data type determines
the MF number for the matrices on the GENDF tape, mfm. As described in the
GROUPR section of this report, the MF assignments are as follows:
MF value Outgoing Particle
6 neutrons
16 photons
21 protons
22 deuterons
23 tritons
24 3He particles
25 alphas
26 photoatomic data
The MF number for the vector data (mfv) is 3, except for the photoatomic case,
where it is 23.
The next step is to search for the desired material imat on the current input
tape. When the first occurrence of imat has been found, mtxdat reads in its
head record, and then it sets up a loop over all the temperatures for this ma-
terial (the loop goes through statement number 300). As it reads through each
temperature, it copies the results to scratch file nscr. The data for the first
temperature is also copied to scratch file iref. File iref will be used for the
higher temperature and σ0values to calculate the delta-sigma values. While the
data are being copied, mtxdat counts the number of one-dimensional reactions,
noned, and the number of two-dimensional reactions, ntwod, for each value of
the background cross section, σ0. When the scratch tapes are complete, the sub-
routine starts a loop over σ0for this material and temperature; it calls vector
to produce the vector cross sections, it calls matrix to produce the matrix cross
sections, and it loads the information on this submaterial into the “Material
Control” record. When the σ0loop is complete, the code jumps back to state-
ment number 300 to get the next temperature. When all the temperatures have
been processed, it reaches statement number 600 and goes back through the
entire process again for the next data type. When the “do 600” loop exits, the
entire “Material Control’ block has been filled in, and the subroutine writes the
record to scratch file nscrt6.
At this point, the processing for material imat is complete. The “do 700”
loop continues until all the requested materials have been found and processed.
486 NJOY2016

15 MATXSR LA-UR-17-20093
Subroutine findg is used to search GENDF file ntape for a specified section
(mat,mf,mt). If it does not find the requested section, a fatal error message is
issued. Materials (mat) do not have to be in order on a GENDF tape. Therefore,
this routine simply reads forward until it comes to the first record matching the
requested mat,mf, and mt values. If the section is not found, it rewinds once
and searches again. When the section is found, it backspaces by one record so
that the next record read will be the desired record.
Subroutine hname is used to construct a Hollerith reaction name hreact from
an ENDF MT number (mt), an ENDF “LR flag” (lr), and an incident particle
name (hp). The definitions of the names were discussed above in connection
with Tables 14–22, and the actual MT numbers and strings used are given in
parameter arrays in this subroutine. If no preset name is found for an MT
number, a default name of the form MTnnn is constructed.
Subroutine vector reads the cross section vectors for one submaterial (that
is, one data type, one temperature, and one σ0). It starts by clearing some flags
that are used to detect the occurrence of particular reactions. For example,
k107 is set if the (n,α) reaction (mt=107) is found. Pointers are assigned for the
vector control and vector data arrays (see ivcon,ivdat). Note that there must
be enough container memory available to hold all the vector data (ning*n1d
words). The routine now starts up a loop over sections on the input scratch tape
(the loop goes through statement number 115). The sections that it processes
are determined by the value of mfd, which will be 3, except for photoatomic
data, when it will be 23. Delayed fission χis a special case; it will be found in
the section with an MT value of mfd+2. As each interesting section is found, the
Hollerith name for the reaction is constructed, and the location of the reaction
relative to ivdat is computed. When the total cross section is found (mt=1),
names and locations are set up for the P`components of the weight function (for
example, nwt0 and nwt1) and for the P`components of the total cross section
(ntot0 and ntot1). If appropriate, the first letter of these names might be p,
d,etc., depending on the incident particle. When the total photoatomic cross
section is found (mt=501), names and locations are defined for the γweight
and the P0cross section (gwt0 and gtot0). When the charged-particle elastic
cross section is found for particle x(mt=2), names and locations are set up for
the weight function xwt0 and the effective charged-particle total cross section
xtot0. Once the name and location have been selected, the code reads the data
for all groups from file nscr and stores them at the selected location. If this
submaterial corresponds to a higher temperature or σ0, the corresponding data
NJOY2016 487

LA-UR-17-20093 15 MATXSR
is also read from file iref and subtracted from the nscr data. As a result,
self-shielding information in the MATXS file is given as differences rather than
f-factors as in the previous CCCC self-shielding file, BRKOXS. The delayed-
neutron spectra are read from mf=5, mt=455; the spectra from the time groups
on the GENDF tape are added to obtain a single spectrum χd.
There is a special feature in vector for incident charged-particle reactions.
Although discrete-ordinates transport codes require a total cross section, it is not
actually possible to compute a total cross section for charged-particle reactions
because Coulomb scattering is singular for straight-ahead scattering (at least
in the absence of electronic screening). The solution to this problem used by
GROUPR is to exclude a range of forward angles from the charged-particle
elastic matrix (this angular range is handled by continuous-slowing-down theory
in the application codes). Therefore, MATXSR can construct an effective total
cross section by adding all the reaction cross sections found to this truncated
elastic cross section. However, it must be careful to watch for possibly redundant
cross sections that must be omitted from the sum; for example, if the total (x,p)
cross section (mt=103) is present for incident particle x, the discrete-level (x,pn)
cross sections and the (x,p) continuum reactions (mt=600-649) must be omitted
from the sum. This is the function of flags like k103.
There is another special feature for nuclide production data. When using
this experimental ENDF format, there may be a number of different sections on
the GENDF file producing the same product. These separate contributions are
added up into one single production cross section in the block of coding starting
at statement number 410.
When all the reactions have been entered, subroutine vector thins the vec-
tor data just loaded by removing unneeded leading or trailing zeros (actually,
numbers less than small=1.e-30) from each reaction. These zeros can arise
from thresholds and upper limits for thermal-range reactions. In addition, since
data for the higher temperatures and σ0values are stored as differences, zero
(or very small) elements can imply that there is no significant temperature or
σ0dependence. The subroutine simply steps through the ivdat data block to
find the band limits nfg and nlg for each reaction, to squeeze out the zeros,
and to record the band limits in the vector control block at ivcon. When all of
the n1d reactions have been processed, the resulting vector data is written out
as a series of “Vector Block” records on scratch tape nscr3. The subblocking is
controlled by maxw (5000 words). The code just steps through the cross section
bands until the next reaction will cause the sum to exceed maxw. It then writes
488 NJOY2016

15 MATXSR LA-UR-17-20093
these reactions to the scratch file, and it repeats the process for the next group
of reactions. Each record will have fewer than maxw words, and the minimum
number of records will be produced within the restriction that no reaction is bro-
ken up between records. The last step in the subroutine is to write the “Vector
Control” record for this submaterial to scratch file nscrt2.
Subroutine matrix reads the group-to-group matrix data for this submate-
rial, converts it to MATXS format, and writes the results to a scratch file. The
pointer imcon is used to accumulate matrix control information, pointer icdat
is used for the low-energy constant spectrum data (if any), ijgll is used for
banding information, and pointer imdat for the actual matrix data. The main
loop is over the n2d matrix reaction types. The head card for the reaction is
read in from nscr, and for higher temperatures and σ0values, from iref also.
Subroutine hname is called to construct the Hollerith reaction name, subroutine
band is called to read through the data and determine the banding parameters
used to remove excess zero elements, and subroutine shufl is called to read
through the input scratch file again and load the data into memory in its final
compact form.
Subroutine band is fairly simple. It loops over all the groups for this reaction
on nscr and/or iref. When the loop is finished, jg1lo(i) and jg1hi(e)
contain lowest and highest initial-group indices found for each final group i.
Note that the actual cross section for a matrix element (or the cross section
difference when iref is being used) is not checked; it is assumed that GROUPR
has done a good job removing excess zeros. This should be improved in a future
version. Before returning, these limiting group indices are used to compute the
MATXS parameters jband and ijj, and to insert them into the accumulating
matrix control block at pointer imcon).
Subroutine shufl starts by initializing a loop through statement number 100
that will be used to produce “Matrix Sub-Block” records. Inside this loop, the
code sums the bandwidths found by band to find out how many final-energy
group bands can fit in a subblock with length less than or equal to maxw words.
The result is a pair of group indices i0 and imax that define the range of groups
to be included in the subblock. Subroutine shufl now makes a pass through
scratch file nscr, and also through scratch file iref for higher temperatures and
σ0values. It stores away the constant subblock data (ig=0 for the constant
spectrum and ig2lo=0 for the production cross section), if found. For each
group-to-group element, it computes the final group index jg2. If the group is
in the allowed range for this subblock, it computes the output location noloc
NJOY2016 489

LA-UR-17-20093 15 MATXSR
and stores the element in memory. For higher temperatures and σ0values, it
subtracts the base value found on file iref. (This step is normally needed for
neutron elastic scattering only.) When the group loops for nscr and iref are
complete, the subroutine writes out the “Matrix Sub-Block” record on a scratch
file, resets the ng2z parameter to the top group of the subblock, and continues
the loop through statement number 100 to produce the rest of the subblocks for
this reaction. The resulting series of subblock records on the scratch file are all
less than maxw words in length, and the number of records is minimal within the
restriction that bands are not split between records.
Returning to matrix, data already in memory are used to complete the “Ma-
trix Control” record, which is written out onto nscrt2. If no matrix data were
found by band and shufl, a dummy matrix control record is written on nscrt2
and a dummy matrix data record is written on nscrt3. Finally, the constant
subblock data saved in shufl (if any) is written to nscrt3.
Returning to subroutine cmatx, after the call to mtxdat, the data stored
in the a,ia,ha equivalenced arrays are written to the output file for the “File
Identification,” “File Control,” “Set Hollerith Identification,” “File Data,” and
“Group Structure” records. In a loop over materials, the “Material Control”
record is copied from nscrt6 to the output file. Then, in a loop over the subma-
terials for this material, the “Vector Control” records are copied from nscrt2,
the “Vector Blocks” are copied from nscrt3, the “Matrix Control” blocks are
copied from nscrt2, and the “Matrix Subblocks” are copied from nscrt3. Sub-
routine cmatx then returns to the main MATXSR routine, files are closed, and
the MATXSR run is complete.
15.7 Error Messages
The fatal-error and warning messages generated by MATXSR are given below,
along with suggested actions to alleviate the problem.
error in mtxdat***input error (nin=0)
No input GENDF tape has been given. Check Card 1 of the user input.
error in mtxdat***too many submaterials
The code is currently limited to 100 submaterials per material. See nsubmx=100
in cmatxs.
error in findg***mat or mf or mt le 0 not allowed
Subroutine findg has been asked to search for an illegal section on the
GENDF tape.
490 NJOY2016

15 MATXSR LA-UR-17-20093
error in findg***mat=nnnn mf=nn mt=nnn not on tape
The requested section was not found on the input GENDF tape. Check
that the correct tape was mounted.
error in vector***exceed input data array size.
Check the parameter maxb=30000 in vector.
error in band***input too large
Check the parameter maxb=30000 in matrix.
error in shufl***input too large
Check the parameter maxb=30000 in shufl.
error in lst1io***storage exceeded
See nbmax=2000 in mtxdat, the size of the array b.
NJOY2016 491

LA-UR-17-20093 15 MATXSR
492 NJOY2016

16 RESXSR LA-UR-17-20093
16 RESXSR
In thermal reactor systems, resonance self-shielding in the near epithermal range
(e.g., 4-200 eV) is often poorly represented by the simple Bondarenko model[39].
The normal form of this model as used by the TRANSX code[41] assumes that all
the absorber resonances are narrow with respect to the energy lost in neutron
scattering. In this near epithermal range, many resonances have widths that
violate this assumption. A number of ways exist to try to compensate for this
problem, one example being intermediate-resonance theory as discussed in the
WIMSR chapter of this manual. The GROUPR flux calculator can also be used
to compensate for wide and intermediate resonances, but only for homogeneous
systems or idealized reactor cells.
One way to solve this problem accurately is to move the flux calculation into
TRANSX, where full information on material mixtures and geometry can be
made available. To test this concept, an experimental version of TRANSX was
created that could do a full pointwise flux solution using collision probabilities
for cylindrical systems with an arbitrary number and arrangement of shells.
It could then take the computed flux by region and generate new, accurate,
self-shielded cross sections for the groups in the near epithermal range.
Of course, this experimental code required pointwise cross sections in the
epithermal range to do these calculations. Since TRANSX uses CCCC standard
interface files[11] for all other communication to the outside world, it was decided
to define an interface format for resonance-region pointwise cross sections, or
RESXS. This RESXSR module was written to produce the RESXS file from
PENDF tapes produced using the other modules of NJOY.
This module and the RESXS format may be of use for other applications
besides TRANSX.
16.1 Method
For each material, the data for elastic (mt=2), fission (mt=18), if present, and
capture (mt=102) for the desired energy range and for all the desired temper-
atures are read in and interpolated onto a single union grid. This large set of
cross sections is then thinned down using an input tolerance EPS. Using a union
grid for all reactions and temperatures makes temperature interpolation and
reconstruction of the total cross section easy.
These data are then written out in the specially defined RESXS format. The
key to this format is the “Cross Section Block.” For each incident energy, it is
NJOY2016 493
LA-UR-17-20093 16 RESXSR
necessary to give two or three cross sections for each temperature. If all the many
energy points were given in one record, the record could be many thousands of
words in length. Therefore, the cross section data are broken up into a set of
blocks, where each block contains NBLOK records, except the last block can be
shorter.
16.2 RESXS Format Specification
The specification for the RESXS format follows in the standard CCCC style[11].
These card images were copied from the comment cards at the beginning of the
RESXSR source.
!***********************************************************************
! proposed 09/24/90 -
! -
!f resxs -
!e resonance cross section file -
! -
!n this file contains pointwise cross -
!n sections for the epithermal resonance -
!n range to be used for hyper-fine flux -
!n calculations. elastic, fission, and -
!n capture cross sections are given vs -
!n temperature. linear interpolation is -
!n assumed. -
! -
!n formats given are for file exchange only -
! -
!***********************************************************************
!
!
!-----------------------------------------------------------------------
!s file structure -
!s -
!s record type present if -
!s ============================== =============== -
!s file identification always -
!s file control always -
!s set hollerith identification always -
!s file data always -
!s -
494 NJOY2016

16 RESXSR LA-UR-17-20093
!s *************(repeat for all materials) -
!s * material control always -
!s * -
!s * ***********(repeat for all cross section blocks) -
!s * * cross section block always -
!s * *********** -
!s ************* -
! -
!-----------------------------------------------------------------------
!
!
!-----------------------------------------------------------------------
!r file identification -
! -
!l hname,(huse(i),i=1,2),ivers -
! -
!w 1+3*mult -
! -
!b format(4h ov ,a8,1h*,2a8,1h*,i6) -
! -
!d hname hollerith file name - resxs - (a8) -
!d huse hollerith user identifiation (a8) -
!d ivers file version number -
!d mult double precision parameter -
!d 1- a8 word is single word -
!d 2- a8 word is double precision word -
! -
!-----------------------------------------------------------------------
!
!
!-----------------------------------------------------------------------
!r file control -
! -
!l efirst,elast,nholl,nmat,nblok
! -
!w 5 -
! -
!b format(4h 1d ,2i6) -
! -
!d efirst lowest energy on file (ev) -
!d elast highest enery on file (ev) -
!d nholl number of words in set hollerith -
NJOY2016 495

LA-UR-17-20093 16 RESXSR
!d identification record -
!d nmat number of materials on file -
!d nblok energy blocking factor -
! -
!-----------------------------------------------------------------------
!
!
!-----------------------------------------------------------------------
!r set hollerith identification -
! -
!l (hsetid(i),i=1,nholl) -
! -
!w nholl*mult -
! -
!b format(4h 2d ,8a8/(9a8)) -
! -
!d hsetid hollerith identification of set (a8) -
!d (to be edited out 72 characters per line) -
! -
!-----------------------------------------------------------------------
!
!
!-----------------------------------------------------------------------
!r file data -
! -
!l (hmatn(i),i=1,nmat),(ntemp(i),i=1,nmat),(locm(i),i=1,nmat) -
! -
!w (mult+2)*nmat -
! -
!b format(4h 3d ,8a8/(9a8)) hmatn -
!b format(12i6) ntemp,locm -
! -
!d hmatn(i) hollerith identification for material i -
!d ntemp(i) number of temperatures for material i -
!d locm(i) location of material i -
! -
!-----------------------------------------------------------------------
!
!
!-----------------------------------------------------------------------
!r material control -
! -
496 NJOY2016

16 RESXSR LA-UR-17-20093
!l hmat,amass,(temp(i),i=1,ntemp),nreac,nener -
! -
!w mult+3+ntemp -
! -
!b format(4h 6d ,a8,1h*,1p1e12.5/(6e12.5)) hmat,temp -
!b format(2i6) nener,blok -
! -
!d hmat hollerith material identifier -
!d amass atomic weight ratio -
!d temp temperature values for this material -
!d nreac number of reactions for this material -
!d (3 for fissionable, 2 for nonfissionable) -
!d nener number of energies for this material -
! -
!-----------------------------------------------------------------------
!
!
!-----------------------------------------------------------------------
!r cross section block -
! -
!l (xsb(i),i=1,imax) -
! -
!c imax=3*ntemp*(number of energies in the block) -
! -
!w imax -
! -
!b format(4h 8d ,1p5e12.5/(6e12.5)) -
! -
!d xsb(i) data for a block of nblok or fewer point energy -
!d values. the data values given for each energy -
!d are nelas, nfis, and ng at temp(1), followed by -
!d nelas, nfis, and ng at temp(2), and so on. -
! -
!-----------------------------------------------------------------------
16.3 User Input
The following input specifications were taken from the comment cards at the
beginning of the RESXSR source. It is always a good idea to check the comment
cards in the current version in case there have been changes.
NJOY2016 497

LA-UR-17-20093 16 RESXSR
! User input:
!
! card 1 units
! nout output unit
!
! card 2 control
! nmat number of materials
! maxt max. number of temperatures
! nholl number of lines of descriptive comments
! efirst lower energy limit (ev)
! elast upper energy limit
! eps thinning tolerance
!
! card 3 user id
! huse hollerith user identification (up to 16 chars)
! ivers file version number
!
! card 4 descriptive data (repeat nholl times)
! holl line of hollerith data (72 chars max)
!
! card 5 material specifications (repeat nmat times)
! hmat hollerith name for material (up to 8 chars)
! mat endf mat number for material
! unit njoy unit number for pendf data
!
The only difficulty in constructing the input file for RESXSR is in choosing
efirst,last, and eps. The goal is to get a set that can be used to generate
reasonably good fluxes and cross sections without being too expensive. Also, the
energy limits should be consistent with the group bounds that will be used for
the multigroup part of the calculation. However, the upper energy limit should
be enough above the highest group to be treated with this method that “Placek”
oscillations from the discontinuity in the source from higher energies have some
chance to die out. It is possible that the values of eps could be somewhat larger
than the value used in RECONR and BROADR to attain additional economy.
In practice, it may be necessary to iterate a few times to get a good compromise.
498 NJOY2016

17 ACER LA-UR-17-20093
17 ACER
The ACER module prepares libraries in ACE format (A Compact ENDF) for
the MCNP continuous-energy neutron-photon Monte Carlo code[18]. One of
the design goals for MCNP has been to use the most detailed representation
of the physics of a problem that is practical. Therefore, the ACE format has
evolved to include all the details of the ENDF[9] representations for neutron
and photon data. However, for the sake of efficiency, the representation of data
in ACE is quite different from that in ENDF. The fundamental difference is
the use of random access with pointers to the various parts of the data. Other
key differences include the use of union energy grids, equal-probability bins, and
cumulative probability distributions.
This chapter describes the ACER module in NJOY2016.0.
17.1 ACER and ACE Data Classes
The ACE format provides for several different “classes” of data, the most popular
being the “continuous-energy neutron” class. Others include include photo-
atomic data, thermal data, and photo-nuclear data. Files for each class of
data are distinguished by a code letter at the end of the ZAID identifier for
each material. For example, a file with a ZAID identifier of “13027.00c” would
contain continuous-energy neutron data. The data classes currently handled by
ACER and the class suffixes are given in Table 23.
For the Fortran-90 version of ACER, each different class of ACE data is
handled by a different sub-module; the module acefc handles the continuous-
Table 23: ACE Data Classes and ZAID suffixes
Suffix ACE Data Class
c continuous-energy neutron data
t thermal S(α, β) data
y dosimetry data
p photo-atomic data (incomplete)
u photonuclear data
h continuous-energy proton data
o continuous-energy deuteron data
r continuous-energy triton data
s continuous-energy 3He data
a continuous-energy alpha data
NJOY2016 499

LA-UR-17-20093 17 ACER
energy neutron data class (and also incident charged particles), the module
aceth handles thermal data, the module acepa handles photo-atomic data, and
the module acepn handles photonuclear data. There is also an acecm module
containing routines common to more than one of the ACER sub-modules. The
main ACER module itself acem is used to read in the user’s input commands and
then to call the main subroutines from the appropriate sub-module to carry out
the ACE library production desired. The following sections of this chapter will
describe the methods used to construct data for each of these classes, discuss
the user input and how to set up ACER jobs, and give coding details for the
ACER set of modules.
17.2 Continuous-Energy Neutron Data
The next few sections will discuss the details of preparing data for this very
important class of ACE data. The module acefc exports two subroutine calls;
namely, acetop for producing the continuous-energy data file, and acefix for
printing or editing continuous-energy data files. The latter function also includes
consistency checking and plotting.
17.3 Energy Grids and Cross Sections
MCNP requires that all the cross sections be given on a single union energy grid
suitable for linear interpolation. This was also true of its predecessor MCN[90],
and this is one of the reasons that the RECONR and BROADR modules of
NJOY are also organized around union grids and linear interpolation.
The energy grid and cross section data on an NJOY PENDF tape are basi-
cally consistent with the requirements of MCNP. In the still recent past, when
computers were smaller, there was a problem that many ENDF evaluations (es-
pecially ENDF/B-VI evaluations) produced energy grids with very large num-
bers of points. A few examples from early ENDF/B-VI releases are shown in
Table 24. Thus, it was considered useful to reduce the size of these data sets by
reducing the number of energy points in the union grid. This kind of thinning is
no longer routinely done for libraries produced by LANL, but it is still available,
if needed.
Of course, any thinning of the energy grid will result in a loss of accuracy.
The goal is to control the accuracy loss and balance it against the memory
requirements. This balance will vary from application to application. For ex-
ample, a user doing fusion calculations may be able to drastically reduce the
500 NJOY2016

17 ACER LA-UR-17-20093
number of resonance points at low energies without affecting the results signifi-
cantly. Similarly, a thermal-reactor designer may be able to reduce the number
of energy points used above 100 to 200 eV with minimal impact on the answers.
The acefc module provides two different thinning algorithms (implemented
in unionx). First, the code can do a very crude removal of points; for example,
it can remove 2 out of every 3 points for all energies between E1 and E2. This is
called the “energy skip” option. It is now obsolete, and it is not recommended.
The second thinning option is “integral fraction” thinning. The idea here
is to attempt to preserve the resonance integral. Two weighting functions are
provided: 1/E and flat. The former is best for thermal-type problems, and the
latter preserves more points in the high-energy range. The user specifies a target
number of points for the final energy grid. The code uses this target number
to estimate an initial thinning tolerance, and it starts moving through the en-
ergy grid and calculating the contributions to the total and capture resonance
integrals from each energy panel. Panels whose contributions to both integrals
are small with respect to the current tolerance are candidates for rejection. The
code has additional tolerances designed to preserve major features and to pre-
serve a reasonable minimum lethargy step; these features keep some of the points
from being rejected. When the entire energy range has been scanned, the code
checks the resulting number of points against the user’s target. If the goal has
not been reached, it doubles the tolerance and repeats the entire process. When
the target has been reached, it prints out the new and original values for the
resonance integrals for several subranges of the total energy range. If the errors
introduced by thinning are too large, the user will have to repeat the ACER run
using a larger target for the final number of energy points. An example of the
printout provided with integral thinning is given below.
Table 24: Union Energy Grid Sizes for Some Evaluations from ENDF/B-V and ENDF/B-VI
Evaluation Union Grid
235U, ENDF/B-V at 300K and 0.5% 7 200
235U, ENDF/B-VI at 300K and 0.5% 49 100
238U, ENDF/B-V at 300K and 0.5% 30 900
238U, ENDF/B-VI at 300K and 0.5% 58 300
NJOY2016 501

LA-UR-17-20093 17 ACER
original grid= 19585 with integrals 5.9781e+07 2.1716e+04
new grid= 18809 with integrals 5.9782e+07 2.1720e+04
new grid= 17842 with integrals 5.9782e+07 2.1724e+04
new grid= 16227 with integrals 5.9782e+07 2.1735e+04
new grid= 13786 with integrals 5.9783e+07 2.1727e+04
new grid= 11033 with integrals 5.9785e+07 2.1762e+04
total
8.0942e+04 5.4213e+05 0.0 0.0 0.0 0.0 0.0
1.7327e+05 4.1284e+05 0.0 0.0 0.0 0.0 0.1
2.5257e+05 3.0142e+05 0.0 0.0 0.0 0.1 0.1
3.2191e+05 1.8647e+05 0.0 0.0 0.0 0.1 0.3
4.4842e+05 5.0962e+05 0.0 0.0 0.0 0.0 0.1
5.5888e+05 3.5549e+05 0.0 0.0 0.0 0.0 0.1
6.5861e+05 2.0999e+05 0.0 0.0 0.0 0.1 0.3
7.8043e+05 4.1624e+05 0.0 0.0 0.0 0.0 0.1
1.1206e+06 9.0192e+05 0.1 0.1 0.1 0.1 0.1
2.0000e+07 5.5945e+07 0.0 0.0 0.0 0.0 0.0
capture
8.0942e+04 1.0141e+03 0.3 0.4 0.8 -0.5 1.5
1.7327e+05 7.3599e+02 0.0 0.2 0.5 0.0 0.2
2.5257e+05 5.4686e+02 0.0 0.0 0.3 0.5 1.3
3.2191e+05 4.2149e+02 0.0 0.1 0.3 1.0 1.4
4.4842e+05 5.9879e+02 0.0 0.1 0.2 0.4 0.7
5.5888e+05 5.7626e+02 0.0 0.0 0.1 0.2 0.4
6.5861e+05 5.5110e+02 0.0 0.1 0.3 0.5 0.8
7.8043e+05 8.4225e+02 0.0 0.0 0.1 0.2 0.4
1.1206e+06 1.3748e+03 0.0 0.0 0.0 0.0 0.1
2.0000e+07 1.5054e+04 0.0 0.0 0.0 0.0 0.0
861 827 825 739 983 1137 867 1262 1575 1956
The numbers at the ends of the first few lines of this listing are the total and
capture resonance integrals computed by ACER. The sections starting with the
502 NJOY2016

17 ACER LA-UR-17-20093
words total and capture give the resonance integrals for a few energy ranges,
and they also show the percentage change caused by thinning for each step of
the process. This sample shows that the capture integral increases by as much
as 1.5% after thinning to 11 000 points. If this seems too large, the user can
repeat the run using a target of 15 000 points; the maximum capture error
will be reduced to 1%. The last line of the listing shows the number of points
remaining in each energy interval with the intervals listed horizontally. In this
case, the original number of points was about 1958 for each interval. The high
energy band has not been thinned much at all, but the low energy band has lost
56% of its points.
The formats for storing energy grid and cross section data in an ACE library
are completely described in Appendix F of the MCNP manual, but they will also
be reviewed briefly here for the reader’s convenience. The principal cross sections
are given in the ESZ block. First, the NES energy values of the union grid are
given, then the NES values of the total cross section. These are followed by
the absorption cross section, elastic cross section, and average heating numbers.
The cross sections for the other NTR reaction types are controlled by a set of
blocks called MTR, LQR, TYR, and LSIG that contain the reaction ENDF MT
numbers, the Q values, the reaction types, and pointers to the cross section
data for each reaction, respectively. The cross section segments addressed by
the pointers in the LSIG block contain a count of values, the energy index from
the main energy grid for the first value, and the actual cross sections for the
reaction.
The energy and cross section values from the input PENDF tape are copied
onto the grid of the total cross section in subroutine unionx . This routine also
handles the thinning as described above. The results are written onto a scratch
tape and passed on to subroutine acelod, which reads in the cross sections
and stores them into the ACE-format blocks. Note that all energy values in
the ACE libraries are given in MeV. The ACE heating numbers are computed
by dividing the heat production cross sections from MT=301 on the PENDF
tape by the corresponding total cross sections to obtain heating in MeV per
reaction. Damage values from MT=444 are converted to MeV-barns. Sometimes
additional cross sections, such as nonelastic or inelastic are needed, and they are
added at the end of the reaction list. Note that there are two reaction counters
used in the ACE format: NTR is the total number of reactions, and NR is the
number of reactions that participate in the transport (i.e., that add up to the
total cross section). Reactions with index values above NR and up to NRT can
NJOY2016 503

LA-UR-17-20093 17 ACER
be used for tallies. This can include reactions like damage or gas production.
17.4 Two-Body Scattering Distributions
Reactions like elastic and discrete-level inelastic scattering are completely de-
scribed by their reaction cross sections, Q values, and angular distributions in
the center-of-mass (CM) system. The ACE locations for the cross sections and
Q values were noted above. The angular distributions are stored in the AND
block using a set of pointers stored in the LAND block. Two different represen-
tations for angular distributions are provided: equally probable cosine bins, and
cumulative distributions. In the older format, which is supported by all versions
of MCNP, the angular distributions are represented by 32 equally probable co-
sine bins for each incident energy (except for isotropic cases). The methods for
doing this calculation in ACER were borrowed from ETOPL[25]. The calcula-
tion is driven by topfil, which uses ptleg for distributions represented using
Legendre coefficients and pttab for distributions given as tabulations of scatter-
ing probability versus scattering cosine P(µ). The ENDF angular distributions
are obtained from File 4 on the input ENDF tape.
The newer representation for angular distributions has been available in
MCNP since version 4C. The ENDF data are converted into cumulative density
functions (CDF) and the corresponding probability density functions (PDF)
versus scattering cosine. This option is triggered by newfor=1 in the User’s
ACER input, and the work is done in subroutine acensd (“nsd”for neutron
scattering distributions) using ptleg2 for Legendre coefficient data and pttab2
for tabulated data. This representation is superior to the 32-bin one for high-
energy evaluations (those that go beyond 20 MeV), which have very sharply
forward-peaked shapes. It also reduces biases in the average cosine for scatter-
ing at lower energies. Even though it is sometimes more bulky than the 32-bin
representation, the newer cumulative format is now the default.
17.5 Secondary-Energy Distributions
In earlier versions of MCNP, and in the original MCN code, tabulated energy
distributions for secondary neutrons from multi-body reactions like (n, 2n) or
composite reactions like (n, n0
c) were represented using equally probable bins (see
LAW=1 in the DLW block). This representation turned out to be poor because
it didn’t sample low-probability important events like those in the high-energy
tails of energy distributions. The current standard representation for tabulated
504 NJOY2016

17 ACER LA-UR-17-20093
energy distributions is LAW=4, the “Continuous Tabular Distribution.” This
scheme is based on sampling from a cumulative density distribution C(E0), which
gives the probability that the energy of the emitted particle will be less than
E0. Since this probability runs from 0 to 1, it is easy to select a random number
in this range and interpolate for the corresponding value of E0. The differential
density distribution P(E0) is also given for use in MCNP’s interpolation scheme.
These quantities are computed in subroutine acelod using acelf5 and stored
into the ACE DLW block using pointers stored in the LDLW block.
Analytic energy distribution laws, such as the LF=7 simple Maxwellian fis-
sion spectrum, the LF=9 evaporation spectrum, or the LF=11 energy-dependent
Watt spectrum, are also stored into the DLW and LDLW blocks. The ACE rep-
resentation is a faithful image of the ENDF representation, so acelod simply
stores the various fields into the correct locations in memory.
17.6 Energy-Angle Distributions
A new feature of the ENDF-6 format is coupled energy-angle distributions in
File 6. (There was a File 6 format available in earlier versions of the ENDF
format, but it was never used. The new ENDF-6 MF=6 format is different.)
For neutrons, there are four different representations to be considered:
•The Kalbach law for σ(E→E0) angular distributions as used in ENDF/B-
VI and later evaluations from Los Alamos;
•Legendre coefficients for σ(E→E0) in the laboratory system as used in
ENDF/B-VI and later evaluations from Oak Ridge;
•Secondary-energy distributions versus laboratory scattering cosine as used
in the Livermore evaluation of 9Be in ENDF/B-VI; and
•The phase-space distribution as used in the Los Alamos evaluation of the
(n, 2n) reaction for 2H in ENDF/B-VI.
New evaluations using tabulations of angular distributions in the laboratory
frame, or coefficients or tabulations in the CM frame, are expected to appear
soon.
Kalbach Systematics. Kalbach and Mann[59] examined a large number of
experimental angular distributions for neutrons and charged particles. They
noticed that each distribution could be divided into two parts: an equilibrium
part symmetric in µ, and a forward-peaked pre-equilibrium part. The relative
NJOY2016 505

LA-UR-17-20093 17 ACER
amount of the two parts depended on a parameter r, the pre-equilibrium frac-
tion, that varied from zero for low E0to 1.0 for large E0. The shapes of the two
parts of the distributions depended most directly on E0. This representation is
very useful for pre-equilibrium statistical-model codes like GNASH[61], because
they can compute the parameter r, and all the rest of the angular informa-
tion comes from simple universal functions. More specifically, Kalbach’s latest
work[60] says that
f(µ) = a
2 sinh(a)hcosh(aµ) + rsinh(aµ)i,(480)
where ais a simple function of E,E0, and Bb, the separation energy of the
emitted particle from the liquid-drop model without pairing and shell terms.
The values for aare computed by subroutine bachaa from the common module
acecm.
A special sampling scheme has been developed for this case. The MCNP
code already had logic to select a secondary energy E0from a distribution. The
problem was to select an emission cosine µfor this E0. First, the Kalbach
distribution is written in the form
f(µ) = a
2 sinh(a)h(1 −r) cosh(aµ) + reaµi.(481)
Now select a random number R1. If R1< r, use the first distribution in Eq. 481.
Select a second random number R2, where
R2=Zµ
−1
acosh(ax)
2 sinh(a)dx =sinh(aµ)
2 sinh(a)+1
2.(482)
Therefore, the emission cosine is
µ=1
asinh−1h(2R2−1) sinh(a)i.(483)
If R1≤r, use the second distribution in Eq. 481. Select a random number R2,
where
R2=Zµ
−1
aeax
2 sinh(a)dx =eaµ −e−a
ea−e−a,(484)
506 NJOY2016

17 ACER LA-UR-17-20093
and emit a particle with cosine
µ=1
alnhR2ea+ (1 −R2) e−ai.(485)
The ACE format for the Kalbach File 6 data is similar to the LAW=4 format
used for other continuous energy distributions, namely, cumulative distribution
functions. To this are added tables for the pre-equilibrium ratio rand the
Kalbach slope parameter a. The result is the LAW=44 format.
Legendre or Tabulated Distributions for E to E0.This option is used
in many of the newer Oak Ridge evaluations, such as the isotopes of chromium,
55Mn, the isotopes of iron, the isotopes of nickel, the isotopes of copper, and the
isotopes of lead. The distribution for outgoing neutrons is given as a set of nor-
malized emission spectra g(E, E0) for various incident energies E. In addition,
an angular distribution is given for each E→E0as a Legendre expansion. Emis-
sion energy and angle are given in the laboratory frame. Some recent European
evaluations use a similar representation in the CM frame.
The last few versions of ACER tried various ways to handle these formats
within the limitations of versions of MCNP up to 4B, but none of them were
very satisfactory. Therefore, we added a new representation for MCNP4C called
LAW=61. This law uses the cumulative density approach for sampling for E0,
just as in LAW=4 or 44. In addition, it gives a cumulative type distribution
in the emission cosine for each E0. This is a bulky representation, but it has
the advantage of not forcing any approximations on MCNP. This format is also
selected by giving newfor=1, which is now the default for ACER.
For users who prefer to use the older versions of MCNP with the older rep-
resentation, the option newfor=0 can be selected. ACER will try to convert
the Legendre data into an equivalent section using ENDF MF=6 format with
33 cosines. This section can then be processed into ACE LAW=67 format as
described below. This process is reasonably straightforward for laboratory data.
If necessary, ACER does attempt to convert CM data to the lab frame when
building one of these MF=6 representations, but the methods used are fairly
rough and approximate. See fix6.
Laboratory Angle-Energy Distributions. The ENDF/B-VI evaluation for
9Be prepared at the Lawrence Livermore National Laboratory uses the angle-
energy option. That is, the outer loop is on incident energy E, the next loop is
NJOY2016 507

LA-UR-17-20093 17 ACER
on laboratory scattering cosine µ, and the inner loop is on secondary energy E0.
In order to sample from data in this form, the first step is to integrate over E0
for each µin order to obtain the differential angular distribution f(E, µ). This
angular distribution is converted into 32 equally probable bins and stored into
the ACE file using the same format used for two-body angular distributions.
The emission spectra for the individual µvalues are normalized and stored into
the file using a format called LAW=67 (named for ENDF File 6, Law 7). MCNP
can sample from this representation as follows: for each emission, first sample
from f(µ) to get an emission angle, then find the corresponding spectrum and
sample from its cumulative probability distribution to get the value of E0.
N-Body Phase-Space Distributions. The phase-space distribution for par-
ticle iin the CM system is given by
PCM
i(µ, E, E0) = Cn√E0(Emax
i−E0)3n/2−4,(486)
where Emax
iis the maximum possible CM energy for particle i,µand E0are in
the CM system, and the Cnare normalization constants. The value of Emax
iis
a fraction of the energy available in the CM:
Emax
i=M−mi
MEa,(487)
where Mis the total mass of the nparticles being treated by this law, and
Ea=mT
mp+mT
E+Q . (488)
Here, mTis the target mass, and mpis the projectile mass. In summary, the
data items required for the phase-space law are
Symbol ENDF Location
nNPSX N2 field of the MF=6 CONT for LAW=6
miAWI C1 field of third card in MF=1
mpAWP C2 field of LAW=6 TAB1 record
mTAWR C2 field of section HEAD record
MAPSX C1 field of LAW=6 CONT record
QQ C1 field of the MF=3 TAB1 record
These equations are sampled with a compact numerical scheme similar to
508 NJOY2016
17 ACER LA-UR-17-20093
LAW=4. Note that all the spectra scale with the maximum possible outgoing
energy. Therefore, it is easy to construct a single normalized distribution with
Emax
i=1 with a reasonable number of x=E0/Emax
ipoints and then to construct
a cumulative distribution function for it. The grid uses uniform spacing above
x= 0.10 and log spacing below. The xgrid, the probability density values P(x),
the cumulative densities C(x), NPXS, and APSX are stored in the Law=66
format. For any given E, the cumulative distribution function is sampled with
a random number between 0 and 1. The resulting xvalue is then multiplied
by Emax
ito get the emitted E0value. The corresponding CM cosine value is
obtained by sampling uniformly in the interval [−1,1].
The CM to lab transformation is carried out by adding the CM velocity of
the initial collision to the emitted particle velocity.
E0
LAB =ECM +E0
CM + 2µCMqECME0
CM ,(489)
and
µLAB =pE0
CM µCM +√ECM
pE0
LAB
,(490)
where the CM energy is
ECM =A
A+ 1 E . (491)
Smoothing. For a number of evaluations (including main actinides), the spec-
tra from continuous reactions like MT=91 are given in histogram form. This
is a natural result of the nuclear model codes used to generate the evaluations.
At low energies, you will typically see one histogram bin extending from zero
energy to keV energies; that is, the emission probability will be constant in that
range. From physics, we expect that the limiting shape at low emission energies
in the CM frame will be pE0
CM (implying a pE0
LAB shape in the laboratory).
Therefore, the histogram shape greatly overestimates the source into low ener-
gies. This problem is somewhat alleviated by the low probability for scattering
into this lowest bin, and the evaluations that use this representation give good
results for criticality calculations. However to improve the physical consistency
of the emission spectra, ACER has an option to convert the low energy part
of the spectra into a new histogram representation with finer steps that does a
better job of approximating the pE0
CM shape. We call this “smoothing” and
it is controlled by the parameter ismooth. For NJOY2012 and NJOY2016 the
NJOY2016 509

LA-UR-17-20093 17 ACER
default is to carry out the smoothing operation. Users are reminded that this is
opposite the NJOY99 default setting.
A similar smoothing operation is applied to the low-energy bin of the delayed
neutron spectra for fission when ismooth is set. A somewhat different problem
occurs at energies above 10 MeV for some of the MF=5 fission spectrum sections.
The energy grid shifts from a reasonable size below 10 MeV to one that is too
coarse above there. The expected shape of the fission spectrum on the high-
energy side is nearly exponential. ACER inserts additional grid points between
the ones in the evaluation using linear-in-E and log-in-probability interpolation
when ismooth is set. Without smoothing the coarse high energy mesh can cause
significant errors in reaction rates for high-threshold reactions.
17.7 Photon Production
Earlier versions of MCNP used a very simple representation for photon pro-
duction from neutron reactions. There was a single total photon production
cross section on the same union grid as the neutron data, and there were 600
words of data describing the spectrum of outgoing neutrons. This table con-
tained 20 equally likely outgoing photon energies for each of 30 incident neutron
groups. This representation did not achieve the MCNP goal of providing the
best possible representation of the physics of the problem. It was inadequate
in representing discrete photons because their real energies were often lost, and
it was inadequate in representing low-probability events from the tails of distri-
butions. This was especially noticeable in capture events because of the high
photon energies possible. It is still possible to use this representation, but it
is no longer recommended. The newer “Expanded Photon Production Data”
option is preferred.
Photon Production Cross Section. In the earlier versions of the ENDF
format, photon production cross section information was given in File 13 (photon
production cross sections), or as a combination of File 3 (reaction cross sections)
and File 12 (photon production yields). With the ENDF-6 format, photon
production can also be computed using a combination of File 3 and File 6
(product yields and energy-angle distributions).
The first step in photon production processing takes place in subroutine
convr. MF=12 on the ENDF tape is examined for transition probability arrays
(LO=2). If they are found, they are converted into the photon yield format
(LO=1). The final photon yield data are written onto a scratch tape. Next, the
510 NJOY2016

17 ACER LA-UR-17-20093
MF=13 data are copied, and MF=14 (photon angular distributions) is updated
to reflect the changes made in MF=12. Finally, if File 6 is present, any photon
production subsections found are converted into a special MF=16 format on the
scratch tape. The next step is performed in gamsum. The scratch tape from
convr is used together with the input PENDF tape to calculate the sum of
MF=13, MF=12×MF=3, and MF=16×MF=3 for all the photon reactions on
the normal union energy grid. Later, this total photon production cross section
is written into the ACE GPD block in acelod.
Photon Production Matrix. The 30-by-20 photon production matrix is
computed from input multi-group data. Therefore, it is necessary to execute
the GROUPR module prior to ACER. This run should use the 30-group option
for neutrons and a photon group structure with many groups (the CSEWG 94-
group structure is normally used). The gamout routine reads the multi-group
data and adds up all the reactions. It then integrates through the photon groups
for each neutron group and finds the equal-probability boundaries. For each of
these equally probable bins, it selects a single photon energy that preserves the
average energy for the bin. The results are written on a scratch tape in a special
ENDF-type format and passed to acelod to be inserted into the GPD block.
Expanded Photon Production Data. This newer representation allows
each discrete photon to be treated with its proper energy, and it allows for a
much better representation of the spectrum of continuum photons. In the ACE
representation, the MTRP block lists all the photon reactions included by ENDF
MT number. Since some reactions may describe more than one photon (for
example, radiative capture reactions usually describe many discrete photons),
the identifier numbers are given as 1000×MT plus a photon index. Thus 102002
would stand for the second photon described under radiative capture (MT=102).
Each of the NMTR photons listed in the MTRP block can have its own cross
section or yield as described in the SIGP and LSIGP blocks, its own angular
distribution as described in the ANDP and LANDP blocks, and its own energy
distribution as described in the DLWP and LDLWP blocks. In addition, the
YP block contains a list of reaction MT numbers that are needed as photon
production yield multipliers.
These expanded photon production data are stored into the ACE-format
blocks in acelod using the information written on a scratch file by convr.
NJOY2016 511

LA-UR-17-20093 17 ACER
17.8 Probability Tables for the Unresolved Region
Starting with Version 4B, MCNP has been able to make use of cross section
probability tables for energies in the unresolved resonance range to get proper
self-shielding effects. These tables are produced by the PURR module of NJOY.
The tables provide a cumulative density function that gives the probability that
the total cross section observed at some energy Ein the unresolved resonance
range will be less than some particular values. MCNP can then throw a random
number and search this table to get a sample value for the total cross section
at each collision. The probability tables also include conditional probability
distributions that give values for scattering, fission, capture, and heating for
each particular value of the total. The probability tables are read from the
input PENDF file and stored into the ACE format in acelod.
17.9 Charged-Particle Production
Another recent addition to the continuous-energy neutron data class for MCNP
is a detailed representation of the emission of light charged particles from neutron-
induced reactions. These kinds of data are now available for a number of ma-
terials in ENDF/B evaluations, including the large set of evaluations originally
added for ENDF/B-VI Release 6 that go to incident neutron energies of 150
MeV.
When present, the charged-particle production data reside in a set of ACE
blocks at the end of the ACE file. There is a set of data given for each charged
particle produced: protons, deuterons, tritons, 3He’s, and alphas. These data
sets give a production cross section and a heating value referenced to the stan-
dard union energy grid from the ESZ block, and they also give the fraction of
the production coming from each reaction producing the particle, together with
the associated angle and energy distribution data for the reaction. These data
are loaded into the ACE format using subroutine acelcp, which support most
of the formats described above, including LAWs 44 and 61.
These charged particle production distributions will be used in advanced
versions of MCNP to provide the source from neutron reactions for subsequent
charged-particle transport, thus providing a true n-particle Monte Carlo capa-
bility.
Care must be taken to handle heating correctly in n-particle transport calcu-
lations. The heating value in the main ESZ block of the ACE format contains
energy deposition resulting from all the charged particles resulting from nuclear
512 NJOY2016

17 ACER LA-UR-17-20093
reactions. If a user wants to do a coupled neutron-gamma-proton calculation,
it is necessary to subtract the proton heating from the main heating value first.
The subsequent non-local energy deposition from the transported protons will
be handled directly. This is why the new charged-particle blocks include the
separate heating contribution associated with each particle.
17.10 Gas Production
During the NJOY run that makes the input for ACER processing, the user can
choose to run the GASPR module. It goes through all the reactions given on
its input ENDF and PENDF files and constructs reaction cross sections for the
production of the light charged particles (p, d, t, 3He, and alpha) and writes
them on a new version of the PENDF file. When acelod processes this PENDF
file, the cross sections are made available in the ACE file for use in MCNP tallies.
Watch for reaction names like “(n,Xp).”
These gas production cross sections are basically the same as the charged-
particle production cross sections in the new charged-particle sections on the
ACE file (except for reactions using the ENDF LR flags), but the latter are not
available for simple tallies.
17.11 Consistency Checks and Plotting
As part of the Quality Assurance (QA) process for producing ACE library files,
ACER has the capability to read in an ACE file and check the data for some
common problems. These are called “consistency checks,” and the checks are
provided for class “c” libraries are as follows:
•check reaction thresholds against Q values,
•check the main energy grid is monotonic,
•check angular distributions for correct reference frame,
•check angular distributions for unreasonable cosine values (µout of range,
µvalues not monotonic, cumulative probability out of range, cumulative
probabilities not monotonic)
•check energy distributions (illegal interpolation, E0greater than the max-
imum possible value, bad cumulative probability, decreasing cumulative
probability, bad Kalbach r, bad angular cumulative probability, decreasing
angular commutative probability),
•check photon production sum,
NJOY2016 513

LA-UR-17-20093 17 ACER
•check photon production distributions (bad cumulative probability, de-
creasing cumulative probability), and
•check particle production sections (bad LAW=4 cumulative probability, de-
creasing LAW=4 cumulative probability, bad LAW=44 cumulative proba-
bility, decreasing LAW=44 cumulative probability, bad LAW=44 Kalbach
r, bad LAW=61 cumulative probability, decreasing LAW=61 cumulative
probability, bad LAW=61 angular cumulative probability, decreasing an-
gular cumulative probability)
When E0values greater than the expected limit are found, the consistency-
check routine can correct them. See the sections on running ACER for the
details.
Another important part of the ACE QA procedure is to prepare an extensive
set of plots and to scan through them for possible problems. The aplots routine
does this, together with a number of subsidiary routines. The plots are generated
in the form of an input file for the VIEWR module, which can then prepare
the final plots as color Postscript files. The plots include pages showing the
principle ACE cross sections (total, elastic, absorption, photon production),
non-threshold reactions (such as capture and heating), and threshold reactions in
log form (to feature the low-energy region) and linear form (for higher energies).
Several reactions are given per page. The routine also prepares expanded views
of the cross sections in the resonance range to make the details of prominent
resonances more apparent. In addition, the plots include 3-D perspective views
of angular distributions for the new format. The 32-bin representation of the
angular distributions is shown as contour plots. The energy and energy-angle
distributions for tabulated representations are also shown as 3-D perspective
plots. Finally, the particle production data, if present, are shown using similar
2-D and 3-D plots. Fig. 54 is an example of the log plot for the principal cross
sections, and Fig. 55 is an example of a 3-D plot for particle emission.
17.12 Thermal Cross Sections
Thermal data is the second class of ACE data to be considered, and they are
handled by the aceth module. This module exports two subroutines: acesix
to process the data into ACE format, and thrfix for edits, listings, and plots.
For energies below several eV, the thermal motions of nuclei can lead to sig-
nificant energy gains in neutron scattering. In addition, the binding of atoms
into liquids and solids begins to affect the scattering cross section and the dis-
tribution of scattered neutrons in angle and energy. MCNP can handle thermal
514 NJOY2016
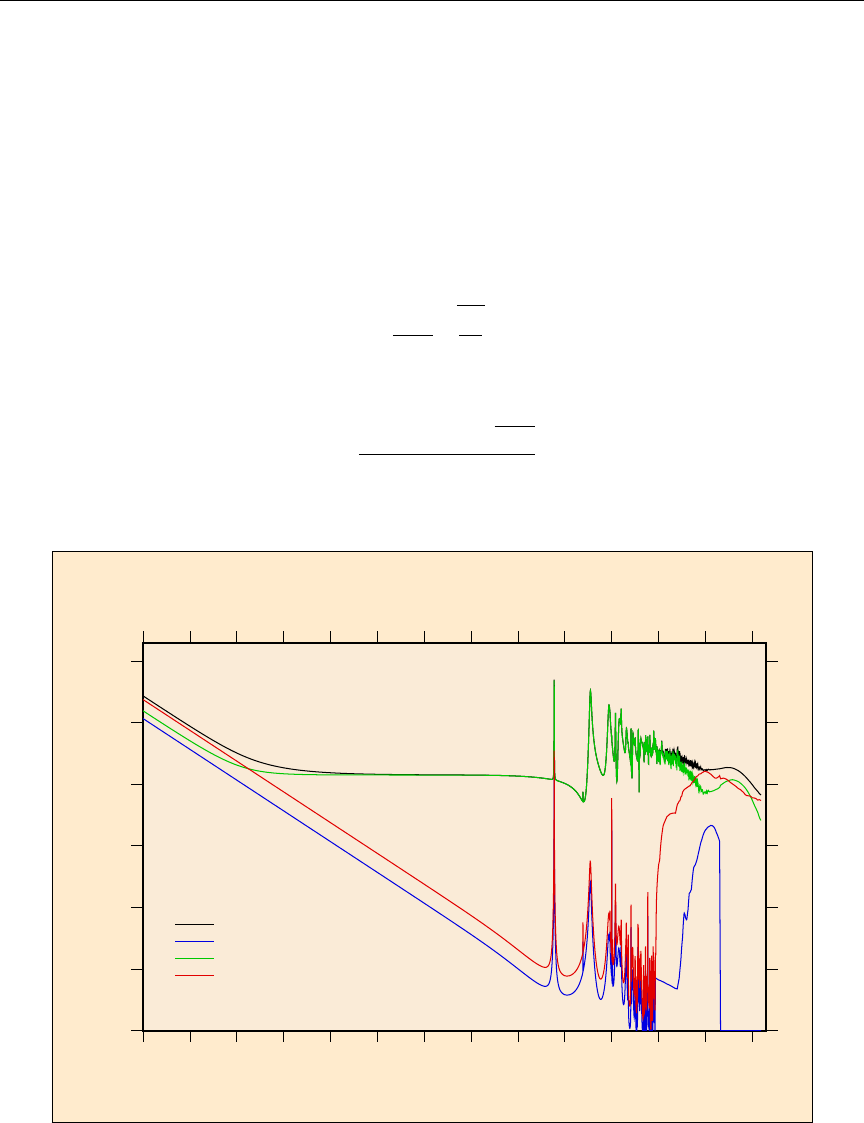
17 ACER LA-UR-17-20093
neutron scattering from the atoms of a free gas using internal kinematic formu-
las that assume a Boltzmann distribution. The bound-atom effects are treated
using thermal data from ENDF evaluations stored in a special MCNP thermal
library.
The ENDF format allows for several thermal processes. Thermal inelastic
scattering is represented using the scattering law S(α, β), where αand βare
dimensionless momentum and energy transfer parameters, respectively:
σ(E→E0, µ) = σb
4πT rE0
Ee−β/2S(α, β),(492)
where
α=E0+E−2µ√EE0
AkT ,(493)
ENDF/B-VII AL-27
Principal cross sections
10-11 10-9 10-7 10-5 10-3 10-1 101
Energy (MeV)
10-4
10-3
10-2
10-1
100
101
102
Cross section (barns)
total
absorption
elastic
gamma production
Figure 54: A log plot of the ACE principal cross sections for 27Al from ENDF/B-VII.0.
Note the extension beyond 20 MeV to 150 MeV.
NJOY2016 515
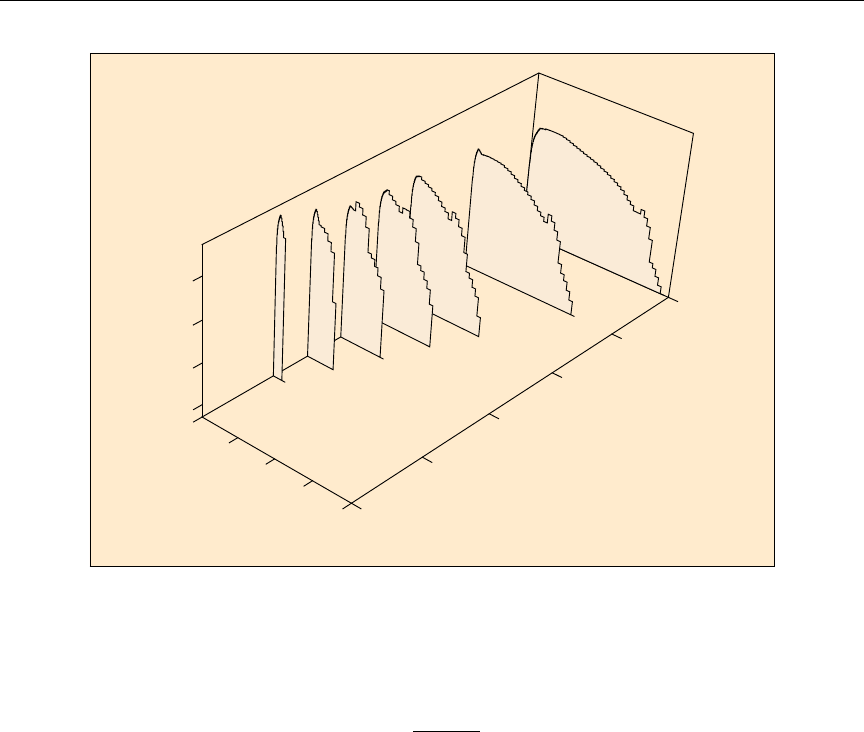
LA-UR-17-20093 17 ACER
ENDF/B-VII AL-27
Neutron emission for (n,n*)a
1
0
-
3
1
0
-
1
P
r
o
b
/
M
e
V
0
2
4
6
8
S
e
c
.
E
n
e
r
g
y
1
0
1
2
1
4
1
6
1
8
2
0
E
n
e
r
g
y
(
M
e
V
)
Figure 55: A 3-D view of the energy distribution for neutrons emitted from the (n,n0α)
reaction on 27Al from ENDF/B-VII.
and
β=E0−E
kT .(494)
Eand E0are the incident and outgoing neutron energies, µis the scattering
cosine, Tis the absolute temperature, Ais the mass ratio to the neutron of the
scatterer, and kis Boltzmann’s constant. This process occurs in all the ENDF
thermal materials, such as water, heavy water, graphite, beryllium, beryllium
oxide, polyethylene, benzine, and zirconium hydride.
The THERMR module of NJOY uses this equation and evaluated S(α, β)
data from an ENDF-format evaluation to compute σ(E→E0, µ). The E0de-
pendence of the integral over µis computed adaptively so as to represent the
function using linear interpolation within a specified tolerance. The angular
distribution at each of these E0values is then calculated in a similar way, but
the curve of σvs. µis then converted into equally probable bins (typically 8),
and a discrete angle is selected for each bin that preserves the average scattering
cosine for that bin. The data are written onto the PENDF tape using special
MF=6-like formats.
516 NJOY2016

17 ACER LA-UR-17-20093
The acesix subroutine reads this thermal section on the input PENDF file.
In older versions of this method, the energy distribution σ(E→E0) is converted
into equally probable bins (typically 16), and a discrete energy is chosen for each
bin that preserves the average energy in that bin. The result of this process is a
set of equally probable events (typically 8 ×16 = 128 events) in E0, µ space for
each incident energy. It is very easy to sample from this representation, and it
is fairly compact. See iwt=0 is the input instructions.
However, it must be recognized that this scheme is only reasonable if each
neutron undergoes several scattering events before being detected. The artificial
discrete lines must be averaged out. Be careful when using this method to an-
alyze experimental arrangements using optically thin elements and small-angle
detectors. In addition, as in all equal-probability bin schemes, the wings of func-
tions (which may be unlikely but important) are not well sampled. ACER in-
cludes a variation to partially relieve this problem: instead of equal bin weights,
the pattern 1, 4, 10, 10,..., 10, 4, 1 is used (see “variable weighting” in the input
instructions). This approach produces some samples fairly far out on the wings
of the energy distribution. Angles are still equally weighted. See iwt=1 in the
input instructions.
In practice, this method using discrete energies can still leave some artificial
peaks in typical thermal neutron spectra. These peaks don’t have much effect
on average quantities for most applications, but they are visually offensive. The
newer versions of MCNP (version 5.1.50 and later) support continuous distri-
butions of σ(E→E0) with PDF and CDF values to drive the sampling. See
iwt=2 in the input instructions. This is the preferred representation. The ther-
mal inelastic data prepared by acesix is loaded into the ACE blocks ITIE and
ITXE by thrlod.
The second ENDF process to consider is “coherent elastic” scattering. This
process occurs in powdered crystalline materials, such as graphite, beryllium,
and beryllium oxide. Bragg scattering from the crystal planes leads to jumps
in the cross section vs. energy curve as scattering from each new set of planes
becomes possible. The formula for this process can be written in the following
form:
σ(E, µ) = σc
π¯h2
4MEV
τ<τmax
X
τ6=0
f(τ)δ(µ−µ0[τ]) ,(495)
NJOY2016 517

LA-UR-17-20093 17 ACER
where
τmax =r8ME
¯h2,(496)
and
µ0= 1 −¯h2τ2
4ME ,(497)
and where Eis the incident neutron energy, E0is the outgoing neutron energy, µ
is the scattering cosine, σcis the characteristic coherent scattering cross section
for the material, Mis the target mass, Vis the volume of the unit cell, τis the
radius of one of the reciprocal lattice shells, and f(τ) is the effective structure
factor for that shell.
Examination of these equations shows that the angle-integrated cross section
will go through a jump proportional to f(µ) when Egets large enough so that
µ0=−1 for a given value of τ. At this energy, a backward directed component of
discrete-angle scattering will appear. As the energy increases, this discrete-angle
line will shift toward the forward direction. It is clear that the only information
that MCNP needs to represent this process in complete detail is a histogram
P(E) tabulated at the values of Ewhere the cross section jumps. The cross
section will then be given by P(E)/E. The intensity and angle of each of the
discrete lines can be deduced from the sizes of the steps in P(E) and the E
values where the steps take place.
The P(E) function is computed from σ(E) in acesix. Subroutine thrlod
stores the number of Bragg edges, the Bragg energies, and the Pvalues at the
Bragg edges into the ACE-format ITCE block.
The third ENDF thermal process is incoherent elastic scattering. It occurs
for hydrogenous solids like polyethylene and zirconium hydride by virtue of
the large incoherent scattering length and small coherent scattering length of
hydrogen. The equation describing this process is
σ(E, µ) = σb
2e−2EW (1−µ)/A ,(498)
where σbis the characteristic bound cross section, and Wis the Debye-Waller
integral. The THERMR module of NJOY computes the integrated cross section
σ(E) for this process and a set of equally probable cosines for each incident
energy E; it writes them onto the PENDF tape using a special format. These
quantities are copied into the ITCE and ITCA blocks of the ACE format in
518 NJOY2016
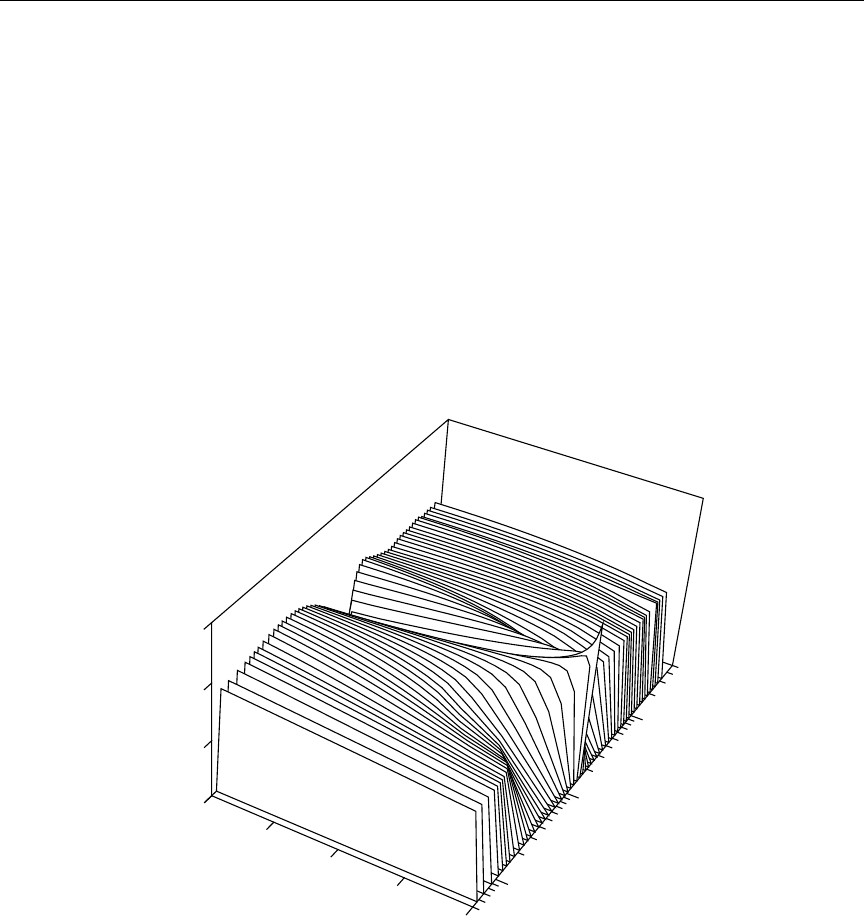
17 ACER LA-UR-17-20093
subroutine thrlod.
No consistency checking is currently available for thermal files, but a set
of plots is provided to help with QA. The plots are prepared as input for the
VIEWR module, which can generate the final color Postscript files for plotting.
A log plot of the total, inelastic, and elastic (if present) cross sections is given
first, followed by by plots of the average scattering cosine, mubar, and the
average energy of the scattering neutrons, ebar. Perspective views of the energy
spectrum for thermal neutron scattering are provided, and several plots of the
angle-energy emission for different incident energies are also present. Fig. 56
shows an example of an angular distribution plot.
1
0
-
1
1
0
0
1
0
1
P
r
o
b
/
c
o
s
i
n
e
-
1
.
0
-
0
.
5
0
.
0
0
.
5
1
.
0
C
o
s
i
n
e
1
0
-
3
1
0
-
2
1
0
-
1
S
e
c
.
E
n
e
r
g
y
Figure 56: A perspective view of an angle-energy distribution for H in H2O.
17.13 Dosimetry Cross Sections
The ACE dosimetry data forms another class of MCNP data, and they are
handled by the acedo sub-module of the ACER group. This class of library
provides cross sections to be used for response functions in MCNP; the data
cannot be used for actual neutron transport. The information on a dosimetry
file is limited to an MTR block, which describes the reactions included in the set,
NJOY2016 519

LA-UR-17-20093 17 ACER
an LSIG block containing pointers to the cross section data for the reactions, and
the SIGD block, which contains the actual data. The format for dosimetry cross
section storage is different from the format for neutron cross sections. The union
grid for linear interpolation is not used; instead, the cross sections are stored
with their ENDF interpolation laws. If the file mounted as the input PENDF
tape is a real PENDF tape (that is, if it has been through RECONR), all the
reactions are already linearized, and the interpolation information stored in the
SIGD block will indicate linear interpolation for a single interpolation range.
However, if the file mounted as NPEND is actually an ENDF file, the SIGD
block may indicate multiple interpolation ranges with nonlinear interpolation
laws.
17.14 Photoatomic Data
Photoatomic data form another ACE class. The data are processed using the
acepa module, which exports the subroutine acepho for formatting the data,
and the subroutine phofix for editing, listing, consistency checks, and plots.
Photons from direct sources and photons produced by neutron reactions are
scattered and absorbed by atomic processes, producing heat at the same time.
The existing MCNP “photon interaction” libraries were based on fairly old cross
section data and assembled by hand[91, 92]. This version of ACER contains the
beginnings of an automated capability to produce these libraries from the latest
ENDF/B photoatomic data.
The cross sections for the basic photoatomic process incoherent scattering,
coherent scattering, pair production, and photoelectric absorption are given on
a union energy grid. Actually, the energies and the cross sections are stored as
logarithms, and MCNP uses linear interpolation on them; therefore, the effective
interpolation law is log-log. MCNP determines the mean-free-path to a reaction
using the sum of these partial cross sections instead of a total cross section.
If the reaction is incoherent (Compton) scattering, the scattering is assumed
to be given by the product of the free-electron Klein-Nishina cross section and
the incoherent scattering function, I(v). MCNP assumes that this function is
tabulated on a given 21-point grid of vvalues, where vis the momentum of the
recoil electron given in inverse angstroms. It is easy to extract the scattering
function from the section MF=26, MT=504 of the photoatomic ENDF library
and to interpolate the function onto the required vgrid.
If the reaction is coherent (Thomson) scattering, the photon will be scattered
without energy loss, and the scattering distribution is given by the Thomson
520 NJOY2016

17 ACER LA-UR-17-20093
cross section times the coherent form factor. The sampling scheme used in
MCNP requires the coherent form factor tabulated on a predefined set of 55 v
values, and it also requires integrated form factors tabulated at 55 values of v2,
where the vvalues are the same set used for the form factors. These values are
extracted from the section MF=26, MT=502, and the integrals are done using
the standard NJOY routine intega.
Photoelectric absorption results in the emission of a complex pattern of dis-
crete “fluorescence” photons and electrons (which lead to heating) due to the
cascades through the atomic levels as the atom de-excites.
The fluorescence part is not coded yet. This section will be completed when
the new fluorescence methods have been developed and installed in MCNP.
In the meantime, ambitious users may be able to meld the new cross sections
computed by the methods discussed in this section with the fluorescence data
from the current MCNP library.
17.15 Photonuclear Data
Photonuclear data forms a new class of ACE data that has just become available
in recent years. These data are handled by the module acepn, which exports the
call acephn for processing the data into ACE format, and the call phnfix for
editing, listing, consistency checks, and plots. A fairly large number of photonu-
clear evaluations is available as of this writing. They were originally collected
by the Data Section of the IAEA, and they then migrated into ENDF/B-VII.0.
The new ACE photonuclear format differs in some ways from the more famil-
iar continuous-energy format (class “c”). In this format, all emissions (neutrons,
photons, and charged particles) are treated symmetrically using blocks with the
style of the particle production blocks from the class “c” format. Each possible
reaction product is described by a production cross section, a partial heating
value, fractions represented by different reaction channels, and angle, energy, or
energy-angle distributions for each reaction channel.
One class of the new evaluations consists of those performed at LANL and a
large set of materials using the same methods generated at the Korea Atomic En-
ergy Research Institute (KAERI). These evaluations lump all the photonuclear
processes into a single reaction with MT=5 and use subsections of MF=6/MT=5
to represent all the neutrons, photons, and charged particles produced. These
are processed by using the energy grid of MT=5 as the union grid. The ACE
total and heating values are constructed on this grid. Then the sections of File
6 are processed to generate production cross sections and partial heating val-
NJOY2016 521

LA-UR-17-20093 17 ACER
ues for each of the emitted species. Each emitted neutron or charged particle
also has an energy-angle distribution associated with it, represented using the
Kalbach LAW=44 format, and emitted photons are represented using LAW=4.
17.16 Type 1 and Type 2
ACE library files come in two different types in order to allow for efficiency and
portability.
•Type 1 is a simple formatted file suitable for exchanging ACE libraries
between different computers.
•Type 2 is a FORTRAN-77 direct-access binary file for efficient use during
actual MCNP runs.
There used to be Type 3 using word-addressable random access methods, but
these methods were machine specific, and the type has been abandoned. ACER
stores all values in memory as real numbers, and it is easy to write them out
in Type-2 format, because all fields in that format are also represented by real
numbers (except for some of the fields in the header record). The Type 1 format
requires that fields that represent integers must be written in integer format,
that is, right justified and without decimal points. The output routines in
the ACER submodules contain logic to perform this step (see aceout,throut,
dosout,phoout, and phnout).
The ACER user can prepare libraries using either Type 1 or Type 2 output.
The advantage of Type 1 is that the files can be easily moved to other machines
or laboratories. The advantage of Type 2 is that it is more compact and can be
used directly by MCNP with no performance penalties. At any time, ACER can
be used to convert one format to another, or to make a listing of the data from
any of the formats (see iopt values from 7 through 9 in the input instructions).
17.17 Running ACER
The following input instructions are copied from the comment cards at the
beginning of the ACER module. Users should always check the actual comment
cards for the current version to see if there have been any changes.
!---input specifications (free format)---------------------------
!
! card 1
522 NJOY2016

17 ACER LA-UR-17-20093
! nendf unit for input endf tape
! npend unit for input pendf tape
! ngend unit for input multigroup photon data
! nace unit for output ace tape
! ndir unit for output mcnp directory
! card 2
! iopt type of acer run option
! 1 fast data
! 2 thermal data
! 3 dosimetry data
! 4 photo-atomic data
! 5 photo-nuclear data
! 7 read type 1 ace files to print or edit
! 8 read type 2 ace files to print or edit
! set iopt negative for mcnpx format
! iprint print control (0 min, 1 max, default=1)
! itype ace output type (1, 2, or 3, default=1)
! suff id suffix for zaid (default=.00)
! nxtra number of iz,aw pairs to read in (default=0)
! card 3
! hk descriptive character string (70 char max)
! delimited by quotes
! card 4 (nxtra.gt.0 only)
! iz,aw nxtra pairs of iz and aw
!
! --- fast data (iopt=1 only) ---
!
! card 5
! matd material to be processed
! tempd temperature desired (kelvin) (default=300)
! card 6
! newfor use new cumulative angle distributions,
! law 61, and outgoing particle distributions.
! (0=no, 1=yes, default=1)
! iopp detailed photons (0=no, 1=yes, default=1)
! ismooth switch on/off smoothing operation (1/0, default=1=on)
! set ismooth to 1 to cause extension of mf6 cm
! distributions to lower energies using a sqrt(E)
! shape, to extend delayed neutron distributions as
! sqrt(E) to lower energies, and to add additional
! points above 10 Mev to some fission spectra assuming
! an exponential shape. otherwise, use ismooth=0.
NJOY2016 523

LA-UR-17-20093 17 ACER
! NOTE: ismooth=0 is the default value in njoy99.
! card 7
! type of thinning is determined by sign of thin(1)
! (pos. or zero/neg.=energy skip/integral fraction)
! (all entries defaulted=no thinning)
! thin(1) e1 energy below which to use all energies (ev)
! or iwtt weighting option (1=flat,2=1/e)
! (1/e actually has weight=10 when e lt .1)
! thin(2) e2 energy above which to use all energies
! or target number of points
! thin(3) iskf skip factor--use every iskf-th energy
! between e1 and e2, or rsigz reference sigma zero
!
! --- thermal data (iopt=2 only) ---
!
! card 8
! matd material to be processed
! tempd temperature desired (kelvin) (default=300)
! tname thermal zaid name ( 6 char max, def=za)
! card 8a
! iza01 moderator component za value
! iza02 moderator component za value (def=0)
! iza03 moderator component za value (def=0)
! card 9
! mti mt for thermal incoherent data
! nbint number of bins for incoherent scattering
! mte mt for thermal elastic data
! ielas 0/1=coherent/incoherent elastic
! nmix number of atom types in mixed moderator
! (default=1, not mixed)
! (example, 2 for beo or c6h6)
! emax maximum energy for thermal treatment (ev)
! (default=1000.=determined from mf3, mti)
! iwt weighting option
! 0/1/2=variable/constant/tabulated (default=variable)
!
! --- dosimetry data (iopt=3 only) ---
!
! card 10
! matd material to be processed
! tempd temperature desired (kelvin) (default=300)
!
524 NJOY2016
17 ACER LA-UR-17-20093
! --- photo-atomic data (iopt=4 only) ---
!
! card 11
! matd material to be processed
! photoatomic data on nendf
! atomic relaxation data on npend
!
! --- photo-nuclear data (iopt=5 only) ---
!
! card 12
! matd material to be processed
!
! --- print or edit existing files (iopt=7-9) ---
!
! No additional input cards are required. Mount the old
! ace tape on "npend". The code can modify zaid, hk,
! the (iz,aw) list, and the type of the file. Use suff<0
! to leave the old zaid unchanged. Use just "/" on
! card 3 to leave the comment field hk unchanged. Use
! nxtra=0 to leave the old iz,aw list unchanged. The
! code can modify zaid, hk, and type of file.
!
! Exhaustive consistency checks are automatically made on
! the input file. If ngend.ne.0, a set of standard ACE plots
! are prepared on unit ngend as plotr input instructions.
!
!--------------------------------------------------------------------
Card 1. ACER uses the information from the ENDF tape mounted on unit
nendf for angle, energy, energy-angle, and photon emission distributions, and
it uses the data on npend for the unionized and linearized cross sections. The
latter file should have been processed through RECONR, and maybe BROADR.
If it wasn’t, ACER will still work, but the energy grids may not be quite right.
The ngend unit is only needed for input if the old 30×20 photon production
matrix is to be constructed; otherwise, set it to zero. In addition, ngend is used
for plotting output (if available) when one of the print or edit options is selected
(see iopt=7 below; set it to zero to suppress plotting output. Unit nace is
the main output tape for the ACE-format library, and unit ndir will contain a
single line of text intended to be edited and incorporated into a directory for a
NJOY2016 525

LA-UR-17-20093 17 ACER
big multi-material ACE library.
Card 2. The value of iopt specifies the kind of ACE data being produced,
as indicated in the instructions. The long print option, iprint=1, produces a
complete, interpreted listing of the ACE data. The shorter print options just
put out progress information from the ACER job and a brief listing of the header
information for the library that was generated. The ntype parameter specifies
whether the output library will be in ASCII or binary form. In MCNP jobs,
materials are identified by their “zaid” numbers (rhymes with “staid”); they
are constructed by using the value 1000×Z+A, appending the value of suff
(the suffix), and then adding a letter that indicates the library class (“c” for
continuous, “t” for thermal, etc. (see Table 23). For example, 92235.70c denotes
a continuous (fast data) library entry for 235U from ENDF/B-VII. Thermal zaids
are actually alphanumeric before the dot; see Card 8. Finally, nxtra is the
number of extra iz,aw pairs of values to be read in on Card 4.
Card 3. This card contains a descriptive character string up to 70 characters
long. It must be delimited by ’ characters and terminated by the / character.
Card 4. Read in nxtra pairs of numbers iz and aw for photoatomic data. Use
as many cards as necessary.
Card 5. This is the first card for a fast data library run. It specifies the ENDF
MAT number and the absolute temperature for the material to be processed.
ENDF MAT numbers are 4-digit numbers. For the earlier versions of ENDF/B,
they were assigned in an arbitrary way; for example, 1276 was 16O for ENDF/B-
IV and 1395 represented 235U for ENDF/B-V. For ENDF/B-VI and later, a
systematic scheme has been selected that allows the same MAT number to be
used for all the various sub-libraries (for example, neutron data, thermal data,
incident proton data, etc.). This scheme is based on using Z to get the first two
digits. The second two digits are chosen to be zero for elements, and for normal
isotopes, they step in units of 3 up and down around 25, the value for the lowest
isotope of the normal stable group of isotopes. This leaves room for two isomers
for each isotope in between. Examples include 9225 for 234U, 9228 for 235U, and
2200 for natural Ti. If the temperature is greater than zero, the input PENDF
tape must have been run through BROADR.
526 NJOY2016

17 ACER LA-UR-17-20093
Card 6. The flag newfor is equal to 1 if the new cumulative format for an-
gular distributions, the LAW=61 format for energy-angle data, and the particle
production sections are desired; otherwise, it is zero. The default is newfor=1,
suitable for use with MCNP4C and subsequent versions. The flag iopp de-
termines whether the newer detailed photon data option is used (preferred),
or whether the older 30×20 photon production matrices are to be generated.
Remember that if the latter option is selected, GROUPR must be run before
ACER to generate multigroup versions of the photon production matrices for
all reactions, and the resulting GENDF tape must be coupled to ACER using
the ngend input parameter.
Card 7. Thinning of the union energy grid can be performed using several
options as described in detail in Section 17.1 above. Defaulting the entire card
by entering only / results in no thinning. This is preferred.
Card 8. This card starts the input of parameters for the thermal library op-
tion. The material MAT number and absolute temperature are given. The
default temperature is 293.6K and the default tname is generated from ZA.
Therefore, the simplest version of this card would consist of a MAT number
followed by /. Check the discussion above for Card 5. In almost all cases, an
entry for tname is desirable. Examples are “LWTR” for H in light water (or
“HH2O” for hydrogen in water), “GRAPH” for graphite, “ZRZRH” for zirco-
nium in zirconium hydride, and so on.
Card 8a. MCNP needs to know the zaid values to get the fast data needed
to go with a particular set of thermal data. For a thermal set like HH2O, only
iza01=1001 would be needed. For a mixed moderator like benzine, values for
both iza01 and iza02 must be given (e.g., 1001 and 6000). See nmix below.
The third input parameter allows for the aliases 6012 and 6000, if needed.
Card 9. The value mti must correspond to one of the values used for this
material in the THERMR runs that generated the input PENDF tape (see Ta-
ble 25). The number of bins to use for the equally probable bins for the outgoing
neutron spectra is defined by nbint; the default value is 16. The parameter mte
defaults to zero; a nonzero value is only needed for materials that show elas-
tic scattering (see Table 25). The value ielas indicates whether this elastic
scattering is coherent or incoherent. In the ENDF/B thermal evaluations, some
NJOY2016 527

LA-UR-17-20093 17 ACER
isotopes for mixtures are represented like water, which describes the scatter-
ing from hydrogen bound in water, and some are given like benzine, which
describes the scattering from the benzine molecule normalized to the hydrogen
cross section. The parameter nmix is used to tell ACER about this effect. For
the existing ENDF/B evaluations, the user should use nmix=2 for benzine; the
user should use nmix=1 for all other materials. The parameter emax defines the
maximum energy to be used for the thermal scattering treatment. This value
should be coordinated with the value of emax in THERMR. A number around
4 eV is reasonable for most problems. The default for this parameter is 1000.,
which means that the code will determine the upper limit from the data in
MF=3 on the PENDF tape. Thus, the value used in THERMR is passed into
ACER without the user having to check it. The last parameter on Card 9 is
iwt. As described in Section 17.12, the weighting pattern for probability bins
for emitted thermal neutrons can be flat (that is, equally probable bins), or it
can be variable in the pattern 1, 4, 10, 10,..., 10, 4, 1 in order to better sample
the outlying wings of the energy distribution. The default is variable. Better
yet, for modern MCNP 5.1.50 and later, use iwt=2, which gives a continuous
distribution in outgoing energy, eliminating the discrete energy spikes.
The simplest version of Card 9 would contain only mti followed by /. This
works for many materials, including water, heavy water, and benzine, but if an
elastic (coherent or incoherent) component is present than the appropriate mte
value must also appear.
Card 10. This card is used for dosimetry libraries only. It specifies the ma-
terial MAT number and absolute temperatures. See the discussion of mat and
tempd for the fast (continuous) libraries.
Card 11. Photoatomic libraries require only the single parameter matd. For
ENDF/B-VII input, this will be a number like 100 for hydrogen or 9200 for
uranium.
Card 12. Photonuclear libraries require only the single parameter matd. See
the discussion of mat for the fast (continuous) libraries.
Editing Runs. No special input cards are required for editing runs. The class
of data in the library is automatically determined from the ZAID suffix. The
type of the output library is determined by ntype on Card 2. Changes can be
528 NJOY2016

17 ACER LA-UR-17-20093
Table 25: Conventional values for the thermal MT numbers (MTI and MTE) used in ACER
and THERMR for ENDF/B-VII
Thermal Material MTI Value MTE Value
H in H2O 222
D in D2O 228
Be metal 231 232
Graphite 229 230
Benzine 227
Zr in ZrH 235 236
H in ZrH 225 226
Be(BeO) 233 234
O(BeO) 237 238
H in Polyethylene 223 224
U(UO2) 241 242
O(UO2) 239 240
Al 243 244
Fe 245 246
made in the fields zaid,hk, and in the (iz,aw) list. One common use for these
editing parameters would be as follows. A user runs several isotopes, one at a
time, using the default ZAID of “.00c”, and 1/E integral thinning. Later, the
user decides that all these materials should go into a particular library with the
suffix “.77c” and the comment field “ENDF/B-VII library 7 for thermal reactor
applications.” ACER can handle these changes.
The following is a typical ACER input deck for producing a continuous-
energy file (class “c”):
acer
20 21 0 31 32/
1 0 1/
’ENDF/B-VII U-238’/
9237 293.6/
/
/
acer
0 31 33 34 35/
7 1 1/
’ENDF/B-VII U-238’/
NJOY2016 529

LA-UR-17-20093 17 ACER
viewr
33 36/
stop
It assumes that the ENDF file for 238U from ENDF/B-VII has been mounted
on unit 20 (tape20) and that the corresponding PENDF tape (after running
through RECONR,BROADR,etc.) has been mounted on unit 21 (tape21).
We have used iopt=1 for fast continuous data, suppressed the output listing
with iprint=1, and requested Type-1 output (itype=1). Any desired descrip-
tive line may be used, but some library schemes might like to define special
arrangements of text. The proper ENDF MAT number for 238U is 9237, and we
are taking the first temperature produced in the BROADR run, namely, 293.6K.
This corresponds to 0.0253e-6 MeV, the standard base temperature for MCNP
data files. We have taken the default values for newfor and iopp, so we expect
to see the new formats and the detailed photon data. We have also taken the
default of no thinning, which is preferred with modern large computers. The
output ACE file and XSDIR line will appears on tape31 and tape32. The sec-
ond ACER run is used to provide QA checks. It reads in the Type-1 file from
tape31 and writes out a new Type-1 file and a new XSDIR line on tape34 and
tape35, respectively. While doing this, it runs the consistency checks and makes
a set of plots on tape33. If the consistency plots find an E0> E0
max error that
can be repaired, the modified result will be on tape34. Finally, the VIEWR
module is run to convert the information on tape33 into color Postscript plots
on tape36. The actual step of reading the ACE file is a useful QA step, as
are the consistency checks and plots. In addition, it is good practice to run the
output ACE file immediately into an simple MCNP test job to see if it really
scans correctly. This is easy to do by incorporating the input example above
and the MCNP test input into a single script.
The second input example for ACER is for producing a thermal class “t”
library for hydrogen in water at a temperature of 800K using continuous energy
distributions:
acer
20 21 0 31 32/
2 0/
’1-h-1 in h2o at 800k from endf-vii’/
125 800 ’hh2o’/
530 NJOY2016
17 ACER LA-UR-17-20093
1001/
222 64 0 0 2/
acer
0 31 22 33 34/
7 1/
’1-h-1 in h2o at 800k from endf-vii’/
viewr
22 23/
stop
Here we have the additional entry tname=’hh2o’, which is used to construct the
ZAID value (which will be “hh2o.00t”). We have used mti=222, the standard
value for hydrogen in water (see Table 25) and requested 64 bins with the con-
tinuous tabulated data the outgoing neutron spectrum. Experience has shown
that more bins than the default of 16 are often desirable.
17.18 Coding Details
ACER begins in the acer routine provided by module acem by reading the user’s
input. The input varies according to whether “fast”, “thermal”, “dosimetry”,
“photoatomic”, or photonuclear” data are wanted, or if editing or type conver-
sion is desired. See iopt. For regular processing runs (iopt=1-5), input ENDF
and PENDF tapes are required, the input GENDF tape is only needed if a pho-
ton production matrix is to be constructed. For edit runs, the input ACE file
is mounted on the PENDF unit, and the GENDF unit is used for plotting out-
put, if desired. The code then branches to a different subroutine (in a different
module) for each different value of iopt.
Processing of fast data is controlled by acetop (which is in the acefc mod-
ule). It begins begins by opening the ENDF, PENDF, and GENDF units, and
by opening a scratch file MSCR used to accumulate the input for the acelod pro-
cedure. Subroutine first is then called to read the MF=1 and MF=2 data from
the input tapes and to prepare the corresponding data on MSCR. It copies the
TAPEID record and Hollerith descriptive data on the PENDF tape to MSCR,
and it processes the directory on the ENDF tape in order to set flags that
depend on which reactions and data types are present. For example, mt19 is
set if a distribution is provided for MT=19, in addition or instead of the more
standard MT=18. The global variables nf12s,mf1x, and gmt are used to keep
track of the reactions involved in computing photon production. For the new
NJOY2016 531

LA-UR-17-20093 17 ACER
format (newfor=1), the MT=3 reactions that imply the production of neutrons
or charged particles (either directly or as a residual) are identified. The MF,
MT, and product identity for each such reaction is stored in the arrays kprod,
mprod, and iprod, respectively, for a total of nprod items. Subroutine first
continues by standardizing and copying the fission neutron yield sections (see
tabize), by writing a dummy File 2 on mscr, and by copying the probability
tables in MT=153, if present. The next step is to read through File 3 on the
input PENDF tape to make an ordered list of all the thresholds in the array
ethr. The thresholds for each particle production are also determined (see t201,
t203,t204,etc., for neutrons, protons, deuterons, etc.). The last step is only
performed if the newfor option has been selected. The routine reads through
the subsections of File 6 on the input ENDF tape and adds any additional
particle production sections found into the arrays kprod,mprod, and iprod,
and it updates the production thresholds t201,t203,etc.. The final total of
nprod elements are sorted into order by first MT and then particle identity, and
subroutine first returns.
If necessary, convr is called next. It converts MF=12 photon transition prob-
ability arrays (lo=2), if present, into the photon yield format (lo=1) by tracing
all the cascades through the photon level structure. The results are written
on NSCR2. Sections of File 13 are simply copied to the scratch tape. While
working, the routine adds any additional thresholds associated with photons in
MF=13 to the ethr list, and it stores any discontinuities found in disc. It is
important to make sure these discontinuities appear in the final energy grid as
sharp steps. If MF=12 was converted, corresponding isotropic photon angular
distribution sections are constructed and written into File 14 on the scratch
tape. Other sections of File 14 are copied. If File 6 is present (ENDF-6 format
evaluations only), convr checks to see whether photon production subsections
are present. If so, it converts them into specially defined MF=16 sections on the
scratch tape. The resulting scratch tape contains sections for MF=12, MF=13,
MF=14, and MF=16. The updated list of threshold and the list of are sorted
into order, and the discontinuities are printed out on the listing for the user’s
information.
Returning to acetop, subroutine unionx is called to construct the union en-
ergy grid. It starts by checking the probability tables, if present, and setting
the flag mtcomp if an overlap with MT=4 is indicated. It continues by reading
in the energy grid of the total cross section on the PENDF tape. In the process,
it watches for energies from the lists of thresholds and photon discontinuities
532 NJOY2016

17 ACER LA-UR-17-20093
and adds corresponding sharp steps by plus and minus one in the seventh sig-
nificant figure to the ACE energy grid. If integral thinning was requested, it
computes the starting weighted integrals for the total cross section. Note that
the energy grid, the total cross sections, and the weighted integrals are stored
on a loada/finda tape for later use. If RECONR and BROADR were used
to produce the PENDF tape, this is the desired union grid. If another file is
used for PENDF input, ACER will still work, but the grid might not be really
correct. If integral thinning was requested, subroutine unionx now reads for-
ward on the PENDF tape to find the capture cross section, MT=102, and read
through the section computing the capture integrals and storing them on the
loada/finda tape. After printing out the original integrals, it carries out the
integral thinning procedure described in Section 17.3, taking care not to remove
the breaks at the thresholds and photon-production discontinuities. When an
energy grid has been found that satisfies the input target, UNIONX prints out a
table of the final resonance integrals by energy bands. This thinning process is
somewhat obsolete with modern large computers, and it probably will not be
maintained in the future.
A different process is used in unionx to generate a union grid for incident
charged-particle data classes. The RECONR module is not used for incident
charged particles, so the routine reads through File 3 and constructs a unionized
grid appropriate for linear-linear interpolation. It then searches forward to find
MF=6/MT=2 and adds in the energy points found there. It then reads back
through the energy grid obtained so far and adds additional energy points to
large intervals. The parameter step=1.2 is used to add these additional grid
energies. The input PENDF file is backed up to MF=3 for the next step.
Now that the complete union energy grid has been determined, unionx reads
through File 3 to write all the other desired reactions onto this new energy
grid. Some reactions are eliminated as “redundant;” for example, MT=4 (total
inelastic) can be removed, unless it will be needed later for photon production.
MCNP is sensitive to errors in the reaction thresholds. RECONR normally
makes sure the the threshold is slightly greater than the theoretical value. This
routine will print out a message if it finds a reaction threshold that is lower than
the theoretical value. While writing out the new sections of File 3, the total cross
section is recomputed to be exactly equal to the sum over the partial reactions
at each energy grid point and stored using loada/finda. When this process
is complete, the file nscr contains all the unionized reaction cross sections.
Subroutine unionx now writes out the new total cross section on the file mscr,
NJOY2016 533

LA-UR-17-20093 17 ACER
and then copies over all the new reaction sections from nscr. The file mscr now
has a complete File 3.
Next, acetop calls topfil to prepare new versions of MF=4, MF=5, and
MF=6 on mscr. First, ptinit is called to precalculate some of the constants
needed for converting angular distributions to equally probable bins. After the
constants have been calculated, topfil starts a loop over all the sections for
Files 4, 5, and 6 on the ENDF tape. Some reactions are just skipped entirely;
for example, if first found a distribution for MF=19 and set the mt19 flag, the
distribution for MT=18 is removed. For the new format (newfor=1), sections
of File 4 (angular distributions) are simply copied for later processing. For the
old format, the sections are converted into a representation giving 32 equally
probable cosine bins for each incident energy (with appropriate exceptions for
completely isotropic sections or energy values). Angular distributions using
Legendre coefficients are converted using ptleg, and tabulated distributions are
converted using pttab. A special ENDF option, flagged by ltt3=3, directs that
the section is divided into low- and high-energy parts. The high-energy part is
always tabulated.
Continuing with topfil, sections of File 5 are just copied for more processing
later. For sections of File 6 with the old format requested (newfor=0), sections
are scanned to see if any use tabulated sections with laws other than the Kalbach
representation (lf=1 and lang=2). If so, the routine backs up and calls fix6
to convert the distribution into lf=7 form, a form the older versions of MCNP
can understand.
Subroutine fix6 produces a section with the E,µ,E0ordering in the labora-
tory frame using 33 equally spaced cosine values for each incident energy. The
original data can be in either Legendre coefficient form or in tabulated form.
If the data are given in the CM frame, a conversion to the laboratory frame
is carried out, but no attempt is made to refine the energy and cosine grids to
provide a really good representation in the laboratory. If the input data are
sufficiently dense, the results are not too bad.
Returning to topfil at “work on file 6,” data for LF=6 (phase-space distri-
butions) are just copied. Sections with LF=1 (tabulated) are also just copied,
except if there is more than one interpolation range, or if nonlinear interpolation
is specified, cptab is called to linearize the representation and reduce it to one
interpolation range as required by the ACE format. For LF=2 (two-body angu-
lar distributions) when the new formats have been requested (newfor=1), the
ENDF data are just copied to the mscr file. For the old formats, the data are
534 NJOY2016

17 ACER LA-UR-17-20093
converted into 32 equally probable cosine bins using either ptleg for Legendre
data or pttab for tabulated distributions. LF=5 sections (charged-particle elas-
tic scattering) are copied. For LF=7 (either original E,µ,E0data from ENDF or
data converted using fix6), the overall angular distribution is computed by in-
tegrating over all outgoing energies. The TAB2 record that defines the loop over
incident energies in the ENDF format is converted to a TAB1 record to hold the
new overall angular distribution. For the old format (newfor=0), this angular
distribution is converted into 32 equally probably cosine bins using pttab. The
TAB1 records for the various cosines described by LF=7 are copied to the out-
put file. Thus, the LF=7 sections on mscr are almost in standard form, except
for the extra overall angular distribution.
When topfil is complete, acetop calls gamsum, which computes the total
photon production cross section on the union grid. It does this by adding the
contributions from the MF=12 photon yields times the corresponding MF=3
cross sections, the MF=13 photon production cross sections, and MF=16 yields
times the corresponding MF=3 cross sections. The results are written out using
MF=13, MT=1.
Next, subroutine gamout is called to add the photon distribution information
to the main scratch tape. If no GENDF tape is available, gamout simply copies
MF=14, MF=15, and MF=16 from the scratch tape prepared by convr. How-
ever, if the GENDF tape is present, it prepares the 600-word photon production
matrix. The first step is to read through the input tape extracting the photon
group boundaries and adding up all the photon production reactions into one
matrix. The code then loops over neutron groups converting the outgoing pho-
ton groups into equal-probability bins and computing the single discrete photon
in each bin that conserves energy. Finally, the resulting 30-by-20 matrix is writ-
ten onto the output tape using the identification MF=15, MT=1. This process
is now obsolete and may not be maintained in future versions.
Upon returning to acetop, the tape mscr is completed by adding a material-
end, or MEND, record. Subroutine acelod is called with mscr as its input file.
It reads through the file in order and stores the numbers into memory in ACE
format. The first step is to define the ACE zaid value based on 1000*Z+A
for this material, plus a numerical suffix provided by the user (the default is
“.00”), plus a letter suffix appropriate for this class of data (see Table 23). For
the acefc module, the data class is completely determined by identity of the
incident particle in izai. The routine than counts all the reactions that survived
unionx, using slightly different rules for the different incident particles. Here,
NJOY2016 535

LA-UR-17-20093 17 ACER
ntr is the count of all the reactions present on the input mscr file, and nr is
the subset of reactions that actually determines the transport and contributes
to the total reaction cross section. The routine then reads through File 1 and
stores the total and prompt fission ¯νdata, if present, into the temporary areas
nut and nup for future use. The routine also reads through File 2 and stores in
unresolved-range probability tables, if present, into a temporary area urd.
Next, the energy grid of the total cross section from MF=3 is read in starting
at pointer esz. This determines the number of energy points in the union grid,
nes, which can then be used to compute the pointers to the other cross sections
in the main cross section block (namely, it for total, ic for absorption, ie for
elastic, and ih for heating). The blocks for supplemental cross sections can
also be assigned; for example, lqr for reaction Q values, or lsig for reaction
cross section pointers. With all these pointers computed, acelod can simply
read through File 3 and store all the cross sections, Q values, and cross section
locators in their assigned slots. The total and absorption cross sections are
summed up from their parts during this process. Because of the complexities
of handling the various possible incident particles, this process is divided into
three parts: a loop over reactions producing the incident particle, a loop over
reactions that do not produce the incident particle, and a pass to go back and
add MT=3 (nonelastic) and MT=4 (inelastic), if they are needed for photon
production. After MF=3 has been read, the fission ¯νdata can be stored in the
main memory block.
The next step is to assign the LAND and AND blocks after the cross section
data, and to read in the angular distribution data, store them in the AND block,
and save the pointers in the LAND block. Coupled energy-angle sections from
File 6 with LF=1 or LF=6 don’t have separate angular distributions, and they
are flagged by putting the value -1 in the LAND block for the reaction. For the
remaining reactions, the TYR block is filled in with the particle yield for the
reaction — for example, 2 for an (n,2n) reaction — and the sign of the TYR
entry is adjusted to be positive for laboratory-frame distributions and negative
for CM-frame distributions. Sections that are completely isotropic are flagged
by putting 0 in the LAND block for the reaction, and anisotropic sections are
processed by calling acensd (for neutron scattering distributions) or acecpe (for
charged-particle elastic distributions).
In acensd, a loop is set up over the incident energies in the section. For
the old format, the first record has always been adjusted to be a TAB1 record
containing the 32-bin angular distribution, and it can be stored directly into the
536 NJOY2016

17 ACER LA-UR-17-20093
cells of the ACE image. For the new format, there are several possibilities. If
LF=7, the distribution in the TAB1 record is already in the desired form. For
tabulated MF=4 data, pttab2 is called to produce a properly normalized dis-
tribution. For MF=4 Legendre coefficient data, ptleg2 is called to reconstruct
the pointwise angular distribution adaptively and make sure it is properly nor-
malized. For Legendre data in File 6, ptleg2 is used in the same way. For
tabulated data in File 6, the LIST representation is transformed into a TAB1
representation, and pttab2 is used to produce the properly normalized distribu-
tion. With a simple tabulated distribution in place, acensd can now integrate to
form the cumulative density distribution, double check the normalization, and
write the results into the proper ACE memory locations. Allowance is made for
the LTT=3 format, where separate low- and high-energy sections are given, and
distributions that are found to be completely isotropic are removed by setting
their entry to zero in the LAND block.
Subroutine acecpe handles charged-particle elastic scattering, supporting the
new ACER capability to produce libraries using charged-particle classes. As this
option is fairly new, the routine prints out a number of intermediate results on
the output listing after the header “working on charged-particle elastic,”
Next, the LDLW and DLW blocks are assigned following the angular data,
and the energy distribution data are read and stored. Reactions from the dif-
ferent ENDF files are processed through different paths. Sections of File 5 go
to acelf5. Sections of File 6 go to acelf6. Sections of File 4 (except for elastic
scattering) are represented by LAW=3 discrete-level distributions that provide
the parameters that MCNP uses to compute emission energy after discrete-
inelastic scattering.
In acelf5, each section of energy distribution data is examined for its “LAW”
and stored accordingly. The analytic laws from ENDF File 5 are simple to store;
there is basically a one-to-one correspondence between the ENDF quantities and
their ACE equivalents (except, eV are converted to MeV). Tabulated sections
in File 5 (LF=1) are converted into the LAW=4 cumulative density function
format by computing the cumulative probability function and storing tables of
E0,P(E0), and C(E0) for each E.
Subroutine acelf6 is used to process energy-angle distributions from sections
of File 6. The particle yield for data from MF=5 is determined by the MT
number; for example, the yield is 2 for MT=16, the (n,2n) reaction. On the other
hand, subsections of File 6 contain explicit values for the particle yield, and the
yield may vary with E. In addition, there may be more than one subsection
NJOY2016 537

LA-UR-17-20093 17 ACER
describing emission for a particle. An example of this is 19F from ENDF/B-
VI, which has two subsections for emitted neutrons (first neutron and second
neutron). To handle all these complications, ACER reads through the entire
section of MF=6 data for a given reaction, looks at all the yield tabulations,
and computes the total yield for the reaction. It types out messages if multiple
subsections are found for one particle, if energy-dependent yields are found, or
if noninteger yields are found.
The case of constant integer yields is simple; the value is stored in the tyr
array just as for MF=5 reactions. The sign of the yield in tyr is positive for
laboratory data and negative for CM data.
Generalized yield data are stored as a table of Eand Y(E) starting at location
ntyr with respect to the start of the DLW block. The value of ntyr is stored
in the tyr array as 100+ntyr. The sign of this value is positive for laboratory
data and negative for CM data. The code then repositions the input file to the
start of the section for the current reaction in order to read in the distributions.
As each subsection is read, the yield tabulation is converted into a fractional
probability for this subsection by dividing by the generalized yield. There are
five different types of secondary particle distributions that must be processed:
Legendre data (LAW=1, LANG=1), Kalbach data (LAW=1, LANG=2), tabu-
lated data (LAW=1, LANG>2), angle-energy data (LAW=7), and phase-space
data (LAW=6).
The first three share the same loop over incident energy E. For each sec-
ondary energy E0, the probability P(E0) and the angular representation are read
from the input file, and the cumulative probability density C(E0) is computed.
For Kalbach data, the only angular parameter is the pre-equilibrium fraction r.
The corresponding slope parameter ais computed using the function bachaa,
and both rand aare stored in the table using the ACE Law 44 format.
Neither Legendre data nor tabulated angular distributions will appear for the
old format (newfor=0), because such sections were intercepted and converted to
LF=7 in topfil. For the new format, the Legendre distributions are converted
to tabulated form using ptleg2 and the tabulated distributions are converted
to properly normalized tabulations. In both cases, the result is integrated to
obtain the cumulative density function. The result is stored using the new ACE
format, LAW=61.
LAW=7 data are handled in a separate incident-energy loop, which stores
data using the ACE Law 67 format. The individual energy distributions on
the input file have already been normalized and are ready to be stored in the
538 NJOY2016

17 ACER LA-UR-17-20093
xss array. Note that the values of intmu and nmu were passed to this part of
the code using two nonstandard locations in the TAB1 record that was origi-
nally the TAB2 record controlling the loop over µbut now contains the angular
distribution in 32 equal-probability bins.
The phase-space distribution doesn’t need an incident-energy loop. It is only
necessary to store the values of apsx and npxs into the xss array and to compute
a single set of E0,P(E0), and C(E0) values for E0
max = 1. The normalization
factor Cnis obtained from the integration over E0in order to guarantee that
C(E0
max = 1).
Once the secondary-particle energy distributions and angle-energy distribu-
tions have all been stored, the GPD pointer is computed to point to the start
of the photon production data. The total photon production cross section itself
is simply read from the section MF=13, MT=1 on the input tape and stored
starting at GPD. The next step depends on whether photon production matri-
ces were requested by giving ACER a nonzero value for the input GENDF tape.
If so, the matrix is read from the section MF=15, MT=1 on the input tape
and stored in memory just after the photon production cross section. If not, a
dummy matrix of 600 zeros is stored. The ACE fast library is finished.
At this point, ntrp is set, acelod calls acelpp to store detailed photon
data. The code goes through the main energy grid changing eV to MeV with all
energies adjusted to have a maximum of nine significant figures. The summation
cross sections, total and absorption, are also truncated to nine-digit precision.
The final step in acelod is to call acelcp to load the particle production
data. For incident neutrons, these are charged-particle production blocks, but
for incident charged particles, these blocks are for all particles not the same as
the incident particle, and neutron emission is included.
Now that all the fast ACE data have been stored into memory, acetop calls
aceprt to print the data on the output listing file. The amount of information
printed depends on the value of the input parameter iprint. Finally, acetop
calls aceout to write out the ACE fast library.
The output library file can be written in Type-1 or Type-2 format, depending
on the value of itype. As described above, Type 1 is a simple formatted file
suitable for exchanging ACE libraries between different computers, and Type 2
is a Fortran direct-access binary file. The problem here is that Type 2 files are
written with all data as real numbers (except for some of the fields in the header
record). Some of these numbers represent integers, and the Type 1 format
requires that these numbers be written into their fields in integer format, that
NJOY2016 539

LA-UR-17-20093 17 ACER
is, right justified and without decimal points. In order to handle both these file
types in a portable way, subroutine acelod first stores all values into memory as
real numbers in the array xss. Therefore, the contents of memory can be written
out in Type 2 format with no further processing. In order to convert to Type-1
formats, subroutine change is used. Subroutine change knows the type (real
or integer) of every word in the ACE format. When converting from internal
Type-2 data to Type-1 output, it uses typen to write the number directly to
nout using the appropriate format (I20 or 1PE20.12).
Processing of thermal data is controlled by subroutine acesix from module
aceth. It starts by finding the desired temperature on the input PENDF tape.
The inelastic and elastic cross sections are copied to a scratch file nscr. The
scratch file is then rewound, and the inelastic cross section is read again to
determine the maximum thermal energy emax.
If the elastic component is coherent, the input cross sections from nin are
divided by Eto get a stair-step function, which is written to the output file. If
the elastic component is incoherent, the incident energies and equally probable
emission cosines are read from MF=6 on nin and the corresponding cross sec-
tions are read from MF=3 on nscr. All data are stored into memory in ACE
format and then written onto nout.
The processing of inelastic scattering is more complex. After the proper sec-
tion on File 6 is located, a uniform or variable pattern of weights is constructed
in wt(i). The energy grid is obtained from File 6 on nin, and the corresponding
cross sections are read from MF=3 on nscr. The secondary-energy spectrum for
each incident energy is converted into bins using the weight pattern in wt(i),
and the single E0that conserves the average energy for the bin is computed.
The nang equally probable cosines for this new E0are obtained by interpo-
lation. Once all of the nbin*nang events have been computed and stored in
memory, they are copied out to nout.
At this point, all the thermal data have been computed, and nout is passed
to subroutine thrlod for storing into memory in ACE format. This memory
image is then printed out using subroutine thrprt, if desired, and written to
the final Type-1 or Type-2 output file using throut.
Subroutine thrfix is the other call exported by module aceth, and it can
be called from ACER for editing or listing thermal files that have already been
produced. It begins by reading the input Type-1 or Type-2 file into memory.
It then allows for editing the ZAID value, the descriptive string, or the (iz,aw)
list. The thermal ACE file can be printed out by using thrprt, and the file can
540 NJOY2016

17 ACER LA-UR-17-20093
be written out in either Type-1 or Type-2 format using throut. If the input
unit normally called ngend is nonzero, it is interpreted as nplot and used by
subroutine tplots to output a file for VIEWR that will generate a set of color
Postscript plots of the thermal scattering data.
Processing of dosimetry data is controlled by subroutine acedos from mod-
ule acedo. It begins by allocating space for the main ACE container array
xss(nxss) and a scratch array scr that will be used to read in the ENDF data
records. It then opens the input file, determines what ENDF version is being
used, and searches for the desired MAT and temperature (matd and tempd). This
option is normally used directly on ENDF-style evaluations for dosimetry cross
sections that just give the cross sections and omit the additional distributions
needed for full transport calculations. These are usually threshold reactions,
and zero temperature works fine. The dosimetry option can also be used with
PENDF-style input containing broadened capture cross sections, and in this
case, a non-zero value for tempd would be appropriate.
The acedos routine the searches for the first reaction in File 3, defines loca-
tors for the MTR, LSIG, and SIG blocks by assuming that there are no more
than nmax=100 reactions present, and it begins a loop over all the reactions in
File 3.
For each reaction, its MT identifier is stored in the MTR block, the current
pointer value is stored in the LSIG block, and the interpolation table and cross
sections are stored in the SIGD block starting at the current pointer value. The
pointer is then increased by the number of words stored, and the reaction loop
continues. Note that if the input tape is real PENDF tape (that is, if it has been
through RECONR), the cross sections will have been linearized onto a union
grid. There will only be a single interpolation range for each reaction. However,
if the input file was an ENDF tape, there may be several interpolation ranges
specifying nonlinear interpolation laws for a given reaction, and the energy grids
for different reactions may be different.
When the reaction loop has been completed, the excess space in the MTR
and LSIG blocks is squeezed out, and the scratch storage array is deallocated.
The final steps are to construct the ZAID value for the material using the “y”
class, to call dosprt to print the results, and to call dosout to write the ACE
dosimetry library file.
Subroutine dosfix is the other call exported by module acedo. It is used
when the user requests editing or printing of an ACE dosimetry file separate
from the production of the file. The routine reads in input Type-1 or Type-2
NJOY2016 541

LA-UR-17-20093 17 ACER
ACE file into memory and allows the user to adjust the ZAID value for the
material or to change the comment string and (iz,aw) list. It calls dosprt to
print the file and dosout to write out the modified file. Note that the type of the
ACE file can be changed from 1 to 2 or from 2 to 1 at this point. No consistency
checks or cross-section plots are currently provided for dosimetry libraries.
The dosout routine calls typen directly to cause Type 1 fields to be written
in the proper floating-point or integer format, if requested.
Processing of photoatomic data is controlled by subroutine acepho in module
acepa. It starts by allocating an area for scratch storage scr and the main ACE
container array xss. The input file is opened and scanned to determine what
ENDF version is being used. The requested material matd is then located, and
acepho reads in the energy grid for the total cross section, mt=501, which will
be used as the union grid for all the photoatomic reactions, starting at pointer
esz. The number of energy points in the union grid is nes, and that value can
now be used to compute the pointers iinc,icoh,iabs, and ipair, representing
incoherent scattering, coherent scattering, photoelectric absorption, and pair
production, respectively. The acepho routine then reads through File 23 on the
input tape, extracts the cross sections for each of the reactions using the energy
points of the union grid, and stores the cross sections at the appropriate pointer
values. Note that the cross sections and energies have not been converted to log
form at this point, but the energies have been converted to MeV. The detailed
sub-shell cross section for photo-ionization supported by the most recent version
of the ENDF-6 photoatomic format are not supported in this version of acepho.
The pointers to the jinc block for incoherent scattering functions, the jcoh
block for coherent form factors, the jflo block for fluorescence data, and the
lhnm block for heating numbers are now computed in the storage area just
following the cross sections.
The jcoh block uses a fixed grid of 55 values for the momentum transfer of
the recoil electron (in inverse Angstroms) specified in the parameter array vc.
The code first reads through MF=27, MT=502 and interpolates for the values
of the coherent form factor at these 55 recoil values. They are stored in the
jcoh block as the second block of 55 numbers. The code then loops through
the 55 recoil values again, computing the cumulative integral of the coherent
form factor for each recoil value and storing them as the first group of 55 words
in jcoh. The anomalous form factors supported by the latest version of the
ENDF-6 format are not yet supported by this version.
The incoherent scattering function is tabulated on a fixed grid of 21 values
542 NJOY2016

17 ACER LA-UR-17-20093
for the momentum of the recoil electron (in inverse Angstroms) that is given in
the parameter array vi. The values are obtained by interpolating in the section
MF=27, MT=504 from the input file. At the same time, the contribution to the
heating from incoherent photon scattering is computed on the union grid with
subroutine iheat.
The calculation of fluorescence data for photoelectric absorption is not com-
plete in this version. A message to the user is provided.
Finally, the scratch storage is deallocated, the ZAID value is generated for
class “p”, phoprt is called to prepare the output listing for the photoatomic
data, and phoout is called to prepare the output library file. Note that typen
is called for each field in order to write it out in Type 1 format with the proper
floating or integer format, if requested.
Subroutine iheat is used to calculate the local heating associated with inco-
herent photon scattering.
The other call exported by module phopa is phofix, which provides for edit-
ing or printing photoatomic libraries when requested by the user from acer.
It reads in the Type-1 or Type-2 input file, and allows the ZAID value, the
comment string, or the (iz,aw) list to be changed, if desired. A listing of the
file can be obtained using phoprt, and the modified ACE file can be written
using phoout. Note the the ACE file type can be changed from 1 to 2, or from
2 to 1 at this point. No consistency checks or plots are currently provided for
photoatomic libraries.
Processing of photonuclear data is controlled by subroutine acephn in module
acepn. The photonuclear format is a little different from the more familiar class
“c” format used for incident neutrons and charged particles. In the class “c”
format, sections describing the emission of the particle that matches the input
particle are treated specially, and photon production is treated specially. The
other emissions are lumped together in the particle production sections. In the
photonuclear format, all the products (neutron, photon, charged particles) are
treated symmetrically, and they all are given in blocks similar to the particle
production blocks used for class “c.”
To begin, storage is allocated for the scratch array used to read in ENDF
records, the ENDF version being used is determined, and the location of the
desired material on the input file is found. The routine then reads through the
ENDF “dictionary,” sets some flags to indicate the presence of some kinds of
data, and save a list of the reactions found (see mfm,mtm, and nr6). If fission
nubar data are available on the input file, they are read into the fnubar array.
NJOY2016 543

LA-UR-17-20093 17 ACER
There is no real distinction made between total and prompt nubar in current
photonuclear evaluations.
The energy grid is taken from the first section of File 3 found. For Los Alamos
evaluations, and others that use that same style, this is MT=5, and that value
is stored in mttot. Some other evaluations will start with MT=1 or MT=3,
and that value is stored in mttot. It is now possible to define the cross section
locators for the ACE file, namely, esz (always 1), tot,non,els, and thn. The
pointer for the elastic cross section, els, is set to zero if elastic data do not
occur on the input file (see ielas). The routine can now assign locators for the
partial cross sections, including mtr for the MT value, lqr for the Q value, and
lsig for pointers to the data in the data block starting at sig. It reads through
File 3 on the input file, stores each cross section in the appropriate locations,
and computes a correct total that is the sum of all the partial cross sections.
With the cross sections in place, aceph makes a pass through the distri-
butions of the input file to count the different particles produced (see nneut,
nphot,nprot,etc.), to determine the production thresholds (see tneut,tphot,
tprot,etc.), and to accumulate the heating from any recoils described in File 6.
For the latter, the average energy of the recoil distribution is computed on its
natural energy grid, and then the results are interpolated onto the ACE energy
grid, converted to “per reaction” units by dividing by the total cross section,
and added into the accumulating total heating at index thn. For photonuclear
capture (MT=102) when no recoil is given, or for sections of File 6 that don’t
define the recoil spectrum, the corresponding recoil energy per reaction is added
into the accumulating heating.
At this point, there is enough information to set up the IXS block and to
fill in the elements that define the particle types emitted and the number of
reactions that contribute to that particle production. The numeric codes used
for the various particles in the ACE file are shown in Table 26.
Now a loop is set up over the particle types that have been found to be
available for this material in the order neutrons, photons, protons, and so on.
For each particle, additional entries are made into the IXS block: the pointer to
the data for the particle pxs, the pointer to the list of MT numbers contributing
mtrp, the pointer to the list of yield/system values tyrp, the pointer to the
list of cross section pointers lsigp, and the pointer to the list of cross section
data blocks sigp. The first two elements in the sigp segment are filled in: the
index to the threshold for the production from the main energy grid it, and the
count of production cross section values (from it to nes). The code now loops
544 NJOY2016

17 ACER LA-UR-17-20093
Table 26: ACE Particle Codes for Photonuclear Files
Code Particle Data Class
1 neutrons
2 photons
9 protons
31 deuterons
32 tritons data
33 3He
34 alphas
through the File 4 and/or File 6 again and treats each section or subsection that
contributes for this particular particle. In each case, the contribution is summed
into the accumulating production cross sections, the data giving the fractional
yield for this reaction to the total production of this particle is stored, and the
heating contribution from this reaction for this particle is added in.
Now that the sigp data are complete, the code can compute the pointer to
the list of LANDP entries and and the pointer to the ANDP data block and store
them in the IXS block. It continues by reading through the sections that con-
tribute angular distributions, storing the data in the normal ACE-format slots,
and adding in the appropriate contributions to the accumulating heating cross
section. Angular distributions are stored using the “new formats”, LAW=61.
They are generated with the help of subroutines ptleg2 and pttab2, just as
described above for class “c” files.
The locators for energy distributions can now be defined and stored into the
IXS block (see ldlwp and dlwp). Subroutine acephn searches through Files
4, 5, and 6 to find sections that contribute energy distributions. Each such
distribution is stored using the appropriate ACE law, and the contribution to
the heating from the distribution is added into the accumulating heating cross
section. The methods are similar to those described for energy and energy-angle
distributions above.
When the loop over all the particle types is complete, the routine converts
the main energy grid to MeV and adjusts the precision of the energies and the
heating to 7 digits. The ZAID value for this material is generated using a class
suffix of “u,” and the results are written to the output file.
The other call exported by module acepn is phnfix, which provides for edit-
ing or printing photonuclear libraries when requested by the user from acer. It
reads in the Type-1 or Type-2 ACE files, and allows for adjustments of the ZAID
NJOY2016 545

LA-UR-17-20093 17 ACER
value, the descriptive text string, or the (iz,aw) list. The ACE photonuclear file
can be printed using phnprt. The data file can be written out in either Type-1
or Type-2 format using phnout. And a input file for the VIEWR module can
be produced that will generate color Postscript plots of all the photonuclear
cross sections, the heating value, the individual particle production and heating
values, and angle or energy distributions as 3-D perspective plots.
17.19 Error Messages
error in acer***illegal iopt
IOPT must be between 1 and 5, 7 and 9.
error in acer***illegal newfor.
Check the input, the value for the format option must be either 0 or 1.
error in acer***illegal iopp.
Check the input, the value for the photon option must be either 0 or 1.
error in acer***illegal ismooth.
Check the input, the value for the smoothing option must be either 0 or 1.
error in first***desired temperature not found
Desired temperature was not found on the input PENDF tape. Check for
an input error or whether the wrong tape was mounted.
error in first***storage exceeded
This can result if there are more than maxpp=250 sections in File 12 on
the input ENDF tape (maxpp is a global parameter at the beginning of
module acefc) or if there are more than ngmtmx=500 different gamma
rays described in the evaluation (ngmtmx is defined in subroutine first).
error in first***too many production items
There isn’t enough space in the global arrays that accumulate particle
production information. See the global parameter maxpr=300 and the be-
ginning of module acefc.
error in first***too many threshold
See nethr=300 in first.
error in topfil***nxc.gt.nxcmax
More than 500 reactions have been found on the input ENDF tape. See
the global parameter nxcmax=500 at the start of module acefc.
error in ptleg2***nord= ...
The maximum Legendre order for the identified MT reaction exceeds ipmax.
This is likely an ENDF file error.
error in pttab***storage exceeded
This routine can process up to 300 secondary angles. See the parameter
npmax=300.
546 NJOY2016

17 ACER LA-UR-17-20093
error in pttab***tab ang dis has more than one terp range
Only one interpolation range is allowed when processing tabulated angular
distributions in pttab. In some cases, two ranges are allowed; see chekit.
error in pttab***tab ang dist not allowed for
Interpolation schemes that use logs for the scattering cosine (int=3 or 5)
are not allowed because µcan take on negative values.
error in chekit***wrong type of nr=2 file 5 mt
Only certain types can be handled here.
error in fix6***storage in a exceeded
See the parameter namax=9000.
error in gamsum***exceeded storage in dictionary
Limited by the global parameter nxcmax=500 at the beginning of module
acefc.
error in convr***storage exceeded for photon data
There is not enough room in the allocatable array tot for the total photon
yield array from MF=12 or MF=13. See nwtot=5000.
error in convr***storage exceeded for edis
The list of discontinuity energies is limited to nned=50 elements in convr.
error in convr***too many lo=2 photons
See lmax=100 in convr.
error in convr***only law=1 allowed for endf6 file6 photons
Photon sections in File 6 should use the tabulated representation only.
error in gamout***expected send card while reading mf14
Sequence of ENDF records is off.
error in gamout***mat not found
The desired material was not found on the input GENDF tape. Make sure
that the correct file was mounted.
error in gamout***storage in a exceeded
Storage exceeded in the dynamic array scr. Check the value for nwamax in
this subroutine.
error in gamout***no gamma groups on ngend
The input GENDF tape does not contain a photon group structure. Re-
member that using the 30×20 matrix option for photon emission requires
that a GROUPR run be made to produce multigroup cross sections for all
of the photon production reactions.
error in gamout***storage in sig exceeded
Storage limit for the allocatable array sig has been exceeded. See nsmax=5000.
error in aceout***not coded for this incident particle
Neutrons, protons, deuterons, tritons, He-3, or alpha are allowed.
NJOY2016 547

LA-UR-17-20093 17 ACER
error in acelod***insufficient storage for esz block
The ESZ block contains 5×NES words, and this value must be less than the
limit of nxss=7 000 000 words, which is set in the global variables at the
start of the acefc module.
error in acelod***insufficient space for cross sections
There is not enough space for the SIG block in the container array xss.
See the discussion for the ESZ block above.
error in acensd***insufficient storage for angular...
There is not enough space for the angular data block in the container array
xss. See the discussion for the ESZ block above.
error in acelod***insufficient space for energy dist
There is not enough space for the DLW block in xss. See the discussion
for the ESZ block above.
error in acelod***insufficient space for photon spectra
There is not enough space in xss. See the discussion for the ESZ block
above.
error in acelod***30 groups are required for ...
The photon production neutron group structure must be 30 groups.
error in acelod***insufficient storage for energy dist
There is not enough space in xss. See the discussion for the ESZ block
above.
error in acelf5***insufficient space for energy dist
There is not enough space for the DLW block in xss. See the discussion
for the ESZ block above.
error in acelf5***scratch storage exceeded reading lf=1
See nwscr=5000.
error in acelf5***sorry acer cannot handle lf=5...
This evaluation contains a bad representation.
error in acelf5***illegal lf=...
The acelf5 routine can process LF=1, 5, 7, 9, and 11 from ENDF File 5.
error in acelf6***illegal law for endf6 file6 neutrons
Only lf=1, 6, or 7 are allowed here.
error in acelf6***insufficient space for mf6 tab2
There is not enough space in xss. See the discussion for the ESZ block
above.
error in acelf6***insufficient space for mf6 neutron yield
There is not enough space in xss. See the discussion for the ESZ block
above.
548 NJOY2016

17 ACER LA-UR-17-20093
error in acelf6***exceeded scratch storage
There is not enough space in xss. See the discussion for the ESZ block
above.
error in acelf6***storage exceeded for generalized yield
See ishift=500.
error in acelf6***only lang=1, 2, 11-13 allowed ...
Others aren’t expected here.
error in ptlegc***too many coulomb angles
The parameter maxang=2000 needs to be adjusted.
error in acelpp***insufficient space for photon production
There is not enough space in xss. See the discussion for the ESZ block
above.
error in acelpp***no. of gamma energies not complete
There is something wrong with the data for this reaction on the main
ACER scratch file.
error in acelpp***insufficient storage for input photon
There is not enough storage in the dynamic array SCR. This size is con-
trolled by the statement nwscr=150 000 in subroutine acelpp.
error in bachaa***dominant isotope not known for ...
The separation energy calculation only works for isotopes. This routine
contains a small table of the dominant isotope in elements that sometimes
appear in evaluations. This message means that the dominant isotope is
not known for this element, and that the table must be extended.
error in acelcp***exceeded scratch storage
See nwscr=5000 in acelcp.
error in acelcp***insufficient storage for angular dist...
There is not enough space in xss. See the discussion for the ESZ block
above.
error in acelcp***unsupported law and lang
Only some combinations of LF=1 and LF=2 are currently handled.
error in acelcp***scratch array overflowing ...
Reduce the number of energy points.
error in acefix***problem with particle id in zaid
Unknown particle type.
error in acefix***illegal file type
Only files of class “c” can be handled here.
error in aplof4***too many e values in angular distribution
Up to 1200 allowed. See parameter maxe=1200.
NJOY2016 549

LA-UR-17-20093 17 ACER
error in acesix***storage exceeded for coherent reactions
There is insufficient space in the six array for the coherent or incoherent
data, respectively. This is a space of 50 000 words. This value is set by the
statement ninmax=50 000 at the beginning of the acesix routine.
error in acesix***exceeded storage for incoherent reactions
See the explanations above.
error in acesix***exceeded storage for incoherent elastic
See the explanations above.
error in acesix***coded for equiprobable angles only
The input thermal File 6 (a nonstandard format) must use the equiprob-
able angle format. Since this is currently the only format produced by
THERMR, this error should not occur.
error in acesix***solution out of range
The routine is not able to find a legal solution while trying to find the
equiprobable bins for inelastic scattering.
error in acedos***desired mat and temp not found
The requested material and temperature were not found on the input
photo-atomic PENDF file. Check for an input error, and make sure that
the correct file has been mounted as npend. Remember that this is nor-
mally the output of a RECONR run to assure correct unionization and
linearization.
error in acedos***too many reactions, need ...
The number of mt values in the ACE output file exceeds acedos’s internal
limits. Increase the value of nmax.
message from acepho---photoelectric processing not complete
This version doesn’t handle fluorescence data as yet.
error in acephn***too many reactions in mtr list
See the parameter mmax=80.
error in acephn***mf=6/mt=201-207 not supported...
Some of the first-generation of photonuclear evaluations represented par-
ticle production from photonuclear reactions using MT=201 through 207,
as for gas production. This does not conform to the ENDF-6 format and
cannot be processed here.
error in acephn***insufficient storage for angular dist...
More space is needed in the main xss array. Adjust the parameter nxss=999
000.
error in acephn***file 5 law not ready
The code can only handle laws 1, 7, and 9 from File 5.
error in phnprt***law not installed
The routine can currently handle the following ACE laws: 4, 7, 9, 33, and
44
550 NJOY2016

18 POWR LA-UR-17-20093
18 POWR
The POWR module is used to prepare libraries for the Electric Power Research
Institute (EPRI) reactor analysis codes EPRI-CELL and EPRI-CPM.11 These
codes were originally developed to provide an alternative to the reactor manu-
facturers’ computer codes for calculating reactor core performance as required
for operating and reloading power reactors run by US electric utility compa-
nies. Because these codes require up-to-date accurate cross sections that were
not controlled by the reactor manufacturers, EPRI contracted with the Los
Alamos National Laboratory to generate new libraries based on the US-standard
Evaluated Nuclear Data Files (ENDF). With this funding, we were able to de-
velop the THERMR module and the associated thermal multigroup methods in
GROUPR. We also developed this POWR module to format cross section data
in GENDF format for use in CELL or CPM. In addition, it was necessary to
make a number of modifications to EPRI-CELL to make it perform well with
unadjusted cross sections. The results of all this work were reported in 1984[62].
This module has not been used at Los Alamos since 1984, although we have
had scattered reports of use elsewhere. A list of the input instructions, without
further comment, follows.
18.1 Input Instructions
As an aid to discussions of the user input to POWR, the input instructions
that appear as comment cards at the beginning of the current version of this
module are listed below. Since code changes are possible, albeit unlikely for
this module, it is always advisable to consult the comment-card instructions
contained in the version of the code actually being used before proceeding with
an actual calculation.
!---input specifications (free format)---------------------------
!
! card 1
! ngendf unit for input gout tape
! nout unit for output tape
! card 2
! lib library option (1=fast, 2=thermal, 3=cpm)
11EPRI-CELL and EPRI-CPM are proprietary products of the Electric Power Research Institute, 3420
Hillview Avenue, Palo Alto, CA 94304. For more information, please contact the owners.
NJOY2016 551

LA-UR-17-20093 18 POWR
! iprint print option (0=minimum, 1=maximum)
! (default=0)
! iclaps group collapsing option (0=collapse from 185 group
! to desired group structure, 1=no collapse)
! (default=0)
!
!---for lib=1----------------------------------------------------
!
! card 3
! matd material to be processed
! if matd lt 0, read-in absorption data only for
! this material with mat=abs(matd) directly from
! input deck (see card 6)
! following three parameters irrelevant for matd lt 0
! rtemp reference temperature (degrees kelvin)
! (default=300 k)
! iff f-factor option
! (0/1=do not calculate f-factors/calculate if found)
! (default=1)
! nsgz no. of sigma zeroes to process for this material
! (default=0=all found on input tape)
! izref ref. sigzero for elastic matrix (default=1)
! cards 4 and 5 for normal run only (matd gt 0)
! card 4
! word description of nuclide (up to 16 characters,
! delimited with *, ended with /) (default=blank)
! card 5
! fsn title of fission spectrum (up to 40 characters,
! delimited with *, ended with /0 (default=blank)
! delimited with *, ended with /) (default=blank)
! card 6 for reading in absorption data only
! abs ngnd absorption values (default values=0)
! repeat cards 3 through 6 for each material desired.
! terminate with matd=0/ (i.e., a 0/ card).
!
!---for lib=2----------------------------------------------------
!
! card 3
! matd material to be processed
! idtemp temperature id (default=300 k)
! name hollerith name of isotope (up to 10 characters,
! delimited with *, ended with /) (default=blank)
552 NJOY2016

18 POWR LA-UR-17-20093
! card 4 default for all values=0.
! itrc transport correction option (0 no, 1 yes)
! mti thermal inelastic mt
! mtc thermal elastic mt
! card 5 default for all values=0.
! xi
! alpha
! mubar
! nu
! kappa fission
! kappa capture
! lambda
! sigma s if 0, set to scattering cross section at group 35
! repeat cards 3 thru 5 for each material and temperature desired
! (maximum number of temperatures allowed is 7.)
! terminate with matd=0/ (i.e., a 0/ card).
!
!---for lib=3----------------------------------------------------
!
! card 3
! nlib number of library.
! idat date library is written (i format).
! newmat number of materials to be added.
! iopt add option (0=mats will be read in,
! 1=use all mats found on ngendf).
! mode 0/1/2=replace isotope(2) in cpmlib/
! add/create a new library (default=0)
! if5 file5 (burnup data) option
! 0/1/2=do not process file5 burnup data/
! process burnup data along with rest of data/
! process burnup data only (default=0)
! (default=0)
! if4 file4 (cross section data) option
! 0/1=do not process/process
! (default=1)
! card 4 for iopt=0 only
! mat endf mat number of all desired materials.
! for materials not on gendf tape, use ident for mat.
! if mat lt 0, add 100 to output ident
! (for second isomer of an isotope)
! card 5
! nina nina indicator.
NJOY2016 553

LA-UR-17-20093 18 POWR
! 0/1/2/3=normal/
! no file2 data, calculate absorption in file4/
! no file2 data, read in absorption in file4/
! read in all file2 and file4 data.
! ntemp no. of temperatures to process for this material
! (default=0=all found on input tape)
! nsigz no. of sigma zeroes to process for this material
! (default=0=all found on input tape)
! sgref reference sigma zero
! following 2 parameters are for nina=0 or nina=3.
! ires resonance absorber indicator (0/1=no/yes)
! sigp potential cross section from endf.
! following 5 parameters are for ntapea=0 only
! mti thermal inelastic mt
! mtc thermal elastic mt
! ip1opt 0/1=calculate p1 matrices/
! correct p0 scattering matrix ingroups.
! ******if a p1 matrix is calculated for one of the isotopes
! having a p1 matrix on the old library, file 6 on the
! new library will be completely replaced.******
! inorf 0/1=include resonance fission if found/
! do not include
! following two parameters for mode=0 only
! pos position of this isotope in cpmlib
! posr (for ires=1) position of this isotope in resonance
! tabulation in cpmlib
! repeat card 5 for each nuclide.
! following three cards are for if5 gt 0 only
! card 6
! ntis no. time-dependent isotopes
! nfis no. fissionable burnup isotopes
! card 7
! identb ident of each of the nfis isotopes
! card 8
! identa ident of time-dependent isotope
! decay decay constant (default=0.)
! yield nfis yields (default=0.)
! repeat card 8 for each of the ntis isotopes.
! card 9 for if5=2 only
! aw atomic weight
! indfis fission indicator
! ntemp no. temperatures on old library
554 NJOY2016

18 POWR LA-UR-17-20093
! repeat card 9 for each of the ntis isotopes.
! card 10
! lambda resonance group goldstein lambdas
! ******remember that the 69-group structure has 13 resonance
! groups while the collapsed 185-group structure has 15.
! use a slash at end of each line of card 10 input.******
! repeat card 10 for each nuclide having nina=0, nina=3, or
! ires=1.
! cards 11 and 11a for nuclides having nina=3 only.
! card 11
! resnu nrg nus values to go with the lambda values
! card 11a
! tot nrg total xsec values to go with the lambda values
! read cards 11 and 11a for each nuclide having nina=3.
! cards 12 for nina gt 2 only
! aw atomic weight
! temp temperature
! fpa ngnd absorption values (default=0.)
! cards 12a, 12b, 12c for nuclides having nina=3 only.
! card 12a
! nus ngnd nus values
! fis ngnd fission values
! xtr ngnd transport values
! card 12b
! ia group. 0 means no scattering from this group
! l1 lowest group to which scattering occurs
! l2 highest group to which scattering occurs
! card 12c for ia gt 0 only
! scat l2-l1+1 scattering values
! repeat card 12b and 12c for each group
! repeat cards 12 for each of the nina gt 2 nuclides
!
!--------------------------------------------------------------------
NJOY2016 555

LA-UR-17-20093 18 POWR
556 NJOY2016

19 WIMSR LA-UR-17-20093
19 WIMSR
The WIMSR module is used to prepare libraries for the reactor-physics code
WIMS[19]. WIMS stands for “Winfrith improved multigroup scheme;” it has
been developed through its various versions at the UK laboratory AEE/Winfrith.
WIMS-E was the Winfrith version circa 1990, and it was distributed commer-
cially. WIMS-D is an older version that is freely available through various dis-
tribution centers; therefore, it is very popular all around the world.
WIMS uses collision-probability methods for computing fluxes in reactor pin
cells and more complicated geometrical arrangements. Therefore, it requires
transport, fission, and capture cross sections, a transfer matrix for epithermal
neutrons, fission-source information (νand χ), and a bound-atom scattering
matrix for thermal neutrons. Self-shielded cross sections are obtained using
equivalence theory from tabulated resonance integrals with intermediate reso-
nance corrections. The resonance integrals can be obtained from the self-shielded
cross sections produced by GROUPR, and the intermediate-resonance λvalues
by group can be computed using the NJOY flux calculator. WIMS libraries
normally use a standard 69-group structure with 14 fast groups, 13 resonance
groups, and 42 thermal groups.
This chapter describes the WIMSR module in NJOY2016.0.
19.1 Resonance Integrals
WIMS computes the self-shielded cross sections for a wide range of mixtures and
fuel geometries using equivalence theory. The GROUPR chapter of this report
describes the narrow-resonance (NR) version of equivalence theory; that is, all
systems with the same value for the “sigma-zero,”
σ0i=1
ni
X
j6=i
njσtj +σe
,(499)
in a group have the same self-shielded cross section in that group. Here, njis
the number density for material jwith cross section σtj, and σeis the escape
cross section (which takes care of the geometry of the fuel).
However, in the near epithermal range (e.g., 4-100 eV), some resonances are
too wide for the NR approximation to apply well. For these resonances, the
effect of a moderator material is reduced, because collisions with the moderator
do not always result in enough energy loss to remove the neutron from the
resonance. For this reason, WIMS uses an intermediate-resonance (IR) extension
NJOY2016 557

LA-UR-17-20093 19 WIMSR
to equivalence theory in which the background cross section is taken to be the
following:
σP i =1
ni
X
j
njλjσpj +σe
,(500)
where the λfactors are numbers between zero and one. Note that σp, the
potential scattering cross section, is used here, and that the sum is now over all
materials. The basic concept is the same: all systems with the same value of
the IR “sigma-P” for a group will have the same self-shielded cross sections for
that group.
WIMS takes the additional step of expressing the self-shielding data in terms
of “resonance integrals,” instead of using the self-shielded cross sections pro-
duced by GROUPR. That is
σx(σ0) = σPIx(σP)
σP−Ia(σP),(501)
and
Ix(σP) = σPσx(σ0)
σP+σa(σ0),(502)
where xdenotes the reaction, either “a” for absorption or “nf” for nu*fission,
and Ixis the corresponding resonance integral.
In order to clarify the meaning of this pair of equations, consider a homo-
geneous mixture of 238U and hydrogen with concentrations such that there are
50 barns of hydrogen scattering per atom of uranium. The GROUPR flux cal-
culator can be used to solve for the flux in this mixture, and GROUPR can
then calculate the corresponding absorption cross section for 238U. Assuming
that λ= 0.1 and σp= 10 for the uranium, the numbers being appropriate for
WIMS group 25, we get σP= 51. This value of σpgoes into the sigz array
in the resonance-integral block on the WIMS library, and the corresponding Ia
goes into the resa array.
At some later time, a WIMS user runs a problem for a homogeneous mixture
of 238U and hydrogen that matches these specifications. WIMS will compute a
value of σPof 51.0, interpolate in the table of resonance integrals, and compute
a new absorption cross section that is exactly equal to the accurate computed
558 NJOY2016

19 WIMSR LA-UR-17-20093
result from the original GROUPR flux-calculator run.
This argument can be extended to more complex systems. For example,
the assembly calculated using the flux calculator could represent an enriched
uranium-oxide fuel pin of a size typical of a user’s reactor system with a water
moderator. The computed absorption cross section is converted to a resonance
integral and stored with the computed value of σP. In any later calculation
that happens to mimic the same composition and geometry, WIMS will return
the accurate calculated absorption cross section. Equivalence theory, with all
its approximations, is only used to interpolate and extrapolate around these
calculated values. This is a powerful approach, because it allows a user to
optimize the library in order to obtain very accurate results for a limited range
of systems without having to modify the methods used in the lattice-physics
code. Unfortunately, the present version of WIMSR does not allow you to enter
σPdirectly; it computes it from input data that only consider one material at
a time. A future version may include the more general capabilities described in
this paragraph.
Let us call the homogeneous uranium-hydrogen case discussed above “case 0.”
Now, consider a homogeneous mixture of 238U, oxygen, and hydrogen. Ratio
the number densities to the uranium density such that there is 1 barn/atom
of oxygen scattering and 50 barn/atom of hydrogen scattering. Carry out an
accurate flux calculation for the mixture, and call the result “case 1.” Also do
an accurate flux calculation with only hydrogen, but at a density corresponding
to 51 barns/atom. Call this result “case 2.” The IR lambda value for oxygen is
then given by
λ=σa(1) −σa(0)
σa(2) −σa(0) .(503)
Note that λwill be 1 if the oxygen and hydrogen have exactly the same effect
on the absorption cross section. In practice, λ=.91 for WIMS group 27 (which
contains the large 6.7 eV resonance of 238U), and λ= 1 for all the other resonance
groups. That is, all the resonances above the 6.7 eV resonance are effectively
narrow with respect to oxygen scattering.
Similarly, do a flux-calculator solution for a homogeneous mixture of 238U
combined with 1 barn/atom of 235U and 50 barn/atom of hydrogen. Call the
NJOY2016 559
LA-UR-17-20093 19 WIMSR
result “case 3.” Now, the lambda value for 235U is given by
λ=σa(3) −σa(0)
σa(2) −σa(0) .(504)
The actual value obtained for WIMS group 27 is .035. Group 26 gives 0.50,
and group 25 gives 0.09. An examination of the flux-calculator equations in the
GROUPR chapter of this manual shows that the effect of the “admixed” mod-
erator term depends only on its atomic mass (through the αvalue); therefore,
the IR λvalues will be the same for all uranium isotopes (and the same values
should work for all the actinides). This conclusion neglects the small effects of
absorption in the admixed isotope on the intraresonance flux for one resonance.
This process can be continued for additional admixed materials from each
important range of atomic mass. The result is the table of λgi values needed as
WIMSR input.
What are the implications of this discussion? Foremost is the observation
that the lambda values for the isotopes are a function of the composition of the
mixture that was used for the base calculation. To make the effect of this clear,
let us consider two different types of cells:
1. a homogeneous mixture of 238U and hydrogen, and
2. a homogeneous mixture of 235U and hydrogen.
A look at the pointwise cross sections in group 27 shows very different pictures
for the two uranium isotopes. The 238U cross section has one large, fairly wide
resonance at 6.7 eV, and the 235U cross section has several narrower resonances
scattered across the group. If the lambda values are computed for these two
different situations, the results in Table 27 are obtained.
Table 27: IR λValues for Several Resonance Groups and Two Different Reactor Systems
WIMS λ(U) λ(O) λ(U) λ(O)
group 238U@50b 238U@50b 235U@200b 235U@200b
27 .035 .91 0.20 1.00
26 .50 1.00 .38 1.00
25 .092 1.00 .44 1.00
24 .090 1.00 .55 1.00
23 .29 1.00 .46 1.00
560 NJOY2016

19 WIMSR LA-UR-17-20093
It is clear that the energy dependence of the two lambda sets is quite different.
This is because of the difference in the resonance structure between 238U and
235U. Clearly, the one resonance in group 27 in 238U is effectively wider than the
group of resonances in group 27 for 235U. Group 26 has essentially no resonance
character for 238U, which reverses the sense of the difference. In groups 24 and
25, the 235U resonances become more narrow, while the 238U resonances stay
fairly wide. Finally, in group 23, the 238U resonances begin to get narrower.
These results imply that completely different sets of lambda values should
be used for different fuel/moderator systems, such as 238U/water, 235U/water,
or 238U/graphite. In practice, this is rarely done.
The remaining question is, “How should the self-shielded cross sections for the
minor isotopes be calculated?” Formally, the best approach using NJOY would
be to first do an accurate flux calculation for pure 238U mixed with hydrogen (or
to be really accurate, a typical reactor cell containing pure 238U oxide), and to
save the resulting flux on a scratch file. This flux would then be used as input
for the 235U calculation. See the GROUPR chapter for details. This approach
takes care of all the complexities of resonance-resonance interference, the drop
in the average flux across the group caused by accumulated 238U absorptions,
and so on. In practice, this is rarely done. Since the self-shielding effects in the
minor actinides are much smaller than those in the main absorber, it is usually
sufficient to do a simple NR calculation for the minor actinides and to convert
them into WIMS resonance integrals with the normal lambda values for heavy
isotopes.
19.2 Cross Sections
The first part of the WIMS cross section data contains σpfor the resonance
groups (15-27 in the normal 69-group structure), the scattering power per unit
lethargy for the resonance groups, the transport cross section for the non-thermal
groups (1-27 normally), the absorption cross section for the non-thermal groups,
an obsolete quantity for the resonance groups (set to zero), and the intermediate-
resonance λvalues for the resonance groups. For WIMS-E, the (n,2n) cross
section is added between the slowing-down power and the transport cross section.
The σpvalue is assumed to be constant (see sigp in the user input instruc-
tions). It must be obtained by finding the scattering length ain the ENDF file
and computing σp= 4πa2. The scattering power per unit lethargy is ξσs/τ ,
where ξis the log energy loss parameter given as MT=252 on the GENDF
file, σsis the elastic scattering cross section (MT=2), and τis the lethargy
NJOY2016 561
LA-UR-17-20093 19 WIMSR
width for the group, which can be calculated from the group structure given
in MF=1/MT=451 on the GENDF file. The (n,2n) cross section is obtained
from MF=3/MT=16 on the GENDF file. The absorption cross section is com-
puted by adding up the fission cross section (MT=18) and all the cross sections
given with MT=102-150. The (n,2n) cross section (MT=16) is then subtracted
from the sum. Finally, the λvalues are obtained from the user’s input. See
Section 19.1 for more details on these intermediate-resonance corrections.
The next part of the WIMS data file contains the fission neutron production
cross section νσfand the fission cross section σffor the non-thermal groups (1-
27 normally). The cross section is always obtained from MT=18 on the GENDF
file, but there are several complications involved in getting ν.
A shortcut for obtaining the fission data is to run MFD=3/MTD=452 and
MFD=5/MTD=452 in GROUPR. This approach ignores the energy dependence
of fission neutron emission at high energies and the effects of delayed neutrons
on the fission spectrum. If these options are used in GROUPR, it is important
not to use the other options described below at the same time. When WIMSR
finds a section on the GENDF file with MF=3/MT=452, it can read in νσf
directly.
A better approach to fission in GROUPR is to prepare a full fission matrix for
MT=18, or to prepare matrices for all the partial fission reactions, MT=19, 20,
21, and 38. The latter is the recommended approach for evaluations with both
MT=18 and MT=19 given in File 5. See the GROUPR chapter for more details.
WIMSR reads in the data given in MF=6/MT=18, or in MF=6/MT=19,20,...,
and sums over all secondary-energy groups to obtain the prompt part of νσf. It
adds in the delayed part of νσffrom MF=3/MT=455. If the input GENDF file
contains both MT=18 and partial fission matrices, a diagnostic message will be
printed, and the partial-fission representation will be used.
The next section of the WIMS data file contains the non-thermal P0scatter-
ing matrix for incident-energy groups in the non-thermal range (1-27 normally).
This matrix is loaded by summing over all of the reactions found on the GENDF
tape except the thermal reactions mti and mtc. If requested, this matrix is trans-
port corrected by subtracting the sum over secondary-energy groups of the P1
matrix for each primary group. When the individual reactions are read, they
are loaded into “full” matrix (typically 69×69). At the same time, a record is
kept of the lowest and highest secondary groups found for each primary group.
These limits are then used to pack the scattering matrix into a more compact
form.
562 NJOY2016

19 WIMSR LA-UR-17-20093
The scattering matrix is not actively self-shielded in WIMS, but WIMSR
allows the user to request that the elastic component be evaluated at some
reference σ0value different from infinity. This option can be useful for the
major fertile component of reactor fuel, that is, for 238U in pins of a uranium
system, or for 232Th for fuel in a Thorium/233U system.
Because the thermal scattering matrix depends on temperature, the next
component of the WIMSR data contains the ntemp versions of the basic cross
sections and the P0scattering matrix for the thermal groups (28-69 normally).
The cross sections included are transport, absorption, nu*fission, and fission.
The transport positions contain the sum of the thermal inelastic cross section
obtained by summing up the P0matrix (MF=6/MT=MTI), the thermal elastic
cross section from the diagonal elements of the P0matrix (MF=6/MT=MTC),
if present, and the absorption cross section. If separate P1matrices are not
given for this material, the P1cross section obtained by summing the P1ma-
trices over secondary groups for each primary group is subtracted. The matrix
data are read from sections on the GENDF file with MF=6/MT=MTI and
MF=6/MT=MTC (if present). As for the temperature-independent matrices,
they can be transport-corrected by subtracting the sum over secondary groups
of the P1matrix for each primary group from the self-scatter position. Also,
minimum and maximum limits on the secondary group are determined for each
primary group, and the matrix is compacted for efficiency.
The next part of the WIMS data file contains the resonance data, which were
discussed in Section 19.1. In some cases, these resonance data are followed by a
fission spectrum block. The complications of obtaining the fission spectrum are
the same as those described above for obtaining the fission neutron production
cross section, νσf. If the short-cut option was used in GROUPR, the fission
spectrum can be read directly from MF=5/MT=452 on the GENDF file. The
sum over groups is also accumulated in cnorm in order to allow the final spec-
trum to be normalized accurately. The shortcut approach neglects the effects of
delayed neutron emission on the fission spectrum.
If fission matrices are available (either MT=18, or MT=19+20+21...), the
prompt part of the fission spectrum is obtained by summing σgg0φgover all
primary groups, g. These numbers are also summed into cnorm for use later in
normalizing χ. The delayed part is obtained as
(X
g
νdσfgφg)χdg0,(505)
NJOY2016 563

LA-UR-17-20093 19 WIMSR
which also contributes to the normalization. Note that the energy dependence
of the fission matrix is factored into the final χin proportion to the weighting
flux used in GROUPR to prepare the WIMSR input file. For thermal reactor
problems, it is easy to provide a good estimate for this weighting flux.
The final block on the WIMS data tape is optional. If present, it contains
P1scattering matrices for each temperature. These matrices are defined over
the entire group range (normally 1-69), and they contain both the temperature-
independent and temperature-dependent reactions in each matrix. The methods
used to build up these matrices are parallel to those discussed above for the P0
matrices. Note that if P1matrices are given, the transport corrections are not
included in the transport cross sections or P0matrices.
19.3 Burn Data
WIMS uses a simplified burn model for tracking the production and depletion
of actinides and fission products, and the chains used are hard-wired into the
code. WIMSR provides a method to enter new fission-yield data into the WIMS
library format, but it has not been used or tested very much so far.
19.4 User Input
The following user input specifications were copied from the comment cards at
the beginning of the WIMSR source. It is always a good idea to check the
comment cards in the current version to see if there have been any changes.
!--------------------------------------------------------------------
!
! Format multigroup cross sections from groupr for WIMS.
!
!---input specifications (free format)----
!
! card 1
! ngendf unit for input gendf tape
! nout unit for output wims tape
!
! card 2
! iprint print option
! 0=minimum (default)
! 1=regular
! 2=1+intermediate results
564 NJOY2016

19 WIMSR LA-UR-17-20093
! iverw wims version
! 4=wims-d (default)
! 5=wims-e
! igroup group option
! 0=69 groups (default)
! 9=user’s choice
!
! card 2a (igroup.eq.9 only)
! ngnd number of groups
! nfg number of fast groups
! nrg number of resonance groups
! igref reference group (default is last fast group)
!
! card 3
! mat endf mat number of the material to be processed
! nfid not used
! rdfid identification of material for the wims library
! iburn burnup data option
! -1=suppress printout of burnup data
! 0=no burnup data is provided (default)
! 1=burnup data is provided in cards 5 and 6
!
! card 4
! ntemp no. of temperatures to process for this material
! in the thermal energy range
! (0=all found on input tape)
! nsigz no. of sigma zeroes to process for this material
! (0=all found on input tape)
! sgref reference sigma zero
! (.ge. 1.e10 to select all cross sect. at inf.dil.*
! but fully shielded elastic x-sect,
! .lt. 1.e10 to select all x-sect at inf.dil.
! =sig0 from the list on groupr input to
! select all x-sect. at that sig0)
! ires resonance absorber indicator
! 0=no resonance tables
! >0=ires temperatures processed
! sigp potential cross section from endf.
! (if zero, replace by the elastic cross section)
! mti thermal inelastic mt (default=0=none)
! mtc thermal elastic mt (default=0=none)
! ip1opt include p1 matrices
NJOY2016 565

LA-UR-17-20093 19 WIMSR
! 0=yes
! 1=no, correct p0 ingroups (default)
! inorf resonance fission (if found)
! 0=include resonance fission (default)
! 1=do not include
! isof fission spectrum
! 0=do not include fission spectrum (default)
! 1=include fission spectrum
! ifprod fission product flag
! 0=not a fission product (default)
! 1=fission product, no resonance tables
! 2=fission product, resonance tables
! jp1 transport correction neutron current spectrum flag
! 0=use p1-flux for transport correction (default)
! >0=read in jp1 values of the neutron current
! spectrum from input
!
! the following cards 5 and 6 are for iburn gt 0 only
! card 5
! ntis no. of time-dependent isotopes
! for burnable materials ntis=2
! for fissile materials ntis>2 when fission product
! yields are given.
! efiss energy released per fission
!
! card 6a
! identa ident of capture product isotope
! yield yield of product identa from capture
!
! card 6b
! identa ident of decay product isotope (zero if stable)
! lambda decay constant (s-1)
!
! card 6c (repeated ntis-2 times, if necessary)
! identa ident of fission product isotope
! yield fission yield of identa from burnup of mat
!
! card 7
! lambda resonance-group goldstein lambdas (13 for
! default 69-group structure, nrg otherwise).
!
! card 8 (only when jp1>0)
566 NJOY2016
19 WIMSR LA-UR-17-20093
! p1flx current spectrum (jp1 entries read, the rest are
! set with the default p1-flux calculated by njoy).
!--------------------------------------------------------------------
The first card specifies the input and output unit numbers, as is normal for
NJOY modules. ngendf comes from a previous GROUPR run, and it can be in
either binary or ASCII mode. nout is always in ASCII mode.
The options card allows the user to select how much detail will be printed
on the output listing (iprint), whether the output is intended for WIMS-D or
WIMS-E (iverw), and how many groups are desired. Currently, the only dif-
ference between WIMS-D and WIMS-E output is that some additional reaction
cross sections are included for the latter. If the user selects some group structure
different from the standard 69-group structure, an additional input card is re-
quired to give the number of groups (ngnd), the number of fast groups (nfg, 14
for 69 groups), the number of resonance groups (nrg, 13 for 69 groups), and the
reference group used for normalizing the flux (igref, normally the low-energy
group of the fast groups).
Card 3 is required. It gives the ENDF MAT number for the materials to
be processed. If this MAT doesn’t appear on the GENDF tape, a fatal error
message will be issued. nfid will be the identification number for this material
used on the output WIMS library, and rdfid will be the identification number
for the resonance data. Formally, WIMS libraries allow for data sets with more
than one version of the resonance-integral tabulation. The last parameter on
this card is iburn to flag whether burn data are included in the input stream.
Card 4 starts out with ntemp and nsigz, which define the size of the resonance-
integral tables. They are normally both set to zero; the code then uses all of
the values computed by GROUPR. The reference sigma-zero value, sgref, is
used for the elastic cross section and matrix, because these quantities are not
normally self-shielded by WIMS. Normally, 1e10 is appropriate, but for the ma-
jor fissionable material in the reactor (i.e., 238U or 232Th), it may be better
to use a realistic number like sgref=50. WIMSR assumes that the potential
scattering cross section for the material is constant, but this constant value is
not available from the GROUPR output. The WIMSR user will have to look in
the ENDF-formatted evaluation for the scattering length a, compute σp= 4πa2,
and enter the value as sigp. As shown in the following ENDF-formatted file
fragment, the scattering length (9.56630- 1 in this case) is the second item on
the fourth line in MF=2, MT=151.
NJOY2016 567

LA-UR-17-20093 19 WIMSR
...
9.22350+ 4 2.33025+ 2 0 0 1 01395 2151
9.22350+ 4 1.00000+ 0 0 1 2 01395 2151
1.00000+ 0 8.20000+ 1 1 1 0 01395 2151
3.50000+ 0 9.56630- 1 0 0 1 01395 2151
2.33025+ 2 0.00000+ 0 0 0 780 1301395 2151
...
The parameters mti and mtc select the thermal inelastic and elastic data from
the sections that might be available on the GENDF tape. Most materials have
only free-gas scattering available, and the appropriate values would be mti=221
and mtc=0. The conventional values to use for reactor moderator materials are
given in Table 28.
Continuing with Card 4, WIMSR allows P1scattering to be treated in two
ways. If ip1opt=0, the P1matrix for the material is written to the WIMS
output file explicitly. This option is normally used only for major moderator
materials, such as the components of water. The other option, ip1opt=1, in-
structs the code to use the P1data to transport-correct the P0elastic scattering
Table 28: Conventional values for thermal MT numbers (mti and mte) used in WIMSR,
GROUPR, and THERMR
Thermal Material MTI Value MTC Value
H in H2O 222
D in D2O 228
Be metal 231 232
Graphite 229 230
Benzine 227
Zr in ZrH 235 236
H in ZrH 225 226
Be(BeO) 233 234
O(BeO) 237 238
O(UO2) 239 240
U(UO2) 241 242
H in Polyethylene 223 224
Al metal 243 244
Fe metal 245 246
568 NJOY2016

19 WIMSR LA-UR-17-20093
matrix; that is, the ingroup elements of the P0matrix are reduced by the sum
over all outgoing groups of the P1matrix for that ingoing group.
The inorf parameter can be set to 1 to eliminate the resonance-integral table
for nu*fission from the WIMS output. Some of the higher actinides are treated
this way for some WIMS libraries. The isof flag is set to 1 to tell WIMSR to
produce a fission spectrum. This is usually done for main fissile materials, such
as 235U and 239Pu. The ifprod flag is used to control whether resonance tables
are included for fission products.
WIMSR has some capability to format burn data for incorporation into a
WIMS library (see cards 5 and 6). This part of the code has not been used or
tested very much.
The final card gives the intermediate-resonance λvalues for each of the res-
onance groups. Methods for obtaining these quantities with NJOY are outlined
in Section 19.1.
19.5 Coding Details
The main entry point for WIMSR is subroutine wimsr exported by module
wimsr. WIMSR starts by reserving the scratch files with unit numbers from
10 through 14. The next step is to read and echo the user’s input. Note that
the array scr is allocated. The code will issue error messages if more than
the default nwscr=30000 words are needed. Subroutine wminit is then called.
It looks at the record MF=1/MT=451 for the desired material on the input
GENDF tape to obtain the group structure. It then reads through the entire
GENDF tape for this material to set the fission flags i318 and i618 and to
count the number of temperatures that are available. The fission flag is used to
handle cases where both MT=18 and the partial fission representation (MT=19,
20, ...) appear on the GENDF tape.
Subroutine resint is called next to compute the WIMS resonance integrals
from the GROUPR self-shielded cross sections. It reads through the entire
GENDF tape and extracts the flux, absorption cross section, fission cross sec-
tion, and elastic cross section versus temperature and sigma-zero for all of the
resonance groups. It also extracts the reference-group flux versus temperature
and sigma-zero and the fission νvalue. The latter is computed from File 6 with
delayed contributions from MT=455 in File 3. Once all the data are in place,
resint uses the νvalues to convert the self-shielded fission cross sections into
self-shielded νσfvalues.
If the user has asked for a value of ntemp that is larger than the number of
NJOY2016 569

LA-UR-17-20093 19 WIMSR
temperatures on the GENDF tape for this material, resint will duplicate the
values from the last temperature given into the higher temperature positions for
the flux and the absorption cross section.
The final step in wminit is to convert the self-shielded cross sections into
resonance integrals using the method described in Section 19.1. These resonance
integrals are written out to a scratch file and displayed on the output listing
using subroutine rsiout. The elastic resonance integrals are only written for
WIMS-E.
Next, the main program calls xsecs to process the cross sections. The out-
ermost loop is over temperature. A distinction has to be made between the
temperature-independent matrix data, such as (n,2n) and (n,n0) reactions, and
the temperature-dependent matrix data, such as thermal scattering. While read-
ing through the GENDF tape, the following quantities are extracted and stored
using the allocatable arrays indicated:
abs1 radiative capture (MT=102);
abs2 other absorption reactions (MT=103-150);
sf0 the fission cross section (MT=18);
ab0 also the fission cross section (MT=18);
sn2n the (n,2n) cross section;
scat the elastic scattering cross section (MT=2), possi-
bly using the value corresponding to the reference
sigma-zero value instead of infinite dilution;
xi the log slowing down ξ(MT=252);
snus the fission yield νσfcomputed from either 3/452
or File 6 plus the delayed part from 3/455;
chi the fission spectrum χcomputed from either 5/455
or File 6 plus the delayed contributions from MT=455;
xs the temperature-dependent scattering matrix, con-
taining mti and mtc, the thermal inelastic and
elastic reactions, respectively;
l1 the smallest group number for a nonzero element
of the nonelastic part of the matrix stored in xs;
l1e the smallest group number for a nonzero element
of the elastic part of the matrix stored in xs;
l2 the largest group number for a nonzero element
of the nonelastic part of the matrix stored in xs;
l2e the largest group number for a nonzero element
of the elastic part of the matrix stored in xs; and
570 NJOY2016
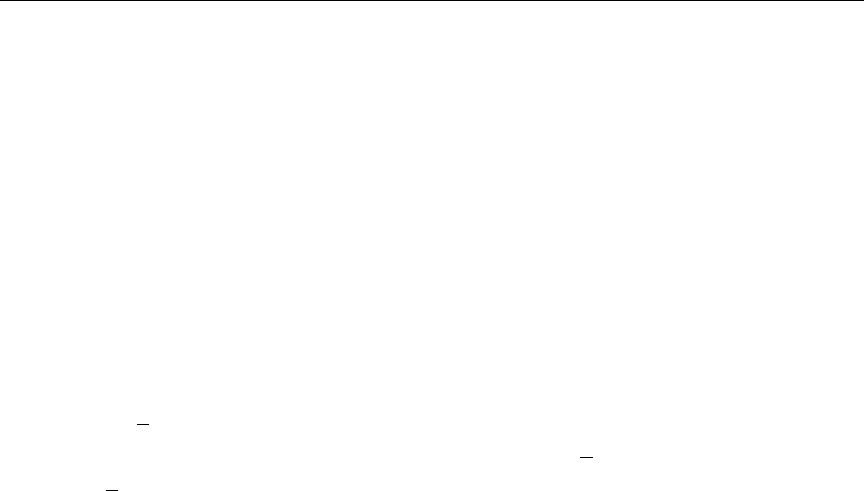
19 WIMSR LA-UR-17-20093
csp1 the P1cross section for the thermal matrix ob-
tained by summing over the P1matrix elements
for scattering from each group.
Once all the data for a temperature have been stored in memory, several ad-
ditional operations are performed on them. The initial absorption cross section
in ab0 contains the fission cross section. The final value is formed by adding the
data in abs1 and abs2, and then subtracting the (n,2n) cross section in sn2n.
The final transport cross section in xtr is formed by adding the absorption and
subtracting the transport correction (csp1). The slowing-down power per unit
lethargy is computed from ξ,σscat, and the group boundary energies at iegb.
As usual, the treatment of fission is more complex. For some combinations of
options, νis computed by dividing the fission neutron production cross section
by the fission cross section, and for others, the value of νσfhas to be computed
from νand σf. In addition, the fission spectrum, if requested, is normalized.
Subroutine xseco starts with a section that writes and prints the temperature-
independent part of the WIMS data. This section is skipped when xseco is
called with itemp>1. It first processes the temperature-independent vectors:
potential scattering, slowing-down power, transport, absorption, IR lambda,
and sometimes (n,2n). Next, it processes the fission vectors nu*sigf and sigf.
The temperature-independent part of the scattering matrix includes the fast
groups and the resonance groups (this normally totals 27 groups). It is packed
by retrieving the low (lone) and high (ltwo) limits for each band of nonzero
elements from l1 and l2, which were loaded in xsecs. They are used to com-
pute the number of elements in the band and the location of the self-scatter
element in the band (always 1 for this part of the matrix, because there is no
upscatter). They are also used to direct how the numbers in xs are moved into
scr with the zeros outside of the band removed. Note that the data are stored
as follows: location of self-scatter for group 1, number of elements in band for
group 1, the band of elements for group 1, location of self-scatter for group 2,
number of elements in group 2, the band of elements for group 2, etc. If the
number of elements in a band is zero, the two counts are there, but no band
data are given. After being printed, the temperature-independent part of the
matrix is written out on a scratch file nscr2.
The next part of xseco is executed for itemp=1 and all the higher tempera-
tures. It prints and writes the temperature-dependent transport, and absorption
cross sections (they are defined in the thermal range only, normally groups 28-
69). Note that the absorption cross section is also written out on scratch file
NJOY2016 571

LA-UR-17-20093 19 WIMSR
nscr3. If available, the temperature-dependent fission neutron production cross
section and fission cross section are also printed and written. The temperature-
dependent scattering matrix is processed as described above, except that the
incident-neutron group range is limited to the thermal range (normally 28-69).
Note that the location of the self-scatter element will no longer be 1 for these
data, because of the presence of upscatter. The packed matrix length and the
packed data are written out to scratch file nscr3.
If the user has requested that P1scattering matrices be constructed for the
material, subroutine p1scat is called. It uses methods similar to those described
above. The results are printed and written onto nscr4 by p1sout.
The last step in WIMSR is to call wimout to prepare the final WIMS data
library. The first card on nout is slightly different for WIMS-D and WIMS-E. It
is followed by lines for the burnup data using numbers obtained from common
storage.
The data needed for the material identifier card are available in global stor-
age. The temperature-independent data are read from nscr2 and written to
nout. Similarly, the temperature-dependent data are read from nscr3 (although
the tempr array is obtained from global storage). For WIMS-D, a record mark
is written at this point.
The resonance data, if needed, are read from nscr1 and written to nout. The
format is slightly different for WIMS-D and WIMS-E. The WIMS-D version has
extra lines containing ntnp, the product of the number of temperatures and the
number of sigma-zero values, and it has a record mark after the resonance data
block. The WIMS-E version has an extra section of resonance-integral data for
computing the self-shielded elastic scattering cross section.
If a fission spectrum was requested, it is written out next by using data from
the allocatable array uff. If a P1matrix was requested, it is read in from nscr4
and written out onto nout.
This completes the entire WIMS library. The final step takes place in the
main WIMSR program, where the normal timing and storage usage messages
are printed.
19.6 WIMS Data File Format
The following section describes the WIMS data output provided by WIMSR. It
consists of a number of logical blocks of information written out in coded form.
The output is intended to be used by a library maintenance code to prepare a
binary library for use by the WIMS code.
572 NJOY2016

19 WIMSR LA-UR-17-20093
Library Header (2I5)
NFID material identifier
NPOS position to insert material on a large multimate-
rial library (given for WIMS-E only)
Burnup Data (3(1PE15.8,I6))
(YIELD(I),IFISP(I),I=1,JCC/2 fission yields and fission product flag
Material Identifier Data (I6,1PE15.8,5I6)
IDENT material identifier
AWR atomic weight ratio to neutron
IZNUM atomic charge number Zfor this material
IFIS fission and resonance flag: 0=non-fissile with no
resonance tabulation, 1=non-fissile with resonance
absorption only, 2=fissile with resonance absorp-
tion only (e.g., 240Pu), 3=fissile with resonance
absorption and fission, 4=fissile with no resonance
tabulations.
NTEMP number of temperatures
NRESTB number of resonance tables included (0 or 1)
ISOF fission spectrum flag (0=no, 1=yes)
Temperature-Independent Vectors (1P5E15.8)
(SIGP(I),I=1,N2) σpfor resonance groups
(XX(I),I=1,N2) ξσs/τ for resonance groups
(XTR(I),I=1,N1+N2) transport cross section for fast and resonance groups
(ABS(I),I=N1+N2) absorption cross section for fast and resonance
groups
(DUM,I=1,N2) unused dummy for resonance groups
(ALAM(I),I=1,N2) IR λvalues for resonance groups
Temperature-Independent Fission (IFIS>1 only) (1P5E15.8)
(NSIGF(I),I=1,N1) νσffor fast and resonance groups
(SIGF(I),I=1,N1) σffor fast and resonance groups
NJOY2016 573

LA-UR-17-20093 19 WIMSR
P0Matrix Length (I15)
NDAT length of P0scattering block to follow
Temperature-Independent P0Matrix (1PE15.8)
(XS(I),I=1,NDAT) packed scattering data: IS for group 1, NS for
group 1, NS scattering elements for group 1, IS
for group 2, NS for group 2, etc., through all of
the fast and resonance groups (normally through
group 27). IS is the position of self-scatter in the
band of scattering elements (always 1 here), and
NS is the number of elements in the band.
Temperature Values (1PE15.8)
(TEMP(I),I=1,NTEMP) temperatures in Kelvin
Repeat the following 4 blocks for
each of the NTEMP temperatures.
Temperature-Dependent Transport and Absorption (1PE15.8)
(XTR(I),I=1,N3) transport cross section for thermal groups
(ABS(I),I=1,N3) absorption cross section for thermal groups
Temperature-Dependent Fission Vectors (1PE15.8)
(NSIGF(I),I=1,N3) fission neutron production cross section νσffor
thermal groups
(SIGF(I),I=1,N3) fission cross section σffor thermal groups
Temperature-Dependent P0Matrix Length (I15)
NDAT length of P0scattering block
Temperature-Dependent P0Matrix (1PE15.8)
XS(I),I=1,NDAT) packed scattering data: IS for group N, NS for
group N, NS scattering elements for group N, IS
for group N+1, NS for group N+1, etc. through
the last group (normally group 69). IS is the
position of self-scatter in the band of scattering
elements, and NS is the number of elements in the
band.
574 NJOY2016

19 WIMSR LA-UR-17-20093
Record Mark (’ 999999999999’), WIMS-D only
Resonance Control Data
RID resonance set identifier
NTEMP number of temperatures for this resonance set
NSIGZ number of background cross section values
Absorption Resonance Data
(TEMP(I),I=1,NTEMP) temperatures
(SIGZ(I),I=1,NSIGZ) background cross section values
(RESA(I),I=1,NTEMP*NSIGZ absorption resonance integrals
Nu*fission Resonance Data
(TEMP(I),I=1,NTEMP) temperatures
(SIGZ(I),I=1,NSIGZ) background cross section values
(RESNF(I),I=1,NTEMP*NSIGZ nu*fission resonance integrals
Scattering Resonance Data, WIMS-E only
(TEMP(I),I=1,NTEMP) temperatures
(SIGZ(I),I=1,NSIGZ) background cross section values
(RESS(I),I=1,NTEMP*NSIGZ scattering resonance integrals
Record Mark (’ 999999999999’), WIMS-D only
Fission Spectrum
(FSPECT(I),I=1,NGND) fission spectrum χ
Repeat the following two blocks
for each of NTEMP temperatures.
P1Matrix Length (I15)
NDAT length of P1scattering block
NJOY2016 575

LA-UR-17-20093 19 WIMSR
P1Matrix (1PE15.8)
XS(I),I=1,NDAT) packed scattering data: IS for group 1, NS for
group 1, NS scattering elements for group 1, IS
for group 2, NS for group 2, etc., through the last
group (normally group 69). IS is the position
of self-scatter in the band of scattering elements,
and NS is the number of elements in the band.
19.7 WIMSR Auxiliary Codes
The WIMSR output as described above is not directly usable by WIMS. Two
library-maintenance codes are used at Los Alamos. An unpublished code called
FIXER is used to modify (fix up) an existing WIMS-D library, or to create a
new one, using WIMSR output. It processes burnup data, main data, resonance
data, and P1matrices. In its fix-up mode, it can replace, delete, or add a
material. another unpublished code called WRITER is a code to read a WIMS-
D library in coded form, convert it to binary form, and list it in a user readable
form.
19.8 Error Messages
error in wimsr***too many time dependent isotopes
See nymax=100 in the global variables at the beginning of the wimsm mod-
ule.
error in wminit***desired material is not on gendf tape
Check whether the right input GENDF input tape was mounted.
error in wminit***incorrect group structure
The group structure on the input GENDF file does not agree with the one
specified in the WIMSR input deck.
message from wminit---mat xxxx mf xx has both mt18 and ...
If both MT=18 and MT=19 are present in File 3 or File 6, WIMSR must
make a choice of which to use. For materials with partial fission reactions,
GROUPR normally does not process the fission matrix from MT=18. It is
more accurate to use the sum of the partial fission matrices.
message from wminit---mat xxxx has no mf3, mt252 ...
In the absence of an input section for µ, it will be computed assuming
isotropic CM scattering.
576 NJOY2016

19 WIMSR LA-UR-17-20093
error in resint***storage exceeded
The size of the allocatable scratch array is set by the global parameter
nwscr=30000.
error in xsecs***storage exceeded
The size of the allocatable scratch array is set by the global parameter
nwscr=30000.
message from xsecs---ref sig0 xxx not on list...
In this case, the first entry will be used as the default.
message from xsecs---nu-bar calculated from fission ....
This is just to alert the user to this situation.
message from xsecs---use only xx temps for mat xxxx
The thermal inelastic sections are missing from some of the higher tem-
peratures on the input GENDF tape. This message tells you how many
temperatures can be used correctly. Check the THERMR and GROUPR
runs if more temperatures are needed.
error in xseco***scratch storage exceeded
The size of the allocatable scratch array is set by the global parameter
nwscr=30000.
error in p1scat***storage exceeded
The size of the allocatable scratch array is set by the global parameter
nwscr=30000.
error in p1scat***no p1 matrices found for mat xxxx
Check the GROUPR run to make sure that P1matrices have been requested
for the desired materials.
error in p1scat***no temperature-dependent reactions ...
Check the GROUPR run to make sure that the elastic scattering matrix
was requested.
NJOY2016 577

LA-UR-17-20093 19 WIMSR
578 NJOY2016

20 PLOTR LA-UR-17-20093
20 PLOTR
The PLOTR module provides a general-purpose plotting capability for ENDF,
PENDF, and GENDF files by generating files that VIEWR can use to generate
high-quality Postscript plots. The following kinds of plots are produced:
•conventional 2-D plots (for example, cross section vs energy) of ENDF,
PENDF, or GENDF data with the normal combinations of linear and log
scales, automatic or user-specified ranges and labels, an optional alternate
right-hand axis, and with one or two title lines;
•a set of experimental data by itself or superimposed on ENDF, PENDF,
or GENDF curves;
•curves of various patterns, labeled with tags and arrows or described in a
legend block;
•data points given with a variety of symbols with error bars (they can be
identified in a legend block);
•detailed 3-D perspective plots of File 4 or File 6 angular distributions with
a choice of a linear or a log axes for incident energy and a choice of energy
range and viewpoint;
•selected 2-D plots of File 5 and File 15 emission spectra for specified in-
cident energies, and selected 2-D emission spectra for given energies and
particle types for File 6 data;
•detailed 3-D perspective plots of File 5, 6, or 15 energy distributions with
a choice of log or linear axes and viewpoint (both EE0θand EθE0laws are
supported);
•3-D plots of GENDF data; and
•various 2-D plots for File 7 data, including both symmetric and asymmetric
S(α, β)vs either αor β.
This section describes the PLOTR module in NJOY2016.0. As in NJOY2012
the basic plotting calls have been moved to the VIEWR module, and the PLOTR
module concentrates exclusively on constructing plots from the data files. The
coding has been converted into a modular Fortran-90 style.
Methods for generating these types of plots will be given in the following
subsections. An attempt has been made to keep the input as simple as possible
by moving the less common options to the right-hand side of each input line so
that they can be easily defaulted. A complete copy of the input instructions
will be found in Section 20.8. It may be useful to refer to it occasionally while
reading the following sections.
NJOY2016 579

LA-UR-17-20093 20 PLOTR
20.1 Simple 2-D Plots
The simplest kind of 2-D plot is for a single reaction from an ENDF, PENDF, or
GENDF file using automatic scales and default labels. For example, to plot the
total cross section of carbon from ENDF/B-VII, use the following input (don’t
type the line numbers; they are inserted here for reference):
1. plotr
2. 31/
3. /
4. 1/
5. ’<endf/b-vii carbon’/
6. ’<t>otal <c>ross <s>ection’/
7. 4/
8. /
9. /
10. /
11. /
12. 6 20 600 3 1/ tape20 is ENDF/B-VII carbon
13. /
14. 99/
15. stop
The data to be plotted are selected in line 12 using the normal MAT, MF,
MT notation of ENDF. The “slash” at the end of the line hides several defaults,
the first of which is the temperature, which defaults to 0K. The “4” in line 7
selects log-log axes (a number of other options are defaulted here also). Lines
8 through 11 are blank, resulting in the choice of automatically defined ranges
and default labels. Two title lines are given on lines 5 and 6. Note the use of
special shift characters to change between lowercase and uppercase. The file
on tape31 should be sent throughVIEWR to generate the Postscript plot. The
result is shown in Fig. 57.
In many cases, the default scales will give reasonable plots. However, in this
case, the low-energy portion of the plot is approximately constant. It makes
sense to change the lower limit of the xaxis in order to expand the amount of
detail shown at higher energies. A slight change in the lower limit of the yaxis
would also be beneficial. It is only necessary to change two lines as follows:
580 NJOY2016
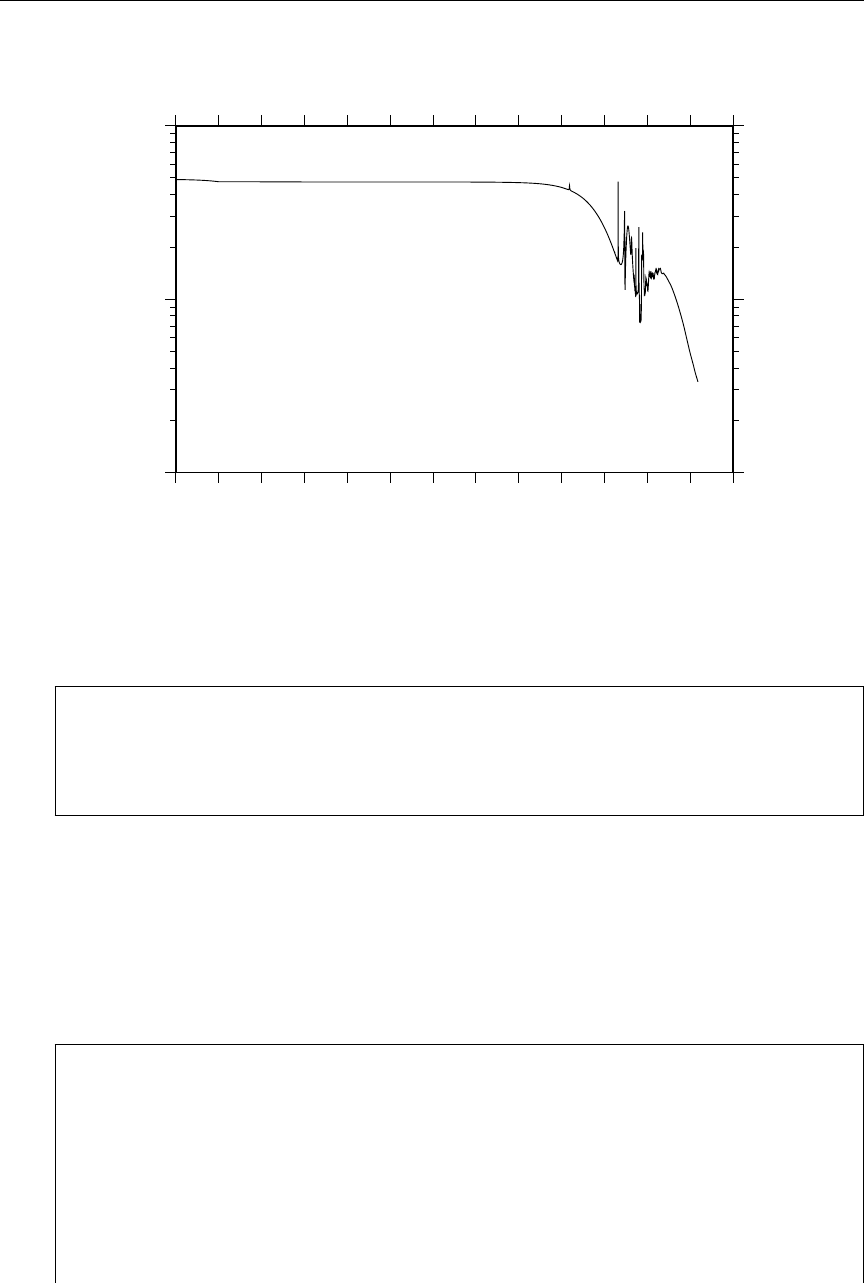
20 PLOTR LA-UR-17-20093
ENDF/B-VII CARBON
Total Cross Section
10-4 10-3 10-2 10-1 100101102103104105106107108109
Energy (eV)
10-1
100
101
Cross section (barns)
Figure 57: Simple 2-D plot of the total cross section of ENDF/B-VII carbon using automatic
log-log axes.
8. 1e3 2e7/
10. .5 10/
Note that the third parameter on these axes cards should always be defaulted
for log scales. The results are shown in Fig. 58. This is a better balanced plot.
If the user needs to emphasize the high-energy region, linear scales are more
appropriate. In addition, some people may prefer a different font. The following
input gives the results shown in Fig. 59. Note how the new font is specified in
line 3. The linear-linear axes option is selected in line 7.
1. plotr
2. 31/
3. 1 1/
4. 1/
5. ’<endf/b-vii carbon’/
6. ’<t>otal <c>ross <s>ection’/
7. 1/
NJOY2016 581
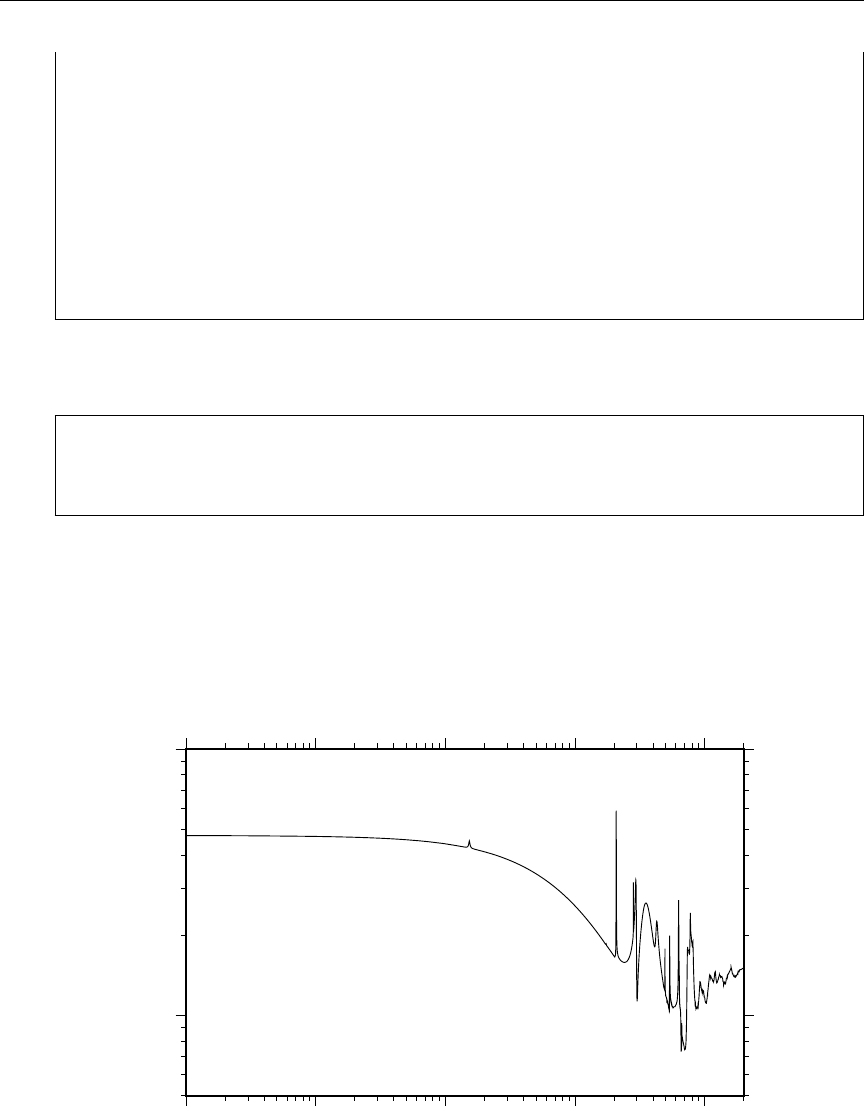
LA-UR-17-20093 20 PLOTR
8. /
9. /
10. /
11. /
12. 6 20 600 3 1/ tape20 is ENDF/B-VII carbon
13. /
14. 99/
15. stop
The limits for the linear xaxis in this example could have been specified by the
user with a card of the form
8. 0 1e7 2e6/
The general rule for linear axes is either give all three parameters explicitly, or
default all three parameters. For log axes, either give the first two parameters
and default the third, or default all three parameters.
ENDF/B-VII CARBON
Total Cross Section
103104105106107
Energy (eV)
100
101
Cross section (barns)
Figure 58: Simple 2-D plot of the total cross section of ENDF/B-VII carbon using log-log
axes with user-selected ranges.
582 NJOY2016
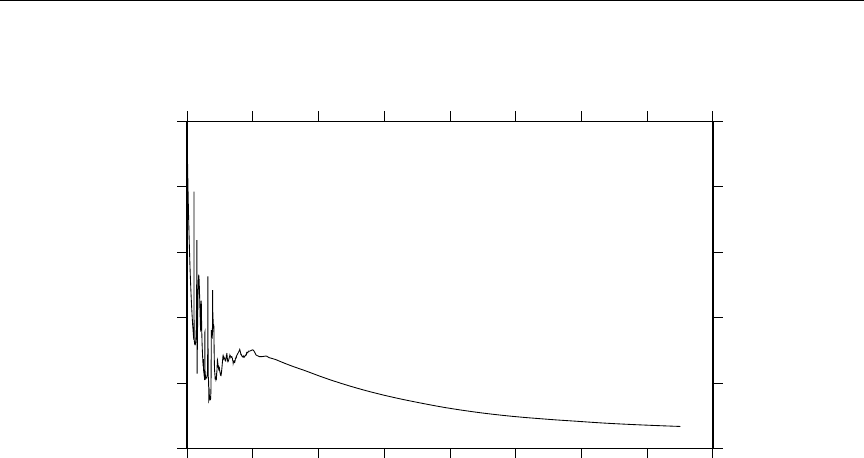
20 PLOTR LA-UR-17-20093
ENDF/B-VII CARBON
Total Cross Section
0 20 40 60 80 100 120 140 160
*106
Energy (eV)
0
1
2
3
4
5
Cross section (barns)
Figure 59: Simple 2-D plot of the total cross section of ENDF/B-VII.0 carbon using linear
axes to emphasize the high-energy region and a more elaborate font.
Most ENDF or PENDF reactions will have many more energy points than can
be shown on a graph like those in these figures. Therefore, PLOTR “thins” the
grid down until there are fewer than max points on the plot (max is currently 10
000). On the other hand, at some energies some ENDF reactions are described
on fairly coarse energy grids using interpolation laws like “lin-lin” or “log-log”.
These representations will look as the evaluator intended if they are plotted using
corresponding scales (for example, log-log interpolation on log-log scales, or log-
lin interpolation on log-lin scales), but if they were to be plotted on a different set
of axes, the cross sections between the grid points would be different from those
intended. Therefore, PLOTR “thickens” the energy grid by adding additional
energy points between the grid points of the evaluation and computing the cross
section at each of these points from the given interpolation law. The resulting
curves will be faithful to the evaluation, but they may exhibit unphysical bumps
and cusps in certain modes of presentation.
20.2 Multicurve and Multigroup Plots
Several curves can be drawn on each set of axes, and each curve can be taken
from a different data source. The following input deck demonstrates how GENDF
data can be compared with PENDF data by overplotting:
NJOY2016 583

LA-UR-17-20093 20 PLOTR
1. plotr
2. 31/
3. /
4. 1/
5. ’ENDF/B-VII #EH.5>241#EXHX>Pu’/
6. /
7. 4 0 2 1 5e3 500/
8. .1 2e7/
9. /
10. 1 1e4/
11. /
12. 6 23 9443 3 18 293.6/
13. /
14. ’pointwise fission’/
15. 2/
16. 1 24 9443 3 18 293.6 1 1 1/
17. 0 0 1/
18. ’multigroup fission’/
19. 99/
20. stop
The result is shown in Fig. 60. The PENDF data are requested on Card 12, and
the GENDF data are requested on Card 16. Note the use of ivers=1 to denote
GENDF data, and also note the settings for nth,ntp, and nkh necessary to select
the P0infinitely dilute cross section for plotting. The GENDF-format data are
automatically converted into histogram form for plotting. This example also
demonstrates using a “legend” block to identify the two curves. The position
for the legend is given on Card 7. These values are normally determined by trial
and error. Note also the presence of a superscript in the title. The superscript
depends on the VIEWR “instruction” mode, which is described in the VIEWR
section of this report.
As another example of a plot of multigroup data, Fig. 61 shows both infinitely
dilute and self-shielded cross sections, and the plot also compares them with the
pointwise cross section. In order to distinguish better between the different
curves, color and double width are used. Here are the curve colors currently
allowed:
curve color (def=black)
584 NJOY2016
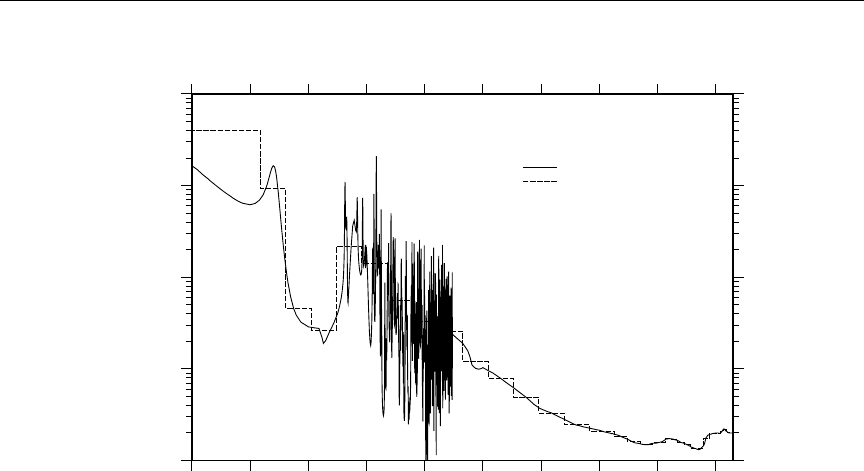
20 PLOTR LA-UR-17-20093
ENDF/B-VII 241Pu
10-2 10-1 100101102103104105106107
Energy (eV)
100
101
102
103
104
Cross section (barns)
pointwise fission
multigroup fission
Figure 60: Comparison of the multigroup fission cross section of ENDF/B-VII.0 241Pu
(dashed curve) with the corresponding pointwise cross section from the PENDF
tape (solid curve).
0=black
1=red
2=green
3=blue
4=magenta
5=cyan
6=brown
7=purple
8=orange
In addition, this plot uses “tags” and arrows to identify the different curves.
The position of the tags and the xlocation for the arrowhead usually must be
determined by trial and error. See lines 15, 20 and 25, which give the x and y
coordinates of the tag and x coordinate where the arrow head meets the curve.
The input for this example follows:
NJOY2016 585
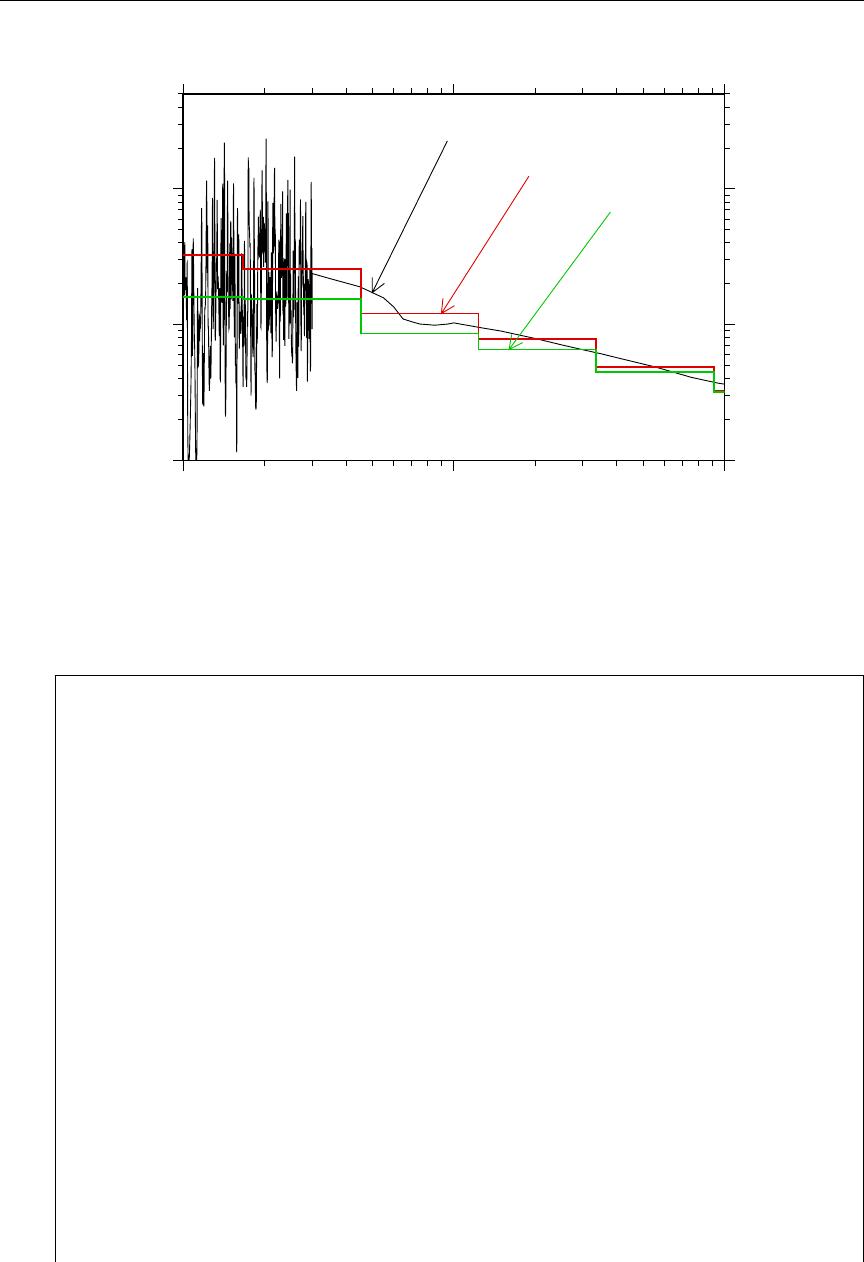
LA-UR-17-20093 20 PLOTR
ENDF/B-VII 235U
102103104
Energy (eV)
100
101
102
Cross section (barns)
pointwise fission
multigroup fission
sigz=10 fission
Figure 61: Multigroup fission cross sections of ENDF/B-VII.0 238U for infinite dilution and
a 10-barn background compared with the corresponding pointwise cross section.
1. plotr
2. 31/
3. /
4. 1/
5. ’ENDF/B-VII #EH.5>235#EXHX>U’/
6. /
7. 4 0 2 2/
8. 100 10000/
9. /
10. 1 500/
11. /
12. 6 23 9443 3 18 293.6/
13. /
14. ’pointwise fission’/
15. 1000 200 500/
16. 2/
17. 1 24 9228 3 18 293.6 1 1 1/
18. 0 0 1 2/
19. ’multigroup fission’/
586 NJOY2016

20 PLOTR LA-UR-17-20093
20. 2000 110 900/
21. 3/
22. 1 24 9228 3 18 293.6 1 3 1/
23. 0 0 2 2/
24. ’]#S+LH.5>0#LXHX>=10 fission’/
25. 4000 60 1600/
26. 99/
27. stop
This example requires 293.6K PENDF data for 235U on the input file tape23
and 293.6K multigroup data for σ0=∞,σ0= 500 barns, and σ0= 10 barns on
tape24. These tapes can be generated with the following NJOY input deck:
1. reconr
2. 20 21/ tape20 is U-235
3. /
4. 9228/
5. .1/
6. 0/
7. broadr
8. 20 21 22/
9. 9228 1/
10. .1/
11. 293.6/
12. 0/
13. unresr
14. 20 22 23/
15. 9228 1 3 1/
16. 293.6/
17. 1e10 500 10/
18. 0/
19. groupr
20. 20 23 0 24/
21. 9228 3 0 3 1 1 3 1/
22. /
23. 293.6/
24. 1e10 500 10/
25. 3 1/
26. 3 18/
27. 3 102/
NJOY2016 587
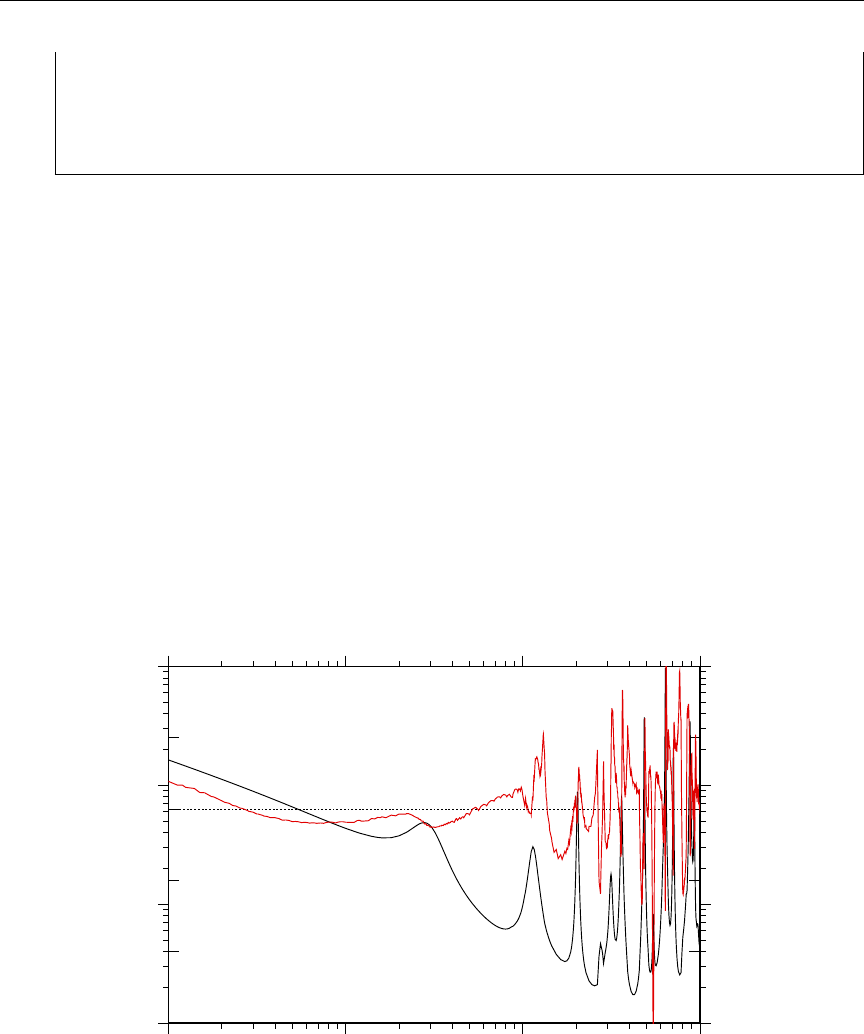
LA-UR-17-20093 20 PLOTR
28. 0/
29. 0/
30. stop
20.3 Right-Hand Axes
PLOTR supports the capability to have different ordinate scales on the left and
right sides of a graph. One place where this can be used is plotting a data
curve and the ratio of another data curve to the first curve. An example of
this is shown in Fig. 62. The input file used to make this plot is shown below.
The RECONR module is run twice to make zero ◦K PENDF files for plotting.
Note the minus signs on lines 28 and 35 — this selects the right-hand scale for
those sections of the input. In line 36, the value of nth of 3 request the ratio
calculation, and the additional input card in line 37 is read to access the second
material for the ratio.
U-235 Capture Comparison
ENDF/B-VII to ENDF/B-V ratio
10-2 10-1 100101
Energy (eV)
100
101
102
103
Cross section (barns)
0.4
0.6
0.8
1.0
1.2
1.4
ratio
0.4
0.6
0.8
1.0
1.2
1.4
ratio
Figure 62: Using a right-hand axis to plot the ratio of the ENDF/B-VII.0 capture cross
section for 235U to the ENDF/B-V value. The black curve is the ENDF/B-V
cross section, and the red curve is the ratio (right-hand axis).
588 NJOY2016

20 PLOTR LA-UR-17-20093
1. reconr
2. 20 22/ tape20 ENDF/B-V U-235
3. /
4. 1395/
5. .02/
6. 0/
7. reconr
8. 21 23/ tape20 ENDF/B-VII U-235
9. /
10. 9228/
11. .02/
12. 0/
13. plotr
14. 31/
15. /
16. 1/
17. ’U-235 Capture Comparison’/
18. ’ENDF/B-VII to ENDF/B-V ratio’/
19. 4 1/
20. 1e-2 10/
21. /
22. /
23. /
24. 0.4 1.4 .2/
25. ’ratio’/
26. 5 22 1395 3 102/ tape20 is carbon from V
27. /
28. -2/
29. 0/
20. 0 0 4/
31. 0/
32. 1e-2 1./
33. 10. 1./
34. /
35. -3/
36. 5 22 1395 3 102 0. 1 3/ tape20 is carbon from V
37. 6 23 9228 3 102 0./
38. 0 0 0 1/
39. 99/
40. stop
NJOY2016 589

LA-UR-17-20093 20 PLOTR
20.4 Plotting Input Data
PLOTR allows the user to insert data directly into the input deck. The main use
of this is to superimpose experimental data over curves obtained from ENDF,
PENDF or GENDF tapes, but reading data directly from the input deck can
also be used to add precalculated curves or eye guides to plots, or to add special
features such as vertical lines to separate regions on plots. Experimental data
points can be plotted with a variety of symbols, and xand/or yerror bars can
be included if desired. The error bars can be either symmetric or asymmetric.
For experimental data, the curves and various sets of data points are normally
identified using a legend block. The following input produces a typical example
of this type of plot:
1. plotr
2. 31/
3. /
4. 1/
5. ’ENDF/B-VII CARBON’/
6. ’(n,]a>) with fake data’/
7. 1 0 2 1 1.3e7 .25/
8. 6e6 18e6/
9. /
10. /
11. /
12. 6 20 600 3 107/
13. /
14. ’ENDF/B-VII MAT 600’/
15. 2/
16. 0/
17. -1 0/
18. ’<s>mith & <s>mith 1914’/
19. 0/
20. 1.1e7 .08 .05 .05/
21. 1.2e7 .10 .05 .05/
22. 1.3e7 .09 .04 .04/
23. 1.4e7 .08 .03 .03/
24. /
25. 3/
26. 0/
27. -1 2/
28. ’Black & Blue 2008’/
590 NJOY2016
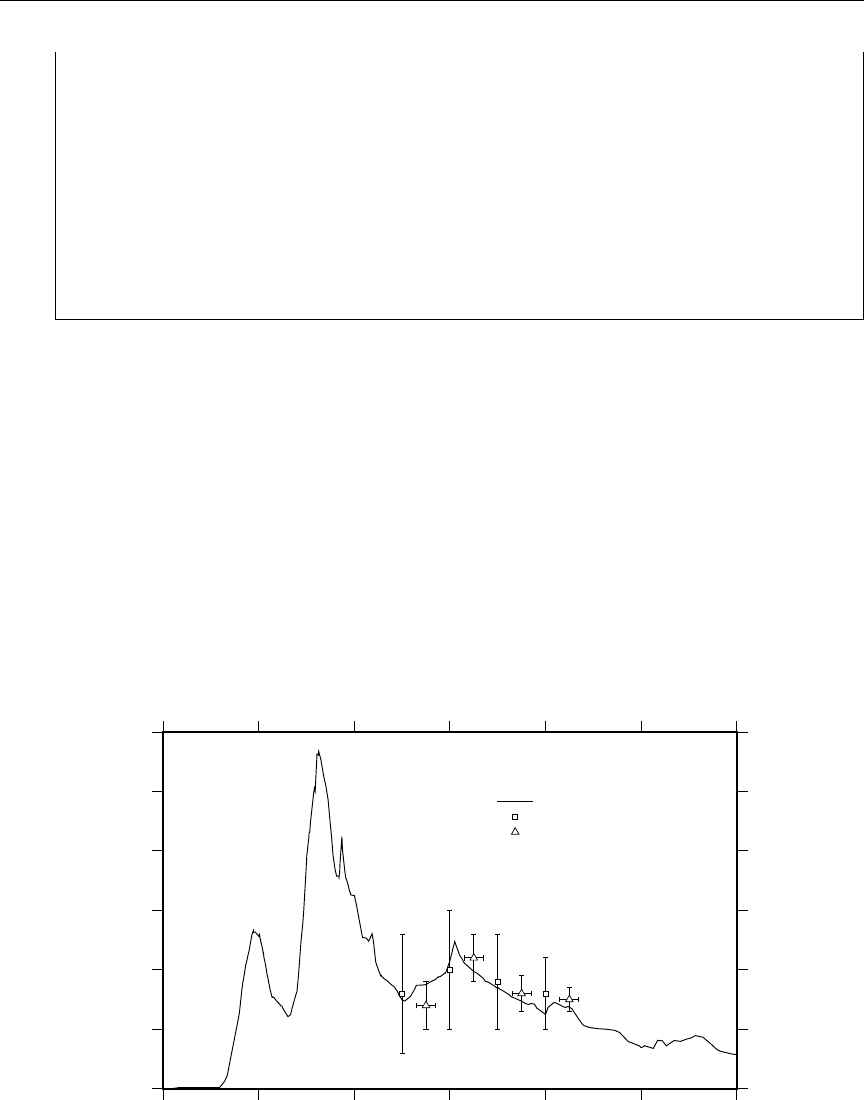
20 PLOTR LA-UR-17-20093
29. 0/
30. 1.15e7 .07 .02 0. .2e6 0./
31. 1.25e7 .11 .02 0. .2e6 0./
32. 1.35e7 .08 .015 0. .2e6 0./
33. 1.45e7 .075 .01 0. .2e6 0./
34. /
35. 99/
36. stop
The results are shown in Fig. 63. The error bars for both of these simulated
data sets are symmetric, as indicated explicitly in Cards 20 through 23, or by
the zeroes in Cards 30 through 33. They can also be asymmetric if the lower
and upper (or right and left) values are nonzero and different.
20.5 Three-D Plots of Angular Distributions
ENDF angular distribution data, whether given in File 4 or File 6, can be very
bulky. Therefore, it is useful to present them in the form of a perspective plot
ENDF/B-VII CARBON
(n,α) with fake data
6 8 10 12 14 16 18
*106
Energy (eV)
0
50
100
150
200
250
300
*10-3
Cross section (barns)
ENDF/B-VII MAT 600
Smith & Smith 1914
Black & Blue 2008
Figure 63: Carbon (n,α) cross section compared with two sets of simulated experimental
data represented with two types of error bars.
NJOY2016 591

LA-UR-17-20093 20 PLOTR
showing a family of angular distribution curves for each value of incident particle
energy. An input deck to make such a perspective plot follows:
1. plotr
2. 31/
3. /
4. 1/
5. ’ENDF/B-V CARBON’/
6. ’Elastic MF4’/
7. -1 2/
8. /
9. /
10. 1e6 5e6 1e6/
11. /
12. /
13. /
14. 5 20 1306 4 2/
15. /
16. 99/
17. stop
Fig. 64 shows the result using a linear axis for incident energy. This axis is
the yaxis, and its range has been limited to expand a particular part of the
distribution. A linear scale emphasizes the high-energy region.
20.6 Three-D Plots of Energy Distributions
Three-D perspective plots are also useful for energy distributions. For the
ENDF-5 and earlier formats, neutron secondary-energy distributions are given
in File 5. The following input deck shows how to request a 3-D plot for File 5:
1. plotr
2. 31/
3. /
4. 1/
5. ’ENDF/B-V Li-6’/
6. ’(n,2n)]a neutron distribution’/
7. -1 2 1/
8. /
9. /
10. 4e6 20e6 2e6/
592 NJOY2016
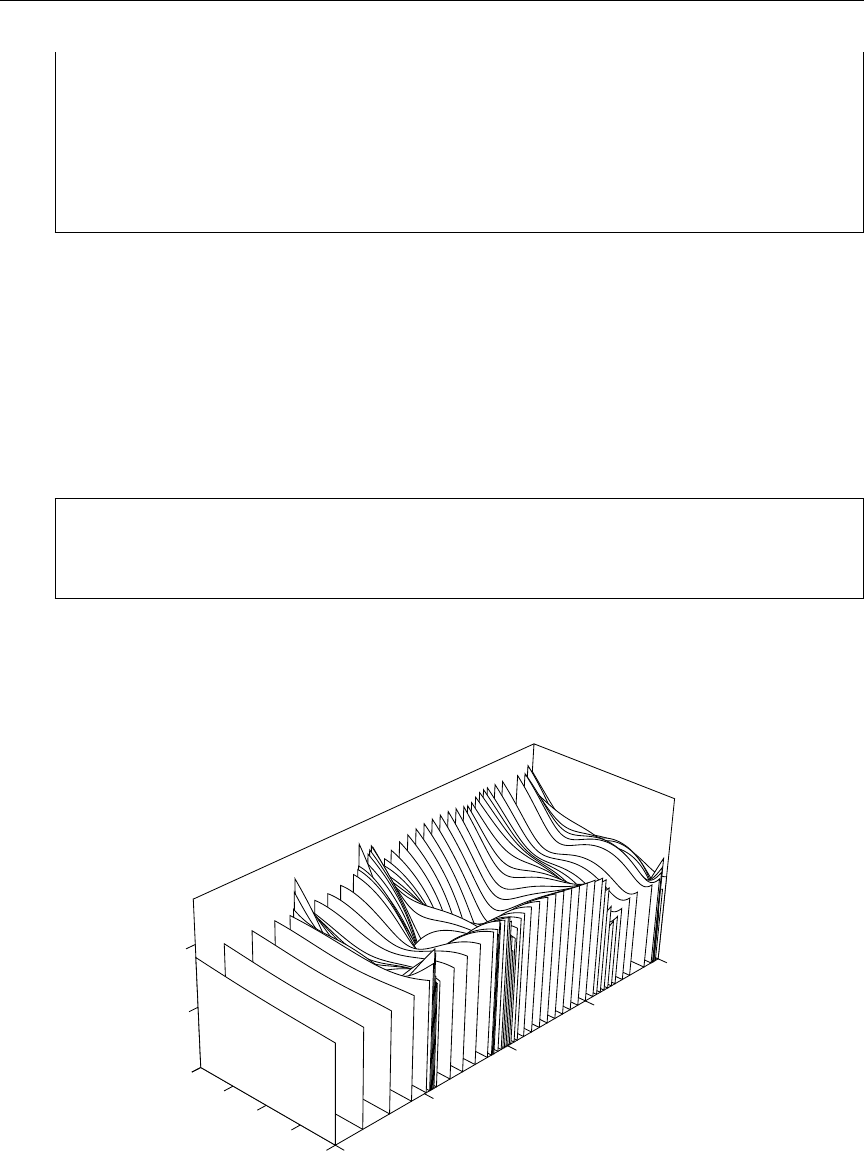
20 PLOTR LA-UR-17-20093
11. /
12. 5 20 1303 5 24/
13. /
14. 99/
15. stop
Grids lines have been requested in Card 7. The result is shown in Fig. 65.
Similar methods can be used to plot photon emission distributions from File 15.
The new ENDF-6 format also provides for giving distributions for other emit-
ted particles, such a protons, alphas, photons, and even recoil nuclei. This com-
plicates the task of selecting which distribution is to be extracted from File
6. The user must specify the index for the particular outgoing particle to be
considered (see nkh). Line 12 might become, for example,
12. 6 20 2437 103 0. 0 0 1/
which would request a plot of the proton distribution for the (n,p) reaction of
54Cr from ENDF/B-VI.
ENDF/B-V CARBON
Elastic MF4
1
0
-
1
1
0
0
P
r
o
b
-
1
.
0
-
0
.
5
0
.
0
0
.
5
1
.
0
C
o
s
i
n
e
1
2
3
4
5
*
1
0
6
E
n
e
r
g
y
(
e
V
)
Figure 64: Perspective view of carbon elastic scattering angular distribution.
NJOY2016 593
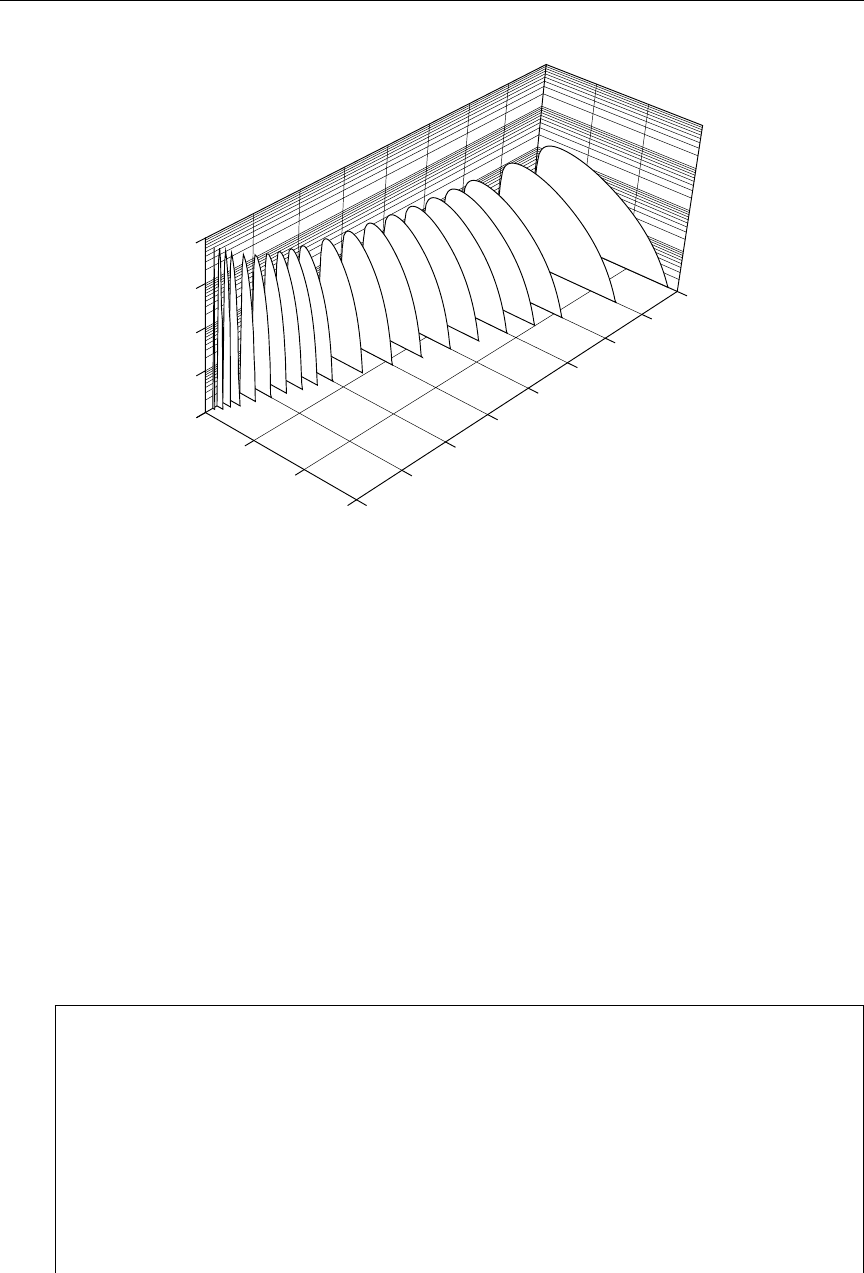
LA-UR-17-20093 20 PLOTR
ENDF/B-V Li-6
(n,2n)α neutron distribution
1
0
-
7
1
0
-
5
P
r
o
b
/
e
V
0
5
1
0
1
5
*
1
0
6
S
e
c
.
e
n
e
r
g
y
4
6
8
1
0
1
2
1
4
1
6
1
8
2
0
*
1
0
6
E
n
e
r
g
y
(
e
V
)
Figure 65: Perspective plot of 6Li (n,2n)αneutron secondary-energy distributions.
For some evaluations, File 6 uses Law 7, where the energy-angle distribution
is represented as E→E0distributions for several emission cosines µ. In these
cases, the ntp parameter may be used to select one of the emission angles, and
the 3-D plot shows the distribution for that angle.
20.7 Two-D Spectra Plots from Files 5 and 6
It is difficult to see real detail on 3-D plots, and the emission spectra cannot be
compared with measurements. Therefore, PLOTR has the capability to extract
the spectrum for a particular particle and incident energy. The following input
deck shows how several such spectra can be plotted on one graph.
1. plotr
2. 31/
3. /
4. 1/
5. ’ENDF/B-V Li-6’/
6. ’(n,2n)]a >neutron spectra vs <E>’/
7. 4 0 2 2/
8. 10. 2.e7/
594 NJOY2016

20 PLOTR LA-UR-17-20093
9. /
10. 1e-11 1e-6/
11. ’<c>ross <s>ection (barns/e<V>)’/
12. 5 20 1303 5 24 0. 12/
13. /
14. ’10 <m>e<v>’/
15. 1e3 2e-11 1e2/
16. 2/
17. 5 20 1303 5 24 0. 16/
18. /
19. ’14 <m>e<v>’/
20. 1e4 2e-10 2e3/
21. 3/
22. 5 20 1303 5 24 0. 20/
23. /
24. ’20 <m>e<v>’/
25. 1e5 2e-9 4e4/
26. 99/
27. stop
The results are shown in Fig. 66. “Tags” are used to distinguish between the
different incident energy values.
The method used for selecting which curve is to be plotted is awkward in the
current version of PLOTR. The user must give the index number of the incident
energy desired (like the value 12 in line 12 of this example).
When an ENDF-6 format File 6 is available, emission spectra will normally
be given for several emitted particles, photons, and recoil nuclei. In addition,
angular data may be given for various E→E0transfers using several different
representations. This complicates the task of selecting which curve is to be
extracted from File 6. For Law 1 data, the user must specify the particular
outgoing particle to be considered (see nkh), the index for the incident energy
desired (see nth), and the dependent variable to plot (see ntp). The result
depends on the representation used. In every case, ntp=1 gives the cross section
versus E0, but for Legendre polynomials, ntp=2 gives the P1component versus
E0, and for Kalbach-Mann, ntp=2 gives the preequilibrium ratio versus E0. For
Law 7, ntp specifies the emission angle. The graph will show a spectrum versus
E0for the specified angle, specified incident energy E, and specified particle.
NJOY2016 595
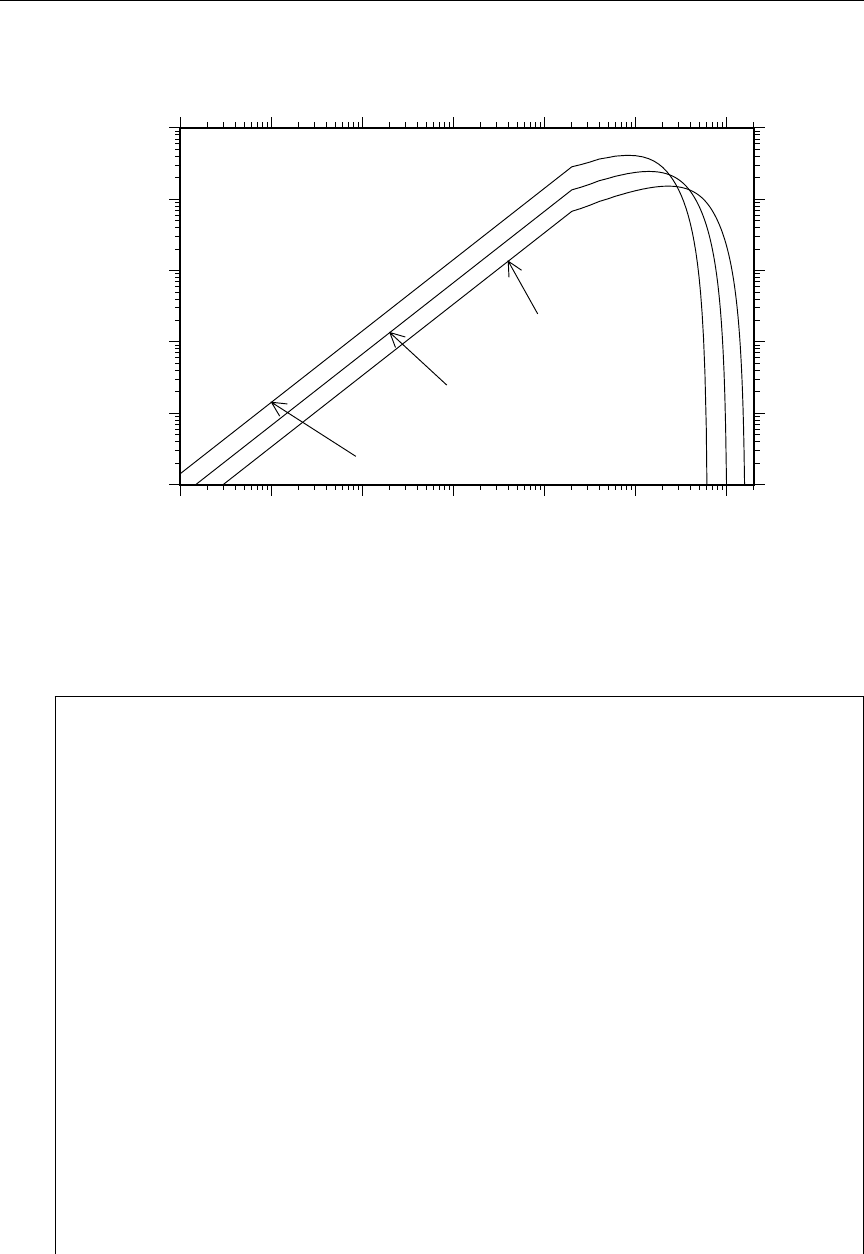
LA-UR-17-20093 20 PLOTR
ENDF/B-V Li-6
(n,2n)α neutron spectra vs E
101102103104105106107
Energy (eV)
10-11
10-10
10-9
10-8
10-7
10-6
Cross Section (barns/eV)
10 MeV
14 MeV
20 MeV
Figure 66: Two-D plot of selected secondary neutron spectra for the 6Li (n,2n)αreaction.
20.8 Input Instructions
!---input--------------------------------------------------------
!
! card 0
! nplt unit for output plot commands
! nplt0 unit for input plot commands
! default=0=none
! output plot commands are appended
! to the input plot commands, if any.
! card 1
! lori page orientation (def=1)
! 0 portrait (7.5x10in)
! 1 landscape (10x7.5in)
! istyle character style (def=2)
! 1 = roman
! 2 = swiss
! size character size option
! pos = height in page units
! neg = height as fraction of subplot size
596 NJOY2016

20 PLOTR LA-UR-17-20093
! (default=0.30)
! ipcol page color (def=white)
! 0=white
! 1=navajo white
! 2=blanched almond
! 3=antique white
! 4=very pale yellow
! 5=very pale rose
! 6=very pale green
! 7=very pale blue
!
! -----repeat cards 2 through 13 for each curve-----
!
! card 2
! iplot plot index
! 99 = terminate plotting job
! 1 = new axes, new page
! -1 = new axes, existing page
! n = nth additional plot on existing axes
! -n = start a new set of curves using
! the alternate y axis
! default = 1
! iwcol window color (def=white)
! color list same as for ipcol above
! factx factor for energies (default=1.)
! facty factor for cross-sections (default=1.)
! xll,yll lower-left corner of plot area
! ww,wh,wr window width, height, and rotation angle
! (plot area defaults to one plot per page)
!
! -----cards 3 thru 7 for iplot = 1 or -1 only-----
!
! card 3
! t1 first line of title
! 60 characters allowed.
! default=none
!
! card 3a
! t2 second line of title
! 60 characters allowed.
! default=none
!
NJOY2016 597

LA-UR-17-20093 20 PLOTR
! card 4
! itype type for primary axes
! 1 = linear x - linear y
! 2 = linear x - log y
! 3 = log x - linear y
! 4 = log x - log y
! set negative for 3d axes
! default=4
! jtype type for alternate y axis or z axis
! 0 = none
! 1 = linear
! 2 = log
! default=0
! igrid grid and tic mark control
! 0 = no grid lines or tic marks
! 1 = grid lines
! 2 = tic marks on outside
! 3 = tic marks on inside
! default=2
! ileg option to write a legend.
! 0 = none
! 1 = write a legend block with upper left
! corner at xtag,ytag (see below)
! 2 = use tag labels on each curve with
! a vector from the tag to the curve
! default=0
! xtag x coordinate of upper left corner
! of legend block
! ytag y coord of upper left corner
! default=upper left corner of plot
!
! card 5
! el lowest energy to be plotted
! eh highest energy to be plotted
! xstep x axis step
! default = automatic scales
! (default all 3, or none)
! (the actual value of xstep is
! ignored for log scales)
!
! card 5a
! xlabl label for x axis
598 NJOY2016

20 PLOTR LA-UR-17-20093
! 60 characters allowed.
! default="energy (ev)"
!
! card 6
! yl lowest value of y axis.
! yh highest value of y axis.
! ystep step for y ayis (linear scales only)
! default = automatic scales
! (default all 3, or none)
! (the actual value of ystep is
! ignored for log scales)
!
! card 6a
! ylabl label for y axis
! 60 characters allowed.
! default="cross section (barns)"
!
! card 7 (jtype.gt.0 only)
! rbot lowest value of secondary y axis or z axis
! rtop highest value of secondary y axis or z axis
! rstep step for secondary y axis or z axis
! default for last three = automatic
!
! card 7a (jtype.gt.0 only)
! rl label for alternate y axis or z axis
! 60 characters allowed.
! default=blank
!
! -----cards 8 thru 9 are always given-----
!
! card 8
! iverf version of endf tape
! set to zero for data on input file
! and ignore rest of parameters on card
! set to 1 for gendf data
! nin input tape
! can change for every curve if desired.
! matd desired material
! mfd desired file
! mtd desired section
! mtd=0 means loop over all reactions in mfd
! (usually one page per mt, but for mf=3,
NJOY2016 599

LA-UR-17-20093 20 PLOTR
! resonance reactions may have several pages)
! temper temperature for endf data (degK, default=0.)
! nth,ntp,nkh see below (defaults=1)
!
! special meanings for nth,ntp,nkh for file 3 or 5 data
! nth number of subsection to plot
! (works for isomer prod, delayed n, etc.)
! ntp not used
! nkh not used
!
! special meanings for nth for file 4 Legendre data
! nth index for Legendre coefficient (p1, p2, ...)
!
! special meanings for nth,ntp,nkh for file 6 data
! nth index for incident energy
! ntp number of dep. variable in cyle to plot
! (or angle number for law 7)
! nkh number of outgoing particle to plot
!
! special meanings for nth,ntp,nkh for gendf mf=3 data
! nth=0 for flux per unit lethargy
! nth=1 for cross section (default)
! ntp=1 for infinite dilution (default)
! ntp=2 for next lowest sigma-zero values, etc.
! nkh=1 for p0 weighting (default)
! nkh=2 for p1 weighting (total only)
!
! special meaning for nth for gendf mf=6 data
! nth=1 plot 2-d spectrum for group 1
! nth=2 plot 2-d spectrum for group 2
! etc.
! no special flags are needed for mf=6 3d plots
!
! special meanings for nth and ntp for mf7 plots
! nth is index for indep. variable (alpha or beta)
! ntp=1 selects alpha as indep. variable (default)
! ntp=2 selects beta as indep. variable
! nkh=1 selects normal s(alpha,beta)
! nkh=2 selects script s(alpha,-beta)
! nkh=3 selects script s(alpha,beta)
!
! -----cards 9 and 10 for 2d plots only-----
600 NJOY2016

20 PLOTR LA-UR-17-20093
!
! card 9
! icon symbol and connection option
! 0 = points connected, no symbols
! -i = points not connected, symbol at every
! ith point
! i = points connected, symbol at every ith
! points
! default=0
! isym no. of symbol to be used
! 0 = square
! 1 = octagon
! 2 = triangle
! 3 = cross
! 4 = ex
! 5 = diamond
! 6 = inverted triangle
! 7 = exed square
! 8 = crossed ex
! 9 = crossed diamond
! 10 = crossed octagon
! 11 = double triangle
! 12 = crossed square
! 13 = exed octagon
! 14 = triangle and square
! 15 = filled circle
! 16 = open circle
! 17 = open square
! 18 = filled square
! default=0
! idash type of line to plot
! 0 = solid
! 1 = dashed
! 2 = chain dash
! 3 = chain dot
! 4 = dot
! default=0
! iccol curve color (def=black)
! 0=black
! 1=red
! 2=green
! 3=blue
NJOY2016 601

LA-UR-17-20093 20 PLOTR
! 4=magenta
! 5=cyan
! 6=brown
! 7=purple
! 8=orange
! ithick thickness of curve (def=1)
! 0 = invisible (for shaded areas)
! ishade shade pattern
! 0 = none
! 1 to 10 = 10\% to 100\% gray
! 11 to 20 = 45 deg right hatching
! 21 to 30 = 45 deg left hatching
! 31 to 40 = 45 deg cross hatching
! 41 to 50 = shades of green
! 51 to 60 = shades of red
! 61 to 70 = shades of brown
! 71 to 80 = shades of blue
! default=0
!
! card 10 ---ileg.ne.0 only---
! aleg title for curve tag or legend block
! 60 characters allowed.
! default=blank
!
! card 10a ---ileg.eq.2 only---
! xtag x position of tag title
! ytag y position of tag title
! xpoint x coordinate of vector point
! (.le.0 to omit vector)
!
! -----card 11 for 3d plots only-----
!
! card 11
! xv,yv,zv abs. coords of view point
! defaults=15.,-15.,15.
! x3,y3,z3 abs. sides of work box volume
! defaults=2.5,6.5,2.5
!
! set x3 or y3 negative to flip the order of the
! axis on that side of the work box.
!
! -----cards 12 thru 13 for iverf = 0 only-----
602 NJOY2016

20 PLOTR LA-UR-17-20093
!
! card 12
! nform format code for input data
! 0 = free format input with
! optional x and y error bars
!
! card 13 ---nform = 0 only---
! xdata dependent value
! terminate with empty card (/)
! ydata independent value
! yerr1 lower y error limit
! no y error bar if zero
! yerr2 upper y error limit
! if zero, equals yerr1
! xerr1 x left error limit
! no x error bar if zero
! xerr2 x right error limit
! if zero, equals xerr1
!
! all curves contain at least 10 points per decade (see delta).
! code can plot curves containing fewer than 2000 points (see
! max) without thinning. curves with more points are thinned
! based on a minimum spacing determined from max and the
! length of the x axis.
!
!--------------------------------------------------------------------
20.9 Coding Details
Subroutine plotr is the only public call in the module plotm. It starts by
setting up the default paper size, margins, working box, and view point. It then
reads in the first two input cards to define the unit for Postscript output and
the parameters for the graphics page, such as orientation, font style, font size,
and page color. The routine can then start the main loop over plots, subplots,
and curves (see statement number 110). The next card is read, which gives the
value of iplot. If iplot=99, the job is complete and the code exits through
statement number 700 by writing an end “99” on the plot file and closing the
open units.
The next step is to start reading the user’s input. For each input line, the
defaults are set and the standard Fortran READ* method is used to read the
NJOY2016 603

LA-UR-17-20093 20 PLOTR
input. Once all the input parameters have been read, the code branches to
different regions for different data types.
For ENDF and PENDF data, PLOTR reads the first part of File 1 and
searches for the desired temperature. It then uses findf to locate the desired
material and reaction. Note that there is an option for an automatic reaction
loop that enters at statement number 320. When mtd=0, plotr automatically
loops over all the MT numbers that it finds in the current file. For 2-D plots,
it is necessary to extract the desired xand yvalues out of a TAB1 or a LIST
record. It is fairly tricky finding this record because of the large number of
possible formats in Files 3, 5, 6, 7, and 15. Some improvements are needed here
to allow PLOTR to construct angular distributions from File 4 and to allow
access by actual values rather than the indexes nth,ntp, and nkh.
Once the appropriate record has been located, PLOTR sets up a process to
extract the xand yvalues from the record either thinning or thickening the given
xgrid as necessary to get a good plot. After all the values have been computed,
the code ends up at statement number 610, and the VIEWR instructions to
make the 2-D plot are written to the output file nplt. Control then loops back
to either statement number 110 (ordinary manual reaction specification) or to
statement number 320 (automatic reaction loop).
For 3-D ENDF or PENDF plots, the code first skips to the desired subsection
of File 4, 5, 6, 15, etc. The structure of a subsection varies with the law used to
describe the data. The format for File 4 and File 6 two-body angular distribution
data is similar, so a common procedure ad3d can be used for these two Files. At
each incident energy, the angular distribution is either obtained by interpolation
in the given tabulation, or it is computed from the given Legendre coefficients.
Once all the numbers have been loaded into the aa array, they are written to
the output nplot file in VIEWR format.
For Files 5, 6, and 15 3-D plots, control is passed to subroutine ed3d. The
data from the desired subsection are extracted and loaded into the aa array.
During this process, the maximum and minimum values on the various axes are
determined. The code determines an appropriate vertical axis range of about 3
decades. It then writes out the VIEWR file for the 3-D energy plot, removing
any zvalues that are too small.
For GENDF 2-D data, PLOTR searches the GENDF tape for the requested
material and temperature. It then reads in the entire MT=451 header record
and sets pointers to the energy boundaries for the particle and photon group
structures. The next step is to loop through the records on the file looking for
604 NJOY2016

20 PLOTR LA-UR-17-20093
the desired reaction. The cross section values are read from the list records,
and energy values for the histogram break points are computed from the group
structure information. The resulting x and y arrays are passed to statement
number 610 and written to the VIEWR file.
For 3-D GENDF plots, subroutine gg3d is used to extract the data for the
distribution, add in the group-boundary energies, set up the axis limits, and
write out the resulting distribution in VIEWR format.
Experimental data are read directly into the xand yarrays from the input
deck. If error bars are present, they are read into the arrays dxm,dxp,dym, and
dyp. The xand yarrays are passed to statement number 610 and written out
in VIEWR format.
There are several remaining routines in PLOTR. Subroutine gety6 is used
to page in data from an ENDF-6 format File 6. Subroutine fixl7 is used to
transform File 6 Law 7 into Law 1 form for plotting. This requires putting the
spectra for all angles onto a common secondary-energy grid, and then integrating
over angle for each energy of this common grid. The result is a P0energy
distribution ready for plotting. Subroutine rname constructs reaction names
from ENDF MT numbers. Subroutine ascale constructs good axis limits and
step sizes for linear axes.
20.10 Storage Allocation
The array a(nwamax) with length nwamax=45 000 words is used for reading
in ENDF-format records. The main container array is aa(maxaa) with length
maxaa=200 000. The maximum number of x, y pairs in any plot is set by data
mmax=20 000. There are several arrays of this length equivalenced to various
regions of the container array aa. See x(mmax),y(mmax),b(mmax),dxm(mmax),
dxp(mmax),dym(mmax), and dyp(mmax). These assignments could be changed, if
necessary, for a very high resolution device. The arrays used to map coordinate
values to curves for 3-D plots are limited to 200. This could be a problem if an
evaluation had more than 200 incident energies in File 4, 5, or 6. There is a
limit of 400 incident or outgoing energy groups for GENDF 3-D distributions.
20.11 Input and Output Units
PLOTR doesn’t use any internal scratch units. The only units used are those
mentioned on cards 0 and 8, and they can be either ASCII (nin positive) or
blocked binary (nin negative) as desired. ASCII and blocked binary units can
NJOY2016 605

LA-UR-17-20093 20 PLOTR
be mixed on a single plot if necessary.
20.12 Error Messages
error in plotr***error in axis input
Check your input Cards 5, 6, and/or 7. Remember that the easiest thing to
do with xstep,ystep, or rstep for log axes is to take the default value. For
linear scales, either give all three parameters, or default all three. Usually
this message means some previous card is missing.
error in plotr***desired mat and temp not found a
Check the input cards against the input tape mounted.
error in plotr***lf=1 only for mf5 or 15.
The analytic secondary distribution laws are not supported by PLOTR.
error in plotr***lf=1 or 7 only for file 6.
Two-D plots from File 6 are currently limited to laws 1 and 7.
error in plotr***illegal ntd for mf7.
The requested value of nth is larger than the number of beta values avail-
able in File 7.
error in plotr***temperature not found.
The requested temperature is not available in File 7.
error in plotr***storage exceeded.
Either there is an undiscovered error in the thinning/thickening logic, or
an attempt has been made to read a GENDF reaction with more than
nwamax=30 000 words.
error in plotr***illegal mf6 law.
Only laws 0, 1, 2, 3, 4, and 7 are currently supported.
error in plotr***3d mf7 plots not available.
This would be a desirable extension for PLOTR.
message from plotr---no distribution, no plot
No distribution was found on the input tape.
error in gg3d***too many incident groups for 3d gendf plot
This is limited to maxx3=400 groups.
error in gg3d***too many data for 3d gendf plot
More than maxaa=100 000 words of GENDF data are needed.
error in gg3d***too many secondary groups for 3d gendf plot
This is controlled by maxy3=400.
error in fixl7***not enough storage to convert file 7
Up to nw7max=6000 words are made available out the the aa array for
converting File 7.
606 NJOY2016

21 VIEWR LA-UR-17-20093
21 VIEWR
The VIEWR module provides a general-purpose plotting capability for NJOY.
It reads in user commands that define a variety of 2-D and 3-D graphs, and then
it writes a Postscript file to display the graphs with high quality. Some of the
capabilities of VIEWR include
•conventional 2-D plots (for example, cross section vs energy) with the nor-
mal combinations of linear and log scales, automatic or user-specified ranges
and labels, an optional alternate right-hand axis, and with one or two title
lines;
•curves of various line patterns, labeled with tags and arrows or described
in a legend block;
•data points given with a variety of symbols with error bars (they can be
identified in a legend block);
•the superposition of several plots on a given set of axes;
•detailed 3-D perspective plots for data such as angular distributions or
energy distributions, with a choice of linear or log axes, with a choice of
working area and viewpoint, and with one or two title lines;
•color can be used to distinguish between different curves, and the graphics
window area and page background can also have selected colors;
•closed regions can be displayed with various kinds of cross hatching for
filled with selected colors; and
•multiple plots can be put on each page.
Many examples of graphs generated by VIEWR can be found elsewhere in this
report.
This chapter describes the VIEWR module in NJOY2016.0.
21.1 Modular Structure
The viewr subroutine is encapsulated into a Fortran-90 module that only makes
public that one subroutine call. This module is supported by module graph,
which makes a number of calls and data structures public. The features in
graph provide the low-level capabilities for generating Postscript graphics that
are used by the routines in VIEWR. We will first describe VIEWR by giving
the user-input specifications and describing the details of the VIEWR coding.
Finally, we will describe the details of the graphics calls as implemented in the
separate graph module.
NJOY2016 607

LA-UR-17-20093 21 VIEWR
21.2 Using VIEWR
The VIEWR module can be used as a general-purpose plotting engine by con-
structing input for it by hand. However, it is more commonly used to dis-
play data assembled by other NJOY modules. For example, PLOTR reads
data in ENDF, PENDF, or GENDF formats and constructs an output file in
VIEWR format. COVR constructs an elaborate set of plots of cross-section
covariance data using color contour maps and rotated subplots. HEATR can
produce graphs showing the heating value, the photon energy production, and
their associated kinematic limits. DTFR and ACER both are capable of gener-
ating VIEWR files that show the cross sections and distributions contained in
the libraries that they produce. See the writeups for these various modules for
examples of these kinds of plots.
21.3 Input Instructions
There is actually only one line of input for the VIEWR module itself:
!---input--------------------------------------------------------
!
! card 1
! infile input file
! nps postscript output file
!
The plotting commands and data are provided on an input file to VIEWR that
use the following format:
!---data file format---------------------------------------------
!
! card 1
! lori page orientation (def=1)
! 0 portrait (7.5x10in)
! 1 landscape (10x7.5in)
! istyle character style (def=2)
! 1 roman
! 2 swiss
! size character size option
! pos = height in page units
608 NJOY2016

21 VIEWR LA-UR-17-20093
! neg = height as fraction of subplot size
! (default=.30)
! ipcol page color (def=white)
! 0=white
! 1=navajo white
! 2=blanched almond
! 3=antique white
! 4=very pale yellow
! 5=very pale rose
! 6=very pale green
! 7=very pale blue
!
! -----repeat cards 2 through 13 for each curve-----
!
! card 2
! iplot plot index
! 99 = terminate plotting job
! 1 = new axes, new page
! -1 = new axes, existing page
! n = nth additional plot on existing axes
! -n = start a new set of curves using
! the alternate y axis
! default = 1
! iwcol window color (def=white)
! color list same as for ipcol above
! factx factor for energies (default=1.)
! facty factor for cross-sections (default=1.)
! xll,yll lower-left corner of plot area
! ww,wh,wr window width, height, and rotation angle
! (plot area defaults to one plot per page)
!
! -----cards 3 thru 7 for iplot = 1 or -1 only-----
!
! card 3
! t1 first line of title
! 60 characters allowed.
! default=none
!
! card 3a
! t2 second line of title
! 60 characters allowed.
! default=none
NJOY2016 609

LA-UR-17-20093 21 VIEWR
!
! card 4
! itype type for primary axes
! 1 = linear x - linear y
! 2 = linear x - log y
! 3 = log x - linear y
! 4 = log x - log y
! set negative for 3d axes
! 0 = no plot, titles only
! default=4
! jtype type for alternate y axis or z axis
! 0 = none
! 1 = linear
! 2 = log
! default=0
! igrid grid and tic mark control
! 0 = no grid lines or tic marks
! 1 = grid lines
! 2 = tic marks on outside
! 3 = tic marks on inside
! default=2
! ileg option to write a legend.
! 0 = none
! 1 = write a legend block with upper left
! corner at xtag,ytag (see below)
! 2 = use tag labels on each curve with
! a vector from the tag to the curve
! default=0
! xtag x coordinate of upper left corner
! of legend block
! ytag y coord of upper left corner
! default=upper left corner of plot
!
! card 5
! xmin lowest energy to be plotted
! xmax highest energy to be plotted
! xstep x axis step
! default = automatic scales
! (for linear, give all 3, or none)
! (for log, give first 2, or none)
!
! card 5a
610 NJOY2016

21 VIEWR LA-UR-17-20093
! xlabl label for x axis
! 60 characters allowed.
! (default = no label, no numbering)
!
! card 6
! ymin lowest value of y axis.
! ymax highest value of y axis.
! ystep step for y ayis (linear scales only)
! default = automatic scales
! (for linear, give all 3, or none)
! (for log, give first 2, or none)
!
! card 6a
! ylabl label for y axis
! 60 characters allowed.
! (default = no label, no numbering)
!
! card 7 (jtype.gt.0 only)
! rmin lowest value of secondary y axis or z axis
! rmax highest value of secondary y axis or z axis
! rstep step for secondary y axis or z axis
! (default = automatic scale)
! (for linear, give all 3, or none)
! (for log, give first 2, or none)
!
! card 7a (jtype.gt.0 only)
! rl label for alternate y axis or z axis
! 60 characters allowed.
! (default = no label, no numbering)
!
! card 8 -- dummy input card for consistency with plotr
! it always should be 0/
!
! -----cards 9 and 10 for 2d plots only-----
!
! card 9
! icon symbol and connection option
! 0 = points connected, no symbols
! -i = points not connected, symbol at every
! ith point
! i = points connected, symbol at every ith
! points
NJOY2016 611

LA-UR-17-20093 21 VIEWR
! default=0
! isym no. of symbol to be used
! 0 = square
! 1 = octagon
! 2 = triangle
! 3 = cross
! 4 = ex
! 5 = diamond
! 6 = inverted triangle
! 7 = exed square
! 8 = crossed ex
! 9 = crossed diamond
! 10 = crossed octagon
! 11 = double triangle
! 12 = crossed square
! 13 = exed octagon
! 14 = triangle and square
! 15 = filled circle
! 16 = open circle
! 17 = open square
! 18 = filled square
! 19 = filled diamond
! 20 = filled triangle
! 21 = filled inverted triangle
! 22 = crossed circle
! 23 = exed circle
! 24 = exed diamond
! default=0
! idash type of line to plot
! 0 = solid
! 1 = dashed
! 2 = chain dash
! 3 = chain dot
! 4 = dot
! 5 = invisible
! default=0
! iccol curve color (def=black)
! 0=black
! 1=red
! 2=green
! 3=blue
! 4=magenta
612 NJOY2016

21 VIEWR LA-UR-17-20093
! 5=cyan
! 6=brown
! 7=purple
! 8=orange
! ithick controls thickness of curve
! 0 = invisible (for shaded areas)
! (default=1)
! ishade shade pattern
! 0 = none
! 1 to 10 = 10\% to 100\% gray
! 11 to 20 = 45 deg right hatching
! 21 to 30 = 45 deg left hatching
! 31 to 40 = 45 deg cross hatching
! 41 to 50 = shades of green
! 51 to 60 = shades of red
! 61 to 70 = shades of brown
! 71 to 80 = shades of blue
! default=0
!
! card 10 ---ileg.ne.0 only---
! aleg title for curve tag or legend block
! 60 characters allowed.
! default=blank
!
! card 10a ---ileg.eq.2 only---
! xtag x position of tag title
! ytag y position of tag title
! xpoint x coordinate of vector point
! (.le.0 to omit vector)
!
! -----card 11 for 3d plots only-----
!
! card 11
! xv,yv,zv abs. coords of view point
! defaults= 15.,-15.,15.
! x3,y3,z3 abs. sides of work box volume
! defaults=2.5,6.5,2.5
!
! set x3 negative to flip the order of the axis on
! that side of the box (secondary energy, cosine).
!
! card 12
NJOY2016 613

LA-UR-17-20093 21 VIEWR
! nform format code for input data
! 0 = free format input with
! optional x and y error bars
! 1 = free format input for a
! 3d family of curves z(x) vs y
!
! card 13 ---nform = 0 only--- 2-d data
! xdata independent value
! terminate with empty card (/)
! ydata dependent value
! yerr1 lower y error limit
! no y error bar if zero
! yerr2 upper y error limit
! if zero, equals yerr1
! xerr1 x left error limit
! no x error bar if zero
! xerr2 x right error limit
! if zero, equals xerr1
!
! card 14 ---nform = 1 only--- 3-d data
! y y value for curve
! repeat cards 13 and 13a for each curve
! terminate with empty card (/)
!
! card14a ---nform = 1 only---
! x x value
! z z value
! repeat card 13a for each point in curve
! terminate with empty card (/)
! disspla version requires same x grid
! for each value of y.
!
!--------------------------------------------------------------------
Card 1 in the data file format sets up the specifications for the graphics page.
The orientation can be either portrait or landscape. Characters can use a serif
style “roman,” implemented by the Postscript Times-Roman font, or sans-serif
“swiss,” implemented by the Postscript Helvetica font. The character size can
be specified in inches or as a fraction of the subplot size. The latter is handy
when subplots are shrunk down to just a fraction of the page. The default
614 NJOY2016

21 VIEWR LA-UR-17-20093
character size is 0.30 inches. The page color set here is the color of the overall
page. See below for the color inside the frame of a subplot. We have provided
a set of pale colors here for these backgrounds.
Card 2 starts a new plot, subplot, or curve on an existing plot. It also
provides the flag indicating the the plotting job is finished; namely, iplot=99/.
The value for nwhen its magnitude is greater than one is arbitrary, but we
often use 2, 3, etc., to indicate the second, third, etc., curves on a set of axes.
You could just use the value n=2 for every additional curve, and it would still
work. The window color ipcol refers to the color inside the axes frame for 2-D
plots and to the color used for the various slices of the function for 3-D plots.
The same set of light colors described for the page background is used here, and
the pages look good if different colors are selected for the page color and the
window color. The parameters factx and facty are handy for changing the x or
y units for a plot or for scaling curves on a multi-curve graph to be closer to each
other. The last few parameters on this card are only needed when several small
subplots are put onto one page. They define the position, size, and rotation of
the subplot. The covariance plots from COVR make use of this feature.
The next few lines of input are only given for new plots or subplots. There
can be zero, one, or two lines of titles provided above the graph. The size of
the plot readjusts to use the space not used by titles. The titles (and all the
other labels in VIEWR) can use some special characters to trigger effects like
subscript, superscript, symbol characters, size changes, or font changes. The
rules for this are defined in the source listing as follows:
!
! Character specifications are similar to DISSPLA, except that
! the default case is lower instead of upper. This allows
! mixed-case strings to be used in Postscript mode. The
! following shift characters are used:
! < = upper-case standard
! > = lower-case or mixed-case standard
! [ = upper-case greek
! ] = lower-case or mixed-case greek
! # = instructions
! Give one of the shift characters twice to get it instead of
! its action. The following instructions are supported:
! Ev = elevate by v as a fraction of the height
! if v is missing or D is given, use .5
! Lv = lower by v as a fraction of the height
NJOY2016 615
LA-UR-17-20093 21 VIEWR
! if v is missing or D is given, use .5
! Hv = change height by v as a fraction of the height
! if v is missing or D is given, use .5
! Fi = change to font number i
! Mi = change mode number, where mode 0 is the lower 128
! postscript characters and mode 1 is the upper 128
! X = reset E, L, or H. Font and Mode must be
! reset explicitly.
! c is a real number, i is an integer.
!
Normal characters are just entered using mixed upper and lower case as desired.
If desired, upper case can be forced using the trigger character. For example,
<p>u-239 from <endf/b-vi>
will have the indicated characters displayed in upper case. Similarly, Greek
letters can be entered using mixed upper and lower case, or they can be given
in all lower case and then forced to upper case with the trigger character:
Display ]a> and ]b>, then ]G> and ]D>
Display ]a< and ]b>, then [g> and [d>
Subscripts and superscripts use the “instruction” trigger character. For example,
ENDF/B-VI #EH<3#HXEX<h>e
displays the isotope name for 3He correctly with a subscript one-half the size
of the main characters. Subscripts lowered by one-quarter of the character size
and with height equal to three-quarters of the character size could be obtained
using
X#L.25H.75<min#HXLX<
616 NJOY2016

21 VIEWR LA-UR-17-20093
For the mapping of the symbols and the other special characters available by
shifting to the upper 128 characters in each font, check the Postscript Red
Book[93].
Returning to the input data, Card 4 sets up the axes for the plot using itype
and jtype. Several choices are allowed for adding grid lines to the axes. There
are two ways available to label the curves in multi-curve graphs, namely, legend
blocks, and curve tags. The default location for the legend block is the upper
left corner of the graph area, but it can be positioned wherever desired using
xtag and ytag. These values use coordinate units. The legend block contains
a line for each curve giving the plotting symbol, curve style or color, and an
identifying string entered below (see aleg). Curve tags are defined below.
Cards 5, 5a, 6, 6a, 7, and 7a define the axis limits, step sizes, and labels. The
limits and step sizes are defined automatically based on the data, but they can
also be defined manually to better control the display. This is often necessary
for multi-curve plots, because the axes are chosen based on the extent of the
first curve, which may not be suitable for all the curves in the graph. The graph
scales are sometimes scaled with a power of ten, and these powers are always
chosen to be divisible by three. Thus, you might have a scale labeled barns with
a factor of 10−3indicated; the numbers on the scale would then by milli-barns.
Note that when no label is given, the numbering for the axis is also omitted.
Card 8 is a dummy card that is only used to make the VIEWR input more
compatible with the PLOTR input. As indicated, it should always contain 0/.
Cards 9, 10, and 10a are used for curves on 2-D plots. You an use the
icon connection parameter to choose simple curves, sets of symbols, or symbols
connected by curves. A variety of symbols and curve types are provided, and
curves can be rendered in color if desired. The colors provided are all darker
than the light backgrounds provided. We do not allow for the light curves on
dark backgrounds that some people like. Another way to distinguish between
different curves is with the weight of the curve (see ithick). If the curve being
plotted is closed, it can be filled with hatching patterns, shades of gray, or colors
(shades of green, red, brown, or blue). The shades of gray could be used to show
a variance band around a curve. The colors are used for the contour plots of
covariances produced by COVR, and many other uses are possible. See Fig. 67
for examples of fills.
Card 10 gives aleg, the identifying string for the curve that is used if legend
blocks or curve tags were requested. The location for the curve tag and the
point where the arrow point touches the curve are defined on Card 10a. The
NJOY2016 617

LA-UR-17-20093 21 VIEWR
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
x
0.0
0.2
0.4
0.6
0.8
1.0
y
Figure 67: Examples of regions filled with gray, cross hatching and outlined, pink, and dark
blue.
arrow from the tag to the curve can be omitted, if desired.
Card 11 is only given for 3-D plots. It defines the imaginary work box that
contains the perspective view of the 3-D function, and it defines the view point
outside of the box where your eye goes. The perspective distortion will be
greater for close viewpoints and less for distant ones. The 3-D coding is not
very sophisticated, and it is best to keep the view point in the octant defined
by the defaults x,y,z=(15,-15,15). That is, you are looking in along the x and z
axes and the y axis is running away from you. You have the option of flipping
the sense of the x axis, which is along the front of the work box as seen from
the view point. This makes it possible to see features on either side of the slices
of the function that are given for different discrete values of y. Fig. 68 may help
to clarify the coordinate system used.
At this point, all the specifications for the 2-D or 3-D graph have been en-
tered, and it is only necessary to enter the actual values to be plotted. The
format to be used is controlled by nform, which currently has only two options.
Option nform=0 is used for 2-D curves with optional error bars. In order to
make the input simple for simple cases, the sequence of the possible x and y
values is arranged to be defaulted at various points. For a simple curve, you can
618 NJOY2016
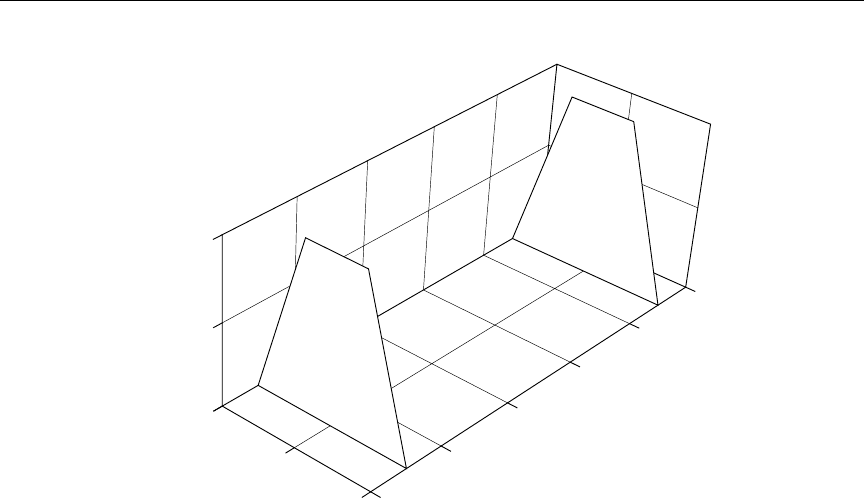
21 VIEWR LA-UR-17-20093
Sample of 3-D axes
with default perspective
0
.
5
1
.
0
Z
A
x
i
s
0
.
0
0
.
5
1
.
0
X
A
x
i
s
0
.
0
0
.
2
0
.
4
0
.
6
0
.
8
1
.
0
Y
A
x
i
s
Figure 68: The 3-D coordinate system using the default work box and view point.
just give x and y, and then terminate the line with /. For the most common case
of error bars (symmetric y errors), just give x, y, delta-y, and the terminating
slash. The next step allows for asymmetric y error bars, then symmetric x error
bars, and finally asymmetric x error bars. Terminate the list with an empty line
(only /).
For 3-D views, the function is represented by giving a set of curves z(x) for
given values of y. The yvalues are given in increasing order, and each yvalue
is followed by lines of xand zvalues terminated by /. The set of lines for each
yis terminated by an empty card (only /). The ylist is also terminated by an
empty line, so there are two lines with only / given at the end of the nform=1
structure.
After the input data are given, the code loops back to search for another
iplot value. If iplot=99, the job is finished.
21.4 Coding Details
The main entry for VIEWR is subroutine viewr, which is exported by module
viewm. It starts up by setting the default values for paper size, margins, font
size, line width, work box, and viewpoint. Sizes are currently given in inches
(with apologies to the rest of the world). The first part of the input is read in
NJOY2016 619

LA-UR-17-20093 21 VIEWR
to determine the page parameters, and then subroutine gplot from the graph
module is called to initialize the plotting system.
The next step is to start the main loop over various plots, subplots, and curves
in plots. The key to this is iplot, and this loop continues until iplot=99. For
other values of iplot, the code reads in the user’s input and stores the values in
global variables for the viewm module. When all of the input values have been
read for this particular plot, subplot, or curve, subroutine viewr call either
set2d or set3d to do the work, and then loops back for the next case. When
it sees iplot=99, it closes the current window (endw), closes the current page
(endp), shuts down the plotting system (gdone), and exits from the VIEWR
module.
Subroutine set2d is used to prepare a 2-D plot or subplot, or to add an-
other curve to an existing set of 2-D axes. The information on the particular
curve being plotted is passed in as parameters to the subroutine, and the other
parameters that describe the plot or curve are available in the global variables
(see the beginning of module viewm). For new plots, the code calls initp from
the graph module to initialize a new page. Then for either a new plot or a new
subplot on this page, it calls init2 to initialize the graph area for a 2-D plot.
The next step takes place if automatic scaling has been requested by leav-
ing the axis limits blank. The code reads through the input data to find the
minimum and maximum values on the axis or axes being scaled. It then choose
the axis limits and step size to have nice even values using either ascalv for
linear axes or direct determination of the axis decades for log scales. With the
axes determined, it calls axis2 to construct and label the axes and to draw the
line and tic marks on the opposite sides to complete the 2-D graph area. If a
right-side axis has been requested, it adds it also. The legend block, if requested,
is located inside the graph frame using either the default location (upper left
corner) or the user’s xtag,ytag choice.
Next, subroutine frame2 is called, which establishes a clipping path just
outside of the frame formed by the axes. This allows for a hint to suggest that a
curve passes outside the specified graph area. Subroutine erbar is called to draw
on the error bars, if any. Subroutine curv2 is called to draw on the curves or the
plotting symbols. Subroutine legndb is called if a legend block was requested,
or tagit is called if curve tags were desired instead. Finally, endfr is called to
close out this graph frame, and subroutine set2d returns to the VIEWR main
routine.
Subroutine erbar draws error bars, either x or y, and either symmetric or
620 NJOY2016

21 VIEWR LA-UR-17-20093
asymmetric. Note that they are drawn before the plotting symbol is drawn.
This makes the opaque plotting symbol appear on top of the error bars for
the expected appearance. The cap size for the error bars is set in this routine
as capd=0.02 in inches. Conversion between the user’s data coordinates and
absolute plot units is done using xscale and yscale. The error bars and caps
are drawn using the routine vect3, which is actually drawing in two dimensions
because the z coordinate is set to zero.
Subroutine legndb constructs the legend block or adds an additional line to
an existing block. Subroutine tagit places a tag string at the desired location
xtag,ytag and optionally draws an arrow from the tag string to meet the curve
at xpoint. The routine interpolates for the y value corresponding to xpoint to
define the position for the point of the arrow.
Subroutine set3d is used to construct a 3-D perspective plot. It first calls
initp to initialize the graphics page, and then it calls init3 to set up the 3-D
perspective projection. Next, it reads through the input data to find the x, y,
and z limits, and to adjust for nice scales. When this is complete, set3d can
start to construct the scales and the opposite axes to complete the entire 3-D
plotting frame. Grids can be added to the bottom and to the back two sides, if
desired.
With the frame in place, subroutine curv3 is called to produce the z(x) curve
for each yvalue. The routine starts at the largest yvalue and works forward.
Each z(x) curve is converted to an opaque panel by completing the polygon to
the bottom and side of the graph area and filling with the window color. In this
way, the curve for each lower value of ysimply paints over the higher values,
and no sophisticed hidden-line removal procedure is required.
Subroutine ascalv is used to adjust the minimum and maximum values for
an axis to nice even values and to choose an appropriate step size. The routine
is set up to prefer multiples of 103for axis limits to suggest our normal micro,
milli, kilo, and mega preferences for numbers, and it tries to use integer type
labels rather than floating-point ones when possible.
21.5 The Graphics Module
The basic graphics calls used by VIEWR are provided by module graph. This
section will describe how they work. There are two logical levels included in
the module. The higher level works with windows, frames, user coordinates,
and the like. Most of these routines are made public by the module. The lower
level works to write the Postscript text itself, and most of these routines are not
NJOY2016 621

LA-UR-17-20093 21 VIEWR
public.
Module graph uses a large number of global variables and arrays. They
are not public, and they are accessed from the outside through various public
subroutines. Note especially the values that describe the fonts, including the
three font names (“Times-Roman,” “Helvetica,” and “Symbol”). There are
tables of character widths for each of the fonts (cs1,cw2,etc.). Also note the
tables that define the light colors for backgrounds and the darker colors for
foregrounds. They are given using RGB values, and they could be customized
to improve the artistic appearance of things.
The graphing logic uses a hierarchy of objects to represent a graph. The
highest level is the graphing “page,” which is initialized by subroutine initp and
ended by subroutine endp. A page is defined by its size, orientation, font style,
font height normal line weight, and page background color. The user’s choices
come in through the parameters to the subroutine, and they are used to set
the appropriate internal global variables. The low-level routine newp is called to
increment the Postscript page number and to write the corresponding Postscript
“Page” comment. A page border is drawn using the low-level command poly2
and the page area is filled with the defined page color.
The next level in the hierarchy is the “window,” which defines the area
enclosing the graph, its titles, and its axis labels. It can have its own border
(see ibord) and it sets up its own clipping path to protect other windows on
the page. A window is initialized using window and ended using endw. Note
that endw calls the low-level routine gend to end the clipping path and to write
a “gend” comment on the Postscript file. The titles for the plot or subplot are
drawn by window. There is also a subroutine called transw associated with a
window. It transforms between the units inside the window and the actual units
on the page, thus allowing for the possibility that the window has been rotated.
The third level of the hierarchy is related to the actual 2-D or 3-D plots.
Subroutine init2 is used to initialize a 2-D plot by choosing an origen and
axis lengths to nicely position the graph in the window. It sets the coordinate
transformation to turn off 3-D perspective. Finally, it draws the graph frame
(see wframe=0.005) and fills it with the specified window color. The 2-D plots
also use a “frame.” Subroutine frame2 initializes a frame by setting a clipping
path just outside the frame boundary. This margin is controlled by grace. A
frame is ended by calling endfr.
A 3-D plot is initialized by calling init3. It sets the color of the 3-D slices to
the window color, sets up the axis parameters, and sets up the 3-D perspective
622 NJOY2016

21 VIEWR LA-UR-17-20093
transformation. It then adjusts the scale and position for the 3-D view to center
the projection in the window. The key to transforming coordinates is subroutine
trans3. It converts x,y,z coordinates in 3-space into u,v coordinates in the
corresponding view plane. Note that trans3 also gets called for lots of 2-D
work, but the parameters that control the transformation are set to appropriate
2-D values by init2 in those cases.
To draw a 2-D vector, vect2 just calls vect3 with the z coordinate set to zero.
The subroutine vect3 uses trans3 to go from x1,y1,z1 to window coordinates
wu1,wv1. Then, transw is used to go from wu1,wv1 to real page coordinates
u1,v1, thereby accounting for any possible rotation of the window on the page.
The point u1,v1 is then passed to the low-level Postscript routine moveh, which
moves the current position to u1,v1. The same process is used for the other
end of the vector, and the low-level routine drawh is used to draw the line with
width w. If this is an arrow (see ivec), the head can be constructed using
suitable geometry.
Similarly, to draw a 2-D axis, axis2 just calls axis3 with the z-axis elements
of the unit vectors set to zero. Subroutine axis3 is a general routine to draw
an axis projected into 3-D perspective. The line of the axis is defined by its
length asize, its x,y,z origen, a unit vector along the length of the axis, and a
unit vector defining the vertical direction for the characters. The subdivision
of linear axis is defined by the minimum value, maximum value, and step size
(amin,amax, and astp), but log axes need only the minimum and maximum
values. Other options control the numbering, the label, and the tic marks. The
axis3 routine also sets up the constants that control the scaling subroutines
xscale,yscale, and zscale, which are used to convert user coordinates into
axis coordinates for plotting curves in either 2-D or 3-D displays. The reverse
transformation can be done in 2-D using xinvrs and yinvrs.
Subroutine grid2 is used to generate a grid for a 2-D case using the 3-D call
with z-axis parameters set to zero. Subroutine grid3 is used to draw a grid in
a plane projected by perspective. The grid can be drawn perpendicular to the
x, the y, or the z axis. It can be located at the minimum or the maximum. This
allows it to be used to subdivide all the back 3 surfaces of the 3-D perspective
box. Both log and linear subdivision is possible. The log grids subdivide each
decade at the 2, 3, 4, 5, etc. values.
Subroutine curv2 is used to draw a curve or plot symbols on a 2-D plot.
It uses the standard trans3 and transw transformations to come up with the
low-level u,v coordinates that go to the Postscript routines. It can also be used
NJOY2016 623

LA-UR-17-20093 21 VIEWR
to fill a curve with color or hatching (see fillh and hatch). Subroutine curv3
draws a 3-D curve by making the perspective transformation, completing the
polygon to the working box bottom and back, and filling the polygon with the
window color to make it opaque.
Subroutine poly2 draws a filled 2-D polygon, with or without an outline.
Similarly, poly3 draws a 3-D polygon. Subroutine hatch will fill the current
path with hatching or cross hatching. The options are left-leaning lines at 45
degrees, right-leaning lines at 45 degrees, or both superimposed.
Subroutine text2 draws a 2-D text string using the 3-D call in the normal
pattern of this module. Subroutine text3 draws a text string projected by
perspective into a 3-D space. The string starts at xo,yo,zo, and its orienta-
tion is controlled by one unit vector along the string, and a second unit vector
that defines the vertical direction for the characters. This routine is compli-
cated because it watches for a variety of trigger characters that enable things
like subscript, superscript, size changes, font changes, and special characters.
Subroutine txtlen is almost identical, but instead of drawing the string, it cal-
culates the space that it will take to help with functions like centering labels. It
uses a private routine ssum to add up character widths. These routines also use
rget to decode real numbers out of a string.
The rest of the routines in module graph are the Postscript-dependent plot-
ting package. The package begins with the public routine gplot, which sets
up for “US letter” (8.5 inches by 11.0 inches) size, defines the page orientation
(portrait or landscape), opens the Postscript output unit (nps), and writes the
Postscript bounding box and page orientation comments. This routine pairs with
gdone, which writes some closing Postscript comments and closes the Postscript
output unit.
Subroutine gset sets up a clipping path, and subroutine gend closes a clip-
ping path.
Subroutine newp starts a new Postscript page, including writing the “Page”
comment that is needed by programs such as ghostview to make it easy to scan
through Postscript files containing many plots (such as ACER output). It is
paired with endp to write the Postscript command “showpage” at the end of
each page.
Subroutines moveh and drawh are routines for drawing lines on the page.
This includes making various kinds of dashed lines, and doing the coordinate
conversion between portrait and landscape orientations. Subroutine fillh is
used to fill the current path with a color. The colors available for filling were
624 NJOY2016

21 VIEWR LA-UR-17-20093
defined in some global arrays as described above.
Subroutine cclip is used to set up a clipping path on the current path, and
nclip is used to terminate it. Subroutine ncurve is used to cancel the current
curve path in order to make a shaded region that doesn’t have a border.
Subroutine dsym is used to generate the symbols used for plotting by drawing
them with low-level Postscript commands. The symbols are made opaque by
filling them with the window color, or filled symbols can be made by filling
polygons with the foreground color. A small routine called circle is used here.
Subroutine dchr is used to draw a Postscript character in perspective by using
basic Postscript transformations. This routine also sets the desired font and
uses the octal character notation to get special characters. Subroutine charw is
also needed for handling character strings; it returns the width for characters
in the built-in fonts using the information from the global arrays of character
widths.
The module ends with subroutine stripv, which is used to strip leading
and trailing blanks from character strings and to return the actual number of
characters found.
21.6 VIEWR Messages
message from viewr***too much 3d data...
The amount of 3-D data allowed is controlled by maxaa=200 000 and the
array aa(maxaa).
message from set3d***curve truncated.
The 3-D plots are limited to kmax=1999 elements. See x(2000),y(2000),
and z(2000).
NJOY2016 625

LA-UR-17-20093 21 VIEWR
626 NJOY2016

22 MIXR LA-UR-17-20093
22 MIXR
The MIXR module will construct a new PENDF tape with a specified set of
reactions that are linear combinations of the cross sections on the input tapes.
MIXR can also be used for ENDF tapes, but the input interpolation laws are
ignored. The output file contains ENDF File 1 and File 3 sections only, and
linear-linear interpolation is assumed.
MIXR can be used for several purposes. When combined with PLOTR,
it can be used to construct mixed cross sections for plotting with VIEWR.
One example would be to combine the isotopic cross sections given in modern
evaluations into elemental cross sections for comparison with older evaluated
elemental data such as found, for example, in ENDF/B-V. Such an example is
provided in the sample deck below. Another would be to compute the difference
between two versions of a particular reaction; plots that simultaneously show
one version of a function and the difference between that version and another are
sometimes very revealing. In both cases, the mixed cross section is computed
on the union grid of its components, and all details are preserved.
Another use for MIXR would be to prepare a new ENDF material to repre-
sent a particular “enriched uranium,” having a particular amount of 235U mixed
with 238U. This file could then be run through the GROUPR flux calculator
to generate an accurate pointwise flux for enriched uranium mixed with water,
or for pins of enriched uranium in a typical reactor lattice. This computed
flux could then be used as the weighting flux for computing the self-shielded
cross sections of both 235U and 238U in two subsequent GROUPR runs. This
approach handles the interference between resonances in 235U and 238U accu-
rately, including proper treatment of all wide and intermediate resonance effects.
This chapter describes the MIXR module in NJOY2016.0.
22.1 User Input
The following input instructions were copied from the comment cards at the
beginning of the MIXR source. It is always a good idea to check the cards in
the current version of the program for possible changes.
NJOY2016 627

LA-UR-17-20093 22 MIXR
! user input --
!
! card 1 -- units
! nout output unit for mixed cross sections
! nin1 first input unit (endf or pendf)
! nin2 second input unit
! ... continue for nnin<=nninmx (=10) input units
!
! card 2 -- reaction list
! mtn list of nmt<=nmtmx (=20) mt numbers for
! the output reactions
!
! card 3 -- material list
! matn, list of nmat<=nmatmx (=nninmx=10) pairs (matn,wtn)
! wtn, of material numbers and associated weighting factors
!
! card 4 -- temperature
! temp temperature (use zero except for pendf tapes)
!
! card 5 -- output material
! matd material number
! za za value
! awr awr value
!
! card 6 -- file 1 comment card
! des description (66 char max)
!
!-------------------------------------------------------------------
Card 1. This card gives the unit numbers for the output that will contain the
mixed cross sections and the input files that contain the materials to be mixed
together. Note that there is a limit of nninmx, currently 10, input files.
Card 2. The code currently allows up to nmtmx, currently 20, mixed reactions
to be generated. This card contains a list of the MT numbers for these reactions.
The number of reactions is counted automatically.
628 NJOY2016

22 MIXR LA-UR-17-20093
Card 3. This card (it may continue onto several lines) contains the MAT
numbers and weights for the materials to be mixed. The first pair matn,wtn
refers to the data on input file nin1; the next pair is for nin2, etc.
Card 4. The same temperature is used for all of the materials, and its value
is given on this card in Kelvin. The appropriate value for ENDF tapes is zero.
The temperatures used for PENDF cases must be in the set included on the
PENDF tape.
Card 5. This card gives some values that are needed to construct the ENDF or
PENDF file for the output material. matd is the conventional material number.
za is 1000 ∗Z+A, where Zis the charge number and Ais the atomic mass
number for the mixture. Finally, awr is the mass ratio to the neutron for the
mixture.
Card 6. This card contains one line of text to be used for the Hollerith de-
scriptive information in MF=1/MT=451 on the new ENDF tape for the fixture.
The final tape on NOUT will contain the section MF=1/MT=451 and sections
MF=3/MT=MTnonly.
The following sample input deck combines the four isotopes of iron to gener-
ate plots for the total cross section (MT=1), the energy-balance heating cross
section (MT=301), and the radiation damage cross section (MT=444). See the
PLOTR section of this report for more information on the part of the input deck
that produces the actual graphs.
cfs get tape21:/pendf/5/fe/natr2
cfs get tape22:/pendf/6/fe/54
cfs get tape23:/pendf/6/fe/56
cfs get tape24:/pendf/6/fe/57
cfs get tape25:/pendf/6/fe/58
cat>input <<EOF
mixr
20 -22 -23 -24 -25/
1 301 444/
2625 .0590/
2631 .9172/
2634 .0210/
2637 .0028/
NJOY2016 629

LA-UR-17-20093 22 MIXR
300/
2600 26000 56./
’Fe-nat for ENDF/B-VI from MIXR’/
plotr
31/
/
1/
’ENDF/B-VI IRON’/
’TOTAL’/
1 0 2 1 13e6 9./
0 20e6 2e6/
/
0 10 2/
/
6 20 2600 3 1 300/
/
’ENDF/B-VI’/
2/
5 -21 1326 3 1 300/
0 0 4/
’ENDF/B-V’/
1/
’ENDF/B-VI IRON’/
’TOTAL’/
4021/
1e2 1e5/
/
/
/
6 20 2600 3 1 300/
/
’ENDF/B-VI’/
2/
5 -21 1326 3 1 300/
0 0 4/
’ENDF/B-V’/
1/
’ENDF/B-VI IRON’/
’HEATING CHECK’/
1 0 2 1 1e6 2.7e6/
0 20e6 2e6/
/
630 NJOY2016

22 MIXR LA-UR-17-20093
0 3e6 .5e6/
*Heating (eV-barns)’/
6 20 2600 3 301 300/
/
’ENDF/B-VI’/
3/
5 -21 1326 3 301 300/
0 0 4/
’ENDF/B-V’/
1/
’ENDF/B-VI IRON’/
’DAMAGE CHECK’/
1 0 2 1 13e6 7e4/
0 20e6 2e6/
/
0 35e4 5e4/
’Damage (eV-barns)’/
6 20 2600 3 444 300/
/
’ENDF/B-VI’/
3/
5 -21 1326 3 444 300/
0 0 4/
’ENDF/B-V’/
99/
viewr
31 32/
stop
EOF
xnjoy<input
cfs store plot:/pendf/6/fe/natplot
The first few lines retrieve ENDF/B-V version of natFe, and the four iron isotopes
for ENDF/B-VI. A c-shell “here file” is then created with the input for MIXR,
PLOTR, and VIEWR. The lines after the EOF line take care of executing NJOY
and saving the plot file for future use.
Returning to the actual NJOY input cards, note that the MIXR output will
be on tape20 in ASCII mode, and the four isotopic input files (in binary mode)
will be on tape22 through tape25. The next input card lists the three reaction
types to be written onto the output file; it is followed by four cards giving the
NJOY2016 631

LA-UR-17-20093 22 MIXR
isotope MAT numbers and the atomic fractions that they are to have in the
mixture. These mix-specification cards are then followed by a card asking for a
temperature of 300K.
The last two cards in the MIXR section specify the ENDF parameters for the
mixed material that will be written on tape20. The MAT number is to be 2600
(the standard ENDF-6 value for natural iron), the ZA value is to be 26000, and
the AWR value is to be 56.0000 (a rather crude choice). The text line shown
will appear in MF=1/MT=451 on the output tape.
At this point, the MIXR module will run and produce its output file. The rest
of the input deck reads in this output file and makes a graphical comparison of
the mixed elemental cross section with the corresponding elemental values from
ENDF/B-V.
22.2 Coding Details
Subroutine mixr is exported by module mixm. The heart of MIXR is subroutine
gety. It is similar to gety1 in the endf module, except that it works with
several TAB1 records in parallel. The routine is initialized for up to nmtmx
input TAB1 records on up to nninmx input tapes by calling it with x=0 for each
tape. It returns the value of xnext for each tabulation. The calling program
can compare these xnext values to determine the lowest energy point for the
mixed reaction (the threshold).
On subsequent calls with x>0, MIXR returns the value of ycorresponding
to xfor the specified tabulation, and it also computes xnext for this tabulation.
The calling program can loop through all the input tapes, compute the mixed
value of yas a linear combination of the separate gety results, and compute
the next energy grid point as the lowest of the values of xnext returned by the
separate gety calls. In this way, the mixed results are obtained on a unionized
grid, and no features are lost.
To do its job, gety has to keep tables of the current location and related
parameters on each of the input tapes. These tables will be found in the sub-
routine, all with dimension nninmx.
22.3 Error Messages
error in mixr***mat and temp not found
There is an inconsistency between the requested matn and temp values and
the materials found on the input files nin1,nin2, ....
632 NJOY2016

22 MIXR LA-UR-17-20093
message from mixr***mt=xxx not present for mat=xxxx
This message is just information. If the user asked for construction of, for
example, an (n,2n) reaction for an element, and if one of the isotopes did
not have an (n,2n) reaction, this message would be issued.
error in gety***not properly initialized
The subroutine gety has to be called with x=0 for each material/section
combination to be introduced into the mixed reaction before it is called
with x>0.
NJOY2016 633

LA-UR-17-20093 22 MIXR
634 NJOY2016

23 PURR LA-UR-17-20093
23 PURR
The unresolved self-shielding data generated by UNRESR are suitable for use
in multigroup methods after processing by GROUPR, but the so-called Bon-
darenko method[39] is not very useful for continuous-energy Monte Carlo codes
like MCNP[18]. As pointed out by Levitt[94], the natural approach for treating
unresolved-resonance self-shielding for Monte Carlo codes is the “Probability Ta-
ble” method. The method requires tables of the probability that the total cross
section will be less than some value σtfor a number of incident energies. Then,
when the Monte Carlo code needs the cross section at E, it selects a random
number between 0 and 1 and looks up the corresponding σtin the appropriate
probability table. The corresponding capture and fission cross sections are ob-
tained from conditional probability tables that give σγand σfversus σt. This
approach allows geometry and mix effects on self-shielding to arise naturally
during the Monte Carlo calculation, and it supplies reasonable variances for the
tallies. The probability table method has been used successfully in a number of
applications, notably the VIM continuous-energy Monte Carlo code[95], which
was developed to solve fast-reactor problems where unresolved effects become
very important.
The PURR module produces probability tables that can be used in versions
of MCNP from 4B on to treat unresolved-resonance self-shielding.
In recent versions of NJOY, the Bondarenko self-shielded cross sections from
PURR will override any previous self-shielded data on the PENDF file coming
from UNRESR.
This chapter describes the PURR module in NJOY2016.0.
23.1 Sampling from Ladders
In the unresolved range, we don’t know the real center energy of any of the
resonances, and we don’t know the partial widths that determine the shape and
strength of any particular resonance. However, the ENDF evaluation provides
us with mean values for the resonance spacings, the probability distribution for
the spacings (the Wigner distribution), the mean values for the resonance partial
widths, and the distributions for the partial widths (chi-square distributions for
various numbers of degrees of freedom). These quantities are given for several
different spin sequences, which are statistically independent, and for a number
of energies spaced through the unresolved energy range. A “narrow-resonance
assumption” is always made in the unresolved range; that is, the energy loss in
NJOY2016 635

LA-UR-17-20093 23 PURR
scattering in the system is assumed to be large with respect to the width of any of
the resonances. Thus, neutrons arrive at random energies that are not correlated
with the resonance structure. The effective cross sections at one of the energies
in the ENDF unresolved grid then depend on a number of resonances in the
vicinity of that energy, all of which are assumed to have resonance parameters
characteristic of that grid energy value.
This allows us to define a plausible set of cross sections in the vicinity of one
of the grid energies. We first define an energy range that will hold a specified
number of resonances, and we randomly choose a set of sampling energies in this
range, avoiding the ends of the range to reduce truncation effects. For each spin
sequence, we start by choosing a center for the starting resonance from a uniform
distribution (this provides a random offset between the various spin sequences
in the ladder). We then choose a set of partial widths for this resonance drawn
from the appropriate distributions. A second resonance is then chosen above
the first using the distribution for resonance spacings, and partial widths are
randomly chosen for it. Then a third resonance is chosen, and so on, until
the energy range defined for the ladder has been filled. We can now compute
the cross section contributions from this spin sequence at each of the sampling
energies. We then step to the next spin sequence and repeat the process. After
looping through all the spin sequences, the accumulated cross sections are one
possible set of plausible cross sections that obey the defined statistics for the
unresolved range.
We can now go through this set of sampled cross sections, determine how
many values of the total cross section hit each bin, and compute the conditional
average for the elastic, fission, and capture cross sections for samples where the
total ends up in each bin. This is the contribution to the probability table from
the particular resonance ladder. However, using only one ladder could result
in average cross sections that differ dramatically from the expected infinitely
dilute averages computed directly from the resonance parameters. Therefore, the
whole sampling process is repeated again for a user-selected number of different
ladders. When enough ladders have been processed, the average cross sections
will begin to converge to the expected results. The following piece of a PURR
output listing shows 16 ladders being processed for 235U from ENDF/B-VII.0:
636 NJOY2016

23 PURR LA-UR-17-20093
e= 2.2500E+03 spot= 1.1700E+01 dbar= 1.6137E-01 sigx= 0.0000E+00
total elastic fission capture
1 1.9471E+01 1.2074E+01 5.3460E+00 2.0507E+00
2 1.9617E+01 1.2041E+01 5.6196E+00 1.9566E+00
3 1.9559E+01 1.2075E+01 5.4597E+00 2.0245E+00
4 1.9458E+01 1.2000E+01 5.5723E+00 1.8859E+00
...
14 1.9456E+01 1.2102E+01 5.3632E+00 1.9905E+00
15 1.9660E+01 1.2082E+01 5.4429E+00 2.1354E+00
16 1.9363E+01 1.2019E+01 5.3736E+00 1.9710E+00
bkgd 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
infd 1.9778E+01 1.2105E+01 5.6364E+00 2.0363E+00
aver 1.9567E+01 1.2068E+01 5.5030E+00 1.9964E+00
pcsd 1.38 0.32 3.28 4.97
nres 3664
Some steps have been eliminated for brevity. The “aver” values computed from
the sampling have converged to be fairly close to the infinitely dilute values
“infd” computed from the resonance parameters. Here spot is the potential
scattering cross section, dbar is the average resonance spacing, and sigx is the
competitive cross section.
The probability table can be used to generate a picture of the probability
distribution for the total cross section as shown in Fig. 69. This example is
for 238U. It demonstrates how the fluctuations get smaller as energy increases,
which means that the self-shielding effect also gets smaller.
The statements that generate the VIEWR input for this kind of plot are
normally commented out.
During the sampling process, PURR also computes Bondarenko-style self-
shielded cross sections just like those produced by UNRESR. These values are
printed out so that they can be compared with the results from other methods.
For recent versions of NJOY, the Bondarenko self-shielded cross sections replace
any previous values on the PENDF file from UNRESR. The Bondarenko cross
NJOY2016 637
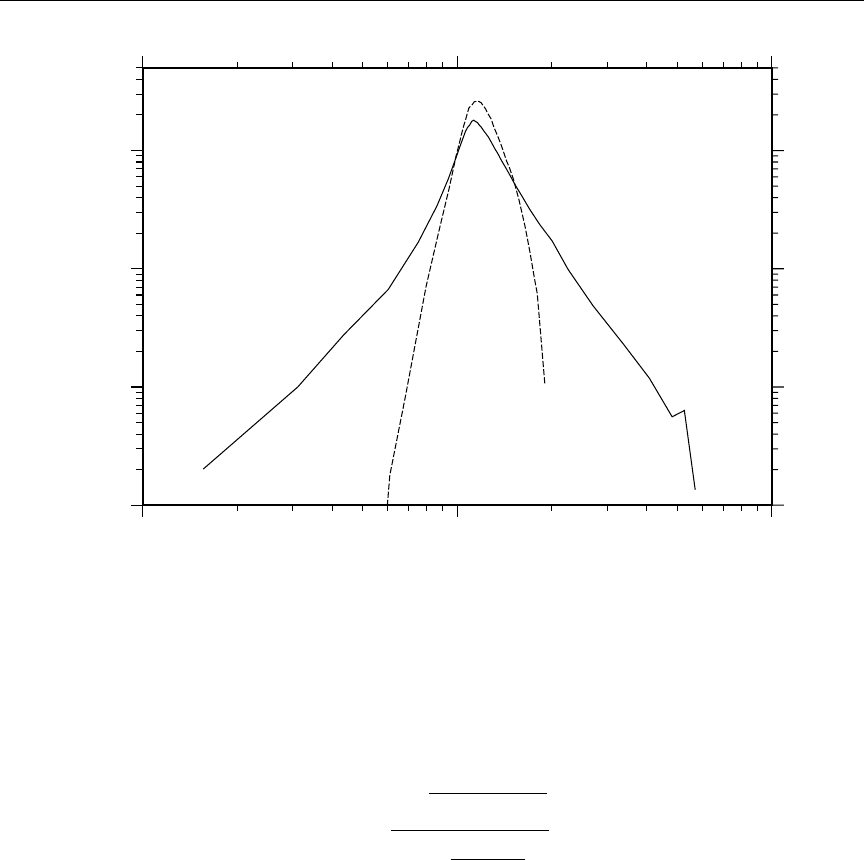
LA-UR-17-20093 23 PURR
100101102
total cross section (barns)
10-4
10-3
10-2
10-1
probability
Figure 69: The probability distribution for the total cross section at 20 keV (solid) and 140
keV (dashed) in the unresolved resonance range of 238U.
sections can also be computed directly from the probability table using
σx(E) = X
i
Pi(E)σxi(E)
σ0+σti(E)
X
i
Pi(E)
σ0+σti
,(506)
where xcan be tfor total, nfor elastic, ffor fission, or γfor capture. These
values are also printed out. They can be compared to the Bondarenko values
from direct sampling to help judge whether adequate convergence has been
obtained.
Fig. 70 shows Bondarenko-style self-shielded curves from PURR for the total
cross section for 238U in the unresolved region at three different values of the
dilution. This kind of plot is included in the standard graphs generated by
ACER. Most of the self shielding comes from the elastic channel in this case.
Fig. 71 shows how the total self-shielding factor for 238U varies with temperature
and dilution at an energy of 20 keV.
PURR uses the Single-Level Breit-Wigner (SLBW) approximation to cal-
638 NJOY2016
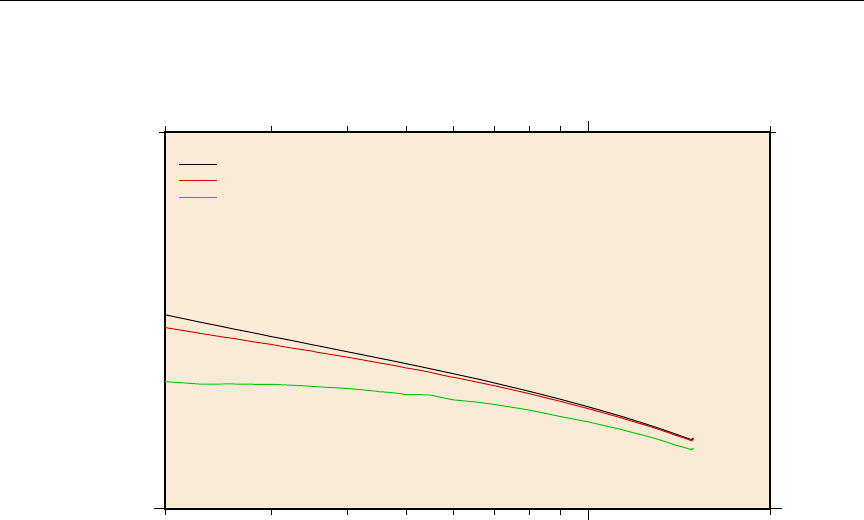
23 PURR LA-UR-17-20093
ENDF/B-VII U-238
UR total cross section
10-1
Energy (MeV)
101
Cross section (barns)
Inf. Dil.
100 b
1 b
Figure 70: Bondarenko-style self-shielded cross sections for the total cross section of 238U
in the unresolved resonance region at three different dilutions.
culate cross sections (as specified for ENDF unresolved data), and it uses the
ψ−χmethod to compute the Doppler broadened values. As is well known, this
method doesn’t always produce reasonable results for the small cross sections
between resonances due to the neglect of interference and multi-channel effects.
It is even possible to get negative elastic cross sections. When comparing Bon-
darenko results from PURR with those from UNRESR, several factors should
be considered. The PURR results may be more reliable at low σ0values than
UNRESR results because of the more complete treatment of resonance over-
lap effects, but the unrealistic cross sections in the dips between resonances
will eventually make even the PURR results suspect at low values. This effect
may be especially apparent for the current-weighted total cross section, which
is especially sensitive to the low cross sections between resonances.
The following piece of a PURR output listing shows the probability table for
the 235U example at an energy of 2.25 keV:
NJOY2016 639
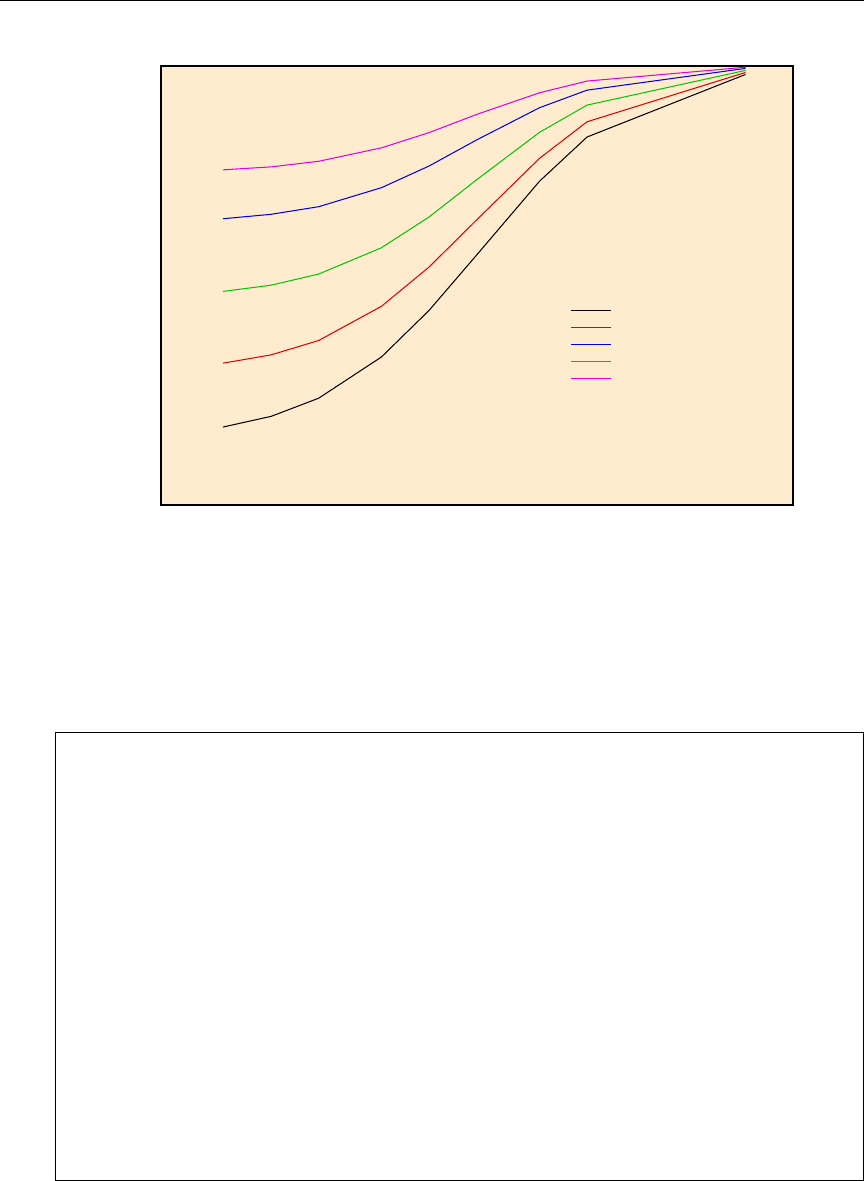
LA-UR-17-20093 23 PURR
100101102103
Sigma_zero
850
900
950
1000
*10-3
Self-shielding Factor
293.6K
400K
1000K
600K
1600K
Figure 71: Self-shielding factors for the total cross section of 238U at 20 keV showing the
variation with temperature and background cross section (dilution).
probability table
tmin 1.162E+01
tmax 1.352E+01 1.428E+01 1.509E+01 1.594E+01 1.683E+01 ...
2.339E+01 2.471E+01 2.611E+01 2.758E+01 2.913E+01 ...
prob 2.084E-02 3.597E-02 5.978E-02 8.244E-02 9.788E-02 ...
6.094E-02 5.269E-02 4.169E-02 3.112E-02 1.806E-02 ...
tot 2.936E+02 1.308E+01 1.393E+01 1.469E+01 1.552E+01 1.639E+01 ...
2.275E+01 2.403E+01 2.537E+01 2.680E+01 2.832E+01 ...
els 2.936E+02 1.114E+01 1.132E+01 1.144E+01 1.151E+01 1.161E+01 ...
1.220E+01 1.230E+01 1.262E+01 1.274E+01 1.287E+01 ...
fis 2.936E+02 1.486E+00 1.976E+00 2.444E+00 3.002E+00 3.582E+00 ...
7.838E+00 8.607E+00 9.206E+00 1.023E+01 1.104E+01 ...
cap 2.936E+02 4.574E-01 6.334E-01 8.095E-01 1.005E+00 1.202E+00 ...
2.711E+00 3.121E+00 3.543E+00 3.832E+00 4.417E+00 ...
The columns give the results for the 20 probability bins, but the rightmost 5
columns of numbers have been removed to make the lines fit this page. Thus,
640 NJOY2016

23 PURR LA-UR-17-20093
we are seeing bins 1-5 and 11-15. The rows for tmax give the upper bounds for
the total cross section bins, and prob gives the probability that the total cross
section lies in the bin. The tot,els,fis, and cap lines give the average cross
section seen when the total lies in that bin, all for a temperature of 293.6K.
The ENDF format contains an option called LSSF. When LSSF=1, the reso-
nance parameters are to be used to compute a fluctuation factor or self-shielding
factor that is to be applied to the cross section given in File 3 of the ENDF tape.
When LSSF=0, the parameters are used to compute cross sections that are to be
added to any possible background corrections that may be given in File 3. The
presence of this option doesn’t effect the table printed out by PURR, but when
LSSF=1, all the cross section values are divided by the corresponding infinitely
dilute cross sections before the output file is written. The bins then contain
dimensionless fluctuation factors instead of cross sections in barns.
23.2 Temperature Correlations
One important feature of PURR is its ability to handle temperature correlations.
If the Monte Carlo code is tracking a particle through a system, it periodically
checks for a total cross section to calculate the range to the next collision.
Consider a collision that takes place in a region at a particular temperature.
The Monte Carlo code samples from the probability table, getting a low cross
section. The mean free path then takes the particle into another region at a
different temperature that contains the same material. The sampled total cross
section there cannot be independent from the first; the resulting cross section
must also be low. PURR handles this kind of correlation. When a particular
ladder of resonances is sampled to obtain a probability table, all the different
temperatures are sampled simultaneously at the same energies to preserve the
correlations. In the Monte Carlo code, it is only necessary to use the same
random number to sample for the cross section in the two different regions to
preserve the proper correlations.
23.3 Self-Shielded Heating Values
PURR can also provide self-shielding effects for the heating if partial heating
cross sections are provided to it from HEATR. Of course, there are no resonance
parameters for heating, but the heating value does depend on the elastic, fission,
and capture cross sections in the unresolved range. It may also have a contribu-
tion from competitive reactions, such as MT=51 discrete inelastic scattering or
NJOY2016 641

LA-UR-17-20093 23 PURR
(n,p) absorption. The general idea is to extract the portion of the heating cor-
responding to elastic, fission, and heating, and to apply the fluctuations in the
probability table to them in order to get an estimate for the possible fluctuations
in the total heating. This requires that HEATR be run to generate the partial
heating values MT=302 (elastic), MT=318 (fission), and MT=402 (capture),
in addition to the normal MT=301 (total heating). With these present, each
partial heating value (eV-barns) can be divided by the corresponding infinitely-
dilute reaction cross section to get eV/reaction for that reaction channel. These
numbers can then be multiplied by the corresponding conditional cross section
in each bin of the probability table and added to the eV-barns from the compet-
itive reaction, if any, to get a value for heating in eV-barns in each bin. Finally,
these values can be divided by the average total for the bin to get a heating
value in eV/reaction that MCNP can use with sampled values of the total cross
section to produce contributions to heating tallies.
23.4 Random Numbers
The version of PURR in NJOY2012 and continuing in NJOY2016 uses the
Fortran-based random number generator rann. Earlier versions relied on ran-
dom number generators from the host systems, but this resulted in different
answers from every machine and made it hard to do Quality Assurance (QA)
on PURR results. The new approach allows comparisons to be made with stan-
dard “diff” utilities. Different machines should give the same results unless real
changes are made.
23.5 User Input
The following user input specification was copied from the comment cards at
the beginning of the PURR source. It is always a good idea to check these
comments in the current version in case there have been changes.
! card 1
! nendf unit for endf tape
! nin unit for input pendf tape
! nout unit for output pendf tape
! card 2
! matd material to be processed
! matd=0 terminates purr
! ntemp no. of temperatures (default=1)
642 NJOY2016
23 PURR LA-UR-17-20093
! nsigz no of sigma zeros (default=1)
! nbin no. of probability bins
! nladr no. of resonance ladders
! iprint print option (0=min, 1=max, def=1)
! nunx no. of energy points desired (def=0=all)
! card 3
! temp temperatures in Kelvin (including zero)
! card 4
! sigz sigma zero values (including infinity)
The following is an example of HEATR and PURR input for a full calculation
of the probability tables for a fissionable material. This would be just a small
part of a sequence for producing a PENDF file for 235U.
...
heatr
-21 -24 -25/
9228 5/
302 318 402 443 444/
purr
-21 -25 -26
9228 8 7 20 32/
293.6 400 600 800 1000 1200 1600 2000/
1e10 1e4 1e3 300 100 30 10/
0/
...
The HEATR run requests partial heating for elastic, fission, capture, kinematic
total, and damage. The total heating, MT=301, is always produced automati-
cally. The PURR run requests 20 bins for the probability table, and 32 ladders
are to be used.
23.6 Coding Details
Subroutine purr is the only exported routine of module purrm. It starts by
setting various parameters, like nermax,nsamp, and maxscr, by reading the first
card of the user input, and by calling uwtab2 to compute the constants needed
for calculating the table for the complex probability integral w. The calculation
of the wtable is the same as in UNRESR. The routine now opens the requested
NJOY2016 643

LA-UR-17-20093 23 PURR
units and makes the first call to the random number generator rann to initialize
the random number sequence.
Now purr can begin the loop over requested materials. Card 2 from the user
input is read to obtain matd. If matd=0, the PURR run is complete. A tape-end
record is written on the PENDF file being generated, and the code closes up.
For a nonzero matd, the input parameters are checked and echoed to the output
listing.
With the size of the problem determined, purr allocates storage for the
elements of the resonance ladder, such as the resonance energies er, the neutron
widths gnr, the fission widths gfr, the sampling arrays es,xs,fis,cap, and
els, and the probability table itself (tabl and tval). Next, it reads through
File 2 on the ENDF file to get the resonance parameters using rdf2un, and it
reads through File 3 on the ENDF tape to find the background cross sections
using rdf3un. It then goes to the PENDF file and searches for the total and
partial heating cross sections that it will need for computing the conditional
average for heating (see rdheat).
At this point, all the data needed to generate the probability tables are in
place. The code sets up a loop over the energies that define the unresolved cross
sections. Note that there is an option for debugging called nunx. If nonzero,
purr skips over some of the incident energies, which can give a faster calculation.
In practice, use nunx=0 to get the full unresolved data. For each energy, unresx
is called to construct the ladder parameters, infinite-dilution cross sections, and
potential scattering. Subroutine unrest is called to generate a set of ladders,
sample from the ladders, and accumulate the probability table. The resulting
probability table for this energy is stored on a scratch file, and the energy loop
continues.
The code now continues by writing the new Bondarenko cross sections to the
output PENDF file using MF=2/MT=152 and the new probability table to the
file using MF=2/MT=153. It writes a report on this material to the listing, and
continues the material loop.
Subroutine rdf2un is very similar to the routine in UNRESR that reads in
unresolved resonance parameter data. All the comments made in the RECONR
and UNRESR sections of this report about the complexities of constructing the
energy grid in the unresolved range apply here also. Subroutine rdf3un is also
very similar to the corresponding routine in UNRESR; it reads any background
cross sections that may exist in the unresolved range from the input ENDF file.
The resulting background cross sections are analyzed to see if any of the non-
644 NJOY2016

23 PURR LA-UR-17-20093
resonant cross sections overlap into the unresolved range. The inelastic overlap
iinel can be equal to 51 if only the first inelastic level overlaps the unresolved
range, or equal to 4 if more levels overlap. The absorption overlap iabso can
be equal to 103 if the (n,p) reaction overlaps, or some higher value for another
reaction, but only one absorption reaction is allowed to overlap the unresolved.
The routine types out “not allowed” messages for overlaps that it can’t handle.
Subroutine rdheat extracts the total heating value (MT=301), the elastic
heating (MT=302), the fission heating (MT=318), and the capture heating
(MT=402) from the input PENDF tape. The results are stored in the array
heat, indexed by reaction type, energy index, and temperature index. If no
total heating value is found on the PENDF tape, a message “no heating found
on pendf, ur heating set to zero” will be issued. If a total heating value is found,
but the partial heating values are missing, the message will read “no partial
heating xsecs found on pendf, ur heating will not selfshield.” For full capabili-
ties, the user should be sure to run HEATR with partial heating cross sections
requested before running PURR.
Subroutine unresx reads through the resonance data in MF=2/MT=151
on the ENDF tape and extracts the resonance parameters for each resonance
sequence that contributes to the unresolved cross sections. These parameters
are stored by their sequence index in a set of arrays that are passed to unrest.
For example, cgg contains the gamma widths for the sequences. At the same
time, unresx uses these parameters to compute the potential scattering cross
sections spot (a global variable), and the infinitely dilute total, elastic, fission,
and capture cross sections. This last is exactly equivalent to the calculation
done in RECONR.
Subroutine ladr2 is the routine that actually constructs a “ladder” of res-
onances for one particular spin sequence. In the unresolved range, it is not
known exactly where a resonance lies on the energy scale or what the resonance
widths are for a particular resonance. But the ENDF format does provide ex-
pectation values for quantities like the resonance spacing and capture width,
and the format specifies the statistical distributions that these quantities should
follow. Therefore, ladr2 can produce a plausible sequence of resonances by
starting with a first energy point chosen randomly (to provide an random offset
between the various spin sequences). Selected partial widths are then assigned
to this resonance using values drawn from the distributions for each type of
width (chi-square distributions). A second resonance energy is chosen above
the first one using a spacing drawn from the distribution of resonance spacings
NJOY2016 645

LA-UR-17-20093 23 PURR
(the Wigner distribution). The partial widths are chosen as before, and a third
resonance is constructed above the first two. This process continues until the
entire energy range specified for the ladder (elow to ehigh) has been filled. The
results are stored in the parameter arrays er for energies, gt for total widths,
gnr for neutron widths, gfr for fission widths, ggr for gamma widths, and gxr
for competitive widths, for a total of nr resonances in this sequence.
Subroutine unrest is the core of the calculation of the probability tables.
It starts by setting up the energy range for the calculation and printing out
the constant values for this energy, namely, the potential scattering cross sec-
tions spot, the average resonance spacing dbar, and the competing cross section
sigx. It then sets up the loop over the number of ladders requested by the user,
nladr. For each different ladder, it chooses a random set of energies in the
energy range of the ladder to be used to calculate cross sections (it avoids 300
resonances on each end to minimize truncation effects). It then starts up a loop
over resonance sequences and generates a ladder for each sequence using ladr2.
For each of these sequence-specific ladders, it loops over temperature. For each
temperature, it loops over all the resonances in the ladder and increments the
accumulating cross sections for each point in the energy grid that is contributed
to by that resonance. The cross sections are computed by the ψ−χmethod us-
ing the different ranges for the wfunction to take advantage of the asymptotic
forms, the rational approximations, and the pre-tabulated values. The formu-
las used here are the same as those used for the quikw routine in UNRESR.
Note that the same set of energies is used for every temperature. This is what
preserves the temperature correlations. When the loop over resonances, tem-
peratures, and spin sequences is complete, the code makes a pass through the
results to eliminate the negative elastic cross sections that can occur with the
Single-Level Breit-Wigner (SLBW) approximation, computes the corresponding
infinitely dilute cross sections, and prints out the results for this particular lad-
der. The infinitely dilute values computed for any given ladder will not equal
the proper results defined by the ENDF parameters, but they should fluctuate
around the proper values to form a normal distribution. There is a unused op-
tion controlled by nmode=1 that will renormalize the results of each ladder to
the proper infinitely dilute values.
Now that we have a set of cross sections samples at various temperatures, the
probability table can be generated. When the first ladder comes through, the
routine uses it to set up the total cross section values that will define the bins of
the table. Then that ladder and each subsequent ladder are used to increment
646 NJOY2016

23 PURR LA-UR-17-20093
the cells for the total cross section and the various reaction cross sections. A set
of Bondarenko self-shielded cross sections are computed at the same time. This
process continues until all the ladders have been processed. The final summary
gives the background cross section, the proper infinitely dilute cross section, the
average of all the ladders (which should converge to the infinite dilution values
when may ladders are used), and the percent standard deviation of the samples
for the cross sections. The code then computes and displays the Bondarenko
table and the the final normalized probability table. As a cross check it also
computes the Bondarenko table from the probability table. It should compare
well with the Bondarenko table generated by direct sampling if enough ladders
have been used.
The last step is to renormalize the probability table and the Bondarenko
table to match the proper infinitely dilute cross sections. This is the result that
is written to the output PENDF tape in purr. The conditional probabilities for
heating are added at this time. It is important to note that the values printed on
the PURR listing won’t be quite the same as those passed on to ACER or other
modules that access the PENDF sections MF=2/MT=152 or MF=2/MT=153.
The format used for the specially-defined MT=152, which contains the Bon-
darenko tables of self-shielded cross sections, is the same as the one described
in the UNRESR chapter. Using the standard ENDF style,
[MAT,2,152/ ZA, AWR, LSSF, 0, 0, INTUNR ] HEAD
[MAT,2,152/ TEMZ, 0, NREAC, NSIGZ, NW, NUNR/
SIGZ(1), SIGZ(2),...,SIGZ(NSIGZ),
EUNR(1),
SIGU(1,1,1), SIGU(1,2,1),...,SIGU(1,NSIGZ,1),
SIGU(2,1,1),...
...
SIGU(NREAC,1,1),...,SIGU(NREAC,NSIGZ,1),
EUNR(2),...
<continue for energies through EUNR(NUNR)>
...SIGU(NREAC,NSIGZ,NUNR) ] LIST
where NREAC is always 5 (for the total, elastic, fission, capture, and current-
weighted total reactions, in that order), NSIGZ is the number of σ0values, NUNR
is the number of unresolved energy grid points, and NW is given by
NJOY2016 647

LA-UR-17-20093 23 PURR
NW=NSIGZ+NUNR*(1+5*NSIGZ)
The format used for the specially-defined MT=153, which contains the prob-
ability tables, is
[MAT,2,153/ ZA, AWR, IINEL, IABSO, 0, NBIN ] HEAD
[MAT,2,153/ TEMZ, 0, LSSF, 0, NW, NUNR/
EUNR(1),
PROB(1,1),...,PROB(1,NBIN),
TOTL(1,1),...,TOTL(1,NBIN),
ELAS(1,1),...,ELAS(1,NBIN),
FISS(1,1),...,FISS(1,NBIN),
CAPT(1,1),...,CAPT(1,NBIN),
HEAT(1,1),...,HEAT(1,NBIN),
EUNR(2),...
<continue for energies through EUNR(NUNR)>
...,HEAT(NUNR,NBIN) ] LIST
IINEL and IABSO are the inelastic and absorption competition flags used to define
the reactions that compete with the unresolved fluctuations. If no competition
is present, the flag is set to -1. If there is only a single reaction that competes
with the unresolved energy region, then the flag is set to be equal to the MT
number of that reaction. For the inelastic competition flag, this would be 4, 51
or 91. If more than one reaction competes with the unresolved resonance region,
the flag is set to 0. In versions of NJOY prior to NJOY 2016.35, these flags were
defined differently and stored in a single ENDF field.
Here NBIN is the number of bins in the probability table, and NUNR is the number
of energies in the unresolved energy grid. The total length of the LIST data is
NW=(1+6*NBIN)*NUNR
There is a section like this added for each temperature TEMZ on the output
PENDF tape. In addition, lssf is the flag that tells whether the quantities given
648 NJOY2016

23 PURR LA-UR-17-20093
are cross sections, or whether they are factors to be applied to the corresponding
infinitely-dilute cross sections.
The heating values read in by rdheat from the input PENDF file are the
heat production in eV-barns for the heating reactions found. If none are found,
ihave=0. If only total heating, MT=301, is found, ihave=1. And if all the
required partial heating values are found (MT=302, 318, and 402), ihave=2.
If ihave=1 and lssf=1, the heating entries in the probability table are set
to one, meaning that the infinitely dilute values from the PENDF file will be
used in calculations. If ihave=1 and lssf=0, then the total heating read in by
rdheat will be divided by the total cross section and the same value of heating in
eV/reaction will be stored in every bin (no fluctuations for heating). If ihave=2,
it is possible to add real fluctuations for heating. The partial heating values are
subtracted from the total heating to obtain the part of the heating coming from
competitive reactions (eV-barns). Then each component of the partial heating
is divided by the corresponding infinitely dilute cross sections to get eV/reaction
for that component. This quantity is multiplied by the conditional cross section
in each bin to get eV-barns for events with the total cross section in this bin, and
that value is added into the accumulating heating value. After all the partials
have been processed, the result is eV-barns in each bin. For lssf=1, this result
is divided by the total heating in eV-barns, which gives a fluctuation factor to
be used with the normal infinitely dilute heating value from the PENDF file.
For lssf=0, the result is divided by the average total cross section for the bin to
get a heating value in eV/reaction appropriate for use in MCNP as a multiplier
for the sampled value of the total cross section.
If the ENDF parameter LSSF is equal to one, the elements of the heating in
the probability table are divided by the infinitely dilute heating cross sections to
give heating fluctuation factors in each bin. If a total heating value is available
on the PENDF file (MT=301), but the partials are missing, the heating elements
in the probability table will be filled in with the same non-fluctuating value in
each bin.
The coding includes two sections of output statements that are normally
commented out. In PURR, there is a block of statements that will print out
the self-shielded cross sections in a form that can be adapted for the VIEWR
module. In unrest, there is a block of coding that will print out VIEWR input
for plotting the probability distribution (see Fig. 69).
NJOY2016 649

LA-UR-17-20093 23 PURR
23.7 Error Messages
error in purr***mode conversion between nin and nout not allowed nin
and nout must both be binary (negative) or ASCII (positive).
error in purr***nbin should be 15 or more
The construction of the cross sections bins requires this.
error in purr***maxscr is too small, increase to at least ...
error in purr***not enough scratch space
The amount of space in the allocatable array ahas been exceeded. See
maxscr=20000 in the subroutine purr.
error in rdf2un***storage in a exceeded
error in rdf2un***storage exceeded
The amount of space in the allocatable array arry has been exceeded. See
the global variable jx=10000 at the start of the purm module.
error in rdf2un***too many ur energy points
The limit meunr=150 defined in the global assignments has been exceeded.
error in unresx***illegal naps
The NAPS parameter on the ENDF file can be 0, 1, or 2 with nro equal
to 1 only. Check the evaluation.
error in unresx***too many sequences, increase mxns0
The limit of 100 spin sequences allowed in subroutine unresx has been
exceeded. See mxns0=100.
error in ladr2***too many resonances in ladder
There is a limit of nermax=1000 resonances in a ladder. This is global
variable defined at the start of module purrm and set in purr. It controls
the length of several allocatable arrays that are defined in subroutine purr,
such as er,gnr, and so on.
error in unrest***bad value for nres or emin>emax, increase dmin
In order to generate the probability table, purr generates a number of
resonances over a given energy range. To determine the value of these
parameters, purr uses the lowest value of the level density. If a negative
value is obtained for nres, or if emin is larger than emax, something has
gone wrong. Adjusting dmin to an even higher value (default of 100000)
might help.
error in rann***failed
The random number generator failed.
message from purr---reset ibin=1 (or =nsamp), consider ...
The nbin size specified is too large for PURR’s internal arrays. Either
decrease the input nbin or increase the PURR’s nsamp variable.
650 NJOY2016

23 PURR LA-UR-17-20093
message from purr---reset ibin=1 (or =nsamp), consider ...
The nbin size specified is too large for PURR’s internal arrays. Either
decrease the input nbin or increase the PURR’s nsamp variable.
message from purr---total xs less than its components at e=...
This message can appear for evaluations using LSSF=1 when the total
cross section is smaller than the sum of its components. Using the data as
is could result in the appearance of negative cross sections in the probability
table, which is why PURR will set all backgrounds to 0 if this happens.
This is an error in the evaluation and it should be corrected.
message from purr---ptable has ... negative xs values
When generating a probability table at a given energy, purr has detected
that some cross section values are actually negative. This is most likely
due to a large negative background cross section defined in MF=3 for the
current energy.
message from purr---no heating found on pendf
message from purr---no partial heating xsecs found on pendf
Heating values are added to the probability tables. These messages indicate
that the user forgot to either include a heatr run or to request partial
KERMA data in the heatr run (e.g. 318 for the fission KERMA).
message from purr---mat has no resonance parameters
message from purr---mat has no unresolved resonance parameters
Probability tables can only be generated when unresolved resonance pa-
rameters are defined for the material.
message from purr---resolved-unresolved overlap energies
The resolved and unresolved energy region appear to overlap. This may
indicate an issue in the evaluation.
NJOY2016 651

LA-UR-17-20093 23 PURR
652 NJOY2016

24 LEAPR LA-UR-17-20093
24 LEAPR
The LEAPR module is used to prepare the scattering law S(α, β), which de-
scribes thermal scattering from bound moderators, in the ENDF-6 format used
by THERMR. The original ENDF thermal scattering data[52] was prepared
by General Atomics (GA) using the GASKET code[96]. This code has dif-
ficulty working with the very large energy and momentum transfers encoun-
tered for large incident energy or very low temperatures. For these reasons,
LEAPR is based on the British code LEAP+ADDELT originally written by
McLatchie at Harwell[97], then implemented by Butland at Winfrith[98], and
finally modified to work better for cold moderators as part of the Ph.D. Thesis
of D. J. Picton[99]. The code that Dr. Picton provided was modified extensively
to fit better into the NJOY environment and to take advantage of modern large
computers. This involved massive rearrangement of storage and routines, up-
dating for first FORTRAN-77, then Fortran-90, and extensive editing of the
comment cards. The original Edgewood expansion and Short Collision Time
(SCT) treatments were removed in favor of using more terms in the phonon
expansion and using the simple ENDF SCT formula[9]. In addition, output in
ENDF-6 format[9] was provided, the capability to include either coherent or
incoherent elastic scattering was added, a major speedup for the diffusion cal-
culation was provided, and a capability to produce a mixed scattering law for
materials like BeO and benzine was developed. In order to improve the numerics
on short-word computers, the code was changed to use the asymmetric scatter-
ing function, the normalization scheme for the phonon expansion was revised,
and the discrete-oscillator calculation was rebuilt to take better advantage of the
convolution properties of the delta function and to use better Bessel Functions.
A complete discussion of the theory used in the code is given below.
LEAPR was used[100] to reevaluate several of the thermal moderator ma-
terials from ENDF/B-VI using the original GA physics[52] but extending the
alpha and beta ranges for incoherent inelastic scattering. The energy range
for coherent scattering was also increased. The code was also used to pre-
pare scattering-law files for several cold moderators of interest for experimental
cold-neutron sources[101, 102]. More recently, some of these materials were up-
dated for ENDF/B-VII.0 and additional materials were added. Several of the
ENDF/B-VII.0 cases are discussed below as examples of how to run LEAPR.
Acknowledgements are due to Gary Russell of the Los Alamos Neutron Sci-
ence Center (LANSCE) for motivating this work, to Drew Kornreich of the
NJOY2016 653

LA-UR-17-20093 24 LEAPR
University of Arizona for his careful study of the water problem, and to Max
Lazo (University of New Mexico, SAIC, and Sandia National Laboratory) for
testing and reviewing the code and documentation. In addition, we thank D.
J. Picton for sending us his cold-moderator version of LEAPR, Rolf Neef of
Julich and Guy Robert of ILL-Grenoble for sending us the initial version of the
cold hydrogen treatment, and M. Mattes and J. Keinert of the University of
Stuttgart for their help with the liquid hydrogen and deuterium models.
This chapter describes the LEAPR module in NJOY2016.0.
24.1 Theory
The following discussion of the theories used in the the code is based on the
original British documentation and the presentation in a standard reference[103].
Coherent and Incoherent Scattering. In practice, the scattering of neu-
trons from a system of N particles with a random distribution of spins or isotope
types can be expressed as the sum of a coherent part and an incoherent part. The
coherent scattering includes the effects from waves that are able to interfere with
each other, and the incoherent part depends on a simple sum of noninterfering
waves from all the N particles. (The spin correlations in ortho and para hydro-
gen violate the assumption of randomness, so liquid hydrogen does not fit into
the model described here. A method for treating them will be described below.)
The cross sections for coherent and incoherent scattering can be considered to
be characteristic properties of the materials. As examples, the scattering from
hydrogen is almost completely incoherent, and the scattering from carbon and
oxygen is almost completely coherent.
Furthermore, the coherent and incoherent scattering include both elastic and
inelastic parts. The elastic scattering takes place with no energy change. It
should not be confused with the elastic scattering from a single particle that
is familiar for higher neutron energies where the neutron loses energy; thermal
elastic scattering can be considered to be scattering from the entire lattice,
thus the effective mass of the target is very large, and the neutron does not
lose energy in the scattering process. Thermal inelastic scattering results in an
energy loss (gain) for the neutron with a corresponding excitation (deexcitation)
of the target. The excitation may correspond to the production of one or more
phonons in a crystalline material, to the production of rotations or vibrations in
molecules, or to the initiation of atomic or molecular recoil motions in a liquid
or gas.
654 NJOY2016

24 LEAPR LA-UR-17-20093
In addition, the coherent inelastic part of the scattering contains both inter-
ference effects between waves scattered by different particles and direct terms.
It turns out that the direct part for gases, liquids and solids consisting of ran-
domly oriented crystallites has approximately the same form as the incoherent
term. The interference is usually neglected.
Therefore, we can usually divide the thermal scattering cross section into
three different parts:
•Coherent elastic. Important for crystalline solids like graphite or beryllium.
•Incoherent elastic. Important for hydrogenous solids like solid methane,
polyethylene, and zirconium hydride.
•Inelastic. Important for all materials (this category includes both incoher-
ent and coherent inelastic).
The absence of interference in incoherent scattering and the neglect of inter-
ference in coherent inelastic scattering allows us to construct thermal scattering
laws for “hydrogen in water” or “hydrogen in solid methane” or “oxygen in
beryllium oxide”. However, this simplification is not possible in general for co-
herent elastic scattering in materials with more that one type of atom in the
unit cell; for coherent elastic scattering, beryllium oxide must be considered as
a unit.
Inelastic Scattering It is shown in the standard references[103] that the
double differential scattering cross section for thermal neutrons for gases, liquids
or solids consisting of randomly ordered microcrystals can be written as
σ(E→E0, µ) = σb
2kT rE0
ES(α, β),(507)
where Eand E0are the incident and secondary neutron energies in the labora-
tory system, µis the cosine of the scattering angle in the laboratory, σbis the
characteristic bound scattering cross section for the material, kT is the thermal
energy in eV, and Sis the asymmetric form of the scattering law. The scattering
law depends on only two variables: the momentum transfer
α=E0+E−2µ√E0E
AkT ,(508)
where Ais the ratio of the scatterer mass to the neutron mass, and the energy
NJOY2016 655

LA-UR-17-20093 24 LEAPR
transfer
β=E0−E
kT .(509)
Note that βis positive for energy gain and negative for energy loss. Working in
the incoherent approximation and the Gaussian approximation, the scattering
law can be written
S(α, β) = 1
2πZ∞
−∞
eiβˆ
te−γ(ˆ
t)dˆ
t , (510)
where ˆ
tis time measured in units of ¯h/(kT ) seconds. The function γ(ˆ
t) is given
by
γ(ˆ
t) = αZ∞
−∞
P(β)1−e−iβˆ
te−β/2dβ , (511)
where
P(β) = ρ(β)
2βsinh(β/2) ,(512)
and where ρ(β) is the frequency spectrum of excitations in the system expressed
as a function of β. The spectrum must be normalized as follows:
Z∞
0
ρ(β)dβ = 1 .(513)
The function P(β) defined by Eq.(512) is used directly in LEAPR, and ρ(β) =
ρ(/kt) is given as a function of in eV. For systems in thermal equilibrium,
there is a relationship between upscatter and downscatter called “detail balance”
that is a consequence of microscopic reversibility. It requires that
S(α, β)=e−βS(α, −β).(514)
Liquid hydrogen and deuterium violate this condition, as will be described below.
In addition, the scattering law satisfies two other important constraints; namely,
normalization,
Z∞
−∞ S(α, β)dβ = 1 ,(515)
656 NJOY2016

24 LEAPR LA-UR-17-20093
and the sum rule
Z∞
−∞
βS(α, β)dβ =−α . (516)
Actually, ENDF works with the so-called “symmetric” S(α, β),
S(α, β) = eβ/2S(α, β) (517)
which (except for liquid hydrogen or deuterium) satisfies the condition
S(α, β) = S(α, −β).(518)
Note that S(α, −β) for positive βdescribes the downscatter side of the function,
and because it is basically proportional to the cross section, it can be represented
by reasonable numbers (say 10−8to 1) for all β. The symmetric S(α, β), on the
other hand, can easily be smaller than S(α, −β) by factors like e−β/2∼e−80 ∼
10−35, which can cause trouble on short-word machines. This kind of numerical
problem is even more severe for cold moderators, where dynamic ranges on
the order of 10100 occur for S(α, β). (The user will have to use some caution
reading this report, because the typographic symbols for S and script-S are very
similar.) By working with S(α, −β), LEAPR can do all of its calculations using
single-precision variables, even on a short-word machine.
The next step is to decompose the frequency spectrum into a sum of simple
spectra
ρ(β) =
K
X
j=1
ρj(β),(519)
where the following possibilities are allowed:
ρj(β) = wjδ(βj) discrete oscillator (520)
ρj(β) = ρs(β) solid-type spectrum (521)
ρj(β) = ρt(β) translational spectrum (522)
The solid-type spectrum must vary as β2as βgoes to zero, and it must integrate
to ws, the weight for the solid-type law. The translational spectrum can be either
a free-gas law or a diffusion-type spectrum represented with the approximation of
Egelstaff and Schofield that will be discussed later. In either case, the spectrum
NJOY2016 657

LA-UR-17-20093 24 LEAPR
must integrate to wt, the translational weight. The sum of all the weights of
the partial spectra must equal 1. Defining γj(ˆ
t) to be the value of γappropriate
for ρj, and Sjto be the corresponding partial scattering law, and using the
convolution theorem for Fourier transforms, leads to a recursive formula for the
scattering law:
S(α, β) = S(K)(α, β),(523)
where
S(J)(α, β) = 1
2πZ∞
−∞
eiβˆ
tJ
Y
j=1
e−γj(ˆ
t)dˆ
t
=Z∞
−∞ SJ(α, β0)S(J−1)(α, β−β0)dβ0.(524)
As an example of the use of this recursive procedure, consider a case where the
desired frequency spectrum is a combination of ρsand two discrete oscillators.
First, calculate S(1)=S1using ρs. Then calculate S2using ρ(β1), the distribution
for the first discrete oscillator, and convolve S2with S(1) to obtain S(2), the
composite scattering law for the first two partial distributions. Repeat the
process with the second discrete oscillator to obtain S(3), which is equal to
S(α, β) for the full distribution.
The Phonon Expansion. Consider first γs(ˆ
t), the Gaussian function for
solid-type frequency spectra. Expanding the time-dependent part of the ex-
ponential gives
e−γs(ˆ
t)= e−αλs
∞
X
n=0
1
n!αZ∞
−∞
Ps(β) e−β/2e−iβˆ
tdβ n
,(525)
where λsis the Debye-Waller coefficient
λs=Z∞
−∞
Ps(β) e−β/2dβ . (526)
The scattering function becomes
658 NJOY2016
24 LEAPR LA-UR-17-20093
Ss(α, β)=e−αλs
∞
X
n=0
1
n!αn
×1
2πZ∞
−∞
eiβˆ
tZ∞
−∞
Ps(β0) e−β0/2e−iβ0ˆ
tdβ0n
dˆ
t . (527)
For convenience, define the quantity in the second line of this equation to be
λn
sTn(β). Then clearly,
Ss(α, β)=e−αλs
∞
X
n=0
1
n![αλs]nTn(β),(528)
where
T0(β) = 1
2πZ∞
−∞
eiβˆ
tdˆ
t=δ(β),(529)
and
T1(β) = Z∞
−∞
Ps(β0) e−β0/2
λs1
2πZ∞
−∞
ei(β−β0)ˆ
tdˆ
tdβ0=Ps(β) e−β/2
λs
,
(530)
In general,
Tn(β) = Z∞
−∞ T1(β0)Tn−1(β−β0)dβ0.(531)
The script-T functions obey the relationship Tn(β) = e−βTn(−β). In addition,
each of the Tnfunctions obeys the following normalization condition:
Z∞
−∞ Tn(β)dβ = 1 .(532)
It guarantees that Eq.515 will be satisfied by the sum in Eq.528. In LEAPR, the
Tn(−β) functions are precomputed on the input βgrid for nup to some specified
maximum value, typically 100. It is then easy to compute the smooth part of
Ss(α, −β) for any sufficiently small value of αusing Eq.528. The corresponding
values of Ss(α, β) can then be obtained by multiplying by e−β. The delta
function arising from the “zero-phonon” term is carried forward separately. The
normalization in Eq.528 has better numerical properties than the one used in
LEAP.
NJOY2016 659

LA-UR-17-20093 24 LEAPR
The Short-Collision-Time Approximation. For larger values of α, the
expansion of Eq.528 requires too many terms. LEAPR uses the simple Short-
Collision-Time (SCT) approximation from ENDF to extend the solid-type scat-
tering law.
Ss(α, −β) = 1
q4πwsαT s/T
exp −(wsα−β)2
wsαT s/T ,(533)
and
Ss(α, β) = e−βSs(α, −β) (534)
where βis positive, and where the effective temperature is given by
Ts=T
2wsZ∞
−∞
β2Ps(β) e−βdβ . (535)
As above, wsis the weight for the solid-type spectrum.
Diffusion and Free-Gas Translation. The neutron scattering from many
important liquids, including water and liquid methane, can be represented using
a solid-type spectrum of rotational and vibrational modes combined with a dif-
fusion term. Egelstaff and Schofield have proposed an especially simple model
for diffusion called the “effective width model”. It has the advantage of having
analytic forms for both S(α, β) and the associated frequency spectrum ρ(β):
St(α, β) = 2cwtα
πexp 2c2wtα−β/2
√c2+.25
pβ2+ 4c2w2
tα2K1npc2+.25qβ2+ 4c2w2
tα2o,(536)
and
ρ(β) = wt
4c
πβ pc2+.25 sinh(β/2) K1npc2+.25 βo.(537)
In these equations, K1(x) is a modified Bessel function of the second kind, and
the translational weight wtand the diffusion constant care provided as inputs.
An alternative for the translational part of the distribution is the free-gas
law. It is clearly appropriate for a gas of molecules, but it has also been used to
660 NJOY2016

24 LEAPR LA-UR-17-20093
represent the translational component for liquid moderators like water[52]. The
scattering law is given by
St(α, −β) = 1
√4πwtαexp −(wtα−β)2
4wtα,(538)
and
St(α, β)=e−βSt(α, −β),(539)
with βpositive. The free-gas law is used in LEAPR if the diffusion coefficient c
is input as zero.
In LEAPR, Ss(α, β), the scattering law for the solid-type modes, is calculated
using the phonon expansion as described above. The translational contribution
St(α, β) is then calculated using one of the formulas above on a βgrid chosen
to represent its shape fairly well. The combined scattering law is then obtained
by convolution as follows:
S(α, β) = St(α, β) e−αλs+Z∞
−∞ St(α, β0)Ss(α, β−β0)dβ0.(540)
The first term arises from the delta function in Eq.528, which isn’t included in
the numerical results for the phonon series calculation. The values for St(β)
and Ss(β−β0) are obtained from the precomputed functions by interpolation.
This makes LEAPR run much faster than LEAP+ADDELT for diffusive cases,
because the original code did direct recalculations of the solid-type scattering
law for all the desired values of β−β0. It also had to take pains to compute Ston
aβgrid that was commensurate with the input grid. This often resulted in more
points for Stthan were necessary to obtain useful accuracy for the convolutions.
The effective temperature for a combination of solid-type and translation
modes is computed using
Ts=wtT+wsTs
wt+ws
.(541)
Discrete Oscillators. Polyatomic molecules normally contain a number of
vibrational modes that can be represented as discrete oscillators. The distribu-
tion function for one oscillator is given by wiδ(βi), where wiis the fractional
weight for mode i, and βiis the energy-transfer parameter computed from the
mode’s vibrational frequency. The corresponding scattering law is given by
NJOY2016 661

LA-UR-17-20093 24 LEAPR
Si(α, β)=e−αλi
∞
X
n=−∞
δ(β−nβi)Inαwi
βisinh(βi/2)e−nβi/2
=
∞
X
n=−∞
Ain(α)δ(β−nβi),(542)
where
λi=wi
coth(βi/2)
βi
.(543)
The combination of a solid-type mode (s) with discrete oscillators (1) and (2)
would give
S(0)(α, β) = Ss(α, β),(544)
S(1)(α, β) = Z∞
−∞ S1(α, β0)S(0)(α, β−β0)dβ0
=
∞
X
n=−∞
A1n(α)S(0)(α, β−nβ1),(545)
S(2)(α, β) = Z∞
−∞ S2(α, β0)S(1)(α, β−β0)dβ0
=
∞
X
m=−∞
A2m(α)
∞
X
n=−∞
A1n(α)S(0)(α, β−nβ1−mβ2).(546)
This process can be continued through S(3)(α, β), S(4)(α, β), etc., until all the
discrete oscillators have been included. The result has the form
S(α, β) = X
k
Wk(α)Ss(α, β −βk),(547)
where the βkand the associated weights Wkare easily generated recursively
using a procedure that throws out small weights at each step. The Debye-Waller
λfor the combined modes is computed using
λ=λs+
N
X
i=1
λi.(548)
662 NJOY2016

24 LEAPR LA-UR-17-20093
The effective temperature for the combined modes is given by
Ts=wtT+wsTs+
N
X
i=1
wi
βi
2coth βi
2T . (549)
If the starting-point scattering law S(0) does not contain a translational con-
tribution (true for hydrogenous solids like polyethylene and frozen methane),
it is important to remember to include the effects of the “zero-phonon” term
exp(−αλs)δ(β). The code does this by adding in triangular peaks with the
proper areas and with their apexes at the βvalue closest to the βkvalues. One
of these peaks is at β=0. This peak is not put into the scattering law as a sharp
triangle; instead, it is handled as “incoherent elastic” scattering in order to take
full advantage of the analytic properties of δ(β).
Incoherent Elastic Scattering. In hydrogenous solids, there is an elastic
(no energy loss) component of scattering arising from the “zero-phonon”, or n=0
term, of Eq.528. In ENDF terminology, this is called the “incoherent elastic”
term. Clearly,
Siel(α, β) = e−αλδ(β).(550)
The corresponding differential scattering cross section is
σ(E, µ) = σb
2e−2WE(1−µ),(551)
and the integrated cross section is
σ(E) = σb
21−e−4WE
2W E .(552)
In these equations, the Debye-Waller coefficient is given by
W=λ
AkT ,(553)
where λis computed from the input frequency spectrum as shown by Eq.526 and
modified by the presence of discrete oscillators (if any) as shown above. LEAPR
writes the bound scattering cross section σband the Debye-Waller coefficient W
as a function of temperature into a section of the ENDF-6 output with MF=7
and MT=2.
NJOY2016 663

LA-UR-17-20093 24 LEAPR
Coherent Elastic Scattering. In solids consisting of coherent scatterers –
for example, graphite – the zero-phonon term leads to interference scattering
from the various planes of atoms of the crystals making up the solid. Once
again, there is no energy loss, and the ENDF term for the process is “coherent
elastic scattering”. The differential scattering cross section is given by
σcoh(E, µ) = σc
EX
Ei<E
fie−4WEiδ(µ−µi),(554)
where
µi= 1 −Ei/E , (555)
and the integrated cross section is given by
σcoh =σc
EX
Ei<E
fie−4WEi.(556)
In these equations, σcis the effective bound coherent scattering cross section
for the material, Wis the effective Debye-Waller coefficient, Eiare the so-called
“Bragg Edges”, and the fiare related to the crystallographic structure factors.
It can be seen from Eq.556 that the coherent elastic cross section is zero below
the first Bragg Edge, E1(typically about 2 to 5 meV). It then jumps sharply
to a value determined by f1and the Debye-Waller term. At higher energies,
the cross section drops off as 1/E until E=E2. It then takes another jump, and
resumes its 1/E drop off. The sizes of the steps in the cross section gradually
get smaller, and at high energies there is nothing left but an asymptotic 1/E
decrease (typically above 1 to 2 eV). LEAPR stores the quantity Eσcoh(E) as
a function of energy and temperature in a section of the ENDF-6 output with
MF=7 and MT=2. The cross section is easily recovered from this representation
by dividing by E(this is done in the THERMR module of NJOY). The angular
distribution of scattered neutrons can be calculated by extracting the fifrom the
steps in σcoh(E) file by subtraction. This process is carried out automatically
in the GROUPR module of NJOY.
The calculation of the Eiand fidepends on a knowledge of the crystal
structure of the scattering material. The methods used are borrowed from
HEXSCAT[32]. In general, the energies of the Bragg edges are given by
Ei=¯h2τ2
i
8m,(557)
664 NJOY2016

24 LEAPR LA-UR-17-20093
where τiis the length of the vectors of one particular “shell” of the reciprocal
lattice, and mis the neutron mass. The fifactors for a material containing a
single atomic species are given by
fi=2π¯h2
4mNV X
τi|F(τ)|2,(558)
where the sum extends over all reciprocal lattice vectors of the given length, and
the crystallographic structure factor is given by
|F(τ)|2=
N
X
j=1
ei2πφj
2,(559)
where Nis the number of atoms in the unit cell, φj=~τ ·~ρjare the phases for
the atoms, and the ~ρjare their positions. The situation is more complicated for
materials containing different atomic species, such as beryllium oxide. In these
cases,
σce−2WEifi=
N
X
j=1
√σje−WjEiei2πφj
2,(560)
where the coherent cross section and Debye-Waller factor can be different for
each site in the unit cell. The effective coherent cross section is clearly given by
σc=
N
X
j=1
σj.(561)
Since LEAPR only works with one material at a time, it doesn’t have access to
different values of Wjfor the atoms in the unit cell. Therefore, it assumes that
either WjEiis small, or the Wjdoesn’t vary much from site to site. This allows
it to calculate the fiusing
|F|2=
N
X
j=1
√σj
√σc
e−2πφj
2.(562)
For hexagonal materials, the lattice is described by the two constants aand c.
The reciprocal lattice vector lengths are given by
τ
2π=4
3a2`2
1+`2
2+`1`2+1
c2`2
3(563)
NJOY2016 665

LA-UR-17-20093 24 LEAPR
where `1, `2,and `3run over all the positive and negative integers, including
zero. The volume of the unit cell is
V=√3a2c/2.(564)
For graphite, there are four atoms in the unit cell at positions[104]
(0,0,0),(−1
3,1
3,0),(−2
3,−1
3,1
2),(−1
3,1
3,1
2).
These positions give the following phases:
φ1= 0 ,(565)
φ2= (−`1+`2)/3,(566)
φ3=−(2/3)`1−(1/3)`2+ (1/2)`3,(567)
φ4=−(1/3)`1+ (1/3)`2+ (1/2)`3.(568)
The form factor for graphite becomes
|F|2=(6 + 10 cos[2π(`1−`2)/3] `3even
4 sin2[π(`1−`2)/3] `3odd (569)
For the hexagonal close packed (hcp) structure, which includes beryllium, there
are two atoms per unit cell at
(0,0,0),(1
3,2
3,1
2),
and the form factor for hcp lattices like beryllium becomes
|F|2= 2 + 2 cosh2π(2`1+ 4`2+ 3`3)/6i.(570)
The beryllium oxide lattice consists of two interpenetrating hcp lattices, one
for the beryllium atoms, and one for the oxygen. There are four atoms per unit
cell with positions
(0,0,0),(1
3,2
3,1
2),(0,0, u),(1
3,2
3, u +1
2),
666 NJOY2016

24 LEAPR LA-UR-17-20093
Using the approximation that the Debye-Waller factor doesn’t vary from position
to position in the unit cell gives the following expression for the structure factor:
|F|2=1 + cos[2π(2`1+ 4`2+ 3`3)/6]r2
1+ 2r1r2cos(3π`3/4),(571)
where r2
1and r2
2are the bound coherent cross sections for beryllium and oxygen,
respectively, and the effective coherent cross section, σc, is to be taken as 1.
LEAPR contains similar logic to handle face-centered cubic (fcc), e.g. alu-
minum, and body-centered cubic (bcc), e.g. iron, lattices. More formulas for
the structure factor can be added to the code when needed.
Liquid Hydrogen and Deuterium. Materials containing hydrogen (H) or
deuterium (D) molecules violate the assumption that spins are distributed ran-
domly that underlies the incoherent approximation used for Eq.528, and an
explicitly quantum-mechanical formula is required to take account of the corre-
lations between the spins of two atoms in the same molecule. This problem was
considered by Young and Koppel[105]. Changing to our notation, the formulas
for the hydrogen molecule (neglecting vibrations) become
Spara(α, β) = X
J=0,2,4,...
PJ
×4π
σbhApara X
J0=0,2,4,...
+Bpara X
J0=1,3,5,...i(2J0+ 1)
× Sf(wα, β+βJJ0)
×
J0+J
X
`=|J0−J|
4j2
`(y)C2(JJ0`; 00) ,(572)
and
Sortho(α, β) = X
J=1,3,5,...
PJ
×4π
σbhAortho X
J0=0,2,4,...
+Bortho X
J0=1,3,5,...i(2J0+ 1)
× Sf(wα, β+βJJ0)
×
J0+J
X
`=|J0−J|
4j2
`(y)C2(JJ0`; 00) .(573)
NJOY2016 667

LA-UR-17-20093 24 LEAPR
The coefficients for the even and odd sums are given in the following table:
Type A(even) B(odd)
H para a2
ca2
i
H ortho a2
c/3a2
c+ 2a2
i/3
D para 3a2
i/4a2
c+a2
i/4
D ortho a2
c+ 5a2
i/8 3a2
i/8
Here acand aiare the coherent and incoherent scattering lengths (note that the
characteristic bound cross section is σb=4π[a2
c+a2
i]), PJis the statistical weight
factor, βJJ0=(E0
J−EJ)/kT is the energy transfer for a rotational transition, j`(x)
is a spherical Bessel function of order `, and C(JJ0`; 00) is a Clebsch-Gordan
coefficient. The parameter yis given by κa/2=(a/2)p4M kT α/2, where ais the
interatomic distance in the molecule. The translational weight wis 1/2 for H2
and 1/4 for D2. The sums over J0are treated as operators into order to keep
the notation compact.
Young and Koppel assumed that the molecular translations were free, so the
equations contain
Sf(α, −β) = 1
√4πα exp −(α−β)2
4α,(574)
and
Sf(α, β)=e−βSf(α, −β),(575)
the free-atom scattering function (with βpositive). Note that αis multiplied
by a translational weight of 0.5 or 0.25 when this equation is used in order to
make the formula apply to a molecule with mass ratio 2 or 4, respectively.
These formulas as stated are appropriate for a gas of hydrogen or deuterium
molecules. In a liquid, there are two additional effects to be considered: in-
terference between the neutron waves scattered from different molecules, and
the fact that the recoil of the hydrogen molecule is not really free. First, we
will consider the latter effect. Experiments by Egelstaff, Haywood, and Webb
at Harwell[106] and Schott at Karlsruhe[107] showed appreciable broadening of
the quasi-elastic scattering peak for liquid hydrogen, and both groups ascribed
this to diffusive effects. Later, Utsuro of Kyoto University constructed a simple
analytic model[108] that included both diffusion and intermolecular vibrations
and showed good agreement with experiment. More recently, Keinert and Sax
of the University of Stuttgart proposed the model[109] that we follow here.
668 NJOY2016

24 LEAPR LA-UR-17-20093
They suggested that the free translation term in the Young and Koppel
formulas be replaced by the superposition of a solid-state like motion and a
diffusive law. One can picture a hydrogen molecule bound in a cluster of about
20 molecules and undergoing vibrations similar to those of a hydrogen molecule
in a solid. These clumps then diffuse through the liquid (hindered translations)
according to the Egelstaff-Schofield effective width model discussed above. The
details of the performance of this model will be discussed further in a subsequent
section.
As mentioned earlier, waves scattered from different molecules can also in-
terfere. Inter-molecular coherence results when there is a correlation between
the positions of nearby molecules. This kind of coherence is described by the
“static structure factor” S(κ). This quantity can be used in an approximation
due to Vineyard as follows:
d2σ
dΩd =d2σcoh
dΩd S(κ) + d2σincoh
dΩd .(576)
This is equivalent to using Eqs.572 and 573 with a2
creplaced by S(κ)a2
cin the
calculation of the coefficients Aand B. The effects of this procedure will be
shown below.
Mixed Moderators. In some cases, thermal evaluations give the scattering
for a principal scatterer as bound in a moderator; for example, H in H2O, or
Zr in ZrH. The other atoms in the molecule are represented by an analytic law
(free-gas O), or by another detailed scattering law (H in ZrH). In other cases,
the scattering from the entire molecule is represented in one file. Examples are
BeO and benzine in earlier versions of ENDF/B, but only benzine remains as a
mixed moderator in ENDF/B-VII.0. The molecular scattering is renormalized
to be used with the principal scatterer (Be or H for these cases); the secondary
scatterer is assumed to have zero scattering in the thermal range.
Taking BeO as an example, the thermal cross section can be represented as
follows:
σBeO =σb,Be
2kT rE0
Ee−β/2
SBe(αBe, β) + σb,O
σb,Be
SO(ABe
AO
αBe, β),(577)
where αBe stands for αcomputed with the atomic mass ratio for Be, ABe. In
practice, LEAPR first computes SBe using the input αgrid, and then it computes
NJOY2016 669
LA-UR-17-20093 24 LEAPR
SOon a new αgrid obtained by transforming the input grid with the indicated
mass ratio. The two parts can now be added up by weighting with the indicated
ratio of the bound cross sections. The method for preparing a mixed S(α, β) for
BeO is shown in detail below.
24.2 Input Instructions
The following listing of input instructions was copied from the comment cards
at the beginning of the LEAPR module. It is always a good idea to check the
current source file in case there have been changes.
!----- user input (free format) ---------------------------------
!
! card 1 - units
! nout endf output unit for thermal file
!
! card 2 - title
!
! card 3 - run control
! ntempr number of temperatures (def=1)
! iprint print control (0=min, 1=more, 2=most, def=1)
! nphon phonon-expansion order (def=100)
!
! card 4 - endf output control
! mat endf mat number
! za 1000*z+a for principal scatterer
! isabt sab type (0=s, 1=ss, def=0)
! ilog log flag (0=s, 1=log10(s), def=0)
! smin minimum S(alpha, beta) stored in file (def=1e-75)
!
! card 5 - principal scatterer control
! awr weight ratio to neutron for principal scatterer
! spr free atom cross section for principal scatterer
! npr number of principal scattering atoms in compound
! iel coherent elastic option
! 0 none (default)
! 1 graphite
! 2 beryllium
! 3 beryllium oxide
! 4 aluminum
! 5 lead
670 NJOY2016

24 LEAPR LA-UR-17-20093
! 6 iron
! ncold cold hydrogen option
! 0 none (default)
! 1 ortho hydrogen
! 2 para hydrogen
! 3 otho deuterium
! 4 para deuterium
! nsk 0 none (default)
! 1 vineyard
! 2 skold
!
! card 6 - secondary scatterer control
! nss number of secondary scatterers (0 or 1)
! b7 secondary scatterer type
! (0=sct only, 1=free, 2=diffusion)
! aws weight ratio to neutron for secondary scatterer
! sps free atoms cross section for secondary scatterer
! mss number of atoms of this type in the compound
!
! card 7 - alpha, beta control
! nalpha number of alpha values
! nbeta number of beta values
! lat if lat.eq.1, alpha and beta values are scaled
! by .0253/tev, where tev is temp in ev. (def=0)
!
! card 8 - alpha values (increasing order)
! card 9 - beta values (increasing order)
!
! scatterer loop, do temperature loop for principal scatterer.
! repeat for secondary scatterer (if any) if b7=0.
!
! temperature loop, repeat cards 10 to 18 for each temperature
!
! card 10 - temperature (k)
! a negative value means skip cards 11 to 18,
! thereby using previous parameters for this temp.
!
! card 11 -- continuous distribution control
! delta interval in ev
! ni number of points
!
! card 12 -- rho(energy) (order of increasing ev)
NJOY2016 671

LA-UR-17-20093 24 LEAPR
!
! card 13 - continuous distribution parameters
! twt translational weight
! c diffusion constant (zero for free gas)
! tbeta normalization for continuous part
!
! card 14 - discrete oscillator control
! nd number of discrete oscillators
!
! card 15 - oscillator energies (ev)
! card 16 - oscillator weights (sum to 1.-tbeta-twt)
!
! card 17 - pair correlation control (nsk.ne.0 only)
! nka number of kappa values
! dka kappa increment (inv. angstroms)
!
! card 18 skappa values in increasing order (inv. ang.)
!
! card 19 coherent scattering fraction for nsk.eq.2 only
! cfrac coherent fraction
!
! card 20 - file 1 comments, repeat until blank line is read.
!
!-------------------------------------------------------------------
Card1. Card 1 is the standard NJOY units card. The value of nout should be
a number from 20 up, and it can be either positive (ASCII) or negative (blocked
binary).
Card 2. Card 2, the title card, is just used to label the input deck and the
output listing for the user’s convenience. The title string does not go into the
output ENDF file.
Card 3. Card 3 contains global parameters that control the run. The meaning
of ntempr is clear. The amount of information printed on the output listing is
controlled by iprint. The default is 1 (a mid-size listing). If you suspect
problems, you can turn on the long listing to see more details. The parameter
nphon gives the order of the phonon expansion. Usually a fairly large number
672 NJOY2016

24 LEAPR LA-UR-17-20093
(such as 100) is suitable. If it is too small, the SCT approximation will be used
to excess.
Card 4. The ENDF MAT number on Card 4 should be one of the numbers
listed in Appendix C of ENDF-102[9]. For the user’s convenience, the numbers
currently (ENDF/B-VII.1) being used are given in the following table:
Compound MAT Compound MAT
Water 1 Liquid Methane 33
Para Hydrogen 2 Solid Methane 34
Ortho Hydrogen 3 Polyethylene 37
H in ZrH 7 Benzine 40
Heavy Water 11 O in BeO 46
Para Deuterium 12 O in SiO247
Ortho Deuterium 13 O in UO248
Be 26 Al metal 53
BeO 27 Fe metal 56
Be2C 28 Zr in ZrH 58
Be in BeO 29 UO275
Graphite 31 UC 76
Some of these files (Al, Fe, U in UO2, and O in UO2) were also available in
ENDF/B-VII.0 with non-standard material numbers. The appropriate value to
be used for za is fairly obvious. The parameter isym controls whether the output
ENDF tape contains the symmetric S(α, β) or the asymmetric S(α, β). The
second option gives much better numerics, especially on short-word machines,
but it is not sanctioned by the ENDF-6 format. Here, ilog controls whether
the output file contains S(or S) or log10 S. Giving the log of S is the ENDF-
sanctioned way of handling very small numbers in File 7.
Card 5. The “principal scatterer” may be hard to select for some compounds.
For water, it is H. For ZrH, it would be H for mat=7 and Zr for mat=58. For
mixed moderators like BeO, it is usually the light material. The value of spr
should be chosen by looking at the low-energy limit for MF=3/MT=2 (elastic
scattering) on the neutron file to be used with the new evaluation. The value
for npr would be 2 for H2O, or 1 for BeO. The elastic option iel would nor-
mally be zero, except for solid moderators. Currently, only the five crystalline
materials graphite, beryllium, beryllium oxide, FCC aluminum, and BCC iron
are supported for coherent elastic scattering. Options for UO2and UC need to
NJOY2016 673

LA-UR-17-20093 24 LEAPR
be added. The current evalution for U in UO2and O in UO2uses the Bragg
edges from the old UO2evaluation divided between the two channels. If iel=0
and twt=0.0, an incoherent elastic section is automatically added to the ENDF
tape. This normally occurs for hydrogenous solids like polyethylene, ZrH, or
frozen methane. The nscold option is set to zero, except when a liquid hy-
drogen or deuterium calculation is desired. The nsk parameter is used when
intermolecular interference is represented. See Cards 17, 18, and 19.
Card 6. The “secondary scatterer” card would be just “0/” for simple materi-
als like graphite or beryllium. The behavior of LEAPR for molecular moderators
is determined by the value of B7. The choice B7=0.0 is for mixed moderators
like BeO and Benzine. In these cases, the entire S(α, β) for the molecule is
given in MF=7/MT=4, and it is intended to be used with the neutron file for
the primary scatterer. The secondary scatterer’s cross section, atomic weight
ratio, and effective temperature are only used for extending S(α, β) with the
SCT approximation (see THERMR). When B7>0.0, only the scattering law for
the primary scatterer is given. The effects of the secondary scatterer are to be
included later by using an analytic law. For example, in the water evaluation,
the S(α, β) is for H in H2O; the oxygen is included later by using a free-gas cross
section using the given sps and aws.
Cards 7, 8 and 9. Cards 7-9 are used to define the αand βgrids for the
LEAPR run. In the ENDF thermal format, the values for S(α, β) for the higher
temperatures are given on the same αand βgrids as for the base temperature,
but since αand βare inversely proportional to T, only the smaller αand β
values would be seen at higher temperatures. The results for the higher values
would normally be zero. This is a waste of space in the fields on the ENDF
evaluation. Using LAT=1 will spread the scattering law values for the higher
temperatures out, thereby giving a more accurate representation.
The range of βhelps determine the high-energy limit for the evaluation. For
example, if Tis 296K, a value of βmax of 160 will allow downscatter events of 4
eV to be represented without recourse to the SCT approximation. This implies
that pretty good results would be obtained for incident neutrons with energies
of 4 eV. If incident energies are limited to βmaxkT , the range of αvalues that
can be obtained using Eq.508 is limited to αmax = 4βmax/A. The specific points
in the αand βgrids are hard to choose. Too many points makes the evaluation
expensive to use; too few lead to inaccurate interpolated results. The low β
674 NJOY2016

24 LEAPR LA-UR-17-20093
grid should probably have about the same detail as the input ρ(β) in order to
reflect all the structure in the frequency distribution. Because of the smoothing
effect of the convolutions, the grid can gradually get coarser as βincreases. GA
traditionally used a log spacing in this higher region. If translational modes are
to be included, a finer βgrid for small βmay be required to get good results at
small α. If discrete oscillators are included, additional βvalues might be needed
near the values ±nβiand their various sums and differences, especially for n=1.
After running LEAPR, the user should examine the results vs βprinted out on
the listing and the results vs αprinted out on the ENDF file to see whether the
features of S(α, β) are being represented well enough. If the normalization and
sum rule checks are not being satisfied well, this may be an indication that the
grids are too coarse.
If a secondary scatterer with B7=0.0 is seen, it is necessary to read two entire
temperature loops, one for the principal scatterer, and one for the secondary
scatterer. See the BeO example below for how this is done.
Cards 10 through 19. LEAPR allows you to change the input frequency
distribution ρ() for every temperature, but for many ENDF/B evaluations, it
is taken to be energy independent. In those cases, Cards 11-19 are given for the
first temperature only. Subsequently, only Card 10 is given to enter the desired
temperature value.
The input distribution is given as a function of energy (eV) on a uniform grid.
It can be in arbitrary units; it will always be normalized to the value tbeta.
If a translational term is desired in addition, set twt to a number greater than
zero. The translational term can be either a free-gas law (c=0.0) or a diffusive
law (c>0.0).
Card 14 is used to enter the number of discrete oscillators desired. Their
energies and weights are given on Cards 15 and 16. It is important to obey the
restriction
wt+ws+
ND
X
i=1
wi= 1 (578)
Of course, if nd=0, the sum over iin this equation is omitted.
Card 17 is only given for the liquid hydrogen or liquid deuterium cases. It
controls the entry of the pair-correlation function used to account for inter-
molecular interference at very low neutron energies. There are two options for
this: Vineyard and Skold. Card 18 gives the actual values for the pair-correlation
NJOY2016 675

LA-UR-17-20093 24 LEAPR
function S(κ). See the liquid hydrogen example below for an example of how
this quantity is entered. Card 19 gives the coherent scattering fraction for use
with the Skold option. See the D in D2O example for how this is entered.
Card 20. The final section of the input deck gives the new comment cards
to be added to the section MF=1/MT=451 on the ENDF file generated by
LEAPR. If this section is to be a part of a standard library like ENDF/B-VII,
there are standard fields that must appear. An example of the appearance of
such a formal section will be found in the graphite example below. Note that the
comment cards are terminated by an empty card; the number of cards entered
is counted by LEAPR.
24.3 LEAPR Examples
The examples that follow were chosen for their practical importance and to
illustrate several important points.
The Model for Graphite. The basic physics for graphite was left unchanged
from the original GA evaluation[52]. A concise account appears in the new
ENDF File 1 comment cards included in the input deck below. The important
changes are the extended αand βgrids, an updated value for the cross section
to match the value in ENDF/B-VII.0, and the use of LEAPR itself. The new
grids were chosen to allow energies up to 4 eV. Note that αvalues are only
needed up to 4βmax/A. The input deck for the LEAPR graphite run follows:
leapr
20/
’graphite, endf model (extended) ’/
10 1/
31 131./
11.898 4.7392 1 1/
0/
72 96 1/
.01008 .015 .0252 .033 .0504 .0756 .1008 .15
2.52030e-1 .33 5.040600-1 7.560900-1 1.008120+0 1.260150+0 1.512180+0
1.76421e+0 2.016240+0 2.273310+0 2.535520+0 2.802970+0 3.075770+0
3.35401e+0 3.637900+0 3.927330+0 4.222710+0 4.523830+0 4.831110+0
5.14443e+0 5.464110+0 5.790130+0 6.122610+0 6.461850+0 6.807830+0
7.16077e+0 7.520670+0 7.887830+0 8.262340+0 8.644320+0 9.033960+0
676 NJOY2016

24 LEAPR LA-UR-17-20093
9.43136e+0 9.836730+0 1.025060+1 1.067190+1 1.110240+1 1.154090+1
1.19886e+1 1.244520+1 1.291100+1 1.338580+1 14. 15. 16. 17. 18.
19. 20. 22. 24. 26. 28. 30. 32.5 35. 37.5 40. 42.5 45. 47.5
50. 52.5 55. 60. /
0.000000+0 1.008120-1 2.016240-1 3.024360-1 4.032480-1 5.040600-1
6.048720-1 7.056840-1 8.064960-1 9.073070-1 1.008120+0 1.108930+0
1.209740+0 1.310550+0 1.411370+0 1.512180+0 1.612990+0 1.713800+0
1.814610+0 1.915430+0 2.016240+0 2.117050+0 2.217860+0 2.318670+0
2.419490+0 2.520300+0 2.621110+0 2.721920+0 2.822730+0 2.923540+0
3.024360+0 3.125170+0 3.225980+0 3.326790+0 3.427600+0 3.528420+0
3.629230+0 3.730040+0 3.830850+0 3.931670+0 4.032480+0 4.133290+0
4.243780+0 4.364850+0 4.497620+0 4.643090+0 4.802480+0 4.977190+0
5.168730+0 5.378620+0 5.608670+0 5.73473 5.860800+0 5.99896
6.137130+0 6.28855 6.439970+0 6.60591
6.771840+0 6.95376 7.135670+0 7.33502 7.534380+0 7.75289
7.971400+0 8.21088 8.450360+0 8.975290+0
9.550520+0 1.018100+1 1.087260+1 1.162970+1 1.245930+1 1.336970+1
1.436670+1 1.545950+1 1.665710+1 1.796970+1 1.940930+1 2.098600+1
2.271390+1 2.460820+1 2.668490+1 2.896020+1 3.145330+1 3.418730+1
3.718250+1 4.046590+1 45. 50. 55. 60. 65. 70. 75. 80. /
293.6/
.005485 40/
0. .346613 1.4135 3.03321 3.25901 3.38468 3.48269
3.76397 4.05025 4.84696 7.35744 5.88224 4.63255
4.48287 5.80642 4.63802 4.28503 3.92079 4.91352
5.53836 7.51076 5.31651 5.40525 5.20376 5.3276
7.17251 3.31813 4.50126 5.04663 4.2089 2.91985
4.65109 13.1324 7.25016 6.5662 5.47181 5.06137
5.19813 .457086 0./
0. 0. 1. 0./
0/
-400/
-500/
-600/
-700/
-800/
-1000/
-1200/
-1600/
-2000/
’ graphite lanl eval-may05 macfarlane ’/
’ ref. 4 dist- ’/
NJOY2016 677

LA-UR-17-20093 24 LEAPR
’ ---- endf/b-6 material 31 ’/
’ ----- thermal neutron scattering data ’/
’ ------ endf-6 ’/
’ ’/
’ temperatures = 293.6, 400, 500, 600, 700, 800, 1000, ’/
’ 1200, 1600, 2000 deg k. ’/
’ ’/
’ history ’/
’ ------- ’/
’ ’/
’ changed temperatures may05’/
’ ’/
’ this evaluation was generated at the los alamos national ’/
’ laboratory (apr 1993) using the leapr code. the physical ’/
’ model is very similar to the one used at general atomic ’/
’ in 1969 to produce the original endf/b-iii evaluations ’/
’ (see ref. 1). tighter grids and extended ranges for alpha ’/
’ and beta were used. a slightly more detailed calculation ’/
’ of the coherent inelastic scattering was generated. of ’/
’ course, the various constants were updated to agree with ’/
’ the endf/b-vi evaluation of natural carbon. ’/
’ ’/
’ theory ’/
’ ------ ’/
’ graphite has an hexagonal close-packed crystal structure. the ’/
’ lattice dynamics is represented using a model with four force ’/
’ constants (refs.2,3). one force constant is used to describe a ’/
’ nearest-neighbor central force that binds two hexagonal planes ’/
’ together, another describes a bond-bending force in an hexagonal ’/
’ plane, the third is for bond-stretching between nearest neighbors ’/
’ in a plane, and the fourth corresponds to a restoring force ’/
’ against bending of the hexagonal plane. the force constants ’/
’ were evaluated numerically using a very precise fit to the ’/
’ high and low temperature specific heat and compressibility ’/
’ of reactor grade graphite. the phonon spectrum was computed ’/
’ from this model using the root sampling method, and then used ’/
’ to compute s(alpha,beta). the coherent elastic scattering ’/
’ cross section was computed using the known lattice ’/
’ structure and the debye-waller integrals from the lattice ’/
’ dynamics model. ’/
’ ’/
’ references ’/
678 NJOY2016

24 LEAPR LA-UR-17-20093
’ ---------- ’/
’ 1. j.u.koppel and d.h.houston, reference manual for endf thermal ’/
’ neutron scattering data, general atomic report ga-8774 ’/
’ revised and reissued as endf-269 by the national nuclear ’/
’ data center, july 1978. ’/
’ 2. j.a.young, n.f.wilkner, and d.e.parks, nukleonik ’/
’ band 1, 295(1965). ’/
’ 3. j.a.young and j.u.koppel, j.chem.phys. 42, 357(1965). ’/
’ 4. r.e.macfarlane, new thermal neutron scattering files for ’/
’ endf/b-vi release 2, los alamos national laboratory report ’/
’ la-12639-ms (march 1994). ’/
’ ’/
/
stop
The first card tells the code to write the S(α, β) output on unit 20. After
the comment card, which is just for the user’s convenience and does not go
into the output file, comes the global options for the run. Here we see that 10
temperatures and a mid-size listing are desired. The default size for the phonon
expansion of 100 is taken. The next card gives the ENDF MAT number to be
used and a substitute for ZA.
The next input line gives information for the primary scatterer. In this case,
there is only a primary; its ZA is 11.898 and its free scattering cross section is
4.7392 barns. These values come from the ENDF/B-VII.0 carbon evaluation.
The next field indicates that there is only one of the primary scatterers in the
compound. The coherent elastic option is set to 1, which means that the code
obtains its information from the ENDF file. The “secondary scatterer” card just
has “0/” for graphite.
The following lines are used to define the αand βgrids for the LEAPR
run. Each list is terminated by a “/” character. The graphite case uses 72 α
values and 96 βvalues. The high upper limits for αand βallow for a high
energy limit in the calculation. The next field gives the LAT parameter. The
frequency distribution was copied directly from the GASKET input in the GA
report, except the last point was changed to satisfy LEAPR input restrictions.
See Fig. 72.
LEAPR allows you to change the input frequency distribution for every tem-
perature, but this has not been done very often. The new ENDF/B-VII.0 evalu-
ations for H in H2O and D in D2O are exceptions. In this case, the distribution
NJOY2016 679
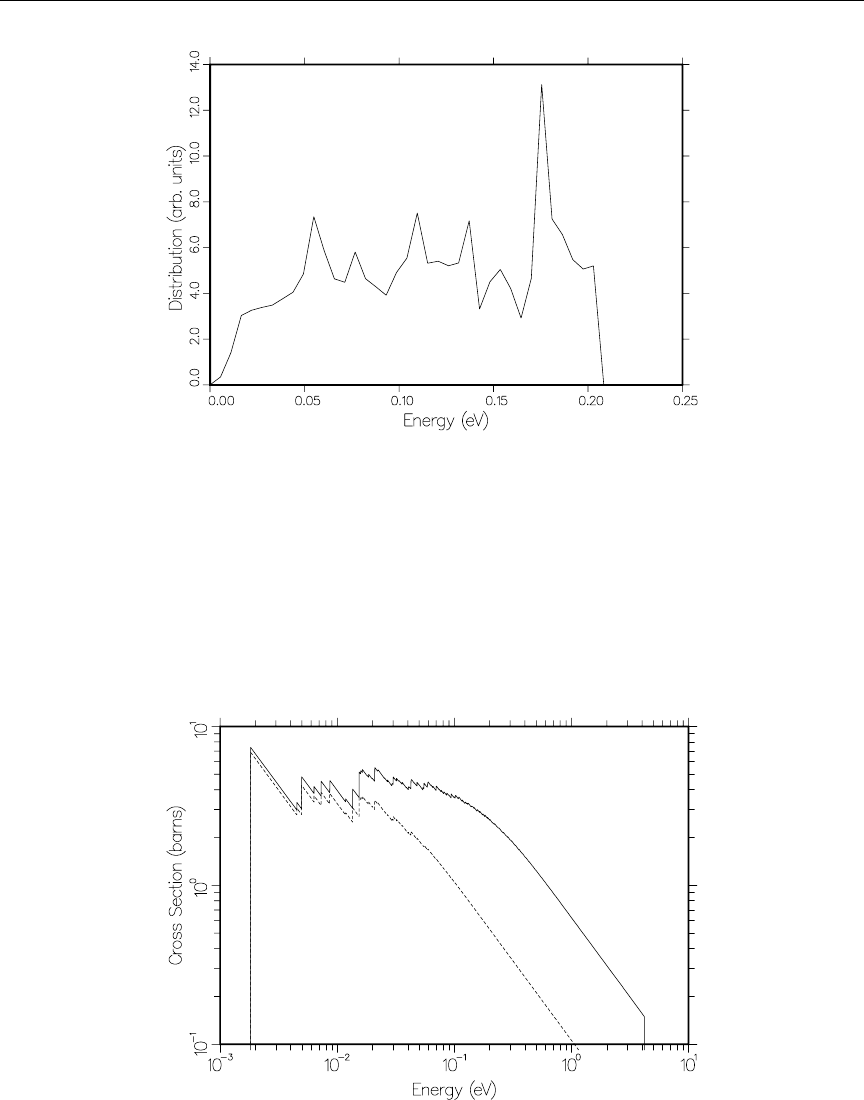
LA-UR-17-20093 24 LEAPR
Figure 72: The phonon frequency spectrum ρ() used for graphite.
is not temperature dependent, and the minus sign in front of each subsequent
temperature indicates that no additional parameters are to be read for that
temperature.
The rest of the sample input for graphite gives comment cards to be entered
into MF1/MT451 in the new evaluation.
Figure 73: The coherent elastic cross section for graphite at temperatures of 293.6K (solid)
and 2000K (dashed) showing the Bragg peaks. Note that the 293.6K cross
section near the 4 eV breakpoint is still an appreciable part of the 4.74 barn free
cross section.
680 NJOY2016
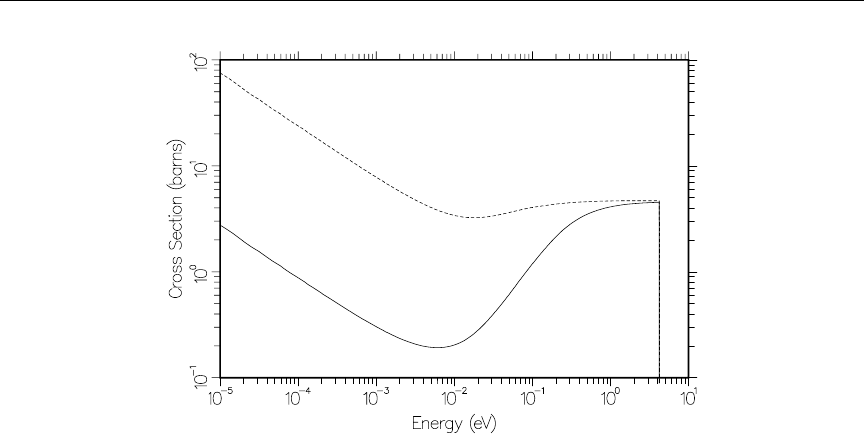
24 LEAPR LA-UR-17-20093
Figure 74: The incoherent inelastic cross section for graphite at temperatures of 293.6K
(solid) and 2000K (dashed). A comparison of the two curves near the 4 eV
breakpoint shows that the 293.6K cross section still has not reached the 4.74
barn free cross section. However, the sum of the elastic and inelastic components
does equal the free value.
After echoing back the input, the code prints out ρ(β), P(β), and T1(β)
in normalized form. It then prints out the effective temperature for the SCT
approximation and the Debye-Waller factor needed for the coherent scattering
cross section calculation. The break points between the phonon expansion and
the SCT are also shown. LEAPR next computes the S(α, β) function for each
α. For quality control, it displays the results of the normalization and sum rule
tests. If these tests are not fairly close to unity, it may be necessary to tighten
up the grids used for the calculation. Don’t worry about test failures at high
values of α; the βgrid will not extend to high enough values to complete the
integral over β.
An examination of the ENDF-6 output on “tape20” will show that both
coherent elastic scattering (MF=7/MT=2) and incoherent inelastic scattering
(MF=7/MT=4) are included in the new evaluation. As shown in Fig. 73, the
the coherent scattering extends all the way to 4 eV, which is an improvement
over the original GA evaluation. There is also enough range in αand βgrids to
compute thermal inelastic cross sections up to 4 eV. See Fig. 74.
The Model for BeO This example demonstrates how to prepare a mixed
S(α, β). Actually, the evaluation used in ENDF/B-VII.0 (and later) splits the
BeO case into separate parts for Be in BeO and O in BeO. This earlier example
NJOY2016 681

LA-UR-17-20093 24 LEAPR
is kept here to demonstrate the methods used for preparing mixed moderators.
The basic physics was left unchanged from the GA evaluation of 1969[52].
Note that the following input deck contains both “Be in BeO” and “O in BeO”.
The mixing option is selected by the “0.” in the second field of input card 6.
682 NJOY2016

24 LEAPR LA-UR-17-20093
leapr
20/
’test of BeO in LEAPR’/
1/
27 4009/
8.93478 6.15 1 3/
1 0. 15.858 3.7481 1/
50 80 1/
.252 .504 .756 1.008 1.260 1.512 1.764 2.016 2.268 2.520 2.772 3.024
3.282 3.544 3.813 4.087 4.366 4.652 4.943 5.241 5.545 5.855 6.172 6.495
6.825 7.162 7.507 7.858 8.217 8.583 8.957 9.339 9.729 10.13 10.53 10.95
11.37 11.81 12.25 12.69 13.16 13.63 14.11 14.60 15.10 15.61 16.13 16.66
17.21 17.76/
0. .1513 .3025 .4537 .6049 .7561 .9073 1.059 1.210 1.361 1.512 1.663
1.815 1.966 2.117 2.268 2.419 2.571 2.722 2.873 3.024 3.176 3.327 3.478
3.629 3.780 3.932 4.083 4.241 4.408 4.583 4.766 4.958 5.159 5.371 5.592
5.825 6.069 6.325 6.593 6.875 7.170 7.480 7.805 8.146 8.504 8.879 9.273
9.686 10.12 10.57 11.05 11.55 12.07 12.62 13.20 13.81 14.44 15.11 15.81
16.54 17.31 18.12 18.96 19.85 20.78 21.76 22.78 23.86 24.99 26.17 27.41
28.71 30.08 31.51 33.01 34.59 36.24 37.98 39.80/
296/ Be in BeO
.0016518 84/
0.0 .3 .7 .9 1. 1.2 1.6 2.0 2.2 3.0 3.5 4.5 5.5 6.8 8.0 9.2 10.9 12.9
15.5 18.6 22.0 26.0 30.5 35.0 39.0 40.0 34.0 28.0 26.0 24.4 23.0
21.3 19.8 17.0 14.1 12.0 10.0 9.0 9.0 8.5 7.5 6.0 4.6 3.1 1.6
0.5 0. 0.0 4.0 15.0 38.0 52.0 70.0 105.0 165.0 230.0 200.0 170.0
145.0 136.0 134.0 112.0 96.0 89.0 84.0 75.0 87.0 81.0 66.0 59.0
68.0 105.0 95.0 97.0 135.0 163.0 130.0 111.0 92.0 67.0 45.0 19.0
7.0 0.0/
0. 0. 1./
0/
296/ O in BeO
.0016518 84/
0.0 0.4 0.8 1.0 1.4 2.0 2.5 3.5 4.8 6.2 8.9 11.0 14.0 17.2 21.5 26.5
34.0 40.0 46.0 58.0 60.0 93.0 110.0 129.0 141.0 142.0 125.0 101.0
93.0 92.0 91.0 95.0 95.0 98.0 108.0 93.0 78.0 98.0 112.0 115.0 145.0
160.0 190.0 190.0 120.0 43.0 0.0 0.0 1.0 9.0 19.0 26.0 35.0 48.0 66.0
92.0 82.0 56.0 44.0 35.0 29.0 21.0 15.0 11.5 9.0 8.0 7.0 6.0 5.2
4.5 5.0 5.9 6.0 5.0 4.0 2.5 1.8 1.0 0.50 0.50 0.20 0.0 0.0 0.0/
0. 0. 1. 0./
NJOY2016 683
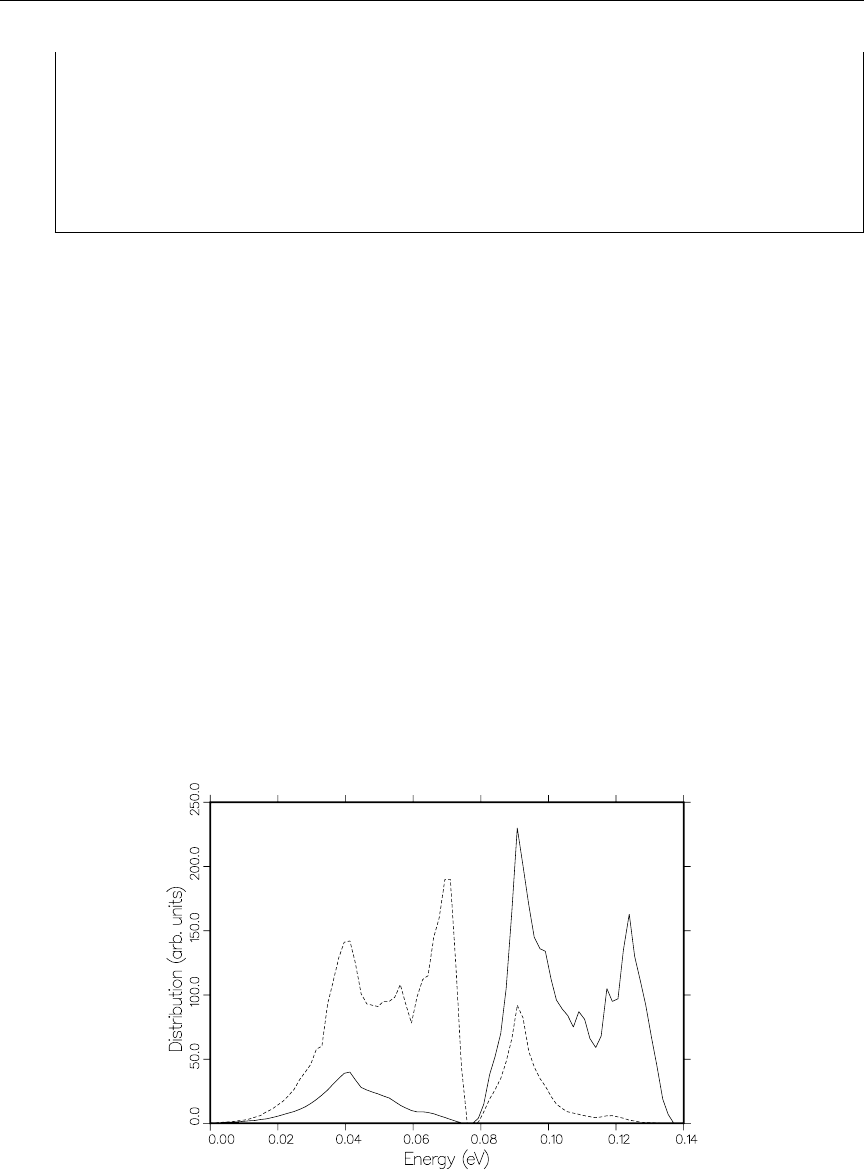
LA-UR-17-20093 24 LEAPR
0/
’TEST COMMENTS’/
’FOR MF1/MT451 OF BEO’/
/
STOP
The output listing for this case starts with the output for the primary scat-
terer “Be in BeO” and continues with results for the secondary scatterer “O in
BeO”. Note that the αvalues for the secondary scatterer have been transformed
by the atomic weight ratio of the two atoms. This allows us to add the S(α, β)
contribution for αifrom Be in BeO to the contribution for αifrom O in BeO
with only a cross-section weighting. The resulting S(α, β) is intended to be used
with the beryllium cross sections. The two frequency distributions are shown in
Fig. 75.
The listing includes effective temperatures and Debye-Waller factors for both
constituents. The average of the Debye-Waller factors is used in computing the
coherent elastic scattering for BeO.
The ENDF output on tape20 looks pretty much like the results for graphite,
except data for two scatterers is given at the start of MF=7/MT=4, and two
effective temperatures are given at the end of the section.
Figure 75: The frequency spectr ρ() used for Be in BeO (solid) and O in BeO (dashed).
684 NJOY2016
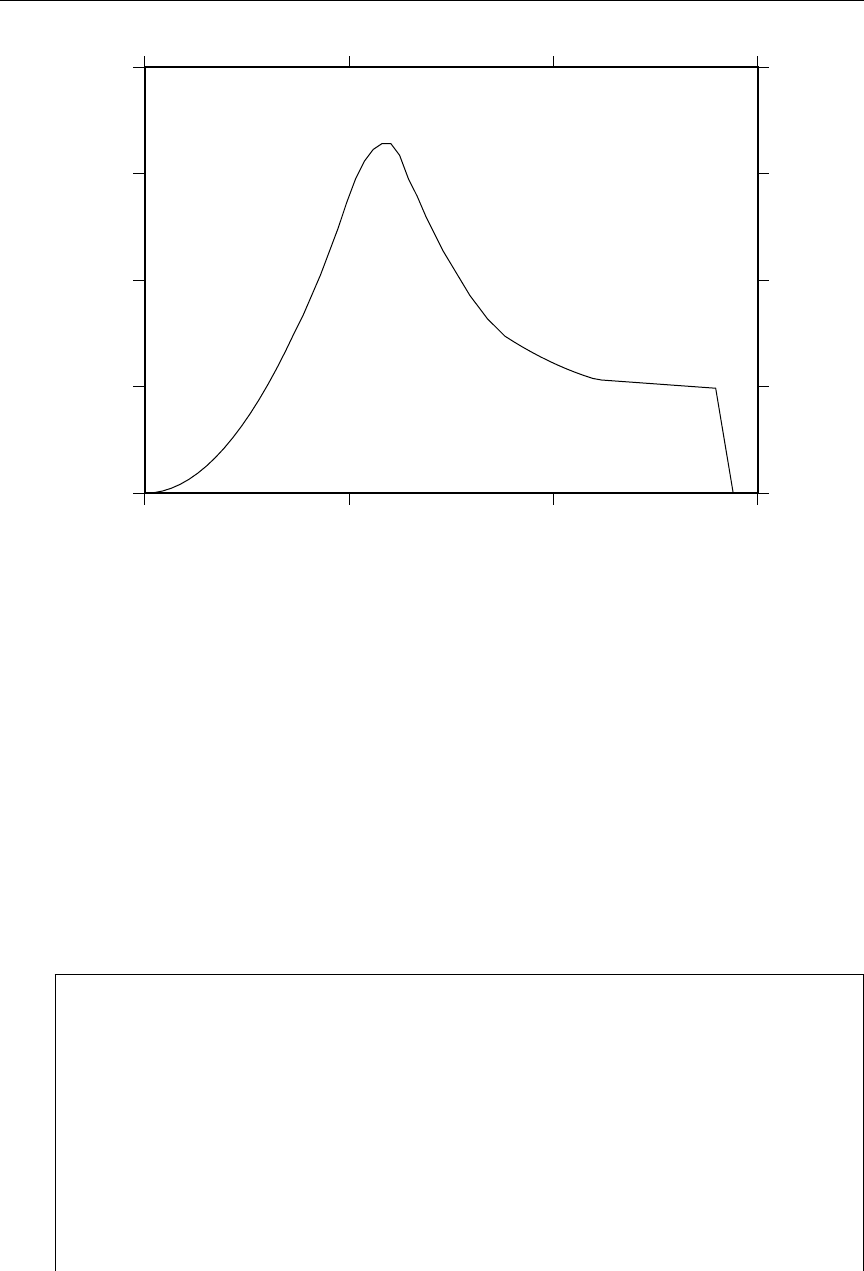
24 LEAPR LA-UR-17-20093
0 50 100 150
*10-3
Energy (eV)
0
2
4
6
8
rho
Figure 76: The frequency spectrum used for H in H2O for ENDF/B-VII.0.
The Model for Water. The current ENDF/B-VII.0 evaluation for the ther-
mal scattering law for H bound in H2O is based on recent work done under
IAEA auspices[110] with some slight modifications. Mainly, the αand βgrids
were extended and enhanced. The temperature grid was modified to be more
like the other ENDF/B cases by interpolating in the original distributions. Note
that the frequency spectrum is temperature dependent in this input. The 296K
spectrum is shown in Fig. 76. In addition, the energy scale of the rotational
spectrum was adjusted slightly to improve agreement with experiment in the
region between 0.01 eV and 0.1 eV. The final input deck is listed below.
leapr
20’
’ H in H2O, IKE model modified at LANL’ /
9 2 200/
1 1001/
0.99917 20.43634 2/ latest Hale values for VII
1 1 1.585751+1 3.842443 1/ oxygen as free gas from VII
187 274 1/ lat=1
.001 .0015 .0025 .0035 .005 .007 .01 .015 .025 .035 .05 .070
NJOY2016 685

LA-UR-17-20093 24 LEAPR
.1 .125 .15 .2 .25 .3 .325
.35 .375 .4 .425 .45 .475 .5
.525 .55 .58 .61 .65 .69 .73
.78 .83 .88 .94 1. 1.08 1.16
1.24 1.33 1.43 1.54 1.66 1.79 1.94
2.09 2.26 2.48 2.7127 2.89 3.11 3.38
3.67 3.98 4.32 4.65 5.0 5.4255 6.
6.56 7.13 7.6 8.1026 8.8 9.5 10.2
10.8152 11.7 12.6 13.528 14.4 15.3 16.2051
17.233 18.2 18.92 20.3 21.63 22.9 24.308
25.6 27.02 28.4 29.73 31. 32.41 33.44
34.466 36.15 37.18 38.8 40.513 41.54 42.57
44.2 46.0 47.0 48.615 49.6 51.2 52.5
54.41 55.2 56.72 58.4 59.80 61.2 62.51
63.8 65.23 66.5 67.90 68.93 70.61 71.64
72.92 75.9 80. 84. 89. 94. 100.
105. 113. 120.63 126. 132. 140. 147.
154. 162. 170. 177. 184. 191. 199.
208. 218. 227. 237. 246. 255. 265.
275.72 284. 293.58 302. 311. 320. 329.
338. 347. 356. 365. 374. 383. 392.
401. 410. 419. 428. 437. 446. 455.
464. 473. 482. 491. 500. 509. 518.
527. 536. 545. 554. 563. 572. 581.
590. 597. 604. 611. 618. 625. 632.9 / alpha
0.0 0.005 0.01 0.015 0.020 0.025 0.030 0.040 0.050
0.06 0.07 0.08 0.1 0.125
0.15 0.175 0.20 0.225 0.250 0.30 0.35 0.40 0.45
0.50 0.55 0.60 0.65 0.70 0.75 0.80
0.85 0.90 0.95 1.0 1.05 1.10 1.15
1.20 1.25 1.30 1.35 1.4 1.45 1.5
1.55 1.6 1.65 1.7 1.75 1.8 1.85
1.9 1.95 2.0 2.05 2.1 2.15 2.2
2.25 2.3 2.35 2.4 2.45 2.5 2.55
2.6 2.65 2.7127 2.77 2.83 2.90 2.96
3.03 3.11 3.18 3.26 3.34 3.43 3.52
3.61 3.71 3.81 3.92 4.03 4.14 4.26
4.39 4.52 4.65 4.80 4.94 5.10 5.26
5.4255 5.60 5.70 5.97 6.17 6.37 6.59
6.81 7.04 7.29 7.54 7.81 7.9 8.0 8.103 8.2 8.28 8.37
8.67 8.98 9.30 9.64 10. 10.4 10.8152
11.16 11.57 12.0 12.46 12.98 13.528 13.94
686 NJOY2016

24 LEAPR LA-UR-17-20093
14.48 15.03 15.62 16.2051 16.8 17. 17.233 17.5 18.2
18.92 19.4 19.95 20.7 21.63 22.1 22.66
23.5 24.308 24.8 25.34 26.2 27.02 27.5
28.05 28.9 29.73 30.2 30.76 31.5 32.41
32.9 33.44 34. 34.466 35.3 36.15 36.6
37.18 37.9 38.8 39.89 40.2 40.513 41.
41.54 42. 42.57 43.2 44.2 45.28 46.0
47.0 47.99 48.3 48.615 49.6 50.67 51.2
51.70 52.5 53.38 53.9 54.41 55.2 56.
56.72 57.12 58.4 59.80 61.2 62.51 63.8
65.23 66.5 67.90 68.4 68.93 69.8 70.61
71.1 71.64 72.2 72.92 73.3340 74. 74.8
75.6 76.4 77.2 78. 78.9 79.8 80.7
81.6 82.5 83.4 84.3 85.2 86.1 87.
88. 89. 90. 91. 92. 93. 94.
95. 96. 97. 98. 99. 100. 101.2
102.4 103.6 104.8 106. 107.2 108.4 109.6
110.8 112. 113.5 115. 116.5 118. 119.5
121. 122.5 124. 125.5 127. 128.5 130.
132. 134. 136. 138. 140. 142. 144.
146. 148. 150. 152. 154. 156. 158.1 / beta
293.6/ temperature (K)
0.00215 68/ frequency distribution
0.00000E+00 1.04170E-02 4.16710E-02 9.37490E-02 1.66682E-01
2.60457E-01 3.74972E-01 5.10341E-01 6.66586E-01 8.43707E-01
1.04169E+00 1.26039E+00 1.49991E+00 1.76047E+00 2.04172E+00
2.34379E+00 2.66665E+00 3.01045E+00 3.33873E+00 3.72164E+00
4.10441E+00 4.54222E+00 4.98019E+00 5.47328E+00 5.91196E+00
6.24071E+00 6.45971E+00 6.56965E+00 6.56980E+00 6.35010E+00
5.91059E+00 5.58143E+00 5.19738E+00 4.86852E+00 4.53952E+00
4.26544E+00 3.99124E+00 3.71714E+00 3.49814E+00 3.27889E+00
3.11484E+00 2.95067E+00 2.84650E+00 2.74784E+00 2.65469E+00
2.56706E+00 2.48495E+00 2.40835E+00 2.33727E+00 2.27169E+00
2.21165E+00 2.15711E+00 2.12732E+00 2.11543E+00 2.10353E+00
2.09165E+00 2.07975E+00 2.06786E+00 2.05596E+00 2.04408E+00
2.03218E+00 2.02029E+00 2.00839E+00 1.99651E+00 1.98461E+00
1.97272E+00 9.86360E-01 0.00000E+00/
0.0192 0. .4904 / weights
2 / discrete oscillators
.205 .436 / oscillator energies (eV)
.163467 .326933 / oscillator weigths
350./
NJOY2016 687

LA-UR-17-20093 24 LEAPR
0.00215 68/
0.00215 68/
0.00000E+00 1.01473E-02 4.05927E-02 9.13258E-02 1.62372E-01
2.53717E-01 3.65283E-01 4.97147E-01 6.49350E-01 8.21883E-01
1.01473E+00 1.22779E+00 1.46112E+00 1.71490E+00 1.98888E+00
2.28315E+00 2.59770E+00 2.93259E+00 3.25984E+00 3.63884E+00
4.02767E+00 4.45671E+00 4.88387E+00 5.34035E+00 5.73991E+00
6.04488E+00 6.25544E+00 6.34641E+00 6.34077E+00 6.15681E+00
5.79298E+00 5.49979E+00 5.16054E+00 4.85982E+00 4.56082E+00
4.31061E+00 4.06087E+00 3.81176E+00 3.60561E+00 3.39981E+00
3.23731E+00 3.06474E+00 2.95935E+00 2.84908E+00 2.74389E+00
2.64100E+00 2.54595E+00 2.45437E+00 2.37253E+00 2.29361E+00
2.22288E+00 2.15259E+00 2.10362E+00 2.07303E+00 2.04091E+00
2.00986E+00 1.98036E+00 1.95997E+00 1.93780E+00 1.91648E+00
1.89595E+00 1.87631E+00 1.86017E+00 1.84223E+00 1.82513E+00
1.80884E+00 8.99437E-01 0.00000E+00/
0.029135 0. .485433 /
2 /
.205 .436 /
.161811 .323622 /
400/
0.00215 68/
0.00000E+00 9.92998E-03 3.97244E-02 8.93749E-02 1.58902E-01
2.48290E-01 3.57482E-01 4.86523E-01 6.35474E-01 8.04310E-01
9.93028E-01 1.20154E+00 1.42988E+00 1.67821E+00 1.94634E+00
2.23432E+00 2.54218E+00 2.86990E+00 3.19677E+00 3.57300E+00
3.96771E+00 4.38985E+00 4.80833E+00 5.23385E+00 5.60019E+00
5.88507E+00 6.08865E+00 6.16336E+00 6.15269E+00 5.99938E+00
5.70048E+00 5.43794E+00 5.13693E+00 4.86008E+00 4.58656E+00
4.35661E+00 4.12764E+00 3.89978E+00 3.70442E+00 3.50993E+00
3.34851E+00 3.16838E+00 3.06178E+00 2.94128E+00 2.82550E+00
2.70924E+00 2.60283E+00 2.49814E+00 2.40685E+00 2.31627E+00
2.23617E+00 2.15212E+00 2.08649E+00 2.03966E+00 1.98998E+00
1.94228E+00 1.89751E+00 1.86973E+00 1.83863E+00 1.80911E+00
1.78107E+00 1.75470E+00 1.73486E+00 1.71165E+00 1.69001E+00
1.66990E+00 8.25640E-01 0.00000E+00/
0.0346475 0. .482676 /
2 /
.205 .436 /
0.160892 0.321784 /
450/
0.00215 68/
688 NJOY2016

24 LEAPR LA-UR-17-20093
0.00000E+00 9.75410E-03 3.90199E-02 8.77925E-02 1.56087E-01
2.43887E-01 3.51155E-01 4.77906E-01 6.24218E-01 7.90054E-01
9.75417E-01 1.18024E+00 1.40455E+00 1.64845E+00 1.91182E+00
2.19470E+00 2.49715E+00 2.81904E+00 3.14676E+00 3.52166E+00
3.92356E+00 4.34050E+00 4.75201E+00 5.14878E+00 5.48392E+00
5.75016E+00 5.94766E+00 6.00672E+00 5.99108E+00 5.86722E+00
5.63083E+00 5.39736E+00 5.13269E+00 4.87821E+00 4.62866E+00
4.41770E+00 4.20824E+00 4.00034E+00 3.81484E+00 3.63071E+00
3.46976E+00 3.28157E+00 3.17338E+00 3.04241E+00 2.91583E+00
2.78605E+00 2.66813E+00 2.55020E+00 2.44932E+00 2.34697E+00
2.25742E+00 2.15958E+00 2.07737E+00 2.01447E+00 1.94741E+00
1.88323E+00 1.82333E+00 1.78821E+00 1.74824E+00 1.71058E+00
1.67508E+00 1.64202E+00 1.61848E+00 1.59002E+00 1.56386E+00
1.53993E+00 7.56386E-01 0.00000E+00/
0.0385185 0. .480741 /
2 /
.205 .436 /
0.160247 0.320494 /
500./
0.00215 68/
0.00000E+00 9.59182E-03 3.83708E-02 8.63356E-02 1.53495E-01
2.39833E-01 3.45330E-01 4.69972E-01 6.13855E-01 7.76930E-01
9.59202E-01 1.16064E+00 1.38122E+00 1.62104E+00 1.88004E+00
2.15823E+00 2.45569E+00 2.77222E+00 3.10113E+00 3.47514E+00
3.88458E+00 4.29687E+00 4.70201E+00 5.07095E+00 5.37579E+00
5.62401E+00 5.81575E+00 5.85948E+00 5.83894E+00 5.74390E+00
5.56870E+00 5.36355E+00 5.13433E+00 4.90155E+00 4.67527E+00
4.48277E+00 4.29224E+00 4.10374E+00 3.92773E+00 3.75358E+00
3.59291E+00 3.39657E+00 3.28670E+00 3.14529E+00 3.00795E+00
2.86472E+00 2.73536E+00 2.60427E+00 2.49386E+00 2.37982E+00
2.28086E+00 2.16936E+00 2.07076E+00 1.99198E+00 1.90775E+00
1.82730E+00 1.75245E+00 1.71007E+00 1.66134E+00 1.61563E+00
1.57276E+00 1.53308E+00 1.50587E+00 1.47223E+00 1.44158E+00
1.41387E+00 6.89143E-01 0.00000E+00/
0.0417390 0. 0.479131 /
2 /
.205 .436 /
.159710 .319420 /
550./
0.00215 68/
0.00000E+00 9.44225E-03 3.77730E-02 8.49922E-02 1.51106E-01
2.36096E-01 3.39961E-01 4.62659E-01 6.04301E-01 7.64830E-01
NJOY2016 689

LA-UR-17-20093 24 LEAPR
9.44252E-01 1.14257E+00 1.35972E+00 1.59577E+00 1.85074E+00
2.12460E+00 2.41747E+00 2.72905E+00 3.05951E+00 3.43307E+00
3.85041E+00 4.25857E+00 4.65785E+00 4.99971E+00 5.27495E+00
5.50565E+00 5.69192E+00 5.72054E+00 5.69514E+00 5.62848E+00
5.51353E+00 5.33613E+00 5.14167E+00 4.93008E+00 4.72654E+00
4.55204E+00 4.38002E+00 4.21047E+00 4.04363E+00 3.87915E+00
3.71857E+00 3.51397E+00 3.40232E+00 3.25044E+00 3.10232E+00
2.94564E+00 2.80482E+00 2.66059E+00 2.54064E+00 2.41493E+00
2.30656E+00 2.18144E+00 2.06653E+00 1.97198E+00 1.87070E+00
1.77407E+00 1.68437E+00 1.63478E+00 1.57734E+00 1.52363E+00
1.47343E+00 1.42716E+00 1.39631E+00 1.35749E+00 1.32239E+00
1.29091E+00 6.23480E-01 0.00000E+00/
0.044466 0. 0.477767 /
2 /
.205 .436 /
0.159256 0.318512 /
600./
0.00215 68/
0.00000E+00 9.30614E-03 3.72301E-02 8.37725E-02 1.48936E-01
2.32702E-01 3.35086E-01 4.56017E-01 5.95626E-01 7.53841E-01
9.30674E-01 1.12615E+00 1.34019E+00 1.57282E+00 1.82412E+00
2.09406E+00 2.38276E+00 2.68985E+00 3.02226E+00 3.39584E+00
3.82152E+00 4.22611E+00 4.62011E+00 4.93565E+00 5.18198E+00
5.39565E+00 5.57674E+00 5.59048E+00 5.56024E+00 5.52153E+00
5.46600E+00 5.31580E+00 5.15545E+00 4.96453E+00 4.78321E+00
4.62629E+00 4.47234E+00 4.32131E+00 4.16331E+00 4.00819E+00
3.84750E+00 3.63447E+00 3.52091E+00 3.35849E+00 3.19952E+00
3.02936E+00 2.87703E+00 2.71964E+00 2.59009E+00 2.45269E+00
2.33489E+00 2.19614E+00 2.06498E+00 1.95472E+00 1.83644E+00
1.72372E+00 1.61923E+00 1.56244E+00 1.49632E+00 1.43462E+00
1.37712E+00 1.32429E+00 1.28978E+00 1.24581E+00 1.20626E+00
1.17101E+00 5.59371E-01 0.00000E+00/
0.046537 0. 0.476732 /
2 /
.205 .436 /
0.158911 0.317821 /
650./
0.00215 68/
0.00000E+00 9.20968E-03 3.68424E-02 8.29024E-02 1.47390E-01
2.30283E-01 3.31608E-01 4.51281E-01 5.89440E-01 7.46008E-01
9.20999E-01 1.11445E+00 1.32627E+00 1.55647E+00 1.80516E+00
2.07229E+00 2.35801E+00 2.66190E+00 2.99405E+00 3.36630E+00
690 NJOY2016

24 LEAPR LA-UR-17-20093
3.79437E+00 4.19585E+00 4.58597E+00 4.88805E+00 5.11997E+00
5.32491E+00 5.50293E+00 5.50965E+00 5.47725E+00 5.45177E+00
5.42426E+00 5.28734E+00 5.14353E+00 4.96297E+00 4.79271E+00
4.64457E+00 4.49963E+00 4.35781E+00 4.20453E+00 4.05433E+00
3.89416E+00 3.67795E+00 3.56391E+00 3.39713E+00 3.23364E+00
3.05777E+00 2.90060E+00 2.73760E+00 2.60402E+00 2.46163E+00
2.33984E+00 2.19520E+00 2.05689E+00 1.93967E+00 1.81386E+00
1.69399E+00 1.58295E+00 1.52299E+00 1.45304E+00 1.38783E+00
1.32711E+00 1.27139E+00 1.23530E+00 1.18907E+00 1.14757E+00
1.11069E+00 5.27354E-01 0.00000E+00/
0.049020 0. 0.47549 /
2 /
.205 .436 /
0.158497 0.316993 /
800./
0.00215 68/
0.00000E+00 9.20968E-03 3.68424E-02 8.29024E-02 1.47390E-01
2.30283E-01 3.31608E-01 4.51281E-01 5.89440E-01 7.46008E-01
9.20999E-01 1.11445E+00 1.32627E+00 1.55647E+00 1.80516E+00
2.07229E+00 2.35801E+00 2.66190E+00 2.99405E+00 3.36630E+00
3.79437E+00 4.19585E+00 4.58597E+00 4.88805E+00 5.11997E+00
5.32491E+00 5.50293E+00 5.50965E+00 5.47725E+00 5.45177E+00
5.42426E+00 5.28734E+00 5.14353E+00 4.96297E+00 4.79271E+00
4.64457E+00 4.49963E+00 4.35781E+00 4.20453E+00 4.05433E+00
3.89416E+00 3.67795E+00 3.56391E+00 3.39713E+00 3.23364E+00
3.05777E+00 2.90060E+00 2.73760E+00 2.60402E+00 2.46163E+00
2.33984E+00 2.19520E+00 2.05689E+00 1.93967E+00 1.81386E+00
1.69399E+00 1.58295E+00 1.52299E+00 1.45304E+00 1.38783E+00
1.32711E+00 1.27139E+00 1.23530E+00 1.18907E+00 1.14757E+00
1.11069E+00 5.27354E-01 0.00000E+00/
0.049020 0. 0.47549 /
2 /
.205 .436 /
0.158497 0.316993 /
’ H(H2O) IKE,LANL EVAL-mar06 MacFarlane,Keinert,Mattes ’/
’ INDC-NDS-0470 DIST- ’/
’----ENDF/B-VII MATERIAL 1 ’/
’-----THERMAL NEUTRON SCATTERING DATA ’/
’------ENDF-6 FORMAT ’/
’ ’/
’ Temperatures (K) ’/
’ 293.6 350 400 450 500 550 600 650 800 ’/
NJOY2016 691

LA-UR-17-20093 24 LEAPR
’ ’/
’ This evaluation[1] was generated at IKE in January of 2004 using ’/
’ the LEAPR module of the NJOY Nuclear Data Processing System[2] ’/
’ and modified at LANL in March of 2006 to use a temperature grid ’/
’ more like the other ENDF evaluations and to fit the experimental ’/
’ data slightly better. The model is improved over the one used ’/
’ at General Atomics in 1969 to produce the original ENDF/B-III ’/
’ evaluation[3]. The alpha and beta grids have been extended to ’/
’ allow for larger incident energies and to properly represent the ’/
’ features of S(alpha,beta) for the various integrations required. ’/
’ The physical constants have been updated for ENDF/B-VII to match ’/
’ the current hydrogen and oxygen evaluations. The LANL changes ’/
’ include some additional alpha and beta points, interpolating the ’/
’ rotational energy distributions and translational masses onto ’/
’ the new temperature grid, and slightly reducing the rotational ’/
’ energies to improve the energy region between .01 and .1 eV. ’/
’ ’/
’ Water is represented by freely moving H2O molecule clusters ’/
’ with some temperature dependence to the clustering effect. ’/
’ Each molecule can undergo torsional harmonic oscillations ’/
’ (hindered rotations) with a broad spectrum of distributed ’/
’ modes. The excitation spectra were improved over the older ’/
’ ENDF model, and they are given with a temperature variation. ’/
’ In addition, there are two internal modes of vibration at ’/
’ 205 and 436 meV. The stretching mode was reduced from the ’/
’ older ENDF value of 480 meV to account for the liquid state. ’/
’ Scattering by the oxygen atoms is not included in the ’/
’ tabulated scattering law data. It should be taken into ’/
’ account by adding the scattering for free oxygen of mass 16. ’/
’ ’/
’ References ’/
’ ---------- ’/
’ 1. M.Mattes and J.Keinert, "Thermal Neutron Scattering Data ’/
’ for the Moderator Materials H2O, D2O, and ZrHx in ENDF-6 ’/
’ Format and as ACE Library for MCNP(X) Codes," INDC/NDS ’/
’ report INDC(NDS)-0470 (April 2005). ’/
’ 2. R.E.MacFarlane, "New Thermal Neutron Scattering Files for ’/
’ ENDF/B-VI Release 2," Los Alamos National Laboratory report ’/
’ LA-12639-MS (March 1994). ’/
’ 3. J.U.Koppel and D.H.Houston, "Reference Manual for ENDF ’/
’ Thermal Neutron Scattering Data," General Atomic report ’/
’ GA-8774 revised and reissued as ENDF-269 by the National ’/
692 NJOY2016
24 LEAPR LA-UR-17-20093
’ Nuclear Data Center, July 1978. ’/
’ ’/
’ ---------------------------------------------------------------- ’/
/ end leapr
stop
These αand βgrids extend to rather high values in order to allow calculations
of water cross sections to energies on the order of 10 eV.
This run specifies iprint=2 to get a more detailed output listing. Note that
the listing now includes checks for the normalization of the phonon expansion
members, Tn. It also prints out the values S(α, β), S(α, β), and S(α, −β) for
each β. Note that only the asymmetric S for −βis actually used and stored
inside the code. The other two versions are computed just before being printed.
On a short-word machine, these first two styles of Smay underflow and be
printed as zero, even though the last column is nonzero. No accuracy is actually
lost at this point.
After the results for the solid-type rotational modes have been printed out,
the code starts a print for the convolution of the translational modes with the
continuous modes. For each α, the values for Sfree are printed out, followed by
the results of the convolution, and the results of the normalization and sum-rule
tests. These results can be examined to see if the βgrid seems to be sufficient
for the problem. The problem here is that the translational peak is very sharp
for small α, and it is difficult to make the βgrid fine enough to represent it well.
Some loss in the normalization and sum-rule accuracies must be accepted.
Next, the code shows similar results for the convolution of the discrete os-
cillators with the current scattering law. Now the problem is that new peaks
appear at the nβivalues and their various sums and differences (see Table 29 for
examples). For small α, these peaks are very sharp. A few additional βpoints
can be added near the peaks to improve the results, but it is usually impractical
to represent them with full fidelity. Once again, some loss in the accuracy of the
checks must be accepted.
Finally, a summary of the effective temperature and Debye-Waller factor is
printed out, and the ENDF output file is constructed. The resulting S(α, β)
can be plotted using capabilities of the PLOTR module. Fig. 77 shows Svs
βfor various αvalues. The high-energy cutoff of the energy distribution for
the rotational modes is visible, as well as the effect of the discrete oscillators.
Fig. 78 shows Svs αfor various βvalues. Note the singularity at low αand β
NJOY2016 693
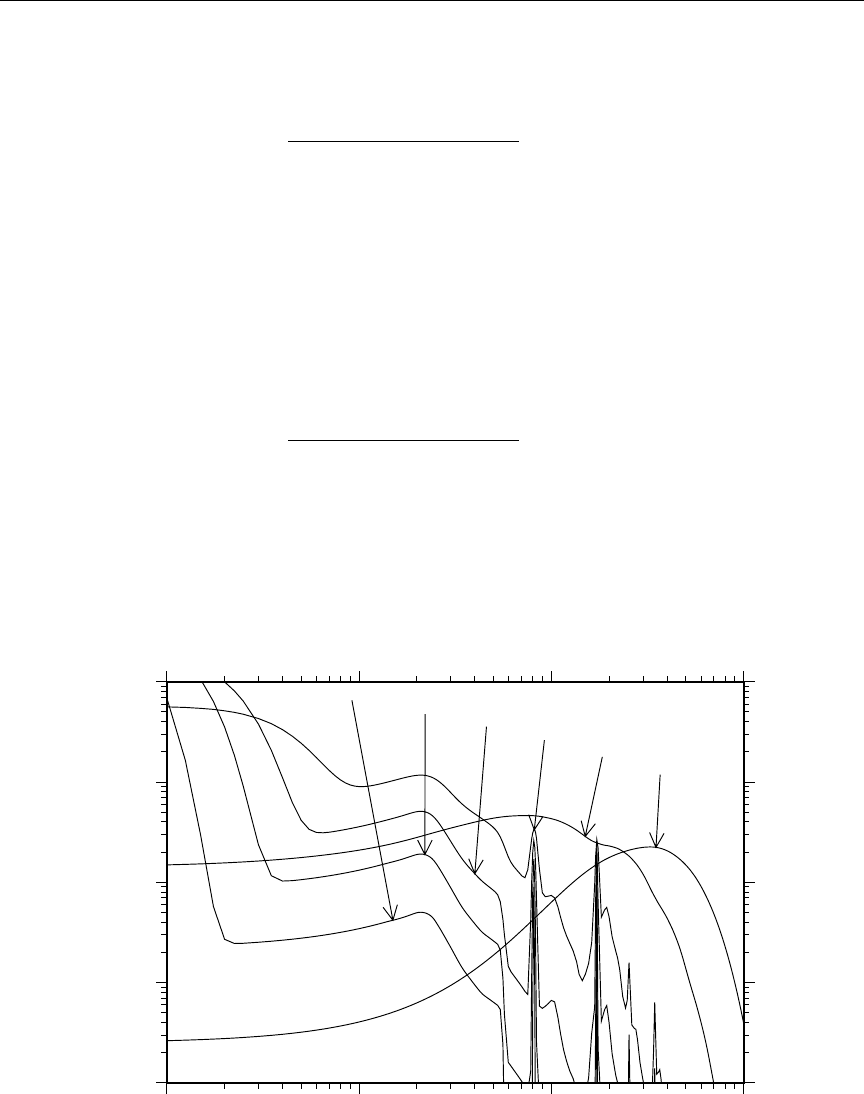
LA-UR-17-20093 24 LEAPR
Table 29: Discrete oscillator βvalues and weights for α= 1 for H in H2O.
Beta Weight
0.0000 9.6160E-01
-8.1026 1.9405E-02
-17.2328 1.8243E-02
-25.3353 3.6814E-04
-16.2051 1.9580E-04
-34.4655 1.7304E-04
8.1026 5.8752E-06
-33.4379 3.7146E-06
-42.5680 4.4920E-06
-24.3077 1.3171E-06
-51.6983 1.0943E-06
where the slope changes sign. This is an effect characteristic of the translational
modes in liquids.
The neutron emission spectra for incoherent inelastic scattering that results
from processing this scattering law is shown in Fig. 79 for several incident ener-
10-1 100101102
β
10-4
10-3
10-2
10-1
100
S-hat(α,−β)
α=.05 α=.20 α=.61 α=2.5
α=15
α=39
Figure 77: S(α, −β) for H in H2O at room temperature plotted versus βfor various values
of α.
694 NJOY2016
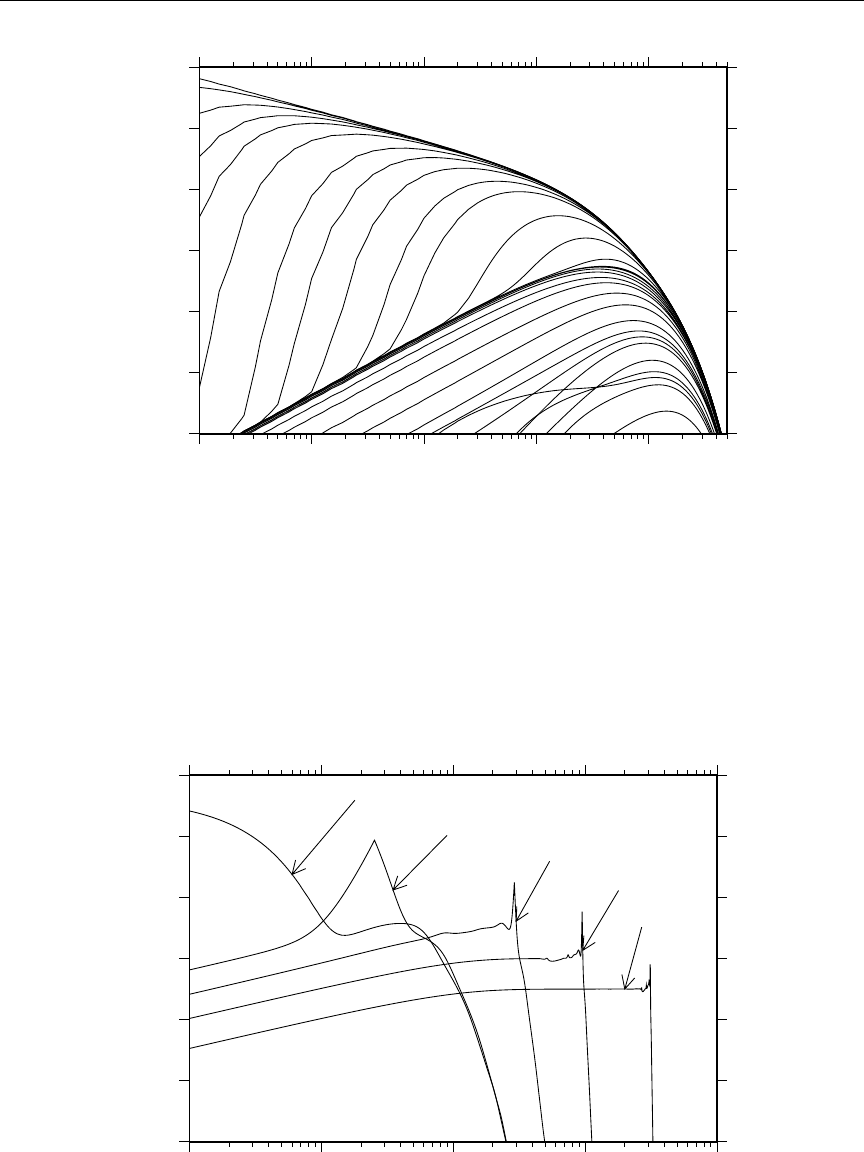
24 LEAPR LA-UR-17-20093
10-3 10-2 10-1 100101
α
10-4
10-3
10-2
10-1
100
101
102
S(α,β)
Figure 78: S(α, −β) vs αfor a number of βvalues.
gies. For very low incident energies, the neutron gains energy from the rotational
modes excited at thermal equilibrium. For higher energies, it is more probable
that the neutron will lose energy, and the effects of exciting translational, rota-
tional and vibrational modes are visible. The down-scatter behavior is shown
10-3 10-2 10-1 100101
Energy (eV)
10-3
10-2
10-1
100
101
102
103
Prob/eV
.0005 eV
.0253 eV
.2907 eV
.95 eV
3.12 eV
Figure 79: Incoherent inelastic spectra for several incident energies for H in H2O.
NJOY2016 695
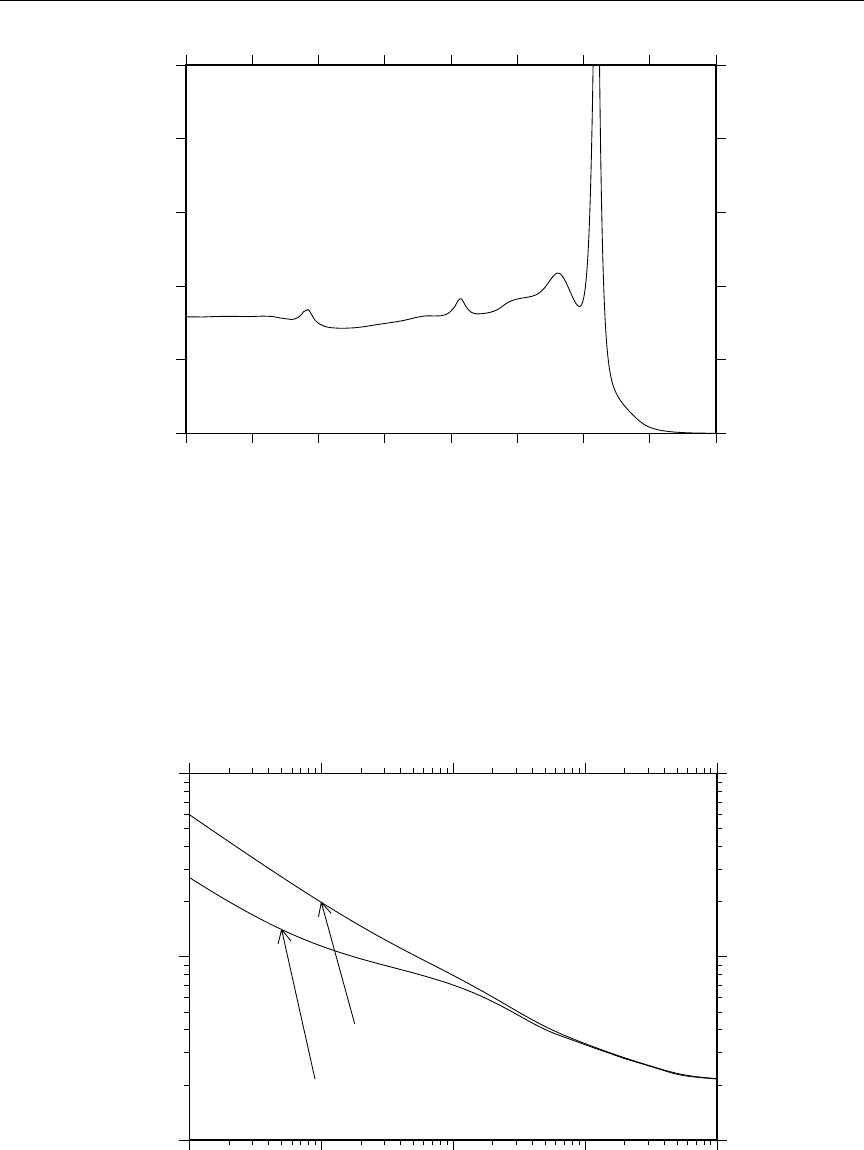
LA-UR-17-20093 24 LEAPR
2.5 2.6 2.7 2.8 2.9 3.0 3.1 3.2 3.3
Energy (eV)
0.0
0.2
0.4
0.6
0.8
1.0
Prob/eV
Figure 80: Detailed view of a neutron emission spectrum for inelastic scattering for H in
H2O.
in more detail in Fig. 80. The sharp peak at E0=Eis the quasi-elastic peak
coming from the diffusive translations. The next lower hump is from rotational
modes, and the other peaks are from vibrational modes.
10-4 10-3 10-2 10-1 100
Energy (eV)
101
102
103
Prob/eV
293.6K
600K
Figure 81: The incoherent inelastic cross section for H in H2O at two temperatures.
696 NJOY2016
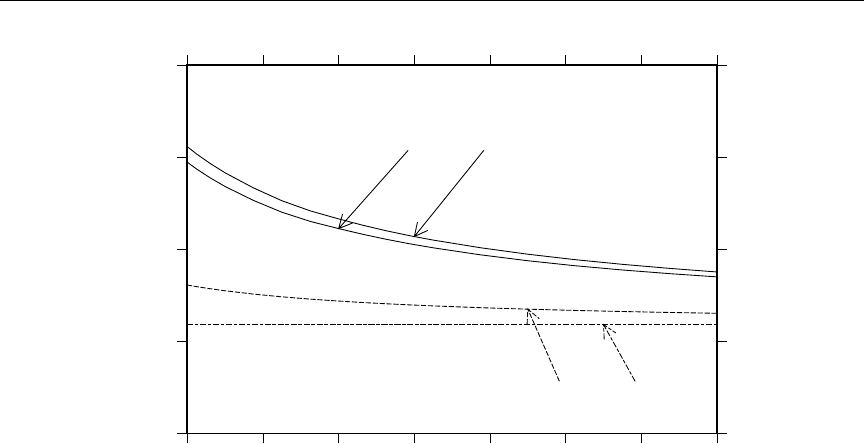
24 LEAPR LA-UR-17-20093
3 4 5 6 7 8 9 10
Energy (eV)
20.2
20.4
20.6
20.8
21.0
Sigma-in (barns)
293.6K 600K
free gas static
Figure 82: The incoherent inelastic cross section for H in H2O for higher incident energies
showing the static limit (scattering from atoms at rest) and the free-gas cross
section.
The integrated cross section is shown in Fig. 81 and Fig. 82 for two temper-
atures. As the incident energy increases, the cross section begins to approach
the free-atom value, as predicted by the theory. In practice, multigroup codes
would normally change from the thermal value to the target-at-rest value at
some particular break-point energy chosen so that error caused by the addi-
tional discontinuity at that energy group was not too significant. Monte Carlo
codes normally change from the thermal cross section to the free-gas cross sec-
tion at some breakpoint energy. There again, it is hoped that the breakpoint
can be made high enough to minimize the adverse effects of the discontinuity.
Another approach that has been used in practice is to shift from the thermal
cross section to an SCT cross section, that is, a free-gas cross section at a
higher temperature than the ambient value. Table 30 shows the effective SCT
temperatures for H in H2O. This approach gives a fairly good integrated cross
section versus energy above the thermal cutoff of the scattering law calculation,
and it gives a good downscatter spectrum, but the up-scatter is too large.
The angular behavior of thermal scattering is also of interest. For H bound
in H2O, the hydrogen atom is not as free to recoil as the free atom. This makes
it look like it has a higher effective mass, and it causes the scattering to be more
isotropic on the average. See Fig. 83. However, as Fig. 84 demonstrates, there
NJOY2016 697
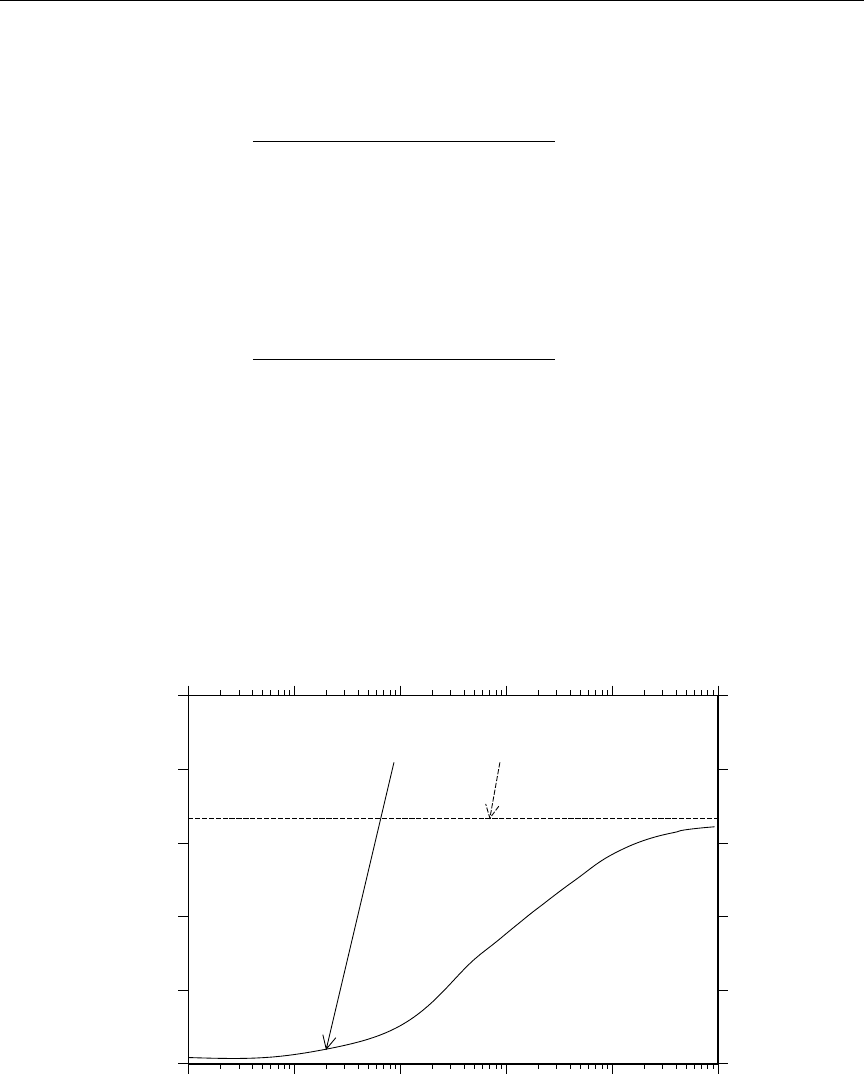
LA-UR-17-20093 24 LEAPR
Table 30: Effective temperatures for the Short Collision Time approximation for H in H2O.
Temp (◦K) Eff Temp (◦K)
293.6 1269
350 1276
400 1289
450 1305
500 1324
550 1344
600 1367
800 1473
are still interesting anisotropies seen, especially near E0=Ewhere translational
effects are important.
Fig. 85 gives an overall view of the isotropic part of the scattering distribution
for H in H2O.
As the description of the evaluation for H in H2O demonstrates, ENDF scat-
tering law data are not obtained directly from experimental measurement as that
requires more complete differential data than are currently available. Instead,
10-4 10-3 10-2 10-1 100101
Energy (eV)
0.0
0.2
0.4
0.6
0.8
1.0
mubar
bound static
Figure 83: The average scattering cosine for H in H2O compared to the static value for
scattering from atoms at rest. The effect of the binding of H in H2O is to make
the scattering more isotropic at thermal energies.
698 NJOY2016
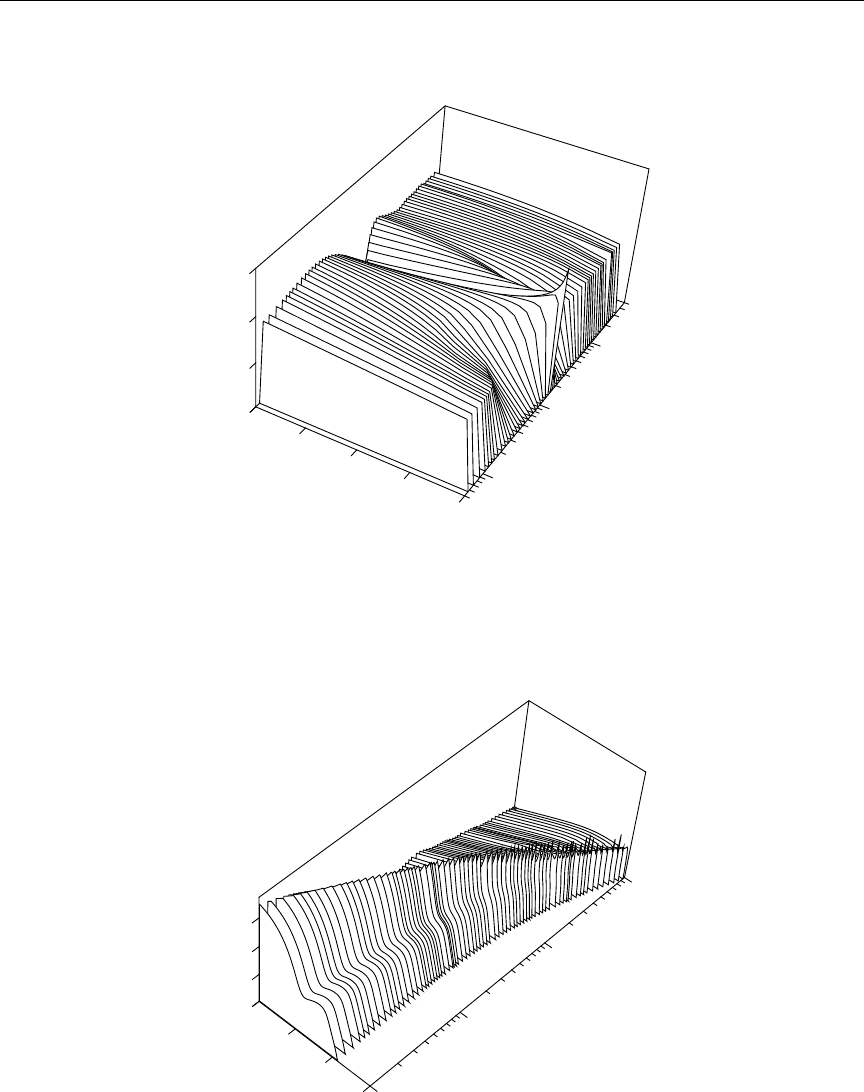
24 LEAPR LA-UR-17-20093
1
0
-
1
1
0
0
1
0
1
P
r
o
b
/
c
o
s
i
n
e
-
1
.
0
-
0
.
5
0
.
0
0
.
5
1
.
0
C
o
s
i
n
e
1
0
-
3
1
0
-
2
1
0
-
1
S
e
c
.
E
n
e
r
g
y
Figure 84: A perspective view of an angle-energy distribution for H in H2O.
1
0
0
1
0
1
1
0
2
P
r
o
b
/
e
V
1
0
-
3
1
0
-
2
1
0
-
1
1
0
0
E
n
e
r
g
y
(
e
V
)
1
0
-
3
1
0
-
2
1
0
-
1
1
0
0
E
n
e
r
g
y
e
V
)
Figure 85: A perspective view of the isotropic part of the incoherent inelastic scattering
from H in H2O. The variations in the size of the quasi-elastic peak are artifacts
of the plotting program.
NJOY2016 699
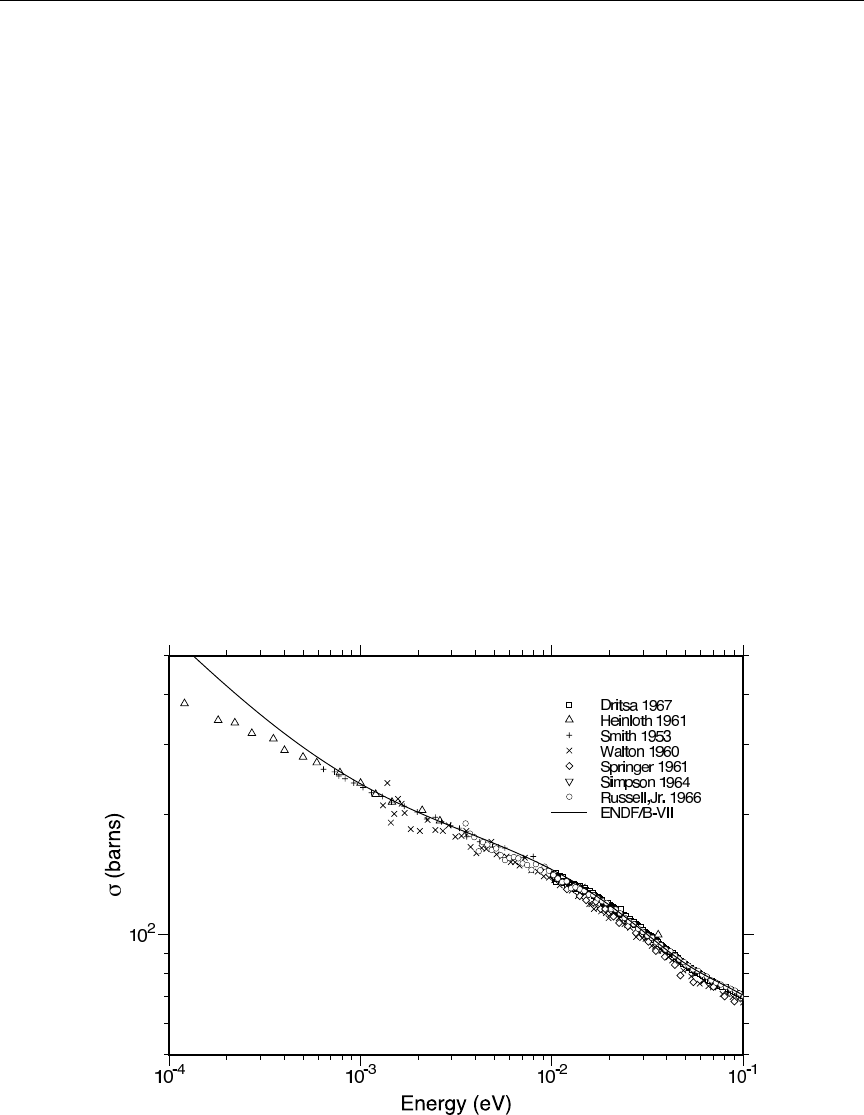
LA-UR-17-20093 24 LEAPR
they are modeled based on various kinds of input data ranging from neutron
scattering measurements to optical results. The model results are then com-
pared to the available experimental data to see how good of a job was done
with the evaluation. Examples of the comparison of the modeled thermal cross
section for water with experiment[111, 112, 113, 114, 115, 116, 117] are shown
in Fig. 86 and Fig. 87. Additional comparisons with differential data are shown
in the report on the IAEA evaluation[110]. The results are fairly good, except
around 300 to 400 meV and below 1 meV. The problem at the lowest energies
comes from the failure of the translational model. This part of the distribution
is not too important in practice due to effects of detail balance.
The Model for Solid Methane. The methane molecule consists of an atom
of carbon surrounded by four atoms of hydrogen placed on the corners of a
tetrahedron. The carbon atom is at the center of mass of the system; because
of its symmetry, the methane molecule is often called a “spherical top”. Op-
tical measurements of methane in the gas phase show four fairly well defined
vibrational modes at 162 meV, 190 meV, 361 meV and 374 meV. Following the
Figure 86: Comparison of the ENDF/B-VII.0 thermal cross section for water at lower inci-
dent energies with experimental results for the CSISRS compilation at the the
National Nuclear Data Center of the Brookhaven National Laboratory. See the
compilation for the references.
700 NJOY2016
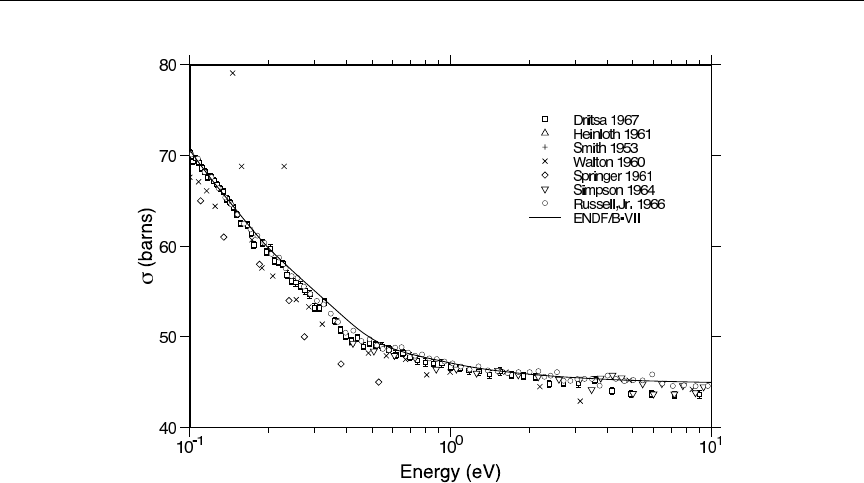
24 LEAPR LA-UR-17-20093
Figure 87: Comparison of the ENDF/B-VII.0 thermal cross section for water at higher
incident energies with experimental results for the CSISRS compilation at the
the National Nuclear Data Center of the Brookhaven National Laboratory. See
the compilation for the references.
lead of Picton, they have been included in this model as discrete oscillators with
weights equal to .308, .186, .042, and .144, respectively.
Specific heat measurements in solid methane near one atmosphere show three
phases with transitions at 8K and 20.4K. The melting point is about 89K. X-
ray measurements show that the carbon atoms are arranged on an fcc lattice for
both of the higher two phases; it has been speculated that the phase transition
is due to a change in the degree of rotational order, or perhaps due to the
onset of a self-diffusion behavior. Because of this interesting question, a series
of slow neutron inelastic scattering experiments were carried out with samples
in each of the phases[118]. Since hydrogen is an incoherent scatterer, it was
possible to analyze the data to obtain a frequency spectrum for hydrogen in
solid methane. The results didn’t really explain what was happening in the 20K
phase transition, but they did provide the data needed for our calculation.
Again following Picton, we chose the spectrum for 22.1K for our model.
Instead of using Picton’s numbers directly, we digitized the curve from the graph
in the reference, plotted it on a large scale, and then smoothed it by hand. Care
was taken to use an ω2variation for low energies. The resulting spectrum
is shown in Fig. 88. As discussed by Harker and Brugger, the appropriate
normalization for this curve is 0.32.
NJOY2016 701
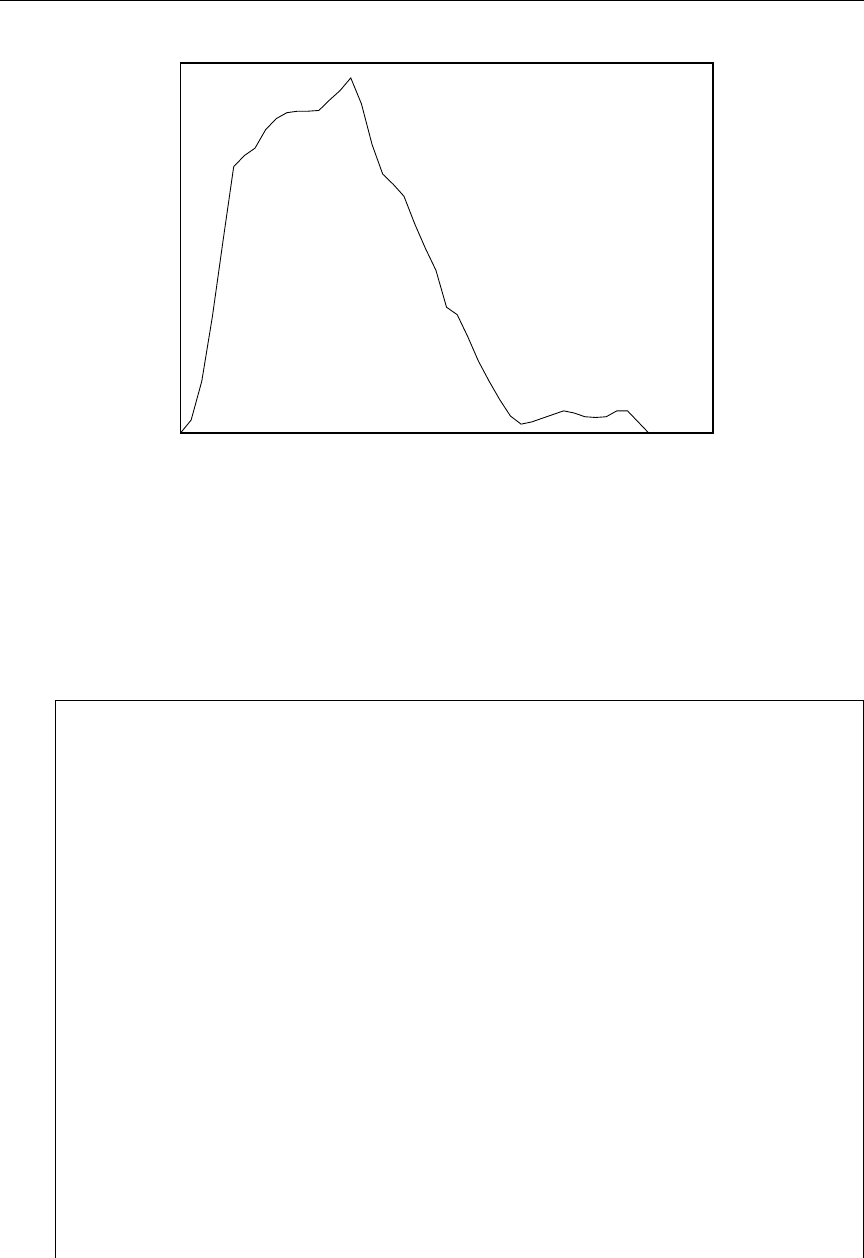
LA-UR-17-20093 24 LEAPR
0 5 10 15 20 25
*10-3
E (meV)
0
10
20
30
40
50
ρ(E) (arb. units)
Figure 88: The Harker-Brugger frequency spectrum used for solid methane. Note the
quadratic shape at low energies.
This spectrum and the four discrete oscillators were then used to calculate
S(α, β) with LEAPR using the αand βgrids of Picton. The input file follows:
leapr
26/
’solid methane at 22K, Harker & Brugger spectrum’/
1 2/
11 1001./
0.9992 20.36 4/
1 1. 11.898 4.7392 1/
70 80/
.1742 .3488 .4059 .4644 .5215 .6386 .7547 .8703
.9860 1.1601 1.3932 1.6245 1.9148 2.2050 2.6105
3.0177 3.5393 4.1198 4.8740 5.6871 6.6159 7.7760
9.0522 10.6200 12.4187 14.5066 16.9443 19.8464 23.2115
27.0995 31.7421 37.0805 43.4052 50.7168 59.1889 69.6343
81.2403 87.0431 94.0059 101.5493 110.2545 120.1198 129.9834
151.4547 177.5682 188.0122 204.2604 207.1629 209.4831 214.7058
217.0265 220.5090 232.1145 242.5599 261.1291 272.7347 282.0199
287.2413 298.2667 304.6496 311.0342 319.1575 327.2810 331.9236
350. 370. 390. 410. 450. 500./
702 NJOY2016

24 LEAPR LA-UR-17-20093
0. .1742 .3488 .4059 .4644 .5215 .6386 .7547 .8703
.9860 1.1601 1.3932 1.6245 1.9148 2.2050 2.6105
3.0177 3.5393 4.1198 4.8740 5.6871 6.6159 7.7760
9.0522 10.6200 12.4187 14.5066 16.9443 19.8464 23.2115
27.0995 31.7421 37.0805 43.4052 50.7168 59.1889 69.6343
81.2403 85.451 89.650 94.0059 96.0 100.221 104.6 110.2545
120.1198 129.9834 151.4547 170.90 177.5682 181.6 185.67 190.419
193.8 197.276 200.8 204.2604 207.1629 209.4831 214.7058
217.0265 220.5090 232.1145 242.5599 261.1291 272.7347 282.0199
287.2413 298.2667 304.6496 311.0342 319.1575 327.2810 331.9236
350. 370. 390. 410. 430. 450./
22/
.0005 45/
0. 1.75 7 15.75 26 36 37.5 38.5 41 42.5 43.3 43.5
43.5 43.6 45 46.3 48 44.5 39 35 33.6 32 28.3 25 22 17 16
13 9.7 7 4.5 2.3 1.2 1.5 2 2.5 3 2.7 2.2 2.1 2.2 3 3 1.5
0./
0. 0. .32/
4/
.162 .190 .361 .374/
.308 .186 .042 .144/
’ S-CH4 LANL EVAL-NOV92 MACFARLANE’/
’ NO REF TO DATE DIST-’/
’----ENDF/B-6 MATERIAL 11’/
’-----THERMAL DATA’/
’------ENDF-6’/
’ SOLID METHANE AT 22K, SPECTRUM OF HARKER AND BRUGGER.’/
/
stop
After the calculation, the moments of Tnand S(α, β) can be checked. The er-
rors should be modest. The output listing for the solid-type part of the problem
should be examined carefully to see that the αand βranges are sufficient and
that the normalization and sum rule checks are reasonably well satisfied. Since
this is a solid, there was no translational calculation. In the discrete-oscillator
calculation the delta functions for β > 0 are put directly into the scattering law
as sharp triangles. The β=0 peak is converted into incoherent elastic scattering.
A listing showing some of the discrete lines is given below:
NJOY2016 703

LA-UR-17-20093 24 LEAPR
alpha= 2.61050
debye-waller factor= 6.0347e-01
discrete lines
beta weight
0.000 9.8340E-01
-85.451 9.2531E-03
-170.903 4.3532E-05
-100.221 4.7644E-03
-185.672 4.4830E-05
-200.441 1.1541E-05
-190.419 5.6623E-04
-197.276 1.8739E-03
-282.728 1.7632E-05
norm check 1.0000
rule check 0.9964
The Debye-Waller factor printed here is the one from the solid-type spectrum,
λs. It defines the total strength of all the discrete lines. All the discrete lines
taken together must satisfy the normalization and sum-rule requirements of any
scattering law. If the number of discrete lines increases above 100, some of them
will begin to be lost, and the checks will begin to decrease below unity. The
listing for the discrete-oscillator calculation should show that the grid specified
does a reasonable job of satisfying the overall normalization and sum-rule checks.
LEAPR automatically prepared an output file in ENDF-6 format. Plots of
S(α, β)vs. βfor several values of αare give in Fig. 89.
Next, the new evaluation for S(α, β) can be processed into integrated cross
sections and double differential cross sections using the THERMR module of
NJOY. A plot of the integrated cross section is given in Fig. 90, and plots of the
outgoing neutron spectrum integrated over angle at several incident energies are
given in Fig. 91.
The Model for Liquid Methane. This example is for liquid methane at
100K. Once again, we use the four discrete oscillators to represent the the molec-
ular vibrations. In addition, we need a continuous frequency distribution to
represent the molecular rotations, and a pair of parameters dand cto represent
704 NJOY2016
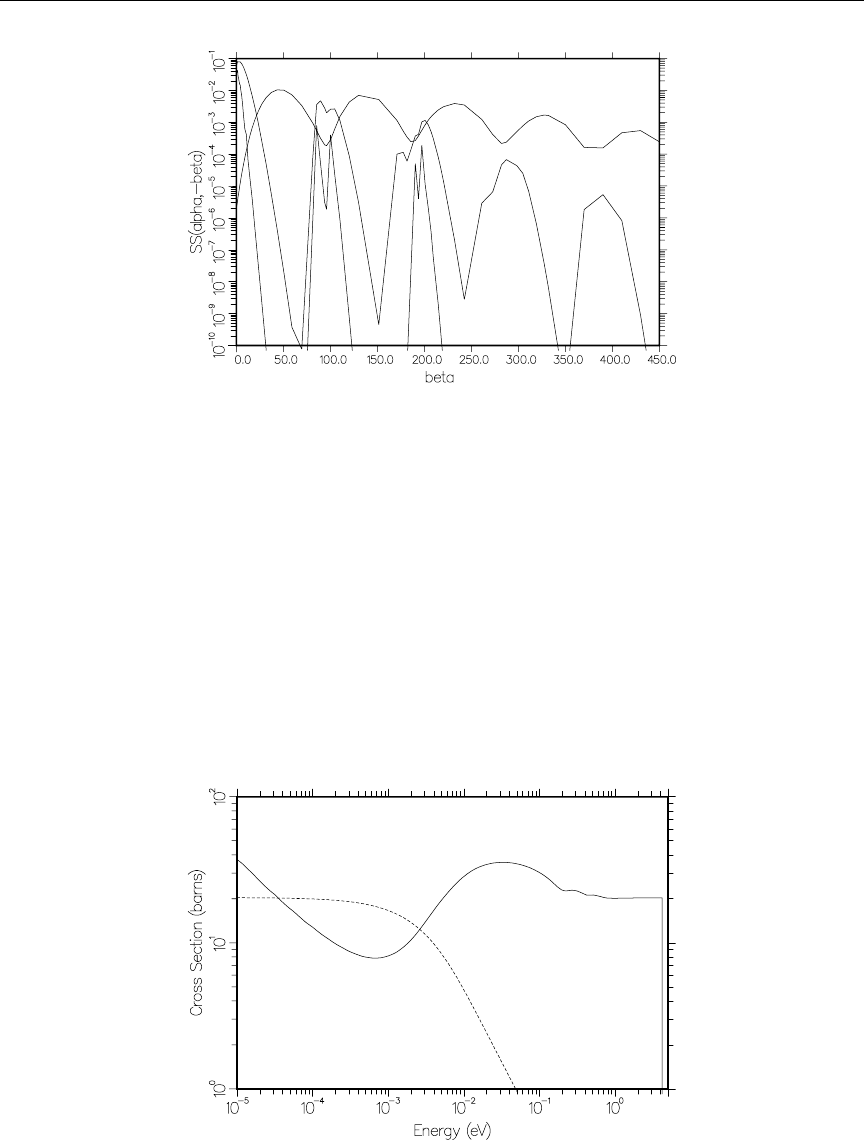
24 LEAPR LA-UR-17-20093
Figure 89: S(α, −β) for solid methane shown as a function of βfor the αvalues 0.986
(lowest), 16.94, and 151.45 (highest). The four discrete levels show up as sharp
triangles in the lowest curve.
diffusion. This latter component was omitted from the earlier model of Picton,
but we felt that it might be needed to obtain a reasonable quasi-elastic peak in
the spectrum of scattered neutrons. Therefore, we couldn’t use the Picton input
directly, and we had to refer to his source[119]. Agrawal and Yip divided the
problem into two parts: translations and rotations.
For translations, they proposed a model for γ(t) that matches the expected
diffusive behavior at long times and provides an oscillatory behavior at short
Figure 90: Inelastic (solid) and incoherent elastic (dashed) cross sections for solid methane.
The small bumps starting at about 0.2 eV are due to the discrete levels at 0.162
eV, 0.190 eV, 0.361 eV, and 0.374 eV.
NJOY2016 705
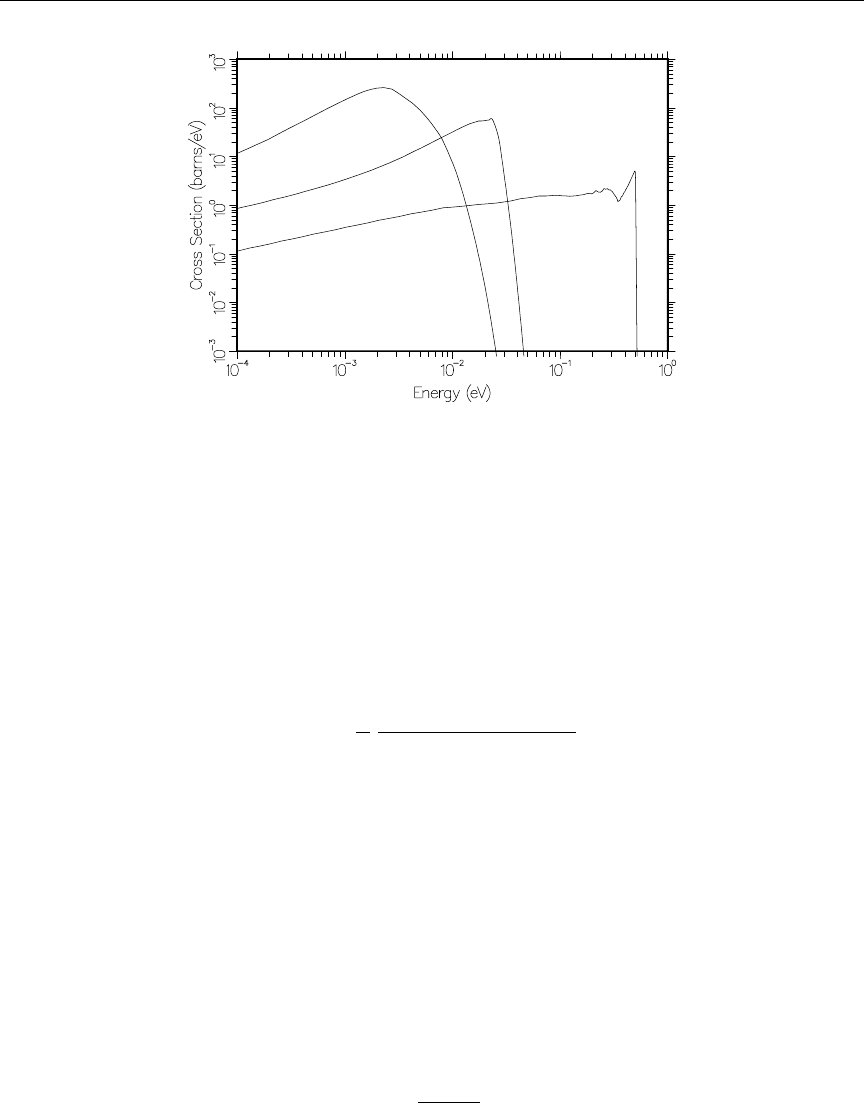
LA-UR-17-20093 24 LEAPR
Figure 91: Neutron spectra σ(E→E0) for solid methane shown as functions of outgoing
neutron energy E0for E=0.0001 eV, 0.0253 eV, and 0.503 eV.
times. Each methane molecule is assumed to move in a “cage” formed by its
neighbors, and the cage itself is allowed to relax with time. As Agrawal and
Yip point out, the molecule will oscillate initially, but gradually as the restoring
forces decay into a frictional background, it will go over into diffusive motions.
The resulting analytic expression for the frequency spectrum is
ft(ω) = 2
π
ω2
0/τ0
(ω2−ω2
0)2+ (ω/τ0)2.(579)
The fact that f(ω) is nonzero at ω=0 indicates that the molecules are capable
of diffusion, and in addition, f(ω) has a resonant behavior near (ω2−τ2
0)1/2, the
characteristic frequency of local oscillations.
For rotations, the argument starts out by recalling that for translations, γ(t)
is related to the mean-square displacement W(t) by
γ(t) = κ2W(t),(580)
where the magnitude of the wave vector is related to αby
α=¯h2κ2
2MkT .(581)
The rotational analog of the mean-square displacement is the mean-square com-
ponent of the bond length ~
balong the the vector ~κ, or
706 NJOY2016

24 LEAPR LA-UR-17-20093
W(t) = <[bκ(t)−bκ(0)] >2
= 2 < b2
κ>1−< bκ(t)bκ(0) >
< b2
κ>
=2b2
3h1−F1(t)i.(582)
The function F1(t) is seen to describe the correlation between a specific direction
in the molecule at t=0 with its direction at a later time t. Therefore, it is called
the “dipole correlation function”. The same function appears in the classical
limit of the theory of optical line shapes for infrared absorption as presented
by Gordon[120]. At frequencies where it is safe to assume that the internal
vibrations of different molecules are uncoupled, the shape of a vibrational line
depends mostly on the reorientation motions of individual molecules, and the
dipole correlation function can be obtained from
F1(t) = Zband
ˆ
I(ω) cos ωt dω. (583)
Gordon has used this method to compute F1(t) for liquid methane at 98K based
on the infrared data of Ewing[121]. In order to link this result to neutron
scattering, we use the high-temperature classical limit of Eq.511 to express W(t);
namely,
W(ˆ
t) = ¯h2
2MkT Z∞
0
ρr
β2h1−cos(βˆ
t)idβ, (584)
which can be inverted to obtain
ρr(β) = 2MkT
¯h2Z∞
−∞
d2γr
dt2eiβˆ
tdˆ
t.(585)
This limit is justified by noting that β<1 for the rotational modes in liquid
methane around 90K. It is now easy to compute ρrby taking two derivatives of
the dipole correlation function graphed by Gordon.
The result is shown in Fig. 92, together with the translational frequency dis-
tribution discussed above. These numbers were generated by digitizing the curve
from Agrawal and Yip, subtracting the translational part, and smoothing the
remainder. Agrawal and Yip compared their model with both double-differential
and integrated cross sections, with very good agreement.
NJOY2016 707
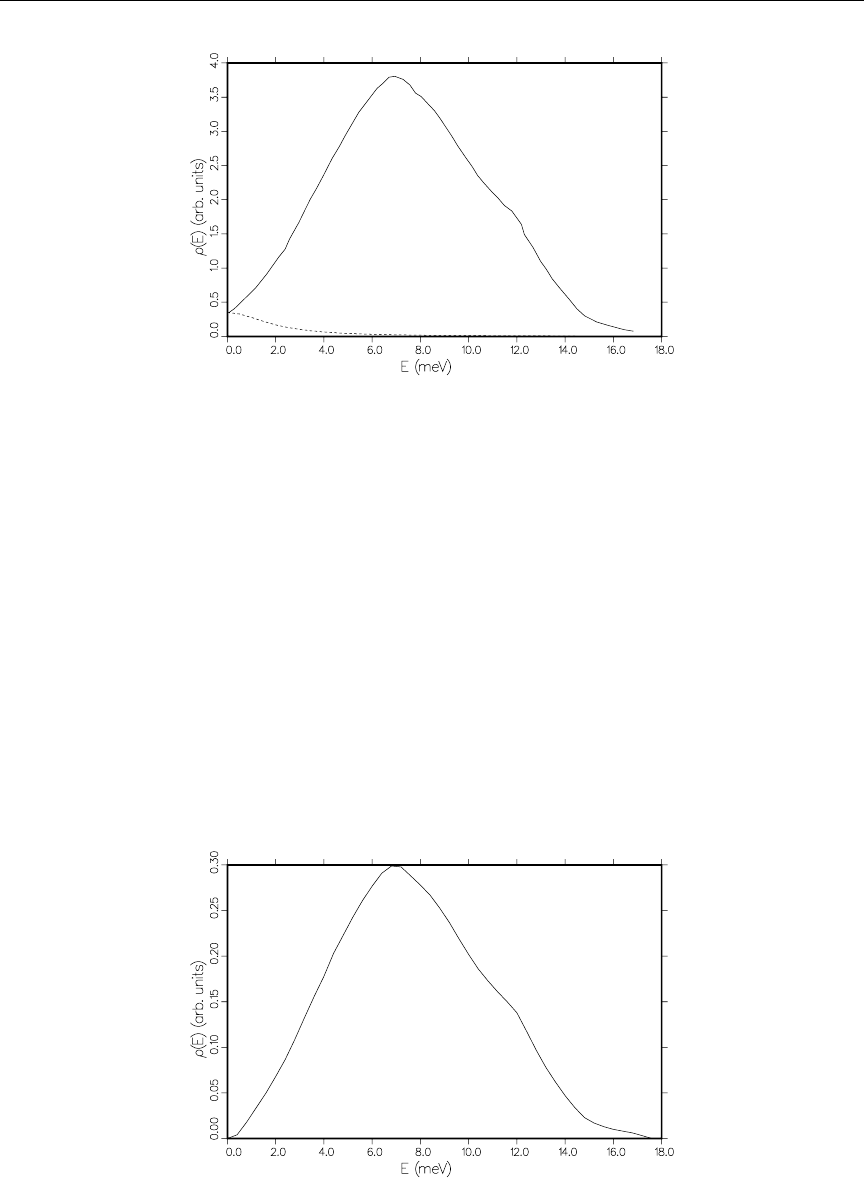
LA-UR-17-20093 24 LEAPR
Figure 92: Frequency spectrum for liquid methane (solid) as given by Agrawal and Yip,
including an analytic translational part (dashed) and a rotational part based on
Gordon’s analysis of the optical measurements of Ewing.
Unfortunately, this model does not match the requirements of LEAPR. The
only type of frequency distribution that is nonzero at ω=0 that can be used
by the code is the diffusive law of Egelstaff and Schofield, which does not have
the short-time oscillatory behavior of Eq. 579. Our main reason for using the
diffusion term in our model for liquid methane was to improve the “quasi-elastic”
peak, which depends mostly on the small-ωpart of the frequency distribution.
Therefore, it seemed reasonable to select diffusion parameters dand cthat gave
a reasonable representation for the full width at half maximum of the quasi-
elastic peak, to subtract the result fdfrom the sum of the two curves shown in
Figure 93: Effective frequency spectrum for methane including both translational and ro-
tational modes, but not including diffusive modes.
708 NJOY2016

24 LEAPR LA-UR-17-20093
Fig. 92, and to use the difference to represent both the translational oscillatory
modes and the rotational modes. Fig. 93 shows this breakdown. Once again,
there has been some hand smoothing, and the low energy part of the distribution
was forced to follow an ω2law. The final breakdown was 1.5% diffusion, 30.5%
rotation, and 68% molecular vibrations.
The LEAPR input for liquid methane at 100K is shown below.
liquid methane at 100k, modified agrawal & yip model
89 81/
.0387 .0775 .0902 .1032 .1159
.1419 .1677 .1934 .2191 .2578 .3096 .3610
.4255 .4900 .5801 .6706 .7865 .9155 1.0831
1.2638 1.4702 1.7280 2.0116 2.3600 2.7597 3.2237
3.7654 4.4103 5.1581 6.0221 7.0538 8.2401 9.6456
11.2704 13.1531 15.4743 18.0534 19.3429 20.8902 22.5665
24.5010 26.6933 28.8852 33.6566 39.4596 41.7805 45.3912
46.0362 46.5518 47.7124 48.2218 49.0020 51.5810 53.9022
58.0287 60.6077 62.6711 63.8314 66.2815 67.6999 69.1187
70.9239 72.7291 73.7608 78.6611 83.5613 86.1404 90.0089
93.2326 96.4566 98.0039 100.8408 104.4516 109.6097 117.8625
137.8503 140.5583 144.6847 149.5850 161.1907 183.4447 208.7711
237.5941 270.3965 307.7273 350.2124 398.5625 453.5881 516.2107/
0.0 .0387 .0775 .0902
.1032 .1159 .1419 .1677 .1934 .2191 .2578
.3096 .3610 .4255 .4900 .5801 .6706 .7865
.9155 1.0831 1.2638 1.4702 1.7280 2.0116 2.3600
2.7598 3.2237 3.7654 4.4103 5.1581 6.0221 7.0538
8.2401 9.6456 11.2704 13.1531 15.4743 18.0538 19.3429
20.8902 22.5665 24.5010 26.6933 28.8852 33.6566 39.4596
41.7805 45.3912 46.0362 46.5518 47.7124 48.2281 49.0020
51.5810 53.9022 58.0287 60.6077 62.6711 63.8314 66.2815
67.6999 69.1187 70.9239 72.7291 73.7608 78.6611 83.5613
86.1404 90.0089 93.2326 96.4566 98.0039 100.8408 104.4516
109.6097 117.8625 137.8503 140.5583 144.6847 149.5850 161.1907/
100/
1 1/
.00040 45/
0. .004 .018 .034 .050 .068 .087 .109
.133 .156 .178 .203 .223 .243 .261 .277 .291 .299
.298 .288 .278 .267 .253 .237 .219 .202 .186 .173
.161 .150 .138 .118 .097 .078 .062 .047 .034 .023
NJOY2016 709
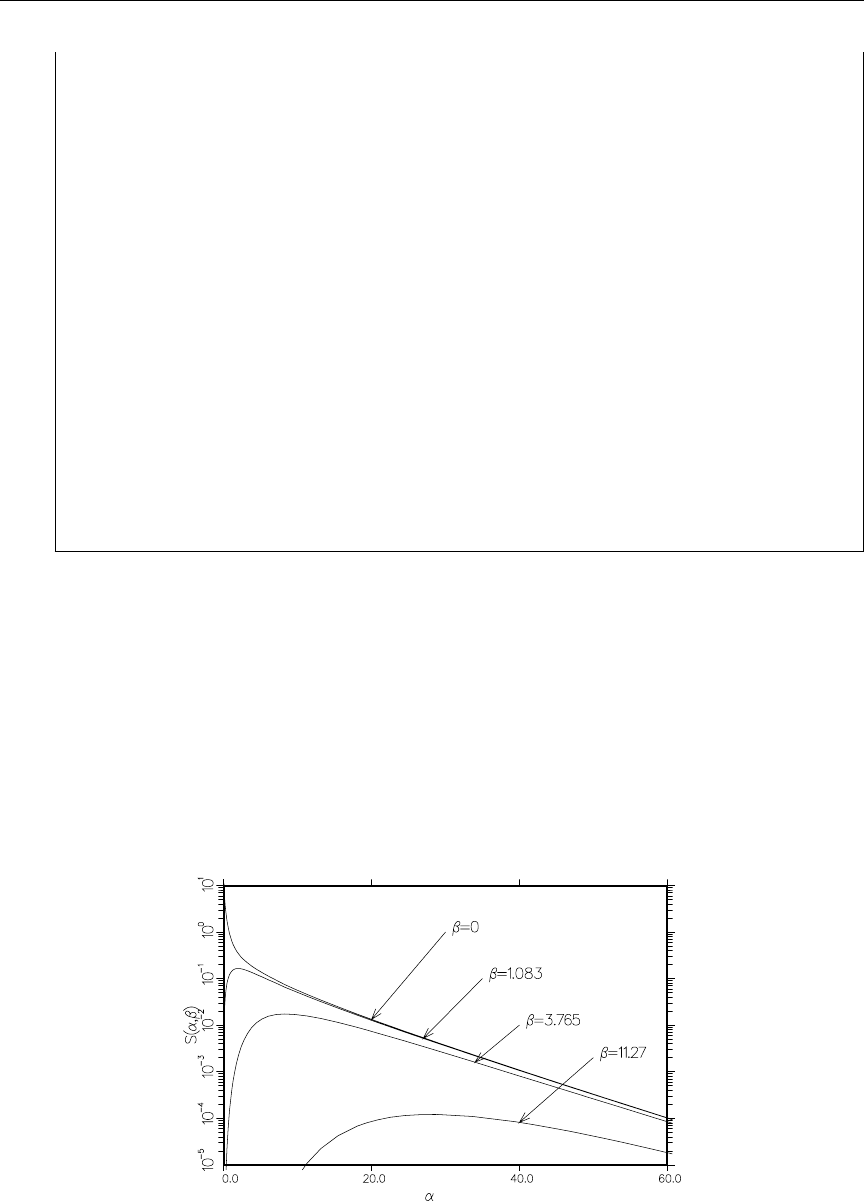
LA-UR-17-20093 24 LEAPR
.017 .013 .010 .008 .006 .003 0./
3. 200. 0 0 .32/
4/
.162 .190 .361 .374/
.308 .186 .042 .144/
0/
10 1001. 1.008 20.3 1 0 8/
’ L-CH4 LANL EVAL-FEB88 MACFARLANE’/
’ NO REF TO DATE DIST-’/
’----ENDF/B-6 MATERIAL’/
’-----THERMAL DATA’/
’------ENDF-6’/
’ LIQUID METHANE AT 100k, MODEL OF AGRAWAL AND YIP’/
’ AS IMPLEMENTED BY D.J.PICTON,’/
’ MODIFIED TO INCLUDE A DIFFUSIVE COMPONENT.’/
/
LEAPR can be run with this input deck. Once again the moments of Tnand
S(β) can be checked, and no great problems should be seen. These checks help
to prove that the grid for the input frequency spectrum and the βgrid for
calculating Sare reasonable. The user should also check the range of αand β
to be sure that no significant cross section contributions were being cut off. The
results should be good for all energy transfers possible with incident neutron
energies up to 1 eV. Once again, LEAPR produces an output file in ENDF-6
format. This time, there will be no elastic contribution at all. Plots of S(α, β)
Figure 94: S(α, β) curves for liquid methane. Note the diffusive behavior at low αand β.
710 NJOY2016
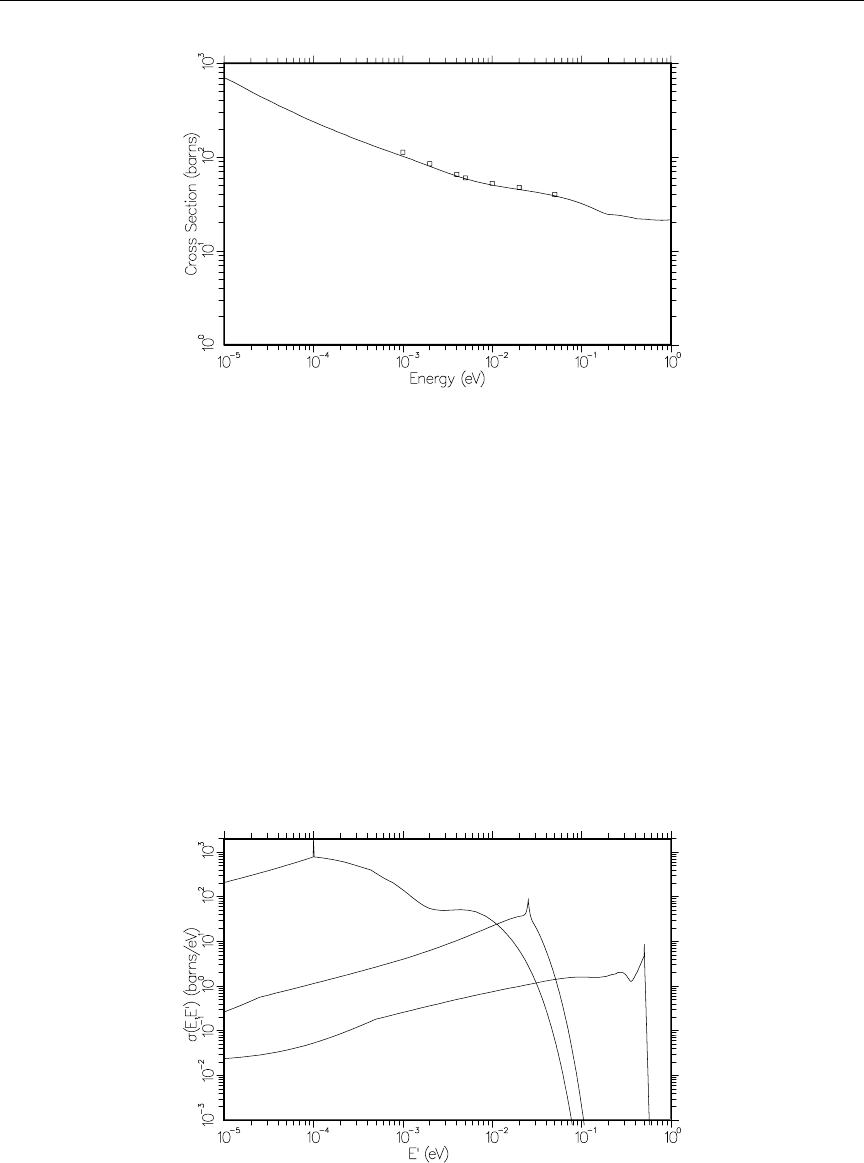
24 LEAPR LA-UR-17-20093
Figure 95: The computed cross section for liquid methane at 100K (solid) is compared to
experimental data at 110K (squares) by Whittemore and by Rogalska as quoted
by Agrawal and Yip.
versus αfor several values of βwith this mode are shown in Fig. 94. Note that
the behavior of the curves for small βis quite different than in Fig. 89. This
reflects the presence of the diffusive component.
The new evaluation for liquid methane can be run through the THERMR
module of NJOY to produce integrated and differential cross sections. Sample
results are given in Figs. 95 and 96. The integrated cross section at 100K is
compared with experimental data at 110K that was quoted in the Agrawal and
Yip paper.
Figure 96: Neutron spectra σ(E→E0) are shown for E= 0.0001 eV, 0.0253 eV, and 0.503
eV. Note the sharp quasi-elastic peak that results from the diffusive term in the
theory used here.
NJOY2016 711
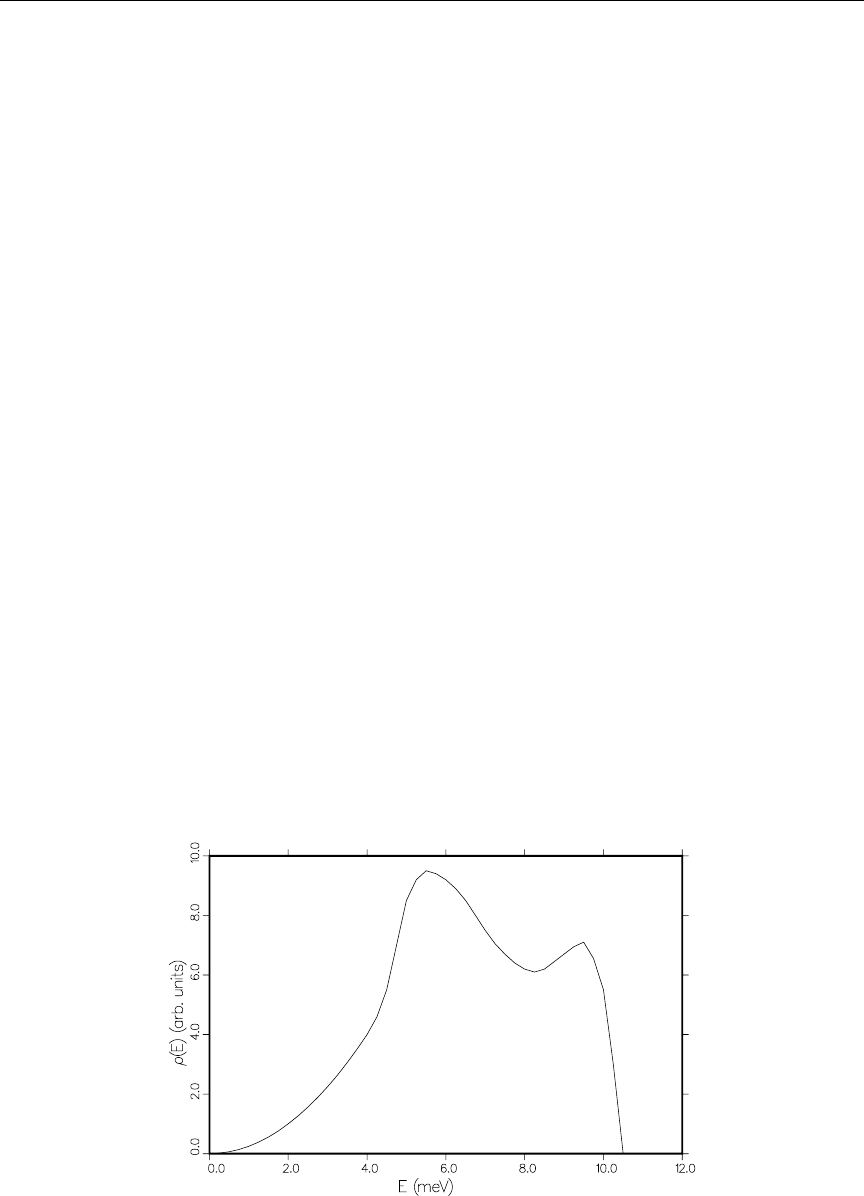
LA-UR-17-20093 24 LEAPR
The Model for Liquid Hydrogen. As discussed above, we picture a hydro-
gen molecule bound in a cluster of about 20 molecules and undergoing vibrations
similar to those of a hydrogen molecule in a solid. These clumps then diffuse
through the liquid (hindered translations) according to the Egelstaff-Schofield
effective width model. This physical situation is described by the Keinert-Sax
distribution function shown in Fig. 97. They assumed a weight of 0.025 for
the hindered translation, leaving a value of 0.475 for the solid-like distribution.
In addition, intermolecular coherence is taken into accound using the Vineyard
approximation. The static structure factor S(κ) was provided by Keinert and
Sax. See Fig. 98.
This model can then be used in LEAPR. Some results for the effective trans-
lational S(α, β) to be used in the Young and Koppel formulas are shown in
Figs. 99 and 100. Because of the spin correlations, S(α, β)6=S(α, −β), and it
is necessary to calculate both sides of the function. Similar results for ortho
hydrogen are shown in Figs. 101 and 102. These results were then passed to
the ENDF output subroutine, which allows for asymmetric scattering functions
through the parameter “LASYM” in the ENDF File 7 format (it is in the “L1”
position of the head card for MF=7, MT=4). When LASYM=1, the βgrid in
File 7 starts with −βmax and increases through zero to +βmax. Some examples
of energy distributions for this asymmetric case computed by THERMR are
shown in Figs. 103 and 104.
A comparison of the computed cross section for para and ortho hydrogen
with experiment is shown in Fig. 105.
Figure 97: The Keinert-Sax frequency distribution for the effective translational modes of
liquid hydrogen.
712 NJOY2016
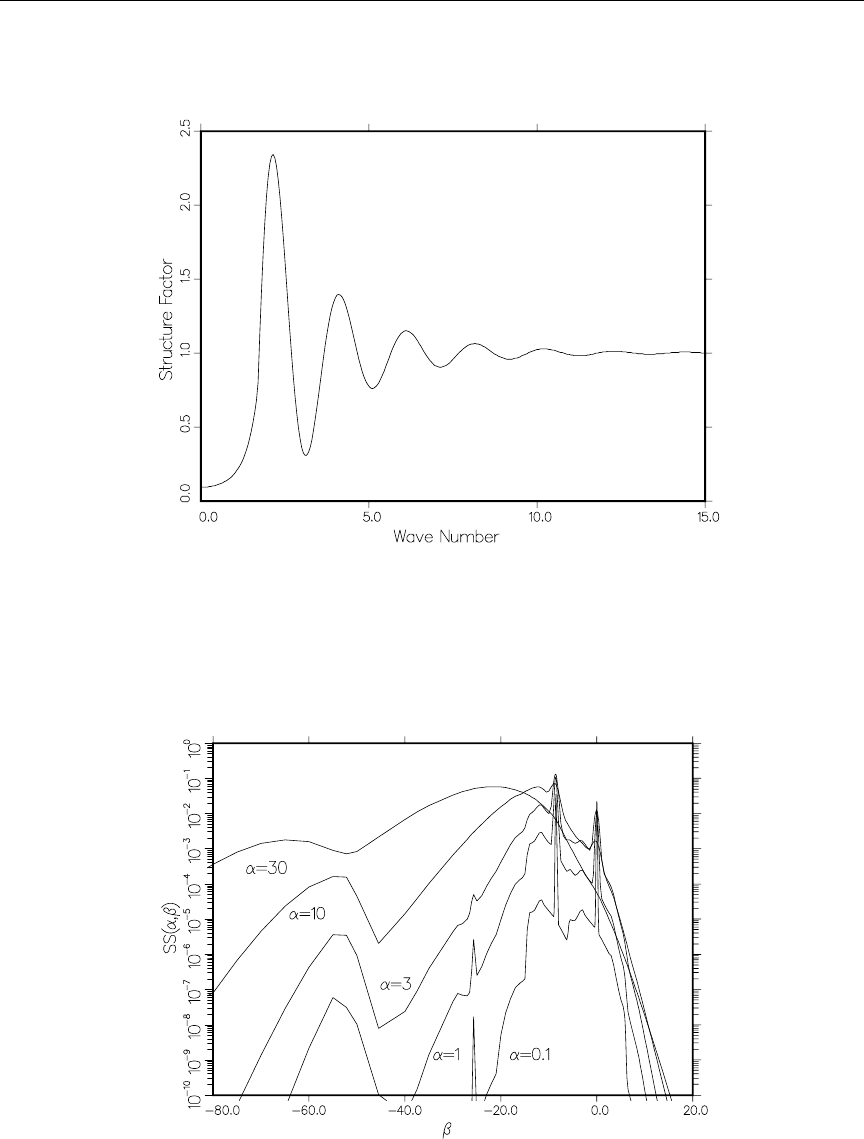
24 LEAPR LA-UR-17-20093
Figure 98: The static structure factor S(κ) for liquid hydrogen.
Figure 99: Script-S for para-hydrogen at 20K is shown as a function of βfor several α
values.
NJOY2016 713
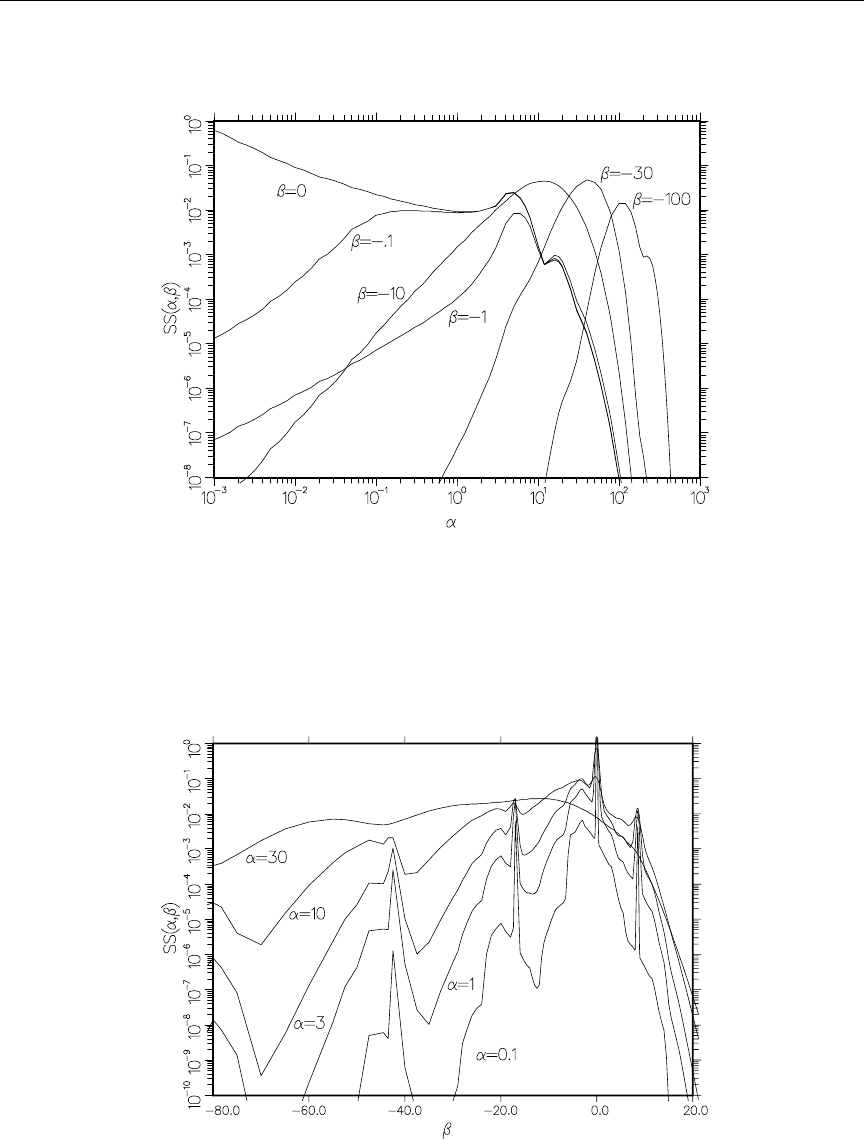
LA-UR-17-20093 24 LEAPR
Figure 100: Script-S for para-hydrogen at 20K is shown as a function of αfor several β
values corresponding to downscatter.
Figure 101: Script-S for ortho-hydrogen at 20K is shown as a function of βfor several α
values.
714 NJOY2016
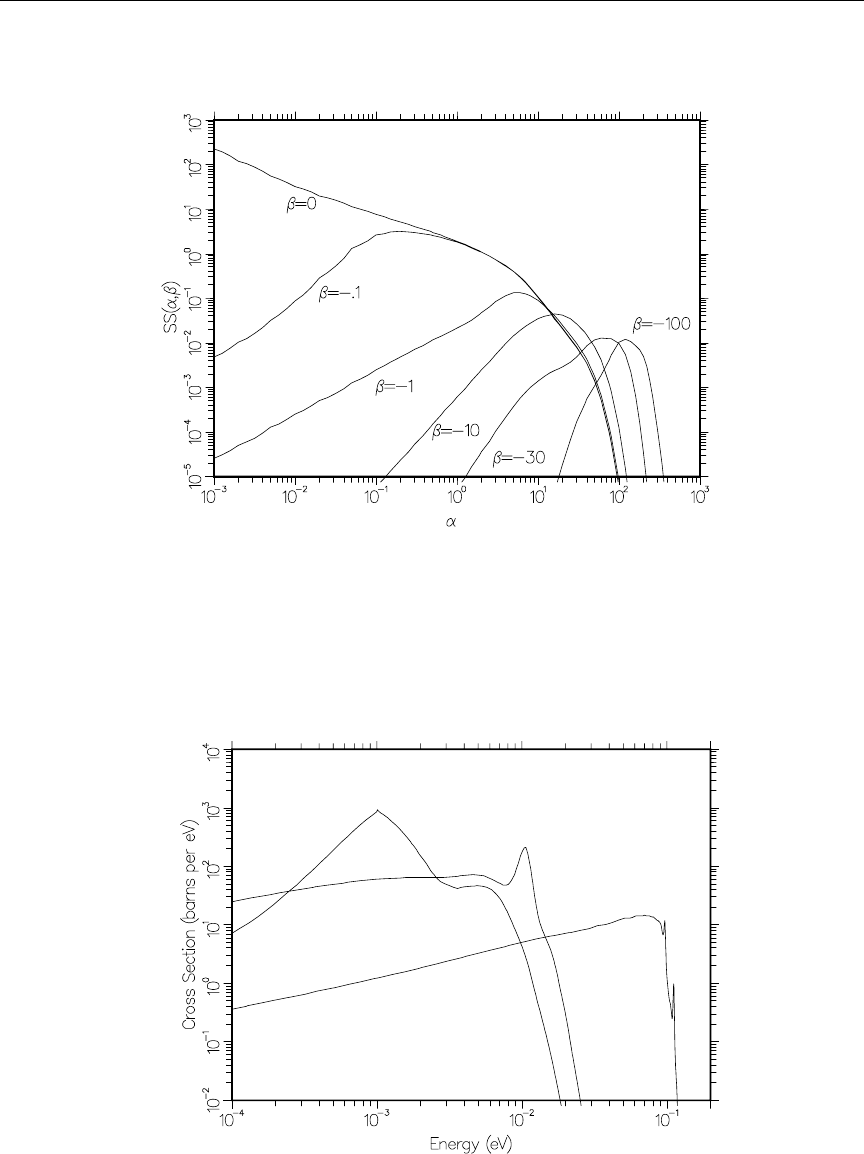
24 LEAPR LA-UR-17-20093
Figure 102: Script-S for ortho-hydrogen at 20K is shown as a function of αfor several β
values corresponding to downscatter.
Figure 103: The spectra σ(E→E0) for liquid para-hydrogen are shown for E= 0.0001 eV,
0.0106 eV, and 0.112 eV.
NJOY2016 715
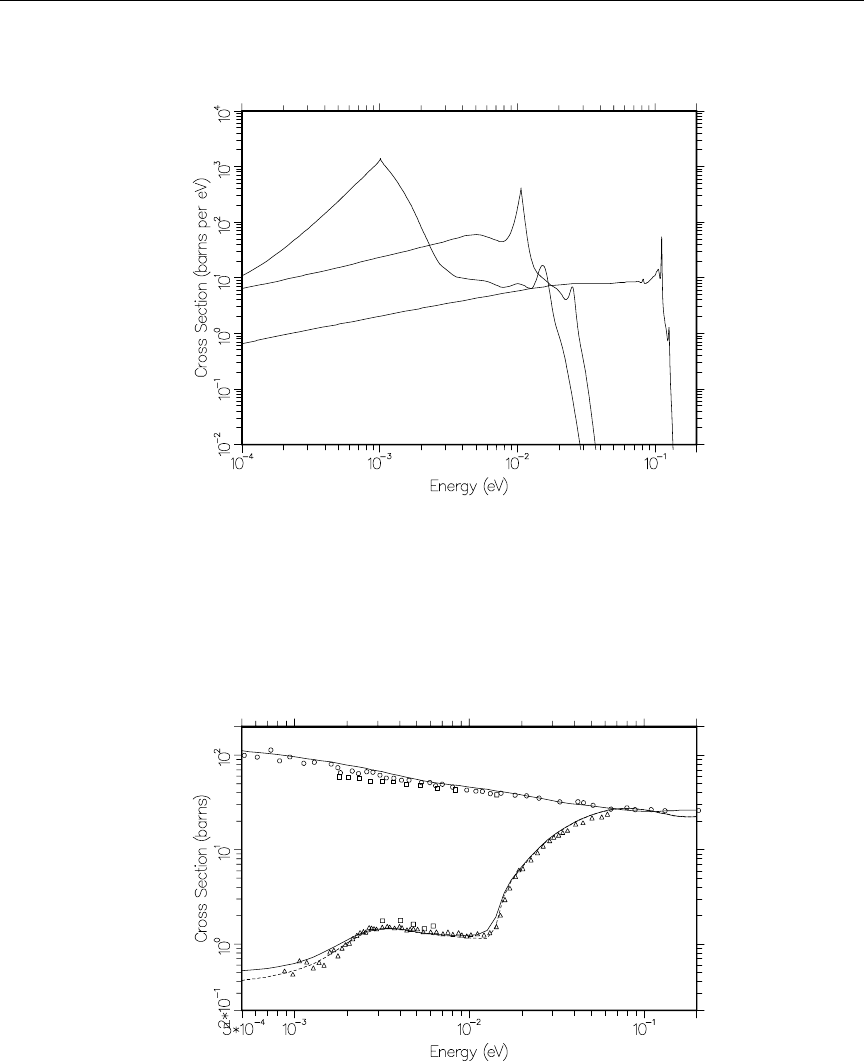
LA-UR-17-20093 24 LEAPR
Figure 104: The spectra σ(E→E0) for liquid ortho-hydrogen are shown for E= 0.0001 eV,
0.0106 eV, and 0.112 eV.
Figure 105: The cross sections for liquid ortho-hydrogen (upper curve) and liquid para-
hydrogen (lower curve) at 20K are compared with experimental data[122] due
to Squires (gas) at 20K (squares), Whittemore at 20K (circles), and Seiffert at
14K (triangles). The solid curves are at 20K and the dashed curve is at 14K.
The sharp drop in the para cross section below 0.05 eV is due to spin coherence,
and the second drop below 0.003 eV is due to intermolecular interference.
716 NJOY2016

24 LEAPR LA-UR-17-20093
24.4 Coding Details
Subroutine leapr is exported by module leapm. It follows the standard pattern
for an NJOY module in that it starts with a group of comment cards describing
the code and giving the input instructions.
LEAPR performs many calculations of exponentials of very small numbers
and of products of small numbers. These calculations will lead to underflow
conditions on many machines. These underflow events are not intercepted or
reset by LEAPR for efficiency. The programmer should use the appropriate
system calls or compiler options to suppress these underflow messages and to
assure that the system does not generate “Not a Number” (NaN) values that
would affect the calculation.
User input is read in using the standard Fortran READ*. With the size of
the problem determined, storage can be allocated for the alpha grid, the beta
grid, and the ssm and ssp array (if needed).
Most of the main program consists of the loops over principal and secondary
scatterers, and the loop over temperatures. If the mixed-moderator option has
been requested, the results for the principal scatterer are written onto a scratch
file on unit 10, and the effective temperature and Debye-Waller factor for the
principal scatterer are stored in the variables tempf1 and dwp1. The code then
loops back to statement 100 to repeat the calculation for the secondary scatterer.
Note the global variable arat. This is the mass ratio that is used to scale the α
grid for the secondary scatterer in the mixed-moderator calculation. If only one
scattering law is being calculated, the code drops through to the ENDF output
section.
Inside the temperature loop, LEAPR first reads in the temperature, the con-
tinuous frequency distribution, the oscillator data, and the pair correlation func-
tion. It then processes the continuous spectrum by calling subroutine contin,
the translational modes (if any) by calling trans, the discrete oscillators (if any)
by calling discre, and the liquid hydrogen or deuterium option using subroutine
coldh.
We next look at contin. The first part of the calculation is performed by
start, which prepares and normalizes the functions ρ(β) and P(β). It also cal-
culates the effective temperature and Debye-Waller λ, and starts the convolution
process for the phonon expansion by computing T1. The results printed out at
this point refer to the continuous part of the distribution only. The effective
temperature and Debye-Waller λmay change as other modes are added.
When start returns to contin, the continuous part of the scattering law
NJOY2016 717

LA-UR-17-20093 24 LEAPR
is computed by carrying out the phonon expansion. At any one time, only T1,
Tlast, and Tnow have to be kept in memory to carry out the convolution. Note
that the number of elements of Tnstarts out equal to the number of βvalues
in ρfor n=1, and then it increases by this number for every subsequent step.
Therefore, the maximum sizes for tlast and tnow are equal to the number of
points in the frequency distribution times nphon.
Each step of the expansion is handled by the convolution routine convol.
The input T arrays tlast and t1 contain only the −βpart of the asymmetric
T functions. This is the part that has the smallest dynamic range, because it is
roughly proportional to the cross section. Really small numbers like those that
occur on the upscatter side of the asymmetric T function cannot significantly
affect the answers. This approach was developed to get good results even on
short-word computers that could not represent numbers less than quantities like
10−31 or 10−45. This is less of a problem with Fortran-90’s “kind” method.
Note that convol also returns the quantity ckk, which is used to check the
normalization condition on the Tn.
Returning to contin, note that the code determines the maximum value of
αthat can be used for each βwithout invoking the SCT approximation. This is
done by checking each term that is accumulated into the phonon expansion to
see if it is smaller than 0.1% of the accumulating S(α, −β). These breakpoints
are summarized on the output listing if iprint=2. Next, contin checks the
computed scattering law to see if it satisfies the normalization and sum rule
requirements. The scattering law may also be printed out by this loop. Note
that the quantity S(α, −β) is the result actually computed by contin. The
corresponding upscatter side of Sand the symmetric S(α, β) are computed just
for the listing. On a short-word machine, these two quantities may underflow
to zero, but that doesn’t affect the accuracy of subsequent calculations. The
denominator of the normalization test with sum0 is 1−exp(−αλ) because the
delta function that represents the “zero-phonon” term is not included in the
calculated scattering law.
When contin returns to leapr, the −βside of the asymmetric scattering
law is safely stored in ssm for this temperature. If translational modes have
been requested by entering a value greater than zero for twt, subroutine trans
is called. The task here to to convolve a free-gas or diffusive shape with the
current scattering law. The approach is to first use stable to compute the
free-gas or diffusive shape on an appropriate βgrid. Then, subroutine sbfill
is called to remap the current scattering law onto the same βgrid. It is then
718 NJOY2016

24 LEAPR LA-UR-17-20093
easy to perform the convolution integral using Simpson’s Rule. The final step is
to add in the convolution of the “zero-phonon” term, which is a delta function,
with the translational term. That step is very easy, because it is only necessary
to interpolate for the translational term at the current βvalue and multiply by
exp(−αλ). When the loop over βis complete, another βloop is used to check the
normalization and sum-rule conditions. Normally, there is some loss in accuracy
at this point, because it is impractical to keep the βgrid fine enough at small β
to represent the very sharp shape of the translational contribution at small α.
When the αloop is complete, a new value for the effective temperature to be
used with the SCT approximation in computed. The Debye-Waller λremains
unchanged.
The next step is to call subroutine discre to add the contributions from the
discrete oscillators, if any. The keys to this calculation are the routine bfact,
which generates the terms
e−αλiInαwi
βisinh(βi/2)e−nβi/2,(586)
and the routine sint, which interpolates for the scattering law at αand β−nβi.
sint uses the arrays bex,rdbex, and sex, which are generated by bfill and
exts. These arrays extend the βgrid and the −βside of the scattering law over
the entire βrange needed for the discrete oscillator calculation. This makes it
easy for sint to interpolate for the scattering law at a given βwithout having
to worry about the asymmetry of the Sfunction. The sum given by
∞
X
n=−∞ ··· ,(587)
is evaluated by first doing the term with n=0, then doing the negative nterms
until add is less than tiny (currently 1.0×10−30), and finally, doing the positive
nterms until the add is less than tiny. This entire process is continued until all
βand αvalues have been processed. The normalization and sum-rule checks are
carried out as before. There is usually some loss in the accuracy of these tests
at high α, because the βgrid doesn’t extend to high enough values to complete
the integrals.
New values for the effective temperature and the Debye-Waller λare also
produced by discre before it returns to the main processing line in contin.
Subroutine bfact computes the factors used to weight the various discrete-
NJOY2016 719

LA-UR-17-20093 24 LEAPR
oscillator contributions to the scattering law. The modified Bessel Functions
I0(x) and I1(x) are computed separately for small xand large xto take ad-
vantage of the factor exat large x. It is easier to control the numerics when
xcan be combined with −αλ and −nβi/2 in the exponent before computing
the factor. The I0(x) and I1(x) are computed using series expansions; higher
orders are generated using reverse recursion[123]. The numerics of the products
In(x)eyis controlled to return all significant values for both + and −n, even for
large x. This is an improvement over the original LEAP code.
Subroutine sint first checks to see if the requested value of βis in the tab-
ulated range. If not, it computes the scattering law using the SCT expression.
Otherwise, the value is computed by finding the appropriate panel in the tabu-
lated function and interpolating on log S. Note that the βgrid has been extended
over the entire range of negative and positive βvalues using bfill and exts.
Subroutine coldh is fairly complicated due to the messy details of following
the quantum mechanics needed to compute the effects of spin correlation. It
starts by setting values for the atomic masses, coherent and incoherent scatter-
ing lengths. The fundamental constants needed are available from the NJOY
physics module. It also sets the translational weight for the free-gas and SCT
formulas and the effective temperature ratio tbart for the SCT approximation.
Of course, all these values depend on whether hydrogen or deuterium are being
processed (see law). Inside the αloop, the even and odd Aand Bcoefficients are
computed for the current molecule from the coherent and incoherent scattering
lengths. The next step is to prepare the arrays for sint, just as was done in
discre.
The βloop is complicated by the fact that it is necessary to keep both the
+βand −βsides of the scattering function, because the principle of detailed
balance doesn’t hold for para or ortho phases treated separately. Note that
the +βterms go into ssp, and the −βterms go into ssm. For each value of
β, the sums over the even values of J0and the odd values of J0are performed
separately using sumh to retrieve the appropriate sums over Bessel Functions
and Clebsch-Gordan coefficients and using sint to get the corresponding values
of the translational scattering law. A hidden option is available to use the free-
gas law instead of the scattering law computed from ρ(β). One has to change
the flag ifree to 1.
The endout routine begins by merging the principal and secondary scatterer,
if the mixed-moderator option was used. It then displays the final values of the
effective temperatures and Debye-Waller coefficients. For comparison with the
720 NJOY2016

24 LEAPR LA-UR-17-20093
GA results, the Debye-Waller terms are printed out as Aλ. For cases with
coherent elastic scattering, subroutine coher is called to construct the Bragg
edges.
The routine can now start to build up the output ENDF-6 file. It starts
by writing the appropriate header cards and the subsection containing the Hol-
lerith description. It then constructs a subsection with MF=7 and MT=2 for
incoherent elastic scattering, if present. Note that this section contains the
Debye-Waller integral obtained from dbw. Next, the code constructs a section
with MF=7 and MT=2 for coherent elastic scattering, if present. Because the
Bragg edges get very small at high energies, it is possible to thin down the
coherent-elastic results slightly. The fractional tolerance for this thinning is set
to 0.9×10−7. The final data are output inside a loop over temperature. For
mixed-moderator cases, the Debye-Waller integral is computed as the average
of the two parts.
The rest of the subroutine outputs the inelastic part. There are a number
of variations possible. Normally, the array ssm contains the −βside of the
asymmetric scattering law. For liquid hydrogen or deuterium, ssm contains
the −βside of the asymmetric scattering law and ssp contains the +βside.
These numbers have reasonable values, even on short-word machines. However,
the ENDF-6 format normally requires you to give the “symmetric” S(α, β) (it
is not really symmetric for liquid hydrogen or deuterium). This function can
require that numbers on the order of 10−50 be kept, if incident energies as high
as 4 eV are needed. For cold moderators, it is necessary to handle numbers
on the order of 10−99. For NJOY2016, this is handled by using the Fortran-90
“kind” mechanism.
24.5 Error Messages
error in sjbes***argument is invalid...
There is a problem with the argument to the Bessel functions used for cold
hydrogen and deuterium calculations.
message from sjbes---value is not accurate...
There is a problem with calculating the Bessel functions.
error in coh***illegal lat
Currently limited to 1 to 6, for graphite, be, and beo, al, pb, and fe,
respectively.
error in coh***storage exceeded
NJOY2016 721

LA-UR-17-20093 24 LEAPR
Currently limited to maxb=60 000, the size of the allocatable array bragg
in subroutine leapr.
error in endout***scratch storage exceeded for hollerith...
This refers to the allocatable array scr with length mscr=4000 in subrou-
tine leapr.
722 NJOY2016

25 GASPR LA-UR-17-20093
25 GASPR
The GASPR module will add gas production reactions (MT=203-207) to the
PENDF file. Any existing gas-production sections on the input PENDF file
are removed, and the file directory is updated to show the new reactions. This
module can be run anywhere in the PENDF preparation sequence, but as a
practical matter is should follow BROADR.
This chapter describes the GASPR module in NJOY2016.0.
25.1 Gas Production
The light products of nuclear reactions – namely, protons, deuterons, tritons,
3He’s, and alphas – can accumulate as gases in a nuclear system. The resulting
hydrogen, deuterium, tritium, 3He, and 4He buildup can have important effects
on the original material, such as causing embrittlement. In other cases, the gas
may even be the desired product, such as in tritium production.
Keeping track of the total production of each gas species is complicated.
Gases can sometimes be determined from the MT number for the reaction; for
example, an (n,α) reaction produces one 4He per reaction. The gas might be a
residual nucleus as in 2H(n,2n)1H or 9Be(n,2n)2α. Sometimes, the ENDF LR
flags are used to indicate that the residual nucleus from a reaction breaks up by
further particle emission. An example of this is 16O(n,n6)αrepresented using
MT=56/LR=22. In other cases, the yield per reaction for the light product
may be tabulated directly (and even be fractional) when File 6 is used for the
reaction. This is common for the high-energy data (150 MeV) introduced for
ENDF/B-VI Release 6. GASPR goes through all the reactions in the evaluation
and adds up all these various contributions to get the net production of each of
the light species.
The ENDF format assigns the MT values from 203 to 207 to represent the
production of hydrogen, deuterium, tritium, 3He, and 4He, but only a few eval-
uators have supplied these data in the past. By using GASPR to generate these
data at the PENDF stage, a number of possible inconsistencies are avoided.
Therefore, when gas-production MT values are found, GASPR removes them in
favor of the ones that it calculates.
When the code runs, it prints out a summary of which reactions contribute
to the production of each gas. Here is an example for aluminum from ENDF/B-
VII.0:
NJOY2016 723

LA-UR-17-20093 25 GASPR
mf6,mt5 found
the gas production threshold is 1.8969E+06 ev
found 1038 points
pendf mt mt203 mt204 mt205 mt206 mt207
________ _____ _____ _____ _____ _____
5 *** *** *** 0.0 ***
22 0.0 0.0 0.0 0.0 1.0
28 1.0 0.0 0.0 0.0 0.0
32 0.0 1.0 0.0 0.0 0.0
33 0.0 0.0 1.0 0.0 0.0
45 1.0 0.0 0.0 0.0 1.0
103 1.0 0.0 0.0 0.0 0.0
104 0.0 1.0 0.0 0.0 0.0
105 0.0 0.0 1.0 0.0 0.0
107 0.0 0.0 0.0 0.0 1.0
108 0.0 0.0 0.0 0.0 2.0
111 2.0 0.0 0.0 0.0 0.0
112 1.0 0.0 0.0 0.0 1.0
117 0.0 1.0 0.0 0.0 1.0
*** means that the yield is energy dependent
found 8 temperatures
25.2 User Input
The following input instructions were copied from the comment cards at the
beginning of the GASPR source. It is always a good idea to check the cards in
the current version of the program for possible changes.
Users are cautioned that only tape numbers are input. GASPR assumes that
the first material read from each tape is the material to be processed. Therefore,
if dealing with multi-material tapes MODER should be run to create a single
material tape for input to GASPR.
724 NJOY2016

25 GASPR LA-UR-17-20093
! card 1
! nendf unit for endf tape
! nin unit for input pendf tape
! nout unit for output pendf tape
25.3 Coding Details
Subroutine gaspr is exported by module gaspm. The code first checks the di-
rectory in File 1 of the ENDF tape to see whether MF=6/MT=5 is present
(see mf6mt5). If so, it reads through the MT=5 section of File 6 and saves the
various light-particle yields in the array six using a set of pointers like l203,
l204, and so on.
GASPR then proceeds to read through the input PENDF tape. It copies
all the sections up to point where the gas production sections will be inserted
to a scratch file. It then goes through all these reactions computing the direct
products and the residual nucleus (with full account of the LR flags) and de-
termines the lowest threshold for gas production. It then goes back through
the scratch file again to get the energy grid for the total cross section starting
at the threshold (see egas). It continues looping over all the reactions on the
file, determining again what the direct products and residual nuclei are, and
accumulating the gas production values in the array sgas(particle,energy).
When all the reactions have been processed, GASPR goes back and updates
the directory in MF=1/MT=451 to reflect the new reactions that have been
added. It copies all the reactions on the scratch file to the output PENDF tape.
It constructs new MF=3 sections for each of the gas-production reactions that
was found. And then it copies the remainder of the input PENDF tape to the
output file.
25.4 Error Messages
error in gaspr***npend and noutp must both be ...
The mode of the PENDF tape must not change, because many of the
sections are simply copied.
error in gaspr***too many gas production energy points.
Should not occur, maxg used to allocate space for egas(maxg) and sgas(5,maxg)
is determined from the input file.
NJOY2016 725

LA-UR-17-20093 25 GASPR
726 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
26 NJOY Maintenance and Testing
There are several components of the NJOY Quality Assurance system: a detailed
code manual (this report), version control software (git) that keeps track of all
changes made to the code, a suite of standard test problems to verify installation,
and extensive application of the code to find special cases that lead to failures.
26.1 Code Maintenance with GIT
Begininng with NJOY2016, git is used for software version control. This is a
significant departure from UPD[88], the local version control program used for
past NJOY versions. git version control software is used virtually everywhere
modern software development is utilized and is available on platforms using
Windows, Linux, and Mac operating systems. git will keep track of the changes
made to all files it is tracking.
This manual is not a proper forum to provide a tutorial on using git. A brief
tutorial is available at https://try.github.io. This introduction provides the
reader with enough understanding to be able to perform basic git operations.
For additional information, we recommend users check the official git website,
https://git-scm.com, or other online resources (e.g., Pro Git[130]).
26.2 Standard Test Problems
Another important part of the NJOY revision control procedure is the set of
standard test problems used to validate each new version. This kind of system-
atic testing is also a key part of any QA program. The NJOY test problems
also act as examples in helping new users to operate the code system. Brief de-
scriptions of the current sec of test problems follow. See the following sections
for details.
Problem 1: Process one ENDF/B-V isotope through pointwise and multigroup
modules. It tests heating and damage calculations, thermal calculations for
free-gas carbon and carbon bound in graphite, and multigroup averaging.
The full PENDF tape is included in the test comparisons. ENDF/B-V Tape
511 and ENDF/B-III thermal tape T322 are provided in the NJOY2016
package.
Problem 2: Process one ENDF/B-IV isotope for a practical CCCC library.
It tests resonance reconstruction, Doppler-broadening to several tempera-
tures, self-shielded unresolved cross sections, self-shielded multigroup cross
NJOY2016 727

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
sections, and the CCCC files ISOTXS, BRKOXS, and DLAYXS. Tape 404
is provided in the NJOY2016 package.
Problem 3: Process photon interaction cross sections into DTF and MATXS
formats. The problem tests photoatomic cross section linearization in
RECONR, multigroup averaging in GAMINR, and output formatting in
DTFR and MATXSR. The DLC7E library is provided in the NJOY2016
package.
Problem 4: ERRORR is tested, including the calculation of covariances for
fission ¯ν. Tape 511 is used.
Problem 5: This run tests COVR, including the plotting capability. Tape 511
is used. This calculation produces a large number of covariance graphs.
Problem 6: Includes a number of 2-D sample problems for PLOTR, and one
3-D case. Plots with special characters, error bars, curve tags, and legend
blocks are demonstrated.
Problem 7: Prepares an ACE-format library for a fissionable material.
Problem 8: Checks the processing of a typical ENDF/B-VI material using
Reich-Moore resonances and File 6 for energy-angle distributions through
PENDF production and ACER formatting.
Problem 9: Demonstrates the use of LEAPR to generate a scattering kernel
for water. The αand βranges have been reduced to make the case run
faster with less output.
Problem 10: The production of unresolved resonance probability tables for
MCNP is demonstrated. UNRESR and PURR are both run to allow com-
parisons of the Bondarenko results, and then ACER is run to format the
results for MCNP.
Problem 11: Demonstrates the production of a library for the WIMS reactor
lattice code using 238Pu from ENDF/B-V. PENDF processing, GROUPR,
and WIMSR are all included.
Problem 12: Shows how to use GASPR to generate gas-production data on the
PENDF file, including color Postscript plots of the resulting cross sections.
Problem 13: Demonstrates the “new” MCNP formats and ACE plotting.
Problem 14: Shows how to prepare ACE incident proton data and demon-
strates the charged-particle format. The necessary evaluation is provided.
Problem 15: Executes MODER/RECONR/BROADR/GROUPR/ERRORR
(once each for MF31, MF33 and MF34). This job illustrates NJOYs ability
to process uncertainty data for ¯ν(MF31), pointwise cross sections (MF33)
and angular distributions (MF4/MT2 P1moment). The “ENDF’ input
tape is the JENDL-3.3 238U evaluation, demonstrating that non-ENDF li-
braries that conform to the ENDF-6 format can be successfully processed
by NJOY. This input tape is provided in the NJOY2016 package.
728 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
Problem 16: This test job is similar to Problem 15, but it omits the GROUPR
module, demonstrating that uncertainty data (MF33 & MF34) processing
can proceed directly from PENDF input. We also append multiple COVR
and VIEWR inputs to this job to illustrate postscript plot generation for a
user-specified set of cross sections (MF33) and automatic plot generation
for MF34.
Problem 17: This is the longest running job in the NJOY test suite, involv-
ing processing of 235,238U and 239Pu. The job suite includes RECONR,
BROADR, and GROUPR for each nuclide, a MODER job to combine the
GENDF files and ERRORR processing that includes correlations among
the isotopes. The necessary JENDL-3.3 input files are provided in the
NJOY2016 package.
Problem 18: Execute MODER/RECONR/BROADR/GROUPR/ERRORR/
COVR and VIEWR to process MF35 (spectrum) uncertainty data. The
multigroup energy boundaries used in GROUPR and ERRORR match
those used to define the uncertainty data on the input tape and allow
for easy comparison of the processed output and the original data. The
“ENDF” input file is a composite of ENDF/B-VII.0 252Cf decay data (for
MF5 & MF35, MT18) and ENDF/B-VII.0 252Cf neutron transport data
(for all other MF/MT data) and given a dummy MATN of 9999.
Problem 19: Tests processing of a Reich-Moore evaluation (241Pu) in an ACE
file for MCNP. An RM evaluation from ORNL is provided.
Problem 20: Tests processing of covariance data from Reich-Moore-Limited
resonance parameters using an experimental 35Cl evaluation from ORNL
that is included in the NJOY2016 package.
26.3 Test Problem 1
This problem demonstrates how to prepare data for natural carbon as given on
the ENDF/B-V “Standards Tape” and one of the ENDF/B-III thermal tapes.
We’ve kept on using these old input libraries for this test over all the versions
of NJOY for consistency.
The input cards for NJOY are listed below in the form of a UNIX shell script.
We normally run this script in a subdirectory called test, and the first few cards
copy the ENDF general-purpose and thermal data from their normal locations
in the next higher directory into the test subdirectory. Note that the data files
are assigned the local names tape20 and tape26. The cat line starts a “here”
file, which continues down to the eof line near the end of the input. The NJOY
code is then run using this new input file, and the output file and PENDF file
are saved in the names out01, and pend01 for later comparisons with previous
runs.
NJOY2016 729

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
echo ’NJOY Test Problem 1’
echo ’getting endf tape 511’
cp ../t511 tape20
echo ’getting thermal tape 322’
cp ../t322 tape26
echo ’running njoy’
ulimit -s 32768
cat>input <<EOF
moder
20 -21
reconr
-21 -22
’pendf tape for c-nat from endf/b tape 511’/
1306 3/
.005/
’6-c-nat from tape 511’/
’processed by the njoy nuclear data processing system’/
’see original endf/b-v tape for details of evaluation’/
0/
broadr
-21 -22 -23
1306 1/
.005/
300.
0/
heatr
-21 -23 -22/
1306 1/
444
thermr
0 -22 -24
013068110012212
300.
.05 1.2/
thermr
26 -24 -23
1065 1306 8 1 2 1 0 1 229 2
300.
.05 1.2/
groupr
730 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
-21 -23 0 -24
13063333111
’carbon in graphite’/
300
1.e10
3 1 ’total’/
3 2 ’elastic’/
3 4 ’inelastic’/
3 51 ’discrete inelastic’/
3 -68 ’continued’/
3 91 ’continuum inelastic’/
3 102 ’n,g’/
3 103 ’(n,p)’/
3 104 ’(n,d)’/
3 107 ’(n,a)’/
3 221 ’free thermal scattering’/
3 229 ’graphite inelastic thermal scattering’/
3 230 ’graphite elastic thermal scattering’/
3 251 ’mubar’/
3 252 ’xi’/
3 253 ’gamma’/
3 301 ’total heat production’/
3 444 ’total damage energy production’/
6 2 ’elastic’/
6 51 ’discrete inelastic’/
6 -68 ’continued’/
6 91 ’continuum inelastic’/
6 221 ’free thermal scattering’/
6 229 ’graphite inelastic thermal scattering’/
6 230 ’graphite elastic thermal scattering’/
17 51 ’inelastic gamma production’/
16 102 ’capture gamma production’/
0/
0/
moder
-23 25
stop
EOF
../xnjoy<input
echo ’saving output and pendf files’
cp output out01
cp tape25 pend01
NJOY2016 731

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
The first step is to run the MODER module to convert the ASCII ENDF
file to binary mode. Using binary mode will often cut the cost of running
NJOY jobs. RECONR is then used to linearize and unionize the cross sections
(no resonance reconstruction is needed for carbon). A tolerance of 0.5% was
requested for this linearization. The BROADR module is used to Doppler-
broaden the carbon cross sections to 300K. It is recommended that the same
thinning and reconstruction tolerances be used in BROADR as are used in
RECONR.
This NJOY run supplements the original ENDF data with computed values
for heating, radiation damage, and thermal scattering. The call to the HEATR
module requests MT444 to get the damage cross section; heating (MT301) is
automatically provided. The first of the two THERMR runs generates thermal
scattering data for a carbon free gas at 300K (MT221). The second THERMR
run generates data for graphite (MT229). The “1” in the sixth field on the
input card directs the module to use the S(α, β) data from MT1065 on tape26
in order to compute the inelastic scattering cross section and scattering matrix,
the next field of “0” requests E, E0, µ ordering, and the following “1” directs
it to compute the coherent elastic scattering cross section using the built-in
parameters for graphite.
When the second THERMR run has finished, tape23 contains the complete
PENDF tape needed by GROUPR. Multigroup neutron reaction and photon
production cross sections are computed using the Los Alamos 30-group structure
for neutrons, the Los Alamos 12-group structure for photons, and the CLAW
weight function. The scattering order is P3. Note that the long-input form
is used to specify the list of reactions to be processed. Most users now prefer
the automatic input option. The user has to carefully look at the reactions
available on the ENDF tape and to consider the additional reactions added by
HEATR and THERMR. Note especially the inclusion of several gas production
reactions from the ENDF tape, the thermal reactions MT221 and MT229 from
the PENDF tape, and MT301 and MT444 as generated by HEATR from the
PENDF tape. The output is easy to read, but remember that groups are given
in the order of increasing energy.
The thermal scattering reactions must also be requested in the scattering
matrix section (MFD=6). MT230 was automatically generated by THERMR
as MT229+1 when coherent elastic scattering for graphite was requested.
732 NJOY2016
26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
Photon production matrices are requested in the lines with mfd=17 and
mfd=16. Actually, the use of “17” to denote data given in MF13 on the ENDF
tape is no longer required by GROUPR.
As a last step, this problem runs MODER once more to convert the binary
PENDF tape to ASCII mode.
26.4 Test Problem 2
The second problem supplements the first by adding resonance reconstruction
and output formatting. The ENDF/B-IV material 238Pu (MAT1050) was orig-
inally chosen for this problem because it was freely available and its execution
time was fairly small.
echo ’NJOY Test Problem 2’
echo ’getting endf tape 404’
cp ../t404 tape20
echo ’running njoy’
cat>input <<EOF
moder
20 -21
reconr
-21 -22
’pendf tape for pu-238 from endf/b-iv tape 404’/
1050 3/
.005/
’94-pu-238 from endf/b tape t404’/
’processed by the njoy nuclear data processing system’/
’see original endf/b-iv tape for details of evaluation’/
0/
broadr
-21 -22 -23
1050 3 0 1 0/
.005/
300. 900. 2100.
0/
moder
-23 33
unresr
-21 -23 -24
1050 3 7 1
300 900 2100
NJOY2016 733

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
1.e10 1.e5 1.e4 1000. 100. 10. 1
0/
groupr
-21 -24 0 -25
10505043371
’94-pu-238’/
300. 900. 2100.
1.e10 1.e5 1.e4 1000. 100. 10. 1
.1 0.025 0.8208e06 1.4e06
3 1 ’total’/
3 2 ’elastic’/
3 16 ’n2n’/
3 17 ’n3n’/
3 18 ’fission’/
3 102 ’capture’/
3 251 ’mubar’/
3 252 ’xi’/
3 253 ’gamma’/
3 259 ’1/v’/
6 2 ’elastic’/
6 16 ’n2n’/
6 17 ’n,3n’/
6 18 ’fission’/
6 51 ’discrete inelastic’/
6 -59 ’continued’/
6 91 ’continuum inelastic’/
0/
3 1 ’total’/
3 2 ’elastic’/
3 18 ’fission’/
3 102 ’capture’/
6 2 ’elastic’/
0/
3 1 ’total’/
3 2 ’elastic’/
3 18 ’fission’/
3 102 ’capture’/
6 2 ’elastic’/
0/
0/
ccccr
-25 26 27 0
734 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
1 1 ’t2lanl njoy’/
’ccccr tests for njoy’/
500141
pu238 pu238 endfb4 ’ 1050 ’ 1050 10.89
1 0 50 -1
0 2.3821e02 3.3003e-11 1.7461e-12 0. 1.e10 0.0
3 6
300 900 2100
1.e5 1.e4 1000. 100. 10. 1
moder
-24 28
stop
EOF
../xnjoy<input
echo ’saving output and pendf files’
cp output out02
cp tape28 pend02
The RECONR input is similar to the one in Problem 1, but reading the
listing file will demonstrate that RECONR added about 2700 points to the
original grid in the resonance region. After a little thinning, it ended up with
about 2800 resonance energy points at 0K for 0.5% reconstruction. The data
from RECONR was then passed to BROADR for preparation of cross sections
at 300, 900, and 2100K. An examination of the output listing shows that some
thinning was possible because of the smoothing effect of Doppler broadening;
the zero degree grid of 3241 points changed to 2341 points at 2100 degrees.
One of the new features of this run is the call to UNRESR. The user will nor-
mally notice that unresolved-resonance parameters are available for a material
by reading the introductory information on the ENDF tape, but UNRESR will
return gracefully if no unresolved data are present in the evaluation. The long
output from UNRESR gives a table of the self-shielded cross sections by reac-
tion (vertical) and sigma-zero value (horizontal) for each point of the unresolved-
range energy grid. The reactions are flux-weighted total, elastic, fission, capture,
and current-weighted total reading from the top down. Heating, damage, and
thermal cross sections were omitted for this particular problem. Therefore, the
final PENDF tape is on tape22, the output from UNRESR.
The GROUPR run shown here adds several new features over the one given
for Problem 1. First, multiple temperatures and sigma-zero values are speci-
NJOY2016 735

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
fied in order to get tables of self-shielded cross sections for the total, elastic,
fission, and capture reactions. It is desirable to use the same sigma-zero grid in
GROUPR that was used in UNRESR, although GROUPR will attempt to inter-
polate if the grids are different. Note that a section of GROUPR input is given
for 300K with complete coverage of all the reactions, and additional sections
are given for the two higher temperatures with only the self-shielded reactions
included. An examination of the output listing will show that self-shielded cross
sections are given for the low-energy reactions (total, elastic, fission, capture),
with group index reading down and sigma-zero value reading across.
Another new feature of this input is the computation of the fission matrix
(mfd=6,mtd=18). More complicated input may be necessary for other materials.
Examination of the output listing will show that GROUPR discovered that the
fission spectrum shape was constant over the entire energy range; therefore, it
only put out a spectrum and a fission-neutron production cross section.
When the GROUPR run is complete, the final GENDF tape will be found on
tape25. This file is used as input to the CCCCR module to produce ISOTXS
and BRKOXS files for 238Pu.
26.5 Test Problem 3
This problem demonstrates the use of GAMINR to prepare photon interaction
(or photoatomic) cross sections. It also demonstrates DTFR, including plotting,
and MATXSR. For the sake of continuity, this test problem uses a rather old
version of the photon interaction files called DLC7E. The MF23 and MF27 parts
of these data are written on two separate files. Later libraries have everything
on a single file.
echo ’NJOY Test Problem 3’
echo ’getting photoatomic tape gam23’
cp ../gam23 tape30
echo ’getting photoatomic tape gam27’
cp ../gam27 tape32
echo ’running njoy’
cat>input <<EOF
reconr
30 31
’pendf tape for photon interaction cross sections from dlc7e’/
110
.001/
736 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
’1-hydrogen’/
92 1 0
.001/
’92-uranium’/
0/
gaminr
32 31 0 33
13341
’12 group photon interaction library’/
-1 0/
92
-1 0/
0/
dtfr
33 34 31 36
110
512451610
’pheat’
1 621 1
0/
’h’ 1 1 0./
’u’ 92 1 0./
/
matxsr
0 33 35/
1 ’t2lanl njoy’/
1112
’12-group photon interaction library’/
’g’
12
’gscat’/
1
1
’h’ 1 1
’u’ 92 92
viewr
36 37/
stop
EOF
../xnjoy<input
echo ’saving output and plot files’
cp output out03
NJOY2016 737
LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
cp tape37 plot03
This run starts with an application of the RECONR module to linearize and
unionize the File 23 cross sections. Of course, there is no resonance reconstruc-
tion required here. This RECONR run demonstrates the use of a material loop;
both hydrogen and uranium are processed in one run. GAMINR is then used
to prepare the multigroup photon interaction cross sections, including heating;
this run also uses a multimaterial loop. The LANL 12-group photon structure
is used. The GENDF tape (tape33) is processed into two completely different
library formats. First, DTFR is called. This is a rather old output module, but
it is still useful for some purposes. For one thing, it automatically produces plots
of the multigroup data overlayed with the PENDF data. Examples of the plots
are given in the DTFR chapter of this manual. The MATXS output is more
useful, because it can be used in a much more flexible way by the TRANSX
code.
26.6 Test Problem 4
This problem illustrates several aspects of the calculation of covariances (un-
certainties) of multigroup data using ERRORR. The first ERRORR problem
produces, on unit 23, a file of multigroup cross section covariances (mfcov=33)
for all reactions present (iread=0) in File 33 for 235U. The group structure
employed is identical to the energy grid selected by the evaluator (ign=19);
however, no covariances are produced for cross sections below 1 eV or above
1 keV. The second ERRORR run adds to the above results a second data set
containing multigroup νcovariances. Note that the use of mfcov=31 dictates
that a GENDF file be produced (ngout=24) prior to the start of ERRORR. In
the νrun, a user-defined group structure is employed (ign=1).
echo ’NJOY Test Problem 4’
echo ’getting endf tape 511’
cp ../t511 tape20
echo ’running njoy...’
cat>input <<EOF
moder
20 -21
reconr
-21 -22
738 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
’u-235 10% pendf for errorr test problem from t511’/
1395/
.10/
0/
errorr
-21 -22 0 23 0/
1395 19 3 1 1/
0 0./
0 33/
1
1.e0 1.e3
groupr
-21 -22 0 24
13953030111
’u-235 multigroup nubar calculation’/
0.
1.e10
3 452 ’total nubar’/
0/
0/
errorr
-21 0 24 25 23/
1395 1 2 1 1/
1 0
0 31/
7
1.e0 1.e1 1.e2 1.e3 1.e4 1.e5 1.e6 1.e7
stop
EOF
../xnjoy<input
echo ’saving output’
cp output out04
26.7 Test Problem 5
This short problem produces multigroup covariances for carbon, again using
ign=19, but here all cross sections from 1E-5 to 2E7 are treated. The COVR
module reads the binary output file from ERRORR and produces publication-
quality plots of all reactions for which covariance data exist. This simple problem
setup could be used with only a few simple changes for any nuclide, in order to
NJOY2016 739
LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
take a quick look at the contents of the covariance files. For applications where
the resonance region is of interest, it is necessary to replace the second MODER
step with a resonance reconstruction step using RECONR, as in the previous
example.
echo ’NJOY Test Problem 5’
echo ’getting endf tape 511’
cp ../t511 tape30
echo ’running njoy...’
cat>input <<EOF
moder
30 -31
moder
-31 -32
errorr
-31 -32 0 33/
1306 19 2 1/
0 0
0 33/
1
1e-5 2e7/
covr
33 0 34/
1/
/
/
1306/
viewr
34 35/
stop
EOF
../xnjoy<input
echo ’saving output and plot files’
cp output out05
cp tape35 plot05
26.8 Test Problem 6
This test problem demonstrates and tests a number of different kinds of plots
using data from ENDF/B-V Tape 511 (the “Standards Tape”). The graphs pro-
740 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
duced and a detailed discussion of the input cards will be found in the PLOTR
chapter of this manual.
echo ’NJOY Test Problem 6’
echo ’getting endf tape 511’
cp ../t511 tape30
echo ’running njoy’
cat>input <<EOF
plotr
31/
/
1/
’<endf/b-v carbon’/
’<t>otal <c>ross <s>ection’/
4/
1e3 2e7/
/
.5 10/
/
5 30 1306 3 1/
/
1/
’<endf/b-v carbon’/
’(n,]a>) with fake data’/
1 0 2 1 1.3e7 .32/
/
/
/
/
5 30 1306 3 107/
/
’<endf/b-v mat1306’/
2/
0/
-1 0/
’<s>mith & <s>mith 1914’/
0/
1.1e7 .08 .05 .05/
1.2e7 .10 .05 .05/
1.3e7 .09 .04 .04/
1.4e7 .08 .03 .03/
NJOY2016 741

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
/
3/
0/
-1 2/
’<b>lack & <b>lue 2008’/
0/
1.15e7 .07 .02 0. .2e6 0./
1.25e7 .11 .02 0. .2e6 0./
1.35e7 .08 .015 0. .2e6 0./
1.45e7 .075 .01 0. .2e6 0./
/
1/
’<endf/b-v carbon’/
’<e>lastic <mf4>’/
-1 2/
/
/
/
/
/
/
5 30 1306 4 2/
/
1/
’<endf/b-v l>i-6’/
’(n,2n)]a >neutron distribution’/
-1 2/
/
/
0 12e6 2e6/
/
/
/
5 30 1303 5 24/
/
1/
’<endf/b-v l>i-6’/
’(n,2n)]a >neutron spectra vs <E>’/
4022/
10. 2.e7/
/
1e-11 1e-6/
742 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
’<c>ross <s>ection (barns/e<v>)’/
5 30 1303 5 24 0. 12/
/
’10 <m>e<v’/
1e3 2e-11 1e2/
2/
5 30 1303 5 24 0. 16/
/
’14 <m>e<v’/
1e4 2e-10 2e3/
3/
5 30 1303 5 24 0. 20/
/
’20 <m>e<v’/
1e5 2e-9 4e4/
99/
viewr
31 32/
stop
EOF
../xnjoy<input
echo ’saving plot file’
cp tape32 plot06
26.9 Test Problem 7
This test problem demonstrates the preparation of ACE format libraries for
the MCNP continuous-energy Monte Carlo code. The material selected for
processing was 235U from ENDF/B-V. The GROUPR run is included to make
a 30x20 photon production matrix for ACER. This is an obsolete method for
handling photon production for MCNP – nowadays, people use the “Detailed
Photon Production” option. This old test problem is kept for consistency with
the testing in previous versions of NJOY.
echo ’NJOY Test Problem 7’
echo ’getting endf tape 511’
cp ../t511 tape20
echo ’running njoy...’
cat>input <<EOF
NJOY2016 743

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
moder
20 -21
reconr
-21 -22
’pendf tape for u-235 from endf/b-v tape 511’ /
1395 3 /
.005 /
’92-u-235 from endf/b-v tape 511 ’ /
’processed by the njoy nuclear data processing system’ /
’see original endf/b-v tape for details of evaluation’ /
0 /
broadr
-21 -22 -23
13951010/
.005 /
300.
0 /
heatr
-21 -23 -24/
1395/
moder
-24 28
groupr
-21 -24 0 -25
13953290111/
’u-235 from tape 511’ /
300.
1.0e10
16 /
0 /
0 /
acer
-21 -24 -25 26 27 /
1/
’njoy test problem 7’/
1395 300. /
0/
/
stop
EOF
../xnjoy<input
echo ’saving output, pendf, and ace files’
744 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
cp output out07
cp tape26 ace07
cp tape28 pend07
26.10 Test Problem 8
This problem was added to the NJOY testing suite to verify the processing of a
typical ENDF/B-VI material with Reich-Moore resonances and File 6 energy-
angle distributions. The 61Ni evaluation is from ORNL, and the file is included
in the NJOY package. The normal processing sequence is used. The GROUPR
run is included to provide additional output for comparing to standard results
or to older testing results. An ACER run is also included.
echo ’NJOY Test Problem 8’
echo ’getting endf tape for ni-61’
cp ../eni61 tape20
cat>input <<EOF
moder
20 -21
reconr
-21 -22
’pendf tape for endf/b-vi.1 28-ni-61a’/
2834 1 0 /
.01/
’28-ni-61a from endf/b-vi.1 t124 (hetrick,fu;ornl)’/
0/
broadr
-21 -22 -23
2834 1/
.01/
300/
0/
heatr
-21 -23 -24/
2834 6 0 1 0 2/
302 303 304 402 443 444
moder
-24 28
groupr
-21 -24 0 -22
NJOY2016 745
LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
28343394111
’ni61a endf/b-vi.1 30x12’/
300
1e10
3/
3 251 ’mubar’/
3 252 ’xi’/
3 253 ’gamma’/
3 259 ’1/v’/
6/
16/
0/
0/
acer
-21 -24 0 25 26
1 1 1/
’28-ni-61a from endf-vi.1’/
2834 300./
0/
/
stop
EOF
echo "running njoy"
../xnjoy<input
echo ’saving output and pendf files’
cp output out08
cp tape28 pend08
26.11 Test Problem 9
This example demonstrates and tests the use of the LEAPR module to generate
thermal scattering data. The material is 1H to be used with 16O for a problem
requiring water. The run starts out with the familiar use of RECONR and
BROADR to construct the basic cross sections at 296K. LEAPR is then used to
generate an S(α, β) scattering kernel on tape24. Shortened αand βgrids are
used for compactness. The THERMR module is then run using tape24 as input
to add the thermal scattering cross section and scattering data to the PENDF
tape on tape23. The new PENDF tape is on tape25, and it can be used as
input to GROUPR for a multigroup library or to ACER for an MCNP Monte
746 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
Carlo library.
echo ’NJOY Test Problem 9’
echo ’getting endf tape 511’
cp ../t511 tape20
echo ’running njoy’
cat>input <<EOF
moder
20 -21
reconr
-21 -22
’pendf tape for h-1 from endf/b tape 511’/
1301 3/
.005/
’1-h-1 from tape 511’/
’processed by the njoy nuclear data processing system’/
’see original endf/b-v tape for details of evaluation’/
0/
broadr
-21 -22 -23
1301 1/
.005/
296.
0/
leapr
24
’h in h2o, shortened endf model’/
1 1/
101 1001./
0.99917 20.449 2 0 0/
1 1. 15.85316 3.8883 1/
65 75 1/
.01008 .015 .0252 .033 0.050406
.0756 0.100812 0.151218 0.201624 0.252030 0.302436 0.352842
0.403248 0.453654 0.504060 0.554466 0.609711 0.670259 0.736623
0.809349 0.889061 0.976435 1.072130 1.177080 1.292110 1.418220
1.556330 1.707750 1.873790 2.055660 2.255060 2.473520 2.712950
2.975460 3.263080 3.578320 3.923900 4.302660 4.717700 5.172560
5.671180 6.217580 6.816500 7.472890 8.192280 8.980730 9.844890
10.79190 11.83030 12.96740 14.21450 15.58150 17.07960 18.72080
20.52030 22.49220 24.65260 27.02160 29.61750 32.46250 35.58160
NJOY2016 747

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
38.99910 42.74530 46.85030 50.0/
0.000000 0.006375 0.012750 0.025500 0.038250 0.051000 0.065750
.0806495 0.120974 0.161299 0.241949 0.322598 0.403248 0.483897
0.564547 0.645197 0.725846 0.806496 0.887145 0.967795 1.048440
1.129090 1.209740 1.290390 1.371040 1.451690 1.532340 1.612990
1.693640 1.774290 1.854940 1.935590 2.016240 2.096890 2.177540
2.258190 2.338840 2.419490 2.500140 2.580790 2.669500 2.767090
2.874450 2.992500 3.122350 3.265300 3.422470 3.595360 3.785490
3.994670 4.224730 4.477870 4.756310 5.062580 5.399390 5.769970
6.177660 6.626070 7.119240 7.661810 8.258620 8.915110 9.637220
10.43200 11.30510 12.26680 13.32430 14.48670 15.76600 17.17330
18.72180 20.42450 22.29760 24.35720 25.0/
296/
.00255 67/
0 .0005 .001 .002 .0035 .005 .0075 .01 .013 .0165 .02 .0245
.029 .034 .0395 .045 .0506 .0562 .0622 .0686 .075 .083 .091
.099 .107 .115 .1197 .1214 .1218 .1195 .1125 .1065 .1005 .09542
.09126 .0871 .0839 .0807 .07798 .07574 .0735 .07162 .06974
.06804 .06652 .065 .0634 .0618 .06022 .05866 .0571 .05586
.05462 .0535 .0525 .0515 .05042 .04934 .04822 .04706 .0459
.04478 .04366 .04288 .04244 .042 0./
0.055556 0. 0.444444 0./ for diffusion, use 120. for second number
2/
.205 .48/
.166667 .333333/
’ h(h2o) thermal scattering ’/
’ ’/
’ temperatures = 296 deg k. ’/
’ ’/
’ shortened version of the endf/b-vi.4 evaluation for ’/
’ hydrogen in water. the energy transfer is limited to ’/
’ 0.625 ev. this is only for njoy testing, not for ’/
’ real applications. ’/
/
thermr
24 -23 -25
10113018121012222
296.
.05 .625
stop
EOF
../xnjoy<input
748 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
echo ’saving output and pendf files’
cp output out09
cp tape24 pend09
26.12 Test Problem 10
This case was constructed to demonstrate unresolved resonance range process-
ing for MCNP libraries. It starts with linearization, unionization, resonance
reconstruction, and Doppler broadening to 300, 900, and 2100K. The UNRESR
module to run to generate one version of the self-shielded unresolved range cross
sections on MF=2/MT152 to tape24 for the three temperatures and seven values
of the background cross section σ0. Then the PURR module is run to generate
probability tables on MF=2/MT153 of the PENDF tape and an alternate set of
self-shielded cross sections. Actually, once PURR has run, the MT152 values for
UNRESR are overwritten with the PURR values. Both methods are provided
on this run to allow them to be compared. Finally, ACER is run to format the
data for MCNP.
echo ’NJOY Test Problem 10’
echo ’getting endf tape 404’
cp ../t404 tape20
echo ’running njoy’
cat>input <<EOF
moder
20 -21
reconr
-21 -22
’pendf tape for pu-238 from endf/b-iv tape 404’/
1050 3/
.005/
’94-pu-238 from endf/b tape t404’/
’processed by the njoy nuclear data processing system’/
’see original endf/b-iv tape for details of evaluation’/
0/
broadr
-21 -22 -23
1050 3 0 1 0/
.005/
300. 900. 2100.
NJOY2016 749

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
0/
unresr
-21 -23 -24
1050 3 7 1
300 900 2100
1.e10 1.e5 1.e4 1000. 100. 10. 1
0/
purr
-21 -24 -25
1050 3 7 20 4/
300 900 2100
1.e10 1.e5 1.e4 1000. 100. 10. 1
0/
acer
-21 -25 0 26 27/
1/
’njoy test problem 10’/
1050 300./
/
/
moder
-25 28
stop
EOF
../xnjoy<input
echo ’saving output, ace, and pendf files’
cp output out10
cp tape26 ace10
cp tape28 pend10
26.13 Test Problem 11
This case demonstrates and tests the construction of a multigroup library for the
WIMS reactor physics code. Here, we will need thermal data, so the THERMR
module is included in the processing path. Once the GROUPR module has been
run, WIMSR is used for the final formatting.
echo ’NJOY Test Problem 11’
echo ’getting endf tape 404’
cp ../t404 tape20
750 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
echo ’running njoy’
cat>input <<EOF
moder
20 -21
reconr
-21 -22
’pendf tape for pu-238 from endf/b-iv tape 404’/
1050 3/
.005/
’94-pu-238 from endf/b tape t404’/
’processed by the njoy nuclear data processing system’/
’see original endf/b-iv tape for details of evaluation’/
0/
broadr
-21 -22 -23
10503010/
.005/
300. 900. 2100.
0/
unresr
-21 -23 -24
1050 3 7 1
300 900 2100
1.e10 1.e5 1.e4 1000. 100. 10. 1
0/
thermr
0 -24 -25
010508310012210
300. 900. 2100.
.05 4.2
groupr
-21 -25 0 -26
10509053371
’94-pu-238’/
300. 900. 2100.
1.e10 1.e5 1.e4 1000. 100. 10. 1
3 1 ’total’/
3 2 ’elastic’/
3 16 ’n2n’/
3 17 ’n3n’/
3 18 ’fission’/
3 102 ’capture’/
NJOY2016 751

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
3 221 ’free gas thermal’/
6 2 ’elastic’/
6 16 ’n2n’/
6 17 ’n,3n’/
6 18 ’fission’/
6 51 ’discrete inelastic’/
6 -59 ’continued’/
6 91 ’continuum inelastic’/
6 221 ’free gas thermal’/
0/
3 1 ’total’/
3 2 ’elastic’/
3 18 ’fission’/
3 102 ’capture’/
3 221 ’free gas thermal’/
6 2 ’elastic’/
6 221 ’free gas thermal’/
0/
3 1 ’total’/
3 2 ’elastic’/
3 18 ’fission’/
3 102 ’capture’/
3 221 ’free gas thermal’/
6 2 ’elastic’/
6 221 ’free gas thermal’/
0/
0/
wimsr
-26 27
1/
1050 1 1050./
3 7 1e10 3 10.890 221 0/
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1./
stop
EOF
../xnjoy<input
echo ’saving output and wims files’
cp output out11
cp tape27 wims11
752 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
26.14 Test Problem 12
This case was constructed to demonstrate the methods for adding gas produc-
tion to a processing stream. The GASPR module doesn’t require any special
input. We then use the PLOTR and VIEWR modules to graph the gas produc-
tion reactions using color Postscript. The gas production reactions have special
MT values in the range 203 to 207. They can also be fed into GROUPR for
multigroup applications and ACER for MCNP Monte Carlo libraries.
echo ’NJOY Test Problem 12’
echo ’getting endf tape for ni-61’
cp ../eni61 tape20
cat>input <<EOF
reconr
20 21
’pendf tape for endf/b-vi.1 28-ni-61a’/
2834 1 0 /
.01/
’28-ni-61a from endf/b-vi.1 t124 (hetrick,fu;ornl)’/
0/
gaspr
20 21 22
plotr
23/
1 1 .3 2/
1 3/
’<endf/b-vi n>i-61’/
’<r>esonance <c>ross <s>ections’/
2 0 3 1 23e3 5e2/
.5e4 3e4 .5e4/
/
1e-3 1e3/
/
6 22 2834 3 2/
00032/
’elastic’/
2/
6 22 2834 3 102/
00012/
’capture’/
1 7/
NJOY2016 753

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
’<endf/b-vi n>i-61’/
’<g>as <p>roduction’/
1031/
0 2e7 5e6/
/
/
/
6 22 2834 3 203 0./
00012/
’hydrogen’/
2/
6 22 2834 3 207 0./
00022/
’helium-4’/
99/
viewr
23 24
stop
EOF
echo "running njoy"
../xnjoy<input
echo ’saving output, pendf, and plot files’
cp output out12
cp tape22 pend12
cp tape24 plot12
26.15 Test Problem 13
This test problem was constructed when Reich-Moore resonance processing and
File 6 energy-angle distributions began to be used in ENDF/B files. The sample
evaluation for 61Ni was generated at ORNL, and it is provided in the NJOY
package. Note that HEATR and GASPR are included to satisfy the expectations
for a complete ACE library. Two ACER runs are used here. The first one
generates an ACE library on tape26. The second one reads in this new ACE
file, does a series of consistency checks, provides an eye-readable listing, and
makes a large set of color Postscript plots showing the various reaction cross
sections and distributions. This is a part of the QA procedure for ACE libraries.
The file tape36 output by VIEWR is the plot file in Postscript format.
754 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
echo ’NJOY Test Problem 13’
echo ’getting endf tape for ni-61’
cp ../eni61 tape20
cat>input <<EOF
moder
20 -21
reconr
-21 -22
’pendf tape for endf/b-vi.1 28-ni-61a’/
2834 1 0 /
.01/
’28-ni-61a from endf/b-vi.1 t124 (hetrick,fu;ornl)’/
0/
broadr
-21 -22 -23
2834 1/
.01/
300/
0/
heatr
-21 -23 -24/
2834 6 0 1 0 2/
302 303 304 402 443 444
gaspr
-21 -24 -25
moder
-25 28
acer
-21 -25 0 26 27
1 0 1/
’28-ni-61a endf-vi.1 njoy99’/
2834 300./
/
/
acer
0 26 33 34 35
7 1 2/
’28-ni-61a endf-vi.1 njoy99’/
viewr
33 36/
NJOY2016 755

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
stop
EOF
echo "running njoy"
../xnjoy<input
echo ’saving output, pendf, ace, and plot files’
cp output out13
cp tape28 pend13
cp tape26 ace13
cp tape36 plot13
26.16 Test Problem 14
This case demonstrates and tests processing for incident charged particles, specif-
ically, protons on 14N. It is not necessary to run reconstruction or Doppler broad-
ening, so the evaluation is read directly into ACER. A copy of the ENDF/B file
is used as the PENDF input. Once again, two ACER runs are used: one to
generate the ACE file, and one to do the checks and make color Postscript
plots.
echo ’NJOY Test Problem 14’
echo ’getting endf tape for p+n14’
cp ../epn14 tape20
cp tape20 tape21
cat>input <<EOF
acer
20 21 0 31 32
1 0 1/
’proton + 7-n-14 apt la150 njoy99 mcnpx’/
725 0./
/
/
acer
0 31 33 34 35
7 1 2/
’proton + 7-n-14 apt la150 njoy99 mcnpx’/
viewr
33 36/
stop
EOF
echo "running njoy"
756 NJOY2016
26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
../xnjoy<input
echo ’saving output, ace, and plot files’
cp output out14
cp tape31 ace14
cp tape36 plot14
26.17 Test Problem 15
This test problem exercises the ERRORR routines used to process MF31 (¯ν),
MF33 (cross sections) and MF34 (MF4/MT2 P1component only) uncertainty
data. We use the JENDL-3.3 238U evaluation for input, demonstrating that
non-ENDF/B libraries that conform to the ENDF-6 format can be processed by
NJOY. The job includes a standard MODER/RECONR/BROADR/GROUPR
sequence to create Doppler broadened PENDF and group-averaged GENDF
tapes followed by a sequence of ERRORR jobs; one for each MF value to be
processed. Use of GROUPR to process ¯ν(MF=3, MT=whatever MF=31 sec-
tions are present) is a pre-requisite for MF=31 processing with ERRORR. The
first ERRORR job processes MF=31 data (specified via the second item on the
third input line (corresponding to card 7 in the ERRORR input description)).
The first input line specifies the various input and output files; tape21 for a
binary ENDF tape, tape91 for a GENDF tape and tape25 for the ERRORR
output tape in this instance. The material number, multigroup energy structure
and weighting function options are specified on the second input line. This in-
put line could have been terminated here, as the fourth and fifth items, related
to printing and selection of relative rather than absolute covariances, are given
their default values. Users will notice that the group structure and weighting
function options differ from those specified in the GROUPR input preceding
ERRORR. NJOY will not flag this as an error, but it is not recommended prac-
tice. The third input card (corresponding to card 7 in the ERRORR input, since
ngout.ne.0, and we are dealing with ENDF-6 format data), specifies iread=0
meaning that all MF=31 (the second item on this input card) MT values found
on the ENDF input tape will be processed. The remaining items on this card are
not germaine to MF=31 processing and could have been omitted. Additional
ERRORR jobs process the cross section uncertainties (MF=33) and elastic scat-
tering Legendre (P1only) moment uncertainty (MF=34) using a combination
of ENDF and GENDF input tapes. Separate output files (tape25,tape26 and
tape27) are created with these three ERRORR executions. These are ASCII
NJOY2016 757

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
files that may be viewed in any text editor or saved for use in a subsequent
NJOY job, such as COVR/VIEWR for plot generation.
echo ’NJOY Test Problem 15’
echo ’getting JENDL-3.3 U-238’
cp ../J33U238 tape20
echo ’running njoy’
ulimit -s 32768
cat>input <<EOF
moder
20 -21 /
reconr
-21 -22 /
’processing of U-238 of jendl-3.3.’
9237 0 0 /
0.001 /
0 /
broadr
-21 -22 -23 /
92371000/
0.001 /
300. /
0 /
groupr
-21 -23 0 91 /
92373021111/
’test’
300. /
1.0e10 /
3 /
3 251 ’mubar’ /
3 252 ’xi’ /
3 452 ’nu’ /
3 455 ’nu’ /
3 456 ’nu’ /
5 18 ’xi’ /
0 /
0 /
--
-- process mf31
errorr
758 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
-210912500/
92373611/
1 300./
03111-1/
--
-- process mf33
errorr
-210912600/
92373611/
1 300./
03311-1/
--
-- process mf34
errorr
-210912700/
92373611/
1 300./
03411-1/
--
-- make mf31 plot file
covr
25 0 35 /
1 /
/
/
9237 /
--
-- make mf33 plot file.
covr
26 0 36 /
1 /
/
1 14 /
9237 1 9237 1 /
9237 1 9237 2 /
9237 2 9237 2 /
9237 2 9237 4 /
9237 2 9237 16 /
9237 2 9237 17 /
9237 2 9237 18 /
9237 2 9237 102 /
9237 4 9237 4 /
NJOY2016 759

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
9237 16 9237 16 /
9237 17 9237 17 /
9237 18 9237 18 /
9237 18 9237 102 /
9237 102 9237 102 /
--
-- make mf34 plot file.
covr
27 0 37 /
1 /
/
/
9237 /
--
-- make mf31 postscript file.
viewr
35 45 /
--
-- make mf33 postscript file.
viewr
36 46 /
--
-- make mf34 postscript file.
viewr
37 47 /
stop
EOF
../xnjoy<input
echo ’saving output file’
cp output out15
cp tape45 plot15-31
cp tape46 plot15-33
cp tape47 plot15-34
26.18 Test Problem 16
This test problem is similar to test 15, but we omit GROUPR and only process
cross section (MF=33) and P1moment (MF=34) uncertainties with ERRORR.
As stated in the previous problem, GROUPR execution is required when using
ERRORR to process MF=31 data but, as shown here, is not required to process
760 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
MF=33 or MF=34 uncertainty data. We also append COVR and VIEWR
to this job to demonstrate Postscript plot generation. The first COVR job
reads tape26, the ERRORR MF=33 processed output tape and will create
tape36 containing the appropriate plot commands that VIEWR uses to create
a Postscript formatted tape46. Additional COVR input includes icolor=1
(card 2) to specify color plots, and a user-specified number of plots, ncase=14,
on the third (card 3a) input card. This is followed by 14 occurrences of card 4.
The second COVR job reads the ERRORR output tape created from MF=34
processing and creates all possible plots as we use the default input values for
the variables defined by the third input card. In reality there will only be a
single plot since MF=34 processing is only performed for the elastic scattering
(MF=4/MT=2) P1Legendre moment. The output of this COVR job, tape37
is fed to VIEWR, which generates a Postscript formatted file, tape47.
echo ’NJOY Test Problem 16’
echo ’getting JENDL-3.3 U-238’
cp ../J33U238 tape20
echo ’running njoy’
ulimit -s 32768
cat>input <<EOF
moder
20 -21 /
reconr
-21 -22 /
’processing of U-238 of jendl-3.3.’
9237 0 0 /
0.001 /
0 /
broadr
-21 -22 -23 /
92371000/
0.001 /
300. /
0 /
--
-- process mf33 with internal group averaging
-- since there is no groupr input tape
errorr
-21 -23 0 26 0 0 /
92373611/
NJOY2016 761

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
0 300. /
0331/
--
-- process mf34
errorr
-21 -23 0 27 0 0 /
92373611/
0 300. /
03411/
--
-- make mf33 plot file.
covr
26 0 36 /
1 /
/
1 14 /
9237 1 9237 1 /
9237 1 9237 2 /
9237 2 9237 2 /
9237 2 9237 4 /
9237 2 9237 16 /
9237 2 9237 17 /
9237 2 9237 18 /
9237 2 9237 102 /
9237 4 9237 4 /
9237 16 9237 16 /
9237 17 9237 17 /
9237 18 9237 18 /
9237 18 9237 102 /
9237 102 9237 102 /
--
-- make mf34 plot file.
covr
27 0 37 /
1 /
/
/
9237 /
--
-- make mf33 postscript file.
viewr
36 46 /
762 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
--
-- make mf34 postscript file.
viewr
37 47 /
stop
EOF
../xnjoy<input
echo ’saving output file’
cp output out16
cp tape46 plot16-33
cp tape47 plot16-34
26.19 Test Problem 17
Test problem 17 is the longest running job in the NJOY test suite, involv-
ing processing of 235,238U and 239Pu. We start with a standard sequence of
RECONR/BROADR/GROUPR for each of these nuclides. Three separate
GENDF files are created (tape91,tape92, and tape93) by these GROUPR ex-
ecutions, followed by a MODER job that merges the three GENDF files onto
a single GENDF tape. MODERs card 1 nin=2 option is specified, followed by
multiple card 3 input to accomplish this merge. ERRORR begins with the stan-
dard input and output tape specifications on card 1 and the material number,
multigroup and weighting function specification on card 2. As we’ve included
an GENDF tape as part of the input and we’re dealing with ENDF-6 formatted
data, the third input card corresponds to card 7 in the ERRORR input descrip-
tion. Here we specify iread=2, indicating that additional MAT/MT data are
to be included over those found on the original ENDF input (tape21). This
additional input follows on the fourth and fifth input cards, corresponding to
repeated use of card 10 from the ERRORR input description. Based upon this
additional input, the effect of 235U (mat=9228) and 239Pu (mat=9437) MT=18
uncertainties are included when processing 238U (mat=9237) uncertainties.
echo ’NJOY Test Problem 17’
echo ’getting JENDL-3.3 U-238’
cp ../J33U238 tape21
echo ’getting JENDL-3.3 U-235’
cp ../J33U235 tape22
echo ’getting JENDL-3.3 Pu-239’
NJOY2016 763

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
cp ../J33Pu239 tape23
echo ’running njoy’
ulimit -s 32768
cat>input <<EOF
reconr
21 41 /
’processing jendl-3.3 238u.’/
9237 0 0 /
0.001 /
0 /
broadr
21 41 31 /
92371000/
0.001 /
300. /
0 /
reconr
22 42 /
’processing jendl-3.3 235u.’/
9228 0 0 /
0.001 /
0 /
broadr
22 42 32 /
92281000/
0.001 /
300. /
0 /
reconr
23 43 /
’processing jendl-3.3 239pu.’/
9437 0 0 /
0.001 /
0 /
broadr
23 43 33 /
94371000/
0.001 /
300. /
0 /
groupr
21 31 0 91 /
764 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
92373061110/
’u-238’ /
300. /
1.0e10 /
3 /
3 251 ’mubar’ /
3 252 ’xi’ /
3 452 ’nu’ /
3 455 ’nu’ /
3 456 ’nu’ /
5 18 ’xi’ /
0 /
0 /
groupr
22 32 0 92 /
92283061110/
’u-235’ /
300. /
1.0e10 /
3 /
0 /
0 /
groupr
23 33 0 93 /
94373061110/
’pu-239’ /
300. /
1.0e10 /
3 /
0 /
0 /
moder
2 99 /
’merge u235, u-238 and pu-239’ /
92 9228 /
91 9237 /
93 9437 /
0 /
errorr
21099260/
9237 3 6 1 /
1 300./
NJOY2016 765
LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
23311-1/
9228 18 /
9437 18 /
0 /
stop
EOF
../xnjoy<input
echo ’saving output file’
cp output out17
26.20 Test Problem 18
This test problem exercises the ERRORR spectrum uncertainty processing rou-
tines followed by a COVR/VIEWR job to produce plots of these data. There
are no spectrum uncertainty data in the ENDF/B-VII.0 neutron transport files,
but such data are provided for the spontaneous fission of 252Cf in the ENDF/B-
VII.0 decay file. Therefore a fictitious transport file has been created containing
MF5 and MF35, MT18 data from the decay file with the remaining MF/MT
data coming from the transport file. This tape serves as the ENDF input to a
MODER/RECONR/BROADR/GROUPR/ERRORR/COVR/VIEWR job.
This job could have started at GROUPR with MF5/MT18 processing. The
multgroup user input mimics the energy structure appearing in the MF35/MT18
input tape and was chosen to allow easy comparison of the final calculated uncer-
tainty with the corresponding data provided in MF1/MT451 by the evaluator.
The GROUPR GENDF output file resides on tape91 which along with the orig-
inal ENDF input (tape20) are input to ERRORR. The ERRORR output will go
on tape28. This tape will contain the results of processing MATN 9999 for the
user-specified multigroup structure with no weighting function (based upon the
ign=1,iwt=2 options specified on card 2). The third line in the ERRORR input
(really card 7 in the ERRORR input description) specifies processing MF35 data
for an incident neutron energy of 1.23 MeV (based upon the -1, 1.23e6 values
appearing as the fourth and fifth items on this input card). The remaining in-
put identifies the user-specified multigroup structure. After ERRORR, we pass
tape28 to COVR, where the appropriate plot commands are generated to pro-
duce the correlation matrix plot, the spectrum plot, and the uncertainty plot.
Card 2 (icolor) requests a color contour plot, and card 3 sets the lower (x-axis)
energy limit to 1 keV with default values used for the other input parameters.
766 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
Card 5 specifies the mat number for the material of interest. Finally, VIEWR
reads the COVR output file, tape38, and produces a postscript-formatted file,
tape39.
echo ’NJOY Test Problem 18’
echo ’getting endf tape for e7 cf252’
cp ../DCf252 tape20
echo ’running njoy’
cat>input <<EOF
--
-- Copy ascii input to binary.
moder
20 -21 /
--
-- Resonance reconstruction, to 0.1%.
reconr
-21 -22 /
’processing e70 252Cf with decay mf5/mt18 & mf35/mt18’
9999 0 0 /
0.001 /
0 /
--
-- Doppler broaden to 300K.
broadr
-21 -22 -23 /
99991000/
0.001 /
300. /
0 /
--
-- Group average, 300K with mf35 group structure.
-- - All file 3 cross sections plus fission spectrum.
groupr
-21 -23 0 91 /
99991021111/
’test’
300. /
1.0e10 /
71 / # of groups, energy boundaries follow:
1.000000-5 1.500000+4 3.500000+4 5.500000+4 7.500000+4
9.500000+4 1.150000+5 1.350000+5 1.650000+5 1.950000+5
NJOY2016 767

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
2.250000+5 2.550000+5 3.050000+5 3.550000+5 4.050000+5
4.550000+5 5.050000+5 5.550000+5 6.050000+5 6.550000+5
7.050000+5 7.550000+5 8.050000+5 8.550000+5 9.050000+5
9.550000+5 1.050000+6 1.150000+6 1.250000+6 1.350000+6
1.450000+6 1.550000+6 1.650000+6 1.750000+6 1.850000+6
1.950000+6 2.150000+6 2.350000+6 2.550000+6 2.750000+6
2.950000+6 3.250000+6 3.550000+6 3.850000+6 4.150000+6
4.450000+6 4.750000+6 5.050000+6 5.550000+6 6.050000+6
6.550000+6 7.050000+6 7.550000+6 8.050000+6 8.550000+6
9.050000+6 9.550000+6 1.005000+7 1.055000+7 1.105000+7
1.155000+7 1.205000+7 1.255000+7 1.305000+7 1.355000+7
1.405000+7 1.460000+7 1.590000+7 1.690000+7 1.790000+7
1.910000+7 2.000000+7
3 /
5 18 ’chi’ /
0 /
0 /
--
-- ERRORJ, mf35
errorr
200912800/
99991211/
1 300./
0 35 1 1 -1 1.23e6 /
71 / # of groups, energy boundaries follow:
1.000000-5 1.500000+4 3.500000+4 5.500000+4 7.500000+4
9.500000+4 1.150000+5 1.350000+5 1.650000+5 1.950000+5
2.250000+5 2.550000+5 3.050000+5 3.550000+5 4.050000+5
4.550000+5 5.050000+5 5.550000+5 6.050000+5 6.550000+5
7.050000+5 7.550000+5 8.050000+5 8.550000+5 9.050000+5
9.550000+5 1.050000+6 1.150000+6 1.250000+6 1.350000+6
1.450000+6 1.550000+6 1.650000+6 1.750000+6 1.850000+6
1.950000+6 2.150000+6 2.350000+6 2.550000+6 2.750000+6
2.950000+6 3.250000+6 3.550000+6 3.850000+6 4.150000+6
4.450000+6 4.750000+6 5.050000+6 5.550000+6 6.050000+6
6.550000+6 7.050000+6 7.550000+6 8.050000+6 8.550000+6
9.050000+6 9.550000+6 1.005000+7 1.055000+7 1.105000+7
1.155000+7 1.205000+7 1.255000+7 1.305000+7 1.355000+7
1.405000+7 1.460000+7 1.590000+7 1.690000+7 1.790000+7
1.910000+7 2.000000+7
--
-- make plot file.
768 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
covr
28 0 38 /
1 /
1.e3 /
/
9999 /
--
-- make postscript file.
viewr
38 39 /
stop
EOF
../xnjoy<input
echo ’saving output, ace, and pendf files’
cp output out18
cp tape39 plot18
26.21 Test Problem 19
The input file for this test is an evaluation for 241Pu using Reich-Moore resonance
parameters.
echo ’NJOY Test Problem 19’
echo ’getting endf tape for e6 pu241c’
cp ../e6pu241c tape20
echo ’running njoy’
cat>input <<EOF
moder
20 -21
reconr
-21 -22
’pendf tape for pu-241 from endf/b-vi.3’/
9443 3/
.02/
’94-pu-241 from endf/b-vi.3’/
’processed by the njoy nuclear data processing system’/
’see original endf/b-iv tape for details of evaluation’/
0/
broadr
-21 -22 -23
NJOY2016 769

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
9443 3 0 1 0/
.02/
293.6 900. 2100.
0/
unresr
-21 -23 -24
9443 3 7 1
293.6 900 2100
1.e10 1.e5 1.e4 1000. 100. 10. 1
0/
heatr
-21 -24 -25/
9443 3/
302 318 402
purr
-21 -25 -26
9443 3 7 20 4/
293.6 900 2100
1.e10 1.e5 1.e4 1000. 100. 10. 1
0/
acer
-21 -26 0 27 28/
1/
’njoy test problem 19’/
9443 293.6/
/
/
moder
-26 29
stop
EOF
../xnjoy<input
echo ’saving output, ace, and pendf files’
cp output out19
cp tape27 ace19
cp tape29 pend19
It starts with a normal RECONR run using 2% reconstruction for economy.
The output file will disclose that Reich-Moore resonances were processed. The
rest of the run follows the pattern of the previous examples.
770 NJOY2016
26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
26.22 Test Problem 20
The input file for this case is an experimental evaluation from ORNL for 35Cl
that uses the Reich-Moore-Limited (RML) format for its resonance parameters
(lrf=7 in MF2/MT151) and for the covariances between resonance parameters
(MF32). Utilizing the multi-channel capabilities of the RML representation,
resonance cross sections and their covariances also include the first two inelastic
levels (MT=51 and 52) in addition to the normal elastic and capture channels.
echo ’NJOY Test Problem 20’
echo ’getting cl35rml’
cp ../cl35rml tape20
echo ’running njoy’
ulimit -s 32768
cat>input <<EOF
errorr
999 / option to insert dummy file 33 data
+20 +21 / input & output tapes
1 / mt to insert,
2 / continue mt list ...
102 /
600 /
0 / terminate mt list with zero
reconr
+21 +22 /
’processing cl35 with rml’
1725 0 0 /
0.01 /
0 /
broadr
+20 +22 +23 /
17251000/
0.01 /
293.6 /
0 /
groupr
+20 +23 0 +91 /
17254021111/
’test of cl35 with rml’
293.6 /
1.0e10 /
NJOY2016 771

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
3 /
3 251 ’mubar’ /
3 252 ’xi’ /
0 /
0 /
errorr
+21 0 +91 +25 0 0 /
17254211/
1 293.6/
03311-1/
covr
+25 0 +26 /
1 /
.01 /
1 /
1725 /
viewr
+26 +27
stop
EOF
../xnjoy<input
echo ’saving output file’
cp output out20
cp tape23 pend20
cp tape27 plot20
The reconr output from this run will show that it used the RML methods and
it will list the reactions treated with resonance methods (MT=2, 51, 52, 102).
BROADR and GROUPR are used in the normal way, ERRORR and COVR are
then run to produce the covariances and prepare plots of the results.
26.23 Application of the NJOY System
There are not enough standard test problems to exercise all the many options
that evaluators manage to use. Therefore, the next step in testing is to run
NJOY on many different evaluations. This has included running all the materials
in recent ENDF/B (as well as many JEFF, JENDL and special purpose libraries
such as the IAEA’s International Reactor Dosimetry and Fusion File, IRDFF)
neutron, thermal, photoatomic, photonuclear, and charged-particle sublibraries
through to MCNP “ACE” files followed by short MCNP runs to make sure
772 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
the data have no obvious flaws that prevent the code from running. The out-
put files were examined for error messages and other indications of problems.
This process also produces a useful set of plots that can be scanned for possible
problems. Plots from some of these tests are available on the web. Browse to
http://t2.lanl.gov and select the “Nuclear Information Service (NIS)”, “Data
area” and “US ENDF/B Libraries” links. Look in “ENDF/B-VII Neutron
Data,” “ENDF/B-VII Thermal Scattering Data,” “ENDF/B-VII Proton Data,”
and “ENDF/B-VII Photonuclear Data.
As discussed in the HEATR section of this report, NJOY has the capability
to examine ENDF-format evaluations for energy balance problems that show
up for nuclear heating calculations. These tests can also reveal problems with
the processing on occasion. A large set of results, including plots, can be found
on the web. As before, browse to http://t2.lanl.gov, again select the “Nuclear
Information Service (NIS)”, “Data area” and “US ENDF/B Libraries” links,
but now scroll down to “Energy Balance of ENDF/B-VII.1,” and click on “sum-
mary.” This page lists the materials with their problems and provides links to
the plots.
Another test of the processing code comes from running criticality bench-
marks such as those defined in the ICSBEP Handbook[125] using the processed
data libraries. If results are consistent, it gives some confidence that the li-
braries don’t contain severe errors. Table 31 shows some benchmark results
using ENDF/B-VII.0 data processed with NJOY and used by MCNP5. The re-
sults are calculated keff values divided by the evaluated model keff value (C/E).
Similarly, we can calculate criticality benchmarks using multigroup libraries
with a discrete-ordinates transport code. The Los Alamos PARTISN code was
used with data prepared using TRANSX. Table 32 shows results for a selection of
fast critical assemblies using three different group structures. Comparing these
results with the previous table shows that multigroup methods can compare
favorably with Monte Carlo when using high-accuracy libraries. IMF007h is
a 2-D cyclindrical homogenized model for Big-10. Table 33 shows results for
two of the thermal solution criticals from Table 31. Once again, the results are
satisfactory. These kinds of tests provide some confidence that the multigroup
processing in NJOY is working properly and is consistent with the Monte Carlo
processing.
As a further verification of NJOY processing, it is useful to do intercom-
parisons with other processing systems. Over the years, we have periodically
compared NJOY results from RECONR and BROADR with the PREPRO sys-
NJOY2016 773

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
Table 31: Criticality benchmark results from MCNP5 using NJOY processed ENDF/B-
VII.0 Cross Sections
Critical keff C/E Description
HMF001 Godiva 0.99986 sphere of 235U
PMF001 Jezebel 1.00006 sphere of 239Pu
UMF001 Jezebel-23 0.99970 sphere of 233U
HMF028 Flattop-25 1.00277 235U core, natU reflector
PMF006 Flattop-Pu 1.00105 239Pu core, natU reflector
UMF006 Flattop-23 0.99937 233U core, natU reflector
IMF007s Bigten 0.99995 10% enr. U core, natU refl.
HST042-02 1.00028 HEU in nitrate solution
HST042-03 1.00065 HEU in nitrate solution
HST042-05 1.00019 HEU in nitrate solution
LCT006-01 0.99995 low enruiched UO2lattice
LCT006-02 1.00052 low enriched UO2lattice
LCT006-03 1.00036 low enriched UO2lattice
Table 32: Benchmark Results for Fast Criticals Using ENDF/B-VII.0 Mulitgroup Libraries
and TRANSX/PARTISN
Critical keff C/E
MCNP 30 gp 80 gp 187 gp
HMF001 Godiva 0.99986 1.00234 1.00091 1.00025
PMF001 Jezebel 1.00006 1.00060 1.00047 1.00036
UMF001 Jezebel-23 0.99970 1.00115 1.00024 0.99992
HMF028 Flattop-25 1.00277 1.00349 1.00343 1.00295
PMF006 Flattop-Pu 1.00105 1.00126 1.00147 1.00134
UMF006 Flattop-23 0.99937 1.00126 1.00010 0.99971
IMF007h Bigten 1.00005 1.00022 1.00001
Table 33: Benchmark Results for Thermal Criticals Using ENDF/B-VII.0 Mulitgroup Li-
braries and TRANSX/PARTISN.
Critical keff C/E
MCNP 69 gp 187 gp
HST042-03 1.00065 0.99931 0.99958
HST042-05 1.00019 0.99946 0.99935
774 NJOY2016

26 NJOY MAINTENANCE AND TESTING LA-UR-17-20093
tem of D. E. Cullen[126], especially when new features have been added to the
ENDF system. We recently did a number of comparisons with ORNL results to
verify the new capabilities for resonance reconstruction and covariance process-
ing imported from the ORNL SAMMY code. In some cases, these comparisons
have been extended to multiple laboratories. An example of that is a recent
comparison of unresolved resonance range processing[127]. This study suggests
that more work is needed in the unresolved resonance range.
The comparisons described above were on cross sections. It is also useful
to do multilab comparisons on integral results. As an example, a LANL-LLNL
comparison[128] shows that we can get good agreement for the fast criticals
Godiva, Jezebel, and Jezebel-23. Another recent multilab comparison involving
LANL, LLNL, ANL, and the CEA demonstrated reasonable results for the softer
spectrum of the Big-10 critical assembly[129].
NJOY2016 775

LA-UR-17-20093 26 NJOY MAINTENANCE AND TESTING
776 NJOY2016

REFERENCES LA-UR-17-20093
References
[1] R. E. MacFarlane and R. M. Boicourt, “NJOY: A Neutron and Photon
Processing System,” Trans. Am. Nucl. Soc. 22, 720 (1975).
[2] R. E. MacFarlane, D. W. Muir, and R. M. Boicourt, “The NJOY Nu-
clear Data Processing System, Volume 1: User’s Manual,” Los Alamos
National Laboratory report LA-9303-M, Vol. I (ENDF-324), (May 1982).
R. E. MacFarlane, D. W. Muir, and R. M. Boicourt, “The NJOY Nuclear
Data Processing System, Volume II: The NJOY, RECONR, BROADR,
HEATR, and THERMR Modules,” Los Alamos National Laboratory re-
port LA-9303-M, Vol. II (ENDF-324) (May 1982). R. E. MacFarlane and
D. W. Muir, “The NJOY Nuclear Data Processing System, Volume III:
The GROUPR, GAMINR, and MODER Modules,” Los Alamos National
Laboratory report LA-9303-M, Vol. III (ENDF-324) (October 1987). D. W.
Muir and R. E. MacFarlane, “The NJOY Nuclear Data Processing System,
Volume IV: The ERRORR and COVR Modules,” Los Alamos National
Laboratory report LA-9303-M, Vol. IV (ENDF-324) (December 1985).
[3] R. E. MacFarlane and D. W. Muir, “The NJOY Nuclear Data Processing
System, Version 91,” Los Alamos National Laboratory report LA-12740-M
(1994).
[4] R. E. MacFarlane and A. C. Kahler, “Methods for Processing ENDF/B-VII
with NJOY,” Nuclear Data Sheets,111, 2739–2890 (2010).
[5] A. C. Kahler, editor, “The NJOY Nuclear Data Processing System, Version
2012,” Los Alamos National Laboratory report LA-UR-12-27079 (2012).
[6] For an online tutorial on NJOY, see http://t2.lanl.gov, and follow links
to the “Nuclear Information Service (NIS)”, “Training area” and “NJOY”
which leads to “Understanding NJOY,” Los Alamos National Laboratory
report LA-UR-00-1538 (March 2000).
[7] M. B. Chadwick et al., “ENDF/B-VII.0: Next Generation Evaluated Nu-
clear Data Library for Nuclear Science and Technology,” Nuclear Data
Sheets,107, 2931–3060 (2006).
[8] M. B. Chadwick et al., “ENDF/B-VII.1 Nuclear Data for Science and Tech-
nology: Cross Sections, Covariances, Fission Product Yields and Decay
Data,” Nuclear Data Sheets,112, 2887–2996 (2011).
[9] A. Trkov, M. Herman and D. A. Brown, Eds., ENDF-6 Formats Man-
ual, Data Formats and Procedures for the Evaluated Nuclear Data Files
ENDF/B-VI and ENDF/B-VII, Brookhaven National Laboratory report
BNL-90365-2009 Rev.2 (CSEWG Document ENDF-102) (October 24,
2012). For the latest version of this report, see http://www.nndc.bnl.gov
and take the CSEWG tab to ENDF-6 Formats Manual.
[10] For an online tutorial on the ENDF formats, see http://t2.lanl.gov, and
follow links to the “Nuclear Information Service (NIS)”, “Training area”
NJOY2016 777

LA-UR-17-20093 REFERENCES
and “ENDF” which leads to “An Introduction to the ENDF Formats,” Los
Alamos National Laboratory report LA-UR-98-1779 (January 1998).
[11] R. D. O’Dell, “Standard Interface Files and Procedures for Reactor Physics
Codes, Version IV,” Los Alamos Scientific Laboratory report LA-6941-MS
(September 1977).
[12] R. E. MacFarlane, “TRANSX-CTR: A Code for Interfacing MATXS Cross-
Section Libraries to Nuclear Transport Codes for Fusion Systems Analysis,”
Los Alamos National Laboratory report LA-9863-MS (February 1984).
[13] W. W. Engle, Jr., “A Users Manual for ANISN, A One-Dimensional Dis-
crete Ordinates Transport Code with Anisotropic Scattering,” Oak Ridge
Gaseous Diffusion Plant Computing Technology Center report K-1693
(1967).
[14] R. D O’Dell, F. W. Brinkley, Jr., D. R. Marr, and R. E. Alcouffe, “Re-
vised User’s Manual for ONEDANT: A Code Package for One-Dimensional,
Diffusion-Accelerated, Neutral-Particle Transport,” Los Alamos National
Laboratory report LA-9184-M, Rev. (December 1989).
[15] R. E. Alcouffe, F. W. Brinkley, D. R. Marr, and R. D. O’Dell, “User’s
Guide for TWODANT: A Code Package for Two-Dimensional, Diffusion-
Accelerated, Neutral-Particle Transport,” Los Alamos National Laboratory
report LA-10049 Revised (February 1990).
[16] K. L. Derstine, “DIF3D: A Code to Solve One-, Two-, and Three-
Dimensional Finite-Difference Diffusion Theory Problems,” Argonne Na-
tional Laboratory report ANL-82-64 (April 1984).
[17] R. E. Alcoufe, R. S. Baker, J. A. Dahl, S. A. Turner, and R. C. Ward,
“PARTISN: A Time-Dependent, Parallel Neutral Particle Transport Code
System,” Los Alamos National Laboratory report LA-UR-05-3925 (Revised
May 2005).
[18] X-5 Monte Carlo Team, “MCNP–A General Monte Carlo N-Particle Trans-
port Code, Version 5,” Los Alamos National Laboratory report LA-UR-03-
1987 (April 2003).
[19] J. R. Askew, F. J. Fayers, and P. B. Kemshell, “A General Description of
the Lattice Code WIMS,” J. Brit. Nucl. Energy Soc. 5, 564 (1966).
[20] Userinput information may be found on the NJOY homepage, found under
the “Nuclear Information Service (NIS)”, “Codes” and “NJOY” links at
http://t2.lanl.gov.
[21] C. R. Weisbin, P. D. Soran, R. E. MacFarlane, D. R. Harris, R. J. LaBauve,
J. S. Hendricks, J. E. White, and R. B. Kidman, “MINX, A Multigroup
Interpretation of Nuclear X-Sections from ENDF/B,” Los Alamos Scientific
Laboratory report LA-6486-MS (ENDF-237) (September 1976).
[22] D. J. Dudziak, R. E. Seamon, and D. V. Susco, “LAPHAN0: A Multigroup
Photon-Production Matrix and Source Code for ENDF,” Los Alamos Sci-
entific Laboratory report LA-4750-MS (ENDF-156) (January 1972).
778 NJOY2016

REFERENCES LA-UR-17-20093
[23] K. D. Lathrop, “GAMLEG–A FORTRAN Code to Produce Multigroup
Cross Sections for Photon Transport Calculations,” Los Alamos Scientific
Laboratory report LA-3267 (April 1965).
[24] K. D. Lathrop, “DTF-IV, A FORTRAN Program for Solving the Multi-
group Transport Equation with Anisotropic Scattering,” Los Alamos Sci-
entific Laboratory report LA-3373 (November 1965).
[25] R. J. LaBauve, C. R. Weisbin, R. E. Seamon, M. E. Battat, D. R. Harris,
P. G. Young, and M. M. Klein, “PENDF: A Library of Nuclear Data for
Monte Carlo Calculations Derived from Data in the ENDF/B Format,” Los
Alamos Scientific Laboratory report LA-5687 (October 1974).
[26] O. Ozer, Ed. “Description of the ENDF/B Processing Codes and Retrieval
Subroutines,” Brookhaven National Laboratory report BNL-50300 (ENDF-
11) (June 1971).
[27] D. E. Cullen, “Program SIGMA1 (Version 74-1),” Lawrence Livermore Lab-
oratory report UCID-16426 (January 1974).
[28] R. E. Schenter, J. L. Baker, and R. B. Kidman, “ETOX, A Code to Cal-
culate Group Constants for Nuclear Reactor Calculations,” Battelle North-
west Laboratory report BNWL-1002 (1969).
[29] B. M. Carmichael, “Standard Interface Files and Procedures for Reactor
Physics Codes, Version III,” Los Alamos Scientific Laboratory report LA-
5486-MS (1974).
[30] M. A. Abdou, C. W. Maynard, and R. Q. Wright, “MACK: A Com-
puter Program to Calculate Neutron Energy Release Parameters (Fluence
to Kerma Factors) and Multigroup Neutron Reaction Cross Sections from
Nuclear Data in ENDF Format,” Oak Ridge National Laboratory report
ORNL-TM-3994 (1973).
[31] H. C. Honek and D. R. Finch, “FLANGE-II (Version 71-1), A Code to
Process Thermal Neutron Data frp, an ENDF/B Tape,” E. I. DuPont de
Nemours and Co. Savannah River Laboratory report DP-1278 (1971).
[32] Y. D. Naliboff and J. U. Koppel, “HEXSCAT, Coherent Elastic Scatter-
ing of Neutrons by Hexagonal Lattices,” General Atomic report GA-6026
(1964).
[33] R. E. MacFarlane, R. J. Barrett, D. W. Muir, and R. M. Boicourt, “NJOY:
A Comprehensive ENDF/B Processing System,” in A Review of Multigroup
Nuclear Cross-Section Processing, Proceedings of a Seminar-Workshop,
Oak Ridge, Tennessee, March 14-16, 1978,” Oak Ridge National Laboratory
report ORNL/RSIC-41 (October 1978).
[34] R. E. MacFarlane, “Introducing NJOY89,” in Proceedings of the Seminar
on NJOY and Themis, 20-21 June 1989, OECD/NEA Data Bank, Saclay,
France (1989). See also “Nuclear Theory and Application Progress Report,
January 1, 1989—April 1, 1990,” pp. 21-38, Los Alamos National Labora-
tory report LA-11972-PR (December 1990).
NJOY2016 779
LA-UR-17-20093 REFERENCES
[35] Go Chiba, “ERRORJ, A Code to Process Neutron-Nuclide Reaction Co-
variance, Version 2.3,” JAEA-Data/Code 2007-007, March 2007.
[36] N.M.Larson, “Updated Users Guide for SAMMY: Multilevel R-Matrix Fits
to Neutron Data Using Bayes Equations,” Oak Ridge National Laboratory
report ORNL/TM-9179/R8 (October 2008).
[37] B. J. Toppel, A. L. Rago, and D. M. O’Shea, “MC2, A Code to Calculate
Multigroup Cross Sections,” Argonne National Laboratory report ANL-
7318 (1967).
[38] H. Henryson II, B. J. Toppel, and C. G. Stenberg, “MC2-2: A Code to
Calculate Fast Neutron Spectra and Multigroup Cross Sections,” Argonne
National Laboratory report ANL-8144 (ENDF-239) (1976).
[39] I. I. Bondarenko, Ed., Group Constants for Nuclear Reactor Calculations
(Consultants Bureau, New York, 1964).
[40] R. B. Kidman, “Cross Section Structure Factor Interpolation Schemes,”
Hanford Engineering Development Laboratory report HEDL-TME-71-40
(1971).
[41] R. E. MacFarlane, “TRANSX 2: A Code for Interfacing MATXS Cross-
Section Libraries to Nuclear Transport Codes,” Los Alamos National Lab-
oratory report LA-12312-MS (July 1992).
[42] D. W. Muir, “Gamma Rays, Q-Values, and Kerma Factors,” Los Alamos
Scientific Laboratory report LA-6258-MS (March 1976).
[43] R. E. MacFarlane, “Energy Balance of ENDF/B-V,” Trans. Am. Nucl. Soc.
33, 681 (1979). See also R. E. MacFarlane, “Energy Balance of ENDF/B-
V.2,” Minutes of the Cross Section Evaluation Working Group (available
from the National Nuclear Data Center, Brookhaven National Laboratory,
Upton, NY) (May 1984).
[44] T. A. Gabriel, J. D. Amburgy, and N. M. Greene, “Radiation-Damage
Calculations: Primary Knock-On Atom Spectra, Displacement Rates, and
Gas Production Rates,” Nucl. Sci. Eng. 61, 21 (1976).
[45] D. G. Doran, “Neutron Displacement Cross Sections for Stainless Steel and
Tantalum Based on a Linhard Model,” Nucl. Sci. Eng. 49, 130 (1972).
[46] L. R. Greenwood and R. K. Smither, “Displacement Damage Calculations
with ENDF/B-V,” in Proceedings of the Advisory Group Meeting on Nu-
clear Data for Radiation Damage Assessment and Reactor Safety Aspects,
October 12-16, 1981, IAEA, Vienna, Austria (October 1981).
[47] M. T. Robinson, in Nuclear Fusion Reactors (British Nuclear Energy Soci-
ety, London, 1970).
[48] J. Lindhard, V. Nielsen, M. Scharff, and P. V. Thomsen, Kgl. Dansk, Vi-
densk. Selsk, Mat-Fys. Medd. 33 (1963).
[49] R. E. MacFarlane, D. W. Muir, and F. M. Mann, “Radiation Damage
Calculations with NJOY,” J. Nucl. Materials 122 and 123, 1041 (1984).
780 NJOY2016

REFERENCES LA-UR-17-20093
[50] R. E. MacFarlane and D. G. Foster, Jr., “Advanced Nuclear Data for Radi-
ation Damage Calculations,” J. Nucl. Materials 122 and 123, 1047 (1984).
[51] R. Kinsey, Ed., “ENDF-102, Data Formats and Procedures for the Evalu-
ated Nuclear Data File, ENDF,” Brookhaven National Laboratory report
BNL-NCS-50496 (ENDF-102) 2nd Edition (ENDF/B-V) (October 1979).
[52] J. U. Koppel and D. H. Houston, “Reference Manual for ENDF Thermal
Neutron Scattering Data,” General Atomic report GA-8774 revised and
reissued as ENDF-269 by the National Nuclear Data Center, Brookhaven
National Laboratory (1978).
[53] G. I. Bell and S. Glasstone, Nuclear Reactor Theory (Van Nostrand Rein-
hold, New York, 1970).
[54] R. W. Hardie and W. W. Little, Jr., “1DX, A One-Dimensional Diffusion
Code for Generating Effective Nuclear Cross Sections,” Battelle Northwest
Laboratory report BNWL-954 (1969).
[55] R. E. MacFarlane, “ENDF/B-IV and -V Cross Sections for Thermal Power
Reactor Analysis,” in Proc. Intl. Conf. of Nuclear Cross Sections for Tech-
nology, Knoxville, TN (October 22-26 1979), National Bureau of Standards
Publication 594 (September 1980).
[56] G. I. Bell, G. E. Hansen, and H. A. Sandmeier, “Multitable Treatments
of Anisotropic Scattering in SNMultigroup Transport Calculations,” Nucl.
Sci. Eng. 28, 376 (1967).
[57] M. Abramowitz and I. Stegun, Handbook of Mathematical Functions (Dover
Publications, New York, 1965).
[58] D. G. Madland, “New Fission Neutron Spectrum Representation for
ENDF,” Los Alamos National Laboratory report LA-9285-MS (ENDF-321)
(April 1982).
[59] C. Kalbach and F. M. Mann, “Phenomenology of Continuum Angular Dis-
tributions. I. Systematics and Parameterization,” Phys. Rev. C. 23, 112
(1981).
[60] C. Kalbach, “Systematics of Continuum Angular Distributions: Extensions
to Higher Energies,” Phys. Rev. C. 37, 2350 (1988).
[61] P. G. Young and E. D. Arthur, “GNASH: A Preequilibrium Statistical Nu-
clear Model Code for Calculation of Cross Sections and Emission Spectra,”
Los Alamos Scientific Laboratory report LA-6947 (1977).
[62] R. E. MacFarlane, “ENDF/B-V Cross-Section Library for Reactor Cell
Analysis,” Electric Power Research Institute report EPRI NP-3418 (Febru-
ary 1984).
[63] R. B. Kidman and R. E. MacFarlane, “LIB-IV, A Library of Group Con-
stants for Nuclear Reactor Calculations,” Los Alamos Scientific Laboratory
report LA-6260-MS (1976).
[64] G. Lehner, “Reaction Rates and Energy Spectra for Nuclear Reactions in
High Energy Plasmas,” Z. Physik 232, 174 (1970).
NJOY2016 781

LA-UR-17-20093 REFERENCES
[65] D. E. Nagle, W. E. Quinn, W. B. Riesenfeld, and W. Leland, “Ion Tem-
perature in Scylla, as Determined from the Reaction D(d,p)T,” Phys. Rev.
Letters 3, 318 (1959).
[66] N. Jarmie and J. D. Seagrave (Eds.), “Charged Particle Cross Sections,”
Los Alamos Scientific Laboratory report LA-2014 (1956).
[67] D. W. Muir, “Sensitivity of Neutron Multigroup Cross Sections to Ther-
mal Broadening of the Fusion Peak,” Proc. 1st Topical Meeting on the
Technology of Controlled Nuclear Fusion, San Diego, Calif., April 1974,
CONF-740402-P2, p.166 (1975).
[68] R. W. Roussin, J. R. Knight, J. H. Hubbell, and R. J. Howerton, “De-
scription of the DLC-99/HUGO Package of Photon Interaction Data in
ENDF/B-V Format,” Oak Ridge National Laboratory report ORNL/RSIC-
46 (ENDF-335) (December 1983).
[69] J. H. Hubbell, Wm. J. Viegle, E. A. Briggs, R. T. Brown, D. T. Cromer, and
R. J. Howerton, “Atomic Form Factors, Incoherent Scattering Functions,
and Photon Scattering Cross Sections,” J. Phys. Chem. Ref. Data 4, 471
(1975).
[70] S. A. W. Gerstl, D. J. Dudziak, and D. W. Muir, “Cross Section Sensitivity
and Uncertainty Analysis with Application to a Fusion Reactor,” Nucl. Sci.
Eng. 62, 137 (January 1977).
[71] W. A. Reupke, D. W. Muir, and J. N. Davidson, “Consistency of Neutron
Cross-Section Data, SnCalculations, and Measured Tritium Production
for a 14-MeV Neutron-Driven Sphere of Natural-Lithium Deuteride,” Nucl.
Sci. Eng. 82, 416 (December 1982).
[72] D. W. Muir, “Evaluation of Correlated Data Using Partitioned Least
Squares: A Minimum-Variance Derivation,” Nucl. Sci. and Eng. 101, 88-93
(January 1989).
[73] C. R. Weisbin, E. M. Oblow, J. Ching, J. E. White, R. Q. Wright, and
J. Drischler, “Cross Section and Method Uncertainties: The Application
of Sensitivity Analysis to Study Their Relationship in Radiation Transport
Benchmark Problems,” Oak Ridge National Laboratory report ORNL-TM-
4847 (ENDF-218) (August 1975). (See especially Chapter IV.)
[74] J. D. Smith III, “Processing ENDF/B-V Uncertainty Data into Multigroup
Covariance Matrices,” Oak Ridge National Laboratory report ORNL/TM-
7221 (ENDF-295) (June 1980).
[75] P. G. Young, “Evaluation of n + 7Li Reactions using Variance-Covariance
Techniques,” Trans. Am. Nucl. Soc. 39, 272 (1981).
[76] P. G. Young, J. W. Davidson, and D. W. Muir, “Evaluation of the
7Li(n,n’t)4He Cross Section for ENDF/B-VI and Application to Uncer-
tainty Analysis,” Fusion Tech. 15, 440-448 (1989).
[77] D. W. Muir and R. J. LaBauve, “COVFILS: A 30-Group Covariance Li-
brary Based on ENDF/B-V,” Los Alamos National Laboratory report LA-
8733-MS (ENDF-306) (March 1981).
782 NJOY2016

REFERENCES LA-UR-17-20093
[78] D. W. Muir, “COVFILS-2: Neutron Data and Covariances for Sensitivity
and Uncertainty Analysis,” Fusion Tech. 10 (3), Part 2B, 1461 (November
1986).
[79] S. A. W. Gerstl, “SENSIT: A Cross-Section and Design Sensitivity and
Uncertainty Analysis Code,” Los Alamos Scientific Laboratory report LA-
8498-MS (August 1980).
[80] M. J. Embrechts, “SENSIT-2D: A Two-Dimensional Cross-Section Sensi-
tivity and Uncertainty Analysis Code,” Los Alamos National Laboratory
report LA-9515-MS (October 1982).
[81] D. W. Muir, R. E. MacFarlane, and R. M. Boicourt, “Multigroup Pro-
cessing of ENDF/B Dosimetry Covariances,” Proc. 4th ASTM-EURATOM
Symp. on Reactor Dosimetry, Gaithersburg, Maryland, March 22-26, 1982,
NUREG/CP-0029 (CONF-820321), p. 655 (1982).
[82] R. J. Barrett and R. E. MacFarlane, “Coupled Neutron and Photon Cross
Sections for Transport Calculations,” Los Alamos Scientific Laboratory re-
port LA-7808-MS (April 1979).
[83] R. E. MacFarlane and R. B. Kidman, “LINX and BINX: CCCC Utility
Codes for the MINX Multigroup Processing Code,” Los Alamos Scientific
Laboratory report LA-6219-MS (February 1976).
[84] “CINX: Collapsed Interpretation of Nuclear X Sections,” Los Alamos Sci-
entific Laboratory report LA-6287-MS (April 1976).
[85] W. J. Davis, M. B. Yarbrough, and A. B. Bortz, “SPHINX: A One Dimen-
sional Diffusion and Transport Nuclear Cross Section Processing Code,”
Westinghouse Advanced Reactors Division report WARD-XS-3045-17 (Au-
gust 1977).
[86] C. L. Cowan, B. A. Hutchins, and J. E. Turner, “TDOWN – A Code to
Generate Composition and Spatially Dependent Cross Sections,” General
Electric report GEAP-13740 (August 1971).
[87] R. J. LaBauve, T. R. England, D. C. George, R. E. MacFarlane, and W. B.
Wilson, “DANDE—A Linked Code System for Core Neutronics/Depletion
Analysis,” Los Alamos National Laboratory report LA-10412-MS (June
1985).
[88] R. E. MacFarlane and D. C. George, “UPD: A Portable Version-Control
Program,” Los Alamos National Laboratory report LA-12057-MS (April
1991).
[89] Y. Farawila, Y. Gohar, and C. Maynard, “KAOS/LIB-V: A Library
of Nuclear Response Functions Generated by KAOS-V Code From
ENDF/B-V and Other Data Files” Argonne National Laboratory report
ANL/FPP/TM-241 (April 1989).
[90] E. D. Cashwell, J. R. Neergaard, W. M. Taylor, and G. D. Turner, “MCN:
A Neutron Monte Carlo Code,” Los Alamos Scientific Laboratory report
LA-4751 (January 1972).
NJOY2016 783

LA-UR-17-20093 REFERENCES
[91] E. D. Cashwell, J. R. Neergaard, C. J. Everett, R. G. Schrandt, W. M.
Taylor, and G. D. Turner, “Monte Carlo Photon Codes MCG and MCP,”
Los Alamos Scientific Laboratory report LA-5157-MS (March 1973).
[92] C. J. Everett and E. D. Cashwell, “MCP Code Fluorescence-Routine Revi-
sion,” Los Alamos Scientific Laboratory report LA-5240-MS (May 1973).
[93] Adobe Systems Incorporated, Postscript Language Reference Manual,
Addison-Wesley Publishing Company, 1985.
[94] L. B. Levitt, “The Probability Table Method for Treating Unresolved Res-
onances in Monte Carlo Criticality Calculations,” Trans. Am. Nucl. Soc.
14, 648 (1971).
[95] R. E. Prael and L. J. Milton, “A User’s Manual for the Monte Carlo Code
VIM,” Argonne National Laboratory report FRA-TM-84 (1976). Also, R.
Blomquist, “VIM continuous energy Monte Carlo transport code,” in Proc.
Inter. Conf. on Mathematics, Computations, Reactor Physics and Environ-
mental Analysis, Portland, OR, April 30 – May 4, 1995.
[96] J. U. Koppel, J. R. Triplett, and Y. D. Naliboff, “GASKET: A Unified
Code for Thermal Neutron Scattering,” General Atomics report GA-7417
(Rev.) (March 1967).
[97] R. C. F. McLatchie, 1962, unpublished.
[98] A. T. Butland, “LEAP and ADDELT, A Users Guide to Two Comple-
mentary Codes on the ICL-470 for Calculating The Scattering Law From
a Phonon Frequency Function,” Atomic Energy Establishment Winfrith
report AEEW-M-1200, 1973.
[99] D. J. Picton, personal communication to G. J. Russell, 1987.
[100] R. E. MacFarlane, “New Thermal Neutron Scattering Files for ENDF/B-
VI Release 2,” Los Alamos National Laboratory report LA-12639-MS
(1994).
[101] R. E. MacFarlane, ”Cold Moderator Scattering Kernels,” in Advanced
Neutron Sources 1988, Proceedings of the 10th Meeting of the Interna-
tional Collaboration on Advanced Neutron Sources (ICANS-X) held at Los
Alamos, 3–7 October 1988, Institute of Physics Conferences Series Number
97 (Institute of Physics, Bristol and New York, 1988), p.157.
[102] R. E. MacFarlane, “Cold Moderator Scattering Kernels,” presented at the
International Workshop on Cold Neutron Sources, March 5–8, 1990, Los
Alamos, New Mexico, Los Alamos National Laboratory report LA-12146-C
(August 1991).
[103] D. E. Parks, M. S. Nelkin, J. R. Beyster, and N. F. Wikner, Slow Neutron
Scattering and Thermalization, W. A. Benjamin, Inc. (New York, 1970).
[104] R. W. G. Wycoff, Crystal Structures, John Wiley & Sons, New York,
London, 1963.
[105] J. A. Young and J. U. Koppel, Phys. Rev. 135, A603(1964).
784 NJOY2016
REFERENCES LA-UR-17-20093
[106] P. A. Egelstaff, B. C. Haywood, and F. J. Webb, Proc. Phys. Soc., 90,
681(1967).
[107] Wolfgang Schott, Z. Physik 231, 243(1970).
[108] Masahiko Utsuro, Z. Physik B 27, 111(1977).
[109] J. Keinert and J. Sax, “Investigation of Neutron Scattering Dynamics in
Liquid Hydrogen and Deuterium for Cold Neutron Sources,” Kerntechnik
51, 19 (1987).
[110] M. Mattes and J. Keinert, “Thermal Neutron Scattering Data for the
Moderator Materials H2O, D2O and ZrHx in ENDF-6 Format and as ACE
Library for MCNP(X)”, IAEA INDC(NDS)-0470, April 2005.
[111] M. Dritsa, report from misc. OECD countries to EANDC, No. 63, 1967.
[112] K. Heinloth, Zeitscrift fur Physik 163, 218 (1961).
[113] R. R. Smith, private communication held at BNL, 1953.
[114] W. Walton, private communication held at BNL, 1960.
[115] V. T. Springer, Nucleonik 3, 110 (1961).
[116] O. D. Simpson, J. Nuclear Instruments and Methods 30, 293 (1964).
[117] J. L. Russell, Jr., General Atomic report 7581, 1966.
[118] Y. D. Harker and R. M. Brugger, “Investigation of the Low-Temperature
Phase Transitions in Solid Methane by Slow Neutron Inelastic Scattering,”
J. Chem. Phys. 46, 2201(1967).
[119] A. K. Agrawal and S. Yip, “Slow-Neutron Scattering by Molecular Liq-
uids,” Nucl. Sci. Eng. 37, 368(1969).
[120] R. G. Gordon, J. Chem. Phys. 43, 1307(1965).
[121] G. E. Ewing, J. Chem. Phys. 40, 179(1964).
[122] These data were obtained from the paper of Keinert and Sax[109] and
converted to the numbers shown by subtracting the hydrogen absorption
cross section. The ortho cross sections were converted from normal 2H cross
sections using the theoretical ortho and para cross sections to produce a con-
version factor. The original references are G. L. Squires and A. T. Stewart,
Proc. Roy. Soc. A230, 19(1955), W. L. Whittemore and A. W. McReynolds,
“Differential Neutron Thermalization,” General Atomic report GA-2505
(1961), and W. D. Seiffert, “Messung der Streuquerschnitte von fl¨ussigem
und festem Wasserstoff, Deuterium, und Deuteriumhydrid f¨ur thermische
Neutronen,” EUR-5566d (1970).
[123] W. H. Press, B. P. Flannery, Saul A. Teukolsky, and William T. Vetterling,
Numerical Recipes in C, Cambridge University Press, 1988.
[124] “UPDATE, VERSION 1, Reference Manual,” Revision 11/23/81, Control
Data Corporation report 60449900 (November 1981).
NJOY2016 785

LA-UR-17-20093 REFERENCES
[125] J. B. Briggs, et al, “International Handbook of Evaluated Criticality Safety
Benchmark Experiments,” Tech. Rep. NEA/NSC/DOC(95)04/I, Nuclear
Energy Agency, Paris, France, 2004. Note that this Handbook is updated
annually.
[126] D. E. Cullen, “PREPRO 2007: 2007 ENDF/B Pre-Processing Codes,”
IAEA-NDS-39, Rev. 13, Nuclear Data Section, International Atomic En-
ergy Agency, Vienna, Austria.
[127] J. C. Sublet, R. N. Blomquest, S. Goluoglu, and R. E. MacFarlane, “Un-
resolved Resonance Range Cross Section Probabiliy and Self Shielding Fac-
tors,” CEA-R-6227 (July 2009).
[128] D. E. Cullen, P. Brown, E. Lent, R. MacFarlane, and S. McKin-
ley, “Criticality Calculations Using LANL and LLNL Neutron Trans-
port Codes,” Lawrence Livermore National Laboratory report UCRL-TR-
237333 (November 22, 2007).
[129] R. E. MacFarlane, R. M. Blomquist (ANL), D. E. Cullen (LLNL), and J.
C. Sublet (CEA), “A Code Comparison Study for the Bigten Critical As-
sembly,” Los Alamos National Laboratory report LA-UR-08-4668 (August
2008).
[130] Scott Chacon and Ben Straub, Pro Git, Apress, Berkeley, CA, USA, 2nd
edition. Downloadable e-book versions are available at https://git-scm.
com/book/en/v2.
786 NJOY2016