Lateral Loads Manual

User Manual: Lateral Loads Manual

Open the PDF directly: View PDF PDF.
Page Count: 252 [warning: Documents this large are best viewed by clicking the View PDF Link!]

Lateral Loads Manual
ISO ETA122815M4 Rev. 1
Proudly developed in the United States of America October 2016
Lateral Loads Manual
For ETABS 2016
Copyright
Copyright Computers & Structures, Inc., 1978-2016
All rights reserved.
The CSI Logo® and ETABS® are registered trademarks of Computers & Structures, Inc.
Watch & LearnTM is a trademark of Computers & Structures, Inc.
The computer program ETABS® and all associated documentation are proprietary and
copyrighted products. Worldwide rights of ownership rest with Computers & Structures,
Inc. Unlicensed use of these programs or reproduction of documentation in any form,
without prior written authorization from Computers & Structures, Inc., is explicitly
prohibited.
No part of this publication may be reproduced or distributed in any form or by any
means, or stored in a database or retrieval system, without the prior explicit written
permission of the publisher.
Further information and copies of this documentation may be obtained from:
Computers & Structures, Inc.
www.csiamerica.com
info@csiamerica.com (for general information)
support@csiamerica.com (for technical support)
DISCLAIMER
CONSIDERABLE TIME, EFFORT AND EXPENSE HAVE GONE INTO THE
DEVELOPMENT AND TESTING OF THIS SOFTWARE. HOWEVER, THE USER
ACCEPTS AND UNDERSTANDS THAT NO WARRANTY IS EXPRESSED OR
IMPLIED BY THE DEVELOPERS OR THE DISTRIBUTORS ON THE ACCURACY
OR THE RELIABILITY OF THIS PRODUCT.
THIS PRODUCT IS A PRACTICAL AND POWERFUL TOOL FOR STRUCTURAL
DESIGN. HOWEVER, THE USER MUST EXPLICITLY UNDERSTAND THE BASIC
ASSUMPTIONS OF THE SOFTWARE MODELING, ANALYSIS, AND DESIGN
ALGORITHMS AND COMPENSATE FOR THE ASPECTS THAT ARE NOT
ADDRESSED.
THE INFORMATION PRODUCED BY THE SOFTWARE MUST BE CHECKED BY
A QUALIFIED AND EXPERIENCED ENGINEER. THE ENGINEER MUST
INDEPENDENTLY VERIFY THE RESULTS AND TAKE PROFESSIONAL
RESPONSIBILITY FOR THE INFORMATION THAT IS USED.
Contents
Chapter 1 Introduction
1.1 About the Manual 1-1
Chapter 2 Automatic Seismic Loads
2.1 Defining Automatic Seismic Load Patterns 2-2
2.2 Automatic Seismic Load Patterns 2-3
2.2.1 Distribution of Automatic Seismic Loads
at a Story Level 2-4
2.2.2 Load Direction and Diaphragm Eccentricity 2-4
2.2.3 Load Direction and Diaphragm Eccentricity 2-4
2.2.3 Story/Elevation Range Data 2-5
2.3 1994 UBC Seismic Loads 2-6
2.3.1 Options for 1994 UBC Building Period 2-6
2.3.2 Other Input Factors and Coefficients 2-7
2.3.3 Algorithm for 1994 UBC Seismic Loads 2-8
2.4 1997 UBC Seismic Loads 2-10
i
Lateral Loads
2.4.1 Options for 1997 UBC Building Period 2-10
2.4.2 Other Input Factors and Coefficients 2-11
2.4.3 Algorithm for 1997 UBC Seismic Loads 2-12
2.5 1997 UBC Isolated Building Seismic Loads 2-15
2.5.1 Other Input Factors and Coefficients 2-15
2.5.2 Algorithm for 1997 UBC Isolated Building
Seismic Loads 2-17
2.6 1996 BOCA Seismic Loads 2-18
2.6.1 Options for 1996 BOCA Building Period 2-18
2.6.2 Other Input Factors and Coefficients 2-20
2.6.3 Algorithm for 1996 BOCA Seismic Loads 2-20
2.7 1995 NBCC Seismic Loads 2-22
2.7.1 Options for 1995 NBCC Building Period 2-22
2.7.2 Other Input Factors and Coefficients 2-23
2.7.3 Algorithm for 1995 NBCC Seismic Loads 2-24
2.8 2005 NBCC Seismic Loads 2-26
2.8.1 Options for 2005 NBCC Building Period 2-26
2.8.2 Other Input Factors and Coefficients 2-27
2.8.3 Algorithm for 2005 NBCC Seismic Loads 2-28
2.9 2010 NBCC Seismic Loads 2-31
2.9.1 Options for 2010 NBCC Building Period 2-31
2.9.2 Other Input Factors and Coefficients 2-32
2.9.3 Algorithm for 2010 NBCC Seismic Loads 2-33
2.10 2015 NBCC Seismic Loads 2-36
2.10.1 Options for 2015 NBCC Building Period 2-36
2.10.2 Other Input Factors and Coefficients 2-37
2.10.3 Algorithm for 2015 NBCC Seismic Loads 2-39
2.11 2003 IBC/ASCE 7-02 Seismic Loads 2-42
2.11.1 Options for 2003 IBC/ASCE 7-02 Building
Period 2-42
ii
Contents
2.11.2 Other Input Factors and Coefficients 2-43
2.11.3 Algorithm for 2003 IBC/ASCE 7-02 Seismic
Loads 2-44
2.12 2006 IBC/ASCE 7-05 Seismic Loads 2-47
2.12.1 Options for 2006 IBC/ASCE 7-05 Building
Period 2-47
2.12.2 Other Input Factors and Coefficients 2-48
2.12.3 Algorithm for ASCE 7-05 Seismic Loads 2-49
2.13 2009 IBC/ASCE 7-05 Seismic Loads 2-52
2.13.1 Options for 2009 IBC/ASCE 7-05 Building
Period 2-52
2.13.2 Other Input Factors and Coefficients 2-53
2.13.3 Algorithm for 2009 IBC/ASCE 7-05 Seismic
Loads 2-55
2.14 2012 IBC/ASCE 7-10 Seismic Loads 2-58
2.14.1 Options for 2012 IBC/ASCE 7-05 Building
Period 2-58
2.14.2 Other Input Factors and Coefficients 2-59
2.14.3 Algorithm for 2012 IBC/ASCE 7-10 Seismic
Loads 2-60
2.15 1997 NEHRP Seismic Loads 2-63
2.15.1 Options for 1997 NEHRP Building Period 2-63
2.15.2 Other Input Factors and Coefficients 2-64
2.15.3 Algorithm for 1997 NEHRP Seismic Loads 2-65
2.16 2010 Chinese Seismic Loads 2-68
2.16.1 Options for 2012 Chinese Building Period 2-68
2.16.2 Other Input Factors and Coefficients 2-69
2.16.3 Algorithm for 2010 Chinese Seismic Loads 2-69
2.17 2004 NZS 1170.5 Seismic Loads 2-72
2.17.1 Options for 2004 NZS 1170.5 Building Period 2-72
2.17.2 Other Input Factors and Coefficients 2-72
iii
Lateral Loads
2.17.3 Algorithm for 2004 NZS 1170.5 Seismic
Loads 2-73
2.18 2007 AS 1170.4 Seismic Loads 2-75
2.18.1 Options for 2007 AS 1170.4 Building Period 2-75
2.18.2 Other Input Factors and Coefficients 2-76
2.18.3 Algorithm for 2007 AS 1170.4 Seismic Loads 2-77
2.19 2004 Eurocode 8 (EN 1998-1) Seismic Loads 2-79
2.19.1 Options for EN 1998-1:2004 Building Period 2-79
2.19.2 Other Input Factors and Coefficients 2-79
2.19.3 Algorithm for EN 1998-1:2004 Seismic Loads 2-80
2.20 2002 Indian IS:1893 2-81
2.20.1 Options for 2002 Indian IS:1893 Building
Period 2-81
2.20.2 Other Input Factors and Coefficients 2-82
2.20.3 Algorithm for IS:1893 Seismic Loads 2-82
2.21 2008 Italian NTC Seismic Loads 2-84
2.21.1 Options for 2008 Italian NTC Building Period 2-84
2.21.2 Other Input Factors and Coefficients 2-85
2.21.3 Algorithm for 2008 Italian NTC Seismic Loads 2-85
2.22 2007 Turkish Seismic Code (TSC) Loads 2-89
2.22.1 Options for 2007 TSC Building Period 2-89
2.22.2 Other Input Factors and Coefficients 2-90
2.22.3 Algorithm for 2007 TSC Seismic Loads 2-91
2.23 2009 Korean Building Code (KBC) Seismic Loads 2-94
2.23.1 Options for 2009 KBC Building Period 2-94
2.23.2 Other Input Factors and Coefficients 2-95
2.23.3 Algorithm for 2009 KBC Seismic Loads 2-96
2.24 2011 Dominican Republic R-001 Seismic Code Loads 2-98
2.24.1 Options for 2011 Dominican Republic R-001
Building Period 2-98
iv
Contents
2.24.2 Other Input Factors and Coefficients 2-98
2.24.3 Algorithm for Dominican Republic R-001
Seismic Loads 2-99
2.25 User Defined Seismic Loads 2-101
2.25.1 Input Factors and Coefficients 2-101
2.25.2 Algorithm for User Defined Seismic Loads 2-101
2.26 Response Spectrum Functions 2-102
2.26.1 From File 2-102
2.26.2 User 2-103
2.26.3 Code Specific 2-103
2.26.4 1994 UBC Parameters for a Response
Spectrum Function 2-104
2.26.5 1997 UBC Parameters for a Response
Spectrum Function 2-104
2.26.6 1996 BOCA Parameters for a Response
Spectrum Function 2-104
2.26.7 1995 NBCC Parameters for a Response
Spectrum Function 2-105
2.26.8 2005 NBCC Parameters for a Response
Spectrum Function 2-105
2.26.9 2010 NBCC Parameters for a Response
Spectrum Function 2-106
2.26.10 2015 NBCC Parameters for a Response
Spectrum Function 2-107
2.26.11 2003 IBC/ASCE 7-02 Parameters for a
Response Spectrum Function 2-107
2.26.12 2006 IBC/ASCE 7-05 Parameters for a
Response Spectrum Function 2-108
2.26.13 2009 IBC/ASCE 7-05 Parameters for a
Response Spectrum Function 2-108
2.26.14 2012 IBC/ASCE 7-10 Parameters for a
Response Spectrum Function 2-109
2.26.15 1997 NEHRP Parameters for a Response
Spectrum Function 2-110
2.26.16 1998 Eurocode 8 Parameters for a
v
Lateral Loads
Response Spectrum Function 2-110
2.26.17 2004 Eurocode 8 Parameters for a
Response Spectrum Function 2-110
2.26.18 1992 NZS 4203 Parameters for a Response
Spectrum Function 2-111
2.26.19 2004 NZS 1170.5 Parameters for a
Response Spectrum Function 2-112
2.26.20 2007 AS 1170.4 Parameters for a Response
Spectrum Function 2-112
2.26.21 2007 AASHTO Parameters for a Response
Spectrum Function 2-113
2.26.22 2012 AASHTO Parameters for a Response
Spectrum Function 2-114
2.26.23 2002 Indian IS:1893 Response Spectrum
Function 2-114
2.26.24 2008 Italian NTC Parameters for
Response Spectrum Function 2-115
2.26.25 2007 TSC Parameters for a Response
Spectrum Function 2-119
2.26.26 2007 TSC Parameters for a Response
Spectrum Function 2-119
2.26.27 2009 KBC Parameters for a Response
Spectrum Function 2-120
2.26.28 20013 Argentina Regulation 103 INPRES-
CIRSOC Parameters for a Response
Spectrum Function 2-120
2.26.291993 Chile Standard NCh433 + DS61
Parameters for a Response Spectrum
Function 2-121
2.26.30 2003 Chile Standard 2369 Parameters
for a Response Spectrum Function 2-121
2.26.31 2010 Colombian Regulations NSR–10
Parameters for a Response Spectrum
Function 2-122
2.26.32 2011 Ecuador Standard NEC–11
Parameters for a Response Spectrum
Function 2-122
2.26.33 2010 Guatemala Standard AGIES
vi
Contents
NSE 2–10 Parameters for a Response
Spectrum Function 2-123
2.26.34 2004 Mexico Standard NTC–2004
Parameters for a Response Spectrum
Function 2-124
2.26.35 2003 Peru Standard E.030 Parameters
for a Response Spectrum Function 2-125
2.26.36 2011 Dominican Republic Standard R–001
Parameters for a Response Spectrum
Function 2-125
2.2637 2001 Venezuela Standard COVENIN
1756–1 Parameters for a Response
Spectrum Function 2-126
2.26.38 2015 Ecuador Standard NEC–SE–DS
Parameters for a Response Spectrum
Function 2-127
2.26.39 2014 Peru Standard E.030 Parameters
for a Response Spectrum Function 2-128
2.26.40 2008 Mexico CFE Parameters for a Response
Spectrum Function 2-128
2.26.41 1993 Mexico CFE Parameters for a Response
Spectrum Function 2-129
2.26.42 2010 Costa Rica Parameters for a Response
Spectrum Function 2-129
2.26.43 SP 14.13330.2014 Response Spectrum Function
2-130
Chapter 3 Automatic Wind Loads
3.1 Defining Automatic Wind Load Patterns 3-2
3.2 Automatic Wind Load Patterns 3-2
3.2.1 Exposure 3-3
3.2.2 Wind Exposure Parameters 3-4
3.2.3 Wind Exposure Height 3-5
vii
Lateral Loads
3.3 1994 UBC Wind Loads 3-7
3.3.1 Input Wind Coefficients 3-7
3.3.2 Algorithm for 1994 UBC Wind Loads 3-7
3.4 1997 UBC Wind Loads 3-9
3.4.1 Input Wind Coefficients 3-9
3.4.2 Algorithm for 1997 UBC Wind Loads 3-9
3.5 1996 BOCA Wind Loads 3-12
3.5.1 Input Wind Coefficients 3-12
3.5.2 Algorithm for 1996 BOCA Wind Loads 3-13
3.6 1995 BS 6399 Wind Loads 3-15
3.6.1 Input Wind Coefficients 3-15
3.6.2 Algorithm for 1995 BS 6399 Wind Loads 3-16
3.7 1995 NBCC Wind Loads 3-18
3.7.1 Input Wind Coefficients 3-18
3.7.2 Algorithm for 1995 NBCC Wind Loads 3-19
3.8 2005 NBCC Wind Loads 3-21
3.8.1 Input Wind Coefficients 3-21
3.8.2 Algorithm for 2005 NBCC Wind Loads 3-22
3.9 2010 NBCC Wind Loads 3-25
3.9.1 Input Wind Coefficients 3-25
3.9.2 Algorithm for 2010 NBCC Wind Loads 3-25
3.10 2015 NBCC Wind Loads 3-28
3.9.1 Input Wind Coefficients 3-28
3.9.2 Algorithm for 2015 NBCC Wind Loads 3-29
3.11 ASCE 7-95 Wind Loads 3-33
3.11.1 Input Wind Coefficients 3-33
3.11.2 Algorithm for ASCE 7-95 Wind Loads 3-33
3.12 ASCE 7-02 Wind Loads 3-37
viii
Contents
3.12.1 Input Exposure 3-37
3.12.2 Algorithm for ASCE 7-02 Wind Loads 3-39
3.13 2006 IBC / ASCE 7-05 Wind Loads 3-45
3.13.1 Input Exposure 3-45
3.13.2 Algorithm for ASCE 7-05 Wind Loads 3-47
3.14 ASCE 7-10 Wind Loads 3-52
3.14.1 Input Exposure 3-52
3.14.2 Algorithm for ASCE 7-10 Wind Loads 3-54
3.15 1987 RCDF Wind Loads 3-60
3.15.1 Input Wind Coefficients 3-60
3.15.2 Algorithm for 1987 RCDF Wind Loads 3-60
3.16 2010 Chinese Wind Loads 3-61
3.16.1 Input Wind Exposure Parameters 3-61
3.16.2 Input Wind Coefficients 3-62
3.16.3 Algorithm for 2010 Chinese Wind Loads 3-63
3.17 2008 API 4F Wind Loads 3-65
3.17.1 Input Exposure 3-66
3.17.2 Algorithm for API 4F-2008 Wind Loads 3-66
3.18 2008 API 4F Wind Loads 3-69
3.18.1 Input Exposure 3-69
3.18.2 Algorithm for API 4F-2008 Wind Loads 3-70
3.19 2005 Eurocode 1 (EN 1991-14) Wind Loads 3-73
3.19.1 Input Wind Coefficients 3-73
3.19.2 Algorithm for EN 1991-1-1:2005 Wind Loads 3-74
3.20 2002 AS/NZS 1170.2 Wind Loads 3-79
3.20.1 Input Wind Coefficients 3-79
3.20.2 Algorithm for AS/NZS 1170.2:2002 Wind
Loads 3-80
ix
Lateral Loads
3.21 2011 AS/NZS 1170.2 Wind Loads 3-85
3.21.1 Input Wind Coefficients 3-85
3.21.2 Algorithm for AS/NZS 1170.2:2011 Wind
Loads 3-86
3.22 1987 Indian IS:875 Part-3Wind Loads 3-91
3.22.1 Input Wind Coefficients 3-91
3.22.2 Exposure from Extents of Diaphragms 3-91
3.22.3 Exposure from Area Objects 3-93
3.23 2008 Italian NTC Wind Loads 3-95
3.23.1 Input Wind Coefficients 3-95
3.23.2 Algorithm for Italian NTC 2008 Wind Loads 3-95
3.24 1997 TS 498Wind Loads 3-99
3.24.1 Input Wind Coefficients 3-99
3.24.2 Algorithm for 1997 TX 498 Wind Loads 3-99
3.25 User-Defined Wind Loads 3-101
References
x
Chapter 1
Introduction
SAP2000, ETABS, and CSiBridge are extremely powerful and productive
structural analysis and design programs, partially due to the high level of intel-
ligence embedded within the software. What this means is that many of the ca-
pabilities are highly automated, allowing the user to create and analyze the
models in such a way that is both natural and efficient for a structural engineer.
This manual seeks to explain the logic behind the automated lateral load gener-
ation so that users can gain greater insight into the behavior of the programs,
and hence, greater confidence in their models and analyses.
1.1 About the Manual
The next chapter will show how seismic loads are generated for various codes,
including a detailed discussion of the algorithms used. Chapter 3 does the same
for automatic wind loads, again describing both the forms used and the accom-
panying algorithms.
It is strongly recommended that you read this manual and review any applica-
ble “Watch & Learn” Series tutorials before attempting to use the automated
features of the software. Additional information can be found in the on-line
Help facility available from within the program’s main menu.
1 - 1
Chapter 2
Automatic Seismic Loads
This chapter documents the automatic seismic lateral load patterns that can be
generated. Automatic seismic loads can be generated in the global X or global
Y directions for the following codes:
1994 UBC
1997 UBC
1997 UBC Isolated Building
1996 BOCA
1995 NBCC
2005 NBCC
2010 NBCC
2015 NBCC
2003 IBC / ASCE 7-02
2006 IBC / ASCE 7-05
2009 IBC / ASCE 7-05
2012 IBC/ ASCE 7-10
1997 NEHRP
2010 Chinese
2004 NZS 1170.5
2007 AS 1170.4
2004 Eurocode 8
2002 Indian IS:1893
2008 Italian NTC
2007 Turkish Seismic Code
(TSC)
2009 Korean Building Code
(KBC)
2009 Korean Building Code
(KBC)
2011 Dominican Republic –R-
001
2 - 1
Automated Lateral Loads
2.1 Defining Automatic Seismic Load Patterns
The automatic seismic static load patterns are defined using the Define menu
> Load Patterns command in SAP2000 and ETABS or the Loads > Load
Patterns > Load Patterns command in CSiBridge. Those commands dis-
play the Define Load Patterns form. Use that form to specify a name for the
load pattern, the type of load, a self-weight multiplier, and in some instances,
specify that the load is an Auto Lateral Load Pattern.
When the load type is specified as Quake, the Auto Lateral Load drop-down
list becomes active; use the list to choose any of the codes identified in the
preceding section. Select None for the Auto Lateral Load to specify that the
Quake load will not be an automatic lateral load.
If a code is selected in the Auto Lateral Load list when the Add New Load
Pattern or Modify Load Pattern button is clicked, the load pattern is added
to the model using default settings that are based on the selected code. To re-
view or modify the parameters for an automatic lateral load, highlight the
load in the Load list and click the Modify Lateral Load Pattern button.
In SAP2000 and CSiBridge, each automatic static lateral load must be in a
separate load pattern. That is, two or more automatic static lateral loads can-
not be specified in the same load pattern. However, additional user defined
loads can be added to a load pattern that includes an automatic static lateral
load.
In SAP2000 and CSiBridge, a separate automatic static load pattern must be
defined for each direction, and, in the case of seismic loading, for each ec-
centricity that is to be considered. For example, to define automatic seismic
lateral loads based on the 1997 UBC for X-direction load with no eccentrici-
ty, X-direction load with +5% eccentricity, and X-direction load with –5%
eccentricity, three separate load patterns must be defined.
Note that the actual forces associated with an automatic static lateral load are
not calculated until an analysis has been run. Thus, the resultant automatic
lateral loads cannot be reviewed until after an analysis has been run.
2 - 2
Chapter 2 - Automatic Seismic Loads
2.2 Automatic Seismic Load Patterns
The forms defining the automatic seismic loads consist of various data
sections, some of which are dependent upon the direction of the loading.
Some of the direction-dependent data is common to all of the codes. This
includes the direction and eccentricity data and the story/elevation range
data. These data are described in the subsections that follow because they
are applicable to all codes. Other direction-dependent data, including
building period information and other factors, and coefficients and the non-
direction-dependent factors and coefficients are described separately for each
code later in this chapter.
The weight of the structure used in the calculation of automatic seismic loads
is based on the specified mass of the structure.
In ETABS, seismic load patterns may become multi-stepped. For example, a
seismic load may be applied in multiple directions with and without
eccentricities. These will be treated as a single load pattern and will be
analyzed in a single load case, producing multiple output steps of response,
one for each separate step of the load.
When a multi-stepped load pattern is applied in a load case, the following
rules govern how it will be handled:
1. In a linear static load case, the load case will internally be run as a multi-
linear static load case, producing multiple output steps.
2. In a nonlinear static load case, the load case will internally be run as a
new type of staged-construction load case, where each stage starts from
the beginning of the load case, producing results similar to the multi-
linear static load case.
3. All other load cases (including staged-construction) are unchanged, and
will treat the load pattern as single-stepped, using the first step of the
multi-stepped load pattern.
4. For cases 1 and 2, if several multi-stepped load patterns are applied in a
single load case, they superpose on a step-wise basis. For example, if
load pattern A has 3 steps and load pattern B has 5 steps, the load case
Automatic Seismic Load Patterns 2 - 3
Automatic Seismic Loads
will apply five independent load steps: A1+B1, A2+B2, A3+B3, B4, B5.
If a non-stepped load pattern is applied, such as Dead, it is applied in
every load step.
2.2.1 Types of Auto Seismic Loads
There are two types of auto seismic load patterns i.e. Seismic and Seismic
(Drift) in ETABS. Seismic type pattern is used for strength design by includ-
ing the load patterns in the default design combinations. The seismic type
load pattern is documented in details in sections 2.3 to 2.21.
Seismic (Drift) patterns can be specified for modeling serviceability cases
where upper limits on time period is waved. Generally, Seismic (Drift) case
is applicable to 1997 UBC, 1997 UBC, 1996 BOCA, 1997 NEHRP, ASCE
7-02, ASCE 7-05 and ASCE 7/10 codes. These auto lateral load patterns do
not enforce the upper limit on time period when time period is “Program
Computed”. For ASCE 7-10 code, in addition the minimum base shear limit
as specified in ASCE 7-10 Eqn. 12.8-5 or Eqn. 12.8-6 is not enforced. The
remaining implementation remains same as Seismic pattern documented in
section 2.3 to 2.21.
2.2.2 Distribution of Automatic Seismic Loads at a Story Level
The method that the program uses to calculate the seismic base shear and the
associated story lateral forces is documented separately for each code later in
this chapter. After the program has calculated a force for each level based on
the automatic seismic load pattern, that force is apportioned to each point at
the level elevation in proportion to its mass.
2.2.3 Load Direction and Diaphragm Eccentricity
Use the direction and eccentricity data to choose the Global X or Global Y
direction of the load and the eccentricity associated with the load pattern for
all diaphragms.
To apply an eccentricity, specify a ratio eccentricity that is applicable to all
diaphragms. The default ratio is 0.05. The eccentricity options have meaning
2 - 4 Automatic Seismic Load Patterns
Chapter 2 - Automatic Seismic Loads
only if the model has diaphragms—the programs ignore eccentricities where
diaphragms are not present.
Where diaphragms are present, the programs calculate a maximum width of
the diaphragm perpendicular to the direction of the seismic loading. This
width is calculated by finding the maximum and minimum X or Y coordi-
nates (depending on direction of load considered) of the points that are part
of the diaphragm constraint and determining the distance between these max-
imum and minimum values.
After the appropriate diaphragm width has been determined, a moment is ap-
plied that is equal to the specified ratio eccentricity times the maximum
width of the diaphragm perpendicular to the direction of the seismic loading
times the total lateral force applied to the diaphragm. This moment is applied
about the diaphragm center of mass to account for the eccentricity.
When defining eccentricities, click the Overwrite button to overwrite the
eccentricity for any diaphragm at any level. Thus, it is possible to have
different eccentricity ratios at different levels. Note that when the
eccentricities are overridden, an actual distance from the center of mass of
the rigid diaphragm, not a ratio, must be input.
When the eccentricities have been overridden, the eccentric moment is calcu-
lated as the specified eccentricity distance times the total lateral force applied
to the diaphragm. This moment is again applied about the diaphragm center
of mass to account for the eccentricity.
2.2.4 Story/Elevation Range Data
In the Story/Elevation range data, specify a top story/maximum elevation and
a bottom story/minimum elevation. This specifies the elevation range over
which the automatic static lateral loads are calculated.
In most instances, the top elevation would be specified as the uppermost lev-
el in the structure, typically the roof in a building. However, in some cases, it
may be advantageous to specify a lower elevation as the top level for auto-
matic seismic loads. For example, if a penthouse is included in a building
model, the automatic lateral load calculation likely should be based on the
building roof level, not the penthouse roof level, as the top elevation, with
Automatic Seismic Load Patterns 2 - 5
Automatic Seismic Loads
additional user-defined load added to the load pattern to account for the
penthouse.
The bottom elevation typically would be the base level, but this may not al-
ways be the case. For example, if a building has several below-grade levels
and it is assumed that the seismic loads are transferred to the ground at
ground level, it would be necessary to specify the bottom elevation to be
above the base level.
Note that no seismic loads are calculated for the bottom story/minimum ele-
vation.
2.3 1994 UBC Seismic Loads
2.3.1 Options for 1994 UBC Building Period
Three options are provided for the building period used in calculating the
1994 UBC automatic seismic loads. They are:
Method A: Calculate the period based on the Method A period discussed in
Section 1628.2.2 of the 1994 UBC. The period is calculated using 1994 UBC
Equation 28-3. The value used for Ct is user input and hn is determined by
ETABS from the input story level heights.
( )
34
A tn
T Ch
=
1994 UBC Equation 28-3
Note that the item Ct is always input in English units as specified in the code.
A typical range of values for Ct is 0.020 to 0.035. The height hn is measured
from the elevation of the (top of the) specified bottom story level to the (top
of the) specified top story level.
Program Calculated: ETABS starts with the period of the mode calculated
to have the largest participation factor in the direction that loads are being
calculated (X or Y). Call this period TETABS. ETABS also calculates a period
based on the Method A period discussed in Section 1628.2.2 of the 1994
UBC. The period is calculated using 1994 UBC Equation 28-3. The value
used for Ct is user input and hn is determined by ETABS from the input story
2 - 6 1994 UBC Seismic Loads
Chapter 2 - Automatic Seismic Loads
level heights. Call this period TA. The building period, T, that ETABS choos-
es depends on the seismic zone factor, Z.
If Z ≥ 0.35 (Zone 4) then:
If TETABS ≤ 1.30TA, then T = TETABS.
If TETABS > 1.30TA, then T = TA.
If Z < 0.35 (Zone 1, 2 or 3) then:
If TETABS ≤ 1.40TA, then T = TETABS.
If TETABS > 1.40TA, then T = TA.
User Defined: In this case, the user inputs a building period. ETABS uses
this period in the calculations. It does not compare it against the Method A
period. It is assumed that the user has completed this comparison before
specifying the period.
2.3.2 Other Input Factors and Coefficients
The Rw factor is direction dependent. It is specified in 1994 UBC Table 16-N.
A typical range of values for Rw is 4 to 12.
The seismic zone factor, Z, can be input in accordance with the code, which
restricts it to one of the following values: 0.075, 0.15, 0.2, 0.3, 0.4 as speci-
fied in 1994 UBC Table 16-I. Alternatively the Z factor can be user-defined,
which allows any value to be input.
The site coefficient for soil characteristics, S, can be 1, 1.2, 1.5 or 2. These
correspond to soil types S1, S2, S3 and S4 in Table 16-J of the 1994 UBC. No
other values can be input.
The seismic importance factor, I can be input as any value. See 1994 UBC
Table 16-K. A typical range of values for I is 1.00 to 1.25.
1994 UBC Seismic Loads 2 - 7
Automatic Seismic Loads
2.3.3 Algorithm for 1994 UBC Seismic Loads
The algorithm for determining 1994 UBC seismic loads is based on Chapter
16, Section 1628 of the 1994 UBC. ETABS calculates a period as described
in a preceding section entitled "Options for 1994 UBC Building Period."
A numerical coefficient, C, is calculated using 1994 UBC Equation 28-2.
23
1.25S
CT
=
1994 UBC Equation 28-2
where,
S = Site coefficient for soil characteristics.
T = Building period.
If the value of C exceeds 2.75, then C is set equal to 2.75 for use in Equation
28-3. If the value of C/Rw is less than 0.075, then it is set equal to 0.075 for
use in Equation 28-3.
The base shear, V, is calculated from 1994 UBC Equation 28-1.
w
ZIC
VW
R
=
Eqn. 281994 UBC Equation 28-1
where,
Z = Seismic zone factor.
I = Importance factor.
C = Numerical coefficient calculated in Equation 28-2.
Rw = Numerical factor specified in UBC Table 16-N.
W = Weight of the building (based on specified mass).
Note that the weight, W, that ETABS uses in Equation 28-3 is derived from
the building mass.
2 - 8 1994 UBC Seismic Loads
Chapter 2 - Automatic Seismic Loads
The total base shear, V, is broken into a concentrated force applied to the top
of the building and forces applied at each story level in accordance with 1994
UBC Equation 28-6:
story
story 1
n
t
VF F
=
= +
∑
1994 UBC Equation 28-6
where,
V = Building base shear.
Ft = Concentrated force at the top of the building.
Fstory = Portion of base shear applied to a story level.
n = Number of story levels in the building.
The concentrated force at the top of the building, Ft, is calculated as shown in
1994 UBC Equation 28-7:
If 0.7 sec, then 0
If 0.7 sec, then 0.07 0.25
t
t
TF
T F TV V
≤=
>=≤
1994 UBC Equation 28-7
where,
T = Building period.
V = Building base shear.
The remaining portion of the base shear, (V − Ft), is distributed over the
height of the building in accordance with 1994 UBC Equation 28-8:
()
story story
story
story story
story 1
t
n
V Fw h
F
wh
=
−
=∑
1994 UBC Equation 28-8
where,
Fstory = Portion of base shear applied to a story level.
V = Building base shear.
1994 UBC Seismic Loads 2 - 9
Automatic Seismic Loads
Ft = Concentrated force at the top of the building.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of building to story level.
n = Number of story levels in the building.
2.4 1997 UBC Seismic Loads
2.4.1 Options for 1997 UBC Building Period
Three options are provided for the building period used in calculating the
1997 UBC automatic seismic loads. They are as follows:
Method A: Calculate the period based on the Method A period discussed
in Section 1630.2.2 of the 1997 UBC. The period is calculated using
1997 UBC Eqn. 30-8. The value used for Ct is user input, and hn is de-
termined from the level heights.
(1997 UBC Eqn. 30-8)
Note that the item Ct is always input in English units as specified in the
code. A typical range of values for Ct is 0.020 to 0.035. The height hn is
measured from the elevation of the specified bottom story/minimum el-
evation level to the (top of the) specified top story/maximum elevation
level.
Program Calculated: The program starts with the period of the mode
calculated to have the largest participation factor in the direction that
loads are being calculated (X or Y). Call this period Tmode. The program
also calculates a period based on the Method A period discussed in Sec-
tion 1630.2.2 of the 1997 UBC. The period is calculated using 1997
UBC Eqn. 30-8. The value used for Ct is user input, and hn is determined
from the level heights. Call this period TA. The building period, T, that
the program chooses depends on the seismic zone factor, Z.
•
If Z ≥ 0.35 (Zone 4) then:
2 - 10 1997 UBC Seismic Loads
Chapter 2 - Automatic Seismic Loads
– If Tmode ≤ 1.30TA, then T = Tmode.
– If Tmode > 1.30TA, then T = TA.
•
If Z < 0.35 (Zone 1, 2 or 3) then:
– If Tmode ≤ 1.40TA, then T = Tmode.
– If Tmode > 1.40TA, then T = TA.
User Defined: With this option, the user inputs a structure period, which
the program uses in the calculations. The program does not compare the
period to the Method A period. It is assumed that this comparison has
been completed before the period is specified.
2.4.2 Other Input Factors and Coefficients
The overstrength factor, R, and the force factor, Ω, are direction dependent.
Both are specified in 1997 UBC Table 16-N. A typical range of values for R
is 2.8 to 8.5. A typical range of values for Ω is 2.2 to 2.8.
The seismic coefficients Ca and Cv can be determined in accordance with the
code or they can be user-defined. If Ca and Cv are user-defined, specify val-
ues for them. A typical range of values for Ca is 0.06 to 0.40 and larger if the
near source factor Na exceeds 1.0. A typical range of values for Cv is 0.06 to
0.96 and larger if the near source factor Nv exceeds 1.0.
If Ca and Cv are determined in accordance with code, specify a soil profile
type and a seismic zone factor. The programs then use these parameters to
determine Ca from 1997 UBC Table 16-Q and Cv from 1997 UBC Table 16-
R.
The soil profile type can be SA, SB, SC, SD or SE. These correspond to soil
types SA, SB, SC, SD and SE in Table 16-J of the 1997 UBC. No other values
can be input. Note that soil profile type SF is not allowed for the automatic
1997 UBC seismic loads.
The seismic zone factor, Z, is restricted to one of the following values, as
specified in 1997 UBC Table 16-I: 0.075, 0.15, 0.2, 0.3, or 0.4.
1997 UBC Seismic Loads 2 - 11
Automatic Seismic Loads
Note that in 1997 UBC Table 16-Q the Ca value for Z = 0.4 has an additional
factor, Na. Similarly, in 1997 UBC Table 16-R, the Cv value for Z = 0.4 has
an additional factor, Nv. The values for the near source factors, Na and Nv, can
be determined in accordance with the code or they can be user-defined. If Na
and Nv are user-defined, specify values for them. If they are determined in
accordance with code, specify a seismic source type and a distance to the
closest known seismic source. On the basis of the input for seismic source
type and distance to the source, the programs determine Na from 1997 UBC
Table 16-S and Nv from 1997 UBC Table 16-T. The programs use linear
interpolation for specified distances between those included in 1997 UBC
Tables 16-S and 16-T.
The seismic source type can be A, B, or C. These correspond to seismic
source types A, B, and C in Table 16-U of the 1997 UBC. No other values
can be input.
The distance to the closest known seismic source should be input in kilome-
ters (km).
The seismic importance factor, I, can be input as any value. See 1997 UBC
Table 16-K. Note that the value from Table 16-K to be input for automatic
seismic loads is I, not Ip or Iw. A typical range of values for I is 1.00 to 1.25.
2.4.3 Algorithm for 1997 UBC Seismic Loads
The algorithm for determining 1997 UBC seismic loads is based on Chapter
16, Section 1630.2 of the 1997 UBC. A period is calculated as described in a
preceding section entitled "Options for 1997 UBC Building Period."
Initially the total design base shear, V, is calculated using (1997 UBC Eqn.
30-4). This base shear value is then checked against the limits specified in
(1997 UBC Eqns. 30-5, 30-6 and 30-7) and modified as necessary to obtain
the final base shear.
v
CI
VW
RT
=
(1997 UBC Eqn. 30-4)
where,
Cv = 1997 UBC seismic coefficient, Cv.
2 - 12 1997 UBC Seismic Loads
Chapter 2 - Automatic Seismic Loads
I = Importance factor.
R = Overstrength factor specified in UBC Table 16-N.
T = Building period.
W = Weight of the building (based on specified mass).
The total design base shear, V, need not exceed that specified in (1997 UBC
Eqn. 30-5). If the base shear calculated in accordance with (1997 UBC Eqn.
30-4) exceeds that calculated in accordance with (1997 UBC Eqn. 30-5), the
base shear is set equal to that calculated in accordance with (1997 UBC Eqn.
30-5).
25 a
.CI
VW
R
=
(1997 UBC Eqn. 30-5)
where,
Ca = 1997 UBC seismic coefficient, Ca.
and all other terms are as described for (1997 UBC Eqn. 30-4).
The total design base shear, V, cannot be less than that specified in (1997
UBC Eqn. 30-6). If the base shear calculated in accordance with (1997 UBC
Eqn. 30-6) exceeds that calculated in accordance with (1997 UBC Eqn. 30-
4), the base shear is set equal to that calculated in accordance with (1997
UBC Eqn. 30-5).
V = 0.11Ca I W (1997 UBC Eqn. 30-6)
where all terms are as described previously for (1997 UBC Eqns. 30-4 and
30-5).
Finally, if the building is in seismic Zone 4, the total design base shear, V,
cannot be less than that specified in (1997 UBC Eqn. 30-7). If the building is
in seismic Zone 4 and the base shear calculated in accordance with (1997
UBC Eqn. 30-7) exceeds that calculated in accordance with (1997 UBC
Eqns. 30-5 and 30-6), the base shear is set equal to that calculated in accord-
ance with (1997 UBC Eqn. 30-7).
1997 UBC Seismic Loads 2 - 13
Automatic Seismic Loads
0.8 v
ZN I
VW
R
=
(1997 UBC Eqn. 30-7)
where,
Z = Seismic zone factor (0.40).
Nv = Near source factor, Nv.
I = Importance factor.
R = Overstrength factor specified in UBC Table 16-N.
W = Weight of the building (based on specified mass).
Note that the programs check (1997 UBC Eqn. 30-7) only if the seismic co-
efficients, Ca and Cv, are determined in accordance with the code and the
seismic zone factor Z is specified as 0.40. If the Ca and Cv coefficients are
user specified, (1997 UBC Eqn. 30-7) is never checked.
Note that the weight, W, that is used in (1997 UBC Eqns. 30-4 through 30-7)
is derived from the building mass.
The total base shear, V, is broken into a concentrated force applied to the top
elevation/story and forces applied at each level/story in accordance with
(1997 UBC Eqn. 30-13):
story
story 1
n
t
VF F
=
= + ∑
(1997 UBC Eqn. 30-13)
where,
V = Building base shear.
Ft = Concentrated force at the top of the building.
Fstory = Portion of base shear applied to a story level.
n = Number of story levels in the building.
The concentrated force at the top of the building, Ft , is calculated as shown
in (1997 UBC Eqn. 30-14):
2 - 14 1997 UBC Seismic Loads
Chapter 2 - Automatic Seismic Loads
T. F
T . F . TV . V
≤=
>=≤
t
t
If 0 7 sec, then 0
If 0 7 sec, then 0 07 0 25
(1997 UBC Eqn. 30-14)
where,
T = Building period.
V = Building base shear.
The remaining portion of the base shear, (V − Ft ), is distributed over the
height of the structure in accordance with (1997 UBC Eqn 30-15):
()
story story
story n
story story
story 1
t
V Fw h
F
wh
=
−
=∑
(1997 UBC Eqn. 30-15)
where,
Fstory = Portion of base shear applied to a story level.
V = Base shear.
Ft = Concentrated force at the top of the structure.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
n = Number of story levels in the structure.
2.5 1997 UBC Isolated Building Seismic Loads
2.5.1 Other Input Factors and Coefficients
For 1997 UBC isolated building seismic loads, the bottom story or minimum
elevation should be input as the story at the top of the isolators.
The overstrength factor, Ri , is direction dependent. It relates to the structure
above the isolation interface. It is specified in 1997 UBC Table A-16-E,
1997 UBC Isolated Building Seismic Loads 2 - 15
Automatic Seismic Loads
which is in Appendix Chapter 16, Division IV. A typical range of values for
Ri is 1.4 to 2.0.
The coefficient for damping, BD , is direction dependent. It should be speci-
fied based on an assumed effective damping using 1997 UBC Table A-16-C,
which is in Appendix Chapter 16, Division IV. A typical range of values for
BD is 0.8 to 2.0.
The maximum effective stiffness and minimum effective stiffness items refer
to the maximum and minimum effective stiffness of the isolation system (not
individual isolators) at the design displacement level (not the maximum dis-
placement level). They correspond to the terms KDmax and KDmin, respectively,
in Appendix Chapter 16, Division IV.
The seismic coefficient CvD can be determined in accordance with the code or
it can be user defined. If CvD is user defined, simply specify a value for it. A
typical range of values for CvD is 0.06 to 0.96 and larger if the near source
factor Nv exceeds 1.0.
If CvD is determined in accordance with the code, specify a soil profile type
and a seismic zone factor. On the basis of the input soil profile type and a
seismic zone factor, the programs determine CvD from 1997 UBC Table 16-
R, which is in Chapter 16, not Appendix Chapter 16, Division IV.
Note that in 1997 UBC Table 16-R, the Cv value for Z = 0.4 has an additional
factor, Nv. The value for this near source factor, Nv, can be determined in ac-
cordance with the code or it can be user defined. If Nv is user defined, simply
specify a value for it. If it is determined in accordance with the code, specify
a seismic source type and a distance to the closest known seismic source. On
the basis of the input seismic source type and distance to the source, the pro-
grams determine Nv from 1997 UBC Table 16-T. The programs use linear
interpolation for specified distances between those included in 1997 UBC
Table 16-T.
2.5.2 Algorithm for 1997 UBC Isolated Building Seismic Loads
The algorithm for determining 1997 UBC seismic loads for isolated build-
ings is based on Appendix Chapter 16, Division IV, Sections 1658.3 and
1658.4 of the 1997 UBC.
2 - 16 1997 UBC Isolated Building Seismic Loads
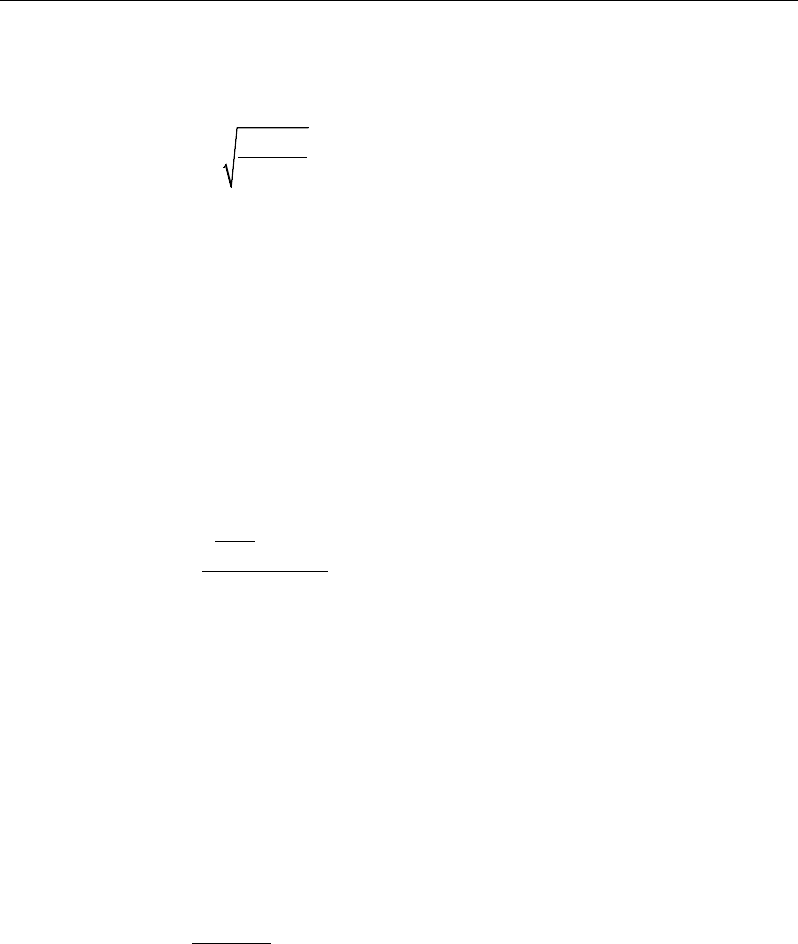
Chapter 2 - Automatic Seismic Loads
The effective period at the design displacement, TD , is determined from
(1997 UBC Eqn. 58-2).
min
DD
W
T2kg
=
π
(1997 UBC Eqn. 58-2)
where,
W = Weight of the building (based on specified mass).
kDmin = Minimum effective stiffness of the isolation system at the design
displacement.
g = Gravity constant, (e.g., 386.4 in/sec2, 9.81 m/sec2, etc.).
The design displacement at the center of rigidity of the isolation system, DD,
is determined from (1997 UBC Eqn. 58-1).
vD D
2
DD
gCT
4
DB



=
π
(1997 UBC Eqn. 58-1)
where,
g = Gravity constant, (e.g., 386.4 in/sec2, 9.81 m/sec2, etc.).
CvD = Seismic coefficient, CvD.
TD = Effective period at the design displacement.
BD = Coefficient for damping.
The base shear, Vs , is calculated from (1997 UBC Eqn. 58-8).
DD
sI
kD
VR
=
max
(1997 UBC Eqn. 58-8)
Note that (1997 UBC Eqn. 58-8) gives a force level that is applicable for the
structure above the isolation system. To use a force level that is applicable to
the isolation system in accordance with (1997 UBC Eqn. 58-7), create a dif-
ferent load combination with a scale factor of RI for the seismic load.
1997 UBC Isolated Building Seismic Loads 2 - 17
Automatic Seismic Loads
Also note that the limits on Vs specified in 1997 UBC section 1658.4.3 are
not considered by the programs.
The total base shear, Vs, is distributed over the height of the structure in
accordance with (1997 UBC Eqn. 58-9):
s
n
i
Vw h
F
wh
=
=
∑
story story
story
story story
story
(1997 UBC Eqn. 58-9)
where,
Fstory = Portion of base shear applied to a story level.
Vs = Base shear in accordance with (1997 UBC Eqn. 58-8).
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
n = Number of story levels in the structure.
2.6 1996 BOCA Seismic Loads
2.6.1 Options for 1996 BOCA Building Period
Three options are provided for the building period used in calculating the
1996 BOCA automatic seismic loads. They are:
Approximate: Calculate the approximate period, Ta, based on the ap-
proximate formula discussed in Section 1610.4.1.2.1 of the 1996 BOCA.
The period is calculated using BOCA 1610.4.1.2.1. The value used for
CT is user input and hn is determined from the input level heights.
()
a Tn
T Ch
=34
(BOCA 1610.4.1.2.1)
Note that the item CT is always input in English units as specified in the
code. A typical range of values for CT is 0.020 to 0.035. The height hn is
2 - 18 1996 BOCA Seismic Loads
Chapter 2 - Automatic Seismic Loads
measured from the elevation of the specified bottom story/minimum ele-
vation level to the (top of the) specified top story/maximum elevation
level.
Program Calculated: The programs start with the period of the mode
calculated to have the largest participation factor in the direction that
loads are being calculated (X or Y). Call this period Tmode. The programs
also calculate a period based on the approximate formula discussed in
Section 1610.4.1.2.1 of 1996 BOCA. The value used for CT is user input
and hn is determined from the level heights. Call this period Ta.
The programs determine a value for the coefficient for the upper limit on
the calculated period, Ca , using Table 1610.4.1.2 in the 1996 BOCA.
Note that the value used for Ca depends on the specified value for the ef-
fective peak velocity-related coefficient, Av. Ca is determined using linear
interpolation if the specified value of Av is not in Table 1610.4.1.2. If Av
exceeds 0.40, Ca is taken as 1.2. If Av is less than 0.05, Ca is taken as 1.7.
The building period, T, that the programs choose is determined as fol-
lows:
– If Tmode > CaTa , then T = CaTa.
– If Tmode ≤ CaTa , then T = Tmode.
User Defined: In this case, input a building period, which the programs
use in the calculations. They do not compare it against the coefficient for
the upper limit on the calculated period times the approximate period
(CaTa). It is assumed that this comparison is performed before the period
is specified.
2.6.2 Other Input Factors and Coefficients
The response modification factor, R, is direction dependent. It is specified in
1996 BOCA Table 1610.3.3. A typical range of values for R is 3 to 8.
Any value can be input for the effective peak acceleration coefficient, Aa. Re-
fer to BOCA section 1610.1.3. A typical range of values for Aa is 0.05 to
0.40.
1996 BOCA Seismic Loads 2 - 19
Automatic Seismic Loads
Any value can be input for the effective peak velocity-related coefficient, Av.
Refer to BOCA section 1610.1.3. A typical range of values for Av is 0.05 to
0.40.
The soil profile type can be S1, S2, S3 or S4. These correspond to soil types S1,
S2, S3 and S4 in Table 1610.3.1 of the 1996 BOCA. No other values can be
input.
2.6.3 Algorithm for 1996 BOCA Seismic Loads
The algorithm for determining 1996 BOCA seismic loads is based on Section
1610.4.1 of 1996 BOCA. A period is calculated as described in the previous
section entitled "Options for 1996 BOCA Building Period."
Initially the seismic coefficient, Cs, is calculated from section 1610.4.1.1.
The value of this coefficient is then checked against the limit specified in
(1996 BOCA Eqn. 1610.4.1.1) and modified as necessary to obtain the seis-
mic coefficient.
23
1.2
v
s
AS
CRT
=
(BOCA 1610.4.1.1(a))
where,
Av = The effective peak velocity-related coefficient.
S = The site coefficient based on the input soil profile type.
R = Response modification factor.
T = Building period.
The seismic coefficient, Cs, need not exceed that specified in section 1610.4.1.1(b). If
the seismic coefficient calculated in accordance with section 1610.4.1.1(a)
exceeds that calculated in accordance with (BOCA Eqn. 1610.4.1.1(b)), the
seismic coefficient is set equal to that calculated in accordance with (BOCA
Eqn. 1610.4.1.1(b)).
25 a
s.A
CR
=
(BOCA 1610.4.1.1(b))
2 - 20 1996 BOCA Seismic Loads
Chapter 2 - Automatic Seismic Loads
where,
Aa = The effective peak acceleration coefficient.
R = Response modification factor.
The base shear is calculated using (BOCA 1610.4.1.1).
V = Cs W (BOCA 1610.4.1.1)
where,
Cs = Seismic coefficient calculated from (BOCA Eqn. 1610.4.1.1(a))
or (BOCA Eqn. 1610.4.1.1(b)) as appropriate.
W = Weight of the structure (based on specified mass).
The base shear, V, is distributed over the height of the structure in accordance
with (BOCA Eqn. 1610.4.2):
story story
story
story story
= story
k
nk
i
Vw h
F
wh
=
∑
(BOCA 1610.4.2)
where,
Fstory = Portion of base shear applied to a story level.
V = Base shear.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
k = Exponent applied to structure height. The value of k depends
on the value of the period, T, used for determining the base
shear. If T ≤ 0.5 seconds, k = 1. If T
≥
2.5 seconds, k = 2. If
0.5 seconds < T < 2.5 seconds, k is linearly interpolated be-
tween 1 and 2.
n = Number of story levels in the structure.
1996 BOCA Seismic Loads 2 - 21
Automatic Seismic Loads
2.7 1995 NBCC Seismic Loads
2.7.1 Options for 1995 NBCC Building Period
Five options are provided for the building period used in calculating the 1995
NBCC automatic seismic loads. They are as follows:
Code - Moment Frame: Calculate the period as 0.1N, where N is the
number of stories in the structure based on the specified top and bottom
story levels.
Code - Other: Calculate the period, T, using section 4.1.9.1(7b):
0 09 n
s
.h
TD
=
(1995 NBCC Section 4.1.9.19(7b))
where,
hn = Height of the structure measured from the elevation of the
specified bottom story/minimum level to the (top of the) speci-
fied top story/maximum level measured in meters.
Ds = Length of wall or braced frame, which constitutes the main lat-
eral-force-resisting system measured in meters.
Program Calculated - Moment Frame: The programs use the period of
the mode calculated to have the largest participation factor in the direc-
tion that loads are being calculated (X or Y). In addition, the programs
run a parallel calculation using a period equal to 0.1N, where N is the
number of stories in the structure based on the specified top and bottom
story levels.
The equivalent lateral force at the base of the structure, Ve , is calculated
using both periods. Call these values Ve-mode and Ve-0.1N. The value of Ve to
use is determined as follows:
– If Ve-mode ≥ 0.8 Ve-0.1N, then Ve = Ve-mode.
– If Ve-mode < 0.8 Ve-0.1N, then Ve = 0.8 Ve-0.1N.
2 - 22 1995 NBCC Seismic Loads
Chapter 2 - Automatic Seismic Loads
Program Calculated - Other: The programs use the period of the mode
calculated to have the largest participation factor in the direction that
loads are being calculated (X or Y). In addition, the programs run a paral-
lel calculation using a period calculated using (1995 NBCC Section
4.1.9.19(7b)).
The equivalent lateral force at the base of the structure, Ve, is calculated
using both periods. Call these values Ve-mode and Ve-Eqn (7b). The value of Ve
to use is determined as follows:
– If Ve-mode ≥ 0.8 Ve-Eqn. (7b), then Ve = Ve-mode.
– If Ve-mode < 0.8 Ve-Eqn. (7b), then Ve = 0.8 Ve-Eqn. (7b).
User Defined: In this case the user inputs a building period, which the
programs use in the calculations. The programs do not calculate other
values of Ve using this method for comparison against the Ve calculated
using the user-specified period. It is assumed that this comparison is
completed before the period is specified.
2.7.2 Other Input Factors and Coefficients
The force modification factor, R, is direction dependent. It is specified in
1995 NBCC Table 4.1.9.1.B. A typical range of values for R is 1.5 to 4.0.
The acceleration-related seismic zone, Za , can be input as 0, 1, 2, 3, 4, 5, or 6.
No other input values are allowed.
The velocity-related seismic zone, Zv , can be input as 0, 1, 2, 3, 4, 5, or 6.
No other input values are allowed.
The zonal velocity ratio, v, can be based on Zv, or a user-specified value can
be input. If it is based on Zv , v is assumed equal to 0.00, 0.05, 0.10, 0.15,
0.20, 0.30, or 0.40 for Zv equal to 0, 1, 2, 3, 4, 5, or 6, respectively.
The importance factor, I, can be input as any value. It is specified in 1995
NBCC Sentence 4.1.9.1(10). A typical range of values for I is 1.0 to 1.5.
The foundation factor, F, can be input as any value. It is specified in 1995
NBCC Table 4.1.9.1.C. A typical range of values for F is 1.0 to 2.0.
1995 NBCC Seismic Loads 2 - 23
Automatic Seismic Loads
2.7.3 Algorithm for 1995 NBCC Seismic Loads
The algorithm for determining 1995 NBCC seismic loads is based on Sub-
section 4.1.9 of the 1995 NBCC. The period is calculated as described in a
preceding section entitled "Options for 1995 NBCC Building Period."
First the programs check if Zv = 0 and Za > 0. If so, then Zv = 1 and v = 0.05
is set for the calculation of the base shear.
The seismic response factor, S, is calculated based on 1995 NBCC Table
4.1.9.1.A.
The programs determine the product of the foundation factor, F, and the
seismic response factor, S. Call this product FS. If necessary, this product is
modified as follows:
– If FS > 3 and Za ≤ Zv , then FS = 3.
– If FS > 4.2 and Za > Zv , then FS = 4.2.
The equivalent lateral force representing elastic response is determined in ac-
cordance with section 4.1.9.1(5):
Ve = v FS I (1995 NBCC Section 4.1.9.1 (5))
Note that in cases where the structure period is program calculated, the value
of Ve is calculated twice and then one of the calculated values is chosen. See
the preceding section entitled "Options for 1995 NBCC Building Period" for
more information.
The minimum lateral seismic force, V, is calculated using section 4.1.9.1(4).
0.6
e
V
VR
=
(1995 NBCC Section 4.1.9.1(4))
The total base shear, V, is broken into a concentrated force applied to the top
of the structure and forces applied at each story level in accordance with sec-
tion 4.1.9.1(13):
n
t
1
VF F
=
= + ∑
story
story
(1995 NBCC Section 4.1.9.1(13))
2 - 24 1995 NBCC Seismic Loads
Chapter 2 - Automatic Seismic Loads
where,
V = Building base shear.
Ft = Concentrated force at the top of the building.
Fstory = Portion of base shear applied to a story level.
n = Number of story levels in the building.
The concentrated force at the top of the structure, Ft , is calculated as shown
in section 4.1.9.1(13):
t
- If 0.7 sec, then 0
- If 0.7 sec, then 0.07 0.25
t
TF
T F TV V
≤=
>=≤
(1995 NBCC Section 4.1.9.1(13))
where,
T = Building period.
V = Building base shear.
The remaining portion of the base shear, (V − Ft ), is distributed over the
height of the structure in accordance with (1995 NBCC Section 4.1.9.1(13)):
( )
t
n
V Fw h
F
wh
−
=
∑
story story
story
story story
story = 1
(1995 NBCC Section 4.1.9.1(13))
where,
Fstory = Portion of base shear applied to a story level.
V = Base shear.
Ft = Concentrated force at the top of the structure.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
n = Number of story levels in the structure.
1995 NBCC Seismic Loads 2 - 25
Automatic Seismic Loads
Note that the torsional moments discussed in 1995 NBCC Section 4.1.9.1(28)
are included automatically when a diaphragm is present and eccentricity is
specified in an auto lateral load pattern. Options are available to overwrite
the eccentricities at each diaphragm to specify these torsional moments.
2.8 2005 NBCC Seismic Loads
2.8.1 Options for 2005 NBCC Building Period
Four options are provided for the building period used in calculating the
2005 NBCC automatic seismic loads. They are as follows:
Code – Steel & Concrete Moment Frames, Shear Wall & Other
Structures: Calculate the approximate period based on section
4.1.8.11(3). The values used for CT and x are user input and hn is deter-
mined by the programs from the input story level heights.
( )
3
4
A Tn
T Ch=
(2005 NBCC Section 4.1.8.11(3))
A typical range of values for CT is 0.025 to 0.085. The height hn is meas-
ured from the elevation of the specified bottom story/minimum level to
the (top of the) specified top story/maximum level measured in meters.
Code – Moment Frames other than Steel & Concrete: Calculate the
approximate period, TA, using section 4.1.8.11(3):
0.1
A
TN=
(2005 NBCC Section 4.1.8.11(3))
where,
N = The number of stories in the structure based on the specified
top and bottom story levels.
Code – Braced Frame: Calculate the approximate period, TA, using sec-
tion 4.1.8.11(3):
()
0.025=
An
Th
(2005 NBCC Section 4.1.8.11(3))
2 - 26 2005 NBCC Seismic Loads
Chapter 2 - Automatic Seismic Loads
Program Calculated: The programs use the period of the mode calcu-
lated to have the largest participation factor in the direction that loads are
being calculated (X or Y). Call this period Tmode. A period is also calculat-
ed based on (NBCC Eqn. 4.1.8.11(3)), as appropriate. Call this period TA.
The building period, T, that the programs choose is determined from sec-
tion 4.1.8.11(d). The values used for Cu are user input, and typically vary
from 1.5 to 2.0 as specified in NBCC 2005 clause 4.1.8.11(3).
– If Tmode ≤ CuTA , then T = Tmode. (NBCC 2005 Section 4.1.8.11(d))
– If Tmode > CuTA , then T = CuTA. (NBCC 2005 Section 4.1.8.11(d))
User Defined: In this case the user inputs a building period, which the
programs use in the calculations. They do not compare it against CuTA. It
is assumed that this comparison has been performed before the period is
specified.
2.8.2 Other Input Factors and Coefficients
The ductility-related force modification factor, Rd , is direction dependent. It
is specified in 2005 NBCC Table 4.1.8.9. A typical range of values for Rd is
1.5 to 5.0.
The overstrength-related force modification factor, Ro , is direction depend-
ent. It is specified in 2005 NBCC Table 4.1.8.9. A typical range of values for
Ro is 1.3 to 1.7.
The 5% damped spectral response acceleration, Sa(T), shall be input for peri-
ods T of 0.2 s, 0.5 s, 1.0 s, and 2.0 s as described in subsection 4.1.8.4 of the
2005 NBCC. The input in the programs is in g.
The higher mode factor, Mv , is direction dependent. It is specified in 2005
NBCC Table 4.1.8.11. A typical range of values for Mv is 1 to 2.5.
The site coefficients can be input in accordance with the code or they can be
user defined. If the site coefficients are in accordance with code, specify a
site class. If site coefficients are user defined, specify Fa and Fv.
2005 NBCC Seismic Loads 2 - 27
Automatic Seismic Loads
The site class can be A, B, C, D, or E. Note that site class F is not allowed for
automatic 2005 NBCC lateral seismic loads. See 2005 NBCC Table
4.1.8.4.A for site class definitions.
Fa is the acceleration-based site coefficient. If the site coefficients are deter-
mined in accordance with code, the software automatically determines Fa
from the site class and Sa(0.2) based on 2005 NBCC Table 4.1.8.4.B. If site
coefficients are user defined, the value for Fa is input directly by the user. A
typical range of values for Fa is 0.7 to 2.1.
Fv is the velocity-based site coefficient. If the site coefficients are determined
in accordance with code, the software automatically determines Fv from the
site class and Sa(1.0) based on 2005 NBCC Table 4.1.8.4.C. If site coeffi-
cients are user defined, the value for Fv is input directly by the user. A typical
range of values for Fv is 0.5 to 2.1.
The importance factor, IE, can be input as any value. It is specified in 2005
NBCC Sentence 4.1.8.5. A typical range of values for IE is 0.8 to 1.5.
2.8.3 Algorithm for 2005 NBCC Seismic Loads
The algorithm for determining 2005 NBCC seismic loads is based on Sub-
section 4.1.8.11 of the 2005 NBCC. The period T is calculated as described
in a preceding section entitled "Options for 2005 NBCC Building Period."
The programs begin by calculating the design spectral acceleration S(T) us-
ing (2005 NBCC Eqns. 4.1.8.4(6)-1 to 4.1.8.4(6)-5). Linear interpolation is
used for intermediate values of T. Eqns. 4.1.8.4(6)-1 to 4.1.8.4(6)-5 are de-
scribed in Section 4.1.8.4 of 2005 NBCC.
( ) (0.2) for 0.2s
aa
ST FS T= ≤
(2005 NBCC Eqn. 4.1.8.4(6)-1)
( ) (0.5) or (0.2),
whichever is smaller for 0.5s
va aa
ST FS FS
T
=
=
(2005 NBCC Eqn. 4.1.8.4(6)-2)
( ) (1.0) for 1.0s
va
ST FS T= =
(2005 NBCC Eqn. 4.1.8.4(6)-3)
( ) (2.0) for 2.0s
va
ST FS T= =
(2005 NBCC Eqn. 4.1.8.4(6)-4)
2 - 28 2005 NBCC Seismic Loads
Chapter 2 - Automatic Seismic Loads
( ) (2.0) 2 for 4.0s
va
ST FS T= ≥
(2005 NBCC Eqn. 4.1.8.4(6)-5)
The minimum lateral earthquake force, V, is determined in accordance with
(2005 NBCC Eqn. 4.1.8.11(2)-2):
() ( )
vE d o
V STMI W RR=
(2005 NBCC Eqn. 4.1.8.11(2)-1)
where,
W = Weight of the building (based on specified mass).
The total design base shear, V, shall not be less than that specified in (2005
NBCC Eqn. 4.1.8.11(2)-2). If the base shear calculated in accordance with
(2005 NBCC Eqn. 4.1.8.11(2)-1) is less than that calculated in accordance
with (2005 NBCC Eqn. 4.1.8.11(2)-2), the base shear is set equal to that cal-
culated in accordance with (2005 NBCC Eqn. 4.1.8.11(2)-2).
(2.0) ( )
vE d o
V S MIW RR
=
(2005 NBCC Eqn. 4.1.8.11(2)-2)
where,
S(2.0) = Design spectral acceleration for a period of 2 s.
The total design base shear, V, for a structure with an Rd ≥ 1.5 need not ex-
ceed that specified in (2005 NBCC Eqn. 4.1.8.11(2)-3). If the base shear cal-
culated in accordance with (2005 NBCC Eqn. 4.1.8.11(2)-1) exceeds that
calculated in accordance with (2005 NBCC Eqn. 24.1.8.11(2)-3), the base
shear is set equal to that calculated in accordance with (2005 NBCC Eqn.
4.1.8.11(2)-3).
2(0.2) ( )
3
=
E do
V S IW RR
(2005 NBCC Eqn. 4.1.8.11(2)-3)
where,
S(0.2) = Design spectral acceleration for 0.2 s.
The total base shear, V, is broken into a concentrated force applied to the top
of the structure and forces applied at each story level in accordance with
(2005 NBCC Eqn. 4.1.8.11(6)-1).
2005 NBCC Seismic Loads 2 - 29
Automatic Seismic Loads
story
story 1
n
t
VF F
=
= +
∑
(2005 NBCC Eqn. 4.1.8.11(6)-1)
where,
V = Building base shear.
Ft = Concentrated force at the top of the building.
Fstory = Portion of base shear applied to a story level.
n = Number of story levels in the building.
The concentrated force at the top of the structure, Ft , is calculated as shown
in (2005 NBCC Eqn. 4.1.8.11(6)-2):
- If 0.7 sec, then 0
- If 0.7 sec, then 0.07 0.25
t
t
TF
T F TV V
≤=
>=≤
(2005 NBCC Eqn. 4.1.8.11(6)-2)
where,
T = Building period.
V = Building base shear.
The remaining portion of the base shear, (V − Ft ), is distributed over the
height of the structure in accordance with (2005 NBCC Eqn. 4.1.8.11(6)-3):
()
t
n
V Fw h
F
wh
−
=
∑
story story
story
story story
story =1
(2005 NBCC Eqn. 4.1.8.11(6)-3)
where,
Fstory = Portion of base shear applied to a story level.
V = Base shear.
Ft = Concentrated force at the top of the structure.
wstory = Weight of story level (based on specified mass).
2 - 30 2005 NBCC Seismic Loads
Chapter 2 - Automatic Seismic Loads
hstory = Story height, distance from base of structure to story level.
n = Number of story levels in the structure.
2.9 2010 NBCC Seismic Loads
2.9.1 Options for 2010 NBCC Building Period
Four options are provided for the building period used in calculating the
2010 NBCC automatic seismic loads. They are as follows:
Code – Steel & Concrete Moment Frames, Braced Frames, Shear
Wall & Other Structures: Calculate the approximate period based on
section 4.1.8.11(3). The values used for CT and x are user input, and hn is
determined by the programs from the input story level heights.
( )
3
4
A Tn
T Ch=
(2010 NBCC Section 4.1.8.11(3))
A typical range of values for CT is 0.025 to 0.085. The height hn is meas-
ured from the elevation of the specified bottom story/minimum level to
the (top of the) specified top story/maximum level measured in meters.
Code – Moment Frames other than Steel & Concrete: Calculate the
approximate period, TA, using section 4.1.8.11(3):
0.1
A
TN=
(2010 NBCC Section 4.1.8.11(3))
where,
N = The number of stories in the structure based on the specified
top and bottom story levels.
Code – Braced Frame: Calculate the approximate period, TA, using sec-
tion 4.1.8.11(3):
( )
0.025=
An
Th
(2005 NBCC Section 4.1.8.11(3))
2010 NBCC Seismic Loads 2 - 31
Automatic Seismic Loads
Program Calculated: The programs use the period of the mode calcu-
lated to have the largest participation factor in the direction that loads are
being calculated (X or Y). Call this period Tmode. A period is also calculat-
ed based on (NBCC Eqn. 4.1.8.11(3)), as appropriate. Call this period TA.
The building period, T, that the programs choose is determined from sec-
tion 4.1.8.11(d). The values used for Cu are user input, and typically vary
from 1.5 to 2.0 as specified in NBCC 2010 clause 4.1.8.11(3).
– If Tmode ≤ CuTA , then T = Tmode. (NBCC 2010 Section 4.1.8.11(d))
– If Tmode > CuTA , then T = CuTA. (NBCC 2010 Section 4.1.8.11(d))
User Defined: In this case the user can input a building period, which
the programs use in the calculations. The programs do not compare it
against CuTA. It is assumed that this comparison has been performed be-
fore specifying the period.
2.9.2 Other Input Factors and Coefficients
The ductility-related force modification factor, Rd , is direction dependent. It
is specified in 2010 NBCC Table 4.1.8.9. A typical range of values for Rd is
1.5 to 5.0.
The overstrength-related force modification factor, Ro , is direction depend-
ent. It is specified in 2010 NBCC Table 4.1.8.9. A typical range of values for
Ro is 1.3 to 1.7.
The 5% damped spectral response acceleration, Sa(T), shall be input for peri-
ods T of 0.2 s, 0.5 s, 1.0 s, and 2.0 s as described in subsection 4.1.8.4 of the
2010 NBCC. The input in the programs is in g.
The higher mode factor, Mv , is direction dependent. It is specified in 2010
NBCC Table 4.1.8.11. A typical range of values for Mv is 1 to 2.5.
The site coefficients can be input in accordance with the code or they can be
user defined. If the site coefficients are in accordance with code, specify a
site class. If site coefficients are user defined, specify Fa and Fv.
2 - 32 2010 NBCC Seismic Loads
Chapter 2 - Automatic Seismic Loads
The site class can be A, B, C, D, or E. Note that site class F requires site spe-
cific evaluation for automatic 2010 NBCC lateral seismic loads. See 2010
NBCC Table 4.1.8.4.A for site class definitions.
Fa is the acceleration-based site coefficient. If the site coefficients are deter-
mined in accordance with code, the software automatically determines Fa
from the site class and Sa(0.2) based on 2010 NBCC Table 4.1.8.4.B. If site
coefficients are user defined, the value for Fa is input directly by the user. A
typical range of values for Fa is 0.7 to 2.1.
Fv is the velocity-based site coefficient. If the site coefficients are determined
in accordance with code, the software automatically determines Fv from the
site class and Sa(1.0) based on 2010 NBCC Table 4.1.8.4.C. If site coeffi-
cients are user defined, the value for Fv is input directly by the user. A typical
range of values for Fv is 0.5 to 2.1.
The importance factor, IE, can be input as any value. It is specified in 2010
NBCC Sentence 4.1.8.5. A typical range of values for IE is 0.8 to 1.5.
2.9.3 Algorithm for 2010 NBCC Seismic Loads
The algorithm for determining 2010 NBCC seismic loads is based on Sub-
section 4.1.8.11 of the 2010 NBCC. The period T is calculated as described
in a preceding section entitled "Options for 2010 NBCC Building Period."
The programs begin by calculating the design spectral acceleration S(T) us-
ing (2010 NBCC Eqns. 4.1.8.4(6)-1 to 4.1.8.4(6)-5). Linear interpolation is
used for intermediate values of T. Eqns. 4.1.8.4(6)-1 to 4.1.8.4(6)-5 are de-
scribed in Section 4.1.8.4 of the 2010 NBCC.
( ) (0.2) for 0.2 s
aa
ST FS T= ≤
(2010 NBCC Eqn. 4.1.8.4(6)-1)
( ) (0.5) or (0.2),
whichever is smaller for 0.5 s
va aa
ST FS FS
T
=
=
(2010 NBCC Eqn. 4.1.8.4(6)-2)
( ) (1.0) for 1.0 s
va
ST FS T= =
(2010 NBCC Eqn. 4.1.8.4(6)-3)
( ) (2.0) for 2.0 s
va
ST FS T= =
(2010 NBCC Eqn. 4.1.8.4(6)-4)
( ) (2.0) / 2 for 4.0 s
va
ST FS T= ≥
(2010 NBCC Eqn. 4.1.8.4(6)-5)
2010 NBCC Seismic Loads 2 - 33
Automatic Seismic Loads
The minimum lateral earthquake force, V, is determined in accordance with
(2010 NBCC Eqn. 4.1.8.11(2)-2):
() ( )
vE d o
V STMIW RR=
(2010 NBCC Eqn. 4.1.8.11(2)-1)
where,
W = Weight of the building (based on specified mass).
The total design base shear, V, shall not be less than that specified in (2010
NBCC Eqn. 4.1.8.11(2)-2). If the base shear calculated in accordance with
(2010 NBCC Eqn. 4.1.8.11(2)-1) is less than that calculated in accordance
with (2010 NBCC Eqn. 4.1.8.11(2)-2), the base shear is set equal to that cal-
culated in accordance with (2010 NBCC Eqn. 4.1.8.11(2)-2).
For walls, coupled walls and wall-frame system:
(4.0) ( )
=vE d o
V S MIW RR
(2010 NBCC Eqn. 4.1.8.11(2)-a)
For moment resisting frame, braced frame and other systems:
(2.0) ( )
vE d o
V S MIW RR=
(2010 NBCC Eqn. 4.1.8.11(2)-b)
where,
S(2.0) = Design spectral acceleration for a period of 2 s.
S(4.0) = Design spectral acceleration for a period of 4 s.
The total design base shear, V, for a structure Other than Site Class F and Rd
≥ 1.5 need not exceed that specified in (2010 NBCC Eqn. 4.1.8.11(2)-3). If
the base shear calculated in accordance with (2010 NBCC Eqn. 4.1.8.11(2)-
1) exceeds that calculated in accordance with (2010 NBCC Eqn.
24.1.8.11(2)-3), the base shear is set equal to that calculated in accordance
with (2010 NBCC Eqn. 4.1.8.11(2)-3).
2(0.2) ( )
3E do
V S IW RR=
(2010 NBCC Eqn. 4.1.8.11(2)-3)
where,
S(0.2) = Design spectral acceleration for 0.2 s.
2 - 34 2010 NBCC Seismic Loads
Chapter 2 - Automatic Seismic Loads
The total base shear, V, is broken into a concentrated force applied to the top
of the structure and forces applied at each story level in accordance with
(2010 NBCC Eqn. 4.1.8.11(6)-1).
t story
story 1
n
VF F
=
= + ∑
(2010 NBCC Eqn. 4.1.8.11(6)-1)
where,
V = Building base shear.
Ft = Concentrated force at the top of the building.
Fstory = Portion of base shear applied to a story level.
n = Number of story levels in the building.
The concentrated force at the top of the structure, Ft , is calculated as shown
in (2010 NBCC Eqn. 4.1.8.11(6)-2):
– If T ≤ 0.7 sec, then F
t
= 0
(2010 NBCC Eqn. 4.1.8.11(6)-2)
– If T > 0.7 sec, then F
t
= 0.7TV ≤ 0.25V
where,
T = Building period.
V = Building base shear.
The remaining portion of the base shear, (V − Ft ), is distributed over the
height of the structure in accordance with (2010 NBCC Eqn. 4.1.8.11(6)-3):
( )
t
n
V Fw h
F
wh
−
=
∑
story story
story
story story
story =1
(2010 NBCC Eqn. 4.1.8.11(6)-3)
where,
Fstory = Portion of base shear applied to a story level.
V = Base shear.
2010 NBCC Seismic Loads 2 - 35
Automatic Seismic Loads
Ft = Concentrated force at the top of the structure.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
n = Number of story levels in the structure.
2.10 2015 NBCC Seismic Loads
2.10.1 Options for 2015 NBCC Building Period
Four options are provided for the building period used in calculating the
2015 NBCC automatic seismic loads. They are as follows:
Code – Steel & Concrete Moment Frames, Braced Frames, Shear
Wall & Other Structures: Calculate the approximate period based on
section 4.1.8.1(7). The values used for CT and x are user input, and hn is
determined by the programs from the input story level heights.
( )
3
4
A Tn
T Ch=
(2015 NBCC Section 4.1.8.11(3))
A typical range of values for CT is 0.025 to 0.085. The height hn is meas-
ured from the elevation of the specified bottom story/minimum level to
the (top of the) specified top story/maximum level measured in meters.
Code – Moment Frames other than Steel & Concrete: Calculate the
approximate period, TA, using section 4.1.8.11(3):
0.1
A
TN
=
(2015 NBCC Section 4.1.8.11(3))
where,
N = The number of stories in the structure based on the specified
top and bottom story levels.
Code – Braced Frame: Calculate the approximate period, TA, using sec-
tion 4.1.8.11(3):
2 - 36 2015 NBCC Seismic Loads
Chapter 2 - Automatic Seismic Loads
( )
0.025=
An
Th
(2005 NBCC Section 4.1.8.11(3))
Program Calculated: The programs use the period of the mode calcu-
lated to have the largest participation factor in the direction that loads are
being calculated (X or Y). Call this period Tmode. A period is also calculat-
ed based on (NBCC Eqn. 4.1.8.11(3)), as appropriate. Call this period TA.
The building period, T, that the programs choose is determined from sec-
tion 4.1.8.11(d). The values used for Cu are user input, and typically vary
from 1.5 to 2.0 as specified in NBCC 2015 clause 4.1.8.11(3).
– If Tmode ≤ CuTA , then T = Tmode. (NBCC 2015 Section 4.1.8.11.3(d))
– If Tmode > CuTA , then T = CuTA. (NBCC 2015 Section 4.1.8.11.3(d))
User Defined: In this case the user can input a building period, which
the programs use in the calculations. The programs do not compare it
against CuTA. It is assumed that this comparison has been performed be-
fore specifying the period.
2.10.2 Other Input Factors and Coefficients
The ductility-related force modification factor, Rd , is direction dependent. It
is specified in 2015 NBCC Table 4.1.8.9. A typical range of values for Rd is
1.5 to 5.0.
The overstrength-related force modification factor, Ro , is direction depend-
ent. It is specified in 2015 NBCC Table 4.1.8.9. A typical range of values for
Ro is 1.3 to 1.7.
The 5% damped spectral response acceleration, Sa(T), shall be input for peri-
ods T of 0.2 s, 0.5 s, 1.0 s, 2.0 s, 5.0 s and 10.0 s as described in subsection
4.1.8.4 of the 2015 NBCC. The input in the programs is in g.
The higher mode factor, Mv , is direction dependent. It is specified in 2015
NBCC Table 4.1.8.11. A typical range of values for Mv is 1 to 4.65.
The site coefficients can be input in accordance with the code or they can be
user defined. If the site coefficients are in accordance with code, specify a
2015 NBCC Seismic Loads 2 - 37
Automatic Seismic Loads
site class. If site coefficients are user defined, specify F(0.2), F(0.5), F(1.0),
F(2.0), F(5.0) and F(10.0).
The site class can be A, B, C, D, or E. Note that site class F requires site spe-
cific evaluation for automatic 2015 NBCC lateral seismic loads. See 2015
NBCC Table 4.1.8.4.A for site class definitions.
F(0.2) is the acceleration-based site coefficient as described in 4.1.8.4(7). If
the site coefficients are determined in accordance with code, the software au-
tomatically determines F(0.2) from the site class and Sa(0.2) based on 2015
NBCC Table 4.1.8.4.B. If site coefficients are user defined, the value for
F(0.2) is input directly by the user. A typical range of values for F(0.2) is
0.69 to 1.64.
F(0.5) is the velocity-based site coefficient as described in 4.1.8.4(7). If the
site coefficients are determined in accordance with code, the software auto-
matically determines F(0.5) from the site class and Sa(0.5) based on 2015
NBCC Table 4.1.8.4.C. If site coefficients are user defined, the value for
F(0.5) is input directly by the user. A typical range of values for F(0.5) is
0.57 to 2.47.
F(1.0) is the velocity-based site coefficient as described in 4.1.8.4(7). If the
site coefficients are determined in accordance with code, the software auto-
matically determines F(1.0) from the site class and Sa(1.0) based on 2015
NBCC Table 4.1.8.4.D. If site coefficients are user defined, the value for
F(1.0) is input directly by the user. A typical range of values for F(1.0) is
0.57 to 2.81.
F(2.0) is the velocity-based site coefficient as described in 4.1.8.4(7). If the
site coefficients are determined in accordance with code, the software auto-
matically determines F(2.0) from the site class and Sa(2.0) based on 2015
NBCC Table 4.1.8.4.E. If site coefficients are user defined, the value for
F(2.0) is input directly by the user. A typical range of values for F(2.0) is
0.58 to 2.90.
F(5.0) is the velocity-based site coefficient as described in 4.1.8.4(7). If the
site coefficients are determined in accordance with code, the software auto-
matically determines F(5.0) from the site class and Sa(5.0) based on 2015
NBCC Table 4.1.8.4.F. If site coefficients are user defined, the value for
2 - 38 2015 NBCC Seismic Loads
Chapter 2 - Automatic Seismic Loads
F(5.0) is input directly by the user. A typical range of values for F(5.0) is
0.61 to 2.93.
F(10.0) is the velocity-based site coefficient as described in 4.1.8.4(7). If the
site coefficients are determined in accordance with code, the software auto-
matically determines F(10.0) from the site class and Sa(10.0) based on 2015
NBCC Table 4.1.8.4.G. If site coefficients are user defined, the value for
F(10.0) is input directly by the user. A typical range of values for F(10.0) is
0.67 to 2.52.
The importance factor, IE, can be input as any value. It is specified in 2015
NBCC Sentence 4.1.8.5. A typical range of values for IE is 0.8 to 1.5.
2.10.3 Algorithm for 2015 NBCC Seismic Loads
The algorithm for determining 2015 NBCC seismic loads is based on Sub-
section 4.1.8.11 of the 2015 NBCC. The period T is calculated as described
in a preceding section entitled "Options for 2015 NBCC Building Period."
The programs begin by calculating the design spectral acceleration S(T) us-
ing (2015 NBCC Eqns. 4.1.8.4(9)-1 to 4.1.8.4(9)-6). Linear interpolation is
used for intermediate values of T. Eqns. 4.1.8.4(9)-1 to 4.1.8.4(9)-6 are de-
scribed in Section 4.1.8.4 of the 2015 NBCC.
( ) (0.2) (0.2) or (0.5) (0.5),
whichever is larger for 0.2 s
aa
ST F S F S
T
=
≤
(2015 NBCC Eqn. 4.1.8.4(9)-1)
( ) (0.5) (0.5) for 0.5 s
a
ST F S T= =
(2015 NBCC Eqn. 4.1.8.4(9)-2)
( ) (1.0) (1.0) for 1.0 s
a
ST F S T= =
(2015 NBCC Eqn. 4.1.8.4(9)-3)
( ) (2.0) (2.0) for 2.0 s
a
ST F S T= =
(2015 NBCC Eqn. 4.1.8.4(9)-4)
( ) (5.0) (5.0) for 5.0 s
a
ST F S T= =
(2015 NBCC Eqn. 4.1.8.4(9)-5)
( ) (10.0) (10.0) for 10.0 s
a
ST F S T= =
(2015 NBCC Eqn. 4.1.8.4(9)-6)
The minimum lateral earthquake force, V, is determined in accordance with
(2015 NBCC Eqn. 4.1.8.11(2)-2):
2015 NBCC Seismic Loads 2 - 39
Automatic Seismic Loads
() ( )
vE d o
V STMIW RR=
(2015 NBCC Eqn. 4.1.8.11(2)-1)
where,
W = Weight of the building (based on specified mass).
The total design base shear, V, shall not be less than that specified in (2015
NBCC Eqn. 4.1.8.11(2)-2). If the base shear calculated in accordance with
(2015 NBCC Eqn. 4.1.8.11(2)-1) is less than that calculated in accordance
with (2015 NBCC Eqn. 4.1.8.11(2)-2), the base shear is set equal to that cal-
culated in accordance with (2015 NBCC Eqn. 4.1.8.11(2)-2).
For walls, coupled walls and wall-frame system:
(4.0) ( )=vE d o
V S MIW RR
(2015 NBCC Eqn. 4.1.8.11(2)-a)
For moment resisting frame, braced frame and other systems:
(2.0) ( )
vE d o
V S MIW RR=
(2015 NBCC Eqn. 4.1.8.11(2)-b)
where,
S(2.0) = Design spectral acceleration for a period of 2 s.
S(4.0) = Design spectral acceleration for a period of 4 s.
The total design base shear, V, for a structure Other than Site Class F and Rd
≥ 1.5 need not exceed that specified in (2015 NBCC Eqn. 4.1.8.11(2)-3). If
the base shear calculated in accordance with (2015 NBCC Eqn. 4.1.8.11(2)-
1) exceeds that calculated in accordance with (2015 NBCC Eqn.
24.1.8.11(2)-3), the base shear is set equal to that calculated in accordance
with (2015 NBCC Eqn. 4.1.8.11(2)-3).
2(0.2) ( )
largerof 3(0.5) ( )
E do
E do
S IW RR
V
S IW RR
=
(2015 NBCC Eqn. 4.1.8.11(2)-3)
where,
S(0.2) = Design spectral acceleration for 0.2 s.
S(0.5) = Design spectral acceleration for 0.5 s.
2 - 40 2015 NBCC Seismic Loads
Chapter 2 - Automatic Seismic Loads
The total base shear, V, is broken into a concentrated force applied to the top
of the structure and forces applied at each story level in accordance with
(2015 NBCC Eqn. 4.1.8.11(7)-1).
t story
story 1
n
VF F
=
= + ∑
(2015 NBCC Eqn. 4.1.8.11(7)-1)
where,
V = Building base shear.
Ft = Concentrated force at the top of the building.
Fstory = Portion of base shear applied to a story level.
n = Number of story levels in the building.
The concentrated force at the top of the structure, Ft , is calculated as shown
in (2015 NBCC Eqn. 4.1.8.11(7)-2):
– If T ≤ 0.7 sec, then F
t
= 0
(2015 NBCC Eqn. 4.1.8.11(7)-2)
– If T > 0.7 sec, then F
t
= 0.7TV ≤ 0.25V
where,
T = Building period.
V = Building base shear.
The remaining portion of the base shear, (V − Ft ), is distributed over the
height of the structure in accordance with (2015 NBCC Eqn. 4.1.8.11(7)-3):
( )
t
n
V Fw h
F
wh
−
=
∑
story story
story
story story
story =1
(2015 NBCC Eqn. 4.1.8.11(7)-3)
where,
Fstory = Portion of base shear applied to a story level.
V = Base shear.
2015 NBCC Seismic Loads 2 - 41
Automatic Seismic Loads
Ft = Concentrated force at the top of the structure.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
n = Number of story levels in the structure.
2.11 2003 IBC/ASCE 7-02 Seismic Loads
2.11.1 Options for 2003 IBC/ASCE 7-02 Building Period
Three options are provided for the building period used in calculating the
2003 IBC automatic seismic loads. They are as follows:
Approximate Period: Calculate the period based on (ASCE 7-02, Eqn.
9.5.5.3.2-1). The value used for CT is user input and hn is determined by
the programs from the input story level heights.
( )
x
A Tn
T Ch=
(ASCE 7-02, Eqn. 9.5.5.3.2-1)
Note that the item CT is always input in English units as specified in the
code. A typical range of values for CT is 0.020 to 0.030. The height hn is
measured from the elevation of the specified bottom story/minimum lev-
el to the (top of the) specified top story/maximum level. x is determined
using table 9.5.5.3.2 of ASCE 7-02.
Program Calculated: The programs start with the period of the mode
calculated to have the largest participation factor in the direction that
loads are being calculated (X or Y). Call this period Tmode. A period is al-
so calculated based on (ASCE Eqn. 9.5.5.3.2-1). The value used for CT is
user input, and hn is determined from the input story level heights. Call
this period TA.
The programs also calculate a coefficient for the upper limit on the calcu-
lated period, Cu. The building period, T, that the programs choose is de-
termined as follows:
– If Tmode ≤ CuTA , then T = Tmode.
2 - 42 2003 IBC/ASCE 7-02 Seismic Loads
Chapter 2 - Automatic Seismic Loads
– If Tmode > CuTA, then T = CuTA.
User Defined: In this case, input a building period, which the programs
use in the calculations. They do not compare it against CuTA. It is as-
sumed that this comparison is performed before the period is specified.
2.11.2 Other Input Factors and Coefficients
The response modification factor, R, and the system overstrength factor, Ω,
are direction dependent. Both are specified in 2003 IBC Table 1617.6.2. A
typical range of values for R is 2 to 8. A typical range of values for Ω is 2 to
3.
The seismic group can be input as I, II or III. No other values are allowed.
See 2003 IBC Section 1616.2 for information about the seismic group. The
programs determine the occupancy importance factor, I, from the input seis-
mic group and 2003 IBC Table 1604.5.
The seismic coefficients can be input in accordance with the code or they can
be user defined. If the seismic coefficients are in accordance with code, spec-
ify a site class, Ss and S1. If seismic coefficients are user defined, specify Ss,
S1, Fa and Fv.
The site class can be A, B, C, D, or E. Note that site class F is not allowed for
automatic 2003 IBC lateral seismic loads. See 2003 IBC Table 1615.1.1 for
site class definitions.
Ss is the mapped spectral acceleration for short periods as determined in 2003
IBC Section 1615.1. A typical range of values for Ss is 0 to 3. Note that the
seismic maps show Ss in % g with a typical range of 0% to 300%. The input
in the programs is in g. Thus the map values should be divided by 100 when
they are input. For example, if the map value is 125%g, it should be input as
1.25g.
S1 is the mapped spectral acceleration for a one second period as determined
in 2003 IBC Section 1615.1. A typical range of values for S1 is 0 to 2. Note
that the seismic maps show S1 in % g with a typical range of 0% to 200%.
The input in the programs is in g. Thus the map values should be divided by
100 when they are input. For example, if the map value is 125%g it should be
input as 1.25g.
2003 IBC/ASCE 7-02 Seismic Loads 2 - 43
Automatic Seismic Loads
Fa is a site coefficient. If the site coefficients are determined in accordance
with code, the software automatically determines Fa from the site class and Ss
based on 2003 IBC Table 1615.1.2(1). If site coefficients are user defined, Fa
is input directly by the user. A typical range of values for Fa is 0.8 to 2.5.
Fv is a site coefficient. If the site coefficients are determined in accordance
with code, the software automatically determines Fv from the site class and S1
based on 2003 IBC Table 1615.1.2(2). If site coefficients are user defined, Fv
is input directly by the user. A typical range of values for Fv is 0.8 to 3.5.
2.11.3 Algorithm for 2003 IBC/ASCE 7-02 Seismic Loads
The algorithm for determining 2003 IBC seismic loads is based on 2003 IBC
Section 1617.4. A period is calculated as described in a preceding section en-
titled "Options for 2003 IBC Building Period."
The programs begin by calculating the design spectral response acceleration
at short periods, SDS , using IBC Eqns. 16-38 and 16-40.
2
3
DS a s
S FS
=
(IBC Eqns. 16-38 and 16-40)
Next, the design spectral response acceleration is calculated at a one second
period, SD1, using IBC Eqns. 16-39 and 16-41.
11
2
3
Dv
S FS=
(IBC Eqns. 16-39 and 16-41)
The programs determine a seismic design category (A, B, C, D, E, or F with
A being the least severe and F being the most severe) based on 2003 IBC
Section 1616.3. A seismic design category is determined based on SDS using
2003 IBC Table 1616.3(1). A seismic design category also is determined
based on SD1 using 2003 IBC Table 1616.3(2). The more severe of the two
seismic categories is chosen as the seismic design category for the building.
Initially a seismic response coefficient, Cs, is calculated using (ASCE 7-02
Eqn. 9.5.5.2.1-1). This base shear value is then checked against the limits
specified in (ASCE Eqns. 9.5.5.2.1-2, 9.5.5.2.1-3, and 9.5.5.2.1-4) and modi-
fied as necessary to obtain the final base shear.
2 - 44 2003 IBC/ASCE 7-02 Seismic Loads
Chapter 2 - Automatic Seismic Loads
DS
s
S
CR
I
=
(ASCE 7-02 Eqn. 9.5.5.2.1-1)
where,
SDS = The design spectral response acceleration at short periods.
R = Response modification factor specified in 2003 IBC Table
1617.6.2.
I = The occupancy importance factor determined in accordance with
2003 IBC Table 1604.5.
The seismic response coefficient, Cs , need not exceed that specified in
(ASCE 7-02 Eqn. 9.5.5.2.1-2). If the seismic response coefficient calculated
in accordance with (ASCE Eqn. 9.5.5.2.1.1-1) exceeds that calculated in ac-
cordance with (ASCE 7-02 Eqn. 9.5.5.2.1-2), the programs set the seismic
response coefficient, Cs, equal to that calculated in accordance with (ASCE
7-02 Eqn. 9.5.5.2.1-2).
D1
s
S
CRT
I
=


(ASCE 7-02 Eqn. 9.5.5.2.1-2)
where,
SD1 = the design spectral response acceleration at a one second period
T = the building period used for calculating the base shear
and all other terms are as described for (ASCE 7-02 Eqn. 9.5.5.2.1-1)
The seismic response coefficient, Cs , cannot be less than that specified in
(ASCE 7-02 Eqn. 9.5.5.2.1-3). If the seismic response coefficient calculated
in accordance with (ASCE 7-02 Eqn. 9.5.5.2.1-3) exceeds that calculated in
accordance with (ASCE 7-02 Eqn. 9.5.5.2.1-1), the programs set the seismic
response coefficient equal to that calculated in accordance with (ASCE 7-02
Eqn. 9.5.5.2.1-3).
Cs = 0.044 SDS I (ASCE 7-02 Eqn. 9.5.5.2.1-3)
2003 IBC/ASCE 7-02 Seismic Loads 2 - 45
Automatic Seismic Loads
where all terms are as previously described for (ASCE 7-02 Eqn. 9.5.5.2.1-1)
Finally, if the building is in seismic design category E or F, the seismic re-
sponse coefficient, Cs, shall not be less than that specified in (ASCE 7-02
Eqn. 9.5.5.2.1-4). If the building is in seismic design category E or F and the
seismic response coefficient calculated in accordance with (ASCE 7-02 Eqn.
9.5.5.2.1-4) exceeds that calculated in accordance with (ASCE 7-02 Eqn.
9.5.5.2.1-1) and (ASCE Eqn. 7-02 9.5.5.2.1-3), the programs set the seismic
response coefficient equal to that calculated in accordance with (ASCE 7-02
Eqn. 9.5.5.2.1-4).
1
0.5
s
S
CR
I
=
(ASCE 7-02 Eqn. 9.5.5.2.1-4)
where,
S1 = the mapped spectral acceleration for a one second period
and all other terms are as previously described for (ASCE 7-02 Eqn.
9.5.5.2.1-1) .
The base shear, V, is calculated using (ASCE 7-02 Eqn. 9.5.5.2.-1)
V = Cs W (ASCE 7-02 Eqn. 9.5.5.2.-1)
Cs = Seismic response coefficient as determined from one of (ASCE 7-
02 Eqns. 9.5.5.2.1-1 through 9.5.5.2.1-4) as appropriate.
W = Weight of the building (based on specified mass).
The base shear, V, is distributed over the height of the building in accordance
with (ASCE 7-02 Eqns. 9.5.5.4-1 and 9.5.5.4-2).
story story
story
story story
story 1
k
nk
Vw h
F
wh
=
=∑
(Eqns. 9.5.5.4.-1 and 9.5.5.4-2)
where,
Fstory = Portion of base shear applied to a story level.
2 - 46 2003 IBC/ASCE 7-02 Seismic Loads
Chapter 2 - Automatic Seismic Loads
V = Building base shear.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
k = Exponent applied to building height. The value of k depends on
the value of the building period, T, used for determining the
base shear. If T ≤ 0.5 seconds, then k = 1. If T ≥ 2.5 seconds,
then k = 2. If 0.5 seconds < T < 2.5 seconds, then k is linearly
interpolated between 1 and 2.
n = Number of story levels in the structure.
2.12 2006 IBC/ASCE 7-05 Seismic Loads
Section 1613 of the 2006 IBC states that earthquake loads shall be deter-
mined in accordance with ASCE Standard 7-05. For the sake of clarity, in the
remainder of this section all references will be made only to the ASCE 7- 05
document, with the understanding that this information is directly applicable
to those using the 2006 IBC as well.
2.12.1 Options for 2006 IBC/ASCE 7-05 Building Period
Three options are provided for the building period used in calculating the
2006 IBC automatic seismic loads. They are as follows:
Approximate Period: Calculate the period based on (ASCE 7-05 Eqn.
12.8-7) The values used for CT and x are user input and hn is determined
by the programs from the input story level heights.
( )
x
A Tn
T Ch=
(ASCE 7-05 Eqn. 12.8-7)
Note that CT is always input in English units, as specified in the code. A
typical range of values for CT is 0.016 to 0.03, while x varies from 0.75
to 0.9. The height hn is measured from the elevation of the specified bot-
tom story/minimum level to the (top of the) specified top story/maximum
level.
2006 IBC/ASCE 7-05 Seismic Loads 2 - 47
Automatic Seismic Loads
Program Calculated: The programs start with the period of the mode
calculated to have the largest participation factor in the direction that
loads are being calculated (X or Y). Call this period Tmode. A period is al-
so calculated based on (ASCE 7-05 Eqn. 12.8-7). The values used for CT
and x are user input, and hn is determined from the input story level
heights. Call this period TA.
The programs also calculate a coefficient for the upper limit on the calcu-
lated period, Cu. The building period, T, that the programs choose is de-
termined as follows:
– If Tmode ≤ CuTA, then T = Tmode.
– If Tmode > CuTA, then T = CuTA.
User Defined: In this case, input a building period, which the programs
use in the calculations. They do not compare it against CuTA. It is as-
sumed that this comparison is performed before the period is specified.
2.12.2 Other Input Factors and Coefficients
The response modification factor, R, and the system overstrength factor, Ω,
are direction dependent. Both are specified in ASCE 7-05 Table 12.2-1. A
typical range of values for R is 2 to 8. A typical range of values for Ω is 2 to
3.
The occupancy category can be input as I, II, III or IV. No other values are
allowed. See ASCE 7-05 Section 11.5 for information about the occupancy
category. The programs determine the occupancy importance factor, I, from
the input occupancy category and ASCE 7-05 Table 11.5-1.
The seismic coefficients can be input in accordance with the code or they can
be user defined. If the seismic coefficients are in accordance with code, spec-
ify a site class, Ss and S1, as well as a long-period transition period, TL. If
seismic coefficients are user defined, specify Ss, S1, TL, Fa and Fv.
The site class can be A, B, C, D, or E. Note that site class F is not allowed for
automatic ASCE 7-05 lateral seismic loads. See ASCE 7-05 Table 20.3-1 for
site class definitions.
2 - 48 2006 IBC/ASCE 7-05 Seismic Loads
Chapter 2 - Automatic Seismic Loads
Ss is the mapped maximum considered earthquake (MCE) spectral accelera-
tion for short periods as determined in ASCE 7-05 Section 11.4.1. A typical
range of values for Ss is 0 to 3. Note that the seismic maps show Ss in % g
with a typical range of 0% to 300%. The input in the programs is in g. Thus
the map values should be divided by 100 when they are input. For example,
if the map value is 125%g it should be input as 1.25g.
S1 is the mapped MCE spectral acceleration for a one second period as de-
termined in ASCE 7-05 Section 11.4.1. A typical range of values for S1 is 0
to 1. Note that the seismic maps show S1 in %g with a typical range of 0% to
100%. The input in the programs is in g. Thus the map values should be di-
vided by 100 when they are input. For example, if the map value is 100%g it
should be input as 1.0g.
Fa is a site coefficient. If the site coefficients are determined in accordance
with code, the software automatically determines Fa from the site class and Ss
based on ASCE 7-05 Table 11.4-1. If site coefficients are user defined, the Fa
is input directly by the user. A typical range of values for Fa is 0.8 to 2.5.
Fv is a site coefficient. If the site coefficients are determined in accordance
with code, the software automatically determines Fv from the site class and S1
based on ASCE 7-05 Table 11.4-2. If site coefficients are user defined, Fv is
input directly by the user. A typical range of values for Fv is 0.8 to 3.5.
TL is the long-period transition period as determined in ASCE 7-05 Section
11.4.5.
2.12.3 Algorithm for ASCE 7-05 Seismic Loads
The algorithm for determining ASCE 7-05 seismic loads is based on ASCE
7-05 Section 12.8. A period is calculated as described in a preceding section
entitled "Options for ASCE 7-05 Building Period."
The programs begin by calculating the design spectral response acceleration
at short period, SDS, using (ASCE 7-05 Eqs. 11.4-1 and 11.4-3).
2
3
DS a s
S FS=
(ASCE 7-05 Eqns. 11.4-1 and 11.4-3)
2006 IBC/ASCE 7-05 Seismic Loads 2 - 49
Automatic Seismic Loads
Next, the design spectral response acceleration is calculated at a one second
period, SD1, using (ASCE 7-05 Eqns. 11.4-2 and 11.4-3).
11
2
3
Dv
S FS=
(ASCE 7-05 Eqns. 11.4-2 and 11.4-3)
The programs determine a seismic design category (A, B, C, D, E, or F with
A being the least severe and F being the most severe) based on ASCE 7-05
Section 11.6. A seismic design category is determined based on SDS using
ASCE 7-05 Table 11.6-1. A seismic design category also is determined based
on SD1 using ASCE 7-05 Table 11.6-2. The more severe of the two seismic
categories is chosen as the seismic design category for the building.
Initially a seismic response coefficient, Cs, is calculated using (ASCE 7-05
Eqn. 12.8-2). This base shear value is then checked against the limits speci-
fied in (ASCE 7-05 Eqns. 12.8-3, 12.8-4, 2.8-5, and 12.8-6) and modified as
necessary to obtain the final base shear.
DS
s
S
CR
I
=
(ASCE 7-05 Eqn. 12.8-2)
where,
SDS = The design spectral response acceleration at short periods.
R = Response modification factor specified in ASCE 7-05 Table 12.2-
1.
I = The occupancy importance factor determined in accordance with
ASCE 7-05 Table 11.5-1.
The seismic response coefficient, Cs , need not exceed that specified in
(ASCE 7-05 Eqns. 12.8-3 ). If the seismic response coefficient calculated in
accordance with (ASCE 7-05 Eqns. 12.8-2) exceeds that calculated in ac-
cordance with (ASCE 7-05 Eqns. 12.8-3 and 12.8-4), the programs set the
seismic response coefficient, Cs, equal to that calculated in accordance with
(ASCE 7-05 Eqns. 12.8-3 and 12.8-4), as appropriate.
2 - 50 2006 IBC/ASCE 7-05 Seismic Loads
Chapter 2 - Automatic Seismic Loads
1
D
s
S
CRT
I
=


for T ≤ TL (ASCE 7-05 Eqn. 12.8-3)
1
2
DL
s
ST
CRT
I
=


for T > TL (ASCE 7-05 Eqn. 12.8-4)
where,
SD1 = the design spectral response acceleration at a one second period
T = the building period used for calculating the base shear
TL = the long-period transition period
and all other terms are as described for (ASCE 7-05 Eqn. 12.8-2).
Cs shall not be less than that shown in (ASCE 7-05 Eqn. 12.8-5).
Cs = 0.044SDSI ≥ 0.01 (ASCE 7-05 Eqn. 12.8-5)
Finally, for structures located where S1 is equal to or greater than 0.6g, Cs
shall not be less than that shown in (ASCE 7-05 Eqn. 12.8-6).
1
0.5
s
S
CR
I
=


(ASCE 7-05 Eqn. 12.8-6)
where,
S1 = the mapped MCE spectral acceleration for a one second period
and all other terms are as described for (ASCE 7-05 Eqn. 12.8-2).
The base shear, V, is calculated using (ASCE 7-05 Eqn. 12.8-1):
V = Cs W (ASCE 7-05 Eqn. 12.8-1)
Cs = Seismic response coefficient as determined from one of (ASCE 7-
05 Eqns. 12.8-2 through 12.8-6) as appropriate.
2006 IBC/ASCE 7-05 Seismic Loads 2 - 51
Automatic Seismic Loads
W = Weight of the building (based on specified mass).
The base shear, V, is distributed over the height of the building in accordance
with (ASCE 7-05 Eqns. 12.8-11 and 12.8-12)
story story
story
story story
story =1
k
nk
Vw h
F
wh
=∑
(ASCE 7-05 Eqns. 12.8-11 and 12.8-12)
where,
Fstory = Portion of base shear applied to a story level.
V = Building base shear.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
k = Exponent applied to building height. The value of k depends
on the value of the building period, T, used to determine the
base shear. If T ≤ 0.5 second, k = 1. If T ≥ 2.5 seconds, k = 2.
If 0.5 second < T < 2.5 seconds, k is linearly interpolated be-
tween 1 and 2.
n = Number of story levels in the structure.
2.13 2009 IBC/ASCE 7-05 Seismic Loads
Section 1613 of the 2009 IBC states that earthquake loads shall be deter-
mined in accordance with ASCE Standard 7-05. For the sake of clarity, in the
remainder of this section all references will be made only to the ASCE 7- 05
document, with the understanding that this information is directly applicable
to those using the 2009 IBC as well.
2.13.1 Options for 2009 IBC/ASCE 7-05 Building Period
Three options are provided for the building period used in calculating the
2009 IBC automatic seismic loads. They are as follows:
2 - 52 2009 IBC/ASCE 7-05 Seismic Loads
Chapter 2 - Automatic Seismic Loads
Approximate Period: Calculate the period based on (ASCE 7-05 Eqn.
12.8-7). The values used for Ct and x are user input, and hn is determined
by the programs from the input story level heights.
()
x
A tn
T Ch=
(ASCE 7-05 Eqn. 12.8-7)
Note that Ct is always input in English units, as specified in the code. A
typical range of values for Ct is 0.016 to 0.03, while x varies from 0.75 to
0.9. The height hn is measured from the elevation of the specified bottom
story/minimum level to the (top of the) specified top story/maximum
level.
Program Calculated: The programs start with the period of the mode
calculated to have the largest participation factor in the direction that
loads are being calculated (X or Y). Call this period Tmode. A period is al-
so calculated based on (ASCE 7-05 Eqn. 12.8-7). The values used for Ct
and x are user input, and hn is determined from the input story level
heights. Call this period TA.
The programs also calculate a coefficient for the upper limit on the calcu-
lated period, Cu. The building period, T, that the programs choose is de-
termined as follows:
– If Tmode ≤ CuTA, then T = Tmode.
– If Tmode > CuTA, then T = CuTA.
User Defined: In this case, input a building period, which the programs
use in the calculations. They do not compare it against CuTA. It is as-
sumed that this comparison is performed before the period is specified.
2.13.2 Other Input Factors and Coefficients
The response modification factor, R, and the system overstrength factor, Ωο,
are direction dependent. Both are specified in ASCE 7-05 Table 12.2-1. A
typical range of values for R is 2 to 8. A typical range of values for Ω ο is 2 to
3.
The occupancy category can be input as I, II, III or IV. No other values are
allowed. See ASCE 7-05 Section 11.5 for information about the occupancy
2009 IBC/ASCE 7-05 Seismic Loads 2 - 53
Automatic Seismic Loads
category. The programs determine the occupancy importance factor, I, from
the input occupancy category and ASCE 7-05 Table 11.5-1.
The seismic coefficients can be input in accordance with the code or they can
be user defined. If the seismic coefficients are in accordance with code, spec-
ify a site class, Ss and S1, as well as a long-period transition period, TL. If
seismic coefficients are user defined, specify Ss, S1, TL, Fa and Fv.
The site class can be A, B, C, D, or E. Note that site class F is not allowed for
automatic ASCE 7-05 lateral seismic loads. See ASCE 7-05 Table 20.3-1 for
site class definitions.
Ss is the mapped maximum considered earthquake (MCE) spectral accelera-
tion for short periods as determined in ASCE 7-05 Section 11.4.1. A typical
range of values for Ss is 0 to 3. Note that the seismic maps show Ss in % g
with a typical range of 0% to 300%. The input in the programs is in g. Thus
the map values should be divided by 100 when they are input. For example,
if the map value is 125%g it should be input as 1.25g.
S1 is the mapped MCE spectral acceleration for a one second period as de-
termined in ASCE 7-05 Section 11.4.1. A typical range of values for S1 is 0
to 1. Note that the seismic maps show S1 in %g with a typical range of 0% to
100%. The input in the programs is in g. Thus the map values should be di-
vided by 100 when they are input. For example, if the map value is 100%g, it
should be input as 1.0g.
Fa is a site coefficient. If the site coefficients are determined in accordance
with code, the software automatically determines Fa from the site class and Ss
based on ASCE 7-05 Table 11.4-1. If site coefficients are user defined, the Fa
is input directly by the user. A typical range of values for Fa is 0.8 to 2.5.
Fv is a site coefficient. If the site coefficients are determined in accordance
with code, the software automatically determines Fv from the site class and S1
based on ASCE 7-05 Table 11.4-2. If site coefficients are user defined, Fv is
input directly by the user. A typical range of values for Fv is 0.8 to 3.5.
TL is the long-period transition period as determined in ASCE 7-05 Section
11.4.5.
2 - 54 2009 IBC/ASCE 7-05 Seismic Loads
Chapter 2 - Automatic Seismic Loads
2.13.3 Algorithm for 2009 IBC/ASCE 7-05 Seismic Loads
The algorithm for determining ASCE 7-05 seismic loads is based on ASCE
7-05 Section 12.8. A period is calculated as described in a preceding section
entitled "Options for ASCE 7-05 Building Period."
The programs begin by calculating the design spectral response acceleration
at short period, SDS, using (ASCE 7-05 Eqs. 11.4-1 and 11.4-3).
2
3
DS a s
S FS=
(ASCE 7-05 Eqns. 11.4-1 and 11.4-3)
Next, the design spectral response acceleration is calculated at a one second
period, SD1, using (ASCE 7-05 Eqns. 11.4-2 and 11.4-3).
11
2
3
Dv
S FS
=
(ASCE 7-05 Eqns. 11.4-2 and 11.4-3)
The programs determine a seismic design category (A, B, C, D, E, or F with
A being the least severe and F being the most severe) based on ASCE 7-05
Section 11.6. A seismic design category is determined based on SDS using
ASCE 7-05 Table 11.6-1. A seismic design category also is determined based
on SD1 using ASCE 7-05 Table 11.6-2. The more severe of the two seismic
categories is chosen as the seismic design category for the building.
Initially a seismic response coefficient, Cs, is calculated using (ASCE 7-05
Eqn. 12.8-2). This base shear value is then checked against the limits speci-
fied in (ASCE 7-05 Eqns. 12.8-3, 12.8-4, 2.8-5, and 12.8-6) and modified as
necessary to obtain the final base shear.
DS
s
e
S
CR
I
=
(ASCE 7-05 Eqn. 12.8-2)
where,
SDS = The design spectral response acceleration at short periods.
R = Response modification factor specified in ASCE 7-05 Table 12.2-
1.
2009 IBC/ASCE 7-05 Seismic Loads 2 - 55
Automatic Seismic Loads
Ie = The occupancy importance factor determined in accordance with
ASCE 7-05 Table 11.5-1.
The seismic response coefficient, Cs, need not exceed that specified in
(ASCE 7-05 Eqns. 12.8-3 and 12.8-4). If the seismic response coefficient
calculated in accordance with (ASCE 7-05 Eqns. 12.8-2) exceeds that calcu-
lated in accordance with (ASCE 7-05 Eqns. 12.8-3 and 12.8-4), the programs
set the seismic response coefficient, Cs, equal to that calculated in accordance
with (ASCE 7-05 Eqns. 12.8-3 and 12.8-4), as appropriate.
1D
s
e
S
CRT
I
=


for T ≤ TL (ASCE 7-05 Eqn. 12.8-3)
1
2
DL
s
e
ST
CRT
I
=


for T > TL (ASCE 7-05 Eqn. 12.8-4)
where,
SD1 = the design spectral response acceleration at a one second period
T = the building period used for calculating the base shear
TL = the long-period transition period
and all other terms are as described for (ASCE 7-05 Eqn. 12.8-2).
Cs shall not be less than that shown in (ASCE 7-05 Eqn. 12.8-5).
Cs = 0.044SDSIe ≥ 0.01 (ASCE 7-05 Eqn. 12.8-5)
Finally, for structures located where S1 is equal to or greater than 0.6g, Cs
shall not be less than that shown in (ASCE 7-05 Eqn. 12.8-6).
1
0.5
s
e
S
CR
I
=


(ASCE 7-05 Eqn. 12.8-6)
where,
2 - 56 2009 IBC/ASCE 7-05 Seismic Loads
Chapter 2 - Automatic Seismic Loads
S1 = the mapped MCE spectral acceleration for a one second period
and all other terms are as described for (ASCE 7-05 Eqn. 12.8-2).
The base shear, V, is calculated using (ASCE 7-05 Eqn. 12.8-1):
V = CsW (ASCE 7-05 Eqn. 12.8-1)
Cs = Seismic response coefficient as determined from one of (ASCE 7-
05 Eqns. 12.8-2 through 12.8-6) as appropriate.
W = Weight of the building (based on specified mass).
The base shear, V, is distributed over the height of the building in accordance
with (ASCE 7-05 Eqns. 12.8-11 and 12.8-12)
story story
story
story story
story =1
k
nk
Vw h
F
wh
=∑
(ASCE 7-05 Eqns. 12.8-11 and 12.8-12)
where,
Fstory = Portion of base shear applied to a story level.
V = Building base shear.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
k = Exponent applied to building height. The value of k depends on
the value of the building period, T, used for determining the base
shear. If T ≤ 0.5 seconds, k = 1. If T ≥ 2.5 seconds, k = 2. If 0.5
seconds < T < 2.5 seconds, k is linearly interpolated between 1
and 2.
n = Number of story levels in the structure.
2009 IBC/ASCE 7-05 Seismic Loads 2 - 57
Automatic Seismic Loads
2.14 2012 IBC/ASCE 7-10 Seismic Loads
Section 1613 of the 2012 IBC states that earthquake loads shall be deter-
mined in accordance with ASCE Standard 7-10. For the sake of clarity, in the
remainder of this section all references will be made only to the ASCE 7-10
document, with the understanding that this information is directly applicable
to those using the 2012 IBC as well.
2.14.1 Options for 2012 IBC/ASCE 7-10 Building Period
Three options are provided for the building period used in calculating the
ASCE 7-10 automatic seismic loads. They are as follows:
Approximate Period: Calculate the period based on (ASCE 7-10 Eqn.
12.8-7). The values used for Ct and x are user input, and hn is determined
by the programs from the input story level heights.
( )
x
A tn
T Ch=
(ASCE 7-10 Eqn. 12.8-7)
Note that Ct is always input in English units, as specified in the code. A
typical range of values for Ct is 0.016 to 0.03, while x varies from 0.75 to
0.9. The height hn is measured from the elevation of the specified bottom
story/minimum level to the (top of the) specified top story/maximum
level.
Program Calculated: The programs start with the period of the mode
calculated to have the largest participation factor in the direction that
loads are being calculated (X or Y). Call this period Tmode. A period is
also calculated based on (ASCE 7-10 Eqn. 12.8-7). The values used for
Ct and x are user input, and hn is determined from the input story level
heights. Call this period TA.
The programs also calculate a coefficient for the upper limit on the calcu-
lated period, Cu. The building period, T, that the programs choose is de-
termined as follows:
– If Tmode ≤ CuTA, then T = Tmode.
– If Tmode > CuTA, then T = CuTA.
2 - 58 2012 IBC/ASCE 7-10 Seismic Loads
Chapter 2 - Automatic Seismic Loads
User Defined: In this case, input a building period, which the programs
use in the calculations. They do not compare it against CuTA. It is as-
sumed that this comparison is performed before the period is specified.
2.14.2 Other Input Factors and Coefficients
The response modification factor, R, and the system overstrength factor, Ωο,
are direction dependent. Both are specified in ASCE 7-10 Table 12.2-1. A
typical range of values for R is 2 to 8. A typical range of values for Ω ο is 2 to
3.
The occupancy category can be input as I, II, III or IV. No other values are
allowed. See ASCE 7-10 Section 11.5 for information about the occupancy
category. The programs determine the occupancy importance factor, I, from
the input occupancy category and ASCE 7-10 Table 1.5-1 and 1.5-2.
The seismic coefficients can be input in accordance with the code or they can
be user defined. If the seismic coefficients are in accordance with code, spec-
ify a site class, Ss and S1, as well as a long-period transition period, TL. If
seismic coefficients are user defined, specify Ss, S1, TL, Fa and Fv.
The site class can be A, B, C, D, or E. Note that site class F is not allowed for
automatic ASCE 7-10 lateral seismic loads. See ASCE 7-10 Table 20.3-1 for
site class definitions.
Ss is the mapped Risk-Targeted Maximum Considered Earthquake (MCER)
spectral acceleration for short periods as determined in ASCE 7-10 Section
11.4.1. A typical range of values for Ss is 0 to 3. Note that the seismic maps
show Ss in % g with a typical range of 0% to 300%. The input in the pro-
grams is in g. Thus the map values should be divided by 100 when they are
input. For example, if the map value is 125%g it should be input as 1.25g.
S1 is the mapped MCE spectral acceleration for a one second period as de-
termined in ASCE 7-10 Section 11.4.1. A typical range of values for S1 is 0
to 1. Note that the seismic maps show S1 in %g with a typical range of 0% to
100%. The input in the programs is in g. Thus the map values should be di-
vided by 100 when they are input. For example, if the map value is 100%g, it
should be input as 1.0g.
2012 IBC/ASCE 7-10 Seismic Loads 2 - 59
Automatic Seismic Loads
Fa is a site coefficient. If the site coefficients are determined in accordance
with code, the software automatically determines Fa from the site class and Ss
based on ASCE 7-10 Table 11.4-1. If site coefficients are user defined, the Fa
is input directly by the user. A typical range of values for Fa is 0.8 to 2.5.
Fv is a site coefficient. If the site coefficients are determined in accordance
with code, the software automatically determines Fv from the site class and S1
based on ASCE 7-10 Table 11.4-2. If site coefficients are user defined, Fv is
input directly by the user. A typical range of values for Fv is 0.8 to 3.5.
TL is the long-period transition period as determined in ASCE 7-10 Section
11.4.5.
2.14.3 Algorithm for 2012 IBC / ASCE 7-10 Seismic Loads
The algorithm for determining ASCE 7-10 seismic loads is based on ASCE
7-10 Section 12.8. A period is calculated as described in a preceding section
entitled "Options for ASCE 7-10 Building Period."
The programs begin by calculating the design spectral response acceleration
at short period, SDS, using (ASCE 7-10 Eqs. 11.4-1 and 11.4-3).
2
3
DS a s
S FS
=
(ASCE 7-10 Eqns. 11.4-1 and 11.4-3)
Next, the design spectral response acceleration is calculated at a one second
period, SD1, using (ASCE 7-10 Eqns. 11.4-2 and 11.4-3).
11
2
3
Dv
S FS=
(ASCE 7-10 Eqns. 11.4-2 and 11.4-3)
The programs determine a seismic design category (A, B, C, D, E, or F with
A being the least severe and F being the most severe) based on ASCE 7-10
Section 11.6. A seismic design category is determined based on SDS using
ASCE 7-10 Table 11.6-1. A seismic design category also is determined based
on SD1 using ASCE 7-10 Table 11.6-2. The more severe of the two seismic
categories is chosen as the seismic design category for the building.
Initially a seismic response coefficient, Cs, is calculated using (ASCE 7-10
Eqn. 12.8-2). This base shear value is then checked against the limits speci-
2 - 60 2012 IBC/ASCE 7-10 Seismic Loads
Chapter 2 - Automatic Seismic Loads
fied in (ASCE 7-10 Eqns. 12.8-3, 12.8-4, 2.8-5, and 12.8-6) and modified as
necessary to obtain the final base shear.
DS
s
e
S
CR
I
= (ASCE 7-10 Eqn. 12.8-2)
where,
SDS = The design spectral response acceleration at short periods.
R = Response modification factor specified in ASCE 7-10 Table 12.2-
1.
Ie = The occupancy importance factor determined in accordance with
ASCE 7-10 Table 1.5-2.
The seismic response coefficient, Cs, need not exceed that specified in
(ASCE 7-10 Eqns. 12.8-3 and 12.8-4). If the seismic response coefficient
calculated in accordance with (ASCE 7-10 Eqns. 12.8-2) exceeds that calcu-
lated in accordance with (ASCE 7-10 Eqns. 12.8-3 and 12.8-4), the programs
set the seismic response coefficient, Cs, equal to that calculated in accordance
with (ASCE 7-10 Eqns. 12.8-3 and 12.8-4), as appropriate.
1D
s
e
S
CRT
I
=


for T ≤ TL (ASCE 7-10 Eqn. 12.8-3)
1
2
DL
s
e
ST
CRT
I
=


for T > TL (ASCE 7-10 Eqn. 12.8-4)
where,
SD1 = the design spectral response acceleration at a one second period
T = the building period used for calculating the base shear
TL = the long-period transition period
and all other terms are as described for (ASCE 7-10 Eqn. 12.8-2).
2012 IBC/ASCE 7-10 Seismic Loads 2 - 61
Automatic Seismic Loads
Cs shall not be less than that shown in (ASCE 7-10 Eqn. 12.8-5).
Cs = 0.044SDSIe ≥ 0.01 (ASCE 7-10 Eqn. 12.8-5)
Finally, for structures located where S1 is equal to or greater than 0.6g, Cs
shall not be less than that shown in (ASCE 7-10 Eqn. 12.8-6).
1
0.5
s
e
S
CR
I
=


(ASCE 7-10 Eqn. 12.8-6)
where,
S1 = the mapped MCER spectral acceleration for a one second period
and all other terms are as described for (ASCE 7-10 Eqn. 12.8-2).
The base shear, V, is calculated using (ASCE 7-10 Eqn. 12.8-1):
V = CsW (ASCE 7-10 Eqn. 12.8-1)
Cs = Seismic response coefficient as determined from one of (ASCE 7-
10 Eqns. 12.8-2 through 12.8-6) as appropriate.
W = Weight of the building (based on specified mass).
The base shear, V, is distributed over the height of the building in accordance
with (ASCE 7-10 Eqns. 12.8-11 and 12.8-12)
story story
story
story story
story =1
k
nk
Vw h
F
wh
=∑
(ASCE 7-10 Eqns. 12.8-11 and 12.8-12)
where,
Fstory = Portion of base shear applied to a story level.
V = Building base shear.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
2 - 62 2012 IBC/ASCE 7-10 Seismic Loads
Chapter 2 - Automatic Seismic Loads
k = Exponent applied to building height. The value of k depends on
the value of the building period, T, used for determining the base
shear. If T ≤ 0.5 seconds, k = 1. If T ≥ 2.5 seconds, k = 2. If 0.5
seconds < T < 2.5 seconds, k is linearly interpolated between 1
and 2.
n = Number of story levels in the structure.
2.15 1997 NEHRP Seismic Loads
2.15.1 Options for 1997 NEHRP Building Period
Three options are provided for the building period used in calculating the
1997 NEHRP automatic seismic loads. They are as follows:
Approximate Period: Calculate the period based on (1997 NEHRP Eqn.
5.3.3.1-1). The value used for CT is user input and hn is determined by the
programs from the input story level heights.
( )
34
A Tn
T Ch=
(1997 NEHRP Eqn. 5.3.3.1-1)
Note that CT is always input in English units as specified in the code. A
typical range of values for CT is 0.020 to 0.035. The height hn is meas-
ured from the elevation of the specified bottom story/minimum level to
the (top of the) specified top story/maximum level.
Program Calculated: The programs start with the period of the mode
calculated to have the largest participation factor in the direction that
loads are being calculated (X or Y). Call this period Tmode. A period also
is calculated based on the (1997 NEHRP Eqn. 5.3.3.1-1). The value used
for CT is user input and hn is determined from the input story level
heights. Call this period TA.
The programs also calculate a coefficient for the upper limit on the calcu-
lated period, Cu, based on 1997 NEHRP Table 5.3.3. Note that linear in-
terpolation is used to calculate values of Cu where the value of SD1 is not
specifically specified in Table 5.3.3.
1997 NEHRP Seismic Loads 2 - 63
Automatic Seismic Loads
The building period, T, that the programs choose is determined as fol-
lows:
– If Tmode ≤ CuTA, then T = Tmode.
– If Tmode > CuTA, then T = CuTA.
User Defined: In this case, input a building period, which the programs
use in the calculations. They do not compare it to CuTA. t is assumed that
this comparison is performed before the period is specified.
2.15.2 Other Input Factors and Coefficients
The response modification coefficient, R, and the system overstrength factor,
Ω, are direction dependent. Both are specified in 1997 NEHRP Table 5.2.2.
A typical range of values for R is 2 to 8. A typical range of values for Ω is 2
to 3.
The seismic group can be input as I, II or III. No other values are allowed.
See 1997 NEHRP Table 1.4 for information about the seismic group. An oc-
cupancy importance factor, I, is determined from the input seismic group and
1997 NEHRP Table 1.4.
The seismic coefficients can be input in accordance with the code or they can
be user defined. If the seismic coefficients are in accordance with code, spec-
ify a site class, Ss and S1. If seismic coefficients are user defined, specify Ss,
S1, Fa and Fv.
The site class can be A, B, C, D or E. Note that site class F is not allowed for
the automatic 1997 NEHRP lateral seismic loads. See 1997 NEHRP Section
4.1.2.1 for site class definitions.
Ss is the mapped maximum considered spectral acceleration for short periods
as determined in 1997 NEHRP Section 4.1.2. A typical range of values for Ss
is 0 to 3. Note that the seismic maps show Ss in %g with a typical range of
0% to 300%. The input is in g. Thus the map values should be divided by
100 when they are input. For example, if the map value is 125%g, it should
be input as 1.25g.
2 - 64 1997 NEHRP Seismic Loads
Chapter 2 - Automatic Seismic Loads
S1 is the mapped maximum considered spectral acceleration for a one second
period as determined in 1997 NEHRP Section 4.1.2. A typical range of val-
ues for S1 is 0 to 2. Note that the seismic maps show S1 in %g with a typical
range of 0% to 200%. The input is in g. Thus the map values should be di-
vided by 100 when they are input. For example, if the map value is 125%g, it
should be input as 1.25g.
Fa is a site coefficient. If the site coefficients are determined in accordance
with code, the programs automatically determine Fa from the site class and Ss
based on 1997 NEHRP Table 4.1.2.4a. If site coefficients are user defined, Fa
is input directly by the user. A typical range of values for Fa is 0.8 to 2.5.
Fv is a site coefficient. If the site coefficients are determined in accordance
with code, the programs automatically determine Fv from the site class and S1
based on 1997 NEHRP Table 4.1.2.4b. If site coefficients are user defined,
the Fv is input directly by the user. A typical range of values for Fv is 0.8 to
3.5.
2.15.3 Algorithm for 1997 NEHRP Seismic Loads
The algorithm for determining 1997 NEHRP seismic loads is based on 1997
NEHRP Section 5.3. A period is calculated as described in a preceding sec-
tion entitled "Options for 1997 NEHRP Building Period."
The programs begin by calculating the design spectral response acceleration
at short periods, SDS, using 1997 NEHRP Eqns. 4.1.2.4-1 and 4.1.2.5-1.
2
3
DS a s
S FS=
(1997 NEHRP Eqns. 4.1.2.4-1 and 4.1.2.5-1.)
Next the programs calculate the design spectral response acceleration at a
one second period, SD1, using 1997 NEHRP Eqns. 4.1.2.4-2 and 4.1.2.5-2.
11
2
3
Dv
S FS=
(1997 NEHRP Eqns. 4.1.2.4-2 and 4.1.2.5-2.)
A seismic design category (A, B, C, D, E, or F with A being the least severe
and F being the most severe) is determined based on 1997 NEHRP Section
4.2.1.A seismic design category is determined based on SDS using 1997
NEHRP Table 4.2.1a. A seismic design category also is determined based on
1997 NEHRP Seismic Loads 2 - 65
Automatic Seismic Loads
SD1 using 1997 NEHRP Table 4.2.1b. The more severe of the two seismic
categories is chosen as the seismic design category for the building.
Initially a seismic response coefficient, Cs
, is calculated using (1997 NEHRP
Eqn. 5.3.2.1-1). This base shear value is then checked against the limits spec-
ified in (1997 NEHRP Eqns. 5.3.2.1-2,5.3.2..1-2, and 5.3.2.1-3) and modified
as necessary to obtain the final base shear.
DS
s
S
CR
I
=
(1997 NEHRP Eqn. 5.3.2.1-1).
where,
SDS = The design spectral response acceleration at short periods.
R = Response modification factor specified in 1997 NEHRP Table
5.2.2.
I = The occupancy importance factor determined in accordance with
1997 NEHRP Table 1.4.
The seismic response coefficient, Cs , need not exceed that specified in (1997
NEHRP Eqn. 5.3.2.1-2). If the seismic response coefficient calculated in
accordance with (1997 NEHRP Eqn. 5.3.2.1-1) exceeds that calculated in
accordance with (1997 NEHRP Eqn. 5.3.2.1-2), the programs set the seismic
response coefficient, Cs , equal to that calculated in accordance with (1997
NEHRP Eqn. 5.3.2.1-2).
D1
s
S
CRT
I
=


(1997 NEHRP Eqn. 5.3.2.1-2)
where,
SD1 = the design spectral response acceleration at a one second period
T = the building period used for calculating the base shear
and all other terms are as described for (1997 NEHRP Eqn. 5.3.2.1-1).
2 - 66 1997 NEHRP Seismic Loads
Chapter 2 - Automatic Seismic Loads
The seismic response coefficient, Cs , shall not be less than that specified in
(1997 NEHRP Eqn. 5.3.2.1-3). If the seismic response coefficient calculated
in accordance with (1997 NEHRP Eqn. 5.3.2.1-3) exceeds that calculated in
accordance with (1997 NEHRP Eqn. 5.3.2.1-1), the programs set the seismic
response coefficient equal to that calculated in accordance with (1997
NEHRP Eqn. 5.3.2.1-3).
Cs = 0.1 SD1 I (1997 NEHRP Eqn. 5.3.2.1-3)
where all terms are as previously described for (1997 NEHRP Eqns. 5.3.2.1-
1 and 5.3.2.1-2).
Finally, if the building is in seismic design category E or F, the seismic re-
sponse coefficient, Cs , shall not be less than that specified in (1997 NEHRP
Eqn. 5.3.2.1-4). If the building is in seismic design category E or F and the
seismic response coefficient calculated in accordance with (1997 NEHRP
Eqn. 5.3.2.1-4) exceeds that calculated in accordance with (1997 NEHRP
Eqns. 5.3.2.1-1 and 5.3.2.1-3), the programs set the seismic response coeffi-
cient equal to that calculated in accordance with (1997 NEHRP Eqn. 2-
58.5.3.2.1-4).
1
0.5
s
S
CR
I
=
(1997 NEHRP Eqn. 5.3.2.1-4)
where,
S1 = the mapped spectral acceleration for a one second period
and all other terms are as previously described for (1997 NEHRP Eqn.
5.3.2.1-1).
The base shear, V, is calculated using (1997 NEHRP Eqn. 5.3.2):
V = Cs W (1997 NEHRP Eqn. 5.3.2)
Cs = Seismic response coefficient as determined from one of (1997
NEHRP Eqns. 5.3.2.1-1 through 5.3.2.1-4) as appropriate.
W = Weight of the building (based on specified mass).
1997 NEHRP Seismic Loads 2 - 67
Automatic Seismic Loads
The base shear, V, is distributed over the height of the building by combining
(1997 NEHRP Eqns. 5.3.4-1 and 5.3.4-2).
story story
story
story story
story 1
k
nk
Vw h
F
wh
=
=∑
where,
Fstory = Portion of base shear applied to a story level.
V = Building base shear.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
k = Exponent applied to building height. The value of k depends
on the value of the building period, T, used for determining the
base shear. If T ≤ 0.5 second, k = 1. If T ≥ 2.5 seconds, k = 2. If
0.5 second < T < 2.5 seconds, k is linearly interpolated be-
tween 1 and 2.
n = Number of story levels in the structure.
2.16 2010 Chinese Seismic Loads
2.16.1 Options for 2010 Chinese Building Period
Two options are provided for the building period used in calculating the 2010
Chinese automatic seismic loads. They are as follows:
Program Calculated: The programs use the longest period mode (fun-
damental) for the calculated time period. This period is T1.
User Defined: In this case, input a building period, which the programs
use in the calculations.
2 - 68 2010 Chinese Seismic Loads
Chapter 2 - Automatic Seismic Loads
2.16.2 Other Input Factors and Coefficients
The maximum value for seismic lateral influence factor, αmax, is used to cal-
culate the factor of seismic lateral influence, α1, obtained from the 2010 Chi-
nese Design Code response spectrum for the fundamental period.
The seismic intensity, SI, has six possible values: 6(0.05g), 7(0.10g),
7(0.15g), 8(0.20g), 8(0.30g) and 9(0.40g).
The damping ratio, ζ, is used to adjust the shape of the response spectrum
curve.
The characteristic ground period, Tg, is entered in units of seconds. The fun-
damental period, T1, is multiplied by the period time discount factor, PTDF,
prior to looking up the value of α1 from the 2010 Chinese Design Code re-
sponse spectrum curve. PTDF typically ranges from 0.5 to 1.0.
The enhancement factor is a multiplier to amplify the value or response spec-
trum curve.
2.16.3 Algorithm for 2010 Chinese Seismic Loads
The algorithm for determining 2010 Chinese seismic loads is based on calcu-
lating a factor of seismic lateral influence, α1, from the response spectrum
curve. The period used for determining this factor, T1, is the fundamental
period as described in a preceding section entitled "Options for 2010 Chinese
Building Period."
The programs calculate the seismic lateral influence factor using (Eqn. 2-1).
2 max
2 max
12 max
2 1 max
[0.45 ( 4.5)] If 0.1s
If 0.1s
If 5
[ 0.2 ( 5 )] If 5 6
g
ggg
g gg
TT
TT
TTTT
T
TT TT T
γ
γ
+ η− α ≤
ηα < <
α= 
ηα < ≤


η −η − α < ≤
(Eqn. 2-1)
where,
α1 = Seismic lateral influence factor.
2010 Chinese Seismic Loads 2 - 69
Automatic Seismic Loads
αmax = Maximum value for the seismic lateral influence factor.
T = PTDF (T1)
T1 = Fundamental period of the structure.
Tg = Characteristic ground period.
PTDF = Period time discount factor.
γ =
0.05
0.9 0.5 5
−ζ
++ζ
(GB50011-2010 Eqn. 5.1.5-1)
η1 =
( )
( )
0.05
0.02 4 32
−ζ
++ζ
( )
1
0η≥
(GB50011-2010 Eqn. 5.1.5-2)
η2 =
0.05
10.08 1.6
−ζ
++ζ
( )
2
0.55
η≥
(GB50011-2010 Eqn. 5.1.5-3)
ζ = Damping ratio.
The total specified load for lateral seismic action, FEk, is calculated using
(Eqn. 2-2):
1Ek Eq
FG= α
(GB50010-2010 Eqn. 5.2.1-1)
where,
α1 = Seismic lateral influence factor calculated in (Eqns. 2-1).
GEq = 0.85GE, GE is total representative gravity load of building.
The total specified load for lateral seismic action, FEk, is broken into a con-
centrated force applied to the top of the structure and forces applied at each
story level in accordance with (Eqn. 2-2):
1
n
Ek n i
i
FF F
=
=∆+
∑
(Eqn. 2-2)
where,
2 - 70 2010 Chinese Seismic Loads
Chapter 2 - Automatic Seismic Loads
FEk = Total specified load for lateral seismic action.
∆Fn = Concentrated force at the top of the building.
Fi = Portion of total specified load applied to a story level.
n = Number of story levels in the building.
The concentrated force at the top of the structure, ∆Fn, is calculated as::
n n Ek
FF∆=δ
(GB50011 2010 Eqn. 5.2.1-3)
where,
FEk = Total specified load for lateral seismic action.
11
11
11
0.08 0.07 If 1.4 and 0.35
0.08 0.01 If 1.4 and 0.35 0.55
0.08 0.02 If 1.4 and 0.55
0 If 1.4
gg
gg
ngg
gg
T TTT
T TT T
T TTT
TT
+ >≤
+ > <≤
δ=
− >≥
≤
The remaining portion of the lateral seismic load, (FEk − ∆Fn), is distributed
over the height of the structure in accordance with:
( )
i
1
1
ii Ek n
n
jj
j
GH
FF
GH
=
= −δ
∑
(GB50010 2010 Eqn.5.2.1-2)
where,
Fi = Portion of lateral seismic load applied to story level i.
FEk = Total specified load for lateral seismic action.
∆Fn = Concentrated force at the top of the structure.
Gi, Gj = Equivalent gravity load of lumped mass for story levels i and j,
respectively.
Hi, Hj = Story heights of lumped masses i and j, respectively, measured
from base of structure to story level.
n = Number of story levels in the structure.
2010 Chinese Seismic Loads 2 - 71
Automatic Seismic Loads
2.17 2004 NZS 1170.5 Seismic Loads
2.17.1 Options for 2004 NZS 1170.5 Building Period
Two options are provided for the building period used in calculating the 2004
NZS automatic seismic loads. They are:
Program Calculated: The programs use the longest period mode calcu-
lated to have the largest participation factor in the direction that loads are
being calculated (X or Y). Call this period T1.
User Defined: In this case, input a building period, which the programs
use in the calculations. They do not compare it against the program cal-
culated period.
2.17.2 Other Input Factors and Coefficients
The structural performance factor, Sp, is based on Section 4.4 of the 2004
NZS 1170.5. A typical range of values for Sp is 0.7 to 1.0.
The structural ductility factor, μ, is based on Section 4.3 of the 2004 NZS
1170.5.
The site subsoil class can be A, B, C, D, or E. See 2004 NZS 1170.5 Subsec-
tion 3.1.3 for site subsoil class definitions. The site subsoil class in combina-
tion with the period, T1, are used to look up the seismic hazard coefficient,
Ch(T1), as described in Subsection 3.1.2 of the 2004 NZS 1170.5.
Z is the hazard factor as determined from Table 3.3 of the 2004 NZS 1170.5.
A typical range of values for Z is 0.13 to 0.55.
R is the return period factor as determined from Table 3.5 of the 2004 NZS
1170.5. A typical range of values for R is 0.2 to 1.8, but should be limited
such that ZR does not exceed 0.7.
D is the shortest distance (in kilometers) from the site to the nearest fault
listed in Table 3.6. The distance, D, is used to compute the near-fault factor,
N(D,T), as given in Subsection 3.1.6.2 of the 2004 NZS 1170.5. A typical
range of values for N(D,T) is 1 to 1.72.
2 - 72 2004 NZS 1170.5 Seismic Loads
Chapter 2 - Automatic Seismic Loads
2.17.3 Algorithm for 2004 NZS 1170.5 Seismic Loads
The algorithm for determining 2004 NZS 1170.5 seismic loads is based on
Section 6.2 of the 2004 NZS 1170.5 entitled “Equivalent Static Method.” A
period is calculated as described in a preceding section entitled "Options for
2004 NZS 1170.5 Building Period."
The programs begin by calculating the elastic site hazard spectrum for hori-
zontal loading, C(T), using (NZS Eqn. 1170.5 3.1(1))
11
() () (,)
hu
CT C T ZRNTD=
(NZS Eqn. 1170.5 3.1(1))
where,
Ch(T1) = Seismic hazard coefficient for period T as determined by the
program from Table 3.1 of the 2004 NZS 1170.5 Commen-
tary.
Z = The hazard factor determined from Clause 3.1.4 taking ac-
count of the limitation on the value of ZRu given by Clause
3.1.1
Ru = Return period factor.
N (T,D) = Near-fault factor determined from clause 3.1.6.2.
max
(, ) ()NTD N T
=
for
2km≤D
( )
max
20
1 () 1 18
−
=+−
D
NT
for
2 20kmD<≤
10
.=
for
20kmD>
where,
D = the shortest distance (in kilometers) from the site to the
nearest fault listed in Table 3.6.
max ()NT
= the maximum near-fault factor and is linearly interpolated
for period T from Table 3.7.
2004 NZS 1170.5 Seismic Loads 2 - 73
Automatic Seismic Loads
Next, the horizontal design action coefficient is calculated at the T period,
Cd(T1), using the following equation:
( )
1
1
( ) 0.02 but not less than 0.03
20
p
d uu
CT S Z
CT R R
kµ

= ≥+


(NZS Eqn. 5.2(1))
where,
C(T1) = elastic site hazard spectrum calculated in (NZS Eqn. 1170.5
3.1(1))
Sp = structural performance factor
For soil Classes A, B, C and D
kμ = μ for T1 ≥ 0.7 s
=
( )
1
11
07
T
.
µ− +
for T1 < 0.7 s
For soil class E
kμ = μ for T1 ≥ 1 s or μ < 1.5
=
( )
1
1 15T.µ− +
for T1 < 1 s and μ ≥ 1.5
provided that for the purposes of calculating kμ, T1 shall not be taken
less than 0.4 s.
μ = structural ductility factor
and for the purposes of calculating kμ, T1 shall not be taken less than 0.4 sec-
ond for site subsoil classes A, B, and C; 0.6 second for site subsoil class D;
or 1.0 second for site subsoil class E.
The horizontal base shear, V, is calculated using (NZS Eqn. 1170.5 6.2(1)):
V = Cd (T1)W (NZS Eqn. 1170.5 6.2(1))
where,
2 - 74 2004 NZS 1170.5 Seismic Loads
Chapter 2 - Automatic Seismic Loads
Cd(T1) = Horizontal design action coefficient calculated in (NZS Eqn.
5.2(1))
W = Weight of the building (based on specified mass).
The horizontal base shear, V, is distributed over the height of the building in
accordance with (NZS Eqn. 1170.5 6.2(2))
story story
story
story story
story =1
+0.92
tn
wh
FFV
wh
=
∑
(NZS Eqn. 1170.5 6.2(2))
where,
Fstory = Portion of base shear applied to a story level.
Ft = 0.08V if story = top level
or
Ft = 0 if story
≠
top level.
V = Horizontal base shear calculated in (NZS Eqn. 6.2(1)).
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
n = Number of story levels in the structure.
2.18 2007 AS 1170.4 Seismic Loads
2.18.1 Options for 2007 AS 1170.4 Building Period
Three options are provided for the building period used in calculating the
2007 AS 1170.4 automatic seismic loads. They are as follows:
Approximate Period: Calculate the fundamental period based on (AS
1170.4 Eqn. 6.2(7)). The value used for hn is determined by the programs
from the input story level heights.
2007 AS 1170.4 Seismic Loads 2 - 75
Automatic Seismic Loads
0.75
1.25
A tn
T kh
=
(AS 1170.4 Eqn. 6.2(7))
where kt is defined as follows (AS 1170.4 section 6.2.3):
kt = 0.11 for moment-resisting steel frames
= 0.075 for moment-resisting concrete frames
= 0.06 for eccentrically braced steel frames
= 0.05 for all other structures
The height hn is measured from the elevation of the specified bottom sto-
ry/minimum level to the (top of the) specified top story/maximum level
and is input in meters.
Program Calculated: The programs start with the period of the mode
calculated to have the largest participation factor in the direction that
loads are being calculated (X or Y). Call this period Tmode.
The base shear obtained using a Program Calculated period cannot be
less than 80% of the base shear obtained using the approximate period
(AS 6.2.3).
User Defined: In this case, input a building period, which the programs
use in the calculations. They do not compare it against TA or Tmode. It is
assumed that this comparison is performed before the period is specified.
2.18.2 Other Input Factors and Coefficients
The structural performance factor, Sp, is based on Section 6.5 of the 2007 AS
1170.4 and Table 6.5(A) and 6.5(B). A typical range of values for Sp is 0.67
to 1.0.
The structural ductility factor, μ, is based on Section 6.5 of the 2007 AS
1170.4 and Table 6.5(A) and 6.5(B). A typical range of values for μ is 2.0 to
3.0 (AS 2.2).
The site subsoil class can be Ae, Be, Ce, De or Ee. See 2007 AS 1170.4 Sub-
section 4.1.1 for site subsoil class definitions. The site subsoil class in com-
2 - 76 2007 AS 1170.4 Seismic Loads
Chapter 2 - Automatic Seismic Loads
bination with the period, T1, are used to look up the spectral shape factor,
Ch(T1), as described in Subsection 6.4 of the 2007 AS 1170.4.
Z is the hazard factor as determined from Table 3.2 of the 2007 AS 1170.4. A
typical range of values for Z is 0.03 to 0. 29 (AS 2.2).
kp is the return period factor as determined from Table 3.1 of the 2007 AS
1170.4. A typical range of values for kp is 0.2 to 1.8.
2.18.3 Algorithm for 2007 AS 1170.4 Seismic Loads
The algorithm for determining 2007 AS 1170.4 seismic loads is based on
Section 6.2 of the 2007 AS 1170.4 entitled “Equivalent Static Analysis.” A
period is calculated as described in a preceding section entitled "Options for
2007 AS 1170.4 Building Period."
The programs begin by calculating the elastic site hazard spectrum for hori-
zontal loading, C(T), using (AS 1170.4 Eqn. 6.2(5))
11
() ()
ph
C T k ZC T=
(AS Eqn. 1170.4 6.2(5))
where,
Ch(T1) = Spectral shape factor for period T as determined by the pro-
gram from Table 6.4 of the 2007 AS 1170.4.
kp = Return period factor as given in AS 1170.4 clause 3.1.
Z = Hazard factor as given in AS 1170.4 clause 3.2.
Sp = Structural performance factor as given in AS 1170.4 clause
6.5.
μ = Structural ductility factor as given in AS 1170.4 clause 6.5.
The horizontal base shear, V, is calculated using (AS 1170.4 Eqn. 6.2(1)):
V = Cd (T1)W (AS 1170.4 Eqn. 6.2(1))
where,
2007 AS 1170.4 Seismic Loads 2 - 77
Automatic Seismic Loads
Cd(T1) = Horizontal design action coefficient calculated in (AS
1170.4 Eqn. 6.2(4))
( )
1
1
() p
d
CT S
CT=µ
(AS 1170.4 Eqn. 6.2(4))
W = Weight of the building (based on specified mass).
The base shear, V, is distributed over the height of the building in accordance
with (AS 1170.4 Eqn. 6.3(1)).
story story
story
story story
story 1
k
nk
wh
FV
wh
=
=
∑
(AS 1170.4 Eqn. 6.3(1))
where,
Fstory = Portion of base shear applied to a story level.
V = Building base shear.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
k = Exponent applied to building height. The value of k depends
on the value of the building period, T, used for determining the
base shear. If T ≤ 0.5 second, k = 1. If T ≥ 2.5 seconds, k = 2.
If 0.5 second < T < 2.5 seconds, k is linearly interpolated be-
tween 1 and 2.
n = Number of story levels in the structure.
2 - 78 2007 AS 1170.4 Seismic Loads
Chapter 2 - Automatic Seismic Loads
2.19 2004 Eurocode 8 (EN 1998-1) Seismic Loads
2.19.1 Options for EN 1998-1:2004 Building Period
Three options are provided for the building period used in calculating the EN
1998-1:2004 automatic seismic loads. They are as follows:
Approximate Period: Calculate the fundamental period based on (EN
1998-1 Eqn. 4.6). The value used for H is determined by the programs
from the input story level heights.
4/3
1
HC
T
t
=
(EN 1998-1 Eqn. 4.6)
where Ct is defined as follows (EN 1998-1 section 4.3.3.2.2(3)):
Ct = 0.085 for moment-resisting steel frames
= 0.075 for moment-resisting concrete frames
= 0.075 for eccentrically braced steel frames
= 0.05 for all other structures
The height H is measured from the elevation of the specified bottom sto-
ry/minimum level to the (top of the) specified top story/maximum level
and is input in meters.
Program Calculated: The programs start with the period of the mode
calculated to have the largest participation factor in the direction that
loads are being calculated (X or Y). Call this period Tmode.
User Defined: In this case, input a building period, which the programs
use in the calculations. They do not compare it against TA or Tmode. It is
assumed that this comparison is performed before the period is specified.
2.19.2 Other Input Factors and Coefficients
The spectral design spectrum, Sd (T1), is based on Section 3.2.2.5(4) of the
EN 1998-1:2004 and Table 3.2 or Table 3.3.
2004 Eurocode 8 (EN 1998-1) Seismic Loads 2 - 79
Automatic Seismic Loads
The recommended choice of spectra is defined in EN 1998-1:2004 Section
3.2.2.2(2)P Table 3.2 and Table 3.3.
The behavior factor, q, is based on Section 3.2.2.5 of the EN 1998-1:2004
which is an approximation of the ratio of the seismic forces that the structure
would experience if its response was completely elastic with 5% viscous
damping, to the seismic forces that may be used in design, with a conven-
tional elastic analysis model. A value for q is generally greater than 1.5.
The lower bound factor for horizontal design spectrum, β, is given in the Na-
tional annex. The default value of β is 0.2.
The ground type can be A, B, C, D or E. See EN 1998-1:2004 Section 3.1.2
for site subsoil class definitions. The ground type in combination with the pe-
riod, T1, are used to look up the spectral design spectrum, Sd(T1), as described
in Subsection 3.2.2.5 of the EN 1998-1:2004.
λ is the correction factor, the value of as λ is equal to 0.85 if T1 ≤ 2Tc and the
building has more than two stories, or λ = 1.0, otherwise.
2.19.3 Algorithm for EN 1998-1:2004 Seismic Loads
The algorithm for determining EN 1998-1:2004 seismic load is based on Sec-
tion 4.3.3.2 of the EN 1998-1:2004 entitled “Lateral Force Method of Analy-
sis.” A period is calculated as described in a preceding section entitled "Op-
tions for EN 1998-1:2004 Building Period."
The programs begin by calculating the spectral design spectrum, Sd (T1) for
horizontal loading based on Section 3.2.2.5(4) of the EN 1998-1:2004 and
Table 3.2 or Table 3.3.
The horizontal base shear, Fb, is calculated using (EN 1998-1 Eqn. 4.5):
Fb = Sd (T1) W λ (EN 1998-1 Eqn. 4.5)
W = Weight of the building (based on specified mass)
λ
= Correction factor.
The base shear, Fb, is distributed over the height of the building in accord-
ance with (EN 1998-1 Eqn. 4.11).
2 - 80 2004 Eurocode 8 (EN 1998-1) Seismic Loads
Chapter 2 - Automatic Seismic Loads
story story
story
story story
story 1
b
n
wh
FF
wh
=
=∑
(EN 1998-1 Eqn. 4.11)
where,
Fstory = Portion of base shear applied to a story level.
V = Building base shear.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
n = Number of story levels in the structure.
2.20 2002 Indian IS:1893
2.20.1 Options for 2002 Indian IS:1893 Building Period
Three options are provided for the building period used in calculating the
IS:1893 automatic seismic loads. These are:
• Approximate: Calculate the approximate period, Ta, based on the formu-
la discussed in Section 7.6.1 of IS:1893 Code. The period is calculated
using following equations given in the IS:1893 code.
Ta=0.075h0.75 For RC framed buildings
Ta=0.085h0.75 For Steel framed buildings
The height h is measured from the elevation of the specified bottom
story/minimum elevation level to the (top of the) specified top story/
maximum elevation level. The user should give the multiplier value as
0.075 or 0.085 in the static earthquake auto lateral load data form
depending on the building type (viz. RC or steel) being modeled.
• Program Calculated: The program uses the period of the mode
calculated to have the largest participation factor in the direction that
2002 Indian IS:1893 2 - 81
Automatic Seismic Loads
loads are being calculated (X or Y). The user must activate the dynamic
analysis option to use the program calculated period for evaluation of
seismic base shear. If no dynamic analysis option is defined, program
assumes a period of 1 second to evaluate the seismic base shear.
• User Defined: In this case, input a building period, which the program
will use in the calculations. For buildings with brick infill frames or
shear walls, the user should calculate the period using the formula
( )
0.09T hd=
, and this period should be given as input.
2.20.2 Other Input Factors and Coefficients
The seismic zone factor, Z, depends on the geographical location of the
building as determined from Table 2, Section 6.4.2 of IS:1893. A typical
range of values for Z is 0.10 to 0.36. As an alternative the user can also spec-
ify a user defined value of Z.
The response reduction factor R is input by the user. Typically R depends on
the choice of lateral load resisting system, and it is specified in IS:1893 Table
7, Section 6.4.2. A typical range of values for R is 3 to 5 for RC and Steel
buildings.
The soil profile type can be I, II or III. These correspond to soil types Rock
or Hard Soil (type I), Medium Soil (type II) and Soft Soil (type III) respec-
tively. No other values can be input.
The importance factor I is input by the user. Typically I depends on the func-
tional use of the structures, characterized by hazardous consequences of its
failure, post-earthquake functional needs, historical value, or economic im-
portance, and it is specified in IS:1893 Table 6, Section 6.4.2.
2.20.3 Algorithm for IS:1893 Seismic Loads
The algorithm for determining IS:1893 seismic loads is based on Sections
6.4.2, 7.5.3 and 7.7 of IS:1893 code. A period is calculated as described in
the previous section entitled Options for IS:1893 Building Period.
2 - 82 2002 Indian IS:1893
Chapter 2 - Automatic Seismic Loads
Next the value of seismic base shear is computed using the following expres-
sion.
Vb = AhW (IS:1893 Section.7.5.3)
and Ah is given be the following equation:
Ah = ZISa /2Rg (IS:1893 Section.6.4.2)
where,
Ah = The design horizontal spectrum value
Sa /g = Spectral acceleration coefficient computed using expressions
given in section 6.4.5 of IS:1893 for 5% damping
R = Response reduction factor.
I = Importance factor.
W = Seismic weight of the building (based on specified mass)
The base shear, Vb, is distributed over the height of the building in accord-
ance with equation given in Section 7.7 of IS:1893.
1
k
ii
iB
nk
ii
i
Wh
QV
Wh
=
=∑
(IS:1893 Section.7.7)
where,
Qi = Portion of base shear applied to ith story level.
Vb = Base shear.
Wi = Weight of ith story level (based on specified mass).
hi = ith Story height, distance from base of building to story level.
k = 2
n = No. of stories in the building
2002 Indian IS:1893 2 - 83
Automatic Seismic Loads
Note: If the user wants to compute the seismic forces for a building with a
damping ratio other than the default 5%, the corresponding multiplier for
converting the default 5% spectral acceleration coefficient to another damp-
ing ratio should be taken from Table 3, Section 6.4.2 of IS:1893 and the mul-
tiplier should be multiplied by the zone factor Z; the resulting value should
be given as the user-defined seismic zone factor in the static earthquake auto
lateral load form.
2.21 2008 Italian NTC Seismic Loads
The algorithm for determining NTC 2008 seismic load is based on Section
7.3.3.2 of NTC 2008 entitled “Analisi lineare statica” (linear static analysis).
2.21.1 Options for 2008 Italian NTC Building Period
Three options are provided for the building period used in calculating the
2008 Italian NTC automatic seismic loads. They are as follows:
Approximate Period: Calculate the period based on NTC 2008 Eq.
7.3.5). The value used for C1 is user input, and H is determined by the
programs from the input story level heights:
34
11
T CH= ⋅
(NTC 2008 Eq. 7.3.5)
C1 is a coefficient that depends on the structure material:
C1 = 0.085 for steel frame structures
= 0.075 for concrete frame structures
= 0.05 for other types of structures
H is the total height of the structure measured from the elevation of the
specified bottom story/minimum level to the (top of the) specified top
story/maximum level.
Program Calculated: The programs start with the period of the mode
calculated to have the largest participation factor in the direction that
loads are being calculated (X or Y). Call this period Tmode.
2 - 84 2008 Italian NTC Seismic Loads
Chapter 2 - Automatic Seismic Loads
User Defined: In this case, input a building period, which the programs
use in the calculations.
2.21.2 Other Input Factors and Coefficients
The parameters specified are Fundamental Parameters, ag, F0 and Tc*, the
spectrum type, the limit state, the soil type, the topography, the ratio for site
altitude at the base of a hill to the height of the hill (h/H), the damping (ξ) for
elastic spectrum and the behavior correction factor (q) for design spectrum,
and a correction factor Lambda (λ) that is equal to 0.85 if the structure has at
least 3 stories or more; otherwise Lambda (λ) is taken as 1. Lambda is a user
input. Any positive, nonzero value can be specified for the Fundamental
Parameters. The behavior factor must satisfy q ≥ 1.0 (the program will accept
any nonzero value). The subsoil type can be input as A, B, C, D or E. The
topography type can be T1, T2, T3 or T4.
2.21.3 Algorithm for 2008 Italian NTC Seismic Loads
The Fundamental Parameters ag (peak ground acceleration), F0 (magnifica-
tion factor), and Tc* (reference period) can be entered based on a given set of
Latitude and Longitude, by Island name or user specified. For the Latitude
and Longitude and Island Name options, the user also needs to input the
Limit State, the Usage Class, and the Nominal Life of the structure. These
parameters are used for computing the Return period, TR.
( )
ln 1
−
=−
R
R
VR
V
TP
and,
=
R UN
V CV
where,
VN = nominal life of the structure
CU = usage coefficient
Usage Class
I
II
III
IV
Coefficient, CU
0.7
1.0
1.5
2.0
2008 Italian NTC Seismic Loads 2 - 85
Automatic Seismic Loads
The Limit State option can be SLO, SLD for elastic spectrum and SLV and
SLC for design spectrum. The PVR parameters are determined from the fol-
lowing table:
Spectrum Type
Limit State
PVR %
Description
Elastic
SLO
81
Immediate Occupancy
SLD
63
Damage Control
Design
SLV
10
Life safety
SLC
5
Collapse Prevention
For a given return period, TR the parameters ag(TR), F0(TR) and Tc*(TR), here
called p, can be calculated as follows:
() ( )
1
1
2
1
1
2
1loglog
loglog
log
−
⋅
⋅
+
=
R
R
R
R
T
T
T
T
p
p
pp
The ordinates of the response spectrum are calculated using the equations
given below. The values of TB, TC, TD, and S depend on the specified soil
type and spectrum type.
2.21.3.1 Horizontal Elastic Response Spectrum
e0
0
1
0 S( ) 1


≤< = η + −


η

g
B
BB
aTT
T T T SF
g TFT
0
()≤< = η
g
B Ce
a
T T T ST SF
g
0
() 
≤< = η

gC
C De
aT
T T T ST SF
gT
02
() 
≤=η


gCD
De
aTT
T T ST SF
gT
()
10 5 0.55= +≥
ηξ
, where ξ is damping in percentage
The S and spectra ordinate are based on the following equations:
2 - 86 2008 Italian NTC Seismic Loads
Chapter 2 - Automatic Seismic Loads
=sT
S SS
*
=
C CC
T CT
;
3
C
B
T
T=
;
4 1.6= +
g
D
a
Tg
The parameter Cc, Ss and ST are obtained using Soil Type and Topography.
Soil Type
Ss
Cc
A
1.00
1.00
B
0
1.00 1.40 0.40 1.20
≤− ≤
g
a
Fg
()
0.20
*
1.10
−
c
T
C
0
1.00 1.70 0.6 1.50≤− ≤
g
a
Fg
( )
0.33
*
1.05
−
c
T
D
0
0.90 2.40 1.5 1.80≤− ≤
g
a
Fg
( )
0.50
*
1.25
−
c
T
E
0
1.00 2.00 1.10 1.60≤− ≤
g
a
Fg
( )
0.40
*
1.15
−
c
T
Topography
ST
T1
1.0
T2
1.0 1 0.2 1.2≤+ ≤
h
H
T3
1.0 1 0.2 1.2≤+ ≤
h
H
T4
1.0 1 0.4 1.4≤+ ≤
h
H
2.21.3.2 Vertical Elastic Response Spectrum
0
1
0 () 1


≤< = η + −


η

g
B ve v
BB
aTT
T T S T SF
g TFT
()≤< = η
g
B C ve v
a
T T T S T SF
g
() 
≤< = η

gC
C D ve v
aT
T T T S T SF
gT
2008 Italian NTC Seismic Loads 2 - 87
Automatic Seismic Loads
2
() 
≤=η


gCD
D ve v
aTT
T T S T SF
gT
( )
10 5 0.55η= +ξ ≥
, where ξ is damping in percent
=sT
S SS
0.5
0
1.35 
=

g
v
a
FF
g
Soil Type
Ss
TB
TC
TD
A, B, C, D, E
1.00
0.05 s
0.15 s
1.0 s
Topography
ST
T1
1.0
T2
1.2
T3
1.2
T4
1.4
2.21.3.3 Design Horizontal Response Spectrum
The Design Horizontal Spectrum is same as the Elastic Horizontal spectrum,
with the exception of the following:
The η parameter for Design spectrum is defined as
h
q/1=
η
where, qh is the structure behavior factor for the horizontal component.
2.21.3.4 Design Vertical Response Spectrum
The Design Vertical Spectrum is same as Elastic Vertical spectrum, with the
exception of the following:
The η parameter for Design spectrum is defined as
v
q/1=
η
where, qv is the structure behavior factor for the vertical component (1.5
for buildings, 1.0 for bridges).
2 - 88 2008 Italian NTC Seismic Loads
Chapter 2 - Automatic Seismic Loads
The programs begin by calculating the spectral design spectrum, Sd(T1) for
horizontal loading based on Section 3.2 of the NTC 2008.
The horizontal base shear, Fh, is calculated using:
( )
1hd
F S TW
g
λ
=
(NTC § 7.3.3.2)
Sd(T1) = spectral acceleration
W = weight of the building
λ = correction factor (user specified)
g = gravity acceleration
The base shear, Fh, is distributed over the height of the building in accord-
ance with (NTC Eq. 7.3.6):
1
ii
ihn
i ii
zW
FF zW
=
=∑
Fi = portion of the base shear applied at the story level
Fh = building base shear
zi = story height, distance from base of structure to story level
Wi = weight of the story level (based on specified mass)
n = number of story levels in the structure
2.22 2007 Turkish Seismic Code (TSC) Loads
2.22.1 Options for 2007 TSC Building Period
Three options are provided for the building period used in calculating the
2007 TSC automatic seismic loads. They are:
Method A: Calculate the approximate period, TA, using section 2.7.4.2
0.1
A
TN
=
(TSC Section 2.7.4.2)
where,
2007 Turkish Seismic Code (TSC) Loads 2 - 89
Automatic Seismic Loads
N = The number of stories in the structure based on the specified
top and bottom story levels.
Program Calculated: ETABS starts with the period of the mode calculated
to have the largest participation factor in the direction that loads are being
calculated (X or Y). Call this period TETABS. ETABS also calculates a period
based on the Method A. Call this period TA. The building period, T, that
ETABS chooses is given as:
If Number of Stories ≤ 13, then T = TETABS.
If Number of Stories > 13 and If TETABS >
0.1N
, then T = TA.
If Number of Stories > 13 and If TETABS <
0.1N
, then T = TETABS.
User Defined: In this case the user inputs a building period. ETABS uses
this period in the calculations. It does not compare it against the Method A
period. It is assumed that this comparison is performed before the period is
specified.
2.22.2 Other Input Factors and Coefficients
The seismic zone factor, Z, can be input in accordance with the code, which
restricts it to one of the following values: 0.10, 0.2, 0.3, 0.4 as specified in
2007 TSC Table 2.2.
The seismic importance factor, I, can be input as any value. See 2007 TSC
Table 2.3. A typical range of values for I is 1.0 to 1.5.
The local site classes for soil characteristics, Z, can be Z1, Z2, Z3 or Z4.
These correspond to spectrum characteristic periods, TA and TB are given in
2007 TSC Table 2.4. No other values can be input.
The R factor is direction dependent. It is specified in 2007 TSC Table 2.5. A
typical range of values for R is 4 to 8.
2 - 90 2007 Turkish Seismic Code (TSC) Loads
Chapter 2 - Automatic Seismic Loads
2.22.3 Algorithm for 2007 Turkish Seismic Code Loads
The algorithm for determining 2007 TSC seismic loads is based on Part II,
Section 2.4 of the 2007 TSC. ETABS calculates a period as described in a
preceding section entitled "Options for 2007 TSC Building Period."
The base shear, V, is calculated from the below equation.
10
1
() 0.10
()
a
AT
V W A IW
RT
= ≥
EDP 2007 Eqn. 2.4
where,
1
()AT
= Spectral Acceleration Coefficient corresponding to 5% elastic
damping
1
()
a
RT
= Seismic Load Reduction Factor
W = Weight of the building (based on specified mass)
The spectral acceleration coefficient 1
()AT
is computed using TSC 2007
Eqn. 2.1.
() ()=AT AIST
10 1
EDP 2007 Eqn. 2.1
where,
0
A
= Effective ground acceleration coefficient corresponding to 5%
elastic damping from 2007 TSC Table 2.2.
Seismic Zone A0
1 0.40
2 0.30
3 0.20
4 0.10
I = Importance factor.
2007 Turkish Seismic Code (TSC) Loads 2 - 91
Automatic Seismic Loads
()ST
1
= Spectral Coefficient determined from TSC 2007 Eqn. 2.2.
1
1
A
( ) 1 1.5 T
ST T
= +
for
1A
0≤≤TT
= 2.5 for
A1B
≤≤T TT
EDP 2007 Eqn. 2.2
=
08
B
1
25 T
T



.
.
for
B1
<
TT
Spectrum Characteristic Periods, TA and TB, are specified in 2007 TSC
Table 2.4.
Local Site Class
TA
Z1
0.10
Z2
0.15
Z3
0.15
Z4
0.20
Ra = Seismic Load Reduction Factor that is determine using 2007 TSC
Eqn. 2.3.
1
A
( ) 1.5 ( 1.5)
=+−
a
T
RT R T
for
1A
0≤≤
TT
1
( ) =
a
RT R
for
1A
>TT
Note that the weight, W, that ETABS uses is derived from the building mass.
The total base shear, V, is broken into a concentrated force applied to the top
of the building and forces applied at each story level in accordance with the
following equations:
story
story 1
N
N
VF F
=
= + ∑
where,
V = Building base shear.
2 - 92 2007 Turkish Seismic Code (TSC) Loads
Chapter 2 - Automatic Seismic Loads
FN = Concentrated force at the top of the building.
Fstory = Portion of base shear applied to a story level.
n = Number of story levels in the building.
The concentrated force at the top of the building, FN, is calculated as:
0.0075=
N
F NV
EDP 2007 Eqn. 2.8
where,
N = Number of story levels in the building.
V = Building base shear.
The remaining portion of the base shear, (V – FN), is distributed over the
height of the building in accordance with the Equation (2007 TSC Equation
2.9):
( )
story story
story
story story
story 1
N
N
VFw h
F
wh
=
−
=∑
where,
Fstory = Portion of base shear applied to a story level.
V = Building base shear.
FN = Concentrated force at the top of the building.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of building to story level.
2007 Turkish Seismic Code (TSC) Loads 2 - 93
Automatic Seismic Loads
2.23 2009 Korean Building Code (KBC) Seismic
Loads
2.23.1 Options for 2009 KBC Building Period
Three options are provided for the building period used in calculating the
2009 KBC automatic seismic loads. They are as follows:
Approximate Period: Calculate the period based on (KBC 2009 Eqn.
0306.5.5). The values used for Ct and x are user input, and hn is deter-
mined by the programs from the input story level heights.
( )
0.75
A tn
T Ch=
(KBC 2009 Eqn. 0306.5.5)
Note that Ct is always input in Metric units, as specified in the code. A
typical range of values for Ct is 0.049 to 0.085. The height hn is measured
from the elevation of the specified bottom story/minimum level to the
(top of the) specified top story/maximum level in meters.
Program Calculated: The programs start with the period of the mode
calculated to have the largest participation factor in the direction that
loads are being calculated (X or Y). Call this period Tmode. A period is al-
so calculated based on (KBC 2009 Eqn. 0306.5.5). The values used for
Ct is user input, and hn is determined from the input story level heights.
Call this period TA.
The programs also calculate a coefficient for the upper limit on the calcu-
lated period, Cu. The building period, T, that the programs choose is de-
termined as follows:
– If Tmode ≤ CuTA, then T = Tmode.
– If Tmode > CuTA, then T = CuTA.
User Defined: In this case, input a building period, which the programs
use in the calculations. They do not compare it against CuTA. It is as-
sumed that this comparison is performed before the period is specified.
2 - 94 2009 Korean Building Code (KBC) Seismic Loads
Chapter 2 - Automatic Seismic Loads
2.23.2 Other Input Factors and Coefficients
The response modification factor, R, and the system overstrength factor, Ωο,
are direction dependent. Both are specified in KBC 2009 Table 0306.6.1. A
typical range of values for R is 1.5 to 8. A typical range of values for Ω ο is 2
to 3.
The programs determine the occupancy importance factor, IE, from the input
occupancy category and KBC 2009 Table 0306.4.1.
The seismic coefficients can be input in accordance with the code or they can
be user defined. If the seismic coefficients are in accordance with code, spec-
ify a site class, Ss and S1. If seismic coefficients are user defined, specify Ss,
S1, Fa and Fv.
The site class can be SA, SB, SC, SD, or SE. See KBC 2009 Table 0306.3.2 for
site class definitions.
Ss is the mapped maximum considered earthquake (MCE) spectral accelera-
tion for short periods as determined in KBC 2009 Section 0306.3.1. A typical
range of values for Ss is 0 to 0.55.
S1 is the mapped MCE spectral acceleration for a one second period as de-
termined in KBC 2009 Section 0306.3.3. A typical range of values for S1 is 0
to 0.22.
Fa is a site coefficient. If the site coefficients are determined in accordance
with code, the software automatically determines Fa from the site class and Ss
based on KBC 2009 Table 0306.3.3. A typical range of values for Fa is 0.8 to
2.5.
Fv is a site coefficient. If the site coefficients are determined in accordance
with code, the software automatically determines Fv from the site class and S1
based on KBC 2009 Table 0306.3.4. A typical range of values for Fv is 0.8 to
3.5.
2009 Korean Building Code (KBC) Seismic Loads 2 - 95
Automatic Seismic Loads
2.23.3 Algorithm for 2009 KBC Seismic Loads
The algorithm for determining KBC 2009 seismic loads is based on KBC
2009 Section 0306. A period is calculated as described in a preceding section
entitled "Options for KBC 2009 Building Period."
The programs begin by calculating the design spectral response acceleration
at short period, SDS, using (KBC 2009 Eqn. 0306.3.1).
2
3
DS a s
S FS=
(KBC 2009 Eqn. 0306.3.1)
Next, the design spectral response acceleration is calculated at a one second
period, SD1, using (KBC 2009 Eqn. 0306.3.2).
11
2
3
Dv
S FS
=
(KBC 2009 Eqn. 0306.3.2)
The programs determine a seismic design category (A, B, C, or D with A be-
ing the least severe and D being the most severe) based on KBC 2009 Sec-
tion 0306.4.3. A seismic design category is determined based on SDS using
KBC 2009 Table 0306.4.2. A seismic design category also is determined
based on SD1 using KBC 2009 Table 0306.4.3. The more severe of the two
seismic categories is chosen as the seismic design category for the building.
Initially a seismic response coefficient, Cs, is calculated using (KBC 2009
Eqn. 0306.5.2). This base shear value is then checked against the limits spec-
ified in (KBC 2009 Eqns. 0306.5.3, and 0306.5.4) and modified as necessary
to obtain the final base shear.
1D
s
E
S
CRT
I
=


(KBC 2009 Eqn. 0306.5.2)
where,
SD1 = the design spectral response acceleration at a one second period.
R = Response modification factor specified in KBC 2009 Table
0306.6.1.
2 - 96 2009 Korean Building Code (KBC) Seismic Loads
Chapter 2 - Automatic Seismic Loads
IE = The occupancy importance factor determined in accordance with
KBC 2009 Table 0306.4.1.
T = the building period used for calculating the base shear
The seismic response coefficient, Cs, need not exceed that specified in (KBC
2009 Eqns. 0306.5.3). If the seismic response coefficient calculated in ac-
cordance with (KBC 2009 Eqns. 0306.5.2) exceeds that calculated in accord-
ance with (KBC 2009 Eqns. 0306.5.3), the programs set the seismic response
coefficient, Cs, equal to that calculated in accordance with (KBC 2009 Eqns.
0306.5.3), as appropriate.
DS
s
E
S
CR
I
=


(KBC 2009 Eqn. 0306.5.3)
where,
SDS = The design spectral response acceleration at short periods.
and all other terms are as described for (KBC 2009 Eqn. 0306.5.2).
Cs shall not be less than that shown in (KBC 2009 Eqn. 0306.5.4).
Cs = 0.01 (KBC 2009 Eqn. 0306.5.4)
The base shear, V, is calculated using (KBC 2009 Eqn. 0306.5.8):
V = CsW (KBC 2009 Eqn. 0306.5.8)
Cs = Seismic response coefficient as determined from one of (KBC
2009 Eqns. 0306.5.2 through 0306.5.4) as appropriate.
W = Weight of the building (based on specified mass).
The base shear, V, is distributed over the height of the building in accordance
with (KBC 2009 Eqn. 0306.5.9)
story story
story
story story
story =1
k
nk
Vw h
F
wh
=∑
(KBC 2009 Eqn. 0306.5.9)
2009 Korean Building Code (KBC) Seismic Loads 2 - 97
Automatic Seismic Loads
where,
Fstory = Portion of base shear applied to a story level.
V = Building base shear.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
k = Exponent applied to building height. The value of k depends on
the value of the building period, T, used for determining the base
shear. If T ≤ 0.5 seconds, k = 1. If T ≥ 2.5 seconds, k = 2. If 0.5
seconds < T < 2.5 seconds, k is linearly interpolated between 1
and 2.
n = Number of story levels in the structure.
2.24 2011 Dominican Republic R-001 Seismic Loads
2.24.1 Options for 2011 Dominican Republic R-001 Seis-
mic Building Period
Two options are provided for the building period used in calculating the 2011
R-001 automatic seismic loads. They are as follows:
Program Calculated: The programs start with the period of the mode
calculated to have the largest participation factor in the direction that
loads are being calculated (X or Y).
User Defined: In this case, input a building period, which the programs
use in the calculations.
2.24.2 Other Input Factors and Coefficients
The response modification factor, Rd, is direction dependent. Rd is specified
in 2011 R-001 Table 8. A typical range of values for R is 2 to 5.5.
2 - 98 2011 Dominican Republic R-001 Seismic Loads
Chapter 2 - Automatic Seismic Loads
The seismic coefficients can be input by user. The seismic coefficients are in
Ss, S1, Fa and Fv.
Ss is the mapped spectral acceleration for short periods as determined in 2011
R-001 Table 1. Ss is 1.55g for Zone I and 0.95g for Zone II. The input in the
programs is in g.
S1 is the mapped spectral acceleration for a one second period as determined
in 2011 R-001 Table 1. S1 is 0.75 g for Zone I and 0.55g for Zone II. The in-
put in the programs is in g.
Fa is a site coefficient for short period as determined in 2011 R-001 Table 4.
Site coefficients are user defined, Fa is input directly by the user. A typical
range of values for Fa is 0.8 to 2.3.
Fv is a site coefficient for long period as determined in 2011 R-001 Table 5.
Site coefficients are user defined, Fv is input directly by the user. A typical
range of values for Fv is 0.8 to 3.2.
U is a use coefficient as determined in 2011 R-001 Table 7. Use coefficient is
user defined, U is input directly by the user. A typical range of values for U
is 0.9 to 1.50.
2.24.3 Algorithm for 2011 Dominican Republic R-001
Seismic Loads
The algorithm for determining 2011 Dominican Republic R-001 seismic
loads is based on 2011 R-001 Section 34. A period is calculated as described
in a preceding section entitled "Options for 2011 Dominican Republic R-001
Building Period."
The programs begin by calculating the design spectral response acceleration
at short periods, SDS.
2
3
DS a s
S FS=
Next, the design spectral response acceleration is calculated at a one second
period, SD1.
2011 Dominican Republic R-001 Seismic Loads 2 - 99
Automatic Seismic Loads
11
2
3
Dv
S FS=
The programs determine T0 and Ts.
1
0
0.2
D
DS
S
TS
=
, and
0
5
s
TT=
The spectral acceleration (Sa(T)) at building period T is determined based on
the expressions:
0
0
0
1
0.6 0.4 if
( ) if
if
DS DS
a DS s
Ds
ST S TT
T
ST S T T T
STT
T
+≤
= <≤
>
,
Initially a seismic response coefficient, Cs, is calculated using Article 35.
This base shear value is then checked against the limits specified.
( )
0.03
a
s
UST
CRd
•
= ≥
The base shear, V, is calculated using Article 39.
V = Cs W
Cs = Seismic response coefficient as determined.
W = Weight of the building (based on specified mass).
The base shear, V, is distributed over the height of the building in accordance
with (Article 44).
story story
story
story story
story 1
n
Vw h
F
wh
=
=∑
2 - 100 2011 Dominican Republic R-001 Seismic Loads
Chapter 2 - Automatic Seismic Loads
where,
Fstory = Portion of base shear applied to a story level.
V = Building base shear.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
n = Number of story levels in the structure.
2.25 User Defined Seismic Loads
2.25.1 Input Factors and Coefficients
The base shear coefficient, C, is direction dependent. This coefficient multi-
plied times the building weight gives the lateral seismic base shear in the
direction specified.
The building height exponent, k, is used as an exponent on the building
height when determining the distribution of the base shear over the height of
the building.
2.25.2 Algorithm for User Defined Seismic Loads
The base shear, V, is calculated using (Eqn. 2-6):
V = C W (Eqn. 2-6)
where,
C = User-defined base shear coefficient.
W = Weight of the building (based on specified mass).
The base shear, V, is distributed over the height of the building in accordance
with (Eqn. 2-7):
User Defined Seismic Loads 2 - 101
Automatic Seismic Loads
story story
story
story story
story =1
k
nk
Vw h
F
wh
=∑
(Eqn. 2-7)
where,
Fstory = Portion of base shear applied to a story level.
V = Building base shear.
wstory = Weight of story level (based on specified mass).
hstory = Story height, distance from base of structure to story level.
k = A user-defined exponent.
n = Number of story levels in the structure.
2.26 Response Spectrum Functions
A response spectrum function is simply a list of period versus spectral accel-
eration values. In the programs, the acceleration values in the function are
assumed to be normalized; that is, the functions themselves are not assumed
to have units. Instead, the units are associated with a scale factor that multi-
plies the function and is specified when the response spectrum case is de-
fined.
Response spectra can be defined in the programs from a text file (From File),
from user specified parameters (User), and based on one of several built-in
code response spectra.
2.26.1 From File
A response spectrum definition can be added from a text file. The text file
should have period and spectral acceleration values. One set of values (peri-
od and spectral acceleration) should be provided on each line. Any line that
has a $ symbol in the first character space is treated as a comment line and
ignored. Any number of header lines at the beginning of the file can be speci-
2 - 102 Response Spectrum Functions
Chapter 2 - Automatic Seismic Loads
fied to be ignored by the program. Those header lines do not need $ symbols
at the beginning of them. The program quits reading the file when it reaches
the end of the file or when it reaches a blank line. Note that the program con-
siders a line with the first character space blank, the second character space a
$ symbol and anything beyond the $ symbol as a blank line.
Typically the program does not import the file into its database. It simply
maintains a link to the file location. Thus, if the response spectrum file is
moved, or if the .model file is moved to another location, the program may
suddenly be unable to locate the response spectrum file. If the response spec-
trum based on a text file is converted to a user-defined response spectrum,
the program imports the response spectrum into its database file and the data
will always be available to the model.
The program reads the response spectrum function file as follows:
o First it skips the specified number of header lines specified by the user.
o Next it checks to see if a line has a $ symbol as the first character. If it
does, then it skips to the next line.
o If there is not a $ symbol as the first character on the line, the program
reads the information on the line.
o If the line is blank or if the end of the file is reached, the program stops
reading and closes the file.
2.26.2 User
When defining a User Spectrum, the period and spectral acceleration values
are input for the function by the user.
2.26.3 Code Specific
The program allows definition of code specific response spectrum functions
for a variety of building codes. The user can apply the program defaults or
specify the parameters that define the code specific response spectrum. These
parameters vary from code to code. The parameters specified for each of the
codes included in the program are identified in sections that follow.
Response Spectrum Functions 2 - 103
Automatic Seismic Loads
2.26.4 1994 UBC Parameters for a Response Spectrum
Function
The 1994 UBC response spectrum function is based on Figure 16-3 in Chap-
ter 16 of the 1994 UBC. The digitization of these response spectra is based
on Section C106.2.1 in the 1996 SEAOC Recommended Lateral Force Re-
quirements and Commentary (more commonly called the SEAOC Blue
Book).
The parameters required are a seismic zone factor, Z and a soil type. Any
positive, nonzero value can be specified for the seismic zone factor; see
Table 16-I in the 1994 UBC for typical values. The soil type can be input as
1, 2 or 3; see Table 16-J in the 1994 UBC for typical values.
2.26.5 1997 UBC Parameters for a Response Spectrum
Function
The 1997 UBC response spectrum function is constructed as shown in Figure
16-3 in Chapter 16 of the 1997 UBC. The parameters required are seismic
coefficients Ca and Cv. Any positive, nonzero value can be specified for the
seismic coefficients. See Tables 16-Q and 16-R in the 1997 UBC for typical
values of these coefficients.
2.26.6 1996 BOCA Parameters for a Response Spectrum
Function
The following parameters are input for the 1996 BOCA response spectrum
function. Any positive, nonzero value can be input for these parameters.
Aa = Seismic coefficient representing the effective peak acceleration
as determined in 1996 BOCA Section 1610.1.3.
Av = Seismic coefficient representing the effective peak velocity-
related acceleration as determined in 1996 BOCA Section
1610.1.3.
R = The response modification factor determined from 1996 BOCA
Table 1610.3.3.
2 - 104 Response Spectrum Functions
Chapter 2 - Automatic Seismic Loads
S = The coefficient for the soil profile characteristics of the site as
determined by 1996 BOCA Table 1610.3.1.
The 1996 BOCA response spectrum function is based on 1996 BOCA Sec-
tion 1610.5.5. The response spectrum is constructed by plotting the modal
seismic design coefficient, Csm, versus the modal period of vibration, Tm. For
a given period, Tm, the value of Csm is determined using (Eqn. 11-3).
23
1.2 2.5
va
sm
m
AS A
CR
RT
= ≤
(Eqn. 11-3)
2.26.7 1995 NBCC Parameters for a Response Spectrum
Function
The following parameters are input for the 1995 NBCC (Canadian) response
spectrum function.
v = Zonal velocity ratio.
Za = Acceleration-related seismic zone.
Zv = Velocity-related seismic zone.
Values for these parameters can be found in Appendix C of the 1995 NBCC.
Any positive, nonzero value can be input for the zonal velocity ratio, v. Any
positive integer, or zero, can be input for the acceleration and velocity-related
seismic zones.
The 1995 NBCC response spectrum function is based on item 44(a) in
Commentary J of the 1995 NBCC.
2.26.8 2005 NBCC Parameters for a Response Spectrum
Function
The following parameters are input for the 2005 NBCC (Canadian) response
spectrum function.
Peak Ground Acceleration (PGA)
Response Spectrum Functions 2 - 105
Automatic Seismic Loads
Sa(0.20) = Spectral Acceleration at 0.2 Sec.
Sa(0.50) = Spectral Acceleration at 0.5 Sec.
Sa(1.0) = Spectral Acceleration at 1.0 Sec.
Sa(2.0) = Spectral Acceleration at 2.0 Secs.
Site Class = A to F.
Values for these parameters can be found in Appendix C of the 2005 NBCC.
Any positive, nonzero value can be input for the peak ground acceleration,
PGA. Any positive integer, or zero, can be input for the spectral acceleration.
The 2005 NBCC response spectrum function is based on item 72 in Com-
mentary J of the 2005 NBCC.
2.26.9 2010 NBCC Parameters for a Response Spectrum
Function
The following parameters are input for the 2010 NBCC (Canadian) response
spectrum function.
Peak Ground Acceleration (PGA)
Sa(0.20) = Spectral Acceleration at 0.2 Sec.
Sa(0.50) = Spectral Acceleration at 0.5 Sec.
Sa(1.0) = Spectral Acceleration at 1.0 Sec.
Sa(2.0) = Spectral Acceleration at 2.0 Secs.
Site Class = A to F.
Values for these parameters can be found in Appendix C of the 2010 NBCC.
Any positive, nonzero value can be input for the peak ground acceleration,
PGA. Any positive integer, or zero, can be input for the spectral acceleration.
The 2010 NBCC response spectrum function is based on item 4.1.8.4(7) Part
4 of Division B of the 2010 NBCC.
2 - 106 Response Spectrum Functions
Chapter 2 - Automatic Seismic Loads
2.26.10 2015 NBCC Parameters for a Response Spectrum
Function
The following parameters are input for the 2015 NBCC (Canadian) response
spectrum function.
Peak Ground Acceleration (PGA)
Sa(0.20) = Spectral Acceleration at 0.2 Sec.
Sa(0.50) = Spectral Acceleration at 0.5 Sec.
Sa(1.0) = Spectral Acceleration at 1.0 Sec.
Sa(2.0) = Spectral Acceleration at 2.0 Secs.
Sa(5.0) = Spectral Acceleration at 5.0 Secs.
Sa(10.0) = Spectral Acceleration at 10.0 Secs.
Site Class = A to F.
Values for these parameters can be found in Appendix C of the 2010 NBCC.
Any positive, nonzero value can be input for the peak ground acceleration,
PGA. Any positive integer, or zero, can be input for the spectral acceleration.
For Site Class F, additional parameters i.e., F(0.20), F(0.50), F(1.0), F(2.0),
F(5.0 and F(10.0) are also required user input.
The 2015 NBCC response spectrum function is based on item 4.1.8.4(7) Part
4 of Division B of the 2015 NBCC.
2.26.11 2003 IBC/ASCE 7-02 Parameters for a Response
Spectrum Function
The following parameters are input for the 2003 IBC response spectrum
function. Any positive, nonzero value can be input for these parameters.
SDS = The 5% damped design spectral response acceleration at short
periods as specified in 2003 IBC Section 1615.1.3.
Response Spectrum Functions 2 - 107
Automatic Seismic Loads
SD1 = The 5% damped design spectral response acceleration at a one
second period as specified in 2003 IBC Section 1615.1.3.
The 2003 IBC response spectrum function is based on the procedure de-
scribed in 2003 IBC Section 1615.1.4.
2.26.12 2006 IBC/ASCE 7-05 Parameters for a Response
Spectrum Function
The following parameters are input for the 2006 IBC response spectrum
function. Any positive, nonzero value can be input for these parameters.
SS = The 5% damped design spectral response acceleration at short
periods as specified in 2006 IBC Section 1613.5.1 (ASCE 7-05
11.4.1).
S1 = The 5% damped design spectral response acceleration at a one
second period as specified in 2006 IBC Section 1613.5.1 (ASCE
7-05 11.4.1).
TL = Long-Period transition period(s) as specified in ASCE 7-05
11.4.5.
Site Class = Site class A to F as specified in IBC 2006 Section 1613.5.2
(ASCE 7-05 11.4.2).
The IBC 2006 response spectrum function is based on the procedure
described in IBC 2006 Section 1613.2.1.4 (ASCE 7-05 11.4).
2.26.13 2009 IBC/ASCE 7-05 Parameters for a Response
Spectrum Function
The following parameters are input for the 2009 IBC response spectrum
function. Any positive, nonzero value can be input for these parameters.
SS = The 5% damped design spectral response acceleration at short
periods as specified in 2009 IBC Section 1613.5.1 (ASCE 7-05
11.4.1).
2 - 108 Response Spectrum Functions
Chapter 2 - Automatic Seismic Loads
S1 = The 5% damped design spectral response acceleration at a one
second period as specified in 2009 IBC Section 1613.5.1 (ASCE
7-05 11.4.1).
TL = Long-Period transition period(s) as specified in ASCE 7-05
11.4.5.
Site Class = Site class A to F as specified in 2009 IBC Section 1613.5.2
(ASCE 7-05 11.4.2).
The 2009 IBC response spectrum function is based on the procedure
described in 2009 IBC Section 1613.2.1.4 (ASCE 7-05 11.4).
2.26.14 2012 IBC/ASCE 7-10 Parameters for a Response
Spectrum Function
The following parameters are input for the 2012 IBC response spectrum
function. Any positive, nonzero value can be input for these parameters.
SS = The 5% damped design spectral response acceleration at
short periods as specified in IBC 2012 Section 1613.3.1
(ASCE 7-10 11.4.1).
S1 = The 5% damped design spectral response acceleration at a
one second period as specified in IBC 2012 Section
1613.3.1 (ASCE 7-10 11.4.1).
TL = Long-Period transition period(s) as specified in ASCE 7-
10 11.4.5.
Site Class = Site class A to F as specified in IBC 2012 Section 1613.3.2
(ASCE 7-10 11.4.2).
The IBC 2012 response spectrum function is based on the procedure
described in IBC 2012 Section 1613.3 (ASCE 7-10 11.4).
Response Spectrum Functions 2 - 109
Automatic Seismic Loads
2.26.15 1997 NEHRP Parameters for a Response Spectrum
Function
The following parameters are input for the 1997 NEHRP response spectrum
function. Any positive, nonzero value can be input for these parameters.
SDS = The design earthquake spectral response acceleration at short
periods as specified in (1997 NEHRP Eqn. 4.1.2.5-1).
SD1 = The design earthquake spectral response acceleration at a one
second period as specified in (1997 NEHRP Eqn. 4.1.2.5-2).
The 1997 NEHRP response spectrum function is based on the procedure
described in 1997 NEHRP Section 4.1.2.6.
2.26.16 1998 Eurocode 8 Parameters for a Response Spec-
trum Function
The 1998 Eurocode 8 response spectrum function is constructed as described
in 1998 Eurocode ENV 1998-1-1:1994 Section 4.2.2. The parameters to be
entered are the design ground acceleration, ag, the subsoil class and the
damping correction factor, η. Any positive, nonzero value can be specified
for the design ground acceleration. The damping correction factor must satis-
fy η ≥ 0.7. The subsoil class can be input as A, B, or C.
The ordinates of the response spectrum are calculated using Eqns. 4.1
through 4.4 in 1998 Eurocode ENV 1998-1-1:1994 Section 4.2.2. The values
of βo, TB, TC, TD, k1, k2, and S are taken from Table 4.1 in 1998 Eurocode
ENV 1998-1-1:1994 Section 4.2.2. Note that the value of these items de-
pends on the specified subsoil class.
2.26.17 2004 Eurocode 8 Parameters for a Response Spec-
trum Function
The 2004 Eurocode 8 response spectrum function is constructed as described
in EN 1998-1-1:2004 Section 3.2.2.5. The parameters to be entered are the
design spectrum type, the ground type, the lower bound factor for the hori-
zontal design spectrum, β and the behavior correction factor, q. Any positive,
2 - 110 Response Spectrum Functions
Chapter 2 - Automatic Seismic Loads
nonzero value can be specified for the design ground acceleration. The be-
havior factor must satisfy q ≥ 1.5 (the program will accept any nonzero val-
ue). The subsoil class can be input as A, B, C, D or E.
The ordinates of the response spectrum are calculated using Eqns. 3.13
through 3.16 in EN 1998-1-1:2004 Section 3.2.2.5. The values of TB, TC, TD,
and S are taken from Table 3.2 or 3.3 in 1998 Eurocode EN 1998-1-1:2004
Section 3.2.2.5. Note that the value of these items depends on the specified
ground type and spectrum type.
2.26.18 1992 NZS 4203 Parameters for a Response Spec-
trum Function
For the 1992 NZS 4203 (New Zealand) response spectrum function, input a
scaling factor and a site subsoil category. Any positive, nonzero value can be
specified for the scaling factor. The site subsoil category can be input as A,
B, or C.
The 1992 NZS 4203 (New Zealand) response spectrum function is construct-
ed as specified in 1992 NZS 4203 Section 4.6.
The ordinates of the response spectrum are calculated using (1992 NZS4203
Eqns. 4.6.3 and 4.6.4). If (1992 NZS4203 Eqn. 4.6.3) is used, input the scal-
ing factor as (Sp)(R)(Z)(Ls). If (1992 NZS4203 Eqn. 4.6.4) is used, input the
scaling factor as (Sm)(Sp)(R)(Z)(Lu).
The program calculates the Ch(T, 1) term in (1992 NZS4203 Eqns. 4.6.3 and
4.6.4) based on the input site subsoil category and the values for µ = 1.0 in
Figures 4.6.1a, b, and c and in Tables 4.6.1a, b, and c. In Table 4.6.1a the co-
efficient values for periods of 0, 0.09, and 0.20 second are taken as 0.40,
0.68, and 0.68, respectively. In Table 4.6.1b the coefficient values for periods
of 0, 0.13, and 0.20 second are taken as 0.42, 0.80 and 0.80, respectively. In
Table 4.6.1c the coefficient values for periods of 0 and 0.10 second are taken
as 0.42 and 0.72, respectively.
Response Spectrum Functions 2 - 111
Automatic Seismic Loads
2.26.19 2004 NZS 1170.5 Parameters for a Response Spec-
trum Function
For the 2004 NZS 1170.5 (New Zealand) response spectrum function, the
following parameters are input. Any positive, nonzero value can be input for
these parameters.
Site Class = Site class A to E as specified in NZS 1170.5 clause 3.1.3.
Z = The hazard factor determined from NZS 1170.5 clause
3.1.4.
R = The return period factor Rs or Ru for the appropriate limit
state determined from NZS 1170.5 clause 3.1.5 but limited
such that ZRu does not exceed 0.7.
D = D is the shortest distance (in kilometers) from the site to
the nearest fault listed in Table 3.6. The distance, D, is
used to compute the near-fault factor, N(D,T), as given in
Subsection 3.1.6.2 of the 2004 NZS 1170.5. A typical
range of values for N(D,T) is 1 to 1.72.
Ch(T) = The spectral shape factor determined from NZS 1170.5
clause 3.1.2 and Table 3.1 (computed by the program
computed based on time period).
The NZS 1170.5:2004 response spectrum function is constructed as specified
in NZS 1170.5:2004 Section 3.1.1.
2.26.20 2007 AS 1170.4 Parameters for a Response Spec-
trum Function
For the 2007 AS 1170.4 (Australia) response spectrum function, the follow-
ing parameters are input. Any positive, nonzero value can be input for these
parameters.
Ch(T) = Spectral shape factor for period T as determined by the
program from Table 6.4 of the AS 1170.4.
2 - 112 Response Spectrum Functions
Chapter 2 - Automatic Seismic Loads
kp = Return period factor as determined for AS 1170.4 clause
3.1.
Z = Hazard factor as determined for AS 1170.4 clause 3.2.
Site Class = Site class Ae to Ee as specified in AS 1170.4 clause 4.1.
Sp = Structural performance factor as given in AS 1170.4 clause 6.5.
μ = Structural ductility factor as given in AS 1170.4 clause 6.5.
The AS 1170.4:2007 response spectrum function is constructed as specified
in AS 1170.4:2007 clause 7.2(a).
2.26.21 2007 AASHTO Parameters for a Response Spec-
trum Function
The AASHTO 2007 ground motion design spectra in CSiBridge is developed
in accordance with the AASHTO Guide Specifications for LRFD Seismic
Bridge Design. The design spectra uses the digitized USGS maps developed
for AASHTO. Those maps were developed for a hazard of 7% probability of
exceedance in 75 years (1000 return period).
The following parameters are input for the AASHTO 2007 response spec-
trum function. Any positive, nonzero value can be input for these parameters.
SS = 0.2-Sec period spectral acceleration coefficient on Class B
rock.
S1 = 1.0-Sec period spectral acceleration coefficient on Class B
rock.
Site Class = Site class A to F as specified in Section 3.4.2.1 and Table 1.
The AASHTO 2007 response spectrum function is based on the procedure
described in AASHTO Guide Specifications for LRFD Seismic Bridge De-
sign, Section 3.4.1.
Response Spectrum Functions 2 - 113
Automatic Seismic Loads
2.26.22 2012 AASHTO Parameters for a Response Spec-
trum Function
The AASHTO 2012 ground motion design spectra in CSiBridge is developed
in accordance with the AASHTO Guide Specifications for LRFD Seismic
Bridge Design. The design spectra uses the digitized USGS maps developed
for AASHTO. Those maps were developed for a hazard of 7% probability of
exceedance in 75 years (1000 return period).
The following parameters are input for the AASHTO 2012 response spec-
trum function. Any positive, nonzero value can be input for these parameters.
SS = 0.2-Sec period spectral acceleration coefficient on Class B
rock.
S1 = 1.0-Sec period spectral acceleration coefficient on Class B
rock.
Site Class = Site class A to F as specified in Section 3.4.2.1 and Table 1.
The AASHTO 2012 response spectrum function is based on the procedure
described in AASHTO Guide Specifications for LRFD Seismic Bridge De-
sign, Section 3.10.2.1.
2.26.23 2002 Indian IS:1893 Response Spectrum Function
The IS:1893 response spectrum function is based on Figure 2 in section 6.4.5
of the IS:1893 code. The digitization of these response spectra is based on
section 6.4.5.
The parameters required are a seismic zone factor Z, soil type and the damp-
ing ratio of the building structure. These values can be selected from relevant
sections of the IS:1893 code.
2 - 114 Response Spectrum Functions
Chapter 2 - Automatic Seismic Loads
2.26.24 2008 Italian NTC Parameters for a Response Spec-
trum Function
The 2008 Italian NTC response spectrum function is constructed as described
in Technical Rules for Construction (NTC 2008). The parameters to be en-
tered are Fundamental Parameters, ag, F0 and Tc*, the spectrum type, the limit
state, the soil type, the topography, the ratio for site altitude at base of hill to
height of hill (h/H), the damping (ξ) for elastic spectrum and the behavior
correction factor (q) for design spectrum. Any positive, nonzero value can be
specified for the Fundamental Parameters. The behavior factor must satisfy q
≥ 1.0 (the program will accept any nonzero value). The subsoil type can be
input as A, B, C, D or E. The topography type can be T1, T2, T3 or T4.
The Fundamental Parameters ag (peak ground acceleration), F0 (magnifica-
tion factor) and Tc* (reference period), can be entered based on a given set of
Latitude and Longitude, by Island name or user specified. For Latitude and
Longitude and Island Name options, user also need to input the Limit State,
the Usage Class and the Nominal Life of the structure. These parameters are
used for computing Return period, TR.
( )
ln 1 R
R
VR
V
TP
−
=−
and,
R UN
V CV=
where,
VN = nominal life of the structure
CU = usage coefficient
Usage Class
I
II
III
IV
Coefficient, CU
0.7
1.0
1.5
2.0
The Limit State option can be SLO, SLD for elastic spectrum and SLV and
SLC for design spectrum. The PVR parameters are determined from the fol-
lowing table:
Response Spectrum Functions 2 - 115
Automatic Seismic Loads
Spectrum Type
Limit State
PVR %
Description
Elastic
SLO
81
Immediate Occupancy
SLD
63
Damage Control
Design
SLV
10
Life safety
SLC
5
Collapse Prevention
For a given return period, TR the parameters ag(TR), F0(TR) and Tc*(TR), here
called p, can be calculated as follows:
( ) ( )
1
1
2
1
1
2
1logloglog
loglog
−
⋅
⋅
+=
R
R
R
R
T
T
T
T
p
p
p
p
The ordinates of the response spectrum are calculated using the equations
given below. The values of TB, TC, TD, and S depend on the specified soil
type and spectrum type.
2.26.24.1 Horizontal Elastic Response Spectrum
e0
0
1
0 S( ) 1


≤< = + −




g
B
BB
aTT
T T T SF
g TFT
ηη
e0
S( )≤< =
g
BC
a
T T T T SF
g
η
e0
S( ) 
≤< = 

gC
CD
aT
T T T T SF
gT
η
e0
2
S( ) 
≤=


gCD
D
aTT
T T T SF
gT
η
( )
10 5 0.55= +≥
ηξ
, where ξ is damping in percent
The S and spectra ordinate are based on the following equations:
=sT
S SS
2 - 116 Response Spectrum Functions
Chapter 2 - Automatic Seismic Loads
*
C CC
T CT=
;
3
C
B
T
T=
;
4 1.6
= +
g
D
a
Tg
The parameter Cc, Ss and ST are obtained using Soil Type and Topography.
Soil Type
Ss
Cc
A
1.00
1.00
B
0
1.00 1.40 0.40 1.20≤− ≤
g
a
Fg
( )
0.20
*
1.10
−
c
T
C
0
1.00 1.70 0.6 1.501≤− ≤
g
a
Fg
( )
0.33
*
1.05
−
c
T
D
0
0.90 2.40 1.5 1.80≤− ≤
g
a
Fg
( )
0.50
*
1.25
−
c
T
E
0
1.00 2.00 1.10 1.60≤− ≤
g
a
Fg
( )
0.40
*
1.15
−
c
T
Topography
ST
T1
1.0
T2
1.0 1 0.2 1.2≤+ ≤
h
H
T3
1.0 1 0.2 1.2≤+ ≤
h
H
T4
1.0 1 0.4 1.4≤+ ≤
h
H
2.26.24.2 Vertical Elastic Response Spectrum
ve
0
1
0 S() 1


≤< = η + −


η

g
Bv
BB
aTT
T T T SF
g TFT
ve
S()≤< = η
g
BC v
a
T T T T SF
g
ve
S() 
≤< = η

gC
CD v
aT
T T T T SF
gT
Response Spectrum Functions 2 - 117
Automatic Seismic Loads
2
S() 
≤=η


gCD
D ve v
aTT
T T T SF
gT
( )
10 5 0.55
= +≥
ηξ
, where ξ is damping in percent
=sT
S SS
0.5
0
1.35 
=

g
v
a
FF
g
Soil Type Ss TB TC TD
A, B, C, D, E 1.00 0.05 s 0.15 s 1.0 s
Topography
ST
T1
1.0
T2
1.2
T3
1.2
T4
1.4
2.26.24.3 Design Horizontal Response Spectrum
The Design Horizontal Spectrum is same as Elastic Horizontal spectrum ex-
cept the following:
The η parameter for Design spectrum is defined as
h
q/
1=
η
where, qh is the structure behavior factor for horizontal component
2.26.24.4 Design Vertical Response Spectrum
The Design Vertical Spectrum is same as Elastic Vertical spectrum except
the followings:
The η parameter for Design spectrum is defined as
1/
v
qη=
2 - 118 Response Spectrum Functions
Chapter 2 - Automatic Seismic Loads
where, qv is the structure behavior factor for vertical component (1.5 for
buildings, 1.0 for bridges).
2.26.25 2007 TSC Parameters for a Response Spectrum
Function
The 2007 TSC response spectrum function is based on Figure 2.5 in Part II of
the 2007 TSC. The digitization of these response spectra is based on Section
2.4.4.
The parameters required are a seismic zone factor, Z, local site classes for
soil characteristics, R and importance factor, I. Any positive, nonzero value
can be specified for the importance and R factor. The local site classes for
soil characteristic can be input as Z1, Z2, Z3 or Z4; see Table 2.2 to 2.5 in
the 2007 TSC for typical values.
2.26.26 1995 SI 413 Parameters for a Response Spectrum
Function
The following parameters are input for the 1995 SI 413 response spectrum
function. Any positive, nonzero value can be input for these parameters.
Z = Ground Acceleration coefficient representing the effective peak
acceleration as determined in 1995 SI 413 Section 202.1.
S = The Soil type of the site as determined by 1995 SI 413 Table
202.2.
I = The Importance factor as determined in 1995 SI 413.
K = The Seismic force reduction factor as determined from 1995 SI
413 Tables 5, 6 or 7.
Response Spectrum Functions 2 - 119
Automatic Seismic Loads
2.26.27 KBC 2009 Parameters for a Response Spectrum
Function
The following parameters are input for the 2009 KBC response spectrum
function. Any positive, nonzero value can be input for these parameters.
S1 = The design spectral response acceleration as specified in 2009
KBC Section 0306.3.1, Table 0306.3.1.
Ss = The design spectral response acceleration at a one second period.
In KBC 2009, Ss is 2.5 times the value S1 from Table 0306.3.1.
Site Class = Site class SA to SE as specified in KBC 2009 Section
0306.3.2.1, Table 0306.3.2.
The KBC 2009 response spectrum function is based on the procedure
described in KBC 2009 Section 0306.3.
2.26.28 2013 Argentina Regulation 103 INPRES-CIRSOC Pa-
rameters for a Response Spectrum Function
The following parameters are input for the 2013 Spectrum of Argentina un-
der Regulation 103 Inpres-CIRSOC response spectrum function. Any posi-
tive, nonzero value can be input for these parameters.
Z = The seismic zone as specified in 2013 Spectrum of Argentina
under Regulation 103 Inpres-CIRSOC Annex A Section 2.2,
Figure 2.
S = The soil type as specified in 2013 Spectrum of Argentina under
Regulation 103 Inpres-CIRSOC Table 2.2.
Group = The occupation category as specified in 2013 Spectrum of Ar-
gentina under Regulation 103 Inpres-CIRSOC Chapter 2.4.
R = The response modification factor as specified in 2013 Spectrum
of Argentina under Regulation 103 Inpres-CIRSOC Table 5.1.
The 2013 Argentina Regulation 03 Inpres-CIRSOC response spectrum func-
tion is based on the procedure described in Inpres-CIRSOC Section 3.5.
2 - 120 Response Spectrum Functions
Chapter 2 - Automatic Seismic Loads
2.26.29 1993 Chile Standard NCh433 + DS61 Parameters for
a Response Spectrum Function
The following parameters are input for the 1993 Chile Standard NCh433 +
DS61 response spectrum function. Any positive, nonzero value can be input
for these parameters.
Z = The seismic zone as specified in 1993 Chile Standard NCh433 +
DS61 Table 4.2.
S = The soil type as specified in 1993 Chile Standard NCh433 +
DS61.
Category = The occupation category as specified in 1993 Chile Standard
NCh433 + DS61 Table 4.1.
The 1993 Chile Standard NCh433 + DS61 response spectrum function is
based on the procedure described in Section 6.3.5.
2.26.30 2003 Chile Standard 2369 Parameters for a Re-
sponse Spectrum Function
The following parameters are input for the 2003 Chile Standard 2369 re-
sponse spectrum function. Any positive, nonzero value can be input for these
parameters.
I = The importance factor as specified in 2003 Chile Standard 2369
Section 4.3.2.
Z = The seismic zone as specified in 2003 Chile Standard 2369 Table
5.2.
S = The soil type as specified in 2003 Chile Standard 2369 Table
5.4.
R = The response modification factor as specified in 2003 Chile
Standard 2369 Table 5.7.
The 2003 Chile Standard 2369 response spectrum function is based on the
procedure described in Section 5.3.3.
Response Spectrum Functions 2 - 121
Automatic Seismic Loads
2.26.31 2010 Colombian Regulations NSR–10 Parameters
for a Response Spectrum Function
The following parameters are input for the 2010 Colombian Regulations
NSR–10 response spectrum function. Any positive, nonzero value can be in-
put for these parameters.
Aa = The effective peak acceleration as specified in 2010 Colombian
Regulations NSR–10 Appendix A4.
Av = The effective peak velocity as specified in 2010 Colombian
Regulations NSR–10 Appendix A4.
Ae = The reduced effective peak acceleration as specified in 2010 Co-
lombian Regulations NSR–10 Appendix A4.
Ad = The effective peak acceleration for the damage threshold as speci-
fied in 2010 Colombian Regulations NSR–10 Appendix A4.
U = The Group of Use as specified in 2010 Colombian Regulations
NSR–10 Section A.2.5.1.
Fa = The amplification factor of the acceleration for short periods as
specified in 2010 Colombian Regulations NSR–10 A.2.4-3.
Fv = The amplification factor of the acceleration for interim periods
as specified in 2010 Colombian Regulations NSR–10 A.2.4-3.
The 2010 Colombian Regulations NSR–10 response spectrum function is
based on the procedure described in Section A2.6.1.
2.26.32 2011 Ecuador Standard NEC–11 Parameters for a
Response Spectrum Function
The following parameters are input for the 2011 Ecuador Standard NEC–11
response spectrum function. Any positive, nonzero value can be input for
these parameters.
Z = The Zone coefficient as specified in 2011 Ecuador Standard
NEC–11 Table 2.2.
2 - 122 Response Spectrum Functions
Chapter 2 - Automatic Seismic Loads
η = The η coefficient as specified in 2011 Ecuador Standard NEC–
11.
TS = The Soil types as specified in 2011 Ecuador Standard NEC–11
Table 2.3.
Fa = The Site factor as specified in 2011 Ecuador Standard NEC–11
Table 2.5.
Fd = The Site factor as specified in 2011 Ecuador Standard NEC–11
Table 2.6.
Fs = The inelastic behavior factor of subsurface as specified in 2011
Ecuador Standard NEC–11 Table 2.7.
I = The Importance factor as specified in 2011 Ecuador Standard
NEC–11 Table 2.9.
R = The Response Modification factor as specified in 2011 Ecuador
Standard NEC–11 Table 2.14.
The 2011 Ecuador Standard NEC–11 response spectrum function is based on
the procedure described in Section 2.5.5.1.
2.26.33 2010 Guatemala Standard AGIES NSE 2–10 Parame-
ters for a Response Spectrum Function
The following parameters are input for the 2010 Guatemala Standard AGIES
NSE 2–10 response spectrum function. Any positive, nonzero value can be
input for these parameters.
I0 = The Seismicity Index as specified in 2010 Guatemala Standard
AGIES NSE 2–10 Annex A.
Scr = The spectral sorted for short period as specified in 2010 Guate-
mala Standard AGIES NSE 2–10 Annex A.
S1r = The spectral sorted for long period as specified in 2010 Guate-
mala Standard AGIES NSE 2–10 Annex A.
Response Spectrum Functions 2 - 123
Automatic Seismic Loads
Fs = The Type of Seismic Source as specified in 2010 Guatemala
Standard AGIES NSE 2–10 Table 4-5.
Dh = The Horizontal distance to seismic source as specified in 2010
Guatemala Standard AGIES NSE 2–10.
TS = The types of earthquake as specified in 2010 Guatemala Stand-
ard AGIES NSE 2–10.
Fa = The Site coefficient as specified in 2010 Guatemala Standard
AGIES NSE 2–10 Table 4.2.
Fv = The Site coefficient as specified in 2010 Guatemala Standard
AGIES NSE 2–10 Table 4.3.
R = The Response modification factor as specified in 2010 Guatema-
la Standard AGIES NSE 2–10 Table 2.14.
The 2010 Guatemala Standard AGIES NSE 2–10 response spectrum function
is based on the procedure described in Section 4.3.4.2.
2.26.34 2004 Mexico Standard NTC–2004 Parameters for a
Response Spectrum Function
The following parameters are input for the 2004 Mexico Standard NTC–
2004 response spectrum function. Any positive, nonzero value can be input
for these parameters.
Z = The Seismicity Zone as specified in Mexico Standard NTC–2004
Section 1.4.
G = The Ranking by Group as specified in Mexico Standard NTC–
2004 chapter 7.
Q = The seismic behavior factor as specified in Mexico Standard
NTC–2004 chapter 5.
I = The correction factor by irregularity as specified in Mexico
Standard NTC–2004 chapter 6.
2 - 124 Response Spectrum Functions
Chapter 2 - Automatic Seismic Loads
The Mexico Standard NTC–2004 response spectrum function is based on the
procedure described in chapter 4.
2.26.35 2003 Peru Standard E.030 Parameters for a Re-
sponse Spectrum Function
The following parameters are input for the 2003 Peru Standard E.030 re-
sponse spectrum function. Any positive, nonzero value can be input for these
parameters.
ZS = The Seismic Zone as specified in 2003 Peru Standard E.030
Chapter 2, Figure 1.
CE = The Occupation category as specified in 2003 Peru Standard
E.030 Chapter 3, Table 3.
TS = The Soil Types as specified in 2003 Peru Standard E.030 Chap-
ter 2, Section 6.
SC = The Structural Configuration as specified in 2003 Peru Standard
E.030 Chapter 3, Section 11.
R = The Response modification factor as specified in 2003 Peru
Standard E.030 Chapter 3, Table 6.
The 2003 Peru Standard E.030 response spectrum function is based on the
procedure described in Chapter 4, section 18.2b.
2.26.36 2011 Dominican Republic Standard R–001 Parame-
ters for a Response Spectrum Function
The following parameters are input for the 2011 Dominican Republic Stand-
ard R–001 response spectrum function. Any positive, nonzero value can be
input for these parameters.
LC = The Location in near field as specified in 2011 Dominican Re-
public Standard R–001.
Response Spectrum Functions 2 - 125
Automatic Seismic Loads
Ss = The sorted spectral reference for short period as specified in
2011 Dominican Republic Standard R–001.
S1 = The sorted spectral reference for long period as specified in 2011
Dominican Republic Standard R–001.
Fa = The Soil factor associated to short period as specified in 2011
Dominican Republic Standard R–001.
Fv = The Soil factor associated to long period as specified in 2011
Dominican Republic Standard R–001.
Use = The Classification by user of structure as specified in 2011 Do-
minican Republic Standard R–001.
Rd = The Response modification factor as specified in 2011 Domini-
can Republic Standard R–001.
The 2011 Dominican Republic Standard R–001 response spectrum function
is based on the procedure described in Chapter 3.
2.26.37 2001 Venezuela Standard COVENIN 1756–1 Parame-
ters for a Response Spectrum Function
The following parameters are input for the 2001 Venezuela Standard
COVENIN 1756–1 response spectrum function. Any positive, nonzero value
can be input for these parameters.
Z = The Seismic Zone as specified in 2001 Venezuela Standard
COVENIN 1756–1 Table 4.2.
S = The Spectral form as specified in 2001 Venezuela Standard
COVENIN 1756–1 Table 5.1.
ρ = The Correction factor as specified in 2001 Venezuela Standard
COVENIN 1756–1 Chapter 6.
U = The Site coefficient as specified in 2001 Venezuela Standard
COVENIN 1756–1 Table 4.3.
2 - 126 Response Spectrum Functions
Chapter 2 - Automatic Seismic Loads
R = The Response modification factor as specified in 2001 Venezue-
la Standard COVENIN 1756–1 Table 6.4.
The 2001 Venezuela Standard COVENIN 1756–1 response spectrum func-
tion is based on the procedure described in Chapter 7.
2.26.38 2015 Ecuador Standard NEC–SE–DS Parameters for
a Response Spectrum Function
The following parameters are input for the 2015 Ecuador Standard NEC–SE–
DS response spectrum function. Any positive, nonzero value can be input for
these parameters.
Z = The Zone coefficient as specified in 2015 Ecuador Standard
NEC–SE–DS Table 1.
Soil Type = The soil type as specified in 2015 Ecuador Standard NEC–SE–
DS Table 2.
η = The η coefficient as specified in 2015 Ecuador Standard NEC–
SE–DS Section 3.3.1.
Fa = The Site factor as specified in 2015 Ecuador Standard NEC–SE–
DS Table 3.
Fd = The Site factor as specified in 2015 Ecuador Standard NEC–SE–
DS Table 4.
Fs = The inelastic behavior factor of subsurface as specified in 2015
Ecuador Standard NEC–SE–DS Table 5.
I = The Importance factor as specified in 2015 Ecuador Standard
NEC–SE–DS Table 6.
R = The Response Modification factor as specified in 2015 Ecuador
Standard NEC–SE–DS Table 15 and 16.
The 2015 Ecuador Standard NEC–SE–DS response spectrum function is
based on the procedure described in Section 3.3.1.
Response Spectrum Functions 2 - 127
Automatic Seismic Loads
2.26.39 2014 Peru Standard E.030 Parameters for a Re-
sponse Spectrum Function
The following parameters are input for the 2014 Peru Standard E.030 re-
sponse spectrum function. Any positive, nonzero value can be input for these
parameters.
ZS = The Seismic Zone as specified in 2014 Peru Standard E.030
Chapter 2, Figure 1, Table 1.
CE = The Occupation category as specified in 2014 Peru Standard
E.030 Chapter 3, Table 5.
SoilType = The soil type as specified in 2014 Peru Standard E.030 Chap-
ter 2, section 2.3.1.
Ia = The irregularity factor as specified in 2014 Peru Standard E.030
Chapter 3, Section 3.6, Table 8.
Ip = The irregularity factor as specified in 2014 Peru Standard E.030
Chapter 3, Section 3.6, Table 9.
R0 = The Response modification factor as specified in 2014 Peru
Standard E.030 Chapter 3, Table 7.
The 2014 Peru Standard E.030 response spectrum function is based on the
procedure described in Chapter 2, section 2.5.
2.26.40 2008 Mexico CFE Parameters for a Response Spec-
trum Function
The following parameters are input for the 2008 Mexico Standard CFE re-
sponse spectrum function. Any positive, nonzero value can be input for these
parameters.
Z = The Seismic Zone as specified in Mexico CFE 2008 code. The
seismic zone are A, B, C or D.
G = The Structural Classification as specified in Mexico CFE 2008
There are two types of structural classification i.e., 1 and 2.
2 - 128 Response Spectrum Functions
Chapter 2 - Automatic Seismic Loads
S = The Soil Type as specified in Mexico CFE 2008. Soil type can
be either I, II or III.
Q = The seismic behavior factor as specified in Mexico CFE 2008.
The values are 1, 1.5, 2, 3 and 4 .
I = The correction factor by irregularity as specified in Mexico CFE
2008. Correction factor can be either 0.8 or 1.0.
2.26.41 1993 Mexico CFE Parameters for a Response Spec-
trum Function
The following parameters are input for the 1993 Mexico Standard CFE re-
sponse spectrum function. Any positive, nonzero value can be input for these
parameters.
Z = The Seismic Zone as specified in Mexico CFE 1993 code. The
seismic zone are A, B, C or D.
G = The Structural Classification as specified in Mexico CFE 1993
There are two types of structural classification i.e., 1 and 2.
S = The Soil Type as specified in Mexico CFE 1993. Soil type can
be either I, II or III.
Q = The seismic behavior factor as specified in Mexico CFE 1993.
The values are 1, 1.5, 2, 3 and 4 .
I = The correction factor by irregularity as specified in Mexico CFE
1993. Correction factor can be either 0.8 or 1.0.
2.26.42 2010 Costa Rica Parameters for a Response Spec-
trum Function
The following parameters are input for the 2010 Costa Rica Seismic Design
code response spectrum function. Any positive, nonzero value can be select-
ed for these parameters.
Response Spectrum Functions 2 - 129
Automatic Seismic Loads
Zone = The Seismic Zone as specified in Costa Rica 2010 seismic
code. The seismic zone are II, III or IV.
Soil = The Soil Type as specified in Costa Rica 2010 seismic code.
Soil type can be either S1, S2, S3 or S4.
Occupancy = There are 4 occupancy Groups i.e., A to D in Costa Rica 2010
seismic code.
Overstrength = The ductility overstrength factor can be 1, 1.5, 2, 3, 4 and 6
as specified in Costa Rica 2010 seismic code.
2.26.43 SP 14.13330.2014 Response Spectrum Function
The Russian SP 14.13330.2014 response spectrum function is constructed
based on input parameters for the spectrum direction, region seismicity at the
construction site, soil category, nonlinear soil deformation factor, and three
additional factors.
The spectrum direction can be horizontal or vertical, for either buildings or
bridges. The region seismicity can be 6, 7, 8, or 9. The soil category can be I,
II, III, or IV.
The factor K0 is only applicable for buildings and should be input with a val-
ue greater than zero and less than or equal to two.
The factor K1 should be greater than zero and less than or equal to one. The
factor K
ψ
is only applicable for horizontal spectra and should be greater than
or equal to 0.5 and less than or equal to 1.5.
Nonlinear soil deformation can be taken into account for buildings with a soil
category of III or IV by inputting a value for asoil that is greater than zero and
less than or equal to one.
The following combinations of the region seismicity and soil category are no
permitted by the code:
• Soil Category – I and Seismicity = 6 or 7
• Soil Category – II and Seismicity = 6
2 - 130 Response Spectrum Functions
Chapter 2 - Automatic Seismic Loads
• Soil Category = III or IV and Seismicity = 9
The spectral acceleration, Sa, is calculated as follows:
Buildings –
Bridges –
where,
adirect = 0.75 for vertical response spectra
adirect = 1.0 for horizontal response spectra
The acceleration value, A, depends on the earthquake intensity and the soil
type, as shown in the following table.
I
II
III or IV
6
N/A
N/A
1 m/s2
7
N/A
1 m/s2
2 m/s2
8
1 m/s2
2 m/s2
4 m/s2
9
2m/s2
4 m/s2
N/A
The value
β
i is calculated based on the period of interest and shall be greater
than or equal to 0.8. The equations used depend on the soil type. For soil
types I and II,
β
i is calculated as:
For soil types III and IV,
β
i is calculated as:
Response Spectrum Functions 2 - 131
Chapter 3
Automatic Wind Loads
This chapter documents the automatic wind lateral static load patterns that can
be generated. Automatic wind loads can be generated in any arbitrary horizon-
tal direction for the following codes:
1994 UBC
1997 UBC
1996 BOCA
BS 6399-95
1995 NBCC
2005 NBCC
2010 NBCC
2015 NBCC
ASCE 7-88
ASCE 7-95
ASCE 7-02
2006 IBC/ASCE 7-05
ASCE 7-10
1987 RCDF (Mexico)
2010 Chinese
API 4F 2008
2005 Eurocode 1, Part 1-4
2011 AS/NZS 1170.2
2002 AS/NZS 1170.2
1987 Indian IS:875
2008 Italian NTC
1997 Turkish 498
3 - 1
Lateral Loads
3.1 Defining Automatic Wind Load Patterns
The commands used to define automatic seismic static load patterns are as
specified in the on-line, program-specific Help.
Each automatic static lateral load must be in a separate load pattern. That is,
two or more automatic static lateral loads cannot be specified in the same load
pattern. However, additional user-defined loads can be added to a load pattern
that includes an automatic static lateral load. A separate automatic static load
pattern must be defined for each direction of wind load.
Note that the actual forces associated with an automatic static lateral load are
not calculated until an analysis has been run. Thus, the resultant automatic
lateral loads cannot be reviewed until after an analysis has been run.
3.2 Automatic Wind Load Patterns
The forms defining the automatic wind loads consist of four data sets; some of
the data sets are dependent on the exposure selected.
One data set defines the exposure by selecting loading based on diaphragms or
area objects. Another data set defines the wind exposure parameters, and a
third set defines the exposure height. The fourth set is for specifying the wind
coefficients. The data in the first three sets is common to all of the codes and is
described in the subsections that follow. The wind coefficient data set is code-
dependent and is described separately for each code later in this chapter.
Wind loads also can be user defined, which is described at the end of this chap-
ter.
When the code is ASCE 7-95, ASCE 7-02, ASCE 7-05, ASCE 7-10 or NBCC
2015, automatic wind load patterns may become multi-stepped. For example, a
wind load may be specified as occurring at multiple angles around the struc-
ture. These will be treated as a single load pattern and will be analyzed in a
single load case, producing multiple output steps of response, one for each sep-
arate step of the load.
3 - 2
Chapter 3 - Automatic Wind Loads
When a multi-stepped load pattern is applied in a load case, the following rules
govern how it will be handled:
1. In a linear static load case, the load case will internally be run as a multi-
linear static load case, producing multiple output steps.
2. In a nonlinear static load case, the load case will internally be run as a new
type of staged-construction load case, where each stage starts from the be-
ginning of the load case, producing results similar to the multi-linear static
load case.
3. All other load cases (including staged-construction) are unchanged, and
will treat the load pattern as single-stepped, using the first step of the mul-
ti-stepped load pattern.
4. For cases 1 and 2, if several multi-stepped load patterns are applied in a
single load case, they superpose on a step-wise basis. For example, if load
pattern A has 3 steps and load pattern B has 5 steps, the load case will ap-
ply five independent load steps: A1+B1, A2+B2, A3+B3, B4, B5. If a non-
stepped load pattern is applied, such as Dead, it is applied in every load
step.
3.2.1 Exposure
The automatically calculated wind loads may be determined by exposure to di-
aphragms or to area objects (i.e., exterior cladding, walls, and roofs).
If exposure from the extents of diaphragms is selected, a separate lateral load is
created for each diaphragm present at a story level. The wind loads calculated
at any story level are based on the story level elevation, the story height above
and below that level, the assumed exposure width for the diaphragm(s) at the
story level, and various code-dependent wind coefficients.
If area objects are used to model the actual in-plane stiffness of the diaphragm
and automatic wind loads are to be created using the diaphragm option, one or
more dummy diaphragms must be defined at each story level. Assign a dummy
diaphragm to just one point object at a story level; that point object becomes
the location where the wind load is applied. However, a diaphragm consisting
of a single point object will have a zero exposure width, so input a user-defined
Exposure from Extents of Diaphragms 3 - 3
Lateral Loads
exposure width for the dummy diaphragm to generate a non-zero wind load
(use the Modify/Show Exposure Widths button on the Wind Loading form).
If exposure from area objects is selected, wind loads will be generated on each
area object that has been assigned a wind pressure coefficient, Cp. The wind
load pattern must be defined before assigning the Cp values to the area objects.
The wind loads calculated at an area object are based on the elevation of the
object, the dimensions of the object, and various code-dependent wind coeffi-
cients.
Unlike the diaphragm exposure option that generates only lateral wind loads,
the exposure from area objects option will generate wind loads normal to any
area object, regardless of its orientation. Thus, this option may be used to gen-
erate vertical as well as lateral loads.
3.2.2 Wind Exposure Parameters
The wind exposure parameters are available only when calculating lateral wind
loads using the exposure from extents of diaphragms option. These input
values are not available when using the exposure from area objects method
because the wind coefficients are assigned directly to the area objects using a
loads command.
When specifying the wind direction, indicate the direction of the wind by an
angle measured in degrees. An angle of 0 degrees means the wind is blowing in
the positive global X-direction; that is, it is blowing from the negative global X-
direction to the positive global X-direction. An angle of 90 degrees means the
wind is blowing in the positive global Y-direction. An angle of 180 degrees
means the wind is blowing in the negative global X-direction. An angle of 270
degrees means the wind is blowing in the negative global Y-direction.
Any angle for the wind direction can be input. The angle is always measured
counterclockwise from the positive global X-axis. A positive angle appears
counterclockwise as you look down on the model in the negative global Z-
direction.
The windward coefficient, Cp, and the leeward coefficient, Cp, are used in
calculating the wind pressures on the windward and leeward sides of the
diaphragms, respectively. The windward side of a diaphragm is the side
exposed to the wind, while the opposite side is the leeward side.
3 - 4 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
Click the Modify/Show Exposure Widths button to review and modify the
exposure widths calculated by the programs for each diaphragm. By default,
the wind exposure width for a diaphragm is equal to the calculated width of the
diaphragm in a direction perpendicular to the direction of the wind load.
The maximum width of the diaphragm perpendicular to the direction of the
wind loading is calculated using the following three-step process.
Transform the coordinates of all of the point objects that are part of the
diaphragm constraint into a system of coordinates that is parallel and per-
pendicular to the specified direction of wind loading.
Find the point objects that have the maximum and minimum coordinates
perpendicular to the direction of the wind load. For example, if the wind
load is in the global X-direction, find the point objects with the maximum
and minimum global Y-coordinates.
Subtract the minimum perpendicular coordinate from the maximum per-
pendicular coordinate to obtain the diaphragm width perpendicular to the
wind load.
By default, the point where the wind load is applied to a diaphragm is the cal-
culated geometric center of the diaphragm. Modify the assumed wind load ap-
plication point and the default exposure width on the Wind Exposure Width
Data form, which displays when the Modify/Show Exposure Widths button is
clicked.
NOTE: It is recommended to only use “Area Exposure Method” for specify-
ing Auto Wind Load when Multiple Towers are present in a single model.
3.2.3 Wind Exposure Height
The top story/maximum elevation and a bottom story/minimum elevation input
values specify the elevation range over which the structure is exposed to wind.
The top story/maximum global Z indicates the highest story level to be
assumed exposed to wind loading for the purposes of calculating the automatic
wind load. In most instances the top story should be the uppermost story
level/elevation in the building and this is the default value.
Exposure from Extents of Diaphragms 3 - 5
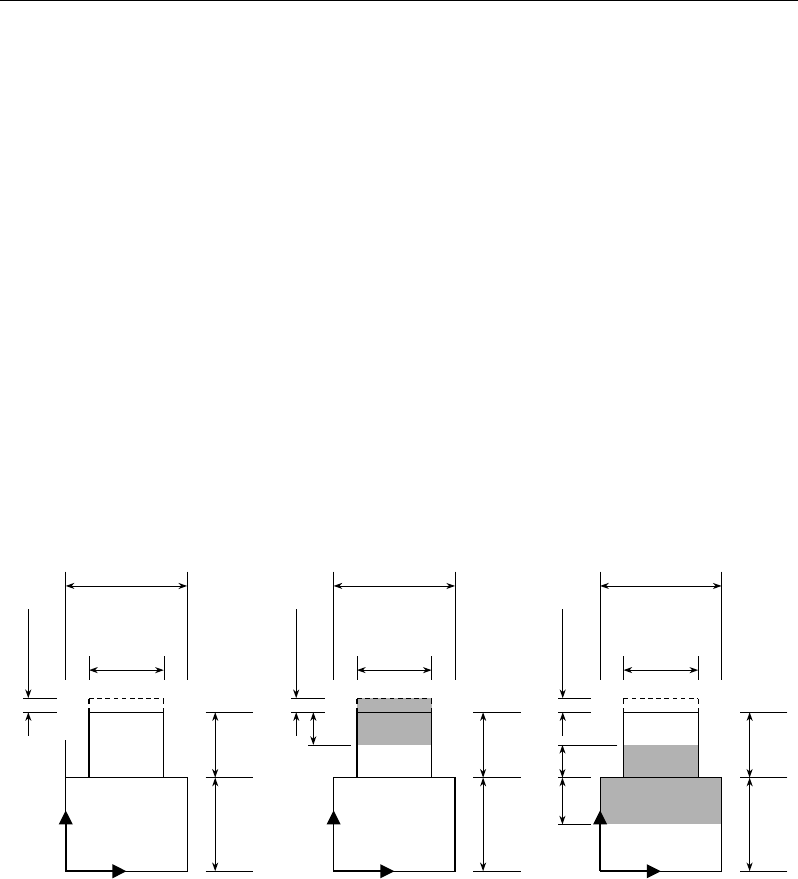
Lateral Loads
In some instances, for example where penthouses are included in the model, it
may be more convenient to indicate that the top story level for automatic wind
loading is the main roof level. User-defined loads can then be added to the load
pattern to account for the wind loads acting on the penthouse.
The bottom story/minimum global Z indicates the lowest story level that is ex-
posed to wind loading. It is assumed that all stories above the bottom story are
loaded by the wind.
By default the bottom story is assumed to be the base level of the structure. In
some cases, it may be advantageous to specify a higher level as the bottom
story for wind loading. One example of this might be if a building has several
below-grade levels that should not receive any wind loading.
Figure 3-1 gives a representation of how loads are distributed to the dia-
phragms when using the exposure from extents of diaphragms method.
Figure 3-1: Example extent of wind loading
Figure 3-1a shows an elevation of a two-story building with diaphragms at
each story level. Assume the wind load is to be automatically calculated for the
Y-direction. Thus, the wind load is acting on the face of the building shown in
Figure 3-1a.
X
Z
Roof
2nd
Base
h
1
h
2
Exposure
width for
Roof level
diaphragm
Exposure width for
2nd level diaphragm
Specified
parapet height
X
Z
Roof
2nd
Base
h
1
h
2
Exposure
width for
Roof level
diaphragm
Exposure width for
2nd level diaphragm
Specified
parapet height
X
Z
Roof
2nd
Base
h
1
h
2
Exposure
width for
Roof level
diaphragm
Exposure width for
2nd level diaphragm
Specified
parapet height
h
2
/2
h
2
/2
h
1
/2
a) Building Elevation b) Wind Loading at Roof Level c) Wind Loading at 2nd Level
3 - 6 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
The shaded area in Figure 3-1b illustrates the extent of the wind load that is
applied to the roof level diaphragm. The shaded area in Figure 3-1c illustrates
the extent of the wind load that is applied to the 2nd level diaphragm.
When using the exposure from area objects method, the exposure heights al-
lows the programs to determine how much of each area object is exposed to
wind.
3.3 1994 UBC Wind Loads
3.3.1 Input Wind Coefficients
Three wind coefficients are input for 1994 UBC wind loads. They are the basic
wind speed in miles per hour (mph), the exposure type, and the wind im-
portance factor, Iw.
The basic wind speed is described in 1994 UBC Sections 1614 and 1616. A
typical range of values for the basic wind speed is 70 to 130 mph.
The exposure types are described in 1994 UBC Sections 1614 and 1617. The
exposure type can be B, C or D. No other values are allowed. The wind im-
portance factor can be found in 1994 UBC Table 16-K. The wind importance
factor, Iw, should be input, not one of the seismic importance factors, I or Ip. A
typical range of values for Iw is 1.00 to 1.15.
3.3.2 Algorithm for 1994 UBC Wind Loads
ETABS automatic wind loads for the 1994 UBC are based on Sections 1614
through 1619 of the 1994 UBC.
The wind loads applied in ETABS are a modified version of the Method 2
(Projected Area Method) as described in Section 1619.3 of the 1994 UBC.
ETABS applies horizontal wind loads on the vertical projected area as de-
scribed in Section 1619.3. ETABS has two modifications to the requirements
of Section 1619.3. The first modification is that ETABS does not automatically
apply vertical wind loads over the projected horizontal area. To include these
vertical wind loads in the load case, the user must manually include them.
Exposure from Extents of Diaphragms 3 - 7
Lateral Loads
The other modification is that ETABS applies the method to structures of any
height. It does not limit it to structures less than 200 feet high as discussed in
1994 UBC Section 1619.3.
The shape of the horizontal projected area is determined based on the story
heights and the input exposure widths for each rigid diaphragm. ETABS uses
1994 UBC Equation 18-1 to determine the wind pressure, P, at any point on the
surface of the horizontal projected area.
P = Ce Cq qs Iw (UBC 94 Eqn. 18-1)
where,
Ce = Combined height, exposure and gust factor coefficient, as given in
1994 UBC Table 16-G.
Cq = Pressure coefficient for the structure, as given in 1994 UBC Table
16-H.
qs = Wind stagnation pressure at the standard height of 33 feet, as giv-
en in 1994 UBC Table 16-F.
Iw = Importance factor, as input by the user.
ETABS determines the Ce coefficient from 1994 UBC Table 16-G using the
input exposure type and the input bottom story. For use in 1994 UBC Table 16-
G the elevation of the input bottom story is assumed to be zero (0). ETABS us-
es linear interpolation to determine the value of the Ce coefficient at heights
above 15 feet that are not listed in 1994 UBC Table 16-G.
ETABS determines the Cq coefficient from 1994 UBC Table 16-H. ETABS us-
es the values for Primary Frames and Systems using Method 2 (the projected
area method). Thus for buildings 40 feet or less in height, ETABS uses Cq =
1.3, and for buildings more than 40 feet in height, ETABS uses Cq = 1.4.
ETABS determines qs from 1994 UBC Table 16-F.
qs = 0.00256 V2 ≥ 10 psf
where,
qs = Wind stagnation pressure at the standard height of 33 feet, psf.
3 - 8 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
V = Basic wind speed as input by the user, mph.
Note the units that are specified for qs and V.
ETABS distributes the pressures, P, on the surface of the horizontal projected
area to each rigid diaphragm on a tributary area basis as shown in Figure 3-1.
3.4 1997 UBC Wind Loads
3.4.1 Input Wind Coefficients
Three wind coefficients are input for 1997 UBC wind loads. They are the basic
wind speed in miles per hour (mph), the exposure type, and the wind im-
portance factor, Iw.
The basic wind speed is described in 1997 UBC Sections 1616 and 1618. A
typical range of values for the basic wind speed is 70 to 130 mph.
The exposure types are described in 1997 UBC Sections 1616 and 1619. The
exposure type can be B, C, or D. No other values are allowed.
The wind importance factor can be found in 1997 UBC Table 16-K. The wind
importance factor, Iw—not one of the seismic importance factors, I or Ip—
should be input. A typical range of values for Iw is 1.00 to 1.15.
3.4.2 Algorithm for 1997 UBC Wind Loads
3.4.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for the 1997 UBC are based on Sections 1616 through
1621 of the 1997 UBC.
The wind loads applied when using the exposure from extents of diaphragms
method are based on a modified version of Method 2 (Projected Area Method)
as described in Section 1621.3 of the 1997 UBC. Horizontal wind loads are ap-
plied on the vertical projected area as described in Section 1621.3. The pro-
grams have two modifications to the requirements of Section 1621.3. The first
modification is that the programs do not automatically apply vertical wind
loads over the projected horizontal area. To include those vertical wind loads in
the same load pattern, the user must manually include them. The other modifi-
Exposure from Extents of Diaphragms 3 - 9
Lateral Loads
cation is that the programs apply the method to structures of any height. The
modification does not limit structures to less than 200 feet high, as discussed in
1997 UBC Section 1621.3.
The shape of the vertical projected area is determined based on the story
heights and the input exposure widths for each diaphragm. (UBC Eqn. 20-1) is
used to determine the wind pressure, P, at any point on the surface of the verti-
cal projected area.
P = qs Iw (Cq-windward Ce-windward + Cq-leeward Ce-leeward) (UBC Eqn. 20-1)
where,
qs = Wind stagnation pressure at the standard height of 33 feet, as
given in 1997 UBC Table 16-F.
Iw = Importance factor as input by the user.
Cq-windward = Windward pressure coefficient as input by the user.
Ce-windward = Windward combined height, exposure and gust factor coeffi-
cient at the height of interest, as given in 1997 UBC Table
16-G.
Cq-leeward = Leeward pressure coefficient as input by the user.
Ce-leeward = Leeward combined height, exposure, and gust factor coeffi-
cient, evaluated at the specified top story level, as given in
1997 UBC Table 16-G.
The Ce coefficient is determined from 1997 UBC Table 16-G using the input
exposure type and the elevation from the input bottom story. Linear interpola-
tion is used to determine the value of the Ce coefficient at heights above 15 feet
that are not listed in 1997 UBC Table 16-G.
qs is determined from the following equation:
qs = 0.00256 V 2 ≥ 10 psf (UBC Table 16-F)
where,
qs = Wind stagnation pressure at the standard height of 33 feet, psf.
V = Basic wind speed as input by the user, mph.
3 - 10 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
Note the units that are specified for qs and V. Also note that the preceding
equation is consistent with 1997 UBC Table 16-F.
The programs distribute the pressures, P, on the surface of the vertical project-
ed area to each diaphragm on a tributary area basis as shown in Figure 3-1.
3.4.2.2 Exposure from Area Objects
Automatic wind loads for the 1997 UBC are based on Sections 1616 through
1621 of the 1997 UBC.
The wind loads applied when using the exposure from area objects method are
based on Method 1 (Normal Force Method) as described in Section 1621.2 of
the 1997 UBC. Wind loads are applied on the vertical and horizontal surfaces
of the user selected area objects as described in Section 1621.2.
(UBC Eqn. 20-1) is used to determine the wind pressure, P, at any point on the
surface of the area objects.
P = Ce Cp qs Iw (UBC Eqn. 20-1)
where,
Ce = Combined height, exposure, and gust factor coefficient as given in
1997 UBC Table 16-G. This value is evaluated at the height of
interest for windward exposures, and at the top story level for lee-
ward objects.
Cp = Windward or leeward pressure coefficient assigned to the area
object by the user.
qs = Wind stagnation pressure at the standard height of 33 feet as given
in 1997 UBC Table 16-F.
Iw = Importance factor as input by the user.
The value for qs is the same as described in the previous section entitled “Ex-
posure from Extents of Diaphragms.”
The programs distribute the pressures, P, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
Exposure from Area Objects 3 - 11
Lateral Loads
3.5 1996 BOCA Wind Loads
3.5.1 Input Wind Coefficients
Four wind coefficients are input for 1996 BOCA wind loads. They are the
basic wind speed in miles per hour (mph), the exposure category, and the wind
importance factor, I, and the gust response factor, Gh.
The basic wind speed is described in 1996 BOCA Section 1609.3. A typical
range of values for the basic wind speed is 70 to 130 mph.
The exposure categories are described in 1996 BOCA Section 1609.4. The
exposure category can be A, B, C or D. No other values are allowed.
The wind importance factor, I, is described in 1996 BOCA Section 1609.5. A
typical range of values for I is 0.90 to 1.23.
The gust response factor, Gh, is discussed in 1996 BOCA Section 1609.7 and in
Table 1609.7(5). Specify that the gust response factor is (a) calculated based on
the height (distance) of the specified top story above the specified bottom story
and the exposure category in accordance with the code using Table 1609.7(5)
or (b) a value input by the user. Note that in 1996 BOCA Section 1609.7, the
following statement is made about Gh.
The gust response factor for buildings which have a height to
least horizontal dimension ratio greater than 5 or a fundamental
frequency less than one cycle per second (period greater than 1
second) shall be calculated by an approved rational analysis that
incorporates the dynamic properties of the main wind force-
resisting system.
When the Per Code option for the gust response factor is selected, the programs
do not check the height-to-least-horizontal-dimension ratio or the building
period and it does not determine the gust factor using an approved rational
analysis incorporating the dynamic properties of the main wind force-resisting
system. It is assumed that the user will do this, if necessary, and provide a user
defined value for Gh. A typical range of values for Gh is 1.00 to 2.36.
3 - 12 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
3.5.2 Algorithm for 1996 BOCA Wind Loads
3.5.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for the 1996 BOCA are based on Section 1609 of the
1996 BOCA.
The wind loads applied are a modified version of those described in 1996
BOCA Section 1609.7. Windward and leeward horizontal wind loads are
applied on the vertical projected area of the building as determined from the
story heights and the input diaphragm exposure widths. The programs do not
apply vertical wind loads automatically over the projected horizontal area of
roof surfaces. To include those vertical wind loads in the same load pattern, the
user must manually include them.
The following equation is used to determine the wind pressure, P, at any point
on the surface of the vertical projected area.
P = Pv I [Kz Gh Cp-windward + Kh Gh Cp-leeward] (Table 1609.7)
where,
Pv = Basic velocity pressure given in 1996 BOCA Table 1609.7(3).
I = Importance factor as input by the user.
Kz = Velocity pressure exposure coefficient at the height of
interest as given in 1996 BOCA Table 1609.7(4).
Gh = Gust response factor as given in 1996 BOCA Table 1609.7(5) or as
user specified.
Cp-windward = Windward pressure coefficient as input by the user.
Kh = Velocity pressure exposure coefficient, evaluated at the specified
top story level, as given in 1996 BOCA Table 1609.7(4).
Cp-leeward = Leeward pressure coefficient as input by the user.
The Pv coefficient is determined from the following equation.
Pv = 0.00256 V2 ≥ 10 psf (Table 1609.7(3))
Exposure from Extents of Diaphragms 3 - 13
Lateral Loads
where,
Pv = Basic velocity pressure, psf.
V = Basic wind speed as input by the user, mph.
Note the units specified for Pv and V.
The Kz coefficient is determined from 1996 BOCA Table 1609.7(4) using the
input exposure category and the input bottom story. For use in 1996 BOCA
Table 1609.7(4), the input bottom story/minimum elevation is assumed to be
ground level. The programs use linear interpolation to determine the value of
the Kz coefficient at heights above 15 feet that are not listed in 1996 BOCA
Table 1609.7(4).
For discussion of the gust response factor, Gh, refer to the previous section enti-
tled "Input Wind Coefficients for 1996 BOCA."
The Kh coefficient is determined from 1996 BOCA Table 1609.7(4) using the
input exposure category and the height of the input top story above the input
bottom story. Linear interpolation is used to determine the value of the Kh
coefficient at heights above 15 feet that are not listed in 1996 BOCA Table
1609.7(4).
The programs distribute the pressures, P, on the surface of the vertical project-
ed area to each diaphragm on a tributary area basis as shown in Figure 3-1.
3.5.2.2 Exposure from Area Objects
Automatic wind loads for the 1996 BOCA are based on Section 1609 of the
1996 BOCA.
The wind loads applied when using the exposure from area objects method are
as described in 1996 BOCA Section 1609.7. Wind loads are applied on the ver-
tical and horizontal surfaces of the user selected area objects as described in
Section 1609.7.
The following equations are used to determine either the windward or leeward
wind pressure, P, at any point on the surface of the area objects.
Pwindward = Pv I Kz Gh Cp-windward (Table 1609.7)
3 - 14 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
or
Pleeward = Pv I Kh Gh Cp-leeward (Table 1609.7)
where,
Pv = Basic velocity pressure given in 1996 BOCA Table 1609.7(3).
I = Importance factor as input by the user.
Kz = Velocity pressure exposure coefficient at the height of interest as
given in 1996 BOCA Table 1609.7(4).
Gh = Gust response factor as given in 1996 BOCA Table 1609.7(5) or as
user specified.
Cp-windward = Windward pressure coefficient as assigned to the area object
by the user.
Kh = Velocity pressure exposure coefficient, evaluated at the specified
top story level, as given in 1996 BOCA Table 1609.7(4).
Cp-leeward = Leeward pressure coefficient as assigned to the area object
by the user.
The values for Pv, Kz, and Kh are the same as described in the previous section
entitled “Exposure from Extents of Diaphragms.”
The programs distribute the pressures, P, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects
3.6 1995 BS 6399 Wind Loads
3.6.1 Input Wind Coefficients
Three wind coefficients are input for 1995 BS 6399 wind loads. They are the
effective wind speed in meters per second (m/s), the size effect factor, and the
dynamic augmentation factor.
The effective wind speed, Ve, is described in 1995 BS 6399 Section 2.2.3.
The size effect factor for external pressures, Ca, is described in 1995 BS 6399
Section 2.1.3.4. A typical range of values for Ca is 0.52 to 1.00.
Exposure from Area Objects 3 - 15
Lateral Loads
The dynamic augmentation factor, Cr, is described in 1995 BS 6399 Section
1.6.1. A typical range of values for Cr is 0 to 0.25.
Note that in 1995 BS 6399 Section 1.6.2 the following statement is made about
Cr:
This part of BS 6399 does not apply when the value of dynamic
augmentation factor exceeds the limits shown in figure 3. Buildings
falling outside these limits should be assessed using established
dynamic methods.
This typically means that when Cr ≥ 0.25, the structure is assumed to be
dynamic and the methodology for establishing wind loads described herein is
not applicable. However, the program allows the user to input any value, and
performs no check to ensure that Cr is less than 0.25.
3.6.2 Algorithm for 1995 BS 6399 Wind Loads
3.6.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for the 1995 BS 6399 are based on 1995 BS 6399 Sec-
tion 2.
The wind loads applied when using the exposure from extents of diaphragms
method are based on a modified version of the Standard method as described in
Section 2.1 of the 1995 BS 6399. Horizontal wind loads are applied on the
vertical projected area as described in Section 2. The programs have two modi-
fications to the requirements of Section 2. The first modification is that the
programs do not apply vertical wind loads automatically over the projected
horizontal area. To include those vertical wind loads in the same load pattern,
the user must include them manually. The other modification is that the
programs apply the method to structures of any height. The modification does
not limit structures to less than 100 meters high, as discussed in 1995 BS
Section 1.8.1.
The shape of the vertical projected area is determined based on the story
heights and the input exposure widths for each diaphragm. Eqn. 2.3.1.6(7) is
used to determine the wind pressure, p, at any point on the surface of the verti-
cal projected area.
3 - 16 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
p = 0.85 qs Ca (Cp-front + Cp-rear) (1 + Cr) (Eqn. 2.3.1.6(7))
where,
qs = Dynamic pressure as given in 1995 BS 6399 Table 2.
Ca = Size effect factor as input by the user.
Cp-front = External pressure coefficient on the windward side as input by
the user.
Cp-rear = External pressure coefficient on the leeward side as input by
the user.
Cr = Dynamic augmentation factor as input by the user.
Note that the factor 0.85 accounts for the non-simultaneous action between the
front and rear faces.
qs is determined from (Eqn. 2.2.2.1(1)).
qs = 0.613
2
e
V
(Eqn. 2.2.2.1(1))
where,
qs = Dynamic pressure, Pa.
Ve = Effective wind speed as input by the user, m/s.
Note the units that are specified for qs and Ve. Also note that (Eqn.
2.2.2.1(1)) is consistent with 1995 BS 6399 Table 2.
The programs distribute the pressures, p, on the surface of the vertical project-
ed area to each diaphragm on a tributary area basis as shown in Figure 3-1.
3.6.2.2 Exposure from Area Objects
Automatic wind loads for 1995 BS 6399 are based on Section 2.
The wind loads applied when using the exposure from area objects method are
based on a modified version of the Standard method as described in Section 2.1
of 1995 BS 6399. Wind loads are applied on the vertical and horizontal surfac-
es of the user selected area objects as described in Section 2.
Exposure from Area Objects 3 - 17
Lateral Loads
Eqn. (2.1.3.6(7)) is used to determine the wind pressure, p, at any point on the
surface of the area objects.
p = 0.85 qs Cp Ca (1 + Cr) (Eqn. 2.1.3.6(7))
where,
qs = Dynamic pressure as given in 1995 BS 6399 Table 2.
Cp = Windward (front) or leeward (rear) external pressure coefficient as-
signed to the area object by the user.
Ca = Size effect factor as input by the user.
Cr = Dynamic augmentation factor as input by the user.
Note that the factor 0.85 accounts for the non-simultaneous action between the
front and rear faces.
The value for qs is the same as described in the previous section entitled “Ex-
posure from Extents of Diaphragms.”
The programs distribute the pressures, p, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3.7 1995 NBCC Wind Loads
3.7.1 Input Wind Coefficients
Two wind coefficients are input for 1995 NBCC wind loads. They are the
velocity pressure, q, in kPa and the gust effect factor, Cg.
The velocity pressure, q, can be obtained from 1995 NBCC Appendix C. A
typical range of values for the velocity pressure is 0.20 to 0.90 kPa. Any posi-
tive value or zero is allowed.
The gust effect factor, Cg, is discussed in 1995 NBCC Sentence 4.1.8.1(6). The
default value is 2.0. Any positive value is allowed.
3 - 18 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
3.7.2 Algorithm for 1995 NBCC Wind Loads
3.7.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for 1995 NBCC are based on Section 4.1.8.1 of the 1995
NBCC.
Windward and leeward horizontal wind loads are applied on the vertical pro-
jected area of the building as determined from the story heights and the input
diaphragm exposure widths. The programs do not apply vertical wind loads au-
tomatically over the projected horizontal area of roof surfaces. To include those
vertical wind loads in the load pattern, the user must include them manually.
The following equation is used to determine the wind pressure, p, at any point
on the surface of the vertical projected area.
p = q Cg [Cp-winward Ce-windward + Cp-leeward Ce-leeward](1995 NBCC Eqn. 4.1.8.1(1))
where,
q = Velocity pressure as input by the user.
Cg = Gust effect factor as input by the user.
Cp-windward = External pressure coefficient for the windward wall as input
by the user.
Ce-windward = Exposure factor for the windward wall.
Cp-leeward = External pressure coefficient for the leeward wall as input by
the user.
Ce-leeward = Exposure factor for the leeward wall.
Ce-windward is determined from (Eqn. 4.1.8.1(5)).
15
windward
0.9
10
e
h
C
−

= ≥


(1995 NBCC Eqn. 4.1.8.1(5))
where,
h = Distance from the input bottom story/minimum level to the eleva-
tion considered, meters.
Exposure from Extents of Diaphragms 3 - 19
Lateral Loads
Ce-leeward is determined from (1995 NBCC Eqn. 4.1.8.1(5)).
15
middle
leeward
0.9
10
e
h
C
−

= ≥


(1995 NBCC Eqn. 4.1.8.1(5))
where,
hmiddle = One-half of the distance from the input bottom story/minimum
level to the input top story/maximum level, meters.
The pressures, p, are distributed on the surface of the vertical projected area to
each diaphragm on a tributary area basis, as shown in Figure 3-1.
3.7.2.2 Exposure from Area Objects
Automatic wind loads for 1995 NBCC are based on Section 4.1.8.1 of the 1995
NBCC.
The wind loads applied when using the exposure from area objects method are
applied on the vertical and horizontal surfaces of the user selected area objects
as described in 1995 NBCC Section 4.1.8.1.
The following equations is used to determine the wind pressure, p, at any point
on the surface of the area objects.
p = q Ce Cg Cp (1995 NBCC Eqn. 4.1.8.1(1))
where,
q = Velocity pressure as input by the user.
Ce = Exposure factor.
Cg = Gust effect factor as input by the user.
Cp = Windward or leeward external pressure coefficient assigned to the
area object by the user.
Ce for a windward facing area object is determined from (1995 NBCC Eqn.
Eqn. 4.1.8.1(5)).
3 - 20 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
15
-windward 0.9
10
eh
C
= ≥


(1995 NBCC Eqn. 4.1.8.1(5))
where,
h = Distance from the input bottom story/minimum level to the eleva-
tion considered, meters.
Ce for a leeward facing area object is determined from (1995 NBCC Eqn.
4.1.8.1(5)).
middle
-leeward
15 0.9
10
eh
C
= ≥


(1995 NBCC Eqn. 4.1.8.1(5))
where,
hmiddle = One-half of the distance from the input bottom story/minimum
level to the input top story/maximum level, meters.
The programs distribute the pressures, p, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3.8 2005 NBCC Wind Loads
3.8.1 Input Wind Coefficients
Three wind coefficients are input for 2005 NBCC wind loads. They are the
velocity pressure, q, in kPa, the gust effect factor, Cg, and the importance fac-
tor, I.
The velocity pressure, q, can be obtained from 2005 NBCC Appendix C. A
typical range of values for the velocity pressure is 0.27 to 1.23 kPa. Any posi-
tive value or zero is allowed.
The gust effect factor, Cg, is discussed in 2005 NBCC Sentence 4.1.7.1(6). The
default value is 2.0. Any positive value is allowed.
The importance factor, I, is described in 2005 NBCC Table 4.1.7.1. A typical
range of values for I is 0.8 to 1.25.
Exposure from Area Objects 3 - 21
Lateral Loads
3.8.2 Algorithm for 2005 NBCC Wind Loads
3.8.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for the 2005 NBCC are based on Section 4.1.7.1 of the
2005 NBCC.
Windward and leeward horizontal wind loads are applied on the vertical pro-
jected area of the building as determined from the story heights and the input
diaphragm exposure widths. The programs do not apply vertical wind loads au-
tomatically over the projected horizontal area of roof surfaces. To include those
vertical wind loads in the load pattern, the user must include them manually.
The following equation is used to determine the wind pressure, p, at any point
on the surface of the vertical projected area.
p = I q Cg [Cp-winward Ce-windward + Cp-leeward Ce-leeward] (2005 NBCC 4.1.7.1(1))
where,
I = Importance factor as input by the user.
q = Velocity pressure as input by the user.
Cg = Gust effect factor as input by the user.
Cp-windward = External pressure coefficient for the windward wall as input
by the user.
Ce-windward = Exposure factor for the windward wall.
Cp-leeward = External pressure coefficient for the leeward wall as input by
the user.
Ce-leeward = Exposure factor for the leeward wall.
Ce-windward is determined from (2005 NBCC Eqn. 4.1.7.1(5).
0.2
-windward 0.9
10
eh
C
= ≥


for Open Terrain (2005 NBCC 4.1.7.1(5))
3 - 22 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
0.3
-windward
0.7 0.7
12

= ≥


e
h
C
for Rough Terrain (2005 NBCC 4.1.7.1(5))
where,
h = Distance from the input bottom story/minimum level to the eleva-
tion considered, meters.
Ce-leeward is determined from (2005 NBCC Eqn. 4.1.7.1(5).
0.2
middle
-leeward 0.9
10
eh
C
= ≥


for Open Terrain (2005 NBCC 4.1.7.1(5))
0.3
middle
-leeward
0.7 0.7
12

= ≥


e
h
C
for Rough Terrain
(2005 NBCC 4.1.7.1(5))
where,
hmiddle = One-half of the distance from the input bottom story/minimum
level to the input top story/maximum level, meters.
The pressures, p, are distributed on the surface of the vertical projected area to
each diaphragm on a tributary area basis as shown in Figure 3-1.
3.8.2.2 Exposure from Area Objects
Automatic wind loads for 2005 NBCC are based on Section 4.1.7.1 of the 2005
NBCC.
The wind loads applied when using the exposure from area objects method are
applied on the vertical and horizontal surfaces of the user selected area objects
as described in 2005 NBCC Section 4.1.7.1.
The following equation is used to determine the wind pressure, p, at any point
on the surface of the area objects.
p = I q Ce Cg Cp (2005 NBCC 4.1.7.1(1))
where,
Exposure from Area Objects 3 - 23
Lateral Loads
I = Importance factor as input by the user.
q = Velocity pressure as input by the user.
Ce = Exposure factor.
Cg = Gust effect factor as input by the user.
Cp = Windward or leeward external pressure coefficient assigned to the
area object by the user.
Ce for a windward facing area object is determined from (2005 NBCC Eqn.
4.1.7.1(5)).
0.2
-windward 0.9
10
eh
C
= ≥


for Open Terrain (2005 NBCC 4.1.7.1(5))
0.3
-windward
0.7 0.7
12

= ≥


e
h
C
for Rough Terrain (2005 NBCC 4.1.7.1(5))
where,
h = Distance from the input bottom story/minimum level to the eleva-
tion considered, meters.
Ce for a leeward facing area object is determined from (2005 NBCC Eqn.
4.1.7.1(5)).
0.2
middle
-leeward 0.9
10
eh
C
= ≥


for Open Terrain (2005 NBCC 4.1.7.1(5))
0.3
middle
-leeward 0.7 0.7
12

= ≥


eh
C
for Rough Terrain
(2005 NBCC 4.1.7.1(5))
where,
hmiddle = One-half of the distance from the input bottom story/minimum
level to the input top story/maximum level, meters.
3 - 24 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
The programs distribute the pressures, p, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3.9 2010 NBCC Wind Loads
3.9.1 Input Wind Coefficients
Three wind coefficients are input for 2010 NBCC wind loads. They are the
velocity pressure, q, in kPa, the gust effect factor, Cg, and the importance fac-
tor, I.
The velocity pressure, q, can be obtained from 2010 NBCC Appendix C. A
typical range of values for the velocity pressure is 0.27 to 1.23 kPa. Any posi-
tive value or zero is allowed.
The gust effect factor, Cg, is discussed in 2010 NBCC Section 4.1.7.1(6). The
default value is 2.0. Any positive value is allowed.
The importance factor, I, is described in 2010 NBCC Table 4.1.7.1. A typical
range of values for I is 0.8 to 1.25.
3.9.2 Algorithm for 2010 NBCC Wind Loads
3.9.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for the 2010 NBCC are based on Section 4.1.7.1 of the
2010 NBCC.
Windward and leeward horizontal wind loads are applied on the vertical pro-
jected area of the building as determined from the story heights and the input
diaphragm exposure widths. The programs do not apply vertical wind loads au-
tomatically over the projected horizontal area of roof surfaces. To include those
vertical wind loads in the load pattern, the user must include them manually.
The following equation is used to determine the wind pressure, p, at any point
on the surface of the vertical projected area.
p = I q Cg [Cp-winward Ce-windward + Cp-leeward Ce-leeward] (2010 NBCC 4.1.7.1(1))
where,
Exposure from Extents of Diaphragms 3 - 25
Lateral Loads
I = Importance factor as input by the user.
q = Velocity pressure as input by the user.
Cg = Gust effect factor as input by the user.
Cp-windward = External pressure coefficient for the windward wall as input
by the user.
Ce-windward = Exposure factor for the windward wall.
Cp-leeward = External pressure coefficient for the leeward wall as input by
the user.
Ce-leeward = Exposure factor for the leeward wall.
Ce-windward is determined from (2010 NBCC Eqn. 4.1.7.1(5) or may be specified
by the user:
0.2
-windward 0.9
10
eh
C
= ≥


for Open Terrain (2010 NBCC 4.1.7.1(5))
0.3
-windward
0.7 0.7
12

= ≥


e
h
C
for Rough Terrain (2010 NBCC 4.1.7.1(5))
where,
h = Distance from the input bottom story/minimum level to the eleva-
tion considered, meters.
Ce-leeward is determined from (2010 NBCC Eqn. 4.1.7.1(5) or may be specified
by the user:
0.2
middle
-leeward 0.9
10
eh
C
= ≥


for Open Terrain (2010 NBCC 4.1.7.1(5))
0.3
middle
-leeward 0.7 0.7
12

= ≥


eh
C
for Rough Terrain (2010 NBCC 4.1.7.1(5))
where,
3 - 26 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
hmiddle = One-half of the distance from the input bottom story/minimum
level to the input top story/maximum level, meters.
The pressures, p, are distributed on the surface of the vertical projected area to
each diaphragm on a tributary area basis as shown in Figure 3-1.
3.9.2.2 Exposure from Area Objects
Automatic wind loads for 2010 NBCC are based on Section 4.1.7.1 of the 2010
NBCC.
The wind loads applied when using the exposure from area objects method are
applied on the vertical and horizontal surfaces of the user selected area objects
as described in 2010 NBCC Section 4.1.7.1.
The following equation is used to determine the wind pressure, p, at any point
on the surface of the area objects.
p = I q Ce Cg Cp (2010 NBCC 4.1.7.1(1))
where,
I = Importance factor as input by the user.
q = Velocity pressure as input by the user.
Ce = Exposure factor.
Cg = Gust effect factor as input by the user.
Cp = Windward or leeward external pressure coefficient assigned to the
area object by the user.
Ce for a windward facing area object is determined from (2010 NBCC Eqn.
4.1.7.1(5)) or may be specified by the user:
0.2
-windward 0.9
10
eh
C
= ≥


for Open Terrain (2010 NBCC 4.1.7.1(5))
0.3
-windward 0.7 0.7
12

= ≥


eh
C
for Rough Terrain (2010 NBCC 4.1.7.1(5))
Exposure from Area Objects 3 - 27
Lateral Loads
where,
h = Distance from the input bottom story/minimum level to the eleva-
tion considered, meters.
Ce for a leeward facing area object is determined from (2010 NBCC Eqn.
4.1.7.1(5)) or may be specified by the user:
0.2
middle
-leeward 0.9
10
eh
C
= ≥


for Open Terrain (2010 NBCC 4.1.7.1(5))
0.3
middle
-leeward 0.7 0.7
12

= ≥


eh
C
for Rough Terrain (2010 NBCC 4.1.7.1(5))
where,
hmiddle = One-half of the distance from the input bottom story/minimum
level to the input top story/maximum level, meters.
The programs distribute the pressures, p, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3.10 2015 NBCC Wind Loads
3.10.1 Input Wind Coefficients
Three wind coefficients are input for 2015 NBCC wind loads. They are the
velocity pressure, q, in kPa, the exposure factor, Ce, the topographic factor, Ct ,
the gust effect factor, Cg, and the importance factor, Iw.
The velocity pressure, q, can be obtained from 2015 NBCC Appendix C. A
typical range of values for the velocity pressure is 0.27 to 1.05 kPa. Any posi-
tive value or zero is allowed.
The exposure factor, Ce, is discussed in 2015 NBCC Section 4.1.7.3(5). The
exposure factor is either internally determined from terrain type or directly
specified by the user. Any positive value is allowed when user specified.
The gust effect factor, Ct, is discussed in 2015 NBCC Section 4.1.7.4. The de-
fault value is 1.0. Any positive value is allowed.
3 - 28 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
The gust effect factor, Cg, is discussed in 2015 NBCC Section 4.1.7.3(10). The
default value is 2.0. Any positive value is allowed.
The importance factor, Iw, is described in 2015 NBCC Table 4.1.7.3. A typical
range of values for Iw is 0.8 to 1.25.
3.10.2 Algorithm for 2015 NBCC Wind Loads
3.10.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for the 2015 NBCC are based on Section 4.1.7.3 of the
2015 NBCC.
Windward and leeward horizontal wind loads are applied on the vertical pro-
jected area of the building as determined from the story heights and the input
diaphragm exposure widths. The programs do not apply vertical wind loads au-
tomatically over the projected horizontal area of roof surfaces. To include those
vertical wind loads in the load pattern, the user must include them manually.
The following equation is used to determine the wind pressure, p, at any point
on the surface of the vertical projected area.
p = Iw q Ct Cg [Cp-winward Ce-windward + Cp-leeward Ce-leeward](2015 NBCC 4.1.7.3(1))
where,
Iw = Importance factor as input by the user.
q = Velocity pressure as input by the user.
Ct = Topographic factor as input by the user.
Cg = Gust effect factor as input by the user.
Cp-windward = External pressure coefficient for the windward wall as input
by the user.
Ce-windward = Exposure factor for the windward wall.
Cp-leeward = External pressure coefficient for the leeward wall as input by
the user.
Ce-leeward = Exposure factor for the leeward wall.
Exposure from Extents of Diaphragms 3 - 29
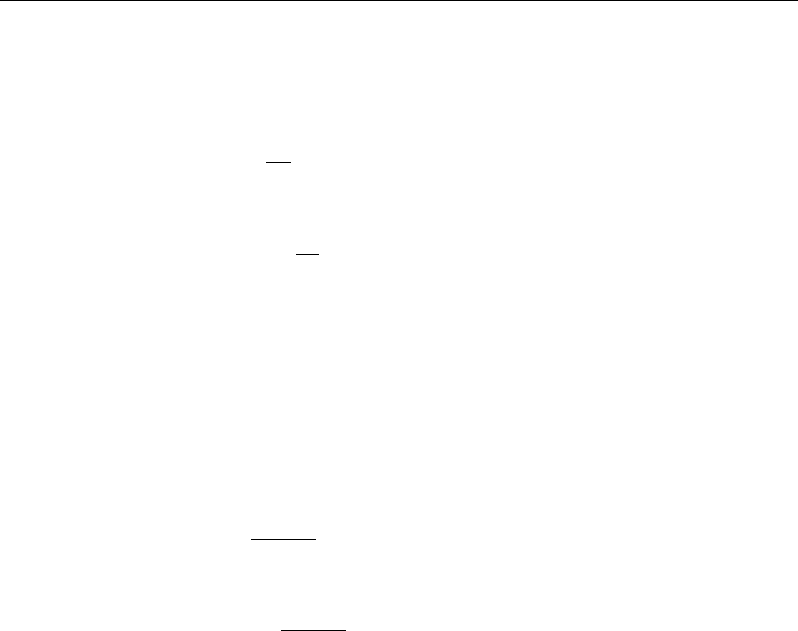
Lateral Loads
Ce-windward is determined from (2015 NBCC Eqn. 4.1.7.3(5) or may be specified
by the user:
0.2
-windward 0.9
10
eh
C
= ≥


for Open Terrain (2015 NBCC 4.1.7.3(5))
0.3
-windward
0.7 0.7
12

= ≥


e
h
C
for Rough Terrain (2015 NBCC 4.1.7.3(5))
where,
h = Distance from the input bottom story/minimum level to the eleva-
tion considered, meters.
Ce-leeward is determined from (2015 NBCC Eqn. 4.1.7.3(5) or may be specified
by the user:
0.2
middle
-leeward 0.9
10
eh
C
= ≥


for Open Terrain (2015 NBCC 4.1.7.1(5))
0.3
middle
-leeward
0.7 0.7
12

= ≥


e
h
C
for Rough Terrain (2015 NBCC 4.1.7.1(5))
where,
hmiddle = One-half of the distance from the input bottom story/minimum
level to the input top story/maximum level, meters.
The pressures, p, are distributed on the surface of the vertical projected area to
each diaphragm on a tributary area basis as shown in Figure 3-1. The applica-
tion of these pressures determines a resultant lateral force in both the x- and y-
directions of the building, Px and Py, at each diaphragm level. Note that one or
the other of these forces may be zero if the wind direction is perfectly aligned
with the x- or y-axis. The program then combines the loads for each of the four
wind load patterns described in NBCC 2015 Figure A-4.1.7.9(1), resulting in
the permutations shown in Table 3-1.
3 - 30 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
Table 3-1: Wind Load Patterns
Case Lateral Force Torsional Moment
1 Px ---
1 Py ---
2 0.75 Px ±0.75 e1 Bx Px
2 0.75 Py ±0.75 e1 By Py
3 0.75(Px + Py) ---
4 0.563(Px + Py) ±0.563(e1BxPx ± e2ByPy)
where,
Px = Resultant wind force in the x-direction.
Py = Resultant wind force in the y-direction.
e1 = Eccentricity for load in the direction of applied load as input by the
user.
Bx = Diaphragm width in the y-direction.
e2 = Eccentricity for load in the transverse direction of applied load as
input by the user.
By = Diaphragm width in the x-direction.
3.10.2.2 Exposure from Area Objects
Automatic wind loads for 2015 NBCC are based on Section 4.1.7.3 of the 2015
NBCC.
The wind loads applied when using the exposure from area objects method are
applied on the vertical and horizontal surfaces of the user selected area objects
as described in 2015 NBCC Section 4.1.7.3.
The following equation is used to determine the wind pressure, p, at any point
on the surface of the area objects.
p = Iw q Ce Ct Cg Cp (2015 NBCC 4.1.7.3(1))
Exposure from Area Objects 3 - 31
Lateral Loads
where,
Iw = Importance factor as input by the user.
q = Velocity pressure as input by the user.
Ce = Exposure factor.
Ct = Topographic factor as input by the user.
Cg = Gust effect factor as input by the user.
Cp = Windward or leeward external pressure coefficient assigned to the
area object by the user.
Ce for a windward facing area object is determined from (2015 NBCC Eqn.
4.1.7.3(5)) or may be specified by the user:
0.2
-windward 0.9
10
eh
C
= ≥


for Open Terrain (2015 NBCC 4.1.7.3(5))
0.3
-windward
0.7 0.7
12

= ≥


e
h
C
for Rough Terrain (2015 NBCC 4.1.7.3(5))
where,
h = Distance from the input bottom story/minimum level to the eleva-
tion considered, meters.
Ce for a leeward facing area object is determined from (2015 NBCC Eqn.
4.1.7.3(5)) or may be specified by the user:
0.2
middle
-leeward 0.9
10
eh
C
= ≥


for Open Terrain (2015 NBCC 4.1.7.3(5))
0.3
middle
-leeward 0.7 0.7
12

= ≥


eh
C
for Rough Terrain (2015 NBCC 4.1.7.1(5))
where,
hmiddle = One-half of the distance from the input bottom story/minimum
level to the input top story/maximum level, meters.
3 - 32 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
The programs distribute the pressures, p, on the surface of each area object,
which in turn creates loads on the joints connected to the area
objects.
3.11 ASCE 7-95 Wind Loads
3.11.1 Input Wind Coefficients
Five wind coefficients are input for ASCE 7-95 wind loads. They are the basic
wind speed in miles per hour (mph), the exposure category, the wind im-
portance factor, I, the topographic factor, Kzt, and the gust factor G.
The basic wind speed is described in ASCE 7-95 Section 6.5.2. A typical range
of values for the basic wind speed is 85 to 150 mph.
The exposure categories are described in ASCE 7-95 Section 6.5.3. The expo-
sure category can be A, B, C, or D. No other values are allowed.
The wind importance factor, I, is described in ASCE 7-95 Table 6-2. Note that
the building and structure classification categories are defined in ASCE 7-95
Table 1-1. A typical range of values for I is 0.87 to 1.15.
The topographic factor Kzt is discussed in ASCE 7-95 Section 6.5.5. The de-
fault value for Kzt is 1.0. Kzt cannot be less than 1.0.
The gust response factor G is discussed in ASCE 7-95 Section 6.6. A typical
range of values for G is 0.80 to 0.85.
3.11.2 Algorithm for ASCE 7-95 Wind Loads
3.11.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for ASCE 7-95 are based on Sections 6.4 through 6.6 of
ASCE 7-95.
The wind loads applied are a modified version of those described in ASCE 7-
95 Sections 6.4 through 6.6. Windward and leeward horizontal wind loads are
applied on the vertical projected area of the building as determined from the
story heights and the input diaphragm exposure widths. The programs do not
apply vertical wind loads automatically over the projected horizontal area of
Exposure from Extents of Diaphragms 3 - 33
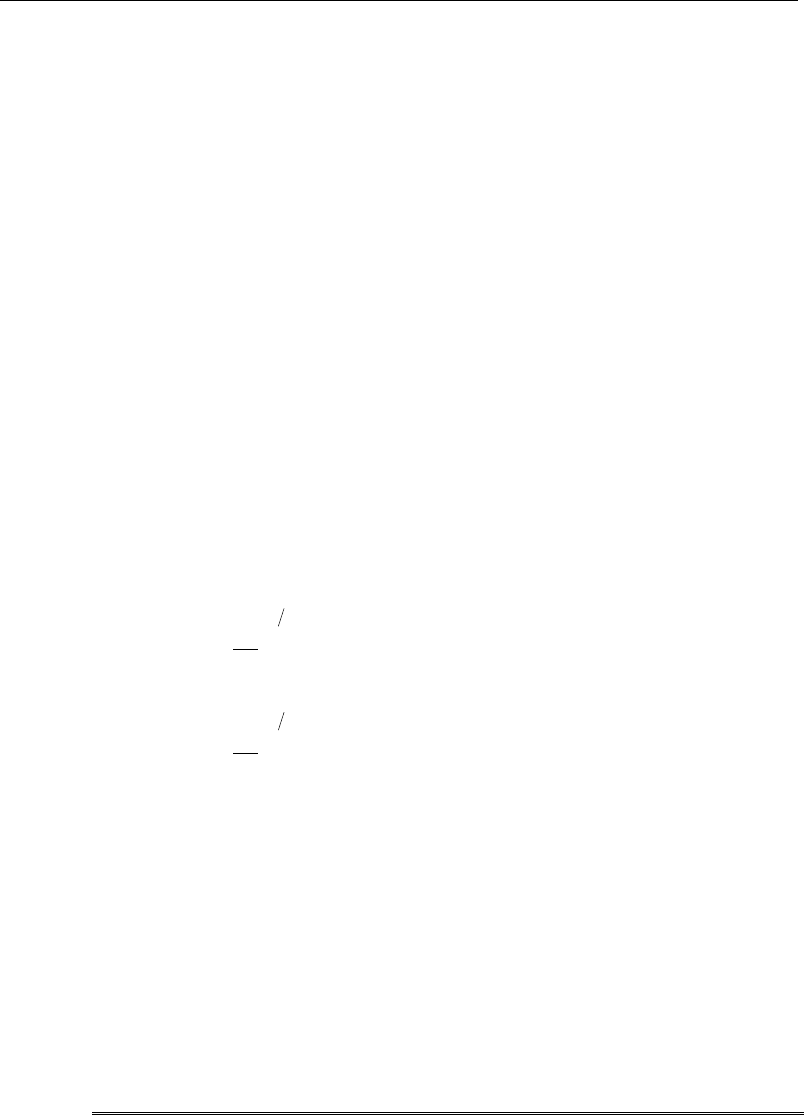
Lateral Loads
roof surfaces. To include those vertical wind loads in the same load pattern, the
user must include them manually.
The following equation is used to determine the velocity pressure, qz, at any
height z on the surface of the vertical projected area in pounds per square foot
(psf).
qz = 0.00256 Kz Kzt V2 I (ASCE 7-95 Eqn 6-1)
where,
Kz = The velocity pressure exposure coefficient. See (ASCE 7-95 Eqns.
C3a and C3b).
Kzt = Topographic factor as input by the user.
V = Basic wind speed in miles per hour (mph) as input by the user.
I = Importance factor as input by the user.
The velocity pressure exposure coefficient, Kz, is obtained using (Eqns. C3a
and C3b in ASCE 7-95 Commentary Section 6.5.1).
2
2.01
zg
z
Kz
α

=


for 15 feet ≤ z ≤ zg
2
15
2.01
zg
Kz
α

=


for z < 15 feet (ASCE 7-95 Eqns. C3a, C3b)
where,
z = Distance (height) from input bottom story/minimum height to point
considered.
zg = As specified in Table 3-2 (ASCE 7-95 Table C6-2 in ASCE 7-95
Commentary Section 6.5.1).
α = As specified in Table 3-2 (ASCE 7-95 Table C6-2 in ASCE 7-95
Commentary Section 6.5.1).
Table 3-2: α and zg factors for use in ASCE 7-95 Equations C3a and C3b
3 - 34 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
Exposure Category α zg (feet)
A 5.0 1500
B 7.0 1200
C 9.5 900
D 11.5 700
The following equation is used to determine the wind pressure, p, at any point
on the surface of the vertical projected area, which is based on ASCE 7-95 Ta-
ble 6-1. In particular, it is based on the row entitled "Main wind force-resisting
systems" under the heading "Buildings of all heights."
p = q G Cp-windward + qh G Cp-leeward (ASCE 7-95 Table 6-1)
where,
q = Velocity pressure, qz, at any height z on the surface of the horizontal
projected area calculated using (ASCE 7-965 Eqn. 6-1).
G = Gust response factor as input by the user.
Cp-windward = Windward external pressure coefficient as input by the user.
qh = Velocity pressure at the top story height on the surface of the verti-
cal projected area calculated using (ASCE 7-965 Eqn. 6-1).
Cp-leeward = Leeward external pressure coefficient as input by the user.
The pressures, p, are distributed on the surface of the vertical projected area to
each diaphragm on a tributary area basis as shown in Figure 3-1.
3.11.2.2 Exposure from Area Objects
Automatic wind loads for ASCE 7-95 are based on Sections 6.4 through 6.6 of
ASCE 7-95.
The wind loads applied when using the exposure from area objects method are
applied on the vertical and horizontal surfaces of the user selected area objects
as described in ASCE 7-95 Section 6.4.2.
Exposure from Area Objects 3 - 35
Lateral Loads
(ASCE 7-95 Eqn. 6-1) is used to determine the velocity pressure, qz, at any
height z on the surface of the user selected area objects in pounds per square
feet (psf).
qz = 0.00256 Kz Kzt V2 I (ASCE 7-95 Eqn. 6-1)
where,
Kz = Velocity pressure exposure coefficient. See (ASCE 7-95 Eqns. C3a
and C3b).
Kzt = Topographic factor as input by the user.
V = Basic wind speed in miles per hour (mph) as input by the user.
I = Importance factor as input by the user.
The value for Kz is the same as described in the previous section entitled “Ex-
posure from Extents of Diaphragms.”
ASCE 7-95 Table 6-1 is used to determine the wind pressure, p, at any point on
the surface of the area objects, which is based on ASCE 7-95 Table 6-1. In
particular it is based on the row entitled "Main wind force-resisting systems"
under the heading entitled "Buildings of all heights."
p = q G Cp (ASCE 7-95 Table 6-1)
where,
q = Velocity pressure, qz, at any height z on the surface of the area ob-
ject calculated using (ASCE 7-95 Table 6-1). For leeward facing ar-
ea objects, q = qh, the velocity pressure at the top story/maximum
height.
G = Gust response factor as input by the user.
Cp = Windward or leeward external pressure coefficient assigned to the
area object by the user.
The programs distribute the pressures, p, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3 - 36 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
3.12 ASCE 7-02 Wind Loads
3.12.1 Input Exposure
In addition to the items discussed in the section entitled “Exposure” earlier in
this chapter, the automatic wind loads for ASCE 7-02 also offers the capability
to generate wind loads on line (frame) objects for use on open or lattice struc-
tures. If the option to include frame objects is checked, wind loads will be
generated on each line object that has been assigned wind parameters. The
wind load pattern must be defined before assigning wind parameters to frame
objects.
Assigning frame load open structure wind parameters allows specification of
three items: the frame object is or is not loaded by wind (the default is that it
is); the thickness of ice, if any; and the net force coefficient, Cf.
The ice thickness for wind load affects the area of the line object to be loaded,
and has a default value of “Program Determined.” The net force coefficient for
wind, Cf, also has a default value of “Program Determined.” The wind loads
calculated at a line object are based on the elevation of the object, the dimen-
sions of the object, and various code-dependent wind coefficients.
3.12.1.1 Input Wind Exposure Parameters
In addition to the items discussed in the section entitled “Wind Exposure
Parameters” earlier in this chapter, the automatic wind loads for ASCE 7-02
allows specification of three additional coefficients when the exposure from
extents of diaphragms is selected: the case type; and the eccentricity factors, e1
and e2.
The case types are described in ASCE 7-02 Figure 6-9. The case type can be 1,
2, 3, or 4.
The eccentricity factors are described in ASCE 7-02 Figure 6-9. A typical val-
ue for e1 and e2 is 0.15.
3.12.1.2 Input Pressure Coefficients
When the Input Pressure Coefficients option is Program Determined, pressure
coefficients, Cp are taken from ASCE 7-02 Figure 6-6, Table for “Wall Pres-
Input Wind Exposure Parameters 3 - 37
Lateral Loads
sure Coefficients” in the windward and leeward directions. The determination
of leeward pressure automatically accounts for the building aspect ratio i.e.,
L/B ratio based on diaphragm extents. When the L/B ratio varies over the
building height, the program uses the smallest L/B ratio for producing a maxi-
mum leeward pressure coefficient. If this effect is not desirable, the User Spec-
ified option provides an alternative way to overwrite the leeward pressure coef-
ficients. A single load pattern with multi-step cases is sufficient for accurately
capturing the variable leeward pressures with the Program Determined Option.
For User Specified Input Pressure Coefficients option, only a single case in
each specific direction is recommended.
3.12.1.3 Input Wind Coefficients
Seven or eight wind coefficients are input for ASCE 7-02 wind loads depend-
ing upon the type of exposure. They are the basic wind speed in miles per hour
(mph), the exposure category, the wind importance factor, I, the topographic
factor, Kzt, the gust factor, G, the directionality factor, kd, the roughness length
parameter, z0, and the solid/gross area ratio if frame objects are exposed to
wind loads.
The basic wind speed is described in ASCE 7-02 Section 6.5.4. A typical range
of values for the basic wind speed is 85 to 150 mph.
The exposure categories are described in ASCE 7-02 Section 6.5.6.3. The
exposure category can be A, B, C or D. No other values are allowed.
The wind importance factor, I, is described in ASCE 7-02 Table 6-1. Note that
the building and structure classification categories are defined in ASCE 7-02
Table 1-1. A typical range of values for I is 0.77 to 1.15.
The topographic factor Kzt is discussed in ASCE 7-02 Section 6.5.7.2. The
default value for Kzt is 1.0. Kzt cannot be less than 1.0.
The gust response factor G is discussed in ASCE 7-02 Section 6.5.8. A typical
value for G is 0.85.
The directionality factor, Kd, is discussed in ASCE 7-02 Section 6.5.4.4. A
typical range of values for Kd is 0.85 to 0.95.
The roughness length parameter, z0, is discussed in ASCE 7-02 Commentary
C6.5.6. A typical range of values for z0 is 0.016 to 6.6.
3 - 38 Input Wind Coefficients
Chapter 3 - Automatic Wind Loads
The ratio of solid area to gross area, ∈, is used in the determination of the net
force coefficient, Cf, as discussed in ASCE 7-02 Section 6.5.13. This ratio
applies only to open structures, and thus is available for user input only when
exposure to frame objects has been selected.
3.12.2 Algorithm for ASCE 7-02 Wind Loads
3.12.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for the ASCE 7-02 are based on Section 6.5 of ASCE 7-
02.
The wind loads applied are a modified version of those described in ASCE 7-
02 Section 6.5 (Method 2 – Analytical Procedure). Windward and leeward hor-
izontal wind loads are applied on the vertical projected area of the building as
determined from the story heights and the input diaphragm exposure widths.
The programs do not apply vertical wind loads automatically over the projected
horizontal area of roof surfaces. To include those vertical wind loads in the
same load pattern, the user must include them manually.
The following equation is used to determine the velocity pressure, qz, at any
height z on the surface of the vertical projected area, in pounds per square foot
(psf).
qz = 0.00256 Kz Kzt Kd V2 I (ASCE 7-02 Eqn 6-15)
where,
Kz = The velocity pressure exposure coefficient. See (ASCE 7-02 Eqns.
C6-3a and C6-3b).
Kzt = Topographic factor as input by the user.
Kd = Directionality factor as input by the user.
V = Basic wind speed in miles per hour (mph) as input by the user.
I = Importance factor as input by the user.
The velocity pressure exposure coefficient, Kz, is obtained using (Eqns. C6-3a
and C6-3b in ASCE 7-02 Commentary Section 6.5.6.4).
Exposure from Extents of Diaphragms 3 - 39
Lateral Loads
2
2.01
zg
z
Kz
α

=


for 15 feet ≤ z ≤ zg
2
15
2.01
zg
Kz
α

=


for z < 15 feet (ASCE 7-02 C6-3a,C6-3b)
where,
z = Distance (height) from input bottom story/minimum height to point
considered.
zg = Gradient height. See (ASCE 7-02 Eqn. C6-5).
α = Empirical exponent. See (ASCE 7-02 Eqn. C6-4).
The gradient height, zg, is obtained using (Eqn. C6-5 in ASCE 7-02 Commen-
tary Section 6.5.6.4).
0.125
0
1273
g
zz
=
(ASCE 7-02 C6-5)
The empirical exponent α is obtained using (Eqn. C6-4 in ASCE 7-02 Com-
mentary Section 6.5.6.4).
(ASCE 7-02 C6-4)
where,
z0 = Roughness length parameter as input by the user.
The following equation is used to determine the wind pressure, p, at any point
on the surface of the vertical projected area.
p = q G Cp-windward + qh G Cp-leeward (ASCE 7-02 Eqn 6-17)
where,
q = Velocity pressure, qz, at any height z on the surface of the horizontal
projected area calculated using (ASCE 7-02 Eqn. 6-15).
G = Gust response factor as input by the user.
3 - 40 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
Cp-windward = Windward external pressure coefficient as input by the user.
qh = Velocity pressure at the top story height on the surface of the verti-
cal projected area calculated using (ASCE 7-02 Eqn. 6-15).
Cp-leeward = Leeward external pressure coefficient as input by the user.
The pressures, p, are distributed on the surface of the vertical projected area to
each diaphragm on a tributary area basis, as shown in Figure 3-1. The applica-
tion of these pressures determines a resultant lateral force in both the x- and y-
directions of the building, Px and Py, at each diaphragm level. Note that one or
the other of these forces may be zero if the wind direction is perfectly aligned
with the x- or y-axis. The program then combines the loads for each of the four
wind load patterns described in ASCE 7-02 Figure 6-9, resulting in the permu-
tations shown in Table 3-3.
Table 3-3: Wind Load Patterns
CASE Lateral Force Torsional Moment
1 Px ---
1 Py ---
2 0.75 Px ±0.75 e1 Bx Px
2 0.75 Py ±0.75 e1 By Py
3 0.75(Px + Py) ---
4 0.563(Px + Py) ±0.563(e1BxPx ± e2ByPy)
where,
Px = Resultant wind force in the x-direction.
Py = Resultant wind force in the y-direction.
e1 = Eccentricity for load in the direction of applied Wind load as input
by the user.
Bx = Diaphragm width in the y-direction.
e2 = Eccentricity for load in the transverse direction of applied load as
input by the user.
By = Diaphragm width in the x-direction.
Exposure from Extents of Diaphragms 3 - 41
Lateral Loads
The design pressure for the parapet is determined by the following equation:
pp = qp G Cpm (ASCE 7-02 Eqn. 6-20)
where,
pp = Combined net pressure on the parapet due to the combination of
net pressure from the front and back parapet surfaces.
qp = Velocity pressure evaluated at the top of the parapet
GCpm = Combined pressure coefficients
= +1.8 psf for Windward parapet
= −1.0 psf for Leeward parapet
3.12.2.2 Exposure from Area Objects
Automatic wind loads for the ASCE 7-02 are based on Section 6.5 of ASCE 7-
02.
The wind loads applied when using the exposure from area objects method are
applied on the vertical and horizontal surfaces of the user selected area objects
as described in ASCE 7-02 Section 6.5.12.
The following equation is used to determine the velocity pressure, qz, at any
height z on the surface of the user selected area objects, in pounds per square
feet (psf).
qz = 0.00256 Kz Kzt Kd V2 I ( ASCE 7-02 Eqn. 6-15)
where,
Kz = The velocity pressure exposure coefficient. See (ASCE 7-02 Eqns.
C6-3a and C6-3b).
Kzt = Topographic factor as input by the user.
Kd = Directionality factor as input by the user.
V = Basic wind speed in miles per hour (mph) as input by the user.
3 - 42 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
I = Importance factor as input by the user.
The value for Kz is the same as described in the previous section entitled “Ex-
posure from Extents of Diaphragms.”
The following equation is used to determine the wind pressure, p, at any point
on the surface of the area objects.
p = q G Cp (ASCE 7-02 Eqn. 6-17)
where,
q = Velocity pressure, qz, at any height z on the surface of the area ob-
ject calculated using (ASCE 7-02 Eqn. 6-15). For leeward facing
area objects, q = qh, the velocity pressure at the top story/maximum
height.
G = Gust response factor as input by the user.
Cp = Windward or leeward external pressure coefficient assigned to the
area object by the user.
The programs distribute the pressures, p, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3.12.2.3 Exposure from Line (Frame) Objects
Automatic wind loads for the ASCE 7-02 are based on Section 6.5 of ASCE 7-
02.
The wind loads applied when using the exposure from frame objects method
are applied on the exposed surfaces of the user selected frame objects as
described in ASCE 7-02 Section 6.5.13.
The following equation is used to determine the velocity pressure, qz, at any
height z on the projected area of the user selected frame objects, in pounds per
square feet (psf).
qz = 0.00256 Kz Kzt Kd V2 I (ASCE 7-02 Eqn. 6-15)
where,
Exposure from Line (Frame) Objects 3 - 43
Lateral Loads
Kz = The velocity pressure exposure coefficient. See (ASCE 7-02 Eqns.
C6-3a and C6-3b).
Kzt = Topographic factor as input by the user.
Kd = Directionality factor as input by the user.
V = Basic wind speed in miles per hour (mph) as input by the user.
I = Importance factor as input by the user.
The value for Kz is the same as described in the previous section entitled “Ex-
posure from Extents of Diaphragms.”
The following equation is used to determine the design wind force, F, on the
surface of the frame objects.
F = qz G Cf Af (ASCE 7-02 Eqn. 6-25)
where,
qz = Velocity pressure, qz, evaluated at height z of the centroid of area Af
using (ASCE 7-02 Eqn. 6-15).
G = Gust response factor as input by the user.
Cf = Net force coefficient, as specified in Table 3-4 (ASCE 7-02 Figure
6-21).
Af = Projected solid area normal to the wind.
Table 3-4: Cf factor for use in (ASCE 7-02 Eqn. 6-25)
Solid/Gross Area Ratio
∈ Cf
< 0.1 2.0
0.1 to 0.29 1.8
0.3 to 0.7 1.6
3 - 44 Exposure from Line (Frame) Objects
Chapter 3 - Automatic Wind Loads
3.13 2006 IBC / ASCE 7-05 Wind Loads
Section 1609.1.1 of the 2006 IBC states that wind loads shall be determined in
accordance with ASCE Standard 7-05. For the sake of clarity, in the remainder
of this section all references will be made only to the ASCE 7-05 document,
with the understanding that this information is directly applicable to those us-
ing the 2006 IBC as well.
3.13.1 Input Exposure
In addition to the items discussed in the section entitled “Exposure” earlier in
this chapter, the automatic wind loads for ASCE 7-05 allows specification of
the generation of wind loads on line (frame) objects for use on open or lattice
structures. If the option to include frame objects is checked, wind loads will be
generated on each line object that has been assigned wind parameters. The
wind load pattern must be defined before assigning wind parameters to frame
objects.
Assigning frame load open structure wind parameters allows specification of
three items: the frame object is or is not loaded by wind (the default is that it
is); the thickness of ice, if any; and the net force coefficient, Cf.
The ice thickness for wind load affects the area of the line (frame) object to be
loaded and has a default value of “Program Determined.” The net force coeffi-
cient for wind, Cf, also has a default value of “Program Determined.” The wind
loads calculated at a line (frame) object are based on the elevation of the object,
the dimensions of the object, and various code-dependent wind coefficients.
3.13.1.1 Input Wind Exposure Parameters
In addition to the items discussed in the section entitled “Wind Exposure Pa-
rameters” earlier in this chapter, the automatic wind loads for ASCE 7-05 also
offers three additional coefficients to input when the exposure from extents of
diaphragms is selected: the case type; and the eccentricity factors, e1 and e2.
The case types are described in ASCE 7-05 Figure 6-9. The case type can be 1,
2, 3, or 4.
The eccentricity factors are described in ASCE 7-05 Figure 6-9. A typical val-
ue for e1 and e2 is 0.15.
Input Wind Exposure Parameters 3 - 45
Lateral Loads
3.13.1.2 Input Pressure Coefficients
When the Input Pressure Coefficients option is Program Determined, pressure
coefficients, Cp are taken from ASCE 7-05 Figure 6-6, Table for “Wall Pres-
sure Coefficients” in the windward and leeward directions. The determination
of leeward pressure automatically accounts for the building aspect ratio i.e.,
L/B ratio based on diaphragm extents. When L/B ratio varies over the building
height, the program uses the smallest L/B ratio for producing a maximum lee-
ward pressure coefficient. If this effect is not desirable, the User specified op-
tion provides an alternative way to overwrite the leeward pressure coefficients.
A single load pattern with multi-step cases is sufficient for accurately capturing
the variable leeward pressures with the Program Determined Option. For the
User Specified Input Pressure Coefficients option, only a single case in each
specific direction is recommended.
3.13.1.3 Input Wind Coefficients
Seven or eight wind coefficients are input for ASCE 7-05 wind loads, depend-
ing on the type of exposure. They are the basic wind speed in miles per hour
(mph), the exposure category, the wind importance factor, I, the topographic
factor, Kzt, the gust factor, G, the directionality factor, kd, the roughness length
parameter, z0, and the solid/gross area ratio if frame objects are exposed to
wind loads.
The basic wind speed is described in ASCE 7-05 Section 6.5.4. A typical range
of values for the basic wind speed is 85 to 150 mph.
The exposure categories are described in ASCE 7-05 Section 6.5.6.3. The ex-
posure category can be B, C, or D. No other values, including exposure A, are
allowed.
The wind importance factor, I, is described in ASCE 7-05 Table 6-1. Note that
the building and structure classification categories are defined in ASCE 7-05
Table 1-1. A typical range of values for I is 0.77 to 1.15.
The topographic factor Kzt is discussed in ASCE 7-05 Section 6.5.7.2. The
default value for Kzt is 1.0. Kzt cannot be less than 1.0.
The gust effect factor G is discussed in ASCE 7-05 Section 6.5.8. A typical
value for G is 0.85.
3 - 46 Input Pressure Coefficients
Chapter 3 - Automatic Wind Loads
The directionality factor, Kd, is discussed in ASCE 7-05 Section 6.5.4.4. A
typical range of values for Kd is 0.85 to 0.95.
The roughness length parameter, z0, is discussed in ASCE 7-05 Commentary
C6.5.6. A typical range of values for z0 is 0.016 to 1.0.
The ratio of solid area to gross area, ∈, is used in the determination of the net
force coefficient, Cf, as discussed in ASCE 7-05 Section 6.5.15. This ratio
applies only to open structures, and thus is available for user input only when
exposure to frame objects has been selected.
3.13.2 Algorithm for ASCE 7-05 Wind Loads
3.13.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for the ASCE 7-05 are based on Section 6.5 of ASCE 7-
05.
The wind loads applied are a modified version of those described in ASCE 7-
05 Section 6.5 (Method 2 – Analytical Procedure). Windward and leeward
horizontal wind loads are applied on the vertical projected area of the building
as determined from the story heights and the input diaphragm exposure widths.
The programs do not apply vertical wind loads automatically over the projected
horizontal area of roof surfaces. To include those vertical wind loads in the
same load pattern, the user must include them manually.
The following equation is used to determine the velocity pressure, qz, at any
height z on the surface of the vertical projected area, in pounds per square foot
(psf).
qz = 0.00256 Kz Kzt Kd V2 I (ASCE 7-05 Eqn. 6-15)
where,
Kz = The velocity pressure exposure coefficient. See (ASCE 7-05 Eqns.
C6-4a and C6-4b).
Kzt = Topographic factor as input by the user.
Kd = Directionality factor as input by the user.
V = Basic wind speed in miles per hour (mph) as input by the user.
Exposure from Extents of Diaphragms 3 - 47
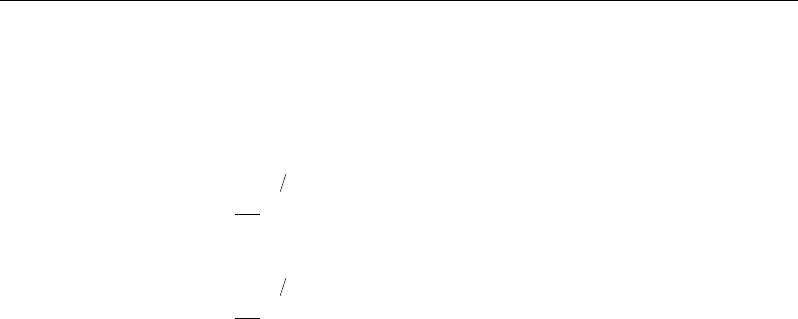
Lateral Loads
I = Importance factor as input by the user.
The velocity pressure exposure coefficient, Kz, is obtained using (Eqns. C6-4a
and C6-4b in ASCE 7-05 Commentary Section 6.5.6.6).
2
2.01
zg
z
Kz
α

=


for 15 feet ≤ z ≤ zg
2
15
2.01
zg
Kz
α

=


for z < 15 feet (ASCE 7-05 Eqn. C6-4a, C6-4b )
where,
z = Distance (height) from input bottom story/minimum height to point
considered.
zg = Gradient height. See (ASCE 7-05 Eqn. C6-6).
α = Empirical exponent. See (ASCE 7-05 Eqn. C6-5).
The gradient height, zg, and the empirical exponent α are obtained ASCE 7-05
Table 6-2.
ASCE 7-05 Eqn. 6-17 is used to determine the wind pressure, p, at any point on
the surface of the vertical projected area.
p = q G Cp-windward + qh G Cp-leeward (ASCE 7-05 Eqn. 6-17)
where,
q = Velocity pressure, qz, at any height z on the surface of the vertical
projected area calculated using (ASCE 7-05 Eqn. 6-15).
G = Gust effect factor as input by the user.
Cp-windward = Windward external pressure coefficient as input by the user.
qh = Velocity pressure at the top story height on the surface of the verti-
cal projected area calculated using (ASCE 7-05 Eqn. 6-15).
Cp-leeward = Leeward external pressure coefficient as input by the user.
3 - 48 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
The pressures, p, are distributed on the surface of the vertical projected area to
each diaphragm on a tributary area basis as shown in Figure 3-1. The applica-
tion of these pressures determines a resultant lateral force in both the x- and y-
directions of the building, Px and Py, at each diaphragm level. Note that one or
the other of these forces may be zero if the wind direction is perfectly aligned
with the x- or y-axis. The program then combines the loads for each of the four
wind load patterns described in ASCE 7-05 Figure 6-9, resulting in the permu-
tations shown in Table 3-5.
Table 3-5: Wind Load Patterns
Case Lateral Force Torsional Moment
1 Px ---
1 Py ---
2 0.75 Px ±0.75 e1 Bx Px
2 0.75 Py ±0.75 e1 By Py
3 0.75(Px + Py) ---
4 0.563(Px + Py) ±0.563(e1BxPx ± e2ByPy)
where,
Px = Resultant wind force in the x-direction.
Py = Resultant wind force in the y-direction.
e1 = Eccentricity for load in the direction of applied load as input by the
user.
Bx = Diaphragm width in the y-direction.
e2 = Eccentricity for load in the transverse direction of applied load as
input by the user.
By = Diaphragm width in the x-direction.
The design pressure for the parapet is determined by the following equation:
pp = qp G Cpm (ASCE 7-05 Eqn. 6-20)
where,
Exposure from Extents of Diaphragms 3 - 49
Lateral Loads
pp = Combined net pressure on the parapet due to the combination of
net pressure from the front and back parapet surfaces.
qp = Velocity pressure evaluated at the top of the parapet
GCpm = Combined pressure coefficients
= +1.5 psf for Windward parapet
= −1.0 psf for Leeward parapet
3.13.2.2 Exposure from Area Objects
Automatic wind loads for the ASCE 7-05 are based on Section 6.5 of ASCE 7-
05.
The wind loads applied when using the exposure from area objects method are
applied on the vertical and horizontal surfaces of the user selected area objects
as described in ASCE 7-05 Section 6.5.12.
The following equation is used to determine the velocity pressure, qz, at any
height z on the surface of the user selected area objects, in pounds per square
feet (psf).
qz = 0.00256 Kz Kzt Kd V2 I (ASCE 7-05 Eqn. 6-15)
where,
Kz = The velocity pressure exposure coefficient. See (ASCE 7-05 Eqns.
C6-4a and C6-4b).
Kzt = Topographic factor as input by the user.
Kd = Directionality factor as input by the user.
V = Basic wind speed in miles per hour (mph) as input by the user.
I = Importance factor as input by the user.
The value for Kz is the same as described in the previous section entitled “Ex-
posure from Extents of Diaphragms.”
The following equation is used to determine the wind pressure, p, at any point
on the surface of the area objects.
3 - 50 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
p = q G Cp (ASCE 7-05 Eqn. 6-17)
where,
q = Velocity pressure, qz, at any height z on the surface of the area ob-
ject calculated using (ASCE 7-05 Eqn. 6-15). For leeward facing
area objects, q = qh, the velocity pressure at the top story/maximum
height.
G = Gust effect factor as input by the user.
Cp = Windward or leeward external pressure coefficient assigned to the
area object by the user.
The programs distribute the pressures, p, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3.13.2.3 Exposure from Line (Frame) Objects
Automatic wind loads for the ASCE 7-05 are based on Section 6.5 of ASCE 7-
05.
The wind loads applied when using the exposure from frame objects method
are applied on the exposed surfaces of the user selected frame objects as de-
scribed in ASCE 7-05 Section 6.5.15.
The following equation is used to determine the velocity pressure, qz, at any
height z on the projected area of the user selected frame objects, in pounds per
square feet (psf).
qz = 0.00256 Kz Kzt Kd V2 I (ASCE 7-05 Eqn. 6-15 )
where,
Kz = The velocity pressure exposure coefficient. See (ASCE 7-05 Eqns.
C6-4a and C6-4b).
Kzt = Topographic factor as input by the user.
Kd = Directionality factor as input by the user.
V = Basic wind speed in miles per hour (mph) as input by the user.
Exposure from Line (Frame) Objects 3 - 51
Lateral Loads
I = Importance factor as input by the user.
The value for Kz is the same as described in the previous section entitled “Ex-
posure from Extents of Diaphragms.”
The following equation is used to determine the design wind force, F, on the
surface of the frame objects.
F = qz G Cf Af (ASCE 7-05 Eqn. 6-28)
where,
qz = Velocity pressure, qz, evaluated at height z of the centroid of area Af
using ASCE 7-05 Eqn. 6-15.
G = Gust effect factor as input by the user.
Cf = Net force coefficient, as specified in Table 3-6 (ASCE 7-05 Figure
6-22).
Af = Projected solid area normal to the wind.
Table 3-6: Cf factor for use in ASCE 7-05 Equation 6-28
Solid/Gross Area Ratio
∈
Cf
< 0.1 2.0
0.1 to 0.29 1.8
0.3 to 0.7 1.6
3.14 ASCE 7-10 Wind Loads
3.14.1 Input Exposure
In addition to the items discussed in the section entitled “Exposure” earlier in
this chapter, the automatic wind loads for ASCE 7-10 allows specification of
the generation of wind loads on line (frame) objects for use on open or lattice
structures. If the option to include frame objects is checked, wind loads will be
generated on each line object that has been assigned wind parameters. The
3 - 52 Exposure from Line (Frame) Objects
Chapter 3 - Automatic Wind Loads
wind load pattern must be defined before assigning wind parameters to frame
objects.
Assigning frame load open structure wind parameters allows specification of
three items: the frame object is or is not loaded by wind (the default is that it
is); the thickness of ice, if any; and the net force coefficient, Cf.
The ice thickness for wind load affects the area of the line object to be loaded
and has a default value of “Program Determined.” The net force coefficient for
wind, Cf, also has a default value of “Program Determined.” The wind loads
calculated at a line object are based on the elevation of the object, the dimen-
sions of the object, and various code-dependent wind coefficients.
3.14.1.1 Input Wind Exposure Parameters
In addition to the items discussed in the section entitled “Wind Exposure Pa-
rameters” earlier in this chapter, the automatic wind loads for ASCE 7-10 also
offers three additional coefficients to input when the exposure from extents of
diaphragms is selected: the case type; and the eccentricity factors, e1 and e2.
The case types are described in ASCE 7-10 Figure 27.4-8. The case type can be
1, 2, 3, or 4.
The eccentricity factors are described in ASCE 7-10 Figure 27.4-8. A typical
value for e1 and e2 is 0.15.
3.14.1.2 Input Pressure Coefficients
When the Input Pressure Coefficients option is Program Determined, pressure
coefficients, Cp are taken from ASCE 7-10 Figure 27.4-1, Table for “Wall
Pressure Coefficients” in the windward and leeward directions. The determina-
tion of the leeward pressure automatically accounts for the building aspect ratio
i.e., L/B ratio based on diaphragm extent. When the L/B ratio varies over the
building height, the program uses the smallest L/B ratio for producing a maxi-
mum leeward pressure coefficient. If this effect is not desirable, the User speci-
fied option provides an alternative way to overwrite the leeward pressure coef-
ficients. A single load pattern with multi-step cases is sufficient for accurately
capturing the variable leeward pressures with the Program Determined Option.
For the User Specified Input Pressure Coefficients option, only a single case in
each specific direction is recommended.
Input Wind Exposure Parameters 3 - 53
Lateral Loads
3.14.1.3 Input Wind Coefficients
Seven or eight wind coefficients are input for ASCE 7-10 wind loads, depend-
ing on the type of exposure. They are the basic wind speed in miles per hour
(mph), the exposure category, the topographic factor, Kzt, the gust factor, G, the
directionality factor, kd, and the solid/gross area ratio if frame objects are ex-
posed to wind loads
The basic wind speed is described in ASCE 7-10 Section 26.5.1. A typical
range of values for the basic wind speed is 85 to 150 mph.
The exposure categories are described in ASCE 7-10 Section 26.7.3. The
exposure category can be B, C, or D. No other values, including exposure A,
are allowed.
The topographic factor Kzt is discussed in ASCE 7-10 Section 26.8.1. The
default value for Kzt is 1.0. Kzt cannot be less than 1.0.
The gust effect factor G is discussed in ASCE 7-10 Section 26.9.1. A typical
value for G is 0.85.
The directionality factor, Kd, is discussed in ASCE 7-10 Section 26.6. A typical
range of values for Kd is 0.85 to 0.95.
The ratio of solid area to gross area, ∈, is used in the determination of the net
force coefficient, Cf, as discussed in ASCE 7-10 Section 29.5. This ratio ap-
plies to open structures only and thus is available for user input only when ex-
posure to frame objects has been selected.
3.14.2 Algorithm for ASCE 7-10 Wind Loads
3.14.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for the ASCE 7-10 are based on Section 27.2 of ASCE
7-10.
The wind loads applied are a modified version of those described in ASCE 7-
10 Section 27.2, Part 1 for Enclosed, Partially Enclosed, and Open Building of
all heights. Windward and leeward horizontal wind loads are applied on the
vertical projected area of the building as determined from the story heights and
the input diaphragm exposure widths. The programs do not apply vertical wind
3 - 54 Input Wind Coefficients
Chapter 3 - Automatic Wind Loads
loads automatically over the projected horizontal area of roof surfaces. To in-
clude those vertical wind loads in the same load pattern, the user must include
them manually.
The following equation is used to determine the velocity pressure, qz, at any
height z on the surface of the vertical projected area, in pounds per square foot
(psf).
qz = 0.00256 Kz Kzt Kd V2 (ASCE 7-10 Eqn. 27.3-1)
where,
Kz = The velocity pressure exposure coefficient. See (ASCE 7-10 Eqns.
27.3.1).
Kzt = Topographic factor as input by the user.
Kd = Directionality factor as input by the user.
V = Basic wind speed in miles per hour (mph) as input by the user.
The velocity pressure exposure coefficient, Kz, is obtained using Table 27.3-1,
Eqns. C27.3-1 and C27.3-2 in ASCE 7-10 Commentary.
2
2.01
zg
z
Kz
α

=


for 15 feet ≤ z ≤ zg
2
15
2.01
zg
Kz
α

=


for z < 15 feet (ASCE 7-10 Eqn. 27.3.1 )
where,
z = Distance (height) from input bottom story/minimum height to point
considered.
zg = Gradient height.
α = Empirical exponent.
The gradient height, zg, and the empirical exponent α are obtained using ASCE
7-10 Table 26.9-1.
Exposure from Extents of Diaphragms 3 - 55
Lateral Loads
ASCE 7-10 Eqn. 27.4-2 is used to determine the wind pressure, p, at any point
on the surface of the vertical projected area.
p = q G Cp-windward + qh G Cp-leeward (ASCE 7-10 Eqn. 27.4-2)
where,
q = Velocity pressure, qz, at any height z on the surface of the vertical
projected area calculated using (ASCE 7-10 Section 27.4.1).
G = Gust effect factor as input by the user.
Cp-windward = Windward external pressure coefficient as input by the user.
qh = Velocity pressure at the top story height on the surface of the verti-
cal projected area calculated using (ASCE 7-10 Section 27.4.1).
Cp-leeward = Leeward external pressure coefficient as input by the user.
The pressures, p, are distributed on the surface of the vertical projected area to
each diaphragm on a tributary area basis as shown in Figure 3-1. The applica-
tion of these pressures determines a resultant lateral force in both the x- and y-
directions of the building, Px and Py, at each diaphragm level. Note that one or
the other of these forces may be zero if the wind direction is perfectly aligned
with the x- or y-axis. The program then combines the loads for each of the four
wind load patterns described in ASCE 7-10 Figure 27.4-8, resulting in the per-
mutations shown in Table 3-7.
Table 3-7: Wind Load Patterns
Case Lateral Force Torsional Moment
1 Px ---
1 Py ---
2 0.75 Px ±0.75 e1 Bx Px
2 0.75 Py ±0.75 e1 By Py
3 0.75(Px + Py) ---
4 0.563(Px + Py) ±0.563(e1BxPx ± e2ByPy)
where,
3 - 56 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
Px = Resultant wind force in the x-direction.
Py = Resultant wind force in the y-direction.
e1 = Eccentricity for load in the direction of applied load as input by the
user.
Bx = Diaphragm width in the y-direction.
e2 = Eccentricity for load in the transverse direction of applied load as
input by the user.
By = Diaphragm width in the x-direction.
The design pressure for the parapet is determined by the following equation:
pp = qp G Cpm (ASCE 7-10 Eqn. 27.4-4)
where,
pp = Combined net pressure on the parapet due to the combination of
net pressure from the front and back parapet surfaces.
qp = Velocity pressure evaluated at the top of the parapet
GCpm = Combined pressure coefficients
= +1.5 psf for Windward parapet
= −1.0 psf for Leeward parapet
3.14.2.2 Exposure from Area Objects
Automatic wind loads for the ASCE 7-10 are based on Section 27.2 of ASCE
7-10.
The wind loads applied when using the exposure from area objects method are
applied on the vertical and horizontal surfaces of the user selected area objects
as described in ASCE 7-10 Section 27.2.
The following equation is used to determine the velocity pressure, qz, at any
height z on the surface of the user selected area objects, in pounds per square
feet (psf).
Exposure from Area Objects 3 - 57
Lateral Loads
qz = 0.00256 Kz Kzt Kd V2 (ASCE 7-10 Eqn. 27.3-1)
where,
Kz = The velocity pressure exposure coefficient. See (ASCE 7-10 Eqns.
Section 27.3-1).
Kzt = Topographic factor as input by the user.
Kd = Directionality factor as input by the user.
V = Basic wind speed in miles per hour (mph) as input by the user.
The value for Kz is the same as described in the previous section entitled “Ex-
posure from Extents of Diaphragms.”
The following equation is used to determine the wind pressure, p, at any point
on the surface of the area objects.
p = q G Cp (ASCE 7-10 Eqn. 27.4-2)
where,
q = Velocity pressure, qz, at any height z on the surface of the area ob-
ject calculated using (ASCE 7-10 Eqn. 27.4-2). For leeward facing
area objects, q = qh, the velocity pressure at the top story/maximum
height.
G = Gust effect factor as input by the user.
Cp = Windward or leeward external pressure coefficient assigned to the
area object by the user.
The programs distribute the pressures, p, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3.14.2.3 Exposure from Line (Frame) Objects
Automatic wind loads for the ASCE 7-10 are based on Section 29.5 of ASCE
7-10.
3 - 58 Exposure from Line (Frame) Objects
Chapter 3 - Automatic Wind Loads
The wind loads applied when using the exposure from frame objects method
are applied on the exposed surfaces of the user selected frame objects as de-
scribed in ASCE 7-10 Section 27.3-1.
The following equation is used to determine the velocity pressure, qz, at any
height z on the projected area of the user selected frame objects, in pounds per
square feet (psf).
qz = 0.00256 Kz Kzt Kd V2 (ASCE 7-10 Eqn. 29.3-1 )
where,
Kz = The velocity pressure exposure coefficient.
Kzt = Topographic factor as input by the user.
Kd = Directionality factor as input by the user.
V = Basic wind speed in miles per hour (mph) as input by the user.
The value for Kz is the same as described in the previous section entitled “Ex-
posure from Extents of Diaphragms.”
The following equation is used to determine the design wind force, F, on the
surface of the frame objects.
F = qz G Cf Af (ASCE 7-10 Eqn. 29.5-1)
where,
qz = Velocity pressure, qz, evaluated at height z of the centroid of area Af
using ASCE 7-10 Eqn. 29.3-1.
G = Gust effect factor as input by the user.
Cf = Net force coefficient, as specified in Table 3-8 (ASCE 7-10 Figure
29.5-2).
Af = Projected solid area normal to the wind.
Table 3-8: Cf factor for use in ASCE 7-10 Equation 29.5-1
Solid/Gross Area Ratio
C
f
Exposure from Line (Frame) Objects 3 - 59
Lateral Loads
∈
< 0.1
2.0
0.1 to 0.29 1.8
0.3 to 0.7
1.6
3.15 1987 RCDF Wind Loads
3.15.1 Input Wind Coefficients
A single wind coefficient, the wind velocity, VD, is input for 1987 Reglamento
de Construcciones para el Distrito Federal (RCDF) wind loads.
The wind velocity is described in 1987 RCDF Section 3.1.
3.15.2 Algorithm for 1987 RCDF Wind Loads
3.15.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for the 1987 RCDF are based on Section 3 of the Nor-
mas Tecnicas Complementarias para Diseno por Viento.
The wind loads applied when using the exposure from extents of diaphragms
method are based on a modified version of the Metodos Simplificado (Simpli-
fied Method) as described in Section 3 of the 1987 RCDF. Windward and lee-
ward horizontal wind loads are applied on the vertical projected area of the
building as determined from the story heights and the input diaphragm expo-
sure widths. The programs do not apply vertical wind loads automatically over
the projected horizontal area of roof surfaces. To include those vertical wind
loads in the same load pattern, the user must include them manually.
(Eqn. 3-1) is used to determine the wind pressure, pz, at any point on the sur-
face of the vertical projected area in pascals (Pa). (Eqn. 3-1) is based on (1987
RCDF Normas Tecnicas Complementarias para Diseno por Viento Eqn. 3.3).
( )
2-windward -leeward
0.47
z Dp p
p VC C= +
(Eqn. 3-1)
where,
VD = Wind velocity as input by the user.
3 - 60 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
Cp-windward = Windward pressure coefficient as input by the user.
Cp-leeward = Leeward pressure coefficient as input by the user.
The programs distribute the pressures, pz, on the surface of the vertical project-
ed area to each diaphragm on a tributary area basis, as shown in Figure 3-1.
3.15.2.2 Exposure from Area Objects
Automatic wind loads for the 1987 RCDF are based on Section 3 of the Nor-
mas Tecnicas Complementarias para Diseno por Viento.
The wind loads applied when using the exposure from area objects method are
based on Metodos Simplificado (Simplified Method) as described in Section 3
of the 1987 RCDF. Wind loads are applied on the vertical and horizontal sur-
faces of the user selected area objects as described in Section 3.
(Eqn. 3-2) is used to determine the wind pressure, pz, at any point on the sur-
face of the area objects in pascals (Pa). (Eqn. 3-2) is based on (1987 RCDF
Normas Tecnicas Complementarias para Diseno por Viento Eqn. 3.3).
2
0 47
z pD
p . CV=
(Eqn. 3-2)
where,
VD = Wind velocity as input by the user.
Cp = Windward or leeward external pressure coefficient assigned to the
area object by the user.
The programs distribute the pressures, pz, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3.16 2010 Chinese Wind Loads
3.16.1 Input Wind Exposure Parameters
In addition to the wind direction angle discussed in the section entitled “Wind
Exposure Parameters” earlier in this chapter, two additional coefficients are
input for the automatic wind loads for 2010 Chinese when the exposure from
extents of diaphragms is selected: the building width, B, and the shape
Exposure from Area Objects 3 - 61
Lateral Loads
coefficient, µs. The building width, B, is also input when the exposure from
area objects is selected.
The building windward width, B, is used in determining the wind vibration co-
efficient
β
z, from the GB50009-2012 (Eqn. 8.4.3).
The shape coefficient for wind load,
µ
s, replaces the windward and leeward co-
efficients previously discussed in this chapter. This coefficient is described in
section 8.3 of GB50009-2012.
When the exposure from extents of diaphragms is selected and across wind or
torsion wind option is selected: building depth D is input. For across wind,
corner modification ratio b/B and lateral period are input. For torsion wind, tor-
sion period is input.
3.16.2 Input Wind Coefficients
Two wind coefficients are input for 2010 Chinese wind loads: the basic wind
pressure, w0, in kN per meter2 (kN/m2); and the ground roughness type, RT.
The basic wind pressure is described in GB5009-2010 appendix E.
The ground roughness types are described in GB50009-2012 Section 8.2. The
roughness type can be A, B, C, or D. No other values are allowed.
3.16.2.1 Input Phi Z Source
Two choices are offered for determining how the mode coefficient, ϕz, shall be
calculated by the program. The first mode of vibration coefficient can be ob-
tained from a modal analysis or by using the Z/H ratio.
3.16.2.2 Input T1 Source
The fundamental period, T1, may be determined by the program from a modal
analysis, or it may be input directly by the user.
3.16.2.3 Input Other Parameters
The damping ratio, ζ, is input for the 2010 Chinese wind loads for use in cal-
culating the fluctuating wind load resonance factor.
3 - 62 Input Phi Z Source
Chapter 3 - Automatic Wind Loads
3.16.3 Algorithm for 2010 Chinese Wind Loads
3.16.3.1 Exposure from Extents of Diaphragms
Automatic wind loads for the 2010 Chinese are based on GB 50009-2012 sec-
tion 8 and appendix H.
Along wind loads, when using the exposure from extents of diaphragms meth-
od, are applied on the vertical projected area as determined based on the story
heights and the input exposure widths for each diaphragm. Wind vibration co-
efficient, βz at height z is determined by:
2
z 10
12 1
z
gI B Rβ=+ +
(GB50009-2012 Eqn.8.4.3)
where,
g = peak factor, g=2.5.
I10 = turbulence intensity at 10m. For roughness type A, B, C, and D, val-
ues are 0.12, 0.14, 0.23 and 0.39 correspondingly.
R = fluctuating wind load resonance factor. (GB50009-2012 8.4.4)
Bz = fluctuating wind load background factor. (GB50009-2012 8.4.5)
The wind pressure, wk (in kN/m2), at any point on the surface of the vertical
projected area, is determined by:
0
w
k zsz
w=βµµ
(GB50009-2012 Eqn. 8.1.1-1)
where,
βz = wind vibration coefficient at height z.
µs = shape coefficient for wind load as input by the user.
µz = wind pressure distribution coefficient at height z (table 7.2.1 GB
50009-2012).
w0 = basic value for wind pressure as input by the user.
Exposure from Extents of Diaphragms 3 - 63
Lateral Loads
The across wind pressure, wLk (in kN/m2), at any point on the surface of the
vertical projected area, is determined by:
2
0'1
Lk z L L
w gw C R=µ+
(GB50009-2012 Eqn. H2.2)
where,
C’L = across wind coefficient. (GB50009-2012 H.2.3)
RL = across wind resonance factor. (GB50009-2012 H.2.4)
Corner modification ratio b/B is used for calculating RL, positive value means
chamfer corner, negative value means concave corner. 0.05≤b/B≤0.2.
The torsion wind pressure, wTk (in kN/m2), at any point on the surface of the
vertical projected area, is determined by:
0.9 2
0
1.8 ' 1
Tk H T T
z
w gw C R
H

=µ+


(GB50009-2012 Eqn. H.3.2)
where,
µH = wind pressure distribution coefficient at structure top.
C’T = torsion wind induced coefficient. (GB50009-2012 H.3.3)
RT = torsion wind resonance factor. (GB50009-2012 H.3.4)
The programs distribute the pressures, wk, wLk and wTk, on the surface of the
vertical projected area to each diaphragm on a tributary area basis, as shown in
Figure 3-1.
If across wind load option selected, the program automatically create sub step
0.6FDk±FLk for across wind load case, where FD is along wind action, FLk is
across wind action. If torsion wind load option selected, the program automati-
cally create torsion wind load sub step. Only rectangular structure plan shape is
considered for across wind effect.
3 - 64 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
3.16.3.2 Exposure from Area Objects
Automatic wind loads for the 2010 Chinese are based on Section 3.2 of the JGJ
3-2002 and Section 7 of GB 50009-2001.
The wind loads applied when using the exposure from area objects method are
as described in Section 8 of GB 50009-2001. Wind loads are applied on the
vertical and horizontal surfaces of the user selected area objects.
The wind pressure, wk (in kN/m2), at any point on the surface of the vertical
projected area, is determined by:
0
w
k zsz
w=βµµ
(GB50009-2012 Eqn. 8.1.1-1)
where,
βz = wind vibration coefficient at height z.
µs = shape coefficient for wind load as input by the user.
µz = wind pressure distribution coefficient at height z (table 7.2.1 GB
50009-2012).
w0 = basic value for wind pressure as input by the user.
The value for βz is the same as described in the previous section entitled “Ex-
posure from Extents of Diaphragms.”
The programs distribute the pressures, wk, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects. As a
general rule, only area objects exposed on the windward side of the building
should be loaded using the exposure from area objects method when using the
2010 Chinese automatic wind load option.
3.17 2008 API 4F Wind Loads
Two wind coefficients are input for 2008 API 4F wind loads. They are the ref-
erence wind speed in knots and the Structural Safety Level (SSL) Multiplier.
Exposure from Area Objects 3 - 65
Lateral Loads
3.17.1 Input Exposure
In addition to the items discussed in the section entitled “Exposure” earlier in
this chapter, the automatic wind loads for API 4F-2008 allows specification of
the generation of wind loads on line (frame) objects for use on open or lattice
structures. If the option to include frame objects is checked, wind loads will be
generated on each line object that has been assigned wind parameters. The
wind load pattern must be defined before assigning wind parameters to frame
objects.
Assigning frame load open structure wind parameters allows specification of
three items: the frame object is or is not loaded by wind (the default is that it
is); the thickness of ice, if any; and the net force coefficient, Cs.
The ice thickness for wind load affects the area of the line object to be loaded,
and has a default value of “Program Determined.” The net force coefficient for
wind, Cs, also has a default value of “Program Determined.” The wind loads
calculated at a line object are based on the elevation of the object, the dimen-
sions of the object, and various code-dependent wind coefficients.
3.17.2 Algorithm for API 4F-2008 Wind Loads
3.17.2.1 Exposure from Area Objects
Automatic wind loads for the API 4F-2008 are based on Section 8.3 of API
Specification 4F.
The wind loads applied when using the exposure from area objects method are
applied on the vertical and horizontal surfaces of the user selected area objects
as described in API 4F-2008 Section 8.3.3.
The following equation is used to determine the velocity pressure, qm, at any
height z on the surface of the user selected area objects, in pounds per square
feet (psf).
qm = 0.00338 Ki Cp Vz2 (API 4F-2008 Section 8.3.3)
where,
Ki = This factor is taken as 1.0,
Cp = Wind pressure coefficient,
3 - 66 Exposure from Area Objects
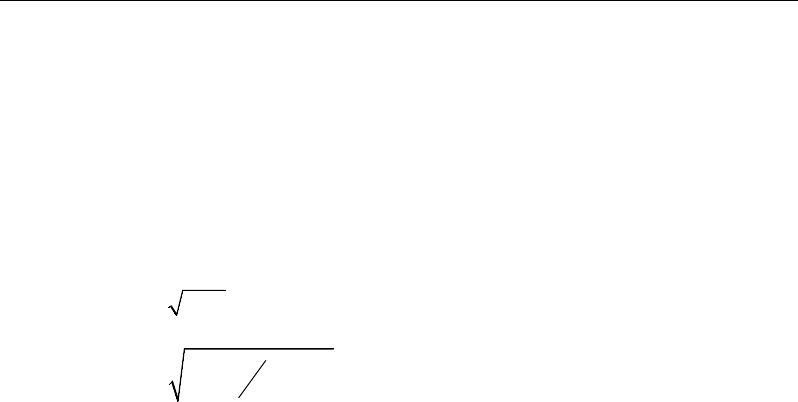
Chapter 3 - Automatic Wind Loads
Vz = Wind speed in knots at height z as computed by API 4F-2008 sec-
tion 8.3.1.3.
The following equation is used to determine the wind speed, Vz, at any point on
the surface of the area objects.
Vz = Vdes β (API 4-2008 Section 8.3.1.3)
where
0.85β=
for heights ≤ 4.6 m (15 ft)
( )
0.211
2.01 900
z
β=
for heights > 4.6 m (15 ft)
and
Vdes = Vref
α
ref (API 4-2008 Section 8.3.1.1 and 8.3.1.2)
where,
Vdes = Maximum design Wind velocity.
β = Elevation factor as determine from API 4F-2008 Table 8.4.
α
ref = Structural Safety Level (SSL) Multiplier as input by the user.
The programs distribute the pressures, qm, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3.17.2.2 Exposure from Line (Frame) Objects
Automatic wind loads for the API 4F-2008 are based on Section 8.3 of API
Specification 4F.
The wind loads applied when using the exposure from frame objects method
are applied on the exposed surfaces of the user selected frame objects as de-
scribed in API 4F-2008 Section 8.3.3.
The following equation is used to determine the velocity pressure, qm, at any
height z on the projected area of the user selected frame objects, in pounds per
square feet (psf).
Exposure from Line (Frame) Objects 3 - 67
Lateral Loads
qm = 0.00338 Ki Cs Vz2 (API 4F-2008 Section 8.3.3)
where,
Ki = A factor to account for angle of inclination φ between the longitudi-
nal axis of an individual area and the wind.
Cs = Shape coefficient in accordance with clause API 4F-2008 8.3.3.4
and Table 8.6.
Vz = Wind speed in knots at height z as computed by API 4F-2008
section 8.3.1.3.
The following equation is used to determine the wind speed, Vz, at any point on
the surface of the area objects.
Vz = Vdes β (API 4-2008 Section 8.3.1.3)
where
0.85β=
for heights ≤ 4.6 m (15 ft)
( )
0.211
2.01 900
z
β=
for heights > 4.6 m (15 ft)
and
Vdes = Vref α ref (API 4-2008 Section 8.3.1.1 and 8.3.1.2)
where,
Vdes = Maximum design Wind velocity.
β = Elevation factor as determine from API 4F-2008 Table 8.4.
α ref = Structural Safety Level (SSL) Multiplier as input by the user.
The following equation is used to determine the member design wind force, Fm,
on the surface of the frame objects.
Fm = qm Cs A (API 4F-2008 Section 8.3.3)
A correction factor Ksh is used to account for global shielding effects and for
changes in airflow around member or appurtenances ends. The Ksh factor ap-
plies to the overall wind load on the building, but does not apply to the load on
the member itself.
3 - 68 Exposure from Line (Frame) Objects
Chapter 3 - Automatic Wind Loads
Ft = Gf Ksh ∑Fm (API 4F-2008 Section 8.3.3)
where,
Gf = Gust effect factor to account for spatial coherence in accordance
with API 4F section 8.3.3.3.
Ksh = A reduction factor to account for global shielding by members or
appurtenances, and for changes in airflow around member or appur-
tenance in accordance with API 4F section 8.3.3.3
qm = Velocity pressure, qm, evaluated at height z of the centroid of area
Af.
Cs = Shape coefficient, as specified in Table 3-9 (API 4F-2008, Table
8.6).
A = Projected solid area normal to the wind.
Table 3-9: Cs Shape Coefficients for use in (API 4F-2008)
Shape Cs
Angles, Channels, Beams, Tees 1.8
Square/Rectangular box 1.5
Round pipes 0.8
Others
2.0
3.18 2013 API 4F Wind Loads
Two wind coefficients are input for 2013 API 4F wind loads. They are the ref-
erence wind speed in knots and the Structural Safety Level (SSL) Multiplier.
3.18.1 Input Exposure
In addition to the items discussed in the section entitled “Exposure” earlier in
this chapter, the automatic wind loads for API 4F-2013 allows specification of
the generation of wind loads on line (frame) objects for use on open or lattice
structures. If the option to include frame objects is checked, wind loads will be
generated on each line object that has been assigned wind parameters. The
wind load pattern must be defined before assigning wind parameters to frame
objects.
Exposure from Line (Frame) Objects 3 - 69
Lateral Loads
Assigning frame load open structure wind parameters allows specification of
three items: the frame object is or is not loaded by wind (the default is that it
is); the thickness of ice, if any; and the net force coefficient, Cs.
The ice thickness for wind load affects the area of the line object to be loaded,
and has a default value of “Program Determined.” The net force coefficient for
wind, Cs, also has a default value of “Program Determined.” The wind loads
calculated at a line object are based on the elevation of the object, the dimen-
sions of the object, and various code-dependent wind coefficients.
3.18.2 Algorithm for API 4F-2013 Wind Loads
3.18.2.1 Exposure from Area Objects
Automatic wind loads for the API 4F-2013 are based on Section 8.3 of API
Specification 4F.
The wind loads applied when using the exposure from area objects method are
applied on the vertical and horizontal surfaces of the user selected area objects
as described in API 4F-2013 Section 8.3.3.
The following equation is used to determine the velocity pressure, qm, at any
height z on the surface of the user selected area objects, in pounds per square
feet (psf).
qm = 0.00338 Ki Cp Vz2 (API 4F-2013 Section 8.3.3)
where,
Ki = This factor is taken as 1.0,
Cp = Wind pressure coefficient,
Vz = Wind speed in knots at height z as computed by API 4F-2013 sec-
tion 8.3.1.3.
The following equation is used to determine the wind speed, Vz, at any point on
the surface of the area objects.
Vz = Vdes β (API 4-2013 Section 8.3.1.4)
where
3 - 70 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
0.85β=
for heights ≤ 4.6 m (15 ft)
( )
0.211
2.01 900
z
β=
for heights > 4.6 m (15 ft)
and
Vdes = Vref
α
ref (API 4-2013 Section 8.3.1.2 and 8.3.1.3)
where,
Vdes = Maximum design Wind velocity.
β = Elevation factor as determine from API 4F-2013 Table 6.
α
ref = Structural Safety Level (SSL) Multiplier as input by the user.
The programs distribute the pressures, qm, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3.18.2.2 Exposure from Line (Frame) Objects
Automatic wind loads for the API 4F-2013 are based on Section 8.3 of API
Specification 4F.
The wind loads applied when using the exposure from frame objects method
are applied on the exposed surfaces of the user selected frame objects as de-
scribed in API 4F-2013 Section 8.3.3.
The following equation is used to determine the velocity pressure, qm, at any
height z on the projected area of the user selected frame objects, in pounds per
square feet (psf).
qm = 0.00338 Ki Cs Vz2 (API 4F-2013 Section 8.3.3)
where,
Ki = A factor to account for angle of inclination φ between the longitudi-
nal axis of an individual area and the wind.
Cs = Shape coefficient in accordance with clause API 4F-2013 8.3.3.5
and Table 8.
Exposure from Line (Frame) Objects 3 - 71
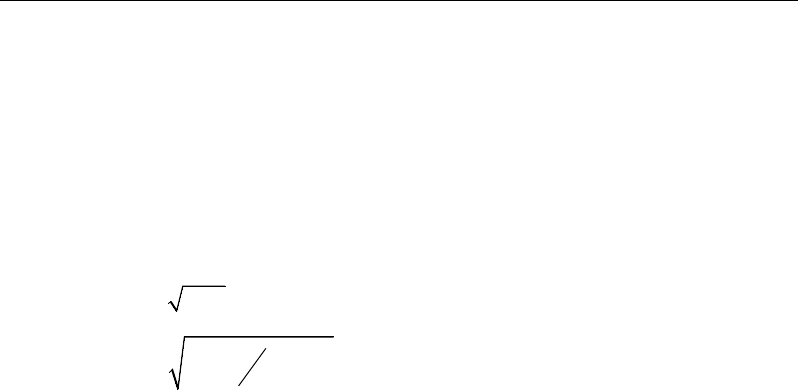
Lateral Loads
Vz = Wind speed in knots at height z as computed by API 4F-2013
section 8.3.1.4.
The following equation is used to determine the wind speed, Vz, at any point on
the surface of the area objects.
Vz = Vdes β (API 4-2013 Section 8.3.1.4)
where
0.85β=
for heights ≤ 4.6 m (15 ft)
( )
0.211
2.01 900
z
β=
for heights > 4.6 m (15 ft)
and
Vdes = Vref α ref (API 4-2013 Section 8.3.1.2 and 8.3.1.3)
where,
Vdes = Maximum design Wind velocity.
β = Elevation factor as determine from API 4F-2013 Table 6.
α ref = Structural Safety Level (SSL) Multiplier as input by the user.
The following equation is used to determine the member design wind force, Fm,
on the surface of the frame objects.
Fm = qm Cs A (API 4F-2013 Section 8.3.3)
A correction factor Ksh is used to account for global shielding effects and for
changes in airflow around member or appurtenances ends. The Ksh factor ap-
plies to the overall wind load on the building, but does not apply to the load on
the member itself.
Ft = Gf Ksh ∑Fm (API 4F-2013 Section 8.3.3)
where,
Gf = Gust effect factor to account for spatial coherence in accordance
with API 4F section 8.3.3.4
3 - 72 Exposure from Line (Frame) Objects
Chapter 3 - Automatic Wind Loads
Exposure from Line (Frame) Objects 3 - 73
Ksh = A reduction factor to account for global shielding by members or
appurtenances, and for changes in airflow around member or appur-
tenance in accordance with API 4F section 8.3.3.4
qm = Velocity pressure, qm, evaluated at height z of the centroid of area
Af.
Cs = Shape coefficient, as specified in Table 3-10 (API 4F-2013, Table
1).
A = Projected solid area normal to the wind.
Table 3-10: Cs Shape Coefficients for use in (API 4F-2013)
Shape
Cs
Angles, Channels, Beams, Tees
1.8
Square/Rectangular box
1.5
Round pipes
0.8
Others
2.0
3.19 2005 Eurocode 1(EN 1991-1-4) Wind Loads
3.19.1 Input Wind Coefficients
Seven wind coefficients are input for EN 1991-1-4:2005 wind loads. They are
the basic wind speed,
b
v
, in meter per second (m/sec), the terrain category, the
terrain orography,
 
o
cz
, turbulence factor,
1
k
, and the structural factor,
sd
cc
.
The basic wind velocity,
b
v
, is described in EN 1991-1-4:2005 Section 4.2
(2)P.
The terrain roughness,
 
zCr
, is described in EN 1991-1-4:2005 Section 4.3.2.
The terrain categories can be 0, I, II, III and IV. The roughness factor,
 
zCr
,
accounts for the variability of the mean wind velocity at the site of the structure
due to:
the height of ground level
Lateral Loads
3 - 74 Exposure from Extents of Diaphragms
the ground roughness of the terrain upwind of the structure in the wind di-
rection considered
The terrain orography,
 
o
cz
, is described in EN 1991-1-4:2005 Section 4.3.3.
The orography factor is taken as 1.0 unless otherwise specified in EN 1991-1-
4:2005 Section 4.3.3.
The wind turbulence factor
1
k
is discussed in EN 1991-1-4:2005 Section 4.4.
The roughness length parameter, z0, is discussed in EN 1991-1-4:2005 Section
4.3.2, Table 4.1. A typical range of values for z0 is 0.003 to 1.0.
3.19.2 Algorithm for EN 1991-1-4:2005 Wind Loads
3.19.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for the EN 1991-1-4:2005 are based on Section 5.3 of
EN 1991-1-4:2005.
Windward and leeward horizontal wind loads are applied on the vertical pro-
jected area of the building as determined from the story heights and the input
diaphragm exposure widths. The programs do not apply vertical wind loads au-
tomatically over the projected horizontal area of roof surfaces. To include those
vertical wind loads in the same load pattern, the user must include them manu-
ally.
The following equation is used to determine the peak velocity pressure, qp(z),
at any height z on the surface of the vertical projected area, in Newton per
square meter (N/m2).
       
2
1
217
p v r o b
q z I z c z c z v
 
 
 
(EN 1991-1-4 Eqn. 4.8)
where,
vb = Basic wind speed in m/sec as input by the user
= The air density. The values for
may be given in the National
Annex. The programs use 1.25 kg/m3 for this item.
Iv(z) = The turbulent intensity at height z
Chapter 3 - Automatic Wind Loads
cr(z) = The roughness factor
co(z) = The orography factor as input by the user
The terrain roughness factor, cr(z), is obtained using (Eqns. 4.4 and 4.5 in EN
1991-1-4:2005 Section 4.3.2).
( )
=
o
rr
z
z
kz
cln
for zmin ≤ z ≤ zmax
where,

=


0.07
0
0,
0.19
r
II
z
kz
() ()
min
z
czc rr =
≤ zmin (EN 1991-1-4 Eqn. 4.4 and 4.5)
where,
z = Distance (height) from input bottom story/minimum height to point
considered
z0 = Roughness length as given in EN 1991-1-4 Table 4.1
z0,II = 0.05 m (terrain category II, EN 1991-1-4 Table 4.1)
zmin = Minimum height as defined in EN 1991-1-4 Table 4.1
zmax = is to be taken as 200 m
The turbulence intensity factor, Iv(z), is obtained using (Eqns. 4.7 in EN 1991-
1-4:2005 Section 4.4).
( ) ( ) ( )
oo
I
v
zzzc
k
zI ln
=
for zmin ≤ z ≤ zmax
() ( )
min
zI
zI vv =
for z ≤ zmin (EN 1991-1-4 Eqn. 4.7)
where,
Exposure from Extents of Diaphragms 3 - 75
Lateral Loads
z = Distance (height) from input bottom story/minimum height to point
considered.
kI = Turbulence factor. The value of kI may be given in the National An-
nex. The default value of kI is 1.0
EN 1991-1-4:2005 Eqn. 5.1 and 5.5 are used to determine the wind pressure, w,
at any point on the surface of the vertical projected area.
w =
-windward
()
sd p p
cc q zc
+
-leeward
()
sd p p
cc q zc
(EN 1991-1-4 Eqn. 5.1 and 5.5)
where,
()
p
qz
= Velocity pressure, qp, at any height z on the surface of the ver-
tical projected area calculated using (EN 1991-1-4 Eqn. 4.8).
sd
cc
= Structural factor as input by the user.
cp-windward = Windward external pressure coefficient as input by the user.
cp-leeward = Leeward external pressure coefficient as input by the user.
The pressures, w, are distributed on the surface of the vertical projected area to
each diaphragm on a tributary area basis as shown in Figure 3-1. The applica-
tion of these pressures determines a resultant lateral force in both the x- and y-
directions of the building, Fx and Fy, at each diaphragm level. Note that one or
the other of these forces may be zero if the wind direction is perfectly aligned
with the x- or y-axis.
3.19.2.2 Exposure from Area Objects
Automatic wind loads for the EN 1991-1-4:2005 are based on Section 5.3 of
EN 1991-1-4:2005.
The wind loads applied when using the exposure from area objects method are
applied on the vertical and horizontal surfaces of the user selected area objects
based on Section 5.3 of EN 1991-1-4:2005.
The following equation is used to determine the peak velocity pressure, qp(z),
at any height z on the surface of the vertical projected area, in Newton per
square meter (N/m2).
3 - 76 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
( ) ( ) ( ) ( )
2
1
2
17
p v rob
q z I z c zc zv
 
=ρ+
 
(EN 1991-1-4 Eqn. 4.8)
where,
vb = Basic wind speed in m/sec as input by the user
ρ
= The air density. The values for
ρ
may be given in the National
Annex. The programs use 1.25 kg/m3 for this item.
Iv(z) = The turbulent intensity at height z
cr(z) = The roughness factor
co(z) = The orography factor as input by the user
The terrain roughness factor, cr(z), is obtained using (Eqns. 4.4 and 4.5 in EN
1991-1-4:2005 Section 4.3.2).
( )
=
o
rr
z
z
kzc ln
for zmin ≤ z ≤ zmax
where,

=


0.07
0
0,
0.19
r
II
z
kz
( ) ( )
min
zczc
rr
=
≤ zmin (EN 1991-1-4 Eqn. 4.4 and 4.5)
where,
z = Distance (height) from input bottom story/minimum height to point
considered.
z0 = Roughness length as given in EN 1991-1-4 Table 4.1
z0,II = 0.05 m (terrain category II, EN 1991-1-4 Table 4.1)
zmin = Minimum height as defined in EN 1991-1-4 Table 4.1
zmax = Is to be taken as 200 m.
Exposure from Area Objects 3 - 77
Lateral Loads
The turbulence intensity factor, Iv(z), is obtained using (Eqns. 4.7 in EN 1991-
1-4:2005 Section 4.4).
( ) ( ) ( )
oo
I
v
zzzc
k
zI ln
=
for zmin ≤ z ≤ zmax
( ) ( )
min
zIzI
vv
=
for z ≤ zmin (EN 1991-1-4 Eqn. 4.7)
where,
z = Distance (height) from input bottom story/minimum height to point
considered.
kI = Turbulence factor. The value of kI may be given in the National An-
nex. The default value of kI is 1.0.
EN 1991-1-4:2005 Eqn. 5.1 and 5.5 are used to determine the wind pressure, w,
at any point on the surface of the vertical projected area.
w =
-windward
()
sd p p
cc q zc
+
-leeward
()
sd p p
cc q zc
(EN 1991-1-4 Eqn. 5.1 and 5.5)
where,
()
p
qz
= Velocity pressure, qp, at any height z on the surface of the ver-
tical projected area calculated using (EN 1991-1-4 Eqn. 4.8)
sd
cc
= Structural factor as input by the user
cp-windward = Windward external pressure coefficient as input by the user.
cp-leeward = Leeward external pressure coefficient as input by the user.
The programs distribute the pressures, w, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3 - 78 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
3.20 2002 AS/NZS 1170.2 Wind Loads
3.20.1 Input Wind Coefficients
Eleven wind coefficients are input for AS/NZS 1170.2:2002 wind loads. They
are the regional wind speed,
R
V
, in meter per second (m/sec), the wind direc-
tion multiplier,
d
M
, the terrain category,
,Z cat
M
, the shielding multiplier,
s
M
,
the topographic multiplier,
t
M
, the identification of region (cyclonic/non-
cyclonic), the dynamic response factor,
dyn
C
and four parameters
( )
,
,,
a cl p
K KKK
that are used to compute aerodynamic shape factor,
fig.C
The regional wind speed,
R
V
, is described in AS/NZS 1170.2:2002 Section
3.2. For regions C and D, regional wind speed,
R
V
, includes additional factors
1.05
c
F=
and
1.1
D
F=
respectively.
The wind direction multiplier,
d
M
, is described in AS/NZS 1170.2:2002 Sec-
tion 3.3. The programs are using
1.0
d
M=
for all wind directions as default.
The terrain category,
,z cat
M
,is described in AS/NZS 1170.2:2002 Section 4.2.
The terrain categories can be 1, 2, 3 and 4. The terrain category,
,Z cat
M
, ac-
counts for the variability of the wind velocity at the site of the structure due to:
the height of ground level
the ground roughness of the terrain upwind of the structure in the wind
direction considered
The shielding multiplier,
,
s
M
is described in AS/NZS 1170.2:2002 Section
4.3.
The topographic multiplier,
,
t
M
is described in AS/NZS 1170.2:2002 Section
4.4.
The aerodynamic shape factor,
fig ,C
is described in AS/NZS 1170.2:2002
Section 5.2.
Exposure from Area Objects 3 - 79
Lateral Loads
The dynamic response factor,
dyn ,C
is described in AS/NZS 1170.2:2002
Section 6.1. For structures with a first mode fundamental frequency greater
than 1Hz,
dyn
1.0.C=
First mode fundamental frequencies between 0.2 Hz and
1Hz should be computed in accordance with AS/NZS 1170.2:2002 Section 6.
Structures with a first mode that is less than 0.2 Hz are not covered by this
Standard.
3.20.2 Algorithm for AS/NZS 1170.2:2002 Wind Loads
3.20.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for the AS/NZS 1170.2:2002 are based on Section 2.4 of
AS/NZS 1170.2:2002.
Windward and leeward horizontal wind loads are applied on the vertical
projected area of the building as determined from the story heights and the
input diaphragm exposure widths. The programs do not apply vertical wind
loads automatically over the projected horizontal area of roof surfaces. To
include those vertical wind loads in the same load pattern, the user must
include them manually.
The following equation is used to determine the design wind pressure, p, at any
height z on the surface of the vertical projected area, in Newton per square
meter (N/m2).
2
1air des, fig dyn
2
p V CC
θ

= ρ 
(AS/NZS 1170.2 Eqn. 2.4(1))
where,
des,
Vθ
= Building Orthogonal design wind speed in m/sec.
air
ρ
= Air density. The values for
air
ρ
is taken as 1.2 kg/m3.
fig
C
= Aerodynamic shape factor.
dyn
C
= Dynamic response factor as input by the user.
3 - 80 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
To simplify design, building orthogonal design wind speed is computed for the
worst direction. Therefore,
des, sit,
VV
θβ
=
in the program.
The site wind speed,
sit,
Vβ
, at the reference height
( )
z
, above ground is com-
puted as follows:
( )
sit, ,cat 30
Rd z st
V VM M MM
β= ≥
m/sec (AS/NZS 1170.2 Eqn. 2.2)
where,
sit,
V
β
= Site wind speed in m/sec at the reference height
( )
z
above
ground
R
V
= Regional 3 seconds gust wind speed in m/sec, for annual proba-
bility of exceedance of 1/R, as input by the user.
d
M
= Wind directional multiplier taken as 1.0 for all directions.
,catz
M
= Terrain/height multiplier.
s
M
= Shielding multiplier as input by the user.
t
M
= Topographic multiplier as input by the user.
The terrain roughness on wind speed factor,
,catz
M
, is obtained using AS/NZS
1170.2 Table 4.1(A) or Table 4.1(B).
The aerodynamic shape factor,
fig
C
, is obtained using Eqns. 5.2(1) in AS/NZS
1170.2:2002 Section 5.2.
fig ,
=pe a c l p
C C KKKK
(AS/NZS 1170.2 Eqn. 5.2(1))
where,
,pe
C
= external pressure coefficient as input by the user.
a
K
= Area reduction factor. The value of
a
K
is given in AS/NZS 1170.2,
Table 5.4. The default value of
a
K
is 1.0.
Exposure from Extents of Diaphragms 3 - 81
Lateral Loads
c
K
= Combination factor. The value of
c
K
is given in AS/NZS 1170.2,
Table 5.5 and for all surfaces,
c
K
should not be less than 0.8/
.
a
K
The default value of
c
K
is 1.0.
l
K
= Local pressure factor. The value of
l
K
is given in AS/NZS 1170.2,
Table 5.6. The local pressure factor
l
K
is 1.0 in all cases.
p
K
= Porous cladding reduction factor. The value of
p
K
is given in
AS/NZS 1170.2, Table 5.8. The default value of
p
K
is 1.0.
AS/NZS 1170.2:2002 Eqn. 2.2, 2.4(1) and 5.2(1) are used to determine the
wind pressure, p, at any point on the surface of the vertical projected area.
()
22
1air dyn des, ( ) , -windward des, ( ) , -leeward
2a c l p z pe h pe
p C KKKK V C V C
θθ

 
=ρ+
 

where,
cp,e-windward = Windward external pressure coefficient as input by the user.
cp,e-leeward = Leeward external pressure coefficient as input by the user.
For leeward sides, wind speed is taken as the value at
.zh=
The
()
( )
des,
,
z
pz V
θ
varies with height, whereas
( )
des, h
V
θ
remains constant.
The pressures, p, are distributed on the surface of the vertical projected area to
each diaphragm on a tributary area basis as shown in Figure 3-1. The applica-
tion of these pressures determines a resultant lateral force in both the x- and y-
directions of the building, Fx and Fy, at each diaphragm level. Note that one or
the other of these forces may be zero if the wind direction is perfectly aligned
with the x- or y-axis.
3.20.2.2 Exposure from Area Objects
Automatic wind loads for the AS/NZS 1170.2:2002 are based on Section 2.4 of
AS/NZS 1170.2:2002.
The wind loads applied when using the exposure from area objects method are
applied on the vertical and horizontal surfaces of the user selected area objects
based on Section 2.4 of AS/NZS 1170.2:2002.
3 - 82 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
The following equation is used to determine the design wind pressure, p, at any
height z on the surface of the vertical projected area, in Newton per square me-
ter (N/m2).
2
1air des, fig dyn
2
p V CC
θ

= ρ 
(AS/NZS 1170.2 Eqn. 2.4(1))
where,
des,
V
θ
= Building Orthogonal design wind speed in m/sec.
air
ρ
= Air density. The values for
air
ρ
is taken as 1.2 kg/m3.
fig
C
= Aerodynamic shape factor.
dyn
C
= Dynamic response factor as input by the user.
To simplify design, building orthogonal design wind speed is computed for the
worst direction. Therefore,
des, sit,
VV
θβ
=
in the program.
The site wind speed,
sit,
Vβ
, at the reference height
()
z
, above ground is com-
puted as follows:
( )
sit, ,cat 30 m/sec
Rd z st
V VM M MM
β= ≥
(AS/NZS 1170.2 Eqn. 2.2)
where,
sit,
Vβ
= Site wind speed in m/sec at the reference height
( )
z
above
ground
R
V
= Regional 3 seconds gust wind speed in m/sec, for annual proba-
bility of exceedance of 1/R, as input by the user.
d
M
= Wind directional multiplier taken as 1.0 for all directions.
,catz
M
= Terrain/height multiplier.
s
M
= Shielding multiplier as input by the user.
t
M
= Topographic multiplier as input by the user.
Exposure from Area Objects 3 - 83
Lateral Loads
The terrain roughness on wind speed factor,
,catz
M
, is obtained using AS/NZS
1170.2 Table 4.1(A) or Table 4.1(B).
The aerodynamic shape factor,
fig
C
, is obtained using Eqns. 5.2(1) in AS/NZS
1170.2:2002 Section 5.2.
fig ,pe a c l p
C C KKKK=
(AS/NZS 1170.2 Eqn. 5.2(1))
where,
,pe
C
= external pressure coefficient as input by the user.
a
K
= Area reduction factor. The value of
a
K
is given in AS/NZS 1170.2,
Table 5.4. The default value of
a
K
is 1.0.
c
K
= Combination factor. The value of
c
K
is given in AS/NZS 1170.2,
Table 5.5 and for all surfaces,
c
K
should not be less than 0.8/
a
K
.
The default value of
c
K
is 1.0.
l
K
= Local pressure factor. The value of
l
K
is given in AS/NZS 1170.2,
Table 5.6. The local pressure factor
l
K
is 1.0 in all cases.
p
K
= Porous cladding reduction factor. The value of
p
K
is given in
AS/NZS 1170.2, Table 5.8. The default value of
p
K
is 1.0.
AS/NZS 1170.2:2002 Eqn. 2.2, 2.4(1) and 5.2(1) are used to determine the
wind pressure, p, at any point on the surface of the vertical projected area.
( )
2
1air des, dyn , -windward , -leeward
2pe pe a c l p
p V C C C KKKK
θ


=ρ+
 
where,
cp,e-windward = Windward external pressure coefficient as input by the user.
cp,e-leeward = Leeward external pressure coefficient as input by the user.
The programs distribute the pressures, p, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3 - 84 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
3.21 2011 AS/NZS 1170.2 Wind Loads
3.21.1 Input Wind Coefficients
Eleven wind coefficients are input for AS/NZS 1170.2:2011 wind loads. They
are the regional wind speed,
R
V
, in meter per second (m/sec), the wind direc-
tion multiplier,
d
M
, the terrain category,
,Z cat
M
, the shielding multiplier,
s
M
,
the topographic multiplier,
t
M
, the identification of region (cyclonic/non-
cyclonic), the dynamic response factor,
dyn
C
and four parameters
( )
,
,,
a cl p
K KKK
that are used to compute aerodynamic shape factor,
fig.C
The regional wind speed,
R
V
, is described in AS/NZS 1170.2:2011 Section
3.2. For regions C and D, regional wind speed,
R
V
, includes additional factors
1.05
c
F=
and
1.1
D
F=
respectively.
The wind direction multiplier,
d
M
, is described in AS/NZS 1170.2:2011 Sec-
tion 3.3. The programs are using
1.0
d
M=
for all wind directions as default.
The terrain category,
,z cat
M
,is described in AS/NZS 1170.2:2011 Section 4.2.
The terrain categories can be 1, 2, 3 and 4. The terrain category,
,Z cat
M
, ac-
counts for the variability of the wind velocity at the site of the structure due to:
the height of ground level
the ground roughness of the terrain upwind of the structure in the wind
direction considered
The shielding multiplier,
,
s
M
is described in AS/NZS 1170.2:2011 Section
4.3.
The topographic multiplier,
,
t
M
is described in AS/NZS 1170.2:2011 Section
4.4.
The aerodynamic shape factor,
fig ,C
is described in AS/NZS 1170.2:2011
Section 5.2.
Exposure from Area Objects 3 - 85
Lateral Loads
The dynamic response factor,
dyn ,C
is described in AS/NZS 1170.2:2011
Section 6.1. For structures with a first mode fundamental frequency greater
than 1Hz,
dyn
1.0.C=
First mode fundamental frequencies between 0.2 Hz and
1Hz should be computed in accordance with AS/NZS 1170.2:2011 Section 6.
Structures with a first mode that is less than 0.2 Hz are not covered by this
Standard.
3.21.2 Algorithm for AS/NZS 1170.2:2011 Wind Loads
3.21.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for the AS/NZS 1170.2:2011 are based on Section 2.4 of
AS/NZS 1170.2:2011.
Windward and leeward horizontal wind loads are applied on the vertical
projected area of the building as determined from the story heights and the
input diaphragm exposure widths. The programs do not apply vertical wind
loads automatically over the projected horizontal area of roof surfaces. To
include those vertical wind loads in the same load pattern, the user must
include them manually.
Buildings with height over 70 m, a torsion force is also required based on the
eccentricity of 0.2b with respect to the center of geometry of each diaphragm.
Program provides an option for activating additional torsional moment for any
building height in positive and negative directions. User must include torsional
moments when building height is greater than 70m.
The following equation is used to determine the design wind pressure, p, at any
height z on the surface of the vertical projected area, in Newton per square
meter (N/m2).
2
1air des, fig dyn
2
p V CC
θ

= ρ 
(AS/NZS 1170.2 Eqn. 2.4(1))
where,
des,
Vθ
= Building Orthogonal design wind speed in m/sec.
air
ρ
= Air density. The values for
air
ρ
is taken as 1.2 kg/m3.
3 - 86 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
fig
C
= Aerodynamic shape factor as input by the user.
dyn
C
= Dynamic response factor as input by the user.
To simplify design, building orthogonal design wind speed is computed for the
worst direction. Therefore,
des, sit,
VV
θβ
=
in the program.
The site wind speed,
sit,
V
β
, at the reference height
( )
z
, above ground is com-
puted as follows:
( )
sit, ,cat
30
Rd z st
V VM M MM
β
= ≥
m/sec (AS/NZS 1170.2 Eqn. 2.2)
where,
sit,
V
β
= Site wind speed in m/sec at the reference height
( )
z
above
ground
R
V
= Regional gust wind speed in m/sec, for annual probability of ex-
ceedance of 1/R, as input by the user.
d
M
= Wind directional multiplier taken as 1.0 for all directions.
,catz
M
= Terrain/height multiplier.
s
M
= Shielding multiplier as input by the user.
t
M
= Topographic multiplier as input by the user.
The terrain roughness on wind speed factor,
,catz
M
, is obtained using AS/NZS
1170.2 Table 4.1.
The aerodynamic shape factor,
fig
C
, is obtained using Eqns. 5.2(1) in AS/NZS
1170.2:2011 Section 5.2.
fig ,
=pe a c l p
C C KKKK
(AS/NZS 1170.2 Eqn. 5.2(1))
where,
Exposure from Extents of Diaphragms 3 - 87
Lateral Loads
,pe
C
= external pressure coefficient as input by the user.
a
K
= Area reduction factor. The value of
a
K
is given in AS/NZS 1170.2,
Table 5.4. The default value of
a
K
is 1.0.
c
K
= Combination factor. The value of
c
K
is given in AS/NZS 1170.2,
Table 5.5 and for all surfaces,
c
K
should not be less than 0.8/
.
a
K
The default value of
c
K
is 1.0.
l
K
= Local pressure factor. The value of
l
K
is given in AS/NZS 1170.2,
Table 5.6. The local pressure factor
l
K
is 1.0 in all cases.
p
K
= Porous cladding reduction factor. The value of
p
K
is given in
AS/NZS 1170.2, Table 5.8. The default value of
p
K
is 1.0.
AS/NZS 1170.2:2011 Eqn. 2.2, 2.4(1) and 5.2(1) are used to determine the
wind pressure, p, at any point on the surface of the vertical projected area.
()
22
1air dyn des, ( ) , -windward des, ( ) , -leeward
2a c l p z pe h pe
p C KKKK V C V C
θθ

 
=ρ+
 

where,
cp,e-windward = Windward external pressure coefficient as input by the user.
cp,e-leeward = Leeward external pressure coefficient as input by the user.
For leeward sides, wind speed is taken as the value at
.zh=
The
( )
()
des,
,z
pz V θ
varies with height, whereas
( )
des, h
V
θ
remains constant.
The pressures, p, are distributed on the surface of the vertical projected area to
each diaphragm on a tributary area basis as shown in Figure 3-1. The applica-
tion of these pressures determines a resultant lateral force in both the x- and y-
directions of the building, Fx and Fy, at each diaphragm level. Note that one or
the other of these forces may be zero if the wind direction is perfectly aligned
with the x- or y-axis.
3 - 88 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
3.21.2.2 Exposure from Area Objects
Automatic wind loads for the AS/NZS 1170.2:2011 are based on Section 2.4 of
AS/NZS 1170.2:2011.
The wind loads applied when using the exposure from area objects method are
applied on the vertical and horizontal surfaces of the user selected area objects
based on Section 2.4 of AS/NZS 1170.2:2011.
The following equation is used to determine the design wind pressure, p, at any
height z on the surface of the vertical projected area, in Newton per square me-
ter (N/m2).
2
1air des, fig dyn
2
p V CC
θ

= ρ 
(AS/NZS 1170.2 Eqn. 2.4(1))
where,
des,
V
θ
= Building Orthogonal design wind speed in m/sec.
air
ρ
= Air density. The values for
air
ρ
is taken as 1.2 kg/m3.
fig
C
= Aerodynamic shape factor.
dyn
C
= Dynamic response factor as input by the user.
To simplify design, building orthogonal design wind speed is computed for the
worst direction. Therefore,
des, sit,
VV
θβ
=
in the program.
The site wind speed,
sit,
Vβ
, at the reference height
( )
z
, above ground is com-
puted as follows:
( )
sit, ,cat 30 m/sec
Rd z st
V VM M MM
β= ≥
(AS/NZS 1170.2 Eqn. 2.2)
where,
sit,
Vβ
= Site wind speed in m/sec at the reference height
( )
z
above
ground
Exposure from Area Objects 3 - 89
Lateral Loads
R
V
= Regional gust wind speed in m/sec, for annual probability of ex-
ceedance of 1/R, as input by the user.
d
M
= Wind directional multiplier taken as 1.0 for all directions.
,cat
z
M
= Terrain/height multiplier.
s
M
= Shielding multiplier as input by the user.
t
M
= Topographic multiplier as input by the user.
The terrain roughness on wind speed factor,
,catz
M
, is obtained using AS/NZS
1170.2 Table 4.1.
The aerodynamic shape factor,
fig
C
, is obtained using Eqns. 5.2(1) in AS/NZS
1170.2:2002 Section 5.2.
fig ,pe a c l p
C C KKKK=
(AS/NZS 1170.2 Eqn. 5.2(1))
where,
,pe
C
= external pressure coefficient as input by the user.
a
K
= Area reduction factor. The value of
a
K
is given in AS/NZS 1170.2,
Table 5.4. The default value of
a
K
is 1.0.
c
K
= Combination factor. The value of
c
K
is given in AS/NZS 1170.2,
Table 5.5 and for all surfaces,
c
K
should not be less than 0.8/
a
K
.
The default value of
c
K
is 1.0.
l
K
= Local pressure factor. The value of
l
K
is given in AS/NZS 1170.2,
Table 5.6. The local pressure factor
l
K
is 1.0 in all cases.
p
K
= Porous cladding reduction factor. The value of
p
K
is given in
AS/NZS 1170.2, Table 5.8. The default value of
p
K
is 1.0.
AS/NZS 1170.2:2011 Eqn. 2.2, 2.4(1) and 5.2(1) are used to determine the
wind pressure, p, at any point on the surface of the vertical projected area.
3 - 90 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
( )
2
1air des, dyn , -windward , -leeward
2pe pe a c l p
p V C C C KKKK
θ


=ρ+
 
where,
cp,e-windward = Windward external pressure coefficient as input by the user.
cp,e-leeward = Leeward external pressure coefficient as input by the user.
The programs distribute the pressures, p, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3.22 1987 Indian IS:875 Part-3 Wind Loads
3.22.1 Input Wind Coefficients
Five wind coefficients are input for IS:875 Indian wind loads. They are the
basic wind speed Vb in meter per second (m/s), the terrain category, the
structure class, Probability coefficient or Risk coefficient (k1 factor) and
topography factor (k3 factor). Terrain, height, and structure size factor (k2
factor) are evaluated by the program automatically from the terrain category
and structure class specified by the user.
The basic wind speed is described in section 5.2 of IS:875 code. A typical
range of values for the basic wind speed is 33 to 55 m/sec.
The terrain categories are described in section 5.3.2.1 of IS:875 code. The ter-
rain category can be 1, 2, 3 or 4. No other values are allowed.
The structure classes are described in section 5.3.2.1 of IS:875 code. The struc-
ture class can be A, B or C. No other values are allowed.
3.22.2 Exposure from Extents of Diaphragms
Automatic wind loads for the IS:875 Indian code are based on section 6 of
IS:875.
The wind load estimation when using the exposure from extents of diaphragms
method is based on IS:875 section 6. The user must have defined diaphragms
in the building model to use this method for wind load computation. Windward
and leeward horizontal wind loads are applied on the vertical projected area of
Exposure from Area Objects 3 - 91
Lateral Loads
the building as determined from the story heights and the input diaphragm ex-
posure widths. The program does not apply vertical wind load automatically
over the projected horizontal area of roof surfaces. To include those vertical
wind loads in the load pattern, the user must include them manually.
If a parapet exists at terrace level, the user can specify the parapet height and
the resulting wind load due to exposure of the parapet wall to wind will be in-
cluded automatically. Such a parapet is assumed to be located at the highest
floor level along the boundary of the diaphragm. There may be certain situa-
tions when a lift machine room or a water tank could be modeled above the ter-
race level. In such a case, the highest floor level will be the floor level with
maximum Z coordinate, which could be the roof of the lift machine room or
the top slab of the water tank. Suppose the parapet exists at the terrace level; in
that case, the program would not be able to identify the location of the parapet
wall to correctly account for the wind load acting on the wall. Such a parapet
wall height should not be specified on the form used to define the wind load.
Wind loads acting on such parapets must be included by manually computing
them, and such a wind load should be applied by the user at the appropriate lo-
cation manually.
The following equation is used to determine the design wind pressure pd, at any
point on the surface of the vertical projected area.
pd = 0.6Vz2 (IS:875 Section 5.4)
where,
pd = Design wind pressure
Vz = Design wind speed in m/sec
Vz = Vb.k1.k2.k3
Other terms have already been explained.
The wind force on a vertical projected area is computed by the following equa-
tion.
F = Cp.A.pd
where,
3 - 92 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
A = Vertical projected area
Cp = Net wind pressure coefficient for the windward or leeward sur-
face
Note: The program does not compute the net wind pressure coefficients. The
user should input net wind pressure coefficients on the windward and the
leeward sides by considering all possibilities of external and internal pressures
existing together or separately and specify them on the form used to define the
wind load pattern. The following equation may be used to determine the
coefficient Cp.
Cp = Cpe − Cpi
Cpe = External wind pressure coefficient
Cpi = Internal wind pressure coefficient
3.22.3 Exposure from Area Objects
Automatic wind loads for the IS:875 Indian code are based on section 6 of
IS:875.
The wind load estimation when using the exposure from area objects method is
based on IS:875 section 6. The user must have defined area objects in a vertical
plane covering the building’s outer surfaces exposed to wind to use this method
of wind load computation. If no such vertical structural elements are present in
the prototype building, the user can add dummy area objects with NULL prop-
erty for the purpose of estimating wind loads acting on outer surfaces of the
building. Typically the user will be applying windward and leeward wind coef-
ficients to such vertical area objects. Windward and leeward horizontal wind
loads are then computed and applied on the vertical area object, which in turn
creates loads on the joints connected to the area objects. The program does not
apply vertical wind load automatically over the projected horizontal area of
roof surfaces. To include those vertical wind loads in the load pattern, the user
must include them manually.
The wind load acting on parapet walls existing above roof level can’t be com-
puted automatically when wind loads are estimated using exposure from area
objects method. Assigning the parapet wall height in wind load definition dia-
Exposure from Area Objects 3 - 93
Lateral Loads
log box will have no effect on wind load in this method. Wind load acting on
parapets must be included by manually computing the wind load on them and
such a wind load should be applied by the user at appropriate location manual-
ly.
The following equation is used to determine the design wind pressure pd, at any
point on the surface of the vertical projected area.
pd=0.6Vz2 (IS:875 Section 5.4)
where,
pd = Design wind pressure
Vz = Design wind speed in m/sec.
Vz=Vb.k1.k2.k3
Other terms have been explained already.
The wind force on a vertical projected area is computed by the following equa-
tion.
F=Cp.A.pd
where,
A = Vertical projected area of area object, including dummy area
Cp= Net wind pressure coefficient for windward or leeward surfaces
Note: The program does not compute net wind pressure coefficients and the
user should input net wind pressure coefficient on windward and leeward sides
by considering all possibilities of external and internal pressures existing
together or separately and specify it in the form used to define the wind load
pattern. The following equation may be used to determine the coefficient Cp.
Cp = Cpe
−
Cpi
where,
Cpe= External wind pressure coefficient
3 - 94 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
Cpi= Internal wind pressure coefficient
Such a wind load coefficient, Cp , must be applied to the area object, including
dummy area objects drawn by the user in elevation, identifying whether it is a
windward or leeward coefficient.
3.23 2008 Italian NTC Wind Loads
3.23.1 Input Wind Coefficients
Six wind coefficients are input for Italian NTC 2008 wind loads. They are the
basic wind speed,
b
V
, in meter per second (m/sec), the exposure category, the
topography factor,
t
c
, Dynamic coefficient,
d
c
, and the shape factor,
p
c
.
The exposure category is described in NTC table 3.3.II. The exposure category
can be I, II, III, IV and V. The topography factor,
t
c
, accounts for the variabil-
ity of the mean wind velocity at the site of the structure due to:
the height of the ground level
the ground roughness of the terrain upwind from the structure in the wind
direction considered
The Dynamic coefficient represents the interaction between the wind action
and the dynamic response of the structure. For common structures it can be
cautionary and taken as 1; for particular structures, it must be determined on
the basis of specific analysis
The shape factor depends on the morphological properties of the structure.
Values for the shape factor (also known as pressure coefficient) are reported in
EC1 part 4 section 7. These values can be used also for the determination of the
shape factor in accordance with NTC 2008.
3.23.2 Algorithm for Italian NTC 2008 Wind Loads
3.23.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for the Italian NTC 2008 are based on Section 3.3 of
Italian NTC 2008.
Exposure from Extents of Diaphragms 3 - 95
Lateral Loads
Windward and leeward horizontal wind loads are applied on the vertical pro-
jected area of the building as determined from the story heights and the input
diaphragm exposure widths. The programs do not apply vertical wind loads au-
tomatically over the projected horizontal area of roof surfaces. To include those
vertical wind loads in the same load pattern, the user must include them manu-
ally.
The following equation is used to determine the peak velocity pressure, qp(z),
at any height z on the surface of the vertical projected area, in Newton per
square meter (N/m2).
2
1
2
ρ
=
bb
qV
(NTC 2008 Eqn. 3.3.4)
where,
Vb = Basic wind speed in m/sec as input by the user
ρ
= The air density. The programs use 1.25 kg/m3 for this item.
The exposure coefficient is obtained using (Eqns. 3.3.5 in NTC 2008).
2min
00
min min
7 for
()
( ) for

 
+≥

 

 

=
<
rt t
e
e
zz
k c ln c ln z z
zz
cz
cz z z
(NTC Eqn. 3.3.5)
where,
is the height of the considered point from the base of the structure
kr, z0, zmin depend on the exposure category of the site as defined in NTC 2008
table 3.3.II
Exposure Category kr Z0 [m] Zmin [m]
I 0.17 0.01 2
II
0.19
0.05
4
III 0.20 0.10 5
3 - 96 Exposure from Extents of Diaphragms
Chapter 3 - Automatic Wind Loads
IV
0.22
0.30
8
V 0.23 0.70 12
ct is the “topography” factor which can be, in general, set equal to 1
EN 1991-1-4:2005 Eqn. 5.1 and 5.5 are used to determine the wind pressure, w,
at any point on the surface of the vertical projected area.
w =
p-windwarded b
cc qc
+
p-leewarded b
cc qc
(NTC 2008 Eqn. 3.3.2)
where,
qb = Velocity pressure, qb, at any height z on the surface of the vertical
projected area calculated using (NTC 2008 Eqn. 3.3.4 ).
ce = Exposure coefficient
cp = Shape factor or pressure coefficient
cd = Dynamic coefficient
qb = Dynamic pressure
cp-windward = Windward external pressure coefficient as input by the user.
cp-leeward = Leeward external pressure coefficient as input by the user.
The pressures, w, are distributed on the surface of the vertical projected area to
each diaphragm on a tributary area basis as shown in Figure 3-1. The applica-
tion of these pressures determines a resultant lateral force in both the x- and y-
directions of the building, Fx and Fy, at each diaphragm level. Note that one or
the other of these forces may be zero if the wind direction is perfectly aligned
with the x- or y-axis.
3.23.2.2 Exposure from Area Objects
Automatic wind loads for the NTC 2008 are based on Section 3.3 of NTC
2008.
The wind loads applied when using the exposure from area objects method are
applied on the vertical and horizontal surfaces of the user selected area objects
are based on Section 3.3 of Italian NTC 2008.
Exposure from Area Objects 3 - 97
Lateral Loads
The following equation is used to determine the peak velocity pressure, qb, at
any height z on the surface of the vertical projected area, in Newton per square
meter (N/m2).
2
1
2
bb
qV= ρ
(NTC 2008 Eqn. 3.3.4)
where,
Vb = Basic wind speed in m/sec as input by the user
ρ
= The air density. The programs use 1.25 kg/m3 for this item.
The exposure coefficient is obtained using (Eqns. 3.3.5 in NTC 2008).
2min
00
min min
7 for
()
( ) for
rt t
e
e
zz
k c ln c ln z z
zz
cz
cz z z

 
+≥

 

 

=
<
(NTC Eqn. 3.3.5)
where,
is the height of the considered point from the base of the structure
kr, z0, zmin, depend on the exposure category of the site as defined in NTC
2008 table 3.3.II
Exposure Category
kr
z0 [m]
zmin [m]
I
0.17
0.01
2
II
0.19
0.05
4
III
0.20
0.10
5
IV
0.22
0.30
8
V
0.23
0.70
12
is the “topography” factor which can be, in general, set equal to 1
EN 1991-1-4:2005 Eqn. 5.1 and 5.5 are used to determine the wind pressure, w,
at any point on the surface of the vertical projected area.
w =
-windwarded bp
cc qc
+
-leewarded bp
cc qc
(NTC 2008 Eqn. 3.3.2)
where,
3 - 98 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
b
q
= Velocity pressure, qb, at any height z on the surface of the vertical
projected area calculated using (NTC 2008 Eqn. 3.3.4 ).
= Exposure coefficient
= Shape factor pressure coefficient
= Dynamic coefficient
= Dynamic pressure
cp-windward = Windward external pressure coefficient as input by the user.
cp-leeward = Leeward external pressure coefficient as input by the user.
The programs distribute the pressures, w, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3.24 1997 TS 498 Wind Loads
3.24.1 Input Wind Coefficients
Two wind coefficients are input for 1997 TS 498 wind loads. They are the
wind speed, V, in m/sec and the coefficient of dynamic, Cr.
The velocity pressure, q, can be obtained from 1997 TS 498 from section 11.3.
The coefficient of dynamic, Cr, is discussed in 1997 TS 498 section 11.2.2.
The default value is 1.0. Any positive value is allowed.
3.24.2 Algorithm for 1997 TS 498 Wind Loads
3.24.2.1 Exposure from Extents of Diaphragms
Automatic wind loads for 1997 TS 498 are based on Section 11.2 of the 1997
TS 498.
Windward and leeward horizontal wind loads are applied on the vertical
projected area of the building as determined from the story heights and the
input diaphragm exposure widths. The programs do not apply vertical wind
loads automatically over the projected horizontal area of roof surfaces. To
Exposure from Extents of Diaphragms 3 - 99
Lateral Loads
include those vertical wind loads in the load pattern, the user must include
them manually.
The following equation is used to determine the peak velocity pressure, q, at
any height z on the surface of the vertical projected area, in Newton per square
meter (N/m2).
2
1600
=V
q
(TS 498 Section 11.3)
where,
V = Basic wind speed in m/sec as input by the user
The following equation is used to determine the wind pressure, p, at any point
on the surface of the vertical projected area.
p = q Cr [Cp-windward + Cp-leeward] (TS 498 Section11.2.3)
where,
q = Velocity pressure.
Cr = Dynamic factor as input by the user.
Cp-windward = External pressure coefficient for the windward wall as input
by the user.
Cp-leeward = External pressure coefficient for the leeward wall as input by
the user.
The pressures, p, are distributed on the surface of the vertical projected area to
each diaphragm on a tributary area basis, as shown in Figure 3-1.
3.24.2.2 Exposure from Area Objects
Automatic wind loads for 1997 TS 498 are based on Section 11.2 of the 1997
TS 498.
Windward and leeward horizontal wind loads are applied on the vertical
projected area of the building as determined from the story heights and the
input diaphragm exposure widths. The programs do not apply vertical wind
loads automatically over the projected horizontal area of roof surfaces. To
3 - 100 Exposure from Area Objects
Chapter 3 - Automatic Wind Loads
include those vertical wind loads in the load pattern, the user must include
them manually.
The following equation is used to determine the peak velocity pressure, q, at
any height z on the surface of the vertical projected area, in Newton per square
meter (N/m2).
2
2
ρ
=V
qg
(TS 498 Section 11.3)
where,
Vb = Basic wind speed in m/sec as input by the user
ρ
= The air density. The programs use 1.25 kg/m3 for this item.
The following equation is used to determine the wind pressure, p, at any point
on the surface of the vertical projected area.
p = q Cr [Cp-winward + Cp-leeward] (TS 498 Section11.2.3)
where,
q = Velocity pressure.
Cr = Dynamic factor as input by the user.
Cp-windward = External pressure coefficient for the windward wall as input
by the user.
Cp-leeward = External pressure coefficient for the leeward wall as input by
the user.
The programs distribute the pressures, p, on the surface of each area object,
which in turn creates loads on the joints connected to the area objects.
3.25 User-Defined Wind Loads
For user-defined loads, define the magnitude of the wind load force in the X-
and Y-directions, the torsional moment, and the location of the wind load force
Exposure from Area Objects 3 - 101
Lateral Loads
to each diaphragm at each story level. On the basis of these data, a point object
is automatically created at the location of the applied load.
3 - 102 Exposure from Area Objects
References
AASHTO 2012. AASHTO LRFD Bridge Design Specifications — U.S.
Units, 6th Edition, American Association of State High way and
Transportation Officials, 2012.
AASHTO 2007 AASHTO LRFD Bridge Design Specifications — U.S.
Units, 4th Edition, American Association of State High way and
Transportation Officials, 2007.
ANSI/ASCE, 7-88. ASCE Standard – Minimum Design Loads for
Buildings and Other Structures, American National Standards Insti-
tute, New York, New York.
API 4F 2008. Specification for drilling and well servicing structures, 3rd
Edition, American Petroleum Institute.
AS 1170.4-2007. Australian Standard – Part 4: Earthquake action in
Australia, Standards Australia, GPO Box 476, Sydney, NSW 2001,
Australia.
AS/NZS 1170.2:2011. Australian/New Zealand Standard, Structural De-
sign Actions – Part 2: Wind Actions, Standards Australia Lim-
ited/Standards New Zealand, GPO Box 476, Sydney, NSW 2001,
Australia.
AS/NZS 1170.2:2002. Australian/New Zealand Standard, Structural De-
sign Actions – Part 2: Wind Actions, Standards Australia Lim-
References i
Automated Lateral Loads
ited/Standards New Zealand, GPO Box 476, Sydney, NSW 2001,
Australia.
ASCE, 7-95. ASCE Standard – Minimum Design Loads for Buildings
and Other Structures, American Society of Civil Engineers, New
York, New York.
ASCE, 7-02. ASCE Standard – Minimum Design Loads for Buildings
and Other Structures, American Society of Civil Engineers, Reston,
Virginia.
ASCE/SEI, 7-05. ASCE Standard – Minimum Design Loads for Build-
ings and Other Structures, American Society of Civil Engineers,
Reston, Virginia.
ASCE/SEI, 7-10. ASCE Standard – Minimum Design Loads for Build-
ings and Other Structures, American Society of Civil Engineers,
Reston, Virginia.
BOCA, 1996. The BOCA National Building Code – 13th Edition, Build-
ing Officials & Code Administrators International, Inc., Country
Club Hills, Illinois.
BS 6399, 1995. British Standard – Loading for Buildings, Part 2, British
Standards Institution, London, England.
Chinese, 2010. GB 50009-2012, Load Code for the Design of Building
Structures.
Chinese, 2002. GB 50009-2001, Load Code for the Design of Building
Structures.
EN 1991-1-4:2005, Eurocode 1: Actions on Structures, European Com-
mittee for Standardization, Management Centre: rue de Stassart, 36
B-1050 Brussels.
ENV 1998-1-1:2004, Eurocode 8: Design of structures for earthquake re-
sistance, European Committee for Standardization, Management
Centre: rue de Stassart, 36 B-1050 Brussels.
ENV 1998-1-1:1994, Eurocode 8: Design of structures for earthquake re-
sistance, European Committee for Standardization, Management
Centre: rue de Stassart, 36 B-1050 Brussels.
ii References
References
IBC, 2012. International Building Code, International Code Council,
Inc., 500 New Jersey Avenue, NW, 6th Floor, Washington, DC
20001.
IBC, 2009. International Building Code, International Code Council,
Inc., 500 New Jersey Avenue, NW, 6th Floor, Washington, DC
20001.
IBC, 2006. International Building Code, International Code Council,
Inc., 500 New Jersey Avenue, NW, 6th Floor, Washington, DC
20001.
IBC, 2003. International Building Code, International Code Council,
Inc., Falls Church, Virginia.
Indian IS:1893, 2002. Criteria for Earthquake Resistant Design of Struc-
tures (Fifth Revision), Bureau of Indian Standards, Manak Bhavan, 9
Bahadur Shah Zafar Marg, New Delhi 110002.
Indian IS:875, 1987. Code of Practice for Design Loads (Other than
Earthquake) for Buildings and Structures (Second Revision), Bureau
of Indian Standards, Manak Bhavan, 9 Bahadur Shah Zafar Marg,
New Delhi 110002.
Italian NTC, 2008. Technical Rules for Construction, D.M. January
2008,
NBCC 2015. National Building Code of Canada, National Research
Council of Canada, Ottawa, Ontario.
NBCC 2010. National Building Code of Canada, National Research
Council of Canada, Ottawa, Ontario.
NBCC 2005. National Building Code of Canada, National Research
Council of Canada, Ottawa, Ontario.
NBCC 1995. National Building Code of Canada, National Research
Council of Canada, Ottawa, Ontario.
NEHRP 1997. NEHRP Recommended Provisions for Seismic Regula-
tions for New Buildings and Other Structures, Building Seismic
Safety Council, Washington, D.C
NZS 1170.5:2004. New Zealand Standard – Part 5: Earthquake Actions
– New Zealand, Standards New Zealand, Wellington, New Zealand.
iii
Automated Lateral Loads
NZS 4203:1992. General structural design and design loadings for build-
ings, Standards New Zealand, Wellington, New Zealand.
RCDF 1987. Reglamento de Construcciones para el Distrito Federal –
Normas Tecnicas Complementarias para Diseno por Viento, RCDF,
Mexico, D.F.
TSC 2007, Turkish Seismic Code, Specification for Structures to be Built
in Seismic Areas, Official Gazette No. 26454 and 26511, Ministry of
Public Works and Settlement,
Government of Republic of Turkey.
Turkish 498, 1997. Design Loads for Buildings. Turkish Standard Insti-
tute, Necatibet Street No. 112 Ministries, Ankara.
UBC, 1997. Uniform Building Code – Structural Engineering Design
Provisions, International Conference of Building Officials, Whittier,
California.
UBC, 1994. Uniform Building Code – Structural Engineering Design
Provisions, International Conference of Building Officials, Whittier,
California.
iv References

Navigation menu