Learning Tensor Flow. A Guide To Building Deep Systems, Tom Hope, Yehezkel S. Resheff,
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 230 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Contents
- Preface
- Introduction
- Up & Running with TensorFlow
- TensorFlow Basics
- Convolutional Neural Networks
- Text & Sequences & Visualization
- Word Vectors, Advanced RNN & embedding Visualization
- TensorFlow Abstractions & Simplification
- Queues Threads & Reading Data
- Distributed TensorFlow
- Exporting & Serving Models
- Model Construction & TensorFlow Serving
- Index

Tom Hope, Yehezkel S. Reshe, and Itay Lieder
Learning TensorFlow
A Guide to Building Deep Learning Systems
Boston Farnham Sebastopol Tokyo
Beijing Boston Farnham Sebastopol Tokyo
Beijing
978-1-491-97851-1
[LSI]
Learning TensorFlow
August 2017: First Edition
Revision History for the First Edition
2017-08-04: First Release
2017-09-15: Second Release
by Tom Hope, Yehezkel S. Resheff, and Itay Lieder
Copyright © 2017 Tom Hope, Itay Lieder, and Yehezkel S. Resheff. All rights reserved.
Printed in the United States of America
Preface. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . vii
1. Introduction. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
Going Deep 1
Using TensorFlow for AI Systems 2
TensorFlow: What’s in a Name? 5
A High-Level Overview 6
Summary 8
2. Go with the Flow: Up and Running with TensorFlow. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Installing TensorFlow 9
Hello World 11
MNIST 13
Softmax Regression 14
Summary 21
3. Understanding TensorFlow Basics. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
Computation Graphs 23
What Is a Computation Graph? 23
The Benefits of Graph Computations 24
Graphs, Sessions, and Fetches 24
Creating a Graph 25
Creating a Session and Running It 26
Constructing and Managing Our Graph 27
Fetches 29
Flowing Tensors 30
Nodes Are Operations, Edges Are Tensor Objects 30
Data Types 32
Contents
Tensor Arrays and Shapes 33
Names 37
Variables, Placeholders, and Simple Optimization 38
Variables 38
Placeholders 39
Optimization 40
Summary 49
4. Convolutional Neural Networks. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
Introduction to CNNs 51
MNIST: Take II 53
Convolution 54
Pooling 56
Dropout 57
The Model 57
CIFAR10 61
Loading the CIFAR10 Dataset 62
Simple CIFAR10 Models 64
Summary 68
5. Text I: Working with Text and Sequences, and TensorBoard Visualization. . . . . . . . . . . 69
The Importance of Sequence Data 69
Introduction to Recurrent Neural Networks 70
Vanilla RNN Implementation 72
TensorFlow Built-in RNN Functions 82
RNN for Text Sequences 84
Text Sequences 84
Supervised Word Embeddings 88
LSTM and Using Sequence Length 89
Training Embeddings and the LSTM Classifier 91
Summary 93
6. Text II: Word Vectors, Advanced RNN, and Embedding Visualization. . . . . . . . . . . . . . . 95
Introduction to Word Embeddings 95
Word2vec 97
Skip-Grams 98
Embeddings in TensorFlow 100
The Noise-Contrastive Estimation (NCE) Loss Function 101
Learning Rate Decay 101
Training and Visualizing with TensorBoard 102
Checking Out Our Embeddings 103
Pretrained Embeddings, Advanced RNN 105
Pretrained Word Embeddings 106
Bidirectional RNN and GRU Cells 110
Summary 112
7. TensorFlow Abstractions and Simplications. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113
Chapter Overview 113
High-Level Survey 115
contrib.learn 117
Linear Regression 118
DNN Classifier 120
FeatureColumn 123
Homemade CNN with contrib.learn 128
TFLearn 131
Installation 131
CNN 131
RNN 134
Keras 136
Pretrained models with TF-Slim 143
Summary 151
8. Queues, Threads, and Reading Data. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 153
The Input Pipeline 153
TFRecords 154
Writing with TFRecordWriter 155
Queues 157
Enqueuing and Dequeuing 157
Multithreading 159
Coordinator and QueueRunner 160
A Full Multithreaded Input Pipeline 162
tf.train.string_input_producer() and tf.TFRecordReader() 164
tf.train.shuffle_batch() 164
tf.train.start_queue_runners() and Wrapping Up 165
Summary 166
9. Distributed TensorFlow. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 167
Distributed Computing 167
Where Does the Parallelization Take Place? 168
What Is the Goal of Parallelization? 168
TensorFlow Elements 169
tf.app.flags 169
Clusters and Servers 170
Replicating a Computational Graph Across Devices 171
Managed Sessions 171
Device Placement 172
Distributed Example 173
Summary 179
10. Exporting and Serving Models with TensorFlow. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 181
Saving and Exporting Our Model 181
Assigning Loaded Weights 182
The Saver Class 185
Introduction to TensorFlow Serving 191
Overview 192
Installation 193
Building and Exporting 194
Summary 201
A. Tips on Model Construction and Using TensorFlow Serving. . . . . . . . . . . . . . . . . . . . . . . 203
Index. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 221
Preface
Deep learning has emerged in the last few years as a premier technology for building
intelligent systems that learn from data. Deep neural networks, originally roughly
inspired by how the human brain learns, are trained with large amounts of data to
solve complex tasks with unprecedented accuracy. With open source frameworks
making this technology widely available, it is becoming a must-know for anybody
involved with big data and machine learning.
TensorFlow is currently the leading open source software for deep learning, used by a
rapidly growing number of practitioners working on computer vision, natural lan‐
guage processing (NLP), speech recognition, and general predictive analytics.
This book is an end-to-end guide to TensorFlow designed for data scientists, engi‐
neers, students, and researchers. The book adopts a hands-on approach suitable for a
broad technical audience, allowing beginners a gentle start while diving deep into
advanced topics and showing how to build production-ready systems.
In this book you will learn how to:
1. Get up and running with TensorFlow, rapidly and painlessly.
2. Use TensorFlow to build models from the ground up.
3. Train and understand popular deep learning models for computer vision and
NLP.
4. Use extensive abstraction libraries to make development easier and faster.
5. Scale up TensorFlow with queuing and multithreading, training on clusters, and
serving output in production.
6. And much more!
This book is written by data scientists with extensive R&D experience in both indus‐
try and academic research. The authors take a hands-on approach, combining practi‐
cal and intuitive examples, illustrations, and insights suitable for practitioners seeking
to build production-ready systems, as well as readers looking to learn to understand
and build flexible and powerful models.
Prerequisites
This book assumes some basic Python programming know-how, including basic
familiarity with the scientific library NumPy.
Machine learning concepts are touched upon and intuitively explained throughout
the book. For readers who want to gain a deeper understanding, a reasonable level of
knowledge in machine learning, linear algebra, calculus, probability, and statistics is
recommended.
Conventions Used in This Book
The following typographical conventions are used in this book:
Italic
Indicates new terms, URLs, email addresses, filenames, and file extensions.
Constant width
Used for program listings, as well as within paragraphs to refer to program ele‐
ments such as variable or function names, databases, data types, environment
variables, statements, and keywords.
Constant width bold
Shows commands or other text that should be typed literally by the user.
Constant width italic
Shows text that should be replaced with user-supplied values or by values deter‐
mined by context.
Using Code Examples
Supplemental material (code examples, exercises, etc.) is available for download at
https://github.com/Hezi-Reshe/Oreilly-Learning-TensorFlow.
This book is here to help you get your job done. In general, if example code is offered
with this book, you may use it in your programs and documentation. You do not
need to contact us for permission unless you’re reproducing a significant portion of
the code. For example, writing a program that uses several chunks of code from this
book does not require permission. Selling or distributing a CD-ROM of examples
from O’Reilly books does require permission. Answering a question by citing this
book and quoting example code does not require permission. Incorporating a signifi‐
cant amount of example code from this book into your product’s documentation does
require permission.
CHAPTER 1
Introduction
This chapter provides a high-level overview of TensorFlow and its primary use:
implementing and deploying deep learning systems. We begin with a very brief intro‐
ductory look at deep learning. We then present TensorFlow, showcasing some of its
exciting uses for building machine intelligence, and then lay out its key features and
properties.
Going Deep
From large corporations to budding startups, engineers and data scientists are col‐
lecting huge amounts of data and using machine learning algorithms to answer com‐
plex questions and build intelligent systems. Wherever one looks in this landscape,
the class of algorithms associated with deep learning have recently seen great success,
often leaving traditional methods in the dust. Deep learning is used today to under‐
stand the content of images, natural language, and speech, in systems ranging from
mobile apps to autonomous vehicles. Developments in this field are taking place at
breakneck speed, with deep learning being extended to other domains and types of
data, like complex chemical and genetic structures for drug discovery and high-
dimensional medical records in public healthcare.
Deep learning methods—which also go by the name of deep neural networks—were
originally roughly inspired by the human brain’s vast network of interconnected neu‐
rons. In deep learning, we feed millions of data instances into a network of neurons,
teaching them to recognize patterns from raw inputs. The deep neural networks take
raw inputs (such as pixel values in an image) and transform them into useful repre‐
sentations, extracting higher-level features (such as shapes and edges in images) that
capture complex concepts by combining smaller and smaller pieces of information to
solve challenging tasks such as image classification (Figure 1-1). The networks auto‐
matically learn to build abstract representations by adapting and correcting them‐
1

selves, fitting patterns observed in the data. The ability to automatically construct
data representations is a key advantage of deep neural nets over conventional
machine learning, which typically requires domain expertise and manual feature
engineering before any “learning” can occur.
Figure 1-1. An illustration of image classication with deep neural networks. e net‐
work takes raw inputs (pixel values in an image) and learns to transform them into use‐
ful representations, in order to obtain an accurate image classication.
This book is about Google’s framework for deep learning, TensorFlow. Deep learning
algorithms have been used for several years across many products and areas at Goo‐
gle, such as search, translation, advertising, computer vision, and speech recognition.
TensorFlow is, in fact, a second-generation system for implementing and deploying
deep neural networks at Google, succeeding the DistBelief project that started in
2011.
TensorFlow was released to the public as an open source framework with an Apache
2.0 license in November 2015 and has already taken the industry by storm, with
adoption going far beyond internal Google projects. Its scalability and flexibility,
combined with the formidable force of Google engineers who continue to maintain
and develop it, have made TensorFlow the leading system for doing deep learning.
Using TensorFlow for AI Systems
Before going into more depth about what TensorFlow is and its key features, we will
briefly give some exciting examples of how TensorFlow is used in some cutting-edge
real-world applications, at Google and beyond.
2 | Chapter 1: Introduction

Pre-trained models: state-of-the-art computer vision for all
One primary area where deep learning is truly shining is computer vision. A funda‐
mental task in computer vision is image classification—building algorithms and sys‐
tems that receive images as input, and return a set of categories that best describe
them. Researchers, data scientists, and engineers have designed advanced deep neural
networks that obtain highly accurate results in understanding visual content. These
deep networks are typically trained on large amounts of image data, taking much
time, resources, and effort. However, in a growing trend, researchers are publicly
releasing pre-trained models—deep neural nets that are already trained and that
users can download and apply to their data (Figure 1-2).
Figure 1-2. Advanced computer vision with pre-trained TensorFlow models.
TensorFlow comes with useful utilities allowing users to obtain and apply cutting-
edge pretrained models. We will see several practical examples and dive into the
details throughout this book.
Generating rich natural language descriptions for images
One exciting area of deep learning research for building machine intelligence systems
is focused on generating natural language descriptions for visual content (Figure 1-3).
A key task in this area is image captioning—teaching the model to output succinct
and accurate captions for images. Here too, advanced pre-trained TensorFlow models
that combine natural language understanding with computer vision are available.
Going Deep | 3

Figure 1-3. Going from images to text with image captioning (illustrative example).
Text summarization
Natural language understanding (NLU) is a key capability for building AI systems.
Tremendous amounts of text are generated every day: web content, social media,
news, emails, internal corporate correspondences, and many more. One of the most
sought-after abilities is to summarize text, taking long documents and generating
succinct and coherent sentences that extract the key information from the original
texts (Figure 1-4). As we will see later in this book, TensorFlow comes with powerful
features for training deep NLU networks, which can also be used for automatic text
summarization.
4 | Chapter 1: Introduction

Figure 1-4. An illustration of smart text summarization.
TensorFlow: What’s in a Name?
Deep neural networks, as the term and the illustrations we’ve shown imply, are all
about networks of neurons, with each neuron learning to do its own operation as part
of a larger picture. Data such as images enters this network as input, and flows
through the network as it adapts itself at training time or predicts outputs in a
deployed system.
Tensors are the standard way of representing data in deep learning. Simply put, ten‐
sors are just multidimensional arrays, an extension of two-dimensional tables (matri‐
ces) to data with higher dimensionality. Just as a black-and-white (grayscale) images
are represented as “tables” of pixel values, RGB images are represented as tensors
(three-dimensional arrays), with each pixel having three values corresponding to red,
green, and blue components.
In TensorFlow, computation is approached as a dataow graph (Figure 1-5). Broadly
speaking, in this graph, nodes represent operations (such as addition or multiplica‐
tion), and edges represent data (tensors) flowing around the system. In the next chap‐
ters, we will dive deeper into these concepts and learn to understand them with many
examples.
TensorFlow: What’s in a Name? | 5

Figure 1-5. A dataow computation graph. Data in the form of tensors ows through a
graph of computational operations that make up our deep neural networks.
A High-Level Overview
TensorFlow, in the most general terms, is a software framework for numerical com‐
putations based on dataflow graphs. It is designed primarily, however, as an interface
for expressing and implementing machine learning algorithms, chief among them
deep neural networks.
TensorFlow was designed with portability in mind, enabling these computation
graphs to be executed across a wide variety of environments and hardware platforms.
With essentially identical code, the same TensorFlow neural net could, for instance,
be trained in the cloud, distributed over a cluster of many machines or on a single
laptop. It can be deployed for serving predictions on a dedicated server or on mobile
device platforms such as Android or iOS, or Raspberry Pi single-board computers.
TensorFlow is also compatible, of course, with Linux, macOS, and Windows operat‐
ing systems.
The core of TensorFlow is in C++, and it has two primary high-level frontend lan‐
guages and interfaces for expressing and executing the computation graphs. The most
developed frontend is in Python, used by most researchers and data scientists. The
C++ frontend provides quite a low-level API, useful for efficient execution in embed‐
ded systems and other scenarios.
Aside from its portability, another key aspect of TensorFlow is its flexibility, allowing
researchers and data scientists to express models with relative ease. It is sometimes
revealing to think of modern deep learning research and practice as playing with
“LEGO-like” bricks, replacing blocks of the network with others and seeing what hap‐
pens, and at times designing new blocks. As we shall see throughout this book, Ten‐
sorFlow provides helpful tools to use these modular blocks, combined with a flexible
API that enables the writing of new ones. In deep learning, networks are trained with
6 | Chapter 1: Introduction

a feedback process called backpropagation based on gradient descent optimization.
TensorFlow flexibly supports many optimization algorithms, all with automatic dif‐
ferentiation—the user does not need to specify any gradients in advance, since Ten‐
sorFlow derives them automatically based on the computation graph and loss
function provided by the user. To monitor, debug, and visualize the training process,
and to streamline experiments, TensorFlow comes with TensorBoard (Figure 1-6), a
simple visualization tool that runs in the browser, which we will use throughout this
book.
Figure 1-6. TensorFlow’s visualization tool, TensorBoard, for monitoring, debugging, and
analyzing the training process and experiments.
Key enablers of TensorFlow’s flexibility for data scientists and researchers are high-
level abstraction libraries. In state-of-the-art deep neural nets for computer vision or
NLU, writing TensorFlow code can take a toll—it can become a complex, lengthy, and
cumbersome endeavor. Abstraction libraries such as Keras and TF-Slim offer simpli‐
fied high-level access to the “LEGO bricks” in the lower-level library, helping to
streamline the construction of the dataflow graphs, training them, and running infer‐
ence. Another key enabler for data scientists and engineers is the pretrained models
that come with TF-Slim and TensorFlow. These models were trained on massive
amounts of data with great computational resources, which are often hard to come by
and in any case require much effort to acquire and set up. Using Keras or TF-Slim, for
example, with just a few lines of code it is possible to use these advanced models for
inference on incoming data, and also to fine-tune the models to adapt to new data.
The flexibility and portability of TensorFlow help make the flow from research to
production smooth, cutting the time and effort it takes for data scientists to push
their models to deployment in products and for engineers to translate algorithmic
ideas into robust code.
A High-Level Overview | 7

TensorFlow abstractions
TensorFlow comes with abstraction libraries such as Keras and TF-
Slim, offering simplified high-level access to TensorFlow. These
abstractions, which we will see later in this book, help streamline
the construction of the dataflow graphs and enable us to train them
and run inference with many fewer lines of code.
But beyond flexibility and portability, TensorFlow has a suite of properties and tools
that make it attractive for engineers who build real-world AI systems. It has natural
support for distributed training—indeed, it is used at Google and other large industry
players to train massive networks on huge amounts of data, over clusters of many
machines. In local implementations, training on multiple hardware devices requires
few changes to code used for single devices. Code also remains relatively unchanged
when going from local to distributed, which makes using TensorFlow in the cloud, on
Amazon Web Services (AWS) or Google Cloud, particularly attractive. Additionally,
as we will see further along in this book, TensorFlow comes with many more features
aimed at boosting scalability. These include support for asynchronous computation
with threading and queues, efficient I/O and data formats, and much more.
Deep learning continues to rapidly evolve, and so does TensorFlow, with frequent
new and exciting additions, bringing better usability, performance, and value.
Summary
With the set of tools and features described in this chapter, it becomes clear why Ten‐
sorFlow has attracted so much attention in little more than a year. This book aims at
first rapidly getting you acquainted with the basics and ready to work, and then we
will dive deeper into the world of TensorFlow with exciting and practical examples.
8 | Chapter 1: Introduction

1We refer the reader to the official TensorFlow install guide for further details, and especially the ever-changing
details of GPU installations.
CHAPTER 2
Go with the Flow: Up and Running
with TensorFlow
In this chapter we start our journey with two working TensorFlow examples. The first
(the traditional “hello world” program), while short and simple, includes many of the
important elements we discuss in depth in later chapters. With the second, a first end-
to-end machine learning model, you will embark on your journey toward state-of-
the-art machine learning with TensorFlow.
Before getting started, we briefly walk through the installation of TensorFlow. In
order to facilitate a quick and painless start, we install the CPU version only, and
defer the GPU installation to later.1 (If you don’t know what this means, that’s OK for
the time being!) If you already have TensorFlow installed, skip to the second section.
Installing TensorFlow
If you are using a clean Python installation (probably set up for the purpose of learn‐
ing TensorFlow), you can get started with the simple pip installation:
$ pip install tensorflow
This approach does, however, have the drawback that TensorFlow will override exist‐
ing packages and install specific versions to satisfy dependencies. If you are using this
Python installation for other purposes as well, this will not do. One common way
around this is to install TensorFlow in a virtual environment, managed by a utility
called virtualenv.
9

Depending on your setup, you may or may not need to install virtualenv on your
machine. To install virtualenv, type:
$ pip install virtualenv
See http://virtualenv.pypa.io for further instructions.
In order to install TensorFlow in a virtual environment, you must first create the vir‐
tual environment—in this book we choose to place these in the ~/envs folder, but feel
free to put them anywhere you prefer:
$ cd ~
$ mkdir envs
$ virtualenv ~/envs/tensorflow
This will create a virtual environment named tensorow in ~/envs (which will mani‐
fest as the folder ~/envs/tensorow). To activate the environment, use:
$ source ~/envs/tensorflow/bin/activate
The prompt should now change to indicate the activated environment:
(tensorflow)$
At this point the pip install command:
(tensorflow)$ pip install tensorflow
will install TensorFlow into the virtual environment, without impacting other pack‐
ages installed on your machine.
Finally, in order to exit the virtual environment, you type:
(tensorflow)$ deactivate
at which point you should get back the regular prompt:
$
TensorFlow for Windows Users
Up until recently TensorFlow had been notoriously difficult to use with Windows
machines. As of TensorFlow 0.12, however, Windows integration is here! It is as sim‐
ple as:
pip install tensorflow
for the CPU version, or:
pip install tensorflow-gpu
for the GPU-enabled version (assuming you already have CUDA 8).
10 | Chapter 2: Go with the Flow: Up and Running with TensorFlow

Adding an alias to ~/.bashrc
The process described for entering and exiting your virtual envi‐
ronment might be too cumbersome if you intend to use it often. In
this case, you can simply append the following command to your
~/.bashrc file:
alias tensorflow="source ~/envs/tensorflow/bin/activate"
and use the command tensorflow to activate the virtual environ‐
ment. To quit the environment, you will still use deactivate.
Now that we have a basic installation of TensorFlow, we can proceed to our first
working examples. We will follow the well-established tradition and start with a
“hello world” program.
Hello World
Our first example is a simple program that combines the words “Hello” and “ World!”
and displays the output—the phrase “Hello World!” While simple and straightfor‐
ward, this example introduces many of the core elements of TensorFlow and the ways
in which it is different from a regular Python program.
We suggest you run this example on your machine, play around with it a bit, and see
what works. Next, we will go over the lines of code and discuss each element sepa‐
rately.
First, we run a simple install and version check (if you used the virtualenv installation
option, make sure to activate it before running TensorFlow code):
import tensorflow as tf
print(tf.__version__)
If correct, the output will be the version of TensorFlow you have installed on your
system. Version mismatches are the most probable cause of issues down the line.
Example 2-1 shows the complete “hello world” example.
Example 2-1. “Hello world” with TensorFlow
import tensorflow as tf
h = tf.constant("Hello")
w = tf.constant(" World!")
hw = h + w
with tf.Session() as sess:
ans = sess.run(hw)
print (ans)
Hello World | 11

We assume you are familiar with Python and imports, in which case the first line:
import tensorflow as tf
requires no explanation.
IDE conguration
If you are running TensorFlow code from an IDE, then make sure
to redirect to the virtualenv where the package is installed. Other‐
wise, you will get the following import error:
ImportError: No module named tensorflow
In the PyCharm IDE this is done by selecting Run→Edit Configu‐
rations, then changing Python Interpreter to point to ~/envs/
tensorow/bin/python, assuming you used ~/envs/tensorow as the
virtualenv directory.
Next, we define the constants "Hello" and " World!", and combine them:
import tensorflow as tf
h = tf.constant("Hello")
w = tf.constant(" World!")
hw = h + w
At this point, you might wonder how (if at all) this is different from the simple
Python code for doing this:
ph = "Hello"
pw = " World!"
phw = h + w
The key point here is what the variable hw contains in each case. We can check this
using the print command. In the pure Python case we get this:
>print phw
Hello World!
In the TensorFlow case, however, the output is completely different:
>print hw
Tensor("add:0", shape=(), dtype=string)
Probably not what you expected!
In the next chapter we explain the computation graph model of TensorFlow in detail,
at which point this output will become completely clear. The key idea behind compu‐
tation graphs in TensorFlow is that we first define what computations should take
place, and then trigger the computation in an external mechanism. Thus, the Tensor‐
Flow line of code:
12 | Chapter 2: Go with the Flow: Up and Running with TensorFlow
hw = h + w
does not compute the sum of h and w, but rather adds the summation operation to a
graph of computations to be done later.
Next, the Session object acts as an interface to the external TensorFlow computation
mechanism, and allows us to run parts of the computation graph we have already
defined. The line:
ans = sess.run(hw)
actually computes hw (as the sum of h and w, the way it was defined previously), fol‐
lowing which the printing of ans displays the expected “Hello World!” message.
This completes the first TensorFlow example. Next, we dive right in with a simple
machine learning example, which already shows a great deal of the promise of the
TensorFlow framework.
MNIST
The MNIST (Mixed National Institute of Standards and Technology) handwritten
digits dataset is one of the most researched datasets in image processing and machine
learning, and has played an important role in the development of artificial neural net‐
works (now generally referred to as deep learning).
As such, it is fitting that our first machine learning example should be dedicated to
the classification of handwritten digits (Figure 2-1 shows a random sample from the
dataset). At this point, in the interest of keeping it simple, we will apply a very simple
classifier. This simple model will suffice to classify approximately 92% of the test set
correctly—the best models currently available reach over 99.75% correct classifica‐
tion, but we have a few more chapters to go until we get there! Later in the book, we
will revisit this data and use more sophisticated methods.
MNIST | 13

Figure 2-1. 100 random MNIST images
Softmax Regression
In this example we will use a simple classifier called somax regression. We will not go
into the mathematical formulation of the model in too much detail (there are plenty
of good resources where you can find this information, and we strongly suggest that
you do so, if you have never seen this before). Rather, we will try to provide some
intuition into the way the model is able to solve the digit recognition problem.
Put simply, the softmax regression model will figure out, for each pixel in the image,
which digits tend to have high (or low) values in that location. For instance, the cen‐
ter of the image will tend to be white for zeros, but black for sixes. Thus, a black pixel
14 | Chapter 2: Go with the Flow: Up and Running with TensorFlow

2It is common to add a “bias term,” which is equivalent to stating which digits we believe an image to be before
seeing the pixel values. If you have seen this before, then try adding it to the model and check how it affects
the results.
3If you are familiar with softmax regression, you probably realize this is a simplification of the way it works,
especially when pixel values are as correlated as with digit images.
in the center of an image will be evidence against the image containing a zero, and in
favor of it containing a six.
Learning in this model consists of finding weights that tell us how to accumulate evi‐
dence for the existence of each of the digits. With softmax regression, we will not use
the spatial information in the pixel layout in the image. Later on, when we discuss
convolutional neural networks, we will see that utilizing spatial information is one of
the key elements in making great image-processing and object-recognition models.
Since we are not going to use the spatial information at this point, we will unroll our
image pixels as a single long vector denoted x (Figure 2-2). Then
xw0 = ∑xiwi
0
will be the evidence for the image containing the digit 0 (and in the same way we will
have wd weight vectors for each one of the other digits, d= 1, . . ., 9).
Figure 2-2. MNIST image pixels unrolled to vectors and stacked as columns (sorted by
digit from le to right). While the loss of spatial information doesn’t allow us to recog‐
nize the digits, the block structure evident in this gure is what allows the somax model
to classify images. Essentially, all zeros (lemost block) share a similar pixel structure, as
do all ones (second block from the le), etc.
All this means is that we sum up the pixel values, each multiplied by a weight, which
we think of as the importance of this pixel in the overall evidence for the digit zero
being in the image.2
For instance, w038 will be a large positive number if the 38th pixel having a high inten‐
sity points strongly to the digit being a zero, a strong negative number if high-
intensity values in this position occur mostly in other digits, and zero if the intensity
value of the 38th pixel tells us nothing about whether or not this digit is a zero.3
Performing this calculation at once for all digits (computing the evidence for each of
the digits appearing in the image) can be represented by a single matrix operation. If
Softmax Regression | 15
we place the weights for each of the digits in the columns of a matrix W, then the
length-10 vector with the evidence for each of the digits is
[xw0···xw9] = xW
The purpose of learning a classifier is almost always to evaluate new examples. In this
case, this means that we would like to be able to tell what digit is written in a new
image we have not seen in our training data. In order to do this, we start by summing
up the evidence for each of the 10 possible digits (i.e., computing xW). The final
assignment will be the digit that “wins” by accumulating the most evidence:
digit = argmax(xW)
We start by presenting the code for this example in its entirety (Example 2-2), then
walk through it line by line and go over the details. You may find that there are many
novel elements or that some pieces of the puzzle are missing at this stage, but our
advice is that you go with it for now. Everything will become clear in due course.
Example 2-2. Classifying MNIST handwritten digits with somax regression
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
DATA_DIR = '/tmp/data'
NUM_STEPS = 1000
MINIBATCH_SIZE = 100
data = input_data.read_data_sets(DATA_DIR, one_hot=True)
x = tf.placeholder(tf.float32, [None, 784])
W = tf.Variable(tf.zeros([784, 10]))
y_true = tf.placeholder(tf.float32, [None, 10])
y_pred = tf.matmul(x, W)
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
logits=y_pred, labels=y_true))
gd_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
correct_mask = tf.equal(tf.argmax(y_pred, 1), tf.argmax(y_true, 1))
accuracy = tf.reduce_mean(tf.cast(correct_mask, tf.float32))
with tf.Session() as sess:
# Train
sess.run(tf.global_variables_initializer())
16 | Chapter 2: Go with the Flow: Up and Running with TensorFlow
for _ in range(NUM_STEPS):
batch_xs, batch_ys = data.train.next_batch(MINIBATCH_SIZE)
sess.run(gd_step, feed_dict={x: batch_xs, y_true: batch_ys})
# Test
ans = sess.run(accuracy, feed_dict={x: data.test.images,
y_true: data.test.labels})
print "Accuracy: {:.4}%".format(ans*100)
If you run the code on your machine, you should get output like this:
Extracting /tmp/data/train-images-idx3-ubyte.gz
Extracting /tmp/data/train-labels-idx1-ubyte.gz
Extracting /tmp/data/t10k-images-idx3-ubyte.gz
Extracting /tmp/data/t10k-labels-idx1-ubyte.gz
Accuracy: 91.83%
That’s all it takes! If you have put similar models together before using other plat‐
forms, you might appreciate the simplicity and readability. However, these are just
side bonuses, with the efficiency and flexibility gained from the computation graph
model of TensorFlow being what we are really interested in.
The exact accuracy value you get will be just under 92%. If you run the program once
more, you will get another value. This sort of stochasticity is very common in
machine learning code, and you have probably seen similar results before. In this
case, the source is the changing order in which the handwritten digits are presented
to the model during learning. As a result, the learned parameters following training
are slightly different from run to run.
Running the same program five times might therefore produce this result:
Accuracy: 91.86%
Accuracy: 91.51%
Accuracy: 91.62%
Accuracy: 91.93%
Accuracy: 91.88%
We will now briefly go over the code for this example and see what is new from the
previous “hello world” example. We’ll break it down line by line:
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
The first new element in this example is that we use external data! Rather than down‐
loading the MNIST dataset (freely available at http://yann.lecun.com/exdb/mnist/) and
loading it into our program, we use a built-in utility for retrieving the dataset on the
fly. Such utilities exist for most popular datasets, and when dealing with small ones
(in this case only a few MB), it makes a lot of sense to do it this way. The second
Softmax Regression | 17

4Here and throughout, before running the example code, make sure DATA_DIR fits the operating system you are
using. On Windows, for instance, you would probably use something like c:\tmp\data instead.
import loads the utility we will later use both to automatically download the data for
us, and to manage and partition it as needed:
DATA_DIR = '/tmp/data'
NUM_STEPS = 1000
MINIBATCH_SIZE = 100
Here we define some constants that we use in our program—these will each be
explained in the context in which they are first used:
data = input_data.read_data_sets(DATA_DIR, one_hot=True)
The read_data_sets() method of the MNIST reading utility downloads the dataset
and saves it locally, setting the stage for further use later in the program. The first
argument, DATA_DIR, is the location we wish the data to be saved to locally. We set this
to '/tmp/data', but any other location would be just as good. The second argument
tells the utility how we want the data to be labeled; we will not go into this right now.4
Note that this is what prints the first four lines of the output, indicating the data was
obtained correctly. Now we are finally ready to set up our model:
x = tf.placeholder(tf.float32, [None, 784])
W = tf.Variable(tf.zeros([784, 10]))
In the previous example we saw the TensorFlow constant element—this is now com‐
plemented by the placeholder and Variable elements. For now, it is enough to
know that a variable is an element manipulated by the computation, while a place‐
holder has to be supplied when triggering it. The image itself (x) is a placeholder,
because it will be supplied by us when running the computation graph. The size
[None, 784] means that each image is of size 784 (28×28 pixels unrolled into a single
vector), and None is an indicator that we are not currently specifying how many of
these images we will use at once:
y_true = tf.placeholder(tf.float32, [None, 10])
y_pred = tf.matmul(x, W)
In the next chapter these concepts will be dealt with in much more depth.
A key concept in a large class of machine learning tasks is that we would like to learn
a function from data examples (in our case, digit images) to their known labels (the
identity of the digit in the image). This setting is called supervised learning. In most
supervised learning models, we attempt to learn a model such that the true labels and
the predicted labels are close in some sense. Here, y_true and y_pred are the ele‐
ments representing the true and predicted labels, respectively:
18 | Chapter 2: Go with the Flow: Up and Running with TensorFlow

5As of TensorFlow 1.0 this is also contained in tf.losses.softmax_cross_entropy.
6As of TensorFlow 1.0 this is also contained in tf.metrics.accuracy.
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
logits=y_pred, labels=y_true))
The measure of similarity we choose for this model is what is known as cross entropy
—a natural choice when the model outputs class probabilities. This element is often
referred to as the loss function:5
gd_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
The final piece of the model is how we are going to train it (i.e., how we are going to
minimize the loss function). A very common approach is to use gradient descent
optimization. Here, 0.5 is the learning rate, controlling how fast our gradient descent
optimizer shifts model weights to reduce overall loss.
We will discuss optimizers and how they fit into the computation graph later on in
the book.
Once we have defined our model, we want to define the evaluation procedure we will
use in order to test the accuracy of the model. In this case, we are interested in the
fraction of test examples that are correctly classified:6
correct_mask = tf.equal(tf.argmax(y_pred, 1), tf.argmax(y_true, 1))
accuracy = tf.reduce_mean(tf.cast(correct_mask, tf.float32))
As with the “hello world” example, in order to make use of the computation graph we
defined, we must create a session. The rest happens within the session:
with tf.Session() as sess:
First, we must initialize all variables:
sess.run(tf.global_variables_initializer())
This carries some specific implications in the realm of machine learning and optimi‐
zation, which we will discuss further when we use models for which initialization is
an important issue
Supervised Learning and the Train/Test Scheme
Supervised learning generally refers to the task of learning a function from data
objects to labels associated with them, based on a set of examples where the correct
labels are already known. This is usually subdivided into the case where labels are
continuous (regression) or discrete (classification).
The purpose of training supervised learning models is almost always to apply them
later to new examples with unknown labels, in order to obtain predicted labels for
Softmax Regression | 19

them. In the MNIST case discussed in this section, the purpose of training the model
would probably be to apply it on new handwritten digit images and automatically
find out what digits they represent.
As a result, we are interested in the extent to which our model will label new examples
correctly. This is reflected in the way we evaluate the accuracy of the model. We first
partition the labeled dataset into train and test partitions. During model training we
use only the train partition, and during evaluation we test the accuracy only on the
test partition. This scheme is generally known as a train/test validation.
for _ in range(NUM_STEPS):
batch_xs, batch_ys = data.train.next_batch(MINIBATCH_SIZE)
sess.run(gd_step, feed_dict={x: batch_xs, y_true: batch_ys})
The actual training of the model, in the gradient descent approach, consists of taking
many steps in “the right direction.” The number of steps we will make, NUM_STEPS,
was set to 1,000 in this case. There are more sophisticated ways of deciding when to
stop, but more about that later! In each step we ask our data manager for a bunch of
examples with their labels and present them to the learner. The MINIBATCH_SIZE con‐
stant controls the number of examples to use for each step.
Finally, we use the feed_dict argument of sess.run for the first time. Recall that we
defined placeholder elements when constructing the model. Now, each time we want
to run a computation that will include these elements, we must supply a value for
them.
ans = sess.run(accuracy, feed_dict={x: data.test.images,
y_true: data.test.labels})
In order to evaluate the model we have just finished learning, we run the accuracy
computing operation defined earlier (recall the accuracy was defined as the fraction
of images that are correctly labeled). In this procedure, we feed a separate group of
test images, which were never seen by the model during training:
print "Accuracy: {:.4}%".format(ans*100)
Lastly, we print out the results as percent values.
Figure 2-3 shows a graph representation of our model.
20 | Chapter 2: Go with the Flow: Up and Running with TensorFlow

Figure 2-3. A graph representation of the model. Rectangular elements are Variables,
and circles are placeholders. e top-le frame represents the label prediction part, and
the bottom-right frame the evaluation.
Model evaluation and memory errors
When using TensorFlow, like any other system, it is important to
be aware of the resources being used, and make sure not to exceed
the capacity of the system. One possible pitfall is in the evaluation
of models—testing their performance on a test set. In this example
we evaluate the accuracy of the models by feeding all the test exam‐
ples in one go:
feed_dict={x: data.test.images, y_true: data.test.labels}
ans = sess.run(accuracy, feed_dict)
If all the test examples (here, data.test.images) are not able to fit
into the memory in the system you are using, you will get a mem‐
ory error at this point. This is likely to be the case, for instance, if
you are running this example on a typical low-end GPU.
The easy way around this (getting a machine with more memory is
a temporary fix, since there will always be larger datasets) is to split
the test procedure into batches, much as we did during training.
Summary
Congratulations! By now you have installed TensorFlow and taken it for a spin with
two basic examples. You have seen some of the fundamental building blocks that will
be used throughout the book, and have hopefully begun to get a feel for TensorFlow.
Next, we take a look under the hood and explore the computation graph model used
by TensorFlow.
Summary | 21
CHAPTER 3
Understanding TensorFlow Basics
This chapter demonstrates the key concepts of how TensorFlow is built and how it
works with simple and intuitive examples. You will get acquainted with the basics of
TensorFlow as a numerical computation library using dataflow graphs. More specifi‐
cally, you will learn how to manage and create a graph, and be introduced to Tensor‐
Flow’s “building blocks,” such as constants, placeholders, and Variables.
Computation Graphs
TensorFlow allows us to implement machine learning algorithms by creating and
computing operations that interact with one another. These interactions form what
we call a “computation graph,” with which we can intuitively represent complicated
functional architectures.
What Is a Computation Graph?
We assume a lot of readers have already come across the mathematical concept of a
graph. For those to whom this concept is new, a graph refers to a set of interconnec‐
ted entities, commonly called nodes or vertices. These nodes are connected to each
other via edges. In a dataflow graph, the edges allow data to “flow” from one node to
another in a directed manner.
In TensorFlow, each of the graph’s nodes represents an operation, possibly applied to
some input, and can generate an output that is passed on to other nodes. By analogy,
we can think of the graph computation as an assembly line where each machine
(node) either gets or creates its raw material (input), processes it, and then passes the
output to other machines in an orderly fashion, producing subcomponents and even‐
tually a final product when the assembly process comes to an end.
23

Operations in the graph include all kinds of functions, from simple arithmetic ones
such as subtraction and multiplication to more complex ones, as we will see later on.
They also include more general operations like the creation of summaries, generating
constant values, and more.
The Benets of Graph Computations
TensorFlow optimizes its computations based on the graph’s connectivity. Each graph
has its own set of node dependencies. When the input of node y is affected by the
output of node x, we say that node y is dependent on node x. We call it a direct
dependency when the two are connected via an edge, and an indirect dependency
otherwise. For example, in Figure 3-1 (A), node e is directly dependent on
node c, indirectly dependent on node a, and independent of node d.
Figure 3-1. (A) Illustration of graph dependencies. (B) Computing node e results in the
minimal amount of computations according to the graph’s dependencies—in this case
computing only nodes c, b, and a.
We can always identify the full set of dependencies for each node in the graph. This is
a fundamental characteristic of the graph-based computation format. Being able to
locate dependencies between units of our model allows us to both distribute compu‐
tations across available resources and avoid performing redundant computations of
irrelevant subsets, resulting in a faster and more efficient way of computing things.
Graphs, Sessions, and Fetches
Roughly speaking, working with TensorFlow involves two main phases: (1) con‐
structing a graph and (2) executing it. Let’s jump into our first example and create
something very basic.
24 | Chapter 3: Understanding TensorFlow Basics

Creating a Graph
Right after we import TensorFlow (with import tensorflow as tf), a specific
empty default graph is formed. All the nodes we create are automatically associated
with that default graph.
Using the tf.<operator> methods, we will create six nodes assigned to arbitrarily
named variables. The contents of these variables should be regarded as the output of
the operations, and not the operations themselves. For now we refer to both the oper‐
ations and their outputs with the names of their corresponding variables.
The first three nodes are each told to output a constant value. The values 5, 2, and 3
are assigned to a, b, and c, respectively:
a = tf.constant(5)
b = tf.constant(2)
c = tf.constant(3)
Each of the next three nodes gets two existing variables as inputs, and performs sim‐
ple arithmetic operations on them:
d = tf.multiply(a,b)
e = tf.add(c,b)
f = tf.subtract(d,e)
Node d multiplies the outputs of nodes a and b. Node e adds the outputs of nodes
b and c. Node f subtracts the output of node e from that of node d.
And voilà! We have our first TensorFlow graph! Figure 3-2 shows an illustration of
the graph we’ve just created.
Figure 3-2. An illustration of our rst constructed graph. Each node, denoted by a lower‐
case letter, performs the operation indicated above it: Const for creating constants and
Add, Mul, and Sub for addition, multiplication, and subtraction, respectively. e inte‐
ger next to each edge is the output of the corresponding node’s operation.
Note that for some arithmetic and logical operations it is possible to use operation
shortcuts instead of having to apply tf.<operator>. For example, in this graph we
Graphs, Sessions, and Fetches | 25

could have used */+/- instead of tf.multiply()/tf.add()/tf.subtract() (like we
did in the “hello world” example in Chapter 2, where we used + instead of tf.add()).
Table 3-1 lists the available shortcuts.
Table 3-1. Common TensorFlow operations and their respective shortcuts
TensorFlow operator Shortcut Description
tf.add() a + b Adds a and b, element-wise.
tf.multiply() a * b Multiplies a and b, element-wise.
tf.subtract() a - b Subtracts a from b, element-wise.
tf.divide() a / b Computes Python-style division of a by b.
tf.pow() a ** b Returns the result of raising each element in a to its corresponding element b,
element-wise.
tf.mod() a % b Returns the element-wise modulo.
tf.logical_and() a & b Returns the truth table of a & b, element-wise. dtype must be tf.bool.
tf.greater() a > b Returns the truth table of a > b, element-wise.
tf.greater_equal() a >= b Returns the truth table of a >= b, element-wise.
tf.less_equal() a <= b Returns the truth table of a <= b, element-wise.
tf.less() a < b Returns the truth table of a < b, element-wise.
tf.negative() -a Returns the negative value of each element in a.
tf.logical_not() ~a Returns the logical NOT of each element in a. Only compatible with Tensor objects
with dtype of tf.bool.
tf.abs() abs(a) Returns the absolute value of each element in a.
tf.logical_or() a | b Returns the truth table of a | b, element-wise. dtype must be tf.bool.
Creating a Session and Running It
Once we are done describing the computation graph, we are ready to run the compu‐
tations that it represents. For this to happen, we need to create and run a session. We
do this by adding the following code:
sess = tf.Session()
outs = sess.run(f)
sess.close()
print("outs = {}".format(outs))
Out:
outs = 5
First, we launch the graph in a tf.Session. A Session object is the part of the Ten‐
sorFlow API that communicates between Python objects and data on our end, and
the actual computational system where memory is allocated for the objects we define,
intermediate variables are stored, and finally results are fetched for us.
sess = tf.Session()
26 | Chapter 3: Understanding TensorFlow Basics

The execution itself is then done with the .run() method of the Session
object. When called, this method completes one set of computations in our graph in
the following manner: it starts at the requested output(s) and then works backward,
computing nodes that must be executed according to the set of dependencies. There‐
fore, the part of the graph that will be computed depends on our output query.
In our example, we requested that node f be computed and got its value, 5, as output:
outs = sess.run(f)
When our computation task is completed, it is good practice to close the session
using the sess.close() command, making sure the resources used by our session are
freed up. This is an important practice to maintain even though we are not obligated
to do so for things to work:
sess.close()
Example 3-1. Try it yourself! Figure 3-3 shows another two graph examples. See if you
can produce these graphs yourself.
Figure 3-3. Can you create graphs A and B? (To produce the sine function, use tf.sin(x)).
Constructing and Managing Our Graph
As mentioned, as soon as we import TensorFlow, a default graph is automatically cre‐
ated for us. We can create additional graphs and control their association with some
given operations. tf.Graph() creates a new graph, represented as a TensorFlow
object. In this example we create another graph and assign it to the variable g:
Graphs, Sessions, and Fetches | 27

import tensorflow as tf
print(tf.get_default_graph())
g = tf.Graph()
print(g)
Out:
<tensorflow.python.framework.ops.Graph object at 0x7fd88c3c07d0>
<tensorflow.python.framework.ops.Graph object at 0x7fd88c3c03d0>
At this point we have two graphs: the default graph and the empty graph in g. Both
are revealed as TensorFlow objects when printed. Since g hasn’t been assigned as the
default graph, any operation we create will not be associated with it, but rather with
the default one.
We can check which graph is currently set as the default by using
tf.get_default_graph(). Also, for a given node, we can view the graph it’s associ‐
ated with by using the <node>.graph attribute:
g = tf.Graph()
a = tf.constant(5)
print(a.graph is g)
print(a.graph is tf.get_default_graph())
Out:
False
True
In this code example we see that the operation we’ve created is associated with the
default graph and not with the graph in g.
To make sure our constructed nodes are associated with the right graph we can con‐
struct them using a very useful Python construct: the with statement.
The with statement
The with statement is used to wrap the execution of a block with
methods defined by a context manager—an object that has the spe‐
cial method functions .__enter__() to set up a block of code
and .__exit__() to exit the block.
In layman’s terms, it’s very convenient in many cases to execute
some code that requires “setting up” of some kind (like opening a
file, SQL table, etc.) and then always “tearing it down” at the end,
regardless of whether the code ran well or raised any kind of excep‐
tion. In our case we use with to set up a graph and make sure every
piece of code will be performed in the context of that graph.
28 | Chapter 3: Understanding TensorFlow Basics
We use the with statement together with the as_default() command, which returns
a context manager that makes this graph the default one. This comes in handy when
working with multiple graphs:
g1 = tf.get_default_graph()
g2 = tf.Graph()
print(g1 is tf.get_default_graph())
with g2.as_default():
print(g1 is tf.get_default_graph())
print(g1 is tf.get_default_graph())
Out:
True
False
True
The with statement can also be used to start a session without having to explicitly
close it. This convenient trick will be used in the following examples.
Fetches
In our initial graph example, we request one specific node (node f) by passing the
variable it was assigned to as an argument to the sess.run() method. This argument
is called fetches, corresponding to the elements of the graph we wish to com‐
pute. We can also ask sess.run() for multiple nodes’ outputs simply by inputting a
list of requested nodes:
with tf.Session() as sess:
fetches = [a,b,c,d,e,f]
outs = sess.run(fetches)
print("outs = {}".format(outs))
print(type(outs[0]))
Out:
outs = [5, 2, 3, 10, 5, 5]
<type 'numpy.int32'>
We get back a list containing the outputs of the nodes according to how they were
ordered in the input list. The data in each item of the list is of type NumPy.
Graphs, Sessions, and Fetches | 29

NumPy
NumPy is a popular and useful Python package for numerical com‐
puting that offers many functionalities related to working with
arrays. We assume some basic familiarity with this package, and it
will not be covered in this book. TensorFlow and NumPy are
tightly coupled—for example, the output returned by sess.run()
is a NumPy array. In addition, many of TensorFlow’s operations
share the same syntax as functions in NumPy. To learn more about
NumPy, we refer the reader to Eli Bressert’s book SciPy and NumPy
(O’Reilly).
We mentioned that TensorFlow computes only the essential nodes according to the
set of dependencies. This is also manifested in our example: when we ask for the out‐
put of node d, only the outputs of nodes a and b are computed. Another example is
shown in Figure 3-1(B). This is a great advantage of TensorFlow—it doesn’t matter
how big and complicated our graph is as a whole, since we can run just a small por‐
tion of it as needed.
Automatically closing the session
Opening a session using the with clause will ensure the session is
automatically closed once all computations are done.
Flowing Tensors
In this section we will get a better understanding of how nodes and edges are actually
represented in TensorFlow, and how we can control their characteristics. To demon‐
strate how they work, we will focus on source operations, which are used to initialize
values.
Nodes Are Operations, Edges Are Tensor Objects
When we construct a node in the graph, like we did with tf.add(), we are actually
creating an operation instance. These operations do not produce actual values until
the graph is executed, but rather reference their to-be-computed result as a handle
that can be passed on—ow—to another node. These handles, which we can think of
as the edges in our graph, are referred to as Tensor objects, and this is where the
name TensorFlow originates from.
TensorFlow is designed such that first a skeleton graph is created with all of its com‐
ponents. At this point no actual data flows in it and no computations take place. It is
only upon execution, when we run the session, that data enters the graph and compu‐
30 | Chapter 3: Understanding TensorFlow Basics

tations occur (as illustrated in Figure 3-4). This way, computations can be much more
efficient, taking the entire graph structure into consideration.
Figure 3-4. Illustrations of before (A) and aer (B) running a session. When the session
is run, actual data “ows” through the graph.
In the previous section’s example, tf.constant() created a node with the corre‐
sponding passed value. Printing the output of the constructor, we see that it’s actually
a Tensor object instance. These objects have methods and attributes that control their
behavior and that can be defined upon creation.
In this example, the variable c stores a Tensor object with the name Const_52:0, des‐
ignated to contain a 32-bit floating-point scalar:
c = tf.constant(4.0)
print(c)
Out:
Tensor("Const_52:0", shape=(), dtype=float32)
A note on constructors
The tf.<operator> function could be thought of as a constructor,
but to be more precise, this is actually not a constructor at all, but
rather a factory method that sometimes does quite a bit more than
just creating the operator objects.
Setting attributes with source operations
Each Tensor object in TensorFlow has attributes such as name, shape, and dtype that
help identify and set the characteristics of that object. These attributes are optional
Flowing Tensors | 31
when creating a node, and are set automatically by TensorFlow when missing. In the
next section we will take a look at these attributes. We will do so by looking at Tensor
objects created by ops known as source operations. Source operations are operations
that create data, usually without using any previously processed inputs. With these
operations we can create scalars, as we already encountered with the tf.constant()
method, as well as arrays and other types of data.
Data Types
The basic units of data that pass through a graph are numerical, Boolean, or string
elements. When we print out the Tensor object c from our last code example, we see
that its data type is a floating-point number. Since we didn’t specify the type of data,
TensorFlow inferred it automatically. For example 5 is regarded as an integer, while
anything with a decimal point, like 5.1, is regarded as a floating-point number.
We can explicitly choose what data type we want to work with by specifying it when
we create the Tensor object. We can see what type of data was set for a given Tensor
object by using the attribute dtype:
c = tf.constant(4.0, dtype=tf.float64)
print(c)
print(c.dtype)
Out:
Tensor("Const_10:0", shape=(), dtype=float64)
<dtype: 'float64'>
Explicitly asking for (appropriately sized) integers is on the one hand more memory
conserving, but on the other may result in reduced accuracy as a consequence of not
tracking digits after the decimal point.
Casting
It is important to make sure our data types match throughout the graph—performing
an operation with two nonmatching data types will result in an exception. To change
the data type setting of a Tensor object, we can use the tf.cast() operation, passing
the relevant Tensor and the new data type of interest as the first and second argu‐
ments, respectively:
x = tf.constant([1,2,3],name='x',dtype=tf.float32)
print(x.dtype)
x = tf.cast(x,tf.int64)
print(x.dtype)
Out:
<dtype: 'float32'>
<dtype: 'int64'>
32 | Chapter 3: Understanding TensorFlow Basics

TensorFlow supports many data types. These are listed in Table 3-2.
Table 3-2. Supported Tensor data types
Data type Python type Description
DT_FLOAT tf.float32 32-bit oating point.
DT_DOUBLE tf.float64 64-bit oating point.
DT_INT8 tf.int8 8-bit signed integer.
DT_INT16 tf.int16 16-bit signed integer.
DT_INT32 tf.int32 32-bit signed integer.
DT_INT64 tf.int64 64-bit signed integer.
DT_UINT8 tf.uint8 8-bit unsigned integer.
DT_UINT16 tf.uint16 16-bit unsigned integer.
DT_STRING tf.string Variable-length byte array. Each element of a Tensor is a byte array.
DT_BOOL tf.bool Boolean.
DT_COMPLEX64 tf.complex64 Complex number made of two 32-bit oating points: real and imaginary parts.
DT_COMPLEX128 tf.complex128 Complex number made of two 64-bit oating points: real and imaginary parts.
DT_QINT8 tf.qint8 8-bit signed integer used in quantized ops.
DT_QINT32 tf.qint32 32-bit signed integer used in quantized ops.
DT_QUINT8 tf.quint8 8-bit unsigned integer used in quantized ops.
Tensor Arrays and Shapes
A source of potential confusion is that two different things are referred to by the
name, Tensor. As used in the previous sections, Tensor is the name of an object used
in the Python API as a handle for the result of an operation in the graph. However,
tensor is also a mathematical term for n-dimensional arrays. For example, a 1×1 ten‐
sor is a scalar, a 1×n tensor is a vector, an n×n tensor is a matrix, and an n×n×n tensor
is just a three-dimensional array. This, of course, generalizes to any dimension. Ten‐
sorFlow regards all the data units that flow in the graph as tensors, whether they are
multidimensional arrays, vectors, matrices, or scalars. The TensorFlow objects called
Tensors are named after these mathematical tensors.
To clarify the distinction between the two, from now on we will refer to the former as
Tensors with a capital T and the latter as tensors with a lowercase t.
As with dtype, unless stated explicitly, TensorFlow automatically infers the shape of
the data. When we printed out the Tensor object at the beginning of this section, it
showed that its shape was (), corresponding to the shape of a scalar.
Using scalars is good for demonstration purposes, but most of the time it’s much
more practical to work with multidimensional arrays. To initialize high-dimensional
arrays, we can use Python lists or NumPy arrays as inputs. In the following example,
Flowing Tensors | 33
we use as inputs a 2×3 matrix using a Python list and then a 3D NumPy array of size
2×2×3 (two matrices of size 2×3):
import numpy as np
c = tf.constant([[1,2,3],
[4,5,6]])
print("Python List input: {}".format(c.get_shape()))
c = tf.constant(np.array([
[[1,2,3],
[4,5,6]],
[[1,1,1],
[2,2,2]]
]))
print("3d NumPy array input: {}".format(c.get_shape()))
Out:
Python list input: (2, 3)
3d NumPy array input: (2, 2, 3)
The get_shape() method returns the shape of the tensor as a tuple of integers. The
number of integers corresponds to the number of dimensions of the tensor, and each
integer is the number of array entries along that dimension. For example, a shape of
(2,3) indicates a matrix, since it has two integers, and the size of the matrix is 2×3.
Other types of source operation constructors are very useful for initializing constants
in TensorFlow, like filling a constant value, generating random numbers, and creating
sequences.
Random-number generators have special importance as they are used in many cases
to create the initial values for TensorFlow Variables, which will be introduced
shortly. For example, we can generate random numbers from a normal distribution
using tf.random.normal(), passing the shape, mean, and standard deviation as the
first, second, and third arguments, respectively. Another two examples for useful ran‐
dom initializers are the truncated normal that, as its name implies, cuts off all values
below and above two standard deviations from the mean, and the uniform initializer
that samples values uniformly within some interval [a,b).
Examples of sampled values for each of these methods are shown in Figure 3-5.
34 | Chapter 3: Understanding TensorFlow Basics

Figure 3-5. 50,000 random samples generated from (A) standard normal distribution,
(B) truncated normal, and (C) uniform [–2,2).
Those who are familiar with NumPy will recognize some of the initializers, as they
share the same syntax. One example is the sequence generator tf.linspace(a, b,
n) that creates n evenly spaced values from a to b.
A feature that is convenient to use when we want to explore the data content of an
object is tf.InteractiveSession(). Using it and the .eval() method, we can get a
full look at the values without the need to constantly refer to the session object:
sess = tf.InteractiveSession()
c = tf.linspace(0.0, 4.0, 5)
print("The content of 'c':\n {}\n".format(c.eval()))
sess.close()
Out:
The content of 'c':
[ 0. 1. 2. 3. 4.]
Interactive sessions
tf.InteractiveSession() allows you to replace the usual tf.Ses
sion(), so that you don’t need a variable holding the session for
running ops. This can be useful in interactive Python environ‐
ments, like when writing IPython notebooks, for instance.
We’ve mentioned only a few of the available source operations. Table 3-2 provides
short descriptions of more useful initializers.
Flowing Tensors | 35

TensorFlow operation Description
tf.constant(value)Creates a tensor populated with the value or values specied by the argument value
tf.fill(shape, value)Creates a tensor of shape shape and lls it with value
tf.zeros(shape)Returns a tensor of shape shape with all elements set to 0
tf.zeros_like(tensor)Returns a tensor of the same type and shape as tensor with all elements set to 0
tf.ones(shape)Returns a tensor of shape shape with all elements set to 1
tf.ones_like(tensor)Returns a tensor of the same type and shape as tensor with all elements set to 1
tf.random_normal(shape,
mean, stddev)
Outputs random values from a normal distribution
tf.truncated_nor
mal(shape, mean,
stddev)
Outputs random values from a truncated normal distribution (values whose magnitude
is more than two standard deviations from the mean are dropped and re-picked)
tf.random_uni
form(shape, minval,
maxval)
Generates values from a uniform distribution in the range [minval, maxval)
tf.random_shuffle(ten
sor)
Randomly shues a tensor along its rst dimension
Matrix multiplication
This very useful arithmetic operation is performed in TensorFlow via the tf.mat
mul(A,B) function for two Tensor objects A and B.
Say we have a Tensor storing a matrix A and another storing a vector x, and we wish
to compute the matrix product of the two:
Ax = b
Before using matmul(), we need to make sure both have the same number of dimen‐
sions and that they are aligned correctly with respect to the intended multiplication.
In the following example, a matrix A and a vector x are created:
A = tf.constant([ [1,2,3],
[4,5,6] ])
print(a.get_shape())
x = tf.constant([1,0,1])
print(x.get_shape())
Out:
(2, 3)
(3,)
In order to multiply them, we need to add a dimension to x, transforming it from a
1D vector to a 2D single-column matrix.
36 | Chapter 3: Understanding TensorFlow Basics
We can add another dimension by passing the Tensor to tf.expand_dims(), together
with the position of the added dimension as the second argument. By adding another
dimension in the second position (index 1), we get the desired outcome:
x = tf.expand_dims(x,1)
print(x.get_shape())
b = tf.matmul(A,x)
sess = tf.InteractiveSession()
print('matmul result:\n {}'.format(b.eval()))
sess.close()
Out:
(3, 1)
matmul result:
[[ 4]
[10]]
If we want to flip an array, for example turning a column vector into a row vector or
vice versa, we can use the tf.transpose() function.
Names
Each Tensor object also has an identifying name. This name is an intrinsic string
name, not to be confused with the name of the variable. As with dtype, we can use
the .name attribute to see the name of the object:
with tf.Graph().as_default():
c1 = tf.constant(4,dtype=tf.float64,name='c')
c2 = tf.constant(4,dtype=tf.int32,name='c')
print(c1.name)
print(c2.name)
Out:
c:0
c_1:0
The name of the Tensor object is simply the name of its corresponding operation (“c”;
concatenated with a colon), followed by the index of that tensor in the outputs of the
operation that produced it—it is possible to have more than one.
Flowing Tensors | 37

Duplicate names
Objects residing within the same graph cannot have the same name
—TensorFlow forbids it. As a consequence, it will automatically
add an underscore and a number to distinguish the two. Of course,
both objects can have the same name when they are associated with
different graphs.
Name scopes
Sometimes when dealing with a large, complicated graph, we would like to create
some node grouping to make it easier to follow and manage. For that we can hier‐
archically group nodes together by name. We do so by using tf.name_scope("pre
fix") together with the useful with clause again:
with tf.Graph().as_default():
c1 = tf.constant(4,dtype=tf.float64,name='c')
with tf.name_scope("prefix_name"):
c2 = tf.constant(4,dtype=tf.int32,name='c')
c3 = tf.constant(4,dtype=tf.float64,name='c')
print(c1.name)
print(c2.name)
print(c3.name)
Out:
c:0
prefix_name/c:0
prefix_name/c_1:0
In this example we’ve grouped objects contained in variables c2 and c3 under the
scope prefix_name, which shows up as a prefix in their names.
Prefixes are especially useful when we would like to divide a graph into subgraphs
with some semantic meaning. These parts can later be used, for instance, for visuali‐
zation of the graph structure.
Variables, Placeholders, and Simple Optimization
In this section we will cover two important types of Tensor objects: Variables and pla‐
ceholders. We then move forward to the main event: optimization. We will briefly
talk about all the basic components for optimizing a model, and then do some simple
demonstration that puts everything together.
Variables
The optimization process serves to tune the parameters of some given model. For
that purpose, TensorFlow uses special objects called Variables. Unlike other Tensor
38 | Chapter 3: Understanding TensorFlow Basics
objects that are “refilled” with data each time we run the session, Variables can main‐
tain a fixed state in the graph. This is important because their current state might
influence how they change in the following iteration. Like other Tensors, Variables
can be used as input for other operations in the graph.
Using Variables is done in two stages. First we call the tf.Variable() function in
order to create a Variable and define what value it will be initialized with. We then
have to explicitly perform an initialization operation by running the session with the
tf.global_variables_initializer() method, which allocates the memory for the
Variable and sets its initial values.
Like other Tensor objects, Variables are computed only when the model runs, as we
can see in the following example:
init_val = tf.random_normal((1,5),0,1)
var = tf.Variable(init_val, name='var')
print("pre run: \n{}".format(var))
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
post_var = sess.run(var)
print("\npost run: \n{}".format(post_var))
Out:
pre run:
Tensor("var/read:0", shape=(1, 5), dtype=float32)
post run:
[[ 0.85962135 0.64885855 0.25370994 -0.37380791 0.63552463]]
Note that if we run the code again, we see that a new variable is created each time, as
indicated by the automatic concatenation of _1 to its name:
pre run:
Tensor("var_1/read:0", shape=(1, 5), dtype=float32)
This could be very inefficient when we want to reuse the model (complex models
could have many variables!); for example, when we wish to feed it with several differ‐
ent inputs. To reuse the same variable, we can use the tf.get_variables() function
instead of tf.Variable(). More on this can be found in “Model Structuring” on page
203 of the appendix.
Placeholders
So far we’ve used source operations to create our input data. TensorFlow, however,
has designated built-in structures for feeding input values. These structures are called
placeholders. Placeholders can be thought of as empty Variables that will be filled with
Variables, Placeholders, and Simple Optimization | 39
data later on. We use them by first constructing our graph and only when it is exe‐
cuted feeding them with the input data.
Placeholders have an optional shape argument. If a shape is not fed or is passed as
None, then the placeholder can be fed with data of any size. It is common to use
None for the dimension of a matrix that corresponds to the number of samples (usu‐
ally rows), while having the length of the features (usually columns) fixed:
ph = tf.placeholder(tf.float32,shape=(None,10))
Whenever we define a placeholder, we must feed it with some input values or else an
exception will be thrown. The input data is passed to the session.run() method as a
dictionary, where each key corresponds to a placeholder variable name, and the
matching values are the data values given in the form of a list or a NumPy array:
sess.run(s,feed_dict={x: X_data,w: w_data})
Let’s see how it looks with another graph example, this time with placeholders for two
inputs: a matrix x and a vector w. These inputs are matrix-multiplied to create a five-
unit vector xw and added with a constant vector b filled with the value -1. Finally, the
variable s takes the maximum value of that vector by using the tf.reduce_max()
operation. The word reduce is used because we are reducing a five-unit vector to a
single scalar:
x_data = np.random.randn(5,10)
w_data = np.random.randn(10,1)
with tf.Graph().as_default():
x = tf.placeholder(tf.float32,shape=(5,10))
w = tf.placeholder(tf.float32,shape=(10,1))
b = tf.fill((5,1),-1.)
xw = tf.matmul(x,w)
xwb = xw + b
s = tf.reduce_max(xwb)
with tf.Session() as sess:
outs = sess.run(s,feed_dict={x: x_data,w: w_data})
print("outs = {}".format(outs))
Out:
outs = 3.06512
Optimization
Now we turn to optimization. We first describe the basics of training a model, giving
a short description of each component in the process, and show how it is performed
in TensorFlow. We then demonstrate a full working example of an optimization pro‐
cess of a simple regression model.
40 | Chapter 3: Understanding TensorFlow Basics
Training to predict
We have some target variable y, which we want to explain using some feature vector
x. To do so, we first choose a model that relates the two. Our training data points will
be used for “tuning” the model so that it best captures the desired relation. In the fol‐
lowing chapters we focus on deep neural network models, but for now we will settle
for a simple regression problem.
Let’s start by describing our regression model:
f(xi) = wTxi + b
yi = f(xi) + εi
f(xi) is assumed to be a linear combination of some input data xi, with a set of
weights w and an intercept b. Our target output yi is a noisy version of f(xi) after being
summed with Gaussian noise εi (where i denotes a given sample).
As in the previous example, we will need to create the appropriate placeholders for
our input and output data and Variables for our weights and intercept:
x = tf.placeholder(tf.float32,shape=[None,3])
y_true = tf.placeholder(tf.float32,shape=None)
w = tf.Variable([[0,0,0]],dtype=tf.float32,name='weights')
b = tf.Variable(0,dtype=tf.float32,name='bias')
Once the placeholders and Variables are defined, we can write down our model. In
this example, it’s simply a multivariate linear regression—our predicted output
y_pred is the result of a matrix multiplication of our input container x and our
weights w plus a bias term b:
y_pred = tf.matmul(w,tf.transpose(x)) + b
Dening a loss function
Next, we need a good measure with which we can evaluate the model’s performance.
To capture the discrepancy between our model’s predictions and the observed tar‐
gets, we need a measure reflecting “distance.” This distance is often referred to as an
objective or a loss function, and we optimize the model by finding the set of parame‐
ters (weights and bias in this case) that minimize it.
There is no ideal loss function, and choosing the most suitable one is often a blend of
art and science. The choice may depend on several factors, like the assumptions of
our model, how easy it is to minimize, and what types of mistakes we prefer to avoid.
MSE and cross entropy
Perhaps the most commonly used loss is the MSE (mean squared error), where for all
samples we average the squared distances between the real target and what our model
predicts across samples:
Variables, Placeholders, and Simple Optimization | 41

L y,y=1
nΣi= 1
nyi−yi2
This loss has intuitive interpretation—it minimizes the mean square difference
between an observed value and the model’s fitted value (these differences are referred
to as residuals).
In our linear regression example, we take the difference between the vector y_true
(y), the true targets, and y_pred (ŷ), the model’s predictions, and use tf.square() to
compute the square of the difference vector. This operation is applied element-wise.
We then average the squared differences using the tf.reduce_mean() function:
loss = tf.reduce_mean(tf.square(y_true-y_pred))
Another very common loss, especially for categorical data, is the cross entropy, which
we used in the softmax classifier in the previous chapter. The cross entropy is given
by
H(p,q)=-Σxp(x) log q(x)
and for classification with a single correct label (as is the case in an overwhelming
majority of the cases) reduces to the negative log of the probability placed by the clas‐
sifier on the correct label.
In TensorFlow:
loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=y_true,logits=y_pred)
loss = tf.reduce_mean(loss)
Cross entropy is a measure of similarity between two distributions. Since the classifi‐
cation models used in deep learning typically output probabilities for each class, we
can compare the true class (distribution p) with the probabilities of each class given
by the model (distribution q). The more similar the two distributions, the smaller our
cross entropy will be.
The gradient descent optimizer
The next thing we need to figure out is how to minimize the loss function. While in
some cases it is possible to find the global minimum analytically (when it exists), in
the great majority of cases we will have to use an optimization algorithm. Optimizers
update the set of weights iteratively in a way that decreases the loss over time.
The most commonly used approach is gradient descent, where we use the loss’s gradi‐
ent with respect to the set of weights. In slightly more technical terms, if our loss is
some multivariate function F(w
̄
), then in the neighborhood of some point w
̄
0, the
“steepest” direction of decrease of F(w
̄
) is obtained by moving from w
̄
0 in the direc‐
tion of the negative gradient of F at w
̄
0.
42 | Chapter 3: Understanding TensorFlow Basics
So if w
̄
1 = w
̄
0-γ∇F(w
̄
0) where
∇
F(w
̄
0) is the gradient of F evaluated at w
̄
0, then for a
small enough γ:
F(w
̄
0) ⩾ F(w
̄
1)
The gradient descent algorithms work well on highly complicated network architec‐
tures and therefore are suitable for a wide variety of problems. More specifically,
recent advances make it possible to compute these gradients by utilizing massively
parallel systems, so the approach scales well with dimensionality (though it can still
be painfully time-consuming for large real-world problems). While convergence to
the global minimum is guaranteed for convex functions, for nonconvex problems
(which are essentially all problems in the world of deep learning) they can get stuck
in local minima. In practice, this is often good enough, as is evidenced by the huge
success of the field of deep learning.
Sampling methods
The gradient of the objective is computed with respect to the model parameters and
evaluated using a given set of input samples, xs. How many of the samples should we
take for this calculation? Intuitively, it makes sense to calculate the gradient for the
entire set of samples in order to benefit from the maximum amount of available
information. This method, however, has some shortcomings. For example, it can be
very slow and is intractable when the dataset requires more memory than is available.
A more popular technique is the stochastic gradient descent (SGD), where instead of
feeding the entire dataset to the algorithm for the computation of each step, a subset
of the data is sampled sequentially. The number of samples ranges from one sample at
a time to a few hundred, but the most common sizes are between around 50 to
around 500 (usually referred to as mini-batches).
Using smaller batches usually works faster, and the smaller the size of the batch, the
faster are the calculations. However, there is a trade-off in that small samples lead to
lower hardware utilization and tend to have high variance, causing large fluctuations
to the objective function. Nevertheless, it turns out that some fluctuations are benefi‐
cial since they enable the set of parameters to jump to new and potentially better local
minima. Using a relatively smaller batch size is therefore effective in that regard, and
is currently overall the preferred approach.
Gradient descent in TensorFlow
TensorFlow makes it very easy and intuitive to use gradient descent algorithms. Opti‐
mizers in TensorFlow compute the gradients simply by adding new operations to the
graph, and the gradients are calculated using automatic differentiation. This means,
in general terms, that TensorFlow automatically computes the gradients on its own,
“deriving” them from the operations and structure of the computation graph.
Variables, Placeholders, and Simple Optimization | 43
An important parameter to set is the algorithm’s learning rate, determining how
aggressive each update iteration will be (or in other words, how large the step will be
in the direction of the negative gradient). We want the decrease in the loss to be fast
enough on the one hand, but on the other hand not large enough so that we over-
shoot the target and end up at a point with a higher value of the loss function.
We first create an optimizer by using the GradientDescentOptimizer() function
with the desired learning rate. We then create a train operation that updates our vari‐
ables by calling the optimizer.minimize() function and passing in the loss as an
argument:
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
train = optimizer.minimize(loss)
The train operation is then executed when it is fed to the sess.run() method.
Wrapping it up with examples
We’re all set to go! Let’s combine all the components we’ve discussed in this section
and optimize the parameters of two models: linear and logistic regression. In these
examples we will create synthetic data with known properties, and see how the model
is able to recover these properties with the process of optimization.
Example 1: linear regression. In this problem we are interested in retrieving a set of
weights w and a bias term b, assuming our target value is a linear combination of
some input vector x, with an additional Gaussian noise εi added to each sample.
For this exercise we will generate synthetic data using NumPy. We create 2,000 sam‐
ples of x, a vector with three features, take the inner product of each x sample with a
set of weights w ([0.3, 0.5, 0.1]), and add a bias term b (–0.2) and Gaussian noise to
the result:
import numpy as np
# === Create data and simulate results =====
x_data = np.random.randn(2000,3)
w_real = [0.3,0.5,0.1]
b_real = -0.2
noise = np.random.randn(1,2000)*0.1
y_data = np.matmul(w_real,x_data.T) + b_real + noise
The noisy samples are shown in Figure 3-6.
44 | Chapter 3: Understanding TensorFlow Basics

Figure 3-6. Generated data to use for linear regression: each lled circle represents a
sample, and the dashed line shows the expected values without the noise component (the
diagonal).
Next, we estimate our set of weights w and bias b by optimizing the model (i.e., find‐
ing the best parameters) so that its predictions match the real targets as closely as
possible. Each iteration computes one update to the current parameters. In this exam‐
ple we run 10 iterations, printing our estimated parameters every 5 iterations using
the sess.run() method.
Don’t forget to initialize the variables! In this example we initialize both the weights
and the bias with zeros; however, there are “smarter” initialization techniques to
choose, as we will see in the next chapters. We use name scopes to group together
parts that are related to inferring the output, defining the loss, and setting and creat‐
ing the train object:
NUM_STEPS = 10
g = tf.Graph()
wb_ = []
with g.as_default():
x = tf.placeholder(tf.float32,shape=[None,3])
y_true = tf.placeholder(tf.float32,shape=None)
with tf.name_scope('inference') as scope:
w = tf.Variable([[0,0,0]],dtype=tf.float32,name='weights')
b = tf.Variable(0,dtype=tf.float32,name='bias')
y_pred = tf.matmul(w,tf.transpose(x)) + b
with tf.name_scope('loss') as scope:
loss = tf.reduce_mean(tf.square(y_true-y_pred))
Variables, Placeholders, and Simple Optimization | 45

with tf.name_scope('train') as scope:
learning_rate = 0.5
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
train = optimizer.minimize(loss)
# Before starting, initialize the variables. We will 'run' this first.
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
for step in range(NUM_STEPS):
sess.run(train,{x: x_data, y_true: y_data})
if (step % 5 == 0):
print(step, sess.run([w,b]))
wb_.append(sess.run([w,b]))
print(10, sess.run([w,b]))
And we get the results:
(0, [array([[ 0.30149955, 0.49303722, 0.11409992]],
dtype=float32), -0.18563795])
(5, [array([[ 0.30094019, 0.49846715, 0.09822173]],
dtype=float32), -0.19780949])
(10, [array([[ 0.30094025, 0.49846718, 0.09822182]],
dtype=float32), -0.19780946])
After only 10 iterations, the estimated weights and bias are w = [0.301, 0.498, 0.098]
and b = –0.198. The original parameter values were w = [0.3,0.5,0.1] and b = –0.2.
Almost a perfect match!
Example 2: logistic regression. Again we wish to retrieve the weights and bias compo‐
nents in a simulated data setting, this time in a logistic regression framework. Here
the linear component wTx + b is the input of a nonlinear function called the logistic
function. What it effectively does is squash the values of the linear part into the inter‐
val [0, 1]:
Pr(yi = 1|xi) = 1
1 + expwxi+b
We then regard these values as probabilities from which binary yes/1 or no/0 out‐
comes are generated. This is the nondeterministic (noisy) part of the model.
The logistic function is more general, and can be used with a different set of parame‐
ters for the steepness of the curve and its maximum value. This special case of a logis‐
tic function we are using is also referred to as a sigmoid function.
We generate our samples by using the same set of weights and biases as in the previ‐
ous example:
46 | Chapter 3: Understanding TensorFlow Basics

N = 20000
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# === Create data and simulate results =====
x_data = np.random.randn(N,3)
w_real = [0.3,0.5,0.1]
b_real = -0.2
wxb = np.matmul(w_real,x_data.T) + b_real
y_data_pre_noise = sigmoid(wxb)
y_data = np.random.binomial(1,y_data_pre_noise)
The outcome samples before and after the binarization of the output are shown in
Figure 3-7.
Figure 3-7. Generated data to use for logistic regression: each circle represents a sample.
In the le plot we see the probabilities generated by inputting the linear combination of
the input data to the logistic function. e right plot shows the binary target output, ran‐
domly sampled from the probabilities in the le image.
The only thing we need to change in the code is the loss function we use.
The loss we want to use here is the binary version of the cross entropy, which is also
the likelihood of the logistic regression model:
y_pred = tf.sigmoid(y_pred)
loss = y_true*tf.log(y_pred) - (1-y_true)*tf.log(1-y_pred)
loss = tf.reduce_mean(loss)
Luckily, TensorFlow already has a designated function we can use instead:
tf.nn.sigmoid_cross_entropy_with_logits(labels=,logits=)
Variables, Placeholders, and Simple Optimization | 47
To which we simply need to pass the true outputs and the model’s linear predictions:
NUM_STEPS = 50
with tf.name_scope('loss') as scope:
loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=y_true,logits=y_pred)
loss = tf.reduce_mean(loss)
# Before starting, initialize the variables. We will 'run' this first.
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
for step in range(NUM_STEPS):
sess.run(train,{x: x_data, y_true: y_data})
if (step % 5 == 0):
print(step, sess.run([w,b]))
wb_.append(sess.run([w,b]))
print(50, sess.run([w,b]))
Let’s see what we get:
(0, [array([[ 0.03212515, 0.05890014, 0.01086476]],
dtype=float32), -0.021875083])
(5, [array([[ 0.14185661, 0.25990966, 0.04818931]],
dtype=float32), -0.097346731])
(10, [array([[ 0.20022796, 0.36665651, 0.06824245]],
dtype=float32), -0.13804035])
(15, [array([[ 0.23269908, 0.42593899, 0.07949805]],
dtype=float32), -0.1608445])
(20, [array([[ 0.2512995 , 0.45984453, 0.08599731]],
dtype=float32), -0.17395383])
(25, [array([[ 0.26214141, 0.47957924, 0.08981277]],
dtype=float32), -0.1816061])
(30, [array([[ 0.26852587, 0.49118528, 0.09207394]],
dtype=float32), -0.18611355])
(35, [array([[ 0.27230808, 0.49805275, 0.09342111]],
dtype=float32), -0.18878292])
(40, [array([[ 0.27455658, 0.50213116, 0.09422609]],
dtype=float32), -0.19036882])
(45, [array([[ 0.27589601, 0.5045585 , 0.09470785]],
dtype=float32), -0.19131286])
(50, [array([[ 0.27656636, 0.50577223, 0.09494986]],
dtype=float32), -0.19178495])
It takes a few more iterations to converge, and more samples are required than in the
previous linear regression example, but eventually we get results that are quite similar
to the original chosen weights.
48 | Chapter 3: Understanding TensorFlow Basics
Summary
In this chapter we learned about computation graphs and what we can use them for.
We saw how to create a graph and how to compute its outputs. We introduced the
main building blocks of TensorFlow—the Tensor object, representing the graph’s
operations, placeholders for our input data, and Variables we tune as part of the
model training process. We learned about tensor arrays and covered the data type,
shape, and name attributes. Finally, we discussed the model optimization process and
saw how to implement it in TensorFlow. In the next chapter we will go into more
advanced deep neural networks used in computer vision.
Summary | 49
CHAPTER 4
Convolutional Neural Networks
In this chapter we introduce convolutional neural networks (CNNs) and the building
blocks and methods associated with them. We start with a simple model for classifica‐
tion of the MNIST dataset, then we introduce the CIFAR10 object-recognition data‐
set and apply several CNN models to it. While small and fast, the CNNs presented in
this chapter are highly representative of the type of models used in practice to obtain
state-of-the-art results in object-recognition tasks.
Introduction to CNNs
Convolutional neural networks have gained a special status over the last few years as
an especially promising form of deep learning. Rooted in image processing, convolu‐
tional layers have found their way into virtually all subfields of deep learning, and are
very successful for the most part.
The fundamental difference between fully connected and convolutional neural net‐
works is the pattern of connections between consecutive layers. In the fully connected
case, as the name might suggest, each unit is connected to all of the units in the previ‐
ous layer. We saw an example of this in Chapter 2, where the 10 output units were
connected to all of the input image pixels.
In a convolutional layer of a neural network, on the other hand, each unit is connec‐
ted to a (typically small) number of nearby units in the previous layer. Furthermore,
all units are connected to the previous layer in the same way, with the exact same
weights and structure. This leads to an operation known as convolution, giving the
architecture its name (see Figure 4-1 for an illustration of this idea). In the next sec‐
tion, we go into the convolution operation in some more detail, but in a nutshell all it
means for us is applying a small “window” of weights (also known as lters) across an
image, as illustrated in Figure 4-2 later.
51

Figure 4-1. In a fully connected layer (le), each unit is connected to all units of the pre‐
vious layers. In a convolutional layer (right), each unit is connected to a constant num‐
ber of units in a local region of the previous layer. Furthermore, in a convolutional layer,
the units all share the weights for these connections, as indicated by the shared linetypes.
There are motivations commonly cited as leading to the CNN approach, coming
from different schools of thought. The first angle is the so-called neuroscientific
inspiration behind the model. The second deals with insight into the nature of
images, and the third relates to learning theory. We will go over each of these shortly
before diving into the actual mechanics.
It has been popular to describe neural networks in general, and specifically convolu‐
tional neural networks, as biologically inspired models of computation. At times,
claims go as far as to state that these mimic the way the brain performs computa‐
tions. While misleading when taken at face value, the biological analogy is of some
interest.
The Nobel Prize–winning neurophysiologists Hubel and Wiesel discovered as early as
the 1960s that the first stages of visual processing in the brain consist of application of
the same local filter (e.g., edge detectors) to all parts of the visual field. The current
understanding in the neuroscientific community is that as visual processing proceeds,
information is integrated from increasingly wider parts of the input, and this is done
hierarchically.
Convolutional neural networks follow the same pattern. Each convolutional layer
looks at an increasingly larger part of the image as we go deeper into the network.
Most commonly, this will be followed by fully connected layers that in the biologically
inspired analogy act as the higher levels of visual processing dealing with global
information.
The second angle, more hard fact engineering–oriented, stems from the nature of
images and their contents. When looking for an object in an image, say the face of a
cat, we would typically want to be able to detect it regardless of its position in the
image. This reflects the property of natural images that the same content may be
found in different locations of an image. This is property is known as an invariance—
52 | Chapter 4: Convolutional Neural Networks

invariances of this sort can also be expected with respect to (small) rotations, chang‐
ing lighting conditions, etc.
Correspondingly, when building an object-recognition system, it should be invariant
to translation (and, depending on the scenario, probably also rotation and deforma‐
tions of many sorts, but that is another matter). Put simply, it therefore makes sense
to perform the same exact computation on different parts of the image. In this view, a
convolutional neural network layer computes the same features of an image, across
all spatial areas.
Finally, the convolutional structure can be seen as a regularization mechanism. In this
view, convolutional layers are like fully connected layers, but instead of searching for
weights in the full space of matrices (of certain size), we limit the search to matrices
describing fixed-size convolutions, reducing the number of degrees of freedom to the
size of the convolution, which is typically very small.
Regularization
The term regularization is used throughout this book. In machine
learning and statistics, regularization is mostly used to refer to the
restriction of an optimization problem by imposing a penalty on
the complexity of the solution, in the attempt to prevent overfitting
to the given examples.
Overfitting occurs when a rule (for instance, a classifier) is compu‐
ted in a way that explains the training set, but with poor generaliza‐
tion to unseen data.
Regularization is most often applied by adding implicit informa‐
tion regarding the desired results (this could take the form of say‐
ing we would rather have a smoother function, when searching a
function space). In the convolutional neural network case, we
explicitly state that we are looking for weights in a relatively low-
dimensional subspace corresponding to fixed-size convolutions.
In this chapter we cover the types of layers and operations associated with convolu‐
tional neural networks. We start by revisiting the MNIST dataset, this time applying a
model with approximately 99% accuracy. Next, we move on to the more interesting
object recognition CIFAR10 dataset.
MNIST: Take II
In this section we take a second look at the MNIST dataset, this time applying a small
convolutional neural network as our classifier. Before doing so, there are several ele‐
ments and operations that we must get acquainted with.
MNIST: Take II | 53

Convolution
The convolution operation, as you probably expect from the name of the architec‐
ture, is the fundamental means by which layers are connected in convolutional neu‐
ral networks. We use the built-in TensorFlow conv2d():
tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
Here, x is the data—the input image, or a downstream feature map obtained further
along in the network, after applying previous convolution layers. As discussed previ‐
ously, in typical CNN models we stack convolutional layers hierarchically, and feature
map is simply a commonly used term referring to the output of each such layer.
Another way to view the output of these layers is as processed images, the result of
applying a filter and perhaps some other operations. Here, this filter is parameterized
by W, the learned weights of our network representing the convolution filter. This is
just the set of weights in the small “sliding window” we see in Figure 4-2.
Figure 4-2. e same convolutional lter—a “sliding window”—applied across an image.
The output of this operation will depend on the shape of x and W, and in our case is
four-dimensional. The image data x will be of shape:
[None, 28, 28, 1]
54 | Chapter 4: Convolutional Neural Networks
meaning that we have an unknown number of images, each 28×28 pixels and with
one color channel (since these are grayscale images). The weights W we use will be of
shape:
[5, 5, 1, 32]
where the initial 5×5×1 represents the size of the small “window” in the image to be
convolved, in our case a 5×5 region. In images that have multiple color channels
(RGB, as briefly discussed in Chapter 1), we regard each image as a three-
dimensional tensor of RGB values, but in this one-channel data they are just two-
dimensional, and convolutional filters are applied to two-dimensional regions. Later,
when we tackle the CIFAR10 data, we’ll see examples of multiple-channel images and
how to set the size of weights W accordingly.
The final 32 is the number of feature maps. In other words, we have multiple sets of
weights for the convolutional layer—in this case, 32 of them. Recall that the idea of a
convolutional layer is to compute the same feature along the image; we would simply
like to compute many such features and thus use multiple sets of convolutional filters.
The strides argument controls the spatial movement of the filter W across the image
(or feature map) x.
The value [1, 1, 1, 1] means that the filter is applied to the input in one-pixel
intervals in each dimension, corresponding to a “full” convolution. Other settings of
this argument allow us to introduce skips in the application of the filter—a common
practice that we apply later—thus making the resulting feature map smaller.
Finally, setting padding to 'SAME' means that the borders of x are padded such that
the size of the result of the operation is the same as the size of x.
MNIST: Take II | 55

Activation functions
Following linear layers, whether convolutional or fully connected,
it is common practice to apply nonlinear activation functions (see
Figure 4-3 for some examples). One practical aspect of activation
functions is that consecutive linear operations can be replaced by a
single one, and thus depth doesn’t contribute to the expressiveness
of the model unless we use nonlinear activations between the linear
layers.
Figure 4-3. Common activation functions: logistic (le), hyperbolic tangent
(center), and rectifying linear unit (right)
Pooling
It is common to follow convolutional layers with pooling of outputs. Technically,
pooling means reducing the size of the data with some local aggregation function, typ‐
ically within each feature map.
The reasoning behind this is both technical and more theoretical. The technical
aspect is that pooling reduces the size of the data to be processed downstream. This
can drastically reduce the number of overall parameters in the model, especially if we
use fully connected layers after the convolutional ones.
The more theoretical reason for applying pooling is that we would like our computed
features not to care about small changes in position in an image. For instance, a fea‐
ture looking for eyes in the top-right part of an image should not change too much if
we move the camera a bit to the right when taking the picture, moving the eyes
slightly to the center of the image. Aggregating the “eye-detector feature” spatially
allows the model to overcome such spatial variability between images, capturing
some form of invariance as discussed at the beginning of this chapter.
In our example we apply the max pooling operation on 2×2 blocks of each feature
map:
tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
Max pooling outputs the maximum of the input in each region of a predefined size
(here 2×2). The ksize argument controls the size of the pooling (2×2), and the
strides argument controls by how much we “slide” the pooling grids across x, just as
56 | Chapter 4: Convolutional Neural Networks
in the case of the convolution layer. Setting this to a 2×2 grid means that the output of
the pooling will be exactly one-half of the height and width of the original, and in
total one-quarter of the size.
Dropout
The final element we will need for our model is dropout. This is a regularization trick
used in order to force the network to distribute the learned representation across all
the neurons. Dropout “turns off” a random preset fraction of the units in a layer, by
setting their values to zero during training. These dropped-out neurons are random
—different for each computation—forcing the network to learn a representation that
will work even after the dropout. This process is often thought of as training an
“ensemble” of multiple networks, thereby increasing generalization. When using the
network as a classifier at test time (“inference”), there is no dropout and the full net‐
work is used as is.
The only argument in our example other than the layer we would like to apply drop‐
out to is keep_prob, the fraction of the neurons to keep working at each step:
tf.nn.dropout(layer, keep_prob=keep_prob)
In order to be able to change this value (which we must do, since for testing we would
like this to be 1.0, meaning no dropout at all), we will use a tf.Variable and pass
one value for train (.5) and another for test (1.0).
The Model
First, we define helper functions that will be used extensively throughout this chapter
to create our layers. Doing this allows the actual model to be short and readable (later
in the book we will see that there exist several frameworks for greater abstraction of
deep learning building blocks, which allow us to concentrate on rapidly designing our
networks rather than the somewhat tedious work of defining all the necessary ele‐
ments). Our helper functions are:
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
MNIST: Take II | 57
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME')
def conv_layer(input, shape):
W = weight_variable(shape)
b = bias_variable([shape[3]])
return tf.nn.relu(conv2d(input, W) + b)
def full_layer(input, size):
in_size = int(input.get_shape()[1])
W = weight_variable([in_size, size])
b = bias_variable([size])
return tf.matmul(input, W) + b
Let’s take a closer look at these:
weight_variable()
This specifies the weights for either fully connected or convolutional layers of the
network. They are initialized randomly using a truncated normal distribution
with a standard deviation of .1. This sort of initialization with a random normal
distribution that is truncated at the tails is pretty common and generally pro‐
duces good results (see the upcoming note on random initialization).
bias_variable()
This defines the bias elements in either a fully connected or a convolutional layer.
These are all initialized with the constant value of .1.
conv2d()
This specifies the convolution we will typically use. A full convolution (no skips)
with an output the same size as the input.
max_pool_2×2
This sets the max pool to half the size across the height/width dimensions, and in
total a quarter the size of the feature map.
conv_layer()
This is the actual layer we will use. Linear convolution as defined in conv2d, with
a bias, followed by the ReLU nonlinearity.
full_layer()
A standard full layer with a bias. Notice that here we didn’t add the ReLU. This
allows us to use the same layer for the final output, where we don’t need the non‐
linear part.
With these layers defined, we are ready to set up our model (see the visualization in
Figure 4-4):
58 | Chapter 4: Convolutional Neural Networks

x = tf.placeholder(tf.float32, shape=[None, 784])
y_ = tf.placeholder(tf.float32, shape=[None, 10])
x_image = tf.reshape(x, [-1, 28, 28, 1])
conv1 = conv_layer(x_image, shape=[5, 5, 1, 32])
conv1_pool = max_pool_2x2(conv1)
conv2 = conv_layer(conv1_pool, shape=[5, 5, 32, 64])
conv2_pool = max_pool_2x2(conv2)
conv2_flat = tf.reshape(conv2_pool, [-1, 7*7*64])
full_1 = tf.nn.relu(full_layer(conv2_flat, 1024))
keep_prob = tf.placeholder(tf.float32)
full1_drop = tf.nn.dropout(full_1, keep_prob=keep_prob)
y_conv = full_layer(full1_drop, 10)
Figure 4-4. A visualization of the CNN architecture used.
Random initialization
In the previous chapter we discussed initializers of several types,
including the random initializer used here for our convolutional
layer’s weights:
initial = tf.truncated_normal(shape, stddev=0.1)
Much has been said about the importance of initialization in the
training of deep learning models. Put simply, a bad initialization
can make the training process “get stuck,” or fail completely due to
numerical issues. Using random rather than constant initializations
helps break the symmetry between learned features, allowing the
model to learn a diverse and rich representation. Using bound val‐
ues helps, among other things, to control the magnitude of the gra‐
dients, allowing the network to converge more efficiently.
MNIST: Take II | 59
We start by defining the placeholders for the images and correct labels, x and y_,
respectively. Next, we reshape the image data into the 2D image format with size
28×28×1. Recall we did not need this spatial aspect of the data for our previous
MNIST model, since all pixels were treated independently, but a major source of
power in the convolutional neural network framework is the utilization of this spatial
meaning when considering images.
Next we have two consecutive layers of convolution and pooling, each with 5×5 con‐
volutions and 64 feature maps, followed by a single fully connected layer with 1,024
units. Before applying the fully connected layer we flatten the image back to a single
vector form, since the fully connected layer no longer needs the spatial aspect.
Notice that the size of the image following the two convolution and pooling layers is
7×7×64. The original 28×28 pixel image is reduced first to 14×14, and then to 7×7 in
the two pooling operations. The 64 is the number of feature maps we created in the
second convolutional layer. When considering the total number of learned parame‐
ters in the model, a large proportion will be in the fully connected layer (going from
7×7×64 to 1,024 gives us 3.2 million parameters). This number would have been 16
times as large (i.e., 28×28×64×1,024, which is roughly 51 million) if we hadn’t used
max-pooling.
Finally, the output is a fully connected layer with 10 units, corresponding to the num‐
ber of labels in the dataset (recall that MNIST is a handwritten digit dataset, so the
number of possible labels is 10).
The rest is the same as in the first MNIST model in Chapter 2, with a few minor
changes:
train_accuracy
We print the accuracy of the model on the batch used for training every 100
steps. This is done before the training step, and therefore is a good estimate of the
current performance of the model on the training set.
test_accuracy
We split the test procedure into 10 blocks of 1,000 images each. Doing this is
important mostly for much larger datasets.
Here’s the complete code:
mnist = input_data.read_data_sets(DATA_DIR, one_hot=True)
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(y_conv,
y_))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
60 | Chapter 4: Convolutional Neural Networks

1In machine learning and especially in deep learning, an epoc refers to a single pass over all the training data;
i.e., when the learning model has seen each training example exactly one time.
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(STEPS):
batch = mnist.train.next_batch(50)
if i % 100 == 0:
train_accuracy = sess.run(accuracy, feed_dict={x: batch[0],
y_: batch[1],
keep_prob: 1.0})
print "step {}, training accuracy {}".format(i, train_accuracy)
sess.run(train_step, feed_dict={x: batch[0], y_: batch[1],
keep_prob: 0.5})
X = mnist.test.images.reshape(10, 1000, 784)
Y = mnist.test.labels.reshape(10, 1000, 10)
test_accuracy = np.mean([sess.run(accuracy,
feed_dict={x:X[i], y_:Y[i],keep_prob:1.0})
for i in range(10)])
print "test accuracy: {}".format(test_accuracy)
The performance of this model is already relatively good, with just over 99% correct
after as little as 5 epocs,1 which are 5,000 steps with mini-batches of size 50.
For a list of models that have been used over the years with this dataset, and some
ideas on how to further improve this result, take a look at http://yann.lecun.com/exdb/
mnist/.
CIFAR10
CIFAR10 is another dataset with a long history in computer vision and machine
learning. Like MNIST, it is a common benchmark that various methods are tested
against. CIFAR10 is a set of 60,000 color images of size 32×32 pixels, each belonging
to one of ten categories: airplane, automobile, bird, cat, deer, dog, frog, horse, ship,
and truck.
State-of-the-art deep learning methods for this dataset are as good as humans at clas‐
sifying these images. In this section we start off with much simpler methods that will
run relatively quickly. Then, we discuss briefly what the gap is between these and the
state of the art.
CIFAR10 | 61

2This is done mostly for the purpose of illustration. There are existing open source libraries containing this
sort of data wrapper built in, for many popular datasets. See, for example, the datasets module in Keras
(keras.datasets), and specifically keras.datasets.cifar10.
Loading the CIFAR10 Dataset
In this section we build a data manager for CIFAR10, similarly to the built-in
input_data.read_data_sets() we used for MNIST.2
First, download the Python version of the dataset and extract the files into a local
directory. You should now have the following files:
•data_batch_1, data_batch_2, data_batch_3, data_batch_4, data_batch_5
•test_batch
•batches_meta
•readme.html
The data_batch_X files are serialized data files containing the training data, and
test_batch is a similar serialized file containing the test data. The batches_meta file
contains the mapping from numeric to semantic labels. The .html file is a copy of the
CIFAR-10 dataset’s web page.
Since this is a relatively small dataset, we load it all into memory:
class CifarLoader(object):
def __init__(self, source_files):
self._source = source_files
self._i = 0
self.images = None
self.labels = None
def load(self):
data = [unpickle(f) for f in self._source]
images = np.vstack([d["data"] for d in data])
n = len(images)
self.images = images.reshape(n, 3, 32, 32).transpose(0, 2, 3, 1)\
.astype(float) / 255
self.labels = one_hot(np.hstack([d["labels"] for d in data]), 10)
return self
def next_batch(self, batch_size):
x, y = self.images[self._i:self._i+batch_size],
self.labels[self._i:self._i+batch_size]
self._i = (self._i + batch_size) % len(self.images)
return x, y
where we use the following utility functions:
DATA_PATH = "/path/to/CIFAR10"
62 | Chapter 4: Convolutional Neural Networks

def unpickle(file):
with open(os.path.join(DATA_PATH, file), 'rb') as fo:
dict = cPickle.load(fo)
return dict
def one_hot(vec, vals=10):
n = len(vec)
out = np.zeros((n, vals))
out[range(n), vec] = 1
return out
The unpickle() function returns a dict with fields data and labels, containing the
image data and the labels, respectively. one_hot() recodes the labels from integers (in
the range 0 to 9) to vectors of length 10, containing all 0s except for a 1 at the position
of the label.
Finally, we create a data manager that includes both the training and test data:
class CifarDataManager(object):
def __init__(self):
self.train = CifarLoader(["data_batch_{}".format(i)
for i in range(1, 6)])
.load()
self.test = CifarLoader(["test_batch"]).load()
Using Matplotlib, we can now use the data manager in order to display some of the
CIFAR10 images and get a better idea of what is in this dataset:
def display_cifar(images, size):
n = len(images)
plt.figure()
plt.gca().set_axis_off()
im = np.vstack([np.hstack([images[np.random.choice(n)] for i in range(size)])
for i in range(size)])
plt.imshow(im)
plt.show()
d = CifarDataManager()
print "Number of train images: {}".format(len(d.train.images))
print "Number of train labels: {}".format(len(d.train.labels))
print "Number of test images: {}".format(len(d.test.images))
print "Number of test images: {}".format(len(d.test.labels))
images = d.train.images
display_cifar(images, 10)
Matplotlib
Matplotlib is a useful Python library for plotting, designed to look
and behave like MATLAB plots. It is often the easiest way to
quickly plot and visualize a dataset.
CIFAR10 | 63

The display_cifar()function takes as arguments images (an iterable containing
images), and size (the number of images we would like to display), and constructs
and displays a size×size grid of images. This is done by concatenating the actual
images vertically and horizontally to form a large image.
Before displaying the image grid, we start by printing the sizes of the train/test sets.
CIFAR10 contains 50K training images and 10K test images:
Number of train images: 50000
Number of train labels: 50000
Number of test images: 10000
Number of test images: 10000
The image produced and shown in Figure 4-5 is meant to give some idea of what
CIFAR10 images actually look like. Notably, these small, 32×32 pixel images each
contain a full single object that is both centered and more or less recognizable even at
this resolution.
Figure 4-5. 100 random CIFAR10 images.
Simple CIFAR10 Models
We will start by using the model that we have previously used successfully for the
MNIST dataset. Recall that the MNIST dataset is composed of 28×28-pixel grayscale
images, while the CIFAR10 images are color images with 32×32 pixels. This will
necessitate minor adaptations to the setup of the computation graph:
64 | Chapter 4: Convolutional Neural Networks

3See Who Is the Best in CIFAR-10? for a list of methods and associated papers.
cifar = CifarDataManager()
x = tf.placeholder(tf.float32, shape=[None, 32, 32, 3])
y_ = tf.placeholder(tf.float32, shape=[None, 10])
keep_prob = tf.placeholder(tf.float32)
conv1 = conv_layer(x, shape=[5, 5, 3, 32])
conv1_pool = max_pool_2x2(conv1)
conv2 = conv_layer(conv1_pool, shape=[5, 5, 32, 64])
conv2_pool = max_pool_2x2(conv2)
conv2_flat = tf.reshape(conv2_pool, [-1, 8 * 8 * 64])
full_1 = tf.nn.relu(full_layer(conv2_flat, 1024))
full1_drop = tf.nn.dropout(full_1, keep_prob=keep_prob)
y_conv = full_layer(full1_drop, 10)
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(y_conv,
y_))
train_step = tf.train.AdamOptimizer(1e-3).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
def test(sess):
X = cifar.test.images.reshape(10, 1000, 32, 32, 3)
Y = cifar.test.labels.reshape(10, 1000, 10)
acc = np.mean([sess.run(accuracy, feed_dict={x: X[i], y_: Y[i],
keep_prob: 1.0})
for i in range(10)])
print "Accuracy: {:.4}%".format(acc * 100)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(STEPS):
batch = cifar.train.next_batch(BATCH_SIZE)
sess.run(train_step, feed_dict={x: batch[0], y_: batch[1],
keep_prob: 0.5})
test(sess)
This first attempt will achieve approximately 70% accuracy within a few minutes
(using a batch size of 100, and depending naturally on hardware and configurations).
Is this good? As of now, state-of-the-art deep learning methods achieve over 95%
accuracy on this dataset,3 but using much larger models and usually many, many
hours of training.
CIFAR10 | 65
There are a few differences between this and the similar MNIST model presented ear‐
lier. First, the input consists of images of size 32×32×3, the third dimension being the
three color channels:
x = tf.placeholder(tf.float32, shape=[None, 32, 32, 3])
Similarly, after the two pooling operations, we are left this time with 64 feature maps
of size 8×8:
conv2_flat = tf.reshape(conv2_pool, [-1, 8 * 8 * 64])
Finally, as a matter of convenience, we group the test procedure into a separate func‐
tion called test(), and we do not print training accuracy values (which can be added
back in using the same code as in the MNIST model).
Once we have a model with some acceptable baseline accuracy (whether derived from
a simple MNIST model or from a state-of-the-art model for some other dataset), a
common practice is to try to improve it by means of a sequence of adaptations and
changes, until reaching what is necessary for our purposes.
In this case, leaving all the rest the same, we will add a third convolution layer with
128 feature maps and dropout. We will also reduce the number of units in the fully
connected layer from 1,024 to 512:
x = tf.placeholder(tf.float32, shape=[None, 32, 32, 3])
y_ = tf.placeholder(tf.float32, shape=[None, 10])
keep_prob = tf.placeholder(tf.float32)
conv1 = conv_layer(x, shape=[5, 5, 3, 32])
conv1_pool = max_pool_2x2(conv1)
conv2 = conv_layer(conv1_pool, shape=[5, 5, 32, 64])
conv2_pool = max_pool_2x2(conv2)
conv3 = conv_layer(conv2_pool, shape=[5, 5, 64, 128])
conv3_pool = max_pool_2x2(conv3)
conv3_flat = tf.reshape(conv3_pool, [-1, 4 * 4 * 128])
conv3_drop = tf.nn.dropout(conv3_flat, keep_prob=keep_prob)
full_1 = tf.nn.relu(full_layer(conv3_drop, 512))
full1_drop = tf.nn.dropout(full_1, keep_prob=keep_prob)
y_conv = full_layer(full1_drop, 10)
This model will take slightly longer to run (but still way under an hour, even without
sophisticated hardware) and achieve an accuracy of approximately 75%.
There is still a rather large gap between this and the best known methods. There are
several independently applicable elements that can help close this gap:
66 | Chapter 4: Convolutional Neural Networks
Model size
Most successful methods for this and similar datasets use much deeper networks
with many more adjustable parameters.
Additional types of layers and methods
Additional types of popular layers are often used together with the layers presen‐
ted here, such as local response normalization.
Optimization tricks
More about this later!
Domain knowledge
Pre-processing utilizing domain knowledge often goes a long way. In this case
that would be good old-fashioned image processing.
Data augmentation
Adding training data based on the existing set can help. For instance, if an image
of a dog is flipped horizontally, then it is clearly still an image of a dog (but what
about a vertical flip?). Small shifts and rotations are also commonly used.
Reusing successful methods and architectures
As in most engineering fields, starting from a time-proven method and adapting
it to your needs is often the way to go. In the field of deep learning this is often
done by fine-tuning pretrained models.
The final model we will present in this chapter is a smaller version of the type of
model that actually produces great results for this dataset. This model is still compact
and fast, and achieves approximately 83% accuracy after ~150 epocs:
C1, C2, C3 = 30, 50, 80
F1 = 500
conv1_1 = conv_layer(x, shape=[3, 3, 3, C1])
conv1_2 = conv_layer(conv1_1, shape=[3, 3, C1, C1])
conv1_3 = conv_layer(conv1_2, shape=[3, 3, C1, C1])
conv1_pool = max_pool_2x2(conv1_3)
conv1_drop = tf.nn.dropout(conv1_pool, keep_prob=keep_prob)
conv2_1 = conv_layer(conv1_drop, shape=[3, 3, C1, C2])
conv2_2 = conv_layer(conv2_1, shape=[3, 3, C2, C2])
conv2_3 = conv_layer(conv2_2, shape=[3, 3, C2, C2])
conv2_pool = max_pool_2x2(conv2_3)
conv2_drop = tf.nn.dropout(conv2_pool, keep_prob=keep_prob)
conv3_1 = conv_layer(conv2_drop, shape=[3, 3, C2, C3])
conv3_2 = conv_layer(conv3_1, shape=[3, 3, C3, C3])
conv3_3 = conv_layer(conv3_2, shape=[3, 3, C3, C3])
conv3_pool = tf.nn.max_pool(conv3_3, ksize=[1, 8, 8, 1], strides=[1, 8, 8, 1],
padding='SAME')
conv3_flat = tf.reshape(conv3_pool, [-1, C3])
CIFAR10 | 67
conv3_drop = tf.nn.dropout(conv3_flat, keep_prob=keep_prob)
full1 = tf.nn.relu(full_layer(conv3_flat, F1))
full1_drop = tf.nn.dropout(full1, keep_prob=keep_prob)
y_conv = full_layer(full1_drop, 10)
This model consists of three blocks of convolutional layers, followed by the fully con‐
nected and output layers we have already seen a few times before. Each block of con‐
volutional layers contains three consecutive convolutional layers, followed by a single
pooling and dropout.
The constants C1, C2, and C3 control the number of feature maps in each layer of each
of the convolutional blocks, and the constant F1 controls the number of units in the
fully connected layer.
After the third block of convolutional layers, we use an 8×8 max pool layer:
conv3_pool = tf.nn.max_pool(conv3_3, ksize=[1, 8, 8, 1], strides=[1, 8, 8, 1],
padding='SAME')
Since at this point the feature maps are of size 8×8 (following the first two poolings
that each reduced the 32×32 pictures by half on each axis), this globally pools each of
the feature maps and keeps only the maximal value. The number of feature maps at
the third block was set to 80, so at this point (following the max pooling) the repre‐
sentation is reduced to only 80 numbers. This keeps the overall size of the model
small, as the number of parameters in the transition to the fully connected layer is
kept down to 80×500.
Summary
In this chapter we introduced convolutional neural networks and the various build‐
ing blocks they are typically made of. Once you are able to get small models working
properly, try running larger and deeper ones, following the same principles. While
you can always have a peek in the latest literature and see what works, a lot can be
learned from trial and error and figuring some of it out for yourself. In the next chap‐
ters, we will see how to work with text and sequence data and how to use TensorFlow
abstractions to build CNN models with ease.
68 | Chapter 4: Convolutional Neural Networks
CHAPTER 5
Text I: Working with Text and Sequences,
and TensorBoard Visualization
In this chapter we show how to work with sequences in TensorFlow, and in particular
text. We begin by introducing recurrent neural networks (RNNs), a powerful class of
deep learning algorithms particularly useful and popular in natural language process‐
ing (NLP). We show how to implement RNN models from scratch, introduce some
important TensorFlow capabilities, and visualize the model with the interactive Ten‐
sorBoard. We then explore how to use an RNN in a supervised text classification
problem with word-embedding training. Finally, we show how to build a more
advanced RNN model with long short-term memory (LSTM) networks and how to
handle sequences of variable length.
The Importance of Sequence Data
We saw in the previous chapter that using the spatial structure of images can lead to
advanced models with excellent results. As discussed in that chapter, exploiting struc‐
ture is the key to success. As we will see shortly, an immensely important and useful
type of structure is the sequential structure. Thinking in terms of data science, this
fundamental structure appears in many datasets, across all domains. In computer
vision, video is a sequence of visual content evolving over time. In speech we have
audio signals, in genomics gene sequences; we have longitudinal medical records in
healthcare, financial data in the stock market, and so on (see Figure 5-1).
69

Figure 5-1. e ubiquity of sequence data.
A particularly important type of data with strong sequential structure is natural lan‐
guage—text data. Deep learning methods that exploit the sequential structure inher‐
ent in texts—characters, words, sentences, paragraphs, documents—are at the
forefront of natural language understanding (NLU) systems, often leaving more tra‐
ditional methods in the dust. There are a great many types of NLU tasks that are of
interest to solve, ranging from document classification to building powerful language
models, from answering questions automatically to generating human-level conversa‐
tion agents. These tasks are fiendishly difficult, garnering the efforts and attention of
the entire AI community in both academia and industry.
In this chapter, we focus on the basic building blocks and tasks, and show how to
work with sequences—primarily of text—in TensorFlow. We take a detailed deep dive
into the core elements of sequence models in TensorFlow, implementing some of
them from scratch, to gain a thorough understanding. In the next chapter we show
more advanced text modeling techniques with TensorFlow, and in Chapter 7 we use
abstraction libraries that offer simpler, high-level ways to implement our models.
We begin with the most important and popular class of deep learning models for
sequences (in particular, text): recurrent neural networks.
Introduction to Recurrent Neural Networks
Recurrent neural networks are a powerful and widely used class of neural network
architectures for modeling sequence data. The basic idea behind RNN models is that
each new element in the sequence contributes some new information, which updates
the current state of the model.
70 | Chapter 5: Text I: Working with Text and Sequences, and TensorBoard Visualization

In the previous chapter, which explored computer vision with CNN models, we dis‐
cussed how those architectures are inspired by the current scientific perceptions of
the way the human brain processes visual information. These scientific perceptions
are often rather close to our commonplace intuition from our day-to-day lives about
how we process sequential information.
When we receive new information, clearly our “history” and “memory” are not wiped
out, but instead “updated.” When we read a sentence in some text, with each new
word, our current state of information is updated, and it is dependent not only on the
new observed word but on the words that preceded it.
A fundamental mathematical construct in statistics and probability, which is often
used as a building block for modeling sequential patterns via machine learning is the
Markov chain model. Figuratively speaking, we can view our data sequences as
“chains,” with each node in the chain dependent in some way on the previous node,
so that “history” is not erased but carried on.
RNN models are also based on this notion of chain structure, and vary in how exactly
they maintain and update information. As their name implies, recurrent neural nets
apply some form of “loop.” As seen in Figure 5-2, at some point in time t, the network
observes an input xt (a word in a sentence) and updates its “state vector” to ht from
the previous vector ht-1. When we process new input (the next word), it will be done
in some manner that is dependent on ht and thus on the history of the sequence (the
previous words we’ve seen affect our understanding of the current word). As seen in
the illustration, this recurrent structure can simply be viewed as one long unrolled
chain, with each node in the chain performing the same kind of processing “step”
based on the “message” it obtains from the output of the previous node. This, of
course, is very related to the Markov chain models discussed previously and their
hidden Markov model (HMM) extensions, which are not discussed in this book.
Figure 5-2. Recurrent neural networks updating with new information received over
time.
Introduction to Recurrent Neural Networks | 71
Vanilla RNN Implementation
In this section we implement a basic RNN from scratch, explore its inner workings,
and gain insight into how TensorFlow can work with sequences. We introduce some
powerful, fairly low-level tools that TensorFlow provides for working with sequence
data, which you can use to implement your own systems.
In the next sections, we will show how to use higher-level TensorFlow RNN modules.
We begin with defining our basic model mathematically. This mainly consists of
defining the recurrence structure—the RNN update step.
The update step for our simple vanilla RNN is
ht = tanh(Wxxt + Whht-1 + b)
where Wh, Wx, and b are weight and bias variables we learn, tanh(·) is the hyperbolic
tangent function that has its range in [–1,1] and is strongly connected to the sigmoid
function used in previous chapters, and xt and ht are the input and state vectors as
defined previously. Finally, the hidden state vector is multiplied by another set of
weights, yielding the outputs that appear in Figure 5-2.
MNIST images as sequences
To get a first taste of the power and general applicability of sequence models, in this
section we implement our first RNN to solve the MNIST image classification task
that you are by now familiar with. Later in this chapter we will focus on sequences of
text, and see how neural sequence models can powerfully manipulate them and
extract information to solve NLU tasks.
But, you may ask, what have images got to do with sequences?
As we saw in the previous chapter, the architecture of convolutional neural networks
makes use of the spatial structure of images. While the structure of natural images is
well suited for CNN models, it is revealing to look at the structure of images from
different angles. In a trend in cutting-edge deep learning research, advanced models
attempt to exploit various kinds of sequential structures in images, trying to capture
in some sense the “generative process” that created each image. Intuitively, this all
comes down to the notion that nearby areas in images are somehow related, and try‐
ing to model this structure.
Here, to introduce basic RNNs and how to work with sequences, we take a simple
sequential view of images: we look at each image in our data as a sequence of rows (or
columns). In our MNIST data, this just means that each 28×28-pixel image can be
viewed as a sequence of length 28, each element in the sequence a vector of 28 pixels
(see Figure 5-3). Then, the temporal dependencies in the RNN can be imaged as a
72 | Chapter 5: Text I: Working with Text and Sequences, and TensorBoard Visualization

scanner head, scanning the image from top to bottom (rows) or left to right (col‐
umns).
Figure 5-3. An image as a sequence of pixel columns.
We start by loading data, defining some parameters, and creating placeholders for our
data:
import tensorflow as tf
# Import MNIST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
# Define some parameters
element_size = 28
time_steps = 28
num_classes = 10
batch_size = 128
hidden_layer_size = 128
# Where to save TensorBoard model summaries
LOG_DIR = "logs/RNN_with_summaries"
# Create placeholders for inputs, labels
_inputs = tf.placeholder(tf.float32,shape=[None, time_steps,
element_size],
name='inputs')
y = tf.placeholder(tf.float32, shape=[None, num_classes],
name='labels')
element_size is the dimension of each vector in our sequence—in our case, a row/
column of 28 pixels. time_steps is the number of such elements in a sequence.
Introduction to Recurrent Neural Networks | 73

As we saw in previous chapters, when we load data with the built-in MNIST data
loader, it comes in unrolled form—a vector of 784 pixels. When we load batches of
data during training (we’ll get to that later in this section), we simply reshape each
unrolled vector to [batch_size, time_steps, element_size]:
batch_x, batch_y = mnist.train.next_batch(batch_size)
# Reshape data to get 28 sequences of 28 pixels
batch_x = batch_x.reshape((batch_size, time_steps, element_size))
We set hidden_layer_size (arbitrarily to 128, controlling the size of the hidden RNN
state vector discussed earlier.
LOG_DIR is the directory to which we save model summaries for TensorBoard visuali‐
zation. You will learn what this means as we go.
TensorBoard visualizations
In this chapter, we will also briefly introduce TensorBoard visuali‐
zations. TensorBoard allows you to monitor and explore the model
structure, weights, and training process, and requires some very
simple additions to the code. More details are provided throughout
this chapter and further along in the book.
Finally, our input and label placeholders are created with the suitable dimensions.
The RNN step
Let’s implement the mathematical model for the RNN step.
We first create a function used for logging summaries, which we will use later in Ten‐
sorBoard to visualize our model and training process (it is not important to under‐
stand its technicalities at this stage):
# This helper function, taken from the official TensorFlow documentation,
# simply adds some ops that take care of logging summaries
def variable_summaries(var):
with tf.name_scope('summaries'):
mean = tf.reduce_mean(var)
tf.summary.scalar('mean', mean)
with tf.name_scope('stddev'):
stddev = tf.sqrt(tf.reduce_mean(tf.square(var - mean)))
tf.summary.scalar('stddev', stddev)
tf.summary.scalar('max', tf.reduce_max(var))
tf.summary.scalar('min', tf.reduce_min(var))
tf.summary.histogram('histogram', var)
Next, we create the weight and bias variables used in the RNN step:
# Weights and bias for input and hidden layer
with tf.name_scope('rnn_weights'):
74 | Chapter 5: Text I: Working with Text and Sequences, and TensorBoard Visualization
with tf.name_scope("W_x"):
Wx = tf.Variable(tf.zeros([element_size, hidden_layer_size]))
variable_summaries(Wx)
with tf.name_scope("W_h"):
Wh = tf.Variable(tf.zeros([hidden_layer_size, hidden_layer_size]))
variable_summaries(Wh)
with tf.name_scope("Bias"):
b_rnn = tf.Variable(tf.zeros([hidden_layer_size]))
variable_summaries(b_rnn)
Applying the RNN step with tf.scan()
We now create a function that implements the vanilla RNN step we saw in the previ‐
ous section using the variables we created. It should by now be straightforward to
understand the TensorFlow code used here:
def rnn_step(previous_hidden_state,x):
current_hidden_state = tf.tanh(
tf.matmul(previous_hidden_state, Wh) +
tf.matmul(x, Wx) + b_rnn)
return current_hidden_state
Next, we apply this function across all 28 time steps:
# Processing inputs to work with scan function
# Current input shape: (batch_size, time_steps, element_size)
processed_input = tf.transpose(_inputs, perm=[1, 0, 2])
# Current input shape now: (time_steps, batch_size, element_size)
initial_hidden = tf.zeros([batch_size,hidden_layer_size])
# Getting all state vectors across time
all_hidden_states = tf.scan(rnn_step,
processed_input,
initializer=initial_hidden,
name='states')
In this small code block, there are some important elements to understand. First, we
reshape the inputs from [batch_size, time_steps, element_size] to
[time_steps, batch_size, element_size]. The perm argument to tf.transpose()
tells TensorFlow which axes we want to switch around. Now that the first axis in our
input Tensor represents the time axis, we can iterate across all time steps by using the
built-in tf.scan() function, which repeatedly applies a callable (function) to a
sequence of elements in order, as explained in the following note.
Introduction to Recurrent Neural Networks | 75

tf.scan()
This important function was added to TensorFlow to allow us to
introduce loops into the computation graph, instead of just
“unrolling” the loops explicitly by adding more and more replica‐
tions of the same operations. More technically, it is a higher-order
function very similar to the reduce operator, but it returns all inter‐
mediate accumulator values over time. There are several advan‐
tages to this approach, chief among them the ability to have a
dynamic number of iterations rather than fixed, computational
speedups and optimizations for graph construction.
To demonstrate the use of this function, consider the following simple example
(which is separate from the overall RNN code in this section):
import numpy as np
import tensorflow as tf
elems = np.array(["T","e","n","s","o","r", " ", "F","l","o","w"])
scan_sum = tf.scan(lambda a, x: a + x, elems)
sess=tf.InteractiveSession()
sess.run(scan_sum)
Let’s see what we get:
array([b'T', b'Te', b'Ten', b'Tens', b'Tenso', b'Tensor', b'Tensor ',
b'Tensor F', b'Tensor Fl', b'Tensor Flo', b'Tensor Flow'],
dtype=object)
In this case, we use tf.scan() to sequentially concatenate characters to a string, in a
manner analogous to the arithmetic cumulative sum.
Sequential outputs
As we saw earlier, in an RNN we get a state vector for each time step, multiply it by
some weights, and get an output vector—our new representation of the data. Let’s
implement this:
# Weights for output layers
with tf.name_scope('linear_layer_weights') as scope:
with tf.name_scope("W_linear"):
Wl = tf.Variable(tf.truncated_normal([hidden_layer_size,
num_classes],
mean=0,stddev=.01))
variable_summaries(Wl)
with tf.name_scope("Bias_linear"):
bl = tf.Variable(tf.truncated_normal([num_classes],
mean=0,stddev=.01))
variable_summaries(bl)
76 | Chapter 5: Text I: Working with Text and Sequences, and TensorBoard Visualization
# Apply linear layer to state vector
def get_linear_layer(hidden_state):
return tf.matmul(hidden_state, Wl) + bl
with tf.name_scope('linear_layer_weights') as scope:
# Iterate across time, apply linear layer to all RNN outputs
all_outputs = tf.map_fn(get_linear_layer, all_hidden_states)
# Get last output
output = all_outputs[-1]
tf.summary.histogram('outputs', output)
Our input to the RNN is sequential, and so is our output. In this sequence classifica‐
tion example, we take the last state vector and pass it through a fully connected linear
layer to extract an output vector (which will later be passed through a softmax activa‐
tion function to generate predictions). This is common practice in basic sequence
classification, where we assume that the last state vector has “accumulated” informa‐
tion representing the entire sequence.
To implement this, we first define the linear layer’s weights and bias term variables,
and create a factory function for this layer. Then we apply this layer to all outputs
with tf.map_fn(), which is pretty much the same as the typical map function that
applies functions to sequences/iterables in an element-wise manner, in this case on
each element in our sequence.
Finally, we extract the last output for each instance in the batch, with negative index‐
ing (similarly to ordinary Python). We will see some more ways to do this later and
investigate outputs and states in some more depth.
RNN classication
We’re now ready to train a classifier, much in the same way we did in the previous
chapters. We define the ops for loss function computation, optimization, and predic‐
tion, add some more summaries for TensorBoard, and merge all these summaries
into one operation:
with tf.name_scope('cross_entropy'):
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(logits=output, labels=y))
tf.summary.scalar('cross_entropy', cross_entropy)
with tf.name_scope('train'):
# Using RMSPropOptimizer
train_step = tf.train.RMSPropOptimizer(0.001, 0.9)\
.minimize(cross_entropy)
with tf.name_scope('accuracy'):
correct_prediction = tf.equal(
tf.argmax(y,1), tf.argmax(output,1))
Introduction to Recurrent Neural Networks | 77
accuracy = (tf.reduce_mean(
tf.cast(correct_prediction, tf.float32)))*100
tf.summary.scalar('accuracy', accuracy)
# Merge all the summaries
merged = tf.summary.merge_all()
By now you should be familiar with most of the components used for defining the
loss function and optimization. Here, we used the RMSPropOptimizer, implementing
a well-known and strong gradient descent algorithm, with some standard hyperpara‐
meters. Of course, we could have used any other optimizer (and do so throughout
this book!).
We create a small test set with unseen MNIST images, and add some more technical
ops and commands for logging summaries that we will use in TensorBoard.
Let’s run the model and check out the results:
# Get a small test set
test_data = mnist.test.images[:batch_size].reshape((-1, time_steps,
element_size))
test_label = mnist.test.labels[:batch_size]
with tf.Session() as sess:
# Write summaries to LOG_DIR -- used by TensorBoard
train_writer = tf.summary.FileWriter(LOG_DIR + '/train',
graph=tf.get_default_graph())
test_writer = tf.summary.FileWriter(LOG_DIR + '/test',
graph=tf.get_default_graph())
sess.run(tf.global_variables_initializer())
for i in range(10000):
batch_x, batch_y = mnist.train.next_batch(batch_size)
# Reshape data to get 28 sequences of 28 pixels
batch_x = batch_x.reshape((batch_size, time_steps,
element_size))
summary,_ = sess.run([merged,train_step],
feed_dict={_inputs:batch_x, y:batch_y})
# Add to summaries
train_writer.add_summary(summary, i)
if i % 1000 == 0:
acc,loss, = sess.run([accuracy,cross_entropy],
feed_dict={_inputs: batch_x,
y: batch_y})
print ("Iter " + str(i) + ", Minibatch Loss= " + \
"{:.6f}".format(loss) + ", Training Accuracy= " + \
"{:.5f}".format(acc))
if i % 10:
# Calculate accuracy for 128 MNIST test images and
78 | Chapter 5: Text I: Working with Text and Sequences, and TensorBoard Visualization
# add to summaries
summary, acc = sess.run([merged, accuracy],
feed_dict={_inputs: test_data,
y: test_label})
test_writer.add_summary(summary, i)
test_acc = sess.run(accuracy, feed_dict={_inputs: test_data,
y: test_label})
print ("Test Accuracy:", test_acc)
Finally, we print some training and testing accuracy results:
Iter 0, Minibatch Loss= 2.303386, Training Accuracy= 7.03125
Iter 1000, Minibatch Loss= 1.238117, Training Accuracy= 52.34375
Iter 2000, Minibatch Loss= 0.614925, Training Accuracy= 85.15625
Iter 3000, Minibatch Loss= 0.439684, Training Accuracy= 82.81250
Iter 4000, Minibatch Loss= 0.077756, Training Accuracy= 98.43750
Iter 5000, Minibatch Loss= 0.220726, Training Accuracy= 89.84375
Iter 6000, Minibatch Loss= 0.015013, Training Accuracy= 100.00000
Iter 7000, Minibatch Loss= 0.017689, Training Accuracy= 100.00000
Iter 8000, Minibatch Loss= 0.065443, Training Accuracy= 99.21875
Iter 9000, Minibatch Loss= 0.071438, Training Accuracy= 98.43750
Testing Accuracy: 97.6563
To summarize this section, we started off with the raw MNIST pixels and regarded
them as sequential data—each column (or row) of 28 pixels as a time step. We then
applied the vanilla RNN to extract outputs corresponding to each time-step and used
the last output to perform classification of the entire sequence (image).
Visualizing the model with TensorBoard
TensorBoard is an interactive browser-based tool that allows us to visualize the learn‐
ing process, as well as explore our trained model.
To run TensorBoard, go to the command terminal and tell TensorBoard where the
relevant summaries you logged are:
tensorboard --logdir=LOG_DIR
Here, LOG_DIR should be replaced with your log directory. If you are on Windows and
this is not working, make sure you are running the terminal from the same drive
where the log data is, and add a name to the log directory as follows in order to
bypass a bug in the way TensorBoard parses the path:
tensorboard --logdir=rnn_demo:LOG_DIR
TensorBoard allows us to assign names to individual log directories by putting a
colon between the name and the path, which may be useful when working with mul‐
tiple log directories. In such a case, we pass a comma-separated list of log directories
as follows:
Introduction to Recurrent Neural Networks | 79

tensorboard --logdir=rnn_demo1:LOG_DIR1, rnn_demo2:LOG_DIR2
In our example (with one log directory), once you have run the tensorboard com‐
mand, you should get something like the following, telling you where to navigate in
your browser:
Starting TensorBoard b'39' on port 6006
(You can navigate to http://10.100.102.4:6006)
If the address does not work, go to localhost:6006, which should always work.
TensorBoard recursively walks the directory tree rooted at LOG_DIR looking for sub‐
directories that contain tfevents log data. If you run this example multiple times,
make sure to either delete the LOG_DIR folder you created after each run, or write the
logs to separate subdirectories within LOG_DIR, such as LOG_DIR/run1/train, LOG_DIR/
run2/train, and so forth, to avoid issues with overwriting log files, which may lead to
some “funky” plots.
Let’s take a look at some of the visualizations we can get. In the next section, we will
explore interactive visualization of high-dimensional data with TensorBoard—for
now, we focus on plotting training process summaries and trained weights.
First, in your browser, go to the Scalars tab. Here TensorBoard shows us summaries
of all scalars, including not only training and testing accuracy, which are usually most
interesting, but also some summary statistics we logged about variables (see
Figure 5-4). Hovering over the plots, we can see some numerical figures.
Figure 5-4. TensorBoard scalar summaries.
In the Graphs tab we can get an interactive visualization of our computation graph,
from a high-level view down to the basic ops, by zooming in (see Figure 5-5).
80 | Chapter 5: Text I: Working with Text and Sequences, and TensorBoard Visualization

Figure 5-5. Zooming in on the computation graph.
Finally, in the Histograms tab we see histograms of our weights across the training
process (see Figure 5-6). Of course, we had to explicitly add these histograms to our
logging in order to view them, with tf.summary.histogram().
Introduction to Recurrent Neural Networks | 81

Figure 5-6. Histograms of weights throughout the learning process.
TensorFlow Built-in RNN Functions
The preceding example taught us some of the fundamental and powerful ways we can
work with sequences, by implementing our graph pretty much from scratch. In prac‐
tice, it is of course a good idea to use built-in higher-level modules and functions.
This not only makes the code shorter and easier to write, but exploits many low-level
optimizations afforded by TensorFlow implementations.
In this section we first present a new, shorter version of the code in its entirety. Since
most of the overall details have not changed, we focus on the main new elements,
tf.contrib.rnn.BasicRNNCell and tf.nn.dynamic_rnn():
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
element_size = 28;time_steps = 28;num_classes = 10
batch_size = 128;hidden_layer_size = 128
_inputs = tf.placeholder(tf.float32,shape=[None, time_steps,
element_size],
name='inputs')
y = tf.placeholder(tf.float32, shape=[None, num_classes],name='inputs')
# TensorFlow built-in functions
rnn_cell = tf.contrib.rnn.BasicRNNCell(hidden_layer_size)
outputs, _ = tf.nn.dynamic_rnn(rnn_cell, _inputs, dtype=tf.float32)
Wl = tf.Variable(tf.truncated_normal([hidden_layer_size, num_classes],
mean=0,stddev=.01))
bl = tf.Variable(tf.truncated_normal([num_classes],mean=0,stddev=.01))
def get_linear_layer(vector):
82 | Chapter 5: Text I: Working with Text and Sequences, and TensorBoard Visualization
return tf.matmul(vector, Wl) + bl
last_rnn_output = outputs[:,-1,:]
final_output = get_linear_layer(last_rnn_output)
softmax = tf.nn.softmax_cross_entropy_with_logits(logits=final_output,
labels=y)
cross_entropy = tf.reduce_mean(softmax)
train_step = tf.train.RMSPropOptimizer(0.001, 0.9).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(final_output,1))
accuracy = (tf.reduce_mean(tf.cast(correct_prediction, tf.float32)))*100
sess=tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
test_data = mnist.test.images[:batch_size].reshape((-1,
time_steps, element_size))
test_label = mnist.test.labels[:batch_size]
for i in range(3001):
batch_x, batch_y = mnist.train.next_batch(batch_size)
batch_x = batch_x.reshape((batch_size, time_steps, element_size))
sess.run(train_step,feed_dict={_inputs:batch_x,
y:batch_y})
if i % 1000 == 0:
acc = sess.run(accuracy, feed_dict={_inputs: batch_x,
y: batch_y})
loss = sess.run(cross_entropy,feed_dict={_inputs:batch_x,
y:batch_y})
print ("Iter " + str(i) + ", Minibatch Loss= " + \
"{:.6f}".format(loss) + ", Training Accuracy= " + \
"{:.5f}".format(acc))
print ("Testing Accuracy:",
sess.run(accuracy, feed_dict={_inputs: test_data, y: test_label}))
tf.contrib.rnn.BasicRNNCell and tf.nn.dynamic_rnn()
TensorFlow’s RNN cells are abstractions that represent the basic operations each
recurrent “cell” carries out (see Figure 5-2 at the start of this chapter for an illustra‐
tion), and its associated state. They are, in general terms, a “replacement” of the
rnn_step() function and the associated variables it required. Of course, there are
many variants and types of cells, each with many methods and properties. We will see
some more advanced cells toward the end of this chapter and later in the book.
Introduction to Recurrent Neural Networks | 83
Once we have created the rnn_cell, we feed it into tf.nn.dynamic_rnn(). This func‐
tion replaces tf.scan() in our vanilla implementation and creates an RNN specified
by rnn_cell.
As of this writing, in early 2017, TensorFlow includes a static and a dynamic function
for creating an RNN. What does this mean? The static version creates an unrolled
graph (as in Figure 5-2) of fixed length. The dynamic version uses a tf.While loop to
dynamically construct the graph at execution time, leading to faster graph creation,
which can be significant. This dynamic construction can also be very useful in other
ways, some of which we will touch on when we discuss variable-length sequences
toward the end of this chapter.
Note that contrib refers to the fact that code in this library is contributed and still
requires testing. We discuss the contrib library in much more detail in Chapter 7.
BasicRNNCell was moved to contrib in TensorFlow 1.0 as part of ongoing develop‐
ment. In version 1.2, many of the RNN functions and classes were moved back to the
core namespace with aliases kept in contrib for backward compatibiliy, meaning that
the preceding code works for all versions 1.X as of this writing.
RNN for Text Sequences
We began this chapter by learning how to implement RNN models in TensorFlow.
For ease of exposition, we showed how to implement and use an RNN for a sequence
made of pixels in MNIST images. We next show how to use these sequence models
on text sequences.
Text data has some properties distinctly different from image data, which we will dis‐
cuss here and later in this book. These properties can make it somewhat difficult to
handle text data at first, and text data always requires at least some basic pre-
processing steps for us to be able to work with it. To introduce working with text in
TensorFlow, we will thus focus on the core components and create a minimal, con‐
trived text dataset that will let us get straight to the action. In Chapter 7, we will apply
RNN models to movie review sentiment classification.
Let’s get started, presenting our example data and discussing some key properties of
text datasets as we go.
Text Sequences
In the MNIST RNN example we saw earlier, each sequence was of fixed size—the
width (or height) of an image. Each element in the sequence was a dense vector of 28
pixels. In NLP tasks and datasets, we have a different kind of “picture.”
Our sequences could be of words forming a sentence, of sentences forming a para‐
graph, or even of characters forming words or paragraphs forming whole documents.
84 | Chapter 5: Text I: Working with Text and Sequences, and TensorBoard Visualization
Consider the following sentence: “Our company provides smart agriculture solutions
for farms, with advanced AI, deep-learning.” Say we obtain this sentence from an
online news blog, and wish to process it as part of our machine learning system.
Each of the words in this sentence would be represented with an ID—an integer,
commonly referred to as a token ID in NLP. So, the word “agriculture” could, for
instance, be mapped to the integer 3452, the word “farm” to 12, “AI” to 150, and
“deep-learning” to 0. This representation in terms of integer identifiers is very differ‐
ent from the vector of pixels in image data, in multiple ways. We will elaborate on this
important point shortly when we discuss word embeddings, and in Chapter 6.
To make things more concrete, let’s start by creating our simplified text data.
Our simulated data consists of two classes of very short “sentences,” one composed of
odd digits and the other of even digits (with numbers written in English). We gener‐
ate sentences built of words representing even and odd numbers. Our goal is to learn
to classify each sentence as either odd or even in a supervised text-classification task.
Of course, we do not really need any machine learning for this simple task—we use
this contrived example only for illustrative purposes.
First, we define some constants, which will be explained as we go:
import numpy as np
import tensorflow as tf
batch_size = 128;embedding_dimension = 64;num_classes = 2
hidden_layer_size = 32;times_steps = 6;element_size = 1
Next, we create sentences. We sample random digits and map them to the corre‐
sponding “words” (e.g., 1 is mapped to “One,” 7 to “Seven,” etc.).
Text sequences typically have variable lengths, which is of course the case for all real
natural language data (such as in the sentences appearing on this page).
To make our simulated sentences have different lengths, we sample for each sentence
a random length between 3 and 6 with np.random.choice(range(3, 7))—the lower
bound is inclusive, and the upper bound is exclusive.
Now, to put all our input sentences in one tensor (per batch of data instances), we
need them to somehow be of the same size—so we pad sentences with a length
shorter than 6 with zeros (or PAD symbols) to make all sentences equally sized (artifi‐
cially). This pre-processing step is known as zero-padding. The following code
accomplishes all of this:
RNN for Text Sequences | 85
digit_to_word_map = {1:"One",2:"Two", 3:"Three", 4:"Four", 5:"Five",
6:"Six",7:"Seven",8:"Eight",9:"Nine"}
digit_to_word_map[0]="PAD"
even_sentences = []
odd_sentences = []
seqlens = []
for i in range(10000):
rand_seq_len = np.random.choice(range(3,7))
seqlens.append(rand_seq_len)
rand_odd_ints = np.random.choice(range(1,10,2),
rand_seq_len)
rand_even_ints = np.random.choice(range(2,10,2),
rand_seq_len)
# Padding
if rand_seq_len<6:
rand_odd_ints = np.append(rand_odd_ints,
[0]*(6-rand_seq_len))
rand_even_ints = np.append(rand_even_ints,
[0]*(6-rand_seq_len))
even_sentences.append(" ".join([digit_to_word_map[r] for
r in rand_odd_ints]))
odd_sentences.append(" ".join([digit_to_word_map[r] for
r in rand_even_ints]))
data = even_sentences+odd_sentences
# Same seq lengths for even, odd sentences
seqlens*=2
Let’s take a look at our sentences, each padded to length 6:
even_sentences[0:6]
Out:
['Four Four Two Four Two PAD',
'Eight Six Four PAD PAD PAD',
'Eight Two Six Two PAD PAD',
'Eight Four Four Eight PAD PAD',
'Eight Eight Four PAD PAD PAD',
'Two Two Eight Six Eight Four']
odd_sentences[0:6]
Out:
['One Seven Nine Three One PAD',
'Three Nine One PAD PAD PAD',
'Seven Five Three Three PAD PAD',
'Five Five Three One PAD PAD',
'Three Three Five PAD PAD PAD',
'Nine Three Nine Five Five Three']
86 | Chapter 5: Text I: Working with Text and Sequences, and TensorBoard Visualization
Notice that we add the PAD word (token) to our data and digit_to_word_map dictio‐
nary, and separately store even and odd sentences and their original lengths (before
padding).
Let’s take a look at the original sequence lengths for the sentences we printed:
seqlens[0:6]
Out:
[5, 3, 4, 4, 3, 6]
Why keep the original sentence lengths? By zero-padding, we solved one technical
problem but created another: if we naively pass these padded sentences through our
RNN model as they are, it will process useless PAD symbols. This would both harm
model correctness by processing “noise” and increase computation time. We resolve
this issue by first storing the original lengths in the seqlens array and then telling
TensorFlow’s tf.nn.dynamic_rnn() where each sentence ends.
In this chapter, our data is simulated—generated by us. In real applications, we would
start off by getting a collection of documents (e.g., one-sentence tweets) and then
mapping each word to an integer ID.
So, we now map words to indices—word identiers—by simply creating a dictionary
with words as keys and indices as values. We also create the inverse map. Note that
there is no correspondence between the word IDs and the digits each word represents
—the IDs carry no semantic meaning, just as in any NLP application with real data:
# Map from words to indices
word2index_map ={}
index=0
for sent in data:
for word in sent.lower().split():
if word not in word2index_map:
word2index_map[word] = index
index+=1
# Inverse map
index2word_map = {index: word for word, index in word2index_map.items()}
vocabulary_size = len(index2word_map)
This is a supervised classification task—we need an array of labels in the one-hot for‐
mat, train and test sets, a function to generate batches of instances, and placeholders,
as usual.
RNN for Text Sequences | 87
First, we create the labels and split the data into train and test sets:
labels = [1]*10000 + [0]*10000
for i in range(len(labels)):
label = labels[i]
one_hot_encoding = [0]*2
one_hot_encoding[label] = 1
labels[i] = one_hot_encoding
data_indices = list(range(len(data)))
np.random.shuffle(data_indices)
data = np.array(data)[data_indices]
labels = np.array(labels)[data_indices]
seqlens = np.array(seqlens)[data_indices]
train_x = data[:10000]
train_y = labels[:10000]
train_seqlens = seqlens[:10000]
test_x = data[10000:]
test_y = labels[10000:]
test_seqlens = seqlens[10000:]
Next, we create a function that generates batches of sentences. Each sentence in a
batch is simply a list of integer IDs corresponding to words:
def get_sentence_batch(batch_size,data_x,
data_y,data_seqlens):
instance_indices = list(range(len(data_x)))
np.random.shuffle(instance_indices)
batch = instance_indices[:batch_size]
x = [[word2index_map[word] for word in data_x[i].lower().split()]
for i in batch]
y = [data_y[i] for i in batch]
seqlens = [data_seqlens[i] for i in batch]
return x,y,seqlens
Finally, we create placeholders for data:
_inputs = tf.placeholder(tf.int32, shape=[batch_size,times_steps])
_labels = tf.placeholder(tf.float32, shape=[batch_size, num_classes])
# seqlens for dynamic calculation
_seqlens = tf.placeholder(tf.int32, shape=[batch_size])
Note that we have created a placeholder for the original sequence lengths. We will see
how to make use of these in our RNN shortly.
Supervised Word Embeddings
Our text data is now encoded as lists of word IDs—each sentence is a sequence of
integers corresponding to words. This type of atomic representation, where each
88 | Chapter 5: Text I: Working with Text and Sequences, and TensorBoard Visualization
word is represented with an ID, is not scalable for training deep learning models with
large vocabularies that occur in real problems. We could end up with millions of such
word IDs, each encoded in one-hot (binary) categorical form, leading to great data
sparsity and computational issues. We will discuss this in more depth in Chapter 6.
A powerful approach to work around this issue is to use word embeddings. The
embedding is, in a nutshell, simply a mapping from high-dimensional one-hot vec‐
tors encoding words to lower-dimensional dense vectors. So, for example, if our
vocabulary has size 100,000, each word in one-hot representation would be of the
same size. The corresponding word vector—or word embedding—would be of size
300, say. The high-dimensional one-hot vectors are thus “embedded” into a continu‐
ous vector space with a much lower dimensionality.
In Chapter 6 we dive deeper into word embeddings, exploring a popular method to
train them in an “unsupervised” manner known as word2vec.
Here, our end goal is to solve a text classification problem, and we will train word
vectors in a supervised framework, tuning the embedded word vectors to solve the
downstream classification task.
It is helpful to think of word embeddings as basic hash tables or lookup tables, map‐
ping words to their dense vector values. These vectors are optimized as part of the
training process. Previously, we gave each word an integer index, and sentences are
then represented as sequences of these indices. Now, to obtain a word’s vector, we use
the built-in tf.nn.embedding_lookup() function, which efficiently retrieves the vec‐
tors for each word in a given sequence of word indices:
with tf.name_scope("embeddings"):
embeddings = tf.Variable(
tf.random_uniform([vocabulary_size,
embedding_dimension],
-1.0, 1.0),name='embedding')
embed = tf.nn.embedding_lookup(embeddings, _inputs)
We will see examples of and visualizations of our vector representations of words
shortly.
LSTM and Using Sequence Length
In the introductory RNN example with which we began, we implemented and used
the basic vanilla RNN model. In practice, we often use slightly more advanced RNN
models, which differ mainly by how they update their hidden state and propagate
information through time. A very popular recurrent network is the long short-term
memory (LSTM) network. It differs from vanilla RNN by having some special mem‐
ory mechanisms that enable the recurrent cells to better store information for long
periods of time, thus allowing them to capture long-term dependencies better than
plain RNN.
RNN for Text Sequences | 89
There is nothing mysterious about these memory mechanisms; they simply consist of
some more parameters added to each recurrent cell, enabling the RNN to overcome
optimization issues and propagate information. These trainable parameters act as fil‐
ters that select what information is worth “remembering” and passing on, and what is
worth “forgetting.” They are trained in exactly the same way as any other parameter
in a network, with gradient-descent algorithms and backpropagation. We don’t go
into the more technical mathematical formulations here, but there are plenty of great
resources out there delving into the details.
We create an LSTM cell with tf.contrib.rnn.BasicLSTMCell() and feed it to
tf.nn.dynamic_rnn(), just as we did at the start of this chapter. We also give
dynamic_rnn() the length of each sequence in a batch of examples, using the _seq
lens placeholder we created earlier. TensorFlow uses this to stop all RNN steps
beyond the last real sequence element. It also returns all output vectors over time (in
the outputs tensor), which are all zero-padded beyond the true end of the sequence.
So, for example, if the length of our original sequence is 5 and we zero-pad it to a
sequence of length 15, the output for all time steps beyond 5 will be zero:
with tf.variable_scope("lstm"):
lstm_cell = tf.contrib.rnn.BasicLSTMCell(hidden_layer_size,
forget_bias=1.0)
outputs, states = tf.nn.dynamic_rnn(lstm_cell, embed,
sequence_length = _seqlens,
dtype=tf.float32)
weights = {
'linear_layer': tf.Variable(tf.truncated_normal([hidden_layer_size,
num_classes],
mean=0,stddev=.01))
}
biases = {
'linear_layer':tf.Variable(tf.truncated_normal([num_classes],
mean=0,stddev=.01))
}
# Extract the last relevant output and use in a linear layer
final_output = tf.matmul(states[1],
weights["linear_layer"]) + biases["linear_layer"]
softmax = tf.nn.softmax_cross_entropy_with_logits(logits = final_output,
labels = _labels)
cross_entropy = tf.reduce_mean(softmax)
We take the last valid output vector—in this case conveniently available for us in the
states tensor returned by dynamic_rnn()—and pass it through a linear layer (and
the softmax function), using it as our final prediction. We will explore the concepts of
90 | Chapter 5: Text I: Working with Text and Sequences, and TensorBoard Visualization
last relevant output and zero-padding further in the next section, when we look at
some outputs generated by dynamic_rnn() for our example sentences.
Training Embeddings and the LSTM Classier
We have all the pieces in the puzzle. Let’s put them together, and complete an end-to-
end training of both word vectors and a classification model:
train_step = tf.train.RMSPropOptimizer(0.001, 0.9).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(_labels,1),
tf.argmax(final_output,1))
accuracy = (tf.reduce_mean(tf.cast(correct_prediction,
tf.float32)))*100
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(1000):
x_batch, y_batch,seqlen_batch = get_sentence_batch(batch_size,
train_x,train_y,
train_seqlens)
sess.run(train_step,feed_dict={_inputs:x_batch, _labels:y_batch,
_seqlens:seqlen_batch})
if step % 100 == 0:
acc = sess.run(accuracy,feed_dict={_inputs:x_batch,
_labels:y_batch,
_seqlens:seqlen_batch})
print("Accuracy at %d: %.5f" % (step, acc))
for test_batch in range(5):
x_test, y_test,seqlen_test = get_sentence_batch(batch_size,
test_x,test_y,
test_seqlens)
batch_pred,batch_acc = sess.run([tf.argmax(final_output,1),
accuracy],
feed_dict={_inputs:x_test,
_labels:y_test,
_seqlens:seqlen_test})
print("Test batch accuracy %d: %.5f" % (test_batch, batch_acc))
output_example = sess.run([outputs],feed_dict={_inputs:x_test,
_labels:y_test,
_seqlens:seqlen_test})
states_example = sess.run([states[1]],feed_dict={_inputs:x_test,
_labels:y_test,
_seqlens:seqlen_test})
As we can see, this is a pretty simple toy text classification problem:
RNN for Text Sequences | 91
Accuracy at 0: 32.81250
Accuracy at 100: 100.00000
Accuracy at 200: 100.00000
Accuracy at 300: 100.00000
Accuracy at 400: 100.00000
Accuracy at 500: 100.00000
Accuracy at 600: 100.00000
Accuracy at 700: 100.00000
Accuracy at 800: 100.00000
Accuracy at 900: 100.00000
Test batch accuracy 0: 100.00000
Test batch accuracy 1: 100.00000
Test batch accuracy 2: 100.00000
Test batch accuracy 3: 100.00000
Test batch accuracy 4: 100.00000
We’ve also computed an example batch of outputs generated by dynamic_rnn(), to
further illustrate the concepts of zero-padding and last relevant outputs discussed in
the previous section.
Let’s take a look at one example of these outputs, for a sentence that was zero-padded
(in your random batch of data you may see different output, of course—look for a
sentence whose seqlen was lower than the maximal 6):
seqlen_test[1]
Out:
4
output_example[0][1].shape
Out:
(6, 32)
This output has, as expected, six time steps, each a vector of size 32. Let’s take a
glimpse at its values (printing only the first few dimensions to avoid clutter):
output_example[0][1][:6,0:3]
Out:
array([[-0.44493711, -0.51363373, -0.49310589],
[-0.72036862, -0.68590945, -0.73340571],
[-0.83176643, -0.78206956, -0.87831545],
[-0.87982416, -0.82784462, -0.91132098],
[ 0. , 0. , 0. ],
[ 0. , 0. , 0. ]], dtype=float32)
We see that for this sentence, whose original length was 4, the last two time steps have
zero vectors due to padding.
Finally, we look at the states vector returned by dynamic_rnn():
92 | Chapter 5: Text I: Working with Text and Sequences, and TensorBoard Visualization
states_example[0][1][0:3]
Out:
array([-0.87982416, -0.82784462, -0.91132098], dtype=float32)
We can see that it conveniently stores for us the last relevant output vector—its values
match the last relevant output vector before zero-padding.
At this point, you may be wondering how to access and manipulate the word vectors
and explore the trained representation. We show how to do so, including interactive
embedding visualization, in the next chapter.
Stacking multiple LSTMs
Earlier, we focused on a one-layer LSTM network for ease of exposition. Adding
more layers is straightforward, using the MultiRNNCell() wrapper that combines
multiple RNN cells into one multilayer cell.
Say, for example, we wanted to stack two LSTM layers in the preceding example. We
can do this as follows:
num_LSTM_layers = 2
with tf.variable_scope("lstm"):
lstm_cell = tf.contrib.rnn.BasicLSTMCell(hidden_layer_size,
forget_bias=1.0)
cell = tf.contrib.rnn.MultiRNNCell(cells=[lstm_cell]*num_LSTM_layers,
state_is_tuple=True)
outputs, states = tf.nn.dynamic_rnn(cell, embed,
sequence_length = _seqlens,
dtype=tf.float32)
We first define an LSTM cell as before, and then feed it into the tf.contrib.rnn.Mul
tiRNNCell() wrapper.
Now our network has two layers of LSTM, causing some shape issues when trying to
extract the final state vectors. To get the final state of the second layer, we simply
adapt our indexing a bit:
# Extract the final state and use in a linear layer
final_output = tf.matmul(states[num_LSTM_layers-1][1],
weights["linear_layer"]) + biases["linear_layer"]
Summary
In this chapter we introduced sequence models in TensorFlow. We saw how to imple‐
ment a basic RNN model from scratch by using tf.scan() and built-in modules, as
well as more advanced LSTM networks, for both text and image data. Finally, we
trained an end-to-end text classification RNN with word embeddings, and showed
Summary | 93
how to handle sequences of variable length. In the next chapter, we dive deeper into
word embeddings and word2vec. In Chapter 7, we will see some cool abstraction lay‐
ers over TensorFlow, and how they can be used to train advanced text classification
RNN models with considerably less effort.
94 | Chapter 5: Text I: Working with Text and Sequences, and TensorBoard Visualization
CHAPTER 6
Text II: Word Vectors, Advanced RNN, and
Embedding Visualization
In this chapter, we go deeper into important topics discussed in Chapter 5 regarding
working with text sequences. We first show how to train word vectors by using an
unsupervised method known as word2vec, and how to visualize embeddings interac‐
tively with TensorBoard. We then use pretrained word vectors, trained on massive
amounts of public data, in a supervised text-classification task, and also introduce
more-advanced RNN components that are frequently used in state-of-the-art sys‐
tems.
Introduction to Word Embeddings
In Chapter 5 we introduced RNN models and working with text sequences in Tensor‐
Flow. As part of the supervised model training, we also trained word vectors—map‐
ping from word IDs to lower-dimensional continuous vectors. The reasoning for this
was to enable a scalable representation that can be fed into an RNN layer. But there
are deeper reasons for the use of word vectors, which we discuss next.
Consider the sentence appearing in Figure 6-1: “Our company provides smart agri‐
culture solutions for farms, with advanced AI, deep-learning.” This sentence may be
taken from, say, a tweet promoting a company. As data scientists or engineers, we
now may wish to process it as part of an advanced machine intelligence system, that
sifts through tweets and automatically detects informative content (e.g., public senti‐
ment).
In one of the major traditional natural language processing (NLP) approaches to text
processing, each of the words in this sentence would be represented with N ID—say,
an integer. So, as we posited in the previous chapter, the word “agriculture” might be
95
mapped to the integer 3452, the word “farm” to 12, “AI” to 150, and “deep-learning”
to 0.
While this representation has led to excellent results in practice in some basic NLP
tasks and is still often used in many cases (such as in bag-of-words text classification),
it has some major inherent problems. First, by using this type of atomic representa‐
tion, we lose all meaning encoded within the word, and crucially, we thus lose infor‐
mation on the semantic proximity between words. In our example, we of course
know that “agriculture” and “farm” are strongly related, and so are “AI” and “deep-
learning,” while deep learning and farms don’t usually have much to do with one
another. This is not reflected by their arbitrary integer IDs.
Another important issue with this way of looking at data stems from the size of typi‐
cal vocabularies, which can easily reach huge numbers. This means that naively, we
could need to keep millions of such word identifiers, leading to great data sparsity
and in turn, making learning harder and more expensive.
With images, such as in the MNIST data we used in the first section of Chapter 5, this
is not quite the case. While images can be high-dimensional, their natural representa‐
tion in terms of pixel values already encodes some semantic meaning, and this repre‐
sentation is dense. In practice, RNN models like the one we saw in Chapter 5 require
dense vector representations to work well.
We would like, therefore, to use dense vector representations of words, which carry
semantic meaning. But how do we obtain them?
In Chapter 5 we trained supervised word vectors to solve a specific task, using labeled
data. But it is often expensive for individuals and organizations to obtain labeled data,
in terms of the resources, time, and effort involved in manually tagging texts or
somehow acquiring enough labeled instances. Obtaining huge amounts of unlabeled
data, however, is often a much less daunting endeavor. We thus would like a way to
use this data to train word representations, in an unsupervised fashion.
There are actually many ways to do unsupervised training of word embeddings,
including both more traditional approaches to NLP that can still work very well and
newer methods, many of which use neural networks. Whether old or new, these all
rely at their core on the distributional hypothesis, which is most easily explained by a
well-known quote by linguist John Firth: “You shall know a word by the company it
keeps.” In other words, words that tend to appear in similar contexts tend to have
similar semantic meanings.
In this book, we focus on powerful word embedding methods based on neural net‐
works. In Chapter 5 we saw how to train them as part of a downstream text-
classification task. We now show how to train word vectors in an unsupervised
manner, and then how to use pretrained vectors that were trained using huge
amounts of text from the web.
96 | Chapter 6: Text II: Word Vectors, Advanced RNN, and Embedding Visualization

Word2vec
Word2vec is a very well-known unsupervised word embedding approach. It is
actually more like a family of algorithms, all based in some way on exploiting the
context in which words appear to learn their representation (in the spirit of the distri‐
butional hypothesis). We focus on the most popular word2vec implementation,
which trains a model that, given an input word, predicts the word’s context by using
something known as skip-grams. This is actually rather simple, as the following exam‐
ple will demonstrate.
Consider, again, our example sentence: “Our company provides smart agriculture sol‐
utions for farms, with advanced AI, deep-learning.” We define (for simplicity) the
context of a word as its immediate neighbors (“the company it keeps”)—i.e., the word
to its left and the word to its right. So, the context of “company” is [our, provides], the
context of “AI” is [advanced, deep-learning], and so on (see Figure 6-1).
Figure 6-1. Generating skip-grams from text.
In the skip-gram word2vec model, we train a model to predict context based on an
input word. All that means in this case is that we generate training instance and label
pairs such as (our, company), (provides, company), (advanced, AI), (deep-learning,
AI), etc.
In addition to these pairs we extract from the data, we also sample “fake” pairs—that
is, for a given input word (such as “AI”), we also sample random noise words as con‐
text (such as “monkeys”), in a process known as negative sampling. We use the true
pairs combined with noise pairs to build our training instances and labels, which we
use to train a binary classifier that learns to distinguish between them. The trainable
parameters in this classifier are the vector representations—word embeddings. We
tune these vectors to yield a classifier able to tell the difference between true contexts
of a word and randomly sampled ones, in a binary classification setting.
TensorFlow enables many ways to implement the word2vec model, with increasing
levels of sophistication and optimization, using multithreading and higher-level
Word2vec | 97
abstractions for optimized and shorter code. We present here a fundamental
approach, which will introduce you to the core ideas and operations.
Let’s dive straight into implementing the core ideas in TensorFlow code.
Skip-Grams
We begin by preparing our data and extracting skip-grams. As in Chapter 5, our data
comprises two classes of very short “sentences,” one composed of odd digits and the
other of even digits (with numbers written in English). We make sentences equally
sized here, for simplicity, but this doesn’t really matter for word2vec training. Let’s
start by setting some parameters and creating sentences:
import os
import math
import numpy as np
import tensorflow as tf
from tensorflow.contrib.tensorboard.plugins import projector
batch_size=64
embedding_dimension = 5
negative_samples =8
LOG_DIR = "logs/word2vec_intro"
digit_to_word_map = {1:"One",2:"Two", 3:"Three", 4:"Four", 5:"Five",
6:"Six",7:"Seven",8:"Eight",9:"Nine"}
sentences = []
# Create two kinds of sentences - sequences of odd and even digits
for i in range(10000):
rand_odd_ints = np.random.choice(range(1,10,2),3)
sentences.append(" ".join([digit_to_word_map[r] for r in rand_odd_ints]))
rand_even_ints = np.random.choice(range(2,10,2),3)
sentences.append(" ".join([digit_to_word_map[r] for r in rand_even_ints]))
Let’s take a look at our sentences:
sentences[0:10]
Out:
['Seven One Five',
'Four Four Four',
'Five One Nine',
'Eight Two Eight',
'One Nine Three',
'Two Six Eight',
'Nine Seven Seven',
'Six Eight Six',
'One Five Five',
'Four Six Two']
98 | Chapter 6: Text II: Word Vectors, Advanced RNN, and Embedding Visualization
Next, as in Chapter 5, we map words to indices by creating a dictionary with words as
keys and indices as values, and create the inverse map:
# Map words to indices
word2index_map ={}
index=0
for sent in sentences:
for word in sent.lower().split():
if word not in word2index_map:
word2index_map[word] = index
index+=1
index2word_map = {index: word for word, index in word2index_map.items()}
vocabulary_size = len(index2word_map)
To prepare the data for word2vec, let’s create skip-grams:
# Generate skip-gram pairs
skip_gram_pairs = []
for sent in sentences:
tokenized_sent = sent.lower().split()
for i in range(1, len(tokenized_sent)-1) :
word_context_pair = [[word2index_map[tokenized_sent[i-1]],
word2index_map[tokenized_sent[i+1]]],
word2index_map[tokenized_sent[i]]]
skip_gram_pairs.append([word_context_pair[1],
word_context_pair[0][0]])
skip_gram_pairs.append([word_context_pair[1],
word_context_pair[0][1]])
def get_skipgram_batch(batch_size):
instance_indices = list(range(len(skip_gram_pairs)))
np.random.shuffle(instance_indices)
batch = instance_indices[:batch_size]
x = [skip_gram_pairs[i][0] for i in batch]
y = [[skip_gram_pairs[i][1]] for i in batch]
return x,y
Each skip-gram pair is composed of target and context word indices (given by the
word2index_map dictionary, and not in correspondence to the actual digit each word
represents). Let’s take a look:
skip_gram_pairs[0:10]
Out:
[[1, 0],
[1, 2],
[3, 3],
[3, 3],
[1, 2],
[1, 4],
[6, 5],
[6, 5],
Word2vec | 99
[4, 1],
[4, 7]]
We can generate batches of sequences of word indices, and check out the original sen‐
tences with the inverse dictionary we created earlier:
# Batch example
x_batch,y_batch = get_skipgram_batch(8)
x_batch
y_batch
[index2word_map[word] for word in x_batch]
[index2word_map[word[0]] for word in y_batch]
x_batch
Out:
[6, 2, 1, 1, 3, 0, 7, 2]
y_batch
Out:
[[5], [0], [4], [0], [5], [4], [1], [7]]
[index2word_map[word] for word in x_batch]
Out:
['two', 'five', 'one', 'one', 'four', 'seven', 'three', 'five']
[index2word_map[word[0]] for word in y_batch]
Out:
['eight', 'seven', 'nine', 'seven', 'eight',
'nine', 'one', 'three']
Finally, we create our input and label placeholders:
# Input data, labels
train_inputs = tf.placeholder(tf.int32, shape=[batch_size])
train_labels = tf.placeholder(tf.int32, shape=[batch_size, 1])
Embeddings in TensorFlow
In Chapter 5, we used the built-in tf.nn.embedding_lookup() function as part of
our supervised RNN. The same functionality is used here. Here too, word embed‐
dings can be viewed as lookup tables that map words to vector values, which are opti‐
mized as part of the training process to minimize a loss function. As we shall see in
the next section, unlike in Chapter 5, here we use a loss function accounting for the
unsupervised nature of the task, but the embedding lookup, which efficiently
retrieves the vectors for each word in a given sequence of word indices, remains the
same:
100 | Chapter 6: Text II: Word Vectors, Advanced RNN, and Embedding Visualization
with tf.name_scope("embeddings"):
embeddings = tf.Variable(
tf.random_uniform([vocabulary_size, embedding_dimension],
-1.0, 1.0),name='embedding')
# This is essentially a lookup table
embed = tf.nn.embedding_lookup(embeddings, train_inputs)
The Noise-Contrastive Estimation (NCE) Loss Function
In our introduction to skip-grams, we mentioned we create two types of context–
target pairs of words: real ones that appear in the text, and “fake” noisy pairs that are
generated by inserting random context words. Our goal is to learn to distinguish
between the two, helping us learn a good word representation. We could draw ran‐
dom noisy context pairs ourselves, but luckily TensorFlow comes with a useful loss
function designed especially for our task. tf.nn.nce_loss() automatically draws
negative (“noise”) samples when we evaluate the loss (run it in a session):
# Create variables for the NCE loss
nce_weights = tf.Variable(
tf.truncated_normal([vocabulary_size, embedding_dimension],
stddev=1.0 / math.sqrt(embedding_dimension)))
nce_biases = tf.Variable(tf.zeros([vocabulary_size]))
loss = tf.reduce_mean(
tf.nn.nce_loss(weights = nce_weights, biases = nce_biases, inputs = embed,
labels = train_labels, num_sampled = negative_samples, num_classes =
vocabulary_size))
We don’t go into the mathematical details of this loss function, but it is sufficient to
think of it as a sort of efficient approximation to the ordinary softmax function used
in classification tasks, as introduced in previous chapters. We tune our embedding
vectors to optimize this loss function. For more details about it, see the official Ten‐
sorFlow documentation and references within.
We’re now ready to train. In addition to obtaining our word embeddings in Tensor‐
Flow, we next introduce two useful capabilities: adjustment of the optimization learn‐
ing rate, and interactive visualization of embeddings.
Learning Rate Decay
As discussed in previous chapters, gradient-descent optimization adjusts weights by
making small steps in the direction that minimizes our loss function. The learn
ing_rate hyperparameter controls just how aggressive these steps are. During
gradient-descent training of a model, it is common practice to gradually make these
steps smaller and smaller, so that we allow our optimization process to “settle down”
as it approaches good points in the parameter space. This small addition to our train‐
Word2vec | 101
ing process can actually often lead to significant boosts in performance, and is a good
practice to keep in mind in general.
tf.train.exponential_decay() applies exponential decay to the learning rate, with
the exact form of decay controlled by a few hyperparameters, as seen in the following
code (for exact details, see the official TensorFlow documentation at http://bit.ly/
2tluxP1). Here, just as an example, we decay every 1,000 steps, and the decayed learn‐
ing rate follows a staircase function—a piecewise constant function that resembles a
staircase, as its name implies:
# Learning rate decay
global_step = tf.Variable(0, trainable=False)
learningRate = tf.train.exponential_decay(learning_rate=0.1,
global_step= global_step,
decay_steps=1000,
decay_rate= 0.95,
staircase=True)
train_step = tf.train.GradientDescentOptimizer(learningRate).minimize(loss)
Training and Visualizing with TensorBoard
We train our graph within a session as usual, adding some lines of code enabling cool
interactive visualization in TensorBoard, a new tool for visualizing embeddings of
high-dimensional data—typically images or word vectors—introduced for Tensor‐
Flow in late 2016.
First, we create a TSV (tab-separated values) metadata file. This file connects embed‐
ding vectors with associated labels or images we may have for them. In our case, each
embedding vector has a label that is just the word it stands for.
We then point TensorBoard to our embedding variables (in this case, only one), and
link them to the metadata file.
Finally, after completing optimization but before closing the session, we normalize
the word embedding vectors to unit length, a standard post-processing step:
# Merge all summary ops
merged = tf.summary.merge_all()
with tf.Session() as sess:
train_writer = tf.summary.FileWriter(LOG_DIR,
graph=tf.get_default_graph())
saver = tf.train.Saver()
with open(os.path.join(LOG_DIR,'metadata.tsv'), "w") as metadata:
metadata.write('Name\tClass\n')
for k,v in index2word_map.items():
metadata.write('%s\t%d\n' % (v, k))
config = projector.ProjectorConfig()
102 | Chapter 6: Text II: Word Vectors, Advanced RNN, and Embedding Visualization
embedding = config.embeddings.add()
embedding.tensor_name = embeddings.name
# Link embedding to its metadata file
embedding.metadata_path = os.path.join(LOG_DIR,'metadata.tsv')
projector.visualize_embeddings(train_writer, config)
tf.global_variables_initializer().run()
for step in range(1000):
x_batch, y_batch = get_skipgram_batch(batch_size)
summary,_ = sess.run([merged,train_step],
feed_dict={train_inputs:x_batch,
train_labels:y_batch})
train_writer.add_summary(summary, step)
if step % 100 == 0:
saver.save(sess, os.path.join(LOG_DIR, "w2v_model.ckpt"), step)
loss_value = sess.run(loss,
feed_dict={train_inputs:x_batch,
train_labels:y_batch})
print("Loss at %d: %.5f" % (step, loss_value))
# Normalize embeddings before using
norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), 1, keep_dims=True))
normalized_embeddings = embeddings / norm
normalized_embeddings_matrix = sess.run(normalized_embeddings)
Checking Out Our Embeddings
Let’s take a quick look at the word vectors we got. We select one word (one) and sort
all the other word vectors by how close they are to it, in descending order:
ref_word = normalized_embeddings_matrix[word2index_map["one"]]
cosine_dists = np.dot(normalized_embeddings_matrix,ref_word)
ff = np.argsort(cosine_dists)[::-1][1:10]
for f in ff:
print(index2word_map[f])
print(cosine_dists[f])
Now let’s take a look at the word distances from the one vector:
Out:
seven
0.946973
three
0.938362
nine
0.755187
five
0.701269
eight
-0.0702622
Word2vec | 103

two
-0.101749
six
-0.120306
four
-0.159601
We see that the word vectors representing odd numbers are similar (in terms of the
dot product) to one, while those representing even numbers are not similar to it (and
have a negative dot product with the one vector). We learned embedded vectors that
allow us to distinguish between even and odd numbers—their respective vectors are
far apart, and thus capture the context in which each word (odd or even
digit) appeared.
Now, in TensorBoard, go to the Embeddings tab. This is a three-dimensional interac‐
tive visualization panel, where we can move around the space of our embedded vec‐
tors and explore different “angles,” zoom in, and more (see Figures 6-2 and 6-3). This
enables us to understand our data and interpret the model in a visually comfortable
manner. We can see, for instance, that the odd and even numbers occupy different
areas in feature space.
Figure 6-2. Interactive visualization of word embeddings.
104 | Chapter 6: Text II: Word Vectors, Advanced RNN, and Embedding Visualization
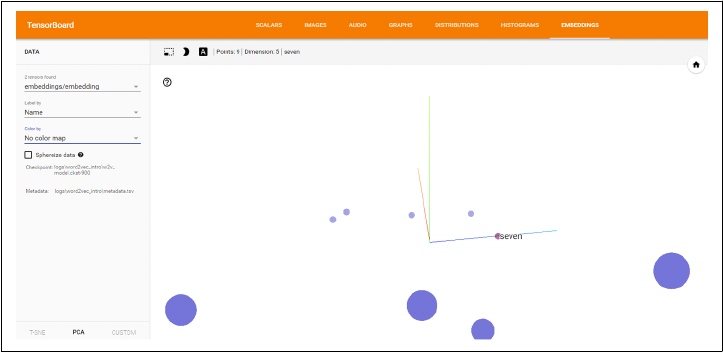
Figure 6-3. We can explore our word vectors from dierent angles (especially useful in
high-dimensional problems with large vocabularies).
Of course, this type of visualization really shines when we have a great number of
embedded vectors, such as in real text classification tasks with larger vocabularies, as
we will see in Chapter 7, for example, or in the Embedding Projector TensorFlow
demo. Here, we just give you a taste of how to interactively explore your data and
deep learning models.
Pretrained Embeddings, Advanced RNN
As we discussed earlier, word embeddings are a powerful component in deep learning
models for text. A popular approach seen in many applications is to first train word
vectors with methods such as word2vec on massive amounts of (unlabeled) text, and
then use these vectors in a downstream task such as supervised document classifica‐
tion.
In the previous section, we trained unsupervised word vectors from scratch. This
approach typically requires very large corpora, such as Wikipedia entries or web
pages. In practice, we often use pretrained word embeddings, trained on such huge
corpora and available online, in much the same manner as the pretrained models pre‐
sented in previous chapters.
In this section, we show how to use pretrained word embeddings in TensorFlow in a
simplified text-classification task. To make things more interesting, we also take this
opportunity to introduce some more useful and powerful components that are fre‐
quently used in modern deep learning applications for natural language understand‐
ing: the bidirectional RNN layers and the gated recurrent unit (GRU) cell.
Pretrained Embeddings, Advanced RNN | 105
We will expand and adapt our text-classification example from Chapter 5, focusing
only on the parts that have changed.
Pretrained Word Embeddings
Here, we show how to take word vectors trained based on web data and incorporate
them into a (contrived) text-classification task. The embedding method is known as
GloVe, and while we don’t go into the details here, the overall idea is similar to that of
word2vec—learning representations of words by the context in which they appear.
Information on the method and its authors, and the pretrained vectors, is available on
the project’s website.
We download the Common Crawl vectors (840B tokens), and proceed to our exam‐
ple.
We first set the path to the downloaded word vectors and some other parameters, as
in Chapter 5:
import zipfile
import numpy as np
import tensorflow as tf
path_to_glove = "path/to/glove/file"
PRE_TRAINED = True
GLOVE_SIZE = 300
batch_size = 128
embedding_dimension = 64
num_classes = 2
hidden_layer_size = 32
times_steps = 6
We then create the contrived, simple simulated data, also as in Chapter 5 (see details
there):
digit_to_word_map = {1:"One",2:"Two", 3:"Three", 4:"Four", 5:"Five",
6:"Six",7:"Seven",8:"Eight",9:"Nine"}
digit_to_word_map[0]="PAD_TOKEN"
even_sentences = []
odd_sentences = []
seqlens = []
for i in range(10000):
rand_seq_len = np.random.choice(range(3,7))
seqlens.append(rand_seq_len)
rand_odd_ints = np.random.choice(range(1,10,2),
rand_seq_len)
rand_even_ints = np.random.choice(range(2,10,2),
rand_seq_len)
if rand_seq_len<6:
rand_odd_ints = np.append(rand_odd_ints,
[0]*(6-rand_seq_len))
rand_even_ints = np.append(rand_even_ints,
106 | Chapter 6: Text II: Word Vectors, Advanced RNN, and Embedding Visualization
[0]*(6-rand_seq_len))
even_sentences.append(" ".join([digit_to_word_map[r] for
r in rand_odd_ints]))
odd_sentences.append(" ".join([digit_to_word_map[r] for
r in rand_even_ints]))
data = even_sentences+odd_sentences
# Same seq lengths for even, odd sentences
seqlens*=2
labels = [1]*10000 + [0]*10000
for i in range(len(labels)):
label = labels[i]
one_hot_encoding = [0]*2
one_hot_encoding[label] = 1
labels[i] = one_hot_encoding
Next, we create the word index map:
word2index_map ={}
index=0
for sent in data:
for word in sent.split():
if word not in word2index_map:
word2index_map[word] = index
index+=1
index2word_map = {index: word for word, index in word2index_map.items()}
vocabulary_size = len(index2word_map)
Let’s refresh our memory of its content—just a map from word to an (arbitrary)
index:
word2index_map
Out:
{'Eight': 7,
'Five': 1,
'Four': 6,
'Nine': 3,
'One': 5,
'PAD_TOKEN': 2,
'Seven': 4,
'Six': 9,
'Three': 0,
'Two': 8}
Now, we are ready to get word vectors. There are 2.2 million words in the vocabulary
of the pretrained GloVe embeddings we downloaded, and in our toy example we have
only 9. So, we take the GloVe vectors only for words that appear in our own tiny
vocabulary:
Pretrained Embeddings, Advanced RNN | 107
def get_glove(path_to_glove,word2index_map):
embedding_weights = {}
count_all_words = 0
with zipfile.ZipFile(path_to_glove) as z:
with z.open("glove.840B.300d.txt") as f:
for line in f:
vals = line.split()
word = str(vals[0].decode("utf-8"))
if word in word2index_map:
print(word)
count_all_words+=1
coefs = np.asarray(vals[1:], dtype='float32')
coefs/=np.linalg.norm(coefs)
embedding_weights[word] = coefs
if count_all_words==vocabulary_size -1:
break
return embedding_weights
word2embedding_dict = get_glove(path_to_glove,word2index_map)
We go over the GloVe file line by line, take the word vectors we need, and normalize
them. Once we have extracted the nine words we need, we stop the process and exit
the loop. The output of our function is a dictionary, mapping from each word to its
vector.
The next step is to place these vectors in a matrix, which is the required format for
TensorFlow. In this matrix, each row index should correspond to the word index:
embedding_matrix = np.zeros((vocabulary_size ,GLOVE_SIZE))
for word,index in word2index_map.items():
if not word == "PAD_TOKEN":
word_embedding = word2embedding_dict[word]
embedding_matrix[index,:] = word_embedding
Note that for the PAD_TOKEN word, we set the corresponding vector to 0. As we saw in
Chapter 5, we ignore padded tokens in our call to dynamic_rnn() by telling it the
original sequence length.
We now create our training and test data:
data_indices = list(range(len(data)))
np.random.shuffle(data_indices)
data = np.array(data)[data_indices]
labels = np.array(labels)[data_indices]
seqlens = np.array(seqlens)[data_indices]
train_x = data[:10000]
train_y = labels[:10000]
train_seqlens = seqlens[:10000]
test_x = data[10000:]
test_y = labels[10000:]
108 | Chapter 6: Text II: Word Vectors, Advanced RNN, and Embedding Visualization
test_seqlens = seqlens[10000:]
def get_sentence_batch(batch_size,data_x,
data_y,data_seqlens):
instance_indices = list(range(len(data_x)))
np.random.shuffle(instance_indices)
batch = instance_indices[:batch_size]
x = [[word2index_map[word] for word in data_x[i].split()]
for i in batch]
y = [data_y[i] for i in batch]
seqlens = [data_seqlens[i] for i in batch]
return x,y,seqlens
And we create our input placeholders:
_inputs = tf.placeholder(tf.int32, shape=[batch_size,times_steps])
embedding_placeholder = tf.placeholder(tf.float32, [vocabulary_size,
GLOVE_SIZE])
_labels = tf.placeholder(tf.float32, shape=[batch_size, num_classes])
_seqlens = tf.placeholder(tf.int32, shape=[batch_size])
Note that we created an embedding_placeholder, to which we feed the word vectors:
if PRE_TRAINED:
embeddings = tf.Variable(tf.constant(0.0, shape=[vocabulary_size,
GLOVE_SIZE]),
trainable=True)
# If using pretrained embeddings, assign them to the embeddings variable
embedding_init = embeddings.assign(embedding_placeholder)
embed = tf.nn.embedding_lookup(embeddings, _inputs)
else:
embeddings = tf.Variable(
tf.random_uniform([vocabulary_size,
embedding_dimension],
-1.0, 1.0))
embed = tf.nn.embedding_lookup(embeddings, _inputs)
Our embeddings are initialized with the content of embedding_placeholder, using
the assign() function to assign initial values to the embeddings variable. We set
trainable=True to tell TensorFlow we want to update the values of the word vectors,
by optimizing them for the task at hand. However, it is often useful to set
trainable=False and not update these values; for example, when we do not have
much labeled data or have reason to believe the word vectors are already “good” at
capturing the patterns we are after.
There is one more step missing to fully incorporate the word vectors into the training
—feeding embedding_placeholder with embedding_matrix. We will get to that soon,
Pretrained Embeddings, Advanced RNN | 109

but for now we continue the graph building and introduce bidirectional RNN layers
and GRU cells.
Bidirectional RNN and GRU Cells
Bidirectional RNN layers are a simple extension of the RNN layers we saw in Chap‐
ter 5. All they consist of, in their basic form, is two ordinary RNN layers: one layer
that reads the sequence from left to right, and another that reads from right to left.
Each yields a hidden representation, the left-to-right vector h, and the right-to-left
vector h. These are then concatenated into one vector. The major advantage of this
representation is its ability to capture the context of words from both directions,
which enables richer understanding of natural language and the underlying seman‐
tics in text. In practice, in complex tasks, it often leads to improved accuracy. For
example, in part-of-speech (POS) tagging, we want to output a predicted tag for each
word in a sentence (such as “noun,” “adjective,” etc.). In order to predict a POS tag for
a given word, it is useful to have information on its surrounding words, from both
directions.
Gated recurrent unit (GRU) cells are a simplification of sorts of LSTM cells. They also
have a memory mechanism, but with considerably fewer parameters than LSTM.
They are often used when there is less available data, and are faster to compute. We
do not go into the mathematical details here, as they are not important for our pur‐
poses; there are many good online resources explaining GRU and how it is different
from LSTM.
TensorFlow comes equipped with tf.nn.bidirectional_dynamic_rnn(), which is
an extension of dynamic_rnn() for bidirectional layers. It takes cell_fw and cell_bw
RNN cells, which are the left-to-right and right-to-left vectors, respectively. Here we
use GRUCell() for our forward and backward representations and add dropout for
regularization, using the built-in DropoutWrapper():
with tf.name_scope("biGRU"):
with tf.variable_scope('forward'):
gru_fw_cell = tf.contrib.rnn.GRUCell(hidden_layer_size)
gru_fw_cell = tf.contrib.rnn.DropoutWrapper(gru_fw_cell)
with tf.variable_scope('backward'):
gru_bw_cell = tf.contrib.rnn.GRUCell(hidden_layer_size)
gru_bw_cell = tf.contrib.rnn.DropoutWrapper(gru_bw_cell)
outputs, states = tf.nn.bidirectional_dynamic_rnn(cell_fw=gru_fw_cell,
cell_bw=gru_bw_cell,
inputs=embed,
sequence_length=
_seqlens,
dtype=tf.float32,
110 | Chapter 6: Text II: Word Vectors, Advanced RNN, and Embedding Visualization
scope="BiGRU")
states = tf.concat(values=states, axis=1)
We concatenate the forward and backward state vectors by using tf.concat() along
the suitable axis, and then add a linear layer followed by softmax as in Chapter 5:
weights = {
'linear_layer': tf.Variable(tf.truncated_normal([2*hidden_layer_size,
num_classes],
mean=0,stddev=.01))
}
biases = {
'linear_layer':tf.Variable(tf.truncated_normal([num_classes],
mean=0,stddev=.01))
}
# extract the final state and use in a linear layer
final_output = tf.matmul(states,
weights["linear_layer"]) + biases["linear_layer"]
softmax = tf.nn.softmax_cross_entropy_with_logits(logits=final_output,
labels=_labels)
cross_entropy = tf.reduce_mean(softmax)
train_step = tf.train.RMSPropOptimizer(0.001, 0.9).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(_labels,1),
tf.argmax(final_output,1))
accuracy = (tf.reduce_mean(tf.cast(correct_prediction,
tf.float32)))*100
We are now ready to train. We initialize the embedding_placeholder by feeding it
our embedding_matrix. It’s important to note that we do so after calling
tf.global_variables_initializer()—doing this in the reverse order would over‐
run the pre-trained vectors with a default initializer:
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
sess.run(embedding_init, feed_dict=
{embedding_placeholder: embedding_matrix})
for step in range(1000):
x_batch, y_batch,seqlen_batch = get_sentence_batch(batch_size,
train_x,train_y,
train_seqlens)
sess.run(train_step,feed_dict={_inputs:x_batch, _labels:y_batch,
_seqlens:seqlen_batch})
if step % 100 == 0:
acc = sess.run(accuracy,feed_dict={_inputs:x_batch,
_labels:y_batch,
_seqlens:seqlen_batch})
print("Accuracy at %d: %.5f" % (step, acc))
Pretrained Embeddings, Advanced RNN | 111
for test_batch in range(5):
x_test, y_test,seqlen_test = get_sentence_batch(batch_size,
test_x,test_y,
test_seqlens)
batch_pred,batch_acc = sess.run([tf.argmax(final_output,1),
accuracy],
feed_dict={_inputs:x_test,
_labels:y_test,
_seqlens:seqlen_test})
print("Test batch accuracy %d: %.5f" % (test_batch, batch_acc))
print("Test batch accuracy %d: %.5f" % (test_batch, batch_acc))
Summary
In this chapter, we extended our knowledge regarding working with text sequences,
adding some important tools to our TensorFlow toolbox. We saw a basic implementa‐
tion of word2vec, learning the core concepts and ideas, and used TensorBoard for 3D
interactive visualization of embeddings. We then incorporated publicly available
GloVe word vectors, and RNN components that allow for richer and more efficient
models. In the next chapter, we will see how to use abstraction libraries, including for
classification tasks on real text data with LSTM networks.
112 | Chapter 6: Text II: Word Vectors, Advanced RNN, and Embedding Visualization
CHAPTER 7
TensorFlow Abstractions and
Simplications
The aim of this chapter is to get you familiarized with important practical extensions
to TensorFlow. We start by describing what abstractions are and why they are useful
to us, followed by a brief review of some of the popular TensorFlow abstraction libra‐
ries. We then go into two of these libraries in more depth, demonstrating some of
their core functionalities along with some examples.
Chapter Overview
As most readers probably know, the term abstraction in the context of programming
refers to a layer of code “on top” of existing code that performs purpose-driven gener‐
alizations of the original code. Abstractions are formed by grouping and wrapping
pieces of code that are related to some higher-order functionality in a way that con‐
veniently reframes them together. The result is simplified code that is easier to write,
read, and debug, and generally easier and faster to work with. In many cases Tensor‐
Flow abstractions not only make the code cleaner, but can also drastically reduce
code length and as a result significantly cut development time.
To get us going, let’s illustrate this basic notion in the context of TensorFlow, and take
another look at some code for building a CNN like we did in Chapter 4:
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
113
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1],
padding='SAME')
def conv_layer(input, shape):
W = weight_variable(shape)
b = bias_variable([shape[3]])
h = tf.nn.relu(conv2d(input, W) + b)
hp = max_pool_2x2(h)
return hp
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME')
x = tf.placeholder(tf.float32, shape=[None, 784])
x_image = tf.reshape(x, [-1, 28, 28, 1])
h1 = conv_layer(x_image, shape=[5, 5, 1, 32])
h2 = conv_layer(h1, shape=[5, 5, 32, 64])
h3 = conv_layer(h2, shape=[5, 5, 64, 32])
In native TensorFlow, in order to create a convolutional layer, we have to define and
initialize its weights and biases according to the shapes of the input and the desired
output, apply the convolution operation with defined strides and padding, and finally
add the activation function operation. It’s easy to either accidentally forget one of
these fundamental components or get it wrong. Also, repeating this process multiple
times can be somewhat laborious and feels as if it could be done more efficiently.
In the preceding code example we created our own little abstraction by using func‐
tions that eliminate some of the redundancies in this process. Let’s compare the read‐
ability of that code with another version of it that does exactly the same, but without
using any of the functions:
x = tf.placeholder(tf.float32, shape=[None, 784])
x_image = tf.reshape(x, [-1, 28, 28, 1])
W1 = tf.truncated_normal([5, 5, 1, 32], stddev=0.1)
b1 = tf.constant(0.1, shape=[32])
h1 = tf.nn.relu(tf.nn.conv2d(x_image, W1,
strides=[1, 1, 1, 1], padding='SAME') + b1)
hp1 = tf.nn.max_pool(h1, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME')
W2 = tf.truncated_normal([5, 5, 32, 64], stddev=0.1)
b2 = tf.constant(0.1, shape=[64])
h2 = tf.nn.relu(tf.nn.conv2d(hp1, W2,
strides=[1, 1, 1, 1], padding='SAME') + b2)
hp2 = tf.nn.max_pool(h2, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME')
W3 = tf.truncated_normal([5, 5, 64, 32], stddev=0.1)
114 | Chapter 7: TensorFlow Abstractions and Simplications
b3 = tf.constant(0.1, shape=[32])
h3 = h1 = tf.nn.relu(tf.nn.conv2d(hp2, W3,
strides=[1, 1, 1, 1], padding='SAME') + b3)
hp3 = tf.nn.max_pool(h3, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME')
Even with just three layers, the resulting code looks pretty messy and confusing.
Clearly, as we progress to larger and more advanced networks, code such as this
would be hard to manage and pass around.
Beyond the more typical medium-sized batching of code, long and complex code is
often “wrapped up” for us in abstraction libraries. This is particularly effective in rela‐
tively simple models where very little customization is ever required. As a preview to
what will follow in the next section, you can already see how in contrib.learn, one
of the abstractions available for TensorFlow, the core of defining and training a linear
regression model similar to the one at the end of Chapter 3 could be done in just two
lines:
regressor = learn.LinearRegressor(feature_columns=feature_columns,
optimizer=optimizer)
regressor.fit(X, Y, steps=200, batch_size=506)
High-Level Survey
More than a few great TensorFlow open source extensions are available at the time of
writing this book. Among the popular ones are:
•tf.contrib.learn
• TFLearn
•TF-Slim
• Keras
While TFLearn needs to be installed, contrib.learn and TF-Slim (now tf.con
trib.slim) are merged with TensorFlow and therefore require no installation. In
2017 Keras gained official Google support, and it has also been moved into tf.con
trib as of version 1.1 (tf.contrib.keras). The name contrib refers to the fact that
code in this library is “contributed” and still requires testing to see if it receives broad
acceptance. Therefore, it could still change, and is yet to be part of the core Tensor‐
Flow.
contrib.learn started as an independent simplified interface for TensorFlow and
was initially called Scikit Flow, with the intention of making the creation of complex
networks with TensorFlow more accessible for those who are transitioning from the
scikit-learn world of “one-liner” machine learning. As is often the case, it was later
merged to TensorFlow and is now regarded as its Learn module, with extensive docu‐
mentation and examples that are available on the official TensorFlow website.
Chapter Overview | 115

Like other libraries, the main goal of contrib.learn is to make it easy to configure,
train, and evaluate our learning models. For very simple models, you can use out-of-
the-box implementations to train with just a few lines of code. Another great advan‐
tage of contrib.learn, as we will see shortly, is functionality with which data features
can be handled very conveniently.
While contrib.learn is more transparent and low-level, the other three extensions
are a bit cleaner and more abstract, and each has its own specialties and little advan‐
tages that might come in handy depending on the needs of the user.
TFLearn and Keras are full of functionality and have many of the elements needed for
various types of state-of-the-art modeling. Unlike all the other libraries, which were
created to communicate solely with TensorFlow, Keras supports both TensorFlow and
Theano (a popular library for deep learning).
TF-Slim was created mainly for designing complex convolutional nets with ease and
has a wide variety of pretrained models available, relieving us from the expensive
process of having to train them ourselves.
These libraries are very dynamic and are constantly changing, with the developers
adding new models and functionalities, and occasionally modifying their syntax.
Theano
eano is a Python library that allows you to manipulate symbolic
mathematical expressions that involve tensor arrays in an efficient
way, and as such it can serve as a deep learning framework, com‐
peting with TensorFlow. Theano has been around longer, and
therefore is a bit more mature than TensorFlow, which is still
changing and evolving but is rapidly becoming the leader of the
pack (it is widely considered by many to already be the leading
library, with many advantages over other frameworks).
In the following sections we demonstrate how to use these extensions, alongside
some examples. We begin by focusing on contrib.learn, demonstrating how easily
it lets us train and run simple regression and classification models. Next we introduce
TFLearn and revisit the more advanced models introduced in the previous chapters—
CNN and RNN. We then give a short introduction to autoencoders and demonstrate
how to create one with Keras. Finally, we close this chapter with brief coverage of TF-
Slim and show how to classify images using a loaded pretrained state-of-the-art CNN
model.
116 | Chapter 7: TensorFlow Abstractions and Simplications

contrib.learn
Using contrib.learn doesn’t require any installation since it’s been merged with Ten‐
sorFlow:
import tensorflow as tf
from tensorflow.contrib import learn
We start with contrib.learn’s out-of-the-box estimators (a fancy name for models),
which we can train in a quick and efficient manner. These predefined estimators
include simple linear and logistic regression models, a simple linear classifier, and a
basic deep neural network. Table 7-1 lists some of the popular estimators we can use.
Table 7-1. Popular built-in contrib.learn estimators
Estimator Description
LinearRegressor() Linear regression model to predict label value given observation of feature values.
LogisticRegressor() Logistic regression estimator for binary classication.
LinearClassifier() Linear model to classify instances into one of multiple possible classes. When the number of
possible classes is 2, this is binary classication.
DNNRegressor() A regressor for TensorFlow deep neural network (DNN) models.
DNNClassifier() A classier for TensorFlow DNN models.
Of course, we would also like to use more-advanced and customized models, and for
that contrib.learn lets us conveniently wrap our own homemade estimators, a fea‐
ture that will be covered as we go along. Once we have an estimator ready for deploy‐
ment, whether it was made for us or we made it ourselves, the steps are pretty much
the same:
1. We instantiate the estimator class to create our model:
model = learn.<some_Estimator>()
2. Then we t it using our training data:
model.fit()
3. We evaluate the model to see how well it does on some given dataset:
model.evaluate()
4. Finally, we use our fitted model to predict outcomes, usually for new data:
model.predict()
These four fundamental stages are also found in other extensions.
contrib offers many other functionalities and features; in particular, contrib.learn
has a very neat way to treat our input data, which will be the focus of the next subsec‐
tion, where we discuss linear models.
contrib.learn | 117
Linear Regression
We start our contrib.learn engagement with one of its strongest features: linear
models. We say that a model is linear whenever it is defined by a function of a weigh‐
ted sum of the features, or more formally f(w1x1 + w2x2 +...+ wnxn), where f could be
any sort of function, like the identity function (as in linear regression) or a logistic
function (as in logistic regression). Although limited in their expressive power, linear
models have lots of advantages, such as clear interpretability, optimization speed, and
simplicity.
In Chapter 3 we created our own linear regression model using native TensorFlow by
first creating a graph with placeholders for the input and target data, Variables for the
set of parameters, a loss function, and an optimizer. After the model was defined, we
ran the session and obtained results.
In the following section we first repeat this full process, and then show how drasti‐
cally easier it is to do with contrib.learn. For this example we use the Boston Hous‐
ing dataset, available to download using the sklearn library. The Boston Housing
dataset is a relatively small dataset (506 samples), containing information concerning
housing in the area of Boston, Massachusetts. There are 13 predictors in this dataset:
1. CRIM: per capita crime rate by town
2. ZN: proportion of residential land zoned for lots over 25,000 sq.ft.
3. INDUS: proportion of nonretail business acres per town
4. CHAS: Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
5. NOX: nitric oxide concentration (parts per 10 million)
6. RM: average number of rooms per dwelling
7. AGE: proportion of owner-occupied units built prior to 1940
8. DIS: weighted distances to five Boston employment centers
9. RAD: index of accessibility to radial highways
10. TAX: full-value property tax rate per $10,000
11. PTRATIO: pupil–teacher ratio by town
12. B: 1000(Bk – 0.63)^2, where Bk is the proportion of blacks by town
13. LSTAT: % lower status of the population
The target variable is the median value of owner-occupied homes in thousands of
dollars. In this example we try to predict the target variable by using some linear
combination of these 13 features.
First, we import the data:
from sklearn import datasets, metrics, preprocessing
boston = datasets.load_boston()
x_data = preprocessing.StandardScaler().fit_transform(boston.data)
y_data = boston.target
118 | Chapter 7: TensorFlow Abstractions and Simplications
Next, we use the same linear regression model as in Chapter 3. This time we track the
“loss” so we can measure the mean squared error (MSE), which is the average of the
squared differences between the real target value and our predicted value. We use this
measure as an indicator of how well our model performs:
x = tf.placeholder(tf.float64,shape=(None,13))
y_true = tf.placeholder(tf.float64,shape=(None))
with tf.name_scope('inference') as scope:
w = tf.Variable(tf.zeros([1,13],dtype=tf.float64,name='weights'))
b = tf.Variable(0,dtype=tf.float64,name='bias')
y_pred = tf.matmul(w,tf.transpose(x)) + b
with tf.name_scope('loss') as scope:
loss = tf.reduce_mean(tf.square(y_true-y_pred))
with tf.name_scope('train') as scope:
learning_rate = 0.1
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
train = optimizer.minimize(loss)
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
for step in range(200):
sess.run(train,{x: x_data, y_true: y_data})
MSE = sess.run(loss,{x: x_data, y_true: y_data})
print(MSE)
Out:
MSE = 21.9036388397
After 200 iterations, we print out the MSE calculated for the training set. Now we per‐
form the exact same process, but using contrib.learn’s estimator for linear regres‐
sion. The whole process of defining, fitting, and evaluating the model comes down to
just a few lines:
1. The linear regression model is instantiated using learn.LinearRegressor() and
fed with knowledge about the data representation and the type of optimizer:
reg = learn.LinearRegressor(
feature_columns=feature_columns,
optimizer=tf.train.GradientDescentOptimizer(
learning_rate=0.1)
)
2. The regressor object is trained using .fit(). We pass the covariates and the tar‐
get variable, and set the number of steps and batch size:
contrib.learn | 119
reg.fit(x_data, boston.target, steps=NUM_STEPS,
batch_size=MINIBATCH_SIZE)
3. The MSE loss is returned by .evaluate():
MSE = regressor.evaluate(x_data, boston.target, steps=1)
Here’s the code in its entirety:
NUM_STEPS = 200
MINIBATCH_SIZE = 506
feature_columns = learn.infer_real_valued_columns_from_input(x_data)
reg = learn.LinearRegressor(
feature_columns=feature_columns,
optimizer=tf.train.GradientDescentOptimizer(
learning_rate=0.1)
)
reg.fit(x_data, boston.target, steps=NUM_STEPS,
batch_size=MINIBATCH_SIZE)
MSE = reg.evaluate(x_data, boston.target, steps=1)
print(MSE)
Out:
{'loss': 21.902138, 'global_step': 200}
Some representation of the input data is passed in the regressor instantiation as a pro‐
cessed variable called feature_columns. We will return to this shortly.
DNN Classier
As with regression, we can use contrib.learn to apply an out-of-the-box classifier.
In Chapter 2 we created a simple softmax classifier for the MNIST data. The DNNClas
sifier estimator allows us to perform a similar task with a considerably reduced
amount of code. Also, it lets us add hidden layers (the “deep” part of the DNN).
As in Chapter 2, we first import the MNIST data:
import sys
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
DATA_DIR = '/tmp/data' if not 'win32' in sys.platform else "c:\\tmp\\data"
data = input_data.read_data_sets(DATA_DIR, one_hot=False)
x_data, y_data = data.train.images,data.train.labels.astype(np.int32)
x_test, y_test = data.test.images,data.test.labels.astype(np.int32)
Note that in this case, due to the requirement of the estimator, we pass the target in its
class label form:
120 | Chapter 7: TensorFlow Abstractions and Simplications
one_hot=False
returning a single integer per sample, corresponding to the correct digit class (i.e.,
values from 0 to [number of classes] – 1), instead of the one-hot form where each
label is a vector with 1 in the index that corresponds to the correct class.
The next steps are similar to the ones we took in the previous example, except that
when we define the model, we add the number of classes (10 digits) and pass a list
where each element corresponds to a hidden layer with the specified number of units.
In this example we use one hidden layer with 200 units:
NUM_STEPS = 2000
MINIBATCH_SIZE = 128
feature_columns = learn.infer_real_valued_columns_from_input(x_data)
dnn = learn.DNNClassifier(
feature_columns=feature_columns,
hidden_units=[200],
n_classes=10,
optimizer=tf.train.ProximalAdagradOptimizer(
learning_rate=0.2)
)
dnn.fit(x=x_data,y=y_data, steps=NUM_STEPS,
batch_size=MINIBATCH_SIZE)
test_acc = dnn.evaluate(x=x_test,y=y_test, steps=1)["accuracy"]
print('test accuracy: {}'.format(test_acc))
Out:
test accuracy: 0.977
Though not as good as our CNN model in Chapter 4 (above 99%), the test accuracy
here (around 98%) is significantly better than it was in the simple softmax example
(around 92%) as a result of adding just a single layer. In Figure 7-1 we see how the
accuracy of the model increases with the number of units in that hidden layer.
contrib.learn | 121
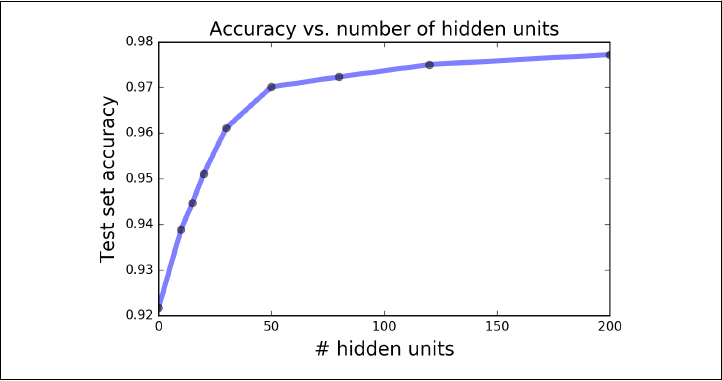
Figure 7-1. MNIST classication test accuracy as a function of units added in a single
hidden layer.
Using the <Estimator>.predict() method, we can predict the classes of new sam‐
ples. Here we will use the predictions to demonstrate how we can analyze our model’s
performance—what classes were best identified and what types of typical errors were
made. Plotting a confusion matrix can help us understand these behaviors. We import
the code to create the confusion matrix from the scikit-learn library:
from sklearn.metrics import confusion_matrix
y_pred = dnn.predict(x=x_test,as_iterable=False)
class_names = ['0','1','2','3','4','5','6','7','8','9']
cnf_matrix = confusion_matrix(y_test, y_pred)
The confusion matrix is shown in Figure 7-2. Its rows correspond to the true digits,
its columns to the predicted digits. We see, for example, that the model sometimes
misclassified 5 as 3 and 9 as 4 and 7.
122 | Chapter 7: TensorFlow Abstractions and Simplications
Figure 7-2. A confusion matrix showing the number of predicted digits (columns) for
each true label (rows).
FeatureColumn
One of contrib.learn’s nicest offerings is handling features of different types, which
can sometimes be a little tricky. To make things easier, contrib.learn offers us the
FeatureColumn abstraction.
With a FeatureColumn we can maintain a representation of a single feature in our
data, while performing a range of transformations defined over it. A FeatureColumn
can be either one of the original columns or any new columns that may be added
depending on our transformations. These may include creating a suitable and effec‐
tive representation for categorical data by encoding it as a sparse vector (often
referred to as dummy encoding), creating feature crosses to look for feature interac‐
tions, and bucketization (discretization of the data). All this can be done while
manipulating the feature as a single semantic unit (encompassing, for example, all
dummy vectors).
We use the FeatureColumn abstraction to specify the form and structure of each fea‐
ture of our input data. For instance, let’s say that our target variable is height, and we
contrib.learn | 123
try to predict it using two features, weight and species. We make our own synthetic
data where heights are generated by dividing each weight by a factor of 100 and
adding a constant that varies according to the species: 1 is added for Humans, 0.9 for
Goblins, and 1.1 for ManBears. We then add normally distributed noise to each
instance:
import pandas as pd
N = 10000
weight = np.random.randn(N)*5+70
spec_id = np.random.randint(0,3,N)
bias = [0.9,1,1.1]
height = np.array([weight[i]/100 + bias[b] for i,b in enumerate(spec_id)])
spec_name = ['Goblin','Human','ManBears']
spec = [spec_name[s] for s in spec_id]
Figure 7-3 shows visualizations of the data samples.
Figure 7-3. Le: A histogram of heights for the three types of species: Goblins, Humans,
and ManBears (distributions centered at 1.6, 1.7, and 1.8, respectively). Right: A scatter
plot of heights vs. weights.
Our target variable is a numeric NumPy array of heights height, and our covariates
are the numeric NumPy array of weights weight and a list of strings denoting the
name of each species spec.
We use the Pandas library to have the data represented as a data frame (table), so that
we can conveniently access each of its columns:
df = pd.DataFrame({'Species':spec,'Weight':weight,'Height':height})
Figure 7-4 shows what our data frame looks like.
124 | Chapter 7: TensorFlow Abstractions and Simplications
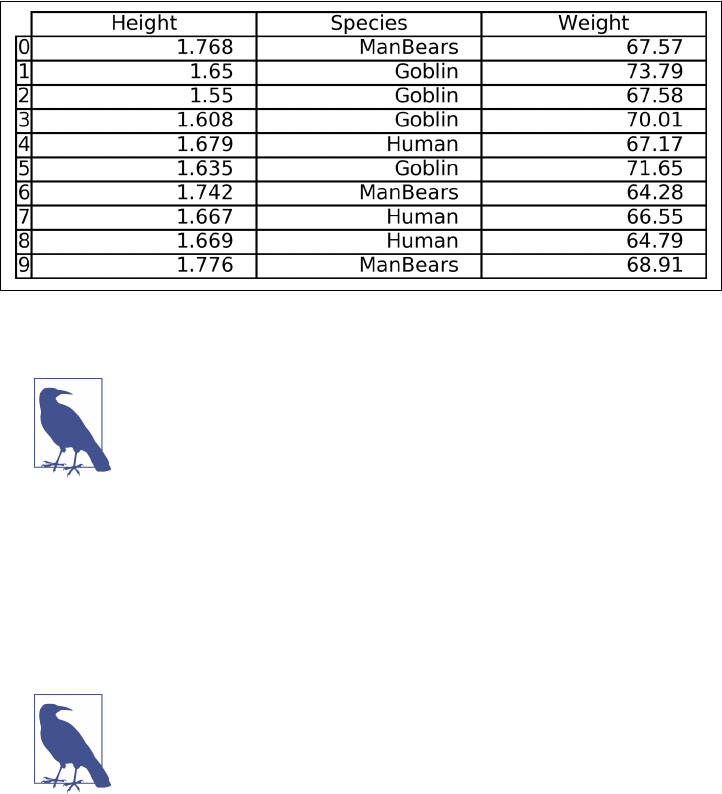
Figure 7-4. Ten rows of the Height–Species–Weight data frame. Heights and Weights are
numeric; Species is categorical with three categories.
Pandas
Pandas is a very popular and useful library in Python for working
with relational or labeled data like tabular data, multidimensional
time series, etc. For more information on how to use Pandas, we
refer the reader to Wes McKinney’s book Python for Data Analysis
(O’Reilly).
We start by specifying the nature of each feature. For Weight we use the following
FeatureColumn command, indicating that it’s a continuous variable:
from tensorflow.contrib import layers
Weight = layers.real_valued_column("Weight")
Layers
contrib.layers is not a part of contrib.learn, but another inde‐
pendent subsection of the TensorFlow Python API that offers high-
level operations and tools for building neural network layers.
The name that was passed to the function (in this case Weight) is crucially important
since it will be used to associate the FeatureColumn representation with the actual
data.
Species is a categorical variable, meaning its values have no natural ordering, and
therefore cannot be represented as a single variable in the model. Instead, it has to be
extended and encoded as several variables, depending on the number of cate‐
gories. FeatureColumn does this for us, so we just have to use the following command
to specify that it is a categorical feature and indicate the name of each category:
contrib.learn | 125
Species = layers.sparse_column_with_keys(
column_name="Species", keys=['Goblin','Human','ManBears'])
Next, we instantiate an estimator class and input a list of our FeatureColumns:
reg = learn.LinearRegressor(feature_columns=[Weight,Species])
Up to now we’ve defined how the data will be represented in the model; in the follow‐
ing stage of fitting the model we need to provide the actual training data. In the Bos‐
ton Housing example, the features were all numeric, and as a result we could just
input them as x_data and target data.
Here, contrib.learn requires that we use an additional encapsulating input function.
The function gets both predictors and target data in their native form (Pandas data
frame, NumPy array, list, etc.) as input, and returns a dictionary of tensors. In these
dictionaries, each key is a name of a FeatureColumn (the names Weight and Species
that were given as input previously), and its value needs to be a Tensor that contains
the corresponding data. This means that we also have to transform the values into a
TensorFlow Tensor inside the function.
In our current example, the function receives our data frame, creates a dictionary fea
ture_cols, and then stores the values of each column in the data frame as a Tensor
for the corresponding key. It then returns that dictionary and the target variable as a
Tensor. The keys have to match the names we used to define our FeatureColumns:
def input_fn(df):
feature_cols = {}
feature_cols['Weight'] = tf.constant(df['Weight'].values)
feature_cols['Species'] = tf.SparseTensor(
indices=[[i, 0] for i in range(df['Species'].size)],
values=df['Species'].values,
dense_shape=[df['Species'].size, 1])
labels = tf.constant(df['Height'].values)
return feature_cols, labels
The values of Species are required by their FeatureColumn specification to be enco‐
ded in a sparse format. For that we use tf.SparseTensor(), where each i index cor‐
responds to a nonzero value (in this case, all the rows in a one-column matrix).
For example, the following:
SparseTensor(indices=[[0, 0], [2, 1], [2, 2]], values=[2, 5, 7],
dense_shape=[3, 3])
represents the dense tensor:
126 | Chapter 7: TensorFlow Abstractions and Simplications

[[2, 0, 0]
[0, 0, 0]
[0, 5, 7]]
We pass it to the .fit() method in the following way:
reg.fit(input_fn=lambda:input_fn(df), steps=50000)
Here, input_fn() is the function we just created, df is the data frame containing the
data, and we also specify the number of iterations.
Note that we pass the function in a form of a lambda function rather than the func‐
tion’s outputs, because the .fit() method requires a function object. Using lambda
allows us to pass our input arguments and keep it in an object form. There are other
workarounds we could use to achieve the same outcome, but lambda does the trick.
The fitting process may take a while. If you don’t want to do it all at once, you can
split it into segments (see the following note).
Splitting the training process
It’s possible to perform the fit iteratively since the state of the model
is preserved in the classifier. For example, instead of performing all
50,000 iterations consecutively like we did, we could split it into
five segments:
reg.fit(input_fn=lambda:input_fn(df), steps=10000)
reg.fit(input_fn=lambda:input_fn(df), steps=10000)
reg.fit(input_fn=lambda:input_fn(df), steps=10000)
reg.fit(input_fn=lambda:input_fn(df), steps=10000)
reg.fit(input_fn=lambda:input_fn(df), steps=10000)
and achieve the same outcome. This could be useful if we want to
have some tracking of the model while training it; however, there
are better ways to do that, as we will see later on.
Now let’s see how well the model does by looking at the estimated weights. We can
use the the .get_variable_value() method to get the variables’ values:
w_w = reg.get_variable_value('linear/Weight/weight')
print('Estimation for Weight: {}'.format(w_w))
s_w = reg.get_variable_value('linear/Species/weights')
b = reg.get_variable_value('linear/bias_weight')
print('Estimation for Species: {}'.format(s_w + b))
Out:
Estimation for Weight: [[0.00992305]]
Estimation for Species: [[0.90493023]
[1.00566959]
[1.10534406]]
contrib.learn | 127

We request the values of the weights for both Weight and Species. Species is a cate‐
gorical variable, so its three weights serve as different bias terms. We see that the
model did quite well in estimating the true weights (0.01 for Weight and 0.9, 1, 1.1
for Goblins, Humans, and ManBears, respectively, for Species). We can get the names
of the variables by using the .get_variable_names() method.
The same process can be used in more complicated scenarios where we want to han‐
dle many types of features and their interactions. Table 7-2 lists some useful opera‐
tions you can do with contrib.learn.
Table 7-2. Useful feature transformation operations
Operation Description
layers.sparse_column_with_keys() Handles the conversion of categorical values
layers.sparse_column_with_hash_bucket() Handles the conversion of categorical features for which you
don’t know all possible values
layers.crossed_column() Sets up feature crosses (interactions)
layers.bucketized_column() Turns a continuous column into a categorical column
Homemade CNN with contrib.learn
We next move on to creating our own estimator by using contrib.learn. To do so,
we first need to construct a model function where our homemade network will reside
and an object containing our training settings.
In the following example we create a custom CNN estimator that is identical to the
one used at the beginning of Chapter 4, and use it again to classify the MNIST data.
We begin by creating a function for our estimator with inputs that include our data,
the mode of operation (training or test), and the parameters of the model.
In the MNIST data the pixels are concatenated in the form of a vector and therefore
require that we reshape them:
x_image = tf.reshape(x_data, [-1, 28, 28, 1])
We build the network by using the contrib.layers functionality, making the process
of layer construction simpler.
Using layers.convolution2d() we can set everything in a one-liner command: we
pass the input (the output of the previous layer), and then indicate the number of fea‐
ture maps (32), the size of the filter (5×5), and the activation function (relu), and ini‐
tialize the weights and biases. The dimensionality of the input is automatically
identified and does not need to be specified. Also, unlike when working in lower-level
TensorFlow, we don’t need to separately define the shapes of the variables and biases:
128 | Chapter 7: TensorFlow Abstractions and Simplications
conv1 = layers.convolution2d(x_image, 32, [5,5],
activation_fn=tf.nn.relu,
biases_initializer=tf.constant_initializer(0.1),
weights_initializer=tf.truncated_normal_initializer(stddev=0.1))
The padding is set to 'SAME' by default (unchanged number of pixels), resulting in an
output of shape 28×28×32.
We also add the standard 2×2 pooling layer:
pool1 = layers.max_pool2d(conv1, [2,2])
We then repeat these steps, this time for 64 target feature maps:
conv2 = layers.convolution2d(pool1, 64, [5,5],
activation_fn=tf.nn.relu,
biases_initializer=tf.constant_initializer(0.1),
weights_initializer=tf.truncated_normal_initializer(stddev=0.1))
pool2 = layers.max_pool2d(conv2, [2,2])
Next, we flatten the 7×7×64 tensor and add a fully connected layer, reducing it to
1,024 entries. We use fully_connected() similarly to convolution2d(), except we
specify the number of output units instead of the size of the filter (there’s just one of
those):
pool2_flat = tf.reshape(pool2, [-1, 7*7*64])
fc1 = layers.fully_connected(pool2_flat, 1024,
activation_fn=tf.nn.relu,
biases_initializer=tf.constant_initializer(0.1),
weights_initializer=tf.truncated_normal_initializer(stddev=0.1))
We then add dropout with keep_prob as set in the parameters given to the function
(train/test mode), and the final fully connected layer with 10 output entries, corre‐
sponding to the 10 classes:
fc1_drop = layers.dropout(fc1, keep_prob=params["dropout"],
is_training=(mode == 'train'))
y_conv = layers.fully_connected(fc1_drop, 10, activation_fn=None)
We complete our model function by defining a training object with the loss and the
learning rate of the optimizer.
We now have one function that encapsulates the entire model:
def model_fn(x, target, mode, params):
y_ = tf.cast(target, tf.float32)
x_image = tf.reshape(x, [-1, 28, 28, 1])
# Conv layer 1
conv1 = layers.convolution2d(x_image, 32, [5,5],
activation_fn=tf.nn.relu,
biases_initializer=tf.constant_initializer(0.1),
weights_initializer=tf.truncated_normal_initializer(stddev=0.1))
contrib.learn | 129
pool1 = layers.max_pool2d(conv1, [2,2])
# Conv layer 2
conv2 = layers.convolution2d(pool1, 64, [5,5],
activation_fn=tf.nn.relu,
biases_initializer=tf.constant_initializer(0.1),
weights_initializer=tf.truncated_normal_initializer(stddev=0.1))
pool2 = layers.max_pool2d(conv2, [2,2])
# FC layer
pool2_flat = tf.reshape(pool2, [-1, 7*7*64])
fc1 = layers.fully_connected(pool2_flat, 1024,
activation_fn=tf.nn.relu,
biases_initializer=tf.constant_initializer(0.1),
weights_initializer=tf.truncated_normal_initializer(stddev=0.1))
fc1_drop = layers.dropout(fc1, keep_prob=params["dropout"],
is_training=(mode == 'train'))
# Readout layer
y_conv = layers.fully_connected(fc1_drop, 10, activation_fn=None)
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(logits=y_conv, labels=y_))
train_op = tf.contrib.layers.optimize_loss(
loss=cross_entropy,
global_step=tf.contrib.framework.get_global_step(),
learning_rate=params["learning_rate"],
optimizer="Adam")
predictions = tf.argmax(y_conv, 1)
return predictions, cross_entropy, train_op
We instantiate the estimator by using contrib.learn.Estimator(), and we’re good
to go. Once defined, we can use it with the same functionalities as before:
from tensorflow.contrib import layers
data = input_data.read_data_sets(DATA_DIR, one_hot=True)
x_data, y_data = data.train.images,np.int32(data.train.labels)
tf.cast(x_data,tf.float32)
tf.cast(y_data,tf.float32)
model_params = {"learning_rate": 1e-4, "dropout": 0.5}
CNN = tf.contrib.learn.Estimator(
model_fn=model_fn, params=model_params)
print("Starting training for %s steps max" % 5000)
CNN.fit(x=data.train.images,
y=data.train.labels, batch_size=50,
max_steps=5000)
test_acc = 0
130 | Chapter 7: TensorFlow Abstractions and Simplications
for ii in range(5):
batch = data.test.next_batch(2000)
predictions = list(CNN.predict(batch[0], as_iterable=True))
test_acc = test_acc + (np.argmax(batch[1],1) == predictions).mean()
print(test_acc/5)
Out:
0.9872
Using contrib.learn and contrib.layers, the number of lines of code was cut
down considerably in comparison to lower-level TensorFlow. More important, the
code is much more organized and easier to follow, debug, and write.
With this example we conclude the contrib.learn portion of this chapter. We’ll now
move on to cover some of the functionalities of the TFLearn library.
TFLearn
TFLearn is another library that allows us to create complex custom models in a very
clean and compressed way, while still having a reasonable amount of flexibility, as we
will see shortly.
Installation
Unlike the previous library, TFLearn first needs to be installed. The installation is
straightforward using pip:
pip install tflearn
If that doesn’t work, it can be downloaded from GitHub and installed manually.
After the library has been successfully installed, you should be able to import it:
import tflearn
CNN
Many of the functionalities of TFLearn resemble those covered in the previous sec‐
tion on contrib.learn; however, creating a custom model is a bit simpler and
cleaner in comparison. In the following code we use the same CNN used earlier for
the MNIST data.
Model construction is wrapped and finalized using regression(), where we set the
loss and optimization configuration as we did previously for the training object in
contrib.learn (here we simply specify 'categorical_crossentreopy' for the loss,
rather than explicitly defining it):
TFLearn | 131
from tflearn.layers.core import input_data, dropout, fully_connected
from tflearn.layers.conv import conv_2d, max_pool_2d
from tflearn.layers.normalization import local_response_normalization
from tflearn.layers.estimator import regression
# Data loading and basic transformations
import tflearn.datasets.mnist as mnist
X, Y, X_test, Y_test = mnist.load_data(one_hot=True)
X = X.reshape([-1, 28, 28, 1])
X_test = X_test.reshape([-1, 28, 28, 1])
# Building the network
CNN = input_data(shape=[None, 28, 28, 1], name='input')
CNN = conv_2d(CNN, 32, 5, activation='relu', regularizer="L2")
CNN = max_pool_2d(CNN, 2)
CNN = local_response_normalization(CNN)
CNN = conv_2d(CNN, 64, 5, activation='relu', regularizer="L2")
CNN = max_pool_2d(CNN, 2)
CNN = local_response_normalization(CNN)
CNN = fully_connected(CNN, 1024, activation=None)
CNN = dropout(CNN, 0.5)
CNN = fully_connected(CNN, 10, activation='softmax')
CNN = regression(CNN, optimizer='adam', learning_rate=0.0001,
loss='categorical_crossentropy', name='target')
# Training the network
model = tflearn.DNN(CNN,tensorboard_verbose=0,
tensorboard_dir = 'MNIST_tflearn_board/',
checkpoint_path = 'MNIST_tflearn_checkpoints/checkpoint')
model.fit({'input': X}, {'target': Y}, n_epoch=3,
validation_set=({'input': X_test}, {'target': Y_test}),
snapshot_step=1000,show_metric=True, run_id='convnet_mnist')
Another layer that’s been added here, and that we briefly mentioned in Chapter 4, is
the local response normalization layer. See the upcoming note for more details about
this layer.
The tflearn.DNN() function is somewhat equivalent to contrib.learn.Estima
tor()—it’s the DNN model wrapper with which we instantiate the model and to
which we pass our constructed network.
Here we can also set the TensorBoard and checkpoints directories, the level of verbo‐
sity of TensorBoard’s logs (0–3, from basic loss and accuracy reports to other meas‐
ures like gradients and weights), and other settings.
Once we have a model instance ready, we can then perform standard operations with
it. Table 7-3 summarizes the model’s functionalities in TFLearn.
132 | Chapter 7: TensorFlow Abstractions and Simplications

Table 7-3. Standard TFLearn operations
Function Description
evaluate(X, Y, batch_size=128)Perform evaluations of the model on given samples.
fit(X, Y, n_epoch=10)Train the model with input features X and target Y to the network.
get_weights(weight_tensor)Get a variable’s weights.
load(model_file)Restore model weights.
predict(X)Get model predictions for the given input data.
save(model_file)Save model weights.
set_weights(tensor, weights)Assign a tensor variable a given value.
Similarly with contrib.learn, the fitting operation is performed by using the .fit()
method, to which we feed the data and control training settings: the number of
epochs, training and validation batch sizes, displayed measures, saved summaries fre‐
quency, and more. During fitting, TFLearn displays a nice dashboard, enabling us to
track the training process online.
Local response normalization
The local response normalization (LRN) layer performs a kind of
lateral inhibition by normalizing over local input regions. This is
done by dividing the input values by the weighted, squared sum of
all inputs within some depth radius, which we can manually
choose. The resulting effect is that the activation contrast between
the excited neurons and their local surroundings increases, pro‐
ducing more salient local maxima. This method encourages inhibi‐
tion since it will diminish activations that are large, but uniform.
Also, normalization is useful to prevent neurons from saturating
when inputs may have varying scale (ReLU neurons have unboun‐
ded activation). There are more modern alternatives for regulariza‐
tion, such as batch normalization and dropout, but it is good to
know about LRN too.
After fitting the model, we evaluate performance on the test data:
evaluation = model.evaluate({'input': X_test},{'target': Y_test})
print(evaluation):
Out:
0.9862
TFLearn | 133
and form new predictions (using them here again as a “sanity check” to the previous
evaluation):
pred = model.predict({'input': X_test})
print((np.argmax(testY,1)==np.argmax(pred,1)).mean())
Out:
0.9862
Iterations training steps and epochs in TFLearn
In TFLearn, each iteration is a full pass (forward and backward)
over one example. The training step is the number of full passes to
perform, determined by the batch size you set (the default is 64),
and an epoch is a full pass over all the training examples (50,000 in
the case of MNIST). Figure 7-5 shows an example of the interactive
display in TFLearn.
Figure 7-5. Interactive display in TFLearn.
RNN
We wrap up our introduction to TFLearn by constructing a fully functioning text
classification RNN model that considerably simplifies the code we saw in Chapters 5
and 6.
The task we perform is a sentiment analysis for movie reviews with binary classifica‐
tion (good or bad). We will use a well-known dataset of IMDb reviews, containing
25,000 training samples and 25,000 test samples:
from tflearn.data_utils import to_categorical, pad_sequences
from tflearn.datasets import imdb
# IMDb dataset loading
train, test, _ = imdb.load_data(path='imdb.pkl', n_words=10000,
valid_portion=0.1)
X_train, Y_train = train
X_test, Y_test = test
We first prepare the data, which has different sequence lengths, by equalizing the
sequences with zero-padding by using tflearn.data_utils.pad_sequences() and
setting 100 as the maximum sequence length:
X_train = pad_sequences(X_train, maxlen=100, value=0.)
X_test = pad_sequences(X_test, maxlen=100, value=0.)
134 | Chapter 7: TensorFlow Abstractions and Simplications
Now we can represent data in one tensor, with samples in its rows and word IDs in its
columns. As was explained in Chapter 5, IDs here are integers that are used to encode
the actual words arbitrarily. In our case, we have 10,000 unique IDs.
Next, we embed each word into a continuous vector space by using tflearn.embed
ding(), transforming our two-dimensional tensor [samples, IDs] into a three-
dimensional tensor, [samples, IDs, embedding-size], where each word ID now
corresponds to a vector of size of 128. Before that we use input_data() to input/feed
data to the network (a TensorFlow placeholder is created with the given shape):
RNN = tflearn.input_data([None, 100])
RNN = tflearn.embedding(RNN, input_dim=10000, output_dim=128)
Finally, we add an LSTM layer and a fully connected layer to output the binary out‐
come:
RNN = tflearn.lstm(RNN, 128, dropout=0.8)
RNN = tflearn.fully_connected(RNN, 2, activation='softmax'
Here’s the full code:
from tflearn.data_utils import to_categorical, pad_sequences
from tflearn.datasets import imdb
# Load data
train, test, _ = imdb.load_data(path='imdb.pkl', n_words=10000,
valid_portion=0.1)
X_train, Y_train = train
X_test, Y_test = test
# Sequence padding and converting labels to binary vectors
X_train = pad_sequences(X_train, maxlen=100, value=0.)
X_test = pad_sequences(X_test, maxlen=100, value=0.)
Y_train = to_categorical(Y_train, nb_classes=2)
Y_test = to_categorical(Y_test, nb_classes=2)
# Building an LSTM network
RNN = tflearn.input_data([None, 100])
RNN = tflearn.embedding(RNN, input_dim=10000, output_dim=128)
RNN = tflearn.lstm(RNN, 128, dropout=0.8)
RNN = tflearn.fully_connected(RNN, 2, activation='softmax')
RNN = tflearn.regression(RNN, optimizer='adam', learning_rate=0.001,
loss='categorical_crossentropy')
# Training the network
model = tflearn.DNN(RNN, tensorboard_verbose=0)
model.fit(X_train, Y_train, validation_set=(X_test, Y_test),
show_metric=True, batch_size=32)
TFLearn | 135
In this section, we had just a quick taste of TFLearn. The library has nice documenta‐
tion and many examples that are well worth looking at.
Keras
Keras is one of the most popular and powerful TensorFlow extension libra‐
ries. Among the extensions we survey in this chapter, Keras is the only one that sup‐
ports both Theano—upon which it was originally built—and TensorFlow. This is
possible because of Keras’s complete abstraction of its backend; Keras has its own
graph data structure for handling computational graphs and communicating with
TensorFlow.
In fact, because of that it could even be possible to define a Keras model with either
TensorFlow or Theano and then switch to the other.
Keras has two main types of models to work with: sequential and functional. The
sequential type is designed for simple architectures, where we just want to stack layers
in a linear fashion. The functional API can support more-general models with a
diverse layer structure, such as multioutput models.
We will take a quick look at the syntax used for each type of model.
Installation
In TensorFlow 1.1+ Keras can be imported from the contrib library; however, for
older versions it needs to be installed externally. Note that Keras requires the numpy,
scipy, and yaml dependencies. Similarly to TFLearn, Keras can either be installed
using pip:
pip install keras
or downloaded from GitHub and installed using:
python setup.py install
By default, Keras will use TensorFlow as its tensor manipulation library. If it is set to
use Theano, it can be switched by changing the settings in the file called
$HOME/.keras/keras.json (for Linux users—modify the path according to your
OS), where the attribute backend appears in addition to other technical settings not
important in this chapter:
{
"image_data_format": "channels_last",
"epsilon": 1e-07,
"floatx": "float32",
"backend": "tensorflow"
}
If we want to access the backend, we can easily do so by first importing it:
136 | Chapter 7: TensorFlow Abstractions and Simplications
from keras import backend as K
We can then use it for most tensor operations as we would in TensorFlow (also for
Theano). For example, this:
input = K.placeholder(shape=(10,32))
is equivalent to:
tf.placeholder(shape=(10,32))
Sequential model
Using the sequential type is very straightforward—we define it and can simply start
adding layers:
from keras.models import Sequential
from keras.layers import Dense, Activation
model = Sequential()
model.add(Dense(units=64, input_dim=784))
model.add(Activation('softmax'))
Or equivalently:
model = Sequential([
Dense(64, input_shape=(784,),activation='softmax')
])
A dense layer is a fully connected layer. The first argument denotes the number of
output units, and the input shape is the shape of the input (in this example the weight
matrix would be of size 784×64). Dense() also has an optional argument where we
can specify and add an activation function, as in the second example.
After the model is defined, and just before training it, we set its learning configura‐
tions by using the .compile() method. It has three input arguments—the loss func‐
tion, the optimizer, and another metric function that is used to judge the
performance of your model (not used as the actual loss when training the model):
model.compile(loss='categorical_crossentropy',
optimizer='sgd',
metrics=['accuracy'])
We can set the optimizer at a finer resolution (learning rate, method,
etc.) using .optimizers. For example:
optimizer=keras.optimizers.SGD(lr=0.02, momentum=0.8, nesterov=True))
Finally, we feed .fit() the data and set the number of epochs and batch size. As with
the previous libraries, we can now easily evaluate how it does and perform predic‐
tions with new test data:
TFLearn | 137

from keras.callbacks import TensorBoard, EarlyStopping, ReduceLROnPlateau
early_stop = EarlyStopping(monitor='val_loss', min_delta=0,
patience=10, verbose=0, mode='auto')
model.fit(x_train, y_train, epochs=10, batch_size=64,
callbacks=[TensorBoard(log_dir='/models/autoencoder',)
early_stop])
loss_and_metrics = model.evaluate(x_test, y_test, batch_size=64)
classes = model.predict(x_test, batch_size=64)
Note that a callbacks argument was added to the fit() method. Callbacks are func‐
tions that are applied during the training procedure, and we can use them to get a
view on statistics and make dynamic training decisions by passing a list of them to
the .fit() method.
In this example we plug in two callbacks: TensorBoard, specifying its output folder,
and early stopping.
Early stopping
Early stopping is used to protect against overfitting by preventing
the learner from further improving its fit to the training data at the
expense of increasing the generalization error. In that sense, it can
be thought of as a form of regularization. In Keras we can specify
the minimum change to be monitored (min_delta), the number of
no-improvement epochs to stop after (patience), and the direction
of wanted change (mode).
Functional model
The main practical difference between the functional model and the sequential model
is that here we first define our input and output, and only then instantiate the model.
We first create an input Tensor according to its shape:
inputs = Input(shape=(784,))
Then we define our model:
x = Dense(64, activation='relu')(inputs)
x = Dense(32, activation='relu')(x)
outputs = Dense(10, activation='softmax')(x)
As we can see, the layers act as functions, giving the functional model its name.
And now we instantiate the model, passing both inputs and outputs to Model:
model = Model(inputs=inputs, outputs=outputs)
138 | Chapter 7: TensorFlow Abstractions and Simplications
The other steps follow as before:
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(x_train, y_train, epochs=10, batch_size=64)
loss_and_metrics = model.evaluate(x_test, y_test, batch_size=64)
classes = model.predict(x_test, batch_size=64)
We will end this section by introducing the concept of autoencoders and then show‐
ing how to implement one using Keras.
Autoencoders
Autoencoders are neural networks that try to output a reconstruction of the input. In
most cases the input is reconstructed after having its dimensionality reduced. Dimen‐
sionality reduction will be our main focus; however, autoencoders can also be used to
achieve “overcomplete” representations (for more stable decomposition), which
actually increases dimensions.
In dimensionality reduction we wish to translate each vector of data with size n to a
vector with size m, where m < n, while trying to keep as much important information
as possible. One very common way to do that is using principal component analysis
(PCA), where we can represent each original data column xj (all data points corre‐
sponding to an original feature) with some linear combination of the new reduced
features, called the principal components, such that xj = Σi=1mwibi.
PCA, however, is limited to only linear transformation of the data vectors.
Autoencoders are more general compressors, allowing complicated nonlinear trans‐
formations and finding nontrivial relations between visible and hidden units (in fact,
PCA is like a one-layer “linear autoencoder”). The weights of the models are learned
automatically by reducing a given loss function with an optimizer (SGD, for exam‐
ple).
Autoencoders that reduce input dimensionality create a bottleneck layer called a hid‐
den layer that has a smaller number of units than the input layer, forcing the data to
be represented in a lower dimension (Figure 7-6) before it is reconstructed. For the
reconstruction (decoding), autoencoders extract representative features that capture
some hidden abstractions, like the shape of an eye, wheel of a car, type of sport, etc.,
with which we can reconstruct the original input.
TFLearn | 139
Figure 7-6. Illustration of an autoencoder—a typical autoencoder will have input and
output layers consisting of the same number of units, and bottleneck hidden layers,
where the dimensionality of the data is reduced (compressed).
Like some of the models we’ve seen so far, autoencoder networks can have layers
stacked on top of each other, and they can include convolutions as in CNNs.
Autoencoders are currently not very suitable for real-world data compression prob‐
lems due to their data specificity—they are best used on data that is similar to what
they were trained on. Their current practical applications are mostly for extracting
lower-dimensional representations, denoising data, and data visualization with
reduced dimensionality. Denoising works because the network learns the important
abstractions of the image, while losing unimportant image-specific signals like noise.
Now let’s build a toy CNN autoencoder with Keras. In this example we will train the
autoencoder on one category of a noisy version of the CIFAR10 data images, and
then use it to denoise a test set of the same category. In this example we will use the
functional model API.
First we load the images by using Keras, and then we choose only the images that cor‐
respond to the label 1 (the automobile class):
from keras.layers import Input, Conv2D, MaxPooling2D, UpSampling2D
from keras.models import Model
from keras.callbacks import TensorBoard, ModelCheckpoint
from keras.datasets import cifar10
import numpy as np
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train = x_train[np.where(y_train==1)[0],:,:,:]
x_test = x_test[np.where(y_test==1)[0],:,:,:]
140 | Chapter 7: TensorFlow Abstractions and Simplications
Next we do a little pre-processing, by first converting our data to float32 and then
normalizing it to a range between [0,1]. This normalization will allow us to perform
an element-wise comparison at the pixel level, as we will see shortly. First, the type
conversion:
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
We then add some Gaussian noise to create the noisy dataset, and clip values that are
either smaller than 0 or larger than 1:
x_train_n = x_train + 0.5 *\
np.random.normal(loc=0.0, scale=0.4, size=x_train.shape)
x_test_n = x_test + 0.5 *\
np.random.normal(loc=0.0, scale=0.4, size=x_test.shape)
x_train_n = np.clip(x_train_n, 0., 1.)
x_test_n = np.clip(x_test_n, 0., 1.)
Now we declare the input layer (every image in the CIFAR10 dataset is 32×32 pixels
with RGB channels):
inp_img = Input(shape=(32, 32, 3))
Next, we start adding our usual “LEGO brick" layers. Our first layer is a 2D convolu‐
tion layer, where the first argument is the number of filters (and thus the number of
output images), and the second is the size of each filter. Like the other libraries, Keras
automatically identifies the shape of the input.
We use a 2×2 pooling layer, which reduces the total number of pixels per channel by
4, creating the desired bottleneck. After another convolutional layer, we regain the
same number of units for each channel by applying an up-sampling layer. This is
done by quadrupling each pixel in a pixel’s near vicinity (repeating the rows and col‐
umns of the data) to get back the same number of pixels in each image.
Finally, we add a convolutional output layer where we go back to three channels:
img = Conv2D(32, (3, 3), activation='relu', padding='same')(inp_img)
img = MaxPooling2D((2, 2), padding='same')(img)
img = Conv2D(32, (3, 3), activation='relu', padding='same')(img)
img = UpSampling2D((2, 2))(img)
decoded = Conv2D(3, (3, 3), activation='sigmoid', padding='same')(img)
We declare the functional model format, passing both inputs and outputs:
autoencoder = Model(inp_img, decoded)
Next we compile the model, defining the loss function and the optimizer—in this case
we use the Adagrad optimizer (just to show another example!). For denoising of the
images, we want our loss to capture the discrepancy between the decoded images and
TFLearn | 141

the original, pre-noise images. For that we use a binary cross-entropy loss, comparing
each decoded pixel to its corresponding original one (it’s now between [0,1]):
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')
After the model is defined, we fit it with 10 training epochs:
tensorboard = TensorBoard(log_dir='<some_path>',
histogram_freq=0, write_graph=True, write_images=True)
model_saver = ModelCheckpoint(
filepath='<some_path>',
verbose=0, period=2)
autoencoder.fit(x_train_n, x_train,
epochs=10,
batch_size=64,
shuffle=True,
validation_data=(x_test_n, x_test),
callbacks=[tensorboard, model_saver])
Hopefully the model will capture some internal structure, which it can later general‐
ize to other noisy images, and denoise them as a result.
We use our test set as validation data for loss evaluation at the end of each epoch (the
model will not be trained on this data), and also for visualization in TensorBoard. In
addition to the TensorBoard callback, we add a model saver callback and set it to save
our weights every two epochs.
Later, when we wish to load our weights, we need to reconstruct the network and
then use the Model.load_weights() method, passing our model as the first argument
and our saved weights file path as the second (more on saving models in Chapter 10):
inp_img = Input(shape=(32, 32, 3))
img = Conv2D(32, (3, 3), activation='relu', padding='same')(inp_img)
img = MaxPooling2D((2, 2), padding='same')(img)
img = Conv2D(32, (3, 3), activation='relu', padding='same')(img)
img = UpSampling2D((2, 2))(img)
decoded = Conv2D(3, (3, 3), activation='sigmoid', padding='same')(img)
autoencoder = Model(inp_img, decoded)
Model.load_weights(autoencoder,'some_path')
h5py requirement
For model saving, it is required that the h5py package is installed.
This package is primarily used for storing large amounts of data
and manipulating it from NumPy. You can install it using pip:
pip install h5py
142 | Chapter 7: TensorFlow Abstractions and Simplications
Figure 7-7 shows the denoised test images of our chosen category for different num‐
bers of training epochs.
Figure 7-7. Noisy CIFAR10 images before autoencoding (upper row) and aer autoen‐
coding (lower rows). e 4 bottom rows show results aer increasing number of training
epochs.
Keras also has a bunch of pretrained models to download, like inception, vgg, and
resnet. In the next and final section of this chapter, we will discuss these models and
show an example of how to download and use a pretrained VGG model for classifica‐
tion using the TF-Slim extension.
Pretrained models with TF-Slim
In this section of the chapter we will introduce the last abstraction to be covered here,
TF-Slim. TF-Slim stands out by offering simplified syntax for defining convolutional
neural networks in TensorFlow—its abstractions make it easy to build complex net‐
works in a clean, streamlined manner. Like Keras, it also offers a nice variety of pre‐
trained CNN models to download and use.
We start this section by learning about some of the general features and benefits of
TF-Slim, and why it’s a great tool to use for building CNNs. In the second part of this
section we will demonstrate how to download and deploy a pretrained model
(VGG) for image classification.
TFLearn | 143
TF-Slim
TF-Slim is a relatively new lightweight extension of TensorFlow that, like other
abstractions, allows us to define and train complex models quickly and
intuitively. TF-Slim doesn’t require any installation since it’s been merged with Ten‐
sorFlow.
This extension is all about convolutional neural networks. CNNs are notorious for
having a lot of messy boilerplate code. TF-Slim was designed with the goal of opti‐
mizing the creation of very complex CNN models so that they could be elegantly
written and easy to interpret and debug by using high-level layers, variable abstrac‐
tions, and argument scoping, which we will touch upon shortly.
In addition to enabling us to create and train our own models, TF-Slim has available
pretrained networks that can be easily downloaded, read, and used: VGG, AlexNet,
Inception, and more.
We start this section by briefly describing some of TF-Slim’s abstraction features.
Then we shift our focus to how to download and use a pretrained model, demonstrat‐
ing it for the VGG image classification model.
Creating CNN models with TF-Slim
With TF-Slim we can create a variable easily by defining its initialization, regulariza‐
tion, and device with one wrapper. For example, here we define weights initialized
from a truncated normal distribution using L2 regularization and placed on the CPU
(we will talk about distributing model parts across devices in Chapter 9):
import tensorflow as tf
from tensorflow.contrib import slim
W = slim.variable('w',shape=[7, 7, 3 , 3],
initializer=tf.truncated_normal_initializer(stddev=0.1),
regularizer=slim.l2_regularizer(0.07),
device='/CPU:0')
Like the other abstractions we’ve seen in this chapter, TF-Slim can reduce a lot of
boilerplate code and redundant duplication. As with Keras or TFLearn, we can define
a layer operation at an abstract level to include the convolution operation, weights
initialization, regularization, activation function, and more in a single command:
net = slim.conv2d(inputs, 64, [11, 11], 4, padding='SAME',
weights_initializer=tf.truncated_normal_initializer(stddev=0.01),
weights_regularizer=slim.l2_regularizer(0.0007), scope='conv1')
TF-Slim extends its elegance even beyond that, providing a clean way to replicate lay‐
ers compactly by using the repeat, stack, and arg_scope commands.
144 | Chapter 7: TensorFlow Abstractions and Simplications
repeat saves us the need to copy and paste the same line over and over so that, for
example, instead of having this redundant duplication:
net = slim.conv2d(net, 128, [3, 3], scope='con1_1')
net = slim.conv2d(net, 128, [3, 3], scope='con1_2')
net = slim.conv2d(net, 128, [3, 3], scope='con1_3')
net = slim.conv2d(net, 128, [3, 3], scope='con1_4')
net = slim.conv2d(net, 128, [3, 3], scope='con1_5')
we could just enter this:
net = slim.repeat(net, 5, slim.conv2d, 128, [3, 3], scope='con1')
But this is viable only in cases where we have layers of the same size. When this does
not hold, we can use the stack command, allowing us to concatenate layers of differ‐
ent shapes. So, instead of this:
net = slim.conv2d(net, 64, [3, 3], scope='con1_1')
net = slim.conv2d(net, 64, [1, 1], scope='con1_2')
net = slim.conv2d(net, 128, [3, 3], scope='con1_3')
net = slim.conv2d(net, 128, [1, 1], scope='con1_4')
net = slim.conv2d(net, 256, [3, 3], scope='con1_5')
we can write this:
slim.stack(net, slim.conv2d, [(64, [3, 3]), (64, [1, 1]),
(128, [3, 3]), (128, [1, 1]),
(256, [3, 3])], scope='con')
Finally, we also have a scoping mechanism referred to as arg_scope, allowing users to
pass a set of shared arguments to each operation defined in the same scope. Say, for
example, that we have four layers having the same activation function, initialization,
regularization, and padding. We can then simply use the slim.arg_scope command,
where we specify the shared arguments as in the following code:
with slim.arg_scope([slim.conv2d],
padding='VALID',
activation_fn=tf.nn.relu,
weights_initializer=tf.truncated_normal_initializer(stddev=0.02)
weights_regularizer=slim.l2_regularizer(0.0007)):
net = slim.conv2d(inputs, 64, [11, 11], scope='con1')
net = slim.conv2d(net, 128, [11, 11], padding='VALID', scope='con2')
net = slim.conv2d(net, 256, [11, 11], scope='con3')
net = slim.conv2d(net, 256, [11, 11], scope='con4')
The individual arguments inside the arg_scope command can still be overwritten,
and we can also nest one arg_scope inside another.
In these examples we used conv2d(): however, TF-Slim has many of the other stan‐
dard methods for building neural networks. Table 7-4 lists some of the available
options. For the full list, consult the documentation.
TFLearn | 145

Table 7-4. Available layer types in TF-Slim
Layer TF-Slim
BiasAdd slim.bias_add()
BatchNorm slim.batch_norm()
Conv2d slim.conv2d()
Conv2dInPlane slim.conv2d_in_plane()
Conv2dTranspose (Deconv) slim.conv2d_transpose()
FullyConnected slim.fully_connected()
AvgPool2D slim.avg_pool2d()
Dropout slim.dropout()
Flatten slim.flatten()
MaxPool2D slim.max_pool2d()
OneHotEncoding slim.one_hot_encoding()
SeparableConv2 slim.separable_conv2d()
UnitNorm slim.unit_norm
To illustrate how convenient TF-Slim is for creating complex CNNs, we will build the
VGG model by Karen Simonyan and Andrew Zisserman that was introduced in
2014 (see the upcoming note for more information). VGG serves as a good illustra‐
tion of how a model with many layers can be created compactly using TF-Slim. Here
we construct the 16-layer version: 13 convolution layers plus 3 fully connected layers.
Creating it, we take advantage of two of the features we’ve just mentioned:
1. We use the arg_scope feature since all of the convolution layers have the same
activation function and the same regularization and initialization.
2. Many of the layers are exact duplicates of others, and therefore we also take
advantage of the repeat command.
The result very compelling—the entire model is defined with just 16 lines of code:
with slim.arg_scope([slim.conv2d, slim.fully_connected],
activation_fn=tf.nn.relu,
weights_initializer=tf.truncated_normal_initializer(0.0, 0.01),
weights_regularizer=slim.l2_regularizer(0.0005)):
net = slim.repeat(inputs, 2, slim.conv2d, 64, [3, 3], scope='con1')
net = slim.max_pool2d(net, [2, 2], scope='pool1')
net = slim.repeat(net, 2, slim.conv2d, 128, [3, 3], scope='con2')
net = slim.max_pool2d(net, [2, 2], scope='pool2')
net = slim.repeat(net, 3, slim.conv2d, 256, [3, 3], scope='con3')
net = slim.max_pool2d(net, [2, 2], scope='pool3')
net = slim.repeat(net, 3, slim.conv2d, 512, [3, 3], scope='con4')
net = slim.max_pool2d(net, [2, 2], scope='pool4')
net = slim.repeat(net, 3, slim.conv2d, 512, [3, 3], scope='con5')
net = slim.max_pool2d(net, [2, 2], scope='pool5')
net = slim.fully_connected(net, 4096, scope='fc6')
146 | Chapter 7: TensorFlow Abstractions and Simplications

net = slim.dropout(net, 0.5, scope='dropout6')
net = slim.fully_connected(net, 4096, scope='fc7')
net = slim.dropout(net, 0.5, scope='dropout7')
net = slim.fully_connected(net, 1000, activation_fn=None, scope='fc8')
VGG and the ImageNet Challenge
The ImageNet project is a large database of images collected for the
purpose of researching visual object recognition. As of 2016 it con‐
tained over 10 million hand-annotated images.
Each year (since 2010) a competition takes place called the Image‐
Net Large Scale Visual Recognition Challenge (ILSVRC), where
research teams try to automatically classify, detect, and localize
objects and scenes in a subset of the ImageNet collection. In the
2012 challenge, dramatic progress occurred when a deep convolu‐
tional neural net called AlexNet, created by Alex Krizhevsky, man‐
aged to get a top 5 (top 5 chosen categories) classification error of
only 15.4%, winning the competition by a large margin.
Over the next couple of years the error rate kept falling, from
ZFNet with 14.8% in 2013, to GoogLeNet (introducing the Incep‐
tion module) with 6.7% in 2014, to ResNet with 3.6% in 2015. The
Visual Geometry Group (VGG) was another CNN competitor in
the 2014 competition that also achieved an impressive low error
rate (7.3%). A lot of people prefer VGG over GoogLeNet because it
has a nicer, simpler architecture.
In VGG the only spatial dimensions used are very small 3×3 filters
with a stride of 1 and a 2×2 max pooling, again with a stride of 1.
Its superiority is achieved by the number of layers it uses, which is
between 16 and 19.
Downloading and using a pretrained model
Next we will demonstrate how to download and deploy a pretrained VGG model.
First we need to clone the repository where the actual models will reside by running:
git clone https://github.com/tensorflow/models
Now we have the scripts we need for modeling on our computer, and we can use
them by setting the path:
import sys
sys.path.append("<some_path> + models/slim")
Next we will download the pretrained VGG-16 (16 layers) model—it is available on
GitHub, as are other models, such as Inception, ResNet, and more:
TFLearn | 147
from datasets import dataset_utils
import tensorflow as tf
target_dir = '<some_path> + vgg/vgg_checkpoints'
The downloaded checkpoint file contains information about both the model and the
variables. Now we want to load it and use it for classification of new images.
However, before that we first have to prepare our input image, turning it into a reada‐
ble TensorFlow format and performing a little pre-processing to make sure that it is
resized to match the size of the images the model was trained on.
We can load the image into TensorFlow either as a URL link or as a desktop image.
For a URL link, we can load the image as a string with urllib2 (this needs to be
imported), and then decode it into a Tensor by using tf.image_decode_jpeg():
import urllib2
url = ("https://somewebpage/somepicture.jpg")
im_as_string = urllib2.urlopen(url).read()
im = tf.image.decode_jpeg(im_as_string, channels=3)
Or, for PNG:
im = tf.image.decode_png(im_as_string, channels=3)
To load an image from our computer, we can create a queue of our filenames in the
target directory, and then read the entire image file by using tf.WholeFileReader():
filename_queue = tf.train.string_input_producer(
tf.train.match_filenames_once("./images/*.jpg"))
image_reader = tf.WholeFileReader()
_, image_file = image_reader.read(filename_queue)
image = tf.image.decode_jpeg(image_file)
Don’t worry about the details for this step; we will discuss queues and reading data in
much more depth in Chapter 8.
Next we want to resize the image so that it matches the size of the images VGG was
trained on. For that, we first extract the desired size from the VGG script (in this case,
it is 224):
from nets import vgg
image_size = vgg.vgg_16.default_image_size
Then we feed the raw image and the image size to the VGG pre-processing unit,
where the image will be resized with a preserved aspect ratio (the width-to-height
ratio of the image) and then cropped:
from preprocessing import vgg_preprocessing
processed_im = vgg_preprocessing.preprocess_image(image,
image_size,
image_size,
is_training=False)
148 | Chapter 7: TensorFlow Abstractions and Simplications
Next we use tf.expand_dims() to insert a dimension of 1 into a tensor’s shape. This
is done to add a batch dimension to a single element (changing [height, width,
channels] to [1, height, width, channels]):
processed_images = tf.expand_dims(processed_im, 0)
Now we create the model from the script we cloned earlier. We pass the model func‐
tion the images and number of classes. The model has shared arguments; therefore,
we call it using arg_scope, as we saw earlier, and use the vgg_arg_scope() function
in the script to define the shared arguments. The function is shown in the following
code snippet.
vgg_16() returns the logits (numeric values acting as evidence for each class), which
we can then turn into probabilities by using tf.nn.softmax(). We use the argument
is_training to indicate that we are interested in forming predictions rather than
training:
with slim.arg_scope(vgg.vgg_arg_scope()):
logits, _ = vgg.vgg_16(processed_images,
num_classes=1000,
is_training=False)
probabilities = tf.nn.softmax(logits)
def vgg_arg_scope(weight_decay=0.0005):
with slim.arg_scope([slim.conv2d, slim.fully_connected],
activation_fn=tf.nn.relu,
weights_regularizer=slim.l2_regularizer(weight_decay),
biases_initializer=tf.zeros_initializer):
with slim.arg_scope([slim.conv2d], padding='SAME') as arg_sc:
return arg_sc
Now, just before starting the session, we need to load the variables we downloaded
using slim.assign_from_checkpoint_fn(), to which we pass the containing direc‐
tory:
import os
load_vars = slim.assign_from_checkpoint_fn(
os.path.join(target_dir, 'vgg_16.ckpt'),
slim.get_model_variables('vgg_16'))
Finally, the main event—we run the session, load the variables, and feed in the images
and the desired probabilities.
We can get the class names by using the following lines:
from datasets import imagenet
imagenet.create_readable_names_for_imagenet_labels()
We extract the five classes with the highest probabilities for our given image, and the
probabilities as well:
TFLearn | 149

names = []
with tf.Session() as sess:
load_vars(sess)
network_input, probabilities = sess.run([processed_images,
probabilities])
probabilities = probabilities[0, 0:]
names_ = imagenet.create_readable_names_for_imagenet_labels()
idxs = np.argsort(-probabilities)[:5]
probs = probabilities[idxs]
classes = np.array(names_.values())[idxs+1]
for c,p in zip(classes,probs):
print('Class: '+ c + ' |Prob: ' + str(p))
In this example we passed the image shown in Figure 7-8 as input to the pretrained
VGG model.
Figure 7-8. A lakeside in Switzerland.
Here are the output results for the top-five chosen classes and their probabilities:
Output:
Class: lakeside, lakeshore |Prob: 0.365693
Class: pelican |Prob: 0.163627
Class: dock, dockage, docking facility |Prob: 0.0608374
Class: breakwater, groin, groyne, mole, bulwark, seawall, jetty |Prob: 0.0393285
Class: speedboat |Prob: 0.0391587
150 | Chapter 7: TensorFlow Abstractions and Simplications
As you can see, the classifier does quite well at capturing different elements in this
image.
Summary
We started this chapter by discussing the importance of abstractions, followed by
high-level coverage and then focusing in on some of the popular TensorFlow exten‐
sions: contrib.learn, TFLearn, Keras, and TF-Slim. We revisited models from previ‐
ous chapters, using out-of-the-box contrib.learn linear regression and linear
classification models. We then saw how to use the FeatureColumn abstraction for fea‐
ture handling and pre-processing, incorporate TensorBoard, and create our own cus‐
tom estimator. We introduced TFLearn and exemplified how easily CNN and RNN
models can be constructed with it. Using Keras, we demonstrated how to implement
an autoencoder. Finally, we created complex CNN models with TF-Slim and deployed
a pretrained model.
In the next chapters we cover scaling up, with queuing and threading, distributed
computing, and model serving.
Summary | 151
CHAPTER 8
Queues, Threads, and Reading Data
In this chapter we introduce the use of queues and threads in TensorFlow, with the
main motivation of streamlining the process of reading input data. We show how to
write and read TFRecords, the efficient TensorFlow file format. We then demonstrate
queues, threads, and related functionalities, and connect all the dots in a full working
example of a multithreaded input pipeline for image data that includes pre-
processing, batching, and training.
The Input Pipeline
When dealing with small datasets that can be stored in memory, such as MNIST
images, it is reasonable to simply load all data into memory, then use feeding to push
data into a TensorFlow graph. For larger datasets, however, this can become
unwieldy. A natural paradigm for handling such cases is to keep the data on disk and
load chunks of it as needed (such as mini-batches for training), such that the only
limit is the size of your hard drive.
In addition, in many cases in practice, a typical data pipeline often includes steps
such as reading input files with different formats, changing the shape or structure of
input, normalizing or doing other forms of pre-processing, and shuffling the input,
all before training has even started.
Much of this process can trivially be decoupled and broken into modular
components. Pre-processing, for example, does not involve training, and thus naively
inputs can be preprocessed all at once and then fed to training. Since our training
works on batches of examples in any case, we could in principle handle batches of
inputs on the fly, reading them from disk, applying pre-processing, and then feeding
them into the computational graph for training.
153
This approach, however, can be wasteful. Because pre-processing is independent of
training, waiting for each batch to be pre-processed would lead to severe I/O latency,
forcing each training step to (impatiently) wait for mini-batches of data to be loaded
and processed. A more scalable practice would be to prefetch the data and use inde‐
pendent threads for loading and processing and for training. But this practice, in
turn, could become messy when working with many files kept on disk that need to be
repeatedly read and shuffled, and require a fair amount of bookkeeping and techni‐
calities to run seamlessly.
It’s important to note that even without taking pre-processing into consideration,
using the standard feeding mechanism (with a feed_dict) we saw in previous chap‐
ters is wasteful in itself. feed_dict does a single-threaded copy of data from the
Python runtime to the TensorFlow runtime, causing further latency and slow‐
downs. We would like to avoid this by somehow reading data directly into native Ten‐
sorFlow.
To make our lives easier (and faster), TensorFlow comes with a set of tools to stream‐
line this input-pipeline process. The main building blocks are a standard TensorFlow
file format, utilities for encoding and decoding this format, queues of data, and multi‐
threading.
We will go over these key components one by one, exploring how they work and
building toward an end-to-end multithreaded input pipeline. We begin by introduc‐
ing TFRecords, the recommended file format for TensorFlow, which will come in
useful later on.
TFRecords
Datasets, of course, can come in many formats, sometimes even mixed (such as
images and audio files). It can often be convenient—and useful—to convert input files
into one unifying format, regardless of their original formats. TensorFlow’s default,
standard data format is the TFRecord. A TFRecord file is simply a binary file, con‐
taining serialized input data. Serialization is based on protocol buffers (proto‐
bufs), which in plain words convert data for storage by using a schema describing the
data structure, independently of what platform or language is being used (much like
XML).
In our setting, using TFRecords (and protobufs/binary files in general) has many
advantages over just working with raw data files. This unified format allows for a tidy
way to organize input data, with all relevant attributes for an input instance kept
together, avoiding the need for many directories and subdirectories. TFRecord files
enable very fast processing. All data is kept in one block of memory, as opposed to
storing each input file separately, cutting the time needed to read data from memory.
It’s also important to note that TensorFlow comes with many implementations and
154 | Chapter 8: Queues, Threads, and Reading Data
utilities optimized for TFRecords, making it well suited for use as part of a multi‐
threaded input pipeline.
Writing with TFRecordWriter
We begin by writing our input files to TFRecord format, to allow us to work with
them (in other cases, we may already have the data stored in this format). In this
example we will convert MNIST images to this format, but the same ideas carry on to
other types of data.
First, we download the MNIST data to save_dir, using a utility function from tensor
flow.contrib.learn:
from __future__ import print_function
import os
import tensorflow as tf
from tensorflow.contrib.learn.python.learn.datasets import mnist
save_dir = "path/to/mnist"
# Download data to save_dir
data_sets = mnist.read_data_sets(save_dir,
dtype=tf.uint8,
reshape=False,
validation_size=1000)
Our downloaded data includes train, test, and validation images, each in a separate
split. We go over each split, putting examples in a suitable format and using TFRecord
Writer() to write to disk:
data_splits = ["train","test","validation"]
for d in range(len(data_splits)):
print("saving " + data_splits[d])
data_set = data_sets[d]
filename = os.path.join(save_dir, data_splits[d] + '.tfrecords')
writer = tf.python_io.TFRecordWriter(filename)
for index in range(data_set.images.shape[0]):
image = data_set.images[index].tostring()
example = tf.train.Example(features=tf.train.Features(feature={
'height': tf.train.Feature(int64_list=
tf.train.Int64List(value=
[data_set.images.shape[1]])),
'width': tf.train.Feature(int64_list=
tf.train.Int64List(value =
[data_set.images.shape[2]])),
'depth': tf.train.Feature(int64_list=
tf.train.Int64List(value =
[data_set.images.shape[3]])),
'label': tf.train.Feature(int64_list=
tf.train.Int64List(value =
TFRecords | 155
[int(data_set.labels[index])])),
'image_raw': tf.train.Feature(bytes_list=
tf.train.BytesList(value =
[image]))}))
writer.write(example.SerializeToString())
writer.close()
Let’s break this code down to understand the different components.
We first instantiate a TFRecordWriter object, giving it the path corresponding to the
data split:
filename = os.path.join(save_dir, data_splits[d] + '.tfrecords')
writer = tf.python_io.TFRecordWriter(filename)
We then go over each image, converting it from a NumPy array to a byte string:
image = data_set.images[index].tostring()
Next, we convert images to their protobuf format. tf.train.Example is a structure
for storing our data. An Example object contains a Features object, which in turn
contains a map from attribute name to a Feature. A Feature can contain an
Int64List, a BytesList, or a FloatList (not used here). For example, here we
encode the label of the image:
tf.train.Feature(int64_list=tf.train.Int64List(value =
[int(data_set.labels[index])]))
And here is the encoding for the actual raw image:
tf.train.Feature(bytes_list=tf.train.BytesList(value =[image]))
Let’s take a look at what our saved data looks like. We do this with
tf.python_io.tf_record_iterator, an iterator that reads records from a TFRecords
file:
filename = os.path.join(save_dir, 'train.tfrecords')
record_iterator = tf.python_io.tf_record_iterator(filename)
seralized_img_example= next(record_iterator)
serialized_img is a byte string. To recover the structure we used when saving the
image to a TFRecord, we parse this byte string, allowing us to access all the attributes
we stored earlier:
example = tf.train.Example()
example.ParseFromString(seralized_img_example)
image = example.features.feature['image_raw'].bytes_list.value
label = example.features.feature['label'].int64_list.value[0]
width = example.features.feature['width'].int64_list.value[0]
height = example.features.feature['height'].int64_list.value[0]
Our image was saved as a byte string too, so we convert it back to a NumPy array and
reshape it back to a tensor with shape (28,28,1):
156 | Chapter 8: Queues, Threads, and Reading Data
img_flat = np.fromstring(image[0], dtype=np.uint8)
img_reshaped = img_flat.reshape((height, width, -1))
This basic example should have given you a feel for TFRecords and how to write and
read them. In practice, we will typically want to read TFRecords into a queue of pre‐
fetched data as part of a multithreaded process. In the next section, we first introduce
TensorFlow queues before showing how to use them with TFRecords.
Queues
A TensorFlow queue is similar to an ordinary queue, allowing us to enqueue new
items, dequeue existing items, etc. The important difference from ordinary queues is
that, just like anything else in TensorFlow, the queue is part of a computational graph.
Its operations are symbolic as usual, and other nodes in the graph can alter its state
(much like with Variables). This can be slightly confusing at first, so let’s walk through
some examples to get acquainted with basic queue functionalities.
Enqueuing and Dequeuing
Here we create a rst-in, rst-out (FIFO) queue of strings, with a maximal number of
10 elements that can be stored in the queue. Since queues are part of a computational
graph, they are run within a session. In this example, we use a tf.InteractiveSes
sion():
import tensorflow as tf
sess= tf.InteractiveSession()
queue1 = tf.FIFOQueue(capacity=10,dtypes=[tf.string])
Behind the scenes, TensorFlow creates a memory buffer for storing the 10 items.
Just like any other operation in TensorFlow, to add items to the queue, we create an
op:
enque_op = queue1.enqueue(["F"])
Since you are by now familiar with the concept of a computational graph in Tensor‐
Flow, it should be no surprise that defining the enque_op does not add anything to
the queue—we need to run the op. So, if we look at the size of queue1 before running
the op, we get this:
sess.run(queue1.size())
Out:
0
After running the op, our queue now has one item populating it:
enque_op.run()
sess.run(queue1.size())
Queues | 157
Out:
1
Let’s add some more items to queue1, and look at its size again:
enque_op = queue1.enqueue(["I"])
enque_op.run()
enque_op = queue1.enqueue(["F"])
enque_op.run()
enque_op = queue1.enqueue(["O"])
enque_op.run()
sess.run(queue1.size())
Out:
4
Next, we dequeue items. Dequeuing too is an op, whose output evaluates to a tensor
corresponding to the dequeued item:
x = queue1.dequeue()
x.eval()
Out: b'F'
x.eval()
Out: b'I'
x.eval()
Out: b'F'
x.eval()
Out: b'O'
Note that if we were to run xs.eval() one more time, on an empty queue, our main
thread would hang forever. As we will see later in this chapter, in practice we use code
that knows when to stop dequeuing and avoid hanging.
Another way to dequeue is by retrieving multiple items at once, with the
dequeue_many() operation. This op requires that we specify the shape of items in
advance:
queue1 = tf.FIFOQueue(capacity=10,dtypes=[tf.string],shapes=[()])
Here we fill the queue exactly as before, and then dequeue four items at once:
inputs = queue1.dequeue_many(4)
inputs.eval()
Out:
array([b'F', b'I', b'F', b'O'], dtype=object)
158 | Chapter 8: Queues, Threads, and Reading Data
Multithreading
A TensorFlow session is multithreaded—multiple threads can use the same session
and run ops in parallel. Individual ops have parallel implementations that are used by
default with multiple CPU cores or GPU threads. However, if a single call to
sess.run() does not make full use of the available resources, one can increase
throughput by making multiple parallel calls. For example, in a typical scenario, we
may have multiple threads apply pre-processing to images and push them into a
queue, while another thread pulls pre-processed images from the queue for training
(in the next chapter, we will discuss distributed training, which is conceptually
related, with important differences).
Let’s walk our way through a few simple examples introducing threading in Tensor‐
Flow and the natural interplay with queues, before connecting all the dots later on in
a full example with MNIST images.
We start by creating a FIFO queue with capacity of 100 items, where each item is a
random float generated with tf.random_normal():
from __future__ import print_function
import threading
import time
gen_random_normal = tf.random_normal(shape=())
queue = tf.FIFOQueue(capacity=100,dtypes=[tf.float32],shapes=())
enque = queue.enqueue(gen_random_normal)
def add():
for i in range(10):
sess.run(enque)
Note, again, that the enque op does not actually add the random numbers to the
queue (and they are not yet generated) prior to graph execution. Items will be
enqueued using the function add() we create that adds 10 items to the queue by call‐
ing sess.run() multiple times.
Next, we create 10 threads, each running add() in parallel, thus each pushing 10
items to the queue, asynchronously. We could think (for now) of these random num‐
bers as training data being added into a queue:
Queues | 159
threads = [threading.Thread(target=add, args=()) for i in range(10)]
threads
Out:
[<Thread(Thread-77, initial)>,
<Thread(Thread-78, initial)>,
<Thread(Thread-79, initial)>,
<Thread(Thread-80, initial)>,
<Thread(Thread-81, initial)>,
<Thread(Thread-82, initial)>,
<Thread(Thread-83, initial)>,
<Thread(Thread-84, initial)>,
<Thread(Thread-85, initial)>,
<Thread(Thread-86, initial)>]
We have created a list of threads, and now we execute them, printing the size of the
queue at short intervals as it grows from 0 to 100:
for t in threads:
t.start()
print(sess.run(queue.size()))
time.sleep(0.01)
print(sess.run(queue.size()))
time.sleep(0.01)
print(sess.run(queue.size()))
Out:
10
84
100
Finally, we dequeue 10 items at once with dequeue_many(), and examine the results:
x = queue.dequeue_many(10)
print(x.eval())
sess.run(queue.size())
Out:
[ 0.05863889 0.61680967 1.05087686 -0.29185265 -0.44238046 0.53796548
-0.24784896 0.40672767 -0.88107938 0.24592835]
90
Coordinator and QueueRunner
In realistic scenarios (as we shall see later in this chapter), it can be more complicated
to run multiple threads effectively. Threads should be able to stop properly (to avoid
“zombie” threads, for example, or to close all threads together when one fails), queues
need to be closed after stopping, and there are other technical but important issues
that need to be addressed.
160 | Chapter 8: Queues, Threads, and Reading Data
TensorFlow comes equipped with tools to help us in this process. Key among them
are tf.train.Coordinator, for coordinating the termination of a set of threads, and
tf.train.QueueRunner, which streamlines the process of getting multiple threads to
enqueue data with seamless cooperation.
tf.train.Coordinator
We first demonstrate how to use tf.train.Coordinator with a simple, toy example.
In the next section, we’ll see how to use it as part of a real input pipeline.
We use the code similar to that in the previous section, altering the add() function
and adding a coordinator:
gen_random_normal = tf.random_normal(shape=())
queue = tf.FIFOQueue(capacity=100,dtypes=[tf.float32],shapes=())
enque = queue.enqueue(gen_random_normal)
def add(coord,i):
while not coord.should_stop():
sess.run(enque)
if i == 11:
coord.request_stop()
coord = tf.train.Coordinator()
threads = [threading.Thread(target=add, args=(coord,i)) for i in range(10)]
coord.join(threads)
for t in threads:
t.start()
print(sess.run(queue.size()))
time.sleep(0.01)
print(sess.run(queue.size()))
time.sleep(0.01)
print(sess.run(queue.size()))
10
100
100
Any thread can call coord.request_stop() to get all other threads to stop. Threads
typically run loops that check whether to stop, using coord.should_stop(). Here, we
pass the thread index i to add(), and use a condition that is never satisfied (i==11) to
request a stop. Thus, our threads complete their job, adding the full 100 items to the
queue. However, if we were to alter add() as follows:
def add(coord,i):
while not coord.should_stop():
sess.run(enque)
if i == 1:
coord.request_stop()
Queues | 161
then thread i=1 would use the coordinator to request all threads to stop, stopping all
enqueueing early:
print(sess.run(queue.size()))
time.sleep(0.01)
print(sess.run(queue.size()))
time.sleep(0.01)
print(sess.run(queue.size()))
Out:
10
17
17
tf.train.QueueRunner and tf.RandomShueQueue
While we can create a number of threads that repeatedly run an enqueue op, it is bet‐
ter practice to use the built-in tf.train.QueueRunner, which does exactly that, while
closing the queue upon an exception.
Here we create a queue runner that will run four threads in parallel to enqueue items:
gen_random_normal = tf.random_normal(shape=())
queue = tf.RandomShuffleQueue(capacity=100,dtypes=[tf.float32],
min_after_dequeue=1)
enqueue_op = queue.enqueue(gen_random_normal)
qr = tf.train.QueueRunner(queue, [enqueue_op] * 4)
coord = tf.train.Coordinator()
enqueue_threads = qr.create_threads(sess, coord=coord, start=True)
coord.request_stop()
coord.join(enqueue_threads)
Note that qr.create_threads() takes our session as an argument, along with our
coordinator.
In this example, we used a tf.RandomShuffleQueue rather than the FIFO queue. A
RandomShuffleQueue is simply a queue with a dequeue op that pops items in random
order. This is useful when training deep neural networks with stochastic gradient-
descent optimization, which requires shuffling the data. The min_after_dequeue
argument specifies the minimum number of items that will remain in the queue after
calling a dequeue op—a bigger number entails better mixing (random sampling), but
more memory.
A Full Multithreaded Input Pipeline
We now put all the pieces together in a working example with MNIST images, from
writing data to TensorFlow’s efficient file format, through data loading and pre-
processing, to training a model. We do so by building on the queuing and multi‐
162 | Chapter 8: Queues, Threads, and Reading Data
threading functionality demonstrated earlier, and along the way introduce some more
useful components for reading and processing data in TensorFlow.
First, we write the MNIST data to TFRecords, with the same code we used at the start
of this chapter:
from __future__ import print_function
import os
import tensorflow as tf
from tensorflow.contrib.learn.python.learn.datasets import mnist
import numpy as np
save_dir = "path/to/mnist"
# Download data to save_dir
data_sets = mnist.read_data_sets(save_dir,
dtype=tf.uint8,
reshape=False,
validation_size=1000)
data_splits = ["train","test","validation"]
for d in range(len(data_splits)):
print("saving " + data_splits[d])
data_set = data_sets[d]
filename = os.path.join(save_dir, data_splits[d] + '.tfrecords')
writer = tf.python_io.TFRecordWriter(filename)
for index in range(data_set.images.shape[0]):
image = data_set.images[index].tostring()
example = tf.train.Example(features=tf.train.Features(feature={
'height': tf.train.Feature(int64_list=
tf.train.Int64List(value=
[data_set.images.shape[1]])),
'width': tf.train.Feature(int64_list=
tf.train.Int64List(value =
[data_set.images.shape[2]])),
'depth': tf.train.Feature(int64_list=
tf.train.Int64List(value =
[data_set.images.shape[3]])),
'label': tf.train.Feature(int64_list=
tf.train.Int64List(value =
[int(data_set.labels[index])])),
'image_raw': tf.train.Feature(bytes_list=
tf.train.BytesList(value =
[image]))}))
writer.write(example.SerializeToString())
writer.close()
A Full Multithreaded Input Pipeline | 163
tf.train.string_input_producer() and tf.TFRecordReader()
tf.train.string_input_producer() simply creates a QueueRunner behind the
scenes, outputting filename strings to a queue for our input pipeline. This filename
queue will be shared among multiple threads:
filename = os.path.join(save_dir ,"train.tfrecords")
filename_queue = tf.train.string_input_producer(
[filename], num_epochs=10)
The num_epochs argument tells string_input_producer() to produce each filename
string num_epochs times.
Next, we read files from this queue using TFRecordReader(), which takes a queue of
filenames and dequeues filename by filename off the filename_queue. Inter‐
nally, TFRecordReader() uses the state of the graph to keep track of the location of
the TFRecord being read, as it loads “chunk after chunk” of input data from the disk:
reader = tf.TFRecordReader()
_, serialized_example = reader.read(filename_queue)
features = tf.parse_single_example(
serialized_example,
features={
'image_raw': tf.FixedLenFeature([], tf.string),
'label': tf.FixedLenFeature([], tf.int64),
})
tf.train.shue_batch()
We decode the raw byte string data, do (very) basic pre-processing to convert pixel
values to floats, and then shuffle the image instances and collect them into
batch_size batches with tf.train.shuffle_batch(), which internally uses a Random
ShuffleQueue and accumulates examples until it contains batch_size +
min_after_dequeue elements:
image = tf.decode_raw(features['image_raw'], tf.uint8)
image.set_shape([784])
image = tf.cast(image, tf.float32) * (1. / 255) - 0.5
label = tf.cast(features['label'], tf.int32)
# Randomly collect instances into batches
images_batch, labels_batch = tf.train.shuffle_batch(
[image, label], batch_size=128,
capacity=2000,
min_after_dequeue=1000)
The capacity and min_after_dequeue parameters are used in the same manner as
discussed previously. The mini-batches that are returned by shuffle_batch() are the
result of a dequeue_many() call on the RandomShuffleQueue that is created internally.
164 | Chapter 8: Queues, Threads, and Reading Data
tf.train.start_queue_runners() and Wrapping Up
We define our simple softmax classification model as follows:
W = tf.get_variable("W", [28*28, 10])
y_pred = tf.matmul(images_batch, W)
loss = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y_pred,
labels=labels_batch)
loss_mean = tf.reduce_mean(loss)
train_op = tf.train.AdamOptimizer().minimize(loss)
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
init = tf.local_variables_initializer()
sess.run(init)
Finally, we create threads that enqueue data to queues by calling
tf.train.start_queue_runners(). Unlike other calls, this one is not symbolic and
actually creates the threads (and thus needs to be done after initialization):
from __future__ import print_function
# Coordinator
coord = tf.train.Coordinator()
threads = tf.train.start_queue_runners(sess=sess,coord=coord)
Let’s take a look at the list of created threads:
threads
Out:
[<Thread(Thread-483, stopped daemon 13696)>,
<Thread(Thread-484, started daemon 16376)>,
<Thread(Thread-485, started daemon 4320)>,
<Thread(Thread-486, started daemon 13052)>,
<Thread(Thread-487, started daemon 7216)>,
<Thread(Thread-488, started daemon 4332)>,
<Thread(Thread-489, started daemon 16820)>]
Having everything in place, we are now ready to run the multithreaded process, from
reading and pre-processing batches into a queue to training a model. It’s important to
note that we do not use the familiar feed_dict argument anymore—this avoids data
copies and offers speedups, as discussed earlier in this chapter:
A Full Multithreaded Input Pipeline | 165

try:
step = 0
while not coord.should_stop():
step += 1
sess.run([train_op])
if step%500==0:
loss_mean_val = sess.run([loss_mean])
print(step)
print(loss_mean_val)
except tf.errors.OutOfRangeError:
print('Done training for %d epochs, %d steps.' % (NUM_EPOCHS, step))
finally:
# When done, ask the threads to stop
coord.request_stop()
# Wait for threads to finish
coord.join(threads)
sess.close()
We train until a tf.errors.OutOfRangeError error is thrown, indicating that queues
are empty and we are done:
Out:
Done training for 10 epochs, 2299500 steps.
Future input pipeline
In mid-2017, the TensorFlow development team announced the
Dataset API, a new preliminary input pipeline abstraction offering
some simplifications and speedups. The concepts presented in this
chapter, such as TFRecords and queues, are fundamental and
remain at the core of TensorFlow and its input pipeline process.
TensorFlow is still very much a work in progress, and exciting and
important changes naturally occur from time to time. See the issue
tracker for an ongoing discussion.
Summary
In this chapter, we saw how to use queues and threads in TensorFlow, and how to cre‐
ate a multithreaded input pipeline. This process can help increase throughput and
utilization of resources. In the next chapter, we take this a step forward and show how
to work in a distributed setting with TensorFlow, across multiple devices and
machines.
166 | Chapter 8: Queues, Threads, and Reading Data
CHAPTER 9
Distributed TensorFlow
In this chapter we discuss the use of TensorFlow for distributed computing. We start
by briefly surveying the different approaches to distributing model training in
machine learning in general, and specifically for deep learning. We then introduce the
elements of TensorFlow designed to support distributed computing, and finally put
everything together with an end-to-end example.
Distributed Computing
Distributed computing, in the most general terms, entails the utilization of more than
one component in order to perform the desired computation or achieve a goal. In our
case, this means using multiple machines in order to speed up the training of a deep
learning model.
The basic idea behind this is that by using more computing power, we should be able
to train the same model faster. This is indeed often the case, although just how much
faster depends on many factors (i.e., if you expect to use 10× resources and get a 10×
speedup, you are most likely going to be disappointed!).
There are many ways to distribute computations in a machine learning setting. You
may want to utilize multiple devices, either on the same machine or across a cluster.
When training a single model, you may want to compute gradients across a cluster to
speed up training, either synchronously or asynchronously. A cluster may also be
used to train multiple models at the same time, or in order to search for the optimal
parameters for a single model.
In the following subsections we map out these many aspects of parallelism.
167
Where Does the Parallelization Take Place?
The first split in the classification of types of parallelization is the location. Are we
using multiple computing devices on a single machine or across a cluster?
It is becoming increasingly common to have powerful hardware with multiple devices
on a single machine. Cloud providers (such as Amazon Web Services) now offer this
sort of platform set up and ready to go.
Whether in the cloud or on premises, a cluster configuration affords more flexibility
in design and evolution, and the setup can grow way beyond what is currently feasi‐
ble with multiple devices on the same board (essentially, you can use a cluster of arbi‐
trary size).
On the other hand, while several devices on the same board can use shared memory,
the cluster approach introduces the time cost of communication between nodes. This
can become a limiting factor, when the amount of information that has to be shared is
large and communication is relatively slow.
What Is the Goal of Parallelization?
The second split is the actual goal. Do we want to use more hardware to make the
same process faster, or in order to parallelize the training of multiple models?
The need to train multiple models often arises in development stages where a choice
needs to be made regarding either the models or the hyperparameters to use. In this
case it is common to run several options and choose the best-performing one. It is
natural to do so in parallel.
Alternatively, when training a single (often large) model, a cluster may be used in
order to speed up training. In the most common approach, known as data parallel‐
ism, the same model structure exists on each computation device separately, and the
data running through each copy is what is parallelized.
For example, when training a deep learning model with gradient descent, the process
is composed of the following steps:
1. Compute the gradients for a batch of training examples.
2. Sum the gradients.
3. Apply an update to the model parameters accordingly.
Clearly, step 1 of this schema lends itself to parallelization. Simply use multiple devi‐
ces to compute the gradients (with respect to different training examples), and then
aggregate the results and sum them up in step 2, just as in the regular case.
168 | Chapter 9: Distributed TensorFlow

Synchronous versus asynchronous data parallelism
In the process just described, gradients from different training
examples are aggregated together, in order to make a single update
to the model parameters. This is what is known as synchronous
training, since the summation step defines a point where the flow
has to wait for all of the nodes to complete the gradient computa‐
tion.
One case where it might be better to avoid this is when there are
heterogeneous computing resources being used together, since the
synchronous option entails waiting for the slowest of the nodes.
The alternative, asynchronous option is to apply the update step
independently after each node finishes computing the gradients for
the training examples it was assigned.
TensorFlow Elements
In this section we go over the TensorFlow elements and concepts that are used in par‐
allel computations. This is not a complete overview, and primarily serves as an intro‐
duction to the parallel example that concludes this chapter.
tf.app.ags
We start with a mechanism that is completely unrelated to parallel computing, but is
essential for our example at the end of the chapter. Indeed, the flags mechanism is
heavily used in TensorFlow examples and deserves to be discussed.
Essentially, tf.app.flags is a wrapper for the Python argparse module, which is
commonly used to process command-line arguments, with some extra and specific
functionality.
Consider, for instance, a Python command-line program with typical command-line
arguments:
'python distribute.py --job_name="ps" --task_index=0'
The program distribute.py is passed the following:
job_name="ps"
task_index=0
This information is then extracted within the Python script, by using:
tf.app.flags.DEFINE_string("job_name", "", "name of job")
tf.app.flags.DEFINE_integer("task_index", 0, "Index of task")
The arguments (both string and integer) are defined by the name in the command
line, a default value, and a description of the argument.
TensorFlow Elements | 169
The flags mechanism allows the following types of arguments:
•tf.app.flags.DEFINE_string defines a string value.
•tf.app.flags.DEFINE_boolean defines a Boolean value.
•tf.app.flags.DEFINE_float defines a floating-point value.
•tf.app.flags.DEFINE_integer defines an integer value.
Finally, tf.app.flags.FLAGS is a structure containing the values of all the arguments
parsed from the command-line input. The arguments are accessed as FLAGS.arg, or
via the dictionary FLAGS.__flags if necessary (it is, however, highly recommended to
use the first option—the way it was designed to be used).
Clusters and Servers
A TensorFlow cluster is simply a set of nodes (a.k.a. tasks) that participate in parallel
processing of a computation graph. Each task is defined by the network address at
which it may be accessed. For example:
parameter_servers = ["localhost:2222"]
workers = ["localhost:2223",
"localhost:2224",
"localhost:2225"]
cluster = tf.train.ClusterSpec({"parameter_server": parameter_servers,
"worker": workers})
Here we defined four local tasks (note that localhost:XXXX points to port XXXX on
the current machine, and in a multiple-computer setting the localhost would be
replaced by an IP address). The tasks are divided into a single parameter server and
three workers. The parameter server/worker assignments are referred to as jobs. We
further describe what each of these does during training later on in the chapter.
Each of the tasks must run a TensorFlow server, in order to both use local resources
for the actual computations and communicate with other tasks in the cluster to facili‐
tate parallelization.
Building on the cluster definition, a server on the first worker node (i.e., localhost:
2223) would be started by:
server = tf.train.Server(cluster,
job_name="worker",
task_index=0)
The arguments received by Server() let it know its identity, as well as the identities
and addresses of the other members in the cluster.
Once we have the clusters and servers in place, we build the computation graph that
will allow us to go forward with the parallel computation.
170 | Chapter 9: Distributed TensorFlow
Replicating a Computational Graph Across Devices
As mentioned previously, there is more than one way to perform parallel training. In
“Device Placement” on page 172, we briefly discuss how to directly place operations
on a specific task in a cluster. In the rest of this section we go over what is necessary
for between-graph replication.
Between-graph replication refers to the common parallelization mode where a sepa‐
rate but identical computation graph is built on each of the worker tasks. During
training, gradients are computed by each of the workers and combined by the param‐
eter server, which also keeps track of the current versions of the parameters, and pos‐
sibly other global elements of training (such as a global step counter, etc.).
We use tf.train.replica_device_setter() in order to replicate the model (com‐
putation graph) on each of the tasks. The worker_device argument should point to
the current task within the cluster. For instance, on the first worker we run this:
with tf.device(tf.train.replica_device_setter(
worker_device="/job:worker/task:%d" % 0,
cluster=cluster)):
# Build model...
The exception is the parameter server, on which we don’t build a computation graph.
In order for the process not to terminate, we use:
server.join()
which will keep the parameter server alive for the duration of the parallel computa‐
tion.
Managed Sessions
In this section we cover the mechanism that we will later use for parallel training of
our model. First, we define a Supervisor:
sv = tf.train.Supervisor(is_chief=...,
logdir=...,
global_step=...,
init_op=...)
As the name suggests, the Supervisor is used to supervise training, providing some
utilities necessary for the parallel setting.
There are four arguments passed:
is_chief (Boolean)
There must be a single chief, which is the task responsible for initialization, etc.
TensorFlow Elements | 171
logdir (string)
Where to store logs.
global_step
A TensorFlow Variable that will hold the current global step during training.
init_op
A TensorFlow op for initializing the model, such as tf.global_variables_ini
tializer().
The actual session is then launched:
with sv.managed_session(server.target) as sess:
# Train ...
At this point the chief will initialize variables, while all other tasks wait for this to be
completed.
Device Placement
The final TensorFlow mechanism we discuss in this section is device placement. While
the full extent of this topic is outside the scope of this chapter, the overview would
not be complete without a mention of this ability, which is mostly useful when engi‐
neering advanced systems.
When operating in an environment with multiple computational devices (CPUs,
GPUs, or any combination of these), it may be useful to control where each operation
in the computational graph is going to take place. This may be done to better utilize
parallelism, exploit the different capabilities of different devices, and overcome limi‐
tations such as memory limits on some devices.
Even when you do not explicitly choose device placement, TensorFlow will output the
placement used if required to. This is enabled while constructing the session:
tf.Session(config=tf.ConfigProto(log_device_placement=True))
In order to explicitly choose a device, we use:
with tf.device('/gpu:0'):
op = ...
The '/gpu:0' points TensorFlow to the first GPU on the system; likewise, we could
have used '/cpu:0' to place the op on the CPUs, or '/gpu:X' on a system with mul‐
tiple GPU devices, where X is the index of the GPU we would like to use.
Finally, placement across a cluster is done by pointing to the specific task. For
instance:
172 | Chapter 9: Distributed TensorFlow

with tf.device("/job:worker/task:2"):
op = ...
This will assign to the second worker task, as defined in the cluster specification.
Placement across CPUs
By default, TensorFlow uses all the CPUs available on the system
and handles the threading internally. For this reason, the device
placement '/cpu:0' is the full CPU power, and '/cpu:1' doesn’t
exist by default, even in a multiple-CPU environment.
In order to manually assign to specific CPUs (which you would
need a very good reason to do—otherwise, let TensorFlow handle
it), a session has to be defined with the directive to separate the
CPUs:
config = tf.ConfigProto(device_count={"CPU": 8},
inter_op_parallelism_threads=8,
intra_op_parallelism_threads=1)
sess = tf.Session(config=config)
Here, we define two parameters:
•inter_op_parallelism_threads=8, meaning we allow eight
threads for different ops
•intra_op_parallelism_threads=1, indicating that each op
gets a single thread
These settings would make sense for an 8-CPU system.
Distributed Example
In this section we put it all together with an end-to-end example of distributed train‐
ing of the MNIST CNN model we saw in Chapter 4. We will use one parameter server
and three worker tasks. In order to make it easily reproducible, we will assume all the
tasks are running locally on a single machine (this is easily adapted to a multiple-
machine setting by replacing localhost with the IP address, as described earlier). As
usual, we first present the full code, and then break it down into elements and explain
it:
import tensorflow as tf
from tensorflow.contrib import slim
from tensorflow.examples.tutorials.mnist import input_data
BATCH_SIZE = 50
TRAINING_STEPS = 5000
PRINT_EVERY = 100
LOG_DIR = "/tmp/log"
Distributed Example | 173
parameter_servers = ["localhost:2222"]
workers = ["localhost:2223",
"localhost:2224",
"localhost:2225"]
cluster = tf.train.ClusterSpec({"ps": parameter_servers, "worker": workers})
tf.app.flags.DEFINE_string("job_name", "", "'ps' / 'worker'")
tf.app.flags.DEFINE_integer("task_index", 0, "Index of task")
FLAGS = tf.app.flags.FLAGS
server = tf.train.Server(cluster,
job_name=FLAGS.job_name,
task_index=FLAGS.task_index)
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
def net(x):
x_image = tf.reshape(x, [-1, 28, 28, 1])
net = slim.layers.conv2d(x_image, 32, [5, 5], scope='conv1')
net = slim.layers.max_pool2d(net, [2, 2], scope='pool1')
net = slim.layers.conv2d(net, 64, [5, 5], scope='conv2')
net = slim.layers.max_pool2d(net, [2, 2], scope='pool2')
net = slim.layers.flatten(net, scope='flatten')
net = slim.layers.fully_connected(net, 500, scope='fully_connected')
net = slim.layers.fully_connected(net, 10, activation_fn=None,
scope='pred')
return net
if FLAGS.job_name == "ps":
server.join()
elif FLAGS.job_name == "worker":
with tf.device(tf.train.replica_device_setter(
worker_device="/job:worker/task:%d" % FLAGS.task_index,
cluster=cluster)):
global_step = tf.get_variable('global_step', [],
initializer=tf.constant_initializer(0),
trainable=False)
x = tf.placeholder(tf.float32, shape=[None, 784], name="x-input")
y_ = tf.placeholder(tf.float32, shape=[None, 10], name="y-input")
y = net(x)
cross_entropy = tf.reduce_mean(
174 | Chapter 9: Distributed TensorFlow
tf.nn.softmax_cross_entropy_with_logits(y, y_))
train_step = tf.train.AdamOptimizer(1e-4)\
.minimize(cross_entropy, global_step=global_step)
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
init_op = tf.global_variables_initializer()
sv = tf.train.Supervisor(is_chief=(FLAGS.task_index == 0),
logdir=LOG_DIR,
global_step=global_step,
init_op=init_op)
with sv.managed_session(server.target) as sess:
step = 0
while not sv.should_stop() and step <= TRAINING_STEPS:
batch_x, batch_y = mnist.train.next_batch(BATCH_SIZE)
_, acc, step = sess.run([train_step, accuracy, global_step],
feed_dict={x: batch_x, y_: batch_y})
if step % PRINT_EVERY == 0:
print "Worker : {}, Step: {}, Accuracy (batch): {}".\
format(FLAGS.task_index, step, acc)
test_acc = sess.run(accuracy, feed_dict={x: mnist.test.images,
y_: mnist.test.labels})
print "Test-Accuracy: {}".format(test_acc)
sv.stop()
In order to run this distributed example, from four different terminals we execute the
four commands for dispatching each of the tasks (we will shortly explain how exactly
this happens):
python distribute.py --job_name="ps" --task_index=0
python distribute.py --job_name="worker" --task_index=0
python distribute.py --job_name="worker" --task_index=1
python distribute.py --job_name="worker" --task_index=2
Alternatively, the following will dispatch the four tasks automatically (depending on
the system you are using, the output may all go to a single terminal or to four sepa‐
rate ones):
Distributed Example | 175
import subprocess
subprocess.Popen('python distribute.py --job_name="ps" --task_index=0',
shell=True)
subprocess.Popen('python distribute.py --job_name="worker" --task_index=0',
shell=True)
subprocess.Popen('python distribute.py --job_name="worker" --task_index=1',
shell=True)
subprocess.Popen('python distribute.py --job_name="worker" --task_index=2',
shell=True)
Next, we go over the code in the preceding example and highlight where this is differ‐
ent from the examples we have seen thus far in the book.
The first block deals with imports and constants:
import tensorflow as tf
from tensorflow.contrib import slim
from tensorflow.examples.tutorials.mnist import input_data
BATCH_SIZE = 50
TRAINING_STEPS = 5000
PRINT_EVERY = 100
LOG_DIR = "/tmp/log"
Here we define:
BATCH_SIZE
The number of examples to use during training in each mini-batch.
TRAINING_STEPS
The total number of mini-batches we will use during training.
PRINT_EVERY
How often to print diagnostic information. Since in the distributed training we
use there is a single counter of the current step for all of the tasks, the print at a
certain step will happen only from a single task.
LOG_DIR
The training supervisor will save logs and temporary information to this loca‐
tion. Should be emptied between runs of the program, since old info could cause
the next session to crash.
Next, we define the cluster, as discussed earlier in this chapter:
parameter_servers = ["localhost:2222"]
workers = ["localhost:2223",
"localhost:2224",
"localhost:2225"]
cluster = tf.train.ClusterSpec({"ps": parameter_servers, "worker": workers})
176 | Chapter 9: Distributed TensorFlow
We run all tasks locally. In order to use multiple computers, replace localhost with
the correct IP address. The ports 2222–2225 are also arbitrary, of course (but natu‐
rally have to be distinct when using a single machine): you might as well use the same
port on all machines in a distributed setting.
In the following, we use the tf.app.flags mechanism to define two parameters that
we will provide through the command line when we call the program on each task:
tf.app.flags.DEFINE_string("job_name", "", "'ps' / 'worker'")
tf.app.flags.DEFINE_integer("task_index", 0, "Index of task")
FLAGS = tf.app.flags.FLAGS
The parameters are as follows:
job_name
This will be either 'ps' for the single-parameter server, or 'worker' for each of
the worker tasks.
task_index
The index of the task in each of the types of jobs. The parameter server will
therefore use task_index = 0, and for the workers we will have 0, 1, and 2.
Now we are ready to use the identity of the current task in the cluster we defined in
order to define the server for this current task. Note that this happens on each of the
four tasks that we run. Each one of the four tasks knows its identity (job_name,
task_index), as well as that of everybody else in the cluster (which is provided by the
first argument):
server = tf.train.Server(cluster,
job_name=FLAGS.job_name,
task_index=FLAGS.task_index)
Before we start the actual training, we define our network and load the data to be
used. This is similar to what we have done in previous examples, so we will not go
into the details again here. We use TF-Slim for the sake of brevity:
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
def net(x):
x_image = tf.reshape(x, [-1, 28, 28, 1])
net = slim.layers.conv2d(x_image, 32, [5, 5], scope='conv1')
net = slim.layers.max_pool2d(net, [2, 2], scope='pool1')
net = slim.layers.conv2d(net, 64, [5, 5], scope='conv2')
net = slim.layers.max_pool2d(net, [2, 2], scope='pool2')
net = slim.layers.flatten(net, scope='flatten')
net = slim.layers.fully_connected(net, 500, scope='fully_connected')
net = slim.layers.fully_connected(net, 10, activation_fn=None, scope='pred')
return net
Distributed Example | 177
The actual processing to do during training depends of the type of task. For the
parameter server, we want the mechanism to, well, serve parameters, for the most
part. This entails waiting for requests and processing them. This is all it takes to ach‐
ieve this:
if FLAGS.job_name == "ps":
server.join()
The .join() method of the server will not terminate even when all other tasks do, so
this process will have to be killed externally once it is no longer needed.
In each of the worker tasks, we define the same computation graph:
with tf.device(tf.train.replica_device_setter(
worker_device="/job:worker/task:%d" % FLAGS.task_index,
cluster=cluster)):
global_step = tf.get_variable('global_step', [],
initializer=tf.constant_initializer(0),
trainable=False)
x = tf.placeholder(tf.float32, shape=[None, 784], name="x-input")
y_ = tf.placeholder(tf.float32, shape=[None, 10], name="y-input")
y = net(x)
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(y, y_))
train_step = tf.train.AdamOptimizer(1e-4)\
.minimize(cross_entropy, global_step=global_step)
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
init_op = tf.global_variables_initializer()
We use tf.train.replica_device_setter() in order to specify this, meaning that
the TensorFlow Variables will be synchronized through the parameter server (which
is the mechanism that allows us to do the distributed computations).
The global_step Variable will hold the total number of steps during training across
the tasks (each step index will occur only on a single task). This creates a timeline so
that we can always know where we are in the grand scheme, from each of the tasks
separately.
The rest of the code is the standard setup we have seen before in numerous examples
throughout the book.
Next, we set up a Supervisor and a managed_session:
sv = tf.train.Supervisor(is_chief=(FLAGS.task_index == 0),
logdir=LOG_DIR,
global_step=global_step,
178 | Chapter 9: Distributed TensorFlow
init_op=init_op)
with sv.managed_session(server.target) as sess:
This is similar to the regular session we use throughout, except it is able to handle
some aspects of the distribution. The initialization of the Variables will be done only
in a single task (the chief designated via the is_chief argument; in our case, this will
be the first worker task). All other tasks will wait for this to happen, then continue.
With the session live, we run training:
while not sv.should_stop() and step <= TRAINING_STEPS:
batch_x, batch_y = mnist.train.next_batch(BATCH_SIZE)
_, acc, step = sess.run([train_step, accuracy, global_step],
feed_dict={x: batch_x, y_: batch_y})
if step % PRINT_EVERY == 0:
print "Worker : {}, Step: {}, Accuracy (batch): {}".\
format(FLAGS.task_index, step, acc)
Every PRINT_EVERY steps, we print the current accuracy on the current mini-batch.
This will go to 100% pretty fast. For instance, the first two rows might be:
Worker : 1, Step: 0.0, Accuracy (batch): 0.140000000596
Worker : 0, Step: 100.0, Accuracy (batch): 0.860000014305
Finally, we run the test accuracy:
test_acc = sess.run(accuracy,
feed_dict={x: mnist.test.images, y_: mnist.test.labels})
print "Test-Accuracy: {}".format(test_acc)
Note that this will execute on each of the worker tasks, and thus the same exact out‐
put will appear three times. In order to save on computation, we could have run this
in only a single task (for instance, in the first worker only).
Summary
In this chapter we covered the main concepts pertaining to parallelization in deep
learning and machine learning in general, and concluded with an end-to-end exam‐
ple of distributed training on a cluster with data parallelization.
Distributed training is a very important tool that is utilized both in order to speed up
training, and to train models that would otherwise be infeasible. In the next chapter
we introduce the serving capabilities of TensorFlow, allowing trained models to be
utilized in production environments.
Summary | 179
CHAPTER 10
Exporting and Serving Models
with TensorFlow
In this chapter we will learn how to save and export models by using both simple and
advanced production-ready methods. For the latter we introduce TensorFlow Serv‐
ing, one of TensorFlow’s most practical tools for creating production environments.
We start this chapter with a quick overview of two simple ways to save models and
variables: first by manually saving the weights and reassigning them, and then by
using the Saver class that creates training checkpoints for our variables and also
exports our model. Finally, we shift to more advanced applications where we can
deploy our model on a server by using TensorFlow Serving.
Saving and Exporting Our Model
So far we’ve dealt with how to create, train, and track models with TensorFlow. Now
we will see how to save a trained model. Saving the current state of our weights is
crucial for obvious practical reasons—we don’t want to have to retrain our model
from scratch every time, and we also want a convenient way to share the state of our
model with others (as in the pretrained models we saw in Chapter 7).
In this section we go over the basics of saving and exporting. We start with a simple
way of saving and loading our weights to and from files. Then we will see how to use
TensorFlow’s Saver object to keep serialized model checkpoints that include informa‐
tion about both the state of our weights and our constructed graph.
181
Assigning Loaded Weights
A naive but practical way to reuse our weights after training is saving them to a file,
which we can later load to have them reassigned to the model.
Let’s look at some examples. Say we wish to save the weights of the basic softmax
model used for the MNIST data in Chapter 2. After fetching them from the ses‐
sion, we have the weights represented as a NumPy array, and we save them in some
format of our choice:
import numpy as np
weights = sess.run(W)
np.savez(os.path.join(path, 'weight_storage'), weights)
Given that we have the exact same graph constructed, we can then load the file and
assign the loaded weight values to the corresponding variables by using
the .assign() method within a session:
loaded_w = np.load(path + 'weight_storage.npz')
loaded_w = loaded_w.items()[0][1]
x = tf.placeholder(tf.float32, [None, 784])
W = tf.Variable(tf.zeros([784, 10]))
y_true = tf.placeholder(tf.float32, [None, 10])
y_pred = tf.matmul(x, W)
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(logits=y_pred,
labels=y_true))
gd_step = tf.train.GradientDescentOptimizer(0.5)\
.minimize(cross_entropy)
correct_mask = tf.equal(tf.argmax(y_pred, 1), tf.argmax(y_true, 1))
accuracy = tf.reduce_mean(tf.cast(correct_mask, tf.float32))
with tf.Session() as sess:
# Assigning loaded weights
sess.run(W.assign(loaded_w))
acc = sess.run(accuracy, feed_dict={x: data.test.images,
y_true: data.test.labels})
print("Accuracy: {}".format(acc))
Out:
Accuracy: 0.9199
Next, we will perform the same procedure, but this time for the CNN model used for
the MNIST data in Chapter 4. Here we have eight different sets of weights: two filter
weights and their corresponding biases for the convolution layers 1 and 2, and two
sets of weights and biases for the fully connected layer. We encapsulate the model
inside a class so we can conveniently keep an updated list of these eight parameters.
182 | Chapter 10: Exporting and Serving Models with TensorFlow
We also add optional arguments for weights to load:
if weights is not None and sess is not None:
self.load_weights(weights, sess)
and a function to assign their values when weights are passed:
def load_weights(self, weights, sess):
for i,w in enumerate(weights):
print("Weight index: {}".format(i),
"Weight shape: {}".format(w.shape))
sess.run(self.parameters[i].assign(w))
In its entirety:
class simple_cnn:
def __init__(self, x_image,keep_prob, weights=None, sess=None):
self.parameters = []
self.x_image = x_image
conv1 = self.conv_layer(x_image, shape=[5, 5, 1, 32])
conv1_pool = self.max_pool_2x2(conv1)
conv2 = self.conv_layer(conv1_pool, shape=[5, 5, 32, 64])
conv2_pool = self.max_pool_2x2(conv2)
conv2_flat = tf.reshape(conv2_pool, [-1, 7*7*64])
full_1 = tf.nn.relu(self.full_layer(conv2_flat, 1024))
full1_drop = tf.nn.dropout(full_1, keep_prob=keep_prob)
self.y_conv = self.full_layer(full1_drop, 10)
if weights is not None and sess is not None:
self.load_weights(weights, sess)
def weight_variable(self,shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial,name='weights')
def bias_variable(self,shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial,name='biases')
def conv2d(self,x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1],
padding='SAME')
def max_pool_2x2(self,x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
Saving and Exporting Our Model | 183
strides=[1, 2, 2, 1], padding='SAME')
def conv_layer(self,input, shape):
W = self.weight_variable(shape)
b = self.bias_variable([shape[3]])
self.parameters += [W, b]
return tf.nn.relu(self.conv2d(input, W) + b)
def full_layer(self,input, size):
in_size = int(input.get_shape()[1])
W = self.weight_variable([in_size, size])
b = self.bias_variable([size])
self.parameters += [W, b]
return tf.matmul(input, W) + b
def load_weights(self, weights, sess):
for i,w in enumerate(weights):
print("Weight index: {}".format(i),
"Weight shape: {}".format(w.shape))
sess.run(self.parameters[i].assign(w))
In this example the model was already trained and the weights were saved as
cnn_weights. We load the weights and pass them to our CNN object. When we run
the model on the test data, it will be using the pretrained weights:
x = tf.placeholder(tf.float32, shape=[None, 784])
x_image = tf.reshape(x, [-1, 28, 28, 1])
y_ = tf.placeholder(tf.float32, shape=[None, 10])
keep_prob = tf.placeholder(tf.float32)
sess = tf.Session()
weights = np.load(path + 'cnn_weight_storage.npz')
weights = weights.items()[0][1]
cnn = simple_cnn(x_image, keep_prob, weights, sess)
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(
logits=cnn.y_conv,
labels=y_))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(cnn.y_conv, 1),
tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
X = data.test.images.reshape(10, 1000, 784)
Y = data.test.labels.reshape(10, 1000, 10)
184 | Chapter 10: Exporting and Serving Models with TensorFlow
test_accuracy = np.mean([sess.run(accuracy,
feed_dict={x:X[i], y_:Y[i],keep_prob:1.0})
for i in range(10)])
sess.close()
print("test accuracy: {}".format(test_accuracy))
Out:
Weight index: 0 Weight shape: (5, 5, 1, 32)
Weight index: 1 Weight shape: (32,)
Weight index: 2 Weight shape: (5, 5, 32, 64)
Weight index: 3 Weight shape: (64,)
Weight index: 4 Weight shape: (3136, 1024)
Weight index: 5 Weight shape: (1024,)
Weight index: 6 Weight shape: (1024, 10)
Weight index: 7 Weight shape: (10,)
test accuracy: 0.990100026131
And we obtain high accuracy without the need to retrain.
The Saver Class
TensorFlow also has a built-in class we can use for the same purpose as in the previ‐
ous examples, offering additional useful features as we will see shortly. This class is
referred to as the Saver class (already briefly presented in Chapter 5).
Saver adds operations that allow us to save and restore the model’s parameters by
using binary files called checkpoint les, mapping the tensor values to the names of
the variables. Unlike the method used in the previous section, here we don’t have to
keep track of our parameters—Saver does it automatically for us.
Using Saver is straightforward. We first create a saver instance by using
tf.train.Saver(), indicating how many recent variable checkpoints we would like
to keep and optionally the time interval at which to keep them.
For example, in the following code we ask that only the seven most recent check‐
points will be kept, and in addition we specify that one checkpoint be kept each half
hour (this can be useful for performance and progression evaluation analysis):
saver = tf.train.Saver(max_to_keep=7,
keep_checkpoint_every_n_hours=0.5)
If no inputs are given, the default is to keep the last five checkpoints, and the
every_n_hours feature is effectively disabled (it’s set to 10000 by default).
Next we save the checkpoint files by using the .save() method of the saver
instance, passing the session argument, the path where the files are to be saved, and
also the step number (global_step), which is automatically concatenated to the
Saving and Exporting Our Model | 185
name of each checkpoint file as an indication of its iteration count. This creates mul‐
tiple checkpoints at different steps while training a model.
In this code example, every 50 training iterations a file will be saved in the designated
directory:
DIR = "path/to/model"
with tf.Session() as sess:
for step in range(1,NUM_STEPS+1):
batch_xs, batch_ys = data.train.next_batch(MINIBATCH_SIZE)
sess.run(gd_step, feed_dict={x: batch_xs, y_true: batch_ys})
if step % 50 == 0:
saver.save(sess, os.path.join(DIR, "model"),
global_step=step)
An additional saved file carrying the name checkpoint contains the list of saved check‐
points, and also the path to the most recent checkpoint:
model_checkpoint_path: "model_ckpt-1000"
all_model_checkpoint_paths: "model_ckpt-700"
all_model_checkpoint_paths: "model_ckpt-750"
all_model_checkpoint_paths: "model_ckpt-800"
all_model_checkpoint_paths: "model_ckpt-850"
all_model_checkpoint_paths: "model_ckpt-900"
all_model_checkpoint_paths: "model_ckpt-950"
all_model_checkpoint_paths: "model_ckpt-1000"
In the following code we use Saver to save the state of the weights:
from tensorflow.examples.tutorials.mnist import input_data
DATA_DIR = '/tmp/data'
data = input_data.read_data_sets(DATA_DIR, one_hot=True)
NUM_STEPS = 1000
MINIBATCH_SIZE = 100
DIR = "path/to/model"
x = tf.placeholder(tf.float32, [None, 784],name='x')
W = tf.Variable(tf.zeros([784, 10]),name='W')
y_true = tf.placeholder(tf.float32, [None, 10])
y_pred = tf.matmul(x, W)
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(logits=y_pred,
186 | Chapter 10: Exporting and Serving Models with TensorFlow
labels=y_true))
gd_step = tf.train.GradientDescentOptimizer(0.5)\
.minimize(cross_entropy)
correct_mask = tf.equal(tf.argmax(y_pred, 1), tf.argmax(y_true, 1))
accuracy = tf.reduce_mean(tf.cast(correct_mask, tf.float32))
saver = tf.train.Saver(max_to_keep=7,
keep_checkpoint_every_n_hours=1)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(1,NUM_STEPS+1):
batch_xs, batch_ys = data.train.next_batch(MINIBATCH_SIZE)
sess.run(gd_step, feed_dict={x: batch_xs, y_true: batch_ys})
if step % 50 == 0:
saver.save(sess, os.path.join(DIR, "model_ckpt"),
global_step=step)
ans = sess.run(accuracy, feed_dict={x: data.test.images,
y_true: data.test.labels})
print("Accuracy: {:.4}%".format(ans*100))
Out:
Accuracy: 90.87%
And now we simply restore the checkpoint we want for the same graph model by
using saver.restore(), and the weights are automatically assigned to the model:
tf.reset_default_graph()
x = tf.placeholder(tf.float32, [None, 784],name='x')
W = tf.Variable(tf.zeros([784, 10]),name='W')
y_true = tf.placeholder(tf.float32, [None, 10])
y_pred = tf.matmul(x, W)
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(logits=y_pred,
labels=y_true))
gd_step = tf.train.GradientDescentOptimizer(0.5)\
.minimize(cross_entropy)
correct_mask = tf.equal(tf.argmax(y_pred, 1), tf.argmax(y_true, 1))
accuracy = tf.reduce_mean(tf.cast(correct_mask, tf.float32))
saver = tf.train.Saver()
with tf.Session() as sess:
saver.restore(sess, os.path.join(DIR,"model_ckpt-1000"))
ans = sess.run(accuracy, feed_dict={x: data.test.images,
y_true: data.test.labels})
print("Accuracy: {:.4}%".format(ans*100))
Saving and Exporting Our Model | 187

Out:
Accuracy: 90.87%
Resetting the graph before restoring
The loaded variables need to be paired with the ones in the current
graph, and thus should have matching names. If for some reason
the names don’t match, then an error similar to this might follow:
NotFoundError: Key W_1 not found in checkpoint
[[Node: save/RestoreV2_2 = RestoreV2[
dtypes=[DT_FLOAT], _device="/job:localhost/replica:0
/task:0/cpu:0"](_recv_save/Const_1_0, save/RestoreV2_2
/tensor_names, save/RestoreV2_2/shape_and_slices)]]
This can happen if the names were used by some old, irrelevant
graph. By using the tf.reset_default_graph() command to reset
the graph, you can solve this issue.
So far, in both methods we needed to re-create the graph for the restored parameters
to be reassigned. Saver, however, also allows us to restore the graph without having
to reconstruct it by generating .meta checkpoint files containing all the required
information about it.
The information about the graph and how to incorporate the saved weights in it
(metainformation) is referred to as the MetaGraphDef. This information is serialized
—transformed to a string—using protocol buffers (see “Serialization and Protocol
Buffers” on page 191), and it includes several parts. The information about the archi‐
tecture of the network is kept in graph_def.
Here is a little sample of textual serialization of the graph information (more about
serialization follows):
meta_info_def {
stripped_op_list {
op {
name: "ApplyGradientDescent"
input_arg {
name: "var"
type_attr: "T"
is_ref: true
}
input_arg {
name: "alpha"
type_attr: "T"
}...
graph_def {
node {
name: "Placeholder"
188 | Chapter 10: Exporting and Serving Models with TensorFlow
op: "Placeholder"
attr {
key: "_output_shapes"
value {
list {
shape {
dim {
size: -1
}
dim {
size: 784
}
}
}
}
}...
In order to load the saved graph, we use tf.train.import_meta_graph(), passing
the name of the checkpoint file we want (with the .meta extension). TensorFlow
already knows what to do with the restored weights, since this information is also
kept:
tf.reset_default_graph()
DIR = "path/to/model"
with tf.Session() as sess:
saver = tf.train.import_meta_graph(os.path.join(
DIR,"model_ckpt-1000.meta"))
saver.restore(sess, os.path.join(DIR,"model_ckpt-1000"))
ans = sess.run(accuracy, feed_dict={x: data.test.images,
y_true: data.test.labels})
print("Accuracy: {:.4}%".format(ans*100))
Simply importing the graph and restoring the weights, however, is not enough and
will result in an error. The reason is that importing the model and restoring the
weights doesn’t give us additional access to the variables used as arguments when
running the session (fetches and keys of feed_dict)—the model doesn’t know what
the inputs and outputs are, what measures we wish to calculate, etc.
One way to solve this problem is by saving them in a collection. A collection is a Ten‐
sorFlow object similar to a dictionary, in which we can keep our graph components
in an orderly, accessible fashion.
In this example we want to have access to the measure accuracy (which we wish to
fetch) and the feed keys x and y_true. We add them to a collection before saving the
model under the name of train_var:
Saving and Exporting Our Model | 189
train_var = [x,y_true,accuracy]
tf.add_to_collection('train_var', train_var[0])
tf.add_to_collection('train_var', train_var[1])
tf.add_to_collection('train_var', train_var[2])
As shown, the saver.save() method automatically saves the graph architecture
together with the weights’ checkpoints. We can also save the graph explicitly using
saver.export_meta.graph(), and then add a collection (passed as the second argu‐
ment):
train_var = [x,y_true,accuracy]
tf.add_to_collection('train_var', train_var[0])
tf.add_to_collection('train_var', train_var[1])
tf.add_to_collection('train_var', train_var[2])
saver = tf.train.Saver(max_to_keep=7,
keep_checkpoint_every_n_hours=1)
saver.export_meta_graph(os.path.join(DIR,"model_ckpt.meta")
,collection_list=['train_var'])
Now we retrieve the graph together with the collection, from which we can extract
the required variables:
tf.reset_default_graph()
DIR = "path/to/model"
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
saver = tf.train.import_meta_graph(os.path.join(
DIR,"model_ckpt.meta")
saver.restore(sess, os.path.join(DIR,"model_ckpt-1000"))
x = tf.get_collection('train_var')[0]
y_true = tf.get_collection('train_var')[1]
accuracy = tf.get_collection('train_var')[2]
ans = sess.run(accuracy, feed_dict={x: data.test.images,
y_true: data.test.labels})
print("Accuracy: {:.4}%".format(ans*100))
Out:
Accuracy: 91.4%
When defining the graph, think about which variables/operations you would like to
retrieve once the graph has been saved and restored, such as the accuracy operation
in the preceding example. In the next section, when we talk about Serving, we’ll see
190 | Chapter 10: Exporting and Serving Models with TensorFlow

that it has built-in functionality for guiding the exported model without the need to
save the variables as we do here.
Serialization and Protocol Buers
When we run a program, the state of our code-produced data structure is stored in
memory. Whenever we want to either make a copy of this data structure, save it to a
file, or transfer it somewhere, we need to translate it to some representation that can
be efficiently saved or sent through a connection in a sequential manner. We do that
by what is referred to as the process of serialization, where we use some function that
flattens our data as a string. This string can then later be deserialized to a code format
by applying the same serializing function in a reversed order.
While in simple data structure instances this may be trivial to do (e.g., representing an
array as a simple concatenation of its values), in complex data structures that have
nested arrays, dictionaries, and objects, the approach to take is not as straightforward.
There are several popular representations for serialization—perhaps the most famous
ones you may have heard of or even worked with are JSON and XML. Both have nes‐
ted elements that belong within a set of delimiters. In JSON all elements are comma-
separated; arrays are denoted with square brackets and objects by curly braces. XML,
which at its core is a markup language, uses tags for the same purpose.
The serialized string can be encoded either in a readable, human-friendly text format,
making it easier to check and debug it with any text editor, or in a machine-friendly
binary format, which can sometimes be more compact.
Protocol buffers, or protobufs for short, is the format TensorFlow uses to transfer
data, developed internally by Google. Protobufs (mentioned in Chapter 8, when read‐
ing data was discussed) can be used either as an uncompressed text format for debug‐
ging and editing or a more compact binary format.
Introduction to TensorFlow Serving
TensorFlow Serving, written in C++, is a high-performance serving framework with
which we can deploy our model in a production setting. It makes our model usable
for production by enabling client software to access it and pass inputs through Ser‐
ving’s API (Figure 10-1). Of course, TensorFlow Serving is designed to have seamless
integration with TensorFlow models. Serving features many optimizations to reduce
latency and increase throughput of predictions, useful for real-time, large-scale appli‐
cations. It’s not only about accessibility and efficient serving of predictions, but also
about flexibility—it’s quite common to want to keep a model updated for various rea‐
sons, like having additional training data for improving the model, making changes
to the network architecture, and more.
Introduction to TensorFlow Serving | 191

Figure 10-1. Serving links our trained model to external applications, allowing client
soware easy access.
Overview
Say that we run a speech-recognition service and we want to deploy our models with
TensorFlow Serving. In addition to optimized serving, it is important for us to update
our models periodically as we obtain more data or experiment with new network
architectures. In slightly more technical terms, we’d like to have the ability to load
new models and serve their outputs, and unload old ones, all while streamlining
model life-cycle management and version policies.
In general terms, we can accomplish this with Serving as follows. In Python, we
define the model and prepare it to be serialized in a way that can be parsed by the
different modules responsible for loading, serving, and managing versions, for exam‐
ple. The core Serving “engine” resides in a C++ module that we will need to access
only if we wish to control specific tuning and customization of Serving behaviors.
In a nutshell, this is how Serving’s architecture works (Figure 10-2):
•A module called Source identifies new models to be loaded by monitoring
plugged-in filesystems, which contain our models and their associated informa‐
tion that we exported upon creation. Source includes submodules that periodi‐
cally inspect the filesystem and determine the latest relevant model versions.
•When it identifies a new model version, source creates a loader. The loader passes
its servables (objects that clients use to perform computations such as predic‐
tions) to a manager. The manager handles the full life cycle of servables (loading,
unloading, and serving) according to a version policy (gradual rollout, reverting
versions, etc.).
• Finally, the manager provides an interface for client access to servables.
Figure 10-2. An outline of the Serving architecture.
192 | Chapter 10: Exporting and Serving Models with TensorFlow
What’s especially nice about how Serving is built is that it’s designed to be flexible and
extendable. It supports building various plug-ins to customize system behavior, while
using the generic builds of other core components.
In the next section we will build and deploy a TensorFlow model with Serving, dem‐
onstrating some of its key functionalities and inner workings. In advanced applica‐
tions it is likely that we may have to control for different types of optimizations and
customization; for example, controlling version policies and more. In this chapter we
show you how to get up and running with Serving and understand its fundamentals,
laying the foundations for production-ready deployment.
Installation
Serving requires several installations, including some third-party components. The
installation can be done from source or using Docker, which we use here to get you
started quickly. A Docker container bundles together a software application with
everything needed to run it (for example, code, files, etc.). We also use Bazel, Google’s
own build tool for building client and server software. In this chapter we only briefly
touch on the technicalities behind tools such as Bazel and Docker. More comprehen‐
sive descriptions appear in the appendix, at the end of the book.
Installing Serving
Docker installation instructions can be found in on the Docker website.
Here, we demonstrate the Docker setup using Ubuntu.
Docker containers are created from a local Docker image, which is built from a dock‐
erfile, and encapsulates everything we need (dependency installations, project code,
etc.). Once we have Docker installed, we need to download the TensorFlow Serving
dockerfile.
This dockerfile contains all of the dependencies needed to build TensorFlow Serving.
First, we produce the image from which we can run containers (this may take some
time):
docker build --pull -t $USER/tensorflow-serving-devel -f
Dockerfile.devel .
Now that we’ve got the image created locally on our machine, we can create and run a
container by using:
docker run -v $HOME/docker_files:/host_files
-p 80:80 -it $USER/tensorflow-serving-devel
The docker run -it $USER/tensorflow-serving-devel command would suffice to
create and run a container, but we make two additions to this command.
Introduction to TensorFlow Serving | 193
First, we add -v $HOME/home_dir:/docker_dir, where -v (volume) indicates a request
for a shared filesystem so we have a convenient way to transfer files between the
Docker container and the host. Here we created the shared folders docker_les on our
host and host_les on our Docker container. Another way to transfer files is simply by
using the command docker cp foo.txt mycontainer:/foo.txt. The second addi‐
tion is -p <host port>:<container port>, which makes the service in the container
accessible from anywhere by having the indicated port exposed.
Once we enter our run command, a container will be created and started, and a ter‐
minal will be opened. We can have a look at our container’s status by using the com‐
mand docker ps -a (outside the Docker terminal). Note that each time we use the
docker run command, we create another container; to enter the terminal of an exist‐
ing container, we need to use docker exec -it <container id> bash.
Finally, within the opened terminal we clone and configure TensorFlow Serving:
git clone --recurse-submodules https://github.com/tensorflow/serving
cd serving/tensorflow
./configure
And that’s it; we’re ready to go!
Building and Exporting
Now that Serving is cloned and operational, we can start exploring its features and
how to use it. The cloned TensorFlow Serving libraries are organized in a Bazel archi‐
tecture. The source code Bazel builds upon is organized in a workspace directory,
inside nested hierarchies of packages that group related source files together. Each
package has a BUILD file, specifying the output to be built from the files inside that
package.
The workspace in our cloned library is located in the /serving folder, containing the
WORKSPACE text file and the /tensorow_serving package, which we will return to
later.
We now turn to look at the Python script that handles the training and exportation of
the model, and see how to export our model in a manner ready for serving.
Exporting our model
As when we used the Saver class, our trained model will be serialized and exported to
two files: one that contains information about our variables, and another that holds
information about our graph and other metadata. As we shall see shortly, Serving
requires a specific serialization format and metadata, so we cannot simply use the
Saver class, as we saw at the beginning of this chapter.
The steps we are going to take are as follows:
194 | Chapter 10: Exporting and Serving Models with TensorFlow
1. Define our model as in previous chapters.
2. Create a model builder instance.
3. Have our metadata (model, method, inputs and outputs, etc.) defined in the
builder in a serialized format (this is referred to as SignatureDef).
4. Save our model by using the builder.
We start by creating a builder instance using Serving’s SavedModelBuilder module,
passing the location to which we want our files to be exported (the directory will be
created if it does not exist). SavedModelBuilder exports serialized files representing
our model in the required format:
builder = saved_model_builder.SavedModelBuilder(export_path)
The serialized model files we need will be contained in a directory whose name will
specify the model and its version:
export_path_base = sys.argv[-1]
export_path = os.path.join(
compat.as_bytes(export_path_base),
compat.as_bytes(str(FLAGS.model_version)))
This way, each version will be exported to a distinct subdirectory with its correspond‐
ing path.
Note that the export_path_base is obtained as input from the command line with
sys.argv, and the version is kept as a flag (presented in the previous chapter). Flag
parsing is handled by tf.app.run(), as we will see shortly.
Next, we want to define the input (shape of the input tensor of the graph) and output
(tensor of the prediction) signatures. In the first part of this chapter we used Tensor‐
Flow collection objects to specify the relation between input and output data and
their corresponding placeholders, and also operations for computing predictions and
accuracy. Here, signatures serve a somewhat analogous purpose.
We use the builder instance we created to add both the variables and meta graph
information, using the SavedModelBuilder.add_meta_graph_and_variables()
method:
Introduction to TensorFlow Serving | 195
builder.add_meta_graph_and_variables(
sess, [tag_constants.SERVING],
signature_def_map={
'predict_images':
prediction_signature,
signature_constants.DEFAULT_SERVING_SIGNATURE_DEF_KEY:
classification_signature,
},
legacy_init_op=legacy_init_op)
We need to pass four arguments: the session, tags (to “serve” or “train”), the signature
map, and some initializations.
We pass a dictionary with the prediction and classification signatures. We start with
the prediction signature, which again can be thought of as analogical to specifying
and saving a prediction op in a TensorFlow collection as we saw earlier:
prediction_signature = signature_def_utils.build_signature_def(
inputs={'images': tensor_info_x},
outputs={'scores': tensor_info_y},
method_name=signature_constants.PREDICT_METHOD_NAME)
images and scores here are arbitrary names that we will use to refer to our x and y
Tensors later. The images and scores are encoded into the required format by using
the following commands:
tensor_info_x = utils.build_tensor_info(x)
tensor_info_y = utils.build_tensor_info(y_conv)
Similar to the prediction signature, we have the classification signature, where we
input the information about the scores (the probability values of the top k classes)
and the corresponding classes:
# Build the signature_def_map
classification_inputs = utils.build_tensor_info(
serialized_tf_example)
classification_outputs_classes = utils.build_tensor_info(
prediction_classes)
classification_outputs_scores = utils.build_tensor_info(values)
classification_signature = signature_def_utils.build_signature_def(
inputs={signature_constants.CLASSIFY_INPUTS:
classification_inputs},
outputs={
signature_constants.CLASSIFY_OUTPUT_CLASSES:
classification_outputs_classes,
signature_constants.CLASSIFY_OUTPUT_SCORES:
classification_outputs_scores
},
method_name=signature_constants.CLASSIFY_METHOD_NAME)
Finally, we save our model by using the save() command:
196 | Chapter 10: Exporting and Serving Models with TensorFlow
builder.save()
This, in a nutshell, wraps all the parts together in a format ready to be serialized and
exported upon execution of the script, as we shall see immediately.
Here is the final code for our main Python model script, including our model (the
CNN model from Chapter 4):
import os
import sys
import tensorflow as tf
from tensorflow.python.saved_model import builder
as saved_model_builder
from tensorflow.python.saved_model import signature_constants
from tensorflow.python.saved_model import signature_def_utils
from tensorflow.python.saved_model import tag_constants
from tensorflow.python.saved_model import utils
from tensorflow.python.util import compat
from tensorflow_serving.example import mnist_input_data
tf.app.flags.DEFINE_integer('training_iteration', 10,
'number of training iterations.')
tf.app.flags.DEFINE_integer(
'model_version', 1, 'version number of the model.')
tf.app.flags.DEFINE_string('work_dir', '/tmp', 'Working directory.')
FLAGS = tf.app.flags.FLAGS
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial,dtype='float')
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial,dtype='float')
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME')
def main(_):
if len(sys.argv) < 2 or sys.argv[-1].startswith('-'):
print('Usage: mnist_export.py [--training_iteration=x] '
'[--model_version=y] export_dir')
sys.exit(-1)
if FLAGS.training_iteration <= 0:
print('Please specify a positive
value for training iteration.')
sys.exit(-1)
if FLAGS.model_version <= 0:
Introduction to TensorFlow Serving | 197
print ('Please specify a positive
value for version number.')
sys.exit(-1)
print('Training...')
mnist = mnist_input_data.read_data_sets(
FLAGS.work_dir, one_hot=True)
sess = tf.InteractiveSession()
serialized_tf_example = tf.placeholder(
tf.string, name='tf_example')
feature_configs = {'x': tf.FixedLenFeature(shape=[784],
dtype=tf.float32),}
tf_example = tf.parse_example(serialized_tf_example,
feature_configs)
x = tf.identity(tf_example['x'], name='x')
y_ = tf.placeholder('float', shape=[None, 10])
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
x_image = tf.reshape(x, [-1,28,28,1])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.matmul(h_fc1_drop, W_fc2) + b_fc2
y = tf.nn.softmax(y_conv, name='y')
cross_entropy = -tf.reduce_sum(y_ * tf.log(y_conv))
198 | Chapter 10: Exporting and Serving Models with TensorFlow
train_step = tf.train.AdamOptimizer(1e-4)\
.minimize(cross_entropy)
values, indices = tf.nn.top_k(y_conv, 10)
prediction_classes = tf.contrib.lookup.index_to_string(
tf.to_int64(indices),
mapping=tf.constant([str(i) for i in xrange(10)]))
sess.run(tf.global_variables_initializer())
for _ in range(FLAGS.training_iteration):
batch = mnist.train.next_batch(50)
train_step.run(feed_dict={x: batch[0],
y_: batch[1], keep_prob: 0.5})
print(_)
correct_prediction = tf.equal(tf.argmax(y_conv,1),
tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, 'float'))
y_: mnist.test.labels})
print('training accuracy %g' % accuracy.eval(feed_dict={
x: mnist.test.images,
y_: mnist.test.labels, keep_prob: 1.0}))
print('training is finished!')
export_path_base = sys.argv[-1]
export_path = os.path.join(
compat.as_bytes(export_path_base),
compat.as_bytes(str(FLAGS.model_version)))
print 'Exporting trained model to', export_path
builder = saved_model_builder.SavedModelBuilder(export_path)
classification_inputs = utils.build_tensor_info(
serialized_tf_example)
classification_outputs_classes = utils.build_tensor_info(
prediction_classes)
classification_outputs_scores = utils.build_tensor_info(values)
classification_signature = signature_def_utils.build_signature_def(
inputs={signature_constants.CLASSIFY_INPUTS:
classification_inputs},
outputs={
signature_constants.CLASSIFY_OUTPUT_CLASSES:
classification_outputs_classes,
signature_constants.CLASSIFY_OUTPUT_SCORES:
classification_outputs_scores
},
Introduction to TensorFlow Serving | 199
method_name=signature_constants.CLASSIFY_METHOD_NAME)
tensor_info_x = utils.build_tensor_info(x)
tensor_info_y = utils.build_tensor_info(y_conv)
prediction_signature = signature_def_utils.build_signature_def(
inputs={'images': tensor_info_x},
outputs={'scores': tensor_info_y},
method_name=signature_constants.PREDICT_METHOD_NAME)
legacy_init_op = tf.group(tf.initialize_all_tables(),
name='legacy_init_op')
builder.add_meta_graph_and_variables(
sess, [tag_constants.SERVING],
signature_def_map={
'predict_images':
prediction_signature,
signature_constants.DEFAULT_SERVING_SIGNATURE_DEF_KEY:
classification_signature,
},
legacy_init_op=legacy_init_op)
builder.save()
print('new model exported!')
if __name__ == '__main__':
tf.app.run()
The tf.app.run() command gives us a nice wrapper that handles parsing command-
line arguments.
In the final part of our introduction to Serving, we use Bazel for the actual exporting
and deployment of our model.
Most Bazel BUILD files consist only of declarations of build rules specifying the rela‐
tionship between inputs and outputs, and the steps to build the outputs.
For instance, in this BUILD file we have a Python rule py_binary to build executable
programs. Here we have three attributes, name for the name of the rule, srcs for the
list of files that are processed to create the target (our Python script), and deps for the
list of other libraries to be linked into the binary target:
py_binary(
name = "serving_model_ch4",
srcs = [
"serving_model_ch4.py",
],
deps = [
":mnist_input_data",
"@org_tensorflow//tensorflow:tensorflow_py",
200 | Chapter 10: Exporting and Serving Models with TensorFlow
"@org_tensorflow//tensorflow/python/saved_model:builder",
"@org_tensorflow//tensorflow/python/saved_model:constants",
"@org_tensorflow//tensorflow/python/saved_model:loader",
"@org_tensorflow//tensorflow/python/saved_model:
signature_constants",
"@org_tensorflow//tensorflow/python/saved_model:
signature_def_utils",
"@org_tensorflow//tensorflow/python/saved_model:
tag_constants",
"@org_tensorflow//tensorflow/python/saved_model:utils",
],
)
Next we run and export the model by using Bazel, training with 1,000 iterations and
exporting the first version of the model:
bazel build //tensorflow_serving/example:serving_model_ch4
bazel-bin/tensorflow_serving/example/serving_model_ch4
--training_iteration=1000 --model_version=1 /tmp/mnist_model
To train the second version of the model, we just use:
--model_version=2
In the designated subdirectory we will find two files, saved_model.pb and variables,
that contain the serialized information about our graph (including metadata) and its
variables, respectively. In the next lines we load the exported model with the standard
TensorFlow model server:
bazel build //tensorflow_serving/model_servers:
tensorflow_model_server
bazel-bin/tensorflow_serving/model_servers/tensorflow_model_server
--port=8000 --model_name=mnist
--model_base_path=/tmp/mnist_model/ --logtostderr
Finally, our model is now served and ready for action at localhost:8000. We can test
the server with a simple client utility, mnist_client:
bazel build //tensorflow_serving/example:mnist_client
bazel-bin/tensorflow_serving/example/mnist_client
--num_tests=1000 --server=localhost:8000
Summary
This chapter dealt with how to save, export, and serve models, from simply saving
and reassigning of weights using the built-in Saver utility to an advanced model-
deployment mechanism for production. The last part of this chapter touched on Ten‐
sorFlow Serving, a great tool for making our models commercial-ready with dynamic
version control. Serving is a rich utility with many functionalities, and we strongly
recommend that readers who are interested in mastering it seek out more in-depth
technical material online.
Summary | 201
APPENDIX A
Tips on Model Construction and
Using TensorFlow Serving
Model Structuring and Customization
In this short section we will focus on two topics that continue from and extend the
previous chapters—how to construct a proper model, and how to customize the
model’s entities. We start by describing how we can effectively reframe our code by
using encapsulations and allow its variables to be shared and reused. In the second
part of this section we will talk about how to customize our own loss functions and
operations and use them for optimization.
Model Structuring
Ultimately, we would like to design our TensorFlow code efficiently, so that it can be
reused for multiple tasks and is easy to follow and pass around. One way to make
things cleaner is to use one of the available TensorFlow extension libraries, which
were discussed in Chapter 7. However, while they are great to use for typical net‐
works, models with new components that we wish to implement may sometimes
require the full flexibility of lower-level TensorFlow.
203
Let’s take another look at the optimization code from the previous chapter:
import tensorflow as tf
NUM_STEPS = 10
g = tf.Graph()
wb_ = []
with g.as_default():
x = tf.placeholder(tf.float32,shape=[None,3])
y_true = tf.placeholder(tf.float32,shape=None)
with tf.name_scope('inference') as scope:
w = tf.Variable([[0,0,0]],dtype=tf.float32,name='weights')
b = tf.Variable(0,dtype=tf.float32,name='bias')
y_pred = tf.matmul(w,tf.transpose(x)) + b
with tf.name_scope('loss') as scope:
loss = tf.reduce_mean(tf.square(y_true-y_pred))
with tf.name_scope('train') as scope:
learning_rate = 0.5
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
train = optimizer.minimize(loss)
.
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
for step in range(NUM_STEPS):
sess.run(train,{x: x_data, y_true: y_data})
if (step % 5 == 0):
print(step, sess.run([w,b]))
wb_.append(sess.run([w,b]))
print(10, sess.run([w,b]))
We get:
(0, [array([[ 0.30149955, 0.49303722, 0.11409992]],
dtype=float32), -0.18563795])
(5, [array([[ 0.30094019, 0.49846715, 0.09822173]],
dtype=float32), -0.19780949])
(10, [array([[ 0.30094025, 0.49846718, 0.09822182]],
dtype=float32), -0.19780946])
The entire code here is simply stacked line by line. This is OK for simple and focused
examples. However, this way of coding has its limits—it’s neither reusable nor very
readable when the code gets more complex.
Let’s zoom out and think about what characteristics our infrastructure should have.
First, we would like to encapsulate the model so it can be used for various tasks like
training, evaluation, and forming predictions. Furthermore, it can also be more effi‐
204 | Appendix A: Tips on Model Construction and Using TensorFlow Serving
cient to construct the model in a modular fashion, giving us specific control over its
subcomponents and increasing readability. This will be the focus of the next few sec‐
tions.
Modular design
A good start is to split the code into functions that capture different elements in the
learning model. We can do this as follows:
def predict(x,y_true,w,b):
y_pred = tf.matmul(w,tf.transpose(x)) + b
return y_pred
def get_loss(y_pred,y_true):
loss = tf.reduce_mean(tf.square(y_true-y_pred))
return loss
def get_optimizer(y_pred,y_true):
loss = get_loss(y_pred,y_true)
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
return train
def run_model(x_data,y_data):
wb_ = []
# Define placeholders and variables
x = tf.placeholder(tf.float32,shape=[None,3])
y_true = tf.placeholder(tf.float32,shape=None)
w = tf.Variable([[0,0,0]],dtype=tf.float32)
b = tf.Variable(0,dtype=tf.float32)
print(b.name)
# Form predictions
y_pred = predict(x,y_true,w,b)
# Create optimizer
train = get_optimizer(y_pred,y_data)
# Run session
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
for step in range(10):
sess.run(train,{x: x_data, y_true: y_data})
if (step % 5 == 0):
print(step, sess.run([w,b]))
wb_.append(sess.run([w,b]))
run_model(x_data,y_data)
run_model(x_data,y_data)
Tips on Model Construction and Using TensorFlow Serving | 205
And here is the result:
Variable_9:0 Variable_8:0
0 [array([[ 0.27383861, 0.48421991, 0.09082422]],
dtype=float32), -0.20805186]
4 [array([[ 0.29868397, 0.49840903, 0.10026278]],
dtype=float32), -0.20003076]
9 [array([[ 0.29868546, 0.49840906, 0.10026464]],
dtype=float32), -0.20003042]
Variable_11:0 Variable_10:0
0 [array([[ 0.27383861, 0.48421991, 0.09082422]],
dtype=float32), -0.20805186]
4 [array([[ 0.29868397, 0.49840903, 0.10026278]],
dtype=float32), -0.20003076]
9 [array([[ 0.29868546, 0.49840906, 0.10026464]],
dtype=float32), -0.20003042]
Now we can reuse the code with different inputs, and this division makes it easier to
read, especially when it gets more complex.
In this example we called the main function twice with the same inputs and printed
the variables that were created. Note that each call created a different set of variables,
resulting in the creation of four variables. Let’s assume, for example, a scenario where
we wish to build a model with multiple inputs, such as two different images. Say we
wish to apply the same convolutional filters to both input images. New variables will
be created. To avoid this, we “share” the filter variables, using the same variables on
both images.
Variable sharing
It’s possible to reuse the same variables by creating them with tf.get_variable()
instead of tf.Variable(). We use this very similarly to tf.Variable(), except that
we need to pass an initializer as an argument:
w = tf.get_variable('w',[1,3],initializer=tf.zeros_initializer())
b = tf.get_variable('b',[1,1],initializer=tf.zeros_initializer())
Here we used tf.zeros_initializer(). This initializer is very similar to
tf.zeros(), except that it doesn’t get the shape as an argument, but rather arranges
the values according to the shape specified by tf.get_variable().
In this example the variable w will be initialized as [0,0,0], as specified by the given
shape, [1,3].
With get_variable() we can reuse variables that have the same name (including the
scope prefix, which can be set by tf.variable_scope()). But first we need to indi‐
cate this intention by either using tf.variable_scope.reuse_variable() or setting
206 | Appendix A: Tips on Model Construction and Using TensorFlow Serving

the reuse flag (tf.variable.scope(reuse=True)). An example of how to share vari‐
ables is shown in the code that follows.
Heads-up for ag misuse
Whenever a variable has the exact same name as another, an excep‐
tion will be thrown when the reuse flag is not set. The same goes
for the opposite scenario—variables with mismatching names that
are expected to be reused (when reuse = True) will cause an
exception as well.
Using these methods, and setting the scope prefix to Regression, by printing their
names we can see that the same variables are reused:
def run_model(x_data,y_data):
wb_ = []
# Define placeholders and variables
x = tf.placeholder(tf.float32,shape=[None,3])
y_true = tf.placeholder(tf.float32,shape=None)
w = tf.get_variable('w',[1,3],initializer=tf.zeros_initializer())
b = tf.get_variable('b',[1,1],initializer=tf.zeros_initializer())
print(b.name,w.name)
# Form predictions
y_pred = predict(x,y_true,w,b)
# Create optimizer
train = get_optimizer(y_pred,y_data)
# Run session
init = tf.global_variables_initializer()
sess.run(init)
for step in range(10):
sess.run(train,{x: x_data, y_true: y_data})
if (step % 5 == 4) or (step == 0):
print(step, sess.run([w,b]))
wb_.append(sess.run([w,b]))
sess = tf.Session()
with tf.variable_scope("Regression") as scope:
run_model(x_data,y_data)
scope.reuse_variables()
run_model(x_data,y_data)
sess.close()
The output is shown here:
Tips on Model Construction and Using TensorFlow Serving | 207

Regression/b:0 Regression/w:0
0 [array([[ 0.27383861, 0.48421991, 0.09082422]],
dtype=float32), array([[-0.20805186]], dtype=float32)]
4 [array([[ 0.29868397, 0.49840903, 0.10026278]],
dtype=float32), array([[-0.20003076]], dtype=float32)]
9 [array([[ 0.29868546, 0.49840906, 0.10026464]],
dtype=float32), array([[-0.20003042]], dtype=float32)]
Regression/b:0 Regression/w:0
0 [array([[ 0.27383861, 0.48421991, 0.09082422]],
dtype=float32), array([[-0.20805186]], dtype=float32)]
4 [array([[ 0.29868397, 0.49840903, 0.10026278]],
dtype=float32), array([[-0.20003076]], dtype=float32)]
9 [array([[ 0.29868546, 0.49840906, 0.10026464]],
dtype=float32), array([[-0.20003042]], dtype=float32)]
tf.get_variables() is a neat, lightweight way to share variables. Another approach
is to encapsulate our model as a class and manage the variables there. This approach
has many other benefits, as described in the following section
Class encapsulation
As with any other program, when things get more complex and the number of code
lines grows, it becomes very convenient to have our TensorFlow code reside within a
class, giving us quick access to methods and attributes that belong to the same model.
Class encapsulation allows us to maintain the state of our variables and then perform
various post-training tasks like forming predictions, model evaluation, further train‐
ing, saving and restoring our weights, and whatever else is related to the specific
problem our model solves.
In the next batch of code we see an example of a simple class wrapper. The model is
created when the instance is instantiated, and the training process is performed by
calling the fit() method.
@property and Python decorators
This code uses a @property decorator. A decorator is simply a func‐
tion that takes another function as input, does something with it
(like adding some functionality), and returns it. In Python, a deco‐
rator is defined with the @ symbol.
@property is a decorator used to handle access to class attributes.
Our class wrapper is as follows:
class Model:
def __init__(self):
# Model
208 | Appendix A: Tips on Model Construction and Using TensorFlow Serving
self.x = tf.placeholder(tf.float32,shape=[None,3])
self.y_true = tf.placeholder(tf.float32,shape=None)
self.w = tf.Variable([[0,0,0]],dtype=tf.float32)
self.b = tf.Variable(0,dtype=tf.float32)
init = tf.global_variables_initializer()
self.sess = tf.Session()
self.sess.run(init)
self._output = None
self._optimizer = None
self._loss = None
def fit(self,x_data,y_data):
print(self.b.name)
for step in range(10):
self.sess.run(self.optimizer,{self.x: x_data, self.y_true: y_data})
if (step % 5 == 4) or (step == 0):
print(step, self.sess.run([self.w,self.b]))
@property
def output(self):
if not self._output:
y_pred = tf.matmul(self.w,tf.transpose(self.x)) + self.b
self._output = y_pred
return self._output
@property
def loss(self):
if not self._loss:
error = tf.reduce_mean(tf.square(self.y_true-self.output))
self._loss= error
return self._loss
@property
def optimizer(self):
if not self._optimizer:
opt = tf.train.GradientDescentOptimizer(0.5)
opt = opt.minimize(self.loss)
self._optimizer = opt
return self._optimizer
lin_reg = Model()
lin_reg.fit(x_data,y_data)
lin_reg.fit(x_data,y_data)
Tips on Model Construction and Using TensorFlow Serving | 209
And we get this:
Variable_89:0
0 [array([[ 0.32110521, 0.4908163 , 0.09833425]],
dtype=float32), -0.18784374]
4 [array([[ 0.30250472, 0.49442694, 0.10041162]],
dtype=float32), -0.1999902]
9 [array([[ 0.30250433, 0.49442688, 0.10041161]],
dtype=float32), -0.19999036]
Variable_89:0
0 [array([[ 0.30250433, 0.49442688, 0.10041161]],
dtype=float32), -0.19999038]
4 [array([[ 0.30250433, 0.49442688, 0.10041161]],
dtype=float32), -0.19999038]
9 [array([[ 0.30250433, 0.49442688, 0.10041161]],
dtype=float32), -0.19999036]
Splitting the code into functions is somewhat redundant in the sense that the same
lines of code are recomputed with every call. One simple solution is to add a condi‐
tion at the beginning of each function. In the next code iteration we will see an even
nicer workaround.
In this setting there is no need to use variable sharing since the variables are kept as
attributes of the model object. Also, after calling the training method model.fit()
twice, we see that the variables have maintained their current state.
In our last batch of code for this section we add another enhancement, creating a cus‐
tom decorator that automatically checks whether the function was already called.
Another improvement we can make is having all of our variables kept in a dictio‐
nary. This will allow us to keep track of our variables after each operation, as we saw
in Chapter 10 when we looked at saving weights and models.
Finally, additional functions for getting the values of the loss function and our
weights are added:
class Model:
def __init__(self):
# Model
self.x = tf.placeholder(tf.float32,shape=[None,3])
self.y_true = tf.placeholder(tf.float32,shape=None)
self.params = self._initialize_weights()
init = tf.global_variables_initializer()
self.sess = tf.Session()
self.sess.run(init)
self.output
self.optimizer
210 | Appendix A: Tips on Model Construction and Using TensorFlow Serving
self.loss
def _initialize_weights(self):
params = dict()
params['w'] = tf.Variable([[0,0,0]],dtype=tf.float32)
params['b'] = tf.Variable(0,dtype=tf.float32)
return params
def fit(self,x_data,y_data):
print(self.params['b'].name)
for step in range(10):
self.sess.run(self.optimizer,{self.x: x_data, self.y_true: y_data})
if (step % 5 == 4) or (step == 0):
print(step,
self.sess.run([self.params['w'],self.params['b']]))
def evaluate(self,x_data,y_data):
print(self.params['b'].name)
MSE = self.sess.run(self.loss,{self.x: x_data, self.y_true: y_data})
return MSE
def getWeights(self):
return self.sess.run([self.params['b']])
@property_with_check
def output(self):
y_pred = tf.matmul(self.params['w'],tf.transpose(self.x)) + \
self.params['b']
return y_pred
@property_with_check
def loss(self):
error = tf.reduce_mean(tf.square(self.y_true-self.output))
return error
@property_with_check
def optimizer(self):
opt = tf.train.GradientDescentOptimizer(0.5)
opt = opt.minimize(self.loss)
return opt
lin_reg = Model()
lin_reg.fit(x_data,y_data)
MSE = lin_reg.evaluate(x_data,y_data)
print(MSE)
print(lin_reg.getWeights())
Tips on Model Construction and Using TensorFlow Serving | 211
Here is the output:
Variable_87:0
0 [array([[ 0.32110521, 0.4908163 , 0.09833425]],
dtype=float32), -0.18784374]
4 [array([[ 0.30250472, 0.49442694, 0.10041162]],
dtype=float32), -0.1999902]
9 [array([[ 0.30250433, 0.49442688, 0.10041161]],
dtype=float32), -0.19999036]
Variable_87:0
0 [array([[ 0.30250433, 0.49442688, 0.10041161]],
dtype=float32), -0.19999038]
4 [array([[ 0.30250433, 0.49442688, 0.10041161]],
dtype=float32), -0.19999038]
9 [array([[ 0.30250433, 0.49442688, 0.10041161]],
dtype=float32), -0.19999036]
Variable_87:0
0.0102189
[-0.19999036]
The custom decorator checks whether an attribute exists, and if not, it sets it accord‐
ing to the input function. Otherwise, it returns the attribute. functools.wrap() is
used so we can reference the name of the function:
import functools
def property_with_check(input_fn):
attribute = '_cache_' + input_fn.__name__
@property
@functools.wraps(input_fn)
def check_attr(self):
if not hasattr(self, attribute):
setattr(self, attribute, input_fn(self))
return getattr(self, attribute)
return check_attr
This was a fairly basic example of how we can improve the overall code for our
model. This kind of optimization might be overkill for our simple linear regression
example, but it will definitely be worth the effort for complicated models with plenty
of layers, variables, and features.
Customization
So far we’ve used two loss functions. In the classification example in Chapter 2 we
used the cross-entropy loss, defined as follows:
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(logits=y_pred, labels=y_true))
212 | Appendix A: Tips on Model Construction and Using TensorFlow Serving
In contrast, in the regression example in the previous section we used the square
error loss, defined as follows:
loss = tf.reduce_mean(tf.square(y_true-y_pred))
These are the most commonly used loss functions in machine learning and deep
learning right now. The purpose of this section is twofold. First, we want to point out
the more general capabilities of TensorFlow in utilizing custom loss functions. Sec‐
ond, we will discuss regularization as a form of extension of any loss function in
order to achieve a specific goal, irrespective of the basic loss function used.
Homemade loss functions
This book (and presumably our readers) takes a specific view of TensorFlow with the
aspect of deep learning in mind. However, TensorFlow is more general in scope, and
most machine learning problems can be formulated in a way that TensorFlow can be
used to solve. Furthermore, any computation that can be formulated in the computa‐
tion graph framework is a good candidate to benefit from TensorFlow.
The predominant special case is the class of unconstrained optimization problems.
These are extremely common throughout scientific (and algorithmic) computing,
and for these, TensorFlow is especially helpful. The reason these problems stand out
is that TensorFlow provides an automatic mechanism for computing gradients, which
affords a tremendous speedup in development time for such problems.
In general, optimization with respect to an arbitrary loss function will be in the form
def my_loss_function(key-variables...):
loss = ...
return loss
my_loss = my_loss_function(key-variables...)
gd_step = tf.train.GradientDescentOptimizer().minimize(my_loss)
where any optimizer could be used in place of the GradientDescentOptimizer.
Regularization
Regularization is the restriction of an optimization problem by imposing a penalty on
the complexity of the solution (see the note in Chapter 4 for more details). In this
section we take a look at specific instances where the penalty is directly added to the
basic loss function in an additive form.
For example, building on the softmax example from Chapter 2, we have this:
x = tf.placeholder(tf.float32, [None, 784])
W = tf.Variable(tf.zeros([784, 10]))
y_true = tf.placeholder(tf.float32, [None, 10])
Tips on Model Construction and Using TensorFlow Serving | 213

y_pred = tf.matmul(x, W)
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(logits=y_pred, labels=y_true))
total_loss = cross_entropy + LAMBDA * tf.nn.l2_loss(W)
gd_step = tf.train.GradientDescentOptimizer(0.5).minimize(total_loss)
The difference between this and the original in Chapter 2 is that we added LAMBDA *
tf.nn.l2_loss(W) to the loss we are optimizing with respect to. In this case, using a
small value of the trade-off parameter LAMBDA will have very little effect on the result‐
ing accuracy (a large value will be detrimental). In large networks, where overfitting
is a serious issue, this sort of regularization can often be a lifesaver.
Regularization of this sort can be done with respect to the weights of the model, as
shown in the previous example (also called weight decay, since it will cause the
weights to have smaller values), as well as to the activations of a specific layer, or
indeed all layers.
Another factor is what function we use—we could have used l1 instead of the l2 reg‐
ularization, or a combination of the two. All combinations of these regularizers are
valid and used in various contexts.
Many of the abstraction layers make the application of regularization as easy as speci‐
fying the number of filters, or the activation function. In Keras (a very popular exten‐
sion reviewed in Chapter 7), for instance, we are provided with the regularizers listed
in Table A-1, applicable to all the standard layers.
Table A-1. Regularization with Keras
Regularizer What it does Example
l1 l1 regularization of weights Dense(100, W_regularizer=l1(0.01))
l2 l2 regularization of weights Dense(100, W_regularizer=l2(0.01))
l1l2 Combined l1 + l2
regularization of weights
Dense(100, W_regularizer=l1l2(0.01))
activity_l1 l1 regularization of
activations
Dense(100, activity_regularizer=activity_l1(0.01))
activity_l2 l2 regularization of
activations
Dense(100, activity_regularizer=activity_l2(0.01))
activity_l1l2 Combined l1 + l2
regularization of activations
Dense(100, activity_regularizer=activity_l1l2(0.01))
Using these shortcuts makes it easy to test different regularization schemes when a
model is overfitting.
214 | Appendix A: Tips on Model Construction and Using TensorFlow Serving
Writing your very own op
TensorFlow comes ready packed with a large number of native ops, ranging from
standard arithmetic and logical operations to matrix operations, deep learning–spe‐
cific functions, and more. When these are not enough, it is possible to extend the sys‐
tem by creating a new op. This is done in one of two ways:
• Writing a “from scratch” C++ version of the operation
•Writing Python code that combines existing ops and Python code to create the
new one
We will spend the remainder of this section discussing the second option.
The main reason to construct a Python op is to utilize NumPy functionality in the
context of a TensorFlow computational graph. For the sake of illustration, we will
construct the regularization example from the previous section by using the NumPy
multiplication function rather than the TensorFlow op:
import numpy as np
LAMBDA = 1e-5
def mul_lambda(val):
return np.multiply(val, LAMBDA).astype(np.float32)
Note that this is done for the sake of illustration, and there is no special reason why
anybody would want to use this instead of the native TensorFlow op. We use this
oversimplified example in order to shift the focus to the details of the mechanism
rather than the computation.
In order to use our new creation from within TensorFlow, we use the py_func()
functionality:
tf.py_func(my_python_function, [input], [output_types])
In our case, this means we compute the total loss as follows:
total_loss = cross_entropy + \
tf.py_func(mul_lambda, [tf.nn.l2_loss(W)], [tf.float32])[0]
Doing this, however, will not be enough. Recall that TensorFlow keeps track of the
gradients of each of the ops in order to perform gradient-based training of our overall
model. In order for this to work with the new Python-based op, we have to specify
the gradient manually. This is done in two steps.
First, we create and register the gradient:
@tf.RegisterGradient("PyMulLambda")
def grad_mul_lambda(op, grad):
return LAMBDA*grad
Tips on Model Construction and Using TensorFlow Serving | 215
Next, when using the function, we point to this function as the gradient of the op.
This is done using the string registered in the previous step:
with tf.get_default_graph().gradient_override_map({"PyFunc": "PyMulLambda"}):
total_loss = cross_entropy + \
tf.py_func(mul_lambda, [tf.nn.l2_loss(W)], [tf.float32])[0]
Putting it all together, the code for the softmax model with regularization through
our new Python-based op is now:
import numpy as np
import tensorflow as tf
LAMBDA = 1e-5
def mul_lambda(val):
return np.multiply(val, LAMBDA).astype(np.float32)
@tf.RegisterGradient("PyMulLambda")
def grad_mul_lambda(op, grad):
return LAMBDA*grad
x = tf.placeholder(tf.float32, [None, 784])
W = tf.Variable(tf.zeros([784, 10]))
y_true = tf.placeholder(tf.float32, [None, 10])
y_pred = tf.matmul(x, W)
cross_entropy =
tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits\
(logits=y_pred, labels=y_true))
with tf.get_default_graph().gradient_override_map({"PyFunc": "PyMulLambda"}):
total_loss = cross_entropy + \
tf.py_func(mul_lambda, [tf.nn.l2_loss(W)], [tf.float32])[0]
gd_step = tf.train.GradientDescentOptimizer(0.5).minimize(total_loss)
correct_mask = tf.equal(tf.argmax(y_pred, 1), tf.argmax(y_true, 1))
accuracy = tf.reduce_mean(tf.cast(correct_mask, tf.float32))
This can now be trained using the same code as in Chapter 2, when this model was
first introduced.
216 | Appendix A: Tips on Model Construction and Using TensorFlow Serving

Using the inputs in the computation of gradients
In the simple example we just showed, the gradient depends only
on the gradient with respect to the input, and not on the input
itself. In the general case, we will need access to the input as well.
This is done easily, using the op.inputs field:
x = op.inputs[0]
Other inputs (if they exist) are accessed in the same way.
Required and Recommended Components for TensorFlow
Serving
In this section, we add details on some of the material covered in Chapter 10 and
review in more depth some of the technical components used behind the scenes in
TensorFlow Serving.
In Chapter 10, we used Docker to run TensorFlow Serving. Those who prefer to avoid
using a Docker container need to have the following installed:
Bazel
Bazel is Google’s own build tool, which recently became publicly available. When
we use the term build, we are referring to using a bunch of rules to create output
software from source code in a very efficient and reliable manner. The build pro‐
cess can also be used to reference external dependencies that are required to
build the outputs. Among other languages, Bazel can be used to build C++ appli‐
cations, and we exploit this to build the C++-written TensorFlow Serving’s pro‐
grams. The source code Bazel builds upon is organized in a workspace directory
inside nested hierarchies of packages, where each package groups related source
files together. Every package consists of three types of files: human-written
source files called targets, generated les created from the source files, and rules
specifying the steps for deriving the outputs from the inputs.
Each package has a BUILD file, specifying the output to be built from the files
inside that package. We use basic Bazel commands like bazel build to build
generated files from targets, and bazel run to execute a build rule. We use the
-bin flag when we want to specify the directories to contain the build outputs.
Downloads and installation instructions can be found on the Bazel website.
gRPC
Remote procedure call (RPC) is a form of client (caller)–server (executer) inter‐
action; a program can request a procedure (for example, a method) that is exe‐
cuted on another computer (commonly in a shared network). gRPC is an open
source framework developed by Google. Like any other RPC framework, gRPC
lets you directly call methods on other machines, making it easier to distribute
Tips on Model Construction and Using TensorFlow Serving | 217
the computations of an application. The greatness of gRPC lies in how it handles
the serialization, using the fast and efficient protocol buffers instead of XML or
other methods.
Downloads and installation instructions can be found on GitHub.
Next, you need to make sure that the necessary dependencies for Serving are installed
with the following command:
sudo apt-get update && sudo apt-get install -y \
build-essential \
curl \
libcurl3-dev \
git \
libfreetype6-dev \
libpng12-dev \
libzmq3-dev \
pkg-config \
python-dev \
python-numpy \
python-pip \
software-properties-common \
swig \
zip \
zlib1g-dev
And lastly, clone Serving:
git clone --recurse-submodules https://github.com/tensorflow/serving
cd serving
As illustrated in Chapter 10, another option is to use a Docker container, allowing a
simple and clean installation.
What Is a Docker Container and Why Do We Use It?
Docker is essentially solving the same problem as Vagrant with VirtualBox, and that
is making sure our code will run smoothly on other machines. Different machines
might have different operating systems as well as different tool sets (installed soft‐
ware, configurations, permissions, etc.). By replicating the same environment—
maybe for production purposes, maybe just to share with others—we guarantee that
our code will run exactly the same way elsewhere as on our original development
machine.
What’s unique about Docker is that, unlike other similarly purposed tools, it doesn’t
create a fully operational virtual machine on which the environment will be built, but
rather creates a container on top of an existing system (Ubuntu, for example), acting
as a virtual machine in a sense and using our existing OS resources. These containers
are created from a local Docker image, which is built from a dockerle and encapsu‐
lates everything we need (dependency installations, project code, etc.). From that
218 | Appendix A: Tips on Model Construction and Using TensorFlow Serving
image we can create as many containers as we want (until we run out of memory, of
course). This makes Docker a very cool tool with which we can easily create complete
multiple environment replicas that contain our code and run them anywhere (very
useful for cluster computing).
Some Basic Docker Commands
To get you a bit more comfortable with using Docker, here’s a quick look at some use‐
ful commands, written in their most simplified form. Given that we have a dockerfile
ready, we can build an image by using docker build <dockerfile>. From that
image we can then create a new container by using the docker run <image> com‐
mand. This command will also automatically run the container and open a terminal
(type exit to close the terminal). To run, stop, and delete existing containers, we use
the docker start <container id>, docker stop <container id>, and docker rm
<container id> commands, respectively. To see the list of all of our instances, both
running and idle, we write docker ps -a.
When we run an instance, we can add the -p flag followed by a port for Docker to
expose, and the -v flag followed by a home directory to be mounted, which will
enable us to work locally (the home directory is addressed via the /mnt/home path in
the container).
Tips on Model Construction and Using TensorFlow Serving | 219
Index
Symbols
.assign(), 109, 182
.compile(), 137
.eval(), 35
.evaluate(), 120
.fit(), 119, 127, 133, 137
.get_variable_value(), 127
.meta checkpoint files, 188
.name attribute, 37
.optimizers, 137
.run() method, 27
.save(), 185
.__enter__(), 28
.__exit__(), 28
<Estimator>.predict(), 122
@property decorator, 208
A
abstraction libraries
abstraction illustration, 113
benefits of, 8, 113
contrib.learn, 117-131
popular libraries, 115
regularization and, 214
TFLearn, 131-151
acknowledgments, x
activation functions, 56
aliases, 11
argparse module, 169
arguments
callbacks, 138
feed_dict argument, 20, 154
fetches argument, 29
ksize argument, 56
num-epochs argument, 164
perm argument, 75
shape argument, 40
strides argument, 55
arrays, 33-38
.assign(), 109, 182
asynchronous training, 169
as_default() command, 29
attributes
.name, 37
<node>.graph attribute, 28
dtype, 32
purpose of, 31
setting with source operations, 31
attributions, viii
autoencoders, 139-142
B
backpropagation, 6
bag-of-words text classification, 96
BasicRNNCell, 84
batch_size, 74
Bazel build tool, 194, 200, 217
between-graph replication, 171
bias_variable(), 58
binary classification, 134
biologically inspired models, 52
C
callbacks argument, 138
casting, 32
chains, 71
CIFAR10 dataset, 61-68
class encapsulation, 208
221
clusters, 170
code examples, obtaining and using, viii
command-line arguments, 169
comments and questions, ix
Common Crawl vectors, 106
.compile(), 137
computation graphs (see dataflow computation
graphs)
computer vision
pretrained models for, 3
sequence data and, 69
confusion matrices, 122
constructors, 31
contact information, ix
context managers, 28
continuous (regression) learning, 19, 41, 117
contrib library, 84, 136
contrib.layers, 125, 128
contrib.learn
built-in estimators, 117
custom CNN estimators, 128-131
deploying custom models, 117
DNN classifier, 120-122
feature transformation operations, 128
FeatureColumn, 123-128
importing, 117
linear regression, 118
overview of, 115
contrib.learn.Estimator(), 130, 132
conv2d(), 54, 58
convolutional neural networks (CNNs)
architecture visualization, 58
CIFAR10 dataset classification, 61-68
convolution operation, 54, 60
creating models with TF-Slim, 144-151
custom estimators using contrib.learn,
128-131
MNIST dataset classification, 53-61
model creation using TFLearn, 131-134
overview of, 51-53
conv_layer(), 58
coord.request_stop(), 161
coord.should_stop(), 161
cross entropy, 19, 42, 212
customization
loss functions, 212
regularization, 213
TensorFlow Ops, 215
D
data augmentation, 67
data frames (tables), 124
data parallelism, 168
data types
changing, 32
choosing explicitly, 32
default data format, 154
labeled vs. unlabeled data, 96
sequence data, 69
supported types, 33
type inference, 33
dataflow computation graphs
benefits of, 24
constructing and managing, 27-29
creating, 25
fetches argument, 29
overview of, 5, 23
replicating across devices, 171
resetting prior to restoring, 188
session closing, 27
session creation, 26
deactivate command, 11
decorators, 208
deep learning
advances in, 1
computer vision, 3, 69
data processing in, 5
image captioning, 3
overview of, 1
sequence data and, 70
supervised learning, 18, 19
unsupervised learning, 97
deep learning models (see models)
deep neural networks (see deep learning)
dense vector representations, 96
Dense(), 137
dequeing and enqueuing, 157
design tips
class encapsulation, 208
model structure, 203
modular design, 205
variable sharing, 206
device placement, 172
digit_to_word_map dictionary, 87
dimensionality reduction, 139
discrete (classification) learning, 19
display_cifar(), 64
DistBelief , 2
222 | Index
distributed computing
distributed example, 173-179
overview of, 167
parallelization and, 168
TensorFlow elements, 169-173
distributional hypothesis, 97
DNN classifier, 120-122
Docker
alternatives to, 217
basic commands, 219
benefits of, 193, 218
container creation, 193
overview of, 218
setup, 193
dropout, 57, 110
DropoutWrapper(), 110
dtype attribute, 32
dynamic_rnn(), 90, 92, 108, 110
E
early stopping, 138
edge detectors, 52
edges, 30
elements (see TensorFlow elements)
element_size, 73
embedding_matrix, 109, 111
embedding_placeholder, 109, 111
enqueuing and dequeuing, 157
.__enter__(), 28
estimators, 117
.eval(), 35
.evaluate(), 120
.__exit__(), 28
external data, 17
F
feature maps, 54
feature_columns, 120, 123-128
feed_dict argument, 20, 154
fetches argument, 29
filters
in CNNs, 51, 54
in human visual processing, 52
.fit(), 119, 127, 133, 137
flags mechanism, 169
fully connected neural networks, 51
full_layer(), 58
functools.wrap(), 212
G
gated recurrent unit (GRU) cells, 110
get_shape(), 34
.get_variable_value(), 127
global_step, 178
GloVe embedding method, 106
gradient descent optimization, 6, 19, 42-44, 78,
101
GradientDescentOptimizer(), 44
graphs (see dataflow computation graphs)
gRPC framework, 217
GRUCell(), 110
H
h5py package, 142
“hello world” program, 11-13
helper functions, 57
hidden layers, 139
hidden Markov model (HMM), 71
hidden_layer_size, 74
I
IDE configuration, 12
image captioning, 3
image classification
CIFAR10, 61-68
illustration of, 1
images as sequences, 72
invariance property, 52
MNIST, 13, 53-61
pretrained models for, 3
softmax regression, 14-20, 101, 165
ImageNet project, 147
IMDb reviews dataset, 134
initializers, 34, 59, 111, 206
input pipeline
full multithreaded, 162-166
overview of, 153
queues, 157-158
redesign of, 166
TFRecords, 154-157
input_data.read_data_sets(), 62
input_fn(), 127
integer IDs, 95
invariance, 52
J
JSON, 191
Index | 223
K
keep_prob, 129
Keras
autoencoders, 139-142
benefits of, 136
functional model, 138
installing, 136
overview of, 115
pre-trained models, 143
regularization with, 214
sequential model, 137
ksize argument, 56
L
labeled data, 96
lambda functions, 127
language models, 70
layers.convolution2d(), 128
learn.LinearRegressor(), 119
learning rates, 19, 44, 101
learning_rate hyperparameter, 101
lifecycle management, 192
linear regression, 44-46, 117
loaded weights, assigning, 182
local response normalization (LRN), 133
logistic regression, 46-48, 117
LOG_DIR, 74, 79
long short-term memory (LSTM), 89-93, 110
loss functions
choosing, 41
cross entropy, 19, 42, 212
customizing, 213
Noise-Contrastive Estimation (NCE), 101
square error loss, 213
M
Markov chain model, 71
Matplotlib, 63
matrices, 33, 122
matrix multiplication, 36
max_pool_2×2, 58
mean squared error (MSE), 41, 119
memory errors, 21
.meta checkpoint files, 188
metadata files, 102
metainformation, 188
mini-batches, 43
MINIBATCH_SIZE, 20
MNIST (Mixed National Institute of Standards
and Technology) , 13, 53-61, 72-74
model.fit(), 210
Model.load_weights(), 142
models
biologically inspired, 52
CNN classification of CIFAR10 dataset,
64-68
CNN classification of MNIST dataset, 57-61
customizing loss functions, 212-217
evaluating, 20
language models, 70
measures of similarity in, 19, 42
optimizing, 40-48
pretrained, 3
regression, 41, 117
saving, 142
saving and exporting, 181-191
sequential model, 137
serving, 191-201
softmax regression, 14-20, 101, 165
structuring, 203-212
training, 19, 41, 59, 127, 134, 167
VGG model, 146
MSE (mean squared error), 41, 119, 213
multiple computational devices , 172
MultiRNNCell(), 93
multithreading
device placement and, 173
full input pipeline example, 162-166
queues and, 159
N
names and naming
duplicate names, 38
.name attribute, 37
name scopes, 38
natural language processing (NLP), 95
natural language understanding (NLU), 4, 70
neuroscientific inspiration, 52
nodes, 30
Noise-Contrastive Estimation (NCE), 101
normal distribution, 34
normalization, 132, 133
np.random.choice(range()), 85
NumPy, 30, 33, 215
num_epochs argument, 164
224 | Index
O
objectives, 41
(see also loss function)
operation instances, 30
operators and shortcuts, 25
ops, 215
optimization
cross entropy loss, 19, 42, 212
gradient descent, 19, 42-44
linear regression example, 44-46, 117
logistic regression example, 46-48, 117
loss function, 41
MSE (mean squared error), 119, 213
MSE loss, 41
training to predict, 41
optimizer.minimize(), 44
.optimizers, 137
overfitting, 53
P
padding, 55, 85
PAD_TOKEN, 108
Pandas library, 124
parallelization, 168, 171
parameter servers, 170
part-of-speech (POS) tagging, 110
perm argument, 75
placeholders
in CNNs, 60
example of, 40
purpose of, 39
shape argument, 40
pooling, 56, 60
pre-processing, 153
pre-trained models, 3, 143-151
principal component analysis (PCA), 139
processed images, 54
@property decorator, 208
protocol buffers (protobufs), 154, 191
PyCharm IDE, 12
Python
argparse module, 169
CIFAR10 dataset version, 62
data types supported in TensorFlow, 33
decorators, 208
ops, 215
vs. TensorFlow programs, 11
Theano library, 116
with statements, 28
Q
qr.create_threads(), 162
questions and comments, ix
queues
enqueuing and dequeuing, 157
multithreading, 159
vs. ordinary queues, 157
tf.train.Coordinator, 161
tf.train.QueueRunner, 162
R
random initializers, 34, 59
read_data_sets() method, 18
recurrent neural networks (RNNs)
basic implementation of, 72-81
bidirectional RNNs, 110
functions built into TensorFlow, 82-84
model creation using TFLearn, 134
overview of, 70
sequence data and, 69, 71
static vs. dynamic creation, 84
for text sequences, 84-93
regression problems
linear, 44-46, 117
logistic, 46-48, 117
simple, 41
regression(), 131
regularization
definition of term, 53, 213
dropout, 57, 110
with Keras, 214
loss functions and, 213
ReLU neurons, 133
remote procedure call (RPC), 217
RGB images, 5
RMSPropOptimizer, 78
rnn_cell, 84
rnn_step(), 83
.run() method, 27
S
sampling methods, 43
.save(), 185
saver.save(), 190
save_dir, 155
saving and exporting, 181-191
assigning loaded weights, 182
Index | 225
required and recommended components
for, 217
resetting graphs prior to restore, 188
Saver class, 185
saving as a collection, 189
serialization and protocol buffers, 191
scalars, 32, 33, 80
Scikit Flow, 115
scikit-learn, 115
sentiment analysis, 134
sequence data, 69, 72
(see also text sequences)
sequential model, 137
serialization, 191
servers, 170
serving output in production, 191-201, 217-219
sess.run() method, 29, 45
session.run(), 40
sessions
closing, 27
creating and running, 26
interactive, 35
managed, 171
pre- and post-run, 30
shape argument, 40
skip-grams, 97-100
slim.assign_from_checkpoint_fn(), 149
softmax regression, 14-20, 101, 165
source operations
descriptions of, 35
purpose of, 30, 32
special method functions, 28
square error loss, 41, 119, 213
stochastic gradient descent (SGD), 43
strides argument, 55
supervised learning, 18, 19, 87
Supervisor, 171
synchronous training, 169
T
tanh(·), 72
tensor (mathematical term), 33
TensorBoard
Embeddings tab, 104
functions of, 74
Graphs tab, 80
Histograms tab, 81
illustration of, 7
log verbosity, 132
logging summaries, 74
LOG_DIR (directory), 74
model visualization using, 79
Scalars tab, 80
tensorboard command, 80
Word2vec training and visualization, 102
TensorFlow
applications of by Google, 2-4
data types supported, 33
documentation, 101
history of, 2
IDE configuration, 12
installing, 9-11
key features, 6-8
main phases of operation, 24
naming of, 30
operators and shortcuts, 25, 35
prerequisites to learning, viii
tensorflow command, 11
TensorFlow elements,
clusters and servers, 170
device placement, 172
managed sessions, 171
replicating computational graphs, 171
tf.app.flags, 169
TensorFlow ops, 215
TensorFlow Serving
benefits of, 191
exporting models, 194-201
installing, 193
overview of, 192
required and recommended components
for, 217-219
workspace directory and packages, 194
tensorflow.contrib.learn, 155
Tensors
attributes, 31
basics of, 30
data types, 32
flowing data through, 30-38
data types, 32
names and naming, 37
nodes and edges, 30
tensor arrays and shapes, 33
names, 37
optimization, 40-48
placeholders, 39
purpose of, 5
Variables, 38
226 | Index
test(), 66
test_accuracy, 60
text sequences
natural language understanding and, 70
RNN for, 84-93
word embeddings and, 95, 105
Word2vec and, 97-105
text summarization, 4
TF-Slim
available layer types, 145
benefits of, 144
creating CNN models with, 144
overview of, 115
pre-trained models, 147
tf.<operator> methods, 25, 31, 35
tf.add(), 30
tf.app.flags, 169
tf.app.flags.FLAGS, 170
tf.cast(), 32
tf.concat(), 111
tf.constant(), 31, 32
tf.contrib.rnn.BasicLSTMCell(), 90
tf.contrib.rnn.BasicRNNCell, 82
tf.contrib.rnn.MultiRNNCell(), 93
tf.expand_dims(), 37, 149
tf.get_variables(), 39, 206
tf.global_variables_initializer(), 39, 111
tf.Graph(), 27
tf.InteractiveSession(), 35
tf.linspace(a, b, n), 35
tf.map_fn(), 77
tf.matmul(A,B), 36
tf.nn.bidirectional_dynamic_rnn(), 110
tf.nn.dynamic_rnn(), 82, 87, 90
tf.nn.embedding_lookup(), 89, 100
tf.nn.nce_loss(), 101
tf.random.normal(), 34
tf.RandomShuffleQueue, 162
tf.reduce_mean(), 42
tf.reset_default_graph(), 188
tf.scan(), 75, 84
tf.Session, 26
tf.SparseTensor(), 126
tf.square(), 42
tf.summary.histogram(), 81
tf.TFRecordReader(), 164
tf.train.Coordinator, 161
tf.train.exponential_decay(), 102
tf.train.import_meta_graph(), 189
tf.train.QueueRunner, 161
tf.train.replica_device_setter(), 171, 178
tf.train.Saver(), 185
tf.train.shuffle_batch(), 164
tf.train.start_queue_runners(), 165
tf.train.string_input_producer(), 164
tf.transpose(), 37
tf.Variable(), 39, 206
tf.variable_scope.reuse_variable(), 206
tf.While, 84
tf.zeros_initializer(), 206
TFLearn
benefits of, 131
custom CNN model creation, 131-134
epochs and iteration in, 134
installing, 131
Keras extension for, 136-143
local response normalization (LRN), 133
overview of, 115
pre-trained models with TF-Slim, 143-151
RNN text classification using, 134
standard operations, 132
tflearn.data_utils.pad_sequences(), 134
tflearn.DNN(), 132
tflearn.embedding(), 135
TFRecords, 154
TFRecordWriter, 155
Theano, 116, 136
three-dimensional arrays, 33
time_steps, 73
train/test validation, 19
train_accuracy, 60
transformations, 128
truncated normal initializers, 34
TSV (tab-separated values), 102
tuning (see optimization)
type inference, 32, 33
typographical conventions, viii
U
unconstrained optimization problems, 213
uniform initializers, 34
unpickle(), 63
unsupervised learning, 97
V
Vagrant, 218
Variables
initializing, 45
Index | 227
purpose of, 38
random number generators and, 34
reusing, 39, 206
storing in dictionaries, 210
using, 39
vectors, 33
versioning, 192
VGG model, 146
virtual environments, 10, 218
VirtualBox, 218
visualizations, using TensorBoard, 7, 74, 102
W
weights, 51, 182
weight_variable(), 58
Windows, 10
with statements, 28
word embeddings
bidirectional RNNs, 110
LSTM classifier, 91
overview of, 95
pretrained, 105-110
RNN example, 89
using Word2vec, 97-105
word vectors (see word embeddings)
Word2vec
embeddings in TensorFlow, 100
examining word vectors, 103
learning rate decay, 101
skip-grams, 98-100
training and visualizing with TensorBoard,
102
workers, 170
X
XML, 191
Z
zero-padding, 85
228 | Index